code
stringlengths 38
801k
| repo_path
stringlengths 6
263
|
|---|---|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Data Preprocessing and Machine Learning with Scikit-Learn
# +
import numpy as np
import pandas as pd
from sklearn.impute import SimpleImputer
from sklearn.pipeline import make_pipeline
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import MinMaxScaler, LabelEncoder, StandardScaler
from sklearn.model_selection import train_test_split, GridSearchCV, PredefinedSplit
# -
PATH = '../data/iris.csv'
# !ls '../data'
# !wc -l {PATH}
# !du -h {PATH}
# !head -n 5 {PATH}
# !tail -n 5 {PATH}
# ## A. Loading Tabular Datasets from Text Files
data_frame = pd.read_csv(filepath_or_buffer = PATH)
data_frame.head()
data_frame.info() # data frame information
# +
memory_series = data_frame.memory_usage(deep = True) / 1024 # show memory usage in KB
display(memory_series)
print(f'Total memory used: {memory_series.sum():.2f} KB')
# -
print(f'The data_frame data type is: {type(data_frame)}')
print(f'The data_frame has {data_frame.shape[0]} rows and {data_frame.shape[1]} columns')
print(f'The data_frame contains {data_frame.size} values (rows x columns)')
print(f'The data_frame index is: {data_frame.index}')
print(f'The data_frame columns are: {data_frame.columns.values}')
# +
class_map = {
'Iris-setosa': 0,
'Iris-versicolor': 1,
'Iris-virginica': 2
}
data_frame['Classes'] = data_frame['Species'].map(class_map) # apply a dictionary mapping on a column
display(data_frame.head(), data_frame.tail(), np.unique(data_frame['Classes']))
# +
series = data_frame['Species']
display(series.head(n = 3), (series.index, series.dtype, series.shape, np.unique(series.values)), series.tail(n = 3))
# -
data_frame.loc[[2, 1, 0], ['PetalLength[cm]', 'PetalWidth[cm]', 'SepalLength[cm]', 'SepalWidth[cm]', 'Species']]
data_frame.iloc[[2, 1, 0], [3, 4, 1, 2, 5]]
data_frame[['PetalLength[cm]', 'PetalWidth[cm]', 'Species']].head()
data_frame[:5]
data_frame = data_frame.drop('Id', axis = 1) # delete `Id` column
data_frame.head()
# ## B. Splitting a Dataset into Train, Validation, and Test Subsets
# +
indices = np.arange(data_frame.shape[0])
rng = np.random.RandomState(123)
permuted_indices = rng.permutation(indices)
permuted_indices
# +
train_size, validation_size = int(.65*data_frame.shape[0]), int(.15*data_frame.shape[0])
test_size = int(data_frame.shape[0] - (train_size + validation_size))
print(train_size, validation_size, test_size)
# -
train_indices = permuted_indices[:train_size]
validation_indices = permuted_indices[train_size:train_size + validation_size]
test_indices = permuted_indices[train_size + validation_size:]
# +
X, y = data_frame.drop(['Species', 'Classes'], axis = 1).values, data_frame['Classes'].values
print(f'Features: {X.shape}')
print(f'Classes: {y.shape}')
# +
X_train, X_valid, X_test = X[train_indices], X[validation_indices], X[test_indices]
y_train, y_valid, y_test = y[train_indices], y[validation_indices], y[test_indices]
print('Training set size: ', X_train.shape, ' -> Class proportions:', np.bincount(y_train))
print('Validation set size:', X_valid.shape, ' -> Class proportions:', np.bincount(y_valid))
print('Test set size:', X_test.shape, ' -> Class proportions:', np.bincount(y_test))
# -
# ### B.1. Stratification
#
# Previously, we wrote our own code to shuffle and split a data set into training, validation, and test subsets, which had one considerable downside.
# If we are working with small datasets and split it randomly into subsets, it will affect the class distribution in the samples - this is problematic since machine learning algorithms/models assume that training, validation, and test samples have been drawn from the same distributions to produce reliable models and estimates of the generalization performance.
#
# 
# The method of ensuring that the class label proportions are the same in each subset after splitting, we use an approach that is usually referred to as **stratification**.
# Stratification is supported in `scikit-learn`'s `train_test_split` method if we pass the class label array to the `stratify` parameter as shown below.
# +
X_temp, X_test, y_temp, y_test = train_test_split(X, y, test_size = .15, shuffle = True, random_state = 123, stratify = y)
X_train, X_valid, y_train, y_valid = train_test_split(X_temp, y_temp, test_size = .15, shuffle = True, random_state = 123, stratify = y_temp)
print('Training set size: ', X_train.shape, ' -> Class proportions:', np.bincount(y_train))
print('Validation set size:', X_valid.shape, ' -> Class proportions:', np.bincount(y_valid))
print('Test set size:', X_test.shape, ' -> Class proportions:', np.bincount(y_test))
# -
# ## C. Data Scaling
#
# Whether or not to scale features depends on the problem at hand and requires your judgement.
# However, there are several algorithms (especially gradient-descent, etc.), which work much better (are more robust, numerically stable, and converge faster) if the data is centered and has a smaller range.
# There are many different ways for scaling features; here, we only cover to of the most common "normalization" schemes: *min-max* scaling and *z-score* standardization.
# ### C.1. Normalization - Min-Max Scaling
#
# Min-max scaling squashes the features into a `[0, 1]` range, which can be achieved via the following equation for a single input:
#
# $$ x^{[i]}_{norm} = \frac{x^{[i]}_{norm} - x_{min}}{x_{max} - x_{min}} $$
# +
x = np.arange(6).astype(np.float16)
display(f'Unnormalized vector: {x}')
display(f'Normalized vector: {(x - x.min()) / (x.max() - x.min())}')
# -
# ### C.2 Standardization
#
# After standardizing a feature, it will have the properties of a standard normal distribution, that is, unit variance and zero mean $\mathcal{N}(\mu = 0, \sigma^2 = 1)$; however, this does not transform a feature from not following a normal distribution to a normal distributed one.
# The formula for standardizing a feature is shown below, for a single data point $x^{[i]}$:
#
# $$ x^{[i]}_{standard} = \frac{x^{[i]} - \mu_x}{\sigma_x} $$
# +
x = np.arange(6).astype(np.float16)
display(f'Unnormalized vector: {x}')
display(f'Standardized vector: {(x - x.mean()) / (x.std())}')
# -
# A concept that is very important though is how we use the estimated normalization parameters (e.g., mean and standard deviation in z-score standardization).
# In particular, it is important that we re-use the parameters estimated from the training set to transfrom validation and test sets - re-estimating the parameters is a common "beginner-mistake".
# +
X_train_example, y_train_example = np.array([10, 20, 30]), np.array([0, 1, 0])
X_valid_example, y_valid_example = np.array([3, 12, 27]), np.array([0, 1, 0])
mu, sigma = X_train_example.mean(), X_train_example.std()
minimum, maximum = X_train_example.min(), X_train_example.max()
X_valid_example_scaled = (X_valid_example - minimum) / (maximum - minimum)
X_valid_example_standardized = (X_valid_example - mu) / sigma # WRONG !!! X_valid = (X_valid - X_valid.mean()) / X_valid.std()
print(f'Scaled: {X_valid_example_scaled}, Standardized: {X_valid_example_standardized}')
# -
# ## D. Scikit-Learn Transformer API
# +
min_max_scaler = MinMaxScaler()
min_max_scaler.fit(X_train_example.reshape(-1, 1))
X_valid_example_scaled = min_max_scaler.transform(X_valid_example.reshape(-1, 1)).reshape(1, -1)[0]
print(f'Scaled: {X_valid_example_scaled}')
# +
standardizer = StandardScaler()
standardizer.fit(X_train_example.reshape(-1, 1))
X_valid_example_standardized = standardizer.transform(X_valid_example.reshape(-1, 1)).reshape(1, -1)[0]
print(f'Standardized: {X_valid_example_standardized}')
# -
# ### D.1 Categorical Data
#
# When we preprocess a dataset as input to a machine learning algorithm, we have to be careful how we treat categorical variables.
# There are two broad categories of categorical variables: **nominal** (no order implied) and **ordinal** (order implied).
data_frame_1 = pd.DataFrame({'Color': ['green', 'red', 'blue'], 'Size': ['M', 'L', 'XXL'], 'Class': ['Class 1', 'Class 2', 'Class 2']})
data_frame_1.head()
# - In the example above, `Size` would be an example of an ordinal variable; i.e., if the letters refer to T-shirt sizes, it would make sense to come up with an ordering like `M < L < XXL`.
#
# - Hence, we can assign increasing values to a ordinal values; however, the range and difference between categories depends on our domain knowledge and judgement.
# +
size_mapper = {
'M': 2,
'L': 3,
'XXL': 5
}
data_frame_1['Size'] = data_frame_1['Size'].map(size_mapper)
data_frame_1.head()
# -
# - Machine learning algorithms do not assume an ordering in the case of class labels.
#
# - Here, we can use the `LabelEncoder` from `scikit-learn` to convert class labels to integers as an alternative to using the `map` method.
# +
label_encoder = LabelEncoder()
label_encoder.fit(data_frame_1['Class'])
data_frame_1['ClassLabels'] = label_encoder.transform(data_frame_1['Class'])
data_frame_1.head()
# -
# - Representing nominal variables properly is a bit more tricky.
#
# - We use "one-hot" encoding - we binarize a nominal variable, as shown below for the color variable (again, we do this because some ordering like `orange < red < blue` would not make sense in many applications).
data_frame_1 = pd.get_dummies(data_frame_1, columns = ['Color'])
data_frame_1.head()
# - Note that executing the code above produced `3` new variables for `Color_*` each of which takes on binary values.
# ### D.2 Missing Data
#
# There are many different ways for dealing with missing data.
# The simplest approaches are removing entire columns or rows.
# Another simple approach is to impute missing values via the feature means, medians, mode, etc.
# There is no rule or best practice, and the choice of the approprite missing data imputation method depends on your judgement and domain knowledge.
data_frame_2 = pd.DataFrame({'A': [1., 5., 10.], 'B': [2., 6., 11.], 'C': [3., np.nan, 12.], 'D': [4., 8., np.nan]})
data_frame_2.head()
display(data_frame_2.isnull(), data_frame_2.isnull().sum())
display(data_frame_2.dropna(axis = 0), data_frame_2.dropna(axis = 1)) # drop rows, columns where there are missing values respectively
# +
imputer_mean = SimpleImputer(missing_values = np.nan, strategy = 'mean')
imputer_median = SimpleImputer(missing_values = np.nan, strategy = 'median')
imputer_mean.fit(data_frame_2['C'].values.reshape(-1, 1))
imputer_median.fit(data_frame_2['D'].values.reshape(-1, 1))
data_frame_2['C'] = imputer_mean.transform(data_frame_2['C'].values.reshape(-1, 1))
data_frame_2['D'] = imputer_median.transform(data_frame_2['D'].values.reshape(-1, 1))
data_frame_2.head()
# -
# ## E. Feature Transformation, Extraction, and Selection
#
# Scikit-learn pipelines are an extremely convenient and powerful concept.
# Pipelines basically let us define a series of perprocessing steps together with fitting an estimator.
# Pipelines will automatically take care of pitfalls like estimating feature scaling parameters from the training set and applying those to scale new data.
# +
pipeline = make_pipeline(StandardScaler(), KNeighborsClassifier(n_neighbors=3))
pipeline
# +
pipeline.fit(X = X_test, y = y_test)
print(f'Predictions: {pipeline.predict(X = X_valid)}'),
print(f'Score (accuracy): {pipeline.score(X = X_test, y = y_test)*100:.2f}%')
# -
# ### E.1 Intro Model Selection - Pipelines and Grid Search
#
# In machine learning practice, we often need to experiment with an machine learning algorithm's hyperparameters to find a good setting.
# The process of tuning hyperparameters and comparing and selecting the resulting models is also called *model selection*.
# Here, we are introducing the simplest way of performing model selection: using the *holdout method.*
# In the holdout method, we split a dataset into 3 subsets: a training, a validation, and a test datatset.
# To avoid biasing the estimate of the generalization performance, we only want to use the test dataset once, which is why we use the validation dataset for hyperparameter tuning (model selection).
# Here, the validation dataset serves as an estimate of the generalization performance, too, but it becomes more biased than the final estimate on the test data because of its repeated re-use during model selection (think of "multiple hypothesis testing").
#
# 
pipeline = make_pipeline(StandardScaler(), KNeighborsClassifier())
pipeline
# +
params = {
'kneighborsclassifier__n_neighbors': [1, 3, 5],
'kneighborsclassifier__p': [1, 2]
}
ps = PredefinedSplit(np.concatenate((np.full(shape = (X_train.shape[0],), fill_value = -1), np.zeros(shape = (X_valid.shape[0],)))))
grid = GridSearchCV(estimator = pipeline, param_grid = params, cv = ps)
grid.fit(X = np.vstack((X_train, X_valid)), y = np.hstack((y_train, y_valid)))
# -
grid.cv_results_
print(f'Best score: {grid.best_score_}')
print(f'Best parameters: {grid.best_params_}')
classifier = grid.best_estimator_
classifier.fit(X_train, y_train)
print(f'Test accuracy: {(classifier.score(X_test, y_test)*100):.2f}%')
|
notebooks/03-data-preprocessing-and-machine-learning-with-sklearn.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# look at tools/set_up_magics.ipynb
yandex_metrica_allowed = True ; get_ipython().run_cell('# one_liner_str\n\nget_ipython().run_cell_magic(\'javascript\', \'\', \n \'// setup cpp code highlighting\\n\'\n \'IPython.CodeCell.options_default.highlight_modes["text/x-c++src"] = {\\\'reg\\\':[/^%%cpp/]} ;\'\n \'IPython.CodeCell.options_default.highlight_modes["text/x-cmake"] = {\\\'reg\\\':[/^%%cmake/]} ;\'\n)\n\n# creating magics\nfrom IPython.core.magic import register_cell_magic, register_line_magic\nfrom IPython.display import display, Markdown, HTML\nimport argparse\nfrom subprocess import Popen, PIPE\nimport random\nimport sys\nimport os\nimport re\nimport signal\nimport shutil\nimport shlex\nimport glob\nimport time\n\n@register_cell_magic\ndef save_file(args_str, cell, line_comment_start="#"):\n parser = argparse.ArgumentParser()\n parser.add_argument("fname")\n parser.add_argument("--ejudge-style", action="store_true")\n args = parser.parse_args(args_str.split())\n \n cell = cell if cell[-1] == \'\\n\' or args.no_eof_newline else cell + "\\n"\n cmds = []\n with open(args.fname, "w") as f:\n f.write(line_comment_start + " %%cpp " + args_str + "\\n")\n for line in cell.split("\\n"):\n line_to_write = (line if not args.ejudge_style else line.rstrip()) + "\\n"\n if line.startswith("%"):\n run_prefix = "%run "\n if line.startswith(run_prefix):\n cmds.append(line[len(run_prefix):].strip())\n f.write(line_comment_start + " " + line_to_write)\n continue\n run_prefix = "%# "\n if line.startswith(run_prefix):\n f.write(line_comment_start + " " + line_to_write)\n continue\n raise Exception("Unknown %%save_file subcommand: \'%s\'" % line)\n else:\n f.write(line_to_write)\n f.write("" if not args.ejudge_style else line_comment_start + r" line without \\n")\n for cmd in cmds:\n display(Markdown("Run: `%s`" % cmd))\n get_ipython().system(cmd)\n\n@register_cell_magic\ndef cpp(fname, cell):\n save_file(fname, cell, "//")\n \n@register_cell_magic\ndef cmake(fname, cell):\n save_file(fname, cell, "#")\n\n@register_cell_magic\ndef asm(fname, cell):\n save_file(fname, cell, "//")\n \n@register_cell_magic\ndef makefile(fname, cell):\n assert not fname\n save_file("makefile", cell.replace(" " * 4, "\\t"))\n \n@register_line_magic\ndef p(line):\n line = line.strip() \n if line[0] == \'#\':\n display(Markdown(line[1:].strip()))\n else:\n try:\n expr, comment = line.split(" #")\n display(Markdown("`{} = {}` # {}".format(expr.strip(), eval(expr), comment.strip())))\n except:\n display(Markdown("{} = {}".format(line, eval(line))))\n \n \ndef show_log_file(file, return_html_string=False):\n obj = file.replace(\'.\', \'_\').replace(\'/\', \'_\') + "_obj"\n html_string = \'\'\'\n <!--MD_BEGIN_FILTER-->\n <script type=text/javascript>\n var entrance___OBJ__ = 0;\n var errors___OBJ__ = 0;\n function halt__OBJ__(elem, color)\n {\n elem.setAttribute("style", "font-size: 14px; background: " + color + "; padding: 10px; border: 3px; border-radius: 5px; color: white; "); \n }\n function refresh__OBJ__()\n {\n entrance___OBJ__ -= 1;\n if (entrance___OBJ__ < 0) {\n entrance___OBJ__ = 0;\n }\n var elem = document.getElementById("__OBJ__");\n if (elem) {\n var xmlhttp=new XMLHttpRequest();\n xmlhttp.onreadystatechange=function()\n {\n var elem = document.getElementById("__OBJ__");\n console.log(!!elem, xmlhttp.readyState, xmlhttp.status, entrance___OBJ__);\n if (elem && xmlhttp.readyState==4) {\n if (xmlhttp.status==200)\n {\n errors___OBJ__ = 0;\n if (!entrance___OBJ__) {\n if (elem.innerHTML != xmlhttp.responseText) {\n elem.innerHTML = xmlhttp.responseText;\n }\n if (elem.innerHTML.includes("Process finished.")) {\n halt__OBJ__(elem, "#333333");\n } else {\n entrance___OBJ__ += 1;\n console.log("req");\n window.setTimeout("refresh__OBJ__()", 300); \n }\n }\n return xmlhttp.responseText;\n } else {\n errors___OBJ__ += 1;\n if (!entrance___OBJ__) {\n if (errors___OBJ__ < 6) {\n entrance___OBJ__ += 1;\n console.log("req");\n window.setTimeout("refresh__OBJ__()", 300); \n } else {\n halt__OBJ__(elem, "#994444");\n }\n }\n }\n }\n }\n xmlhttp.open("GET", "__FILE__", true);\n xmlhttp.setRequestHeader("Cache-Control", "no-cache");\n xmlhttp.send(); \n }\n }\n \n if (!entrance___OBJ__) {\n entrance___OBJ__ += 1;\n refresh__OBJ__(); \n }\n </script>\n\n <p id="__OBJ__" style="font-size: 14px; background: #000000; padding: 10px; border: 3px; border-radius: 5px; color: white; ">\n </p>\n \n </font>\n <!--MD_END_FILTER-->\n <!--MD_FROM_FILE __FILE__.md -->\n \'\'\'.replace("__OBJ__", obj).replace("__FILE__", file)\n if return_html_string:\n return html_string\n display(HTML(html_string))\n\n \nclass TInteractiveLauncher:\n tmp_path = "./interactive_launcher_tmp"\n def __init__(self, cmd):\n try:\n os.mkdir(TInteractiveLauncher.tmp_path)\n except:\n pass\n name = str(random.randint(0, 1e18))\n self.inq_path = os.path.join(TInteractiveLauncher.tmp_path, name + ".inq")\n self.log_path = os.path.join(TInteractiveLauncher.tmp_path, name + ".log")\n \n os.mkfifo(self.inq_path)\n open(self.log_path, \'w\').close()\n open(self.log_path + ".md", \'w\').close()\n\n self.pid = os.fork()\n if self.pid == -1:\n print("Error")\n if self.pid == 0:\n exe_cands = glob.glob("../tools/launcher.py") + glob.glob("../../tools/launcher.py")\n assert(len(exe_cands) == 1)\n assert(os.execvp("python3", ["python3", exe_cands[0], "-l", self.log_path, "-i", self.inq_path, "-c", cmd]) == 0)\n self.inq_f = open(self.inq_path, "w")\n interactive_launcher_opened_set.add(self.pid)\n show_log_file(self.log_path)\n\n def write(self, s):\n s = s.encode()\n assert len(s) == os.write(self.inq_f.fileno(), s)\n \n def get_pid(self):\n n = 100\n for i in range(n):\n try:\n return int(re.findall(r"PID = (\\d+)", open(self.log_path).readline())[0])\n except:\n if i + 1 == n:\n raise\n time.sleep(0.1)\n \n def input_queue_path(self):\n return self.inq_path\n \n def wait_stop(self, timeout):\n for i in range(int(timeout * 10)):\n wpid, status = os.waitpid(self.pid, os.WNOHANG)\n if wpid != 0:\n return True\n time.sleep(0.1)\n return False\n \n def close(self, timeout=3):\n self.inq_f.close()\n if not self.wait_stop(timeout):\n os.kill(self.get_pid(), signal.SIGKILL)\n os.waitpid(self.pid, 0)\n os.remove(self.inq_path)\n # os.remove(self.log_path)\n self.inq_path = None\n self.log_path = None \n interactive_launcher_opened_set.remove(self.pid)\n self.pid = None\n \n @staticmethod\n def terminate_all():\n if "interactive_launcher_opened_set" not in globals():\n globals()["interactive_launcher_opened_set"] = set()\n global interactive_launcher_opened_set\n for pid in interactive_launcher_opened_set:\n print("Terminate pid=" + str(pid), file=sys.stderr)\n os.kill(pid, signal.SIGKILL)\n os.waitpid(pid, 0)\n interactive_launcher_opened_set = set()\n if os.path.exists(TInteractiveLauncher.tmp_path):\n shutil.rmtree(TInteractiveLauncher.tmp_path)\n \nTInteractiveLauncher.terminate_all()\n \nyandex_metrica_allowed = bool(globals().get("yandex_metrica_allowed", False))\nif yandex_metrica_allowed:\n display(HTML(\'\'\'<!-- YANDEX_METRICA_BEGIN -->\n <script type="text/javascript" >\n (function(m,e,t,r,i,k,a){m[i]=m[i]||function(){(m[i].a=m[i].a||[]).push(arguments)};\n m[i].l=1*new Date();k=e.createElement(t),a=e.getElementsByTagName(t)[0],k.async=1,k.src=r,a.parentNode.insertBefore(k,a)})\n (window, document, "script", "https://mc.yandex.ru/metrika/tag.js", "ym");\n\n ym(59260609, "init", {\n clickmap:true,\n trackLinks:true,\n accurateTrackBounce:true\n });\n </script>\n <noscript><div><img src="https://mc.yandex.ru/watch/59260609" style="position:absolute; left:-9999px;" alt="" /></div></noscript>\n <!-- YANDEX_METRICA_END -->\'\'\'))\n\ndef make_oneliner():\n html_text = \'("В этот ноутбук встроен код Яндекс Метрики для сбора статистики использований. Если вы не хотите, чтобы по вам собиралась статистика, исправьте: yandex_metrica_allowed = False" if yandex_metrica_allowed else "")\'\n html_text += \' + "<""!-- MAGICS_SETUP_PRINTING_END -->"\'\n return \'\'.join([\n \'# look at tools/set_up_magics.ipynb\\n\',\n \'yandex_metrica_allowed = True ; get_ipython().run_cell(%s);\' % repr(one_liner_str),\n \'display(HTML(%s))\' % html_text,\n \' #\'\'MAGICS_SETUP_END\'\n ])\n \n\n');display(HTML(("В этот ноутбук встроен код Яндекс Метрики для сбора статистики использований. Если вы не хотите, чтобы по вам собиралась статистика, исправьте: yandex_metrica_allowed = False" if yandex_metrica_allowed else "") + "<""!-- MAGICS_SETUP_PRINTING_END -->")) #MAGICS_SETUP_END
# # FUSE
#
# <table width=100% > <tr>
# <th width=15%> <b>Видео с семинара → </b> </th>
# <th>
# <a href="https://www.youtube.com/watch?v=__RuADlaK0k&list=PLjzMm8llUm4CL-_HgDrmoSTZBCdUk5HQL&index=5"><img src="video.jpg" width="320"
# height="160" align="left" alt="Видео с семинара"></a>
# </th>
# <th> </th>
# </table>
#
# Сегодня в программе:
# * <a href="#fs_posix" style="color:#856024"> Работа с файловой системой POSIX </a>
# * <a href="#opendir" style="color:#856024"> Просмотр содержимого директории c фильтрацией по регулярке </a>
# * <a href="#glob" style="color:#856024"> glob или история о том, как вы пишете *.cpp в терминале </a>
# * <a href="#ftw" style="color:#856024"> Рекурсивный просмотр. Правда с помощью устаревшей функции. </a>
# * <a href="#fs_stat" style="color:#856024"> Информация о файловой системе. </a>
#
# * <a href="#fusepy" style="color:#856024"> Примонтируем json как read-only файловую систему. Python + fusepy </a>
# * <a href="#fuse_с" style="color:#856024"> Файловая система с одним файлом на C </a>
#
#
# https://ru.wikipedia.org/wiki/FUSE_(модуль_ядра)
#
# 
#
#
# https://habr.com/ru/post/315654/ - на питоне
#
# https://engineering.facile.it/blog/eng/write-filesystem-fuse/
#
#
#
#
# [<NAME>](https://github.com/victor-yacovlev/mipt-diht-caos/tree/master/practice/fuse)
#
#
# <a href="#hw" style="color:#856024">Комментарии к ДЗ</a>
#
#
# ## <a name="fs_posix"></a> Работа с файловой системой в POSIX
#
#
#
#
# Заголовочные файлы, в которых есть функции для работы с файловой системой ([wiki-источник](https://en.wikipedia.org/wiki/C_POSIX_library)):
#
# | Header file | Description |
# |-------------|-------------|
# | `<fcntl.h>` | File opening, locking and other operations |
# | `<fnmatch.h>` | Filename matching |
# | `<ftw.h>` | File tree traversal |
# | `<sys/stat.h>` | File information (stat et al.) |
# | `<sys/statvfs.h>` | File System information |
# | `<dirent.h>` | Directories opening, traversing |
#
#
# read, write, stat, fstat - это все было раньше
#
# ## <a name="opendir"></a> Просмотр содержимого директории с фильтрацией по регулярке
# +
# %%cpp traverse_dir.c
# %run gcc -Wall -Werror -fsanitize=address traverse_dir.c -lpthread -o traverse_dir.exe
# %run ./traverse_dir.exe ..
#include <stdio.h>
#include <dirent.h>
#include <assert.h>
#include <fnmatch.h>
int main(int argc, char** argv) {
assert(argc == 2);
const char* dir_path = argv[1];
DIR *pDir = opendir(dir_path);
if (pDir == NULL) {
fprintf(stderr, "Cannot open directory '%s'\n", dir_path);
return 1;
}
int limit = 4;
for (struct dirent *pDirent; (pDirent = readdir(pDir)) != NULL && limit > 0;) {
// + Регулярочки
if (fnmatch("sem2*", pDirent->d_name, 0) == 0) {
printf("%s\n", pDirent->d_name);
--limit;
}
}
closedir(pDir);
return 0;
}
# -
# ## <a name="glob"></a> glob или история о том, как вы пишете *.cpp в терминале
#
# Это не совсем про файловую систему, но тем не менее интересно
#
# glob хорошо сочетается с exec, пример тут http://man7.org/linux/man-pages/man3/glob.3.html
# +
# %%cpp traverse_dir.c
# %run gcc -Wall -Werror -fsanitize=address traverse_dir.c -lpthread -o traverse_dir.exe
# %run ./traverse_dir.exe .. | head -n 5
#include <stdio.h>
#include <assert.h>
#include <glob.h>
int main() {
glob_t globbuf = {0};
glob("*.c", GLOB_DOOFFS, NULL, &globbuf);
glob("../*/*.c", GLOB_DOOFFS | GLOB_APPEND, NULL, &globbuf);
for (char** path = globbuf.gl_pathv; *path; ++path) {
printf("%s\n", *path);;
}
globfree(&globbuf);
return 0;
}
# -
import glob
glob.glob("../*/*.c")[:4]
# ## <a name="ftw"></a> Рекурсивный просмотр. Правда с помощью устаревшей функции.
# +
# %%cpp traverse_dir_2.c
# %run gcc -Wall -Werror -fsanitize=address traverse_dir_2.c -lpthread -o traverse_dir_2.exe
# %run ./traverse_dir_2.exe ..
#include <stdio.h>
#include <ftw.h>
#include <assert.h>
int limit = 4;
int callback(const char* fpath, const struct stat* sb, int typeflag) {
printf("%s %ld\n", fpath, sb->st_size);
return (--limit == 0);
}
int main(int argc, char** argv) {
assert(argc == 2);
const char* dir_path = argv[1];
ftw(dir_path, callback, 0);
return 0;
}
# -
# ## <a name="fs_stat"></a> Информация о файловой системе
# +
# %%cpp fs_stat.c
# %run gcc -Wall -Werror -fsanitize=address fs_stat.c -lpthread -o fs_stat.exe
# %run ./fs_stat.exe ..
# %run ./fs_stat.exe /dev
#include <stdio.h>
#include <sys/statvfs.h>
#include <assert.h>
int main(int argc, char** argv) {
assert(argc == 2);
const char* dir_path = argv[1];
struct statvfs stat;
statvfs(dir_path, &stat);
printf("Free 1K-blocks %lu/%lu", stat.f_bavail * stat.f_bsize / 1024, stat.f_blocks * stat.f_bsize / 1024);
return 0;
}
# -
# !df
# # FUSE
#
# Важные опции
# * `-f` - запуск в синхронном режиме (без этой опции будет создан демон, а сама программа почти сразу завершится)
# * `-s` - запуск в однопоточном режиме.
#
# В этом месте что-нибудь про демонизацию стоит расскзать, наверное.
# ## <a name="fusepy"></a> Python + fusepy
#
# Установк: `pip2 install --user fusepy`
# +
# %%writefile fuse_json.py
from __future__ import print_function
import logging
import os
import json
from errno import EIO, ENOENT, EROFS
from stat import S_IFDIR, S_IFREG
from sys import argv, exit
from time import time
from fuse import FUSE, FuseOSError, LoggingMixIn, Operations
NOW = time()
DIR_ATTRS = dict(st_mode=(S_IFDIR | 0o555), st_nlink=2)
FILE_ATTRS = dict(st_mode=(S_IFREG | 0o444), st_nlink=1)
def find_json_path(j, path):
for part in path.split('/'):
if len(part) > 0:
if part == '__json__':
return json.dumps(j)
if part not in j:
return None
j = j[part]
return j
class FuseOperations(LoggingMixIn, Operations):
def __init__(self, j):
self.j = j
self.fd = 0
def open(self, path, flags):
self.fd += 1
return self.fd
def read(self, path, size, offset, fh):
logging.debug("Read %r %r %r", path, size, offset)
node = find_json_path(self.j, path)
if not isinstance(node, str):
raise FuseOSError(EIO)
return node[offset:offset + size]
def readdir(self, path, fh):
logging.debug("Readdir %r %r", path, fh)
node = find_json_path(self.j, path)
if node is None:
raise FuseOSError(EROFS)
return ['.', '..', '__json__'] + list(node.keys())
def getattr(self, path, fh=None):
node = find_json_path(self.j, path)
if isinstance(node, dict):
return DIR_ATTRS
elif isinstance(node, str):
attrs = dict(FILE_ATTRS)
attrs["st_size"] = len(node)
return attrs
else:
raise FuseOSError(ENOENT)
if __name__ == '__main__':
logging.basicConfig(level=logging.INFO)
j = {
'a': 'b',
'c': {
'c1': '234'
}
}
FUSE(FuseOperations(j), "./fuse_json", foreground=True)
# -
# !mkdir fuse_json 2>&1 | grep -v "File exists" || true
a = TInteractiveLauncher("python2 fuse_json.py example.txt fuse_json 2>&1")
# !ls fuse_json
# !cat fuse_json/c/__json__
# + language="bash"
# echo -n -e "\n" > new_line
# exec 2>&1 ; set -o xtrace
#
# tree fuse_json --noreport
#
# cat fuse_json/__json__ new_line
# cat fuse_json/a new_line
# cat fuse_json/c/__json__ new_line
# -
# !fusermount -u fuse_json
a.close()
# `sudo apt install tree`
# + language="bash"
# tree fuse_json --noreport
# -
# ## <a name="fuse_c"></a> fuse + с
#
# Надо поставить `libfuse-dev`. Возможно, для этого нужно подаунгрейдить `libfuse2`.
#
# Да, обращаю внимание, что у Яковлева в ридинге используется fuse3. Но что-то его пока не очень тривиально поставить в Ubuntu 16.04 (за час не справился) и мне не хочется ненароком себе что-нибудь сломать в системе :)
#
# fuse3 немного отличается по API. В примере я поддержал компилируемость и с fuse2, и с fuse3.
# Для установки на Ubuntu может оказаться полезным [Официальный репозиторий Fuse](https://github.com/libfuse/libfuse).
# В нём указаны шаги установки. Правда, может понадобиться поставить ещё [*Ninja*](https://ninja-build.org/) и [*Meson*](https://mesonbuild.com/).
# +
# %%cmake with_fuse_1.cmake
cmake_minimum_required(VERSION 3.15)
project(hw23 CXX)
set(CMAKE_CXX_STANDARD 11)
set(CMAKE_CXX_FLAGS "${CMAKE_CXX_FLAGS} -fsanitize=address -fsanitize=leak -g")
set(FUSE_PATH "downloads/fuse")
add_executable(hw23 task.cpp)
target_include_directories(hw23 PUBLIC ${FUSE_PATH}/include) # -I/usr/include/fuse3
target_link_libraries(hw23 ${FUSE_PATH}/build/lib/libfuse3.so) # -lfuse3 -lpthread
# -
# Либо, если следовать скрипту ниже, то может помочь такой CMake
# +
# %%cmake with_fuse_2.cmake
cmake_minimum_required(VERSION 2.7)
find_package(PkgConfig REQUIRED)
pkg_check_modules(FUSE REQUIRED fuse3)
include_directories(${FUSE_INCLUDE_DIRS})
add_executable(main main.c)
target_link_libraries(main ${FUSE_LIBRARIES})
# -
# Код во многом взят отсюда: https://github.com/fntlnz/fuse-example
# !mkdir fuse_c_example 2>&1 | grep -v "File exists" || true
# !mkdir fuse_c_example/CMake 2>&1 | grep -v "File exists" || true
# +
# %%cmake fuse_c_example/CMake/FindFUSE.cmake
# copied from https://github.com/fntlnz/fuse-example/blob/master/CMake/FindFUSE.cmake
# Кстати, вот пример модуля CMake который умеет искать библиотеку
IF (FUSE_INCLUDE_DIR)
SET (FUSE_FIND_QUIETLY TRUE)
ENDIF (FUSE_INCLUDE_DIR)
FIND_PATH (FUSE_INCLUDE_DIR fuse.h /usr/local/include/osxfuse /usr/local/include /usr/include)
if (APPLE)
SET(FUSE_NAMES libosxfuse.dylib fuse)
else (APPLE)
SET(FUSE_NAMES fuse)
endif (APPLE)
FIND_LIBRARY(FUSE_LIBRARIES NAMES ${FUSE_NAMES} PATHS /lib64 /lib /usr/lib64 /usr/lib /usr/local/lib64 /usr/local/lib /usr/lib/x86_64-linux-gnu)
include ("FindPackageHandleStandardArgs")
find_package_handle_standard_args ("FUSE" DEFAULT_MSG FUSE_INCLUDE_DIR FUSE_LIBRARIES)
mark_as_advanced (FUSE_INCLUDE_DIR FUSE_LIBRARIES)
# +
# %%cmake fuse_c_example/CMakeLists.txt
# copied from https://github.com/fntlnz/fuse-example/blob/master/CMakeLists.txt
cmake_minimum_required(VERSION 3.0 FATAL_ERROR)
project(fuse_c_example)
set(CMAKE_C_FLAGS "${CMAKE_C_FLAGS} -D_FILE_OFFSET_BITS=64 -DFUSE2 -g -fsanitize=address")
set(CMAKE_MODULE_PATH "${CMAKE_CURRENT_SOURCE_DIR}/CMake" ${CMAKE_MODULE_PATH}) # Говорим, где еще можно искать модули
find_package(FUSE REQUIRED)
include_directories(${FUSE_INCLUDE_DIR})
add_executable(fuse-example main.c)
target_link_libraries(fuse-example ${FUSE_LIBRARIES})
# -
# ---
# Чтобы пользователь мог пользоваться вашим модулем Fuse, нужно добавить основные операции для взаимодействия. Они реализуются в виде колбэков, которые Fuse будет вызывать при выполнении определённого действия пользователем.
# В C/C++ это реализуется путём заполнения структурки [fuse_operations](http://libfuse.github.io/doxygen/structfuse__operations.html).
# ---
# +
# %%cpp fuse_c_example/main.c
# %run mkdir fuse_c_example/build 2>&1 | grep -v "File exists"
# %run cd fuse_c_example/build && cmake .. > /dev/null && make
#include <string.h>
#include <errno.h>
#include <stddef.h>
#include <stdlib.h>
#include <stdio.h>
#include <unistd.h>
#ifdef FUSE2
#define FUSE_USE_VERSION 26
#else
#define FUSE_USE_VERSION 30
#endif
#include <fuse.h>
typedef struct {
char* filename;
char* filecontent;
char* log;
} my_options_t;
my_options_t my_options;
void print_cwd() {
if (my_options.log) {
FILE* f = fopen(my_options.log, "at");
char buffer[1000];
getcwd(buffer, sizeof(buffer));
fprintf(f, "Current working dir: %s\n", buffer);
fclose(f);
}
}
// Самый важный колбэк. Вызывается первым при любом другом колбэке.
// Заполняет структуру stbuf.
int getattr_callback(const char* path, struct stat* stbuf
#ifndef FUSE2
, struct fuse_file_info *fi
#endif
) {
#ifndef FUSE2
(void) fi;
#endif
if (strcmp(path, "/") == 0) {
// st_mode(тип файла, а также права доступа)
// st_nlink(количество ссылок на файл)
// Интересный факт, что количество ссылок у папки = 2 + n, где n -- количество подпапок.
*stbuf = (struct stat) {.st_nlink = 2, .st_mode = S_IFDIR | 0755};
return 0;
}
if (path[0] == '/' && strcmp(path + 1, my_options.filename) == 0) {
*stbuf = (struct stat) {.st_nlink = 2, .st_mode = S_IFREG | 0777, .st_size = (__off_t)strlen(my_options.filecontent)};
return 0;
}
return -ENOENT; // При ошибке, вместо errno возвращаем (-errno).
}
// filler(buf, filename, stat, flags) -- заполняет информацию о файле и вставляет её в buf.
int readdir_callback(const char* path, void* buf, fuse_fill_dir_t filler, off_t offset, struct fuse_file_info* fi
#ifndef FUSE2
, enum fuse_readdir_flags flags
#endif
) {
#ifdef FUSE2
(void) offset; (void) fi;
filler(buf, ".", NULL, 0);
filler(buf, "..", NULL, 0);
filler(buf, my_options.filename, NULL, 0);
#else
(void) offset; (void) fi; (void)flags;
filler(buf, ".", NULL, 0, (enum fuse_fill_dir_flags)0);
filler(buf, "..", NULL, 0, (enum fuse_fill_dir_flags)0);
filler(buf, my_options.filename, NULL, 0, (enum fuse_fill_dir_flags)0);
#endif
return 0;
}
// Вызывается после успешной обработки open.
int read_callback(const char* path, char* buf, size_t size, off_t offset, struct fuse_file_info* fi) {
// "/"
if (strcmp(path, "/") == 0) {
return -EISDIR;
}
print_cwd();
// "/my_file"
if (path[0] == '/' && strcmp(path + 1, my_options.filename) == 0) {
size_t len = strlen(my_options.filecontent);
if (offset >= len) {
return 0;
}
size = (offset + size <= len) ? size : (len - offset);
memcpy(buf, my_options.filecontent + offset, size);
return size;
}
return -EIO;
}
// Структура с колбэками.
struct fuse_operations fuse_example_operations = {
.getattr = getattr_callback,
.read = read_callback,
.readdir = readdir_callback,
};
struct fuse_opt opt_specs[] = {
{ "--file-name %s", offsetof(my_options_t, filename), 0 },
{ "--file-content %s", offsetof(my_options_t, filecontent), 0 },
{ "--log %s", offsetof(my_options_t, log), 0 },
FUSE_OPT_END // Структурка заполненная нулями. В общем такой типичный zero-terminated массив
};
int main(int argc, char** argv) {
struct fuse_args args = FUSE_ARGS_INIT(argc, argv);
/*
* Если не хотите создавать структурку с данными, а нужно только распарсить одну строку,
* То можно вторым аргументом передать char*.
* Тогда в opt_specs это можно указать как {"--src %s", 0, 0}
*
* ВАЖНО: заполняемые поля должны быть инициализированы нулями.
* (В противном случае fuse3 может делать что-то очень плохое. TODO)
*/
my_options.filename = "asdfrgt";
fuse_opt_parse(&args, &my_options, opt_specs, NULL);
print_cwd();
int ret = fuse_main(args.argc, args.argv, &fuse_example_operations, NULL);
fuse_opt_free_args(&args);
return ret;
}
# -
# Запустим в синхронном режиме (программа работает, пока `fusermount -u` не будет сделан)
# !mkdir fuse_c 2>&1 | grep -v "File exists" || true
# !fusermount -u fuse_c
# !truncate --size=0 err.txt || true
a = TInteractiveLauncher("fuse_c_example/build/fuse-example fuse_c -f "
"--file-name my_file --file-content 'My file content\n' --log `pwd`/err.txt")
# + language="bash"
# exec 2>&1 ; set -o xtrace
#
# tree fuse_c --noreport
#
# cat fuse_c/my_file
# -
# !fusermount -u fuse_c
a.close()
# + language="bash"
# tree fuse_c --noreport
# cat err.txt
# -
# А теперь в асинхронном (в режиме демона, в параметрах запуска нет `-f`):
# !mkdir fuse_c 2>&1 | grep -v "File exists" || true
# !fusermount -u fuse_c
# !truncate --size=0 err.txt || true
a = TInteractiveLauncher("fuse_c_example/build/fuse-example fuse_c "
"--file-name my_file --file-content 'My file content\n' --log `pwd`/err.txt")
# + language="bash"
# exec 2>&1 ; set -o xtrace
#
# tree fuse_c --noreport
#
# cat fuse_c/my_file
#
# fusermount -u fuse_c
# -
a.close()
# + language="bash"
# tree fuse_c --noreport
# cat err.txt
# -
# Парам-пам-пам, изменилась текущая директория! Учиытвайте это в ДЗ
# # <a name="hw"></a> Комментарии к ДЗ
#
# * Пример входных данных в первой задаче:
#
# ```
# 2
# a.txt 3
# b.txt 5
#
# AaAbBbBb
# ```
#
# * В ejudge fuse запускается без опции `-f` поэтому текущая директория будет меняться и относительные пути могут становиться невалидными. Рекомендую: `man 3 realpath`
# 1) В задачах на fuse основная цель -- реализовать 3 метода(read, readdir, getattr).
# Для этого может понадобиться сохранить свои данные в какую-то глобальную переменную и доставать их оттуда в вызовах колбэка.
#
# 2) В 23-1 Чтобы не усложнять себе жизнь, можно ходить по папкам при каждом вызове.
# Тогда задача сводится к поиску конкретного файла в каждой папке из условия и выборе из этих файлов последнего.
# Либо, в случае readdir, можно вызвать opendir/readdir/closedir к каждому пути и сформировать словарик из уникальных файлов в папках.
|
caos_2019-2020/sem26-fs-fuse/fs_fuse.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # L8 - Inheritance
# ---
# As in any object-oriented programming language, you can inherit from other classes when creating a new one.
# For example, imagine you want to create both a `Fish` class and a `Bird` class. Both of these classes will probably have many things in common, since both are animals.
# Instead of duplicating methods and/or attributes in both of these classes, it's preferable to create a base class with all the things that they'll share, and then inherit from this class when creating the `Fish` and `Bird` classes.
class Animal:
def __init__(self, name):
self.name = name
self.is_sleeping = False
def sleep(self):
self.is_sleeping = True
def wake_up(self):
self.is_sleeping = False
def talk(self):
return
# Now we can create the other classes by inheriting from the `Animal` class.
# ### 8.1 Syntax
class Fish(Animal):
def __init__(self, name):
super().__init__(name)
def swim(self):
print(self.name, 'is swimming')
class Bird(Animal):
def __init__(self, name, max_speed):
super().__init__(name)
self.max_speed = max_speed
def fly(self):
print(self.name, 'is flying')
def talk(self):
print('cheep cheep!')
# ---
# ### 8.2 Creating and using `Fish`
# And now we can create objects from these classes.
myTuna = Fish('Darold')
# Darold will have the attributes and methods that are common to all `Animal`s.
myTuna.name
myTuna.is_sleeping
myTuna.talk()
myTuna.sleep()
myTuna.is_sleeping
myTuna.wake_up()
myTuna.is_sleeping
# And also everything that's specific to `Fish`.
myTuna.swim()
# ---
# ### 8.3 Creating and using `Bird`s
# Creating a member of the `Bird` class is almost the same, but we also require a second positional argument.
myCanary = Bird('Quinn', 100)
# Just like before, Quinn has all attributes and methods that `Animal`s have.
myCanary.sleep()
print(myCanary.is_sleeping)
myCanary.wake_up()
print(myCanary.is_sleeping)
# But one of them behaves differently:
myCanary.talk()
# And Quinn also has everything from `Bird`s as well.
myCanary.fly()
# ---
# But obviously, `Bird`s don't have access to methods/attributes from `Fish`es.
#
myCanary.swim()
# Neither `Fish`es have access to methods/attributes from `Bird`s.
myTuna.fly()
myTuna.max_speed
# ---
# Finally, inheritance can also be used for providing users of your code with a "template" class.
#
# This is enables users to modify the behavior of your code, but without breaking the rest of it (and without having to know exactly how everything works under the hood).
#
# One great example of this is how [we create our own Neural Network layers in Keras](https://keras.io/layers/writing-your-own-keras-layers/). We'll talk more about this during the DL course.
# ---
|
Python Crash Course/Module 1 - Core Language/L8 Python.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Recommendations with IBM
#
# In this notebook, you will be putting your recommendation skills to use on real data from the IBM Watson Studio platform.
#
#
# You may either submit your notebook through the workspace here, or you may work from your local machine and submit through the next page. Either way assure that your code passes the project [RUBRIC](https://review.udacity.com/#!/rubrics/2322/view). **Please save regularly.**
#
# By following the table of contents, you will build out a number of different methods for making recommendations that can be used for different situations.
#
#
# ## Table of Contents
#
# I. [Exploratory Data Analysis](#Exploratory-Data-Analysis)<br>
# II. [Rank Based Recommendations](#Rank)<br>
# III. [User-User Based Collaborative Filtering](#User-User)<br>
# IV. [Content Based Recommendations (EXTRA - NOT REQUIRED)](#Content-Recs)<br>
# V. [Matrix Factorization](#Matrix-Fact)<br>
# VI. [Extras & Concluding](#conclusions)
#
# At the end of the notebook, you will find directions for how to submit your work. Let's get started by importing the necessary libraries and reading in the data.
# +
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import project_tests as t
import pickle
import seaborn as sns
# %matplotlib inline
# -
df = pd.read_csv('data/user-item-interactions.csv')
df_content = pd.read_csv('data/articles_community.csv')
del df['Unnamed: 0']
del df_content['Unnamed: 0']
# Show df to get an idea of the data
df.head()
# Show df_content to get an idea of the data
df_content.head()
# ### <a class="anchor" id="Exploratory-Data-Analysis">Part I : Exploratory Data Analysis</a>
#
# Use the dictionary and cells below to provide some insight into the descriptive statistics of the data.
#
# `1.` What is the distribution of how many articles a user interacts with in the dataset? Provide a visual and descriptive statistics to assist with giving a look at the number of times each user interacts with an article.
sort_interactions_count_per_user = df.groupby(['email'])['article_id'].count().sort_values(ascending=False)
sort_interactions_count_per_user.median(),sort_interactions_count_per_user.max()
# +
# Fill in the median and maximum number of user_article interactios below
median_val = 3 # 50% of individuals interact with ____ number of articles or fewer.
max_views_by_user = 364 # The maximum number of user-article interactions by any 1 user is ______.
# -
# `2.` Explore and remove duplicate articles from the **df_content** dataframe.
# Find and explore duplicate articles
article_count = df_content.groupby('article_id')['article_id'].count().sort_values(ascending=False)
duplicate_articles=article_count[article_count>1]
duplicate_articles
df_content[df_content['article_id'].isin(duplicate_articles.index.values)].sort_values(by='article_id')
print("before removing duplicates {}".format(len(df_content)))
# Remove any rows that have the same article_id - only keep the first
df_content = df_content.drop_duplicates(subset=['article_id'], keep='first', inplace=False)
print("after removing duplicates {}".format(len(df_content)))
# `3.` Use the cells below to find:
#
# **a.** The number of unique articles that have an interaction with a user.
# **b.** The number of unique articles in the dataset (whether they have any interactions or not).<br>
# **c.** The number of unique users in the dataset. (excluding null values) <br>
# **d.** The number of user-article interactions in the dataset.
df['article_id'].nunique()
df_content['article_id'].nunique()
df['email'].nunique()
len(df)
unique_articles = 714 # The number of unique articles that have at least one interaction
total_articles = 1051 # The number of unique articles on the IBM platform
unique_users = 5148 # The number of unique users
user_article_interactions = 45993# The number of user-article interactions
# `4.` Use the cells below to find the most viewed **article_id**, as well as how often it was viewed. After talking to the company leaders, the `email_mapper` function was deemed a reasonable way to map users to ids. There were a small number of null values, and it was found that all of these null values likely belonged to a single user (which is how they are stored using the function below).
df.groupby('article_id')['email'].count().sort_values(ascending=False)
most_viewed_article_id = '1429.0' # The most viewed article in the dataset as a string with one value following the decimal
max_views = 937 # The most viewed article in the dataset was viewed how many times?
# +
## No need to change the code here - this will be helpful for later parts of the notebook
# Run this cell to map the user email to a user_id column and remove the email column
def email_mapper():
coded_dict = dict()
cter = 1
email_encoded = []
for val in df['email']:
if val not in coded_dict:
coded_dict[val] = cter
cter+=1
email_encoded.append(coded_dict[val])
return email_encoded
email_encoded = email_mapper()
del df['email']
df['user_id'] = email_encoded
# show header
df.head()
# +
## If you stored all your results in the variable names above,
## you shouldn't need to change anything in this cell
sol_1_dict = {
'`50% of individuals have _____ or fewer interactions.`': median_val,
'`The total number of user-article interactions in the dataset is ______.`': user_article_interactions,
'`The maximum number of user-article interactions by any 1 user is ______.`': max_views_by_user,
'`The most viewed article in the dataset was viewed _____ times.`': max_views,
'`The article_id of the most viewed article is ______.`': most_viewed_article_id,
'`The number of unique articles that have at least 1 rating ______.`': unique_articles,
'`The number of unique users in the dataset is ______`': unique_users,
'`The number of unique articles on the IBM platform`': total_articles
}
# Test your dictionary against the solution
t.sol_1_test(sol_1_dict)
# -
# ### <a class="anchor" id="Rank">Part II: Rank-Based Recommendations</a>
#
# Unlike in the earlier lessons, we don't actually have ratings for whether a user liked an article or not. We only know that a user has interacted with an article. In these cases, the popularity of an article can really only be based on how often an article was interacted with.
#
# `1.` Fill in the function below to return the **n** top articles ordered with most interactions as the top. Test your function using the tests below.
def get_top_articles(n, df=df):
'''
INPUT:
n - (int) the number of top articles to return
df - (pandas dataframe) df as defined at the top of the notebook
OUTPUT:
top_articles - (list) A list of the top 'n' article titles
'''
# Your code here
temp = df.groupby('article_id')['user_id'].count().sort_values(ascending=False)
temp = temp.iloc[0:n].index.values
df_temp = df[df['article_id'].isin(temp)][['article_id','title']]
df_temp = df_temp.drop_duplicates(subset=['article_id'],keep="first",inplace=False)
top_articles = list(df_temp['title'])
return top_articles # Return the top article titles from df (not df_content)
def get_top_article_ids(n, df=df):
'''
INPUT:
n - (int) the number of top articles to return
df - (pandas dataframe) df as defined at the top of the notebook
OUTPUT:
top_articles - (list) A list of the top 'n' article titles
'''
# Your code here
temp = df.groupby('article_id')['user_id'].count().sort_values(ascending=False)
temp = temp.iloc[0:n].index.values
top_articles = list(temp)
return top_articles # Return the top article ids
print(get_top_articles(10))
print(get_top_article_ids(10))
# +
# Test your function by returning the top 5, 10, and 20 articles
top_5 = get_top_articles(5)
top_10 = get_top_articles(10)
top_20 = get_top_articles(20)
# Test each of your three lists from above
t.sol_2_test(get_top_articles)
# -
# ### <a class="anchor" id="User-User">Part III: User-User Based Collaborative Filtering</a>
#
#
# `1.` Use the function below to reformat the **df** dataframe to be shaped with users as the rows and articles as the columns.
#
# * Each **user** should only appear in each **row** once.
#
#
# * Each **article** should only show up in one **column**.
#
#
# * **If a user has interacted with an article, then place a 1 where the user-row meets for that article-column**. It does not matter how many times a user has interacted with the article, all entries where a user has interacted with an article should be a 1.
#
#
# * **If a user has not interacted with an item, then place a zero where the user-row meets for that article-column**.
#
# Use the tests to make sure the basic structure of your matrix matches what is expected by the solution.
# +
# create the user-article matrix with 1's and 0's
def create_user_item_matrix(df):
'''
INPUT:
df - pandas dataframe with article_id, title, user_id columns
OUTPUT:
user_item - user item matrix
Description:
Return a matrix with user ids as rows and article ids on the columns with 1 values where a user interacted with
an article and a 0 otherwise
'''
# Fill in the function here
temp = df.groupby(['user_id','article_id'])['user_id'].count().unstack()
temp[temp>1] = 1
temp = temp.fillna(0)
user_item = temp
return user_item # return the user_item matrix
user_item = create_user_item_matrix(df)
# -
## Tests: You should just need to run this cell. Don't change the code.
assert user_item.shape[0] == 5149, "Oops! The number of users in the user-article matrix doesn't look right."
assert user_item.shape[1] == 714, "Oops! The number of articles in the user-article matrix doesn't look right."
assert user_item.sum(axis=1)[1] == 36, "Oops! The number of articles seen by user 1 doesn't look right."
print("You have passed our quick tests! Please proceed!")
# `2.` Complete the function below which should take a user_id and provide an ordered list of the most similar users to that user (from most similar to least similar). The returned result should not contain the provided user_id, as we know that each user is similar to him/herself. Because the results for each user here are binary, it (perhaps) makes sense to compute similarity as the dot product of two users.
#
# Use the tests to test your function.
def get_user_similar_users(user_id, user_item=user_item):
# compute similarity of each user to the provided user
transposed_users_items = user_item.T
given_user_items = user_item.loc[user_id]
similarity_matrix = given_user_items.dot(transposed_users_items)
# sort by similarity
similarity_matrix = similarity_matrix[similarity_matrix.index != user_id]
similarity_matrix = similarity_matrix.sort_values(ascending=False)
return similarity_matrix
def find_similar_users(user_id, user_item=user_item):
'''
INPUT:
user_id - (int) a user_id
user_item - (pandas dataframe) matrix of users by articles:
1's when a user has interacted with an article, 0 otherwise
OUTPUT:
similar_users - (list) an ordered list where the closest users (largest dot product users)
are listed first
Description:
Computes the similarity of every pair of users based on the dot product
Returns an ordered
'''
similar_user_similarity = get_user_similar_users(user_id, user_item=user_item)
most_similar_users = list(similar_user_similarity.index.values)
return most_similar_users # return a list of the users in order from most to least similar
# Do a spot check of your function
print("The 10 most similar users to user 1 are: {}".format(find_similar_users(1)[:10]))
print("The 5 most similar users to user 3933 are: {}".format(find_similar_users(3933)[:5]))
print("The 3 most similar users to user 46 are: {}".format(find_similar_users(46)[:3]))
# `3.` Now that you have a function that provides the most similar users to each user, you will want to use these users to find articles you can recommend. Complete the functions below to return the articles you would recommend to each user.
def get_article_names(article_ids, df=df):
'''
INPUT:
article_ids - (list) a list of article ids
df - (pandas dataframe) df as defined at the top of the notebook
OUTPUT:
article_names - (list) a list of article names associated with the list of article ids
(this is identified by the title column)
'''
# Your code here
article_ids = [int(float(i)) for i in article_ids]
unique_article_names = df[['article_id','title']].drop_duplicates(subset=['article_id'],keep="first",inplace=False)
temp = unique_article_names.set_index('article_id')
temp_result = temp.loc[article_ids,'title'].values
article_names = temp_result
return article_names # Return the article names associated with list of article ids
def get_user_articles(user_id, user_item=user_item):
'''
INPUT:
user_id - (int) a user id
user_item - (pandas dataframe) matrix of users by articles:
1's when a user has interacted with an article, 0 otherwise
OUTPUT:
article_ids - (list) a list of the article ids seen by the user
article_names - (list) a list of article names associated with the list of article ids
(this is identified by the doc_full_name column in df_content)
Description:
Provides a list of the article_ids and article titles that have been seen by a user
'''
# Your code here
user_articles = user_item.loc[user_id]
article_ids = user_articles[user_articles>0].index.values.astype('str')
article_names = get_article_names(article_ids)
return article_ids, article_names # return the ids and names
def Diff(list1, list2):
return (list(set(list1) - set(list2)))
def append_unseen_article_from_similar_user(articles_id_list,user_id,neighbor_id):
this_user_articles_ids,_ = get_user_articles(user_id)
other_user_articles_ids,_ = get_user_articles(neighbor_id)
recommended_articles = Diff(other_user_articles_ids, this_user_articles_ids)
articles_id_list.extend(recommended_articles)
return articles_id_list
def user_user_recs(user_id, m=10):
'''
INPUT:
user_id - (int) a user id
m - (int) the number of recommendations you want for the user
OUTPUT:
recs - (list) a list of recommendations for the user
Description:
Loops through the users based on closeness to the input user_id
For each user - finds articles the user hasn't seen before and provides them as recs
Does this until m recommendations are found
Notes:
Users who are the same closeness are chosen arbitrarily as the 'next' user
For the user where the number of recommended articles starts below m
and ends exceeding m, the last items are chosen arbitrarily
'''
# Your code here
similar_users = find_similar_users(user_id)
recommendations = []
for other_user in similar_users:
recommendations = append_unseen_article_from_similar_user(recommendations,user_id,other_user)
if len(recommendations)>m: break
recs = recommendations[0:m]
return recs # return your recommendations for this user_id
# + active=""
# # Your code here
# similar_users = find_similar_users(user_id)
# this_user_articles_ids,_ = get_user_articles(user_id)
# recommendations = []
# for other_user in similar_users:
# recommendations = append_unseen_article_from_similar_user(recommendations,user_id,neighbor_id)
# other_user_articles_ids,_ = get_user_articles(other_user)
# recommended_articles = Diff(other_user_articles_ids, this_user_articles_ids)
# recommendations.extend(recommended_articles)
# if len(recommendations)>m: break
# recs = recommendations[0:m]
#
# -
# Check Results
get_article_names(user_user_recs(1, 10)) # Return 10 recommendations for user 1
# Test your functions here - No need to change this code - just run this cell
assert set(get_article_names(['1024.0', '1176.0', '1305.0', '1314.0', '1422.0', '1427.0'])) == set(['using deep learning to reconstruct high-resolution audio', 'build a python app on the streaming analytics service', 'gosales transactions for naive bayes model', 'healthcare python streaming application demo', 'use r dataframes & ibm watson natural language understanding', 'use xgboost, scikit-learn & ibm watson machine learning apis']), "Oops! Your the get_article_names function doesn't work quite how we expect."
assert set(get_article_names(['1320.0', '232.0', '844.0'])) == set(['housing (2015): united states demographic measures','self-service data preparation with ibm data refinery','use the cloudant-spark connector in python notebook']), "Oops! Your the get_article_names function doesn't work quite how we expect."
assert set(get_user_articles(20)[0]) == set(['1320.0', '232.0', '844.0'])
assert set(get_user_articles(20)[1]) == set(['housing (2015): united states demographic measures', 'self-service data preparation with ibm data refinery','use the cloudant-spark connector in python notebook'])
assert set(get_user_articles(2)[0]) == set(['1024.0', '1176.0', '1305.0', '1314.0', '1422.0', '1427.0'])
assert set(get_user_articles(2)[1]) == set(['using deep learning to reconstruct high-resolution audio', 'build a python app on the streaming analytics service', 'gosales transactions for naive bayes model', 'healthcare python streaming application demo', 'use r dataframes & ibm watson natural language understanding', 'use xgboost, scikit-learn & ibm watson machine learning apis'])
print("If this is all you see, you passed all of our tests! Nice job!")
# `4.` Now we are going to improve the consistency of the **user_user_recs** function from above.
#
# * Instead of arbitrarily choosing when we obtain users who are all the same closeness to a given user - choose the users that have the most total article interactions before choosing those with fewer article interactions.
#
#
# * Instead of arbitrarily choosing articles from the user where the number of recommended articles starts below m and ends exceeding m, choose articles with the articles with the most total interactions before choosing those with fewer total interactions. This ranking should be what would be obtained from the **top_articles** function you wrote earlier.
def get_users_total_interactions(user_ids,df=df):
all_user_interaction_count = df.groupby('user_id')['article_id'].count()
subset_interaction_count = all_user_interaction_count.loc[user_ids]
return subset_interaction_count
def get_top_sorted_users(user_id, df=df, user_item=user_item):
'''
INPUT:
user_id - (int)
df - (pandas dataframe) df as defined at the top of the notebook
user_item - (pandas dataframe) matrix of users by articles:
1's when a user has interacted with an article, 0 otherwise
OUTPUT:
neighbors_df - (pandas dataframe) a dataframe with:
neighbor_id - is a neighbor user_id
similarity - measure of the similarity of each user to the provided user_id
num_interactions - the number of articles viewed by the user - if a u
Other Details - sort the neighbors_df by the similarity and then by number of interactions where
highest of each is higher in the dataframe
'''
# Your code here
similar_users_similarity = get_user_similar_users(user_id, user_item=user_item)
similar_user_interaction_count = get_users_total_interactions(similar_users_similarity.index.values,df=df)
neighbors_df = similar_users_similarity.to_frame().join(similar_user_interaction_count)
neighbors_df.columns = ['similarity','num_interactions']
neighbors_df = neighbors_df.sort_values(by=['similarity','num_interactions'],ascending=False)
neighbors_df.index = neighbors_df.index.rename('neighbor_id')
return neighbors_df # Return the dataframe specified in the doc_string
def sort_articles_by_interaction_count(articles_ids,df=df):
articles_ids = [int(float(i)) for i in articles_ids]
article_interactions = df.groupby('article_id')['user_id'].count()
article_interactions = article_interactions.loc[articles_ids].sort_values(ascending=False)
return article_interactions.index.values.astype(float).astype(str)
def user_user_recs_part2(user_id, m=10):
'''
INPUT:
user_id - (int) a user id
m - (int) the number of recommendations you want for the user
OUTPUT:
recs - (list) a list of recommendations for the user by article id
rec_names - (list) a list of recommendations for the user by article title
Description:
Loops through the users based on closeness to the input user_id
For each user - finds articles the user hasn't seen before and provides them as recs
Does this until m recommendations are found
Notes:
* Choose the users that have the most total article interactions
before choosing those with fewer article interactions.
* Choose articles with the articles with the most total interactions
before choosing those with fewer total interactions.
'''
# Your code here
similar_users = get_top_sorted_users(user_id).index.values
recommendations = []
for other_user in similar_users:
recommendations = append_unseen_article_from_similar_user(recommendations,user_id,other_user)
if len(recommendations)>m:break
recommendations = sort_articles_by_interaction_count(recommendations,df=df)
recommendations = recommendations[0:m]
recs = recommendations
rec_names = get_article_names(recommendations)
return recs, rec_names
# Quick spot check - don't change this code - just use it to test your functions
rec_ids, rec_names = user_user_recs_part2(20, 10)
print("The top 10 recommendations for user 20 are the following article ids:")
print(rec_ids)
print()
print("The top 10 recommendations for user 20 are the following article names:")
print(rec_names)
# `5.` Use your functions from above to correctly fill in the solutions to the dictionary below. Then test your dictionary against the solution. Provide the code you need to answer each following the comments below.
# +
### Tests with a dictionary of results
user1_most_sim = get_top_sorted_users(1).index.values[0] # Find the user that is most similar to user 1
user131_10th_sim = get_top_sorted_users(131).index.values[9]# Find the 10th most similar user to user 131
# +
## Dictionary Test Here
sol_5_dict = {
'The user that is most similar to user 1.': user1_most_sim,
'The user that is the 10th most similar to user 131': user131_10th_sim,
}
t.sol_5_test(sol_5_dict)
# -
# `6.` If we were given a new user, which of the above functions would you be able to use to make recommendations? Explain. Can you think of a better way we might make recommendations? Use the cell below to explain a better method for new users.
# Since the new user will have no recorded interactions in the system, it would not make any sense to find similar users to him; hence, no collaborative filtered recommendations can be made.
#
# The best way to go about this situation is to recommend the most popular articles for the new user (by total number of interactions with the articles).
# `7.` Using your existing functions, provide the top 10 recommended articles you would provide for the a new user below. You can test your function against our thoughts to make sure we are all on the same page with how we might make a recommendation.
def get_most_popular_articles(m=10,df=df):
article_interactions = df.groupby('article_id')['user_id'].count()
article_interactions = article_interactions.sort_values(ascending=False)
recommendations = article_interactions.iloc[:10]
recommendations = recommendations.index.values.astype(float).astype(str)
return recommendations
# +
new_user = '0.0'
# What would your recommendations be for this new user '0.0'? As a new user, they have no observed articles.
# Provide a list of the top 10 article ids you would give to
new_user_recs = get_most_popular_articles(10) # Your recommendations here
# +
assert set(new_user_recs) == set(['1314.0','1429.0','1293.0','1427.0','1162.0','1364.0','1304.0','1170.0','1431.0','1330.0']), "Oops! It makes sense that in this case we would want to recommend the most popular articles, because we don't know anything about these users."
print("That's right! Nice job!")
# -
# ### <a class="anchor" id="Matrix-Fact">Part V: Matrix Factorization</a>
#
# In this part of the notebook, you will build use matrix factorization to make article recommendations to the users on the IBM Watson Studio platform.
#
# `1.` You should have already created a **user_item** matrix above in **question 1** of **Part III** above. This first question here will just require that you run the cells to get things set up for the rest of **Part V** of the notebook.
# Load the matrix here
user_item_matrix = pd.read_pickle('user_item_matrix.p')
# quick look at the matrix
user_item_matrix.head()
# `2.` In this situation, you can use Singular Value Decomposition from [numpy](https://docs.scipy.org/doc/numpy-1.14.0/reference/generated/numpy.linalg.svd.html) on the user-item matrix. Use the cell to perform SVD, and explain why this is different than in the lesson.
# +
# Perform SVD on the User-Item Matrix Here
u, s, vt = np.linalg.svd(user_item_matrix)# use the built in to get the three matrices
# -
print("U.shape =",u.shape)
print("S.shape =",s.shape)
print("Vt.shape =",vt.shape)
# Since our user_item_matrix has no missing values (it shows 1 if at least a single interaction exists or 0 otherwise), we don't have to use FunkSVD (which is needed when the matrix has missing values). We can go ahead and use the standard SVD function with no worries.
# `3.` Now for the tricky part, how do we choose the number of latent features to use? Running the below cell, you can see that as the number of latent features increases, we obtain a lower error rate on making predictions for the 1 and 0 values in the user-item matrix. Run the cell below to get an idea of how the accuracy improves as we increase the number of latent features.
# +
num_latent_feats = np.arange(10,700+10,20)
sum_errs = []
for k in num_latent_feats:
# restructure with k latent features
s_new, u_new, vt_new = np.diag(s[:k]), u[:, :k], vt[:k, :]
# take dot product
user_item_est = np.around(np.dot(np.dot(u_new, s_new), vt_new))
# compute error for each prediction to actual value
diffs = np.subtract(user_item_matrix, user_item_est)
# total errors and keep track of them
err = np.sum(np.sum(np.abs(diffs)))
sum_errs.append(err)
plt.plot(num_latent_feats, 1 - np.array(sum_errs)/df.shape[0]);
plt.xlabel('Number of Latent Features');
plt.ylabel('Accuracy');
plt.title('Accuracy vs. Number of Latent Features');
# -
# `4.` From the above, we can't really be sure how many features to use, because simply having a better way to predict the 1's and 0's of the matrix doesn't exactly give us an indication of if we are able to make good recommendations. Instead, we might split our dataset into a training and test set of data, as shown in the cell below.
#
# Use the code from question 3 to understand the impact on accuracy of the training and test sets of data with different numbers of latent features. Using the split below:
#
# * How many users can we make predictions for in the test set?
# * How many users are we not able to make predictions for because of the cold start problem?
# * How many articles can we make predictions for in the test set?
# * How many articles are we not able to make predictions for because of the cold start problem?
user_item_test = create_user_item_matrix(df)
# +
df_train = df.head(40000)
df_test = df.tail(5993)
def create_test_and_train_user_item(df_train, df_test):
'''
INPUT:
df_train - training dataframe
df_test - test dataframe
OUTPUT:
user_item_train - a user-item matrix of the training dataframe
(unique users for each row and unique articles for each column)
user_item_test - a user-item matrix of the testing dataframe
(unique users for each row and unique articles for each column)
test_idx - all of the test user ids
test_arts - all of the test article ids
'''
# Your code here
user_item_train = create_user_item_matrix(df_train) # this is the user_item matrix for the training dataset
#train_idx = user_item_train.index.values # this is the list of users in the training dataset
#train_arts = user_item_train.columns.values # this is the list of articles in the training dataset
user_item_test = create_user_item_matrix(df_test) # this is the user_item matrix for the testing dataset
test_idx = user_item_test.index.values # this is the list of users in the testing dataset
test_arts = user_item_test.columns.values # this is the list of articles in the testing dataset
return user_item_train, user_item_test, test_idx, test_arts
user_item_train, user_item_test, test_idx, test_arts = create_test_and_train_user_item(df_train, df_test)
# -
# these users are the only users available across both training and testing datasets
# these are the only users for which we will be able to make predictions in testing
len(np.intersect1d(test_idx,user_item_train.index.values))
# these test users are not in the training dataset;hence, we cannot make predictions for them in the testing process
len(test_idx)-len(np.intersect1d(test_idx,user_item_train.index.values))
# these articles are the only articles available across both training and testing datasets
# these are the only articles for which we will be able to make predictions in testing
len(np.intersect1d(test_arts,user_item_train.columns.values))
# these test articles are not in the training dataset;hence, we cannot make predictions for them in the testing process
len(test_arts)-len(np.intersect1d(test_arts,user_item_train.columns.values))
# +
# Replace the values in the dictionary below
a = 662
b = 574
c = 20
d = 0
sol_4_dict = {
'How many users can we make predictions for in the test set?':c,
'How many users in the test set are we not able to make predictions for because of the cold start problem?':a,
'How many movies can we make predictions for in the test set?':b,
'How many movies in the test set are we not able to make predictions for because of the cold start problem?':d
}
t.sol_4_test(sol_4_dict)
# -
# `5.` Now use the **user_item_train** dataset from above to find U, S, and V transpose using SVD. Then find the subset of rows in the **user_item_test** dataset that you can predict using this matrix decomposition with different numbers of latent features to see how many features makes sense to keep based on the accuracy on the test data. This will require combining what was done in questions `2` - `4`.
#
# Use the cells below to explore how well SVD works towards making predictions for recommendations on the test data.
# +
# Use these cells to see how well you can use the training
# decomposition to predict on test data
# -
def u_s_vt_dot_product(u,s,vt):
return np.around(np.dot(np.dot(u, s),vt))
def slice_by_k_features(u,s,vt,k):
u_new = u[:, :k]
s_new = np.diag(s[:k])
vt_new = vt[:k, :]
return u_new, s_new, vt_new
def find_and_track_error(errors,user_item_matrix,user_item_est):
diffs = np.subtract(user_item_matrix, user_item_est)
err = np.sum(np.sum(np.abs(diffs)))
errors.append(err)
return errors
# fit SVD on the user_item_train matrix
u_train, s_train, vt_train = np.linalg.svd(user_item_train)# fit svd similar to above then use the cells below
p_test_idx = np.intersect1d(test_idx,user_item_train.index.values)
p_test_arts = np.intersect1d(test_arts,user_item_train.columns.values)
user_item_test = user_item_test.loc[p_test_idx, p_test_arts]
common_user_rows = user_item_train.index.isin(test_idx)
common_article_columns = user_item_train.columns.isin(test_arts)
u_test = u_train[common_user_rows, :]
vt_test = vt_train[:,common_article_columns]
# +
num_latent_feats = np.arange(10,700+10,20)
train_error_sum = []
test_error_sum = []
for k in num_latent_feats:
# restructure with k latent features
u_train_slice, s_train_slice, vt_train_slice = slice_by_k_features(u_train,s_train,vt_train,k)
u_test_slice, s_test_slice, vt_test_slice = slice_by_k_features(u_test,s_train,vt_test,k)
# take dot product
user_item_train_preds = u_s_vt_dot_product(u_train_slice,s_train_slice,vt_train_slice)
user_item_test_preds = u_s_vt_dot_product(u_test_slice,s_test_slice,vt_test_slice)
# compute error for each prediction to actual value and add it to error tracker
train_error_sum = find_and_track_error(train_error_sum,user_item_train,user_item_train_preds)
test_error_sum = find_and_track_error(test_error_sum,user_item_test,user_item_test_preds)
# -
plt.plot(num_latent_feats, 1 - np.array(train_error_sum)/(user_item_train.shape[0]*user_item_test.shape[1]));
plt.plot(num_latent_feats, 1 - np.array(test_error_sum)/(user_item_test.shape[0]*user_item_test.shape[1]), label='Test');
plt.xlabel('Number of Latent Features');
plt.ylabel('Accuracy');
plt.title('Accuracy vs. Number of Latent Features');
# `6.` Use the cell below to comment on the results you found in the previous question. Given the circumstances of your results, discuss what you might do to determine if the recommendations you make with any of the above recommendation systems are an improvement to how users currently find articles?
# - As per the scree plot above, we can see that the accuracy of the training set increases as we introduce more latent features. This is expected as more latent features allow for parameters to the predictions; hence, increasing the granularity and accuracy.
# - Countrary to intituition, the accuracy of the testing set has been decreasing rapidly as more latent features are introduced. This is most likely due to the fact that our user_item test matrix is based on a seperate subset of the recorded interactions, leading to a completely different interaction set that was not predictable to by the trainin_set decomposition; hence, the higher error and lower accuracy.
# - A suggestion to properly test this the prformance of our training decomposition is to rebuild the test user_item test matrix in a way that caters for the interactions we already trained for. This will give us a clearer understanding of the overall accuracy changes when predicting the test set performance.
# - Another suggestion is to resort to f1-scores instead of the simple accuracy score as it reflects a more honest picture of precision and recall.
# - Last but not least, we should also be concerned about the class representation across our training and testing sets in order not to produce biased results.
# <a id='conclusions'></a>
#
# ## Conclusion
#
# > Congratulations! You have reached the end of the Recommendations with IBM project!
#
# > **Tip**: Once you are satisfied with your work here, check over your report to make sure that it is satisfies all the areas of the [rubric](https://review.udacity.com/#!/rubrics/2322/view). You should also probably remove all of the "Tips" like this one so that the presentation is as polished as possible.
#
#
# ## Directions to Submit
#
# > Before you submit your project, you need to create a .html or .pdf version of this notebook in the workspace here. To do that, run the code cell below. If it worked correctly, you should get a return code of 0, and you should see the generated .html file in the workspace directory (click on the orange Jupyter icon in the upper left).
#
# > Alternatively, you can download this report as .html via the **File** > **Download as** submenu, and then manually upload it into the workspace directory by clicking on the orange Jupyter icon in the upper left, then using the Upload button.
#
# > Once you've done this, you can submit your project by clicking on the "Submit Project" button in the lower right here. This will create and submit a zip file with this .ipynb doc and the .html or .pdf version you created. Congratulations!
from subprocess import call
call(['python', '-m', 'nbconvert', 'Recommendations_with_IBM.ipynb'])
|
Recommendations_with_IBM.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Non Linear regression using the diabetes dataset
# This example follows on from the previous [linear regression](https://github.com/morganics/bayesianpy/blob/master/examples/notebook/diabetes_linear_regression.ipynb) example, to demonstrate how additional latent states are synonymous with the number of degrees of freedom in traditional non-linear regression (e.g. non-linear least squares).
#
# I'm not going to spend much time explaining the code. The only difference to the linear regression is the additional 'Cluster' variable specified in the MixtureNaiveBayes template. I can start off with 2 latent states.
# +
# %matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn.metrics import r2_score
import sys
sys.path.append("../../../bayesianpy")
import bayesianpy
import pandas as pd
import logging
from sklearn.model_selection import train_test_split
# Load the diabetes dataset
diabetes = datasets.load_diabetes()
# Use only one feature
diabetes_X = diabetes.data[:, np.newaxis, 2]
df = pd.DataFrame({'A': [x[0] for x in diabetes_X], 'target': diabetes.target})
train, test = train_test_split(df, test_size=0.4)
logger = logging.getLogger()
bayesianpy.jni.attach(logger)
f = bayesianpy.utils.get_path_to_parent_dir('')
with bayesianpy.data.DataSet(df, f, logger) as dataset:
tpl = bayesianpy.template.MixtureNaiveBayes(logger, continuous=df, latent_states=2)
network = tpl.create(bayesianpy.network.NetworkFactory(logger))
plt.figure()
layout = bayesianpy.visual.NetworkLayout(network)
graph = layout.build_graph()
pos = layout.fruchterman_reingold_layout(graph)
layout.visualise(graph, pos)
model = bayesianpy.model.NetworkModel(network, logger)
model.train(dataset.subset(train.index.tolist()))
results = model.batch_query(dataset.subset(test.index.tolist()),
[bayesianpy.model.QueryMeanVariance('target',output_dtype=df['target'].dtype)])
results.sort_values(by='A', ascending=True, inplace=True)
plt.figure(figsize=(10, 10))
plt.scatter(df['A'].tolist(), df['target'].tolist(), label='Actual')
plt.plot(results['A'], results['target_mean'], 'ro-', label='Predicted')
plt.fill_between(results.A,
results.target_mean-results.target_variance.apply(np.sqrt),
results.target_mean+results.target_variance.apply(np.sqrt),
color='darkgrey', alpha=0.4,
label='Variance'
)
plt.xlabel("A")
plt.ylabel("Predicted Target")
plt.legend()
plt.show()
print("R2 score: {}".format(r2_score(results.target.tolist(), results.target_mean.tolist())))
# -
# With 5 latent states:
with bayesianpy.data.DataSet(df, f, logger) as dataset:
tpl = bayesianpy.template.MixtureNaiveBayes(logger, continuous=df, latent_states=5)
network = tpl.create(bayesianpy.network.NetworkFactory(logger))
model = bayesianpy.model.NetworkModel(network, logger)
model.train(dataset.subset(train.index.tolist()))
results = model.batch_query(dataset.subset(test.index.tolist()),
[bayesianpy.model.QueryMeanVariance('target',output_dtype=df['target'].dtype)])
results.sort_values(by='A', ascending=True, inplace=True)
plt.figure(figsize=(10, 10))
plt.scatter(df['A'].tolist(), df['target'].tolist(), label='Actual')
plt.plot(results['A'], results['target_mean'], 'ro-', label='Predicted')
plt.fill_between(results.A,
results.target_mean-results.target_variance.apply(np.sqrt),
results.target_mean+results.target_variance.apply(np.sqrt),
color='darkgrey', alpha=0.4,
label='Variance'
)
plt.xlabel("A")
plt.ylabel("Predicted Target")
plt.legend()
plt.show()
print("R2 score: {}".format(r2_score(results.target.tolist(), results.target_mean.tolist())))
# Finally 10 latent states:
with bayesianpy.data.DataSet(df, f, logger) as dataset:
tpl = bayesianpy.template.MixtureNaiveBayes(logger, continuous=df, latent_states=10)
network = tpl.create(bayesianpy.network.NetworkFactory(logger))
model = bayesianpy.model.NetworkModel(network, logger)
model.train(dataset.subset(train.index.tolist()))
results = model.batch_query(dataset.subset(test.index.tolist()),
[bayesianpy.model.QueryMeanVariance('target',output_dtype=df['target'].dtype)])
results.sort_values(by='A', ascending=True, inplace=True)
plt.figure(figsize=(10, 10))
plt.scatter(df['A'].tolist(), df['target'].tolist(), label='Actual')
plt.plot(results['A'], results['target_mean'], 'ro-', label='Predicted')
plt.fill_between(results.A,
results.target_mean-results.target_variance.apply(np.sqrt),
results.target_mean+results.target_variance.apply(np.sqrt),
color='darkgrey', alpha=0.4,
label='Variance'
)
plt.xlabel("A")
plt.ylabel("Predicted Target")
plt.legend()
plt.show()
print("R2 score: {}".format(r2_score(results.target.tolist(), results.target_mean.tolist())))
# Obviously, the R2 score doesn't take variance in to account, but it looks like we've reached peak R2 at around 5 latent states (incidentally, a similar iteration can be used to select the optimal number of latent states).
#
# Our base R2 was around 0.34, so it seems like a linear regression model fits the data better than a non-linear regressor.
|
examples/notebook/diabetes_non_linear_regression.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import torch as t
from torch import nn
from torch.autograd import Variable
from torch.optim import RMSprop
from torchvision import transforms
from torchvision.utils import make_grid
from torchvision.datasets import CIFAR10
from pylab import plt
# %matplotlib inline
import os
os.environ['CUDA_VISIBLE_DEVICES']='1'
# +
'''
https://zhuanlan.zhihu.com/p/25071913
WGAN modified of DCGAN in:
1. remove sigmoid in the last layer of discriminator(classification -> regression) # 回归问题,而不是二分类概率
2. no log Loss (Wasserstein distance)
3. clip param norm to c (Wasserstein distance and Lipschitz continuity)
4. No momentum-based optimizer, use RMSProp,SGD instead
explanation of GAN:
collapse mode ->KL diverse
digit unstability-> comflict between KL Divergence and JS Divergence
'''
class Config:
lr = 0.00005
nz = 100 # noise dimension
image_size = 64
image_size2 = 64
nc = 3 # chanel of img
ngf = 64 # generate channel
ndf = 64 # discriminative channel
beta1 = 0.5
batch_size = 32
max_epoch = 50 # =1 when debug
workers = 2
gpu = True # use gpu or not
clamp_num=0.01# WGAN clip gradient
opt=Config()
# +
# data preprocess
transform=transforms.Compose([
transforms.Resize(opt.image_size) ,
transforms.ToTensor(),
transforms.Normalize([0.5]*3,[0.5]*3)
])
dataset=CIFAR10(root='cifar10/',transform=transform,download=True)
# dataloader with multiprocessing
dataloader=t.utils.data.DataLoader(dataset,
opt.batch_size,
shuffle = True,
num_workers=opt.workers)
# +
netg = nn.Sequential(
nn.ConvTranspose2d(opt.nz,opt.ngf*8,4,1,0,bias=False),
nn.BatchNorm2d(opt.ngf*8),
nn.ReLU(True),
nn.ConvTranspose2d(opt.ngf*8,opt.ngf*4,4,2,1,bias=False),
nn.BatchNorm2d(opt.ngf*4),
nn.ReLU(True),
nn.ConvTranspose2d(opt.ngf*4,opt.ngf*2,4,2,1,bias=False),
nn.BatchNorm2d(opt.ngf*2),
nn.ReLU(True),
nn.ConvTranspose2d(opt.ngf*2,opt.ngf,4,2,1,bias=False),
nn.BatchNorm2d(opt.ngf),
nn.ReLU(True),
nn.ConvTranspose2d(opt.ngf,opt.nc,4,2,1,bias=False),
nn.Tanh()
)
netd = nn.Sequential(
nn.Conv2d(opt.nc,opt.ndf,4,2,1,bias=False),
nn.LeakyReLU(0.2,inplace=True),
nn.Conv2d(opt.ndf,opt.ndf*2,4,2,1,bias=False),
nn.BatchNorm2d(opt.ndf*2),
nn.LeakyReLU(0.2,inplace=True),
nn.Conv2d(opt.ndf*2,opt.ndf*4,4,2,1,bias=False),
nn.BatchNorm2d(opt.ndf*4),
nn.LeakyReLU(0.2,inplace=True),
nn.Conv2d(opt.ndf*4,opt.ndf*8,4,2,1,bias=False),
nn.BatchNorm2d(opt.ndf*8),
nn.LeakyReLU(0.2,inplace=True),
nn.Conv2d(opt.ndf*8,1,4,1,0,bias=False),
# Modification 1: remove sigmoid
# nn.Sigmoid()
)
def weight_init(m):
# weight_initialization: important for wgan
class_name=m.__class__.__name__
if class_name.find('Conv')!=-1:
m.weight.data.normal_(0,0.02)
elif class_name.find('Norm')!=-1:
m.weight.data.normal_(1.0,0.02)
# else:print(class_name)
netd.apply(weight_init)
netg.apply(weight_init)
# +
# modification 2: Use RMSprop instead of Adam
# optimizer
optimizerD = RMSprop(netd.parameters(),lr=opt.lr )
optimizerG = RMSprop(netg.parameters(),lr=opt.lr )
# modification3: No Log in loss
# criterion
# criterion = nn.BCELoss()
fix_noise = Variable(t.FloatTensor(opt.batch_size,opt.nz,1,1).normal_(0,1))
if opt.gpu:
fix_noise = fix_noise.cuda()
netd.cuda()
netg.cuda()
# +
# begin training
print('begin training, be patient...')
one=t.FloatTensor([1])
mone=-1*one
for epoch in range(opt.max_epoch):
for ii, data in enumerate(dataloader,0):
real,_=data
input = Variable(real)
noise = t.randn(input.size(0),opt.nz,1,1)
noise = Variable(noise)
if opt.gpu:
one = one.cuda()
mone = mone.cuda()
noise = noise.cuda()
input = input.cuda()
# modification: clip param for discriminator
for parm in netd.parameters():
parm.data.clamp_(-opt.clamp_num,opt.clamp_num)
# ----- train netd -----
netd.zero_grad()
## train netd with real img
output=netd(input)
output.backward(one)
## train netd with fake img
fake_pic=netg(noise).detach()
output2=netd(fake_pic)
output2.backward(mone)
optimizerD.step()
# ------ train netg -------
# train netd more: because the better netd is,
# the better netg will be
if (ii+1)%5 ==0:
netg.zero_grad()
noise.data.normal_(0,1)
fake_pic=netg(noise)
output=netd(fake_pic)
output.backward(one)
optimizerG.step()
if ii%100==0:pass
fake_u=netg(fix_noise)
imgs = make_grid(fake_u.data*0.5+0.5).cpu() # CHW
plt.imshow(imgs.permute(1,2,0).numpy()) # HWC
plt.show()
# -
t.save(netd.state_dict(),'epoch_wnetd.pth')
t.save(netg.state_dict(),'epoch_wnetg.pth')
netd.load_state_dict(t.load('epoch_wnetd.pth'))
netg.load_state_dict(t.load('epoch_wnetg.pth'))
noise = t.randn(64,opt.nz,1,1).cuda()
noise = Variable(noise)
fake_u=netg(noise)
imgs = make_grid(fake_u.data*0.5+0.5).cpu() # CHW
plt.figure(figsize=(5,5))
plt.imshow(imgs.permute(1,2,0).numpy()) # HWC
plt.show()
|
WGAN.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Instructions
# * **<font color="red">When you load this page, go to "Cell->Run All" to start the program running. After that point, you should be able to use the sliders and buttons to manipulate the output.</font>**
# * If things go totally awry, you can go to "Kernel->Restart" and then "Cell->Run All". A more drastic solution would be to close and reload the page, which will reset the code to its initial state.
# * If you're interested in programming, click the "Toggle raw code" button. This will expose the underlying program, written in the Python3 programming language. You can edit the code to your heart's content: just go to "Cell->Run All" after you modify things so the changes will be incorporated. Text in the code blocks preceded by `#` are comments to guide you through the excercise and/or explain the code
#
# +
# -----------------------------------------------------------------------------------
# Javascript that gives us a cool hide-the-code button
from IPython.display import HTML
HTML('''
<script>
code_show=true;
function code_toggle() {
if (code_show){
$('div.input').hide();
} else {
$('div.input').show();
}
code_show = !code_show
}
$( document ).ready(code_toggle);
</script>
<form action="javascript:code_toggle()">
<input type="submit" value="Toggle raw code">
</form>
''')
# ------------------------------------------------------------------------------------
# -
#
# # Amino acid titration explorer
# +
#Import libraries that do things like plot data and handle arrays
# %matplotlib inline
from matplotlib import pyplot as plt
import numpy as np
# libraries for making pretty sliders and interactive graphs
import ipywidgets as widgets
from ipywidgets import interactive
from IPython.display import display
def fractional_protonation(pKa,pH):
"""
Calculate the protonation state of a titratable group versus pH given its pKa.
"""
theta_protonated = 1/(1 + 10**(pH-pKa))
return theta_protonated
def fractional_charge(pKa,charge_when_protonated,pH):
"""
Cacluate the fractional charge on a molecule given its pKa value, charge when ionized, and pH
"""
theta_protonated = 1/(1 + 10**(pH-pKa))
if charge_when_protonated == 0:
theta_charge = -1*(1-theta_protonated)
else:
theta_charge = theta_protonated
return theta_charge
def titrate_amino_acid(sidechain_pKa=4,charge_when_protonated=0,titratable_sidechain=True):
"""
Calculate the total charge on a free amino acid as a function of pH.
"""
# N- and C-terminal groups
pKas = [9.0,2.0]
charges = [1,0]
# Are we adding a titratable sidec chain?
if titratable_sidechain == True:
pKas.append(sidechain_pKa)
charges.append(charge_when_protonated)
# Create a vector of pH values and a vector of zeros to hold total charge state vs. pH
pH_list = np.arange(0,14,0.25)
total_charge = np.zeros(len(pH_list))
total_protonation = np.zeros(len(pH_list))
# For every titratable group, calculate charge vs. pH and append to the total charge
for i in range(len(pKas)):
total_charge = total_charge + fractional_charge(pKas[i],charges[i],pH_list)
total_protonation = total_protonation + fractional_protonation(pKas[i],pH_list)
fig, ax = plt.subplots(1,2)
ax[0].plot(pH_list,total_protonation,color="black")
ax[0].axhline(y=0,color="gray",linestyle="dashed")
ax[0].set_xlabel("pH")
ax[0].set_ylabel("total protonation")
ax[0].set_title("protonation state")
ax[1].plot(pH_list,total_charge,color="green")
ax[1].axhline(y=0,color="gray",linestyle="dashed")
ax[1].set_xlabel("pH")
ax[1].set_ylabel("total charge")
ax[1].set_title("charge state")
fig.set_figwidth(10)
fig.tight_layout()
plt.show()
titratable_sc_widget = widgets.Checkbox(description="amino acid sidechain titrable?",value=True)
pKa_widget = widgets.FloatText(description="pKa of sidechain",value=4.5)
charge_widget = widgets.IntSlider(description="charge of protonated sidechain",min=0,max=1,step=1,value=0)
container = widgets.interactive(titrate_amino_acid,
titratable_sidechain=titratable_sc_widget,
sidechain_pKa=pKa_widget,
charge_when_protonated=charge_widget)
display(container)
# -
# # Appendix: the Henderson-Hasselbalch Equation and Fractional Charge
#
#
# ## Derive HH:
# Start with the definition of an acid dissocation constant:
#
# $$\frac{[H^{+}][A]}{[HA]}=K_{acid}$$
#
# Rearrange and take the $-log_{10}$ of both sides:
#
# $$[H^{+}]=\frac{K_{acid}[HA]}{[A]}$$
#
# $$-log_{10}([H^{+}]) = -log_{10}\Big(\frac{K_{acid}[HA]}{[A]}\Big)$$
#
# Apply the log rule that $log(XY) = log(X) + log(Y)$:
#
# $$-log_{10}([H^{+}]) = -log_{10}(K_{acid}) -log_{10}\Big(\frac{[HA]}{[A]}\Big)$$
#
# Recalling that $pX \equiv -log_{10}(X)$ we can write:
#
# $$pH = pK_{a} - log_{10} \Big (\frac{[HA]}{[A]} \Big)$$
#
# Then apply the log rule that $ -log(X) = log(1/X)$ to get:
#
# $$pH = pK_{a} + log_{10} \Big (\frac{[A]}{[HA]} \Big)$$
#
# This is the Henderson-Hasselbalch equation.
#
# ## Derive fractional protonation
#
# Now let's think about $\theta$, the fraction of some molecule $A$ that is protonated as a function of $pH$. This is simply the concentration of protonated molecules ($[HA]$) over all possible molecules:
#
# $$\theta \equiv \frac{[HA]}{[HA] + [A]}$$
#
# We can rearrange Henderson-Hasselbalch to solve for $[A]$:
#
# $$pH - pK_{a} = log_{10} \Big (\frac{[A]}{[HA]} \Big)$$
#
# $$10^{(pH-pK_{a})} = \frac{[A]}{[HA]}$$
#
# $$[HA] 10^{(pH-pK_{a})} = [A]$$
#
# And then substitute into the equation for $\theta$:
#
# $$\theta = \frac{[HA]}{[HA] + [HA] 10^{(pH-pK_{a})}}$$
#
# $$\theta = \frac{1}{1 + 10^{(pH-pK_{a})}}$$
#
# We now have an equation that relates the $pK_{a}$ and $pH$ to the saturation of a molecule.
#
# ## Relate fractional protonation to fractional charge
#
# To relate fractional protonation to the fractional charge, we need to know some chemistry.
# For example, a protonated carboxylic acid ($R-COOH$) is neutral, while a protonated amine ($NH^{+}_{4}$) is charged. If you know the chemical structures of your amino acids, you should be able to reason about charge vs. pH given information about _protonation_ vs. pH. The titration behaviors of the groups that titrate at reasonable pH values are shown below:
#
# **Charge on protonated state = 0**
#
# Aspartic acid/glutamic acid/C-terminus ($pK_{a} \approx 2-4$): $R-COOH \rightleftharpoons \color{red}{R-COO^{-}} + \color{blue}{H^{+}}$
#
# Tyrosine ($pK_{a} = 10.5 $): $R-OH \rightleftharpoons \color{red}{R-O^{-}} + \color{blue}{H^{+}}$
#
# Cysteine ($pK_{a} = 8.4 $): $R-SH \rightleftharpoons \color{red}{R-S^{-}} + \color{blue}{H^{+}}$
#
#
#
# **Charge on protonated state = 1**
#
# Lysine/N-terminus ($pK_{a} \approx 10 $): $\color{blue}{R-NH^{+}_{3}} \rightleftharpoons R-NH_{2} + \color{blue}{H^{+}}$
#
# Histidine ($pK_{a} = 6.0 $): $\color{blue}{R-C_{3}H_{4}N_{2}^{+}} \rightleftharpoons R-C_{3}H_{3}N_{2} + \color{blue}{H^{+}}$
#
# Arginine ($pK_{a} = 12.5 $): $\color{blue}{R-C_{1}H_{5}N_{3}^{+}} \rightleftharpoons R-C_{1}H_{4}N_{3} + \color{blue}{H^{+}}$
#
|
pH-Titration.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# default_exp l10_anneal
# +
#export
from pathlib import Path
from IPython.core.debugger import set_trace
import pickle, gzip, math, torch, matplotlib as mpl
import matplotlib.pyplot as plt
from torch import tensor
from torch import nn
from torch.utils.data import DataLoader, SequentialSampler, RandomSampler
from tensorflow.keras.datasets import mnist
import torch.nn.functional as F
from torch.utils.data import DataLoader, SequentialSampler, RandomSampler
def get_data():
(x_train,y_train),(x_valid,y_valid)= mnist.load_data()
x_train,y_train, x_valid, y_valid = map(torch.from_numpy,(x_train,y_train,x_valid,y_valid))
l=[x_train, y_train,x_valid, y_valid]
for i in range(len(l)):
sh=l[i].shape
l[i]=l[i].reshape(sh[0],-1)
return l[0].float()/255,l[1].squeeze(-1).long(), l[2].float()/255,l[3].squeeze(-1).long()
class Dataset():
def __init__(self, x,y): self.x, self.y= x,y
def __len__(self): return len(self.x)
def __getitem__(self, n): return self.x[n], self.y[n]
class DataBunch():
def __init__(self, train_dl, valid_dl, c=None): self.train_dl, self.valid_dl, self.c = train_dl, valid_dl, c
@property
def train_ds(self): return self.train_dl.dataset
@property
def valid_ds(self): return self.valid_dl.dataset
class Learner():
def __init__(self, model, opt, loss_func, data):
self.model, self.opt, self.loss_func,self.data = model, opt, loss_func, data
def get_dls(train_ds, valid_ds, bs, **kwargs):
return (DataLoader(train_ds, batch_size=bs, shuffle=True, **kwargs),
DataLoader(valid_ds, batch_size=bs*2, **kwargs))
# +
#export
from torch import optim
def get_model(data, lr=0.5,nh=50):
m=data.train_ds.x.shape[1]
model=nn.Sequential(nn.Linear(m,nh),nn.ReLU(), nn.Linear(nh, data.c))
return model, optim.SGD(model.parameters(), lr=lr)
def get_learner(model_func, loss_func, data):
return Learner(*model_func(data), loss_func, data)
# -
#export
def accuracy(out, yb): return (torch.argmax(out, dim=1)==yb).float().mean()
x_train, y_train, x_valid, y_valid=get_data()
bs=32
# +
cat=y_train.max().item()+1
train_ds=Dataset(x_train, y_train)
valid_ds=Dataset(x_valid, y_valid)
data = DataBunch(*get_dls(train_ds, valid_ds, bs), cat)
loss_func = F.cross_entropy
# +
#export
import re
_camel_re1 = re.compile('(.)([A-Z][a-z]+)')
_camel_re2 = re.compile('([a-z0-9])([A-Z])')
def camel2snake(name):
s1 = re.sub(_camel_re1, r'\1_\2', name)
return re.sub(_camel_re2, r'\1_\2', s1).lower()
class Callback():
_order=0
def set_runner(self, run): self.run=run
def __getattr__(self, k): return getattr(self.run, k)
@property
def name(self):
name = re.sub(r'Callback$', '', self.__class__.__name__)
return camel2snake(name or 'callback')
# +
#export
class TrainEvalCallback(Callback):
def begin_fit(self):
self.run.n_epochs=0.
self.run.n_iter=0
def after_batch(self):
if not self.in_train: return
self.run.n_epochs += 1./self.iters
self.run.n_iter += 1
def begin_epoch(self):
self.run.n_epochs=self.epoch
self.model.train()
self.run.in_train=True
def begin_validate(self):
self.model.eval()
self.run.in_train=False
from typing import *
def listify(o):
if o is None: return []
if isinstance(o, list): return o
if isinstance(o, str): return [o]
if isinstance(o, Iterable): return list(o)
return [o]
# +
#export
class Runner():
def __init__(self, cbs=None, cb_funcs=None):
cbs = listify(cbs)
for cbf in listify(cb_funcs):
cb = cbf()
setattr(self, cb.name, cb)
cbs.append(cb)
self.stop,self.cbs = False,[TrainEvalCallback()]+cbs
@property
def opt(self): return self.learn.opt
@property
def model(self): return self.learn.model
@property
def loss_func(self): return self.learn.loss_func
@property
def data(self): return self.learn.data
def one_batch(self, xb, yb):
self.xb,self.yb = xb,yb
if self('begin_batch'): return
self.pred = self.model(self.xb)
if self('after_pred'): return
self.loss = self.loss_func(self.pred, self.yb)
if self('after_loss') or not self.in_train: return
self.loss.backward()
if self('after_backward'): return
self.opt.step()
if self('after_step'): return
self.opt.zero_grad()
def all_batches(self, dl):
self.iters = len(dl)
for xb,yb in dl:
if self.stop: break
self.one_batch(xb, yb)
self('after_batch')
self.stop=False
def fit(self, epochs, learn):
self.epochs,self.learn = epochs,learn
try:
for cb in self.cbs: cb.set_runner(self)
if self('begin_fit'): return
for epoch in range(epochs):
self.epoch = epoch
if not self('begin_epoch'): self.all_batches(self.data.train_dl)
with torch.no_grad():
if not self('begin_validate'): self.all_batches(self.data.valid_dl)
if self('after_epoch'): break
finally:
self('after_fit')
self.learn = None
def __call__(self, cb_name):
for cb in sorted(self.cbs, key=lambda x: x._order):
f = getattr(cb, cb_name, None)
if f and f(): return True
return False
# +
#export
class AvgStats():
def __init__(self, metrics, in_train): self.metrics,self.in_train = listify(metrics),in_train
def reset(self):
self.tot_loss,self.count = 0.,0
self.tot_mets = [0.] * len(self.metrics)
@property
def all_stats(self): return [self.tot_loss.item()] + self.tot_mets
@property
def avg_stats(self): return [o/self.count for o in self.all_stats]
def __repr__(self):
if not self.count: return ""
return f"{'train' if self.in_train else 'valid'}: {self.avg_stats}"
def accumulate(self, run):
bn = run.xb.shape[0]
self.tot_loss += run.loss * bn
self.count += bn
for i,m in enumerate(self.metrics):
self.tot_mets[i] += m(run.pred, run.yb) * bn
class AvgStatsCallback(Callback):
def __init__(self, metrics):
self.train_stats,self.valid_stats = AvgStats(metrics,True),AvgStats(metrics,False)
def begin_epoch(self):
self.train_stats.reset()
self.valid_stats.reset()
def after_loss(self):
stats = self.train_stats if self.in_train else self.valid_stats
with torch.no_grad(): stats.accumulate(self.run)
def after_epoch(self):
print(self.train_stats)
print(self.valid_stats)
# -
learn=get_learner(get_model,loss_func, data)
run= Runner(AvgStatsCallback([accuracy]))
run.fit(2,learn)
#export
from functools import partial
# +
#export
class Recorder(Callback):
def begin_fit(self): self.lrs, self.losses=[],[]
def after_batch(self):
if not self.in_train: return
self.lrs.append(self.opt.param_groups[-1]['lr'])
self.losses.append(self.loss.detach().cpu())
def plot_lr(self): plt.plot(self.lrs)
def plot_loss(self): plt.plot(self.losses)
class ParamScheduler(Callback):
_order=1
def __init__(self,pname, sched_func): self.pname, self.sched_func = pname, sched_func
def set_param(self):
for pg in self.opt.param_groups:
pg[self.pname]=self.sched_func(self.n_epochs/self.epochs)
def begin_batch(self):
if self.in_train: self.set_param()
# -
def sched_lin(start,end):
def _inner(start, end, pos): return start+ pos*(end-start)
return partial(_inner, start,end)
#export
def annealer(f):
def _inner(start, end): return partial(f, start, end)
return _inner
@annealer
def sched_lin(start,end,pos): return start+ pos*(end-start)
f=sched_lin(1,2)
f(0.5)
# +
#export
@annealer
def sched_cos(start,end,pos):return start+(1+math.cos(math.pi*(1-pos)))*(end-start)/2
@annealer
def sched_no(start, end, pos): return start
@annealer
def sched_expo(start,end, pos): return (end/start)**pos
def cos_1cycle_anneal(start, high,end):
return [sched_cos(start, high),sched_cos(high, end)]
torch.Tensor.ndim=property(lambda x: len(x.shape))
# +
annealings='LINEAR COS NO EXPO'.split()
a = torch.arange(0,100)
p = torch.linspace(0.01,1,100)
fns = [sched_lin, sched_cos, sched_no, sched_expo]
for fn, t in zip(fns, annealings):
f=fn(2,1e-2)
plt.plot(a, [f(o) for o in p], label=t)
plt.legend()
# +
#export
def combine_scheds(pcts, scheds):
assert sum(pcts)==1.
pcts=tensor([0]+listify(pcts))
assert torch.all(pcts>=0)
pcts= torch.cumsum(pcts,0)
def _inner(pos):
idx = (pos>=pcts).nonzero().max()
actual_pos=(pos-pcts[idx])/(pcts[idx+1]-pcts[idx])
return scheds[idx](actual_pos)
return _inner
# -
sched = combine_scheds([0.3, 0.7], [sched_cos(0.3, 0.6), sched_cos(0.6, 0.2)])
plt.plot(a, [sched(o) for o in p])
cbfs=[Recorder, partial(AvgStatsCallback,accuracy), partial(ParamScheduler, 'lr', sched)]
learn=get_learner(get_model,loss_func, data)
run=Runner(cb_funcs=cbfs)
run.fit(3,learn)
run.recorder.plot_lr()
run.recorder.plot_loss()
|
01_core.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# soc.030 http://sedac.ciesin.columbia.edu/data/set/spatialecon-gecon-v4
# Downloaded to RW_Data/Rasters/spatialecon-gecon-v4-gis-ascii
# File type: asc
# +
# Libraries for downloading data from remote server (may be ftp)
import requests
from urllib.request import urlopen
from contextlib import closing
import shutil
# Library for uploading/downloading data to/from S3
import boto3
# Libraries for handling data
import rasterio as rio
import numpy as np
# from netCDF4 import Dataset
# import pandas as pd
# import scipy
# Libraries for various helper functions
# from datetime import datetime
import os
import threading
import sys
from glob import glob
# -
# s3
# +
s3_upload = boto3.client("s3")
s3_download = boto3.resource("s3")
s3_bucket = "wri-public-data"
s3_folder = "resourcewatch/raster/soc_030_gross_domestic_product/"
s3_file1 = "soc_030_mer_1990_sum.asc"
s3_file2 = "soc_030_mer_1995_sum.asc"
s3_file3 = "soc_030_mer_2000_sum.asc"
s3_file4 = "soc_030_mer_2005_sum.asc"
s3_file5 = "soc_030_ppp_1990_sum.asc"
s3_file6 = "soc_030_ppp_1995_sum.asc"
s3_file7 = "soc_030_ppp_2000_sum.asc"
s3_file8 = "soc_030_ppp_2005_sum.asc"
s3_key_orig1 = s3_folder + s3_file1
s3_key_edit1 = s3_key_orig1[0:-4] + "_edit.tif"
s3_key_orig2 = s3_folder + s3_file2
s3_key_edit2 = s3_key_orig2[0:-4] + "_edit.tif"
s3_key_orig3 = s3_folder + s3_file3
s3_key_edit3 = s3_key_orig3[0:-4] + "_edit.tif"
s3_key_orig4 = s3_folder + s3_file4
s3_key_edit4 = s3_key_orig4[0:-4] + "_edit.tif"
s3_key_orig5 = s3_folder + s3_file5
s3_key_edit5 = s3_key_orig5[0:-4] + "_edit.tif"
s3_key_orig6= s3_folder + s3_file6
s3_key_edit6 = s3_key_orig6[0:-4] + "_edit.tif"
s3_key_orig7 = s3_folder + s3_file7
s3_key_edit7 = s3_key_orig7[0:-4] + "_edit.tif"
s3_key_orig8 = s3_folder + s3_file8
s3_key_edit8 = s3_key_orig8[0:-4] + "_edit.tif"
class ProgressPercentage(object):
def __init__(self, filename):
self._filename = filename
self._size = float(os.path.getsize(filename))
self._seen_so_far = 0
self._lock = threading.Lock()
def __call__(self, bytes_amount):
# To simplify we'll assume this is hooked up
# to a single filename.
with self._lock:
self._seen_so_far += bytes_amount
percentage = (self._seen_so_far / self._size) * 100
sys.stdout.write("\r%s %s / %s (%.2f%%)"%(
self._filename, self._seen_so_far, self._size,
percentage))
sys.stdout.flush()
# -
# Define local file locations
# +
local_folder = "/Users/Max81007/Desktop/Python/Resource_Watch/Raster/soc_030/"
file_name1 = "mer1990sum.asc"
file_name2 = "mer1995sum.asc"
file_name3 = "mer2000sum.asc"
file_name4 = "mer2005sum.asc"
file_name5 = "ppp1990sum.asc"
file_name6 = "ppp1995sum.asc"
file_name7 = "ppp2000sum.asc"
file_name8 = "ppp2005sum.asc"
local_orig1 = local_folder + file_name1
local_orig2 = local_folder + file_name2
local_orig3 = local_folder + file_name3
local_orig4 = local_folder + file_name4
local_orig5 = local_folder + file_name5
local_orig6 = local_folder + file_name6
local_orig7 = local_folder + file_name7
local_orig8 = local_folder + file_name8
orig_extension_length = 4 #4 for each char in .tif
local_edit1 = local_orig1[:-orig_extension_length] + "edit.tif"
local_edit2 = local_orig2[:-orig_extension_length] + "edit.tif"
local_edit3 = local_orig3[:-orig_extension_length] + "edit.tif"
local_edit4 = local_orig4[:-orig_extension_length] + "edit.tif"
local_edit5 = local_orig5[:-orig_extension_length] + "edit.tif"
local_edit6 = local_orig6[:-orig_extension_length] + "edit.tif"
local_edit7 = local_orig7[:-orig_extension_length] + "edit.tif"
local_edit8 = local_orig8[:-orig_extension_length] + "edit.tif"
# -
# Use rasterio to reproject and compress
files = [local_orig1, local_orig2]
for file in files:
with rio.open(file, 'r') as src:
profile = src.profile
print(profile)
# +
os.getcwd()
os.chdir(local_folder)
os.environ["local_orig1"] =local_orig1
os.environ["local_orig2"] =local_orig2
os.environ["local_orig3"] =local_orig3
os.environ["local_orig4"] =local_orig4
os.environ["local_orig5"] =local_orig5
os.environ["local_orig6"] =local_orig6
os.environ["local_orig7"] =local_orig7
os.environ["local_orig8"] =local_orig8
os.environ["local_edit1"] =local_edit1
os.environ["local_edit2"] =local_edit2
os.environ["local_edit3"] =local_edit3
os.environ["local_edit4"] =local_edit4
os.environ["local_edit5"] =local_edit5
os.environ["local_edit6"] =local_edit6
os.environ["local_edit7"] =local_edit7
os.environ["local_edit8"] =local_edit8
# -
# !gdalwarp -overwrite -t_srs epsg:4326 -co compress=lzw %local_orig1% %local_edit1%
# !gdalwarp -overwrite -t_srs epsg:4326 -co compress=lzw %local_orig2% %local_edit2%
# !gdalwarp -overwrite -t_srs epsg:4326 -co compress=lzw %local_orig3% %local_edit3%
# !gdalwarp -overwrite -t_srs epsg:4326 -co compress=lzw %local_orig4% %local_edit4%
# !gdalwarp -overwrite -t_srs epsg:4326 -co compress=lzw %local_orig5% %local_edit5%
# !gdalwarp -overwrite -t_srs epsg:4326 -co compress=lzw %local_orig6% %local_edit6%
# !gdalwarp -overwrite -t_srs epsg:4326 -co compress=lzw %local_orig7% %local_edit7%
# !gdalwarp -overwrite -t_srs epsg:4326 -co compress=lzw %local_orig8% %local_edit8%
# Upload orig and edit files to s3
# +
# Original
s3_upload.upload_file(local_orig1, s3_bucket, s3_key_orig1,
Callback=ProgressPercentage(local_orig1))
s3_upload.upload_file(local_orig2, s3_bucket, s3_key_orig2,
Callback=ProgressPercentage(local_orig2))
s3_upload.upload_file(local_orig3, s3_bucket, s3_key_orig3,
Callback=ProgressPercentage(local_orig3))
s3_upload.upload_file(local_orig4, s3_bucket, s3_key_orig4,
Callback=ProgressPercentage(local_orig4))
s3_upload.upload_file(local_orig5, s3_bucket, s3_key_orig5,
Callback=ProgressPercentage(local_orig5))
s3_upload.upload_file(local_orig6, s3_bucket, s3_key_orig6,
Callback=ProgressPercentage(local_orig6))
s3_upload.upload_file(local_orig7, s3_bucket, s3_key_orig7,
Callback=ProgressPercentage(local_orig7))
s3_upload.upload_file(local_orig8, s3_bucket, s3_key_orig8,
Callback=ProgressPercentage(local_orig8))
# Edit
s3_upload.upload_file(local_edit1, s3_bucket, s3_key_edit1,
Callback=ProgressPercentage(local_edit1))
s3_upload.upload_file(local_edit2, s3_bucket, s3_key_edit2,
Callback=ProgressPercentage(local_edit2))
s3_upload.upload_file(local_edit3, s3_bucket, s3_key_edit3,
Callback=ProgressPercentage(local_edit3))
s3_upload.upload_file(local_edit4, s3_bucket, s3_key_edit4,
Callback=ProgressPercentage(local_edit4))
s3_upload.upload_file(local_edit5, s3_bucket, s3_key_edit5,
Callback=ProgressPercentage(local_edit5))
s3_upload.upload_file(local_edit6, s3_bucket, s3_key_edit6,
Callback=ProgressPercentage(local_edit6))
s3_upload.upload_file(local_edit7, s3_bucket, s3_key_edit7,
Callback=ProgressPercentage(local_edit7))
s3_upload.upload_file(local_edit8, s3_bucket, s3_key_edit8,
Callback=ProgressPercentage(local_edit8))
# -
band_ids = ["mer_1990","mer_1995","mer_2000", "mer_2005","ppp_1990","ppp_1995","ppp_2000", "ppp_2005" ]
merge_name = "soc_030_gross_domestic_product.tif"
s3_key_merge = s3_folder + merge_name
# +
merge_files = [local_edit1, local_edit2, local_edit3, local_edit4, local_edit5, local_edit6, local_edit7, local_edit8]
tmp_merge = local_folder + merge_name
# -
# +
with rio.open(merge_files[0]) as src:
kwargs = src.profile
kwargs.update(
count=len(merge_files)
)
with rio.open(tmp_merge, 'w', **kwargs) as dst:
for idx, file in enumerate(merge_files):
print(idx)
with rio.open(file) as src:
band = idx+1
windows = src.block_windows()
for win_id, window in windows:
src_data = src.read(1, window=window)
dst.write_band(band, src_data, window=window)
# -
s3_upload.upload_file(tmp_merge, s3_bucket, s3_key_merge,
Callback=ProgressPercentage(tmp_merge))
os.environ["Zs3_key"] = "s3://wri-public-data/" + s3_key_merge
os.environ["Zgs_key"] = "gs://resource-watch-public/" + s3_key_merge
# !gsutil cp %Zs3_key% %Zgs_key%
os.environ["asset_id"] = "users/resourcewatch/soc_030_gross_domestic_product"
# !earthengine upload image --asset_id=%asset_id% %Zgs_key%
os.environ["band_names"] = str(band_ids)
# !earthengine asset set -p band_names="%band_names%" %asset_id%
files = [local_edit1, local_edit2, local_edit3, local_edit4, local_edit5, local_edit6, local_edit7, local_edit8]
for file in files:
with rio.open(file, 'r') as src:
profile = src.profile
print(profile)
|
.ipynb_checkpoints/ene.023-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Pore Scale Imaging and Modeling Section I
# In this project, we have selected a comprehensive paper related to [pore scale imaging and modeling](https://www.sciencedirect.com/science/article/pii/S0309170812000528). The goal of this example is to investigate the permeability of different rock samples. As there are different samples, we just put the general code here which can be applicable for other samples as well. Therefore, the results will be given in figures.
#
# The structure of this report goes as follows:
#
# - Pore Newtork Extraction Method
# - Applying Stokes flow for permeability estimation
# + language="html"
# <style>
# table {float:left}
# </style>
# -
# ## Pore Newtork Extraction Method
# In this project, we have used [SNOW algorithm](https://journals.aps.org/pre/abstract/10.1103/PhysRevE.96.023307) in [Porespy](http://porespy.org/) which is a network extraction method based on marker-based watershed segmentation. The SNOW algorithm concludes four main steps:
#
# - Prefiltering the distance map
# - Eliminating peaks on saddles and plateaus
# - Merging peaks that are too near each other
# - Assigning void voxels to the appropriate pore using a marker-based watershed.
# ### Effect of prefiltering parameters
# In the first step, use of right parameters for filtering may enhance the reliablity of the results. We use a gaussian filter with a spherical
# structuring element of radius R. The sigma or
# standard deviation of the convolution kernel is an adjustable
# parameter, the effect of which can be studied with the following code. Another parameter to be considered is the radius R, which is also investigated for the same sample. Choosing the right value affects the smoothness of the resulting partitioned regions. In other words, this will prevent oversmoothing and loss of a great amount of data from the original image. There is a trade off between preserving the data and filtering. We should find an optimum point for this parameters. The idea have been shown in Fig.4 of the paper. We have used the same idea to change the snowpartitioning algorithm so that we can have our desired output for this part. As long as Network extraction will take more time, we first investigate the effect of choosing different R and sigma as a preprocess, then use the righ parameters for network extraction and call SNOW algorithm.
# The following piece of code is related to this prefiltering step (this is a part of the whole code which is related to prefiltering)Changes in the filtering functions so that we can have the initial and final number of local maxima in a dictionarry array resultsB:
def snow_partitioning_test(im, r_max=4, sigma=0.4, return_all=False):
tup = namedtuple('results', field_names=['im', 'dt', 'peaks', 'regions'])
results = {
'r_max': r_max, 'sigma': sigma,
'Initial number of peaks:': [],
'Peaks after trimming saddle points:': [],
'Peaks after trimming nearby peaks:':[]
}
print('-' * 80)
print("Beginning SNOW Algorithm")
im_shape = np.array(im.shape)
if im.dtype == 'bool':
print('Peforming Distance Transform')
if np.any(im_shape == 1):
ax = np.where(im_shape == 1)[0][0]
dt = spim.distance_transform_edt(input=im.squeeze())
dt = np.expand_dims(dt, ax)
else:
dt = spim.distance_transform_edt(input=im)
else:
dt = im
im = dt > 0
tup.im = im
tup.dt = dt
if sigma > 0:
print('Applying Gaussian blur with sigma =', str(sigma))
dt = spim.gaussian_filter(input=dt, sigma=sigma)
peaks = find_peaks(dt=dt, r_max=r_max)
print('Initial number of peaks: ', spim.label(peaks)[1])
resultsB['Initial number of peaks:']=spim.label(peaks)[1]
peaks = trim_saddle_points(peaks=peaks, dt=dt, max_iters=500)
print('Peaks after trimming saddle points: ', spim.label(peaks)[1])
resultsB['Peaks after trimming saddle points:']=spim.label(peaks)[1]
peaks = trim_nearby_peaks(peaks=peaks, dt=dt)
peaks, N = spim.label(peaks)
print('Peaks after trimming nearby peaks: ', N)
resultsB['Peaks after trimming nearby peaks:']=N
tup.peaks = peaks
regions = watershed(image=-dt, markers=peaks, mask=dt > 0)
regions = randomize_colors(regions)
if return_all:
tup.regions = regions
return tup
else:
return results
imageinit = im
Resultslast = {}
R_max = [2,4,6,8,12,15,20]
Sigmax = [0.25,0.35,0.5,0.65]
c = -1
for j in range(len(Sigmax)):
for i in range(len(R_max)):
c = c+1
r_max = R_max[i]
sigma = Sigmax[j]
results = snow_partitioning(im=imageinit,r_max=r_max, sigma=sigma, return_all=False)
Resultslast[c] = results
# ### Marching Cube Algorithm
# Based on new porespy package, there is also some changes in SNOW algorithm previous version. In the previous version the area was estimated as the number of voxels on the surface multiplied by the area of
# one voxel face. Now the user can have the chance to use [Marching Cube](https://en.wikipedia.org/wiki/Marching_cubes) algorithm. The idea ofd the algorithm is to find what portion of the cube is inside the image by using a triangular mesh marching through the cube to fine the best interface between inner and outer part of the image. Generally speaking this will decrease the voxelated representation of the image which itself increase the accuracy of the calculations. In the voxel based surface area calculation, we assign the whole voxel to the surface even though only half of that voxel might be within the surface. So it may lead to overestimation. It may make the process slower, but provides better results. To understand the algorithm, we have shown here a [2D example](http://www.cs.carleton.edu/cs_comps/0405/shape/marching_cubes.html). Imagine an aritrary shaped image. If we mesh the area with a square mesh (representative as pixels which will be cubes in 3D as voxels), we have the follwing image:
# 
# The red corners are within the image, the blue ones are outside. Each square which has not 4 same color corner will be marched until get the most precise triangular mesh as the boundary. First the purple dots locate the center of each edge, which we know this is a rough estimation. Then the connecting line (surface in 3D) will march through the square area so that finds its way through the boundary at an optimum location. Implementation of the algorithm in the 3D follows the same idea. The following picture is a sketch of [3D implementation](http://www.cs.carleton.edu/cs_comps/0405/shape/marching_cubes.html).
# 
# Although this option will give better results, we can still turn it off in SNOW algorithm for the sake of time efficiency and still have good results.
# ### Validation of the code
# To ensure that our scriopt for the network extraction is correcrt, we first implemented the same code on Berea Sandstone, the validity of which can be prooved by comparing the results given in the paper. We have additional boundary face pores, but internal pores are approximately the sam as that of SNOW paper.
# permeabilities are: 1.20607725e-12, 1.0525892e-12, 1.18140011e-12
#
# average permeability is: 1.1466888534117068e-12
#
# The results are very close to the SNOW paper (which was 1.29e-12 from Image Analysis) . This will ensure us about our script written for the network extraction and permeability calculation.
# ### Extracted Networks
# The following figures illustrate one segment of CT images of rock samples (MG and Bentheimer) in binarized version:
# <img src="https://i.imgur.com/sZoo5xO.jpg" style="width: 30%" align="left"/>
# <img src="https://i.imgur.com/TwAvbcu.jpg" style="width: 30%" align="left"/>
# <img src="https://i.imgur.com/ls3ar6c.jpg" style="width: 30%" align="left"/>
# | Sample | Size | Resolution | Porosity |
# | :--- | :--- |:--- |:--- |
# | Mount Gambier (our model) | 512 512 512 | 3.024 μm | 0.436 |
# | Mount Gambier (paper) | 350 350 350 | 9 μm | 0.556 |
# | Bentheimer Sandstone (our model) | 300 300 300 | 3 μm | 0.2 |
# | Bentheimer Sandstone (paper) | 1000 1000 1000 | 3.0035 μm | 0.217 |
# The following code is the script we have written for MG sample. The same code have been applied on other samples.
import porespy as ps
import matplotlib.pyplot as plt
import openpnm as op
import numpy as np
import scipy as sp
ws = op.Workspace()
ws.clear()
ws.keys()
proj = ws.new_project()
from skimage import io
im = io.imread('MG.tif')
imtype=im.view()
print(imtype)
digits = np.prod(np.array(im.shape))
logi = (np.sum(im==0)+np.sum(im==1))==digits
if logi == True:
print('There is no noise')
else:
print('Please check your input image for noise')
print(im.shape)
imtype = im.view()
print(imtype)
im = np.array(im, dtype=bool)
# Inversion of 0s and 1s in binarized image to represent 1 for pores and 0 for solids
im = ~im
print(ps.metrics.porosity(im))
plt.imshow(ps.visualization.sem(im), cmap=plt.cm.bone)
net = ps.network_extraction.snow(im, voxel_size=3.024e-6,
boundary_faces=['top', 'bottom', 'left', 'right', 'front', 'back'],
marching_cubes_area=False) # voxel size and marching cube can be changed for each specific sample
pn = op.network.GenericNetwork()
pn.update(net)
print(pn)
a = pn.check_network_health()
op.topotools.trim(network=pn,pores=a['trim_pores'])
print(pn)
ps.io.to_vtk(path='MGvt',im=im.astype(sp.int8))
mgr = op.Workspace()
# The generated .pnm file will be used as input for simulations (permeability calculation, etc.)
mgr.save_workspace('MountGampn.pnm')
# Now that we ensure the validity of our script, we implement the network extraction on the samples of the study. Their network properties are given in the following table:
# | Model | Number of pores | Number of throats | Volume (mm3) | Coordination number |
# | --- | --- | --- | --- | --- |
# | Mount Gambier Carbonate (512) | 5780 (4679 internal) | 10128 (9027 internal) | 27.65 | 3.504 |
# | MG Paper (350) | 22665 (257 elements isolated) | 84593 | 31.3 | 7.41 |
# | Bentheimer Sandstone (1000) | 26588 (23329 internal) | 48911 (45652 internal) | 27.1 | 3.68 |
# | Bentheimer Paper (300) | Not given | Not given | 19.68 | Not given |
#
# #### Some Comments:
#
# As shown in the table, we have a good match on the average coordination numbers, but the number of pores and throats are different. This is related to the difference between SNOW and maximall method which have been done in the ICL. The snow algorithm will have larger pores which decreases the number of pores and throats.
#
# The porosity is being calculated from the voxelated image in a similar manner of the paper. The permeabilities have been calculated using stokes flow algorithm. The difference might be related to the error which lays behind the parameters in filtering process (sigma, R). We have used default values of sigma=0.4 and R=5 in all samples, which may lead to misrepresentation of the network.
#
# The difference in permeability may also be related to the different conduit lengths. In the Blunt's paper they have defined a shape factor to account for the non-cylindrical deviation of the throats. This shape factor is whithin the maximal extraction method. In the SNOW algorithm, using the equivalent diameter rather than inscribed diameter for the hydraulic conductance (assumming no P loss in the pores) will provide better results in the permeability calculation.
#
# From the Berea sandstone results, we can also comment on the effect of the structures of the rock sample. For sandstones, the morphology is more ideal than carbonates for network extractions. We also get a good result for Bentheimer Sandstone permeability. But for the carbonate cases, it is different. As we see in their CT images, there are Fossil grains (Pebbles in ketton, other fossil shells in two other sample) which provide different length scales of micro to macro pores. For example it is recommended to use multiscale pore network extraction.
#
# As long as not any of our sample is the same sample in the Blunt's paper (they are from the same rock but different resolution and size), the slight difference in results is acceptable.
#
# Isolated pores and throats will be trimmed using "topotools" trimming method after the network extraction.
#
# -For the permeability calculation, we need to set inlets and outlets of the media, both of which can be defined by introducing some pores as boundary surface pores.
#
# ## Static parameters assignment
# We redefine some parameters of the network by deleting them from the pn dictionary and adding models for them in the geomety:
import openpnm as op
import numpy as np
import matplotlib.pyplot as plt
import math
import random
from pathlib import Path
mgr = op.Workspace()
mgr.clear()
mgr.keys()
path = Path('../fixtures/PoreScale Imaging/MountGampn.pnm')
mgr.load_workspace(path)
pn = mgr['proj_03']['net_01']
a = pn.check_network_health()
op.topotools.trim(network=pn,pores=a['trim_pores'])
proj = pn.project
print(pn)
coord_num_avg=np.mean(pn.num_neighbors(pores=pn.Ps))
del pn['pore.area']
del pn['throat.conduit_lengths.pore1']
del pn['throat.conduit_lengths.pore2']
del pn['throat.conduit_lengths.throat']
del pn['throat.endpoints.tail']
del pn['throat.endpoints.head']
del pn['throat.volume']
# In this section we implement the assignment of Geometry, Phase, and Physics to the Network.
# +
geom = op.geometry.GenericGeometry(network=pn, pores=pn['pore.all'], throats=pn['throat.all'],project=proj)
geom.add_model(propname='throat.endpoints',
model=op.models.geometry.throat_endpoints.spherical_pores)
geom.add_model(propname='pore.area',
model=op.models.geometry.pore_area.sphere)
geom.add_model(propname='throat.volume',
model=op.models.geometry.throat_volume.cylinder)
geom.add_model(propname='throat.conduit_lengths',
model=op.models.geometry.throat_length.conduit_lengths)
oil = op.phases.GenericPhase(network=pn,project=proj)
water = op.phases.GenericPhase(network=pn,project=proj)
oil['pore.viscosity']=0.547e-3
oil['throat.contact_angle'] =180
oil['throat.surface_tension'] = 0.072
oil['pore.surface_tension']=0.072
oil['pore.contact_angle']=180
water['throat.contact_angle'] = 0 # first assumming highly water-wet
water['pore.contact_angle'] = 0
water['throat.surface_tension'] = 0.0483
water['pore.surface_tension'] = 0.0483
water['pore.viscosity']=0.4554e-3
phys_water= op.physics.GenericPhysics(network=pn, phase=water, geometry=geom,project=proj)
phys_oil = op.physics.GenericPhysics(network=pn, phase=oil, geometry=geom,project=proj)
mod = op.models.physics.hydraulic_conductance.hagen_poiseuille
phys_oil.add_model(propname='throat.hydraulic_conductance',
model=mod)
phys_oil.add_model(propname='throat.entry_pressure',
model=op.models.physics.capillary_pressure.washburn)
phys_water.add_model(propname='throat.hydraulic_conductance',
model=mod)
phys_water.add_model(propname='throat.entry_pressure',
model=op.models.physics.capillary_pressure.washburn)
# -
# ## Permeability Calculation Algorithm
# The StokesFlow class is for simulation of viscous flow. In this class default property names will be set. The main role of this class would be calculation of the hydraulic permeability. Having its effective permeability calculation method, it can deal with nonuniform medias.
#
# We first find single phase permeability where the stokes flow is implemented for each phase as if it is the only phase flowing through the porous media. Theis is done as the conductance is the hydraulic conductance. Otherwise, it will change to multiphase conduit conductance. Note that we have defined perm_water and perm_oil in a dictionary so that we have a permeability tensor (directional permeability).
# As we have mentioned the permeability will be a tensor, which represents $K_x,K_y,K_z$. Permeability tensor plays an important role in anisotropic medias charactarization. We have also defined relative permeabilities in three directions. We only show the relative permeabilities for one direction in the report, but the code gives us the results for all three directions in the oil and water perm dictionary.
#
# We also define methods in which the domain length and area will be calculated. These methods are called within the permeability calculation loop.
# +
K_water_single_phase = [None,None,None]
K_oil_single_phase = [None,None,None]
bounds = [ ['top', 'bottom'], ['left', 'right'],['front', 'back']]
[amax, bmax, cmax] = np.max(pn['pore.coords'], axis=0)
[amin, bmin, cmin] = np.min(pn['pore.coords'], axis=0)
lx = amax-amin
ly = bmax-bmin
lz = cmax-cmin
da = lx*ly
dl = lz
def top_b(lx,ly,lz):
da = lx*ly
dl = lz
res_2=[da,dl]
return res_2
def left_r(lx,ly,lz):
da = lx*lz
dl = ly
res_2=[da,dl]
return res_2
def front_b(lx,ly,lz):
da = ly*lz
dl = lx
res_2=[da,dl]
return res_2
options = {0 : top_b(lx,ly,lz),1 : left_r(lx,ly,lz),2 : front_b(lx,ly,lz)}
for bound_increment in range(len(bounds)):
BC1_pores = pn.pores(labels=bounds[bound_increment][0])
BC2_pores = pn.pores(labels=bounds[bound_increment][1])
[da,dl]=options[bound_increment]
# Permeability - water
sf_water = op.algorithms.StokesFlow(network=pn, phase=water)
sf_water.setup(conductance='throat.hydraulic_conductance')
sf_water._set_BC(pores=BC1_pores, bctype='value', bcvalues=100000)
sf_water._set_BC(pores=BC2_pores, bctype='value', bcvalues=1000)
sf_water.run()
K_water_single_phase[bound_increment] = sf_water.calc_effective_permeability(domain_area=da,
domain_length=dl,
inlets=BC1_pores,
outlets=BC2_pores)
proj.purge_object(obj=Stokes_alg_single_phase_water)
# Permeability - oil
sf_oil = op.algorithms.StokesFlow(network=pn, phase=oil)
sf_oil.setup(conductance='throat.hydraulic_conductance')
sf_oil._set_BC(pores=BC1_pores, bctype='value', bcvalues=1000)
sf_oil._set_BC(pores=BC2_pores, bctype='value', bcvalues=0)
sf_oil.run()
K_oil_single_phase[bound_increment] = sf_oil.calc_effective_permeability(domain_area=da,
domain_length=dl,
inlets=BC1_pores,
outlets=BC2_pores)
proj.purge_object(obj=Stokes_alg_single_phase_oil)
# -
# Results for permeability calculation of four samples are given in the following. As we see the results for Bentheimer which is a sand stone rock is very close to the value given in the paper. We have also adjusted the permeabilities of the MGambier by using equivalent diameter instead of pore and throat diameter for the conductance calculation.
# | Sample | Mount Gambier 512 | Bentheimer 1000 |
# | --- | --- | --- |
# |K1 (e-12) |18.93 | 1.57|
# |K2 (e-12) |23.96 | 1.4|
# |K3 (e-12) | 12.25| 1.64|
# | Kavg | 18.38| 1.53 |
# |Sample paper | Mount Gambier 350 | Bentheimer 300 |
# |Kavg (from image)| 19.2 | 1.4 |
#
#
#
|
examples/paper_recreations/Blunt et al. (2013)/Pore-scale Imaging and Modeling - Part A.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="_as3tyDPAvzM"
# ##### Copyright 2021 The TensorFlow Authors.
# + cellView="form" id="-CoWjX1EBXJX"
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# + [markdown] id="7hQmWrtkBBQB"
# # Converting TensorFlow Text operators to TensorFlow Lite
# + [markdown] id="qmGnheU8BPKN"
# <table class="tfo-notebook-buttons" align="left">
# <td>
# <a target="_blank" href="https://www.tensorflow.org/text/guide/text_tf_lite"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
# </td>
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/tensorflow/text/blob/master/docs/guide/text_tf_lite.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
# </td>
# <td>
# <a target="_blank" href="https://github.com/tensorflow/text/blob/master/docs/guide/text_tf_lite.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View on GitHub</a>
# </td>
# <td>
# <a href="https://storage.googleapis.com/tensorflow_docs/text/docs/guide/text_tf_lite.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
# </td>
# </table>
# + [markdown] id="hz1hOEHPTF2n"
# ## Overview
#
# Machine learning models are frequently deployed using TensorFlow Lite to mobile, embedded, and IoT devices to improve data privacy and lower response times. These models often require support for text processing operations. TensorFlow Text version 2.7 and higher provides improved performance, reduced binary sizes, and operations specifically optimized for use in these environments.
#
# + [markdown] id="_mdIyFfqTMjc"
# ## Text operators
#
# The following TensorFlow Text classes can be used from within a TensorFlow Lite model.
#
# * `FastWordpieceTokenizer`
# * `WhitespaceTokenizer`
#
# + [markdown] id="x6NAs1fcUwUn"
# ## Model Example
# + id="8ZalFZQvTJf5"
# !pip install -U tensorflow-text==2.7.3
# + id="uL-I0CyPTXnN"
from absl import app
import numpy as np
import tensorflow as tf
import tensorflow_text as tf_text
from tensorflow.lite.python import interpreter
# + [markdown] id="qj_bJ-xVTfU1"
# The following code example shows the conversion process and interpretation in Python using a simple test model. Note that the output of a model cannot be a `tf.RaggedTensor` object when you are using TensorFlow Lite. However, you can return the components of a `tf.RaggedTensor` object or convert it using its `to_tensor` function. See [the RaggedTensor guide](https://www.tensorflow.org/guide/ragged_tensor) for more details.
# + id="nqQjBcXqTf_0"
class TokenizerModel(tf.keras.Model):
def __init__(self, **kwargs):
super().__init__(**kwargs)
self.tokenizer = tf_text.WhitespaceTokenizer()
@tf.function(input_signature=[
tf.TensorSpec(shape=[None], dtype=tf.string, name='input')
])
def call(self, input_tensor):
return { 'tokens': self.tokenizer.tokenize(input_tensor).flat_values }
# + id="jsPFI-55TiF_"
# Test input data.
input_data = np.array(['Some minds are better kept apart'])
# Define a Keras model.
model = TokenizerModel()
# Perform TensorFlow Text inference.
tf_result = model(tf.constant(input_data))
print('TensorFlow result = ', tf_result['tokens'])
# + [markdown] id="YKpFsvJGTlPq"
# ## Convert the TensorFlow model to TensorFlow Lite
#
# When converting a TensorFlow model with TensorFlow Text operators to TensorFlow Lite, you need to
# indicate to the `TFLiteConverter` that there are custom operators using the
# `allow_custom_ops` attribute as in the example below. You can then run the model conversion as you normally would. Review the [TensorFlow Lite converter](https://www.tensorflow.org/lite/convert) documentation for a detailed guide on the basics of model conversion.
# + id="6hYWezs1Tndo"
# Convert to TensorFlow Lite.
converter = tf.lite.TFLiteConverter.from_keras_model(model)
converter.target_spec.supported_ops = [tf.lite.OpsSet.TFLITE_BUILTINS]
converter.allow_custom_ops = True
tflite_model = converter.convert()
# + [markdown] id="cxCdhrHATpSR"
# ## Inference
#
# For the TensorFlow Lite interpreter to properly read your model containing TensorFlow Text operators, you must configure it to use these custom operators, and provide registration methods for them. Use `tf_text.tflite_registrar.SELECT_TFTEXT_OPS` to provide the full suite of registration functions for the supported TensorFlow Text operators to `InterpreterWithCustomOps`.
#
# Note, that while the example below shows inference in Python, the steps are similar in other languages with some minor API translations, and the necessity to build the `tflite_registrar` into your binary. See [TensorFlow Lite Inference](https://www.tensorflow.org/lite/guide/inference) for more details.
# + id="kykFg2pXTriw"
# Perform TensorFlow Lite inference.
interp = interpreter.InterpreterWithCustomOps(
model_content=tflite_model,
custom_op_registerers=tf_text.tflite_registrar.SELECT_TFTEXT_OPS)
interp.get_signature_list()
# + [markdown] id="rNGPpHCCTxVX"
# Next, the TensorFlow Lite interpreter is invoked with the input, providing a result which matches the TensorFlow result from above.
# + id="vmSbfbgJTyKY"
tokenize = interp.get_signature_runner('serving_default')
output = tokenize(input=input_data)
print('TensorFlow Lite result = ', output['tokens'])
|
docs/guide/text_tf_lite.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Background
#
# This notebook walks through the creation of a fastai [DataBunch](https://docs.fast.ai/basic_data.html#DataBunch) object. This object contains a pytorch dataloader for the train, valid and test sets. From the documentation:
#
# ```
# Bind train_dl,valid_dl and test_dl in a data object.
#
# It also ensures all the dataloaders are on device and applies to them dl_tfms as batch are drawn (like normalization). path is used internally to store temporary files, collate_fn is passed to the pytorch Dataloader (replacing the one there) to explain how to collate the samples picked for a batch.
# ```
#
# Because we are training the language model, we want our dataloader to construct the target variable from the input data. The target variable for language models are the next word in a sentence. Furthermore, there are other optimizations with regard to the sequence length and concatenating texts together that avoids wasteful padding. Luckily the [TextLMDataBunch](https://docs.fast.ai/text.data.html#TextLMDataBunch) does all this work for us (and more) automatically.
from fastai.text import TextLMDataBunch as lmdb
from fastai.text.transform import Tokenizer
import pandas as pd
from pathlib import Path
# ### Read in Data
# You can download the above saved dataframes (in pickle format) from Google Cloud Storage:
#
# **train_df.pkl (9GB)**:
#
# `https://storage.googleapis.com/issue_label_bot/pre_processed_data/2_partitioned_df/train_df.pkl`
#
# **valid_df.pkl (1GB)**
#
# `https://storage.googleapis.com/issue_label_bot/pre_processed_data/2_partitioned_df/valid_df.pkl`
# +
# note: download the data and place in right directory before running this code!
valid_df = pd.read_pickle(Path('../data/2_partitioned_df/valid_df.pkl'))
train_df = pd.read_pickle(Path('../data/2_partitioned_df/train_df.pkl'))
# -
print(f'rows in train_df:, {train_df.shape[0]:,}')
print(f'rows in valid_df:, {valid_df.shape[0]:,}')
train_df.head(3)
# ## Create The [DataBunch](https://docs.fast.ai/basic_data.html#DataBunch)
# #### Instantiate The Tokenizer
#
def pass_through(x):
return x
# only thing is we are changing pre_rules to be pass through since we have already done all of the pre-rules.
# you don't want to accidentally apply pre-rules again otherwhise it will corrupt the data.
tokenizer = Tokenizer(pre_rules=[pass_through], n_cpus=31)
# Specify path for saving language model artifacts
path = Path('../model/lang_model/')
# #### Create The Language Model Data Bunch
#
# **Warning**: this steps builds the vocabulary and tokenizes the data. This procedure consumes an incredible amount of memory. This took 1 hour on a machine with 72 cores and 400GB of Memory.
# Note you want your own tokenizer, without pre-rules
data_lm = lmdb.from_df(path=path,
train_df=train_df,
valid_df=valid_df,
text_cols='text',
tokenizer=tokenizer,
chunksize=6000000)
data_lm.save() # saves to self.path/data_save.pkl
# ### Location of Saved DataBunch
#
# The databunch object is available here:
#
# `https://storage.googleapis.com/issue_label_bot/model/lang_model/data_save.pkl`
#
# It is a massive file of 27GB so proceed with caution when downlaoding this file.
|
Issue_Embeddings/notebooks/02_fastai_DataBunch.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Think Bayes
#
# This notebook presents example code and exercise solutions for Think Bayes.
#
# Copyright 2016 <NAME>
#
# MIT License: https://opensource.org/licenses/MIT
# +
# Configure Jupyter so figures appear in the notebook
# %matplotlib inline
# Configure Jupyter to display the assigned value after an assignment
# %config InteractiveShell.ast_node_interactivity='last_expr_or_assign'
# import classes from thinkbayes2
from thinkbayes2 import Pmf, Beta, MakeBinomialPmf
import thinkplot
import numpy as np
# -
beta = Beta(5, 5)
prior = beta.MakePmf()
thinkplot.Pdf(prior)
thinkplot.decorate(xlabel='Prob Red Sox win (x)',
ylabel='PDF')
# %psource beta.Update
# +
beta.Update((15, 0))
posterior = beta.MakePmf()
thinkplot.Pdf(prior, color='gray', label='prior')
thinkplot.Pdf(posterior, label='posterior')
thinkplot.decorate(xlabel='Prob Red Sox win (x)',
ylabel='PDF')
# -
posterior.Mean()
posterior.MAP()
posterior.CredibleInterval()
x = posterior.Random()
np.sum(np.random.random(7) < x)
# +
def simulate(k, dist):
x = dist.Random()
return np.sum(np.random.random(k) <= x)
simulate(7, posterior)
# -
sample = [simulate(7, posterior) for i in range(100000)];
thinkplot.Hist(Pmf(sample))
np.mean(np.array(sample) >= 4)
|
examples/red_sox.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import matplotlib as mpl
from matplotlib import pyplot as plt
import matplotlib.patheffects as path_effects
from matplotlib.patches import Rectangle,Polygon
from matplotlib.gridspec import GridSpec
typeface='Helvetica Neue'
mpl.rcParams['font.weight']=300
mpl.rcParams['axes.labelweight']=300
mpl.rcParams['font.family']=typeface
mpl.rcParams['font.size']=22
mpl.rcParams['pdf.fonttype']=42
import os,glob,re
import numpy as np
from Bio import SeqIO
from collections import Counter
import baltic as bt
travel={}
for line in open('/Users/evogytis/Documents/manuscripts/SARS-CoV-2_kitenis/data/travel_qc_info.csv','r'):
l=line.strip('\n').split('\t')
# print(l[3])
if l[0]!='Virus name' and l[4]!='':
travel[l[0]]=l[4]
base_path='/Users/evogytis/Documents/manuscripts/SARS-CoV-2_kitenis/data/alignments/B.1.620_repr_Cameroon_wRef.fasta'
seqs={}
seq_order=[]
for seq in SeqIO.parse(base_path,format='fasta'):
seqs[seq.id]=str(seq.seq).replace('U','T')
seq_order.append(seq.id)
# print(seq.id,len(seq.seq))
ref='NC_045512'
ll=bt.loadNexus('/Users/evogytis/Documents/manuscripts/SARS-CoV-2_kitenis/data/trees/B.1.620_repr_Cameroon_wRef_renamed.tre',absoluteTime=False,tip_regex='[A-Za-z0-9]+',treestring_regex='tree con_50_majrule =')
rename={}
for line in open('/Users/evogytis/Documents/manuscripts/SARS-CoV-2_kitenis/data/trees/B.1.620_repr_Cameroon_wRef.fasta_names_keyfile.txt','r'):
key,val=line.strip('\n').split('@')
rename[key[1:]]=val[1:]
for k in ll.getExternal():
k.name=rename[k.name]
for k in ll.Objects:
k.length=k.length*len(seq.seq)
ll=ll.collapseBranches(lambda k: k.length==0)
ll.sortBranches(descending=False)
# ll.treeStats()
alnL=max(list(map(len,seqs.values())))
variable=[]
# focus_sequences=[f for f in seqs if f.split('|')[0] in travel]
travel_cases=[s for s in seqs if s.split('|')[0] in travel]
ca=ll.commonAncestor(ll.getExternal(lambda k: k.name in travel_cases))
focus_sequences=list(ca.leaves)
for i in range(alnL): ## iterate over alignment columns
if len(set([s[i] for s in seqs.values() if s[i] in ['A','C','T','G','-']]))>1: ## polymorphic site
column=[s[i] for s in seqs.values() if s[i] in ['A','C','T','G','-']] ## get column states
VOI_column=[seqs[s][i] for s in focus_sequences if seqs[s][i] in ['A','C','T','G','-']]
# print(i,VOI_column)
if min(Counter(column).values())>1 and min(Counter(VOI_column).values())>1: ## column polymorphic and shared by at least two sequences
variable.append(i)
variable=list(filter(lambda i: i>100,variable))
variable=list(filter(lambda i: i<29903-50,variable))
# SNPs={s: {i: seqs[s][i] for i in variable} for s in seqs} ## get all variable sites
SNPs={s: {i: seqs[s][i] for i in variable if any([seqs[f][i]!=seqs[ref][i] and seqs[f][i] in ['A','C','T','G','-'] for f in focus_sequences])} for s in seqs}
variable=sorted(list(SNPs[ref].keys()))
print(variable)
# +
def convert_deletions(deletions):
formatted=[]
if len(dels)>0:
for d in dels:
ds=d.split('-')
if len(ds)>1:
# print('span',ds)
b,e=map(int,ds)
for i in range(b,e):
formatted.append('X%s-'%(i))
return formatted
ORFs={"E": (26244,26472),
"M": (26522,27191),
"N": (28273,29533),
"ORF10": (29557,29674),
# "ORF14": (28733,28955),
"ORF1a": (265,13468),
"ORF1b": (13467,21555),
"ORF3a": (25392,26220),
"ORF6": (27201,27387),
"ORF7a": (27393,27759),
"ORF7b": (27755,27887),
"ORF8": (27893,28259),
"ORF9b": (28283,28577),
"S": (21562,25384)}
def id_orf(site):
orf={}
for gene in ORFs:
m,M=ORFs[gene]
if m<=site<=M:
orf[gene]=[m,M]
return orf
def match_aa(nt,aa):
matched={}
for mut in nt:
site=int(mut[1:-1])
orfs=id_orf(site)
if len(orfs)==0: ## no orf, nucleotide
matched[site]='%s'%(site) ## just site, no aa change
for gene in orfs: ## iterate over ORFs
m,M=orfs[gene] ## beginning and end of ORF
codon=(((site-m-1))//3)+1 ## get codon in ORF
mut_search=re.compile('%s:[A-Z*-]%d[A-Z*-]'%(gene,codon)) ## form regex search for match
search=[mut_search.match(aa_mut) for aa_mut in aa] ## search amongst aa mutations for match
candidates=[]
for candidate in search: ## iterate over searches
if candidate: ## match is not None
candidates.append(candidate.group()) ## remember candidate
if len(candidates)==1: ## one candidate found - great
# print(mut,gene,codon,candidates[0])
# if site in nt2aa and site-1 in variable:
# if '%s (%s)'%(site,candidates[0])!=nt2aa[site]:
# print('different mutation: %s %s'%('%s (%s)'%(site,candidates[0]),nt2aa[site]))
# print(nt2aa[site],)
matched[site]='%s (%s)'%(site,candidates[0])
elif len(candidates)==0: ## no good candidates found - synonymous
matched[site]='%s'%(site)
else:
print('problematic mutation %s with multiple candidates %s'%(mut,candidates))
return matched
nt2aa={}
for line in open('/Users/evogytis/Documents/manuscripts/SARS-CoV-2_kitenis/data/alignments/B.1.620_repr_Cameroon_wRef.nextclade.tsv','r'):
l=line.strip('\n').split('\t')
# print(l)
# print(l)
if l[0]=='seqName':
header={x: i for i,x in enumerate(l)}
elif l[0]!=ref:
# print(l[0])
AAs=l[header['aaSubstitutions']].split(',')+l[header['aaDeletions']].split(',')
NTs=l[header['substitutions']].split(',')
dels=l[header['deletions']].split(',')
# print(convert_deletions(dels))
NTs+=convert_deletions(dels)
keep_nt=[]
for nt in NTs:
site=int(nt[1:-1])
if site-1 not in variable: ## not interested in converting, not in plot
# print('%s not in variable'%(nt))
pass
else: ## site is in plot, need to convert
pass
keep_nt.append(nt)
# print('%s in plot'%(nt))
matched_up=match_aa(keep_nt,AAs)
# print(l[0])
for i in matched_up:
if i not in nt2aa:
nt2aa[i]=matched_up[i]
elif nt2aa[i]!=matched_up[i]:
print('different',nt2aa[i],matched_up[i])
else:
pass
print(nt2aa)
nt2aa[21765]='21765' ## beginning of H69 deletion
nt2aa[21991]='21991 (S:Y144-)' ## Y144 deletion missed entirely
nt2aa[21992]='21992 (S:Y144-)'
nt2aa[21993]='21993 (S:Y144-)'
nt2aa[22295]='22295 (S:H245Y)'
nt2aa[22281]='22281' ## beginning of L241 deletion
nt2aa[22282]='22282'
nt2aa[22283]='22283 (S:L241-)'
nt2aa[22284]='22284 (S:L241-)'
nt2aa[22285]='22285 (S:L241-)'
nt2aa[22287]='22287 (S:L242-)'
nt2aa[22288]='22288 (S:L242-)'
nt2aa[25432]='25432 (ORF3a:T14-)'
nt2aa[25433]='25433 (ORF3a:T14-)'
nt2aa[25434]='25434 (ORF3a:T14-)'
inter_orf_breaks=[]
store=None
for i in variable:
Os=id_orf(i)
orf=list(Os.keys())[0] if len(Os)>0 else None
if store and store!=orf:
inter_orf_breaks.append(i)
store=orf
print(inter_orf_breaks)
# +
fig = plt.subplots(figsize=(20,20),facecolor='w')
gs = GridSpec(1,2,width_ratios=[8,2],hspace=0.01,wspace=0.01)
ax=plt.subplot(gs[0])
colours={'A': '#D0694A', 'C': '#77BEDB', 'T': '#48A365', 'G': '#E1C72F',
'-':'w','N':'dimgrey',
'K': 'dimgrey', 'Y': 'dimgrey', 'M': 'dimgrey', 'W': 'dimgrey', 'R': 'dimgrey'}
# seq_order=list(SNPs.keys())
# seq_order=sorted(list(SNPs.keys()),key=lambda w: w.split('|')[0])
window=3
ll.sortBranches()
seq_order=[k.name for k in sorted(ll.getExternal(),key=lambda w: w.y)]
for s,S in enumerate(seq_order):
cumulative_x=-1
store_site=0
xticks=[]
h=0.95
w=1.0
for i,nt in enumerate(SNPs[S]):
fc=colours[seqs[S][nt]]
if store_site+window<nt: ## next site is beyond window
cumulative_x+=1+(nt-store_site)*0.0002
else:
cumulative_x+=1
if S==ref or SNPs[S][nt]==SNPs[ref][nt]:
fc='lightgrey'
rect=Rectangle((cumulative_x,s),w,h,facecolor=fc,edgecolor='none')
ax.add_patch(rect)
if S==ref or SNPs[S][nt]!=SNPs[ref][nt]: ## nucleotide different from reference or at reference
ax.text(cumulative_x+0.5,s+0.5,seqs[S][nt],size=10,ha='center',va='center')
xticks.append(cumulative_x)
store_site=nt
if S=='MN908947.3' or S==ref:
ax.add_patch(Rectangle((0,s),cumulative_x+1.1,h,facecolor='none',edgecolor='k',lw=2))
ax.add_patch(Rectangle((0,0),cumulative_x+1.1,len([k for k in ll.getExternal() if k.name in focus_sequences]),facecolor='none',edgecolor='k',lw=2,ls='--',zorder=1000))
norm=mpl.colors.Normalize(1,alnL)
for site,nt in zip(xticks,variable):
y=-1
skip=1
tick_size=0.4
low_y=y-skip
f=0.02
point=(nt/alnL)*(cumulative_x+1)
A=(site+f,0)
B=(site+f,y)
C=(point-0.05,low_y)
D=(point+0.05,low_y)
E=(site+1-f,y)
F=(site+1-f,0)
ax.add_patch(Polygon([A,B,C,D,E,F],facecolor='lightgrey',edgecolor='none',clip_on=False))
ax.plot([point,point],[low_y,low_y-tick_size],color='k',clip_on=False)
ax.plot([0,cumulative_x+1],[low_y-tick_size/2,low_y-tick_size/2],color='k',clip_on=False)
for o in sorted(ORFs,key=lambda s: s[0]):
b,e=ORFs[o]
begin=(b/alnL)*(cumulative_x+1)
end=(e/alnL)*(cumulative_x+1)
offset=2.4
w=1.5
kwargs={'width': w,
'length_includes_head': True,
'head_width': w,
'head_length': 0.3,
'clip_on': False}
if (e-b)<200:
offset=3.4
elif '7' in o or '8' in o or '9' in o:
pass
# ax.text(np.mean([begin,end]),y-offset-w,o,size=20,color='k',ha='center',va='top',zorder=1000,clip_on=False)
elif '3' in o:
ax.text(np.mean([begin,end]),y-offset-w,o,size=16,color='k',ha='center',va='center',zorder=1000,clip_on=False)
else:
ax.text(np.mean([begin,end]),y-offset,o,size=16,color='k',ha='center',va='center',zorder=1000,clip_on=False)
ax.arrow(begin,y-offset,end-begin,0,facecolor='lightgrey',edgecolor='none',**kwargs)
ax.xaxis.tick_top()
ax.set_xticks([x+0.55 for x in xticks])
### ax.set_xticklabels([site+1 for site in variable],size=14,rotation=90)
ax.set_xticklabels([nt2aa[site+1] if site+1 in nt2aa else 'XXXXXXX absent %s'%(site+1) for site in variable],size=12,rotation=90)
ax.set_yticks([y+0.5 for y in range(len(seqs))])
yticklabels=[]
for y in seq_order:
lin=None
if y!=ref:
if len(y.split('|'))==4:
strain=y.split('|')[1]
acc=y.split('|')[2]
lin=y.split('|')[0]
elif len(y.split('|'))==3:
strain=y.split('|')[0]
acc=y.split('|')[1]
lin='B.1.620' if y in focus_sequences else ''
country=strain.split('/')[1]
country=country.replace('_',' ')
y='%s\t\t%s\t\t%s'%(country,acc,lin)
elif len(y.split('|'))==3:
acc=y.split('|')[1]
y=y.split('|')[0] ## strain name
country=y.split('/')[1] ## country
y='%s\t\t%s\t\t%s'%(country,acc,' ')
yticklabels.append(y)
ax.set_yticklabels(yticklabels,size=14)
ax.tick_params(size=0)
ax.set_xlim(min(xticks)-0.2,cumulative_x+1.2)
ax.set_ylim(-0.1,len(seqs)+0.1)
[ax.spines[loc].set_visible(False) for loc in ax.spines]
ax2=plt.subplot(gs[1])
ll.plotTree(ax2,width=4)
colours={}
for line in open('/Users/evogytis/Documents/manuscripts/SARS-CoV-2_kitenis/colours.csv','r'):
loc,colour=line.strip('\n').split('\t')
colours[loc]=colour
for k in ll.getExternal():
ax2.plot([k.height,50],[k.y,k.y],ls='--',color='grey',zorder=90)
s=80
ec='none'
country=None
if len(k.name.split('|'))==4:
strain=k.name.split('|')[1]
country=strain.split('/')[1]
lin=k.name.split('|')[0]
elif len(k.name.split('|'))==3:
strain=k.name.split('|')[0]
lin='B.1.620' if strain in travel else ''
country=strain.split('/')[1]
if country:
country=country.replace('_',' ')
fc=colours[country] if country in colours else 'lightgrey'
ax2.scatter(k.height,k.y,s=s,facecolor=fc,edgecolor=ec,zorder=100)
ax2.scatter(k.height,k.y,s=s*2,facecolor='k',edgecolor=ec,zorder=99)
for k in ll.getInternal():
if len(k.leaves.intersection(set(focus_sequences)))>0 and len(k.leaves)>=len(focus_sequences) and len(k.traits)>0:
effects=[path_effects.Stroke(linewidth=4, foreground='white'),
path_effects.Stroke(linewidth=0, foreground='k')] ## black text, white outline
prob='%.2f'%(k.traits['prob']) if k.traits['prob']<1.0 else '1'
ax2.text(k.height-0.8,k.y-0.4,prob,size=22,path_effects=effects,ha='left',va='top')
if len(k.leaves.intersection(set(focus_sequences)))==len(focus_sequences)==len(k.leaves):
ax2.text(k.height-0.8,k.y+0.2,'B.1.620',ha='left',va='bottom',size=20)
ax2.invert_xaxis()
ax2.plot()
ax2.xaxis.set_major_locator(mpl.ticker.MultipleLocator(10))
ax2.xaxis.set_minor_locator(mpl.ticker.MultipleLocator(2))
[ax2.spines[loc].set_visible(False) for loc in ax2.spines if loc not in ['bottom']]
ax2.tick_params(axis='y',size=0,labelsize=0)
ax2.set_ylim(-0.1,len(seqs)+0.1)
ax2.set_xlim(37.5,-1)
ax2.grid(axis='x',ls='--')
ax2.set_xlabel('mutations',size=26)
# plt.savefig('/Users/evogytis/Documents/manuscripts/SARS-CoV-2_kitenis/figures/Fig1_mutations.png',dpi=100,bbox_inches='tight')
plt.savefig('/Users/evogytis/Documents/manuscripts/SARS-CoV-2_kitenis/figures/Fig1_mutations.pdf',dpi=100,bbox_inches='tight')
plt.show()
# -
|
scripts/B.1.620-lineage-SNPs-main.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## NumPy Indexing and Selection
import numpy as np
arr = np.arange(0,17)
arr
# #### Bracket Indexing and Selection
arr[5]
arr[9:]
# ### Indexing a 2D array (matrices)
#
# using one subscript comma approach i.e. **arr_2d[row,col]**.
arr_2d = np.array(([3,6,9],[10,15,20],[20,25,30],[90,67,56]))
arr_2d
arr_2d[2]
#Indexing multiple rows
arr_2d[2:4]
# Format is arr_2d[row][col] or arr_2d[row,col]
# Getting individual element value
arr_2d[2,0]
# 2D array slicing
#Shape (2,2) from top right corner
arr_2d[:2,1:]
#Shape bottom row
arr_2d[2:5,4:7]
# ## Quiz 5
#
# What will the output of follwoing lines of code?
#
# arr_2d = np.arange(16).reshape(4,4)
# arr_2d[2:4][1:2]
#
# * array( [[ 8, 9, 10, 11],
# [12, 13, 14, 15]] )
# * array( [[12, 13, 14, 15]] )
# * array([], shape=(0, 4), dtype=int64)
# * None of these
# ### Selection
#
# Selecting/Filtering data based on some conditions.
arr1 = np.arange(1,21)
arr1
arr1 > 7
bool1 = arr>7
bool1
arr1[arr1>7]
arr1[arr1==12]
arr1
# ### np.where() function
#
# syntax - **numpy.where(condition[, x, y])**
#
# * It returns the indices of elements in an input array where the given condition is satisfied.
#
# * If both x and y are specified, the output array contains elements of x where condition is True, and elements from y elsewhere.
np.where(arr1>7) #indices
arr1[np.where(arr1>7)] #values
# case 2
np.where(arr1>7, arr1, 1)
|
04 Numpy and Pandas/NumPy/Numpy Indexing and Selection.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
import plotly.express as px
df=pd.read_csv('WA_Fn-UseC_-HR-Employee-Attrition.csv')
df.head(5)
df.dtypes
df.isnull().sum()
df_DistanceFromHome=df.groupby(['JobRole','Attrition'])['DistanceFromHome'].sum().reset_index()
df_DistanceFromHome
fig=px.bar(df_DistanceFromHome,x='JobRole',y='DistanceFromHome',hover_data=['Attrition'],color='Attrition',title='Breakdown of distance from home by job role and attrition',height=700)
fig.show()
df_MonthlyIncome_avg=df.groupby(['Education','Attrition'])['MonthlyIncome'].mean().reset_index()
df_MonthlyIncome_avg
fig=px.bar(df_MonthlyIncome_avg,x='Education',y='MonthlyIncome',hover_data=['Attrition'],color='Attrition',title='Comparision of average monthly income by education and attrition',height=500)
fig.show()
|
ADS-Assignment-2-3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# # Introduction to MOOG
#
# > MOOG is a code that performs a variety of LTE line analysis and spectrum synthesis tasks. The typical use of MOOG is to assist in the determination of the chemical composition of a star.
# > -- from [MOOG website](http://www.as.utexas.edu/~chris/moog.html) by <NAME>
#
#
# Simply speaking, MOOG is a old fashion (Fortran) but effective code to ceate normalized stellar synthetic spectra.
# By comparing the synthetic spectra with observed one, we can determine the stellar parameters (effective temperature, surface gravity and metallicity) and abundance ratios (e.g., \[Mg/Fe\], \[Al/Fe\] and \[Si/Fe\]) of a star because we know these parameters of synthetic spectra.
#
# 
# ** Figure of solar synthetic spectra and observed spectra from [BASS2000](http://bass2000.obspm.fr/solar_spect.php).**
#
# However, it is not so easy to use MOOG with the following reasons:
# - It is written in Fortran, an old programm lagnuage with strict format, which means it is not as flexiable as python;
# - It requires a commerical plotting module, SuperMongo to be installed in the machine, which is not open source;
# - The calculation requires external information, i.e., **a stellar atmosphere model and a line list **.
#
# As a result, it is necessary to construct a python wrapper for MOOG to make it more simple to use.
# Actually some large scale stellar survey (such as SDSS/APOGEE) also use MOOG to determine stellar parameters and they have their own version of MOOG, but there is only [one attempt](https://github.com/andycasey/moog) for simplify the install process of MOOG by <NAME>.
#
# ## Package goal
#
# Our pymoog package is aiming to make the use of MOOG more easily.
# With a time of a week we will only go for the `SYNTH` driver - the most fundamental driver for creating the synthetic sectra.
#
# Example (only for reference):
# ```py
# spec = pymoog.synth(Teff=5000, logg=4.0, m_h=-0.5, wavelength_range=[9500, 9550])
# spec.create_synth_spectra()
#
# print(spec.synth_spec_wav, spec.synth_spec_flux)
# >>> np.array([9500, 9501, 9502, ... , 9550]), np.array([1.0, 1.0, 0.9, ... , 1.0])
#
# ```
#
# ## To dos
#
# 1. Install MOOG automatically.
# 1. Prepare a model file accoring to the specified stellar parameters (Teff, logg and m_h)
# - This can be done with the help of other packages; there is a package provide the download of some models.
# - The whole set of atmosphere model is in GB level, so it may not be precticle to store all the models in the package.
# 2. Prepare a line list according to the specified wavelength_range.
# 3. Construct the control file (`batch.par`)
# 4. Feed MOOG with the files mentioned above
# 5. Extract the output of moog and plot the synthetic spectra in python.
#
# The standard format of atmosphere model, line list and `batch.par` is described in the [documetation of MOOG](http://www.as.utexas.edu/~chris/codes/WRITEnov2019.pdf), and we will constrict these files based on this documation.
#
#
#
# ## Things done
#
# We are not starting from nothing when creating synthetic spectra.
# There are lots of stellar atmosphere model atlas available, such as those from [Kurucz](http://kurucz.harvard.edu/grids.html) and [MARCS](https://marcs.astro.uu.se/).
# These are pre-calculated models, so we only need to dwonload the right one and that's all.
# For simplicity I suggest we only focus on one type of model (maybe Kurucz)
# The situation for line list is similar, with many choices available.
# The one I am most familiar with is the [Vienna Atomic Line Database](http://vald.astro.uu.se/~vald/php/vald.php) (VALD).
# It can be used after some simple format or unit convertion.
# For the code of MOOG itself, MJ have done some modification to remove its dependence on SuperMongo (see [this repo](https://github.com/MingjieJian/moog_nosm)).
# Also see the codes for using MOOG in `moog.py`; they works **but only work in MJ's working environment**, so large amount of modification needed to perform.
#
#
# ## How to use
#
# ```python
# pymoog.line_data.vald2moog_format('../vald_init', 'files/linelist/vald_')
# ```
#
# ```python
# synth_spec = synth.synth(5750,4.0,0, 3800,3805, 2800000)
# synth_spec.prepare_file(loggf_cut=-1)
# synth_spec.run_moog(output=True)
# synth_spec.read_spectra()
# plt.plot(synth_spec.wav, synth_spec.flux)
# ```
|
docs/Introduction to MOOG.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import tensorflow as tf
from tensorflow import keras
import numpy as np
import matplotlib.pyplot as pyplot
import image
import cv2
import os
scale=4
(x_train,y_train),(x_test,y_test)=keras.datasets.mnist.load_data()
datagen=keras.preprocessing.image.ImageDataGenerator(rescale=1/255.,horizontal_flip=True,vertical_flip=True)
x_train=x_train.reshape((x_train.shape[0],28,28,1))
y_train.shape
wres=scale*x_train.shape[2]
hres=scale*x_train.shape[1]
npic=x_train.shape[0]
nchan=x_train.shape[3]
x_train_aug=np.full((npic,wres,hres,nchan),0)
for i in range(0,(x_train.shape[0])):
pic=x_train[i]
pic=cv2.resize(pic,(wres,hres),interpolation=cv2.INTER_AREA)
pic=np.expand_dims(pic,axis=2)
x_train_aug[i]=pic
datagen.fit(x_train_aug)
os.makedirs('images')
for x_batch, y_batch in datagen.flow(x_train_aug,y_train,batch_size=9,save_to_dir='images',save_prefix='aug',save_format='png'):
for i in range(0,9):
pyplot.subplot(3,3,i+1)
pyplot.imshow(x_batch[i].reshape(wres,hres), cmap=pyplot.get_cmap('gray'))
pyplot.show()
if i == 9:
print(i)
break
break
|
augtest.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # INTRODUÇÃO
# ------------
#
# O Python é uma linguagem de programação conhecida como **OOP (_Object Oriented Programming_)**, de **alto nível** e **interpretada**.
# ## COMPILADA x INTERPRETADA
# ------------------------------
#
# Em qualquer linguagem de programação estamos escrevendo um código que será convertido para linguagem de máquina, sendo possível então a utilização desse programa pelo computador ou outros dispositivos eletrônicos.
#
# <br>
#
# ### COMPILADA
#
# Em uma linguagem compilada, após concluir um programa, precisamos passar por um programa chamado "compilador" que irá ler o programa, verificar algum erro estrutural e criar um arquivo executável para a plataforma desejada. Dessa forma, com esse novo arquivo, não conseguimos mais editar o código (partindo apenas desse material) e não precisamos de mais nenhum outro programa para rodar o script.
#
# **Vantagem:** Depois de compilado, o programa pode rodar em outros dispositivos (sem a interface de desenvolvedor).
# **Desvantagem:** Não é possível verificar ou editá-lo possuindo apenas o arquivo compilado.
# **Exemplos:** C, C++, Fortran, Visual Basic
#
# <br>
#
# ### INTERPRETADA
#
# Em uma linguagem interpretada, o código não precisa passar por esse compilador, mas para o programa funcionar é necessário executar o programa utilizando um "interpretador" que irá ler o programa enquanto está rodando o código.
#
# **Vantagem:** O programa pode ser executado linha a linha, sendo para o processo de *debugging* ou ainda utilizar os *notebooks*.
# **Desvantagem:** O programa só poderá rodar possuindo um interpretador compatível com a versão utilizada e costuma ser bem mais lento (em ordens de magnitude).
# **Exemplos:** Python, R, JavaScript
# ## BAIXO NÍVEL x ALTO NÍVEL
# ---------------------------
#
# No tópico anterior foi comentado que qualquer código deve passar por um procedimento para a máquina conseguir ler o programa (deixar em linguagem de máquina). Da mesma forma, podemos programar, conforme a linguagem, de uma maneira mais "próxima" dessa conversão ou mais parecido com uma linguagem humana, criando assim um espectro conhecido como "nível" da linguagem dentro da programação.
#
# <br>
#
# ### BAIXO NÍVEL
#
# Uma linguagem de baixo nível significa que está muito próxima do comportamento tomado pela máquina. Dessa forma, a linguagem costuma apresentar uma interpretação mais diícil, mas permite mais controle do sistema. Além disso, funções mais complexas podem ser difícil de implementar sem cair em várias de linhas de código.
#
# **Vantagem:** Os programadores costumam ter mais controle do funcionamento da máquina e o código de execução, o que também compromete a performance durante a execução do *script*.
# **Desvantagem:** Possui uma sintaxe mais complicada e pouco ágil para os programadores.
# **Exemplos:** Assembly e binário
#
# <br>
#
# ### ALTO NÍVEL
#
# Uma linguagem de alto nível significar que está mais próxima da fala/escrita humana. Assim, essas linguagens são mais fáceis de aprender e trabalhar. Fora isso, possuem uma sintaxe mais variada e abertura para diversas outras funcionalidades.
#
# **Vantagem:** Costumam-se ser mais fáceis de aprender e ágeis de programar, pela simplicidade da sintaxe.
# **Desvantagem:** Precisam passar pelo procedimento de compilação ou interpretação, se tornando programas mais lentos.
# **Exemplos:** Python e Java
# ## PROGRAMAÇÃO ORIENTADA A OBJETOS
# ----------------------------------
#
# Esse já é um tópico mais avançado, mas certamente é uma das funcionalidades mais fascinantes e poderosas em algumas linguagens. Basicamente, um programa pode ser escrito em torno de objetos, que representam o mundo real, que podem carregar atributos (informações) e métodos (funções). Embora isso provavelmente não esteja claro, você verá que em programas mais complexos, esse mecanismo se torna mais comum pelas suas capacidades e diversidades de uso.
#
# Mais informações no vídeo: https://youtu.be/QY0Kdg83orY
# ## OBSERVAÇÕES
# --------------
#
# O que acha de já comentarmos de tópicos comuns na linguagem Python?
# Vamos para a lista:
# ### 1. VERSÕES
#
# O Python possui duas versões principais: Python 2 e Python 3. Contudo, o Python 2 não possui mais suporte e deve ser evitado sempre que possível (até porque o "3" possui mais funcionalidades). Além disso, dentro do Python 3.x, por exemplo, ainda temos outras "sub-versões" do interpretador. Dessa forma, preste atenção ao utilizar a versão recomendada ou exigida, principalmente quando estiver utilizando bibliotecas externas (veremos isso em breve).
# ### 2. EXPERIENTES
#
# Aos que já mexeram em outras linguagens de programação, podem acabar percebendo duas principais diferenças na sintaxe em relação ao Python. A primeira e mais óbvia é a exclusão da utilização do famoso `;`. A segunda, relacionada com a primeira, é a importância da indentação na nova linguagem que você está aprendendo. Isto pois, em outras linguagens, é muito comum a utilização de parênteses e chaves para agrupar um "bloco" de conteúdo, não sendo (sempre) exigida alguma formatação específica. Já no Python, esses "blocos" são inexistentes, de forma que precisamos respeitar uma tabulação do conteúdo para o interpretador compreender corretamente o programa.
# ### 3. COMENTÁRIOS
#
# Os comentários durante o código possuem duas funcionalidades principais: acrescentar explicações ao longo do programa ou colocar uma parte do programa para ser "pulada" (ao invés de deletar e perder uma parte do código). As duas opções são boas práticas de programação em qualquer linguagem e podem ser feitas de várias formas no Python.
# +
# Podemos usar o símbolo de "#" antes do texto e tudo que vier em seguida será desconsiderada pelo interpretador
'Podemos também usar aspas simples'
"Aspas duplas também podem ser utilizadas"
'''
Para comentários com
mais de uma linha, devemos
repetir o par de aspas 3 vezes.
'''
"""
O mesmo vale para
aspas duplas.
"""
# -
# ### 4. FORMATAÇÃO
#
# Como boa prática de programação é recomendado seguir uma formação para o código, de forma a deixá-lo "legível" para todos os usuários. Existe uma "norma" chamada **PEP 8** que traz um guia de dicas úteis para esse procedimento, mas isso se pega com a experiência também.
# ### 5. DÚVIDAS
#
# O Python é uma linguagem em alta no momento e possui muita documentação por aí: fóruns, wikis, canais no YouTube, cursos, etc. Então, se tiver alguma dúvida ou problema, generealize-o (ou seja, não deixe ele específico para o seu projeto) e procure na internet. Você provavelmente vai encontrar algum material a respeito.
# Você provavelmente conhecerá o StackOverFlow muito em breve 😂
# ## TRADIÇÃO
# -----------
#
# Existe uma tradição ao aprender uma nova linguagem de programação em fazer um programa simples: mostrar ao usuário a frase "Hello, World!" ("Olá, Mundo!"). Rés a lenda que dá azar não fazer esse procedimento, então, vamos lá né 😅
# +
# O "print" é um método que retorna no terminal o valor dentro dos "parênteses".
# Para retornar um texto, precisamos adioná-lo entre aspas simples ou duplas.
print('Hello, World!')
print("Olá, Mundo!")
# -
# # TIPOS DE DADOS
# ----------------
#
# Dados servem para guardar informações, mas nem toda informação pertence a uma mesma categoria. Um exemplo simples são os números e palavras, quando eu digo "quatro" e "4", mesmo você lendo isso da mesma forma, você possivelmente interpretaria isso de maneira diferente dependendo do contexto. E sobre isso que veremos nesta seção: principais tipos de dados, sua estrutura e suas principais utilizações.
#
# **Observação:** para verificar a tipagem de uma variável, você pode usar o comando abaixo:
#
# `print(type(<variável>))`
#
# onde:
# `<variável>` deve ser a variável em questão;
# `type` retorna o tipo da `<variável>`;
# `print` retorna no terminal o valor encontrado.
# ## TEXTO
# --------
#
# Qualquer tipo de texto: caracteres, palavras, frases, etc.
# ### str
#
# Qualquer tipo de texto: caracteres, palavras, frases, etc.
#
# **Representação**
# Sempre por aspas, sejam simples ou duplas (mesma lógica dos comentários que utilizam esse símbolo).
# +
# A variável 'texto' receberá o valor "Olá, mundo!"
texto = "Olá, Mundo!"
# texto = str("Olá, Mundo!")
# Retorna o valor da variável
print(texto) # Olá, Mundo!
# Retorna o tipo
print(type(texto)) # <class 'str'>
# -
# ## NUMÉRICO
# -----------
#
# Registram diferentes tipos de números, conforme a necessidade: apenas inteiros, reais ou complexos.
# ### int
#
# Número inteiro.
#
# **Representação**
# Valor inteiro, sem pontuação, relacionado com a variável (depois do `=`).
# +
# A variável 'x' recebe o valor 10
x = 10
# x = int(10)
# Retorna o valor da variável
print(x) # 10
# Retorna o tipo
print(type(x)) # <class 'int'>
# -
# ### float
#
# Ponto flutuante, números reais que aceitam a parte decimal.
#
# **Representação**
# Valor numérico com a parte decimal, indicado pelo sistema americano como `.` (separador decimal).
# +
# A variável 'y' recebe o valor 7.0 (note que não é necessário adionar o 0 depois do ponto)
y = 7. # y = float(7)
# Retorna o valor da variável
print(y) # 7.0
# Retorna o tipo
print(type(y)) # <class 'float'>
# -
# ### complex
#
# Números complexos: parte real e parte imaginária (utilizando o `j` ou `J`). O motivo para ser `j` é não `i` vem da engenharia elétrica que utiliza a primeira letra para representar o número imaginário. Além disso, é muito comum a letra `i` ser usada nos *loops*. Por último, dependendo da fonte, a letra maiúscula, `I`, com o `l`.
#
# **Representação**
# Valor numérico com a parte real e a parte imaginária, esta última com a letra J (minúsculo ou maiúscula).
# +
# A variável 'z' recebe o valor 2 + 3i
z = 2 + 3j # z = complex(2, 3)
# Retorna o valor da variável
print(z) # (2+3j)
# Retorna o tipo
print(type(z)) # <class 'complex'>
# -
# ## SEQUENCIAL
# -------------
#
# Possuem várias dados que podem ser acessados através de uma sequência.
# ### list
#
# Listas são conjuntos de dados indexados, iniciando pelo índice 0. Além disso, as listas são modeláveis, podendo ser editadas após a sua criação (acrescentando ou removendo itens, por exemplo).
#
# **Representação**
# Itens separados por vírgula dentro de `[]`.
# +
# A variável 'primos' recebe os valores 2, 3, 5, 7, 11
primos = [2, 3, 5, 7, 11] # primos = list((2, 3, 5, 7, 11))
# Retorna o valor da variável
print(primos) # [2, 3, 5, 7, 11]
# Podemos retornar um(alguns) valor(es) da lista a partir dos seus índices
print(primos[2]) # Apenas o valor de índice 2 --> 5
print(primos[0:3]) # Valores entre o índice 0 até 2 --> [2, 3, 5]
# Retorna o tipo
print(type(primos)) # <class 'list'>
# -
# As sequências também podem conter diferentes tipos de valores.
ficha = ['Fulano', 22, 'Masculino'] # Poderia ser: [nome, ano, sexo]
print(ficha) # ['Fulano', 22, 'Masculino']
# Também é possível ter listas dentro de listas. Essa prática é conhecida como _nested lists_ ou _nD-lists_ (_n_ sendo o valor da dimensão da lista).
# +
# Matriz identidade 3x3
matriz_I = [
[1, 0, 0],
[0, 1, 0],
[0, 0, 1]
]
print(matriz_I) # [[1, 0, 0], [0, 1, 0], [0, 0, 1]]
# Podemos retornar uma célula específica especiicando a linha e depois a coluna
print(matriz_I[1][1]) # 1
# -
# ### tuple
#
# Tuplas são muito semelhantes as `list`, porém imutáveis, isto é, não podem ser modificadas após a sua criação.
#
# **Representação**
# Itens separados por vírgula dentro de `()`.
# +
# Tuplas devem ser uma sequência de itens separados por vírgula e dentro de ().
# A variável 'CONSTANTES' recebe os valores 3.1415, 9.81, 1.6
CONSTANTES = (3.1415, 9.81, 1.6) # CONSTANTES = tuple((3.1415, 9.81, 1.6))
'Quando escrevemos uma variável em toda em maiúscula, ela é considerada uma constante.'
# Retorna o valor da variável
print(CONSTANTES) # (3.1415, 9.81, 1.6)
# Todas as aplicações apresentadas anteriormente para listas se aplicam nas tuplas.
# Retorna o tipo
print(type(CONSTANTES)) # <class 'tuple'>
# -
# ### range
#
# Arranjo de valores, podendo configurar o valor de início, final ($*n-1*$) e o passo. Em outras palavras, é possível fazer uma progressão aritmética, muito útil para *loops*.
#
# **Representação**
# Método `range()` com até 3 parâmetros:
# - 1 parâmetro - `range(n)` - valor final, $n-1$.
# - 2 parâmetros - `range(start, end)` - valor inicial (`start`) e final (`end`), $n-1$.
# - 3 parâmetros - `range(start, end, step)` - valor inicial (`start`) e final (`end`), $n-1$, e o passo (`step`).
# +
# range pode receber até 3 parâmetros
# Apenas 1 parâmetro diz que a variável vai de 0 até o valor estipulado (-1)
arr1 = range(5) # 0, 1, 2, 3, 4
# Se utilizar dois argumentos, o primeiro será o início e o segundo o fim do arranjo
arr2 = range(2, 6) # 2, 3, 4, 5
# O terceiro argumento é o espaçamento do arranjo
arr3 = range(1, 8, 2) # 1, 3, 5, 7
arr4 = range(5, 0, -1) # 5, 4, 3, 2, 1
# Retorna o valor da variável
print(arr1, arr2, arr3, arr4) # range(0, 5) range(2, 6) range(1, 8, 2) range(5, 0, -1)
# Retorna o tipo
print(type(arr1)) # <class 'range'>
# -
# ## MAPEÁVEL
# -----------
#
# Possuem vários dados que podem ser acessados através de um "endereço" (chave).
# ### dict
#
# Dicionários são estruturas de dados que possuem uma lista pareada de chaves e valores. Da mesma forma que podemos chamar um valor de uma lista pelo seu índice, nos dicionários podemos retornar um valor baseado em sua chave associada.
#
# **Representação**
# Valores pareados, chave e valor, com a dupla separada por `:` e novos itens separados por `,` dentro de `{}`.
# +
# A variável 'telefones' guarda uma lista de nomes com os seus valores de número de telefone
telefones = {
'Fulano' : '(XX) XXXX-XXXX',
'Ciclano' : '(YY) YYYY-YYYY',
'Beltrano' : '(ZZ) ZZZZ-ZZZZ'
}
# telefones = dict(Fulano = '(XX) XXXX-XXXX', Ciclano = '(YY) YYYY-YYYY', Beltrano = '(ZZ) ZZZZ-ZZZZ')
# Retorna o valor da variável
print(telefones) # {'Fulano': '(XX) XXXX-XXXX', 'Ciclano': '(YY) YYYY-YYYY', 'Beltrano': '(ZZ) ZZZZ-ZZZZ'}
# Podemos retornar um valor do dicionário a partir dos seus índices
print(telefones['Beltrano']) # (ZZ) ZZZZ-ZZZZ
# Retorna o tipo
print(type(telefones)) # <class 'dict'>
# -
# ## CONJUNTO
# -----------
#
# Conjunto de valores que não possuem sequência definida.
# ### set
#
# Esse conjunto também é capaz de armazenar diversos valores em uma única variável (como as listas), mas não é ordenável, nem indexado. Isso quer dizer que os valores não podem ser "chamados" utilizando algum índice e toda vez estes são mostrados podem estar "misturados". Além disso, esse tipo de dado não pode remover algum item e não aceita valores duplicados.
#
# **Representação**
# Os valores são separados por `,` dentro de `{}`. Contudo, não deve ser vazio, por esse método, caso contrário, vai criar um dicionário).
# +
# A variável 'frutas' recebe os valores 'maçã', 'melancia', 'pêra', 'uva'
frutas = {'maçã', 'melancia', 'pêra', 'uva'}
# frutas = set(('maçã', 'melancia', 'pêra', 'uva'))
# Retorna o valor da variável
print(frutas) # Possível retorno --> {'pêra', 'uva', 'maçã', 'melancia'}
# Retorna o tipo
print(type(frutas)) # <class 'set'>
# -
# ### frozenset
#
# Muito parecido com o `set`, mas não pode ser modificado (acrescentar itens).
#
# **Representação**
# Método `frozenset()` com uma lista de valores dentro dos `()`.
# +
# A variável 'materias' recebe os valores 'matemática', 'física', 'química', 'biologia'
matérias = frozenset({'matemática', 'física', 'química', 'biologia'})
# Retorna o valor da variável
print(matérias) # Possível retorno --> frozenset({'química', 'biologia', 'física', 'matemática'})
# Retorna o tipo
print(type(matérias)) # <class 'frozenset'>
# -
# ## BOOLEANO
# -----------
#
# Valores booleanos: verdadeiro/falso, 0/1, sim/não, etc.
# ### bool
#
# Valores booleanos ( `True` | `False` ).
#
# **Representação**
# Valor `True` (verdadeiro) e `False` (falso).
# +
# A variável 'passei' recebe True (verdadeiro)
passei = True
# passei = bool(1) # Qualquer coisa diferente de 0
# não_passei = False
# não_passei = bool(0)
# Retorna o valor da variável
print(passei) # True
# Retorna o tipo
print(type(passei)) # <class 'bool'>
# -
# ## BINÁRIO
# ----------
#
# Valores ligados a memória do dispositivo.
# ### bytes
#
# Retorna um objeto feito de bytes imutável com um dado tamanho e informação.
#
# **Representação**
# Valor antecedido por um `b` e entre aspas.
# +
# A variável "oi" recebe o valor "Hi" em bytes
oi = b'Hi'
# Retorna o valor da variável
print(oi) # b'Hi'
# Retorna o tipo
print(type(oi)) # <class 'bytes'>
# -
# ### bytearray
#
# Semelhante ao `bytes`, mas é um array mutável.
#
# **Representação**
# Método `bytearray()` com o tamanho do array dentro dos `()`.
# +
# A variável array recebe um array de bytes de tamanho 5
array = bytearray(5)
# Retorna o valor da variável
print(array) # bytearray(b'\x00\x00\x00\x00\x00')
# Retorna o tipo
print(type(array)) # <class 'bytearray'>
# -
# ### memoryview
#
# Retorna o local de memória de um objeto.
#
# **Representação**
# Objeto do tipo `byte` dentro do método `memoryview()`.
# +
# A variável "vis" recebe a posição na memória do bytes(5)
vis = memoryview(bytes(5))
# Retorna o valor da variável
print(vis) # Possível retorno --> <memory at 0x0000024B2DBA4D00>
# Retorna o tipo
print(type(vis)) # <class 'memoryview'>
# -
# # PRINCIPAIS MÉTODOS
# --------------------
#
# Métodos são funções que podem receber algum tipo de dado e argumentos a fim de retornar algum novo valor ou dado.
# Nesta seção, vamos conferir os métodos mais comuns utilizados no dia-a-dia da programação.
#
# Os métodos costumam aparecer de duas formas principais: `método(argumentos)` ou `dado.método(argumentos)`. Isso ficará mais claro com o passar do tempo.
# ## Print
# --------
#
# Sim, você já viu esse método antes. Como você deve saber, ele retorna o valor passado para o terminal.
#
# Além disso, vamos ver outras opções interessantes para o `print`.
# ### f-strings
#
# Essa na verdade não é uma propriedade do método `print`, mas da própria `str`. Basicamente, podemos mesclar um texto com valores de outras variáveis, de forma que um mesmo texto pode ter valores diferentes conforme os valores de entrada.
#
# Para isso, iniciamos uma `str` com um `f` na frente e o espaço que vai receber a variável deve possuir um `{}`.
# +
nome = 'João'
idade = 27
print(f'Olá, meu nome é {nome} e tenho {idade} anos.') # Olá, meu nome é João e tenho 27 anos.
# Alternativamente...
print('Olá, meu nome é {} e tenho {} anos.'.format(nome, idade)) # Olá, meu nome é João e tenho 27 anos.
# -
# ## Input
# --------
#
# Muitas vezes queremos que o usuário nos forneça algum tipo de informação ou dado. Para isso, podemos usar o método `input` que registrar o que for digitado no terminal.
#
# Cuidado: esse método registra por padrão uma `str`, então se você está esperando um número, por exemplo, acrescente o `int()`, `float()` e assim por diante.
# +
# Registra o que o usuário digitar na variável 'mensagem'
mensagem = input('Digite alguma coisa (depois dê enter): ')
# Printa o que foi registrado
print(f'Você digitou a seguinte mensagem: {mensagem}')
# -
# ## Split
# --------
#
# Também é utilizado para `str`, caso se deseja separar um conjunto de palavras em uma lista de palavras.
# +
frase = "Rosas são vermelhas. Violetas são azuis."
separado = frase.split() # Veja que estamos passando o método tendo primeiro definido a variável
print(separado) # ['Rosas', 'são', 'vermelhas.', 'Violetas', 'são', 'azuis.']
# -
# O método `split` pode receber também um parâmetro para indicar qual será o separador da `str`. Um exemplo prático é usar o ponto final para separar frases de um parágrafo.
# +
poema_autopsicografia = """
O poeta é um fingidor.
Finge tão completamente
Que chega a fingir que é dor
A dor que deveras sente.
E os que lêem o que escreve,
Na dor lida sentem bem,
Não as duas que ele teve,
Mas só a que eles não têm.
E assim nas calhas da roda
Gira, a entreter a razão,
Esse comboio de corda
Que se chama o coração."""
print(poema_autopsicografia.split('.'))
# ['\nO poeta é um fingidor', '\nFinge tão completamente\nQue chega a fingir que é dor\nA dor que deveras sente', '\n\nE os que lêem o que escreve,\nNa dor lida sentem bem,\nNão as duas que ele teve,\nMas só a que eles não têm', '\n\nE assim nas calhas da roda\nGira, a entreter a razão,\nEsse comboio de corda\nQue se chama o coração', '']
# -
# Note que a saída produziu vários `\n` que, nas `str`, são interpretados como nova linha (parágrafo).
# ## Len
# ------
#
# Utilizado em qualquer tipo de estrutura de dados (`list`, `tuple`, `set`, `str`) para retornar o seu tamanho.
# +
pontos = [1, 4, 7, 3, 10]
print(len(pontos)) # 5
# -
# ## Append
# ---------
#
# Adiciona um valor ao final de uma lista.
# +
pontos = [1, 4, 7, 3, 10]
pontos.append(55)
print(pontos)
# [1, 4, 7, 3, 10, 55]
# -
# Lembra que as tuplas são imutáveis?
# +
países = ('Brasil', 'EUA', 'Alemanha', 'Canadá', 'Itália')
países.append('Japão')
# AttributeError: 'tuple' object has no attribute 'append'
# -
# ## Remove
# ---------
#
# Remove um item de uma lista dado o seu valor.
# +
pontos = [1, 4, 7, 3, 10, 55]
pontos.remove(7)
print(pontos)
# [1, 4, 3, 10, 55]
# -
# Lembra que as tuplas são imutáveis?
# +
países = ('Brasil', 'EUA', 'Alemanha', 'Canadá', 'Itália')
países.remove('EUA')
# AttributeError: 'tuple' object has no attribute 'remove'
# -
# ## Sum
# ------
#
# Soma o valor de todos os itens em um conjunto numérico.
# +
pontos = [1, 4, 3, 10, 55]
soma = sum(pontos)
print(soma) # 73
# -
# ## Operações básicas
# --------------------
#
# Esse não se trata de um método, mas acredito que seja importante mostrar as principais operações numéricas.
# +
x = 6
y = 2
# Soma
print(f'{x}+{y} = {x + y}')
# 6+2 = 8
# Subtração
print(f'{x}-{y} = {x - y}')
# 6-2 = 4
# Multiplicação
print(f'{x}x{y} = {x * y}')
# 6x2 = 12
# Divisão
print(f'{x}/{y} = {x / y}')
# 6/2 = 3.0
# Note que o resuldo será um float, mesmo o resultando sendo inteiro.
# Potência
print(f'{x}^{y} = {x ** y}') # Alternativamente: pow(x,y)
# 6^2 = 36
# Divisão inteira
print(f'Parte inteira de {x}/{y} é {x // y}')
# Parte inteira de 6/2 é 3
# Resto da divisão
print(f'Resto de {x}/{y} é {x % y}')
# Resto de 6/2 é 0
# -
# ## Map
# ------
#
# Permite processar e transformar todos os itens de um iterável sem a necessidade de um *loop*.
# +
# map(função, iterável)
quadrados = tuple(map(lambda x: x**2, range(10)))
print(quadrados)
# (0, 1, 4, 9, 16, 25, 36, 49, 64, 81)
# -
# ---
# Existem diversos métodos para cada um dos tipos de dados já apresentados e muito disso você pode facilmente encontrar pela internet, conforme a sua necessidade.
# # BIBLIOTECAS
# -------------
#
# As bibliotecas servem para poder adicionar funcionalidades diversas no programa, sendo utilizando códigos produzidos por você ou pela comunidade. Vejamos como podemos estar "chamando" essas bibliotecas e quais são as mais utilizadas.
#
# **Observações:** Sempre importe as bibliotecas que serão utilizadas na parte superior do código.
#
# Tendo a biblioteca instalada em seu ambiente de trabalho, podemos importar as bibliotecas ou funções de duas formas:
#
# 1. Importar todas as funções disponíveis no pacote.
#
# `import <biblioteca>`
#
# Desse jeito, teremos que chamar uma função desta biblioteca pelo seguinte formato: `biblioteca.função()`.
#
# 2. Importar apenas algumas funções específicas.
#
# `from <biblioteca> import <função>`
#
# Desta forma, basta chamar a função importada no formato: `função()`.
#
# Uma prática comum é renomear as bibliotecas ou funções, geralmente para deixar em uma forma mais enxuta. Assim, ao invés de chamarmos uma função por `biblioteca.função()`, por exemplo, chamamos por `<novo nome>.função()`. Para isso, usamos a expressão as `<novo nome>`:
#
# `import <biblioteca> as <novo nome>`
# `from <biblioteca> import <função> as <novo nome>`
# ## Bibliotecas comuns
# ---------------------
#
# - **math**: Funções matemáticas complexas;
# - **random**: Números aleatórios;
# - **os**: Controle de arquivos do sistema;
# - **sys**: Controle de sistema do computador;
# - **time**: Medir o tempo, hora, etc;
# - **timeit**: Tempo de execução;
# - **tkinter**: Criação de GUI;
# - **pygame**: Craiçao de jogos;
# - **numpy**: Manipulação de *arrays*, vetores e matrizes;
# - **pandas**: Manipulação e visualização de tabelas de dados;
# - **scipy**: Operações da área científica;
# - **matplotlib**: Criação e visualização de gráficos;
# - **seaborn**: Criação e visualização de gráficos;
# - **scikit-learn**: Modelos para *data science*;
# - **tensorflow**: *Framework* para *deep learning*;
# ## Instalação de bibliotecas
# ----------------------------
#
# Existem dois métodos principais para a instalação de bibliotecas a partir de comandos no terminal. Não se preocupem, pois não é nada demais.
# ### pip
#
# O mais comum é utilizando o **PyPI** que é um repositório de diversas bibliotecas para Python. Se você fez uma instalação comum do Python em seu computador, você deve ter instalado junto o `pip`. A partir desse comando, iremos instalar uma biblioteca, basta digitar (o '$' quer dizer que é um comando para terminal, ignore-o na digitação):
#
# `$ pip install <biblioteca>`
#
# Caso você esteja utilizando um sistema Linux, o comando é alterado para:
#
# `$ pip3 install <biblioteca>`
#
# O motivo do acréscimo desse "3" é pelo fato de o Linux já vir com o Python2 que é chamado de `python` e `pip` por padrão. Você pode modificar isso utilizando um `alias`.
#
# Caso esse procedimento não funcione, tente as seguintes opções:
#
# `$ python -m pip install <biblioteca>`
# `$ python3 -m pip install <biblioteca>`
# ### conda
#
# Caso você esteja utilizando o software **Anaconda**, que contem diversos recursos para *data science* no geral (Python e R), você pode utilizar o próprio repositório deles para fazer a instalação de bibliotecas. Existem duas opções nesse caso: utilizar a interface gráfica do Anaconda para instalar novas bibliotecas em *packages* ou digitar o comando no terminal:
#
# ```bash
# $ conda activate <ambiente>
# $ conda install <biblioteca>
# ```
#
# O primeiro comando é para certificar que o ambiente esteja ativo, caso você esteja utilizando o padrão, basta substituir por *base*. O segundo faz a instalação da biblioteca no ambiente ativo. Lembrando que o Anaconda já instala por padrão diversas bibliotecas comuns no *base*, dessa forma, raramente será necessário instalar um novo pacote.
#
# Caso encontre dificuldade nesses processos, existem diversos tutoriais na internet dedicados a explicar esses procedimentos.
# **Gráfico da função seno**
# +
# Bibliotecas
import numpy as np
import matplotlib.pyplot as plt
# Valores de x e y para o gráfico
x = np.linspace(-5, 5, 100) # Array com 100 valores indo de -5 até 5
y = np.sin(x) # Array com os valores da função seno em 'x'
plt.plot(x, y) # Gera o gráfico de linha
plt.show() # Mostra o gráfico produzido
# -
# # CONDIÇÕES
# -----------
#
# As condições são verificações lógicas, dessa forma, baseado na resposta de uma pergunta no estilo "sim ou não" (verdadeiro ou falso), executamos determinadas partes do código.
# No Python, utilizamos o `if` ("se") para criar uma estrutura condicional e os operadores condicionais para fazer a verificação lógica, como veremos a seguir. Caso o retorno seja verdadeiro, aquilo que estiver abaixo e deslocado à direita (indentação) será executado. Em caso contrário, essa parte do código será desconsiderada. Contudo, podemos fazer condições mais complexas com mais de uma verificação.
# ## Operadores lógicos
# ---------------------
#
# **SE:** `if`
# **SE-SENÃO:** `elif`
# **SENÃO:** `else`
#
# **Igual a:** `a == b`
# **Diferente de:** `a != b`
# **Menor que:** `a < b`
# **Menor ou igual a:** `a <= b`
# **Maior que:** `a > b`
# **Maior ou igual a:** `a >= b`
#
# **E:** `and`
# **OU:** `or`
# **NÂO:** `not`
# **EM:** `in`
# **MESMO:** `is`
# **Qual número é maior?**
# +
# Entrada do usuário
a = float(input('Digite o primeiro número: '))
b = float(input('Digite o segundo número: '))
# if <arg> <operador> <arg>:
if a > b:
print(f'{a} é maior que {b}')
# Só será testado se a condição anterior for falsa
# elif <arg> <operador> <arg>:
elif a == b:
print(f'{a} é igual a {b}')
# 'else' não leva nenhum argumento e só será executado
# se nenhuma condição for atendida
else:
print(f'{a} é menor que {b}')
# -
# **Estados brasileiros**
# +
# Siglas dos estados brasileiros em um 'frozenset'
estados = frozenset({
'AC', 'AL', 'AP', 'AM', 'BA', 'CE',
'DF', 'ES', 'GO', 'MA', 'MT', 'MS',
'MG', 'PA', 'PB', 'PR', 'PE', 'PI',
'RJ', 'RN', 'RS', 'RO', 'RR', 'SC',
'SP', 'SE', 'TO'
})
# Entrada do usuário
resposta = str(input('Digite a sigla de um estado brasileiro: '))
resposta = resposta.upper() # Coloca o texto em maísculo
resposta = resposta.replace(" ","") # Tira os espaços em branco
# Verifica se a entrada do usuário está no conjunto
if resposta in estados:
print('Muito bem! 😃')
else:
print(f"'{resposta}' não é um estado brasileiro válido.")
# -
# ## Tentativa e erro
# -------------------
#
# Dependendo do procedimento do código, receber uma variável errada, algum erro de utilização do usuário, pode quebrar o programa. Para evitar (ou minimizar) isso e deixar o programa mais "inteligente", podemos preparar o código para tais situações a partir dos comandos `try` e `except`.
#
# **TENTE:** `try`
# **EXCEÇÃO:** `except <erro>`
# **Digite um número inteiro**
# +
# Tenta executar as seguintes linhas
try:
# Entrada do usuário
num = int(input('Digite um número inteiro: '))
print(f'O número digitado foi: {num}')
# Se a qualquer momento dentro de 'try' der um erro do tipo explícito,
# as seguintes linhas são executadas
except ValueError:
print('Erro de entrada')
# -
# ### Múltiplos erros
#
# A estrutura `try` e `except` aceita um retorno dierente para cada tipo de erro e também uma mesma exceção para diferentes tipos de erros, como veremos no exemplo.
# **Dividir números**
# +
try:
# Entrada do usuário
num1 = float(input('Digite o numerador: '))
num2 = float(input('Digite o denominador: '))
print(f'O resultado da divisão é: {num1 / num2}')
# Caso dê um erro de valor ou de interrupção via teclado
# except (<erro1>, <erro2>, ...) as <alguma coisa>:
# Assim, ele salva essa tupla de erros em uma variável
except (ValueError, KeyboardInterrupt) as erro:
print('Erro de entrada')
# Caso o denominador seja igual a zero
except ZeroDivisionError:
print('Não é possível dividir por zero')
# -
# # ESTRUTURA DE REPETIÇÃO
# ------------------------
#
# As estruturas de repetição são expressões capazes de repetir por um número determinado ou indeterminado de vezes uma parte do código. Dessa forma, somos capazes de evitar repetições desnecessárias na escrita do código ou até mesmo apenas prosseguir um procedimento a partir de uma condição, como veremos a seguir.
# ## while
# --------
#
# A *keyword* `while` é equivalente a uma expressão de "ENQUANTO". Ou seja, enquanto um condição for satisfeita (verdadeira), o *loop* será mantido.
#
# ```
# while <condição>:
# ...
# ...
# ```
#
# ⚠️ ATENÇÃO: Cuidado para não criar um loop infinito!
# **Decolagem**
# +
# Biblioteca
import time
# Varíavel
i = 10
# Mensagem inicial
print('Decolagem em:')
# Enquanto 'i' for maior que 0...
while i > 0:
# Espera 1 segundo
time.sleep(1)
print(f'{i}...')
# A cada passagem no loop, i perde uma unidade
i -= 1 # i = i - 1
# Só será acionado depois que o loop acabar
print('DECOLAR!!! 🚀')
# -
# **Descubra o número**
# +
# Biblioteca
from random import randint
# Número escolhido
num = randint(1, 10) # Número aleatório entre 1 e 10
# Escolha do usuário
chute = 0
# Enquanto a escolha for diferente do número escolhido...
while chute != num:
# Recebe uma nova tentativa do usuário
chute = int(input('Tente adivinhar o número (entre 1 e 10):'))
print(f'Você apostou no número {chute}')
# Parabeniza o jogador
print('Parabéns, você acertou!')
# -
# ## for
# ------
#
# A *keyword* `for` é equivalente a expressão "PARA". Ou seja, para "alguma coisa" em determinada sequência, faça algo.
#
# ```
# for <variável> in <sequência>:
# ...
# ...
# ```
# ### Operadores comuns
#
# `in range()` - Sequência usando o `range` visto em *tipos de dados*`in len()` - Sequência utilizando o tamanho do conteúdo dentro de `lenin enumerate()` - Retorna tanto o índice quanto o valor da sequência, respectivamente
# **Decolagem - versão `for` _loop_**
# +
# Biblioteca
import time
# Mensagem inicial
print('Decolagem em:')
# Para 'i' entre 10 até 1...
for i in range(10, 0, -1):
# Espera 1 segundo
time.sleep(1)
print(f'{i}...')
# Só será acionado depois que o loop acabar
print('DECOLAR!!! 🚀')
# -
# **Lista de chamada**
# +
# Lista de nomes
chamada = (
'Ana', 'Bianca', 'Gabriel', 'Helen', 'Kevin'
)
# Enumarate retorna, respectivamente, o índice e o valor da lista 'chamada'
for índice, valor in enumerate(chamada):
print(f'{índice + 1} - {valor}')
# -
# ### *List comprehensions*
#
# "Compreensões de lista" proporciona a criação de listas a partir de uma operação dentro de uma própria lista. Esse método não adiciona de fato algo novo, mas pode deixar o código mais *clean* e enxuto.
# **Quadrados**
# Vamos usar o mesmo exemplo dos quadrados, $x^2$.
# **Usando `for loop`**
# +
# Cria uma lista vazia
quadrados = []
# Loop de 0 até 9
for x in range(10):
quadrados.append(x**2)
# Adiciona o quadrado desse número para a lista
print(quadrados)
# [0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
# -
# **Usando `map`**
# +
quadrados = list(map(lambda x: x**2, range(10)))
print(quadrados)
# [0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
# -
# **Usando _list comprehension_**
# +
quadrados = [i**2 for i in range(10)]
print(quadrados)
# [0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
# -
# ## Alterar o *loop*
# -------------------
#
# Dependendo da necessidade do nosso código, um fator externo pode influenciar o funcionamento do programa. Para isso, podemos adicionar algumas expressões que realizam diferentes ações dentro de estruturas de repetição.
#
# **QUEBRAR:** `break`
# Ao adicionar essa expressão, toda vez que uma condição acionar essa ação, todo a estrutura de repetição é interrompida.
#
# **CONTINUAR:** `continue`
# Utilizando essa ação, o pedaço posterior do código será interrompido, mas o *loop* ainda será preservado.
#
# **IGNORAR:** `pass`
# Essa expressão permite que o programa continue a rodar, mesmo que uma condição foi atendida.
# ### `break`
# +
# Para 'i' de 0 até 9
for i in range(10):
# Se i for igual a 5...
if i == 5:
break # Quebra o loop
print('Número é ' + str(i))
print('Fim do loop!')
# Número é 0
# Número é 1
# Número é 2
# Número é 3
# Número é 4
# Fim do loop!
# -
# ### `continue`
# +
# Para 'i' de 0 até 9
for i in range(10):
# Se i for igual a 5...
if i == 5:
continue # Pula apenas essa "rodada"
print('Número é ' + str(i))
print('Fim do loop!')
# Número é 0
# Número é 1
# Número é 2
# Número é 3
# Número é 4
# Número é 6
# Número é 7
# Número é 8
# Número é 9
# Fim do loop!
# -
# ### `pass`
# +
# Para 'i' de 0 até 9
for i in range(10):
# Se i for igual a 5...
if i == 5:
pass # Só ignora
print('Número é ' + str(i))
print('Fim do loop!')
# Número é 0
# Número é 1
# Número é 2
# Número é 3
# Número é 4
# Número é 5
# Número é 6
# Número é 7
# Número é 8
# Número é 9
# Fim do loop!
# -
# # FUNÇÕES
# ---------
#
# Seguindo essa *playlist* de Python, você já utilizou diversas funções *build-in* (ou seja, da própria ferramenta) e externas usando as bibliotecas. Contudo, não acha que seria muito útil você criar as suas próprias funções? Existem alguns motivos principais para criar uma função personalizada:
#
# - Executar algum procedimento muito específico para o seu projeto;
# - Possuir alguma etapa ou processo repetitivo;
# - Conseguir chamar essa função para outros projetos (criar um biblioteca própria);
#
# Além disso, vale reforçar que as funções são muito poderosas pela forma que podemos trabalhar com os dados de entrada e saída.
#
# A estrutura básica de uma função é dada pelo exemplo abaixo:
#
# ```
# def <função>(<parâmetros>):
#
# """
# <docstring>
# """
#
# ...
# ...
#
# return <valor>
# ```
#
# **`def`**: Define a estrutura de uma função;
#
# **`<função>`**: Este será o nome da função e como ela será chamada ao longo do código (não pode conter espaços em branco);
#
# **`<parâmetros>`**: (Opcional) Responsável pela entrada de informação utilizada dentro da função, como veremos em breve;
#
# **`<docstring>`**: (Opcional) Todo texto comentado por parênteses no topo da função se torna a documentação dessa função, essa é uma prática altamente recomendada (comente o que a função faz, brevemente, o que ela recebe e o que retorna);
#
# **`return`**: (Opcional) Toda função retorna algum valor (saída), caso nada seja declarado ela retornará `None`;
#
# **`<valor>`** O que será retornado.
# **Função mínima**
# Definimos que a função chama `olá_mundo` e recebe nenhum argumento.
# +
def olá_mundo():
print('Olá, Mundo!')
# Como não existe o return, vai retornar None
print(olá_mundo())
# Olá, Mundo!
# None
# -
# É um péssimo hábito "retornar" um print!
# **Função mínima 2**
# Definimos que a função chama `olá_mundo` e recebe nenhum parâmetro.
# +
def olá_mundo():
return 'Olá, Mundo!'
print(olá_mundo())
# Olá, Mundo!
# -
# ## Parâmetros
# -------------
#
# Primeiro, vamos desmistificar uma confusão comum quando estamos trabalhando com funções: a diferença entre **argumentos** e **parâmetros**. Quando estamos construindo uma função, as variáveis que definimos para serem as entradas são definidas como "parâmetros". Contudo, quando chamamos esse método estamos passando "argumentos" para rodar essa função. Ou seja, parâmetro é a variável declarada na função e o argumento e o valor de fato da variável que será utilizado na função.
#
# Vejamos um exemplo básico para entender o funcionamento dos parâmetros/argumentos.
# **Bom dia**
# +
# Criamos a função
# Ela recebe um parâmetro obrigatório chamado 'nome'
# Dessa forma, a partir dessa variável, podemos utilizá-la ao longo da função (sabendo que ela será um str)
def bom_dia(nome):
"Dado um nome, retorna uma mensagem de bom dia para esse nome."
return f'Bom dia, {nome}!'
# Passamos o argumento "Fulano" para a função (parâmetro posicional)
print(bom_dia('Fulano'))
# Podemos também definir que "nome" deve ser igual a "Ciclano"
print(bom_dia(nome='Ciclano'))
# -
# ### `args`
#
# Parâmetros obrigatórios, mas podem ter valores padrão.
# **Calculadora básica**
# +
# Definimos que a função 'calculadora' possui dois parâmetros, 'x' e 'y'
# Por padrão, x = 1 e y = 1, dessa forma, se nenhum argumento for passado, estes srão os seus valores
def calculadora(x = 1, y = 1):
# Docstring
"""
Calculadora
-----------
Cria um dicionário com as principais operações matemáticas, dado dois números.
args
----
x : int ou float
Primeiro número de entrada
y : int ou float
Segundo número de entrada
return
------
dict
{'operação' : valor}
"""
# Retornamos um dicionário com as operações básicas
return {
'soma' : x + y,
'subtração' : x - y,
'divisão' : x / y,
'multiplicação' : x * y,
'potência' : x ** y
}
a = 3
b = 5
# 'resultado' recebe o 'return' da função 'calculadora'
resultado = calculadora(a, b)
# resultado = calculadora(x = a, y = b)
print(resultado)
# {'soma': 8, 'subtração': -2, 'divisão': 0.6, 'multiplicação': 15, 'potência': 243}
# Caso nenhum argumento seja passado, x = 1 e y = 1
print(calculadora())
# {'soma': 2, 'subtração': 0, 'divisão': 1.0, 'multiplicação': 1, 'potência': 1}
# -
# ### `*argv`
#
# Lista de valores com tamanho indeterminado. `*argv` é apenas um nome comum para esse tipo de parâmetro, o necessário é utilizar o `*`.
# **Mensagem para todos**
# +
# 'mensagem' é um argumento posicional
# Tudo que vier depois vai se tornar uma lista salva em 'nomes'
def mensagem(mensagem, *nomes):
"Manda uma 'mensagem' para a lista de 'nomes'"
for i in nomes:
print(f'{mensagem}, {i}.')
mensagem('Oi', 'Carol', 'Beatriz', 'Pedro', 'Carlos')
# -
# ### `**kwargs`
#
# Dicionário de parâmetros opcionais e devem ser chamados no formato `<parâmetro> = <argumento>`. `**kwargs` é apenas um nome comum para esse tipo de parâmetro, o necessário é utilizar o `**`.
# **Preço de produto**
# +
# 'preço' é o parâmetro posicional
# '**kwargs' vai receber os demais parâmetros em formato de dicionário
def preço_final(preço, **kwargs):
"""
Preço final
-----------
Calcula o valor final de um produto.
args
----
preço : float
Preço inicial do produto
**kwargs
--------
imposto : float
Imposto sobre o preço (%)
desconto : float
Desconto sobre o preço (%)
return
------
float
Valor final do valor do produto
"""
# Resgata os valores do dicionário 'kwargs'
imposto = kwargs.get('imposto')
desconto = kwargs.get('desconto')
# Se 'imposto' não for vazio (existir)
if imposto:
preço += preço * (imposto/100)
# Se 'desconto' não for vazio (existir)
if desconto:
preço -= preço * (desconto/100)
# Retorna o preço calculado
return preço
valor_inicial = 80
imposto = 12.5
desconto = 5
# Mesmo não passando todas os possíveis parâmetros para **kwargs, a função ainda funciona
print(preço_final(valor_inicial, imposto = imposto, desconto = desconto))
# 85.5
# Teste mudando os valores ou comentando os parâmetros opcionais
# -
# A combinação de todos esses tipos de parâmetros também é possível, seguindo a ordem: `(args, *argv, **kwargs)`.
# ## Variáveis globais e locais
# -----------------------------
#
# Uma variável global é uma variável definida que vale para todo o código.
#
# Uma variável local é uma variável definida no escopo de uma função e só possui esse valor durante a execução desse método.
# +
# Variável global
x = 50
def f():
# Variável local
x = 20
print(x)
print(x) # 50
f() # 20
print(x) # 50
# -
# ## Funções anônimas (`lambda`)
# ------------------------------
#
# Caso precisamos fazer uma operação simples, podemos construir uma função anônima: podem ter qualquer número de argumentos, mas só podem ter uma expressão.
#
# `lambda <argumentos> : <expressão>`
# **Multiplicação**
# +
# A variável 'vezes' vai "segurar" a função anônima
vezes = lambda a, b : a * b
# Utiliza a função
print(vezes(3, 17)) # 51
# -
# **Potência**
# Vamos misturar as funções "normais" e anônimas.
# +
# Função potência
def potência(n):
"Retorna uma função anônima que vai ser a potência de 'n'"
return lambda a : a ** n
# Função x^2
ao_quadrado = potência(2)
# Função x^3
ao_cubo = potência(3)
# Testa as funções
print(ao_quadrado(5)) # 25
print(ao_cubo(5)) # 125
# -
# # CLASSES
# ---------
#
# **PLOT-TWIST**: Estamos usando as classes desde o início desse material 🤯
#
# Se você lembrar da saída do comando `type` que utilizamos na seção de *tipos de dados*, ela era no estilo `<class ...>`. Então, cada tipo de dado na verdade é uma classe, conhecido também como "objeto". Um objeto é uma estrutura de informação capaz de possuir dados, chamados de atributos, e código, conhecido como métodos (semelhantes as funções que já estudamos, mas funcionam apenas para os objetos criados a partir dessa classe).
#
# Ao criar uma nova classe, podemos criar um objeto com uma estrutura de dados única e com métodos bem definidos que, em programas mais complexos, se torna muito útil.
#
# Formato padrão:
#
# ```
# class <Nome>(<herança>):
#
# """
# <docstring>
# """
#
# def <função1>(self, <parâmetros>):
# ...
# ...
#
# ...
# ...
# ```
#
# **`class`**: Define a estrutura de uma classe;
#
# **`<Nome>`**: Este será o nome da classe e como ela será chamada ao longo do código (não pode conter espações em branco);
#
# **`<herança>`**: (Opcional) Herda os métodos e parâmetros da classe <herança>;
#
# **`<docstring>`**: (Opcional) Todo texto comentado por parênteses no topo da classe se torna a documentação dessa classe, essa é uma prática altamente recomendada;
#
# **`<função1>`**: (Opcional) Função/método da classe;
#
# **`self`**: Atributo que chama os demais atributos do objeto e os métodos da classe;
#
# **`<parâmetros>`**: (Opcional) Responsável pela entrada de informação utilizada dentro da função;
# ## _Magic methods_
# ------------------
#
# Existem alguns métodos especiais com nomes pré-definidos que possuem propriedades únicas. Por exemplo, a concatenação de duas `str` a partir do sinal `+` é definida no método `__add__`. Você pode encontrar uma lista completa desses métodos pelo nome *magic methods*.
#
# Um método comum em classes é o `__init__` que é iniciado na criação do objeto.
# ## Dados protegidos
# -------------------
#
# Nas linguagens orientada a objetos é comum existir o conceito de campos públicos, privados e protegidos. Esses conceitos se referem se um dado atributo ou método é acessível fora do escopo da classe. No caso do Python, não existe nenhum método para evidentemente atribuir esses status aos dados da classe. Contudo, existe um consenso de adicionar um `_` na frente dos nomes dos atributos e métodos para identificá-los como privados, ou seja, acesso apenas para dentro da classe.
#
# Apenas para deixar um pouco mais claro, essa prática pode controlar quando o usuário tem permissão ou não para fazer uma atribuição. Por exemplo:
#
# `objeto.atributo = novo_valor`
#
# Por esse motivo, é muito comum ver que algumas classes possuem vários métodos com o único propósito de retornar um valor de um atributo, de forma que assim não é possível escrever, apenas ler o que está registrado.
#
# ```
# def get_value(self):
# return self._value # Atributo "privado"
# ```
# ## Herança
# ----------
#
# As classes apresentam uma "hierarquia", na qual uma *classe secundária* pode adquirir os atributos e métodos da *classe principal*.
# **RPG Simples**
# +
# BIBLIOTECAS
import os # Sistema operacional
import sys # Sistema-interpretador
from random import random # Gerador de números aleatórios [0,1)
from time import sleep # Aguardar
# CLASSES
class Jogador():
"""
# JOGADOR
---------
Classe primária para criar um objeto do tipo `jogador`.
## ATRIBUTOS
- Vida
- Mana
- Ataque
## MÉTODOS
- `atacar()`: Retorna um valor (inteiro) correspondente ao dano físico.
- `magia()`: Retorna um valor (inteiro) correspondente ao dano por magia.
- `descanso()`: Recupera uma fraçã de alguns status do personagem.
- `status()`: Retorna um texto com os atributos do personagem.
"""
# Atributos básicos do personagem
# Aqui é possível configurar o balenceamento do jogo
ATRIBUTOS = {
"Vida" : 500,
"Mana" : 200,
"Ataque" : 100
}
# Valor que será aplicado nos atributos do personagem
# conforme a especialidade/classe de cada um
VANTAGENS = {
"Fraqueza" : 0.8,
"Normal" : 1.0,
"Força" : 1.2
}
# Fração mínima e máxima de dano, respectivamente
DANO_AMPLITUDE = (0.5, 1.5)
# Custo no uso de magia para a mana
MAGIA_CUSTO = 50
# Fração de vida e mana recuperada ao final de uma batalha
RECUPERAÇÃO = 0.1
def __init__(self):
"Configura os atributos básicos."
self.max_vida = self.ATRIBUTOS["Vida"]
self.vida = self.max_vida
self.max_mana = self.ATRIBUTOS["Mana"]
self.mana = self.max_mana
self.ataque = self.ATRIBUTOS["Ataque"]
def atacar(self):
"Calcula o valor de dano físico que o personagem vai infligir nesse turno."
return round(((self.DANO_AMPLITUDE[1]-self.DANO_AMPLITUDE[0])*random()+self.DANO_AMPLITUDE[0])*self.ataque)
def magia(self):
"Calcula o valor de dano mágico que o personagem vai infligir nesse turno."
# Custo do uso da magia
self.mana -= self.MAGIA_CUSTO
return round(((self.DANO_AMPLITUDE[1]-self.DANO_AMPLITUDE[0])*random()+self.DANO_AMPLITUDE[0])*self.max_mana)
def descanso(self):
"Recupera uma parte das estatísticas do jogador: vida e mana."
# Recuperação da vida
self.vida += round(self.max_vida * self.RECUPERAÇÃO)
if self.vida > self.max_vida:
self.vida = self.max_vida
# Recuperação da mana
self.mana += round(self.max_mana * self.RECUPERAÇÃO)
if self.mana > self.max_mana:
self.mana = self.max_mana
def status(self):
"Retorna uma `str` com as estatísticas do personagem."
return f"Vida: {self.vida}/{self.max_vida} | Mana: {self.mana}/{self.max_mana} | Ataque: {self.ataque}"
class Guerreiro(Jogador):
"""
# GUERREIRO
-----------
Classe forte e resistente, com muitos pontos de vida.
- Vida: +++
- Mana: +
- Ataque: ++
"""
def __init__(self):
"Atualiza os atributos básicos."
# Resgata os atributos da classe pai.
# Nese caso, não é necessário, pois não possuiu parâmetros.
super().__init__()
self.max_vida = round(self.max_vida * self.VANTAGENS["Força"])
self.vida = self.max_vida
self.max_mana = round(self.max_mana * self.VANTAGENS["Fraqueza"])
self.mana = self.max_mana
self.ataque = round(self.ataque * self.VANTAGENS["Normal"])
class Ninja(Jogador):
"""
# NINJA
-------
Classe preparada para o dano físico, com muitos pontos de ataque.
- Vida: +
- Mana: ++
- Ataque: +++
"""
def __init__(self):
"Atualiza os atributos básicos."
# Resgata os atributos da classe pai.
# Nese caso, não é necessário, pois não possuiu parâmetros.
super().__init__()
self.max_vida = round(self.max_vida * self.VANTAGENS["Fraqueza"])
self.vida = self.max_vida
self.max_mana = round(self.max_mana * self.VANTAGENS["Normal"])
self.mana = self.max_mana
self.ataque = round(self.ataque * self.VANTAGENS["Força"])
class Mago(Jogador):
"""
# MAGO
------
Classe especializada em magia, com muitos pontos de mana.
- Vida: ++
- Mana: +++
- Ataque: +
"""
def __init__(self):
"Atualiza os atributos básicos."
# Resgata os atributos da classe pai.
# Nese caso, não é necessário, pois não possuiu parâmetros.
super().__init__()
self.max_vida = round(self.max_vida * self.VANTAGENS["Normal"])
self.vida = self.max_vida
self.max_mana = round(self.max_mana * self.VANTAGENS["Força"])
self.mana = self.max_mana
self.ataque = round(self.ataque * self.VANTAGENS["Fraqueza"])
class Inimigo():
"""
# INIMIGO
---------
Classe primária para criar um objeto do tipo `inimigo`.
## ATRIBUTOS
- Vida
- Ataque
## MÉTODOS
- `atacar()`: Retorna um valor (inteiro) correspondente ao dano físico.
- `status()`: Retorna um texto com os atributos do personagem.
"""
ATRIBUTOS = dict(zip(
Jogador().ATRIBUTOS.keys(),
list(map(lambda x: x*0.65, list(Jogador.ATRIBUTOS.values())))
))
DANO_AMPLITUDE = (0.5, 1.5)
def __init__(self):
"Configura os atributos básicos."
self.max_vida = round(self.ATRIBUTOS["Vida"] * (0.5 + random()))
self.vida = self.max_vida
# self.max_mana = self.ATRIBUTOS["Mana"]
# self.mana = self.max_mana
self.ataque = round(self.ATRIBUTOS["Ataque"] * (0.5 + random()))
def atacar(self):
"Calcula o valor de dano físico que o inimgo vai infligir nesse turno."
return round(((self.DANO_AMPLITUDE[1]-self.DANO_AMPLITUDE[0])*random()+self.DANO_AMPLITUDE[0])*self.ataque)
def status(self):
"Retorna uma `str` com as estatísticas do inimigo."
# return f"Vida: {self.vida}/{self.max_vida} | Mana: {self.mana}/{self.max_mana} | Ataque: {self.ataque}"
return f"Vida: {self.vida}/{self.max_vida} | Ataque: {self.ataque}"
# FUNÇÕES
def clear():
"Limpa o terminal."
os.system('cls' if os.name=='nt' else 'clear')
# MAIN
# Roda apenas se este programa que está em execução e não caso tenha sido importado.
if __name__ == '__main__':
# Opções de clases
CLASSES = {
"Guerreiro" : Guerreiro(),
"Ninja" : Ninja(),
"Mago" : Mago()
}
clear() # Limpa o terminal
print("Classes disponíveis:")
# Mostra as classes disponíveis
for i in CLASSES:
print(f"- {i}")
# Escolha de classe
while True:
# Já "limpa" a string de entrada
escolha = input("\nEscolha a sua classe:").capitalize().replace(" ","")
try:
player = CLASSES[escolha]
break
except:
print("\nEscolha inválida!")
# Pontuação do jogador
score = 0
while True:
clear() # Limpa o terminal
print("Um novo inimigo aparece!\n")
inimigo = Inimigo() # Gera um novo inimigo
while True:
# Estatística dos objetos
print(f"INIMIGO: {inimigo.status()}")
print(f"JOGADOR: {player.status()}")
# Opções de ações
print("\nATACAR | MAGIA | SAIR")
while True:
# Escolha de ação do usuário
evento = input("\nO que fazer? ").lower().replace(" ","")
# ATACAR
if evento == "atacar":
dano = player.atacar() # Calcula o dano
print(f"\nVocê ataca o inimigo e inflige {dano} de dano.")
inimigo.vida -= dano # Aplica o dano
break
# MAGIA
elif evento == "magia":
# Verifica se possui mana suficiente
if player.mana >= player.MAGIA_CUSTO:
dano = player.magia() # Calcula o dano
print(f"\nVocê usa uma magia no inimigo e inflige {dano} de dano.")
inimigo.vida -= dano # Aplica o dano
break
else:
print("Mana insuficiente!")
# SAIR
elif evento == "sair":
print(f"\nFim de jogo!\nPontuação: {score}")
sys.exit() # Fecha o interpretador
else:
print("\nComando inválido!")
# Inimigo vivo, ataca
if inimigo.vida > 0:
sleep(1) # Espera
dano = inimigo.atacar() # Calcula o dano
print(f"O inimigo te ataca e inflige {dano} de dano.\n")
sleep(1) # Espera
player.vida -= dano # Aplica o dano
# Inimigo morto
else:
score += 1 # Aumenta pontuação
print("\nVocê aniquilou o inimigo!")
sleep(1) # Espera
player.descanso() # Restaura um pouco o player
print("\nVocê consegue descansar um pouco.")
sleep(2) # Espera
break
# Se jogador está sem vida
if player.vida <= 0:
print(f"\nFim de jogo!\nPontuação: {score}")
sys.quit() # Fecha o interpretador
|
Completo.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import sqlite3
import pandas as pd
cnx = sqlite3.connect('billboard-200.db')
df = pd.read_sql_query("""SELECT albums.date as date,
albums.artist,
albums.album,
acoustic_features.song,
acoustic_features.valence,
albums.rank
FROM albums
left join acoustic_features
on albums.album = acoustic_features.album
order by date asc""", cnx)
# -
#convert date to datetime object to extract year.
df['date'] = pd.to_datetime(df['date'])
#extract & append year on df
df['year'] = df['date'].dt.year
#remove 2019 (it's only January data) & get the mean of each year.
#songs' valences are obviously included multiple times a year.
valence_by_year = df[df.year != 2019.0].groupby('year').mean()
valence_by_year
|
Billboard Data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Importing the required functions to simulate the circuit.
# +
import matplotlib.pyplot as plt
import numpy as np
from qiskit import IBMQ, Aer, QuantumCircuit, ClassicalRegister, QuantumRegister, execute
from qiskit.providers.ibmq import least_busy
from qiskit.quantum_info import Statevector
from qiskit.visualization import plot_histogram
from qiskit.extensions import UnitaryGate
from math import sqrt
# -
# The value of n can be changed over here depending upon the number of qubits to simulate.
n = 5
N = 2 ** n
# This initalises the qubits in the uniform state by applying a Hadamard gate to every qubit in the zero state.
def initialize(qc, qubits):
for q in qubits:
qc.h(q)
return qc
# The matrix that simulates the amplitude negation behaviour of the provided black box.
def get_oracle_matrix(N, values):
oracle_matrix = np.identity(N)
for value in values:
oracle_matrix[value][value] = -1
return oracle_matrix
# The matrix that simulates inversion across mean.
def get_diffusion_matrix(N):
diffusion_matrix = np.zeros((N, N), dtype = float)
diffusion_matrix.fill(2 / N)
diffusion_matrix -= np.identity(N)
return diffusion_matrix
# Here the values array can be edited and the desirables values in the range $[0, N - 1]$ can be entered.
values = [2, 3, 4]
# Make a Gate out of the unitary matrices.
oracle_matrix = get_oracle_matrix(N, values)
oracle_unitary_gate = UnitaryGate(oracle_matrix)
diffusion_matrix = get_diffusion_matrix(N)
diffusion_unitary_gate = UnitaryGate(diffusion_matrix)
# Initalise the Quantum Circuit and run the negation, inversion iterations for the required number of times.
# +
qc = QuantumCircuit(n)
qc = initialize(qc, [x for x in range(n)])
for i in range(int(sqrt(N / len(values)))):
qc.unitary(oracle_matrix, [x for x in range(n)])
qc.unitary(diffusion_matrix, [x for x in range(n)])
qc.draw()
# -
# Display result.
# +
qc.measure_all()
qasm_simulator = Aer.get_backend('qasm_simulator')
shots = 1024
results = execute(qc, backend=qasm_simulator, shots=shots).result()
answer = results.get_counts()
plot_histogram(answer, figsize = (15, 12))
# -
# ### Going beyond $\sqrt{(N)}$ queries.
# Enter the number of extra queries to see the result as mentioned in the tutorial sheet.
extra_queries = 3
# +
qc = QuantumCircuit(n)
qc = initialize(qc, [x for x in range(n)])
for i in range(int(sqrt(N / len(values))) + extra_queries):
qc.unitary(oracle_matrix, [x for x in range(n)])
qc.unitary(diffusion_matrix, [x for x in range(n)])
qc.measure_all()
qasm_simulator = Aer.get_backend('qasm_simulator')
shots = 1024
results = execute(qc, backend=qasm_simulator, shots=shots).result()
answer = results.get_counts()
plot_histogram(answer, figsize = (10, 8))
|
Code/src/Grover's Algorithm/GroversAlgorithm.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Scikit-Learn: un API de python para el aprendizaje automatico
# Scikit-Learn, libreria de python, combina una interfaz intuitiva con una implementacion altamente optimizada de varios algoritmos de clasificacion y regresion. No solo ofrece una amplia variedad de algoritmos de aprendizaje, sino tambien diferentes funciones sencillas para el preprocesamiento de datos y para la evaluacion de los modelos.
#
# Los cinco pasos principales que se dan en el entrenamiento de un algoritmo de aprendizaje automatica se pueden resumir en:
#
# 1. Seleccionar caracteristicas y recopilar muestras de entrenamiento.
# 2. Elegir una medicion del rendimiento.
# 3. Eligir un algoritmo optimizador y de clasificacion.
# 4. Evaluar el rendimiento del modelo.
# 5. Afinar el algoritmo.
#
# Siempre sera necesario aprender a manejar varios algoritmos de clasificacion, debido a que no todos funcionan de la misma manera ni son aptos para todos los conjuntos de datos; inclusive sus restricciones matematicas suelen ser diferentes, y por, lo tanto pueden producir resultados erroneos de no utilizarse con los datos adecuados. Mas aun, algunos de llos dependen de los llamadas _hiperparametros_ , siendo estos diferentes entre los distintos algoritmos, lo cual implica una dificultad mayor, la cual puede ser subsanada con la practica.
# Para introducirnos adecuadamente en el tema, iniciaremos con la implementacion del modelo **Perceptron** de clasificacion lineal visto la semana pasada, pero esta vez implementado a traves de _scikit learn_. Primero debemos recordar y agregar lo siguiente:
#
# 1. El modelo es de clasificacion lineal, lo que significa que tratara de separar las clases por medio de lineas rectas.
# 2. El modelo, al ser de clasificacion, puede manejar distintas clases, y no solo dos, como se vio en la clase de la semana pasada, en la cual se manejo unicamente clasificacion binaria. Para lograr la clasificacion de mas de dos clases, utilizara un metodo llamada **OvR: One versus All**.
# 3. El escalado de variables, que favorecia al metodo del Descenso del gradiente usado en el modelo Adaline, tambien puede ser usado con el modelo del Perceptron a traves de la libreria scikit learn.
# 4. El modelo de Perceptron requiere para su convergencia que las clases sean linealmente separables, de lo contrario nunca terminar de clasificar. Para solventar esto, se introduce un numero predeterminado de iteraciones y asi asegurar su finalizacion, mas no su convergencia. Es de aclarar que el numero de iteraciones elegido no garantiza que los errores sean minimos, y en clases que no son linealmente separables, puede llegar a ser demandante encontrar este minimo. Esto representa un defecto de la funcion de activacion del Perceptron.
#
# Scikit Learn ademas proporciona acceso a conjuntos de datos precargados, los cuales, por su popularidad, se ganaron su lugar dentro de la libreria. Otra librerias que permiten algo similar son Pandas y Numpy.
# +
# Cargando el conjunto de datos Iris
# =========================================================
from sklearn import datasets
import numpy as np
iris = datasets.load_iris()
X = iris.data[:, [2, 3]]
y = iris.target
print(f'Etiquetas de clase: {np.unique(y)}')
# +
# Division del conjunto de datos en entrenamiento y test
# =========================================================
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3, stratify = y)
print(f'Tamaño del conjunto X_train: {X_train.shape}')
print(f'Tamaño del conjunto X_test: {X_test.shape}')
print(f'Tamaño del conjunto y_train: {y_train.shape}')
print(f'Tamaño del conjunto y_test: {y_test.shape}')
print(f'\nConteo de etiquetas en y: {np.bincount(y)}')
print(f'Conteo de etiquetas en y_train: {np.bincount(y_train)}')
print(f'Conteo de etiquetas en y_test: {np.bincount(y_test)}')
# -
# Escalado de variables
# =========================================================
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
sc.fit(X_train) # Calculo de mu y sigma para cada caracteristica
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test) # X_test se escala con los mismos parametros de X_train, para que sean comparables
# Creacion del modelo de perceptron
# =========================================================
from sklearn.linear_model import Perceptron
modelo = Perceptron(max_iter = 40, eta0 = 0.1, random_state = 1)
modelo.fit(X_train_std, y_train)
# Prediccion de resultados
# =========================================================
y_pred = modelo.predict(X_test_std)
print(f'Valores mal clasificados: {(y_test != y_pred).sum()}')
print(f'Cantidad de valores en y_test: {y_test.shape[0]}')
proporcion = (y_test != y_pred).sum()/y_test.shape[0]
print(f'Proporcion de valores mal clasificados: {np.round(proporcion, 3)}')
print(f'Precision de la clasificacion: {1 - np.round(proporcion, 3)}')
# Calculo de la precision usando accuracy_score
# =========================================================
from sklearn.metrics import accuracy_score
print(f'Precision: {np.round(accuracy_score(y_test, y_pred), 3)}')
# Calculo de la precision usando score
# =========================================================
print(f'Precision: {np.round(modelo.score(X_test_std, y_test), 3)}')
# +
# Graficando las regiones
# =========================================================
from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
def plot_decision_regions(X, y, classifier, test_idx=None, resolution=0.02):
# setup marker generator and color map
markers = ('s', 'x', 'o', '^', 'v')
colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
cmap = ListedColormap(colors[:len(np.unique(y))])
# plot the decision surface
x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
np.arange(x2_min, x2_max, resolution))
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1, xx2, Z, alpha=0.3, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x=X[y == cl, 0],
y=X[y == cl, 1],
alpha=0.8,
c=colors[idx],
marker=markers[idx],
label=cl,
edgecolor='black')
# highlight test samples
if test_idx:
# plot all samples
X_test, y_test = X[test_idx, :], y[test_idx]
plt.scatter(X_test[:, 0],
X_test[:, 1],
c='',
edgecolor='black',
alpha=1.0,
linewidth=1,
marker='o',
s=100,
label='test set')
# +
# %matplotlib notebook
X_combined_std = np.vstack((X_train_std, X_test_std))
y_combined = np.hstack((y_train, y_test))
plot_decision_regions(X=X_combined_std, y=y_combined,
classifier=modelo, test_idx=range(105, 150))
plt.xlabel('petal length [estandarizado]')
plt.ylabel('petal width [estandarizado]')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()
# -
# <span class="burk">EJERCICIO</span>
#
# 1. Volver a usar el modelo de Perceptron con todas las caracteristicas del dataset. Calcular la precision.
# 2. Tomar el dataset `Social_Network_Ads.csv` y clasificar los datos de compra y no compra usando las variables 'Age' y 'EstimatedSalary'. Calcular el score y graficar para visualizar las regiones.
# # Regresion Logistica
# La regresion logistica es uno de los algoritmos de clasificacion mas populares, que no se usa para regresion, como su nombre pareciera indicar. Su metodo se basa en el establecimiento de probabilidades a partir de un valor de entra da de red $z$, el cual se representa de forma lineal, como en el caso del perceptron:
#
# $$z=w_0+w_1x_1+w_2x_x+\dots+w_mx_m$$
#
# Por lo tanto, la regresion logistica tambien es un algoritmo de clasificacion lineal, que tratara de separar las clases por un limite o frentera lineal; su ventaja sobre el modelo de Perceptron es similar a la ventaja mostrada por Adaline, la cual es la posibilidad de hallar un minimo de la funcion de costo sin depender de la convergencia del algoritmo; recordemos que Perceptron es un modelo que depende la separacion lineal de clases para su convergencia, lo cual es una limitante del modelo.
#
# La definicion matematica de la regresion logistica es:
#
# $$\phi(z)=\frac{1}{1+e^{-z}}$$
#
# Para entender mejor como funciona, vamos a graficar su forma en python:
# +
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn')
# %matplotlib notebook
def sigmoid(z):
return 1./(1.+np.exp(-z))
x = np.linspace(-7, 7, 100)
y = sigmoid(x)
fig, ax = plt.subplots(figsize = (8, 5))
ax.plot(x, y, color = 'red')
plt.axhline(y = 0.5, color = 'gray', linewidth = 0.5)
plt.axhline(y = 1, color = 'gray', linewidth = 0.5)
plt.axhline(y = 0, color = 'gray', linewidth = 0.5)
plt.axvline(x = 0, color = 'k')
ax.set_xlabel('z')
ax.set_ylabel('sigmoid(z)')
ax.set_title('Comportamiento de la funcion sigmoide');
# -
# Como se puede ver, a medida que x se acrca a infinito, la funcion se acerca a 1; cuando la funcion se acerca a menos infinito, la funcion se acerca a -1. La funcion se puede entender como que toma valores numero numericos en el intervalo $(-\infty, \infty)$ y los transforma al intervalo $[0, 1]$.
# ###### Comparacion entre Adaline y Regresion logistica
#
# 
# La salida de la funcion sigmoide se lee como: La probabilidad de que la muestra pertenezca a la clase 1, dados los valores $\vec{x}$ y $\vec{w}$ de entrada. En terminos mas formales, se escribe como $P(y=1|\vec{x},\vec{w})$. Por ejemplo, si $\phi(z)=0.8$, significa que la probabilidad de que la flor de entrada sea `Iris-versicolor` (etiqueta 1) es del 80%, y por lo tanto la probabilidad de que se `Iris-Setosa` es del 20%.
#
# Lo interesante de la regresion logistica es que no solo brinda la etiqueta de clase, sino que ademas brinda la probabilidad de esta etiqueta sea la correcta; por esta razon es bastante popular en calculos meteorologicos y en medicina.
#
# La probabilidad predicha se puede, simplemete, convertir despues en un resultado binario mediante la funcion umbral:
#
# \begin{equation}
# \hat{y} = \left\{
# \begin{array}{ll}
# 1 & \mathrm{si\ } \phi(z) \geq 0.5 \\
# 0 & \text{en otros casos}
# \end{array}
# \right.
# \end{equation}
#
# Tambien, a partir del grafico, se puede deducir que:
#
# \begin{equation}
# \hat{y} = \left\{
# \begin{array}{ll}
# 1 & \mathrm{si\ } z \geq 0.0 \\
# 0 & \text{en otros casos}
# \end{array}
# \right.
# \end{equation}
# ## Aprender los pesos para la funcion logistica
#
# Para aprender los pesos, haremos uso de la tecnica de maximizacion de la funcion de coste apropiada para la regresion logistica:
#
# $$J(\textbf{w})=\sum_{i=1}^n \big [-y^{(i)}\log(\phi(z^{(i)}))-(1-y^{(i)})\log(1-\phi(z^{(i)})) \big]$$
#
# Tener en cuenta que la siguiente propiedad se cumple para $J$:
#
# \begin{equation}
# J(\phi(z), y; \textbf{w}) = \left\{
# \begin{array}{ll}
# -\log(\phi(z)) & \mathrm{si\ } y = 1 \\
# -\log(1-\phi(z)) & \mathrm{si\ } y = 0
# \end{array}
# \right.
# \end{equation}
# +
def cost_1(z):
return - np.log(sigmoid(z))
def cost_0(z):
return - np.log(1 - sigmoid(z))
z = np.arange(-10, 10, 0.1)
phi_z = sigmoid(z)
fig, ax = plt.subplots(figsize = (5, 3))
c1 = [cost_1(x) for x in z]
plt.plot(phi_z, c1, label='J(w) if y=1')
c0 = [cost_0(x) for x in z]
plt.plot(phi_z, c0, linestyle='--', label='J(w) if y=0')
plt.ylim(0.0, 5.1)
plt.xlim([0, 1])
plt.xlabel('$\phi$(z)')
plt.ylabel('J(w)')
plt.legend(loc='best')
plt.tight_layout()
plt.show()
# -
# ## Implementando el algoritmo de regresion logistica
class LogisticRegressionGD:
"""Logistic Regression Classifier using gradient descent.
Parametros
------------
eta : float
Rango de aprendizaje (entre 0.0 1 1.0)
n_iter : int
Iteracion sobre el datset de entrenamiento completo.
random_state : int
Semilla de numeros aleatorios
Atributos
-----------
w_ : 1d-array
Pesos de las caracteristicas.
cost_ : list
Suma de cuadrados de la funcion de costo en cada epoca.
"""
def __init__(self, eta=0.05, n_iter=100, random_state=1):
self.eta = eta
self.n_iter = n_iter
self.random_state = random_state
def fit(self, X, y):
""" Fit de datos de entrenamiento.
Parametros
----------
X : {array-like}, shape = [n_samples, n_features]
y : array-like, shape = [n_samples]
Returno
-------
self : object
"""
rgen = np.random.RandomState(self.random_state)
self.w_ = rgen.normal(loc=0.0, scale=0.01, size=1 + X.shape[1])
self.cost_ = []
for i in range(self.n_iter):
net_input = self.net_input(X)
output = self.activation(net_input)
errors = (y - output)
self.w_[1:] += self.eta * X.T.dot(errors)
self.w_[0] += self.eta * errors.sum()
cost = -y.dot(np.log(output)) - ((1 - y).dot(np.log(1 - output)))
self.cost_.append(cost)
return self
def net_input(self, X):
"""Calcular la entrada de red"""
return np.dot(X, self.w_[1:]) + self.w_[0]
def activation(self, z):
"""Calcular la activaciond e la funcion sigmoide"""
return 1. / (1. + np.exp(-np.clip(z, -250, 250)))
def predict(self, X):
"""Retornar la etiqueta de clase despues de cada paso"""
return np.where(self.net_input(X) >= 0.0, 1, 0)
# Es importante tener en cuenta que la regresion logistica solo sirve para clasificaciones binarias.
# +
from sklearn import datasets
import numpy as np
iris = datasets.load_iris()
X = iris.data[:, [2, 3]]
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=1, stratify=y)
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
sc.fit(X_train)
X_train = sc.transform(X_train)
X_test = sc.transform(X_test)
# +
X_train_01_subset = X_train[(y_train == 0) | (y_train == 1)]
y_train_01_subset = y_train[(y_train == 0) | (y_train == 1)]
lrgd = LogisticRegressionGD(eta=0.05, n_iter=1000, random_state=1)
lrgd.fit(X_train_01_subset, y_train_01_subset)
fig, ax = plt.subplots(figsize = (6, 4))
plot_decision_regions(X=X_train_01_subset, y=y_train_01_subset, classifier=lrgd)
plt.xlabel('petal length [normalizado]')
plt.ylabel('petal width [normalizado]')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()
# -
y = lrgd.cost_
x = np.arange(1, len(y)+1)
fig, ax = plt.subplots()
ax.plot(x,y);
# <span class="burk">EJERCICIOS</span>
#
# 1. Realice la clasificacion de todo el dataset usando la regresion logistica. Compare los resultados con el modelo del perceptron.
# 2. De nuevo realice el ejericicio 2 pero con esta regresion. Verifique sus resultados y grafique.
|
Semana-12/scikit-learn.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/project-ccap/project-ccap.github.io/blob/master/notebooks/2020_0722transformer_tutorial.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="izhB0L2VCvCj" colab_type="code" colab={}
# %matplotlib inline
# + [markdown] id="tOAm7nfcCvCo" colab_type="text"
#
# # Sequence-to-Sequence Modeling with nn.Transformer and TorchText
#
# This is a tutorial on how to train a sequence-to-sequence model
# that uses the
# [`nn.Transformer`](https://pytorch.org/docs/master/nn.html?highlight=nn%20transformer#torch.nn.Transformer) module.
#
# PyTorch 1.2 release includes a standard transformer module based on the paper [Attention is All You Need](https://arxiv.org/pdf/1706.03762.pdf).
# The transformer model has been proved to be superior in quality for many sequence-to-sequence problems while being more parallelizable.
# The `nn.Transformer` module relies entirely on an attention mechanism (another module recently implemented as [`nn.MultiheadAttention`](https://pytorch.org/docs/master/nn.html?highlight=multiheadattention#torch.nn.MultiheadAttention) to draw global dependencies between input and output.
# The `nn.Transformer` module is now highly modularized such that a single component (like [`nn.TransformerEncoder`](https://pytorch.org/docs/master/nn.html?highlight=nn%20transformerencoder#torch.nn.TransformerEncoder) in this tutorial) can be easily adapted/composed.
#
# 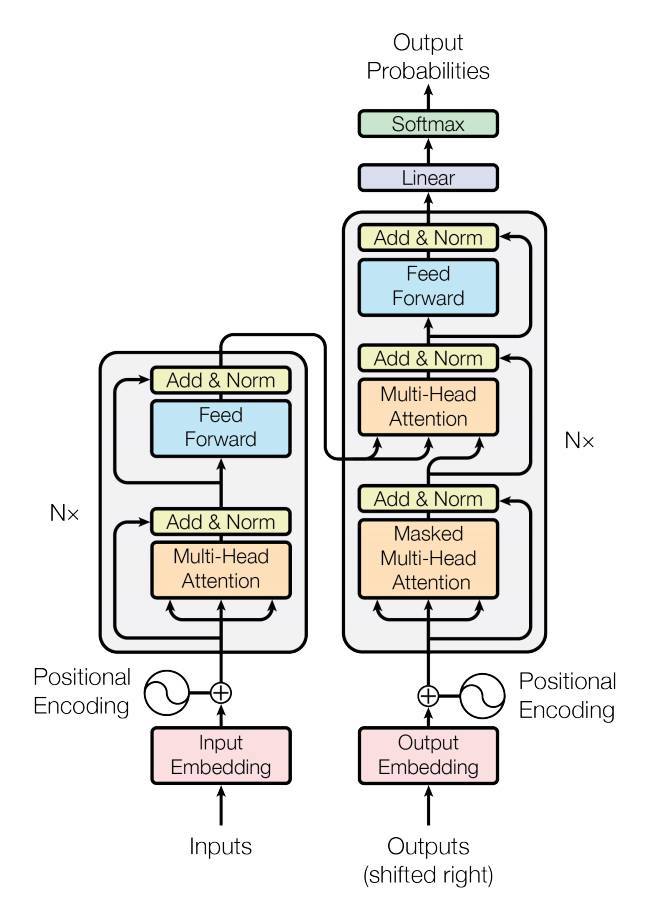
#
#
# + [markdown] id="Ltgk212dCvCp" colab_type="text"
# ## Define the model
#
#
#
# + [markdown] id="40TisKhiCvCq" colab_type="text"
# In this tutorial, we train ``nn.TransformerEncoder`` model on a language modeling task.
# The language modeling task is to assign a probability for the likelihood of a given word (or a sequence of words) to follow a sequence of words.
# A sequence of tokens are passed to the embedding layer first, followed by a positional encoding layer to account for the order of the word (see the next paragraph for more details).
# The ``nn.TransformerEncoder`` consists of multiple layers of [`nn.TransformerEncoderLayer`](https://pytorch.org/docs/master/nn.html?highlight=transformerencoderlayer#torch.nn.TransformerEncoderLayer).
# Along with the input sequence, a square attention mask is required because the self-attention layers in ``nn.TransformerEncoder`` are only allowed to attend the earlier positions in the sequence.
# For the language modeling task, any tokens on the future positions should be masked. To have the actual words, the output of ``nn.TransformerEncoder`` model is sent to the final Linear layer, which is followed by a log-Softmax function.
#
#
#
# + id="2yXdwL9dCvCq" colab_type="code" colab={}
import math
import torch
import torch.nn as nn
import torch.nn.functional as F
class TransformerModel(nn.Module):
def __init__(self, ntoken, ninp, nhead, nhid, nlayers, dropout=0.5):
super(TransformerModel, self).__init__()
from torch.nn import TransformerEncoder, TransformerEncoderLayer
self.model_type = 'Transformer'
self.src_mask = None
self.pos_encoder = PositionalEncoding(ninp, dropout)
encoder_layers = TransformerEncoderLayer(ninp, nhead, nhid, dropout)
self.transformer_encoder = TransformerEncoder(encoder_layers, nlayers)
self.encoder = nn.Embedding(ntoken, ninp)
self.ninp = ninp
self.decoder = nn.Linear(ninp, ntoken)
self.init_weights()
def _generate_square_subsequent_mask(self, sz):
mask = (torch.triu(torch.ones(sz, sz)) == 1).transpose(0, 1)
mask = mask.float().masked_fill(mask == 0, float('-inf')).masked_fill(mask == 1, float(0.0))
return mask
def init_weights(self):
initrange = 0.1
self.encoder.weight.data.uniform_(-initrange, initrange)
self.decoder.bias.data.zero_()
self.decoder.weight.data.uniform_(-initrange, initrange)
def forward(self, src):
if self.src_mask is None or self.src_mask.size(0) != len(src):
device = src.device
mask = self._generate_square_subsequent_mask(len(src)).to(device)
self.src_mask = mask
src = self.encoder(src) * math.sqrt(self.ninp)
src = self.pos_encoder(src)
output = self.transformer_encoder(src, self.src_mask)
output = self.decoder(output)
return output
# + [markdown] id="p0I8drH4CvCt" colab_type="text"
# ``PositionalEncoding`` module injects some information about the relative or absolute position of the tokens in the sequence.
# The positional encodings have the same dimension as the embeddings so that the two can be summed. Here, we use ``sine`` and ``cosine`` functions of different frequencies.
#
#
#
# + id="wj8gcDb3CvCu" colab_type="code" colab={}
class PositionalEncoding(nn.Module):
def __init__(self, d_model, dropout=0.1, max_len=5000):
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(p=dropout)
pe = torch.zeros(max_len, d_model)
position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)
div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model))
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
pe = pe.unsqueeze(0).transpose(0, 1)
self.register_buffer('pe', pe)
def forward(self, x):
x = x + self.pe[:x.size(0), :]
return self.dropout(x)
# + [markdown] id="OpMw1tp4CvCx" colab_type="text"
# Load and batch data
# -------------------
#
#
#
# + [markdown] id="EuSyJAbICvCx" colab_type="text"
# The training process uses Wikitext-2 dataset from ``torchtext``.
# The vocab object is built based on the train dataset and is used to numericalize tokens into tensors.
# Starting from sequential data, the ``batchify()`` function arranges the dataset into columns, trimming off any tokens remaining after the data has been divided into batches of size ``batch_size``.
# For instance, with the alphabet as the sequence (total length of 26) and a batch size of 4, we would divide the alphabet into 4 sequences of length 6:
#
# \begin{align}\begin{bmatrix}
# \text{A} & \text{B} & \text{C} & \ldots & \text{X} & \text{Y} & \text{Z}
# \end{bmatrix}
# \Rightarrow
# \begin{bmatrix}
# \begin{bmatrix}\text{A} \\ \text{B} \\ \text{C} \\ \text{D} \\ \text{E} \\ \text{F}\end{bmatrix} &
# \begin{bmatrix}\text{G} \\ \text{H} \\ \text{I} \\ \text{J} \\ \text{K} \\ \text{L}\end{bmatrix} &
# \begin{bmatrix}\text{M} \\ \text{N} \\ \text{O} \\ \text{P} \\ \text{Q} \\ \text{R}\end{bmatrix} &
# \begin{bmatrix}\text{S} \\ \text{T} \\ \text{U} \\ \text{V} \\ \text{W} \\ \text{X}\end{bmatrix}
# \end{bmatrix}\end{align}
#
# These columns are treated as independent by the model, which means that the dependence of ``G`` and ``F`` can not be learned, but allows more efficient batch processing.
#
#
#
# + id="LifyGl02CvCy" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 68} outputId="08872458-807e-4541-99e7-4b8bf10487c7"
import torchtext
from torchtext.data.utils import get_tokenizer
#TEXT = torchtext.data.Field(tokenize=get_tokenizer("basic_english"),
TEXT = torchtext.data.Field(tokenize=get_tokenizer("spacy"),
#TEXT = torchtext.data.Field(tokenize=get_tokenizer("moses"),
init_token='<sos>',
eos_token='<eos>',
lower=True)
train_txt, val_txt, test_txt = torchtext.datasets.WikiText2.splits(TEXT)
TEXT.build_vocab(train_txt)
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
def batchify(data, bsz):
data = TEXT.numericalize([data.examples[0].text])
# Divide the dataset into bsz parts.
nbatch = data.size(0) // bsz
# Trim off any extra elements that wouldn't cleanly fit (remainders).
data = data.narrow(0, 0, nbatch * bsz)
# Evenly divide the data across the bsz batches.
data = data.view(bsz, -1).t().contiguous()
return data.to(device)
batch_size = 20
eval_batch_size = 10
train_data = batchify(train_txt, batch_size)
val_data = batchify(val_txt, eval_batch_size)
test_data = batchify(test_txt, eval_batch_size)
# + [markdown] id="EyBA19PSCvC1" colab_type="text"
# ### Functions to generate input and target sequence
#
#
#
# + [markdown] id="TxLN81NVCvC2" colab_type="text"
# ``get_batch()`` function generates the input and target sequence for the transformer model.
# It subdivides the source data into chunks of length ``bptt``.
# For the language modeling task, the model needs the following words as ``Target``.
# For example, with a ``bptt`` value of 2, we’d get the following two Variables for ``i`` = 0:
#
# 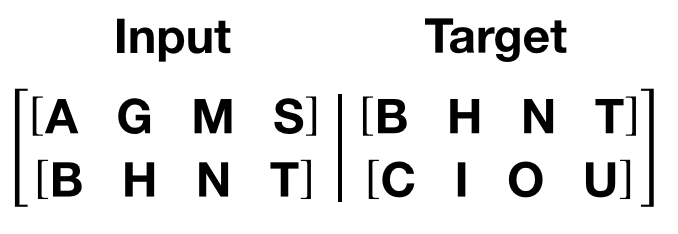
# <!--
# 
# -->
#
# It should be noted that the chunks are along dimension 0, consistent with the ``S`` dimension in the Transformer model. The batch dimension ``N`` is along dimension 1.
#
#
#
# + id="AtpupptMCvC2" colab_type="code" colab={}
bptt = 35
def get_batch(source, i):
seq_len = min(bptt, len(source) - 1 - i)
data = source[i:i+seq_len]
target = source[i+1:i+1+seq_len].view(-1)
return data, target
# + [markdown] id="35lvEX4hCvC5" colab_type="text"
# Initiate an instance
# --------------------
#
#
#
# + [markdown] id="8XJBZYkCCvC6" colab_type="text"
# The model is set up with the hyperparameter below. The vocab size is
# equal to the length of the vocab object.
#
#
#
# + id="rEgBjoSxCvC7" colab_type="code" colab={}
ntokens = len(TEXT.vocab.stoi) # the size of vocabulary
emsize = 200 # embedding dimension
nhid = 200 # the dimension of the feedforward network model in nn.TransformerEncoder
nlayers = 2 # the number of nn.TransformerEncoderLayer in nn.TransformerEncoder
nhead = 2 # the number of heads in the multiheadattention models
dropout = 0.2 # the dropout value
model = TransformerModel(ntokens, emsize, nhead, nhid, nlayers, dropout).to(device)
# + [markdown] id="H9QbhiBvCvC-" colab_type="text"
# Run the model
# -------------
#
#
#
# + [markdown] id="CDcuL_V9CvC-" colab_type="text"
# [`CrossEntropyLoss`](https://pytorch.org/docs/master/nn.html?highlight=crossentropyloss#torch.nn.CrossEntropyLoss) is applied to track the loss and [`SGD`](https://pytorch.org/docs/master/optim.html?highlight=sgd#torch.optim.SGD) implements stochastic gradient descent method as the optimizer.
# The initial learning rate is set to 5.0.
# [`StepLR`](https://pytorch.org/docs/master/optim.html?highlight=steplr#torch.optim.lr_scheduler.StepLR) is applied to adjust the learn rate through epochs.
# During the training, we use [`nn.utils.clip_grad_norm_`](https://pytorch.org/docs/master/nn.html?highlight=nn%20utils%20clip_grad_norm#torch.nn.utils.clip_grad_norm_) function to scale all the gradient together to prevent exploding.
#
#
#
# + id="RXaeIhfiCvC_" colab_type="code" colab={}
criterion = nn.CrossEntropyLoss()
lr = 5.0 # learning rate
optimizer = torch.optim.SGD(model.parameters(), lr=lr)
scheduler = torch.optim.lr_scheduler.StepLR(optimizer, 1.0, gamma=0.95)
import time
def train():
model.train() # Turn on the train mode
total_loss = 0.
start_time = time.time()
ntokens = len(TEXT.vocab.stoi)
for batch, i in enumerate(range(0, train_data.size(0) - 1, bptt)):
data, targets = get_batch(train_data, i)
optimizer.zero_grad()
output = model(data)
loss = criterion(output.view(-1, ntokens), targets)
loss.backward()
torch.nn.utils.clip_grad_norm_(model.parameters(), 0.5)
optimizer.step()
total_loss += loss.item()
log_interval = 200
if batch % log_interval == 0 and batch > 0:
cur_loss = total_loss / log_interval
elapsed = time.time() - start_time
print('| epoch {:3d} | {:5d}/{:5d} batches | '
'lr {:02.2f} | ms/batch {:5.2f} | '
'loss {:5.2f} | ppl {:8.2f}'.format(
epoch, batch, len(train_data) // bptt, scheduler.get_lr()[0],
elapsed * 1000 / log_interval,
cur_loss, math.exp(cur_loss)))
total_loss = 0
start_time = time.time()
def evaluate(eval_model, data_source):
eval_model.eval() # Turn on the evaluation mode
total_loss = 0.
ntokens = len(TEXT.vocab.stoi)
with torch.no_grad():
for i in range(0, data_source.size(0) - 1, bptt):
data, targets = get_batch(data_source, i)
output = eval_model(data)
output_flat = output.view(-1, ntokens)
total_loss += len(data) * criterion(output_flat, targets).item()
return total_loss / (len(data_source) - 1)
# + [markdown] id="dqeJZzj_CvDC" colab_type="text"
# Loop over epochs. Save the model if the validation loss is the best
# we've seen so far. Adjust the learning rate after each epoch.
#
#
# + id="XQGWaf-wCvDC" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="aae43d48-fb28-4bce-a0f1-0a6db14ddf23"
best_val_loss = float("inf")
epochs = 10 # The number of epochs
best_model = None
for epoch in range(1, epochs + 1):
epoch_start_time = time.time()
train()
val_loss = evaluate(model, val_data)
print('-' * 89)
print('| end of epoch {:3d} | time: {:5.2f}s | valid loss {:5.2f} | '
'valid ppl {:8.2f}'.format(epoch, (time.time() - epoch_start_time),
val_loss, math.exp(val_loss)))
print('-' * 89)
if val_loss < best_val_loss:
best_val_loss = val_loss
best_model = model
scheduler.step()
# + [markdown] id="58Fw_MNrCvDF" colab_type="text"
# Evaluate the model with the test dataset
# -------------------------------------
#
# Apply the best model to check the result with the test dataset.
#
#
# + id="VSnoui7nCvDF" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 68} outputId="c9b8ae93-ea47-45c3-d411-7d8fcc8892e3"
test_loss = evaluate(best_model, test_data)
print('=' * 89)
print('| End of training | test loss {:5.2f} | test ppl {:8.2f}'.format(
test_loss, math.exp(test_loss)))
print('=' * 89)
# + id="aTqwSbxiITkb" colab_type="code" colab={}
|
notebooks/2020_0722transformer_tutorial.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="TA21Jo5d9SVq"
#
#
# 
#
# [](https://colab.research.google.com/github/JohnSnowLabs/spark-nlp-workshop/blob/master/tutorials/streamlit_notebooks/healthcare/CLINICAL_CLASSIFICATION.ipynb)
#
#
#
# + [markdown] id="CzIdjHkAW8TB"
# # **How to use Licensed Classification models in Spark NLP**
# + [markdown] id="RuZr5fPZ4Jwa"
# ### Spark NLP documentation and instructions:
# https://nlp.johnsnowlabs.com/docs/en/quickstart
#
# ### You can find details about Spark NLP annotators here:
# https://nlp.johnsnowlabs.com/docs/en/annotators
#
# ### You can find details about Spark NLP models here:
# https://nlp.johnsnowlabs.com/models
#
# + [markdown] id="6uDmeHEFW7_h"
# To run this yourself, you will need to upload your license keys to the notebook. Otherwise, you can look at the example outputs at the bottom of the notebook. To upload license keys, open the file explorer on the left side of the screen and upload `workshop_license_keys.json` to the folder that opens.
# + [markdown] id="wIeCOiJNW-88"
# ## 1. Colab Setup
# + [markdown] id="HMIDv74CYN0d"
# Import license keys
# + colab={"base_uri": "https://localhost:8080/"} id="ttHPIV2JXbIM" outputId="004068ac-9191-4f95-9f02-1d600648efda"
import os
import json
with open('/content/spark_nlp_for_healthcare.json', 'r') as f:
license_keys = json.load(f)
license_keys.keys()
secret = license_keys['SECRET']
os.environ['SPARK_NLP_LICENSE'] = license_keys['SPARK_NLP_LICENSE']
os.environ['AWS_ACCESS_KEY_ID'] = license_keys['AWS_ACCESS_KEY_ID']
os.environ['AWS_SECRET_ACCESS_KEY'] = license_keys['AWS_SECRET_ACCESS_KEY']
sparknlp_version = license_keys["PUBLIC_VERSION"]
jsl_version = license_keys["JSL_VERSION"]
print ('SparkNLP Version:', sparknlp_version)
print ('SparkNLP-JSL Version:', jsl_version)
# + [markdown] id="rQtc1CHaYQjU"
#
# Install dependencies
# + colab={"base_uri": "https://localhost:8080/"} id="CGJktFHdHL1n" outputId="69c06067-3b73-4fe3-f024-0f608436ecb7"
# Install Java
# ! apt-get update -qq
# ! apt-get install -y openjdk-8-jdk-headless -qq > /dev/null
# ! java -version
# Install pyspark
# ! pip install --ignore-installed -q pyspark==2.4.4
# Install Spark NLP
# ! pip install --ignore-installed spark-nlp==$sparknlp_version
# ! python -m pip install --upgrade spark-nlp-jsl==$jsl_version --extra-index-url https://pypi.johnsnowlabs.com/$secret
# + [markdown] id="Hj5FRDV4YSXN"
# Import dependencies into Python and start the Spark session
# + colab={"base_uri": "https://localhost:8080/", "height": 86} id="qUWyj8c6JSPP" outputId="b83a58a9-c278-4cc3-92fb-92f702815231"
os.environ['JAVA_HOME'] = "/usr/lib/jvm/java-8-openjdk-amd64"
os.environ['PATH'] = os.environ['JAVA_HOME'] + "/bin:" + os.environ['PATH']
import pandas as pd
from pyspark.ml import Pipeline
from pyspark.sql import SparkSession
import pyspark.sql.functions as F
import sparknlp
from sparknlp.annotator import *
from sparknlp_jsl.annotator import *
from sparknlp.base import *
import sparknlp_jsl
spark = sparknlp_jsl.start(secret)
# manually start session
'''
builder = SparkSession.builder \
.appName('Spark NLP Licensed') \
.master('local[*]') \
.config('spark.driver.memory', '16G') \
.config('spark.serializer', 'org.apache.spark.serializer.KryoSerializer') \
.config('spark.kryoserializer.buffer.max', '2000M') \
.config('spark.jars.packages', 'com.johnsnowlabs.nlp:spark-nlp_2.11:' +sparknlp.version()) \
.config('spark.jars', f'https://pypi.johnsnowlabs.com/{secret}/spark-nlp-jsl-{jsl_version}.jar')
'''
# + [markdown] id="9RgiqfX5XDqb"
# ## 2. Usage Guidelines
# + [markdown] id="AVKr8C2SrkZQ"
# 1. **Selecting the correct Classification Model**
#
# > a. To select from all the Classification models available in Spark NLP please go to https://nlp.johnsnowlabs.com/models
#
# > b. Read through the model descriptions to select desired model
#
# > c. Some of the available models:
# >> classifierdl_pico_biobert
#
# >> classifierdl_ade_biobert
# ---
# 2. **Selecting correct embeddings for the chosen model**
#
# > a. Models are trained on specific embeddings and same embeddings should be used at inference to get best results
#
# > b. If the name of the model contains "**biobert**" (e.g: *ner_anatomy_biobert*) then the model is trained using "**biobert_pubmed_base_cased**" embeddings. Otherwise, "**embeddings_clinical**" was used to train that model.
#
# > c. Using correct embeddings
#
# >> To use *embeddings_clinical* :
#
# >>> word_embeddings = WordEmbeddingsModel.pretrained("embeddings_clinical", "en", "clinical/models")
# .setInputCols(["sentence", "token"]) \
# .setOutputCol("embeddings")
#
# >> To use *Bert* Embeddings:
#
# >>> embeddings = BertEmbeddings.pretrained('biobert_pubmed_base_cased')\
# .setInputCols(["document", 'token'])\
# .setOutputCol("word_embeddings")
# > d. You can find list of all embeddings at https://nlp.johnsnowlabs.com/models?tag=embeddings
#
# + [markdown] id="zweiG2ilZqoR"
# Create the pipeline
# + colab={"base_uri": "https://localhost:8080/"} id="LLuDz_t40be4" outputId="3f85f688-ae9b-423b-8db1-80d292a09a05"
document_assembler = DocumentAssembler()\
.setInputCol("text")\
.setOutputCol("document")
tokenizer = Tokenizer() \
.setInputCols(["document"]) \
.setOutputCol("token")
embeddings = BertEmbeddings.pretrained('biobert_pubmed_base_cased')\
.setInputCols(["document", 'token'])\
.setOutputCol("word_embeddings")
sentence_embeddings = SentenceEmbeddings() \
.setInputCols(["document", "word_embeddings"]) \
.setOutputCol("sentence_embeddings") \
.setPoolingStrategy("AVERAGE").setStorageRef('SentenceEmbeddings_5d018a59d7c3')
åå
classifier = ClassifierDLModel.pretrained('classifierdl_pico_biobert', 'en', 'clinical/models')\
.setInputCols(['document', 'token', 'sentence_embeddings']).setOutputCol('class')
pipeline = Pipeline(stages=[
document_assembler,
tokenizer,
embeddings,
sentence_embeddings,
classifier])
empty_data = spark.createDataFrame([[""]]).toDF("text")
pipeline_model = pipeline.fit(empty_data)
lmodel = LightPipeline(pipeline_model)
# + [markdown] id="2Y9GpdJhXIpD"
# ## 3. Create example inputs
# + id="vBOKkB2THdGI"
# Enter examples as strings in this array
input_list = [
"""A total of 10 adult daily smokers who reported at least one stressful event and coping episode and provided post-quit data.""",
]
# + [markdown] id="mv0abcwhXWC-"
# ## 4. Use the pipeline to create outputs
# + [markdown] id="27rHwCk4ODFr"
# Full Pipeline (Expects a Spark Data Frame)
# + id="TK1DB9JZaPs3"
df = spark.createDataFrame(pd.DataFrame({"text": input_list}))
result = pipeline_model.transform(df)
# + [markdown] id="FFq4QRXjOEeG"
# Light Pipeline (Expects a list of string
# + id="NzFUrSmkOFfs"
lresult = lmodel.fullAnnotate(input_list)
# + [markdown] id="UQY8tAP6XZJL"
# ## 5. Visualize results
# + [markdown] id="0vhxZgvibTi3"
# Full Pipeline Results
# + colab={"base_uri": "https://localhost:8080/", "height": 35} id="2EXCQGCMbTKT" outputId="74433ac8-a41e-4c71-fb74-8eee7e2732e5"
result.toPandas()['class'].iloc[0][0].result
# + [markdown] id="hnsMLq9gctSq"
# Light Pipeline Results
# + colab={"base_uri": "https://localhost:8080/", "height": 35} id="Ar32BZu7J79X" outputId="33c26ac9-fdb7-43eb-b57e-3f75e0fd7f74"
lresult[0]['class'][0].result
|
tutorials/streamlit_notebooks/healthcare/CLINICAL_CLASSIFICATION.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.8.5 64-bit (''3.8.5'': pyenv)'
# metadata:
# interpreter:
# hash: 40f0aa7cb53c514384145c8233a75c82c384db7f0b9e58264fdf777852089e81
# name: python3
# ---
a = 1
print(a)
a
1 < 2
a = 3
a < 2
a == 3
a == 4
a != 3
print("aaaaaaaaa \n bbbbbbbbb")
List = [1, 2, 3, 4 ,5 ,6 ,7 ,8]
List
List[0:3]
List[:3]
List[3:]
List[1] = 10
List
words = ["Hello", "World", 3 , 3.14]
words
tuple_1 = (4, 5, 6, 7)
tuple_1
#辞書型
results = {"Math": 90, "Sience": 80, "English": 75}
results
results["Math"]
#For文
for i in range(5):
print(i)
names = ["Sato", "Suzuki", "Takahashi"]
for i in range(3):
print(names[i] + "-san")
names = ["Sato", "Suzuki", "Takahashi", "Yoshida"]
for i in range(len(names)):
print(names[i] + "-san")
for a in names:
print(a)
for name in names:
print(name + "-san")
# +
# if文
val = 0
if val > 0:
print("It's positive")
elif val==0:
print("It's Zero")
else:
print("It's negative")
# +
#関数
def say_hello():
print("Hello!!")
say_hello()
# +
#引数のある関数
def say_hello2(name):
print("Hello!!" + name + " san")
say_hello2("Suzuki")
# +
#出力(返り値)のある関数
def add(a, b):
return a + b
result = add(3 ,5)
result
# +
def abs(num):
if num < 0:
return num * -1
else:
return num
result = abs(-1)
result
# +
import numpy as np
#ベクトルの定義
x = np.array([1, 2, 3])
y = np.array([2., 3.9, 6.1])
x_ave = x.mean()
y_ave = y.mean()
x_center = x - x_ave
y_center = y - y_ave
xx = x_center * x_center
xy = x_center * y_center
a = xy.sum() / xx.sum()
a
# +
import pandas as pd
# data frame
df = pd.read_csv('sample.csv')
print(df)
# -
x = df['x']
y = df['y']
# +
import matplotlib.pyplot as plt
#散布図
plt.scatter(x,y)
plt.grid()
plt.show()
# -
|
kikagaku/Sesson5.ipynb
|
# ---
# jupyter:
# jupytext:
# formats: ipynb,md
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Introduction
#
# This notebook introduces `jupyter_ui_poll` library.
#
# This library allows one to implement a "blocking GUI" inside a Jupyter
# environment. It does not implement new GUI primitives, rather it allows use of
# existing `ipywidgets` based libraries in a blocking fashion. It also gives you
# mechanisms to maintain interactivity of widgets while executing a long-running
# cell.
#
# After going through this notebook you should also checkout a more [complex
# example](ComplexUIExample.ipynb), it demonstrates implementation a blocking UI
# primitive as a library.
# +
import asyncio
import time
import ipywidgets as w
from IPython.display import display
from jupyter_ui_poll import run_ui_poll_loop, ui_events, with_ui_events
# -
# ## Simplest UI widget
#
# Create a button that displays number of times it was clicked. We will be using it for testing.
#
# Go on, run the cell below and click the button few times.
# +
def on_click(btn):
n = int(btn.description)
btn.description = str(n + 1)
def test_button():
"""
Create button that displays number of times it was clicked
"""
btn = w.Button(description="0")
btn.on_click(on_click)
return btn
display(test_button())
# -
# ## Waiting for user action
#
# Example of using `ui_events` function. This is the foundational function in
# `jupyter-ui-poll` library, all other methods use it under the hood. `ui_events`
# returns a function your code should call to process UI events that happened so
# far while executing a long-running cell. This requires temporarily modifying
# internals of the running IPython kernel, hence this function needs to be used
# inside `with` statement, so that IPython state can be restored to normal once
# your code is done, even if errors have happened.
#
# You can supply how many events should be processed every time you call `ui_poll`
# function, default is `1`. You probably want to use larger value if you have
# highly interactive widgets that generate a lot of events, like a map, or if your
# poll frequency is low. One should aim for something like 100 events per second.
# If you notice that UI lags and is not responsive try increasing poll frequency
# and if that is not possible, increase number of UI events you process per
# polling interval.
#
# - Cell below presents a button with click count display
# - Roughly ten times a second we print click count so far
# - When click count reaches 10, we stop
# +
btn = test_button()
print("Press this button 10 times to terminate")
display(btn)
with ui_events() as ui_poll:
while int(btn.description) < 10:
print(btn.description, end="")
ui_poll(11) # Process upto 11 ui events per iteration
time.sleep(0.1)
print("... done")
# -
# ## Process Long Sequence while Responding to UI events
#
# Sometimes you want to process a large number of small jobs in the notebook, but
# still want to respond to UI events, like button clicks. Maybe you want to
# terminate computation early and get the result so far, or change some parameter
# mid-flight. Providing interactive feedback to the user about the state of the
# computation is another example.
#
# Just wrap an iterator in `with_ui_events` function, you will get the same data
# out, but also UI events will be processed in between each item.
# +
btn = test_button()
print("Press this button a few times")
display(btn)
for i in with_ui_events(range(55), 10): # Process upto 10 ui events per iteration
if int(btn.description) >= 5:
print("✋", end="")
break # Test early exit
print(btn.description, end="") # Verify UI state changes
time.sleep(0.1) # Simulate blocking computation
print("... done")
# -
# Try changing code in the cell above to run without `with_ui_events`
#
# ```diff
# - for i in with_ui_events(range(55), 10):
# + for i in range(55):
# ```
#
# You will see that the button text no longer updates as you click it, but instead
# `on_click` events will be processed as soon as the cell finishes executing.
# ## Example using run_ui_poll_loop
#
# A common scenario is to wait for some input from the user, validate it, and if
# successful continue with the execution of the rest of the notebook.
# `run_ui_poll_loop` is handy in this case. You give it a function to call at a
# regular interval. This function should return `None` while user input is still
# incomplete. Once all data is entered this function should extract it from the UI
# and return as python construct of some sort (tuple, dictionary, single number,
# anything but `None`) to be used by the rest of the notebook.
#
# Cell below will:
#
# - Display a button
# - Ask user to press it 10 times
# - Report how many seconds it took
#
# Try using `Cell->Run All Below`, everything should still work as expected.
# +
t0 = time.time()
xx = ["-_-", "o_o"]
def on_poll():
"""This is called repeatedly by run_ui_poll_loop
Return None if condition hasn't been met yet
Return some result once done, in this example result
is a number of seconds it took to press the button 10 times.
"""
if int(btn.description) < 10:
print(xx[0], end="\r", flush=True)
xx[:] = xx[::-1]
return None # Continue polling
# Terminate polling and return final result
return time.time() - t0
btn = test_button()
print("Press button 10 times")
display(btn)
dt = run_ui_poll_loop(on_poll, 1 / 15)
print("._.") # This should display the text in the output of this cell
n_times = "10 times" # To verify that the rest of this cell executes before executing cells below
# -
# Cell below uses `dt` and `n_times` that are set in the cell above, so it's
# important that it doesn't execute until `dt` is known.
print(f"Took {dt:.1f} seconds to click {n_times}")
# Cell below contains intentional error.
#
# Cells below this one should not execute as part of `Run All Below` command you can still run them later of course.
this_will_raise_an_error()
# ## Async Operations
#
# We also support async mode of operation if desired. Just use `async with` or `async for`.
# +
btn = test_button()
print("Press this button 10 times to terminate")
display(btn)
async with ui_events() as ui_poll:
while int(btn.description) < 10:
print(btn.description, end="")
await ui_poll(11) # Process upto 11 ui events per iteration
await asyncio.sleep(0.1) # Simulate async processing
print("... done")
# -
# ### Async Iterable
#
# Iterable returned from `with_ui_events` can also be used in async context. It can wrap async/sync iterators, the result can be iterated with either plain `for` or `async for` when wrapping normal iterators, and only with `async for` when wrapping `async` iterators.
# +
btn = test_button()
print("Press this button a few times")
display(btn)
async for i in with_ui_events(range(55), 10): # Process upto 10 ui events per iteration
if int(btn.description) >= 5:
print("✋", end="")
break # Test early exit
print(btn.description, end="") # Verify UI state changes
await asyncio.sleep(0.1) # Simulate Async computation
print("... done")
# -
# ### Test Async Iterable wrapping
# +
from collections import abc
async def async_range(n):
for i in range(n):
yield i
its0 = async_range(55)
its = with_ui_events(its0, 10)
print(
f"""Iterable: {isinstance(its0, abc.Iterable)}, {isinstance(its, abc.Iterable)}
AsyncIterable: {isinstance(its0, abc.AsyncIterable)}, {isinstance(its, abc.AsyncIterable)}"""
)
# -
# One can create and wrap iterator in an earlier cell and use it later.
# +
btn = test_button()
print("Press this button a few times")
display(btn)
async for i in its: # Process upto 10 ui events per iteration
if int(btn.description) >= 5:
print("✋", end="")
break # Test early exit
print(btn.description, end="") # Verify UI state changes
await asyncio.sleep(0.1) # Simulate Async computation
print("... done")
# -
# ------------------------------------------------------------
|
notebooks/Examples.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import numpy as np
import matplotlib.pyplot as plt
from fst_pso.benchmark_functions import Rastrigin, Squared, numpyWrapper
from fst_pso.pso import FSTPSO
import benchmark_functions as bf
from scipy.spatial import distance
from tqdm import tqdm
func = bf.Schwefel(n_dimensions=4)
point = [25, -34.6, -112.231, 242]
# results: -129.38197657025287
print(func(point))
# +
# SWARM INITALIZATION
# Number of dimensions
DIM_NUM = 2
iterations = 400
numOfTests = 30
FNC_OPTIM_list = [
bf.Ackley(n_dimensions=DIM_NUM),
bf.Griewank(n_dimensions=DIM_NUM),
bf.Michalewicz(n_dimensions=DIM_NUM),
bf.Rastrigin(n_dimensions=DIM_NUM),
# bf.Rosenbrock(n_dimensions=DIM_NUM),
# bf.Schwefel(n_dimensions=DIM_NUM),
# bf.EggHolder(n_dimensions=DIM_NUM),
# bf.Keane(n_dimensions=DIM_NUM),
# bf.Rana(n_dimensions=DIM_NUM),
# bf.Easom(n_dimensions=DIM_NUM),
# bf.DeJong3(n_dimensions=DIM_NUM),
# bf.GoldsteinAndPrice(n_dimensions=DIM_NUM)
]
# Hyper-square Boundaries for each FNC_OPTIM
DIM_SIZE_list = [30,
600,
np.pi,
5.12]
# -
cnt=0
for FNC_OPTIM_RAW in FNC_OPTIM_list:
print("\nFUNCTION {} --------------------------------\nMIN.: {}".format(FNC_OPTIM_RAW.name,FNC_OPTIM_RAW.getMinimum()))
DIM_SIZE = DIM_SIZE_list[cnt]
cnt+=1
bestSolutionMat = []
bestSolutionMatPSO = []
for testNum in tqdm(range(0, numOfTests)):
swarm_size = int(np.floor(10+2*np.sqrt(DIM_NUM)))
swarm_x = 2 * DIM_SIZE * np.random.rand(swarm_size, DIM_NUM) - DIM_SIZE
swarm_v = 2 * DIM_SIZE * np.random.rand(swarm_size, DIM_NUM) - DIM_SIZE
FNC_OPTIM = numpyWrapper(FNC_OPTIM_RAW)
optimizer = FSTPSO(DIM_NUM, DIM_SIZE, FNC_OPTIM, True,swarm_x,swarm_v, interia_mode=True)
optimizer_PSO = FSTPSO(DIM_NUM, DIM_SIZE, FNC_OPTIM, False,swarm_x,swarm_v, interia_mode=False)
bestSolutionVec = []
bestSolutionVecPSO = []
bestSolutionVec.append(FNC_OPTIM(optimizer.swarm_opt_g))
bestSolutionVecPSO.append(FNC_OPTIM(optimizer_PSO.swarm_opt_g))
for i in range(1, iterations+1):
for p in range(optimizer.get_swarm_size()):
optimizer.update_particle(p, plot=False)
optimizer_PSO.update_particle(p, plot=False)
bestSolutionVec.append(FNC_OPTIM(optimizer.swarm_opt_g))
bestSolutionVecPSO.append(FNC_OPTIM(optimizer_PSO.swarm_opt_g))
bestSolutionMat.append(bestSolutionVec)
bestSolutionMatPSO.append(bestSolutionVecPSO)
ABF_list = []
ABF_listPSO = []
for it in range(0,iterations):
suma = 0
sumaPSO = 0
for testId in range(0,numOfTests):
suma += bestSolutionMat[testId][it]
sumaPSO += bestSolutionMatPSO[testId][it]
ABF = suma/numOfTests
ABF_list.append(suma/numOfTests)
ABF_listPSO.append(sumaPSO/numOfTests)
plt.figure()
fig, ax = plt.subplots(figsize=(12, 6))
plt.plot(ABF_list,'k')
plt.title(FNC_OPTIM_RAW.name)
plt.xlabel("Iteration")
plt.ylabel("Average Best Fitness")
plt.plot(ABF_listPSO,'b')
plt.title(FNC_OPTIM_RAW.name)
plt.xlabel("Iteration")
plt.ylabel("Average Best Fitness")
plt.legend(['FST PSO','PSO'])
plt.grid()
plt.savefig('./{}.png'.format(FNC_OPTIM_RAW.name))
plt.show()
|
FST-PSO.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Temporary vs. Permanent Methods
#
# ### Temporary Methods
#
# When you use a method on an object (e.g. a DataFrame) in python, `<object>.<method>(<args>)` performs the method on the object and returns the modified object, as you can see here:
#
# +
import pandas as pd
# define a df
df = pd.DataFrame({'height':[72,60,68],'gender':['M','F','M'],'weight':[175,110,150]})
# call method on df and print - df.assign yields the modified object!
df.assign(feet=df['height']//12)
# -
# This is useful if you want to alter the variable **temporarily** (e.g. for a graph, or to just print it out, like I literally just did!).
#
# **But the object in memory wasn't changed when I used `df.<method>`. See, here is the df in memory, and it wasn't changed:**
print(df) # see, the object has no feet! this is the original obj!
# ### Permanent changes
#
# If you want to change the object permanently, you have two options[^caveat]
# +
# option 1: explicitly define the df as the prior df after the method was called
# here, that means to add "df = " before the df.method
df = df.assign(feet1=df['height']//12)
# option 2: define a new feature of the df
# here, "df['newcolumnname'] = " (some operation)
df['feet2']=df['height']//12
print(df) # both of these added to obj in memory
# -
#
# [^caveat]: You can also do some pandas operations "in place", without explicitly writing `df = ` at the start of the line. However, I discourage this for reasons I won't belabor here.
|
content/03/02d_temp.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import os
import sys
ROOT_DIR = os.path.abspath("../")
os.chdir(ROOT_DIR)
sys.path.append(ROOT_DIR)
from utils import resources
from preprocessing import conversion
from preprocessing import chips
conversion.convert_LAZ_to_LAS_mt(resources.laz, resources.las, 12)
conversion.convert_LAS_to_TIFF_mt(resources.las, resources.images, 12)
conversion.check_nulldata(resources.images_dgm)
conversion.check_nulldata(resources.images_dom)
conversion.calculate_ndom_mt(resources.images_dom, resources.images_dgm, resources.images_ndom)
chips.create_training_chips(resources.images_ndom,
resources.images_chips_esri,
resources.shapefile,
"dachform",
512, 256,
rotation=0,
num_threads=12)
chips.unique_colors_to_masks_mt(resources.images_chips_esri, resources.images_chips_single_masks, 12)
|
notebooks/01_prepare_data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + _cell_guid="79c7e3d0-c299-4dcb-8224-4455121ee9b0" _uuid="d629ff2d2480ee46fbb7e2d37f6b5fab8052498a"
# %matplotlib inline
import os
import multiprocessing
from multiprocessing import Pool
import numpy as np
import pandas as pd
from tqdm import tqdm
import mlcrate as mlc
from bayes_opt import BayesianOptimization
from trackml.dataset import load_event
from trackml.dataset import load_dataset
from trackml.score import score_event
from sklearn.utils import shuffle
from sklearn.preprocessing import StandardScaler
from sklearn.cluster.dbscan_ import dbscan
import matplotlib
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# import hdbscan
class Config():
ROOT_PATH = '/home/bilal/.kaggle/competitions/trackml-particle-identification'
DATA_FOLDERS = {
'train': 'train_100_events',
'test': 'test'
}
EVENT = 'event000001000'
OUTPUT_FOLDER = './data'
SPLIT = 0.75
THETA = 75
config = Config()
event_path = os.path.join(config.ROOT_PATH, config.DATA_FOLDERS['train'], config.EVENT)
hits, cells, particles, truth = load_event(event_path)
# + _uuid="a6033df117e0b8800f9572208c37ffa5ccf653ff"
def preprocess(hits):
hits['r1'] = np.sqrt(np.square(hits['x']) + np.square(hits['y']))
hits['r2'] = np.sqrt(np.square(hits['x']) + np.square(hits['y']) + np.square(hits['z']))
hits['x2'] = hits['x'] / hits['r1']
hits['y2'] = hits['y'] / hits['r1']
hits['z1'] = hits['z'] / hits['r1']
hits['z2'] = hits['z'] / hits['r2']
hits['rho'] = np.sqrt(np.square(hits['x']) + np.square(hits['y']))
hits['phi'] = np.arctan2(hits['y'], hits['x'])
hits['s'] = np.sin(hits['phi'])
hits['c'] = np.cos(hits['phi'])
hits['arctan2'] = np.arctan2(hits['z'], hits['rho'])
hits['log1p'] = np.log1p(np.abs(hits['z2'])) * np.sign(hits['z2'])
hits['r-abs'] = (hits['r2'] - np.abs(hits['z'])) / hits['r2']
return hits
def get_preds(x):
w1, w2, w3, param = x[0], x[1], x[2], x[3]
hits, mm, ii = param[0], param[1], param[2]
hits['aa'] = hits['phi'] + mm * (hits['r1'] + 0.000005 * np.square(hits['r1'])) / 1000 * (ii / 2) / 180 * np.pi
hits['cosaa'] = np.cos(hits['aa'])
hits['sinaa'] = np.sin(hits['aa'])
# x = StandardScaler().fit_transform(np.column_stack([hits['cosaa'], hits['sinaa'], hits['z1'], hits['z2']]))
x = StandardScaler().fit_transform(np.column_stack([hits['cosaa'], hits['sinaa'], hits['arctan2'], hits['log1p'], hits['z1']]))
x[:,0] = x[:,0] * w1
x[:,1] = x[:,1] * w1
x[:,2] = x[:,2] * w2
x[:,3] = x[:,3] * w3
_, preds = dbscan(x, eps=0.0035, min_samples=1, n_jobs=4)
return preds
def get_params(hits, niter):
params = []
for i in range(0, int(niter)):
ii = i
if i % 2 == 0:
mm = 1
else:
mm = -1
params.append((hits, mm, ii))
return params
def train(hits, w1, w2, w3, niter, optimize=False):
params = get_params(hits, niter)
for i, param in enumerate(params):
params[i] = (w1, w2, w3, param)
pool = Pool(processes=4)
preds = pool.map(get_preds, params)
pool.close()
return preds
def add_count(l):
# unique: sorted unique values; reverse: indicies of unique to reconstruct l; count: num times each unique appears
unique, reverse, count = np.unique(l, return_counts=True, return_inverse=True)
# get num times each unique l appears
c = count[reverse]
# unassign any tracks with either 0 or > 20 hits
c[np.where(l == 0)] = 0
c[np.where(c > 20)] = 0
return (l, c)
def postprocess(hits, preds, event):
results = [add_count(l) for l in preds]
preds, counts = results[0]
for i in range(1, len(results)):
l, c = results[i]
idx = np.where((c - counts > 0))[0]
preds[idx] = l[idx] + preds.max()
counts[idx] = c[idx]
hits['track_id'] = preds
hits['event_id'] = event
return hits
def predict(w1, w2, w3, niter=10, optimize=True, visualize=False, test=False, hits=hits, event='000001000'):
hits = preprocess(hits)
preds = train(hits, w1, w2, w3, niter, optimize=optimize)
hits = postprocess(hits, preds, event)
if not test:
score = score_event(truth, hits)
if visualize:
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
hits = hits[hits['track_id'] != 0]
for particle in hits['track_id'][:100].unique():
hit = hits[hits['track_id'] == particle]
ax.scatter(hit.x, hit.y, hit.z, marker='o')
ax.plot(hit.x, hit.y, hit.z)
ax.set_xlabel('X Label')
ax.set_ylabel('Y Label')
ax.set_zlabel('Z Label')
plt.show()
if test:
return hits
else:
if optimize:
return score
else:
return hits, score
# -
# cos(aa) sin(aa) z1 z2
# + _uuid="23e8c1b4fea19b41be0ea9e6c1d3162e6b1ce589"
hits, score = predict(1, 1, 1, niter=100, optimize=False, visualize=True)
print(score)
# -
# cos(aa) sin(aa) log1p z2
hits, score = predict(1, 1, 1, niter=100, optimize=False, visualize=True)
print(score)
# ## Try:
# cos(aa) sin(aa) z1 log1p
hits, score = predict(1, 1, 1, niter=100, optimize=False, visualize=True)
print(score)
# ## Best:
# cos(aa) sin(aa) arctan2
hits, score = predict(1, 1, 1, niter=100, optimize=False, visualize=True)
print(score)
# cos(aa) sin(aa) r-abs
hits, score = predict(1, 1, 1, niter=100, optimize=False, visualize=True)
print(score)
# cos(aa) sin(aa) z1 r-abs
hits, score = predict(1, 1, 1, niter=100, optimize=False, visualize=True)
print(score)
# cos(aa) sin(aa) z2 r-abs
hits, score = predict(1, 1, 1, niter=100, optimize=False, visualize=True)
print(score)
# cos(aa) sin(aa) log1p r-abs
hits, score = predict(1, 1, 1, niter=100, optimize=False, visualize=True)
print(score)
# cos(aa) sin(aa) arctan2 log1p r-abs
hits, score = predict(1, 1, 1, niter=100, optimize=False, visualize=True)
print(score)
# cos(aa) sin(aa) log1p z1; Weights: 1 1 0.5
hits, score = predict(1, 1, 0.5, niter=100, optimize=False, visualize=True)
print(score)
# cos(aa) sin(aa) log1p z1; Weights: 1 1 1.5
hits, score = predict(1, 1, 1.5, niter=100, optimize=False, visualize=True)
print(score)
# +
submissions = []
for event_id, hits, cells in tqdm(load_dataset(os.path.join(config.ROOT_PATH, config.DATA_FOLDERS['test']), parts=['hits', 'cells'])):
# for event_id, hits, cells in tqdm(load_dataset(os.path.join(config.ROOT_PATH, config.DATA_FOLDERS['test']), parts=['hits', 'cells'], nevents=2)):
hits = predict(1.0438, 0.3795, 0.2350, niter=214, optimize=False, visualize=False, test=True, hits=hits, event=event_id)
sub = hits[['hit_id', 'track_id', 'event_id']]
submissions.append(sub)
# -
submission = pd.concat(submissions, axis=0)
len(submission)
mlc.kaggle.save_sub(submission, 'submission.csv.gz')
submission
|
attempt-8/feature-exploration.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Load Data from File
# +
from pyspark.sql.types import *
raw_data = sc.textFile('/user/cloudera/data/bike-sharing/hour_nohead.csv')
column_data = raw_data.map(lambda x: x.split(','))
schema = StructType([
StructField('row_id',StringType(),True),
StructField('date',StringType(), True),
StructField('season',StringType(), True),
StructField('year',StringType(), True),
StructField('month',StringType(), True),
StructField('hour',StringType(), True),
StructField('holiday',StringType(), True),
StructField('weekday',StringType(), True),
StructField('workingday',StringType(), True),
StructField('weather',StringType(), True),
StructField('temperature',StringType(), True),
StructField('apparent_temperature',StringType(), True),
StructField('humidity',StringType(), True),
StructField('wind_speed',StringType(), True),
StructField('casual',StringType(), True),
StructField('registered',StringType(), True),
StructField('counter',StringType(), True)
])
structured_data = sqlContext.createDataFrame(column_data, schema)
data = structured_data.select(
structured_data.row_id.cast('int'),
structured_data.date.cast('string'),
structured_data.season.cast('int'),
structured_data.year.cast('int'),
structured_data.month.cast('int'),
structured_data.hour.cast('int'),
structured_data.holiday.cast('int'),
structured_data.weekday.cast('int'),
structured_data.workingday.cast('int'),
structured_data.weather.cast('int'),
structured_data.temperature.cast('double'),
structured_data.apparent_temperature.cast('double'),
structured_data.humidity.cast('double'),
structured_data.wind_speed.cast('double'),
structured_data.casual.cast('int'),
structured_data.registered.cast('int'),
structured_data.counter.cast('int')
)
# -
# # Prepare Data
# +
from pyspark.sql.functions import *
ddata = data.select(
data.date,
unix_timestamp(data.date, "yyyy-MM-dd").alias('ts'),
data.season.cast("double"),
data.year.cast("double"),
data.month.cast("double"),
data.hour.cast("double"),
data.holiday.cast("double"),
data.weekday.cast("double"),
data.workingday.cast("double"),
data.weather.cast("double"),
data.temperature,
data.apparent_temperature,
data.humidity,
data.wind_speed,
data.casual.cast("double"),
data.registered.cast("double"),
data.counter.cast("double")
)
# -
# # Make some Pictures
# First we need to import matplotlib.pyplot and also make all plots appear inline in the notebook
# %matplotlib inline
import matplotlib.pyplot as plt
# ## Make a Plot of Rents per Day
# The original data contains rents per hour, we want to have the data per day
# +
# Generate Pandas DataFrame with summed data per day
pdf = ...
plt.figure(figsize=(16, 6), dpi=80, facecolor='w', edgecolor='k')
plt.plot(pdf['ts'],pdf['sum(counter)'])
# +
# Now only look at casual renters
pdf = ...
plt.figure(figsize=(16, 6), dpi=80, facecolor='w', edgecolor='k')
plt.plot(pdf['ts'],pdf['sum(casual)'])
# +
# Now only look at registered renters
pdf = ...
plt.figure(figsize=(16, 6), dpi=80, facecolor='w', edgecolor='k')
plt.plot(pdf['ts'],pdf['sum(registered)'])
# -
# # Initial Statistics
#
# Of course we are interested in some initial statistics on all columns.
# +
schema = ddata.schema
for field in schema.fields:
# Print statistcs for field if field is Double Type
# -
# # Extract Vectors for Regression
#
# Spark ML needs a special data type (Vector) for most operations. So we need to transform columns of interest into that special data type.
#
# A Vector can be created from a double Array via
#
# from pyspark.mllib.linalg import Vectors
# Vectors.dense([1.0,2.0,3.0])
# +
def extract_vector(row, cols):
pass
print extract_vector(Row('name','age')('Bob',23), [1])
# -
# ## Transform DataFrame
#
# Now that we have extract_vector, we can use it in order to extract the relevant features from our DataFrame
# +
# Use the following columns
cols = [1,2,3,4,5,6,7,8,9,10,11,12,13]
# Transform all records ddata into vectors [feature, counter]
# counter can be found in column row[16]
rdd = ...
# Now create new DataFrame
features_labels = sqlContext.createDataFrame(rdd, ['features','counter'])
# Peek inside, convert first 10 rows to Pandas
# -
# # Split Data into Training and Test Set
train_data, test_data = ...
print train_data.count()
print test_data.count()
# # Perform Linear Regression
from pyspark.ml.regression import *
# ### Peek into the Model
#
# Let us have a look at the coefficients and at the intercept
# # Perform Prediction
#
# Predict new Data by applying the model to the test data
# # Evaluate Model
# # Use VectorAssembler
#
# Manual feature extraction (i.e. creation of the Vector) is a little bit tedious and not very comfortable. But luckily, there is a valuable helper called VectorAssembler.
#
# We use it to automatically extract the columns
#
# season, year, month, hour, holiday, weekday, workingday, weather,
# temperature, apparent_temperature, humidity, wind_speed
#
# into the new output column 'features'
# ## Split Train and Test Data
#
# Since we found an easier way to generate features, we split incoming data first and apply the VectorAssembler
train_data, test_data = ddata.randomSplit([0.8,0.2], seed=0)
print train_data.count()
print test_data.count()
# ## Perform Regression
#
# 1. Apply VectorAssembler
# 2. Perform Fitting
asm = ...
regression = ...
model = ...
# ## Predict
#
# Make predictions from test data and print some results
p
# ## Evaluation
#
# Finally lets evaluate the prediction
# # Make New Pictures of Regression
# +
tmp = prediction \
.groupBy('ts').agg({'counter':'sum', 'prediction':'sum'}) \
.orderBy('ts')
pdf = tmp.toPandas()
min_ts,max_ts = prediction.agg(min('ts'), max('ts')).collect()[0]
plt.figure(figsize=(16, 6), dpi=80, facecolor='w', edgecolor='k', tight_layout=True)
plt.plot(pdf['ts'],pdf['sum(counter)'])
plt.plot(pdf['ts'],pdf['sum(prediction)'])
axes = plt.gca()
axes.set_xlim([min_ts,max_ts])
# -
|
spark-training/spark-python/jupyter-ml-bike-sharing/PySpark Bike Sharing Regression Skeleton.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Convolution of astronomical data
#
# The [astropy.convolution](https://docs.astropy.org/en/stable/convolution/) sub-package provides convolution functions that can correctly handle NaN/missing values, and also provides common convolution kernels and functionality to create custom kernels. Packages such as SciPy also include functionality for convolution (see e.g. [scipy.ndimage](https://docs.scipy.org/doc/scipy/reference/ndimage.html)), but these do not typically treat NaN/missing values properly.
#
# <section class="objectives panel panel-warning">
# <div class="panel-heading">
# <h2><span class="fa fa-certificate"></span> Objectives</h2>
# </div>
#
#
# <div class="panel-body">
#
# <ul>
# <li>Use built-in kernels and understand discretization options</li>
# <li>Use NaN-friendly convolution functions</li>
# </ul>
#
# </div>
#
# </section>
#
# ## Documentation
#
# This notebook only shows a subset of the functionality in astropy.convolution. For more information about the features presented below as well as other available features, you can read the
# [astropy.convolution documentation](https://docs.astropy.org/en/stable/convolution/).
# %matplotlib inline
import matplotlib.pyplot as plt
plt.rc('image', origin='lower')
plt.rc('figure', figsize=(10, 6))
# ## Convolution kernels
#
# A number of convolution kernels are provided by default - these are classes that support several options for discretization onto a pixel grid. An example of such a kernel is [Gaussian2DKernel](https://docs.astropy.org/en/stable/api/astropy.convolution.Gaussian2DKernel.html#astropy.convolution.Gaussian2DKernel):
from astropy.convolution import Gaussian2DKernel
kernel1 = Gaussian2DKernel(2)
# Kernels have a ``.array`` attribute that can be used to access the discretized values:
plt.imshow(kernel1.array)
# By default, the kernel is discretized by sampling the values of the Gaussian (or whatever kernel function is used) at the center of each pixel. However this can cause issues if the kernel is not very well resolved by the grid:
from astropy import units as u
kernel2 = Gaussian2DKernel(x_stddev=0.3, y_stddev=5, theta=30 * u.deg)
plt.imshow(kernel2.array)
kernel3 = Gaussian2DKernel(x_stddev=0.3, y_stddev=5, theta=30 * u.deg, mode='oversample')
plt.imshow(kernel3.array)
plt.imshow(kernel3.array - kernel2.array)
# A list of available kernels can be found [in the documentation](https://docs.astropy.org/en/stable/convolution/kernels.html#available-kernels). If you are interested in constructing your own kernels, you can make use of any astropy model, and make use of the [Model1DKernel](http://docs.astropy.org/en/stable/api/astropy.convolution.Model1DKernel.html#astropy.convolution.Model1DKernel) and [Model2DKernel](http://docs.astropy.org/en/stable/api/astropy.convolution.Model1DKernel.html#astropy.convolution.Model2DKernel) classes.
# ## Convolution functions
#
# The two main convolution functions provided are [convolve](https://docs.astropy.org/en/stable/api/astropy.convolution.convolve.html#astropy.convolution.convolve) and [convolve_fft](https://docs.astropy.org/en/stable/api/astropy.convolution.convolve_fft.html#astropy.convolution.convolve_fft) - the former implements direct convolution (more efficient for small kernels), and the latter FFT convolution (more efficient for large kernels)
from astropy.convolution import convolve, convolve_fft
# To understand how the NaN treatment differs from SciPy, let's take a look at a simple example:
import numpy as np
data = [1, 2, np.nan, 4, 5]
kernel = [0.5, 1.0, 0.5]
from scipy.ndimage import convolve as scipy_convolve
scipy_convolve(data, kernel)
convolve(data, kernel)
# In short, the way this works is, prior to the convolution, to replace NaNs with the average of nearby pixels weighted by the kernel. The astropy convolution functions can work for data in 1-, 2- and 3-dimensions.
#
# We can take a look at an example for an image, using one of the FITS images used previously:
from astropy.io import fits
gaia_map = fits.getdata('data/LMCDensFits1k.fits')
# This image doesn't contain any NaN values, but we can sprinkle some NaN values throughout with:
gaia_map[np.random.random((750, 1000)) > 0.999] = np.nan
plt.imshow(gaia_map)
# Let's construct a small Gaussian kernel:
gauss = Gaussian2DKernel(3)
# And we can now compare the convolution from scipy.ndimage and astropy.convolution:
plt.imshow(scipy_convolve(gaia_map, gauss.array))
plt.imshow(convolve(gaia_map, gauss))
#
# <section class="challenge panel panel-success">
# <div class="panel-heading">
# <h2><span class="fa fa-pencil"></span> Challenge</h2>
# </div>
#
#
# <div class="panel-body">
#
# <p>Using a simple 1D dataset as done above, can you determine whether the kernel is automatically normalized by default? How can you change this behavior? And how does this compare to SciPy's convolve function?</p>
#
# </div>
#
# </section>
#
#1a
convolve([0, 1, 0], [1, 2, 1]) # normalized kernel
#1b
convolve([0, 1, 0], [1, 2, 1], normalize_kernel=False) # normalized kernel
#1c
scipy_convolve([0, 1, 0], [1, 2, 1]) # unnormalized kernel
# <center><i>This notebook was written by <a href="https://aperiosoftware.com/">Aperio Software Ltd.</a> © 2019, and is licensed under a <a href="https://creativecommons.org/licenses/by/4.0/">Creative Commons Attribution 4.0 International License (CC BY 4.0)</a></i></center>
#
# 
|
instructor/10-convolution_instructor.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import pandera as pa
# +
#a limpeza de dados sera feita na parte da leitura dos dados com o parametro na_values
valores_ausentes = ['**','###!','####','****','*****','NULL']
caminho_dados = 'ocorrencia_2010_2020.csv'
df = pd.read_csv(caminho_dados, sep=';', parse_dates=['ocorrencia_dia'], dayfirst=True, na_values=valores_ausentes)
df.head(10)
# +
#a principio essa validaçao dara erro, isso porque fizemos ela apos a limpeza parcial
#ou seja apareceram valores que nao podem ser carregados de acordo com as regras da validaçao
#entao a validaçao impede que o codigo continue
schema = pa.DataFrameSchema(
columns={
'codigo': pa.Column(pa.Int, required=False),
#essa coluna nao exise, mas como ela pode aparecer em alguns df e outros nao
#podemmos adiciona-la com o parametro required=false, esse parmetro é true como padrao
'codigo_ocorrencia': pa.Column(pa.Int),
'codigo_ocorrencia2': pa.Column(pa.Int),
'ocorrencia_classificacao': pa.Column(pa.String),
'ocorrencia_cidade': pa.Column(pa.String),
'ocorrencia_uf': pa.Column(pa.String, pa.Check.str_length(2,2), nullable=True), #validaçao de tamanho
'ocorrencia_aerodromo': pa.Column(pa.String, nullable=True),
'ocorrencia_dia': pa.Column(pa.DateTime),
'ocorrencia_hora': pa.Column(pa.String, pa.Check.str_matches(r'^([0-1]?[0-9]|[2][0-3]):([0-5][0-9])(:[0-5][0-9])?$'), nullable=True),
#nullable permite valores nulos, senao ocorreria erro na validaçao
#check vai fazer a validaçao da hora a partir de uma regex, para nao ter horarios omo 25h, etc
'total_recomendacoes': pa.Column(pa.Int)
}
)
schema.validate(df)
# na linha de validaçao da coluna "ocorrencias_uf" colocando o parametro nulable, e rodando o codigo de novo
#o erro deixa de aparecer, pois agora os NA que apareceraam sao permitidos na validaçao
#porem aparecerao erros de outras validaçoes, na coluna "ocorrencia_aerodromo"
# +
df.loc[1]
#df.loc[-1]
#loc busca por label
# +
df.iloc[1]
df.iloc[-1]
#iloc busca por indice, possui os metodos de lista, é usado quando precisamos manipular o df pelos numeros das linhas e colunas
# -
filtro = df.ocorrencia_uf.isnull()
df.loc[filtro]
filtro = df.ocorrencia_hora.isnull()
df.loc[filtro]
#nao considera os valores NA na contagem
df.count()
#filtro que exibe as linhas com mais de 10 recomendaçoes
filtro = df.total_recomendacoes > 10
df.loc[filtro, ['ocorrencia_cidade', 'total_recomendacoes']]
#filtro que exibe as linhas com acidente grave
filtro = df.ocorrencia_classificacao == 'INCIDENTE GRAVE'
df.loc[filtro, ['ocorrencia_cidade', 'total_recomendacoes']]
# +
#filtro que exibe as linhas com acidente grave e estado SP
filtro1 = (df.ocorrencia_classificacao == 'INCIDENTE GRAVE') | (df.ocorrencia_classificacao == 'INCIDENTE')
#filtro1 = df.ocorrencia_classificacao.isin(['INCIDENTE GRAVE', 'INCIDENTE']) alternativa ao comando de cima
filtro2 = df.ocorrencia_uf == 'RJ'
df.loc[filtro1 & filtro2, ['ocorrencia_cidade', 'ocorrencia_hora']]
# -
#filtro que busca cidades que o nome comecem com a letra C
filtro = df.ocorrencia_cidade.str[0] == 'C'
df.loc[filtro]
#filtro que busca cidades que o nome termine com ma
filtro = df.ocorrencia_cidade.str[-2:] == 'MA'
df.loc[filtro]
#filtro que busca cidades que o nome termine com MA
filtro = df.ocorrencia_cidade.str.contains('MA')
df.loc[filtro]
#filtro que busca cidades que o nome tem MA ou AL
filtro = df.ocorrencia_cidade.str.contains('MA|AL')
df.loc[filtro]
#filtro que busca ano de 2015
filtro = df.ocorrencia_dia.dt.year == 2015 #operador dt usado em datas nos permite acessar os dados
df.loc[filtro]
#filtro que busca ano de 2015 e mes 1
filtro = (df.ocorrencia_dia.dt.year == 2015) & (df.ocorrencia_dia.dt.month == 1)
df.loc[filtro]
# +
#filtro que busca ano de 2015 e mes 1, entre os dias 1 e 10
filtro = (df.ocorrencia_dia.dt.year == 2015) & (df.ocorrencia_dia.dt.month == 1)
filtro_dia_inicio = df.ocorrencia_dia.dt.day > 0
filtro_dia_fim = df.ocorrencia_dia.dt.day < 11
df.loc[filtro & filtro_dia_inicio & filtro_dia_fim]
# +
#em determinadas situaçoes é util juntar dauas colunas em uma nova
#primeiro é necessario mudar a data do tipo data para tipo string para poder fazer a concatenaçao
#depois transformar tudo em data novamente
df['ocorrencia_dia_hora'] = pd.to_datetime(df.ocorrencia_dia.astype(str) + ' ' + df.ocorrencia_hora)
df.loc[:, 'ocorrencia_dia_hora']
# +
#filtro que busca ano de 2015 e mes 1, entre os dias 1 e 10 e horario da noite
filtro = (df.ocorrencia_dia.dt.year == 2015) & (df.ocorrencia_dia.dt.month == 1)
filtro_dia_inicio = df.ocorrencia_dia.dt.day > 0
filtro_dia_fim = df.ocorrencia_dia.dt.day < 11
# filtro_hora1 = df.ocorrencia_dia_hora >= '2015-01-01 12:00:00'
# filtro_hora2 = df.ocorrencia_dia_hora <= '2015-01-09 12:00:00'
df.loc[filtro & filtro_dia_inicio & filtro_dia_fim]
# +
filtro_hora1 = df.ocorrencia_dia_hora >= '2015-01-01 12:00:00'
filtro_hora2 = df.ocorrencia_dia_hora <= '2015-01-09 12:00:00'
df.loc[filtro_hora1 & filtro_hora2]
#juntando dia e hora podemos faer filtros mais facilmente
# +
#vamos criar um novo df
filtro1 = df.ocorrencia_dia.dt.year == 2015
filtro2 = df.ocorrencia_dia.dt.month == 3
df201503 = df.loc[filtro1 & filtro2]
df201503
# -
#verificando falta de dados
df201503.count()
df201503.groupby(['codigo_ocorrencia']).count()
#nessa contagem agrupamos pelo codigo, como é unico entao as somas serao 1 ou 0 no caso do dado estar faltando
df201503.groupby(['ocorrencia_classificacao']).codigo_ocorrencia.count()
#aqui se conta quantos codigos de ocorrencia diferentes tem para cada tipo de classificaçao
# ou seja, houve 15 ocorrencias diferentes que foram acidentes, 5 que foram incidente grave, etc
df201503.groupby(['ocorrencia_classificacao']).ocorrencia_aerodromo.count()
#aqui se conta quantas ocorrencias no aerodromo tem para cada tipo de classificaçao
#deve se evitar contar por colunas que contenham dados nulos, como essa
df201503.groupby(['ocorrencia_classificacao']).size()
#size conta as linhas com valores
df201503.groupby(['ocorrencia_classificacao']).size().sort_values()
# +
filtro1 = df.ocorrencia_dia.dt.year == 2010
filtro2 = df.ocorrencia_uf.isin(['SP', 'MG', 'ES', 'RJ'])
dfsudeste2010 = df.loc[filtro1 & filtro2]
dfsudeste2010
# -
dfsudeste2010.groupby(['ocorrencia_classificacao']).size()
dfsudeste2010.count()
#
dfsudeste2010.groupby(['ocorrencia_uf', 'ocorrencia_classificacao']).size()
dfsudeste2010.groupby(['ocorrencia_cidade']).size().sort_values(ascending=False)
filtro = dfsudeste2010.ocorrencia_cidade == 'RIO DE JANEIRO'
dfsudeste2010.loc[filtro].total_recomendacoes.sum()
# total de recomendaçoes do Rio deu 25, para confirmar podemos buscar onde estao as recomendaçoes
# +
filtro1 = dfsudeste2010.ocorrencia_cidade == 'RIO DE JANEIRO'
filtro2 = dfsudeste2010.total_recomendacoes > 0
dfsudeste2010.loc[filtro1 & filtro2]
#filtrando as recomendaçoes
# -
dfsudeste2010.groupby(['ocorrencia_cidade']).total_recomendacoes.sum()
dfsudeste2010.groupby(['ocorrencia_aerodromo'], dropna=False).total_recomendacoes.sum()
filtro = dfsudeste2010.total_recomendacoes > 0
dfsudeste2010.loc[filtro].groupby(['ocorrencia_cidade']).total_recomendacoes.sum()
#filtramos o df so com valores a cima de 0 para recomendacoes e em seguida ordenamos pela cidade
dfsudeste2010.loc[filtro].groupby(['ocorrencia_cidade', dfsudeste2010.ocorrencia_dia.dt.month]).total_recomendacoes.sum()
#depois de filtrar o df agrupamos por cidade e mes, como nao temos coluna pro mes separada temos que usar dessa forma
#verificando as ocorrencias em SP para ver se os valores batem com as da celula anterior
filtro1 = dfsudeste2010.total_recomendacoes > 0
filtro2 = dfsudeste2010.ocorrencia_cidade == 'SÃO PAULO'
dfsudeste2010.loc[filtro1 & filtro2]
|
fundamentos_ETL/projeto/03-transformacao.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Installer for Email Notification Scheduler
# ⚠️ Only Seeq Administrators can run this installer to completion, since only Administrators can install Add-ons.
#
# This notebook will walk you through the steps needed to install the Email Notification Scheduler as a Data Lab Tool in Workbench. If you are fine with the defaults and have never installed the scheduler before, you should be able to leave everything as is, running all cells in order.
#
# At the end, if you have encountered no errors:
# * in the folder you've specified using the `path_to_notifications_folder`, you should find all files listed as `source_files` below
# * the Tools tab in Workbench should have a tool grouping named `Add-ons`
# * there should be a tool named `Email Notification Scheduler` among the `Add-ons`.
#
# There is ONE MORE STEP that must be done to complete installation - after running all steps in this installer, one must complete the SMTP server and account configuration in `Email Notifier.ipynb` within the target folder (`Email Notifications` if `path_to_notifications_folder` is not changed below). Please note that anyone that has access to this project will be able to see the account information provided there. If using the gmail SMTP server, it is preferred to use an app password rather than the actual password for the account, and the port should be set to 587 to use STARTTLS. You can find out more about gmail app passwords in the [Google Account Help](https://support.google.com/accounts/answer/185833?hl=en#zippy=%2Cwhy-you-may-need-an-app-password).
#
# See the [Add-on Tools KB article](https://telemetry.seeq.com/support-link/wiki/spaces/KB/pages/961675391) for further details of Add-on tools.
# ### Installation Folder
#
# The path to the Notifications folder is set in the next cell. It should be specified relative to the root of the project and should use forward slashes ( / ) for path separators. The folder should be created before proceeding with installation.
path_to_notifications_folder = 'Email Notifications'
# ### How to handle existing files
# If the following parameter is changed to `True`, any existing files in the target folder will be overwritten. You
# may want to do this if you wish to discard changes to the installed notebooks or if you wish to upgrade the notebooks
# with the versions found in this folder (e.g., after upgrading the Data Lab server).
overwrite_existing_files = False
# ### How to handle existing versions of Scheduler in Add-on Tools
# If the following parameter is `True`, any already-installed tools with the same name as shown in the `name` field of
# the `tool_with_permissions` dictionary below will be removed before the new tool is installed. By default, the
# `name` of the scheduler is `Email Notification Scheduler`. Be careful! If you change this parameter to `True`, you
# will be replacing the existing version of the Add-on Tool with the version found at the
# `path_to_notifications_folder` in this project for _all users_ of the Add-on Tool. You may want to change the `name`
# field in the `tool_with_permissions` dictionary instead.
remove_existing_versions = False
# ### Tool Configuration
# Check the output of the following cell to confirm the desired configuration for the Add-on Tool. The resulting JSON object will be used to create or update the existing tool.
# +
import urllib.parse as urlparse
target_path_encoded = urlparse.quote(path_to_notifications_folder)
project_id = spy.utils.get_data_lab_project_id()
project_url = spy.utils.get_data_lab_project_url()
notebook_name = 'Email Notification Scheduler.ipynb'
query_parameters = '?workbookId={workbookId}&worksheetId={worksheetId}&workstepId={workstepId}&seeqVersion={seeqVersion}'
install_url = f'{project_url}/apps/{path_to_notifications_folder}/{notebook_name}/{query_parameters}'
tool_with_permissions = {
'name': 'Email Notification Scheduler',
'description': 'Data Lab Notebook-based Email Notification Scheduling tool',
'iconClass': 'fa fa-envelope',
'targetUrl': install_url,
'linkType': 'window',
'windowDetails': 'toolbar=0,location=0,scrollbars=1,statusbar=0,menubar=0,resizable=1,height=700,width=600',
'sortKey' : 'e',
'reuseWindow': 'false', # but not relevant, since linkType is 'tab'
'permissions': {
'groups': [],
'users': [spy.user.email]
}
}
print('The following parameters will be used to define the add-on:\n')
tool_with_permissions
# -
# # ⚠️ Advanced Configuration and Automated Installation Beyond This Point
# If you are just running this notebook to install or update the Email Notifications Scheduler in a typical fashion, you can just run the remaining cells as is, checking the output of each to confirm the expected results. Contact support if any problems are encountered.
import os
import requests
import shutil
from datetime import datetime, timezone
from pathlib import Path
from seeq import sdk
try:
spy_version = seeq.__version__
except:
spy_version = spy.__version__
print(f'Seeq PyPI package version: {spy_version}')
# ### Check whether the required source files and target folder exist
# The source files should be in the same folder as this installer. The target folder for the installation should already exist by the time this installer is run.
home_path = os.environ['HOME']
all_required_paths_exist = False
source_files = [
'Email Notification Scheduler.ipynb',
'Email Notifier.ipynb',
'Email Unsubscriber.ipynb',
'Seeq Data Lab.jpg'
]
source_paths = [
f'{os.getcwd()}/{source_file}' for source_file in source_files
]
target_folder_path = Path(home_path, path_to_notifications_folder)
os.makedirs(target_folder_path, exist_ok=True)
target_folder_exists = os.path.exists(target_folder_path)
all_source_paths_exist = all(iter([os.path.exists(source_path) for source_path in source_paths]))
status_message = ''
if not all_source_paths_exist:
files_string = "\n".join(source_paths)
status_message += f'Not all source files exist. Check for the presence of the following files ' \
f'in the folder that contains this notebook:\n{source_files}'
if not target_folder_exists:
status_message += f'Target folder not found. Add a folder at {path_to_notifications_folder} relative to ' \
f'the root of the Data Lab Project'
if status_message:
print(status_message)
else:
print('All required paths exist. Installation may proceed.')
target_paths = []
if all_source_paths_exist:
existing_files_not_overwritten = False
for source_path in source_paths:
source_file = source_path.split('/').pop()
target_path = Path(home_path, path_to_notifications_folder, source_file)
target_paths.append(target_path)
if overwrite_existing_files or not target_path.exists():
shutil.copyfile(source_path, target_path)
else:
existing_files_not_overwritten = True
if existing_files_not_overwritten:
print(f'Warning! One or more files were not overwritten. Change overwrite_existing_files to True '
f'or delete the files in the target folder to ensure the latest versions.')
all_target_files_exist = all(iter([os.path.exists(target_path) for target_path in target_paths]))
print(f'{"All" if all_target_files_exist else "Not all"} target files exist. '
f'Installation may{" " if all_target_files_exist else " not "}proceed.')
else:
all_target_files_exist = False
print('Please check results of previous step')
# ### Configuration update and tool installation
# The following cell enables the Add-on Tools and ScheduledNotebooks features and adds the Email Notifications Scheduler to the Add-on Tools.
# +
# Adapted from the Notebook Add-on Tool Management UI-TEST.ipynb, available at
# https://seeq.atlassian.net/wiki/spaces/SQ/pages/961675391/Add-on+Tools
def create_add_on_tool(tool_with_permissions):
# Create add-on tool
tool = tool_with_permissions.copy()
tool.pop("permissions")
tool_id = sdk.SystemApi(spy.client).create_add_on_tool(body = tool).id
items_api = sdk.ItemsApi(spy.client)
# assign group permissions to add-on tool and data lab project
groups = tool_with_permissions["permissions"]["groups"]
for group_name in groups:
group = sdk.UserGroupsApi(spy.client).get_user_groups(name_search=group_name)
if group:
ace_input = { 'identityId': group.items[0].id, 'permissions': { 'read': True } }
# Add permissions to add-on tool item
items_api.add_access_control_entry(id=tool_id, body=ace_input)
# Add permissions to data lab project if target URL references one
ace_input['permissions']['write'] = True # Data lab project also needs write permission
items_api.add_access_control_entry(id=project_id, body=ace_input)
# assign user permissions to add-on tool and data lab project
users = tool_with_permissions["permissions"]["users"]
for user_name in users:
user = sdk.UsersApi(spy.client).get_users(username_search=user_name)
if user:
ace_input = { 'identityId': user.users[0].id, 'permissions': { 'read': True } }
items_api.add_access_control_entry(id=tool_id, body=ace_input)
# Add permissions to data lab project if target URL references one
ace_input['permissions']['write'] = True # Data lab project also needs write permission
items_api.add_access_control_entry(id=project_id, body=ace_input)
system_api = sdk.SystemApi(spy.client)
if all_target_files_exist:
if not spy.user.is_admin:
raise RuntimeError('Only Administrators can install Add-on Tools')
if int(spy_version.split('.')[0]) >= 54:
configuration_output = system_api.get_configuration_options(limit=5000)
else:
configuration_output = system_api.get_configuration_options()
add_on_tools_already_enabled = next((option.value for option in configuration_output.configuration_options
if option.path == 'Features/AddOnTools/Enabled'), False)
scheduled_notebooks_already_enabled = next((option.value for option in configuration_output.configuration_options
if option.path == 'Features/DataLab/ScheduledNotebooks/Enabled'), False)
configuration_options_update = []
if not add_on_tools_already_enabled:
configuration_options_update.append(
sdk.ConfigurationOptionInputV1(
note = f'Set to true by Email Notifications Installer user {spy.user.email} {datetime.now(timezone.utc)}',
path = 'Features/AddOnTools/Enabled',
value = True
)
)
if not scheduled_notebooks_already_enabled:
configuration_options_update.append(
sdk.ConfigurationOptionInputV1(
note = f'Set to true by Email Notifications Installer user {spy.user.email} {datetime.now(timezone.utc)}',
path = 'Features/DataLab/ScheduledNotebooks/Enabled',
value = True
)
)
if configuration_options_update:
config_options = sdk.ConfigurationInputV1(configuration_options = configuration_options_update)
system_api.set_configuration_options(body=config_options)
existing_tools_output = system_api.get_add_on_tools()
existing_tools = [add_on_tool for add_on_tool in existing_tools_output.add_on_tools
if add_on_tool.name == tool_with_permissions['name']]
if len(existing_tools) > 0:
if not remove_existing_versions:
raise RuntimeError(f'One or more tools exist with name {tool_with_permissions["name"]}, '
f'and remove_existing_versions is False; Cannot create add-on tool')
else:
# Delete existing tools
for existing_tool in existing_tools:
system_api.delete_add_on_tool(id=existing_tool.id)
print(f'Removed {len(existing_tools)} existing tools with name {tool_with_permissions["name"]}')
# Create new tool
create_add_on_tool(tool_with_permissions)
print(f'Success! Check Workbench for the {tool_with_permissions["name"]} tool in the Add-on Tools collection')
else:
print('Not all target files exist; cannot complete installation.')
# -
|
Email Notification Add-on Installer.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.6
# language: python
# name: python36
# ---
# Copyright (c) Microsoft Corporation. All rights reserved.
#
# Licensed under the MIT License.
# 
# # Train using Azure Machine Learning Compute
#
# * Initialize a Workspace
# * Create an Experiment
# * Introduction to AmlCompute
# * Submit an AmlCompute run in a few different ways
# - Provision as a run based compute target
# - Provision as a persistent compute target (Basic)
# - Provision as a persistent compute target (Advanced)
# * Additional operations to perform on AmlCompute
# * Download model explanation data from the Run History Portal
# * Print the explanation data
# ## Prerequisites
# If you are using an Azure Machine Learning Notebook VM, you are all set. Otherwise, make sure you go through the [configuration notebook](../../../configuration.ipynb) first if you haven't.
# +
# Check core SDK version number
import azureml.core
print("SDK version:", azureml.core.VERSION)
# -
# ## Initialize a Workspace
#
# Initialize a workspace object from persisted configuration
# + tags=["create workspace"]
from azureml.core import Workspace
ws = Workspace.from_config()
print(ws.name, ws.resource_group, ws.location, ws.subscription_id, sep='\n')
# -
# ## Create An Experiment
#
# **Experiment** is a logical container in an Azure ML Workspace. It hosts run records which can include run metrics and output artifacts from your experiments.
from azureml.core import Experiment
experiment_name = 'explainer-remote-run-on-amlcompute'
experiment = Experiment(workspace=ws, name=experiment_name)
# ## Introduction to AmlCompute
#
# Azure Machine Learning Compute is managed compute infrastructure that allows the user to easily create single to multi-node compute of the appropriate VM Family. It is created **within your workspace region** and is a resource that can be used by other users in your workspace. It autoscales by default to the max_nodes, when a job is submitted, and executes in a containerized environment packaging the dependencies as specified by the user.
#
# Since it is managed compute, job scheduling and cluster management are handled internally by Azure Machine Learning service.
#
# For more information on Azure Machine Learning Compute, please read [this article](https://docs.microsoft.com/azure/machine-learning/service/how-to-set-up-training-targets#amlcompute)
#
# If you are an existing BatchAI customer who is migrating to Azure Machine Learning, please read [this article](https://aka.ms/batchai-retirement)
#
# **Note**: As with other Azure services, there are limits on certain resources (for eg. AmlCompute quota) associated with the Azure Machine Learning service. Please read [this article](https://docs.microsoft.com/azure/machine-learning/service/how-to-manage-quotas) on the default limits and how to request more quota.
#
#
# The training script `run_explainer.py` is already created for you. Let's have a look.
# ## Submit an AmlCompute run in a few different ways
#
# First lets check which VM families are available in your region. Azure is a regional service and some specialized SKUs (especially GPUs) are only available in certain regions. Since AmlCompute is created in the region of your workspace, we will use the supported_vms () function to see if the VM family we want to use ('STANDARD_D2_V2') is supported.
#
# You can also pass a different region to check availability and then re-create your workspace in that region through the [configuration notebook](../../../configuration.ipynb)
# +
from azureml.core.compute import ComputeTarget, AmlCompute
AmlCompute.supported_vmsizes(workspace=ws)
# AmlCompute.supported_vmsizes(workspace=ws, location='southcentralus')
# -
# ### Create project directory
#
# Create a directory that will contain all the necessary code from your local machine that you will need access to on the remote resource. This includes the training script, and any additional files your training script depends on
# +
import os
import shutil
project_folder = './explainer-remote-run-on-amlcompute'
os.makedirs(project_folder, exist_ok=True)
shutil.copy('run_explainer.py', project_folder)
# -
# ### Provision as a run based compute target
#
# You can provision AmlCompute as a compute target at run-time. In this case, the compute is auto-created for your run, scales up to max_nodes that you specify, and then **deleted automatically** after the run completes.
# +
from azureml.core.runconfig import RunConfiguration
from azureml.core.conda_dependencies import CondaDependencies
from azureml.core.runconfig import DEFAULT_CPU_IMAGE
# create a new runconfig object
run_config = RunConfiguration()
# signal that you want to use AmlCompute to execute script.
run_config.target = "amlcompute"
# AmlCompute will be created in the same region as workspace
# Set vm size for AmlCompute
run_config.amlcompute.vm_size = 'STANDARD_D2_V2'
# enable Docker
run_config.environment.docker.enabled = True
# set Docker base image to the default CPU-based image
run_config.environment.docker.base_image = DEFAULT_CPU_IMAGE
# use conda_dependencies.yml to create a conda environment in the Docker image for execution
run_config.environment.python.user_managed_dependencies = False
azureml_pip_packages = [
'azureml-defaults', 'azureml-contrib-explain-model', 'azureml-core', 'azureml-telemetry',
'azureml-explain-model'
]
# specify CondaDependencies obj
run_config.environment.python.conda_dependencies = CondaDependencies.create(conda_packages=['scikit-learn'],
pip_packages=azureml_pip_packages)
# Now submit a run on AmlCompute
from azureml.core.script_run_config import ScriptRunConfig
script_run_config = ScriptRunConfig(source_directory=project_folder,
script='run_explainer.py',
run_config=run_config)
run = experiment.submit(script_run_config)
# Show run details
run
# -
# Note: if you need to cancel a run, you can follow [these instructions](https://aka.ms/aml-docs-cancel-run).
# %%time
# Shows output of the run on stdout.
run.wait_for_completion(show_output=True)
# ### Provision as a persistent compute target (Basic)
#
# You can provision a persistent AmlCompute resource by simply defining two parameters thanks to smart defaults. By default it autoscales from 0 nodes and provisions dedicated VMs to run your job in a container. This is useful when you want to continously re-use the same target, debug it between jobs or simply share the resource with other users of your workspace.
#
# * `vm_size`: VM family of the nodes provisioned by AmlCompute. Simply choose from the supported_vmsizes() above
# * `max_nodes`: Maximum nodes to autoscale to while running a job on AmlCompute
# +
from azureml.core.compute import ComputeTarget, AmlCompute
from azureml.core.compute_target import ComputeTargetException
# Choose a name for your CPU cluster
cpu_cluster_name = "cpu-cluster"
# Verify that cluster does not exist already
try:
cpu_cluster = ComputeTarget(workspace=ws, name=cpu_cluster_name)
print('Found existing cluster, use it.')
except ComputeTargetException:
compute_config = AmlCompute.provisioning_configuration(vm_size='STANDARD_D2_V2',
max_nodes=4)
cpu_cluster = ComputeTarget.create(ws, cpu_cluster_name, compute_config)
cpu_cluster.wait_for_completion(show_output=True)
# -
# ### Configure & Run
# +
from azureml.core.runconfig import RunConfiguration
from azureml.core.conda_dependencies import CondaDependencies
# create a new RunConfig object
run_config = RunConfiguration(framework="python")
# Set compute target to AmlCompute target created in previous step
run_config.target = cpu_cluster.name
# enable Docker
run_config.environment.docker.enabled = True
azureml_pip_packages = [
'azureml-defaults', 'azureml-contrib-explain-model', 'azureml-core', 'azureml-telemetry',
'azureml-explain-model'
]
# specify CondaDependencies obj
run_config.environment.python.conda_dependencies = CondaDependencies.create(conda_packages=['scikit-learn'],
pip_packages=azureml_pip_packages)
from azureml.core import Run
from azureml.core import ScriptRunConfig
src = ScriptRunConfig(source_directory=project_folder,
script='run_explainer.py',
run_config=run_config)
run = experiment.submit(config=src)
run
# -
# %%time
# Shows output of the run on stdout.
run.wait_for_completion(show_output=True)
run.get_metrics()
# ### Provision as a persistent compute target (Advanced)
#
# You can also specify additional properties or change defaults while provisioning AmlCompute using a more advanced configuration. This is useful when you want a dedicated cluster of 4 nodes (for example you can set the min_nodes and max_nodes to 4), or want the compute to be within an existing VNet in your subscription.
#
# In addition to `vm_size` and `max_nodes`, you can specify:
# * `min_nodes`: Minimum nodes (default 0 nodes) to downscale to while running a job on AmlCompute
# * `vm_priority`: Choose between 'dedicated' (default) and 'lowpriority' VMs when provisioning AmlCompute. Low Priority VMs use Azure's excess capacity and are thus cheaper but risk your run being pre-empted
# * `idle_seconds_before_scaledown`: Idle time (default 120 seconds) to wait after run completion before auto-scaling to min_nodes
# * `vnet_resourcegroup_name`: Resource group of the **existing** VNet within which AmlCompute should be provisioned
# * `vnet_name`: Name of VNet
# * `subnet_name`: Name of SubNet within the VNet
# +
from azureml.core.compute import ComputeTarget, AmlCompute
from azureml.core.compute_target import ComputeTargetException
# Choose a name for your CPU cluster
cpu_cluster_name = "cpu-cluster"
# Verify that cluster does not exist already
try:
cpu_cluster = ComputeTarget(workspace=ws, name=cpu_cluster_name)
print('Found existing cluster, use it.')
except ComputeTargetException:
compute_config = AmlCompute.provisioning_configuration(vm_size='STANDARD_D2_V2',
vm_priority='lowpriority',
min_nodes=2,
max_nodes=4,
idle_seconds_before_scaledown='300',
vnet_resourcegroup_name='<my-resource-group>',
vnet_name='<my-vnet-name>',
subnet_name='<my-subnet-name>')
cpu_cluster = ComputeTarget.create(ws, cpu_cluster_name, compute_config)
cpu_cluster.wait_for_completion(show_output=True)
# -
# ### Configure & Run
# +
from azureml.core.runconfig import RunConfiguration
from azureml.core.conda_dependencies import CondaDependencies
# create a new RunConfig object
run_config = RunConfiguration(framework="python")
# Set compute target to AmlCompute target created in previous step
run_config.target = cpu_cluster.name
# enable Docker
run_config.environment.docker.enabled = True
azureml_pip_packages = [
'azureml-defaults', 'azureml-contrib-explain-model', 'azureml-core', 'azureml-telemetry',
'azureml-explain-model'
]
# specify CondaDependencies obj
run_config.environment.python.conda_dependencies = CondaDependencies.create(conda_packages=['scikit-learn'],
pip_packages=azureml_pip_packages)
from azureml.core import Run
from azureml.core import ScriptRunConfig
src = ScriptRunConfig(source_directory=project_folder,
script='run_explainer.py',
run_config=run_config)
run = experiment.submit(config=src)
run
# -
# %%time
# Shows output of the run on stdout.
run.wait_for_completion(show_output=True)
run.get_metrics()
# +
from azureml.contrib.explain.model.explanation.explanation_client import ExplanationClient
client = ExplanationClient.from_run(run)
# Get the top k (e.g., 4) most important features with their importance values
explanation = client.download_model_explanation(top_k=4)
# -
# ## Additional operations to perform on AmlCompute
#
# You can perform more operations on AmlCompute such as updating the node counts or deleting the compute.
# Get_status () gets the latest status of the AmlCompute target
cpu_cluster.get_status().serialize()
# Update () takes in the min_nodes, max_nodes and idle_seconds_before_scaledown and updates the AmlCompute target
# cpu_cluster.update(min_nodes=1)
# cpu_cluster.update(max_nodes=10)
cpu_cluster.update(idle_seconds_before_scaledown=300)
# cpu_cluster.update(min_nodes=2, max_nodes=4, idle_seconds_before_scaledown=600)
# +
# Delete () is used to deprovision and delete the AmlCompute target. Useful if you want to re-use the compute name
# 'cpu-cluster' in this case but use a different VM family for instance.
# cpu_cluster.delete()
# -
# ## Download Model Explanation Data
# +
from azureml.contrib.explain.model.explanation.explanation_client import ExplanationClient
# Get model explanation data
client = ExplanationClient.from_run(run)
explanation = client.download_model_explanation()
local_importance_values = explanation.local_importance_values
expected_values = explanation.expected_values
# -
# Or you can use the saved run.id to retrive the feature importance values
client = ExplanationClient.from_run_id(ws, experiment_name, run.id)
explanation = client.download_model_explanation()
local_importance_values = explanation.local_importance_values
expected_values = explanation.expected_values
# Get the top k (e.g., 4) most important features with their importance values
explanation = client.download_model_explanation(top_k=4)
global_importance_values = explanation.get_ranked_global_values()
global_importance_names = explanation.get_ranked_global_names()
print('global importance values: {}'.format(global_importance_values))
print('global importance names: {}'.format(global_importance_names))
# ## Success!
# Great, you are ready to move on to the remaining notebooks.
|
how-to-use-azureml/explain-model/explain-on-amlcompute/regression-sklearn-on-amlcompute.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Genetic Algorithms with pyevolve
#
# <img src="img/logo.png" align="center">
#
# [Pyevolve](http://pyevolve.sourceforge.net/0_6rc1/) was developed to be a complete genetic algorithm framework written in pure python. The main objectives were:
#
# * **written in pure python**, to maximize the cross-platform issue;
# * **easy to use** API;
# * **see the evolution**, the user can and must see and interact with the evolution statistics, graphs, etc;
# * **extensible**, the user can create new representations, genetic operators like crossover, mutation, etc;
# * **fast**, the design must be optimized for performance;
# * **common features**, the framework must implement the most common features: selectors like roulette wheel, tournament, ranking, uniform; scaling schemes like linear scaling, etc;
# * **default parameters**, we must have default operators, settings, etc in all options;
# * **open-source**, the source is for everyone, not for only one.
#
# ## Aim of these notebooks
#
# You will learn the basic functioning of Pyevolve. You will make scripts for using genetic algorithms in simple problems.
#
# * [First Example](First%20Example.ipynb)
# * [Graphical Analysis](Graphical%20Analysis.ipynb)
# * [Rastrigin Function](Rastrigin.ipynb)
# * [Travelling Salesman Problem](TSP.ipynb)
|
index.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] deletable=false editable=false nbgrader={"checksum": "75c86807402955e4c01ac1ce25306bd7", "grade": false, "grade_id": "cell-649fd0b1aa7ccb0f", "locked": true, "schema_version": 1, "solution": false}
# # Assignment 2: Optimal Policies with Dynamic Programming
#
# Welcome to Assignment 2. This notebook will help you understand:
# - Policy Evaluation and Policy Improvement.
# - Value and Policy Iteration.
# - Bellman Equations.
# - Synchronous and Asynchronous Methods.
# + [markdown] deletable=false editable=false nbgrader={"checksum": "20729884a9ceb3804a03589ce5938a2d", "grade": false, "grade_id": "cell-9aafac39a58eeca4", "locked": true, "schema_version": 1, "solution": false}
# ## Gridworld City
#
# Gridworld City, a thriving metropolis with a booming technology industry, has recently experienced an influx of grid-loving software engineers. Unfortunately, the city's street parking system, which charges a fixed rate, is struggling to keep up with the increased demand. To address this, the city council has decided to modify the pricing scheme to better promote social welfare. In general, the city considers social welfare higher when more parking is being used, the exception being that the city prefers that at least one spot is left unoccupied (so that it is available in case someone really needs it). The city council has created a Markov decision process (MDP) to model the demand for parking with a reward function that reflects its preferences. Now the city has hired you — an expert in dynamic programming — to help determine an optimal policy.
# + [markdown] deletable=false editable=false nbgrader={"checksum": "77a7b97ee700b6ce77ed26bd22749e80", "grade": false, "grade_id": "cell-28ccff8d1e663850", "locked": true, "schema_version": 1, "solution": false}
# ## Preliminaries
# You'll need two imports to complete this assigment:
# - numpy: The fundamental package for scientific computing with Python.
# - tools: A module containing an environment and a plotting function.
#
# There are also some other lines in the cell below that are used for grading and plotting — you needn't worry about them.
#
# In this notebook, all cells are locked except those that you are explicitly asked to modify. It is up to you to decide how to implement your solution in these cells, **but please do not import other libraries** — doing so will break the autograder.
# + deletable=false editable=false nbgrader={"checksum": "f70cbdcd1e273dfc166b366836a4136f", "grade": false, "grade_id": "cell-c11ff54faaf3fd89", "locked": true, "schema_version": 1, "solution": false}
# %%capture
# %matplotlib inline
import numpy as np
import pickle
import tools
# + [markdown] deletable=false editable=false nbgrader={"checksum": "596fffc2a1391897952fcabe2a8db930", "grade": false, "grade_id": "cell-4c7c5c4373be59ff", "locked": true, "schema_version": 1, "solution": false}
# In the city council's parking MDP, states are nonnegative integers indicating how many parking spaces are occupied, actions are nonnegative integers designating the price of street parking, the reward is a real value describing the city's preference for the situation, and time is discretized by hour. As might be expected, charging a high price is likely to decrease occupancy over the hour, while charging a low price is likely to increase it.
#
# For now, let's consider an environment with three parking spaces and three price points. Note that an environment with three parking spaces actually has four states — zero, one, two, or three spaces could be occupied.
# + deletable=false editable=false nbgrader={"checksum": "c2e5b06e5166bc03c5075db981280485", "grade": false, "grade_id": "cell-d25d06a8bafc4c26", "locked": true, "schema_version": 1, "solution": false}
num_spaces = 3
num_prices = 3
env = tools.ParkingWorld(num_spaces, num_prices)
V = np.zeros(num_spaces + 1)
pi = np.ones((num_spaces + 1, num_prices)) / num_prices
# + [markdown] deletable=false editable=false nbgrader={"checksum": "0813b0f481e1f2f90e12f38456781410", "grade": false, "grade_id": "cell-57212e031233c500", "locked": true, "schema_version": 1, "solution": false}
# The value function is a one-dimensional array where the $i$-th entry gives the value of $i$ spaces being occupied.
# + deletable=false editable=false nbgrader={"checksum": "6e59c4a32939d9211dfc0f8fdd939780", "grade": false, "grade_id": "cell-c5f693a5ff49a888", "locked": true, "schema_version": 1, "solution": false}
V
# + deletable=false editable=false nbgrader={"checksum": "559643d84ae07b1b499ec4c6b9af40bc", "grade": false, "grade_id": "cell-ac2f8ec29c0c9ab6", "locked": true, "schema_version": 1, "solution": false}
state = 0
V[state]
# + deletable=false editable=false nbgrader={"checksum": "29380e07e1a4da60134db6949d7eb772", "grade": false, "grade_id": "cell-c829e4ece8bf9412", "locked": true, "schema_version": 1, "solution": false}
state = 0
value = 10
V[state] = value
V
# + deletable=false editable=false nbgrader={"checksum": "a296188c40952607943d9eddbd021f81", "grade": false, "grade_id": "cell-cb5bc5279787faad", "locked": true, "schema_version": 1, "solution": false}
for s, v in enumerate(V):
print(f'State {s} has value {v}')
# + [markdown] deletable=false editable=false nbgrader={"checksum": "cb305ee8a8d6e293a48b96ace69bfb53", "grade": false, "grade_id": "cell-57154206afc97770", "locked": true, "schema_version": 1, "solution": false}
# The policy is a two-dimensional array where the $(i, j)$-th entry gives the probability of taking action $j$ in state $i$.
# + deletable=false editable=false nbgrader={"checksum": "d732d93b6545408fa819526c2e52a0cf", "grade": false, "grade_id": "cell-85c017bb1e6fe4df", "locked": true, "schema_version": 1, "solution": false}
pi
# + deletable=false editable=false nbgrader={"checksum": "3b5bc8eebf9c09786a2a966cadcf0400", "grade": false, "grade_id": "cell-92a61a07d9f0bf04", "locked": true, "schema_version": 1, "solution": false}
state = 0
pi[state]
# + deletable=false editable=false nbgrader={"checksum": "4780c63332dfc7f65a998403c2a4bf21", "grade": false, "grade_id": "cell-0e224545b27d80c7", "locked": true, "schema_version": 1, "solution": false}
state = 0
action = 1
pi[state, action]
# + deletable=false editable=false nbgrader={"checksum": "ba7a14554c52279e4cfe7818982b914e", "grade": false, "grade_id": "cell-1f5e3fcf8d0384b9", "locked": true, "schema_version": 1, "solution": false}
pi[state] = np.array([0.75, 0.21, 0.04])
pi
# + deletable=false editable=false nbgrader={"checksum": "1cf19333d9690caba29729b2d8fed55c", "grade": false, "grade_id": "cell-d7d514ba81bc686c", "locked": true, "schema_version": 1, "solution": false}
for s, pi_s in enumerate(pi):
print(f''.join(f'pi(A={a}|S={s}) = {p.round(2)}' + 4 * ' ' for a, p in enumerate(pi_s)))
# + deletable=false editable=false nbgrader={"checksum": "cdff0c353f33f3cfd7413c141fa4d317", "grade": false, "grade_id": "cell-46b46b0dc80c68c7", "locked": true, "schema_version": 1, "solution": false}
tools.plot(V, pi)
# + [markdown] deletable=false editable=false nbgrader={"checksum": "4f450ea0212f959d952e9b0272e57cf3", "grade": false, "grade_id": "cell-ce3ac9318671059d", "locked": true, "schema_version": 1, "solution": false}
# We can visualize a value function and policy with the `plot` function in the `tools` module. On the left, the value function is displayed as a barplot. State zero has an expected return of ten, while the other states have an expected return of zero. On the right, the policy is displayed on a two-dimensional grid. Each vertical strip gives the policy at the labeled state. In state zero, action zero is the darkest because the agent's policy makes this choice with the highest probability. In the other states the agent has the equiprobable policy, so the vertical strips are colored uniformly.
# + [markdown] deletable=false editable=false nbgrader={"checksum": "049e3d7344e203034323e1f86a503ee4", "grade": false, "grade_id": "cell-3975c91dbe24e9e8", "locked": true, "schema_version": 1, "solution": false}
# You can access the state space and the action set as attributes of the environment.
# + deletable=false editable=false nbgrader={"checksum": "4fafc756424773278069199ff876300e", "grade": false, "grade_id": "cell-94d868709c1a9eba", "locked": true, "schema_version": 1, "solution": false}
env.S
# + deletable=false editable=false nbgrader={"checksum": "dc72712f4890361c35c0b19f0df5befd", "grade": false, "grade_id": "cell-6f16d9e8ebf01b60", "locked": true, "schema_version": 1, "solution": false}
env.A
# + [markdown] deletable=false editable=false nbgrader={"checksum": "12e6b88d7cf8ec6d20c7e14e3d43b5e2", "grade": false, "grade_id": "cell-927e52efe516a816", "locked": true, "schema_version": 1, "solution": false}
# You will need to use the environment's `transitions` method to complete this assignment. The method takes a state and an action and returns a 2-dimensional array, where the entry at $(i, 0)$ is the reward for transitioning to state $i$ from the current state and the entry at $(i, 1)$ is the conditional probability of transitioning to state $i$ given the current state and action.
# + deletable=false editable=false nbgrader={"checksum": "4d32e329bafe53f2061e6b577751f291", "grade": false, "grade_id": "cell-4185982b1a21cd04", "locked": true, "schema_version": 1, "solution": false}
state = 3
action = 1
transitions = env.transitions(state, action)
transitions
# + deletable=false editable=false nbgrader={"checksum": "768d9dfafd5bb70c8d3641fb6fb17ce3", "grade": false, "grade_id": "cell-379fdb797cae3afb", "locked": true, "schema_version": 1, "solution": false}
for s_, (r, p) in enumerate(transitions):
print(f'p(S\'={s_}, R={r} | S={state}, A={action}) = {p.round(2)}')
# + [markdown] deletable=false editable=false nbgrader={"checksum": "0869f6736a9ab680b0c82dccf72ba11c", "grade": false, "grade_id": "cell-141d4e3806427283", "locked": true, "schema_version": 1, "solution": false}
# ## Section 1: Policy Evaluation
#
# You're now ready to begin the assignment! First, the city council would like you to evaluate the quality of the existing pricing scheme. Policy evaluation works by iteratively applying the Bellman equation for $v_{\pi}$ to a working value function, as an update rule, as shown below.
#
# $$\large v(s) \leftarrow \sum_a \pi(a | s) \sum_{s', r} p(s', r | s, a)[r + \gamma v(s')]$$
# This update can either occur "in-place" (i.e. the update rule is sequentially applied to each state) or with "two-arrays" (i.e. the update rule is simultaneously applied to each state). Both versions converge to $v_{\pi}$ but the in-place version usually converges faster. **In this assignment, we will be implementing all update rules in-place**, as is done in the pseudocode of chapter 4 of the textbook.
#
# We have written an outline of the policy evaluation algorithm described in chapter 4.1 of the textbook. It is left to you to fill in the `bellman_update` function to complete the algorithm.
# + deletable=false editable=false nbgrader={"checksum": "732aa9563f9fa2209380be4dcfc22c31", "grade": false, "grade_id": "cell-8d04cf6f6f397e17", "locked": true, "schema_version": 1, "solution": false}
def evaluate_policy(env, V, pi, gamma, theta):
while True:
delta = 0
for s in env.S:
v = V[s]
bellman_update(env, V, pi, s, gamma)
delta = max(delta, abs(v - V[s]))
if delta < theta:
break
return V
# + deletable=false nbgrader={"checksum": "c8aad24b28e1eaf3fd87481be87f89e1", "grade": false, "grade_id": "cell-4113388a5f8401b6", "locked": false, "schema_version": 1, "solution": true}
# [Graded]
def bellman_update(env, V, pi, s, gamma):
"""Mutate ``V`` according to the Bellman update equation."""
### START CODE HERE ###
actions = pi[s]
G = [0]*len(actions)
for action in env.A:
transitions = env.transitions(s, action)
for s_, (r, p) in enumerate(transitions):
G[action] += p*(r + gamma * V[s_])
V[s] = np.sum(G*actions)
### END CODE HERE ###
# + [markdown] deletable=false editable=false nbgrader={"checksum": "4d9639225bc3d57f1079ceab1d57d411", "grade": false, "grade_id": "cell-5c1f3ff4b0e1b0bf", "locked": true, "schema_version": 1, "solution": false}
# The cell below uses the policy evaluation algorithm to evaluate the city's policy, which charges a constant price of one.
# + deletable=false editable=false nbgrader={"checksum": "7cd01aaa12fdfc50a4764d069b7a95fe", "grade": false, "grade_id": "cell-4b69f06bc67962af", "locked": true, "schema_version": 1, "solution": false}
num_spaces = 10
num_prices = 4
env = tools.ParkingWorld(num_spaces, num_prices)
V = np.zeros(num_spaces + 1)
city_policy = np.zeros((num_spaces + 1, num_prices))
city_policy[:, 1] = 1
gamma = 0.9
theta = 0.1
V = evaluate_policy(env, V, city_policy, gamma, theta)
# + [markdown] deletable=false editable=false nbgrader={"checksum": "0f19b2dc70097c6425bbc3bd25a2a500", "grade": false, "grade_id": "cell-b612ffe570dd7e29", "locked": true, "schema_version": 1, "solution": false}
# You can use the ``plot`` function to visualize the final value function and policy.
# + deletable=false editable=false nbgrader={"checksum": "1dd55a310f0d18634f95c4dd3dc19da3", "grade": false, "grade_id": "cell-fe5cf61a03a028fc", "locked": true, "schema_version": 1, "solution": false}
tools.plot(V, city_policy)
# + [markdown] deletable=false editable=false nbgrader={"checksum": "33d9d76d53c4cd379e8b7b0c6ecd5cc6", "grade": false, "grade_id": "cell-7dbb5974798259f7", "locked": true, "schema_version": 1, "solution": false}
# You can check the output (rounded to one decimal place) against the answer below:<br>
# State $\quad\quad$ Value<br>
# 0 $\quad\quad\quad\;$ 80.0<br>
# 1 $\quad\quad\quad\;$ 81.7<br>
# 2 $\quad\quad\quad\;$ 83.4<br>
# 3 $\quad\quad\quad\;$ 85.1<br>
# 4 $\quad\quad\quad\;$ 86.9<br>
# 5 $\quad\quad\quad\;$ 88.6<br>
# 6 $\quad\quad\quad\;$ 90.1<br>
# 7 $\quad\quad\quad\;$ 91.6<br>
# 8 $\quad\quad\quad\;$ 92.8<br>
# 9 $\quad\quad\quad\;$ 93.8<br>
# 10 $\quad\quad\;\;\,\,$ 87.8<br>
#
# Observe that the value function qualitatively resembles the city council's preferences — it monotonically increases as more parking is used, until there is no parking left, in which case the value is lower. Because of the relatively simple reward function (more reward is accrued when many but not all parking spots are taken and less reward is accrued when few or all parking spots are taken) and the highly stochastic dynamics function (each state has positive probability of being reached each time step) the value functions of most policies will qualitatively resemble this graph. However, depending on the intelligence of the policy, the scale of the graph will differ. In other words, better policies will increase the expected return at every state rather than changing the relative desirability of the states. Intuitively, the value of a less desirable state can be increased by making it less likely to remain in a less desirable state. Similarly, the value of a more desirable state can be increased by making it more likely to remain in a more desirable state. That is to say, good policies are policies that spend more time in desirable states and less time in undesirable states. As we will see in this assignment, such a steady state distribution is achieved by setting the price to be low in low occupancy states (so that the occupancy will increase) and setting the price high when occupancy is high (so that full occupancy will be avoided).
# + [markdown] deletable=false editable=false nbgrader={"checksum": "c954d5fee584058d6cff61e3274c2e8b", "grade": false, "grade_id": "cell-eb62290c37932db0", "locked": true, "schema_version": 1, "solution": false}
# The cell below will check that your code passes the test case above. (Your code passed if the cell runs without error.) Your solution will also be checked against hidden test cases for your final grade. (So don't hard code parameters into your solution.)
# + deletable=false editable=false nbgrader={"checksum": "b096086d94a387a1b453e2592c687575", "grade": true, "grade_id": "cell-8ff996ea5428abf6", "locked": true, "points": 1, "schema_version": 1, "solution": false}
## Test Code for bellman_update() ##
with open('section1', 'rb') as handle:
V_correct = pickle.load(handle)
np.testing.assert_array_almost_equal(V, V_correct)
# + [markdown] deletable=false editable=false nbgrader={"checksum": "f0d6665789065c7bfa797664e0f43c8c", "grade": false, "grade_id": "cell-45d6a1c8f905e939", "locked": true, "schema_version": 1, "solution": false}
# ## Section 2: Policy Iteration
# Now the city council would like you to compute a more efficient policy using policy iteration. Policy iteration works by alternating between evaluating the existing policy and making the policy greedy with respect to the existing value function. We have written an outline of the policy iteration algorithm described in chapter 4.3 of the textbook. We will make use of the policy evaluation algorithm you completed in section 1. It is left to you to fill in the `q_greedify_policy` function, such that it modifies the policy at $s$ to be greedy with respect to the q-values at $s$, to complete the policy improvement algorithm.
# + deletable=false editable=false nbgrader={"checksum": "92679d89cf740af64cdc7d37193608cf", "grade": false, "grade_id": "cell-15ec36bbf7a6fdc6", "locked": true, "schema_version": 1, "solution": false}
def improve_policy(env, V, pi, gamma):
policy_stable = True
for s in env.S:
old = pi[s].copy()
q_greedify_policy(env, V, pi, s, gamma)
if not np.array_equal(pi[s], old):
policy_stable = False
return pi, policy_stable
def policy_iteration(env, gamma, theta):
V = np.zeros(len(env.S))
pi = np.ones((len(env.S), len(env.A))) / len(env.A)
policy_stable = False
while not policy_stable:
V = evaluate_policy(env, V, pi, gamma, theta)
pi, policy_stable = improve_policy(env, V, pi, gamma)
return V, pi
# + deletable=false nbgrader={"checksum": "54f69a62cbb1dfbccfb9fafd6c3cc77a", "grade": false, "grade_id": "cell-43cadb209544e857", "locked": false, "schema_version": 1, "solution": true}
# [Graded]
def q_greedify_policy(env, V, pi, s, gamma):
"""Mutate ``pi`` to be greedy with respect to the q-values induced by ``V``."""
### START CODE HERE ###
actions = pi[s]
G = [0]*len(env.A)
for action in env.A:
transitions = env.transitions(s, action)
for s_, (r, p) in enumerate(transitions):
G[action] += p*(r + gamma * V[s_])
best_action = np.argmax(G)
pi[s,:] = 0
pi[s,best_action] = 1
return pi
### END CODE HERE ###
# + [markdown] deletable=false editable=false nbgrader={"checksum": "b70073346d140503e1572043f2be5c7e", "grade": false, "grade_id": "cell-d82e51ee8122647c", "locked": true, "schema_version": 1, "solution": false}
# When you are ready to test the policy iteration algorithm, run the cell below.
# + deletable=false editable=false nbgrader={"checksum": "aeedaa745e6dc30ebbc6b822c670c9b3", "grade": false, "grade_id": "cell-6939985ef9ad58a3", "locked": true, "schema_version": 1, "solution": false}
env = tools.ParkingWorld(num_spaces=10, num_prices=4)
gamma = 0.9
theta = 0.1
V, pi = policy_iteration(env, gamma, theta)
# + [markdown] deletable=false editable=false nbgrader={"checksum": "dcd619f8fcc010b6933b2bba4ce9f9e7", "grade": false, "grade_id": "cell-acd7f476ed298570", "locked": true, "schema_version": 1, "solution": false}
# You can use the ``plot`` function to visualize the final value function and policy.
# + deletable=false editable=false nbgrader={"checksum": "da17cf77a51f4fabd0ce3a93e2803af8", "grade": false, "grade_id": "cell-73a1da64ca84a151", "locked": true, "schema_version": 1, "solution": false}
tools.plot(V, pi)
# + [markdown] deletable=false editable=false nbgrader={"checksum": "0943d42dc7e60e40739b606700125da1", "grade": false, "grade_id": "cell-92139bf490757a44", "locked": true, "schema_version": 1, "solution": false}
# You can check the value function (rounded to one decimal place) and policy against the answer below:<br>
# State $\quad\quad$ Value $\quad\quad$ Action<br>
# 0 $\quad\quad\quad\;$ 81.6 $\quad\quad\;$ 0<br>
# 1 $\quad\quad\quad\;$ 83.3 $\quad\quad\;$ 0<br>
# 2 $\quad\quad\quad\;$ 85.0 $\quad\quad\;$ 0<br>
# 3 $\quad\quad\quad\;$ 86.8 $\quad\quad\;$ 0<br>
# 4 $\quad\quad\quad\;$ 88.5 $\quad\quad\;$ 0<br>
# 5 $\quad\quad\quad\;$ 90.2 $\quad\quad\;$ 0<br>
# 6 $\quad\quad\quad\;$ 91.7 $\quad\quad\;$ 0<br>
# 7 $\quad\quad\quad\;$ 93.1 $\quad\quad\;$ 0<br>
# 8 $\quad\quad\quad\;$ 94.3 $\quad\quad\;$ 0<br>
# 9 $\quad\quad\quad\;$ 95.3 $\quad\quad\;$ 3<br>
# 10 $\quad\quad\;\;\,\,$ 89.5 $\quad\quad\;$ 3<br>
# + [markdown] deletable=false editable=false nbgrader={"checksum": "6baffe56fd26c8c0fb1db1409801a308", "grade": false, "grade_id": "cell-c3aed944e874ac92", "locked": true, "schema_version": 1, "solution": false}
# The cell below will check that your code passes the test case above. (Your code passed if the cell runs without error.) Your solution will also be checked against hidden test cases for your final grade. (So don't hard code parameters into your solution.)
# + deletable=false editable=false nbgrader={"checksum": "8135eb9fffa77e2554bb0e5892525988", "grade": true, "grade_id": "cell-8b8cce6304cb8bfe", "locked": true, "points": 1, "schema_version": 1, "solution": false}
## Test Code for q_greedify_policy() ##
with open('section2', 'rb') as handle:
V_correct, pi_correct = pickle.load(handle)
np.testing.assert_array_almost_equal(V, V_correct)
np.testing.assert_array_almost_equal(pi, pi_correct)
# + [markdown] deletable=false editable=false nbgrader={"checksum": "e59b175ca7605a8002c2040043f7b1af", "grade": false, "grade_id": "cell-e7628124eafb2fc2", "locked": true, "schema_version": 1, "solution": false}
# ## Section 3: Value Iteration
# The city has also heard about value iteration and would like you to implement it. Value iteration works by iteratively applying the Bellman optimality equation for $v_{\ast}$ to a working value function, as an update rule, as shown below.
#
# $$\large v(s) \leftarrow \max_a \sum_{s', r} p(s', r | s, a)[r + \gamma v(s')]$$
# We have written an outline of the value iteration algorithm described in chapter 4.4 of the textbook. It is left to you to fill in the `bellman_optimality_update` function to complete the value iteration algorithm.
# + deletable=false editable=false nbgrader={"checksum": "3743399285b929801497af405783d06e", "grade": false, "grade_id": "cell-75baf962376afa7c", "locked": true, "schema_version": 1, "solution": false}
def value_iteration(env, gamma, theta):
V = np.zeros(len(env.S))
while True:
delta = 0
for s in env.S:
v = V[s]
bellman_optimality_update(env, V, s, gamma)
delta = max(delta, abs(v - V[s]))
if delta < theta:
break
pi = np.ones((len(env.S), len(env.A))) / len(env.A)
for s in env.S:
q_greedify_policy(env, V, pi, s, gamma)
return V, pi
# + deletable=false nbgrader={"checksum": "53654ee726c72456f461afd5a44aa5dc", "grade": false, "grade_id": "cell-f2c6a183cc0923fb", "locked": false, "schema_version": 1, "solution": true}
# [Graded]
def bellman_optimality_update(env, V, s, gamma):
"""Mutate ``V`` according to the Bellman optimality update equation."""
### START CODE HERE ###
G = [0]*len(env.A)
for action in env.A:
transitions = env.transitions(s, action)
for s_, (r,p) in enumerate(transitions):
G[action] += p* (r + gamma*V[s_])
V[s] = np.max(G)
### END CODE HERE ###
# + [markdown] deletable=false editable=false nbgrader={"checksum": "c5020582c7de3757fa3ece73983b61d9", "grade": false, "grade_id": "cell-d472d58e936b371e", "locked": true, "schema_version": 1, "solution": false}
# When you are ready to test the value iteration algorithm, run the cell below.
# + deletable=false editable=false nbgrader={"checksum": "cd8be31ddef5580d095a7e861e52a479", "grade": false, "grade_id": "cell-f609be2c58adc3e2", "locked": true, "schema_version": 1, "solution": false}
env = tools.ParkingWorld(num_spaces=10, num_prices=4)
gamma = 0.9
theta = 0.1
V, pi = value_iteration(env, gamma, theta)
# + [markdown] deletable=false editable=false nbgrader={"checksum": "8c88ac444253a80a377a7dce46e0c606", "grade": false, "grade_id": "cell-cba784b8d158758b", "locked": true, "schema_version": 1, "solution": false}
# You can use the ``plot`` function to visualize the final value function and policy.
# + deletable=false editable=false nbgrader={"checksum": "d18a2592a3bac43de72e18cb54357ac9", "grade": false, "grade_id": "cell-086e26bfb519a017", "locked": true, "schema_version": 1, "solution": false}
tools.plot(V, pi)
# + [markdown] deletable=false editable=false nbgrader={"checksum": "f7ee7bba538aa9300cd636c99403fd72", "grade": false, "grade_id": "cell-066f9bbdc057115b", "locked": true, "schema_version": 1, "solution": false}
# You can check your value function (rounded to one decimal place) and policy against the answer below:<br>
# State $\quad\quad$ Value $\quad\quad$ Action<br>
# 0 $\quad\quad\quad\;$ 81.6 $\quad\quad\;$ 0<br>
# 1 $\quad\quad\quad\;$ 83.3 $\quad\quad\;$ 0<br>
# 2 $\quad\quad\quad\;$ 85.0 $\quad\quad\;$ 0<br>
# 3 $\quad\quad\quad\;$ 86.8 $\quad\quad\;$ 0<br>
# 4 $\quad\quad\quad\;$ 88.5 $\quad\quad\;$ 0<br>
# 5 $\quad\quad\quad\;$ 90.2 $\quad\quad\;$ 0<br>
# 6 $\quad\quad\quad\;$ 91.7 $\quad\quad\;$ 0<br>
# 7 $\quad\quad\quad\;$ 93.1 $\quad\quad\;$ 0<br>
# 8 $\quad\quad\quad\;$ 94.3 $\quad\quad\;$ 0<br>
# 9 $\quad\quad\quad\;$ 95.3 $\quad\quad\;$ 3<br>
# 10 $\quad\quad\;\;\,\,$ 89.5 $\quad\quad\;$ 3<br>
# + [markdown] deletable=false editable=false nbgrader={"checksum": "3b65819e3413c5a6d4b8d9859f69e5b7", "grade": false, "grade_id": "cell-7408f0fb3e078296", "locked": true, "schema_version": 1, "solution": false}
# The cell below will check that your code passes the test case above. (Your code passed if the cell runs without error.) Your solution will also be checked against hidden test cases for your final grade. (So don't hard code parameters into your solution.)
# + deletable=false editable=false nbgrader={"checksum": "8330fadde649c957ab85437d34d62829", "grade": true, "grade_id": "cell-2fa266149b9ff1b1", "locked": true, "points": 1, "schema_version": 1, "solution": false}
## Test Code for bellman_optimality_update() ##
with open('section3', 'rb') as handle:
V_correct, pi_correct = pickle.load(handle)
np.testing.assert_array_almost_equal(V, V_correct)
np.testing.assert_array_almost_equal(pi, pi_correct)
# + [markdown] deletable=false editable=false nbgrader={"checksum": "167e35e35d0d33a6e9b26413281e4592", "grade": false, "grade_id": "cell-12976ff0ac11680d", "locked": true, "schema_version": 1, "solution": false}
# In the value iteration algorithm above, a policy is not explicitly maintained until the value function has converged. Below, we have written an identically behaving value iteration algorithm that maintains an updated policy. Writing value iteration in this form makes its relationship to policy iteration more evident. Policy iteration alternates between doing complete greedifications and complete evaluations. On the other hand, value iteration alternates between doing local greedifications and local evaluations.
# + deletable=false editable=false nbgrader={"checksum": "335160bd36744265e1ac43bd4305766b", "grade": false, "grade_id": "cell-e7940cfb801649be", "locked": true, "schema_version": 1, "solution": false}
def value_iteration2(env, gamma, theta):
V = np.zeros(len(env.S))
pi = np.ones((len(env.S), len(env.A))) / len(env.A)
while True:
delta = 0
for s in env.S:
v = V[s]
q_greedify_policy(env, V, pi, s, gamma)
bellman_update(env, V, pi, s, gamma)
delta = max(delta, abs(v - V[s]))
if delta < theta:
break
return V, pi
# + [markdown] deletable=false editable=false nbgrader={"checksum": "795713d092ebf77dbe0f17c46d4286cd", "grade": false, "grade_id": "cell-de841fb4eb290d56", "locked": true, "schema_version": 1, "solution": false}
# You can try the second value iteration algorithm by running the cell below.
# + deletable=false editable=false nbgrader={"checksum": "09b1fda9c335946b52cae6c8a55e80fb", "grade": false, "grade_id": "cell-2ace3a0ae8ee2e72", "locked": true, "schema_version": 1, "solution": false}
env = tools.ParkingWorld(num_spaces=10, num_prices=4)
gamma = 0.9
theta = 0.1
V, pi = value_iteration2(env, gamma, theta)
tools.plot(V, pi)
# + [markdown] deletable=false editable=false nbgrader={"checksum": "a946352618aa97fbc96962a39c135080", "grade": false, "grade_id": "cell-6bee5739d8d8ffb4", "locked": true, "schema_version": 1, "solution": false}
# ## Section 4: Asynchronous Methods
# So far in this assignment we've been working with synchronous algorithms, which update states in systematic sweeps. In contrast, asynchronous algorithms are free to update states in any order. Asynchronous algorithms can offer significant advantages in large MDPs, where even one synchronous sweep over the state space may be prohibitively expensive. One important type of asynchronous value iteration is known as real-time dynamic programming. Like sychronous value iteration, real-time dynamic programming updates a state by doing a local greedification followed by a local evaluation; unlike synchronous value iteration, real-time dynamic programming determines which state to update using the stream of experience generated by its policy. An outline of the algorithm is written below. Complete it by filling in the helper function. Remember that you are free to reuse functions that you have already written!
# + deletable=false editable=false nbgrader={"checksum": "137229f2262baebc95bb69bc7efc148b", "grade": false, "grade_id": "cell-7713cc5a92c248ea", "locked": true, "schema_version": 1, "solution": false}
def real_time_dynamic_programming(env, gamma, horizon):
V = np.zeros(len(env.S))
pi = np.ones((len(env.S), len(env.A))) / len(env.A)
s = env.random_state()
for t in range(horizon):
real_time_dynamic_programming_helper(env, V, pi, s, gamma)
a = np.random.choice(env.A, p=pi[s])
s = env.step(s, a)
return V, pi
# + deletable=false nbgrader={"checksum": "627d471847b27241a1f5b66b701b1c53", "grade": false, "grade_id": "cell-6e4cd97c16c01c1e", "locked": false, "schema_version": 1, "solution": true}
# [Graded]
def real_time_dynamic_programming_helper(env, V, pi, s, gamma):
"""Mutate ``pi`` and ``V`` appropriately."""
### START CODE HERE ###
q_greedify_policy(env, V, pi, s, gamma)
bellman_update(env, V, pi, s, gamma)
### END CODE HERE ###
# + [markdown] deletable=false editable=false nbgrader={"checksum": "5f7a90c3de0d99582546873bd9d67cdd", "grade": false, "grade_id": "cell-743c978fb8c173a8", "locked": true, "schema_version": 1, "solution": false}
# When you are ready to test the real-time dynamic programming algorithm, run the cell below.
# + deletable=false editable=false nbgrader={"checksum": "9c979297385bcf9ce4fdfbaf3ea1e45a", "grade": false, "grade_id": "cell-1e094e30adc885a5", "locked": true, "schema_version": 1, "solution": false}
env = tools.ParkingWorld(num_spaces=10, num_prices=4)
gamma = 0.9
horizon = 500
np.random.seed(101)
V, pi = real_time_dynamic_programming(env, gamma, horizon)
# + [markdown] deletable=false editable=false nbgrader={"checksum": "aec75705d27771e9ffeff3c51846f2bc", "grade": false, "grade_id": "cell-7db6a9982ded6e40", "locked": true, "schema_version": 1, "solution": false}
# You can use the ``plot`` function to visualize the final value function and policy.
# + deletable=false editable=false nbgrader={"checksum": "4673d5ded4f273d15c37366620b6c33b", "grade": false, "grade_id": "cell-bf8edaf9a039f267", "locked": true, "schema_version": 1, "solution": false}
tools.plot(V, pi)
# + [markdown] deletable=false editable=false nbgrader={"checksum": "15822b15b22c9c530798a4ab561c7739", "grade": false, "grade_id": "cell-9be12918d67720d8", "locked": true, "schema_version": 1, "solution": false}
# You can check your value function (rounded to one decimal place) and policy against the answer below:<br>
# State $\quad\quad$ Value $\quad\quad$ Action<br>
# 0 $\quad\quad\quad\;$ 79.7 $\quad\quad\;$ 0<br>
# 1 $\quad\quad\quad\;$ 81.3 $\quad\quad\;$ 0<br>
# 2 $\quad\quad\quad\;$ 83.2 $\quad\quad\;$ 0<br>
# 3 $\quad\quad\quad\;$ 84.7 $\quad\quad\;$ 0<br>
# 4 $\quad\quad\quad\;$ 86.5 $\quad\quad\;$ 0<br>
# 5 $\quad\quad\quad\;$ 87.4 $\quad\quad\;$ 0<br>
# 6 $\quad\quad\quad\;$ 89.8 $\quad\quad\;$ 0<br>
# 7 $\quad\quad\quad\;$ 91.3 $\quad\quad\;$ 0<br>
# 8 $\quad\quad\quad\;$ 91.9 $\quad\quad\;$ 0<br>
# 9 $\quad\quad\quad\;$ 93.0 $\quad\quad\;$ 3<br>
# 10 $\quad\quad\;\;\,\,$ 87.6 $\quad\quad\;$ 3<br>
#
# Notice that these values differ from those of the synchronous methods we ran to convergence, indicating that the real-time dynamic programming algorithm needs more than 500 steps to converge. One takeaway from this result is that, while asychronous methods scale better to larger MDPs, they are not always the right choice — in small MDPs in which all states are visited frequently, such as the Gridworld City parking MDP, synchronous methods may offer better performance.
# + [markdown] deletable=false editable=false nbgrader={"checksum": "58adf9da7fb4a9543b0790162648eb7f", "grade": false, "grade_id": "cell-e02c91090dc88cfb", "locked": true, "schema_version": 1, "solution": false}
# The cell below will check that your code passes the test case above. (Your code passed if the cell runs without error.) Your solution will also be checked against hidden test cases for your final grade. (So don't hard code parameters into your solution.)
# + deletable=false editable=false nbgrader={"checksum": "2549d8bea6de373349fd36d057303260", "grade": true, "grade_id": "cell-37df874cf4ed9492", "locked": true, "points": 1, "schema_version": 1, "solution": false}
## Test Code for real_time_dynamic_programming_helper() ##
with open('section4', 'rb') as handle:
V_correct, pi_correct = pickle.load(handle)
np.testing.assert_array_almost_equal(V, V_correct)
np.testing.assert_array_almost_equal(pi, pi_correct)
# + [markdown] deletable=false editable=false nbgrader={"checksum": "71b40821df7749eb1fecf4f83af1388c", "grade": false, "grade_id": "cell-6025f917f706302b", "locked": true, "schema_version": 1, "solution": false}
# ## Wrapping Up
# Congratulations, you've completed assignment 2! In this assignment, we investigated policy evaluation and policy improvement, policy iteration and value iteration, Bellman operators, and synchronous methods and asynchronous methods. Gridworld City thanks you for your service!
# -
|
C1-Fundamentals/Dynamic-Programming/C1M4_Assignment2-v2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import os
import numpy as np
import pylab
import imageio
from matplotlib import pyplot as plt
import cv2
import time
from os.path import isfile, join
from keras.applications import mobilenet
from keras.models import load_model
from scipy.ndimage.measurements import label
from scipy.ndimage.measurements import center_of_mass
from matplotlib import colors
import skimage
from keras.preprocessing.image import ImageDataGenerator
print(os.listdir('.'))
# +
# normalization
# normalize each chip
samplewise_center = True
samplewise_std_normalization = True
# normalize by larger batches
featurewise_center = False
featurewise_std_normalization = False
# adjacent pixel correllation reduction
# never explored
zca_whitening = False
zca_epsilon = 1e-6
# data augmentation
# training only
transform = 0
zoom_range = 0
color_shift = 0
rotate = 0
flip = False
datagen_test = ImageDataGenerator(
samplewise_center=samplewise_center,
featurewise_center=featurewise_center,
featurewise_std_normalization=featurewise_std_normalization,
samplewise_std_normalization=samplewise_std_normalization,
zca_whitening=zca_whitening,
zca_epsilon=zca_epsilon,
rotation_range=rotate,
width_shift_range=transform,
height_shift_range=transform,
shear_range=transform,
zoom_range=zoom_range,
channel_shift_range=color_shift,
fill_mode='constant',
cval=0,
horizontal_flip=flip,
vertical_flip=flip,
rescale=1./255,
preprocessing_function=None)
# + active=""
# generator_test = datagen_test.flow(
# 'Training_Data',
# target_size=(image_dimensions,image_dimensions),
# color_mode="rgb",
# batch_size=training_batch_size,
# class_mode='categorical',
# shuffle=True)
#
# -
# **Module to operate on each individual frame of the video**
#Load Weights
model = load_model('bebop_mobilenet_v0.h5', custom_objects={
'relu6': mobilenet.relu6,
'DepthwiseConv2D': mobilenet.DepthwiseConv2D})
def ProcessChip (frame):
#result_feature_map = np.zeros((9,16,7)) #CNN feature map to be returned
values = np.zeros((9,16,3))
chips = np.zeros((144,120,120,3))
for i in range(0,9):
for j in range(0,16):
chips[16*i+j] = frame[120*i:120*(i+1), 120*j:120*(j+1), :]
generator_test = datagen_test.flow(
chips,
batch_size=144,
shuffle=False)
#return values
return model.predict_generator(generator_test,
steps = 1)
# +
#All Decision Algo Definition
#Function to find the closest roof/driveway
def closest(list,img_center):
closest=list[0]
for c in list:
if np.linalg.norm(c-img_center) < np.linalg.norm(closest-img_center):
closest = c
return closest
#Sliding window function
def sliding_window_view(arr, shape):
n = np.array(arr.shape)
o = n - shape + 1 # output shape
strides = arr.strides
new_shape = np.concatenate((o, shape), axis=0)
new_strides = np.concatenate((strides, strides), axis=0)
return np.lib.stride_tricks.as_strided(arr ,new_shape, new_strides)
# -
##Decision algo with input of 9x16 array at which image was taken.
def decision_algo(image_frame):
image_frame[image_frame==0]=3
### READ THE ALTITUDE FROM CSV FILE ###
#Read alt.csv
with open('alt.csv', 'r') as csvfile:
alt_list = [line.rstrip('\n') for line in csvfile]
#Choose last value in alt_list
altitude=int(alt_list[-1]) #in meters
### ALGORITHM TO FIND CLOSEST DRIVEWAY ###
#Center of the 9x16 array
img_center=np.array([4,7.5])
#Label all the driveways and roofs
driveway, num_driveway = label(image_frame==1)
roof, num_roof = label(image_frame==2)
#Save number of driveways and roofs into array
d=np.arange(1,num_driveway+1)
r=np.arange(1,num_roof+1)
if(len(d)<1):
print("No driveway found, return to base")
else:
#Find the center of the all the driveways
driveway_center=center_of_mass(image_frame,driveway,d)
roof_center=center_of_mass(image_frame,roof,r)
#Find the closest roof to the center of the image
if(len(roof_center)>0):
closest_roof=closest(roof_center,img_center)
else:
#if no roof is found, set closest_roof as center of image
closest_roof=img_center
print("Roof center list empty")
#Find the closest driveway to the closest roof
closest_driveway=closest(driveway_center,np.asarray(closest_roof))
### ALGORITHM TO FIND 3x3 DRIVEWAY TO LAND ###
#If altitude is 5m or less, look for a 3x3 sliding window of 1's, if found, Land.
#At 5m, a 3x3 will be equivalent to 1.5m x 1.5m.
if(altitude<=5.0):
#Creates a 7x10 ndarray with all the 3x3 submatrices
sub_image=sliding_window_view(image_frame,(3,3))
#Empty list
driveway_list=[]
#Loop through the 7x14 ndarray
for i in range(0,7):
for j in range(i,14):
#Calculate the total of the submatrices
output=sum(sum(sub_image[i,j]))
#if the output is 9, that means we have a 3x3 that is all driveway
if output==9:
#append the i(row) and j(column) to a list declared previously
#we add 1 to the i and j to find the center of the 3x3
driveway_list.append((i+1,j+1))
if(len(driveway_list)>0):
#Call closest function to find driveway closest to house.
closest_driveway=closest(driveway_list,np.asarray(closest_roof))
print(closest_driveway)
print("Safe to land")
else:
print("Need to fly lower")
### SCALE CLOSEST DRIVEWAY CENTER TO REAL WORLD COORDINATES AND SAVE TO CSV ###
scaler=0.205/(216.26*altitude**-0.953) #m/pixel
if(len(driveway_center)>0):
print (closest_driveway)
move_coordinates=([4,7.5]-np.asarray(closest_driveway)) #Find coordinates relative to center of image
move_coordinates=np.asarray(move_coordinates)*np.asarray(scaler)*120 #60 is the center of the 120x120 superpixel
move_coordinates=np.append(move_coordinates,(altitude-2)) #Add altitude to array
print (move_coordinates)
with open('coords.csv', 'w') as csvfile:
filewriter = csv.writer(csvfile, delimiter=',')
filewriter.writerow(move_coordinates)
with open('coordinates_history.csv', 'a', newline='') as csvfile:
filewriter = csv.writer(csvfile, delimiter=',')
filewriter.writerow(move_coordinates)
return
def heatmap (feature_map, frame):
color_mask = np.zeros((1080,1920,3))
temp_frame = skimage.img_as_float(frame)
alpha = 0.6
for i in range (0,9):
for j in range (0,16):
if feature_map[i][j] == 2:
color_mask[120*i:120*(i+1), 120*j:120*(j+1), :] = [0, 0, 1] #Blue, House
elif feature_map[i][j] == 1:
color_mask[120*i:120*(i+1), 120*j:120*(j+1), :] = [0, 1, 0] #Green, Concrete
else:
color_mask[120*i:120*(i+1), 120*j:120*(j+1), :] = [1, 0, 0] #Red, Don't Care
color_mask_hsv = colors.rgb_to_hsv(color_mask)
frame_hsv = colors.rgb_to_hsv(temp_frame)
frame_hsv[..., 0] = color_mask_hsv[..., 0]
frame_hsv[..., 1] = color_mask_hsv[..., 1] * alpha
frame_masked = colors.hsv_to_rgb(frame_hsv)
return frame_masked
def correct_arr (arr) :
arr = arr + 1
arr[arr>2] = 0
return arr
# **Module to iterate through each frame in video**
def VideoToFrames (vid):
count = 0 # Can be removed. Just to verify number of frames
#count_pavement = []
t = time.time()
for image in vid.iter_data(): #Iterate through every frame in Video
#image: numpy array containing image information
if count % 100 == 0:
feature_map = ProcessChip(image)
arr = heatmap(np.reshape(correct_arr(np.argmax(ProcessChip(image), axis=1)), (9,16)), image)
cv2.imwrite('./Frames_New//frame%d.jpg'%count, arr*255)
count += 1
elapsed = time.time() - t
return elapsed
# + active=""
# if count % 600 == 0:
# print (count)
# feature_map = ProcessChip(image)
# arr = correct_arr(np.argmax(ProcessChip(image), axis=1))
# arr = np.reshape(arr,(9,16))
# plt.imshow(heatmap(arr, image), interpolation='nearest')
# plt.show()
# -
def convert_frames_to_video(pathIn,pathOut,fps):
frame_array = []
files = [f for f in os.listdir(pathIn) if isfile(join(pathIn, f))]
#for sorting the file names properly
files.sort(key = lambda x: int(x[5:-4]))
for i in range(len(files)):
filename=pathIn + files[i]
#reading each file
img = cv2.imread(filename)
height, width, layers = img.shape
size = (width,height)
print(filename)
#inserting the frames into an image array
frame_array.append(img)
out = cv2.VideoWriter(pathOut,cv2.VideoWriter_fourcc(*'DIVX'), fps, size)
for i in range(len(frame_array)):
# writing to a image array
out.write(frame_array[i])
out.release()
filename = './Bebop/Bebop2_20180422173922-0700.mp4' #Add path to video file
vid = imageio.get_reader(filename, 'ffmpeg') #You can use any reader of your choice
#print (vid.iter_data())
time_taken = VideoToFrames(vid) #Passing the video to be analyzed frame by frame
print ('Total time taken %s'%time_taken)
convert_frames_to_video('./Frames_New/', 'out1.mp4', 2.5)
|
Working CNN (Clean).ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# +
import sys
sys.path.append('../')
from torch.utils.data import TensorDataset
from torch import Tensor
from torch.distributions.multivariate_normal import MultivariateNormal
import matplotlib
import seaborn as sns; sns.set_style('white')
from main import *
plt = matplotlib.pyplot
# + [markdown] pycharm={"name": "#%% md\n"}
# MathJax.Hub.Config({
# TeX: { equationNumbers: { autoNumber: "AMS" } }
# });
#
# # Introduction
# Though the Bayesian paradigm is theoretically appealing, it has proved difficult to apply in deep learning.
# Consider a neural network $f_\theta: X \to Y$. For illustrative purposes, suppose the model is given by
# $$
# p(y|x,\theta) \propto \exp\{-|| y - f_\theta(x) ||^2/2\}
# $$
# Let $\varphi(\theta)$ be the prior distribution and $p(\mathcal D_n |\theta) = \Pi_{i=1}^n p(y_i | x_i, \theta)$ be the likelihood of the data $\mathcal D_n = \{(x_i,y_i)\}_{i=1}^n$. Then the posterior distribution of $\theta$ is given by
# $$
# p(\theta | \mathcal D_n) \propto p(\mathcal D_n | \theta) \varphi(\theta).
# $$
# The normalizing constant in the posterior distribution is an intractable integral. Many methods for sampling from the posterior, e.g., MCMC, variational inference, will encounter extra difficulty when $\theta$ is a high dimensional neural network weight.
#
# Leaving aside the fact that the posterior is hard to sample, let's see why we should care about the posterior distribution in the first place. In the Bayesian paradigm, we predict using a distribution
# $$
# p(y|x, \mathcal D_n) = \int p(y|x,\theta) p(\theta|\mathcal D_n) \,d\theta
# $$
# Thus instead of providing a point estimate $\hat y$ for input $\hat x$, we can form an entire distribution estimate which lends itself naturally to uncertainty quantification.
#
# There is yet another advantage to Bayesian prediction, perhaps less well documented in the deep learning community. Neural networks are singular models. In terms of generalization, Bayesian prediction is better than MAP or MLE for singular models. This phenomenon is what we seek to elucidate in this work.
#
# # Generalization error
#
#
# Suppose $\hat q_n(y|x)$ is some estimate of the true unknown conditional density $q(y|x)$. The generalization error of the prediction $\hat q(y|x)$ is defined as
# $$
# G(n) = KL (q(y|x) || \hat q(y|x) ) = \int \int q(y|x) \log \frac{q(y|x)}{\hat q_n(y|x)} \,dy q(x) \,dx
# $$
# We've written this in terms of the sample size $n$ to remind ourselves that $\hat q_n$ is formed using $\mathcal D_n$.
#
# We will consider three predictors of $q(y|x)$:
# # + Bayesian predictive distribution $\hat q(y|x) = p(y|x,\mathcal D_n)$
# # + MAP $\hat q(y|x) = p(y|x,\theta_n^{MAP}$)
# # + MLE $\hat q(y|x) = p(y|x,\theta_n^{MLE}$)
#
# To average out the randomness in the dataset $\mathcal D_n$ used to form the predictors, we will ultimately look at the average generalization error
# \begin{equation}
# E_n G(n)
# \label{eq:avgGn}
# \end{equation}
# where $E_n$ denotes expectation over the dataset $\mathcal D_n$. In simulations, we calculate the average generalization error using a held-out-test set $T_{n'} = \{(x_i',y_i')\}_{i=1}^{n'}$ as
# \begin{equation}
# \frac{1}{n'} \sum_{i=1}^{n'} \log q(y_i'|x_i') - E_n \frac{1}{n'} \sum_{i=1}^{n'} \log \hat q_n(y_i'|x_i')
# \label{eq:computed_avgGn}
# \end{equation}
# Assume the held-out test set is large enough so that the difference between \eqref{eq:avgGn} and \eqref{eq:computed_avgGn} is negligible. We will refer to them interchangeably as the average generalization error.
#
# # Bayes versus MAP versus MLE in singular models
#
# A singular model is ...
#
# Neural networks are singular models because ...
#
# Since $p(y|x,\theta)$ is singular, we look to Watanabe's singular learnng theory to understand the generalization error of the various predictors considered. Assume the true distribution is realizable by the model, i.e., $q(y|x) = p(y|x,\theta_0)$ for some $\theta_0$ (though we will investigate violations of this assumption in the experiments).
#
# We have the following asymptotic expansions of the generalization error for singular models.
# # + For Bayes, $E_n G(n) = \lambda/n + o(1/n)$ where $\lambda \in \mathbb Q^+$ is a positive rational number known as the learning coefficient. The learning coefficient is completely determined by the the truth-model-prior triplet $( q(y|x), p(y|x,\theta), \varphi(\theta) )$. Most of the time $\lambda << dim(\theta)/2$
# # + For MAP and MLE, $E_n G(n) = C/n + o(1/n)$ (different $C$'s for MAP and MLE). Basically $C$ is the maximum of some Gaussian process, which can easily be greater than $dim(\theta)/2$. Watanabe's Main Theorem 6.4 gives the precise formulation.
#
# # Last layer Bayesian
#
# Though the Bayes predictive distribution is provably superior to MAP and MLE, it relies on the intractable posterior distribution. As a workaround, we form the predictive distribution only in the last layer(s) of a deep neural network. Since a neural network $f_\theta$ is naturally hierarchical, we break it up into $f_\theta = h_w \circ g_v$ where $\theta = (v,w)$ with $dim(w)$ being small enough to manageably perform MCMC.
#
# Let $\theta_{map} = (v_{map},w_{map})$. Let $\tilde x_i = g_{v_{map}}(x_i)$. Define a new transformed dataset $\tilde{\mathcal D_n} = \{(\tilde x_i, y_i) \}_{i=1}^n$. We perform MCMC to sample the posterior over $w$:
# $$
# p(w | \tilde{\mathcal D_n}) \propto p(\tilde{\mathcal D_n} | w) \varphi(w) = \Pi_{i=1}^n \exp\{-|| y_i - h_w \circ g_{v_{map}}(x_i) ||^2/2\} \varphi(w)
# $$
#
# Define the last layer Bayesian predictive distribution to be
# $$
# p_{LLB}(y|x, \mathcal D_n) = \int p(y|x,(v_{map},w)) p(w|\tilde{\mathcal D_n}) \,dw
# $$
# We have to be careful when we speak of the generalization error of the LLB predictive distribution. For a proper comparison to $E_n G_{map}(n)$ or $E_n G_{mle}(n)$, we have to look at
# \begin{equation}
# E_n G_{LLB}(n) = KL (q(y|x) || p_{LLB}(y|x, \mathcal D_n) )
# \label{G_LLB}
# \end{equation}
# where $E_n$ averages out the randomness of both $D_n$ and $v_{map}$.
#
# An alternative is to condition on $v_{map}$, using $g_{v_{map}}$ as a feature extractor in a preprocessing step. Then, assuming realizability $q(y|x) = p(y|x,(v_0,w_0))$ we may examine the generalizaton error
# \begin{equation}
# E_{\mathcal D_n | v_{map}} KL( p(y|x,(v_{map},w_0)) || p_{LLB}(y|x, \mathcal D_n) )
# \label{G_LLB_vfixed}
# \end{equation}
# The average generalization error in \eqref{G_LLB_vfixed} is distinctly different from the one for LLB in \eqref{G_LLB}. The nice thing about \eqref{G_LLB_vfixed} is that we know its asymptotic expansion is $\lambda/n$ where $\lambda$ corresponds to the triplet $( p(y|x,(v_{map},w_0)), p(y| x, (v_{map},w)), \varphi(w))$. For certain functions $h_w$ where the true $\lambda$ is known, we can verify this in the experiments. (Not implemented yet).
#
# So we have various (average) generalization errors we are interested in
# # + $E_n G_{post}(n)$ corresponding to the full posterior over $\theta$
# # + $E_n G_{map}(n)$
# # + $E_n G_{mle}(n)$
# # + $E_n G_{LLB}(n)$
# # + Generalization error in \eqref{G_LLB_vfixed}. (don't have a name for it yet)
#
#
# Theory guarantees the following relationships:
# # + $E_n G_{post}(n)$ has smaller learning coefficient than either $E_n G_{map}(n)$ or $E_n G_{mle}(n)$
# # + \eqref{G_LLB_vfixed} = known $\lambda$/n + o(1/n) for certain $h_w$.
#
# The question is, what is the behavior of $E_n G_{LLB}(n)$? Two hunches
# # + Though LLB is different from full posterior predictive distribution, it's still better than map or mle, i.e., $E_n G_{LLB}(n) \le E_n G_{map}(n)$.
# # + $E_n G_{LLB}(n)$ is different from \eqref{G_LLB_vfixed} but perhaps asymptotially they share the same leading term $\lambda/n$?
# We'll set out to investigate these conjectures in the following experiment.
# -
# # Experiments
#
# Consider a neural network where $h_w$ is a reduced-rank regression network and $g_v$ is a block of linear composed with ReLU layers.
#
class Model(nn.Module):
def __init__(self, input_dim, output_dim, ffrelu_hidden, rr_hidden):
super(Model, self).__init__()
self.feature_map = nn.Sequential(
nn.Linear(input_dim, ffrelu_hidden),
nn.ReLU(),
nn.Linear(ffrelu_hidden, ffrelu_hidden),
nn.ReLU(),
nn.Linear(ffrelu_hidden, input_dim),
)
self.rr = nn.Sequential(
nn.Linear(input_dim, rr_hidden, bias=False),
nn.Linear(rr_hidden, output_dim, bias=False)
)
def forward(self, x):
x = self.feature_map(x)
return self.rr(x)
# We use the following values for the parameters
# + input_dim = output_dim = rr_hidden = 3
# + ffrelu_hidden = 5
#
#
# We generate the training data as follows:
# + $X \sim N(0,\sigma_x^2 I_3)$
# + realizability
# + realizable $Y \sim N(f_{\theta_0}(X),\sigma_y^2 I_3)$
# + not realizable $Y \sim N(h_{w_0}(X),\sigma_y^2 I_3)$
#
# For the testing data, we consider a possible change in the support of $X$:
# + $X \sim \alpha N(0,\sigma_x^2 I_3)$ for some scale $\alpha \in \mathbb R^+$.
def get_data(args):
train_size = int(args.n)
valid_size = int(args.n * 0.5)
test_size = int(10000)
a = Normal(0.0, 1.0)
a_params = 0.2 * a.sample((args.input_dim, args.rr_hidden))
b = Normal(0.0, 1.0)
b_params = 0.2 * b.sample((args.rr_hidden, args.output_dim))
X_rv = MultivariateNormal(torch.zeros(args.input_dim), torch.eye(args.input_dim))
y_rv = MultivariateNormal(torch.zeros(args.output_dim), torch.eye(args.output_dim))
true_model = Model(args.input_dim, args.output_dim, args.ffrelu_hidden, args.rr_hidden)
true_model.eval()
with torch.no_grad():
# training +valid data
X = X_rv.sample(torch.Size([train_size+valid_size]))
if args.realizable:
true_mean = true_model(X)
else:
true_mean = torch.matmul(torch.matmul(X, a_params), b_params)
y = true_mean + y_rv.sample(torch.Size([train_size+valid_size]))
dataset_train, dataset_valid = torch.utils.data.random_split(TensorDataset(X, y),[train_size,valid_size])
# testing data
X = args.X_test_std * X_rv.sample(torch.Size([test_size]))
if args.realizable:
true_mean = true_model(X)
else:
true_mean = torch.matmul(torch.matmul(X, a_params), b_params)
y = true_mean + y_rv.sample(torch.Size([test_size]))
dataset_test = TensorDataset(X, y)
oracle_mse = (torch.norm(y - true_mean, dim=1)**2).mean()
entropy = -torch.log((2 * np.pi) ** (-args.output_dim / 2) * torch.exp(
-(1 / 2) * torch.norm(y - true_mean, dim=1) ** 2)).mean()
train_loader = torch.utils.data.DataLoader(dataset_train, batch_size=args.batchsize, shuffle=True)
valid_loader = torch.utils.data.DataLoader(dataset_valid, batch_size=args.batchsize, shuffle=True)
test_loader = torch.utils.data.DataLoader(dataset_test, batch_size=args.batchsize, shuffle=True)
return train_loader, valid_loader, test_loader, oracle_mse, entropy
# Note that the way MAP training is usually conducted in deep learning may involve early stopping. Watanabe's theory does not account for early stopping. We will try MAP training with and without early stopping.
#
def map_train(args, X_train, Y_train, X_valid, Y_valid, X_test, Y_test, oracle_mse):
model = Model(args.input_dim, args.output_dim, args.ffrelu_hidden, args.rr_hidden)
opt = optim.SGD(model.parameters(), lr=1e-3, momentum=0.9, weight_decay=5e-4)
early_stopping = EarlyStopping(patience=10, verbose=False, taskid=args.taskid)
# TODO: is it necessary to implement mini batch SGD?
for it in range(5000):
model.train()
y_pred = model(X_train).squeeze()
l = (torch.norm(y_pred - Y_train, dim=1)**2).mean()
l.backward()
opt.step()
opt.zero_grad()
model.eval()
with torch.no_grad():
valid_loss = (torch.norm(model(X_valid).squeeze() - Y_valid, dim=1)**2).mean()
if it % 100 == 0:
model.eval()
ytest_pred = model(X_test).squeeze()
test_loss = (torch.norm(ytest_pred - Y_test, dim=1)**2).mean()
print('MSE: train {:.3f}, validation {:.3f}, test {:.3f}, oracle on test set {:.3f}'.format(l.item(), valid_loss, test_loss.item(), oracle_mse))
if args.early_stopping:
early_stopping(valid_loss, model)
if early_stopping.early_stop:
print("Early stopping")
break
return model
# The last function we will need is for drawing samples from the last layers. Although the code supports implicit variational inference (and even explicit variational inference), only the MCMC (NUTS) will be considered in the experiments.
def lastlayer_approxinf(model, args, X_train, Y_train, X_valid, Y_valid, X_test, Y_test):
transformed_X_train = model.feature_map(X_train)
transformed_X_valid = model.feature_map(X_valid)
transformed_X_test = model.feature_map(X_test)
transformed_train_loader = torch.utils.data.DataLoader(
TensorDataset(Tensor(transformed_X_train), torch.as_tensor(Y_train, dtype=torch.long)),
batch_size=args.batchsize, shuffle=True)
transformed_valid_loader = torch.utils.data.DataLoader(
TensorDataset(Tensor(transformed_X_valid), torch.as_tensor(Y_valid, dtype=torch.long)),
batch_size=args.batchsize, shuffle=True)
if args.posterior_method == 'ivi':
# parameters for train_implicitVI
mc = 1
beta_index = 0
args.betas = [1.0]
saveimgpath = None
args.dataset = 'reducedrank_synthetic'
args.H = args.rr_hidden
# TODO: strip train_implicitVI to simplest possible inputs
G = train_implicitVI(transformed_train_loader, transformed_valid_loader, args, mc, beta_index, saveimgpath)
eps = torch.randn(args.R, args.epsilon_dim)
sampled_weights = G(eps)
list_of_param_dicts = weights_to_dict(args, sampled_weights)
pred_prob = 0
output_dim = transformed_X_test.shape[1]
for param_dict in list_of_param_dicts:
mean = torch.matmul(torch.matmul(transformed_X_test, param_dict['a']), param_dict['b'])
pred_prob += (2 * np.pi) ** (-output_dim / 2) * torch.exp(-(1 / 2) * torch.norm(Y_test - mean, dim=1) ** 2)
elif args.posterior_method == 'mcmc':
wholex = transformed_train_loader.dataset[:][0]
wholey = transformed_train_loader.dataset[:][1]
beta = 1.0
kernel = NUTS(conditioned_pyro_rr, adapt_step_size=True)
mcmc = MCMC(kernel, num_samples=args.R, warmup_steps=args.num_warmup, disable_progbar=True)
mcmc.run(pyro_rr, wholex, wholey, args.rr_hidden, beta)
sampled_weights = mcmc.get_samples()
pred_prob = 0
output_dim = wholey.shape[1]
for r in range(0, args.R):
mean = torch.matmul(torch.matmul(transformed_X_test, sampled_weights['a'][r,:,:]), sampled_weights['b'][r,:,:])
pred_prob += (2 * np.pi) ** (-output_dim / 2) * torch.exp(-(1 / 2) * torch.norm(Y_test - mean, dim=1) ** 2)
return -torch.log(pred_prob / args.R).mean()
# We set the arguments below. We are interested in examining the following three factors
# + realizability or not
# + support of $X_{test}$
# + early stopping or not
#
# For the realizable plus non-early-stopping setting, we expect the learning coefficient for the last layer Bayes predictive distribution to match the theoretically known values of $\lambda$ for reduced rank regression. Watanabe's theory, as it stands, seems unable to say anything meaningful in the case $q$ is unrealizable by the model or in the case that MAP is trained using early stopping.
#
# The computational overhead comes from the following variables:
# + num_warmup: burn-in for MCMC
# + MCs: number of training datasets for assessing $E_n$
# + num_n: number of sample sizes considered for drawing learning curve $1/n$ versus $E_n G(n)$
# + R: number of MCMC samples from the posterior
#
# We've set these numbers to be very small for the purpose of running quickly in the notebook.
# + pycharm={"name": "#%%\n"}
class Args:
taskid = 1
input_dim = 3
output_dim = 3
X_test_std = 1.0 # play around with
realizable = 1 # play around with
ffrelu_hidden = 5
rr_hidden = 3
early_stopping = 0 # play around with
posterior_method = 'mcmc'
num_warmup = 10
batchsize = 50
# epsilon_mc = 100
# epochs = 100
# pretrainDepochs = 100
# trainDepochs = 20
# n_hidden_D = 128
# num_hidden_layers_D = 1
# n_hidden_G = 128
# num_hidden_layers_G = 1
# lr_primal = 0.01
# lr_dual = 0.001
MCs = 5
R = 10
num_n = 10
no_cuda = True
log_interval = 500
args=Args()
args.cuda = not args.no_cuda and torch.cuda.is_available()
# change to boolean
if args.early_stopping == 0:
args.early_stopping = False
else:
args.early_stopping = True
if args.realizable == 0:
args.realizable = False
else:
args.realizable = True
args.epsilon_dim = args.rr_hidden*(args.input_dim + args.output_dim)
# TODO: w_dim and total_param_count depend on model and shouldn't be hardcoded as follows
args.w_dim = args.rr_hidden*(args.input_dim + args.output_dim)
total_param_count = (args.input_dim + args.rr_hidden + args.input_dim) * args.rr_hidden + args.w_dim
# -
# Below we plot the learning curve, i.e., $n$ versus $E_n G(n)$. (Actually we'll plot $1/n$ versus $E_n G(n)$ to easily assess whether the slope matches the theoretical $\lambda$.)
# + pycharm={"name": "#%%\n"}
avg_lastlayerbayes_gen_err = np.array([])
std_lastlayerbayes_gen_err = np.array([])
avg_map_gen_err = np.array([])
std_map_gen_err = np.array([])
avg_entropy = np.array([])
std_entropy = np.array([])
n_range = np.round(1/np.linspace(1/200,1/10000,args.num_n))
for n in n_range:
map_gen_err = np.empty(args.MCs)
lastlayerbayes_gen_err = np.empty(args.MCs)
entropy_array = np.empty(args.MCs)
args.n = n
for mc in range(0, args.MCs):
train_loader, valid_loader, test_loader, oracle_mse, entropy = get_data(args)
entropy_array[mc] = entropy
X_train = train_loader.dataset[:][0]
Y_train = train_loader.dataset[:][1]
X_valid = valid_loader.dataset[:][0]
Y_valid = valid_loader.dataset[:][1]
X_test = test_loader.dataset[:][0]
Y_test = test_loader.dataset[:][1]
model = map_train(args, X_train, Y_train, X_valid, Y_valid, X_test, Y_test, oracle_mse)
model.eval()
map_gen_err[mc] = -torch.log((2*np.pi)**(-args.output_dim /2) * torch.exp(-(1/2) * torch.norm(Y_test-model(X_test), dim=1)**2)).mean() - entropy
Bmap = list(model.parameters())[-1]
Amap = list(model.parameters())[-2]
params = (args.input_dim, args.output_dim, np.linalg.matrix_rank(torch.matmul(Bmap, Amap).detach().numpy()), args.rr_hidden)
trueRLCT = theoretical_RLCT('rr', params)
print('true RLCT {}'.format(trueRLCT))
lastlayerbayes_gen_err[mc] = lastlayer_approxinf(model, args, X_train, Y_train, X_valid, Y_valid, X_test, Y_test) - entropy
print('n = {}, mc {}, gen error: map {}, bayes last layer {}'
.format(n, mc, map_gen_err[mc], lastlayerbayes_gen_err[mc]))
print('average gen error: MAP {}, bayes {}'
.format(map_gen_err.mean(), lastlayerbayes_gen_err.mean()))
avg_lastlayerbayes_gen_err = np.append(avg_lastlayerbayes_gen_err, lastlayerbayes_gen_err.mean())
std_lastlayerbayes_gen_err = np.append(std_lastlayerbayes_gen_err, lastlayerbayes_gen_err.std())
avg_map_gen_err = np.append(avg_map_gen_err, map_gen_err.mean())
std_map_gen_err = np.append(std_map_gen_err, map_gen_err.std())
avg_entropy = np.append(avg_entropy, entropy_array.mean())
std_entropy = np.append(std_entropy, entropy_array.std())
print('avg LLB gen err {}, std {}'.format(avg_lastlayerbayes_gen_err, std_lastlayerbayes_gen_err))
print('avg MAP gen err {}, std {}'.format(avg_map_gen_err, std_map_gen_err))
if args.realizable:
ols_map = OLS(avg_map_gen_err, 1 / n_range).fit()
map_slope = ols_map.params[0]
ols_llb = OLS(avg_lastlayerbayes_gen_err, 1 / n_range).fit()
llb_intercept = 0.0
llb_slope = ols_llb.params[0]
else:
ols_map = OLS(avg_map_gen_err, add_constant(1 / n_range)).fit()
map_slope = ols_map.params[1]
ols_llb = OLS(avg_lastlayerbayes_gen_err, add_constant(1 / n_range)).fit()
llb_intercept = ols_llb.params[0]
llb_slope = ols_llb.params[1]
print('estimated RLCT {}'.format(llb_slope))
#
fig, ax = plt.subplots()
ax.errorbar(1/n_range, avg_lastlayerbayes_gen_err, yerr=std_lastlayerbayes_gen_err, fmt='-o', c='r', label='En G(n) for last layer Bayes predictive')
ax.errorbar(1/n_range, avg_map_gen_err, yerr=std_map_gen_err, fmt='-o', c='g', label='En G(n) for MAP')
plt.plot(1 / n_range, llb_intercept + llb_slope / n_range, 'r--', label='ols fit for last-layer-Bayes')
plt.xlabel('1/n')
plt.title('map slope {:.2f}, parameter count {}, LLB slope {:.2f}, true RLCT {}'.format(map_slope, total_param_count, llb_slope, trueRLCT))
plt.legend()
plt.savefig('taskid{}.png'.format(args.taskid))
plt.show()
# -
# The graph produced plots $1/n$ versus average generalizaton error $E_n G(n)$ for MAP predictor and LLB predictive distribution. Vertical bars indicate 1 std deviation over the different Monte Carlo training-testing sets. The LLB learning coefficient (LLB slope) indicated in the title of the graph should match the "true RLCT." In addition, the MAP learning coefficient (map slope) should be bigger than the LLB slope according to theory.
# + pycharm={"name": "#%%\n"}
# -
# Below we plot the learning curve, i.e., $n$ versus $E_n G(n)$. (Actually we'll plot $1/n$ versus $E_n G(n)$ to easily assess whether the slope matches the theoretical $\lambda$.)
# +
avg_lastlayerbayes_gen_err = np.array([])
std_lastlayerbayes_gen_err = np.array([])
avg_map_gen_err = np.array([])
std_map_gen_err = np.array([])
avg_entropy = np.array([])
std_entropy = np.array([])
n_range = np.round(1/np.linspace(1/200,1/10000,args.num_n))
for n in n_range:
map_gen_err = np.empty(args.MCs)
lastlayerbayes_gen_err = np.empty(args.MCs)
entropy_array = np.empty(args.MCs)
args.n = n
for mc in range(0, args.MCs):
train_loader, valid_loader, test_loader, oracle_mse, entropy = get_data(args)
entropy_array[mc] = entropy
X_train = train_loader.dataset[:][0]
Y_train = train_loader.dataset[:][1]
X_valid = valid_loader.dataset[:][0]
Y_valid = valid_loader.dataset[:][1]
X_test = test_loader.dataset[:][0]
Y_test = test_loader.dataset[:][1]
model = map_train(args, X_train, Y_train, X_valid, Y_valid, X_test, Y_test, oracle_mse)
model.eval()
map_gen_err[mc] = -torch.log((2*np.pi)**(-args.output_dim /2) * torch.exp(-(1/2) * torch.norm(Y_test-model(X_test), dim=1)**2)).mean() - entropy
Bmap = list(model.parameters())[-1]
Amap = list(model.parameters())[-2]
params = (args.input_dim, args.output_dim, np.linalg.matrix_rank(torch.matmul(Bmap, Amap).detach().numpy()), args.rr_hidden)
trueRLCT = theoretical_RLCT('rr', params)
print('true RLCT {}'.format(trueRLCT))
lastlayerbayes_gen_err[mc] = lastlayer_approxinf(model, args, X_train, Y_train, X_valid, Y_valid, X_test, Y_test) - entropy
print('n = {}, mc {}, gen error: map {}, bayes last layer {}'
.format(n, mc, map_gen_err[mc], lastlayerbayes_gen_err[mc]))
print('average gen error: MAP {}, bayes {}'
.format(map_gen_err.mean(), lastlayerbayes_gen_err.mean()))
avg_lastlayerbayes_gen_err = np.append(avg_lastlayerbayes_gen_err, lastlayerbayes_gen_err.mean())
std_lastlayerbayes_gen_err = np.append(std_lastlayerbayes_gen_err, lastlayerbayes_gen_err.std())
avg_map_gen_err = np.append(avg_map_gen_err, map_gen_err.mean())
std_map_gen_err = np.append(std_map_gen_err, map_gen_err.std())
avg_entropy = np.append(avg_entropy, entropy_array.mean())
std_entropy = np.append(std_entropy, entropy_array.std())
print('avg LLB gen err {}, std {}'.format(avg_lastlayerbayes_gen_err, std_lastlayerbayes_gen_err))
print('avg MAP gen err {}, std {}'.format(avg_map_gen_err, std_map_gen_err))
if args.realizable:
ols_map = OLS(avg_map_gen_err, 1 / n_range).fit()
map_slope = ols_map.params[0]
ols_llb = OLS(avg_lastlayerbayes_gen_err, 1 / n_range).fit()
llb_intercept = 0.0
llb_slope = ols_llb.params[0]
else:
ols_map = OLS(avg_map_gen_err, add_constant(1 / n_range)).fit()
map_slope = ols_map.params[1]
ols_llb = OLS(avg_lastlayerbayes_gen_err, add_constant(1 / n_range)).fit()
llb_intercept = ols_llb.params[0]
llb_slope = ols_llb.params[1]
print('estimated RLCT {}'.format(llb_slope))
#
fig, ax = plt.subplots()
ax.errorbar(1/n_range, avg_lastlayerbayes_gen_err, yerr=std_lastlayerbayes_gen_err, fmt='-o', c='r', label='En G(n) for last layer Bayes predictive')
ax.errorbar(1/n_range, avg_map_gen_err, yerr=std_map_gen_err, fmt='-o', c='g', label='En G(n) for MAP')
plt.plot(1 / n_range, llb_intercept + llb_slope / n_range, 'r--', label='ols fit for last-layer-Bayes')
plt.xlabel('1/n')
plt.title('map slope {:.2f}, parameter count {}, LLB slope {:.2f}, true RLCT {}'.format(map_slope, total_param_count, llb_slope, trueRLCT))
plt.legend()
plt.savefig('taskid{}.png'.format(args.taskid))
plt.show()
# -
# The graph produced plots $1/n$ versus average generalizaton error $E_n G(n)$ for MAP predictor and LLB predictive distribution. Vertical bars indicate 1 std deviation over the different Monte Carlo training-testing sets. The LLB learning coefficient (LLB slope) indicated in the title of the graph should match the "true RLCT." In addition, the MAP learning coefficient (map slope) should be bigger than the LLB slope according to theory.
# # Related work
#
# Is this last-layer-Bayesian approach common? Has anyone written about this formally? In a quick search, I can only find rough heuristics similar in spirit to what I'm doing:
#
# + [blog post](https://towardsdatascience.com/probabilistic-machine-learning-series-post-1-c8809652dd60) uses LSTM as feature extractor then performs Bayesian inference on linear last layer
# + [Snoek et. al 2017 ICML](http://proceedings.mlr.press/v37/snoek15.pdf) calls this approach the well-known adaptive basis regression
# + [Kristiadi et. al 2020 ICML](https://arxiv.org/pdf/2002.10118.pdf) appends linear last layer to beginning ReLU blocks, then uses Laplace approximation to perform Bayesian inference in the last layer.
|
notebooks/lastlayerbayesian.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="JmkqzqUpw-Hd"
# # Session 6: Encoder-Decoder
# ---
# + colab={"base_uri": "https://localhost:8080/"} id="GDaLXki6pgJ2" outputId="500c3a2d-e522-479f-c7cd-838c89781d04"
from google.colab import drive
drive.mount('/content/gdrive', force_remount=True)
# + [markdown] id="EAILL4Ffw9x4"
# ## Import libraries
# + colab={"base_uri": "https://localhost:8080/"} id="PWMvOrzPeopS" outputId="95d2a8a1-fdff-4217-d02e-a956fb3a36c4"
# Download these NLTK packages
import nltk
nltk.download('punkt')
nltk.download('stopwords')
nltk.download('averaged_perceptron_tagger')
nltk.download('maxent_ne_chunker')
nltk.download('words')
nltk.download('wordnet')
# + id="av7eDoJAhHhq"
# Import necessary libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
import nltk, time
from nltk.tokenize import word_tokenize
from nltk.corpus import stopwords
from collections import Counter
from nltk.stem import WordNetLemmatizer
import collections, itertools
# + id="f5gvZJGsI504"
import os
base_path = 'gdrive/MyDrive/TSAI_END2/Session6/'
data_path = base_path + 'data/'
data_filename = 'tweets.csv'
# + [markdown] id="6ZXjJ8j7xL-2"
# ## Dataset Creation
# ---
# + id="IImUW6D8VTvV"
import pandas as pd
tweets_data = pd.read_csv(os.path.join(data_path,data_filename))
# + colab={"base_uri": "https://localhost:8080/", "height": 417} id="ywVu1CVBY-oO" outputId="be6c1072-6d72-447c-8d74-5526e8139849"
tweets_data
# + [markdown] id="FBc_eSRxxSVD"
# ### EDA
# ---
# + colab={"base_uri": "https://localhost:8080/"} id="x6sWQrZ6ZGmc" outputId="b4c2d95f-d954-400f-9a86-de2504499997"
tweets_data.info()
# + colab={"base_uri": "https://localhost:8080/"} id="E-wzQPN8Zmx4" outputId="bad64753-9e0c-42f9-82a0-e6ba2be53d8e"
tweets_data.value_counts()
# + colab={"base_uri": "https://localhost:8080/", "height": 418} id="bMRY2FE4bj04" outputId="8285f577-71b8-4815-b1a7-6b6172201d6c"
unique_tweets_data = tweets_data.value_counts().reset_index()
unique_tweets_data.columns = ['tweets','labels','count']
unique_tweets_data
# + colab={"base_uri": "https://localhost:8080/", "height": 513} id="TrSOFYWS3Svy" outputId="0728abad-93aa-49d2-90d7-24764166df76"
fig = plt.figure(figsize=(12,8))
fig = sns.barplot(x=unique_tweets_data[unique_tweets_data['count']>1]['count'], y=[str(i) for i in range(len(unique_tweets_data[unique_tweets_data['count']>1]))])
fig = plt.xlabel("Count")
fig = plt.ylabel('Sentences')
fig = plt.title('Duplicate Sentences')
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 513} id="zCqUou3KdWg7" outputId="577adad0-2001-4e46-dd74-338c1282a232"
fig = plt.figure(figsize=(12,8))
fig = sns.barplot(x=unique_tweets_data[:20]['count'], y=[str(i) for i in range(20)])
fig = plt.xlabel("Count")
fig = plt.ylabel('Sentences')
fig = plt.title('Top 20 Duplicate Sentences')
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 417} id="9hOWn-02aCEj" outputId="fb211689-093c-4c96-8812-e68ed9f8e8dd"
tweets_data[tweets_data['tweets'] == unique_tweets_data.loc[0,'tweets']]
# + id="hTrAiC0_bE74"
# Function to tokenize the tweets
def custom_tokenize(text, tokenize=False):
"""Function that tokenizes text"""
from nltk.tokenize import word_tokenize
if not text:
print('The text to be tokenized is a None type. Defaulting to blank string.')
text = ''
if tokenize:
return word_tokenize(text)
else:
return text.split(' ')
# Function that applies the cleaning steps
def clean_up(data1):
"""Function that cleans up the data into a shape that can be further used for modeling"""
data = data1.copy()
data.drop_duplicates(inplace=True) # drop duplicate tweets
tokenized = data['tweets'].apply(custom_tokenize) # Tokenize tweets
lower_tokens = tokenized.apply(lambda x: [t.lower() for t in x]) # Convert tokens into lower case
alpha_only = lower_tokens.apply(lambda x: [t for t in x if t.isalpha()]) # Remove punctuations
no_stops = alpha_only.apply(lambda x: [t for t in x if t not in stopwords.words('english')]) # remove stop words
no_stops.apply(lambda x: [x.remove(t) for t in x if t=='rt']) # remove acronym "rt"
no_stops.apply(lambda x: [x.remove(t) for t in x if t=='https']) # remove acronym "https"
no_stops.apply(lambda x: [x.remove(t) for t in x if t=='twitter']) # remove the word "twitter"
no_stops.apply(lambda x: [x.remove(t) for t in x if t=='retweet'])
data['cleaned_tweets'] = no_stops
return data
# + colab={"base_uri": "https://localhost:8080/", "height": 417} id="cVsy3Pzlgubi" outputId="da03ac16-0c8a-4c2f-8dd3-3eaaa867071f"
clean_up(tweets_data)
# + [markdown] id="WLWTkCboxZ6i"
# ## Dataset Creation
# ---
# + id="6jCPYddCg47C" colab={"base_uri": "https://localhost:8080/"} outputId="cc980622-f3fc-4297-e921-65711ab5b1fa"
# Import Library
import random
import torch, torchtext
from torchtext.legacy import data
# Manual Seed
SEED = 42
torch.manual_seed(SEED)
# + id="D3ogPfUO6JFe"
Tweet = data.Field(sequential = True, tokenize = 'spacy', batch_first =True)#, include_lengths=True)
Label = data.LabelField(dtype = torch.int64)
# + id="rffOYhgE6ylO"
fields = [('tweets', Tweet),('labels',Label)]
# + id="B2xEdzUe89NT"
example = [data.Example.fromlist([tweets_data.tweets[i],tweets_data.labels[i]], fields) for i in range(tweets_data.shape[0])]
# + id="Tw2l3t_m9XsW"
twitterDataset = data.Dataset(example, fields)
# + id="m-9-6OaJ9dPV"
(train_data, valid_data) = twitterDataset.split(split_ratio=[0.85, 0.15], random_state=random.seed(SEED))
# + id="eKN3vdpz9gNs" colab={"base_uri": "https://localhost:8080/"} outputId="2d55599a-89df-41b3-98ae-3858bac4fa0a"
(len(train_data), len(valid_data))
# + id="FZPozyoY9iz1" colab={"base_uri": "https://localhost:8080/"} outputId="5c963377-d2d4-4772-c1e7-87a41ad2a72b"
vars(train_data.examples[10])
# + id="-PS9FL2c9pGj"
Tweet.build_vocab(train_data)
Label.build_vocab(train_data)
# + id="Vt0dv2-Z94eA" colab={"base_uri": "https://localhost:8080/"} outputId="d58b05df-2c06-4d38-8ae4-124074b47323"
print('Size of input vocab : ', len(Tweet.vocab))
print('Size of label vocab : ', len(Label.vocab))
print('Top 10 words appreared repeatedly :', list(Tweet.vocab.freqs.most_common(10)))
print('Labels : ', Label.vocab.stoi)
# + id="0gaTFMKl-DFX"
BATCH_SIZE = 64
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# + id="VIOojo5l-GTG"
train_iterator, valid_iterator = data.BucketIterator.splits((train_data, valid_data), batch_size = BATCH_SIZE,
sort_key = lambda x: len(x.tweets),
sort_within_batch=True, device = device)
# + id="I9zZpHvm-7KF"
import os, pickle
with open(os.path.join(data_path,'tokenizer.pkl'), 'wb') as tokens:
pickle.dump(Tweet.vocab.stoi, tokens)
# + [markdown] id="c1tNJX0O_DcI"
# ## Model Building
# + id="ow87D_oGyJe2"
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.nn.utils.rnn import pack_padded_sequence, pad_packed_sequence
# + [markdown] id="gOTmf98CyLLq"
# #### Encoder
# + id="dk8Iu2AJyKJu"
class EncoderLSTM(nn.Module):
def __init__(self, vocab_size, embedding_dim, hidden_dim, output_dim, n_layers=1):
super().__init__()
self.hidden_dim = hidden_dim
self.n_layers = n_layers
# embedding layer
self.embedding = nn.Embedding(vocab_size, embedding_dim)
# lstm layer
self.lstm = nn.LSTM(embedding_dim,
hidden_dim,
num_layers=n_layers,
batch_first=True)
self.enc_context = nn.Linear(hidden_dim, output_dim)
def initHidden(self, batch_size, device):
return (torch.zeros(1, batch_size, self.hidden_dim, device=device), torch.zeros(1, batch_size, self.hidden_dim, device=device))
def forward(self, text, enc_hidden, visualize=False, verbose=False):
# hidden, cell = enc_hidden
embedded = self.embedding(text)
lstm_output, (hidden, cell) = self.lstm(embedded, enc_hidden)
output = self.enc_context(hidden.squeeze(0))
if verbose:
print('inside encoder:-')
print(f'shape of text input to encoder: {text.shape}')
print(f'shape of Embedding layer output: {embedded.shape}')
print(f'shape of lstm layer output: {hidden.shape}')
print(f'shape of fc layer output: {output.shape}')
print(f'shape of encoder output: {output.shape}')
if visualize:
enc_op = lstm_output[0].detach().cpu().numpy()
fig, ax = plt.subplots(figsize=(20,10))
sns.heatmap(enc_op, fmt=".2f", vmin=-1, vmax=1, annot=True, cmap="YlGnBu", ax=ax)
plt.title('Hidden State in each time step of Encoder', fontsize = 20) # title with fontsize 20
plt.xlabel('Hidden state', fontsize = 15) # x-axis label with fontsize 15
plt.ylabel('Time Step', fontsize = 15) # y-axis label with fontsize 15
plt.show()
enc_op = output.detach().cpu().numpy()
fig, ax = plt.subplots(figsize=(20,4))
sns.heatmap(enc_op, fmt=".2f", vmin=-1, vmax=1, annot=True, cmap="YlGnBu", ax=ax, annot_kws={"size": 20})
plt.title('Encoded Representation from Encoder', fontsize = 20) # title with fontsize 20
plt.show()
return output, (hidden, cell)
# + [markdown] id="9fh5biutyNmR"
# #### Decoder
# + id="Z7E97LnoyPQR"
class DecoderLSTM(nn.Module):
def __init__(self, enc_dim, hidden_dim, output_dim, n_layers=1):
super().__init__()
# lstm layer
self.lstm = nn.LSTMCell(enc_dim,
hidden_dim,
bias=False)
# num_layers=n_layers,
# batch_first=True)
self.decoded_op = nn.Linear(hidden_dim, output_dim)
def forward(self, enc_context, enc_hidden, dec_steps=2, visualize=False, verbose=False):
dec_input = enc_context.unsqueeze(1)
hidden, cell = enc_hidden
hidden = hidden.squeeze(0)
cell = cell.squeeze(0)
dec_outputs = []
for i in range(dec_steps):
hidden, cell = self.lstm(enc_context, (hidden, cell))
dec_outputs.append(hidden)
dec_output = torch.stack(dec_outputs, dim=1)
output = self.decoded_op(hidden)
if verbose:
print('inside decoder:-')
print(f'shape of output from encoder which goes as input to decoder: {enc_context.shape}')
print(f'shape of lstm layer output: {hidden.shape}')
print(f'shape of fc layer output: {output.shape}')
print(f'shape of decoder output: {output.shape}')
if visualize:
enc_op = dec_output[0].detach().cpu().numpy()
fig, ax = plt.subplots(figsize=(50,4))
sns.heatmap(enc_op, fmt=".2f", vmin=-1, vmax=1, annot=True, cmap="YlGnBu", ax=ax, annot_kws={"size": 20})
plt.title('Hidden State in each time step of Decoder', fontsize = 20) # title with fontsize 20
plt.xlabel('Hidden State', fontsize = 15) # x-axis label with fontsize 15
plt.ylabel('Time Step', fontsize = 15) # y-axis label with fontsize 15
plt.show()
enc_op = output.detach().cpu().numpy()
fig, ax = plt.subplots(figsize=(20,4))
sns.heatmap(enc_op, fmt=".2f", vmin=-1, vmax=1, annot=True, cmap="YlGnBu", ax=ax, annot_kws={"size": 20})
plt.title('Decoded Representation from Decoder', fontsize = 20) # title with fontsize 20
plt.show()
return output
# + [markdown] id="wbebVbH4yJFN"
# #### Encoder Decoder Model
# + id="dz0zgMXpPYZv"
class LSTMEncoderDecoderClassifier(nn.Module):
# Define all the layers used in model
def __init__(self, device, vocab_size, embedding_dim, hidden_enc_dim, hidden_dec_dim, context_dim, output_dim, n_classes, n_enc_layers=1, n_dec_layers=1):
# Constructor
super().__init__()
self.device = device
# encoder layer
self.encoder = EncoderLSTM(vocab_size, embedding_dim, hidden_enc_dim, context_dim, n_enc_layers)
# decoder layer
self.decoder = DecoderLSTM(context_dim, hidden_dec_dim, output_dim, n_dec_layers)
# output layer
self.linear_output = nn.Linear(output_dim, n_classes)
def forward(self, text, dec_steps=2, visualize=False, verbose=False): #, text_lengths):
# text = [batch size,sent_length]
enc_h = self.encoder.initHidden(text.shape[0], self.device)
encoded_context, encoded_hidden = self.encoder(text, enc_h, visualize, verbose)#, text_lengths)
decoded = self.decoder(encoded_context, encoded_hidden, dec_steps, visualize, verbose)
prediction = self.linear_output(decoded)
if verbose:
print(f'shape of final output: {prediction.shape}')
if visualize:
enc_op = prediction.detach().cpu().numpy()
fig, ax = plt.subplots(figsize=(20,4))
sns.heatmap(enc_op, fmt=".2f", vmin=-1, vmax=1, annot=True, cmap="YlGnBu", ax=ax)#.set(title=f"Encoded Representation from Encoder")
plt.title('Final Prediction', fontsize = 20) # title with fontsize 20
plt.show()
return prediction
# + id="3ghjQ2ZMPzYu"
# Define hyperparameters
size_of_vocab = len(Tweet.vocab)
embedding_dim = 100
hidden_enc_dim = 24
hidden_dec_dim = 24
context_dim = 16
output_dim = 16
n_classes = 3
n_enc_layers = 1
n_dec_layers = 1
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# Instantiate the model
model = LSTMEncoderDecoderClassifier(device, size_of_vocab, embedding_dim, hidden_enc_dim, hidden_dec_dim, context_dim, output_dim, n_classes, n_enc_layers, n_dec_layers)
# + id="Ja6F2c5cP7OS" colab={"base_uri": "https://localhost:8080/"} outputId="1aa5125d-5a58-439f-db7b-815c8a2d845e"
print(model)
#No. of trianable parameters
def count_parameters(model):
return sum(p.numel() for p in model.parameters() if p.requires_grad)
print(f'The model has {count_parameters(model):,} trainable parameters')
# + [markdown] id="1u5Dkyp2_HyB"
# ## Model Training and Testing
# ---
# + id="-5I6x3jg_G_r"
import torch.optim as optim
# define optimizer and loss
optimizer = optim.Adam(model.parameters())
criterion = nn.CrossEntropyLoss()
# define metric
def categorical_accuracy(preds, y):
"""
Returns accuracy per batch, i.e. if you get 8/10 right, this returns 0.8, NOT 8
"""
top_pred = preds.argmax(1, keepdim = True)
correct = top_pred.eq(y.view_as(top_pred)).sum()
acc = correct.float() / y.shape[0]
return acc
# push to cuda if available
model = model.to(device)
criterion = criterion.to(device)
# + id="RdKmLUq0A7G7"
def train(model, iterator, optimizer, criterion):
# initialize every epoch
epoch_loss = 0
epoch_acc = 0
# set the model in training phase
model.train()
for batch in iterator:
# print(batch.tweets.shape)
# resets the gradients after every batch
optimizer.zero_grad()
# retrieve text and no. of words
text = batch.tweets #, text_lengths = batch.tweet
# convert to 1D tensor
predictions = model(text)#, text_lengths)
# print('in train')
# print(predictions.shape)
# print(batch.labels.shape)
# compute the loss
loss = criterion(predictions, batch.labels)
# compute the categorical accuracy
acc = categorical_accuracy(predictions, batch.labels)
# backpropage the loss and compute the gradients
loss.backward()
# update the weights
optimizer.step()
# loss and accuracy
epoch_loss += loss.item()
epoch_acc += acc.item()
return epoch_loss / len(iterator), epoch_acc / len(iterator)
# + id="EyzUhtdrBAix"
def evaluate(model, iterator, criterion):
# initialize every epoch
epoch_loss = 0
epoch_acc = 0
# deactivating dropout layers
model.eval()
# deactivates autograd
with torch.no_grad():
for batch in iterator:
# retrieve text and no. of words
text = batch.tweets #, text_lengths = batch.text
# convert to 1D tensor
predictions = model(text).squeeze(1) #, text_lengths).squeeze(1)
# compute loss and accuracy
loss = criterion(predictions, batch.labels)
acc = categorical_accuracy(predictions, batch.labels)
# keep track of loss and accuracy
epoch_loss += loss.item()
epoch_acc += acc.item()
return epoch_loss / len(iterator), epoch_acc / len(iterator)
# + id="hIjfJGzlBG8D"
import time
def epoch_time(start_time, end_time):
elapsed_time = end_time - start_time
elapsed_mins = int(elapsed_time / 60)
elapsed_secs = int(elapsed_time - (elapsed_mins * 60))
return elapsed_mins, elapsed_secs
# + id="m5Us_U9MBNKR" colab={"base_uri": "https://localhost:8080/"} outputId="659137d1-8048-423e-ed19-1ccc46f04066"
N_EPOCHS = 10
best_valid_loss = float('inf')
train_losses = []
train_accs = []
valid_losses = []
valid_accs = []
for epoch in range(N_EPOCHS):
start_time = time.time()
# train the model
train_loss, train_acc = train(model, train_iterator, optimizer, criterion)
# evaluate the model
valid_loss, valid_acc = evaluate(model, valid_iterator, criterion)
end_time = time.time()
epoch_mins, epoch_secs = epoch_time(start_time, end_time)
# save the best model
if valid_loss < best_valid_loss or epoch == N_EPOCHS:
best_valid_loss = valid_loss
torch.save(model.state_dict(), os.path.join(base_path, 'saved_weights.pt'))
train_losses.append(train_loss)
train_accs.append(train_acc)
valid_losses.append(valid_loss)
valid_accs.append(valid_acc)
print(f'Epoch: {epoch+1:02} | Epoch Time: {epoch_mins}m {epoch_secs}s')
print(f'\tTrain Loss: {train_loss:.3f} | Train Acc: {train_acc*100:.2f}%')
print(f'\t Val. Loss: {valid_loss:.3f} | Val. Acc: {valid_acc*100:.2f}% \n')
# + id="EqcwIW5m8z-o"
torch.save(model.state_dict(), os.path.join(base_path, 'lepoch10_saved_weights.pt'))
# + [markdown] id="Rrc82i1BxhbK"
# ## Visualization
# ---
# + id="aSswDN2fkFZ1"
# visualize accuracy and loss graph
def visualize_graph(train_losses, train_acc, test_losses, test_acc):
fig, axs = plt.subplots(2,2,figsize=(15,10))
axs[0, 0].plot(train_losses)
axs[0, 0].set_title("Training Loss")
axs[1, 0].plot(train_acc)
axs[1, 0].set_title("Training Accuracy")
axs[0, 1].plot(test_losses)
axs[0, 1].set_title("Test Loss")
axs[1, 1].plot(test_acc)
axs[1, 1].set_title("Test Accuracy")
def visualize_save_train_vs_test_graph(EPOCHS, dict_list, title, xlabel, ylabel, PATH, name="fig"):
plt.figure(figsize=(20,10))
#epochs = range(1,EPOCHS+1)
for label, item in dict_list.items():
x = np.linspace(1, EPOCHS+1, len(item))
plt.plot(x, item, label=label)
plt.title(title)
plt.xlabel(xlabel)
plt.ylabel(ylabel)
plt.legend()
plt.savefig(PATH+"/"+name+".png")
# + [markdown] id="Wzo7PwxkxlmV"
# #### Training and Testing Accuracy and Loss
# + colab={"base_uri": "https://localhost:8080/", "height": 607} id="Q3Z0biLn2DqW" outputId="907e6449-3c64-4450-aae0-393f783148d6"
visualize_graph(train_losses, train_accs, valid_losses, valid_accs)
# + [markdown] id="I5yIKJ1ExsKk"
# #### Train vs Test Accuracy Comparison
# + colab={"base_uri": "https://localhost:8080/", "height": 621} id="KQhc4AJ4nr-h" outputId="30ce7e7e-a46e-46f2-862f-f8af8c154497"
dict_list = {'Training Accuracy': train_accs, 'Test Accuracy': valid_accs}
title = "Training vs Test Accuracy"
xlabel = "Epochs"
ylabel = "Accuracy(in Percentage)"
name = "train_vs_test_acc_comparison_graph"
visualize_save_train_vs_test_graph(N_EPOCHS, dict_list, title, xlabel, ylabel, base_path, name=name)
# + [markdown] id="EgfHl3p_x3_y"
# #### Train vs Test Loss Comparison
# + colab={"base_uri": "https://localhost:8080/", "height": 621} id="ZE2N4NLBn1eF" outputId="b31fd560-a1ef-4d8a-9e47-86f9474a1d01"
dict_list = {'Training Loss': train_losses, 'Test Loss': valid_losses}
title = "Training vs Test Loss"
xlabel = "Epochs"
ylabel = "Loss"
name = "train_vs_test_loss_comparison_graph"
visualize_save_train_vs_test_graph(N_EPOCHS, dict_list, title, xlabel, ylabel, base_path, name=name)
# + [markdown] id="nAxiXJIJx9z-"
# ## Evaluation
# ---
# + id="3-puuitPt9nP"
from sklearn.metrics import f1_score, accuracy_score
def print_accuracy(df, target_col, pred_column):
"Print f1 score and accuracy after making predictions"
f1_macro = f1_score(df[target_col].astype(int), df[pred_column].astype(int), average='macro')
acc = accuracy_score(df[target_col].astype(int), df[pred_column].astype(int))*100
return f1_macro, acc
# + id="GTP_DwmFqNiW"
def evaluation_pred(model, iterator):
# initialize every epoch
epoch_loss = 0
epoch_acc = 0
# deactivating dropout layers
model.eval()
eval_df = pd.DataFrame(columns=['label','pred'])
# deactivates autograd
with torch.no_grad():
for batch in iterator:
# retrieve text and no. of words
text = batch.tweets #, text_lengths = batch.text
label = batch.labels.cpu().numpy()
# convert to 1D tensor
predictions = model(text)
top_pred = predictions.argmax(1, keepdim = True).cpu().numpy()
batch_df = pd.DataFrame(top_pred, columns=['pred'])
batch_df['label'] = label
batch_df['pred'] = batch_df['pred'].astype(int)
batch_df['label'] = batch_df['label'].astype(int)
eval_df = pd.concat([eval_df, batch_df])
return eval_df
# + id="s-573X44n-Oa"
from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
import numpy as np
def plot_confusion_matrix(y_true, y_pred,
classes=['Positive','Neutral','Negative'],
normalize=False,
cmap=plt.cm.YlOrBr):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
(Adapted from scikit-learn docs).
"""
# Compute confusion matrix
cm = confusion_matrix(y_true, y_pred)
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
fig, ax = plt.subplots()
im = ax.imshow(cm, interpolation='nearest', origin='lower', cmap=cmap)
ax.figure.colorbar(im, ax=ax)
# Show all ticks
ax.set(xticks=np.arange(cm.shape[1]),
yticks=np.arange(cm.shape[0]),
# Label with respective list entries
xticklabels=classes, yticklabels=classes,
ylabel='True label',
xlabel='Predicted label')
# Set alignment of tick labels
plt.setp(ax.get_xticklabels(), rotation=0, ha="right",
rotation_mode="anchor")
# Loop over data dimensions and create text annotations
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i in range(cm.shape[0]):
for j in range(cm.shape[1]):
ax.text(j, i, format(cm[i, j], fmt),
ha="center", va="center",
color="white" if cm[i, j] > thresh else "black")
return fig, ax
# + id="yMaZZy81oKTt"
import pickle
model.eval()
tokenizer_file = open(os.path.join(data_path,'tokenizer.pkl'), 'rb')
tokenizer = pickle.load(tokenizer_file)
#inference
import spacy
nlp = spacy.load('en')
def classify_text(tweet, visualize=True, verbose=False):
categories = {0: 0, 1:1, 2:2}
# tokenize the tweet
tokenized = [tok.text for tok in nlp.tokenizer(tweet)]
# convert to integer sequence using predefined tokenizer dictionary
indexed = [tokenizer[t] for t in tokenized]
# compute no. of words
length = [len(indexed)]
# convert to tensor
tensor = torch.LongTensor(indexed).to(device)
# reshape in form of batch, no. of words
tensor = tensor.unsqueeze(1).T
print(tensor.shape)
# convert to tensor
length_tensor = torch.LongTensor(length)
# Get the model prediction
prediction = model(tensor, visualize=visualize, verbose=verbose) #, length_tensor)
# print(prediction)
# _, pred = torch.max(prediction, 1)
pred = prediction.argmax(keepdim = True)
return categories[pred.item()]
# + id="aVUHNb-8pIRi"
plt.rcParams["figure.figsize"] = (8,8)
# + [markdown] id="1sQgeexIyW2d"
# #### Encoder-Decoder Visualization of each step
#
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="TrnzuZ23sg-i" outputId="b4ecf68b-d925-4551-adbe-e0388f8a0b94"
label, tweet = tweets_data.loc[0]['labels'], tweets_data.loc[0]['tweets']
print(tweet)
print(f'Target Label: {label}')
pred = classify_text(tweet)
print(f'Predicted Label: {pred}')
# + [markdown] id="4yzygatLzdeU"
# #### Evaluation Result
# + id="mO7wumr1lRdt"
eval_df = evaluation_pred(model, valid_iterator)
# + colab={"base_uri": "https://localhost:8080/", "height": 506} id="q86kCBedqHvg" outputId="81900f32-a2a4-4129-8325-a57ee2af6d2c"
plot_confusion_matrix(eval_df['label'].values.tolist(), eval_df['pred'].values.tolist())
# + colab={"base_uri": "https://localhost:8080/"} id="7qcokgmJuzSP" outputId="4e52b426-df99-4f65-da55-718f81f6b595"
f1_macro, acc = print_accuracy(eval_df, 'label', 'pred')
print(f'F1 Macro Score: {f1_macro}')
print(f'Accuracy: {acc} %')
# + id="zSc8P39fkYNk"
# model.load_state_dict(torch.load(os.path.join(base_path, 'lepoch10_saved_weights.pt')))
# model = model.to(device)
|
Session6-GRUs,Seq2SeqandIntroductiontoAttentionMechanism/Session6_LSTM_Encoder_Decoder_TweeterDataset.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 11장 자연어처리 3부
# **감사말**: 프랑소와 숄레의 [Deep Learning with Python, Second Edition](https://www.manning.com/books/deep-learning-with-python-second-edition?a_aid=keras&a_bid=76564dff) 10장에 사용된 코드에 대한 설명을 담고 있으며 텐서플로우 2.6 버전에서 작성되었습니다. 소스코드를 공개한 저자에게 감사드립니다.
#
# **tensorflow 버전과 GPU 확인**
# - 구글 코랩 설정: '런타임 -> 런타임 유형 변경' 메뉴에서 GPU 지정 후 아래 명령어 실행 결과 확인
#
# ```
# # !nvidia-smi
# ```
#
# - 사용되는 tensorflow 버전 확인
#
# ```python
# import tensorflow as tf
# tf.__version__
# ```
# - tensorflow가 GPU를 사용하는지 여부 확인
#
# ```python
# tf.config.list_physical_devices('GPU')
# ```
# + [markdown] colab_type="text"
# ## 11.4 트랜스포머 아키텍처
# -
# 2017년 논문
# ["Attention is all you need"](https://arxiv.org/abs/1706.03762)에서
# 소개된 트랜스포머(Transformer) 아키텍처는 자연어처리 분야에서 혁명을 불러왔다.
# 트랜스포머는 "**뉴럴 어텐션**(Neural Attention)" 기법을 이용하여
# 순환층 또는 합성곱 층과는 다르게 작동하는 순차 모델(sequence model)을 구현한다.
#
# 여기서는 뉴럴 어텐션의 작동법을 설명한 후에
# 트랜스포머 인코더를 이용하여 IMDB 영화 리뷰 모델을 구현한다.
# + [markdown] colab_type="text"
# ### 11.4.1 셀프 어텐션(self-attention)
# -
# 입력값의 특성 중에 보다 중요한 특성에 **집중(attention)**하면 보다 효율적으로
# 훈련이 진행될 수 있다.
# 아래 그림이 집중(attention)이 어떻게 활용되는지 잘 보여준다.
# <div align="center"><img src="https://drek4537l1klr.cloudfront.net/chollet2/Figures/11-05.png" style="width:60%;"></div>
#
# 그림 출처: [Deep Learning with Python(Manning MEAP)](https://www.manning.com/books/deep-learning-with-python-second-edition)
# 앞서 유사한 아이디어를 활용한 적이 있다.
#
# - 합성곱 신경망의 맥스 풀링(max pooling): 지역적으로 가장 중요한 특성만 사용한다.
# - TF-IDF 정규화: 텍스트 벡터화를 위해 사용되는 TF-IDF 정규화는
# 사용되는 토큰(tokens)에 포함된 정보의 중요도를 평가하여
# 보다 중요한 정보를 담은 토큰에 집중한다.
# **셀프 어텐션**(self-attention)은 주어진 문장에 사용된 단어들의 연관성을 평가하여
# 그 결과를 해당 문장에 적용하여 입력값을 변환하는 기법을
# 가리킨다.
# 즉, **문맥**(context)를 활용한다.
# 아래 그림은 "The train left the station on time." 이라는 문장에
# 셀프 어텐션을 적용하여 입력값을 변환하는 과정을 나타낸다.
#
# - 1단계: 문장에 사용된 각 토큰들 사이의 연관성 계산.
# - 2단계: 계산된 연관성을 (토큰) 벡터와 결합시킨 후 새로운
# 토큰 벡터들의 시퀀스 생성.
# 아래 그림에서는 "station" 단어에 해당하는 벡터가 변환되는 과정을 보여줌.
# <div align="center"><img src="https://drek4537l1klr.cloudfront.net/chollet2/Figures/11-06.png" style="width:70%;"></div>
#
# 그림 출처: [Deep Learning with Python(Manning MEAP)](https://www.manning.com/books/deep-learning-with-python-second-edition)
# + [markdown] colab_type="text"
# **질문-키-값(query-key-value) 모델**
# -
# 셀프 어텐션의 작동 과정을 식으로 표현하면 다음과 같다.
#
# outputs = sum(inputs * pairwise_scores(inputs, inputs))
# | | |
# (C) (A) (B)
#
# 위 식은 원래 검색 엔진 또는 추천 시스템에 사용되는
# 보다 일반화된 셀프 어텐션의 작동과정을 표현한 식의 특별한 경우를 보여준다.
#
# outputs = sum(values * pairwise_scores(query, keys))
# | | |
# (C) (A) (B)
# 예를 들어, 아래 그림은 "dogs on the beach." 질문(query)에 가장
# 적절한 사신을 검색한다면 각 사진과의 연관성(keys) 점수를
# 해당 사진(values)과 결합하여 가장 높은 점수를 갖는 사진을
# 추천하는 것을 보여준다.
# <div align="center"><img src="https://drek4537l1klr.cloudfront.net/chollet2/Figures/11-07.png" style="width:60%;"></div>
#
# 그림 출처: [Deep Learning with Python(Manning MEAP)](https://www.manning.com/books/deep-learning-with-python-second-edition)
# 질문-키-값(query-key-value) 모델을 실전에 적용할 때 많은 경우 키(keys)와 값(values)가 동일하다.
#
# - 기계 번역:
# "How's the weather today?"를 스페인어로 기계 번역하려 할 경우
# 스페인어로 날씨에 해당하는 "tiempo"를 키(key)로 해서 주어진 영어 문장(query)에
# 사용된 단어들과 비교해야 한다.
# - 텍스트 분류:
# 앞서 셀프 어텐션 설명을 위해 사용된 그림에서처럼 query, keys, values 모두 동일하다.
# + [markdown] colab_type="text"
# ### 11.4.2 멀티헤드 어텐션
# -
# 단어들 사이의 연관성을 다양한 방식으로 알아내기 위해 셀프 어텐션을 수행하는
# **헤드**(head)를 여러 개 병렬로 처리한 후에 다시 합치는 기법을
# **멀티헤드 어텐션**(multi-head attention)이다.
# 아래 그림은 두 개의 헤드를 사용하는 것을 보여주며 각각의 헤드가 하는 일은 다음과 같다.
#
# - 질문, 키, 값을 각각 서로 다른 밀집 밀집 층으로 구성된 블록을 통과 시킨다.
# - 이후 변환된 질문, 키, 값에 셀프 어텐션을 적용한다.
#
# 각 헤드에 포함된 밀집 층 블록으로 인해 멀티헤드 어텐션 층에서도
# 학습이 이루어진다.
#
# **참고**: 채널 분리 합성곱 층의 알고리즘과 기본 아이디어가 유사하다.
# <div align="center"><img src="https://drek4537l1klr.cloudfront.net/chollet2/Figures/11-08.png" style="width:70%;"></div>
#
# 그림 출처: [Deep Learning with Python(Manning MEAP)](https://www.manning.com/books/deep-learning-with-python-second-edition)
# + [markdown] colab_type="text"
# ### 11.4.2 트랜스포머 인코더
# -
# 멀티헤드 어텐션을 밀집(dense) 층, 정규화 층, 잔차 연결 등과 조합하여
# **트랜스포머 인코더**(transformer encoder)를 생성한다.
#
# 아래 그림에서 사용되는 정규화 층인 케라스의 `LayerNormalization`은
# 정규화를 배치 단위가 아닌 시퀀스 단위로 정규화를 실행한다.
# 시퀀스 데이터를 처리할 때는 `BatchNormalization` 보다 잘 작동한다.
# <div align="center"><img src="https://drek4537l1klr.cloudfront.net/chollet2/Figures/11-09.png" style="width:35%;"></div>
#
# 그림 출처: [Deep Learning with Python(Manning MEAP)](https://www.manning.com/books/deep-learning-with-python-second-edition)
# + [markdown] colab_type="text"
# **예제: IMDB 데이터셋**
# -
# 데이터셋을 준비하는 과정은 이전과 동일하다.
# + colab_type="code"
# !curl -O https://ai.stanford.edu/~amaas/data/sentiment/aclImdb_v1.tar.gz
# !tar -xf aclImdb_v1.tar.gz
if 'google.colab' in str(get_ipython()):
# !rm -r aclImdb/train/unsup
else:
import shutil
unsup_path = './aclImdb/train/unsup'
shutil.rmtree(unsup_path)
# + colab_type="code"
import os, pathlib, shutil, random
from tensorflow import keras
batch_size = 32
base_dir = pathlib.Path("aclImdb")
val_dir = base_dir / "val"
train_dir = base_dir / "train"
for category in ("neg", "pos"):
os.makedirs(val_dir / category)
files = os.listdir(train_dir / category)
random.Random(1337).shuffle(files)
num_val_samples = int(0.2 * len(files))
val_files = files[-num_val_samples:]
for fname in val_files:
shutil.move(train_dir / category / fname,
val_dir / category / fname)
train_ds = keras.utils.text_dataset_from_directory(
"aclImdb/train", batch_size=batch_size
)
val_ds = keras.utils.text_dataset_from_directory(
"aclImdb/val", batch_size=batch_size
)
test_ds = keras.utils.text_dataset_from_directory(
"aclImdb/test", batch_size=batch_size
)
text_only_train_ds = train_ds.map(lambda x, y: x)
# + [markdown] colab_type="text"
# 텍스트 벡터화는 정수들의 벡터를 사용하며, 리뷰의 최대 길이를 600 단어로 제한한다.
#
# - `output_mode="int"`
# - `output_sequence_length=600`
# + colab_type="code"
from tensorflow.keras import layers
max_length = 600
max_tokens = 20000
text_vectorization = layers.TextVectorization(
max_tokens=max_tokens,
output_mode="int",
output_sequence_length=max_length,
)
# 어휘 색인화
text_vectorization.adapt(text_only_train_ds)
int_train_ds = train_ds.map(lambda x, y: (text_vectorization(x), y))
int_val_ds = val_ds.map(lambda x, y: (text_vectorization(x), y))
int_test_ds = test_ds.map(lambda x, y: (text_vectorization(x), y))
# + [markdown] colab_type="text"
# **트랜스포머 구현**
# -
# 위 그림에서 설명된 트랜스포머 인코더를 층(layer)으로 구현하면 다음과 같다.
# 생성자의 입력값을 예를 들어 설명하면 다음과 같다.
#
# - `embed_dim`
# - 트랜스포머 인코더는 "단어 임베딩" 층을 통과한 값을 받음.
# - 예를 들어 `embed_dim=256`은 단어 임베딩이
# `(600, 256)` 모양의 샘플을 생성할 것을 기대함.
# - `dense_dim`: 밀집 층에서 사용되는 유닛(unit) 수
# - `num_heads`: 헤드(head) 수
# + colab_type="code"
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
class TransformerEncoder(layers.Layer):
def __init__(self, embed_dim, dense_dim, num_heads, **kwargs):
super().__init__(**kwargs)
self.embed_dim = embed_dim
self.dense_dim = dense_dim
self.num_heads = num_heads
self.attention = layers.MultiHeadAttention(
num_heads=num_heads, key_dim=embed_dim)
self.dense_proj = keras.Sequential(
[layers.Dense(dense_dim, activation="relu"),
layers.Dense(embed_dim),]
)
self.layernorm_1 = layers.LayerNormalization()
self.layernorm_2 = layers.LayerNormalization()
def call(self, inputs, mask=None):
if mask is not None:
mask = mask[:, tf.newaxis, :]
attention_output = self.attention(
inputs, inputs, attention_mask=mask)
proj_input = self.layernorm_1(inputs + attention_output)
proj_output = self.dense_proj(proj_input)
return self.layernorm_2(proj_input + proj_output)
def get_config(self):
config = super().get_config()
config.update({
"embed_dim": self.embed_dim,
"num_heads": self.num_heads,
"dense_dim": self.dense_dim,
})
return config
# + [markdown] colab_type="text"
# **트랜스포머 인코더 활용 모델**
# -
# 훈련 데이터셋이 입력되면 먼저 단어 임베딩을 이용하여
# 단어들 사이의 연관성을 찾는다.
# 이후 트랜스포머 인코더로 셀프 어텐션을 적용한다.
#
# 사용되는 변수들은 다음과 같다.
#
# - `vocab_size = 20000`: 어휘 색인 크기
# - `embed_dim = 256`: 단어 임베딩 특성 수
# - `dense_dim = 32`: 트랜스포머 인코더에 사용되는 밀집층의 유닛(unit) 수
# - `num_heads = 2`: 트랜스포머 인코더에 사용되는 밀집층의 헤드(head) 수
# + colab_type="code"
vocab_size = 20000
embed_dim = 256
num_heads = 2
dense_dim = 32
inputs = keras.Input(shape=(None,), dtype="int64")
x = layers.Embedding(vocab_size, embed_dim)(inputs)
x = TransformerEncoder(embed_dim, dense_dim, num_heads)(x)
x = layers.GlobalMaxPooling1D()(x)
x = layers.Dropout(0.5)(x)
outputs = layers.Dense(1, activation="sigmoid")(x)
model = keras.Model(inputs, outputs)
model.compile(optimizer="rmsprop",
loss="binary_crossentropy",
metrics=["accuracy"])
model.summary()
# + [markdown] colab_type="text"
# 훈련 과정은 특별한 게 없다.
# 테스트셋에 대한 정확도가 87.5% 정도로 바이그램 모델보다 좀 더 낮다.
# + colab_type="code"
callbacks = [
keras.callbacks.ModelCheckpoint("transformer_encoder.keras",
save_best_only=True)
]
model.fit(int_train_ds, validation_data=int_val_ds, epochs=20, callbacks=callbacks)
model = keras.models.load_model(
"transformer_encoder.keras",
custom_objects={"TransformerEncoder": TransformerEncoder})
print(f"Test acc: {model.evaluate(int_test_ds)[1]:.3f}")
# -
# **모델 비교**
# 자연어처리와 관련된 모델을 단어 순서 인식과 문맥 이해 차원에서 비교하면 다음과 같다.
#
# | | 단어순서 인식 | 문맥 이해 |
# | :---: | :---: | :---: |
# | 유니그램 주머니 모델 | X | X |
# | 바이그램 주머니 모델 | $\triangle$ | X |
# | RNN | O | X |
# | 셀프 어텐션 | X | O |
# | 트랜스포머 | O | O |
# + [markdown] colab_type="text"
# **단어 위치 인코딩**
# -
# 앞서 살펴 본 트랜스포머 인코더는 셀프 어텐션과 밀집층을 사용하기에
# 단어순서를 제대로 활용하지는 못한다.
# 하지만 단어 인코딩 과정에서 단어순서 정보를 활용하도록 하는 기능을 추가하면
# 트랜스포머가 알아서 단어위치 정보를 활용한다.
#
# 다음 `PositionalEmbedding` 층 클래스는 두 개의 임베딩 클래스를 사용한다.
# 하나는 보통의 단어 임베딩이며,
# 다른 하나는 단어의 위치 정보를 임베딩한다.
# 각 임베딩의 출력값을 합친 값을 트랜스포머에게 전달하는 역할을 수행한다.
# + colab_type="code"
class PositionalEmbedding(layers.Layer):
def __init__(self, sequence_length, input_dim, output_dim, **kwargs):
super().__init__(**kwargs)
self.token_embeddings = layers.Embedding(
input_dim=input_dim, output_dim=output_dim)
self.position_embeddings = layers.Embedding(
input_dim=sequence_length, output_dim=output_dim)
self.sequence_length = sequence_length
self.input_dim = input_dim
self.output_dim = output_dim
def call(self, inputs):
length = tf.shape(inputs)[-1]
positions = tf.range(start=0, limit=length, delta=1)
embedded_tokens = self.token_embeddings(inputs)
embedded_positions = self.position_embeddings(positions)
return embedded_tokens + embedded_positions
def compute_mask(self, inputs, mask=None):
return tf.math.not_equal(inputs, 0)
def get_config(self):
config = super().get_config()
config.update({
"output_dim": self.output_dim,
"sequence_length": self.sequence_length,
"input_dim": self.input_dim,
})
return config
# + [markdown] colab_type="text"
# **단어위치인식 트랜스포머 아키텍처**
# + [markdown] colab_type="text"
# 아래 코드는 `PositionalEmbedding` 층을 활용하여 트랜스포머 인코더가
# 단어위치를 활용할 수 있도록 한다.
# 최종 모델의 테스트셋에 대한 정확도가 88.3%까지 향상됨을 확인할 수 있다.
# + colab_type="code"
vocab_size = 20000
sequence_length = 600
embed_dim = 256
num_heads = 2
dense_dim = 32
inputs = keras.Input(shape=(None,), dtype="int64")
x = PositionalEmbedding(sequence_length, vocab_size, embed_dim)(inputs)
x = TransformerEncoder(embed_dim, dense_dim, num_heads)(x)
x = layers.GlobalMaxPooling1D()(x)
x = layers.Dropout(0.5)(x)
outputs = layers.Dense(1, activation="sigmoid")(x)
model = keras.Model(inputs, outputs)
model.compile(optimizer="rmsprop",
loss="binary_crossentropy",
metrics=["accuracy"])
model.summary()
callbacks = [
keras.callbacks.ModelCheckpoint("full_transformer_encoder.keras",
save_best_only=True)
]
model.fit(int_train_ds, validation_data=int_val_ds, epochs=20, callbacks=callbacks)
model = keras.models.load_model(
"full_transformer_encoder.keras",
custom_objects={"TransformerEncoder": TransformerEncoder,
"PositionalEmbedding": PositionalEmbedding})
print(f"Test acc: {model.evaluate(int_test_ds)[1]:.3f}")
# + [markdown] colab_type="text"
# ### 11.4.4 트랜스포머 사용 기준
# -
# 단어주머니 모델이 여전히 유용하게 활용된다.
# 실제로 IMDB 데이터셋에 대한 성능도 단어주머니 모델이 가장 좋았다.
# 그리고 많은 실험 결과 "훈련셋의 크기"와 "텍스트의 평균 단어 수"의 비율이 모델 선택에
# 결정적인 역할을 수행한다는 경험 법칙이 알려졌다.
#
# - ("훈련셋의 크기" $/$ "텍스트의 평균 단어 수") $>$ 1500 인 경우: 트랜스포머 등 순차 모델
# - ("훈련셋의 크기" $/$ "텍스트의 평균 단어 수") $<$ 1500 인 경우: 바이그램 단어주머니 모델
# **예제 1**
# 1천개의 단어를 포함한 텍스트 십만 개로 이루어진 훈련셋을 사용하는 경우 비율이 100이기에 바이그램 모델을 사용하는 것이 좋다.
# **예제 2**
# 평균 40개의 단어를 포함하는 트윗(tweets) 5만 개로 이루어진 훈련셋을 사용하는 경우 비율이 1,250이기에 역시 바이그램 모델을 사용하는 것이 좋다.
# **예제 3**
# 평균 40개의 단어를 포함하는 트윗(tweets) 50만 개로 이루어진 훈련셋을 사용하는 경우 비율이 12,500이기에 이번엔 트랜스포머 인코더를 활용하는 것이 좋다.
# **예제 4**
# IMDB 훈련셋은 2만 개의 리뷰로 구성되며 리뷰 한 개는 평균 233 개의 단어를 포함한다. 비율이 85.84 정도이기에 바이그램 모델이 보다 적합해야 하는데
# 지금까지 살펴본 결과가 이에 입증한다.
# **경험 법칙의 직관적 이해**
# 짧은 문장이 많을 수록 문맥을 파악하려면 단어들의 순서가 중요하며,
# 문장에 사용된 단어들 사이의 복잡한 연관성을 보다 주의깊게 살펴볼 필요가 있다.
# 예를 들어, "그 영화는 실패야"와 "그 영화는 실패였어"는 분명 다른 의미를 가지지만
# 단어주머니 모델은 차이점을 파악하기 어렵다.
# 반면에 보다 긴 문장의 주제와 긍정/부정 등의 감성에 대한 분류는
# 단어 관련 통계의 중요성이 보다 크다.
# **주의사항**
#
# 앞서 설명한 경험 법칙은은 텍스트 분류(text classification)에 한정된다.
# 예를 들어 기계 번역(machine translation)의 경우 매우 긴 문장을 다룰 때
# 트랜스포머가 가본적으로 가장 강력한 성능의 모델을 생성한다.
|
notebooks/dlp11_part03_transformer.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # <font color=darkblue>ENGR 1330-2022 Exam 3 - Laboratory Portion </font>
#
# **LAST NAME, FIRST NAME**
#
# **R00000000**
#
# ENGR 1330 Exam 3A - Demonstrate Laboratory/Programming Skills
#
# ---
#
#
# **If you are unable to download the file, create an empty notebook and copy paste the problems into Markdown cells and Code cells (problem-by-problem)**
#
#
# ## Problem 0 (5 pts) : <font color = 'magenta'>*Profile your computer*</font>
#
# Execute the code cell below exactly as written. If you get an error just continue to the remaining problems.
# Preamble script block to identify host, user, and kernel
import sys
# ! hostname
# ! whoami
print(sys.executable)
print(sys.version)
print(sys.version_info)
# ## Exercise 1 (5 pts) Download the datafile
# The file [http://54.243.252.9/engr-1330-webroot/5-ExamProblems/Exam3/spring2022/boxes.csv](http://5172.16.17.32/engr-1330-webroot/5-ExamProblems/Exam3/spring2022/boxes.csv) below contains values of impact strength of packaging materials in foot-pounds of branded boxes.
#
# Download the file and read it into a dataframe.
#
# <!--```
# import requests
# remote_url="http://5172.16.17.32/engr-1330-webroot/5-ExamProblems/Exam3/spring2022/boxes.csv" # set the url
# rget = requests.get(remote_url, allow_redirects=True) # get the remote resource, follow imbedded links
# localfile = open('boxes.csv','wb') # open connection to a local file same name as remote
# localfile.write(rget.content) # extract from the remote the contents,insert into the local file same name
# localfile.close() # close connection to the local file
# ```-->
# #### Download the necessary datafile
# download the datafile
import requests
remote_url="http://192.168.127.12/engr-1330-webroot/5-ExamProblems/Exam3/spring2022/boxes.csv" # set the url
rget = requests.get(remote_url, allow_redirects=True) # get the remote resource, follow imbedded links
localfile = open('boxes.csv','wb') # open connection to a local file same name as remote
localfile.write(rget.content) # extract from the remote the contents,insert into the local file same name
localfile.close() # close connection to the local file
# #### Store the datafile into a datafrome
# +
# your script/answers go here
# -
# #### Describe the dataframe, how many columns are in the dataframe? What are the column names?
# +
# your script/answers go here
# -
# ## Exercise 2 (15 pts.) Produce a histogram of the Amazon series and the USPS series on the same plot. Plot Amazon using red, and USPS using blue.
#
# > - Import suitable package to build histograms
# > - Apply package with plotting call to prodice two histograms on same figure space
# > - Label plot and axes with suitable annotation
# #### Plot the histograms with proper formatting
# +
# your script goes here
# -
# #### Comment on the histograms, do they overlap?
# TYPE HERE: Your comments regarding the histograms here
#
# ## Exercise 3 (5 pts.) Summary Statistics for the Amazon and USPS Brands
# > - Compute the mean strength and the standard deviation of the Amazon and USPS brands
# > - Identify which series has a greater mean value
# > - Identify which series has the greater standard deviation
# #### Compute the means and standard deviations
# +
# your script goes here
# -
# #### Identify which has the largest mean
# TYPE HERE: Your comments regarding which has a greater mean
#
# #### Identify which has the largest standard deviation
# TYPE HERE: Your comments regarding which has a greater standard deviation
#
# ## Exercise 4 (5 pts.) Test the Amazon data for normality, interpret the results.
# #### Build your test below
# +
# your script goes here
# -
# #### Interpret the results
# Type your interpretation here
# ## Exercise 5 (5 pts.) Test the USPS data for normality, interpret the results.
# #### Build your test below
# +
# your script goes here
# -
# #### Interpret the results
# Type your interpretation here
#
# ## Exercise 6 (10 pts.) Determine if there is evidence of a difference in mean strength between the two brands.
# Use an appropriate hypothesis test to support your assertion at a level of significance of $\alpha = 0.10$.
#
# > - Choose a test and justify choice
# > - Import suitable package to run the test
# > - Apply the test and interpret the results
# > - Report result with suitable annotation
# #### Build your hypothesis test below
# +
# your script here
# -
# #### Interpret the results
# Type your interpretation here
#
|
5-ExamProblems/Exam3/spring2022/src/.ipynb_checkpoints/s22-ex3-deployA-jd-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # "Solving the Problem of the K Parameter in the KNN Classifier Using an Ensemble Learning Approach"
#
# # Ideea principala a acestui articol este utilizarea algoritmului KNN fara a specifica parametrul k in mod empiric.
#
#
# # Metoda propusa in acest articol a fost asamblarea clasificatoarelor KNN cu k=1, 3, 5, 7 ... n (unde n reprezinta radacina patrata a dimensiunii setului de date) intr-un singur clasificator care va clasifica in urma deciziei majoritare
#
# # Pasul 1: importam librariile necesare
# +
#import subprocess
import pandas as pd
import numpy as np
from numpy import mean
from numpy import std
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.preprocessing import LabelEncoder
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score, precision_score
from sklearn.utils import shuffle
from matplotlib import pyplot
from sklearn.ensemble import VotingClassifier
import math
# -
# # Pasul 2: definim metoda de instantiere a clasificatorului asamblat
# get a voting ensemble of models
def get_voting(n):
k=-1; count=0; models = list(); label="-NN"; labelList=[];
while k<n:
k=k+2;
count=count+1;
labelList.append(str(k)+label)
# define the base models
models.append((str(k)+label, KNeighborsClassifier(n_neighbors=k)))
# define the voting ensemble
ensemble = VotingClassifier(estimators=models, voting='hard')
return ensemble
# # Pasul 3: vom crea o lista cu clasificatorii care vor fi evaluati, aceasta lista contine clasificatorii 1NN, 3NN, 5NN.... nNN (unde n reprezinta radacina patrata a dimensiunii setului de date), si clasificatorul care asambleaza toti clasificatorii mentionati anterior
# get a list of models to evaluate
def get_models(n):
models = dict()
k=-1; count=0; label="-NN"; labelList=[];
while k<n:
k=k+2;
count=count+1;
labelList.append(str(k)+label)
# define the base models
if(k<10):
models[' '+str(k)+label] = KNeighborsClassifier(n_neighbors=k)
elif(k>10 and k<100):
models[' '+str(k)+label] = KNeighborsClassifier(n_neighbors=k)
else:
models[str(k)+label] = KNeighborsClassifier(n_neighbors=k)
models['ensemble'] = get_voting(n)
return models
# # Pasul 4: vom crea o metoda care va evalua fiecare model individual, metrica de interes fiind acuratetea. Pentru testare am impartit setul de date in 70% date de antrenare si 30% date de testare cum a specificat autorul documentului
# evaluate a give model using cross-validation
def evaluate_model(model):
cv = RepeatedStratifiedKFold(n_splits=5, n_repeats=1, random_state=1)
scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
return scores
# # Un exemplu propus de autor foloseste setul de date QSAR.csv care contine 43 de feature-uri, din care primele 42 sunt date de intrare, iar al 43-lea feature reprezinta clasa din care face parte obiectul interogat.
# # Dimensiunea setului de date este de 1055 de unde tragem concluzia ca vom utiliza clasificatorii 1NN, 3NN, 5NN, 7NN, 9NN, 11NN, 13NN, 15NN, 17NN, 19NN, 21NN, 23NN, 25NN, 27NN, 29NN, 31NN(deoarece 31 este cel mai apropiat numar impar de radical(1055)) in cadrul clasificatorului asamblat.
# +
input_file = "QSAR .csv"
data = pd.read_csv(input_file, header = 0)
X, y = data[data.columns.drop('F43')], data['F43']
n=int(math.sqrt(1055))
if(n % 2 == 0):
n=n-1
models = get_models(n)
# -
# # Datorita unui bug modelele sunt analizate intr-o ordine aleatoare, motiv pentru care voi introduce o sortare alfabetica a numelor clasificatoriilor care va ordona indirect si lista performantelor obtinute
#
# +
# evaluate the models and store results (unsorted)
results, names = list(), list()
for name, model in models.items():
scores = evaluate_model(model)
results.append(scores)
names.append(name)
for x in range (len(names)):
print('%s %.4f ' % (names[x], mean(results[x])))
# +
# evaluate the models and store results (sorted)
results, names = list(), list()
for name, model in models.items():
scores = evaluate_model(model)
results.append(scores)
names.append(name)
zipped= zip(names, results)
names, results = zip(*sorted(zipped))
for x in range (len(names)):
print('%s %.4f ' % (names[x], mean(results[x])))
# -
# # Australian data set contine 690 randuri de date, 42 de feature-uri, feature-ul pe care il vom clasifica este F15 care are 2 posibile clase
# +
print('Evaluate Australian dataset')
input_file = "australian.csv"
data = pd.read_csv(input_file, header = 0)
X, y = data[data.columns.drop('F15')], data['F15']
n=int(math.sqrt(690))
if(n % 2 == 0):
n=n-1
models = get_models(n)
# evaluate the models and store results
results, names = list(), list()
bestName="1NN"; bestAccuracy=0;
for name, model in models.items():
scores = evaluate_model(model)
results.append(scores)
names.append(name)
zipped= zip(names, results)
names, results = zip(*sorted(zipped))
for x in range (len(names)):
print('%s %.4f ' % (names[x], mean(results[x])))
if(mean(results[x])> bestAccuracy):
bestName= names[x];
bestAccuracy= mean(results[x]);
print('Best accuracy :%s with accuracy %.4f '% (bestName, bestAccuracy))
# -
# # Balance data set contine 625 randuri de date, 4 feature-uri, feature-ul pe care il vom clasifica este F1 care are 3 posibile clase
# +
print('Evaluate Balance dataset')
input_file = "balance.csv"
data = pd.read_csv(input_file, header = 0)
X, y = data[data.columns.drop('F1')], data['F1']
n=int(math.sqrt(625))
if(n % 2 == 0):
n=n-1
models = get_models(n)
# evaluate the models and store results
results, names = list(), list()
bestName="1NN"; bestAccuracy=0;
for name, model in models.items():
scores = evaluate_model(model)
results.append(scores)
names.append(name)
zipped= zip(names, results)
names, results = zip(*sorted(zipped))
for x in range (len(names)):
print('%s %.4f ' % (names[x], mean(results[x])))
if(mean(results[x])> bestAccuracy):
bestName= names[x];
bestAccuracy= mean(results[x]);
print('Best accuracy :%s with accuracy %.4f '% (bestName, bestAccuracy))
# -
# # Banknote data set contine 1372 randuri de date, 5 feature-uri, feature-ul pe care il vom clasifica este F5 care are 2 posibile clase
# +
print('Evaluate Banknote dataset')
input_file = "banknote.csv"
data = pd.read_csv(input_file, header = 0)
X, y = data[data.columns.drop('F5')], data['F5']
n=int(math.sqrt(1372))
if(n % 2 == 0):
n=n-1
models = get_models(n)
# evaluate the models and store results
results, names = list(), list()
bestName="1NN"; bestAccuracy=0;
for name, model in models.items():
scores = evaluate_model(model)
results.append(scores)
names.append(name)
zipped= zip(names, results)
names, results = zip(*sorted(zipped))
for x in range (len(names)):
print('%s %.4f ' % (names[x], mean(results[x])))
if(mean(results[x])> bestAccuracy):
bestName= names[x];
bestAccuracy= mean(results[x]);
print('Best accuracy :%s with accuracy %.4f '% (bestName, bestAccuracy))
# -
# # Haberman data set contine 306 randuri de date, 4 feature-uri, feature-ul pe care il vom clasifica este F4 care are 2 posibile clase
# +
print('Evaluate Haberman dataset')
input_file = "haberman.csv"
data = pd.read_csv(input_file, header = 0)
X, y = data[data.columns.drop('F4')], data['F4']
n=int(math.sqrt(306))
if(n % 2 == 0):
n=n-1
models = get_models(n)
# evaluate the models and store results
results, names = list(), list()
bestName="1NN"; bestAccuracy=0;
for name, model in models.items():
scores = evaluate_model(model)
results.append(scores)
names.append(name)
zipped= zip(names, results)
names, results = zip(*sorted(zipped))
for x in range (len(names)):
print('%s %.4f ' % (names[x], mean(results[x])))
if(mean(results[x])> bestAccuracy):
bestName= names[x];
bestAccuracy= mean(results[x]);
print('Best accuracy :%s with accuracy %.4f '% (bestName, bestAccuracy))
# -
# # Heart data set contine 271 randuri de date, 14 feature-uri, feature-ul pe care il vom clasifica este F14 care are 2 posibile clase
# +
print('Evaluate Heart dataset')
input_file = "heart.csv"
data = pd.read_csv(input_file, header = 0)
X, y = data[data.columns.drop('F14')], data['F14']
n=int(math.sqrt(271))
if(n % 2 == 0):
n=n-1
models = get_models(n)
# evaluate the models and store results
results, names = list(), list()
bestName="1NN"; bestAccuracy=0;
for name, model in models.items():
scores = evaluate_model(model)
results.append(scores)
names.append(name)
zipped= zip(names, results)
names, results = zip(*sorted(zipped))
for x in range (len(names)):
print('%s %.4f ' % (names[x], mean(results[x])))
if(mean(results[x])> bestAccuracy):
bestName= names[x];
bestAccuracy= mean(results[x]);
print('Best accuracy :%s with accuracy %.4f '% (bestName, bestAccuracy))
# -
# # Ionosphere data set contine 351 randuri de date, 35 feature-uri, feature-ul pe care il vom clasifica este F35 care are 2 posibile clase
# +
print('Evaluate Ionosphere dataset')
input_file = "ionosphere.csv"
data = pd.read_csv(input_file, header = 0)
X, y = data[data.columns.drop('F35')], data['F35']
n=int(math.sqrt(351))
if(n % 2 == 0):
n=n-1
models = get_models(n)
# evaluate the models and store results
results, names = list(), list()
bestName="1NN"; bestAccuracy=0;
for name, model in models.items():
scores = evaluate_model(model)
results.append(scores)
names.append(name)
zipped= zip(names, results)
names, results = zip(*sorted(zipped))
for x in range (len(names)):
print('%s %.4f ' % (names[x], mean(results[x])))
if(mean(results[x])> bestAccuracy):
bestName= names[x];
bestAccuracy= mean(results[x]);
print('Best accuracy :%s with accuracy %.4f '% (bestName, bestAccuracy))
# -
# # Iris data set contine 151 randuri de date, 5 feature-uri, feature-ul pe care il vom clasifica este F5 care are 3 posibile clase
# +
print('Evaluate Iris dataset')
input_file = "iris.csv"
data = pd.read_csv(input_file, header = 0)
X, y = data[data.columns.drop('F5')], data['F5']
n=int(math.sqrt(151))
if(n % 2 == 0):
n=n-1
models = get_models(n)
# evaluate the models and store results
results, names = list(), list()
bestName="1NN"; bestAccuracy=0;
for name, model in models.items():
scores = evaluate_model(model)
results.append(scores)
names.append(name)
zipped= zip(names, results)
names, results = zip(*sorted(zipped))
for x in range (len(names)):
print('%s %.4f ' % (names[x], mean(results[x])))
if(mean(results[x])> bestAccuracy):
bestName= names[x];
bestAccuracy= mean(results[x]);
print('Best accuracy :%s with accuracy %.4f '% (bestName, bestAccuracy))
# -
# # Liver data set contine 345 randuri de date, 7 feature-uri, feature-ul pe care il vom clasifica este F7 care are 2 posibile clase
# +
print('Evaluate Liver dataset')
input_file = "liver.csv"
data = pd.read_csv(input_file, header = 0)
X, y = data[data.columns.drop('F7')], data['F7']
n=int(math.sqrt(345))
if(n % 2 == 0):
n=n-1
models = get_models(n)
# evaluate the models and store results
results, names = list(), list()
bestName="1NN"; bestAccuracy=0;
for name, model in models.items():
scores = evaluate_model(model)
results.append(scores)
names.append(name)
zipped= zip(names, results)
names, results = zip(*sorted(zipped))
for x in range (len(names)):
print('%s %.4f ' % (names[x], mean(results[x])))
if(mean(results[x])> bestAccuracy):
bestName= names[x];
bestAccuracy= mean(results[x]);
print('Best accuracy :%s with accuracy %.4f '% (bestName, bestAccuracy))
# -
# # Parkinson data set contine 1040 randuri de date, 27 feature-uri, feature-ul pe care il vom clasifica este F1 care are 2 posibile clase
# +
print('Evaluate Parkinson dataset')
input_file = "parkinson.csv"
data = pd.read_csv(input_file, header = 0)
X, y = data[data.columns.drop('F1')], data['F1']
n=int(math.sqrt(168))
if(n % 2 == 0):
n=n-1
models = get_models(n)
# evaluate the models and store results
results, names = list(), list()
bestName="1NN"; bestAccuracy=0;
for name, model in models.items():
scores = evaluate_model(model)
results.append(scores)
names.append(name)
zipped= zip(names, results)
names, results = zip(*sorted(zipped))
for x in range (len(names)):
print('%s %.4f ' % (names[x], mean(results[x])))
if(mean(results[x])> bestAccuracy):
bestName= names[x];
bestAccuracy= mean(results[x]);
print('Best accuracy :%s with accuracy %.4f '% (bestName, bestAccuracy))
# -
# # Sonar data set contine 209 randuri de date, 61 feature-uri, feature-ul pe care il vom clasifica este F61 care are 2 posibile clase
# +
print('Evaluate Sonar dataset')
input_file = "sonar.csv"
data = pd.read_csv(input_file, header = 0)
X, y = data[data.columns.drop('F61')], data['F61']
n=int(math.sqrt(209))
if(n % 2 == 0):
n=n-1
models = get_models(n)
# evaluate the models and store results
results, names = list(), list()
bestName="1NN"; bestAccuracy=0;
for name, model in models.items():
scores = evaluate_model(model)
results.append(scores)
names.append(name)
zipped= zip(names, results)
names, results = zip(*sorted(zipped))
for x in range (len(names)):
print('%s %.4f ' % (names[x], mean(results[x])))
if(mean(results[x])> bestAccuracy):
bestName= names[x];
bestAccuracy= mean(results[x]);
print('Best accuracy :%s with accuracy %.4f '% (bestName, bestAccuracy))
# -
# # Wine data set contine 179 randuri de date, 13 feature-uri, feature-ul pe care il vom clasifica este F1 care are 3 posibile clase
# +
print('Evaluate Wine dataset')
input_file = "wine.csv"
data = pd.read_csv(input_file, header = 0)
X, y = data[data.columns.drop('F1')], data['F1']
n=int(math.sqrt(179))
if(n % 2 == 0):
n=n-1
models = get_models(n)
# evaluate the models and store results
results, names = list(), list()
bestName="1NN"; bestAccuracy=0;
for name, model in models.items():
scores = evaluate_model(model)
results.append(scores)
names.append(name)
zipped= zip(names, results)
names, results = zip(*sorted(zipped))
for x in range (len(names)):
print('%s %.4f ' % (names[x], mean(results[x])))
if(mean(results[x])> bestAccuracy):
bestName= names[x];
bestAccuracy= mean(results[x]);
print('Best accuracy :%s with accuracy %.4f '% (bestName, bestAccuracy))
# -
# # EEG data set contine 14980 randuri de date, 15 feature-uri, feature-ul pe care il vom clasifica este F15 care are 2 posibile clase (loading time > 5 minutes)
# +
print('Evaluate EEG dataset')
input_file = "EEG.csv"
data = pd.read_csv(input_file, header = 0)
X, y = data[data.columns.drop('F15')], data['F15']
n=int(math.sqrt(14980))
if(n % 2 == 0):
n=n-1
models = get_models(n)
# evaluate the models and store results
results, names = list(), list()
bestName="1NN"; bestAccuracy=0;
for name, model in models.items():
scores = evaluate_model(model)
results.append(scores)
names.append(name)
zipped= zip(names, results)
names, results = zip(*sorted(zipped))
for x in range (len(names)):
print('%s %.4f ' % (names[x], mean(results[x])))
if(mean(results[x])> bestAccuracy):
bestName= names[x];
bestAccuracy= mean(results[x]);
print('Best accuracy :%s with accuracy %.4f '% (bestName, bestAccuracy))
# -
# # Letter recognition data set contine 20000 randuri de date, 16 feature-uri, feature-ul pe care il vom clasifica este F1 care are 26 posibile clase (loading time > 5 minutes)
# +
print('Evaluate Letter-Recognition dataset')
input_file = "letter-recognition.csv"
data = pd.read_csv(input_file, header = 0)
X, y = data[data.columns.drop('F1')], data['F1']
n=int(math.sqrt(20000))
if(n % 2 == 0):
n=n-1
models = get_models(n)
# evaluate the models and store results
results, names = list(), list()
bestName="1NN"; bestAccuracy=0;
for name, model in models.items():
scores = evaluate_model(model)
results.append(scores)
names.append(name)
zipped= zip(names, results)
names, results = zip(*sorted(zipped))
for x in range (len(names)):
print('%s %.4f ' % (names[x], mean(results[x])))
if(mean(results[x])> bestAccuracy):
bestName= names[x];
bestAccuracy= mean(results[x]);
print('Best accuracy :%s with accuracy %.4f '% (bestName, bestAccuracy))
# -
# # Concluzii:
# # Toate seturile de date evaluate anterior au fost evaluate si in articolul ales de mine, restul seturilor de date care sunt prezentate in articol si nu sunt regasite mai sus nu mai sunt disponibile pe site-ul din bibliografie.
#
# # In urma experimentelor am remarcat ca desi clasificatorul asamblat descris in articol nu depaseste performanta celui mai bun clasificator KNN din ansamblul sau performanta ansamblului este foarte apropiata de cea mai buna performanta, scutundu-ne de cautarea parametrului k care ar avea cea mai buna performanta.
#
# # De asemenea am remarcat ca performantele optinute ruland codul python din terminal(folosind versiunea 2.7.3) si cea optinuta din acest notebook(care foloseste versiunea 3) sunt diferite
|
KNN EnsembleClassifieR.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] application/vnd.databricks.v1+cell={"inputWidgets": {}, "nuid": "3e8921b5-ae3e-4df0-9f5c-8e62ceaf18c4", "showTitle": false, "title": ""}
# # [Model] Data Analytics Test - iFood
# ###### [By <NAME>](https://github.com/israelmendez232)
#
# This notebook was generated locally, because of the complexity to run the models that won't work for the [Databricks](https://databricks.com/) Community Edition.
#
# The main library used here is [PyCaret](https://pycaret.readthedocs.io/en/latest/) to generate the model and tuning because is very practical and productive. The summary:
# 1. Train the model and explorations;
# 2. Validate the results;
# 3. Evaluate the return;
# 4. [EXTRA] Results
# -
# ## 1. Train the model
# Bring more explorations.
# + application/vnd.databricks.v1+cell={"inputWidgets": {}, "nuid": "6e52ae10-d4c7-4184-8ed9-482335d82128", "showTitle": false, "title": ""}
import pandas as pd
from pycaret.classification import *
df = pd.read_csv("../data/data_analytics_cleaned.csv")
df.head(10)
# -
# Selecting only the best variables stipulated on the 02-EDA phase.
df_focused = df[["ID", "AcceptedCmp5", "AcceptedCmp1", "MntWines", "AcceptedCmp3", "MntMeatProducts", "NumCatalogPurchases", "Recency", "Teenhome", "Kidhome", "Response"]]
df_focused.head()
df_focused.describe()
# +
# Defining the rows for testing and prediction
df_train = df_focused.sample(frac = 0.9, random_state = 786)
df_prediction = df_focused.drop(df_train.index)
df_train.reset_index(drop = True, inplace = True)
df_prediction.reset_index(drop = True, inplace = True)
print('Data for Training/Modeling: ' + str(df_train.shape))
print('Data For Predictions: ' + str(df_prediction.shape))
# + application/vnd.databricks.v1+cell={"inputWidgets": {}, "nuid": "2efd1296-f0d3-4a6b-b186-0f2e75e3207d", "showTitle": false, "title": ""}
# Setup for the classification model
setup_sample = setup(df_train, target = 'Response')
# + application/vnd.databricks.v1+cell={"inputWidgets": {}, "nuid": "c3acad40-a74a-4bde-9885-f35cb39bcacf", "showTitle": false, "title": ""}
# Compare different models
best_model = compare_models()
# -
# The best models are highlighted in yellow. Decided to move with CatBoost, Light Gradient Boosting, and Naive Bayes.
# + application/vnd.databricks.v1+cell={"inputWidgets": {}, "nuid": "72367126-e6b5-4965-987b-329d793e5cb0", "showTitle": false, "title": ""}
catboost = create_model('catboost')
# -
lightgbm = create_model('lightgbm')
nb = create_model('nb')
# + application/vnd.databricks.v1+cell={"inputWidgets": {}, "nuid": "5103de87-5b2a-4fa4-8a74-889e3532c584", "showTitle": false, "title": ""}
# Using Hyperparameters
tuned_catboost = tune_model(catboost)
# -
# Using Hyperparameters
tuned_lightgbm = tune_model(lightgbm)
# Using Hyperparameters
tuned_nb = tune_model(nb)
# Blending the models
blender = blend_models(estimator_list = [tuned_catboost, tuned_lightgbm, tuned_nb], method = 'soft')
stacker = stack_models(estimator_list = [tuned_catboost, tuned_lightgbm, tuned_nb], meta_model = catboost)
# Choosing stacker over blender because of significantly better performance on stacker based on Recall, Kappa, and MCC.
plot_model(stacker)
plot_model(stacker, plot = 'confusion_matrix')
plot_model(stacker, plot = 'boundary')
# ## 2. Validate the results
# Save the model
predict_new = predict_model(stacker, data = df_prediction)
predict_new.tail()
predict_new['result'] = predict_new['Response'] == predict_new['Label']
predict_new.tail()
# +
lost = predict_new[predict_new['result'] == False]['result'].count()
won = predict_new[predict_new['result'] == True]['result'].count()
end_result = won / (won + lost)
print(f"Right predictions: {won}")
print(f"Wrong predictions: {lost}")
print(f"End result in % of the predictions: {end_result}")
# -
# Saving locally the model
save_model(stacker, model_name='end-classifier-model')
# ## 3. Evaluate the return
# Now it's time to validate if the insights are accurate based on the **prediction sample**. Main points to evaluate:
# - Prove that the insight could have a **campaign rate beyond 15%**, which was the standard for this campaign;
# - Considering the 6.720MU spent on this "sample", with 2.213 (not counting the null and outliers). This campaign has **invested 3.03MU/customer**;
# - The **total received** by each Response was: 3.674MU / 333 (not counting the null and outliers) => **11.03MU/customer**;
# - To be successful, the **campaign rate needs to be 28% or higher** (3.03 / 11.03) based on the cost and return over customer;
# - The **R.O.I.** was (3.674MU / 6.720MU) - 1 => **-45,32%**;
#
# Since we can't change the price or the campaign, we can focus more on segmentation and the historical data of those customers. And to provide better insights to overcome the standard elements mentioned earlier.
# Considering we will only impact the customers that were predicted as 1, avoiding the 0 ones.
validation = predict_new.copy()
validation = validation[validation['Label'] == 1]
validation.head()
# +
base_total_customers = predict_new['result'].count()
customers_impactated = validation['result'].count()
rel_customers_imp_total_base = customers_impactated / base_total_customers
customers_positive = validation[predict_new['result'] == True]['result'].count()
total_spend = customers_impactated * 3.03
total_return = customers_positive * 11.03
campaign_rate = customers_positive / customers_impactated
roi = (total_return / total_spend) - 1
print("# Results from the prediction sample \n")
print(f"Total customers impactated: {customers_impactated}")
print(f"Customers impactated and positive response: {customers_positive}")
print(f"Customers impactated / total customers: {rel_customers_imp_total_base}")
print(f"Total spend on campaign: {total_spend}")
print(f"Total return on the campaign: {total_return}")
print(f"Campaign rate: {campaign_rate}")
print(f"ROI: {roi}")
# -
# ## [EXTRA] Results
#
# The model was responsable to:
# - Increase the **Campaign Rate** to 15% up to **100%**;
# - Deliver a **ROI** to **+264,02%**, compared to -45,32% of the starndart campaign.
#
# ---
#
# If we extrapolate the results from this model, it would generate the following results in the whole base:
# - 2,213 (whole base) * 0.054 (rate from impactated customers) * 3.03 (cost by customer) => **362MU in costs;**
# - 2,213 (whole base) * 0.054 (rate from impactated customers) * 1 (campaign rate) * 11.03 (return by customer) => **1.318MU in profit;**
# - The model would save up to **6.358MU**;
# - Also, the model would bring 35.87% of the standard results of the campaign with ONLY 5.38% of the total budget!
#
|
notebooks/03-model-data-analytics-test-ifood-israel-mendes.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### Machine Learning for Engineers: [GaussianMixtureModel](https://www.apmonitor.com/pds/index.php/Main/GaussianMixtureModel)
# - [Gaussian Mixture Model](https://www.apmonitor.com/pds/index.php/Main/GaussianMixtureModel)
# - Source Blocks: 1
# - Description: Introduction to Gaussian Mixture Models
# - [Course Overview](https://apmonitor.com/pds)
# - [Course Schedule](https://apmonitor.com/pds/index.php/Main/CourseSchedule)
#
from sklearn.mixture import GaussianMixture
gmm = GaussianMixture(n_components=2)
gmm.fit(XA)
yP = gmm.predict_proba(XB) # produces probabilities
# Arbitrary labels with unsupervised clustering may need to be reversed
if len(XB[np.round(yP[:,0])!=yB]) > n/4: yP = 1 - yP
|
All_Source_Code/GaussianMixtureModel/GaussianMixtureModel.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
def truth_table(gate):
print("*{}*".format(gate.__name__))
print("|x1|x2|y|")
print("|0 |0 |{}|".format(gate(0, 0)))
print("|0 |1 |{}|".format(gate(0, 1)))
print("|1 |0 |{}|".format(gate(1, 0)))
print("|1 |1 |{}|".format(gate(1, 1)))
def and_gate(x1, x2):
w1, w2, theta, = 0.5, 0.5, 0.75
if theta < x1 * w1 + x2 * w2:
y = 1
else:
y = 0
return y
truth_table(and_gate)
def or_gate(x1, x2):
w1, w2, theta, = 0.5, 0.5, 0.25
if theta < x1 * w1 + x2 * w2:
y = 1
else:
y = 0
return y
truth_table(or_gate)
def nand_gate(x1, x2):
w1, w2, theta, = -0.5, -0.5, -0.75
if theta < x1 * w1 + x2 * w2:
y = 1
else:
y = 0
return y
truth_table(nand_gate)
def xor_gate(x1, x2):
s1 = or_gate(x1, x2)
s2 = nand_gate(x1, x2)
y = and_gate(s1, s2)
return y
truth_table(xor_gate)
|
python/gate.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Training Keras model on Cloud AI Platform.
#
# **Learning Objectives**
#
# 1. Setup up the environment
# 1. Create trainer module's task.py to hold hyperparameter argparsing code
# 1. Create trainer module's model.py to hold Keras model code
# 1. Run trainer module package locally
# 1. Submit training job to Cloud AI Platform
# 1. Submit hyperparameter tuning job to Cloud AI Platform
#
#
# ## Introduction
# After having testing our training pipeline both locally and in the cloud on a susbset of the data, we can submit another (much larger) training job to the cloud. It is also a good idea to run a hyperparameter tuning job to make sure we have optimized the hyperparameters of our model.
#
# In this notebook, we'll be training our Keras model at scale using Cloud AI Platform.
#
# In this lab, we will set up the environment, create the trainer module's task.py to hold hyperparameter argparsing code, create the trainer module's model.py to hold Keras model code, run the trainer module package locally, submit a training job to Cloud AI Platform, and submit a hyperparameter tuning job to Cloud AI Platform.
#
# Each learning objective will correspond to a __#TODO__ in this student lab notebook -- try to complete this notebook first and then review the [solution notebook](../solutions/5a_train_keras_ai_platform_babyweight.ipynb).
# + [markdown] colab_type="text" id="hJ7ByvoXzpVI"
# ## Set up environment variables and load necessary libraries
# -
# Import necessary libraries.
import os
# ### Lab Task #1: Set environment variables.
#
# Set environment variables so that we can use them throughout the entire lab. We will be using our project name for our bucket, so you only need to change your project and region.
# + language="bash"
# export PROJECT=$(gcloud config list project --format "value(core.project)")
# echo "Your current GCP Project Name is: "${PROJECT}
# -
# TODO: Change these to try this notebook out
PROJECT = "cloud-training-demos" # Replace with your PROJECT
BUCKET = PROJECT # defaults to PROJECT
REGION = "us-central1" # Replace with your REGION
os.environ["PROJECT"] = PROJECT
os.environ["BUCKET"] = BUCKET
os.environ["REGION"] = REGION
os.environ["TFVERSION"] = "2.0"
# + language="bash"
# gcloud config set project $PROJECT
# gcloud config set compute/region $REGION
# + language="bash"
# if ! gsutil ls | grep -q gs://${BUCKET}; then
# gsutil mb -l ${REGION} gs://${BUCKET}
# fi
# -
# ## Check data exists
#
# Verify that you previously created CSV files we'll be using for training and evaluation. If not, go back to lab [prepare_data_babyweight.ipynb](../solutions/prepare_data_babyweight.ipynb) to create them.
# + language="bash"
# gsutil ls gs://${BUCKET}/babyweight/data/*000000000000.csv
# -
# Now that we have the [Keras wide-and-deep code](../solutions/4c_keras_wide_and_deep_babyweight.ipynb) working on a subset of the data, we can package the TensorFlow code up as a Python module and train it on Cloud AI Platform.
#
# ## Train on Cloud AI Platform
#
# Training on Cloud AI Platform requires:
# * Making the code a Python package
# * Using gcloud to submit the training code to [Cloud AI Platform](https://console.cloud.google.com/ai-platform)
#
# Ensure that the AI Platform API is enabled by going to this [link](https://console.developers.google.com/apis/library/ml.googleapis.com).
#
# ### Move code into a Python package
#
# A Python package is simply a collection of one or more `.py` files along with an `__init__.py` file to identify the containing directory as a package. The `__init__.py` sometimes contains initialization code but for our purposes an empty file suffices.
#
# The bash command `touch` creates an empty file in the specified location, the directory `babyweight` should already exist.
# + language="bash"
# mkdir -p babyweight/trainer
# touch babyweight/trainer/__init__.py
# -
# We then use the `%%writefile` magic to write the contents of the cell below to a file called `task.py` in the `babyweight/trainer` folder.
# ### Lab Task #2: Create trainer module's task.py to hold hyperparameter argparsing code.
#
# The cell below writes the file `babyweight/trainer/task.py` which sets up our training job. Here is where we determine which parameters of our model to pass as flags during training using the `parser` module. Look at how `batch_size` is passed to the model in the code below. Use this as an example to parse arguements for the following variables
# - `nnsize` which represents the hidden layer sizes to use for DNN feature columns
# - `nembeds` which represents the embedding size of a cross of n key real-valued parameters
# - `train_examples` which represents the number of examples (in thousands) to run the training job
# - `eval_steps` which represents the positive number of steps for which to evaluate model
#
# Be sure to include a default value for the parsed arguments above and specfy the `type` if necessary.
# +
# %%writefile babyweight/trainer/task.py
import argparse
import json
import os
from babyweight.trainer import model
import tensorflow as tf
if __name__ == "__main__":
parser = argparse.ArgumentParser()
parser.add_argument(
"--job-dir",
help="this model ignores this field, but it is required by gcloud",
default="junk"
)
parser.add_argument(
"--train_data_path",
help="GCS location of training data",
required=True
)
parser.add_argument(
"--eval_data_path",
help="GCS location of evaluation data",
required=True
)
parser.add_argument(
"--output_dir",
help="GCS location to write checkpoints and export models",
required=True
)
parser.add_argument(
"--batch_size",
help="Number of examples to compute gradient over.",
type=int,
default=512
)
# TODO: Add nnsize argument
# TODO: Add nembeds argument
# TODO: Add num_epochs argument
# TODO: Add train_examples argument
# TODO: Add eval_steps argument
# Parse all arguments
args = parser.parse_args()
arguments = args.__dict__
# Unused args provided by service
arguments.pop("job_dir", None)
arguments.pop("job-dir", None)
# Modify some arguments
arguments["train_examples"] *= 1000
# Append trial_id to path if we are doing hptuning
# This code can be removed if you are not using hyperparameter tuning
arguments["output_dir"] = os.path.join(
arguments["output_dir"],
json.loads(
os.environ.get("TF_CONFIG", "{}")
).get("task", {}).get("trial", "")
)
# Run the training job
model.train_and_evaluate(arguments)
# -
# In the same way we can write to the file `model.py` the model that we developed in the previous notebooks.
#
# ### Lab Task #3: Create trainer module's model.py to hold Keras model code.
#
# Complete the TODOs in the code cell below to create our `model.py`. We'll use the code we wrote for the Wide & Deep model. Look back at your [9_keras_wide_and_deep_babyweight](../solutions/9_keras_wide_and_deep_babyweight.ipynb) notebook and copy/paste the necessary code from that notebook into its place in the cell below.
# +
# %%writefile babyweight/trainer/model.py
import datetime
import os
import shutil
import numpy as np
import tensorflow as tf
# Determine CSV, label, and key columns
# TODO: Add CSV_COLUMNS and LABEL_COLUMN
# Set default values for each CSV column.
# Treat is_male and plurality as strings.
# TODO: Add DEFAULTS
def features_and_labels(row_data):
# TODO: Add your code here
pass
def load_dataset(pattern, batch_size=1, mode='eval'):
# TODO: Add your code here
pass
def create_input_layers():
# TODO: Add your code here
pass
def categorical_fc(name, values):
# TODO: Add your code here
pass
def create_feature_columns(nembeds):
# TODO: Add your code here
pass
def get_model_outputs(wide_inputs, deep_inputs, dnn_hidden_units):
# TODO: Add your code here
pass
def rmse(y_true, y_pred):
# TODO: Add your code here
pass
def build_wide_deep_model(dnn_hidden_units=[64, 32], nembeds=3):
# TODO: Add your code here
pass
def train_and_evaluate(args):
model = build_wide_deep_model(args["nnsize"], args["nembeds"])
print("Here is our Wide-and-Deep architecture so far:\n")
print(model.summary())
trainds = load_dataset(
args["train_data_path"],
args["batch_size"],
'train')
evalds = load_dataset(
args["eval_data_path"], 1000, 'eval')
if args["eval_steps"]:
evalds = evalds.take(count=args["eval_steps"])
num_batches = args["batch_size"] * args["num_epochs"]
steps_per_epoch = args["train_examples"] // num_batches
checkpoint_path = os.path.join(args["output_dir"], "checkpoints/babyweight")
cp_callback = tf.keras.callbacks.ModelCheckpoint(
filepath=checkpoint_path, verbose=1, save_weights_only=True)
history = model.fit(
trainds,
validation_data=evalds,
epochs=args["num_epochs"],
steps_per_epoch=steps_per_epoch,
verbose=2, # 0=silent, 1=progress bar, 2=one line per epoch
callbacks=[cp_callback])
EXPORT_PATH = os.path.join(
args["output_dir"], datetime.datetime.now().strftime("%Y%m%d%H%M%S"))
tf.saved_model.save(
obj=model, export_dir=EXPORT_PATH) # with default serving function
print("Exported trained model to {}".format(EXPORT_PATH))
# -
# ## Train locally
#
# After moving the code to a package, make sure it works as a standalone. Note, we incorporated the `--train_examples` flag so that we don't try to train on the entire dataset while we are developing our pipeline. Once we are sure that everything is working on a subset, we can change it so that we can train on all the data. Even for this subset, this takes about *3 minutes* in which you won't see any output ...
# ### Lab Task #4: Run trainer module package locally.
#
# Fill in the missing code in the TODOs below so that we can run a very small training job over a single file with a small batch size, 1 epoch, 1 train example, and 1 eval step.
# + language="bash"
# OUTDIR=babyweight_trained
# rm -rf ${OUTDIR}
# export PYTHONPATH=${PYTHONPATH}:${PWD}/babyweight
# python3 -m trainer.task \
# --job-dir=./tmp \
# --train_data_path=gs://${BUCKET}/babyweight/data/train*.csv \
# --eval_data_path=gs://${BUCKET}/babyweight/data/eval*.csv \
# --output_dir=${OUTDIR} \
# --batch_size=# TODO: Add batch size
# --num_epochs=# TODO: Add the number of epochs to train for
# --train_examples=# TODO: Add the number of examples to train each epoch for
# --eval_steps=# TODO: Add the number of evaluation batches to run
# -
# ## Dockerized module
#
# Since we are using TensorFlow 2.0 and it is new, we will use a container image to run the code on AI Platform.
#
# Once TensorFlow 2.0 is natively supported on AI Platform, you will be able to simply do (without having to build a container):
# <pre>
# gcloud ai-platform jobs submit training ${JOBNAME} \
# --region=${REGION} \
# --module-name=trainer.task \
# --package-path=$(pwd)/babyweight/trainer \
# --job-dir=${OUTDIR} \
# --staging-bucket=gs://${BUCKET} \
# --scale-tier=STANDARD_1 \
# --runtime-version=${TFVERSION} \
# -- \
# --train_data_path=gs://${BUCKET}/babyweight/data/train*.csv \
# --eval_data_path=gs://${BUCKET}/babyweight/data/eval*.csv \
# --output_dir=${OUTDIR} \
# --num_epochs=10 \
# --train_examples=20000 \
# --eval_steps=100 \
# --batch_size=32 \
# --nembeds=8
# </pre>
# ### Create Dockerfile
#
# We need to create a container with everything we need to be able to run our model. This includes our trainer module package, python3, as well as the libraries we use such as the most up to date TensorFlow 2.0 version.
# +
# %%writefile babyweight/Dockerfile
FROM gcr.io/deeplearning-platform-release/tf2-cpu
COPY trainer /babyweight/trainer
RUN apt update && \
apt install --yes python3-pip && \
pip3 install --upgrade --quiet tensorflow==2.0
ENV PYTHONPATH ${PYTHONPATH}:/babyweight
ENTRYPOINT ["python3", "babyweight/trainer/task.py"]
# -
# ### Build and push container image to repo
#
# Now that we have created our Dockerfile, we need to build and push our container image to our project's container repo. To do this, we'll create a small shell script that we can call from the bash.
# +
# %%writefile babyweight/push_docker.sh
export PROJECT_ID=$(gcloud config list project --format "value(core.project)")
export IMAGE_REPO_NAME=babyweight_training_container
export IMAGE_URI=gcr.io/${PROJECT_ID}/${IMAGE_REPO_NAME}
# echo "Building $IMAGE_URI"
docker build -f Dockerfile -t ${IMAGE_URI} ./
# echo "Pushing $IMAGE_URI"
docker push ${IMAGE_URI}
# -
# **Note:** If you get a permissions/stat error when running push_docker.sh from Notebooks, do it from CloudShell:
#
# Open CloudShell on the GCP Console
# * git clone https://github.com/GoogleCloudPlatform/training-data-analyst
# * cd training-data-analyst/courses/machine_learning/deepdive2/structured/solutions/babyweight
# * bash push_docker.sh
#
# This step takes 5-10 minutes to run.
# + language="bash"
# cd babyweight
# bash push_docker.sh
# -
# ### Test container locally
#
# Before we submit our training job to Cloud AI Platform, let's make sure our container that we just built and pushed to our project's container repo works perfectly. We can do that by calling our container in bash and passing the necessary user_args for our task.py's parser.
# + language="bash"
# export PROJECT_ID=$(gcloud config list project --format "value(core.project)")
# export IMAGE_REPO_NAME=babyweight_training_container
# export IMAGE_URI=gcr.io/${PROJECT_ID}/${IMAGE_REPO_NAME}
# echo "Running $IMAGE_URI"
# docker run ${IMAGE_URI} \
# --train_data_path=gs://${BUCKET}/babyweight/data/train*.csv \
# --train_data_path=gs://${BUCKET}/babyweight/data/train*.csv \
# --eval_data_path=gs://${BUCKET}/babyweight/data/eval*.csv \
# --output_dir=gs://${BUCKET}/babyweight/trained_model \
# --batch_size=10 \
# --num_epochs=10 \
# --train_examples=1 \
# --eval_steps=1
# -
# ## Lab Task #5: Train on Cloud AI Platform.
#
# Once the code works in standalone mode, you can run it on Cloud AI Platform. Because this is on the entire dataset, it will take a while. The training run took about <b> two hours </b> for me. You can monitor the job from the GCP console in the Cloud AI Platform section. Complete the __#TODO__s to make sure you have the necessary user_args for our task.py's parser.
# + language="bash"
# OUTDIR=gs://${BUCKET}/babyweight/trained_model
# JOBID=babyweight_$(date -u +%y%m%d_%H%M%S)
# echo ${OUTDIR} ${REGION} ${JOBNAME}
# gsutil -m rm -rf ${OUTDIR}
#
# IMAGE=gcr.io/${PROJECT}/babyweight_training_container
#
# gcloud ai-platform jobs submit training ${JOBID} \
# --staging-bucket=gs://${BUCKET} \
# --region=${REGION} \
# --master-image-uri=${IMAGE} \
# --master-machine-type=n1-standard-4 \
# --scale-tier=CUSTOM \
# -- \
# --train_data_path=# TODO: Add path to training data in GCS
# --eval_data_path=# TODO: Add path to evaluation data in GCS
# --output_dir=${OUTDIR} \
# --num_epochs=# TODO: Add the number of epochs to train for
# --train_examples=# TODO: Add the number of examples to train each epoch for
# --eval_steps=# TODO: Add the number of evaluation batches to run
# --batch_size=# TODO: Add batch size
# --nembeds=# TODO: Add number of embedding dimensions
# -
# When I ran it, I used train_examples=2000000. When training finished, I filtered in the Stackdriver log on the word "dict" and saw that the last line was:
# <pre>
# Saving dict for global step 5714290: average_loss = 1.06473, global_step = 5714290, loss = 34882.4, rmse = 1.03186
# </pre>
# The final RMSE was 1.03 pounds.
# ## Lab Task #6: Hyperparameter tuning.
#
# All of these are command-line parameters to my program. To do hyperparameter tuning, create `hyperparam.yaml` and pass it as `--config hyperparam.yaml`.
# This step will take <b>up to 2 hours</b> -- you can increase `maxParallelTrials` or reduce `maxTrials` to get it done faster. Since `maxParallelTrials` is the number of initial seeds to start searching from, you don't want it to be too large; otherwise, all you have is a random search. Complete __#TODO__s in yaml file and gcloud training job bash command so that we can run hyperparameter tuning.
# %%writefile hyperparam.yaml
trainingInput:
scaleTier: STANDARD_1
hyperparameters:
hyperparameterMetricTag: # TODO: Add metric we want to optimize
goal: # TODO: MAXIMIZE or MINIMIZE?
maxTrials: 20
maxParallelTrials: 5
enableTrialEarlyStopping: True
params:
- parameterName: batch_size
type: # TODO: What datatype?
minValue: # TODO: Choose a min value
maxValue: # TODO: Choose a max value
scaleType: # TODO: UNIT_LINEAR_SCALE or UNIT_LOG_SCALE?
- parameterName: nembeds
type: # TODO: What datatype?
minValue: # TODO: Choose a min value
maxValue: # TODO: Choose a max value
scaleType: # TODO: UNIT_LINEAR_SCALE or UNIT_LOG_SCALE?
# + language="bash"
# OUTDIR=gs://${BUCKET}/babyweight/hyperparam
# JOBNAME=babyweight_$(date -u +%y%m%d_%H%M%S)
# echo ${OUTDIR} ${REGION} ${JOBNAME}
# gsutil -m rm -rf ${OUTDIR}
#
# IMAGE=gcr.io/${PROJECT}/babyweight_training_container
#
# gcloud ai-platform jobs submit training ${JOBNAME} \
# --staging-bucket=gs://${BUCKET} \
# --region=${REGION} \
# --master-image-uri=${IMAGE} \
# --master-machine-type=n1-standard-4 \
# --scale-tier=CUSTOM \
# --# TODO: Add config for hyperparam.yaml
# -- \
# --train_data_path=gs://${BUCKET}/babyweight/data/train*.csv \
# --eval_data_path=gs://${BUCKET}/babyweight/data/eval*.csv \
# --output_dir=${OUTDIR} \
# --num_epochs=10 \
# --train_examples=20000 \
# --eval_steps=100
# -
# ## Repeat training
#
# This time with tuned parameters for `batch_size` and `nembeds`.
# + language="bash"
# OUTDIR=gs://${BUCKET}/babyweight/trained_model_tuned
# JOBNAME=babyweight_$(date -u +%y%m%d_%H%M%S)
# echo ${OUTDIR} ${REGION} ${JOBNAME}
# gsutil -m rm -rf ${OUTDIR}
#
# IMAGE=gcr.io/${PROJECT}/babyweight_training_container
#
# gcloud ai-platform jobs submit training ${JOBNAME} \
# --staging-bucket=gs://${BUCKET} \
# --region=${REGION} \
# --master-image-uri=${IMAGE} \
# --master-machine-type=n1-standard-4 \
# --scale-tier=CUSTOM \
# -- \
# --train_data_path=gs://${BUCKET}/babyweight/data/train*.csv \
# --eval_data_path=gs://${BUCKET}/babyweight/data/eval*.csv \
# --output_dir=${OUTDIR} \
# --num_epochs=10 \
# --train_examples=20000 \
# --eval_steps=100 \
# --batch_size=32 \
# --nembeds=8
# -
# ## Lab Summary:
# In this lab, we set up the environment, created the trainer module's task.py to hold hyperparameter argparsing code, created the trainer module's model.py to hold Keras model code, ran the trainer module package locally, submitted a training job to Cloud AI Platform, and submitted a hyperparameter tuning job to Cloud AI Platform.
# Copyright 2019 Google Inc. Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.apache.org/licenses/LICENSE-2.0 Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License
|
courses/machine_learning/deepdive2/end_to_end_ml/labs/train_keras_ai_platform_babyweight.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Рекуррентные нейронных сетей
# +
import tensorflow as tf
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import os
import pandas as pd
mpl.rcParams['figure.figsize'] = (8, 6)
mpl.rcParams['axes.grid'] = False
# -
df = pd.read_csv("C:/Users/Zhastay/Downloads/jena_climate_2009_2016/data.csv")
df.head()
def univariate_data(dataset, start_index, end_index, history_size, target_size):
data = []
labels = []
start_index = start_index + history_size
if end_index is None:
end_index = len(dataset) - target_size
for i in range(start_index, end_index):
indices = range(i-history_size, i)
# Reshape data from (history_size,) to (history_size, 1)
data.append(np.reshape(dataset[indices], (history_size, 1)))
labels.append(dataset[i+target_size])
return np.array(data), np.array(labels)
uni_data = df['temp']
uni_data.index = df['id']
uni_data.head()
TRAIN_SPLIT = 11000
tf.random.set_seed(13)
uni_data = df['temp']
uni_data.index = df['id']
uni_data.head()
uni_data.plot(subplots=True)
uni_data = uni_data.values
uni_train_mean = uni_data[:TRAIN_SPLIT].mean()
uni_train_std = uni_data[:TRAIN_SPLIT].std()
uni_data = (uni_data-uni_train_mean)/uni_train_std
# +
univariate_past_history = 100
univariate_future_target = 0
x_train_uni, y_train_uni = univariate_data(uni_data, 0, TRAIN_SPLIT,
univariate_past_history,
univariate_future_target)
x_val_uni, y_val_uni = univariate_data(uni_data, TRAIN_SPLIT, None,
univariate_past_history,
univariate_future_target)
print ('Single window of past history')
print (x_train_uni[0])
print ('\n Target temperature to predict')
print (y_train_uni[0])
# -
print (len(x_train_uni))
def create_time_steps(length):
return list(range(-length, 0))
def show_plot(plot_data, delta, title):
labels = ['History', 'True Future', 'Model Prediction']
marker = ['.-', 'rx', 'go']
time_steps = create_time_steps(plot_data[0].shape[0])
if delta:
future = delta
else:
future = 0
plt.title(title)
for i, x in enumerate(plot_data):
if i:
plt.plot(future, plot_data[i], marker[i], markersize=10,
label=labels[i])
else:
plt.plot(time_steps, plot_data[i].flatten(), marker[i], label=labels[i])
plt.legend()
plt.xlim([time_steps[0], (future+5)*2])
plt.xlabel('Time-Step')
return plt
show_plot([x_train_uni[0], y_train_uni[0]], 0, 'Sample Example')
def baseline(history):
return np.mean(history)
show_plot([x_train_uni[0], y_train_uni[0], baseline(x_train_uni[0])], 0,
'Baseline Prediction Example')
# # LSTM-модель для прогнозирование
# +
simple_lstm_model = tf.keras.models.Sequential([
tf.keras.layers.LSTM(8, input_shape=x_train_uni.shape[-2:]),
tf.keras.layers.Dense(1)
])
simple_lstm_model.compile(optimizer='adam', loss='mae')
# +
BATCH_SIZE = 256
BUFFER_SIZE = 10000
train_univariate = tf.data.Dataset.from_tensor_slices((x_train_uni, y_train_uni))
train_univariate = train_univariate.cache().shuffle(BUFFER_SIZE).batch(BATCH_SIZE).repeat()
val_univariate = tf.data.Dataset.from_tensor_slices((x_val_uni, y_val_uni))
val_univariate = val_univariate.batch(BATCH_SIZE).repeat()
# -
for x, y in val_univariate.take(1):
print(simple_lstm_model.predict(x).shape)
print(x_train_uni.shape)
# +
EVALUATION_INTERVAL = 200
EPOCHS = 10
simple_lstm_model.fit(train_univariate, epochs=EPOCHS,
steps_per_epoch=EVALUATION_INTERVAL,
validation_data=val_univariate, validation_steps=50)
# -
for x, y in val_univariate.take(3):
plot = show_plot([x[0].numpy(), y[0].numpy(),
simple_lstm_model.predict(x)[0]], 0, 'Simple LSTM model')
plot.show()
# # Прогнозирование на основе многомерного временного ряда
features_considered = ['temp', 'gas', 'humid']
features = df[features_considered]
features.index = df['id']
features.head()
features.plot(subplots=True)
dataset = features.values
data_mean = dataset[:TRAIN_SPLIT].mean(axis=0)
data_std = dataset[:TRAIN_SPLIT].std(axis=0)
dataset = (dataset-data_mean)/data_std
# Точечное прогнозирование
def multivariate_data(dataset, target, start_index, end_index, history_size,
target_size, step, single_step=False):
data = []
labels = []
start_index = start_index + history_size
if end_index is None:
end_index = len(dataset) - target_size
for i in range(start_index, end_index):
indices = range(i-history_size, i, step)
data.append(dataset[indices])
if single_step:
labels.append(target[i+target_size])
else:
labels.append(target[i:i+target_size])
return np.array(data), np.array(labels)
# Настроить надо правильно! Step шаги переход, например если каждые 10 минут шаг 6 = каждые 60 минут
# +
past_history = 720
future_target = 72
STEP = 6
x_train_single, y_train_single = multivariate_data(dataset, dataset[:, 1], 0,
TRAIN_SPLIT, past_history,
future_target, STEP,
single_step=True)
x_val_single, y_val_single = multivariate_data(dataset, dataset[:, 1],
TRAIN_SPLIT, None, past_history,
future_target, STEP,
single_step=True)
# -
print ('Single window of past history : {}'.format(x_train_single[0].shape))
# +
train_data_single = tf.data.Dataset.from_tensor_slices((x_train_single, y_train_single))
train_data_single = train_data_single.cache().shuffle(BUFFER_SIZE).batch(BATCH_SIZE).repeat()
val_data_single = tf.data.Dataset.from_tensor_slices((x_val_single, y_val_single))
val_data_single = val_data_single.batch(BATCH_SIZE).repeat()
# +
single_step_model = tf.keras.models.Sequential()
single_step_model.add(tf.keras.layers.LSTM(32,
input_shape=x_train_single.shape[-2:]))
single_step_model.add(tf.keras.layers.Dense(1))
single_step_model.compile(optimizer=tf.keras.optimizers.RMSprop(), loss='mae')
# -
for x, y in val_data_single.take(1):
print(single_step_model.predict(x).shape)
single_step_history = single_step_model.fit(train_data_single, epochs=EPOCHS,
steps_per_epoch=EVALUATION_INTERVAL,
validation_data=val_data_single,
validation_steps=50)
def plot_train_history(history, title):
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(loss))
plt.figure()
plt.plot(epochs, loss, 'b', label='Training loss')
plt.plot(epochs, val_loss, 'r', label='Validation loss')
plt.title(title)
plt.legend()
plt.show()
plot_train_history(single_step_history,
'Single Step Training and validation loss')
# Выполнение точечного прогноза
for x, y in val_data_single.take(3):
plot = show_plot([x[0][:, 1].numpy(), y[0].numpy(),
single_step_model.predict(x)[0]], 1,
'Single Step Prediction')
plot.show()
# Интервальное прогнозирование
future_target = 72
x_train_multi, y_train_multi = multivariate_data(dataset, dataset[:, 1], 0,
TRAIN_SPLIT, past_history,
future_target, STEP)
x_val_multi, y_val_multi = multivariate_data(dataset, dataset[:, 1],
TRAIN_SPLIT, None, past_history,
future_target, STEP)
print ('Single window of past history : {}'.format(x_train_multi[0].shape))
print ('\n Target temperature to predict : {}'.format(y_train_multi[0].shape))
# +
train_data_multi = tf.data.Dataset.from_tensor_slices((x_train_multi, y_train_multi))
train_data_multi = train_data_multi.cache().shuffle(BUFFER_SIZE).batch(BATCH_SIZE).repeat()
val_data_multi = tf.data.Dataset.from_tensor_slices((x_val_multi, y_val_multi))
val_data_multi = val_data_multi.batch(BATCH_SIZE).repeat()
# -
def multi_step_plot(history, true_future, prediction):
plt.figure(figsize=(12, 6))
num_in = create_time_steps(len(history))
num_out = len(true_future)
plt.plot(num_in, np.array(history[:, 1]), label='History')
plt.plot(np.arange(num_out)/STEP, np.array(true_future), 'bo',
label='True Future')
if prediction.any():
plt.plot(np.arange(num_out)/STEP, np.array(prediction), 'ro',
label='Predicted Future')
plt.legend(loc='upper left')
plt.show()
for x, y in train_data_multi.take(1):
multi_step_plot(x[0], y[0], np.array([0]))
# +
multi_step_model = tf.keras.models.Sequential()
multi_step_model.add(tf.keras.layers.LSTM(32,
return_sequences=True,
input_shape=x_train_multi.shape[-2:]))
multi_step_model.add(tf.keras.layers.LSTM(16, activation='relu'))
multi_step_model.add(tf.keras.layers.Dense(72))
multi_step_model.compile(optimizer=tf.keras.optimizers.RMSprop(clipvalue=1.0), loss='mae')
# -
for x, y in val_data_multi.take(1):
print (multi_step_model.predict(x).shape)
multi_step_history = multi_step_model.fit(train_data_multi, epochs=EPOCHS,
steps_per_epoch=EVALUATION_INTERVAL,
validation_data=val_data_multi,
validation_steps=50)
plot_train_history(multi_step_history, 'Multi-Step Training and validation loss')
# Выполнение интервального прогноза
for x, y in val_data_multi.take(3):
multi_step_plot(x[0], y[0], multi_step_model.predict(x)[0])
|
Neural network in FPGA.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Apply logistic regression to categorize whether a county had high mortality rate due to contamination
# ## 1. Import the necessary packages to read in the data, plot, and create a logistic regression model
import pandas as pd
# %matplotlib inline
import numpy as np
from sklearn.linear_model import LogisticRegression
# cd C:\Users\<NAME>\Desktop\algorithms\class7
# ## 2. Read in the hanford.csv file in the `data/` folder
df=pd.read_csv('data/hanford.csv')
len(df)
# <img src="../../images/hanford_variables.png"></img>
# ## 3. Calculate the basic descriptive statistics on the data
df.describe()
df['Mortality'].hist(bins=5)
# ## 4. Find a reasonable threshold to say exposure is high and recode the data
df['Mort_high']=df['Mortality'].apply(lambda x:1 if x>=147.1 else 0)
df['Exposure_high']=df['Exposure'].apply(lambda x:1 if x>=3.41 else 0)
df
df exposure_high(x):
if x >=3.41
return 1
else:
return 0
# THIS IS THE FUNCTION ONE HAD TO USE IF IT WASNT FOR LAMBDA FUNCTION
# ## 5. Create a logistic regression model
from sklearn.linear_model import LogisticRegression
lm = LogisticRegression()
x = np.asarray(df[['Exposure_high']])
y = np.asarray(df['Mort_high'])
lm = lm.fit(x,y)
# ## 6. Predict whether the mortality rate (Cancer per 100,000 man years) will be high at an exposure level of 50
lm.predict([50])
|
07 Teaching Machines/donow/Devulapalli_Harsha_7_donow.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %matplotlib inline
#
# # Blob Detection
#
# Blobs are bright on dark or dark on bright regions in an image. In
# this example, blobs are detected using 3 algorithms. The image used
# in this case is the Hubble eXtreme Deep Field. Each bright dot in the
# image is a star or a galaxy.
#
# ## Laplacian of Gaussian (LoG)
# This is the most accurate and slowest approach. It computes the Laplacian
# of Gaussian images with successively increasing standard deviation and
# stacks them up in a cube. Blobs are local maximas in this cube. Detecting
# larger blobs is especially slower because of larger kernel sizes during
# convolution. Only bright blobs on dark backgrounds are detected. See
# :py:meth:`skimage.feature.blob_log` for usage.
#
# ## Difference of Gaussian (DoG)
# This is a faster approximation of LoG approach. In this case the image is
# blurred with increasing standard deviations and the difference between
# two successively blurred images are stacked up in a cube. This method
# suffers from the same disadvantage as LoG approach for detecting larger
# blobs. Blobs are again assumed to be bright on dark. See
# :py:meth:`skimage.feature.blob_dog` for usage.
#
# ## Determinant of Hessian (DoH)
# This is the fastest approach. It detects blobs by finding maximas in the
# matrix of the Determinant of Hessian of the image. The detection speed is
# independent of the size of blobs as internally the implementation uses
# box filters instead of convolutions. Bright on dark as well as dark on
# bright blobs are detected. The downside is that small blobs (<3px) are not
# detected accurately. See :py:meth:`skimage.feature.blob_doh` for usage.
#
# +
from math import sqrt
from skimage import data
from skimage.feature import blob_dog, blob_log, blob_doh
from skimage.color import rgb2gray
import matplotlib.pyplot as plt
image = data.hubble_deep_field()[0:500, 0:500]
image_gray = rgb2gray(image)
blobs_log = blob_log(image_gray, max_sigma=30, num_sigma=10, threshold=.1)
# Compute radii in the 3rd column.
blobs_log[:, 2] = blobs_log[:, 2] * sqrt(2)
blobs_dog = blob_dog(image_gray, max_sigma=30, threshold=.1)
blobs_dog[:, 2] = blobs_dog[:, 2] * sqrt(2)
blobs_doh = blob_doh(image_gray, max_sigma=30, threshold=.01)
blobs_list = [blobs_log, blobs_dog, blobs_doh]
colors = ['yellow', 'lime', 'red']
titles = ['Laplacian of Gaussian', 'Difference of Gaussian',
'Determinant of Hessian']
sequence = zip(blobs_list, colors, titles)
fig, axes = plt.subplots(1, 3, figsize=(9, 3), sharex=True, sharey=True)
ax = axes.ravel()
for idx, (blobs, color, title) in enumerate(sequence):
ax[idx].set_title(title)
ax[idx].imshow(image)
for blob in blobs:
y, x, r = blob
c = plt.Circle((x, y), r, color=color, linewidth=2, fill=False)
ax[idx].add_patch(c)
ax[idx].set_axis_off()
plt.tight_layout()
plt.show()
|
digital-image-processing/notebooks/features_detection/plot_blob.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "slide"}
#
# ### Research Data Management in Neuroscience
#
# # An introduction to BIDS
#
# The Brain Imaging Data Structure
#
# <NAME>
#
# Department Biologie II
# Ludwig-Maximilians-Universität München
#
# Friday, 12 June, 2020
#
#
# 
# + [markdown] slideshow={"slide_type": "slide"}
# ## Take home message
#
# BIDS
# - can help you organise (imaging) data
# - exposes you to a community standard of data organisation
# - exposes you to a standard of project and metadata organisation
# + [markdown] slideshow={"slide_type": "slide"}
# ## BIDS background
#
# - inspired by addressing problems at openNeuro.org
# - developed in Stanford at the Poldrack lab in 2016
#
# + [markdown] slideshow={"slide_type": "fragment"}
# > <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., Rokem,
# A., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., 2016. The brain imaging data structure, a format for organizing and describing outputs of neuroimaging experiments. Sci Data 3, 160044.
#
# Research Resource Identifier RRID:SCR_016124
# + [markdown] slideshow={"slide_type": "fragment"}
# - orignally aimed to document MRI and fMRI data
# - data structure specification to consistently organize and document neuroimaging and connected behavioral data
# - out of this developed the larger BIDS project: https://bids.neuroimaging.io
# + [markdown] slideshow={"slide_type": "slide"}
# ### The BIDS specification
#
# - BIDS provides a specification but is not a standard
# - it should be viewed as a best practice in project structure and documentation
# + [markdown] slideshow={"slide_type": "fragment"}
# To this end the BIDS standard specifies
# - the naming convention for files and directories
# - which file formats are to be used for a use case (i.e. Nifti, json, tsv)
# - core metadata and how they are to be stored e.g. about participants, stimuli and key recording settings
# + [markdown] slideshow={"slide_type": "fragment"}
# Besides the imaging aspect it tries to cover
# - behavior
# - physiology
#
# + [markdown] slideshow={"slide_type": "slide"}
# ### The BIDS specification
#
# So far full BIDS specifications exist for
# - MRI (2016)
# - fMRI (2016)
# - MEG (2018)
# - EEG (2019)
# - iEEG (2019)
# + [markdown] slideshow={"slide_type": "fragment"}
# Specification extensions e.g. for PET or CT are currently being developed by the community.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Introduction to the standard specification
# ### The BIDS structure
# BIDS specifies
# - folder structures
# - supported file types for different types of (neuroimaging) data
# - file naming
# - partially file content
#
# The specification can be found at https://bids-specification.readthedocs.io/en/stable.
# + [markdown] slideshow={"slide_type": "fragment"}
# ### BIDS file type support
# - `.json` files to document metadata
# - `.tsv` files containing tab separated tabular metadata - no CSV, no excel, only true tabs, no spacing
# - raw data files specific to the modality that the project contains
# - e.g. nii.gz files for an anatomical MRI project
# - only NIFTI files are supported
# + [markdown] slideshow={"slide_type": "slide"}
# ### BIDS general folder structure
#
#
# project exampleProjectName
# └── subject └── sub-subject_id_01
# └── session └── ses-session_number_01
# └── datatype └── anat
# └── datatype └── func
#
# + [markdown] slideshow={"slide_type": "fragment"}
# #### BIDS folder names and contrstraints
# - `project` ... can have any name but should be descriptive
# - `subject` ... `sub-<participant label>`
# - Label has to be specific for each subject
# - Only one folder per subject per dataset
# - `session` ... `sub-<session label>`
# - Each folder represents a recording session
# - If required use multiple sessions per subject
# - The session label has to be unique per subject
# - `datatype` ... `func`, `dwi`, `fmap`, `anat`, `meg`, `eeg`, `ieeg`, `beh`
# - defines the types of data contained in this dataset
# + [markdown] slideshow={"slide_type": "slide"}
# ### BIDS general folder structure
#
#
# project exampleProjectName
# └── subject └── sub-subject_id_01
# └── session └── ses-session_number_01
# └── datatype └── anat
# └── datatype └── func
#
# #### BIDS datatypes
#
# - `func` ... functional MRI data
# - `dwi` ... diffusion Imaging Data
# - `fmap` ... fieldmap MRI data
# - `anat` ... anatomical MRI data
# - `meg` ... MEG data
# - `eeg` ... EEG Data
# - `ieeg` ... intracranial EEG data
# - `beh` ... behavior
#
# Folders of these datatypes allow only specific files that are named according to the BIDS specificiation.
# + [markdown] slideshow={"slide_type": "slide"}
# ### BIDS general folder structure
#
# #### File naming contstraints
#
# Metadata and data file names depend on the project type and the folder names!
#
# + [markdown] slideshow={"slide_type": "fragment"}
#
# Anatomical MRI data example: `anat`
#
# Folder structure and naming constraints
# `./myProject/sub-01/ses-01/anat/`
#
# + [markdown] slideshow={"slide_type": "fragment"}
#
# Data file naming constraints in an anatomical MRI data project:
# - `sub-<>_ses-<>_T1w.nii.gz`
#
# Metadata file naming constraints:
# - `sub-<>_ses-<>_T1w.json`
#
# Other files are not allowed in an `anat` folder.
#
# + [markdown] slideshow={"slide_type": "slide"}
# ### BIDS general folder structure - full example
#
# ds001
# ├── dataset_description.json
# ├── participants.tsv
# ├── sub-01
# │ ├── anat
# │ │ ├── sub-01_inplaneT2.nii.gz
# │ │ └── sub-01_T1w.nii.gz
# │ └── func
# │ ├── sub-01_task-balloonanalogrisktask_run-01_bold.nii.gz
# │ ├── sub-01_task-balloonanalogrisktask_run-01_events.tsv
# │ ├── sub-01_task-balloonanalogrisktask_run-02_bold.nii.gz
# │ ├── sub-01_task-balloonanalogrisktask_run-02_events.tsv
# ├── sub-02
# │ ├── anat
# │ │ ├── sub-02_inplaneT2.nii.gz
# │ │ └── sub-02_T1w.nii.gz
# │ └── func
# │ ├── sub-02_task-balloonanalogrisktask_run-01_bold.nii.gz
# │ ├── sub-02_task-balloonanalogrisktask_run-01_events.tsv
# │ ├── sub-02_task-balloonanalogrisktask_run-02_bold.nii.gz
# │ ├── sub-02_task-balloonanalogrisktask_run-02_events.tsv
# ...
# └── task-balloonanalogrisktask_bold.json
# + [markdown] slideshow={"slide_type": "slide"}
# ### BIDS general folder structure - BIDS is rigid
# - folder structure and naming scheme has to be followed
# - empty or additional files as well as unsupported file types are not allowed
#
# + [markdown] slideshow={"slide_type": "fragment"}
# #### Adding additional files
# The root of the project folder may (and should) contain the following files
# - `README`
# - `dataset_description.json`
# - `participants.tsv`
#
# + [markdown] slideshow={"slide_type": "fragment"}
# #### Dealing with unsupported files
# - keep unsupported files one level above the project root
# - add non-BIDS files to `.bidsignore` at the project root; works like `.gitignore`.
#
# *_not_bids.txt
# extra_data/
#
# + [markdown] slideshow={"slide_type": "slide"}
# ### BIDS validation
#
# Core of BIDS is a validation service
# - needs to be run on a regular basis to ensure adherence to specification
# - online service at https://bids-standard.github.io/bids-validator
#
# + [markdown] slideshow={"slide_type": "fragment"}
# - local service installation at https://github.com/bids-standard/bids-validator
# - nodejs (full functionality, commandline tool)
# - Python (reduced functionality)
# - docker
#
# + [markdown] slideshow={"slide_type": "slide"}
# ### BIDS usage example
#
# We will now use the online validator to build and troubleshoot a BIDS project from scratch.
#
# https://bids-standard.github.io/bids-validator
#
# Find step by step example directories in the RDM course folder on gin:
# https://gin.g-node.org/RDMcourse2020/Lectures/Lecture04/BIDS_validation_examples
#
# The folder contains four BIDS projects with various validation issues:
#
# 01_empty_example/
# 02_invalid_structure/
# 03_invalid_file_annotation/
# 04_invalid_additional_file/
#
# The folders can be uploaded to the validator and will return the individual issues.
# + [markdown] slideshow={"slide_type": "slide"}
# ### BIDS troubleshooting: use the specification
#
# - BIDS is available for fMRI, MRI, EEG, iEEG and other data sources
# - the exact specification, allowed structure, naming and file format varies
# - use the specification for all details to get to a valid BIDS structure
#
# https://bids-specification.readthedocs.io/en/stable
#
# - use the specification to collect and document metadata
#
# + [markdown] slideshow={"slide_type": "slide"}
# ### BIDS specifications in the making - get involved
#
# Besides the published supported data many more are currently in development
#
# e.g. BIDS for PET is close to finishing:
# https://docs.google.com/document/d/1mqMLnxVdLwZjDd4ZiWFqjEAmOmfcModA_R535v3eQs0/edit
#
# Everyone can look up the status of a project and also contribute:
# https://bids.neuroimaging.io/get_involved.html
#
#
#
# + [markdown] slideshow={"slide_type": "slide"}
# # BIDS converters, tools and apps
#
# List of tools
# - https://bids.neuroimaging.io/benefits.html
#
# Example tool: Raw data to BIDS converter
# - https://github.com/Donders-Institute/bidscoin
#
# BIDS apps - applications that work with BIDS datasets
# - https://bids-apps.neuroimaging.io/about
#
# Example app
# - https://github.com/poldracklab/fmriprep
#
# + [markdown] slideshow={"slide_type": "slide"}
# # Linklist
#
# BIDS home page
# - https://bids.neuroimaging.io
#
# BIDS specification
# - https://bids-specification.readthedocs.io/en/stable/
#
# BIDS validator
# - https://bids-standard.github.io/bids-validator/
# - https://github.com/bids-standard/bids-validator
#
# Introductions and examples
# - https://github.com/bids-standard/bids-starter-kit
# - https://github.com/bids-standard/bids-starter-kit/wiki/Tutorials
# - https://github.com/bids-standard/bids-examples
#
# + [markdown] slideshow={"slide_type": "slide"}
# ## BIDS papers
#
# BIDS
# https://doi.org/10.1038/sdata.2016.44
#
# EEG-BIDS
# https://doi.org/10.1038/s41597-019-0104-8
#
# iEEG BIDS
# https://doi.org/10.1038/s41597-019-0105-7
#
# MEG BIDS
# https://doi.org/10.1038/sdata.2018.110
#
# BIDS apps
# https://doi.org/10.1371/journal.pcbi.1005209
#
# + [markdown] slideshow={"slide_type": "slide"}
# # Assignment
#
# - read through https://github.com/bids-standard/bids-starter-kit
# - try to map your data to the BIDS structure
# - if you have problems check
# - the specification: https://bids-specification.readthedocs.io/en/stable/
# - the examples page: https://github.com/bids-standard/bids-examples
# - make sure your example is valid using the online validator
# - read through the specification for your dataset and try to find some metadata, validate again
#
|
courses/2020-LMU-RDM/BIDS/BIDS_introduction.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Introduction
#
# This notebook will include experimental results on the Actor-Critic agent specified in the RL book by <NAME> on the smart vacuum environment but with added memory.
# +
# import needed libs
# %load_ext autoreload
# Auto reloading causes the kernel to reload the libraries we have
# %autoreload 2
# usual imports for visualization, etc.
import numpy as np
import matplotlib.pyplot as plt
import datetime
# make it reproducible
np.random.seed(0)
# show plots inline
# %matplotlib inline
# +
# Some initializations
from envs import SmartVac
from agents import ActorCriticMemoryAgent
max_episode_steps = 1000
results_folder = 'res/'
figs_folder = 'figs/'
# +
AgentClass = ActorCriticMemoryAgent
best_performance = 0.74
env = SmartVac()
num_of_tests = 1
episode_count = 10000
plot_count = int(episode_count / 100)
alpha_theta = np.power(2.0, -2)
alpha_w = np.power(2.0, -2)
params_str = f'alpha_theta_{alpha_theta}_alpha_w_{alpha_w}_episodes_{episode_count}'
agent_name = AgentClass.__name__
mult_avgs = []
mult_probs1 = []
mult_probs2 = []
for i_test in range(num_of_tests):
print()
print(i_test + 1, end=' ')
# Initialize the agent
agent = AgentClass(alpha_w=alpha_w, alpha_theta=alpha_theta)
avgs = []
probs1 = []
probs2 = []
episode_rewards = np.zeros(episode_count)
for i_episode in range(episode_count):
done = False
totalReward = 0
if i_episode >= plot_count and (i_episode % plot_count == 0):
avg = np.average(episode_rewards[i_episode - plot_count:i_episode])
avgs.append(avg)
# deterministic position
env.x = 0
env.y = 1
obs = env.get_obs()
prob = agent.get_action_vals_for_obs(obs)
probs1.append(prob)
# stochastic position
env.x = 1
env.y = 1
obs = env.get_obs()
prob = agent.get_action_vals_for_obs(obs)
probs2.append(prob)
print('#', end='', flush=True)
if len(avgs) % 100 == 0:
print(i_episode)
obs = env.reset()
action = agent.start(obs)
step = 0
while not done:
obs, reward, done = env.step(action)
action = agent.step(obs, reward, done)
totalReward += reward
step += 1
if step > max_episode_steps:
done = True
episode_rewards[i_episode] = totalReward
agent.update_for_episode()
mult_avgs.append(avgs)
mult_probs1.append(probs1)
mult_probs2.append(probs2)
avgs = np.mean(np.array(mult_avgs), axis=0)
probs1 = np.mean(np.array(mult_probs1), axis=0)
probs2 = np.mean(np.array(mult_probs2), axis=0)
# +
plt.figure(1, figsize=(14,10))
plt.plot(avgs)
plt.title(f'Average Return in {episode_count} episodes')
plt.xlabel(f'index')
plt.ylabel(f'Average Return per {plot_count} episodes')
plt.axhline(y=best_performance, linewidth=1, color="g", linestyle='--')
# plt.savefig(f'{figs_folder}agent_{agent_name}_{params_str}.png')
plt.show()
plt.figure(2, figsize=(14,10))
plt.subplot(211)
plt.plot(probs1)
plt.title(f'Probs for (0,0) in {episode_count} episodes')
plt.xlabel(f'index')
plt.ylabel(f'Probability')
plt.legend(['UP', 'RIGHT', 'DOWN', 'LEFT'])
plt.axhline(y=1, linewidth=1, color="g", linestyle='--')
plt.subplot(212)
plt.plot(probs2)
plt.title(f'Probs for (0,1) in {episode_count} episodes')
plt.xlabel(f'index')
plt.ylabel(f'Probability')
plt.legend(['UP', 'RIGHT', 'DOWN', 'LEFT'])
plt.axhline(y=.5, linewidth=1, color="g", linestyle='--')
plt.show()
print('')
results = f'Average: \t\t{np.mean(avgs):5.3f}'
results += f'\nBest {plot_count} Average: \t{np.max(avgs):5.3f}'
results += f'\nLast {plot_count} Average: \t{avgs[-1]:5.3f}'
# print(agent.theta)
# print(agent.v_hat)
results += f'\n\nAgent: {agent_name} \tAlpha_w: {alpha_w}\tAlpha_theta: {alpha_theta}'
test_xs = [0, 1, 2, 3, 4]
test_ys = [1, 1, 1, 1, 1]
for i in range(len(test_xs)):
env.x = test_xs[i]
env.y = test_ys[i]
obs = env.get_obs()
probs = agent.get_action_vals_for_obs(obs)
results += f'\nx: {env.x}, y:{env.y}, probs: [{probs[0]:4.2f},{probs[1]:4.2f},{probs[2]:4.2f},{probs[3]:4.2f}]'
print(results)
# Write to file if needed
# file = open(f'{results_folder}agent_{agent_name}_{params_str}.txt', 'w')
# file.write(results)
# file.close()
# +
AgentClass = ActorCriticMemoryAgent
best_performance = -1.26
env = SmartVac(terminal_rewards=(-1,-3))
num_of_tests = 1
episode_count = 10000
plot_count = int(episode_count / 100)
alpha_theta = np.power(2.0, -2)
alpha_w = np.power(2.0, -2)
params_str = f'alpha_theta_{alpha_theta}_alpha_w_{alpha_w}_episodes_{episode_count}'
agent_name = AgentClass.__name__
mult_avgs = []
mult_probs1 = []
mult_probs2 = []
for i_test in range(num_of_tests):
print()
print(i_test + 1, end=' ')
# Initialize the agent
agent = AgentClass(alpha_w=alpha_w, alpha_theta=alpha_theta)
avgs = []
probs1 = []
probs2 = []
episode_rewards = np.zeros(episode_count)
for i_episode in range(episode_count):
done = False
totalReward = 0
if i_episode >= plot_count and (i_episode % plot_count == 0):
avg = np.average(episode_rewards[i_episode - plot_count:i_episode])
avgs.append(avg)
# deterministic position
env.x = 0
env.y = 1
obs = env.get_obs()
prob = agent.get_action_vals_for_obs(obs)
probs1.append(prob)
# stochastic position
env.x = 1
env.y = 1
obs = env.get_obs()
prob = agent.get_action_vals_for_obs(obs)
probs2.append(prob)
print('#', end='', flush=True)
if len(avgs) % 100 == 0:
print(i_episode)
obs = env.reset()
action = agent.start(obs)
step = 0
while not done:
obs, reward, done = env.step(action)
action = agent.step(obs, reward, done)
totalReward += reward
step += 1
if step > max_episode_steps:
done = True
episode_rewards[i_episode] = totalReward
agent.update_for_episode()
mult_avgs.append(avgs)
mult_probs1.append(probs1)
mult_probs2.append(probs2)
avgs = np.mean(np.array(mult_avgs), axis=0)
probs1 = np.mean(np.array(mult_probs1), axis=0)
probs2 = np.mean(np.array(mult_probs2), axis=0)
# +
plt.figure(1, figsize=(14,10))
plt.plot(avgs)
plt.title(f'Average Return in {episode_count} episodes')
plt.xlabel(f'index')
plt.ylabel(f'Average Return per {plot_count} episodes')
plt.axhline(y=best_performance, linewidth=1, color="g", linestyle='--')
# plt.savefig(f'{figs_folder}agent_{agent_name}_{params_str}.png')
plt.show()
plt.figure(2, figsize=(14,10))
plt.subplot(211)
plt.plot(probs1)
plt.title(f'Probs for (0,0) in {episode_count} episodes')
plt.xlabel(f'index')
plt.ylabel(f'Probability')
plt.legend(['UP', 'RIGHT', 'DOWN', 'LEFT'])
plt.axhline(y=1, linewidth=1, color="g", linestyle='--')
plt.subplot(212)
plt.plot(probs2)
plt.title(f'Probs for (0,1) in {episode_count} episodes')
plt.xlabel(f'index')
plt.ylabel(f'Probability')
plt.legend(['UP', 'RIGHT', 'DOWN', 'LEFT'])
plt.axhline(y=.5, linewidth=1, color="g", linestyle='--')
plt.show()
print('')
results = f'Average: \t\t{np.mean(avgs):5.3f}'
results += f'\nBest {plot_count} Average: \t{np.max(avgs):5.3f}'
results += f'\nLast {plot_count} Average: \t{avgs[-1]:5.3f}'
# print(agent.theta)
# print(agent.v_hat)
results += f'\n\nAgent: {agent_name} \tAlpha_w: {alpha_w}\tAlpha_theta: {alpha_theta}'
test_xs = [0, 1, 2, 3, 4]
test_ys = [1, 1, 1, 1, 1]
for i in range(len(test_xs)):
env.x = test_xs[i]
env.y = test_ys[i]
obs = env.get_obs()
probs = agent.get_action_vals_for_obs(obs)
results += f'\nx: {env.x}, y:{env.y}, probs: [{probs[0]:4.2f},{probs[1]:4.2f},{probs[2]:4.2f},{probs[3]:4.2f}]'
print(results)
# Write to file if needed
# file = open(f'{results_folder}agent_{agent_name}_{params_str}.txt', 'w')
# file.write(results)
# file.close()
|
step11_actor_critic_with_mem.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Creation of synthetic data for a stroke thrombolysis pathway data set using CTGAN Generative Advesarial Network (GAN). Tested using a logistic regression model.
# ## Aim
#
# To test CT-Generative Advesarial Network (GAN) for synthesising data that can be used to train a logistic regression machine learning model.
#
# Generative Advesarial Networks (GANs) are composed of two competing networks:
#
# * A *descriminator* network: This produces an output (0-1) that determines whether a particular example is fake (output=0) or real (output=1).
# * A *generator* network: This network produces synthetic (fake) examples
#
# The networks are trained together. With each iteration:
#
# * The *descriminator* network is trained on a set of labelled examples (real examples have a label of 1, those produced by the gernator network have a label of 0).
# * The *generator* network is trained by passing generated examples to the *descriminator* network. The loss function is the difference between the *descriminator* output and a value of 1 (for an example which is classified as 100% probability of being real by the *descriminator network*). The *descriminator* output is passed to the *generator network* complete with *gradients*, so that the *generator network* can be trained with gradients back from the *descriminator* output (see figure below).
#
# Improvement in the *descriminator* network provides a better feedback to the *generator network*, producing better examples.
#
# 
#
# Goodfellow I, <NAME>, <NAME>, et al. Generative Adversarial Nets. In: <NAME>, <NAME>, <NAME>, et al., eds. Advances in Neural Information Processing Systems 27. Curran Associates, Inc. 2014. 2672–2680.http://papers.nips.cc/paper/5423-generative-adversarial-nets.pdf
#
# ### CTGAN
#
# CTGAN is a Python/PyTorch package developed to make it easy to use GANs for tabular data.
#
# GitHub page: https://github.com/sdv-dev/CTGAN
#
# Key features of CTGAN include:
#
# * *Preprocessing*: CTGAN uses more sophisticated Variational Gaussian Mixture Model to detect modes of continuous columns.
# * *Network structure*: TGAN uses LSTM to generate synthetic data column by column. CTGAN uses Fully-connected networks which is more efficient.
# * Features to prevent mode collapse*: We design a conditional generator and resample the training data to prevent model collapse on discrete columns. We use WGANGP and PacGAN to stabilize the training of GAN.
# * *Data types*: CTGAN can handle continuous and discrete/categorical data (interger data needs an additional step to convert from float to integer).
# * *Source data*: CTGAN works from NumPy or Pandas source data.
#
# <NAME>, <NAME>, <NAME>, <NAME>. Modeling Tabular data using Conditional GAN. NeurIPS, 2019.
#
# Xu, Lei, <NAME>, <NAME>, and <NAME> (2019). ‘Modeling Tabular Data Using Conditional GAN’. ArXiv:1907.00503 http://arxiv.org/abs/1907.00503.
#
# ## Data
#
# Raw data is avilable at:
#
# https://raw.githubusercontent.com/MichaelAllen1966/1807_stroke_pathway/master/machine_learning/data/data_for_ml_clin_only.csv
# ## Basic methods description
#
# * Create synthetic data by use of a Generative Adversarial Network (GAN)
# * Train logistic regression model on synthetic data and test against held-back raw data
# ### Import modules
# +
from IPython.display import clear_output
from ctgan import CTGANSynthesizer
ctgan = CTGANSynthesizer()
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
# Turn warnings off for notebook publication
import warnings
warnings.filterwarnings("ignore")
# +
## Function to turn an array of float values into one-hot
# -
def make_one_hot(x):
"""
Takes a list/array/series and returns 1 for highest value and 0 for all
others
"""
# Get argmax
highest = np.argmax(x)
# Set all values to zero
x *= 0.0
# Set argmax to one
x[highest] = 1.0
return x
# ### Import Data
#
# Data is imported from local wisconsin.csv file (held in same directory as this notebook). Data can also be accessed here: https://www.kaggle.com/uciml/breast-cancer-wisconsin-data
def load_data():
""""
Load Stroke Pathway data set
Inputs
------
None
Returns
-------
X: NumPy array of X
y: Numpy array of y
col_names: column names for X
"""
# Load data
data = pd.read_csv('./stroke_pathway.csv')
# Shuffle data
data = data.sample(frac=1)
# Change 'Thrombolysis given' column to 'thrombolysis', and put last
data['label'] = data['Thrombolysis given']
data.drop('Thrombolysis given', axis=1, inplace=True)
# Split data in X and y
X = data.drop(['label'], axis=1)
y = data['label']
# Get col names and convert to NumPy arrays
X_col_names = list(X)
X = X.values
y = y.values
return data, X, y, X_col_names
# ### Data processing
# Function for splitting X and y into training and test sets.
def split_into_train_test(X, y, test_proportion=0.25):
""""
Randomly split X and y numpy arrays into training and test data sets
Inputs
------
X and y NumPy arrays
Returns
-------
X_test, X_train, y_test, y_train Numpy arrays
"""
X_train, X_test, y_train, y_test = \
train_test_split(X, y, shuffle=True, test_size=test_proportion)
return X_train, X_test, y_train, y_test
# Function to standardise data (based on mean and dtandard deviation of training data).
def standardise_data(X_train, X_test):
""""
Standardise training and tets data sets according to mean and standard
deviation of test set
Inputs
------
X_train, X_test NumPy arrays
Returns
-------
X_train_std, X_test_std
"""
mu = X_train.mean(axis=0)
std = X_train.std(axis=0)
X_train_std = (X_train - mu) / std
X_test_std = (X_test - mu) /std
return X_train_std, X_test_std
# ### Calculate accuracy measures
#
# Function to calculate a range of accuracy scores.
def calculate_diagnostic_performance(actual, predicted):
"""
Inputs
------
actual, predted numpy arrays (1 = +ve, 0 = -ve)
Returns
-------
A dictionary of results:
1) accuracy: proportion of test results that are correct
2) sensitivity: proportion of true +ve identified
3) specificity: proportion of true -ve identified
4) positive likelihood: increased probability of true +ve if test +ve
5) negative likelihood: reduced probability of true +ve if test -ve
6) diagnostic odds ratio: positive likelihood / negative likelihood
7) true positive rate: same as sensitivity
8) true negative rate: same as specificity
9) false positive rate: proportion of false +ves in true -ve patients
10) false negative rate: proportion of false -ves in true +ve patients
11) positive predictive value: chance of true +ve if test +ve
12) negative predictive value: chance of true -ve if test -ve
13) actual positive rate: proportion of actual values that are +ve
14) predicted positive rate: proportion of predicted vales that are +ve
15) recall: same as sensitivity
16) precision: the proportion of predicted +ve that are true +ve
17) f1: 2 * ((precision * recall) / (precision + recall))
*false positive rate is the percentage of healthy individuals who
incorrectly receive a positive test result
* alse neagtive rate is the percentage of diseased individuals who
incorrectly receive a negative test result
"""
# Calculate results
actual_positives = actual == 1
actual_negatives = actual == 0
test_positives = predicted == 1
test_negatives = predicted == 0
test_correct = actual == predicted
accuracy = test_correct.mean()
true_positives = actual_positives & test_positives
false_positives = test_positives & actual_negatives
true_negatives = actual_negatives & test_negatives
false_negatives = test_negatives & actual_positives
sensitivity = true_positives.sum() / actual_positives.sum()
specificity = true_negatives.sum() / actual_negatives.sum()
true_positive_rate = sensitivity
true_negative_rate = specificity
false_positive_rate = 1 - specificity
false_negative_rate = 1 - sensitivity
positive_likelihood = true_positive_rate / false_positive_rate
negative_likelihood = false_positive_rate / true_negative_rate
diagnostic_odds_ratio = positive_likelihood / negative_likelihood
positive_predictive_value = true_positives.sum() / test_positives.sum()
negative_predicitive_value = true_negatives.sum() / test_negatives.sum()
actual_positive_rate = actual.mean()
predicted_positive_rate = predicted.mean()
recall = sensitivity
precision = true_positives.sum() / actual_positives.sum()
f1 = 2 * ((precision * recall) / (precision + recall))
# Add results to dictionary
results = dict()
results['accuracy'] = accuracy
results['sensitivity'] = sensitivity
results['specificity'] = specificity
results['positive_likelihood'] = positive_likelihood
results['negative_likelihood'] = negative_likelihood
results['diagnostic_odds_ratio'] = diagnostic_odds_ratio
results['true_positive_rate'] = true_positive_rate
results['true_negative_rate'] = true_negative_rate
results['false_positive_rate'] = false_positive_rate
results['false_negative_rate'] = false_negative_rate
results['positive_predictive_value'] = positive_predictive_value
results['negative_predicitive_value'] = negative_predicitive_value
results['actual_positive_rate'] = actual_positive_rate
results['predicted_positive_rate'] = predicted_positive_rate
results['recall'] = recall
results['precision'] = precision
results['f1'] = f1
return results
# ### Logistic Regression Model
#
# Function to fit and test a logistic regression model (when synthetic data is used the model is fitted on synthetic data but tested on real data).
def fit_and_test_logistic_regression_model(X_train, X_test, y_train, y_test):
""""
Fit and test logistic regression model.
Return a dictionary of accuracy measures.
Calls on `calculate_diagnostic_performance` to calculate results
Inputs
------
X_train, X_test NumPy arrays
Returns
-------
A dictionary of accuracy results.
"""
# Fit logistic regression model
lr = LogisticRegression(C=0.1)
lr.fit(X_train,y_train)
# Predict tets set labels
y_pred = lr.predict(X_test_std)
# Get accuracy results
accuracy_results = calculate_diagnostic_performance(y_test, y_pred)
return accuracy_results
# ## Synthetic Data Method - CTGAN
# #### Putting it all together: Training network and getting synthetic data
def make_synthetic_data_gan(X_original, y_original, number_of_samples=1000,
epochs=1000):
"""
Synthetic data generation, using a GAN
Inputs
------
original_data: X, y numpy arrays
batch_size: batch size to use when training networks
latent_dim: input dimension for generator network
number_of_samples: number of synthetic samples to generate
n_components: number of principal components to use for data synthesis
Returns
-------
X_synthetic: NumPy array
y_synthetic: NumPy array
"""
# Split the training data into positive and negative
mask = y_original == 1
X_pos = X_original[mask]
mask = y_original == 0
X_neg = X_original[mask]
# Set up list for positive and negative synthetic data sets
synthetic_X_sets = []
# Generate positive class data
ctgan.fit(X_pos, epochs=epochs)
x_fake_pos = ctgan.sample(number_of_samples)
synthetic_X_sets.append(x_fake_pos)
# Generate negative class data
ctgan.fit(X_neg, epochs=epochs)
x_fake_neg = ctgan.sample(number_of_samples)
synthetic_X_sets.append(x_fake_neg)
# Combine positive and negative and shuffle rows
X_synthetic = np.concatenate(
(synthetic_X_sets[0], synthetic_X_sets[1]), axis=0)
y_synthetic_pos = np.ones((number_of_samples, 1))
y_synthetic_neg = np.zeros((number_of_samples, 1))
y_synthetic = np.concatenate((y_synthetic_pos, y_synthetic_neg), axis=0)
# Randomise order of X, y
synthetic = np.concatenate((X_synthetic, y_synthetic), axis=1)
shuffle_index = np.random.permutation(np.arange(X_synthetic.shape[0]))
synthetic = synthetic[shuffle_index]
X_synthetic = synthetic[:,0:-1]
y_synthetic = synthetic[:,-1]
return X_synthetic, y_synthetic
# ### Main code
# +
# Load data
original_data, X, y, X_col_names = load_data()
# Set up results DataFrame
results = pd.DataFrame()
# +
# Set one hot columns
one_hot_cols = [[x for x in X_col_names if x[0:4] == 'Hosp'],
[x for x in X_col_names if x[0:21] == 'Onset Time Known Type'],
[x for x in X_col_names if x[0:21] == 'Stroke severity group'],
[x for x in X_col_names if x[0:11] == 'Stroke Type'],
[x for x in X_col_names if x[0:12] == 'Antiplatelet'],
[x for x in X_col_names if x[0:22] == 'Anticoag before stroke']]
# +
# Set integer and binary columns
integer_cols = ['Male',
'Age',
'Age_80',
'# Comorbidities',
'2+ comorbidotes',
'Congestive HF',
'Hypertension',
'Atrial Fib',
'Diabetes',
'TIA',
'Co-mordity',
'S2RankinBeforeStroke',
'S2NihssArrival',
'S2NihssArrivalLocQuestions',
'S2NihssArrivalLocCommands',
'S2NihssArrivalBestGaze',
'S2NihssArrivalVisual',
'S2NihssArrivalFacialPalsy',
'S2NihssArrivalMotorArmLeft',
'S2NihssArrivalMotorArmRight',
'S2NihssArrivalMotorLegLeft',
'S2NihssArrivalMotorLegRight',
'S2NihssArrivalLimbAtaxia',
'S2NihssArrivalSensory',
'S2NihssArrivalBestLanguage',
'S2NihssArrivalDysarthria',
'S2NihssArrivalExtinctionInattention']
binary_cols = ['Male',
'Age_80',
'2+ comorbidotes',
'Congestive HF',
'Hypertension',
'Atrial Fib',
'Diabetes',
'TIA',
'Co-mordity']
# -
# Fitting classification model to raw data
# +
# Set number of replicate runs
number_of_runs = 5
# Set up lists for results
accuracy_measure_names = []
accuracy_measure_data = []
for run in range(number_of_runs):
# Print progress
print (run + 1, end=' ')
# Split training and test set
X_train, X_test, y_train, y_test = split_into_train_test(X, y)
# Standardise data
X_train_std, X_test_std = standardise_data(X_train, X_test)
# Get accuracy of fitted model
accuracy = fit_and_test_logistic_regression_model(
X_train_std, X_test_std, y_train, y_test)
# Get accuracy measure names if not previously done
if len(accuracy_measure_names) == 0:
for key, value in accuracy.items():
accuracy_measure_names.append(key)
# Get accuracy values
run_accuracy_results = []
for key, value in accuracy.items():
run_accuracy_results.append(value)
# Add results to results list
accuracy_measure_data.append(run_accuracy_results)
# Output accuracy
percent_accuracy = accuracy['accuracy'] * 100
print(f'Accuracy: {percent_accuracy:3.1f}')
# Strore mean and sem in results DataFrame
accuracy_array = np.array(accuracy_measure_data)
results['raw_mean'] = accuracy_array.mean(axis=0)
results['raw_sem'] = accuracy_array.std(axis=0)/np.sqrt(number_of_runs)
results.index = accuracy_measure_names
# -
# Fitting classification model to synthetic data
# +
# Set up lists for results
accuracy_measure_names = []
accuracy_measure_data = []
synthetic_data = []
# Set number of replicate runs
number_of_runs = 5
for run in range(number_of_runs):
# Print progress
print (run + 1, end=' ')
# Make synthetic data
X_synthetic, y_synthetic = make_synthetic_data_gan(X, y)
clear_output(wait=True)
# Split training and test set
X_train, X_test, y_train, y_test = split_into_train_test(X, y)
# Standardise data (using synthetic data)
X_train_std, X_test_std = standardise_data(X_synthetic, X_test)
# Get accuracy of fitted model
accuracy = fit_and_test_logistic_regression_model(
X_train_std, X_test_std, y_synthetic, y_test)
# Get accuracy measure names if not previously done
if len(accuracy_measure_names) == 0:
for key, value in accuracy.items():
accuracy_measure_names.append(key)
# Get accuracy values
run_accuracy_results = []
for key, value in accuracy.items():
run_accuracy_results.append(value)
# Add results to results list
accuracy_measure_data.append(run_accuracy_results)
# Output accuracy
percent_accuracy = accuracy['accuracy'] * 100
print(f'Accuracy: {percent_accuracy:3.1f}')
# Save synthetic data set
# -----------------------
# Create a data frame with id
synth_df = pd.DataFrame()
# Transfer X values to DataFrame
synth_df=pd.concat([synth_df,
pd.DataFrame(X_synthetic, columns=X_col_names)],
axis=1)
# Make one hot as necessary
for one_hot_list in one_hot_cols:
for index, row in synth_df.iterrows():
x = row[one_hot_list]
x_one_hot = make_one_hot(x)
row[x_one_hot.index]= x_one_hot.values
# Make integer as necessary
for col in integer_cols:
synth_df[col] = synth_df[col].round(0)
# Clip binary cols
for col in binary_cols:
synth_df[col] = np.clip(synth_df[col],0,1)
# Add a label
y_list = list(y_synthetic)
synth_df['label'] = y_list
# Shuffle data
synth_df = synth_df.sample(frac=1.0)
# Add to synthetic data results list
synthetic_data.append(synth_df)
# Store mean and sem in results DataFrame
accuracy_array = np.array(accuracy_measure_data)
results['gan_mean'] = accuracy_array.mean(axis=0)
results['gan_sem'] = accuracy_array.std(axis=0)/np.sqrt(number_of_runs)
# -
# ### Show results
results
# ## Compare raw and synthetic data means and standard deviations
# +
descriptive_stats_all_runs = []
for run in range(number_of_runs):
synth_df = synthetic_data[run]
descriptive_stats = pd.DataFrame()
descriptive_stats['Original pos_label mean'] = \
original_data[original_data['label'] == 1].mean()
descriptive_stats['Synthetic pos_label mean'] = \
synth_df[synth_df['label'] == 1].mean()
descriptive_stats['Original neg_label mean'] = \
original_data[original_data['label'] == 0].mean()
descriptive_stats['Synthetic neg_label mean'] = \
synth_df[synth_df['label'] == 0].mean()
descriptive_stats['Original pos_label std'] = \
original_data[original_data['label'] == 1].std()
descriptive_stats['Synthetic pos_label std'] = \
synth_df[synth_df['label'] == 1].std()
descriptive_stats['Original neg_label std'] = \
original_data[original_data['label'] == 0].std()
descriptive_stats['Synthetic neg_label std'] = \
synth_df[synth_df['label'] == 0].std()
descriptive_stats_all_runs.append(descriptive_stats)
# +
colours = ['k', 'b', 'g', 'r', 'y', 'c', 'm']
fig = plt.figure(figsize=(10,10))
# Note: Set x and y limits to avoid plotting values that are very close to zero
# Negative mean
ax1 = fig.add_subplot(221)
for run in range(number_of_runs):
x = descriptive_stats_all_runs[0]['Original neg_label mean'].copy()
y = descriptive_stats_all_runs[run]['Synthetic neg_label mean'].copy()
x.drop(labels ='label', inplace=True)
y.drop(labels ='label', inplace=True)
colour = colours[run % 7] # Cycle through 7 colours
ax1.scatter(x,y, color=colour, alpha=0.5)
ax1.set_xlabel('Original data')
ax1.set_ylabel('Synthetic data')
ax1.set_xlim(1e-3, 1e2)
ax1.set_ylim(1e-3, 1e2)
ax1.set_title('Negative label samples mean')
ax1.set_xscale('log')
ax1.set_yscale('log')
ax1.grid()
# Positive mean
ax2 = fig.add_subplot(222)
for run in range(number_of_runs):
x = descriptive_stats_all_runs[0]['Original pos_label mean'].copy()
y = descriptive_stats_all_runs[run]['Synthetic pos_label mean'].copy()
x.drop(labels ='label', inplace=True)
y.drop(labels ='label', inplace=True)
colour = colours[run % 7] # Cycle through 7 colours
ax2.scatter(x,y, color=colour, alpha=0.5)
ax2.set_xlabel('Original data')
ax2.set_ylabel('Synthetic data')
ax2.set_title('Positive label samples mean')
ax2.set_xlim(1e-3, 1e2)
ax2.set_ylim(1e-3, 1e2)
ax2.set_xscale('log')
ax2.set_yscale('log')
ax2.grid()
# Negative standard deviation
ax3 = fig.add_subplot(223)
for run in range(number_of_runs):
x = descriptive_stats_all_runs[0]['Original neg_label std'].copy()
y = descriptive_stats_all_runs[run]['Synthetic neg_label std'].copy()
x.drop(labels ='label', inplace=True)
y.drop(labels ='label', inplace=True)
colour = colours[run % 7] # Cycle through 7 colours
ax3.scatter(x,y, color=colour, alpha=0.5)
ax3.set_xlabel('Original data')
ax3.set_ylabel('Synthetic data')
ax3.set_title('Negative label standard deviation')
ax3.set_xlim(1e-2, 1e2)
ax3.set_ylim(1e-2, 1e2)
ax3.set_xscale('log')
ax3.set_yscale('log')
ax3.grid()
# Positive standard deviation
ax4 = fig.add_subplot(224)
for run in range(number_of_runs):
x = descriptive_stats_all_runs[0]['Original pos_label std'].copy()
y = descriptive_stats_all_runs[run]['Synthetic pos_label std'].copy()
x.drop(labels ='label', inplace=True)
y.drop(labels ='label', inplace=True)
colour = colours[run % 7] # Cycle through 7 colours
ax4.scatter(x,y, color=colour, alpha=0.5)
ax4.set_xlabel('Original data')
ax4.set_ylabel('Synthetic data')
ax4.set_title('Positive label standard deviation')
ax4.set_xlim(1e-2, 1e2)
ax4.set_ylim(1e-2, 1e2)
ax4.set_xscale('log')
ax4.set_yscale('log')
ax4.grid()
plt.tight_layout(pad=2)
plt.savefig('Output/ctgan_correls.png', facecolor='w', dpi=300)
plt.show()
# -
# Calculate correlations between means and standard deviations for negative and positive classes.
# +
correl_mean_neg = []
correl_std_neg = []
correl_mean_pos = []
correl_std_pos = []
for run in range(number_of_runs):
# Get correlation of means
x = descriptive_stats_all_runs[run]['Original neg_label mean']
y = descriptive_stats_all_runs[run]['Synthetic neg_label mean']
correl_mean_neg.append(np.corrcoef(x,y)[0,1])
x = descriptive_stats_all_runs[run]['Original pos_label mean']
y = descriptive_stats_all_runs[run]['Synthetic pos_label mean']
correl_mean_pos.append(np.corrcoef(x,y)[0,1])
# Get correlation of standard deviations
x = descriptive_stats_all_runs[run]['Original neg_label std']
y = descriptive_stats_all_runs[run]['Synthetic neg_label std']
correl_std_neg.append(np.corrcoef(x,y)[0,1])
x = descriptive_stats_all_runs[run]['Original pos_label std']
y = descriptive_stats_all_runs[run]['Synthetic pos_label std']
correl_std_pos.append(np.corrcoef(x,y)[0,1])
# Get correlation of means
mean_r_square_mean_neg = np.mean(np.square(correl_mean_neg))
mean_r_square_mean_pos = np.mean(np.square(correl_mean_pos))
sem_square_mean_neg = np.std(np.square(correl_mean_neg))/np.sqrt(number_of_runs)
sem_square_mean_pos = np.std(np.square(correl_mean_pos))/np.sqrt(number_of_runs)
print ('R-square of means (negative), mean (std): ', end='')
print (f'{mean_r_square_mean_neg:0.3f} ({sem_square_mean_neg:0.3f})')
print ('R-square of means (positive), mean (std): ', end='')
print (f'{mean_r_square_mean_pos:0.3f} ({sem_square_mean_pos:0.3f})')
# Get correlation of standard deviations
mean_r_square_sd_neg = np.mean(np.square(correl_std_neg))
mean_r_square_sd_pos = np.mean(np.square(correl_std_pos))
sem_square_sd_neg = np.std(np.square(correl_std_neg))/np.sqrt(number_of_runs)
sem_square_sd_pos = np.std(np.square(correl_std_pos))/np.sqrt(number_of_runs)
print ('R-square of standard deviations (negative), mean (sem): ', end='')
print (f'{mean_r_square_sd_neg:0.3f} ({sem_square_sd_neg:0.3f})')
print ('R-square of standard deviations (positive), mean (sem): ', end='')
print (f'{mean_r_square_sd_pos:0.3f} ({sem_square_sd_pos:0.3f})')
# -
# ## Single run example
descriptive_stats_all_runs[0]
# ## Correlation between features
#
# Here we calculate a correlation matric between all features for original and synthetic data.
# +
neg_correlation_original = []
neg_correlation_synthetic = []
pos_correlation_original = []
pos_correlation_synthetic = []
correl_coeff_neg = []
correl_coeff_pos= []
# Original data
mask = original_data['label'] == 0
neg_o = original_data[mask].copy()
neg_o.drop('label', axis=1, inplace=True)
neg_correlation_original = neg_o.corr().values.flatten()
mask = original_data['label'] == 1
pos_o = original_data[mask].copy()
pos_o.drop('label', axis=1, inplace=True)
pos_correlation_original = pos_o.corr().values.flatten()
# Synthetic data
for i in range (number_of_runs):
data_s = synthetic_data[i]
mask = data_s['label'] == 0
neg_s = data_s[mask].copy()
neg_s.drop('label', axis=1, inplace=True)
corr_neg_s = neg_s.corr().values.flatten()
neg_correlation_synthetic.append(corr_neg_s)
mask = data_s['label'] == 1
pos_s = data_s[mask].copy()
pos_s.drop('label', axis=1, inplace=True)
corr_pos_s = pos_s.corr().values.flatten()
pos_correlation_synthetic.append(corr_pos_s)
# Get correlation coefficients
df = pd.DataFrame()
df['original'] = neg_correlation_original
df['synthetic'] = corr_neg_s
correl_coeff_neg.append(df.corr().loc['original']['synthetic'])
df = pd.DataFrame()
df['original'] = pos_correlation_original
df['synthetic'] = corr_pos_s
correl_coeff_pos.append(df.corr().loc['original']['synthetic'])
# +
colours = ['k', 'b', 'g', 'r', 'y', 'c', 'm']
fig = plt.figure(figsize=(10,5))
ax1 = fig.add_subplot(121)
for run in range(number_of_runs):
colour = colours[run % 7] # Cycle through 7 colours
ax1.scatter(
neg_correlation_original,
neg_correlation_synthetic[run],
color=colour,
alpha=0.25)
ax1.grid()
ax1.set_xlabel('Original data correlation')
ax1.set_ylabel('Synthetic data correlation')
ax1.set_title('Negative label samples correlation of features')
ax2 = fig.add_subplot(122)
for run in range(number_of_runs):
colour = colours[run % 7] # Cycle through 7 colours
ax2.scatter(
pos_correlation_original,
pos_correlation_synthetic[run],
color=colour,
alpha=0.25)
ax2.grid()
ax2.set_xlabel('Original data correlation')
ax2.set_ylabel('Synthetic data correlation')
ax2.set_title('Positive label samples correlation of features')
plt.tight_layout(pad=2)
plt.savefig('Output/ctgan_cov.png', facecolor='w', dpi=300)
plt.show()
# +
r_square_neg_mean = np.mean(np.square(correl_coeff_neg))
r_square_pos_mean = np.mean(np.square(correl_coeff_pos))
r_square_neg_sem = np.std(np.square(correl_coeff_neg))/np.sqrt(number_of_runs)
r_square_pos_sem = np.std(np.square(correl_coeff_pos))/np.sqrt(number_of_runs)
print ('Corrleation of correlations (negative), mean (sem): ', end='')
print (f'{r_square_neg_mean:0.3f} ({r_square_neg_sem:0.3f})')
print ('Corrleation of correlations (positive), mean (sem): ', end = '')
print (f'{r_square_pos_mean:0.3f} ({r_square_pos_sem:0.3f})')
|
02_stroke_pathway/03b_CTGAN_log_regression.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # SVI Part I: An Introduction to Stochastic Variational Inference in Pyro
#
# Pyro has been designed with particular attention paid to supporting stochastic variational inference as a general purpose inference algorithm. Let's see how we go about doing variational inference in Pyro.
#
# ## Setup
#
# We're going to assume we've already defined our model in Pyro (for more details on how this is done see [Intro Part I](intro_part_i.ipynb)).
# As a quick reminder, the model is given as a stochastic function `model(*args, **kwargs)`, which, in the general case takes arguments. The different pieces of `model()` are encoded via the mapping:
#
# 1. observations $\Longleftrightarrow$ `pyro.sample` with the `obs` argument
# 2. latent random variables $\Longleftrightarrow$ `pyro.sample`
# 3. parameters $\Longleftrightarrow$ `pyro.param`
#
# Now let's establish some notation. The model has observations ${\bf x}$ and latent random variables ${\bf z}$ as well as parameters $\theta$. It has a joint probability density of the form
#
# $$p_{\theta}({\bf x}, {\bf z}) = p_{\theta}({\bf x}|{\bf z}) p_{\theta}({\bf z})$$
#
# We assume that the various probability distributions $p_i$ that make up $p_{\theta}({\bf x}, {\bf z})$ have the following properties:
#
# 1. we can sample from each $p_i$
# 2. we can compute the pointwise log pdf $p_i$
# 3. $p_i$ is differentiable w.r.t. the parameters $\theta$
#
#
# ## Model Learning
#
# In this context our criterion for learning a good model will be maximizing the log evidence, i.e. we want to find the value of $\theta$ given by
#
# $$\theta_{\rm{max}} = \underset{\theta}{\operatorname{argmax}} \log p_{\theta}({\bf x})$$
#
# where the log evidence $\log p_{\theta}({\bf x})$ is given by
#
# $$\log p_{\theta}({\bf x}) = \log \int\! d{\bf z}\; p_{\theta}({\bf x}, {\bf z})$$
#
# In the general case this is a doubly difficult problem. This is because (even for a fixed $\theta$) the integral over the latent random variables $\bf z$ is often intractable. Furthermore, even if we know how to calculate the log evidence for all values of $\theta$, maximizing the log evidence as a function of $\theta$ will in general be a difficult non-convex optimization problem.
#
# In addition to finding $\theta_{\rm{max}}$, we would like to calculate the posterior over the latent variables $\bf z$:
#
# $$ p_{\theta_{\rm{max}}}({\bf z} | {\bf x}) = \frac{p_{\theta_{\rm{max}}}({\bf x} , {\bf z})}{
# \int \! d{\bf z}\; p_{\theta_{\rm{max}}}({\bf x} , {\bf z}) } $$
#
# Note that the denominator of this expression is the (usually intractable) evidence. Variational inference offers a scheme for finding $\theta_{\rm{max}}$ and computing an approximation to the posterior $p_{\theta_{\rm{max}}}({\bf z} | {\bf x})$. Let's see how that works.
#
# ## Guide
#
# The basic idea is that we introduce a parameterized distribution $q_{\phi}({\bf z})$, where $\phi$ are known as the variational parameters. This distribution is called the variational distribution in much of the literature, and in the context of Pyro it's called the **guide** (one syllable instead of nine!). The guide will serve as an approximation to the posterior.
#
# Just like the model, the guide is encoded as a stochastic function `guide()` that contains `pyro.sample` and `pyro.param` statements. It does _not_ contain observed data, since the guide needs to be a properly normalized distribution. Note that Pyro enforces that `model()` and `guide()` have the same call signature, i.e. both callables should take the same arguments.
#
# Since the guide is an approximation to the posterior $p_{\theta_{\rm{max}}}({\bf z} | {\bf x})$, the guide needs to provide a valid joint probability density over all the latent random variables in the model. Recall that when random variables are specified in Pyro with the primitive statement `pyro.sample()` the first argument denotes the name of the random variable. These names will be used to align the random variables in the model and guide. To be very explicit, if the model contains a random variable `z_1`
#
# ```python
# def model():
# pyro.sample("z_1", ...)
# ```
#
# then the guide needs to have a matching `sample` statement
#
# ```python
# def guide():
# pyro.sample("z_1", ...)
# ```
#
# The distributions used in the two cases can be different, but the names must line-up 1-to-1.
#
# Once we've specified a guide (we give some explicit examples below), we're ready to proceed to inference.
# Learning will be setup as an optimization problem where each iteration of training takes a step in $\theta-\phi$ space that moves the guide closer to the exact posterior.
# To do this we need to define an appropriate objective function.
#
# ## ELBO
#
# A simple derivation (for example see reference [1]) yields what we're after: the evidence lower bound (ELBO). The ELBO, which is a function of both $\theta$ and $\phi$, is defined as an expectation w.r.t. to samples from the guide:
#
# $${\rm ELBO} \equiv \mathbb{E}_{q_{\phi}({\bf z})} \left [
# \log p_{\theta}({\bf x}, {\bf z}) - \log q_{\phi}({\bf z})
# \right]$$
#
# By assumption we can compute the log probabilities inside the expectation. And since the guide is assumed to be a parametric distribution we can sample from, we can compute Monte Carlo estimates of this quantity. Crucially, the ELBO is a lower bound to the log evidence, i.e. for all choices of $\theta$ and $\phi$ we have that
#
# $$\log p_{\theta}({\bf x}) \ge {\rm ELBO} $$
#
# So if we take (stochastic) gradient steps to maximize the ELBO, we will also be pushing the log evidence higher (in expectation). Furthermore, it can be shown that the gap between the ELBO and the log evidence is given by the KL divergence between the guide and the posterior:
#
# $$ \log p_{\theta}({\bf x}) - {\rm ELBO} =
# \rm{KL}\!\left( q_{\phi}({\bf z}) \lVert p_{\theta}({\bf z} | {\bf x}) \right) $$
#
# This KL divergence is a particular (non-negative) measure of 'closeness' between two distributions. So, for a fixed $\theta$, as we take steps in $\phi$ space that increase the ELBO, we decrease the KL divergence between the guide and the posterior, i.e. we move the guide towards the posterior. In the general case we take gradient steps in both $\theta$ and $\phi$ space simultaneously so that the guide and model play chase, with the guide tracking a moving posterior $\log p_{\theta}({\bf z} | {\bf x})$. Perhaps somewhat surprisingly, despite the moving target, this optimization problem can be solved (to a suitable level of approximation) for many different problems.
#
# So at high level variational inference is easy: all we need to do is define a guide and compute gradients of the ELBO. Actually, computing gradients for general model and guide pairs leads to some complications (see the tutorial [SVI Part III](svi_part_iii.ipynb) for a discussion). For the purposes of this tutorial, let's consider that a solved problem and look at the support that Pyro provides for doing variational inference.
#
# ## `SVI` Class
#
# In Pyro the machinery for doing variational inference is encapsulated in the `SVI` class.
#
# The user needs to provide three things: the model, the guide, and an optimizer. We've discussed the model and guide above and we'll discuss the optimizer in some detail below, so let's assume we have all three ingredients at hand. To construct an instance of `SVI` that will do optimization via the ELBO objective, the user writes
#
# ```python
# import pyro
# from pyro.infer import SVI, Trace_ELBO
# svi = SVI(model, guide, optimizer, loss=Trace_ELBO())
# ```
#
# The `SVI` object provides two methods, `step()` and `evaluate_loss()`, that encapsulate the logic for variational learning and evaluation:
#
# 1. The method `step()` takes a single gradient step and returns an estimate of the loss (i.e. minus the ELBO). If provided, the arguments to `step()` are piped to `model()` and `guide()`.
#
# 2. The method `evaluate_loss()` returns an estimate of the loss _without_ taking a gradient step. Just like for `step()`, if provided, arguments to `evaluate_loss()` are piped to `model()` and `guide()`.
#
# For the case where the loss is the ELBO, both methods also accept an optional argument `num_particles`, which denotes the number of samples used to compute the loss (in the case of `evaluate_loss`) and the loss and gradient (in the case of `step`).
#
# ## Optimizers
#
# In Pyro, the model and guide are allowed to be arbitrary stochastic functions provided that
#
# 1. `guide` doesn't contain `pyro.sample` statements with the `obs` argument
# 2. `model` and `guide` have the same call signature
#
# This presents some challenges because it means that different executions of `model()` and `guide()` may have quite different behavior, with e.g. certain latent random variables and parameters only appearing some of the time. Indeed parameters may be created dynamically during the course of inference. In other words the space we're doing optimization over, which is parameterized by $\theta$ and $\phi$, can grow and change dynamically.
#
# In order to support this behavior, Pyro needs to dynamically generate an optimizer for each parameter the first time it appears during learning. Luckily, PyTorch has a lightweight optimization library (see [torch.optim](http://pytorch.org/docs/master/optim.html)) that can easily be repurposed for the dynamic case.
#
# All of this is controlled by the `optim.PyroOptim` class, which is basically a thin wrapper around PyTorch optimizers. `PyroOptim` takes two arguments: a constructor for PyTorch optimizers `optim_constructor` and a specification of the optimizer arguments `optim_args`. At high level, in the course of optimization, whenever a new parameter is seen `optim_constructor` is used to instantiate a new optimizer of the given type with arguments given by `optim_args`.
#
# Most users will probably not interact with `PyroOptim` directly and will instead interact with the aliases defined in `optim/__init__.py`. Let's see how that goes. There are two ways to specify the optimizer arguments. In the simpler case, `optim_args` is a _fixed_ dictionary that specifies the arguments used to instantiate PyTorch optimizers for _all_ the parameters:
#
# ```python
# from pyro.optim import Adam
#
# adam_params = {"lr": 0.005, "betas": (0.95, 0.999)}
# optimizer = Adam(adam_params)
# ```
#
# The second way to specify the arguments allows for a finer level of control. Here the user must specify a callable that will be invoked by Pyro upon creation of an optimizer for a newly seen parameter. This callable must have the following signature:
#
# 1. `module_name`: the Pyro name of the module containing the parameter, if any
# 2. `param_name`: the Pyro name of the parameter
#
# This gives the user the ability to, for example, customize learning rates for different parameters. For an example where this sort of level of control is useful, see the [discussion of baselines](svi_part_iii.ipynb). Here's a simple example to illustrate the API:
#
# ```python
# from pyro.optim import Adam
#
# def per_param_callable(param_name):
# if param_name == 'my_special_parameter':
# return {"lr": 0.010}
# else:
# return {"lr": 0.001}
#
# optimizer = Adam(per_param_callable)
# ```
#
# This simply tells Pyro to use a learning rate of `0.010` for the Pyro parameter `my_special_parameter` and a learning rate of `0.001` for all other parameters.
#
# ## A simple example
#
# We finish with a simple example. You've been given a two-sided coin. You want to determine whether the coin is fair or not, i.e. whether it falls heads or tails with the same frequency. You have a prior belief about the likely fairness of the coin based on two observations:
#
# - it's a standard quarter issued by the US Mint
# - it's a bit banged up from years of use
#
# So while you expect the coin to have been quite fair when it was first produced, you allow for its fairness to have since deviated from a perfect 1:1 ratio. So you wouldn't be surprised if it turned out that the coin preferred heads over tails at a ratio of 11:10. By contrast you would be very surprised if it turned out that the coin preferred heads over tails at a ratio of 5:1—it's not _that_ banged up.
#
# To turn this into a probabilistic model we encode heads and tails as `1`s and `0`s. We encode the fairness of the coin as a real number $f$, where $f$ satisfies $f \in [0.0, 1.0]$ and $f=0.50$ corresponds to a perfectly fair coin. Our prior belief about $f$ will be encoded by a beta distribution, specifically $\rm{Beta}(10,10)$, which is a symmetric probability distribution on the interval $[0.0, 1.0]$ that is peaked at $f=0.5$.
# + raw_mimetype="text/html" active=""
# <center><figure><img src="_static/img/beta.png" style="width: 300px;"><figcaption> <font size="-1"><b>Figure 1</b>: The distribution Beta that encodes our prior belief about the fairness of the coin. </font></figcaption></figure></center>
# -
# To learn something about the fairness of the coin that is more precise than our somewhat vague prior, we need to do an experiment and collect some data. Let's say we flip the coin 10 times and record the result of each flip. In practice we'd probably want to do more than 10 trials, but hey this is a tutorial.
#
# Assuming we've collected the data in a list `data`, the corresponding model is given by
#
# ```python
# import pyro.distributions as dist
#
# def model(data):
# # define the hyperparameters that control the beta prior
# alpha0 = torch.tensor(10.0)
# beta0 = torch.tensor(10.0)
# # sample f from the beta prior
# f = pyro.sample("latent_fairness", dist.Beta(alpha0, beta0))
# # loop over the observed data
# for i in range(len(data)):
# # observe datapoint i using the bernoulli
# # likelihood Bernoulli(f)
# pyro.sample("obs_{}".format(i), dist.Bernoulli(f), obs=data[i])
# ```
#
# Here we have a single latent random variable (`'latent_fairness'`), which is distributed according to $\rm{Beta}(10, 10)$. Conditioned on that random variable, we observe each of the datapoints using a bernoulli likelihood. Note that each observation is assigned a unique name in Pyro.
#
# Our next task is to define a corresponding guide, i.e. an appropriate variational distribution for the latent random variable $f$. The only real requirement here is that $q(f)$ should be a probability distribution over the range $[0.0, 1.0]$, since $f$ doesn't make sense outside of that range. A simple choice is to use another beta distribution parameterized by two trainable parameters $\alpha_q$ and $\beta_q$. Actually, in this particular case this is the 'right' choice, since conjugacy of the bernoulli and beta distributions means that the exact posterior is a beta distribution. In Pyro we write:
#
# ```python
# def guide(data):
# # register the two variational parameters with Pyro.
# alpha_q = pyro.param("alpha_q", torch.tensor(15.0),
# constraint=constraints.positive)
# beta_q = pyro.param("beta_q", torch.tensor(15.0),
# constraint=constraints.positive)
# # sample latent_fairness from the distribution Beta(alpha_q, beta_q)
# pyro.sample("latent_fairness", dist.Beta(alpha_q, beta_q))
# ```
#
# There are a few things to note here:
#
# - We've taken care that the names of the random variables line up exactly between the model and guide.
# - `model(data)` and `guide(data)` take the same arguments.
# - The variational parameters are `torch.tensor`s. The `requires_grad` flag is automatically set to `True` by `pyro.param`.
# - We use `constraint=constraints.positive` to ensure that `alpha_q` and `beta_q` remain non-negative during optimization.
#
# Now we can proceed to do stochastic variational inference.
#
# ```python
# # set up the optimizer
# adam_params = {"lr": 0.0005, "betas": (0.90, 0.999)}
# optimizer = Adam(adam_params)
#
# # setup the inference algorithm
# svi = SVI(model, guide, optimizer, loss=Trace_ELBO())
#
# n_steps = 5000
# # do gradient steps
# for step in range(n_steps):
# svi.step(data)
# ```
#
# Note that in the `step()` method we pass in the data, which then get passed to the model and guide.
#
# The only thing we're missing at this point is some data. So let's create some data and assemble all the code snippets above into a complete script:
# +
import math
import os
import torch
import torch.distributions.constraints as constraints
import pyro
from pyro.optim import Adam
from pyro.infer import SVI, Trace_ELBO
import pyro.distributions as dist
# this is for running the notebook in our testing framework
smoke_test = ('CI' in os.environ)
n_steps = 2 if smoke_test else 2000
assert pyro.__version__.startswith('1.6.0')
# clear the param store in case we're in a REPL
pyro.clear_param_store()
# create some data with 6 observed heads and 4 observed tails
data = []
for _ in range(6):
data.append(torch.tensor(1.0))
for _ in range(4):
data.append(torch.tensor(0.0))
def model(data):
# define the hyperparameters that control the beta prior
alpha0 = torch.tensor(10.0)
beta0 = torch.tensor(10.0)
# sample f from the beta prior
f = pyro.sample("latent_fairness", dist.Beta(alpha0, beta0))
# loop over the observed data
for i in range(len(data)):
# observe datapoint i using the bernoulli likelihood
pyro.sample("obs_{}".format(i), dist.Bernoulli(f), obs=data[i])
def guide(data):
# register the two variational parameters with Pyro
# - both parameters will have initial value 15.0.
# - because we invoke constraints.positive, the optimizer
# will take gradients on the unconstrained parameters
# (which are related to the constrained parameters by a log)
alpha_q = pyro.param("alpha_q", torch.tensor(15.0),
constraint=constraints.positive)
beta_q = pyro.param("beta_q", torch.tensor(15.0),
constraint=constraints.positive)
# sample latent_fairness from the distribution Beta(alpha_q, beta_q)
pyro.sample("latent_fairness", dist.Beta(alpha_q, beta_q))
# setup the optimizer
adam_params = {"lr": 0.0005, "betas": (0.90, 0.999)}
optimizer = Adam(adam_params)
# setup the inference algorithm
svi = SVI(model, guide, optimizer, loss=Trace_ELBO())
# do gradient steps
for step in range(n_steps):
svi.step(data)
if step % 100 == 0:
print('.', end='')
# grab the learned variational parameters
alpha_q = pyro.param("alpha_q").item()
beta_q = pyro.param("beta_q").item()
# here we use some facts about the beta distribution
# compute the inferred mean of the coin's fairness
inferred_mean = alpha_q / (alpha_q + beta_q)
# compute inferred standard deviation
factor = beta_q / (alpha_q * (1.0 + alpha_q + beta_q))
inferred_std = inferred_mean * math.sqrt(factor)
print("\nbased on the data and our prior belief, the fairness " +
"of the coin is %.3f +- %.3f" % (inferred_mean, inferred_std))
# -
# ### Sample output:
#
# ```
# based on the data and our prior belief, the fairness of the coin is 0.532 +- 0.090
# ```
#
# This estimate is to be compared to the exact posterior mean, which in this case is given by $16/30 = 0.5\bar{3}$.
# Note that the final estimate of the fairness of the coin is in between the the fairness preferred by the prior (namely $0.50$) and the fairness suggested by the raw empirical frequencies ($6/10 = 0.60$).
# ## References
#
# [1] `Automated Variational Inference in Probabilistic Programming`,
# <br/>
# <NAME>, <NAME>
#
# [2] `Black Box Variational Inference`,<br/>
# <NAME>, <NAME>, <NAME>
#
# [3] `Auto-Encoding Variational Bayes`,<br/>
# <NAME>, <NAME>
|
tutorial/source/svi_part_i.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import requests
import pandas as pd
page = requests.get("https://solicitors.lawsociety.org.uk/person/130616")
page.content
data = {'index': index, 'status': page.status_code, 'content': page.content}
df_new = pd.DataFrame.from_records([data])
df_new.info()
df_new
df_new = df_new.append(df_new)
# +
df_summary = pd.DataFrame()
for index in range(2000, 2010):
page = requests.get("https://solicitors.lawsociety.org.uk/person/"+str(index))
data = {'index': index, 'status': page.status_code}
df_new = pd.DataFrame.from_records([data])
df_summary = df_summary.append(df_new)
print(index, end=', ')
# -
range(1000, 2000)[0]
# +
df_summary = pd.DataFrame()
for index in range(1000, 2000):
page = requests.get("https://solicitors.lawsociety.org.uk/person/"+str(index))
data = {'index': index, 'status': page.status_code}
df_new = pd.DataFrame.from_records([data])
df_summary = df_summary.append(df_new)
print(index, end=', ')
# -
page.content
# +
df = pd.DataFrame()
for index in range(1000):
data = {'index': index, 'status': df_summary.iloc[index, index]}
df_new = pd.DataFrame.from_records([data])
df = df.append(df_new)
# -
df.loc[df.status == 200]
# +
from bs4 import BeautifulSoup
soup = BeautifulSoup(page.content, 'html.parser')
# -
soup.find('div', id='languages-spoken-accordion')
|
Notebooks/Law Professionals - Web Query Test - Request Multiple Pages in Loop.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import re
import seaborn as sns
import string
import nltk
import warnings
#nltk.download('stopwords')
#nltk.download('wordnet')
from wordcloud import WordCloud
df = pd.read_csv(r"C:\Users\<NAME>\Desktop\sanketf1data.csv",low_memory=False)
df
df.info()
df.columns
df['label'] = df['reviews.rating'].apply(lambda x : 1 if x > 4 else 0)
df["comb_review"]=df[["reviews.title","reviews.text"]].apply(lambda x:' '.join(x),axis=1)
# +
df[['text', 'rating']] = df[['comb_review', 'reviews.rating']]
df.head(119)
# -
df.columns
df.drop(df.columns[0], axis=1)
# +
def remove_pattern(text, pattern):
# find all the pattern in the input text and return a list of postion indeces
r = re.findall(pattern, text)
# replace the pattern with an empty space
for i in r: text = re.sub(pattern, '', text)
return text
# +
# lower case every word to ease the upcoming processes
df['text'] = df['text'].str.lower()
# tokenize the text to search for any stop words to remove it
df['tokenized_text'] = df.text.apply(lambda x : x.split())
# removing stop words
stopWords = set(nltk.corpus.stopwords.words('english'))
df['tokenized_text'] = df['tokenized_text'].apply(lambda x : [word for word in x if not word in stopWords])
# create a word net lemma
lemma = nltk.stem.WordNetLemmatizer()
pos = nltk.corpus.wordnet.VERB
df['tokenized_text'] = df['tokenized_text'].apply(lambda x : [lemma.lemmatize(word, pos) for word in x])
# remove any punctuation
df['tokenized_text'] = df['tokenized_text'].apply(lambda x : [ remove_pattern(word,'\.') for word in x])
# rejoin the text again to get a cleaned text
df['cleaned_text'] = df['tokenized_text'].apply(lambda x : ' '.join(x))
df.drop(labels=['tokenized_text'], axis=1, inplace=True)
df.head()
# +
from sklearn.feature_extraction.text import TfidfVectorizer
tfidf_Vectorizer = TfidfVectorizer(max_df=0.9, min_df=2, max_features=1000, stop_words='english')
tfidf_features = tfidf_Vectorizer.fit_transform(df['cleaned_text'])
tfidf_df = pd.DataFrame(tfidf_features.toarray(), columns=tfidf_Vectorizer.get_feature_names())
tfidf_df.head()
# +
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(tfidf_df, df['label'], test_size=0.2, random_state=42)
#X_test, X_valid, y_test, y_valid = train_test_split(X_metric, y_metric, test_size=0.5, random_state=42)
# +
from sklearn.neighbors import KNeighborsClassifier
clf_tfidf_knn = KNeighborsClassifier()
clf_tfidf_knn.fit(X_train, y_train)
# +
pred_tfidf_knn = clf_tfidf_knn.predict(X_test)
# +
from sklearn.metrics import classification_report, accuracy_score, f1_score,confusion_matrix
print("using TF-IDF")
print("Accuracy Socre: ",(100 * accuracy_score(y_test, pred_tfidf_knn)))
print(classification_report(y_test, pred_tfidf_knn))
# -
print(confusion_matrix(y_test, pred_tfidf_knn))
from wordcloud import WordCloud
reviews_great = str(df['cleaned_text'][df['label']==0])
greatcloud = WordCloud(width=1200,height=800).generate(reviews_great)
plt.imshow(greatcloud,interpolation='bilinear')
plt.axis('off')
plt.show()
from wordcloud import WordCloud
reviews_great = str(df['cleaned_text'][df['label']==1])
greatcloud = WordCloud(width=1200,height=800).generate(reviews_great)
plt.imshow(greatcloud,interpolation='bilinear')
plt.axis('off')
plt.show()
df['label'][5]
review=pd.DataFrame(df.groupby('reviews.rating').size().sort_values(ascending=False).rename('No of Users').reset_index())
review.head()
|
KNN usinf TD-IDF.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
pickle_file = '../dataset/arbimon_0.pickle'
# +
from six.moves import cPickle as pickle
with open(pickle_file, 'rb') as f:
save = pickle.load(f)
train_dataset = save['train_dataset']
train_labels = save['train_labels']
test_dataset = save['test_dataset']
test_labels = save['test_labels']
del save
# -
import numpy as np
def svm_reformat(dataset):
dataset = dataset.reshape((len(dataset), -1)).astype(np.float32)
return dataset
train_dataset = svm_reformat(train_dataset)
test_dataset = svm_reformat(test_dataset)
# +
from sklearn.svm import SVC
clf = SVC(kernel='sigmoid')
clf.fit(train_dataset, train_labels)
# -
clf.score(test_dataset, test_labels)
|
Jupyter Notebooks/SVM-SOLO_0.1707.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %matplotlib inline
#
# # With Clipping
#
# Removes unseen data points.
#
# Look at the examples below.
#
# +
import pandas as pd
from lets_plot import *
from lets_plot.geo_data import *
LetsPlot.setup_html()
# -
df = pd.read_csv('https://raw.githubusercontent.com/JetBrains/lets-plot-docs/master/data/midwest.csv')
states = geocode('state', df.state.unique(), scope='US').get_boundaries(9)
states.head(2)
# +
p = ggplot() + geom_map(data=states, tooltips=layer_tooltips().line('@{found name}'))
p1 = p + ggtitle('Default')
p2 = p + scale_x_continuous(limits=[-92, -82]) + ylim(36, 43) + ggtitle('Zoom With Clipping')
w, h = 400, 300
bunch = GGBunch()
bunch.add_plot(p1, 0, 0, w, h)
bunch.add_plot(p2, w, 0, w, h)
bunch
|
docs/_downloads/23e60af26d9bec72e2475f36b70fa6af/plot__with_clipping.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="ggpPusBoxZt8"
# # Computational and Numerical Methods
# ## Group 16
# ### Set 16 (12-11-2018): Runge-Kutta Method to Solve Ordinary Differential Equations
# #### <NAME> 201601003
# #### <NAME> 201601086
# + colab_type="text" id="a50RW7-JxysE" active=""
# <script>
# function code_toggle() {
# if (code_shown){
# $('div.input').hide('500');
# $('#toggleButton').val('Show Code')
# } else {
# $('div.input').show('500');
# $('#toggleButton').val('Hide Code')
# }
# code_shown = !code_shown
# }
#
# $( document ).ready(function(){
# code_shown=false;
# $('div.input').hide()
# });
# </script>
# <form action="javascript:code_toggle()"><input type="submit" id="toggleButton" value="Show Code"></form>
# + colab={} colab_type="code" id="EuL2kN0sksoq"
# %matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from math import sqrt
# +
def rk2(f, x0, y0, x1, h):
n = int((x1 - x0)/h)
vx = [0] * (n + 1)
vy = [0] * (n + 1)
vx[0] = x = x0
vy[0] = y = y0
for i in range(1, n + 1):
k1 = h * f(x, y)
k2 = h * f(x + 0.5 * h, y + 0.5 * k1)
vx[i] = x = x0 + i * h
vy[i] = y = y + (k1 + k2) / 2
return vx, vy
def rk4(f, x0, y0, x1, h):
n = int((x1 - x0)/h)
vx = [0] * (n + 1)
vy = [0] * (n + 1)
vx[0] = x = x0
vy[0] = y = y0
for i in range(1, n + 1):
k1 = h * f(x, y)
k2 = h * f(x + 0.5 * h, y + 0.5 * k1)
k3 = h * f(x + 0.5 * h, y + 0.5 * k2)
k4 = h * f(x + h, y + k3)
vx[i] = x = x0 + i * h
vy[i] = y = y + (k1 + k2 + k2 + k3 + k3 + k4) / 6
return vx, vy
def f(x, y):
return -y + 2*np.cos(x)
vx2, vy2 = rk2(f, 0, 1, 10, 0.1)
vx4, vy4 = rk4(f, 0, 1, 10, 0.1)
plt.xlabel("x")
plt.ylabel("y")
plt.grid(True)
plt.plot(vx2,vy2,label = "Second order Rungekutta")
plt.legend(loc = 'best')
plt.xlabel("x")
plt.ylabel("y")
plt.grid(True)
plt.plot(vx4,vy4, label = "Fourth order Rungekutta")
plt.legend(loc = 'best')
plt.xlabel("x")
plt.ylabel("y")
plt.grid(True)
plt.plot(vx2, np.sin(vx2) + np.cos(vx2), label = "Analytic Solution")
plt.legend(loc = 'best')
plt.show()
plt.grid(True)
plt.xlabel("x")
plt.ylabel("y")
plt.title("Error for Second order Rungekutta, h = 0.1")
plt.plot(vx2, np.sin(vx2) + np.cos(vx2) - vy2)
plt.show()
plt.xlabel("x")
plt.ylabel("y")
plt.grid(True)
plt.title("Error for Fourth order Rungekutta, h = 0.1")
plt.plot(vx4, np.sin(vx4) + np.cos(vx4) - vy4)
plt.show()
# +
vx2, vy2 = rk2(f, 0, 1, 10, 0.05)
vx4, vy4 = rk4(f, 0, 1, 10, 0.05)
plt.xlabel("x")
plt.ylabel("y")
plt.grid(True)
plt.plot(vx2,vy2,label = "Second order Rungekutta")
plt.legend(loc = 'best')
plt.xlabel("x")
plt.ylabel("y")
plt.grid(True)
plt.plot(vx4,vy4, label = "Fourth order Rungekutta")
plt.legend(loc = 'best')
plt.xlabel("x")
plt.ylabel("y")
plt.grid(True)
plt.plot(vx2, np.sin(vx2) + np.cos(vx2), label = "Analytic Solution")
plt.legend(loc = 'best')
plt.show()
plt.grid(True)
plt.xlabel("x")
plt.ylabel("y")
plt.title("Error for Second order Rungekutta, h = 0.05")
plt.plot(vx2, np.sin(vx2) + np.cos(vx2) - vy2)
plt.show()
plt.xlabel("x")
plt.ylabel("y")
plt.grid(True)
plt.title("Error for Fourth order Rungekutta, h = 0.05")
plt.plot(vx4, np.sin(vx4) + np.cos(vx4) - vy4)
plt.show()
# -
# # Q2
# +
def f(x, y):
return -y + (x**0.1)*(1.1+x)
for h in [0.1, 0.05, 0.025, 0.0125, 0.00625]:
vx2, vy2 = rk2(f, 0, 0, 5, h)
vx4, vy4 = rk4(f, 0, 0, 5, h)
plt.xlabel("x")
plt.ylabel("y")
plt.grid(True)
plt.plot(vx2,vy2,label = "Second order Rungekutta")
plt.legend(loc = 'best')
plt.xlabel("x")
plt.ylabel("y")
plt.grid(True)
plt.plot(vx4,vy4, label = "Fourth order Rungekutta")
plt.legend(loc = 'best')
plt.xlabel("x")
plt.ylabel("y")
plt.grid(True)
plt.plot(vx2, np.power(vx2, (1.1)), label = "Analytic Solution")
plt.legend(loc = 'best')
plt.show()
plt.grid(True)
plt.xlabel("x")
plt.ylabel("y")
plt.title("Error for Second order Rungekutta, h = " + str(h))
plt.plot(vx2, np.power(vx2, (1.1)) - vy2)
plt.show()
plt.xlabel("x")
plt.ylabel("y")
plt.grid(True)
plt.title("Error for Fourth order Rungekutta, h = " + str(h))
plt.plot(vx4, np.power(vx4, (1.1)) - vy4)
plt.show()
|
src/Set_16.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# +
import pandas as pd
import numpy as np
import time
today = time.strftime('%Y%m%d')
# +
# bring in zoningmods fields from FBP as place holders
# read these fields in s24
lookup_fbp = pd.read_csv(r'C:\Users\blu\Documents\GitHub\bayarea_urbansim\data\zoning_mods_24.csv',
usecols = ['fbpzoningmodcat', 'add_bldg', 'drop_bldg', 'dua_up', 'far_up',
'dua_down', 'far_down', 'subsidy', 'notes', 'res_rent_cat', 'job_out_cat'])
print('zoning_mods_24 has {} unique fbpzoningmodcat'.format(lookup_fbp.shape[0]))
display(lookup_fbp.head())
#print(list(lookup_fbp))
print('dua_up has the following values: {}'.format(list(lookup_fbp.dua_up.unique())))
print('dua_down has the following values: {}'.format(list(lookup_fbp.dua_down.unique())))
print('far_up has the following values: {}'.format(list(lookup_fbp.far_up.unique())))
print('far_down has the following values: {}'.format(list(lookup_fbp.far_down.unique())))
print('add_bldg has the following values: {}'.format(list(lookup_fbp.add_bldg.unique())))
print('drop_bldg has the following values: {}'.format(list(lookup_fbp.drop_bldg.unique())))
# -
# read parcel-level EIR zoningmods master file
p10_pba50_EIR_attr = pd.read_csv('C:\\Users\\blu\\Box\\Modeling and Surveys\\Urban Modeling\\Bay Area UrbanSim\\PBA50\\Policies\\Zoning Modifications\\p10_pba50_EIR_attr_20210224.csv')
p10_pba50_EIR_attr_modcat = p10_pba50_EIR_attr.merge(lookup_fbp,
left_on='fbpzoningm',
right_on='fbpzoningmodcat', how='left')
print('p10_pba50_EIR_attr_modcat has {} rows'.format(p10_pba50_EIR_attr_modcat.shape[0]))
# +
# collapsed to lookup table based on 'eirzoningm' and EIR geography fields, 'fbpzoningmodcat'
# was kept to inherent Final Blueprint values
EIR_modcat_df = p10_pba50_EIR_attr_modcat[['ACRES', 'fbpzoningmodcat', 'eirzoningm', 'juris',
'eir_gg_id', 'eir_tra_id', 'eir_sesit_', 'eir_coc_id',
'eir_ppa_id', 'eir_exp202', 'ex_res_bldg',
'add_bldg', 'drop_bldg', 'dua_up', 'far_up',
'dua_down', 'far_down', 'subsidy', 'res_rent_cat', 'job_out_cat']]
EIR_modcat_df = EIR_modcat_df[['eirzoningm', 'juris',
'eir_gg_id', 'eir_tra_id', 'eir_sesit_', 'eir_coc_id',
'eir_ppa_id', 'eir_exp202', 'ex_res_bldg',
'add_bldg', 'drop_bldg', 'dua_up', 'far_up',
'dua_down', 'far_down', 'subsidy','res_rent_cat', 'job_out_cat']].drop_duplicates()
# rename columns
EIR_modcat_df.rename(columns = {'eir_gg_id': 'gg_id',
'eir_tra_id': 'tra_id',
'eir_sesit_': 'sesit_id',
'eir_coc_id': 'coc_id',
'eir_ppa_id': 'ppa_id',
'eir_exp202': 'exp2020_id'}, inplace=True)
# add 'manual_county' column
juris_county = pd.read_csv(r'C:\Users\blu\Documents\GitHub\petrale\zones\jurisdictions\juris_county_id.csv',
usecols = ['juris_name_full', 'county_id'])
juris_county.columns = ['juris','manual_county']
EIR_modcat_df = EIR_modcat_df.merge(juris_county, on='juris', how='left')
# -
EIR_modcat_df.juris.unique()
# ## create zoning_mods lookup table for Alt2 (repeat steps above)
# ### Major changes in EIR Alt2 H3 strategy:
# #### 1. allow residential development in GGs for res and non_res parcels
# #### 2. change upzoning levels for different jurisdiction categories
# #### 3. don't allow upzoning for res parcels in CoCs
# +
#list of job Job-Rich & High-Resource Juris and Adjacent Juris
jlist = ['menlo_park', 'palo_alto', 'cupertino', 'milpitas',
'atherton', 'belmont', 'campbell', 'east_palo_alto',
'fremont', 'hayward', 'los_altos', 'los_altos_hills',
'los_gatos', 'monte_sereno', 'mountain_view', 'newark',
'redwood_city', 'portola_valley', 'san_carlos', 'san_jose',
'santa_clara', 'saratoga', 'sunnyvale', 'union_city', 'woodside']
#second version of the list
#job rich and high resource additions: pleasanton and st. Helena
#adjacency addition: Calistoga, Dublin, livermore, san ramon
jlist2 = ['menlo_park', 'palo_alto', 'cupertino', 'milpitas',
'st_helena', 'pleasanton',
'atherton', 'belmont', 'calistoga', 'campbell', 'dublin', 'east_palo_alto',
'fremont', 'hayward', 'livermore', 'los_altos', 'los_altos_hills',
'los_gatos', 'monte_sereno', 'mountain_view', 'newark',
'redwood_city', 'portola_valley', 'san_carlos', 'san_jose', 'san_ramon',
'santa_clara', 'saratoga', 'sunnyvale', 'union_city', 'woodside']
print ('There are {} cities in the list'.format(len(jlist2)))
# +
EIR_modcat_alt2 = EIR_modcat_df.copy()
# first, set to nan
EIR_modcat_alt2.dua_up = np.nan
EIR_modcat_alt2.far_up = np.nan
EIR_modcat_alt2.add_bldg = np.nan
# create an HRA list
hra_list = ['HRA','HRADIS']
# update values for Residential zoning change
#tra1
## no difference among juris categories in tra1
EIR_modcat_alt2.loc[(EIR_modcat_alt2.gg_id=='GG') & (
EIR_modcat_alt2.tra_id=='tra1'), 'add_bldg'] = 'HM'
EIR_modcat_alt2.loc[(EIR_modcat_alt2.gg_id=='GG') & (
EIR_modcat_alt2.tra_id=='tra1'), 'dua_up'] = 125
#tra2
## first add HM to all parcels in tra2
EIR_modcat_alt2.loc[(EIR_modcat_alt2.gg_id=='GG') & (
EIR_modcat_alt2.tra_id.str.contains('tra2', na = False)), 'add_bldg'] = 'HM'
## HRA upzoning
EIR_modcat_alt2.loc[(EIR_modcat_alt2.gg_id=='GG') & (
EIR_modcat_alt2.tra_id.str.contains('tra2', na = False)) & (
EIR_modcat_alt2.sesit_id.isin(hra_list)), 'dua_up'] = 75
## adjust for juris in the list
### note: the following code doesn't differentiate HRA or nonHRA, because in the next step
### nonHRA gets lower upzoning, so the nonHRA in this juris list would get
### revised from 100 to 55 too
EIR_modcat_alt2.loc[(EIR_modcat_alt2.gg_id=='GG') & (
EIR_modcat_alt2.tra_id.str.contains('tra2', na = False)) & (
EIR_modcat_alt2.juris.isin(jlist2)), 'dua_up'] = 100
## nonHRA upzoning
EIR_modcat_alt2.loc[(EIR_modcat_alt2.gg_id=='GG') & (
EIR_modcat_alt2.tra_id.str.contains('tra2', na = False)) & (
(EIR_modcat_alt2.sesit_id=='DIS') | (
EIR_modcat_alt2.sesit_id.isnull())), 'dua_up'] = 55
#tra3
## first add HM to all parcels in tra3
EIR_modcat_alt2.loc[(EIR_modcat_alt2.gg_id=='GG') & (
EIR_modcat_alt2.tra_id=='tra3'), 'add_bldg'] = 'HM'
## HRA upzoning
EIR_modcat_alt2.loc[(EIR_modcat_alt2.gg_id=='GG') & (
EIR_modcat_alt2.tra_id == 'tra3') & (
EIR_modcat_alt2.sesit_id.isin(hra_list)), 'dua_up'] = 50
## adjust for juris in the list
### note: the following code doesn't differentiate HRA or nonHRA, because in the next step
### nonHRA gets lower upzoning, so the nonHRA in this juris list would get
### revised from 75 to 50 too
EIR_modcat_alt2.loc[(EIR_modcat_alt2.gg_id=='GG') & (
EIR_modcat_alt2.tra_id == 'tra3') & (
EIR_modcat_alt2.juris.isin(jlist2)), 'dua_up'] = 75
## nonHRA upzoning
EIR_modcat_alt2.loc[(EIR_modcat_alt2.gg_id=='GG') & (
EIR_modcat_alt2.tra_id == 'tra3') & (
(EIR_modcat_alt2.sesit_id=='DIS') | (
EIR_modcat_alt2.sesit_id.isnull())), 'dua_up'] = 35
# non-TRA
EIR_modcat_alt2.loc[(EIR_modcat_alt2.gg_id=='GG') & (
EIR_modcat_alt2.tra_id.isnull()) & (
EIR_modcat_alt2.sesit_id.isin(hra_list)), 'add_bldg'] = 'HM'
## HRA upzoning
EIR_modcat_alt2.loc[(EIR_modcat_alt2.gg_id=='GG') & (
EIR_modcat_alt2.tra_id.isnull()) & (
EIR_modcat_alt2.sesit_id.isin(hra_list)), 'dua_up'] = 50
## adjust for juris in the list
### note: the following code doesn't differentiate HRA or nonHRA, because in the next step
### nonHRA gets lower upzoning, so the nonHRA in this juris list would get
### revised from 75 to 50 too
EIR_modcat_alt2.loc[(EIR_modcat_alt2.gg_id=='GG') & (
EIR_modcat_alt2.tra_id.isnull()) & (
EIR_modcat_alt2.juris.isin(jlist2)), 'dua_up'] = 75
## nonHRA upzoning
EIR_modcat_alt2.loc[(EIR_modcat_alt2.gg_id=='GG') & (
EIR_modcat_alt2.tra_id.isnull()) & (
(EIR_modcat_alt2.sesit_id=='DIS') | (
EIR_modcat_alt2.sesit_id.isnull())), 'dua_up'] = 35
# -
#Unincorporated w/in UGB upzoning
EIR_modcat_alt2.loc[EIR_modcat_alt2.exp2020_id == 'inun', 'dua_up'] = 2
EIR_modcat_alt2.loc[EIR_modcat_alt2.exp2020_id == 'inun', 'add_bldg'] = 'HS'
#check that that only areas outside UGB has dua_down == 0
EIR_modcat_alt2.loc[EIR_modcat_alt2.dua_down == 0].exp2020_id.unique()
#removing dua_up and add_bldg for areas outside UGB
EIR_modcat_alt2.loc[EIR_modcat_alt2.dua_down == 0, 'dua_up'] = np.nan
EIR_modcat_alt2.loc[EIR_modcat_alt2.dua_down == 0, 'add_bldg'] = np.nan
# +
# zoningmod for PPA
#1) dua_up and add_bldg = HM doesn't apply PPAs;
#2) all parcels within PPAs have drop_bldg = HM
EIR_modcat_alt2.loc[EIR_modcat_alt2.ppa_id=='ppa', 'dua_up'] = np.nan
EIR_modcat_alt2.loc[EIR_modcat_alt2.ppa_id=='ppa', 'add_bldg'] = np.nan
EIR_modcat_alt2.loc[EIR_modcat_alt2.ppa_id=='ppa', 'drop_bldg'] = 'HM'
# Then modify PPA zoning changes in FBP
# remove this one below to make sure housing gets built in core area first given the lower upzoning
# EIR_modcat_alt2.loc[(EIR_modcat_alt2.gg_id=='GG') & (EIR_modcat_alt2.tra_id=='tra1'), 'far_up'] = 9
EIR_modcat_alt2.loc[(EIR_modcat_alt2.gg_id=='GG') & (
EIR_modcat_alt2.ppa_id=='ppa') & (
EIR_modcat_alt2.tra_id != 'tra1'), 'far_up'] = 2
EIR_modcat_alt2.loc[(EIR_modcat_alt2.gg_id=='GG') & (
EIR_modcat_alt2.ppa_id=='ppa') & (
EIR_modcat_alt2.tra_id != 'tra1'), 'add_bldg'] = 'IW'
# -
#check that that only areas outside UGB has far_down == 0
EIR_modcat_alt2.loc[EIR_modcat_alt2.far_down == 0].exp2020_id.unique()
#removing far_up and add_bldg for areas outside UGB
EIR_modcat_alt2.loc[EIR_modcat_alt2.far_down == 0, 'far_up'] = np.nan
EIR_modcat_alt2.loc[EIR_modcat_alt2.far_down == 0, 'add_bldg'] = np.nan
# limit development in CoCs
EIR_modcat_alt2.loc[(EIR_modcat_alt2.coc_id=='CoC') & (
EIR_modcat_alt2.ex_res_bldg =='res'), 'dua_up'] = np.nan
EIR_modcat_alt2.loc[(EIR_modcat_alt2.coc_id=='CoC') & (
EIR_modcat_alt2.ex_res_bldg =='res'), 'add_bldg'] = np.nan
# +
# drop duplicates
EIR_modcat_alt2 = EIR_modcat_alt2.drop_duplicates()
print('EIR_modcat_alt2 has {} rows'.format(EIR_modcat_alt2.shape[0]))
# add 'FREQUENCE', 'SUM_ACRES' columns
EIR_modcat_stats = p10_pba50_EIR_attr_modcat.groupby('eirzoningm').agg({'ACRES': ['count','sum']}).reset_index()
EIR_modcat_stats.columns = ['eirzoningm', 'FREQUENCY', 'SUM_ACRES']
print('EIR_modcat_stats has {} rows'.format(EIR_modcat_stats.shape[0]))
EIR_modcat_alt2 = EIR_modcat_alt2.merge(EIR_modcat_stats, on='eirzoningm', how='left')
print('p10_pba50_EIR_modcat_df has {} rows'.format(EIR_modcat_alt2.shape[0]))
# add 'modcat_id' column
EIR_modcat_alt2['modcat_id'] = EIR_modcat_alt2.index + 1
# recoder the fields
EIR_modcat_alt2 = EIR_modcat_alt2[['eirzoningm', 'modcat_id', 'FREQUENCY', 'SUM_ACRES', 'manual_county', 'juris',
'gg_id', 'tra_id', 'sesit_id', 'coc_id', 'ppa_id', 'exp2020_id', 'ex_res_bldg',
'add_bldg', 'drop_bldg', 'dua_up', 'far_up', 'dua_down', 'far_down', 'subsidy', 'res_rent_cat', 'job_out_cat']]
# +
#check
# PPA parcels should have no dua_up
ppa_chk = EIR_modcat_alt2.loc[EIR_modcat_alt2.ppa_id == 'ppa']
display(ppa_chk.dua_up.unique()) # should only contain nan
# PPA parcels should have drop_bldg = HM
display(ppa_chk.drop_bldg.unique()) # should only contain 'HM'
# -
# export
EIR_modcat_alt2.rename(columns={'eirzoningm': 'eirzoningmodcat'}, inplace=True)
print('export zoning_mods lookup table of {} rows'.format(EIR_modcat_alt2.shape[0]))
EIR_modcat_alt2.to_csv('C:\\Users\\blu\\Box\\Modeling and Surveys\\Urban Modeling\\Bay Area UrbanSim\\PBA50\\Policies\\Zoning Modifications\\BAUS input files\\zoning_mods_28_{}.csv'.format(today), index=False)
|
policies/plu/update_EIR_zoningmods_lookup_Alt2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
#
# ## The highlighter extension:
#
# - Firstable, the extension provides <span class="mark">several toolbar buttons</span> for highlighting a selected text _within a markdown cell_. Three different \`color schemes' are provided, which can be easily customized in the \textit{stylesheet} `highlighter.css`. The last button enables to remove all highlightings in the current cell.
# - This works both <span class="burk">when the cell is _rendered_ and when the cell is in edit mode</span>;
# - In both modes, it is possible to highlight formatted portions of text (In rendered mode, since the selected text loose its formatting, an heuristic is applied to find the best alignment with the actual text)
# - When no text is selected, the whole cell is highlighted;
# - The extension also provides two keyboard shortcuts (Alt-G and Alt-H) which fire the highlighting of the selected text.
# - Highlights can be preserved when exporting to html or to LaTeX -- details are provided in [export_highlights](export_highlights.ipynb)
#
#
# 
#
# ## Installation:
#
# The extension can be installed with the nice UI available on IPython-notebook-extensions website, which also allows to enable/disable the extension.
#
# You may also install the extension from the original repo: issue
# ```bash
# jupyter nbextension install https://rawgit.com/jfbercher/small_nbextensions/master/highlighter.zip --user
#
# ```
# at the command line.
#
# ### Testing:
#
# Use a code cell with
# ```javascript
# # %%javascript
# require("base/js/utils").load_extensions("usability/highlighter/highlighter")
# ```
#
# ### Automatic load
# You may also automatically load the extension for any notebook via
# ```bash
# jupyter nbextension enable usability/highlighter/highlighter
# ```
#
# + language="javascript"
# require("base/js/utils").load_extensions("usability/highlighter/highlighter")
|
nbextensions/usability/highlighter/demo_highlighter.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Maxwell's equations
#
# Maxwell's equation are some of the most important equation in physics as form the understanding behind essentially all applications of electrical or magnetic systems in the modern world. Despite being devised in the $19th$ century, they obey the laws of relativity. This notebook will introduce the 4 Maxwell equations in both their intergral and differential form.
# (gauss_law)=
# ## Gauss's law
#
# Gauss’s law is the first of Maxwell’s equations, and ultimately encapsulates the idea that charged particles are a source of electric field. In order to derive Gauss’s law, we first have to introduce the concept of electric flux, $\Phi_\mathbf{E}$. This is equivalent to the magnetic flux and is defined as
#
# $$\Phi_\mathbf{E} = \iint_{\mathbf{S}}^{} \mathbf{E} \cdot d\mathbf{S}$$
#
# where for a closed surface, $d\mathbf{S}$ points outwards by convention. To better understand the electric flux from a point charge, we will introduce the concept of *Solid Angles*. The solid angle is a generalisation of the ordinary angle between two lines. Consider a surface element, i.e., a small vector area $d\mathbf{S}$ which is distance r from point P. The surface element is defined to subtend a solid angle $d\Omega$ as follows:
#
# $$d\Omega = \frac{d\mathbf{S} \cdot \mathbf{\hat{r}}} {r^2}$$
#
# where $\mathbf{\hat{r}}$ is the unit vector along the direction from P to the surface element. It should be noted that just as there are 2π radians in a circle, there are 4π steradians covering the surface of a sphere.
#
# Consider a point charge $Q$. The electric flux through a spherical surface $S_1$, radius $r_1$, is
#
# $$\Phi_{\mathbf{E},1} = 4\pi r_1^2 E_{r_1} = \frac{Q}{\epsilon_0}$$
#
# Now we consider the flux $d\Phi_{\mathbf{E},1}$ through the surface element $dS_1$. This is given by
#
# $$d\Phi_{\mathbf{E},1} = \mathbf{E}_{r_1} \cdot d\mathbf{S}_1 = \frac {\Phi_{\mathbf{E},1}} {4\pi r_1^2} dS_1$$
#
# where we have used the fact that $\frac {d\Phi_{\mathbf{E},1}} {\Phi_{\mathbf{E},1}} = \frac {dS_1} {4\pi r_1^2}$ and the fact that $\mathbf{E}$ is radial. Now, using the above definition of the solid angle, we can write
#
# $$\frac {\Phi_{\mathbf{E},1}} {4\pi r_1^2} dS_1 = \frac {\Phi_{\mathbf{E},1}} {4\pi} d\Omega = \frac{Q}{4\pi \epsilon_0} d\Omega$$
#
# Thus, we can finally write
#
# $$d\Phi_{\mathbf{E},1} = \frac{Q}{4\pi \epsilon_0} d\Omega$$
#
# Now consider $S_2$, an arbitrary surface enclosing $S_1$. The corresponding element of flux $d\Phi_{\mathbf{E},2}$ through $dS_2$ is given by
#
# $$d\Phi_{\mathbf{E},2} = \mathbf{E}_{r_2} \cdot d\mathbf{S}_2 = \frac{Q}{4\pi \epsilon_0 r_2^2} \mathbf{\hat{r}} \cdot d\mathbf{S}_2$$
#
# and using the definition of the solid angle we can write
#
# $$d\Phi_{\mathbf{E},2} = \frac{Q}{4\pi \epsilon_0}d\Omega = d\Phi_{\mathbf{E},1}$$
#
# Thus, the flux through the two surface elements is the same, even though the orientation of $dS_2$ is arbitrary and consequently, the flux through any closed surface is always $\frac{Q}{\epsilon_0}$
#
# Now consider an arbitrary closed surface surrounding a collection of charges $Q_1$, $Q_2$, ..., $Q_N$. Using the supeposition principle, the electric flux through the surface is given by
#
# $$\Phi_{\mathbf{E}} = \frac{Q_1}{\epsilon_0}, \frac{Q_2}{\epsilon_0}, ..., \frac{Q_N}{\epsilon_0}$$
#
# Since $Q$ = $Q_1$ + $Q_2$ + ... + $Q_N$ we can write
#
# $$\oint_S \mathbf{E} \cdot d\mathbf{S} = \frac{Q}{\epsilon_0}$$
#
# This is the integral form of Gauss's law! By considering a region of space with uniform charge density instead of point charges we can write Gauss's law in a different form. Consider a volume, $V$, with total charge, $Q$, and charge density, $\rho$. The total charge can then be written in terms of the charge density:
#
# $$Q = \iiint_V \rho dV$$
#
# Substituting this to Gauss's law:
#
# $$\oint_S \mathbf{E} \cdot d\mathbf{S} = \frac {1}{\epsilon_0} \iiint_V \rho dV$$
#
# where $V$ is the volume enclosed by the closed surface $S$.
#
# Applying the Divergence theorem we get
#
# $$\iiint_V \nabla \cdot \mathbf{E} \,dV = \frac {1}{\epsilon_0} \iiint_V \rho dV$$
#
# By applying this to an infinitesimal volume, we can remove the integrals such that
#
# $$ \nabla \cdot \mathbf{E} = \frac {\rho}{\epsilon_0} $$
#
# This is Gauss's law in differential form!
# (gauss_magnetism)=
# ## Gauss’s law for magnetism
#
# This is essentially the same law as Gauss's law for electricity, but unlike electricity, there are no magnetic monopoles in nature, as magnetic pole always exist in pairs - dipoles. Thus, magnetic field lines are loops, with no beginning or end, unlike electric field lines. This is described mathematically by
#
# $$\nabla \cdot \mathbf{B} = 0 \, \ \mbox{(differential form)}$$
#
# $$\oint_{Closed} \mathbf{B} \cdot d\mathbf{S} = 0 \, \ \mbox{(integral form)}$$
#
# This is Maxwell's second equation.
# (faraday_law)=
# ## Faraday's law
#
# We know by Faraday's law of induction that when the magnetic flux changes through a wire loop an electromotive force ($EMF$) is acquired by the wire loop given by
#
# $$EMF = - \frac {d\mathbf{\Phi_B}}{dt}$$
#
# The $EMF$ and the electric field generated around the wire loop are essentially the same and thus
#
# $$EMF = \int_{circuit} \mathbf{E} \cdot d\boldsymbol{l}$$
#
# Thus, using Faraday's law
#
# $$ \int_{circuit} \mathbf{E} \cdot d\boldsymbol{l} = - \frac {d}{dt} \iint_{S}^{} \mathbf{B} \cdot d\mathbf{S}$$
#
# This is the third Maxwell equation, in integral form. To get the differntial form we can use Stoke's Theorem such that
#
# $$\iint_{S} \nabla \times \mathbf{E} \cdot d\mathbf{S} = - \frac {d}{dt} \iint_{S}^{} \mathbf{B} \cdot d\mathbf{S}$$
#
# $$\nabla \times \mathbf{E} = - \frac {d\mathbf{B}}{dt}$$
# (ampere_law)=
# ## Ampere - Maxwell equation
#
# The Biot-Savart law provides a general expression for the magnetic field from a current element:
#
# $$d\mathbf{B} = \frac{\mu_0 I} {4\pi} \frac{d\boldsymbol{l} \times \mathbf{\hat{r}}} {r^2}$$
#
# where $d\boldsymbol{l}$ is the line element, d$\mathbf{B}$ is the magnetic field by the current element $Id\boldsymbol{l}$ and $\mathbf{\hat{r}}$ is the unit vector from the line element to the location where we want the $\mathbf{B}$ field. Thus the total field at this point is given by
#
# $$\mathbf{B} = \frac{\mu_0} {4\pi} \int \frac{Id\boldsymbol{l} \times \mathbf{\hat{r}}} {r^2}$$
#
# Ampere's law is just another formulation of the Biot-Savart law. Using Biot-Savart, we can write
#
# $$\int_L \mathbf{B} \cdot d\boldsymbol{l} = \frac{\mu_0 I} {2\pi r} \int_L d\boldsymbol{l} = \mu_0 I$$
#
# since $ \int_L d\boldsymbol{l}$ is just the circumference. It should be noted that the line integral does not depend on the shape of path or the position of the wire within it. If the current in the wire is in the opposite direction, the integral has a negative sign.
#
# Rather than using a single current, we can introduce a new quantity called the *current density*, $\mathbf{J}$, related to $I$ by
#
# $$I = \iint_S \mathbf{J} \cdot d\mathbf{S}$$
#
# Using this definition we can write
#
# $$\int_L \mathbf{B} \cdot d\boldsymbol{l} = \mu_0 \iint_S \mathbf{J} \cdot d\mathbf{S}$$
#
# and using Stoke's Theorem we get
#
# $$\iint_S \nabla \times \mathbf{B} \cdot d\mathbf{S} = \mu_0 \iint_S \mathbf{J} \cdot d\mathbf{S}$$
#
# $$\nabla \times \mathbf{B} = \mu_0\mathbf{J}$$
#
# This is Ampere's law in differential form, but it is not quite yet a Maxwell equation, as it is not valid for a time-varying electric fields (not constant current). Another term needs to be added into the equation that takes into account the time-varying electric fields. Doing so yields the fourth Maxwell equation:
#
# $$\int_L \mathbf{B} \cdot d\boldsymbol{l} = \mu_0 \iint_S \mathbf{J} \cdot d\mathbf{S} + \mu_0 \epsilon_0 \iint_S \frac {d\mathbf{E}}{dt} \cdot d\mathbf{S} \, \ \mbox{(integral form)}$$
#
# $$\nabla \times \mathbf{B} = \mu_0\mathbf{J} + \mu_0 \epsilon_0 \frac {d\mathbf{E}}{dt} \, \ \mbox{(differential form)}$$
|
notebooks/d_geosciences/Electromagnetism/2_maxwell_eqs.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernel_info:
# name: python3-azureml
# kernelspec:
# display_name: Python 3.6 - AzureML
# language: python
# name: python3-azureml
# ---
# + gather={"logged": 1638378338753}
from azureml.core import Experiment, Environment, Workspace, Datastore, Dataset, Model, ScriptRunConfig
import os
import glob
# get the current workspace
ws = Workspace.from_config()
# + jupyter={"source_hidden": false, "outputs_hidden": false} nteract={"transient": {"deleting": false}}
# %cd Satellite_ComputerVision
# !git pull
# %cd ..
# + jupyter={"source_hidden": false, "outputs_hidden": false} nteract={"transient": {"deleting": false}} gather={"logged": 1638378354914}
# access our registered data share containing image data in this workspace
datastore = Datastore.get(workspace = ws, datastore_name = 'solardatafilestore')
cpk_train_path = (datastore, 'CPK_solar/training/')
cpk_eval_path = (datastore, 'CPK_solar/eval/')
nc_train_path = (datastore, 'NC_solar/training/')
nc_eval_path = (datastore, 'NC_solar/eval/')
test_path = (datastore, 'CPK_solar/predict/testpred5')
# cpk_train_dataset = Dataset.File.from_files(path = [cpk_train_path])
# cpk_eval_dataset = Dataset.File.from_files(path = [cpk_eval_path])
# nc_train_dataset = Dataset.File.from_files(path = [nc_train_path])
# nc_eval_dataset = Dataset.File.from_files(path = [nc_eval_path])
# when we combine datasets the selected directories and relative paths to the datastore are brought in
# mount folder
# |-cddatafilestore
# | |-GEE
# | | |-training
# | | |-eval
# | |-Onera
# | | |-training
# | | |-eval
train_dataset = Dataset.File.from_files(path = [cpk_train_path, nc_train_path])
eval_dataset = Dataset.File.from_files(path = [cpk_eval_path, nc_eval_path])
test_dataset = Dataset.File.from_files(path = [test_path])
# + jupyter={"source_hidden": false, "outputs_hidden": false} nteract={"transient": {"deleting": false}} gather={"logged": 1637721743359}
# FInd the run corresponding to the model we want to register
run_id = 'solar-nc-cpk_1624989679_f59da7cf'
run = ws.get_run(run_id)
# + jupyter={"source_hidden": false, "outputs_hidden": false} nteract={"transient": {"deleting": false}} gather={"logged": 1638378394414}
model_name = 'solar_Nov21'
# + jupyter={"source_hidden": false, "outputs_hidden": false} nteract={"transient": {"deleting": false}} gather={"logged": 1625103322523}
model = run.register_model(model_name=model_name,
tags=run.tags,
description = 'UNET model delineating ground mounted solar arrays in S2 imagery. Trained on multi-season data from Chesapeake Bay and NC',
model_path='outputs/',
model_framework = 'Tensorflow',
model_framework_version= '2.0',
datasets = [('training', train_dataset), ('evaluation', eval_dataset), ('testing', test_dataset)])
print(model.name, model.id, model.version, sep='\t')
# + jupyter={"source_hidden": false, "outputs_hidden": false} nteract={"transient": {"deleting": false}} gather={"logged": 1638378482125}
# use the azure folder as our script folder
source = 'Satellite_ComputerVision'
util_folder = 'utils'
script_folder = f'{source}/azure'
script_file = 'train_solar.py'
# + jupyter={"source_hidden": false, "outputs_hidden": false} nteract={"transient": {"deleting": false}} gather={"logged": 1638378416579}
# get our environment
envs = Environment.list(workspace = ws)
env = envs.get('solar-training')
# + jupyter={"source_hidden": false, "outputs_hidden": false} nteract={"transient": {"deleting": false}} gather={"logged": 1638378418660}
# define the compute target
compute_target = ws.compute_targets['mevans1']
# + jupyter={"source_hidden": false, "outputs_hidden": false} nteract={"transient": {"deleting": false}} gather={"logged": 1638378420398}
experiment_name = 'solar-nc-cpk'
exp = Experiment(workspace = ws, name = experiment_name)
# + jupyter={"source_hidden": false, "outputs_hidden": false} nteract={"transient": {"deleting": false}} gather={"logged": 1638378455879}
args = [
'--train_data', train_dataset.as_mount(),
'--eval_data', eval_dataset.as_mount(),
'--test_data', test_dataset.as_mount(),
'--model_id', model_name,
'--weight', 0.7,
'-lr', 0.0005,
'--epochs', 50,
'--batch', 16,
'--size', 7755,
'--kernel_size', 256,
'--response', 'landcover']
# + jupyter={"source_hidden": false, "outputs_hidden": false} nteract={"transient": {"deleting": false}} gather={"logged": 1638381137340}
src = ScriptRunConfig(source_directory=script_folder,
script=script_file,
arguments=args,
compute_target=compute_target,
environment=env)
# + jupyter={"source_hidden": false, "outputs_hidden": false} nteract={"transient": {"deleting": false}} gather={"logged": 1638381147221}
# run the training job
run = exp.submit(config=src, tags = dict({'splits':'None', 'model':'Unet', 'dataset':'CPK+NC', 'normalization':'pixel', 'epochs':'100-150'}))
run
|
re-train.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
import pandas as pd
dados = pd.read_csv('aluguel.csv', sep = ';')
dados.head(10)
# Criar um distribuição de frequência dos imoveis com quantidades determinadas de quartos
# 1 e 2 quartos
# 3 e 4 quartos
# 5 e 6 quartos
# 7 ou mais quartos
# lista em que passaremos os valores mínimos (0) e máximos (2,4,6,100)
classes = [0, 2, 4, 6, 100]
quartos = pd.cut(dados['Quartos'], classes)
quartos
pd.value_counts(quartos)
labels = ['1 e 2 quartos','3 e 4 quartos', '5 e 6 quartos','7 ou mais quartos']
quartos = pd.cut(dados['Quartos'], classes, labels = labels)
quartos
pd.value_counts(quartos)
quartos = pd.cut(dados['Quartos'], classes, labels = labels, include_lowest=True)
quartos
pd.value_counts(quartos)
|
pacote/Python Pandas - Tratando e analisando dados/extras/Criando faixas de valor.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda root]
# language: python
# name: conda-root-py
# ---
# +
import numpy as np
import pandas as pd
import math
from sklearn import svm
df_train = pd.read_csv("../data/mnist_train.csv").sample(n=10000)
df_train['intercept'] = 1
trainingData = df_train.drop("label", axis = 1).values
trainingResults = df_train["label"].values
df_test = pd.read_csv("../data/mnist_test.csv").sample(n=2000)
df_test['intercept'] = 1
testData = df_test.drop("label", axis=1).values
testResults = df_test["label"].values
Cvals = [1, 10, 100, 1000, 5000, 10000]
rbfSVMErrors = []
linearSVMErrors = []
for i in range(len(Cvals)):
Cval = Cvals[i]
# build the validation set
# build the validation set
start_index = i * len(trainingData)//len(Cvals)
end_index = len(trainingData)//len(Cvals) * (i + 1)
validation_data = trainingData[start_index:end_index]
validation_classifications = trainingResults[start_index:end_index]
# build the model
model = np.concatenate((trainingData[:start_index], trainingData[end_index:]), axis=0)
model_classifications = np.concatenate((trainingResults[:start_index], trainingResults[end_index:]), axis=0)
svm1 = svm.SVC(C=Cval)
svm1.fit(model, model_classifications)
rbfScore = svm1.score(validation_data, validation_classifications)
rbfSVMErrors.append(1 - rbfScore)
svm3 = svm.LinearSVC(C=Cval)
svm3.fit(model, model_classifications)
linearScore = svm3.score(validation_data, validation_classifications)
linearSVMErrors.append(1 - linearScore)
# +
from matplotlib import pyplot as plt
plt.plot(Cvals, rbfSVMErrors)
plt.title("C vs. Validation Error on RBF SVMs")
plt.xscale('log')
plt.xlabel("C")
plt.ylabel("error")
plt.savefig('rbf_svm_CvsError.png')
plt.show()
plt.plot(Cvals, linearSVMErrors)
plt.title("C vs. Validation Error on Linear SVMs")
plt.xscale('log')
plt.xlabel("C")
plt.ylabel("error")
plt.savefig('linear_svm_CvsError.png')
plt.show()
# -
# We found that the Linear SVM had a markedly lower validation error than the RBF SVM. We were surprised by this. The best C value, according to our cross-validation, was C = 1, but we're skeptical that variations in validation error are due to variations in validation blocks rather than any impact our C value might have because the differences in error are so small. Thus, we'll build a Linear SVM model with C = 1 with our training set against the test set to get our test error.
# +
import numpy as np
import pandas as pd
import math
from sklearn import svm
df_train = pd.read_csv("../data/mnist_train.csv").sample(n=20000)
df_train['intercept'] = 1
trainingData = df_train.drop("label", axis = 1).values
trainingResults = df_train["label"].values
df_test = pd.read_csv("../data/mnist_test.csv")
df_test['intercept'] = 1
testData = df_test.drop("label", axis=1).values
testResults = df_test["label"].values
classifier = svm.SVC(C=100)
classifier.fit(trainingData, trainingResults)
print("The test error of the RBF SVM is", 1 - classifier.score(testData, testResults))
classifier = svm.LinearSVC(C=1)
classifier.fit(trainingData, trainingResults)
print("The test error of the Linear SVM is", 1 - classifier.score(testData, testResults))
|
notebook/SciKit SVM.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Bibliotecas
import pandas as pd
import numpy as np
import yfinance as yf
import datetime as datetime
import matplotlib.pyplot as plt
import statsmodels.api as sm
from sklearn.linear_model import LinearRegression
plt.style.use('fivethirtyeight')
# ## Buscando dados
# +
inicio = datetime.datetime(2019, 1, 1)
fim = datetime.datetime(2021, 12, 31)
tickers = ['PETR4.SA', '^BVSP']
dados = pd.DataFrame()
for i in tickers:
dados[i] = yf.download(i, start=inicio, end=fim, interval='1wk')['Adj Close']
dados.head()
# -
# ## Beta: yfinance
beta = yf.Ticker("PETR4.SA")
beta.info['beta']
# ## Retorno simples
retorno_simples = np.log(dados / dados.shift()).dropna()
retorno_simples.tail()
# ## Beta: CAPM - Capital Asset Pricing Model
# +
#Dados da Selic
url = 'http://api.bcb.gov.br/dados/serie/bcdata.sgs.432/dados?formato=json'
selic_meta = pd.read_json(url)
#Adaptando a base de dados
selic_meta['data'] = pd.to_datetime(selic_meta['data'], dayfirst=True)
selic_meta.set_index('data', inplace=True)
selic_meta.tail()
# +
#Ativo livre de risco
rf = selic_meta.iloc[-1]
rf
retorno_simples['Selic'] = 0
for i in retorno_simples['Selic']:
retorno_simples['Selic'] = rf[0]
retorno_simples.head()
# +
#Utilizando a biblioteca Statsmodels
y = retorno_simples['PETR4.SA']
x = retorno_simples['^BVSP']
#c = retorno_simples['Selic']
X = sm.add_constant(x)
resultado = sm.OLS(y, X).fit()
# -
print(resultado.summary())
# +
#Utilizando a biblioteca Sklearn
X = x.values.reshape(-1, 1)
# +
#Estimação do modelo
reg = LinearRegression()
reg.fit(X, y)
# +
#R-square
reg.score(X, y)
# +
#Intercepto
reg.intercept_
# +
#Coeficiente
reg.coef_[0]
# +
#Previsão do modelo
y_chapeu = reg.predict(X)
# +
#Visualização
plt.figure(figsize=(16, 8));
plt.plot(x, y_chapeu, label='Reta de regressão (predição)', color='#ed1118', linewidth=3);
plt.scatter(x, y, label='Dispersão', color='#2424ed', linewidth=0.8);
plt.title('Beta PETR4');
plt.ylabel('Retorno do ativo');
plt.xlabel('Retorno do mercado');
plt.text(0.05, 0.2, f'ŷ = {np.round(reg.intercept_, 0)} + {np.round(reg.coef_[0], 3)} * Rm');
plt.text(0.10, -0.3, f'Beta: {np.round(reg.coef_[0], 4)}');
plt.legend();
# -
# SCRIPT FINALIZADO!
|
capm2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Hill Climbing
#
# ---
#
# In this notebook, we will train hill climbing with adaptive noise scaling with OpenAI Gym's Cartpole environment.
# ### 1. Import the Necessary Packages
import gym
import numpy as np
from collections import deque
import matplotlib.pyplot as plt
# %matplotlib inline
# ### 2. Define the Policy
# +
env = gym.make('CartPole-v0')
print('observation space:', env.observation_space)
print('action space:', env.action_space)
class Policy():
def __init__(self, s_size=4, a_size=2):
self.w = 1e-4*np.random.rand(s_size, a_size) # weights for simple linear policy: state_space x action_space
def forward(self, state):
x = np.dot(state, self.w)
return np.exp(x)/sum(np.exp(x))
def act(self, state):
probs = self.forward(state)
#action = np.random.choice(2, p=probs) # option 1: stochastic policy
action = np.argmax(probs) # option 2: deterministic policy
return action
# -
# ### 3. Train the Agent with Stochastic Policy Search
# +
env = gym.make('CartPole-v0')
env.seed(0)
np.random.seed(0)
policy = Policy()
def hill_climbing(n_episodes=1000, max_t=1000, gamma=1.0, print_every=100, noise_scale=1e-2):
"""Implementation of hill climbing with adaptive noise scaling.
Params
======
n_episodes (int): maximum number of training episodes
max_t (int): maximum number of timesteps per episode
gamma (float): discount rate
print_every (int): how often to print average score (over last 100 episodes)
noise_scale (float): standard deviation of additive noise
"""
scores_deque = deque(maxlen=100)
scores = []
best_R = -np.Inf
best_w = policy.w
for i_episode in range(1, n_episodes+1):
rewards = []
state = env.reset()
for t in range(max_t):
action = policy.act(state)
state, reward, done, _ = env.step(action)
rewards.append(reward)
if done:
break
scores_deque.append(sum(rewards))
scores.append(sum(rewards))
discounts = [gamma**i for i in range(len(rewards)+1)]
R = sum([a*b for a,b in zip(discounts, rewards)])
if R >= best_R: # found better weights
best_R = R
best_w = policy.w
noise_scale = max(1e-3, noise_scale / 2)
policy.w += noise_scale * np.random.rand(*policy.w.shape)
else: # did not find better weights
noise_scale = min(2, noise_scale * 2)
policy.w = best_w + noise_scale * np.random.rand(*policy.w.shape)
if i_episode % print_every == 0:
print('Episode {}\tAverage Score: {:.2f}'.format(i_episode, np.mean(scores_deque)))
if np.mean(scores_deque)>=195.0:
print('Environment solved in {:d} episodes!\tAverage Score: {:.2f}'.format(i_episode-100, np.mean(scores_deque)))
policy.w = best_w
break
return scores
scores = hill_climbing()
# -
# ### 4. Plot the Scores
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(np.arange(1, len(scores)+1), scores)
plt.ylabel('Score')
plt.xlabel('Episode #')
plt.show()
# ### 5. Watch a Smart Agent!
# +
env = gym.make('CartPole-v0')
state = env.reset()
for t in range(200):
action = policy.act(state)
env.render()
state, reward, done, _ = env.step(action)
if done:
break
env.close()
|
hill-climbing/Hill_Climbing.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# !pip install mxnet-cu101
# !pip install gluonnlp pandas tqdm
# !pip install sentencepiece==0.1.85
# !pip install transformers==2.1.1
# !pip install torch==1.3.1
# !pip install git+https://git@github.com/SKTBrain/KoBERT.git@master
import torch
from torch import nn
import torch.nn.functional as F
import torch.optim as optim
from torch.utils.data import Dataset, DataLoader
import gluonnlp as nlp
import numpy as np
from tqdm import tqdm, tqdm_notebook
from kobert.utils import get_tokenizer
from kobert.pytorch_kobert import get_pytorch_kobert_model
from transformers import AdamW
from transformers.optimization import WarmupLinearSchedule
##GPU 사용 시
device = torch.device("cuda:0")
bertmodel, vocab = get_pytorch_kobert_model()
# !wget https://www.dropbox.com/s/374ftkec978br3d/ratings_train.txt?dl=1
# !wget https://www.dropbox.com/s/977gbwh542gdy94/ratings_test.txt?dl=1
dataset_train = nlp.data.TSVDataset("ratings_train.txt?dl=1", field_indices=[1,2], num_discard_samples=1)
dataset_test = nlp.data.TSVDataset("ratings_test.txt?dl=1", field_indices=[1,2], num_discard_samples=1)
tokenizer = get_tokenizer()
tok = nlp.data.BERTSPTokenizer(tokenizer, vocab, lower=False)
class BERTDataset(Dataset):
def __init__(self, dataset, sent_idx, label_idx, bert_tokenizer, max_len,
pad, pair):
transform = nlp.data.BERTSentenceTransform(
bert_tokenizer, max_seq_length=max_len, pad=pad, pair=pair)
self.sentences = [transform([i[sent_idx]]) for i in dataset]
self.labels = [np.int32(i[label_idx]) for i in dataset]
def __getitem__(self, i):
return (self.sentences[i] + (self.labels[i], ))
def __len__(self):
return (len(self.labels))
## Setting parameters
max_len = 64
batch_size = 64
warmup_ratio = 0.1
num_epochs = 5
max_grad_norm = 1
log_interval = 200
learning_rate = 5e-5
data_train = BERTDataset(dataset_train, 0, 1, tok, max_len, True, False)
data_test = BERTDataset(dataset_test, 0, 1, tok, max_len, True, False)
train_dataloader = torch.utils.data.DataLoader(data_train, batch_size=batch_size, num_workers=5)
test_dataloader = torch.utils.data.DataLoader(data_test, batch_size=batch_size, num_workers=5)
class BERTClassifier(nn.Module):
def __init__(self,
bert,
hidden_size = 768,
num_classes=2,
dr_rate=None,
params=None):
super(BERTClassifier, self).__init__()
self.bert = bert
self.dr_rate = dr_rate
self.classifier = nn.Linear(hidden_size , num_classes)
if dr_rate:
self.dropout = nn.Dropout(p=dr_rate)
def gen_attention_mask(self, token_ids, valid_length):
attention_mask = torch.zeros_like(token_ids)
for i, v in enumerate(valid_length):
attention_mask[i][:v] = 1
return attention_mask.float()
def forward(self, token_ids, valid_length, segment_ids):
attention_mask = self.gen_attention_mask(token_ids, valid_length)
_, pooler = self.bert(input_ids = token_ids, token_type_ids = segment_ids.long(), attention_mask = attention_mask.float().to(token_ids.device))
if self.dr_rate:
out = self.dropout(pooler)
return self.classifier(out)
model = BERTClassifier(bertmodel, dr_rate=0.5).to(device)
# Prepare optimizer and schedule (linear warmup and decay)
no_decay = ['bias', 'LayerNorm.weight']
optimizer_grouped_parameters = [
{'params': [p for n, p in model.named_parameters() if not any(nd in n for nd in no_decay)], 'weight_decay': 0.01},
{'params': [p for n, p in model.named_parameters() if any(nd in n for nd in no_decay)], 'weight_decay': 0.0}
]
optimizer = AdamW(optimizer_grouped_parameters, lr=learning_rate)
loss_fn = nn.CrossEntropyLoss()
t_total = len(train_dataloader) * num_epochs
warmup_step = int(t_total * warmup_ratio)
scheduler = WarmupLinearSchedule(optimizer, warmup_steps=warmup_step, t_total=t_total)
def calc_accuracy(X,Y):
max_vals, max_indices = torch.max(X, 1)
train_acc = (max_indices == Y).sum().data.cpu().numpy()/max_indices.size()[0]
return train_acc
for e in range(num_epochs):
train_acc = 0.0
test_acc = 0.0
model.train()
for batch_id, (token_ids, valid_length, segment_ids, label) in enumerate(tqdm_notebook(train_dataloader)):
optimizer.zero_grad()
token_ids = token_ids.long().to(device)
segment_ids = segment_ids.long().to(device)
valid_length= valid_length
label = label.long().to(device)
out = model(token_ids, valid_length, segment_ids)
loss = loss_fn(out, label)
loss.backward()
torch.nn.utils.clip_grad_norm_(model.parameters(), max_grad_norm)
optimizer.step()
scheduler.step() # Update learning rate schedule
train_acc += calc_accuracy(out, label)
if batch_id % log_interval == 0:
print("epoch {} batch id {} loss {} train acc {}".format(e+1, batch_id+1, loss.data.cpu().numpy(), train_acc / (batch_id+1)))
print("epoch {} train acc {}".format(e+1, train_acc / (batch_id+1)))
model.eval()
for batch_id, (token_ids, valid_length, segment_ids, label) in enumerate(tqdm_notebook(test_dataloader)):
token_ids = token_ids.long().to(device)
segment_ids = segment_ids.long().to(device)
valid_length= valid_length
label = label.long().to(device)
out = model(token_ids, valid_length, segment_ids)
test_acc += calc_accuracy(out, label)
print("epoch {} test acc {}".format(e+1, test_acc / (batch_id+1)))
|
scripts/NSMC/naver_review_classifications_pytorch_kobert.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] colab_type="text" id="view-in-github"
# <a href="https://colab.research.google.com/github/NeuromatchAcademy/course-content-dl/blob/main/tutorials/W1D2_LinearDeepLearning/W1D2_Tutorial2.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# -
# # Tutorial 2: Learning Hyperparameters
# **Week 1, Day 2: Linear Deep Learning**
#
# **By Neuromatch Academy**
#
# __Content creators:__ <NAME>, <NAME>
#
# __Content reviewers:__ <NAME>, <NAME>
#
# __Content editors:__ <NAME>
#
# __Production editors:__ <NAME>, <NAME>
#
# **Our 2021 Sponsors, including Presenting Sponsor Facebook Reality Labs**
#
# <p align='center'><img src='https://github.com/NeuromatchAcademy/widgets/blob/master/sponsors.png?raw=True'/></p>
# ---
# # Tutorial Objectives
#
# * Training landscape
# * The effect of depth
# * Choosing a learning rate
# * Initialization matters
#
# + cellView="form"
# @title Tutorial slides
# @markdown These are the slides for the videos in the tutorial
from IPython.display import IFrame
IFrame(src=f"https://mfr.ca-1.osf.io/render?url=https://osf.io/sne2m/?direct%26mode=render%26action=download%26mode=render", width=854, height=480)
# -
# ---
# # Setup
#
# This a GPU-Free tutorial!
# +
# Imports
import time
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
# !pip install git+https://github.com/NeuromatchAcademy/evaltools --quiet
from evaltools.airtable import AirtableForm
# + cellView="form"
# @title Figure settings
from ipywidgets import interact, IntSlider, FloatSlider, fixed
from ipywidgets import HBox, interactive_output, ToggleButton, Layout
from mpl_toolkits.axes_grid1 import make_axes_locatable
# %config InlineBackend.figure_format = 'retina'
plt.style.use("https://raw.githubusercontent.com/NeuromatchAcademy/content-creation/main/nma.mplstyle")
# + cellView="form"
# @title Plotting functions
def plot_x_y_(x_t_, y_t_, x_ev_, y_ev_, loss_log_, weight_log_):
"""
"""
plt.figure(figsize=(12, 4))
plt.subplot(1, 3, 1)
plt.scatter(x_t_, y_t_, c='r', label='training data')
plt.plot(x_ev_, y_ev_, c='b', label='test results', linewidth=2)
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.subplot(1, 3, 2)
plt.plot(loss_log_, c='r')
plt.xlabel('epochs')
plt.ylabel('mean squared error')
plt.subplot(1, 3, 3)
plt.plot(weight_log_)
plt.xlabel('epochs')
plt.ylabel('weights')
plt.show()
def plot_vector_field(what, init_weights=None):
"""
"""
n_epochs=40
lr=0.15
x_pos = np.linspace(2.0, 0.5, 100, endpoint=True)
y_pos = 1. / x_pos
xx, yy = np.mgrid[-1.9:2.0:0.2, -1.9:2.0:0.2]
zz = np.empty_like(xx)
x, y = xx[:, 0], yy[0]
x_temp, y_temp = gen_samples(10, 1.0, 0.0)
cmap = matplotlib.cm.plasma
plt.figure(figsize=(8, 7))
ax = plt.gca()
if what == 'all' or what == 'vectors':
for i, a in enumerate(x):
for j, b in enumerate(y):
temp_model = ShallowNarrowLNN([a, b])
da, db = temp_model.dloss_dw(x_temp, y_temp)
zz[i, j] = temp_model.loss(temp_model.forward(x_temp), y_temp)
scale = min(40 * np.sqrt(da**2 + db**2), 50)
ax.quiver(a, b, - da, - db, scale=scale, color=cmap(np.sqrt(da**2 + db**2)))
if what == 'all' or what == 'trajectory':
if init_weights is None:
for init_weights in [[0.5, -0.5], [0.55, -0.45], [-1.8, 1.7]]:
temp_model = ShallowNarrowLNN(init_weights)
_, temp_records = temp_model.train(x_temp, y_temp, lr, n_epochs)
ax.scatter(temp_records[:, 0], temp_records[:, 1],
c=np.arange(len(temp_records)), cmap='Greys')
ax.scatter(temp_records[0, 0], temp_records[0, 1], c='blue', zorder=9)
ax.scatter(temp_records[-1, 0], temp_records[-1, 1], c='red', marker='X', s=100, zorder=9)
else:
temp_model = ShallowNarrowLNN(init_weights)
_, temp_records = temp_model.train(x_temp, y_temp, lr, n_epochs)
ax.scatter(temp_records[:, 0], temp_records[:, 1],
c=np.arange(len(temp_records)), cmap='Greys')
ax.scatter(temp_records[0, 0], temp_records[0, 1], c='blue', zorder=9)
ax.scatter(temp_records[-1, 0], temp_records[-1, 1], c='red', marker='X', s=100, zorder=9)
if what == 'all' or what == 'loss':
contplt = ax.contourf(x, y, np.log(zz+0.001), zorder=-1, cmap='coolwarm', levels=100)
divider = make_axes_locatable(ax)
cax = divider.append_axes("right", size="5%", pad=0.05)
cbar = plt.colorbar(contplt, cax=cax)
cbar.set_label('log (Loss)')
ax.set_xlabel("$w_1$")
ax.set_ylabel("$w_2$")
ax.set_xlim(-1.9, 1.9)
ax.set_ylim(-1.9, 1.9)
plt.show()
def plot_loss_landscape():
"""
"""
x_temp, y_temp = gen_samples(10, 1.0, 0.0)
xx, yy = np.mgrid[-1.9:2.0:0.2, -1.9:2.0:0.2]
zz = np.empty_like(xx)
x, y = xx[:, 0], yy[0]
for i, a in enumerate(x):
for j, b in enumerate(y):
temp_model = ShallowNarrowLNN([a, b])
zz[i, j] = temp_model.loss(temp_model.forward(x_temp), y_temp)
temp_model = ShallowNarrowLNN([-1.8, 1.7])
loss_rec_1, w_rec_1 = temp_model.train(x_temp, y_temp, 0.02, 240)
temp_model = ShallowNarrowLNN([1.5, -1.5])
loss_rec_2, w_rec_2 = temp_model.train(x_temp, y_temp, 0.02, 240)
plt.figure(figsize=(12, 8))
ax = plt.subplot(1, 1, 1, projection='3d')
ax.plot_surface(xx, yy, np.log(zz+0.5), cmap='coolwarm', alpha=0.5)
ax.scatter3D(w_rec_1[:, 0], w_rec_1[:, 1], np.log(loss_rec_1+0.5),
c='k', s=50, zorder=9)
ax.scatter3D(w_rec_2[:, 0], w_rec_2[:, 1], np.log(loss_rec_2+0.5),
c='k', s=50, zorder=9)
plt.axis("off")
ax.view_init(45, 260)
plt.show()
def depth_widget(depth):
if depth == 0:
depth_lr_init_interplay(depth, 0.02, 0.9)
else:
depth_lr_init_interplay(depth, 0.01, 0.9)
def lr_widget(lr):
depth_lr_init_interplay(50, lr, 0.9)
def depth_lr_interplay(depth, lr):
depth_lr_init_interplay(depth, lr, 0.9)
def depth_lr_init_interplay(depth, lr, init_weights):
n_epochs = 600
x_train, y_train = gen_samples(100, 2.0, 0.1)
model = DeepNarrowLNN(np.full((1, depth+1), init_weights))
plt.figure(figsize=(10, 5))
plt.plot(model.train(x_train, y_train, lr, n_epochs),
linewidth=3.0, c='m')
plt.title("Training a {}-layer LNN with"
" $\eta=${} initialized with $w_i=${}".format(depth, lr, init_weights), pad=15)
plt.yscale('log')
plt.xlabel('epochs')
plt.ylabel('Log mean squared error')
plt.ylim(0.001, 1.0)
plt.show()
def plot_init_effect():
depth = 15
n_epochs = 250
lr = 0.02
x_train, y_train = gen_samples(100, 2.0, 0.1)
plt.figure(figsize=(12, 6))
for init_w in np.arange(0.7, 1.09, 0.05):
model = DeepNarrowLNN(np.full((1, depth), init_w))
plt.plot(model.train(x_train, y_train, lr, n_epochs),
linewidth=3.0, label="initial weights {:.2f}".format(init_w))
plt.title("Training a {}-layer narrow LNN with $\eta=${}".format(depth, lr), pad=15)
plt.yscale('log')
plt.xlabel('epochs')
plt.ylabel('Log mean squared error')
plt.legend(loc='lower left', ncol=4)
plt.ylim(0.001, 1.0)
plt.show()
class InterPlay:
def __init__(self):
self.lr = [None]
self.depth = [None]
self.success = [None]
self.min_depth, self.max_depth = 5, 65
self.depth_list = np.arange(10, 61, 10)
self.i_depth = 0
self.min_lr, self.max_lr = 0.001, 0.105
self.n_epochs = 600
self.x_train, self.y_train = gen_samples(100, 2.0, 0.1)
self.converged = False
self.button = None
self.slider = None
def train(self, lr, update=False, init_weights=0.9):
if update and self.converged and self.i_depth < len(self.depth_list):
depth = self.depth_list[self.i_depth]
self.plot(depth, lr)
self.i_depth += 1
self.lr.append(None)
self.depth.append(None)
self.success.append(None)
self.converged = False
self.slider.value = 0.005
if self.i_depth < len(self.depth_list):
self.button.value = False
self.button.description = 'Explore!'
self.button.disabled = True
self.button.button_style = 'danger'
else:
self.button.value = False
self.button.button_style = ''
self.button.disabled = True
self.button.description = 'Done!'
time.sleep(1.0)
elif self.i_depth < len(self.depth_list):
depth = self.depth_list[self.i_depth]
# assert self.min_depth <= depth <= self.max_depth
assert self.min_lr <= lr <= self.max_lr
self.converged = False
model = DeepNarrowLNN(np.full((1, depth), init_weights))
self.losses = np.array(model.train(self.x_train, self.y_train, lr, self.n_epochs))
if np.any(self.losses < 1e-2):
success = np.argwhere(self.losses < 1e-2)[0][0]
if np.all((self.losses[success:] < 1e-2)):
self.converged = True
self.success[-1] = success
self.lr[-1] = lr
self.depth[-1] = depth
self.button.disabled = False
self.button.button_style = 'success'
self.button.description = 'Register!'
else:
self.button.disabled = True
self.button.button_style = 'danger'
self.button.description = 'Explore!'
else:
self.button.disabled = True
self.button.button_style = 'danger'
self.button.description = 'Explore!'
self.plot(depth, lr)
def plot(self, depth, lr):
fig = plt.figure(constrained_layout=False, figsize=(10, 8))
gs = fig.add_gridspec(2, 2)
ax1 = fig.add_subplot(gs[0, :])
ax2 = fig.add_subplot(gs[1, 0])
ax3 = fig.add_subplot(gs[1, 1])
ax1.plot(self.losses, linewidth=3.0, c='m')
ax1.set_title("Training a {}-layer LNN with"
" $\eta=${}".format(depth, lr), pad=15, fontsize=16)
ax1.set_yscale('log')
ax1.set_xlabel('epochs')
ax1.set_ylabel('Log mean squared error')
ax1.set_ylim(0.001, 1.0)
ax2.set_xlim(self.min_depth, self.max_depth)
ax2.set_ylim(-10, self.n_epochs)
ax2.set_xlabel('Depth')
ax2.set_ylabel('Learning time (Epochs)')
ax2.set_title("Learning time vs depth", fontsize=14)
ax2.scatter(np.array(self.depth), np.array(self.success), c='r')
# ax3.set_yscale('log')
ax3.set_xlim(self.min_depth, self.max_depth)
ax3.set_ylim(self.min_lr, self.max_lr)
ax3.set_xlabel('Depth')
ax3.set_ylabel('Optimial learning rate')
ax3.set_title("Empirically optimal $\eta$ vs depth", fontsize=14)
ax3.scatter(np.array(self.depth), np.array(self.lr), c='r')
plt.show()
# + cellView="form"
# @title Helper functions
atform = AirtableForm('appn7VdPRseSoMXEG','W1D2_T2','https://portal.neuromatchacademy.org/api/redirect/to/9c55f6cb-cdf9-4429-ac1c-ec44fe64c303')
def gen_samples(n, a, sigma):
"""
Generates `n` samples with `y = z * x + noise(sgma)` linear relation.
Args:
n : int
a : float
sigma : float
Retutns:
x : np.array
y : np.array
"""
assert n > 0
assert sigma >= 0
if sigma > 0:
x = np.random.rand(n)
noise = np.random.normal(scale=sigma, size=(n))
y = a * x + noise
else:
x = np.linspace(0.0, 1.0, n, endpoint=True)
y = a * x
return x, y
class ShallowNarrowLNN:
"""
Shallow and narrow (one neuron per layer) linear neural network
"""
def __init__(self, init_ws):
"""
init_ws: initial weights as a list
"""
assert isinstance(init_ws, list)
assert len(init_ws) == 2
self.w1 = init_ws[0]
self.w2 = init_ws[1]
def forward(self, x):
"""
The forward pass through netwrok y = x * w1 * w2
"""
y = x * self.w1 * self.w2
return y
def loss(self, y_p, y_t):
"""
Mean squared error (L2) with 1/2 for convenience
"""
assert y_p.shape == y_t.shape
mse = ((y_t - y_p)**2).mean()
return mse
def dloss_dw(self, x, y_t):
"""
partial derivative of loss with respect to weights
Args:
x : np.array
y_t : np.array
"""
assert x.shape == y_t.shape
Error = y_t - self.w1 * self.w2 * x
dloss_dw1 = - (2 * self.w2 * x * Error).mean()
dloss_dw2 = - (2 * self.w1 * x * Error).mean()
return dloss_dw1, dloss_dw2
def train(self, x, y_t, eta, n_ep):
"""
Gradient descent algorithm
Args:
x : np.array
y_t : np.array
eta: float
n_ep : int
"""
assert x.shape == y_t.shape
loss_records = np.empty(n_ep) # pre allocation of loss records
weight_records = np.empty((n_ep, 2)) # pre allocation of weight records
for i in range(n_ep):
y_p = self.forward(x)
loss_records[i] = self.loss(y_p, y_t)
dloss_dw1, dloss_dw2 = self.dloss_dw(x, y_t)
self.w1 -= eta * dloss_dw1
self.w2 -= eta * dloss_dw2
weight_records[i] = [self.w1, self.w2]
return loss_records, weight_records
class DeepNarrowLNN:
"""
Deep but thin (one neuron per layer) linear neural network
"""
def __init__(self, init_ws):
"""
init_ws: initial weights as a numpy array
"""
self.n = init_ws.size
self.W = init_ws.reshape(1, -1)
def forward(self, x):
"""
x : np.array
input features
"""
y = np.prod(self.W) * x
return y
def loss(self, y_t, y_p):
"""
mean squared error (L2 loss)
Args:
y_t : np.array
y_p : np.array
"""
assert y_p.shape == y_t.shape
mse = ((y_t - y_p)**2 / 2).mean()
return mse
def dloss_dw(self, x, y_t, y_p):
"""
analytical gradient of weights
Args:
x : np.array
y_t : np.array
y_p : np.array
"""
E = y_t - y_p # = y_t - x * np.prod(self.W)
Ex = np.multiply(x, E).mean()
Wp = np.prod(self.W) / (self.W + 1e-9)
dW = - Ex * Wp
return dW
def train(self, x, y_t, eta, n_epochs):
"""
training using gradient descent
Args:
x : np.array
y_t : np.array
eta: float
n_epochs : int
"""
loss_records = np.empty(n_epochs)
loss_records[:] = np.nan
for i in range(n_epochs):
y_p = self.forward(x)
loss_records[i] = self.loss(y_t, y_p).mean()
dloss_dw = self.dloss_dw(x, y_t, y_p)
if np.isnan(dloss_dw).any() or np.isinf(dloss_dw).any():
return loss_records
self.W -= eta * dloss_dw
return loss_records
# + cellView="form"
#@title Set random seed
#@markdown Executing `set_seed(seed=seed)` you are setting the seed
# for DL its critical to set the random seed so that students can have a
# baseline to compare their results to expected results.
# Read more here: https://pytorch.org/docs/stable/notes/randomness.html
# Call `set_seed` function in the exercises to ensure reproducibility.
import random
import torch
def set_seed(seed=None, seed_torch=True):
if seed is None:
seed = np.random.choice(2 ** 32)
random.seed(seed)
np.random.seed(seed)
if seed_torch:
torch.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
torch.cuda.manual_seed(seed)
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.deterministic = True
print(f'Random seed {seed} has been set.')
# In case that `DataLoader` is used
def seed_worker(worker_id):
worker_seed = torch.initial_seed() % 2**32
np.random.seed(worker_seed)
random.seed(worker_seed)
# + cellView="form"
#@title Set device (GPU or CPU). Execute `set_device()`
# especially if torch modules used.
# inform the user if the notebook uses GPU or CPU.
def set_device():
device = "cuda" if torch.cuda.is_available() else "cpu"
if device != "cuda":
print("GPU is not enabled in this notebook. \n"
"If you want to enable it, in the menu under `Runtime` -> \n"
"`Hardware accelerator.` and select `GPU` from the dropdown menu")
else:
print("GPU is enabled in this notebook. \n"
"If you want to disable it, in the menu under `Runtime` -> \n"
"`Hardware accelerator.` and select `None` from the dropdown menu")
return device
# -
SEED = 2021
set_seed(seed=SEED)
DEVICE = set_device()
# ---
# # Section 1: A Shallow Narrow Linear Neural Network
# ## Section 1.1: A neural network from scratch
# + cellView="form"
# @title Video 1: Shallow Narrow Linear Net
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1F44y117ot", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"6e5JIYsqVvU", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
#add event to airtable
atform.add_event('video 1: Shallow Narrow Linear Net')
display(out)
# -
# To better understand the behavior of neural network training with gradient descent, we start with the incredibly simple case of a shallow narrow linear neural net, since state-of-the-art models are impossible to dissect and comprehend with our current mathematical tools.
#
# The model we use has one hidden layer, with only one neuron, and two weights. We consider the squared error (or L2 loss) as the cost function. As you may have already guessed, we can visualize the model as a neural network:
#
# <center><img src="https://raw.githubusercontent.com/ssnio/statics/main/neuromatch/shallow_narrow_nn.png" width="400"/></center>
#
# <br/>
#
# or by its computation graph:
#
# <center><img src="https://raw.githubusercontent.com/ssnio/statics/main/neuromatch/shallow_narrow.png" alt="Shallow Narrow Graph" width="400"/></center>
#
# or on a rare occasion, even as a reasonably compact mapping:
#
# $$ loss = (y - w_1 \cdot w_2 \cdot x)^2 $$
#
# <br/>
#
# ### Analytical Exercise 1.1: Loss Gradients
#
# #### Part i: Calculate gradients (Optional)
# Once again, we ask you to calculate the network gradients analytically, since you will need them for the next exercise. We understand how annoying this is.
#
# $\dfrac{\partial{loss}}{\partial{w_1}} = ?$
#
# $\dfrac{\partial{loss}}{\partial{w_2}} = ?$
#
# <br/>
#
# ---
# #### Solution
#
# $\dfrac{\partial{loss}}{\partial{w_1}} = -2 \cdot w_2 \cdot x \cdot (y - w_1 \cdot w_2 \cdot x)$
#
# $\dfrac{\partial{loss}}{\partial{w_2}} = -2 \cdot w_1 \cdot x \cdot (y - w_1 \cdot w_2 \cdot x)$
#
# ---
#
# ### Coding Exercise 1.1: Implement simple narrow LNN
#
# Next, we ask you to implement the `forward` pass for our model from scratch without using PyTorch.
#
# Also, although our model gets a single input feature and outputs a single prediction, we could calculate the loss and perform training for multiple samples at once. This is the common practice for neural networks, since computers are incredibly fast doing matrix (or tensor) operations on batches of data, rather than processing samples one at a time through `for` loops. Therefore, for the `loss` function, please implement the **mean** squared error (MSE), and adjust your analytical gradients accordingly when implementing the `dloss_dw` function.
#
# Finally, complete the `train` function for the gradient descent algorithm:
#
# \begin{equation}
# \mathbf{w}^{(t+1)} = \mathbf{w}^{(t)} - \eta \nabla loss (\mathbf{w}^{(t)})
# \end{equation}
# +
class ShallowNarrowExercise:
"""Shallow and narrow (one neuron per layer) linear neural network
"""
def __init__(self, init_weights):
"""
Args:
init_weights (list): initial weights
"""
assert isinstance(init_weights, (list, np.ndarray, tuple))
assert len(init_weights) == 2
self.w1 = init_weights[0]
self.w2 = init_weights[1]
def forward(self, x):
"""The forward pass through netwrok y = x * w1 * w2
Args:
x (np.ndarray): features (inputs) to neural net
returns:
(np.ndarray): neural network output (prediction)
"""
#################################################
## Implement the forward pass to calculate prediction
## Note that prediction is not the loss
# Complete the function and remove or comment the line below
raise NotImplementedError("Forward Pass `forward`")
#################################################
y = ...
return y
def dloss_dw(self, x, y_true):
"""Gradient of loss with respect to weights
Args:
x (np.ndarray): features (inputs) to neural net
y_true (np.ndarray): true labels
returns:
(float): mean gradient of loss with respect to w1
(float): mean gradient of loss with respect to w2
"""
assert x.shape == y_true.shape
#################################################
## Implement the gradient computation function
# Complete the function and remove or comment the line below
raise NotImplementedError("Gradient of Loss `dloss_dw`")
#################################################
dloss_dw1 = ...
dloss_dw2 = ...
return dloss_dw1, dloss_dw2
def train(self, x, y_true, lr, n_ep):
"""Training with Gradient descent algorithm
Args:
x (np.ndarray): features (inputs) to neural net
y_true (np.ndarray): true labels
lr (float): learning rate
n_ep (int): number of epochs (training iterations)
returns:
(list): training loss records
(list): training weight records (evolution of weights)
"""
assert x.shape == y_true.shape
loss_records = np.empty(n_ep) # pre allocation of loss records
weight_records = np.empty((n_ep, 2)) # pre allocation of weight records
for i in range(n_ep):
y_prediction = self.forward(x)
loss_records[i] = loss(y_prediction, y_true)
dloss_dw1, dloss_dw2 = self.dloss_dw(x, y_true)
#################################################
## Implement the gradient descent step
# Complete the function and remove or comment the line below
raise NotImplementedError("Training loop `train`")
#################################################
self.w1 -= ...
self.w2 -= ...
weight_records[i] = [self.w1, self.w2]
return loss_records, weight_records
def loss(y_prediction, y_true):
"""Mean squared error
Args:
y_prediction (np.ndarray): model output (prediction)
y_true (np.ndarray): true label
returns:
(np.ndarray): mean squared error loss
"""
assert y_prediction.shape == y_true.shape
#################################################
## Implement the MEAN squared error
# Complete the function and remove or comment the line below
raise NotImplementedError("Loss function `loss`")
#################################################
mse = ...
return mse
#add event to airtable
atform.add_event('Coding Exercise 1.1: Implement simple narrow LNN')
set_seed(seed=SEED)
n_epochs = 211
learning_rate = 0.02
initial_weights = [1.4, -1.6]
x_train, y_train = gen_samples(n=73, a=2.0, sigma=0.2)
x_eval = np.linspace(0.0, 1.0, 37, endpoint=True)
## Uncomment to run
# sn_model = ShallowNarrowExercise(initial_weights)
# loss_log, weight_log = sn_model.train(x_train, y_train, learning_rate, n_epochs)
# y_eval = sn_model.forward(x_eval)
# plot_x_y_(x_train, y_train, x_eval, y_eval, loss_log, weight_log)
# +
# to_remove solution
class ShallowNarrowExercise:
"""Shallow and narrow (one neuron per layer) linear neural network
"""
def __init__(self, init_weights):
"""
Args:
init_weights (list): initial weights
"""
assert isinstance(init_weights, (list, np.ndarray, tuple))
assert len(init_weights) == 2
self.w1 = init_weights[0]
self.w2 = init_weights[1]
def forward(self, x):
"""The forward pass through netwrok y = x * w1 * w2
Args:
x (np.ndarray): features (inputs) to neural net
returns:
(np.ndarray): neural network output (prediction)
"""
y = x * self.w1 * self.w2
return y
def dloss_dw(self, x, y_true):
"""Gradient of loss with respect to weights
Args:
x (np.ndarray): features (inputs) to neural net
y_true (np.ndarray): true labels
returns:
(float): mean gradient of loss with respect to w1
(float): mean gradient of loss with respect to w2
"""
assert x.shape == y_true.shape
dloss_dw1 = - (2 * self.w2 * x * (y_true - self.w1 * self.w2 * x)).mean()
dloss_dw2 = - (2 * self.w1 * x * (y_true - self.w1 * self.w2 * x)).mean()
return dloss_dw1, dloss_dw2
def train(self, x, y_true, lr, n_ep):
"""Training with Gradient descent algorithm
Args:
x (np.ndarray): features (inputs) to neural net
y_true (np.ndarray): true labels
lr (float): learning rate
n_ep (int): number of epochs (training iterations)
returns:
(list): training loss records
(list): training weight records (evolution of weights)
"""
assert x.shape == y_true.shape
loss_records = np.empty(n_ep) # pre allocation of loss records
weight_records = np.empty((n_ep, 2)) # pre allocation of weight records
for i in range(n_ep):
y_prediction = self.forward(x)
loss_records[i] = loss(y_prediction, y_true)
dloss_dw1, dloss_dw2 = self.dloss_dw(x, y_true)
self.w1 -= lr * dloss_dw1
self.w2 -= lr * dloss_dw2
weight_records[i] = [self.w1, self.w2]
return loss_records, weight_records
def loss(y_prediction, y_true):
"""Mean squared error
Args:
y_prediction (np.ndarray): model output (prediction)
y_true (np.ndarray): true label
returns:
(np.ndarray): mean squared error loss
"""
assert y_prediction.shape == y_true.shape
mse = ((y_true - y_prediction)**2).mean()
return mse
#add event to airtable
atform.add_event('Coding Exercise 1.1: Implement simple narrow LNN')
set_seed(seed=SEED)
n_epochs = 211
learning_rate = 0.02
initial_weights = [1.4, -1.6]
x_train, y_train = gen_samples(n=73, a=2.0, sigma=0.2)
x_eval = np.linspace(0.0, 1.0, 37, endpoint=True)
## Uncomment to run
sn_model = ShallowNarrowExercise(initial_weights)
loss_log, weight_log = sn_model.train(x_train, y_train, learning_rate, n_epochs)
y_eval = sn_model.forward(x_eval)
with plt.xkcd():
plot_x_y_(x_train, y_train, x_eval, y_eval, loss_log, weight_log)
# -
# ## Section 1.2: Learning landscapes
# + cellView="form"
# @title Video 2: Training Landscape
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1Nv411J71X", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"k28bnNAcOEg", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
#add event to airtable
atform.add_event('Video 2: Training Landscape')
# -
# As you may have already asked yourself, we can analytically find $w_1$ and $w_2$ without using gradient descent:
#
# \begin{equation}
# w_1 \cdot w_2 = \dfrac{y}{x}
# \end{equation}
#
# In fact, we can plot the gradients, the loss function and all the possible solutions in one figure. In this example, we use the $y = 1x$ mapping:
#
# **Blue ribbon**: shows all possible solutions: $~ w_1 w_2 = \dfrac{y}{x} = \dfrac{x}{x} = 1 \Rightarrow w_1 = \dfrac{1}{w_2}$
#
# **Contour background**: Shows the loss values, red being higher loss
#
# **Vector field (arrows)**: shows the gradient vector field. The larger yellow arrows show larger gradients, which correspond to bigger steps by gradient descent.
#
# **Scatter circles**: the trajectory (evolution) of weights during training for three different initializations, with blue dots marking the start of training and red crosses ( **x** ) marking the end of training. You can also try your own initializations (keep the initial values between `-2.0` and `2.0`) as shown here:
# ```python
# plot_vector_field('all', [1.0, -1.0])
# ```
#
# Finally, if the plot is too crowded, feel free to pass one of the following strings as argument:
#
# ```python
# plot_vector_field('vectors') # for vector field
# plot_vector_field('trajectory') # for training trajectory
# plot_vector_field('loss') # for loss contour
# ```
#
# **Think!**
#
# Explore the next two plots. Try different initial values. Can you find the saddle point? Why does training slow down near the minima?
plot_vector_field('all')
# Here, we also visualize the loss landscape in a 3-D plot, with two training trajectories for different initial conditions.
# Note: the trajectories from the 3D plot and the previous plot are independent and different.
plot_loss_landscape()
# + cellView="form"
# @title Student Response
from ipywidgets import widgets
text=widgets.Textarea(
value='Type your here and Push submit',
placeholder='Type something',
description='',
disabled=False
)
button = widgets.Button(description="Submit!")
display(text,button)
def on_button_clicked(b):
atform.add_answer('q1', text.value)
print("Submission successful!")
button.on_click(on_button_clicked)
# + cellView="form"
# @title Video 3: Training Landscape - Discussion
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1py4y1j7cv", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"0EcUGgxOdkI", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
#add event to airtable
atform.add_event('Video 3: Training Landscape - Discussiond')
display(out)
# -
# ---
# # Section 2: Depth, Learning rate, and initialization
#
# Successful deep learning models are often developed by a team of very clever people, spending many many hours "tuning" learning hyperparameters, and finding effective initializations. In this section, we look at three basic (but often not simple) hyperparameters: depth, learning rate, and initialization.
# ## Section 2.1: The effect of depth
# + cellView="form"
# @title Video 4: Effect of Depth
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1z341167di", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"Ii_As9cRR5Q", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
#add event to airtable
atform.add_event('Video 4: Effect of Depth')
display(out)
# -
# In 1989, <NAME> published the paper *Approximation by superpositions of a sigmoidal function*, mathematically proving that:
#
# > arbitrary decision regions can be arbitrarily well approximated by continuous feedforward neural networks with only a single internal, hidden layer and any continuous sigmoidal nonlinearity.
#
# So if a neural net with a single hidden layer can approximate any function, why might depth be useful? What makes a network or learning system "deep"? The reality is that shallow neural nets are often incapable of learning complex functions due to data limitations. On the other hand, depth seems like magic. Depth can change the functions a network can represent, the way a network learns, and how a network generalizes to unseen data.
#
# So let's look at the challenges that depth poses in training a neural network. Imagine a single input, single output linear network with 50 hidden layers and only one neuron per layer (i.e. a narrow deep neural network). The output of the network is easy to calculate:
#
# $$ prediction = x \cdot w_1 \cdot w_2 \cdot \cdot \cdot w_{50} $$
#
# If the initial value for all the weights is $w_i = 2$, the prediction for $x=1$ would be **exploding**: $y_p = 2^{50} \approx 1.1256 \times 10^{15}$. On the other hand, for weights initialized to $w_i = 0.5$, the output is **vanishing**: $y_p = 0.5^{50} \approx 8.88 \times 10^{-16}$. Similarly, if we recall the chain rule, as the graph gets deeper, the number of elements in the chain multiplication increases, which could lead to exploding or vanishing gradients. To avoid such numerical vulnerablities that could impair our training algorithm, we need to understand the effect of depth.
#
# ### Interactive Demo 2.1: Depth widget
#
# Use the widget to explore the impact of depth on the training curve (loss evolution) of a deep but narrow neural network.
#
# **Think!**
#
# Which networks trained the fastest? Did all networks eventually "work" (converge)? What is the shape of their learning trajectory?
# + cellView="form"
# @markdown Make sure you execute this cell to enable the widget!
_ = interact(depth_widget,
depth = IntSlider(min=0, max=51,
step=5, value=0,
continuous_update=False))
# + cellView="form"
# @title Video 5: Effect of Depth - Discussion
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1Qq4y1H7uk", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"EqSDkwmSruk", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
#add event to airtable
atform.add_event('Video 5: Effect of Depth - Discussion')
display(out)
# -
# ## Section 2.2: Choosing a learning rate
# The learning rate is a common hyperparameter for most optimization algorithms. How should we set it? Sometimes the only option is to try all the possibilities, but sometimes knowing some key trade-offs will help guide our search for good hyperparameters.
# + cellView="form"
# @title Video 6: Learning Rate
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV11f4y157MT", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"w_GrCVM-_Qo", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
#add event to airtable
atform.add_event('Video 6: Learning Rate')
display(out)
# -
# ### Interactive Demo 2.2: Learning rate widget
#
# Here, we fix the network depth to 50 layers. Use the widget to explore the impact of learning rate $\eta$ on the training curve (loss evolution) of a deep but narrow neural network.
#
# **Think!**
#
# Can we say that larger learning rates always lead to faster learning? Why not?
# + cellView="form"
# @markdown Make sure you execute this cell to enable the widget!
_ = interact(lr_widget,
lr = FloatSlider(min=0.005, max=0.045, step=0.005, value=0.005,
continuous_update=False, readout_format='.3f',
description='eta'))
# + cellView="form"
# @title Video 7: Learning Rate - Discussion
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1Aq4y1p7bh", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"cmS0yqImz2E", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
#add event to airtable
atform.add_event('Video 7: Learning Rate')
display(out)
# -
# ## Section 2.3: Depth vs Learning Rate
# + cellView="form"
# @title Video 8: Depth and Learning Rate Interplay
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1V44y1177e", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"J30phrux_3k", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
#add event to airtable
atform.add_event('Video 8: Depth and Learning Rate Interplay')
display(out)
# -
# ### Interactive Demo 2.3: Depth and Learning-Rate
#
# **Important instruction**
# The exercise starts with 10 hidden layers. Your task is to find the learning rate that delivers fast but robust convergence (learning). When you are confident about the learning rate, you can **Register** the optimal learning rate for the given depth. Once you press register, a deeper model is instantiated, so you can find the next optimal learning rate. The Register button turns green only when the training converges, but does not imply the fastest convergence. Finally, be patient :) the widgets are slow.
#
#
# **Think!**
#
# Can you explain the relationship between the depth and optimal learning rate?
# + cellView="form"
# @markdown Make sure you execute this cell to enable the widget!
intpl_obj = InterPlay()
intpl_obj.slider = FloatSlider(min=0.005, max=0.105, step=0.005, value=0.005,
layout=Layout(width='500px'),
continuous_update=False,
readout_format='.3f',
description='eta')
intpl_obj.button = ToggleButton(value=intpl_obj.converged, description='Register')
widgets_ui = HBox([intpl_obj.slider, intpl_obj.button])
widgets_out = interactive_output(intpl_obj.train,
{'lr': intpl_obj.slider,
'update': intpl_obj.button,
'init_weights': fixed(0.9)})
display(widgets_ui, widgets_out)
# + cellView="form"
# @title Video 9: Depth and Learning Rate - Discussion
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV15q4y1p7Uq", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"7Fl8vH7cgco", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
display(out)
# -
# ## Section 2.4: Why initialization is important
# + cellView="form"
# @title Video 10: Initialization Matters
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1UL411J7vu", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"KmqCz95AMzY", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
#add event to airtable
atform.add_event('Video 10: Initialization Matters')
display(out)
# -
# We’ve seen, even in the simplest of cases, that depth can slow learning. Why? From the chain rule, gradients are multiplied by the current weight at each layer, so the product can vanish or explode. Therefore, weight initialization is a fundamentally important hyperparameter.
#
# Although in practice initial values for learnable parameters are often sampled from different $\mathcal{Uniform}$ or $\mathcal{Normal}$ probability distribution, here we use a single value for all the parameters.
#
# The figure below shows the effect of initialization on the speed of learning for the deep but narrow LNN. We have excluded initializations that lead to numerical errors such as `nan` or `inf`, which are the consequence of smaller or larger initializations.
# + cellView="form"
# @markdown Make sure you execute this cell to see the figure!
plot_init_effect()
# + cellView="form"
# @title Video 11: Initialization Matters Explained
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1hM4y1T7gJ", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"vKktGdiQDsE", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
#add event to airtable
atform.add_event('Video 11: Initialization Matters Explained')
display(out)
# -
# ---
# # Summary
#
# In the second tutorial, we have learned what is the training landscape, and also we have see in depth the effect of the depth of the network and the learning rate, and their interplay. Finally, we have seen that initialization matters and why we need smart ways of initialization.
# + cellView="form"
# @title Video 12: Tutorial 2 Wrap-up
from ipywidgets import widgets
out2 = widgets.Output()
with out2:
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id=f"BV1P44y117Pd", width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
display(video)
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"r3K8gtak3wA", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
out = widgets.Tab([out1, out2])
out.set_title(0, 'Youtube')
out.set_title(1, 'Bilibili')
#add event to airtable
atform.add_event('Video 11: Initialization Matters Explained')
display(out)
# + cellView="form"
# @title Airtable Submission Link
from IPython import display as IPydisplay
IPydisplay.HTML(
f"""
<div>
<a href= "{atform.url()}" target="_blank">
<img src="https://github.com/NeuromatchAcademy/course-content-dl/blob/main/tutorials/static/AirtableSubmissionButton.png?raw=1"
alt="button link to Airtable" style="width:410px"></a>
</div>""" )
# -
# ---
# # Appendix
# ## Hyperparameter interaction
#
# Finally, let's put everything we learned together and find best initial weights and learning rate for a given depth. By now you should have learned the interactions and know how to find the optimal values quickly. If you get `numerical overflow` warnings, don't be discouraged! They are often caused by "exploding" or "vanishing" gradients.
#
# **Think!**
#
# Did you experience any surprising behaviour
# or difficulty finding the optimal parameters?
# + cellView="form"
# @markdown Make sure you execute this cell to enable the widget!
_ = interact(depth_lr_init_interplay,
depth = IntSlider(min=10, max=51, step=5, value=25,
continuous_update=False),
lr = FloatSlider(min=0.001, max=0.1,
step=0.005, value=0.005,
continuous_update=False,
readout_format='.3f',
description='eta'),
init_weights = FloatSlider(min=0.1, max=3.0,
step=0.1, value=0.9,
continuous_update=False,
readout_format='.3f',
description='initial weights'))
|
tutorials/W1D2_LinearDeepLearning/W1D2_Tutorial2.ipynb
|
/ ---
/ jupyter:
/ jupytext:
/ text_representation:
/ extension: .q
/ format_name: light
/ format_version: '1.5'
/ jupytext_version: 1.14.4
/ ---
/ + cell_id="00000-fda1f226-c8bc-4c39-a67f-fded5c44dd0b" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 0} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=14802 execution_start=1634620396378 source_hash="b1539fef" tags=[]
# import standard scientific libraries
import os
import math
import numpy as np
import pandas as pd
# import ML models from scikit-learn
from sklearn.linear_model import LinearRegression
from sklearn.kernel_ridge import KernelRidge
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn import svm
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import mean_absolute_error
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from tensorflow.keras.layers.experimental import preprocessing
import matplotlib.pyplot as plt
/ + cell_id="00001-d4de8640-6558-4b7f-8c2e-45c19558be6a" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 6} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=22 execution_start=1634620411195 source_hash="1a411e4d" tags=[]
def plot_loss(history):
plt.plot(history.history['loss'], label='loss')
plt.legend()
plt.grid(True)
/ + cell_id="00002-309f1656-9bc1-456a-80ec-012722d4b488" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 12} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=13 execution_start=1634620411238 source_hash="9ec6a611" tags=[]
RANDOM_SEED = 4
np.random.seed(RANDOM_SEED)
pd.set_option('max_columns', None)
pd.set_option("display.precision", 8)
dataset = "../dataset/"
/ + cell_id="00003-98e304ca-4ad8-4b79-8e19-1ef66ae6453a" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 18} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=682 execution_start=1634620411272 source_hash="92c98152" tags=[]
train = pd.read_csv("train.csv")#[:66000]
train.shape
train
/ + cell_id="00004-b995193c-6551-4f57-9ab9-c1e1cda2faaa" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 24} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=45 execution_start=1634620412001 source_hash="fea28bdd" tags=[]
train.info()
/ + cell_id="00005-974490de-8736-4898-ad10-f21bd25da5f5" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 30} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=58 execution_start=1634620412046 source_hash="a32e1fc8" tags=[]
train = train.replace([np.inf, -np.inf], np.nan)
#train = train[train['heat_adsorption_CO2_P0.15bar_T298K [kcal/mol]'].notna()]
train = train[train['functional_groups'].notna()]
/ + cell_id="00006-dbb601a4-2f9e-4399-add3-630f28c067fd" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 36} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=2 execution_start=1634620412176 source_hash="fea28bdd" tags=[]
train.info()
/ + cell_id="00007-b1c136e2-8c99-4439-8954-aaf2c23703d7" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 42} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=1 execution_start=1634620412221 source_hash="c2383418" tags=[]
# train = pd.get_dummies(train, columns=["functional_groups"])
# train = pd.get_dummies(train, columns=["topology"])
# train
col = ["functional_groups", "topology"]
for i in col:
train[i] = train[i].astype("category").cat.codes
/ + cell_id="00008-30121c42-9e49-472f-81cb-ae4ac738fdc2" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 48} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=68 execution_start=1634620412222 source_hash="c85f75f2" tags=[]
train = train.drop(['MOFname'],axis=1)
train= train[train['void_fraction'] > 0]
train= train[train['void_volume [cm^3/g]'] > 0]
#train train[train['CO2/N2_selectivity'] > 0]
train = train[train['heat_adsorption_CO2_P0.15bar_T298K [kcal/mol]'].notna()]
train= train[train['surface_area [m^2/g]'] > 0]
/ + cell_id="00009-d78d3581-cc7a-4856-94d7-aacdf712966c" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 54} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=223 execution_start=1634620412307 source_hash="7f737f25" tags=[]
train
/ + cell_id="00010-cfb9174d-ad5c-4b2a-8521-d1b85d1114f6" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 60} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=10115228 execution_start=1634620412545 source_hash="fea28bdd" tags=[]
train.info()
/ + cell_id="00011-219603a7-9df8-4060-ad06-9c795b27fddd" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 66} deepnote_cell_type="code" deepnote_output_heights=[268] deepnote_to_be_reexecuted=false execution_millis=10115248 execution_start=1634620412578 source_hash="548b7dd5" tags=[]
# find rows having NaN
train.isnull().any(axis=0)
#train.fillna(method='pad', inplace=True)
#train.groupby('functional_groups')['functional_groups'].count()
/ + cell_id="00012-d6beaaf0-cd39-43df-b3bd-2a9bddca6169" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 72} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=6 execution_start=1634620412638 source_hash="3f3220ba" tags=[]
count = 0
for i in train['functional_groups']:
if i == 240:
count = count+1
print(count)
/ + cell_id="00012-b5ee45f7-d6aa-4c59-9736-ce3c63946841" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 78} deepnote_cell_type="code" deepnote_output_heights=[268] deepnote_to_be_reexecuted=false execution_millis=46 execution_start=1634620412639 source_hash="e7d885b7" tags=[]
# find row having inf
np.isinf(train).any(axis=0)
/ + cell_id="00015-c2e82662-93a6-4960-aa1d-05873bf79718" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 84} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=179 execution_start=1634620412685 source_hash="7f737f25" tags=[]
train
/ + cell_id="00014-c980df3c-6f98-4b7a-9304-d770a4a2a2b0" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 90} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=6 execution_start=1634620412871 source_hash="73ee89bf" tags=[]
x = train.drop(['CO2_working_capacity [mL/g]'],axis=1)
y = train['CO2_working_capacity [mL/g]']
/ + cell_id="00015-f72c4b2a-acab-4caf-aa53-48cf836bdfcf" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 96} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=0 execution_start=1634620412929 source_hash="8ee3cb9e" tags=[]
x_train, x_test, y_train, y_true = train_test_split(x, y, test_size=0.2,random_state=RANDOM_SEED)
/ + cell_id="00016-43560f5c-fbdd-4689-a2f7-35af8973cb80" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 102} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=253 execution_start=1634620412930 source_hash="90563ec2" tags=[]
scaler = StandardScaler()
import tensorflow as tf
x_train = pd.DataFrame(scaler.fit_transform(x_train), columns = x_train.columns)
x_test = pd.DataFrame(scaler.fit_transform(x_test), columns = x_test.columns)
normalizer = preprocessing.Normalization(axis=-1)
normalizer.adapt(np.array(x_train))
print(normalizer.mean.numpy())
/ + cell_id="00017-d2872d03-0f86-4af9-aaaf-ddb397b47506" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 108} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=0 execution_start=1634620413192 source_hash="ee30f5cd" tags=[]
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
/ + cell_id="00018-4994e830-7248-4052-be37-0d7bd842ed40" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 114} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=192 execution_start=1634620413248 source_hash="a0d18130" tags=[]
from tensorflow.keras import datasets, layers, models
import tensorflow as tf
from tensorflow.keras import regularizers
from tensorflow.keras.layers import BatchNormalization
initializer = tf.keras.initializers.VarianceScaling(
scale=0.1, mode='fan_in', distribution='uniform',seed = RANDOM_SEED)
tf.random.set_seed(RANDOM_SEED)
model = Sequential(normalizer)
model.add(Dense(416,kernel_initializer=initializer, kernel_regularizer=regularizers.l2(0.0001),input_dim=(x_train.shape[1]), activation='relu')) # input
model.add(layers.Dropout(0.2))
model.add(Dense(416,kernel_initializer=initializer, kernel_regularizer=regularizers.l2(0.0001),activation='relu')) # hidden 1
model.add(layers.Dropout(0.2))
model.add(Dense(416,kernel_initializer=initializer, kernel_regularizer=regularizers.l2(0.0001),activation='relu')) # hidden 2
model.add(layers.Dropout(0.2))
model.add(Dense(416,kernel_initializer=initializer, kernel_regularizer=regularizers.l2(0.0001),activation='relu')) # hidden 3
model.add(layers.Dropout(0.2))
model.add(Dense(1))# output
/ + cell_id="00019-5335bf85-6fcb-42a3-a57a-ac76c9338af4" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 120} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=59 execution_start=1634620413451 source_hash="4e6a3b95" tags=[]
model.summary()
/ + cell_id="00020-6bc9a7bc-f800-45a2-90a2-6a98bbc9e19d" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 126} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=1286537 execution_start=1634620413509 source_hash="3792178a" tags=[]
import tensorflow as tf
lr_schedule = tf.keras.optimizers.schedules.InverseTimeDecay(
0.001,
decay_steps=x_train.shape[0]*1000,
decay_rate=0.1,
staircase=False)
opt = tf.keras.optimizers.Adamax(lr_schedule)
# stop_early = tf.keras.callbacks.EarlyStopping(monitor='loss', patience=5)
model.compile(loss='mean_absolute_error',optimizer=opt)
history = model.fit(x_train, y_train, epochs=98, batch_size=128)
/ + cell_id="00025-b842db18-d8af-4b00-a318-c06b705c93a0" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 132} deepnote_cell_type="code" deepnote_output_heights=[250] deepnote_to_be_reexecuted=false execution_millis=487 execution_start=1634621700046 source_hash="39089663" tags=[]
plot_loss(history)
/ + cell_id="00026-87b8194c-9e5d-4967-8449-659b1027e2b9" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 138} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=10507546 execution_start=1634621700541 source_hash="398a801f" tags=[]
val_acc_per_epoch = history.history['loss']
best_epoch = val_acc_per_epoch.index(min(val_acc_per_epoch)) + 1
print('Best epoch: %d' % (best_epoch,))
/ + cell_id="00021-d9c5d821-2f56-4794-b5ee-498cff2907eb" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 144} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=5930 execution_start=1634621700592 source_hash="2703c5a1" tags=[]
y_pred = model.predict(x_train)
/ + cell_id="00024-4d65323f-ac5c-4ff4-9d58-adbda0eee671" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 150} deepnote_cell_type="code" deepnote_output_heights=[21] deepnote_to_be_reexecuted=false execution_millis=12 execution_start=1634621706559 source_hash="4da7eb4d" tags=[]
log_mae = np.log(mean_absolute_error(y_pred, y_train))
log_mae
/ + cell_id="00023-31f174e2-77a1-4774-9d75-2d9df553f15c" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 156} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=1450 execution_start=1634621706598 source_hash="5406791e" tags=[]
y_pred = model.predict(x_test)
/ + cell_id="00026-8fc39b38-8ff9-4b69-a8b1-17e2e0f6e73e" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 162} deepnote_cell_type="code" deepnote_output_heights=[21] deepnote_to_be_reexecuted=false execution_millis=11 execution_start=1634621708067 source_hash="77d8642f" tags=[]
log_mae = np.log(mean_absolute_error(y_pred, y_true))
log_mae
/ + cell_id="00027-a0743982-85dc-4e90-b14d-b9a7a8e9e905" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 168} deepnote_cell_type="code" deepnote_output_heights=[21] deepnote_to_be_reexecuted=false execution_millis=94 execution_start=1634621708088 source_hash="92590d40" tags=[]
pretest = pd.read_csv("test.csv")
pretest.shape
/ + cell_id="00028-0df3fd96-4599-45b0-a142-251429246254" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 174} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=44 execution_start=1634621708196 source_hash="c74d4493" tags=[]
pretest.info()
/ + cell_id="00029-6d074981-4882-4179-a8b5-bd752e4bf4b2" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 180} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=13 execution_start=1634621708247 source_hash="3c628f36" tags=[]
pretest['functional_groups'] = pretest['functional_groups'].replace({np.nan:0})
# train['void_fraction'] = train['void_fraction'].replace({'0':np.nan, 0:np.nan})
# train['void_volume [cm^3/g]'] = train['void_volume [cm^3/g]'].replace({'0':np. nan, 0:np.nan})
#train['functional_groups'] = train['functional_groups'].fillna(train.groupby('functional_groups')['functional_groups'].transform('mean'))
# train['void_fraction'] = train['void_fraction'].fillna(train.groupby('functional_groups')['void_fraction'].transform('mean'))
# train['void_volume [cm^3/g]'] = train['void_volume [cm^3/g]'].fillna(train.groupby('functional_groups')['void_volume [cm^3/g]'].transform('mean'))
/ + cell_id="00030-b20642d2-9803-4d89-a498-a649e05fee83" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 186} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=75 execution_start=1634621708270 source_hash="c74d4493" tags=[]
pretest.info()
/ + cell_id="00031-86d59262-fd6a-4f86-838f-91380a6d945a" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 192} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=0 execution_start=1634621708342 source_hash="bacc5471" tags=[]
col = ["functional_groups", "topology"]
for i in col:
pretest[i] = pretest[i].astype("category").cat.codes
/ + cell_id="00032-7334b882-30eb-4b3a-a928-420957fce3b2" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 198} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=350 execution_start=1634621708342 source_hash="4506e71d" tags=[]
pretest
/ + cell_id="00033-08fca710-3432-41e0-bf63-886e9822ae9b" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 204} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=10510455 execution_start=1634621708680 source_hash="4484f095" tags=[]
pretest = pretest.drop(['MOFname'],axis=1)
/ + cell_id="00034-97d5d41e-912e-4131-99f8-87219d4c988f" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 210} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=19 execution_start=1634621708725 source_hash="5bc40c87" tags=[]
scaler = StandardScaler()
pretest = pd.DataFrame(scaler.fit_transform(pretest), columns = pretest.columns)
pretest = scaler.inverse_transform(pretest)
/ + cell_id="00035-bdde1cb9-b2bd-4d10-bec8-edc25086760c" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 216} deepnote_cell_type="code" deepnote_output_heights=[249] deepnote_to_be_reexecuted=false execution_millis=3 execution_start=1634621708756 source_hash="4506e71d" tags=[]
pretest
/ + cell_id="00036-dbae053a-3e23-44bd-8f74-59ba6a15dad6" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 222} deepnote_cell_type="code" deepnote_output_heights=[135] deepnote_to_be_reexecuted=false execution_millis=2663 execution_start=1634621708816 source_hash="9aa6f43b" tags=[]
pretest_pred = model.predict(pretest)
pretest_pred
/ + cell_id="00037-5d64133c-0cec-4a26-8b59-0d2a9ab455cb" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 228} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=123 execution_start=1634621711506 source_hash="cdb37d67" tags=[]
submission = pd.DataFrame({
"id": [str(i) for i in range(68614,85614)],
"CO2_working_capacity [mL/g]": pretest_pred.T[0]
})
submission.to_csv("submission.csv", index=False)
/ + cell_id="00038-77d18b49-e397-4282-855f-b475cfd2c103" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 234} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=550 execution_start=1634621711643 source_hash="ad8f3ca4" tags=[]
!ls
/ + cell_id="00039-74b378d3-4084-4ac9-8ede-d637616e9675" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 240} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=7507 execution_start=1634621712200 source_hash="aa79ceb7" tags=[]
/ %%capture
!sudo apt-get update
!sudo apt-get install zip
/ + cell_id="00040-44055291-5b93-4365-8a7f-396e1ff1c62b" deepnote_app_coordinates={"h": 5, "w": 12, "x": 0, "y": 246} deepnote_cell_type="code" deepnote_to_be_reexecuted=false execution_millis=480 execution_start=1634621719749 source_hash="e3e8edcd" tags=[]
!zip submission_NN.zip submission.csv
/ + [markdown] created_in_deepnote_cell=true deepnote_cell_type="markdown" tags=[]
/ <a style='text-decoration:none;line-height:16px;display:flex;color:#5B5B62;padding:10px;justify-content:end;' href='https://deepnote.com?utm_source=created-in-deepnote-cell&projectId=679677c2-c780-422a-a432-9f2ffeaad3b4' target="_blank">
/ <img alt='Created in deepnote.com' style='display:inline;max-height:16px;margin:0px;margin-right:7.5px;' src='data:image/svg+xml;base64,PD94bWwgdmVyc2lvbj0iMS4wIiBlbmNvZGluZz0iVVRGLTgiPz4KPHN2ZyB3aWR0aD0iODBweCIgaGVpZ2h0PSI4MHB4IiB2aWV3Qm94PSIwIDAgODAgODAiIHZlcnNpb249IjEuMSIgeG1sbnM9Imh0dHA6Ly93d3cudzMub3JnLzIwMDAvc3ZnIiB4bWxuczp4bGluaz0iaHR0cDovL3d3dy53My5vcmcvMTk5OS94bGluayI+CiAgICA8IS0tIEdlbmVyYXRvcjogU2tldGNoIDU0LjEgKDc2NDkwKSAtIGh0dHBzOi8vc2tldGNoYXBwLmNvbSAtLT4KICAgIDx0aXRsZT5Hcm91cCAzPC90aXRsZT4KICAgIDxkZXNjPkNyZWF0ZWQgd2l0aCBTa2V0Y2guPC9kZXNjPgogICAgPGcgaWQ9IkxhbmRpbmciIHN0cm9rZT0ibm9uZSIgc3Ryb2tlLXdpZHRoPSIxIiBmaWxsPSJub25lIiBmaWxsLXJ1bGU9ImV2ZW5vZGQiPgogICAgICAgIDxnIGlkPSJBcnRib2FyZCIgdHJhbnNmb3JtPSJ0cmFuc2xhdGUoLTEyMzUuMDAwMDAwLCAtNzkuMDAwMDAwKSI+CiAgICAgICAgICAgIDxnIGlkPSJHcm91cC0zIiB0cmFuc2Zvcm09InRyYW5zbGF0ZSgxMjM1LjAwMDAwMCwgNzkuMDAwMDAwKSI+CiAgICAgICAgICAgICAgICA8cG9seWdvbiBpZD0iUGF0aC0yMCIgZmlsbD0iIzAyNjVCNCIgcG9pbnRzPSIyLjM3NjIzNzYyIDgwIDM4LjA0NzY2NjcgODAgNTcuODIxNzgyMiA3My44MDU3NTkyIDU3LjgyMTc4MjIgMzIuNzU5MjczOSAzOS4xNDAyMjc4IDMxLjY4MzE2ODMiPjwvcG9seWdvbj4KICAgICAgICAgICAgICAgIDxwYXRoIGQ9Ik0zNS4wMDc3MTgsODAgQzQyLjkwNjIwMDcsNzYuNDU0OTM1OCA0Ny41NjQ5MTY3LDcxLjU0MjI2NzEgNDguOTgzODY2LDY1LjI2MTk5MzkgQzUxLjExMjI4OTksNTUuODQxNTg0MiA0MS42NzcxNzk1LDQ5LjIxMjIyODQgMjUuNjIzOTg0Niw0OS4yMTIyMjg0IEMyNS40ODQ5Mjg5LDQ5LjEyNjg0NDggMjkuODI2MTI5Niw0My4yODM4MjQ4IDM4LjY0NzU4NjksMzEuNjgzMTY4MyBMNzIuODcxMjg3MSwzMi41NTQ0MjUgTDY1LjI4MDk3Myw2Ny42NzYzNDIxIEw1MS4xMTIyODk5LDc3LjM3NjE0NCBMMzUuMDA3NzE4LDgwIFoiIGlkPSJQYXRoLTIyIiBmaWxsPSIjMDAyODY4Ij48L3BhdGg+CiAgICAgICAgICAgICAgICA8cGF0aCBkPSJNMCwzNy43MzA0NDA1IEwyNy4xMTQ1MzcsMC4yNTcxMTE0MzYgQzYyLjM3MTUxMjMsLTEuOTkwNzE3MDEgODAsMTAuNTAwMzkyNyA4MCwzNy43MzA0NDA1IEM4MCw2NC45NjA0ODgyIDY0Ljc3NjUwMzgsNzkuMDUwMzQxNCAzNC4zMjk1MTEzLDgwIEM0Ny4wNTUzNDg5LDc3LjU2NzA4MDggNTMuNDE4MjY3Nyw3MC4zMTM2MTAzIDUzLjQxODI2NzcsNTguMjM5NTg4NSBDNTMuNDE4MjY3Nyw0MC4xMjg1NTU3IDM2LjMwMzk1NDQsMzcuNzMwNDQwNSAyNS4yMjc0MTcsMzcuNzMwNDQwNSBDMTcuODQzMDU4NiwzNy43MzA0NDA1IDkuNDMzOTE5NjYsMzcuNzMwNDQwNSAwLDM3LjczMDQ0MDUgWiIgaWQ9IlBhdGgtMTkiIGZpbGw9IiMzNzkzRUYiPjwvcGF0aD4KICAgICAgICAgICAgPC9nPgogICAgICAgIDwvZz4KICAgIDwvZz4KPC9zdmc+' > </img>
/ Created in <span style='font-weight:600;margin-left:4px;'>Deepnote</span></a>
|
TMLCC-Chem bot.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Descriptive
# +
import pandas as pd
import numpy as np
import scipy.stats as stats
import statsmodels.stats.api as sm
# %matplotlib inline
data = np.arange(10,14)
mean_val = np.mean(data) # mean
sem_val = stats.sem(data) # standard error of mean
print(mean_val, sem_val)
def mean_confidence_interval(data, confidence=0.95):
a = 1.0*np.array(data)
n = len(a)
m, se = np.mean(a), stats.sem(a)
h = se * stats.t._ppf((1+confidence)/2., n-1)
return m, m-h, m+h
# correct
temp = stats.t.interval(0.95, len(data)-1, loc=np.mean(data), scale=stats.sem(data))
print(temp)
temp = sm.DescrStatsW(data).tconfint_mean()
print(temp)
temp = mean_confidence_interval(data)
print(temp)
#incorrect
temp = stats.norm.interval(0.95, loc=np.mean(data), scale=stats.sem(data))
print(temp)
# +
def cilen(arr, alpha=0.95):
if len(arr) <= 1:
return 0
m, e, df = np.mean(arr), stats.sem(arr), len(arr) - 1
interval = stats.t.interval(alpha, df, loc=m, scale=e)
cilen = np.max(interval) - np.mean(interval)
return cilen
df = pd.DataFrame(np.array([data, data]).T, columns=['x', 'y'])
m = df.pivot_table(index='x', values='y', aggfunc='mean')
e = df.pivot_table(index='x', values='y', aggfunc=cilen)
# e = df.pivot_table(index='x', values='y', aggfunc='sem')
m.plot(xlim=[0.8, 3.2], yerr=e)
# -
# ### proportion confidence interval
#
# http://www.statsmodels.org/dev/generated/statsmodels.stats.proportion.proportion_confint.html
#
# Returns:
# ci_low, ci_upp : float
#
# scipy.stats module has a method .interval() to compute the equal tails confidence,
# # Compare mean
#
# Normal Distribution = True and Homogeneity of Variance = True
#
# scipy.stats.ttest_ind(sample_1, sample_2)
# Normal Distribution = True and Homogeneity of Variance = False
#
# scipy.stats.ttest_ind(sample_1, sample_2, equal_var = False)
# Normal Distribution = False and Homogeneity of Variance = True
#
# scipy.stats.mannwhitneyu(sample_1, sample_2)
# Normal Distribution = False and Homogeneity of Variance = False
#
# ???
# +
import numpy as np
from scipy.stats import ttest_ind
sample_1 = np.random.normal(0.04,0.1,120)
sample_2 = np.random.normal(0.02,0.1,1200)
ttest_ind(sample_1, sample_2)
# -
# ### one sample t test
rvs = stats.norm.rvs(loc=5, scale=10, size=(50))
stats.ttest_1samp(rvs,5.0)
stats.ttest_1samp(rvs,0.0)
# # compare proportion
#
# https://onlinecourses.science.psu.edu/stat414/node/268
#
# ### one sample
# https://docs.scipy.org/doc/scipy-0.14.0/reference/generated/scipy.stats.binom_test.html
#
#
# ### two samples
# http://www.statsmodels.org/dev/generated/statsmodels.stats.proportion.proportions_ztest.html
#
# +
import statsmodels.api as sm
import numpy as np
# import rpy2.robjects.packages as rpackages
# import rpy2.robjects as robjects
# rstats = rpackages.importr('stats')
s1 = 1556 # success
n1 = 2455 # sample size
s2 = 1671
n2 = 2730
# manual calculation
p1 = s1 / n1
p2 = s2 / n2
p = (s1 + s2) / (n1 + n2)
z = (p1 - p2) / (p*(1-p)*((1/n1)+(1/n2)))**0.5
# using R in Python with rpy2
# rmatrix = robjects.r.matrix(robjects.IntVector([s1, n1-s1, s2,n2-s2]), nrow=2)
# fisher_test = rstats.fisher_test(rmatrix, alternative="two.sided")
# statsmodels
zscore, pval = sm.stats.proportions_ztest([s1, s2], [n1, n2], alternative='two-sided')
print('Manual calculation of z: {:.6f}'.format(z))
print('Z-score from statsmodels: {:.6f}'.format(zscore))
# print('R pvalue from fisher.test: {:.6f}'.format(fisher_test[0][0]))
print('Statsmodels pvalue: {:.6f}'.format(pval))
# +
from scipy.stats import norm, chi2_contingency
import scipy.stats as stats
import statsmodels.api as sm
# from rpy2.robjects import IntVector
# from rpy2.robjects.packages import importr
import numpy as np
s1 = 135
n1 = 1781
s2 = 47
n2 = 1443
p1 = s1/n1
p2 = s2/n2
p = (s1 + s2)/(n1+n2)
z = (p2-p1)/ ((p*(1-p)*((1/n1)+(1/n2)))**0.5)
p_value = norm.cdf(z)
print(['{:.12f}'.format(a) for a in (abs(z), p_value * 2)])
z1, p_value1 = sm.stats.proportions_ztest([s1, s2], [n1, n2])
print(['{:.12f}'.format(b) for b in (z1, p_value1)])
# stats = importr('stats')
# r_result = stats.prop_test(IntVector([s1, s2]), IntVector([n1, n2]), correct=False)
# z2 = r_result[0][0]**0.5
# p_value2 = r_result[2][0]
# print(['{:.12f}'.format(c) for c in (z2, p_value2)])
arr = np.array([[s1, n1-s1], [s2, n2-s2]])
chi2, p_value3, dof, exp = chi2_contingency(arr, correction=False)
print(['{:.12f}'.format(d) for d in (chi2**0.5, p_value3)])
# -
# # Correlation
pearsonr(x, y)
# # Chi-Square Test contingency
# ### Chi-Square Goodness of Fit Test
#
# For example, suppose a company printed baseball cards. It claimed that 30% of its cards were rookies; 60%, veterans; and 10%, All-Stars. We could gather a random sample of baseball cards and use a chi-square goodness of fit test to see whether our sample distribution differed significantly from the distribution claimed by the company. The sample problem at the end of the lesson considers this example.
#
#
# ### Chi-Square Test of Homogeneity
#
# For example, in a survey of TV viewing preferences, we might ask respondents to identify their favorite program. We might ask the same question of two different populations, such as males and females. We could use a chi-square test for homogeneity to determine whether male viewing preferences differed significantly from female viewing preferences. The sample problem at the end of the lesson considers this example.
#
#
# ### Chi-Square Test for Independence
#
# For example, in an election survey, voters might be classified by gender (male or female) and voting preference (Democrat, Republican, or Independent). We could use a chi-square test for independence to determine whether gender is related to voting preference. The sample problem at the end of the lesson considers this example.
#
# http://stattrek.com/chi-square-test/homogeneity.aspx?Tutorial=AP
#
#
# ### so... how they are different?
#
# 1) A goodness of fit test is for testing whether a set of multinomial counts is distributed according to a prespecified (i.e. before you see the data!) set of population proportions.
#
# 2) A test of homogeneity tests whether two (or more) sets of multinomial counts come from different sets of population proportions.
#
# 3) A test of independence tests is for a bivariate** multinomial, of whether pijpij is different from pipjpipj.
#
# **(usually)
# https://stats.stackexchange.com/questions/91970/chi-square-test-difference-between-goodness-of-fit-test-and-test-of-independenc
# +
### Chi-Square Goodness of Fit Test
import scipy.stats as stats
chi2, p = stats.chisquare(f_obs=[11294, 11830, 10820, 12875], f_exp=[10749, 10940, 10271, 11937])
msg = "Test Statistic: {}\np-value: {}"
print(msg.format(chi2, p))
# -
# +
### Chi-Square Test for Independence
from scipy.stats import chi2_contingency
import numpy as np
row1 = [91,90,51]
row2 = [150,200,155]
row3 = [109,198,172]
data = [row1, row2, row3]
print(chi2_contingency(data))
chi2, p_value, dfreedom, expected = chi2_contingency(data)
# -
|
stats_method.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
from sqlalchemy import create_engine
from config import password
# %load_ext sql
# +
DB_ENDPOINT = "localhost"
DB = 'bags_db'
DB_USER = 'postgres'
DB_PASSWORD = password
DB_PORT = '5432'
# postgresql://username:password@host:port/database
conn_string = "postgresql://{}:{}@{}:{}/{}" \
.format(DB_USER, DB_PASSWORD, DB_ENDPOINT, DB_PORT, DB)
print(conn_string)
# -
# %sql $conn_string
csv_file = "./all_bags.csv"
all_bags_df = pd.read_csv(csv_file)
all_bags_df.head()
# +
rds_connection_string = DB_USER + ":" + password + "@localhost:5432/bags_db"
engine = create_engine(f'postgresql://{rds_connection_string}')
# -
engine.table_names()
all_bags_df.to_sql(name='all_bags', con=engine, if_exists='append', index=False)
pd.read_sql_query('select * from all_bags', con=engine).head()
csv_file = "./bag_summary.csv"
bag_summary_df = pd.read_csv(csv_file)
bag_summary_df.head()
bag_summary_df.to_sql(name='bag_summary', con=engine, if_exists='append', index=False)
pd.read_sql_query('select * from bag_summary', con=engine).head()
engine.table_names()
# # Schema
# ``` sql
# CREATE TABLE public.all_bags
# (
# "Unnamed: 0" bigint,
# "Name" text COLLATE pg_catalog."default",
# "Brand" text COLLATE pg_catalog."default",
# "Price" double precision,
# "Type" text COLLATE pg_catalog."default",
# "Material" text COLLATE pg_catalog."default",
# "Source" text COLLATE pg_catalog."default"
# );
# ```
#
|
3. Load data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Principi AI
#
# L'intelligenza artificiale dalla sua definizione significa avere la capacità di apprendere e di eseguire compiti in maniera simile a quella umana, è presente però la necessità di usare la programmazione per fare in modo che un calcolatore esibisca queste caratteristiche.
#
# ## Differenze tra programmazione classica e machine learning
#
# Sorge quindi la necessità di capire quale sia la differenza tra la programmazione classica vista fino ad ora e il machine learning, la differenza principale tra le due è che nella prima la **macchina è esplicitamente programmata ad eseguire delle specifiche azioni, mentre nel machine learning la macchina usa una serie di metodi programmati per capire quale sia l'azione migliore da eseguire**.
# Qualora questo possa sembrare complicato da capire pensate ad esempio alla necessità di classificare delle foglie in base alle dimensione, colore, ecc... .
# Ora voi potete programmare esplicitamente che qualora certi parametri siano più gradi di valori a voi assegnati esse siano un tipo di foglia o potete fare in modo che quei valori siano determinata dalla macchina con un certo criterio, nel secondo caso avete vissto un'applicazione del machine learning.
#
# ## Metodi di apprendimento
#
# I metodi di apprendimento dell'AI sono 3 e sono:
#
# - Apprendimento supervisionato
# - Apprendimento non supervisionato
# - Apprendimento per rinforzo
#
# Questi tipi di apprendimento hanno in comune il fattore che dovendo necessariamente girare su un calcolatore debbano essere convertiti in **linguaggio matematico** altrimenti essi non sarebbero in grado di applicarli.
#
#
# ## Dati per l'AI
#
# L'AI necessita di dati, dati che però devono essere "buoni" ovvero devono contenere poco rumore, mancanza di presenza di errori quanto possibile e devono essere adattati alla capacità della macchina di apprendere, qualora i dati non siano "pronti" per l'apprendimento è necessario **preprocessarli** ovvero **modificare i dati in modo tale che possano essere processabili in seguito dal modello**.
# La decisione su quale metodo usare per processare i dati può essere **determinante sulle capacità del modello** infatti anche se sono presenti dei metodi generali per capire quale sia un modo universale di processare i dati, dalle **condizioni dei tipi di dati è possibile ipotizzare che alcuni siano più adatti di altri**.
#
# ## Allenare l'AI in base ai dati
#
# I modelli di AI come prima condizione devono mettere in relazione **complessità e mole di dati** come vedremo in seguito un modello con pochi dati è ***molto probabile*** che performi in maniera peggiore rispetto ad uno più semplice, mentre una grande mole di dati permetterà ad un modello più complesso di essere più preciso. In genere il processo di allenamento è sempre quello più costoso a livello computazionale.
#
# ## Valutare l'AI
#
# La valutazione dell'AI è difficile, in particolare poiché è difficile comprendere come l'AI abbia imparato ad eseguire una particolare azione e su quali principi o assiomi si stia basando(su questo è presente il campo dell' EX_AI ovvero explainable AI), in genere però sono presenti quasi sempre due aspetti in comune:
#
# - la presenza di un dataset per il testing dell'apprendimento
# - la presenza di una metrica per la valutazione quantitativa del testing
#
# La metrica è quella che in genere influisce maggiormente sulla definizione del modello a causa del fatto che penalizziamo certi comportamenti, mentre ne concediamo altri!
#
# ## Uso dell'AI
#
# Al momento sono pochi i modelli in grado di compiere azioni anche al di fuori di quello per cui sono stati allenati e in genere sono sempre richiesti ulteriori allenamenti, qualora però il modello sia allenato in molti casi le performance risultano simili o maggiori rispetto a quelle umane in larga parte grazie alla velocità dei processori.
#
# Quindi ora che abbiamo capito cerchiamo di usare le principali librerie python usate per il machine learning e la data science!
#
# 
#
# ***
#
# Principi AI finito!
|
3.machine learning/1-Principi_AI.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
import featuretools as ft
from featuretools.primitives import Percentile
import composeml as cp
import pandas as pd
# # Load in data
cyber_df = pd.read_csv("data/CyberFLTenDays.csv").sample(10000)
cyber_df.index.name = "log_id"
cyber_df.reset_index(inplace=True, drop=False)
cyber_df['label'] = cyber_df['label'].map({'N': False, 'A': True}, na_action='ignore')
# # Create an EntitySet with many different dataframes
#
# Each dataframe is a different definition of "connection"
es = ft.EntitySet("CyberLL")
# create an index column
cyber_df["name_host_pair"] = cyber_df["src_name"].str.cat(
[cyber_df["dest_name"],
cyber_df["src_host"],
cyber_df["dest_host"]],
sep=' / ')
cyber_df["src_pair"] = cyber_df["src_name"].str.cat(
cyber_df["src_host"],
sep=' / ')
cyber_df["dest_pair"] = cyber_df["dest_name"].str.cat(
cyber_df["dest_host"],
sep=' / ')
es.add_dataframe(dataframe_name="log",
dataframe=cyber_df,
index="log_id",
time_index="secs")
es.normalize_dataframe(base_dataframe_name="log",
new_dataframe_name="name_host_pairs",
index="name_host_pair",
additional_columns=["src_name", "dest_name",
"src_host", "dest_host",
"src_pair",
"dest_pair",
"label"])
es.normalize_dataframe(base_dataframe_name="name_host_pairs",
new_dataframe_name="src_pairs",
index="src_pair",
additional_columns=["src_name", "src_host"])
es.normalize_dataframe(base_dataframe_name="src_pairs",
new_dataframe_name="src_names",
index="src_name")
es.normalize_dataframe(base_dataframe_name="src_pairs",
new_dataframe_name="src_hosts",
index="src_host")
es.normalize_dataframe(base_dataframe_name="name_host_pairs",
new_dataframe_name="dest_pairs",
index="dest_pair",
additional_columns=["dest_name", "dest_host"])
es.normalize_dataframe(base_dataframe_name="dest_pairs",
new_dataframe_name="dest_names",
index="dest_name")
es.normalize_dataframe(base_dataframe_name="dest_pairs",
new_dataframe_name="dest_hosts",
index="dest_host")
# ## Visualize EntitySet
es.plot()
# # Define function to generate labels and cutoff times
# We use [Compose](https://compose.featurelabs.com/) to define our labeling function.
# +
def malicious_connection(df, lead):
if (len(df.index) > lead + 1):
return df.iloc[lead:]['label'].any()
def label_generator(cyber_df, index_col, after_n_obs, lead, prediction_window):
lm = cp.LabelMaker(
target_dataframe_name=index_col,
time_index="secs",
labeling_function=malicious_connection,
window_size=window + lead
)
label_times = lm.search(
cyber_df.sort_values('secs'),
minimum_data=after_n_obs,
gap=after_n_obs + lead + window,
num_examples_per_instance=1,
lead=lead,
verbose=False
)
label_times['time'] = pd.to_numeric(label_times['time'])
return label_times
# +
# predict after 3 observations
after_n_obs = 3
# predict 2 observations out
lead = 2
# predict if any malicious attacks in a 10-observation window
window = 10
# -
# # Compute features for various types of connections
# features on src_name
cutoffs = label_generator(cyber_df, "src_name", after_n_obs, lead, window)
fm, fl = ft.dfs(entityset=es, target_dataframe_name="src_names", cutoff_time=cutoffs, verbose=True, max_depth=3)
## features on src_host
cutoffs = label_generator(cyber_df, "src_host", after_n_obs, lead, window)
fm, fl = ft.dfs(entityset=es, target_dataframe_name="src_hosts", cutoff_time=cutoffs, verbose=True, max_depth=3)
## features on dest_name
cutoffs = label_generator(cyber_df, "dest_name", after_n_obs, lead, window)
fm, fl = ft.dfs(entityset=es, target_dataframe_name="dest_names", cutoff_time=cutoffs, verbose=True, max_depth=3)
## features on dest_host
cutoffs = label_generator(cyber_df, "dest_host", after_n_obs, lead, window)
fm, fl = ft.dfs(entityset=es, target_dataframe_name="dest_hosts", cutoff_time=cutoffs, verbose=True, max_depth=3)
# features on src_name/dest_name/src_host/dest_host
cutoffs = label_generator(cyber_df, "name_host_pair", after_n_obs, lead, window)
fm, fl = ft.dfs(entityset=es, target_dataframe_name="name_host_pairs", cutoff_time=cutoffs, verbose=True, max_depth=2, trans_primitives=[Percentile])
# merge dataframes together to access the index columns created in the process of normalizing
merged = (es['log'].merge(es['name_host_pairs'])
.merge(es['src_pairs'])
.merge(es['dest_pairs']))
# features on src_name/src_host
cutoffs = label_generator(merged, 'src_pair', after_n_obs, lead, window)
fm, fl = ft.dfs(entityset=es, target_dataframe_name="src_pairs", cutoff_time=cutoffs, verbose=True, max_depth=2, trans_primitives=[Percentile])
# features on dest_name/dest_host
cutoffs = label_generator(merged, 'dest_pair', after_n_obs, lead, window)
fm, fl = ft.dfs(entityset=es, target_dataframe_name="dest_pairs", cutoff_time=cutoffs, verbose=True, max_depth=2, trans_primitives=[Percentile])
# ## Built at Alteryx Innovation Labs
#
# <p>
# <a href="https://www.alteryx.com/innovation-labs">
# <img width="75%" src="https://evalml-web-images.s3.amazonaws.com/alteryx_innovation_labs.png" alt="Alteryx Innovation Labs" />
# </a>
# </p>
|
predict-malicious-cyber-connections/Create Feature Matrices from LL Cyber Data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
## creo dos variables que empiezan en 0, los dias y la distancia recorrida
# -
dias=0
distancia=0
# +
### mientras la variable distancia sea menor que 125, se suma 30
while distancia <125:
{distancia== distancia +30
if distancia>=125 ## si ahora es mayor a 125, se imprime el numero de dias
print("El caracol ha tardado " dias "dias en escapar")
else:
dias==(dias+1) ### si distancia es menor a 125, se suma un dia y se restan 20 cm
distancia==(distancia-20)
}
# -
|
01-intro-101/python/practices/01-snail-and-well/your-solution-here/Practica_01_snail_and_well_Raquel.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import glob
import numpy as np
import pandas as pd
# +
df = pd.DataFrame()
for npy in sorted(glob.iglob('data/features/*.npy')):
df1 = pd.DataFrame(np.load(npy)).T
df1['name'] = npy[-21:-7]
df = pd.concat([df, df1], ignore_index=True)
df['class'] = df.index/80
df['class'] = df['class'].astype('int')
df
# -
# # Why stratified train-val-test split?
#
# We split the dataset classwise instead of randomly into 50-25-25 splits, because of the chance that a class could be underrepresented in the randomized split. If there are unequal representations of classes between train and test sets, the model trained on the train set would not perform as well on the test set. This is especially pronounced on a relatively smaller dataset such as this one, where the number of samples from each class is fairly small and equal. An extreme example could be one class not being represented at all in the training set for the randomized split, resulting in no training being done for sample of that class, resulting in poor classification for that class.
# +
from sklearn.model_selection import train_test_split
train, test = train_test_split(df, train_size=0.5, test_size=0.5, stratify=df['class'])
val, test = train_test_split(test, train_size=0.5, test_size=0.5, stratify=test['class'])
with open('splits/train.npy', 'wb') as np_file:
np.save(np_file, train)
with open('splits/val.npy', 'wb') as np_file:
np.save(np_file, val)
with open('splits/test.npy', 'wb') as np_file:
np.save(np_file, test)
val.sort_values('class')
# +
from sklearn.svm import SVC
from sklearn.multiclass import OneVsRestClassifier
c_list = [0.01, 0.1, 0.1**0.5, 1, 10**0.5, 10, 100**0.5]
scores = []
for c in c_list:
svm = OneVsRestClassifier(estimator=SVC(C=c, kernel="linear"))
svm.fit(train.iloc[:, :-2].values, train.iloc[:, -1].values)
scores.append(svm.score(val.iloc[:, :-2].values, val.iloc[:, -1].values))
best_c = c_list[np.argmax(scores)]
best_score = np.max(scores)
print("Best c={}, score={}".format(best_c, best_score))
# +
from sklearn.metrics import classification_report, accuracy_score
best_svm = OneVsRestClassifier(estimator=SVC(C=best_c, kernel="linear"))
best_svm.fit(pd.concat([train.iloc[:, :-2], val.iloc[:, :-2]]).values, pd.concat([train.iloc[:, -1], val.iloc[:, -1]]).values)
test_pred = best_svm.predict(test.iloc[:, :-2])
print("final test accuracy: {}".format(accuracy_score(test.iloc[:, -1], test_pred)))
print(classification_report(test.iloc[:, -1], test_pred))
# +
import math
import matplotlib.pyplot as plt
failed = np.where(test.iloc[:, -1] != test_pred)[0]
fig = plt.figure(figsize=(20,20))
plt.subplots_adjust(hspace=1)
num_rows = math.ceil(len(failed)/4)
results = []
for i in range(len(failed)):
img = test.iloc[failed[i]]['name']
pred = test_pred[failed[i]]
actual = test.iloc[failed[i]]['class']
results.append({'image': img,
'pred': pred,
'actual': actual})
results = sorted(results, key=lambda k: k['image'])
for i in range(len(results)):
fig.add_subplot(num_rows, 4, i+1)
plt.xticks([]), plt.yticks([])
image = '{}'.format(results[i]['image'])
pred = 'Predicted: {}'.format(results[i]['pred'])
actual = 'Actual: {}'.format(results[i]['actual'])
plt.xlabel(image + '\n' + pred + '\n' + actual)
plt.imshow(plt.imread('data/images/' + results[i]['image']))
plt.show()
# -
|
flower_svm.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.8.8 64-bit (''base'': conda)'
# name: python3
# ---
# ## Covid Project
#
# In this data science project we want to use data from the COWAS data base (uploaded at Kaggle: https://www.kaggle.com/praveengovi/coronahack-respiratory-sound-dataset) to make a
#
#
# ### Data Structure
#
# There are 1397 cases of which 56 are positive ones. Each case is composed of 9 independing recordings
# ['counting-normal','counting-fast','breathing-deep','breathing-shallow','cough-heavy','cough-shallow','vowel-a','vowel-e','vowel-o']
#
# ### Potential Solution
#
# Using an auto-encoder approach (out of distribution), training on "healthy" cases.
# Proposed solution (https://github.com/moiseshorta/MelSpecVAE).
# ## #Chunk 1
# ### Libraries
# +
#Data visualization
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score
#Audio Analysis
import glob
import IPython
import tensorflow as tf
from tensorflow import keras
import tensorflow_io as tfio
from random import shuffle
from statistics import mean
from data_prepration import Data
from models import decode, encode, VAE
# names_input = ['counting-normal','counting-fast','breathing-deep','breathing-shallow','cough-heavy','cough-shallow','vowel-a','vowel-e','vowel-o']
name = ['breathing-shallow']
weights_name = 'vaebreathing-shallow-48000_checkpoint'
latent_dim = 2
image_target_height = 28
image_target_width = 28
def get_spectrogram(sample):
audio = sample
audio = tf.reshape(sample, [-1])
audio = tf.cast(audio, tf.float32) # set audio file as float
# generate the mel spectrogram
spectrogram = tfio.audio.spectrogram(audio, nfft=1024, window=1024, stride=64)
spectrogram = tfio.audio.melscale(
spectrogram,
rate=48000,
mels=64,
fmin=0,
fmax=2000, # mels = bins, fmin,fmax = frequences
)
spectrogram /= tf.math.reduce_max(spectrogram) # normalization
spectrogram = tf.expand_dims(spectrogram, axis=-1) # add dimension 2D -> 3D
spectrogram = tf.image.resize(
spectrogram, (image_target_height, image_target_height)
) # resize in two dimensions
spectrogram = tf.transpose(
spectrogram, perm=(1, 0, 2)
) # transpose the first two axis
spectrogram = spectrogram[::-1, :, :] # flip the first axis(frequency)
return spectrogram
# +
file_name = ( "data/Corona-Hack-Respiratory-Sound-Metadata.csv" )
base_path = "data/CoronaHack-Respiratory-Sound-Dataset"
data_obj = Data(filename=file_name)
train_df, test_df = data_obj.create_df()
train_df = train_df.iloc[:100]
def get_paths(df):
paths_vector = df[name]
paths_list = df[name].values.tolist()
path_name = []
# Standard approach
print("paths_vector LENGTH", len(paths_vector))
for dir_name in paths_list:
if dir_name is not None:
path_name.append(base_path + str(dir_name[0]))
# DF approach
test_df['full_path'] = base_path + paths_vector
print("full_path LENGTH", len(test_df['full_path']))
return path_name
train_paths = get_paths(train_df)
test_paths = get_paths(test_df)
# +
# print(test_df[name].values)
# print("Sound File List Len", len(path_name))
# print("Sound File List ", path_name)
# Cut tensors longer than 300k to 300k
# print([sound_path for sound_path in path_name])
test_df['sound_tensors'] = test_df['full_path'].apply(lambda sound_path: tfio.audio.AudioIOTensor(sound_path).to_tensor()[:300000])
# print("sound_tensors LENGTH", len(test_df['sound_tensors']))
# print('sound_tensors', test_df['sound_tensors'][0])
def get_sound_tensors(sound_paths):
sound_tensor_list = [
tfio.audio.AudioIOTensor(sound_path).to_tensor()[:300000]
for sound_path in sound_paths
]
# print("Sound Tensor List Len", sound_tensor_list)
sound_tensor_list = [
sound_tensor
for sound_tensor in sound_tensor_list
if (np.sum(sound_tensor.numpy()) != 0)
# if ((sound_tensor.shape[0] == 300000) and (np.sum(sound_tensor.numpy()) != 0))
]
print('spectrograms LENGTH > 0 REAL', len(sound_tensor_list))
return sound_tensor_list
train_sound_tensors = get_sound_tensors(train_paths)
test_sound_tensors = get_sound_tensors(test_paths)
# print("Tensor list", sound_tensor_list[0])
# sound_slices_train = tf.data.Dataset.from_tensor_slices(sound_tensor_list_clean_train)
test_df = test_df.loc[test_df['sound_tensors'].apply(lambda sound_tensors: np.sum(sound_tensors)) != 0]
print('spectrograms LENGTH > 0', len(test_df))
y_test = test_df['split'].tolist()
# test_df['spectrograms'] = test_df['sound_tensors'].apply(lambda sound_tensor: get_spectrogram(sound_tensor))
# test_df['spectrograms'] = test_df['spectrograms'].apply(lambda spectrogram: tf.expand_dims(spectrogram, axis=0))
# # print('spectrograms', test_df['spectrograms'][1])
# print('spectrograms LENGTH', len(test_df['spectrograms']))
def get_samples_from_tensor(sound_tensors):
test_samples = [get_spectrogram(sound_tensor) for sound_tensor in sound_tensors]
test_samples = [tf.expand_dims(test_sample, axis=0) for test_sample in test_samples]
return test_samples
# +
train_samples = get_samples_from_tensor(train_sound_tensors)
test_samples = get_samples_from_tensor(test_sound_tensors)
# print("Test Sample ", test_samples)
encoder = encode(
latent_dim, image_target_height, image_target_width
)
decoder = decode(latent_dim)
model = VAE(encoder, decoder)
model.load_weights(weights_name)
# x_train = test_df['spectrograms'].to_numpy()
# +
# print("PREDICTION ", x_output)
def find_threshold(model, train_samples):
reconstructions = [model.predict(x_input) for x_input in train_samples]
# provides losses of individual instances
reconstruction_errors = tf.keras.losses.msle(train_samples, reconstructions)
# threshold for anomaly scores
threshold = np.mean(reconstruction_errors.numpy()) \
+ np.std(reconstruction_errors.numpy())
return threshold
def get_predictions(model, test_samples, threshold):
predictions = [model.predict(x_input) for x_input in test_samples]
# provides losses of individual instances
test_samples = [tf.reshape(t, [-1]) for t in test_samples]
predictions = [tf.reshape(p, [-1]) for p in predictions]
errors = tf.keras.losses.msle(test_samples, predictions)
print("ERRORS. ", errors)
print("ERRORS.shape ", errors.shape)
anomaly_mask = pd.Series(errors) > threshold
preds = anomaly_mask.map(lambda x: 0.0 if x == True else 1.0)
return preds
# print("test_df['spectrograms'] ", train_samples )
# print("x_train TYPE ", type(train_samples) )
threshold = find_threshold(model, train_samples)
# threshold = 0.01313
print(f"Threshold: {threshold}")
# Threshold: 0.01001314025746261
predictions = get_predictions(model, test_samples, threshold)
accuracy_score(predictions, y_test)
print(f"Accuracy: {accuracy_score(predictions, y_test)}")
# -
# ## #Chunk 2
# ### Import Meta data (file path information)
# import meta data
# Meta data csv contain different additional information about each case.
# One column contains the path to the .wav files of each case
df_meta = pd.read_csv('./CoronaHack-Respiratory-Sound-Dataset/Corona-Hack-Respiratory-Sound-Metadata.csv')
df_meta.info(), df_meta.shape
df_meta.head()
# ## #Chunk 3
# ### Get the label for each case
# +
#Get the label (healthy / COVID)
#split COVID STATUS column to get labels in column 'split'
df_meta['split'] = df_meta['COVID_STATUS'].str.split('_').str.get(0)
#Check for NA
df_meta.loc[:,'counting-normal'].isna().sum()
df_meta.loc[:,'split'].value_counts()
#Generate a dict to re-categorize the split column
cat_dict = {'healthy':0,'no':0,'resp':0,'recovered':0,'positive':1}
#map cat_dict to split column
df_meta.loc[:,'split'] = df_meta.loc[:,'split'].map(cat_dict)
df_meta2 = df_meta.dropna(subset=['split'])
df_meta2.loc[:,'split'] = df_meta2.loc[:,'split'].astype('int32')
#Extract positive USER ID
df_meta_positives = df_meta[df_meta['split'] == 1]
df_meta_negatives = df_meta[df_meta['split'] == 0]
positives = list(df_meta_positives['USER_ID'])
negatives = list(df_meta_negatives['USER_ID'])
len(positives),len(negatives)
#positives
# -
# ## #Chunk 5
# ### generate Function to create the input data for auto-encoder
# +
# Create function to load and prepare data for input
# here we want to use the 9 recordings as separate features but grouped per case as input to the auto-encoder
#names of 9 recordings per each case (extracted from the csv meta data file from )
#names_input = ['counting-normal','counting-fast','breathing-deep','breathing-shallow','cough-heavy','cough-shallow','vowel-a','vowel-e','vowel-o']
#label column from the meta data csv (#Chunk 3)
name_label = 'split'
def create_input_label(df=df_meta2,names=names_input,name_label=name_label):
input_dic = {} #Use a dictionnary to put in the 9 records per case
base_path = './CoronaHack-Respiratory-Sound-Dataset'
for index,name in enumerate(names):
#print(index,name)
print("Create input run")
path_list = df[name].tolist()
print(path_list[:10])
path_name = []
for dir_name in path_list:
path_name.append(base_path+str(dir_name))
print(path_name[:10])
print("Sound paths convert to tensor")
sound_paths_tensor = tf.convert_to_tensor(path_name, dtype=tf.string) #convert to tensor
print("Sound PATH", sound_paths_tensor[0])
print("Sound Dataset from tensor slices")
sound = tf.data.Dataset.from_tensor_slices(sound_paths_tensor)
print("Sound PATH from slices", sound[0])
#sound = tf.data.Dataset.from_generator(lambda sample: preprocess_other(sample).batch(32), output_types=tf.int32, output_shapes = (64,64,1),)
print("Calling preprocessing")
print("SOUNDD", sound)
input_dic['x_{}'.format(index)] = sound.map(lambda sample: preprocess_other(sample)) #generating the names of recordings(features x_0 till x_8) in batch mode
path_label = df[name_label]
#print(path_label)
y = tf.convert_to_tensor(path_label, dtype=tf.int16)
return input_dic,y
# -
x,y = create_input_label()
x = list(x.values())
x
# ## #Chunk 4
# ### Define Function for .wav import and preprocessing
# +
# Write function for import and preprocessing of all 9 .wav files per case (code adapted from Tristan classes)
import cv2
def preprocess_other(sample):
print("Start preprocessing, setting up the shape of sample")
print("Sample", sample)
audio = sample
#label = sample['label']
audio = tf.reshape(sample, [-1])
print("PY-PREPROCESS set audio file as float", type(audio))
audio = tf.cast(audio, tf.float32) #set audio file as float
#audio = audio[24500:5000+len(audio)//10]
# Plot audio amplitude
# plt.figure(figsize=(10,15))
# plt.plot(audio)
# plt.show()
# plt.close()
print(audio)
print("PY-PREPROCESS generate the mel spectrogram")
#generate the mel spectrogram
spectrogram = tfio.audio.spectrogram(
audio, nfft=1024, window=1024, stride=64
)
spectrogram = tfio.audio.melscale(
spectrogram, rate=8000, mels=64, fmin=0, fmax=2000 #mels = bins, fmin,fmax = frequences
)
print("PY-PREPROCESS devide by np.max(audio)")
spectrogram /= tf.math.reduce_max(spectrogram) #normalization
spectrogram = tf.expand_dims(spectrogram, axis=-1) #add dimension 2D -> 3D
spectrogram = tf.image.resize(spectrogram, (image_target_height, image_target_height)) #resize in two dimensions
spectrogram = tf.transpose(spectrogram, perm=(1, 0, 2)) #transpose the first two axis
spectrogram = spectrogram[::-1, :, :] #flip the first axis(frequency)
# plt.figure(figsize=(10,15))
# plt.imshow(spectrogram[::-1,:], cmap='inferno') #flipping upside down
# plt.show()
# plt.close()
# RESHAPE TO FIT VAE MODEL, RESHAPING THE NORMAL FINAL OUTPUT (DATASET) IS NOT POSSIBLE SO WE DO IT HERE
# WHILE IT´S STILL A TENSOR
#
#spectrogram = tf.reshape(spectrogram, [-1 ,28, 28, 1])
print("SPRECTROGRAM: ", spectrogram)
return spectrogram
print("PREPROCESS - apply py_preprocess_audio function")
spectrogram = tf.py_function(py_preprocess_audio, [audio], tf.float32) #apply py_process_audio function
print("PREPROCESS - set shape, include channel dimension")
spectrogram.set_shape((image_target_height, image_target_width, 1)) #set shape, include channel dimension
return spectrogram#, label
# +
# Experimental version of above
import matplotlib.pyplot as plt
import tensorflow_io as tfio
# Create function to load and prepare data for input
# here we want to use the 9 recordings as separate features but grouped per case as input to the auto-encoder
#names of 9 recordings per each case (extracted from the csv meta data file from )
#names_input = ['counting-normal','counting-fast','breathing-deep','breathing-shallow','cough-heavy','cough-shallow','vowel-a','vowel-e','vowel-o']
names_input = ['counting-normal']
#label column from the meta data csv (#Chunk 3)
name_label = 'split'
image_target_height, image_target_width = 28, 28
IS_VAE = True
def create_input_label2(df=df_meta2,names=names_input,name_label=name_label):
input_dic = {} #Use a dictionnary to put in the 9 records per case
base_path = './CoronaHack-Respiratory-Sound-Dataset'
for index,name in enumerate(names):
print(index,name)
print("create path list")
path_list = df[name].tolist()
print(path_list[:10])
path_name = []
print("create path name")
for dir_name in path_list:
if dir_name is not None:
path_name.append(base_path+str(dir_name))
#path_name = base_path+str(path_list[0])
print("create sound tensor")
sound_tensor_list = [tfio.audio.AudioIOTensor(sound_path).to_tensor()[:300000] for sound_path in path_name]
sound_rate_tensor_list = tfio.audio.AudioIOTensor(path_name[0]).rate
print("DIRTY", len(sound_tensor_list))
sound_tensor_list_clean = [sound_tensor for sound_tensor in sound_tensor_list if sound_tensor.shape[0] == 300000]
print("CLEAN", len(sound_tensor_list_clean))
print("SHAPE ME", sound_tensor_list[0][:100000].shape)
print("RATE ME", sound_rate_tensor_list)
print("create Sound Slices")
sound_slices = tf.data.Dataset.from_tensor_slices(sound_tensor_list_clean)
print("create input dictionary")
input_dic['x_{}'.format(index)] = sound_slices.map(lambda sample: preprocess_other(sample)) #generating the names of recordings(features x_0 till x_8) in batch mode
break
path_label = df[name_label]
print(path_label)
y = tf.convert_to_tensor(path_label, dtype=tf.int16)
return input_dic, y
# -
# ## #Chunk 6
# ### test the output from function
x_, y = create_input_label2()
x_ = list(x_.values())
x_[0].batch(256)
# ## #Chunk 7
# ### Built the auto-encoder architecture (code adapted from Tristan Class)
# +
from tensorflow.keras import models, layers
image_target_height, image_target_width
class AutoEncoder(tf.keras.Model):
def __init__(self, latent_dim):
super().__init__()
self.latent_dim = latent_dim
# Encoder
self.encoder_reshape = layers.Reshape((image_target_height * image_target_width,)) #Shape as 64,64,1
self.encoder_fc1 = layers.Dense(32, activation="relu")
self.encoder_fc2 = layers.Dense(latent_dim, activation="relu")
# Decoder
self.decoder_fc1 = layers.Dense(32, activation='relu')
self.decoder_fc2 = layers.Dense(image_target_height * image_target_width, activation='sigmoid')
self.decoder_reshape = layers.Reshape((image_target_height, image_target_width,1))
self._build_graph()
def _build_graph(self):
input_shape = (image_target_height, image_target_width, 1)
self.build((None,)+ input_shape)
inputs = tf.keras.Input(shape=input_shape)
_= self.call(inputs)
def call(self, x):
z = self.encode(x)
x_new = self.decode(z)
return x_new
def encode(self, x):
x = self.encoder_reshape(x)
x = self.encoder_fc1(x)
z = self.encoder_fc2(x)
return z
def decode(self, z):
z = self.decoder_fc1(z)
z = self.decoder_fc2(z)
x = self.decoder_reshape(z)
return x
autoencoder = AutoEncoder(32)
autoencoder.summary()
autoencoder.compile(
optimizer='rmsprop',
loss='binary_crossentropy'
)
# -
autoencoder.summary
# ## #Chunk 8
# ### Train the model
#
# Here we try to input the 9 features (recordings per case) into the model architecture
#list(x[0].as_numpy_iterator())
print(x[0])
print(x[0].batch(256))
print(x[0].take(6))
#dataset
# +
history_list = {}
#dataset = tf.data.Dataset.from_tensor_slices((x[0],x[0]))
dataset = tf.data.Dataset.zip((x[0],x[0]))
history = autoencoder.fit(
dataset.batch(256),
epochs = 20
)
history_list['base'] = history
# -
# ## #Chunk 9
# ### Variatioal Auto-Encoder Architecture
# +
from tensorflow import keras
from tensorflow.keras import layers
class Sampling(layers.Layer):
"""Uses (z_mean, z_log_var) to sample z, the vector encoding a digit."""
def call(self, inputs):
z_mean, z_log_var = inputs
batch = tf.shape(z_mean)[0]
dim = tf.shape(z_mean)[1]
epsilon = tf.keras.backend.random_normal(shape=(batch, dim))
return z_mean + tf.exp(0.5 * z_log_var) * epsilon
# +
latent_dim = 2
encoder_inputs = keras.Input(shape=(28, 28, 1))
x = layers.Conv2D(32, 3, activation="relu", strides=2, padding="same")(encoder_inputs)
x = layers.Conv2D(64, 3, activation="relu", strides=2, padding="same")(x)
x = layers.Flatten()(x)
x = layers.Dense(16, activation="relu")(x)
z_mean = layers.Dense(latent_dim, name="z_mean")(x)
z_log_var = layers.Dense(latent_dim, name="z_log_var",activation="relu")(x)
z = Sampling()([z_mean, z_log_var])
encoder = keras.Model(encoder_inputs, [z_mean, z_log_var, z], name="encoder")
encoder.summary()
# -
latent_inputs = keras.Input(shape=(latent_dim,))
x = layers.Dense(7 * 7 * 64, activation="relu")(latent_inputs)
x = layers.Reshape((7, 7, 64))(x)
x = layers.Conv2DTranspose(64, 3, activation="relu", strides=2, padding="same")(x)
x = layers.Conv2DTranspose(32, 3, activation="relu", strides=2, padding="same")(x)
decoder_outputs = layers.Conv2DTranspose(1, 3, activation="sigmoid", padding="same")(x)
decoder = keras.Model(latent_inputs, decoder_outputs, name="decoder")
decoder.summary()
# +
class VAE(keras.Model):
def __init__(self, encoder, decoder, **kwargs):
super(VAE, self).__init__(**kwargs)
self.encoder = encoder
self.decoder = decoder
self.total_loss_tracker = keras.metrics.Mean(name="total_loss")
self.reconstruction_loss_tracker = keras.metrics.Mean(
name="reconstruction_loss"
)
self.kl_loss_tracker = keras.metrics.Mean(name="kl_loss")
@property
def metrics(self):
return [
self.total_loss_tracker,
self.reconstruction_loss_tracker,
self.kl_loss_tracker,
]
def train_step(self, data):
with tf.GradientTape() as tape:
z_mean, z_log_var, z = self.encoder(data)
reconstruction = self.decoder(z)
reconstruction_loss = tf.reduce_mean(
tf.reduce_sum(
keras.losses.binary_crossentropy(data, reconstruction), axis=(1, 2)
)
)
kl_loss = -0.5 * (1 + z_log_var - tf.square(z_mean) - tf.exp(z_log_var))
kl_loss = tf.reduce_mean(tf.reduce_sum(kl_loss, axis=1))
total_loss = reconstruction_loss + kl_loss
grads = tape.gradient(total_loss, self.trainable_weights)
self.optimizer.apply_gradients(zip(grads, self.trainable_weights))
self.total_loss_tracker.update_state(total_loss)
self.reconstruction_loss_tracker.update_state(reconstruction_loss)
self.kl_loss_tracker.update_state(kl_loss)
return {
"loss": self.total_loss_tracker.result(),
"reconstruction_loss": self.reconstruction_loss_tracker.result(),
"kl_loss": self.kl_loss_tracker.result(),
}
# -
vae_input = x_[0].batch(256)
vae_input
#vae_input.reshape(None, 28, 28, 1)
# +
vae_input = x_[0].batch(5500)
mymodel = VAE(encoder, decoder)
mymodel.compile(optimizer=keras.optimizers.Adam(learning_rate=1e-6))
mymodel.fit(
vae_input,
epochs = 20
)
mymodel.summary()
# +
history_list = {}
history = mymodel.fit(
x[0],
epochs = 20,
batch_size=32
)
history_list['base'] = history
# -
|
2021-10-04-Corona-V6.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# %matplotlib inline
# %load_ext autoreload
# %autoreload 2
import seaborn as sns
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
# -
df = pd.read_csv('tune_random_forest.csv')
df.shape
df.columns
print("features {}".format(df['feature'].value_counts().to_dict().keys()))
print("depth {}".format(list(df['depth'].value_counts().to_dict().keys())))
print("trees {}".format(list(df['trees'].value_counts().to_dict().keys())))
df['rmse'].describe()
df.ix[df['rmse'].idxmin()]
rdkit = df.loc[df['feature'] == 'rdkit']
rdkit.shape
cdk = df.loc[df['feature'] == 'cdk']
cdk.shape
# +
fig, axes = plt.subplots(nrows=3, ncols=2, figsize=(12, 15))
sns.pointplot(x='trees', y='rmse', hue='depth', data=rdkit, ax=axes[0][0])
sns.pointplot(x='depth', y='rmse', hue='trees', data=rdkit, ax=axes[0][1])
sns.pointplot(x='trees', y='rmse', hue='depth', data=cdk, ax=axes[1][0])
sns.pointplot(x='depth', y='rmse', hue='trees', data=cdk, ax=axes[1][1])
sns.pointplot(x='feature', y='rmse', hue='trees', data=df, ax=axes[2][0])
sns.pointplot(x='feature', y='rmse', hue='depth', data=df, ax=axes[2][1])
# -
rdkit['rmse'].describe()
cdk['rmse'].describe()
|
jupyter-notebooks/Random forest pipeline analysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="cAJ1JuabN2Tc" colab_type="code" colab={}
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# %config InlineBackend.figure_format = 'retina'
# + [markdown] id="ItlhPB2oSx8f" colab_type="text"
# # Confirmados
# + id="YX88cZ-ON8TM" colab_type="code" colab={}
# Bing
# url = 'https://raw.githubusercontent.com/microsoft/Bing-COVID-19-Data/master/data/Bing-COVID19-Data.csv'
# df = pd.read_csv(url)
# + id="eG7Su9gnPV6T" colab_type="code" colab={}
# Johns Hopkins
url = 'https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_confirmed_global.csv'
df = pd.read_csv(url)
# + id="7wvix8ZQRNBz" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 284} outputId="979ee8af-e633-49f6-b92b-ae0c67116b00"
confirmed = df.groupby(['Country/Region']).sum()
confirmed = confirmed.drop(columns=['Lat', 'Long'])
confirmed.head()
# + [markdown] id="6e5uMSRkS1z9" colab_type="text"
# # Mortes
# + id="njgyeRV_S1OY" colab_type="code" colab={}
url = 'https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_deaths_global.csv'
df = pd.read_csv(url)
# + id="AAjQolUoTKSF" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 284} outputId="f2c6c932-2c8a-44bf-fc73-25bb8c13e8c4"
deaths = df.groupby(['Country/Region']).sum()
deaths = deaths.drop(columns=['Lat', 'Long'])
deaths.head()
# + [markdown] id="rB5BuooYTeLy" colab_type="text"
# # Recuperados
# + id="Za92aHh_Tdfl" colab_type="code" colab={}
url = 'https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_recovered_global.csv'
df = pd.read_csv(url)
# + id="rtAid2xnTda9" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 284} outputId="03f4bf52-ee47-4909-caa1-5c7a0afb4f9d"
recovered = df.groupby(['Country/Region']).sum()
recovered = recovered.drop(columns=['Lat', 'Long'])
recovered.head()
# + [markdown] id="QF7uPg3IULQs" colab_type="text"
# # Visualização
# + id="anseuh59UN11" colab_type="code" colab={}
pais = 'Brazil'
# + id="UW9jWpEsUXUU" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 385} outputId="29c54fa3-65ed-4327-df80-8650c71fffc8"
# agrupado
fig, ax = plt.subplots(figsize=(8, 6))
sel = confirmed.loc[pais].T
sel.index = pd.to_datetime(sel.index)
sel.plot(ax=ax, label='Confirmados')
sel = deaths.loc[pais].T
sel.index = pd.to_datetime(sel.index)
sel.plot(ax=ax, label='Mortes')
sel = recovered.loc[pais].T
sel.index = pd.to_datetime(sel.index)
sel.plot(ax=ax, label='Recuperados')
plt.legend()
plt.grid()
plt.show()
# + id="4odg3elIRN6i" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 385} outputId="4eddd17a-65b3-4e9f-c12a-02d6794848d4"
# confirmados
fig, ax = plt.subplots(figsize=(8, 6))
sel = confirmed.loc[pais].T
sel.index = pd.to_datetime(sel.index)
sel.plot(ax=ax)
plt.show()
# + id="mYlauTUORmV6" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 385} outputId="f64b9a07-2a6b-4a42-f705-9188e75ccd88"
# mortes
fig, ax = plt.subplots(figsize=(8, 6))
sel = deaths.loc[pais].T
sel.index = pd.to_datetime(sel.index)
sel.plot(ax=ax)
plt.show()
# + id="1q_xacI6TWh8" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 385} outputId="1f64b8c7-8dd4-4ff2-dbe7-ce1f371de879"
# recuperados
fig, ax = plt.subplots(figsize=(8, 6))
sel = recovered.loc[pais].T
sel.index = pd.to_datetime(sel.index)
sel.plot(ax=ax)
plt.show()
# + id="C5XeSxoyUI2p" colab_type="code" colab={}
|
notebooks/COVID_JohnsHopkins.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: conda_mxnet_p36
# language: python
# name: conda_mxnet_p36
# ---
# ## MNIST Training, Compilation and Deployment with MXNet Module and Sagemaker Neo
#
# The **SageMaker Python SDK** makes it easy to train and deploy MXNet models. In this example, we train a simple neural network using the Apache MXNet [Module API](https://mxnet.apache.org/api/python/module/module.html) and the MNIST dataset. The MNIST dataset is widely used for handwritten digit classification, and consists of 70,000 labeled 28x28 pixel grayscale images of hand-written digits. The dataset is split into 60,000 training images and 10,000 test images. There are 10 classes (one for each of the 10 digits). The task at hand is to train a model using the 60,000 training images and subsequently test its classification accuracy on the 10,000 test images.
#
# ### Setup
#
# First we need to define a few variables that will be needed later in the example.
# + isConfigCell=true
from sagemaker import get_execution_role
from sagemaker.session import Session
# S3 bucket for saving code and model artifacts.
# Feel free to specify a different bucket here if you wish.
bucket = Session().default_bucket()
# Location to save your custom code in tar.gz format.
custom_code_upload_location = 's3://{}/customcode/mxnet'.format(bucket)
# Location where results of model training are saved.
model_artifacts_location = 's3://{}/artifacts'.format(bucket)
# IAM execution role that gives SageMaker access to resources in your AWS account.
# We can use the SageMaker Python SDK to get the role from our notebook environment.
role = get_execution_role()
# -
# ### The training script
#
# The ``mnist.py`` script provides all the code we need for training and hosting a SageMaker model. The script we will use is adaptated from Apache MXNet [MNIST tutorial](https://mxnet.incubator.apache.org/tutorials/python/mnist.html).
# !cat mnist.py
# In the training script, there are two additional functions, to be used with Neo Deep Learning Runtime:
# * `neo_preprocess(payload, content_type)`: Function that takes in the payload and Content-Type of each incoming request and returns a NumPy array. Here, the payload is byte-encoded NumPy array, so the function simply decodes the bytes to obtain the NumPy array.
# * `neo_postprocess(result)`: Function that takes the prediction results produced by Deep Learining Runtime and returns the response body
# ### SageMaker's MXNet estimator class
# The SageMaker ```MXNet``` estimator allows us to run single machine or distributed training in SageMaker, using CPU or GPU-based instances.
#
# When we create the estimator, we pass in the filename of our training script, the name of our IAM execution role, and the S3 locations we defined in the setup section. We also provide a few other parameters. ``train_instance_count`` and ``train_instance_type`` determine the number and type of SageMaker instances that will be used for the training job. The ``hyperparameters`` parameter is a ``dict`` of values that will be passed to your training script -- you can see how to access these values in the ``mnist.py`` script above.
#
# For this example, we will choose one ``ml.m4.xlarge`` instance.
# +
from sagemaker.mxnet import MXNet
mnist_estimator = MXNet(entry_point='mnist.py',
role=role,
output_path=model_artifacts_location,
code_location=custom_code_upload_location,
train_instance_count=1,
train_instance_type='ml.m4.xlarge',
framework_version='1.4.0',
distributions={'parameter_server': {'enabled': True}},
hyperparameters={'learning-rate': 0.1})
# -
# ### Running the Training Job
# After we've constructed our MXNet object, we can fit it using data stored in S3. Below we run SageMaker training on two input channels: **train** and **test**.
#
# During training, SageMaker makes this data stored in S3 available in the local filesystem where the mnist script is running. The ```mnist.py``` script simply loads the train and test data from disk.
# +
# %%time
import boto3
region = boto3.Session().region_name
train_data_location = 's3://sagemaker-sample-data-{}/mxnet/mnist/train'.format(region)
test_data_location = 's3://sagemaker-sample-data-{}/mxnet/mnist/test'.format(region)
mnist_estimator.fit({'train': train_data_location, 'test': test_data_location})
# -
# ### Opimtize your model with Neo API
# Neo API allows to optimize our model for a specific hardware type. When calling `compile_model()` function, we specify the target instance family (C5) as well as the S3 bucket to which the compiled model would be stored.
#
# **Important. If the following command result in a permission error, scroll up and locate the value of execution role returned by `get_execution_role()`. The role must have access to the S3 bucket specified in ``output_path``.**
output_path = '/'.join(mnist_estimator.output_path.split('/')[:-1])
compiled_model = mnist_estimator.compile_model(target_instance_family='ml_c5',
input_shape={'data':[1, 784]},
role=role,
output_path=output_path)
# ### Creating an inference Endpoint
#
# We can deploy this compiled model, note that we need to use the same instance that the target we used for compilation. This creates a SageMaker endpoint that we can use to perform inference.
#
# The arguments to the ``deploy`` function allow us to set the number and type of instances that will be used for the Endpoint. Make sure to choose an instance for which you have compiled your model, so in our case `ml_c5`. Neo API uses a special runtime (DLR runtime), in which our optimzed model will run.
predictor = compiled_model.deploy(initial_instance_count = 1, instance_type = 'ml.c5.4xlarge')
# This endpoint will receive uncompressed NumPy arrays, whose Content-Type is given as `application/vnd+python.numpy+binary`:
# +
import io
import numpy as np
def numpy_bytes_serializer(data):
f = io.BytesIO()
np.save(f, data)
f.seek(0)
return f.read()
predictor.content_type = 'application/vnd+python.numpy+binary'
predictor.serializer = numpy_bytes_serializer
# -
# ### Making an inference request
#
# Now that our Endpoint is deployed and we have a ``predictor`` object, we can use it to classify handwritten digits.
#
# To see inference in action, draw a digit in the image box below. The pixel data from your drawing will be loaded into a ``data`` variable in this notebook.
#
# *Note: after drawing the image, you'll need to move to the next notebook cell.*
from IPython.display import HTML
HTML(open("input.html").read())
# Now we can use the ``predictor`` object to classify the handwritten digit:
# +
data = np.array(data)
response = predictor.predict(data)
print('Raw prediction result:')
print(response)
labeled_predictions = list(zip(range(10), response))
print('Labeled predictions: ')
print(labeled_predictions)
labeled_predictions.sort(key=lambda label_and_prob: 1.0 - label_and_prob[1])
print('Most likely answer: {}'.format(labeled_predictions[0]))
# -
# ## Conclusion
# ---
# SageMaker Neo automatically optimizes machine learning models to perform at up to fourth the speed with no loss in accuracy. In the diagram below shows you how our neo-optimized model performs better than the original mxnet mnist model. The originl model stands for the uncompiled model deployed on Flask container on May 26th, 2019 and neo-optimized model stands for the compiled model deployed on Neo-AI-DLR container. The data for each trial is the average of 1000 trys for each endpoint.
# 
# # (Optional) Delete the Endpoint
#
# After you have finished with this example, remember to delete the prediction endpoint to release the instance(s) associated with it.
print("Endpoint name: " + predictor.endpoint)
import sagemaker
predictor.delete_endpoint()
|
sagemaker_neo_compilation_jobs/mxnet_mnist/mxnet_mnist_neo.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernel_info:
# name: work
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
## Import all dependencies
from splinter import Browser
from bs4 import BeautifulSoup as bs
import pandas as pd
import time
from webdriver_manager.chrome import ChromeDriverManager
## Set up Splinter
executable_path = {'executable_path': ChromeDriverManager().install()}
browser = Browser('chrome', **executable_path, headless=False)
## Visit redplanetscience.com
url = "https://redplanetscience.com/"
browser.visit(url)
time.sleep(1)
## Scrape webpage into BSoup
html = browser.html
soup = bs(html, "html.parser")
## Establish Soup Variables for first result for webscrape
news_title = soup.find_all('div', class_='content_title')[0].text
news_p = soup.find_all('div', class_='article_teaser_body')[0].text
# +
## Print first news title
print(news_title)
# +
## Print first news paragraph
print(news_p)
# -
# ## Visit Mars Space Images - Featured Image
## Visit redplanetscience.com
url = "https://spaceimages-mars.com"
browser.visit(url)
time.sleep(1)
## Scrape webpage into BSoup
html = browser.html
soup = bs(html, "html.parser")
## find the image url link
image_link = soup.find('img', class_='headerimage fade-in').get('src')
image_link
## Establish Image URL with scraped HREF
featured_image_url = f'https://spaceimages-mars.com/{image_link}'
featured_image_url
# ### Mars Facts
### Visit galaxyfacts-mars.com
url = 'https://galaxyfacts-mars.com'
## Establish variable to containe pd df data
tables = pd.read_html(url)
tables
## Establish DF
df = tables[0]
df.head()
## convert the data to a HTML table string
html_table = df.to_html()
html_table
# ### Mars Hemispheres
url = 'https://marshemispheres.com/'
browser.visit(url)
html=browser.html
soup=bs(html,'html.parser')
## Scrape hemispheres image elements in to variables
mars_spheres = soup.find('div',class_='collapsible results')
mars_images = mars_spheres.find_all('div',class_='item')
## Establish List to hold all image urls
mars_image_urls=[]
# +
## Begin Loop cycling through all hemisphere imagess
for images in mars_images:
try:
## scrape title
hem_sphere=images.find('div',class_='description')
title=hem_sphere.h3.text
## scrape image url
hem_sphere_url=hem_sphere.a['href']
browser.visit(url+hem_sphere_url)
html = browser.html
soup = bs(html,'html.parser')
image_src = soup.find('li').a['href']
if (title and image_src):
## Print results
print('-----------------')
print('Title: '+ title)
print(url + image_src)
## Create dict (title and url)
hem_sphere_dict={
'title':title,
'image_url':image_src}
mars_image_urls=[].append(hem_sphere_dict)
except Exception as error:
print(error)
# -
|
Mission_to_Mars.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Numpy Review
# # 1- Basic Introduction
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
print(np.__version__)
# ## NumPy Creating Arrays
# +
# Creat Object array in numpy (ndarray)
arr = np.array([0, 1, 2, 3, 4, 5])
print(arr)
print(type(arr))
# +
# 0-D Arrays
arr = np.array(5)
print(arr)
print(arr.ndim)
# +
# 1-D Arrays
arr = np.array([0, 1, 2, 3, 4, 5])
print(arr)
print(arr.ndim)
# +
# 2-D Arrays
arr = np.array([[0, 1, 2, 3], [4, 5, 6, 7]])
print(arr)
print(arr.ndim)
# +
# 3-D Arrays
arr = np.array([[[0, 1, 2], [3, 4, 5]], [[6, 7, 8], [9, 10, 11]]])
print(arr)
print(arr.ndim)
# +
# Higher Dimensional Arrays
arr = np.array([0, 1, 2, 3, 4, 5], ndmin=5)
print(arr)
print(arr.ndim)
# -
# ## NumPy Array Indexing
arr = np.array([0, 1, 2, 3, 4, 5, 6,7, 8, 9, 10, 11, 12, 13, 14, 15])
print(arr)
# +
# Accessing the elements of 1-D Arrays using a positive index
print(arr[0])
print(arr[1])
print(arr[2])
print(arr[3])
print(arr[4])
# Accessing the elements of 1-D matrices using the negative index
print(arr[-1])
print(arr[-2])
print(arr[-3])
print(arr[-4])
print(arr[-5])
# -
arr = np.array([[0, 1, 2, 3, 4], [5, 6, 7, 8, 9], [10, 11, 12, 13, 14]])
print(arr)
# +
# Accessing the elements of 2-D Arrays using a positive index
print(arr[0, 0])
print(arr[0, 1])
print(arr[0, 2])
print(arr[1, 0])
print(arr[1, 1])
print(arr[1, 2])
print(arr[2, 0])
print(arr[2, 1])
print(arr[2, 2])
# Accessing the elements of 1-D matrices using the negative index
print(arr[-1, -1])
print(arr[-1, -2])
print(arr[-1, -3])
print(arr[-2, -1])
print(arr[-2, -2])
print(arr[-2, -3])
print(arr[-3, -1])
print(arr[-3, -2])
print(arr[-3, -3])
# Accessing the elements of 1-D matrices using the negative and positive index
print(arr[1, -1])
print(arr[1, -2])
print(arr[1, -3])
print(arr[-2, 0])
print(arr[-2, 1])
print(arr[-2, 2])
print(arr[-3, 0])
print(arr[2, -2])
print(arr[-3, 2])
# -
arr = np.array([[[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]], [[10, 11, 12, 13, 14], [15, 16, 17, 18, 19]]])
print(arr)
# +
# Accessing the elements of 3-D Arrays using a positive index
print(arr[0, 0, 0])
print(arr[0, 1, 1])
print(arr[1, 1, 2])
print(arr[1, 0, 0])
print(arr[1, 1, 1])
print(arr[1, 0, 3])
# Accessing the elements of 3-D matrices using the negative index
print(arr[-1, -1, -1])
print(arr[-1, -2, -3])
print(arr[-1, -1, -2])
print(arr[-2, -1, -1])
print(arr[-2, -2, -3])
print(arr[-2, --1, -4])
# Accessing the elements of 3-D matrices using the negative and positive index
print(arr[1, -1, 0])
print(arr[1, -2, -3])
print(arr[1, -1, 2])
print(arr[-2, 0, 0])
print(arr[-2, 1, -2])
print(arr[-2, 1, 3])
# -
# ## NumPy Array Slicing
arr = np.array([0, 1, 2, 3, 4, 5, 6,7, 8, 9, 10, 11, 12, 13, 14, 15])
print(arr)
# +
print(arr[1:10])
print(arr[2:13])
print(arr[:10])
print(arr[5:])
print(arr[:])
print(arr[-10:-2])
print(arr[-14:-8])
print(arr[::3])
# -
arr = np.array([[0, 1, 2, 3, 4], [5, 6, 7, 8, 9], [10, 11, 12, 13, 14]])
print(arr)
# +
print(arr[0, 2:4])
print(arr[1, 0:3])
print(arr[-1, 2:4])
print(arr[-2, 0:3])
print(arr[0, -4:-1])
print(arr[-2, :-1])
print(arr[:, -3])
print(arr[:1, 2])
print(arr[-2:, :])
# -
# ## NumPy Data Types
# +
# i - integer
# b - boolean
# u - unsigned integer
# f - float
# c - complex float
# m - timedelta
# M - datetime
# O - object
# S - string
# U - unicode string
# V - fixed chunk of memory for other type ( void )
# +
arr = np.array([0, 1, 2, 3, 4, 5])
print(arr)
print(arr.dtype)
# +
arr = np.array(['A', 'B', 'C'])
print(arr)
print(arr.dtype)
# +
arr = np.array([0, 1, 2, 3, 4], dtype='S')
print(arr)
print(arr.dtype)
# +
arr = np.array(['', 'A', 'B', 'C'], dtype=bool)
print(arr)
print(arr.dtype)
# +
arr = np.array([0, 1, 2, 3, 4, 5])
arr_S = arr.astype('S')
arr_bool = arr.astype(bool)
print(f"arr: {arr} type array: {arr.dtype}")
print(f"arr_S: {arr_S} type array: {arr_S.dtype}")
print(f"arr_bool: {arr_bool} type array: {arr_bool.dtype}")
# -
# ## NumPy Array Copy vs View
# +
# Copy
arr = np.array([0, 1, 2, 3, 4, 5])
print(arr)
copy = arr.copy()
arr[0] = 10
copy[1] = 20
print(arr)
print(copy)
# +
# View
arr = np.array([0, 1, 2, 3, 4, 5])
print(arr)
view = arr.view()
arr[0] = 10
view[1] = 20
print(arr)
print(view)
# -
# Copy VS View
print(view.base)
print(copy.base)
# ## NumPy Array Shape
arr = np.array([1, 2, 3, 4, 5])
print(arr.shape)
arr = np.array([[1, 2, 3, 4, 5], [6, 7, 8, 9, 10], [11, 12, 13, 14, 15]])
print(arr.shape)
arr = np.array([[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]], [[1, 2, 3], [4, 5, 6]]])
print(arr.shape)
arr = np.array([1, 2, 3, 4, 5], ndmin=10)
print(arr.shape)
# ## NumPy Array Reshaping
arr = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20])
print(f"Array: {arr}")
# +
# ERROR 4 * 6 != 20
# re = arr.reshape(4, 6)
# print(f"Array: {re}")
# +
re = arr.reshape(4, 5)
print(f"1- Array: {re}")
re = arr.reshape(5, 4)
print(f"2- Array: {re}")
re = arr.reshape(2, 2, 5, 1)
print(f"3- Array: {re}")
re = arr.reshape(2, 2, -1)
print(f"4- Array: {re}")
arr = np.array([[1, 2, 3, 4, 5], [6, 7, 8, 9, 10], [11, 12, 13, 14, 15], [16, 17, 18, 19, 20]])
print(f"5- Array: {arr}")
re = arr.reshape(-1)
print(f"6- Array: {re}")
print(f"7- Copy OR View: {re.base} Hmmmm (-_-) 'View'!!!")
# -
# ## NumPy Array Iterating
# +
arr = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
for i in np.nditer(arr):
print(i)
print("Lterating Other Data Type:")
for i in np.nditer(arr, flags=['buffered'], op_dtypes=['S']):
print(i)
# +
arr = np.array([[1, 2, 3, 4, 5], [6, 7, 8, 9, 10], [11, 12, 13, 14, 15]])
for i in np.nditer(arr):
print(i)
print("Lterating Other Data Type:")
for i in np.nditer(arr, flags=['buffered'], op_dtypes=['S']):
print(i)
# +
arr = np.array([[[1, 2, 3, 4, 5], [6, 7, 8, 9, 10]], [[11, 12, 13, 14, 15], [16, 17, 18, 19, 20]]])
for i in np.nditer(arr):
print(i)
print("Lterating Other Data Type:")
for i in np.nditer(arr, flags=['buffered'], op_dtypes=['S']):
print(i)
# -
arr = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
for i, j in np.ndenumerate(arr):
print(f"index: {i}, eleme: {j}")
arr = np.array([[1, 2, 3, 4, 5], [6, 7, 8, 9, 10], [11, 12, 13, 14, 15]])
for i, j in np.ndenumerate(arr):
print(f"index: {i}, eleme: {j}")
arr = np.array([[[1, 2, 3, 4, 5], [6, 7, 8, 9, 10]], [[11, 12, 13, 14, 15], [16, 17, 18, 19, 20]]])
for i, j in np.ndenumerate(arr):
print(f"index: {i}, eleme: {j}")
# ## NumPy Joining Array
# +
# Joining Arrays Using concatenate Functions
a = np.array([1, 2, 3, 4])
b = np.array([5, 6, 7, 8])
c = np.concatenate((a, b)) # a and b they have 1 dimansion beyt default axis=0
print(f"1- Array: \n{c}")
# +
a = np.array([[1, 2, 3, 4],
[5, 6, 7, 8]])
b = np.array([[9, 10, 11, 12],
[13, 14, 15, 16]])
c = np.concatenate((a, b)) # defauld axis = 0 = -1
print(f"2 A- Array: \n{c}")
c = np.concatenate((a, b), axis=0) # defauld axis = 0 = -1
print(f"2 B- Array: \n{c}")
c = np.concatenate((a, b), axis=1) # axis = 1 = -1
print(f"3- Array: \n{c}")
# +
a = np.array([[[1, 2, 3, 4, 5],
[6, 7, 8, 9, 10]],
[[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20]]])
b = np.array([[[21, 22, 23, 24, 25],
[26, 27, 28, 29, 30]],
[[31, 32, 33, 34, 35],
[36, 37, 38, 39, 40]]])
c = np.concatenate((a, b), axis=0) # defauld axis = 0 = -1
print(f"4- Array: \n{c}")
c = np.concatenate((a, b), axis=1) # axis 1 = -2
print(f"5- Array: \n{c}")
# +
# Joining Arrays Using stack Functions
a = np.array([1, 2, 3, 4])
b = np.array([5, 6, 7, 8])
c = np.stack((a, b)) # a and b they have 2 dimansion beyt default axis=0 = -1
print(f"6- Array: \n{c}")
c = np.stack((a, b), axis=1) # axis =1 = -2
print(f"7- Array: \n{c}")
# +
a = np.array([[1, 2, 3, 4],
[5, 6, 7, 8]])
b = np.array([[9, 10, 11, 12],
[13, 14, 15, 16]])
c = np.stack((a, b), axis=0)
print(f"8- Array: \n{c}")
c = np.stack((a, b), axis=1)
print(f"9- Array: \n{c}")
# +
a = np.array([[[1, 2, 3, 4, 5],
[6, 7, 8, 9, 10]],
[[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20]]])
b = np.array([[[21, 22, 23, 24, 25],
[26, 27, 28, 29, 30]],
[[31, 32, 33, 34, 35],
[36, 37, 38, 39, 40]]])
c = np.stack((a, b), axis=0)
print(f"10- Array: \n{c}")
c = np.stack((a, b), axis=1)
print(f"11- Array: \n{c}")
# +
# Joining Arrays Using hstack - vstack - dstack Functions
a = np.array([[[1, 2, 3, 4, 5],
[6, 7, 8, 9, 10]],
[[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20]]])
b = np.array([[[21, 22, 23, 24, 25],
[26, 27, 28, 29, 30]],
[[31, 32, 33, 34, 35],
[36, 37, 38, 39, 40]]])
c = np.hstack((a, b)) # hstack == concatenate with axis=1
print(f"12- Array: \n{c}")
c = np.vstack((a, b)) # hstack == concatenate with axis=0
print(f"13- Array: \n{c}")
c = np.dstack((a, b))
print(f"14- Array: \n{c}")
a = np.array([1, 2, 3, 4])
b = np.array([5, 6, 7, 8])
c = np.hstack((a, b)) # hstack == concatenate with axis=1
print(f"15- Array: \n{c}")
c = np.vstack((a, b)) # hstack == concatenate with axis=0
print(f"16- Array: \n{c}")
c = np.dstack((a, b))
print(f"17- Array: \n{c}")
# -
# ## NumPy Splitting Array
# +
arr = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15])
print(f'Array: \n{arr}')
print(f"1- Array: {np.array_split(arr, 5)}")
print(f"2- Array: {np.array_split(arr, 3)}")
print(f"3- Array: {np.array_split(arr, 4)}")
print(f"4- Array: {np.array_split(arr, 2)}")
print(f"5- Array: {np.array_split(arr, 6)}")
arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12], [13, 14, 15], [16, 17, 18]])
print(f"Array: \n{arr}")
print(f"1- Array: {np.array_split(arr, 6)}")
print(f"2- Array: {np.array_split(arr, 5)}")
print(f"3- Array: {np.array_split(arr, 3, axis=0)}")
print(f"4- Array: {np.array_split(arr, 3, axis=1)}")
print(f"5- Array: {np.hsplit(arr, 3)}")
print(f"6- Array: {np.vsplit(arr, 3)}")
# -
# ## NumPy Searching Arrays
# +
arr = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
print(f"1- {np.where(arr == 5)}")
print(f"2- {np.where(arr == 4)}")
print(f"3- {np.where(arr % 2 == 0)}")
print(f"4- {np.where(arr % 2 != 0)}")
print(f"5- {np.where(arr != 5)}")
print(f"6- {np.where(arr > 5)}")
arr = np.array([[0, 1, 2], [3, 4, 5], [6, 7, 8]])
print(f"1- {np.where(arr == 5)}")
print(f"2- {np.where(arr == 4)}")
print(f"3- {np.where(arr % 2 == 0)}")
print(f"4- {np.where(arr % 2 != 0)}")
print(f"5- {np.where(arr != 5)}")
print(f"6- {np.where(arr > 5)}")
# +
arr = np.array([1, 2, 3, 4, 5, 5])
print(f"1- {np.searchsorted(arr, 3)}")
print(f"2- {np.searchsorted(arr, 4, side='rigth')}")
print(f"3- {np.searchsorted(arr, 5)}")
print(f"4- {np.searchsorted(arr, [1, 2, 4])}")
arr = np.array([2, 1, 3, 5])
print(f"1- {np.searchsorted(arr, 1)}")
print(f"2- {np.searchsorted(arr, 2)}")
print(f"3- {np.searchsorted(arr, [1, 2, 5])}")
# -
# ## NumPy Sorting Arrays
# +
arr = np.array([4, 1, 5, 2, 3])
print(np.sort(arr))
print(arr)
print(np.sort(arr).base)
arr = np.array([True, False, True, False])
print(np.sort(arr))
arr = np.array(['Python', 'C', 'Java', 'SQL'])
print(np.sort(arr))
# -
# ## NumPy Filter Array
# +
# 1-
arr = np.array([1, 2, 3, 4, 5])
filter = [True, False, False, True, True]
new_arr = arr[filter]
print(new_arr)
# +
# 2- Creating the Filter Array
arr = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
filter = []
for i in arr:
if i % 2 == 0:
filter.append(True)
else:
filter.append(False)
new_arr = arr[filter]
print(new_arr)
filter = []
for i in arr:
if i % 2 != 0:
filter.append(True)
else:
filter.append(False)
new_arr = arr[filter]
print(new_arr)
# +
# 3- Creating Filter Directly From Array
new_arr = arr[arr % 2 == 0]
print(new_arr)
new_arr = arr[arr > 5]
print(new_arr)
new_arr = arr[arr < 5]
print(new_arr)
# -
# ## Some different things !!
# +
a = np.array([1, 2, 3, 4, 5], dtype='int16')
print(a)
print(a.itemsize) # 2byte > int16: 1byte = 8bet
print(a.size) # Nembers of items array
print(a.itemsize * a.size) # Totl Size of bytes
print(a.nbytes) # Total Size of bytes
b = np.array([[[1, 2], [3, 4]], [[5, 6], [7, 8]]])
print(b)
print(b[0, 0, 0])
b[0, 0, 0] = 0
print(b)
b[:, 1, :] = [[8,8], [9,9]]
print(b)
z = np.zeros((2, 5))
print(z)
o = np.ones((2, 5))
print(o)
f = np.full((2, 5), 95)
print(f)
f = np.full(b.shape, 95)
print(f)
fl = np.full_like(b, 77)
print(fl)
r = np.random.random_sample(b.shape)
print(r)
i = np.identity(5)
print(i)
r = np.repeat(b, 3, axis=0)
print(r)
a = np.array([1, 2, 3, 4, 5])
print(a + 2) # a += 2
print(a - 2) # a -= 2
print(a / 2) # a /= 2
print(a * 2) # a *= 2
a = np.array([1, 2, 3, 4])
b = np.array([5, 6, 7, 8])
print(a + b)
print(a - b)
print(a * b)
print(a / b)
print(a ** b)
a = np.array([1, 2, 3, 4, 5])
print(np.min(a)) # axis=(0,1,-1,-2) in array > 1 dimantion
print(np.max(a)) # axis=(0,1,-1,-2) in array > 1 dimantion
print(a > 2)
print(a%2 == 0)
b = np.array([[[1, 2, 9], [3, 4, 9]], [[5, 6, 7], [8, 7, 8]]])
print(b)
print(np.any(b > 5, axis=1))
print(np.all(b > 5, axis=1))
print((b >= 5) & (b < 9)) # ~((b >= 5) & (b < 9))
## read data from file
## text = np.genfromtext('path.extation', delimiter=',')
## cv = np.loadtext('path.extaion', dtype='O', delimiter=',', unpack=True, skiprows=1)
# -
# # 2- Random Data Sets
# ## Random Numbers in NumPy
# +
## 1- Create Random Number
# 1- Random Number Between 0 and 1
arr = np.random.rand()
print(f"1- Random Number: {arr}")
# 2- Random Number Between 0 and any Number
arr = np.random.randint(10)
print(f"2- Random Number: {arr}")
# 3- Choice Random Number from list, tuple,...
arr = np.random.choice([1, 2, 3, 4, 5])
print(f"3- Random Number: {arr}")
# +
## 2- Crate Array
# 1-
arr = np.random.rand(5)
print(f"1- Array: {arr}")
arr = np.random.rand(2, 5)
print(f"2- Array: {arr}")
# 2-
arr = np.random.randint(10, size=5)
print(f"3- Array: {arr}")
arr = np.random.randint(100, size=(2, 5))
print(f"4- Array: {arr}")
# 3-
arr = np.random.choice([1, 2, 3, 4, 5, 6, 7, 8, 9, 10], size=5)
print(f"5- Array: {arr}")
arr = np.random.choice(np.random.randint(1000, size=100), size=(2, 5))
print(f"6- Array: {arr}")
# -
# ## Random Data Distribution
# +
arr = np.random.choice([1, 2, 3, 4, 5], p=[0.4, 0.2, 0.0, 0.2, 0.2], size=100)
print(f"Array: {arr}")
# -
# ## Random Permutations
# +
import numpy as np
## 1- Shuffle
arr = np.array([1, 2, 3, 4, 5])
print(f"shuffle: {np.random.shuffle(arr)}")
print(f"Array: {arr}")
## 2- permutation
arr = np.array([1, 2, 3, 4, 5])
print(f"permutation: {np.random.permutation(arr)}")
print(f"Array: {arr}")
# -
# ## Normal (Gaussian) Distribution
# +
normal = np.random.normal(loc=0, scale=1, size=100)
print(normal)
# Visualization of Normal Distribution
normal = np.random.normal(size=1000)
sns.distplot(normal, hist=False)
plt.show()
# -
# ## Binomial Distribution
# +
binomial = np.random.binomial(n=100, p=0.5, size=10)
print(binomial)
# Visualization of Binomial Distribution
binomial = np.random.binomial(n=10000, p=0.5, size=1000)
sns.distplot(binomial, kde=False)
plt.show()
# -
# ## Poisson Distribution
# +
poisson = np.random.poisson(lam=2, size=10)
print(poisson)
# Visualization of Poisson Distribution
poisson = np.random.poisson(lam=2, size=1000)
sns.distplot(poisson, hist=False)
plt.show()
# -
# ## Uniform Distribution
# +
uniform = np.random.uniform(low=0, high=1000, size=100)
print(uniform)
# Visualization of Uniform Distribution
uniform= np.random.uniform(low=0, high=10000, size=1000)
sns.distplot(uniform, hist=False)
plt.show()
# -
# ## Logistic Distribution
# +
logistic = np.random.logistic(loc=0, scale=1, size=100)
print(logistic)
# Visualization of Logistic Distribution
logistic = np.random.logistic(loc=0, scale=1, size=1000)
sns.distplot(logistic, hist=False)
plt.show()
# -
# ## Multinomial Distribution
# +
multinomial = np.random.multinomial(n=6, pvals=[1/6, 1/6, 1/6, 1/6, 1/6, 1/6])
print(multinomial)
# Visualization of Multinomial Distribution
sns.distplot(multinomial, hist=False)
plt.show()
# -
# ## Exponential Distribution
# +
exponential = np.random.exponential(scale=1, size=100)
print(exponential)
# Visualization of Exponential Distribution
exponential = np.random.exponential(scale=1, size=1000)
sns.distplot(exponential, hist=False)
plt.show()
# -
# ## Chi Square Distribution
# +
chisquare = np.random.chisquare(df=3, size=10)
print(chisquare)
# Visualization of Chi Square Distribution
chisquare = np.random.chisquare(df=2, size=1000)
sns.distplot(chisquare, hist=False)
plt.show()
# -
# ## Rayleigh Distribution
# +
rayleigh = np.random.rayleigh(scale=1, size=10)
print(rayleigh)
# Visualization of Rayleigh Distribution
rayleigh = np.random.rayleigh(scale=1.0, size=1000)
sns.distplot(rayleigh, hist=False)
plt.show()
# -
# ## Pareto Distribution
# +
pareto = np.random.pareto(a=2, size=10)
print(pareto)
# Visualization of Pareto Distribution
pareto = np.random.pareto(a=3, size=1000)
sns.distplot(pareto, hist=False)
plt.show()
# -
# ## Zipf Distribution
# +
zipf = np.random.zipf(a=3, size=10)
print(zipf)
# Visualization of Zipf Distribution
zipf = np.random.zipf(a=2, size=1000)
sns.distplot(zipf, hist=False)
plt.show()
# -
# # 3- NumPy ufunc
# ## Create Your Own ufunc
# +
# 1- Create Ufunc
def add_num(x, y):
return x + y
add_num = np.frompyfunc(add_num, 2, 1)
a = [1, 2, 3]
b = [4, 5, 6]
c = add_num(a, b)
print(c)
# 2- check if a function or ufunc
print(np.ufunc)
print(type(np.add))
print(type(add_num))
print(type(np.where))
# -
# ## Simple Arithmetic
# +
a = np.array([9, 5, 6])
b = np.array([3, 4, 2])
# 1- Addition
c = np.add(a, b)
print(f"Addition: {c}")
# 2- Subtraction
c = np.subtract(a, b)
print(f"Subtraction: {c}")
# 3- Multiplication
c = np.multiply(a, b)
print(f"Multiplication: {c}")
# 4- Division
c = np.divide(a, b)
print(f"Division: {c}")
# 5- Remainder
c = np.mod(a, b)
print(f"Mod: {c}")
c = np.remainder(a, b)
print(f"Remainder: {c}")
# 6- Quotient and Mod
c = np.divmod(a, b)
print(f"Quotient and Mod: {c}")
# 7- Power
c = np.power(a, b)
print(f"Power: {c}")
# 8- Absolute Values
c = np.absolute(a, b)
print(f"Absolute Values: {c}")
# -
# ## Rounding Decimals
# +
a = np.array([1.4, 1.5, -1.4, -1.5])
# 1- Truncation and Fix
c = np.trunc(a)
print(f"Trunc: {c}")
c = np.fix(a)
print(f"Fix: {c}")
# 2- Rounding
c = np.around(a)
print(f"Round: {c}")
# 3- Floor
c = np.floor(a)
print(f"Floor: {c}")
# 4- Ceil
c = np.ceil(a)
print(f"Ceil: {c}")
# -
# ## NumPy Logs
# +
import math
a = np.array([1, 2, 3, 4, 5])
# 1- Log at Base 2
c = np.log2(a)
print(f"Log at Base 2: {c}")
# 2- Log at Base 10
c = np.log10(c)
print(f"Log at Base 10: {c}")
# 3- Log at Base e
c = np.log(c)
print(f"Log at Base e: {c}")
# 4- Log at Any Base
log = np.frompyfunc(math.log, 2, 1)
c = log(a, 5)
print(f"Log at Any Base: {c}")
# -
# ## NumPy Summations
# +
# Summations
# What is the difference between summation and addition?
# Addition is done between two arguments whereas summation happens over n elements.
a = np.array([1, 2, 3, 4])
b = np.array([5, 6, 7, 8])
c = np.add(a, b)
print(c)
c = np.sum(a)
print(c)
c = np.sum(b)
print(c)
c = np.sum((a, b))
print(c)
c = np.sum([a, b], axis=0)
print(c)
c = np.sum([a, b], axis=1)
print(c)
c = np.cumsum(a)
print(c)
c = np.cumsum(b)
print(c)
# -
# ## NumPy Products
# +
a = np.array([1, 2, 3, 4])
b = np.array([5, 6, 7, 8])
c = np.prod(a)
print(c)
c = np.prod(b)
print(c)
c = np.prod([a, b])
print(c)
c = np.prod([a, b], axis=0)
print(c)
c = np.prod([a, b], axis=1)
print(c)
c = np.cumprod(a)
print(c)
c = np.cumprod(b)
print(c)
# -
# ## NumPy Differences
# +
a = np.array([4, 9, 10, 5])
c = np.diff(a)
print(c)
c = np.diff(a, 2)
print(c)
c = np.diff(a, 3)
print(c)
# -
# ## NumPy LCM Lowest Common Multiple
# +
a = 4
b = 9
c = np.lcm(a, b)
print(c)
a = np.array([1, 2, 4, 5])
c = np.lcm.reduce(a)
print(c)
# -
# ## NumPy GCD Greatest Common Denominator
# +
a = 25
b = 35
c = np.gcd(a, b)
print(c)
a = np.array([21, 77, 35, 28, 70])
c = np.gcd.reduce(a)
print(c)
# -
# ## NumPy Trigonometric Functions
# +
arr = np.array([np.pi/2, np.pi/3, np.pi/4, np.pi/5])
a = np.pi/2
c = np.sin(a)
print(f"Sin {a}: {c}")
c = np.tan(a)
print(f"Tan {a}: {c}")
c = np.cos(a)
print(f"Cos {a}: {c}")
c = np.sin(arr)
print(f"Sin {arr}: {c}")
c = np.tan(arr)
print(f"Tan {arr}: {c}")
c = np.cos(arr)
print(f"Cos {arr}: {c}")
# Convert Degrees Into Radians
c = np.deg2rad(a)
print(f"deg2rad {a}: {c}")
c = np.deg2rad(arr)
print(f"deg2rad {arr}: {c}")
# Radians to Degrees
a = 1.633123935319537e+16
arr = np.array([6.12323400e-17, 5.00000000e-01, 7.07106781e-01, 8.09016994e-01])
c = np.rad2deg(a)
print(f"rad2deg {a}: {c}")
c = np.rad2deg(arr)
print(f"rad2deg {arr}: {c}")
# Finding Angles
a = 1.0
arr = np.array([6.12323400e-17, 5.00000000e-01, 7.07106781e-01, 8.09016994e-01])
c = np.arcsin(a)
print(f"Sin {a}: {c}")
c = np.arctan(a)
print(f"Tan {a}: {c}")
c = np.arccos(a)
print(f"Cos {a}: {c}")
c = np.arcsin(arr)
print(f"Sin {arr}: {c}")
c = np.arctan(arr)
print(f"Tan {arr}: {c}")
c = np.arccos(arr)
print(f"Cos {arr}: {c}")
hypot = np.hypot(4, 5)
print(f"Hypot :{hypot}")
# -
# ## NumPy Hyperbolic Functions
# +
# Hyperbolic Functions
arr = np.array([np.pi/2, np.pi/3, np.pi/4, np.pi/5])
a = np.pi/2
c = np.sinh(a)
print(f"Sinh {a}: {c}")
c = np.tanh(a)
print(f"Tanh {a}: {c}")
c = np.cosh(a)
print(f"Cosh {a}: {c}")
c = np.sinh(arr)
print(f"Sinh {arr}: {c}")
c = np.tanh(arr)
print(f"Tanh {arr}: {c}")
c = np.cosh(arr)
print(f"Cosh {arr}: {c}")
# Finding Angles
a = np.pi/2
arr = np.array([0.1, 0.2, 0.3])
c = np.arcsinh(a)
print(f"arcSinh {a}: {c}")
c = np.arctanh(a)
print(f"arcTanh {a}: {c}")
c = np.arccosh(a)
print(f"arcCosh {a}: {c}")
c = np.arcsinh(arr)
print(f"Sinh {arr}: {c}")
c = np.arctanh(arr)
print(f"Tanh {arr}: {c}")
c = np.arccosh(arr)
print(f"Cosh {arr}: {c}")
# -
# ## Hmmmm(=_=)
|
Tutorial/Jupyter/Numpy Review.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Regression Week 3: Assessing Fit (polynomial regression)
# In this notebook you will compare different regression models in order to assess which model fits best. We will be using polynomial regression as a means to examine this topic. In particular you will:
# * Write a function to take an SArray and a degree and return an SFrame where each column is the SArray to a polynomial value up to the total degree e.g. degree = 3 then column 1 is the SArray column 2 is the SArray squared and column 3 is the SArray cubed
# * Use matplotlib to visualize polynomial regressions
# * Use matplotlib to visualize the same polynomial degree on different subsets of the data
# * Use a validation set to select a polynomial degree
# * Assess the final fit using test data
#
# We will continue to use the House data from previous notebooks.
# # Fire up graphlab create
import graphlab
# Next we're going to write a polynomial function that takes an SArray and a maximal degree and returns an SFrame with columns containing the SArray to all the powers up to the maximal degree.
#
# The easiest way to apply a power to an SArray is to use the .apply() and lambda x: functions.
# For example to take the example array and compute the third power we can do as follows: (note running this cell the first time may take longer than expected since it loads graphlab)
tmp = graphlab.SArray([1., 2., 3.])
tmp_cubed = tmp.apply(lambda x: x**3)
print tmp
print tmp_cubed
# We can create an empty SFrame using graphlab.SFrame() and then add any columns to it with ex_sframe['column_name'] = value. For example we create an empty SFrame and make the column 'power_1' to be the first power of tmp (i.e. tmp itself).
ex_sframe = graphlab.SFrame()
ex_sframe['power_1'] = tmp
print ex_sframe
# # Polynomial_sframe function
# Using the hints above complete the following function to create an SFrame consisting of the powers of an SArray up to a specific degree:
def polynomial_sframe(feature, degree):
# assume that degree >= 1
# initialize the SFrame:
poly_sframe = graphlab.SFrame()
# and set poly_sframe['power_1'] equal to the passed feature
poly_sframe['power_1'] = feature
# first check if degree > 1
if degree > 1:
# then loop over the remaining degrees:
# range usually starts at 0 and stops at the endpoint-1. We want it to start at 2 and stop at degree
for power in range(2, degree+1):
# first we'll give the column a name:
name = 'power_' + str(power)
# then assign poly_sframe[name] to the appropriate power of feature
poly_sframe[name] = feature.apply(lambda x: x ** power)
return poly_sframe
# To test your function consider the smaller tmp variable and what you would expect the outcome of the following call:
print polynomial_sframe(tmp, 3)
# # Visualizing polynomial regression
# Let's use matplotlib to visualize what a polynomial regression looks like on some real data.
sales = graphlab.SFrame('kc_house_data.gl/')
# As in Week 3, we will use the sqft_living variable. For plotting purposes (connecting the dots), you'll need to sort by the values of sqft_living. For houses with identical square footage, we break the tie by their prices.
sales = sales.sort(['sqft_living', 'price'])
# Let's start with a degree 1 polynomial using 'sqft_living' (i.e. a line) to predict 'price' and plot what it looks like.
poly1_data = polynomial_sframe(sales['sqft_living'], 1)
poly1_data['price'] = sales['price'] # add price to the data since it's the target
# NOTE: for all the models in this notebook use validation_set = None to ensure that all results are consistent across users.
model1 = graphlab.linear_regression.create(poly1_data, target = 'price', features = ['power_1'], validation_set = None)
#let's take a look at the weights before we plot
model1.get("coefficients")
import matplotlib.pyplot as plt
# %matplotlib inline
plt.plot(poly1_data['power_1'],poly1_data['price'],'.',
poly1_data['power_1'], model1.predict(poly1_data),'-')
# Let's unpack that plt.plot() command. The first pair of SArrays we passed are the 1st power of sqft and the actual price we then ask it to print these as dots '.'. The next pair we pass is the 1st power of sqft and the predicted values from the linear model. We ask these to be plotted as a line '-'.
#
# We can see, not surprisingly, that the predicted values all fall on a line, specifically the one with slope 280 and intercept -43579. What if we wanted to plot a second degree polynomial?
poly2_data = polynomial_sframe(sales['sqft_living'], 2)
my_features = poly2_data.column_names() # get the name of the features
poly2_data['price'] = sales['price'] # add price to the data since it's the target
model2 = graphlab.linear_regression.create(poly2_data, target = 'price', features = my_features, validation_set = None)
model2.get("coefficients")
plt.plot(poly2_data['power_1'],poly2_data['price'],'.',
poly2_data['power_1'], model2.predict(poly2_data),'-')
# The resulting model looks like half a parabola. Try on your own to see what the cubic looks like:
poly3 = polynomial_sframe(sales['sqft_living'], 3) # create the cubic sframe with sqft_living
my_features = poly3.column_names() # get the features to use in polynomial regression
poly3['price'] = sales['price'] # add the price column becuase it is the target
model3 = graphlab.linear_regression.create(poly3, target='price', features=my_features, validation_set=None)
model3.coefficients
plt.plot(poly3['power_1'], poly3['price'], ".",
poly3['power_1'], model3.predict(poly3), "-")
# Now try a 15th degree polynomial:
poly15 = polynomial_sframe(sales['sqft_living'], 15) # create the cubic sframe with sqft_living
my_features = poly15.column_names() # get the features to use in polynomial regression
poly15['price'] = sales['price'] # add the price column becuase it is the target
model15 = graphlab.linear_regression.create(poly15, target='price', features=my_features, validation_set=None)
model15.coefficients
plt.plot(poly15['power_1'], poly15['price'], ".",
poly15['power_1'], model15.predict(poly15), "-")
# What do you think of the 15th degree polynomial? Do you think this is appropriate? If we were to change the data do you think you'd get pretty much the same curve? Let's take a look.
# The polynomial with degree 15 is not appropriate because it overfits the training data. This model is too complex for the data and has high variance. If the subset of data used were to change, the model would differ substantially. This model would not generalize well to new data.
# # Changing the data and re-learning
# We're going to split the sales data into four subsets of roughly equal size. Then you will estimate a 15th degree polynomial model on all four subsets of the data. Print the coefficients (you should use .print_rows(num_rows = 16) to view all of them) and plot the resulting fit (as we did above). The quiz will ask you some questions about these results.
#
# To split the sales data into four subsets, we perform the following steps:
# * First split sales into 2 subsets with `.random_split(0.5, seed=0)`.
# * Next split the resulting subsets into 2 more subsets each. Use `.random_split(0.5, seed=0)`.
#
# We set `seed=0` in these steps so that different users get consistent results.
# You should end up with 4 subsets (`set_1`, `set_2`, `set_3`, `set_4`) of approximately equal size.
# +
tmp_set_1, tmp_set_2= sales.random_split(0.5, seed=0)
set_1, set_2 = tmp_set_1.random_split(0.5, seed=0)
set_3, set_4 = tmp_set_2.random_split(0.5, seed=0)
# -
# Fit a 15th degree polynomial on set_1, set_2, set_3, and set_4 using sqft_living to predict prices. Print the coefficients and make a plot of the resulting model.
def make_and_plot_poly(data, degree, feature='sqft_living'):
sframe = polynomial_sframe(data[feature], degree)
my_features = sframe.column_names()
sframe['price'] = data['price']
model = graphlab.linear_regression.create(sframe, target='price', features=my_features, validation_set=None, verbose=False)
plt.plot(sframe['power_1'], sframe['price'], ".",
sframe['power_1'], model.predict(sframe), "-");
plt.xlabel(feature); plt.ylabel('Price'), plt.legend(['raw_data', 'model_predictions']);
print("Model Coefficients")
print(model.coefficients.print_rows(num_rows=16))
make_and_plot_poly(set_1, 15)
make_and_plot_poly(set_2, 15)
make_and_plot_poly(set_3, 15)
make_and_plot_poly(set_4, 15)
# Some questions you will be asked on your quiz:
#
# **Quiz Question: Is the sign (positive or negative) for power_15 the same in all four models?**
#
# No, it is positive for sets 1, 2, 3 but negative for set 4.
#
# **Quiz Question: (True/False) the plotted fitted lines look the same in all four plots**
#
# False, the plotted fit lines differ substantially in shape.
# # Selecting a Polynomial Degree
# Whenever we have a "magic" parameter like the degree of the polynomial there is one well-known way to select these parameters: validation set. (We will explore another approach in week 4).
#
# We split the sales dataset 3-way into training set, test set, and validation set as follows:
#
# * Split our sales data into 2 sets: `training_and_validation` and `testing`. Use `random_split(0.9, seed=1)`.
# * Further split our training data into two sets: `training` and `validation`. Use `random_split(0.5, seed=1)`.
#
# Again, we set `seed=1` to obtain consistent results for different users.
training_and_validation, testing = sales.random_split(0.9, seed=1)
training, validation = training_and_validation.random_split(0.5, seed=1)
# Next you should write a loop that does the following:
# * For degree in [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15] (to get this in python type range(1, 15+1))
# * Build an SFrame of polynomial data of train_data['sqft_living'] at the current degree
# * hint: my_features = poly_data.column_names() gives you a list e.g. ['power_1', 'power_2', 'power_3'] which you might find useful for graphlab.linear_regression.create( features = my_features)
# * Add train_data['price'] to the polynomial SFrame
# * Learn a polynomial regression model to sqft vs price with that degree on TRAIN data
# * Compute the RSS on VALIDATION data (here you will want to use .predict()) for that degree and you will need to make a polynmial SFrame using validation data.
# * Report which degree had the lowest RSS on validation data (remember python indexes from 0)
#
# (Note you can turn off the print out of linear_regression.create() with verbose = False)
validation_scores = {}
for power in range(1, 16):
sframe = polynomial_sframe(training['sqft_living'], degree=power)
my_features = sframe.column_names()
sframe['price'] = training['price']
model = graphlab.linear_regression.create(sframe, target='price', features=my_features, validation_set=None, verbose=False)
validation_sframe = polynomial_sframe(validation['sqft_living'], degree=power)
validation_predictions = model.predict(validation_sframe)
RSS = ((validation_predictions - validation['price'])**2).sum()
validation_scores[power] = RSS
validation_scores = [(power, RSS) for power, RSS in validation_scores.items()]
validation_scores = sorted(validation_scores, key=lambda x: x[1], reverse=False)
validation_scores
# **Quiz Question: Which degree (1, 2, …, 15) had the lowest RSS on Validation data?**
#
# 6 had the lowest validation error
# Now that you have chosen the degree of your polynomial using validation data, compute the RSS of this model on TEST data. Report the RSS on your quiz.
# +
poly6 = polynomial_sframe(training['sqft_living'], degree=6)
my_features = poly6.column_names()
poly6['price'] = training['price']
model6 = graphlab.linear_regression.create(poly6, target='price', features=my_features, validation_set=None, verbose=False)
test_sframe = polynomial_sframe(testing['sqft_living'], degree=6)
predictions = model6.predict(test_sframe)
RSS = ((predictions - testing['price']) **2).sum()
# -
print('RSS using a model with degree 6: {}'.format(str(RSS)))
# **Quiz Question: what is the RSS on TEST data for the model with the degree selected from Validation data?**
# 1.255E14
|
Studying Materials/Course 2 Regression/Assessing Performance/week-3-polynomial-regression-assignment-blank.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Gender Classification Using Names
#
# ### This project aims to detect/predict gender of individuals from their names using Machine Learning.
# #### The dataset contains Indian as well as English names
#
# - Sklearn
# - Pandas
# - Text Extraction
# Importing EDA packages
import pandas as pd
import numpy as np
# Importing ML Packages
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction import DictVectorizer
# Load our data
df = pd.read_csv('dataset/Names_dataset.csv')
df.head()
df.size
# Data Cleaning
# Checking for column name consistency
df.columns
# Data Types
df.dtypes
# Checking for Missing Values
df.isnull().isnull().sum()
# Number of Female Names
df[df.gender == 'f'].size
# Number of Female Names
df[df.gender == 'm'].size
df_names = df
# Replacing All 'f' and 'm' with 0 and 1 respectively
df_names.gender.replace({'f':0,'m':1}, inplace=True)
df_names.gender.unique()
df_names.dtypes
Xfeatures = df_names['name']
# Feature Extraction
cv = CountVectorizer()
X = cv.fit_transform(Xfeatures.values.astype('U'))
# Save Our Vectorizer
import joblib
gender_vectorizer = open("gender_vectorizer.pkl","wb")
joblib.dump(cv,gender_vectorizer)
gender_vectorizer.close()
cv.get_feature_names()
from sklearn.model_selection import train_test_split
# Features
X
# Labels
y = df_names.gender
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)
# Naive Bayes Classifier
from sklearn.naive_bayes import MultinomialNB
clf = MultinomialNB()
clf.fit(X_train,y_train)
clf.score(X_test,y_test)
# Accuracy of our Model
# test
print("Accuracy of Model",clf.score(X_test,y_test)*100,"%")
# Accuracy of our Model
# train
print("Accuracy of Model",clf.score(X_train,y_train)*100,"%")
# ### Sample Prediction
# Sample1 Prediction
sample_name = ["Kanchi"]
vect = cv.transform(sample_name).toarray()
vect
# Female is 0, Male is 1
clf.predict(vect)
# Sample2 Prediction
sample_name1 = ["Vandan"]
vect1 = cv.transform(sample_name1).toarray()
clf.predict(vect1)
# Sample3 Prediction of Russian Names
sample_name2 = ["Natasha"]
vect2 = cv.transform(sample_name2).toarray()
clf.predict(vect2)
# Sample3 Prediction of Random Names
sample_name3 = ["Tejas", "Nefertiti","Nasha","Anaisha","Kabir","Ovetta","Tathiana","Xia","Joseph","Drishti", "Yuvaan"]
vect3 = cv.transform(sample_name3).toarray()
clf.predict(vect3)
# A function to do it
def genderpredictor(a):
test_name = [a]
vector = cv.transform(test_name).toarray()
if clf.predict(vector) == 0:
return("Female")
else:
return("Male")
genderpredictor("Priti")
namelist = ["Nitin","Gigi", "Zayn","Rihanna","Masha", "Rohit"]
for i in namelist:
print(i, "->", genderpredictor(i))
# ### Using a custom function for feature analysis
# By Analogy most female names ends in 'A' or 'I' or has the sound of 'A'
def features(name):
name = str(name)
name = name.lower()
return {
'first-letter': name[0], # First letter
'first2-letters': name[0:2], # First 2 letters
'first3-letters': name[0:3], # First 3 letters
'last-letter': name[-1],
'last2-letters': name[-2:],
'last3-letters': name[-3:],
}
# Vectorize the features function
features = np.vectorize(features)
print(features(["Anna", "Kanchi", "Prathmesh", "Saloni", "Trupti", "Hannah", "Peter", "John", "Vladmir"]))
# Extract the features for the dataset
df_X = features(df_names['name'])
df_y = df_names['gender']
# +
from sklearn.feature_extraction import DictVectorizer
corpus = features(["Aarav", "Julia"])
dv = DictVectorizer()
dv.fit(corpus)
transformed = dv.transform(corpus)
print(transformed)
# -
dv.get_feature_names()
# Train Test Split
dfX_train, dfX_test, dfy_train, dfy_test = train_test_split(df_X, df_y, test_size=0.33, random_state=42)
dfX_train
dv = DictVectorizer()
dv.fit_transform(dfX_train)
# +
# Model building Using DecisionTree
from sklearn.tree import DecisionTreeClassifier
dclf = DecisionTreeClassifier()
my_xfeatures =dv.transform(dfX_train)
dclf.fit(my_xfeatures, dfy_train)
# -
# Build Features and Transform them
sample_name_eg = ["Vandan"]
transform_dv =dv.transform(features(sample_name_eg))
vect3 = transform_dv.toarray()
# Predicting Gender of Name
# Male is 1, Female = 0
dclf.predict(vect3)
if dclf.predict(vect3) == 0:
print("Female")
else:
print("Male")
# Second Prediction With Nigerian Name
name_eg1 = ["Chioma"]
transform_dv =dv.transform(features(name_eg1))
vect4 = transform_dv.toarray()
if dclf.predict(vect4) == 0:
print("Female")
else:
print("Male")
# A function to do it
def genderpredictor1(a):
test_name1 = [a]
transform_dv =dv.transform(features(test_name1))
vector = transform_dv.toarray()
if dclf.predict(vector) == 0:
return("Female")
else:
return("Male")
random_name_list = ["Alex","Alice","Parth", "Chioma", "Kriti", "Vitalic", "Shruti", "Clairese", "Chan", "Divya"]
for n in random_name_list:
print(n, "->", genderpredictor1(n))
## Accuracy of Models Decision Tree Classifier Works better than Naive Bayes
# Accuracy on training set
print(dclf.score(dv.transform(dfX_train), dfy_train))
# Accuracy on test set
print(dclf.score(dv.transform(dfX_test), dfy_test))
# ### Saving Our Model
import joblib
decisiontreModel = open("decisiontreemodel.pkl","wb")
joblib.dump(dclf,decisiontreModel)
decisiontreModel.close()
#Alternative to Model Saving
import pickle
dctreeModel = open("namesdetectormodel.pkl","wb")
pickle.dump(dclf,dctreeModel)
dctreeModel.close()
# ### Save Multinomial NB Model
NaiveBayesModel = open("naivebayesgendermodel.pkl","wb")
joblib.dump(clf,NaiveBayesModel)
NaiveBayesModel.close()
# +
# By <NAME>
# -
|
ML_models_Flask/Kanchi_Tank/data/Gender-Classification.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
# +
#definiciòn de matriz de coeficientes y vector de terminos ind
A = [[1,1,1],[2,3,-4],[1,-1,1]]
A = np.array(A)
B = [1,9,-1]
B = np.array(B)
# -
#Retorna la fila en la que se encuantra el pivote de una columna
def row_pivote(A,fil,col):
max_value = max(A[fil:,col])
min_value = min(A[fil:,col])
if(abs(max_value)>abs(min_value)):
pivote = max_value
else:
pivote = min_value
for i in range(0,A.shape[0]):
if(A[i][col] == pivote):
fila_pivote = i
return fila_pivote
# +
def GaussSolver(A,B):
#dimenciones de matriz de coeficientes
n = A.shape[0]
m = A.shape[1]
AB = np.zeros((n,m+1))
AB[:,0:m] = A
for i in range(0,n):
AB[i][m] = b[i]
#inicia eliminaciòn
i= 0 #sobre filas
j= 0 #sobre columnas
#recorriendo columnas
for h in range(j,m-1):
#Determinando fila del pivote
fila_pivote=row_pivote(AB,i,h)
pivote = AB[fila_pivote][h]
if(fila_pivote!= i):
#Intercambio de filas
AB[[fila_pivote,i]] = AB[[i,fila_pivote]]
#Luego el pivote està en la fila i-èsima
for k in range(i+1,n):
x = -AB[k][h]/pivote
AB[k] = AB[k] + x*AB[i]
i= i + 1
j= j + 1
#Vector soluciòn
x_sol= np.zeros(m)
for i in range(n-1,-1,-1):
if(i==n-1):
x_sol[i] = AB[i,m]/AB[i][i]
else:
sum= 0.0
for j in range(i+1,m):
sum += AB[i][j]*x_sol[j]
x_sol = (AB[i][m]-sum)/(AB[i][i]
return x_sol
# -
print(GaussSolver(A,B))
|
algebra_lineal/sln_ecuaciones/gauss_solver.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="CZLeOG22FAqa"
# !python -m pip install konlpy
# + id="u4Tp2RA-FYVh"
# from preprocess import *
import preprocess as pp
# + id="VhILsB5WN09m"
path_csv='./ChatBotData.csv_short'
inputs, outputs = pp.load_data(path_csv)
type(inputs), type(outputs)
# + id="iDHWQSoJOKbq"
inputs[7], outputs[7] # 대화내용
# + id="Hcmoh6jlN6JS"
path_vocab = './vocabulary.txt'
char2idx, idx2char, vocab_size = pp.load_vocabulary(path_csv, path_vocab) # preprocess 내 function
type(char2idx), type(idx2char), type(vocab_size)
# + id="pUNvjYM_Q9Or"
print(char2idx)
print(idx2char)
print(vocab_size)
# + id="o3UOidv-P3Sc"
idx_inputs, input_seq_len = pp.enc_processing(inputs, char2idx)
type(idx_inputs), len(input_seq_len)
# + id="2j3GN042SWhy"
idx_inputs[3:5]
# + id="LdVoyHl9O9Rn"
idx_outputs, output_seq_len = pp.dec_output_processing(outputs. char2idx)
type(idx_outputs), len(output_seq_len)
# + id="VKiMvNGvSWHR"
idx_outputs[3:5]
# + id="vysz8jcBSanP"
idx_targets = pp.dec_target_processing(outputs, char2idx)
type(idx_targets), len(idx_targets)
# + id="C6JmhV24SjN9"
idx_targets[3:5]
# + id="mpgmy8tmSlaX"
data_configs = dict()
# + id="xXk5wUKhTpyq"
data_configs['char2idx'] = char2idx
data_configs['idx2char'] = idx2char
data_configs['vocab_size'] = vocab_size
# + id="Fch057HgUkvR"
import numpy as np
# + id="5aD-78CZUksz"
np.save(open('./train_inputs.npy','wb'), idx_inputs)
# + id="umdGJiXdUrfy"
# !file ./train_inputs.npy
# + id="HTc04OYoUrdi"
np.save(open('./train_outputs.npy','wb'), idx_outputs)
# + id="9jeuLQU4VT92"
data_configs['char2idx'] = char2idx
data_configs['idx2char'] = idx2char
data_configs['vocab_size'] = vocab_size
data_configs['pad_symbol'] = PAD
data_configs['std_symbol'] = STD
data_configs['end_symbol'] = END
data_configs['unk_symbol'] = UNK
# + id="zwejk2fHVTcf"
pp.json.dump(data_configs, open('./data_configs.json', 'w'))
|
NLP/seq2seq_preprocess.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="WzfdUE-RDKZe" colab_type="text"
# #Face Recognition using Deep Learning (IoT project)
# + id="y6_UOrhYOyHX" colab_type="code" outputId="f82f10ed-4d28-4e08-beb7-ed75a073deae" colab={"base_uri": "https://localhost:8080/", "height": 638}
# !pip install tensorflow==1.8
# + id="weuAoWzzAu_w" colab_type="code" outputId="55a882e1-b6b0-4df2-d262-a3b635f2049e" colab={"base_uri": "https://localhost:8080/", "height": 54}
import matplotlib.pyplot as plt
import numpy as np
import os
import tensorflow as tf
import zipfile
import keras
from keras.applications import MobileNet
from keras.layers import Conv2D, Dense, Dropout, Flatten, MaxPooling2D
from keras.models import Sequential
from keras.preprocessing.image import ImageDataGenerator
from keras import optimizers
print(keras.__version__)
# + [markdown] id="6Jvxio08wbUG" colab_type="text"
# ##Build dataset
#
# We have taken photos of our group members mixed with public face dataset . I took a video of the landmarks and used FFmpeg to extract 4 images(frames) per second. Finally I shuffle the dataset and split them into train, validation and test dataset.
# + id="gZHxl2dESMpg" colab_type="code" outputId="b7543693-4dea-4fc4-b722-d51ca8f1b910" colab={"base_uri": "https://localhost:8080/", "height": 35}
# !ls
# + id="LKqy9HGQBQIj" colab_type="code" colab={}
local_zip = 'face.zip'
zip_ref = zipfile.ZipFile(local_zip, 'r')
zip_ref.extractall('face')
zip_ref.close()
base_dir = 'face'
train_dir = os.path.join(base_dir, 'train')
validation_dir = os.path.join(base_dir, 'val')
test_dir = os.path.join(base_dir, 'test')
train_owner_dir = os.path.join(train_dir, 'owner')
train_breaker_dir = os.path.join(train_dir, 'breaker')
validation_owner_dir = os.path.join(validation_dir, 'owner')
validation_breaker_dir = os.path.join(validation_dir, 'breaker')
test_owner_dir = os.path.join(test_dir, 'owner')
test_breaker_dir = os.path.join(test_dir, 'breaker')
# + id="maha4K_3BQLK" colab_type="code" colab={}
num_owner_tr = len(os.listdir(train_owner_dir))
num_breaker_tr = len(os.listdir(train_breaker_dir))
num_owner_val = len(os.listdir(validation_owner_dir))
num_breaker_val = len(os.listdir(validation_breaker_dir))
num_owner_test = len(os.listdir(test_owner_dir))
num_breaker_test = len(os.listdir(test_breaker_dir))
total_train = num_owner_tr + num_breaker_tr
total_val = num_owner_val + num_breaker_val
total_test = num_owner_test + num_breaker_test
# + id="MQ65ATMiBQNy" colab_type="code" outputId="bdf37960-d5ff-4648-f178-b3ba682086e6" colab={"base_uri": "https://localhost:8080/", "height": 199}
print('Training owner images:', num_owner_tr)
print('Training breaker images:', num_breaker_tr)
print('Validation owner images:', num_owner_val)
print('Validation breaker images:', num_breaker_val)
print('Test owner images:', num_owner_test)
print('Test breaker images:', num_breaker_test)
print("--")
print("Total training images:", total_train)
print("Total validation images:", total_val)
print("Total test images:", total_test)
# + [markdown] id="ZTmsWSd27dx6" colab_type="text"
# ##Data augmentation
# + id="3fUE42H1aqvE" colab_type="code" outputId="9699bd1b-acef-4344-c05e-f9c2f814d5f8" colab={"base_uri": "https://localhost:8080/", "height": 72}
TARGET_SHAPE = 160
BATCH_SIZE = 32
image_gen_train = ImageDataGenerator(
rescale=1./255,
rotation_range=40,
width_shift_range=0.2,
height_shift_range=0.2,
shear_range=0.2,
zoom_range=0.2,
horizontal_flip=True,
fill_mode='nearest')
train_data_gen = image_gen_train.flow_from_directory(
batch_size=BATCH_SIZE,
directory=train_dir,
shuffle=True,
target_size=(TARGET_SHAPE,TARGET_SHAPE),
class_mode='binary')
image_gen_val = ImageDataGenerator(rescale=1./255)
val_data_gen = image_gen_val.flow_from_directory(
batch_size=BATCH_SIZE,
directory=validation_dir,
target_size=(TARGET_SHAPE, TARGET_SHAPE),
class_mode='binary')
image_gen_test = ImageDataGenerator(rescale=1./255)
test_data_gen = image_gen_val.flow_from_directory(
batch_size=BATCH_SIZE,
directory=test_dir,
target_size=(TARGET_SHAPE, TARGET_SHAPE),
class_mode='binary')
# + [markdown] id="-p_mE4Gmya_c" colab_type="text"
# ## Display Sample Training Images
# + id="nWeQxPmryba0" colab_type="code" colab={}
sample_training_images, sample_training_labels = next(train_data_gen)
# + id="w2T5e-x_ysN3" colab_type="code" colab={}
def plotImages(images_arr):
fig, axes = plt.subplots(1, 5, figsize=(20,20))
axes = axes.flatten()
for img, ax in zip( images_arr, axes):
ax.grid(False)
ax.imshow(img)
plt.tight_layout()
plt.show()
# + id="WrAYXQvwysQn" colab_type="code" outputId="8366b06f-a764-42c8-897f-acab4a57c08a" colab={"base_uri": "https://localhost:8080/", "height": 317}
plotImages(sample_training_images[:5])
# + [markdown] id="ridXwziwyb3c" colab_type="text"
# # Part2 transfer learning
# First I chosen MobileNet as the model, and I apply the transfer learning onto the Mobilenet model trained on my own Dataset.
# + id="Mtp9BqPZ0BSC" colab_type="code" colab={}
vgg16_conv_base = MobileNet(weights='imagenet',include_top=False, input_shape=(160, 160, 3))
# + id="DCoyxHb90BsD" colab_type="code" outputId="e258f1ee-141b-431a-9667-e4636ccbae7d" colab={"base_uri": "https://localhost:8080/", "height": 3308}
vgg16_conv_base.summary()
# + id="E2jde6qb0By4" colab_type="code" colab={}
vgg16_conv_base.trainable = False
vgg16_model = Sequential()
vgg16_model.add(vgg16_conv_base)
vgg16_model.add(Flatten())
vgg16_model.add(Dense(512, activation='relu'))
vgg16_model.add(Dense(1, activation='sigmoid'))
# + id="XA6mKtoLz9Bq" colab_type="code" outputId="abfb73b2-94a1-469d-9503-e44119fdfa40" colab={"base_uri": "https://localhost:8080/", "height": 290}
vgg16_model.summary()
# + id="ZkKVaCtZb-C5" colab_type="code" colab={}
EPOCHS = 5
# + id="PeaLKrspaqxr" colab_type="code" outputId="0ff1693c-3558-497e-9e02-b392abd30085" colab={"base_uri": "https://localhost:8080/", "height": 219}
vgg16_model.compile(loss='binary_crossentropy',
optimizer='adam',
metrics=['acc'])
vgg16_history = vgg16_model.fit_generator(
train_data_gen,
steps_per_epoch=int(np.ceil(total_train / float(BATCH_SIZE))),
epochs=EPOCHS,
validation_data=val_data_gen,
validation_steps=int(np.ceil(total_val / float(BATCH_SIZE))),
verbose=1)
# + [markdown] id="FIhThbSJ4XH6" colab_type="text"
# ## Plot Training and Validation Loss and Accuracy
# + id="1BjJ4R_uaq0r" colab_type="code" outputId="f226a5f5-407e-4874-efc6-03ae05055684" colab={"base_uri": "https://localhost:8080/", "height": 791}
acc = vgg16_history.history['acc']
val_acc = vgg16_history.history['val_acc']
loss = vgg16_history.history['loss']
val_loss = vgg16_history.history['val_loss']
epochs_range = range(1, EPOCHS+1)
plt.figure(figsize=(13,13))
plt.subplot(1, 2, 1)
plt.plot(epochs_range, acc, label='Training Accuracy')
plt.plot(epochs_range, val_acc, label='Validation Accuracy')
plt.legend(loc='lower right')
plt.title('Training and Validation Accuracy from Transfer Learning on VGG16')
plt.subplot(1, 2, 2)
plt.plot(epochs_range, loss, label='Training Loss')
plt.plot(epochs_range, val_loss, label='Validation Loss')
plt.legend(loc='upper right')
plt.title('Training and Validation Loss from Transfer Learning on VGG16')
plt.show()
# + [markdown] id="LFZun68z4b2z" colab_type="text"
# ## Show Testing Loss and Accuracy
# + id="GYItoZm-aq3L" colab_type="code" outputId="0edfa5ce-42ff-4747-cc8a-4f2ff4b3a1fc" colab={"base_uri": "https://localhost:8080/", "height": 345}
vgg16_test_loss, vgg16_test_accuracy = vgg16_model.evaluate(test_data_gen, verbose=1)
# + id="u-kw_jFLaq6E" colab_type="code" colab={}
print('The test loss is '+ str(round(vgg16_test_loss,2))+' and the test accracy is '+ str(round(vgg16_test_accuracy,2)))
# + id="oZb16Wj5oBSx" colab_type="code" colab={}
vgg16_model.save("model1.h5")
# + [markdown] id="NWwX6iL-dUeg" colab_type="text"
# #part3: self-defined CNN
# + id="04UFK-TcK00x" colab_type="code" outputId="91b08510-6807-477f-8555-f6fe4639a59c" colab={"base_uri": "https://localhost:8080/", "height": 72}
TARGET_SHAPE = 150
BATCH_SIZE = 32
image_gen_train = ImageDataGenerator(
rescale=1./255,
rotation_range=40,
width_shift_range=0.2,
height_shift_range=0.2,
shear_range=0.2,
zoom_range=0.2,
horizontal_flip=True,
fill_mode='nearest')
train_data_gen = image_gen_train.flow_from_directory(
batch_size=BATCH_SIZE,
directory=train_dir,
shuffle=True,
target_size=(TARGET_SHAPE,TARGET_SHAPE),
class_mode='binary')
image_gen_val = ImageDataGenerator(rescale=1./255)
val_data_gen = image_gen_val.flow_from_directory(
batch_size=BATCH_SIZE,
directory=validation_dir,
target_size=(TARGET_SHAPE, TARGET_SHAPE),
class_mode='binary')
image_gen_test = ImageDataGenerator(rescale=1./255)
test_data_gen = image_gen_val.flow_from_directory(
batch_size=BATCH_SIZE,
directory=test_dir,
target_size=(TARGET_SHAPE, TARGET_SHAPE),
class_mode='binary')
# + id="AvXjmqjVfshF" colab_type="code" colab={}
inc_model = Sequential()
inc_model.add(Conv2D(32, (3, 3), activation='relu',
input_shape=(480, 480, 3)))
inc_model.add(MaxPooling2D((2, 2)))
inc_model.add(Conv2D(64, (3, 3), activation='relu'))
inc_model.add(MaxPooling2D((2, 2)))
inc_model.add(Conv2D(128, (3, 3), activation='relu'))
inc_model.add(MaxPooling2D((2, 2)))
inc_model.add(Conv2D(128, (3, 3), activation='relu'))
inc_model.add(MaxPooling2D((2, 2)))
inc_model.add(Flatten())
inc_model.add(Dense(512, activation='relu'))
inc_model.add(Dense(1, activation='sigmoid'))
# + id="9AsfAdiSi-cL" colab_type="code" outputId="cfa03d4c-34da-4755-8983-528a7a75fd06" colab={"base_uri": "https://localhost:8080/", "height": 401}
EPOCHS = 10
inc_model.compile(loss='binary_crossentropy',
optimizer='adam',
metrics=['acc'])
# Train Transfer Learning
inc_history = inc_model.fit_generator(
train_data_gen,
steps_per_epoch=int(np.ceil(total_train / float(BATCH_SIZE))),
epochs=EPOCHS,
validation_data=val_data_gen,
validation_steps=int(np.ceil(total_val / float(BATCH_SIZE))),
verbose=1)
# + id="2C3GwvfFlpgT" colab_type="code" outputId="728d3db5-728d-482e-e815-9081e399e6d8" colab={"base_uri": "https://localhost:8080/", "height": 499}
acc = inc_history.history['acc']
val_acc = inc_history.history['val_acc']
loss = inc_history.history['loss']
val_loss = inc_history.history['val_loss']
epochs_range = range(1, EPOCHS+1)
plt.figure(figsize=(8, 8))
plt.subplot(1, 2, 1)
plt.plot(epochs_range, acc, label='Training Accuracy')
plt.plot(epochs_range, val_acc, label='Validation Accuracy')
plt.legend(loc='lower right')
plt.title('Training and Validation Accuracy')
plt.subplot(1, 2, 2)
plt.plot(epochs_range, loss, label='Training Loss')
plt.plot(epochs_range, val_loss, label='Validation Loss')
plt.legend(loc='upper right')
plt.title('Training and Validation Loss')
plt.show()
# + id="fauEIos5l2FG" colab_type="code" outputId="1de2e583-a8b0-4b32-855e-3d000eb008f6" colab={"base_uri": "https://localhost:8080/", "height": 363}
inc_test_loss, inc_test_accuracy = inc_model.evaluate(test_data_gen, verbose=1)
print('The test loss is '+ str(round(inc_test_loss,2))+' and the test accracy is '+ str(round(inc_test_accuracy,2)))
# + id="KOhdhh3DmD7a" colab_type="code" colab={}
inc_model.save_weights("model.h5")
# + id="KYi9SCarmM_J" colab_type="code" outputId="a4a03597-f0b3-4dba-de48-49f5210e0d63" colab={"base_uri": "https://localhost:8080/", "height": 72}
import PIL
from PIL import Image
img = Image.open("/content/face/test/owner/IMG_20190428_164249.jpg")
img = img.resize((150,150), PIL.Image.ANTIALIAS)
image = np.asarray(img)
shape1 = image.shape
print(shape1)
image = np.expand_dims(image, axis=0)
print(image.shape)
result = inc_model.predict(image)
print(result)
|
face_recognition_.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:anaconda]
# language: python
# name: conda-env-anaconda-py
# ---
# +
import quandl
import numpy as np
import pandas as pd
import talib
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import linear_model
from statistics import mean, stdev
from sklearn.preprocessing import scale
# +
SOXL = pd.read_csv('/Users/josephseverino/Downloads/SOXL.csv') #ETF growth cycle
Nasdaq = pd.read_csv('/Users/josephseverino/Downloads/Nasdaq.csv') #Index
TQQQ = pd.read_csv('/Users/josephseverino/Downloads/TQQQ.csv') #3X Index
MU = pd.read_csv('/Users/josephseverino/Downloads/MU.csv') #high Beta
AMD = pd.read_csv('/Users/josephseverino/Downloads/AMD.csv') # high beta
NFLX = pd.read_csv('/Users/josephseverino/Downloads/NFLX.csv') #High growth
AMZN = pd.read_csv('/Users/josephseverino/Downloads/AMZN.csv') #High growth
V = pd.read_csv('/Users/josephseverino/Downloads/V.csv') #low volalitity
YINN = pd.read_csv('/Users/josephseverino/Downloads/YINN.csv') #looks like bell curve
NVDA = pd.read_csv('/Users/josephseverino/Downloads/NVDA.csv') #high growth
WTW = pd.read_csv('/Users/josephseverino/Downloads/WTW.csv') #high beta
F = pd.read_csv('/Users/josephseverino/Downloads/F.csv') #highly traded
MSFT = pd.read_csv('/Users/josephseverino/Downloads/MSFT.csv') #high traded
HNGR = pd.read_csv('/Users/josephseverino/Downloads/HNGR.csv') #high beta cyclic
VIX = pd.read_csv('/Users/josephseverino/Downloads/VIX.csv') #high beta cyclic
stocks = [SOXL, Nasdaq, TQQQ, MU, AMD, NFLX, AMZN, V, YINN, NVDA, WTW, F, MSFT, HNGR]
# -
print('SOXL: ',SOXL.shape,
'Nasdaq: ', Nasdaq.shape,
'TQQQ: ',TQQQ.shape,
'MU: ',MU.shape,
'Visa: ', V.shape,
'Amazon: ',AMZN.shape,
'Netflix: ',NFLX.shape,
'AMD: ',AMD.shape,
'YINN: ',YINN.shape,
'NVDA: ', NVDA.shape,
'WTW: ', WTW.shape,
'F: ', F.shape,
'MSFT: ', MSFT.shape,
'HNGR: ', HNGR.shape,
'VIX: ', VIX.shape)
# # Below is my Feature Engineering
adj_return = lambda x: x + 1
for df in stocks:
#previous day percentage return
df['Day_previous_roi'] = df['Open'].pct_change(1)
#adding a 1 to return for easier calculations
df['Day_previous_roi'] = df['Day_previous_roi'].apply(adj_return)
#current day percentage return
df['current_roi'] = df['Day_previous_roi'].shift(-1)
for df in stocks:
for n in [10,20,60,200]:
# Create the moving average indicator and divide by Adj_Close
df['ma' + str(n)] = talib.SMA(df['Adj Close'].values,timeperiod=n) / df['Adj Close']
#PCT of MA
df['ma_chg' + str(n)] = df['ma' + str(n)].pct_change()
# Create the RSI indicator
df['rsi' + str(n)] = talib.RSI(df['Adj Close'].values, timeperiod=n)
#CHG of rsi
# Create the RSI indicator
df['rsi_chg' + str(n)] = df['rsi' + str(n)].pct_change()
# time series predictor
df['tsf' + str(n)] = talib.TSF(df['Adj Close'].values, timeperiod=n)
# Normalize tsf to price
df['tsf' + str(n)] = df['tsf' + str(n)].values/df['Adj Close'].values
for df in stocks:
#MACD signals
df['macd'], df['macdsignal'], df['macdhist'] = talib.MACD(df['Close'].values,
fastperiod=12,
slowperiod=26,
signalperiod=9)
#AROON signals
df['aroondown'], df['aroonup'] = talib.AROON(df['High'].values,
df['Low'].values,
timeperiod=14)
#OBV
volume_data = np.array(df['Volume'].values, dtype='f8')
df['obv'] = talib.OBV(df['Close'].values,
volume_data)
#candle stick pattern
df['shawman'] = talib.CDLRICKSHAWMAN(df['Open'].values, df['High'].values,
df['Low'].values, df['Close'].values)
#candle stick pattern
df['hammer'] = talib.CDLHAMMER(df['Open'].values, df['High'].values,
df['Low'].values, df['Close'].values)
#cyclical indicator
df['sine'], df['leadsine'] = talib.HT_SINE(df['Close'].values)
# +
#normalizing features
for df in stocks:
df['macd_diff'] = df['macd'] - df['macdsignal']
df['macd_diff_hist'] = df['macd'] - df['macdhist']
df['aroon_diff'] = df['aroonup'] - df['aroondown']
df['obv'] = df['obv'].pct_change(1)
# +
#looking at the percent difference between the high, low and open close of a
#day
def dt(start,diff):
diff = (diff-start)/start
return diff
for df in stocks:
df['open_H_ratio'] = dt(df['Open'].values,df['High'].values)
df['open_L_ratio'] = dt(df['Open'].values,df['Low'].values)
df['close_H_ratio'] = dt(df['Close'].values,df['High'].values)
df['close_L_ratio'] = dt(df['Close'].values,df['Low'].values)
# +
# trend line slope
for df in stocks:
for n in [3,5,10,60]:
#print(n)
slope = []
r_sqr = []
for i in range(len(df['Open'])):
if i > n:
X = (np.array(range(n))).reshape(-1,1)
y = df['Open'][(i-n):i]
lm = linear_model.LinearRegression()
model = lm.fit(X,y)
slope.append(model.coef_[0])
r_sqr.append(model.score(X,y))
else:
slope.append(np.nan)
r_sqr.append(np.nan)
if i == (len(df['Open'])-1):
df['slope' + str(n)] = slope
df['r_sqr_' + str(n)] = r_sqr
# +
#20 day moving distribution to see if ROI goes outside of standard deviation
n = 20
for df in stocks:
std_dev = []
for i in range(len(df['Open'])):
if i > n:
sample = df['current_roi'][i]
pop_mean = mean(df['current_roi'][(i-n):i])
pop_std = stdev(df['current_roi'][(i-n):i])
if sample > ( pop_mean +5*pop_std ): #5 deviation above
std_dev.append(5)
elif sample > ( pop_mean +4*pop_std ): #4 deviation above
std_dev.append(4)
elif sample > ( pop_mean +3*pop_std ): #3 deviation above
std_dev.append(3)
elif sample > ( pop_mean +2*pop_std ): #2 deviation above
std_dev.append(2)
elif sample > ( pop_mean + pop_std ): #1 deviation above
std_dev.append(1)
elif sample > ( pop_mean - pop_std ): #within 1 deviation
std_dev.append(0)
elif sample > ( pop_mean - 2* pop_std ): #1 deviation below
std_dev.append(-1)
elif sample > ( pop_mean - 3* pop_std ): #2 deviation below
std_dev.append(-2)
elif sample > ( pop_mean - 4* pop_std ): #3 deviation below
std_dev.append(-3)
elif sample > ( pop_mean - 5* pop_std ): #4 deviation below
std_dev.append(-4)
else: #5 deviation below
std_dev.append(-5)
else:
std_dev.append(np.nan)
if i == (len(df['Open'])-1):
df['stDev' + str(n)] = std_dev
# +
#below 10 or more
#I plan on using this category to train my models
end = Nasdaq.shape[0]
max_price = Nasdaq['Open'][0]
down_array = []
for n in range(end):
if Nasdaq['Close'][n] > max_price:
#setting the all-time highest price
max_price = Nasdaq['Close'][n]
#setting percent down form highest price
down_from_top_percent = 1 + ((Nasdaq['Close'][n] - max_price)/max_price)
#print(down)
if down_from_top_percent < .8:
#bear market
down_array.append('#ff543a')
elif down_from_top_percent < .9:
#correction
down_array.append('#eeff32')
else:
#bull market
down_array.append('#71f442')
Nasdaq['down_market'] = down_array
# -
#recursion from the peak
for df in stocks:
end = df.shape[0]
max_price = df['Open'][0]
down_array = []
for n in range(end):
if df['Close'][n] > max_price:
#setting the all-time highest price
max_price = df['Close'][n]
#setting percent down form highest price
down_from_top_percent = 1 + ((df['Close'][n] - max_price)/max_price)
#print(down)
down_array.append(down_from_top_percent)
df['percent_down'] = down_array
# +
#dummy variable 1 if it's all time high and 0 if not
for df in stocks:
end = df.shape[0]
max_price = df['Open'][0]
max_array = []
for n in range(end):
if n % 60 == 0:
max_price = df['Open'][n]
if df['Open'][n] > max_price:
max_array.append(1)
#setting the all-time highest price
max_price = df['Open'][n]
else:
max_array.append(0)
df['semi_pk_pr'] = max_array
# -
#consecutive days up or day
#this will likely only be used for EDA later on
for df in stocks:
end = df.shape[0]
counter = 0
counter_array = []
for n in range(end):
if n > 1: #here we reset counter if not consistent
if counter > 1 and df['Day_previous_roi'][n] <= 1:
counter = 0
elif counter < 1 and df['Day_previous_roi'][n] >= 1:
counter = 0
elif counter == 1 and df['Day_previous_roi'][n] != 1:
counter
if df['Day_previous_roi'][n] > 1:
counter += 1
elif df['Day_previous_roi'][n] == 1:
counter = 0
else:
counter -= 1
counter_array.append(counter)
df['up_dwn_prev'] = counter_array
#consecutive days up or day
#this will likely only be used for EDA later on
for df in stocks:
end = df.shape[0]
counter = 0
counter_array = []
for n in range(end):
if n > 1: #here we reset counter if not consistent
if counter > 1 and df['current_roi'][n] <= 1:
counter = 0
elif counter < 1 and df['current_roi'][n] >= 1:
counter = 0
elif counter == 1 and df['current_roi'][n] != 1:
counter
if df['current_roi'][n] > 1:
counter += 1
elif df['current_roi'][n] == 1:
counter = 0
else:
counter -= 1
counter_array.append(counter)
df['up_dwn_curr'] = counter_array
# # Creating My target Variables
#Lets make a few target regression variables
for df in stocks:
for i in [1,3,5,10,20]:
end = df.shape[0]
target = 0
target_array = []
for n in range(end):
target = df['current_roi'][n:(n+i)].prod()
target_array.append(target)
df['target_' + str(i) +'roi'] = target_array
# +
#now lets do some categorical data
for df in stocks:
for i in [1,3,5,10,20]:
end = df.shape[0]
target_array = []
for n in range(end):
if n >= (end - i):
target_array.append(np.nan)
else: #try .max for np arrays
target = 1 + (max(df['High'][n:(n+i+1)]) - df['Open'][n])/df['Open'][n]
if target == 1.0:
target = df['target_' + str(i) +'roi'][n]
target_array.append(target)
df['tar_' + str(i) +'best_roi'] = target_array
# +
#now lets do some categorical data
for df in stocks:
for i in [1,3,5,10,20]:
end = df.shape[0]
qtile = (df['tar_' +str(i) + 'best_roi'].quantile([0.25,0.5,0.75])).values
class_array = []
q1 = str(round(qtile[0],4))
q2 = str(round(qtile[1],4))
q3 = str(round(qtile[2],4))
for n in range(end):
if n >= (end - 1):
class_array.append(np.nan)
else:
target = 1 + (max(max(df['High'][n:(n+i+1)]),df['Open'][n+1]) - df['Open'][n])/df['Open'][n]
if target > qtile[2]:
class_array.append('abv_' + q3)
elif target > qtile[1]:
class_array.append('abv_' + q2)
elif target > qtile[0]:
class_array.append('abv_' + q1)
elif target <= qtile[0]:
class_array.append('bel_'+ q1)
df['tar_' + str(i) +'best_class'] = class_array
# -
(V['tar_1best_roi'].quantile([0.25,0.5,0.75])).values
from collections import Counter
Counter(V['tar_1best_class'])
for df in stocks:
end = df.shape[0]
t_array = []
for row in df.current_roi:
if row > 1:
t_array.append('buy')
else:
t_array.append('sell')
df['easy_buy'] = t_array
# +
for df in stocks:
#print(qtile[1])
for i in [1,3,5,10,20]:
qtile = (df['tar_' +str(i) + 'best_roi'].quantile([0.25,0.5,0.75])).values
end = df.shape[0]
target = 0
label = ''
target_array = []
#print(i)
for n in range(end):
if n >= (end - i):
target_array.append(np.nan)
else: #try .max for np arrays
target = 1 + (max(df['High'][n:(n+i+1)]) - df['Open'][n])/df['Open'][n]
if target <= 1.0:
target = 1 + ((df['Close'][n+i] - df['Open'][n])/df['Open'][n])
#print(n,t)
if target > qtile[1]:
label = 'above_'+ str(qtile[1])
else:
label = 'below_'+ str(qtile[1])
target_array.append(label)
df['tar_' + str(i) +'new_high'] = target_array
# -
for df in stocks:
for i in [1,3,5,10,20]:
df['tar_' + str(i) +'new_high'] = df['tar_' + str(i) +'new_high'].shift(-1)
df['tar_' + str(i) +'best_class'] = df['tar_' + str(i) +'best_class'].shift(-1)
df['tar_' + str(i) +'best_roi'] = df['tar_' + str(i) +'best_roi'].shift(-1)
df['target_' + str(i) +'roi'] = df['target_' + str(i) +'roi'].shift(-1)
for df in stocks:
df['easy_buy'] = df['easy_buy'].shift(-1)
# # Saving My dataframes as CSVs to use in Analysis
# +
#Drop all NaN values form dataframes
for df in stocks:
df.replace(-np.inf, np.nan,inplace=True)
df.replace(np.inf, np.nan,inplace=True)
df.dropna(inplace=True)
df.reset_index(inplace=True)
# +
SOXL.name = 'soxl'
Nasdaq.name = 'nasdaq'
TQQQ.name = 'tqqq'
MU.name = 'mu'
AMD.name = 'amd'
NFLX.name = 'nflx'
AMZN.name = 'amzn'
V.name = 'visa'
YINN.name = 'yinn'
NVDA.name = 'nvda'
WTW.name = 'wtw'
F.name = 'f'
MSFT.name = 'mfst'
HNGR.name = 'hngr'
# +
import glob
for df in stocks:
# Give the filename you wish to save the file to
filename = df.name + '_new.csv'
# Use this function to search for any files which match your filename
files_present = glob.glob(filename)
# if no matching files, write to csv, if there are matching files, print statement
if not files_present:
df.to_csv(filename)
else:
print('WARNING: This file already exists!' )
# -
# # Feature Importance Testing
# +
#MU_cln.columns.values.tolist()
features = ['Day_previous_roi','ma10','rsi10','ma20','rsi20','ma_chg20',
'ma60','rsi60','ma200','rsi200','obv','macd_diff','ma_chg10',
'macd_diff_hist','aroon_diff','slope60','r_sqr_60','ma_chg60',
'slope10','r_sqr_10','slope5','slope3','r_sqr_5','stDev20','ma_chg200',
'rsi_chg10','rsi_chg20','rsi_chg60','rsi_chg200',
'percent_down','sine','leadsine','tsf10','tsf20','tsf60','tsf200',
'up_dwn_prev','shawman','hammer','semi_pk_pr','open_H_ratio',
'open_L_ratio','close_H_ratio','close_L_ratio']
feature_best = ['Day_previous_roi','ma10','rsi10','ma20','rsi20',
'ma60','rsi60','ma200','rsi200','obv','macd_diff',
'macd_diff_hist','aroon_diff','slope60','r_sqr_60',
'slope10','r_sqr_10','slope5','r_sqr_5',
'percent_down','sine','leadsine','tsf10',
'tsf20','tsf60','tsf200',
'up_dwn_prev','open_H_ratio',
'open_L_ratio','close_H_ratio','close_L_ratio']
corr_ft = ['Day_previous_roi','ma10','rsi10','ma20','rsi20',
'ma60','rsi60','ma200','rsi200','obv','macd_diff',
'macd_diff_hist','aroon_diff','slope60','r_sqr_60',
'slope10','r_sqr_10','slope5','r_sqr_5','stDev20',
'percent_down','sine','leadsine','tsf10','tsf20','tsf60','tsf200',
'up_dwn_prev','shawman','hammer','semi_pk_pr','current_roi']
targets_cat = ['up_dwn_curr',
'tar_3best_roi',
'tar_5best_roi',
'tar_10best_roi',
'tar_20best_roi',
'tar_1best_roi',
'tar_1best_class',
'tar_3best_class',
'tar_5best_class',
'tar_10best_class',
'tar_20best_class',
'easy_buy',
'tar_3new_high',
'tar_5new_high',
'tar_10new_high',
'tar_20new_high']
targets_reg = ['target_3roi',
'target_5roi',
'target_10roi',
'target_20roi']
#Set stock or dataframe
df_cln = NFLX
target_name = 'tar_3best_class'
#.75 make a 25/75 split
stop = round(.9*len(df_cln))
#set features
feature_train = df_cln.loc[:stop,features]
feature_test = df_cln.loc[stop:,features]
#set my targets
target_train = df_cln.loc[:stop,[target_name]]
target_test = df_cln.loc[stop:,[target_name]]
# +
#MU.columns.values.tolist()
# -
print(target_train.shape,target_test.shape,feature_train.shape,feature_test.shape)
# +
from sklearn.ensemble import RandomForestClassifier
from sklearn.feature_selection import SelectFromModel
from sklearn.metrics import accuracy_score
# Create a random forest classifier
rf2 = RandomForestClassifier(n_estimators=1100,
max_features=6,
max_depth=11,
n_jobs=-1,
random_state=42)
# Train the classifier
rf2.fit(feature_train, target_train)
feature_imp = pd.Series(rf2.feature_importances_,index=features).sort_values(ascending=False)
feature_imp
#rf.feature_importances_
# -
# %matplotlib inline
# Creating a bar plot
sns.barplot(x=feature_imp, y=feature_imp.index)
# Add labels to your graph
plt.xlabel('Feature Importance Score')
plt.ylabel('Features')
plt.title("Visualizing Important Features")
plt.legend()
plt.show()
# +
# prediction on test set
target_pred=rf2.predict(feature_test)
#Import scikit-learn metrics module for accuracy calculation
from sklearn import metrics
# Model Accuracy, how often is the classifier correct?
print("Cohen Kappa:",metrics.cohen_kappa_score(target_test, target_pred),'\n'
"Accuracy:",metrics.accuracy_score(target_test, target_pred))
# +
df_cln[target_name].value_counts()
# -
from collections import Counter
Counter(target_test[target_name])
plt.subplots(figsize=(30,25))
sns.set(style="whitegrid")
ax = sns.violinplot(x="stDev20", y="target_3roi", data=Nasdaq,palette="Set3")
|
data_ingest_&_clean.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: DESI master
# language: python
# name: desi-master
# ---
# # Notebook showing some very basic QA on main survey reduced data so far
from astropy.table import Table
import fitsio
import numpy as np
from matplotlib import pyplot as plt
import os,sys
from desitarget import targetmask
ff = fitsio.read('/global/cfs/cdirs/desi/spectro/redux/everest/zcatalog/ztile-main-dark-cumulative.fits')
wp = ff['PRIORITY'] == 3400
print(len(ff[wp]))
wq = ff['DESI_TARGET'] & 2**2 != 0
print(len(ff[wq]),len(ff[wq&wp]))
ws = ff['DESI_TARGET'] & 2**62 != 0
print(len(ff[wp&ws&~wq]))
np.unique(ff['PRIORITY'],return_counts=True)
w = ff['PRIORITY'] == 0
print(np.unique(ff[w]['OBJTYPE'],return_counts=True))
ff.dtype.names
sys.path.append('../py') #this works if you are in the LSS/Sandbox directory, check with os.getcwd()
from LSS.main import cattools as ct
import importlib
importlib.reload(ct)
mt = Table.read('/global/cfs/cdirs/desi/survey/ops/surveyops/trunk/ops/tiles-main.ecsv')
mt.columns
len(mt)
wd = mt['DONEFRAC'] > 1
print(len(mt[wd]))
#use this to test a specific tile
tdir = '/global/cfs/cdirs/desi/spectro/redux/daily/tiles/cumulative/1895'
subsets = [x[0][len(tdir):].strip('/') for x in os.walk(tdir)]
zt = ct.combspecdata('1895',max(subsets),md='') #zt becomes table with redshift info
wt = zt['FIBERSTATUS'] == 0
np.median(zt[wt]['TSNR2_QSO'])
#look at number of quasars
wq = zt['SPECTYPE'] == 'QSO'
wq &= zt['FIBERSTATUS'] == 0
wq &= zt['ZWARN'] == 0
wq &= zt['DESI_TARGET'] & targetmask.desi_mask['QSO'] > 0
print(len(zt[wq]))
# ### below goes through all tiles with donefrac > 1 and compares "good" to total
tps = ['LRG','ELG','QSO','BGS_ANY','MWS_ANY']
elgt = []
elgg = []
lrgt = []
lrgg = []
qsot = []
qsog = []
bgst = []
bgsg = []
mwst = []
mwsg = []
bt = []
n = 0
for tid,pr in zip(mt[wd]['TILEID'],mt[wd]['PROGRAM']):
n += 1
tdir = '/global/cfs/cdirs/desi/spectro/redux/daily/tiles/cumulative/'+str(tid)
subsets = [x[0][len(tdir):].strip('/') for x in os.walk(tdir)]
zt = ct.combspecdata(str(tid),max(subsets),md='')
print(n,len(mt[wd]))
print('tile is '+str(tid)+' and program is '+pr)
for tp in tps:
selt = (zt['DESI_TARGET'] & targetmask.desi_mask[tp]) > 0
selt &= (zt['FIBERSTATUS'] == 0)
wzg = selt & (zt['ZWARN'] == 0)
#print(tp,len(zt[selt]),len(zt[wzg]))
if pr == 'DARK':
if tp == 'ELG':
selt &= (zt['DESI_TARGET'] & targetmask.desi_mask['QSO']) == 0
wzg &= (zt['DESI_TARGET'] & targetmask.desi_mask['QSO']) == 0
elgt.append(len(zt[selt]))
elgg.append(len(zt[wzg]))
if tp == 'LRG':
lrgt.append(len(zt[selt]))
lrgg.append(len(zt[wzg]))
if tp == 'QSO':
qsot.append(len(zt[selt]))
qsog.append(len(zt[wzg]))
if len(zt[wzg])/len(zt[selt]) < 0.75:
bt.append(tid)
if pr == 'BRIGHT':
if tp == 'BGS_ANY':
wzg &= (zt['DELTACHI2'] > 40)
bgst.append(len(zt[selt]))
bgsg.append(len(zt[wzg]))
if tp == 'MWS_ANY':
mwst.append(len(zt[selt]))
mwsg.append(len(zt[wzg]))
plt.hist(np.array(elgg)/np.array(elgt))
plt.xlabel('fraction with zwarn == 0')
plt.ylabel('# of tiles')
plt.title('ELGs (not QSO) on first '+str(len(elgg))+' dark tiles with donefrac>1')
plt.show()
plt.hist(np.array(lrgg)/np.array(lrgt))
plt.xlabel('fraction with zwarn == 0')
plt.ylabel('# of tiles')
plt.title('LRGs on first '+str(len(elgg))+' dark tiles with donefrac>1')
plt.show()
plt.hist(np.array(qsog)/np.array(qsot))
plt.xlabel('fraction with zwarn == 0')
plt.ylabel('# of tiles')
plt.title('QSO targets on first '+str(len(elgg))+' dark tiles with donefrac>1')
plt.show()
plt.hist(np.array(bgsg)/np.array(bgst))
plt.xlabel('fraction with zwarn == 0 and DELTACHI2 > 40')
plt.ylabel('# of tiles')
plt.title('BGS_ANY targets on first '+str(len(bgsg))+' bright tiles with donefrac>1')
plt.show()
plt.hist(np.array(mwsg)/np.array(mwst))
plt.xlabel('fraction with zwarn == 0')
plt.ylabel('# of tiles')
plt.title('MWS_ANY targets on first '+str(len(elgg))+' bright tiles with donefrac>1')
plt.show()
print(sum(elgg),sum(lrgg),sum(qsog),len(elgg))
print(sum(elgt),sum(lrgt),sum(qsot))
print(sum(bgsg),sum(mwsg),len(bgsg))
print(sum(bgst),sum(mwst),len(bgst))
wb = np.isin(mt['TILEID'],bt)
mt[wb]
sum(qsot)/66
|
Sandbox/Main_explore.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # [LEGALST-123] Lab 11: Math in Scipy
#
#
# This lab will provide an introduction to numpy and scipy library of Python, preparing you for optimization and machine learning.
#
#
# *Estimated Time: 30-40 minutes*
#
# ---
#
# ### Topics Covered
# - Numpy Array
# - Numpy matrix
# - Local minima/maxima
# - Scipy optimize
# - Scipy integrate
#
# ### Table of Contents
#
# 1 - [Intro to Numpy](#section 1)<br>
#
# 3 - [Maxima and Minima](#section 2)<br>
#
# 2 - [Intro to Scipy](#section 3)<br>
#
# ## Intro to Numpy <a id='section 1'></a>
# Numpy uses its own data structure, an array, to do numerical computations. The Numpy library is often used in scientific and engineering contexts for doing data manipulation.
#
# For reference, here's a link to the official [Numpy documentation](https://docs.scipy.org/doc/numpy/reference/routines.html).
## An import statement for getting the Numpy library:
import numpy as np
## Also import csv to process the data file (black magic for now):
import csv
# ### Numpy Arrays
#
# Arrays can hold many different data types, which makes them useful for many different purposes. Here's a few examples.
# create an array from a list of integers
lst = [1, 2, 3]
values = np.array(lst)
print(values)
print(lst)
# nested array
lst = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
values = np.array(lst)
print(values)
# What does the below operation do?
values > 3
# **Your answer:** changes all matrix values that are greater than three to 'True', and all other values to 'False'
"""
Here, we will generate a multidimensional array of zeros. This might be
useful as a starting value that could be filled in.
"""
z = np.zeros((10, 2))
print(z)
# ### Matrix
#
# A **matrix** is a rectangular array- in Python, it looks like an array of arrays. We say that a matrix $M$ has shape ** $m$x$n$ **; that is, it has $m$ rows (different smaller arrays inside of it) and $n$ columns (elements in each smaller matrix.
#
# Matrices are used a lot in machine learning to represent sets of features and train models. Here, we'll give you some practice with manipulating them.
#
# The **identity matrix** is a square matrix (i.e. size $n$x$n$) with all elements on the main diagonal equal to 1 and all other elements equal to zero. Make one below using `np.eye(n)`.
# identity matrix I of dimension 4x4
np.eye(4)
# Let's do some matrix manipulation. Here are two sample matrices to use for practice.
# +
m1 = np.array([[1, 3, 1], [1, 0, 0]])
m2 = np.array([[0, 0, 5], [7, 5, 0]])
print("matrix 1 is:\n", m1)
print("matrix 2 is:\n", m2)
# -
# You can add two matrices together if they have the same shape. Add our two sample matrices using the `+` operator.
# matrix sum
m1 + m2
# A matrix can also be multiplied by a number, also called a **scalar**. Multiply one of the example matrices by a number using the `*` operator and see what it outputs.
# scale a matrix
m1 * 3
# You can sum all the elements of a matrix using `.sum()`.
# sum of all elements in m1
m1.sum()
# And you can get the average of the elements with `.mean()`
# mean of all elements in m2
m2.mean()
# Sometimes it is necessary to **transpose** a matrix to perform operations on it. When a matrix is transposed, its rows become its columns and its columns become its rows. Get the transpose by calling `.T` on a matrix (note: no parentheses)
# transpose of m1
m1.T
# Other times, you may need to rearrange an array of data into a particular shape of matrix. Below, we've created an array of 16 numbers:
H = np.arange(1, 17)
H
# Use `.reshape(...)` on H to change its shape. `.reshape(...)` takes two arguments: the first is the desired number of rows, and the second is the desired number of columns. Try changing H to be a 4x4 matrix.
#
# Note: if you try to make H be a 4x3 matrix, Python will error. Why?
# make H a 4x4 matrix
H = H.reshape(4, 4)
H
# Next, we'll talk about **matrix multiplication**. First, assign H_t below to be the transpose of H.
# assign H_t to the transpose of H
H_t = H.T
H_t
# The [matrix product](https://en.wikipedia.org/wiki/Matrix_multiplication#Matrix_product_.28two_matrices.29) get used a lot in optimization problems, among other things. It takes two matrices (one $m$x$n$, one $n$x$p$) and returns a matrix of size $m$x$p$. For example, the product of a 2x3 matrix and a 3x4 matrix is a 2x4 matrix (click the link for a visualization of what goes on with each individual element).
#
# You can use the matrix product in numpy with `matrix1.dot(matrix2)` or `matrix1 @ matrix2`.
#
# Note: to use the matrix product, the two matrices must have the same number of elements and the number of *rows* in the first matrix must equal the number of *columns* in the second. This is why it's important to know how to reshape and transpose matrices!
#
# A property of the matrix product is that the product of a matrix and the identity matrix is just the first matrix. Check that that is the case below for the matrix `H`.
# matrix product
I = np.eye(4)
# a matrix m's matrix product with the identity matrix is matrix m
H.dot(I)
# Note that we keep using the term 'product', but we don't use the `*` operator. Try using `*` to multiply `H` and `I` together.
# matrix multiplication
H * I
# How is the matrix product different from simply multiplying two matrices together?
#
# **YOUR ANSWER:** The matrix product does row-by-column products and summation (i.e. the dot product). Using `*` in numpy does element-wise multiplication (e.g. element i, j in the first matrix is multiplied by element i, j of the second).
# #### Matrix inverse
# #### Theorem: the product of a matrix m and its inverse is an identity matrix
#
# Using the above theorem, to solve for x in Ax=B where A and B are matrices, what do we want to multiply both sides by?
# Your answer here: $A^{-1}$
# You can get the inverse of a matrix with `np.linalg.inv(my_matrix)`. Try it in the cell below.
#
# Note: not all matrices are invertible.
# +
m3 = np.array([[1, 0, 0, 0], [0, 2, 0, 0], [0, 0, 3, 0], [0, 0, 0, 4]])
# calculate the inverse of m3
m3_inverse = np.linalg.inv(m3)
print("matrix m3:\n", m3)
print("\ninverse matrix m3:\n", m3_inverse)
# -
# do we get the identity matrix?
m3_inverse.dot(m3)
# #### exercise
# In machine learning, we often try to predict a value or category given a bunch of data. The essential model looks like this:
# $$ \large
# Y = X^T \theta
# $$
# Where $Y $ is the predicted values (a vector with one value for every row of X)), $X$ is a $m$x$n$ matrix of data, and $\theta$ (the Greek letter 'theta') is a **parameter** (an $n$-length vector). For example, X could be a matrix where each row represents a person, and it has two columns: height and age. To use height and age to predict a person's weight (our $y$), we could multiply the height and the age by different numbers ($\theta$) then add them together to make a prediction($y$).
#
# The fundamental problem in machine learning is often how to choose the best $\theta$. Using linear algebra, we can show that the optimal theta is:
# $$\large
# \hat{\theta{}} = \left(X^T X\right)^{-1} X^T Y
# $$
#
# You now know all the functions needed to find theta. Use transpose, inverse, and matrix product operations to calculate theta using the equation above and the X and y data given below.
# +
# example real values (the numbers 0 through 50 with random noise added)
y = np.arange(50)+ np.random.normal(scale = 10,size=50)
# example data
x = np.array([np.arange(50)]).T
# add a column of ones to represent an intercept term
X = np.hstack([x, np.ones(x.shape)])
# find the best theta
theta = np.linalg.inv(X.T @ X) @ X.T @ y
theta
# -
# In this case, our X is a matrix where the first column has values representing a feature, and the second column is entirely ones to represent an intercept term. This means our theta is a vector [m, b] for the equation y=mx[0]+b, which you might recognize from algebra as the equation for a line. Let's see how well our predictor line fits the data.
# +
import matplotlib.pyplot as plt
# %matplotlib inline
#plot the data
plt.scatter(x.T,y)
#plot the fit line
plt.plot(x.T[0], X @ theta);
# -
# Not bad!
#
# While it's good to know what computation goes into getting optimal parameters, it's also good that scipy has a function that will take in an X and a y and return the best theta. Run the cell below to use scikit-learn to estimate the parameters. It should output values very near to the ones you found. We'll learn how to use scikit-learn in the next lab!
# +
# find optimal parameters for linear regression
from sklearn import linear_model
lin_reg = linear_model.LinearRegression(fit_intercept=True)
lin_reg.fit(x, y)
print(lin_reg.coef_[0], lin_reg.intercept_)
# -
# ## Maxima and Minima <a id='section 2'></a>
# The extrema of a function are the largest value (maxima) and smallest value (minima) of the function.
#
# We say that f(a) is a **local maxima** if $f(a)\geq f(x)$ when x is near a.
#
# We say that f(a) is a **local minima** if $f(a)\leq f(x)$ when x is near a.
# Global vs local extrema (credit: Wikipedia)
# <img src="https://upload.wikimedia.org/wikipedia/commons/thumb/6/68/Extrema_example_original.svg/440px-Extrema_example_original.svg.png" style="width: 500px; height: 275px;" />
# By looking at the diagram , how are local maxima and minima of a function related to its derivative?
# **YOUR ANSWER**: Local minima and maxima occur when the derivative is zero- i.e. when the slope is zero, or when the tangent line is horizontal.
# Are global maxima also local maixma? Are local maxima global maxima?
# **YOUR ANSWER**: Yes, global maxima are also local maxima.
#
# No, a local maxima may not be a global maxima.
# ## Intro to Scipy <a id='section 3'></a>
# ### Optimize
# Scipy.optimize is a package that provides several commonly used optimization algorithms. Today we'll learn minimize.
# insert concepts about local minima
# importing minimize function
from scipy.optimize import minimize
# Let's define a minimization problem:
#
# minimize $x_1x_4(x_1+x_2+x_3)+x_3$ under the conditions:
# 1. $x_1x_2x_3x_4\geq 25$
# 2. $x_1+x_2+x_3+2x_4 = 14$
# 3. $1\leq x_1,x_2,x_3,x_4\leq 5$
# Hmmm, looks fairly complicated, but don't worry, scipy's got it
# let's define our function
def objective(x):
x1 = x[0]
x2 = x[1]
x3 = x[2]
x4 = x[3]
return x1*x4*(x1+x2+x3)+x3
# +
# define constraints
def con1(x):
return x[0]*x[1]*x[2]*x[3] - 25
def con2(x):
return 14 - x[0] - x[1] - x[2] - 2*x[3]
constraint1 = {'type': 'ineq', 'fun': con1} # constraint 1 is an inequality constraint
constraint2 = {'type': 'eq', 'fun': con2} # constraint 2 is an equality constraint
cons = [constraint1, constraint2]
# -
# define bounds
bound = (1, 5)
bnds = (bound, bound, bound, bound) #the same bound applies to all four variables
# We need to supply initial values as a starting point for minimize function
x0 = [3, 4, 2, 3]
print(objective(x0))
# Overall, we defined objective function, constraints, bounds, and initial values. Let's get to work.
#
# We'll use Sequential Least Squares Programming optimization algorithm (SLSQP)
solution = minimize(objective, x0, method='SLSQP', bounds=bnds, constraints=cons)
print(solution)
# Display optimal values of each variable
solution.x
# #### exercise
# Find the optimal solution to the following problem:
#
# minimize $x_1^2+x_2^2+x_3^2$, under conditions:
# 1. $x_1 + x_2\geq 6$
# 2. $x_3 + 2x_2\geq 4$
# 3. $1.5\leq x_1, x_2, x_3\leq 8$
#
# Tip: 3**2 gives square of 3
def func(x):
x1 = x[0]
x2 = x[1]
x3 = x[2]
return x1**2 + x2**2 + x3**2
def newcon1(x):
return x[0] + x[1] - 6
def newcon2(x):
return x[2] + 2*x[1] - 4
# Take note of scipy's documentation on constraints:
#
# > "Equality constraint means that the constraint function result is to be zero whereas inequality means that it is to be non-negative."
# +
newcons1 = {'type': 'ineq', 'fun': newcon1}
newcons2 = {'type': 'ineq', 'fun': newcon2}
newcons = [newcons1, newcons2]
bd = (1.5, 8)
bds = (bd, bd, bd)
newx0 = [1, 4, 3]
sum_square_solution = minimize(func, newx0, method='SLSQP', bounds=bds, constraints=newcons)
sum_square_solution
# -
# ### Integrate
# scipy.integrate.quad is a function that tntegrates a function from a to b using a technique from QUADPACK library.
# importing integrate package
from scipy import integrate
# define a simple function
def f(x):
return np.sin(x)
# integrate sin from 0 to pi
integrate.quad(f, 0, np.pi)
# Our quad function returned two results, first one is the result, second one is an estimate of the absolute error
# #### exercise
# Find the integral of $x^2 + x$ from 3 to 10
# +
#define the function
def f1(x):
return x ** 2 + x
#find the integral
integrate.quad(f1, 3, 10)
# -
# #### Integrate a normal distribution
# +
# let's create a normal distribution with mean 0 and standard deviation 1 by simpy running the cell
mu, sigma = 0, 1
s = np.random.normal(mu, sigma, 100000)
import matplotlib.pyplot as plt
count, bins, ignored = plt.hist(s, 30, density=True)
plt.plot(bins, 1/(sigma * np.sqrt(2 * np.pi)) *np.exp( - (bins - mu)**2 / (2 * sigma**2) ),linewidth=2, color='r')
plt.show()
# -
# importing normal d
from scipy.stats import norm
# CDF is cumulative distribution function. CDF(x) is the probability that a normal distribution takes on value less than or equal to x.
#
# For a standard normal distribution, what would CDF(0) be? (Hint: how is CDF related to p-values or confidence intervals?)
# 0.5
# Run the cell below to confirm your answer
norm.cdf(0)
# Using the cdf, integrate the normal distribution from -0.5 to 0.5
norm.cdf(0.5) - norm.cdf(-0.5)
# ---
# Notebook developed by: <NAME>
#
# Data Science Modules: http://data.berkeley.edu/education/modules
#
|
labs/11_Math in Scipy/11_Math_in_scipy_solutions.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Distributions
# + [markdown] tags=["remove-cell"]
# Think Bayes, Second Edition
#
# Copyright 2020 <NAME>
#
# License: [Attribution-NonCommercial-ShareAlike 4.0 International (CC BY-NC-SA 4.0)](https://creativecommons.org/licenses/by-nc-sa/4.0/)
# + tags=["remove-cell"]
# If we're running on Colab, install empiricaldist
# https://pypi.org/project/empiricaldist/
import sys
IN_COLAB = 'google.colab' in sys.modules
if IN_COLAB:
# !pip install empiricaldist
# + tags=["remove-cell"]
# Get utils.py
import os
if not os.path.exists('utils.py'):
# !wget https://github.com/AllenDowney/ThinkBayes2/raw/master/soln/utils.py
# + tags=["remove-cell"]
from utils import set_pyplot_params
set_pyplot_params()
# -
# In the previous chapter we used Bayes's Theorem to solve a cookie problem; then we solved it again using a Bayes table.
# In this chapter, at the risk of testing your patience, we will solve it one more time using a `Pmf` object, which represents a "probability mass function".
# I'll explain what that means, and why it is useful for Bayesian statistics.
#
# We'll use `Pmf` objects to solve some more challenging problems and take one more step toward Bayesian statistics.
# But we'll start with distributions.
# ## Distributions
#
# In statistics a **distribution** is a set of possible outcomes and their corresponding probabilities.
# For example, if you toss a coin, there are two possible outcomes with
# approximately equal probability.
# If you roll a six-sided die, the set of possible outcomes is the numbers 1 to 6, and the probability associated with each outcome is 1/6.
#
# To represent distributions, we'll use a library called `empiricaldist`.
# An "empirical" distribution is based on data, as opposed to a
# theoretical distribution.
# We'll use this library throughout the book. I'll introduce the basic features in this chapter and we'll see additional features later.
# ## Probability Mass Functions
#
# If the outcomes in a distribution are discrete, we can describe the distribution with a **probability mass function**, or PMF, which is a function that maps from each possible outcome to its probability.
#
# `empiricaldist` provides a class called `Pmf` that represents a
# probability mass function.
# To use `Pmf` you can import it like this:
from empiricaldist import Pmf
# + [markdown] tags=["remove-cell"]
# If that doesn't work, you might have to install `empiricaldist`; try running
#
# ```
# # # !pip install empiricaldist
# ```
#
# in a code cell or
#
# ```
# pip install empiricaldist
# ```
#
# in a terminal window.
# -
# The following example makes a `Pmf` that represents the outcome of a
# coin toss.
coin = Pmf()
coin['heads'] = 1/2
coin['tails'] = 1/2
coin
# `Pmf` creates an empty `Pmf` with no outcomes.
# Then we can add new outcomes using the bracket operator.
# In this example, the two outcomes are represented with strings, and they have the same probability, 0.5.
# You can also make a `Pmf` from a sequence of possible outcomes.
#
# The following example uses `Pmf.from_seq` to make a `Pmf` that represents a six-sided die.
die = Pmf.from_seq([1,2,3,4,5,6])
die
# In this example, all outcomes in the sequence appear once, so they all have the same probability, $1/6$.
#
# More generally, outcomes can appear more than once, as in the following example:
letters = Pmf.from_seq(list('Mississippi'))
letters
# The letter `M` appears once out of 11 characters, so its probability is $1/11$.
# The letter `i` appears 4 times, so its probability is $4/11$.
#
# Since the letters in a string are not outcomes of a random process, I'll use the more general term "quantities" for the letters in the `Pmf`.
#
# The `Pmf` class inherits from a Pandas `Series`, so anything you can do with a `Series`, you can also do with a `Pmf`.
#
# For example, you can use the bracket operator to look up a quantity and get the corresponding probability.
letters['s']
# In the word "Mississippi", about 36% of the letters are "s".
#
# However, if you ask for the probability of a quantity that's not in the distribution, you get a `KeyError`.
#
#
# + tags=["hide-cell"]
try:
letters['t']
except KeyError as e:
print(type(e))
# -
# You can also call a `Pmf` as if it were a function, with a letter in parentheses.
letters('s')
# If the quantity is in the distribution the results are the same.
# But if it is not in the distribution, the result is `0`, not an error.
letters('t')
# With parentheses, you can also provide a sequence of quantities and get a sequence of probabilities.
die([1,4,7])
# The quantities in a `Pmf` can be strings, numbers, or any other type that can be stored in the index of a Pandas `Series`.
# If you are familiar with Pandas, that will help you work with `Pmf` objects.
# But I will explain what you need to know as we go along.
# ## The Cookie Problem Revisited
#
# In this section I'll use a `Pmf` to solve the cookie problem from <<_TheCookieProblem>>.
# Here's the statement of the problem again:
#
# > Suppose there are two bowls of cookies.
# >
# > * Bowl 1 contains 30 vanilla cookies and 10 chocolate cookies.
# >
# > * Bowl 2 contains 20 vanilla cookies and 20 chocolate cookies.
# >
# > Now suppose you choose one of the bowls at random and, without looking, choose a cookie at random. If the cookie is vanilla, what is the probability that it came from Bowl 1?
#
# Here's a `Pmf` that represents the two hypotheses and their prior probabilities:
prior = Pmf.from_seq(['Bowl 1', 'Bowl 2'])
prior
# This distribution, which contains the prior probability for each hypothesis, is called (wait for it) the **prior distribution**.
#
# To update the distribution based on new data (the vanilla cookie),
# we multiply the priors by the likelihoods. The likelihood
# of drawing a vanilla cookie from Bowl 1 is `3/4`. The likelihood
# for Bowl 2 is `1/2`.
likelihood_vanilla = [0.75, 0.5]
posterior = prior * likelihood_vanilla
posterior
# The result is the unnormalized posteriors; that is, they don't add up to 1.
# To make them add up to 1, we can use `normalize`, which is a method provided by `Pmf`.
posterior.normalize()
# The return value from `normalize` is the total probability of the data, which is $5/8$.
#
# `posterior`, which contains the posterior probability for each hypothesis, is called (wait now) the **posterior distribution**.
posterior
# From the posterior distribution we can select the posterior probability for Bowl 1:
posterior('Bowl 1')
# And the answer is 0.6.
#
# One benefit of using `Pmf` objects is that it is easy to do successive updates with more data.
# For example, suppose you put the first cookie back (so the contents of the bowls don't change) and draw again from the same bowl.
# If the second cookie is also vanilla, we can do a second update like this:
posterior *= likelihood_vanilla
posterior.normalize()
posterior
# Now the posterior probability for Bowl 1 is almost 70%.
# But suppose we do the same thing again and get a chocolate cookie.
#
# Here are the likelihoods for the new data:
likelihood_chocolate = [0.25, 0.5]
# And here's the update.
posterior *= likelihood_chocolate
posterior.normalize()
posterior
# Now the posterior probability for Bowl 1 is about 53%.
# After two vanilla cookies and one chocolate, the posterior probabilities are close to 50/50.
# ## 101 Bowls
#
# Next let's solve a cookie problem with 101 bowls:
#
# * Bowl 0 contains 0% vanilla cookies,
#
# * Bowl 1 contains 1% vanilla cookies,
#
# * Bowl 2 contains 2% vanilla cookies,
#
# and so on, up to
#
# * Bowl 99 contains 99% vanilla cookies, and
#
# * Bowl 100 contains all vanilla cookies.
#
# As in the previous version, there are only two kinds of cookies, vanilla and chocolate. So Bowl 0 is all chocolate cookies, Bowl 1 is 99% chocolate, and so on.
#
# Suppose we choose a bowl at random, choose a cookie at random, and it turns out to be vanilla. What is the probability that the cookie came from Bowl $x$, for each value of $x$?
#
# To solve this problem, I'll use `np.arange` to make an array that represents 101 hypotheses, numbered from 0 to 100.
# +
import numpy as np
hypos = np.arange(101)
# -
# We can use this array to make the prior distribution:
prior = Pmf(1, hypos)
prior.normalize()
# As this example shows, we can initialize a `Pmf` with two parameters.
# The first parameter is the prior probability; the second parameter is a sequence of quantities.
#
# In this example, the probabilities are all the same, so we only have to provide one of them; it gets "broadcast" across the hypotheses.
# Since all hypotheses have the same prior probability, this distribution is **uniform**.
#
# Here are the first few hypotheses and their probabilities.
prior.head()
# The likelihood of the data is the fraction of vanilla cookies in each bowl, which we can calculate using `hypos`:
likelihood_vanilla = hypos/100
likelihood_vanilla[:5]
# Now we can compute the posterior distribution in the usual way:
#
posterior1 = prior * likelihood_vanilla
posterior1.normalize()
posterior1.head()
# The following figure shows the prior distribution and the posterior distribution after one vanilla cookie.
# + tags=["hide-cell"]
from utils import decorate
def decorate_bowls(title):
decorate(xlabel='Bowl #',
ylabel='PMF',
title=title)
# + tags=["hide-input"]
prior.plot(label='prior', color='C5')
posterior1.plot(label='posterior', color='C4')
decorate_bowls('Posterior after one vanilla cookie')
# -
# The posterior probability of Bowl 0 is 0 because it contains no vanilla cookies.
# The posterior probability of Bowl 100 is the highest because it contains the most vanilla cookies.
# In between, the shape of the posterior distribution is a line because the likelihoods are proportional to the bowl numbers.
#
# Now suppose we put the cookie back, draw again from the same bowl, and get another vanilla cookie.
# Here's the update after the second cookie:
# + tags=["hide-output"]
posterior2 = posterior1 * likelihood_vanilla
posterior2.normalize()
# -
# And here's what the posterior distribution looks like.
# + tags=["hide-input"]
posterior2.plot(label='posterior', color='C4')
decorate_bowls('Posterior after two vanilla cookies')
# -
# After two vanilla cookies, the high-numbered bowls have the highest posterior probabilities because they contain the most vanilla cookies; the low-numbered bowls have the lowest probabilities.
#
# But suppose we draw again and get a chocolate cookie.
# Here's the update:
# + tags=["hide-output"]
likelihood_chocolate = 1 - hypos/100
posterior3 = posterior2 * likelihood_chocolate
posterior3.normalize()
# -
# And here's the posterior distribution.
# + tags=["hide-input"]
posterior3.plot(label='posterior', color='C4')
decorate_bowls('Posterior after 2 vanilla, 1 chocolate')
# -
# Now Bowl 100 has been eliminated because it contains no chocolate cookies.
# But the high-numbered bowls are still more likely than the low-numbered bowls, because we have seen more vanilla cookies than chocolate.
#
# In fact, the peak of the posterior distribution is at Bowl 67, which corresponds to the fraction of vanilla cookies in the data we've observed, $2/3$.
#
# The quantity with the highest posterior probability is called the **MAP**, which stands for "maximum a posteori probability", where "a posteori" is unnecessary Latin for "posterior".
#
# To compute the MAP, we can use the `Series` method `idxmax`:
posterior3.idxmax()
# Or `Pmf` provides a more memorable name for the same thing:
posterior3.max_prob()
# As you might suspect, this example isn't really about bowls; it's about estimating proportions.
# Imagine that you have one bowl of cookies.
# You don't know what fraction of cookies are vanilla, but you think it is equally likely to be any fraction from 0 to 1.
# If you draw three cookies and two are vanilla, what proportion of cookies in the bowl do you think are vanilla?
# The posterior distribution we just computed is the answer to that question.
#
# We'll come back to estimating proportions in the next chapter.
# But first let's use a `Pmf` to solve the dice problem.
# ## The Dice Problem
#
# In the previous chapter we solved the dice problem using a Bayes table.
# Here's the statement of the problem:
#
# > Suppose I have a box with a 6-sided die, an 8-sided die, and a 12-sided die.
# > I choose one of the dice at random, roll it, and report that the outcome is a 1.
# > What is the probability that I chose the 6-sided die?
#
# Let's solve it using a `Pmf`.
# I'll use integers to represent the hypotheses:
hypos = [6, 8, 12]
# We can make the prior distribution like this:
#
prior = Pmf(1/3, hypos)
prior
# As in the previous example, the prior probability gets broadcast across the hypotheses.
# The `Pmf` object has two attributes:
#
# * `qs` contains the quantities in the distribution;
#
# * `ps` contains the corresponding probabilities.
prior.qs
prior.ps
# Now we're ready to do the update.
# Here's the likelihood of the data for each hypothesis.
likelihood1 = 1/6, 1/8, 1/12
# And here's the update.
posterior = prior * likelihood1
posterior.normalize()
posterior
# The posterior probability for the 6-sided die is $4/9$.
#
# Now suppose I roll the same die again and get a 7.
# Here are the likelihoods:
likelihood2 = 0, 1/8, 1/12
# The likelihood for the 6-sided die is 0 because it is not possible to get a 7 on a 6-sided die.
# The other two likelihoods are the same as in the previous update.
#
# Here's the update:
posterior *= likelihood2
posterior.normalize()
posterior
# After rolling a 1 and a 7, the posterior probability of the 8-sided die is about 69%.
# ## Updating Dice
#
# The following function is a more general version of the update in the previous section:
def update_dice(pmf, data):
"""Update pmf based on new data."""
hypos = pmf.qs
likelihood = 1 / hypos
impossible = (data > hypos)
likelihood[impossible] = 0
pmf *= likelihood
pmf.normalize()
# The first parameter is a `Pmf` that represents the possible dice and their probabilities.
# The second parameter is the outcome of rolling a die.
#
# The first line selects quantities from the `Pmf` which represent the hypotheses.
# Since the hypotheses are integers, we can use them to compute the likelihoods.
# In general, if there are `n` sides on the die, the probability of any possible outcome is `1/n`.
#
# However, we have to check for impossible outcomes!
# If the outcome exceeds the hypothetical number of sides on the die, the probability of that outcome is 0.
#
# `impossible` is a Boolean `Series` that is `True` for each impossible outcome.
# I use it as an index into `likelihood` to set the corresponding probabilities to 0.
#
# Finally, I multiply `pmf` by the likelihoods and normalize.
#
# Here's how we can use this function to compute the updates in the previous section.
# I start with a fresh copy of the prior distribution:
#
pmf = prior.copy()
pmf
# And use `update_dice` to do the updates.
update_dice(pmf, 1)
update_dice(pmf, 7)
pmf
# The result is the same. We will see a version of this function in the next chapter.
# ## Summary
#
# This chapter introduces the `empiricaldist` module, which provides `Pmf`, which we use to represent a set of hypotheses and their probabilities.
#
# `empiricaldist` is based on Pandas; the `Pmf` class inherits from the Pandas `Series` class and provides additional features specific to probability mass functions.
# We'll use `Pmf` and other classes from `empiricaldist` throughout the book because they simplify the code and make it more readable.
# But we could do the same things directly with Pandas.
#
# We use a `Pmf` to solve the cookie problem and the dice problem, which we saw in the previous chapter.
# With a `Pmf` it is easy to perform sequential updates with multiple pieces of data.
#
# We also solved a more general version of the cookie problem, with 101 bowls rather than two.
# Then we computed the MAP, which is the quantity with the highest posterior probability.
#
# In the next chapter, I'll introduce the Euro problem, and we will use the binomial distribution.
# And, at last, we will make the leap from using Bayes's Theorem to doing Bayesian statistics.
#
# But first you might want to work on the exercises.
# ## Exercises
# **Exercise:** Suppose I have a box with a 6-sided die, an 8-sided die, and a 12-sided die.
# I choose one of the dice at random, roll it four times, and get 1, 3, 5, and 7.
# What is the probability that I chose the 8-sided die?
#
# You can use the `update_dice` function or do the update yourself.
# +
# Solution
pmf = prior.copy()
for data in [1, 3, 5, 7]:
update_dice(pmf, data)
pmf
# -
# **Exercise:** In the previous version of the dice problem, the prior probabilities are the same because the box contains one of each die.
# But suppose the box contains 1 die that is 4-sided, 2 dice that are 6-sided, 3 dice that are 8-sided, 4 dice that are 12-sided, and 5 dice that are 20-sided.
# I choose a die, roll it, and get a 7.
# What is the probability that I chose an 8-sided die?
#
# Hint: To make the prior distribution, call `Pmf` with two parameters.
# +
# Solution
# Notice that I don't bother to normalize the prior.
# The `Pmf` gets normalized during the update, so we
# don't have to normalize it before.
ps = [1,2,3,4,5]
qs = [4,6,8,12,20]
pmf = Pmf(ps, qs)
update_dice(pmf, 7)
pmf
# -
# **Exercise:** Suppose I have two sock drawers.
# One contains equal numbers of black and white socks.
# The other contains equal numbers of red, green, and blue socks.
# Suppose I choose a drawer at random, choose two socks at random, and I tell you that I got a matching pair.
# What is the probability that the socks are white?
#
# For simplicity, let's assume that there are so many socks in both drawers that removing one sock makes a negligible change to the proportions.
# +
# Solution
# In the BlackWhite drawer, the probability of getting a match is 1/2
# In the RedGreenBlue drawer, the probability of a match is 1/3
hypos = ['BlackWhite', 'RedGreenBlue']
prior = Pmf(1/2, hypos)
likelihood = 1/2, 1/3
posterior = prior * likelihood
posterior.normalize()
posterior
# +
# Solution
# If I drew from the BlackWhite drawer, the probability the
# socks are white is 1/2
posterior['BlackWhite'] / 2
# -
# **Exercise:** Here's a problem from [Bayesian Data Analysis](http://www.stat.columbia.edu/~gelman/book/):
#
# > <NAME> had a twin brother (who died at birth). What is the probability that Elvis was an identical twin?
#
# Hint: In 1935, about 2/3 of twins were fraternal and 1/3 were identical.
# +
# Solution
# The trick to this question is to notice that Elvis's twin was a brother.
# If they were identical twins, it is certain they would be the same sex.
# If they were fraternal twins, the likelihood is only 50%.
# Here's a solution using a Bayes table
import pandas as pd
table = pd.DataFrame(index=['identical', 'fraternal'])
table['prior'] = 1/3, 2/3
table['likelihood'] = 1, 1/2
table['unnorm'] = table['prior'] * table['likelihood']
prob_data = table['unnorm'].sum()
table['posterior'] = table['unnorm'] / prob_data
table
# +
# Solution
# Here's a solution using a Pmf
hypos = ['identical', 'fraternal']
prior = Pmf([1/3, 2/3], hypos)
prior
# +
# Solution
likelihood = 1, 1/2
posterior = prior * likelihood
posterior.normalize()
posterior
|
soln/chap03.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# +
import pandas as pd
import matplotlib.pyplot as plt
data1 = pd.read_csv('1-1_swp-thc_trial1.xvg', comment='@', skiprows=13, names=['phi','psi','ram'], delim_whitespace=True)
data1
plt.scatter(data1.phi[::50], data1.psi[::50])
plt.show()
# +
import numpy as np
import numpy.random
import matplotlib.pyplot as plt
# Generate some test data
x = data1.phi
y = data1.psi
heatmap, xedges, yedges = np.histogram2d(x, y, bins=200)
extent = [xedges[0], xedges[-1], yedges[0], yedges[-1]]
plt.clf()
plt.imshow(heatmap.T, extent=extent, origin='lower', cmap='inferno') #cmap changes color, I like 'inferno' or 'plasma'
plt.show()
# -
|
.ipynb_checkpoints/step_verification-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# +
import numpy as np
import os
import matplotlib.pyplot as plt
from imutils import paths ## pip install --upgrade imutils
from tensorflow.keras.applications.mobilenet import MobileNet
from tensorflow.keras.layers import Dense
from tensorflow.keras.layers import AveragePooling2D
from tensorflow.keras.layers import Dropout
from tensorflow.keras.layers import Flatten
from tensorflow.keras.layers import Input
from tensorflow.keras.models import Model
from tensorflow.keras.optimizers import Adam
from tensorflow.keras.applications.mobilenet import preprocess_input
from tensorflow.python.keras.layers import Lambda
from tensorflow.keras.preprocessing.image import ImageDataGenerator
from tensorflow.keras.preprocessing.image import img_to_array
from tensorflow.keras.preprocessing.image import load_img
from tensorflow.keras.utils import to_categorical
from sklearn.preprocessing import LabelBinarizer
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
# +
# #!pip show tensorflow
# -
dataset = r"C:\Users\mdowrla\.ipynb_checkpoints\Cat_Dog_Dataset\Dataset"
imagepaths = list(paths.list_images(dataset))
imagepaths
# +
data = []
labels = []
for i in imagepaths:
label = i.split(os.path.sep)[-2]
labels.append(label)
image = load_img(i, target_size=(224,224))
image = img_to_array(image)
image = preprocess_input(image)
data.append(image)
# -
#print(data)
print(labels)
data = np.array(data,dtype='float32')
labels = np.array(labels)
labels
print(data.shape)
print(labels.shape)
Lb = LabelBinarizer()
labels = Lb.fit_transform(labels)
labels.shape
labels = to_categorical(labels)
labels
train_X, test_X ,train_Y , test_Y = train_test_split(data, labels, test_size=0.2 , random_state=10, stratify = labels)
labels.shape
train_X.shape , train_Y.shape
test_X.shape , test_Y.shape
aug=ImageDataGenerator(rotation_range=20,zoom_range=0.15,width_shift_range=0.2,height_shift_range=0.2,shear_range=0.15,horizontal_flip=True,vertical_flip=True,fill_mode='nearest')
baseModel = MobileNet(weights='imagenet', include_top=False, input_tensor= Input(shape=(224,224,3)))
baseModel.summary()
# +
headModel = baseModel.output
headModel = AveragePooling2D(pool_size=(7,7))(headModel)
headModel = Flatten(name='Flatten')(headModel)
headModel = Dense(128,activation = 'relu')(headModel)
headModel = Dropout(0.5)(headModel)
headModel = Dense(2 ,activation = 'softmax')(headModel)
model = Model(inputs=baseModel.input, outputs=headModel)
# -
for layer in baseModel.layers:
layer.trainable = False
model.summary()
# +
from tensorflow.keras.callbacks import EarlyStopping
lr = 0.001
ep = 10
bs = 80
base_path = r"C:\Users\mdowrla\.ipynb_checkpoints\Cat_Dog_Dataset\Dataset"
opt = Adam(learning_rate=lr)
er = EarlyStopping(monitor='accuracy', mode='max', patience=2, restore_best_weights=True)
model.compile(loss='binary_crossentropy', optimizer=opt, metrics=['accuracy'])
Md = model.fit(
aug.flow(train_X,train_Y,batch_size=bs),
steps_per_epoch = len(train_X)//bs,
validation_data = (test_X,test_Y),
validation_steps = len(test_X)//bs,
epochs = ep,callbacks = [er])
model.save(os.path.join(base_path,'model.h5'))
# -
predict = model.predict(test_X, batch_size=bs)
predict = np.argmax(predict, axis=1) #target_names= Lb.classes_
print(classification_report(test_Y.argmax(axis=1),predict))
# +
# plot the training loss and accuracy
## I used call backs so training has stopped without completing the all epochs, In the absence of callsbacks we can use
# the below plots on following metrics wrt to epochs
N = 8
plt.style.use("ggplot")
plt.figure()
plt.plot(np.arange(0, N), Md.history["loss"], label="train_loss")
plt.plot(np.arange(0, N), Md.history["val_loss"], label="val_loss")
plt.plot(np.arange(0, N), Md.history["accuracy"], label="train_acc")
plt.plot(np.arange(0, N), Md.history["val_accuracy"], label="val_acc")
plt.title("Training Loss and Accuracy")
plt.xlabel("Epoch #")
plt.ylabel("Loss/Accuracy")
plt.legend()
# -
# ### Testing using images
# +
from tensorflow.keras.applications.mobilenet import preprocess_input
from tensorflow.keras.preprocessing.image import img_to_array
from tensorflow.keras.models import load_model
from matplotlib import pyplot as plt
import numpy as np
import os
import cv2
# -
model =load_model(r"C:\Users\mdowrla\.ipynb_checkpoints\Cat_Dog_Dataset\Dataset\model.h5")
# +
import warnings
warnings.filterwarnings('ignore')
import matplotlib.image as mpimg
path = r"C:\Users\mdowrla\.ipynb_checkpoints\Cat_Dog_Dataset\Test_Dog.jpg"
plt.imshow(mpimg.imread(path))
image = load_img(path, target_size=(224,224))
image= img_to_array(image)
image=preprocess_input(image)
image=np.expand_dims(image,axis=0)
result = model.predict(image)
print(result)
# -
if result[0][0] > result[0][1]:
print("Cat")
else:
print("Dog")
|
Documents/PreTrainedAPI/usecase3 backup/Cat vs Dog-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import tensorflow as tf
import numpy as np
import time
import os
from sklearn.preprocessing import LabelEncoder
import re
import collections
import random
import pickle
maxlen = 20
location = os.getcwd()
num_layers = 3
size_layer = 256
learning_rate = 0.0001
batch = 100
with open('dataset-emotion.p', 'rb') as fopen:
df = pickle.load(fopen)
with open('vector-emotion.p', 'rb') as fopen:
vectors = pickle.load(fopen)
with open('dataset-dictionary.p', 'rb') as fopen:
dictionary = pickle.load(fopen)
label = np.unique(df[:,1])
from sklearn.cross_validation import train_test_split
train_X, test_X, train_Y, test_Y = train_test_split(df[:,0], df[:, 1].astype('int'), test_size = 0.2)
class Model:
def __init__(self, num_layers, size_layer, dimension_input, dimension_output, learning_rate):
def lstm_cell():
return tf.nn.rnn_cell.LSTMCell(size_layer)
self.rnn_cells = tf.nn.rnn_cell.MultiRNNCell([lstm_cell() for _ in range(num_layers)])
self.X = tf.placeholder(tf.float32, [None, None, dimension_input])
self.Y = tf.placeholder(tf.float32, [None, dimension_output])
drop = tf.contrib.rnn.DropoutWrapper(self.rnn_cells, output_keep_prob = 0.5)
self.outputs, self.last_state = tf.nn.dynamic_rnn(drop, self.X, dtype = tf.float32)
self.rnn_W = tf.Variable(tf.random_normal((size_layer, dimension_output)))
self.rnn_B = tf.Variable(tf.random_normal([dimension_output]))
self.logits = tf.matmul(self.outputs[:, -1], self.rnn_W) + self.rnn_B
self.cost = tf.losses.hinge_loss(logits = self.logits, labels = self.Y)
self.optimizer = tf.train.AdamOptimizer(learning_rate = learning_rate).minimize(self.cost)
self.correct_pred = tf.equal(tf.argmax(self.logits, 1), tf.argmax(self.Y, 1))
self.accuracy = tf.reduce_mean(tf.cast(self.correct_pred, tf.float32))
tf.reset_default_graph()
sess = tf.InteractiveSession()
model = Model(num_layers, size_layer, vectors.shape[1], label.shape[0], learning_rate)
sess.run(tf.global_variables_initializer())
dimension = vectors.shape[1]
saver = tf.train.Saver(tf.global_variables())
EARLY_STOPPING, CURRENT_CHECKPOINT, CURRENT_ACC, EPOCH = 10, 0, 0, 0
while True:
lasttime = time.time()
if CURRENT_CHECKPOINT == EARLY_STOPPING:
print('break epoch:', EPOCH)
break
train_acc, train_loss, test_acc, test_loss = 0, 0, 0, 0
for i in range(0, (train_X.shape[0] // batch) * batch, batch):
batch_x = np.zeros((batch, maxlen, dimension))
batch_y = np.zeros((batch, len(label)))
for k in range(batch):
tokens = train_X[i + k].split()[:maxlen]
emb_data = np.zeros((maxlen, dimension), dtype = np.float32)
for no, text in enumerate(tokens[::-1]):
try:
emb_data[-1 - no, :] += vectors[dictionary[text], :]
except Exception as e:
print(e)
continue
batch_y[k, int(train_Y[i + k])] = 1.0
batch_x[k, :, :] = emb_data[:, :]
loss, _ = sess.run([model.cost, model.optimizer], feed_dict = {model.X : batch_x, model.Y : batch_y})
train_loss += loss
train_acc += sess.run(model.accuracy, feed_dict = {model.X : batch_x, model.Y : batch_y})
for i in range(0, (test_X.shape[0] // batch) * batch, batch):
batch_x = np.zeros((batch, maxlen, dimension))
batch_y = np.zeros((batch, len(label)))
for k in range(batch):
tokens = test_X[i + k].split()[:maxlen]
emb_data = np.zeros((maxlen, dimension), dtype = np.float32)
for no, text in enumerate(tokens[::-1]):
try:
emb_data[-1 - no, :] += vectors[dictionary[text], :]
except:
continue
batch_y[k, int(test_Y[i + k])] = 1.0
batch_x[k, :, :] = emb_data[:, :]
loss, acc = sess.run([model.cost, model.accuracy], feed_dict = {model.X : batch_x, model.Y : batch_y})
test_loss += loss
test_acc += acc
train_loss /= (train_X.shape[0] // batch)
train_acc /= (train_X.shape[0] // batch)
test_loss /= (test_X.shape[0] // batch)
test_acc /= (test_X.shape[0] // batch)
if test_acc > CURRENT_ACC:
print('epoch:', EPOCH, ', pass acc:', CURRENT_ACC, ', current acc:', test_acc)
CURRENT_ACC = test_acc
CURRENT_CHECKPOINT = 0
saver.save(sess, os.getcwd() + "/model-rnn-vector-huber.ckpt")
else:
CURRENT_CHECKPOINT += 1
EPOCH += 1
print('time taken:', time.time()-lasttime)
print('epoch:', EPOCH, ', training loss:', train_loss, ', training acc:', train_acc, ', valid loss:', test_loss, ', valid acc:', test_acc)
|
classification-comparison/Deep-learning/rnn-vector-hinge.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import re
import os
import json
import time
from shutil import copy2, rmtree
import shutil
import hashlib
# +
data = pd.read_json('silkroad2.json', orient='index')
len(data)
# -
len(data.seller.unique())
# +
# df_unique = data.drop_duplicates(['seller', 'title'])
# len(df_unique)
# -
data = data[data.img.notnull()].copy()
d = [int(x.split('|')[0].split('/')[-1]) for x in data.img.values]
data['itemID'] = d
# +
# df_unique = df_unique[df_unique.img.notnull()]
# df_unique = df_unique.sort_index()
# -
root_path = '/media/intel/m2/silkroad2/'
data['image_location'] = root_path + data.date.astype(str) + data.img
# +
# seller_name_list = list(df_unique.seller)
# image_location = list(df_unique.image_location)
# itemID = [hashlib.md5(x).hexdigest() for x in df_unique.index.astype(str)]
# -
data['seller_path'] = data.seller.apply(lambda x: os.path.join(target_path, x))
len(data)
product_count = 0
img_count = []
for index, row in data.iterrows():
product_count += 1
if product_count % 20000 == 0:
print product_count,
img_f, _ = row.image_location.split('######')
if not os.path.isfile(img_f):
continue
with open(img_f) as fp:
image_files = fp.read()
imgbase64 = re.findall("content: url\('data:image/jpeg;base64,(.*)'", image_files)
img_count.append(len(imgbase64))
from collections import Counter
Counter(img_count)
target_path = '/media/intel/m2/imgs/SilkRoad2'
try:
rmtree(target_path)
except:
pass
try:
os.mkdir(target_path)
except:
pass
product_count = 0
for index, row in data.iterrows():
product_count += 1
if product_count % 20000 == 0:
print product_count,
img_f, _ = row.image_location.split('######')
if not os.path.isfile(img_f):
continue
with open(img_f) as fp:
image_files = fp.read()
imgbase64 = re.findall("content: url\('data:image/jpeg;base64,(.*)'", image_files)
for i in range(len(imgbase64)):
if not os.path.isdir(row.seller_path):
os.makedirs(row.seller_path)
image_name = "%d%2.2d.jpg" % (row.itemID, i)
image_tar_path = os.path.join(row.seller_path, image_name)
with open(image_tar_path, "wb") as fp:
fp.write(imgbase64[i].decode('base64'))
row
|
parser/silkroad2/silkroad_additional.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# 1、线图效果(关系图改造)
# ======
# +
import tushare as ts
import pandas as pd
from IPython.display import HTML
stock_selected='600487'
#历年前十大股东持股情况
#df1为季度统计摘要,data1为前十大持股明细统计
df1, data1 = ts.top10_holders(code=stock_selected, gdtype='0') #gdtype等于1时表示流通股,默认为0
#df1, data1 = ts.top10_holders(code='002281', year=2015, quarter=1, gdtype='1')
df1 = df1.sort_values('quarter', ascending=True)
df1.tail(10)
qts = list(df1['quarter'])
data = list(df1['props'])
name = ts.get_realtime_quotes(stock_selected)['name'][0]
# +
lgdstr = """
var axisData = """ + str(qts) + """;
var data = """ + str(data) + """;
var links = data.map(function (item, i) {
return {
source: i,
target: i + 1
};
});
links.pop();
option = {
title: {
text: 'stockname:前十大流通股东持股占比'
},
tooltip: {
trigger: 'item'
},
xAxis: {
type : 'category',
boundaryGap : false,
data : axisData
},
yAxis: {
type : 'value'
},
series: [
{
type: 'line',
layout: 'none',
coordinateSystem: 'cartesian2d',
symbolSize: 10,
label: {
normal: {
show: true
}
},
edgeSymbol: ['circle', 'arrow'],
edgeSymbolSize: [2, 5],
data: data,
links: links,
lineStyle: {
normal: {
color: '#2f4554'
}
}
}
]
};
"""
lgdstr=lgdstr.replace('stockname',name)
headstr = """
<div id="showhere" style="width:800px; height:600px;"></div>
<script>
require.config({ paths:{ echarts: '//cdn.bootcss.com/echarts/3.2.3/echarts.min', } });
require(['echarts'],function(ec){
var myChart = ec.init(document.getElementById('showhere'));
"""
tailstr = """
myChart.setOption(option);
});
</script>
"""
# -
HTML(headstr + lgdstr+tailstr)
# 2、饼图效果
# ======
# +
import tushare as ts
import pandas as pd
from IPython.display import HTML
#浦发银行2016三季度前十大流通股东情况
df2, data2 = ts.top10_holders(code=stock_selected, year=2016, quarter=3, gdtype='1')
#取前十大流通股东名称
top10name = str(list(data2['name']))
# +
valstrs = ''
for idx in data2.index:
s = '{value: %s, name: \'%s\'}' % (data2.ix[idx]['h_pro'], data2.ix[idx]['name'])
valstrs += s + ','
valstrs = valstrs[:-1]
datacontent = """
option = {
tooltip: {
trigger: 'item',
formatter: "{a} <br/>{b}: {c} ({d}%)"
},
legend: {
orient: 'vertical',
x: 'left',
data: """ + top10name +"""
},
series: [
{
name:'前十大流通股东:',
type:'pie',
radius: ['50%', '70%'],
avoidLabelOverlap: false,
label: {
normal: {
show: false,
position: 'center'
},
emphasis: {
show: true,
textStyle: {
fontSize: '30',
fontWeight: 'bold'
}
}
},
labelLine: {
normal: {
show: false
}
},
data:[
""" + valstrs + """
]
}
]
};
"""
headstr = """
<div id="mychart" style="width:800px; height:600px;"></div>
<script>
require.config({ paths:{ echarts: '//cdn.bootcss.com/echarts/3.2.3/echarts.min', } });
require(['echarts'],function(ec){
var myChart = ec.init(document.getElementById('mychart'));
"""
tailstr = """
myChart.setOption(option);
});
</script>
"""
# -
HTML(headstr + datacontent + tailstr)
# 3、K线效果演示
# =========
import tushare as ts
import pandas as pd
from IPython.display import HTML
#中国联通前复权数据
#df = ts.get_k_data(stock_selected, start='2016-01-01', end='2016-12-02')
df = ts.get_k_data(stock_selected, start='2016-01-01')
# +
datastr = ''
for idx in df.index:
rowstr = '[\'%s\',%s,%s,%s,%s]' % (df.ix[idx]['date'], df.ix[idx]['open'],
df.ix[idx]['close'], df.ix[idx]['low'],
df.ix[idx]['high'])
datastr += rowstr + ','
datastr = datastr[:-1]
#取股票名称
name = ts.get_realtime_quotes(stock_selected)['name'][0]
datahead = """
<div id="chart" style="width:800px; height:600px;"></div>
<script>
require.config({ paths:{ echarts: '//cdn.bootcss.com/echarts/3.2.3/echarts.min', } });
require(['echarts'],function(ec){
var myChart = ec.init(document.getElementById('chart'));
"""
datavar = 'var data0 = splitData([%s]);' % datastr
funcstr = """
function splitData(rawData) {
var categoryData = [];
var values = []
for (var i = 0; i < rawData.length; i++) {
categoryData.push(rawData[i].splice(0, 1)[0]);
values.push(rawData[i])
}
return {
categoryData: categoryData,
values: values
};
}
function calculateMA(dayCount) {
var result = [];
for (var i = 0, len = data0.values.length; i < len; i++) {
if (i < dayCount) {
result.push('-');
continue;
}
var sum = 0;
for (var j = 0; j < dayCount; j++) {
sum += data0.values[i - j][1];
}
result.push((sum / dayCount).toFixed(2));
}
return result;
}
option = {
title: {
"""
namestr = 'text: \'%s\',' %name
functail = """
left: 0
},
tooltip: {
trigger: 'axis',
axisPointer: {
type: 'line'
}
},
legend: {
data: ['日K', 'MA5', 'MA10', 'MA20', 'MA30']
},
grid: {
left: '10%',
right: '10%',
bottom: '15%'
},
xAxis: {
type: 'category',
data: data0.categoryData,
scale: true,
boundaryGap : false,
axisLine: {onZero: false},
splitLine: {show: false},
splitNumber: 20,
min: 'dataMin',
max: 'dataMax'
},
yAxis: {
scale: true,
splitArea: {
show: true
}
},
dataZoom: [
{
type: 'inside',
start: 50,
end: 100
},
{
show: true,
type: 'slider',
y: '90%',
start: 50,
end: 100
}
],
series: [
{
name: '日K',
type: 'candlestick',
data: data0.values,
markPoint: {
label: {
normal: {
formatter: function (param) {
return param != null ? Math.round(param.value) : '';
}
}
},
data: [
{
name: '标点',
coord: ['2013/5/31', 2300],
value: 2300,
itemStyle: {
normal: {color: 'rgb(41,60,85)'}
}
},
{
name: 'highest value',
type: 'max',
valueDim: 'highest'
},
{
name: 'lowest value',
type: 'min',
valueDim: 'lowest'
},
{
name: 'average value on close',
type: 'average',
valueDim: 'close'
}
],
tooltip: {
formatter: function (param) {
return param.name + '<br>' + (param.data.coord || '');
}
}
},
markLine: {
symbol: ['none', 'none'],
data: [
[
{
name: 'from lowest to highest',
type: 'min',
valueDim: 'lowest',
symbol: 'circle',
symbolSize: 10,
label: {
normal: {show: false},
emphasis: {show: false}
}
},
{
type: 'max',
valueDim: 'highest',
symbol: 'circle',
symbolSize: 10,
label: {
normal: {show: false},
emphasis: {show: false}
}
}
],
{
name: 'min line on close',
type: 'min',
valueDim: 'close'
},
{
name: 'max line on close',
type: 'max',
valueDim: 'close'
}
]
}
},
{
name: 'MA5',
type: 'line',
data: calculateMA(5),
smooth: true,
lineStyle: {
normal: {opacity: 0.5}
}
},
{
name: 'MA10',
type: 'line',
data: calculateMA(10),
smooth: true,
lineStyle: {
normal: {opacity: 0.5}
}
},
{
name: 'MA20',
type: 'line',
data: calculateMA(20),
smooth: true,
lineStyle: {
normal: {opacity: 0.5}
}
},
{
name: 'MA30',
type: 'line',
data: calculateMA(30),
smooth: true,
lineStyle: {
normal: {opacity: 0.5}
}
},
]
};
myChart.setOption(option);
});
</script>
"""
# -
HTML(datahead + datavar + funcstr + namestr + functail)
|
sample_code/echartsDemo.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Introduction
# -----
# You (an electrical engineer) wish to determine the resistance of an electrical component by using Ohm's law. You remember from your high school circuit classes that $$V = RI$$ where $V$ is the voltage in volts, $R$ is resistance in ohms, and $I$ is electrical current in amperes. Using a multimeter, you collect the following data:
#
# | Current (A) | Voltage (V) |
# |-------------|-------------|
# | 0.2 | 1.23 |
# | 0.3 | 1.38 |
# | 0.4 | 2.06 |
# | 0.5 | 2.47 |
# | 0.6 | 3.17 |
#
# Your goal is to
# 1. Fit a line through the origin (i.e., determine the parameter $R$ for $y = Rx$) to this data by using the method of least squares. You may assume that all measurements are of equal importance.
# 2. Consider what the best estimate of the resistance is, in ohms, for this component.
#
# ## Getting Started
# ----
#
# First we will import the neccesary Python modules and load the current and voltage measurements into numpy arrays:
# +
import numpy as np
from numpy.linalg import inv
import matplotlib.pyplot as plt
# Store the voltage and current data as column vectors.
I = np.mat([0.2, 0.3, 0.4, 0.5, 0.6]).T
V = np.mat([1.23, 1.38, 2.06, 2.47, 3.17]).T
# -
# Now we can plot the measurements - can you see the linear relationship between current and voltage?
# +
plt.scatter(np.asarray(I), np.asarray(V))
plt.xlabel('Current (A)')
plt.ylabel('Voltage (V)')
plt.grid(True)
plt.show()
# -
# ## Estimating the Slope Parameter
# ----
# Let's try to estimate the slope parameter $R$ (i.e., the resistance) using the least squares formulation from Module 1, Lesson 1 - "The Squared Error Criterion and the Method of Least Squares":
#
# \begin{align}
# \hat{R} = \left(\mathbf{H}^T\mathbf{H}\right)^{-1}\mathbf{H}^T\mathbf{y}
# \end{align}
#
# If we know that we're looking for the slope parameter $R$, how do we define the matrix $\mathbf{H}$ and vector $\mathbf{y}$?
# +
# Define the H matrix, what does it contain?
H = I
y = V
# Now estimate the resistance parameter.
R = np.dot(np.dot(np.linalg.inv(np.dot(H.T, H)), H.T), y)
R = np.asscalar(R)
print('The slope parameter (i.e., resistance) for the best-fit line is:')
print(R)
# -
# ## Plotting the Results
# ----
# Now let's plot our result. How do we relate our linear parameter fit to the resistance value in ohms?
# +
I_line = np.arange(0, 0.8, 0.1)
V_line = R*I_line
plt.scatter(np.asarray(I), np.asarray(V))
plt.plot(I_line, V_line)
plt.xlabel('current (A)')
plt.ylabel('voltage (V)')
plt.grid(True)
plt.show()
# -
# If you have implemented the estimation steps correctly, the slope parameter $\hat{R}$ should be close to the actual resistance value of $R = 5~\Omega$. However, the estimated value will not match the true resistance value exactly, since we have only a limited number of noisy measurements.
|
Notebooks/C2M1L1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Collections Module
# Counter
from collections import Counter
list=['a','s','l','a','n']
Counter(list)
#number of element in list
name='himanshu'
Counter(name)
strs='hey this is rover and i like to play vedio games i like it'
strs=strs.split()
Counter(strs)
cou=Counter(strs)
cou.most_common(2)
cou.update('i')
cou
sum(cou.values())
cou.clear()
cou.most_common(5)
# defaultdict
from collections import defaultdict
d = {'k1':'Rover'}
d['k1']
# +
#d['not_defined_key'] will generate error.
# -
d = defaultdict(object)
d['one']
for item in d:
print(item)
di=defaultdict(lambda :45)
di['2']=3
di['3']
di
# +
d={}
d['a']='Nitro'
d['b']='Strix'
d['c']='prestige'
d['d']='rog'
# -
d
for key,val in d.items():
print(key,':',val)
# Named Tuple
t=(1,2,3,4)
t[0]
from collections import namedtuple
Dog=namedtuple('Dog','age breed name')
liz=Dog(age=2,breed = 'lab',name='Lizzy')
liz
liz[2]
# Datetime
import datetime
t=datetime.time(1,44,1)
print(t)
t.hour
t.minute
print(datetime.time.min)
print(datetime.time.max)
datetime.date(2,1,12)
td=datetime.date.today()
print(td)
td.day
|
15-modules.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# python version : 3.x
import tensorflow as tf
# placeholder 를 통해 tensor - 데이터를 입력받을 공간(노드, 변수)을 만든다.
input1 = tf.placeholder(tf.float32)
input2 = tf.placeholder(tf.float32)
# 2개를 입력 받아서 곱하는 tensor 를 만든다.
output = tf.multiply(input1, input2)
# tensor print 하면 내용만 tensor 의 형식만 보인다.
print (input1)
print (input1)
print (output)
# 입력노드 input1, input2 를 곱한 결과 노드 output 라는 그래프를 만들었다.
# 이 그래프를 실행하기 위해 세션을 사용한다.
sess = tf.Session()
# session 의 run 을 통해 위에서 만들 그래프(모델)을 실행한다.
# input1:3.0 intput2:7.0 으로 두고 output:3.0*7.0=21.0 을 계산한다.
print(sess.run([output], feed_dict={input1: [3.], input2: [7.]}))
# +
# python version : 3.x
import tensorflow as tf
import numpy as np
# Create 100 phony x, y data points in NumPy, y = x * 0.1 + 0.3
x_data = np.random.rand(100).astype(np.float32)
y_data = x_data * 0.1 + 0.3
# Try to find values for W and b that compute y_data = W * x_data + b
# (We know that W should be 0.1 and b 0.3, but TensorFlow will
# figure that out for us.)
# variable 는 weight 를 저장할때 사용한다.
W = tf.Variable(tf.random_uniform([1], -1.0, 1.0))
b = tf.Variable(tf.zeros([1]))
y = W * x_data + b
# Minimize the mean squared errors.
loss = tf.reduce_mean(tf.square(y - y_data))
optimizer = tf.train.GradientDescentOptimizer(0.5)
train = optimizer.minimize(loss)
# Before starting, initialize the variables. We will 'run' this first.
init = tf.global_variables_initializer()
# Launch the graph.
sess = tf.Session()
sess.run(init)
# Fit the line.
for step in range(201):
sess.run(train)
if step % 20 == 0:
print(step, sess.run(W), sess.run(b))
# Learns best fit is W: [0.1], b: [0.3]
|
MachineLearning/placeholder_variable.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Ray Concepts - Data Parallelism (Part 1)
#
# Now let's explore Ray's core concepts and understand how they work. As much as possible, Ray tries to leverage familiar Python idioms, extending them as necessary.
#
# This lesson covers how to define Ray _tasks_, run them, and retrieve the results. We'll also end with an optional section to help you understand how Ray schedules tasks in a distributed environment.
#
# The next lesson will complete the discussion of Ray tasks by exploring how task dependencies are handled and look under the hood at Ray's architecture and runtime behavior.
# First, we need to import `ray` and we'll also import the `time` API. (If you get an error in the next cell, make sure you set up the tutorial as described in the project [README](../README.md).
#
# > **Tip:** The [Ray Package Reference](https://ray.readthedocs.io/en/latest/package-ref.html) in the [Ray Docs](https://ray.readthedocs.io/en/latest/) is useful for exploring the API features we'll learn.
import ray, time, sys
sys.path.append('..') # Import our own libraries starting in the project root directory
# We've implemented a convience function `p()` for printing a number and time duration. It's in a library, so we can just import it, since we set the `sys.path` above.
#
# For reference, the function is defined as follows:
# ```python
# def p(n, duration):
# print('{:2d}: {:6.3f} seconds'.format(n, duration))
# ```
from util.printing import p
# Now consider the following Python function, where we simulate doing something that's slow to complete, using the `sleep` method. A real world example might do a complex calculation (like a training step for machine learning) or call an external web service where a response could take many milliseconds. We'll use more interesting examples later.
def expensive(n):
start = time.time() # Let's time how long this takes.
time.sleep(n) # Sleep for n seconds
return (n, time.time() - start) # Return n and the duration in seconds
(n, duration) = expensive(2)
p(n, duration)
# You should see the output `2: 2.00X seconds`, where `X` is an integer. As we might expect, it took about two seconds to execute.
#
# Now suppose we need to fire off five of these at once:
start_all = time.time()
for n in range(5):
n2, duration = expensive(n)
p(n, duration)
print("Total time:")
p(10, time.time() - start_all)
# It takes about 10 seconds to run, because we do this process _synchronously_, but we don't need to do this. Each call to `expensive()` is independent of the others, so ideally we should run them in _parallel_, i.e., _asynchronously_, so all of them finish more quickly.
#
# Ray makes this easy. Let's define a new function and annotate it with `@ray.remote`. In Ray terminology, the annotation converts the function to a _task_, because we'll now be able to let Ray schedule this "task" (i.e., unit of work) on any CPU core in our laptop or in our cluster when we use one.
@ray.remote
def expensive_task(n):
return expensive(n)
# Note that we could simply call `expensive()`, we don't have to redefine it.
#
# Now when we invoke `expensive_task`, we have to use `expensive_task.remote(n)` instead of `expensive_task(n)`, like before. Python is malleable; the Ray team could have instrumented `expensive_task` so that we can call it like a normal function, but the explicit `.remote` is reminder to the reader what code is using Ray vs. normal Python code.
#
# Okay, let's try the same loop as before. But first, we have to initialize Ray with `ray.init()`. There are optional key-value pairs you can provide. We'll explore many of them later, but for now, we'll just pass an option that allows us to re-initialize Ray without triggering an error. It would be useful if you decided to reevalute the following cell for some reason.
ray.init(ignore_reinit_error=True)
# > **Troubleshooting**
# >
# > 1. If you get an error like `... INFO services.py:... -- Failed to connect to the redis server, retrying.`, it probably means you are running a VPN on your machine. [At this time](https://github.com/ray-project/ray/issues/6573), you can't use `ray.init()` with a VPN running. You'll have to stop your VPN for now.
# >
# > 2. If `ray.init()` worked (for example, you see a message like _View the Ray dashboard at localhost:8265_) and you're using a Mac, you may get several annoying dialogs asking you if you want to allow incoming connections for Python and/or Redis. Click "Accept" for each one and they shouldn't appear again during this lesson. MacOS is trying to verify if these executables have been properly signed. Ray uses Redis. If you installed Python using Anaconda or other mechanism, then it probably isn't properly signed from the point of view of MacOS. To permanently fix this problem, [see this StackExchange post](https://apple.stackexchange.com/questions/3271/how-to-get-rid-of-firewall-accept-incoming-connections-dialog).
# If `ray.init()` worked successfully, you'll see a JSON block with information such as the `node_ip_address` and `webui_rul`.
#
# A separate message tells you that URL is for the Ray dashboard. Open it now in a separate browser tab. It should look something like this:
# 
# > **Tip:** You can ask Ray for this URL later if needed. Use `ray.get_webui_url()`.
# >
# > **Note:** There are many options you can pass to `ray.init()`. See [the docs](https://ray.readthedocs.io/en/latest/configure.html) for details, some of which we'll explore in later modules.
# My laptop has four cores, each of which has a hardware _thread_, for a total of eight. Ray started a `ray` worker process for each hardware thread. These workers are used to run tasks. Click around the dashboard, especially when we run tasks like we're about to do. We'll explore the dashboard more later on. Many laptops have eight cores, so if you may see 16 ray processes.
#
# Now let's run our new Ray task!
expensive_task.remote(2)
# What's this `ObjectID` thing? Recall that `expensive()` returned `(n, seconds)`. Now, when we invoke a task, it will be executed _asynchronously_, so instead of the tuple we will eventually want, we get a reference to a Python [Future](https://docs.python.org/3/library/asyncio-future.html), which we'll use to retrieve the tuple when the task has completed. One way to do this is to use `ray.get()`. So, let's modify our previous loop to use the task and retrieve the values using the futures.
start_all = time.time()
for n in range(5):
id = expensive_task.remote(n) # Call the remote task
n2, duration = ray.get(id) # Retrieve the value using the future
p(n, duration)
print("Total time:")
p(10, time.time() - start_all)
# I said that Ray would make everything go faster, but the performance is the same. The reason is because we used `ray.get()` incorrectly. This is a _blocking call_; we're telling Ray, "I need the value and I'm going to wait until the task is done and you can return it to me." Making this blocking call in the loop defeats the goal of leveraging asynchrony.
#
# Instead, we need to "fire off" all the asynchronous calls, building up a list of futures, then wait for all of them at once. We'll do that as follows, where for this purposes we'll introduce a list comprehension to call the tasks:
# +
start_all = time.time()
ids = []
for n in range(5):
id = expensive_task.remote(n)
ids.append(id)
p(n, time.time() - start_all)
for n2, duration in ray.get(ids): # Retrieve all the values for a list of futures
p(n2, duration)
print("Total time:")
p(10, time.time() - start_all)
# -
# Notice what happened. In the first loop, when we called `expensive_task.remote(n)`, each call returned immediately, so the "durations" were tiny. Then you probably noticed that nothing happend for about four seconds, then suddenly everything was printed, for a total elapsed time of about four seconds.
#
# Why four? When we pass a list of futures to `ray.get()`, it blocks until the results are available for _all_ of them. Our longest task was four seconds, so once that one finished, the others were already done and all could be returned immediately.
# Run the next cell, which is basically the same calculation, but it uses a more idiomatic list comprehension for the `expensive_task` invocations and doesn't log the times for those calls, as we now know these times are trivial.
#
# **However**, as soon as the call starts, switch to the Ray Dashboard browser tab and watch what happens (or use separate windows for these two tabs). You notice instances of `expensive_task` being executed by the different `ray` processes. You'll note that Try using a larger number than `5` so it's easier
start_all = time.time()
ids = [expensive_task.remote(n) for n in range(5)] # Fire off the asynchronous tasks
for n2, duration in ray.get(ids): # Retrieve all the values from the list of futures
p(n2, duration)
print("Total time:")
p(10, time.time() - start_all)
# ## Exercise 1
#
# Let's make sure you understand how to use Ray's task parallelism. In the following two cells, we define a new Python function and then use it several times to perform work. Modify both cells to use Ray. The third cell uses `assert` statements to check your work.
#
# > **Tip:** The solution is in the `solutions` folder.
def slow_square(n):
time.sleep(n)
return n*n
start = time.time()
squares = [slow_square(n) for n in range(4)]
duration = time.time() - start
assert squares == [0, 1, 4, 9]
# should fail until the code modifications are made:
assert duration < 4.1, f'duration = {duration}'
# ## A Closer Look at Scheduling
#
# > **Note:** If you just want to learn the Ray API, you can safely skip the rest of this lesson (notebook) for now. It begins our exploration of how Ray works internally. However, you should come back to it at some point, so you'll develop a better understanding of how Ray works.
# To better see what's happening with the dashboard, run the following cells to determine the number of CPU hardware threads on your laptop, each of which is running a `ray` process. We've expanded this code over several cells so you can see what each step returns, but you could write it all at once, `num_cpus = ray.nodes()[0]['Resources']['CPU']`.
import json
nodes = ray.nodes() # Get a JSON object with metadata about all the nodes in your "cluster".
nodes # On your laptop, a list with one node.
node = nodes[0] # Get the single node
node
resources = node['Resources'] # Get the resources for the node
resources
num_cpus = resources['CPU'] # Get the number of CPU hardware threads
num_cpus
# The final number will be `8.0`, `16.0`, etc. The next cell is one of our previous examples of calling `expensive_task`, but now the loop counter is `2*int(num_cpus)` instead of `5`. This will mean that half of the tasks will have to wait for an open slot. Now run the following cell and watch the Ray dashboard. (You'll know the cell is finished when all the `ray` workers return to `IDLE`.)
#
# What's the total time now? How about the individual times?
# +
start_all = time.time()
ids = []
for n in range(2*int(num_cpus)): # What's changed!
id = expensive_task.remote(n)
ids.append(id)
p(n, time.time() - start_all)
for n2, duration in ray.get(ids): # Retrieve all the values for a list of futures
p(n2, duration)
print("Total time:")
p(10, time.time() - start_all)
# -
# On my 8-worker machine, 16 tasks were run.
#
# Look at the first set of times, for the submissions. They are still fast and nonblocking, but on my machine they took about ~0.02 seconds to complete, so some competition for CPU time occurred.
#
# As before, each asynchronous task still takes roughly `n` seconds to finish (for `n` equals 0 through 15). This makes sense, because each `expensive_task` does essentially nothing but sleep, and since there's only one task per worker, there should be no apreciable difference for the individual times, as before.
#
# However, the whole process took about 22 seconds, not 16, as we might have expected from our previous experience (i.e., the time for the longest task). This reflects the fact that half the tasks had to wait for an available worker.
#
# In fact, we can explain the 22 seconds exactly. Here is how my 16 tasks, with durations 0 to 15 seconds, were allocated to the 8 workers. Keep in mind that the scheduling happened in order for increasing `n`.
#
# The first 8 tasks, of duration 0 to 7 seconds, where scheduled immediately in the 8 available workers. The 0-second task finished immediately, so the next waiting task, the 8-second task was scheduled on that worker. It finished in 8 seconds, so the _total_ time for the 0-second and 8-second tasks was about 8 seconds. Similarly, after the 1-second task finished, the 9-second task was scheduled. Total time: 10 seconds. Using induction ;), the last worker started with the 7-second task followed by the 15-second task for a total of 22 seconds!
#
# Here's a table showing this in detail. where `n1` and `n2` refers to the first and second tasks, with durations `n1` seconds and `n2` seconds, for a total of `n1+n2` seconds. For consistency, the `ray` workers are numbered from zero:
#
# | Worker | n1 | n2 | Total Time |
# | -----: | -: | -: | ---------: |
# | 0 | 0 | 8 | 8 |
# | 1 | 1 | 9 | 10 |
# | 2 | 2 | 10 | 12 |
# | 3 | 3 | 11 | 14 |
# | 4 | 4 | 12 | 16 |
# | 5 | 5 | 13 | 18 |
# | 6 | 6 | 14 | 20 |
# | 7 | 7 | 15 | 22 |
#
#
# Of course a real-world scheduling scenario would be more complicated, but hopefully you have a better sense of how Ray distributes work, whether you're working on a single laptop or a large cluster!
import numpy as np
@ray.remote
def make_array(n):
return np.random.standard_normal(n)
@ray.remote
def add_array(a1, a2):
return np.add(a1, a2)
start = time.time()
id1 = make_array.remote(50)
id2 = make_array.remote(50)
id3 = add_array.remote(id1, id2)
p(0, time.time() - start)
ray.get(id3)
p(1, time.time() - start)
make_array2(5)
np.random.standard_normal(10)
|
ray-core/02-DataParallelism-Part1.ipynb
|