code
stringlengths 38
801k
| repo_path
stringlengths 6
263
|
|---|---|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="oyRf9FDZquq8"
# ### Preparing Environment
# -
# #### This FIle has been run on Google COLAB, please make necessary changes
# + colab={"base_uri": "https://localhost:8080/", "height": 35} id="-JeGVikTqs2i" outputId="8bc856e5-900a-4bac-ed5c-58657bbb22aa"
# !ls
# + [markdown] colab={"base_uri": "https://localhost:8080/", "height": 426} id="JrdX061KrBFa" outputId="490bba35-6894-45d1-efd6-07c61c15bfe3"
# ### Steps to import the Dataset directly from Kaggle
#
# #importing data from Kaggle
#
# # # !mkdir ~/.kaggle
#
# # # !echo '{"username":"YOUR USERNAME","key":"YOUR KEY"}' > /root/.kaggle/kaggle.json #Confidential KEY // Please do not share this section furthur!
#
# # # !kaggle competitions download -c data-science-bowl-2018
# + [markdown] id="KuomYbu4qpjK"
# ### IMPORTS
# + id="aIy09qJhpq_V"
import os
import time
import copy
from collections import defaultdict
import torch
import shutil
import pandas as pd
from skimage import io, transform
import numpy as np
from PIL import Image
#import matplotlib.pyplot as plt
from torch.utils.data import Dataset, DataLoader, random_split
from torchvision import transforms, utils
from torch import nn
from albumentations import (HorizontalFlip, Normalize, Resize, Compose)
import cv2
from albumentations.pytorch import ToTensor
from torch.autograd import Variable
from torch.nn import Linear, ReLU, CrossEntropyLoss, Sequential, Conv2d, MaxPool2d, Module, Softmax, BatchNorm2d, Dropout
from torch.optim import Adam, SGD
import torch.nn.functional as F
from PIL import Image
from torch import nn
import zipfile
from torchsummary import summary
# + colab={"base_uri": "https://localhost:8080/", "height": 35} id="2p2aKDCPq2ae" outputId="74f3c29b-b38c-40df-95fd-96f200adeb4d"
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
print(device)
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="G3RRU7S0rJeM" outputId="d93c8700-7704-4edf-99c3-e552836bb728"
# UNCOMMENT TO UNZIP
# # !mkdir data
# # !unzip stage1_train.zip -d data/stage1_train/
# # !unzip stage1_test.zip -d data/stage1_test/
# + colab={"base_uri": "https://localhost:8080/", "height": 35} id="06vxZZ9_rMNH" outputId="048e2495-de48-4954-a423-a963dd2ac92f"
# !ls data/stage1_train | wc -l #No of Training Samples
# + [markdown] id="GXzJgScpLAtu"
# ### DATASET
# + id="AyR-epxwrPxZ"
def get_transforms(mean, std):
list_transforms = []
list_transforms.extend(
[
HorizontalFlip(p=0.5),
])
list_transforms.extend(
[
Normalize(mean=mean, std=std, p=1),
ToTensor(),
])
list_trfms = Compose(list_transforms)
return list_trfms
class Nuclie_data(Dataset):
def __init__(self,path):
self.path = path
self.folders = os.listdir(path)
self.transforms = get_transforms(0.5, 0.5)
def __len__(self):
return len(self.folders)
def __getitem__(self,idx):
image_folder = os.path.join(self.path,self.folders[idx],'images/')
mask_folder = os.path.join(self.path,self.folders[idx],'masks/')
image_path = os.path.join(image_folder,os.listdir(image_folder)[0])
img = io.imread(image_path)[:,:,:3].astype('float32')
img = transform.resize(img,(128,128))
mask = self.get_mask(mask_folder, 128, 128 ).astype('float32')
augmented = self.transforms(image=img, mask=mask)
img = augmented['image']
mask = augmented['mask']
mask = mask[0].permute(2, 0, 1)
return (img,mask)
def get_mask(self,mask_folder,IMG_HEIGHT, IMG_WIDTH):
mask = np.zeros((IMG_HEIGHT, IMG_WIDTH, 1), dtype=np.bool)
for mask_ in os.listdir(mask_folder):
mask_ = io.imread(os.path.join(mask_folder,mask_))
mask_ = transform.resize(mask_, (IMG_HEIGHT, IMG_WIDTH))
mask_ = np.expand_dims(mask_,axis=-1)
mask = np.maximum(mask, mask_)
return mask
# + id="_pYkPDOmrThQ"
#loading the data
base_dir = 'data/stage1_train/'
data = Nuclie_data(base_dir)
# + colab={"base_uri": "https://localhost:8080/", "height": 568} id="ruIbx9fbrbi7" outputId="582b6ad7-34c4-4d65-e464-98a0aeda3bf2"
# Checking Sample data
print(data.__len__())
data.__getitem__(0)
# + colab={"base_uri": "https://localhost:8080/", "height": 52} id="46MLzaY_rdFX" outputId="b25642c6-1418-48cd-e006-1d650798eba7"
for img, msk in data:
print(img.shape)
print(msk.shape)
break
# + [markdown] id="GcWbtfxpLEsY"
# ### UTILITY FUNCTIONS
# + id="CWmGTaegrfA7"
#Utility function for Plotting
def mask_convert(mask):
mask = mask.clone().cpu().detach().numpy()
mask = mask.transpose((1,2,0))
std = np.array((0.5))
mean = np.array((0.5))
mask = std * mask + mean
mask = mask.clip(0,1)
mask = np.squeeze(mask)
return mask
# converting tensor to image
def image_convert(image):
image = image.clone().cpu().numpy()
image = image.transpose((1,2,0))
std = np.array((0.5,0.5,0.5))
mean = np.array((0.5,0.5,0.5))
image = std * image + mean
image = image.clip(0,1)
image = (image * 255).astype(np.uint8)
return image
def plot_img(no_):
iter_ = iter(train_loader)
images,masks = next(iter_)
images = images.to(device)
masks = masks.to(device)
plt.figure(figsize=(10,6))
for idx in range(0,no_):
image = image_convert(images[idx])
plt.subplot(2,no_,idx+1)
plt.title('image')
plt.imshow(image)
for idx in range(0,no_):
mask = mask_convert(masks[idx])
plt.subplot(2,no_,idx+no_+1)
plt.title('mask')
plt.imshow(mask,cmap='gray')
plt.show()
# + [markdown] id="fuAFDy8ELIV0"
# ### SPLITTING FOR TRAINING
# + id="BaDapOukrk2i"
# splitting to trainset and validation set and loading the data with batch size of 10
trainset, valset = random_split(data, [580, 90])
train_loader = torch.utils.data.DataLoader(dataset=trainset, batch_size=10, shuffle=True)
val_loader = torch.utils.data.DataLoader(dataset=valset, batch_size=10)
# + colab={"base_uri": "https://localhost:8080/", "height": 338} id="OOY8wsJbrmeP" outputId="1603b730-8d0b-4e96-c349-ae5ce48e852d"
# we will try visualizing images and corresponding masks
plot_img(5)
# + [markdown] id="Naiv-016LM0B"
# ### UNET MODEL
# + id="8lzq0iGernl2"
def double_conv(in_channels, out_channels):
return nn.Sequential(
nn.Conv2d(in_channels, out_channels, 3, padding=1),
nn.ReLU(inplace=True),
nn.Conv2d(out_channels, out_channels, 3, padding=1),
nn.ReLU(inplace=True)
)
class Unet(nn.Module):
def __init__(self):
super().__init__()
self.dblock1 = double_conv(3, 64)
self.dblock2 = double_conv(64, 128)
self.dblock3 = double_conv(128,256)
self.dblock4 = double_conv(256,512)
self.pool = nn.MaxPool2d(2)
#self.upsample = nn.Upsample(scale_factor=2, mode='bilinear', align_corners=True)
self.up_trans_1 = nn.ConvTranspose2d(in_channels= 512,out_channels= 256,kernel_size= 2,stride= 2)
self.up_trans_2 = nn.ConvTranspose2d(in_channels= 256,out_channels= 128,kernel_size= 2,stride= 2)
self.up_trans_3 = nn.ConvTranspose2d(in_channels= 128,out_channels= 64,kernel_size= 2,stride= 2)
self.dblock5 = double_conv(256 + 256, 256)
self.dblock6 = double_conv(128 + 128, 128)
self.dblock7 = double_conv(64 + 64, 64)
self.last_layer = nn.Conv2d(64,1,1)
self.sigmoid = nn.Sigmoid()
def forward(self,x):
#decoder
conv1 = self.dblock1(x) #3 #64x128x128
x = self.pool(conv1) #64x64x64
conv2 = self.dblock2(x) #2 #128x64x64
x = self.pool(conv2) #128xx32x32
conv3 = self.dblock3(x) #1 #256x32x32
x = self.pool(conv3) #256x16x16
conv4 = self.dblock4(x) #512x16x16
#encoder
x = self.up_trans_1(conv4) #256x32x32
x = torch.cat([x,conv3], dim=1) #1 #(256+256)x32x32
x = self.dblock5(x) #256x32x32
x = self.up_trans_2(x) #128x64x64
x = torch.cat([x,conv2], dim=1) #2 #(128+128)x64x64
x = self.dblock6(x) #128x64x64
x = self.up_trans_3(x) #64x128x128
x = torch.cat([x,conv1], dim=1) #3 #(64+64)x128x128
x = self.dblock7(x) #64x128x128
out = self.last_layer(x)
#out = self.sigmoid(x)
return out
# + colab={"base_uri": "https://localhost:8080/", "height": 870} id="aPpzZK3usSj5" outputId="684e59d8-f958-4d68-e656-c59188a77034"
model = Unet().to(device)
summary(model, (3,128,128))
# + [markdown] id="akHBcVg3Lc5N"
# ### LOSS + IOU METRICS
# + id="f-OptiH8sihp"
#https://www.kaggle.com/bigironsphere/loss-function-library-keras-pytorch
class DiceBCELoss(nn.Module):
def __init__(self, weight=None, size_average=True):
super(DiceBCELoss, self).__init__()
def forward(self, inputs, targets, smooth=1):
#comment out if your model contains a sigmoid or equivalent activation layer
inputs = F.sigmoid(inputs)
bce_weight = 0.5
#flatten label and prediction tensors
inputs = inputs.view(-1)
targets = targets.view(-1)
intersection = (inputs * targets).sum()
dice_loss = 1 - (2.*intersection + smooth)/(inputs.sum() + targets.sum() + smooth)
BCE = F.binary_cross_entropy(inputs, targets, reduction='mean')
loss_final = BCE * bce_weight + dice_loss * (1 - bce_weight)
return loss_final
## IOU computation
def iou_(y_pred,y):
inputs = y_pred.reshape(-1)
targets = y.reshape(-1)
intersection = (inputs * targets).sum()
total = (inputs + targets).sum()
union = total - intersection
smooth = 1
iou = (intersection + smooth)/(union + smooth)
return iou
def iou_batch(y_pred,y):
'''computes mean iou for a batch of ground truth masks and predicted masks'''
ious = []
y_pred = F.sigmoid(y_pred)
y_pred = y_pred.clone().cpu().detach().numpy()
y = y.clone().cpu().detach().numpy()
for pred, label in zip(y_pred, y):
ious.append(iou_(pred, label))
iou = np.nanmean(ious)
return iou
# + [markdown] id="XaVz7gOhLhrw"
# ### CHECKPOINT UTILITY FUNCTION
# + id="Sf_oShMHy0IZ"
#https://towardsdatascience.com/how-to-save-and-load-a-model-in-pytorch-with-a-complete-example-c2920e617dee
def save_ckp(state, is_best, checkpoint_path, best_model_path):
"""
state: checkpoint we want to save
is_best: is this the best checkpoint; min validation loss
checkpoint_path: path to save checkpoint
best_model_path: path to save best model
"""
# save checkpoint data to the path given, checkpoint_path
torch.save(state, checkpoint_path)
# if it is a best model, min validation loss
if is_best:
# copy that checkpoint file to best path given, best_model_path
shutil.copyfile(checkpoint_path, best_model_path)
def load_ckp(checkpoint_fpath, model, optimizer):
"""
checkpoint_path: path to save checkpoint
model: model that we want to load checkpoint parameters into
optimizer: optimizer we defined in previous training
"""
# load check point
checkpoint = torch.load(checkpoint_fpath)
# initialize state_dict from checkpoint to model
model.load_state_dict(checkpoint['state_dict'])
# initialize optimizer from checkpoint to optimizer
optimizer.load_state_dict(checkpoint['optimizer'])
# initialize valid_loss_min from checkpoint to valid_loss_min
valid_loss_min = checkpoint['valid_loss_min']
# return model, optimizer, epoch value, min validation loss
return model, optimizer, checkpoint['epoch'], valid_loss_min.item()
# + colab={"base_uri": "https://localhost:8080/", "height": 35} id="cj1FK66vy1sR" outputId="20134e0d-e707-498b-b2fd-de0b5dce81ac"
# !pwd
# + [markdown] id="Mup5KKzlLx4V"
# ### TRAINING 50 EPOCHS
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="7kijI55XLqen" outputId="c4a4d6fa-7b83-4592-fe8a-8c5a219f8754"
#https://discuss.pytorch.org/t/how-are-optimizer-step-and-loss-backward-related/7350/6
checkpoint_path = '/content/data/chkpoint2_'
best_model_path = '/content/data/bestmodel2.pt'
epochs = 50
criterion = DiceBCELoss()
learning_rate = 1e-3
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
valid_loss_min = 3.95275 #org np.Inf //
train_loss,val_loss = [],[]
train_iou,val_iou = [],[]
for epoch in range(epochs):
print('Epoch {}/{}'.format(epoch + 1, epochs))
start_time = time.time()
running_train_loss = []
running_train_score = []
#tk0 = tqdm(train_loader, total=int(len(train_loader)))
for image,mask in train_loader:
image = image.to(device,dtype=torch.float)
mask = mask.to(device,dtype=torch.float)
pred_mask = model.forward(image) # forward propogation
loss = criterion(pred_mask,mask)
score = iou_batch(pred_mask,mask)
optimizer.zero_grad() # setting gradient to zero
loss.backward()
optimizer.step()
running_train_loss.append(loss.item())
running_train_score.append(score)
else:
running_val_loss = []
running_val_score = []
with torch.no_grad():
for image,mask in val_loader:
image = image.to(device,dtype=torch.float)
mask = mask.to(device,dtype=torch.float)
pred_mask = model.forward(image)
loss = criterion(pred_mask,mask)
score = iou_batch(pred_mask,mask)
running_val_loss.append(loss.item())
running_val_score.append(score)
epoch_train_loss,epoch_train_score = np.mean(running_train_loss) ,np.mean(running_train_score)
print('Train loss : {} iou : {}'.format(epoch_train_loss,epoch_train_score))
train_loss.append(epoch_train_loss)
train_iou.append(epoch_train_score)
epoch_val_loss,epoch_val_score = np.mean(running_val_loss),np.mean(running_val_score)
print('Validation loss : {} iou : {}'.format(epoch_val_loss,epoch_val_score))
val_loss.append(epoch_val_loss)
val_iou.append(epoch_val_score)
#create checkpoint variable and add important data
checkpoint = {
'epoch': epoch + 1,
'valid_loss_min': epoch_val_loss,
'state_dict': model.state_dict(),
'optimizer': optimizer.state_dict(),
}
# save checkpoint
save_ckp(checkpoint, False, checkpoint_path, best_model_path)
#https://towardsdatascience.com/how-to-save-and-load-a-model-in-pytorch-with-a-complete-example-c2920e617dee
if epoch_val_loss <= valid_loss_min:
print('Validation loss decreased ({:.6f} --> {:.6f}). Saving model ...'.format(valid_loss_min,epoch_val_loss))
# save checkpoint as best model
save_ckp(checkpoint, True, checkpoint_path, best_model_path)
valid_loss_min = epoch_val_loss
time_elapsed = time.time() - start_time
print('{:.0f}m {:.0f}s'.format(time_elapsed // 60, time_elapsed % 60))
# -
# ### VISUALIZING SOME IMAGES FROM TRAINED MODEL
# + id="lIFNiKq-MUI4"
#loading the saved model
model, optimizer, start_epoch, valid_loss_min = load_ckp(checkpoint_path, model, optimizer)
# + colab={"base_uri": "https://localhost:8080/", "height": 832} id="aMA0fbKIm8Tw" outputId="30ac507d-10c9-4f23-edc8-548e24a4a402"
iter_ = iter(val_loader)
image,mask = next(iter_)
image = image.to(device,dtype=torch.float)
mask = mask.to(device,dtype=torch.float)
y_pred = model.forward(image)
plt.figure(figsize=(20,15))
for i in range(0,5):
plt.subplot(3,5,i+1)
plt.title('Actual image')
plt.imshow(image_convert(image[i]))
for i in range(0,5):
plt.subplot(3,5,i+5+1)
plt.title('Actual mask')
plt.imshow(mask_convert(mask[i]),cmap='gray')
for i in range(0,5):
plt.subplot(3,5,i+10+1)
plt.title('Predicted mask')
plt.imshow(mask_convert(y_pred[i]),cmap='gray')
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 607} id="wRV8Wm5noF8Z" outputId="b681ba3e-2acf-4a43-b65a-0d422b345d5f"
plt.figure(figsize=(20,10))
plt.subplot(1,2,1)
plt.plot(train_loss,label='train_loss')
plt.plot(val_loss,label='val_loss')
plt.legend()
plt.title('Loss Plot')
plt.subplot(1,2,2)
plt.plot(train_iou,label='train_iou')
plt.plot(val_iou,label='val_iou')
plt.legend()
plt.title('IOU Plot')
plt.show()
# + id="nEEIRfY4oPda"
# WORK IN PROGRESS
# -
|
Unet_3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: conda_amazonei_mxnet_p36
# language: python
# name: conda_amazonei_mxnet_p36
# ---
# # Plagiarism Text Data
#
# In this project, you will be tasked with building a plagiarism detector that examines a text file and performs binary classification; labeling that file as either plagiarized or not, depending on how similar the text file is when compared to a provided source text.
#
# The first step in working with any dataset is loading the data in and noting what information is included in the dataset. This is an important step in eventually working with this data, and knowing what kinds of features you have to work with as you transform and group the data!
#
# So, this notebook is all about exploring the data and noting patterns about the features you are given and the distribution of data.
#
# > There are not any exercises or questions in this notebook, it is only meant for exploration. This notebook will note be required in your final project submission.
#
# ---
# ## Read in the Data
#
# The cell below will download the necessary data and extract the files into the folder `data/`.
#
# This data is a slightly modified version of a dataset created by <NAME> (Information Studies) and <NAME> (Computer Science), at the University of Sheffield. You can read all about the data collection and corpus, at [their university webpage](https://ir.shef.ac.uk/cloughie/resources/plagiarism_corpus.html).
#
# > **Citation for data**: <NAME>. and <NAME>. Developing A Corpus of Plagiarised Short Answers, Language Resources and Evaluation: Special Issue on Plagiarism and Authorship Analysis, In Press. [Download]
# + jupyter={"outputs_hidden": true}
# !wget https://s3.amazonaws.com/video.udacity-data.com/topher/2019/January/5c4147f9_data/data.zip
# !unzip data
# -
# import libraries
import pandas as pd
import numpy as np
import os
# This plagiarism dataset is made of multiple text files; each of these files has characteristics that are is summarized in a `.csv` file named `file_information.csv`, which we can read in using `pandas`.
# +
csv_file = 'data/file_information.csv'
plagiarism_df = pd.read_csv(csv_file)
# print out the first few rows of data info
plagiarism_df.head(10)
# -
# ## Types of Plagiarism
#
# Each text file is associated with one **Task** (task A-E) and one **Category** of plagiarism, which you can see in the above DataFrame.
#
# ### Five task types, A-E
#
# Each text file contains an answer to one short question; these questions are labeled as tasks A-E.
# * Each task, A-E, is about a topic that might be included in the Computer Science curriculum that was created by the authors of this dataset.
# * For example, Task A asks the question: "What is inheritance in object oriented programming?"
#
# ### Four categories of plagiarism
#
# Each text file has an associated plagiarism label/category:
#
# 1. `cut`: An answer is plagiarized; it is copy-pasted directly from the relevant Wikipedia source text.
# 2. `light`: An answer is plagiarized; it is based on the Wikipedia source text and includes some copying and paraphrasing.
# 3. `heavy`: An answer is plagiarized; it is based on the Wikipedia source text but expressed using different words and structure. Since this doesn't copy directly from a source text, this will likely be the most challenging kind of plagiarism to detect.
# 4. `non`: An answer is not plagiarized; the Wikipedia source text is not used to create this answer.
# 5. `orig`: This is a specific category for the original, Wikipedia source text. We will use these files only for comparison purposes.
#
# > So, out of the submitted files, the only category that does not contain any plagiarism is `non`.
#
# In the next cell, print out some statistics about the data.
# print out some stats about the data
print('Number of files: ', plagiarism_df.shape[0]) # .shape[0] gives the rows
# .unique() gives unique items in a specified column
print('Number of unique tasks/question types (A-E): ', (len(plagiarism_df['Task'].unique())))
print('Unique plagiarism categories: ', (plagiarism_df['Category'].unique()))
# You should see the number of text files in the dataset as well as some characteristics about the `Task` and `Category` columns. **Note that the file count of 100 *includes* the 5 _original_ wikipedia files for tasks A-E.** If you take a look at the files in the `data` directory, you'll notice that the original, source texts start with the filename `orig_` as opposed to `g` for "group."
#
# > So, in total there are 100 files, 95 of which are answers (submitted by people) and 5 of which are the original, Wikipedia source texts.
#
# Your end goal will be to use this information to classify any given answer text into one of two categories, plagiarized or not-plagiarized.
# ### Distribution of Data
#
# Next, let's look at the distribution of data. In this course, we've talked about traits like class imbalance that can inform how you develop an algorithm. So, here, we'll ask: **How evenly is our data distributed among different tasks and plagiarism levels?**
#
# Below, you should notice two things:
# * Our dataset is quite small, especially with respect to examples of varying plagiarism levels.
# * The data is distributed fairly evenly across task and plagiarism types.
# +
# Show counts by different tasks and amounts of plagiarism
# group and count by task
counts_per_task=plagiarism_df.groupby(['Task']).size().reset_index(name="Counts")
print("\nTask:")
display(counts_per_task)
# group by plagiarism level
counts_per_category=plagiarism_df.groupby(['Category']).size().reset_index(name="Counts")
print("\nPlagiarism Levels:")
display(counts_per_category)
# group by task AND plagiarism level
counts_task_and_plagiarism=plagiarism_df.groupby(['Task', 'Category']).size().reset_index(name="Counts")
print("\nTask & Plagiarism Level Combos :")
display(counts_task_and_plagiarism)
# -
# It may also be helpful to look at this last DataFrame, graphically.
#
# Below, you can see that the counts follow a pattern broken down by task. Each task has one source text (original) and the highest number on `non` plagiarized cases.
# +
import matplotlib.pyplot as plt
% matplotlib inline
# counts
group = ['Task', 'Category']
counts = plagiarism_df.groupby(group).size().reset_index(name="Counts")
plt.figure(figsize=(8,5))
plt.bar(range(len(counts)), counts['Counts'], color = 'blue')
# -
# ## Up Next
#
# This notebook is just about data loading and exploration, and you do not need to include it in your final project submission.
#
# In the next few notebooks, you'll use this data to train a complete plagiarism classifier. You'll be tasked with extracting meaningful features from the text data, reading in answers to different tasks and comparing them to the original Wikipedia source text. You'll engineer similarity features that will help identify cases of plagiarism. Then, you'll use these features to train and deploy a classification model in a SageMaker notebook instance.
|
1_Data_Exploration.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Run this again after editing submodules so Colab uses the updated versions
from citylearn import CityLearn
from pathlib import Path
from agent import Agent
import numpy as np
import torch
# +
# Load environment
climate_zone = 5
params = {'data_path':Path("data/Climate_Zone_"+str(climate_zone)),
'building_attributes':'building_attributes.json',
'weather_file':'weather_data.csv',
'solar_profile':'solar_generation_1kW.csv',
'carbon_intensity':'carbon_intensity.csv',
'building_ids':["Building_"+str(i) for i in [1,2,3,4,5,6,7,8,9]],
'buildings_states_actions':'buildings_state_action_space.json',
'simulation_period': (0, 8760*4-1),
'cost_function': ['ramping','1-load_factor','average_daily_peak','peak_demand','net_electricity_consumption','carbon_emissions'],
'central_agent': False,
'save_memory': False }
# Contain the lower and upper bounds of the states and actions, to be provided to the agent to normalize the variables between 0 and 1.
env = CityLearn(**params)
observations_spaces, actions_spaces = env.get_state_action_spaces()
# Provides information on Building type, Climate Zone, Annual DHW demand, Annual Cooling Demand, Annual Electricity Demand, Solar Capacity, and correllations among buildings
building_info = env.get_building_information()
# +
params_agent = {'building_ids':["Building_"+str(i) for i in [1,2,3,4,5,6,7,8,9]],
'buildings_states_actions':'buildings_state_action_space.json',
'building_info':building_info,
'observation_spaces':observations_spaces,
'action_spaces':actions_spaces}
# Instantiating the control agent(s)
agents = Agent(**params_agent)
state = env.reset()
done = False
action, coordination_vars = agents.select_action(state)
while not done:
next_state, reward, done, _ = env.step(action)
action_next, coordination_vars_next = agents.select_action(next_state)
agents.add_to_buffer(state, action, reward, next_state, done, coordination_vars, coordination_vars_next)
coordination_vars = coordination_vars_next
state = next_state
action = action_next
env.cost()
# -
|
main.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Predicting house prices using k-nearest neighbors regression
# In this notebook, you will implement k-nearest neighbors regression. You will:
# * Find the k-nearest neighbors of a given query input
# * Predict the output for the query input using the k-nearest neighbors
# * Choose the best value of k using a validation set
# # Fire up GraphLab Create
import graphlab
# # Load in house sales data
# For this notebook, we use a subset of the King County housing dataset created by randomly selecting 40% of the houses in the full dataset.
sales = graphlab.SFrame('kc_house_data_small.gl/kc_house_data_small.gl')
# # Import useful functions from previous notebooks
# To efficiently compute pairwise distances among data points, we will convert the SFrame into a 2D Numpy array. First import the numpy library and then copy and paste `get_numpy_data()` from the second notebook of Week 2.
import numpy as np # note this allows us to refer to numpy as np instead
def get_numpy_data(data_sframe, features, output):
data_sframe['constant'] = 1 # this is how you add a constant column to an SFrame
# add the column 'constant' to the front of the features list so that we can extract it along with the others:
features = ['constant'] + features # this is how you combine two lists
# select the columns of data_SFrame given by the features list into the SFrame features_sframe (now including constant):
features_sframe = data_sframe[features]
# the following line will convert the features_SFrame into a numpy matrix:
feature_matrix = features_sframe.to_numpy()
# assign the column of data_sframe associated with the output to the SArray output_sarray
output_sarray = data_sframe['price']
# the following will convert the SArray into a numpy array by first converting it to a list
output_array = output_sarray.to_numpy()
return(feature_matrix, output_array)
# We will also need the `normalize_features()` function from Week 5 that normalizes all feature columns to unit norm. Paste this function below.
def normalize_features(feature_matrix):
norms = np.linalg.norm(feature_matrix, axis=0)
features = feature_matrix / norms
return features, norms
# # Split data into training, test, and validation sets
(train_and_validation, test) = sales.random_split(.8, seed=1) # initial train/test split
(train, validation) = train_and_validation.random_split(.8, seed=1) # split training set into training and validation sets
# # Extract features and normalize
# Using all of the numerical inputs listed in `feature_list`, transform the training, test, and validation SFrames into Numpy arrays:
feature_list = ['bedrooms',
'bathrooms',
'sqft_living',
'sqft_lot',
'floors',
'waterfront',
'view',
'condition',
'grade',
'sqft_above',
'sqft_basement',
'yr_built',
'yr_renovated',
'lat',
'long',
'sqft_living15',
'sqft_lot15']
features_train, output_train = get_numpy_data(train, feature_list, 'price')
features_test, output_test = get_numpy_data(test, feature_list, 'price')
features_valid, output_valid = get_numpy_data(validation, feature_list, 'price')
# In computing distances, it is crucial to normalize features. Otherwise, for example, the `sqft_living` feature (typically on the order of thousands) would exert a much larger influence on distance than the `bedrooms` feature (typically on the order of ones). We divide each column of the training feature matrix by its 2-norm, so that the transformed column has unit norm.
#
# IMPORTANT: Make sure to store the norms of the features in the training set. The features in the test and validation sets must be divided by these same norms, so that the training, test, and validation sets are normalized consistently.
features_train, norms = normalize_features(features_train) # normalize training set features (columns)
features_test = features_test / norms # normalize test set by training set norms
features_valid = features_valid / norms # normalize validation set by training set norms
# # Compute a single distance
# To start, let's just explore computing the "distance" between two given houses. We will take our **query house** to be the first house of the test set and look at the distance between this house and the 10th house of the training set.
#
# To see the features associated with the query house, print the first row (index 0) of the test feature matrix. You should get an 18-dimensional vector whose components are between 0 and 1.
print features_test[0]
# Now print the 10th row (index 9) of the training feature matrix. Again, you get an 18-dimensional vector with components between 0 and 1.
print features_train[9]
# ***QUIZ QUESTION ***
#
# What is the Euclidean distance between the query house and the 10th house of the training set?
#
# Note: Do not use the `np.linalg.norm` function; use `np.sqrt`, `np.sum`, and the power operator (`**`) instead. The latter approach is more easily adapted to computing multiple distances at once.
print np.sqrt(np.sum((features_train[9]-features_test[0])**2))
# # Compute multiple distances
# Of course, to do nearest neighbor regression, we need to compute the distance between our query house and *all* houses in the training set.
#
# To visualize this nearest-neighbor search, let's first compute the distance from our query house (`features_test[0]`) to the first 10 houses of the training set (`features_train[0:10]`) and then search for the nearest neighbor within this small set of houses. Through restricting ourselves to a small set of houses to begin with, we can visually scan the list of 10 distances to verify that our code for finding the nearest neighbor is working.
#
# Write a loop to compute the Euclidean distance from the query house to each of the first 10 houses in the training set.
for i in range(0,10):
print str(i) + " : " + str(np.sqrt(np.sum((features_train[i]-features_test[0])**2)))
# *** QUIZ QUESTION ***
#
# Among the first 10 training houses, which house is the closest to the query house?
for i in range(0,10):
print str(i) + " : " + str(np.sqrt(np.sum((features_train[i]-features_test[2])**2)))
# It is computationally inefficient to loop over computing distances to all houses in our training dataset. Fortunately, many of the Numpy functions can be **vectorized**, applying the same operation over multiple values or vectors. We now walk through this process.
#
# Consider the following loop that computes the element-wise difference between the features of the query house (`features_test[0]`) and the first 3 training houses (`features_train[0:3]`):
for i in xrange(3):
print features_train[i]-features_test[0]
# should print 3 vectors of length 18
# The subtraction operator (`-`) in Numpy is vectorized as follows:
print features_train[0:3] - features_test[0]
# Note that the output of this vectorized operation is identical to that of the loop above, which can be verified below:
# verify that vectorization works
results = features_train[0:3] - features_test[0]
print results[0] - (features_train[0]-features_test[0])
# should print all 0's if results[0] == (features_train[0]-features_test[0])
print results[1] - (features_train[1]-features_test[0])
# should print all 0's if results[1] == (features_train[1]-features_test[0])
print results[2] - (features_train[2]-features_test[0])
# should print all 0's if results[2] == (features_train[2]-features_test[0])
# Aside: it is a good idea to write tests like this cell whenever you are vectorizing a complicated operation.
# # Perform 1-nearest neighbor regression
#
# Now that we have the element-wise differences, it is not too hard to compute the Euclidean distances between our query house and all of the training houses. First, write a single-line expression to define a variable `diff` such that `diff[i]` gives the element-wise difference between the features of the query house and the `i`-th training house.
diff = features_train[0:len(features_train)] - features_test[0]
# To test the code above, run the following cell, which should output a value -0.0934339605842:
print diff[-1].sum() # sum of the feature differences between the query and last training house
# should print -0.0934339605842
# The next step in computing the Euclidean distances is to take these feature-by-feature differences in `diff`, square each, and take the sum over feature indices. That is, compute the sum of square feature differences for each training house (row in `diff`).
#
# By default, `np.sum` sums up everything in the matrix and returns a single number. To instead sum only over a row or column, we need to specifiy the `axis` parameter described in the `np.sum` [documentation](http://docs.scipy.org/doc/numpy-1.10.1/reference/generated/numpy.sum.html). In particular, `axis=1` computes the sum across each row.
#
# Below, we compute this sum of square feature differences for all training houses and verify that the output for the 16th house in the training set is equivalent to having examined only the 16th row of `diff` and computing the sum of squares on that row alone.
print np.sum(diff**2, axis=1)[15] # take sum of squares across each row, and print the 16th sum
print np.sum(diff[15]**2) # print the sum of squares for the 16th row -- should be same as above
# With this result in mind, write a single-line expression to compute the Euclidean distances between the query house and all houses in the training set. Assign the result to a variable `distances`.
#
# **Hint**: Do not forget to take the square root of the sum of squares.
distances = np.sqrt(np.sum(diff**2, axis=1))
# To test the code above, run the following cell, which should output a value 0.0237082324496:
print distances[100] # Euclidean distance between the query house and the 101th training house
# should print 0.0237082324496
# Now you are ready to write a function that computes the distances from a query house to all training houses. The function should take two parameters: (i) the matrix of training features and (ii) the single feature vector associated with the query.
def compute_distances(features_instances, features_query):
diff = features_instances[0:len(features_instances)] - features_query
distances = np.sqrt(np.sum(diff**2, axis=1))
return distances
# *** QUIZ QUESTIONS ***
#
# 1. Take the query house to be third ho
# use of the test set (`features_test[2]`). What is the index of the house in the training set that is closest to this query house?
# 2. What is the predicted value of the query house based on 1-nearest neighbor regression?
# +
distances = compute_distances(features_train, features_test[2])
min = distances[0]
index = 0
for i in xrange(len(distances)):
if(distances[i] < min):
min = distances[i]
index = i
print min
print index
# -
print output_train[382]
# # Perform k-nearest neighbor regression
# For k-nearest neighbors, we need to find a *set* of k houses in the training set closest to a given query house. We then make predictions based on these k nearest neighbors.
# ## Fetch k-nearest neighbors
#
# Using the functions above, implement a function that takes in
# * the value of k;
# * the feature matrix for the training houses; and
# * the feature vector of the query house
#
# and returns the indices of the k closest training houses. For instance, with 2-nearest neighbor, a return value of [5, 10] would indicate that the 6th and 11th training houses are closest to the query house.
#
# **Hint**: Look at the [documentation for `np.argsort`](http://docs.scipy.org/doc/numpy/reference/generated/numpy.argsort.html).
def k_nearest_neighbors(k, feature_train, features_query):
distances = compute_distances(features_train, features_query)
neighbors = np.argsort(distances)[0:k]
return neighbors
# *** QUIZ QUESTION ***
#
# Take the query house to be third house of the test set (`features_test[2]`). What are the indices of the 4 training houses closest to the query house?
print k_nearest_neighbors(4, features_train, features_test[2])
# ## Make a single prediction by averaging k nearest neighbor outputs
# Now that we know how to find the k-nearest neighbors, write a function that predicts the value of a given query house. **For simplicity, take the average of the prices of the k nearest neighbors in the training set**. The function should have the following parameters:
# * the value of k;
# * the feature matrix for the training houses;
# * the output values (prices) of the training houses; and
# * the feature vector of the query house, whose price we are predicting.
#
# The function should return a predicted value of the query house.
#
# **Hint**: You can extract multiple items from a Numpy array using a list of indices. For instance, `output_train[[6, 10]]` returns the prices of the 7th and 11th training houses.
def predict_output_of_query(k, features_train, output_train, features_query):
neighbors = k_nearest_neighbors(k, features_train, features_query)
prices = output_train[neighbors]
prediction = np.sum(prices)/k
return prediction
# *** QUIZ QUESTION ***
#
# Again taking the query house to be third house of the test set (`features_test[2]`), predict the value of the query house using k-nearest neighbors with `k=4` and the simple averaging method described and implemented above.
print predict_output_of_query(4, features_train, output_train, features_test[2])
# Compare this predicted value using 4-nearest neighbors to the predicted value using 1-nearest neighbor computed earlier.
# ## Make multiple predictions
# Write a function to predict the value of *each and every* house in a query set. (The query set can be any subset of the dataset, be it the test set or validation set.) The idea is to have a loop where we take each house in the query set as the query house and make a prediction for that specific house. The new function should take the following parameters:
# * the value of k;
# * the feature matrix for the training houses;
# * the output values (prices) of the training houses; and
# * the feature matrix for the query set.
#
# The function should return a set of predicted values, one for each house in the query set.
#
# **Hint**: To get the number of houses in the query set, use the `.shape` field of the query features matrix. See [the documentation](http://docs.scipy.org/doc/numpy-1.10.1/reference/generated/numpy.ndarray.shape.html).
def predict_output(k, features_train, output_train, features_query):
predictions = []
for i in xrange(len(features_query)):
prediction = predict_output_of_query(k, features_train, output_train, features_query[i])
predictions.append(prediction)
return predictions
# *** QUIZ QUESTION ***
#
# Make predictions for the first 10 houses in the test set using k-nearest neighbors with `k=10`.
#
# 1. What is the index of the house in this query set that has the lowest predicted value?
# 2. What is the predicted value of this house?
print predict_output(10, features_train, output_train,features_test[0:10])
# ## Choosing the best value of k using a validation set
# There remains a question of choosing the value of k to use in making predictions. Here, we use a validation set to choose this value. Write a loop that does the following:
#
# * For `k` in [1, 2, ..., 15]:
# * Makes predictions for each house in the VALIDATION set using the k-nearest neighbors from the TRAINING set.
# * Computes the RSS for these predictions on the VALIDATION set
# * Stores the RSS computed above in `rss_all`
# * Report which `k` produced the lowest RSS on VALIDATION set.
# (Depending on your computing environment, this computation may take 10-15 minutes.)
# To visualize the performance as a function of `k`, plot the RSS on the VALIDATION set for each considered `k` value:
# +
import matplotlib.pyplot as plt
# %matplotlib inline
kvals = range(1, 16)
plt.plot(kvals, rss_all,'bo-')
# -
# ***QUIZ QUESTION ***
#
# What is the RSS on the TEST data using the value of k found above? To be clear, sum over all houses in the TEST set.
|
Regression/Assignment_six/week-6-local-regression-assignment-blank.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="aZfhY-rNme8c"
# # Beginner's Python—Session Three and Four Finance/Economics Exercises
# + [markdown] id="mz4BiqG2me8e"
# ## Inflation in Leamington
# + [markdown] id="T0KAtvl4me8f"
# Run the code in the cell below to display Table 1. This table below contains 2016-2020 price data on the five products purchased by Leamington students that serve as a
# representative “typical basket of goods”. We will use this data to determine insights on the level of inflation during recent years in Leamington.
# +
# Run this cell to display Table 1. DO NOT MODIFY THE CODE ON THIS CELL
items = ["Pints of beer", "Smack tickets", "Neon tickets", "Vialis meals", "Pret a Manger coffee"]
prices_2016 = [3.00, 4.00, 4.00, 5.00, 3.00]
prices_2017 = [3.24, 4.50, 5.00, 5.55, 3.30]
prices_2018 = [3.20, 4.50, 4.75, 5.40, 3.24]
prices_2019 = [3.50, 5.75, 5.00, 6.30, 3.65]
prices_2020 = [3.75, 6.50, 5.00, 6.90, 4.25]
quantities = [6, 2, 1, 2, 5]
import pandas as pd
table_1 = pd.DataFrame(data = {"Item": items,
"Average price per unit (2016, £)": prices_2016,
"Average price per unit (2017, £)": prices_2017,
"Average price per unit (2018, £)": prices_2018,
"Average price per unit (2019, £)": prices_2019,
"Average price per unit (2020, £)": prices_2020,
"Weekly quantity purchased by the average student": quantities
}).set_index("Item")
quantities = [6, 2, 1, 2, "???"]
prices_2019 = [3.50, 5.75, 5.75, 5.00, 6.30, 3.65]
table_1
# + [markdown] id="0T5qTb7Xme8f"
# To help you out in this analysis, we have stored the columns of the table into the following lists:
#
# - `prices_2016`
# - `prices_2017`
# - `prices_2018`
# - `prices_2019`
# - `prices_2020`
# - `quantities`
#
# Print out these lists to check that they match the data provided in the table.
#
# -
# + [markdown] id="WWGhCqLcme8j"
# You may have noticed that we are missing data for the weekly average number of Pret coffees consumed per student and have _"???"_ instead of 5. Missing data is a problem that many economists and data scientists face regularly.
#
# Alter the 5th element of list `quantities` by assinging it 5, and print out the list before and after this assingment to check that the change has been made.
# -
# Furthermore, it is evident that we have an extra value in the `prices_2019` list since it contains 6 elements whilst there are only 5 products. Upon inspection, it is clear that a duplicate value has been entered for the price of Smack tickets.
#
# Remove either the second or third element of the `prices_2019` list. Print out the list before and after doing this to ensure the change has been made appropiately and the list matches the 5th column in the table at the top.
# Now that we have complete data we can begin analysing inflation! To do this we will compute the Consumer Price Index (CPI) for Leamington in 2019 using the following formula:
# $$CPI_t = \frac{C_t}{C_0} \times 100$$
#
# Where $C_t$ denotes the cost of the market basket in period $t$ and $C_0$ denotes the cost of the market basket in the base period (we will use 2016 as our base period). The cost of the market basket is determined by summing the average expenditure on each good during that year.
#
# To make our work easier, we will combine all of our price lists into one iterable data structure. Create a tuple named `prices` composed of all of the price lists 2016-2020.
#
# We will now compute the cost of market baskets for every year in the 2016-2020 period. To do this, we iterate over the `prices` tuple, get the average expenditure on each good that year, and then add these expenditures up.
#
# First, we want to be able to iterate through our `prices` tuple. Follow the instructions below
#
# 1. Create an empty list named `baskets` and a variable named `counter` and assign it 0.
# 2. Create a 'while' loop that iterates through `prices`. (Hint: use the variable `counter` to tell the loop when to stop.)
# 3. Inside the 'while' loop, use the variable `counter` to index the `prices` tuple and assign the corresponding element to variable `current_prices`.
# 4. Print variable `current_prices` at each iteration.
# Next, we want to be able to compute the average expenditure on each good in a given year. To do this, follow the instructions below:
#
# 1. Copy and paste the code you wrote in the previous cell, deleting only the 'print' statement.
# 2. Inside the 'while' loop, after the assingment of `current_prices` , create variables `item_index` and `basket_cost` and assign 0 to both of them.
# 3. After the assignment of these variables, create another 'while' loop inside the first one to iterate through the `current_prices` list. (Hint: use the variable `item_index` as a counter variable to tell the loop when to stop).
# 4. At each iteration of the `current_prices` list, create a new variable called `avg_expend_on_item` and assign to it the product of the corresponding element in `current_prices` and `quantities` for that item. (Hint: use variable `item_index` to index both `current_prices` and `quantities`).
# 5. At the end of each iteration of `current_prices`, increment variable `basket_cost` by `avg_expend_on_item`.
# 6. At the end of each iteration of `prices` (inside the first 'while' loop but outside the second) append `basket_cost` to the list `baskets`.
# Now that we have the market basket costs for every year, we're interested in computing the CPI.
#
# 1. Create an empty list called `cpis`.
# 3. Iterate through the list `baskets` using a 'while' loop and, with the formula above, compute the CPI for Leamington for each year (given 2016 as the base year). Round this result to two decimal places and append it to`cpis`.
# 4. At each iteration: print the year and the CPI for that year. (Hint: To compute the year, try adding 2016 to the counter variable used to iterate in the while loop)
# Using CPI data above, answer the following questions:
#
# - What was the rate of inflation in 2017?
# - During which year did Leamington experience deflation?
# - During which year did Leamington experience disinflation?
|
session-four/subject_questions/session_three&four_finecon_exercises.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # LeetCode #844. Backspace String Compare
#
# ## Question
#
# https://leetcode.com/problems/backspace-string-compare/
#
# Given two strings S and T, return if they are equal when both are typed into empty text editors. # means a backspace character.
#
# Example 1:
#
# Input: S = "ab#c", T = "ad#c"
# Output: true
# Explanation: Both S and T become "ac".
#
# Example 2:
#
# Input: S = "ab##", T = "c#d#"
# Output: true
# Explanation: Both S and T become "".
#
# Example 3:
#
# Input: S = "a##c", T = "#a#c"
# Output: true
# Explanation: Both S and T become "c".
#
# Example 4:
#
# Input: S = "a#c", T = "b"
# Output: false
# Explanation: S becomes "c" while T becomes "b".
#
# Note:
#
# 1 <= S.length <= 200
# 1 <= T.length <= 200
# S and T only contain lowercase letters and '#' characters.
#
# Follow up:
#
# Can you solve it in O(N) time and O(1) space?
#
# ## My Solution
import re
def backspaceCompare(S, T):
todel = re.findall('\w#', S)
while todel:
S = S.replace(todel[0], "")
todel.pop(0)
todel = re.findall('\w#', S)
S = S.replace('#', '')
todel = re.findall('\w#', T)
while todel:
T = T.replace(todel[0], "")
todel.pop(0)
todel = re.findall('\w#', T)
T = T.replace('#', '')
print(S, T)
return S == T
# test code
S = "e##e#o##oyof##q"
T = "e##e##o##oyof##q"
backspaceCompare(S, T)
# ## My Result
#
# __Runtime__ : 40 ms, faster than 5.45% of Python3 online submissions for Backspace String Compare.
#
# __Memory Usage__ : 12.8 MB, less than 100.00% of Python3 online submissions for Backspace String Compare.
# ## @jackspp's Solution
def backspaceCompare(S, T):
def str2stack(str_, stack_):
for s in str_:
if s != '#':
stack_ += [s,]
elif len(stack_) >= 1:
stack_.pop(-1)
sStack, tStack = list(), list()
str2stack(S, sStack); str2stack(T, tStack)
#print(sStack, tStack)
return (sStack == tStack)
S = "e##e#o##oyof##q"
T = "e##e#fq##o##oyof##q"
backspaceCompare(S, T)
# ## @jackspp's Result
#
# __Runtime__ : 28 ms, faster than 70.90% of Python3 online submissions for Backspace String Compare.
#
# __Memory Usage__ : 12.7 MB, less than 100.00% of Python3 online submissions for Backspace String Compare.
|
LeetCode/LeetCode_844BackspaceStringCompare.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Figure 4: Grism Dispersions Within a Grism Detector Subarray
# ***
# ### Table of Contents
#
# 1. [Information](#Information)
# 2. [Imports](#Imports)
# 3. [Data](#Data)
# 4. [Generate the Grism Dispersions Within Subarrays Plot](#Generate-the-Grism-Dispersions-Within-Subarrays-Plot)
# 5. [Issues](#Issues)
# 6. [About this Notebook](#About-this-Notebook)
# ***
# ## Information
# #### JDox links:
# * [NIRCam Grism Time Series](https://jwst-docs.stsci.edu/display/JTI/NIRCam+Grism+Time+Series#NIRCamGrismTimeSeries-#DispersionDispersion)
# * Figure 4. Grism dispersions within a grism detector subarray
# ## Imports
# +
import os
import numpy as np
import pandas as pd
from astropy.io import ascii, fits
import matplotlib.patches as patches
import matplotlib.pyplot as plt
import grismconf
from itertools import product
# %matplotlib notebook
# -
# ## Data
# #### Data Location:
#
# In notebook (TBD: use Nor Pirzkal's [grismconf](https://github.com/npirzkal/GRISMCONF) code to create figure parameters)
datadir = '/user/gennaro/Functional_work/NIRCam_GRISM_viz/GRISM_NIRCAM_config_data/'
# ### Initial Setup
# ### Define the wavelength range as the range for which the sensitivity is larger than a given fraction of the maximum
# +
facs = [0.5,0.01]
exts = [{} for fac in facs]
filters = ["F277W","F322W2","F356W","F444W"]
orders = ['1st']
modules = ['A']
orients = ['R']
for fac, ext in zip(facs,exts):
for j,filt in enumerate(filters):
for orient,module, order in product(orients,modules,orders):
fname = 'NIRCam.{}.{}.{}.{}.sensitivity.fits'.format(filt,orient,module,order)
h = fits.open(datadir+fname)
imax = np.argmax(h[1].data['SENSITIVITY'])
BM = h[1].data['SENSITIVITY'] >= fac*h[1].data['SENSITIVITY'][imax]
ilow = np.nonzero(BM)[0][0]
ihigh = np.nonzero(BM)[0][-1]
if ( (orient == 'R') and (module=='A') and (order == '1st')):
# if ( (orient == 'R') and (module=='A')):
ext[filt] = [h[1].data['WAVELENGTH'][ilow],h[1].data['WAVELENGTH'][ihigh]]
# -
# #### For the given filter/module/order/orient combo, use grismconf to get the (x,y) position of the spectra extrema w.r.t. the undeflected wavelength of 3.95 $\mu$m
xys = {"F277W":(1581,280),
"F322W2":(1581,280),
"F356W":(1581,280),
"F444W":(952,280),
}
orders = ['+1']
# +
positions = {}
configs = {}
for (ext,fac),filt,orient,module, order in product(zip(exts,facs),filters,orients,modules,orders):
pos = {}
C = grismconf.Config(datadir+'/NIRCAM_{}_mod{}_{}.conf'.format(filt,module,orient))
x,y = xys[filt]
tmin = C.INVDISPL("+1",100,100,ext[filt][0])
tmax = C.INVDISPL("+1",100,100,ext[filt][1])
dx0 = C.DISPX(order,x,y,tmin)
dx1 = C.DISPX(order,x,y,tmax)
dy0 = C.DISPY(order,x,y,tmin)
dy1 = C.DISPY(order,x,y,tmax)
mu0 = C.DISPL(order,x,y,tmin)
mu1 = C.DISPL(order,x,y,tmax)
pos['xstart'] = x+dx0
pos['ystart'] = y+dy0
pos['xend'] = x+dx1
pos['yend'] = y+dy1
pos['mustart'] = mu0
pos['muend'] = mu1
print(fac,filt,module,orient,order)
print(pos)
key = '{}_{}_{}_{}_{}'.format(fac,filt,module,orient,order)
positions[key] = pos
configs[key] = C
# +
fac,filt,module,orient,order = facs[0],"F444W","A","R","+1"
key = '{}_{}_{}_{}_{}'.format(fac,filt,module,orient,order)
C = configs[key]
ts = C.INVDISPX("+1",952,100,2044-952)
wave = C.DISPL(order,952,100,ts)
print(ts)
print(wave)
fname = 'NIRCam.{}.{}.{}.{}.sensitivity.fits'.format(filt,orient,module,'1st')
h = fits.open(datadir+fname)
imax = np.argmax(h[1].data['SENSITIVITY'])
BM = h[1].data['WAVELENGTH'] >= wave
print(h[1].data['SENSITIVITY'][np.nonzero(BM)[0][0]]/h[1].data['SENSITIVITY'][imax])
# +
### Function to make the top axis (micron) relate to the botoom one (pixels)
def pixtomu(dxvals,x0,y0,C,order):
ts = C.INVDISPX(order,x0,y0,dxvals)
# Compute wavelength of each of the pixels
wavs = C.DISPL(order,x0,y0,ts)
return np.array(wavs)
def mutopix(muvals,x0,y0,C,order):
ts = C.INVDISPL(order,x0,y0,muvals)
dxs = C.DISPX(order,x0,y0,ts)
return x0+np.array(dxs)
# +
plt.style.use('bmh')
plt.rcParams['font.family'] = 'Times New Roman'
plt.rcParams['font.size'] = 18
plt.rcParams['axes.labelsize'] = 18
plt.rcParams['axes.labelweight'] = 'normal'
plt.rcParams['xtick.labelsize'] = 16
plt.rcParams['ytick.labelsize'] = 16
plt.rcParams['legend.fontsize'] = 12
plt.rcParams['figure.titlesize'] = 16
# +
aspectratio =2.
figside = 12
f, ax = plt.subplots(1,figsize=(figside, figside/aspectratio))
ax2 = ax.twiny()
pixvals = np.array([0,2048])
muvals = np.arange(2.,5.01,0.5)
fac,filt,module,orient,order = facs[0],"F277W","A","R","+1"
key = '{}_{}_{}_{}_{}'.format(fac,filt,module,orient,order)
C = configs[key]
x,y = xys[filt]
ax2.set_xticks(muvals)
ax2.set_xlim(1.95,5.4)
ax.set_xlim(mutopix(ax2.get_xlim(),x,y,C,order))
xlims = ax.get_xlim()
xsize = xlims[1]-xlims[0]
ax.set_ylim(0,xsize/aspectratio)
for j,filt in enumerate(filters[:3]):
for orient,module, order in product(orients,modules,orders):
for k,fac in enumerate(facs):
key = '{}_{}_{}_{}_{}'.format(fac,filt,module,orient,order)
pos = positions[key]
x,y = xys[filt]
yref = j*500+150
dy = 256
ax.plot(x, yref+dy/2, 'kx',ms=15)
if order == '+2':
ax.plot([pos['xstart'],pos['xend']],[yref+dy/2,yref+dy/2], 'grey', lw=7/(1+k))
else:
ax.plot([pos['xstart'],pos['xend']],[yref+dy/2,yref+dy/2], 'k', lw=7/(1+k))
ax.add_patch(patches.Rectangle((4, yref),2044, dy,fill=False,color='red',lw=4))
ax2.text(1.99,yref+dy/2, filt, va='center', fontsize=18)
ax.set_xlabel('Science pixels',fontsize=18)
ax2.set_xlabel('Wavelength [$\mu$m]',fontsize=18)
ax.axvline(x,linestyle=':',color='black')
ax.set_xticks(np.append(x,pixvals))
ax.set_facecolor('#FFFFFF')
ax2.set_facecolor('#FFFFFF')
ax.grid(False)
ax2.grid(False)
ax.axes.get_yaxis().set_visible(False)
f.tight_layout()
# # f.savefig("img1.png")
# +
aspectratio = 3.
figside = 12
f, ax = plt.subplots(1,figsize=(figside, figside/aspectratio))
ax2 = ax.twiny()
pixvals = np.array([0,2048])
muvals = np.arange(2.,5.01,0.5)
filt,module,orient,order = "F444W","A","R","+1"
key = '{}_{}_{}_{}_{}'.format(fac,filt,module,orient,order)
C = configs[key]
x,y = xys[filt]
ax2.set_xticks(muvals)
ax2.set_xlim(1.95,5.4)
ax.set_xlim(mutopix(ax2.get_xlim(),x,y,C,order))
xlims = ax.get_xlim()
xsize = xlims[1]-xlims[0]
ax.set_ylim(150,xsize/aspectratio)
for j,filt in enumerate(filters[3:]):
for orient,module, order in product(orients,modules,orders):
for k,fac in enumerate(facs):
key = '{}_{}_{}_{}_{}'.format(fac,filt,module,orient,order)
pos = positions[key]
x,y = xys[filt]
yref = j*500+500
dy = 256
ax.plot(x, yref+dy/2, 'kx',ms=15)
ax.plot([pos['xstart'],pos['xend']],[yref+dy/2,yref+dy/2], 'k', lw=7/(1+k))
ax.add_patch(patches.Rectangle((4, yref),2044, dy,fill=False,color='red',lw=4))
ax2.text(2.2,yref+dy/2, filt, va='center', fontsize=18)
ax.axvline(x,linestyle=':',color='black')
ax.set_xticks(np.append(x,pixvals))
ax.set_xlabel('Science pixels',fontsize=18)
ax2.set_xlabel('Wavelength [$\mu$m]',fontsize=18)
ax.axvline(x,linestyle=':',color='black')
ax.set_xticks(np.append(x,pixvals))
ax.set_facecolor('#FFFFFF')
ax2.set_facecolor('#FFFFFF')
ax.grid(False)
ax2.grid(False)
ax.axes.get_yaxis().set_visible(False)
f.tight_layout()
# f.savefig("img1.png")
# -
# ## Issues
# * Need to add data to the Box directory (https://stsci.box.com/s/tf6049a75u6f3uc26q3xu6w8tv456pk7)
# ## About this Notebook
# **Authors:**
# * <NAME>
# * <NAME>
# * <NAME>
#
# **Updated On:**
# December 30, 2019
|
nircam_jdox/nircam_grism_time_series/figure4_dispersions_subarrays.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Logistic regression tutorial
# +
## Do **not** change this cell, and do **not** import
## any other modules anywhere in the notebook.
import numpy as np
import numpy.random as rn
from scipy import optimize, stats
import scipy.linalg as linalg
import matplotlib.pyplot as plt
# %matplotlib inline
# -
# In this tutorial we're going to cover the basics behind logistic regression. For simplicity we will only consider the binary classification case, in which target variables are $y \in \{0,1\}$.
#
# In logistic regression, the probability of a data point $\boldsymbol x$ being of class 1 is given by
#
# $$p(y = 1 | \boldsymbol x, \boldsymbol\theta) = \sigma (\boldsymbol x^\top \boldsymbol\theta) ~ ,$$
#
# where $\sigma(z) = 1/(1+\exp(-z))$ is the _sigmoid_ function.
#
# Combining this with a Bernoulli likelihood and summing over all datapoints $\{\boldsymbol x_i, y_i\}_{i=1}^N$ we end up with a negative log-likelihood function that looks like this:
#
# $$-\log p(\boldsymbol y|\boldsymbol X, \boldsymbol\theta) = -\sum_i\left(y_i \log \sigma(\boldsymbol x_i^\top \boldsymbol\theta) + (1 - y_i) \log ( 1 - \sigma(\boldsymbol x_i^\top \boldsymbol\theta))\right)$$
#
# You will see this expression in many other classification problems, especially in deep learning, where it's known as the _cross-entropy loss_.
#
# Your goal in this tutorial is to learn how to perform inference over the parameters $\boldsymbol\theta$ in logistic regression, including point estimates $\boldsymbol\theta_{\mathrm{ML}}$ and $\boldsymbol\theta_{\mathrm{MAP}}$ and approximations to the posterior $p(\boldsymbol\theta | \boldsymbol X, \boldsymbol y)$.
#
# Let's do it.
# ## Maximum likelihood estimate
# Let's start easy. First, let's generate a toy 1D binary dataset with two paramaters:
#
# * A **jitter** parameter that controls how noisy the data are; and
# * An **offset** parameter that controls the separation between the two classes.
# +
# Data generation parameters
N = 50
D = 2
jitter = 0.7
offset = 1.2
np.random.seed(43)
# Generate the data
x = np.vstack([rn.normal(0, jitter, (N//2,1)), rn.normal(offset, jitter, (N//2,1))])
y = np.vstack([np.zeros((N//2, 1)), np.ones((N//2, 1))])
x_test = np.linspace(-2, offset + 2).reshape(-1,1)
# Make the augmented data matrix by adding a column of ones
x = np.hstack([np.ones((N,1)), x])
x_test = np.hstack([np.ones((N,1)), x_test])
# -
# Now on to the regression. First, let's code up the logistic log-likelihood as a separate function. This will come in handy.
#
# **Task 1**
#
# * Write a function to calculate the log-likelihood of a dataset given a value of $\boldsymbol\theta$.
x.shape
# +
## EDIT THIS FUNCTION
def log_likelihood(X, y, theta):
# X: N x D matrix of training inputs
# y: N x 1 vector of training targets/observations
# theta: parameters (D x 1)
# returns: log likelihood, scalar
L = 0
# mu = 1/(1+ np.exp(-(np.dot(X, theta))))
mu = 1/(1+ np.exp(-(X @ theta)))
# print('mu :', mu)
# mu_n = 1+ np.exp(-(np.dot(X, theta)))
L = sum(y* (np.log(mu)) + (1-y)*np.log(1-mu))
# for n in range(N):
# mu_n = 1/(1+ np.exp(-(np.dot(X[i], theta[i]))))
# L += y[n]* np.log(mu_n) + (1-y[n])*np.log(1-mu_n) ## <-- EDIT THIS LINE
return L[0]
# -
theta = np.array(([2],[2]))
log_likelihood(x,y, theta)
# Now it's time to optimize it to fit the maximum likelihood parameter,
#
# $$\boldsymbol\theta_{\mathrm{ML}} = \mathrm{arg}_\theta \max p(\boldsymbol y | \boldsymbol X, \boldsymbol\theta)$$
#
# For linear regression, the likelihood function had a closed-form minimum, which made our lives easy. Alas, that is not the case for logistic regression. We will have to resort to _numerical optimization_.
#
# In the lectures you saw how to derive the gradient and all that jazz. For this tutorial you can do it that way, or any other way you want. The optimization is convex, so this should be easy peasy.
#
# **Task 2**
#
# * Write a function to optimize the log-likelihood function you've written above an obtain $\boldsymbol\theta_{\mathrm{ML}}$. Use any optimizer of your choice.
## EDIT THIS FUNCTION
def max_lik_estimate(X, y):
# X: N x D matrix of training inputs
# y: N x 1 vector of training targets/observations
# returns: maximum likelihood parameters (D x 1)
N, D = X.shape
# theta = np.zeros((D,1))
theta = np.random.randn(D,1)
lr = .1
eps = 1e-15
old_ll = 1
new_ll = 0
#setup cost iter
cost_iter = []
cost_iter.append([0, old_ll])
i = 1
while (np.abs(new_ll - old_ll) > eps):
old_ll = -log_likelihood(X, y, theta)
mu = 1/(1+ np.exp(-(np.dot(X, theta))))
gradient = np.dot(X.T, (mu-y))
theta -= lr * gradient
new_ll = -log_likelihood(X, y, theta)
cost_iter.append([i, old_ll])
i+=1
theta_ml = theta
# theta_ml = np.zeros((D,1)) ## <-- EDIT THIS LINE
return theta_ml
# **Task 3**
#
# * Write a predict function to evaluate your estimate.
## EDIT THIS FUNCTION
def predict(X, theta):
# Xtest: K x D matrix of test inputs
# theta: D x 1 vector of parameters
# returns: prediction of f(Xtest); K x 1 vector
threshold = .5
prob = 1/(1+ np.exp(-(np.dot(X, theta))))
predi = prob >= threshold ## <-- EDIT THIS LINE
prediction = np.zeros((X.shape[0],1))
for i in range(len(prediction)):
prediction[i][0] = 0 if (predi[i] == False) else 1
return prediction
# With this we're in a good position to fit a logistic regression to our toy dataset and start visualising the results. Have a go.
#
# 1. Use the function you wrote above to estimate $\boldsymbol\theta_{\mathrm{ML}}$ on the toy dataset.
# 2. Visualize the results, including:
# 1. The data $x$ and target labels $y$.
# 2. The labels predicted by the model.
# 3. The probability assigned by the model, $\sigma(x\theta)$ as a function of $x$.
plt.figure(figsize=(10,8))
plt.scatter(x[:,1], x[:,0], marker='o')
# plt.plot(x[:,1])
# +
# theta_ml, cost_iter = max_lik_estimate(x, y)
# # print('theta_ml : ', theta_ml)
# +
# plt.plot(cost_iter[:,0], cost_iter[:,1])
# plt.ylabel("Cost")
# plt.xlabel("Iteration")
# -
theta_ml = max_lik_estimate(x, y)
print('theta_ml : ', theta_ml)
prediction = predict(x, theta_ml)
log_likelihood(x, y, theta_ml)
# +
# optimize.minimize(lambda theta : -log_likelihood(x, y, theta), np.random.randn(D), method='BFGS')
# +
# theta_ml1 = optimize.minimize(lambda theta: -log_likelihood(x, y, theta) ,np.zeros(D), method ='BFGS')
# +
# theta_ml1
# -
#accuracy
print('{} points over {} have been well predict'.format(sum(prediction == y), len(x)))
print('the accuracy is', (prediction == y).mean())
print('the likelihood is', np.exp(log_likelihood(x,y,theta_ml)))
plt.figure(figsize=(10,8))
label = [0,1]
colors = []
for i in range(len(prediction)):
if prediction[i] == 0:
colors.append('red')
else:
colors.append('green')
plt.scatter(x[:,1], prediction, marker='o', c = colors)
plt.figure(figsize=(10,8))
label = [0,1]
colors = []
for i in range(len(prediction)):
if y[i] == 0:
colors.append('red')
else:
colors.append('green')
plt.scatter(x[:,1], y, marker='o', c = colors)
plt.figure(figsize=(10,8))
label = [0,1]
colors = []
for i in range(len(prediction)):
if y[i] == 0:
colors.append('red')
else:
colors.append('green')
theta = theta_ml[:,0] # Make theta a 1-d array.
t = -(theta[0])/theta[1]
plt.figure(figsize=(10,8))
#u = [i for i in range(len(x))]
#u = range(len(x))
plt.axvline(t)
#plt.plot(t,u)
plt.scatter(x[:,1], y, marker='o', c = colors)
# +
# theta = theta_ml[:,0] # Make theta a 1-d array.
# t = [-(theta[0])/theta[1] for i in range(len(x))]
# plt.figure(figsize=(10,8))
# u = [i for i in range(len(x))]
# plt.plot(t,u)
# plt.scatter(x[:,1], x[:,0], marker='o', c = colors)
# -
prob = 1/(1+ np.exp(-(np.dot(x, theta_ml))))
plt.figure(figsize=(10,8))
plt.plot(x[:,1],prob, '.')
# max(x[:,1]), min(x[:,1])
# max(prob), min(prob)
# +
# prediction = predict(x_test, theta_ml)
# plt.figure(figsize=(10,8))
# colors = []
# for i in range(len(prediction)):
# if prediction[i] == 0:
# colors.append('red')
# else:
# colors.append('green')
# t = [-(theta[1])/theta[0] for i in range(len(x))]
# plt.figure(figsize=(10,8))
# u = [i for i in range(len(x))]
# plt.plot(t,u)
# plt.scatter(x_test[:,1], prediction, marker='o', c = colors)
# -
## ADD CODE HERE
# Fit and plot the logistic regression
theta_ml = max_lik_estimate(x, y)
prediction = predict(x, theta_ml)
# There you go! That should be a nice and easy fit. There are a few things we can start playing with at this point:
#
# * Evaluate the performance of your model: plot the decision boundary, likelihood and accuracy on held-out test sets, etc.
# * Write a gradient-based and a non-gradient-based optimizer. Do they arrive at the same result? Which one takes longer? Which one evaluates the likelihood function more times?
#
# (Warning: if the plot looks odd and you get several warnings, it may be that the data is linearly separable and the sigmoid is saturating, leading to `np.log(0)` numerical problems. Add more noise and retry.)
# ## Bayesian logistic regression
# ### MAP estimate
# Now let's move to Bayesian inference on the parameters $\boldsymbol\theta$. Let's put a prior on them. Because that's what we do. We put priors on things.
#
# More specifically, let's use a Gaussian prior parametrized by a mean $\boldsymbol m$ and a variance $\boldsymbol S$:
#
# $$\boldsymbol\theta \sim \mathcal{N}(\boldsymbol m, \boldsymbol S)$$
#
# Given that $\boldsymbol\theta_{\mathrm{ML}}$ had no analytical solution, it should really come as no surprise that $\boldsymbol\theta_{\mathrm{MAP}}$ doesn't either. That should be no problem for a machine learning expert like you:
#
# **Task 4**
#
# 1. Write down the equation for the full unnormalized posterior $p(\boldsymbol\theta | \boldsymbol X, \boldsymbol y) \propto p(\boldsymbol y | \boldsymbol\theta, \boldsymbol X) p(\boldsymbol\theta)$.
# 2. Write a separate function for it, as we did with the log-likelihood above.
# 3. Optimize it to find $\boldsymbol\theta_{\mathrm{MAP}}$ and use it to make predictions.
## added by me
def unnormalized_log_posterior(X, y, m, S):
# X: N x D matrix of training inputs
# y: N x 1 vector of training targets/observations
# m: D x 1 prior mean of parameters
# S: D x D prior covariance of parameters
# returns: log likelihood, scalar
theta = np.random.randn(D,1)
L = log_likelihood(X, y, theta)
# print('L :',L)
# prior = np.random.multivariate_normal(m.squeeze(), S, (X.shape[1],1))
log_prior = (-0.5 * (theta- m).T @ (np.linalg.solve(S,(theta - m))))[0]
# print('log_prior : ', log_prior)
unnormalized_log_posterior = log_prior + L
# print('unnormalized_log_posterior : ', unnormalized_log_posterior)
return unnormalized_log_posterior[0]
# +
# def map_estimate(X, y, m, S):
# # X: N x D matrix of training inputs
# # y: N x 1 vector of training targets/observations
# # m: D x 1 prior mean of parameters
# # S: D x D prior covariance of parameters
# # returns: maximum a posteriori parameters (D x 1)
# N, D = X.shape
# theta = np.random.randn(D,1)
# log_prior = lambda theta: (-0.5 * (theta- m).T @ (np.linalg.solve(S,(theta - m))))[0][0]
# log_post = lambda theta : -log_likelihood(X, y, theta) - log_prior(theta)
# print('log ',log_post(np.zeros(D)))
# theta_map = optimize.minimize(log_post, np.zeros((D,1)), method='BFGS')
# return theta_map
# +
# m = np.zeros((D, 1))
# S = 5*np.eye(D)
# +
# ## EDIT THIS FUNCTION
# def map_estimate(X, y, m, S):
# # X: N x D matrix of training inputs
# # y: N x 1 vector of training targets/observations
# # m: D x 1 prior mean of parameters
# # S: D x D prior covariance of parameters
# # returns: maximum a posteriori parameters (D x 1)
# N, D = X.shape
# theta_map = np.random.randn(D) ## <-- EDIT THIS LINE
# def logprior(theta):
# A = (theta.reshape(-1,1) - m)
# logprior = (-0.5 * A.T@ np.linalg.solve(S,A)).ravel()[0]
# return logprior
# logpost = lambda theta : -log_likelihood(X,y, theta) - logprior(theta)
# print('log ',logpost(np.zeros(D)))
# theta_map = optimize.minimize(logpost, np.zeros(D), method ='BFGS')
# return theta_map.x.reshape(-1,1)
# +
# map_estimate(x, y, m, S)
# +
# f = lambda x: x**3+ 2*x +1
# optimize.minimize(f, 0, method ='BFGS')
# -
## EDIT THIS FUNCTION
def map_estimate(X, y, m, S):
# X: N x D matrix of training inputs
# y: N x 1 vector of training targets/observations
# m: D x 1 prior mean of parameters
# S: D x D prior covariance of parameters
# returns: maximum a posteriori parameters (D x 1)
N, D = X.shape
theta_map = np.zeros((D,1)) ## <-- EDIT THIS LINE
theta = np.random.randn(D,1)
lr = 1e-2
eps = 1e-6
old_ll = 1
new_ll = 0
niter = 0
epochs = 1000
mu = 1/(1+ np.exp(-(X @ theta)))
while (niter < epochs):
old_ll = -unnormalized_log_posterior(X, y, m, S)
mu = 1/(1+ np.exp(-(np.dot(X, theta))))
gradient = ((mu-y).T @ X + ( (theta - m).T @ np.linalg.inv(S) )).T #np.dot(X.T, (mu-y)) - ( (theta - m).T @ np.linalg.inv(S) )
theta -= lr * gradient
new_ll = -unnormalized_log_posterior(X, y, m, S)
niter += 1
theta_map =theta
return theta_map
# Now you can perform a similar model evaluation as you did before. How does your prior influence the MAP estimate and the model's performance?
# +
## ADD CODE HERE
# Fit and plot the MAP logistic regression estimate
m = np.zeros((D, 1))
S = 5*np.eye(D)
##### my code
unn_log_posterior = unnormalized_log_posterior(x, y, m, S);unn_log_posterior
# -
theta_map = map_estimate(x, y, m, S)
theta_map
# ### The Laplace approximation
# As we have hinted above, in logistic regression the posterior distribution over $\boldsymbol\theta$ doesn't have an analytical solution. This is the first example in the course of _approximate Bayesian inference_: The exact posterior is analytically intractable so that we have to approximate it using one of various techniques. The one we'll use in this part of the tutorial is called the **Laplace approximation**.
#
# In brief, **the Laplace approximation is a Gaussian centered at the peak of the pdf of interest with the same curvature**. Let's make this a bit more rigorous below.
#
# Let's say we have a probability distribution $p(\boldsymbol z)$ we want to approximate. The distribution $p(\boldsymbol z)$ is of the form
#
# $$p(\boldsymbol z) = \frac{1}{Z} \tilde{p}(\boldsymbol z) ~ ,$$
#
# where $\tilde{p}(\boldsymbol z)$ is an unnormalized distribution that we can evaluate easily, but $Z$ is unknown. Formally, the Laplace approximation results from a second-order Taylor expansion of $\log \tilde{p}(\boldsymbol z)$ around $\boldsymbol z_0$:
#
# $$\log \tilde{p}(\boldsymbol z) \approx \log \tilde{p}(\boldsymbol z_0) + \frac{d}{d\boldsymbol z}\log \tilde{p}(\boldsymbol z)\Big|_{\boldsymbol z=\boldsymbol z_0}(\boldsymbol z -\boldsymbol z_0) + \frac{1}{2}(\boldsymbol z-\boldsymbol z_0)^\top\frac{d^2}{d\boldsymbol z^2} \log \tilde{p}(\boldsymbol z)\Big|_{\boldsymbol z=\boldsymbol z_0}(\boldsymbol z-\boldsymbol z_0)$$
#
# Now let's evaluate this expression at the mode of $p(\boldsymbol z)$ – which is the same as the mode of $\tilde{p}(\boldsymbol z)$. We define the mode $\boldsymbol z^*$ such that
#
# $$\frac{d}{d\boldsymbol z} \tilde{p}(\boldsymbol z) \Big|_{\boldsymbol z = \boldsymbol z^*} = \boldsymbol 0 ~ .$$
#
# At this point, the $\mathcal{O}(\boldsymbol z)$ term of the expansion vanishes and we are left with
#
# $$\log \tilde{p}(\boldsymbol z) \approx \log \tilde{p}(\boldsymbol z^*) - \frac{1}{2}(\boldsymbol z-\boldsymbol z^*)^\top\boldsymbol A(\boldsymbol z-\boldsymbol z^*)$$
#
# Or, equivalently,
#
# $$\tilde{p}(\boldsymbol z) \approx \tilde{p}(\boldsymbol z^*) \exp\big(-\tfrac{1}{2}(\boldsymbol z - \boldsymbol z^*)^\top\boldsymbol A(\boldsymbol z - \boldsymbol z^*)\big) ~ ,$$
#
# where
#
# $$\boldsymbol A = - \frac{d^2}{d\boldsymbol z^2} \log \tilde{p}(\boldsymbol z)\Big|_{\boldsymbol z=\boldsymbol z^*} ~ .$$
#
# And now this distribution we know how to normalize, because it's one of those Gaussians we know and love. By inspection, we can identify the mean and the covariance, and write down the Laplace approximation of $p(\boldsymbol z)$ as
#
# $$q(\boldsymbol z) = \mathcal{N}(\boldsymbol z | \boldsymbol z^*, \boldsymbol A^{-1})$$
# As an example, let's use the unnormalized distribution $\tilde{p}(z) = x e^{-x/2}$. When normalized properly, this is in fact the $\chi^2$ distribution with $k=4$ degrees of freedom. Have a go yourself:
#
# 1. Plot $p(z)$.
# 2. Take the first derivative of $\tilde{p}(z)$ (or the first derivative of its log), and find its maximum $z^*$ analytically.
# 3. In the same plot, draw a vertical line at $z = z^*$ to verify you got the right answer.
# 4. Take the second derivative of $\log \tilde{p}(z)$ and evaluate it at $z^*$.
# 5. Plot the corresponding Gaussian $q(z)$ and verify the approximation looks reasonable.
#
# **Task 5**
#
# * Write a function that evaluates the Laplace approximation $q(z)$.
## EDIT THIS FUNCTION
def laplace_q(z):
# z: double array of size (T,)
# returns: array with Laplace approximation q evaluated
# at all points in z
q = 0*z
q = stats.multivariate_normal.pdf(z, 2, 4)
return q
## ADD CODE HERE
# Find the Laplace approximation of x*exp(-x/2) with pen and paper and then plot it.
z = np.linspace(0,10)
p = stats.chi2.pdf(z, 4)
plt.figure(figsize=(10,8))
plt.plot(z, p)
plt.axvline(x=2)
plt.plot(z, laplace_q(z))
# ### Bayesian logistic regression (for real this time)
# Now we have obtained the mode (peak) of the posterior through the MAP estimate above, it's time to go all the way and calculate the posterior over $\boldsymbol\theta$. However, as we mentioned above the posterior doesn't have an analytical form, so we'll use – you guessed it – the Laplace transform.
#
# **Task 6**
#
# * Write a function, based on your previous code, that will calculate the Laplace approximation $q(\boldsymbol\theta)$ of the true posterior $p(\boldsymbol\theta | \boldsymbol X, \boldsymbol y)$ and return the mean and variance of $q$.
#
# To visualize the behavior and the diversity of $q$, draw a number $j = 1, ..., J$ of samples $\boldsymbol\theta_j \sim q(\boldsymbol\theta)$. For each sample, plot its predicted class probabilities $\sigma(x \boldsymbol\theta_j)$.
#
# _Hint_: the extension of the Laplace approximation to multivariate distributions is straightforward, and in this case the variance of the Gaussian is the Hessian of the negative log likelihood $\boldsymbol A = - \nabla_\theta \nabla_\theta \log p(\boldsymbol\theta | \boldsymbol X, \boldsymbol y)$.
# +
# def hessian(X):
# h = 1e-6
# mu = 1/(1+ np.exp(-(np.dot(X, theta))))
# mu_h = 1/(1+ np.exp(-(np.dot(X, theta+h))))
# v_h= ((mu_h-y).T @ X + ( (theta+h - m).T @ np.linalg.inv(S) )).T
# v = ((mu-y).T @ X + ( (theta+h - m).T @ np.linalg.inv(S) )).T
# return X.T @ X
# -
hessian(x)
## EDIT THIS FUNCTION
def get_posterior(X, y, m, S):
# X: N x D matrix of training inputs
# y: N x 1 vector of training targets/observations
# m: D x 1 prior mean of parameters
# S: D x D prior covariance of parameters
# returns: maximum a posteriori parameters (D x 1)
# covariance of Laplace approximation (D x D)
N, D = X.shape
mu_post = np.zeros((D, 1)) ## <-- EDIT THESE LINES
S_post = np.eye(D)
mu_post = map_estimate(X, y, m, S)
mu = 1/(1+ np.exp(-(X @ mu_post)))
hss = np.diag((mu * (1 - mu)).reshape(-1,))
S_post = np.linalg.inv(X.T @ hss @ X + np.linalg.inv(S))
return mu_post, S_post
theta_map, S_post = get_posterior(x, y, m, S)
print('theta_map : ', theta_map)
print('S_post : ', S_post)
np.diag(np.array([1,2,3]).reshape(-1,))
theta_map, S_post = get_posterior(x, y, m, S)
print('theta_map : ', theta_map)
print('S_post : ', S_post)
# +
## ADD CODE HERE
# Calculate the Laplace approximation of the posterior for theta,
# draw a few samples and plot the corresponding likelihood functions
# for each one.
m = np.zeros((D, 1))
S = 5*np.eye(D)
nb_samples = 5
theta_map, S_post = get_posterior(x, y, m, S)
plt.scatter(x[:,1], y)
for i in range(nb_samples):
data = np.random.multivariate_normal(theta_map,S_post)
plt.plot(0, 0) ## <--EDIT THIS LINE
plt.show()
# -
# ## Comparing posterior approximations
# The Laplace approximation is part of a family of methods known as _deterministic approximate inference_. In addition, there's another set of methods known as _stochastic approximate inference_ which, as you can guess includes most of the sampling techniques you have studied.
#
# You must be an expert in sampling by now. Let's actually go and check whether this Laplace approximation we just made is legit.
#
# * What sampling methods do you know to sample from an unnormalized distribution?
#
# For example, let's try the Metropolis algorithm.
#
# 1. Write a proposal function to move in $\boldsymbol\theta$-space.
# 2. Write a function to accept or reject new proposals based on the Metropolis criterion.
# 3. Write a loop and run the Markov chain for a few thousand iterations.
# 4. Check that the sampling worked: did the Markov chain mix properly? What's the acceptance rate? How does it depend on the proposal function?
#
# **Task 7**
#
# * Write a function to sample from the true posterior $p(\boldsymbol\theta | \boldsymbol X, \boldsymbol y)$.
# +
## EDIT THIS FUNCTION
def posterior_sample(X, y, m, S, nb_iter):
# X: N x D matrix of training inputs
# y: N x 1 vector of training targets/observations
# m: D x 1 prior mean of parameters
# S: D x D prior covariance of parameters
# returns: nb_iter x D matrix of posterior samples
D = X.shape[1]
samples = np.zeros((nb_iter, D))
N = X.shape[0]
sigma = np.eye(D,D)
xt = np.random.randn(D)
# print('xt : ',xt)
m = m.ravel()
for i in range(nb_iter):
xprime = np.random.multivariate_normal(xt.ravel(), sigma)
a = stats.multivariate_normal.pdf(xt, xprime, sigma)
b = stats.multivariate_normal.pdf(xprime, m, S)
c, c1 = 0, 0
mu = 1/(1+ np.exp(-X @ xprime))
mu1 = 1/(1+ np.exp(-X @ xt))
for j in range(N):
c += np.log(stats.bernoulli.pmf(y[j], mu[j]))
c1 += np.log(stats.bernoulli.pmf(y[j], mu1[j]))
q = a * b * np.exp(c)
a1 = stats.multivariate_normal.pdf(xprime, xt, sigma)
b1 = stats.multivariate_normal.pdf(xt, m, S)
q1 = a1 * b1 * np.exp(c1)
u = np.random.uniform(0,1)
if (q /q1 >= u) :
# print('True')
samples[i,:] = xprime
xt = xprime
else:
# print('False')
samples[i,:] = xt
return samples
# -
# Finally, let's plot the results and see if both inference methods arrive at roughly the same posterior.
#
# In the same axis, plot
#
# * The histogram pdf of the MCMC samples (you may want to look at the `density` option in `plt.hist`); and
# * The Laplace posterior.
#
# Make one plot for the intercept ($\theta_0$) and one for the slope ($\theta_1$). What do they look like? Do they match? What kinds of posteriors do you think the Laplace approximation will be good or bad at approximating?
# +
## ADD CODE HERE
# Plot a histogram of the MCMC posterior samples and the
# analytical expression for the Laplace posterior. If
# everything went well, the peaks should coincide and
# their widths should be comparable.
nb_iter = 10000
samples = posterior_sample(x, y, m, S, nb_iter)
plt.figure(figsize=(10,8))
plt.hist(samples[:,0], 20 , normed=True);
plt.hist(samples[:,1], 20 , normed=True);
# -
# Et violà! Now you're an expert in logistic regression. (Wait, I think that's a big violin. I meant to say: et voilà!)
#
# Now we can visualize the posterior we can play around with the data and the inference parameters:
#
# * Play around with the data generation process. What happens as you increase/decrease $N$ and the jitter parameter?
# * What does the joint posterior look like? Make a visualization of the MCMC and Laplace approximations in the $(\theta_0, \theta_1)$ plane.
# * What happens if the model is misspecified? Take out the intercept term in the model (i.e., remove the column of ones in $\boldsymbol X$), but set the `offset` in the data generation process to non-zero. What happens to the posterior and its Laplace approximation?
#
# +
plt.figure(figsize=(10,8))
plt.hist(samples[:,0], 20 , normed=True);
plt.hist(samples[:,1], 20 , normed=True);
z = np.linspace(-6,6, 100)
pz = stats.multivariate_normal.pdf(z,theta_map[0], S_post[0,0])
plt.plot(z,pz)
pz = stats.multivariate_normal.pdf(z,theta_map[1], S_post[1,1])
plt.plot(z,pz);
# -
|
Machine-Learning-Codes/seventh assignment-logistic_regression/logistic_regression_assignment.template-Copy1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # NMT-Keras tutorial
# In this module, we are going to create an encoder-decoder model with:
# * A bidirectional GRU encoder and a GRU decoder
# * An attention model
# * The previously generated word feeds back de decoder
# * MLPs for initializing the initial RNN state
# * Skip connections from inputs to outputs
# * Beam search.
# As usual, first we import the necessary stuff.
from keras.layers import *
from keras.models import model_from_json, Model
from keras.optimizers import Adam, RMSprop, Nadam, Adadelta, SGD, Adagrad, Adamax
from keras.regularizers import l2
from keras_wrapper.cnn_model import Model_Wrapper
from keras_wrapper.extra.regularize import Regularize
# And define the dimesnions of our model. For instance, a word embedding size of 50 and 100 units in RNNs. The inputs/outpus are defined as in previous tutorials.
ids_inputs = ['source_text', 'state_below']
ids_outputs = ['target_text']
word_embedding_size = 50
hidden_state_size = 100
input_vocabulary_size=686 # Autoset in the library
output_vocabulary_size=513 # Autoset in the library
# Now, let's define our encoder. First, we have to create an Input layer to connect the input text to our model. Next, we'll apply a word embedding to the sequence of input indices. This word embedding will feed a Bidirectional GRU network, which will produce our sequence of annotations:
# 1. Source text input
src_text = Input(name=ids_inputs[0],
batch_shape=tuple([None, None]), # Since the input sequences have variable-length, we do not retrict the Input shape
dtype='int32')
# 2. Encoder
# 2.1. Source word embedding
src_embedding = Embedding(input_vocabulary_size, word_embedding_size,
name='source_word_embedding', mask_zero=True # Zeroes as mask
)(src_text)
# 2.2. BRNN encoder (GRU/LSTM)
annotations = Bidirectional(GRU(hidden_state_size,
return_sequences=True # Return the full sequence
),
name='bidirectional_encoder',
merge_mode='concat')(src_embedding)
# Once we have built the encoder, let's build our decoder. First, we have an additional input: The previously generated word (the so-called state_below). We introduce it by means of an Input layer and a (target language) word embedding:
# 3. Decoder
# 3.1.1. Previously generated words as inputs for training -> Teacher forcing
next_words = Input(name=ids_inputs[1], batch_shape=tuple([None, None]), dtype='int32')
# 3.1.2. Target word embedding
state_below = Embedding(output_vocabulary_size, word_embedding_size,
name='target_word_embedding',
mask_zero=True)(next_words)
# The initial hidden state of the decoder's GRU is initialized by means of a MLP (in this case, single-layered) from the average of the annotations:
# +
ctx_mean = MaskedMean()(annotations)
annotations = MaskLayer()(annotations) # We may want the padded annotations
initial_state = Dense(hidden_state_size, name='initial_state',
activation='tanh')(ctx_mean)
# -
# So, we have the input of our decoder:
input_attentional_decoder = [state_below, annotations, initial_state]
# Note that, for a sample, the sequence of annotations and initial state is the same, independently of the decoding time-step. In order to avoid computation time, we build two models, one for training and the other one for sampling. They will share weights, but the sampling model will be made up of two different models. One (model_init) will compute the sequence of annotations and initial_state. The other model (model_next) will compute a single recurrent step, given the sequence of annotations, the previous hidden state and the generated words up to this moment.
#
# Therefore, now we slightly change the form of declaring layers. We must share layers between the decoding models.
#
# So, let's start by building the attentional-conditional GRU:
# Define the AttGRUCond function
sharedAttGRUCond = AttGRUCond(hidden_state_size,
return_sequences=True,
return_extra_variables=True, # Return attended input and attenton weights
return_states=True # Returns the sequence of hidden states (see discussion above)
)
[proj_h, x_att, alphas, h_state] = sharedAttGRUCond(input_attentional_decoder) # Apply shared_AttnGRUCond to our input
# Now, we set skip connections between input and output layer. Note that, since we have a temporal dimension because of the RNN decoder, we must apply the layers in a TimeDistributed way. Finally, we will merge all skip-connections and apply a 'tanh' no-linearlity:
# +
# Define layer function
shared_FC_mlp = TimeDistributed(Dense(word_embedding_size, activation='linear',),
name='logit_lstm')
# Apply layer function
out_layer_mlp = shared_FC_mlp(proj_h)
# Define layer function
shared_FC_ctx = TimeDistributed(Dense(word_embedding_size, activation='linear'),
name='logit_ctx')
# Apply layer function
out_layer_ctx = shared_FC_ctx(x_att)
shared_Lambda_Permute = PermuteGeneral((1, 0, 2))
out_layer_ctx = shared_Lambda_Permute(out_layer_ctx)
# Define layer function
shared_FC_emb = TimeDistributed(Dense(word_embedding_size, activation='linear'),
name='logit_emb')
# Apply layer function
out_layer_emb = shared_FC_emb(state_below)
shared_additional_output_merge = Add(name='additional_input')
additional_output = shared_additional_output_merge([out_layer_mlp, out_layer_ctx, out_layer_emb])
shared_activation_tanh = Activation('tanh')
out_layer = shared_activation_tanh(additional_output)
# -
# Now, we'll' apply a deep output layer, with linear activation:
shared_deep_out = TimeDistributed(Dense(word_embedding_size, activation='linear', name='maxout_layer'))
out_layer = shared_deep_out(out_layer)
# Finally, we apply a softmax function for obtaining a probability distribution over the target vocabulary words at each timestep.
shared_FC_soft = TimeDistributed(Dense(output_vocabulary_size,
activation='softmax',
name='softmax_layer'),
name=ids_outputs[0])
softout = shared_FC_soft(out_layer)
model = Model(inputs=[src_text, next_words], outputs=softout)
# That's all! We built a NMT Model!
# Now, let's build the models required for sampling. Recall that we are building two models, one for encoding the inputs and the other one for advancing steps in the decoding stage.
# Let's start with model_init. It will take the usual inputs (src_text and state_below) and will output:
# 1) The vector probabilities (for timestep 1)
# 2) The sequence of annotations (from encoder)
# 3) The current decoder's hidden state
#
# The only restriction here is that the first output must be the output layer (probabilities) of the model.
# +
model_init = Model(inputs=[src_text, next_words], outputs=[softout, annotations, h_state])
# Store inputs and outputs names for model_init
ids_inputs_init = ids_inputs
# first output must be the output probs.
ids_outputs_init = ids_outputs + ['preprocessed_input', 'next_state']
# -
# Next, we will be the model_next. It will have the following inputs:
# * Preprocessed input
# * Previously generated word
# * Previous hidden state
#
# And the following outputs:
# * Model probabilities
# * Current hidden state
#
#
# First, we define the inputs:
preprocessed_size = hidden_state_size*2
preprocessed_annotations = Input(name='preprocessed_input', shape=tuple([None, preprocessed_size]))
prev_h_state = Input(name='prev_state', shape=tuple([hidden_state_size]))
input_attentional_decoder = [state_below, preprocessed_annotations, prev_h_state]
# And now, we build the model, using the functions stored in the 'shared*' variables declared before:
# Apply decoder
[proj_h, x_att, alphas, h_state] = sharedAttGRUCond(input_attentional_decoder)
out_layer_mlp = shared_FC_mlp(proj_h)
out_layer_ctx = shared_FC_ctx(x_att)
out_layer_ctx = shared_Lambda_Permute(out_layer_ctx)
out_layer_emb = shared_FC_emb(state_below)
additional_output = shared_additional_output_merge([out_layer_mlp, out_layer_ctx, out_layer_emb])
out_layer = shared_activation_tanh(additional_output)
out_layer = shared_deep_out(out_layer)
softout = shared_FC_soft(out_layer)
model_next = Model(inputs=[next_words, preprocessed_annotations, prev_h_state],
outputs=[softout, preprocessed_annotations, h_state])
# Finally, we store inputs/outputs for model_next. In addition, we create a couple of dictionaries, matching inputs/outputs from the different models (model_init->model_next, model_nex->model_next):
#
#
# +
# Store inputs and outputs names for model_next
# first input must be previous word
ids_inputs_next = [ids_inputs[1]] + ['preprocessed_input', 'prev_state']
# first output must be the output probs.
ids_outputs_next = ids_outputs + ['preprocessed_input', 'next_state']
# Input -> Output matchings from model_init to model_next and from model_next to model_nextxt
matchings_init_to_next = {'preprocessed_input': 'preprocessed_input', 'next_state': 'prev_state'}
matchings_next_to_next = {'preprocessed_input': 'preprocessed_input', 'next_state': 'prev_state'}
# -
# And that's all! For using this model together with the facilities provided by the staged_model_wrapper library, we should declare the model as a method of a Model_Wrapper class. A complete example of this can be found at `model_zoo.py`.
|
examples/4_nmt_model_tutorial.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/Zeuqram07/Linear-Algebra-58020/blob/main/Midterm_Exam.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="KEF_D8uSFlZX"
# ## Midterm Exam
# + [markdown] id="jI-yuGRgAUV_"
# Answer for question 1
# + colab={"base_uri": "https://localhost:8080/"} id="19uN1EX997vb" outputId="95544980-cf17-4c0e-c5bc-06dc613b8c8e"
import numpy as np
A = np.array([[2,4,6,8,10],[1,3,5,7,9],[1,2,3,4,5],[10,9,8,7,6],[5,10,15,20,25]]) #5x5 matrix
print(A)
# + [markdown] id="_o-IYaIlBAMU"
# Answer for question 2
# + colab={"base_uri": "https://localhost:8080/"} id="O-0wC044Bc4m" outputId="1f285c5b-301b-44c3-a68b-f04f4c52c61b"
import numpy as np
A = np.array([[1,1,1,1],[0,1,1,1],[0,0,1,1],[0,0,0,1]]) #4x4 matrix
print(A)
# + [markdown] id="2PF5kO8fBo5V"
# Answer for question 3
# + colab={"base_uri": "https://localhost:8080/"} id="EFvmdOo5BqzJ" outputId="d1fa2d71-bb78-4ffc-dd8e-d910b4979089"
import numpy as np
A =np.array([[6,1,6],[1,5,2],[6,2,7]])
print(A)
print("/n")
#prints transpose matrix
print(np.transpose(A))
# + [markdown] id="2FOH54esBrOS"
# Answer for question 4
# + colab={"base_uri": "https://localhost:8080/"} id="bLSh7nHmBteN" outputId="7be522c3-eaf0-4a4c-e37d-1f5ffcbc0e02"
import numpy as np
A=np.array(([[1,2,3],[2,3,3],[3,4,-2]]))
B=(np.linalg.inv(A))
print(B)
# + [markdown] id="juSVBwwUB76m"
# Answer for question 5
# + colab={"base_uri": "https://localhost:8080/"} id="PKnK3hZ0B--_" outputId="9bcc90fa-9149-4a21-9e37-21f3a68edbcc"
import numpy as np
A = np.array([[1,2,3],[2,3,3],[3,4,-2]])
print(A)
print(np.linalg.det(A))
print(round(np.linalg.det(A))) #inverse of the matrix
# + [markdown] id="3FZEZtHBDqpO"
# Answer for question 6
# + colab={"base_uri": "https://localhost:8080/"} id="mK1iaYtvDsxP" outputId="c538e08d-fe76-421f-c391-1d7be475df79"
import numpy as np
c = np.array([[5,4,1],[10,9,4],[10,13,15]])
inv_c = np.linalg.inv(c)
print(c)
print()
print(inv_c)
d = np.array([[3.4],[8.8],[19.2]])
x = np.dot(inv_c,d)
print("roots =")
print(x) #prints the roots of the linear equations
z = np.dot(c,x) #checking
print("checking =")
print(z)
|
Midterm_Exam.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Boolean Datatypes
x =1
x == 0
type(False)
bool(x>=1)
bool(0)
# # Operators
# <html>
# <b> Comparison Operators </b>
# </html>
# <div class="table-contents"><table summary="Comparison Operators" style="border-collapse: collapse;border-top: 0.5pt solid ; border-bottom: 0.5pt solid ; border-left: 0.5pt solid ; border-right: 0.5pt solid ; "><colgroup><col><col></colgroup><thead><tr><th style="border-right: 0.5pt solid ; border-bottom: 0.5pt solid ; " valign="top"><p>Operator</p></th><th style="border-bottom: 0.5pt solid ; " valign="top"><p>Meaning</p></th></tr></thead><tbody><tr><td style="border-right: 0.5pt solid ; border-bottom: 0.5pt solid ; " valign="top"><p><code class="literal">==</code></p></td><td style="border-bottom: 0.5pt solid ; " valign="top"><p>Equal to</p></td></tr><tr><td style="border-right: 0.5pt solid ; border-bottom: 0.5pt solid ; " valign="top"><p><code class="literal">!=</code></p></td><td style="border-bottom: 0.5pt solid ; " valign="top"><p>Not equal to</p></td></tr><tr><td style="border-right: 0.5pt solid ; border-bottom: 0.5pt solid ; " valign="top"><p><code class="literal"><</code></p></td><td style="border-bottom: 0.5pt solid ; " valign="top"><p>Less than</p></td></tr><tr><td style="border-right: 0.5pt solid ; border-bottom: 0.5pt solid ; " valign="top"><p><code class="literal">></code></p></td><td style="border-bottom: 0.5pt solid ; " valign="top"><p>Greater than</p></td></tr><tr><td style="border-right: 0.5pt solid ; border-bottom: 0.5pt solid ; " valign="top"><p><code class="literal"><=</code></p></td><td style="border-bottom: 0.5pt solid ; " valign="top"><p>Less than or equal to</p></td></tr><tr><td style="border-right: 0.5pt solid ; " valign="top"><p><code class="literal">>=</code></p></td><td style="" valign="top"><p>Greater than or equal to</p></td></tr></tbody></table></div></div>
# + tags=[]
print(bool.__doc__)
# -
type(True)
# ## Integer Comparison
x = 5
y = 6
x_dec = x <= y
x = y
x is y
y = 1247492
x = 1247492
id(x),id(y)
x == y
x is y
id(x) == id(y)
# ## Strings
x_str = 'hello'
y_str = 'helloooo'
x_str > y_str
x_str is y_str
'l' in x_str
# ## Lists
lst_x = [25,2,3,10,5]
lst_y = [12.3,3.4,5.7,7.3]
lst_x[3] < lst_y[0]
2 == 2
2 is lst_x[1]
lst_str = ['hello','python','pandas','numpy']
'pandas' in lst_str
lst_z = lst_x
lst_z is lst_x
# ## Tuples
tup_a = (1,2,3,4,5)
tup_b = tup_a
tup_b is tup_a
5 in tup_b
# ## Sets
set_a = {1,2,3,4,5}
set_b = set_a.copy()
set_a is set_b
1 in set_a
# ## Dictionary
dict_num = {1:'one',2:'two',3:'three',4:'four'}
dict_num.values()
# ## And ,Or operator
x,y =6,5
type(x >0 and y==0)
# + tags=[]
if x >0 and y>0:
print(x,y)
|
Day_5/.ipynb_checkpoints/Boolean_Datatypes-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Cross Entropy
# ====
#
# There's an excellent explanation of Cross-Entropy and related functions on https://machinelearningmastery.com/cross-entropy-for-machine-learning/ (Brownlee, 2019)
#
# Brownlee has some good explanation with code on cross-entropy from scratch, lets first look at how it's implemented in PyTorch and how to use it.
# # Cross-Entropy Loss (with torch)
# +
import torch
from torch import nn
from torch import optim
# +
criterion = nn.CrossEntropyLoss()
# Assuming, batch first, we have
# 5 data points, with 2 real number output each.
# Each output representing perceptron's prediction for one label.
last_layer = torch.randn(5, 2)
predictions = torch.sigmoid(last_layer)
# Correspondingly, we have 5 data points with 1 label each.
# Each label has its corresponding integer to represent.
truth = torch.LongTensor(5, 1).random_(0,2).squeeze(1)
# -
last_layer
# For each data point, we output the
# sigmoidal output per label.
predictions
# Each data point has a label and our label space
# is made up of labels 0s and 1s.
truth
loss = criterion(predictions, truth)
loss
# # Binary Cross-Entropy Loss (with torch)
# +
criterion = nn.BCELoss()
# Assuming, batch first, we have
# 5 data points, with 3 real number output each.
last_layer = torch.randn(5, 3)
predictions = torch.sigmoid(last_layer)
# Correspondingly, we have 5 data points,
# with 3 boolean labels each.
truth = torch.LongTensor(5, 3).random_(0,2).float()
# -
last_layer # Before activation function.
predictions # After activation function.
# This is kind of special such that for each
# data point we have 3 labels. And within
# torch.autograd, it's design to compute any arbitrary label spaces.
# Here, we're "cheating" the outputs by saying the space is 0s or 1s.
truth
loss = criterion(predictions, truth)
loss
# # What happens when the space isn't just 0s or 1s?
# +
criterion = nn.BCELoss()
# Assuming, batch first, we have
# 5 data points, with 3 real number output each.
last_layer = torch.randn(5, 3)
predictions = torch.sigmoid(last_layer)
# Correspondingly, we have 5 data points,
# with 3 boolean labels each.
truth = torch.LongTensor(5, 3).random_(0,5).float()
# -
predictions
# This is kind of special such that for each
# data point we have 3 labels. And within
# torch.autograd, it's design to compute any arbitrary label spaces.
# Here, we're "cheating" the outputs by saying the space is 0s or 1s.
truth
loss = criterion(predictions, truth)
loss
# # But how does that single scalar do backpropagation?
#
# We don't do backpropagation on that sum loss =)
#
# When we log the sum loss over all the data points, we get a scalar but because we have the loss for all labels in the label space, we actually get a vector back for every data point.
predictions
truth
torch.nn.functional.one_hot(truth)
# If we iterate through each data point.
for row_pred, row_truth in zip(predictions, torch.nn.functional.one_hot(truth)):
row_entropy = [-1 * float(t * math.log2(p)) for p, t in zip(row_pred, row_truth)]
print(row_pred, '\t', row_truth)
print(row_entropy)
print()
# +
X = xor_input = np.array([[0,0], [0,1], [1,0], [1,1]])
Y = xor_output = np.array([0,1,1,0]).T
X_pt = torch.tensor(X).float()
Y_pt = torch.tensor(Y, requires_grad=False).squeeze(0)
# -
X_pt
Y_pt
# +
hidden_dim = 5
num_data, input_dim = 4, 2
num_data, output_dim = 4, 2
model = nn.Sequential(nn.Linear(input_dim, hidden_dim),
nn.Sigmoid(),
nn.Linear(hidden_dim, output_dim),
nn.Sigmoid())
optimizer = optim.SGD(model.parameters(), lr=0.03)
# -
predictions = model(X_pt)
predictions
truth = Y_pt
truth
criterion = nn.CrossEntropyLoss()
loss = criterion(predictions, truth)
loss
list(model.parameters())
list(model.parameters())[0]
list(model.parameters())[0].grad == None
loss.backward()
loss.grad
list(model.parameters())[0].grad
|
Cross-Entropy.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import os
PATH='C:/Users/gptjd/OneDrive/Desktop/tflite_data/test'
file=os.listdir(PATH)
f=open('C:/Users/gptjd/OneDrive/Desktop/tflite_data/test.txt','w')
for i in file:
f.write('/content/drive/MyDrive/darknet/build/darknet/x64/data/obj/'+i+'\n')
f.close()
# -
|
make_train_file_list.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## 5.3.2 Gamma distribution and Laguerre Chaos
#
# $$ f(k) = \frac{e^{-k} k^{\alpha}}{\Gamma(\alpha+1)} = gamma(\alpha+1, 1)$$
#
# [Wiki - Gamma Distribution](https://en.wikipedia.org/wiki/Gamma_distribution)
#
# When $\alpha=0$, then $f(k) = e^{-k}$; when $\alpha=1$, then $f(k)=e^{-k}k$
# $$ \zeta \sim gamma(\alpha+1, 1)$$
#
# [Gamma in Python](https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.gamma.html)
#
# $$ gamma.pdf(x, a) = \frac{\lambda^a x^{a-1} e^{-\lambda x} }{ \Gamma(a)}$$
#
# where scale = 1.0 / lambda.
#
# [Wiki - Laguerre Distribution](https://en.wikipedia.org/wiki/Laguerre_polynomials) Weight function is exp(1) pdf.
#
# [Laguerre in Python](https://docs.scipy.org/doc/numpy-1.15.0/reference/routines.polynomials.laguerre.html)
#
# **In Wiki and python package, they all treat Laguerre distribution with weight function to be exp(1) pdf. But here, the weight function is $g(\zeta)$**
#
# **Laguerre Polynomial: ($\alpha = 0$)** (Python also uses this system, no sign switch)
# $$
# \begin{align*}
# L_0 &= 1\\
# L_1 &= -x + 1\\
# L_2 &= \frac{1}{2}(x^2 - 4x + 2)\\
# L_3 &= \frac{1}{6}(-x^3 + 9x^2 - 18x + 6)\\
# L_4 &= \frac{1}{24}(x^4 - 16x^3 + 72x^2 - 96x + 24)\\
# &\cdots
# \end{align*}
# $$
# Corresponding Hypergeometric orthogonal polynomial
# $$ L_n^{\alpha}(x) = \frac{(\alpha+1)_n}{n!}\ _1F_1(-n;\alpha+1;x)$$
# +
import numpy as np
import numpy.polynomial.laguerre as La
from matplotlib import pyplot as plt
from scipy.integrate import odeint
from scipy.special import gamma #gamma function
from scipy.stats import gamma as Gamma #gamma distribution
from math import factorial
# %matplotlib notebook
# -
# `scipy.special.eval_genlaguerre`
def Lague_gen(params):
'''
The first 4 (degree from 0 to 4) Generalized Laguerre polynomial
Follow definition on P642
'''
n = params[0] #degree
a = params[1] #parameter alpha value
if n==0:
return lambda u: 1
elif n==1:
return lambda u: a+1-u
elif n==2:
return lambda u: (a+1)*(a+2)/2 - (a+2)*u + u**2/2
elif n==3:
return lambda u: (a+1)*(a+2)*(a+3)/6 - (a+2)*(a+3)*u/2 + (a+3)*u**2/2 - u**3/6
else: #this actually means n=4
return lambda u: (a+1)*(a+2)*(a+3)*(a+4)/24 - (a+2)*(a+3)*(a+4)*u/6 + (a+3)*(a+4)*u**2/4 - (a+4)*u**3/6 + u**4/24
# +
def Phi(n):
#define H_n
coeffs = [0]*(n+1)
coeffs[n] = 1
return coeffs
def inner2_la(params):
n = params[0]
a = params[1] #store the value of alpha
return gamma(n+a+1)/(factorial(n))
def product3_la(alpha,i,j,l):
#compute \Phi_i*\Phi_j*\Phi_l
if alpha==0:
return lambda x: La.lagval(x, La.lagmul(La.lagmul(Phi(i),Phi(j)),Phi(l)))
else:
return lambda x: Lague_gen((i,alpha))(x)*Lague_gen((j,alpha))(x)*Lague_gen((l,alpha))(x)
def inner3_la(alpha,P,i,j,l):
#compute <\Phi_i\Phi_j\Phi_l>
'''
a indicates alpha in gamma distribution
P indicates the number of expansion
'''
if alpha==0:
#a=0, this is Laguerre poly, we can directly use gauss-laguerre quadrature
#Set up Gauss-Laguerre quadrature, weighting function is exp^{-x}
m=(P+1)**2
x, w=La.laggauss(m)
inner=sum([product3_la(alpha,i,j,l)(x[idx]) * w[idx] for idx in range(m)])
else:
#crude Monte Carlo
nsample = 10000
#rv = np.zeros(nsample)
rv = Gamma.rvs(alpha+1, loc=0, scale=1, size=nsample)
inner = np.mean(product3_la(alpha,i,j,l)(rv))*gamma(alpha+1)
return inner
# -
def ode_system_la(y, t, P, alpha):
#P indicates the highest degree
dydt = np.zeros(P+1)
for l in range(len(dydt)):
dydt[l] = -(sum(sum(inner3_la(alpha,P,i,j,l)*ki_la[i]*y[j] for j in range(P+1)) for i in range(P+1)))/inner2_la((l,alpha))
return dydt
# <font color = red>This is $\alpha=0$
# $\downarrow$
P = 4
alpha = 0
ki_la = [alpha+1, -1]+[0]*(P-1)
sol_la = odeint(ode_system_la, [1.0]+[0.0]*P, np.linspace(0,1,101), args=(P, alpha))
def y_determ_la(x):
return np.e**(-x)
# +
plt.figure()
plt.ylim([0,1])
plt.xlim([0,1])
x= np.linspace(0,1,101)
for i in range(P+1):
plt.plot(x,sol_la[:,i],label=i)
plt.plot(x, y_determ_la(x), color='r', linestyle='-.',label='Deterministic')
plt.legend(prop={'size': 8})
# -
# ### Error plot
# $$
# \bar{y}_{exact}(t) = \frac{\hat{y_0}}{(1+t)^{\alpha+1}} \ \ \ \ \ \ \ \ \bar{y}(t) = y_0
# $$
# So
# $$
# \epsilon_{mean}(t) = \left| \frac{\bar{y}(t) - \bar{y}_{exact}(t)}{\bar{y}_{exact}(t)}\right|
# $$
#
# $$
# \sigma_{exact}(t) = \frac{\hat{y_0}^2}{(2t+1)^{\alpha+1}} - \frac{\hat{y_0}^2}{(t+1)^{2\alpha+2}} \ \ \ \ \ \ \ \ \sigma(t) = a_1y_1^2 +a_2y_2^2+a_3y_3^2+a_4y_4^2
# $$
# The coefficients $(a_1, a_2, a_3, a_4)$ in $\sigma(t)$ can be obtained by code below.
#
# So
# $$
# \epsilon_{variance}(t) = \left| \frac{\sigma(t) - \sigma_{exact}(t)}{\sigma_{exact}(t)} \right|= \ldots
# $$
# `expect(func, args=(a,), loc=0, scale=1, lb=None, ub=None, conditional=False, **kwds)`
# <font color = red>This is $\alpha=0$
# $\downarrow$
# +
alpha = 0
allcoeff_532_0 = np.zeros((5,4))
#532 indicates example 5.3.2, 0 indicates \alpha=0
#store ki value/ column 0 stores ki when P=1; column 1 stores ki when P=2
allcoeff_532_0[0,:]=np.ones(4) + alpha
allcoeff_532_0[1,:]=-1*np.ones(4)
y_532_0 = np.zeros((5,4)) #row 0 stores y0 for each P from 1-4; row 1 stores y1 for P from 1-4;...
alpha = 0
for i in range(4):
P=i+1
ki_la = allcoeff_532_0[:,i]
y_mid=odeint(ode_system_la, [1.0]+[0.0]*P, np.linspace(0,1,2), args=(P, alpha))[1,:]
y_532_0[:,i] = y_mid.tolist()+[0]*(4-P)
# -
print(y_532_0)
for i in range(9):
#to compute $\bar{y}(t)$
print(Gamma.expect(Lague_gen((i,0)), args=(1,), loc=0, lb=None, ub=None, conditional=False))
# +
def g(params):
n = params
return lambda u: (Lague_gen((n,0))(u))**2
for i in range(1,5):
print(Gamma.expect(g(i), args=(1,), loc=0, scale=1, lb=None, ub=None, conditional=False))
# +
############# alpha = 0 ################
error_mean_532_0=np.abs(2*y_532_0[0,:]-1)
sigma2_532_0=np.zeros(4)
for i in range(4):
sigma2_532_0[i]=y_532_0[1,i]**2+y_532_0[2,i]**2+y_532_0[3,i]**2+y_532_0[4,i]**2
sigma2_exact_532_0 = 1/12
error_var_532_0=np.abs((sigma2_532_0-sigma2_exact_532_0)/sigma2_exact_532_0)
# -
# <font color = red>This is $\alpha=1$
# $\downarrow$
# +
alpha = 1
allcoeff_532_1 = np.zeros((5,4))
allcoeff_532_1[0,:]=np.ones(4) + alpha
allcoeff_532_1[1,:]=-1*np.ones(4)
y_532_1 = np.zeros((5,4)) #row 0 stores y0 for each P from 1-4; row 1 stores y1 for P from 1-4;...
for i in range(4):
P=i+1
ki_la = allcoeff_532_1[:,i]
y_mid=odeint(ode_system_la, [1.0]+[0.0]*P, np.linspace(0,1,2), args=(P, alpha))[1,:]
y_532_1[:,i] = y_mid.tolist()+[0]*(4-P)
# -
print(y_532_1)
for i in range(9):
#to compute $\bar{y}(t)$
print(Gamma.expect(Lague_gen((i,1)), args=(2,), loc=0, lb=None, ub=None, conditional=False))
# +
def g(params):
n = params
return lambda u: (Lague_gen((n,1))(u))**2
for i in range(1,5):
print(Gamma.expect(g(i), args=(2,), loc=0, scale=1, lb=None, ub=None, conditional=False))
# +
############# alpha = 1 ################
error_mean_532_1=np.abs(4*y_532_1[0,:]-1)
sigma2_532_1=np.zeros(4)
for i in range(4):
sigma2_532_1[i]=2*y_532_1[1,i]**2+3*y_532_1[2,i]**2+4*y_532_1[3,i]**2+5*y_532_1[4,i]**2
sigma2_exact_532_1 = 7/144
error_var_532_1=np.abs((sigma2_532_1-sigma2_exact_532_1)/sigma2_exact_532_1)
# -
# ### <font color = red> The error plots when $\alpha=0$ are correct, I am using Laguerre package in python since $\alpha=0$.
#
# ### <font color = red> But when $\alpha=1$, the error plots are so strange, I am using the Laguerre functions I defined by myself
plt.figure()
plt.xlim([0,5])
plt.semilogy([1,2,3,4],error_mean_532_0,'-bs',label= 'mean, alpha=0')
plt.semilogy([1,2,3,4],error_var_532_0,'-rs',label='variance, alpha=0')
plt.semilogy([1,2,3,4],error_mean_532_1,'-.b^',label='mean, alpha=1')
plt.semilogy([1,2,3,4],error_var_532_1,'-.r^',label='variance, alpha=1')
plt.legend()
|
Example 5.3.2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## 1.[enumerate](#1)
# ## 2.[lambda](#2)
# ## 3.[pandas](#3)
# ## 4.[numpy](#4)
# ## 5.[markdown](#5)
# ## 6.[pytorch](#6)
# ## 7.[plot](#7)
# ## L.[其他操作](#last)
import math
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import torch
from torchviz import make_dot
from colorama import Fore, Back
import seaborn as sns; sns.set(color_codes=True)
# ## <span id ="1">1.enumerate</span>
#枚举
LL = ['a','b','c']
aa = enumerate(LL)
print(aa, type(aa))
for i ,e in enumerate(LL):
print(i,e)
for e in enumerate(LL,3):
print(e)
# ## <span id ="2">2.lambda</span>
# * 快速构建函数
epsilon_by_frame = lambda frame_idx:math.exp(-frame_idx/100)
plt.plot([epsilon_by_frame(i) for i in range(500)])
# * 多返回值
multi_return_value = lambda a, b :(a+1,b+2)
a, b =multi_return_value(1,1)
print(a,b)
# * 和map连用快速定义并返回
L = [1,2,3,4]
list(map(lambda x : x**3, L))
# * 和filter连用进行数据的挑选
list(filter(lambda x: x>=2, L))
# ## <span id ="3">3.pandas</span>
# * pd.qcut根据值均匀分配将数据分为n个梯度
pd.qcut(range(6),3)
pd.qcut(range(5), 3, labels=["good", "medium", "bad"])
# ## <span id ="4">4.numpy</span>
# * np.random.choice进行选择
# np.random.choice(a,size=None,replace=True,p=None)
# a:一维数组(表示在其中选一个)或者int数(表示在[0,i-1]中选一个)
# size:int数代表一维数组,也可返回指定大小的多维矩阵
# replace=True 表示可能会返回重复的项
# p:对a中的每个数设置权重,即被选中的概率
print(np.random.choice(range(6)))
print(np.random.choice(["a","b","c","d"]))
print(np.random.choice(["a","b","c","d"],p = [0,1,0,0]))
# * 图片的numpy和torch.Tensor之间的转化要用到transpose()函数<br>
# 对于numpy 的图片:H x W x C<br>
# 对于$\;$torch$\;$ 的图片:C x H x W
# ## <span id = "5">5.markdown</span>
# $${\max_{a'}}$$
# ## <span id='6'>6.pytorch</span>
# * pytorch 使用 **(a)** torch.tensor.item()和 **(b)** torch.tensor.cpu().numpy()的异同<br>
# 同 : 都是将tensor张量转化为python标量值<br>
# 异 : (a)只能对单个张量操作 | (b)既可以对单个张量操作也可以对进行数组操作
test = torch.tensor(5)
print("test :", test)
print(".item() :", test.item())
print(".cpu().numpy() :", test.cpu().numpy())
test = torch.tensor([1,2])
print("test :", test)
print(".cpu().numpy() :",test.cpu().numpy())
print("")
try:
print(".item() :", test.item())
except ValueError :
print(Fore.WHITE + Back.RED + "ValueError: only one element tensors can be converted to Python scalars")
# * torchviz画图<br>
# 该包有两个方法,make_dot_from_trace和make_dot。感觉我只用到了第一个<br>
# 其中,make_dot(model).render("picture")保存的是pdf文档<br>
# make_dot(model).render("picture", format="png")保存的是png格式图片和图片信息文件
lstm_cell = torch.nn.LSTMCell(128, 128)
x = torch.randn(3, 128)
make_dot(lstm_cell(x), params=dict(list(lstm_cell.named_parameters())))
# * 理解.detach()<br>
# 1. 简单理解为该tensor的复制,且require_grad = False
# 2. 通常我们使用到model里输出的量是require_grad = True的,也就是说其包含原始梯度,而这时我们又需要用其计算Loss,此时便需要重置其梯度,使其不受原始梯度的影响。所以.detach()也就起到了重置梯度的作用
# 3. 下图的演示展示了.detach(),require_grad = False
# 4. detach()不能乱用,在计算loss function时,根据是不是需要求导(论文中的求导公式)来使用.detach()
x = torch.ones(10, requires_grad=True)
y = x**2
z = x**3
r = (y + z).sum()
r.backward()
print("x.grad:", x.grad)
make_dot(r)
x = torch.ones(10, requires_grad=True)
y = x**2
z = x.detach()**3
r = (y + z).sum()
r.backward()
print("x.grad:", x.grad)
make_dot(r)
# ## <span id = "last">plot</span>
# * 使用seaborn画出论文里带有置信区间的图
num_fig = 5
start, end = -1, 1
x_list_sub = lambda x, y : np.arange(x, y, 0.1)
x_list_target = np.stack((x_list_sub(start, end) for _ in range(num_fig)), axis=1).flatten()
y_list_target = x_list_target ** 2 + np.random.randn(x_list_target.shape[0]) * 0.2
data = pd.DataFrame(data=dict(x=x_list_target, y=y_list_target))
sns.lineplot(x="x", y="y", data=data, color="g")
# ## <span id = "last">其他操作</span>
# * 对axis = 0,或axis = 1 的理解<br>
# 都表示跨越,0跨行,1跨列
a = np.arange(9).reshape(3,3)
print(a)
print("0跨行:",a.sum(0))
print("1跨列:",a.sum(1))
print("总和:",a.sum())
# * 对函数中\__len__(self)的理解<br>
# 重写len方法供调用
# +
class Test():
def __init__(self, *num):
self.nums = num
def __len__(self):
return len(self.nums)
test = Test("A","B","C")
print(len(test),test.__len__())
# -
# * \*args 和 \*\*kwargs的异同(some code reference Geeks for Geeks)<br>
# 都是可变参数的传值,两者都可当正常函数的传值处理<br>
# \*args是不定长的可变参数,而\*\*kwargs使用的是类似于元组的key to value的可变参数
# +
#对于*args
def myFun(*argv):
for arg in argv:
print(arg)
myFun('Hello', 'Welcome', 'to', 'HHQ\'utils')
# +
#对于**kwargs我分为了两种情况:
#第一种(定义可变参数函数):
def myFun(**kwargs):
for key, value in kwargs.items():
print("%s == %s"%(key, value))
myFun(first ='Geeks', mid ='for', last='Geeks')
# +
#第二种(传入可变参数的字典):
def myFun(first_list, last_list):
print("the first_list is {}, last_list is {}".format(first_list, last_list))
sample = {"first_list":[1,2],"last_list":[3,4]}
myFun(**sample)
# -
# * 提取list中索引值为奇数或者偶数的数<br>
# some_list[start:stop:step]
np.arange(8)[::2]
# * 关于类中方法的错误使用(DDPG 添加Noise的时候发现的)
# +
class Test:
def __init__(self):
self.state = np.zeros(1)
def sample_right(self):
self.state = self.state + np.random.randn(1)
return self.state
def sample_error(self):
self.state += np.random.randn(1)
return self.state
plt.figure(figsize=(16, 6))
plt.subplot(121)
test = Test()
right_sample = [test.sample_right() for _ in range(1000)]
error_sample = [test.sample_error() for _ in range(1000)]
plt.plot(right_sample, label="a")
plt.plot(error_sample, label="b")
plt.legend()
plt.subplot(122)
test1 = Test()
right_sample = [test1.sample_right()[0] for _ in range(1000)]
error_sample = [test1.sample_error()[0] for _ in range(1000)]
plt.plot(right_sample, label="a")
plt.plot(error_sample, label="b")
plt.legend()
plt.show()
# -
# 从一个.py文件中引入其中的类使用:<br>
# from xx import class_name<br>
# 使用import xxx<br>
# 都在__init__()写了东西<br>
# ### 值得去查查
|
.ipynb_checkpoints/utils-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# %matplotlib inline
# ### Import the data
data = pd.read_csv('PHASEdata.csv',header=None, skiprows=1)
data.head()
z = data[0]
#print(z)
z_approach = z[:500]
z_retract = z[500:]
#print(z_approach)
#print(z_retract)
z_approach_as_numpy = z_approach.as_matrix(columns=None)
#phase shift
for k in range(len(z)):
pslist = []
phaseshift = data.iloc[k,1:] #[from zero row to the end row, from second column to the last column]
#print(phaseshift)
ps = np.array(phaseshift)
ps_reshape = np.reshape(ps,(48,48))
#print(ps)
pslist.append(ps_reshape)
#print(pslist)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
a = np.linspace(0, 48, 20)
b = np.linspace(0, 48, 20)
c = z_approach_as_numpy
x, y, z = np.meshgrid(a, b, c)
l = np.linspace(0, 48, 200000)
fig = plt.figure(figsize=(15,15))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x, y, z, c=l)
plt.show()
|
doc/Notebooks/AFM_3dplot.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Naïve Bayes Classifier
# http://scikit-learn.org/stable/modules/naive_bayes.html
#
# https://www.countbayesie.com/blog/2015/2/18/bayes-theorem-with-lego
import pandas as pd
import numpy as np
# ## Importar los datos en Pandas
dataframe = pd.read_excel('https://benlarsonsite.files.wordpress.com/2016/05/logi21.xlsx')
dataframe.head()
# ##### Columnas:
#
# - Score – Puntuación del examen
# - ExtraCir – El estudiante estaba involucrado en actividades extra-curriculares
# - Accepted – El estudiante fue aceptado
#
# ## Split the data
# +
y = dataframe.pop('Accepted')
X = dataframe
y.head()
# -
X.head()
# #### Scikit-learn
#
#
# 1 - Importar algoritmo
#
# 2 - Instanciar clasificador
#
# 3 - Entrenar
#
# 4 - Predecir
# +
# 1 - Importar algoritmo
from sklearn.naive_bayes import MultinomialNB
# +
# 2 - Instanciar clasificador
classifier = MultinomialNB()
# +
# 3 - Entrenar
classifier.fit(X,y)
# -
# ## Predict and profit 📈💸💪
# +
#--score: 1200, ExtraCir = 1
sample_1 = np.array([1200,1]).reshape((1, -1))
print(classifier.predict(sample_1))
print(classifier.predict_proba(sample_1))
# +
#--score: 1000, ExtraCir = 0
sample_2 = np.array([2,1]).reshape((1, -1))
print(classifier.predict(sample_2))
print(classifier.predict_proba(sample_2))
# -
|
Python_para_ciencia_de_datos/4ta_clase/NaiveBayes.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] tags=["remove_cell"]
# # Solving combinatorial optimization problems using QAOA
# -
# In this tutorial, we introduce combinatorial optimization problems, explain approximate optimization algorithms, explain how the Quantum Approximate Optimization Algorithm (QAOA) works and present the implementation of an example that can be run on a simulator or on a 5 qubit quantum chip
#
# ## Contents
# 1. [Introduction](#introduction)
# 2. [Examples](#examples)
# 3. [Approximate optimization algorithms](#approximateOPT)
# 4. [The QAOA algorithm](#QAOA)
# 5. [Qiskit Implementation](#implementation)
# 5.1 [Running QAOA on a simulator](#implementationsim)
# 5.2 [Running QAOA on a real quantum device](#implementationdev)
# 6. [Problems](#problems)
# 7. [References](#references)
# ## 1. Introduction <a id='introduction'></a>
#
# Combinatorial optimization [1](#references) means searching for an optimal solution in a finite or countably infinite set of potential solutions. Optimality is defined with respect to some criterion function, which is to be minimized or maximized, which is typically called the cost function.
#
# There are various types of optimization problems. These include Minimization: cost, distance, length of a traversal, weight, processing time, material, energy consumption, number of objects. Maximization: profit, value, output, return, yield, utility, efficiency, capacity, number of objects. Any maximization problem can be cast in terms of a minimization problem and vice versa. Hence the general form a combinatorial optimization problem is given by
#
#
#
# $$ \text{maximize } \;\; C(x)$$
#
#
#
#
# $$ \text{subject to } \;\; x \in S $$
#
#
#
# where $x \in S$, is a discrete variable and $C : D \rightarrow \mathbb{R}$ is the cost function, that maps from some domain $S$ in to the real numbers $\mathbb{R}$. The variable $x$ can be subject to a set of constraints and lies within the set $S \subset D$ of feasible points.
#
# In binary combinatorial optimization problems, the cost function $C$ can typically be expressed as a sum of terms that only involve a subset $Q \subset[n]$ of the $n$ bits in the string $x \in \{0,1\}^n$ and is written in the canonical form
#
#
#
# $$ C(x) = \sum_{(Q,\overline{Q}) \subset [n]} w_{(Q,\overline{Q})} \; \prod_{i\in Q} x_i \; \prod_{j\in \overline{Q}} (1- x_j), $$
#
#
#
# where $x_i \in \{0,1\}$ and $w_{(Q,\overline{Q})}\in \mathbb{R}$. We want to find the n-bit string $x$ for which $C(x)$ is the maximal.
# ### 1.1 Diagonal Hamiltonians
#
# This cost function can be mapped to a Hamiltonian that is diagonal in the computational basis. Given the cost-function $C$ this Hamiltonian is then written as
#
#
#
# $$ H = \sum_{x \in \{0,1\}^n} C(x) |x \rangle\langle x| $$
#
#
#
# where $x \in \{0,1\}^n$ labels the computational basis states $|x \rangle \in \mathbb{C}^{2^n}$. If the cost function only has at most weight $k$ terms, i.e. when only $Q$ contribute that involve at most $Q \leq k$ bits, then this diagonal Hamiltonian is also only a sum of weight $k$ Pauli $Z$ operators.
#
# The expansion of $H$ in to Pauli $Z$ operators can be obtained from the canonical expansion of the cost-function $C$ by substituting for every binary variable $x_i \in \{0,1\}$ the matrix $x_i \rightarrow 2^{-1}(1 - Z_i)$. Here $Z_i$ is read as the Pauli $Z$ operator that acts on qubit $i$ and trivial on all others, i.e.
#
#
#
# $$ Z_i = \left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right). $$
#
#
#
# This means that the spin Hamiltonian encoding the classical cost function is written as a $|Q|$ - local quantum spin Hamiltonian only involving Pauli $Z$- operators.
#
#
#
# $$ H = \sum_{(Q,\overline{Q}) \subset [n]} w_{(Q,\overline{Q})} \; \frac{1}{2^{|Q| + |\overline{Q}|}}\prod_{i\in Q} \left(1 - Z_i\right) \; \prod_{j\in \overline{Q}} \left(1 + Z_j\right).$$
#
#
#
# Now, we will assume that only a few (polynomially many in $n$) $w_{(Q,\overline{Q})}$ will be non-zero. Moreover we will assume that the set $|(Q,\overline{Q})|$ is bounded and not too large. This means we can write the cost function as well as the Hamiltonian $H$ as the sum of $m$ local terms $\hat{C}_k$,
#
#
#
# $$ H = \sum_{k = 1}^m \hat{C}_k, $$
#
#
#
# where both $m$ and the support of $\hat{C}_k$ is reasonably bounded.
# ## 2 Examples: <a id='examples'></a>
#
# We consider 2 examples to illustrate combinatorial optimization problems. We will only implement the first example as in Qiskit, but provide a sequence of exercises that give the instructions to implement the second example as well.
#
#
# ### 2.1 (weighted) $MAXCUT$
#
# Consider an $n$-node non-directed graph *G = (V, E)* where *|V| = n* with edge weights $w_{ij}>0$, $w_{ij}=w_{ji}$, for $(j,k)\in E$. A cut is defined as a partition of the original set V into two subsets. The cost function to be optimized is in this case the sum of weights of edges connecting points in the two different subsets, *crossing* the cut. By assigning $x_i=0$ or $x_i=1$ to each node $i$, one tries to maximize the global profit function (here and in the following summations run over indices 0,1,...n-1)
#
#
#
# $$C(\textbf{x}) = \sum_{i,j = 1}^n w_{ij} x_i (1-x_j).$$
#
#
#
# To simplify notation, we assume uniform weights $ w_{ij} = 1$ for $(i,j) \in E$. In order to find a solution to this problem on a quantum computer, one needs first to map it to a diagonal Hamiltonian as discussed above. We write the sum as a sum over edges in the set $(i,j) = E$
#
#
#
# $$C(\textbf{x}) = \sum_{i,j = 1}^n w_{ij} x_i (1-x_j) = \sum_{(i,j) \in E} \left( x_i (1-x_j) + x_j (1-x_i)\right)$$
#
#
#
# To map is to a spin Hamiltonian we make the assignment $x_i\rightarrow (1-Z_i)/2$, where $Z_i$ is the Pauli Z operator that has eigenvalues $\pm 1$ and obtain $X \rightarrow H$
#
#
#
# $$ H = \sum_{(j,k) \in E} \frac{1}{2}\left(1 - Z_j Z_k \right).$$
#
#
#
# This means that the Hamiltonian can be written as a sum of $m = |E|$ local terms $\hat{C}_e = \frac{1}{2}\left(1 - Z_{e1}Z_{e2}\right)$ with $e = (e1,e2) \in E$.
#
#
# ### 2.2 Constraint satisfaction problems and $MAX \; 3-SAT$.
#
# Another example of a combinatorial optimization problem is $3-SAT$. Here the cost function $C(\textbf{x}) = \sum_{k = 1}^m c_k(\textbf{x})$ is a sum of clauses $c_k(\textbf{x})$ that constrain the values of $3$ bits of some $\textbf{x} \in \{0,1\}^n$ that participate in the clause. Consider for instance this example of a $3-SAT$ clause
#
#
#
# $$ c_1(\textbf{x}) = (1-x_1)(1-x_3)x_{132} $$
#
#
#
# for a bit string $\textbf{x} \in \{0,1\}^{133}$. The clause can only be satisfied by setting the bits $x_1 = 0$,$x_3 = 0$ and $x_{132} = 1$. The $3-SAT$ problem now asks whether there is a bit string that satisfies all of the $m$ clauses or whether no such string exists. This decision problem is the prime example of a problem that is $NP$-complete.
#
# The closely related optimization problem $MAX \; 3-SAT$ asks to find the bit string $\textbf{x}$ that satisfies the maximal number of of clauses in $C(\textbf{x})$. This can of course be turned again in to a decision problem if we ask where there exists a bit string that satisfies more than $\tilde{m}$ of the $m$ clauses, which is again $NP$-complete.
# ## 3. Approximate optimization algorithms <a id='approximateOPT'></a>
#
# Both the previously considered problems $MAXCUT$ and $MAX \; 3-SAT$ are actually known to be a NP-hard problems [1](#references). In fact it turns out that many combinatorial optimization problems are computationally hard to solve in general. In light of this fact, we can't expect to find a provably efficient algorithm, i.e. an algorithm with polynomial runtime in the problem size, that solves these problems. This also applies to quantum algorithms. There are two main approaches to dealing with such problems. First approach is approximation algorithms that are guaranteed to find solution of specified quality in polynomial time. The second approach are heuristic algorithms that don't have a polynomial runtime guarantee but appear to perform well on some instances of such problems.
#
# Approximate optimization algorithms are efficient and provide a provable guarantee on how close the approximate solution is to the actual optimum of the problem. The guarantee typically comes in the form of an approximation ratio, $\alpha \leq 1$. A probabilistic approximate optimization algorithm guarantees that it produces a bit-string $\textbf{x}^* \in \{0,1\}^n$ so that *with high probability* we have that with a positive $C_{max} = \max_{\textbf{x}}C(\textbf{x})$
#
#
#
# $$ C_{max} \geq C(\textbf{x}^*) \geq \alpha C_{max}. $$
#
#
#
# For the $MAXCUT$ problem there is a famous approximate algorithm due to Goemans and Williamson [2](#references) . This algorithm is based on an SDP relaxation of the original problem combined with a probabilistic rounding technique that yields an with high probability approximate solution $\textbf{x}^*$ that has an approximation ratio of $\alpha \approx 0.868$. This approximation ratio is actually believed to optimal so we do not expect to see an improvement by using a quantum algorithm.
# ## 4. The QAOA algorithm <a id="QAOA"></a>
# The Quantum approximate optimization algorithm (QAOA) by Farhi, Goldstone and Gutmann [3](#references) is an example of a heuristic algorithm. Unlike Goemans-Williamson algorithm, QAOA does not come with performance guarantees.
# QAOA takes the approach of classical approximate algorithms and looks for a quantum analogue that will likewise produce a classical bit string $x^*$ that with high probability is expected to have a good approximation ratio $\alpha$. Before discussing the details, let us first present the general idea of this approach.
#
# ### 4.1 Overview:
#
# We want to find a quantum state $|\psi_p(\vec{\gamma},\vec{\beta})\rangle$, that depends on some real parameters $\vec{\gamma},\vec{\beta} \in \mathbb{R}^p$, which has the property that it maximizes the expectation value with respect to the problem Hamiltonian $H$. Given this trial state we search for parameters $\vec{\gamma}^*,\vec{\beta}^*$ that maximize $F_p(\vec{\gamma},\vec{\beta}) = \langle \psi_p(\vec{\gamma},\vec{\beta})|H|\psi_p(\vec{\gamma},\vec{\beta})\rangle$.
#
# Once we have such a state and the corresponding parameters we prepare the state $|\psi_p(\vec{\gamma}^*,\vec{\beta}^*)\rangle$ on a quantum computer and measure the state in the $Z$ basis $|x \rangle = |x_1,\ldots x_n \rangle$ to obtain a random outcome $x^*$.
#
# We will see that this random $x^*$ is going to be a bit string that is with high probability close to the expected value $M_p = F_p(\vec{\gamma}^*,\vec{\beta}^*)$. Hence, if $M_p$ is close to $C_{max}$ so is $C(x^*)$.
#
# ### 4.2 The components of the QAOA algorithm.
#
# ### 4.2.1 The QAOA trial state <a id="section_421"></a>
# Central to QAOA is the trial state $|\psi_p(\vec{\gamma},\vec{\beta})\rangle$ that will be prepared on the quantum computer. Ideally we want this state to give rise to a large expectation value $F_p(\vec{\gamma},\vec{\beta}) = \langle \vec{\gamma},\vec{\beta})|H|\psi_p(\vec{\gamma},\vec{\beta})\rangle$ with respect to the problem Hamiltonian $H$. In Farhi [3](#references), the trial states $|\psi_p(\vec{\gamma},\vec{\beta})\rangle$ are constructed from the problem Hamiltonian $H$ together with single qubit Pauli $X$ rotations. That means, given a problems Hamiltonian
#
#
# $$ H = \sum_{k = 1}^m \hat{C}_k $$
#
#
# diagonal in the computational basis and a transverse field Hamiltonian
#
#
# $$ B = \sum_{i = 1}^n X_i $$
#
#
# the trial state is prepared by applying $p$ alternating unitaries
#
#
#
# $$ |\psi_p(\vec{\gamma},\vec{\beta})\rangle = e^{ -i\beta_p B } e^{ -i\gamma_p H } \ldots e^{ -i\beta_1 B } e^{ -i\gamma_1 H } |+\rangle^n $$
#
#
#
# to the product state $|+\rangle^n$ with $ X |+\rangle = |+\rangle$.
#
# This particular ansatz has the advantage that there exists an explicit choice for the vectors $\vec{\gamma}^*,\vec{\beta}^*$ such that for $M_p = F_p(\vec{\gamma}^*,\vec{\beta}^*)$ when we take the limit $\lim_{p \rightarrow \infty} M_p = C_{max}$. This follows by viewing the trial state $|\psi_p(\vec{\gamma},\vec{\beta}) \rangle$ as the state that follows from troterizing the adiabatic evolution with respect to $H$ and the transverse field Hamiltonian $B$, c.f. Ref [3](#references).
#
# Conversely the disadvantage of this trial state is one would typically want a state that has been generated from a quantum circuit that is not too deep. Here depth is measured with respect to the gates that can be applied directly on the quantum chip. Hence there are other proposals that suggest using Ansatz trial state that are more tailored to the Hardware of the quantum chip Ref. [4](#references), Ref. [5](#references).
#
#
# ### 4.2.2 Computing the expectation value <a id="section_422"></a>
# An important component of this approach is that we will have to compute or estimate the expectation value
#
# $$
# F_p(\vec{\gamma},\vec{\beta}) = \langle \psi_p(\vec{\gamma},\vec{\beta})|H|\psi_p(\vec{\gamma},\vec{\beta})\rangle
# $$
#
# so we can optimize the parameters $\vec{\gamma},\vec{\beta}$. We will be considering two scenarios here.
#
# #### Classical evaluation
# Note that when the circuit to prepare $|\psi_p(\vec{\gamma},\vec{\beta})\rangle$ is not too deep it may be possible to evaluate the expectation value $F_p$ classically.
#
# This happens for instance when one considers $MAXCUT$ for graphs with bounded degree and one considers a circuit with $p=1$. We will see an example of this in the Qiskit implementation below (section 5.2) and provide an exercise to compute the expectation value.
#
# To illustrate the idea, recall that the Hamiltonian can be written as a sum of individual terms $H = \sum_{k = 1}^m \hat{C}_k$. Due to the linearity of the expectation value, it is sufficient to consider the expectation values of the individual summands. For $p = 1$ one has that
#
#
#
# $$ \langle \psi_1(\vec{\gamma},\vec{\beta})|\hat{C}_k|\psi_1(\vec{\gamma},\vec{\beta})\rangle = \langle +^n | e^{ i\gamma_1 H } e^{ i\beta_1 B } | \hat{C}_k | e^{ -i\beta_1 B } e^{ -i\gamma_1 H } |+^n\rangle.$$
#
#
#
# Observe that with $B = \sum_{i = 1}^n X_i$ the unitary $e^{ -i\beta_1 B }$ is actually a product of single qubit rotations about $X$ with an angle $\beta$ for which we will write $X(\beta)_k = \exp(i\beta X_k)$.
#
# All the individual rotations that don't act on the qubits where $\hat{C}_k$ is supported commute with $\hat{C}_k$ and therefore cancel. This does not increase the support of the operator $\hat{C}_k$. This means that the second set of unitary gates $e^{ -i\gamma_1 H } = \prod_{l=1}^m U_l(\gamma)$ have a large set of gates $U_l(\gamma) = e^{ -i\gamma_1 \hat{C}_l }$ that commute with the operator $e^{ i\beta_1 B } \hat{C}_k e^{ -i\beta_1 B }$. The only gates $U_l(\gamma) = e^{ -i\gamma_1 \hat{C}_l }$ that contribute to the expectation value are those which involve qubits in the support of the original $\hat{C}_k$.
#
# Hence, for bounded degree interaction the support of $e^{ i\gamma_1 H } e^{ i\beta_1 B } \hat{C}_k e^{ -i\beta_1 B } e^{ -i\gamma_1 H }$ only expands by an amount given by the degree of the interaction in $H$ and is therefore independent of the system size. This means that for these smaller sub problems the expectation values are independent of $n$ and can be evaluated classically. The case of a general degree $3$ is considered in [3](#references).
#
# This is a general observation, which means that if we have a problem where the circuit used for the trial state preparation only increases the support of each term in the Hamiltonian by a constant amount the cost function can be directly evaluated.
#
# When this is the case, and only a few parameters $\beta, \gamma$ are needed in the preparation of the trial state,
# these can be found easily by a simple grid search. Furthermore, an exact optimal value of $M_p$ can be used to bound the approximation ratio
#
#
#
# $$ \frac{M_p}{C_{max}} \geq \alpha $$
#
#
#
# to obtain an estimate of $\alpha$. For this case the QAOA algorithm has the same characteristics as a conventional approximate optimization algorithm that comes with a guaranteed approximation ratio that can be obtained with polynomial efficiency in the problem size.
#
#
# #### Evaluation on a quantum computer
#
# When the quantum circuit becomes too deep to be evaluated classically, or when the connectivity of the Problem Hamiltonian is too high we can resort to other means of estimating the expectation value. This involves directly estimating $F_p(\vec{\gamma},\vec{\beta})$ on the quantum computer. The approach here follows the path of the conventional expectation value estimation as used in VQE [4](#references), where a trial state $| \psi(\vec{\gamma},\vec{\beta})$ is prepared directly on the quantum computer and the expectation value is obtained from sampling.
#
# Since QAOA has a diagonal Hamiltonian $H$ it is actually straight forward to estimate the expectation value. We only need to obtain samples from the trial state in the computational basis. Recall that $H = \sum_{x \in \{0,1\}^n} C(x) |x \rangle\langle x|$ so that we can obtain the sampling estimate of
#
#
#
# $$ \langle \psi_p(\vec{\gamma},\vec{\beta})|H|\psi_p(\vec{\gamma},\vec{\beta})\rangle = \sum_{x \in \{0,1\}^n} C(x) |\langle x| \psi_p(\vec{\gamma},\vec{\beta}) \rangle |^2$$
#
#
#
# by repeated single qubit measurements of the state $| \psi_p(\vec{\gamma},\vec{\beta}) \rangle $ in the $Z$ basis. For every bit string $x$ obtained from the distribution $|\langle x| \psi_p(\vec{\gamma},\vec{\beta}) \rangle |^2$ we evaluate the cost function $C(x)$ and average it over the total number of samples. The resulting empirical average approximates the expectation value up to an additive sampling error that lies within the variance of the state. The variance will be discussed below.
#
# With access to the expectation value, we can now run a classical optimization algorithm, such as [6](#references),
# to optimize the $F_p$.
#
# While this approach does not lead to an a-priori approximation guarantee for $x^*$, the optimized function value
# can be used later to provide an estimate for the approximation ratio $\alpha$.
#
#
# ### 4.3.3 Obtaining a solution with a given approximation ratio with high probability
# The algorithm is probabilistic in nature and produces random bit strings from the distribution $|\langle x| \psi_p(\vec{\gamma},\vec{\beta}) \rangle |^2$. So how can we be sure that we will sample an approximation $x^*$ that is close to the value of the optimized expectation value $M_p$? Note that this question is also relevant to the estimation of $M_p$ on a quantum computer in the first place. If the samples drawn from $|\langle x| \psi_p(\vec{\gamma},\vec{\beta}) \rangle |^2$ have too much variance, many samples are necessary to determine the mean.
#
# We will draw a bit string $x^*$ that is close to the mean $M_p$ with high probability when the energy as variable has little variance.
#
# Note that the number of terms in the Hamiltonian $H = \sum_{k=1}^m \hat{C}_k$ are bounded by $m$. Say each individual
# summand $\hat{C}_k$ has an operator norm that can be bounded by a universal constant $\|\hat{C}_k\| \leq \tilde{C}$ for all $k = 1\ldots m$. Then consider
#
# $$
# \begin{eqnarray}
# \langle \psi_p(\vec{\gamma},\vec{\beta})|H^2|\psi_p(\vec{\gamma},\vec{\beta})\rangle - \langle \psi_p(\vec{\gamma},\vec{\beta})|H|\psi_p(\vec{\gamma},\vec{\beta})\rangle^2 &\leq & \langle \psi_p(\vec{\gamma},\vec{\beta})|H^2|\psi_p(\vec{\gamma},\vec{\beta})\rangle \\\nonumber
# &=& \sum_{k,l =1}^m \langle \psi_p(\vec{\gamma},\vec{\beta})|\hat{C}_k \hat{C}_l |\psi_p(\vec{\gamma},\vec{\beta})\rangle \\\nonumber
# &\leq& m^2 \tilde{C}^2 \\\nonumber
# \end{eqnarray}
# $$
#
#
# where we have used that
# $\langle \psi_p(\vec{\gamma},\vec{\beta})|\hat{C}_k \hat{C}_l |\psi_p(\vec{\gamma},\vec{\beta})\rangle \leq \tilde{C}^2$.
#
#
# This means that the variance of any expectation $F_p(\vec{\gamma},\vec{\beta})$ is bounded by $m^2 \tilde{C}^2$. Hence this in particular applies for $M_p$. Furthermore if $m$ only grows polynomially in the number of qubits $n$, we know that taking polynomially growing number of samples $s = O\left(\frac{\tilde{C}^2 m^2}{\epsilon^2}\right)$ from $|\langle x| \psi_p(\vec{\gamma},\vec{\beta}) \rangle |^2$ will be sufficient to obtain a $x^*$ that leads to an $C(x^*)$ that will be close to $M_p$.
# ## 5. Qiskit Implementation<a id='implementation'></a>
#
# As the example implementation we consider the $MAXCUT$ problem on the butterfly graph of the openly available IBMQ 5-qubit chip. The graph will be defined below and corresponds to the native connectivity of the device. This allows us to implement the original version of the $QAOA$ algorithm, where the cost function $C$ and the Hamiltonian $H$ that is used to generate the state coincide. Moreover, for such a simple graph the exact cost function can be calculated analytically, avoiding the need to find optimal parameters variationally [7](#references). To implement the circuit, we follow the notation and gate definitions from the [Qiskit Documentation](https://qiskit.org/documentation/).
# As the first step will will load Qiskit and additional python packages.
# +
import numpy as np
import networkx as nx # tool to handle general Graphs
import matplotlib.pyplot as plt
from matplotlib import cm
from matplotlib.ticker import LinearLocator, FormatStrFormatter
from qiskit import Aer, IBMQ
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, transpile, assemble
from qiskit.providers.ibmq import least_busy
from qiskit.tools.monitor import job_monitor
from qiskit.visualization import plot_histogram
# -
# ### 5.1 Problem definition
#
# We define the cost function in terms of the butterfly graph of the superconducting chip. The graph has $n = 5$ vertices $ V = \{0,1,2,3,4,5\}$ and six edges $E = \{(0,1),(0,2),(1,2),(3,2),(3,4),(4,2)\}$, which will all carry the same unit weight $w_{ij} = 1$. We load an additional network package to encode the graph and plot connectivity below.
# +
# Generating the butterfly graph with 5 nodes
n = 5
V = np.arange(0,n,1)
E =[(0,1,1.0),(0,2,1.0),(1,2,1.0),(3,2,1.0),(3,4,1.0),(4,2,1.0)]
G = nx.Graph()
G.add_nodes_from(V)
G.add_weighted_edges_from(E)
# Generate plot of the Graph
colors = ['r' for node in G.nodes()]
default_axes = plt.axes(frameon=True)
pos = nx.spring_layout(G)
nx.draw_networkx(G, node_color=colors, node_size=600, alpha=1, ax=default_axes, pos=pos)
# -
# ### 5.2 Optimal trial state parameters<a id="implementation_sec52"></a>
#
# In this example we consider the case for $p = 1$, i.e. only layer of gates. The expectation value $F_1(\gamma,\beta) = \langle \psi_1(\gamma,\beta))|H|\psi_1(\gamma,\beta) \rangle$ can be calculated analytically for this simple setting. Let us discuss the steps explicitly for the Hamiltonian $H = \sum_{(j,k) \in E} \frac{1}{2}\left(1 - Z_i Z_k\right)$. Due to the linearity of the expectation value we can compute the expectation value for the edges individually
#
#
#
# $$f_{(i,k)}(\gamma,\beta) = \langle \psi_1(\gamma,\beta)|\;\frac{1}{2}\left(1 - Z_i Z_k\right)\;|\psi_1(\gamma,\beta)\rangle. $$
#
#
#
# For the butterfly graph as plotted above, we observe that there are only two kinds of edges $A = \{(0,1),(3,4)\}$ and
# $B = \{(0,2),(1,2),(2,3),(2,4)\}$. The edges in $A$ only have two neighboring edges, while the edges in $B$ have four. You can convince yourself that we only need to compute the expectation of a single edge in each set since the other expectation values will be the same. This means that we can compute $F_1(\gamma,\beta) = 2 f_A(\gamma,\beta) + 4f_B(\gamma,\beta)$ by evaluating only computing two expectation values. Note, that following the argument as outlined in [section 4.2.2](#section_422), all the gates that do not intersect with the Pauli operator $Z_0Z_1$ or $Z_0Z_2$ commute and cancel out so that we only need to compute
#
#
#
# $$f_A(\gamma,\beta) = \frac{1}{2}\left(1 - \langle +^3|U_{21}(\gamma)U_{02}(\gamma)U_{01}(\gamma)X_{0}(\beta)X_{1}(\beta)\;Z_0Z_1\; X^\dagger_{1}(\beta)X^\dagger_{0}(\beta)U^\dagger_{01}(\gamma)U^\dagger_{02}(\gamma)U^\dagger_{12}(\gamma) | +^3 \rangle \right)$$
#
#
#
# and
#
#
#
# $$f_B(\gamma,\beta) = \frac{1}{2}\left(1 - \langle +^5|U_{21}(\gamma)U_{24}(\gamma)U_{23}(\gamma)U_{01}(\gamma)U_{02}(\gamma)X_{0}(\beta)X_{2}(\beta)\;Z_0Z_2\; X^\dagger_{0}(\beta)X^\dagger_{2}(\beta)U^\dagger_{02}(\gamma)U^\dagger_{01}(\gamma)U^\dagger_{12}(\gamma)U^\dagger_{23}(\gamma)U^\dagger_{24}(\gamma) | +^5 \rangle \right)$$
#
#
#
# How complex these expectation values become in general depend only on the degree of the graph we are considering and is independent of the size of the full graph if the degree is bounded. A direct evaluation of this expression with $U_{k,l}(\gamma) = \exp\frac{i\gamma}{2}\left(1 - Z_kZ_l\right)$ and
# $X_k(\beta) = \exp(i\beta X_k)$ yields
#
#
#
# $$f_A(\gamma,\beta) = \frac{1}{2}\left(sin(4\gamma)sin(4\beta) + sin^2(2\beta)sin^2(2\gamma)\right)$$
#
#
#
# and
#
#
#
# $$f_B(\gamma,\beta) = \frac{1}{2}\left(1 - sin^2(2\beta)sin^2(2\gamma)cos^2(4\gamma) - \frac{1}{4}sin(4\beta)sin(4\gamma)(1+cos^2(4\gamma))\right) $$
#
#
#
# These results can now be combined as described above, and the expectation value is therefore given by
#
#
#
# $$ F_1(\gamma,\beta) = 3 - \left(sin^2(2\beta)sin^2(2\gamma)- \frac{1}{2}sin(4\beta)sin(4\gamma)\right)\left(1 + cos^2(4\gamma)\right),$$
#
#
#
# We plot the function $F_1(\gamma,\beta)$ and use a simple grid search to find the parameters $(\gamma^*,\beta^*)$
# that maximize the expectation value.
# +
# Evaluate the function
step_size = 0.1;
a_gamma = np.arange(0, np.pi, step_size)
a_beta = np.arange(0, np.pi, step_size)
a_gamma, a_beta = np.meshgrid(a_gamma,a_beta)
F1 = 3-(np.sin(2*a_beta)**2*np.sin(2*a_gamma)**2-0.5*np.sin(4*a_beta)*np.sin(4*a_gamma))*(1+np.cos(4*a_gamma)**2)
# Grid search for the minimizing variables
result = np.where(F1 == np.amax(F1))
a = list(zip(result[0],result[1]))[0]
gamma = a[0]*step_size;
beta = a[1]*step_size;
# Plot the expetation value F1
fig = plt.figure()
ax = fig.gca(projection='3d')
surf = ax.plot_surface(a_gamma, a_beta, F1, cmap=cm.coolwarm, linewidth=0, antialiased=True)
ax.set_zlim(1,4)
ax.zaxis.set_major_locator(LinearLocator(3))
ax.zaxis.set_major_formatter(FormatStrFormatter('%.02f'))
plt.show()
#The smallest parameters and the expectation can be extracted
print('\n --- OPTIMAL PARAMETERS --- \n')
print('The maximal expectation value is: M1 = %.03f' % np.amax(F1))
print('This is attained for gamma = %.03f and beta = %.03f' % (gamma,beta))
# -
# ### 5.3 Quantum circuit<a id="implementation_sec53"></a>
#
# With these parameters we can now construct the circuit that prepares the trial state for the Graph
# or the Graph $G = (V,E)$ described above with vertex set $V = \{0,1,2,3,4\}$ and the edges are $E = \{(0,1),(0,2),(1,2),(3,2),(3,4),(4,2)\}$. The circuit is going to require $n = 5$ qubits and we prepare the state
#
#
#
# $$ |\psi_1(\gamma ,\beta)\rangle = e^{ -i\beta B } e^{ -i\gamma H } |+\rangle^n. $$
#
#
#
# Recall that the terms are given by $B = \sum_{k \in V} X_k$ and $H = \sum_{(k,m) \in E} \frac{1}{2}\left(1 - Z_kZ_m\right)$. To generate the circuit we follow these steps:
#
# - We first implement 5 Hadamard $H$ gates to generate the uniform superposition.
#
#
# - This is follow by $6$ Ising type gates $U_{k,l}(\gamma)$ with angle $\gamma$ along the edges $(k,l) \in E$. This gate can be expressed in terms of the native Qiskit gates as
#
#
#
# $$ U_{k,l}(\gamma) = C_{u1}(-2\gamma)_{k,l}u1(\gamma)_k u1(\gamma)_l$$
#
#
#
#
# - Lastly we apply single qubit $X$ rotations $X_k(\beta)$ for every vertex $k \in V$ with $\beta$ as angle. This gate directly parametrized as $X_k(\beta) = R_x(2\beta)_k$ in Qiskit.
#
#
# - In the last step we measure the qubits in the computational basis, i.e. we perform a $Z$ measurement and record the resulting bit-string $x \in \{0,1\}^5$.
# +
# prepare the quantum and classical resisters
QAOA = QuantumCircuit(len(V), len(V))
# apply the layer of Hadamard gates to all qubits
QAOA.h(range(len(V)))
QAOA.barrier()
# apply the Ising type gates with angle gamma along the edges in E
for edge in E:
k = edge[0]
l = edge[1]
QAOA.cp(-2*gamma, k, l)
QAOA.p(gamma, k)
QAOA.p(gamma, l)
# then apply the single qubit X rotations with angle beta to all qubits
QAOA.barrier()
QAOA.rx(2*beta, range(len(V)))
# Finally measure the result in the computational basis
QAOA.barrier()
QAOA.measure(range(len(V)),range(len(V)))
### draw the circuit for comparison
QAOA.draw()
# -
# ### 5.4 Cost function evaluation<a id="implementation_sec54"></a>
#
# Finally, we need a routine to compute the cost function value from the bit string.
# This is necessary to decide whether we have found a "good candidate" bit string $x$ but could also
# be used to estimate the expectation value $F_1(\gamma,\beta)$ in settings where the expectation value can not be evaluated directly.
# Compute the value of the cost function
def cost_function_C(x,G):
E = G.edges()
if( len(x) != len(G.nodes())):
return np.nan
C = 0;
for index in E:
e1 = index[0]
e2 = index[1]
w = G[e1][e2]['weight']
C = C + w*x[e1]*(1-x[e2]) + w*x[e2]*(1-x[e1])
return C
# ## 5a. Running QAOA on a simulator<a id="implementationsim"></a>
#
# We first run the algorithm on a local QASM simulator.
# +
# run on local simulator
backend = Aer.get_backend("qasm_simulator")
shots = 10000
TQAOA = transpile(QAOA, backend)
qobj = assemble(TQAOA, shots=shots)
QAOA_results = backend.run(qobj).result()
plot_histogram(QAOA_results.get_counts(),figsize = (8,6),bar_labels = False)
# -
# #### Evaluate the date from the simulation
#
# Let us now proceed to calculate the relevant information from the simulated data. We will use the
# obtained results to
#
# - Compute the mean energy and check whether it agrees with the theoretical prediction
# - Report the sampled bit string $x^*$ with the largest observed cost function $C(x^*)$
# - Plot the Histogram of the energies to see whether it indeed concentrates around the predicted mean
# +
# Evaluate the data from the simulator
counts = QAOA_results.get_counts()
avr_C = 0
max_C = [0,0]
hist = {}
for k in range(len(G.edges())+1):
hist[str(k)] = hist.get(str(k),0)
for sample in list(counts.keys()):
# use sampled bit string x to compute C(x)
x = [int(num) for num in list(sample)]
tmp_eng = cost_function_C(x,G)
# compute the expectation value and energy distribution
avr_C = avr_C + counts[sample]*tmp_eng
hist[str(round(tmp_eng))] = hist.get(str(round(tmp_eng)),0) + counts[sample]
# save best bit string
if( max_C[1] < tmp_eng):
max_C[0] = sample
max_C[1] = tmp_eng
M1_sampled = avr_C/shots
print('\n --- SIMULATION RESULTS ---\n')
print('The sampled mean value is M1_sampled = %.02f while the true value is M1 = %.02f \n' % (M1_sampled,np.amax(F1)))
print('The approximate solution is x* = %s with C(x*) = %d \n' % (max_C[0],max_C[1]))
print('The cost function is distributed as: \n')
plot_histogram(hist,figsize = (8,6),bar_labels = False)
# -
# ## 5b. Running QAOA on a real quantum device<a id="implementationdev"></a>
# We then see how the same circuit can be executed on real-device backends.
# + tags=["uses-hardware"]
# Use the IBMQ essex device
provider = IBMQ.load_account()
backend = provider.get_backend('ibmq_santiago')
shots = 2048
TQAOA = transpile(QAOA, backend)
qobj = assemble(TQAOA, shots=shots)
job_exp = backend.run(qobj)
job_monitor(job_exp)
# + tags=["uses-hardware"]
exp_results = job_exp.result()
plot_histogram(exp_results.get_counts(),figsize = (10,8),bar_labels = False)
# -
# #### Evaluate the data from the experiment
#
# We can now repeat the same analysis as before and compare the experimental result.
# + tags=["uses-hardware"]
# Evaluate the data from the experiment
counts = exp_results.get_counts()
avr_C = 0
max_C = [0,0]
hist = {}
for k in range(len(G.edges())+1):
hist[str(k)] = hist.get(str(k),0)
for sample in list(counts.keys()):
# use sampled bit string x to compute C(x)
x = [int(num) for num in list(sample)]
tmp_eng = cost_function_C(x,G)
# compute the expectation value and energy distribution
avr_C = avr_C + counts[sample]*tmp_eng
hist[str(round(tmp_eng))] = hist.get(str(round(tmp_eng)),0) + counts[sample]
# save best bit string
if( max_C[1] < tmp_eng):
max_C[0] = sample
max_C[1] = tmp_eng
M1_sampled = avr_C/shots
print('\n --- EXPERIMENTAL RESULTS ---\n')
print('The sampled mean value is M1_sampled = %.02f while the true value is M1 = %.02f \n' % (M1_sampled,np.amax(F1)))
print('The approximate solution is x* = %s with C(x*) = %d \n' % (max_C[0],max_C[1]))
print('The cost function is distributed as: \n')
plot_histogram(hist,figsize = (8,6),bar_labels = False)
# -
# ## 6. Problems<a id="problems"></a>
# 0. The QAOA algorithm produces a bit string, is this string the optimal solution for this graph? Compare the experimental results from the superconducting chip with the results from the local QASM simulation.
#
#
# 1. We have computed the cost function $F_1$ analytically in [section 5.2](#implementation_sec52). Verify the steps and compute $f_A(\gamma,\beta)$ as well $f_B(\gamma,\beta)$.
#
#
# 2. We have given an exact expression for $F_1$ in the Qiskit implementation.
#
# -Write a routine to estimate the expectation value $F_1(\gamma,\beta)$ from the samples obtained in the result (hint: use the function cost_function_C(x,G) from [section 5.4](#implementation_sec54) and the evaluation of the data in both section [5.a / 5.b](#implementationsim))
#
# -Use an optimization routine,e.g. SPSA from the VQE example in this tutorial, to optimize the parameters in the sampled $F_1(\gamma,\beta)$ numerically. Do you find the same values for $\gamma^*,\beta^*$ ?
#
#
# 3. The Trial circuit in [section 5.3](#implementation_sec53) corresponds to depth $p=1$ and was directly aimed at being compatible with the Hardware.
#
# -Use the routine from exercise 2 to evaluate the cost functions $F_p(\gamma,\beta)$ for $p=2,3$. What do you expect to see in the actual Hardware?
#
# -Generalize this class of trial state to other candidate wave functions, such as the Hardware efficient ansatz of Ref. [4](#references).
#
#
# 4. Consider an example of $MAX \;\; 3-SAT$ as discussed in the example section and modify the function cost_function_C(c,G) from [section 5.4](#implementation_sec54) you have used to compute $F_p$ accordingly. Run the QAOA algorithm for this instance of $MAX \; 3-SAT$ using the hardware efficient algorithm and analyze the results.
# ## 7. References<a id="references"></a>
# 1. Garey, <NAME>.; <NAME> (1979). Computers and Intractability: A Guide to the Theory of NP-Completeness. W. H. Freeman. ISBN 0-7167-1045-5
# 2. Goemans, <NAME>., and <NAME>. [Journal of the ACM (JACM) 42.6 (1995): 1115-1145](http://www-math.mit.edu/~goemans/PAPERS/maxcut-jacm.pdf).
# 3. Farhi, Edward, <NAME>, and <NAME>. "A quantum approximate optimization algorithm." arXiv preprint [arXiv:1411.4028 (2014)](https://arxiv.org/abs/1411.4028).
# 4. Kandala, Abhinav, et al. "Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets." [Nature 549.7671 (2017): 242](https://www.nature.com/articles/nature23879).
# 5. <NAME>, et al. "Quantum algorithms for fixed qubit architectures." arXiv preprint [arXiv:1703.06199 (2017)](https://arxiv.org/abs/1703.06199).
# 6. <NAME>. (1992), [IEEE Transactions on Automatic Control, vol. 37(3), pp. 332–341](https://ieeexplore.ieee.org/document/119632).
# 7. <NAME> and <NAME> "Training the quantum approximate optimization algorithm without access to a quantum processing unit" (2020) [Quantum Sci. Technol. 5 034008](https://doi.org/10.1088/2058-9565/ab8c2b)
import qiskit
qiskit.__qiskit_version__
|
content/ch-applications/qaoa.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import pandas as pd
from tabulate import tabulate
df = pd.read_csv('../CleanedData/betas.csv', delimiter = ',')
df.head()
len(df.columns)
df1 = df.iloc[:, range(4, 5605)]
df1.head()
df['mean']df1.mean(axis=1)
|
Python/Untitled.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] deletable=true editable=true
# # Building deep retrieval models
#
# **Learning Objectives**
#
# 1. Converting raw input examples into feature embeddings.
# 2. Splitting the data into a training set and a testing set.
# 3. Configuring the deeper model with losses and metrics.
#
#
#
#
#
# ## Introduction
# In [the featurization tutorial](https://www.tensorflow.org/recommenders/examples/featurization) we incorporated multiple features into our models, but the models consist of only an embedding layer. We can add more dense layers to our models to increase their expressive power.
#
# In general, deeper models are capable of learning more complex patterns than shallower models. For example, our [user model](fhttps://www.tensorflow.org/recommenders/examples/featurization#user_model) incorporates user ids and timestamps to model user preferences at a point in time. A shallow model (say, a single embedding layer) may only be able to learn the simplest relationships between those features and movies: a given movie is most popular around the time of its release, and a given user generally prefers horror movies to comedies. To capture more complex relationships, such as user preferences evolving over time, we may need a deeper model with multiple stacked dense layers.
#
# Of course, complex models also have their disadvantages. The first is computational cost, as larger models require both more memory and more computation to fit and serve. The second is the requirement for more data: in general, more training data is needed to take advantage of deeper models. With more parameters, deep models might overfit or even simply memorize the training examples instead of learning a function that can generalize. Finally, training deeper models may be harder, and more care needs to be taken in choosing settings like regularization and learning rate.
#
# Finding a good architecture for a real-world recommender system is a complex art, requiring good intuition and careful [hyperparameter tuning](https://en.wikipedia.org/wiki/Hyperparameter_optimization). For example, factors such as the depth and width of the model, activation function, learning rate, and optimizer can radically change the performance of the model. Modelling choices are further complicated by the fact that good offline evaluation metrics may not correspond to good online performance, and that the choice of what to optimize for is often more critical than the choice of model itself.
#
#
# Each learning objective will correspond to a __#TODO__ in the [student lab notebook](https://github.com/GoogleCloudPlatform/training-data-analyst/blob/master/courses/machine_learning/deepdive2/recommendation_systems/labs/deep_recommenders.ipynb) -- try to complete that notebook first before reviewing this solution notebook.
# + [markdown] colab_type="text" id="D7RYXwgbAcbU"
# ## Preliminaries
#
# We first import the necessary packages.
# + colab={} colab_type="code" id="dgFBaQZEbw3O"
# !pip install -q tensorflow-recommenders
# !pip install -q --upgrade tensorflow-datasets
# + [markdown] id="m7KBpffWzlxH"
# **NOTE: Please ignore any incompatibility warnings and errors and re-run the above cell before proceeding.**
#
# + colab={} colab_type="code" id="XbwMjnLP5nZ_"
import os
import tempfile
# %matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
import tensorflow_datasets as tfds
import tensorflow_recommenders as tfrs
plt.style.use('seaborn-whitegrid')
# -
# This notebook uses TF2.x.
# Please check your tensorflow version using the cell below.
# Show the currently installed version of TensorFlow
print("TensorFlow version: ",tf.version.VERSION)
# + [markdown] colab_type="text" id="tgKIjpQLAiax"
# In this tutorial we will use the models from [the featurization tutorial](https://www.tensorflow.org/recommenders/examples/featurization) to generate embeddings. Hence we will only be using the user id, timestamp, and movie title features.
# + colab={} colab_type="code" id="kc2REbOO52Fl"
ratings = tfds.load("movielens/100k-ratings", split="train")
movies = tfds.load("movielens/100k-movies", split="train")
ratings = ratings.map(lambda x: {
"movie_title": x["movie_title"],
"user_id": x["user_id"],
"timestamp": x["timestamp"],
})
movies = movies.map(lambda x: x["movie_title"])
# + [markdown] colab_type="text" id="5YZ2q5RXYNI6"
# We also do some housekeeping to prepare feature vocabularies.
# + colab={} colab_type="code" id="G5CVveCS9Doq"
timestamps = np.concatenate(list(ratings.map(lambda x: x["timestamp"]).batch(100)))
max_timestamp = timestamps.max()
min_timestamp = timestamps.min()
timestamp_buckets = np.linspace(
min_timestamp, max_timestamp, num=1000,
)
unique_movie_titles = np.unique(np.concatenate(list(movies.batch(1000))))
unique_user_ids = np.unique(np.concatenate(list(ratings.batch(1_000).map(
lambda x: x["user_id"]))))
# + [markdown] colab_type="text" id="mFJcCVMUQou3"
# ## Model definition
# + [markdown] colab_type="text" id="PtS6a4sgmI-c"
# ### Query model
#
# We start with the user model defined in [the featurization tutorial](https://www.tensorflow.org/recommenders/examples/featurization) as the first layer of our model, tasked with converting raw input examples into feature embeddings.
# + colab={} colab_type="code" id="_ItzYwMW42cb"
class UserModel(tf.keras.Model):
def __init__(self):
super().__init__()
self.user_embedding = tf.keras.Sequential([
tf.keras.layers.experimental.preprocessing.StringLookup(
vocabulary=unique_user_ids, mask_token=None),
tf.keras.layers.Embedding(len(unique_user_ids) + 1, 32),
])
self.timestamp_embedding = tf.keras.Sequential([
tf.keras.layers.experimental.preprocessing.Discretization(timestamp_buckets.tolist()),
tf.keras.layers.Embedding(len(timestamp_buckets) + 1, 32),
])
self.normalized_timestamp = tf.keras.layers.experimental.preprocessing.Normalization()
self.normalized_timestamp.adapt(timestamps)
def call(self, inputs):
# Take the input dictionary, pass it through each input layer,
# and concatenate the result.
return tf.concat([
self.user_embedding(inputs["user_id"]),
self.timestamp_embedding(inputs["timestamp"]),
self.normalized_timestamp(inputs["timestamp"]),
], axis=1)
# + [markdown] colab_type="text" id="hMQzxLqh42on"
# Defining deeper models will require us to stack mode layers on top of this first input. A progressively narrower stack of layers, separated by an activation function, is a common pattern:
#
# ```
# +----------------------+
# | 128 x 64 |
# +----------------------+
# | relu
# +--------------------------+
# | 256 x 128 |
# +--------------------------+
# | relu
# +------------------------------+
# | ... x 256 |
# +------------------------------+
# ```
# Since the expressive power of deep linear models is no greater than that of shallow linear models, we use ReLU activations for all but the last hidden layer. The final hidden layer does not use any activation function: using an activation function would limit the output space of the final embeddings and might negatively impact the performance of the model. For instance, if ReLUs are used in the projection layer, all components in the output embedding would be non-negative.
#
# We're going to try something similar here. To make experimentation with different depths easy, let's define a model whose depth (and width) is defined by a set of constructor parameters.
# + colab={} colab_type="code" id="5qfPi4I-Z0ph"
class QueryModel(tf.keras.Model):
"""Model for encoding user queries."""
def __init__(self, layer_sizes):
"""Model for encoding user queries.
Args:
layer_sizes:
A list of integers where the i-th entry represents the number of units
the i-th layer contains.
"""
super().__init__()
# TODO 1a
# We first use the user model for generating embeddings.
self.embedding_model = UserModel()
# TODO 1b
# Then construct the layers.
self.dense_layers = tf.keras.Sequential()
# Use the ReLU activation for all but the last layer.
for layer_size in layer_sizes[:-1]:
self.dense_layers.add(tf.keras.layers.Dense(layer_size, activation="relu"))
# No activation for the last layer.
for layer_size in layer_sizes[-1:]:
self.dense_layers.add(tf.keras.layers.Dense(layer_size))
def call(self, inputs):
feature_embedding = self.embedding_model(inputs)
return self.dense_layers(feature_embedding)
# + [markdown] colab_type="text" id="B9IqNTLmpJzs"
# The `layer_sizes` parameter gives us the depth and width of the model. We can vary it to experiment with shallower or deeper models.
# + [markdown] colab_type="text" id="XleMceZNHC__"
# ### Candidate model
#
# We can adopt the same approach for the movie model. Again, we start with the `MovieModel` from the [featurization](https://www.tensorflow.org/recommenders/examples/featurization) tutorial:
# + colab={} colab_type="code" id="oQZHX8bEHPOk"
class MovieModel(tf.keras.Model):
def __init__(self):
super().__init__()
max_tokens = 10_000
self.title_embedding = tf.keras.Sequential([
tf.keras.layers.experimental.preprocessing.StringLookup(
vocabulary=unique_movie_titles,mask_token=None),
tf.keras.layers.Embedding(len(unique_movie_titles) + 1, 32)
])
self.title_vectorizer = tf.keras.layers.experimental.preprocessing.TextVectorization(
max_tokens=max_tokens)
self.title_text_embedding = tf.keras.Sequential([
self.title_vectorizer,
tf.keras.layers.Embedding(max_tokens, 32, mask_zero=True),
tf.keras.layers.GlobalAveragePooling1D(),
])
self.title_vectorizer.adapt(movies)
def call(self, titles):
return tf.concat([
self.title_embedding(titles),
self.title_text_embedding(titles),
], axis=1)
# + [markdown] colab_type="text" id="x6vssqPYp-gY"
# And expand it with hidden layers:
# + colab={} colab_type="code" id="l1gTXkvQqHGA"
class CandidateModel(tf.keras.Model):
"""Model for encoding movies."""
def __init__(self, layer_sizes):
"""Model for encoding movies.
Args:
layer_sizes:
A list of integers where the i-th entry represents the number of units
the i-th layer contains.
"""
super().__init__()
self.embedding_model = MovieModel()
# Then construct the layers.
self.dense_layers = tf.keras.Sequential()
# Use the ReLU activation for all but the last layer.
for layer_size in layer_sizes[:-1]:
self.dense_layers.add(tf.keras.layers.Dense(layer_size, activation="relu"))
# No activation for the last layer.
for layer_size in layer_sizes[-1:]:
self.dense_layers.add(tf.keras.layers.Dense(layer_size))
def call(self, inputs):
feature_embedding = self.embedding_model(inputs)
return self.dense_layers(feature_embedding)
# + [markdown] colab_type="text" id="Cc4KbTNwHSvD"
# ### Combined model
#
# With both `QueryModel` and `CandidateModel` defined, we can put together a combined model and implement our loss and metrics logic. To make things simple, we'll enforce that the model structure is the same across the query and candidate models.
# + colab={} colab_type="code" id="26_hNJPKIh4-"
class MovielensModel(tfrs.models.Model):
def __init__(self, layer_sizes):
super().__init__()
self.query_model = QueryModel(layer_sizes)
self.candidate_model = CandidateModel(layer_sizes)
self.task = tfrs.tasks.Retrieval(
metrics=tfrs.metrics.FactorizedTopK(
candidates=movies.batch(128).map(self.candidate_model),
),
)
def compute_loss(self, features, training=False):
# We only pass the user id and timestamp features into the query model. This
# is to ensure that the training inputs would have the same keys as the
# query inputs. Otherwise the discrepancy in input structure would cause an
# error when loading the query model after saving it.
query_embeddings = self.query_model({
"user_id": features["user_id"],
"timestamp": features["timestamp"],
})
movie_embeddings = self.candidate_model(features["movie_title"])
return self.task(
query_embeddings, movie_embeddings, compute_metrics=not training)
# + [markdown] colab_type="text" id="8YXjsRsLTVzt"
# ## Training the model
# + [markdown] colab_type="text" id="QY7MTwMruoKh"
# ### Prepare the data
#
# We first split the data into a training set and a testing set.
# + colab={} colab_type="code" id="wMFUZ4dyTdYd"
tf.random.set_seed(42)
shuffled = ratings.shuffle(100_000, seed=42, reshuffle_each_iteration=False)
# TODO 2a
train = shuffled.take(80_000)
test = shuffled.skip(80_000).take(20_000)
cached_train = train.shuffle(100_000).batch(2048)
cached_test = test.batch(4096).cache()
# + [markdown] colab_type="text" id="I2HEuTBzJ9w5"
# ### Shallow model
#
# We're ready to try out our first, shallow, model!
# + [markdown] id="m7KBpffWzlxH"
# **NOTE: The below cell will take approximately 15~20 minutes to get executed completely.**
#
# + colab={} colab_type="code" id="NkoLkiQdK4Um"
num_epochs = 300
model = MovielensModel([32])
model.compile(optimizer=tf.keras.optimizers.Adagrad(0.1))
one_layer_history = model.fit(
cached_train,
validation_data=cached_test,
validation_freq=5,
epochs=num_epochs,
verbose=0)
accuracy = one_layer_history.history["val_factorized_top_k/top_100_categorical_accuracy"][-1]
print(f"Top-100 accuracy: {accuracy:.2f}.")
# + [markdown] colab_type="text" id="p90vFk8LvJXp"
# This gives us a top-100 accuracy of around 0.27. We can use this as a reference point for evaluating deeper models.
#
#
# + [markdown] colab_type="text" id="BjJ1anzuLXgN"
# ### Deeper model
#
# What about a deeper model with two layers?
# + [markdown] id="m7KBpffWzlxH"
# **NOTE: The below cell will take approximately 15~20 minutes to get executed completely.**
#
# + colab={} colab_type="code" id="11qAr5gGMUxE"
model = MovielensModel([64, 32])
model.compile(optimizer=tf.keras.optimizers.Adagrad(0.1))
two_layer_history = model.fit(
cached_train,
validation_data=cached_test,
validation_freq=5,
epochs=num_epochs,
verbose=0)
accuracy = two_layer_history.history["val_factorized_top_k/top_100_categorical_accuracy"][-1]
print(f"Top-100 accuracy: {accuracy:.2f}.")
# + [markdown] colab_type="text" id="NHnzYfQrOj8I"
# The accuracy here is 0.29, quite a bit better than the shallow model.
#
# We can plot the validation accuracy curves to illustrate this:
# + colab={} colab_type="code" id="xzriiDRlHEvo"
num_validation_runs = len(one_layer_history.history["val_factorized_top_k/top_100_categorical_accuracy"])
epochs = [(x + 1)* 5 for x in range(num_validation_runs)]
plt.plot(epochs, one_layer_history.history["val_factorized_top_k/top_100_categorical_accuracy"], label="1 layer")
plt.plot(epochs, two_layer_history.history["val_factorized_top_k/top_100_categorical_accuracy"], label="2 layers")
plt.title("Accuracy vs epoch")
plt.xlabel("epoch")
plt.ylabel("Top-100 accuracy");
plt.legend()
# + [markdown] colab_type="text" id="5ItwGCpXj9YF"
# Even early on in the training, the larger model has a clear and stable lead over the shallow model, suggesting that adding depth helps the model capture more nuanced relationships in the data.
#
# However, even deeper models are not necessarily better. The following model extends the depth to three layers:
# + [markdown] id="m7KBpffWzlxH"
# **NOTE: The below cell will take approximately 15~20 minutes to get executed completely.**
#
# + colab={} colab_type="code" id="es9k4o0ROt0l"
# TODO 3a
model = MovielensModel([128, 64, 32])
model.compile(optimizer=tf.keras.optimizers.Adagrad(0.1))
three_layer_history = model.fit(
cached_train,
validation_data=cached_test,
validation_freq=5,
epochs=num_epochs,
verbose=0)
accuracy = three_layer_history.history["val_factorized_top_k/top_100_categorical_accuracy"][-1]
print(f"Top-100 accuracy: {accuracy:.2f}.")
# + [markdown] colab_type="text" id="gLJV8jut40Ur"
# In fact, we don't see improvement over the shallow model:
# + colab={} colab_type="code" id="pIoVoMO1Kav6"
plt.plot(epochs, one_layer_history.history["val_factorized_top_k/top_100_categorical_accuracy"], label="1 layer")
plt.plot(epochs, two_layer_history.history["val_factorized_top_k/top_100_categorical_accuracy"], label="2 layers")
plt.plot(epochs, three_layer_history.history["val_factorized_top_k/top_100_categorical_accuracy"], label="3 layers")
plt.title("Accuracy vs epoch")
plt.xlabel("epoch")
plt.ylabel("Top-100 accuracy");
plt.legend()
# + [markdown] colab_type="text" id="wC95C1anA5Gx"
# This is a good illustration of the fact that deeper and larger models, while capable of superior performance, often require very careful tuning. For example, throughout this tutorial we used a single, fixed learning rate. Alternative choices may give very different results and are worth exploring.
#
# With appropriate tuning and sufficient data, the effort put into building larger and deeper models is in many cases well worth it: larger models can lead to substantial improvements in prediction accuracy.
#
#
# + [markdown] colab_type="text" id="dB09crfpgBx7"
# ## Next Steps
#
# In this tutorial we expanded our retrieval model with dense layers and activation functions. To see how to create a model that can perform not only retrieval tasks but also rating tasks, take a look at [the multitask tutorial](https://www.tensorflow.org/recommenders/examples/multitask).
|
courses/machine_learning/deepdive2/recommendation_systems/solutions/deep_recommenders.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
# # Data representation and interaction
# ## The pandas data-frame
# ### Creating dataframes: reading data files or converting arrays
data = pd.read_csv('data/brain_size.csv', sep=';', na_values='.')
data
# ### Manipulating data
data.shape
data.columns
data['Gender']
# +
# Simpler selection
data[data['Gender'] == 'Female']['VIQ'].mean()
# -
data.describe()
# #### groupby: splitting a dataframe on values of categorical variables:
# +
groupby_gender = data.groupby('Gender')
for gender, value in groupby_gender['VIQ']:
print((gender, value.mean()))
# -
groupby_gender.mean()
# ## Plotting data
# +
groupby_gender.boxplot(column=['FSIQ', 'VIQ', 'PIQ'])
# Scatter matrices for different columns
pd.plotting.scatter_matrix(data[['Weight', 'Height', 'MRI_Count']])
pd.plotting.scatter_matrix(data[['PIQ', 'VIQ', 'FSIQ']])
plt.show()
# -
# # Hypothesis testing: comparing two groups
from scipy import stats
# ## Student’s t-test: the simplest statistical test
# ### 1-sample t-test: testing the value of a population mean
# **scipy.stats.ttest_1samp()** tests if the population mean of data is likely to be equal to a given value (technically if observations are drawn from a Gaussian distributions of given population mean). It returns the T statistic, and the p-value
stats.ttest_1samp(data['VIQ'], 0)
# With a p-value of 10^-28 we can claim that the population mean for the IQ (VIQ measure) is not 0.
# ### 2-sample t-test: testing for difference across populations
# We have seen above that the mean VIQ in the male and female populations were different. To test if this is significant, we do a 2-sample t-test with **scipy.stats.ttest_ind():**
# +
female_viq = data[data['Gender'] == 'Female']['VIQ']
male_viq = data[data['Gender'] == 'Male']['VIQ']
stats.ttest_ind(female_viq, male_viq)
# -
# ## Paired tests: repeated measurements on the same indivuals
stats.ttest_ind(data['FSIQ'], data['PIQ'])
# The problem with this approach is that it forgets that there are links between observations: FSIQ and PIQ are measured on the same individuals. Thus the variance due to inter-subject variability is confounding, and can be removed, using a “paired test”, or “repeated measures test”:
stats.ttest_rel(data['FSIQ'], data['PIQ'])
# This is equivalent to a 1-sample test on the difference:
stats.ttest_1samp(data['FSIQ'] - data['PIQ'], 0)
# **T-tests assume Gaussian errors. We can use a Wilcoxon signed-rank test, that relaxes this assumption:**
stats.wilcoxon(data['FSIQ'], data['PIQ'])
# **Note:** The corresponding test in the non paired case is the Mann–Whitney U test, **scipy.stats.mannwhitneyu().**
# +
female_wt = data[data['Gender'] == 'Female']['Weight']
male_wt = data[data['Gender'] == 'Male']['Weight']
stats.mannwhitneyu(male_wt, female_wt)
# -
stats.mannwhitneyu(male_viq, female_viq)
# # Linear models, multiple factors, and analysis of variance
# ## “formulas” to specify statistical models in Python
# ### A simple linear regression
# Given two set of observations, x and y, we want to test the hypothesis that y is a linear function of x. In other terms:
#
# y = x * coef + intercept + e
#
# where e is observation noise. We will use the statsmodels module to:
# 1. Fit a linear model. We will use the simplest strategy, ordinary least squares (OLS).
# 2. Test that coef is non zero.
# **First, we generate simulated data according to the model:**
# +
x = np.linspace(-5, 5, 20)
np.random.seed(1)
# normal distributed noise
y = -5 + 3*x + 4*np.random.normal(size=x.shape)
# Create a data frame containing all the relevant variables
df = pd.DataFrame({'x': x, 'y': y})
df
# -
# **Then we specify an OLS model and fit it:**
# +
from statsmodels.formula.api import ols
model = ols("y~x", df).fit()
# -
model.summary()
# **Terminology:**
#
# Statsmodels uses a statistical terminology: the y variable in statsmodels is called ‘endogenous’ while the x variable is called exogenous.
#
# To simplify, y (endogenous) is the value you are trying to predict, while x (exogenous) represents the features you are using to make the prediction.
#
#
model.params
# ### Categorical variables: comparing groups or multiple categories
data = pd.read_csv('data/brain_size.csv', sep=';', na_values=".")
model = ols("VIQ ~ Gender + 1", data).fit()
model.summary()
# #### Tips on specifying model
#
# **Forcing categorical:**
#
# the ‘Gender’ is automatically detected as a categorical variable, and thus each of its different values are treated as different entities.
#
# An integer column can be forced to be treated as categorical using:
model = ols('VIQ ~ C(Gender)', data).fit()
model.summary()
# ### Link to t-tests between different FSIQ and PIQ
# To compare different types of IQ, we need to create a “long-form” table, listing IQs, where the type of IQ is indicated by a categorical variable:
# +
data_fisq = pd.DataFrame({'iq': data['FSIQ'], 'type': 'fsiq'})
data_piq = pd.DataFrame({'iq': data['PIQ'], 'type': 'piq'})
data_long = pd.concat((data_fisq, data_piq))
data_long
# -
model = ols("iq ~ type", data_long).fit()
model.summary()
# We can see that we retrieve the same values for t-test and corresponding p-values for the effect of the type of iq than the previous t-test:
stats.ttest_ind(data['FSIQ'], data['PIQ'])
# ### Multiple Regression: including multiple factors
# Consider a linear model explaining a variable z (the dependent variable) with 2 variables x and y:
#
# z = $x \, c_1 + y \, c_2 $+ i + e
# Example: the iris data (data/iris.csv)
data = pd.read_csv('data/iris.csv')
data
data.columns
pd.plotting.scatter_matrix(data[['sepal_length', 'sepal_width', 'petal_length', 'petal_width']])
plt.show()
model = ols("sepal_width ~ name + petal_length", data).fit()
model.summary()
# ### Post-hoc hypothesis testing: analysis of variance (ANOVA)
# In the above iris example, we wish to test if the petal length is different between versicolor and virginica, after removing the effect of sepal width. This can be formulated as testing the difference between the coefficient associated to versicolor and virginica in the linear model estimated above (it is an Analysis of Variance, ANOVA). For this, we write a vector of ‘contrast’ on the parameters estimated: we want to test "name[T.versicolor] - name[T.virginica]", with an F-test:
model.f_test([0, 1, -1, 0])
# # More visualization: seaborn for statistical exploration
# Seaborn combines simple statistical fits with plotting on pandas dataframes.
import urllib
import os
# **Load the data**
# +
# Give names to the columns
names = [
'EDUCATION: Number of years of education',
'SOUTH: 1=Person lives in South, 0=Person lives elsewhere',
'SEX: 1=Female, 0=Male',
'EXPERIENCE: Number of years of work experience',
'UNION: 1=Union member, 0=Not union member',
'WAGE: Wage (dollars per hour)',
'AGE: years',
'RACE: 1=Other, 2=Hispanic, 3=White',
'OCCUPATION: 1=Management, 2=Sales, 3=Clerical, 4=Service, 5=Professional, 6=Other',
'SECTOR: 0=Other, 1=Manufacturing, 2=Construction',
'MARR: 0=Unmarried, 1=Married',
]
short_names = [n.split(':')[0] for n in names]
data = pd.read_csv('data/wages.txt', skiprows=27, skipfooter=6, sep=None,
header=None, engine='python')
data.columns = short_names
data['WAGE'] = np.log10(data['WAGE'])
data
# -
data.columns
# #### Pairplot: scatter matrices
# +
import seaborn
seaborn.pairplot(data, vars=['WAGE', 'AGE', 'EDUCATION'], kind='reg')
# -
# #### Categorical variables can be plotted as the hue:
# +
seaborn.pairplot(data, vars=['WAGE', 'AGE', 'EDUCATION'],
kind='reg', hue='SEX')
# -
# ### lmplot: plotting a univariate regression
# A regression capturing the relation between one variable and another, eg wage and eduction, can be plotted using **seaborn.lmplot():**
seaborn.lmplot(y='WAGE', x='EDUCATION', data=data, hue='SEX')
# #### Robust regression
#
# Given that, in the above plot, there seems to be a couple of data points that are outside of the main cloud to the right, they might be outliers, not representative of the population, but driving the regression.
#
# To compute a regression that is less sentive to outliers, one must use a robust model. This is done in seaborn using robust=True in the plotting functions, or in statsmodels by replacing the use of the OLS by a “Robust Linear Model”, **statsmodels.formula.api.rlm().**
seaborn.lmplot(y='WAGE', x='EDUCATION', data=data, hue='SEX', robust=True)
# # Testing for interactions
# Do wages increase more with education for males than females?
#
# The plot above is made of two different fits. We need to formulate a single model that tests for a variance of slope across the to population. This is done via an **“interaction”**.
# +
result = ols(formula='WAGE ~ EDUCATION + SEX + EDUCATION * SEX', data=data).fit()
# -
result.summary()
# ### Take home messages
#
# * Hypothesis testing and p-value give you the **significance** of an effect / difference
# * **Formulas** (with categorical variables) enable you to express rich links in your data
# * **Visualizing** your data and simple model fits matters!
# * **Conditionning** (adding factors that can explain all or part of the variation) is important modeling aspect that changes the interpretation.
|
Statistics_in_Python/statistics_in_py.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import datetime
# +
aaxis_df=pd.read_csv('ICICIBANK.NS.csv')
aaxis_df[['Open', 'High','Low', 'Close','Adj Close','Volume']] = aaxis_df[['Open', 'High','Low', 'Close','Adj Close','Volume']].apply(pd.to_numeric, errors='coerce')
aaxis_df["Open"].fillna(value=aaxis_df["Open"].mean(), inplace=True)
aaxis_df["High"].fillna(value=aaxis_df["High"].mean(), inplace=True)
aaxis_df["Low"].fillna(value=aaxis_df["Low"].mean(), inplace=True)
aaxis_df["Close"].fillna(value=aaxis_df["Close"].mean(), inplace=True)
aaxis_df["Adj Close"].fillna(value=aaxis_df["Adj Close"].mean(), inplace=True)
aaxis_df["Volume"].fillna(value=aaxis_df["Volume"].mean(), inplace=True)
date_column=aaxis_df["Date"]
# +
from sklearn import preprocessing, cross_validation, svm
from sklearn.linear_model import LinearRegression
#Visualization
import matplotlib
import matplotlib.pyplot as plt
# %matplotlib inline
#aaxis_df.set_index("Date", inplace = True)
aaxis_df[['Adj Close','Open','High','Low','Close']].plot(figsize=(20,10), linewidth=1.5)
plt.legend(loc=2, prop={'size':20})
plt.ylabel('Price')
# +
from sklearn import preprocessing, cross_validation, svm
from sklearn.linear_model import LinearRegression
#Visualization
import matplotlib
import matplotlib.pyplot as plt
# %matplotlib inline
# +
#Moving Average
def MA(df, n):
name = 'SMA_' + str(n)
#MA = pd.Series(pd.rolling_mean(df['Close'], n), name = 'SMA_' + str(n))
#df = df.join(MA)
df[name]=pd.rolling_mean(df['Adj Close'],n)
return df
#Exponential Moving Average
def EMA(df, n):
name = 'EMA_' + str(n)
#MA = pd.Series(pd.rolling_mean(df['Close'], n), name = 'SMA_' + str(n))
#df = df.join(MA)
df[name]=pd.ewma(df['Adj Close'], span = n, min_periods = n - 1)
return df
# +
for i in [30,40,50]:
MA(aaxis_df,i)
for i in [30,40,50]:
EMA(aaxis_df,i)
# -
aaxis_df[['Adj Close', 'Close']].plot(figsize=(20,10), linewidth=1.5)
plt.legend(loc=2, prop={'size':20})
dates = np.array(aaxis_df["Date"])
#print(dates)
dates_check = dates[-30:]
dates = dates[:-30]
# +
# define a new feature, HL_PCT
aaxis_df['HL_PCT'] = (aaxis_df['High'] - aaxis_df['Low'])/(aaxis_df['Low']*100)
# define a new feature percentage change
aaxis_df['PCT_CHNG'] = (aaxis_df['Close'] - aaxis_df['Open'])/(aaxis_df['Open']*100)
# -
# +
columns_main=['Adj Close', 'HL_PCT', 'PCT_CHNG', 'Volume' ,'SMA_30', 'SMA_40', 'SMA_50', 'EMA_30', 'EMA_40', 'EMA_50']
aaxis_df = aaxis_df[columns_main]
# -
aaxis_df.fillna( value=0, inplace=True)
aaxis_df.isnull().sum()
# +
# pick a forecast column
forecast_col = 'Adj Close'
# Chosing 30 days as number of forecast days
forecast_out = int(30)
print('length =',len(aaxis_df), "and forecast_out =", forecast_out)
# -
# Creating label by shifting 'Adj. Close' according to 'forecast_out'
aaxis_df['label'] = aaxis_df[forecast_col].shift(-forecast_out)
print(aaxis_df.head(2))
print('\n')
# If we look at the tail, it consists of n(=forecast_out) rows with NAN in Label column
print(aaxis_df.tail(2))
# +
# Define features Matrix X by excluding the label column which we just created
X = np.array(aaxis_df.drop(['label'], 1))
# Using a feature in sklearn, preposessing to scale features
X = preprocessing.scale(X)
print(X[1,:])
# -
X_forecast_out = X[-forecast_out:]
X = X[:-forecast_out]
print ("Length of X_forecast_out:", len(X_forecast_out), "& Length of X :", len(X))
# A good test is to make sure length of X and y are identical
y = np.array(aaxis_df['label'])
y = y[:-forecast_out]
print('Length of y: ',len(y))
# +
X_train, X_test, y_train, y_test = cross_validation.train_test_split(X, y, test_size = 0.2)
print('length of X_train and x_test: ', len(X_train), len(X_test))
# -
# Train
from sklearn.ensemble import RandomForestRegressor
clf = RandomForestRegressor()
clf.fit(X_train,y_train)
# Test
accuracy = clf.score(X_test, y_test)
print("Accuracy of Linear Regression: ", accuracy)
forecast_prediction = clf.predict(X_forecast_out)
print(forecast_prediction)
#Make the final DataFrame containing Dates, ClosePrices, and Forecast values
actual = pd.DataFrame(dates, columns = ["Date"])
actual["ClosePrice"] = aaxis_df["Adj Close"]
actual["Forecast"] = np.nan
actual.set_index("Date", inplace = True)
forecast = pd.DataFrame(dates_check, columns=["Date"])
forecast["Forecast"] = forecast_prediction
forecast["ClosePrice"] = np.nan
forecast.set_index("Date", inplace = True)
var = [actual, forecast]
result = pd.concat(var) #This is the final DataFrame
result.info()
#Plot the results
result.plot(figsize=(20,10), linewidth=1.5)
plt.legend(loc=2, prop={'size':20})
plt.xlabel('Date')
plt.ylabel('Price')
a=result['ClosePrice'].iloc[-31]
b=result['Forecast'].iloc[-1]
ret=((b-a)/a)*100
ret
sub=pd.read_csv('submission.csv')
sub
sub=pd.read_csv('submission.csv')
sub.iloc[2,2]
for i in range(12):
if sub.loc[i]['Symbol']=='ICICIBANK.NS':
sub.iloc[i,2]="{0:.2f}".format(ret)
sub.to_csv('submission.csv',index=False)
sub
|
FORECASTING MODELS/ICICIBANK.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# MIT License
#
# Copyright (c) 2018-2021 <NAME>
#
# Permission is hereby granted, free of charge, to any person obtaining a copy
# of this software and associated documentation files (the "Software"), to deal
# in the Software without restriction, including without limitation the rights
# to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
# copies of the Software, and to permit persons to whom the Software is
# furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in all
# copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
# AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
# OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
# SOFTWARE.
# -
"""
File: Compute Accurate P.ipynb
Author: <NAME>
Date: 2018
Calculate the accurate version of the pressure correlation, based on the results from the least-squares analysis.
"""
# +
# Imports.
# %matplotlib inline
from sympy import *
init_printing(use_latex=True) # Make printing pretty
import mpmath
import cathode.constants as cs
import cathode.models.flow as cmf
import numpy as np
# -
# Define symbols we will use
P,do,dc,q,mdot,Id,mu,mu0,eps,a,M,Lo,pi = symbols('P,d_o,d_c,q,\dot{m},I_d,\mu,\mu0,\epsilon,a,M,L_o,\pi',real=True,positive=True)
# +
# Define the Pi products
PI1 = (P/(mu0*Id**2/(pi**2*do**2)))
PI2 = (do/dc)
PI3 = (do/Lo)
PI4 = ((mdot*q/(M*Id))**2 * (M*do/(mu0*q**2)))
PI5 = (mdot*a/(mu0*Id**2)) * 4*pi
PI6 = (q*eps/(do**2*Lo))*1/(mu0*Id**2/do**2) * (Lo/do) * 4*pi
PI7 = (mdot/(pi*(do/2)**2)*do/mu)
# +
### LEAST SQUARES METHOD
### Exponents from the least squares analysis (beta vector)
Cfit_l = 10**7.0639102021599545
e1 = 0.78967753163551446
e2 = 0.22577194077376095
e3 = -0.26766913155894489
e4 = 0.81622790719254079
e5 = 0.25441804916181782
e6 = 0.40591950688859579
### Power law
prod = (mu0*Id**2.0/(pi**2.0*do**2.0))*PI2**e1*PI3**e2*PI4**e3*PI5**e4*PI6**e5*PI7**e6
# -
### Pressure expression without the speed of sound
gam,kb,Tg,Mamu,C_fit = symbols('\gamma,k_B,Tg,M_a,C_f',real=True,positive=True)
prod_noa = C_fit*prod.subs(a,sqrt(gam*kb/M*Tg))
#prod_noa = C_fit*prod.subs(a,sqrt(gam*cs.gas_constant*1e3/(M/cs.atomic_mass)*Tg))
prod_noa.subs([(mu0,4*np.pi*10**(-7)),(q,cs.e),(pi,np.pi),(gam,5/3),(kb,cs.Boltzmann),(C_fit,Cfit_l)])
### Same as above
prod_SI = prod_noa.subs([(mu0,4*np.pi*10**(-7)),(q,cs.e),(pi,np.pi),(gam,5/3),(kb,cs.Boltzmann),(C_fit,Cfit_l)])
### Pressure expression, in Torr
Locm,docm,dccm,mdsccm = symbols('L_{ocm},d_{ocm},d_{ccm},\dot{m}_s')
prod_Torr = prod_SI.subs([(mdot,mdsccm*0.07174496*M/cs.e),(M,Mamu*cs.atomic_mass),(do,docm*1e-2),(dc,dccm*1e-2),(Lo,Locm*1e-2)])*760/101325
prod_Torr = prod_SI.subs([(mdot,mdsccm*0.07174496*M/cs.e),(M,Mamu*cs.atomic_mass),(do,docm*1e-2),(dc,dccm*1e-2),(Lo,Locm*1e-2)])*760/101325
prod_Torr
# +
### Below are example calculations using the correlations and other models
# -
prod_Torr.subs([(Id,10),(Tg,4443.663),(mdsccm,10),(Locm,0.074),(Mamu,131.293),(eps,12.1298),(mu,1.6538e-4),(dccm,0.38),(docm,0.104)])
mu_n = cmf.viscosity(3000,'Xe',units='Pa-s')
prod_Torr.subs([(Id,22),(Tg,3000),(mdsccm,5.5),(Locm,0.074),(Mamu,131.293),(eps,12.128),(mu,mu_n),(dccm,1.27),(docm,0.25)])
mu_n
mdot_sccm = 5.5
M_n = 131.293*cs.atomic_mass
mdot_n = mdot_sccm *M_n/cs.e * cs.sccm2eqA
prod_SI.subs([(Id,22),(Tg,3000),(mdot,mdot_n),(Lo,0.74e-3),(M,M_n),(eps,12.128),(mu,mu_n),(dc,1.27e-2),(do,2.5e-3)])*760/101325
prod_SI
TgK = 4000
mu_n = cmf.viscosity(TgK,'Xe',units='Pa-s')
Idvec = np.arange(8.0,27.0,1)
resvec = np.zeros_like(Idvec)
for idx,Idv in enumerate(Idvec):
resvec[idx] = prod_Torr.subs([(Id,Idv),(Tg,TgK),(mdsccm,5.5),(Locm,0.074),(Mamu,131.293),(eps,12.128),(mu,mu_n),(dccm,1.27),(docm,0.25)])
print(Idv,resvec[idx])
TgK = 4000
mu_n = cmf.viscosity(TgK,'Xe',units='Pa-s')
mdotvec = np.arange(4.0,11.0,1)
resvec = np.zeros_like(mdotvec)
for idx,mdot in enumerate(mdotvec):
resvec[idx] = prod_Torr.subs([(Id,22),(Tg,TgK),(mdsccm,mdot),(Locm,0.074),(Mamu,131.293),(eps,12.128),(mu,mu_n),(dccm,1.27),(docm,0.25)])
print(mdot,resvec[idx])
mu_n = cmf.viscosity(4000,'Xe',units='Pa-s')
mdotvec = np.arange(4.0,12.0,1)
resvec = np.zeros_like(mdotvec)
for idx,mdot in enumerate(mdotvec):
resvec[idx] = prod_Torr.subs([(Id,22),(Tg,4000),(mdsccm,mdot),(Locm,0.074),(Mamu,131.293),(eps,12.128),(mu,mu_n),(dccm,1.27),(docm,0.25)])
print(mdot,resvec[idx])
Cfit_l*1e-7
# NSTAR at 4000 K
TgK = 4000
P_outlet = 0.0
mu_n = cmf.viscosity(TgK,'Xe',units='Pa-s')
Lo = 0.74 # mm
do = 1.02 # mm
dc = 3.8 # mm
Lc = 25.4 # mm
mdotvec = np.array([2.47,2.47,2.81,3.7])
for mdot in mdotvec:
Po = cmf.poiseuille_flow(Lo*1e-3, do*1e-3, mdot, TgK, P_outlet, species='Xe')
Pu = cmf.poiseuille_flow(Lc*1e-3, dc*1e-3, mdot, TgK, Po, species='Xe')
Pud = cmf.modified_poiseuille_flow(Lo*1e-3,do*1e-3,mdot,TgK)
print(Pu,Pud)
# +
# PLHC @ 2000 K
TgK = 3000
mu_n = cmf.viscosity(TgK,'Ar',units='Pa-s')
Idvec = np.arange(100,301,25,dtype=np.float64)
resvec = np.zeros_like(Idvec)
for idx,Idv in enumerate(Idvec):
resvec[idx] = prod_Torr.subs([(Id,Idv),(Tg,TgK),(mdsccm,145),(Locm,0.15),(Mamu,39.948),(eps,15.7596),(mu,mu_n),(dccm,2.715),(docm,0.56)])
print(Idv,resvec[idx])
Lo = 1.5e-3
do = 5.6e-3
mdot = 145
Ppois = cmf.poiseuille_flow(Lo, do, mdot, TgK, 0, species='Ar')
Pdom = cmf.modified_poiseuille_flow(Lo,do,mdot,TgK)
print(Ppois,Pdom)
# -
mu_n
# +
# NEXIS @ 3000 K
TgK = 3000
mu_n = cmf.viscosity(TgK,'Xe',units='Pa-s')
Idvec = np.linspace(8,26,10)
resvec = np.zeros_like(Idvec)
for idx,Idv in enumerate(Idvec):
resvec[idx] = prod_Torr.subs([(Id,Idv),(Tg,TgK),(mdsccm,5.5),(Locm,0.074),(Mamu,131.293),(eps,12.198),(mu,mu_n),(dccm,1.27),(docm,0.275)])
print(Idv,resvec[idx])
Lo = 0.74e-3
do = 2.75e-3
mdot = 5.5
Ppois = cmf.poiseuille_flow(Lo, do, mdot, TgK, 0, species='Ar')
Pdom = cmf.modified_poiseuille_flow(Lo,do,mdot,TgK)
print(Ppois,Pdom)
# -
|
applications/Compute accurate P.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Estimating with DataExpansionFitter
# ## Estimation
# In the following we apply the estimation method of Lee et al. (2018). Note that the data dataframe must not contain a column named 'C'.
# +
from pydts.fitters import DataExpansionFitter
fitter = DataExpansionFitter()
fitter.fit(df=patients_df.drop(['C', 'T'], axis=1))
fitter.print_summary()
# -
from pydts.examples_utils.plots import plot_first_model_coefs
plot_first_model_coefs(models=fitter.event_models, times=fitter.times, train_df=patients_df, n_cov=5)
# ## Prediction
# Full prediction is given by the method predict_cumulative_incident_function()
#
# The input is a pandas.DataFrame() containing for each observation the covariates columns which were used in the fit() method (Z1-Z5 in our example).
#
# The following columns will be added:
#
# 1. The overall survival at each time point t
# 2. The hazard for each failure type $j$ at each time point t
# 3. The probability of event type $j$ at time t
# 4. The Cumulative Incident Function (CIF) of event type $j$ at time t
#
# In the following, we provide predictions for the individuals with ID values (pid) 0, 1 and 2. We transposed the output for easy view.
pred_df = fitter.predict_cumulative_incident_function(
patients_df.drop(['J', 'T', 'C', 'X'], axis=1).head(3)).set_index('pid').T
pred_df.index.name = ''
pred_df.columns = ['ID=0', 'ID=1', 'ID=2']
pred_df
|
docs/UsageExample-FittingDataExpansionFitter.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# ## Tutorial on how to combine different Fields for advection into a `SummedField` object
# In some oceanographic applications, you may want to advect particles using a combination of different velocity data sets. For example, particles at the surface are transported by a combination of geostrophic, Ekman and Stokes flow. And often, these flows are not even on the same grid.
#
# One option would be to write a `Kernel` that computes the movement of particles due to each of these flows. However, in Parcels it is possible to directly combine different flows (without interpolation) and feed them into the built-in `AdvectionRK4` kernel. For that, we use so-called `SummedField` objects.
#
# This tutorial shows how to use these `SummedField` with a very idealised example. We start by importing the relevant modules.
# %matplotlib inline
from parcels import Field, FieldSet, ParticleSet, JITParticle, plotTrajectoriesFile, AdvectionRK4
import numpy as np
# Now, let's first define a zonal and meridional velocity field on a 1kmx1km grid with a flat mesh. The zonal velocity is uniform and 1 m/s, and the meridional velocity is zero everywhere.
xdim, ydim = (10, 20)
Uflow = Field('U', np.ones((ydim, xdim), dtype=np.float32),
lon=np.linspace(0., 1e3, xdim, dtype=np.float32),
lat=np.linspace(0., 1e3, ydim, dtype=np.float32))
Vflow = Field('V', np.zeros((ydim, xdim), dtype=np.float32), grid=Uflow.grid)
fieldset_flow = FieldSet(Uflow, Vflow)
# We then run a particle and plot its trajectory
pset = ParticleSet(fieldset_flow, pclass=JITParticle, lon=[0], lat=[900])
output_file = pset.ParticleFile(name='SummedFieldParticle_flow.nc', outputdt=1)
pset.execute(AdvectionRK4, runtime=10, dt=1, output_file=output_file)
output_file.export() # export the trajectory data to a netcdf file
plotTrajectoriesFile('SummedFieldParticle_flow.nc');
# The trajectory plot shows a particle moving eastward on the 1 m/s flow, as expected
# Now, let's define another set of velocities (`Ustokes, Vstokes`) on a different, higher-resolution grid. This flow is southward at -0.2 m/s.
gf = 10 # factor by which the resolution of this grid is higher than of the original one.
Ustokes = Field('U', np.zeros((ydim*gf, xdim*gf), dtype=np.float32),
lon=np.linspace(0., 1e3, xdim*gf, dtype=np.float32),
lat=np.linspace(0., 1e3, ydim*gf, dtype=np.float32))
Vstokes = Field('V', -0.2*np.ones((ydim*gf, xdim*gf), dtype=np.float32), grid=Ustokes.grid)
fieldset_stokes=FieldSet(Ustokes, Vstokes)
# We run a particle in this `FieldSet` and also plot its trajectory
pset = ParticleSet(fieldset_stokes, pclass=JITParticle, lon=[0], lat=[900])
output_file = pset.ParticleFile(name='SummedFieldParticle_stokes.nc', outputdt=1)
pset.execute(AdvectionRK4, runtime=10, dt=1, output_file=output_file)
output_file.export() # export the trajectory data to a netcdf file
plotTrajectoriesFile('SummedFieldParticle_stokes.nc');
# Now comes the trick of the `SummedFields`. We can simply define a new `FieldSet` with a summation of different `Fields`, as in `U=fieldset_flow.U+fieldset_stokes.U`.
fieldset_sum = FieldSet(U=fieldset_flow.U+fieldset_stokes.U, V=fieldset_flow.V+fieldset_stokes.V)
# And if we then run the particle again and plot its trajectory, we see that it moves southeastward!
pset = ParticleSet(fieldset_sum, pclass=JITParticle, lon=[0], lat=[900])
output_file = pset.ParticleFile(name='SummedFieldParticle_sum.nc', outputdt=1)
pset.execute(AdvectionRK4, runtime=10, dt=1, output_file=output_file)
output_file.export() # export the trajectory data to a netcdf file
plotTrajectoriesFile('SummedFieldParticle_sum.nc');
# What happens under the hood is that each `Field` in the `SummedField` is interpolated separately to the particle location, and that the different velocities are added in each step of the RK4 advection. So `SummedFields` are effortless to users.
#
# Note that `SummedFields` work for any type of `Field`, not only for velocities. Any call to a `Field` interpolation (`fieldset.fld[time, lon, lat, depth]`) will return the sum of all `Fields` in the list if `fld` is a `SummedField`.
|
parcels/examples/tutorial_SummedFields.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Welcome to Marketing Report
# author: <NAME> <br>
# last edit: 13/10/19 <br>
# purpose: this report is use to show the advertising spending and pricing info in intopia
import pandas as pd
import os
from intopia_analysis import *
# +
path = r'%s' % os.getcwd().replace('\\','/')
df_contact = pd.read_csv('Intopia - Contact List - Sheet1.csv')
df_price = get_live_price_data(path,'phase2/period3/') #<---- ademend path between library
df_ad = get_advertising_data(path,'phase2/period4/') #<---- ademend path between library
# -
# # Team Tracking
team_tracker(df_contact, 17) #<-- admend the team you want information regarding
# # Marketing Expense Tracking
# ## Central Canada Marketing Expese
df_ad[df_ad['region'] == 'cc'].sort_values(by='Total', ascending=False)
# ## Western Canada Marketing Expese
df_ad[df_ad['region'] == 'wc'].sort_values(by=['type','Total'], ascending=False)
# # Pricing Information
print('Central Canada Price')
df_price[df_price['region'] == 'cc'].sort_values(by='Standard Price Cannabis', ascending=False)
print('Western Canada Price')
df_price[df_price['region'] == 'wc'].sort_values(by='Standard Price Cannabis', ascending=False)
print('Eastern Canada Price')
df_price[df_price['region'] == 'ec'].sort_values(by='Standard Price Cannabis', ascending=False)
|
.ipynb_checkpoints/marketing_report-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.8.10 64-bit (''base'': conda)'
# name: python3
# ---
# # Datetimes and timedeltas
#
# Python has several ways of representing datetimes and timedelta. This notebook shows the three most common ways and how to convert between them.
#
# Our general advice: *use pandas whenever you can*.
from datetime import datetime, timedelta
import numpy as np
import pandas as pd
# ## Datetime/timestamp
#
# The most common datetime representations in Python:
#
# * [datetime.datetime](https://docs.python.org/3/library/datetime.html#datetime-objects) (Python build-in)
# * [pd.Timestamp](https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.Timestamp.html)
# * [np.datetime64](https://numpy.org/doc/stable/reference/arrays.datetime.html)
#
# For string representations of datetimes use [ISO 8601](https://en.wikipedia.org/wiki/ISO_8601) (e.g. 2021-09-07T19:03:12Z) when possible.
#
# See [Python Pandas For Your Grandpa - 4.2 Dates and Times](https://www.youtube.com/watch?v=2VyOsBTWLOI) for a 18-min video introduction to three datetime representations (including time-zone handling).
# ### datetime.datetime
#
# The build-in datetime representation is quite simple.
dt_dt = datetime(2018,1,1,19,3,1)
dt_dt
# ### NumPy: np.datetime64
#
# np.datetime64 is essentially an integer (np.int64) representing the time since [epoch time](https://en.wikipedia.org/wiki/Unix_time) 1970-01-01 00:00:00 in a specified **unit** e.g. days, seconds or nano-seconds.
dt_np = np.datetime64('2018-01-01 19:03:01') # implicitly [s]
dt_np
np.int64(dt_np)
np.datetime64('1970-01-01 00:00:00') + np.int64(dt_np)
dt_np.dtype.name
dt_np.astype(datetime) # np.datetime64 -> datetime.datetime
# ### Pandas: pd.Timestamp
#
# pd.Timestamp uses np.datetime64[ns] under the hood. Pandas is good at recognizing various string representations of datetimes:
dt_pd = pd.Timestamp("2018/8/1") # equivalent to pd.to_datetime()
dt_pd
dt_pd.to_numpy() # pd.Timestamp -> np.datetime64
dt_pd.to_pydatetime() # pd.Timestamp -> datetime.datetime
pd.Timestamp(dt_np) # np.datetime64 -> pd.Timestamp
pd.Timestamp(dt_dt) # datetime.datetime -> pd.Timestamp
# ## Timedeltas
#
# We often need to represent differences between two timestamps. The most common representations are:
#
# * [datetime.timedelta](https://docs.python.org/3/library/datetime.html#timedelta-objects)
# * [pd.Timedelta](https://pandas.pydata.org/docs/reference/api/pandas.Timedelta.html)
# * [np.timedelta64](https://numpy.org/doc/stable/reference/arrays.datetime.html)
#
# Which corresponds to the above three representations of datetimes.
# ### datetime.timedelta
#
# The Python build-in way of working with differences between two datetimes.
del_dt = timedelta(days=6)
del_dt
dt_dt + del_dt # datetime.datetime + datetime.timedelta
dt_dt2 = datetime(2018,2,3,11,3,1)
dt_dt2 - dt_dt # datetime.datetime - datetime.datetime
# ### Numpy: np.timedelta64
#
# np.timedelta64 is an int64 in a specific unit e.g. seconds or nanoseconds.
dt_np2 = np.datetime64('2018-02-02 16:21:11')
del_np = dt_np2 - dt_np # np.datetime64 - np.datetime64
del_np
dt_np + del_np
np.int64(del_np), np.dtype(del_np).name
del_np.astype(timedelta) # np.timedelta64 -> datetime.timedelta
# ### Pandas: pd.Timedelta
dt_pd2 = pd.Timestamp("2018/8/4 23:01:03")
del_pd = dt_pd2 - dt_pd # pd.Timedelta - pd.Timedelta
del_pd
dt_pd + del_pd
del_pd.total_seconds()
print(pd.Timedelta(del_dt)) # datetime.timedelta -> pd.Timedelta
print(pd.Timedelta(del_np)) # np.datetime64 -> pd.Timedelta
print(del_pd.to_pytimedelta()) # pd.Timedelta -> datetime.timedelta
print(del_pd.to_timedelta64()) # pd.Timedelta -> np.timedelta64
# ## Datetime ranges
#
# Pandas is very powerful for vectors of datetimes. Use the pd.date_range() method for creating a pd.DatetimeIndex
dti = pd.date_range('2018', periods=8, freq='5D')
dti
tdi = dti - dti[0]
tdi
tdi.total_seconds().to_numpy()
# ### Slicing with DatetimeIndex
df = pd.DataFrame(np.ones(8), index=dti, columns=['one'])
df
df.loc["2018-01-05":"2018-01-21"] # notice that end of slice is included!!!
df.loc["2018-01-26":]
df.loc["2018-02"]
|
mini_book/datetime_timedelta.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from keras.preprocessing.image import ImageDataGenerator, array_to_img, img_to_array, load_img
# +
datagen = ImageDataGenerator(
rotation_range=40,
width_shift_range=0.2,
height_shift_range=0.2,
shear_range=0.2,
zoom_range=0.2,
horizontal_flip=True,
fill_mode='nearest')
img = load_img('data/train/cats/cat.10.jpg')
x = img_to_array(img)
x = x.reshape((1, ) + x.shape)
# -
x.shape
i = 0
for batch in datagen.flow(x, batch_size=1,
save_to_dir='preview',
save_prefix='cat',
save_format='jpeg'):
i += 1
if i > 20:
break
# +
from keras.models import Sequential
from keras.layers import Conv2D, MaxPooling2D
from keras.layers import Activation, Dropout, Flatten, Dense
model = Sequential()
model.add(Conv2D(32, (3, 3), input_shape=(150, 150, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Conv2D(32, (3,3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Conv2D(64, (3,3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Flatten())
model.add(Dense(64))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(1))
model.add(Activation('sigmoid'))
model.summary()
# -
model.compile(loss='binary_crossentropy',
optimizer='rmsprop',
metrics=['accuracy'])
# +
batch_size=16
train_datagen = ImageDataGenerator(
rescale=1./255,
shear_range=0.2,
zoom_range=0.2,
horizontal_flip=True)
test_datagen = ImageDataGenerator(rescale=1./255)
train_generator = train_datagen.flow_from_directory(
'data/train',
target_size=(150, 150),
batch_size=batch_size,
class_mode='binary')
validation_generator = test_datagen.flow_from_directory(
'data/validation',
target_size=(150, 150),
batch_size=batch_size,
class_mode='binary')
# +
from keras.callbacks import ModelCheckpoint
import os
save_checkpoint = ModelCheckpoint('weights-best.hdf5', monitor='val_acc', verbose=1, save_best_only=True, mode='max')
try:
model.load_weights('weights-best.hdf5')
except OSError:
pass
hist = model.fit_generator(
train_generator,
steps_per_epoch= 2000 // batch_size,
epochs = 50,
validation_data=validation_generator,
validation_steps=800 // batch_size,
callbacks=[save_checkpoint])
# +
from keras import applications
datagen = ImageDataGenerator(rescale=1./255)
model = applications.VGG16(include_top=False, weights='imagenet')
generator = datagen.flow_from_directory(
'data/train',
target_size=(150, 150),
batch_size=1,
class_mode=None,
shuffle=None)
bottleneck_features_train = model.predict_generator(
generator, 2000, verbose=1)
np.save(open('bottleneck_train_features.npy', 'w'), bottleneck_features_train)
generator = datagen.flow_from_directory(
'data/validation',
target_size=(150, 150),
batch_size=1,
class_mode=None,
shuffle=False)
bottleneck_features_validation = model.predict_generator(
generator, 800, verbose=1)
np.save(open('bottleneck_validation_features.npy', 'w'), bottleneck_features_validation)
# +
from keras.callbacks import ModelCheckpoint
train_data = np.load(open('bottleneck_train_features.npy', 'rb'))
train_labels = np.array([0] * 1000 + [1] * 1000)
validation_data = np.load(open('bottleneck_validation_features.npy', 'rb'))
validation_labels = np.array([0] * 400 + [1] * 400)
model = Sequential()
model.add(Flatten(input_shape=train_data.shape[1:]))
model.add(Dense(256, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(1, activation='sigmoid'))
model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['accuracy'])
save_checkpoint = ModelCheckpoint('weights-best-vgg.hdf5', monitor='val_acc', verbose=1, save_best_only=True, mode='max')
model.fit(train_data, train_labels,
epochs=50,
batch_size=16,
validation_data=(validation_data, validation_labels),
callbacks=[save_checkpoint])
# +
model.load_weights('weights-best-vgg.hdf5')
test_datagen = ImageDataGenerator(rescale=1./255)
test_generator = test_datagen.flow_from_directory('data/test_single', target_size=(150, 150),
batch_size=1,
class_mode=None,
shuffle=False)
predict = model.predict_generator(test_generator, steps=len(test_generator.filenames))
# -
|
ImageAugmentation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: env_implicit
# language: python
# name: env_implicit
# ---
# +
import pandas as pd
import numpy as np
import pickle
import sys
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.linear_model import LogisticRegression
import nltk
from nltk.stem.porter import *
import string
import re
import os
from vaderSentiment.vaderSentiment import SentimentIntensityAnalyzer as VS
from textstat.textstat import *
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report, accuracy_score, confusion_matrix, recall_score, ConfusionMatrixDisplay
from sklearn.utils import shuffle
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix
import warnings
warnings.simplefilter(action='ignore', category=FutureWarning)
import gc
import random
import matplotlib.pyplot as plt
from sklearn.model_selection import StratifiedKFold, GridSearchCV
from sklearn.pipeline import Pipeline
from sklearn.feature_selection import SelectFromModel
# +
import warnings
warnings.simplefilter(action='ignore', category=FutureWarning)
# +
stopwords = stopwords = nltk.corpus.stopwords.words("english")
other_exclusions = ["#ff", "ff", "rt"]
stopwords.extend(other_exclusions)
stemmer = PorterStemmer()
def preprocess(text_string):
"""
Accepts a text string and replaces:
1) urls with URLHERE
2) lots of whitespace with one instance
3) mentions with MENTIONHERE
This allows us to get standardized counts of urls and mentions
Without caring about specific people mentioned
"""
space_pattern = '\s+'
giant_url_regex = ('http[s]?://(?:[a-zA-Z]|[0-9]|[$-_@.&+]|'
'[!*\(\),]|(?:%[0-9a-fA-F][0-9a-fA-F]))+')
mention_regex = '@[\w\-]+'
parsed_text = re.sub(space_pattern, ' ', text_string)
parsed_text = re.sub(giant_url_regex, '', parsed_text)
parsed_text = re.sub(mention_regex, '', parsed_text)
return parsed_text
def tokenize(tweet):
"""Removes punctuation & excess whitespace, sets to lowercase,
and stems tweets. Returns a list of stemmed tokens."""
tweet = " ".join(re.split("[^a-zA-Z]+", tweet.lower())).strip()
tokens = [stemmer.stem(t) for t in tweet.split()]
return tokens
def basic_tokenize(tweet):
"""Same as tokenize but without the stemming"""
tweet = " ".join(re.split("[^a-zA-Z.,!?]+", tweet.lower())).strip()
return tweet.split()
vectorizer_david = TfidfVectorizer(tokenizer=tokenize,
preprocessor=preprocess,
ngram_range=(1, 3),
stop_words=stopwords,
use_idf=True,
smooth_idf=False,
norm=None,
decode_error='replace',
max_features=10000,
min_df=5,
max_df=0.75)
pos_vectorizer_david = TfidfVectorizer(
tokenizer=None,
lowercase=False,
preprocessor=None,
ngram_range=(1, 3),
stop_words=None,
use_idf=False,
smooth_idf=False,
norm=None,
decode_error='replace',
max_features=5000,
min_df=5,
max_df=0.75,
)
sentiment_analyzer = VS()
def count_twitter_objs(text_string):
"""
Accepts a text string and replaces:
1) urls with URLHERE
2) lots of whitespace with one instance
3) mentions with MENTIONHERE
4) hashtags with HASHTAGHERE
This allows us to get standardized counts of urls and mentions
Without caring about specific people mentioned.
Returns counts of urls, mentions, and hashtags.
"""
space_pattern = '\s+'
giant_url_regex = ('http[s]?://(?:[a-zA-Z]|[0-9]|[$-_@.&+]|'
'[!*\(\),]|(?:%[0-9a-fA-F][0-9a-fA-F]))+')
mention_regex = '@[\w\-]+'
hashtag_regex = '#[\w\-]+'
parsed_text = re.sub(space_pattern, ' ', text_string)
parsed_text = re.sub(giant_url_regex, 'URLHERE', parsed_text)
parsed_text = re.sub(mention_regex, 'MENTIONHERE', parsed_text)
parsed_text = re.sub(hashtag_regex, 'HASHTAGHERE', parsed_text)
return (parsed_text.count('URLHERE'), parsed_text.count('MENTIONHERE'),
parsed_text.count('HASHTAGHERE'))
def other_features(tweet):
"""This function takes a string and returns a list of features.
These include Sentiment scores, Text and Readability scores,
as well as Twitter specific features"""
sentiment = sentiment_analyzer.polarity_scores(tweet)
words = preprocess(tweet) #Get text only
syllables = textstat.syllable_count(words)
num_chars = sum(len(w) for w in words)
num_chars_total = len(tweet)
num_terms = len(tweet.split())
num_words = len(words.split())
avg_syl = round(float((syllables + 0.001)) / float(num_words + 0.001), 4)
num_unique_terms = len(set(words.split()))
###Modified FK grade, where avg words per sentence is just num words/1
FKRA = round(
float(0.39 * float(num_words) / 1.0) + float(11.8 * avg_syl) - 15.59,
1)
##Modified FRE score, where sentence fixed to 1
FRE = round(
206.835 - 1.015 * (float(num_words) / 1.0) - (84.6 * float(avg_syl)),
2)
twitter_objs = count_twitter_objs(tweet)
retweet = 0
if "rt" in words:
retweet = 1
features = [
FKRA, FRE, syllables, avg_syl, num_chars, num_chars_total, num_terms,
num_words, num_unique_terms, sentiment['neg'], sentiment['pos'],
sentiment['neu'], sentiment['compound'], twitter_objs[2],
twitter_objs[1], twitter_objs[0], retweet
]
#features = pandas.DataFrame(features)
return features
def get_feature_array(tweets):
feats = []
for t in tweets:
feats.append(other_features(t))
return np.array(feats)
# +
stopwords = nltk.corpus.stopwords.words("english")
other_exclusions = ["#ff", "ff", "rt"]
stopwords.extend(other_exclusions)
stemmer = PorterStemmer()
sentiment_analyzer = VS()
pos_vectorizer = TfidfVectorizer(
tokenizer=None,
lowercase=False,
preprocessor=None,
ngram_range=(1, 3),
stop_words=None,
use_idf=False,
smooth_idf=False,
norm=None,
decode_error='replace',
max_features=5000,
min_df=5,
max_df=0.75,
)
vectorizer = TfidfVectorizer(tokenizer=basic_tokenize,
preprocessor=preprocess,
ngram_range=(1, 3),
stop_words=stopwords,
use_idf=True,
smooth_idf=False,
norm=None,
decode_error='replace',
max_features=10000,
min_df=5,
max_df=0.75)
davidson_model = LogisticRegression(class_weight='balanced', penalty='l2')
hate_map = {0: "NON HATE", 1: "HATE"}
# +
def get_vectorisers(train_tweets):
global vectorizer_david, pos_vectorizer_david
vectorizer_david = vectorizer_david.fit(train_tweets)
train_tweet_tags = get_tag_list(train_tweets)
pos_vectorizer_david = pos_vectorizer_david.fit(
pd.Series(train_tweet_tags))
def reset_vectorisers():
global vectorizer_david, pos_vectorizer_david
vectorizer_david = TfidfVectorizer(tokenizer=tokenize,
preprocessor=preprocess,
ngram_range=(1, 3),
stop_words=stopwords,
use_idf=True,
smooth_idf=False,
norm=None,
decode_error='replace',
max_features=10000,
min_df=5,
max_df=0.75)
pos_vectorizer_david = TfidfVectorizer(
tokenizer=None,
lowercase=False,
preprocessor=None,
ngram_range=(1, 3),
stop_words=None,
use_idf=False,
smooth_idf=False,
norm=None,
decode_error='replace',
max_features=5000,
min_df=5,
max_df=0.75,
)
def get_tag_list(tweets):
tweet_tags = []
for tweet in tweets:
tokens = basic_tokenize(preprocess(tweet))
tags = nltk.pos_tag(tokens)
tag_list = [x[1] for x in tags]
tag_str = " ".join(tag_list)
tweet_tags.append(tag_str)
return tweet_tags
def return_feature_set(tweets):
global vectorizer_david, pos_vectorizer_david
tfidf = vectorizer_david.transform(tweets).toarray()
tweet_tags = get_tag_list(tweets)
pos = pos_vectorizer_david.transform(pd.Series(tweet_tags)).toarray()
feats = get_feature_array(tweets)
feat_M = np.concatenate([tfidf, pos, feats], axis=1)
del tfidf, pos, feats, tweet_tags
gc.collect()
return feat_M
def run_model(train_texts, train_labels):
reset_vectorisers()
get_vectorisers(train_texts)
X_train = return_feature_set(train_texts)
y_train = np.asarray(train_labels)
base_model = LogisticRegression()
base_model.fit(X_train, y_train)
print("TRAIN ACCURACY")
y_preds = base_model.predict(X_train)
report = classification_report(y_train, y_preds)
print(report)
return base_model
# +
folder = "ext_eval"
david = pd.read_csv(os.path.join(folder, "davidson_raw_labeled_data.csv"))
david['class'].hist()
plt.show()
print(david.groupby('class').count())
train_text = david['tweet']
train_label = david['class']
train_label_final = []
for i in train_label:
if i == 1 or i == 0:
train_label_final.append(1) # hate is 1
else:
train_label_final.append(0)
plt.hist(train_label_final)
plt.show()
c = list(zip(train_text, train_label_final))
random.shuffle(c)
train_texts, train_labels = zip(*c)
train_texts = list(train_texts)
train_labels = list(train_labels)
model = run_model(train_texts, train_labels)
# -
# ## Results
# +
def ext_eval_probs(yg, yp):
diff = []
for g, p in zip(yg, yp):
if g >= 0.5 and p >= 0.5: ## 0 is hate label so we take <0.5
diff.append(g - p)
return np.mean(diff)
def run_for_test(model_name):
folder = "ext_eval"
print(model_name)
file = os.path.join(folder, model_name + "_for_ext_eval.pkl")
with open(file, "rb") as f:
data = pickle.load(f)
xg = data["ground"]
xp = data["pred"]
xg = return_feature_set(xg)
xp = return_feature_set(xp)
yg = model.predict_proba(xg)[:, 1]
yp = model.predict_proba(xp)[:, 1]
print(ext_eval_probs(yg, yp))
def run_for_test_dict(model_name):
folder = "ext_eval"
print(model_name)
file = os.path.join(folder, model_name + "_for_ext_eval.pkl")
with open(file, "rb") as f:
data = pickle.load(f)
for k in data:
print("------k-----", k)
xg = data[k]["ground"]
xp = data[k]["pred"]
xg = return_feature_set(xg)
xp = return_feature_set(xp)
yg = model.predict_proba(xg)[:, 1]
yp = model.predict_proba(xp)[:, 1]
print(ext_eval_probs(yg, yp))
def execute_():
run_for_test("neutral")
run_for_test("drgpreds")
run_for_test("ntpcares")
run_for_test_dict("fgst")
run_for_test_dict("style")
run_for_test("nacl")
# -
execute_()
|
ext_eval/ext_eval_davidson.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Last Mile Delivery
# This is very famous and recurring problem in logistics and supply chain management. The problem is about how you can find the optimal schedule for delivering goods from transportation hub to delivery destination. The optimality criteria of this problem and its objectives are very diverse and contradicting like we want to look at the cost of the delivery routes and the time window of the delivery to many destinations and don't forget the dynamic nature of navigation and routing problems and what if the vehicle needs to go back .
#
# This is problem is pretty much like traveling salesman problem in the sense that you need to visit all delivery destination only once in the most optimal way based on your objectives. There is only one relaxed condition in TSP formulation which is that you can visit the transportation hub multiple times because you probably can't serve all delivery destinations demands with loading the vehicle one time, so you need to go back to the transportation hub multiple times between deliveries to load more goods.
#
# ---
#
# If the description above is a little confusing, we will formulate the problem step by step explaining the constraints and objectives of the problem and how you can make it more sophisticated and realistice. We also made some utilities in `utilities/src/poi.py` that would help you in this and future case studies and it is first time introduced in the course, so please bear with us.
from utilities import *
import networkx as nx
from tqdm import tqdm
from random import shuffle, randint
# ### Problem definition
#
# Imagine that we have medical supplies that we want to deliver to some hospitals in Toronto so these are the delivery destinations and the transportation hub would be the King subway station. We want to find the best schedule for our delivering vehicle to follow.
#
# Our deliveing vehicle should visit hospitals only once so we can't deliver hospital's demand of medical supplies in multiple deliveries, so we could go to our transportation hub to get more supplies to distribute to hospitals because the vehicle can't carry unlimited quantities of medical supplies.
# ---
#
# We will get the data of POIs (point of interest) using `poi` class which takes the name of the place (as saved in OSM databases) and the country of the place to limit the search space and that object will contains the coordinates of that POI and its full address and its OSM id.
#
# We are using [Nominatim](https://nominatim.org/) to do the geodecoding and getting the coordinates of POIs.
# +
sickChildren = poi("Hospital for Sick Children", "canada")
princessMargaret = poi("princess margaret hospital", "canada")
addictionCenter = poi("center for addiction and mental health", "canada")
torontoWestern = poi("toronto western hospital", "canada")
hillcrest = poi("hillcrest reactivation center", "canada")
runnymede = poi("Runnymede Healthcare Centre", "canada")
salvationArmy = poi("Salvation Army Toronto Grace Health Centre", "canada")
michaelGarron = poi("Michael Garron Hospital", "canada")
hollandBloorview = poi("Holland Bloorview Kids Rehabilitation Hospital", "canada")
northYork = poi("North York General Hospital", "canada")
scarborough = poi("Scarborough Health Network - Birchmount", "canada")
kingStation = poi("King Station", "canada")
POIS = [
# hospitals around UofT -- delivery destination
sickChildren,
princessMargaret,
addictionCenter,
torontoWestern,
hillcrest,
runnymede,
salvationArmy,
michaelGarron,
hollandBloorview,
northYork,
scarborough,
# king station -- transportation hub
kingStation
]
# -
# Let's explore `poi` object
print(sickChildren.address)
print(sickChildren.coordinates)
# if you print the object as it is, it will print the name of the place and its osmid
print(sickChildren)
# Drawing the POIs on the map for which we only need their coordinates and thanks to nominatim we get them.
# every marker contains a popup with the name of the POI
drawPOIS(POIS, zoom=10)
# We will construct a graph between all of the POIs to save the route data between every pair of nodes.
G = nx.DiGraph()
G.add_nodes_from(POIS)
# We will be using a method defined for `poi` object that retrieve the route between the object as a source and another object as destination and save it as an edge in the graph.
#
# The method `route_to` uses [OSRM](http://project-osrm.org/) as a routing engine, which returns the coordinates of the route between two coordinates and the length of the route and the expected duration for a vehicle (car-bicycle-foot) to travel that route.
#
# `OSRM` calculates the duration of a route based on multiple criteria like the max speed of the sub-routes and how many turns in the route and how much traffic lights and other obstacles are in the route.
#
# Its calculation is very close to what you would get from google or apple maps, and for how they do that exacly go to [`Project-OSRM/osrm-backend/profiles`](https://github.com/Project-OSRM/osrm-backend/tree/master/profiles) and check how they calculate the traveling time for cars, bicycles, and foot travel.
# this will take 1-2 minutes because you need to find
# two routes between each pair of POIs
for source in G.nodes():
for destination in G.nodes():
if source == destination: continue
G.add_edge(source, destination, route = source.route_to(destination))
# Let's see the route object between the nodes
G[sickChildren][princessMargaret]['route']
# So each edge in the graph has a route object the connects the two adjacent nodes to that edge, which contains the coordinates of that route and its length and estimated travel time.
# ---
# ---
#
# ### Problem Formulation
#
# We will define a list of delivery destinations which consists of an object/dictionary that describes the POI and its demand and some time interval that the delivery should arrive in.
#
# We are treating the transportation hub the same as delivery destinations but with a negative demand, so when we visit it the capacity of the vehicle increases and arbitrary big time interval so we don't penalize the vehicle any time it returns back to the transportation hub to get more goods.
#
# The following heuristic can solve the problem for arbitrary number of delivery destinations, but with only a single transportation hub. We will talk at the end how to solve the problem with arbitrary number of delivery destionations **and** transportation hubs.
# +
delivery_destinations = [
{
'POI':sickChildren,
'demand': 50,
'time_interval':(0, 300),
},
{
'POI':princessMargaret,
'demand':60,
'time_interval':(300, 500),
},
{
'POI':addictionCenter,
'demand':40,
'time_interval':(500, 700),
},
{
'POI':torontoWestern,
'demand':85,
'time_interval':(700, 900),
},
{
'POI':hillcrest,
'demand':100,
'time_interval':(900, 1200),
},
{
'POI':runnymede,
'demand':120,
'time_interval':(1200, 1700),
},
{
'POI':salvationArmy,
'demand':200,
'time_interval':(1700, 2100),
},
{
'POI':michaelGarron,
'demand':100,
'time_interval':(2400, 3100),
},
{
'POI':hollandBloorview,
'demand': 90,
'time_interval':(3100, 4000),
},
{
'POI':northYork,
'demand':30,
'time_interval':(4000, 4500),
},
{
'POI':scarborough,
'demand':200,
'time_interval':(4700, 5200),
},
]
#####################################################
transportation_hub = {
'POI': kingStation,
'demand': -200,
'time_interval': (-999999, 999999)
}
# -
# As any NP-hard problem we can only solve the problem by approximation, that usually happens by generating solutions and evaluates these solutions by some criteria and hopefully choose the best one.
#
# Our solution would be a certain permutation for the list of delivery destinations with the oocusional occurence of the vehicle returning back to the transportation hub to load some goods, so at the end would be a list of POIs that starts and ends with the transportation hub and in the middle of the list we would have permutation of the delivery destinations and some occusional visits to the transportation hub.
#
# ---
#
# ### the heuristic function
#
# The heuristic function takes a permutation for the delivery destinations and add the appropriate number of times that the vehicle needs to return to the transportation hub to get more goods, while that it computes the cost of that tour by penalizing when the goods delivered are not withing the time interval and the length of all routes the vehicle between the POIs.
def evaluate_cost(G, delivery_destinations, transportation_hub):
# accumulative cost of all the moves that would be returned
cost = 0
# the starting of the clock
time = 0
schedule = list()
# we will begine the schedule by visiting the transportation hub
schedule.append((transportation_hub['POI'], time))
# -1 * negative demand of transportation hub so the capacity increase
current_capacity = -1 * transportation_hub['demand']
# we will assume at first that the vehicle don't need to go back
# to the transportation hub and we will add more as needed while
# the algorithm is running based on the demand of next stopping point
complete_tour = [transportation_hub] + delivery_destinations + [transportation_hub]
i = 0
j = 1
while j < len(complete_tour):
start_subroute = complete_tour[i]
end_subroute = complete_tour[j]
# check if the demand of the next goal
# could be fulfilled, if not add transportation
# hub node in the tour and repeat the iteration
if end_subroute['demand'] > current_capacity:
complete_tour = complete_tour[:j] + [transportation_hub] + complete_tour[j:]
continue
# if we are going to deliver goods to destination point
# deduct its demand from vehicle capacity, but if we
# are going to visit transportation hub the capacity will
# increase
current_capacity -= end_subroute['demand']
# retrieve the time interval
time_of_arrival = end_subroute['time_interval']
# calculate the current time of arrival to the destination
time += G[start_subroute['POI']][end_subroute['POI']]['route']['duration']
# If the time is not within the interval we penalize that
# The penalization function doesn't discern if you
# arrived before or after the interval
if int(time) not in range(*time_of_arrival):
cost += (time - min(time_of_arrival))**2
# add the length of the route to the cost
cost += G[start_subroute['POI']][end_subroute['POI']]['route']['duration']
cost += G[start_subroute['POI']][end_subroute['POI']]['route']['length']
# add the visited POI to the scedule and its time
schedule.append((end_subroute['POI'], time))
# move to the next iteration
i += 1
j += 1
return cost, schedule
# we will need an independent function to calculate the duration
# of the whole schedule so a give solution cost value would make
# sense for us
def calculate_duration(G, schedule):
# remember that the schedule is
# a list of tuples (POI, time) so we need
# to fix that first
POIs = [pair[0] for pair in schedule]
cost = 0
for u, v in zip(POIs, POIs[1:]):
cost += G[u][v]['route']['duration']
return cost
# We will be be solving the problem using simulated annealing so you start with a random solution and try to change it a little bit every iterations to find the best answer possible
# temperature scheduling function
schedule = exp_schedule(200, 0.05, 10000)
# +
# %%time
current = delivery_destinations[:]
states = []
# shuffle the first list
# to get our random solution
shuffle(current)
for t in tqdm(range(sys.maxsize)):
T = schedule(t)
if T < 0.01:
# when we arrive at the solution we only need to see the schedule
# the cost of the schedule is a little bit irrelevant outside the
# function
_, solution = evaluate_cost(G, current, transportation_hub)
break
# generate 5 more random permutations
# by swapping two children
neighbors = list()
for _ in range(5):
child = current[:]
i = randint(0, len(child)-1)
j = randint(0, len(child)-1)
child[i], child[j] = child[j], child[i]
neighbors.append(child)
next_choice = random.choice(neighbors)
delta_e = evaluate_cost(G, next_choice, transportation_hub)[0] - evaluate_cost(G, current, transportation_hub)[0]
if delta_e < 0 or probability(np.exp(-1 * delta_e/T)):
current = next_choice
# would be used to visualize the convergence of the algorithm
_, solution = evaluate_cost(G, current, transportation_hub)
states.append(calculate_duration(G, solution))
# -
# the solution converged after 100 iterations
import matplotlib.pyplot as plt
plt.xlabel("# iterations")
plt.ylabel("cost (seconds)")
plt.plot(states)
plt.show()
# The schedule
solution
# As you can see we start and finished at King station and hit all the delivery destinations once with occusional returns to the station to get more goods and supplies.
#
# ---
#
# Let's visualize the first sub-routes in the schedule
POIs = [pair[0] for pair in solution]
POIs
first_route = G[POIs[0]][POIs[1]]['route']['coords']
drawRoute(first_route)
second_route = G[POIs[1]][POIs[2]]['route']['coords']
drawRoute(second_route)
third_route = G[POIs[2]][POIs[3]]['route']['coords']
drawRoute(third_route)
fourth_route = G[POIs[3]][POIs[4]]['route']['coords']
drawRoute(fourth_route)
# ## Dealing with multiple transportation hubs
# As you probably see, the last mile delivery problem with a single transportation hub and arbitrary number of delivery destinations is trivial and its running time for generating new solutions and getting their cost was rather fast because all you have to do is just manipulating a single array of objects.
#
# But handling multiple transportation hubs is completely different beast. The problem could be solved by reducing the problem to a network flow problem, where we would have bipartite graph with two different vertex sets: the first one is the set containing all the delivery destinations and the other set containing all transportation hubs. Your problem is to find the maximum flow and maximum matching between the tranportation hub vertices and delivery destinations vertices and you can add the constraints like time windows and capacity of the vehicles as extra layer of vertices between the layer of transportation hubs and the layer of vertices of delivery destinations.
#
# Solving your problem as flow problem will give you the **exact** solution for the scheduling and you don't need to resort for approximations most of the time. Linear programming is used to solve these kind of problems, but you need to be aware that linear programming solutions sometimes under some conditions can degenerate to exponential and intractable problems, in that case we resort to approximation search algorithms like SA and genetic algorithm.
|
last_mile.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.9.4 64-bit
# name: python3
# ---
import matplotlib
import pandas as pd
import numpy as np
import numpy.linalg as LA
from scipy import stats
import math
import numpy.ma as ma
import matplotlib.pyplot as plt
import numpy.ma as ma
from pathlib import Path
import sys
import qualities
import plotting_func
import glob
files = glob.glob("./outputs/*")
print(files)
# + tags=[]
files = glob.glob("./outputs/*")
print(files)
#print(len(files))
models = ['NATST','NATSS']
file12 = {}
file90 = {}
results12 = {}
results90 = {}
sorted_dict12 = {}
sorted_dict90 = {}
plot12 = {}
plot90 = {}
title = {}
for model in models:
datasets = ['cifar10','cifar100']
file12[model] = {}
file90[model] = {}
results12[model] = {}
results90[model] = {}
sorted_dict12[model] = {}
sorted_dict90[model] = {}
plot12[model] = {}
plot90[model] = {}
title[model] = {}
for dataset in datasets:
for x in files:
if(dataset + "-" in x and model in x and "-12.csv" in x):
file12[model][dataset] = x
print(x)
if(dataset + "-" in x and model in x and "-200.csv" in x):
file90[model][dataset] = x
print(x)
if(dataset + "-" in x and model in x and "-90.csv" in x):
file90[model][dataset] = x
print(x)
#print(results12)
results12[model][dataset] = qualities.correlate(file12[model][dataset].split(os.sep)[-1][0:-4])
sorted_dict12[model][dataset] = results12[model][dataset]["spearman"]
results90[model][dataset] = qualities.correlate(file90[model][dataset].split(os.sep)[-1][0:-4])
sorted_dict90[model][dataset] = results90[model][dataset]["spearman"]
'''
after_process = ["0", "1", "2", "3", "4", "5", "6", "7"]
sorted_dict12[dataset], title[dataset] = plotting_func.rename_dict(sorted_dict12[dataset], after_process[6], "gap") #"test", "gap"
sorted_dict90[dataset], title[dataset] = plotting_func.rename_dict(sorted_dict90[dataset], after_process[6], "gap") #"test", "gap"
#Remove all agg methods except L2 and L3
plot12[dataset] = {}
plot90[dataset] = {}
for x in sorted_dict90[dataset].keys():
if("L2" in x or "L3" in x):
plot12[dataset][x] = sorted_dict12[dataset][x]
plot90[dataset][x] = sorted_dict90[dataset][x]
'''
# +
#Debugging
for x in results90['NATSS']['cifar100']['spearman'].keys(): # spearman
if("spec" in x and "L3_7" in x):
print(x, results90['NATST']['cifar100']['spearman'][x])
for x in results90['NATST']['cifar100']['pearson'].keys(): # spearman
if("spec" in x and "L3_7" in x):
print(x, results90['NATST']['cifar100']['pearson'][x])
# -
newgap90 = dict()
newgap12 = dict()
newtest90 = dict()
newtest12 = dict()
for model in models:
newgap90[model] = dict()
newgap12[model] = dict()
newtest90[model] = dict()
newtest12[model] = dict()
for dataset in datasets:
for x in results90[model][dataset]["spearman"]:
if("gap" in x):
if("QE" in x and "L2_6" in x):
newgap90[model][x+"-"+dataset] = results90[model][dataset]["spearman"][x]
newgap12[model][x+"-"+dataset] = results12[model][dataset]["spearman"][x]
if("QS" in x and "L3_0" in x):
newgap90[model][x+"-"+dataset] = results90[model][dataset]["spearman"][x]
newgap12[model][x+"-"+dataset] = results12[model][dataset]["spearman"][x]
if("spec" in x and "L3_7" in x):
newgap90[model][x+"-"+dataset] = results90[model][dataset]["spearman"][x]
newgap12[model][x+"-"+dataset] = results12[model][dataset]["spearman"][x]
if("fro" in x and "L3_7" in x):
newgap90[model][x+"-"+dataset] = results90[model][dataset]["spearman"][x]
newgap12[model][x+"-"+dataset] = results12[model][dataset]["spearman"][x]
elif("test" in x):
if("QE" in x and "L2_6" in x):
newtest90[model][x+"-"+dataset] = results90[model][dataset]["spearman"][x]
newtest12[model][x+"-"+dataset] = results12[model][dataset]["spearman"][x]
if("QS" in x and "L3_0" in x):
newtest90[model][x+"-"+dataset] = results90[model][dataset]["spearman"][x]
newtest12[model][x+"-"+dataset] = results12[model][dataset]["spearman"][x]
if("spec" in x and "L3_7" in x):
newtest90[model][x+"-"+dataset] = results90[model][dataset]["spearman"][x]
newtest12[model][x+"-"+dataset] = results12[model][dataset]["spearman"][x]
if("fro" in x and "L3_7" in x):
newtest90[model][x+"-"+dataset] = results90[model][dataset]["spearman"][x]
newtest12[model][x+"-"+dataset] = results12[model][dataset]["spearman"][x]
# if("QS" in x):
# if("L3" in x and "_0" in x):
# newgap90[model][x+"-"+dataset] = results90[model][dataset]["spearman"][x]
# newgap12[model][x+"-"+dataset] = results12[model][dataset]["spearman"][x]
# # elif("path" in x):
# # newgap90[model][x+"-"+dataset] = results90[model][dataset]["spearman"][x]
# # newgap12[model][x+"-"+dataset] = results12[model][dataset]["spearman"][x]
# else:
# if("L2" in x and "_6" in x):
# newgap90[model][x+"-"+dataset] = results90[model][dataset]["spearman"][x]
# newgap12[model][x+"-"+dataset] = results12[model][dataset]["spearman"][x]
# elif("test" in x):
# if("QS" in x):
# if("L3" in x and "_0" in x):
# newtest90[model][x+"-"+dataset] = results90[model][dataset]["spearman"][x]
# newtest12[model][x+"-"+dataset] = results12[model][dataset]["spearman"][x]
# # elif("path" in x):
# # newtest90[model][x+"-"+dataset] = results90[model][dataset]["spearman"][x]
# # newtest12[model][x+"-"+dataset] = results12[model][dataset]["spearman"][x]
# else:
# if("L2" in x and "_6" in x):
# newtest90[model][x+"-"+dataset] = results90[model][dataset]["spearman"][x]
# newtest12[model][x+"-"+dataset] = results12[model][dataset]["spearman"][x]
print(newtest12)
# +
def rename_dict(sorted_dict):
#Renames dict to latex
temp = {}
for x in sorted_dict.keys():
#print(x)
#Translate Name to Latex
name = '${'
if('AE' in x):
name += '\widehat{'
elif('BE' in x):
name += '{'
if('QS' in x):
name += 'Q}_{SQ}'
elif('QE' in x):
name += 'Q}_{E}'
elif('fro' in x):
name += 'Q}_{F}'
elif('spec' in x):
name += 'Q}_{S}'
elif('path' in x):
name += '{Q}_{P}'
if('L1' in x):
name += '^{L1}'
elif('L2' in x):
name += '^{L2}'
elif('L3' in x):
name += '^{p}'
elif('L4' in x):
name += '^{L4}'
elif('L5' in x):
name += '^{L5}'
name += '}$'
name += "-"+(x.split("-")[-1]).upper()
#print(name)
temp[name] = sorted_dict[x]
return temp
# +
for model in models:
newgap12[model] = rename_dict(newgap12[model])
newgap90[model] = rename_dict(newgap90[model])
newtest12[model] = rename_dict(newtest12[model])
newtest90[model] = rename_dict(newtest90[model])
labels = []
for x in newtest12[model].keys():
labels.append(x.split('-')[0])
#labels.extend(labels)
print(labels)
# +
width = 0.45
x_size = 18
y_size = 16
title_size = 17
y_label = 'CIFAR10 CIFAR100'
figsize=(6.5,8)
plt.figure(figsize=figsize)
model = 'NATST' #NATST, NATSS
x = np.arange(len(newtest90[model].values()))
plt.barh(x + width/2, newtest90[model].values(), width, label='200', color = "red")
plt.barh(x - width/2, newtest12[model].values(), width, label='12', color = "orange")
plt.yticks(x, labels = labels, fontsize = y_size)
plt.title("NATS Topology Search Space with Test Accuracy", fontsize = title_size)
plt.xlabel('Spearman Correlation', fontsize = x_size)
plt.ylabel(y_label, fontsize = y_size)
plt.xticks(fontsize = x_size)
plt.xlim([0, 1])
#plt.legend()
plt.savefig('figures/' + model[-1] + '_Test.png', dpi = 500)
plt.show()
model = 'NATSS'
plt.figure(figsize=figsize)
x = np.arange(len(newtest90[model].values()))
plt.barh(x + width/2, newtest90[model].values(), width, label='200', color = "red")
plt.barh(x - width/2, newtest12[model].values(), width, label='12', color = "orange")
plt.yticks(x, labels = labels, fontsize = y_size)
plt.title("NATS Size Search Space with Test Accuracy", fontsize = title_size)
plt.xlabel('Spearman Correlation', fontsize = x_size)
plt.ylabel(y_label, fontsize = y_size)
plt.xlim([0, 1])
plt.xticks(fontsize = x_size)
#plt.legend()
plt.savefig('figures/' + model[-1] + '_Test.png', dpi = 500)
plt.show()
# +
model = 'NATST'
plt.figure(figsize=figsize)
x = np.arange(len(newgap90[model].values()))
plt.barh(x + width/2, newgap90[model].values(), width, label='200', color = "red")
plt.barh(x - width/2, newgap12[model].values(), width, label='12', color = "orange")
plt.yticks(x, labels = labels, fontsize = y_size)
plt.title("NATS Topology Search Space with Generalization Gap", fontsize = title_size)
plt.xlabel('spearman Correlation', fontsize = x_size)
plt.ylabel(y_label, fontsize = y_size)
plt.xlim([0, 1])
plt.xticks(fontsize = x_size)
#plt.legend()
plt.savefig('figures/' + model[-1] + '_Gap.png', dpi = 500)
plt.show()
model = 'NATSS'
plt.figure(figsize=figsize)
x = np.arange(len(newgap90[model].values()))
plt.barh(x + width/2, newgap90[model].values(), width, label='200', color = "red")
plt.barh(x - width/2, newgap12[model].values(), width, label='12', color = "orange")
plt.yticks(x, labels = labels, fontsize = y_size)
plt.title("NATS Size Search Space with Generalization Gap", fontsize = title_size)
plt.xlabel('Spearman Correlation', fontsize = x_size)
plt.ylabel(y_label, fontsize = y_size)
plt.xlim([0, 1])
plt.xticks(fontsize = x_size)
#plt.legend()
plt.savefig('figures/' + model[-1] + '_Gap.png', dpi = 500)
plt.show()
# +
#Legend
import pylab
fig = pylab.figure()
figlegend = pylab.figure(figsize=(3,2))
ax = fig.add_subplot(111)
lines = ax.plot(range(10), pylab.randn(10), range(10), pylab.randn(10))
figlegend.legend(lines, ('one', 'two'), 'center')
#fig.show()
#figlegend.show()
#figlegend.savefig('legend.png')
# -
for dataset in datasets:
x = np.arange(len(plot12[dataset].values())) # the label locations
width = 0.35 # the width of the bars
#print(plot12[dataset])
#fig, ax = plt.plot()
plt.barh(x - width/2, plot12[dataset].values(), width, label='12', color = "orange")
plt.barh(x + width/2, plot90[dataset].values(), width, label='90', color = "red")
plt.xlabel('spearman Correlation')
plt.title(title[dataset], fontsize = 9)
plt.yticks(x, labels = plot12[dataset].keys(), fontsize = 7)
plt.legend()
#fi.tight_layout()
plt.savefig('figures/' + dataset + 'Gap_6.png', dpi=300)
plt.show()
# + tags=[]
#correlations['spearman'].keys()
sorted_values = sorted(results['spearman'].values()) # Sort the values
sorted_values.reverse()
sorted_dict = {}
for i in sorted_values:
for k in results['spearman'].keys():
if results['spearman'][k] == i:
sorted_dict[k] = abs(results['spearman'][k])
number = 0
n = '6'
for x in sorted_dict.keys():
if('_' + n in x):
number += 1
#print(x)
print(number)
#print(sorted_dict.keys())
number = 0
for x in results["spearman"].keys():
if('_' + n in x):
number += 1
#print(x)
print(number)
#print(sorted_dict.keys())
# +
agg = ['L1', 'L2', 'L3', 'L4', 'L5']
aft = ['0' , '1' , '2' , '3' , '4' , '5' , '6' , '7']
vss = ['test', 'gap']
for i in aft:
for v in vss:
#Create Temp Dict
temp = {}
for x in sorted_dict.keys():
#print(x)
if(("_" + i) in x and v in x):
#Translate Name to Latex
name = '${'
if('AE' in x):
name += '\widehat{'
elif('BE' in x):
name += '{'
if('QS' in x):
name += 'Q}_{S}'
elif('QE' in x):
name += 'Q}_{E}'
elif('fro' in x):
name += '\mu}_{frob}'
elif('spec' in x):
name += '\mu}_{spec}'
if('L1' in x):
name += '^{L1}'
elif('L2' in x):
name += '^{L2}'
elif('L3' in x):
name += '^{L3}'
elif('L4' in x):
name += '^{L4}'
elif('L5' in x):
name += '^{L5}'
name += '}$'
#print(name)
temp[name] = sorted_dict[x]
#Create Title:
if(v == 'test'):
title = "Spearman Correlation of Metrics Alongside Test Accuracy "
elif(v == 'gap'):
title = "Spearman Correlation of Metrics Alongside Generalization Gap "
title += "Using " + i + " Afterprocessing"
#Plot
matplotlib.rc('ytick', labelsize=3)
matplotlib.rc('xtick', labelsize=10)
plt.barh(range(len(temp)), list(temp.values()), align='center');
#print(title, list(temp.keys()), len(list(temp.keys())))
plt.yticks(range(len(temp)), list(temp.keys()),rotation='horizontal');
plt.title(title, fontsize = 7)
plt.xlim([0,1])
plt.show()
#Merics_Before/After EVBMF_Test / Gap_L1 to L5 (agg)_ (8 afterprocessing) (Only look at 0 and 7)
#4 x 2 x 5 x 8 = 320.
#Split by aft: 4 x 2 x 5 = 40 bars, 8 graphs
# -
print(sorted_dict.keys())
|
source/plotting.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="Y26YW3Mj2LHI" colab_type="text"
# <figure>
# <center>
# <img src='https://raw.githubusercontent.com/alexsnowschool/Python-Basics/master/cover-ppt.png' width = '800px'/>
# </center>
# </figure>
# + [markdown] id="6VwQJVb9oQDe" colab_type="text"
# ## Assignment 1 (Pass >= 7)
# **Assigned Date - 5 July 2020 (9:00 PM)**
#
# **Self-Interactive Due Date - 11 July 2020 (11:59:59 AM)**
#
# **Self-Paced Due Date - Infinity**
#
# + [markdown] id="3t-IGFgS0TQT" colab_type="text"
# ### Description
#
# + [markdown] id="lp25lrzp08ew" colab_type="text"
# In this Assignment, you have to answer all of our questions and write appropriate coding answers in already declared functions to practice how well you understood
# about previous lectures and get hands on code with small problems exercise to gain more experience about python programming language.
#
# Once you've completed the assignment,
#
# 1. Rename this file "PythonBasics - Assignment1.ipynb" to this file naming format (Eg, **A1 - NyanSwanAung.ipynb**)
#
# 2. Upload your renamed answer file to our google drive folder (see [this video](https://www.alexsnowschool.org/courses/take/intro-to-python/lessons/14303017-how-to-upload-your-assignment-files-to-our-avairds-google-drive-folder) for demo)
#
#
# ---
#
#
# Rules
#
# In order to complete the Assignment 1, you have to answer **ALL OF THE QUESTIONS**. Your answers will be graded and stored in our system once we view your code and your certification depends on how well you answered the Assignment questions. **Submit your answer before deadline**.
#
# Tips for answering Assignment
#
# 1. Write your coding answer in related already declared functions
# 2. Once you've done the coding, run the cell and see if your output matches with expected output.
# 3. You can use Google to search python built-in libraries/functions and python syntax
#
# 4. Start Coding! 👨💻 👩💻🤓
# + [markdown] id="Rl7XHezP1ffk" colab_type="text"
# ### Example Question
#
# Write a string with this value "Hello World" by using `print()` function.
# + id="LM2AD7ob1nHV" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="697f605f-6c74-411a-8b29-b37d50de1f8d"
def example_1():
#Start your coding below
print('Hello World')
example_1()
# Expected Output: Hello World
# + [markdown] id="Y9szuueEyZ1n" colab_type="text"
# ### No. 1
#
# Write a Python program which accepts the radius of a circle from the user and compute the area.
#
# **Hint** : use pi value from `math library` and search it on google
# + id="WH1z5e_Tyl7H" colab_type="code" colab={}
from math import pi
def no_1():
# Start your coding below
no_1()
# Expected Output
# Enter the radius of a circle: user input
# Area : result
# + [markdown] id="ibWG7NoaxMWT" colab_type="text"
# ### No. 2
#
# No(2_1)
#
# Write a Python program to find whether a given number (accept from the user) is even or odd, print out an appropriate message to the user.
#
# No(2_2)
#
# Write a Python program to test whether given letters(a, c) are vowels or not.
#
# **Hint** : use keyword `in`
#
#
# + id="2rJ9WFUrxRQ7" colab_type="code" colab={}
def no_2_1():
# Start your coding below
def no_2_2():
char1, char2 = 'a', 'c'
all_vowels = 'aeiou'
# Start your coding below
no_2_1()
# Expected Output
# Enter a number : user input
# This is an odd number
no_2_2()
# Expected Output
# a is a vowel
# c is not a vowel
# + [markdown] id="WqW6-0yzzL8Z" colab_type="text"
# ### No. 3
# Write a Python program to print out all even numbers from a given numbers list in the same order and stop the printing if any numbers that come after 237 in the sequence.
#
# **Hint** : search python `break` keyword on google to quit from the loop
# + id="SIJ3mwcTzQJj" colab_type="code" colab={}
numbers = [
386, 462, 47, 418, 907, 344, 236, 375, 823, 566, 597, 978, 328, 615, 953, 345,
399, 162, 758, 219, 918, 237, 412, 566, 826, 248, 866, 950, 626, 949, 687, 217,
815, 67, 104, 58, 512, 24, 892, 894, 767, 553, 81, 379, 843, 831, 445, 742, 717,
958,743, 527
]
def no_3():
# Start your coding below
no_3()
# Expected Output : 386, 462, 418, 344, .... ,758, 918
# + [markdown] id="YcDJB666zTvg" colab_type="text"
# ### No. 4
#
# Write a Python program to calculate the sum of three given numbers. If the values are equal, then return thrice of their sum, if not return the sum
#
# Sample Numbers: 1, 2, 3
#
# Sample Numbers: 3, 3, 3
# + id="S8ZmgXWJzVrN" colab_type="code" colab={}
def no_4(x, y, z):
sum = 0
# Start your coding below
return sum
print(no_4(1, 2, 3))
# Expected Output
# 6
print(no_4(3, 3, 3))
# Expected Output
# 27
# + [markdown] id="w__EYuIwzb7_" colab_type="text"
# ### No. 5
#
# Write a Python program which accepts a sequence of comma-separated numbers from user and generate a list and a tuple with those numbers.
# **Hint**: search python `split()` method in google
#
# + id="3ezLhb8pzdbZ" colab_type="code" colab={}
def no_5():
# Start your coding below
no_5()
# Expected Output
# Enter some comma seperated numbers: 3, 5, 7, 23
# List : ['3', ' 5', ' 7', ' 23']
# Tuple : ('3', ' 5', ' 7', ' 23')
# + [markdown] id="LGd7mr_6znKj" colab_type="text"
# ### No. 6
#
# Write a Python program to display the current date and time.
# After that, calculate the day difference between 11/7/2020 and today's date
#
# **Hint** : search python `datetime` built-in library in google
# + id="DeSM2AXfzp-G" colab_type="code" colab={}
def no_6():
# Start your coding below
no_6()
# Expected Output
# Today's date: date
# Day difference: date
# + [markdown] id="vfTGm5qbzu0U" colab_type="text"
# ### No. 7
# Write a Python program to get the difference between a given number and 17. If the given number is greater than 17, return the double of differenc or else return the difference.
#
# Given Number : 22, 14
# + id="t2rBoa2zhlO9" colab_type="code" colab={}
def no_7(given_num):
# Start your coding below
print(no_7(22))
# Expected Output
# 10
print(no_7(14))
# Expected Output
# 3
# + [markdown] id="SoH9l3m6z3N4" colab_type="text"
# ### No. 8
#
# Write a Python function that takes a sequence of numbers and determines whether all the numbers are different from each other and return True or False
#
# Sample Data : 1, 5, 7, 9
#
# Sample Data : 2, 4, 5, 5, 7, 9
#
# **Hint** : `Set` do not contain repeated items
# + id="_FyhNPVlz4eq" colab_type="code" colab={}
def no_8(data):
# Start your coding below
print(no_8([1, 5, 7, 9]))
# Expected Output
# True
print(no_8([2, 4, 5, 5, 7, 9]))
# Expected Output
# False
# + [markdown] id="Kv1bbkWoz_gB" colab_type="text"
# ### No. 9
#
# Write a Python program to find those numbers which are divisible by 7 and 5, between 1500 and 2700 (both included).
#
# **Hint** : Use `for in range()` as a loop
# + id="0x6sW0WO0A8e" colab_type="code" colab={}
def no_9():
# Start your coding below
no_9()
# Expected Output
# 1505,1540,1575,1610, ..., 2625,2660,2695
# + [markdown] id="cGEikE6x0IAm" colab_type="text"
# ### No. 10
# Write a Python program to guess a number between 1 to 9.
#
# Note : User is prompted to enter a guess. If the user guesses wrong then the prompt appears again until the guess is correct, on successful guess, user will get a "Well guessed!" message, and the program will exit.
#
# **Hint** : Use `randint` from `random` library to get randomly generated number for target num
#
# **Hint** : Use `while loop`, see how to use while loop in lecture pdf
# + id="rUN0Zurt0Jco" colab_type="code" colab={}
import random
def no_10():
target_num = random.randint( , )
guess_num = 0
# Start your coding below
no_10()
# Expected Output
# Guess a number between 1 and 10 until you get it right: user input
# Well guessed
|
assignments/python-basics-assignment-1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Анализ временных рядов
# ## <NAME>
# # Знакомство с данными
# Во всех процедурах проверки гипотез уровень значимости $\alpha$ принимается равным $0.05$.
import pandas as pd
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import statsmodels.api as sm
# %matplotlib inline
matplotlib.rcParams['figure.figsize'] = (12, 8)
ts = pd.Series.from_csv('ts.txt', index_col=None)
val_obs = ts[-1:] #221.2744
ts = ts[:-1] # last observation for validation of prediction
ts.head()
ts.tail()
plt.title('Observed')
plt.grid()
plt.plot(ts, label='Observed')
plt.xlabel('t')
plt.ylabel('x_t')
# Нужно удалить детерминированные составляющие. Из графика очевидно наличие линейного тренда. Позже будет заметно, что сезонности нет.
# # Детрендирование
x = sm.add_constant(ts.index)
tr = sm.OLS(ts, x).fit()
tr.summary()
print('Equation of linear trend: f(t) =', tr.params['x1'],'*t +',tr.params['const'])
# +
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(20,8))
axes[0].set_title('Time Series and linear trend')
axes[0].grid()
axes[0].plot(ts, label='Observed')
axes[0].plot(tr.fittedvalues, label='Linear trend')
axes[0].legend(loc='best')
u = ts - tr.predict() # residuals <=> detrended TS
axes[1].set_title('Detrended TS (residuals)')
axes[1].grid()
axes[1].plot(u)
# -
# Теперь отдельно рассмотрим ряд остатков.
#
# Изначальная модель: $x_t = \mu + bt + u_t$<br>
# $u_t$ — детрендированный ряд.
# # Идентификация модели детрендированного ряда
def acfpacf(res,name):
nlags=60; z=1.96
borderline = z/np.sqrt(res.shape[0])
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(20,8))
extraticks=[-borderline, borderline]
acf = sm.tsa.stattools.acf(res, nlags=nlags)
pacf = sm.tsa.stattools.pacf(res, nlags=nlags)
axes[0].set_title('ACF for '+name)
axes[0].grid()
axes[0].plot(acf,marker = 'o', linestyle=':', color='magenta')
axes[0].axhspan(-borderline, borderline, alpha=0.15, color='blue')
axes[0].set_yticks(list(axes[0].get_yticks()) + extraticks)
axes[0].set_xlabel('lag')
axes[1].set_title('PACF for '+name)
axes[1].grid()
axes[1].plot(pacf, marker = 'o', linestyle='-.', color='green')
axes[1].axhspan(-borderline, borderline, alpha=0.15, color='blue')
axes[1].set_yticks(list(axes[1].get_yticks()) + extraticks)
axes[1].set_xlabel('lag')
return
acfpacf(u,'detrended TS')
# Некоррелированность $u_t$ можно увидеть из корреллограмм. А именно, начиная с некоторого номера почти все значения выборочной АКФ должны попадать в трубку $[\frac{-1.96}{\sqrt{n}}; +\frac{-1.96}{\sqrt{n}}] = [-0.139; 0.139]$ (допускается редкое несистемное незначительное нарушение границ). В данном случае значения выборочной АКФ попадют в трубку с номера 3, выборочной ЧАКФ — с номера 4. Раз ряд без тренда не автокоррелирует, значит, сезонности нет и нет смысла её убирать.
# ## AR(2)
#
# Рассмотрим модель $u_t=\alpha_1 u_{t-1} + \alpha_2 u_{t-2}+\varepsilon_t$
#AR(2)
x = np.column_stack((u[1:ts.shape[0]-1], u[0:ts.shape[0]-2])) # [u_{t-1}, u_{t-2}]
y = u[2:ts.shape[0]] # u_t
y_ar2 = y
ar2 = sm.OLS(y,x).fit() # u_t ~ u_{t-1} u_{t-2}
eps_ar2 = ar2.resid
ar2.summary('u_t', ['u_(t-1)','u_(t-2)'])
# Из таблицы сразу же можно получить некоторую информацию о модели.
# ### Проверка остатков:
#
# Нужно проверить ряд $\varepsilon_t$ на три свойства:
#
# 1. Некоррелированность
# 2. Гауссовость
# 3. Гомоскедастичность
# **Некоррелированность**
#
# Используем сразу несколько инструментов для проверки некоррелированности. Для начала построим выборочные АКФ и ЧАКФ для ряда $\varepsilon_{t}$.
acfpacf(eps_ar2, 'residuals of U [AR(2)]')
# Некоррелированность остатков можно увидеть из корреллограмм. А именно, начиная с некоторого номера почти все значения АКФ должны попадать в трубку $[\frac{-1.96}{\sqrt{n}}; +\frac{-1.96}{\sqrt{n}}] = [-0.14; 0.14]$. В данном случае это происходит практически сразу же, что говорит о некоррелированности $\varepsilon_t$
#
# Проверим гипотезу с помощью критерия Дарбина-Уотсона. Формальная запись:
#
# $H_0: \forall i={1,\dots,n} \quad \rho(\varepsilon_i, \varepsilon_{i-1}) = 0$<br>
# $H_A: \exists i: \rho(\varepsilon_i, \varepsilon_{i-1}) ≠ 0$
#
# $p=2, \quad n = |U|-p$
#
# Значение статистики, полученное из таблицы: $DW = 1.927$.<br>
# Статистики распределения Дарбина-Уотсона при количестве регрессоров $m=2$:
#
# $d_L =1.748; d_U = 1.789$, причём:
# * $[0; d_L], [4-d_L;4]$ — критические области
# * $[d_U; 4-d_U]$ — доверительная область
# * $[d_L;d_U], [4-d_U; 4-d_L]$ — области неопределённости.
#
# $DW$ попадает в доверительную область, а значит, принимаем гипотезу о некоррелированности остатков.
# ** Гауссовость **
#
# <NAME>.
#
# <cite>$p$-значение — вероятность ошибиться, отвергнув нулевую гипотезу. Если p(t) меньше заданного уровня значимости, то нулевая гипотеза отвергается в пользу альтернативной. В противном случае она не отвергается.</cite>
#
# Проверяем гипотезу о нормальности остатков, выраженную через коэффициенты ассиметрии (**S**kew) и эксцесса (**K**).
#
# $H_0: S=0, K=3$<br>
# $H_A: S≠0, K≠3$
#
#
# $p$-$value = 0.358 > \alpha = 0.05$, а значит, нет оснований для отклонения нулевой гипотезы.
#
# $JB_{|H_0} \sim \chi^2(2)$. $\chi_{\alpha}^2=6$
#
# $JB = 2.054 < 6$, попали в доверительную область. Обе процедуры проверки гипотезы подтверждают гауссовость остатков.
#
# **Гомоскедастичность**
#
# Воспользуемся критерием Голдфельда-Куандта в предположении, что остатки имеют нормальное распределение.
#
# $H_0: \sigma_1 = \dots = \sigma_n = \sigma $<br>
# $H_A: {\exists k: \sigma_i = \sigma_0u_{t-k}^{i}}$
#
#
# $p=2, \quad n = |U|-p$<br>
# $i={1,\dots,n},\quad k={1, \dots, p}$.
#
# Выбрасываем $d$ средних наблюдений. Важно, чтобы выполнялось условие $\frac{n-d}{2} > m$. Пусть $d=71$.
#
# $T_{|H_0} \sim F(\frac{n-d}{2}-m;\ \frac{n-d}{2}-m); \quad \frac{n-d}{2}-m = 60$
#
#
# $F_{0.95}(60;60) = 1.53$, критическая область справа.
T_ar2, pv_ar2 = sm.stats.diagnostic.het_goldfeldquandt(eps_ar2,ar2.model.exog,split=71)[:-1]
print('T =',T_ar2)
print('p-value =', pv_ar2)
# Значение статистики попало в доверительную область.<br>
# $p$-$value > \alpha$, нет оснований для отклонения нулевой гипотезы.
#
# Делаем вывод, что ряд $\varepsilon_t$ действительно является гауссовским белым шумом.
# ### Проверка значимости коэффициентов
# Проверим гипотезу о значимости коэффициентов детрендированного ряда, в данном случае $\hat{\alpha} = \alpha_{k} \quad \forall k=1, \dots, p$
#
# $H_0: \hat{\alpha}=0$<br>
# $H_A: \hat{\alpha}≠0$
#
# Статистика критерия Стьюдента $t = \frac{\hat{\alpha}}{\sqrt{\hat{D}\hat{\alpha}}} |_{H_0} \sim t(n-2)$
#
# Из таблицы видим, что $t_{\alpha_1} = 9.33, \quad t_{\alpha_2} = -5.141$
#
# Критические точки: $t_{0.025; 195} = -1.973 \quad t_{0.975; 195} = 1.973$.
#
# Статистики для обоих коэффициентов попали в критическую область, значит, все коэффициенты значимы.
#
# ### Проверка наличия единичного корня
# $u_t=\alpha_1 u_{t-1} + \alpha_2 u_{t-2}+\varepsilon_t$<br>
# $u_t = (\alpha_1 +\alpha_2 ) u_{t-1} - \alpha_2\Delta u_{t-1} = \gamma u_{t-1} - \alpha_2\Delta u_{t-1}$
#
# $H_0: \gamma = 1$<br>
# $H_A: \gamma<1$
#
# Статистика расширенного критерия Дики-Фуллера $t = \frac{\hat{\gamma}}{\sqrt{\hat{D}\hat{\gamma}}} |_{H_0} \sim DF_0(n)$, так как ряд уже детрендировали.
print('t=', sm.tsa.stattools.adfuller(y)[0])
print('DF0 critical (5%):', sm.tsa.stattools.adfuller(y)[4]['5%'])
# Попали в критическую область (слева от $DF_0$), не можем принять гипотезу о DS-природе ряда.
# ### Информационные критерии
# Из таблицы:
# $AIC = 1453, \quad BIC =1460$
# ## AR(3)
# $u_t=\alpha_1 u_{t-1} + \alpha_2 u_{t-2} + \alpha_3 u_{t-3} +\varepsilon_t$
#
# Будем использовать те же критерии и вышеописанные гипотезы (при $p=3$)
x = np.column_stack((u[2:ts.shape[0]-1], u[1:ts.shape[0]-2], u[0:ts.shape[0]-3])) # [u_{t-1}, u_{t-2} u_{t-3}]
y = u[3:ts.shape[0]] # u_t
ar3 = sm.OLS(y,x).fit() # u_t ~ u_{t-1} u_{t-2} u_{t-3}
eps_ar3 = ar3.resid
ar3.summary('u_t', ['u_(t-1)','u_(t-2)', 'u_(t-3)'])
# ### Проверка остатков:
acfpacf(eps_ar3, 'residuals of U [AR(3)]')
# **Некоррелированность**
#
#
# $m=3; p=3; n=196$ <br>
# $DW=1.927$ <br>
# $d_L = 1.738,\quad d_U = 1.799$
#
# Попадаем в доверительную область. Остатки не корреллированы.
#
# **Гауссовость**
#
# $JB = 1.59<6 \quad p$-$value = 0.451 > \alpha$.
# Попадаем в доверительную область, $p$-значение больше уровня значимости. Остатки распределены нормально.
#
# **Гомоскедастичность**
#
# $d=70$<br>
# $F_{0.95}(60;60) = 1.53$, критическая область справа.
T_ar3, pv_ar3 = sm.stats.diagnostic.het_goldfeldquandt(eps_ar3,ar3.model.exog,split=70)[:-1]
print('T =',T_ar3)
print('p-value =', pv_ar3)
# Значение статистики попало в доверительную область.<br>
# $p$-$value > \alpha$, нет оснований для отклонения нулевой гипотезы.
#
# Делаем вывод, что ряд $\varepsilon_t$ действительно является гауссовским белым шумом.
# ### Проверка значимости коэффициентов
# Из таблицы видим, что:<br>
# $t_{\alpha_1} = 9.217, \quad t_{\alpha_2} = -5.025, \quad t_{\alpha_3}=1.367$
#
# Критические точки: $t_{0.025; 194} = -1.973 \quad t_{0.975; 194} = 1.973$.
#
# Статистики для первых двух коэффициентов попали в критическую область, значит, они значимы. Статистика третьего коэффициента попала в доверительную область, значит, принимаем гипотезу о его незначимости.
#
# ### Проверка наличия единичного корня
print('t=', sm.tsa.stattools.adfuller(y)[0])
print('DF0 critical (5%):', sm.tsa.stattools.adfuller(y)[4]['5%'])
# Попали в критическую область (слева от $DF_0$), не можем принять гипотезу о DS-природе ряда.
# ### Информационные критерии
# Из таблицы:
# $AIC = 1447, \quad BIC =1457$
# ## AR(4)
# $u_t=\alpha_1 u_{t-1} + \alpha_2 u_{t-2} + \alpha_3 u_{t-3} +\alpha_4 u_{t-4} +\varepsilon_t$
#
# Будем использовать те же критерии и вышеописанные гипотезы (при $p=4$)
x = np.column_stack((u[3:ts.shape[0]-1], u[2:ts.shape[0]-2], u[1:ts.shape[0]-3], u[0:ts.shape[0]-4]))
y = u[4:ts.shape[0]] # u_t
ar4 = sm.OLS(y,x).fit() # u_t ~ u_{t-1} u_{t-2} u_{t-3} u_{t-4}
eps_ar4 = ar4.resid
ar4.summary('u_t', ['u_(t-1)','u_(t-2)', 'u_(t-3)', 'u_(t-4)'])
# ### Проверка остатков:
acfpacf(eps_ar4, 'residuals of U [AR(4)]')
# **Некоррелированность**
#
#
# $m=4; p=4; n=195$ <br>
# $DW=1.927$ <br>
# $d_L = 1.728,\quad d_U = 1.81$
#
# Попадаем в доверительную область. Остатки не корреллированы.
#
# **Гауссовость**
#
# $JB = 1.349<6 \quad p$-$value = 0.509 > \alpha$.
# Попадаем в доверительную область, $p$-значение больше уровня значимости. Остатки распределены нормально.
#
# **Гомоскедастичность**
#
# $d=67$<br>
# $F_{0.95}(60;60) = 1.53$, критическая область справа.
T_ar4, pv_ar4 = sm.stats.diagnostic.het_goldfeldquandt(eps_ar4,ar4.model.exog,split=67)[:-1]
print('T =',T_ar4)
print('p-value =', pv_ar4)
# Значение статистики попало в доверительную область.<br>
# $p$-$value > \alpha$, нет оснований для отклонения нулевой гипотезы.
#
# Делаем вывод, что ряд $\varepsilon_t$ действительно является гауссовским белым шумом.
# ### Проверка значимости коэффициентов
# Из таблицы видим, что:<br>
# $t_{\alpha_1} = 9.362, \quad t_{\alpha_2} = -5.221, \quad t_{\alpha_3}=1.850, \quad t_{\alpha_4}= -1.308$
#
# Критические точки: $t_{0.025; 194} = -1.973 \quad t_{0.975; 194} = 1.973$.
#
# Статистики для первых двух коэффициентов попали в критическую область, значит, они значимы.
#
# Статистики третьего и четвёртого коэффициентов попали в доверительную область, значит, принимаем гипотезу об их незначимости.
#
# ### Проверка наличия единичного корня
print('t=', sm.tsa.stattools.adfuller(y)[0])
print('DF0 critical (5%):', sm.tsa.stattools.adfuller(y)[4]['5%'])
# Попали в критическую область (слева от $DF_0$), не можем принять гипотезу о DS-природе ряда.
# ### Информационные критерии
#
# Из таблицы:
# $AIC = 1437, \quad BIC =1450$
# # Выбор лучшей модели
# Так как в моделях AR(3), AR(4) принималась гипотеза о незначимости регрессоров $u_{t-3}, u_{t-4}$, то основной моделью остаётся AR(2), хоть и значения информационных критериев для AR(3), AR(4) меньше.
#
# Таким образом,
#
# $x_t = \hat{\mu} + \hat{b} t+ \hat{\alpha}_1(x_{t-1} - \hat{\mu} - \hat{b}(t-1)) + \hat{\alpha}_2(x_{t-2} - \hat{\mu} - \hat{b}(t-2))$
#
# $x_t = \mu + bt + \alpha_1 u_{t-1} + \alpha_2 u_{t-2} + \varepsilon_t$, где $\varepsilon_t$ — гауссовский белый шум.
#
# Итого:
#
# $x_t = -4.48 + 0.87t + 0.63 x_{t-1} -0.35 x_{t-2} $
# # Прогноз
# Попробуем предсказать последнее значение ряда с помощью этой модели и сравним его с истинным.
pred = -6.1+ 1.21*(198+1) + 0.6280*(ts[198] +6.1 -1.21*198) - 0.3483*(ts[197]+6.1-1.21*(198-1))
print('Predicted value: ', pred)
print('True value:', val_obs.values[0])
print('Absolute error:', abs(pred-val_obs.values[0]))
plt.title('Time Series and Predictive Model')
plt.grid()
plt.plot(ts, color='red', label='Observed')
plt.plot(y_ar2+tr.predict()[:-2], linestyle=':', color='blue', label='Predicted')
plt.legend(loc='best')
# Как видим, модель подогналась довольно точно.
|
TimeSeries/TimeSeries.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/raj-gupta1/MNIST-CNN-Keras-implementation/blob/main/HW_CNN__5VARIENTS_MNIST_DATASET.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="Ag0blEpudle2"
#
# #**MNIST DATASET IMPLEMENTATION IN CNN**
# + [markdown] id="mSXRW3wKdwJ1"
# #1. IMPORTING THE MNIST DATASET
# + id="ASVPVUsCcyEm"
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import matplotlib.cm as cm
# %matplotlib inline
# + colab={"base_uri": "https://localhost:8080/"} id="gYPpwgdRdp3k" outputId="9be4a868-ce66-45e8-df0b-2964a01640e9"
from tensorflow.keras.datasets import mnist
(x_train, y_train), (x_test,y_test) = mnist.load_data()
print("length of training dataset is %d" % len(x_train))
print("length of testing dataset is %d" % len(x_test))
# + colab={"base_uri": "https://localhost:8080/", "height": 206} id="9icqg6iTdqlK" outputId="77895591-cfbb-420d-a0c8-06debc8741e8"
fig = plt.figure(figsize=(20,20))
for i in range(6):
ax = fig.add_subplot(1,6, i+1, xticks=[], yticks=[])
ax.imshow(x_train[i], cmap='gray')
ax.set_title(str(y_train[i]))
# + colab={"base_uri": "https://localhost:8080/", "height": 863} id="HTZiGR1tdrL1" outputId="1c94fa11-13f9-44af-8bb8-9488d2559e2b"
def visualize_input(img, ax):
ax.imshow(img, cmap='gray')
width, height = img.shape
thresh = img.max()/2.5
for x in range(width):
for y in range(height):
ax.annotate(str(round(img[x][y])), xy=(y,x),
horizontalalignment='center',
verticalalignment='center',
color='white' if img[x][y]<thresh else 'black')
fig= plt.figure(figsize=(15,15))
ax= fig.add_subplot(111)
visualize_input(x_train[2], ax)
# + [markdown] id="oxaQBZ-pkppW"
# #2. PREPROCESSING THE IMAGE
# + colab={"base_uri": "https://localhost:8080/"} id="DkbfHoMXdrOt" outputId="3c657cdc-f144-4e33-9a32-a6630771b471"
x_train = x_train.astype('float32')/255
x_test = x_test.astype('float32')/255
print("x_train shape is" ,x_train.shape)
print("x_test shape is " , x_test.shape)
# + [markdown] id="HaBqsljKmDs4"
# #3. USING ONE HOT ENCODING TO LABEL THE DATA
# + colab={"base_uri": "https://localhost:8080/"} id="Ils9vUgVkiFT" outputId="da58acdd-bc20-4312-eb79-065b84a921ef"
from keras.utils import np_utils
num_classes = 10
print('Integer values labelled are :')
print(y_train[:10])
y_train = np_utils.to_categorical(y_train, num_classes)
y_test = np_utils.to_categorical(y_test, num_classes)
print('ONE-HOT labelled are :')
print(y_train[:10])
# + [markdown] id="s6Uqcr_BnuWD"
# #4. RESHAPING INPUT SHAPE
# + colab={"base_uri": "https://localhost:8080/"} id="bxwkxvUSkiIP" outputId="6f54c05d-d791-4d5d-aea5-6aa13eb34fd6"
img_rows, img_cols = 28,28
x_train = x_train.reshape(x_train.shape[0], img_rows, img_cols, 1)
x_test = x_test.reshape(x_test.shape[0], img_rows, img_cols, 1)
input_shape = (img_rows, img_cols, 1)
print("input_shape ", input_shape)
print("x_test shape ", x_test.shape)
print("x_train shape ", x_train.shape)
# + [markdown] id="7FulHkKApQwD"
# #**5. CREATING THE MODEL**
# + [markdown] id="iQFoDMiHpvcI"
# #MODEL 1
# + colab={"base_uri": "https://localhost:8080/"} id="piQ_QNY9kiLK" outputId="7c02401d-b72a-42f0-d19e-74c94fb04402"
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Conv2D, MaxPooling2D, Flatten, Dense, Dropout, GlobalAveragePooling2D
model1 = Sequential()
# layer 1
model1.add(Conv2D(32, kernel_size=(3, 3), padding='same',activation='relu',input_shape=(28,28,1))) # 28*28*1
model1.add(MaxPooling2D(pool_size=(2,2))) # 14*14*1
# layer 2
model1.add(Conv2D(64, kernel_size=(3, 3), padding='same',activation='relu')) # 14*14*1
model1.add(MaxPooling2D(pool_size=(2,2))) # 7*7*1
# layer 3
model1.add(Flatten())
# layer 4
model1.add(Dense(64, activation='relu'))
model1.add(Dense(10, activation='softmax'))
model1.summary()
# + [markdown] id="Pi5fU8BJu43o"
# #6. COMPILING THE MODEL
#
#
# + id="fsSkYUOqdrRo"
model1.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
# + [markdown] id="QocptWiO9UDF"
# #7. TRAINING THE MODEL
#
#
# + colab={"base_uri": "https://localhost:8080/"} id="t7Mxhh9bdrUi" outputId="0c558eca-09c3-494a-f8a1-b9c9d275942f"
from tensorflow.keras.callbacks import ModelCheckpoint
path = 'model1.weights.best.hdf5'
checkpointer = ModelCheckpoint(filepath= path, verbose=1, save_best_only=True)
hist = model1.fit(x_train, y_train,
batch_size=64, epochs=10,
validation_data=(x_test, y_test), callbacks=[checkpointer],
verbose=2, shuffle=True)
# + [markdown] id="Pn_3GUL2ARXg"
# #8. Loading the Model with the Best Classification Accuracy on the Validation Set
# + id="lLnqOCeWdrZ7"
model1.load_weights(path)
# + [markdown] id="sjXN2Y9VAxHH"
# #9. Calculating the model accuracy on test data
# + colab={"base_uri": "https://localhost:8080/"} id="xqWX7t5qdrdA" outputId="2c3dbffe-d236-4ecf-d54e-3b8bbc64dc17"
score = model1.evaluate(x_test, y_test, verbose=0)
accuracy = 100*score[1]
print('Test accuracy = %.4f%% ' % accuracy)
# + id="bbpsMmFOUcpI"
# + [markdown] id="UKVsccDbCts4"
# #MODEL 2
# + colab={"base_uri": "https://localhost:8080/"} id="41sGMc0ndrm3" outputId="b89ab211-30ca-4253-8412-29a205951d94"
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Conv2D, MaxPooling2D, Flatten, Dense, Dropout, GlobalAveragePooling2D
model2 = Sequential()
# layer 1
model2.add(Conv2D(32, kernel_size=(3, 3), padding='same',activation='relu',input_shape=(28,28,1))) # 28*28*1 as padding is same
model2.add(Conv2D(32, kernel_size=(3, 3), padding='same',activation='relu')) # 28*28*1 as padding is same
model2.add(Conv2D(32, kernel_size=(3, 3), padding='same',activation='relu')) # 28*28*1 as padding is same
model2.add(MaxPooling2D(pool_size=(2,2) )) # 14*14*1
# layer 2
model2.add(Conv2D(64, kernel_size=(3, 3), padding='same',activation='relu')) # 14*14*1 as padding is same
model2.add(Conv2D(64, kernel_size=(3, 3), padding='same',activation='relu')) # 14*14*1 as padding is same
model2.add(Conv2D(64, kernel_size=(3, 3), padding='same',activation='relu')) # 14*14*1 as padding is same
model2.add(MaxPooling2D(pool_size=(2,2))) # 7*7*1
# layer 3
model2.add(Flatten())
# layer 4
model2.add(Dense(64, activation='relu'))
model2.add(Dense(10, activation='softmax'))
model2.summary()
# + colab={"base_uri": "https://localhost:8080/"} id="J3sa7NWkdrpi" outputId="a8844557-86c2-455d-d6bf-d1ed4ab26df7"
model2.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
from tensorflow.keras.callbacks import ModelCheckpoint
path = 'model2.weights.best.hdf5'
checkpointer = ModelCheckpoint(filepath= path,
verbose=1,
save_best_only=True)
hist = model2.fit(x_train, y_train,
batch_size=64, epochs=10,
validation_data=(x_test, y_test), callbacks=[checkpointer],
verbose=2, shuffle=True)
model2.load_weights(path)
# + colab={"base_uri": "https://localhost:8080/"} id="5FIGiJfkdrsT" outputId="3403c1dd-f482-4da8-e013-1bebbcf541f3"
score = model2.evaluate(x_test, y_test, verbose=0)
accuracy = 100*score[1]
print('Test accuracy = %.4f%% ' % accuracy)
# + id="pFyUVcRpDEKW"
# + [markdown] id="GAY-AsyaTuMO"
# #MODEL 3
# + colab={"base_uri": "https://localhost:8080/"} id="0-0RUaCbTuMO" outputId="365d7fa6-2254-4304-b9f1-e7ef4e298d32"
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Conv2D, MaxPooling2D, Flatten, Dense, Dropout, GlobalAveragePooling2D
model3 = Sequential()
# layer 1
model3.add(Conv2D(32, kernel_size=(3, 3), padding='valid',activation='selu',input_shape=(28,28,1))) # 26*26*1 as padding is same
model3.add(Conv2D(32, kernel_size=(3, 3), padding='valid',activation='selu')) # 24*24*1 as padding is same
model3.add(Conv2D(32, kernel_size=(3, 3), padding='valid',activation='selu')) # 22*22*1 as padding is same
model3.add(MaxPooling2D(pool_size=(2,2) )) # 11*11*1
# layer 2
model3.add(Conv2D(64, kernel_size=(3, 3), padding='valid',activation='selu')) # 9*9*1 as padding is same
model3.add(Conv2D(64, kernel_size=(3, 3), padding='valid',activation='selu')) # 7*7*1 as padding is same
model3.add(Conv2D(64, kernel_size=(3, 3), padding='valid',activation='selu')) # 5*5*1 as padding is same
model3.add(MaxPooling2D(pool_size=(2,2))) # 2*2*1
# layer 3
model3.add(Flatten())
# layer 4
model3.add(Dense(64, activation='selu'))
model3.add(Dense(10, activation='softmax'))
model3.summary()
# + colab={"base_uri": "https://localhost:8080/"} id="AMj_v95qTuMQ" outputId="f40a4751-e91d-41ae-d780-8164ac68dc52"
model3.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
from tensorflow.keras.callbacks import ModelCheckpoint
path = 'model3.weights.best.hdf5'
checkpointer = ModelCheckpoint(filepath= path,
verbose=1,
save_best_only=True)
hist = model3.fit(x_train, y_train,
batch_size=64, epochs=10,
validation_data=(x_test, y_test), callbacks=[checkpointer],
verbose=2, shuffle=True)
model3.load_weights(path)
# + colab={"base_uri": "https://localhost:8080/"} id="LiDSCTx1dryK" outputId="8863fd7c-463b-4c9a-ad4d-99a989436d04"
score = model3.evaluate(x_test, y_test, verbose=0)
accuracy = 100*score[1]
print('Test accuracy = %.4f%% ' % accuracy)
# + id="Lg8LvnYKJVAy"
# + [markdown] id="XZJvVsbz1Ouc"
# #MODEL 4
# + colab={"base_uri": "https://localhost:8080/"} id="ensLGlHkdr07" outputId="59fe8db4-1dc4-40ea-f269-42727ca7dfda"
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Conv2D, MaxPooling2D, Flatten, Dense, Dropout, GlobalAveragePooling2D
model4 = Sequential()
# layer 1
model4.add(Conv2D(32, kernel_size=(3, 3), padding='same',activation='tanh',input_shape=(28,28,1))) # 28*28*1 as padding is same
model4.add(Conv2D(32, kernel_size=(3, 3), padding='same',activation='tanh')) # 28*28*1 as padding is same
model4.add(MaxPooling2D(pool_size=(2,2) )) # 14*14*1
# layer 2
model4.add(Conv2D(64, kernel_size=(3, 3), padding='same',activation='relu')) # 14*14*1 as padding is same
model4.add(Conv2D(64, kernel_size=(3, 3), padding='same',activation='relu')) # 14*14*1 as padding is same
model4.add(MaxPooling2D(pool_size=(2,2))) # 7*7*1
# layer 2
model4.add(Conv2D(128, kernel_size=(3, 3), padding='same',activation='selu')) # 7*7*1 as padding is same
model4.add(Conv2D(128, kernel_size=(3, 3), padding='same',activation='selu')) # 7*7*1 as padding is same
model4.add(MaxPooling2D(pool_size=(2,2))) # 3*3*1
# layer 3
model4.add(Flatten())
# layer 4
model4.add(Dense(128, activation='relu'))
model4.add(Dense(10, activation='softmax'))
model4.summary()
# + colab={"base_uri": "https://localhost:8080/"} id="XlezM6DfTzkx" outputId="10f424d4-d5a7-49a7-a9bd-abb708e4628e"
model4.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
from tensorflow.keras.callbacks import ModelCheckpoint
path = 'model4.weights.best.hdf5'
checkpointer = ModelCheckpoint(filepath= path,
verbose=1,
save_best_only=True)
hist = model4.fit(x_train, y_train,
batch_size=64, epochs=10,
validation_data=(x_test, y_test), callbacks=[checkpointer],
verbose=2, shuffle=True)
model4.load_weights(path)
# + colab={"base_uri": "https://localhost:8080/"} id="oA0qPSDKT0IP" outputId="4f746b97-6a9f-4430-f38c-2305af360c9e"
score = model4.evaluate(x_test, y_test, verbose=0)
accuracy = 100*score[1]
print('Test accuracy = %.4f%% ' % accuracy)
# + id="AX2ObvUZdr3m"
# + [markdown] id="6xhRNTTN4GKW"
# #MODEL 5
# + colab={"base_uri": "https://localhost:8080/"} id="u0R84UWWdr_-" outputId="f9b4b251-97da-4125-ce3a-b3f8df227d3d"
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Conv2D, MaxPooling2D, Flatten, Dense, Dropout, GlobalAveragePooling2D
model5 = Sequential()
# layer 1
model5.add(Conv2D(16, kernel_size=(3, 3), padding='valid',activation='relu',input_shape=(28,28,1))) # 28*28*1 as padding is same
model5.add(Conv2D(32, kernel_size=(3, 3), padding='valid',activation='relu')) # 28*28*1 as padding is same
model5.add(Conv2D(64, kernel_size=(3, 3), padding='valid',activation='relu')) # 28*28*1 as padding is same
model5.add(MaxPooling2D(pool_size=(2,2) )) # 14*14*1
# layer 2
model5.add(Conv2D(64, kernel_size=(3, 3), padding='valid',activation='selu')) # 12*12*1
model5.add(Conv2D(128, kernel_size=(3, 3), padding='valid',activation='selu')) # 10*10*1 as padding is same
model5.add(Conv2D(256, kernel_size=(3, 3), padding='valid',activation='selu')) # 8*8*1 as padding is same
model5.add(MaxPooling2D(pool_size=(2,2))) # 4*4*1
# layer 3
model5.add(Flatten())
# layer 4
model5.add(Dense(64, activation='relu'))
model5.add(Dense(10, activation='softmax'))
model5.summary()
# + id="Y_cEHv9TdsCp" colab={"base_uri": "https://localhost:8080/"} outputId="cf499957-df93-4739-a25e-4f6585c8046c"
model5.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
from tensorflow.keras.callbacks import ModelCheckpoint
path = 'model5.weights.best.hdf5'
checkpointer = ModelCheckpoint(filepath= path,
verbose=1,
save_best_only=True)
hist = model5.fit(x_train, y_train,
batch_size=64, epochs=10,
validation_data=(x_test, y_test), callbacks=[checkpointer],
verbose=2, shuffle=True)
model5.load_weights(path)
# + id="5oJAQseEdsFa" colab={"base_uri": "https://localhost:8080/"} outputId="2f8831b1-6a87-4d37-f7e1-4ddf9f3a504e"
score = model5.evaluate(x_test, y_test, verbose=0)
accuracy = 100*score[1]
print('Test accuracy = %.4f%% ' % accuracy)
# + id="qxFOQYr2dsIM"
|
HW_CNN__5VARIENTS_MNIST_DATASET.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
from ete3 import Tree, faces, TreeStyle, COLOR_SCHEMES, CircleFace,TextFace, NodeStyle
from pylab import *
dfs = pd.read_excel('data4Joon.xlsx', sheet_name=None)
sheet_names = list(dfs.keys())
sheet_labels = ['Isolate01_Rep01','Isolate01_Rep02','Isolate01_Rep03',
'Isolate02_Rep01','Isolate02_Rep02',
'Isolate03_Rep01','Isolate03_Rep02','Isolate03_Rep03',
'Isolate04_Rep01','Isolate04_Rep02','Isolate04_Rep03',
'Isolate05_Rep01','Isolate05_Rep02','Isolate05_Rep03',
'Isolate06_Rep01','Isolate06_Rep02','Isolate06_Rep03']
cmap = cm.get_cmap('tab20', 17)
colors = []
for i in range(cmap.N):
rgb = cmap(i)[:3] # will return rgba, we take only first 3 so we get rgb
colors.append(matplotlib.colors.rgb2hex(rgb))
cmap = cm.get_cmap('tab20c', 15)
cmap_ee = cm.get_cmap('tab20')
colors = []
for i in range(cmap.N):
rgb = cmap(i)[:3] # will return rgba, we take only first 3 so we get rgb
if (i==3):
colors += [matplotlib.colors.rgb2hex(cmap_ee(i)[:3]) for i in [10,11]]
colors.append(matplotlib.colors.rgb2hex(rgb))
colors = []
# 'Purples', 'Blues', 'Greens', 'Oranges', 'Reds'
cmap = cm.get_cmap('Purples', 5)
colors += [matplotlib.colors.rgb2hex(cmap(3-i)[:3]) for i in range(3)]
cmap = cm.get_cmap('Blues', 5)
colors += [matplotlib.colors.rgb2hex(cmap(3-i)[:3]) for i in range(2)]
cmap = cm.get_cmap('Greens', 5)
colors += [matplotlib.colors.rgb2hex(cmap(3-i)[:3]) for i in range(3)]
cmap = cm.get_cmap('Oranges', 5)
colors += [matplotlib.colors.rgb2hex(cmap(3-i)[:3]) for i in range(3)]
cmap = cm.get_cmap('Reds', 5)
colors += [matplotlib.colors.rgb2hex(cmap(3-i)[:3]) for i in range(3)]
cmap = cm.get_cmap('Greys', 5)
colors += [matplotlib.colors.rgb2hex(cmap(3-i)[:3]) for i in range(3)]
# +
# cordination of the tree branches could be varing when you run the script.
# sheet_names = ['GAS474_2690315640_01',
# 'GAS474_2690315640_02',
# 'GAS474_2690315640_03']
ntops=5
def collect_scores(dfs, sheet_names, node):
scores = [0]*len(sheet_names)
for i, name in enumerate(sheet_names):
df = dfs[name]
temp = df[df.lineage.str.endswith(node)]
if (temp.shape[0] == 1):
scores[i] = temp.sample1.tolist()[0]
elif temp.shape[0] > 1:
print(name, node, "same species more than once?")
return scores
table = []
nodes = []
for s in sheet_names:
branches = dfs[s].iloc[0:ntops].lineage.str.split(';').tolist()
for b in branches:
table += [(b[i],b[i+1],1.0) for i in range(len(b)-1)]
if b[-1] not in nodes: nodes.append(b[-1])
table = set(table)
### collect scores
scores = {}
max_sum = 0
min_sum = 1e10
for node in nodes:
s = collect_scores(dfs, sheet_names, node)
_sum = np.sum(s)
if max_sum < _sum: max_sum = _sum
if min_sum > _sum: min_sum = _sum
scores[node] = collect_scores(dfs, sheet_names, node)
def layout(node):
if node.name in scores:
score = np.array(scores[node.name])
_sum = np.sum(score)
size = 10 + 100 * (np.sum(score) - min_sum)/(max_sum - min_sum)
F= faces.PieChartFace(100*score/_sum,
colors=colors,
width=size, height=size)
F.border.width = None
F.opacity = 0.6
#faces.add_face_to_node(F, node, 0, position="float-behind")
faces.add_face_to_node(F, node, 1, position="float")
if node.is_leaf():
faces.add_face_to_node(TextFace(node.name.split("__")[1].split("(")[0], fsize=13), node, column=1)
def get_tree():
t = Tree.from_parent_child_table(table)
thick_hz_line = NodeStyle()
thick_hz_line["hz_line_width"] = 4
t.children[0].set_style(thick_hz_line)
t.children[1].set_style(thick_hz_line)
thick_vt_line = NodeStyle()
thick_vt_line["vt_line_width"] = 1
thick_vt_line["hz_line_width"] = 1
thick_vt_line["size"] = 4
t.set_style(thick_vt_line)
for n in t.traverse():
n.set_style(thick_vt_line)
ts = TreeStyle()
for i, s in enumerate(sheet_names):
ts.legend.add_face(CircleFace(10, colors[i]), column=0)
ts.legend.add_face(TextFace(sheet_labels[i]), column=1)
ts.layout_fn = layout
ts.mode = "c"
ts.show_leaf_name = False
ts.min_leaf_separation = 14
return t, ts
t, ts = get_tree()
# t.show(tree_style=ts)
# t.render("float_piechart_all_5.pdf", tree_style=ts, w=800, units="mm") # render to the file
t.render("%%inline", tree_style=ts, w=300, units="mm") # render to the notebook
|
taxon_identification/fig5.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Finding Unusual Words in Given Language
from nltk import word_tokenize
from nltk.corpus import words
import nltk
nltk.download('words')
text = "Truly Kryptic is the best puzzle game. It's browser-based and free. Google it."
# ## 1. Tokenizing text
text_tokenized = word_tokenize(text.lower())
text_tokenized
# ## 2. Importing and exploring the words corpus
words.readme().replace('\n', ' ')
words
words.fileids()
words.words('en')[:10]
words.words('en-basic')[:10]
len(words.words('en'))
len(words.words('en-basic'))
# ## 3. Finding unusual words
english_vocab = set(w.lower() for w in words.words())
text_vocab = set(w.lower() for w in text_tokenized if w.isalpha()) # Note .isalpha() removes punctuation tokens. However, tokens with a hyphen like 'browser-based' are totally skipped over because .isalpha() would be false.
unusual = text_vocab.difference(english_vocab)
unusual
|
3-2-Finding-Unusual-Words-in-Given-Language.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from torch.distributions import MultivariateNormal
import torch
# + pycharm={"name": "#%%\n"}
class_dim = 512
K = 10
# + pycharm={"name": "#%%\n"}
def reparameterize(mu, var):
"""
Samples z from a multivariate Gaussian with diagonal covariance matrix using the
reparameterization trick.
"""
std = var.sqrt()
eps = torch.FloatTensor(std.size()).normal_()
z = eps.mul(std).add_(mu)
return z
def reparameterize_witheps(mu, var, eps):
std = var.sqrt()
z = eps.mul(std).add_(mu)
return z
# + pycharm={"name": "#%%\n"}
eps_1 = MultivariateNormal(torch.zeros(class_dim),
torch.eye(class_dim)). \
sample((K,)).reshape((K, class_dim))
mu = torch.zeros(class_dim)
var = torch.ones(class_dim)
print(mu.shape, var.shape)
std_norm_samples = torch.cat([reparameterize(mu, var).unsqueeze(dim=0) for eps in eps_1], dim = 0)
std_norm_samples_sorted = torch.cat([reparameterize_witheps(mu, var, eps).unsqueeze(dim=0) for eps in eps_1], dim = 0)
print(std_norm_samples_sorted.shape)
unsorted_div = torch.nn.functional.kl_div(eps_1, std_norm_samples, reduce=False, log_target=True).sum(-1).mean()
sorted_div = torch.nn.functional.kl_div(eps_1, std_norm_samples_sorted, reduce=False, log_target=True).sum(-1).mean()
print('unsorted_div: ',unsorted_div)
print('sorted_div: ',sorted_div)
# + pycharm={"name": "#%%\n"}
mu = torch.rand(class_dim)
var = torch.rand(class_dim)
logvar = var.log()
KLD = -0.5 * torch.sum(1 - var - mu.pow(2) + logvar)
print(KLD)
# + pycharm={"name": "#%%\n"}
unsorted_samples = torch.cat([reparameterize(mu, var).unsqueeze(dim=0) for eps in eps_1], dim = 0)
# + pycharm={"name": "#%%\n"}
unsorted_div = torch.nn.functional.kl_div(eps_1, unsorted_samples, reduce=False, log_target=True).sum(-1).mean()
print(unsorted_div)
# + pycharm={"name": "#%%\n"}
sorted_samples = torch.cat([reparameterize_witheps(mu, var, eps).unsqueeze(dim=0) for eps in eps_1], dim = 0)
sorted_sampled_div = torch.nn.functional.kl_div(eps_1, sorted_samples, reduce=False, log_target=True).sum(-1).mean()
print(sorted_sampled_div)
# + pycharm={"name": "#%%\n"}
|
mmvae_hub/notebooks/kl__div_exploration.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.6
# language: python
# name: python36
# ---
# Copyright (c) Microsoft Corporation. All rights reserved.
#
# Licensed under the MIT License.
# 
# # Automated Machine Learning
# _**Orange Juice Sales Forecasting**_
#
# ## Contents
# 1. [Introduction](#Introduction)
# 1. [Setup](#Setup)
# 1. [Compute](#Compute)
# 1. [Data](#Data)
# 1. [Train](#Train)
# 1. [Predict](#Predict)
# 1. [Operationalize](#Operationalize)
# ## Introduction
# In this example, we use AutoML to train, select, and operationalize a time-series forecasting model for multiple time-series.
#
# Make sure you have executed the [configuration notebook](../../../configuration.ipynb) before running this notebook.
#
# The examples in the follow code samples use the University of Chicago's Dominick's Finer Foods dataset to forecast orange juice sales. Dominick's was a grocery chain in the Chicago metropolitan area.
# ## Setup
# +
import azureml.core
import pandas as pd
import numpy as np
import logging
from azureml.core.workspace import Workspace
from azureml.core.experiment import Experiment
from azureml.train.automl import AutoMLConfig
from azureml.automl.core.featurization import FeaturizationConfig
# -
# This sample notebook may use features that are not available in previous versions of the Azure ML SDK.
print("This notebook was created using version 1.30.0 of the Azure ML SDK")
print("You are currently using version", azureml.core.VERSION, "of the Azure ML SDK")
# As part of the setup you have already created a <b>Workspace</b>. To run AutoML, you also need to create an <b>Experiment</b>. An Experiment corresponds to a prediction problem you are trying to solve, while a Run corresponds to a specific approach to the problem.
# +
ws = Workspace.from_config()
# choose a name for the run history container in the workspace
experiment_name = 'automl-ojforecasting'
experiment = Experiment(ws, experiment_name)
output = {}
output['Subscription ID'] = ws.subscription_id
output['Workspace'] = ws.name
output['SKU'] = ws.sku
output['Resource Group'] = ws.resource_group
output['Location'] = ws.location
output['Run History Name'] = experiment_name
pd.set_option('display.max_colwidth', -1)
outputDf = pd.DataFrame(data = output, index = [''])
outputDf.T
# -
# ## Compute
# You will need to create a [compute target](https://docs.microsoft.com/en-us/azure/machine-learning/service/how-to-set-up-training-targets#amlcompute) for your AutoML run. In this tutorial, you create AmlCompute as your training compute resource.
#
# > Note that if you have an AzureML Data Scientist role, you will not have permission to create compute resources. Talk to your workspace or IT admin to create the compute targets described in this section, if they do not already exist.
#
# #### Creation of AmlCompute takes approximately 5 minutes.
# If the AmlCompute with that name is already in your workspace this code will skip the creation process.
# As with other Azure services, there are limits on certain resources (e.g. AmlCompute) associated with the Azure Machine Learning service. Please read [this article](https://docs.microsoft.com/en-us/azure/machine-learning/service/how-to-manage-quotas) on the default limits and how to request more quota.
# +
from azureml.core.compute import ComputeTarget, AmlCompute
from azureml.core.compute_target import ComputeTargetException
# Choose a name for your CPU cluster
amlcompute_cluster_name = "oj-cluster"
# Verify that cluster does not exist already
try:
compute_target = ComputeTarget(workspace=ws, name=amlcompute_cluster_name)
print('Found existing cluster, use it.')
except ComputeTargetException:
compute_config = AmlCompute.provisioning_configuration(vm_size='STANDARD_D2_V2',
max_nodes=6)
compute_target = ComputeTarget.create(ws, amlcompute_cluster_name, compute_config)
compute_target.wait_for_completion(show_output=True)
# -
# ## Data
# You are now ready to load the historical orange juice sales data. We will load the CSV file into a plain pandas DataFrame; the time column in the CSV is called _WeekStarting_, so it will be specially parsed into the datetime type.
# +
time_column_name = 'WeekStarting'
data = pd.read_csv("dominicks_OJ.csv", parse_dates=[time_column_name])
# Drop the columns 'logQuantity' as it is a leaky feature.
data.drop('logQuantity', axis=1, inplace=True)
data.head()
# -
# Each row in the DataFrame holds a quantity of weekly sales for an OJ brand at a single store. The data also includes the sales price, a flag indicating if the OJ brand was advertised in the store that week, and some customer demographic information based on the store location. For historical reasons, the data also include the logarithm of the sales quantity. The Dominick's grocery data is commonly used to illustrate econometric modeling techniques where logarithms of quantities are generally preferred.
#
# The task is now to build a time-series model for the _Quantity_ column. It is important to note that this dataset is comprised of many individual time-series - one for each unique combination of _Store_ and _Brand_. To distinguish the individual time-series, we define the **time_series_id_column_names** - the columns whose values determine the boundaries between time-series:
time_series_id_column_names = ['Store', 'Brand']
nseries = data.groupby(time_series_id_column_names).ngroups
print('Data contains {0} individual time-series.'.format(nseries))
# For demonstration purposes, we extract sales time-series for just a few of the stores:
use_stores = [2, 5, 8]
data_subset = data[data.Store.isin(use_stores)]
nseries = data_subset.groupby(time_series_id_column_names).ngroups
print('Data subset contains {0} individual time-series.'.format(nseries))
# ### Data Splitting
# We now split the data into a training and a testing set for later forecast evaluation. The test set will contain the final 20 weeks of observed sales for each time-series. The splits should be stratified by series, so we use a group-by statement on the time series identifier columns.
# +
n_test_periods = 20
def split_last_n_by_series_id(df, n):
"""Group df by series identifiers and split on last n rows for each group."""
df_grouped = (df.sort_values(time_column_name) # Sort by ascending time
.groupby(time_series_id_column_names, group_keys=False))
df_head = df_grouped.apply(lambda dfg: dfg.iloc[:-n])
df_tail = df_grouped.apply(lambda dfg: dfg.iloc[-n:])
return df_head, df_tail
train, test = split_last_n_by_series_id(data_subset, n_test_periods)
# -
# ### Upload data to datastore
# The [Machine Learning service workspace](https://docs.microsoft.com/en-us/azure/machine-learning/service/concept-workspace), is paired with the storage account, which contains the default data store. We will use it to upload the train and test data and create [tabular datasets](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.data.tabulardataset?view=azure-ml-py) for training and testing. A tabular dataset defines a series of lazily-evaluated, immutable operations to load data from the data source into tabular representation.
train.to_csv (r'./dominicks_OJ_train.csv', index = None, header=True)
test.to_csv (r'./dominicks_OJ_test.csv', index = None, header=True)
datastore = ws.get_default_datastore()
datastore.upload_files(files = ['./dominicks_OJ_train.csv', './dominicks_OJ_test.csv'], target_path = 'dataset/', overwrite = True,show_progress = True)
# ### Create dataset for training
from azureml.core.dataset import Dataset
train_dataset = Dataset.Tabular.from_delimited_files(path=datastore.path('dataset/dominicks_OJ_train.csv'))
train_dataset.to_pandas_dataframe().tail()
# ## Modeling
#
# For forecasting tasks, AutoML uses pre-processing and estimation steps that are specific to time-series. AutoML will undertake the following pre-processing steps:
# * Detect time-series sample frequency (e.g. hourly, daily, weekly) and create new records for absent time points to make the series regular. A regular time series has a well-defined frequency and has a value at every sample point in a contiguous time span
# * Impute missing values in the target (via forward-fill) and feature columns (using median column values)
# * Create features based on time series identifiers to enable fixed effects across different series
# * Create time-based features to assist in learning seasonal patterns
# * Encode categorical variables to numeric quantities
#
# In this notebook, AutoML will train a single, regression-type model across **all** time-series in a given training set. This allows the model to generalize across related series. If you're looking for training multiple models for different time-series, please see the many-models notebook.
#
# You are almost ready to start an AutoML training job. First, we need to separate the target column from the rest of the DataFrame:
target_column_name = 'Quantity'
# ## Customization
#
# The featurization customization in forecasting is an advanced feature in AutoML which allows our customers to change the default forecasting featurization behaviors and column types through `FeaturizationConfig`. The supported scenarios include:
#
# 1. Column purposes update: Override feature type for the specified column. Currently supports DateTime, Categorical and Numeric. This customization can be used in the scenario that the type of the column cannot correctly reflect its purpose. Some numerical columns, for instance, can be treated as Categorical columns which need to be converted to categorical while some can be treated as epoch timestamp which need to be converted to datetime. To tell our SDK to correctly preprocess these columns, a configuration need to be add with the columns and their desired types.
# 2. Transformer parameters update: Currently supports parameter change for Imputer only. User can customize imputation methods. The supported imputing methods for target column are constant and ffill (forward fill). The supported imputing methods for feature columns are mean, median, most frequent, constant and ffill (forward fill). This customization can be used for the scenario that our customers know which imputation methods fit best to the input data. For instance, some datasets use NaN to represent 0 which the correct behavior should impute all the missing value with 0. To achieve this behavior, these columns need to be configured as constant imputation with `fill_value` 0.
# 3. Drop columns: Columns to drop from being featurized. These usually are the columns which are leaky or the columns contain no useful data.
# + tags=["sample-featurizationconfig-remarks"]
featurization_config = FeaturizationConfig()
# Force the CPWVOL5 feature to be numeric type.
featurization_config.add_column_purpose('CPWVOL5', 'Numeric')
# Fill missing values in the target column, Quantity, with zeros.
featurization_config.add_transformer_params('Imputer', ['Quantity'], {"strategy": "constant", "fill_value": 0})
# Fill missing values in the INCOME column with median value.
featurization_config.add_transformer_params('Imputer', ['INCOME'], {"strategy": "median"})
# Fill missing values in the Price column with forward fill (last value carried forward).
featurization_config.add_transformer_params('Imputer', ['Price'], {"strategy": "ffill"})
# -
# ## Forecasting Parameters
# To define forecasting parameters for your experiment training, you can leverage the ForecastingParameters class. The table below details the forecasting parameter we will be passing into our experiment.
#
#
# |Property|Description|
# |-|-|
# |**time_column_name**|The name of your time column.|
# |**forecast_horizon**|The forecast horizon is how many periods forward you would like to forecast. This integer horizon is in units of the timeseries frequency (e.g. daily, weekly).|
# |**time_series_id_column_names**|The column names used to uniquely identify the time series in data that has multiple rows with the same timestamp. If the time series identifiers are not defined, the data set is assumed to be one time series.|
# |**freq**|Forecast frequency. This optional parameter represents the period with which the forecast is desired, for example, daily, weekly, yearly, etc. Use this parameter for the correction of time series containing irregular data points or for padding of short time series. The frequency needs to be a pandas offset alias. Please refer to [pandas documentation](https://pandas.pydata.org/pandas-docs/stable/user_guide/timeseries.html#dateoffset-objects) for more information.
# ## Train
#
# The [AutoMLConfig](https://docs.microsoft.com/en-us/python/api/azureml-train-automl-client/azureml.train.automl.automlconfig.automlconfig?view=azure-ml-py) object defines the settings and data for an AutoML training job. Here, we set necessary inputs like the task type, the number of AutoML iterations to try, the training data, and cross-validation parameters.
#
# For forecasting tasks, there are some additional parameters that can be set in the `ForecastingParameters` class: the name of the column holding the date/time, the timeseries id column names, and the maximum forecast horizon. A time column is required for forecasting, while the time_series_id is optional. If time_series_id columns are not given, AutoML assumes that the whole dataset is a single time-series. We also pass a list of columns to drop prior to modeling. The _logQuantity_ column is completely correlated with the target quantity, so it must be removed to prevent a target leak.
#
# The forecast horizon is given in units of the time-series frequency; for instance, the OJ series frequency is weekly, so a horizon of 20 means that a trained model will estimate sales up to 20 weeks beyond the latest date in the training data for each series. In this example, we set the forecast horizon to the number of samples per series in the test set (n_test_periods). Generally, the value of this parameter will be dictated by business needs. For example, a demand planning application that estimates the next month of sales should set the horizon according to suitable planning time-scales. Please see the [energy_demand notebook](https://github.com/Azure/MachineLearningNotebooks/tree/master/how-to-use-azureml/automated-machine-learning/forecasting-energy-demand) for more discussion of forecast horizon.
#
# We note here that AutoML can sweep over two types of time-series models:
# * Models that are trained for each series such as ARIMA and Facebook's Prophet.
# * Models trained across multiple time-series using a regression approach.
#
# In the first case, AutoML loops over all time-series in your dataset and trains one model (e.g. AutoArima or Prophet, as the case may be) for each series. This can result in long runtimes to train these models if there are a lot of series in the data. One way to mitigate this problem is to fit models for different series in parallel if you have multiple compute cores available. To enable this behavior, set the `max_cores_per_iteration` parameter in your AutoMLConfig as shown in the example in the next cell.
#
#
# Finally, a note about the cross-validation (CV) procedure for time-series data. AutoML uses out-of-sample error estimates to select a best pipeline/model, so it is important that the CV fold splitting is done correctly. Time-series can violate the basic statistical assumptions of the canonical K-Fold CV strategy, so AutoML implements a [rolling origin validation](https://robjhyndman.com/hyndsight/tscv/) procedure to create CV folds for time-series data. To use this procedure, you just need to specify the desired number of CV folds in the AutoMLConfig object. It is also possible to bypass CV and use your own validation set by setting the *validation_data* parameter of AutoMLConfig.
#
# Here is a summary of AutoMLConfig parameters used for training the OJ model:
#
# |Property|Description|
# |-|-|
# |**task**|forecasting|
# |**primary_metric**|This is the metric that you want to optimize.<br> Forecasting supports the following primary metrics <br><i>spearman_correlation</i><br><i>normalized_root_mean_squared_error</i><br><i>r2_score</i><br><i>normalized_mean_absolute_error</i>
# |**experiment_timeout_hours**|Experimentation timeout in hours.|
# |**enable_early_stopping**|If early stopping is on, training will stop when the primary metric is no longer improving.|
# |**training_data**|Input dataset, containing both features and label column.|
# |**label_column_name**|The name of the label column.|
# |**compute_target**|The remote compute for training.|
# |**n_cross_validations**|Number of cross-validation folds to use for model/pipeline selection|
# |**enable_voting_ensemble**|Allow AutoML to create a Voting ensemble of the best performing models|
# |**enable_stack_ensemble**|Allow AutoML to create a Stack ensemble of the best performing models|
# |**debug_log**|Log file path for writing debugging information|
# |**featurization**| 'auto' / 'off' / FeaturizationConfig Indicator for whether featurization step should be done automatically or not, or whether customized featurization should be used. Setting this enables AutoML to perform featurization on the input to handle *missing data*, and to perform some common *feature extraction*.|
# |**max_cores_per_iteration**|Maximum number of cores to utilize per iteration. A value of -1 indicates all available cores should be used
# +
from azureml.automl.core.forecasting_parameters import ForecastingParameters
forecasting_parameters = ForecastingParameters(
time_column_name=time_column_name,
forecast_horizon=n_test_periods,
time_series_id_column_names=time_series_id_column_names,
freq='W-THU' # Set the forecast frequency to be weekly (start on each Thursday)
)
automl_config = AutoMLConfig(task='forecasting',
debug_log='automl_oj_sales_errors.log',
primary_metric='normalized_mean_absolute_error',
experiment_timeout_hours=0.25,
training_data=train_dataset,
label_column_name=target_column_name,
compute_target=compute_target,
enable_early_stopping=True,
featurization=featurization_config,
n_cross_validations=3,
verbosity=logging.INFO,
max_cores_per_iteration=-1,
forecasting_parameters=forecasting_parameters)
# -
# You can now submit a new training run. Depending on the data and number of iterations this operation may take several minutes.
# Information from each iteration will be printed to the console. Validation errors and current status will be shown when setting `show_output=True` and the execution will be synchronous.
remote_run = experiment.submit(automl_config, show_output=False)
remote_run.wait_for_completion()
# ### Retrieve the Best Model
# Each run within an Experiment stores serialized (i.e. pickled) pipelines from the AutoML iterations. We can now retrieve the pipeline with the best performance on the validation dataset:
best_run, fitted_model = remote_run.get_output()
print(fitted_model.steps)
model_name = best_run.properties['model_name']
# ## Transparency
#
# View updated featurization summary
custom_featurizer = fitted_model.named_steps['timeseriestransformer']
custom_featurizer.get_featurization_summary()
# # Forecasting
#
# Now that we have retrieved the best pipeline/model, it can be used to make predictions on test data. First, we remove the target values from the test set:
X_test = test
y_test = X_test.pop(target_column_name).values
X_test.head()
# To produce predictions on the test set, we need to know the feature values at all dates in the test set. This requirement is somewhat reasonable for the OJ sales data since the features mainly consist of price, which is usually set in advance, and customer demographics which are approximately constant for each store over the 20 week forecast horizon in the testing data.
# forecast returns the predictions and the featurized data, aligned to X_test.
# This contains the assumptions that were made in the forecast
y_predictions, X_trans = fitted_model.forecast(X_test)
# If you are used to scikit pipelines, perhaps you expected `predict(X_test)`. However, forecasting requires a more general interface that also supplies the past target `y` values. Please use `forecast(X,y)` as `predict(X)` is reserved for internal purposes on forecasting models.
#
# The [forecast function notebook](../forecasting-forecast-function/auto-ml-forecasting-function.ipynb).
# # Evaluate
#
# To evaluate the accuracy of the forecast, we'll compare against the actual sales quantities for some select metrics, included the mean absolute percentage error (MAPE). For more metrics that can be used for evaluation after training, please see [supported metrics](https://docs.microsoft.com/en-us/azure/machine-learning/how-to-understand-automated-ml#regressionforecasting-metrics), and [how to calculate residuals](https://docs.microsoft.com/en-us/azure/machine-learning/how-to-understand-automated-ml#residuals).
#
# We'll add predictions and actuals into a single dataframe for convenience in calculating the metrics.
assign_dict = {'predicted': y_predictions, target_column_name: y_test}
df_all = X_test.assign(**assign_dict)
# +
from azureml.automl.core.shared import constants
from azureml.automl.runtime.shared.score import scoring
from matplotlib import pyplot as plt
# use automl scoring module
scores = scoring.score_regression(
y_test=df_all[target_column_name],
y_pred=df_all['predicted'],
metrics=list(constants.Metric.SCALAR_REGRESSION_SET))
print("[Test data scores]\n")
for key, value in scores.items():
print('{}: {:.3f}'.format(key, value))
# Plot outputs
# %matplotlib inline
test_pred = plt.scatter(df_all[target_column_name], df_all['predicted'], color='b')
test_test = plt.scatter(df_all[target_column_name], df_all[target_column_name], color='g')
plt.legend((test_pred, test_test), ('prediction', 'truth'), loc='upper left', fontsize=8)
plt.show()
# -
# # Operationalize
# _Operationalization_ means getting the model into the cloud so that other can run it after you close the notebook. We will create a docker running on Azure Container Instances with the model.
# +
description = 'AutoML OJ forecaster'
tags = None
model = remote_run.register_model(model_name = model_name, description = description, tags = tags)
print(remote_run.model_id)
# -
# ### Develop the scoring script
#
# For the deployment we need a function which will run the forecast on serialized data. It can be obtained from the best_run.
script_file_name = 'score_fcast.py'
best_run.download_file('outputs/scoring_file_v_1_0_0.py', script_file_name)
# ### Deploy the model as a Web Service on Azure Container Instance
# +
from azureml.core.model import InferenceConfig
from azureml.core.webservice import AciWebservice
from azureml.core.webservice import Webservice
from azureml.core.model import Model
inference_config = InferenceConfig(environment = best_run.get_environment(),
entry_script = script_file_name)
aciconfig = AciWebservice.deploy_configuration(cpu_cores = 1,
memory_gb = 2,
tags = {'type': "automl-forecasting"},
description = "Automl forecasting sample service")
aci_service_name = 'automl-oj-forecast-01'
print(aci_service_name)
aci_service = Model.deploy(ws, aci_service_name, [model], inference_config, aciconfig)
aci_service.wait_for_deployment(True)
print(aci_service.state)
# -
aci_service.get_logs()
# ### Call the service
import json
X_query = X_test.copy()
# We have to convert datetime to string, because Timestamps cannot be serialized to JSON.
X_query[time_column_name] = X_query[time_column_name].astype(str)
# The Service object accept the complex dictionary, which is internally converted to JSON string.
# The section 'data' contains the data frame in the form of dictionary.
test_sample = json.dumps({'data': X_query.to_dict(orient='records')})
response = aci_service.run(input_data = test_sample)
# translate from networkese to datascientese
try:
res_dict = json.loads(response)
y_fcst_all = pd.DataFrame(res_dict['index'])
y_fcst_all[time_column_name] = pd.to_datetime(y_fcst_all[time_column_name], unit = 'ms')
y_fcst_all['forecast'] = res_dict['forecast']
except:
print(res_dict)
y_fcst_all.head()
# ### Delete the web service if desired
serv = Webservice(ws, 'automl-oj-forecast-01')
serv.delete() # don't do it accidentally
|
how-to-use-azureml/automated-machine-learning/forecasting-orange-juice-sales/auto-ml-forecasting-orange-juice-sales.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import tensorflow as tf
import numpy as np
from tensorflow import keras
import matplotlib.pyplot as plt
# %matplotlib inline
import tensorflow_datasets as tfds
import random
from numba import cuda
tf.keras.backend.clear_session()
print(tf.__version__)
# -
from tensorflow.keras.preprocessing.image import ImageDataGenerator
mnist = tf.keras.datasets.mnist
(X_train_images,y_train_labels), (X_test_images,y_test_labels) = mnist.load_data()
X_train_images = np.array(X_train_images) / 255.0
X_test_images = np.array(X_test_images) / 255.0
# +
for y in range(4):
for grid in range(4):
plt.figure()
plt.imshow(X_train_images[random.randint(0,(len(X_train_images)))])
# -
model = tf.keras.Sequential([tf.keras.layers.Flatten(input_shape = (28,28)),
tf.keras.layers.Dense(128,activation='relu'),
tf.keras.layers.Dense(10,activation='softmax')])
model.compile(loss='sparse_categorical_crossentropy',optimizer='adam',metrics=['acc'])
class MyCallback(tf.keras.callbacks.Callback):
def on_epoch_end(self,epoch,logs):
if logs.get('acc')>0.99:
print("Reached 99% accuracy so cancelling training!")
self.model.stop_training = True
callbacks = MyCallback()
history = model.fit(X_train_images,y_train_labels,epochs=15,callbacks=[callbacks])
model.evaluate(X_test_images,y_test_labels)
cuda.close()
|
Course-1/exercise-2-HandwritingRecognitionDNN.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Data Structure with Python Week 8
# ### Input a dataset in csv form and then do the following question.
# https://www.kaggle.com/gustavomodelli/forest-fires-in-brazil use this link to download the dataset.
# ## <NAME>
# CSE2H Roll 29
import pandas as pd
import numpy as np
df = pd.read_csv("amazon.csv", encoding='cp1252')
df.head()
# ## 1. Find out the row and column name of the dataset.
df.columns # 1a
df.index.values # 1b
# ## 2. How fire occurred in the 2016 .
# +
fire_2016 = 0 # 2
year_filter = df['year'] == 2016
df_2016 = df[year_filter]
print(df_2016['number'].sum())
# -
# ## 4. Find out many rows are there in the dataset.
len(list(df.index.values)) # 4
|
Week 8/1-4.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import requests
import time
from fair_research_login import NativeClient
client = NativeClient(client_id='7414f0b4-7d05-4bb6-bb00-076fa3f17cf5')
tokens = client.login(
requested_scopes=['urn:globus:auth:scope:transfer.api.globus.org:all',
"https://auth.globus.org/scopes/facd7ccc-c5f4-42aa-916b-a0e270e2c2a9/all",
'email', 'openid'],
no_local_server=True,
no_browser=True)
transfer_token = tokens['transfer.api.globus.org']['access_token']
funcx_token = tokens['funcx_service']['access_token']
headers = {'Authorization': f"Bearer {funcx_token}",'Transfer': transfer_token, 'FuncX': f"{funcx_token}"}
print(f"Headers: {headers}")
# -
from xtracthub.xcs import XtractConnection
xconn = XtractConnection(funcx_token)
import matplotlib.pyplot as plt
import csv
# ### Plotting Threads vs. Time for Sigularity and Docker
# For this experiment I will measure the time that it takes for XCS to build a fixed number of containers for various numbers of threads. I will then scale up the number of containers. The upload speed will be capped in order to prevent too much variance for Docker.
# +
import os
csv_name = f'thread_time_results_v2.csv'
if os.path.exists("./" + csv_name):
print(f"{csv_name} already exists, do you want to overwrite?")
if input() == "no":
csv_name = None
else:
pass
with open(csv_name, mode='w') as f:
csv_writer = csv.writer(f, delimiter=',', quotechar='"', quoting=csv.QUOTE_MINIMAL)
csv_writer.writerow(["type", "threads", "containers", "time", "fails"])
# +
import datetime
import time
import uuid
from IPython.display import clear_output
with open(csv_name, mode='a') as f:
csv_writer = csv.writer(f, delimiter=',', quotechar='"', quoting=csv.QUOTE_MINIMAL)
for containers in range(10, 60, 10):
for threads in range(5, 55, 5):
print(f"Containers {containers}")
print(f"Threads {threads}")
requests.post("http://1172.16.31.10/change_thread", json={"threads": threads})
print("Starting Singularity")
definition_ids = []
for i in range(containers):
file_name = "my_test.def"
file_path = "./examples/my_example.txt"
definition_id = xconn.register_container(file_name, file_path)
definition_ids.append(definition_id)
build_ids = []
start_time = datetime.datetime.now()
for idx, definition_id in enumerate(definition_ids):
build_id = xconn.build(definition_id, "singularity", "my_test_{}.sif".format(idx))
build_ids.append(build_id)
print(build_id)
keep_printing = True
while keep_printing:
clear_output(True)
is_done = []
statuses = []
finish_times = []
for idx, build_id in enumerate(build_ids):
status = xconn.get_status(build_id)
print(status)
if status["build_status"] == "success":
is_done.append(True)
finish_times.append(status["build_time"])
statuses.append("success")
elif status["build_status"] == "failed":
is_done.append(True)
statuses.append("failed")
else:
is_done.append(False)
if all(is_done):
keep_printing = False
time.sleep(1)
finish_times = list(map(lambda x: datetime.datetime.strptime(x, "%m/%d/%Y, %H:%M:%S"), finish_times))
finish_times = list(map(lambda x: x - datetime.timedelta(hours=1), finish_times))
total_time = max(list(map(lambda x: (x - start_time).total_seconds(), finish_times)))
csv_writer.writerow(["singularity", threads, containers, total_time, statuses.count("failed")])
# +
import time
import uuid
from IPython.display import clear_output
results = []
with open(f'thread_time_results.csv', mode='a') as f:
csv_writer = csv.writer(f, delimiter=',', quotechar='"', quoting=csv.QUOTE_MINIMAL)
containers=10
threads=5
print("Starting Docker")
requests.post("http://149.165.168.132/change_thread", json={"threads": threads})
definition_ids = []
for i in range(containers):
file_name = "Dockerfile"
file_path = "./examples/matio_dockerfile"
definition_id = xconn.register_container(file_name, file_path)
definition_ids.append(definition_id)
build_ids = []
for idx, definition_id in enumerate(definition_ids):
build_id = xconn.build(definition_id, "docker", "my_test_{}".format(idx))
build_ids.append(build_id)
print(build_id)
keep_printing = True
start_time = time.time()
while keep_printing:
clear_output(True)
is_done = []
statuses = []
for idx, build_id in enumerate(build_ids):
status = xconn.get_status(build_id)
print(status)
if status["build_status"] == "success":
is_done.append(True)
statuses.append("success")
elif status["build_status"] == "failed":
is_done.append(True)
statuses.append("failed")
else:
is_done.append(False)
if all(is_done):
keep_printing = False
time.sleep(1)
csv_writer.writerow(["docker", threads, containers, time.time() - start_time, statuses.count("failed")])
print("Starting Singularity")
definition_ids = []
for i in range(containers):
file_name = "my_test.def"
file_path = "./examples/my_example.txt"
definition_id = xconn.register_container(file_name, file_path)
definition_ids.append(definition_id)
build_ids = []
for idx, definition_id in enumerate(definition_ids):
build_id = xconn.build(definition_id, "singularity", "my_test_{}.sif".format(idx))
build_ids.append(build_id)
print(build_id)
keep_printing = True
start_time = time.time()
while keep_printing:
clear_output(True)
is_done = []
statuses = []
for idx, build_id in enumerate(build_ids):
status = xconn.get_status(build_id)
print(status)
if status["build_status"] == "success":
is_done.append(True)
statuses.append("success")
elif status["build_status"] == "failed":
is_done.append(True)
statuses.append("failed")
else:
is_done.append(False)
if all(is_done):
keep_printing = False
time.sleep(1)
csv_writer.writerow(["singularity", threads, containers, time.time() - start_time, statuses.count("failed")])
# +
data = []
with open('thread_time_results_v2.csv') as csv_file:
csv_reader = csv.reader(csv_file, delimiter=',')
line_count = 0
for row in csv_reader:
data.append(row)
data.pop(0)
data = list(filter(lambda x: x[0] == "singularity", data))
for i in list(set([x[2] for x in data])):
cont_data = list(filter(lambda x: x[2] == i, data))
x = [i[1] for i in cont_data]
y = [i[3] for i in cont_data]
print(y)
y = list(map(int, list(map(float, y))))
print(y)
plt.scatter(x, y)
plt.title(f"{i} containers, Singularity")
plt.xlabel("Threads")
plt.ylabel("Time")
plt.show()
# +
definition_ids = []
for i in range(10):
file_name = "Dockerfile"
file_path = "./examples/matio_dockerfile"
definition_id = xconn.register_container(file_name, open(file_path, "rb"))
definition_ids.append(definition_id)
print(definition_id)
# +
build_ids = []
for idx, definition_id in enumerate(definition_ids):
build_id = xconn.build(definition_id, "docker", "my_test_{}".format(idx))
build_ids.append(build_id)
print(build_id)
print(build_ids)
# -
keep_printing = True
import time
from IPython.display import clear_output
while keep_printing:
clear_output(True)
is_done = []
for idx, build_id in enumerate(build_ids):
status = xconn.get_status(build_id)
print(status)
if status["build_status"] in ["success", "failed"]:
is_done.append(True)
else:
is_done.append(False)
print(time.time())
if all(is_done):
keep_printing = False
time.sleep(5)
import os
t0 = time.time()
# Example for pulling a container
for build_id in build_ids:
container_path = os.path.join(os.path.abspath("."), "my_test.tar")
response = xconn.pull(build_id, container_path)
if os.path.exists(container_path):
print("Successfully pulled container to {}".format(container_path))
else:
print(response)
print("Pulled in {}".format(time.time() - t0))
t0 = time.time()
build_ids = []
# Example for building a Docker container with a git repo
for i in range(10):
git_repo = "https://github.com/rewong03/xtract_file_service"
container_name = f"xfs{i}"
build_id = xconn.repo2docker(container_name, git_repo=git_repo)
build_ids.append(build_id)
print(build_id)
print("Response received in {}".format(time.time() - t0))
t0 = time.time()
# Example for getting the status of a container
status = xconn.get_status(build_id)
print(status)
print("Got status in {}".format(time.time() - t0))
build_ids = ['26bda2ab-1bd1-4bb1-be04-20f4e243f47b']
|
threading_experiments.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.8.3 ('base')
# language: python
# name: python3
# ---
class Solution:
def isValid(self, s: str) -> bool:
stack = []
left = ["(", "{", "["]
for char in s:
if char in left:
stack.append(char) ## append all left-hand characters
else:
if stack:
current = stack.pop() ## grab top
if current == '(':
if char != ')':
return False
if current == '{':
if char != '}':
return False
if current == '[':
if char != ']':
return False
else:
return False
print(stack)
if stack:
return False
return True
s = "()"
Solution().isValid(s)
s = "()[]{}"
Solution().isValid(s)
s = "(]"
Solution().isValid(s)
s = ']'
Solution().isValid(s)
|
20validParen.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# +
# %matplotlib inline
import numpy as np
import arrayfire as af
from scipy import ndimage
import matplotlib.pyplot as plt
from LearnAF import *
import tqdm
import pandas as pd
af.set_backend('cpu')
#af.set_device(1)
f = np.load('/home/narsi/Downloads/mnist.npz')
Data = f['x_train']
y_train = f['y_train']
Data = Data.reshape(60000, 784)
Data = Data.astype('float32')/255.0
classes = np.asarray(to_categorical(y_train), dtype = np.float32)
# initialize weights randomly with mean 0
syn0 = np.array(2*np.random.random((Data.shape[1],64)) - 1, dtype = np.float32)
W1 = Variable(af.np_to_af_array(syn0),name='W1')
b1 = Variable(af.constant(0,1),name='b1')
syn0 = np.array(2*np.random.random((64,16)) - 1, dtype = np.float32)
W2 = Variable(af.np_to_af_array(syn0),name='W2')
b2 = Variable(af.constant(0,1),name='b2')
syn0 = np.array(2*np.random.random((16,10)) - 1, dtype = np.float32)
W3 = Variable(af.np_to_af_array(syn0),name='W3')
b3 = Variable(af.constant(0,1),name='b3')
w = [W1,b1,W2,b2,W3,b3]
# -
# # Model
def learner(X,W):
# 784 -> 64
X1 = relu(add(matmul(X,W[0]),W[1]))
# 64 -> 16
X2 = relu(add(matmul(X1,W[2]),W[3]))
# 16 -> 10
YP = softmax(add(matmul(X2,W[4]),W[5]))
return YP
# # Place Holders
batch = 64
Xin = Constant(af.np_to_af_array(np.random.random((batch,Data.shape[1])).astype(np.float32)))
Y = Constant(af.np_to_af_array(np.random.random((batch,10)).astype(np.float32)))
YP = learner(Xin,w)
e = CrossEntropy(Y,YP)
acc = accuracy(Y,YP)
sgd = SGD(lr = 0.01,momentum=0.9)
for i in range(1):
epoch_acc = []
epoch_loss = []
total_batchs = int(Data.shape[0]/batch)
for j in tqdm.tqdm(range(total_batchs)):
X_np = Data[j*batch:(j+1)*batch,:]
Xin.value = af.np_to_af_array(X_np)
Y_np = classes[j*batch:(j+1)*batch,:]
Y.value = af.np_to_af_array(Y_np)
(l,w) = sgd.update(e, w, i)
acc = accuracy(Y,YP)
epoch_acc.append(acc)
epoch_loss.append(np.asarray(l)[0])
print('Accuracy :'+str(np.mean(epoch_acc)))
print('Loss :'+str(np.mean(epoch_loss)))
|
Layers.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import cv2
from cv2.ximgproc import createFastLineDetector
import utils.visualization as vis
im_fn = "../../data/California Museum of Photography/0/07941.jpg"
im = cv2.imread(im_fn, 0)
# im = cv2.resize(im, None, fx=0.5, fy=0.5)
fld = createFastLineDetector(_length_threshold = 30, _distance_threshold = 5, _do_merge = True,
_canny_th1 = 10, _canny_th2=10)
lines = fld.detect(im)
im_vis = fld.drawSegments(im, lines)
vis.imshow([im_vis])
cv2.imwrite('/Users/xuanluo/Downloads//test.png', im_vis)
cv2.imwrite('/Users/xuanluo/Downloads//test2.png', im)
# -
# # lsd = cv2.createLineSegmentDetector(_scale=0.2, _refine = True, _log_eps=10)
# lines, width, precision, nfa = lsd.detect(im)
# im_vis = lsd.drawSegments(im, lines)
# vis.imshow([im_vis])
# cv2.imwrite('/Users/xuanluo/Downloads//test_lsd.png', im_vis)
help(createFastLineDetector)
# +
img1, img2 = im, im
# Initiate feature detector, fd
# fd = cv2.ORB_create() # too few matches
# fd = cv2.xfeatures2d.SIFT_create()
fd = cv2.xfeatures2d.SURF_create(100)
# find the keypoints and descriptors with SIFT
kp1, des1 = fd.detectAndCompute(img1,None)
kp2, des2 = fd.detectAndCompute(img2,None)
# BFMatcher with default params
bf = cv2.BFMatcher()
matches = bf.knnMatch(des1,des2, k=3)
R = 100
# Apply ratio test
good = []
for match in matches:
non_id_matches = []
for m in match:
if kp1[m.queryIdx].pt[0] - kp2[m.trainIdx].pt[0] >= R:
non_id_matches.append(m)
if len(non_id_matches)< 2:
continue
m, n = non_id_matches[:2]
if m.distance < 0.7*n.distance:
good.append([m])
print('#good matches', len(good))
# cv2.drawMatchesKnn expects list of lists as matches.
img3 = cv2.drawMatchesKnn(img1,kp1,img2,kp2,good, None, flags=2)
vis.imshow([img3])
cv2.imwrite('/Users/xuanluo/Downloads//test3.png', img3)
# +
from numpy import linalg
from pdb import set_trace as st
import numpy as np
def line_direction(line_seg):
return line_seg[2:4] - line_seg[:2]
def angle(dir1, dir2):
c = dir1.T.dot(dir2)/linalg.norm(dir1)/linalg.norm(dir2)
a = np.rad2deg(np.arccos(c))
if a > 90:
a = 180-a
return a
def select_lines(lines, direction, degree_threshold):
lines = lines.squeeze().astype(float)
result = []
for l in lines:
if angle(line_direction(l), direction) < degree_threshold:
result.append(l)
return result
v_lines = select_lines(lines, np.array((0,1)), 5)
h_lines = select_lines(lines, np.array((1,0)), 5)
im_vis = fld.drawSegments(im, np.array([v_lines]).astype(np.float32))
vis.imshow([im_vis])
# -
cv2.imwrite('/Users/xuanluo/Downloads//test_select.png',im_vis)
# +
from sklearn.linear_model import LinearRegression
def get_match_points(matches, kp_list1, kp_list2):
N = len(matches)
p1, p2 = np.zeros((N,2)), np.zeros((N,2))
for i, ml in enumerate(matches):
m = ml[0]
p1[i,:] = kp_list1[m.queryIdx].pt
p2[i,:] = kp_list2[m.trainIdx].pt
return p1, p2
def pad_ones(points):
return np.concatenate((points,np.ones((points.shape[0],1))), axis=1)
def line_eq_from_a_line_seg(line_seg):
points = pad_ones(np.array([line_seg[:2], line_seg[2:]]))
return np.cross(points[0,:], points[1,:])
def line_eq_from_line_segs(line_seg):
points = np.concatenate(([line_seg[:,:2], line_seg[:,2:]]), axis=0)
return fit_line_eq(points)
# get line_eq from points (not homogeneous)
# fit s.t., <(w,b), (x,y, 1)>=1
# so line_eq = <(wx, wy, b-1), (x,y,1)> = 0
def fit_line_eq(points):
# convert to homogeneous coordinates
X = pad_ones(points)
y = np.ones(X.shape[0])
cls = LinearRegression(fit_intercept = True)
model = cls.fit(X,y)
print(model.coef_, model.intercept_)
return np.array((model.coef_, model.intercept_-1))
# kp1 and kp2 are np array
def num_match_cut(line_eq, kp1, kp2):
dist1 = pad_ones(kp1).dot(line_eq)
dist2 = pad_ones(kp2).dot(line_eq)
num_cut = np.sum(dist1 * dist2 <= 0)
return num_cut
def point_to_line_dist(line_eq, points):
points = pad_ones(points)
dist = points.dot(line_eq)
return dist/linalg.norm(line_eq[:2])
def get_inliers(line_eq, lines, dist_th):
d1 = np.abs(point_to_line_dist(line_eq, lines[:, :2]))
d2 = np.abs(point_to_line_dist(line_eq, lines[:, 2:]))
ix = np.logical_and(d1 <= dist_th, d2 <= dist_th)
return lines[ix]
def max_distance(inliers):
diff = inliers[:,:2]-inliers[:,2:]
return np.sum(linalg.norm(diff, axis=-1))
kp1_np, kp2_np = get_match_points(good, kp1, kp2)
lines = np.array(v_lines)
dist_th = 5
best_line, best_inliers = None, None
max_num_cut, max_length = 0, 0
cut_inlier_ratio = 0.9
for l in lines:
line_eq = line_eq_from_a_line_seg(l)
num_cut = num_match_cut(line_eq, kp1_np, kp2_np)
inliers = get_inliers(line_eq, lines, dist_th)
length = max_distance(inliers)
max_num_cut = max(num_cut, max_num_cut)
if num_cut >= max_num_cut*cut_inlier_ratio and length > max_length:
best_line, best_inliers = l, inliers
max_length, max_num_cut = length, num_cut
# line_seg = fit_line_seg(inliers)
# im_vis = fld.drawSegments(im, line_seg)
print(best_inliers.shape, max_num_cut, max_length)
print(best_inliers)
im_vis = fld.drawSegments(im, np.array([best_inliers]).astype(np.float32))
vis.imshow([im_vis])
cv2.imwrite('/Users/xuanluo/Downloads/inliers.png', im_vis)
# +
# get line_eq from points (not homogeneous)
# fit s.t., <(w,b), (x,y, 1)>=1
# so line_eq = <(wx, wy, b-1), (x,y,1)> = 0
def fit_line_eq(points, vertical = True):
# convert to homogeneous coordinates
X = points[:,1 if vertical else 0][:,None]
y = points[:,0 if vertical else 1]
cls = LinearRegression(fit_intercept = True)
model = cls.fit(X,y)
w = (-1, model.coef_, model.intercept_) if vertical else (model.coef_, -1, model.intercept_)
return np.array(w)
def get_line_seg(line_eq, ys):
a, b, c = line_eq
xs = (b*ys+c)/(-a)
print(xs, ys)
line_seg = np.array([[[xs[0], ys[0], xs[1], ys[1]]]], dtype=np.float32)
return line_seg
line_eq = line_eq_from_line_segs(best_inliers)
line_seg = get_line_seg(line_eq, np.array((0, im.shape[0]-1)))
im_vis = fld.drawSegments(im, line_seg)
vis.imshow([im_vis])
cv2.imwrite('/Users/xuanluo/Downloads/line.png', im_vis)
# -
line_eq
|
linedect/line_detection.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/Manvikaul/corona-chatbot/blob/master/chatbot_improved.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="g9aTSOlv-jUg" colab_type="code" outputId="8bdc6ff3-f297-4241-ea8f-d938b26bd1d5" colab={"base_uri": "https://localhost:8080/", "height": 51}
pip install nltk
# + id="Z5MmH0sd__S0" colab_type="code" outputId="6e7e220a-26fe-4f36-ccbe-97ddc00bd2e7" colab={"base_uri": "https://localhost:8080/", "height": 870}
pip install newspaper3k
# + id="7wBvZdq2AHQq" colab_type="code" colab={}
#IMPORTS
from newspaper import Article
import random
import string
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.metrics.pairwise import cosine_similarity
import nltk
import numpy as np
import warnings
# + id="AaAkVEI4KUHA" colab_type="code" colab={}
#Ignoring warnings
warnings.filterwarnings('ignore')
# + id="umANhsMjKuaK" colab_type="code" outputId="8500a4a9-855c-405e-974b-0e1563999e65" colab={"base_uri": "https://localhost:8080/", "height": 102}
nltk.download('punkt')
nltk.download('wordnet')
# + id="Wv1WNTJ-XC1z" colab_type="code" outputId="efc75c77-ee4c-4f69-e1a0-0f749f4661c5" colab={"base_uri": "https://localhost:8080/", "height": 1000}
#article=Article('https://www.resmed.com/in/en/consumer/blogs/coronavirus-infection.html')
article=Article('https://www.medicalnewstoday.com/articles/256521')
article.download()
article.parse()
article.nlp()
corpus=article.text
print(corpus)
# + id="6Zz_KIJ-YWPp" colab_type="code" outputId="aa5b0ccd-151b-4600-ff75-eaf810e13999" colab={"base_uri": "https://localhost:8080/", "height": 54}
text=corpus
sent_tokens=nltk.sent_tokenize(text)
print(sent_tokens)
# + id="2jtbnkdBbZpb" colab_type="code" outputId="a20fd6f1-de28-4b34-8629-7aae3456d29c" colab={"base_uri": "https://localhost:8080/", "height": 34}
remove_punct_dict=dict((ord(punct),None) for punct in string.punctuation)
print(string.punctuation)
# + id="5JDptqPWczFo" colab_type="code" outputId="5a0c2d2d-15eb-4645-dbac-d98d7dd0d944" colab={"base_uri": "https://localhost:8080/", "height": 54}
print(remove_punct_dict)
# + id="oFPX_gNPcXLa" colab_type="code" outputId="1ce4918c-d7fb-420b-ffec-8e4c308adadd" colab={"base_uri": "https://localhost:8080/", "height": 54}
def LemNormalize(text):
return nltk.word_tokenize(text.lower().translate(remove_punct_dict))
print(LemNormalize(text))
# + id="HbFX8SPurhxu" colab_type="code" colab={}
GREETING_INPUTS=['hey','hi','hello','heya','howdy','whatsup','wassup','hola']
GREETING_OUTPUTS=['hey!','hello!','heya!','howdy!','hey there!','holaa!']
# + id="luXX68PIt0iR" colab_type="code" colab={}
def greeting(sentence):
for word in sentence.split():
if word.lower() in GREETING_INPUTS:
return random.choice(GREETING_OUTPUTS)
# + id="NRc9ZeIQZeno" colab_type="code" colab={}
def response(user_response):
user_response.lower()
#print(user_response)
robo_response=''
sent_tokens.append(user_response)
#print(sent_tokens)
tfidfvec=TfidfVectorizer(tokenizer=LemNormalize,stop_words='english')
tfidf=tfidfvec.fit_transform(sent_tokens)
#print(tfidf)
#Get similarity scores (user's response with all other tokens)
vals=cosine_similarity(tfidf[-1],tfidf)
#print(vals)
idx=vals.argsort()[0][-2]
#we give -2 as argument since -1 will give the sentence with max similarity, and that would be the sentence itself(since it is appended at the end)
#hence we use -2 which give the second most similar sentence
#reduce the dimensionality of vals
flat=vals.flatten()
#sort the list in ascending order
flat.sort()
#Get the most similar score to user response
score=flat[-2]
#print(score)
#if score==0 => no text similar to user response
if(score==0):
robo_response=robo_response+"I am sorry, I don't quite understand"
else:
robo_response=robo_response+sent_tokens[idx]
#print(robo_response)
sent_tokens.remove(user_response)
return robo_response
# + id="Sg0mJxjOb1fM" colab_type="code" outputId="680075ab-80eb-4c59-e0a3-1aa53c4e3c54" colab={"base_uri": "https://localhost:8080/", "height": 836}
flag=True
print("Bot: Hey! I'm M.A.R.T.I.N. I'm here to clear your doubts on corona virus. If you wish to exit, type 'bye'.")
while(flag==True):
user_response=input()
user_response=user_response.lower()
if(user_response!='bye'):
if(user_response=='thanks' or user_response=='thank you'):
print("Bot: You're welcome!")
else:
if(greeting(user_response)!=None):
print("Bot: "+greeting(user_response ))
else:
print("Bot: "+response(user_response))
else:
flag=False
print("Bot: Talk to ya later!")
|
chatbot_improved.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 1.6.1
# language: julia
# name: julia-1.6
# ---
# # Basic Plot
using PyPlot
x = 1:100
y = rand(100)
p = PyPlot.plot(x,y)
xlabel("x")
ylabel("y")
title("basic plot")
# +
using PyPlot
x = range(0,stop=2*pi,length=10)
xlabel("x-axis")
y = cos(pi + sin.(x))
ylabel("y-axis")
plot(x, y, color="red")
title("using sin and cos functions")
# -
x = [1:1:10;]
y = ones(10)
for i = 1:1:10
y[i] = pi + i*i
end
xkcd()
xlabel("x-axis")
ylabel("y-axis")
title("XKCD")
p = PyPlot.plot(x,y)
x = [10,20,30,40,50]
y = [2,4,6,8,10]
xlabel("x-axis")
ylabel("y-axis")
title("Vertical bar graph")
PyPlot.bar(x, y, color="red")
x = [10,20,30,40,50]
y = [2,4,6,8,10]
title("Horizontal bar graph")
xlabel("x-axis")
ylabel("y-axis")
PyPlot.barh(x,y,color="red")
x = rand(1000)
y = rand(1000)
xlabel("x-axis")
ylabel("y-axis")
title("2D Histograph")
hist2D(x, y, bins=50)
labels = ["Fruits";"Vegetables";"Wheat"]
colors = ["Orange";"Blue";"Red"]
sizes = [25;40;35]
explode = zeros(length(sizes))
fig = figure("piechart", figsize=(10,10))
p = PyPlot.pie(sizes, labels=labels, shadow=true, startangle=90, colors = colors)
title("Pie charts")
using PyPlot
fig = figure("scatterplot", figsize = (10,10))
x = rand(50)
y = rand(50)
areas = 1000*rand(50);
PyPlot.scatter(x, y, s=areas, alpha=0.5)
xlabel("x-axis")
ylabel("y-axis")
title("Scatter Plot")
# +
#3-d surface plot
using PyPlot
a = range(0,stop=2*pi,length=10)
b = range(0,stop=2*pi,length=10)
len_a = length(a)
len_b = length(b)
x = ones(len_a, len_b)
y = ones(len_a, len_b)
z = ones(len_a, len_b)
for i=1:len_a
for j=1:len_b
x[i,j] = sin(a[i])
y[i,j] = cos(a[i])
z[i,j] = sin(b[j])
end
end
colors = rand(len_a, len_b, 3)
fig = figure()
surf(x, y, z, facecolors=colors)
fig[:canvas][:draw]()
# -
Pkg.add("Vega")
Pkg.add("KernelDensity")
Pkg.add("Distributions")
# +
using Vega, KernelDensity, Distributions
# -
|
Notebooks/Data Visualization.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: pysciws
# language: python
# name: sciws
# ---
# +
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.optim.lr_scheduler import ReduceLROnPlateau
from torch.utils.data import DataLoader
from torch.utils.data import Dataset
from torch.utils.tensorboard import SummaryWriter
import numpy as np
import pandas as pd
import hashlib
import shutil
import glob
import time
import re
import os
from tqdm import tqdm
from datetime import datetime
from sklearn.metrics import f1_score, recall_score, precision_score, accuracy_score
class Net(nn.Module):
def __init__(self, sequenceSize=20000, embeddingDim=128, vocabularySize=2**16, filterWidth=5, filterNumber=1024):
super(Net, self).__init__()
self.sequenceSize = sequenceSize
self.embeddingDim = embeddingDim
self.vocabularySize = vocabularySize
self.filterWidth = filterWidth
self.filterNumber = filterNumber
self.embedding = nn.Embedding(self.vocabularySize, self.embeddingDim)
self.conv = nn.Sequential(
nn.Conv2d(1, self.filterNumber, (self.filterWidth, self.embeddingDim)),
nn.BatchNorm2d(self.filterNumber),
nn.ReLU()
)
self.fc = nn.Sequential(
nn.Linear(self.filterNumber , 512),
nn.BatchNorm1d(512),
nn.ReLU(),
nn.Linear(512, 256),
nn.BatchNorm1d(256),
nn.ReLU(),
nn.Linear(256, 1),
nn.Sigmoid()
)
def forward(self, x):
x = self.embedding(x)
#print(x.size())
x = self.conv(x)
#print(x.size())
x = x.max(dim=2)[0]
#print(x.size())
x = x.view(-1, self.filterNumber)
x = self.fc(x)
return x
class SampleDataset(Dataset):
def __init__(self, filePathList, labels, sequenceSize=20000, featureName='functionMethodCallsArgs'):
self.filePathList = filePathList
self.labels = labels
self.sequenceSize = sequenceSize
self.featureName = featureName
def __len__(self):
return len(self.filePathList)
def __getitem__(self, idx):
df = pd.read_parquet(self.filePathList[idx])
seed = int(round(time.time()%1, 6) * 1000000)
x = np.concatenate(df.iloc[np.random.RandomState(seed).permutation(len(df))][self.featureName].values)
if len(x) > self.sequenceSize:
x = x[:self.sequenceSize]
else:
x = np.concatenate((x, np.zeros([self.sequenceSize - len(x)])))
sample = torch.from_numpy(x)
return (sample.long(), self.labels[idx], self.filePathList[idx])
def train(model, optimizer, dataLoader, device):
running_loss = 0.0
label_lst = list()
predicted_lst = list()
model.train()
for inputs, labels, _ in dataLoader:
#
inputs = inputs.unsqueeze(1).to(device)
labels = labels.to(device)
#
optimizer.zero_grad()
#
outputs = model(inputs)
predicted = (outputs > 0.5).squeeze().long()
loss = F.binary_cross_entropy(outputs.squeeze(), labels.float())
#
loss.backward()
optimizer.step()
#
label_lst.append(labels.cpu().numpy())
predicted_lst.append(predicted.cpu().numpy())
running_loss += loss.item()
labels = np.concatenate(label_lst)
predicted = np.concatenate(predicted_lst)
loss = running_loss / len(predicted)
return labels, predicted, loss
def assess(model, dataLoader, device):
running_loss = 0.0
label_lst = list()
predicted_lst = list()
proba_lst = list()
path_lst = list()
with torch.no_grad():
model.eval()
for inputs, labels, paths in dataLoader:
#
inputs = inputs.unsqueeze(1).to(device)
labels = labels.to(device)
#
outputs = model(inputs)
predicted = (outputs > 0.5).squeeze().long()
loss = F.binary_cross_entropy(outputs.squeeze(), labels.float())
#
if len(inputs) > 1:
label_lst.append(labels.cpu().numpy())
predicted_lst.append(predicted.cpu().numpy())
proba_lst.append(outputs.squeeze().cpu().numpy())
path_lst.append(paths)
running_loss += loss.item()
labels = np.concatenate(label_lst)
predicted = np.concatenate(predicted_lst)
proba = np.concatenate(proba_lst)
paths = np.concatenate(path_lst)
loss = running_loss / len(predicted)
return labels, predicted, loss, proba, paths
def trainModel(ws, modelTag, epochNum, trainLoader, validLoader, device, lr=3e-4, weightDecay=9e-5):
#
model = Net()
model = model.to(device)
optimizer = optim.Adam(model.parameters(), lr=lr, weight_decay=weightDecay)
scheduler = ReduceLROnPlateau(optimizer, 'min', verbose=True, patience=5, factor=0.8)
outputlogFilePath = f'./traces/{ws}/logs'
outputtracesPath = f'./traces/{ws}'
#shutil.rmtree(outputtracesPath)
#os.mkdir(outputtracesPath)
result_lst = list()
message = '----------'
with open(outputlogFilePath, 'a') as writer:
writer.write(message + '\n')
print(message)
for epoch in range(epochNum):
tlabel, tpredicted, tloss = train(model, optimizer, trainLoader, device)
vlabel, vpredicted, vloss, vproba, vproba = assess(model, validLoader, device)
message = f'Train: {modelTag} '
message += '[{:04d}] '.format(epoch)
tf1score = f1_score(tlabel, tpredicted)
message += 'TF1: {:2.4f}, '.format(tf1score*100)
message += 'Tloss: {:2.8f}, '.format(tloss)
vf1score = f1_score(vlabel, vpredicted)
message += 'VF1: {:2.4f}, '.format(vf1score*100)
message += 'VLoss: {:2.8f},'.format(vloss)
with open(outputlogFilePath, 'a') as writer:
writer.write(message + '\n')
print(message)
modelOutputPath = f'{outputtracesPath}/model_{modelTag}_{epoch:03d}.pth'
torch.save(model.state_dict(), modelOutputPath)
result_lst.append((epoch, modelOutputPath, vlabel, vpredicted, vproba, vf1score, vloss, tf1score, tloss))
scheduler.step(tloss)
df = pd.DataFrame(result_lst,
columns=['epoch', 'path', 'labels', 'predicted', 'proba', 'vf1score', 'vloss', 'tf1score', 'tloss'])
df.to_parquet(f'{outputtracesPath}/{modelTag}.parquet')
message = '----------'
with open(outputlogFilePath, 'a') as writer:
writer.write(message + '\n')
print(message)
return df
def evaluate(ws, modelPathList, dataloader, device, numberFragments=1):
modelResultList = []
outputlogFilePath = f'./traces/{ws}/logs'
for modelPath in modelPathList:
for fragment in range(numberFragments):
mdl = Net().to(device)
mdl.load_state_dict(torch.load(modelPath))
mdl.eval()
modelResult = assess(mdl, dataloader, device)
modelF1Score = f1_score(modelResult[0], modelResult[1])
modelResultList.append((modelPath, modelF1Score,) + modelResult)
message = f'Evaluate: '
message += f'ModelPath={modelPath} Fragment={fragment:02d} '
message += f'score={modelF1Score}'
print(message)
with open(outputlogFilePath, 'a') as writer:
writer.write(message + '\n')
return pd.DataFrame(modelResultList, columns=['name', 'f1score', 'Truth', 'Predicted', 'loss', 'Proba', 'Path'])
def extendDataset(ws, result_df, probaUpperBorn = 0.8, probaLowerBorn = 0.2):
outputlogFilePath = f'./traces/{ws}/logs'
results = np.vstack(result_df.Proba.values)
truth = result_df.Truth.iloc[0]
paths = result_df.Path.iloc[0]
result_mean = results.mean(axis=0)
predicted = (result_mean > 0.5).astype('int')
f1score = f1_score(truth, predicted)
vtruth = truth[(result_mean >= probaUpperBorn) | (result_mean <= probaLowerBorn)]
vpaths = paths[(result_mean >= probaUpperBorn) | (result_mean <= probaLowerBorn)]
vresult_prob = result_mean[(result_mean >= probaUpperBorn) | (result_mean <= probaLowerBorn)]
vpredicted = (vresult_prob > 0.5).astype('int')
vcoverage = (len(vtruth)/len(truth))
vextendSize = len(vtruth)
vf1score = f1_score(vtruth, vpredicted)
etruth = truth[(result_mean < probaUpperBorn) & (result_mean > probaLowerBorn)]
epaths = paths[(result_mean < probaUpperBorn) & (result_mean > probaLowerBorn)]
eresult_prob = result_mean[(result_mean < probaUpperBorn) & (result_mean > probaLowerBorn)]
epredicted = (eresult_prob > 0.5).astype('int')
ecoverage = (len(etruth)/len(truth))
erestSize = len(etruth)
ef1score = f1_score(etruth, epredicted)
message = f'Extend: '
message += f'f1score={f1score*100:2.4f}, '
message += f'vcoverage={vcoverage*100:2.4f}, vf1score={vf1score*100:2.4f}, vexentdSize={vextendSize}, '
message += f'ecoverage={ecoverage*100:2.4f}, ef1score={ef1score*100:2.4f}, erestSize={erestSize}'
print(message)
with open(outputlogFilePath, 'a') as writer:
writer.write(message + '\n')
extend_df = dataset_df = pd.DataFrame( {'filePath': vpaths,
'label' : vtruth })
rest_df = dataset_df = pd.DataFrame( {'filePath': vpaths,
'label' : vtruth })
return extend_df, rest_df
def getDataloaders(dataset_df, otest_df, ntest_df, batchSize=32, numWorkers=16, trainPercentage = 0.8):
rand_idx = np.random.RandomState(seed=54).permutation(len(dataset_df))
train_df = dataset_df.iloc[rand_idx[:int(trainPercentage * len(dataset_df))]]
valid_df = dataset_df.iloc[rand_idx[int(trainPercentage * len(dataset_df)):]]
print(len(train_df))
print(train_df.label.value_counts())
print(len(valid_df))
print(valid_df.label.value_counts())
print(len(otest_df))
print(otest_df.label.value_counts())
print(len(ntest_df))
print(ntest_df.label.value_counts())
trainDataset = SampleDataset(train_df.filePath.values, train_df.label.values)
trainLoader = DataLoader(trainDataset, batch_size=batchSize, shuffle=True, num_workers=numWorkers)
validDataset = SampleDataset(valid_df.filePath.values, valid_df.label.values)
validLoader = DataLoader(validDataset, batch_size=2*batchSize, shuffle=False, num_workers=numWorkers)
otestDataset = SampleDataset(otest_df.filePath.values, otest_df.label.values)
otestLoader = DataLoader(otestDataset, batch_size=2*batchSize, shuffle=False, num_workers=numWorkers)
ntestDataset = SampleDataset(ntest_df.filePath.values, ntest_df.label.values)
ntestLoader = DataLoader(ntestDataset, batch_size=2*batchSize, shuffle=False, num_workers=numWorkers)
return trainLoader, validLoader, otestLoader, ntestLoader
# +
mdataset_df = pd.read_parquet('dataset/mdataset.parquet')
print(len(mdataset_df))
mdataset_df = mdataset_df[mdataset_df.vt_scan_date.dt.year == 2019]
print(len(mdataset_df))
malware_overtime = mdataset_df.resample('1m', on='vt_scan_date', convention='end')
print(len(malware_overtime.count()))
malware_overtime.count()
# -
#
ws = 'ws063'
epochNum = 30
dataset_rootDir = '/ws/mnt/local/data/zoo/'
device = torch.device('cuda:7')
ensembleSize = 6
# +
dataset_lst = list()
overtime_result = list()
initial_df = pd.DataFrame( {'filePath': malware_overtime['filePath'].apply(list).iloc[0],
'label' : malware_overtime['label'].apply(list).iloc[0] })
dataset_lst.append(initial_df)
timeTags = list(malware_overtime.count().index)
outputlogFilePath = f'./traces/{ws}/logs'
outputtracesPath = f'./traces/{ws}'
os.mkdir(outputtracesPath)
# -
for idx in range(1, len(timeTags)):
currentTag = timeTags[idx].isoformat().split('T')[0].replace('-', '')
message = '######## '
message += currentTag
with open(outputlogFilePath, 'a') as writer:
writer.write(message + '\n')
print(message)
#
otest_df = pd.DataFrame( {'filePath': malware_overtime['filePath'].apply(list).iloc[idx-1],
'label' : malware_overtime['label'].apply(list).iloc[idx-1] })
#
ntest_df = pd.DataFrame( {'filePath': malware_overtime['filePath'].apply(list).iloc[idx],
'label' : malware_overtime['label'].apply(list).iloc[idx] })
dataset_df = pd.concat(dataset_lst)
trainLoader, validLoader, otestLoader, ntestLoader = getDataloaders(dataset_df, otest_df, ntest_df, trainPercentage=0.8)
#
models_df = trainModel(ws, f'train_{currentTag}', epochNum, trainLoader, validLoader, device)
models_df.sort_values(by=['vloss', 'tloss'], inplace=True)
selectedModelPaths = models_df.path.iloc[:ensembleSize].tolist()
evalresult_df = evaluate(ws, selectedModelPaths, ntestLoader, device)
exresult_df = evaluate(ws, selectedModelPaths, otestLoader, device)
extend_df, _ = extendDataset(ws, evalresult_df, probaUpperBorn = 0.9, probaLowerBorn = 0.1)
_, rest_df = extendDataset(ws, exresult_df, probaUpperBorn = 0.9, probaLowerBorn = 0.1)
#
dataset_lst.append(extend_df)
#
currentResults = pd.DataFrame([(currentTag, models_df, evalresult_df, exresult_df, dataset_lst, rest_df)],
columns=['TimeTag', 'models', 'evalResuls',
'extendResults', 'datasetList',
'restDataset'])
#
outputPath = f'traces/{ws}/{currentTag}.pickle'
currentResults.to_pickle(outputPath)
message = '########'
with open(outputlogFilePath, 'a') as writer:
writer.write(message + '\n')
print(message)
#break
#
|
zz_study_ws_04.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## how to plot millions of points?
import datashader as ds
import datashader.transfer_functions as tf
import dask.dataframe as dd
import numpy as np
from astroML.plotting import scatter_contour
# +
### data input for 5 million Sloan objects
# -
from astropy.table import Table
sdss = Table.read('data/sdss_5M_gmr_rmi.fits').to_pandas()
sdss.head()
len(sdss)
sdss = sdss[(np.abs(sdss['g_minus_r']) < 5) & (np.abs(sdss['r_minus_i']) < 5)]
# # scatter contour from astroML
from astroML.plotting import scatter_contour
import matplotlib.pyplot as plt
# +
# #scatter_contour?
# +
#------------------------------------------------------------
# plot the results
# %matplotlib inline
#fig, ax = plt.subplots(figsize=(5, 3.75))
fig, ax = plt.subplots(figsize=(10, 7.5))
scatter_contour(sdss['g_minus_r'], sdss['r_minus_i'], threshold=200, log_counts=True, ax=ax,
histogram2d_args=dict(bins=100),
plot_args=dict(marker=',', linestyle='none', color='black'),
contour_args=dict(cmap=plt.cm.bone))
ax.set_xlabel(r'${\rm g - r}$')
ax.set_ylabel(r'${\rm r - i}$')
ax.set_xlim(-0.6, 3.0)
ax.set_ylim(-0.6, 2.5)
plt.show()
# -
# ## A nicer-looking example
# +
# Author: <NAME>
# License: BSD
# The figure produced by this code is published in the textbook
# "Statistics, Data Mining, and Machine Learning in Astronomy" (2013)
# For more information, see http://astroML.github.com
# To report a bug or issue, use the following forum:
# https://groups.google.com/forum/#!forum/astroml-general
from matplotlib import pyplot as plt
from astroML.plotting import scatter_contour
from astroML.datasets import fetch_sdss_S82standards
# +
#----------------------------------------------------------------------
# This function adjusts matplotlib settings for a uniform feel in the textbook.
# Note that with usetex=True, fonts are rendered with LaTeX. This may
# result in an error if LaTeX is not installed on your system. In that case,
# you can set usetex to False.
from astroML.plotting import setup_text_plots
setup_text_plots(fontsize=8, usetex=True)
#------------------------------------------------------------
# Fetch the Stripe 82 standard star catalog
data = fetch_sdss_S82standards()
g = data['mmu_g']
r = data['mmu_r']
i = data['mmu_i']
# -
len(data)
# +
#------------------------------------------------------------
# plot the results
# %matplotlib inline
#fig, ax = plt.subplots(figsize=(5, 3.75))
fig, ax = plt.subplots(figsize=(10, 7.5))
scatter_contour(g - r, r - i, threshold=200, log_counts=True, ax=ax,
histogram2d_args=dict(bins=40),
plot_args=dict(marker=',', linestyle='none', color='black'),
contour_args=dict(cmap=plt.cm.bone))
ax.set_xlabel(r'${\rm g - r}$')
ax.set_ylabel(r'${\rm r - i}$')
ax.set_xlim(-0.6, 2.5)
ax.set_ylim(-0.6, 2.5)
plt.show()
# -
# ## experiments with datashader
# %%time
cvs = ds.Canvas(600, 600, (-1, 3), (-1, 2.5))
agg = cvs.points(sdss, 'g_minus_r', 'r_minus_i')
# +
black_background = True
#from IPython.core.display import HTML, display
#display(HTML("<style>.container { width:50% !important; }</style>"))
# +
def export(img,filename,fmt=".png",_return=True):
"""Given a datashader Image object, saves it to a disk file in the requested format"""
if black_background: # Optional; removes transparency to force background for exported images
img=tf.set_background(img,"black")
img.to_pil().save(filename+fmt)
return img if _return else None
def cm(base_colormap, start=0, end=1.0, reverse=not black_background):
"""
Given a colormap in the form of a list, such as a Bokeh palette,
return a version of the colormap reversed if requested, and selecting
a subset (on a scale 0,1.0) of the elements in the colormap list.
For instance:
>>> cmap = ["#000000", "#969696", "#d9d9d9", "#ffffff"]
>>> cm(cmap,reverse=True)
['#ffffff', '#d9d9d9', '#969696', '#000000']
>>> cm(cmap,0.3,reverse=True)
['#d9d9d9', '#969696', '#000000']
"""
full = list(reversed(base_colormap)) if reverse else base_colormap
num = len(full)
return full[int(start*num):int(end*num)]
from datashader.colors import Greys9, Hot, viridis, inferno
# +
#export(tf.interpolate(agg, cmap=cm(viridis), how='eq_hist'),"gmr_rmi_eq_hist.png")
# -
x_range,y_range = ((-1,3), (-1,3))
# +
import bokeh.plotting as bp
bp.output_notebook()
#bp.output_file('sdss_color_color_datashader.html')
def base_plot(tools='pan,wheel_zoom,box_zoom,reset',webgl=False):
p = bp.figure(tools=tools,
plot_width=int(400), plot_height=int(400),
x_range=x_range, y_range=y_range, outline_line_color=None,
min_border=10, min_border_left=10, min_border_right=10,
min_border_top=10, min_border_bottom=10, webgl=webgl)
p.axis.visible = True
p.xgrid.grid_line_color = 'gray'
p.ygrid.grid_line_color = 'gray'
p.responsive = True
return p
# +
# #InteractiveImage?
# +
from datashader.callbacks import InteractiveImage
def image_callback2(x_range, y_range, w, h):
cvs = ds.Canvas(plot_width=w, plot_height=h, x_range=x_range, y_range=y_range)
agg = cvs.points(sdss, 'g_minus_r', 'r_minus_i')
img = tf.interpolate(agg, cmap = list(reversed(Greys9)))
return tf.dynspread(img,threshold=0.75, max_px=12)
#return tf.spread(img, mask=mask, how='over', px=5)
#return tf.spread(img, how='over', px=3)
p = base_plot(webgl=False)
InteractiveImage(p, image_callback2, throttle=500)
# -
|
Datashader_on_SDSS.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Install Olliepy
# %%capture
# !pip install -U Olliepy
# # Import packages
# +
import pandas as pd
from sklearn.ensemble import RandomForestRegressor
from sklearn.compose import make_column_transformer
from sklearn.pipeline import make_pipeline
from sklearn.metrics import mean_absolute_error, r2_score, make_scorer
from sklearn.model_selection import cross_val_score
from sklearn.preprocessing import StandardScaler, OneHotEncoder
from olliepy import RegressionErrorAnalysisReport
# -
# # Import data
train_df = pd.read_csv('./data/BMI_train.csv')
test_df = pd.read_csv('./data/BMI_test.csv')
train_df.head()
# # Build model
def plot_error_distribution(y_true, y_pred):
error_df = pd.Series(data=y_pred-y_true, name='Error')
error_df.hist(bins=100)
def score_model(X_test, y_true, y_pred):
r2 = r2_score(y_true, y_pred)
adj_r2 = 1 - (1-r2)*(X_test.shape[0] - 1) / (X_test.shape[0] - (X_test.shape[1] - 1) - 1)
print('MAE: {}'.format(mean_absolute_error(y_true, y_pred)))
print('R^2: {}'.format(r2))
print('Adjusted R^2: {}'.format(adj_r2))
# + slideshow={"slide_type": "slide"}
categorical_features = ['gender']
numerical_features = ['weight', 'height']
target_feature = 'BMI'
# +
transformation_pipeline = make_column_transformer(
(OneHotEncoder(handle_unknown='ignore'), categorical_features),
remainder=StandardScaler()
)
pipeline = make_pipeline(transformation_pipeline,
RandomForestRegressor(random_state=77, n_jobs=-1))
# -
X_train = train_df.drop(target_feature, axis=1)
X_test = test_df.drop(target_feature, axis=1)
y_train = train_df.loc[:, target_feature]
y_test = test_df.loc[:, target_feature]
pipeline.fit(X_train, y_train);
# # Train results
y_train_pred = pipeline.predict(X_train)
plot_error_distribution(y_train, y_train_pred)
train_df['error'] = y_train_pred - y_train
# # test results
y_test_pred = pipeline.predict(X_test)
score_model(X_test, y_test, y_test_pred)
# # Calculate test error classes
test_df['error'] = y_test_pred - y_test
plot_error_distribution(y_test, y_test_pred)
error_classes = {
'EXTREME_UNDER_ESTIMATION': (-8.0, -4.0),
'HIGH_UNDER_ESTIMATION': (-4.0, -3.0),
'MEDIUM_UNDER_ESTIMATION': (-3.0, -1.0),
'LOW_UNDER_ESTIMATION': (-1.0, -0.5),
'ACCEPTABLE': (-0.5, 0.5),
'OVER_ESTIMATING': (0.5, 3.0)
}
# # OlliePy Report
from olliepy import RegressionErrorAnalysisReport
report = RegressionErrorAnalysisReport(
train_df=train_df,
test_df=test_df,
target_feature_name='BMI',
error_column_name='error',
error_classes=error_classes,
acceptable_error_class='ACCEPTABLE',
numerical_features=numerical_features,
categorical_features=categorical_features,
title='BMI Regression Report',
subtitle='BMI distribution shift',
output_directory='.',
report_folder_name='BMI_REPORT',
generate_encryption_secret=False)
report.create_report()
# ## Serve report and display in a new browser tab
report.serve_report_from_local_server(mode='server')
# ## Serve report and display in jupyter
report.serve_report_from_local_server(mode='jupyter')
# ## Save report and zip it to share it with someone or download it and display it locally if you are using a cloud solution
report.save_report(zip_report=True)
|
examples/regression_error_analysis_report.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Height-Balance Binary Sort Tree
#
# Given a sorted array, convert it into a height-balanced binary search tree.
#
# - since the list is sorted, we know that the root should be the element in the middle of hte list, which we call M. Also, the left subtree will be a balanced binary search tree created from the first M - 1 elements in the list.
# - Therefore you can create this tree recursively
# +
class Node:
def __init__(self, data, left=None, right=None):
self.data = data
self.left = left
self.right = right
def make_bst(array):
if not array:
return None
mid = len(array) // 2
root = Node(array[mid])
root.left = make_bst(array[:mid])
root.right = make_bst(array[mid+1:]) # wow that's interesting syntax
return root
# +
# O(N) time and space
|
Daily/Height Balanced Binary Sort.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import yaml
#export
class AppConfig():
def __init__(self, file_name):
with open(file_name) as f:
self.config = yaml.safe_load(f)
self.database_user = self.config["database_user"]
self.database_password = self.config["database_password"]
self.database_name = self.config["database_name"]
self.database_host = self.config["database_host"]
self.table_index_values_name = self.config["table_index_values_name"]
self.table_base_rates_name = self.config["table_base_rates_name"]
|
40_Config.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .r
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: KnowRob
# language: ''
# name: jknowrob
# ---
# Tutorial: jupyter_knowrob
# ===
#
# In this tutorial we describe how to use jupyter_knowrob.
#
#
# ## Writing queries
#
# You can use the code cells here in jupyter to send queries to KnowRob:
A is 5 + 3.
# ## Writing rules
#
# ### Loading own modules
#
# You can write your own modules by adding Prolog modules to the prolog subdirectory that is loaded as a volume in docker. We recommend using the `cloud_consult/1` command to load the modules:
cloud_consult('/prolog/example.pl')
# We can test if the consult was successful by running this query:
example_rule(A).
# ### Adding single rules
#
# It is also possible to assert single rules instead of adding complete modules by writing the rule with the `:-` operator
own_rule(A) :-
A = 'Hello World3'.
# Now we can test the query:
own_rule(A).
|
lectures/tut0-jupyter-knowrob.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np #importing numpy package for scientific computing
import matplotlib.pyplot as plt #importing matplotlib package for plots
import scipy.signal #importing scipy.signal package for detrending
from scipy.fftpack import fft #importing Fourier transform package
from scipy.stats import chi2 #importing confidence interval package
# %matplotlib inline
# # Voorwaards
x = np.arange(0,100,0.1 )
d = np.ones(1000)*10.000000000001
dd = 0.1
de = 10
dg = 2
for i in range(len(d) -1):
d[i+1] = d[i] + dd * (d[i] ** 3 - de ** 3)/(d[i] ** 3 - dg ** 3)
plt.figure()
plt.plot(x,d,"b")
plt.axhline(de, color = 'r')
plt.axhline(dg, color = 'm')
plt.ylim(ymin=0)
plt.xlabel("x (m)")
plt.ylabel("d (m)");
# # Achterwaards
L = 100
dd = 0.01
h = 2.0
dgG= (5/9.81) ** (1/3)
deG= dgG * (0.005/2E-4) ** (1/3)
x = np.arange(0,L,dd )
d = np.zeros(int(L/dd))
d[len(d)-1] = 0.8*deG + h
de = np.ones(int(L/dd))*(deG+h)
dg = np.ones(int(L/dd))*(dgG+h)
B = np.ones(int(L/dd))*h
#de[L/(3*dd):2*L/(3*dd)] =deG
#dg[L/(3*dd):2*L/(3*dd)] =dgG
#B[L/(3*dd):2*L/(3*dd)] = 0
print(deG,dgG)
# +
for i in range(len(d) -1):
d[len(d)- i -2] = d[len(d)- i-1] - dd * (d[len(d)-i-1]**3-de[len(d)- i-1]**3)/(d[len(d)-i-1]**3 - dg[len(d)- i-1] ** 3)
#print(d[len(d)- i -2])
plt.figure()
plt.figure(figsize=(20,6))
plt.plot(x,d,"b")
plt.plot(x,de,"r")
plt.plot(x,dg,"m")
plt.plot(x,B,"k")
plt.ylim(ymin=-0.5)
plt.xlabel("x (m)")
plt.ylabel("d (m)");
# -
|
Python/Notebooks/Backwater curves.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import math as math
get_ipython().magic('matplotlib inline')
#Macrostate calculation
def macrostates(qt):
return qt+1
#Omega
def microstates(n, q):
omega = math.factorial(n+q-1)/(math.factorial(q)*math.factorial(n-1))
return omega
#Entropy
k = 1.38e-23
def entropy(n,q):
Sk = math.log(microstates(n,q)) #S in units of S/k
return Sk
#Temp calculation
def temp(N,q):
if(q!=0):
T = (2)/(entropy(N,q+1)-entropy(N,q-1))
else:
T = 0
return T
#Cv Calculation
def cv(N,q):
Cv = 2/(temp(N,q+1)-temp(N,q-1))
return Cv
# +
# N = 50
# qt = 100
# q = 0
NA = 300
NB = 200
NT = NA+NB
qT = 100
qA = 0
qB = 0
#h = 6.626e-34
#U = qt*h*f
# -
#elements1 = []
elements = []
# +
while qA < macrostates(qT)-1:
if(qA!=0):
##Things for A
omegaA = microstates(NA,qA)
#q cannot equal 0 for the rest
SkA = entropy(NA,qA)
#q cannot equal the final value for the rest
TA = temp(NA,qA)
CvA = cv(NA,qA)
##Things for B
omegaB = microstates(NB,qT-qA)
#q cannot equal 0 for the rest
SkB = entropy(NB,qT-qA)
#q cannot equal the final value for the rest
TB = temp(NB,qT-qA)
CvB = cv(NB,qT-qA)
##Things for both
SkAB = SkA+SkB
elements.append([qA, omegaA, SkA, TA, CvA, qT-qA, omegaB, SkB, TB, CvB, SkAB])
else:
omegaA = microstates(NA,qA)
omegaB = microstates(NB, qT-qA)
elements.append([qA, omegaA, 0, 0, 0, qT-qA, omegaB, 0, 0, 0, 0])
qA = qA+1
print(elements)
dataFrame = pd.DataFrame(elements)
# while q < macrostates(qt):
# if(q!=0):
# omega = microstates(N,q)
# #q cannot equal 0 for the rest
# Sk = entropy(N,q)
# #q cannot equal the final value for the rest
# T = temp(N,q)
# Cv = cv(N,q)
# elements1.append([q, omega, Sk, T, Cv])
# else:
# omega = microstates(N,q)
# elements1.append([q, omega, 0, 0, 0])
# q = q+1
# print(elements1)
# dataFrame1 = pd.DataFrame(elements1)
# -
#dataFrame1
dataFrame
# +
##ENTROPY VS U
data = microstates(NA, qA)
qList = []
SkAList = []
SkBList = []
SkABList = []
for i in range(0, macrostates(qT)):
qList.append(i)
SkAList.append(entropy(NA,i))
SkBList.append(entropy(NB,qT-i))
SkABList.append(entropy(NA,i)+entropy(NB,qT-i))
yval1 = SkAList
yval2 = SkBList
yval3 = SkABList
xval = qList
fig = plt.figure(figsize=(10,10))
plt.plot(xval,yval1)
plt.plot(xval,yval2)
plt.plot(xval,yval3)
#plt.ylim(-0.5e-18,0.5e-18)
#plt.xlim(66400,70000)
# +
##TEMPERATURE VS U
qList = []
TAList = []
TBList = []
#TABList = []
for i in range(0, macrostates(qT)):
qList.append(i)
TAList.append(temp(NA,i))
TBList.append(temp(NB,qT-i))
#SkABList.append(entropy(NA,i)+entropy(NB,qT-i))
yval4 = TAList
yval5 = TBList
#yval6 = SkABList
xval = qList
fig = plt.figure(figsize=(10,10))
plt.plot(xval,yval4)
plt.plot(xval,yval5)
#plt.plot(xval,yval6)
#plt.ylim(-0.5e-18,0.5e-18)
#plt.xlim(66400,70000)
eqTemp = 0
for i in range(0, len(qList)):
if(round(TAList[i],2) == round(TBList[i], 2)):
eqTemp = TAList[i]
print(eqTemp)
# +
#This temperature does make sense. The final temperature is 0.56 times the maximum temperature of the smaller
# object, Object B. The same amount of energy in both objects would increase the temperature of B more, as it had
# fewer oscillators and therefore fewer places to distribute that energy.
#Because of this, when both objects are placed in thermal contact and more towards thermal equilibrium,
# the temperature is balanced at a point in which Object A has more energy (60 units) than Object B (40 units).
#The final temperature of 0.56 is this point of intersection.
# -
|
physics/thermal/Roth-Lab-4-MAIN.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Welcome in the introductory template of the python graph gallery. Here is how to proceed to add a new `.ipynb` file that will be converted to a blogpost in the gallery!
# ## Notebook Metadata
# It is very important to add the following fields to your notebook. It helps building the page later on:
# - **slug**: the URL of the blogPost. It should be exactly the same as the file title. Example: `70-basic-density-plot-with-seaborn`
# - **chartType**: the chart type like density or heatmap. For a complete list see [here](https://github.com/holtzy/The-Python-Graph-Gallery/blob/master/src/util/sectionDescriptions.js), it must be one of the `id` options.
# - **title**: what will be written in big on top of the blogpost! use html syntax there.
# - **description**: what will be written just below the title, centered text.
# - **keyword**: list of keywords related with the blogpost
# - **seoDescription**: a description for the bloppost meta. Should be a bit shorter than the description and must not contain any html syntax.
# ## Add a chart description
# A chart example always come with some explanation. It must:
#
# contain keywords
# link to related pages like the parent page (graph section)
# give explanations. In depth for complicated charts. High level for beginner level charts
# ## Add a chart
import seaborn as sns, numpy as np
np.random.seed(0)
x = np.random.randn(100)
ax = sns.distplot(x)
|
src/notebooks/243-area-chart-with-white-grid.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Motions with visous damping from Ikeda
# # Purpose
# Motions simulation were conducted with visous damping from Ikeda.
# # Setup
# +
# # %load imports.py
"""
These is the standard setup for the notebooks.
"""
# %matplotlib inline
# %load_ext autoreload
# %autoreload 2
from jupyterthemes import jtplot
jtplot.style(theme='onedork', context='notebook', ticks=True, grid=False)
import pandas as pd
pd.options.display.max_rows = 999
pd.options.display.max_columns = 999
pd.set_option("display.max_columns", None)
import numpy as np
import os
import matplotlib.pyplot as plt
from collections import OrderedDict
#plt.style.use('paper')
from reports.paper_writing import save_fig
#import data
import copy
from mdldb.run import Run
from sklearn.pipeline import Pipeline
from rolldecayestimators.transformers import CutTransformer, LowpassFilterDerivatorTransformer, ScaleFactorTransformer, OffsetTransformer
from rolldecayestimators.direct_estimator_cubic import EstimatorQuadraticB, EstimatorCubic
from rolldecayestimators.ikeda_estimator import IkedaQuadraticEstimator
import src.equations as equations
import rolldecayestimators.lambdas as lambdas
from rolldecayestimators.substitute_dynamic_symbols import lambdify
import rolldecayestimators.symbols as symbols
import sympy as sp
from sympy.physics.vector.printing import vpprint, vlatex
from IPython.display import display, Math, Latex
from sklearn.metrics import r2_score
from src.data import database
from mdldb import tables
import shipflowmotionshelpers.shipflowmotionshelpers as helpers
import src.visualization.visualize as visualize
# -
from copy import deepcopy
import joblib
from rolldecayestimators import measure
from src.helpers import get_ikeda, calculate_ikeda, get_estimator_variation, get_data_variation , get_variation, hatify
# ## Load data from Motions:
file_paths = [
'../data/external/kvlcc2_rolldecay_15-5kn_const_large',
'../data/external/kvlcc2_rolldecay_15-5kn_const_large2',
'../data/external/kvlcc2_rolldecay_15-5kn_const_large_5deg',
'../data/external/kvlcc2_rolldecay_15-5kn_const_large_ikeda',
'../data/external/kvlcc2_rolldecay_15-5kn_ikeda_dev',
]
df_parameters = pd.DataFrame()
df_parameters = helpers.load_parameters(file_path=file_paths)
df_parameters
# +
time_series = helpers.load_time_series(df_parameters=df_parameters)
time_series_raw = deepcopy(time_series)
for key,df in time_series.items():
if df.mean().abs()['V1'] > 0.01:
#X = preprocess.remove_acceleration_part(df=df, q=0.99, steady_ratio=0.01)
phi1d_limit = 10**-2
index0 = (df['phi1d'].abs() > phi1d_limit).argmax()
X = df.iloc[index0:].copy()
#mask = X.index < 110
#X = X.loc[mask].copy()
time_series[key] = X
X = time_series['kvlcc2_rolldecay_15-5kn_const_large_ikeda']
time_series['kvlcc2_rolldecay_15-5kn_const_large_ikeda'] = X.loc[0:110]
# -
for key, df in time_series.items():
fig,ax = plt.subplots()
time_series_raw[key].plot(y='phi', ax=ax)
df.plot(y='phi', ax=ax)
## MDL:
pipeline_mdl = joblib.load('../models/KVLCC2_speed.pkl')
model_mdl = pipeline_mdl['estimator']
# +
motions_run_name = 'kvlcc2_rolldecay_15-5kn_const_large_ikeda'
motions_run_name = 'kvlcc2_rolldecay_15-5kn_ikeda_dev'
X = time_series[motions_run_name]
pre_model= EstimatorQuadraticB(fit_method='derivation')
pre_model.fit(X)
model_motions = EstimatorQuadraticB(p0=pre_model.parameters)
model_motions.fit(X)
model_motions.parameters['C_1A'] = model_mdl.parameters['C_1A'] ## Stealing the stiffness from MDL
model_motions.calculate_amplitudes_and_damping()
# +
fig,ax=plt.subplots()
model_mdl.plot_damping(ax=ax, label='MDL')
model_motions.plot_damping(ax=ax, label='Motions + Ikeda')
ylims = ax.get_ylim()
ax.set_ylim(0,ylims[1])
# +
df_motions = model_motions.predict(model_mdl.X)
fig,ax=plt.subplots()
model_mdl.X.plot(y='phi', label='MDL', ax=ax)
df_motions.plot(y='phi', style='--', label='Motions + Ikeda', ax=ax)
# -
fig,ax=plt.subplots()
model_mdl.plot_omega0(label='MDL', ax=ax)
model_motions.plot_omega0(label='Motions + Ikeda', ax=ax)
# +
fig,ax=plt.subplots()
df_amplitude_MDL = measure.calculate_amplitudes_and_damping(X=model_mdl.X)
df_amplitude_motions = measure.calculate_amplitudes_and_damping(X=df_motions)
df_amplitude_MDL.plot(y='phi_a', label='MDL', ax=ax)
df_amplitude_motions.plot(y='phi_a', label='Motions + Ikeda', ax=ax)
# +
parameters = df_parameters.loc[motions_run_name]
scale_factor = 68
GM = 5.737/scale_factor
meta_data={
'Volume' : parameters.V,
'rho' : parameters.dens,
'g' : parameters.gravi,
'GM' : GM,
}
results = model_motions.result_for_database(meta_data=meta_data)
results
# -
results_mdl = model_mdl.result_for_database(meta_data=meta_data)
results_mdl
# +
fig,ax=plt.subplots()
A_44 = 135.00020704200577
omega0= results_mdl['omega0']
df_amplitude_motions['B'] = df_amplitude_motions['zeta_n']*A_44*2*omega0
df_amplitude_motions['B_model'] = lambdas.B_e_lambda(B_1=results['B_1'], B_2=results['B_2'], omega0=omega0, phi_a=df_amplitude_motions['phi_a'])
df_amplitude_motions['B_model'] = df_amplitude_motions['B_model'].astype(float)
df_amplitude_MDL['B'] = df_amplitude_MDL['zeta_n']*A_44*2*omega0
df_amplitude_MDL['B_model'] = lambdas.B_e_lambda(B_1=results_mdl['B_1'], B_2=results_mdl['B_2'], omega0=omega0, phi_a=df_amplitude_MDL['phi_a'])
df_amplitude_MDL['B_model'] = df_amplitude_MDL['B_model'].astype(float)
df_amplitude_MDL.plot(x='phi_a', y='B', style='.:', label='MDL', ax=ax)
color = ax.get_lines()[-1].get_color()
df_amplitude_MDL.plot(x='phi_a', y='B_model', style='-', color=color, label='MDL', ax=ax)
df_amplitude_motions.plot(x='phi_a', y='B', style='.:', label='Motions + Ikeda', ax=ax)
color = ax.get_lines()[-1].get_color()
df_amplitude_motions.plot(x='phi_a', y='B_model', style='-', color=color, label='Motions + Ikeda', ax=ax)
ylim = ax.get_ylim()
ax.set_ylim((0,ylim[1]))
# +
df_amplitude_motions = measure.calculate_amplitudes_and_damping(X=model_motions.X)
df_amplitude_motions['B_model'] = lambdas.B_e_lambda(B_1=results['B_1'], B_2=results['B_2'], omega0=results['omega0'], phi_a=df_amplitude_motions['phi_a'])
df_amplitude_motions['B_model']=df_amplitude_motions['B_model'].astype(float)
df_amplitude_motions['B_ikeda'] = lambdas.B_e_lambda(B_1=parameters['b4l'], B_2=parameters['b4q'], omega0=results['omega0'], phi_a=df_amplitude_motions['phi_a'])
df_amplitude_motions['B_ikeda']=df_amplitude_motions['B_ikeda'].astype(float)
B_W_1 = results['B_1'] - parameters['b4l']
B_W_2 = results['B_2'] - parameters['b4q']
df_amplitude_motions['B_W'] = lambdas.B_e_lambda(B_1=B_W_1, B_2=B_W_2, omega0=results['omega0'], phi_a=df_amplitude_motions['phi_a'])
df_amplitude_motions['B_W']=df_amplitude_motions['B_W'].astype(float)
df_amplitude_motions['B_'] = df_amplitude_motions['B_W'] + df_amplitude_motions['B_ikeda']
# +
A_44 = 135.00020704200577
#omega = 2.4675051745904346
omega = df_amplitude_motions['omega0']
df_amplitude_motions['B'] = df_amplitude_motions['zeta_n']*A_44*2*omega
df_amplitude_motions['B_W_'] = df_amplitude_motions['B'] - df_amplitude_motions['B_ikeda']
fig,ax=plt.subplots()
df_amplitude_motions.plot(x='phi_a', y='B', style='.', ax=ax)
df_amplitude_motions.plot(x='phi_a', y='B_model', label='model', ax=ax)
df_amplitude_motions.plot(x='phi_a', y='B_ikeda', label='ikeda', ax=ax)
df_amplitude_motions.plot(x='phi_a', y='B_W', label='B_W', ax=ax)
df_amplitude_motions.plot(x='phi_a', y='B_W_', label='B_W', style='.', ax=ax)
df_amplitude_motions.plot(x='phi_a', y='B_', style='--', label='B_', ax=ax)
df_amplitude_motions_pred = measure.calculate_amplitudes_and_damping(X=model_motions.predict(X=model_motions.X))
omega = df_amplitude_motions_pred['omega0']
df_amplitude_motions_pred['B'] = df_amplitude_motions_pred['zeta_n']*A_44*2*omega
#df_amplitude_motions_pred.plot(x='phi_a', y='B', style='-', label='B_pred', ax=ax)
# -
df_hat = hatify(df=df_amplitude_motions[['B_W']], Disp=meta_data['Volume'], beam=parameters.B, g=meta_data['g'], rho=meta_data['rho'])
df_hat['phi_a'] = df_amplitude_motions['phi_a']
df_hat.plot(x='phi_a', y='B_W_hat')
# ## Comparing with the Motions results without viscous damping
# +
motion_models = {}
for motions_file_path,X in time_series.items():
parameters = df_parameters.loc[motions_file_path]
pre_model = EstimatorQuadraticB(fit_method='derivation')
pre_model.fit(X=X)
model = EstimatorQuadraticB(fit_method='integration', p0=pre_model.parameters)
try:
model.fit(X=X)
except scipy.linalg.LinAlgError:
model.fit(X=X) # Retry
if pre_model.score() > model.score():
model = pre_model
motion_models[motions_file_path] = model
# +
df_amplitudes = pd.DataFrame()
for motions_file_path, model in motion_models.items():
amplitudes = measure.calculate_amplitudes_and_damping(X=model.X)
omega = amplitudes['omega0']
amplitudes['B'] = amplitudes['zeta_n']*A_44*2*omega
amplitudes['name'] = motions_file_path
df_amplitudes = df_amplitudes.append(amplitudes, ignore_index=True)
# -
runs = df_amplitudes.groupby(by='name')
amplitudes = runs.get_group('kvlcc2_rolldecay_15-5kn_const_large_ikeda')
B_ikeda = lambdas.B_e_lambda(B_1=parameters['b4l'], B_2=parameters['b4q'], omega0=results['omega0'], phi_a=amplitudes['phi_a'])
df_amplitudes.loc[amplitudes.index,'B']=amplitudes['B']-B_ikeda
# +
import seaborn as sns
sns.relplot(data=df_amplitudes, x='phi_a', y='B', kind='line', hue='name', height=5, aspect=3)
# -
|
notebooks/12.1_motions_ikeda.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import astropy
import regions
import matplotlib.pyplot as plt
from astropy.io import ascii
from astropy.io import fits
from astropy import units as u
from regions import read_ds9, write_ds9
from astropy.coordinates import SkyCoord
import glob, os
from astropy.coordinates import Angle, SkyCoord
from regions import CircleSkyRegion
from astropy.coordinates import SkyOffsetFrame
from astropy import cosmology
import math
from astropy.table import Table, Column, unique
from matplotlib import pyplot
import random
import scipy
import collections
from collections import Counter
# +
file = 'C://Users/Janel/Desktop/master_BCG_Cluster_Data2.txt' #master cluster data
file2 = 'C://Users/Janel/Documents/Duplicates.txt' #names of duplicates that I found in previous code
file3 = 'C://Users/Janel/Desktop/all_BCG_coords.txt'#original BCG coordinates
outfil = 'C://Users/Janel/Desktop/Multiple_BCGs.txt'#writing info of multiple BCGs in this
data =ascii.read(file,format = 'basic') #opening master file for reading
data2 = ascii.read(file3) #opening BCG coordinaates for reading
dup = open(file2, 'r') #opening duplicates file
# setting table names for the new data
newdata = Table(names=('Name','SZ_RA','SZ_Dec','Xpeak_RA','Xpeak_Dec', 'BCG_RA', 'BCG_Dec', 'Redshift'), dtype=('U17','f8','f8','f8','f8','f8','f8','f8'))
#indexing needed data in which we want to find dubplicates for
cnames = data['Name']
szra = data['SZ_RA']
szdec = data['SZ_Dec']
xra = data['Xpeak_RA']
xdec = data['Xpeak_Dec']
bra = data ['BCG_RA']
bdec = data ['BCG_Dec']
z_cl = data['Redshift']
doubles = [] #defining array
for i in range(len(data)): #for the length of the data
doubles = Counter(cnames).most_common() #identifying and counting the duplicate data
for lines in dup:
dup_names1 = lines.split() #splitting the data into columns
dup_names = '/n'.join(dup_names1) #getting the names for the duplicates
for i in range(len(data)): #for the length og data
if cnames[i] == dup_names: #if cnames matches dup_name
newdata.add_row((cnames[i], szra[i], szdec[i], xra[i], xdec[i],bra[i],bdec[i], z_cl[i])) #write the data into the new file
print(newdata)
#print([19:21])
#newdata.write(outfil,format='ascii',overwrite=True)
#cluster names of doubles were copied and pasted into a new text document called, "duplicates".
#newdata stores all the information for the duplicates from the master sheet
# +
#Midpoint separation calculations
file4 = 'C://Users/Janel/Documents/Midpoint_Coordinates.txt'
file5 = 'C://Users/Janel/Desktop/Multiple_BCGs.txt'
file6 = 'C://Users/Janel/Documents/Average_Separations.txt'
file7 = 'C://Users/Janel/Documents/Duplicate_Redshift.txt'
data2 = ascii.read(file4) #reading into ascii files
data3 = ascii.read(file5)
data4 = ascii.read(file6)
data5 = ascii.read(file7)
#Indexing the midpoint data:
cnames = data2['Name']
BCG_RA = data2['RA_mp'] #midpoint coordinate for BCG RAs
BCG_Dec = data2['Dec_mp'] #midpoint coordinate for BCG Dec
SZ_RA = data2['SZ_RA_mp'] #midpoint coordinate for SZ center RA
SZ_Dec = data2['SZ_Dec_mp'] #midpoint coordinate for SZ center Dec
Xpeak_RA = data2['Xpeak_RA_mp'] #midpoint coordinate for Xpeak RA
Xpeak_Dec = data2['Xpeak_Dec_mp'] #midpoint coordinate for xpeak Dec
redshift = data5['Redshift']
#Indexing BCG average sep data
BCG_avg_SZ = data4['SZ_avg_sep']
BCG_avg_Xp = data4['Xp_avg_sep']
cos = astropy.cosmology.FlatLambdaCDM(H0 = 70, Om0 = 0.3, Tcmb0 = 2.725) #defining cosomology
adj = cos.angular_diameter_distance(redshift).value
#midpoint SZ separations
c1 = SkyCoord(BCG_RA, BCG_Dec, unit='deg', frame = 'fk5')
c2 = SkyCoord(SZ_RA, SZ_Dec, unit='deg', frame = 'fk5')
sep = c2.separation(c1)
nsep = sep.rad
mid_aSZ = sep.arcsec
mid_SZ_kpc = []
for values in nsep:
sin = math.sin(values)
distance = np.multiply(sin,adj)
ndistance = abs(np.multiply(distance,1000))
mid_SZ_kpc = ndistance
#midpoint Xp separations
c3 = SkyCoord(BCG_RA, BCG_Dec, unit='deg', frame = 'fk5')
c4 = SkyCoord(Xpeak_RA, Xpeak_Dec, unit='deg', frame = 'fk5')
sep1 = c3.separation(c4)
nsep1 = sep1.rad
mid_aXp = sep1.arcsec
mid_Xp_kpc = []
for values in nsep1:
sin = math.sin(values)
distance = np.multiply(sin,adj)
ndistance = abs(np.multiply(distance,1000))
mid_Xp_kpc = ndistance
# +
x = mid_Xp_kpc
a = np.array(BCG_avg_Xp)
print(a)
print(x)
plt.scatter(a,x, c= 'orange')
# x-axis label
plt.xlabel('Average Separation Value (kpc)')
# frequency labe
plt.ylabel('Midpoint Separation Value (kpc)')
# plot title
plt.title('BCG and Xray Peak Duplicate Offsets (needs revising)')
plt.savefig('C://Users/Janel/Documents/BCG_Xray_Peak_Duplicates.png')
# +
b = np.array(BCG_avg_SZ)
y = mid_SZ_kpc
plt.scatter(b,y, c = 'blue')
# x-axis label
plt.xlabel('BCG Average Seperation Value (kpc)')
# frequency labe
plt.ylabel('Midpoint')
# plot title
plt.title('BCG and SZ Duplicate Offsets')
plt.savefig('C://Users/Janel/Documents/BCG_SZ_Duplicates.png')
# +
#avg sep as input value for one
#midpt sep as input value for another
#chosen BCGs as the last one
#midpoints might turn up 0 if bcgs are on opposite sides of cluster
#one case seems to bracket the cluster, midpoint is very small comment on it
# -
|
Finding_Calculating_Duplicates.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# !pip install deeppavlov
from deeppavlov import build_model, configs
# We download and build model from configuration file.
model = build_model(configs.morpho_tagger.UD2_0.morpho_ru_syntagrus_pymorphy, download=True)
# Let us parse several example sentences.
# +
sentences = ["Я шёл домой по незнакомой улице.", "Девушка пела в церковном хоре о всех уставших в чужом краю."]
for parse in model(sentences):
print(parse)
# -
# Model also works with already tokenized sentences.
# +
sentences = [["Я", "шёл", "домой", "по", "незнакомой", "улице", "."]]
for parse in model(sentences):
print(parse)
# -
# We need to change output prettifier parameters to get UD output. The same result is obtained by editing the configuration file (see http://docs.deeppavlov.ai/en/master/components/morphotagger.html).
# +
prettifier = model.pipe[-1][-1]
prettifier.set_format_mode("ud")
for parse in model(sentences):
print(parse)
# -
|
examples/morphotagger_example.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pickle
import numpy as np
def load_obj(name):
with open(name + '.pkl', 'rb') as f:
return pickle.load(f)
# +
# generate QA pairs
what_pokemon = ["What pokemon is there in the image",
"What kind of pokemon is there in the picture",
"What pokemon can you see in the image",
"Can you tell what pokemon you see in this picture"]
what_attack = ["What attack is being performed by the pokemon",
"The pokemon is performing which attack",
"What kind of attack is in the picture",
"What sort of attack is there in this image",
"Can you tell what attack you see in this picture"]
what_type = ["What type of pokemon is it",
"The image contains what type of pokemon",
"Can you identify the type of pokemon",
"What type of pokemon can you see in this picture"]
is_legendary = ["Is the pokemon legendary",
"The pokemon in the image is legendary or not",
"Does the picture contain a legendery pokemon",
"Can you spot any powerful legendery pokemons here"]
what_color = ["What is the color of the pokemon in the image",
"What color of pokemon can you spot in this picture",
"What color of pokemon do you perceive in this image",
"What shading or color can you see in the pokemon"]
all_questions = [what_pokemon, what_attack, what_type, is_legendary, what_color]
# -
pairs_to_image_map = load_obj("battle_scenes_data/pairs_to_image_map")
pairs_to_image_map[355]
pokemon_list = open("pokemon_attacks_classifier/Kanto.txt", "r").readlines()
name_to_id = dict()
for i, p in enumerate(pokemon_list):
name_to_id[p.lower().strip()] = i+1
import pandas as pd
stats_df = pd.read_csv("pokemon_stats.csv")
poke_stats_map = dict()
for p in name_to_id:
temp = dict()
temp["name"] = stats_df.loc[[name_to_id[p]-1]]["Name"].to_string(index=False)
temp["type"] = stats_df.loc[[name_to_id[p]-1]]["Type_1"].to_string(index=False)
temp["legendary"] = stats_df.loc[[name_to_id[p]-1]]["isLegendary"].to_string(index=False) == "True"
temp["color"] = stats_df.loc[[name_to_id[p]-1]]["Color"].to_string(index=False)
poke_stats_map[p] = temp
print(poke_stats_map["mew"])
qa_map_train = list()
qa_map_test = list()
for data in pairs_to_image_map:
qid = -1
wp = list(set(what_pokemon))
for q in wp[:-1]:
qid += 1
qa_map_train.append({"question": q, "answer": data["pokemon"].lower(), "image_id": data["image_id"], "ques_id": qid})
for q in wp[-1:]:
qid += 1
qa_map_test.append({"question": q, "answer": data["pokemon"].lower(), "image_id": data["image_id"], "ques_id": qid})
wa = list(set(what_attack))
for q in wa[:-2]:
qid += 1
qa_map_train.append({"question": q, "answer": data["attack"].lower(), "image_id": data["image_id"], "ques_id": qid})
for q in wa[-2:]:
qid += 1
qa_map_test.append({"question": q, "answer": data["attack"].lower(), "image_id": data["image_id"], "ques_id": qid})
wt = list(set(what_type))
for q in wt[:-1]:
qid += 1
qa_map_train.append({"question": q, "answer": poke_stats_map[data["pokemon"].lower()]["type"], "image_id": data["image_id"], "ques_id": qid})
for q in wt[-1:]:
qid += 1
qa_map_test.append({"question": q, "answer": poke_stats_map[data["pokemon"].lower()]["type"], "image_id": data["image_id"], "ques_id": qid})
il = list(set(is_legendary))
for q in il[:-1]:
qid += 1
qa_map_train.append({"question": q, "answer": poke_stats_map[data["pokemon"].lower()]["legendary"], "image_id": data["image_id"], "ques_id": qid})
for q in il[-1:]:
qid += 1
qa_map_test.append({"question": q, "answer": poke_stats_map[data["pokemon"].lower()]["legendary"], "image_id": data["image_id"], "ques_id": qid})
wc = list(set(what_colour))
for q in wc[:-1]:
qid += 1
qa_map_train.append({"question": q, "answer": poke_stats_map[data["pokemon"].lower()]["color"], "image_id": data["image_id"], "ques_id": qid})
for q in wc[-1:]:
qid += 1
qa_map_test.append({"question": q, "answer": poke_stats_map[data["pokemon"].lower()]["color"], "image_id": data["image_id"], "ques_id": qid})
[q for q in qa_map_train if q["image_id"] == 10355]
[q for q in qa_map_test if q["image_id"] == 10355]
# +
# vqa_raw_train.json and vqa_raw_test.json
# Format:
# {
# "ques_id": image_id + qid,
# "img_path": path/image_id.jpg,
# "question": "",
# "MC_ans": [ans],
# "ans": ""
# }
# +
vqa_raw_train = list()
vqa_raw_test = list()
for q_data in qa_map_train:
temp = dict()
temp["ques_id"] = int(str(q_data["image_id"]) + str(q_data["ques_id"]))
temp["img_path"] = "battle_scenes/" + str(q_data["image_id"]) + ".jpg"
temp["question"] = q_data["question"]
temp["MC_ans"] = [q_data["answer"]]*5
temp["ans"] = q_data["answer"]
vqa_raw_train.append(temp)
for q_data in qa_map_test:
temp = dict()
temp["ques_id"] = int(str(q_data["image_id"]) + str(q_data["ques_id"]))
temp["img_path"] = "battle_scenes/" + str(q_data["image_id"]) + ".jpg"
temp["question"] = q_data["question"]
temp["MC_ans"] = [q_data["answer"]]*5
temp["ans"] = q_data["answer"]
vqa_raw_test.append(temp)
# -
print(vqa_raw_test[0])
# total classes/ans in our system
a = set([i["ans"]for i in vqa_raw_test])
b = set([i["ans"]for i in vqa_raw_train])
print(len(set(a.union(b))))
# +
import json
with open('data/vqa_raw_train.json', 'w') as outfile:
json.dump(vqa_raw_train, outfile)
with open('data/vqa_raw_test.json', 'w') as outfile:
json.dump(vqa_raw_test, outfile)
# +
# params.json OR use neural-vqa-attention/prepro.py
# python prepro.py --input_train_json vqa_raw_train.json --input_test_json vqa_raw_test.json --num_ans 304
# params = dict()
# params["unique_img_train"] = list()
# for d in vqa_raw_train:
# params["unique_img_train"].append(d["img_path"])
# params["unique_img_test"] = list()
# for d in vqa_raw_train:
# params["unique_img_test"].append(d["img_path"])
# with open('data/params.json', 'w') as outfile:
# json.dump(params, outfile)
# +
# questions and validation
# annotations.json
data = dict()
data["annotations"] = list()
for qa in (vqa_raw_train + vqa_raw_test):
data["annotations"].append({"multiple_choice_answer": qa["ans"], "question_id": qa["ques_id"], "image_id": qa["img_path"]})
with open('data/annotations.json', 'w') as outfile:
json.dump(data, outfile)
# questions.json
data = dict()
data["questions"] = list()
for qa in (vqa_raw_train + vqa_raw_test):
data["questions"].append({"question": qa["question"], "question_id": qa["ques_id"], "image_id": qa["img_path"]})
with open('data/questions.json', 'w') as outfile:
json.dump(data, outfile)
# -
# +
results = json.load(open("results/results_best.json", "r"))
qa_map = dict()
for i in vqa_raw_test:
qa_map[i["ques_id"]] = i
c = 0
for result in results:
if qa_map[result["question_id"]]["ans"] == result["answer"]:
c+=1
print((c/len(results))*100)
# -
import matplotlib.pyplot as plt
values = [[float(i) for i in line.split()] for line in open("results/train.log").readlines()][1:]
[iter, epoch, loss] = list(zip(*values))
plt.plot(iter[:80], loss[:80])
plt.title("Avg. Training Loss | Pokemon VQA Model")
plt.xlabel("Iterations")
plt.ylabel("Loss")
plt.show()
# +
# For generating img_train.h5 and img_test.h5
# Steps
# instance creation - get gpus
# after that run the instance and install the nvidia driver
# pull the docker and run it, install luarocks and loadcaffe after which you will be able to generate the image features
# once you get the image features, put them in the same directlry as the preprocessed sata obtained from prepro.py
# install rnn from luarocks
# run the training after setting the batch size, iterations and checkpoints
# +
# 0. /opt/deeplearning/install-driver.sh
# 1. nvidia-docker run -it --rm --name lua-env -v /home/jupyter:/root chaneyk/torch-cuda9:latest-gpu /bin/bash
# 2. apt-get install libprotobuf-dev protobuf-compiler
# 3. luarocks install loadcaffe (rnn in case of rnn)
# 4. th prepro_img.lua -input_json params.json -image_root ./ -gpuid 0
# +
# sh scripts/download_vgg19.sh
# +
# th prepro_img.lua -image_root /path/to/coco/images/ -gpuid 0
# +
# th train.lua
# +
# model_path=checkpoints/<time_stamp>/iter_800.t7 qa_h5=data/qa.h5 params_json=data/params.json img_test_h5=data/img_test.h5 th eval.lua
# -
|
generate_data_files.ipynb
|
# + colab={} colab_type="code" id="AiWokO5On8Rr"
import tensorflow as tf
import numpy as np
from matplotlib import pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets('/tmp/mnist', one_hot=True)
# + colab={} colab_type="code" id="3GTOW509quc0"
num_row, num_col = 1, 10
f,subplots = plt.subplots(num_row, num_col, sharex='col', sharey='row')
X,y = mnist.train.images, mnist.train.labels
X = np.reshape(X,(-1,28,28))
for i in range(num_col):
X_img = X[np.argmax(y,axis=1) == i].reshape((-1,28,28))
idx = np.random.choice(np.arange(0, X_img.shape[0]))
subplots[i].imshow(X_img[idx], cmap='gray', interpolation='nearest', aspect='auto')
title = 'Digit {}'.format(i)
subplots[i].set_title(title, fontweight="bold")
subplots[i].grid(b=False)
subplots[i].axis('off')
f.set_size_inches(18.5, 4.5)
# + colab={} colab_type="code" id="ec9ZoLWHqL09"
# Placeholders
x = tf.placeholder(dtype=tf.float32, shape=[None, 784]) # input placeholder
# Placeholder for targets
targets = tf.placeholder(dtype=tf.float32, shape=[None, 10])
# + colab={} colab_type="code" id="X4XwOiaBoJhG"
def inference(x):
input_dim = 784
n_classes = 10
n_hidden = 256
with tf.variable_scope('network'):
"""
Write HERE your multi layer perceptron, with one hidden layer
characterised by n_hidden neurons. Note that the last layer
should be followed by a softmax activation, the latter giving
a conditional distribution across n_classes.
"""
return y
# Define model output
y = inference(x)
# + [markdown] colab_type="text" id="jv049ulr6wxE"
# # My solution
# + colab={} colab_type="code" id="udEgtxEI6uOs"
def inference(x):
input_dim = 784
n_classes = 10
n_hidden = 256
with tf.variable_scope('network'):
W1 = tf.Variable(initial_value=tf.random_normal(shape=[input_dim, n_hidden]), name='weights1')
b1 = tf.Variable(initial_value=tf.zeros(shape=[n_hidden]), name='biases1')
W2 = tf.Variable(initial_value=tf.random_normal(shape=[n_hidden, n_classes]), name='weights2')
b2 = tf.Variable(initial_value=tf.zeros(shape=[n_classes]), name='biases2')
x1 = tf.matmul(x, W1) + b1
x1 = tf.nn.sigmoid(x1)
x2 = tf.matmul(x1, W2) + b2
y = tf.nn.softmax(x2)
return y
# Define model output
y = inference(x)
# + [markdown] colab_type="text" id="DWjW2vGU62sz"
# # Training Procedure
# + colab={} colab_type="code" id="sBH4vJ3Io1X_"
# Define loss function
loss = tf.reduce_mean(-tf.reduce_sum(targets * tf.log(y + np.finfo('float32').eps), axis=1))
# Define train step
train_step = tf.train.AdamOptimizer(learning_rate=0.001).minimize(loss)
init_op = tf.global_variables_initializer()
# Define metrics
correct_predictions = tf.equal(tf.argmax(y, axis=1), tf.argmax(targets, axis=1))
accuracy = tf.reduce_mean(tf.cast(correct_predictions, tf.float32))
with tf.Session() as sess:
# Initialize all variables
sess.run(init_op)
# Training parameters
training_epochs = 20
batch_size = 128
# Number of batches to process to see whole dataset
batches_each_epoch = mnist.train.num_examples // batch_size
for epoch in range(training_epochs):
# During training measure accuracy on validation set to have an idea of what's happening
val_accuracy = sess.run(fetches=accuracy,
feed_dict={x: mnist.validation.images, targets: mnist.validation.labels})
print('Epoch: {:06d} - VAL accuracy: {:.03f}'.format(epoch, val_accuracy))
for _ in range(batches_each_epoch):
# Load a batch of training data
x_batch, target_batch = mnist.train.next_batch(batch_size)
# Actually run one training step here
sess.run(fetches=[train_step],
feed_dict={x: x_batch, targets: target_batch})
# # Eventually evaluate on whole test set when training ends
# test_accuracy = sess.run(fetches=accuracy,
# feed_dict={x: mnist.test.images, targets: mnist.test.labels})
# print('*' * 50)
# print('Training ended. TEST accuracy: {:.03f}'.format(test_accuracy))
# + colab={} colab_type="code" id="TpgU7rZaok3R"
|
logistic_tensorflow/mlp.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# import networkx as nx
import numpy as np
import scipy.io as scio
import matplotlib.pyplot as plt
import random
import time
# %matplotlib inline
# -
def check_symmetric(a, tol=1e-8):
return np.allclose(a, a.T, atol=tol)
# +
# 网络数据导入为numpy数组
dataFile_1 = '../data/BA_2000_3.mat'
data_1 = scio.loadmat(dataFile_1)
network_scale_1 = data_1['A'].shape
network_physical = np.array(data_1['A'])
# network_physical = nx.Graph(data['A'])
dataFile_2 = '../data/BA_2000_3_add_400_edges.mat'
data_2 = scio.loadmat(dataFile_2)
network_scale_2 = data_2['B'].shape
network_information = np.array(data_2['B'])
# network_information = nx.Graph(data['A'])
assert network_scale_1 == network_scale_2, "networks\' size don\'t match!"
assert check_symmetric(network_physical), "network_physical doesn\'t symmetry!"
assert check_symmetric(network_information), "network_information doesn\'t symmetry!"
np.sum(np.sum(network_physical, axis=0)==0)
# +
# 参数设置
# 公共参数
Monte_Carlo_loop = 20 # 蒙特卡洛模拟次数
time_steps = 50 # 总的时间步数
N = network_scale_1[0] # 网络节点数
p = random.randint(0, N-1) # 初始始随机选出一个感染节点,四舍五入
# SIR参数
bata = 0.2 # 感染概率
mu = 0.1 # 免疫概率
Nodes_SIR = np.zeros([Monte_Carlo_loop, time_steps, N]) # N行代表时间步数,T列代表节点数,记录每步所有节点的状态
infective_count = np.zeros([Monte_Carlo_loop, time_steps]) # 每步感染节点数,用于最终统计
infective_count_average = np.zeros([1, time_steps])
immune_count = np.zeros([Monte_Carlo_loop, time_steps]) # 每步免疫节点数,用于最终统计
immune_count_average = np.zeros([1, time_steps])
s_count = np.zeros([Monte_Carlo_loop, time_steps]) # 每步易感节点数,用于最终统计
s_count_average = np.zeros([1, time_steps])
# UAU参数
lamda = 0.4 # 传播率
delta = 0.15 # 遗忘率
Nodes_UAU = np.zeros([Monte_Carlo_loop, time_steps, N]) # 存储网络中每个节点的状态快照
awareness_count = np.zeros([Monte_Carlo_loop, time_steps]) # 每步知晓节点数量,用于最终统计
awareness_count_average = np.zeros([1, time_steps])
# 其他参数
aplha = 0.6 # 信息上传率
sigma_S = 0.7 # S节点在知道信息后的防御系数/感染率衰减, 相当于减少与周围人的接触
# +
time_start = time.time()
for loop in range(Monte_Carlo_loop):
Nodes_SIR[loop, 0, p] = 1 # 第一步标出初始感染节点的位置
Nodes_UAU[loop, 0, p] = 1 # 随机初始化一个节点使其处于感染状态,当前可感染状态节点的快照
for t in range(time_steps-1):
# UAU演化
# 找到可以传播的活跃节点
active_node = np.where((Nodes_UAU[loop, t, :] == 1))[0] # 找到当前有传播力的节点的位置
# awareness_count[loop] = len(active_node) # 统计这一刻有传播力节点的数量
# UAU传播过程
for i in active_node:
spread_rate_current = lamda # 这个暂时放这里,看能不能省掉
forget_rate_current = delta
# UAU传播过程
neighbor_total = np.where(network_information[i, :] == 1)[0] # 找到第i个有传染力节点的邻居
neighbor_listener = np.setdiff1d(neighbor_total, active_node) # 从neighbor_total去除active_node的节点,应是排除已经感染的邻?
for j in neighbor_listener:
p1 = np.random.rand(1)
if p1 <= spread_rate_current:
Nodes_UAU[loop, t+1, j] = 1 # 这个节点已知
# UAU遗忘过程
p2 = np.random.rand(1)
if p2 <= forget_rate_current:
Nodes_UAU[loop, t+1, i] = 0 # 这个节点遗忘
else:
Nodes_UAU[loop, t+1, i] = 1
# SIR演化
for i in range(N):
if Nodes_SIR[loop, t, i] == 0: # 0代表易感(S),如果上一步节点i健康,就看他的邻居有没有被感染的
neighbor_total = np.where((network_physical[i, :] == 1))[0] # 查找其邻居
infective_nodes = np.where((Nodes_SIR[loop, t, :] == 1))[0]
neighbor_infective = np.intersect1d(infective_nodes, neighbor_total) # 取交集,真正可以感染它的邻居
Num_neighbor_infective = len(neighbor_infective) # 统计
infect_rate_current = bata # 当前临时感染率
rate_temp = 1 # 用于计算感染率
# SIR感染率改变规则
if Nodes_UAU[loop, t, i] == 0:
rate_temp = (1 - infect_rate_current) ** Num_neighbor_infective
elif Nodes_UAU[loop, t, i] == 1:
infect_rate_current = infect_rate_current * sigma_S # 当前临时感染率
rate_temp = (1 - infect_rate_current) ** Num_neighbor_infective
# SIR感染过程
v1 = 1 - rate_temp # 这是最终计算的感染率?
x1 = np.random.rand(1)
if x1 <= v1:
Nodes_SIR[loop, t+1, i] = 1
# 感染节点信息上传(知晓)
x2 = np.random.rand(1)
if x2 <= aplha:
Nodes_UAU[loop, t+1, i] = 1
# SIR康复过程
elif Nodes_SIR[loop, t, i] == 1:
immune_rate_current = mu
x3 = np.random.rand(1)
if x3 <= immune_rate_current:
Nodes_SIR[loop, t+1, i] = 2
else:
Nodes_SIR[loop, t+1, i] = 1
elif Nodes_SIR[loop, t, i] == 2:
Nodes_SIR[loop, t+1, i] = 2
else:
print("There is an else condition happened.")
print("loop {} - time has passed: {} ".format(loop, time.time()-time_start))
# +
# datasave = '../results/result.mat'
# scio.savemat(datasave, {'NodesSIR':Nodes_SIR, 'NodeUAU':Nodes_UAU})
# # print("Nodes_SIS: ", Nodes_SIS)
# # print("Nodes_UAU: ", Nodes_UAU)
# +
# 处理数据
for i in range(Monte_Carlo_loop):
awareness_count[i,:] = np.sum(Nodes_UAU[i,:,:], axis=1)
# infective_count[i,:] = np.sum(Nodes_SIR[i,:,:], axis=1)
for j in range(time_steps):
infective_count[i,j] = np.sum(Nodes_SIR[i, j, :] == 1)
immune_count[i,j] = np.sum(Nodes_SIR[i, j, :] == 2)
s_count[i,j] = np.sum(Nodes_SIR[i, j, :] == 0)
awareness_count_average = np.mean(awareness_count, axis=0)
infective_count_average = np.mean(infective_count, axis=0)
immune_count_average = np.mean(immune_count, axis=0)
s_count_average = np.mean(s_count, axis=0)
assert infective_count_average.shape == (time_steps,), "infective_count_average\' size don\'t match!"
assert immune_count_average.shape == (time_steps,), "immune_count_average\' size don\'t match!"
assert awareness_count_average.shape == (time_steps,), "awareness_count_average\' size don\'t match!"
# print("infective_count_average: ", infective_count_average)
# print("awareness_count_average: ", awareness_count_average)
## 规模参照
# Nodes_SIR = np.zeros([Monte_Carlo_loop, time_steps, N])
# infective_count = np.zeros([Monte_Carlo_loop, time_steps])
# infective_count_average = np.zeros([1, time_steps])
# -
plt.plot(s_count_average/N, label='SIR-S')
plt.plot(infective_count_average/N, label='SIR-I')
plt.plot(immune_count_average/N, label='SIR-R')
plt.plot(awareness_count_average/N, label='UAU')
# +
# 数据可视化
t = (1 : 1 : total_steps);
# SIS统计
plot(t,infective_count_average, '-o', 'color', 'y', 'linewidth', 1.2);
hold on;
# UAU统计
plot(t, awareness_count_average, '-o', 'color', 'k', 'linewidth', 1.2);
hold on;
xlabel('steps');ylabel('density of nodes');
legend('SIS_I(t)','UAU_I(t)');
hold off;
# +
import time
print ("time.time(): %f " %time.time())
time_start=time.time()
time.sleep(1)
time_end=time.time()
print('totally cost',time_end-time_start)
# -
a = np.array([[1,2],[3,4],[5,6]])
datasave = './results/result.mat'
scio.savemat(datasave, {'A':a})
data_1 = scio.loadmat(datasave)
|
Python/Baseline_model/SIR_UAU.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Using HEPData
# +
import json
import pyhf
import pyhf.contrib.utils
# -
# ## Preserved on HEPData
# As of this tutorial, ATLAS has [published 18 full statistical models to HEPData](https://scikit-hep.org/pyhf/citations.html#published-statistical-models)
#
# <p align="center">
# <a href="https://www.hepdata.net/record/ins1755298?version=3"><img src="https://raw.githubusercontent.com/matthewfeickert/talk-SciPy-2020/e0c509cd0dfef98f5876071edd4c60aff9199a1b/figures/HEPData_likelihoods.png"></a>
# </p>
#
# Let's explore the 1Lbb workspace a little bit shall we?
# ### Getting the Data
#
# We'll use the `pyhf[contrib]` extra (which relies on `requests` and `tarfile`) to download the HEPData minted DOI and extract the files we need.
pyhf.contrib.utils.download(
"https://doi.org/10.17182/hepdata.90607.v3/r3", "1Lbb-likelihoods"
)
# This will nicely download and extract everything we need.
# !ls -lavh 1Lbb-likelihoods
# ## Instantiate our objects
#
# We have a background-only workspace `BkgOnly.json` and a signal patchset collection `patchset.json`. Let's create our python objects and play with them:
spec = json.load(open("1Lbb-likelihoods/BkgOnly.json"))
patchset = pyhf.PatchSet(json.load(open("1Lbb-likelihoods/patchset.json")))
# So what did the analyzers give us for signal patches?
# ## Patching in Signals
#
# Let's look at this [`pyhf.PatchSet`](https://pyhf.readthedocs.io/en/v0.6.3/_generated/pyhf.patchset.PatchSet.html#pyhf.patchset.PatchSet) object which provides a user-friendly way to interact with many signal patches at once.
#
# ### PatchSet
patchset
# Oh wow, we've got 125 patches. What information does it have?
print(f"description: {patchset.description}")
print(f" digests: {patchset.digests}")
print(f" labels: {patchset.labels}")
print(f" references: {patchset.references}")
print(f" version: {patchset.version}")
# So we've got a useful description of the signal patches... there's a digest. Does that match the background-only workspace we have?
pyhf.utils.digest(spec)
# It does! In fact, this sort of verification check will be done automatically when applying patches using `pyhf.PatchSet` as we will see shortly. To manually verify, simply run `pyhf.PatchSet.verify` on the workspace. No error means everything is fine. It will loudly complain otherwise.
patchset.verify(spec)
# No error, whew. Let's move on.
#
# The labels `m1` and `m2` tells us that we have the signal patches parametrized in 2-dimensional space, likely as $m_1 = \tilde{\chi}_1^\pm$ and $m_2 = \tilde{\chi}_1^0$... but I guess we'll see?
#
# The references list the references for this dataset, which is pointing at the hepdata record for now.
#
# Next, the version is the version of the schema set we're using with `pyhf` (`1.0.0`).
#
# And last, but certainly not least... its patches:
patchset.patches
# So we can see all the patches listed both by name such as `C1N2_Wh_hbb_900_250` as well as a pair of points `(900, 250)`. Why is this useful? The `PatchSet` object acts like a special dictionary look-up where it will grab the patch you need based on the unique key you provide it.
#
# For example, we can look up by name
patchset["C1N2_Wh_hbb_900_250"]
# or by the pair of points
patchset[(900, 250)]
# ### Patches
#
# A `pyhf.PatchSet` is a collection of `pyhf.Patch` objects. What is a patch indeed? It contains enough information about how to apply the signal patch to the corresponding background-only workspace (matched by digest).
patch = patchset["C1N2_Wh_hbb_900_250"]
print(f" name: {patch.name}")
print(f"values: {patch.values}")
# Most importantly, it contains the patch information itself. Specifically, this inherits from the `jsonpatch.JsonPatch` object, which is a 3rd party module providing native support for json patching in python. That means we can simply apply the patch to our workspace directly!
print(f" samples pre-patch: {pyhf.Workspace(spec).samples}")
print(f"samples post-patch: {pyhf.Workspace(patch.apply(spec)).samples}")
# Or, more quickly, from the `PatchSet` object:
print(f" samples pre-patch: {pyhf.Workspace(spec).samples}")
print(f"samples post-patch: {pyhf.Workspace(patchset.apply(spec, (900, 250))).samples}")
# ### Patching via Model Creation
#
# One last way to apply the patching is to, instead of patching workspaces, we patch the models as we build them from the background-only workspace. This maybe makes it easier to treat the background-only workspace as immutable, and patch in signal models when grabbing the model. Check it out.
workspace = pyhf.Workspace(spec)
# First, load up our background-only spec into the workspace. Then let's create a model.
model = workspace.model(patches=[patchset["C1N2_Wh_hbb_900_250"]])
print(f"samples (workspace): {workspace.samples}")
print(f"samples ( model ): {model.config.samples}")
# ## Doing Physics
#
# So we want to try and reproduce part of the contour. At least convince ourselves we're doing *physics* and not *fauxsics*. ... Anyway... Let's remind ourselves of the 1Lbb contour as we don't have the photographic memory of the ATLAS SUSY conveners
#
# <img alt="1Lbb exclusion contour" src="https://atlas.web.cern.ch/Atlas/GROUPS/PHYSICS/PAPERS/SUSY-2019-08/fig_06.png" width="600" />
#
# So let's work around the 700-900 GeV $\tilde{\chi}_1^\pm, \tilde{\chi}_2^0$ region. We'll look at two points here:
#
# * `C1N2_Wh_hbb_650_0(650, 0)` which is below the contour and excluded
# * `C1N2_Wh_hbb_1000_0(1000, 0)` which is above the contour and not excluded
#
# Let's perform a "standard" hypothesis test (with $\mu = 1$ null BSM hypothesis) on both of these and use the $\text{CL}_\text{s}$ values to convince ourselves that we just did reproducible physics!?!
# ### Doing Physics, for real now
# +
model_below = workspace.model(patches=[patchset["C1N2_Wh_hbb_650_0"]])
model_above = workspace.model(patches=[patchset["C1N2_Wh_hbb_1000_0"]])
# -
# We've made our models. Let's test hypotheses!
#
# *Note: this will not be as instantaneous as our simple models...but it should still be pretty fast!*
# +
test_poi = 1.0
result_below = pyhf.infer.hypotest(
test_poi,
workspace.data(model_below),
model_below,
test_stat="qtilde",
return_expected_set=True,
)
print(f"Observed CLs: {result_below[0]}")
print(f"Expected CLs band: {[exp.tolist() for exp in result_below[1]]}")
# +
result_above = pyhf.infer.hypotest(
test_poi,
workspace.data(model_above),
model_above,
test_stat="qtilde",
return_expected_set=True,
)
print(f"Observed CLs: {result_above[0]}")
print(f"Expected CLs band: {[exp.tolist() for exp in result_above[1]]}")
# -
# And as you can see, we're getting results that we generally expect. Excluded models are those for which $\text{CL}_\text{s} < 0.05$. Additionally, you can see that the expected bands $-2\sigma$ for the $(1000, 0)$ point is just slightly below the observed result for the $(650, 0)$ point which is what we observe in the figure above.
|
book/SerializationAndPatching.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # A/B Testing - Pt. 1
#
# ## What is A/B testing?
# Whether adding a new feature to a product or trying a new form of online advertising we need to know if a change we're going to make is going to make a imapact, usually we hope this will be in a positive direction and increase some metric of interest click through rate, conversions etc. When running an A/B test experiment we need to use some statistical significance test, generally a hypothesis test (depending on what it is we wish to test), to truely prove the effect and ensure the results we observe are not caused by chance variation.
#
# ## Hypothesis Testing
# When testing a hypothesis we have a __null hypothesis__ which will account for all scenarios that the __alternate hypothesis__ does not account for. The null hypothesis will essentially embody the notion that nothing special is happening (there is no effect), so in the simple case of changing the color of a button we might hypothesise that the new color increases clicks (our alternate hypothesis), our null will be that it performs worse or the same.
#
# We usually use notation to express these hypothesis as:
#
# $H_0$: $\mu \geq \overline{X}$
#
# $H_A$: $\mu < \overline{X}$
#
# where:
# - $\mu$ is the population mean.
# - $\overline{X}$ is the sample mean.
#
# 
# +
from IPython.display import HTML
HTML('''<script>
code_show=true;
function code_toggle() {
if (code_show){
$('div.input').hide();
} else {
$('div.input').show();
}
code_show = !code_show
}
$( document ).ready(code_toggle);
</script>
<form action="javascript:code_toggle()"><input type="submit" value="Click here to toggle on/off the raw code."></form>''')
# -
display(HTML("""
<style>
.output {
display: flex;
align-items: justify;
text-align: justify;
}
</style>
"""))
# +
import matplotlib.pyplot as plt
import numpy as np
import random
p = 0.5
n = 100
mu = p * n
sigma = (n * p * (1 - p))**0.5
population_data = np.random.normal(mu, sigma, 20000)
plt.clf()
plt.figure(figsize=(10, 6))
plt.hist(population_data, 40, histtype='bar', label='Population')
plt.axvline(0.6*100, color='red', label='Sample')
plt.axvline(mu, color='black', label='Population')
min_ylim, max_ylim = plt.ylim()
plt.text(mu*.75, max_ylim*0.95, f'Population Mean ($\mu$): {int(mu)}')
plt.text(mu*1.22, max_ylim*0.5, 'Sample Mean ($\overline{X}$): 60')
plt.show()
# -
# In this example we're comparing a sample mean ($\overline{X}$) to a population mean ($\mu$), which is a hypothesis test we might perform if we know the population parameters $\mu, \sigma$, but our A/B is a comparison of 2 or more sample means so our hypothesis is something more like:
#
# $H_0$: $\mu_{control} \geq \mu_{treatment} $
#
# $H_A$: $\mu_{control} < \mu_{treatment}$
#
# _NOTE: We initially used $\mu$ to denote the population mean, moving forward when we are talking about two sample tests it will represent the sample mean._
#
# 
#
# Where our test groups are randomly assigned and our control gets the existing button and the treatment group gets the new version. To compare these two populations we take the sample mean or proportion (eg. click thorugh rate or click through probability) and compare. If the size of the difference exceeds some significance threshold ($\alpha$) then we can reject the null hypothesis and conclude that the result is not due to chance variation and is statistically significant. We call a hypothesis test like this a two sample test.
# +
import matplotlib.pyplot as plt
import numpy as np
import warnings
warnings.filterwarnings('ignore')
p = 0.5
n = 100
mu = p * n
sigma = (n * p * (1 - p))**0.5
control_data = np.random.normal(mu, sigma, 20000)
treatment_data = np.random.normal(60, 5, 20000)
plt.figure(figsize=(10, 6))
plt.hist(control_data, 40, histtype='bar', label='Control Group')
plt.hist(treatment_data, 40, histtype='bar', label='Treatment Group', alpha=0.4)
plt.axvline(0.6*100, color='red', label='Treatment Mean ($\mu_{treatment}$)')
plt.axvline(mu, color='black', label='Control Mean ($\mu_{control}$)')
min_ylim, max_ylim = plt.ylim()
plt.title("Control and Treatment Sampling Distributions")
plt.legend()
plt.show()
# -
# ## Z-tests & T-tests
#
# There are two main type of statistical tests we use for hypothesis testing with 1 or 2 samples. This the z-test and t-test. Generally we use t-tests if we have a small sample size < 30 or if we do not know the population parameters ($\sigma, \mu$). The t-distribution for which we use to determine critical values is more conservative than the z, it has fatter tails as we expect that when n is small the variance will be large so distribution spreads probability wider and is less concentrated around the mean. However when n is large the t-distribution approximates the z-distribution (normal distribution).
#
# Generally in A/B tests we do not know the population parameters because most the time we are running the expermient with the randomly assigned experiemntal groups, testing under the same conditions, but with on or more groups exposed to some different treatment. However, in large web experiments you will often see the z-test used, this is simply because as n becomes large the t-distribution approximates the z so you may see examples of both being used and if n is large the results should be quite similar.
# +
from scipy.stats import t, norm
rv = t(df=5, loc=0, scale=1)
x = np.linspace(rv.ppf(0.0001), rv.ppf(0.9999), 100)
y = rv.pdf(x)
x_norm = np.linspace(-5,5,100)
nd = norm.pdf(x)
plt.figure(figsize=(10, 6))
plt.plot(x_norm, nd, color='red', label='Normal Distribution')
plt.xlim(-5,5)
plt.plot(x,y, label='T-Distribution')
plt.title("Normal vs T Distribution")
min_ylim, max_ylim = plt.ylim()
plt.legend()
plt.show()
# -
# ## One way, Two way Tests
# As the intial example outlined often we want to know if some treatment will increase or decrease some metric. To prove that a result is significant and to not be fooled by the new treatment we have to formulate our hypothesis to support this.
#
# In a one way test we are interested in a treatment that either has a:
#
# __Positive effect__ (treatment mean is greater than the control):
#
# $H_0$: $\mu_{control} \geq \mu_{treatment} $
#
# $H_A$: $ \mu_{control} < \mu_{treatment} $
#
# __Negative effect__ (treatment mean is less than the control):
#
# $H_0$: $\mu_{control} \leq \mu_{treatment} $
#
# $H_A$: $ \mu_{control} > \mu_{treatment} $
#
# In one way test we are often comparing a well test baseline or existing solution to something new. There is always a chance when using a one way test that we might miss an effect going the opposite direction.
#
# Two way tests are more concervative and try to ensure we don't get fooled in either direction.
#
# $H_0$: $\mu_{control} = \mu_{treatment} $
#
# $H_A$: $ \mu_{control} \neq \mu_{treatment} $
#
# There is some debate around what we should use in A/B tests, One way v Two way, often one way fits the nature of A/B tests given we usually run experiments to see if a new feature or product change performs better than the existing, however lots of testing software uses two way as it is more conservative (eg. $\alpha$ = 0.05 gets spread between 2 tails (0.025 in each) instead of one).
# ## Critical Values, Alpha ($\alpha$) and The Normal Distribution
# Critical values are determined by using the significance threshold (refered to as $\alpha$, generally $\alpha=0.05$) we set to ensure we aren't tricked by chance variation (try to ensure we don't make a type 1 error - reject the null when the null is true). Now we can either calculate the critical value using an inverse cdf function or we can use a generic table thats commonly available.
#
# Before we go into the normal distribution we need to be aware of the theorm that underpins why we use the normal distribution that is very important, that is the __Central Limit Theorm__ (CLT). The CLT is one of the most import theories in statistics, and is critical for hypothesis testing. The key points of the CLT:
# - The distribution of sample means is approximately normal.
# - The standard deviation of sample means $\approx \frac{\sigma}{\sqrt{n}}$
# - The mean of the sample mean is $\approx \mu$
#
# So in other words, the relation this has to all we've mentioned is that if we have a distribution of sample means we can determine whether a given sample mean is weird or not by where it lies on that distribution. If a random variable (RV) defined as the average of a large number of idependent and identically distributed RVs, is itself approximately normally distributed, despite shape of the original population distribution. This is a very important for hypothesis testing and for statistical inference.
#
# While we're at this point let's do a tiny bit of background on the normal distribution (often denoted $N(\mu, \sigma^2)$).
#
# Hopefully you've seen the common bell shaped curve which has the __probability density function (PDF)__:
#
# $f(x|\mu, \sigma) = \frac{1}{\sqrt{2 \pi \sigma}} \exp\left(-\frac{(x - \mu)^2}{2\sigma^2}\right)\, \hspace{20pt}$
#
# in code:
# ```python
# def normal_pdf(x, mu=0, sigma=1):
# sqrt_two_pi = math.sqrt(2 * math.pi)
# return (math.exp(-(x-mu) ** 2 / 2 / sigma ** 2) / (sqrt_two_pi * sigma))
# ```
#
# We can visualize an alpha of 0.05 of a normal distribution, and the location of the critical reigon depends upon the type of test you are running, below we show a one way test. Any result to the right of our critical value ($\alpha = 0.05$) would be statistically significant.
# +
import math
def normal_pdf(x, mu, sigma):
sqrt_two_pi = math.sqrt(2 * math.pi)
return (math.exp(-(x-mu) ** 2 / 2 / sigma ** 2) / (sqrt_two_pi * sigma))
x = [x / 10.0 for x in range(-40, 40)]
plt.figure(figsize=(10, 6))
plt.plot(x,[normal_pdf(i, 0, 1) for i in x])
plt.axvline(1.645, color='red', label='$\\alpha=0.05$')
plt.legend()
plt.title("Normal PDF")
plt.ylabel("Probability Density")
plt.xlabel("Z")
plt.show()
# -
# The PDF encompasses the probability that a variate has the value x. The PDF is a continuous function/distribution, meaning that a single point on the probability distribution will be zero (the total probability 1, is the area under the curve, a line has no area), so generally we need to find the integral (area under the curve) to estimate the probability that x is within some range. For our hypothesis tests, our alpha values related to probability density, for our example one way test at $\alpha = 0.05$, the critical region encompases 5% of the probability density.
#
# When $\sigma = 1$ and $\mu = 0$, this distribution is called the __standard normal distribution__ (often denoted $N(0, 1)$).
#
# If $Z$ is a standard normal random variable, with $\mu$ (mean) and $\sigma$ (standard deviation) ($N(0, 1)$), and $X$ is a general normal random variable $N(\mu, \sigma^2)$, $X$ is just a scaled and shifted normal random varialble:
#
# $X = \sigma Z + \mu$ in other words, this can be seen as a representation of random variable $X$ where $Z$ is the standard normal random variable.
#
# If $X$ is a normal random variable with $\mu$ (mean) and $\sigma$ (standard deviation) then we can convert or __standardize__ $X$ to a standard normal random variable $Z$ by:
#
# $Z = \displaystyle \frac{(X - \mu)}{\sigma}$
#
# Let's look at this a little further, just to clarify. To do this we'll use binomial random variables, which has two parameters n and p. A Binomial(n,p) random variable is simply the sum of n independent Bernoulli(p) random variables, each of which equals 1 with probability p and 0 with probability $1 - p$:
# +
import random, collections
def bernoulli(p):
return 1 if random.random() < p else 0
def binomial(p, n):
return sum(bernoulli(p) for _ in range(n))
p = 0.5
n = 100
repeats = 100000
X = [binomial(p, n) for _ in range(repeats)]
freqs = collections.Counter(X)
mu = p * n
sigma = (n * p * (1 - p))**0.5
f, (ax1, ax2) = plt.subplots(1, 2, figsize=(12,5))
ax1.bar([x for x in freqs.keys()], [v for v in freqs.values()], 1)
ax1.set_title('Normal Random Variable')
ax1.set_xlabel('X')
ax2.bar([round((x - mu)/sigma, 1) for x in freqs.keys()], [v / repeats for v in freqs.values()], 0.2)
ax2.set_title('Standardized Random Variable')
ax2.set_xlabel('Z')
plt.show()
# -
# ### Fitting our normal PDF to our experiment data.
f, (ax1, ax2) = plt.subplots(1, 2, figsize=(12,5))
plt.plot(sorted(X),[normal_pdf(i, mu, sigma) for i in sorted(X)], color='red')
ax1.bar([x for x in freqs.keys()], [v for v in freqs.values()], 1)
ax1.set_title('Normal Random Variable')
ax2.bar([x for x in freqs.keys()], [v / repeats for v in freqs.values()], 1)
ax2.set_title('Normal PDF')
plt.show()
# The __cumulative distribution function (CDF)__ gives us the cumulative probabilty associated with a function. The CDF gives us the probability that a variable takes on a value less that or equal to the x. For the normal distribution is not as straightforward to write but we can code it as:
#
# ```python
# def cdf_normal_dist(x: float, mu: float, sigma: float) -> float:
# return (1 + math.erf((x - mu) / 2**0.5 / sigma)) / 2
# ```
# $CDF: F(x) = P[X \leq x]$
#
# In other words we can map a given z score to a probability. $Z \to P$
# +
def cdf_normal_dist(x: float, mu: float, sigma: float) -> float:
return (1 + math.erf((x - mu) / 2**0.5 / sigma)) / 2
x = [x / 10.0 for x in range(-50, 50)]
plt.figure(figsize=(10, 6))
plt.plot(x,[normal_cdf(i, 0, 1) for i in x])
plt.title("Normal CDF")
plt.ylabel("Probability")
plt.show()
# -
cdf_normal_dist(1.645, 0, 1)
# ### Now, the CDF of our observed experiment data.
f, (ax1, ax2) = plt.subplots(1, 2, figsize=(12,5))
ax1.plot(sorted(X),[cdf_normal_dist(i, mu, sigma) for i in sorted(X)])
ax1.set_title('Experiment CDF')
ax1.set_xlabel('X')
ax1.set_ylabel('Probability')
ax2.plot([(x-mu)/sigma for x in sorted(X)],[cdf_normal_dist(i, mu, sigma) for i in sorted(X)])
ax2.set_title('Experiment Standardized CDF')
ax2.set_xlabel('Z')
plt.show()
# To go the other way we use the __Inverse CDF__ (or quantile function) which tells us what $X$ would make some $F(X)$ return some $P$, $P \to Z$.
#
# The inverse CDF function is only a simple binary search using probabilities and Z-scores (we use our cdf function to get the probability for each mid Z point we search) and is an approximation.
# +
def quantile_function(prob: float, mu: float = 0, sigma: float = 1):
# If not standard normal we'll normalize the result.
if mu != 0 or sigma != 1:
return (mu + sigma) * quantile_function(prob)
# Use binary search to find the z that matches our prob.
# Our probability interval is of course (0, 1).
l_p = 0
r_p = 1
# Our Z interval is (-12, 12).
l_z = -12.00
r_z = 12.00
while l_z <= r_z:
mid = l_z + (r_z - l_z) / 2
# Calculate the probability of our mid.
p_mid = cdf_normal_dist(mid, mu, sigma)
# If the mid prob is < our target, target must be to the right.
if p_mid < prob:
l_p, l_z = p_mid, mid
# If the mid prob is > our target, target must be to the left.
elif p_mid > prob:
r_p, r_z = p_mid, mid
# Else mid prob == target, return the z.
else:
return mid
quantile_funtion(0.95)
# -
# In another post we'll look at these functions again and run some simulation experiments.
# ## Why A/B test?
#
# We have to prove that our change (or our hypothesis) has a significant difference, humans are very succeptable to believing changes that are simply due to chance variation, so we must rule this out. We can asses the probability of achieving a result as significant as the one obtained in the experiment by calculating a p-value, which by definition, given a chance model that embodies the null hypothesis, is the probability of obtaining a result as or more extreme than the observed.
#
# Doing a controlled experiments such as an A/B allows us infer things about our overall population. For example, if we run and A/B test we can calculate at __Confidence Interval (CI)__ that at some level of confidence tells us the range of where the population mean would lie, so we can make statements like "given the new treatment x which at 95% confidence we'd expect the population mean to be between X & Y." aka given a treatment that is statistically signifcant and applying that to the entire population we can infer or we would be 95% confident that the mean would be within the range X, Y. This of course helps us decide what to do, for example whether to adopt a change or not.
# ## Considerations for A/B Tests
#
# ### Formulate
# First we need to formualte what our experiment will look like and whether we are going to want to run a one way or two way test. As mentioned previously, when conducting these online experiments we are often comparing an existing treatment of some kind to a new alternate. This naturally fits a one way test, but there is still debate about whether the more conservative two way test should be a default for these kinds of experiments.
#
# ### Design
# #### Selecting a Test Metric
# We are going to need to select a test metric, something that quantitatively will allow us to measure the difference between the treatments. In hypothesis tests this usually comes in terms of proportions or means. In web tests this can be reflected as metrics like click through rate or click through probability, conversion rate etc. Our metric needs to be sensisitive enough to detect change, but also rebust at the same time. We should have confidence in our metric of choice, if we aren't we may wish to perform an A/A test prior to running our experiment to ensure the metric will be reliable come experiment time. The A/A test is simply selecting two sample populations and confirming there's no significant difference between these populations when tested under the same conditions.
# #### Unit of Diversion
# Selecting an appropriate unit of diversion is very important for our experiment. We will need to select this based on consistency for what we wish to measure, we also need to think about the consequences of select a given unit as well. For example, if we are condicting an experiment for a visual change we are most likely going to want to select a unit that is going to ensure consistency for a given test subject/user so they aren't left wondering about what is happening, something like a userid or cookies can help ensure consistent UX for our test subjects.
#
# ### Collect
#
# ### Infer/Conclude
# ## Parametric & Non-Parametric
# Calculating results from A/B tests can be done using two main methodologies;
# - __Parametric/Statistically:__ Here we use methods that make underlying assumptions about distributions (eg. the population is normally distributed) and we use reference tables to perform calculations to determine the significance of our results.
# - __Non-Parametric/Emperically:__ We run resampling methods with the results obtained to make the calculations (eg. exact tests).
#
# So which to choose? Both! The parametric methods were vital in earlier years, but with modern computing we can run non-parametric methods quickly! We can compare results from both and hope they align, if they don't this might suggest there is something wrong and further investigationing should be done!
# ## When should we consider Bandits instead?
#
# When considering running an A/B test there are a number of things we should think about before the start preparing for the experiment. One of the big things to consider is whether we actually need an A/B test, whether we can actually run an A/B experiement properly and whether implementing a MAB instead might be a better choice for our experimentation framework.
#
# 1. What are we hoping to achieve with the A/B test?
# - Are we hoping to try to answer a research questions or are we hoping to select a purely optimimal solution?
# - An A/B test is the right framework to use if we are hoping to validate a hypothesis, statistically prove something.
# - A MAB will help us determine the most optimal treatment/solution.
# 2. Do the requirements for a proper A/B test experiment align with what the experiment setting?
# - Eg. does the website/service etc. have enough traffic with a suffice/allowable time window to reach significance?
# - If sizing doesn't fit the significance requirements does increasing the minimum effect size, power or alpha make sense, can we change our unit of diversion?
# 3. Are we okay with the with exposing a significant proportion of the population to a potentially negative treatment?
# - With A/B we randomly split test subjects into two or more groups, if one of the treatments has a negative effect there can be a significant cost associated the most obvious example is loss of business/users etc, dissatified with their experience.
# - With a MAB we are dynamically allocating test subjects between optimal and potentially optimal solutions (exploitation and exploration) this means that we can hopefully earn while we learn given that we allocating more subjects to the most optimal solution while routinely exploring other treatments to ensure we've converged to the optimal treatment.
|
ab_testing.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
#X: MxN
#y: M
class MultinomialLogisticRegression:
def __init__(self, C, alpha = 0.01, lam = 1, n_iters = 500):
self.C = C
self.alpha = alpha
self.lam = lam
self.n_iters = n_iters
def fit(self, X, y):
M = X.shape[0]
#intercept
X = np.hstack([np.ones((M,1)), X])
N = X.shape[1]
#y:M -> MxC
#one hot encoding for y
y = pd.Series(y)
y = pd.get_dummies(y).to_numpy()
self.W = np.zeros((N,self.C))
for i in range(self.n_iters):
if(i>44 or i%5 == 0):
print(self.W)
grad = (X.T @ (np.exp(X @ self.W) / np.sum(np.exp(X @ self.W), axis=1)[np.newaxis,1] - y)) / M \
+ (self.lam * np.linalg.norm(self.W))
grad[:,self.C-1] = 0
self.W -= self.alpha * grad
def predict(self, X):
M = X.shape[0]
X = np.hstack([np.ones((M,1)), X])
return this.W
model = MultinomialLogisticRegression(C = 2)
model.fit(X, y)
model.W
lineX = np.array([-3.5, 3.5])
print(model.W[:,0].shape)
print(lineX.shape)
lineY = (-model.W[0,0] - model.W[1,0]*lineX)/model.W[2,0]
print(lineY)
plt.plot(lineX, lineY)
# Testing on toy data
# +
from sklearn.datasets import make_classification
X, y = make_classification(n_samples=100, n_features=2, n_redundant=0, random_state=35)
X[0:5]
# +
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state = 35)
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# -
plt.scatter(X[:,0], X[:,1], c = y)
|
Multinomial_logistic_regression.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import numpy as np
import pandas as pd
from ipysheet import from_dataframe, to_dataframe
dates = pd.date_range('20130101', periods=6)
df = pd.DataFrame(np.random.randn(6, 26), index=dates, columns=list(chr(ord('A') + i) for i in range(26)))
sheet = from_dataframe(df)
sheet
# +
df2 = pd.DataFrame({'A': 1.,
'B': pd.Timestamp('20130102'),
'C': pd.Series(1, index=list(range(4)), dtype='float32'),
'D': np.array([False, True, False, False], dtype='bool'),
'E': pd.Categorical(["test", "train", "test", "train"]),
'F': 'foo'})
sheet2 = from_dataframe(df2)
sheet2
# -
df3 = to_dataframe(sheet2)
df3
|
examples/pandas.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import copy
import keras
import numpy as np
from model import get_model
from scripts.data_preprocess import get_data
# ## Load the data
x_train, x_test, y_train, y_test = get_data('sudoku.csv')
# ## Train your own Model
# +
model = get_model()
adam = keras.optimizers.Adam(lr=.001)
model.compile(loss='sparse_categorical_crossentropy', optimizer=adam)
model.fit(x_train, y_train, batch_size=32, epochs=2)
# -
# ## Or load pretrained model
model = keras.models.load_model('model/sudoku.model')
# ## Solve Sudoku by filling blank positions one by one
def norm(a):
return (a/9)-.5
def denorm(a):
return (a+.5)*9
def inference_sudoku(sample):
'''
This function solve the sudoku by filling blank positions one by one.
'''
feat = copy.copy(sample)
while(1):
out = model.predict(feat.reshape((1,9,9,1)))
out = out.squeeze()
pred = np.argmax(out, axis=1).reshape((9,9))+1
prob = np.around(np.max(out, axis=1).reshape((9,9)), 2)
feat = denorm(feat).reshape((9,9))
mask = (feat==0)
if(mask.sum()==0):
break
prob_new = prob*mask
ind = np.argmax(prob_new)
x, y = (ind//9), (ind%9)
val = pred[x][y]
feat[x][y] = val
feat = norm(feat)
return pred
# ## Testing 100 games
def test_accuracy(feats, labels):
correct = 0
for i,feat in enumerate(feats):
pred = inference_sudoku(feat)
true = labels[i].reshape((9,9))+1
if(abs(true - pred).sum()==0):
correct += 1
print(correct/feats.shape[0])
test_accuracy(x_test[:100], y_test[:100])
# ## Test your own game
def solve_sudoku(game):
game = game.replace('\n', '')
game = game.replace(' ', '')
game = np.array([int(j) for j in game]).reshape((9,9,1))
game = norm(game)
game = inference_sudoku(game)
return game
# +
game = '''
0 8 0 0 3 2 0 0 1
7 0 3 0 8 0 0 0 2
5 0 0 0 0 7 0 3 0
0 5 0 0 0 1 9 7 0
6 0 0 7 0 9 0 0 8
0 4 7 2 0 0 0 5 0
0 2 0 6 0 0 0 0 9
8 0 0 0 9 0 3 0 5
3 0 0 8 2 0 0 1 0
'''
game = solve_sudoku(game)
print('solved puzzle:\n')
print(game)
# -
np.sum(game, axis=1)
|
sudoku.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Batched example 2
# This notebook is the second of a series that shows how [GSSHA_Workflow.ipynb](../GSSHA_Workflow.ipynb) can be parameterized at the command line that builds on [GSSHA_Workflow_Batched_Example1](GSSHA_Workflow_Batched_Example1.ipynb). This notebook uses the same principles as the first example but makes the interface more user friendly and Windows compatible.
#
# As in the first example, the two parameters we choose to expose are ``rain_intensity`` and ``rain_duration``. As before, the notebook is configured to use these parameters in three steps.
#
# 1. <a href="#Declare_nbparams">Declare the command line parameters</a>
# 2. <a href="#Display_nbparams">Display the notebook parameter widgets</a>
# 3. <a href="#Apply_nbparams">Apply notebook parameters and display</a>
#
# Only the first step <a href="#Declare_nbparams">Declare the command line parameters</a> is different from the first example; the second step is identical and the third step is only different by a trivial variable name change.
#
# The main improvement presented here is in the interface used to set parameters at the command line:
#
# ```bash
# param -cmd 'jupyter nbconvert --execute GSSHA_Workflow_Batched_Example2.ipynb' -p rain_intensity=25 -p rain_duration=3600
# ```
#
# As in the first example, an arbitrary command can be executed but in this instance a nicer syntax is used to specify the desired parameters. The ``param`` command generates the appropriate environment variable and makes it available to the execution context in a way that is cross platform, allowing this utility to be used on Windows.
# +
from datetime import datetime, timedelta
import os
import glob
import param
import panel as pn
import numpy as np
import xarray as xr
import geoviews as gv
import holoviews as hv
import earthsim.gssha as esgssha
import earthsim.gssha.model as models
import cartopy.crs as ccrs
from panel.param import JSONInit
from earthsim.gssha import download_data, get_file_from_quest
from earthsim.gssha.model import UniformRoughness, CreateGSSHAModel
from holoviews.streams import PolyEdit, BoxEdit, PointDraw, CDSStream
from holoviews.operation.datashader import regrid, shade
from earthsim.io import save_shapefile, open_gssha, get_ccrs
regrid.aggregator = 'max'
hv.extension('bokeh')
# %output holomap='scrubber' fps=2
# -
# rm -r ./vicksburg_south/
# ## Declare the command line parameters <a id="Declare_nbparams"></a>
# As in the previous example, the ``rain_intensity`` and ``rain_duration`` of ``Simulation`` are exposed. The change here is that instead of explicitly defining the ``NotebookParams`` class, a helper function called ``global_params`` is used instead.
#
# This utility makes the definition of notebook parameters more concise and readable. In addition to parameter objects, you can simply use literals for quick parameter definitions. For instance, the literal ``5`` is promoted to a ``param.Integer``, the literal ``6.2`` is promoted to a ``param.Number``, ``'example'`` is promoted to a ``param.String`` etc.
from earthsim import parameters
nbparams = parameters(
rain_intensity = param.Number(default=24, bounds=(0,None), softbounds=(0,75)),
rain_duration = 60
)
# Note that the literal specification is shorter and easier to read but is lacking documentation and numeric bounds declarations. This may also result in less user-friendly widgets: ``rain_duration`` is displayed with a text box in the next code cell instead of a slider. Using literals to define notebook parameters is most appropriate for generating static HTML reports from the command line where the widgets won't be used.
# ## Display the notebook parameter widgets <a id="Display_nbparams"></a>
# This step makes the notebook parameters available to change at the start of the notebook, parameterizing the interactive workflow. In addition, using ``initializer=JSONInit()`` allows these parameters to be set from the command line.
pn.panel(nbparams, initializer=JSONInit())
# ## Configure model parameters
model_creator = esgssha.CreateGSSHAModel(name='Vicksburg South Model Creator',
mask_shapefile='../../data/vicksburg_watershed/watershed_boundary.shp',
grid_cell_size=90)
pn.panel(model_creator)
# ### Setting the parameters of the ``roughness``
model_creator.roughness = UniformRoughness()
pn.panel(model_creator.roughness)
# ## Draw bounds to compute watershed
# Allows drawing a bounding box and adding points to serve as input to compute a watershed:
# %%opts Polygons [width=900 height=500] (fill_alpha=0 line_color='black')
# %%opts Points (size=10 color='red')
tiles = gv.WMTS('http://c.tile.openstreetmap.org/{Z}/{X}/{Y}.png',
crs=ccrs.PlateCarree(), extents=(-91, 32.2, -90.8, 32.4))
box_poly = hv.Polygons([])
points = hv.Points([])
box_stream = BoxEdit(source=box_poly)
point_stream = PointDraw(source=points)
tiles * box_poly * points
# +
if box_stream.element:
element = gv.operation.project(box_stream.element, projection=ccrs.PlateCarree())
xs, ys = element.array().T
bounds = (xs[0], ys[1], xs[2], ys[0])
print("BOUNDS", bounds)
if point_stream.element:
projected = gv.operation.project(point_stream.element, projection=ccrs.PlateCarree())
print("COORDINATE:", projected.iloc[0]['x'][0], projected.iloc[0]['y'][0])
# -
# ## Inspect and edit shapefile
#
# The plot below allows editing the shapefile using a set of tools. The controls for editing are as follows:
#
# * Double-clicking the polygon displays the vertices
# * After double-clicking the point tool is selected and vertices can be dragged around
# * By tapping on a vertex it can be selected, tapping in a new location while a single point is selected inserts a new vertex
# * Multiple points can be selected by holding shift and then tapping or using the box_select tool
# * Once multiple vertices are selected they can be deleted by selecting the point editing tool and pressing ``backspace``
# %%opts Shape [width=900 height=500 tools=['box_select']] (alpha=0.5)
mask_shape = gv.Shape.from_shapefile(model_creator.mask_shapefile)
tiles = gv.WMTS('http://c.tile.openstreetmap.org/{Z}/{X}/{Y}.png')
vertex_stream = PolyEdit(source=mask_shape)
tiles * mask_shape
# If any edits were made to the polygon in the plot above we save the ``watershed_boundary.shp`` back out and redisplay it to confirm our edits were applied correctly:
# %%opts Shape [width=600 height=400] (alpha=0.5)
if vertex_stream.data:
edited_shape_fname = '../vicksburg_watershed_edited/watershed_boundary.shp'
dir_name = os.path.dirname(edited_shape_fname)
if not os.path.isdir(dir_name): os.makedirs(dir_name)
save_shapefile(vertex_stream.data, edited_shape_fname, model_creator.mask_shapefile)
model_creator.mask_shapefile = edited_shape_fname
mask_shape = gv.Shape.from_shapefile(edited_shape_fname)
mask_shape = mask_shape.opts() # Clear options
mask_shape
# ## Configure simulation parameters
sim = esgssha.Simulation(name='Vicksburg South Simulation', simulation_duration=60*60,
rain_duration=30*60, model_creator=model_creator)
# ## Apply notebook parameters and display<a id="Apply_nbparams"></a>
# This is the point at which the notebook parameters hook into the workflow. In this example, the two chosen parameters ``rain_duration`` and ``rain_intensity`` are simply set on ``sim``. In more complex examples, you may decide to compute the parameters set in the workflow as a function of the availabel notebook parameters.
sim.rain_duration = nbparams.rain_duration
sim.rain_intensity = nbparams.rain_intensity
pn.panel(sim)
# ## Create the model
#
# Note that the above code demonstrates how to collect user input, but it has not yet been connected to the remaining workflow, which uses code-based specification for the parameters.
pn.panel(sim.model_creator)
# +
# temporary workaround until workflow cleanup/parameterization is done
if sim.model_creator.project_name == 'test_philippines_small':
sim.model_creator.roughness = models.GriddedRoughnessTable(
land_use_grid=get_file_from_quest(sim.model_creator.project_name, sim.land_use_service, 'landuse', sim.model_creator.mask_shapefile),
land_use_to_roughness_table='../philippines_small/land_cover_glcf_modis.txt')
else:
sim.model_creator.roughness = models.GriddedRoughnessID(
land_use_grid=get_file_from_quest(sim.model_creator.project_name, sim.land_use_service, 'landuse', sim.model_creator.mask_shapefile),
land_use_grid_id=sim.land_use_grid_id)
sim.model_creator.elevation_grid_path = get_file_from_quest(sim.model_creator.project_name, sim.elevation_service, 'elevation', sim.model_creator.mask_shapefile)
# -
model = sim.model_creator()
# +
# add card for max depth
model.project_manager.setCard('FLOOD_GRID',
'{0}.fgd'.format(sim.model_creator.project_name),
add_quotes=True)
# Add time-based depth grids to simulation
"""
See: http://www.gsshawiki.com/Project_File:Output_Files_%E2%80%93_Required
Filename or folder to output MAP_TYPE maps of overland flow depth (m)
every MAP_FREQ minutes. If MAP_TYPE=0, then [value] is a folder name
and output files are called "value\depth.####.asc" **
"""
model.project_manager.setCard('DEPTH', '.', add_quotes=True)
model.project_manager.setCard('MAP_FREQ', '1')
# add event for simulation (optional)
"""
model.set_event(simulation_start=sim.simulation_start,
simulation_duration=timedelta(seconds=sim.simulation_duration),
rain_intensity=sim.rain_intensity,
rain_duration=timedelta(seconds=sim.rain_duration))
"""
# write to disk
model.write()
# -
# ## Review model inputs
# ### Load inputs to the simulation
# +
name = sim.model_creator.project_name
CRS = get_ccrs(os.path.join(name, name+'_prj.pro'))
roughness_arr = open_gssha(os.path.join(name,'roughness.idx'))
msk_arr = open_gssha(os.path.join(name, name+'.msk'))
ele_arr = open_gssha(os.path.join(name, name+'.ele'))
roughness = gv.Image(roughness_arr, crs=CRS, label='roughness.idx')
mask = gv.Image(msk_arr, crs=CRS, label='vicksburg_south.msk')
ele = gv.Image(ele_arr, crs=CRS, label='vicksburg_south.ele')
# -
# #### Shapefile vs. Mask
tiles * regrid(mask) * mask_shape
# #### Elevation
tiles * regrid(ele) * mask_shape
# #### Roughness
tiles * regrid(roughness) * mask_shape
# # Run Simulation
from gsshapy.modeling import GSSHAFramework
# +
# TODO: how does the info here relate to that set earlier?
# TODO: understand comment below
# assuming notebook is run from examples folder
project_path = os.path.join(sim.model_creator.project_base_directory, sim.model_creator.project_name)
gr = GSSHAFramework("gssha",
project_path,
"{0}.prj".format(sim.model_creator.project_name),
gssha_simulation_start=sim.simulation_start,
gssha_simulation_duration=timedelta(seconds=sim.simulation_duration),
# load_simulation_datetime=True, # use this if already set datetime params in project file
)
# http://www.gsshawiki.com/Model_Construction:Defining_a_uniform_precipitation_event
gr.event_manager.add_uniform_precip_event(sim.rain_intensity,
timedelta(seconds=sim.rain_duration))
gssha_event_directory = gr.run()
# -
# # Visualizing the outputs
# ### Load and visualize depths over time
# +
depth_nc = os.path.join(gssha_event_directory, 'depths.nc')
if not os.path.isfile(depth_nc):
# Load depth data files
depth_map = hv.HoloMap(kdims=['Minute'])
for fname in glob.glob(os.path.join(gssha_event_directory, 'depth.*.asc')):
depth_arr = open_gssha(fname)
minute = int(fname.split('.')[-2])
# NOTE: Due to precision issues not all empty cells match the NaN value properly, fix later
depth_arr.data[depth_arr.data==depth_arr.data[0,0]] = np.NaN
depth_map[minute] = hv.Image(depth_arr)
# Convert data to an xarray and save as NetCDF
arrays = []
for minute, img in depth_map.items():
ds = hv.Dataset(img)
arr = ds.data.z.assign_coords(minute=minute)
arrays.append(arr)
depths = xr.concat(arrays, 'minute')
depths.to_netcdf(depth_nc)
else:
depths = xr.open_dataset(depth_nc)
depth_ds = hv.Dataset(depths)
depth_ds.data
# -
# Now that we have a Dataset of depths we can convert it to a series of Images.
# %%opts Image [width=600 height=400 logz=True xaxis=None yaxis=None] (cmap='viridis') Histogram {+framewise}
regrid(depth_ds.to(hv.Image, ['x', 'y'])).redim.range(z=(0, 0.04)).hist(bin_range=(0, 0.04))
# We can also lay out the plots over time to allow for easier comparison.
# %%opts Image [width=300 height=300 logz=True xaxis=None yaxis=None] (cmap='viridis')
regrid(depth_ds.select(minute=range(10, 70, 10)).to(hv.Image, ['x', 'y']).redim.range(z=(0, 0.04))).layout().cols(3)
# ### Flood Grid Depth
#
# (Maximum flood depth over the course of the simulation)
# %%opts Image [width=600 height=400] (cmap='viridis')
fgd_arr = open_gssha(os.path.join(gssha_event_directory,'{0}.fgd'.format(sim.model_creator.project_name)))
fgd = gv.Image(fgd_arr, crs=CRS, label='vicksburg_south.fgd').redim.range(z=(0, 0.04))
regrid(fgd, streams=[hv.streams.RangeXY]).redim.range(z=(0, 0.04))
# ### Analyzing the simulation speed
# %%opts Spikes [width=600]
times = np.array([os.path.getmtime(f) for f in glob.glob(os.path.join(gssha_event_directory, 'depth*.asc'))] )
minutes = (times-times[0])/60
hv.Spikes(minutes, kdims=['Real Time (minutes)'], label='Time elapsed for each minute of simulation time') +\
hv.Curve(np.diff(minutes), kdims=['Simulation Time (min)'], vdims=[('runtime', 'Runtime per minute simulation time')]).redim.range(runtime=(0, None))
# Here if the "spikes" are regularly spaced, simulation time is regularly scaled with real time, and so you should be able read out the approximate time to expect per unit of simulation time.
|
examples/topics/batched_example/GSSHA_Workflow_Batched_Example2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Assignment 3
# ES15BTECH11002
# ## Base class
# +
import numpy as np
import random
import time
import matplotlib.pyplot as plt
num_chars = 256
class RNN:
def __init__(self, num_hidden):
self.num_hidden = num_hidden
#input to hidden
self.U = np.random.uniform(-np.sqrt(1./num_chars), np.sqrt(1./num_chars), (num_hidden, num_chars))
#hidden to output
self.V = np.random.uniform(-np.sqrt(1./num_hidden), np.sqrt(1./num_hidden), (num_chars, num_hidden))
#recurrent connection in the hidden
self.W = np.random.uniform(-np.sqrt(1./num_hidden), np.sqrt(1./num_hidden), (num_hidden, num_hidden))
#cross entropy loss
def loss(self, x):
N = len(x)
x = x[0:len(x)-1]
y = x[1:len(x)]
o, h = self.forward_propagation(x)
correct_word_predictions = o[np.arange(len(y)), y]
L = -1 *np.sum(np.log(correct_word_predictions))
return L/N
def forward_propagation(self, x, temp=1):
T = len(x)
# we need one extra hidden, we initialize all to zero and save them for later
hidden = np.zeros((T+1, self.num_hidden))
hidden[-1] = np.zeros(self.num_hidden)
# we set T outputs to 0 and save them for later
out = np.zeros((T, num_chars))
#computing forward prop
for t in np.arange(T):
hidden[t] = np.tanh(self.U[:,x[t]] + np.dot(self.W, hidden[t-1]))
out[t] = softmax(np.dot(self.V, hidden[t]), temp)
return out, hidden
def bptt(self, x, y):
T = len(y)
# Perform forward propagation
o, h = self.forward_propagation(x)
# We accumulate the gradients in these variables
dLdU = np.zeros(self.U.shape)
dLdV = np.zeros(self.V.shape)
dLdW = np.zeros(self.W.shape)
delta_out = o
delta_out[np.arange(len(y)),y] -= 1
# For each output backwards...
for t in np.arange(T)[::-1]:
dLdV += np.outer(delta_out[t], h[t].T)
# Initial delta calculation: dL/dz
delta_t = np.dot(self.V.T, delta_out[t]) * (1 - (h[t] ** 2))
# Backpropagation through time (for at most self.bptt_truncate steps)
for step in np.arange(max(0, t), t+1)[::-1]:
# Add to gradients at each previous step
dLdW += np.outer(delta_t, h[step-1])
dLdU[:,x[step]] += delta_t
# Update delta for next step dL/dz at t-1
delta_t = np.dot(self.W.T, delta_t) * (1 - (h[step-1] ** 2))
return dLdU, dLdV, dLdW
def predict(self, x, temp=1):
out, hidden_states = self.forward_propagation(x, temp)
ascii_number = np.argmax(out[-1])
return ascii_number
def sgd_step(self, x, y, lr):
dLdU, dLdV, dLdW = self.bptt(x,y)
self.U -= lr * dLdU
self.V -= lr * dLdV
self.W -= lr * dLdW
# -
# ### Function to plot
def graph(toplot, labels, title, xlabel, ylabel, no_epoch):
plt.title(title)
plt.xlabel(xlabel)
plt.ylabel(ylabel)
for i in range(len(toplot)):
plt.plot(no_epoch, toplot[i], label = labels[i])
plt.legend(loc = 'best')
plt.show()
# ### Training Method
def train(model, x, lr, sequence_len, num_epochs, print_freq, breakpoint = False):
train_loss = []
no_epoch = []
for epoch in range(1,num_epochs+1):
i = 0
no_epoch += [epoch]
trainloss = model.loss(x[:1000])
train_loss += [trainloss]
while (i+1+sequence_len) < len(x):
model.sgd_step(x[i:i+sequence_len],x[i+1:i+1+sequence_len], lr)
i += sequence_len
if epoch % print_freq == 0:
print time.strftime("%Y-%m-%d %H:%M:%S")
print ('\tepoch #%d: \tloss = %f' %(epoch, trainloss))
if(breakpoint):
text = generate(model, start = ord('T'), length = 100, temperature = 1, sequence_len = 50)
print 'Generated text for epoch', epoch
display(text)
toplot = [train_loss]
labels = ['Training loss']
graph(toplot, labels, 'Training Loss vs epochs', 'epochs', 'Training Loss', no_epoch)
# ### Softmax with temperature
def softmax(a,temp): # softmax with temperature
numer = np.exp(a/temp)
out = numer / numer.sum()
return out
# # 1
#
# ### Method to read file
def read_file(filename):
with open(filename, 'rb') as f:
x = f.read()
x_train = [ord(letter) for letter in x]
unique = len(set(x))
print ('There are %d unique characters\n' %unique)
return x_train
# ### Method to generate text
def generate(model, start, length, temperature, sequence_len):
text = []
text.append(start)
for i in range(length-1):
begin = max(0, len(text)-sequence_len)
end = len(text)
next_char = model.predict(text[begin:end], temperature)
text.append(next_char)
return text
# ### Method to display text
def display(text):
print ('\nGenerating text of length %d' %len(text))
gen = [str(chr(x)) for x in text] # convert ascii number to corresponding character
#join list of chars and print
print 'Generated text: '
print ''.join(gen)
print "\ndone!"
# ### Hyperparameters
filename = 'novel.txt'
hidden_size = 100
learning_rate = 0.01
num_epochs = 24
print_freq = 4
# __________----------------------------------------------------------------------------------------------___________
#
# ## 2b
# ### 2b i) and ii)
net = RNN(hidden_size)
start = ord('l') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 1 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50
# +
x = read_file(filename)
print 'Training with'
print ('hidden_size = %d, learning_rate = %f, sequence_len = %d, num_epochs = %d\n' \
%(hidden_size, learning_rate, sequence_len, num_epochs))
train(net, x, learning_rate, sequence_len, num_epochs, print_freq, breakpoint = True)
# -
gen_text = generate(net, start, gen_length, temperature, sequence_len)
display(gen_text)
# ## Report
# + active=""
# A total of 24 epochs were run to train the model.
#
# Breaking points were kept after every 4 iterations.
#
# The network learnt more words thorugh epochs and does not print the same words again.
# It also learned grammar rules as it puts a space after a comma.
#
# The general structure of the senetences improved a lot during the eopchs.
# -
# ### 2b iii)
# #### Temp1
# ##### text1
start = ord('a') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 1 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50
# +
print ('Generated text of length = %d, temperature = %d, start letter = %d\n'\
%(gen_length, temperature, start)
)
gen_text = generate(net, start, gen_length, temperature, sequence_len)
display(gen_text)
# -
# ##### text2
start = ord('b') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 1 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50
# +
print ('Generated text of length = %d, temperature = %d, start letter = %d\n'\
%(gen_length, temperature, start)
)
gen_text = generate(net, start, gen_length, temperature, sequence_len)
display(gen_text)
# -
# ##### text3
start = ord('h') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 1 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50
# +
print ('Generated text of length = %d, temperature = %d, start letter = %d\n'\
%(gen_length, temperature, start)
)
gen_text = generate(net, start, gen_length, temperature, sequence_len)
display(gen_text)
# -
# ##### text4
start = ord('i') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 1 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50
# +
print ('Generated text of length = %d, temperature = %d, start letter = %d\n'\
%(gen_length, temperature, start)
)
gen_text = generate(net, start, gen_length, temperature, sequence_len)
display(gen_text)
# -
# ##### text5
start = ord('n') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 1 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50
# +
print ('Generated text of length = %d, temperature = %d, start letter = %d\n'\
%(gen_length, temperature, start)
)
gen_text = generate(net, start, gen_length, temperature, sequence_len)
display(gen_text)
# -
# #### Temp2
# ##### text1
start = ord('v') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 10 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50
# +
print ('Generated text of length = %d, temperature = %d, start letter = %d\n'\
%(gen_length, temperature, start)
)
gen_text = generate(net, start, gen_length, temperature, sequence_len)
display(gen_text)
# -
# ##### text2
start = ord('r') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 10 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50
# +
print ('Generated text of length = %d, temperature = %d, start letter = %d\n'\
%(gen_length, temperature, start)
)
gen_text = generate(net, start, gen_length, temperature, sequence_len)
display(gen_text)
# -
# ##### text3
start = ord('u') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 10 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50
# +
print ('Generated text of length = %d, temperature = %d, start letter = %d\n'\
%(gen_length, temperature, start)
)
gen_text = generate(net, start, gen_length, temperature, sequence_len)
display(gen_text)
# -
# ##### text4
start = ord('t') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 10 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50
# +
print ('Generated text of length = %d, temperature = %d, start letter = %d\n'\
%(gen_length, temperature, start)
)
gen_text = generate(net, start, gen_length, temperature, sequence_len)
display(gen_text)
# -
# ##### text5
start = ord('q') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 10 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50
# +
print ('Generated text of length = %d, temperature = %d, start letter = %d\n'\
%(gen_length, temperature, start)
)
gen_text = generate(net, start, gen_length, temperature, sequence_len)
display(gen_text)
# -
# #### Temp3
# ##### text1
start = ord('f') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 100 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50
# +
print ('Generated text of length = %d, temperature = %d, start letter = %d\n'\
%(gen_length, temperature, start)
)
gen_text = generate(net, start, gen_length, temperature, sequence_len)
display(gen_text)
# -
# ##### text2
start = ord('p') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 100 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50
# +
print ('Generated text of length = %d, temperature = %d, start letter = %d\n'\
%(gen_length, temperature, start)
)
gen_text = generate(net, start, gen_length, temperature, sequence_len)
display(gen_text)
# -
# ##### text3
start = ord('x') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 100 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50
# +
print ('Generated text of length = %d, temperature = %d, start letter = %d\n'\
%(gen_length, temperature, start)
)
gen_text = generate(net, start, gen_length, temperature, sequence_len)
display(gen_text)
# -
# ##### text4
start = ord('y') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 100 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50
# +
print ('Generated text of length = %d, temperature = %d, start letter = %d\n'\
%(gen_length, temperature, start)
)
gen_text = generate(net, start, gen_length, temperature, sequence_len)
display(gen_text)
# -
# ##### text5
start = ord('z') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 100 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50
# +
print ('Generated text of length = %d, temperature = %d, start letter = %d\n'\
%(gen_length, temperature, start)
)
gen_text = generate(net, start, gen_length, temperature, sequence_len)
display(gen_text)
# -
# ## Report
# + active=""
# As the temperaure is increased we expect to see more randomness in the text produced as the probability of a character choosed becomes more uniform, compared to lower temperatures where only the most probable character is chosen.
#
# Higher temperatures thereby increase the diversity of the results
#
# Similar trends were observed and the network seemed to explore rather than predict the most probable letters.
# -
# ## 2c
# ### i)
#
#
# ### Doubling hidden layer size
net2 = RNN(hidden_size*2)
start = ord('l') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 1 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50
# +
x = read_file(filename)
print 'Training with'
print ('hidden_size = %d, learning_rate = %f, sequence_len = %d, num_epochs = %d\n' \
%(hidden_size, learning_rate, sequence_len, num_epochs))
train(net2, x, learning_rate, sequence_len, num_epochs, print_freq, breakpoint = True)
# -
gen_text = generate(net2, start, gen_length, temperature, sequence_len)
display(gen_text)
# #### Temp1
# ##### text1
start = ord('l') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 1 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50
# +
print ('Generated text of length = %d, temperature = %d, start letter = %d\n'\
%(gen_length, temperature, start)
)
gen_text = generate(net2, start, gen_length, temperature, sequence_len)
display(gen_text)
# -
# #### Temp2
# ##### text1
start = ord('a') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 10 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50
# +
print ('Generated text of length = %d, temperature = %d, start letter = %d\n'\
%(gen_length, temperature, start)
)
gen_text = generate(net2, start, gen_length, temperature, sequence_len)
display(gen_text)
# -
# #### Temp3
# ##### text1
start = ord('p') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 100 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50
# +
print ('Generated text of length = %d, temperature = %d, start letter = %d\n'\
%(gen_length, temperature, start)
)
gen_text = generate(net2, start, gen_length, temperature, sequence_len)
display(gen_text)
# -
# ### Halving hidden layer size
net5 = RNN(hidden_size/2)
start = ord('l') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 1 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50
# +
x = read_file(filename)
print 'Training with'
print ('hidden_size = %d, learning_rate = %f, sequence_len = %d, num_epochs = %d\n' \
%(hidden_size, learning_rate, sequence_len, num_epochs))
train(net5, x, learning_rate, sequence_len, num_epochs, print_freq, breakpoint = True)
# -
gen_text = generate(net5, start, gen_length, temperature, sequence_len)
display(gen_text)
# #### Temp1
# ##### text1
start = ord('l') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 1 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50
# +
print ('Generated text of length = %d, temperature = %d, start letter = %d\n'\
%(gen_length, temperature, start)
)
gen_text = generate(net5, start, gen_length, temperature, sequence_len)
display(gen_text)
# -
# #### Temp2
# ##### text1
start = ord('a') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 10 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50
# +
print ('Generated text of length = %d, temperature = %d, start letter = %d\n'\
%(gen_length, temperature, start)
)
gen_text = generate(net5, start, gen_length, temperature, sequence_len)
display(gen_text)
# -
# #### Temp3
# ##### text1
start = ord('p') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 100 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50
# +
print ('Generated text of length = %d, temperature = %d, start letter = %d\n'\
%(gen_length, temperature, start)
)
gen_text = generate(net5, start, gen_length, temperature, sequence_len)
display(gen_text)
# -
# ## Observations
# + active=""
# The network learns a richer vocabulary upon increasing the hidden layer size, as now it can learn more richer dependencies from the sequence length of previous characters.
#
# The network performs worse upon halving the hidden layer size, maybe because it was not able to learn the dependancies because of less training data.
# -
# ### 2c ii)
# ### Doubling sequence
net22 = RNN(hidden_size)
start = ord('l') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 1 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50*2
# +
x = read_file(filename)
print 'Training with'
print ('hidden_size = %d, learning_rate = %f, sequence_len = %d, num_epochs = %d\n' \
%(hidden_size, learning_rate, sequence_len, num_epochs))
train(net22, x, learning_rate, sequence_len, num_epochs, print_freq, breakpoint = True)
# -
gen_text = generate(net22, start, gen_length, temperature, sequence_len)
display(gen_text)
# #### Temp1
# ##### text1
start = ord('r') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 1 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50
# +
print ('Generated text of length = %d, temperature = %d, start letter = %d\n'\
%(gen_length, temperature, start)
)
gen_text = generate(net22, start, gen_length, temperature, sequence_len)
display(gen_text)
# -
# #### Temp2
# ##### text1
start = ord('s') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 10 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50
# +
print ('Generated text of length = %d, temperature = %d, start letter = %d\n'\
%(gen_length, temperature, start)
)
gen_text = generate(net22, start, gen_length, temperature, sequence_len)
display(gen_text)
# -
# #### Temp3
# ##### text1
start = ord('t') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 100 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50
# +
print ('Generated text of length = %d, temperature = %d, start letter = %d\n'\
%(gen_length, temperature, start)
)
gen_text = generate(net22, start, gen_length, temperature, sequence_len)
display(gen_text)
# -
# ### Halving sequence
net25 = RNN(hidden_size)
start = ord('l') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 1 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50/2
# +
x = read_file(filename)
print 'Training with'
print ('hidden_size = %d, learning_rate = %f, sequence_len = %d, num_epochs = %d\n' \
%(hidden_size, learning_rate, sequence_len, num_epochs))
train(net25, x, learning_rate, sequence_len, num_epochs, print_freq, breakpoint = True)
# -
gen_text = generate(net25, start, gen_length, temperature, sequence_len)
display(gen_text)
# #### Temp1
# ##### text1
start = ord('l') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 1 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50
# +
print ('Generated text of length = %d, temperature = %d, start letter = %d\n'\
%(gen_length, temperature, start)
)
gen_text = generate(net25, start, gen_length, temperature, sequence_len)
display(gen_text)
# -
# #### Temp2
# ##### text1
start = ord('a') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 10 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50
# +
print ('Generated text of length = %d, temperature = %d, start letter = %d\n'\
%(gen_length, temperature, start)
)
gen_text = generate(net25, start, gen_length, temperature, sequence_len)
display(gen_text)
# -
# #### Temp3
# ##### text1
start = ord('r') #start character of generated text
gen_length = 100 # number of characters to generate
temperature = 100 # temperature to bias the predictions to most probable or to uniformly predict every char
sequence_len = 50
# +
print ('Generated text of length = %d, temperature = %d, start letter = %d\n'\
%(gen_length, temperature, start)
)
gen_text = generate(net25, start, gen_length, temperature, sequence_len)
display(gen_text)
# -
# ## Observations
# + active=""
# Similar observations to 2c i) were made here.
#
# Doubling the sequence made the model learn better whereas halving the sequence made it perform worse.
# -
# ## Refrence taken from:
#
# http://wildml.com/2015/09/recurrent-neural-networks-tutorial-part-2-implementing-a-language-model-rnn-with-python-numpy-and-theano/
# # 2a
# ## Forward
# +
st = tanh(U*xt + W*st-1)
ot = softmax(Vst)
# -
# ## Backward
# + active=""
# d(Et)/d(V) = (yt - ot) x st
#
# here d is the partial derivative, yt is the predicted output, ot is the actual label, x is the cross product, E is the error
#
# d(Et)/d(W) = sum(t = k to T)((dEk/dyk)*(dyk/dsk)(pi(j=k+1 to T)(dsj/dsj-1))* dsk/dW)
#
#
#
#
|
Asn3/es15btech11002_Assign3(1 and 2).ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Equilibration detection figure generation notebook
# The code was taken from [this paper](https://github.com/choderalab/automatic-equilibration-detection) and was adapted to work with python 3
# %pylab inline
import seaborn as sbn
sbn.set_context("notebook", font_scale=1.5, rc={"lines.linewidth": 2})
sbn.set_style( {'font.family':'sans-serif', 'font.sans-serif':'Helvetica'})
ti = np.loadtxt('ti.dat')
mbar = np.loadtxt('mbar.dat')
fig=figure(figsize=(4,4))
plt.plot(ti[:,0],ti[:,1],'--', marker='*', lw=2, label='TI')
plt.errorbar(mbar[:,0], mbar[:,1], yerr=mbar[:,2], marker='.', lw=1, color='crimson',label='MBAR')
sbn.despine()
xlabel(r'$\vec{\lambda}$')
ylabel(r'PMF in [kcal/mol]')
legend()
|
paper/figures/fig_pmf/PMF_plots.ipynb
|
# ---
# layout: post
# title: "한장간 - 네트워크와 모델"
# author: 김태영
# date: 2017-01-27 04:00:00
# categories: Study
# comments: true
# image: http://tykimos.github.io/warehouse/2017-1-27_CNN_Layer_Talk_lego_10.png
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# 간(GAN)을 시작하기에 앞서 케라스에서 네트워크와 모델 개념 정립을 먼저 한 후에 간단한 간모델을 만들어보겠습니다. 네트워크와 모델 개념을 레고 사람에 비유를 들어보겠습니다. 초반부는 귀엽겠지만 후반부에는 조금 무서울 수 있으니 노약자나 임산부는 주의해서 보시기 바랍니다.
# ---
#
# ### 간(GAN)보기에 앞서
#
# 간관련 공부를 하다보면 네트워크도 여러개 나오고 모델과 손실함수도 여러개라서 상당히 헷갈렸습니다. 기초적인 딥러닝이나 케라스 개념을 익히셨다면 간보기에 앞서 네트워크와 모델 개념을 분리하고, 모델에서도 손실함수와 최적화기도 분리해서 개념을 정립하면 기본 간 모델은 물론 복잡한 간 모델을 이해하는 데 도움이 많이 될 것 같습니다.
# ---
#
# ### 네트워크
#
# 신경망에서 가장 기본적인 요소가 '뉴론'입니다. 이러한 뉴론 여러개가 구성된 것이 '레이어'이고 레이어가 여러 층으로 쌓여있는 것을 '네트워크'라 합니다. 입력 뉴런과 출력 뉴런 간에 연결선을 시냅스라 부르고 이 연결 강도를 '가중치'라고 합니다. 아래 그림은 입력 4개에 출력 3개 뉴런을 가진 전결합층을 표한한 것입니다. (a)에서 보면 학습해야할 녹색 가중치 블록이 12개가 있습니다. 이를 좀 더 간단하게 표시한 것이 (b)인데, 여기서는 가중치가 연결선으로만 표시되어 있습니다. (c)는 (b)를 좀 더 간략하게 표시한 것입니다. (c)의 아래 그림을 보면 '3'으로 표기되어 있는 데, 이는 출력 뉴런의 수를 표기한 것입니다. 케라스에서는 입력 뉴런 수는 입력에 따라 정해지기 때문에 입력층이 아닌 은닉층에서는 따로 지정할 필요는 없습니다.
#
# 
# 여러개의 층을 쌓아보자
#
# 
# +
from keras.models import Sequential
from keras.layers.core import Dense
from keras.layers.advanced_activations import LeakyReLU
generator = Sequential()
generator.add(Dense(256, input_dim=100))
generator.add(LeakyReLU(0.2))
generator.add(Dense(512))
generator.add(LeakyReLU(0.2))
generator.add(Dense(1024))
generator.add(LeakyReLU(0.2))
generator.add(Dense(784, activation='tanh'))
# -
# 입출력에 대한 설명.
#
# 
# +
import numpy as np
random_latent_vectors = np.random.normal(0, 1, size=[1, 100])
generated_data = generator.predict(random_latent_vectors)
generated_images = generated_data.reshape(1, 28, 28)
# +
# %matplotlib inline
import matplotlib.pyplot as plt
plt.imshow(generated_images[0], interpolation='nearest')
plt.axis('off')
# +
import os
os.environ["KERAS_BACKEND"] = "tensorflow"
import numpy as np
from tqdm import tqdm
import matplotlib.pyplot as plt
from keras.layers import Input
from keras.models import Model, Sequential
from keras.layers.core import Reshape, Dense, Dropout, Flatten
from keras.layers.advanced_activations import LeakyReLU
from keras.layers.convolutional import Convolution2D, UpSampling2D
from keras.layers.normalization import BatchNormalization
from keras.datasets import mnist
from keras.optimizers import Adam
from keras import backend as K
from keras import initializers
K.set_image_dim_ordering('th')
# Deterministic output.
# Tired of seeing the same results every time? Remove the line below.
np.random.seed(1000)
# The results are a little better when the dimensionality of the random vector is only 10.
# The dimensionality has been left at 100 for consistency with other GAN implementations.
randomDim = 100
# 1. 데이터셋 생성하기
# Load MNIST data
(X_train, y_train), (X_test, y_test) = mnist.load_data()
X_train = (X_train.astype(np.float32) - 127.5)/127.5
X_train = X_train.reshape(60000, 784)
# 2. 모델 구성하기
# 2.1 생성기 모델
generator = Sequential()
generator.add(Dense(256, input_dim=latent_dim))
generator.add(LeakyReLU(0.2))
generator.add(Dense(512))
generator.add(LeakyReLU(0.2))
generator.add(Dense(1024))
generator.add(LeakyReLU(0.2))
generator.add(Dense(784, activation='tanh'))
# 2.2 판별기 모델
discriminator = Sequential()
discriminator.add(Dense(1024, input_dim=784))
discriminator.add(LeakyReLU(0.2))
discriminator.add(Dropout(0.3))
discriminator.add(Dense(512))
discriminator.add(LeakyReLU(0.2))
discriminator.add(Dropout(0.3))
discriminator.add(Dense(256))
discriminator.add(LeakyReLU(0.2))
discriminator.add(Dropout(0.3))
discriminator.add(Dense(1, activation='sigmoid'))
# 2.3 간 모델
ganInput = Input(shape=(randomDim,))
x = generator(ganInput)
ganOutput = discriminator(x)
gan = Model(inputs=ganInput, outputs=ganOutput)
# 3. 모델 학습과정 설정하기
# Optimizer
adam = Adam(lr=0.0002, beta_1=0.5)
# 3.1 판별기 모델 학습과정 설정
discriminator.compile(loss='binary_crossentropy', optimizer=adam)
# 3.2 간 모델 학습과정 설정
discriminator.trainable = False
gan.compile(loss='binary_crossentropy', optimizer=adam)
dLosses = []
gLosses = []
# Plot the loss from each batch
def plotLoss(epoch):
plt.figure(figsize=(10, 8))
plt.plot(dLosses, label='Discriminitive loss')
plt.plot(gLosses, label='Generative loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend()
plt.savefig('./warehouse/simplegan/images/gan_loss_epoch_%d.png' % epoch)
# Create a wall of generated MNIST images
def plotGeneratedImages(epoch, examples=100, dim=(10, 10), figsize=(10, 10)):
noise = np.random.normal(0, 1, size=[examples, randomDim])
generatedImages = generator.predict(noise)
generatedImages = generatedImages.reshape(examples, 28, 28)
plt.figure(figsize=figsize)
for i in range(generatedImages.shape[0]):
plt.subplot(dim[0], dim[1], i+1)
plt.imshow(generatedImages[i], interpolation='nearest', cmap='gray_r')
plt.axis('off')
plt.tight_layout()
plt.savefig('./warehouse/simplegan/images/gan_generated_image_epoch_%d.png' % epoch)
# Save the generator and discriminator networks (and weights) for later use
def saveModels(epoch):
generator.save('./warehouse/simplegan/models/gan_generator_epoch_%d.h5' % epoch)
discriminator.save('./warehouse/simplegan/models/gan_discriminator_epoch_%d.h5' % epoch)
def train(epochs=1, batchSize=128):
batchCount = X_train.shape[0] / batchSize
print 'Epochs:', epochs
print 'Batch size:', batchSize
print 'Batches per epoch:', batchCount
for e in xrange(1, epochs+1):
print '-'*15, 'Epoch %d' % e, '-'*15
for _ in tqdm(xrange(batchCount)):
# Get a random set of input noise and images
noise = np.random.normal(0, 1, size=[batchSize, randomDim])
imageBatch = X_train[np.random.randint(0, X_train.shape[0], size=batchSize)]
# Generate fake MNIST images
generatedImages = generator.predict(noise)
# print np.shape(imageBatch), np.shape(generatedImages)
X = np.concatenate([imageBatch, generatedImages])
# Labels for generated and real data
yDis = np.zeros(2*batchSize)
# One-sided label smoothing
yDis[:batchSize] = 0.9
# Train discriminator
dloss = discriminator.train_on_batch(X, yDis)
# Train generator
noise = np.random.normal(0, 1, size=[batchSize, randomDim])
yGen = np.ones(batchSize)
gloss = gan.train_on_batch(noise, yGen)
# Store loss of most recent batch from this epoch
dLosses.append(dloss)
gLosses.append(gloss)
plotGeneratedImages(e)
if e == 1 or e % 20 == 0:
saveModels(e)
# Plot losses from every epoch
plotLoss(e)
if __name__ == '__main__':
train(200, 128)
# -
# ---
#
# ### 사소한 변화를 무시해주는 맥스풀링(Max Pooling) 레이어
#
# 컨볼루션 레이어의 출력 이미지에서 주요값만 뽑아 크기가 작은 출력 영상을 만듭니다. 이것은 지역적인 사소한 변화가 영향을 미치지 않도록 합니다.
#
# MaxPooling2D(pool_size=(2, 2))
#
# 주요 인자는 다음과 같습니다.
# * pool_size : 수직, 수평 축소 비율을 지정합니다. (2, 2)이면 출력 영상 크기는 입력 영상 크기의 반으로 줄어듭니다.
#
# 예를 들어, 입력 영상 크기가 4 x 4이고, 풀 크기를 (2, 2)로 했을 때를 도식화하면 다음과 같습니다. 녹색 블록은 입력 영상을 나타내고, 노란색 블록은 풀 크기에 따라 나눈 경계를 표시합니다. 해당 풀에서 가장 큰 값을 선택하여 파란 블록으로 만들면, 그것이 출력 영상이 됩니다. 가장 오른쪽은 맥스풀링 레이어를 약식으로 표시한 것입니다.
#
# 
#
# 이 레이어는 영상의 작은 변화라던지 사소한 움직임이 특징을 추출할 때 크게 영향을 미치지 않도록 합니다. 영상 내에 특징이 세 개가 있다고 가정했을 때, 아래 그림에서 첫 번째 영상을 기준으로 두 번째 영상은 오른쪽으로 이동하였고, 세 번째 영상은 약간 비틀어 졌고, 네 번째 영상은 조금 확대되었지만, 맥스풀링한 결과는 모두 동일합니다. 얼굴 인식 문제를 예를 들면, 맥스풀링의 역할은 사람마다 눈, 코, 입 위치가 조금씩 다른데 이러한 차이가 사람이라고 인식하는 데 있어서는 큰 영향을 미치지 않게 합니다.
#
# 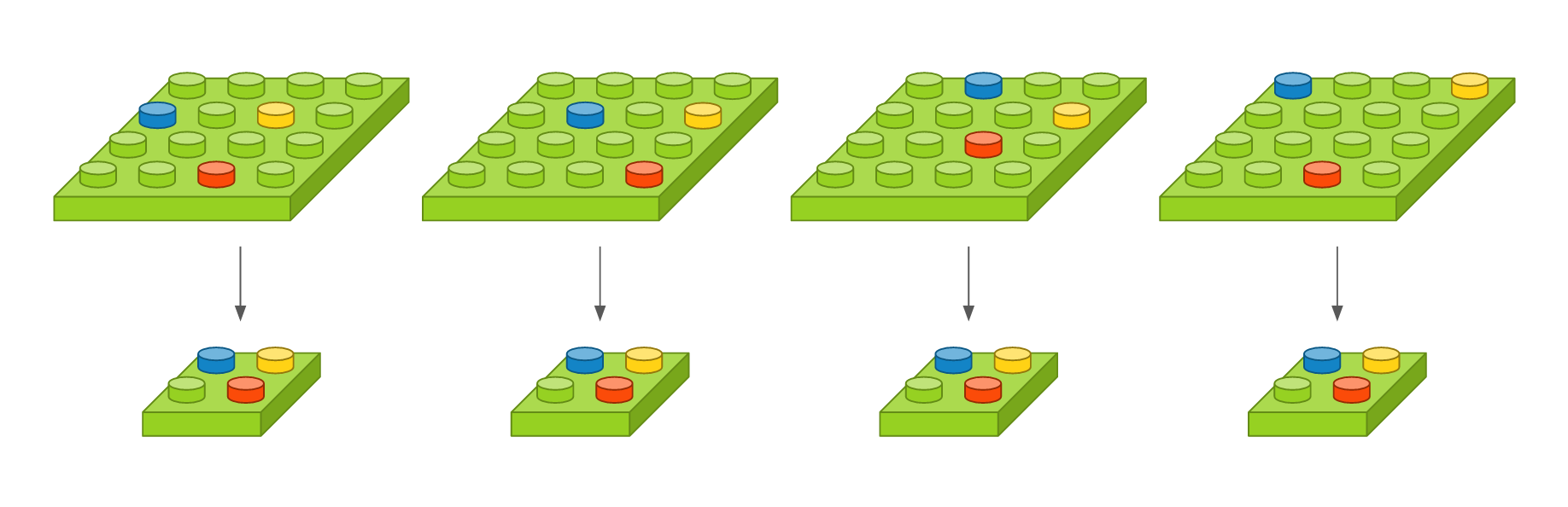
# ---
#
# ### 영상을 일차원으로 바꿔주는 플래튼(Flatten) 레이어
#
# CNN에서 컨볼루션 레이어나 맥스풀링 레이어를 반복적으로 거치면 주요 특징만 추출되고, 추출된 주요 특징은 전결합층에 전달되어 학습됩니다. 컨볼루션 레이어나 맥스풀링 레이어는 주로 2차원 자료를 다루지만 전결합층에 전달하기 위해선 1차원 자료로 바꿔줘야 합니다. 이 때 사용되는 것이 플래튼 레이어입니다. 사용 예시는 다음과 같습니다.
#
# Flatten()
#
# 이전 레이어의 출력 정보를 이용하여 입력 정보를 자동으로 설정되며, 출력 형태는 입력 형태에 따라 자동으로 계산되기 때문에 별도로 사용자가 파라미터를 지정해주지 않아도 됩니다. 크기가 3 x 3인 영상을 1차원으로 변경했을 때는 도식화하면 다음과 같습니다.
#
# 
# ---
#
# ### 한 번 쌓아보기
#
# 지금까지 알아본 레이어를 이용해서 간단한 컨볼루션 신경망 모델을 만들어보겠습니다. 먼저 간단한 문제를 정의해봅시다. 손으로 삼각형, 사각형, 원을 손으로 그린 이미지가 있고 이미지 크기가 8 x 8이라고 가정해봅니다. 삼각형, 사각형, 원을 구분하는 3개의 클래스를 분류하는 문제이기 때문에 출력 벡터는 3개여야 합니다. 필요하다고 생각하는 레이어를 구성해봤습니다.
#
# 
#
# * 컨볼루션 레이어 : 입력 이미지 크기 8 x 8, 입력 이미지 채널 1개, 필터 크기 3 x 3, 필터 수 2개, 경계 타입 'same', 활성화 함수 'relu'
#
# 
#
# * 맥스풀링 레이어 : 풀 크기 2 x 2
#
# 
#
# * 컨볼루션 레이어 : 입력 이미지 크기 4 x 4, 입력 이미지 채널 2개, 필터 크기 2 x 2, 필터 수 3개, 경계 타입 'same', 활성화 함수 'relu'
#
# 
#
# * 맥스풀링 레이어 : 풀 크기 2 x 2
#
# 
#
# * 플래튼 레이어
#
# 
#
# * 댄스 레이어 : 입력 뉴런 수 12개, 출력 뉴런 수 8개, 활성화 함수 'relu'
#
# 
#
# * 댄스 레이어 : 입력 뉴런 수 8개, 출력 뉴런 수 3개, 활성화 함수 'softmax'
#
# 
#
# 모든 레이어 블록이 준비되었으니 이를 조합해 봅니다. 입출력 크기만 맞으면 블록 끼우듯이 합치면 됩니다. 참고로 케라스 코드에서는 가장 첫번째 레이어를 제외하고는 입력 형태를 자동으로 계산하므로 이 부분은 신경쓰지 않아도 됩니다. 레이어를 조립하니 간단한 컨볼루션 모델이 생성되었습니다. 이 모델에 이미지를 입력하면, 삼각형, 사각형, 원을 나타내는 벡터가 출력됩니다.
#
# 
# 그럼 케라스 코드로 어떻게 구현하는 지 알아봅니다. 먼저 필요한 패키지를 추가하는 과정입니다. 케라스의 레이어는 'keras.layers'에 정의되어 있으며, 여기서 필요한 레이어를 추가합니다.
import numpy
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import Flatten
from keras.layers.convolutional import Conv2D
from keras.layers.convolutional import MaxPooling2D
from keras.utils import np_utils
# Sequential 모델을 하나 생성한 뒤 위에서 정의한 레이어를 차례차레 추가하면 컨볼루션 모델이 생성됩니다.
# +
model = Sequential()
model.add(Conv2D(2, (3, 3), padding='same', activation='relu', input_shape=(8, 8, 1)))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Conv2D(3, (2, 2), padding='same', activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Flatten())
model.add(Dense(8, activation='relu'))
model.add(Dense(3, activation='softmax'))
# -
# 생성한 모델을 케라스에서 제공하는 함수를 이용하여 가시화 시켜봅니다.
# +
from IPython.display import SVG
from keras.utils.vis_utils import model_to_dot
# %matplotlib inline
SVG(model_to_dot(model, show_shapes=True).create(prog='dot', format='svg'))
# -
# 
# ---
#
# ### 요약
#
# 컨볼루션 신경망 모델에서 사용되는 주요 레이어의 원리와 역할에 대해서 알아보았고 레이어를 조합하여 간단한 컨볼루션 신경망 모델을 만들어봤습니다.
# ---
#
# ### 같이 보기
#
# * [강좌 목차](https://tykimos.github.io/lecture/)
# * 이전 : [딥러닝 이야기/다층 퍼셉트론 모델 만들어보기](https://tykimos.github.io/2017/02/04/MLP_Getting_Started/)
# * 다음 : [딥러닝 이야기/컨볼루션 신경망 모델 만들어보기](https://tykimos.github.io/2017/03/08/CNN_Getting_Started/)
|
_writing/2018-1-2-One_Slide_GAN_Network_and_Model.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Want to guess what the most popular pandas-related question on StackOverflow is about? http://stackoverflow.com/questions/14262433/large-data-work-flows-using-pandas
#
# The strength of pandas really is in medium-data analytics, which can roughly be described as "datasets that fit in memory, comfortable".
# Depending on your data needs (and ability to buy time on a big [EC2 instance](https://aws.amazon.com/ec2/instance-types/) with, say, 244 GiB of RAM), this section may not apply to you.
#
# Pandas is not meant for "Big Data", but then again you probably don't have big data.
# # Chunking and Iteration
#
# The first potential operation for handling larger-than-memory data is chunking or batching your data, and iterating over each batch.
# This immediately rules out algorithms that require the full dataset to be in memory at once, but with a bit of cleverness you can work around that limitation for many problems.
import pandas as pd
import numpy as np
# %matplotlib inline
pd.Timestamp('2014-01-01').strftime("%Y%m")
# +
from distributed import Client
# executor = Client('127.0.0.1:8786')
# -
from distributed.diagnostics import progress
# +
# progress?
# -
import os
import requests
# +
def download_month(month):
os.makedirs('comext', exist_ok=True)
base = ("http://ec.europa.eu/eurostat/estat-navtree-portlet-prod/"
"BulkDownloadListing?sort=1&"
"downfile=comext%2F2015S1%2Fdata%2Fnc{:%Y%m}.7z")
r = requests.get(base.format(month), stream=True)
filename = 'comext/{:%Y-%m}.tsv.7z'.format(month)
with open(filename, 'wb') as f:
for chunk in r.iter_content(chunk_size=1024):
if chunk:
f.write(chunk)
return filename
# -
dates = pd.date_range(start='2012-01-01', end='2014-12-01', freq='m')
futures = executor.map(download_month, dates)
progress(*futures)
# !rename -S .gz .7z comext/*.gz
# rm nc201401.dat
!7z x -ocomext comext/*.7z
df = pd.read_csv('comext/nc201401.dat', dtype={'DECLARANT': 'object'})
df.head()
import dask.dataframe as dd
import zipfile
# +
zf = zipfile.ZipFile('ml-latest.zip')
zf.extractall()
# -
# ls ml-latest/
df = pd.read_csv('ml-latest/ratings.csv')
df['timestamp'] = pd.to_datetime(df.timestamp, unit='s')
ratings = dd.from_pandas(df, npartitions=100)
ratings.head()
s = df.head(1000000)
s2 = dd.from_pandas(s, npartitions=20)
def sessionize(ts):
return (ts.sort_values().diff() >= pd.Timedelta(1, unit='h')).fillna(True).cumsum()
from dask.diagnostics import Profiler, ResourceProfiler, CacheProfiler
with Profiler() as prof, ResourceProfiler() as rprof:
out = ratings.groupby('userId').timestamp.apply(sessionize, columns='timstamp').compute()
prof.visualize()
rprof.visualize()
# %%time
s.groupby('userId').timestamp.apply(sessionize)
# %%time
s2.groupby(level=0).timestamp.apply(sessionize)
df.groupby(['userId']).timestamp.apply(sessionize)
ratings.groupby('userId').rating.apply(np.mean)
df
# +
# # %load ml-latest/README.txt
Summary
=======
This dataset (ml-latest) describes 5-star rating and free-text tagging activity from [MovieLens](http://movielens.org), a movie recommendation service. It contains 22884377 ratings and 586994 tag applications across 34208 movies. These data were created by 247753 users between January 09, 1995 and January 29, 2016. This dataset was generated on January 29, 2016.
Users were selected at random for inclusion. All selected users had rated at least 1 movies. No demographic information is included. Each user is represented by an id, and no other information is provided.
The data are contained in four files, `links.csv`, `movies.csv`, `ratings.csv` and `tags.csv`. More details about the contents and use of all these files follows.
This is a *development* dataset. As such, it may change over time and is not an appropriate dataset for shared research results. See available *benchmark* datasets if that is your intent.
This and other GroupLens data sets are publicly available for download at <http://grouplens.org/datasets/>.
Usage License
=============
Neither the University of Minnesota nor any of the researchers involved can guarantee the correctness of the data, its suitability for any particular purpose, or the validity of results based on the use of the data set. The data set may be used for any research purposes under the following conditions:
* The user may not state or imply any endorsement from the University of Minnesota or the GroupLens Research Group.
* The user must acknowledge the use of the data set in publications resulting from the use of the data set (see below for citation information).
* The user may not redistribute the data without separate permission.
* The user may not use this information for any commercial or revenue-bearing purposes without first obtaining permission from a faculty member of the GroupLens Research Project at the University of Minnesota.
* The executable software scripts are provided "as is" without warranty of any kind, either expressed or implied, including, but not limited to, the implied warranties of merchantability and fitness for a particular purpose. The entire risk as to the quality and performance of them is with you. Should the program prove defective, you assume the cost of all necessary servicing, repair or correction.
In no event shall the University of Minnesota, its affiliates or employees be liable to you for any damages arising out of the use or inability to use these programs (including but not limited to loss of data or data being rendered inaccurate).
If you have any further questions or comments, please email <<EMAIL>>
Citation
========
To acknowledge use of the dataset in publications, please cite the following paper:
> <NAME> and <NAME>. 2015. The MovieLens Datasets: History and Context. ACM Transactions on Interactive Intelligent Systems (TiiS) 5, 4, Article 19 (December 2015), 19 pages. DOI=<http://dx.doi.org/10.1145/2827872>
Further Information About GroupLens
===================================
GroupLens is a research group in the Department of Computer Science and Engineering at the University of Minnesota. Since its inception in 1992, GroupLens's research projects have explored a variety of fields including:
* recommender systems
* online communities
* mobile and ubiquitious technologies
* digital libraries
* local geographic information systems
GroupLens Research operates a movie recommender based on collaborative filtering, MovieLens, which is the source of these data. We encourage you to visit <http://movielens.org> to try it out! If you have exciting ideas for experimental work to conduct on MovieLens, send us an email at <<EMAIL>> - we are always interested in working with external collaborators.
Content and Use of Files
========================
Formatting and Encoding
-----------------------
The dataset files are written as [comma-separated values](http://en.wikipedia.org/wiki/Comma-separated_values) files with a single header row. Columns that contain commas (`,`) are escaped using double-quotes (`"`). These files are encoded as UTF-8. If accented characters in movie titles or tag values (e.g. Misérables, Les (1995)) display incorrectly, make sure that any program reading the data, such as a text editor, terminal, or script, is configured for UTF-8.
User Ids
--------
MovieLens users were selected at random for inclusion. Their ids have been anonymized. User ids are consistent between `ratings.csv` and `tags.csv` (i.e., the same id refers to the same user across the two files).
Movie Ids
---------
Only movies with at least one rating or tag are included in the dataset. These movie ids are consistent with those used on the MovieLens web site (e.g., id `1` corresponds to the URL <https://movielens.org/movies/1>). Movie ids are consistent between `ratings.csv`, `tags.csv`, `movies.csv`, and `links.csv` (i.e., the same id refers to the same movie across these four data files).
Ratings Data File Structure (ratings.csv)
-----------------------------------------
All ratings are contained in the file `ratings.csv`. Each line of this file after the header row represents one rating of one movie by one user, and has the following format:
userId,movieId,rating,timestamp
The lines within this file are ordered first by userId, then, within user, by movieId.
Ratings are made on a 5-star scale, with half-star increments (0.5 stars - 5.0 stars).
Timestamps represent seconds since midnight Coordinated Universal Time (UTC) of January 1, 1970.
Tags Data File Structure (tags.csv)
-----------------------------------
All tags are contained in the file `tags.csv`. Each line of this file after the header row represents one tag applied to one movie by one user, and has the following format:
userId,movieId,tag,timestamp
The lines within this file are ordered first by userId, then, within user, by movieId.
Tags are user-generated metadata about movies. Each tag is typically a single word or short phrase. The meaning, value, and purpose of a particular tag is determined by each user.
Timestamps represent seconds since midnight Coordinated Universal Time (UTC) of January 1, 1970.
Movies Data File Structure (movies.csv)
---------------------------------------
Movie information is contained in the file `movies.csv`. Each line of this file after the header row represents one movie, and has the following format:
movieId,title,genres
Movie titles are entered manually or imported from <https://www.themoviedb.org/>, and include the year of release in parentheses. Errors and inconsistencies may exist in these titles.
Genres are a pipe-separated list, and are selected from the following:
* Action
* Adventure
* Animation
* Children's
* Comedy
* Crime
* Documentary
* Drama
* Fantasy
* Film-Noir
* Horror
* Musical
* Mystery
* Romance
* Sci-Fi
* Thriller
* War
* Western
* (no genres listed)
Links Data File Structure (links.csv)
---------------------------------------
Identifiers that can be used to link to other sources of movie data are contained in the file `links.csv`. Each line of this file after the header row represents one movie, and has the following format:
movieId,imdbId,tmdbId
movieId is an identifier for movies used by <https://movielens.org>. E.g., the movie Toy Story has the link <https://movielens.org/movies/1>.
imdbId is an identifier for movies used by <http://www.imdb.com>. E.g., the movie Toy Story has the link <http://www.imdb.com/title/tt0114709/>.
tmdbId is an identifier for movies used by <https://www.themoviedb.org>. E.g., the movie Toy Story has the link <https://www.themoviedb.org/movie/862>.
Use of the resources listed above is subject to the terms of each provider.
Cross-Validation
----------------
Prior versions of the MovieLens dataset included either pre-computed cross-folds or scripts to perform this computation. We no longer bundle either of these features with the dataset, since most modern toolkits provide this as a built-in feature. If you wish to learn about standard approaches to cross-fold computation in the context of recommender systems evaluation, see [LensKit](http://lenskit.org) for tools, documentation, and open-source code examples.
# -
|
modern_8_out_of_core.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### DSPT6 - Adding Data Science to a Web Application
#
# The purpose of this notebook is to demonstrate:
# - Simple online analysis of data from a user of the Twitoff app or an API
# - Train a more complicated offline model, and serialize the results for online use
import sqlite3
import pickle
import pandas as pd
# Connect to sqlite database
conn = sqlite3.connect('<path to your db>')
# + colab={} colab_type="code" id="vS_A9hjG1HGD"
def get_data(query, conn):
'''Function to get data from SQLite DB'''
cursor = conn.cursor()
result = cursor.execute(query).fetchall()
# Get columns from cursor object
columns = list(map(lambda x: x[0], cursor.description))
# Assign to DataFrame
df = pd.DataFrame(data=result, columns=columns)
return df
# + colab={} colab_type="code" id="pVapHGy7gEFx"
# -
|
notebooks/LS333_DSPT7_Model_Demo_InClass.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
from math import pow, sqrt
import time
import numpy as np
from sklearn.metrics.pairwise import cosine_similarity
from sklearn.feature_extraction.text import CountVectorizer
# +
ratings = pd.read_csv('./ml-latest-small/ratings.csv')
movies = pd.read_csv('./ml-latest-small/movies.csv')
movies
# -
# users_id has list of unique userids, same goes to movies_id
users_id = ratings.userId.unique().tolist()
movies_id = ratings.movieId.unique().tolist()
print("# of users: ", len(users_id))
print('# of movies: ', len(movies_id))
# given user id and movie id, it returns its corresponding rating
def get_rating(userId, movieId):
return (ratings.loc[(ratings.userId==userId) & (ratings.movieId==movieId), 'rating'].iloc[0]) # --> 4.0
print(get_rating(1,1))
# given user id, returns list of all movies(movieId) the user has rated
def get_movieIds(userId):
return (ratings.loc[(ratings.userId==userId), 'movieId']).tolist()
print(get_movieIds(2))
# given movie id, returns corresponding movie title
def get_movie_title(movieId):
return (movies.loc[(movies.movieId == movieId), 'title'].iloc[0])
print(get_movie_title(2))
# +
# calculate euclidean distance between 2 users by finding the common movies they have rated and applying euclidean
# distance formula between the 2 users' ratings.
from scipy.spatial import distance
def euclidean_dist(user1_id, user2_id):
user1_movie_list = ratings.loc[ratings.userId == user1_id, 'movieId'].tolist()
user2_movie_list = ratings.loc[ratings.userId == user2_id, 'movieId'].tolist()
dist = 0
for movie in user1_movie_list:
if movie in user2_movie_list:
user1_rating = get_rating(user1_id, movie)
user2_rating = get_rating(user2_id, movie)
dist += pow((user1_rating-user2_rating),2) # (x-y)^2
dist = sqrt(dist)
return dist
print("distance=",euclidean_dist(1,500))
# +
# calculate pearson coefficient between 2 users by finding the common movies they have rated and applying pearson
# formula between the 2 users' ratings.
def pearson_coeff(user1_id, user2_id):
movies_common = []
user1_movie_list = ratings.loc[ratings.userId == user1_id, 'movieId'].tolist()
user2_movie_list = ratings.loc[ratings.userId == user2_id, 'movieId'].tolist()
for movie in user1_movie_list:
if movie in user2_movie_list:
movies_common.append(movie)
n = len(movies_common)
if (n == 0):
return 0
sum_x = sum([get_rating(user1_id, movie) for movie in movies_common])
sum_y = sum([get_rating(user2_id, movie) for movie in movies_common])
sum_x2 = sum([pow(get_rating(user1_id, movie),2) for movie in movies_common])
sum_y2 = sum([pow(get_rating(user2_id, movie),2) for movie in movies_common])
numerator = sum([get_rating(user1_id, movie) * get_rating(user2_id, movie) for movie in movies_common]) - ((sum_x*sum_y)/n)
denominator = sqrt((sum_x2-pow(sum_x, 2)/n) * (sum_y2 - pow(sum_y,2)/n))
if denominator == 0:
return 0
return numerator/denominator
print('{0}'.format(pearson_coeff(11, 30)))
# -
# returns recommended list of movies according to pearson coefficient by calculating similarity between the given users
# and all the other users and then sorting the list in the reverse order to get movies with highest correlations first.
def movie_recommendation(user_id):
user_list = ratings.userId.unique().tolist()
movies_watched_by_user_id = get_movieIds(user_id)
# print("movies watched by user: ")
# for movie in movies_watched_by_user_id:
# print(get_movie_title(movie))
total = {}
similarity_sum = {}
for user in user_list[:100]:
if user != user_id:
r = pearson_coeff(user_id, user)
if r > 0:
for movie in get_movieIds(user):
# get movies that are not watched by user_id
if movie not in movies_watched_by_user_id or get_rating(user_id, movie) == 0:
total[movie] = 0
total[movie] += get_rating(user, movie) * r
similarity_sum[movie] = 0
similarity_sum[movie] += r
ranking = [(tot/similarity_sum[movie],movie) for movie,tot in total.items()]
# print(ranking)
ranking.sort()
# print(ranking)
ranking.reverse()
# print(ranking)
recommendations = [get_movie_title(movie) for r, movie in ranking]
return recommendations[:10]
# +
# returns recommended list of movies according to euclidean distance by calculating similarity between the given users
# and all the other users and then sorting the list to get movies with lowest distance first.
def movie_recommendation_euclidean(user_id):
user_list = ratings.userId.unique().tolist()
movies_watched_by_user_id = get_movieIds(user_id)
total = {}
similarity_sum = {}
for user in user_list[:100]:
if user != user_id:
r = euclidean_dist(user_id, user)
if r > 0:
for movie in get_movieIds(user):
# get movies that are not watched by user_id
if movie not in movies_watched_by_user_id or get_rating(user_id, movie) == 0:
total[movie] = 0
total[movie] += get_rating(user, movie) * r
similarity_sum[movie] = 0
similarity_sum[movie] += r
ranking = [(tot/similarity_sum[movie],movie) for movie,tot in total.items()]
ranking.sort()
ranking.reverse()
recommendations = [get_movie_title(movie) for r, movie in ranking]
return recommendations[:10]
return 0
print("euclidean recommendation example")
print(movie_recommendation_euclidean(2))
# -
# ## Content Based Filtering
# Below code we use to cauculate the similarity between two movies using cosine similarity.We take the genre as the feature.We combine it to a single string seperated by space and apply CountVectorizer on it. We make use of Cosine_similarity from sklearn to create a similarity matrix for each movie.
# The diagnol elements are 1,as the movie is similar to itself.We index to the matrix for each movie and obtain the similarity vector to all movies.We sort it by the value in descending order and return the top 10 similar movies ,again getting the title via the index.
# We Call this method for the all the movies in the user watched list.
# +
#Reading movie csv file ,into a different dataframe
movies2 = pd.read_csv('./ml-latest-small/movies.csv')
#Cleaning and removing the year from the movie titles
split_values = movies2['title'].str.split("(", n = 1, expand = True)
movies2.title= split_values[0]
#Iterating through the rows and removing any white space characters at the end and processing genre ,to replace '|'
#with white space and converting it to lower characters.
for index,row in movies2.iterrows():
movies2.loc[index,'title']=row['title'].rstrip()
movies2.loc[index,'genres']=row['genres'].replace('|',' ').lower()
movies2
# -
#We set the index to title and delete other columns ,and have only one column genre which is used for vectorization.
del movies2['movieId']
movies2.set_index('title',inplace=True)
movies2
# +
#Calling CountVectorizer from sklearn and calculating cosine similarity which is stored in a matrix.Diagnol elments are one because
#the movie is similar to itself.
count = CountVectorizer()
count_matrix = count.fit_transform(movies2['genres'])
# generating the cosine similarity matrix
cosine_sim = cosine_similarity(count_matrix, count_matrix)
cosine_sim
# -
#Creating a series for the movie titles so that they are matched with ordered numerical list used later
indices = pd.Series(movies2.index)
def content_recommendation(title, cosine_sim = cosine_sim):
recommended_movies=[]
#Finding the index of the title in the series created initially.
idx = indices[indices == title].index[0]
#Indexing into the similarity matrix and sorting the values in descending order.
score_series = pd.Series(cosine_sim[idx]).sort_values(ascending = False)
#Selecting the top 10 most similar movies ,excluding the first index,as it is the movie itself.
top_10_indexes = list(score_series.iloc[1:11].index)
#Appending the movie titles and returning
for i in top_10_indexes:
recommended_movies.append(list(movies2.index)[i])
return recommended_movies
#Merging user rating and movies table,so that we get the movie title along with the movieId and the rating
usr_rat=pd.merge(ratings,movies,how='left',on='movieId')[['userId','movieId','rating','title']]
usr_rat
#Function to add new user to the rating table ,which takes a userId movieIds and rating for the repective movies.
#We are adding a new user with id 612 who likes crime movies and has watched Goodfellas and Heat
def add_user(userid,movies,usr_rating):
for mov_idx in range(len(movies)):
row=[]
row.append(userid)
row.append(movies[mov_idx])
row.append(usr_rating[mov_idx])
row.append(time.time())
ratings.loc[ratings.index.max() + 1]=row
#Adding the User
add_user(612,[1213,6],[4,5])
#Outputing the respective user in ratings table
ratings.loc[ratings['userId']==612]
#Making recommendation for the new user using collaborative filtering.
movie_recommendation(612)
#Making recommendatio using content based approach
content_recommendation('Goodfellas')
content_recommendation('Heat')
movies=['Goodfellas','Heat']
final=[]
#Taking 5 movies from each movies watched
for mov in movies:
final=final+content_recommendation(mov)[:6]
for mov in final:
print(mov)
|
movie_final.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Qcodes+broadbean example with Tektronix AWG5208
# +
# %matplotlib notebook
from qcodes.instrument_drivers.tektronix.AWG5208 import AWG5208
import broadbean as bb
ramp = bb.PulseAtoms.ramp
sine = bb.PulseAtoms.sine
# -
# ## Part 1: Make a complicated sequence
#
# Keeping in mind that no waveform can be shorter than 2400 points (hardware limitation).
#
# We have an element corresponding to a measurement that we'd like to repeat N times followed by a "reset" element. The master sequence should then repeat that whole thing with different measurement frequencies. We therefore make the measurement into a subsequence.
# +
# First we form the measurement sequence
SR = 1e9
N = 3 # the number of times we repeat the first part
measurement_freqs = [5e4, 1e5, 2e5]
meas_bp_ch1 = bb.BluePrint()
meas_bp_ch1.insertSegment(0, sine, (1e5, 0.1, 0, 0), dur=200e-6)
meas_bp_ch1.insertSegment(-1, ramp, (0, 0), dur=40e-6)
meas_bp_ch1.setSR(SR)
meas_bp_ch2 = bb.BluePrint()
meas_bp_ch2.insertSegment(0, ramp, (0, 0), dur=200e-6)
meas_bp_ch2.insertSegment(-1, ramp, (0.1, 0.1), dur=20e-6)
meas_bp_ch2.insertSegment(-1, ramp, (0, 0), dur=20e-6)
meas_bp_ch2.setSR(SR)
meas_elem = bb.Element()
meas_elem.addBluePrint('signal_channel', meas_bp_ch1)
meas_elem.addBluePrint('trigger_channel', meas_bp_ch2)
reset_bp = bb.BluePrint()
reset_bp.insertSegment(0, ramp, (0, 0.05), dur=120e-6)
reset_bp.insertSegment(1, ramp, (0.05, 0), dur=120e-6)
reset_bp.setSR(SR)
reset_elem = bb.Element()
reset_elem.addBluePrint('signal_channel', reset_bp)
reset_elem.addBluePrint('trigger_channel', reset_bp)
measureseq = bb.Sequence()
measureseq.setSR(SR)
measureseq.addElement(1, meas_elem)
measureseq.addElement(2, reset_elem)
measureseq.setSequencingNumberOfRepetitions(1, N)
measureseq.plotSequence()
# +
# And then we turn that into a master sequence
mainseq = bb.Sequence()
mainseq.setSR(SR)
for pos, freq in enumerate(measurement_freqs):
subseq = measureseq.copy()
subseq.element(1).changeArg('signal_channel', 'sine',
'freq', freq)
mainseq.addSubSequence(pos+1, subseq)
mainseq.plotSequence()
# The visualisation is not terribly helpful in this case, but
# we see that three subsequences are present
# -
# ## Part 2: Get the sequence onto the instrument
# +
# Connect
awg = AWG5208('awg', 'TCPIP0::192.168.15.118::inst0::INSTR')
# +
# forge the sequence
fs = mainseq.forge()
# send it to the instrument
seqname = 'mytestseq'
amplitudes = [ch.awg_amplitude() for ch in awg.channels][:2]
channel_mapping = {'trigger_channel': 2, 'signal_channel': 1}
seqx_file = AWG5208.makeSEQXFileFromForgedSequence(fs,
amplitudes=amplitudes,
seqname=seqname,
channel_mapping=channel_mapping)
# load it and assign its tracks to the channels
filename = 'mainplussub.seqx'
awg.clearSequenceList()
awg.clearWaveformList()
awg.sendSEQXFile(seqx_file, filename=filename)
awg.loadSEQXFile(filename)
awg.ch1.setSequenceTrack(seqname, 1)
awg.ch2.setSequenceTrack(seqname, 2)
# -
# # Part 3: Play it and capture it on a scope
# Pending... Manually verified.
|
docs/examples/driver_examples/Qcodes+broadbean_example_with_Tektronix_AWG5208.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Regression techniques for the classic house price prediction problem.
# +
import pandas as pd
import numpy as np
from scipy.stats import norm
from sklearn.preprocessing import StandardScaler
from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns
import missingno as mno
import warnings
warnings.filterwarnings('ignore')
# %matplotlib inline
# -
train = pd.read_csv('train.csv')
test = pd.read_csv('test.csv')
train.head()
train.shape
train.columns
# # EDA
mno.matrix(train)
train.isnull().sum().sort_values(ascending=False)[:19]
train['SalePrice'].hist()
for i in ['GrLivArea','TotalBsmtSF']:
data = pd.concat([train['SalePrice'], train[i]], axis=1)
data.plot.scatter(x=i, y='SalePrice', ylim=(0,800000))
var = "OverallQual"
f, ax = plt.subplots(figsize=(16, 8))
data = pd.concat([train['SalePrice'], train[var]], axis=1)
fig = sns.boxplot(x=var, y="SalePrice", data=data)
var = 'YearBuilt'
data = pd.concat([train['SalePrice'], train[var]], axis=1)
f, ax = plt.subplots(figsize=(16, 8))
fig = sns.boxplot(x=var, y="SalePrice", data=data)
fig.axis(ymin=0, ymax=800000);
plt.xticks(rotation=90);
# +
sns.distplot(train['SalePrice'] , fit=norm);
(mu, sigma) = norm.fit(train['SalePrice'])
print( '\n mu = {:.2f} and sigma = {:.2f}\n'.format(mu, sigma))
#Now plot the distribution
plt.legend(['Normal dist. ($\mu=$ {:.2f} and $\sigma=$ {:.2f} )'.format(mu, sigma)],
loc='best')
plt.ylabel('Frequency')
plt.title('SalePrice distribution')
#Get also the QQ-plot
fig = plt.figure()
res = stats.probplot(train['SalePrice'], plot=plt)
plt.show()
# -
train["SalePrice"] = np.log1p(train["SalePrice"])
# +
sns.distplot(train['SalePrice'] , fit=norm);
(mu, sigma) = norm.fit(train['SalePrice'])
print( '\n mu = {:.2f} and sigma = {:.2f}\n'.format(mu, sigma))
#Now plot the distribution
plt.legend(['Normal dist. ($\mu=$ {:.2f} and $\sigma=$ {:.2f} )'.format(mu, sigma)],
loc='best')
plt.ylabel('Frequency')
plt.title('SalePrice distribution')
#Get also the QQ-plot
fig = plt.figure()
res = stats.probplot(train['SalePrice'], plot=plt)
plt.show()
# -
corrmat = train.corr()
plt.subplots(figsize=(12,9))
sns.heatmap(corrmat, vmax=0.9, square=True)
ntrain = train.shape[0]
ntest = test.shape[0]
y_train = train.SalePrice.values
train.drop("Id", axis = 1, inplace = True)
test.drop("Id", axis = 1, inplace = True)
all_data = pd.concat((train, test)).reset_index(drop=True)
all_data.drop(['SalePrice'], axis=1, inplace=True)
print("all_data size is : {}".format(all_data.shape))
k = 10 #number of variables for heatmap
cols = corrmat.nlargest(k, 'SalePrice')['SalePrice'].index
cm = np.corrcoef(train[cols].values.T)
sns.set(font_scale=1.25)
hm = sns.heatmap(cm, cbar=True, annot=True, square=True, fmt='.2f', annot_kws={'size': 10}, yticklabels=cols.values, xticklabels=cols.values)
plt.show()
sns.set()
cols = ['SalePrice', 'OverallQual', 'GrLivArea', 'GarageCars', 'TotalBsmtSF', 'FullBath', 'YearBuilt']
sns.pairplot(train[cols], size = 2.5)
plt.show();
all_data_na = (all_data.isnull().sum() / len(all_data)) * 100
all_data_na = all_data_na.drop(all_data_na[all_data_na == 0].index).sort_values(ascending=False)[:30]
missing_data = pd.DataFrame({'Missing Ratio' :all_data_na})
missing_data.head(20)
f, ax = plt.subplots(figsize=(15, 12))
plt.xticks(rotation='90')
sns.barplot(x=all_data_na.index, y=all_data_na)
plt.xlabel('Features', fontsize=15)
plt.ylabel('Percent of missing values', fontsize=15)
plt.title('Percent missing data by feature', fontsize=15)
# # Missing Value Entry
# +
all_data["PoolQC"] = all_data["PoolQC"].fillna("None")
all_data["MiscFeature"] = all_data["MiscFeature"].fillna("None")
all_data["Alley"] = all_data["Alley"].fillna("None")
all_data["Fence"] = all_data["Fence"].fillna("None")
all_data["FireplaceQu"] = all_data["FireplaceQu"].fillna("None")
#missing value means not available. So None
# -
#Group by neighborhood and fill in missing value by the median LotFrontage of all the neighborhood
all_data["LotFrontage"] = all_data.groupby("Neighborhood")["LotFrontage"].transform(
lambda x: x.fillna(x.median()))
for col in ('GarageType', 'GarageFinish', 'GarageQual', 'GarageCond'):
all_data[col] = all_data[col].fillna('None')
for col in ('GarageYrBlt', 'GarageArea', 'GarageCars'):
all_data[col] = all_data[col].fillna(0)
for col in ('BsmtFinSF1', 'BsmtFinSF2', 'BsmtUnfSF','TotalBsmtSF', 'BsmtFullBath', 'BsmtHalfBath'):
all_data[col] = all_data[col].fillna(0)
for col in ('BsmtQual', 'BsmtCond', 'BsmtExposure', 'BsmtFinType1', 'BsmtFinType2'):
all_data[col] = all_data[col].fillna('None')
all_data["MasVnrType"] = all_data["MasVnrType"].fillna("None")
all_data["MasVnrArea"] = all_data["MasVnrArea"].fillna(0)
all_data['MSZoning'] = all_data['MSZoning'].fillna(all_data['MSZoning'].mode()[0])
all_data = all_data.drop(['Utilities'], axis=1)
all_data["Functional"] = all_data["Functional"].fillna("Typ")
all_data['Electrical'] = all_data['Electrical'].fillna(all_data['Electrical'].mode()[0])
all_data['KitchenQual'] = all_data['KitchenQual'].fillna(all_data['KitchenQual'].mode()[0])
all_data['Exterior1st'] = all_data['Exterior1st'].fillna(all_data['Exterior1st'].mode()[0])
all_data['Exterior2nd'] = all_data['Exterior2nd'].fillna(all_data['Exterior2nd'].mode()[0])
all_data['SaleType'] = all_data['SaleType'].fillna(all_data['SaleType'].mode()[0])
all_data['MSSubClass'] = all_data['MSSubClass'].fillna("None")
all_data_na = (all_data.isnull().sum() / len(all_data)) * 100
all_data_na = all_data_na.drop(all_data_na[all_data_na == 0].index).sort_values(ascending=False)
missing_data = pd.DataFrame({'Missing Ratio' :all_data_na})
missing_data.head()
# +
#MSSubClass=The building class
all_data['MSSubClass'] = all_data['MSSubClass'].apply(str)
#Changing OverallCond into a categorical variable
all_data['OverallCond'] = all_data['OverallCond'].astype(str)
#Year and month sold are transformed into categorical features.
all_data['YrSold'] = all_data['YrSold'].astype(str)
all_data['MoSold'] = all_data['MoSold'].astype(str)
# -
final_all_data = all_data
saleprice_scaled = StandardScaler().fit_transform(train['SalePrice'][:,np.newaxis]);
low_range = saleprice_scaled[saleprice_scaled[:,0].argsort()][:10]
high_range= saleprice_scaled[saleprice_scaled[:,0].argsort()][-10:]
# # Label Encoding Data
# +
from sklearn.preprocessing import LabelEncoder
cols = ('FireplaceQu', 'BsmtQual', 'BsmtCond', 'GarageQual', 'GarageCond',
'ExterQual', 'ExterCond','HeatingQC', 'PoolQC', 'KitchenQual', 'BsmtFinType1',
'BsmtFinType2', 'Functional', 'Fence', 'BsmtExposure', 'GarageFinish', 'LandSlope',
'LotShape', 'PavedDrive', 'Street', 'Alley', 'CentralAir', 'MSSubClass', 'OverallCond',
'YrSold', 'MoSold')
# process columns, apply LabelEncoder to categorical features
for c in cols:
lbl = LabelEncoder()
lbl.fit(list(all_data[c].values))
all_data[c] = lbl.transform(list(all_data[c].values))
# shape
str_cols = all_data.select_dtypes(include = 'object').columns
for c in str_cols:
lbl = LabelEncoder()
lbl.fit(list(all_data[c].values))
all_data[c] = lbl.transform(list(all_data[c].values))
print('Shape all_data: {}'.format(all_data.shape))
# -
# # Data Set Split
train_x.shape
train_y.shape
train_x.head()
# +
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
#splitting the dataset as training and testing dataset
X_train, X_test, y_train, y_test = train_test_split(train_x,train_y)
y_train = pd.DataFrame(y_train)
y_test = pd.DataFrame(y_test)
# -
# # Models Used:
#
# * Linear Regression
# * Ridge Regression
# * Min Max Scaler
# * Lasso Regression
# * Random Forest
# +
#linear regression
linreg = LinearRegression()
linreg.fit(X_train, y_train)
#Accuracy
print("R-Squared Value for Training Set: {:.3f}".format(linreg.score(X_train, y_train)))
print("R-Squared Value for Test Set: {:.3f}".format(linreg.score(X_test, y_test)))
# +
#ridge regression
from sklearn.linear_model import Ridge
ridge = Ridge()
ridge.fit(X_train, y_train)
print('R-squared score (training): {:.3f}'.format(ridge.score(X_train, y_train)))
print('R-squared score (test): {:.3f}'.format(ridge.score(X_test, y_test)))
# +
#min max scaler
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
ridge = Ridge(alpha=20)
ridge.fit(X_train_scaled, y_train)
print('R-squared score (training): {:.3f}'.format(ridge.score(X_train_scaled, y_train)))
print('R-squared score (test): {:.3f}'.format(ridge.score(X_test_scaled, y_test)))
# +
#lasso regression
from sklearn.linear_model import Lasso
lasso = Lasso(max_iter = 10000)
lasso.fit(X_train, y_train)
print('R-squared score (training): {:.3f}'.format(lasso.score(X_train, y_train)))
print('R-squared score (test): {:.3f}'.format(lasso.score(X_test, y_test)))
# +
#random Forest
from sklearn.ensemble import RandomForestRegressor
regressor = RandomForestRegressor()
from sklearn.model_selection import RandomizedSearchCV
n_estimators = [100, 500, 900]
depth = [3,5,10,15]
min_split=[2,3,4]
min_leaf=[2,3,4]
bootstrap = ['True', 'False']
verbose = [5]
hyperparameter_grid = {
'n_estimators': n_estimators,
'max_depth':depth,
#'criterion':criterion,
'bootstrap':bootstrap,
'verbose':verbose,
'min_samples_split':min_split,
'min_samples_leaf':min_leaf
}
random_cv = RandomizedSearchCV(estimator=regressor,
param_distributions=hyperparameter_grid,
cv=5,
scoring = 'neg_mean_absolute_error',
n_jobs = -1,
return_train_score = True,
random_state=42)
# -
random_cv.fit(X_train,y_train)
random_cv.best_estimator_
regressor = RandomForestRegressor(bootstrap='False', ccp_alpha=0.0, criterion='mse',
max_depth=10, max_features='auto', max_leaf_nodes=None,
max_samples=None, min_impurity_decrease=0.0,
min_impurity_split=None, min_samples_leaf=3,
min_samples_split=4, min_weight_fraction_leaf=0.0,
n_estimators=100, n_jobs=None, oob_score=False,
random_state=None, verbose=5, warm_start=False)
regressor.fit(X_train,y_train)
print('R-squared score (training): {:.3f}'.format(regressor.score(X_train, y_train)))
regressor.fit(X_test,y_test)
print('R-squared score (test): {:.3f}'.format(regressor.score(X_test, y_test)))
Test_X = all_data[1460:]
y_pred = regressor.predict(Test_X)
pred=pd.DataFrame(y_pred)
samp = pd.read_csv('sample_submission.csv')
sub = pd.concat([samp['Id'],pred], axis=1)
sub.columns=['Id','SalePrice']
sub
sub.to_csv('submission.csv',index=False)
|
Housing Price Prediction/Project.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Fixing mistakes
# We're still in our git working directory:
import os
top_dir = os.getcwd()
git_dir = os.path.join(top_dir, 'learning_git')
working_dir = os.path.join(git_dir, 'git_example')
os.chdir(working_dir)
working_dir
# ### Referring to changes with HEAD and ^
#
# The commit we want to revert to is the one before the latest.
#
# `HEAD` refers to the latest commit. That is, we want to go back to the change before the current `HEAD`.
#
# We could use the hash code (e.g. 73fbeaf) to reference this, but you can also refer to the commit before the `HEAD` as `HEAD^`, the one before that as `HEAD^^`, the one before that as `HEAD~3`.
# ### Reverting
#
# Ok, so now we'd like to undo the nasty commit with the lie about Mount Fictional.
# + language="bash"
# git revert HEAD^
# -
# An editor may pop up, with some default text which you can accept and save.
# ### Conflicted reverts
#
# You may, depending on the changes you've tried to make, get an error message here.
#
# If this happens, it is because git could not automagically decide how to combine the change you made after the change you want to revert, with the attempt to revert the change: this could happen, for example, if they both touch the same line.
#
# If that happens, you need to manually edit the file to fix the problem. Skip ahead to the section on resolving conflicts, or ask a demonstrator to help.
# ### Review of changes
#
# The file should now contain the change to the title, but not the extra line with the lie. Note the log:
# + language="bash"
# git log --date=short
# -
# ### Antipatch
#
# Notice how the mistake has stayed in the history.
#
# There is a new commit which undoes the change: this is colloquially called an "antipatch".
# This is nice: you have a record of the full story, including the mistake and its correction.
# ### Rewriting history
#
# It is possible, in git, to remove the most recent change altogether, "rewriting history". Let's make another bad change, and see how to do this.
# ### A new lie
# %%writefile test.md
Mountains and Hills in the UK
===================
Engerland is not very mountainous.
But has some tall hills, and maybe a
mountain or two depending on your definition.
# + attributes={"classes": [" Bash"], "id": ""} language="bash"
# cat test.md
# + language="bash"
# git diff
# + language="bash"
# git commit -am "Add a silly spelling"
# + attributes={"classes": [" Bash"], "id": ""} language="bash"
# git log --date=short
# -
# ### Using reset to rewrite history
# + attributes={"classes": [" Bash"], "id": ""} language="bash"
# git reset HEAD^
# + attributes={"classes": [" Bash"], "id": ""} language="bash"
# git log --date=short
# -
# ### Covering your tracks
#
# The silly spelling *is no longer in the log*. This approach to fixing mistakes, "rewriting history" with `reset`, instead of adding an antipatch with `revert`, is dangerous, and we don't recommend it. But you may want to do it for small silly mistakes, such as to correct a commit message.
# ### Resetting the working area
#
# When `git reset` removes commits, it leaves your working directory unchanged -- so you can keep the work in the bad change if you want.
# + language="bash"
# cat test.md
# -
# If you want to lose the change from the working directory as well, you can do `git reset --hard`.
#
# I'm going to get rid of the silly spelling, and I didn't do `--hard`, so I'll reset the file from the working directory to be the same as in the index:
# + attributes={"classes": [" Bash"], "id": ""} language="bash"
# git checkout test.md
# + language="bash"
# cat test.md
# -
# We can add this to our diagram:
message="""
Working Directory -> Staging Area : git add
Staging Area -> Local Repository : git commit
Working Directory -> Local Repository : git commit -a
Local Repository -> Working Directory : git checkout
Local Repository -> Staging Area : git reset
Local Repository -> Working Directory: git reset --hard
"""
from wsd import wsd
# %matplotlib inline
wsd(message)
# We can add it to Jim's story:
message="""
participant "Jim's repo" as R
participant "Jim's index" as I
participant Jim as J
note right of J: git revert HEAD^
J->R: Add new commit reversing change
R->I: update staging area to reverted version
I->J: update file to reverted version
note right of J: vim test.md
note right of J: git commit -am "Add another mistake"
J->I: Add mistake
I->R: Add mistake
note right of J: git reset HEAD^
J->R: Delete mistaken commit
R->I: Update staging area to reset commit
note right of J: git checkout test.md
I->J: Update file to reverted version
"""
wsd(message)
|
ch02git/03Mistakes.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# name: python2
# ---
# + [markdown] colab_type="text" id="KFPcBuVFw61h"
# # Overview
#
# This colab demonstrates the steps to use the DeepLab model to perform semantic segmentation on a sample input image. Expected outputs are semantic labels overlayed on the sample image.
#
# ### About DeepLab
# The models used in this colab perform semantic segmentation. Semantic segmentation models focus on assigning semantic labels, such as sky, person, or car, to multiple objects and stuff in a single image.
# + [markdown] colab_type="text" id="t3ozFsEEP-u_"
# # Instructions
# <h3><a href="https://cloud.google.com/tpu/"><img valign="middle" src="https://raw.githubusercontent.com/GoogleCloudPlatform/tensorflow-without-a-phd/master/tensorflow-rl-pong/images/tpu-hexagon.png" width="50"></a> Use a free TPU device</h3>
#
# 1. On the main menu, click Runtime and select **Change runtime type**. Set "TPU" as the hardware accelerator.
# 1. Click Runtime again and select **Runtime > Run All**. You can also run the cells manually with Shift-ENTER.
# + [markdown] colab_type="text" id="7cRiapZ1P3wy"
# ## Import Libraries
# + cellView="code" colab={} colab_type="code" id="kAbdmRmvq0Je"
import os
from io import BytesIO
import tarfile
import tempfile
from six.moves import urllib
from matplotlib import gridspec
from matplotlib import pyplot as plt
import numpy as np
from PIL import Image
import tensorflow as tf
# + [markdown] colab_type="text" id="p47cYGGOQE1W"
# ## Import helper methods
# These methods help us perform the following tasks:
# * Load the latest version of the pretrained DeepLab model
# * Load the colormap from the PASCAL VOC dataset
# * Adds colors to various labels, such as "pink" for people, "green" for bicycle and more
# * Visualize an image, and add an overlay of colors on various regions
# + cellView="code" colab={} colab_type="code" id="vN0kU6NJ1Ye5"
class DeepLabModel(object):
"""Class to load deeplab model and run inference."""
INPUT_TENSOR_NAME = 'ImageTensor:0'
OUTPUT_TENSOR_NAME = 'SemanticPredictions:0'
INPUT_SIZE = 513
FROZEN_GRAPH_NAME = 'frozen_inference_graph'
def __init__(self, tarball_path):
"""Creates and loads pretrained deeplab model."""
self.graph = tf.Graph()
graph_def = None
# Extract frozen graph from tar archive.
tar_file = tarfile.open(tarball_path)
for tar_info in tar_file.getmembers():
if self.FROZEN_GRAPH_NAME in os.path.basename(tar_info.name):
file_handle = tar_file.extractfile(tar_info)
graph_def = tf.GraphDef.FromString(file_handle.read())
break
tar_file.close()
if graph_def is None:
raise RuntimeError('Cannot find inference graph in tar archive.')
with self.graph.as_default():
tf.import_graph_def(graph_def, name='')
self.sess = tf.Session(graph=self.graph)
def run(self, image):
"""Runs inference on a single image.
Args:
image: A PIL.Image object, raw input image.
Returns:
resized_image: RGB image resized from original input image.
seg_map: Segmentation map of `resized_image`.
"""
width, height = image.size
resize_ratio = 1.0 * self.INPUT_SIZE / max(width, height)
target_size = (int(resize_ratio * width), int(resize_ratio * height))
resized_image = image.convert('RGB').resize(target_size, Image.ANTIALIAS)
batch_seg_map = self.sess.run(
self.OUTPUT_TENSOR_NAME,
feed_dict={self.INPUT_TENSOR_NAME: [np.asarray(resized_image)]})
seg_map = batch_seg_map[0]
return resized_image, seg_map
def create_pascal_label_colormap():
"""Creates a label colormap used in PASCAL VOC segmentation benchmark.
Returns:
A Colormap for visualizing segmentation results.
"""
colormap = np.zeros((256, 3), dtype=int)
ind = np.arange(256, dtype=int)
for shift in reversed(range(8)):
for channel in range(3):
colormap[:, channel] |= ((ind >> channel) & 1) << shift
ind >>= 3
return colormap
def label_to_color_image(label):
"""Adds color defined by the dataset colormap to the label.
Args:
label: A 2D array with integer type, storing the segmentation label.
Returns:
result: A 2D array with floating type. The element of the array
is the color indexed by the corresponding element in the input label
to the PASCAL color map.
Raises:
ValueError: If label is not of rank 2 or its value is larger than color
map maximum entry.
"""
if label.ndim != 2:
raise ValueError('Expect 2-D input label')
colormap = create_pascal_label_colormap()
if np.max(label) >= len(colormap):
raise ValueError('label value too large.')
return colormap[label]
def vis_segmentation(image, seg_map):
"""Visualizes input image, segmentation map and overlay view."""
plt.figure(figsize=(15, 5))
grid_spec = gridspec.GridSpec(1, 4, width_ratios=[6, 6, 6, 1])
plt.subplot(grid_spec[0])
plt.imshow(image)
plt.axis('off')
plt.title('input image')
plt.subplot(grid_spec[1])
seg_image = label_to_color_image(seg_map).astype(np.uint8)
plt.imshow(seg_image)
plt.axis('off')
plt.title('segmentation map')
plt.subplot(grid_spec[2])
plt.imshow(image)
plt.imshow(seg_image, alpha=0.7)
plt.axis('off')
plt.title('segmentation overlay')
unique_labels = np.unique(seg_map)
ax = plt.subplot(grid_spec[3])
plt.imshow(
FULL_COLOR_MAP[unique_labels].astype(np.uint8), interpolation='nearest')
ax.yaxis.tick_right()
plt.yticks(range(len(unique_labels)), LABEL_NAMES[unique_labels])
plt.xticks([], [])
ax.tick_params(width=0.0)
plt.grid('off')
plt.show()
LABEL_NAMES = np.asarray([
'background', 'aeroplane', 'bicycle', 'bird', 'boat', 'bottle', 'bus',
'car', 'cat', 'chair', 'cow', 'diningtable', 'dog', 'horse', 'motorbike',
'person', 'pottedplant', 'sheep', 'sofa', 'train', 'tv'
])
FULL_LABEL_MAP = np.arange(len(LABEL_NAMES)).reshape(len(LABEL_NAMES), 1)
FULL_COLOR_MAP = label_to_color_image(FULL_LABEL_MAP)
# + [markdown] colab_type="text" id="nGcZzNkASG9A"
# ## Select a pretrained model
# We have trained the DeepLab model using various backbone networks. Select one from the MODEL_NAME list.
# + colab={} colab_type="code" id="c4oXKmnjw6i_"
MODEL_NAME = 'mobilenetv2_coco_voctrainaug' # @param ['mobilenetv2_coco_voctrainaug', 'mobilenetv2_coco_voctrainval', 'xception_coco_voctrainaug', 'xception_coco_voctrainval']
_DOWNLOAD_URL_PREFIX = 'http://download.tensorflow.org/models/'
_MODEL_URLS = {
'mobilenetv2_coco_voctrainaug':
'deeplabv3_mnv2_pascal_train_aug_2018_01_29.tar.gz',
'mobilenetv2_coco_voctrainval':
'deeplabv3_mnv2_pascal_trainval_2018_01_29.tar.gz',
'xception_coco_voctrainaug':
'deeplabv3_pascal_train_aug_2018_01_04.tar.gz',
'xception_coco_voctrainval':
'deeplabv3_pascal_trainval_2018_01_04.tar.gz',
}
_TARBALL_NAME = 'deeplab_model.tar.gz'
model_dir = tempfile.mkdtemp()
tf.gfile.MakeDirs(model_dir)
download_path = os.path.join(model_dir, _TARBALL_NAME)
print('downloading model, this might take a while...')
urllib.request.urlretrieve(_DOWNLOAD_URL_PREFIX + _MODEL_URLS[MODEL_NAME],
download_path)
print('download completed! loading DeepLab model...')
MODEL = DeepLabModel(download_path)
print('model loaded successfully!')
# + [markdown] colab_type="text" id="SZst78N-4OKO"
# ## Run on sample images
#
# Select one of sample images (leave `IMAGE_URL` empty) or feed any internet image
# url for inference.
#
# Note that this colab uses single scale inference for fast computation,
# so the results may slightly differ from the visualizations in the
# [README](https://github.com/tensorflow/models/blob/master/research/deeplab/README.md) file,
# which uses multi-scale and left-right flipped inputs.
# + cellView="form" colab={} colab_type="code" id="edGukUHXyymr"
SAMPLE_IMAGE = 'image1' # @param ['image1', 'image2', 'image3']
IMAGE_URL = '' #@param {type:"string"}
_SAMPLE_URL = ('https://github.com/tensorflow/models/blob/master/research/'
'deeplab/g3doc/img/%s.jpg?raw=true')
def run_visualization(url):
"""Inferences DeepLab model and visualizes result."""
try:
f = urllib.request.urlopen(url)
jpeg_str = f.read()
original_im = Image.open(BytesIO(jpeg_str))
except IOError:
print('Cannot retrieve image. Please check url: ' + url)
return
print('running deeplab on image %s...' % url)
resized_im, seg_map = MODEL.run(original_im)
vis_segmentation(resized_im, seg_map)
image_url = IMAGE_URL or _SAMPLE_URL % SAMPLE_IMAGE
run_visualization(image_url)
# + [markdown] colab_type="text" id="aUbVoHScTJYe"
# ## What's next
#
# * Learn about [Cloud TPUs](https://cloud.google.com/tpu/docs) that Google designed and optimized specifically to speed up and scale up ML workloads for training and inference and to enable ML engineers and researchers to iterate more quickly.
# * Explore the range of [Cloud TPU tutorials and Colabs](https://cloud.google.com/tpu/docs/tutorials) to find other examples that can be used when implementing your ML project.
# * For more information on running the DeepLab model on Cloud TPUs, see the [DeepLab tutorial](https://cloud.google.com/tpu/docs/tutorials/deeplab).
#
|
research/deeplab/deeplab_demo.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="xD8tM1pd2NAu"
# # Song Embeddings - Skipgram Recommender
# > In this notebook, we'll use human-made music playlists to learn song embeddings. We'll treat a playlist as if it's a sentence and the songs it contains as words. We feed that to the word2vec algorithm which then learns embeddings for every song we have. These embeddings can then be used to recommend similar songs.
#
# - toc: true
# - badges: true
# - comments: true
# - categories: [Word2Vec, Embedding, Music, Sequence]
# - author: "<a href='https://github.com/jalammar/jalammar.github.io'><NAME></a>"
# - image:
# + [markdown] id="yucM-N8R2VaN"
# This technique is used by Spotify, AirBnB, Alibaba, and others. It accounts for a vast portion of their user activity, user media consumption, and/or sales (in the case of Alibaba). The dataset we'll use was collected by Shuo Chen from Cornell University. The [dataset](https://www.cs.cornell.edu/~shuochen/lme/data_page.html) contains playlists from hundreds of radio stations from around the US.
# + [markdown] id="sHZo-F6427A5"
# ## Downloading data
# + id="wu70B8qy-zj1"
# !wget -q https://www.cs.cornell.edu/~shuochen/lme/dataset.tar.gz
# !tar -xf dataset.tar.gz
# + [markdown] id="otMF4HUD3bg2"
# ## Setup
# + id="pV4KRkN4gRec"
import numpy as np
import pandas as pd
import gensim
from gensim.models import Word2Vec
from urllib import request
# + id="duIxrTrfgNPt"
import warnings
warnings.filterwarnings('ignore')
# + [markdown] id="XhjskIqm3X4e"
# ## Training dataset
# + id="AWj3LOqmgmGh"
with open("/content/dataset/yes_complete/train.txt", 'r') as f:
# skipping first 2 lines as they contain only metadata
lines = f.read().split('\n')[2:]
# select playlists with at least 2 songs, a minimum threshold for sequence learning
playlists = [s.rstrip().split() for s in lines if len(s.split()) > 1]
# + colab={"base_uri": "https://localhost:8080/"} id="JbNTSuUHhQar" outputId="fb7a7f90-898e-40ed-8fc2-ef7d3e0ed6a4"
print( 'Playlist #1:\n ', playlists[0], '\n')
print( 'Playlist #2:\n ', playlists[1])
# + [markdown] id="7ulE0Sei3A5P"
# ## Training Word2vec
# + [markdown] id="iLphAx7n3guD"
# Our dataset is now in the shape the the Word2Vec model expects as input. We pass the dataset to the model, and set the following key parameters:
#
# - size: Embedding size for the songs.
# - window: word2vec algorithm parameter -- maximum distance between the current and predicted word (song) within a sentence
# - negative: word2vec algorithm parameter -- Number of negative examples to use at each training step that the model needs to identify as noise
# + id="c3ETOmmrhm9c"
model = Word2Vec(playlists, size=32, window=20, negative=50, min_count=1, workers=-1)
# + [markdown] id="FcxLNCTU3lH6"
# The model is now trained. Every song has an embedding. We only have song IDs, though, no titles or other info. Let's grab the song information file.
# + [markdown] id="HVJexXVa3DmX"
# ## Prepare songs metadata
# + [markdown] id="Z2NaoFA23PUS"
# ### Title and artist
# + colab={"base_uri": "https://localhost:8080/"} id="WIz9OQcHfDzd" outputId="09f74766-35a0-4d5d-8f85-b2ffa3c9861e"
# !head /content/dataset/yes_complete/song_hash.txt
# + id="NlIxHUCiiFnP"
with open("/content/dataset/yes_complete/song_hash.txt", 'r') as f:
songs_file = f.read().split('\n')
songs = [s.rstrip().split('\t') for s in songs_file]
# + colab={"base_uri": "https://localhost:8080/", "height": 235} id="OyN_asrNitmC" outputId="fdf09d8e-08ed-4e22-d979-20b44fe5f4fc"
songs_df = pd.DataFrame(data=songs, columns = ['id', 'title', 'artist'])
songs_df = songs_df.set_index('id')
songs_df.head()
# + colab={"base_uri": "https://localhost:8080/", "height": 173} id="vhW9oqJAn6wn" outputId="0963aa4a-7c8e-44ad-c3b1-dc80f9b2aeda"
songs_df.iloc[[1,10,100]]
# + colab={"base_uri": "https://localhost:8080/", "height": 235} id="4vEME6TgqIcl" outputId="493e5e4e-37bc-4894-eba1-e16857d7af2b"
songs_df[songs_df.artist == 'Rush'].head()
# + [markdown] id="QnE1OWrx3TIU"
# ### Tags
# + colab={"base_uri": "https://localhost:8080/"} id="jfLq2JosfHfp" outputId="14b6c27c-8239-4e42-b0fd-3546ba0ac379"
# !head /content/dataset/yes_complete/tag_hash.txt
# + id="DMBHRM6mh_5N"
with open("/content/dataset/yes_complete/tag_hash.txt", 'r') as f:
tags_file = f.read().split('\n')
tags = [s.rstrip().split(',') for s in tags_file]
tag_name = {a:b.strip() for a,b in tags}
tag_name['#'] = 'no tag'
# + colab={"base_uri": "https://localhost:8080/"} id="WyKDo9aql0KJ" outputId="f4af9da6-6237-4ef9-b3d2-77a2b25541ae"
print('Tag name for tag id {} is "{}"\n'.format('10', tag_name['10']))
print('Tag name for tag id {} is "{}"\n'.format('80', tag_name['80']))
print('There are total {} tags'.format(len(tag_name.items())))
# + colab={"base_uri": "https://localhost:8080/"} id="s9fh6c7L_Dbv" outputId="8c8e29cf-43d9-4332-9de2-b21d03fb2c4a"
# !head /content/dataset/yes_complete/tags.txt
# + id="7nR06ogPjidw"
with open("/content/dataset/yes_complete/tags.txt", 'r') as f:
song_tags = f.read().split('\n')
song_tags = [s.split(' ') for s in song_tags]
song_tags = {a:b for a,b in enumerate(song_tags)}
# + id="_XGMxG7el4ib"
def tags_for_song(song_id=0):
tag_ids = song_tags[int(song_id)]
return [tag_name[tag_id] for tag_id in tag_ids]
# + colab={"base_uri": "https://localhost:8080/"} id="gm6i0HlMk6jZ" outputId="65da0c9a-3225-4969-d8a8-25c4b936a374"
print('Tags for song "{}" : {}\n'.format(songs_df.iloc[0].title, tags_for_song(0)))
# + [markdown] id="iyqhTWtn3Jil"
# ## Recommend
# + id="xlGQ4iygoL2i"
def recommend(song_id=0, topn=5):
# song info
song_info = songs_df.iloc[song_id]
song_tags = [', '.join(tags_for_song(song_id))]
query_song = pd.DataFrame({'title':song_info.title,
'artist':song_info.artist,
'tags':song_tags})
# similar songs
similar_songs = np.array(model.wv.most_similar(positive=str(song_id), topn=topn))[:,0]
recommendations = songs_df.iloc[similar_songs]
recommendations['tags'] = [tags_for_song(i) for i in similar_songs]
recommendations = pd.concat([query_song, recommendations])
axis_name = ['Query'] + ['Recommendation '+str((i+1)) for i in range(topn)]
# recommendations.index = axis_name
recommendations = recommendations.style.set_table_styles([{'selector': 'th', 'props': [('background-color', 'gray')]}])
return recommendations
# + colab={"base_uri": "https://localhost:8080/", "height": 387} id="F0qBm76OtzBV" outputId="06120e62-fecb-4b27-d821-cc9f9169092e"
recs = recommend(10)
recs
# + [markdown] id="qYFrMdrZzlFD"
# ### Paranoid Android - Radiohead
# + colab={"base_uri": "https://localhost:8080/", "height": 370} id="bctpVSM3znHy" outputId="3c5d212d-eac5-4172-a79f-1c32004d807f"
recommend(song_id=19563)
# + [markdown] id="4oYa1QAT14DD"
# ### California Love - 2Pac
# + colab={"base_uri": "https://localhost:8080/", "height": 268} id="4DjOvrZb16LE" outputId="026fa5ed-53d0-4c80-8af3-1d29d8c50ca5"
recommend(song_id=842)
# + [markdown] id="Uw6x-wFV17m5"
# ### <NAME> - <NAME>
# + colab={"base_uri": "https://localhost:8080/", "height": 370} id="X7nA4NWdz22W" outputId="095ba4ad-56b9-4c63-e7ea-b6e6d4087ad1"
recommend(song_id=3822)
|
_notebooks/2021-07-10-songs-embedding-skipgram-recommender.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # 과제 - Transfer Learning
#
# 여기서 풀고자 하는 문제는 개미 와 벌 을 분류하는 모델을 학습하는 것이다.
#
# 개미와 벌 각각의 학습용 이미지는 대략 120장 정도 있고, 75개의 검증용 이미지가 있다. 일반적으로 맨 처음부터 학습을 한다면 이는 일반화하기에는 아주 작은 데이터셋이다. 하지만 Transfer learning을 사용한다면 작은 양의 데이터로도 성능이 좋은 이미지 분류 모형을 생성할 수 있다.
#
# ---
# ## 데이터 준비하기
#
# 데이터 다운로드 하기
# ==> http://download.pytorch.org/tutorial/hymenoptera_data.zip
#
# 제공되는 hymenoptera_data.zip 파일을 현재 directory에 압축해제 한다.
#
#
# +
import tensorflow as tf
from tensorflow import keras
print("TensorFlow version is ", tf.__version__)
import os
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
# -
train_dir = './hymenoptera_data/train'
validation_dir = './hymenoptera_data/val'
train_ants_dir = os.path.join(train_dir, 'ants') # directory with our training cat pictures
train_bees_dir = os.path.join(train_dir, 'bees') # directory with our training dog pictures
validation_ants_dir = os.path.join(validation_dir, 'ants') # directory with our validation cat pictures
validation_bees_dir = os.path.join(validation_dir, 'bees') # directory with our validation dog pictures
# +
num_ants_tr = len(os.listdir(train_ants_dir))
num_bees_tr = len(os.listdir(train_bees_dir))
num_ants_val = len(os.listdir(validation_ants_dir))
num_bees_val = len(os.listdir(validation_bees_dir))
print('total training ants images:', num_ants_tr)
print('total training bees images:', num_bees_tr)
print('total validation ants images:', num_ants_val)
print('total validation bees images:', num_bees_val)
# -
# ### 문제1.
#
# 디렉토리의 이미지를 dataset으로 생성한다.
# +
from tensorflow.keras.preprocessing.image import ImageDataGenerator
train_datagen = ImageDataGenerator(rescale=1./255) # Generator for our training data
validation_datagen = ImageDataGenerator(rescale=1./255) # Generator for our validation data
# +
image_size = 160 # All images will be resized to 160x160
batch_size = None # 적당한 batch size를 정하시오.
train_generator = None # data generator의 flow_from_directory메소드를 사용하여 train set을 생성하시오
validation_generator = None # data generator의 flow_from_directory메소드를 사용하여 validationset을 생성하시오.
# -
# ### 문제 2.
#
# pre trained model을 다운로드 한다.
# https://www.tensorflow.org/api_docs/python/tf/keras/applications 을 참조하면 다양한 pretrained model을 선택 다운로드 할 수 있다.
# +
image_size = 160
IMG_SHAPE = (image_size, image_size, 3)
base_model = None # 원하는 pre trained model을 다운로드 하는 코드를 작성하시오.
# -
# > 문제 2-1 해당 pre trained model을 선택한 이유가 무엇인지 간단하게 설명하시오.
# * 이곳을 더블클릭하여 답변을 작성하시오.
# ### 문제 3.
#
# 선택한 Pre-trained model의 가중치 freeze하시오.
#
base_model.trainable = None # 해당 코드를 작성하시오.
# ### 문제 4.
#
# 마지막에 이미지 분류를 위한 layer를 추가하시오.
model = None # tf.keras.Sequential 을 사용하여 base_model에 layer를 추가하는 코드를 작성하시오.
# ### 문제 5.
#
# 생성한 모형을 compile 하시오. 적당한 optimizer, loss, metric을 선택하시오.
model.compile(optimizer=None,
loss=None,
metrics=None)
model.summary()
# ### 문제 6.
#
# 생성한 모형을 훈련하시오.
epochs = None # 모형을 훈련하기 위한 epochs를 적당히 선택하여 작성하시오.
history = model.fit(train_generator,
epochs=epochs,
validation_data=validation_generator
)
# ### 문제 7.
#
# 훈련된 모형으로 예측을 수행하시오.
# +
imgs, labels = validation_generator.next()
# model.predict() 메소드는 확률을 리턴한다. 확률을 class(0=ants, 1=bees)로 리턴하는 코드를 작성하시오.
preds = None
# -
classes = ['ants','bees'] # class의 이름
# 예측결과를 화면에 출력한다.
idx = 10
plt.title("pred={}(label={})".format(classes[preds[idx].item()],classes[int(labels[idx])]))
plt.imshow(imgs[idx])
plt.show()
# ### 문제 8.
#
# Transfer Learning 이 무엇인지 간략하게 정리하여 설명하시오.
# > 이곳을 더블클릭하여 답변을 작성하시오.
|
02CNN/transfer_learning_ex.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Constructing a Cancer-Specific Network
#
# __Introduction:__
# This notebook uses [__PCNet__](http://www.ndexbio.org/#/network/f93f402c-86d4-11e7-a10d-0ac135e8bacf) from (Huang, Carlin, et al. in press) and various collections of cancer-related genes (see below) to construct a cancer-specific subnetwork that can be used in the pyNBS algorithm to stratify patients with sparse mutational profiles. This method also uses a module wrapping the [MyGene.info](http://mygene.info/) Python API (developed by Huang et al.) to normalize all gene names to HUGO symbols.
#
# __Steps to construct Cancer Subnetwork:__
# 1. Load network
# 2. Compile all cancer genes from cancer-related gene sets into a single list
# 3. Extract only edges from network connecting cancer genes together, remove all other nodes and edges from the network
# 4. Write the filtered network to file as an edge list.
#
# __The following is a list of the four cancer-related gene sets used to filter PCNet:__
#
# |File Name|Cancer Gene Set Description|Citation|
# |:---|:---|:---|
# |hallmarks.txt|Genes from hallmark cancer pathways|Hanahan D and Weinberg RA (2011) Hallmarks of Cancer: The Next Generation. Cell. 144(5), 646-674.|
# |vogelstein.txt|List of tumor suppressor and oncogenes from Vogelstein et al.|Vogelstein B, et al. (2013) Cancer genome landscapes. Science. 339(6127), 1546-1558.|
# |sanger_CL_genes.txt|Recurrently mutated cancer genes discovered from cancer cell lines (Sanger UK)|Iorio F, et al. (2016) A Landscape of Pharmacogenomic Interactions in Cancer. Cell. 166(3), 740-754.|
# |cgc.txt|Genes from the Cancer Gene Census (COSMIC v81)|Forbes SA, et al. (2017) COSMIC: somatic cancer genetics at high-resolution. Nucleic Acids Res. 45(D1), D777-D783.|
#
import pandas as pd
import networkx as nx
from pyNBS import gene_conversion_tools as gct
# ## Load Network
network_file = './CancerSubnetwork_Data/PCNet.txt'
network = nx.read_edgelist(network_file, delimiter='\t', data=True)
# ## Get all cancer-related genes
#
# #### Get genes from all cancer hallmark pathways and convert them from Entrez to HUGO Symbols (Hanahan, Weinberg 2011)
# Load pathway gene sets
f = open('./Supplementary_Notebook_Data/CancerSubnetwork_Data/hallmarks.txt')
lines = f.read().splitlines()
hallmark_genesets = {}
for line in lines:
if '\t' in line:
hallmark_genesets[line.split('\t')[0].split('|')[1]] = line.split('\t')[2:]
# Convert cancer-hallmark gene set genes to HUGO with MyGene.info
all_hallmark_genes_entrez = []
for hallmark in hallmark_genesets:
all_hallmark_genes_entrez = all_hallmark_genes_entrez + hallmark_genesets[hallmark]
all_hallmark_genes_entrez = list(set(all_hallmark_genes_entrez))
# Get gene conversion query string
query_string, valid_genes, invalid_genes = gct.query_constructor(all_hallmark_genes_entrez)
# Set scopes (gene naming systems to search)
scopes = "entrezgene, retired"
# Set fields (systems from which to return gene names from)
fields = "symbol, entrezgene"
# Query MyGene.Info
match_list = gct.query_batch(query_string, scopes=scopes, fields=fields)
# Get gene conversion maps
match_table_trim, query_to_symbol, query_to_entrez = gct.construct_query_map_table(match_list, valid_genes, display_unmatched_queries=True)
# Collapse cancer-hallmark gene set genes as HUGO Symbols only
all_hallmark_genes_symbol = [str(query_to_symbol[gene]) for gene in all_hallmark_genes_entrez]
# #### Load genes determined by Vogelstein as tumor suppressors or oncogenes (Vogelstein et al 2013)
# Vogelstein cancer genes list
f = open('./Supplementary_Notebook_Data/CancerSubnetwork_Data/vogelstein.txt')
lines = f.read().splitlines()
Vogelstein_genes = [line.split('\t')[0] for line in lines]
# #### Load genes determined as recurrently mutated across 1,001 cancer cell lines (Iorio et al 2016)
f = open('./Supplementary_Notebook_Data/CancerSubnetwork_Data/sanger_CL_genes.txt')
Sanger_genes = f.read().splitlines()
# #### Load genes from the Cancer Gene Census from COSMIC v81 (Forbes et al 2017)
COSMIC_table = pd.read_csv('./Supplementary_Notebook_Data/CancerSubnetwork_Data/cgc_v81.txt')
COSMIC_genes = list(COSMIC_table['Gene Symbol'])
# #### Combine all cancer gene lists together
cancer_genes = list(set(all_hallmark_genes_symbol+Vogelstein_genes+Sanger_genes+COSMIC_genes))
print "Number of HUGO Cancer Genes:", len(cancer_genes)
# ### Generate Cancer Gene Network
# Note: The resulting network may not be **exactly** the same as the Cancer Subnetwork found in ```'~/Examples/Example_Data/Network_Files/CancerSubnetwork.txt'``` due to the fact that [MyGene.Info](http://mygene.info/) may be updating gene name mappings over time.
# Filter PCNet to only contain genes from the combined cancer gene list and the edges between those genes
cancer_subnetwork = network.subgraph(cancer_genes)
gene_degree = pd.Series(cancer_subnetwork.degree(), name='degree')
print "Number of connected genes in Cancer Subnetwork:", len(cancer_subnetwork.nodes())-len(gene_degree[gene_degree==0])
print "Number of interactions in Cancer Subnetwork:", len(cancer_subnetwork.edges())
# Write the filtered cancer subnetwork to file
# Note: Genes with no edges connecting them to any other gene will be removed during this step
gct.write_edgelist(cancer_subnetwork.edges(), './Supplementary_Notebook_Results/CancerSubnetwork.txt', binary=True)
|
Supplementary_Notebooks/Cancer Subnetwork Construction.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # RBF Network
# ### 1. Implementation and study of Radial Basis Function (RBF) Network - (7)
# A manufacturing company has collected a large amount of data in the form of pairs of real valued input and output vectors, and wants you to build a system that will predict the outputs for new inputs. Design an appropriate Radial Basis Function (RBF) network for them. Explain what will be computed at each network layer.Describe how you would determine the weights/parameters for such a network and print the weights/ parameters?
# RBF Network Method 1
# %cd "/home/mona/3074 ML Lab/Datasets"
import math
import pandas as pd
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
import numpy as numpy
Data= pd.read_table("bank-full.csv", sep= None, engine= "python")
cols= ["age","balance","day","duration","campaign","pdays","previous"]
data_encode= Data.drop(cols, axis= 1)
data_encode= data_encode.apply(LabelEncoder().fit_transform)
data_rest= Data[cols]
Data= pd.concat([data_rest,data_encode], axis= 1)
data_train, data_test= train_test_split(Data, test_size= 0.33, random_state= 4)
X_train= data_train.drop("Target", axis= 1)
Y_train= data_train["Target"]
X_test= data_test.drop("Target", axis=1)
Y_test= data_test["Target"]
scaler= StandardScaler()
scaler.fit(X_train)
X_train= scaler.transform(X_train)
X_test= scaler.transform(X_test)
K_cent= 8
km= KMeans(n_clusters= K_cent, max_iter= 100)
km.fit(X_train)
cent= km.cluster_centers_
# +
max=0
for i in range(K_cent):
for j in range(K_cent):
d= numpy.linalg.norm(cent[i]-cent[j])
if(d> max):
max= d
d= max
sigma= d/math.sqrt(2*K_cent)
# -
shape= X_train.shape
row= shape[0]
column= K_cent
G= numpy.empty((row,column), dtype= float)
for i in range(row):
for j in range(column):
dist= numpy.linalg.norm(X_train[i]-cent[j])
G[i][j]= math.exp(-math.pow(dist,2)/math.pow(2*sigma,2))
GTG= numpy.dot(G.T,G)
GTG_inv= numpy.linalg.inv(GTG)
fac= numpy.dot(GTG_inv,G.T)
W= numpy.dot(fac,Y_train)
row= X_test.shape[0]
column= K_cent
G_test= numpy.empty((row,column), dtype= float)
for i in range(row):
for j in range(column):
dist= numpy.linalg.norm(X_test[i]-cent[j])
G_test[i][j]= math.exp(-math.pow(dist,2)/math.pow(2*sigma,2))
# +
prediction= numpy.dot(G_test,W)
prediction= 0.5*(numpy.sign(prediction-0.5)+1)
score= accuracy_score(prediction,Y_test)
print(score.mean())
# -
# RBF Network Method 2
# ### 2. Comparison of performance with MLP - (3)
# Compare the performance of Radial Basis Function (RBF) network with Multilayer Perceptron (MLP) network designed for the same task?
# Link to data:
# Use train.csv and test.csv in the following link.
# https://github.com/eugeniashurko/rbfnnpy/tree/master/examples
# ### MPL Code:
# +
# Backprop on the Seeds Dataset
from random import seed
from random import randrange
from random import random
from csv import reader
from math import exp
# Load a CSV file
def load_csv(filename):
dataset = list()
with open(filename, 'r') as file:
csv_reader = reader(file)
for row in csv_reader:
if not row:
continue
dataset.append(row)
return dataset
# Convert string column to float
def str_column_to_float(dataset, column):
for row in dataset:
row[column] = float(row[column].strip())
# Convert string column to integer
def str_column_to_int(dataset, column):
class_values = [row[column] for row in dataset]
unique = set(class_values)
lookup = dict()
for i, value in enumerate(unique):
lookup[value] = i
for row in dataset:
row[column] = lookup[row[column]]
return lookup
# Find the min and max values for each column
def dataset_minmax(dataset):
minmax = list()
stats = [[min(column), max(column)] for column in zip(*dataset)]
return stats
# Rescale dataset columns to the range 0-1
def normalize_dataset(dataset, minmax):
for row in dataset:
for i in range(len(row)-1):
row[i] = (row[i] - minmax[i][0]) / (minmax[i][1] - minmax[i][0])
# Split a dataset into k folds
def cross_validation_split(dataset, n_folds):
dataset_split = list()
dataset_copy = list(dataset)
fold_size = int(len(dataset) / n_folds)
for i in range(n_folds):
fold = list()
while len(fold) < fold_size:
index = randrange(len(dataset_copy))
fold.append(dataset_copy.pop(index))
dataset_split.append(fold)
return dataset_split
# Calculate accuracy percentage
def accuracy_metric(actual, predicted):
correct = 0
for i in range(len(actual)):
if actual[i] == predicted[i]:
correct += 1
return correct / float(len(actual)) * 100.0
# Evaluate an algorithm using a cross validation split
def evaluate_algorithm(dataset, algorithm, n_folds, *args):
folds = cross_validation_split(dataset, n_folds)
scores = list()
for fold in folds:
train_set = list(folds)
train_set.remove(fold)
train_set = sum(train_set, [])
test_set = list()
for row in fold:
row_copy = list(row)
test_set.append(row_copy)
row_copy[-1] = None
predicted = algorithm(train_set, test_set, *args)
actual = [row[-1] for row in fold]
accuracy = accuracy_metric(actual, predicted)
scores.append(accuracy)
return scores
# Calculate neuron activation for an input
def activate(weights, inputs):
activation = weights[-1]
for i in range(len(weights)-1):
activation += weights[i] * inputs[i]
return activation
# Transfer neuron activation
def transfer(activation):
return 1.0 / (1.0 + exp(-activation))
# Forward propagate input to a network output
def forward_propagate(network, row):
inputs = row
for layer in network:
new_inputs = []
for neuron in layer:
activation = activate(neuron['weights'], inputs)
neuron['output'] = transfer(activation)
new_inputs.append(neuron['output'])
inputs = new_inputs
return inputs
# Calculate the derivative of an neuron output
def transfer_derivative(output):
return output * (1.0 - output)
# Backpropagate error and store in neurons
def backward_propagate_error(network, expected):
for i in reversed(range(len(network))):
layer = network[i]
errors = list()
if i != len(network)-1:
for j in range(len(layer)):
error = 0.0
for neuron in network[i + 1]:
error += (neuron['weights'][j] * neuron['delta'])
errors.append(error)
else:
for j in range(len(layer)):
neuron = layer[j]
errors.append(neuron['output'] - expected[j])
for j in range(len(layer)):
neuron = layer[j]
neuron['delta'] = errors[j] * transfer_derivative(neuron['output'])
# Update network weights with error
def update_weights(network, row, l_rate):
for i in range(len(network)):
inputs = row[:-1]
if i != 0:
inputs = [neuron['output'] for neuron in network[i - 1]]
for neuron in network[i]:
for j in range(len(inputs)):
neuron['weights'][j] -= l_rate * neuron['delta'] * inputs[j]
neuron['weights'][-1] -= l_rate * neuron['delta']
# Train a network for a fixed number of epochs
def train_network(network, train, l_rate, n_epoch, n_outputs):
for epoch in range(n_epoch):
for row in train:
outputs = forward_propagate(network, row)
expected = [0 for i in range(n_outputs)]
expected[row[-1]] = 1
backward_propagate_error(network, expected)
update_weights(network, row, l_rate)
# Initialize a network
def initialize_network(n_inputs, n_hidden, n_outputs):
network = list()
hidden_layer = [{'weights':[random() for i in range(n_inputs + 1)]} for i in range(n_hidden)]
network.append(hidden_layer)
output_layer = [{'weights':[random() for i in range(n_hidden + 1)]} for i in range(n_outputs)]
network.append(output_layer)
return network
# Make a prediction with a network
def predict(network, row):
outputs = forward_propagate(network, row)
return outputs.index(max(outputs))
# Backpropagation Algorithm With Stochastic Gradient Descent
def back_propagation(train, test, l_rate, n_epoch, n_hidden):
n_inputs = len(train[0]) - 1
n_outputs = len(set([row[-1] for row in train]))
network = initialize_network(n_inputs, n_hidden, n_outputs)
train_network(network, train, l_rate, n_epoch, n_outputs)
predictions = list()
for row in test:
prediction = predict(network, row)
predictions.append(prediction)
return(predictions)
# Test Backprop on Seeds dataset
seed(1)
# load and prepare data
filename = 'seeds.csv'
dataset = load_csv(filename)
dataset = dataset[1: ]
for i in range(len(dataset[0])-1):
str_column_to_float(dataset, i)
# convert class column to integers
str_column_to_int(dataset, len(dataset[0])-1)
# normalize input variables
minmax = dataset_minmax(dataset)
normalize_dataset(dataset, minmax)
# evaluate algorithm
n_folds = 5
l_rate = 0.3
n_epoch = 500
n_hidden = 5
scores = evaluate_algorithm(dataset, back_propagation, n_folds, l_rate, n_epoch, n_hidden)
print('Scores: %s' % scores)
print('Mean Accuracy: %.3f%%' % (sum(scores)/float(len(scores))))
# -
# %cd "/home/mona/3074 ML Lab/Datasets"
# +
import numpy as np
import pcn #using perceptron network
import kmeans # and kmeans clustering algorithm
class rbf:
""" The Radial Basis Function network
Parameters are number of RBFs, and their width, how to train the network
(pseudo-inverse or kmeans) and whether the RBFs are normalised"""
def __init__(self,inputs,targets,nRBF,sigma=0,usekmeans=0,normalise=0):
self.nin = np.shape(inputs)[1]
self.nout = np.shape(targets)[1]
self.ndata = np.shape(inputs)[0]
self.nRBF = nRBF
self.usekmeans = usekmeans
self.normalise = normalise
if usekmeans:
self.kmeansnet = kmeans.kmeans(self.nRBF,inputs)
self.hidden = np.zeros((self.ndata,self.nRBF+1))
if sigma==0:
# Set width of Gaussians
d = (inputs.max(axis=0)-inputs.min(axis=0)).max()
self.sigma = d/np.sqrt(2*nRBF)
else:
self.sigma = sigma
self.perceptron = pcn.pcn(self.hidden[:,:-1],targets)
# Initialise network
self.weights1 = np.zeros((self.nin,self.nRBF))
def rbftrain(self,inputs,targets,eta=0.25,niterations=100):
if self.usekmeans==0:
# Version 1: set RBFs to be datapoints
indices = range(self.ndata)
np.random.shuffle(indices)
for i in range(self.nRBF):
self.weights1[:,i] = inputs[indices[i],:]
else:
# Version 2: use k-means
self.weights1 = np.transpose(self.kmeansnet.kmeanstrain(inputs))
for i in range(self.nRBF):
self.hidden[:,i] = np.exp(-np.sum((inputs - np.ones((1,self.nin))*self.weights1[:,i])**2,axis=1)/(2*self.sigma**2))
if self.normalise:
self.hidden[:,:-1] /= np.transpose(np.ones((1,np.shape(self.hidden)[0]))*self.hidden[:,:-1].sum(axis=1))
# Call Perceptron without bias node (since it adds its own)
self.perceptron.pcntrain(self.hidden[:,:-1],targets,eta,niterations)
def rbffwd(self,inputs):
hidden = np.zeros((np.shape(inputs)[0],self.nRBF+1))
for i in range(self.nRBF):
hidden[:,i] = np.exp(-np.sum((inputs - np.ones((1,self.nin))*self.weights1[:,i])**2,axis=1)/(2*self.sigma**2))
if self.normalise:
hidden[:,:-1] /= np.transpose(np.ones((1,np.shape(hidden)[0]))*hidden[:,:-1].sum(axis=1))
# Add the bias
hidden[:,-1] = -1
outputs = self.perceptron.pcnfwd(hidden)
return outputs
def confmat(self,inputs,targets):
"""Confusion matrix"""
outputs = self.rbffwd(inputs)
nClasses = np.shape(targets)[1]
if nClasses==1:
nClasses = 2
outputs = np.where(outputs>0,1,0)
else:
# 1-of-N encoding
outputs = np.argmax(outputs,1)
targets = np.argmax(targets,1)
cm = np.zeros((nClasses,nClasses))
for i in range(nClasses):
for j in range(nClasses):
cm[i,j] = np.sum(np.where(outputs==i,1,0)*np.where(targets==j,1,0))
output = cm
print("Confusion matrix is:")
print(cm)
print("Percentage Correct: ", np.trace(cm) / np.sum(cm) * 100)
return output
# -
iris = np.loadtxt('train.csv',delimiter=',')
iris[:,:-1] = iris[:,:-1]-iris[:,:-1].mean(axis=0)
imax = np.concatenate((iris.max(axis=0)*np.ones((1,5)),iris.min(axis=0)*np.ones((1,5))),axis=0).max(axis=0)
iris[:,:-1] = iris[:,:-1]/imax[:-1]
print (iris[0:5,:])
iris.shape
target = np.zeros((np.shape(iris)[0], 2))
indices = np.where(iris[:,-1]==0)
target[indices,0] = 1
indices = np.where(iris[:,-1]==1)
target[indices,1] = 1
'''
indices = np.where(iris[:,9]==2)
target[indices,2] = 1
indices = np.where(iris[:,9]==3)
target[indices,0] = 1
indices = np.where(iris[:,9]==4)
target[indices,1] = 1
indices = np.where(iris[:,9]==5)
target[indices,2] = 1
indices = np.where(iris[:,9]==5)
target[indices,2] = 1
'''
order = np.arange(np.shape(iris)[0])
np.random.shuffle(order)
iris = iris[order,:]
target = target[order,:]
train = iris[::2,0:4]
traint = target[::2]
valid = iris[1::4,0:4]
validt = target[1::4]
test = iris[3::4,0:4]
testt = target[3::4]
print (train.max(axis=0), train.min(axis=0))
# +
net = rbf(train,traint,5,1,1)
net.rbftrain(train,traint,0.25,5000)
print("Train data:-")
net.confmat(train,traint)
print("Test data:-")
cm = net.confmat(test,testt)
# -
cm
# +
import seaborn as sn
import pandas as pd
import matplotlib.pyplot as plt
cm = np.array(cm)
df_cm = pd.DataFrame(cm)
plt.figure(figsize=(10,7))
sn.set(font_scale=1.4) # for label size
sn.heatmap(df_cm, annot=True, annot_kws={"size": 14}) # font size
plt.show()
# +
from sklearn.metrics import classification_report
targets=testt
inputs = test
nClasses = np.shape(targets)[1]
outputs = net.rbffwd(inputs)
if nClasses==1:
nClasses = 2
outputs = np.where(outputs>0,1,0)
else:
# 1-of-N encoding
outputs = np.argmax(outputs,1)
targets = np.argmax(targets,1)
print(classification_report(targets, outputs))
# -
# # ------
import math
import pandas as pd
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
import numpy as numpy
Data= pd.read_table("train.csv", sep= None, engine= "python")
#cols= ["age","balance","day","duration","campaign","pdays","previous"]
#data_encode= Data.drop(cols, axis= 1)
data_encode= Data.apply(LabelEncoder().fit_transform)
#data_rest= Data[cols]
#Data= pd.concat([data_rest,data_encode], axis= 1)
data_train, data_test= train_test_split(Data.iloc[:1000], test_size= 0.33, random_state= 4)
X_train= data_train.drop(columns=data_train.columns[-1], axis= 1)
Y_train= data_train.iloc[:, :-1]
X_test= data_test.drop(columns=data_test.columns[-1], axis=1)
Y_test= data_test.iloc[:, :-1]
scaler= StandardScaler()
scaler.fit(X_train)
X_train= scaler.transform(X_train)
X_test= scaler.transform(X_test)
K_cent= 8
km= KMeans(n_clusters= K_cent, max_iter= 100)
km.fit(X_train)
cent= km.cluster_centers_
# +
max=0
for i in range(K_cent):
for j in range(K_cent):
d= numpy.linalg.norm(cent[i]-cent[j])
if(d> max):
max= d
d= max
sigma= d/math.sqrt(2*K_cent)
# -
shape= X_train.shape
row= shape[0]
column= K_cent
G= numpy.empty((row,column), dtype= float)
for i in range(row):
for j in range(column):
dist= numpy.linalg.norm(X_train[i]-cent[j])
G[i][j]= math.exp(-math.pow(dist,2)/math.pow(2*sigma,2))
GTG= numpy.dot(G.T,G)
GTG_inv= numpy.linalg.inv(GTG)
fac= numpy.dot(GTG_inv,G.T)
W= numpy.dot(fac,Y_train)
row= X_test.shape[0]
column= K_cent
G_test= numpy.empty((row,column), dtype= float)
for i in range(row):
for j in range(column):
dist= numpy.linalg.norm(X_test[i]-cent[j])
G_test[i][j]= math.exp(-math.pow(dist,2)/math.pow(2*sigma,2))
# +
prediction= numpy.dot(G_test,W)
prediction= 0.5*(numpy.sign(prediction-0.5)+1)
score= accuracy_score(prediction,Y_test)
print(score.mean())
# -
# # *||||||
# +
import numpy as np
import matplotlib.pyplot as plt
def rbf(x, c, s):
return np.exp(-1 / (2 * s**2) * (x-c)**2)
def kmeans(X, k):
"""Performs k-means clustering for 1D input
Arguments:
X {ndarray} -- A Mx1 array of inputs
k {int} -- Number of clusters
Returns:
ndarray -- A kx1 array of final cluster centers
"""
# randomly select initial clusters from input data
clusters = np.random.choice(np.squeeze(X), size=k)
prevClusters = clusters.copy()
stds = np.zeros(k)
converged = False
while not converged:
"""
compute distances for each cluster center to each point
where (distances[i, j] represents the distance between the ith point and jth cluster)
"""
distances = np.squeeze(np.abs(X[:, np.newaxis] - clusters[np.newaxis, :]))
# find the cluster that's closest to each point
closestCluster = np.argmin(distances, axis=1)
# update clusters by taking the mean of all of the points assigned to that cluster
for i in range(k):
pointsForCluster = X[closestCluster == i]
if len(pointsForCluster) > 0:
clusters[i] = np.mean(pointsForCluster, axis=0)
# converge if clusters haven't moved
converged = np.linalg.norm(clusters - prevClusters) < 1e-6
prevClusters = clusters.copy()
distances = np.squeeze(np.abs(X[:, np.newaxis] - clusters[np.newaxis, :]))
closestCluster = np.argmin(distances, axis=1)
clustersWithNoPoints = []
for i in range(k):
pointsForCluster = X[closestCluster == i]
if len(pointsForCluster) < 2:
# keep track of clusters with no points or 1 point
clustersWithNoPoints.append(i)
continue
else:
stds[i] = np.std(X[closestCluster == i])
# if there are clusters with 0 or 1 points, take the mean std of the other clusters
if len(clustersWithNoPoints) > 0:
pointsToAverage = []
for i in range(k):
if i not in clustersWithNoPoints:
pointsToAverage.append(X[closestCluster == i])
pointsToAverage = np.concatenate(pointsToAverage).ravel()
stds[clustersWithNoPoints] = np.mean(np.std(pointsToAverage))
return clusters, stds
class RBFNet(object):
"""Implementation of a Radial Basis Function Network"""
def __init__(self, k=2, lr=0.01, epochs=100, rbf=rbf, inferStds=True):
self.k = k
self.lr = lr
self.epochs = epochs
self.rbf = rbf
self.inferStds = inferStds
self.w = np.random.randn(k)
self.b = np.random.randn(1)
def fit(self, X, y):
if self.inferStds:
# compute stds from data
self.centers, self.stds = kmeans(X, self.k)
else:
# use a fixed std
self.centers, _ = kmeans(X, self.k)
dMax = max([np.abs(c1 - c2) for c1 in self.centers for c2 in self.centers])
self.stds = np.repeat(dMax / np.sqrt(2*self.k), self.k)
# training
for epoch in range(self.epochs):
for i in range(X.shape[0]):
# forward pass
a = np.array([self.rbf(X[i], c, s) for c, s, in zip(self.centers, self.stds)])
F = a.T.dot(self.w) + self.b
loss = (y[i] - F).flatten() ** 2
#commented this print('Loss: {0:.2f}'.format(loss[0]))
# backward pass
error = -(y[i] - F).flatten()
# online update
self.w = self.w - self.lr * a * error
self.b = self.b - self.lr * error
def predict(self, X):
y_pred = []
for i in range(X.shape[0]):
a = np.array([self.rbf(X[i], c, s) for c, s, in zip(self.centers, self.stds)])
F = a.T.dot(self.w) + self.b
y_pred.append(F)
return np.array(y_pred)
# sample inputs and add noise
NUM_SAMPLES = 100
X = np.random.uniform(0., 1., NUM_SAMPLES)
X = np.sort(X, axis=0)
noise = np.random.uniform(-0.1, 0.1, NUM_SAMPLES)
y = np.sin(2 * np.pi * X) + noise
rbfnet = RBFNet(lr=1e-2, k=2, inferStds=True)
rbfnet.fit(X, y)
y_pred = rbfnet.predict(X)
plt.plot(X, y, '-o', label='true')
plt.plot(X, y_pred, '-o', label='RBF-Net')
plt.legend()
plt.tight_layout()
plt.show()
# -
# ### 3. Implementation of XOR gate? (5)
# Demonstrate the capability of an RBF network to model XOR logic gate. Generate the performance curves for these RBF models as the inputs vay continuously from 0.0 to 1.0?
import numpy as np
import matplotlib.pyplot as plt
def gaussian_rbf(x, landmark, gamma=1):
return np.exp(-gamma * np.linalg.norm(x - landmark)**2)
def end_to_end(X1, X2, ys, mu1, mu2):
from_1 = [gaussian_rbf(i, mu1) for i in zip(X1, X2)]
from_2 = [gaussian_rbf(i, mu2) for i in zip(X1, X2)]
# plot
plt.figure(figsize=(13, 5))
plt.subplot(1, 2, 1)
plt.scatter((x1[0], x1[3]), (x2[0], x2[3]), label="Class_0")
plt.scatter((x1[1], x1[2]), (x2[1], x2[2]), label="Class_1")
plt.xlabel("$X1$", fontsize=15)
plt.ylabel("$X2$", fontsize=15)
plt.title("Xor: Linearly Inseparable", fontsize=15)
plt.legend()
plt.subplot(1, 2, 2)
plt.scatter(from_1[0], from_2[0], label="Class_0")
plt.scatter(from_1[1], from_2[1], label="Class_1")
plt.scatter(from_1[2], from_2[2], label="Class_1")
plt.scatter(from_1[3], from_2[3], label="Class_0")
plt.plot([0, 0.95], [0.95, 0], "k--")
plt.annotate("Seperating hyperplane", xy=(0.4, 0.55), xytext=(0.55, 0.66),
arrowprops=dict(facecolor='black', shrink=0.05))
plt.xlabel(f"$mu1$: {(mu1)}", fontsize=15)
plt.ylabel(f"$mu2$: {(mu2)}", fontsize=15)
plt.title("Transformed Inputs: Linearly Seperable", fontsize=15)
plt.legend()
# solving problem using matrices form
# AW = Y
A = []
for i, j in zip(from_1, from_2):
temp = []
temp.append(i)
temp.append(j)
temp.append(1)
A.append(temp)
A = np.array(A)
W = np.linalg.inv(A.T.dot(A)).dot(A.T).dot(ys)
print(np.round(A.dot(W)))
print(ys)
print(f"Weights: {W}")
return W
def predict_matrix(point, weights):
gaussian_rbf_0 = gaussian_rbf(np.array(point), mu1)
gaussian_rbf_1 = gaussian_rbf(np.array(point), mu2)
A = np.array([gaussian_rbf_0, gaussian_rbf_1, 1])
return np.round(A.dot(weights))
# +
# points
x1 = np.array([0, 0, 1, 1])
x2 = np.array([0, 1, 0, 1])
ys = np.array([0, 1, 1, 0])
# centers
mu1 = np.array([0, 1])
mu2 = np.array([1, 0])
w = end_to_end(x1, x2, ys, mu1, mu2)
# testing
print(f"Input:{np.array([0, 0])}, Predicted: {predict_matrix(np.array([0, 0]), w)}")
print(f"Input:{np.array([0, 1])}, Predicted: {predict_matrix(np.array([0, 1]), w)}")
print(f"Input:{np.array([1, 0])}, Predicted: {predict_matrix(np.array([1, 0]), w)}")
print(f"Input:{np.array([1, 1])}, Predicted: {predict_matrix(np.array([1, 1]), w)}")
# +
# centers
mu1 = np.array([0, 0])
mu2 = np.array([1, 1])
w = end_to_end(x1, x2, ys, mu1, mu2)
# testing
print(f"Input:{np.array([0, 0])}, Predicted: {predict_matrix(np.array([0, 0]), w)}")
print(f"Input:{np.array([0, 1])}, Predicted: {predict_matrix(np.array([0, 1]), w)}")
print(f"Input:{np.array([1, 0])}, Predicted: {predict_matrix(np.array([1, 0]), w)}")
print(f"Input:{np.array([1, 1])}, Predicted: {predict_matrix(np.array([1, 1]), w)}")
# -
# ### Spot
# Implement a handwritten character recognition algorithm using RBF neural networks?.Use your own dataset.
# +
import numpy as np
def get_distance(x1, x2):
sum = 0
for i in range(len(x1)):
sum += (x1[i] - x2[i]) ** 2
return np.sqrt(sum)
def kmeans(X, k, max_iters):
centroids = X[np.random.choice(range(len(X)), k, replace=False)]
# centroids = [np.random.uniform(size=len(X[0])) for i in range(k)]
converged = False
current_iter = 0
while (not converged) and (current_iter < max_iters):
cluster_list = [[] for i in range(len(centroids))]
for x in X: # Go through each data point
distances_list = []
for c in centroids:
distances_list.append(get_distance(c, x))
cluster_list[int(np.argmin(distances_list))].append(x)
cluster_list = list((filter(None, cluster_list)))
prev_centroids = centroids.copy()
centroids = []
for j in range(len(cluster_list)):
centroids.append(np.mean(cluster_list[j], axis=0))
pattern = np.abs(np.sum(prev_centroids) - np.sum(centroids))
print('K-MEANS: ', int(pattern))
converged = (pattern == 0)
current_iter += 1
return np.array(centroids), [np.std(x) for x in cluster_list]
class RBF:
def __init__(self, X, y, tX, ty, num_of_classes,
k, std_from_clusters=True):
self.X = X
self.y = y
self.tX = tX
self.ty = ty
self.number_of_classes = num_of_classes
self.k = k
self.std_from_clusters = std_from_clusters
def convert_to_one_hot(self, x, num_of_classes):
arr = np.zeros((len(x), num_of_classes))
for i in range(len(x)):
c = int(x[i])
arr[i][c] = 1
return arr
def get_rbf(self, x, c, s):
distance = get_distance(x, c)
return 1 / np.exp(-distance / s ** 2)
def get_rbf_as_list(self, X, centroids, std_list):
RBF_list = []
for x in X:
RBF_list.append([self.get_rbf(x, c, s) for (c, s) in zip(centroids, std_list)])
return np.array(RBF_list)
def fit(self):
self.centroids, self.std_list = kmeans(self.X, self.k, 1000)
if not self.std_from_clusters:
dMax = np.max([get_distance(c1, c2) for c1 in self.centroids for c2 in self.centroids])
self.std_list = np.repeat(dMax / np.sqrt(2 * self.k), self.k)
RBF_X = self.get_rbf_as_list(self.X, self.centroids, self.std_list)
self.w = np.linalg.pinv(RBF_X.T @ RBF_X) @ RBF_X.T @ self.convert_to_one_hot(self.y, self.number_of_classes)
RBF_list_tst = self.get_rbf_as_list(self.tX, self.centroids, self.std_list)
self.pred_ty = RBF_list_tst @ self.w
self.pred_ty = np.array([np.argmax(x) for x in self.pred_ty])
diff = self.pred_ty - self.ty
print('Accuracy: ', len(np.where(diff == 0)[0]) / len(diff))
##################################
data = np.load('mnist_data.npy',).astype(float)
train_y = data[0:500, 0]
train_x = data[0:500, 1:]
test_y = data[0:100, 0]
test_x = data[0:100, 1:]
RBF_CLASSIFIER = RBF(train_x, train_y, test_x, test_y, num_of_classes=10,
k=10, std_from_clusters=False)
RBF_CLASSIFIER.fit()
# +
import numpy as np
def get_distance(x1, x2):
sum = 0
for i in range(len(x1)):
sum += (x1[i] - x2[i]) ** 2
return np.sqrt(sum)
def kmeans(X, k, max_iters):
centroids = X[np.random.choice(range(len(X)), k, replace=False)]
converged = False
current_iter = 0
while (not converged) and (current_iter < max_iters):
cluster_list = [[] for i in range(len(centroids))]
for x in X: # Go through each data point
distances_list = []
for c in centroids:
distances_list.append(get_distance(c, x))
cluster_list[int(np.argmin(distances_list))].append(x)
cluster_list = list((filter(None, cluster_list)))
prev_centroids = centroids.copy()
centroids = []
for j in range(len(cluster_list)):
centroids.append(np.mean(cluster_list[j], axis=0))
pattern = np.abs(np.sum(prev_centroids) - np.sum(centroids))
print('K-MEANS: ', int(pattern))
converged = (pattern == 0)
current_iter += 1
return np.array(centroids), [np.std(x) for x in cluster_list]
|
Lab07.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## ***<NAME>***
# ### ***Question 1***
# ### ***a)***
# +
import random #This code imports random integers so that I can use them to flip the coin
n = int(input("Number of times to flip coin: ")) #This code ask the user the n number of times they want to flip the coin
count_tails = 0 #This code counts the number of tails that appeared #This code initialise the number of tails in the fair coin and I choose 1 to be tails
for i in range(n): #This will repeat the coin flip n number of times
flip = random.randint(0, 1) #This randomise my coin flips with 1 being the Tails 0 is heads
if (flip == 1): #This condiion checks if the flip matches the 1
count_tails +=1 #This code right here counts the number of Tails that appeared in the flip
print("Tails produced was {} times.".format(count_tails)) #This code have count in function to count how many times did Tails appear in the appended list
# -
# ### ***b)***
# +
import random #This code imports random integers so that I can use them to flip the coin
n = int(input("Enter the number of times you want to flip the coin: ")) #This code ask the user the n number of times they want to flip the coin
X = [] #This creates an empty list so that we can store our outcomes
N = int(input("Enter the number of times you want repeat the experiment: ")) #This code will ask the user how many times they want to repeat the experiment
for j in range(N): #This loop will repeat the experiment N times
count_tails = 0 #This initials the counts of how many times did tails appear
for i in range(n): #This will repeat the coin flip n number of times
flip = random.randint(0, 1) #This randomise my coin flips with 1 being the Tails
if (flip == 1): #This condiion checks if the flip matches the 1 for Tails so that it can append to the list for counting
count_tails += 1
X.append(count_tails) #This code right here appends the number of Tails that appeared in the n flips and N repeated times
# -
# ### ***c)***
# +
import random #This code imports random integers so that I can use them to flip the coin
n = int(input("Enter the number of times you want to flip the coin: ")) #This code ask the user the n number of times they want to flip the coin
X = [] #This creates an empty list so that we can store our outcomes
N = int(input("Enter the number of times you want repeat the experiment: "))
for j in range(N):
count_tails = 0 #This initials
for i in range(n): #This will repeat the coin flip n number of times
flip = random.randint(0, 1) #This randomise my coin flips with 1 being the Tails
if (flip == 1):
count_tails += 1
#This condiion checks if the flip matches the 1 for Tails so that it can append to the list for counting
X.append(count_tails) #This code right here appends the number of Tails that appeared in the flip
print(X) #This code prints out how the frequency of tail show up in x times
# -
# ### ***d)***
# +
import random #This code imports random integers so that I can use them to flip the coin
import matplotlib.pyplot as plt
n = int(input("Enter the number of times you want to flip the coin: ")) #This code ask the user the n number of times they want to flip the coin
X = [] #This creates an empty list so that we can store our outcomes
N = int(input("Enter the number of times you want repeat the experiment: "))
for j in range(N):
count_tails = 0
for i in range(n): #This will repeat the coin flip n number of times
flip = random.randint(0, 1) #This randomise my coin flips with 1 being the Tails
if (flip == 1):
count_tails += 1
#This condiion checks if the flip matches the 1 for Tails so that it can append to the list for counting
X.append(count_tails) #This code right here appends the number of Tails that appeared in the flip
x = np.random.normal(size = N) #This is the random variable x which iis plotted on the graph as the frequency
plt.hist(x,bins = 10,label = 'random variable $x$',alpha=0.3) #This code plots the random variable x with auto color from kwargs
plt.hist(X, bins = 10,color = 'm', label = 'Tails frequency $F(x)$',alpha=0.3) #This code plots the frequency F(x) with auto color from kwardgs
plt.legend(loc = 'upper right') #This sets the location of the legends to upper left to show the difference in graphs
plt.gca().set(title='Frequency $F(x)$ and random viriable $x$', ylabel='Frequency', xlabel ='Multi Histogram') #This code sets the title, the x and y axes labels.
# -
# ### ***Question 2***
# ### ***first bullet***
# +
import matplotlib.pyplot as plt #This code import a library matplotlib so that we can use it to visualise our graphs.
import numpy as np #This code will a library numpy which is used for mathematical functions like pi, sin, cos etc.
x = np.linspace(1,2) #This code will creates an interval of [1,2].
h_1 = x**3 -2*x + 1 #This is a function h_1(x) that is going to be plotted.
h_2 = -2*(x**2) + x + 3 #This is a function h_2(x) that is going to be plotted.
plt.plot(x,h_1, color = 'green', label = '$h_1(x) = x^3 -2x + 1$') #This code plots the graph of h_1(x) against the interval [1,2].
plt.plot(x,h_2, color = 'red', label = '$h_2(x) = -2x^2 + x + 3$') #This code plots the graph of h_2(x) against the interval [1,2].
plt.legend(loc = 'upper left') #This code sets the location of the legends in the graph.
plt.gca().set(title='Graph $h_2(x) = -2x^2 + x + 3$ and $h_1(x) = x^3 -2x + 1$', ylabel='y - axis', xlabel ='x - axis') #This code sets the title, the x and y axes labels.
plt.grid() #This code gives a grid
# -
# ## ***(a) to (d)***
# ### ***second bullet point***
# +
a = 1 #This initialise the interval [1,2] where a = 1.
b = 2 #This initialise the interval [1,2] where b = 2.
n = 100 #This will set the iterations to be 100 as specified.
for i in range(n): #This code will create a loop that will repeat n = 100 times.
p = (b + a) /2 #This code calculates p for (a) and (d).
f_a = a**3 -2*a +2*(a**2) - a - 2 #This is obtained from function equating h_1 and h_2, and the inserting a=1 into the function.
f_c = p**3 -2*p +2*(p**2) - p - 2 #This is obtained from function equating h_1 and h_2, and the inserting p into the function.
if f_a*f_c < 0: #This code checks if the condition f(a)xf(p) < 0 is mantained .
b = p #This code shrink the interval from right if the condition is met.
else:
a = p #This code equates a to p if the condition f(a)xf(p) < 0 is not met.
print("The estimate root of the non-linear equation h_1(x) = h_2(x) is {}".format(p)) #This prints out the estimation of the root of the non-linear equation h_1(x)=h_2(x)
# -
# ### ***Question 3***
# +
def nGrams(InputString, n, end = ""): #This line of code creates the a function which takes two arguements
"""
In this code the arguements are 'InputString' and 'n'.
InputString is a string variable in which our user should put in.
n is a integer variable which is what will split our string to given n.
end = "" helps to print out the list in a horizontal list
"""
StringList = [] #This code creates a list where the split string will be store in order to print out at the end
for i in range(len(InputString)-(n-1)): #This code creates a loop that will loop through a given string in a range of the length of the string minus n-1 to gives us an even number of splits of the string
Grams_splits = InputString[i:i+n] #This code splits the string to different parts
StringList.append(Grams_splits) #This code appends the splited parts of the string to StringList that we created earlier
return StringList #This code returns the appended list which will give us the clear view of the variables
nGrams(string, n) #This is just a test to see if my code produce what I inteded in to do.
# +
fname = 'PlagiarismTexts.txt' #This code assign the file name so that we can read it later
P_file = open(fname, 'r') #This code opens a file for reading
Read_lines = P_file.readlines() #This code reads in, line-by-line; p_file is a list
P_file.close() #This code closes the stream
#print(Read_lines)
Clear_paragraph =[Read_lines[1][:-1],Read_lines[4][:-1],Read_lines[7][:-1],Read_lines[10][:-1],] #This code uses slicing to remove all the unwanted parts of my code in the begining and the end.
def similarity(s,r,n=3): #This code creates a function that we check the similarity in a file using the nGram function
'''
This function return the similarity as the fraction
of intersection and the union of the strings r and s
It takes the input strings s & r and n numbers of ngrams from the function created earlier
The function returns the fraction of string r intersection string s over string r union string s
'''
A=len(set.intersection(set(nGrams(s,n)),set(nGrams(r,n)))) #This code takes the length of a set of intersection of string r and s from the input
B=len(set.union(set(nGrams(s,n)),set(nGrams(r,n)))) #This code takes the length of a set of union of string r and s from the input
return A/B
#This code below check if there is any similarities in the file given
for i in range(4):
for j in range(i,4):
print('similarity between (Text{} , Text{}) = {}'.format(i+1,j+1,similarity(Clear_paragraph[i],Clear_paragraph[j])))
# -
# ### ***Question 4***
# ### ***a)***
# +
import numpy as np #This code will a library numpy which is used for mathematical functions like pi, sin, cos etc.
#The parameters r and K represent the growth rate and carrying capacity respectively
r = 0.4
K = 20
y_0 = 2.44 #The initial population at t=0
h = 0.01 #step size of the estimation
x_n = 50 #This is the end interval of the function
n = int(x_n/h) #This code calculates n = x_n - x_0/h to find the range of out iterations
for i in range(n+1): #This loop repeats the Runga-kutta method for 5001 times as specified by the n calculations
k_1 = h*(r*y_0*(1-y_0/K)-y_0**2/(1+y_0**2)) #This code calculates the first k value(k1) of the Runga-kutta method
y_1 = y_0 + k_1/2 #This code updates the function i.e hf(t_i+1/2*h,y_i + 1/2*k1)
k_2 = h*(r*y_1*(1-y_1/K) - y_1**2/(1 + y_1**2)) #This code calculates the second k value(k2) of the Runga-kutta method
y_2 = y_0 + k_2/2 #This code updates the function i.e hf(t_i+1/2*h,y_i + 1/2*k2)
k_3 = h*(r*y_2*(1-y_2/K) - y_2**2/(1 + y_2**2)) #This code calculates the third k value(k3) of the Runga-kutta method
y_3 = y_0 +k_3 #This code updates the function i.e hf(t_i+1/2*h,y_i + 1/2*k3)
k_4 = h*(r*y_3*(1-y_3/K) - y_3**2/(1 + y_2**2)) #This code calculates the fourth k value(k4) of the Runga-kutta method
k = (k_1/6 + k_2/3 + k_3/3 + k_4/6) #This is just the sum of all the k value in the method
y = y_0 + k #This code updates the f(t,y) function so that it can iterate the runga-kutta method
y_0 = y #This assign the new y_0 from the y above
print("The Runga-kutta four-order approximation for the population at t = 50 is {}".format(y)) #This code just print out the Runga-kutta approximation
# -
# ### ***b)***
# +
import numpy as np #This code will a library numpy which is used for mathematical functions like pi, sin, cos etc.
import matplotlib.pyplot as plt #This code import the matplotlib.pyplot library which will give the visuals of our approximation.
x_axis = [] #This code creates an empty list so that I can append the number of iterations from the loop.
y_axis = [] #This code creates an empty list for appending Runga-kutta approximation after every loop.
#The parameters r and K represent the growth rate and carrying capacity respectively.
r = 0.4
K = 20
y_0 = 2.44 #The initial population at t=0.
h = 0.01 #step size of the estimation.
x_n = 80 #This is the end interval of the function.
n = int(x_n/h) #This code calculates n = x_n - x_0/h to find the range of out iterations.
for i in range(n):
k_1 = h*(r*y_0*(1-y_0/K)-y_0**2/(1+y_0**2)) #This code calculates the first k value(k1) of the Runga-kutta method.
y_1 = y_0 + k_1/2 #This code updates the function i.e hf(t_i+1/2*h,y_i + 1/2*k1).
k_2 = h*(r*y_1*(1-y_1/K) - y_1**2/(1 + y_1**2)) #This code calculates the second k value(k2) of the Runga-kutta method.
y_2 = y_0 + k_2/2 #This code updates the function i.e hf(t_i+1/2*h,y_i + 1/2*k2).
k_3 = h*(r*y_2*(1-y_2/K) - y_2**2/(1 + y_2**2)) #This code calculates the third k value(k3) of the Runga-kutta method.
y_3 = y_0 +k_3 #This code updates the function i.e hf(t_i+1/2*h,y_i + 1/2*k3).
k_4 = h*(r*y_3*(1-y_3/K) - y_3**2/(1 + y_2**2)) #This code calculates the fourth k value(k4) of the Runga-kutta method.
k = (k_1/6 + k_2/3 + k_3/3 + k_4/6) #This is just the sum of all the k value in the method.
y = y_0 + k #This code updates the f(t,y) function so that it can iterate the runga-kutta method.
y_0 = y #This assign the new y_0 from the y above.
x_axis.append(i) #This line appends the number of iterations to plot against the Runga-kutta approximation.
y_axis.append(y) #This code appends all the Runga-kutta approximation.
plt.plot(x_axis,y_axis) #This code plot out graph for the approximation.
plt.title('Approximate solution') #This line creates the title of the plot.
plt.xlabel('x-axis') #This creates the x-axis of the graph.
plt.ylabel('y-axis') #This creates the y-axis of the graph.
plt.legend(['Runge-kutta four order']) #This line creates the legend of the approximation.
plt.grid() #This line will create the grid on the plane.
# -
# ### ***c)***
# +
import numpy as np #This code will a library numpy which is used for mathematical functions like pi, sin, cos etc.
import matplotlib.pyplot as plt #This code import the matplotlib.pyplot library which will give the visuals of our approximation.
x_axis = [] #This code creates an empty list so that I can append the number of iterations from the loop with harvesting term.
y_axis = [] #This code creates an empty list for appending Runga-kutta approximation after every loop with harvesting term.
x_axis_1 = [] #This code creates an empty list so that I can append the number of iterations from the loop without harvesting term.
y_axis_1 = [] #This code creates an empty list for appending Runga-kutta approximation after every loop without harvesting term.
#The parameters r and K represent the growth rate and carrying capacity respectively
r = 0.4
K = 20
#The initial population at t=0
y_0 = 2.44
#step size of the estimation
h = 0.01
#n = x_n - x_0/h
n = int(80/h)
for i in range(n):
k_1 = h*(r*y_0*(1-y_0/K)-y_0**2/(1+y_0**2)) #This code calculates the first k value(k1) of the Runga-kutta method.
y_1 = y_0 + k_1/2 #This code updates the function i.e hf(t_i+1/2*h,y_i + 1/2*k1).
k_2 = h*(r*y_1*(1-y_1/K) - y_1**2/(1 + y_1**2)) #This code calculates the second k value(k2) of the Runga-kutta method.
y_2 = y_0 + k_2/2 #This code updates the function i.e hf(t_i+1/2*h,y_i + 1/2*k2).
k_3 = h*(r*y_2*(1-y_2/K) - y_2**2/(1 + y_2**2)) #This code calculates the third k value(k3) of the Runga-kutta method.
y_3 = y_0 +k_3 #This code updates the function i.e hf(t_i+1/2*h,y_i + 1/2*k3).
k_4 = h*(r*y_3*(1-y_3/K) - y_3**2/(1 + y_2**2)) #This code calculates the fourth k value(k4) of the Runga-kutta method.
k = (k_1/6 + k_2/3 + k_3/3 + k_4/6) #This is just the sum of all the k value in the method.
y = y_0 + k #This code updates the f(t,y) function so that it can iterate the runga-kutta method.
y_0 = y #This assign the new y_0 from the y above.
x_axis_1.append(i) #This line appends the number of iterations to plot against the Runga-kutta approximation with harvesting term.
y_axis_1.append(y) #This code appends all the Runga-kutta approximation with harvesting term.
h = 0.01
n = int(80/h)
y_0 = 2.44
r = 0.4
K = 20
for i in range(n):
k_1 = h*(r*y_0*(1-y_0/K)) #This code calculates the first k value(k1) of the Runga-kutta method without harvesting term.
y_1 = y_0 + k_1/2 #This code updates the function i.e hf(t_i+1/2*h,y_i + 1/2*k1) without harvesting term.
k_2 = h*(r*y_1*(1-y_1/K)) #This code calculates the second k value(k2) of the Runga-kutta method without harvesting term.
y_2 = y_0 + k_2/2 #This code updates the function i.e hf(t_i+1/2*h,y_i + 1/2*k2) without harvesting term.
k_3 = h*(r*y_2*(1-y_2/K)) #This code calculates the third k value(k3) of the Runga-kutta method without harvesting term.
y_3 = y_0 +k_3 #This code updates the function i.e hf(t_i+1/2*h,y_i + 1/2*k3) without harvesting term.
k_4 = h*(r*y_3*(1-y_3/K)) #This code calculates the fourth k value(k4) of the Runga-kutta method without harvesting term.
k = (k_1/6 + k_2/3 + k_3/3 + k_4/6) #This is just the sum of all the k value in the method.
y = y_0 + k #This code updates the f(t,y) function so that it can iterate the runga-kutta method without harvesting term.
y_0 = y #This assign the new y_0 from the y above.
x_axis.append(i) #This line appends the number of iterations to plot against the Runga-kutta approximation without harvesting term.
y_axis.append(y) #This code appends all the Runga-kutta approximation without harvesting term.
plt.plot(x_axis,y_axis, color = 'r') #This code plot out graph for the approximation without the harvesting term.
plt.plot(x_axis_1,y_axis_1, color = 'k') #This code plot out graph for the approximation with the harvesting term.
plt.title('Approximate solution with and without harvesting term') #This line creates the title of the plot.
plt.xlabel('x-axis') #This creates the x-axis of the graph.
plt.ylabel('y-axis') #This creates the y-axis of the graph.
plt.legend(['RK4 without harvesting term','RK4 with harvesting term']) #This line creates the legend of the approximation with distintion from the approximation with and without the harvesting term.
plt.grid() #This line will create the grid on the plane.
# -
|
musawenkosi-python-assignment3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
#imports
import os
import tarfile
from six.moves import urllib
import pandas as pd
#Constants
DOWNLOAD_ROOT = "https://raw.githubusercontent.com/ageron/handson-ml/master/"
HOUSING_PATH = os.path.join("datasets", "housing")
HOUSING_URL = DOWNLOAD_ROOT + "datasets/housing/housing.tgz"
# +
#Utility functions
def fetch_housing_data(housing_url=HOUSING_URL, housing_path = HOUSING_PATH):
if not os.path.isdir(housing_path):
os.makedirs(housing_path)
tgz_path = os.path.join(housing_path, "housing.tgz")
urllib.request.urlretrieve(housing_url, tgz_path)
housing_tgz = tarfile.open(tgz_path)
housing_tgz.extractall(path=housing_path)
housing_tgz.close()
def load_housing_data(housing_path=HOUSING_PATH):
csv_path = os.path.join(housing_path, "housing.csv")
return pd.read_csv(csv_path)
# -
#fectch housing data.
fetch_housing_data()
# Data exploration
housing = load_housing_data()
housing.head()
#Variable information
housing.info()
# Note data type for ocean_proximity is object (text) and total_bedrooms is missing some values
#Ocean_proximity details
housing["ocean_proximity"].value_counts()
#Summary
housing.describe()
#Plot histograms for numerical values
# %matplotlib inline #This tells jupyter to use its own backend to render the plot
import matplotlib.pyplot as plt
housing.hist(bins=50, figsize=(20,15))
plt.show() #optional in jupyter
#split into train and test
#Stratify using medium income
housing["income_cat"] = pd.cut(housing["median_income"], bins = [0., 1.5, 3.0, 4.5, 6., np.inf], labels=[1, 2, 3, 4, 5])
housing["income_cat"].hist()
# +
from sklearn.model_selection import StratifiedShuffleSplit
split = StratifiedShuffleSplit(n_splits=1, test_size = 0.2, random_state=42)
for train_index, test_index in split.split(housing, housing["income_cat"]):
strat_train_set = housing.loc[train_index]
strat_test_set = housing.loc[test_index]
print(strat_train_set["income_cat"].value_counts() / len(strat_train_set))
print(housing["income_cat"].value_counts() / len(housing))
for set_ in (strat_train_set, strat_test_set):
set_.drop("income_cat", axis=1, inplace=True)
strat_test_set.to_csv("housing_test.csv")
# -
# Data Exploration (more in depth)
# +
housing=strat_train_set.copy()
#Longtitude Latitude
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.4, s=housing["population"]/100,
label="population", figsize=(10,7), c="median_house_value", cmap=plt.get_cmap("jet"),
colorbar=True) #Alpha makes density more visible
plt.legend()
# -
#Compute Pearson's r (standard correlation coefficient)
corr_matrix = housing.corr()
corr_matrix["median_house_value"].sort_values(ascending=False)
# From here, we see that median_income has the highest correlation, and the further north you go, the cheaper it gets
#Visualize the correlation
from pandas.plotting import scatter_matrix
attributes = ["median_house_value", "median_income", "total_rooms", "housing_median_age"]
scatter_matrix(housing[attributes], figsize=(12,8))
# The median_income seems to be the most correlated
#Take closer look
housing.plot(kind="scatter", x="median_income", y="median_house_value", alpha=0.1)
# Note the horizontal lines. At 500000, it is the price cap in the dataset. However, there are other barely apparent horizontal lines at 450000 and 350000
# +
#combine to see if new variables work better
housing["rooms_per_household"] = housing["total_rooms"]/housing["households"]
housing["bedrooms_per_room"] = housing["total_bedrooms"]/housing["total_rooms"]
housing["population_per_household"] = housing["population"]/housing["households"]
corr_matrix = housing.corr()
corr_matrix["median_house_value"].sort_values(ascending=False)
# -
# rooms_per_household did pretty good.
#Data preparation for model
housing = strat_train_set.drop("median_house_value", axis=1)
housing_labels = strat_train_set["median_house_value"].copy()
# +
#Replace missing values
from sklearn.impute import SimpleImputer
imputer = SimpleImputer(strategy="median")
housing_num = housing.drop("ocean_proximity", axis=1)
imputer.fit(housing_num)
print(imputer.statistics_)
print(housing_num.median().values)
X = imputer.transform(housing_num)
housing_tr = pd.DataFrame(X, columns=housing_num.columns)
housing_tr.info()
# +
#Convert ocean_proximity to numbers
from sklearn.preprocessing import OrdinalEncoder
ordinal_encoder = OrdinalEncoder()
housing_cat = housing[["ocean_proximity"]]
housing_cat_encoded_ordinal = ordinal_encoder.fit_transform(housing_cat)
print(ordinal_encoder.categories_) #view list of categories
#One hot encoder
from sklearn.preprocessing import OneHotEncoder
oneHot_encoder = OneHotEncoder()
housing_cat_encoded_oneHot = oneHot_encoder.fit_transform(housing_cat)
oneHot_encoder.categories_
# -
# Custom Transformers
# +
#BaseEstimator gives you 'get_params()' and 'set_params()' that are
#helpful for automatic parameter tuning, if you avoid *args and **kargs
#TransformerMixin gets you fit_transform()
from sklearn.base import BaseEstimator, TransformerMixin
rooms_ix, bedrooms_ix, population_ix, households_ix = 3, 4, 5, 6
class CombinedAttributeAdder(BaseEstimator, TransformerMixin):
def __init__(self, add_bedrooms_per_room = True):
self.add_bedrooms_per_room = add_bedrooms_per_room
def fit(self, X, y=None):
return self
def transform(self, X, y=None):
rooms_per_household = X[:,rooms_ix] / X[:,households_ix]
population_per_household = X[:, population_ix] / X[:, households_ix]
if self.add_bedrooms_per_room:
bedrooms_per_room = X[:, bedrooms_ix] / X[:, rooms_ix]
return np.c_[X, rooms_per_household, population_per_household, bedrooms_per_room]
else:
return np.c_[X, rooms_per_household, population_per_household]
#Try it out
attr_adder = CombinedAttributeAdder(add_bedrooms_per_room=False)
housing_extra_attribs = attr_adder.transform(housing.values)
housing_extra_attribs
# +
#Pipelines and feature scaling
#MinMaxScaler (range) and StandardScaler (handles outliers well)
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
num_pipeline = Pipeline([
('imputer', SimpleImputer(strategy="median")),
('attribs_adder', CombinedAttributeAdder()),
('std_scaler', StandardScaler())
])
housing_num_tr = num_pipeline.fit_transform(housing_num)
# +
#Applying appropriate transforms to columns
from sklearn.compose import ColumnTransformer
num_attribs = list(housing_num)
cat_attribs = ["ocean_proximity"]
full_pipeline = ColumnTransformer([
("num", num_pipeline, num_attribs),
("cat", OneHotEncoder(), cat_attribs)
])
full_pipeline.fit(housing)
housing_prepared = full_pipeline.transform(housing)
# +
#Try different models on the prepared data
#Try linear regression model
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(housing_prepared, housing_labels)
#Root mean square error
from sklearn.metrics import mean_squared_error
housing_predictions = lin_reg.predict(housing_prepared)
lin_mse = mean_squared_error(housing_labels, housing_predictions)
lin_rmse = np.sqrt(lin_mse)
print("Linear regression RMSE:", lin_rmse)
#Decision Tree regressor
from sklearn.tree import DecisionTreeRegressor
tree_reg = DecisionTreeRegressor()
tree_reg.fit(housing_prepared, housing_labels)
housing_predictions_tree = tree_reg.predict(housing_prepared)
tree_mse = mean_squared_error(housing_labels, housing_predictions_tree)
tree_rmse = np.sqrt(tree_mse)
print("Decision tree RMSE:", tree_rmse)
# -
# Note underfitting in the case of Linear regression and over fitting in the case of the Decision tree
# +
#Evaluation using cross validation
from sklearn.model_selection import cross_val_score
tree_scores = cross_val_score(tree_reg, housing_prepared, housing_labels, scoring="neg_mean_squared_error", cv=10)
tree_rmse_scores = np.sqrt(-tree_scores) #negative because cross_val_score expects a utility function (greater is better)
lin_scores = cross_val_score(lin_reg, housing_prepared, housing_labels, scoring="neg_mean_squared_error", cv=10)
lin_rmse_scores = np.sqrt(-lin_scores)
def display_scores(scores):
print("Scores:", scores)
print("mean:", scores.mean())
print("Standard deviation:", scores.std())
display_scores(tree_rmse_scores)
display_scores(lin_rmse_scores)
#Saving models (you can also use pickle module)
from sklearn.externals import joblib
def save_model(model, model_name):
joblib.dump(model, model_name)
def load_model(model_name):
return joblib.load(model_name)
# +
#Random forest tree
from sklearn.ensemble import RandomForestRegressor
forest_reg = RandomForestRegressor()
forest_reg.fit(housing_prepared, housing_labels)
forest_reg_scores = cross_val_score(forest_reg, housing_prepared, housing_labels, scoring="neg_mean_squared_error", cv=10)
forest_reg_rmse_scores = np.sqrt(-forest_reg_scores)
display_scores(forest_reg_rmse_scores)
# +
#Gridsearch to fine-tune hyperparameters
from sklearn.model_selection import GridSearchCV
param_grid = [
{'n_estimators':[3, 10, 30], 'max_features':[2, 4, 6, 8]},
{'bootstrap': [False], 'n_estimators':[3, 10], 'max_features':[2,3,4]}
]
forest_reg = RandomForestRegressor()
grid_search = GridSearchCV(forest_reg, param_grid, cv=5, scoring='neg_mean_squared_error', return_train_score=True)
grid_search.fit(housing_prepared, housing_labels)
grid_search.best_params_
# +
#Getting the best estimator directly(??)
grid_search.best_estimator_
# +
#Evaluation scores
cvres=grid_search.cv_results_
for mean_score, params in zip(cvres["mean_test_score"], cvres["params"]):
print(np.sqrt(-mean_score), params)
# -
#See importance of features for making predictions
feature_importance = grid_search.best_estimator_.feature_importances_
extra_attribs = ["rooms_per_hhold", "pop_per_hhold", "bedrooms_per_room"]
cat_encoder = full_pipeline.named_transformers_["cat"]
cat_one_hot_attribs = list(cat_encoder.categories_[0])
print(cat_one_hot_attribs)
attributes = num_attribs + extra_attribs + cat_one_hot_attribs
sorted(zip(feature_importance, attributes), reverse=True)
# +
#Evaluate on the test set
final_model = grid_search.best_estimator_
X_test = strat_test_set.drop("median_house_value", axis=1)
y_test = strat_test_set["median_house_value"].copy()
X_test_prepared = full_pipeline.transform(X_test)
final_predictions = final_model.predict(X_test_prepared)
final_mse = mean_squared_error(y_test, final_predictions)
final_rmse = np.sqrt(final_mse)
final_rmse
# -
|
HousingPrices/Housing.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import pandas as pd
trade = pd.read_csv('comtrade.csv')[['Year', 'Trade Flow', 'Partner', 'Commodity', 'Trade Value (US$)']]
trade.head()
# +
files = ['comtrade (1).csv', 'comtrade (2).csv', 'comtrade (3).csv']
for f in files:
df = pd.read_csv(f)[['Year', 'Trade Flow', 'Partner', 'Commodity', 'Trade Value (US$)']]
trade = pd.concat([trade, df])
trade.Partner.unique()
# -
trade.head()
trade.info()
trade.to_excel('Final Trade.xlsx', index=False)
trade['Year'] = trade['Year'].astype(str)
trade['Key'] = trade['Year'] + '_' + trade['Partner'] + '_' + trade['Commodity']
trade.info()
trade2 = pd.pivot_table(trade, values='Trade Value (US$)', index='Key', columns = 'Trade Flow', aggfunc=np.sum).reset_index()
trade2.head()
trade2['Year'] = trade2['Key'].apply(lambda x: x.split('_')[0])
trade2['Partner'] = trade2['Key'].apply(lambda x: x.split('_')[1])
trade2['Commodity'] = trade2['Key'].apply(lambda x: x.split('_')[2])
trade2.head()
trade2.drop(columns='Key', inplace=True)
trade2.Year = trade2.Year.astype('int64')
trade2.info()
trade2.to_excel('Final Trade2.xlsx', index=False)
trade2.Year.unique()
# # World
# +
files = []
for i in range(5, 8, 1):
file = "comtrade (" + str(i) + ").csv"
files.append(file)
files
# -
world = pd.read_csv('comtrade (4).csv')[['Year', 'Reporter', 'Commodity', 'Trade Value (US$)']]
world.head()
# +
for f in files:
df = pd.read_csv(f)[['Year', 'Reporter', 'Commodity', 'Trade Value (US$)']]
world = pd.concat([world, df])
world.Commodity.unique()
# -
world.to_excel('world.xlsx')
world.columns
|
Data Prep.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Importing Libraries
import numpy as np
import gdal
import ogr, osr
import matplotlib.pyplot as plt
import geoconvert
# ### Supporting Functions
# #### To remap array
def remap_array(arr):
"""
Remapping [3, 256,256] to [256,256,3]
"""
return np.moveaxis(arr, 0, 2)
# #### WKT to EPSG conversion
def wkt2epsg(wkt):
"""
From https://gis.stackexchange.com/questions/20298/is-it-possible-to-get-the-epsg-value-from-an-osr-spatialreference-class-using-th
Transform a WKT string to an EPSG code
Arguments
---------
wkt: WKT definition
Returns: EPSG code
"""
p_in = osr.SpatialReference()
s = p_in.ImportFromWkt(wkt)
if s == 5: # invalid WKT
return None
if p_in.IsLocal() == 1: # this is a local definition
return p_in.ExportToWkt()
if p_in.IsGeographic() == 1: # this is a geographic srs
cstype = 'GEOGCS'
else: # this is a projected srs
cstype = 'PROJCS'
an = p_in.GetAuthorityName(cstype)
ac = p_in.GetAuthorityCode(cstype)
if an is not None and ac is not None: # return the EPSG code
return int(p_in.GetAuthorityCode(cstype))
# ### Path location of raster dataset and shapefiles
path_tif = '../data/City.tif'
path_shp = '../data/clip_shp_geo.shp'
# ### Path location of output raster dataset
dst_path = '../data/City_clipped.tif'
dat_path_bbox = '../data/City_clipped_bbox.tif'
dst_shp = '../data/shp_proj.shp'
# ### Defining formats of datasets
RasterFormat = 'GTiff'
VectorFormat = 'ESRI Shapefile'
# ### Reading input raster dataset
src_ds = gdal.Open(path_tif)
if src_ds is not None:
print('Source raster dataset loaded')
else:
raise(Exception('Error loading data'))
# ### Checking projection system of input raster and vector file
# These projection must be same else clipping is not possible
VectorDriver = ogr.GetDriverByName(VectorFormat)
VectorDataset = VectorDriver.Open(path_shp, 0) # 0=Read-only, 1=Read-Write
layer = VectorDataset.GetLayer()
vector_proj = layer.GetSpatialRef().ExportToWkt()
Projection = src_ds.GetProjectionRef()
if not int(wkt2epsg(Projection)) == int(wkt2epsg(vector_proj)):
data = geoconvert.vector()
# Loading data
data.path_input = path_shp
data.config()
# Converting data
data.toshp(epsg=int(wkt2epsg(Projection)), path_toshp=dst_shp)
path_shp = dst_shp
# ### Reading projection information of raster dataset
# Open datasets
Projection = src_ds.GetProjectionRef()
# ### Clipping exactly as shapefile given
OutTile = gdal.Warp(dst_path, src_ds,
format=RasterFormat,
dstSRS=Projection,
cutlineDSName=path_shp,
cropToCutline=True,
multithread=True)
# ### Visualizing results
arr = remap_array(OutTile.ReadAsArray())
plt.imshow(arr)
# ### Saving to Disk
OutTile.FlushCache()
OutTile = None # Close dataset
Raster = None
print("Done.")
# ### Clipping as bounding box of shapefile given
# #### Reading vector data to extract bounds
VectorDriver = ogr.GetDriverByName(VectorFormat)
VectorDataset = VectorDriver.Open(path_shp, 0) # 0=Read-only, 1=Read-Write
layer = VectorDataset.GetLayer()
feature = layer.GetFeature(0)
geom = feature.GetGeometryRef()
minX, maxX, minY, maxY = geom.GetEnvelope() # Get bounding box of the shapefile feature
# #### Clipping from datasource
OutTile = gdal.Warp(dat_path_bbox, src_ds,
format=RasterFormat,
outputBounds=[minX, minY, maxX, maxY],
dstSRS=Projection,
multithread=True)
# #### Visualizing results
arr = remap_array(OutTile.ReadAsArray())
plt.imshow(arr)
# #### Saving to Disk
# +
OutTile.FlushCache()
OutTile = None # Close dataset
Raster = None
VectorDataset.Destroy()
print("Done.")
# -
|
notebooks/Clipping Raster.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] colab_type="text" id="2bhiZKFiIWbK"
# # Non-Federated EMNIST Baseline Training
#
# This colab has three main parts:
#
# * It trains a non-federated model on a flattened and shuffled (that is,
# non-federated) view of the the
# [Federated EMNIST](https://www.tensorflow.org/federated/api_docs/python/tff/simulation/datasets/emnist/load_data)
# dataset. The model architecture matches the simple CNN from the paper
# [Communication-Efficient Learning of Deep Networks from Decentralized Data](https://arxiv.org/abs/1602.05629).
# This (currently untuned) training reaches an accuracy of about 97% with
# vanilla SGD. (Note these accuracy numbers are not directly comparable to
# MNIST results, as the train and test datasets are different). This is
# intended to serve as a baseline for simulated federated training on the Fed
# EMNIST dataset.
#
# * It uses this model to examine the Fed EMNIST dataset, showing it has
# interesting variation across users.
#
# * As a sanity check, it shows an equivalent model can be trained using the
# `Federated Averaging` implementation from `tff.learning` applied to a
# non-federated (that is, flattened and shuffled) view of the data.
#
#
# **Note:** This notebook will probably take ~25 minutes to fully execute.
# + colab_type="code" id="CZ2s96PebCkJ" colab={}
# !pip install tensorflow_federated
# !pip install tensorflow_gan
# + colab_type="code" id="h2CQ4u1H0I_B" colab={}
from __future__ import absolute_import, division, print_function
import collections
import functools
import numpy as np
import time
import matplotlib.pyplot as plt
import pandas as pd
import tensorflow as tf
import tensorflow_federated as tff
import tensorflow_gan as tfgan
tf.compat.v1.enable_v2_behavior()
# + [markdown] colab_type="text" id="w3q3XlRja0tn"
# # Training a baseline model with Keras
# + [markdown] colab_type="text" id="sPSSgR7kRv0z"
# ## Data
#
# Download the data, and lightly reformat for use in Keras.
# + colab_type="code" id="lr7O_KnZR1jW" colab={}
emnist_train, emnist_test = tff.simulation.datasets.emnist.load_data()
# + colab_type="code" id="I9HmvLs_R7dK" colab={}
Example = collections.namedtuple('Example', ['x', 'y'])
BATCH_SIZE = 10
SHUFFLE_BUFFER = 50000
def element_fn(element):
return Example(
x=tf.reshape(element['pixels'], [-1]),
y=tf.reshape(element['label'], [1]))
def preprocess_train(dataset, batch_size=BATCH_SIZE):
return dataset.map(element_fn).apply(
tf.data.experimental.shuffle_and_repeat(
buffer_size=SHUFFLE_BUFFER, count=-1)).batch(batch_size)
def preprocess_test(dataset):
return dataset.map(element_fn).batch(100, drop_remainder=False)
# TODO(b/135021147): Use the seed kwarg once it is supported in
# create_tf_dataset_from_all_clients to ensure clients are
# produced in a random order in the raw dataset. The SHUFFLE_BUFFER
# can probably be decreased in size once this is done.
flat_train_data = preprocess_train(
emnist_train.create_tf_dataset_from_all_clients())
flat_test_data = preprocess_test(
emnist_test.create_tf_dataset_from_all_clients())
# + [markdown] colab_type="text" id="Sg31X5CLRu4m"
# ## Model
# + colab_type="code" id="K7MG76AhjxxL" colab={}
def build_cnn():
"""The CNN model used in https://arxiv.org/abs/1602.05629.
The number of parameters (1,663,370) matches what is reported in the paper.
"""
data_format = 'channels_last'
input_shape = [28, 28, 1]
# Alternatively:
# data_format = 'channels_first'
# input_shape = [1, 28, 28]
max_pool = lambda: tf.keras.layers.MaxPooling2D(
pool_size=(2, 2), padding='same', data_format=data_format)
conv2d = functools.partial(
tf.keras.layers.Conv2D,
kernel_size=5,
padding='same',
data_format=data_format,
activation=tf.nn.relu)
model = tf.keras.models.Sequential([
tf.keras.layers.Reshape(target_shape=input_shape, input_shape=(28 * 28,)),
conv2d(filters=32),
max_pool(),
conv2d(filters=64),
max_pool(),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(512, activation=tf.nn.relu),
tf.keras.layers.Dense(10, activation=tf.nn.softmax),
])
model.compile(
loss=tf.keras.losses.sparse_categorical_crossentropy,
# This learning rate has not been tuned.
optimizer=tf.keras.optimizers.SGD(learning_rate=0.02),
metrics=[tf.keras.metrics.SparseCategoricalAccuracy()])
return model
build_cnn().summary()
# + [markdown] colab_type="text" id="JCBszLXUTzTP"
# ## Training and evaluation
# + colab_type="code" id="W1QJ4WPosLGC" colab={}
NUM_ROUNDS = 10
BATCHES_PER_ROUND = 1000
# + colab_type="code" id="jlq0KEy3RndT" colab={}
model = build_cnn()
# We set steps_per_epoch and epochs just to break training up in reasonable "chunks".
# These aren't really epochs over the full dataset.
# Training could take about 8 minutes.
model.fit(flat_train_data, steps_per_epoch=BATCHES_PER_ROUND, epochs=NUM_ROUNDS)
# + [markdown] colab_type="text" id="3eV1He4dfuRf"
# There are 40,832 test examples, so we take 409 eval steps with a test batch size
# of 100:
# + colab_type="code" id="bB1g32bFRpSC" colab={}
_ = model.evaluate(flat_test_data)
# + [markdown] colab_type="text" id="_dwWV0jqy-Y-"
# # Aside: Do some users have hard-to-classify data?
#
# Since this is a public dataset intended for research, one interesting thing we
# can do with the model is to use it to see if some users
# have hard-to-classify data. This is way of verifying that the Federated EMNIST
# dataset has interesting variation across users.
# + colab_type="code" id="Dcsg0IUb0o77" colab={}
def display_raw_emnist(data, grid_width=25):
"""A helper function to display images from Fed EMNIST datasets."""
# List of numpy images
img_data = np.array([x['pixels'].numpy() for x in data])
img_data = np.reshape(img_data, (-1, 28, 28, 1))
num_rows = int(np.ceil(len(img_data) / grid_width))
# Pad to rectangular since tfgan.eval.python_image_grid
# expects this.
needed_images = num_rows * grid_width
tmp = np.zeros((needed_images, 28, 28, 1))
s = img_data.shape
tmp[:s[0], :s[1], :s[2]] = img_data
img_data = tmp
img_grid = tfgan.eval.python_image_grid(
img_data, grid_shape=(num_rows, grid_width))
h = 20
w = h * (grid_width / num_rows)
plt.figure(figsize=(h, w))
plt.axis('off')
plt.imshow(np.squeeze(img_grid), cmap='binary')
plt.show()
# + [markdown] colab_type="text" id="xCfC_ro25y31"
# Display the data from clients with accuracy below a threshold.
# + colab_type="code" id="e6RZHtMjzDOL" colab={}
accuracy_by_client_id = {}
THRESHOLD = 0.82
for i, client_id in enumerate(emnist_train.client_ids):
raw_data = emnist_train.create_tf_dataset_for_client(client_id)
num_examples = sum([1 for _ in raw_data])
loss, accuracy = model.evaluate(preprocess_test(raw_data), verbose=0)
accuracy_by_client_id[client_id] = accuracy
if accuracy < THRESHOLD:
print('client {} ({}) with {:3d} examples has accuracy {:6.2f}%'.format(
i, client_id, num_examples, 100 * accuracy))
display_raw_emnist(raw_data)
# + [markdown] id="EnwfiozoYXzP" colab_type="text"
# ## Accuracy vs client_id
# Now, let's plot accuracy versus the (sorted) `client_id`s. We are interested in the general trend, so we use a moving average over clients.
# + id="Qp-E4z6h_sJq" colab_type="code" colab={}
client_ids = sorted(list(emnist_train.client_ids))
y = [accuracy_by_client_id[client_id] for client_id in client_ids]
y = pd.Series(y).rolling(window=50).mean(center=True)
plt.figure(figsize=(15, 3))
plt.plot(range(len(y)), y)
plt.title('Rolling mean accuracy vs client_id')
plt.xlabel('client_id')
plt.ylabel('Accuracy')
plt.ylim(0.9, 1.0)
s1 = client_ids.index('f2100_97')
s2 = client_ids.index('f3100_44')
x_loc = [500, 1000, 1500, s1, s2, 3000]
plt.xticks(x_loc, [str(client_ids[x]) for x in x_loc])
plt.vlines([s1, s2], 0.9, 1.0)
plt.show()
# + [markdown] id="5TBfxMytU7iC" colab_type="text"
# There appears to be a correlation between the (sorted) `client_id`s and accuracy. This is likely due to the client_ids indicating the source; see Table 2 in the [User's Guide](https://s3.amazonaws.com/nist-srd/SD19/1stEditionUserGuide.pdf) for the NIST Special Database 19. Writers `f0000` - `f2099` were Census Bureau field personal, `f2100` - `f3099` were high school students, and `f3100` - `f4099` were Census Bureau employees in Maryland.
#
# This finding implies that for centralized baseline training (as we did above), sufficient shuffling of the data is important (see also the TODO(b/135021147) above to improve this).
#
# For federated training, randomly sampling users is important; alternatively, this data could be used to simulate three different "blocks" of users to test the behavior of [Semi-Cyclic Stochastic Gradient Descent](https://arxiv.org/abs/1904.10120) as well as the mitigations suggested in the linked paper; non-federated experiments can be found [here](https://github.com/tensorflow/federated/tree/master/tensorflow_federated/python/research/semi_cyclic_sgd).
# + [markdown] colab_type="text" id="v-ZmqrkufEz6"
# # Replicating the baseline with `tff.learning`
#
# Here we show how to use `tff.learning` to replicate the non-federated
# baseline. However, critically *the training is still essentially
# non-federated* --- that is, this is a santiy check, not a proper simulation of
# federated learning.
#
# The approach is based on the fact that if each "client" has IID shuffled data
# from a centralized training set, and we use the `FederatedAveraging` algorithm
# with one client per round (so there is no actual averaging), then this is
# algorithmically equivalent to running SGD centrally.
#
# + [markdown] id="567-s6ogbm-p" colab_type="text"
#
# ## Construct the `federated_averaging_process`
# + colab_type="code" id="1IoZ-T3g7kwT" colab={}
dummy_batch = tf.nest.map_structure(lambda x: x.numpy(),
next(iter(flat_train_data.take(1))))
def create_tff_model():
keras_model = build_cnn()
return tff.learning.from_compiled_keras_model(
build_cnn(), dummy_batch=dummy_batch)
fed_avg_process = tff.learning.build_federated_averaging_process(
model_fn=create_tff_model)
# + [markdown] colab_type="text" id="NFom89Rg6X2I"
# ## Helper for selecting datasets for each "round"
# We work around a dataset issue to construct a sequence of Datasets each containing
# `BATCHES_PER_ROUND` batches of size `BATCH_SIZE` from the flat shuffled
# training data.
#
# TODO(b/134945216): Once supported, use `tf.data.Dataset.window()` instead.
# + colab_type="code" id="QcXJcjuP6VXp" colab={}
# Dataset of "big" batches to work around window issue (b/134945216)
tff_train_data = preprocess_train(
emnist_train.create_tf_dataset_from_all_clients(),
batch_size=BATCH_SIZE * BATCHES_PER_ROUND)
tff_train_data_iter = iter(tff_train_data)
def next_client_dataset():
# Grab the next "big" batch, create a dataset, and split into regular batches.
client_data = tf.data.Dataset.from_tensor_slices(next(tff_train_data_iter))
return client_data.batch(BATCH_SIZE)
# + [markdown] colab_type="text" id="wDojCQ2O6j_W"
# ## Training and evaluation
#
# Now we are ready to do some training. We do 10 rounds of 1000 batches per round,
# but the split between rounds doesn't really matter.
# + colab_type="code" id="--5NwJKrqX0N" colab={}
state = fed_avg_process.initialize()
print('Running Federated Averaging')
start_time = time.time()
for i in range(NUM_ROUNDS):
# Run one round of FederatedAveraging, on a single client.
round_start_time = time.time()
state, metrics = fed_avg_process.next(state, [next_client_dataset()])
finish_time = time.time()
print('Round {:3d} took {:6.2f} seconds (total {:4.0f} seconds). '
'Training metrics: {}'.format(i, finish_time - round_start_time,
finish_time - start_time, metrics))
# + colab_type="code" id="PuJhFT8L7VPj" colab={}
print('Final model evaluation on test data')
keras_model = build_cnn()
tff.learning.assign_weights_to_keras_model(keras_model, state.model)
_ = keras_model.evaluate(flat_test_data)
|
tensorflow_federated/python/research/emnist_baseline/non_federated_emnist_baseline.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] deletable=false name="Ent\u00eate, Ph\u00e9nom\u00e8nes d'\u00e9changes 1"
# |<img style="float:left;" src="http://pierreproulx.espaceweb.usherbrooke.ca/images/usherb_transp.gif" > |<NAME>, ing, professeur|
# |:---|:---|
# |Département de génie chimique et de génie biotechnologique |** GCH200-Phénomènes d'échanges I **|
#
#
# -
# ### Section 18-2, diffusion binaire dans un milieu stagnant
#
# <img src='http://pierreproulx.espaceweb.usherbrooke.ca/images/Chap-18-Section-18-2.png'>
#
# Voir les hypothèses dans le livre de Transport Phenomena.
#
#
# <NAME>
#
#
# Préparation de l'affichage et des outils de calcul symbolique
#
import sympy as sp
from IPython.display import *
sp.init_printing(use_latex=True)
# %matplotlib inline
# +
# Paramètres, variables et fonctions
z_1,z_2,z,D_AB,X_A1,X_A2,S,delta_z,C1,C2=sp.symbols('z_1,z_2,z,D_AB,X_A1,X_A2,S,delta_z,C1,C2')
N_A=sp.symbols('N_A')
X_A=sp.Function('X_A')(z)
# -
#
# Bilan sur la colonne de diffusion
#
eq=(S*N_A(z)-S*N_A(z+delta_z))/(S*delta_z)
display(eq)
eq=sp.limit(eq,delta_z,0).doit()
display(eq)
fick=-D_AB/(1-X_A)*sp.diff(X_A,z)
eq=eq.subs(N_A(z),fick)
display(eq)
X_A=sp.dsolve(eq,X_A)
display(X_A)
X_A=X_A.rhs
# Pose et solution des 2 équations de conditions aux limites pour C1 et C2
condition_1=sp.Eq(X_A.subs(z,z_1)-X_A1,0)
condition_2=sp.Eq(X_A.subs(z,z_2)-X_A2,0)
constantes=sp.solve([condition_1,condition_2],sp.symbols('C1,C2'),dict=True) # C1 et C2
constantes=constantes[0] # ramener la liste contenant le dictionnaire des constantes
display(constantes) # sous forme de dictionnaire
X_A=X_A.subs(constantes) #
display(X_A.simplify())
#
# La forme de l'équation est lourde, voir plus bas pour formuler de façon plus simple.
#
#
# Tracons avec des valeurs réalistes
#
dico={'z_1':0.00,'z_2':0.2,'X_A1':0.5,'X_A2':0.1}
X_Aplot=X_A.subs(dico)
display(X_Aplot)
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize']=10,8
sp.plot(X_Aplot,(z,0.0,0.2),ylabel='X_A',ylim=[0,1],adaptive=False)
### Ici on peut regarder le profil de concentration en choisissant une géométrie
### un peu simplifiée, par exemple z1=0 et z2=L. Regardons si le profil serait plus simple
### à lire
X_As=X_A.subs(sp.symbols('z_1'),0)
X_As=X_As.subs(sp.symbols('z_2'),sp.symbols('L'))
display(X_As)
### De plus, on pourrait utiliser XB=XA-1
X_As=X_As.subs(sp.symbols('X_A1'),1-sp.symbols('X_B1'))
X_As=X_As.subs(sp.symbols('X_A2'),1-sp.symbols('X_B2'))
display(X_As.simplify())
### en effet, on aurait intérêt à utiliser une notation simplifiée ou z2-z1=L et z1=0.
|
Chap-18-Section-18-2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Dependent density regression
# In another [example](dp_mix.ipynb), we showed how to use Dirichlet processes to perform Bayesian nonparametric density estimation. This example expands on the previous one, illustrating dependent density regression.
#
# Just as Dirichlet process mixtures can be thought of as infinite mixture models that select the number of active components as part of inference, dependent density regression can be thought of as infinite [mixtures of experts](https://en.wikipedia.org/wiki/Committee_machine) that select the active experts as part of inference. Their flexibility and modularity make them powerful tools for performing nonparametric Bayesian Data analysis.
# +
# %matplotlib inline
import pymc3 as pm
import numpy as np
import pandas as pd
from matplotlib import animation as ani, pyplot as plt
import seaborn as sns
from theano import shared, tensor as tt
from IPython.display import HTML
plt.style.use('seaborn-darkgrid')
print('Running on PyMC3 v{}'.format(pm.__version__))
# -
plt.rc('animation', writer='ffmpeg')
blue, *_ = sns.color_palette()
SEED = 972915 # from random.org; for reproducibility
np.random.seed(SEED)
# We will use the LIDAR data set from <NAME>'s excellent book, [_All of Nonparametric Statistics_](http://www.stat.cmu.edu/~larry/all-of-nonpar/). We standardize the data set to improve the rate of convergence of our samples.
# +
DATA_URI = 'http://www.stat.cmu.edu/~larry/all-of-nonpar/=data/lidar.dat'
def standardize(x):
return (x - x.mean()) / x.std()
df = (pd.read_csv(DATA_URI, sep=' *', engine='python')
.assign(std_range=lambda df: standardize(df.range),
std_logratio=lambda df: standardize(df.logratio)))
# -
df.head()
# We plot the LIDAR data below.
# +
fig, ax = plt.subplots(figsize=(8, 6))
ax.scatter(df.std_range, df.std_logratio,
c=blue);
ax.set_xticklabels([]);
ax.set_xlabel("Standardized range");
ax.set_yticklabels([]);
ax.set_ylabel("Standardized log ratio");
# -
# This data set has a two interesting properties that make it useful for illustrating dependent density regression.
#
# 1. The relationship between range and log ratio is nonlinear, but has locally linear components.
# 2. The observation noise is [heteroskedastic](https://en.wikipedia.org/wiki/Heteroscedasticity); that is, the magnitude of the variance varies with the range.
#
# The intuitive idea behind dependent density regression is to reduce the problem to many (related) density estimates, conditioned on fixed values of the predictors. The following animation illustrates this intuition.
# +
fig, (scatter_ax, hist_ax) = plt.subplots(ncols=2, figsize=(16, 6))
scatter_ax.scatter(df.std_range, df.std_logratio,
c=blue, zorder=2);
scatter_ax.set_xticklabels([]);
scatter_ax.set_xlabel("Standardized range");
scatter_ax.set_yticklabels([]);
scatter_ax.set_ylabel("Standardized log ratio");
bins = np.linspace(df.std_range.min(), df.std_range.max(), 25)
hist_ax.hist(df.std_logratio, bins=bins,
color='k', lw=0, alpha=0.25,
label="All data");
hist_ax.set_xticklabels([]);
hist_ax.set_xlabel("Standardized log ratio");
hist_ax.set_yticklabels([]);
hist_ax.set_ylabel("Frequency");
hist_ax.legend(loc=2);
endpoints = np.linspace(1.05 * df.std_range.min(), 1.05 * df.std_range.max(), 15)
frame_artists = []
for low, high in zip(endpoints[:-1], endpoints[2:]):
interval = scatter_ax.axvspan(low, high,
color='k', alpha=0.5, lw=0, zorder=1);
*_, bars = hist_ax.hist(df[df.std_range.between(low, high)].std_logratio,
bins=bins,
color='k', lw=0, alpha=0.5);
frame_artists.append((interval,) + tuple(bars))
animation = ani.ArtistAnimation(fig, frame_artists,
interval=500, repeat_delay=3000, blit=True)
plt.close(); # prevent the intermediate figure from showing
# -
HTML(animation.to_html5_video())
# As we slice the data with a window sliding along the x-axis in the left plot, the empirical distribution of the y-values of the points in the window varies in the right plot. An important aspect of this approach is that the density estimates that correspond to close values of the predictor are similar.
#
# In the previous example, we saw that a Dirichlet process estimates a probability density as a mixture model with infinitely many components. In the case of normal component distributions,
#
# $$y \sim \sum_{i = 1}^{\infty} w_i \cdot N(\mu_i, \tau_i^{-1}),$$
#
# where the mixture weights, $w_1, w_2, \ldots$, are generated by a [stick-breaking process](https://en.wikipedia.org/wiki/Dirichlet_process#The_stick-breaking_process).
#
# Dependent density regression generalizes this representation of the Dirichlet process mixture model by allowing the mixture weights and component means to vary conditioned on the value of the predictor, $x$. That is,
#
# $$y\ |\ x \sim \sum_{i = 1}^{\infty} w_i\ |\ x \cdot N(\mu_i\ |\ x, \tau_i^{-1}).$$
#
# In this example, we will follow Chapter 23 of [_Bayesian Data Analysis_](http://www.stat.columbia.edu/~gelman/book/) and use a probit stick-breaking process to determine the conditional mixture weights, $w_i\ |\ x$. The probit stick-breaking process starts by defining
#
# $$v_i\ |\ x = \Phi(\alpha_i + \beta_i x),$$
#
# where $\Phi$ is the cumulative distribution function of the standard normal distribution. We then obtain $w_i\ |\ x$ by applying the stick breaking process to $v_i\ |\ x$. That is,
#
# $$w_i\ |\ x = v_i\ |\ x \cdot \prod_{j = 1}^{i - 1} (1 - v_j\ |\ x).$$
#
# For the LIDAR data set, we use independent normal priors $\alpha_i \sim N(0, 5^2)$ and $\beta_i \sim N(0, 5^2)$. We now express this this model for the conditional mixture weights using `pymc3`.
# +
def norm_cdf(z):
return 0.5 * (1 + tt.erf(z / np.sqrt(2)))
def stick_breaking(v):
return v * tt.concatenate([tt.ones_like(v[:, :1]),
tt.extra_ops.cumprod(1 - v, axis=1)[:, :-1]],
axis=1)
# +
N, _ = df.shape
K = 20
std_range = df.std_range.values[:, np.newaxis]
std_logratio = df.std_logratio.values[:, np.newaxis]
x_lidar = shared(std_range, broadcastable=(False, True))
with pm.Model() as model:
alpha = pm.Normal('alpha', 0., 5., shape=K)
beta = pm.Normal('beta', 0., 5., shape=K)
v = norm_cdf(alpha + beta * x_lidar)
w = pm.Deterministic('w', stick_breaking(v))
# -
# We have defined `x_lidar` as a `theano` [`shared`](http://deeplearning.net/software/theano/library/compile/shared.html) variable in order to use `pymc3`'s posterior prediction capabilities later.
#
# While the dependent density regression model theoretically has infinitely many components, we must truncate the model to finitely many components (in this case, twenty) in order to express it using `pymc3`. After sampling from the model, we will verify that truncation did not unduly influence our results.
#
# Since the LIDAR data seems to have several linear components, we use the linear models
#
# $$
# \begin{align*}
# \mu_i\ |\ x
# & \sim \gamma_i + \delta_i x \\
# \gamma_i
# & \sim N(0, 10^2) \\
# \delta_i
# & \sim N(0, 10^2)
# \end{align*}
# $$
#
# for the conditional component means.
with model:
gamma = pm.Normal('gamma', 0., 10., shape=K)
delta = pm.Normal('delta', 0., 10., shape=K)
mu = pm.Deterministic('mu', gamma + delta * x_lidar)
# Finally, we place the prior $\tau_i \sim \textrm{Gamma}(1, 1)$ on the component precisions.
with model:
tau = pm.Gamma('tau', 1., 1., shape=K)
obs = pm.NormalMixture('obs', w, mu, tau=tau, observed=std_logratio)
# We now sample from the dependent density regression model.
# +
SAMPLES = 20000
BURN = 10000
with model:
step = pm.Metropolis()
trace = pm.sample(SAMPLES, step, chains=1, tune=BURN, random_seed=SEED)
# -
# To verify that truncation did not unduly influence our results, we plot the largest posterior expected mixture weight for each component. (In this model, each point has a mixture weight for each component, so we plot the maximum mixture weight for each component across all data points in order to judge if the component exerts any influence on the posterior.)
# +
fig, ax = plt.subplots(figsize=(8, 6))
ax.bar(np.arange(K) + 1,
trace['w'].mean(axis=0).max(axis=0));
ax.set_xlim(1 - 0.5, K + 0.5);
ax.set_xticks(np.arange(0, K, 2) + 1);
ax.set_xlabel('Mixture component');
ax.set_ylabel('Largest posterior expected\nmixture weight');
# -
# Since only three mixture components have appreciable posterior expected weight for any data point, we can be fairly certain that truncation did not unduly influence our results. (If most components had appreciable posterior expected weight, truncation may have influenced the results, and we would have increased the number of components and sampled again.)
#
# Visually, it is reasonable that the LIDAR data has three linear components, so these posterior expected weights seem to have identified the structure of the data well. We now sample from the posterior predictive distribution to get a better understand the model's performance.
# +
PP_SAMPLES = 5000
lidar_pp_x = np.linspace(std_range.min() - 0.05, std_range.max() + 0.05, 100)
x_lidar.set_value(lidar_pp_x[:, np.newaxis])
with model:
pp_trace = pm.sample_posterior_predictive(trace, PP_SAMPLES, random_seed=SEED)
# -
# Below we plot the posterior expected value and the 95% posterior credible interval.
# +
fig, ax = plt.subplots(figsize=(8, 6))
ax.scatter(df.std_range, df.std_logratio,
c=blue, zorder=10,
label=None);
low, high = np.percentile(pp_trace['obs'], [2.5, 97.5], axis=0)
ax.fill_between(lidar_pp_x, low, high,
color='k', alpha=0.35, zorder=5,
label='95% posterior credible interval');
ax.plot(lidar_pp_x, pp_trace['obs'].mean(axis=0),
c='k', zorder=6,
label='Posterior expected value');
ax.set_xticklabels([]);
ax.set_xlabel('Standardized range');
ax.set_yticklabels([]);
ax.set_ylabel('Standardized log ratio');
ax.legend(loc=1);
ax.set_title('LIDAR Data');
# -
# The model has fit the linear components of the data well, and also accomodated its heteroskedasticity. This flexibility, along with the ability to modularly specify the conditional mixture weights and conditional component densities, makes dependent density regression an extremely useful nonparametric Bayesian model.
#
# To learn more about depdendent density regression and related models, consult [_Bayesian Data Analysis_](http://www.stat.columbia.edu/~gelman/book/), [_Bayesian Nonparametric Data Analysis_](http://www.springer.com/us/book/9783319189673), or [_Bayesian Nonparametrics_](https://www.google.com/webhp?sourceid=chrome-instant&ion=1&espv=2&ie=UTF-8#q=bayesian+nonparametrics+book).
#
# This example first appeared [here](http://austinrochford.com/posts/2017-01-18-ddp-pymc3.html).
#
# Author: [<NAME>](https://github.com/AustinRochford/)
|
docs/source/notebooks/dependent_density_regression.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] toc=true
# <h1>Table of Contents<span class="tocSkip"></span></h1>
# <div class="toc"><ul class="toc-item"><li><span><a href="#Python" data-toc-modified-id="Python-1">Python</a></span><ul class="toc-item"><li><ul class="toc-item"><li><span><a href="#Are-tuples-immutable?" data-toc-modified-id="Are-tuples-immutable?-1.0.1">Are tuples immutable?</a></span></li><li><span><a href="#Are-variables-and-objects-the-same-in-Python?" data-toc-modified-id="Are-variables-and-objects-the-same-in-Python?-1.0.2">Are variables and objects the same in Python?</a></span></li><li><span><a href="#Are-variables-Typed?" data-toc-modified-id="Are-variables-Typed?-1.0.3">Are variables Typed?</a></span></li><li><span><a href="#What's-the-difference-between-a-list-and-a-tuple-in-Python?" data-toc-modified-id="What's-the-difference-between-a-list-and-a-tuple-in-Python?-1.0.4">What's the difference between a list and a tuple in Python?</a></span></li><li><span><a href="#What's-the-difference-between-Python-and-other-languages?" data-toc-modified-id="What's-the-difference-between-Python-and-other-languages?-1.0.5">What's the difference between Python and other languages?</a></span></li><li><span><a href="#What-is-a-PYTHONPATH?" data-toc-modified-id="What-is-a-PYTHONPATH?-1.0.6">What is a PYTHONPATH?</a></span></li><li><span><a href="#What-are-modules?" data-toc-modified-id="What-are-modules?-1.0.7">What are modules?</a></span></li><li><span><a href="#What's-the-difference-between-local-and-global-variables-in-Python?" data-toc-modified-id="What's-the-difference-between-local-and-global-variables-in-Python?-1.0.8">What's the difference between local and global variables in Python?</a></span></li><li><span><a href="#What-is-type-conversion?" data-toc-modified-id="What-is-type-conversion?-1.0.9">What is type conversion?</a></span></li><li><span><a href="#What-is-the-difference-between-an-array-and-lists?" data-toc-modified-id="What-is-the-difference-between-an-array-and-lists?-1.0.10">What is the difference between an array and lists?</a></span></li><li><span><a href="#What-is-a-function?" data-toc-modified-id="What-is-a-function?-1.0.11">What is a function?</a></span></li><li><span><a href="#What-is-the-meaning-of-__-init-__-?" data-toc-modified-id="What-is-the-meaning-of-__-init-__-?-1.0.12">What is the meaning of __ init __ ?</a></span></li><li><span><a href="#What-is-self-?" data-toc-modified-id="What-is-self-?-1.0.13">What is self ?</a></span></li><li><span><a href="#What-is-a-lambda-function?" data-toc-modified-id="What-is-a-lambda-function?-1.0.14">What is a lambda function?</a></span></li><li><span><a href="#What-are-generators?" data-toc-modified-id="What-are-generators?-1.0.15">What are generators?</a></span></li><li><span><a href="#What-are-iterators?" data-toc-modified-id="What-are-iterators?-1.0.16">What are iterators?</a></span></li><li><span><a href="#Why-use-yield?" data-toc-modified-id="Why-use-yield?-1.0.17">Why use yield?</a></span></li></ul></li></ul></li><li><span><a href="#SQL" data-toc-modified-id="SQL-2">SQL</a></span><ul class="toc-item"><li><ul class="toc-item"><li><span><a href="#What-is-the-difference-between-SQL-and-MySQL?" data-toc-modified-id="What-is-the-difference-between-SQL-and-MySQL?-2.0.1">What is the difference between SQL and MySQL?</a></span></li><li><span><a href="#What's-the-difference-between-a-table,-field-and-a-record?" data-toc-modified-id="What's-the-difference-between-a-table,-field-and-a-record?-2.0.2">What's the difference between a table, field and a record?</a></span></li><li><span><a href="#What-is-a-JOIN-clause?-Explain-the-different-types." data-toc-modified-id="What-is-a-JOIN-clause?-Explain-the-different-types.-2.0.3">What is a JOIN clause? Explain the different types.</a></span></li><li><span><a href="#What's-the-difference-between-CHAR-and-VARCHAR2?" data-toc-modified-id="What's-the-difference-between-CHAR-and-VARCHAR2?-2.0.4">What's the difference between CHAR and VARCHAR2?</a></span></li><li><span><a href="#What-are-constraints?" data-toc-modified-id="What-are-constraints?-2.0.5">What are constraints?</a></span></li><li><span><a href="#What-is-the-difference-between-DELETE-and-TRUNCATE?" data-toc-modified-id="What-is-the-difference-between-DELETE-and-TRUNCATE?-2.0.6">What is the difference between DELETE and TRUNCATE?</a></span></li></ul></li><li><span><a href="#PRIMARY,-UNIQUE-&-FOREIGN-KEYS" data-toc-modified-id="PRIMARY,-UNIQUE-&-FOREIGN-KEYS-2.1">PRIMARY, UNIQUE & FOREIGN KEYS</a></span><ul class="toc-item"><li><span><a href="#What-is-a-PRIMARY-KEY?" data-toc-modified-id="What-is-a-PRIMARY-KEY?-2.1.1">What is a PRIMARY KEY?</a></span></li><li><span><a href="#What-is-a-UNIQUE-key?" data-toc-modified-id="What-is-a-UNIQUE-key?-2.1.2">What is a UNIQUE key?</a></span></li><li><span><a href="#What-is-a-FOREIGN-key?" data-toc-modified-id="What-is-a-FOREIGN-key?-2.1.3">What is a FOREIGN key?</a></span></li><li><span><a href="#What's-the-difference-between-a-PRIMARY-KEY-and-a-UNIQUE-KEY?" data-toc-modified-id="What's-the-difference-between-a-PRIMARY-KEY-and-a-UNIQUE-KEY?-2.1.4">What's the difference between a PRIMARY KEY and a UNIQUE KEY?</a></span></li></ul></li><li><span><a href="#General" data-toc-modified-id="General-2.2">General</a></span></li></ul></li></ul></div>
# -
# A collection of interview questions organised into two categories:
# - Python
# - SQL
# ## Python
# #### Are tuples immutable?
# - Immutable means they cannot be changed, after being created in the memory
# - Mutable objects are ones that can be changed after they've been created in the memory
tuple = ('a', 'b')
print(tuple)
print(tuple[1])
tuple[1] = 'c'
# +
tuple_two = ('a', {'b': 'bee'})
tuple_two[1]['b'] = 'changed_char'
print(tuple_two)
# -
# Tuple objects are data containers, so if a tuple has an object in it such as a list or a dict, then we can change the data inside the list or dict without changing the tuple (where it's stored in memory itself).
#
# So (as we will see below), updating the data in the dictionary above has no change on the object stored in memory.
#
# So, tuples are **relatively immutable** if they hold mutable objects (dicts, list) and we can change their values.
#
# However, we cannot change the tuples' underlying objects that they hold, as they are immutable by definition, and always contain the same objects no matter whether its possible to change contained data.
# #### Are variables and objects the same in Python?
# - In python everything is an object, including data type instances, modules, functions and classes
# - Variables can be viewed as labels associated with specific objects defined
# - Objects are data stored in memory when created
a = 1000
print(id(a)) # memory address
a = 'word'
print(id(a)) # new memory address
# So, when **a** is originally created, it has an address in memory. Then it is changed and has a different memory address.
#
# The memory addresses for these two cases are distinct, and reference the distinct underlying objects in memory.
#
# So, variables and objects are **not the same** since objects are data saved in memory. A new variable in this case is a label referencing a value.
# #### Are variables Typed?
# - Not as they are in other languages, in Python both are valid:
# - a=3
# - a='three'
# - Python is dynamically typed
# - One doesn't have to declare the type of variable when declaring the variable
# - Python variables have types, determined by the values they're bound to
# #### What's the difference between a list and a tuple in Python?
# - A tuple has **( )** brackets, list **[ ]**
# - List is **mutable** and can be changed
# - Tuple is **immutable** and cannot be edited
# #### What's the difference between Python and other languages?
# - Python is dynamically typed
# - Python is an interpreted language (no need to compile code)
# #### What is a PYTHONPATH?
# - This is the path looked at by the intrepreter when looking for modules imported in a script.
# #### What are modules?
# - These are files containing Python code that can contain functions, classes or variables
# - a ".py" file with executable code
# #### What's the difference between local and global variables in Python?
# - Variables declared outside a function or in global space are **GLOBAL VARIABLES**. Can be accessed by any fucntion in the program.
# - Any variable declared inside a function is known as a **LOCAL VARIABLE**, as it is present in local, not global space.
#
# #### What is type conversion?
# Conversion of data from one type to another.
# #### What is the difference between an array and lists?
# - Arrays can only hold one data type element (more useful for arithmetic functions)
# - Lists can hold more than one data type, any data type
import numpy
numpy.array([['i'], [1]])
[1, 'abc', 1.20]
# #### What is a function?
# - A block of code defined using a **def** keyword, only executed when called
# #### What is the meaning of __ init __ ?
# - This is a method or constructor, automatically called to allocate mmeory when an object/instance of a class is created
# - All classes have an __ init __ method
# #### What is self ?
# - This is an instance of an object of a class, explicitly excluded as a first parameter
# - It helps to differentiate between methods and attributes of a class and local variables
# - In the __ init __ method, **self** refers to a newly created object, whilst in other methods it refers to the object whose method is called
# #### What is a lambda function?
# - This is an anonymous function that can have any number of parameters, but just one statement
# #### What are generators?
# - These are functions that return an iterable set of items, often denoted with a **yield** statement
# #### What are iterators?
# - These are objects that can be traversed through/iterated upon
# #### Why use yield?
# - Yield will result in a generator object
# - A generator is advantageous for large amounts of data, so using a for loop and a return object means storing the entire object being iterated through in memory
# - Whereas using a generator, return each element as needed, and then when finished, the computer can free up memory in the program
# - It is slow to do a return, but yield will take each key in turn, and won't iterate through all results
# - If you don't need to allocate a big list in memory for results, you don't have to process all results before you can start using the result
# ## SQL
# #### What is the difference between SQL and MySQL?
# - SQL is a querying language used for accessing data in a database
# - MySQL is a database management system. This is a software allowing the user, applications, and the database to capture and analyse data.
# #### What's the difference between a table, field and a record?
# - A table is a collection of data organised into rows and columns
# - A field is the columns of the table
# - A record is an individual entry in a table
# #### What is a JOIN clause? Explain the different types.
#
# A JOIN clause combines rows from two or more tables, based on a related column between them.
#
# 
# As shown above:
# - **INNER JOIN**: return the rows from multiple tables where the values in the common column overlap
# - **OUTER JOIN**: return all records in both table if there are any matches
# - **LEFT JOIN**: return all the rows from the left table, and entries from the right table matching the entries in the shared column
# - **RIGHT JOIN**: return all rows from the right table, and only matching rows from the left table.
# #### What's the difference between CHAR and VARCHAR2?
# - VARCHAR2 is for character strings of variable length
# - CHAR is for strings of a fixed length only, cannot store a value if it's of a different length
# #### What are constraints?
# - Constraints are used to specify limits on the data type of a table, specified when creating/altering the table.
# - For example: NOT NULL, CHECK, PRIMARY KEY
# #### What is the difference between DELETE and TRUNCATE?
# - DELETE is used for a single row in a table, and you can roll back data
# - TRUNCATE deletes all rows from a table, and cannot be rolled back
# ### PRIMARY, UNIQUE & FOREIGN KEYS
# #### What is a PRIMARY KEY?
# - This is a column or set of columns identifying each row in the table uniquely
# - It isn't allowed to take a null value
# - There is only one primary key in a table
# #### What is a UNIQUE key?
# - This is a key that uniquely identifies a single row in a table.
# - Multiple values are allowed
# #### What is a FOREIGN key?
# - This enforces a link between data in two tables
# - A FOREIGN key in a child table references the PRIMARY KEY in a parent table
# - The table containing the FOREIGN KEY is called the child table, whilst that with the PRIMARY KEY is the parent table
# - The FOREIGN KEY constraint is used to prevent actions that would destroy links between tables, whilst also preventing invalid data from being inserted into the FOREIGN KEY column
# #### What's the difference between a PRIMARY KEY and a UNIQUE KEY?
# - Both can uniquely idenitfy a row in a table
# - UNIQUE KEY can be null, and only one null values in a table
# - PRIMARY KEY cannot be null
# - PRIMARY KEY can be a combination of more than one unique key in the same table
# - There can only be one PRIMARY KEY per table
# - There can be more than one UNIQUE KEY per table
# ### General
# - The `UPDATE` statement is used to update data in a database (not the **MODIFY** statement)
# - `DELETE` statement is used to delete data from a database
# - `INSERT INTO` statement is used to insert new data into a database
# - `DISTINCT` statement returns only unique values
# - `ORDER BY` statement sorts the result set
# - `BETWEEN` statement is used to select values within a range
# - `LIKE` operator is used to search for a specified pattern in a column
# - `CREATE TABLE TableName` statement creates a database table
# - `INSTR` statement returns the position of the first occurrence of a string in another string
# - `CONCAT SUBSTR INSTR` are all character manipulation functions
# - `NVL(expr1, expr2)` function converts a null value to an actual value
# - `ALTER TABLE` statement can add a new column, modify existing columns, and define default values for the new column. It **cannot** add a new row
# - `COUNT(exp)` returns the number of rows with non-null values for the exp
# - `COUNT(DISTINCT exp)` returns the number of unique, non-null values in the column
# - `DROP TABLE` statement will delete a table
# - `CONSTRAINTS` can be created at the same time as the table is created, or after the table is created. The constraints are stored in the data dictionary
# - The `MERGE` statement allows simultaneous (conditional) update, or insertion of data into a table simultaneously.
# - `DELETE` statement can be used to remove existing rows from a table
#
# Examples
# - Select all records from the table `Persons` where the value of column 'FirstName' starts with 'a':
# - `SELECT * FROM Persons WHERE FirstName LIKE 'a%'`
# - Select all records from the table `Persons` where the value of column 'LastName' alphabetically lies between (and includes) 'Hansen' and 'Pettersen':
# - `SELECT * FROM Persons WHERE LastName BETWEEN 'Hansen' AND 'Pettersen'`
# - Select all records from the table `Persons` sorted by descending 'FirstName'
# - `SELECT * FROM Persons ORDER BY FirstName DESC`
# - Insert a new record into the 'Persons' table
# - `INSERT INTO Persons (LastName) VALUES ('Olsen')`
# - Change 'Hansen' to 'Nielsen' in the 'LastName' column in the 'Persons' table
# - `UPDATE Persons SET LastName = 'Nielsen' WHERE LastName = 'Hansen'`
# - Delete the records where 'FirstName' is 'Peter' in the Persons table
# - `DELETE FROM Persons WHERE FirstName = 'Peter'`
# - Return the number of records in the Persons table
# - `SELECT COUNT(*) FROM Persons`
# - Return all unique values for Honours_Subject from the table:
# - `SELECT DISTINCT FROM table`
|
src/jupyter-notebooks/python_sql_interview_questions.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Part 1: What Does `TRTF` Look Like?
#
# **Tensor factorization**for any given tensor $\mathcal{Y}\in\mathbb{R}^{M\times N\times T}$ with rank $R$:
# $$y_{ijt}\approx\sum_{r=1}^{R}u_{ir}v_{jr}x_{tr}\\=\left(\boldsymbol{u}_{i}\circledast\boldsymbol{v}_{j}\right)^{\top}\boldsymbol{x}_{t}\\=\left(\boldsymbol{u}_{i}\circledast\boldsymbol{x}_{t}\right)^{\top}\boldsymbol{v}_{j}\\=\left(\boldsymbol{v}_{j}\circledast\boldsymbol{x}_{t}\right)^{\top}\boldsymbol{u}_{i}$$
#
# **Temporal regularized tensor factorization (TRMF)**:
# $$\min_{U,V,X}~~\sum_{(i,j,t)\in\Omega}\left(y_{ijt}-\sum_{r=1}^{R}u_{ir}v_{jr}x_{tr}\right)^2\\
# +\lambda_{u}\sum_{i=1}^{M}\left\|\boldsymbol{u}_{i}\right\|_{2}^{2}+\lambda_{v}\sum_{j=1}^{N}\left\|\boldsymbol{v}_{j}\right\|_{2}^{2}+\lambda_{x}\sum_{t=1}^{T}\left\|\boldsymbol{x}_{t}\right\|_{2}^{2}\\
# +\lambda_{ar}\sum_{t=h_d+1}^{T}\left\|\boldsymbol{x}_{t}-\sum_{k=1}^{d}\boldsymbol{\theta}_{k}\circledast\boldsymbol{x}_{t-h_k}\right\|_{2}^{2}+\lambda_{\theta}\sum_{l\in\mathcal{L}}\left\|\boldsymbol{\theta}_{l}\right\|_{2}^{2}$$
# # Part 2: Alternative Minimization for `TRTF`
#
# ## Optimizing $\boldsymbol{u}_{i},i\in\left\{1,2,...,M\right\}$:
#
# **Optimization problem**:
# $$\min_{\boldsymbol{u}_{i}}\sum_{j,t:(i,j,t)\in\Omega}\left(y_{ijt}-\left(\boldsymbol{v}_{j}\circledast\boldsymbol{x}_{t}\right)^{\top}\boldsymbol{u}_{i}\right)^{\top}\left(y_{ijt}-\left(\boldsymbol{v}_{j}\circledast\boldsymbol{x}_{t}\right)^{\top}\boldsymbol{u}_{i}\right)+\lambda_{u}\boldsymbol{u}_{i}^{\top}\boldsymbol{u}_{i}$$
#
# **Solution**:
# $$\boldsymbol{u}_{i}\Leftarrow\left(\sum_{j,t:(i,j,t)\in\Omega}\left(\boldsymbol{v}_{j}\circledast\boldsymbol{x}_{t}\right)\left(\boldsymbol{v}_{j}\circledast\boldsymbol{x}_{t}\right)^{\top}+\lambda_{u}I_{R}\right)^{-1}\sum_{j,t:(i,j,t)\in\Omega}\left(\boldsymbol{v}_{j}\circledast\boldsymbol{x}_{t}\right)y_{ijt}$$
# ## Optimizing $\boldsymbol{v}_{j},j\in\left\{1,2,...,N\right\}$:
#
# **Optimization problem**:
# $$\min_{\boldsymbol{v}_{j}}\sum_{i,t:(i,j,t)\in\Omega}\left(y_{ijt}-\left(\boldsymbol{u}_{i}\circledast\boldsymbol{x}_{t}\right)^{\top}\boldsymbol{v}_{j}\right)^{\top}\left(y_{ijt}-\left(\boldsymbol{u}_{i}\circledast\boldsymbol{x}_{t}\right)^{\top}\boldsymbol{v}_{j}\right)+\lambda_{v}\boldsymbol{v}_{j}^{\top}\boldsymbol{v}_{j}$$
#
# **Solution**:
# $$\boldsymbol{v}_{j}\Leftarrow\left(\sum_{i,t:(i,j,t)\in\Omega}\left(\boldsymbol{u}_{i}\circledast\boldsymbol{x}_{t}\right)\left(\boldsymbol{u}_{i}\circledast\boldsymbol{x}_{t}\right)^{\top}+\lambda_{v}I_{R}\right)^{-1}\sum_{i,t:(i,j,t)\in\Omega}\left(\boldsymbol{u}_{i}\circledast\boldsymbol{x}_{t}\right)y_{ijt}$$
# ## Optimizing $\boldsymbol{x}_{t},t\in\left\{1,2,...,T\right\}$:
#
# ### Case #1: $t\in\left\{1,2,...,h_d\right\}$
#
# **Optimization problem**:
# $$\min_{\boldsymbol{x}_{t}}\sum_{i,j:(i,j,t)\in\Omega}\left(y_{ijt}-\left(\boldsymbol{u}_{i}\circledast\boldsymbol{v}_{j}\right)^{\top}\boldsymbol{x}_{t}\right)^{\top}\left(y_{ijt}-\left(\boldsymbol{u}_{i}\circledast\boldsymbol{v}_{j}\right)^{\top}\boldsymbol{x}_{t}\right)+\lambda_{x}\boldsymbol{x}_{t}^{\top}\boldsymbol{x}_{t}$$
#
# **Solution**:
# $$\boldsymbol{x}_{t}\Leftarrow\left(\sum_{i,j:(i,j,t)\in\Omega}\left(\boldsymbol{u}_{i}\circledast\boldsymbol{v}_{j}\right)\left(\boldsymbol{u}_{i}\circledast\boldsymbol{v}_{j}\right)^{\top}+\lambda_{x}I_{R}\right)^{-1}\sum_{i,j:(i,j,t)\in\Omega}\left(\boldsymbol{u}_{i}\circledast\boldsymbol{v}_{j}\right)y_{ijt}$$
#
#
# ### Case #2: $t\in\left\{h_d+1,h_d+2,...,T\right\}$
#
# **Optimization problem**:
# $$\min_{\boldsymbol{x}_{t}}\sum_{i,j:(i,j,t)\in\Omega}\left(y_{ijt}-\left(\boldsymbol{u}_{i}\circledast\boldsymbol{v}_{j}\right)^{\top}\boldsymbol{x}_{t}\right)^{\top}\left(y_{ijt}-\left(\boldsymbol{u}_{i}\circledast\boldsymbol{v}_{j}\right)^{\top}\boldsymbol{x}_{t}\right)+\lambda_{x}\boldsymbol{x}_{t}^{\top}\boldsymbol{x}_{t}\\
# +\lambda_{ar}\sum_{k=1,t+h_{k}\leq T}^{d}\left(\boldsymbol{x}_{t+h_k}-\sum_{l=1}^{d}\boldsymbol{\theta}_{l}\circledast\boldsymbol{x}_{t+h_{k}-h_l}\right)^{\top}\left(\boldsymbol{x}_{t+h_k}-\sum_{l=1}^{d}\boldsymbol{\theta}_{l}\circledast\boldsymbol{x}_{t+h_{k}-h_l}\right)$$
#
# **Solution**:
# $$\boldsymbol{x}_{t}\Leftarrow\left(\sum_{i,j:(i,j,t)\in\Omega}\left(\boldsymbol{u}_{i}\circledast\boldsymbol{v}_{j}\right)\left(\boldsymbol{u}_{i}\circledast\boldsymbol{v}_{j}\right)^{\top}+\lambda_{x}I_{R}+\lambda_{ar}\sum_{k=1,t+h_k\leq T}^{d}\text{diag}\left(\boldsymbol{\theta}_{k}\circledast\boldsymbol{\theta}_{k}\right)\right)^{-1}\\
# \times\left(\sum_{i,j:(i,j,t)\in\Omega}\left(\boldsymbol{u}_{i}\circledast\boldsymbol{v}_{j}\right)y_{ijt}+\lambda_{ar}\sum_{k=1,t+h_k\leq T}^{d}\text{diag}\left(\boldsymbol{\theta}_{k}\right)\boldsymbol{\psi}_{t+h_k}\right)$$
# where
# $$\boldsymbol{\psi}_{t+h_{k}}=\boldsymbol{x}_{t+h_k}-\sum_{l=1,l\neq k}^{d}\boldsymbol{\theta}_{l}\circledast\boldsymbol{x}_{t+h_k-h_l}.$$
# # Part 3: Matrix/Tensor Computation Concepts
#
# ## Khatri-Rao product (`kr_prod`)
#
# - **Definition**:
#
# Given two matrices $A=\left( \boldsymbol{a}_1,\boldsymbol{a}_2,...,\boldsymbol{a}_r \right)\in\mathbb{R}^{m\times r}$ and $B=\left( \boldsymbol{b}_1,\boldsymbol{b}_2,...,\boldsymbol{b}_r \right)\in\mathbb{R}^{n\times r}$ with same number of columns, then, the **Khatri-Rao product** (or **column-wise Kronecker product**) between $A$ and $B$ is given as follows,
#
# $$A\odot B=\left( \boldsymbol{a}_1\otimes \boldsymbol{b}_1,\boldsymbol{a}_2\otimes \boldsymbol{b}_2,...,\boldsymbol{a}_r\otimes \boldsymbol{b}_r \right)\in\mathbb{R}^{(mn)\times r}$$
# where the symbol $\odot$ denotes Khatri-Rao product, and $\otimes$ denotes Kronecker product.
#
# - **Example**:
#
# If $A=\left[ \begin{array}{cc} 1 & 2 \\ 3 & 4 \\ \end{array} \right]=\left( \boldsymbol{a}_1,\boldsymbol{a}_2 \right) $ and $B=\left[ \begin{array}{cc} 5 & 6 \\ 7 & 8 \\ 9 & 10 \\ \end{array} \right]=\left( \boldsymbol{b}_1,\boldsymbol{b}_2 \right) $, then, we have
#
# $$A\odot B=\left( \boldsymbol{a}_1\otimes \boldsymbol{b}_1,\boldsymbol{a}_2\otimes \boldsymbol{b}_2 \right) $$
#
# $$=\left[ \begin{array}{cc} \left[ \begin{array}{c} 1 \\ 3 \\ \end{array} \right]\otimes \left[ \begin{array}{c} 5 \\ 7 \\ 9 \\ \end{array} \right] & \left[ \begin{array}{c} 2 \\ 4 \\ \end{array} \right]\otimes \left[ \begin{array}{c} 6 \\ 8 \\ 10 \\ \end{array} \right] \\ \end{array} \right]$$
#
# $$=\left[ \begin{array}{cc} 5 & 12 \\ 7 & 16 \\ 9 & 20 \\ 15 & 24 \\ 21 & 32 \\ 27 & 40 \\ \end{array} \right]\in\mathbb{R}^{6\times 2}.$$
#
# ## CP combination (`cp_combine`)
#
# - **Definition**:
#
# The CP decomposition factorizes a tensor into a sum of outer products of vectors. For example, for a third-order tensor $\mathcal{Y}\in\mathbb{R}^{m\times n\times f}$, the CP decomposition can be written as
#
# $$\hat{\mathcal{Y}}=\sum_{s=1}^{r}\boldsymbol{u}_{s}\circ\boldsymbol{v}_{s}\circ\boldsymbol{x}_{s},$$
# or element-wise,
#
# $$\hat{y}_{ijt}=\sum_{s=1}^{r}u_{is}v_{js}x_{ts},\forall (i,j,t),$$
# where vectors $\boldsymbol{u}_{s}\in\mathbb{R}^{m},\boldsymbol{v}_{s}\in\mathbb{R}^{n},\boldsymbol{x}_{s}\in\mathbb{R}^{f}$ are columns of factor matrices $U\in\mathbb{R}^{m\times r},V\in\mathbb{R}^{n\times r},X\in\mathbb{R}^{f\times r}$, respectively. The symbol $\circ$ denotes vector outer product.
#
# - **Example**:
#
# Given matrices $U=\left[ \begin{array}{cc} 1 & 2 \\ 3 & 4 \\ \end{array} \right]\in\mathbb{R}^{2\times 2}$, $V=\left[ \begin{array}{cc} 1 & 2 \\ 3 & 4 \\ 5 & 6 \\ \end{array} \right]\in\mathbb{R}^{3\times 2}$ and $X=\left[ \begin{array}{cc} 1 & 5 \\ 2 & 6 \\ 3 & 7 \\ 4 & 8 \\ \end{array} \right]\in\mathbb{R}^{4\times 2}$, then if $\hat{\mathcal{Y}}=\sum_{s=1}^{r}\boldsymbol{u}_{s}\circ\boldsymbol{v}_{s}\circ\boldsymbol{x}_{s}$, then, we have
#
# $$\hat{Y}_1=\hat{\mathcal{Y}}(:,:,1)=\left[ \begin{array}{ccc} 31 & 42 & 65 \\ 63 & 86 & 135 \\ \end{array} \right],$$
# $$\hat{Y}_2=\hat{\mathcal{Y}}(:,:,2)=\left[ \begin{array}{ccc} 38 & 52 & 82 \\ 78 & 108 & 174 \\ \end{array} \right],$$
# $$\hat{Y}_3=\hat{\mathcal{Y}}(:,:,3)=\left[ \begin{array}{ccc} 45 & 62 & 99 \\ 93 & 130 & 213 \\ \end{array} \right],$$
# $$\hat{Y}_4=\hat{\mathcal{Y}}(:,:,4)=\left[ \begin{array}{ccc} 52 & 72 & 116 \\ 108 & 152 & 252 \\ \end{array} \right].$$
#
# ## Tensor unfolding (`ten2mat`)
#
# Using numpy reshape to perform 3rd rank tensor unfold operation. [[**link**](https://stackoverflow.com/questions/49970141/using-numpy-reshape-to-perform-3rd-rank-tensor-unfold-operation)]
import numpy as np
from numpy.linalg import inv as inv
def kr_prod(a, b):
return np.einsum('ir, jr -> ijr', a, b).reshape(a.shape[0] * b.shape[0], -1)
def cp_combine(U, V, X):
return np.einsum('is, js, ts -> ijt', U, V, X)
import numpy as np
def ten2mat(tensor, mode):
return np.reshape(np.moveaxis(tensor, mode, 0), (tensor.shape[mode], -1), order = 'F')
def TRTF(dense_tensor, sparse_tensor, U, V, X, theta, time_lags,
lambda_u, lambda_v, lambda_ar, eta, lambda_theta, maxiter):
dim1, dim2, dim3 = dense_tensor.shape
binary_tensor = np.zeros((dim1, dim2, dim3))
position = np.where(sparse_tensor > 0)
binary_tensor[position] = 1
pos = np.where((dense_tensor > 0) & (sparse_tensor == 0))
d = len(time_lags)
rank = U.shape[1]
for iters in range(maxiter):
var1 = kr_prod(X, V).T
var2 = kr_prod(var1, var1)
var3 = (np.matmul(var2, ten2mat(binary_tensor, 0).T).reshape([rank, rank, dim1])
+ np.dstack([lambda_u * np.eye(rank)] * dim1))
var4 = np.matmul(var1, ten2mat(sparse_tensor, 0).T)
for i in range(dim1):
var_Lambda1 = var3[ :, :, i]
inv_var_Lambda1 = inv((var_Lambda1 + var_Lambda1.T)/2)
U[i, :] = np.matmul(inv_var_Lambda1, var4[:, i])
var1 = kr_prod(X, U).T
var2 = kr_prod(var1, var1)
var3 = (np.matmul(var2, ten2mat(binary_tensor, 1).T).reshape([rank, rank, dim2])
+ np.dstack([lambda_v * np.eye(rank)] * dim2))
var4 = np.matmul(var1, ten2mat(sparse_tensor, 1).T)
for j in range(dim2):
var_Lambda1 = var3[ :, :, j]
inv_var_Lambda1 = inv((var_Lambda1 + var_Lambda1.T)/2)
V[j, :] = np.matmul(inv_var_Lambda1, var4[:, j])
var1 = kr_prod(V, U).T
var2 = kr_prod(var1, var1)
var3 = np.matmul(var2, ten2mat(binary_tensor, 2).T).reshape([rank, rank, dim3])
var4 = np.matmul(var1, ten2mat(sparse_tensor, 2).T)
for t in range(dim3):
Mt = np.zeros((rank, rank))
Nt = np.zeros(rank)
if t < max(time_lags):
Pt = np.zeros((rank, rank))
Qt = np.zeros(rank)
else:
Pt = np.eye(rank)
Qt = np.einsum('ij, ij -> j', theta, X[t - time_lags, :])
if t < dim3 - np.min(time_lags):
if t >= np.max(time_lags) and t < dim3 - np.max(time_lags):
index = list(range(0, d))
else:
index = list(np.where((t + time_lags >= np.max(time_lags)) & (t + time_lags < dim3)))[0]
for k in index:
theta0 = theta.copy()
theta0[k, :] = 0
Mt = Mt + np.diag(theta[k, :] ** 2);
Nt = Nt + np.multiply(theta[k, :], (X[t + time_lags[k], :]
- np.einsum('ij, ij -> j', theta0, X[t + time_lags[k] - time_lags, :])))
X[t, :] = np.matmul(inv(var3[:, :, t] + lambda_ar * Pt + lambda_ar * Mt + lambda_ar * eta * np.eye(rank)),
(var4[:, t] + lambda_ar * Qt + lambda_ar * Nt))
elif t >= dim3 - np.min(time_lags):
X[t, :] = np.matmul(inv(var3[:, :, t] + lambda_ar * Pt + lambda_ar * eta * np.eye(rank)), (var4[:, t] + Qt))
for k in range(d):
theta0 = theta.copy()
theta0[k, :] = 0
mat0 = np.zeros((dim3 - np.max(time_lags), rank))
for L in range(d):
mat0 += np.matmul(X[np.max(time_lags) - time_lags[L] : dim3 - time_lags[L] , :], np.diag(theta0[L, :]))
VarPi = X[np.max(time_lags) : dim3, :] - mat0
var1 = np.zeros((rank, rank))
var2 = np.zeros(rank)
for t in range(np.max(time_lags), dim3):
B = X[t - time_lags[k], :]
var1 += np.diag(np.multiply(B, B))
var2 += np.matmul(np.diag(B), VarPi[t - np.max(time_lags), :])
theta[k, :] = np.matmul(inv(var1 + lambda_theta * np.eye(rank)/lambda_ar), var2)
tensor_hat = cp_combine(U, V, X)
mape = np.sum(np.abs(dense_tensor[pos] - tensor_hat[pos])/dense_tensor[pos])/dense_tensor[pos].shape[0]
rmse = np.sqrt(np.sum((dense_tensor[pos] - tensor_hat[pos])**2)/dense_tensor[pos].shape[0])
if (iters + 1) % 200 == 0:
print('Iter: {}'.format(iters + 1))
print('MAPE: {:.6}'.format(mape))
print('RMSE: {:.6}'.format(rmse))
print()
return U, V, X, theta
# +
import scipy.io
tensor = scipy.io.loadmat('../NYC-data-set/tensor.mat')
dense_tensor = tensor['tensor']
rm_tensor = scipy.io.loadmat('../NYC-data-set/rm_tensor.mat')
rm_tensor = rm_tensor['rm_tensor']
nm_tensor = scipy.io.loadmat('../NYC-data-set/nm_tensor.mat')
nm_tensor = nm_tensor['nm_tensor']
missing_rate = 0.1
# =============================================================================
### Random missing (RM) scenario
### Set the RM scenario by:
binary_tensor = np.round(rm_tensor + 0.5 - missing_rate)
# =============================================================================
sparse_tensor = np.multiply(dense_tensor, binary_tensor)
# -
import time
start = time.time()
pred_time_steps = 24 * 7
rank = 30
time_lags = np.array([1, 2, 24])
maxiter = 1000
dim1, dim2, dim3 = dense_tensor.shape
U = 0.1 * np.random.rand(dim1, rank)
V = 0.1 * np.random.rand(dim2, rank)
X = 0.1 * np.random.rand(dim3, rank)
theta = 0.1 * np.random.rand(time_lags.shape[0], rank)
lambda_u = 500
lambda_v = 500
lambda_ar = 500
eta = 2e-2
lambda_theta = 100
TRTF(dense_tensor, sparse_tensor, U, V, X, theta, time_lags,
lambda_u, lambda_v, lambda_ar, eta, lambda_theta, maxiter)
end = time.time()
print('Running time: %d seconds'%(end - start))
# +
import scipy.io
tensor = scipy.io.loadmat('../NYC-data-set/tensor.mat')
dense_tensor = tensor['tensor']
rm_tensor = scipy.io.loadmat('../NYC-data-set/rm_tensor.mat')
rm_tensor = rm_tensor['rm_tensor']
nm_tensor = scipy.io.loadmat('../NYC-data-set/nm_tensor.mat')
nm_tensor = nm_tensor['nm_tensor']
missing_rate = 0.3
# =============================================================================
### Random missing (RM) scenario
### Set the RM scenario by:
binary_tensor = np.round(rm_tensor + 0.5 - missing_rate)
# =============================================================================
sparse_tensor = np.multiply(dense_tensor, binary_tensor)
# -
import time
start = time.time()
pred_time_steps = 24 * 7
rank = 30
time_lags = np.array([1, 2, 24])
maxiter = 1000
dim1, dim2, dim3 = dense_tensor.shape
U = 0.1 * np.random.rand(dim1, rank)
V = 0.1 * np.random.rand(dim2, rank)
X = 0.1 * np.random.rand(dim3, rank)
theta = 0.1 * np.random.rand(time_lags.shape[0], rank)
lambda_u = 500
lambda_v = 500
lambda_ar = 500
eta = 2e-2
lambda_theta = 100
TRTF(dense_tensor, sparse_tensor, U, V, X, theta, time_lags,
lambda_u, lambda_v, lambda_ar, eta, lambda_theta, maxiter)
end = time.time()
print('Running time: %d seconds'%(end - start))
# +
import scipy.io
tensor = scipy.io.loadmat('../NYC-data-set/tensor.mat')
dense_tensor = tensor['tensor']
rm_tensor = scipy.io.loadmat('../NYC-data-set/rm_tensor.mat')
rm_tensor = rm_tensor['rm_tensor']
nm_tensor = scipy.io.loadmat('../NYC-data-set/nm_tensor.mat')
nm_tensor = nm_tensor['nm_tensor']
missing_rate = 0.1
# =============================================================================
### Non-random missing (NM) scenario
### Set the NM scenario by:
binary_tensor = np.zeros(dense_tensor.shape)
for i1 in range(dense_tensor.shape[0]):
for i2 in range(dense_tensor.shape[1]):
for i3 in range(61):
binary_tensor[i1, i2, i3 * 24 : (i3 + 1) * 24] = np.round(nm_tensor[i1, i2, i3]
+ 0.5 - missing_rate)
# =============================================================================
sparse_tensor = np.multiply(dense_tensor, binary_tensor)
# -
import time
start = time.time()
pred_time_steps = 24 * 7
rank = 30
time_lags = np.array([1, 2, 24])
maxiter = 1000
dim1, dim2, dim3 = dense_tensor.shape
U = 0.1 * np.random.rand(dim1, rank)
V = 0.1 * np.random.rand(dim2, rank)
X = 0.1 * np.random.rand(dim3, rank)
theta = 0.1 * np.random.rand(time_lags.shape[0], rank)
lambda_u = 500
lambda_v = 500
lambda_ar = 500
eta = 2e-2
lambda_theta = 100
TRTF(dense_tensor, sparse_tensor, U, V, X, theta, time_lags,
lambda_u, lambda_v, lambda_ar, eta, lambda_theta, maxiter)
end = time.time()
print('Running time: %d seconds'%(end - start))
# +
import scipy.io
tensor = scipy.io.loadmat('../NYC-data-set/tensor.mat')
dense_tensor = tensor['tensor']
rm_tensor = scipy.io.loadmat('../NYC-data-set/rm_tensor.mat')
rm_tensor = rm_tensor['rm_tensor']
nm_tensor = scipy.io.loadmat('../NYC-data-set/nm_tensor.mat')
nm_tensor = nm_tensor['nm_tensor']
missing_rate = 0.3
# =============================================================================
### Non-random missing (NM) scenario
### Set the NM scenario by:
binary_tensor = np.zeros(dense_tensor.shape)
for i1 in range(dense_tensor.shape[0]):
for i2 in range(dense_tensor.shape[1]):
for i3 in range(61):
binary_tensor[i1, i2, i3 * 24 : (i3 + 1) * 24] = np.round(nm_tensor[i1, i2, i3]
+ 0.5 - missing_rate)
# =============================================================================
sparse_tensor = np.multiply(dense_tensor, binary_tensor)
# -
import time
start = time.time()
pred_time_steps = 24 * 7
rank = 30
time_lags = np.array([1, 2, 24])
maxiter = 1000
dim1, dim2, dim3 = dense_tensor.shape
U = 0.1 * np.random.rand(dim1, rank)
V = 0.1 * np.random.rand(dim2, rank)
X = 0.1 * np.random.rand(dim3, rank)
theta = 0.1 * np.random.rand(time_lags.shape[0], rank)
lambda_u = 500
lambda_v = 500
lambda_ar = 500
eta = 2e-2
lambda_theta = 100
TRTF(dense_tensor, sparse_tensor, U, V, X, theta, time_lags,
lambda_u, lambda_v, lambda_ar, eta, lambda_theta, maxiter)
end = time.time()
print('Running time: %d seconds'%(end - start))
# #### **Experiment results** of missing data imputation using TRTF:
#
# | scenario |`lambda_u`|`lambda_v`|`lambda_ar`|`lambda_theta`|`eta`|`rank`|`time_lags`| `maxiter` | mape | rmse |
# |:----------|-----:|-----:|-----:|-----:|-----:|-----:|---------:|---------:|-----------:|----------:|
# |**10%, RM**|500|500|500|100|0.02| 30 | (1,2,24) | 1000 | 0.5139 | **4.7506**|
# |**30%, RM**|500|500|500|100|0.02| 30 | (1,2,24) | 1000 | 0.5142 | **4.8262**|
# |**10%, NM**|500|500|500|100|0.02| 30 | (1,2,24) | 1000 | 0.5160 | **4.9067**|
# |**30%, NM**|500|500|500|100|0.02| 30 | (1,2,24) | 1000 | 0.5279 | **5.0799**|
#
|
experiments/Imputation-TRTF.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="EpYPi_UAlsnP" colab_type="code" colab={}
# !pip install datadotworld
# !pip install datadotworld[pandas]
# + id="pOoLiG_fmgzg" colab_type="code" colab={}
# !dw configure
# + id="E1f7A-G-lHfA" colab_type="code" colab={}
from google.colab import drive
import pandas as pd
import numpy as np
import datadotworld as dw
# + id="wTf3BxsJm0I6" colab_type="code" colab={}
drive.mount("/content/drive")
# + id="83b644csm5n9" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="d402b72b-4574-4d36-ff08-64e0b82d86d4" executionInfo={"status": "ok", "timestamp": 1581548057250, "user_tz": -60, "elapsed": 2485, "user": {"displayName": "\u0141uk<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AAuE7mDNiK3273nPNgrUX71EsMK77MgQFzCt2Hjt6lEQZaQ=s64", "userId": "04727839156927387844"}}
# ls
# + id="FIWnA11QnCes" colab_type="code" colab={}
# cd "drive/My Drive/Colab Notebooks/dw_matrix/"
# + id="9hO9mIdvnoXc" colab_type="code" colab={}
# !mkdir data
# + id="FEEYM5NvntSn" colab_type="code" colab={}
# !echo 'data' >> .gitignore
# + id="jL5d4N4FoA8u" colab_type="code" colab={}
# !git add .gitignore
# + id="fNDA9Oi_oHWp" colab_type="code" colab={}
data = dw.load_dataset('datafiniti/mens-shoe-prices')
# + id="BTJ-OnP5ooLi" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="7b657920-1d75-4826-a43c-a508a258dad3" executionInfo={"status": "ok", "timestamp": 1581548519928, "user_tz": -60, "elapsed": 553, "user": {"displayName": "\u0141<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AAuE7mDNiK3273nPNgrUX71EsMK77MgQFzCt2Hjt6lEQZaQ=s64", "userId": "04727839156927387844"}}
df = data.dataframes['7004_1']
df.shape
# + id="FEAja-rXow8h" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 496} outputId="e0963f86-3af6-4bc2-9988-2418e6557caf" executionInfo={"status": "ok", "timestamp": 1581548559150, "user_tz": -60, "elapsed": 871, "user": {"displayName": "\u0141<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AAuE7mDNiK3273nPNgrUX71EsMK77MgQFzCt2Hjt6lEQZaQ=s64", "userId": "04727839156927387844"}}
df.sample(5)
# + id="92tpl-Pko9bC" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 233} outputId="212fb8f3-79f3-4d5d-b6e6-6f30eff6b591" executionInfo={"status": "ok", "timestamp": 1581548589461, "user_tz": -60, "elapsed": 686, "user": {"displayName": "\u0141uk<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AAuE7mDNiK3273nPNgrUX71EsMK77MgQFzCt2Hjt6lEQZaQ=s64", "userId": "04727839156927387844"}}
df.columns
# + id="UebAI_z-pE2v" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 107} outputId="3aba4593-33f1-431b-9751-63bf9a864d21" executionInfo={"status": "ok", "timestamp": 1581548674043, "user_tz": -60, "elapsed": 557, "user": {"displayName": "\u0141<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AAuE7mDNiK3273nPNgrUX71EsMK77MgQFzCt2Hjt6lEQZaQ=s64", "userId": "04727839156927387844"}}
df.prices_currency.unique()
# + id="3xyLmS-QpSim" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 269} outputId="30219d4f-f995-4152-d577-cde19f6799f4" executionInfo={"status": "ok", "timestamp": 1581548683065, "user_tz": -60, "elapsed": 724, "user": {"displayName": "\u0141ukasz Szeremeta", "photoUrl": "https://lh3.googleusercontent.com/a-/AAuE7mDNiK3273nPNgrUX71EsMK77MgQFzCt2Hjt6lEQZaQ=s64", "userId": "04727839156927387844"}}
df.prices_currency.value_counts()
# + id="lmoXWGXgpbsP" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 269} outputId="c50eb475-07c6-42d9-c525-318bbd63f200" executionInfo={"status": "ok", "timestamp": 1581548721150, "user_tz": -60, "elapsed": 625, "user": {"displayName": "\u0141ukasz Szeremeta", "photoUrl": "https://lh3.googleusercontent.com/a-/AAuE7mDNiK3273nPNgrUX71EsMK77MgQFzCt2Hjt6lEQZaQ=s64", "userId": "04727839156927387844"}}
df.prices_currency.value_counts(normalize=True)
# + id="ywKueFTApi9-" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="932dc99e-0d70-497e-f477-671899224759" executionInfo={"status": "ok", "timestamp": 1581548847411, "user_tz": -60, "elapsed": 618, "user": {"displayName": "\u0141<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AAuE7mDNiK3273nPNgrUX71EsMK77MgQFzCt2Hjt6lEQZaQ=s64", "userId": "04727839156927387844"}}
df_usd = df[df.prices_currency == 'USD'].copy()
df_usd.shape
# + id="k1dfBeJ5qD2O" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 125} outputId="d85b216b-0017-40ba-c4ab-877124ff1a3d" executionInfo={"status": "ok", "timestamp": 1581548917860, "user_tz": -60, "elapsed": 740, "user": {"displayName": "\u0141<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AAuE7mDNiK3273nPNgrUX71EsMK77MgQFzCt2Hjt6lEQZaQ=s64", "userId": "04727839156927387844"}}
df_usd.prices_amountmin.head()
# + id="g6cueuiIqVBl" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 283} outputId="e99383cc-d90f-4502-dba7-69aedbad3ee9" executionInfo={"status": "ok", "timestamp": 1581549104650, "user_tz": -60, "elapsed": 699, "user": {"displayName": "\u0141<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AAuE7mDNiK3273nPNgrUX71EsMK77MgQFzCt2Hjt6lEQZaQ=s64", "userId": "04727839156927387844"}}
df_usd['prices_amountmin'] = df_usd.prices_amountmin.astype(np.float)
df_usd['prices_amountmin'].hist()
# + id="RVmTSOdCrCnn" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="a187539c-6b2a-4427-f5b6-a0c8fa0dcfa4" executionInfo={"status": "ok", "timestamp": 1581549300745, "user_tz": -60, "elapsed": 620, "user": {"displayName": "\u0141<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AAuE7mDNiK3273nPNgrUX71EsMK77MgQFzCt2Hjt6lEQZaQ=s64", "userId": "04727839156927387844"}}
# In 99% of cases, shoes cost X or less
filter_max = np.percentile(df_usd['prices_amountmin'], 99)
filter_max
# + id="cJX88XuarUse" colab_type="code" colab={}
df_usd_filter = df_usd[df_usd['prices_amountmin'] < filter_max]
# + id="v5dsm9nhsL1b" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 283} outputId="6b8e26f8-7ec2-4bc5-bf42-156884934e32" executionInfo={"status": "ok", "timestamp": 1581549548036, "user_tz": -60, "elapsed": 938, "user": {"displayName": "\u0141uk<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AAuE7mDNiK3273nPNgrUX71EsMK77MgQFzCt2Hjt6lEQZaQ=s64", "userId": "04727839156927387844"}}
df_usd_filter.prices_amountmin.hist(bins=100)
# + id="0vS8k-RHsYKD" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="95a14d0f-25bb-4f0f-aa35-723d6665327a" executionInfo={"status": "ok", "timestamp": 1581549747619, "user_tz": -60, "elapsed": 2363, "user": {"displayName": "\u0141<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AAuE7mDNiK3273nPNgrUX71EsMK77MgQFzCt2Hjt6lEQZaQ=s64", "userId": "04727839156927387844"}}
# ls
# + id="SaOqmfBqtfKY" colab_type="code" colab={}
df.to_csv('data/mens_shoe_prices.csv', index=False)
# + id="HFxmJxWWt9Ga" colab_type="code" colab={}
# !git add matrix_one/day3.ipynb
# + id="L9tsj5dGuDMI" colab_type="code" colab={}
# #!git config --global user.email E-MAIL
# #!git config --global user.name NAME
# + id="OWbdzJeju2Xw" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 71} outputId="915a1b26-6873-4397-e0e9-baf186f42605" executionInfo={"status": "ok", "timestamp": 1581551039747, "user_tz": -60, "elapsed": 2238, "user": {"displayName": "\u0141uk<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AAuE7mDNiK3273nPNgrUX71EsMK77MgQFzCt2Hjt6lEQZaQ=s64", "userId": "04727839156927387844"}}
# !git reset HEAD~2
# + id="65j_hUEfyci3" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 71} outputId="7515a6b1-f096-4d7a-e2d2-162b9ef8aa05" executionInfo={"status": "ok", "timestamp": 1581551063268, "user_tz": -60, "elapsed": 5005, "user": {"displayName": "\u0141<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AAuE7mDNiK3273nPNgrUX71EsMK77MgQFzCt2Hjt6lEQZaQ=s64", "userId": "04727839156927387844"}}
# !git push origin +master
# + id="NRh-zY9hwmGu" colab_type="code" colab={}
# !git commit -m "Read Men's Shoe Prices dataset from data.world"
# + id="v2lzQ6z6wvdz" colab_type="code" colab={}
# !git push --all
# + id="5NQwP41CwzLV" colab_type="code" colab={}
|
matrix_one/day3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# Team Deep Divers submission for
# Brown Data Science DATA2040 Deep Learning course.
# Authors: <NAME>, <NAME>, <NAME>
# The Kaggle notebook structure is based on the example created by <NAME> and Dr.<NAME>
import pandas as pd
import numpy as np
from sklearn.dummy import DummyClassifier
import json
import tensorflow as tf
from functools import partial
import tensorflow.keras as keras
import keras
from keras.layers import Dense, Dropout, Input, MaxPooling2D, ZeroPadding2D, Conv2D, Flatten
from keras.models import Sequential, Model
from keras.losses import categorical_crossentropy
from keras.optimizers import Adam, SGD
from keras.callbacks import EarlyStopping
from keras.preprocessing.image import img_to_array, load_img, ImageDataGenerator
from keras.utils import to_categorical
from tensorflow.keras import regularizers
from tensorflow.keras.layers import MaxPool2D, AveragePooling2D, GlobalAveragePooling2D
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1 import ImageGrid
from zipfile import ZipFile
import time
from datetime import timedelta
from io import BytesIO
# Image manipulation.
import PIL.Image
import pickle
import os
import random
import cv2
# -
# # Exploratory Data Analysis
train_labels = pd.read_csv("../input/cassava-leaf-disease-classification/train.csv")
csv_df = pd.read_csv("../input/cassava-leaf-disease-classification/train.csv")
train_labels.head()
# ### Class0: Cassava Bacterial Blight (CBB)
# + _kg_hide-input=true
labels = pd.read_csv(os.path.join("../input/cassava-leaf-disease-classification/train.csv"))
sample0 = labels[labels.label == 0].sample(4)
plt.figure(figsize=(15, 5))
for ind, (image_id, label) in enumerate(zip(sample0.image_id, sample0.label)):
plt.subplot(1, 4, ind + 1)
img = cv2.imread(os.path.join('../input/cassava-leaf-disease-classification', "train_images", image_id))
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
plt.imshow(img)
plt.show()
# -
# ### Class1: Cassava Brown Streak Disease (CBSD)
# + _kg_hide-input=true
sample1 = labels[labels.label == 1].sample(4)
plt.figure(figsize=(15, 5))
for ind, (image_id, label) in enumerate(zip(sample1.image_id, sample1.label)):
plt.subplot(1, 4, ind + 1)
img = cv2.imread(os.path.join('../input/cassava-leaf-disease-classification', "train_images", image_id))
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
plt.imshow(img)
plt.show()
# -
# ### Class2: Cassava Green Mottle (CGM)
# + _kg_hide-input=true
sample2 = labels[labels.label == 2].sample(4)
plt.figure(figsize=(15, 5))
for ind, (image_id, label) in enumerate(zip(sample2.image_id, sample2.label)):
plt.subplot(1, 4, ind + 1)
img = cv2.imread(os.path.join('../input/cassava-leaf-disease-classification', "train_images", image_id))
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
plt.imshow(img)
plt.show()
# -
# ### Class3: Cassava Mosaic Disease (CMD)
# + _kg_hide-input=true
sample3 = labels[labels.label == 3].sample(4)
plt.figure(figsize=(15, 5))
for ind, (image_id, label) in enumerate(zip(sample3.image_id, sample3.label)):
plt.subplot(1, 4, ind + 1)
img = cv2.imread(os.path.join('../input/cassava-leaf-disease-classification', "train_images", image_id))
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
plt.imshow(img)
plt.show()
# -
# ### Class4: Healthy
# + _kg_hide-input=true
sample4 = labels[labels.label == 4].sample(4)
plt.figure(figsize=(15, 5))
for ind, (image_id, label) in enumerate(zip(sample4.image_id, sample4.label)):
plt.subplot(1, 4, ind + 1)
img = cv2.imread(os.path.join('../input/cassava-leaf-disease-classification', "train_images", image_id))
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
plt.imshow(img)
plt.show()
# -
# Citation: [Cassava Leaf Disease: Best Keras CNN](https://www.kaggle.com/maksymshkliarevskyi/cassava-leaf-disease-best-keras-cnn)
# ### Class Distributions
# +
train_labels['label']=train_labels['label'].astype(str)
with open('/kaggle/input/cassava-leaf-disease-classification/label_num_to_disease_map.json') as f:
disease_dict = json.load(f)
disease_df = pd.DataFrame(list(disease_dict.items()),columns = ['label','real_label'])
for i in range(len(disease_df)):
disease_df['label'][i] = int(i)
actual_class = pd.merge(csv_df,disease_df,on='label')
#Count the number of images in each disease
obs_in_actual = actual_class.groupby(['label','real_label']).size()
print(obs_in_actual)
# +
ax = (actual_class.value_counts(actual_class['real_label'], ascending=True)
.plot(kind='barh', fontsize="20",
title="Class Distribution", figsize=(8,5)))
ax.set(xlabel="Images per class", ylabel="Classes")
ax.xaxis.label.set_size(15)
ax.yaxis.label.set_size(15)
ax.title.set_size(15)
plt.show()
# -
# We calculated our baseline accuracy based on the calss with the largest proportion (class 3)
num_class3 = 13158
num_total = len(train_labels.label)
baseline_acc = num_class3/num_total
print("Baseline Accuracy:",baseline_acc) #0.6150
# # TFRecord Data
# We know the truth that Class Three have the much larger proportion than other classes so our data is imbalanced and our prediction would be biased if we only split the original data randomly. However, we cannot balance the tradeoffs between image resizing (256 x 256 and above) and handling imblanced images due to the limitations of RAM and the stratified method. Therefore, we used the Stratified data in TFRecords format generated by the Kagglor,DimitreOliveira. The details could be checked by the public notebook, [Cassava Leaf Disease-Stratified TFRecords 256x256](https://www.kaggle.com/dimitreoliveira/cassava-leaf-disease-stratified-tfrecords-256x256).
# This dataset contains 15 files with similar proportion of each class. Each file contains around 1427 eaxamples.
#All files have the similar structures so we chose 12 files as training set and 3 files as validation set.
import glob
train_dir = '../input/stratifiedtf/StratifiedTF/train_newtf/*'
test_dir = '../input/stratifiedtf/StratifiedTF/val_newtf/*'
train_list = glob.glob(train_dir)
test_list = glob.glob(test_dir)
print("train: " + str(len(train_list)) + "\ntest: " + str(len(test_list)))
# +
#Read TFrecords
#the functions are adapted from the examples provided by keras reference site:
#https://keras.io/examples/keras_recipes/tfrecord/
def decode_image(image):
image = tf.image.decode_jpeg(image, channels=3)
image = tf.cast(image, tf.float32) / 255.0
image = tf.reshape(image, [*IMAGE_SIZE, 3])
return image
def read_tfrecord(example, labeled):
tfrecord_format = {
"image": tf.io.FixedLenFeature([], tf.string),
"target": tf.io.FixedLenFeature([], tf.int64)
} if labeled else {
"image": tf.io.FixedLenFeature([], tf.string),
"image_name": tf.io.FixedLenFeature([], tf.string)
}
example = tf.io.parse_single_example(example, tfrecord_format)
image = decode_image(example['image'])
if labeled:
label = tf.cast(example['target'], tf.int32)
return image, label
idnum = example['image_name']
return image, idnum
def load_dataset(filenames, labeled=True, ordered=False):
ignore_order = tf.data.Options()
if not ordered:
ignore_order.experimental_deterministic = False
dataset = tf.data.TFRecordDataset(filenames, num_parallel_reads=AUTOTUNE)
dataset = dataset.with_options(ignore_order)
dataset = dataset.map(partial(read_tfrecord, labeled=labeled), num_parallel_calls=AUTOTUNE)
dataset=dataset.batch(BATCH_SIZE)
return dataset
# +
AUTOTUNE = tf.data.experimental.AUTOTUNE
BATCH_SIZE = 16
IMAGE_SIZE = [256, 256]
dataset_train=load_dataset(train_list,labeled=True)
dataset_val=load_dataset(test_list,labeled=True)
# -
labels = train_labels
DATASET_SIZE=len(labels)
train_size = int(0.8 * DATASET_SIZE)
val_size = int(0.2 * DATASET_SIZE)
print("Training data size:",train_size)
print("Validation data size:",val_size)
# # Models
# We implemented four different models, including our baseline CNN model, ResNet50, ResNet architecture, self-designed (ResNet + VGG architechture) and EfficientNet B0. Our results shows EfficientNetB0 gives the best accuracy as well as the best training performance.
# ## Baseline CNN Model
def build_baseline():
inputs = Input(shape = (256,256,3))
model = Conv2D(filters=32, kernel_size=(3, 3),activation='relu',
input_shape=(256,256,3))(inputs)
model = AveragePooling2D(pool_size=(2, 2))(model)
model = Conv2D(filters=64, kernel_size=(3, 3), activation='relu')(model)
model = AveragePooling2D(pool_size=(2, 2))(model)
model = Dropout(0.5)(model)
model = Conv2D(filters=128, kernel_size=(3, 3), activation='relu')(model)
model = MaxPool2D(pool_size=(2, 2))(model)
model = Conv2D(filters=256, kernel_size=(3, 3), activation='relu')(model)
model = Dropout(0.5)(model)
model = Flatten()(model)
model = Dense(512, activation = "relu")(model)
out = Dense(5, activation = 'softmax')(model)
model = Model(inputs=inputs, outputs=out)
model.compile(loss='sparse_categorical_crossentropy',
optimizer=keras.optimizers.Adam(lr=0.001),
metrics=["sparse_categorical_accuracy"])
return model
# + _kg_hide-output=true
model = build_baseline()
model.summary()
# + _kg_hide-output=true
from tensorflow.keras.callbacks import EarlyStopping, ReduceLROnPlateau
early_stop = EarlyStopping(monitor = 'val_loss', min_delta = 0.001,
patience = 5, mode = 'min', verbose = 1,
restore_best_weights = True)
reduce_lr = ReduceLROnPlateau(monitor = 'val_loss', factor = 0.3,
patience = 5, min_delta = 0.001,
mode = 'min', verbose = 1)
history = model.fit(
dataset_train.repeat(),
steps_per_epoch = train_size//BATCH_SIZE,
validation_data= dataset_val.repeat(),
validation_steps=val_size//BATCH_SIZE,
epochs=20,
callbacks = [early_stop, reduce_lr],
verbose=True
)
# -
import matplotlib.pyplot as plt
N = 9
plt.style.use("ggplot")
plt.figure()
plt.plot(np.arange(0, N), history.history["sparse_categorical_accuracy"], label="Train Accuracy")
plt.plot(np.arange(0, N), history.history["val_sparse_categorical_accuracy"], label="Validation Accuracy")
plt.plot(np.arange(0, N), history.history["loss"], label="Train Loss")
plt.plot(np.arange(0, N), history.history["val_loss"], label="Validation Loss")
plt.title("Baseline CNN Loss and Accuracy Plot")
plt.xlabel("Epoch")
plt.legend(bbox_to_anchor=(1.05, 1.0), loc='upper left')
plt.show()
# For our baseline CNN model, overfitting occurs at epoch 5 due to the trends of training and validation losses. Therefore, the baseline CNN achieved 0.66 validation accuracy. We hope the further models would make improvements.
from keras.models import load_model
import os
def save_model(model, name):
model_name = '{}.h5'.format(name)
save_dir = os.path.join(os.getcwd(), 'saved_models')
# Save model and weights
if not os.path.isdir(save_dir):
os.makedirs(save_dir)
model_path = os.path.join(save_dir, model_name)
model.save(model_path)
print('Saved trained model at %s ' % model_path)
save_model(model, 'baseCNN_model') #save baseline CNN model
# ## Self-Designed (ResNet + VGG architechture)
# + _kg_hide-output=false
#The functions are written by
#https://colab.research.google.com/github/d2l-ai/d2l-tensorflow-colab/blob/master/chapter_convolutional-modern/resnet.ipynb
# !pip install d2l==0.16.1
from d2l import tensorflow as d2l
import tensorflow as tf
class Residual(tf.keras.Model): #@save
"""The Residual block of ResNet."""
def __init__(self, num_channels, use_1x1conv=False, strides=1):
super().__init__()
self.conv1 = tf.keras.layers.Conv2D(
num_channels, padding='same', kernel_size=3, strides=strides)
self.conv2 = tf.keras.layers.Conv2D(
num_channels, kernel_size=3, padding='same')
self.conv3 = None
if use_1x1conv:
self.conv3 = tf.keras.layers.Conv2D(
num_channels, kernel_size=1, strides=strides)
self.bn1 = tf.keras.layers.BatchNormalization()
self.bn2 = tf.keras.layers.BatchNormalization()
def call(self, X):
Y = tf.keras.activations.relu(self.bn1(self.conv1(X)))
Y = self.bn2(self.conv2(Y))
if self.conv3 is not None:
X = self.conv3(X)
Y += X
return tf.keras.activations.relu(Y)
class ResnetBlock(tf.keras.layers.Layer):
def __init__(self, num_channels, num_residuals, first_block=False,
**kwargs):
super(ResnetBlock, self).__init__(**kwargs)
self.residual_layers = []
for i in range(num_residuals):
if i == 0 and not first_block:
self.residual_layers.append(
Residual(num_channels, use_1x1conv=True, strides=2))
else:
self.residual_layers.append(Residual(num_channels))
def call(self, X):
for layer in self.residual_layers.layers:
X = layer(X)
return X
# -
sd_model = tf.keras.Sequential([
tf.keras.layers.Input(shape=(256,256,3)),
tf.keras.layers.Conv2D(64, kernel_size=7, strides=2, padding='same'),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Activation('relu'),
tf.keras.layers.MaxPool2D(pool_size=3, strides=2, padding='same'),
ResnetBlock(64, 2, first_block=True),
ResnetBlock(128, 2),
ResnetBlock(256, 2),
tf.keras.layers.Conv2D(128, kernel_size=7, strides=2, padding='same'),
tf.keras.layers.Conv2D(128, kernel_size=7, strides=2, padding='same'),
tf.keras.layers.Conv2D(128, kernel_size=7, strides=2, padding='same'),
tf.keras.layers.MaxPooling2D(),
tf.keras.layers.Conv2D(256, kernel_size=7, strides=2, padding='same'),
tf.keras.layers.Conv2D(256, kernel_size=7, strides=2, padding='same'),
tf.keras.layers.Conv2D(256, kernel_size=7, strides=2, padding='same'),
tf.keras.layers.GlobalAvgPool2D(),
tf.keras.layers.Dense(units=5, activation="softmax")])
# + _kg_hide-output=false
sd_model.summary()
# + _kg_hide-output=true
sd_model.compile(loss='sparse_categorical_crossentropy',
optimizer=keras.optimizers.Adam(lr=0.0001),
metrics=['sparse_categorical_accuracy'])
early_stop = EarlyStopping(monitor = 'val_loss', min_delta = 0.001,
patience = 5, mode = 'min', verbose = 1,
restore_best_weights = True)
reduce_lr = ReduceLROnPlateau(monitor = 'val_loss', factor = 0.3,
patience = 5, min_delta = 0.001,
mode = 'min', verbose = 1)
sd_history = sd_model.fit(
dataset_train.repeat(),
steps_per_epoch = train_size//BATCH_SIZE,
validation_data = dataset_val.repeat(),
validation_steps= val_size//BATCH_SIZE,
callbacks=[reduce_lr, early_stop],
epochs = 20,
verbose = True)
# -
import matplotlib.pyplot as plt
N = 7
plt.style.use("ggplot")
plt.figure()
plt.plot(np.arange(0, N), sd_history.history["sparse_categorical_accuracy"], label="Train Accuracy")
plt.plot(np.arange(0, N), sd_history.history["val_sparse_categorical_accuracy"], label="Validation Accuracy")
plt.plot(np.arange(0, N), sd_history.history["loss"], label="Train Loss")
plt.plot(np.arange(0, N), sd_history.history["val_loss"], label="Validation Loss")
plt.title("Self-Designed Model Loss and Accuracy Plot")
plt.xlabel("Epoch")
plt.legend(bbox_to_anchor=(1.05, 1.0), loc='upper left')
plt.show()
# Our self-designed model which combines Residual blocks and VGG architectures performs better than our baseline CNN model. This model gives us 0.689 as the best validation accuracy at epoch 4 and then overfitting happens due to the trends of training and validation losses.
# ## ResNet50
# +
from tensorflow.keras.applications import ResNet50
from tensorflow.keras.layers import Input
base_res = ResNet50(weights="imagenet", include_top=False, input_shape=(256, 256, 3))
head_res = base_res.output
head_res = GlobalAveragePooling2D()(head_res)
head_res = Dense(5, activation= "softmax")(head_res)
resnet50 = Model(inputs=base_res.input, outputs=head_res)
# -
for layer in base_res.layers:
layer.trainable = False
# + _kg_hide-output=true
resnet50.summary()
# +
resnet50.compile(optimizer = Adam(lr = 0.01),
loss = 'sparse_categorical_crossentropy',
metrics = ['sparse_categorical_accuracy'])
reduce_lr = ReduceLROnPlateau(monitor = 'val_loss', factor = 0.3,
patience = 5, min_delta = 0.001,
mode = 'min', verbose = 1)
early_stop = EarlyStopping(monitor = 'val_loss', min_delta = 0.001,
patience = 10, mode = 'min', verbose = 1,
restore_best_weights = True)
history_resnet50 = resnet50.fit(
dataset_train.repeat(),
steps_per_epoch = train_size//BATCH_SIZE,
validation_data= dataset_val.repeat(),
validation_steps=val_size//BATCH_SIZE,
epochs=30,
callbacks = [reduce_lr, early_stop],
verbose=True
)
# -
N = 29
plt.style.use("ggplot")
plt.figure()
plt.plot(np.arange(0, N), history_resnet50.history["sparse_categorical_accuracy"], label="Train Accuracy")
plt.plot(np.arange(0, N), history_resnet50.history["val_sparse_categorical_accuracy"], label="Validation Accuracy")
plt.plot(np.arange(0, N), history_resnet50.history["loss"], label="Train Loss")
plt.plot(np.arange(0, N), history_resnet50.history["val_loss"], label="Validation Loss")
plt.title("ResNet50 Loss and Accuracy Plot")
plt.xlabel("Epoch")
plt.legend(bbox_to_anchor=(1.05, 1.0), loc='upper left')
plt.show()
# At epoch 18 and later, the validation accuracy converges to 0.64. It means the model based on pre-trained ResNet50 performs worse than our baseline CNN model and we decided to swich on other models.
# ## ResNet architecture
resarc = tf.keras.Sequential([
tf.keras.layers.Input(shape=(256,256,3)),
tf.keras.layers.Conv2D(64, kernel_size=7, strides=2, padding='same'),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Activation('relu'),
tf.keras.layers.MaxPool2D(pool_size=3, strides=2, padding='same'),
ResnetBlock(64, 2, first_block=True),
ResnetBlock(128, 2),
ResnetBlock(256, 2),
ResnetBlock(512, 2),
tf.keras.layers.GlobalAvgPool2D(),
tf.keras.layers.Dense(units=5, activation="softmax")])
resarc.summary()
# + _kg_hide-output=true
resarc.compile(optimizer = Adam(lr = 0.001),
loss = 'sparse_categorical_crossentropy',
metrics = ['sparse_categorical_accuracy'])
history_resarc = resarc.fit(
dataset_train.repeat(),
steps_per_epoch = train_size//BATCH_SIZE,
validation_data= dataset_val.repeat(),
validation_steps=val_size//BATCH_SIZE,
epochs=20,
callbacks = [reduce_lr, early_stop],
verbose=True
)
# -
N = 16
plt.style.use("ggplot")
plt.figure()
plt.plot(np.arange(0, N), history_resarc.history["sparse_categorical_accuracy"], label="Train Accuracy")
plt.plot(np.arange(0, N), history_resarc.history["val_sparse_categorical_accuracy"], label="Validation Accuracy")
plt.plot(np.arange(0, N), history_resarc.history["loss"], label="Train Loss")
plt.plot(np.arange(0, N), history_resarc.history["val_loss"], label="Validation Loss")
plt.title("ResNet(Arc) Loss and Accuracy Plot")
plt.xlabel("Epoch")
plt.legend(bbox_to_anchor=(1.05, 1.0), loc='upper left')
plt.show()
# The simple ResNet architecture achieves 0.67 accuracy which is higher than baseline accuracy (0.6150) but the improvement is not big enough to conclude the final model. At the epoch 8, the model begins to overfit the training dataset.
# ## EfficientNet B0
# +
from tensorflow.keras.applications import EfficientNetB0
effb0_model = tf.keras.Sequential()
effb0_model.add(EfficientNetB0(include_top = False, weights = 'imagenet',
input_shape = (256, 256, 3)))
effb0_model.add(tf.keras.layers.GlobalAveragePooling2D())
effb0_model.add(tf.keras.layers.Dense(5, activation = "softmax"))
effb0_model.compile(optimizer = Adam(lr = 0.001),
loss = 'sparse_categorical_crossentropy',
metrics = ['sparse_categorical_accuracy'])
# + _kg_hide-output=true
effb0_model.summary()
# +
# from tensorflow.keras.callbacks import EarlyStopping, ReduceLROnPlateau
# reduce_lr = ReduceLROnPlateau(monitor = 'val_loss', factor = 0.3,
# patience = 5, min_delta = 0.001,
# mode = 'min', verbose = 1)
# early_stop = EarlyStopping(monitor = 'val_loss', min_delta = 0.001,
# patience = 10, mode = 'min', verbose = 1,
# restore_best_weights = True)
# history_effb0 = effb0_model.fit(
# dataset_train.repeat(),
# steps_per_epoch = train_size//BATCH_SIZE,
# validation_data= dataset_val.repeat(),
# validation_steps=val_size//BATCH_SIZE,
# epochs=100,
# callbacks = [reduce_lr, early_stop],
# verbose=True
# )
# -
#Import the local trained EfficientNetB0 model.
effnetb0 = keras.models.load_model("../input/effnetb0/EffNetB0.h5")
# EffNetb0.png
# EfficientNetB0 gives us around 0.8 validation accuracy score (Within the range: 0.79 - 0.82). Comparing to our baeline model, EfficientNetB0 improved 0.185 validation accuracy with an excellent training process. Therefore, we decided to use the EfficientNet50 as our final model to make the prediction on test set.
# +
import pandas as pd
import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras.preprocessing.image import smart_resize
preds = []
sample_sub = pd.read_csv('/kaggle/input/cassava-leaf-disease-classification/sample_submission.csv')
for image in sample_sub.image_id:
img = keras.preprocessing.image.load_img('/kaggle/input/cassava-leaf-disease-classification/test_images/' + image)
img = img_to_array(img)
img = smart_resize(img, (256,256))
img = tf.reshape(img, (-1, 256, 256, 3))
# Now apply your model and save your prediction:
prediction = effnetb0.predict(img)
preds.append(np.argmax(prediction))
my_submission = pd.DataFrame({'image_id': sample_sub.image_id, 'label': preds})
my_submission.to_csv('/kaggle/working/submission.csv', index=False)
# -
sample_submission=pd.read_csv("../input/cassava-leaf-disease-classification/sample_submission.csv")
sample_submission #True label
submission=pd.read_csv("./submission.csv")
submission #Predicted Label
|
src/Data2040MidProj_part3_Final.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/gist/dsp196/70f15a7e712882b92ea092a873abbbed/-pneumonia_detection102.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="W33lkRkfxxvZ"
from google.colab import files
# + colab={"resources": {"http://localhost:8080/nbextensions/google.colab/files.js": {"data": "<KEY>", "ok": true, "headers": [["content-type", "application/javascript"]], "status": 200, "status_text": ""}}, "base_uri": "https://localhost:8080/", "height": 73} id="XnFtArLvozNN" outputId="2696c823-0f0b-4dc7-daf1-da0bac53afd9"
data = files.upload()
# !mkdir -p ~/.kaggle
# !cp kaggle.json ~/.kaggle/
#change permission
# !chmod 600 ~/.kaggle/kaggle.json
# + colab={"base_uri": "https://localhost:8080/"} id="VOV-Th3UxxUp" outputId="e16377e2-332d-4260-b516-c2f0ad590ff9"
# !kaggle datasets download -d paultimothymooney/chest-xray-pneumonia
# + id="OjwFgIJIxwOZ"
from zipfile import ZipFile
file_name = "chest-xray-pneumonia.zip"
# + colab={"base_uri": "https://localhost:8080/"} id="xf0SmhWTzl95" outputId="2b786a07-8bec-41a1-c098-5ef1923910dc"
with ZipFile(file_name,'r') as zip:
zip.extractall()
print('Done')
# + id="3o3ENtpj1l44"
import glob
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Conv2D, MaxPool2D, Flatten, Dropout
from tensorflow.keras.callbacks import ReduceLROnPlateau ,EarlyStopping,ModelCheckpoint
from tensorflow.keras.preprocessing.image import ImageDataGenerator
from tensorflow import keras
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split
import cv2 as cv
import os
# %matplotlib inline
import warnings
warnings.filterwarnings('ignore')
# + id="ct8G0908HoJV"
image_size =180
batch_size =64
epochs =50
# + id="YCOTPYzY0bR4"
base_dir = '/content/chest_xray/'
pneumonia_files = glob.glob(base_dir + '/**/PNEUMONIA/*.jpeg')
normal_files = glob.glob(base_dir + '/**/NORMAL/*.jpeg')
# + colab={"base_uri": "https://localhost:8080/"} id="R5dBmcXb0boY" outputId="9c5a9432-bd4b-4da8-e6e0-17eab2450f58"
print('pneumonia files : {}'.format(len(pneumonia_files)))
print('normal_files : {}'.format(len(normal_files)))
# + colab={"base_uri": "https://localhost:8080/", "height": 487} id="z7qc3c9nyVgJ" outputId="49693477-ba24-4ef0-dbaf-68591a8a1f9c"
fig, ax = plt.subplots(2, 3, figsize = (15, 9))
ax = ax.ravel()
plt.tight_layout()
for i, _set in enumerate(['train', 'val', 'test']):
set_path = base_dir + _set
ax[i].imshow(plt.imread(set_path + '/NORMAL/' + os.listdir(set_path + '/NORMAL')[0]), cmap = 'gray')
ax[i].set_title('Data: {} \n Type: Normal'.format(_set), fontsize = 13)
ax[i+3].imshow(plt.imread(set_path + '/PNEUMONIA/' + os.listdir(set_path + '/PNEUMONIA')[0]), cmap = 'gray')
ax[i+3].set_title('Data: {} \n Type: Pneumonia'.format(_set), fontsize = 13)
# + id="tx2g0G0v0b3I"
# Data Splitting
train_pneumonia , test_pneumonia = train_test_split(pneumonia_files,test_size = 0.2)
train_pneumonia , val_pneumonia = train_test_split(train_pneumonia,test_size =0.2)
# + id="-_Iz9AkZ3qbn"
train_normal, test_normal = train_test_split(normal_files , test_size = 0.2)
train_normal , val_normal = train_test_split(train_normal , test_size = 0.2)
# + colab={"base_uri": "https://localhost:8080/"} id="5vLccPFV3q13" outputId="4ce65b34-c68e-40a4-ff29-d8882d9ab631"
print('Pneumonia files have {0} training examples ,{1} testing examples ,{2} validation examples'.format(len(train_pneumonia),len(test_pneumonia),len(val_pneumonia)))
print('Normal files have {0} training examples ,{1} testing examples ,{2} validation examples'.format(len(train_normal),len(test_normal),len(val_normal)))
# + id="5d_zqzuI39-4"
# + colab={"base_uri": "https://localhost:8080/"} id="JIa0M2Xp8PB3" outputId="10956e33-4a3b-4bef-90bf-217df20b65bc"
# adding labels (pneumonia: 1, normal: 0)
train_data = []
val_data = []
test_data = []
for sample in train_pneumonia:
train_data.append([sample, '1'])
for sample in val_pneumonia:
val_data.append([sample, '1'])
for sample in test_pneumonia:
test_data.append([sample, '1'])
for sample in train_normal:
train_data.append([sample, '0'])
for sample in val_normal:
val_data.append([sample, '0'])
for sample in test_normal:
test_data.append([sample, '0'])
# convert them into dataframes
train_df = pd.DataFrame(train_data, columns=['image', 'label'])
val_df = pd.DataFrame(val_data, columns=['image', 'label'])
test_df = pd.DataFrame(test_data, columns=['image', 'label'])
print(len(train_df), len(val_df), len(test_df))
# + id="ShpMOyn3BD6J"
train_img_gen = ImageDataGenerator(rescale=1./255,
rotation_range =10,
zoom_range =0.2,
width_shift_range =0.1,
height_shift_range =0.1)
test_img_gen = ImageDataGenerator(
rescale=1./255
)
val_img_gen = ImageDataGenerator(
rescale =1./255
)
# + colab={"base_uri": "https://localhost:8080/"} id="q8R1bsqWBEO2" outputId="347f39fa-6f14-434b-8d97-a739515283fc"
train_set_gen = train_img_gen.flow_from_dataframe(train_df,x_col = 'image',y_col ='label',target_size=(image_size,image_size),batch_size=batch_size,shuffle =True ,class_mode ='binary',color_mode='grayscale')
test_set_gen = test_img_gen.flow_from_dataframe(test_df,x_col = 'image',y_col = 'label',target_size= (image_size,image_size),batch_size=1,class_mode='binary',shuffle =False,color_mode='grayscale')
val_set_gen = val_img_gen.flow_from_dataframe(val_df,x_col = 'image',y_col ='label',target_size=(image_size,image_size),batch_size =batch_size,shuffle=True,class_mode='binary',color_mode ='grayscale')
# + colab={"base_uri": "https://localhost:8080/"} id="V-VYnP9Yesf8" outputId="9372e497-c52a-4c77-b0d8-b3e5c69a42a3"
# + id="vYJeSfRCBEaG"
model = tf.keras.models.Sequential([
tf.keras.layers.Conv2D(32,(3,3),input_shape = (180,180,1),activation='relu',padding ='same'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(32,(3,3),activation='relu',padding='same'),
tf.keras.layers.MaxPooling2D((2,2)),
tf.keras.layers.Conv2D(64,(3,3),activation='relu',padding='same'),
tf.keras.layers.MaxPooling2D((2,2)),
tf.keras.layers.Dropout(0.2),
tf.keras.layers.Conv2D(64,(3,3),activation='relu',padding='same'),
tf.keras.layers.MaxPooling2D((2,2)),
tf.keras.layers.Dropout(0.2),
tf.keras.layers.Conv2D(64,(3,3),activation='relu',padding='same'),
tf.keras.layers.MaxPooling2D((2,2)),
tf.keras.layers.Dropout(0.3),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(64,activation = 'relu'),
tf.keras.layers.Dropout(0.5),
tf.keras.layers.Dense(1,activation = 'sigmoid'),
])
# + id="dqbkxWdVTd6T"
loaded_model = tf.keras.models.load_model('/content/Cnn_xray_103.h5')
# + id="MHdndJ6SUjsR"
#METRICS =[tf.keras.metrics.BinaryAccuracy(),tf.keras.metrics.Accuracy(),tf.keras.metrics.Precision(name = 'precision'),tf.keras.metrics.Recall(name ='recall')]
# + id="Wzuur1DBBEem"
model.compile(optimizer = 'adam',loss = 'binary_crossentropy',metrics=['accuracy'])
# + id="z6WrGy_LqBXV"
lr_reduction = ReduceLROnPlateau(monitor='val_accuracy', patience = 3,
verbose=1,factor=0.5, min_lr=0.000001)
# + colab={"base_uri": "https://localhost:8080/"} id="Js2-Nn56q3LK" outputId="8088055b-1a44-4c58-e4c7-450f25668958"
history = model.fit_generator(train_set_gen,
steps_per_epoch=len(train_set_gen),
epochs=epochs,
validation_data=val_set_gen,
validation_steps=len(val_set_gen),
callbacks=[lr_reduction])
# + id="HfsFhdimxfM0" colab={"base_uri": "https://localhost:8080/"} outputId="d96f2b21-551f-4317-a218-3eef55d7d788"
Predict_score = model.evaluate(test_set_gen)
print(Predict_score)
# + colab={"base_uri": "https://localhost:8080/", "height": 360} id="EJc58lPKktP6" outputId="0275cb6b-7527-4800-e9c4-74a044065d13"
figure, axis = plt.subplots(1, 2, figsize=(10, 5))
for i, e in enumerate(['accuracy', 'loss']):
axis[i].plot(history.history[e])
axis[i].plot(history.history['val_' + e])
axis[i].set_title(e, fontsize=20)
axis[i].set_xlabel('epochs', fontsize=15)
axis[i].set_ylabel(e, fontsize=15)
axis[i].legend(['train', 'val'])
# + id="icdAr9vz3pln"
model.save('Cnn_xray_104.h5')
# + id="pCv0cpY7BEjm"
model.save_weights('Cnn_xray_104_weights.h5')
# + id="NTE1o4tdBEnY"
model_json = model.to_json()
with open("Cnn_xray_104.json", "w") as json_file:
json_file.write(model_json)
# + id="3frOLTwgBEq3"
predictions=model.predict(test_set_gen)
classes_x=np.where(predictions > 0.5, 1,0)
cm = confusion_matrix(test_set_gen.classes, classes_x)
# + id="IHqeRDz-wn2M"
cm_pd = pd.DataFrame(cm , index = ['0','1'] , columns = ['0','1'])
# + colab={"base_uri": "https://localhost:8080/", "height": 320} id="EUPfpkBAwFAE" outputId="cda07377-5241-46c5-fb57-b3ab620ef052"
plt.figure(figsize = (6,5))
sns.heatmap(cm_pd,cmap= "Blues", linecolor = 'black' ,
linewidth = 1 , annot = True, fmt='',
xticklabels = ['Predicted Normal', 'Predicted Pneumonia'],
yticklabels = ['Actual Normal', 'Actual Pneumonia'])
plt.yticks(rotation=0)
plt.show()
# + id="EExwbu96wkes"
|
-pneumonia_detection102.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .sh
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Bash
# language: bash
# name: bash
# ---
sign () { echo "$(( $1 < 0 ? -1 : 1 ))"; }
x=0
y=$(($(sign "$x") ))
echo $y
function add()
{
sum=$(($1 + $2))
echo "Sum = $sum"
}
y = add 32 2
my_function () {
echo "some result"
return $1 + $2
}
x=hello_world
echo $x
my_function 1 2
x=-$y
echo $x
source /home/m/Mert.Kurttutan/Academia/Codes/Physics/Projects/qh_fm_01/codes/excs/FH_job_autoCaller_flux_plaq_fix_pin_02.sh
|
notebooks/Untitled.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.6
# language: python
# name: python3
# ---
# 学习和使用支持向量机
#
# - 学习教材6.3、6.4节内容,调试运行相关代码。
# - 查阅scikit-learn工具包中支持向量机的相关说明,了解分类器函数使用方法。
# - 完成作业二
#
# # SMO高效优化算法
#
# > 书本代码参考仓库[Machine Learning in Action](https://github.com/TeFuirnever/Machine-Learning-in-Action)
#
# SMO算法的目标是求出一系列alpha和b,便于计算权重向量并得到分隔超平面。
#
# 工作原理:选择两个alpha进行优化处理,一旦找到一对合适的alpha,那么就增大一个减少另一个。
#
# > “合适”:①alpha须在间隔边界之外;②alpha没有进行过区间化处理或者不在边界上。
#
#
# ## 简化版SMO
#
# 量少,但执行速度慢。跳过SMO的外循环(确定最佳alpha对),遍历每个alpha随机选择另一个。
import numpy as np
import random
# +
## 6-1 SMO算法中的辅助函数
"""
函数说明:读取数据
Parameters:
fileName - 文件名
Returns:
dataMat - 数据矩阵
labelMat - 数据标签
"""
def loadDataSet(fileName):
dataMat = []; labelMat = []
fr = open(fileName)
for line in fr.readlines(): #逐行读取,滤除空格等
lineArr = line.strip().split('\t')
dataMat.append([float(lineArr[0]), float(lineArr[1])]) #添加数据
labelMat.append(float(lineArr[2])) #添加标签
return dataMat,labelMat
"""
函数说明:随机选择alpha
Parameters:
i - alpha
m - alpha参数个数
Returns:
j -
"""
def selectJrand(i, m):
j = i #选择一个不等于i的j
while (j == i):
j = int(random.uniform(0, m))
return j
"""
函数说明:修剪alpha
Parameters:
aj - alpha值
H - alpha上限
L - alpha下限
Returns:
aj - alpah值
"""
def clipAlpha(aj,H,L):
if aj > H:
aj = H
if L > aj:
aj = L
return aj
# -
dataArr, labelArr = loadDataSet('./data/testSet.txt')
print(labelArr[:5])
# 该数据集中类别标签为1,-1。
#
# SMO的伪代码大致如下:
#
# > * 创建一个alpha向量并将其初始化为0向量
# >
# > * 当迭代次数小于最大迭代次数时:
# >
# > * 对数据集中的每个数据向量(外循环):
# >
# > * 如果该向量可以被优化:
# >
# > * 随机选择另外一个数据向量(内循环)
# >
# > * 同时优化这两个向量
# >
# > * 如果两个向量都不能被优化,退出内循环
# >
# > * 如果所有向量都没有被优化,增加迭代数目,继续下一次循环
#
# $$
# fXi = \sum_{j=1}^N \alpha_j y_j X_j \cdot X_i
# $$
#
# 步骤1:计算误差Ei=f(x)-y
#
# 步骤2:计算上下界L和H
# $$
# L = \max{(0,\alpha_2^{\text{old}}-\alpha_1^{\text{old}})}, \ \ \ H=\min{(C,C+\alpha_2^{\text{old}}-\alpha_1^{\text{old}})}\\
# 或\\
# L = \max{(0,\alpha_2^{\text{old}}+\alpha_1^{\text{old}}-C)}, \ \ \ H=\min{(C,\alpha_2^{\text{old}}+\alpha_1^{\text{old}})}
# $$
#
# 步骤3:计算eta(η)
# $$
# \eta = K_{11} + K_{22} - 2K_{12} = ||\phi(x_1)-\phi(x_2)||^2
# $$
#
# 步骤4:更新alpha_j
# $$
# \alpha_2^{\text{new,unc}} = \alpha_2^{\text{old}} + \dfrac{y_2(E_1-E_2)}{\eta}
# $$
#
# 步骤5:修剪alpha_j
# $$
# \alpha_2^{new} = \left\{
# \begin{align}
# &H, &\alpha_2^{\text{new,unc}}\gt H \\
# &\alpha_2^{\text{new,unc}}, & L \le\alpha_2^{\text{new,unc}}\le H \\
# &L, &\alpha_2^{\text{new,unc}}\lt L
# \end{align}
# \right.
# $$
#
# 步骤6:更新alpha_i
# $$
# \alpha_1^{\text{new}} = \alpha_1^{\text{old}} + y_1y_2(\alpha_2^{\text{old}}-\alpha_2^{\text{new}})
# $$
#
# 步骤7:更新b_1和b_2
# $$
# b_1^{\text{new}} = b^{\text{old}} - E_1 - y_1K_{11}(\alpha_1^{\text{new}}-\alpha_1^{\text{old}}) - y_2K_{21}(\alpha_2^{\text{new}}-\alpha_2^{\text{old}})\\
# b_2^{\text{new}} = b^{\text{old}} - E_2 - y_1K_{12}(\alpha_1^{\text{new}}-\alpha_1^{\text{old}}) - y_2K_{22}(\alpha_2^{\text{new}}-\alpha_2^{\text{old}})\\
# $$
#
# 步骤8:根据b_1和b_2更新b
"""
函数说明:简化版SMO算法
Parameters:
dataMatIn - 数据矩阵
classLabels - 数据标签
C - 松弛变量
toler - 容错率
maxIter - 最大迭代次数
Returns:
无
"""
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
#转换为numpy的mat存储
dataMatrix = np.mat(dataMatIn); labelMat = np.mat(classLabels).transpose()
#初始化b参数,统计dataMatrix的维度
b = 0; m,n = np.shape(dataMatrix)
#初始化alpha参数,设为0
alphas = np.mat(np.zeros((m,1)))
#初始化迭代次数
iter_num = 0
#最多迭代matIter次
while (iter_num < maxIter):
alphaPairsChanged = 0
for i in range(m):
#步骤1:计算误差Ei
fXi = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b
##fXi = \sum_{j=1}^N \alpha_j y_j X_j \cdot X_i X:Vector
Ei = fXi - float(labelMat[i])
#优化alpha,更设定一定的容错率。
if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
#随机选择另一个与alpha_i成对优化的alpha_j
j = selectJrand(i,m)
#步骤1:计算误差Ej
fXj = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b
Ej = fXj - float(labelMat[j])
#保存更新前的aplpha值,使用深拷贝
alphaIold = alphas[i].copy(); alphaJold = alphas[j].copy();
#步骤2:计算上下界L和H
if (labelMat[i] != labelMat[j]):
L = max(0, alphas[j] - alphas[i])
H = min(C, C + alphas[j] - alphas[i])
else:
L = max(0, alphas[j] + alphas[i] - C)
H = min(C, alphas[j] + alphas[i])
## L = \max{(0,\alpha_2^{\text{old}}-\alpha_1^{\text{old}})}, \ \ \ H=\min{(C,C+\alpha_2^{\text{old}}-\alpha_1^{\text{old}})}
## L = \max{(0,\alpha_2^{\text{old}}+\alpha_1^{\text{old}}-C)}, \ \ \ H=\min{(C,\alpha_2^{\text{old}}+\alpha_1^{\text{old}})}
if L==H: print("L==H"); continue
#步骤3:计算eta(η)
eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T
## \eta = K_{11} + K_{22} - 2K_{12} = ||\phi(x_1)-\phi(x_2)||^2
if eta >= 0: print("eta>=0"); continue
#步骤4:更新alpha_j
alphas[j] -= labelMat[j]*(Ei - Ej)/eta
## \alpha_2^{\text{new,unc}} = \alpha_2^{\text{old}} + \dfrac{y_2(E_1-E_2)}{\eta}
#步骤5:修剪alpha_j
alphas[j] = clipAlpha(alphas[j],H,L)
if (abs(alphas[j] - alphaJold) < 0.00001): print("alpha_j变化太小"); continue
#步骤6:更新alpha_i
alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])
## \alpha_1^{\text{new}} = \alpha_1^{\text{old}} + y_1y_2(\alpha_2^{\text{old}}-\alpha_2^{\text{new}})
#步骤7:更新b_1和b_2
b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
##b_1^{\text{new}} = b^{\text{old}} - E_1 - y_1K_{11}(\alpha_1^{\text{new}}-\alpha_1^{\text{old}}) - y_2K_{21}(\alpha_2^{\text{new}}-\alpha_2^{\text{old}})\\
##b_2^{\text{new}} = b^{\text{old}} - E_2 - y_1K_{12}(\alpha_1^{\text{new}}-\alpha_1^{\text{old}}) - y_2K_{22}(\alpha_2^{\text{new}}-\alpha_2^{\text{old}})\\
#步骤8:根据b_1和b_2更新b
if (0 < alphas[i]) and (C > alphas[i]): b = b1
elif (0 < alphas[j]) and (C > alphas[j]): b = b2
else: b = (b1 + b2)/2.0
#统计优化次数
alphaPairsChanged += 1
#打印统计信息
print("第%d次迭代 样本:%d, alpha优化次数:%d" % (iter_num,i,alphaPairsChanged))
#更新迭代次数
if (alphaPairsChanged == 0): iter_num += 1
else: iter_num = 0
print("迭代次数: %d" % iter_num)
return b,alphas
# 进行简单的测试:
# %%time
b, alphas = smoSimple(dataArr, labelArr, 0.6, 0.001, 40)
b
alphas[alphas>0]
# ## 完整Platt SMO
#
# 简化版SMO中,外层循环是遍历所有样本点作为 $\alpha_i$ ,内层循环则是随机选择 $\alpha_j$ 更新这两个 $\alpha$ 。这样做计算速度较慢,在较大量数据集或维度较高数据集中很可能耗时过多。
#
# 完整版的Platt SMO的外层循环是遍历所有样本点和遍历非边界点交替进行,遍历所有样本点之后就遍历所有非边界点,遍历非边界点之后如果没有 $\alpha$ 被更新则重新遍历所有样本点;否则继续遍历非边界点。
#
# 内循环则不是随机选择,是通过计算最大化步长 $|E_i-E_j|$ 来进行选择,选择使得 $|E_i-E_j|$ 最大的点作为 $\alpha_j$。
#
# 简化版和完整版仅在 $\alpha$ 的选择上有所不同,内部计算和更新方法相同,不再赘述。但是后者的计算效率相对较高。
# +
## 6-3 完整版SMO的支持函数
"""
数据结构,维护所有需要操作的值
Parameters:
dataMatIn - 数据矩阵
classLabels - 数据标签
C - 松弛变量
toler - 容错率
"""
class optStruct:
def __init__(self, dataMatIn, classLabels, C, toler):
self.X = dataMatIn #数据矩阵
self.labelMat = classLabels #数据标签
self.C = C #松弛变量
self.tol = toler #容错率
self.m = np.shape(dataMatIn)[0] #数据矩阵行数
self.alphas = np.mat(np.zeros((self.m,1))) #根据矩阵行数初始化alpha参数为0
self.b = 0 #初始化b参数为0
self.eCache = np.mat(np.zeros((self.m,2))) #根据矩阵行数初始化虎误差缓存,第一列为是否有效的标志位,第二列为实际的误差E的值。
"""
读取数据
Parameters:
fileName - 文件名
Returns:
dataMat - 数据矩阵
labelMat - 数据标签
"""
def loadDataSet(fileName):
dataMat = []; labelMat = []
fr = open(fileName)
for line in fr.readlines(): #逐行读取,滤除空格等
lineArr = line.strip().split('\t')
dataMat.append([float(lineArr[0]), float(lineArr[1])]) #添加数据
labelMat.append(float(lineArr[2])) #添加标签
return dataMat,labelMat
"""
计算误差
Parameters:
oS - 数据结构
k - 标号为k的数据
Returns:
Ek - 标号为k的数据误差
"""
def calcEk(oS, k):
fXk = float(np.multiply(oS.alphas,oS.labelMat).T*(oS.X*oS.X[k,:].T) + oS.b)
Ek = fXk - float(oS.labelMat[k])
return Ek
"""
内循环启发方式2
Parameters:
i - 标号为i的数据的索引值
oS - 数据结构
Ei - 标号为i的数据误差
Returns:
j, maxK - 标号为j或maxK的数据的索引值
Ej - 标号为j的数据误差
"""
def selectJ(i, oS, Ei):
maxK = -1; maxDeltaE = 0; Ej = 0 #初始化
oS.eCache[i] = [1,Ei] #根据Ei更新误差缓存
validEcacheList = np.nonzero(oS.eCache[:,0].A)[0] #返回误差不为0的数据的索引值
if (len(validEcacheList)) > 1: #有不为0的误差
for k in validEcacheList: #遍历,找到最大的Ek
if k == i: continue #不计算i,浪费时间
Ek = calcEk(oS, k) #计算Ek
deltaE = abs(Ei - Ek) #计算|Ei-Ek|
if (deltaE > maxDeltaE): #找到maxDeltaE
maxK = k; maxDeltaE = deltaE; Ej = Ek
return maxK, Ej #返回maxK,Ej
else: #没有不为0的误差
j = selectJrand(i, oS.m) #随机选择alpha_j的索引值
Ej = calcEk(oS, j) #计算Ej
return j, Ej #j,Ej
"""
计算Ek,并更新误差缓存
Parameters:
oS - 数据结构
k - 标号为k的数据的索引值
Returns:
无
"""
def updateEk(oS, k):
Ek = calcEk(oS, k) #计算Ek
oS.eCache[k] = [1,Ek] #更新误差缓存
# -
## 6-4 完整Platt SMO算法中的优化例程
"""
优化的SMO算法
Parameters:
i - 标号为i的数据的索引值
oS - 数据结构
Returns:
1 - 有任意一对alpha值发生变化
0 - 没有任意一对alpha值发生变化或变化太小
"""
def innerL(i, oS):
#步骤1:计算误差Ei
Ei = calcEk(oS, i)
#优化alpha,设定一定的容错率。
if ((oS.labelMat[i] * Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i] * Ei > oS.tol) and (oS.alphas[i] > 0)):
#使用内循环启发方式2选择alpha_j,并计算Ej
j,Ej = selectJ(i, oS, Ei)
#保存更新前的aplpha值,使用深拷贝
alphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy();
#步骤2:计算上下界L和H
if (oS.labelMat[i] != oS.labelMat[j]):
L = max(0, oS.alphas[j] - oS.alphas[i])
H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
else:
L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
H = min(oS.C, oS.alphas[j] + oS.alphas[i])
if L == H:
print("L==H")
return 0
#步骤3:计算eta
eta = 2.0 * oS.X[i,:] * oS.X[j,:].T - oS.X[i,:] * oS.X[i,:].T - oS.X[j,:] * oS.X[j,:].T
if eta >= 0:
print("eta>=0")
return 0
#步骤4:更新alpha_j
oS.alphas[j] -= oS.labelMat[j] * (Ei - Ej)/eta
#步骤5:修剪alpha_j
oS.alphas[j] = clipAlpha(oS.alphas[j],H,L)
#更新Ej至误差缓存
updateEk(oS, j)
if (abs(oS.alphas[j] - alphaJold) < 0.00001):
print("alpha_j变化太小")
return 0
#步骤6:更新alpha_i
oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])
#更新Ei至误差缓存
updateEk(oS, i)
#步骤7:更新b_1和b_2
b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[i,:].T - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.X[i,:]*oS.X[j,:].T
b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[j,:].T - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.X[j,:]*oS.X[j,:].T
#步骤8:根据b_1和b_2更新b
if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1
elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2
else: oS.b = (b1 + b2)/2.0
return 1
else:
return 0
"""
完整的线性SMO算法
Parameters:
dataMatIn - 数据矩阵
classLabels - 数据标签
C - 松弛变量
toler - 容错率
maxIter - 最大迭代次数
Returns:
oS.b - SMO算法计算的b
oS.alphas - SMO算法计算的alphas
"""
def smoP(dataMatIn, classLabels, C, toler, maxIter):
oS = optStruct(np.mat(dataMatIn), np.mat(classLabels).transpose(), C, toler) #初始化数据结构
iter = 0 #初始化当前迭代次数
entireSet = True; alphaPairsChanged = 0
while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)): #遍历整个数据集都alpha也没有更新或者超过最大迭代次数,则退出循环
alphaPairsChanged = 0
if entireSet: #遍历整个数据集
for i in range(oS.m):# 对数据集中的所有行
alphaPairsChanged += innerL(i,oS) #使用优化的SMO算法
print("全样本遍历:第%d次迭代 样本:%d, alpha优化次数:%d" % (iter,i,alphaPairsChanged))
iter += 1
else: #遍历非边界值
nonBoundIs = np.nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0] #遍历不在边界0和C的alpha
for i in nonBoundIs:
alphaPairsChanged += innerL(i,oS)
print("非边界遍历:第%d次迭代 样本:%d, alpha优化次数:%d" % (iter,i,alphaPairsChanged))
iter += 1
if entireSet: #遍历一次后改为非边界遍历
entireSet = False
elif (alphaPairsChanged == 0): #如果alpha没有更新,计算全样本遍历
entireSet = True
print("迭代次数: %d" % iter)
return oS.b,oS.alphas #返回SMO算法计算的b和alphas
# 测试
# %%time
dataArr, labelArr = loadDataSet('./data/testSet.txt')
b, alphas = smoP(dataArr, labelArr, 0.6, 0.001, 40)
# 用时方面,在相同配置的主机上,时间从7秒下降到了不到0.3秒。
# 利用计算得到的alpha值,可以计算w用于构建超平面。
def calcWs(alphas, dataArr, classLabels):
X = np.mat(dataArr); labelMat = np.mat(classLabels).transpose()
m,n = X.shape
w = np.zeros((n,1))
for i in range(m):
w += np.multiply(alphas[i]*labelMat[i],X[i,:].T)
return w
ws = calcWs(alphas,dataArr,labelArr)
ws
# 分类
datMat = np.mat(dataArr)
print(datMat[0]*np.mat(ws)+b)
# 若该值大于0,其属于1类;若该值小于0,属于-1类,这里得到的分类结果是-1,我们验证一下是不是一样的:
labelArr[0]
# # SVM in scikit-learn
#
# 查阅scikit-learn工具包中支持向量机的相关说明,了解分类器函数使用方法。
#
# 参考这一篇进行学习:[机器学习笔记3-sklearn支持向量机](https://www.jianshu.com/p/a9f9954355b3?utm_campaign=maleskine&utm_content=note&utm_medium=seo_notes&utm_source=recommendation)
# 调包当然是非常简单的拉~
# +
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(dataArr, labelArr, test_size = 0.2, random_state = 100,stratify=labelArr)
clf = SVC()
clf.fit(X_train, y_train)
print('预测样例:')
print(clf.predict(np.array(X_test[0:5])))
print(y_test[0:5])
train_score = clf.score(X_train,y_train)
test_score = clf.score(X_test,y_test)
print("Train Score: %.3f; Test Score %.3f." % (train_score,test_score))
# -
# 好屌,难道是因为是二分类,或者这个样本集很好分吗?什么参数都没有调,准确率达到了100\%。
#
# 因为准确率过高,所以后续对SVM的优化需要基于新的数据集,否则无法评判优化的效果。
# 官方源码:
#
# ```Python
# sklearn.svm.SVC(C=1.0, kernel='rbf', degree=3, gamma='auto', coef0=0.0, shrinking=True,
# probability=False, tol=0.001, cache_size=200, class_weight=None,
# verbose=False, max_iter=-1, decision_function_shape='ovr',
# random_state=None)
# ```
#
# 参考官方源码给出的参数,可以对其进行一定的优化,主要调节的参数有:C、kernel、degree、gamma、coef0。
#
# * C:C-SVC的惩罚参数C,默认值是1.0
# > C越大,相当于惩罚松弛变量,希望松弛变量接近0,即对误分类的惩罚增大,趋向于对训练集全分对的情况,这样对训练集测试时准确率很高,但泛化能力弱。C值小,对误分类的惩罚减小,允许容错,将他们当成噪声点,泛化能力较强。
#
# * kernel :核函数,默认是rbf,可以是`linear`, `poly`, `rbf`, `sigmoid`
# > 线性:$\kappa(\boldsymbol{x}_i,\boldsymbol{x}_j)=\boldsymbol{x}_i^T\boldsymbol{x}_j$
# >
# > 多项式: $\kappa(\boldsymbol{x}_i,\boldsymbol{x}_j)=(\boldsymbol{x}_i^T\boldsymbol{x}_j)^d$
# >
# > RBF函数/高斯核函数: $\kappa(\boldsymbol{x}_i,\boldsymbol{x}_j)=\exp\left(-\dfrac{||\boldsymbol{x}_i-\boldsymbol{x}_j||^2}{2\sigma^2}\right)$
# >
# > sigmoid:$\kappa(\boldsymbol{x}_i,\boldsymbol{x}_j)=\tanh{(\beta\boldsymbol{x}_i^T\boldsymbol{x}_j+\theta)}$
#
# * degree :多项式poly函数的维度,默认是3,选择其他核函数时会被忽略。
#
# * gamma : `rbf`,`poly` 和`sigmoid`的核函数参数。默认是`auto`,则会选择1/n_features
#
# * coef0 :核函数的常数项。对于`poly`和 `sigmoid`有用。
# # 作业二:
# 已知正例点 $x_1=(1,2)^T$ , $x_2=(2,3)^T$ , $x_3=(3,3)^T$,负例点 $x_4=(2,1)^T$ , $x_5=(3,2)^T$ ,试求最大间隔分离超平面和分类决策函数,并在图上画出分离超平面,间隔边界以及支持向量。
#
# (统计学习方法第七章课后习题2)
# **解**
#
# 参考最大间隔算法,根据训练数据集构造约束最优化问题
#
# $$
# \min\frac{1}{2}(w_1^2+w_2^2)\\
# s.t. \left\{
# \begin{align}
# w_1+2w_2+b&\ge 1 \tag{1}\\
# 2w_1+3w_2+b&\ge 1 \tag{2}\\
# 3w_1+3w_2+b&\ge 1 \tag{3}\\
# -2w_1-w_2-b&\ge 1 \tag{4}\\
# -3w_1-2w_2-b&\ge 1 \tag{5}
# \end{align}
# \right.
# $$
#
# 求得此最优化问题的解$w_1=-1,\ w_2=2,\ b=-2$。于是最大间隔分离超平面为
# $$
# -x^{(1)}+2x^{(2)}-2=0
# $$
# 支持向量 $x_1=(1,2)^T$ , $x_3=(3,3)^T$ , $x_5=(3,2)^T$.
# 分类决策函数
# $$
# f(x)=\text{sign}(-x^{(1)}+2x^{(2)}-2)
# $$
#
# <img src="https://downloads.mariozzj.cn/img/picgo/1616823918946.jpg" style="zoom:10%"/>
# 用程序进行同等的求解验证:
from sklearn import svm
x=[[1, 2], [2, 3], [3, 3], [2, 1], [3, 2]]
y=[1, 1, 1, -1, -1]
clf = svm.SVC(kernel='linear',C=10000)
clf.fit(x, y)
print(clf.coef_)
print(clf.intercept_)
# 得到的解相同,接下来可以进行一定的可视化:
import matplotlib.pyplot as plt
import numpy as np
plt.scatter([i[0] for i in x], [i[1] for i in x], c=y)
xaxis = np.linspace(0, 3.5)
w = clf.coef_[0]
a = -w[0] / w[1]
y_sep = a * xaxis - (clf.intercept_[0]) / w[1]
b = clf.support_vectors_[0]
yy_down = a * xaxis + (b[1] - a * b[0])
b = clf.support_vectors_[-1]
yy_up = a * xaxis + (b[1] - a * b[0])
plt.plot(xaxis, y_sep, 'k-')
plt.plot(xaxis, yy_down, 'k--')
plt.plot(xaxis, yy_up, 'k--')
plt.scatter (clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=150, facecolors='none', edgecolors='k')
plt.show()
# # + 另一种SMO
#
# 另一种参考统计学习方法上的思路,
#
# 外层循环选择**违背KKT条件最严重**的 $\alpha$ 作为 $\alpha_i$,首先遍历间隔边界上的点( $0 \lt \alpha_i \lt C$ ),如果这些点都满足KKT条件,则遍历所有样本点。
#
# 内层循环选择启发式方法选择:
#
# * 如果 $E_i$ 为正,选择最小的 $E$ 作为 $E_j$;如果 $E_i$ 为负,选择最大的 $E$ 作为 $E_j$。(总之使步长最大)
# * 如果上一步都不能使目标函数有足够的下降,则遍历间隔边界上的支持向量点,依次将其作为 $\alpha_j$ 使用。
# * 如果都不能使目标函数有足够的下降,则遍历训练集的所有向量点,依次将其作为 $\alpha_j$ 使用。
# * 如果所有点都不能使目标函数有足够的下降,则放弃当前 $\alpha_i$ ,通过外层循环生成新的 $\alpha_i$ 。
#
#
# 参考[fengdu78/lihang-code](https://github.com/fengdu78/lihang-code)的实现代码:
class SVM:
def __init__(self, max_iter=100, kernel='linear'):
self.max_iter = max_iter
self._kernel = kernel
def init_args(self, features, labels):
self.m, self.n = features.shape
self.X = features
self.Y = labels
self.b = 0.0
# 将Ei保存在一个列表里
self.alpha = np.ones(self.m)
self.E = [self._E(i) for i in range(self.m)]
# 松弛变量
self.C = 1.0
def _KKT(self, i):
y_g = self._g(i) * self.Y[i]
if self.alpha[i] == 0:
return y_g >= 1
elif 0 < self.alpha[i] < self.C:
return y_g == 1
else:
return y_g <= 1
# g(x)预测值,输入xi(X[i])
def _g(self, i):
r = self.b
for j in range(self.m):
r += self.alpha[j] * self.Y[j] * self.kernel(self.X[i], self.X[j])
return r
# 核函数
def kernel(self, x1, x2):
if self._kernel == 'linear':
return sum([x1[k] * x2[k] for k in range(self.n)])
elif self._kernel == 'poly':
return (sum([x1[k] * x2[k] for k in range(self.n)]) + 1)**2
return 0
# E(x)为g(x)对输入x的预测值和y的差
def _E(self, i):
return self._g(i) - self.Y[i]
def _init_alpha(self):
# 外层循环首先遍历所有满足0<a<C的样本点,检验是否满足KKT
index_list = [i for i in range(self.m) if 0 < self.alpha[i] < self.C]
# 否则遍历整个训练集
non_satisfy_list = [i for i in range(self.m) if i not in index_list]
index_list.extend(non_satisfy_list)
for i in index_list:
if self._KKT(i):
continue
E1 = self.E[i]
# 如果E2是+,选择最小的;如果E2是负的,选择最大的
if E1 >= 0:
j = min(range(self.m), key=lambda x: self.E[x])
else:
j = max(range(self.m), key=lambda x: self.E[x])
return i, j
def _compare(self, _alpha, L, H):
if _alpha > H:
return H
elif _alpha < L:
return L
else:
return _alpha
def fit(self, features, labels):
self.init_args(features, labels)
for t in range(self.max_iter):
# train
i1, i2 = self._init_alpha()
# 边界
if self.Y[i1] == self.Y[i2]:
L = max(0, self.alpha[i1] + self.alpha[i2] - self.C)
H = min(self.C, self.alpha[i1] + self.alpha[i2])
else:
L = max(0, self.alpha[i2] - self.alpha[i1])
H = min(self.C, self.C + self.alpha[i2] - self.alpha[i1])
E1 = self.E[i1]
E2 = self.E[i2]
# eta=K11+K22-2K12
eta = self.kernel(self.X[i1], self.X[i1]) + self.kernel(
self.X[i2],
self.X[i2]) - 2 * self.kernel(self.X[i1], self.X[i2])
if eta <= 0:
# print('eta <= 0')
continue
alpha2_new_unc = self.alpha[i2] + self.Y[i2] * (
E1 - E2) / eta #此处有修改,根据书上应该是E1 - E2,书上130-131页
alpha2_new = self._compare(alpha2_new_unc, L, H)
alpha1_new = self.alpha[i1] + self.Y[i1] * self.Y[i2] * (
self.alpha[i2] - alpha2_new)
b1_new = -E1 - self.Y[i1] * self.kernel(self.X[i1], self.X[i1]) * (
alpha1_new - self.alpha[i1]) - self.Y[i2] * self.kernel(
self.X[i2],
self.X[i1]) * (alpha2_new - self.alpha[i2]) + self.b
b2_new = -E2 - self.Y[i1] * self.kernel(self.X[i1], self.X[i2]) * (
alpha1_new - self.alpha[i1]) - self.Y[i2] * self.kernel(
self.X[i2],
self.X[i2]) * (alpha2_new - self.alpha[i2]) + self.b
if 0 < alpha1_new < self.C:
b_new = b1_new
elif 0 < alpha2_new < self.C:
b_new = b2_new
else:
# 选择中点
b_new = (b1_new + b2_new) / 2
# 更新参数
self.alpha[i1] = alpha1_new
self.alpha[i2] = alpha2_new
self.b = b_new
self.E[i1] = self._E(i1)
self.E[i2] = self._E(i2)
return 'train done!'
def predict(self, data):
r = self.b
for i in range(self.m):
r += self.alpha[i] * self.Y[i] * self.kernel(data, self.X[i])
return 1 if r > 0 else -1
def score(self, X_test, y_test):
right_count = 0
for i in range(len(X_test)):
result = self.predict(X_test[i])
if result == y_test[i]:
right_count += 1
return right_count / len(X_test)
def _weight(self):
# linear model
yx = self.Y.reshape(-1, 1) * self.X
self.w = np.dot(yx.T, self.alpha)
return self.w
from sklearn.model_selection import train_test_split
svm = SVM(max_iter=200)
svm.fit(np.array(X_train), np.array(y_train))
svm.score(X_test, y_test)
# 感觉比sklearn的默认状态要弱很多。。
|
L4-Support_Vector_Machine.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Here goes the title
# ---
#
# Some description.
#
# *Code made by [You](https://github.com/@you) - YYYY.*
# ## Importing Standard Libraries
# %load first_cell.py
display_custom_scales() # To check custom colorscales!
plotly.__version__, cf.__version__
# ### Import Scripts
#
# Here you can import any python file that is on the `scripts/` folder.
import example
# # Tips
# ## Colorful anotations
# <div class="alert alert-block alert-info">
# <b>Tip:</b> Try alert-info, alert-warning, alert-danger and alert-success.
# </div>
# ## Profiling
df = pd.DataFrame({'a': [1,2,3], 'b': [1,1,3]})
pandas_profiling.ProfileReport(df)
# ## Printing all outputs
# +
from IPython.core.interactiveshell import InteractiveShell
# Activate
InteractiveShell.ast_node_interactivity = "all"
# Deactivate
InteractiveShell.ast_node_interactivity = "last_expr"
# -
# ## Plotting
# Using custom theme
df[['a', 'b']].iplot(theme='custom', colorscale='my_scale',
title=iplottitle('Plotting a graph with custom theme and a really long title to test it'))
|
notebooks/example.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # 10 Aves Dataset
#
# In this case we use more classes
# +
import pandas as pd
import numpy as np
import torchaudio
import torchaudio.transforms as T
from tqdm.notebook import tqdm
import matplotlib.pyplot as plt
import librosa
# -
df = pd.read_csv("../datasets/AnimalSoundFull.csv")
df.head()
families = ["Alaudidae", "Bucerotidae", "Cardinalidae", "Cisticolidae", "Corvidae",
"Estrildidae", "Falconidae", "Laridae", "Phasianidae", "Thraupidae"]
df_10aves = df[df["family"].isin(families)].reset_index(drop=True)
df_10aves.head()
df_10aves.shape
# +
num_samples = df_10aves.shape[0]
np.random.seed(42)
df_10aves = df_10aves.drop(columns=["identifier",
"species",
"genus",
"class",
"phylum"
])
df_10aves
# -
def getSpectrogram(row):
wf, sample_rate = torchaudio.load("../data/" + row.file_name)
n_fft = 1024
win_length = None
hop_length = 512
n_mels = 128
mel_spectrogram = T.MelSpectrogram(
sample_rate=sample_rate,
n_fft=n_fft,
win_length=win_length,
hop_length=hop_length,
center=True,
pad_mode="reflect",
power=2.0,
norm='slaney',
onesided=True,
n_mels=n_mels,
mel_scale="htk",
)
melspec = mel_spectrogram(wf)[0]
height = 128*2
width = height*4
dpi = 100
fig = plt.figure(frameon=False, figsize=(width/dpi, height/dpi), dpi=dpi)
ax = plt.Axes(fig, [0., 0., 1., 1.])
ax.set_axis_off()
fig.add_axes(ax)
im = ax.imshow(librosa.power_to_db(melspec), origin='lower', aspect="auto")
file_name = "../spectrograms/10aves_dataset/" + str(row["gbifID"]) + ".jpg"
plt.savefig(file_name)
plt.close()
return
tqdm.pandas(desc="Creating Spectrograms")
_ = df_10aves.progress_apply(getSpectrogram, axis=1)
df_10aves.to_csv("../datasets/10Aves.csv", index=False)
|
data_processing/create10AvesDataset.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] pycharm={"name": "#%% md\n"}
# # Shapely
#
# [Shapely](https://shapely.readthedocs.io/en/latest/manual.html) is a powerful computational geometry often useful for generative art. Vsketch directly supports Shapely objects with the `Vsketch.geometry()` function.
# +
import numpy as np
from shapely.affinity import translate
from shapely.geometry import Point
from shapely.ops import unary_union
import vsketch
vsk = vsketch.Vsketch()
vsk.size("a4")
vsk.scale("4mm")
for i in range(5):
for j in range(7):
shape = unary_union(
[
Point(*np.random.random(2) * 5).buffer(np.random.random())
for _ in range(15)
]
)
vsk.geometry(translate(shape, i * 8, j * 8))
vsk.display(mode="matplotlib")
vsk.save("shapely.svg")
|
examples/_notebooks/shapely.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 1章 機械学習入門
# 必要ライブラリの宣言
# %matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# PDF出力用
from IPython.display import set_matplotlib_formats
set_matplotlib_formats('png', 'pdf')
# サンプルデータの宣言
sampleData1 = np.array([[166, 58.7],[176.0, 75.7],[171.0, 62.1],[173.0, 70.4],[169.0,60.1]])
print(sampleData1)
# 散布図表示
for p in sampleData1:
plt.scatter(p[0], p[1], c='k', s=10)
plt.grid()
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.show()
plt.figure(figsize=(10,5))
for p in sampleData1:
plt.scatter(p[0], p[1], c='k', s=50)
plt.grid()
plt.plot([0,0],[-10,80],c='k',lw=1)
plt.plot([171,171],[-10,80],c='k')
plt.plot([-10,180],[0,0],c='k',lw=1)
plt.plot([-10,180],[65.4,65.4],c='k')
plt.xlim(-10,180)
plt.ylim(-10,80)
plt.show()
# 平均値の計算
means = sampleData1.mean(axis=0)
print(means)
# 座標系を平均値=0に変換する
sampleData2 = sampleData1 - means
print(sampleData2)
# 新しい座標系での散布図表示
for p in sampleData2:
plt.scatter(p[0], p[1], c='k', s=50)
plt.grid()
plt.xlabel('$X$')
plt.ylabel('$Y$')
plt.plot([-6,6],[0,0], c='k')
plt.plot([0,0],[-7.5,11],c='k')
plt.xlim(-5.2,5.2)
plt.show()
# 予測関数の定義
def L(W0, W1):
return(5*W0**2 + 58*W1**2 - 211.2*W1 + 214.96)
# L(0, W1)のグラフ
plt.figure(figsize=(6,6))
W1 = np.linspace(0, 4, 501)
#plt.ylim(1,3)
plt.plot(W1, L(0,W1))
plt.scatter(1.82,22.69,s=30)
plt.xlabel('$W_1$')
plt.ylabel('$L(0,W_1)$')
plt.grid()
plt.xlim(0,3.5)
plt.ylim(0,200)
plt.show()
def pred1(X):
return 1.82*X
# 散布図と回帰直線(変換後)
for p in sampleData2:
plt.scatter(p[0], p[1], c='k', s=50)
X=np.array([-6,6])
plt.plot(X, pred1(X), lw=1)
plt.plot([-6,6],[0,0], c='k')
plt.plot([0,0],[-11,11],c='k')
plt.xlim(-5.2,5.2)
plt.grid()
plt.xlabel('$X$')
plt.ylabel('$Y$')
plt.show()
def pred2(x):
return 1.82*x - 245.9
# 散布図と回帰直線(オリジナル)
for p in sampleData1:
plt.scatter(p[0], p[1], c='k', s=50)
x=np.array([166,176])
plt.plot(x, pred2(x), lw=1)
plt.grid()
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.show()
|
notebooks/ch01-entry.ipynb
|
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: julia 1.5.2
# language: julia
# name: julia-1.5
# ---
# # Probabilistic Programming 2: Message Passing & Analytical Solutions
#
# #### Goal
# - Understand when and how analytical solutions to Bayesian inference can be obtained.
# - Understand how to perform message passing in a Forney-style factor graph.
#
# #### Materials
# - Mandatory
# - This notebook
# - Lecture notes on factor graphs
# - Lecture notes on continuous data
# - Lecture notes on discrete data
# - Optional
# - Chapters 2 and 3 of [Model-Based Machine Learning](http://www.mbmlbook.com/LearningSkills.html).
# - [Differences between Julia and Matlab / Python](https://docs.julialang.org/en/v1/manual/noteworthy-differences/index.html).
# Note that none of the material below is new. The point of the Probabilistic Programming sessions is to solve practical problems so that the concepts from Bert's lectures become less abstract.
using Pkg
Pkg.activate("./workspace/")
Pkg.instantiate();
IJulia.clear_output();
using LinearAlgebra
using SpecialFunctions
using ForneyLab
using PyCall
using Plots
pyplot();
# We'll be using the toolbox [ForneyLab.jl](https://github.com/biaslab/ForneyLab.jl) to visualize factor graphs and compute messages passed within the graph.
# ## Problem: A Job Interview
#
# After you finish your master's degree, you will need to start looking for jobs. You will get one or more job interviews and some will be fun while others will be frustrating. The company you applied at wants a talented and skilled employee, but measuring a person's skill is tricky. Even a highly-skilled person makes mistakes and people with few skills can get lucky. In this session, we will look at various ways to assess skills using questions and test assignments. Along the way, you will gain experience with message passing, factor graphs and working with discrete vs continuous data.
# ### 1: Right or wrong
#
# Suppose you head to a job interview for a machine learning engineer position. The company is interested in someone who knows Julia and has set up a test with syntax questions. We will first look at a single question, which we treat as an outcome variable $X_1$. You can either get this question right or wrong, which means we're dealing with a Bernoulli likelihood. The company assumes you have a skill level, denoted $\theta$, and the higher the skill, the more likely you are to get the question right. Since the company doesn't know anything about you, they chose an uninformative prior distribution: the Beta(1,1). We can write the generative model for answering this question as follows:
#
# $$\begin{align*}
# p(X_1, \theta) =&\ p(X_1 \mid \theta) \cdot p(\theta) \\
# =&\ \text{Bernoulli}(X_1 \mid \theta) \cdot \text{Beta}(\theta \mid \alpha = 1, \beta=1) \, .
# \end{align*}$$
#
# The factor graph for this model is:
#
# <!-- <img align="left" width=50 src="../figures/ffg-PP2-01.png"> -->
# 
#
# where $f_b(X_1, \theta) \triangleq \text{Bernoulli}(X_1 \mid \theta)$ and $f_a(\theta) \triangleq \text{Beta}(\theta \mid 1,1)$. We are now going to construct this factor graph using the toolbox ForneyLab.
# +
# Start building a model by setting up a FactorGraph structure
factor_graph1 = FactorGraph()
# Add the prior over
@RV θ ~ Beta(1.0, 1.0, id=:f_a)
# Add the question correctness likelihood
@RV X1 ~ Bernoulli(θ, id=:f_b)
# The outcome X1 is going to be observed, so we set up a placeholder for the data entry
placeholder(X1, :X1)
# Visualize the graph
ForneyLab.draw(factor_graph1)
# -
# Code notes:
# - @RV is a macro that lets you add Random Variables as nodes to your factor graph.
# - The symbol ~ means "is distributed as". For example, $\theta \sim \text{Beta}(1,1)$ should be read as "$\theta$ is distributed according to a Beta($\theta$ | $a$=1, $b$=1) probability distribution".
#
# ----
# Above you can see the factor graph that ForneyLab has generated. It is not as clean as the ones in the theory lectures. For example, ForneyLab generates nodes for the clamped parameters of the Beta prior ($\alpha = 1$ and $\beta = 1$), while we ignore these in the manually constructed graphs. Nonetheless, ForneyLab's version is very useful for debugging later on.
#
# We are now going to tell ForneyLab to generate a message passing procedure for us.
# +
# Indicate which variables you want posteriors for
q = PosteriorFactorization(θ, ids=[:θ])
# Generate a message passing inference algorithm
algorithm = messagePassingAlgorithm(θ, q)
# Compile algorithm code
source_code = algorithmSourceCode(algorithm)
# Bring compiled code into current scope
eval(Meta.parse(source_code))
# Visualize message passing schedule
pfθ = q.posterior_factors[:θ]
ForneyLab.draw(pfθ, schedule=pfθ.schedule);
# -
# Code notes:
# - ForneyLab.jl compiles the specified model and inference procedure into a string. This string is human-readable and portable across devices. The functions `eval(Meta.parse())` are used to bring that string into the current scope, so the generated code can be used.
# - In `ForneyLab.draw()`, only the edge of interest is shown with the two connecting nodes and their inputs. All other parts of the graph are ignored.
#
# ----
# ForneyLab's visualization of the message passing procedure for a specific variable isolates that variable in the graph and shows where the incoming messages come from. In this case, we are interested in $\theta$ (your skill level), which receives message ((2)) from the likelihood node (the "Ber" node above $\theta$) and message ((1)) from the prior node (the "Beta" node below $\theta$).
#
# In the message passing framework, the combination of these two messages produces the "marginal" distribution for $\theta$. We are using message passing to do Bayesian inference, so note that the "marginal" for $\theta$ corresponds to the posterior distribution $p(\theta \mid X_1)$.
#
# Let's inspect these messages.
# +
# Initialize data structure for messages
messages = Array{Message}(undef, 2)
# Initalize data structure for marginal distributions
marginals = Dict()
# Suppose you got question 1 correct
data = Dict(:X1 => 1)
# Update coefficients
stepθ!(data, marginals, messages);
# Print messages
print("\nMessage ((1)) = "*string(messages[1].dist))
println("Message ((2)) = "*string(messages[2].dist))
# -
# Code notes:
# - A `Dict` is a [dictionary data structure](https://docs.julialang.org/en/v1/base/collections/#Base.Dict). In the `marginals` dictionary we only have one entry: the key is the variable `θ` (as a Symbol, i.e. as `:θ`) and the value is a `ProbabilityDistribution` object. It is the initial distribution for that variable. In the `data` dictionary, we also only have one entry: the key is the variable `X1` and the value is a Float. This is because `X1` is observed. We know its value without uncertainty.
# - The `stepθ!` function comes from the algorithm compilation.
#
# ----
# Alright. So, they are both Beta distributions. Do they actually make sense? Where do these parameters come from?
#
# Recall from the lecture notes that the formula for messages sent by factor nodes is:
#
# $$ \boxed{
# \underbrace{\overrightarrow{\mu}_{Y}(y)}_{\substack{ \text{outgoing}\\ \text{message}}} = \sum_{x_1,\ldots,x_n} \underbrace{\overrightarrow{\mu}_{X_1}(x_1)\cdots \overrightarrow{\mu}_{X_n}(x_n)}_{\substack{\text{incoming} \\ \text{messages}}} \cdot \underbrace{f(y,x_1,\ldots,x_n)}_{\substack{\text{node}\\ \text{function}}} }
# $$
#
# <p style="text-align:center;"><img src="../figures/ffg-sum-product.png" width="500px"></p>
#
# The prior node is not connected to any other unknown variables and so does not receive incoming messages. Its outgoing message is therefore:
#
# $$\begin{align}
# \overrightarrow{\mu}(\theta) =&\ f(\theta) \\
# =&\ \text{Beta}(\theta \mid 1,1) \, .
# \end{align}$$
#
# So that confirms the correctness of Message ((1)).
#
# Similarly, we can also derive the message from the likelihood node by hand. For this, we need to know that the message coming from the observation $\overleftarrow{\mu}(x)$ is a delta function, which, if you gave the right answer ($X_1 = 1$), has the form $\delta(X_1 - 1)$. The "node function" is the Bernoulli likelihood $\text{Bernoulli}(X_1 \mid \theta)$. Another thing to note is that this is essentially a convolution with respect to a delta function and that its [sifting property](https://en.wikipedia.org/wiki/Dirac_delta_function#Translation) holds: $\int_{X_1} \delta(X_1 - x) \ f(X_1, \theta) \mathrm{d}X_1 = f(x, \theta)$. The fact that $X_1$ is a discrete variable instead of a continuous one, does not negate this. Using these facts, we can perform the message computation by hand:
#
# $$\begin{align}
# \overleftarrow{\mu}(\theta) =&\ \sum_{X_1} \overleftarrow{\mu}(X_1) \ f(X_1, \theta) \\
# =&\ \sum_{X_1} \delta(X_1 - 1) \ \text{Bernoulli}(X_1 \mid \theta) \\
# =&\ \sum_{X_1} \delta(X_1 - 1) \ \theta^{X_1} (1 - \theta)^{1-X_1} \\
# =&\ \theta^{1} (1 - \theta)^{1-1} \, .
# \end{align}$$
#
# Remember that the pdf of a Beta distribution is proportional to $\theta^{\alpha-1} (1 - \theta)^{\beta-1}$. So, if you read the second-to-last line above as $\theta^{2-1} (1 - \theta)^{1-1}$, then the outgoing message $\overleftarrow{\mu}(\theta)$ is proportional to a Beta distribution with $\alpha=2$ and $\beta=1$. So, our manual derivation verifies ForneyLab's Message ((2)).
#
# Let's now look at these messages visually.
# +
# Probability density function of a Beta distribution
Beta(θ, α, β) = 1/beta(α,β) * θ^(α-1) * (1-θ)^(β-1)
# Extract parameters from message ((1))
α1 = messages[1].dist.params[:a]
β1 = messages[1].dist.params[:b]
# Extract parameters from message ((2))
α2 = messages[2].dist.params[:a]
β2 = messages[2].dist.params[:b]
# Plot messages
θ_range = range(0, step=0.01, stop=1.0)
plot(θ_range, Beta.(θ_range, α1, β1), color="red", linewidth=3, label="Message ((1))", xlabel="θ", ylabel="p(θ)")
plot!(θ_range, Beta.(θ_range, α2, β2), color="blue", linewidth=3, label="Message ((2))")
# -
# The marginal distribution for $\theta$, representing the posterior $p(\theta \mid X_1)$, is obtained by taking the product (followed by normalization) of the two messages: $\overrightarrow{\mu}(\theta) \cdot \overleftarrow{\mu}(\theta)$. Multiplying two Beta distributions produces another Beta distribution with parameter:
#
# $$\begin{align}
# \alpha \leftarrow&\ \alpha_1 + \alpha_2 - 1 \\
# \beta \leftarrow&\ \beta_1 + \beta_2 - 1 \, ,
# \end{align}$$
#
# In our case, the new parameters would be $\alpha = 1 + 2 - 1 = 2$ and $\beta = 1 + 1 - 1 = 1$. Let's check with ForneyLab what it computed.
marginals[:θ]
# Again, ForneyLab matches our manual derivations. Let's visualize the messages as well as the marginal.
# +
# Extract marginal's parameters
α_marg = marginals[:θ].params[:a]
β_marg = marginals[:θ].params[:b]
# Plot messages
θ_range = range(0, step=0.01, stop=1.0)
plot(θ_range, Beta.(θ_range, α1, β1), color="red", linewidth=3, label="Message ((1))", xlabel="θ", ylabel="p(θ)")
plot!(θ_range, Beta.(θ_range, α2, β2), color="blue", linewidth=3, label="Message ((2))")
plot!(θ_range, Beta.(θ_range, α_marg, β_marg), color="purple", linewidth=6, linestyle=:dash, label="Marginal")
# -
# The pdf of the marginal distribution lies on top of the pdf of Message ((2)). That's not always going to be the case; the Beta(1,1) distribution is special in that when you multiply Beta(1,1) with a general Beta(a,b) the result will always be Beta(a,b), kinda like multiplying by $1$. We call prior distributions that have this special effect "non-informative priors".
# #### Multiple questions
#
# Of course, you won't be evaluated on just a single question: it's still possible for you to get one question wrong even if you have a high skill level. You would consider it unfair to be rejected based on only one question. So, we are going to add another question. We're also going to change the prior: the company now assumes that you must have _some_ skill if you applied for the position. This is reflected in a prior Beta distributions with $\alpha = 3.0$ and $\beta = 2.0$.
#
# For now, the second question is also a right-or-wrong question. The outcome of this new question is denoted with variable $X_2$. With this addition, the generative model becomes
#
# $$p(X_1, X_2, \theta) = p(X_1 \mid \theta) p(X_2 \mid \theta) p(\theta) \, ,$$
#
# with the accompanying factor graph
#
# 
#
# where $f_c \triangleq \text{Bernoulli}(X_2 \mid \theta)$ and $f_a, f_b$ are still the same. Notice that we now have an equality node as well. That is because the variable $\theta$ is used in three factor nodes. ForneyLab automatically generates the same factor graph:
# +
# Start building a model
factor_graph2 = FactorGraph()
# Add the prior
@RV θ ~ Beta(3.0, 2.0, id=:f_a)
# Add question 1 correctness likelihood
@RV X1 ~ Bernoulli(θ, id=:f_b)
# Add question 2 correctness likelihood
@RV X2 ~ Bernoulli(θ, id=:f_c)
# The question outcomes are going to be observed
placeholder(X1, :X1)
placeholder(X2, :X2)
# Visualize the graph
ForneyLab.draw(factor_graph2)
# -
# We will go through the message passing operations below. First, we generate an algorithm and visualize where all the messages for $\theta$ come from.
# +
# Indicate which variables you want posteriors for
q = PosteriorFactorization(θ, ids=[:θ])
# Generate a message passing inference algorithm
algorithm = messagePassingAlgorithm(θ, q)
# Compile algorithm code
source_code = algorithmSourceCode(algorithm)
# Bring compiled code into current scope
eval(Meta.parse(source_code))
# Visualize message passing schedule
pfθ = q.posterior_factors[:θ]
ForneyLab.draw(pfθ, schedule=pfθ.schedule);
# -
# There are 4 messages, one from the prior ((1)), one from the first likelihood ((2)), one from the second likelihood ((3)) and one from the equality node ((4)). ForneyLab essentially combines messages 2 and 3 into message 4 and then multiplies messages 1 and 4 to produce the marginal. We can see this if we look in the source code:
println(source_code)
# You can see that `messages[4]` is a function of `messages[2]` and `messages[3]` and that `marginals[:θ]` is the product of `messages[1]` and `messages[4]`.
#
#
# Suppose you got the first question right and the second question wrong. Let's execute the message passing procedure and take a look at the functional form of the messages.
# +
# Initialize a message data structure
messages = Array{Message}(undef, 4)
# Initalize marginal distributions data structure
marginals = Dict()
# Suppose you got question 1 right and question 2 wrong
data = Dict(:X1 => 1,
:X2 => 0)
# Update coefficients
stepθ!(data, marginals, messages);
# Print messages
print("\nMessage ((1)) = "*string(messages[1].dist))
print("Message ((2)) = "*string(messages[2].dist))
print("Message ((3)) = "*string(messages[3].dist))
println("Message ((4)) = "*string(messages[4].dist))
# -
# Messages ((1)) and ((2)) are clear, but Message ((3)) and Message ((4)) are new.
#
# ---
#
# ### $\ast$ **Try for yourself**
#
# Try deriving the functional form of Message ((3)) for yourself.
# Tip: the derivation is very similar to that of Message ((2)). The most important change is to use $\delta(X_2 - 0)$ instead of $\delta(X_1 - 1)$.
#
# ---
# Message ((4)) is the result of the standard message computation formula for the case of an equality node:
#
# $$\begin{align}
# \downarrow \mu(\theta) =&\ \sum_{\theta',\ \theta''} \overrightarrow{\mu}(\theta'')\ f_{=}(\theta, \theta', \theta'') \ \overleftarrow{\mu}(\theta') \\
# =&\ \overrightarrow{\mu}(\theta) \cdot \overleftarrow{\mu}(\theta) \\
# =&\ \text{Beta}(\theta \mid 2, 1) \cdot \text{Beta}(\theta \mid 1, 2) \\
# =&\ \text{Beta}(\theta \mid 2, 2) \quad .
# \end{align}$$
#
# Let's visualize the messages and the marginal again.
# +
# Extract parameters from message ((2))
α2 = messages[2].dist.params[:a]
β2 = messages[2].dist.params[:b]
# Extract parameters from message ((3))
α3 = messages[3].dist.params[:a]
β3 = messages[3].dist.params[:b]
# Extract parameters from message ((4))
α4 = messages[4].dist.params[:a]
β4 = messages[4].dist.params[:b]
plot(θ_range, Beta.(θ_range, α2, β2), color="black", linewidth=3, label="Message ((2))")
plot!(θ_range, Beta.(θ_range, α3, β3), color="green", linewidth=3, label="Message ((3))")
plot!(θ_range, Beta.(θ_range, α4, β4), color="blue", linewidth=3, label="Message ((4))")
xlabel!("θ")
ylabel!("p(θ)")
# -
# Message ((2)) and Message ((3)) are direct opposites: ((2)) increases the estimate and ((3)) decreases the estimate of your skill level. Message ((4)) end up being centered on $0.5$. With one question right and one question wrong, you have essentially been guessing at random.
# +
# Extract parameters from message ((1))
α1 = messages[1].dist.params[:a]
β1 = messages[1].dist.params[:b]
# Extract parameters from message ((4))
α4 = messages[4].dist.params[:a]
β4 = messages[4].dist.params[:b]
# Extract parameters
α_marg = marginals[:θ].params[:a]
β_marg = marginals[:θ].params[:b]
plot(θ_range, Beta.(θ_range, α1, β1), color="red", linewidth=3, label="Message ((1))")
plot!(θ_range, Beta.(θ_range, α4, β4), color="blue", linewidth=3, label="Message ((4))")
plot!(θ_range, Beta.(θ_range, α_marg, β_marg), color="purple", linewidth=4, linestyle=:dash, label="Marginal")
xlabel!("θ")
ylabel!("p(θ)")
# -
# If we now combine the prior (Message ((1)) in red above) with the combined message from both likelihood terms (Message ((4)) in blue), we get the new marginal (purple dotted line). The mean of the marginal lies above $0.5$, which is due to the prior assumption that you must have _some_ skill if you applied.
# ### 2. Score questions
#
# So far, the models we have been looking at have been quite simple; they are Beta-Bernoulli combinations which is exactly what we did for the Beer Tasting Experiment. We will now move on to more complicated distributions. These will enrich your toolbox and allow you to do much more.
#
# Suppose you are not tested on a right-or-wrong question, but on a score question. For instance, you have to complete a piece of code for which you get a score. If all of it was wrong you get a score of $0$, if some of it was correct you get a score of $1$ and if all of it was correct you get a score $2$. That means we have a likelihood with three outcomes: $X_1 = \{ 0,1,2\}$. Suppose we once again ask two questions, $X_1$ and $X_2$. The order in which we ask these questions does not matter, so that means we choose Categorical distributions for these likelihood functions: $X_1, X_2 \sim \text{Categorical}(\theta)$. The parameter $\theta$ is no longer a single parameter, indicating the probability of getting the question right, but a vector of three parameters: $\theta = (\theta_1, \theta_2, \theta_3)$. Each $\theta_k$ indicates the probability of getting the $k$-th outcome. In other words, $\theta_1$ indicates the probability of getting $0$ points, $\theta_2$ of getting $1$ point and $\theta_3$ of getting two points. A highly-skilled applicant will have a parameter vector of $(0.05, 0.1, 0.85)$, for example. The prior distribution conjugate to the Categorical distribution is the Dirichlet distribution.
#
# Let's look at the generative model:
#
# $$p(X_1, X_2, \theta) = p(X_1 \mid \theta) p(X_2 \mid \theta) p(\theta) \, .$$
#
# It's the same as before. The only difference is that:
#
# $$\begin{align}
# p(X_1 \mid \theta) =&\ \text{Categorical}(X_1 \mid \theta) \\
# p(X_2 \mid \theta) =&\ \text{Categorical}(X_2 \mid \theta) \\
# p(\theta) =&\ \text{Dirichlet}(\theta)
# \end{align}$$
#
# The factor graph has the same structure as before. The only change is that the factor nodes $f_a, f_b, f_c$ are now parameterized differently.
# +
# Start building a model
factor_graph3 = FactorGraph()
# Add the prior
@RV θ ~ Dirichlet([1.0, 3.0, 2.0], id=:f_a)
# Add question 1 correctness likelihood
@RV X1 ~ Categorical(θ, id=:f_b)
# Add question 2 correctness likelihood
@RV X2 ~ Categorical(θ, id=:f_c)
# The question outcomes are going to be observed
placeholder(X1, dims=(3,), :X1)
placeholder(X2, dims=(3,), :X2)
# Visualize the graph
ForneyLab.draw(factor_graph3)
# -
# The only difference with the previous graph is the fact that the node called "prior" is a 'Dir', short for Dirichlet, and that the two nodes called "likelihood1" and "likelihood2" are 'Cat' types, short for Categorical. Let's look at the message passing schedule:
# +
# Indicate which variables you want posteriors for
q = PosteriorFactorization(θ, ids=[:θ])
# Generate a message passing inference algorithm
algorithm = messagePassingAlgorithm(θ, q)
# Compile algorithm code
source_code = algorithmSourceCode(algorithm)
# Bring compiled code into current scope
eval(Meta.parse(source_code))
# Visualize message passing schedule
pfθ = q.posterior_factors[:θ]
ForneyLab.draw(pfθ, schedule=pfθ.schedule);
# -
# That's the same as before as well: 2 messages from the likelihoods, 1 combined likelihood message from the equality node and 1 message from the prior.
#
# If we now setup the message passing procedure, we have to be a little bit more careful. We cannot feed the scores $\{ 0,1,2\}$ as outcomes directly. We have to encode them in one-hot vectors (see Bert's lecture notes on discrete distributions). Suppose you had a score of $1$ for the first question and a score of $2$ for the second one. That translates into a vector $[0, 1, 0]$ and $[0, 0, 1]$, respectively. These we enter into the `data` dictionary:
# +
# Initialize a message data structure
messages = Array{Message}(undef, 4)
# Initalize marginal distributions data structure
marginals = Dict()
# Enter the observed outcomes in the placeholders
data = Dict(:X1 => [0, 1, 0],
:X2 => [0, 0, 1])
# Update coefficients
stepθ!(data, marginals, messages);
# Print messages
print("\nMessage ((1)) = "*string(messages[1].dist))
print("Message ((2)) = "*string(messages[2].dist))
print("Message ((3)) = "*string(messages[3].dist))
print("Message ((4)) = "*string(messages[4].dist))
println("Marginal of θ = "*string(marginals[:θ]))
# -
# Visualizing a Dirichlet distribution is a bit tricky. In the special case of $3$ parameters, we can plot the probabilities on a simplex. As a reminder, a [simplex](https://en.wikipedia.org/wiki/Simplex) in 3-dimensions is the triangle between the coordinates $[0,0,1]$, $[0,1,0]$ and $[1,0,0]$:
#
# <p style="text-align:center;"><img src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/2D-simplex.svg/150px-2D-simplex.svg.png" width="150px"></p>
#
# Each vector $\theta$ is a point on that triangle and its elements sum to $1$. Since the triangle is 2-dimensional, we can plot the Dirichlet's probability density over it.
# +
# Import matplotlib
plt = pyimport("matplotlib.pyplot")
# Include helper function
include("../scripts/dirichlet_simplex.jl")
# Extract parameters of Message ((1))
α1 = messages[1].dist.params[:a]
# Compute pdf contour lines on the simplex
trimesh, pvals = pdf_contours_simplex(α1)
# Plot using matplotlib's tricontour
plt.tricontourf(trimesh, pvals, nlevels=200, cmap="jet");
plt.title("Message ((1)) = "*string(messages[1].dist));
# -
# Code notes:
# - `pyimport` allows you to import Python modules.
# - When you `include()` another julia file, it is as if you wrote it at that point in your script.
# - `tricontourf` is a function from Matplolib, where you create a contour plot over a triangulated mesh (here, the simplex).
#
# ----
# The red spot is the area of high probability, with the contours around indicating increasing uncertainty. The prior, with concentration parameters $[1, 3, 2]$, reflects the belief that applicants are least likely to get the question completely wrong ($\alpha_1$ = 1, score = 0), most likely to get the question partly right ($\alpha_2$ = 3, score = 1) and moderately likely to get the question completely correct ($\alpha_3$ = 2, score = 2).
# +
# Extract parameters
α4 = messages[4].dist.params[:a]
# Compute pdf contour lines on the simplex
trimesh, pvals = pdf_contours_simplex(α4)
# Plot using matplotlib's tricontour
plt.tricontourf(trimesh, pvals, nlevels=200, cmap="jet")
plt.title("Message ((4)) = "*string(messages[4].dist));
# -
# Since we got scores $X_1 = 1$ and $X_2 = 2$, the combined message from both likelihoods has concentration parameters $[1,2,2]$.
# +
# Extract parameters
α_marg = marginals[:θ].params[:a]
# Compute pdf contour lines on the simplex
trimesh, pvals = pdf_contours_simplex(α_marg)
# Plot using matplotlib's tricontour
plt.tricontourf(trimesh, pvals, nlevels=200, cmap="jet")
plt.title("Marginal of θ = "*string(marginals[:θ]));
# -
# The posterior is the combination of Messages ((1)) and ((4)) and focuses much more strongly in the area where the two messages overlap.
# ---
#
# ### $\ast$ **Try for yourself**
#
# Play around with the prior parameters and your responses to the questions. See how they change your posterior.
#
# ---
# ### 3. Rating scale
#
# You might want to evaluate someone by an even finer metric. For example, in oral exams you need to provide a score based on a conversation which is hard to quantify. You could do this by taking away the discrete set of responses and replacing it with a continuous response variable. For example, rating scales are forms of continuous response models. You would mark the applicant's performance on a question as a cross on a line:
#
# <p style="text-align:center;"><img src="https://images.slideplayer.com/15/4506022/slides/slide_19.jpg" width="400px"></p>
#
# It is still the case that there is some underlying level of skill, that we'll call $\theta$, and that the performance on each question is a noisy measurement of that skill, that we'll call $X$. We argue that performance noise is symmetric: the probability of performing a little better than their skill level is equal to performing a little worse. We will therefore use Gaussian, or Normal, likelihood functions: $p(X \mid \theta) = \text{Normal}(X \mid \theta, \sigma^2)$. The conjugate prior to the mean in Gaussian likelihoods is another Gaussian distribution: $p(\theta) = \text{Normal}(\theta \mid 60, 20)$. Say that we rate performance on a scale from $0$ to $100$, then it makes sense to use a mean of $60$ and a variance of $20$ for the prior.
#
# We'll keep the same generative model as before, with new definitions for each distribution:
#
# $$\begin{align}
# p(X_1 \mid \theta) =&\ \text{Normal}(X_1 \mid \theta, 10) \\
# p(X_2 \mid \theta) =&\ \text{Normal}(X_2 \mid \theta, 15) \\
# p(\theta) =&\ \text{Normal}(\theta \mid 60, 20)
# \end{align}$$
#
# The factor graph will again be the same, but with different parameterizations of factor nodes:
# +
# Start building a model
factor_graph4 = FactorGraph()
# Add the prior
@RV θ ~ GaussianMeanVariance(60, 20, id=:f_a)
# Add question 1 likelihood
@RV X1 ~ GaussianMeanVariance(θ, 10, id=:f_b)
# Add question 2 likelihood
@RV X2 ~ GaussianMeanVariance(θ, 15, id=:f_c)
# Outcomes are going to be observed
placeholder(X1, :X1)
placeholder(X2, :X2)
# Visualize the graph
ForneyLab.draw(factor_graph4)
# +
# Indicate which variables you want posteriors for
q = PosteriorFactorization(θ, ids=[:θ])
# Generate a message passing inference algorithm
algorithm = messagePassingAlgorithm(θ, q)
# Compile algorithm code
source_code = algorithmSourceCode(algorithm)
# Bring compiled code into current scope
eval(Meta.parse(source_code))
# Visualize message passing schedule
pfθ = q.posterior_factors[:θ]
ForneyLab.draw(pfθ, schedule=pfθ.schedule);
# -
# The message passing schedule is still exactly the same.
# +
# Initialize a message data structure
messages = Array{Message}(undef, 4)
# Initalize marginal distributions data structure
marginals = Dict()
# Enter the scores in the data dictionary
data = Dict(:X1 => 61.5,
:X2 => 72)
# Update coefficients
stepθ!(data, marginals, messages);
# Print messages
print("\nMessage ((1)) = "*string(messages[1].dist))
print("Message ((2)) = "*string(messages[2].dist))
print("Message ((3)) = "*string(messages[3].dist))
print("Message ((4)) = "*string(messages[4].dist))
print("Marginal of θ = "*string(marginals[:θ]))
# -
# Message ((4)) has a somewhat unusual form in that uses `xi` as a parameter instead of `m`. When you take the product of Messages ((2)) and ((3)), the resulting mean is the sum of the precision-weighted means of Messages ((2)) and ((3)), normalized by the total precision (see [Bert's lecture](http://nbviewer.ipython.org/github/bertdv/BMLIP/blob/master/lessons/notebooks/The-Gaussian-Distribution.ipynb)). `xi` represents the sum of precision-weighted means of the two messages. Let's look for the mean:
# Extract parameters from message ((4))
m4 = mean(messages[4].dist)
v4 = var(messages[4].dist)
println("Mean of Message ((4)) = "*string(m4))
println("Variance of Message ((4)) = "*string(v4))
# As you can see, the mean of Message ((4)) lies in between the means of Messages ((2)) and ((3)). Note that the variance is much lower than that of Messages ((2)) or ((3)).
# +
# Define probability density function for Gaussian distribution
pdf_Normal(θ, m, v) = 1/sqrt(2*π*v) * exp( -(θ - m)^2/(2*v))
# Extract parameters from message ((2))
m2 = messages[2].dist.params[:m]
v2 = messages[2].dist.params[:v]
# Extract parameters from message ((3))
m3 = messages[3].dist.params[:m]
v3 = messages[3].dist.params[:v]
# Extract parameters from message ((4))
m4 = mean(messages[4].dist)
v4 = var(messages[4].dist)
# Define new range for skill level θ
θ_range = range(0.0, step=0.1, stop=100.0)
plot(θ_range, pdf_Normal.(θ_range, m2, v2), color="black", linewidth=3, label="Message ((2))", xlabel="θ", ylabel="p(θ)")
plot!(θ_range, pdf_Normal.(θ_range, m3, v3), color="green", linewidth=3, label="Message ((3))")
plot!(θ_range, pdf_Normal.(θ_range, m4, v4), color="blue", linewidth=3, label="Message ((4))", xlims=[50., 80.])
# -
# Message ((4)) is really a weighted average of Messages ((2)) and ((3)).
# +
# Extract parameters from message ((1))
m1 = messages[1].dist.params[:m]
v1 = messages[1].dist.params[:v]
# Extract parameters from message ((4))
m4 = mean(messages[4].dist)
v4 = var(messages[4].dist)
# Extract parameters from marginal
m_marg = mean(marginals[:θ])
v_marg = var(marginals[:θ])
# Define new range for skill level θ
plot(θ_range, pdf_Normal.(θ_range, m1, v1), color="red", linewidth=3, label="Message ((1))", xlabel="θ", ylabel="p(θ)")
plot!(θ_range, pdf_Normal.(θ_range, m4, v4), color="blue", linewidth=3, label="Message ((4))")
plot!(θ_range, pdf_Normal.(θ_range, m_marg, v_marg), color="purple", linewidth=6, linestyle=:dash, label="Marginal", xlims=[50., 80.])
# -
# The posterior is also a weighted average of two incoming messages. Notice that it is much closer to Message ((4)) than Message ((1)). That is because the variance of Message ((1)) (the prior) is much higher than that of Message ((4)) (the combination of likelihoods). The prior has a smaller weight in the weighted average.
# ---
#
# ### $\ast$ **Try for yourself**
#
# Play around with different values for the prior's variance and the variance of the likelihoods. What happens when you make the variance of $p(X_1 \mid \theta)$ different from that of $p(X_2 \mid \theta)$?
#
# ---
|
lessons/notebooks/probprog/Probabilistic-Programming-2.ipynb
|