code
stringlengths 38
801k
| repo_path
stringlengths 6
263
|
|---|---|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# + [markdown] pycharm={"name": "#%% md\n"}
# # Lab 07 - Bagging Decision Trees
# In the previous lab we discussed the [bias-variance tradeoff](https://github.com/GreenGilad/IML.HUJI/blob/master/lab/Lab%2007%20-%20Bias-Variance%20Trade-off.ipynb) and saw how:
# - The less complex a model is the higher is its variance and lower is its bias. We say in this case that the model is underfitted.
# - The more complex a model is the higher is its bias and lower is its variance. We say in this case that the model is overfitted.
#
# In this lab we will use the power of ensemble methods to fit a set of models, each with a low complexity, to achieve better performances while avoiding overfitting. We use the hypothesis class of decision trees and *bag* multiple trees into a single ensemble.
# -
import sys
sys.path.append("../")
from utils import *
# +
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.utils import resample
import matplotlib.pyplot as plt
import itertools
symbols = np.array(["circle", "x"])
# -
# ???????????????????????????
# +
d, n_train, n_test = 8, 3000, 500
X, y = create_data_bagging_utils(d=d, n_samples = n_train + n_test)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=n_test, random_state=42)
go.Figure(data=go.Scatter(x=X[:,0], y=X[:,1], mode="markers", showlegend=False,
marker=dict(color=y, symbol=symbols[y], colorscale=[custom[0], custom[-1]])),
layout=go.Layout(title=rf"$\textbf{{(1) Tree Dataset - True Depth {d}}}$",
xaxis_title=r"$x_1$",
yaxis_title=r"$x_2$"))
# -
# Creation of bootstrap samples
#
# Now, after we understand better the different datasets we're creating for the bootstrap algorithm, let's see the different models (trees) that are created from these datasets. We'll take 2 bootstrap datasets, fit a decision tree of depth of 2 to each dataset and plot the trees
_, axes = plt.subplots(nrows = 1, ncols = 2, figsize = (10,2), dpi=300)
for i in range(2):
idx = resample(range(len(X_train)), replace = True, n_samples = len(X_train))
fit = DecisionTreeClassifier(max_depth=2).fit(X_train[idx], y_train[idx])
plot_tree(fit, filled = True, impurity=False, class_names=["O", "X"], ax = axes[i])
plt.show()
# Now, Let's create 11 bootstrap datasets from our train data, each with 1000 samples.
# Each bootstrap dataset is built by choosing samples from the train data randomly with replcement, that means it is built in the next way:
# 1. choose a sample randomly from the train data and add it to the bootstrap dataset
# 2. keep the sample in the train data so that it can be re-selected to the same bootstrap dataset (and of course to the other bootstrap datasets)
# +
bootstrap_sets = [set(resample(range(len(X_train)), replace = True, n_samples = len(X_train))) for _ in range(100)]
overlap = [len(bootstrap_sets[i].intersection(bootstrap_sets[j])) / len(X_train)
for i, j in (itertools.combinations(range(len(bootstrap_sets)), 2))]
print(f"Average overlap between bootstrap samples of {round(100*np.mean(overlap), 2)}% " +
f"with variance of {round(np.var(overlap), 7)}")
# -
# Construct trees
#
# +
from multiprocessing import Pool
def fit_bootstrap_tree(depth, X, y):
idx = resample(range(len(X)), replace = True, n_samples = len(X))
return DecisionTreeClassifier(max_depth=depth).fit(X[idx], y[idx])
trees = [fit_bootstrap_tree(2, X_train, y_train) for _ in range(50)]
preds = np.array([t.predict(X_test) for t in trees])
np.mean((np.cumsum(preds, axis=0) >= len(trees)/2) == 1, axis=1)
# +
# num_of_trees = 400 # number of weak learners
# iterations = np.arange(0, num_of_trees, 5)
# depth = 3
# def train_bootstrap():
# all_indexes = np.arange(len(samples_train))
# train_errors = []
# test_errors = []
# train_var = []
# test_var = []
# trees = np.zeros(shape = num_of_trees, dtype=object)
# for t in range(num_of_trees):
# # resample new dataset(with replacement)
# indexes = resample(all_indexes, replace = True, n_samples = 1000)
# new_x_train, new_y_train = samples_train[indexes], tags_train[indexes]
# ensemble_learner = tree.DecisionTreeClassifier(max_depth=depth)
# ensemble_learner.fit(new_x_train, new_y_train)
# trees[t] = ensemble_learner
# for T in iterations:
# # predicting with weak leaners (small trees)
# train_pred = np.sign(np.sum([trees[t].predict(samples_train) for t in range(T)], axis = 0))
# train_errors.append (1 - np.mean(train_pred == tags_train))
# train_var.append(train_pred.var())
# test_pred = np.sign(np.sum([trees[t].predict(samples_test) for t in range(T)], axis = 0))
# test_errors.append (1 - np.mean(test_pred == tags_test))
# test_var.append(test_pred.var())
# return train_errors, test_errors, train_var, test_var, trees
# train_errors, test_errors, train_var, test_var, trees = train_bootstrap()
# # line - train error
# train_error = train_errors[-1]
# # lines - test errors
# single_stump_test_error = test_errors[0]
# deep_tree_test_error = 1 - np.mean(tree.DecisionTreeClassifier(max_depth=250).fit(samples_train, tags_train).predict(samples_test) == tags_test)
# +
# # Form grid of points to use for plotting decision boundaries
# lims = np.array([samples_train.min(axis=0), samples_train.max(axis=0)]).T + np.array([-.2, .2])
# xx, yy = list(map(np.ravel, np.meshgrid(np.arange(*lims[0], .2), np.arange(*lims[1], .2))))
# # # Retrieve model train error at each iteration of fitting
# # staged_scores = test_errors
# # # Predict labels of grid points at each iteration of fitting
# # staged_predictions = np.array(list(model.staged_predict(np.vstack([xx, yy]).T)))
# # Create animation frames
# # frames = []
# # for i in range(num_of_trees):
# # frames.append(go.Frame(
# # data=[
# # # Scatter of sample weights
# # go.Scatter(x=samples_train[:,0], y= samples_train[:,1], mode='markers', showlegend=False, marker=dict(color=tags_train, colorscale=class_colors(2),
# # size=np.maximum(2, np.ones(8*5))),
# # xaxis="x", yaxis="y"),
# # # Staged decision surface
# # go.Scatter(x=xx, y=yy, marker=dict(symbol = "square", colorscale=custom, color=trees[i].predict(np.vstack([xx, yy]).T)),
# # mode='markers', opacity = 0.4, showlegend=False, xaxis="x2", yaxis="y2"),
# # # Scatter of train samples with true class
# # go.Scatter(x=samples_train[:,0], y=samples_train[:,1], mode='markers', showlegend=False, xaxis="x2", yaxis="y2",
# # marker=dict(color=tags_train, colorscale=class_colors(2), symbol=class_symbols[tags_train])),
# # # Scatter of staged score
# # go.Scatter(x=list(range(i)), y=test_errors[:i], mode='lines+markers', showlegend=False, marker_color="black",
# # xaxis="x3", yaxis="y3")
# # ],
# # layout = go.Layout(title = rf"hh"),
# # traces=[0, 1, 2, 3]))
# # fig = make_subplots(rows=2, cols=2, row_heights=[350, 200],
# # subplot_titles=(r"$\hh",
# # r"$\hh"),
# # specs=[[{}, {}], [{"colspan": 2}, None]])\
# # .add_traces(data=frames[0].data, rows=[1,1,1,2], cols=[1,2,2,1])\
# # .update(frames = frames)\
# # .update_layout(title=frames[0].layout.title,
# # updatemenus = [dict(type="buttons", buttons=[AnimationButtons.play(), AnimationButtons.pause()])],
# # width=600, height=550, margin=dict(t=100))\
# # .update_yaxes(range=[min(staged_scores)-.1, 1.1], autorange=False, row=2, col=1)\
# # .update_xaxes(range=[0, len(frames)], autorange=False, row=2, col=1)
# # fig.show()
# -
|
lab/Lab 07 - Bagging Decision Trees.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:abc4py]
# language: python
# name: conda-env-abc4py-py
# ---
# +
# You need to install the latest version of dask and distributed
# pip install git+https://github.com/dask/dask.git (--upgrade)
# pip install git+https://github.com/dask/distributed.git (--upgrade)
# +
import sys
# Assuming we are in the notebook directory add this so that we can import the library
sys.path.append('..')
from abcpy.core import *
from abcpy.distributions import *
from distributed import Client
from dask.dot import dot_graph
# -
c = Client()
c
# +
tau = NumpyRV('tau', 'normal', 5)
values = tau.generate(9, batch_size=3)
# Draw the dask graph
dot_graph(values.dask)
# -
# You can see the dask graph dictionary with
values.dask
# Finally compute the values
c.compute(values, sync=True)
|
notebooks/distributed.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.7.10 64-bit (''toymodel0'': conda)'
# name: python3710jvsc74a57bd062830951d42064a77ddcbbe50cc184bfba2fd47286e32c34434c4d86c0a784dc
# ---
# Downloading the data for running the models
#
# # Set up
#
# ## Step 1: import the necessary packages
import os
from datetime import datetime, timedelta
import psycopg2
import pandas as pd
#import matplotlib
print(pd.__version__)
print(psycopg2.__version__)
# ## Step 2: connect to the database
crop_host = "cropapptestsqlserver.postgres.database.azure.com"
crop_port = "5432"
crop_dbname = "app_db"
crop_user = "cropreader@cropapptestsqlserver"
crop_password = "<PASSWORD>"
print(psycopg2.__version__)
conn = psycopg2.connect(host=crop_host, port=crop_port, dbname=crop_dbname, user=crop_user, password=crop_password)
cur = conn.cursor()
# # Access latest environmental and energy data
# In this section we access the latest data from the relevant tables for the last 2 years.
# +
# select your date range
# we want the last 2 years
dt_to = datetime.now()
dt_from = dt_to + timedelta(days=-366)
print(dt_from)
# -
# ## Data from zensie platform
# +
## 30 MHz Data Access Example
sql_command = """SELECT sensors.name, zensie_trh_data.* FROM sensor_types, sensors, zensie_trh_data WHERE sensors.id = zensie_trh_data.sensor_id AND zensie_trh_data.timestamp >= '%s' AND zensie_trh_data.timestamp < '%s'""" % (dt_from, dt_to)
df_30MHz = pd.read_sql(sql_command, conn)
df_30MHz.tail()
# -
# ## Data from Stark
# +
## Accessing new energy data
sql_command = """SELECT * FROM utc_energy_data WHERE utc_energy_data.timestamp >= '%s' AND utc_energy_data.timestamp < '%s'""" % (dt_from, dt_to)
df_energy_utc = pd.read_sql(sql_command, conn)
df_energy_utc.tail()
# -
# # Save the data in LatestData folder
# +
data_folder = "C:/Users/mkj32/OneDrive - UIS/GU/Models_Live/LatestData"
os.chdir(data_folder)
# -
# save zensie data to csv file
df_30MHz.to_csv(data_folder +"\Env_30MHz_raw.csv")
# save utc energy
df_energy_utc.to_csv(data_folder +"\Energy_utc.csv")
|
__app__/crop/Donwload_latest_data_May.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Tutorial 08: Creating Custom Environments
#
# This tutorial walks you through the process of creating custom environments in Flow. Custom environments contain specific methods that define the problem space of a task, such as the state and action spaces of the RL agent and the signal (or reward) that the RL algorithm will optimize over. By specifying a few methods within a custom environment, individuals can use Flow to design traffic control tasks of various types, such as optimal traffic light signal timing and flow regulation via mixed autonomy traffic (see the figures below). Finally, these environments are compatible with OpenAI Gym.
#
# The rest of the tutorial is organized as follows: in section 1 walks through the process of creating an environment for mixed autonomy vehicle control where the autonomous vehicles perceive all vehicles in the network, and section two implements the environment in simulation.
#
# <img src="img/sample_envs.png">
#
#
# ## 1. Creating an Environment Class
#
# In this tutorial we will create an environment in which the accelerations of a handful of vehicles in the network are specified by a single centralized agent, with the objective of the agent being to improve the average speed of all vehicle in the network. In order to create this environment, we begin by inheriting the base environment class located in *flow.envs*:
# +
# import the base environment class
from flow.envs import Env
# define the environment class, and inherit properties from the base environment class
class myEnv(Env):
pass
# -
# `Env` provides the interface for running and modifying a SUMO simulation. Using this class, we are able to start sumo, provide a network to specify a configuration and controllers, perform simulation steps, and reset the simulation to an initial configuration.
#
# By inheriting Flow's base environment, a custom environment for varying control tasks can be created by adding the following functions to the child class:
# * **action_space**
# * **observation_space**
# * **apply_rl_actions**
# * **get_state**
# * **compute_reward**
#
# Each of these components are covered in the next few subsections.
#
# ### 1.1 ADDITIONAL_ENV_PARAMS
#
# The features used to parametrize components of the state/action space as well as the reward function are specified within the `EnvParams` input, as discussed in tutorial 1. Specifically, for the sake of our environment, the `additional_params` attribute within `EnvParams` will be responsible for storing information on the maximum possible accelerations and decelerations by the autonomous vehicles in the network. Accordingly, for this problem, we define an `ADDITIONAL_ENV_PARAMS` variable of the form:
ADDITIONAL_ENV_PARAMS = {
"max_accel": 1,
"max_decel": 1,
}
# All environments presented in Flow provide a unique `ADDITIONAL_ENV_PARAMS` component containing the information needed to properly define some environment-specific parameters. We assume that these values are always provided by the user, and accordingly can be called from `env_params`. For example, if we would like to call the "max_accel" parameter, we simply type:
#
# max_accel = env_params.additional_params["max_accel"]
#
# ### 1.2 action_space
#
# The `action_space` method defines the number and bounds of the actions provided by the RL agent. In order to define these bounds with an OpenAI gym setting, we use several objects located within *gym.spaces*. For instance, the `Box` object is used to define a bounded array of values in $\mathbb{R}^n$.
from gym.spaces.box import Box
# In addition, `Tuple` objects (not used by this tutorial) allow users to combine multiple `Box` elements together.
from gym.spaces import Tuple
# Once we have imported the above objects, we are ready to define the bounds of our action space. Given that our actions consist of a list of n real numbers (where n is the number of autonomous vehicles) bounded from above and below by "max_accel" and "max_decel" respectively (see section 1.1), we can define our action space as follows:
class myEnv(myEnv):
@property
def action_space(self):
num_actions = self.initial_vehicles.num_rl_vehicles
accel_ub = self.env_params.additional_params["max_accel"]
accel_lb = - abs(self.env_params.additional_params["max_decel"])
return Box(low=accel_lb,
high=accel_ub,
shape=(num_actions,))
# ### 1.3 observation_space
# The observation space of an environment represents the number and types of observations that are provided to the reinforcement learning agent. For this example, we will be observe two values for each vehicle: its position and speed. Accordingly, we need a observation space that is twice the size of the number of vehicles in the network.
class myEnv(myEnv): # update my environment class
@property
def observation_space(self):
return Box(
low=0,
high=float("inf"),
shape=(2*self.initial_vehicles.num_vehicles,),
)
# ### 1.4 apply_rl_actions
# The function `apply_rl_actions` is responsible for transforming commands specified by the RL agent into actual actions performed within the simulator. The vehicle kernel within the environment class contains several helper methods that may be of used to facilitate this process. These functions include:
# * **apply_acceleration** (list of str, list of float) -> None: converts an action, or a list of actions, into accelerations to the specified vehicles (in simulation)
# * **apply_lane_change** (list of str, list of {-1, 0, 1}) -> None: converts an action, or a list of actions, into lane change directions for the specified vehicles (in simulation)
# * **choose_route** (list of str, list of list of str) -> None: converts an action, or a list of actions, into rerouting commands for the specified vehicles (in simulation)
#
# For our example we consider a situation where the RL agent can only specify accelerations for the RL vehicles; accordingly, the actuation method for the RL agent is defined as follows:
class myEnv(myEnv): # update my environment class
def _apply_rl_actions(self, rl_actions):
# the names of all autonomous (RL) vehicles in the network
rl_ids = self.k.vehicle.get_rl_ids()
# use the base environment method to convert actions into accelerations for the rl vehicles
self.k.vehicle.apply_acceleration(rl_ids, rl_actions)
# ### 1.5 get_state
#
# The `get_state` method extracts features from within the environments and provides then as inputs to the policy provided by the RL agent. Several helper methods exist within flow to help facilitate this process. Some useful helper method can be accessed from the following objects:
# * **self.k.vehicle**: provides current state information for all vehicles within the network
# * **self.k.traffic_light**: provides state information on the traffic lights
# * **self.k.network**: information on the network, which unlike the vehicles and traffic lights is static
# * More accessor objects and methods can be found within the Flow documentation at: http://berkeleyflow.readthedocs.io/en/latest/
#
# In order to model global observability within the network, our state space consists of the speeds and positions of all vehicles (as mentioned in section 1.3). This is implemented as follows:
# +
import numpy as np
class myEnv(myEnv): # update my environment class
def get_state(self, **kwargs):
# the get_ids() method is used to get the names of all vehicles in the network
ids = self.k.vehicle.get_ids()
# we use the get_absolute_position method to get the positions of all vehicles
pos = [self.k.vehicle.get_x_by_id(veh_id) for veh_id in ids]
# we use the get_speed method to get the velocities of all vehicles
vel = [self.k.vehicle.get_speed(veh_id) for veh_id in ids]
# the speeds and positions are concatenated to produce the state
return np.concatenate((pos, vel))
# -
# ### 1.6 compute_reward
#
# The `compute_reward` method returns the reward associated with any given state. These value may encompass returns from values within the state space (defined in section 1.5) or may contain information provided by the environment but not immediately available within the state, as is the case in partially observable tasks (or POMDPs).
#
# For this tutorial, we choose the reward function to be the average speed of all vehicles currently in the network. In order to extract this information from the environment, we use the `get_speed` method within the Vehicle kernel class to collect the current speed of all vehicles in the network, and return the average of these speeds as the reward. This is done as follows:
# +
import numpy as np
class myEnv(myEnv): # update my environment class
def compute_reward(self, rl_actions, **kwargs):
# the get_ids() method is used to get the names of all vehicles in the network
ids = self.k.vehicle.get_ids()
# we next get a list of the speeds of all vehicles in the network
speeds = self.k.vehicle.get_speed(ids)
# finally, we return the average of all these speeds as the reward
return np.mean(speeds)
# -
# ## 2. Testing the New Environment
#
#
# ### 2.1 Testing in Simulation
# Now that we have successfully created our new environment, we are ready to test this environment in simulation. We begin by running this environment in a non-RL based simulation. The return provided at the end of the simulation is indicative of the cumulative expected reward when jam-like behavior exists within the netowrk.
# +
from flow.controllers import IDMController, ContinuousRouter
from flow.core.experiment import Experiment
from flow.core.params import SumoParams, EnvParams, \
InitialConfig, NetParams
from flow.core.params import VehicleParams
from flow.networks.ring import RingNetwork, ADDITIONAL_NET_PARAMS
sim_params = SumoParams(sim_step=0.1, render=True)
vehicles = VehicleParams()
vehicles.add(veh_id="idm",
acceleration_controller=(IDMController, {}),
routing_controller=(ContinuousRouter, {}),
num_vehicles=22)
env_params = EnvParams(additional_params=ADDITIONAL_ENV_PARAMS)
additional_net_params = ADDITIONAL_NET_PARAMS.copy()
net_params = NetParams(additional_params=additional_net_params)
initial_config = InitialConfig(bunching=20)
flow_params = dict(
exp_tag='ring',
env_name=myEnv, # using my new environment for the simulation
network=RingNetwork,
simulator='traci',
sim=sim_params,
env=env_params,
net=net_params,
veh=vehicles,
initial=initial_config,
)
# number of time steps
flow_params['env'].horizon = 1500
exp = Experiment(flow_params)
# run the sumo simulation
_ = exp.run(1)
# -
# ### 2.2 Training the New Environment
#
# Next, we wish to train this environment in the presence of the autonomous vehicle agent to reduce the formation of waves in the network, thereby pushing the performance of vehicles in the network past the above expected return.
#
# The below code block may be used to train the above environment using the Proximal Policy Optimization (PPO) algorithm provided by RLlib. In order to register the environment with OpenAI gym, the environment must first be placed in a separate ".py" file and then imported via the script below. Then, the script immediately below should function regularly.
#############################################################
####### Replace this with the environment you created #######
#############################################################
from flow.envs import AccelEnv as myEnv
# **Note**: We do not recommend training this environment to completion within a jupyter notebook setting; however, once training is complete, visualization of the resulting policy should show that the autonomous vehicle learns to dissipate the formation and propagation of waves in the network.
# +
import json
import ray
from ray.rllib.agents.registry import get_agent_class
from ray.tune import run_experiments
from ray.tune.registry import register_env
from flow.networks.ring import RingNetwork, ADDITIONAL_NET_PARAMS
from flow.utils.registry import make_create_env
from flow.utils.rllib import FlowParamsEncoder
from flow.core.params import SumoParams, EnvParams, InitialConfig, NetParams
from flow.core.params import VehicleParams, SumoCarFollowingParams
from flow.controllers import RLController, IDMController, ContinuousRouter
# time horizon of a single rollout
HORIZON = 1500
# number of rollouts per training iteration
N_ROLLOUTS = 20
# number of parallel workers
N_CPUS = 2
# We place one autonomous vehicle and 22 human-driven vehicles in the network
vehicles = VehicleParams()
vehicles.add(
veh_id="human",
acceleration_controller=(IDMController, {
"noise": 0.2
}),
car_following_params=SumoCarFollowingParams(
min_gap=0
),
routing_controller=(ContinuousRouter, {}),
num_vehicles=21)
vehicles.add(
veh_id="rl",
acceleration_controller=(RLController, {}),
routing_controller=(ContinuousRouter, {}),
num_vehicles=1)
flow_params = dict(
# name of the experiment
exp_tag="stabilizing_the_ring",
# name of the flow environment the experiment is running on
env_name=myEnv, # <------ here we replace the environment with our new environment
# name of the network class the experiment is running on
network=RingNetwork,
# simulator that is used by the experiment
simulator='traci',
# sumo-related parameters (see flow.core.params.SumoParams)
sim=SumoParams(
sim_step=0.1,
render=True,
),
# environment related parameters (see flow.core.params.EnvParams)
env=EnvParams(
horizon=HORIZON,
warmup_steps=750,
clip_actions=False,
additional_params={
"target_velocity": 20,
"sort_vehicles": False,
"max_accel": 1,
"max_decel": 1,
},
),
# network-related parameters (see flow.core.params.NetParams and the
# network's documentation or ADDITIONAL_NET_PARAMS component)
net=NetParams(
additional_params=ADDITIONAL_NET_PARAMS.copy()
),
# vehicles to be placed in the network at the start of a rollout (see
# flow.core.params.VehicleParams)
veh=vehicles,
# parameters specifying the positioning of vehicles upon initialization/
# reset (see flow.core.params.InitialConfig)
initial=InitialConfig(
bunching=20,
),
)
def setup_exps():
"""Return the relevant components of an RLlib experiment.
Returns
-------
str
name of the training algorithm
str
name of the gym environment to be trained
dict
training configuration parameters
"""
alg_run = "PPO"
agent_cls = get_agent_class(alg_run)
config = agent_cls._default_config.copy()
config["num_workers"] = N_CPUS
config["train_batch_size"] = HORIZON * N_ROLLOUTS
config["gamma"] = 0.999 # discount rate
config["model"].update({"fcnet_hiddens": [3, 3]})
config["use_gae"] = True
config["lambda"] = 0.97
config["kl_target"] = 0.02
config["num_sgd_iter"] = 10
config['clip_actions'] = False # FIXME(ev) temporary ray bug
config["horizon"] = HORIZON
# save the flow params for replay
flow_json = json.dumps(
flow_params, cls=FlowParamsEncoder, sort_keys=True, indent=4)
config['env_config']['flow_params'] = flow_json
config['env_config']['run'] = alg_run
create_env, gym_name = make_create_env(params=flow_params, version=0)
# Register as rllib env
register_env(gym_name, create_env)
return alg_run, gym_name, config
alg_run, gym_name, config = setup_exps()
ray.init(num_cpus=N_CPUS + 1)
trials = run_experiments({
flow_params["exp_tag"]: {
"run": alg_run,
"env": gym_name,
"config": {
**config
},
"checkpoint_freq": 20,
"checkpoint_at_end": True,
"max_failures": 999,
"stop": {
"training_iteration": 200,
},
}
})
# -
|
tutorials/tutorial08_environments.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ¡Holaaaaaa!
#
# En esta ocasión vamos a trabajar con una [API Financiera](https://financialmodelingprep.com/developer/docs)
#
# La razón de este proyecto es mostrarles una manera rapida de analizar cuantitativamente empresas. He pasado el ultimo año desarrollando modelos financieros, soy un "hobbyista" de las finanzas. Siempre me intereso el mundo de las finanzas corporativas y las valuaciones como un mero pasatiempo.
#
# 
#
# 
#
# 
#
# 
#
# Se el dolor y el amor que uno puede sentir al buscar datos financieros dentro de un reporte anual K10. Por eso hice este proyecto. Hay maneras rapidas de sacar datos financieros sin necesidad de copiar y pegarlos a mano en nuestro Excel.
#
# En este proyecto aprenderas sobre:
#
# 1. Que son las API REST
# 2. Como extraer datos de una API
# 3. Transformar los datos de JSON de una API a un dataframe de Pandas
# 4. Como graficar los datos con Matplotlib y Numpy
# 5. Como guardar los datos dentro de un CSV para que los en Excel o R
#
# ---
# #### ¿Que es una API?
#
# Una API es una interfaz que ofrece un servicio de comunicación. A diferencia de una UI (interfaz de usuario) que conecta a una persona con una computadora, una API conecta computadoras o software entre ellos mismos.
#
# Estan hechas de diferentes partes que actuan como herramientas o servicios. Un programador puede llamar a uno de estos servicios a traves de metodos, requests o endpoints que estan definidas en las espicificaciones de una API.
#
# Pero la API como tal no es practica de usar, debe diseñarse a través de una arquitectura llamada REST que ayuda a manejar la información.
#
# REST fue propuesta por <NAME> en un paper titulado " Architectural Styles and the Design of Network-based Software Architectures", y una idea basica detras de REST es tratar a los datos como objetos que puedes llamar, crear o destruir y a través de metodos y que son representados en formato JSON, XML o RDF.
#
# | Metodo | Descripcion |
# | ----------- | ----------- |
# | GET | Trae informacion |
# | POST | Crea informacion |
# | PUT | Actualiza informacion |
# | DELETE | Borra informacion |
#
# [Como explicarle REST a tu esposa](http://www.looah.com/source/view/2284)
#
#
# Esto es justo lo que haremos ahora. Imaginemos a una API Rest como un ente que nos ayuda a traer datos desde una base externa. Nuestra computadora necesita comunicarse con otra y REST es la mejor forma de hacerlo.
#
# ¡Es hora de empezar!
#
# Utilizaremos el modulo **requests** para enviar pedimentos HTTP de manera sencilla.
#
# HTTP o Hypertext Transfer Protocol es un protocolo Request-Response (pedido y respuesta) cuya funcion principal es establecer una comunicación entre sistemas de la Internet que conforman el World Wide Web (WWW).
#
# Fue diseñado y creado para ser un puente entre los clientes y servidores. Este "puente" tiene metodos definidos que indican acciones deseadas por parte de un cliente hacia un recurso especifico. Lo que el recurso represente depende de lo que se implemento en el servidor.
#
# Basicamente REST es la manera en que HTTP se debe usar.
#
# #### Extrayendo datos de una API
#
# Hay 3 reglas que se deben seguir para usar una API REST.
# 1. Definir el metodo
# 2. Definir los parametros
# 3. Hacer el request
#
# Nuestro metodo sera de tipo GET que es lo mismo a pedir informacion de la API.
# Nuestros parametros seran:
# 1. La llave de la API (la puedes conseguir creando una cuenta en el portal de la API)
# 2. El ticket en la bolsa de la empresa de nuestro interes
# 3. Los años
#
# En esta ocasion haremos un request de datos financieros del Income Statement de NVDA.
# Si lo que quieres es su Balance Sheet o Cash Flow solo cambia esto la parte de income-statement en la URL por balance-sheet o cash-flow
import requests
import json
# +
# DEFINIENDO PARAMETROS #
api_key = '<KEY>'
company = "NVDA"
years = 5
# REQUEST GET con el package Requests.
r = requests.get(f'https://financialmodelingprep.com/api/v3/income-statement/{company}?limit={years}&apikey={api_key}')
data = r.json()
print(data)
# CON ESTO CREAMOS UN OBJETO de datos tipo lista.
# -
# #### Transformando los datos JSON a un DF
#
# La razón por la cual queremos transformar estos datos es por el proposito de manupilación. Trabajar con un JSON no es recomendable pues es dificil analizarlo cuando esta en su estado natural, solo son buenos para pasar información entre servidores. Pandas nos permite transformarlos de una manera super sencilla, solo necesitamos el siguiente pedazo de codigo.
import pandas as pd
df = pd.DataFrame(data)
df.info()
# Listo. Los datos vienen sin valores nulos y estan en buen estado así que podemos manejarlos a partir de ahora en adelante.
# Lo unico que hare es quitar quitar algunas columnas como los ratios pero no es necesario que tu lo hagas si no es necesario. Lo que si es necesario es que apliques un SORT. Esto te permite cambiar el orden del frame a partir de sus fechas, esto con el objetivo de graficar.
df = df.drop(columns=['reportedCurrency',
'fillingDate',
'acceptedDate',
'period',
'link',
'finalLink',
'symbol',
'grossProfitRatio',
'incomeBeforeTaxRatio',
'netIncomeRatio',
'eps',
'epsdiluted'])
df = df.sort_values("date")
# #### Graficando los datos
#
# Bueno, es hora de hacer algnos plots para que veas lo facil que es graficar los datos.
# Primero voy a cargar las librerias, despues aplicare una configuración para el tamaño de los plots y por ultimo dividire las columnas de mi interes para que el axis de Y no arroje visualizaciones raras.
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
### Este codigo establece la anchura y la altura de los plots (bastante util)
# %matplotlib inline
plt.rcParams['figure.figsize'] = (12, 10)
## Este codigo te permite seleccionar las columnas de tu interes con el proposito
## de dividirlas y mejorar la visualización del plot
df[["revenue", "costOfRevenue"]] = df[["revenue", "costOfRevenue"]] / 1000000000
plt.bar(df['date'], df['revenue'])
plt.title('Crecimiento en las ventas de NVDA', fontsize=14)
plt.xlabel('Año', fontsize=14)
plt.ylabel('Ventas totales en miles de millones de USD', fontsize=14)
plt.xticks(df['date'],['2017', '2018', '2019', '2020', '2021'])
plt.show()
# +
### Localizando los datos
descripcion = ['2017', '2018', '2019', '2020', '2021']
revenue = df["revenue"]
costOfRevenue = df["costOfRevenue"]
### Recorriendo la descripcion
x = np.arange(len(descripcion))
width = 0.35
### Configurando los plots
fig, ax = plt.subplots()
plot1 = ax.bar(x - width/2, revenue, width, label='Ventas')
plot2 = ax.bar(x + width/2, costOfRevenue, width, label='Costo de ventas')
### Añadiendo la descripcion
ax.set_ylabel('Miles de millones de USD')
ax.set_title('Revenue vs CostOfRevenue')
ax.set_xticks(x)
ax.set_xticklabels(descripcion)
ax.legend()
plt.show()
# -
# #### Creando un csv
#
# Si lo anterior te parecio dificil, no te preocupes. Siempre existen soluciones y de hecho me parece que utilizar Python para este tipo de cosas (visualizar frames tan pequeños) es innecesario. Para eso tenemos Excel.
#
# Con el siguiente pedazo de codigo vas a poder crear un csv con los datos que sacaste del API.
df.to_csv('NVDA.csv', index = False)
# Bueno, esto es todo! Espero que este proyecto te ayude con tus objetivos profesionales y no profesionales. Si necesitas ayuda siempre puedes mandarme un mensaje a <EMAIL>.
#
# Un abrazo!
|
Financial_API/Working with a Financial API.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
from sklearn.model_selection import cross_val_score
from preproc3 import preprocessing
from sklearn.ensemble import StackingClassifier
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import HistGradientBoostingClassifier
# +
gb1=GradientBoostingClassifier(n_estimators=500, learning_rate=0.12, subsample=0.9)
gb2=GradientBoostingClassifier(n_estimators=550, learning_rate=0.1, subsample=0.9)
gb3=GradientBoostingClassifier(n_estimators=600, learning_rate=0.08, subsample=0.9)
hist1=HistGradientBoostingClassifier(max_iter=100)
hist2=HistGradientBoostingClassifier(max_iter=150)
hist3=HistGradientBoostingClassifier(max_iter=200)
lr=LogisticRegression(max_iter=1000)
estimators=[('gb1',gb1),('gb2',gb2),('gb3',gb3),('hist1', hist1), ('hist2', hist2), ('hist3', hist3)]
model=StackingClassifier(estimators=estimators,final_estimator=lr,n_jobs=4,verbose=100)
# +
DATA='ugrin2020-vehiculo-usado-multiclase/'
TRAIN=DATA+'train.csv'
TEST=DATA+'test.csv'
RESULTS='../results/'
# +
train = pd.read_csv(TRAIN) # Cargo datos de entrenamiento
test = pd.read_csv(TEST) # Cargo datos de test
# Eliminamos el campo id ya que no se debe usar para predecir
test_ids = test['id']
del test['id']
del train['id']
# Cambiamos el nombre a la columna Año para poder manejarla correctamente
train.rename(columns = {'Año':'Anio'}, inplace = True)
test.rename(columns = {'Año':'Anio'}, inplace = True)
# -
train, label, test = preprocessing(train, test)
scores=cross_val_score(model, train, label, cv=5)
print(scores)
print(np.mean(scores))
model.fit(train,label)
# Ahora predecimos
predict = model.predict(test)
predict = list(map(int,predict))
# Generamos
df_result = pd.DataFrame({'id': test_ids, 'Precio_cat': predict})
df_result.to_csv(RESULTS+"try19.csv", index=False)
|
practica3/intentos/try19.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Score : 0.76555
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# ## Load data
test_df = pd.read_csv('./data/test.csv')
train_df = pd.read_csv('./data/train.csv')
train_df.head()
test_df.head()
train_df.set_index('PassengerId', inplace=True)
test_df.set_index('PassengerId', inplace=True)
train_df.head()
train_index = train_df.index
test_index = test_df.index
train_index, test_index
# ## Data processing
#
# ### 1. null drop
pd.set_option('display.float_format', lambda x: '%.2f' % x)
test_df.isnull().sum() / len(test_df)
train_df.isnull().sum() / len(train_df) * 100
## Cabin 번역
test_df['Cabin'] = test_df.Cabin.fillna('').apply(lambda x: len(x.split()))
train_df['Cabin'] = train_df.Cabin.fillna('').apply(lambda x: len(x.split()))
train_df['Cabin'].head()
train_df.head()
all_df = train_df.append(test_df, sort=False)
all_df
sex_dict = {'male': 0, 'female': 1}
all_df['Sex'] = all_df['Sex'].apply(lambda x: sex_dict[x])
all_df.head()
del all_df['Name']
del all_df['Ticket']
all_df.Embarked.unique()
embarked_dict = {'S':1, 'C':2, 'Q':3, '0': 0}
all_df['Embarked'] = all_df['Embarked'].fillna('0').apply(lambda x: embarked_dict[x])
all_df.head()
all_df.describe()
all_df.isnull().sum()
all_df.groupby(['Pclass', 'Sex', 'SibSp', 'Cabin'])['Age'].mean()
all_df.groupby(['Pclass', 'Sex', 'SibSp', 'Cabin'])['Age'].apply(lambda x: x.fillna(x.mean())).head()
all_df['Age'] = all_df.groupby(['Pclass', 'Sex', 'SibSp', 'Cabin'])['Age'].apply(lambda x: x.fillna(x.mean()))
all_df['Age'] = all_df.groupby(['Pclass'])['Age'].apply(lambda x: x.fillna(x.mean()))
all_df.isnull().sum()
all_df['Fare'] = all_df['Fare'].fillna(all_df['Fare'].mean())
all_df.isnull().sum()
all_df.describe()
all_df.corr()
fig, ax = plt.subplots(figsize=(7,7))
ax.matshow(all_df.dropna().corr())
all_df.dropna().corr()
# +
from pandas.plotting import scatter_matrix
scatter_matrix(all_df.dropna(), alpha=0.2, figsize=(20, 20), diagonal='kde')
'''
corr check
'''
# +
from pandas.plotting import radviz
plt.figure(figsize=(10,10))
radviz(all_df.dropna(), 'Survived', color=['red', 'green'], alpha=0.2)
# -
# ## Build model
# all_df => test_df
train_df = all_df[all_df.index.isin(train_index)]
test_df = all_df[all_df.index.isin(test_index)]
test_df.pop('Survived')
y_train_df = train_df.pop('Survived')
y_train_df.head()
x_data = train_df.values
y_data = y_train_df.values
x_data.shape, y_data.shape
test_df
from sklearn.linear_model import LogisticRegression
cls = LogisticRegression()
cls.fit(x_data, y_data)
cls.intercept_
cls.coef_
cls.predict(test_df.values)
test_df.index
x_test = test_df.values
y_test = cls.predict(x_test)
y_test
test_values = test_index.values.reshape(-1, 1)
predict_values = cls.predict(x_test).reshape(-1, 1)
result = np.concatenate((test_values, predict_values), axis = 1)
result = result.astype(np.int32)
result[:5]
df_sub = pd.DataFrame(result, columns=['PassengerId', 'Survived'])
df_sub
df_sub.to_csv("sub_result.csv", index=False)
|
01_titanic/teamlab_solution.ipynb
|
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 1.5.0
# language: julia
# name: julia-1.5
# ---
# + active=""
# Text provided under a Creative Commons Attribution license, CC-BY, Copyright (c) 2020, Cysor. All code is made available under the FSF-approved BSD-3 license. Adapted from CFDPython Copyright (c) Barba group - https://github.com/barbagroup/CFDPython
# -
# 12 steps to Navier–Stokes
# =====
# ***
# In the previous step, we solved the [2D Burgers' equation](./10_Step_8.ipynb): an important equation in the study of fluid mechanics because it contains the full convective nonlinearity of the flow equations. With that exercise, we also build the experience to incrementatlly code a Navier–Stokes solver.
#
# In the next two steps, we will solve Laplace and then Poisson equation. We will then put it all together!
# Step 9: 2D Laplace Equation
# ----
# ***
# Here is Laplace's equation in 2D:
#
# $$\frac{\partial ^2 p}{\partial x^2} + \frac{\partial ^2 p}{\partial y^2} = 0$$
#
# We know how to discretize a 2nd order derivative. But think about this for a minute — Laplace's equation has the features typical of diffusion phenomena. For this reason, it has to be discretized with *central differences*, so that the discretization is consistent with the physics we want to simulate.
#
# The discretized equation is:
#
# $$\frac{p_{i+1, j}^n - 2p_{i,j}^n + p_{i-1,j}^n}{\Delta x^2} + \frac{p_{i,j+1}^n - 2p_{i,j}^n + p_{i, j-1}^n}{\Delta y^2} = 0$$
#
# Notice that the Laplace Equation does not have a time dependence — there is no $p^{n+1}$. Instead of tracking a wave through time (like in the previous steps), the Laplace equation calculates the equilibrium state of a system under the supplied boundary conditions.
#
# If you have taken coursework in Heat Transfer, you will recognize the Laplace Equation as the steady-state heat equation.
#
# Instead of calculating where the system will be at some time $t$, we will iteratively solve for $p_{i,j}^n$ until it meets a condition that we specify. The system will reach equilibrium only as the number of iterations tends to $\infty$, but we can approximate the equilibrium state by iterating until the change between one iteration and the next is *very* small.
#
# Let's rearrange the discretized equation, solving for $p_{i,j}^n$:
#
# $$p_{i,j}^n = \frac{\Delta y^2(p_{i+1,j}^n+p_{i-1,j}^n)+\Delta x^2(p_{i,j+1}^n + p_{i,j-1}^n)}{2(\Delta x^2 + \Delta y^2)}$$
#
# Using second-order central-difference schemes in both directions is the most widely applied method for the Laplace operator. It is also known as the **five-point difference operator**, alluding to its stencil.
# We are going to solve Laplace's equation numerically by assuming an initial state of $p=0$ everywhere. Then we add boundary conditions as follows:
#
# $p=0$ at $x=0$
#
# $p=y$ at $x=2$
#
# $\frac{\partial p}{\partial y}=0$ at $y=0, \ 1$
#
# Under these conditions, there is an analytical solution for Laplace's equation:
#
# $$p(x,y)=\frac{x}{4}-4\sum_{n=1,odd}^{\infty}\frac{1}{(n\pi)^2\sinh2n\pi}\sinh n\pi x\cos n\pi y$$
# ##### Exercise
# Write your own code to solve Poisson's equation using loops, in the style of coding used in our first lessons. Then, consider the demonstration of how to write it using functions (below) and modify your code in that style. Can you think of reasons to abandon the old style and adopt modular coding?
#
# Other tips:
#
# + Visualize each step of the iterative process
# + Think about what the boundary conditions are doing
# + Think about what the PDE is doing
# ### Using functions
# Remember the lesson on writing [functions with Python](./11_Defining_Function_in_Python.ipynb)? We will use that style of code in this exercise.
#
# We're going to define two functions: one that plots our data in a 3D projection plot and the other that iterates to solve for $p$ until the change in the [L1 Norm][1] of $p$ is less than a specified value.
#
# [1]: http://en.wikipedia.org/wiki/Norm_(mathematics)#Taxicab_norm_or_Manhattan_norm
# + jupyter={"outputs_hidden": false}
using Plots
function plot2D(x, y, p)
surface(x,y,p,
colour=:viridis,
xlims=(0,2),
ylims=(0,1),
ylabel="y",
xlabel="x",
camera = (30,60)
)
end
# -
# The function `plot2D` takes three arguments, an x-vector, a y-vector and our p matrix. Given these three values, it produces a 3D projection plot, sets the plot limits and gives us a nice viewing angle.
# $$p_{i,j}^n = \frac{\Delta y^2(p_{i+1,j}^n+p_{i-1,j}^n)+\Delta x^2(p_{i,j+1}^n + p_{i,j-1}^n)}{2(\Delta x^2 + \Delta y^2)}$$
# + jupyter={"outputs_hidden": false}
function laplace2D(p, y, Δx, Δy, l1norm_target)
l1norm = 1
pⁿ = similar(p)
while l1norm > l1norm_target
pⁿ = copy(p)
row, col = size(pⁿ)
for j ∈ 1:row
for i ∈ 1:col
# Implement boundary conditions
if i == 1 # @ x = 0, p = 0
p[j,i] = 0
elseif i == col # @ x = 2 , p=y
p[j,i] = y[j]
elseif j == 1 # @ y = 0, dp/dy = 0
p[j,i] == p[j+1,i]
elseif j == row # @ y = 2, dp/dy = 0
p[j,i] = p[j-1,i]
else
# Solve Equation
p[j,i] = ((Δy^2*(pⁿ[j,i+1] + pⁿ[j,i-1]) +
Δx^2*(pⁿ[j+1,i] + pⁿ[j-1,i])) /
(2*(Δx^2+Δy^2)))
end
end
end
# Calculate l1norm of current itteration
l1norm = sum(abs.(p) - abs.(pⁿ)) / sum(abs.(pⁿ))
end
return p
end
# -
# `laplace2d` takes five arguments, the `p` matrix, the `y`-vector, `dx`, `dy` and the value `l1norm_target`. This last value defines how close the `p` matrix should be in two consecutive iterations before the loop breaks and returns the calculated `p` value.
#
# Note that when executing the cells above in your own notebook, there will be no output. You have *defined* the function but you have not yet *called* the function. It is now available for you to use, the same as `numpy.linspace` or any other function in our namespace.
# + jupyter={"outputs_hidden": false}
##variable declarations
nx = 31
ny = 31
c = 1
Δx = 2/(nx-1)
Δy = 2/(ny-1)
##inital conditions
p = zeros(ny,nx)
x = range(0, stop=2, length=nx)
y = range(0, stop=1, length=ny)
##boundary conditions
p[:, x .== 0] .= 0
p[:, x .== 2] = y
p[y .== 0,:] = p[2,:]
p[y .== 1,:] = p[end-1,:];
# The above syntax puts into context the boundary conditions but the notation is a bit messy.
# An alternative syntax is shown below
#p[:, 1] .= 0
#p[:, end] = y
#p[1,:] = p[2,:]
#p[end,:] = p[end-1,:]
# -
# Now let's try using our `plot2D` function to look at our initial conditions. If the function has been correctly defined, you should be able to begin typing `plot2D` and hit the **tab** key for auto-complete options.
# + jupyter={"outputs_hidden": false}
plot2D(x, y, p)
# -
# It worked! This is the initial state of our problem, where the value of `p` is zero everywhere except for along $x=2$ where $p=y$. Now let's try to run our `laplace2d` function with a specified L1 target of .01
#
# [Hint: if you are having trouble remembering the order in which variables are sent to a function, you can just type `laplace2d(` and the iPython Notebook will put up a little popup box to remind you]
# + jupyter={"outputs_hidden": false}
p = laplace2D(p, y, Δx, Δy, 1e-4)
# -
# Now try plotting this new value of `p` with our plot function.
# + jupyter={"outputs_hidden": false}
plot2D(x, y, p)
# -
# ***
# ## Learn More
# The [next step](./13_Step_10.ipynb) will be to solve Poisson's equation. Watch **Video Lesson [11](https://youtube.com/watch?v=ZjfxA3qq2Lg)** on You Tube to understand why we need Poisson's equation in CFD.
# And for a detailed walk-through of the discretization of Laplace and Poisson equations (steps 9 and 10), watch **Video Lesson [12](https://youtube.com/watch?v=iwL8ashXhWU)** on You Tube:
|
Lessons/12_Step_9.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <a id='top'></a>
# + [markdown] hideCode=false hidePrompt=false
# # Db2 Statistical Functions
# + [markdown] hideCode=false hidePrompt=false
# Db2 already has a variety of Statistical functions built in. In Db2 11.1, a number of new
# functions have been added including:
#
# - [*COVARIANCE_SAMP*](#covariance) - The COVARIANCE_SAMP function returns the sample covariance of a set of number pairs
# - [*STDDEV_SAMP*](#stddev) - The STDDEV_SAMP column function returns the sample standard deviation (division by [n-1]) of a set of numbers.
# - [*VARIANCE_SAMP*](#variance) or VAR_SAMP - The VARIANCE_SAMP column function returns the sample variance (division by [n-1]) of a set of numbers.
# - [*CUME_DIST*](#cume) - The CUME_DIST column function returns the cumulative distribution of a row that is hypothetically inserted into a group of rows
# - [*PERCENT_RANK*](#rank) - The PERCENT_RANK column function returns the relative percentile rank of a row that is hypothetically inserted into a group of rows.
# - [*PERCENTILE_DISC*](#disc), [*PERCENTILE_CONT*](#cont) - Returns the value that corresponds to the specified percentile given a sort specification by using discrete (DISC) or continuous (CONT) distribution
# - [*MEDIAN*](#median) - The MEDIAN column function returns the median value in a set of values
# - [*WIDTH_BUCKET*](#width) - The WIDTH_BUCKET function is used to create equal-width histograms
# -
# ## Sampling Functions
# The traditional VARIANCE, COVARIANCE, and STDDEV functions have been available in Db2 for a long time. When computing these values, the formulae assume that the entire population has been counted (N). The traditional formula for standard deviation is:
# $$\sigma=\sqrt{\frac{1}{N}\sum_{i=1}^N(x_{i}-\mu)^{2}}$$
# N refers to the size of the population and in many cases, we only have a sample, not the entire population of values.
# In this case, the formula needs to be adjusted to account for the sampling.
# $$s=\sqrt{\frac{1}{N-1}\sum_{i=1}^N(x_{i}-\bar{x})^{2}}$$
# + [markdown] hideCode=false hidePrompt=false
# Set up the connection to the database.
# -
# %run db2.ipynb
# We populate the database with the EMPLOYEE and DEPARTMENT tables so that we can run the various examples.
# %sql -sampledata
# <a id="covariance"></a>
# + [markdown] hideCode=false hidePrompt=false
# ## COVARIANCE_SAMP
#
# The COVARIANCE_SAMP function returns the sample covariance of a set of number pairs.
# + hideCode=false hidePrompt=false language="sql"
# SELECT COVARIANCE_SAMP(SALARY, BONUS)
# FROM EMPLOYEE
# WHERE WORKDEPT = 'A00'
# -
# <a id="stddev"></a>
# + [markdown] hideCode=false hidePrompt=false
# ## STDDEV_SAMP
#
# The STDDEV_SAMP column function returns the sample standard deviation (division by [n-1]) of a set of numbers.
# + hideCode=false hidePrompt=false language="sql"
# SELECT STDDEV_SAMP(SALARY)
# FROM EMPLOYEE
# WHERE WORKDEPT = 'A00'
# -
# <a id="variance"></a>
# + [markdown] hideCode=false hidePrompt=false
# ## VARIANCE_SAMP
# The VARIANCE_SAMP column function returns the sample variance (division by [n-1]) of a set of numbers.
# + hideCode=false hidePrompt=false language="sql"
# SELECT VARIANCE_SAMP(SALARY)
# FROM EMPLOYEE
# WHERE WORKDEPT = 'A00'
# -
# <a id="median"></a>
# + [markdown] hideCode=false hidePrompt=false
# ## MEDIAN
#
# The MEDIAN column function returns the median value in a set of values.
# + hideCode=false hidePrompt=false language="sql"
# SELECT MEDIAN(SALARY) AS MEDIAN, AVG(SALARY) AS AVERAGE
# FROM EMPLOYEE
# WHERE WORKDEPT = 'E21'
# -
# <a id="cume"></a>
# + [markdown] hideCode=false hidePrompt=false
# ## CUME_DIST
#
# The CUME_DIST column function returns the cumulative distribution of a row that is hypothetically inserted into
# a group of rows.
# + hideCode=false hidePrompt=false language="sql"
# SELECT CUME_DIST(47000) WITHIN GROUP (ORDER BY SALARY)
# FROM EMPLOYEE
# WHERE WORKDEPT = 'A00'
# -
# <a id="rank"></a>
# + [markdown] hideCode=false hidePrompt=false
# ## PERCENT_RANK
#
# The PERCENT_RANK column function returns the relative percentile rank of a
# row that is hypothetically inserted into a group of rows.
# + hideCode=false hidePrompt=false language="sql"
# SELECT PERCENT_RANK(47000) WITHIN GROUP (ORDER BY SALARY)
# FROM EMPLOYEE
# WHERE WORKDEPT = 'A00'
# -
# <a id="disc"></a>
# + [markdown] hideCode=false hidePrompt=false
# ## PERCENTILE_DISC
#
# The PERCENTILE_DISC/CONT returns the value that corresponds to the specified percentile
# given a sort specification by using discrete (DISC) or continuous (CONT) distribution.
# + hideCode=false hidePrompt=false language="sql"
# SELECT PERCENTILE_DISC(0.75) WITHIN GROUP (ORDER BY SALARY)
# FROM EMPLOYEE
# WHERE WORKDEPT = 'E21'
# -
# <a id="cont"></a>
# + [markdown] hideCode=false hidePrompt=false
# ## PERCENTILE_CONT
#
# This is a function that gives you a continuous percentile calculation.
# + hideCode=false hidePrompt=false language="sql"
# SELECT PERCENTILE_CONT(0.75) WITHIN GROUP (ORDER BY SALARY)
# FROM EMPLOYEE
# WHERE WORKDEPT = 'E21'
# -
# <a id="width"></a>
# + [markdown] hideCode=false hidePrompt=false
# ## WIDTH BUCKET and Histogram Example
#
# The WIDTH_BUCKET function is used to create equal-width histograms. Using the EMPLOYEE table,
# This SQL will assign a bucket to each employee's salary using a range of 35000 to 100000 divided into 13 buckets.
# + hideCode=false hidePrompt=false language="sql"
# SELECT EMPNO, SALARY, WIDTH_BUCKET(SALARY, 35000, 100000, 13)
# FROM EMPLOYEE
# ORDER BY EMPNO
# + [markdown] hideCode=false hidePrompt=false
# We can plot this information by adding some more details to the bucket output.
# + hideCode=false hidePrompt=false magic_args="-a" language="sql"
# WITH BUCKETS(EMPNO, SALARY, BNO) AS
# (
# SELECT EMPNO, SALARY,
# WIDTH_BUCKET(SALARY, 35000, 100000, 9) AS BUCKET
# FROM EMPLOYEE ORDER BY EMPNO
# )
# SELECT BNO, COUNT(*) AS COUNT FROM BUCKETS
# GROUP BY BNO
# ORDER BY BNO ASC
# + [markdown] hideCode=false hidePrompt=false
# And here is a plot of the data to make sense of the histogram.
# + hideCode=false hidePrompt=false magic_args="-pb" language="sql"
# WITH BUCKETS(EMPNO, SALARY, BNO) AS
# (
# SELECT EMPNO, SALARY,
# WIDTH_BUCKET(SALARY, 35000, 100000, 9) AS BUCKET
# FROM EMPLOYEE ORDER BY EMPNO
# )
# SELECT BNO, COUNT(*) AS COUNT FROM BUCKETS
# GROUP BY BNO
# ORDER BY BNO ASC
# -
# [Back to Top](#top)
# #### Credits: IBM 2018, <NAME> [<EMAIL>]
|
Db2 Statistical Functions.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Import necessary dependencies and settings
# +
import pandas as pd
import numpy as np
import re
import nltk
import matplotlib.pyplot as plt
pd.options.display.max_colwidth = 200
# %matplotlib inline
# -
# # Sample corpus of text documents
# +
corpus = ['The sky is blue and beautiful.',
'Love this blue and beautiful sky!',
'The quick brown fox jumps over the lazy dog.',
"A king's breakfast has sausages, ham, bacon, eggs, toast and beans",
'I love green eggs, ham, sausages and bacon!',
'The brown fox is quick and the blue dog is lazy!',
'The sky is very blue and the sky is very beautiful today',
'The dog is lazy but the brown fox is quick!'
]
labels = ['weather', 'weather', 'animals', 'food', 'food', 'animals', 'weather', 'animals']
corpus = np.array(corpus)
corpus_df = pd.DataFrame({'Document': corpus,
'Category': labels})
corpus_df = corpus_df[['Document', 'Category']]
corpus_df
# -
# # Simple text pre-processing
# +
wpt = nltk.WordPunctTokenizer()
stop_words = nltk.corpus.stopwords.words('english')
def normalize_document(doc):
# lower case and remove special characters\whitespaces
doc = re.sub(r'[^a-zA-Z\s]', '', doc, re.I|re.A)
doc = doc.lower()
doc = doc.strip()
# tokenize document
tokens = wpt.tokenize(doc)
# filter stopwords out of document
filtered_tokens = [token for token in tokens if token not in stop_words]
# re-create document from filtered tokens
doc = ' '.join(filtered_tokens)
return doc
normalize_corpus = np.vectorize(normalize_document)
# -
norm_corpus = normalize_corpus(corpus)
norm_corpus
# # Bag of Words Model
# +
from sklearn.feature_extraction.text import CountVectorizer
cv = CountVectorizer(min_df=0., max_df=1.)
cv_matrix = cv.fit_transform(norm_corpus)
cv_matrix = cv_matrix.toarray()
cv_matrix
# -
# get all unique words in the corpus
vocab = cv.get_feature_names()
# show document feature vectors
pd.DataFrame(cv_matrix, columns=vocab)
# # Bag of N-Grams Model
# +
# you can set the n-gram range to 1,2 to get unigrams as well as bigrams
bv = CountVectorizer(ngram_range=(2,2))
bv_matrix = bv.fit_transform(norm_corpus)
bv_matrix = bv_matrix.toarray()
vocab = bv.get_feature_names()
pd.DataFrame(bv_matrix, columns=vocab)
# -
# # TF-IDF Model
# +
from sklearn.feature_extraction.text import TfidfVectorizer
tv = TfidfVectorizer(min_df=0., max_df=1., use_idf=True)
tv_matrix = tv.fit_transform(norm_corpus)
tv_matrix = tv_matrix.toarray()
vocab = tv.get_feature_names()
pd.DataFrame(np.round(tv_matrix, 2), columns=vocab)
# -
# # Document Similarity
# +
from sklearn.metrics.pairwise import cosine_similarity
similarity_matrix = cosine_similarity(tv_matrix)
similarity_df = pd.DataFrame(similarity_matrix)
similarity_df
# -
# ## Clustering documents using similarity features
# +
from scipy.cluster.hierarchy import dendrogram, linkage
Z = linkage(similarity_matrix, 'ward')
pd.DataFrame(Z, columns=['Document\Cluster 1', 'Document\Cluster 2',
'Distance', 'Cluster Size'], dtype='object')
# -
plt.figure(figsize=(8, 3))
plt.title('Hierarchical Clustering Dendrogram')
plt.xlabel('Data point')
plt.ylabel('Distance')
dendrogram(Z)
plt.axhline(y=1.0, c='k', ls='--', lw=0.5)
# +
from scipy.cluster.hierarchy import fcluster
max_dist = 1.0
cluster_labels = fcluster(Z, max_dist, criterion='distance')
cluster_labels = pd.DataFrame(cluster_labels, columns=['ClusterLabel'])
pd.concat([corpus_df, cluster_labels], axis=1)
# -
# # Topic Models
# +
from sklearn.decomposition import LatentDirichletAllocation
lda = LatentDirichletAllocation(n_topics=3, max_iter=10000, random_state=0)
dt_matrix = lda.fit_transform(cv_matrix)
features = pd.DataFrame(dt_matrix, columns=['T1', 'T2', 'T3'])
features
# -
# ## Show topics and their weights
tt_matrix = lda.components_
for topic_weights in tt_matrix:
topic = [(token, weight) for token, weight in zip(vocab, topic_weights)]
topic = sorted(topic, key=lambda x: -x[1])
topic = [item for item in topic if item[1] > 0.6]
print(topic)
print()
# ## Clustering documents using topic model features
# +
from sklearn.cluster import KMeans
km = KMeans(n_clusters=3, random_state=0)
km.fit_transform(features)
cluster_labels = km.labels_
cluster_labels = pd.DataFrame(cluster_labels, columns=['ClusterLabel'])
pd.concat([corpus_df, cluster_labels], axis=1)
|
bonus content/feature engineering text data/Feature Engineering Text Data - Traditional Strategies.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:cme193]
# language: python
# name: conda-env-cme193-py
# ---
# # Lecture 4: Optimization Using Python - SciPy
# In this lecture / tutorial, we will learn how to solve some simple optimization problems using Python. This involves a brief introduction to the various optimization libraries available, such as ```scipy.optimize```, ```ortools```, and ```cplex```. We will solve an example optimization problem using each library.
#
# ***
#
# ## Learning goals
# - Obtain an overview of optimization problems that can be easily solved using Python.
# - Know about some of the popular optimization libraries which have easy to use Python interfaces.
# - Learn the syntax to solve some simple optimization problems using at least a couple of the libraries discussed in this tutorial.
# - Test your understanding by solving a few of the practice problems in each section.
# ***
# # Prerequisites for running this notebook
#
# You should have Python 3.6 installed on your computer, with all necessary packages installed.
#
# We recommend that you install Anaconda (Python 3.6 version) from the following links depending on your OS:
# - For Windows: https://www.anaconda.com/download/#windows
# - For macOS: https://www.anaconda.com/download/#macos
# - For Linux: https://www.anaconda.com/download/#linux
#
# **If you are not using Anaconda, it is your responsibility to make sure that Python and all necessary packages are correctly installed and configured to be able to run this notebook.**
#
# ***
#
# Once Anaconda is installed, open a **Terminal** (if you are using macOS / Linux), or **Anaconda Prompt** (if you are using Windows), and then create a new Python environment called **cme193**, by running the following command:<br>
# > ```conda create -n cme193 python=3.6```
#
# Next, change to the newly created virtual environment by running the command:
#
# On Windows
# > ```activate cme193``` <br>
#
# On macOS or Linux
# > ```source activate cme193```
#
# Next install all the necessary packages by running the following commands:
#
# > ```conda install nb_conda``` <br>
# > ```conda install -c anaconda scipy``` <br>
# > ```conda install -c conda-forge matplotlib``` <br>
#
# Now navigate to the directory containing this .ipynb file, from inside the terminal, and start jupyter notebook by typing the following command:
# > ```jupyter notebook```
#
# You should now be able to launch the .ipynb file from the browser. For more information on jupyter notebooks, read the <a href="https://jupyter-notebook.readthedocs.io/en/stable/notebook.html" style="text-decoration: none;">user documentation</a>.
# ***
# # Introduction to scipy.optimize
#
# In this section we will learn how to solve some simple optimization problems using ```scipy```. The ```scipy.optimize``` package already gives us a lot of basic tools to solve a wide variety of important optimization problems. For more information please read the <a href="https://docs.scipy.org/doc/scipy/reference/tutorial/optimize.html" style="text-decoration: none;">documentation</a>.
#
# We can import the module as follows (henceforth to be referred to as ```sciopt```). We also import some other modules we will use in this notebook.
import scipy.optimize as sciopt
import numpy as np
import matplotlib.pyplot as plt
# ***
# ## Solving a linear program
#
# The first example we will look at is that of solving a **linear program (LP)**. A linear program is any optimization problem of the following form:
#
# $$
# \begin{equation}
# \begin{split}
# \text{minimize} \;\; & c^{T}x \\
# \text{subject to} \;\; & A_{ub}x \leq b_{ub} \\
# & A_{eq}x = b_{eq}
# \end{split}
# \end{equation}
# $$
#
# where $c, x \in \mathbb{R}^n$, $A_{ub} \in \mathbb{R}^{m \times n}$, $A_{eq} \in \mathbb{R}^{p \times n}$, $b_{ub} \in \mathbb{R}^{m}$, and $b_{eq} \in \mathbb{R}^{p}$. It should be noted that all LP can be put in this form.
#
# ```scipy.optimize``` provides a simple function ```scipy.optimize.linprog``` to solve such problems, which is documented <a href="https://docs.scipy.org/doc/scipy-0.15.1/reference/generated/scipy.optimize.linprog.html#scipy.optimize.linprog" style="text-decoration: none;">here</a>. Currently, the only available algorithm that is implemented are the **simplex method**, and the **interior point method**. We will demonstrate its usage using a few examples.
# ***
# ### Example 1
# Let us consider the problem
#
# $$
# \begin{equation}
# \begin{split}
# \text{minimize} \;\; & x_1 + 2 x_2 \\
# \text{subject to} \;\; & x_1 \leq 1 \\
# & 5 x_1 + x_2 \geq 0
# \end{split}
# \end{equation}
# $$
#
# In order to solve it, we first need to transform it to the form that ```scipy.optimize.linprog``` requires. The problem is clearly equivalent to
#
# $$
# \begin{equation}
# \begin{split}
# \text{minimize} \;\; & x_1 + 2 x_2 \\
# \text{subject to} \;\; & x_1 \leq 1 \\
# & -5 x_1 - x_2 \leq 0
# \end{split}
# \end{equation}
# $$
#
# The following Python code then solves this problem.
# +
# Define problem parameters
c = [1, 2]
A_ub = [[1, 0], [-5, -1]]
b_ub = [1, 0]
bounds = ((None, None), (None, None))
# Solve the LP
result = sciopt.linprog(c=c, A_ub=A_ub, b_ub=b_ub, bounds=bounds)
# -
# Print the result
print(result)
# ***
# Notice that we must explicitly set the ```bounds``` parameter in the above problem. If we don't pass this parameter, the default assumption is that the variables are non-negative.
#
# You can additionally pass the parameter ```options={"disp": True}``` to print convergence messages from the solver. **Solver method specific parameters can also be passed as optional parameters in** ```options```.
# Solve the LP and print convergence messages
result = sciopt.linprog(c=c, A_ub=A_ub, b_ub=b_ub, bounds=bounds, options={"disp": True})
# Extract the solution and print it
obj_optimal = result['fun']
x = result['x']
print("Optimal solution: x1 = ", x[0], ", x2 = ", x[1])
print("Optimal value = ", obj_optimal)
# ***
# ### Example 2
# Let us change the problem by adding an equality constraint
#
# $$
# \begin{equation}
# \begin{split}
# \text{minimize} \;\; & x_1 + 2 x_2 \\
# \text{subject to} \;\; & x_1 \leq 1 \\
# & 5 x_1 + x_2 \geq 0 \\
# & x_1 + x_2 = 3.
# \end{split}
# \end{equation}
# $$
#
# In order to solve it, we first need to transform it to the form that ```scipy.optimize.linprog``` requires. The problem is clearly equivalent to
#
# $$
# \begin{equation}
# \begin{split}
# \text{minimize} \;\; & x_1 + 2 x_2 \\
# \text{subject to} \;\; & x_1 \leq 1 \\
# & -5 x_1 - x_2 \leq 0 \\
# & x_1 + x_2 = 3.
# \end{split}
# \end{equation}
# $$
#
# The following Python code then solves this problem.
# +
# Define problem parameters
c = [1, 2]
A_ub = [[1, 0], [-5, -1]]
b_ub = [1, 0]
A_eq = [[1, 1]]
b_eq = [3]
bounds = ((None, None), (None, None))
# Solve the LP
print("Solving the LP")
result = sciopt.linprog(c=c, A_ub=A_ub, b_ub=b_ub, A_eq=A_eq, b_eq=b_eq, bounds=bounds, options={"disp": True})
# Extract the solution and print it
obj_optimal = result['fun']
x = result['x']
print("\n")
print("Optimal solution: x1 = ", x[0], ", x2 = ", x[1])
print("Optimal value = ", obj_optimal)
# -
# #### Alternate way of solving the problem
# Notice that the inequality constraint ```x1 <= 1``` is a **bound constraint**. Hence, an alternate way to solve **Example 2** is as follows:
# +
# Define problem parameters
c = [1, 2]
A_ub = [[-5, -1]]
b_ub = [0]
A_eq = [[1, 1]]
b_eq = [3]
bounds = ((None, 1), (None, None))
# Solve the LP
print("Solving the LP")
result = sciopt.linprog(c=c, A_ub=A_ub, b_ub=b_ub, A_eq=A_eq, b_eq=b_eq, bounds=bounds, options={"disp": True})
# Extract the solution and print it
obj_optimal = result['fun']
x = result['x']
print("\n")
print("Optimal solution: x1 = ", x[0], ", x2 = ", x[1])
print("Optimal value = ", obj_optimal)
# -
# ***
# ### Example 3
# Some special problems can be reduced to a LP. Consider the following optimization problem
#
# $$
# \begin{equation}
# \begin{split}
# \text{minimize} \;\; & x_1 + 2 x_2 - 3 x_3 \\
# \text{subject to} \;\; & |x_1| \leq 1 \\
# & |x_2| \leq 2 \\
# & |x_3| \leq 1 \\
# & x_1 + x_2 + x_3 = 1.
# \end{split}
# \end{equation}
# $$
#
# But this is just equivalent to
#
# $$
# \begin{equation}
# \begin{split}
# \text{minimize} \;\; & x_1 + 2 x_2 - 3 x_3 \\
# \text{subject to} \;\; & -1 \leq x_1 \leq 1 \\
# & -2 \leq x_2 \leq 2 \\
# & -1 \leq x_3 \leq 1 \\
# & x_1 + x_2 + x_3 = 1.
# \end{split}
# \end{equation}
# $$
#
# The following Python code then solves this problem.
# +
# Define problem parameters
c = [1, 2, -3]
A_eq = [[1, 1, 1]]
b_eq = [1]
bounds = ((-1, 1), (-2, 2), (-1, 1))
# Solve the LP
print("Solving the LP")
result = sciopt.linprog(c=c, A_eq=A_eq, b_eq=b_eq, bounds=bounds, method="interior-point", options={"disp": True})
# Extract the solution and print it
obj_optimal = result['fun']
x = result['x']
print("\n")
print("Optimal solution: x1 = ", x[0], ", x2 = ", x[1], ", x3 = ", x[2])
print("Optimal value = ", obj_optimal)
# -
# ***
# ### Example 4
# Here is another interesting example. Consider the following optimization problem
#
# $$
# \begin{equation}
# \begin{split}
# \text{minimize} \;\; & \max \{|x_1|, |x_2|, |x_3|\} \\
# \text{subject to} \;\; & x_1 + x_2 + x_3 \geq 1.
# \end{split}
# \end{equation}
# $$
#
# It is easy to show that this problem is equivalent to the problem (this is called the **epigraph form** of the problem)
#
# $$
# \begin{equation}
# \begin{split}
# \text{minimize} \;\; & s \\
# \text{subject to} \;\; & |x_1| \leq s \\
# & |x_2| \leq s \\
# & |x_3| \leq s \\
# & s \geq 0 \\
# & x_1 + x_2 + x_3 \geq 1
# \end{split}
# \end{equation}
# $$
#
# where the minimization is now over the variables $x_1, x_2, x_3,$ and $s$.
#
# As before we need to change this problem into a form that is suitable for ```scipy.optimize.linprog```. The problem can be written equivalently as
#
# $$
# \begin{equation}
# \begin{split}
# \text{minimize} \;\; & s \\
# \text{subject to} \;\; & x_1 - s \leq 0 \\
# & x_2 - s \leq 0 \\
# & x_3 - s \leq 0 \\
# & - x_1 - s \leq 0 \\
# & - x_2 - s \leq 0 \\
# & - x_3 - s \leq 0 \\
# & - x_1 - x_2 - x_3 \leq -1 \\
# & s \geq 0 .
# \end{split}
# \end{equation}
# $$
#
# The following Python code then solves this problem.
# +
# Define problem parameters
c = [0, 0, 0, 1]
A_ub = [[1, 0, 0, -1], [0, 1, 0, -1], [0, 0, 1, -1], [-1, 0, 0, -1], [0, -1, 0, -1], [0, 0, -1, -1], [-1, -1, -1, 0]]
b_ub = [0, 0, 0, 0, 0, 0, -1]
bounds = ((None, None), (None, None),(None, None), (0, None))
# Solve the LP
print("Solving the LP")
result = sciopt.linprog(c=c, A_ub=A_ub, b_ub=b_ub, bounds=bounds, method="interior-point", options={"disp": True})
# Extract the solution and print it
obj_optimal = result['fun']
x = result['x']
print("\n")
print("Optimal solution: x1 = ", x[0], ", x2 = ", x[1], ", x3 = ", x[2], ", s = ", x[3])
print("Optimal value = ", obj_optimal)
# -
# ***
# ### Exercise 1
# Compare the efficiency of the **simplex method** and the **interior point method** at solving linear programs, by generating some random LPs, and then solving them using both options. Plot the timing results as a function of problem size.
# +
# Write your solution here
# -
# ***
# ## Minimum weight matching in bipartite graphs
#
# Given an (undirected) **complete bipartite graph** $G = (V_1, V_2, E)$, with an edge cost function $C : E \rightarrow \mathbb{R}$, the goal is to find a minimum weight **matching** $M \subset E$ that covers the smaller of the two sets $V_1$ or $V_2$. Thus $V_1$ and $V_2$ need not be of the same sizes. $G$ being complete bipartite graph means that there is an edge $e \in E$ between every pair of vertices $v_1 \in V_1$, and $v_2 \in V_2$. A matching refers to a selection of edges such that no vertex is covered more than once. This problem is also known as the **linear sum assignment** problem.
#
# Let $|V_1| = N_1$, and $|V_2| = N_2$, and without loss of generality assume that $N_1 \leq N_2$. If we index the vertices in $V_1$ by $i$, and those in $V_2$ by $j$, then $e_{ij}$ will refer to the edge between $i$ and $j$, and similarly $C_{ij}$ will refer to the cost of the edge $e_{ij}$. Let $X_{ij}$ be a boolean $\{0,1\}$ variable that indicates whether edge $e_{ij}$ is selected or not. Then our goals can be represented by the following optimization problem:
#
# $$
# \begin{equation}
# \begin{split}
# \text{minimize} \;\; & \sum_{i=1}^{N_1} \sum_{j=1}^{N_2} C_{ij} X_{ij} \\
# \text{subject to} \;\; & X_{ij} \in \{0, 1\}, \;\; \forall \;\; i, j \\
# & \sum_{j=1}^{N_2} X_{ij} = 1, \;\; \forall \;\; i \\
# & \sum_{i=1}^{N_1} X_{ij} \leq 1, \;\; \forall \;\; j.
# \end{split}
# \end{equation}
# $$
#
# ```scipy.optimize``` provides an inbuilt function ```scipy.optimize.linear_sum_assignment``` that solves exactly this problem, which is documented <a href="https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.linear_sum_assignment.html#scipy.optimize.linear_sum_assignment" style="text-decoration: none;">here</a>. The algorithm used to solve this problem is the famous **Hungarian algorithm**, also known as the **Kuhn-Munkres algorithm**, although it was discovered in 2006 that <a href="https://en.wikipedia.org/wiki/Carl_Gustav_Jacob_Jacobi" style="text-decoration: none;"><NAME></a> had solved the problem in 1840s (published only posthumously in 1890).
# ***
# Let us see an example.
#
# ### Example 1
# Consider the following $C$ matrix
#
# $$
# C =
# \begin{bmatrix}
# 2 & 1 & -1 & 1 \\
# 4 & 5 & -2 & -3 \\
# 1 & 2 & -1 & 5 \\
# -2 & 3 & 4 & 0
# \end{bmatrix}
# \;\;.
# $$
#
# This problem is easily solved using the following Python code.
# +
# Define problem parameters
cost_matrix = [[2, 1, -1, 1], [4, 5, -2, -3], [1, 2, -1, 5], [-2, 3, 4, 0]]
# Solve the linear sum assignment problem
print("Solving the linear sum assignment problem")
row_ind, col_ind = sciopt.linear_sum_assignment(cost_matrix=cost_matrix)
# Print the solution
print("\n")
print("Row index : ", row_ind)
print("Col index : ", col_ind)
# Print selected edges and the costs
print("\n")
print("The selected edges in the optimal assignment and their costs are:")
cost_opt = 0
for ind, row in enumerate(row_ind):
col = col_ind[ind]
cost_opt += cost_matrix[row][col]
print("Edge (" + str(row) + "," + str(col) + ") , Cost = " + str(cost_matrix[row][col]))
# Print optimal cost
print("\n")
print("The optimal cost is : ", cost_opt)
# -
# ***
# ### Example 2
#
# Consider the following $C$ matrix
#
# $$
# C =
# \begin{bmatrix}
# 2 & 1 & -1 & 1 \\
# 4 & 5 & -2 & -3 \\
# 1 & 2 & -1 & 5
# \end{bmatrix}
# \;\;.
# $$
#
# This problem is easily solved using the following Python code.
# +
# Define problem parameters
cost_matrix = [[2, 1, -1, 1], [4, 5, -2, -3], [1, 2, -1, 5]]
# Solve the linear sum assignment problem
print("Solving the linear sum assignment problem")
row_ind, col_ind = sciopt.linear_sum_assignment(cost_matrix=cost_matrix)
# Print the solution
print("\n")
print("Row index : ", row_ind)
print("Col index : ", col_ind)
# Print selected edges and the costs
print("\n")
print("The selected edges in the optimal assignment and their costs are:")
cost_opt = 0
for ind, row in enumerate(row_ind):
col = col_ind[ind]
cost_opt += cost_matrix[row][col]
print("Edge (" + str(row) + "," + str(col) + ") , Cost = " + str(cost_matrix[row][col]))
# Print optimal cost
print("\n")
print("The optimal cost is : ", cost_opt)
# -
# ***
# ## Root finding problems - univariate rootfinding
#
# ```scipy.optimize``` provides a bunch of functions for finding the roots of a **continuous** univariate function $f$. $x$ is a root of $f$ if and only if $f(x) = 0$. We illustrate some of the important ones with an example.
#
# Consider the function $f(x) = x^4 - x^2$. The function has 3 roots ${-1,0,1}$. The function is graphed below.
# +
# %matplotlib inline
def func(x):
return x**4 - x**2
step = 0.01
max_x = 1.2
x = np.arange(-max_x, max_x + step, step)
y = func(x)
plt.plot(x, y, "-r")
plt.grid()
plt.xlabel("x", fontsize=16)
plt.ylabel("$x^4 - x^2$", fontsize=16)
# -
# The important functions in ```scipy.optimize``` for finding the roots of $f$ can be divided into two categories:
# - **Root finding on an interval**: Requires that an interval $[a,b]$ be specified such that $f(a)f(b) < 0$, i.e. the function has different signs at the end points of the interval. The methods that can be used in this setting are ```scipy.optimize.brentq```, ```scipy.optimize.brenth```, ```scipy.optimize.bisect```, ```scipy.optimize.ridder```.
# - **Root finding near a point**: Requires a starting point $x_0$. The method that can be used in this setting is ```scipy.optimize.newton```.
#
# More information on these methods can be obtained by clicking on each of these functions, starting from the <a href="https://docs.scipy.org/doc/scipy/reference/optimize.html#module-scipy.optimize" style="text-decoration: none;">documentation page</a> for ```scipy.optimize```.
# ***
# ### Root finding in an interval
# Let us first try to search for a root in the interval $[-1.5, 0.5]$ using the different methods, and print some performance metrics related to convergence.
# +
# Set a, b
a = -1.5
b = 0.5
# Solve using different methods
root1, result1 = sciopt.brentq(f=func, a=a, b=b, full_output=True, disp=True)
root2, result2 = sciopt.brenth(f=func, a=a, b=b, full_output=True, disp=True)
root3, result3 = sciopt.ridder(f=func, a=a, b=b, full_output=True, disp=True)
root4, result4 = sciopt.bisect(f=func, a=a, b=b, full_output=True, disp=True)
# Print messages
print("\n\nbrentq method results\n")
print("Root detected at x = ", root1)
print("Performance parameters:")
print(result1)
print("\n\nbrenth method results\n")
print("Root detected at x = ", root2)
print("Performance parameters:")
print(result2)
print("\n\nridder method results\n")
print("Root detected at x = ", root3)
print("Performance parameters:")
print(result3)
print("\n\nbisect method results\n")
print("Root detected at x = ", root4)
print("Performance parameters:")
print(result4)
# -
# ***
# ### Exercise 2
# Try different values of $[a,b]$ and check the performance comparison as above.
# +
# Write your code here
# -
# ***
# ### Root finding near a point
# Next let us try to search for a root of the same function $f(x) = x^4 - x^2$ near a point, using the Newton algorithm. The Newton algorithm ```scipy.optimize.newton``` can take in optional parameters which are the first and second derivatives of the function. When derivatives are not provided the **secant method** is used. When the first derivative is provided, the algorithm used is called **Newton-Raphson**. When both first and second derivatives are provided, the algorithm used is called **Halley's algorithm**.
#
# **Note: It is very important to check the result $x$ from this algorithm, i.e, if $f(x) = 0$, as convergence is only guaranteed when one starts near a zero**.
#
# We first code up the function first and second derivatives.
# +
def func_prime(x):
return 4 * (x ** 3) - 2 * x
def func_prime2(x):
return 12 * (x ** 2) - 2
# -
# Let us see the effect of running these different algorithms for finding a root of our function, starting from the point $x_0 = 0.5$.
# +
# Define starting point
x0 = 0.5
# Solve using secant method
root_secant = sciopt.newton(func=func, x0=x0)
# Solve using Newton-Rapheson method
root_newton = sciopt.newton(func=func, x0=x0, fprime=func_prime)
# Solve using Halley's method
root_halley = sciopt.newton(func=func, x0=x0, fprime=func_prime, fprime2=func_prime2)
# Print results
print("\nPrinting the roots :")
print("Secant method : ", root_secant)
print("Newton-Rapheson method : ", root_newton)
print("Halley's method : ", root_halley)
# -
# ***
# ### Exercise 3
# Try different values of $x_0$ and check what happens with each root finding method. Do you see something strange for $x_0 = 0.7$? If yes, can you explain it?
# +
# Write your code here
# -
# ***
# ## Root finding problems - multivariate rootfinding
#
# We now turn to the much harder problem of finding zeros of functions of the form $f : \mathbb{R}^m \rightarrow \mathbb{R}^n$. ```scipy.optimize``` provides a single function ```scipy.optimize.root```, through which all the other functions listed in the <a href="https://docs.scipy.org/doc/scipy/reference/optimize.html#module-scipy.optimize" style="text-decoration: none;">documentation page</a> for multivariate root finding are accessible. All the algorithms require an initial guess (or starting point) $x_0$. The syntax for the function ```scipy.optimize.root``` can be found <a href="https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.root.html#scipy.optimize.root" style="text-decoration: none;">here</a>.
#
# The important parameters that this function accepts, and about which you should be aware of are:
# - ```fun```: A function that implements $f$. The function can optionally return the Jacobian as well.
# - ```x0```: Initial guess.
# - ```method```: The type of solver to use. Options include ```hybr```, ```krylov```, ```broyden1``` etc.
# - ```jac```: Either a ```bool```, or a callable function that returns the Jacobian. In this case, it must accept the same arguments as fun.
# - ```options```: A dictionary with optional arguments for the solver ```method```.
#
# **Note:** If ```jac``` is a Boolean and is True, ```fun``` is assumed to return the value of Jacobian along with the objective function. If False, the Jacobian will be estimated numerically. Also one should be aware that many methods do not need the Jacobian implemented; they approximate the Jacobian internally.
#
# We will learn to use some of the features of ```scipy.optimize.root``` using an example.
# ***
# ### Example 1
# Consider the function $f : \mathbb{R}^2 \rightarrow \mathbb{R}^2$ defined as
#
# $$
# f(x,y) = ((x - x_t)^2 - (y - y_t)^2, 2(x - x_t)(y - y_t)),
# $$
#
# for some $(x_t, y_t) \in \mathbb{R}^2$.
#
# Alternatively you can also think of this function as $f : \mathbb{C} \rightarrow \mathbb{C}$, defined as $f(z) = (z - z_t)^2$, where $z = x + i y$, and $z_t = x_t + i y_t$. Clearly this function has only one root $z = z_t$, i.e. $(x, y) = (x_t, y_t)$.
#
# Let us code up the function and its Jacobian. The Jacobian is given by
#
# $$
# J(x,y) =
# \begin{bmatrix}
# 2(x - x_t) & 2(y - y_t) \\
# -2(y - y_t) & 2(x - x_t)
# \end{bmatrix}
# .
# $$
#
# Set $x_t = 1, y_t = 1$.
# +
# Define xt, yt
xt = 1
yt = 1
# Define the function
def fun(x):
return [(x[0] - xt) ** 2 - (x[1] - yt) ** 2, 2 * (x[0] - xt) * (x[1] - yt)]
# Define the Jacobian
def jac(x):
return [[2 * (x[0] - xt), 2 * (x[1] - yt)], [-2 * (x[1] - yt), 2 * (x[0] - xt)]]
# Define the function that also returns the Jacobian
def fun1(x):
return (
[(x[0] - xt) ** 2 - (x[1] - yt) ** 2, 2 * (x[0] - xt) * (x[1] - yt)],
[[2 * (x[0] - xt), 2 * (x[1] - yt)], [-2 * (x[1] - yt), 2 * (x[0] - xt)]]
)
# -
# Define a starting guess of the root $(x_0, y_0) = (0.5, 0.5)$, and lets demonstrate how the Jacobian can be passed.
# +
# Define starting guess
x0 = [0.5, 0.5]
# Demonstrate usage using different ways to supply function and Jacobian
print("Method 1", "\n")
sol = sciopt.root(fun=fun1, x0=x0, jac=True, method='hybr')
print(sol, "\n")
print("Solution : x = ", sol.x[0], ", y = ", sol.x[1], "\n\n\n")
print("Method 2", "\n")
sol = sciopt.root(fun=fun, x0=x0, jac=False, method='hybr')
print(sol, "\n")
print("Solution : x = ", sol.x[0], ", y = ", sol.x[1], "\n\n\n")
print("Method 3", "\n")
sol = sciopt.root(fun=fun, x0=x0, jac=jac, method='hybr')
print(sol, "\n")
print("Solution : x = ", sol.x[0], ", y = ", sol.x[1], "\n\n\n")
# -
# ***
# ### Exercise 4
# 1. Try different values of the starting guess $(x_0, y_0)$, and see the impact on performance, as measured by the number of function and Jacobian evaluations.
# 2. Repeat the experiment with different values of $(x_t, y_t)$. What happens as you approach $x_t = 0, y_t = 0$?
# +
# Write your code here
# -
# ***
# ### Example 2
# Consider the following system of nonlinear equations
#
# $$
# \begin{split}
# x + \frac{(x - y)^3}{2} - 1 &= 0 \\
# \frac{(y - x)^3}{2} + y &= 0 \;.
# \end{split}
# $$
#
# We can try to solve this system by trying to find the roots of the function $f : \mathbb{R}^2 \rightarrow \mathbb{R}^2$ defined as
#
# $$
# f(x,y) = \left( x + \frac{(x - y)^3}{2} - 1, \frac{(y - x)^3}{2} + y \right).
# $$
#
# We code up the function, its Jacobian, and solve the problem using a few different methods.
# +
# Define the function
def fun_nonlinear_eq(x):
return [x[0] + 0.5 * ((x[0] - x[1]) ** 3) - 1, 0.5 * ((x[1] - x[0]) ** 3) + x[1]]
# Define the Jacobian
def jac_nonlinear_eq(x):
return [
[1 + 1.5 * ((x[0] - x[1]) ** 2), -1.5 * ((x[1] - x[0]) ** 2)],
[-1.5 * ((x[0] - x[1]) ** 2), 1 + 1.5 * ((x[1] - x[0]) ** 2)]
]
# Define starting guess
x0 = [1, 1]
# Solve using method 'hybr'
name = 'hybr'
print("Method " + name, "\n")
sol = sciopt.root(fun=fun_nonlinear_eq, x0=x0, jac=jac_nonlinear_eq, method=name)
print(sol, "\n")
print("Solution : x = ", sol.x[0], ", y = ", sol.x[1], "\n\n\n")
# Solve using method 'lm'
name = 'lm'
print("Method " + name, "\n")
sol = sciopt.root(fun=fun_nonlinear_eq, x0=x0, jac=jac_nonlinear_eq, method=name)
print(sol, "\n")
print("Solution : x = ", sol.x[0], ", y = ", sol.x[1], "\n\n\n")
# Methods below do not use Jacobian -- should throw an warning if Jacobian is passed
# Solve using method 'broyden1'
name = 'broyden1'
print("Method " + name, "\n")
sol = sciopt.root(fun=fun_nonlinear_eq, x0=x0, jac=jac_nonlinear_eq, method=name)
print(sol, "\n")
print("Solution : x = ", sol.x[0], ", y = ", sol.x[1], "\n\n\n")
# Solve using method 'anderson'
name = 'anderson'
print("Method " + name, "\n")
sol = sciopt.root(fun=fun_nonlinear_eq, x0=x0, method=name)
print(sol, "\n")
print("Solution : x = ", sol.x[0], ", y = ", sol.x[1], "\n\n\n")
# Solve using method 'krylov'
name = 'krylov'
print("Method " + name, "\n")
sol = sciopt.root(fun=fun_nonlinear_eq, x0=x0, method=name)
print(sol, "\n")
print("Solution : x = ", sol.x[0], ", y = ", sol.x[1], "\n\n\n")
# -
# ***
# ### Exercise 5
# 1. Increase the maximum number of iterations for the 'krylov' method and see if there is an impact on the solution.
# 2. Try different starting guesses for $(x_0, y_0)$, for e.g. try $(0.8, 0.2)$ for the 'krylov' method. Does it help?
# +
# Write your code here
# -
# ***
# ## Fixed point iterations
#
# ```scipy.optimize``` provides a special function ```scipy.optimize.fixed_point``` for finding fixed points of functions of the form $f : \mathbb{R}^m \rightarrow \mathbb{R}^m$. $x \in \mathbb{R}^m$ is a fixed point of $f$ if and only if $f(x) = x$. The syntax for the function ```scipy.optimize.fixed_point``` can be found <a href="https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.fixed_point.html#scipy.optimize.fixed_point" style="text-decoration: none;">here</a>.
#
# There are two main algorithms which are supported by this function: ```iteration``` and ```del2```. The default method is ```del2``` which uses Steffensen’s Method with Aitken’s convergence acceleration. The ```iteration``` method simply iterates the function until convergence is detected, without attempting to accelerate the convergence.
#
# We demonstrate the usage of this method with a few examples.
# ***
# ### Example 1
# Let us consider the problem of finding a solution to the equation $\sin (\alpha x) = \beta x$, for $\alpha, \beta \in \mathbb{R}$. The roots of this equation can be expressed as fixed points of the function $f(x) = \frac{\sin (\alpha x)}{\beta}$.
#
# Let us plot the functions $\sin(\alpha x)$ and $\beta x$ below. You can change $\alpha$ and $\beta$ and see the changes in the plots.
# +
# %matplotlib inline
alpha = 1
beta = 0.5
step = 0.01
max_x = 5
x = np.arange(-max_x, max_x + step, step)
y1 = np.sin(alpha * x)
y2 = beta * x
plt.plot(x, y1, "-r", label="$\sin$(" + str(alpha) + "x)")
plt.plot(x, y2, "-b", label=str(beta) + "x")
plt.grid()
plt.xlabel("x", fontsize=16)
plt.legend(fontsize=16)
# -
# The following code solves the problem for $\alpha = 1, \beta = 1$, with a starting guess $x_0 = 0.5$.
# +
# Define the function
def func_sinx(x, alpha, beta):
return np.sin(alpha * x) / beta
# Define alpha, beta
alpha = 1
beta = 1
# Define initial guess
x0 = 0.5
# Solve
fp = sciopt.fixed_point(func=func_sinx, x0=x0, args=(alpha, beta), method="del2")
# Print result
print("Fixed point detected : x = ", fp)
# -
# ***
# ### Exercise 6
# Experiment with different values of $\alpha, \beta, x_0$ in the above example.
# +
# Write your code here
# -
# ***
# ### Example 2
# Consider the function $f : \mathbb{R}^2 \rightarrow \mathbb{R}^2$, defined as
#
# $$
# f(x_1, x_2) = \left( \frac{a_1}{x_1 + b_1}, \frac{a_2}{x_2 + b_2} \right),
# $$
#
# for some $a_1, b_1, a_2, b_2 \in \mathbb{R}$.
#
# The following Python code finds a fixed point of $f$ for $a_1 = 10, b_1 = 3, a_2 = 12, b_2 = 5$, and starting guess $(0,0)$. You can vary these parameters and see the changes in the solution.
# +
# Define the function
def func_fixed_point(x, a, b):
return np.sqrt(a / (x + b))
# Define the parameters
a = [10, 12]
b = [3, 5]
# Define starting guess
x0 = [0, 0]
# Solve the problem
fp = sciopt.fixed_point(func=func_fixed_point, x0=x0, args=(a, b), method="del2")
# Print result
print("Fixed point detected : x1 = ", fp[0], ", x2 = ", fp[1])
# -
# ***
# ### Exercise 7
# 1. Formulate the above example as a multivariate root finding problem and solve it.
# 2. Formulate the above example as a scalar root finding problem and solve it.
# 3. Compare the performance of the two strategies.
# +
# Write your code here
# -
# ***
# # Local optimization
|
nb/2018_Autumn/Lecture4-Optimization-Using-Python-SciPy.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %matplotlib inline
#
# Compile Tensorflow Models
# =========================
# This article is an introductory tutorial to deploy tensorflow models with TVM.
#
# For us to begin with, tensorflow python module is required to be installed.
#
# Please refer to https://www.tensorflow.org/install
#
# +
# tvm, relay
import tvm
from tvm import te
from tvm import relay
# os and numpy
import numpy as np
import os.path
# Tensorflow imports
import tensorflow as tf
try:
tf_compat_v1 = tf.compat.v1
except ImportError:
tf_compat_v1 = tf
# Tensorflow utility functions
import tvm.relay.testing.tf as tf_testing
# Base location for model related files.
repo_base = "https://github.com/dmlc/web-data/raw/main/tensorflow/models/InceptionV1/"
# Test image
img_name = "elephant-299.jpg"
image_url = os.path.join(repo_base, img_name)
# -
# Tutorials
# ---------
# Please refer docs/frontend/tensorflow.md for more details for various models
# from tensorflow.
#
#
# +
model_name = "classify_image_graph_def-with_shapes.pb"
model_url = os.path.join(repo_base, model_name)
# Image label map
map_proto = "imagenet_2012_challenge_label_map_proto.pbtxt"
map_proto_url = os.path.join(repo_base, map_proto)
# Human readable text for labels
label_map = "imagenet_synset_to_human_label_map.txt"
label_map_url = os.path.join(repo_base, label_map)
# Target settings
# Use these commented settings to build for cuda.
# target = 'cuda'
# target_host = 'llvm'
# layout = "NCHW"
# ctx = tvm.gpu(0)
target = "llvm"
target_host = "llvm"
layout = None
ctx = tvm.cpu(0)
# -
# Download required files
# -----------------------
# Download files listed above.
#
#
# +
from tvm.contrib.download import download_testdata
img_path = download_testdata(image_url, img_name, module="data")
model_path = download_testdata(model_url, model_name, module=["tf", "InceptionV1"])
map_proto_path = download_testdata(map_proto_url, map_proto, module="data")
label_path = download_testdata(label_map_url, label_map, module="data")
# -
# Import model
# ------------
# Creates tensorflow graph definition from protobuf file.
#
#
with tf_compat_v1.gfile.GFile(model_path, "rb") as f:
graph_def = tf_compat_v1.GraphDef()
graph_def.ParseFromString(f.read())
graph = tf.import_graph_def(graph_def, name="")
# Call the utility to import the graph definition into default graph.
graph_def = tf_testing.ProcessGraphDefParam(graph_def)
# Add shapes to the graph.
with tf_compat_v1.Session() as sess:
graph_def = tf_testing.AddShapesToGraphDef(sess, "softmax")
# Decode image
# ------------
# <div class="alert alert-info"><h4>Note</h4><p>tensorflow frontend import doesn't support preprocessing ops like JpegDecode.
# JpegDecode is bypassed (just return source node).
# Hence we supply decoded frame to TVM instead.</p></div>
#
#
#
# +
from PIL import Image
image = Image.open(img_path).resize((299, 299))
x = np.array(image)
# -
# Import the graph to Relay
# -------------------------
# Import tensorflow graph definition to relay frontend.
#
# Results:
# sym: relay expr for given tensorflow protobuf.
# params: params converted from tensorflow params (tensor protobuf).
#
#
# +
shape_dict = {"DecodeJpeg/contents": x.shape}
dtype_dict = {"DecodeJpeg/contents": "uint8"}
mod, params = relay.frontend.from_tensorflow(graph_def, layout=layout, shape=shape_dict)
print("Tensorflow protobuf imported to relay frontend.")
# -
# Relay Build
# -----------
# Compile the graph to llvm target with given input specification.
#
# Results:
# graph: Final graph after compilation.
# params: final params after compilation.
# lib: target library which can be deployed on target with TVM runtime.
#
#
with tvm.transform.PassContext(opt_level=3):
lib = relay.build(mod, target=target, target_host=target_host, params=params)
# Execute the portable graph on TVM
# ---------------------------------
# Now we can try deploying the compiled model on target.
#
#
# +
from tvm.contrib import graph_runtime
dtype = "uint8"
m = graph_runtime.GraphModule(lib["default"](ctx))
# set inputs
m.set_input("DecodeJpeg/contents", tvm.nd.array(x.astype(dtype)))
# execute
m.run()
# get outputs
tvm_output = m.get_output(0, tvm.nd.empty(((1, 1008)), "float32"))
# -
# Process the output
# ------------------
# Process the model output to human readable text for InceptionV1.
#
#
# +
predictions = tvm_output.asnumpy()
predictions = np.squeeze(predictions)
# Creates node ID --> English string lookup.
node_lookup = tf_testing.NodeLookup(label_lookup_path=map_proto_path, uid_lookup_path=label_path)
# Print top 5 predictions from TVM output.
top_k = predictions.argsort()[-5:][::-1]
for node_id in top_k:
human_string = node_lookup.id_to_string(node_id)
score = predictions[node_id]
print("%s (score = %.5f)" % (human_string, score))
# -
# Inference on tensorflow
# -----------------------
# Run the corresponding model on tensorflow
#
#
# +
def create_graph():
"""Creates a graph from saved GraphDef file and returns a saver."""
# Creates graph from saved graph_def.pb.
with tf_compat_v1.gfile.GFile(model_path, "rb") as f:
graph_def = tf_compat_v1.GraphDef()
graph_def.ParseFromString(f.read())
graph = tf.import_graph_def(graph_def, name="")
# Call the utility to import the graph definition into default graph.
graph_def = tf_testing.ProcessGraphDefParam(graph_def)
def run_inference_on_image(image):
"""Runs inference on an image.
Parameters
----------
image: String
Image file name.
Returns
-------
Nothing
"""
if not tf_compat_v1.gfile.Exists(image):
tf.logging.fatal("File does not exist %s", image)
image_data = tf_compat_v1.gfile.GFile(image, "rb").read()
# Creates graph from saved GraphDef.
create_graph()
with tf_compat_v1.Session() as sess:
softmax_tensor = sess.graph.get_tensor_by_name("softmax:0")
predictions = sess.run(softmax_tensor, {"DecodeJpeg/contents:0": image_data})
predictions = np.squeeze(predictions)
# Creates node ID --> English string lookup.
node_lookup = tf_testing.NodeLookup(
label_lookup_path=map_proto_path, uid_lookup_path=label_path
)
# Print top 5 predictions from tensorflow.
top_k = predictions.argsort()[-5:][::-1]
print("===== TENSORFLOW RESULTS =======")
for node_id in top_k:
human_string = node_lookup.id_to_string(node_id)
score = predictions[node_id]
print("%s (score = %.5f)" % (human_string, score))
run_inference_on_image(img_path)
|
_downloads/e09aef52edc37570c0178591a87d328c/from_tensorflow.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # List comprehension
#
# List comprehension is an elegant way to define and create list in Python. These lists have often the qualities of sets, but are not in all cases sets.
#
# List comprehension is a complete substitute for the lambda function as well as the functions map(), filter() and reduce(). For most people the syntax of list comprehension is easier to be grasped
Celsius = [39.2, 36.5, 37.3, 37.8]
Fahrenheit = [ ((float(9)/5)*x + 32) for x in Celsius ]
print(Fahrenheit)
# A Pythagorean triple consists of three positive integers a, b, and c, such that
# a2 + b2 = c2.
# Such a triple is commonly written (a, b, c), and the best known example is (3, 4, 5).
# The following list comprehension creates the Pythagorean triples:
[(x,y,z) for x in range(1,30)\
for y in range(x,30) for z in range(y,30) if x**2 + y**2 == z**2 ]
#coventional method
numbers = []
for x in range(1,30):
for y in range(x,30):
for z in range(y,30):
if x**2 + y**2 == z**2:
numbers.append((x,y,z))
numbers
# Another example: Let A and B be two sets, the cross product (or Cartesian product) of A and B, written A×B, is the set of all pairs wherein the first element is a member of the set A and the second element is a member of the set B.
colours = [ "red", "green", "yellow", "blue" ]
things = [ "house", "car", "tree" ]
coloured_things = [ (x,y) for x in colours for y in things ]
print(coloured_things)
#Convetional method
coloured_things2 = []
for i in colours:
for j in things:
coloured_things2.append((i,j))
print(coloured_things2)
# ### If else outside
# +
# Create a list of strings: fellowship
fellowship = ['frodo', 'samwise', 'merry', 'aragorn', 'legolas', 'boromir', 'gimli']
# Create list comprehension: new_fellowship
new_fellowship = [member for member in fellowship if len(member)>=7]
# Print the new list
print(new_fellowship)
# +
# Create a list of strings: fellowship
fellowship = ['frodo', 'samwise', 'merry', 'aragorn', 'legolas', 'boromir', 'gimli']
# Create list comprehension: new_fellowship
new_fellowship = [member if len(member)>=7 else '' for member in fellowship]
# Print the new list
print(new_fellowship)
# -
# ### Dict Comprehensions
# We also can create dictionaries from list comprehensions
# +
# Create a list of strings: fellowship
fellowship = ['frodo', 'samwise', 'merry', 'aragorn', 'legolas', 'boromir', 'gimli']
# Create dict comprehension: new_fellowship
new_fellowship = {member:len(member) for member in fellowship}
# Print the new list
print(new_fellowship)
# -
# # Generators
#
# On the surface generators in Python look like functions, but there is both a syntactic and a semantic difference. One distinguishing characteristic is the yield statements. The yield statement turns a functions into a generator. A generator is a function which returns a generator object. This generator object can be seen like a function which produces a sequence of results instead of a single object. This sequence of values is produced by iterating over it, e.g. with a for loop. The values, on which can be iterated, are created by using the yield statement. The value created by the yield statement is the value following the yield keyword. The execution of the code stops when a yield statement has been reached. The value behind the yield will be returned. The execution of the generator is interrupted now. As soon as "next" is called again on the generator object, the generator function will resume execution right after the yield statement in the code, where the last call exited. The execution will continue in the state in which the generator was left after the last yield. This means that all the local variables still exists, because they are automatically saved between calls. This is a fundamental difference to functions: functions always start their execution at the beginning of the function body, regardless where they had left in previous calls. They don't have any static or persistent values. There may be more than one yield statement in the code of a generator or the yield statement might be inside the body of a loop. If there is a return statement in the code of a generator, the execution will stop with a StopIteration exception error if this code is executed by the Python interpreter. The word "generator" is sometimes ambiguously used to mean both the generator function itself and the objects which are generated by a generator.
|
3Toolbox/.ipynb_checkpoints/3List_comprehensions_and_Generators-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 1.5.2
# language: julia
# name: julia-1.5
# ---
# Import necessary libraries
using AlgebraicRelations.DB,
AlgebraicRelations.Queries,
AlgebraicRelations.Interface,
AlgebraicRelations.Presentations;
# ## Define the Schema
# We need to define the data types, the table column names, and the syntax of our schema
# +
# Initialize presentation object
present = Presentation()
# Add types to presentation
Person, ID, Name, Salary = add_types!(present, [(:Person, Int),
(:ID, Int),
(:Name, String),
(:Salary, Real)]);
# Add Processes to presentation
get_employees, get_manager,
get_salary, get_name = add_processes!(present, [(:get_employees, Person, ID),
(:get_manager, Person, Person),
(:get_salary, Person, Salary),
(:get_name, Person, Name)]);
Workplace = present_to_schema(present)
schema = Workplace();
# -
print(generate_schema_sql(schema));
# ## Generate the Query
# We are now able to generate queries based off of this schema which we defined.
# We generate a query that gets all employees make a salary within some range
q1 = @query schema (emp_name, salary) where
(p, emp_name,
salary,
_sallower, _salupper) begin
# Define name relationships
get_name(p, emp_name)
# Define salary relationships (with input range)
get_salary(p,salary)
<=(salary, _salupper)
>=(salary, _sallower)
end;
print(to_sql(q1))
draw_query(q1)
# We generate a second query that gets all employees whose managers make a salary within some range
q2 = @query schema (emp_name, man_name,salary) where
(p, m, emp_name,
man_name, salary,
_slower, _supper) begin
# Define name relationships
get_name(p, emp_name)
get_name(m, man_name)
# Define manager relationships
get_manager(p,m)
# Define salary relationships (with input range)
get_salary(m,salary)
<=(salary, _supper)
>=(salary, _slower)
end;
print(to_sql(q2))
draw_query(q2)
|
examples/company_demo/concise_demo_ACT.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Import dependencies
import matplotlib.pyplot as plt
from scipy import stats
import pandas as pd
import numpy as np
import psycopg2
# +
#postgresql://sofia:4991@localhost:5432/EmployeeSQL
# -
from sqlalchemy import create_engine
engine = create_engine('postgresql://postgres:4991@localhost:5432/EmployeeSQL')
connection = engine.connect()
df = pd.read_sql("SELECT salary FROM \"Salaries\"", connection)
df.head()
# +
# Histogram to Visualize salaries
df.hist('salary')
plt.savefig("Images/salary_histogram.png")
# +
#Writing the query
query="SELECT t.title, round(avg(s.salary)) AS \"Average Salary\" \
FROM \"Salaries\" s\
LEFT JOIN \"Employee\" e \
ON e.emp_no = s.emp_no\
LEFT JOIN \"Titles\" t \
ON e.emp_title_id = t.title_id\
GROUP BY t.title;"
# Get data from DB
salary_by_title_data = pd.read_sql(query, connection)
salary_by_title_data.head()
# -
|
Bonus.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 0.5.0
# language: julia
# name: julia-0.5
# ---
# # Collective.jl: A tool for finding patterns
#
# Collective.jl is a Julia package designed to identify interesting *features* from a collection of words. This is a common mechanic in puzzles you might find at, for example, the MIT Mystery Hunt.
#
# This is a Jupyter notebook using the Julia programming language to run Collective.jl. You can learn more about Jupyter notebooks at <http://jupyter.org/> and about Julia at [julialang.org](http://docs.julialang.org/en/stable/manual/introduction/).
#
# If you want to use this package without installing Julia, you can use [juliabox](https://juliabox.com/). Just sign in at [juliabox.com](https://juliabox.com/) and upload this file.
#
# ## Features
#
# A *feature* is just a boolean property of a word, like `"contains the letter 'a'"` or `"is a palindrome"`. Many features can also include scalar quantities. For example, we might want to compute a family of features for a word's Scrabble score. Those features would look like: `"scrabble score == 1"`, `"scrabble score == 2"`, ..., `"scrabble score == n".`
#
# ## Interestingness
#
# A particular set of words can satisfy many features. For example, if I give you the list of words: `["questionable", "businesswoman", "exhaustion", "discouraged", "communicated", "hallucinogen", "sequoia"]`, you might tell me that they all contain the letter 'a'. That's true, but it's much more interesting to notice that they all contain *all 5 vowels*. We measure this degree of interestingness using the standard binomial probability distribution: given `n` words, we can compute the probability that `k` of them satisfy some feature `F` as:
#
# (n choose k) * f^k * (1 - f)^(n - k)
#
# where `f` is the frequency with wich feature `F` occurs in the population of words (in this case, the dictionary). The most interesting feature is the one whose probability of `k` occurrences is smallest.
# # Installation
# If you don't have Collective.jl already, this will install it
# directly from github (even on JuliaBox):
isdir(Pkg.dir("Collective")) || Pkg.clone("https://github.com/rdeits/Collective.jl.git")
# # Usage
# Load the package
using Collective
# To determine the frequency distribution of each feature, we'll need a population of English words:
const words = wordlist(open(joinpath(Pkg.dir("Collective"),
"data",
"113809of.fic")));
# Constructing a `Corpus` does all the hard work of compiling functions for every feature and testing their frequencies (this will take a few seconds):
corpus = Corpus(words)
# Now we can use that corpus to solve puzzles. Here's a set of words:
puzzle = ["questionable", "businesswoman", "exhaustion", "discouraged", "communicated", "hallucinogen", "sequoia"]
# We can run the feature statistics with `analyze()`:
results = analyze(corpus, puzzle)
results[1:5]
# Analyze returns a vector of `FeatureResult`s, each of which contains:
#
# * A human-readable description of the feature
# * A function to evaluate that feature
# * The number of words in the puzzle which match that feature
# * The binomial probability of that number of matches
#
# To get the best features, we can just sort that list:
sort(results)[1:5]
# That first feature has a probability of about $1$ in $6 \times 10^{15}$. It's extremely unlikely that 7 randomly chosen words would have 5 unique vowels each. So that's the feature we should use for whatever the next step of the puzzle is!
#
# If we don't want the whole sorted list of features, we can just get the single best one:
best_feature = minimum(results)
# ## More examples
#
# There are a variety of puzzles used for testing Collective, and they show off some of the interesting patterns it can detect. The full list can be found here: <https://github.com/rdeits/Collective.jl/tree/master/test/puzzles>
#
# Some of those examples are reproduced below:
# # Clockwork Orange (2013)
# <http://web.mit.edu/puzzle/www/2013/coinheist.com/rubik/clockwork_orange/index.html>
minimum(analyze(corpus, ["armoredrecon", "hypapante", "commemorativebats", "derricktruck", "brownrot", "attorneysgeneral", "sacrosanct", "impromptu"]))
# # Venntersections (2014)
# <http://www.mit.edu/~puzzle/2014/puzzle/venntersections/>
minimum(analyze(corpus, ["grimaced", "formally", "questionable", "discouraged", "communicated", "chrysalis", "saccharin"]))
minimum(analyze(corpus, ["thumbtacks", "monologue", "testimony", "camel", "meteorology", "trampoline", "achievement"]))
minimum(analyze(corpus, ["philharmonic", "mischievous", "alphabet", "restaurant", "leeching", "mushroom", "pioneer"]))
# ## Clustering
#
# Collective also knows how to cluster words. Specifically, given a list of M words, and a number N < M, it will try to find the group of N words which are related by a single very interesting feature. For example:
#
puzzle = shuffle(["hugoweaving",
"mountaindew",
"mozambique",
"sequoia",
"annotation",
"artificial",
"individual",
"omnivorous",
"onlocation",
"almost",
"biopsy",
"chimp",
"films",
"ghost",
"tux",
"balked",
"highnoon",
"posted"]);
# Find the best cluster of size 6 from the list in puzzle, using
# statistics from corpus
cluster = best_cluster(corpus, puzzle, 6)
# The 6 words which were identified are: `["biopsy","films","chimp","almost","tux","ghost"]`. The feature which was returned says that all 6 words have no reverse alphabetical bigrams, and that the probability of such an occurrence is 1 in 2e-14. Putting it another way, it says that *every* word has only alphabetical bigrams, or, more plainly, every word has all of its letters in alphabetical order.
|
collective.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Day20-1.Homework.ipynb
import sqlite3 as lite
import pandas as pd
import requests
from pymongo import MongoClient
pd.options.display.max_colwidth = 200
db = lite.connect('./products.db')
# SQL
# products.db에 대해
# Employees 의 월별 생일의 분포를 구하세요
# OrderDetails 의 OrderID 별 주문 금액의 합을 구하세요
query = """
SELECT substr(BirthDate, 6,2) "MONTH", count(*) "COUNT"
FROM
Employees
GROUP BY substr(BirthDate, 6,2)
;
"""
pd.read_sql(query, db)
query = """
SELECT D.OrderID, sum(D.Quantity * P.Price) "TOTAL"
FROM
OrderDetails D
JOIN
Products P
ON
D.ProductID = P.ProductID
GROUP BY
D.OrderID
;
"""
pd.read_sql(query, db).head()
# noSQL
# 앞서 저장한 매물정보에서
# 4층 이상인 건물 중 3층 이상인 매물의 목록을 구하세요
# 면적이 33 이상이거나, 조회수가 50 이상인 매물의 목록을 구하세요
mongo_uri = "mongodb://strongadmin:admin1234@ds135844.mlab.com:35844/mydbinstance"
client = MongoClient(mongo_uri)
client.mydbinstance.collection_names()
db = client.mydbinstance
items = db.bigbang
items.find_one({})
# +
# pymongo 라이브러리 만으로는 너무 복잡해지므로, 모든 아이템을 불러온 뒤, 전처리 후 카운트
# mongoDB client로는 javaScript문법으로 db.find().forEach()를 활용하여 각 document에 대해 작업지시 가능
# regex 또한 python의 regex와 문법이 달라 regex compile이 불가
# query가 너무 복잡해지지 않는 선에서 가능한 만큼 수행 한 뒤, python으로 추가 수행을 하는 것이 깔끔합니다.
query = {}
count = 0
for item in items.find(query):
floor = int(item["item"]["floor"].replace("층","").replace("반지하","0"))
floor_all = int(item["item"]["floor_all"].replace("층",""))
if floor>=2 and floor_all>=4:
count+=1
print(count)
# +
#위와 같은 이유로 가능한 조건에 대하여 먼저 필터링 한 후, list comprehension으로 재구성
query={
"$or":[
{"item.size_m2":{"$gte":33}},
#{"item.view_count":{"$gte":50}},
]
}
result = [
(item["item"]["size_m2"], item["item"]["view_count"])
for item in items.find(query) if int(item["item"]["view_count"]) >= 50
]
len(result)
# -
|
SQL/Day20-1.Homework.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 利用PCA来简化数据
# **降维(dimensionality reduction)**
#
# 在低维下,数据更容易处理。我们在应用机器学习算法之前,必须先识别出其相关的特征。
# ## 降维技术
# * **PCA(Principal Component Analysis)主成分分析**
#
# 将原坐标系转换,第一个坐标轴选择方差最大的方向,第二个坐标系选择与第一个坐标系正交(orthogonal)且方差最大的方向,以此类推。
#
# * **FA(Factor Analysis)因子分析**
#
# 假设数据是隐变量(latent variable)和某些噪声的线性组合。
#
# * **ICA(Independent Component Analysis)独立成分分析**
#
# 假设数据是有N个数据源生成的,这些数据源之间相互独立。
# ## 在Numpy中实现PCA
# 伪代码:
#
# 去除平均值
# 计算协方差矩阵
# 计算协方差矩阵的特征值和特征向量
# 将特征值从大到小排序
# 保留最上面的N个特征向量
# 将数据转换到上述N个特征向量构建的新空间中
from numpy import *
def load_dataset(filename, delim='\t'):
fr = open(filename)
str_arr = [line.strip().split(delim) for line in fr.readlines()]
data_arr = [list(map(float, line)) for line in str_arr]
return mat(data_arr)
datamat = load_dataset('testSet.txt')
datamat
def pca(datamat, topNfeat=9999999):
mean_val = mean(datamat, axis=0)
mean_removed = datamat - mean_val
covmat = cov(mean_removed, rowvar=0)
print('covmat:\n',covmat)
# covmat = (mean_removed.T * mean_removed) / len(mean_removed[:, 0])
eig_vals, eig_vec = linalg.eig(covmat)
print('eig_vals:\n',eig_vals)
eig_vals_index = argsort(eig_vals)
eig_vals_index = eig_vals_index[:-(topNfeat+1):-1]
print('eig_vals_index:\n',eig_vals_index)
reg_eig_vec = eig_vec[:, eig_vals_index]
print('reg_eig_vec:\n',reg_eig_vec)
low_datamat = mean_removed * reg_eig_vec
reconmat = (low_datamat * reg_eig_vec.T) + mean_val
return low_datamat, reconmat
lowmat, reconmat = pca(datamat, 1)
shape(lowmat)
import matplotlib.pyplot as plt
fig = plt.figure()
ax = plt.subplot(111)
# print('datamat[:, 1].T.A:\n',datamat[:, 1].T.A)
ax.scatter(datamat[:, 0].T.A[0], datamat[:, 1].T.A[0], marker='s', s=10)
ax.scatter(reconmat[:, 0].T.A[0], reconmat[:, 1].T.A[0], marker='o', s=10)
lowmat, reconmat = pca(datamat, 2)
fig.clf()
ax = plt.subplot(111)
ax.scatter(datamat[:, 0].T.A[0], datamat[:, 1].T.A[0], marker='s', s=10)
ax.scatter(reconmat[:, 0].T.A[0], reconmat[:, 1].T.A[0], marker='o', s=10)
# ## 示例:利用PCA对半导体制造数据降维
#
# ### 处理数据中的缺失值
# * 使用可用特征的均值填补
# * 使用特殊值来填补,如0,-1
# * 忽略有缺失值的样本
# * 使用相似样本的均值填补
# * 使用另外的机器学习预测缺失值
#
# 在这里,我们用平均值代替。
def replace_NaN_with_mean():
datamat = load_dataset('secom.data', ' ')
numfeat = shape(datamat)[1]
for i in range(numfeat):
# print('~isnan(datamat[:, i]).A:\n', ~isnan(datamat[:, i]))
mean_val = mean(datamat[nonzero(~isnan(datamat[:, i]).A)[0], i])
datamat[nonzero(isnan(datamat[:, i]).A)[0], i] = mean_val
return datamat
datamat = replace_NaN_with_mean()
mean_val = mean(datamat, axis=0)
mean_removed = datamat - mean_val
covmat = cov(mean_removed, rowvar=0)
eig_val, eig_vec = linalg.eig(covmat)
eig_val
# +
eig_val_index = argsort(eig_val)
eig_val_index = eig_val_index[::-1]#reverse
sorted_eig_vals = eig_val[eig_val_index]
total = sum(sorted_eig_vals)
varPercentage = sorted_eig_vals / total * 100
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(range(1, 21), varPercentage[:20], marker='^')
plt.xlabel('Principal Component Number')
plt.ylabel('Percentage of Variance')
# -
|
PCA/PCA.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="WMucfLUS1yhH"
# # LSTM IMDB Sentiment Example.ipynb
#
# ## Learning Objectives
#
# 1. Create map for converting IMDB dataset to readable reviews
# 2. Create and build LSTM Recurrent Neural Network
# 3. Visualise the Model and train the LSTM
# 4. Evaluate model with test data and view results
#
#
# ## What is this?
#
# This Jupyter Notebook contains Python code for building a LSTM Recurrent Neural Network that gives 87-88% accuracy on the IMDB Movie Review Sentiment Analysis Dataset.
#
# More information is given on [this blogpost](https://www.bouvet.no/bouvet-deler/explaining-recurrent-neural-networks).
#
# ## Introduction
# Long Short Term Memory networks – usually just called “LSTMs” – are a special kind of RNN, capable of learning long-term dependencies. They were introduced by Hochreiter & Schmidhuber (1997), and were refined and popularized by many people in following work. They work tremendously well on a large variety of problems, and are now widely used.
#
# LSTMs are explicitly designed to avoid the long-term dependency problem. Remembering information for long periods of time is practically their default behavior, not something they struggle to learn!
#
#
# Each learning objective will correspond to a _#TODO_ in this student lab notebook -- try to complete this notebook first and then review the [solution notebook](https://github.com/GoogleCloudPlatform/training-data-analyst/blob/master/courses/machine_learning/deepdive2/text_classification/solutions/LSTM_IMDB_Sentiment_Example.ipynb)
# + [markdown] id="WP1VrbVp3sVu"
# ## Setting up
#
# When running this for the first time you may get a warning telling you to restart the Runtime. You can ignore this, but feel free to select "Kernel->Restart Kernel" from the overhead menu if you encounter problems.
# + id="2e3txwbh3q76" colab={"base_uri": "https://localhost:8080/", "height": 531} outputId="e42b88ff-fa1d-4b9c-df9f-c5b7557ce2fb"
# keras.datasets.imdb is broken in TensorFlow 1.13 and 1.14 due to numpy 1.16.3
# !pip install numpy==1.16.2
# All the imports!
import tensorflow as tf
import numpy as np
from tensorflow.keras.preprocessing import sequence
from numpy import array
# Supress deprecation warnings
import logging
logging.getLogger('tensorflow').disabled = True
# Fetch "IMDB Movie Review" data, constraining our reviews to
# the 10000 most commonly used words
vocab_size = 10000
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.imdb.load_data(num_words=vocab_size)
# Map for readable classnames
class_names = ["Negative", "Positive"]
# + [markdown] id="sawo1x8kQk9b"
# **Note: Please ignore any incompatibility errors or warnings as it does not impact the notebooks functionality.**
# -
# This notebook uses TF2.x.
# Please check your tensorflow version using the cell below.
# Show the currently installed version of TensorFlow
print("TensorFlow version: ",tf.version.VERSION)
# + [markdown] id="hdyHL8FF0JJy"
# ## Create map for converting IMDB dataset to readable reviews
#
# Reviews in the IMDB dataset have been encoded as a sequence of integers. Luckily the dataset also
# contains an index for converting the reviews back into human readable form.
# + id="E05AweFu0Imt" colab={"base_uri": "https://localhost:8080/"} outputId="d4c48cc1-1549-42b3-ddd9-abb3f343d6ab"
# Get the word index from the dataset
word_index = tf.keras.datasets.imdb.get_word_index()
# Ensure that "special" words are mapped into human readable terms
word_index = {k:(v+3) for k,v in word_index.items()}
word_index["<PAD>"] = 0
word_index["<START>"] = 1
word_index["<UNKNOWN>"] = 2
word_index["<UNUSED>"] = 3
# Perform reverse word lookup and make it callable
# TODO -- your code goes here
# + [markdown] id="fFXK-g6G81sC"
# ## Data Insight
#
# Here we take a closer look at our data. How many words do our reviews contain?
#
# And what do our review look like in machine and human readable form?
#
# + id="yD1qHVBn81Y_" colab={"base_uri": "https://localhost:8080/"} outputId="b313242c-0536-4b4d-d9ec-d895cfdc7c35"
# Concatonate test and training datasets
allreviews = np.concatenate((x_train, x_test), axis=0)
# Review lengths across test and training whole datasets
print("Maximum review length: {}".format(len(max((allreviews), key=len))))
print("Minimum review length: {}".format(len(min((allreviews), key=len))))
result = [len(x) for x in allreviews]
print("Mean review length: {}".format(np.mean(result)))
# Print a review and it's class as stored in the dataset. Replace the number
# to select a different review.
print("")
print("Machine readable Review")
print(" Review Text: " + str(x_train[60]))
print(" Review Sentiment: " + str(y_train[60]))
# Print a review and it's class in human readable format. Replace the number
# to select a different review.
print("")
print("Human Readable Review")
print(" Review Text: " + decode_review(x_train[60]))
print(" Review Sentiment: " + class_names[y_train[60]])
# + [markdown] id="mF-Votm66zD5"
# ## Pre-processing Data
#
# We need to make sure that our reviews are of a uniform length. This is for the LSTM's parameters.
#
# Some reviews will need to be truncated, while others need to be padded.
# + id="uNtJTLJA6gaT" colab={"base_uri": "https://localhost:8080/"} outputId="bb552c79-32d9-4a4c-d102-b3f56dfa4bb0"
# The length of reviews
review_length = 500
# Padding / truncated our reviews
x_train = sequence.pad_sequences(x_train, maxlen = review_length)
x_test = sequence.pad_sequences(x_test, maxlen = review_length)
# Check the size of our datasets. Review data for both test and training should
# contain 25000 reviews of 500 integers. Class data should contain 25000 values,
# one for each review. Class values are 0 or 1, indicating a negative
# or positive review.
print("Shape Training Review Data: " + str(x_train.shape))
print("Shape Training Class Data: " + str(y_train.shape))
print("Shape Test Review Data: " + str(x_test.shape))
print("Shape Test Class Data: " + str(y_test.shape))
# Note padding is added to start of review, not the end
print("")
print("Human Readable Review Text (post padding): " + decode_review(x_train[60]))
# + [markdown] id="BfOdV_VCCFee"
# ## Create and build LSTM Recurrent Neural Network
# + id="8nmO8M4aCKwT" colab={"base_uri": "https://localhost:8080/"} outputId="365cce8d-be9a-427e-89bc-3a9940689edd"
# We begin by defining the a empty stack. We'll use this for building our
# network, later by layer.
model = tf.keras.models.Sequential()
# The Embedding Layer provides a spatial mapping (or Word Embedding) of all the
# individual words in our training set. Words close to one another share context
# and or meaning. This spatial mapping is learning during the training process.
model.add(
tf.keras.layers.Embedding(
input_dim = vocab_size, # The size of our vocabulary
output_dim = 32, # Dimensions to which each words shall be mapped
input_length = review_length # Length of input sequences
)
)
# Dropout layers fight overfitting and forces the model to learn multiple
# representations of the same data by randomly disabling neurons in the
# learning phase.
# TODO -- your code goes here
# We are using a fast version of LSTM whih is optimised for GPUs. This layer
# looks at the sequence of words in the review, along with their word embeddings
# and uses both of these to determine to sentiment of a given review.
# TODO -- your code goes here
# Add a second dropout layer with the same aim as the first.
# TODO -- your code goes here
# All LSTM units are connected to a single node in the dense layer. A sigmoid
# activation function determines the output from this node - a value
# between 0 and 1. Closer to 0 indicates a negative review. Closer to 1
# indicates a positive review.
model.add(
tf.keras.layers.Dense(
units=1, # Single unit
activation='sigmoid' # Sigmoid activation function (output from 0 to 1)
)
)
# Compile the model
model.compile(
loss=tf.keras.losses.binary_crossentropy, # loss function
optimizer=tf.keras.optimizers.Adam(), # optimiser function
metrics=['accuracy']) # reporting metric
# Display a summary of the models structure
model.summary()
# + [markdown] id="8Xx1Q2I8WNI9"
# ## Visualise the Model
# + id="cz0Erj2WU3Vh" colab={"base_uri": "https://localhost:8080/", "height": 644} outputId="0b9d22da-1f99-4662-b535-51bbf9a12fc4"
tf.keras.utils.plot_model(model, to_file='model.png', show_shapes=True, show_layer_names=False)
# + [markdown] id="5KdfAoHsGwzo"
# ## Train the LSTM
# + id="rEN1vV4nG1V3" colab={"base_uri": "https://localhost:8080/"} outputId="d9dbba03-32c0-4aa5-e9a8-e5f6d29962d1"
# Train the LSTM on the training data
history = model.fit(
# Training data : features (review) and classes (positive or negative)
x_train, y_train,
# Number of samples to work through before updating the
# internal model parameters via back propagation. The
# higher the batch, the more memory you need.
batch_size=256,
# An epoch is an iteration over the entire training data.
epochs=3,
# The model will set apart his fraction of the training
# data, will not train on it, and will evaluate the loss
# and any model metrics on this data at the end of
# each epoch.
validation_split=0.2,
verbose=1
)
# + [markdown] id="rpCS2-jFH1KY"
# ## Evaluate model with test data and view results
# + id="nPnfxwbnITqV" colab={"base_uri": "https://localhost:8080/"} outputId="8cf4f12d-f801-4317-a49f-c9ec2b0abbb9"
# Get Model Predictions for test data
# TODO -- your code goes here
# + [markdown] id="CkfHCIVHrJni"
# ## View some incorrect predictions
#
# Lets have a look at some of the incorrectly classified reviews. For readability we remove the padding.
#
#
# + id="bwKLBwBbp7zg" colab={"base_uri": "https://localhost:8080/"} outputId="75830a56-10dd-4a3e-c013-8272328ba1aa"
predicted_classes_reshaped = np.reshape(predicted_classes, 25000)
incorrect = np.nonzero(predicted_classes_reshaped!=y_test)[0]
# We select the first 10 incorrectly classified reviews
for j, incorrect in enumerate(incorrect[0:20]):
predicted = class_names[predicted_classes_reshaped[incorrect]]
actual = class_names[y_test[incorrect]]
human_readable_review = decode_review(x_test[incorrect])
print("Incorrectly classified Test Review ["+ str(j+1) +"]")
print("Test Review #" + str(incorrect) + ": Predicted ["+ predicted + "] Actual ["+ actual + "]")
print("Test Review Text: " + human_readable_review.replace("<PAD> ", ""))
print("")
# + [markdown] id="OlAfxIoTrtYa"
# ## Run your own text against the trained model
#
# This is a fun way to test out the limits of the trained model. To avoid getting errors - type in lower case only and do not use punctuation!
#
# You'll see the raw prediction from the model - basically a value between 0 and 1.
#
#
# + id="UEKEB0DpD_8P" colab={"base_uri": "https://localhost:8080/"} outputId="975a5f72-6253-4a83-f403-ad1fc58ced92"
# Write your own review
review = "this was a terrible film with too much sex and violence i walked out halfway through"
#review = "this is the best film i have ever seen it is great and fantastic and i loved it"
#review = "this was an awful film that i will never see again"
# Encode review (replace word with integers)
tmp = []
for word in review.split(" "):
tmp.append(word_index[word])
# Ensure review is 500 words long (by padding or truncating)
tmp_padded = sequence.pad_sequences([tmp], maxlen=review_length)
# Run your processed review against the trained model
rawprediction = model.predict(array([tmp_padded][0]))[0][0]
prediction = int(round(rawprediction))
# Test the model and print the result
print("Review: " + review)
print("Raw Prediction: " + str(rawprediction))
print("Predicted Class: " + class_names[prediction])
|
courses/machine_learning/deepdive2/text_classification/labs/LSTM_IMDB_Sentiment_Example.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # ImagingLSS on NERSC Jupyter Portal
#
# This example will guide you setup imaginglss at NERSC with Jupyter.
#
# https://jupyter.nersc.gov
#
# This guide will not work on Cori or Edison.
# Refer to the documentation for using imaginglss in a Batch environment.
# ## First time install
#
# This will checkout the imaginglss source code to ~/imaginglss
#
# If you'd like to put the code some other places, change the path.
# + language="bash"
#
# cd ~
#
# git clone https://github.com/desihub/imaginglss
# cd imaginglss
#
# /anaconda/bin/pip install --user -e .
#
# -
# ## Update
#
# This will abandon all of your local changes!
#
# + language="bash"
#
# cd ~/imaginglss
#
# git stash
# git pull
#
# -
# ## Head start for Developers
#
# For developers, it is preferable to do updates with `git pull`
# from a true terminal window, or follow other standard git practice of
# merging in upstream changes. (e.g. `git fetch`)
#
# The main development of imaginglss is done this way:
#
# - One terminal window connected to NERSC
# - One notebook connected to http://jupyter.nersc.gov
# - Write up some ideas in the notebook
# - `git checkout -b mybigidea`
# - implement it from the terminal window
# - Reload the notebook kernel and test the implementation
# - If it works, `git add`, `git commit`, `git push`, and file a Pull Request.
# - If it does not work, go to 'implement' step.
# - Wait till the feature is merged,
# - `git checkout master`; `git branch -d mybigidea`.
#
# ## Reinstall
#
# Usually not needed, but if things go severely wrong, try this.
# + language="bash"
#
# cd ~/imaginglss
# /anaconda/bin/pip uninstall imaginglss
# /anaconda/bin/pip install --user -e .
#
# -
import imaginglss
print imaginglss
decals = imaginglss.DECALS('/global/project/projectdirs/m779/imaginglss/dr2.conf.py')
|
NERSCJupyterGuide.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import tweepy
import pandas as pd
from dotenv import load_dotenv
import os
load_dotenv()
# +
CONSUMER_KEY = os.getenv("CONSUMER_KEY")
CONSUMER_SECRET = os.getenv("CONSUMER_SECRET")
ACCESS_KEY = os.getenv("ACCESS_KEY")
ACCESS_SECRET = os.getenv("ACCESS_SECRET")
auth = tweepy.OAuthHandler(CONSUMER_KEY, CONSUMER_SECRET)
auth.set_access_token(ACCESS_KEY, ACCESS_SECRET)
api = tweepy.API(auth)
try:
api.verify_credentials()
print('Authentication OK')
except:
print('Error during authentication')
# + pycharm={"name": "#%%\n"}
## Twitter bot will search for mentions
def get_mentions():
return api.mentions_timeline()
mentions = get_mentions()
# + pycharm={"name": "#%%\n"}
for x in mentions:
print(x)
# + [markdown] pycharm={"name": "#%% md\n"}
# ## Twitter bot will search for replies to a certain tweet
# + pycharm={"name": "#%%\n"}
def get_tweet_comments(input_tweet):
"""
Args:
input_tweet: A Twitter API response object
Returns: A list of the text for all found replies.
"""
comments = []
name = input_tweet._json['user']['screen_name']
tweet_id = input_tweet._json['id']
for tweet in tweepy.Cursor(api.search,q=f"to:{name}", result_type = 'recent',tweet_mode = 'extended').items(100):
if hasattr(tweet, 'in_reply_to_status_id_str'):
if str(tweet.in_reply_to_status_id_str) == str(tweet_id):
comments.append(tweet._json['full_text'])
return tweet
return comments
# -
# ## Twitter bot will reply to the tweet
# +
def twitter_reply(status_id, text):
if text == "":
reply_text = '''
------- test -------
We noticed that you are reporting a police incident.
'''
else:
reply_text = text
tweet = api.update_status(status = reply_text, in_reply_to_status_id=status_id,tweet_mode = 'extended')
return tweet
#twitter_reply(1395143654331744256)
# -
df_data = []
for tweet in api.search(q='police', lang='en', rpp=5)[:5]:
test_data = [tweet.user.screen_name, tweet.id, tweet.text]
df_data.append(test_data)
df = pd.DataFrame(data=df_data, columns=['username', 'id', 'tweet'])
df
# ## Twitter bot will reply to the user through DM
# +
def direct_message(username):
user = api.get_user(username)
message = '''
Just testing some features.
This sends a direct message to the person
'''
api.send_direct_message(user.id, message)
return 'direct message sent'
direct_message('@JoanVillar14')
# -
# Improvements:
#
# 1. Depending on the reply, gather more information such as:
# - did it really happen?
# - where did it happen
#
# 2. They pin the place of incident on a map
# - If tweet's geolocation is on, get the coordinates
#
# -------
#
#
# * There are a few things to keep in mind in designing a model that replies to specific replies. This might be another project in the future.
# * Since the incidents are already identified, it might be best to just get the location from the user.
# + [markdown] pycharm={"name": "#%% md\n"}
# ## The original tweet id will contain the tweet object
#
# ## The bot initial response tweet id will store the tweet id for the original tweet
#
# ## When someone responds to the bot, store the tweet id as key and use the responded to id as value
# + pycharm={"name": "#%%\n"}
|
notebooks/labs34_notebooks/twitter_reply.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import statsmodels.api as sm
from matplotlib import pyplot as plt
import numpy as np
data = sm.datasets.longley.load()
data.exog = sm.add_constant(data.exog)
model = sm.OLS(data.endog, data.exog)
mod_fit = model.fit()
res = mod_fit.resid # residuals
probplot = sm.ProbPlot(res)
probplot.qqplot()
plt.show()
import scipy.stats as stats
probplot = sm.ProbPlot(res, stats.t, distargs=(4,))
fig = probplot.qqplot()
plt.show()
probplot = sm.ProbPlot(res, stats.t, distargs=(4,), loc=3, scale=10)
fig = probplot.qqplot()
plt.show()
probplot = sm.ProbPlot(res, stats.gamma, fit=True)
fig = probplot.qqplot(line='45')
plt.show()
import numpy as np
x = np.random.normal(loc=8.25, scale=2.75, size=37)
y = np.random.normal(loc=8.75, scale=3.25, size=37)
pp_x = sm.ProbPlot(x, fit=True)
pp_y = sm.ProbPlot(y, fit=True)
fig = pp_x.qqplot(line='45', other=pp_y)
plt.show()
nobs = 300
np.random.seed(1234) # Seed random generator
dens = sm.nonparametric.KDEUnivariate(np.random.beta(0.5,1.0,size=nobs))
dens.fit()
plt.plot(dens.cdf)
plt.show()
x=np.random.normal(size=nobs)+2*np.random.uniform(size=nobs)
dens = sm.nonparametric.KDEUnivariate(x)
dens.fit()
plt.plot(dens.cdf)
plt.show()
plt.plot(dens.density)
plt.show()
dens.entropy
|
Q-Q plots.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Q-Learning for FrozenLake 4x4
#
# Based on https://colab.research.google.com/drive/1oqon14Iq8jzx6PhMJvja-mktFTru5GPl#scrollTo=5aQKQMJTJBPH
# 
import numpy as np
import gym
import random
# +
# Create environment
from gym.envs.registration import register
register(
id='FrozenLakeNotSlippery-v0',
entry_point='gym.envs.toy_text:FrozenLakeEnv',
kwargs={'map_name' : '4x4', 'is_slippery': False},
max_episode_steps=100,
reward_threshold=0.8196, # optimum = .8196, changing this seems have no influence
)
# -
env = gym.make("FrozenLakeNotSlippery-v0")
# +
# Create Q-table
action_size = env.action_space.n
state_size = env.observation_space.n
print(f'aciton size: {action_size}, state size: {state_size}')
state = env.observation_space
# -
state = env.observation_space
state
qtable = np.zeros((state_size, action_size))
print(qtable)
# +
# Set hyperparameters
# @hyperparameters
total_episodes = 200 # Total episodes
learning_rate = 0.8 # Learning rate
max_steps = 99 # Max steps per episode
gamma = 0.95 # Discounting rate
# Exploration parameters
epsilon = 1.0 # Exploration rate
max_epsilon = 1.0 # Exploration probability at start
min_epsilon = 0.01 # Minimum exploration probability
decay_rate = 0.001 # Exponential decay rate for exploration prob
#I find that decay_rate=0.001 works much better than 0.01
# +
# Learn
# List of rewards
rewards = []
# 2 For life or until learning is stopped
for episode in range(total_episodes):
# Reset the environment
state = env.reset()
# print(f"state: {state}")
step = 0
done = False
total_rewards = 0
for step in range(max_steps):
# print(f"start step...")
# 3. Choose an action a in the current world state (s)
## First we randomize a number
exp_exp_tradeoff = random.uniform(0, 1)
# print(f"exp_exp_tradeoff: {exp_exp_tradeoff}")
## If this number > greater than epsilon --> exploitation
#(taking the biggest Q value for this state)
if exp_exp_tradeoff > epsilon:
# print(f"qtable[state,:] {qtable[state,:]}")
action = np.argmax(qtable[state,:])
# Else doing a random choice --> exploration
else:
action = env.action_space.sample()
# print(f"action is {action}")
# Take the action (a) and observe the outcome state(s') and reward (r)
new_state, reward, done, info = env.step(action)
# print(f"new_state: {new_state}, reward: {reward}, done: {done}, info: {info}")
# Update Q(s,a):= Q(s,a) + lr [R(s,a) + gamma * max Q(s',a') - Q(s,a)]
# qtable[new_state,:] : all the actions we can take from new state
qtable[state, action] = qtable[state, action] + learning_rate * (reward + gamma * np.max(qtable[new_state, :]) - qtable[state, action])
# print(f'qtable: {qtable}')
total_rewards = total_rewards + reward
# print(f'total_rewards {total_rewards}')
# Our new state is state
state = new_state
# print(f'new state: {state}')
# If done (if we're dead) : finish episode
if done == True:
break
episode += 1
# Reduce epsilon (because we need less and less exploration)
epsilon = min_epsilon + (max_epsilon - min_epsilon)*np.exp(-decay_rate*episode)
rewards.append(total_rewards)
print ("Score over time: " + str(sum(rewards)/total_episodes))
print(qtable)
print(epsilon)
# +
# Visualize learning outcome
env.reset()
env.render()
# Print the action in every place
#LEFT = 0 DOWN = 1 RIGHT = 2 UP = 3
print(np.argmax(qtable,axis=1).reshape(4,4))
# +
# Exploit!
#All the episoded is the same
# taking the maximum of Qtable value every time.
env.reset()
for episode in range(5):
state = env.reset()
step = 0
done = False
print("****************************************************")
print("EPISODE ", episode)
for step in range(max_steps):
env.render()
# Take the action (index) that have the maximum expected future reward given that state
action = np.argmax(qtable[state,:])
new_state, reward, done, info = env.step(action)
if done:
break
state = new_state
env.render()
env.close()
|
notebooks/OpenAIGym_FrozenLake.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="uQJ6xfn_HlSP"
# # CS271P - Lab #1 - Lets get collabing
# + id="yKE-jNq7HTS7"
# !pip install torch matplotlib sklearn scipy sklearn pandas numpy
# + [markdown] id="u1WyjJPqHfj3"
# ## Lets setup dependencies
# + id="8m8AytE6HhE7"
from google.colab import drive
drive.mount('/content/gdrive')
# + id="NT4VABuMITpb"
# #! mkdir -p cs271p
# + id="vzLOy4ZLIX5B"
# %cd /content/gdrive/MyDrive/cs271p
# + id="5hbAwngX_hms"
# !ls data
# + [markdown] id="nnSSGOlvdH0Q"
# -------------------------------------------------------------------------------------------------------------------------------------
#
# If FIW is used or found useful please cite related, https://web.northeastern.edu/smilelab/fiw/publications.html
# -------------------------------------------------------------------------------------------------------------------------------------
#
# 6 July 2020 (v 0.2.0)
#
# RFIW 2020 (https://web.northeastern.edu/smilelab/rfiw2020/), held as an IEEE FG Challenge, is made up of 3 tasks. Specifically, kinship verification (T-1), Tri-Subject Verification (T-2), and Search & Retrieval (T-3). For this, Family IDs are split into 3 sets (i.e., train, val, and test). Train and val were provided for development purposes, while the test was reserved for "blind" evaluation. Now, data and labels are provided for each. As reported in the white paper (downloadable via https://arxiv.org/abs/2002.06303 or https://www.computer.org/csdl/proceedings-article/fg/2020/307900a877/1kecJ3M0dZC), the test set is used to report the final performance. Thus, both train and validation are designated for training the final models deployed for evaluating the test set.
#
# Here we provide downloadable links for each task, along with links to learn more about the tasks (i.e., as reported in white paper pointed to above):
#
# ====================
# Kinship Verification (T-1)
# ====================
# Original Codalab portal, https://competitions.codalab.org/competitions/21843
#
# TRAIN :
# - Images: https://www.dropbox.com/s/k7uest3kzfqfejd/train-faces.zip?dl=0
# - Pair List (CSV): https://www.dropbox.com/s/b6sak9ztgqpjalm/train-pairs.csv?dl=0
#
# VALIDATION:
# - Images: https://www.dropbox.com/s/vnplu700aj6myj2/val-faces.zip?dl=0
# - Pair List (CSV): https://1drv.ms/u/s!AkDk_XdBkJ9wgocNDTeTlxm_gMyr_w?e=EJC5Ow
#
# ====================
# Tri-subject Verification (T-2)
# ====================
# Original Codalab portal, https://competitions.codalab.org/competitions/22117
#
# TRAIN
# - Images: https://1drv.ms/u/s!AkDk_XdBkJ9whucTlnSpGRK0PERUmQ?e=t46GLs
# - Triplet list (CSV), https://1drv.ms/u/s!AkDk_XdBkJ9whucPNNCLTLdVASCpmQ?e=TJrWdb
#
# VAL
# - Images: https://1drv.ms/u/s!AkDk_XdBkJ9whucUb_esMg9C74-lGw?e=1em9Qv
# - Triplet List (CSV): https://1drv.ms/u/s!AkDk_XdBkJ9whucS8n6_PNSyZuQclA?e=LzcK5h
#
#
# TEST
# - Images: https://www.dropbox.com/sh/fnkyhmh6hsv9dur/AADfrejH6lnpblB6XjlS5au2a?dl=0
# - Triplet List (CSV): https://1drv.ms/u/s!AkDk_XdBkJ9wh5BKGCXNuF1kRd3gNw?e=36c1eu
#
#
# ====================
# Search and Retrieval (T-3)
# ====================
# Original Codalab portal, https://competitions.codalab.org/competitions/22152
#
# --- README (MARKDOWN), https://1drv.ms/u/s!AkDk_XdBkJ9wgat1WAl87XfYbMwDqg?e=rJbop9
#
# *TRAIN
# -- Face Data, https://1drv.ms/u/s!AkDk_XdBkJ9wgatyw-PBj1RCh3x9yQ?e=ufdqkm
# --- Triplet list (CSV),
#
# *VAL
# --- Face Data, https://1drv.ms/u/s!AkDk_XdBkJ9wgbklQJ85kYZEHcMPPQ?e=hkNgLp (Probes) and https://1drv.ms/u/s!AkDk_XdBkJ9wgbkkA1QMlrxpZuZj1Q?e=ILUSIb (Gallery)
# --- Probes Labeled (CSV), https://1drv.ms/x/s!AkDk_XdBkJ9wgdp223FQO1FMAViTCA?e=6gmyC2 (Probes, unlabled) https://1drv.ms/u/s!AkDk_XdBkJ9wgdFPn8YdEFfhC_65yw?e=3FoHzF (Gallery)
# --- List Unlabeled (CSV), https://1drv.ms/u/s!AkDk_XdBkJ9wgbklQJ85kYZEHcMPPQ?e=hkNgLp (Probes) and https://1drv.ms/u/s!AkDk_XdBkJ9wgbkkA1QMlrxpZuZj1Q?e=ILUSIb (Gallery)
# --- Probes Labeled (CSV), https://1drv.ms/x/s!AkDk_XdBkJ9whucS8n6_PNSyZuQclA?e=T2H9i6
#
# *TEST
# --- Face Data, https://1drv.ms/u/s!AkDk_XdBkJ9wh5AbPxntsKa1dEyw6w?e=XeZO5l (Probes) and https://1drv.ms/u/s!AkDk_XdBkJ9wh5AaXtnDqwmUTCVo_w?e=vuvNq9 (Gallery)
# --- Face List (CSV), https://1drv.ms/x/s!AkDk_XdBkJ9wh5AeUdNM2nZq0m5Ngw?e=dyu7gt (Probes) and https://1drv.ms/x/s!AkDk_XdBkJ9wh5AczwHPRVKrNP9_ig?e=e1eFAX (Gallery)
# --- Ground-truth labeled (CSV), https://1drv.ms/x/s!AkDk_XdBkJ9wh5AdoeaaNepWFYOTJQ?e=ogqZFC
# --- Sample output (CSV), https://1drv.ms/u/s!AkDk_XdBkJ9wh5Af-M3YY2MZiaEYJQ?e=nan0q2
#
#
# ---------------------------------------------------------------------------------------------------------------------
# ------
# -------------------------------------------------------------------------------------------------------------------------------------
# 4 December 2019 (v 0.1.2)
# Family Face Data, verification pair lists, and protocols, along with face encodings, available on One Drive, https://1drv.ms/u/s!AkDk_XdBkJ9wh5AgFLcx9r_J4ky6Rg?e=fy3lPV
#
# Codalabs competition hosted as a data challenge workshop in conjunction with the 2020 IEEE FG Conference:
#
# Kinship Verification (T-1)
# https://competitions.codalab.org/competitions/21843
#
# Tri-Subject Verification (T-2)
# https://competitions.codalab.org/competitions/22117
#
# Workshop website:
# https://web.northeastern.edu/smilelab/rfiw2020/
#
#
#
# -------------------------------------------------------------------------------------------------------------------------------------
# 2017 (v 0.1.1)
# Data
# Family List:
# https://1drv.ms/u/s!AkDk_XdBkJ9whk2vCAgT7ly1q85J (csv)
# https://1drv.ms/u/s!AkDk_XdBkJ9whk47NQfRPKLudWPt (numbers)
#
# Family Photo List:
# https://1drv.ms/u/s!AkDk_XdBkJ9whk_6ssK-Z7lOqjN0 (csv)
# https://1drv.ms/u/s!AkDk_XdBkJ9whlHmdLKKTM-GqAhH (numbers)
#
# Relationship LUT
# https://1drv.ms/u/s!AkDk_XdBkJ9whlBp-Ej6Z1QdzNvk (csv)
#
# Face Data
# https://1drv.ms/u/s!AkDk_XdBkJ9whlQQkd2rOXSREro-
#
# Photo-level Labels,
# https://1drv.ms/u/s!AkDk_XdBkJ9whlMaiPhsQuY1P_y8
#
# Family-level Labels
# https://1drv.ms/u/s!AkDk_XdBkJ9whlLtkhZM8c6B-EZh
#
#
#
# Task Evaluations
#
# Kinship Verification (5-fold, no family overlap)
# https://1drv.ms/u/s!AkDk_XdBkJ9whlVoqEj8xx7DJh9z (csv)</a>, <a
# https://1drv.ms/u/s!AkDk_XdBkJ9whldXl5q-zjsqKCXd (mat)
#
# Family Classification (5-fold, no member overlap)
# https://1drv.ms/u/s!AkDk_XdBkJ9whlYaGENBR-nguc1j
#
# + id="P8iGTZKwJEHM"
# ! unzip data/train-faces.zip
# + id="tYBLUvlUBSqi"
# !unzip data/val-faces.zip
# + id="WNIB_0D2Myrk"
# !find ./train-faces -mindepth 1 -type f -name "*.jpg" -printf x | wc -c
# + id="FuJkfAljB_fM"
# !find ./val-faces -mindepth 1 -type f -name "*.jpg" -printf x | wc -c
# + id="JY9rsPyyXZzz"
import os
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import cv2
from sklearn.decomposition import PCA
from mpl_toolkits.mplot3d import Axes3D
from mpl_toolkits.mplot3d import proj3d
from imageio import imread
from skimage.transform import resize
from scipy.spatial import distance
from tqdm import tqdm
# + id="WB8GhSKlTSxT"
train_df = pd.read_csv('./data/train-pairs.csv')
val_df = pd.read_csv('./data/val-pairs.csv')
# + id="PeM8Q8ulXKd2"
train_df.head()
# + id="ytVea2HVXL18"
train_df.info()
# + id="rI_M2IwMCWcq"
train_df.describe()
# + id="jzzAV9RtCYnv"
val_df.head()
# + id="-TfRaiwlChIR"
val_df.info()
# + id="uEl934qpCjX5"
val_df.describe()
# + id="RN7kbbJ9CnmO"
print(f"Train Rows: {train_df.shape[0]}")
print(f"Validation Rows: {val_df.shape[0]}")
# + id="Q99etQVpC5BO"
|
nbs/CS271P_Lab_1_Setup_and_Quick_EDA.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import cv2,os
import numpy as np
from PIL import Image
#
# recognizer = cv2.face.LBPHFaceRecognizer_create()
recognizer=cv2.face.createFisherFaceRecognizer_create()
detector= cv2.CascadeClassifier("haarcascade_frontalface_default.xml")
def getImagesAndLabels(path):
#get the path of all the files in the folder
imagePaths=[os.path.join(path,f) for f in os.listdir(path)]
#create empth face list
faceSamples=[]
#create empty ID list
Ids=[]
#now looping through all the image paths and loading the Ids and the images
for imagePath in imagePaths:
#loading the image and converting it to gray scale
pilImage=Image.open(imagePath).convert('L')
#Now we are converting the PIL image into numpy array
imageNp=np.array(pilImage,'uint8')
#getting the Id from the image
Id = int(os.path.split(imagePath)[-1].split(".")[1])
# extract the face from the training image sample
faces=detector.detectMultiScale(imageNp)
#If a face is there then append that in the list as well as Id of it
for (x,y,w,h) in faces:
faceSamples.append(imageNp[y:y+h,x:x+w])
Ids.append(Id)
return faceSamples,Ids
faces,Ids = getImagesAndLabels('TrainingImage')
recognizer.train(faces, np.array(Ids))
recognizer.save('TrainingImageLabel/trainner.yml')
|
training.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import os
import sys
sys.path.append('../')
import numpy as np
from matplotlib.dates import DateFormatter
import matplotlib.pyplot as plt
import pandas as pd
from pprint import pprint
import datetime
import matplotlib
import src.io as sio
import src.preprocessing as spp
import src.fitting as sft
import ipympl
# -
FIRST_COOLDOWN_FOLDER = sio.get_folderpath("20201217_FirstCooldown")
# +
# Temperature
df1 = sio.read_tm224_data("temperature-monitoring01_LN2.xls", FIRST_COOLDOWN_FOLDER)
df2 = sio.read_tm224_data("temperature-monitoring02_LN2.xls", FIRST_COOLDOWN_FOLDER)
dft = pd.concat([df1])
df1 = sio.read_tpg_data("pressure-monitoring01_LN2", FIRST_COOLDOWN_FOLDER)
dfp = pd.concat([df1])
# +
fig, ax = plt.subplots()
myFmt = DateFormatter("%H:%M\n%a %d")
ax.xaxis.set_major_formatter(myFmt)
ax.set_ylabel(r"Temperature (K)")
ax.plot(dft["MPL_datetimes"], dft["Baseplate"], color="C1", label="Baseplate")
# Sensor location was changed
ax.plot(dft["MPL_datetimes"], dft["Input C1"], color="C1")
ax.plot(dft["MPL_datetimes"], dft["Magnet Base"], color="C3", label="Magnet Base")
ax.plot(dft["MPL_datetimes"], dft["Tip Holder"], color="C2", label="Tip Holder")
ax.legend()
ax.set_ylim([290, 310])
ax2 = ax.twinx()
myFmt = DateFormatter("%H:%M\n%a-%d")
ax2.xaxis.set_major_formatter(myFmt)
# Pressure
ax2.set_ylabel(r"Main Pressure (mbar)", color="C0")
ax2.set_yscale("log", base=10)
ax2.tick_params(axis='y', labelcolor="C0")
ax2.plot(dfp["MPL_datetimes"], dfp["Main"], "-", color="C0")
sio.savefig("cooldown_LN2_outer_bath", FIRST_COOLDOWN_FOLDER)
# -
# +
fig, ax = plt.subplots(figsize=(10, 8))
myFmt = DateFormatter("%H:%M\n%a-%d")
ax.xaxis.set_major_formatter(myFmt)
# Pressure
ax.set_ylabel(r"Main Pressure (mbar)", color="C0")
ax.set_yscale("log", base=10)
ax.tick_params(axis='y', labelcolor="C0")
ax.plot(dfp["MPL_datetimes"], dfp["Main"], "-", color="C0")
# -
# # Cooling from 300 K to 80 K (LN2)
# Temperature
df1 = sio.read_tm224_data("temperature-monitoring01_LN2.xls", FIRST_COOLDOWN_FOLDER)
df2 = sio.read_tm224_data("temperature-monitoring02_LN2.xls", FIRST_COOLDOWN_FOLDER)
df3 = sio.read_tm224_data("temperature-monitoring03_LN2.xls", FIRST_COOLDOWN_FOLDER)
df4 = sio.read_tm224_data("temperature-monitoring04_LN2.xls", FIRST_COOLDOWN_FOLDER)
df5 = sio.read_tm224_data("temperature-monitoring05_LN2.xls", FIRST_COOLDOWN_FOLDER)
df6 = sio.read_tm224_data("temperature-monitoring06_LN2.xls", FIRST_COOLDOWN_FOLDER)
dft = pd.concat([df1, df2, df3, df4, df5, df6])
# +
fig, ax = plt.subplots()
myFmt = DateFormatter("%H:%M\n%a %d")
ax.xaxis.set_major_formatter(myFmt)
ax.set_ylabel(r"Temperature (K)")
ax.plot(dft["MPL_datetimes"], dft["Baseplate"], color="C1", label="Baseplate")
# Sensor location was changed
ax.plot(dft["MPL_datetimes"], dft["Input C1"], color="C1")
ax.plot(dft["MPL_datetimes"], dft["Magnet Base"], color="C3", label="Magnet Base")
ax.plot(dft["MPL_datetimes"], dft["Tip Holder"], color="C2", label="Tip Holder")
ax.legend()
sio.savefig("cooldown_300K_to80K_LN2", FIRST_COOLDOWN_FOLDER)
# -
# # Cooling from 80 K to 4 K (LHe)
# +
# Temperature
df7 = sio.read_tm224_data("temperature-monitoring07_LN2.xls", FIRST_COOLDOWN_FOLDER)
df8 = sio.read_tm224_data("temperature-monitoring08_LN2.xls", FIRST_COOLDOWN_FOLDER)
df9 = sio.read_tm224_data("temperature-monitoring09_LN2.xls", FIRST_COOLDOWN_FOLDER)
df10 = sio.read_tm224_data("temperature-monitoring10_LN2.xls", FIRST_COOLDOWN_FOLDER)
df11 = sio.read_tm224_data("temperature-monitoring11_LN2.xls", FIRST_COOLDOWN_FOLDER)
df12 = sio.read_tm224_data("temperature-monitoring12_LN2.xls", FIRST_COOLDOWN_FOLDER)
df13 = sio.read_tm224_data("temperature-monitoring13_LN2.xls", FIRST_COOLDOWN_FOLDER)
df14 = sio.read_tm224_data("temperature-monitoring14_LN2.xls", FIRST_COOLDOWN_FOLDER)
df15 = sio.read_tm224_data("temperature-monitoring15_LN2.xls", FIRST_COOLDOWN_FOLDER)
df16 = sio.read_tm224_data("temperature-monitoring16_LHe.xls", FIRST_COOLDOWN_FOLDER)
dft = pd.concat([df7, df8, df9, df10, df11, df12, df13, df14, df15, df16])
# +
fig, ax = plt.subplots()
myFmt = DateFormatter("%H:%M\n%a %d")
ax.xaxis.set_major_formatter(myFmt)
ax.set_ylabel(r"Temperature (K)")
ax.plot(dft["MPL_datetimes"], dft["Baseplate"], color="C1", label="Baseplate")
ax.plot(dft["MPL_datetimes"], dft["Magnet Base"], color="C3", label="Magnet Base")
ax.plot(dft["MPL_datetimes"], dft["Tip Holder"], color="C2", label="Tip Holder")
ax.legend()
sio.savefig("cooldown_80K_emptyLN2_LHe", FIRST_COOLDOWN_FOLDER)
# -
# # Hold time at 4 K (LHe)
# +
# Temperature
df17 = sio.read_tm224_data("temperature-monitoring17_LHe.xls", FIRST_COOLDOWN_FOLDER)
df18 = sio.read_tm224_data("temperature-monitoring18_LHe.xls", FIRST_COOLDOWN_FOLDER)
dft = pd.concat([df17, df18])
# +
fig, ax = plt.subplots()
myFmt = DateFormatter("%H:%M\n%a %d")
ax.xaxis.set_major_formatter(myFmt)
ax.set_ylabel(r"Temperature (K)")
ax.plot(dft["MPL_datetimes"], dft["Baseplate"], color="C1", label="Baseplate")
ax.plot(dft["MPL_datetimes"], dft["Magnet Base"], color="C3", label="Magnet Base")
ax.plot(dft["MPL_datetimes"], dft["Tip Holder"], color="C2", label="Tip Holder")
ax.legend()
sio.savefig("holdtime_LHe", FIRST_COOLDOWN_FOLDER)
# -
# # Base pressure
df1 = sio.read_tpg_data("pressure-monitoring04_LHe", FIRST_COOLDOWN_FOLDER)
df2 = sio.read_tpg_data("pressure-monitoring05_LHe", FIRST_COOLDOWN_FOLDER)
df3 = sio.read_tpg_data("pressure-monitoring06_LHe", FIRST_COOLDOWN_FOLDER)
dfp = pd.concat([df2, df3])
# +
fig, ax = plt.subplots()
myFmt = DateFormatter("%H:%M\n%a %d")
ax.xaxis.set_major_formatter(myFmt)
# Pressure
ax.set_ylabel(r"Main Pressure (mbar)")
ax.set_yscale("log", base=10)
ax.plot(dfp["MPL_datetimes"], dfp["Main"], "-", color="C0")
ax.set_ylim([5e-10, 4e-9])
sio.savefig("pressure_LHe", FIRST_COOLDOWN_FOLDER)
# -
# # Other stuff
# +
df1 = sio.read_tpg_data("pressure-monitoring01_LN2", FIRST_COOLDOWN_FOLDER)
df2 = sio.read_tpg_data("pressure-monitoring02_LN2", FIRST_COOLDOWN_FOLDER)
df3 = sio.read_tpg_data("pressure-monitoring03_LN2", FIRST_COOLDOWN_FOLDER)
dfp = pd.concat([df1, df2, df3])
# Temperature
df1 = sio.read_tm224_data("temperature-monitoring01_LN2.xls", FIRST_COOLDOWN_FOLDER)
df2 = sio.read_tm224_data("temperature-monitoring02_LN2.xls", FIRST_COOLDOWN_FOLDER)
df3 = sio.read_tm224_data("temperature-monitoring03_LN2.xls", FIRST_COOLDOWN_FOLDER)
df4 = sio.read_tm224_data("temperature-monitoring04_LN2.xls", FIRST_COOLDOWN_FOLDER)
df5 = sio.read_tm224_data("temperature-monitoring05_LN2.xls", FIRST_COOLDOWN_FOLDER)
df6 = sio.read_tm224_data("temperature-monitoring06_LN2.xls", FIRST_COOLDOWN_FOLDER)
dft = pd.concat([df1, df2, df3, df4, df5, df6])
# -
# ## Alternative way using text matching
# Note that this is slow and expensive
dfp = pd.DataFrame()
for file in sio.get_filenames_matching("pressure-monitoring", FIRST_COOLDOWN_FOLDER):
dfp = dfp.append(sio.read_tpg_data(file, FIRST_COOLDOWN_FOLDER), ignore_index=True)
dft = pd.DataFrame()
for file in sio.get_filenames_matching("temperature-monitoring", FIRST_COOLDOWN_FOLDER):
dft = dft.append(sio.read_tm224_data(file, FIRST_COOLDOWN_FOLDER), ignore_index=True)
# +
fig, ax2 = plt.subplots(figsize=(10, 8))
myFmt = DateFormatter("%H:%M\n%a")
ax2.xaxis.set_major_formatter(myFmt)
ax2.set_ylabel(r"Temperature (K)")
ax2.plot(dft["MPL_datetimes"], dft["Baseplate"], color="C1", label="Baseplate T")
# Sesnor location was changed
ax2.plot(dft["MPL_datetimes"], dft["Input C1"], color="C1")
ax2.plot(dft["MPL_datetimes"], dft["Magnet Base"], color="C3", label="Magnet Base T")
ax2.plot(dft["MPL_datetimes"], dft["Tip Holder"], color="C2", label="Tip Holder T")
ax2.legend()
# +
fig, ax = plt.subplots(figsize=(10, 8))
myFmt = DateFormatter("%H:%M\n%a")
ax.xaxis.set_major_formatter(myFmt)
# Pressure
ax.set_ylabel(r"Main Pressure (mbar)", color="C0")
ax.set_yscale("log", base=10)
ax.tick_params(axis='y', labelcolor="C0")
ax.plot(dfp["MPL_datetimes"], dfp["Main"], "-", color="C0")
x, y = sft.time_extrapolation(dfp, "Main", end_date="19-Dec-20 15:00", start_index=95000, fit="logarithmic")
ax.plot(x, y, "--")
# +
x = np.linspace(10, 1e5, 1000)
a, b = 1e2, -1
y = a + b * np.log(x)
fig, ax = plt.subplots()
ax.set_yscale("log", base=10)
ax.plot(x, y)
def func(x, a, b, c):
return a + b * np.log(c*x)
from scipy.optimize import curve_fit
popt, pcov = curve_fit(func, xdata=x, ydata=y)
x = np.linspace(5e4, 5e5, 1000)
ax.plot(x, func(x, *popt), "--")
print(popt)
# -
# # LHe level and temperature
# +
fig, (ax, ax2) = plt.subplots(nrows=2, sharex=True, figsize=(10, 8))
dft = sio.read_tm224_data("temperature-monitoring16_LHe.xls", FIRST_COOLDOWN_FOLDER)
myFmt = DateFormatter("%H:%M")
ax.xaxis.set_major_formatter(myFmt)
ax.set_ylabel(r"Temperature (K)")
ax.plot(dft["MPL_datetimes"], dft["Baseplate"], color="C1", label="Baseplate")
ax.plot(dft["MPL_datetimes"], dft["Magnet Base"], color="C3", label="Magnet Base")
ax.plot(dft["MPL_datetimes"], dft["Tip Holder"], color="C2", label="Tip Holder")
x, y, _mod, y_mod = sft.time_extrapolation_lmfit(dft, "Baseplate", end_date="24-Dec-20 10:00", start_index=19000, fit="linear")
ax.plot(x, y, "-o", color="C1")
sft.setpointy_reach_time(x, y, 4.5)
ax.legend()
ax2.set_ylabel(r"LHe level (mm)")
time_strings = ["23-Dec-20 22:10", "23-Dec-20 22:24", "23-Dec-20 22:48", "23-Dec-20 22:58", "23-Dec-20 23:45", "24-Dec-20 00:20", "24-Dec-20 00:43"]
level = [326, 318, 310, 309, 282, 260, 238]
time_object_mpl = []
for time_string in time_strings:
time_object_mpl.append(matplotlib.dates.date2num(datetime.datetime.strptime(time_string, "%d-%b-%y %H:%M")))
ax2.plot(time_object_mpl, level, "--o", color="C0", label="LHe level")
#sio.savefig("temperature-monitoring_level-monitoring", FIRST_COOLDOWN_FOLDER)
# -
|
notebooks/20201217_FirstCooldown.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.6
# language: python
# name: python3.6
# ---
# # Cell Migration Quantification
# <div class="alert alert-info">
# <h3 style="margin-top: 0;"> Instructions <i class="fa fa-info-circle"></i></h3>
# Run each cell. More useful instructions will be added later.
# </div>
# + genepattern={"name": "Login", "server": "https://cloud.genepattern.org/gp", "type": "auth"}
# Requires GenePattern Notebook: pip install genepattern-notebook
import gp
import genepattern
# Username and password removed for security reasons.
genepattern.display(genepattern.session.register("https://cloud.genepattern.org/gp", "", ""))
# + [markdown] heading_collapsed=true
# # Requirements
# + [markdown] heading_collapsed=true hidden=true
# ## For developers
# + [markdown] hidden=true
# <div class="alert alert-warning">
# <h3 style="margin-top: 0;"> Warning <i class="fa fa-exclamation-triangle"></i></h3>
# LMFIT has been removed --> No need to install it anymore!
# </div>
# + [markdown] hidden=true
# ```
# Python 3.6 Kernel, but no reason why this won't work on 3.7 if these libraries are present
# Collecting lmfit==0.9.12
# Collecting uncertainties>=3.0 (from lmfit==0.9.12)
# Collecting scipy>=0.17 (from lmfit==0.9.12)
# Downloading https://files.pythonhosted.org/packages/7f/5f/c48860704092933bf1c4c1574a8de1ffd16bf4fde8bab190d747598844b2/scipy-1.2.1-cp36-cp36m-manylinux1_x86_64.whl (24.8MB)
# 100% |████████████████████████████████| 24.8MB 236kB/s eta 0:00:01 68% |██████████████████████ | 17.0MB 41.9MB/s eta 0:00:01
# Collecting six>1.10 (from lmfit==0.9.12)
# Downloading https://files.pythonhosted.org/packages/73/fb/00a976f728d0d1fecfe898238ce23f502a721c0ac0ecfedb80e0d88c64e9/six-1.12.0-py2.py3-none-any.whl
# Collecting asteval>=0.9.12 (from lmfit==0.9.12)
# Collecting numpy>=1.10 (from lmfit==0.9.12)
# Downloading https://files.pythonhosted.org/packages/35/d5/4f8410ac303e690144f0a0603c4b8fd3b986feb2749c435f7cdbb288f17e/numpy-1.16.2-cp36-cp36m-manylinux1_x86_64.whl (17.3MB)
# 100% |████████████████████████████████| 17.3MB 247kB/s eta 0:00:01
# Installing collected packages: uncertainties, numpy, scipy, six, asteval, lmfit
# Found existing installation: numpy 1.14.0
# Uninstalling numpy-1.14.0:
# Successfully uninstalled numpy-1.14.0
# The scripts f2py, f2py3 and f2py3.6 are installed in '/home/jovyan/.local/bin' which is not on PATH.
# Consider adding this directory to PATH or, if you prefer to suppress this warning, use --no-warn-script-location.
# Found existing installation: scipy 1.0.0
# Uninstalling scipy-1.0.0:
# Successfully uninstalled scipy-1.0.0
# Found existing installation: lmfit 0.9.12
# Uninstalling lmfit-0.9.12:
# Successfully uninstalled lmfit-0.9.12
# Successfully installed asteval-0.9.13 lmfit-0.9.12 numpy-1.16.2 scipy-1.2.1 six-1.12.0 uncertainties-3.0.3
# also:
#
# opencv-python 192.168.3.11
# seaborn == 0.9.0
# ```
# + [markdown] heading_collapsed=true hidden=true
# ## Define some functions and import some others
# + hidden=true
# %matplotlib inline
# from lmfit import Minimizer, Parameters, report_fit
import cv2
import numpy as np
from skimage import draw
from skimage import io
import matplotlib.pyplot as plt
from scipy import optimize
import humanfriendly
from timeit import default_timer as timer
import os
import pandas as pd
import seaborn as sns
from cuzcatlan import add_stat_annotation
# + hidden=true
def cost(params):
global im2
maxy, maxx = im2.shape
maxr = min(maxx,maxy)/2
area = maxy*maxx
x0= params[0]
y0 = params[1]
r0 = params[2]
coords = draw.circle(y0, x0, r0, shape=im2.shape)
template = np.zeros_like(im2) #set all values to be zero
template[coords] = 1
mask_size = np.sum(template)
cell_pixels_covered_by_mask = np.sum(template&im2)
penalty_harshness = 10
score = mask_size - penalty_harshness*cell_pixels_covered_by_mask
score = score/area
return -score
# -
# # Analyses
# ## Find cells on control
# + nbtools={"description": "", "name": "create_mask", "param_values": {"control": "analyses/MDA231_stopper_1_c3.tif", "kernel_size": "2", "output_var": "setup", "setup": "setup"}, "show_code": false, "type": "uibuilder"}
setup = {}
@genepattern.build_ui
def create_mask(control='analyses/MDA231_stopper_1_c3.tif',kernel_size=2,setup='setup'):
beginning_of_time = timer()
# Read image
im_in = cv2.imread(control, cv2.IMREAD_GRAYSCALE)
# Threshold. ==> These could be parameters
# Set values equal to or above 20 to 0.
# Set values below 20 to 255.
th, im_th = cv2.threshold(im_in, 20, 255, cv2.THRESH_BINARY_INV)
# Copy the thresholded image.
im_floodfill = im_th.copy()
# Mask used to flood filling.
# Notice the size needs to be 2 pixels than the image.
h, w = im_th.shape[:2]
mask = np.zeros((h+2, w+2), np.uint8)
# Floodfill from point (0, 0)
cv2.floodFill(im_floodfill, mask, (0,0), 255);
# Invert floodfilled image
im_floodfill_inv = cv2.bitwise_not(im_floodfill)
# Combine the two images to get the foreground.
im_out = im_th | im_floodfill_inv
io.imsave(fname='temp_output.png', arr=im_out)
# im_out_inv = cv2.bitwise_not(im_out)
# dilate the mask:
k_size = kernel_size
k_half = k_size/2
kernel = np.ones((k_size,k_size),np.uint8)
coords = draw.circle(k_half, k_half, k_half, shape=im_th.shape)
kernel[coords] = 1
erosion = cv2.erode(im_out,kernel,iterations = 1)
dilation = cv2.dilate(cv2.bitwise_not(erosion),kernel,iterations = 1)
# cells_mask = cv2.bitwise_not(dilation)
cells_mask = dilation/255
setup['control_grayscale'] = im_in
setup['mask'] = cells_mask
io.imshow(cells_mask)
plt.show()
print("Note that a value of ~1 means that pixel belongs to the mask and it is rendered as white.")
print("A value of 0 means it deos not belong the mask and it is rendered as black.")
end_of_time = timer()
spanned = end_of_time - beginning_of_time
print(f"\nDone with this part of the workflow. Elapsed time: {humanfriendly.format_timespan(spanned)}.")
return setup
# -
# ## Find migration region
# + nbtools={"description": "", "name": "find_migration_region", "param_values": {"finesse": "6", "output_var": "setup", "setup": "setup"}, "show_code": false, "type": "uibuilder"}
@genepattern.build_ui
def find_migration_region(setup='setup',finesse=20):
beginning_of_time = timer()
global im2
im2 = setup['control_grayscale']>0.2
im2 = im2.astype(int)
maxy, maxx = im2.shape
minx, miny = (0,0)
maxr = min(maxx,maxy)/2
x0 = im2.shape[1]/2
y0 = im2.shape[0]/2
r0 = min(im2.shape[1],im2.shape[0])/4
xmid = im2.shape[1]/2
ymid = im2.shape[0]/2
rmid = min(xmid,ymid)
coarse = finesse*1/3
# do fit, here with leastsq model
# minner = Minimizer(cost_obj, params)
x_slice = slice(xmid-x0/4, xmid+x0/4, (x0/2)/coarse)
y_slice = slice(ymid-x0/4, ymid+x0/4, (y0/2)/coarse)
r_slice = slice(rmid-x0/4, rmid+x0/4, (r0/2)/finesse)
rranges = (x_slice,y_slice, r_slice)
print('About to perform optimization. This would take a few seconds to a few minutes.')
resbrute = optimize.brute(cost, rranges,full_output=True)
# result = minner.minimize(method='brute',ranges=rranges)
# report_fit(result)
print('############')
method = 'scipy.brute'
opt_params = resbrute[0]
x_opt = opt_params[0]
y_opt = opt_params[1]
r_opt = opt_params[2]
print("Optimal paramters are", [x_opt,y_opt,r_opt])
f, ax = plt.subplots()
circle = plt.Circle((x_opt, y_opt), r_opt, alpha = 0.5)
ax.imshow(im2, cmap='gray', interpolation='nearest')
ax.add_artist(circle)
print('############')
print(f'Method "{method}""\tobjective={cost([x_opt,y_opt,r_opt])}')
print('############')
plt.show()
coords = draw.circle(y0, x0, r0, shape=im2.shape)
template = np.zeros_like(im2) #set all values to be zero
template[coords] = 1
setup['im2'] = im2
setup['opt_params'] = opt_params
setup['x_opt'] = x_opt
setup['y_opt'] = y_opt
setup['r_opt'] = r_opt
setup['circle'] = circle
setup['coords'] = coords
setup['template'] = template
end_of_time = timer()
spanned = end_of_time - beginning_of_time
print(f"\nDone with this part of the workflow. Elapsed time: {humanfriendly.format_timespan(spanned)}.")
return setup
# -
# ## Quantify migration (load images & make final plot)
# + nbtools={"description": "", "name": "load_images", "param_values": {"folder": "images", "list_of_groups": "stopper, untreated, AGR2ab, Taxol, IgG", "output_var": "", "setup": "setup", "verbose": "false"}, "show_code": false, "type": "uibuilder"}
@genepattern.build_ui
def load_images(list_of_groups,folder='images',setup=setup,verbose=False):
all_files = sorted(os.listdir(folder))
filename = []
condition = []
percent_covered = []
if isinstance(list_of_groups, str):
list_of_groups = list_of_groups.split(', ')
for category in list_of_groups:
curr_files = [i for i in all_files if category in i]
if verbose:
print(category,curr_files)
for image in curr_files:
if verbose:
print(f"\tWorking with {image}")
current_filename = os.path.join(folder,image)
im = io.imread(current_filename,as_gray=True)
im01 = im>0
im01 = im01.astype(int)
if False:
f, ax = plt.subplots()
ax.imshow(im01, cmap='gray')
circle = plt.Circle((setup['x_opt'], setup['y_opt']), setup['r_opt'], alpha = 0.5)
ax.add_artist(circle)
plt.show()
# create the mask on top of this image
coords = draw.circle(setup['y_opt'], setup['x_opt'], setup['r_opt'], shape=im01.shape)
template = np.zeros_like(im01) #set all values to be zero
template[coords] = 1
cell_pixels_covered_by_mask = np.sum(template&im01)
# print(100*cell_pixels_covered_by_mask/np.sum(template))
filename.append(image)
condition.append(category)
percent_covered.append(100*cell_pixels_covered_by_mask/np.sum(template))
df = pd.DataFrame({"condition": condition, "percent_covered": percent_covered, "filename" : filename})
f, ax = plt.subplots(figsize=(16,9))
ax=sns.barplot(x="condition", y="percent_covered", data=df, dodge=1, ax=ax, ci=None)
ax=sns.stripplot(x="condition", y="percent_covered", data=df, ax=ax, linewidth=2, edgecolor='gray')
add_stat_annotation(ax, data=df, x='condition', y='percent_covered',
boxPairList=[("untreated", "AGR2ab"),("untreated", "Taxol"),("untreated", "IgG")],
test='Mann-Whitney', textFormat='star', loc='inside', verbose=2)
return
# -
|
Cell Migration Quantification.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Practical example
# ## Importing the relevant libraries
import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
import seaborn as sns
sns.set()
# ## Loading the raw data
raw_data = pd.read_csv('1.04. Real-life example.csv')
raw_data.head()
# ## Preprocessing
# ### Exploring the descriptive statistics of the variables
raw_data.describe(include='all')
# ### Determining the variables of interest
data = raw_data.drop(['Model'],axis=1)
data.describe(include='all')
# ### Dealing with missing values
data.isnull().sum()
data_no_mv = data.dropna(axis=0)
data_no_mv.describe(include='all')
# ### Exploring the PDFs
sns.distplot(data_no_mv['Price'])
# ### Dealing with outliers
q = data_no_mv['Price'].quantile(0.99)
data_1 = data_no_mv[data_no_mv['Price']<q]
data_1.describe(include='all')
sns.distplot(data_1['Price'])
sns.distplot(data_no_mv['Mileage'])
q = data_1['Mileage'].quantile(0.99)
data_2 = data_1[data_1['Mileage']<q]
sns.distplot(data_2['Mileage'])
sns.distplot(data_no_mv['EngineV'])
data_3 = data_2[data_2['EngineV']<6.5]
sns.distplot(data_3['EngineV'])
sns.distplot(data_no_mv['Year'])
q = data_3['Year'].quantile(0.01)
data_4 = data_3[data_3['Year']>q]
sns.distplot(data_4['Year'])
data_cleaned = data_4.reset_index(drop=True)
data_cleaned.describe(include='all')
# ## Checking the OLS assumptions
# +
f, (ax1, ax2, ax3) = plt.subplots(1, 3, sharey=True, figsize =(15,3))
ax1.scatter(data_cleaned['Year'],data_cleaned['Price'])
ax1.set_title('Price and Year')
ax2.scatter(data_cleaned['EngineV'],data_cleaned['Price'])
ax2.set_title('Price and EngineV')
ax3.scatter(data_cleaned['Mileage'],data_cleaned['Price'])
ax3.set_title('Price and Mileage')
plt.show()
# -
sns.distplot(data_cleaned['Price'])
# ### Relaxing the assumptions
log_price = np.log(data_cleaned['Price'])
data_cleaned['log_price'] = log_price
data_cleaned
# +
f, (ax1, ax2, ax3) = plt.subplots(1, 3, sharey=True, figsize =(15,3))
ax1.scatter(data_cleaned['Year'],data_cleaned['log_price'])
ax1.set_title('Log Price and Year')
ax2.scatter(data_cleaned['EngineV'],data_cleaned['log_price'])
ax2.set_title('Log Price and EngineV')
ax3.scatter(data_cleaned['Mileage'],data_cleaned['log_price'])
ax3.set_title('Log Price and Mileage')
plt.show()
# -
data_cleaned = data_cleaned.drop(['Price'],axis=1)
# ### Multicollinearity
data_cleaned.columns.values
from statsmodels.stats.outliers_influence import variance_inflation_factor
variables = data_cleaned[['Mileage','Year','EngineV']]
vif = pd.DataFrame()
vif["VIF"] = [variance_inflation_factor(variables.values, i) for i in range(variables.shape[1])]
vif["features"] = variables.columns
vif
data_no_multicollinearity = data_cleaned.drop(['Year'],axis=1)
# ## Create dummy variables
data_with_dummies = pd.get_dummies(data_no_multicollinearity, drop_first=True)
data_with_dummies.head()
# ### Rearrange a bit
data_with_dummies.columns.values
cols = ['log_price', 'Mileage', 'EngineV', 'Brand_BMW',
'Brand_Mercedes-Benz', 'Brand_Mitsubishi', 'Brand_Renault',
'Brand_Toyota', 'Brand_Volkswagen', 'Body_hatch', 'Body_other',
'Body_sedan', 'Body_vagon', 'Body_van', 'Engine Type_Gas',
'Engine Type_Other', 'Engine Type_Petrol', 'Registration_yes']
data_preprocessed = data_with_dummies[cols]
data_preprocessed.head()
# ## Linear regression model
# ### Declare the inputs and the targets
targets = data_preprocessed['log_price']
inputs = data_preprocessed.drop(['log_price'],axis=1)
# ### Scale the data
# +
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(inputs)
# -
inputs_scaled = scaler.transform(inputs)
# ### Train Test Split
# +
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(inputs_scaled, targets, test_size=0.2, random_state=365)
# -
# ### Create the regression
reg = LinearRegression()
reg.fit(x_train,y_train)
y_hat = reg.predict(x_train)
plt.scatter(y_train, y_hat)
plt.xlabel('Targets (y_train)',size=18)
plt.ylabel('Predictions (y_hat)',size=18)
plt.xlim(6,13)
plt.ylim(6,13)
plt.show()
sns.distplot(y_train - y_hat)
plt.title("Residuals PDF", size=18)
reg.score(x_train,y_train)
# ### Finding the weights and bias
reg.intercept_
reg.coef_
reg_summary = pd.DataFrame(inputs.columns.values, columns=['Features'])
reg_summary['Weights'] = reg.coef_
reg_summary
data_cleaned['Brand'].unique()
|
Resources/Data-Science/Machine-Learning/Multiple-Linear-Regression/sklearn - Linear Regression - Practical Example (Part 4).ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 0.5.2
# language: julia
# name: julia-0.5
# ---
# +
using QuantEcon
using Interpolations
using Distributions
"""
Job Search with Permanent and Transient Components
Authors: <NAME> and <NAME>
transition function of the state process:
w_t = eta_t + thet_t * xi_t,
ln (thet_t) = ln (thet_{t-1}) + ln (u_t).
"""
type Search_Problem_SV
bet::Float64 # the discount factor
c0_tilde::Float64 # the unemployment compensation
sig::Float64 # the coefficient of relative risk aversion
rho::Float64 # the autoregressiion coefficient
gam_u::Float64 # variance of the shock process w.r.t (theta_t) process
gam_xi::Float64 # variance of the (xi_t) process
mu_eta::Float64 # mean of the (eta_t) process
gam_eta::Float64 # variance of the (eta_t) process
thet_min::Float64 # minimum of the thet grid point
thet_max::Float64 # maximum of the thet grid point
thet_size::Int # grid size of thet
thet_grids::Vector{Float64} # grid points of thet
w_min::Float64 # munimum of the w grid point
w_max::Float64 # maximum of the w grid point
w_size::Int # grid size of w
w_grids::Vector{Float64} # grid points of w
mc_size::Int # size of Monte Carlo draws
draws::Vector{Float64} # Monte carlo draws
function Search_Problem_SV(;bet=.95,
c0_tilde=.6,
sig=1.,
rho=.75,
gam_u=1e-4,
gam_xi=5e-4,
mu_eta=0.,
gam_eta=1e-6,
thet_min=1e-3,
thet_max=10.,
thet_size=200,
thet_grids=Array{Float64}(100),
w_min=1e-3,
w_max=10.,
w_size=100,
w_grids=Array{Float64}(100),
mc_size=1000,
draws=Array{Float64}(1000))
# making grid points for (thet, w)
thet_grids = linspace(thet_min, thet_max, thet_size)
w_grids = linspace(w_min, w_max, w_size)
# making Monte Carlo samples
draws = randn(mc_size)
return new(bet, c0_tilde, sig, rho, gam_u, gam_xi, mu_eta, gam_eta,
thet_min, thet_max, thet_size, thet_grids,
w_min, w_max, w_size, w_grids, mc_size, draws)
end
end
# the CRRA utility function
function util_func(w, sigma)
if sigma == 1.0
uw = log.(w)
else
uw = w.^(1. - sigma) / (1. - sigma)
end
return uw
end
# =================== The Bellman Operator ==================== #
function Bellman_operator(sp::Search_Problem_SV, v)
# simplify names
bet, c0_tilde, sig = sp.bet, sp.c0_tilde, sp.sig
rho, gam_u, gam_xi = sp.rho, sp.gam_u, sp.gam_xi
mu_eta, gam_eta = sp.mu_eta, sp.gam_eta
thet_size, thet_grids = sp.thet_size, sp.thet_grids
w_size, w_grids = sp.w_size, sp.w_grids
mc_size, draws = sp.mc_size, sp.draws
# interpolate (and extrapolate) to obtain a function
vf = extrapolate(interpolate((thet_grids, w_grids), v,
Gridded(Linear())), Flat())
c0 = util_func(c0_tilde, sig) # the flow continuation reward
# create empty matrix to store T(v)
new_v = Array{Float64}(thet_size, w_size)
for j = 1:w_size
w = w_grids[j]
# the exit reward at grid point w_j
v1 = util_func(w, sig) / (1. - bet)
# MC samples : eta'
eta_draws = exp.(mu_eta + sqrt(gam_eta) * draws)
# MC samples : xi'
xi_draws = exp.(sqrt(gam_xi) * draws)
for i = 1:thet_size
thet = thet_grids[i]
# MC samples : thet'
thet_draws = exp.(rho * log(thet) + sqrt(gam_u) * draws)
# MC samples : w'
w_draws = eta_draws + thet_draws .* xi_draws
# MC samples : v(thet', w')
intg_draws = Array{Float64}(mc_size)
for k = 1:mc_size
intg_draws[k] = vf[thet_draws[k], w_draws[k]]
end
# the continuation value at grid point (thet_i, w_j)
v2 = c0 + bet * mean(intg_draws)
# the value function at grid point (thet_i, w_j)
new_v[i,j] = max(v1, v2)
end
end
return new_v
end
# ====================== The Jovanovic Operator ======================= #
function Jovanovic_operator(sp::Search_Problem_SV, psi)
# simplify names
bet, c0_tilde, sig = sp.bet, sp.c0_tilde, sp.sig
rho, gam_u, gam_xi = sp.rho, sp.gam_u, sp.gam_xi
mu_eta, gam_eta = sp.mu_eta, sp.gam_eta
thet_size, thet_grids = sp.thet_size, sp.thet_grids
w_size, w_grids = sp.w_size, sp.w_grids
mc_size, draws = sp.mc_size, sp.draws
# interpolate (and extrapolate) to obtain a function
#psi_f = extrapolate(interpolate(thet_grids, psi,
# Gridded(Linear())), Flat())
psi_f = LinInterp(thet_grids, psi)
c0 = util_func(c0_tilde, sig) # the flow continuation reward
# MC samples : eta'
eta_draws = exp.(mu_eta + sqrt(gam_eta) * draws)
# MC samples : xi'
xi_draws = exp.(sqrt(gam_xi) * draws)
# create empty vector (thet_size * 1) to store Q (psi)
new_psi = Array{Float64}(thet_size)
for i = 1:thet_size
# MC samples : thet'
thet = thet_grids[i]
thet_draws = exp.(rho * log(thet) + sqrt(gam_u) * draws)
# MC samples : r(w'), the exit reward
integ_1 = util_func(eta_draws + thet_draws .* xi_draws, sig) / (1. - bet)
# MC samples : psi(thet')
integ_2 = Array{Float64}(mc_size)
for k = 1:mc_size
integ_2[k] = psi_f(thet_draws[k])
end
# MC samples : max{r(w'), psi(thet')}
integ = max.(integ_1, integ_2)
# the i-th element of the vector Q(psi)
new_psi[i] = c0 + bet * mean(integ)
end
return new_psi
end
# +
# Computation time of CVI : different grid sizes
thet_size_vals = [200, 200, 300, 300, 400, 400] # the list of thet grid points
w_size_vals = [200, 400, 200, 400, 200, 400] # the list of w grid points
loops_cvi = 50 # the number of iterations performed for each case
# create empty matrix to store the time taken of CVI
time_cvi = Array{Float64}(loops_cvi, length(thet_size_vals))
# store the sig values used in each simulation
sig_vals = Array{Float64}(length(thet_size_vals))
for j=1:length(thet_size_vals)
sp = Search_Problem_SV(sig=1., thet_size=thet_size_vals[j],
w_size=w_size_vals[j])
psi_0 = ones(sp.thet_size) # initial guess
for i=1:loops_cvi
tic() # start the clock
psi_new = Jovanovic_operator(sp, psi_0)
time_cvi[i,j] = toq() # calculate the time elapsed
psi_0 = psi_new
end
sig_vals[j] = sp.sig
println("Loop $j finished ... ")
end
# key loops for which we want to calculate the time elapsed (CVI)
keyloops_cvi = [10, 20, 50]
# create a vector to store the time elapsed (CVI) for the selected key loops
time_cvi_keyloops = Array{Float64}(length(keyloops_cvi), length(thet_size_vals))
for i=1:length(keyloops_cvi)
for j=1:length(thet_size_vals)
time_cvi_keyloops[i,j] = sum(time_cvi[1:keyloops_cvi[i], j])
end
end
row_1 = time_cvi_keyloops[1,:] # time taken : loop 10, all cases (grid sizes)
row_2 = time_cvi_keyloops[2,:] # time taken : loop 20, all cases (grid sizes)
row_3 = time_cvi_keyloops[3,:] # time taken : loop 50, all cases (grid sizes)
println("")
println("----------------------------------------------------------------")
println(" Computation time CVI : different grid sizes")
println("")
println(" Key parameters : sig = $sig_vals")
println("")
println(" thet_sizes : $thet_size_vals")
println(" w_sizes : $w_size_vals")
println("")
println(" Key loops : $keyloops_cvi")
println("")
println(" Time of CVI (column: grid sizes) : ")
println("")
println(" Loop 10 : $row_1")
println(" Loop 20 : $row_2")
println(" Loop 50 : $row_3")
println("")
println("----------------------------------------------------------------")
println("")
# +
# Computation time of VFI : different grid sizes
thet_size_vals = [200, 200, 300, 300, 400, 400] # the list of thet grid points
w_size_vals = [200, 400, 200, 400, 200, 400] # the list of w grid points
loops_vfi = 50 # the number of iterations performed for each case
# create empty matrix to store the time taken of VFI
time_vfi = Array{Float64}(loops_vfi, length(thet_size_vals))
# store the sig values used in each simulation
sig_vals = Array{Float64}(length(thet_size_vals))
for j=1:length(thet_size_vals)
sp = Search_Problem_SV(sig=1., thet_size=thet_size_vals[j],
w_size=w_size_vals[j])
v_0 = ones(sp.thet_size, sp.w_size) # initial guess (VFI)
for i=1:loops_vfi
tic() # start the clock
v_new = Bellman_operator(sp, v_0)
time_vfi[i,j] = toq() # calculate the time elapsed
v_0 = v_new
end
sig_vals[j] = sp.sig
println("Loop $j finished ... ")
end
# key loops for which we want to calculate the time elapsed (VFI)
keyloops_vfi = [10, 20, 50]
# create a vector to store the time elapsed (VFI) for the selected key loops
time_vfi_keyloops = Array{Float64}(length(keyloops_vfi), length(thet_size_vals))
for i=1:length(keyloops_vfi)
for j=1:length(thet_size_vals)
time_vfi_keyloops[i,j] = sum(time_vfi[1:keyloops_vfi[i], j])
end
end
row_1 = time_vfi_keyloops[1,:] # time taken : loop 10, all cases (grid sizes)
row_2 = time_vfi_keyloops[2,:] # time taken : loop 20, all cases (grid sizes)
row_3 = time_vfi_keyloops[3,:] # time taken : loop 50, all cases (grid sizes)
println("")
println("----------------------------------------------------------------")
println(" Computation time VFI : different grid sizes")
println("")
println(" Key parameters : sig = $sig_vals")
println("")
println(" thet_sizes : $thet_size_vals")
println(" w_sizes : $w_size_vals")
println("")
println(" Key loops : $keyloops_vfi")
println("")
println(" Time of VFI (column: grid sizes) : ")
println("")
println(" Loop 10 : $row_1")
println(" Loop 20 : $row_2")
println(" Loop 50 : $row_3")
println("")
println("----------------------------------------------------------------")
println("")
# +
# Computation time of CVI : different parameter values
sig_vals = [2., 2., 2., 3., 3., 3., 4., 4., 4.] # the list of sig values
rho_vals = [.8, .7, .6, .8, .7, .6, .8, .7, .6] # the list of rho values
loops_cvi = 50 # the number of iterations performed for each case
# create empty matrix to store the time taken of CVI
time_cvi = Array{Float64}(loops_cvi, length(sig_vals))
# create empty matrix to store the grid sizes used for simulation
grid_sizes = Array{Float64}(2)
for j=1:length(sig_vals)
sp = Search_Problem_SV(sig=sig_vals[j], rho=rho_vals[j],
thet_size=300, w_size=300)
psi_0 = ones(sp.thet_size) # initial guess (CVI)
for i=1:loops_cvi
tic() # start the clock
psi_new = Jovanovic_operator(sp, psi_0)
time_cvi[i,j] = toq() # calculate the time elapsed
psi_0 = psi_new
end
println("Loop $j finished ... ")
# record the grid sizes used in simulation
grid_sizes[1], grid_sizes[2] = sp.thet_size, sp.w_size
end
# key loops for which we want to calculate the time elapsed (CVI)
keyloops_cvi = [10, 20, 50]
# create a vector to store the time elapsed (CVI) for the selected key loops
time_cvi_keyloops = Array{Float64}(length(keyloops_cvi), length(sig_vals))
for i=1:length(keyloops_cvi)
for j=1:length(sig_vals)
time_cvi_keyloops[i,j] = sum(time_cvi[1:keyloops_cvi[i], j])
end
end
row_1 = time_cvi_keyloops[1,:] # time taken : loop 10, all cases (grid sizes)
row_2 = time_cvi_keyloops[2,:] # time taken : loop 20, all cases (grid sizes)
row_3 = time_cvi_keyloops[3,:] # time taken : loop 50, all cases (grid sizes)
println("")
println("----------------------------------------------------------------")
println(" Computation time CVI : different parameter values")
println("")
println(" Key parameters : ")
println(" sig = $sig_vals")
println(" rho = $w_size_vals")
println("")
println(" Grid sizes (thet, w) : $grid_sizes")
println("")
println(" Key loops : $keyloops_cvi")
println("")
println(" Time of CVI (column: parameter values) : ")
println("")
println(" Loop 10 : $row_1")
println(" Loop 20 : $row_2")
println(" Loop 50 : $row_3")
println("")
println("----------------------------------------------------------------")
println("")
# +
# Computation time of VFI : different parameter values
sig_vals = [2., 2., 2., 3., 3., 3., 4., 4., 4.] # the list of sig values
rho_vals = [.8, .7, .6, .8, .7, .6, .8, .7, .6] # the list of rho values
loops_vfi = 50 # the number of iterations performed for each case
# create empty matrix to store the time taken of VFI
time_vfi = Array{Float64}(loops_vfi, length(sig_vals))
# create empty matrix to store the grid sizes used for simulation
grid_sizes = Array{Float64}(2)
for j=1:length(sig_vals)
sp = Search_Problem_SV(sig=sig_vals[j], rho=rho_vals[j],
thet_size=300, w_size=300)
v_0 = ones(sp.thet_size, sp.w_size) # initial guess (VFI)
for i=1:loops_vfi
tic() # start the clock
v_new = Bellman_operator(sp, v_0)
time_vfi[i,j] = toq() # calculate the time elapsed
v_0 = v_new
end
println("Loop $j finished ... ")
# record the grid sizes used in simulation
grid_sizes[1], grid_sizes[2] = sp.thet_size, sp.w_size
end
# key loops for which we want to calculate the time elapsed (VFI)
keyloops_vfi = [10, 20, 50]
# create a vector to store the time elapsed (VFI) for the selected key loops
time_vfi_keyloops = Array{Float64}(length(keyloops_vfi), length(sig_vals))
for i=1:length(keyloops_vfi)
for j=1:length(sig_vals)
time_vfi_keyloops[i,j] = sum(time_vfi[1:keyloops_vfi[i], j])
end
end
row_1 = time_vfi_keyloops[1,:] # time taken : loop 10, all cases (grid sizes)
row_2 = time_vfi_keyloops[2,:] # time taken : loop 20, all cases (grid sizes)
row_3 = time_vfi_keyloops[3,:] # time taken : loop 50, all cases (grid sizes)
println("")
println("----------------------------------------------------------------")
println(" Computation time VFI : different parameter values")
println("")
println(" Key parameters : ")
println(" sig = $sig_vals")
println(" rho = $rho_vals")
println("")
println(" Grid sizes (thet, w) : $grid_sizes")
println("")
println(" Key loops : $keyloops_vfi")
println("")
println(" Time of VFI (row: key loops, column: parameter values) : ")
println("")
println(" Loop 10 : $row_1")
println(" Loop 20 : $row_2")
println(" Loop 50 : $row_3")
println("")
println("----------------------------------------------------------------")
println("")
# -
|
code/Julia/js_sv.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
df = pd.read_csv("WHO_first9cols.csv")
df.head()
country_series = df['Country']
type(country_series)
print('Shape: ', df.shape)
print('List of columns: ', df.columns)
print("Data types: \n", df.dtypes)
country_series
country_series[-5:]
pip3 install Quandl
# !pip3 install Quandl
import quandl
sunspots = quandl.get("SIDC/SUNSPOTS_A")
sunspots.head()
sunspots.tail()
sunspots_filtered = sunspots[['Yearly Mean Total Sunspot Number', 'Definitive/Provisional Indicator']]
sunspots_filtered.head()
sunspots['20020101': '20131231']
sunspots[sunspots['Yearly Mean Total Sunspot Number'] > sunspots['Yearly Mean Total Sunspot Number'].mean()]
df
df.describe()
df.count()
df.median()
df.std()
df.groupby('Continent').mean()
df.head()
df.groupby('Continent').mean()['Adult literacy rate (%)']
df.groupby('Continent').mean()
dest = pd.read_csv('dest.csv')
dest.head()
tips = pd.read_csv('tips.csv')
tips.head()
df_inner = pd.merge(dest, tips, on='EmpNr', how='inner')
df_inner.head()
df_outer = pd.merge(dest, tips, on='EmpNr', how='outer')
df_outer.head()
df_right = pd.merge(dest, tips, on = 'EmpNr', how='right')
df_right.head()
df_left = pd.merge(dest, tips, on='EmpNr', how='left')
df_left.head()
pd.isnull(df).sum()
df.isnull().sum()
df.dropna(inplace=True)
df.info()
df.shape
df.head()
df.shape
df.isnull().sum()
df.fillna(0,inplace=True)
df.shape
df.info()
purchase = pd.read_csv("purchase.csv")
purchase.head(10)
import numpy as np
pd.pivot_table(purchase, values='Price', index=['Weather',], columns=['Food'], aggfunc=np.sum)
pd.date_range('01-01-2000', periods=45, freq='MS')
pd.to_datetime('1/1/1970')
pd.to_datetime(['20200101', '20200102'], format='%Y%m%d')
pd.to_datetime(['20200101', 'not a date'], errors='coerce')
|
Chapter02 Numpy Pandas/Untitled.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import datalabframework as dlf
from datalabframework import utils
dlf.project.info()
metadata = dlf.params.metadata()
utils.pretty_print(metadata)
import datalabframework as dlf
from datalabframework import utils
engine = dlf.engines.get('spark-local')
df = engine.read(".products")
df.printSchema()
df.show()
df.printSchema()
df.columns
from pyspark.sql.types import *
supportedTypes = [
ByteType.typeName(),
ShortType.typeName(),
IntegerType.typeName(),
LongType.typeName(),
FloatType.typeName(),
DoubleType.typeName(),
DecimalType.typeName(),
StringType.typeName(),
BooleanType.typeName(),
TimestampType.typeName(),
DateType.typeName(),
ArrayType.typeName()
]
supportedTypes
# +
import datalabframework as dlf
from datalabframework import utils
engine = dlf.engines.get('spark-local')
df = engine.read(".sales_origin")
df.printSchema()
df.show(truncate = False)
# +
import datalabframework as dlf
from datalabframework import utils
engine = dlf.engines.get('spark-local')
df = engine.read(".sales")
df.printSchema()
df.show(truncate = False)
# -
from pyspark.sql import functions as F
from pyspark.sql import types
df.schema["sku"].dataType == types.StringType()
df.withColumn("abc", F.expr("name")).show()
|
demos/mapping/mapping.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Pre-processing, dimensionalization, visualization and image sorting
import numpy as np
import pandas as pd
import random
import cv2
import matplotlib.pylab as plt
import os
from os import listdir, path
from PIL import Image as PImage # converting images into arrays
def load_images(path, width=100, height=100, inter=cv2.INTER_LANCZOS4) :
"""Read all images from a directory, converts them to all to the same dimensions,
and return a DataFrame where each row corresponds to an image.
Parameters
----------
path (str): path (abolute or relative in the current working directory) of the directory of the images
width (int): (default=100)
height (int): (default=100)
inter : flag that takes one of the following cv2 interpolation methods/algorithm for image resize:
cv2.INTER_LANCZOS4
cv2.INTER_NEAREST (default)
cv2.INTER_LINEAR
cv2.INTER_AREA
cv2.INTER_CUBIC
Returns
------
df (pandas DataFrame):
rows : images
columns: 1st) integers representing the season each photo was taken
corresponding to the inital letter of each image file
(0:winter:W, 1:fall:F, 2:spring:S)
rest) RGB color data for each pixel
"""
path_abs = os.getcwd()+path
images = os.listdir(path_abs)
paths=[str(path_abs)+'/'+img for img in images]
seasons=[]
for filename in images:
seasons.append(filename[0])
dic = {'W':0, 'F':1, 'S':2}
seasons=[dic.get(n, n) for n in seasons]
dim = (width, height)
x = [] # images as arrays
for i,patth in enumerate(paths):
# Read and resize image
img_size_full = cv2.imread(patth)
img_size_new = cv2.resize(img_size_full, dim, interpolation=inter)
img_flat = img_size_new.reshape(-1,width*height*3).tolist()[0]
obs_full = np.append(seasons[i], img_flat)
x.append(obs_full)
df = pd.DataFrame(x)
names=['label']
for i in range(1,(width+1)):
for j in range(1,(height+1)):
for c in ('B', 'G', 'R'):
names.append(str(i)+','+str(j)+':'+c)
df.columns = names
df.index = [str(path)+'/'+img for img in os.listdir(path_abs)]
return(df)
df=load_images('/images')
df
def pca_image_space_visualization(x, width=16., height=8.):
"""Read a labeled dataframe, calculate the two first principal components of the data
and return a plot representing the 2-dimensional data.
Parameters
----------
x (pandas DataFrame) : dataframe i) labeled with label in column 0
ii) in the form of output of function load_images
representing flattened image data
width (float) : width of the plot (default=16.)
height (float) : height of the plot (default=8.)
Returns
------
plot : in which images are visualized in the two-dimensional space resulting
from the projection of the data in the first two principal components
"""
from sklearn.preprocessing import StandardScaler
# Standardizing the features
features = x.iloc[:,1:].values
features_st = StandardScaler().fit_transform(features)
from sklearn.decomposition import PCA
# initalize and apply PCA transformation
pca = PCA(n_components=2)
principalComponents = pca.fit_transform(features_st)
# create new DataFrame with PCA values
principalDf = pd.DataFrame(data = principalComponents
, columns = ['principal component 1', 'principal component 2'])
paths = principalDf.index = list(x.index)
finalDf = pd.concat([principalDf, x.iloc[:,0]], axis = 1)
pca_image_space_visualization.explained_variance_ratio = pca.explained_variance_ratio_
import matplotlib.pyplot as plt
from matplotlib.offsetbox import OffsetImage, AnnotationBbox
pca1=list(finalDf.iloc[:,0].values)
pca2=list(finalDf.iloc[:,1].values)
img_paths=[os.getcwd()+patth for patth in paths]
fig, ax = plt.subplots(figsize = (width, height))
ax.scatter(pca1, pca2)
ax.axis('off')
for pca1, pca2, img_path in zip(pca1, pca2, img_paths):
ab = AnnotationBbox(OffsetImage(plt.imread(img_path), zoom=0.25), (pca1, pca2))
ax.add_artist(ab)
pca_image_space_visualization(df)
# In the above plot, the images located closer together are positively related to each other in some way, while images located far apart across the PCs are negatively related (always in respect of the linearly uncorrelated variables PC1 and PC2).
#
# But what about generalization of these or other conclusions from this plot for the original image space?
print('The above plot represents image data that explain only the',
"{:.2%}".format(pca_image_space_visualization.explained_variance_ratio.sum()),
'of the variance/information of the initial data.')
# In that sense, we can say that the 2-D graph, using just PC1 and PC2, would be a 50.94% approximation or 50.94% accurate representation of the original image space.
#
# Let's insist a bit more:
print('We can see that the x axis —corresponding to the first principal component— represents the',
"{:.2%}".format(pca_image_space_visualization.explained_variance_ratio[0]),
', \nwhile the y axis —corresponding to the second principal component— represents the',
"{:.2%}".format(pca_image_space_visualization.explained_variance_ratio[1]),
'\nof the variance(information) of the initial data.')
# At this point, we should keep in mind two facts and a graph:
# - The PCs are ranked (as first, second and so on) based on the percentage of variance/information of the original data explained by them. Thus the first principal component retains always more data information than the second one.
# - The PCs are linearly uncorrelated; the second principal component does not explain variance that has retained earlier by the first one.
# +
#variance0=[]
#for i in range(1,30):
# pca = PCA(n_components=i)
# pca.fit_transform(X)
# variance0.append(pca.explained_variance_ratio_[i-1])
plt.grid(b=True, which='major', color='#666666', linestyle='-')
# Show the minor grid lines with very faint and almost transparent grey lines
plt.minorticks_on()
plt.grid(b=True, which='minor', color='#999999', linestyle='-', alpha=0.2)
plt.title('Scree plot (data variance explained by each PC)')
plt.xlabel('Sequence of PC')
plt.ylabel('Explained Variance')
plt.plot(range(1,30), variance0)
# -
# Given, all the more, that in our case the first principal component explains/retains 3.75 times more information than the second one, then it is expected that is along this axis we perceive a much more semantically meaningful variance of its values, or else, it's logical it's along this axis that we have a separable clustering of winter images (obviously PC1 tends to be interpreted as the amount of white colour) even if fall and spring remain inseparable in a unified cluster.
# In that sense, it may be more correct and useful to have a graphical representation where the length of the axes is not set randomly but based justly on this ratio of retained variance between of the first two principal components
pc1_exlained_variance = pca_image_space_visualization.explained_variance_ratio[0]
pc2_exlained_variance = pca_image_space_visualization.explained_variance_ratio[1]
r=pc2_exlained_variance/pc1_exlained_variance
pca_image_space_visualization(df, 16, 16*r)
# ### 1-nn classification with the large data
# We will first develop a 1-nn classifier, so, in the first place we have to standarize our data
from sklearn.preprocessing import StandardScaler
# standardize the features
X = df.iloc[:,1:].values
X = StandardScaler().fit_transform(X)
y= df.iloc[:,0].values
# +
# import the knn classifier library and the cross-validation library
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import cross_val_score
# perform 5-fold cross-validation 1-nn classification and calculate the average accuracy
knn = KNeighborsClassifier(n_neighbors=1)
accuracy_1nn = cross_val_score(knn, X, y, cv=5, scoring='accuracy').mean()
print('for an 5-fold cross-validaiton 1-nn classification the average accuracy is:\n', accuracy_1nn)
# -
# At this point, we have to be careful because accuracy with a binary classifier is measured as:
#
# \begin{equation*}
# Acc =
# \frac{\text{Number of correct predictions}}{\text{Total number of predictions}} =
# \frac{TP + TN}{P + N} =
# \frac{TP + TN}{TP + FP + TN +FP}
# \end{equation*}
#
# Where P = Positives, N = Negatives, TP = True Positives, TN = True Negatives, FP = False Positives, and FN = False Negatives.
#
# <div class="alert alert-block alert-warning">
# <b>But</b> that is not our case, since we have to deal with a problem of a multiclass/3-class classification problem.
# </div>
#
# The **multiclass classification accuracy** is calculated as the average accuracy per class:
#
# \begin{equation*}
# Acc =
# \frac{\sum_{i=1}^k \frac{tp_i+tn_i}{tp_i+tn_i+fp_i+fn_i}}{k},
# \quad\quad \text{for $k:$ total number of classes}.
# \end{equation*}
# ---
# ### 1-nn classification with the low-dimensional data (using PCA decomposition)
# \begin{equation*}
# || X - W[t] C [t] || _F ^ 2 / || X || _F ^ 2
# \end{equation*}
#
# \begin{equation*}
# ε (|| Χ - W [t] C [t] || _F ^ 2 - || Χ - W [t-1] C [t-1] || _F ^ 2) / || X || _F ^ 2 <ε \text{ with ε = 0.01 or 0.001 or 0.0001)}
# \end{equation*}
# At this point we should note that we will choose the number of components so as to retain at least 95% of the data variance:
#
# +
# import PCA decomposition algorithm from the appropriate scikit-learn module
from sklearn.decomposition import PCA
# the data (X,y) are already standarized so we proceed directly to the decomposition
pca = PCA(n_components=.95)
principal_components = pca.fit_transform(X)
print('The minimun number of principal components that explain at least 95% of data variance is:\n',
pca.n_components_,
',\nand indeed, the retained data variance (information) is:\n',
"{:.2%}".format(pca.explained_variance_ratio_.sum()),
'.\nSo, we have here a percentage significantly higher compared to the ',
"{:.2%}".format(pca.explained_variance_ratio_[0:2].sum()),
' of the two prncipal components we saw above, as well as a significant reduction',
' in the number of features/estimators, from 30,000 to',
pca.n_components_)
# -
# With these 22-dimensional data we proceed again with the development of a 1-nn classifier.
# perform 5-fold cross-validation 1-nn classification and calculate the average accuracy
knn_pca = KNeighborsClassifier(n_neighbors=1)
accuracy_1nn_pca = cross_val_score(knn_pca, principal_components, y, cv=5, scoring='accuracy').mean()
print('for a 5-fold cross-validaiton 1-nn classification (PCA-95%variance) the average accuracy is:\n',
accuracy_1nn_pca)
# We thus observe a reduction in the average classification accuracy, that is not only expected, but also very similar to the reduction in the variance of the data with which we trained the *1-nn_pca* classifier.
# ---
# ### SVM classification with the large data
# This time we will try the four different kernel functions so as to choose the best one base on their classification accuracy
from sklearn import svm
svm_rbf = svm.SVC(kernel='rbf', random_state=0, gamma='auto')
svm_linear = svm.SVC(kernel='linear', random_state=0, gamma='auto')
svm_poly = svm.SVC(kernel='poly', random_state=0, gamma='auto')
svm_sigmoid = svm.SVC(kernel='sigmoid', random_state=0, gamma='auto')
accuracy_svm_rbf = cross_val_score(svm_rbf, X, y, cv=5, scoring='accuracy').mean()
accuracy_svm_linear = cross_val_score(svm_linear, X, y, cv=5, scoring='accuracy').mean()
accuracy_svm_poly = cross_val_score(svm_poly, X, y, cv=5, scoring='accuracy').mean()
accuracy_svm_sigmoid = cross_val_score(svm_sigmoid, X, y, cv=5, scoring='accuracy').mean()
print('accuracy_svm_rbf : ',
"{:.2f}".format(accuracy_svm_rbf),
'\naccuracy_svm_linear : ',
"{:.2f}".format(accuracy_svm_linear),
'\naccuracy_svm_poly : ',
"{:.2f}".format(accuracy_svm_poly),
'\naccuracy_svm_sigmoid: ',
"{:.2f}".format(accuracy_svm_sigmoid))
# ---
# ### SVM classification with the low-dimensional data (using PCA decomposition)
# And we will do the same but this time with the 22-dimensional data from the PCA decomposition:
accuracy_svm_pca_rbf = cross_val_score(svm_rbf, principal_components, y, cv=5, scoring='accuracy').mean()
accuracy_svm_pca_linear = cross_val_score(svm_linear, principal_components, y, cv=5, scoring='accuracy').mean()
accuracy_svm_pca_poly = cross_val_score(svm_poly, principal_components, y, cv=5, scoring='accuracy').mean()
accuracy_svm_pca_sigmoid = cross_val_score(svm_sigmoid, principal_components, y, cv=5, scoring='accuracy').mean()
print('accuracy_svm_pca_rbf : ',
"{:.2f}".format(accuracy_svm_pca_rbf),
'\naccuracy_svm_pca_linear : ',
"{:.2f}".format(accuracy_svm_pca_linear),
'\naccuracy_svm_pca_poly : ',
"{:.2f}".format(accuracy_svm_pca_poly),
'\naccuracy_svm_pca_sigmoid: ',
"{:.2f}".format(accuracy_svm_pca_sigmoid))
# # Further Investigation and Discussion
#
# From the accuracy scores of the eight SVM classifiers we end up with two remarks:
# - considering altogether, both approaches andd all the kernel functions, the linear and sigmoid kernel functions seem to have better accuracy scores than the radial basis and the polynomial one,
# - regarding the accuracy score, the classification using linear and sigmoid kernel functions doesn't seem to be affected by whether we rely on all image data information or only on 95.6% of it.
#
# The second remark makes us wonder if there is a limit of retained data variance and number of principal components below which the performance of the classifiers (in terms of at least of accuracy) is lower than that of the classifiers trained with all the information and if there is, in general, some pattern (linear or not) that characterises this relation "number of PC/explained data variance ~ accuracy of the classifier".
# After all, although we chose the number of principal components with a solid and widely accepted reasoning (selecting those that hold a minimum of 95% of the information), it would not be bad to be able to take advantage of even more of the basic advantages of PCA approach (especially the reduction in training time, in noise and overfitting, as well as from feature extraction aspect) without losing in terms of prediction performance.
# +
variance1=[]
variance2=[]
for i in range(1,23):
pca = PCA(n_components=i)
pca.fit_transform(X)
variance1.append(pca.explained_variance_ratio_.sum())
variance2.append(pca.explained_variance_ratio_.sum()/i)
# +
plt.figure(figsize=(12,5))
plt.subplot(1, 2, 1)
# Show the major grid lines with dark grey lines
plt.grid(b=True, which='major', color='#666666', linestyle='-')
# Show the minor grid lines with very faint and almost transparent grey lines
plt.minorticks_on()
plt.grid(b=True, which='minor', color='#999999', linestyle='-', alpha=0.2)
plt.axhline(y=0.95, color='r', linestyle='-')
plt.text(4.5, 0.96, '95% cut-off threshold', color = 'red', fontsize=11)
plt.title('Total Variance retained vs. number of PCs')
plt.xlabel('Number of PCs')
plt.ylabel('Total Explained Variance')
plt.plot(range(1,23), variance1)
plt.subplot(1, 2, 2)
# Show the major grid lines with dark grey lines
plt.grid(b=True, which='major', color='#666666', linestyle='-')
# Show the minor grid lines with very faint and almost transparent grey lines
plt.minorticks_on()
plt.grid(b=True, which='minor', color='#999999', linestyle='-', alpha=0.2)
plt.axhline(y=.9559/22, color='r', linestyle='-')
plt.text(.5, 0.051, '95% cut-off threshold', color = 'red', fontsize=11)
plt.title('Average Explained Variance per PC vs. number of PCs')
plt.xlabel('Number of PCs')
plt.ylabel('Average Explained Variance per PC')
plt.plot(range(1,23), variance2)
# -
# To this end, the two above graphs:
#
# - the cumulative sum of data variance (eigenvalues) for different numbers of principal components (eigenvectors),
# - the average (per PC) cumulative sum of data variance of the above eigenvalues against the number of PCs (dividing each sum of eigenvalues by the number of corresponding PCs (eigenvectors) before plotting it against the PCs' number)
#
# provide a good indication of when we hit the point of diminishing returns (i.e., little variance is gained by retaining additional eigenvalues), and that is around the number 5 of PCs.
#
# After all, given the size of our data set, we are able to calculate (always with a 5-fold cross-validation) the accuracy of the SVM classifier for the four different kernel functions for all different numbers of principal components.
# +
svm_rbf = svm.SVC(kernel='rbf', random_state=0, gamma='auto')
accuracies_svm_rbf = []
svm_linear = svm.SVC(kernel='linear', random_state=0, gamma='auto')
accuracies_svm_linear = []
svm_poly = svm.SVC(kernel='poly', random_state=0, gamma='auto')
accuracies_svm_poly = []
svm_sigmoid = svm.SVC(kernel='sigmoid', random_state=0, gamma='auto')
accuracies_svm_sigmoid = []
for i in range(1,23):
pcs = PCA(n_components=i).fit_transform(X)
accuracies_svm_rbf.append(cross_val_score(svm_rbf, pcs, y, cv=5,scoring='accuracy').mean())
accuracies_svm_linear.append(cross_val_score(svm_linear, pcs, y, cv=5, scoring='accuracy').mean())
accuracies_svm_poly.append(cross_val_score(svm_poly, pcs, y, cv=5, scoring='accuracy').mean())
accuracies_svm_sigmoid.append(cross_val_score(svm_sigmoid, pcs, y, cv=5, scoring='accuracy').mean())
# -
line1, = plt.plot(range(1,23), accuracies_svm_rbf, label="rbf", color='blue')
line2, = plt.plot(range(1,23), accuracies_svm_poly, label="poly", color='red')
line3, = plt.plot(range(1,23), accuracies_svm_linear, label="linear", color='green')
line4, = plt.plot(range(1,23), accuracies_svm_sigmoid, label="sigmoid", color='orange')
# Create a legend for the first line.
first_legend = plt.legend(bbox_to_anchor=(1, 1), title="Kernel functions")
# Add the legend manually to the current Axes.
ax = plt.gca().add_artist(first_legend)
# Show the major grid lines with dark grey lines
plt.grid(b=True, which='major', color='#666666', linestyle='-')
# Show the minor grid lines with very faint and almost transparent grey lines
plt.minorticks_on()
plt.grid(b=True, which='minor', color='#999999', linestyle='-', alpha=0.2)
plt.title('Classification Accuracy per number of PCs')
plt.xlabel('Number of PCs')
plt.ylabel('Classification Accuracy')
plt.show()
# From the above, it follows that the most satisfactory in our case kernel function is the linear while the worst is the radial basis. It is also confirmed that indeed for the efficient in our case kernel functions (linear, sigmoid, polynomial) the peak of the accuracy performance of the SVM classifier is taking place around 5 or 6 principal components. Also of interest is the generally declining course of classification accuracy after these first 6 principal components, despite the fluctuations, which is probably due to overfitting because of the inclusion of noise information (phenomenon from which we try to escape with PCA approach).
# # Conclusions
#
# Trying to sum up our conclusions, we would say that between a simple 1-nn classifier (either with the large data or after a decomposition that will maintain only the principal components that correpsond to 95% of the data variance) is inferior in terms of classification accuracy to a Support Vector Machine classification — at least to a SVM with linear or a sigmoid kernel function. We can also note that the accuracy score of SVM with these two kernel functions is not affected by the dimensions reduction after the PCA decomposition with 95% of variance retained. Even more, the accuracy score with the three most favourable kernel functions (linear, sigmoid, polynomial) is even better if we choose even fewer PCs, in other words, if we rely on even less image data variance/information (but now decorrelated data). More precisely, even with 64% of variance retained, with a peak at 67% and 70% (respectively 4, 5 and 6 PCs), the classification accuracy of the SVM classifiers is significantly better and from that point on continuously decreasing (despite the turbulence) going towards 95% (22 PCs), the percentage we initially chose to use. It is therefore normal to end up with a combination of SVM algorithm, linear kernel function and 5 or 6 Principal Components decompostion for the optimisation of our image data 3-class classification model.
|
Image_Processing---3-class_Season_Classification.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Graph Coloring Oracle
# +
from tweedledum.bool_function_compiler import BitVec
invalid = BitVec('00')
red = BitVec('01')
blue = BitVec('10')
purple = BitVec('11')
# -
# ## Configurations
# +
oracle_type = 'naive' # (naive, fancy)
syntehsis_method = 'xag' # (pkrm, xag)
# Optimization options
use_barenco_decomp = True
use_linear_resynth = False
use_diagonal_synth = True
# -
# ## Oracles
# +
from tweedledum.bool_function_compiler import BoolFunction
def naive(v0, v1, v2, v3 : BitVec(2)) -> BitVec(1):
c_01 = (v0 != v1)
c_123 = (v1 != v2) and (v1 != v3) and (v2 != v3)
color_00 = (v0 != BitVec('00')) and (v1 != BitVec('00')) and (v2 != BitVec('00')) and (v3 != BitVec('00'))
return c_01 and c_123 and color_00
def fancy(v0, v1, v2, v3 : BitVec(2)) -> BitVec(1):
c_01 = (v0 != v1)
c_123 = (v1 != v2) and (v1 != v3) and (v2 != v3)
return c_01 and c_123
oracle_func = BoolFunction(naive) if oracle_type == 'naive' else BoolFunction(fancy)
# -
print(f"Try 1: {oracle_func.simulate(red, red, blue, purple)}")
print(f"Try 2: {oracle_func.simulate(blue, red, blue, purple)}")
if oracle_type == 'naive':
print(f"Try 3: {oracle_func.simulate(invalid, red, blue, purple)}")
# When using the fancy oracle, we promise to not query it with 'invalid'
# If we do, the result will be garbage!
# +
# Using l337 programming skills:
search_space_size = 0
num_solutions = 0
for i in range(2**(2*4)):
v = BitVec(8, i)
if oracle_type == 'fancy' and BitVec('00') in [v[2:0], v[4:2], v[6:4], v[8:6]]:
continue
search_space_size += 1
result = oracle_func.simulate(v[2:0], v[4:2], v[6:4], v[8:6])
if result:
num_solutions += 1
print(v[2:0], v[4:2], v[6:4], v[8:6])
print(f"Search space size: {search_space_size}")
print(f"Number of solutions: {num_solutions}")
# +
from tweedledum.synthesis import xag_synth, pkrm_synth
def use_pkrm(bool_function):
return pkrm_synth(bool_function.truth_table(output_bit=0))
def use_xag(bool_function):
from tweedledum.passes import parity_decomp
circuit = xag_synth(bool_function.logic_network())
return parity_decomp(circuit)
# -
oracle_circuit = use_pkrm(oracle_func) if syntehsis_method == 'pkrm' else use_xag(oracle_func)
if use_barenco_decomp:
from tweedledum.passes import barenco_decomp
oracle_circuit = barenco_decomp(oracle_circuit, {'max_qubits' : 16})
print(f"Number of qubits: {oracle_circuit.num_qubits()}")
print(f"Number of instructions: {len(oracle_circuit)}")
# ## Initialization subcircuit
# +
import numpy as np
from tweedledum.ir import Circuit
from tweedledum.operators import H, Ry, X, Measure
from tweedledum.passes import inverse
def naive_init():
circuit = Circuit()
qubits = [circuit.create_qubit() for i in range(8)]
for qubit in qubits:
circuit.apply_operator(H(), [qubit])
return circuit
def fancy_init():
theta = 2 * np.arccos(1 / np.sqrt(3))
circuit = Circuit()
qubits = [circuit.create_qubit() for i in range(8)]
for i in range(0, 8, 2):
circuit.apply_operator(Ry(theta), [qubits[i]])
circuit.apply_operator(H(), [qubits[i], qubits[i + 1]])
circuit.apply_operator(X(), [qubits[i + 1]])
return circuit
init_subcircuit = naive_init() if oracle_type == 'naive' else fancy_init()
init_adj_subcircuit = inverse(init_subcircuit)
# -
# ## Diffuser subcircuit
# +
from tweedledum.operators import X, Z
diffuser_subcircuit = Circuit()
qubits = [diffuser_subcircuit.create_qubit() for i in range(9)]
# Why 9? I need to account for the output qubit! Also if barenco is used
# this qubit should be left alone as it where the output rests!
diffuser_subcircuit.append(init_adj_subcircuit, qubits[0:init_subcircuit.num_qubits()], [])
for qubit in qubits[0:8]:
diffuser_subcircuit.apply_operator(X(), [qubit])
diffuser_subcircuit.apply_operator(Z(), qubits[0:8])
for qubit in qubits[0:8]:
diffuser_subcircuit.apply_operator(X(), [qubit])
diffuser_subcircuit.append(init_subcircuit, qubits[0:init_adj_subcircuit.num_qubits()], [])
if use_barenco_decomp:
from tweedledum.passes import barenco_decomp
diffuser_subcircuit = barenco_decomp(diffuser_subcircuit, {'max_qubits' : 16})
# -
# ## Grover circuit
# +
# Initialize
num_qubits = max(oracle_circuit.num_qubits(), diffuser_subcircuit.num_qubits())
circuit = Circuit()
qubits = [circuit.create_qubit() for i in range(num_qubits)]
cbits = [circuit.create_cbit() for i in range(8)]
circuit.apply_operator(X(), [qubits[8]])
circuit.apply_operator(H(), [qubits[8]])
circuit.append(init_subcircuit, qubits[0:init_subcircuit.num_qubits()], [])
# Grover iteration
num_iterations = int(np.floor(np.sqrt(search_space_size / num_solutions)))
for i in range(num_iterations):
circuit.append(oracle_circuit, qubits[0:oracle_circuit.num_qubits()], [])
circuit.append(diffuser_subcircuit, qubits[0:diffuser_subcircuit.num_qubits()], [])
if use_diagonal_synth:
from tweedledum.ir import rotation_angle
from tweedledum.passes import shallow_duplicate
from tweedledum.synthesis import diagonal_synth
new_circuit = shallow_duplicate(circuit)
for instruction in circuit:
if instruction.kind() == 'std.rx':
angle = rotation_angle(instruction)
qs = instruction.qubits()
angles = [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, -angle/2, angle/2]
new_circuit.apply_operator(H(), [qs[-1]])
diagonal_synth(new_circuit, qs, instruction.cbits(), angles)
new_circuit.apply_operator(H(), [qs[-1]])
else:
new_circuit.apply_operator(instruction)
circuit = new_circuit
for i in range(circuit.num_cbits()):
circuit.apply_operator(Measure(), [qubits[i]], [cbits[i]])
print(f"Number of qubits: {circuit.num_qubits()}")
print(f"Number of instructions: {len(circuit)}")
# -
# ## Local simulation
# +
from tweedledum.converters_qiskit import tweedledum_to_qiskit_qc
qiskit_circuit = tweedledum_to_qiskit_qc(circuit)
# +
import qiskit
from qiskit.providers.aer import QasmSimulator
# Construct an ideal simulator
sim = QasmSimulator()
# Perform an ideal simulation
result_ideal = qiskit.execute(qiskit_circuit, sim).result()
counts_ideal = result_ideal.get_counts(0)
# +
# Sort count
count_sorted = sorted(counts_ideal.items(), key=lambda x:x[1], reverse=True)
for bit_string, count in count_sorted:
v = BitVec(bit_string)
print(v[2:0], v[4:2], v[6:4], v[8:6], f'({count})', (oracle_func.simulate(v[2:0], v[4:2], v[6:4], v[8:6])))
# -
|
libs/tweedledum/python/notebooks/oracles/graph_coloring.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + colab={"base_uri": "https://localhost:8080/", "height": 206} executionInfo={"elapsed": 655, "status": "ok", "timestamp": 1641588073453, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a/default-user=s64", "userId": "07041918671559436153"}, "user_tz": 300} id="dA58NEPnZB3x" outputId="68fa48ce-6078-48e8-c2d0-e65ff4feb27f"
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
sns.set(style="darkgrid")
plt.style.use("seaborn-pastel")
# -
df = pd.read_ex
# + colab={"base_uri": "https://localhost:8080/", "height": 206} executionInfo={"elapsed": 260, "status": "ok", "timestamp": 1641588075757, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a/default-user=s64", "userId": "07041918671559436153"}, "user_tz": 300} id="fSsYccmCzb_T" outputId="64cf5ef7-70f4-4b97-8ae1-d3b6e17201ad"
df.Rank = df.Rank.apply(lambda x: int(x.split("#")[1]) if type(x) == np.str else x)
df.Pay = df.Pay.apply(lambda x: float(x.split(" ")[0].split("$")[1]))
df.Endorsements = df.Endorsements.apply(lambda x: float(x.split(" ")[0].split("$")[1]))
df["Salary/Winnings"].replace("-", "$nan M", inplace=True)
df["Salary/Winnings"] = df["Salary/Winnings"].apply(lambda x: float(x.split(" ")[0].split("$")[1]))
df.Sport.replace({"Mixed Martial Arts": "MMA",
"Auto racing": "Racing",
"Auto Racing": "Racing",
"Basketbal": "Basketball"}, inplace=True)
df.columns=["Rank", "Name", "Pay", "Salary_Winnings", "Endorsements", "Sport", "Year"]
df.head()
# + colab={"base_uri": "https://localhost:8080/"} executionInfo={"elapsed": 267, "status": "ok", "timestamp": 1641588078811, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a/default-user=s64", "userId": "07041918671559436153"}, "user_tz": 300} id="MXtgVB8-RTLu" outputId="7e536d85-159a-4004-e910-d51b55b0d061"
df.isnull().any()
# + colab={"base_uri": "https://localhost:8080/", "height": 81} executionInfo={"elapsed": 250, "status": "ok", "timestamp": 1641588081181, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a/default-user=s64", "userId": "07041918671559436153"}, "user_tz": 300} id="v8b9JvkoQ1_2" outputId="b3fb1337-a5d1-4895-8d0a-9f7c21b712df"
df[df["Salary_Winnings"].isnull()]
# + executionInfo={"elapsed": 175, "status": "ok", "timestamp": 1641588084104, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a/default-user=s64", "userId": "07041918671559436153"}, "user_tz": 300} id="pwR1hz2uQ6ze"
df.drop(520, inplace=True)
# + colab={"base_uri": "https://localhost:8080/"} executionInfo={"elapsed": 237, "status": "ok", "timestamp": 1641588090566, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a/default-user=s64", "userId": "07041918671559436153"}, "user_tz": 300} id="FwBlGZR0PQX1" outputId="611d8588-e5c4-48b2-94df-af9d3df1f369"
df.isnull().any()
# + colab={"base_uri": "https://localhost:8080/", "height": 858} executionInfo={"elapsed": 665, "status": "ok", "timestamp": 1641588123463, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a/default-user=s64", "userId": "07041918671559436153"}, "user_tz": 300} id="o2V105AI6XkN" outputId="42daf209-f8f5-4451-d2db-b6a57075ffcd"
df.groupby("Name")["Sport"].first().value_counts().plot(kind="pie", autopct="%.0f%%", figsize=(20,20), fontsize=16, wedgeprops=dict(width=0.5), pctdistance=0.8)
plt.ylabel(None)
plt.title("Atletas mejor pagados por deporte", fontsize=26)
plt.show()
# + executionInfo={"elapsed": 238, "status": "ok", "timestamp": 1641588127526, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a/default-user=s64", "userId": "07041918671559436153"}, "user_tz": 300} id="hjwGSfop_LcP"
df = df[(df["Sport"] != "MMA") & (df["Sport"] != "Track") & (df["Sport"] != "Motorcycle")]
# + colab={"base_uri": "https://localhost:8080/", "height": 875} executionInfo={"elapsed": 579, "status": "ok", "timestamp": 1641588130328, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a/default-user=s64", "userId": "07041918671559436153"}, "user_tz": 300} id="iFAI5DbKBEqS" outputId="6d7780c6-0353-40eb-93e7-6c4cf0838991"
df.groupby("Name")["Sport"].first().value_counts().plot(kind="pie", autopct="%.0f%%", figsize=(20,20), fontsize=16, wedgeprops=dict(width=0.5), pctdistance=0.8)
plt.ylabel(None)
plt.title("Atletas mejor pagados por deporte", fontsize=26)
plt.show()
# + executionInfo={"elapsed": 168, "status": "ok", "timestamp": 1641588134685, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a/default-user=s64", "userId": "07041918671559436153"}, "user_tz": 300} id="MJLmS-f0MnDc"
df.Year = pd.to_datetime(df.Year, format="%Y")
# + colab={"base_uri": "https://localhost:8080/", "height": 460} executionInfo={"elapsed": 208, "status": "ok", "timestamp": 1641589141703, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a/default-user=s64", "userId": "07041918671559436153"}, "user_tz": 300} id="0gWdM7gqR8Df" outputId="b4de9ba2-0609-4e4f-9441-421927f6490a"
racing_bar_data = df.pivot_table(values="Pay", index="Year", columns="Name")
racing_bar_data
# + colab={"base_uri": "https://localhost:8080/"} executionInfo={"elapsed": 179, "status": "ok", "timestamp": 1641588648731, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a/default-user=s64", "userId": "07041918671559436153"}, "user_tz": 300} id="9CgofCMvSMRE" outputId="e68a0f83-3903-41a0-a5b7-913b2fb47ed1"
racing_bar_data.columns[racing_bar_data.isnull().sum() == 0]
# + colab={"base_uri": "https://localhost:8080/", "height": 460} executionInfo={"elapsed": 210, "status": "ok", "timestamp": 1641589097317, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a/default-user=s64", "userId": "07041918671559436153"}, "user_tz": 300} id="F0ZIZGQsTxQT" outputId="176c0e8d-5aab-46aa-c303-2c7cea5008c1"
racing_bar_completa = racing_bar_data.interpolate(method="linear").fillna(method="bfill")
#racing_bar_completa = racing_bar_completa.cumsum()
racing_bar_completa
# + colab={"base_uri": "https://localhost:8080/", "height": 554} executionInfo={"elapsed": 433, "status": "ok", "timestamp": 1641589345561, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a/default-user=s64", "userId": "07041918671559436153"}, "user_tz": 300} id="lFTZnrYOUhIN" outputId="8d5279bf-609b-45b7-c730-dd8a05c53b4e"
racing_bar_completa = racing_bar_completa.resample("1D").interpolate(method="linear")[::7]
racing_bar_completa
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} executionInfo={"elapsed": 1146, "status": "error", "timestamp": 1641592452581, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a/default-user=s64", "userId": "07041918671559436153"}, "user_tz": 300} id="unIRzNAaWaSj" outputId="e44f0211-10a1-47df-8c7d-1cdfeb005642"
from matplotlib.animation import FuncAnimation, FFMpegWriter
seleccion = racing_bar_completa.iloc[-1,:].sort_values(ascending=False)[:20].index
data = racing_bar_completa[seleccion].round()
fig, ax = plt.subplots(figsize=(12, 8))
fig.subplots_adjust(left=0.18)
no_of_frames = data.shape[0]
barras = sns.barplot(x=data.iloc[0,:], y=data.columns, orient="h", ax=ax)
ax.set_xlim(0, 1500)
texto = [ax.text(0, i, 0, va="center") for i in range(data.shape[1])]
titulo = ax.text(650, -1, "Date: ", fontsize=16)
ax.set_xlabel("Ganancia (USD)")
ax.set_ylabel(None)
def animate(i):
y = data.iloc[i, :]
titulo.set_txt(f"Date: {str(data.index[i].date())}")
for j, b in enumerate(barras.patches):
b.set_width(y[j])
texto[j].set_text(f"${y[j].astype(int)}M")
texto[j].set_x(y[j])
animacion = FuncAnimation(fig, animate, repeat=False, frames=no_of_frames,
interval=1, blit=False)
animacion.save("atletas.gif",writer="imagemagick", fps=120)
plt.close(fig)
|
notebooks/.ipynb_checkpoints/atletas-mejor-pagados-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Welcome to fastai
# + hide_input=true
from fastai.vision import *
from fastai.gen_doc.nbdoc import *
from fastai.core import *
from fastai.basic_train import *
# -
# The fastai library simplifies training fast and accurate neural nets using modern best practices. It's based on research in to deep learning best practices undertaken at [fast.ai](http://www.fast.ai), including "out of the box" support for [`vision`](/vision.html#vision), [`text`](/text.html#text), [`tabular`](/tabular.html#tabular), and [`collab`](/collab.html#collab) (collaborative filtering) models. If you're looking for the source code, head over to the [fastai repo](https://github.com/fastai/fastai) on GitHub. For brief examples, see the [examples](https://github.com/fastai/fastai/tree/master/examples) folder; detailed examples are provided in the full documentation (see the sidebar). For example, here's how to train an MNIST model using [resnet18](https://arxiv.org/abs/1512.03385) (from the [vision example](https://github.com/fastai/fastai/blob/master/examples/vision.ipynb)):
path = untar_data(URLs.MNIST_SAMPLE)
data = ImageDataBunch.from_folder(path)
learn = cnn_learner(data, models.resnet18, metrics=accuracy)
learn.fit(1)
# + hide_input=true
jekyll_note("""This documentation is all built from notebooks;
that means that you can try any of the code you see in any notebook yourself!
You'll find the notebooks in the <a href="https://github.com/fastai/fastai/tree/master/docs_src">docs_src</a> folder of the
<a href="https://github.com/fastai/fastai">fastai</a> repo. For instance,
<a href="https://nbviewer.jupyter.org/github/fastai/fastai/blob/master/docs_src/index.ipynb">here</a>
is the notebook source of what you're reading now.""")
# -
# ## Installation and updating
# To install or update fastai, we recommend `conda`:
#
# ```
# conda install -c pytorch -c fastai fastai pytorch
# ```
# For troubleshooting, and alternative installations (including pip and CPU-only options) see the [fastai readme](https://github.com/fastai/fastai/blob/master/README.md).
# ## Reading the docs
# To get started quickly, click *Applications* on the sidebar, and then choose the application you're interested in. That will take you to a walk-through of training a model of that type. You can then either explore the various links from there, or dive more deeply into the various fastai modules.
#
# We've provided below a quick summary of the key modules in this library. For details on each one, use the sidebar to find the module you're interested in. Each module includes an overview and example of how to use it, along with documentation for every class, function, and method. API documentation looks, for example, like this:
#
# ### An example function
# + hide_input=true
show_doc(rotate, full_name='rotate')
# -
# ---
#
# Types for each parameter, and the return type, are displayed following standard Python [type hint syntax](https://www.python.org/dev/peps/pep-0484/). Sometimes for compound types we use [type variables](/fastai_typing.html). Types that are defined by fastai or Pytorch link directly to more information about that type; try clicking *Image* in the function above for an example. The docstring for the symbol is shown immediately after the signature, along with a link to the source code for the symbol in GitHub. After the basic signature and docstring you'll find examples and additional details (not shown in this example). As you'll see at the top of the page, all symbols documented like this also appear in the table of contents.
#
# For inherited classes and some types of decorated function, the base class or decorator type will also be shown at the end of the signature, delimited by `::`. For `vision.transforms`, the random number generator used for data augmentation is shown instead of the type, for randomly generated parameters.
# ## Module structure
# ### Imports
# fastai is designed to support both interactive computing as well as traditional software development. For interactive computing, where convenience and speed of experimentation is a priority, data scientists often prefer to grab all the symbols they need, with `import *`. Therefore, fastai is designed to support this approach, without compromising on maintainability and understanding.
#
# In order to do so, the module dependencies are carefully managed (see next section), with each exporting a carefully chosen set of symbols when using `import *`. In general, for interactive computing, you'll want to import from both `fastai`, and from one of the *applications*, such as:
from fastai.vision import *
# That will give you all the standard external modules you'll need, in their customary namespaces (e.g. `pandas as pd`, `numpy as np`, `matplotlib.pyplot as plt`), plus the core fastai libraries. In addition, the main classes and functions for your application ([`fastai.vision`](/vision.html#vision), in this case), e.g. creating a [`DataBunch`](/basic_data.html#DataBunch) from an image folder and training a convolutional neural network (with [`cnn_learner`](/vision.learner.html#cnn_learner)), are also imported. If you don't wish to import any application, but want all the main functionality from fastai, use `from fastai.basics import *`. Of course, you can also just import the specific symbols that you require, without using `import *`.
#
# If you wish to see where a symbol is imported from, either just type the symbol name (in a REPL such as Jupyter Notebook or IPython), or (in most editors) wave your mouse over the symbol to see the definition. For instance:
Learner
# ### Dependencies
# At the base of everything are the two modules [`core`](/core.html#core) and [`torch_core`](/torch_core.html#torch_core) (we're not including the `fastai.` prefix when naming modules in these docs). They define the basic functions we use in the library; [`core`](/core.html#core) only relies on general modules, whereas [`torch_core`](/torch_core.html#torch_core) requires pytorch. Most type-hinting shortcuts are defined there too (at least the one that don't depend on fastai classes defined later). Nearly all modules below import [`torch_core`](/torch_core.html#torch_core).
#
# Then, there are three modules directly on top of [`torch_core`](/torch_core.html#torch_core):
# - [`data`](/vision.data.html#vision.data), which contains the class that will take a [`Dataset`](https://pytorch.org/docs/stable/data.html#torch.utils.data.Dataset) or pytorch [`DataLoader`](https://pytorch.org/docs/stable/data.html#torch.utils.data.DataLoader) to wrap it in a [`DeviceDataLoader`](/basic_data.html#DeviceDataLoader) (a class that sits on top of a [`DataLoader`](https://pytorch.org/docs/stable/data.html#torch.utils.data.DataLoader) and is in charge of putting the data on the right device as well as applying transforms such as normalization) and regroup then in a [`DataBunch`](/basic_data.html#DataBunch).
# - [`layers`](/layers.html#layers), which contains basic functions to define custom layers or groups of layers
# - [`metrics`](/metrics.html#metrics), which contains all the metrics
#
# This takes care of the basics, then we regroup a model with some data in a [`Learner`](/basic_train.html#Learner) object to take care of training. More specifically:
# - [`callback`](/callback.html#callback) (depends on [`data`](/vision.data.html#vision.data)) defines the basis of callbacks and the [`CallbackHandler`](/callback.html#CallbackHandler). Those are functions that will be called every step of the way of the training loop and can allow us to customize what is happening there;
# - [`basic_train`](/basic_train.html#basic_train) (depends on [`callback`](/callback.html#callback)) defines [`Learner`](/basic_train.html#Learner) and [`Recorder`](/basic_train.html#Recorder) (which is a callback that records training stats) and has the training loop;
# - [`callbacks`](/callbacks.html#callbacks) (depends on [`basic_train`](/basic_train.html#basic_train)) is a submodule defining various callbacks, such as for mixed precision training or 1cycle annealing;
# - `learn` (depends on [`callbacks`](/callbacks.html#callbacks)) defines helper functions to invoke the callbacks more easily.
#
# From [`data`](/vision.data.html#vision.data) we can split on one of the four main *applications*, which each has their own module: [`vision`](/vision.html#vision), [`text`](/text.html#text) [`collab`](/collab.html#collab), or [`tabular`](/tabular.html#tabular). Each of those submodules is built in the same way with:
# - a submodule named <code>transform</code> that handles the transformations of our data (data augmentation for computer vision, numericalizing and tokenizing for text and preprocessing for tabular)
# - a submodule named <code>data</code> that contains the class that will create datasets specific to this application and the helper functions to create [`DataBunch`](/basic_data.html#DataBunch) objects.
# - a submodule named <code>models</code> that contains the models specific to this application.
# - optionally, a submodule named <code>learn</code> that will contain [`Learner`](/basic_train.html#Learner) specific to the application.
#
# Here is a graph of the key module dependencies:
# 
|
docs_src/index.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# # Derivatives with respect to matrices
#
# What is the gradient of a scalar function with respect to a matrix argument?
#
# Remember that the gradient of a scalar valued function with respect to a vector argument is a vector of the same size, similarly the derivative of a scalar with respect to a matrix is a matrix of the same size.
#
# The trace (sum of diagonal elements) appears often in scalar valued functions of matrices, so we start with its definition and an example:
# $\newcommand{\trace}{\mathop{\text{Tr}}}$
# \begin{eqnarray}
# \trace X = \sum_i X(i,i)
# \end{eqnarray}
#
# \begin{eqnarray}
# f(X) & = & \trace \left( \begin{array}{cc} X_{1,1} & X_{1,2} \\ X_{2,1} & X_{2,2} \end{array} \right) = X_{1,1} + X_{2,2} \\
# \frac{df}{dX} & = & \left( \begin{array}{cc} \partial{f}/\partial X_{1,1} & \partial{f}/\partial X_{1,2} \\ \partial{f}/\partial X_{2,1} & \partial{f}/\partial X_{2,2} \end{array} \right) = \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right)
# \end{eqnarray}
# The trace is like the inner product of the matrix $X$ (viewed as a vector) and the identity matrix (viewed as a vector). In the following, we will introduce a systematic way for computing these defivatives where
# we will make use of the Kronecker delta symbol that is defined as
# $$
# \delta(i, j) = \delta(j, i) = \left\{ \begin{array}{cc} 1 & i = j \\0 & i\neq j \end{array} \right.
# $$
#
# Before delving into the business of computing the derivatives, let us warm up a little. An important property of the trace is that the matrices can be rotated in a trace
# \begin{eqnarray}
# \trace A X = \trace X A
# \end{eqnarray}
#
# Using the Kronecker delta, the trace operator can be written as
# \begin{eqnarray}
# \trace X = \sum_i \sum_j X(i,j) \delta(i, j)
# \end{eqnarray}
#
# To prove this result, we will write the product explicitly using the index notation
# \begin{eqnarray}
# (A X)(i,j) &=& \sum_k A(i, k) X(k, j)
# \end{eqnarray}
# \begin{eqnarray}
# \trace A X & = & \sum_i \sum_j \left(\sum_k A(i, k) X(k, j) \right) \delta(i, j) \\
# & = & \sum_k \sum_i A(i, k) X(k, i) \\
# & = & \sum_k \sum_i X(k, i) A(i, k) \\
# & = & \sum_k \sum_r \sum_i X(k, i) A(i, r) \delta(r,k) \\
# & = & \sum_k \sum_r (X A)(k, r) \delta(r,k) = \trace X A
# \end{eqnarray}
#
# Let's now focus on the derivative of the trace of a product. We define
# \begin{eqnarray}
# f(X) = \trace A X & = & \sum_i \sum_j \left(\sum_k A(i, k) X(k, j) \right) \delta(i, j)
# \end{eqnarray}
# where $A$ is $I \times K$ and $X$ is $K \times I$. Note that the result matrix in the trace must be a square matrix as otherwise the result is rectangular matrix and the trace does not make any sense.
#
# The gradient with respect to $X$ will be a object of the same size as $X$, with each entry defined by
# $$
# \frac{d f}{d X} = [\frac{\partial f(X)}{\partial X(u, r)}]
# $$
# Formally, by the chain rule we have
# \begin{eqnarray}
# \frac{\partial f(X)}{\partial X(u, r)} & = & \frac{\partial f(X)}{\partial X(k, j)}\frac{\partial X(k, j)}{\partial X(u, r)} = \frac{\partial f(X)}{\partial X(k, j)} \delta(u, k) \delta(r, j)
# \end{eqnarray}
#
# We can now sum over the indices to remove the Kronecker delta symbols
# \begin{eqnarray}
# \frac{\partial f(X)}{\partial X(u, r)} & = & \sum_i \sum_j \sum_k A(i, k) \delta(u, k) \delta(r, j) \delta(i, j) \\
# & = & \sum_i \sum_j A(i, u) \delta(r, j) \delta(i, j) \\
# & = & \sum_j A(j, u) \delta(r, j) = A(r, u) = (A^\top)(u, r) \\
# \end{eqnarray}
#
# We have just shown that
# \begin{eqnarray}
# \frac{d f}{d X} = A^\top
# \end{eqnarray}
#
#
# ## Example: Derivative of $\trace A^\top X A$
# We will use the results above
# \begin{eqnarray}
# f(X) & = & \trace A^\top X A = \trace A A^\top X \\
# \frac{d f}{d X} &= & (A A^\top)^\top = A A^\top
# \end{eqnarray}
#
# Now, this quantity isnew.
# \begin{eqnarray}
# f(X) & = & \trace A^\top X A = \trace A A^\top X \\
# \frac{d f}{d A} &= & ?
# \end{eqnarray}
#
# \begin{eqnarray}
# f(A) = \trace A^\top X A & = & \sum_i \sum_j \left(\sum_k \sum_l (A^\top)(i, k) X(k, l) A(l, j) \right) \delta(i, j) \\
# \frac{d f}{d A} &= &[\frac{\partial f(A)}{\partial A(u, r)}] \\
# \frac{\partial f}{\partial A(u,r)} & = & \frac{\partial}{\partial A(u,r)} \sum_i \sum_j \left(\sum_k \sum_l (A^\top)(i, k) X(k, l) A(l, j) \right) \delta(i, j) \\
# & = & \sum_i \sum_j \left(\sum_k \sum_l \delta(k, u) \delta(i, r) X(k, l) A(l, j) \right) \delta(i, j) \\
# & & + \sum_i \sum_j \left(\sum_k \sum_l A(k, i) X(k, l) \delta(l, u) \delta(j, r) \right) \delta(i, j) \\
# & = & \sum_i \sum_j \sum_k \sum_l \delta(k, u) \delta(i, r) X(k, l) A(l, j) \delta(i, j) \\
# & & + \sum_i \sum_j \sum_k \sum_l A(k, i) X(k, l) \delta(l, u) \delta(j, r) \delta(i, j) \\
# & = & \sum_i \sum_j \sum_l \delta(i, r) X(u, l) A(l, j) \delta(i, j) \\
# & & + \sum_i \sum_j \sum_k A(k, i) X(k, u) \delta(j, r) \delta(i, j) \\
# & = & \sum_j \sum_l X(u, l) A(l, j) \delta(r, j) + \sum_j \sum_k A(k, j) X(k, u) \delta(j, r) \\
# & = & \sum_l X(u, l) A(l, r) + \sum_k A(k, r) X(k, u) \\
# & = & \sum_l X(u, l) A(l, r) + \sum_k (X^\top)(u,k) A(k, r) \\
# & = & (X A)(u, r) + (X^\top A)(u,r) \\
# & = & (X+X^\top) A
# \end{eqnarray}
# ## Example: Derivative of $\trace A X A^\top$
# This looks quite similar
#
# \begin{eqnarray}
# f(A) & = & \trace A X A^\top = \sum_i \sum_j \left(\sum_k \sum_l A (i, k) X(k, l) (A^\top)(l, j) \right) \delta(i, j) \\
# & = & \sum_i \sum_j \sum_k \sum_l A (i, k) X(k, l) A(j, l) \delta(i, j) \\
# \frac{\partial f}{\partial A(u,r)} & = & \sum_i \sum_j \sum_k \sum_l \delta(u,i) \delta(r,k) X(k, l) A(j, l) \delta(i, j) + \sum_i \sum_j \sum_k \sum_l A (i, k) X(k, l) \delta(u,j) \delta(r,l) \delta(i, j) \\
# & = & \sum_l X(r, l) A(u, l) + \sum_k A (u, k) X(k, r) \\
# & = & \sum_l A(u, l) (X^\top)(l, r) + \sum_k A (u, k) X(k, r) \\
# & = & (A X^\top)(u,r) + (A X)(u, r)
# \end{eqnarray}
#
# So the derivative is
# $$
# \frac{d f(A)}{d A} = A (X^\top + X)
# $$
#
# ## Matrix Factorization by Alternating Least Squares (ALS)
#
# We define the Frobenious norm
# $$
# \|E\|_F = \sqrt{\trace E^\top E}
# $$
#
# By using the results that we have just derived we obtain we can derive the derivative of the
# Frobenious norm of the error matrix $E$ as
#
# \begin{eqnarray}
# E^\top E &= & (X - M C)^\top (X - M C) \\
# & = & X^\top X + C^\top M^\top M C - X^\top M C - C^\top M^\top X \\
# \|E\|_F^2 & = & \trace \left( X^\top X + C^\top M^\top M C - 2 X^\top M C \right)
# \end{eqnarray}
#
# By the linearity of the trace
# \begin{eqnarray}
# \|E\|_F^2 & = & \trace \left( X^\top X + C^\top M^\top M C - 2 X^\top M C \right) \\
# \frac{d\|E\|_F^2}{d C} & = & 2 M^\top M C - 2 M^\top X \\
# C & = & (M^\top M)^{-1} M^\top X
# \end{eqnarray}
#
# \begin{eqnarray}
# \|E\|_F^2 & = & \trace X^\top X + \trace C^\top M^\top M C - 2 \trace X^\top M C \\
# & = & \trace X^\top X + \trace M C C^\top M^\top - 2 \trace C X^\top M \\
# \frac{d\|E\|_F^2}{d M} & = & 2 M C C^\top - 2 X C^\top \\
# M & = & X C^\top (C C^\top)^{-1}
# \end{eqnarray}
#
#
#
#
# $B = (A^\top A)^{-1} A^\top X$
#
# $A = X B^\top (B B^\top)^{-1}$
|
Matrix Calculus.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### DSPT6 - Adding Data Science to a Web Application
#
# The purpose of this notebook is to demonstrate:
# - Simple online analysis of data from a user of the Twitoff app or an API
# - Train a more complicated offline model, and serialize the results for online use
import sqlite3
import pickle
import pandas as pd
# Connect to sqlite database
conn = sqlite3.connect('C:\\Users\\bruno\\Desktop\\twitoff.sqlite3')
# + colab={} colab_type="code" id="vS_A9hjG1HGD"
def get_data(query, conn):
'''Function to get data from SQLite DB'''
cursor = conn.cursor()
result = cursor.execute(query).fetchall()
# Get columns from cursor object
columns = list(map(lambda x: x[0], cursor.description))
# Assign to DataFrame
df = pd.DataFrame(data=result, columns=columns)
return df
# + colab={} colab_type="code" id="pVapHGy7gEFx" tags=[]
import pickle
sql = '''
SELECT
tweet.id,
tweet.tweet,
tweet.embedding,
user.username
FROM tweet
JOIN user on tweet.user_id = user.id;
'''
df = get_data(sql, conn)
df['embedding_decoded'] = df.embedding.apply(lambda x: pickle.loads(x))
print(df.shape)
df.head(3)
# -
df.username.value_counts()
# + tags=[]
import numpy as np
user1_embeddings = df.embedding_decoded[df.username == 'barackobama']
user2_embeddings = df.embedding_decoded[df.username == 'jimmyfallon']
embeddings = pd.concat([user1_embeddings, user2_embeddings])
embeddings_df = pd.DataFrame(embeddings.to_list(),
columns=[f'dom{i}' for i in range(300)])
labels = np.concatenate([np.ones(len(user1_embeddings)),
np.zeros(len(user2_embeddings))])
print(embeddings_df.shape, labels.shape)
# + tags=[]
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
embeddings_df, labels, test_size=0.25, random_state=42
)
print(X_train.shape, X_test.shape)
# + tags=[]
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression(max_iter=1000)
# %timeit log_reg.fit(X_train, y_train)
# + tags=[]
from sklearn.metrics import classification_report, plot_confusion_matrix
y_pred = log_reg.predict(X_test)
print(classification_report(y_test, y_pred))
# +
import matplotlib.pyplot as plt
# %matplotlib inline
fig, ax = plt.subplots(figsize=(8,8))
plot_confusion_matrix(log_reg, X_test, y_test,
normalize='true', cmap='Blues',
display_labels=['<NAME>', '<NAME>'], ax=ax)
plt.title(f'LogReg Confusion Matrix (N={X_test.shape[0]})');
# +
import spacy
# Load SpaCy pre-trained model
nlp = spacy.load('en_core_web_md', disable=['tagger', 'parser'])
def vectorize_tweet(nlp, tweet_text):
'''This function returns the SpaCy embeddings for an input text'''
return list(nlp(tweet_text).vector)
# -
new_embedding = vectorize_tweet(nlp, "The innovation displayed during this pandemic is unprecedented.")
new_embedding[0:5]
log_reg.predict([new_embedding])
pickle.dump(log_reg, open("../models/log_reg.pkl", "wb"))
unpickled_lr = pickle.load(open("../models/log_reg.pkl", "rb"))
unpickled_lr.predict([new_embedding])
|
notebooks/LS333_DSPT7_Model_Demo_InClass.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Archivos & Sistema Operativo
# ## Abrir Archivos
# Se usa la función `open`, esta funciona con rutas absolutas o relativas.
path = 'untexto.txt'
f = open(path)
# Se puede tratar como una lista y se itera sobre las líneas.
for line in f:
print(line)
[x.rstrip() for x in open(path)]
# ### Modos de archivo
# Los archivos pueden abrirse con diferentes modos.
f = open(path, 'r') # Modo de lectura
f = open(path, 'w') # Modo de escritura
f = open(path, 'x') # Modo de lecto-escritura
# * `read` devuelve un cierto número de caracteres del archivo
# * Lo que constituye un "carácter" está determinado por la codificación del archivo, o simplemente bytes sin formato en modo binario
# +
f_binary = open(path, 'rb')
f_binary.seek(0)
f_binary.seek(10)
# -
# ## Cerrar archivos
# Cuando se crean archivos con `open`, es importante cerrarlos al finalizar el trabajo.
# Cuando el archivo se cierra con `close`, sus recursos vuelven al sistema operativo
f.close()
# ## Escribir Archivos
# ### Paso a Paso
# +
list(x for x in open(path) if len(x) > 1)
path_nuevo = 'nuevo_texto.txt'
f_escritura = open(path_nuevo, 'w')
f_escritura.writelines(x for x in open(path)if len(x) > 1)
f_escritura.close()
# -
# ### Forma Compacta
with open('tmp.txt', 'w') as handle:
handle.writelines(x for x in open(path) if len(x) > 1)
f.close()
# ### Ejercicio
#
# Crear un archivo y escribir un texto en el.
|
05_Archivos&SO.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import os
import csv
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
def get_file_names(dir_name):
file_names = []
for root, dirs, files in os.walk(dir_name, topdown = False):
for name in files:
new_name = "_".join(name.split("_")[:-1]) + ".png"
file_names.append(new_name)
return file_names
image_paths_expressions_csv_path = "/home/steffi/dev/independent_study/FairFace/expw_image_paths_expressions.csv"
expw_img_ex = pd.read_csv(image_paths_expressions_csv_path, delimiter=',')
labels_csv = '/home/steffi/dev/data/ExpW/labels_clean.csv'
expw = pd.read_csv(labels_csv, delimiter=',')
expw.head()
# ## Check expressions of selected images
# ### Black disgust
black_disgust_files = get_file_names("/home/steffi/dev/data/ExpW/ExpwHandSelected/Black/disgust")
expw[expw['Image name'].isin(black_disgust_files)]
# ### Black angry
black_angry_files = get_file_names("/home/steffi/dev/data/ExpW/ExpwHandSelected/Black/angry")
pd.set_option('display.max_rows', 70)
expw[expw['Image name'].isin(black_angry_files)]
|
notebooks/ExpW-check-handselected.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from plotly import __version__
from plotly.offline import download_plotlyjs, init_notebook_mode, plot, iplot
import plotly.graph_objs as go
# -
import pandas as pd
import numpy as np
df = pd.read_excel('books_variation.xlsx')
df.head()
book1 = df.loc[df['title'] == '<NAME> DAD']
book1 = book1.drop(columns='title')
book1
book1['date'] = pd.to_datetime(df['date'], infer_datetime_format=True)
indexed_book1 = book1.set_index(['date'])
indexed_book1.index
data = [go.Scatter(x= indexed_book1.index, y= indexed_book1.price)]
plot(data, filename='basic-line')
#Determining rolling statistics
rollmean = indexed_book1.rolling(window='14d').mean() #monthly basis
rollstd = indexed_book1.rolling(window='14d').std()
rollmean, rollstd
# +
#Plotting Rolling Statistics
trace1 = go.Scatter(x= indexed_book1.index, y= indexed_book1.price, name='Original')
trace2 = go.Scatter(x= rollmean.index , y= rollmean.price, name= 'Rolling Mean')
trace3 = go.Scatter(x= rollstd.index , y= rollstd.price, name= 'Rolling Std')
data = [trace1, trace2, trace3]
# Edit the layout
layout = dict(title = 'Rolling Mean and Standard Deviation',
xaxis = dict(title = 'Date'),
yaxis = dict(title = 'Price')
)
fig = dict(data=data, layout=layout)
plot(fig, filename='styled-line')
# +
#Dickey-Fuller test
from statsmodels.tsa.stattools import adfuller
dftest = adfuller(indexed_book1['price'], autolag='AIC')
dfout = pd.Series(dftest[0:4], index= ['Test statistic','p-value','lags used','number of observations used'])
for key,value in dftest[4].items():
dfout['Critical value (%s)'%key] = value
print(dfout)
# +
#The test statistic is positive, meaning we are much less likely to reject the null hypothesis (it looks non-stationary).
#Comparing the test statistic to the critical values, it looks like we would have to fail to reject the null hypothesis
#that the time series is non-stationary and does have time-dependent structure.
# +
#log transform the dataset to make the distribution of values more linear and better meet the expectations of this statistical test
import numpy as np
indexed_book1_logscale = np.log(indexed_book1)
data = [go.Scatter(x= indexed_book1_logscale.index, y= indexed_book1_logscale.price)]
plot(data, filename='line-mode')
# +
# Moving Average with log timeseries
moving_avg = indexed_book1_logscale.rolling(window='14d').mean()
moving_std = indexed_book1_logscale.rolling(window='14d').std()
moving_avg, moving_std
# -
trace1 = go.Scatter(x= indexed_book1_logscale.index, y= indexed_book1_logscale.price)
trace2 = go.Scatter(x= moving_avg.index , y= moving_avg.price)
data = [trace1, trace2]
plot(data, filename='basic-line')
# +
#Difference between log timeseries and moving average
logminusMA = indexed_book1_logscale - moving_avg
logminusMA
# +
#Determining the Stationarity of data
moving_avg = logminusMA.rolling(window='14d').mean()
moving_std = logminusMA.rolling(window='14d').std()
trace1 = go.Scatter(x= logminusMA.index, y= logminusMA.price, name='Original')
trace2 = go.Scatter(x= moving_avg.index , y= moving_avg.price, name= 'Rolling Mean')
trace3 = go.Scatter(x= moving_std.index , y= moving_std.price, name= 'Rolling Std')
data = [trace1, trace2, trace3]
# Edit the layout
layout = dict(title = 'Rolling Mean and Standard Deviation',
xaxis = dict(title = 'Date'),
yaxis = dict(title = 'Price'))
fig = dict(data=data, layout=layout)
plot(fig, filename='styled-line')
# -
print("Results of Dickey-Fuller test: ")
dftest = adfuller(logminusMA['price'], autolag='AIC')
dfout = pd.Series(dftest[0:4], index= ['Test statistic','p-value','lags used','number of observations used'])
for key,value in dftest[4].items():
dfout['Critical value (%s)'%key] = value
print(dfout)
# +
#Calculate the weighted average to see the trend
#DataFrame.ewm : Provides exponential weighted functions
weighted_avg = indexed_book1_logscale.ewm(com=0.5).mean()
weighted_avg
# +
trace1 = go.Scatter(x= indexed_book1_logscale.index, y= indexed_book1_logscale.price)
trace2 = go.Scatter(x= weighted_avg.index , y= weighted_avg.price)
data = [trace1, trace2]
plot(data, filename='basic-line')
#As you can see, the trend is moving with the logged data with respect to time
# +
#Difference between log timeseries and weighted average
logminusWA = indexed_book1_logscale - weighted_avg
print(logminusWA)
#Determining the Stationarity of data
moving_avg = logminusWA.rolling(window='14d').mean()
moving_std = logminusWA.rolling(window='14d').std()
trace1 = go.Scatter(x= logminusWA.index, y= logminusWA.price, name='Original')
trace2 = go.Scatter(x= moving_avg.index , y= moving_avg.price, name= 'Rolling Mean')
trace3 = go.Scatter(x= moving_std.index , y= moving_std.price, name= 'Rolling Std')
data = [trace1, trace2, trace3]
# Edit the layout
layout = dict(title = 'Rolling Mean and Standard Deviation',
xaxis = dict(title = 'Date'),
yaxis = dict(title = 'Price'))
fig = dict(data=data, layout=layout)
plot(fig, filename='styled-line')
# -
print("Results of Dickey-Fuller test: ")
dftest = adfuller(logminusWA['price'], autolag='AIC')
dfout = pd.Series(dftest[0:4], index= ['Test statistic','p-value','lags used','number of observations used'])
for key,value in dftest[4].items():
dfout['Critical value (%s)'%key] = value
print(dfout)
# +
# No difference in the p-value from original data and weighted average data
# Here timeseries is not stationary
# +
#Shifting the values
indexed_book1_logscale_diffshift = indexed_book1_logscale - indexed_book1_logscale.shift()
data = [go.Scatter(x= indexed_book1_logscale_diffshift.index, y= indexed_book1_logscale_diffshift.price)]
plot(data, filename='basic-line')
# +
indexed_book1_logscale_diffshift.dropna(inplace=True)
#Determining the Stationarity of data
moving_avg = indexed_book1_logscale_diffshift.rolling(window='14d').mean()
moving_std = indexed_book1_logscale_diffshift.rolling(window='14d').std()
trace1 = go.Scatter(x= indexed_book1_logscale_diffshift.index, y= indexed_book1_logscale_diffshift.price, name='Original')
trace2 = go.Scatter(x= moving_avg.index , y= moving_avg.price, name= 'Rolling Mean')
trace3 = go.Scatter(x= moving_std.index , y= moving_std.price, name= 'Rolling Std')
data = [trace1, trace2, trace3]
# Edit the layout
layout = dict(title = 'Rolling Mean and Standard Deviation',
xaxis = dict(title = 'Date'),
yaxis = dict(title = 'Price'))
fig = dict(data=data, layout=layout)
plot(fig, filename='styled-line')
# +
print("Results of Dickey-Fuller test: ")
dftest = adfuller(indexed_book1_logscale_diffshift['price'], autolag='AIC')
dfout = pd.Series(dftest[0:4], index= ['Test statistic','p-value','lags used','number of observations used'])
for key,value in dftest[4].items():
dfout['Critical value (%s)'%key] = value
print(dfout)
# Here timeseries is stationary and null-hypothesis is rejected
# +
from statsmodels.tsa.seasonal import seasonal_decompose
decomposition = seasonal_decompose(indexed_book1_logscale)
trend = decomposition.trend
seasonal = decomposition.seasonal
residual = decomposition.resid
from plotly import tools
trace1 = go.Scatter(x= indexed_book1_logscale.index, y= indexed_book1_logscale.price, name='Original')
trace2 = go.Scatter(x= trend.index, y= trend.price, name='Trend')
trace3 = go.Scatter(x= seasonal.index, y= seasonal.price, name='Seasonality')
trace4 = go.Scatter(x= residual.index, y= residual.price, name='Residual')
fig = tools.make_subplots(rows=4, cols=1)
fig.append_trace(trace1, 1, 1)
fig.append_trace(trace2, 2, 1)
fig.append_trace(trace3, 3, 1)
fig.append_trace(trace4, 4, 1)
fig['layout'].update(title='Stacked subplots')
plot(fig, filename='stacked-subplots')
# +
#Residuals are irregualr in nature
#So checking noise stationarity
decomposed_logdata = residual
decomposed_logdata.dropna(inplace=True)
#Determining the Stationarity of data
moving_avg = decomposed_logdata.rolling(window='14d').mean()
moving_std = decomposed_logdata.rolling(window='14d').std()
trace1 = go.Scatter(x= decomposed_logdata.index, y= decomposed_logdata.price, name='Original')
trace2 = go.Scatter(x= moving_avg.index , y= moving_avg.price, name= 'Rolling Mean')
trace3 = go.Scatter(x= moving_std.index , y= moving_std.price, name= 'Rolling Std')
data = [trace1, trace2, trace3]
# Edit the layout
layout = dict(title = 'Rolling Mean and Standard Deviation',
xaxis = dict(title = 'Date'),
yaxis = dict(title = 'Price'))
fig = dict(data=data, layout=layout)
plot(fig, filename='styled-line')
# +
#ACF and PACF plots
from statsmodels.tsa.stattools import acf, pacf
lag_acf = acf(indexed_book1_logscale_diffshift)
lag_pacf = pacf(indexed_book1_logscale_diffshift)
#lag_acf,lag_pacf
#ACF
#trace1 = go.Scatter(y= lag_acf, name='Autocorrelation Function', type='bar')
trace1 = {"y": lag_acf, "name": "Autocorrelation Function", "type": "bar"}
trace2 = {"y": lag_pacf, "name": "Partial Autocorrelation Function", "type": "bar"}
#trace2 = go.Scatter(y= lag_pacf, name='Partial Autocorrelation Function', type='bar')
data = [trace1, trace2]
layout = dict(title = 'ACF and PACF Plots')
fig = dict(data=data, layout=layout)
plot(fig)
# +
#AR Model
from statsmodels.tsa.arima_model import ARIMA
model = ARIMA(indexed_book1_logscale, order= (3,1,0))
results_AR = model.fit(disp=-1)
print("Plotting AR Model...")
trace1 = go.Scatter(x= indexed_book1_logscale_diffshift.index, y= indexed_book1_logscale_diffshift.price, name='Original')
trace2 = go.Scatter(y=results_AR.fittedvalues, name='AR fitted values')
data = [trace1, trace2]
layout = dict(title = 'RSS: %.4f'%sum((results_AR.fittedvalues-indexed_book1_logscale_diffshift.price)**2))
fig = dict(data=data, layout=layout)
plot(fig)
# +
#MA Model
from statsmodels.tsa.arima_model import ARIMA
model = ARIMA(indexed_book1_logscale, order= (0,1,0))
results_MA = model.fit(disp=-1)
print("Plotting MA Model...")
trace1 = go.Scatter(x= indexed_book1_logscale_diffshift.index, y= indexed_book1_logscale_diffshift.price, name='Original')
trace2 = go.Scatter(y=results_MA.fittedvalues, name='MA fitted values')
data = [trace1, trace2]
layout = dict(title = 'RSS: %.4f'%sum((results_MA.fittedvalues-indexed_book1_logscale_diffshift.price)**2))
fig = dict(data=data, layout=layout)
plot(fig)
# +
#AR Model is better as it has less RSS value than MA Model
# +
prediction = pd.Series(results_AR.fittedvalues, copy=True)
print(prediction)
prediction_cumsum = prediction.cumsum()
print(prediction_cumsum)
# -
prediction_log = pd.Series(indexed_book1_logscale.price.ix[0], index = indexed_book1_logscale.index)
prediction_log = prediction_log.add(prediction_cumsum, fill_value=0)
prediction_log
# +
prediction_ARIMA = np.exp(prediction_log)
trace1 = go.Scatter(x= indexed_book1.index, y= indexed_book1.price, name='Original data')
trace2 = go.Scatter(y=prediction_ARIMA, name='prdiction')
data = [trace1, trace2]
layout = dict(title = "Predictions")
fig = dict(data=data, layout=layout)
plot(fig)
# -
indexed_book1_logscale
# +
forecast = results_AR.forecast(steps=7)
#print(results_AR.forecast(steps=7))
results_AR.plot_predict(1,21)
results_AR.forecast(steps=7)
# -
|
TS Analysis for each book/#9.Rich Dad Poor DAD.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import geemap
geemap.show_youtube('9EUTX8j-YVM')
Map = geemap.Map()
Map.split_map()
Map
Map = geemap.Map()
Map.split_map(left_layer='HYBRID', right_layer='ROADMAP')
Map
basemaps = geemap.ee_basemaps.keys()
print(basemaps)
for basemap in basemaps:
print(basemap)
Map = geemap.Map()
Map.split_map(left_layer='NLCD 2016 CONUS Land Cover', right_layer='NLCD 2001 CONUS Land Cover')
Map
import ee
# https://developers.google.com/earth-engine/datasets/catalog/USGS_NLCD
collection = ee.ImageCollection("USGS/NLCD")
print(collection.aggregate_array('system:id').getInfo())
# +
nlcd_2001 = ee.Image('USGS/NLCD/NLCD2001').select('landcover')
nlcd_2016 = ee.Image('USGS/NLCD/NLCD2016').select('landcover')
left_layer = geemap.ee_tile_layer(nlcd_2001, {}, 'NLCD 2001')
right_layer = geemap.ee_tile_layer(nlcd_2016, {}, 'NLCD 2016')
Map = geemap.Map()
Map.split_map(left_layer, right_layer)
Map
# -
|
examples/notebooks/04_split_panel_map.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
"""
Illustrate finite element function over 2D mesh with triangles.
Good set of parameters for f1 function:
nx = 4; ny = 3
view: 58, 345
"""
from fe_approx2D import mesh, np
import os
class Gnuplotter:
def __init__(self):
self.fc = 0 # file counter
import io
self.commands = io.StringIO()
self._gnuwrite('unset border\nunset xtics\nunset ytics\nunset ztics\nset parametric\n')
self._plot = []
def _gnuwrite(self, command):
import builtins
builtins.str = str
self.commands.write(str(command))
def hold(self, mode):
pass
def plot3(self, x, y, z, style):
if '--' in style or '..' in style:
gnustyle = 'linespoints'
lt = 2
else:
gnustyle = 'lines'
lt = 1
filename = '_tmp_%04d.dat' % self.fc
self.fc += 1
f = open(filename, 'w')
for xi, yi, zi in zip(x, y, z):
f.write('%g %g %g\n' % (xi, yi, zi))
f.close()
self._plot.append('"%s" using 1:2:3 with %s lt %d lw 2 title ""' %
(filename, gnustyle, lt))
def view(self, angle1, angle2):
self._gnuwrite('set view %d,%d\n' % (angle1, angle2))
def axis(self, a):
self._gnuwrite('set xrange [%g:%g]\nset yrange [%g:%g]\nset zrange [%g:%g]\n' % tuple(a))
def savefig(self, filename):
self._gnuwrite('splot %s\n' % ', '.join(self._plot))
self._gnuwrite('set output "%s.eps"\n' % filename)
self._gnuwrite('set terminal postscript eps enhanced monochrome\n')
self._gnuwrite('replot\n')
self._gnuwrite('set output "%s.png"\n' % filename)
self._gnuwrite('set terminal png\n')
self._gnuwrite('replot\n')
def show(self):
self._gnuwrite('replot\npause 3\n')
text = self.commands.getvalue()
f = open('_tmp.gnu', 'w')
f.write(text)
f.close()
os.system('gnuplot _tmp.gnu')
class Matplotlibplotter:
# http://matplotlib.org/examples/mplot3d/lines3d_demo.html
pass
def f1(x, y):
return 1 + 4*x*(1-x)*y + (1 - y)*(1-x**2)
def fill(f, vertices):
values = np.zeros(vertices.shape[0])
for i, point in enumerate(vertices):
values[i] = f(point[0], point[1])
return values
def draw_mesh(vertices, cells, plt, style='g--'):
for local_vertices in cells:
local_vertices = local_vertices.tolist()
local_vertices.append(local_vertices[0]) # closed polygon
x = [vertices[vertex,0] for vertex in local_vertices]
y = [vertices[vertex,1] for vertex in local_vertices]
z = [0 for vertex in local_vertices]
plt.plot3(x, y, z, style)
plt.hold('on')
return
def draw_surface(zvalues, vertices, cells, plt, style='r-'):
for local_vertices in cells:
local_vertices = local_vertices.tolist()
local_vertices.append(local_vertices[0]) # closed polygon
x = [vertices[vertex,0] for vertex in local_vertices]
y = [vertices[vertex,1] for vertex in local_vertices]
z = [zvalues[vertex] for vertex in local_vertices]
plt.plot3(x, y, z, style)
plt.hold('on')
return
def demo1(f=f1, nx=4, ny=3, viewx=58, viewy=345, plain_gnuplot=True):
vertices, cells = mesh(nx, ny, x=[0,1], y=[0,1], diagonal='right')
if f == 'basis':
# basis function
zvalues = np.zeros(vertices.shape[0])
zvalues[int(round(len(zvalues)/2.)) + int(round(nx/2.))] = 1
else:
zvalues = fill(f1, vertices)
if plain_gnuplot:
plt = Gnuplotter()
else:
import scitools.std as plt
"""
if plt.backend == 'gnuplot':
gpl = plt.get_backend()
gpl('unset border; unset xtics; unset ytics; unset ztics')
#gpl('replot')
"""
draw_mesh(vertices, cells, plt)
draw_surface(zvalues, vertices, cells, plt)
plt.axis([0, 1, 0, 1, 0, zvalues.max()])
plt.view(viewx, viewy)
if plain_gnuplot:
plt.savefig('tmp')
else:
plt.savefig('tmp.pdf')
plt.savefig('tmp.eps')
plt.savefig('tmp.png')
plt.show()
#demo1()
demo1(f='basis', nx=4, ny=3, viewx=72)
# -
|
Data Science and Machine Learning/Machine-Learning-In-Python-THOROUGH/EXAMPLES/FINITE_ELEMENTS/INTRO/SRC/33_PLOT_FE_APPROX2D.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
from astropy.io import fits
import astropy
astropy.__version__
from spicer import spicer, kernels
import math
import spiceypy as spice
v = (1,0,0)
spice.vrotv(v, (0,0,1), np.radians(90))
s = spicer.Spicer('2015-10-18T23:50:24.747598')
s.utc
planets = 'earth moon venus mercury mars saturn jupiter neptune uranus pluto'.split()
for planet in planets:
s.target=planet+' barycenter'
s.ref_frame ='IAU_'+planet.upper()
# s.ref_frame = "j2000"
s.corr = 'lt+s'
print(planet)
try:
print(spice.vnorm(s.center_to_sun)/1e6)
except:
print('failed')
s.target='mars'
s.ref_frame = 'iau_mars'
s.corr = 'none'
s.center_to_sun
s.solar_constant
s.target = 'mars'
s.set_spoint_by(lat=0, lon=0)
s.spoint
s.south_pole
|
notebooks/2015-10-18 first dabbles.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from sympy import *
from pylab import *
init_printing(use_unicode=True)
a1 = Symbol("a1")
a2 = Symbol("a2")
a3 = Symbol("a3")
b1 = Symbol("b1")
b2 = Symbol("b2")
A = Matrix([[a1,0,0],[0,a2,0],[0,0,a3]])
B = Matrix([[b1,0,0],[0,0,b2],[0,b2,0]])
#A = Operator("A")
#B = Operator("B")
A
B
A*B - B*A
A.eigenvects()
B.eigenvects()
btwo = Bra(np.exp(a1))
btwo
ktwo = Ket("2")
ktwo
InnerProduct(btwo,ktwo)
btwo*A*ktwo
btwo*B*ktwo
a = Symbol("a")
A = Matrix([[0,a],[a,0]])
A.eigenvects()
A.norm()
E1 = Symbol("E1")
E2 = Symbol("E2")
H = Matrix([[E1,0],[0,E2]])
H.eigenvects()
am = matrix([[1],[1]])
E0 = Symbol("E0")
E1 = Symbol("E1")
A = Symbol("A")
H = Matrix([[E0,0,A],[0,E1,0],[A,0,E0]])
H.eigenvects()
# +
def spinx(s):
n = int(2.0*s+1)
sx = matrix(zeros((n,n)))
for a in range(0,n):
for b in range(0,n):
if (a==b+1):
sx[a,b] = sx[a,b] + 0.5*sqrt((s+1)*(a+b+1)-(a+1)*(b+1))
elif (a==b-1):
sx[a,b] = sx[a,b] + 0.5*sqrt((s+1)*(a+b+1)-(a+1)*(b+1))
return sx
def spiny(s):
n = int(2.0*s+1)
sy = matrix(zeros((n,n),dtype='complex'))
for a in range(0,n):
for b in range(0,n):
if (a==b+1):
sy[a,b] = sy[a,b] + 0.5j*sqrt((s+1)*(a+b+1)-(a+1)*(b+1))
elif (a==b-1):
sy[a,b] = sy[a,b] - 0.5j*sqrt((s+1)*(a+b+1)-(a+1)*(b+1))
return sy
def spinz(s):
n = int(2.0*s+1)
sz = matrix(zeros((n,n)))
for a in range(0,n):
for b in range(0,n):
if (a==b):
sz[a,b] = (s+1-b-1)
return sz
# -
# Sx = Sx1+Sx2+Sx3
# Sy = ...
# Sz = ...
s = 0.5
I = eye(2)
Sx = spinx(s)
Sy = spiny(s)
Sz = spinz(s)
Sx = kron(Sx,kron(I,I)) + kron(I,kron(Sx,I)) + kron(I,kron(I,Sx))
Sy = kron(Sy,kron(I,I)) + kron(I,kron(Sy,I)) + kron(I,kron(I,Sy))
Sz = kron(Sz,kron(I,I)) + kron(I,kron(Sz,I)) + kron(I,kron(I,Sz))
S = Sx**2 + Sy**2 + Sz**2
Ssym = Matrix(S)
Ssym.eigenvals()
print(eigh(S))
a = Symbol("a")
sqrt2 = Symbol("sqrt(2)")
H = Matrix([[1,1],[1,-1]])
Heig = H.eigenvects()
Heig
# +
npH = matrix([[1,1,],[1,-1]])
npHeig = eigh(npH)
test = np.linalg.norm(npHeig[1])
#matrix(Heig[0][2])
# -
np.linalg.norm(matrix(Heig[0][2]))
|
physics/quant/QuantumSet3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # GraphQL
#
# If you want to try out this notebook with a live Python kernel, use mybinder:
#
# <a class="reference external image-reference" href="https://mybinder.org/v2/gh/vaexio/vaex/latest?filepath=docs%2Fsource%2Fexample_graphql.ipynb"><img alt="https://mybinder.org/badge_logo.svg" src="https://mybinder.org/badge_logo.svg" width="150px"></a>
#
# vaex-graphql is a plugin package that exposes a DataFrame via a GraphQL interface. This allows easy sharing of data or aggregations/statistics or machine learning models to frontends or other programs with a standard query languages.
#
# (Install with `$ pip install vaex-graphql`, no conda-forge support yet)
import vaex.ml
df = vaex.ml.datasets.load_titanic()
df
result = df.graphql.execute("""
{
df {
min {
age
fare
}
mean {
age
fare
}
max {
age
fare
}
groupby {
sex {
count
mean {
age
}
}
}
}
}
""")
result.data
# ## Pandas support
# After importing vaex.graphql, vaex also installs a pandas accessor, so it is also accessible for Pandas DataFrames.
df_pandas = df.to_pandas_df()
df_pandas.graphql.execute("""
{
df(where: {age: {_gt: 20}}) {
row(offset: 3, limit: 2) {
name
survived
}
}
}
"""
).data
# ## Server
#
#
# The easiest way to learn to use the GraphQL language/vaex interface is to launch a server, and play with the GraphiQL graphical interface, its autocomplete, and the schema explorer.
#
# We try to stay close to the Hasura API: https://docs.hasura.io/1.0/graphql/manual/api-reference/graphql-api/query.html
#
#
# A server can be started from the command line:
#
# `$ python -m vaex.graphql myfile.hdf5`
#
# Or from within Python using [df.graphql.serve](api.html#vaex.graphql.DataFrameAccessorGraphQL.serve)
# ## GraphiQL
# See https://github.com/mariobuikhuizen/ipygraphql for a graphical widget, or a [mybinder to try out a live example](https://mybinder.org/v2/gh/mariobuikhuizen/ipygraphql/master?filepath=example.ipynb).
# 
|
docs/source/example_graphql.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="iC3ijHEQeQmH" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 666} outputId="c26dc2f0-ef9b-430e-bba9-e82b8ee0e838"
'''Transfer learning toy example.
1 - Train a simple convnet on the MNIST dataset the first 5 digits [0..4].
2 - Freeze convolutional layers and fine-tune dense layers
for the classification of digits [5..9].
Get to 99.8% test accuracy after 5 epochs
for the first five digits classifier
and 99.2% for the last five digits after transfer + fine-tuning.
'''
from __future__ import print_function
import datetime
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras import backend as K
now = datetime.datetime.now
batch_size = 128
num_classes = 5
epochs = 5
# input image dimensions
img_rows, img_cols = 28, 28
# number of convolutional filters to use
filters = 32
# size of pooling area for max pooling
pool_size = 2
# convolution kernel size
kernel_size = 3
if K.image_data_format() == 'channels_first':
input_shape = (1, img_rows, img_cols)
else:
input_shape = (img_rows, img_cols, 1)
def train_model(model, train, test, num_classes):
x_train = train[0].reshape((train[0].shape[0],) + input_shape)
x_test = test[0].reshape((test[0].shape[0],) + input_shape)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
# convert class vectors to binary class matrices
y_train = keras.utils.to_categorical(train[1], num_classes)
y_test = keras.utils.to_categorical(test[1], num_classes)
model.compile(loss='categorical_crossentropy',
optimizer='adadelta',
metrics=['accuracy'])
t = now()
model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
verbose=1,
validation_data=(x_test, y_test))
print('Training time: %s' % (now() - t))
score = model.evaluate(x_test, y_test, verbose=0)
print('Test score:', score[0])
print('Test accuracy:', score[1])
# the data, split between train and test sets
(x_train, y_train), (x_test, y_test) = mnist.load_data()
# create two datasets one with digits below 5 and one with 5 and above
x_train_lt5 = x_train[y_train < 5]
y_train_lt5 = y_train[y_train < 5]
x_test_lt5 = x_test[y_test < 5]
y_test_lt5 = y_test[y_test < 5]
x_train_gte5 = x_train[y_train >= 5]
y_train_gte5 = y_train[y_train >= 5] - 5
x_test_gte5 = x_test[y_test >= 5]
y_test_gte5 = y_test[y_test >= 5] - 5
# define two groups of layers: feature (convolutions) and classification (dense)
feature_layers = [
Conv2D(filters, kernel_size,
padding='valid',
input_shape=input_shape),
Activation('relu'),
Conv2D(filters, kernel_size),
Activation('relu'),
MaxPooling2D(pool_size=pool_size),
Dropout(0.25),
Flatten(),
]
classification_layers = [
Dense(128),
Activation('relu'),
Dropout(0.5),
Dense(num_classes),
Activation('softmax')
]
# create complete model
model = Sequential(feature_layers + classification_layers)
# train model for 5-digit classification [0..4]
train_model(model,
(x_train_lt5, y_train_lt5),
(x_test_lt5, y_test_lt5), num_classes)
# freeze feature layers and rebuild model
for l in feature_layers:
l.trainable = False
# transfer: train dense layers for new classification task [5..9]
train_model(model,
(x_train_gte5, y_train_gte5),
(x_test_gte5, y_test_gte5), num_classes)
# + id="GgrgCtlqesWJ" colab_type="code" colab={}
|
9_Deep_Learning/Artificial_Neural_Networks/Use cases for ANN/MNIST_Digits_Classifer_with_Only_5_digits.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# 
# # Practical Assignment - Programming for Data Analysis 2018
# By <NAME> G00263352
#
#
#
# # Numpy.Random Package
# In this notebook I will answer and discuss following points:
# 1. The purpose of Numpy.Random package
# 2. Explanation of 'Simple random data' and 'Permutations' functions
# 3. Use and purpose of 'Distributions' functions such as uniform, normal, logistic, geometric, exponential and more.
# 4. Why use seeds in generating pseudorandom numbers.
# ## 1. Purpose of Numpy.Random package
#
# Before diving deep into the numpy.random package, here is some background information on Numpy as a package.
#
# It is a Python Package, specialized for building and manipulating large, multidimensional arrays. NumPy has built-in functions for linear alegbra and random number generation.
# It's an important library because a lot of the other Python packages such as SciPy, Matplotlib depend on Numpy to function (to a reasonable extent.)
#
# The numpy.random module supplements the built-in Python random with functions for efficiently generating whole arrays of sample values from many kinds of probability distributions. Source [Python for Data Analysis by <NAME>ey](https://www.oreilly.com/library/view/python-for-data/9781449323592/ch04.html)
#
#
# Numpy has some benefits over Python lists such as: being more compact, faster access in reading and writing items, being more convenient and more efficient.
# **Numpy array** is a powerful N-dimensional array object which is in the form of rows and columns.
# +
# Import libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from matplotlib.ticker import FuncFormatter
# %matplotlib inline
# -
# ## 1.1 Types of Arrays
# **Single-dimensional Numpy Array**
a=np.array([1,2,3])
print(a)
# **Multi Dimentional Numpy Array**
a=np.array([(1,2,3),(4,5,6)])
print(a)
# ## 2. Permutations & Simple Random Data
#
# #### 2.1 What is permutation?
#
# A permutation is a method to calculate the number of events occurring where order matters.
#
# Use of Permutations
# * **permutation(x)** Randomly permute a sequence, or return a permuted range.
# * **shuffle(x)** Modify a sequence in-place by shuffling its contents.
# +
# Import a Python module to print permutations
from itertools import permutations
# Get all permutations of [1, 2, 3]
p = permutations([1, 2, 3])
# Print the permutations
for i in list(p):
print(i)
# -
# I can see from example above that the outcome of obtained result did in fact come out in an order.
# #### 2.2 What does Shuffle function do?
#
# The method shuffle() randomizes the items of a list in place.
# +
# Testing a Python library to shuffle all values
from random import shuffle
x = [12, 15, 77, 298];
# Shuffle and print the outcome
shuffle(x)
print ("Reshuffled values : ", x)
# +
# Testing shuffle function with strings
names = ["Simona", "Elena", "Pat", "Dave"]
shuffle(names) # Shuffle all strings
print ("New shuffled name order : ", names) # Print shuffled strings
# -
# #### 2.3 Sample Random Data
# Import random function
import random
# **random.sample**
#
# sample() is an inbuilt function of random module in Python that returns a particular length list of items chosen from the sequence i.e. list, tuple, string or set. Used for random sampling without replacement.
# Below I will test a few types of sequences and see what outcome the function returns.
# +
# Print list of random items of length 3 from the given list.
list1 = [5, 6, 7, 8, 9, 11]
print("With list:", random.sample(list1, 3))
# Print list of random items of length 4 from the given string.
string = "Computer"
print("With string:", random.sample(string, 4))
# Print list of random items of length 2 from the given tuple.
tuple1 = ("college" , "work" , "pc" , "study" , "science")
print("With tuple:", random.sample(tuple1, 2))
# Print list of random items of length 3 from the given set.
set1 = {"a", "b", "c", "d", "e"}
print("With set:", random.sample(set1, 3))
# -
# **random.randint**
#
# Returns a random element from the non-empty sequence seq. If seq is empty, raises IndexError.
#
# Randint accepts two parameters: a lowest and a highest number.
# +
from random import randint
# Generate integers between 1,5
a = random.randint(0, 5)
print(a)
# -
# **random.choice**
# +
# Generate a random sample from a 1-D array
letters = ['a', 'b', 'c', 'd', 'e']
print("Random choice:", random.choice(letters)) # Print generated random sample
# -
# ## 3. Probability Distributions & Their Relationships
#
# Probability distributions are a fundamental concept in statistics. They are used both on a theoretical level and a practical level.
#
# #### 3.1 Common Data Types
#
# The data can be discrete or continuous.
#
# * Discrete Data can take only specified values.
#
# Discrete probability functions are also known as probability mass functions and can assume a discrete number of values. For example, coin tosses and counts of events are discrete functions. These are discrete distributions because there are no in-between values. [Source](http://statisticsbyjim.com/basics/probability-distributions/)
#
# * Continuous Data can take any value within a given range. The range may be finite or infinite.
#
# Continuous probability functions are also known as probability density functions. You know that you have a continuous distribution if the variable can assume an infinite number of values between any two values. Continuous variables are often measurements on a scale, such as height, weight, and temperature. [Source](http://statisticsbyjim.com/basics/probability-distributions/)
#
# Probabilities for continuous distributions are measured over ranges of values rather than single points. A probability indicates the likelihood that a value will fall within an interval.
#
# #### 3.2 Density Functions
#
# Distributions are often described in terms of their density or density functions.
#
# Density functions are functions that describe how the proportion of data or likelihood of the proportion of observations change over the range of the distribution.
#
# Two types of density functions are **probability density functions** and **cumulative density functions.**
#
# * Probability Density function: calculates the probability of observing a given value.
# * Cumulative Density function: calculates the probability of an observation equal or less than a value. [Source](https://machinelearningmastery.com/statistical-data-distributions/)
#
# Below is a graph of some of the common distributions and the arrows inidicate which distributions relate to each other.
#
# I will now compare some common distributions and their relationships with one another.
#
#
# 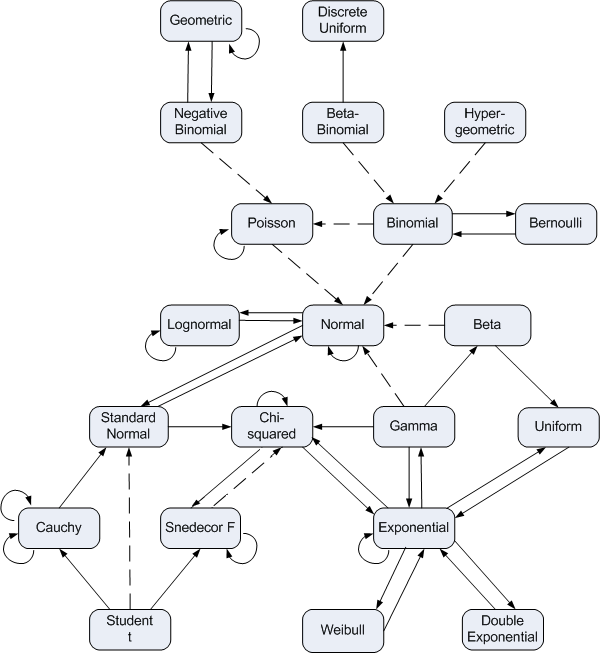 [Source](https://www.johndcook.com)
#
# I also found this graph below very interesting as it shows similarities between some common distributions and I will try to compare my analysis of these distribution relationships to what this graph suggests and draw a conclusion.
#
# 
#
# [Source](https://analyticsbuddhu.com/2017/02/26/how-many-types-of-continuous-probability-distribution/)
# ### 3.3 Discrete Distributions
# * Poisson
#
# **Poisson distribution** shows number of times an event occurs in fixed time interval. It is a binomial approximated distribution which occurs when number of trials (n) becomes sufficiently large and probability of success (p) successively becomes small.
# +
# Intializing the parameters for Poisson distribution
s = np.random.poisson(5, 10000) # Draw samples from the parameterized Poisson distribution
count, bins, ignored = plt.hist(s, 14, density=True, facecolor='green', alpha=0.5)
plt.title('Poisson Distribution') # Give this graph a title
plt.ylabel("Frequency") # Label the y axis
plt.show() # Display histogram of the sample
# -
# * Binomial
#
# A **binomial distribution** is simply the probability of a success or failure outcome in an experiment that is repeated multiple times.
# +
# Initializing the parameters 'number of trials' and 'probability of success'
n, p = 17, 0.7 # number of trials, probability of each trial
s = np.random.binomial(n, p, 1000)
count, bins, ignored = plt.hist(s, 14, density=True, facecolor='pink', alpha=0.77)
plt.title('Binomial Distribution') # Give this graph a title
plt.ylabel("Probability of Success") # Give y axis a title
plt.xlabel("No. of Trials") # Give X axis a title
plt.show() # Display histogram of the sample
# -
# Similarities & differences between Binominal & Poisson Distributions
#
#
# * Binomial Distribution is biparametric, i.e. it is featured by two parameters n and p whereas Poisson distribution is uniparametric, i.e. characterised by a single parameter m.
# * There are a fixed number of attempts in the binomial distribution. On the other hand, an unlimited number of trials are there in a poisson distribution.
# * The success probability is constant in binomial distribution but in poisson distribution, there are an extremely small number of success chances.
# * In a binomial distribution, there are only two possible outcomes, i.e. success or failure. Conversely, there are an unlimited number of possible outcomes in the case of poisson distribution. [Source](https://keydifferences.com/difference-between-binomial-and-poisson-distribution.html)
#
# ### 3.3 Continuous Distribution
# * Uniform
#
# **Uniform distribution** is probability associated with each data points within a fixed interval is equal.
# +
# Parameters low and high have been assigned the values 1 and 6
s = np.random.uniform(1, 6, 500000)
count, bins, ignored = plt.hist(s, 14, density=True, facecolor='yellow', alpha=0.77)
plt.title('Uniform Continuous Distribution') # Give this graph a titles
plt.ylabel("Frequency") # Label y axis
plt.show() # Display histogram of the sample
# -
# * Normal
# The probability density function of the **normal distribution** is often called the bell curve because of its characteristic shape. It can take on values anywhere on the real line.
# +
mu, sigma = 0, 0.1 # mean and standard deviation
s = np.random.normal(mu, sigma, 1000)
abs(mu - np.mean(s)) < 0.01 # find mean
abs(sigma - np.std(s, ddof=1)) < 0.01 # find standard deviation
count, bins, ignored = plt.hist(s, 30, density=True, facecolor="grey")
plt.plot(bins, 1/(sigma * np.sqrt(2 * np.pi)) *
np.exp( - (bins - mu)**2 / (2 * sigma**2) ),
linewidth=2, color='r')
plt.title("Normal Distribution") # Give graph a title
plt.show() # Show graph
# -
# * Gamma
#
# **Gamma distribution** is a right skewed distribution used for continuous variables. This is due to its flexibility in the choice of the shape and scale parameters. The scale parameter determines where the bulk of the observations lies and the shape parameter determines how the distribution will look.
# +
#Initializing the parameters for Gamma distribution
shape, scale = 1, 2.
s = np.random.gamma(shape, scale, 50000)
count, bins, ignored = plt.hist(s, density=True, facecolor='pink')
plt.title('Gamma Distribution') # Give graph a title
plt.ylabel("Frequency") # Label y axis
plt.show() # Display histogram of the sample
# -
# ## 4. Use of Seed
#
# Random number generation (RNG) is the process by which a string of random numbers may be drawn. The numbers are not completely random for several reasons.
#
# 1. They are drawn from a probability distribution. The most common one is the uniform distribution on the domain 0≤x<1 , i.e., random numbers between zero and one.
#
# 2. In most computer applications, the random numbers are actually pseudorandom. They depend entirely on an input seed and are then generated by a deterministic algorithm from that seed. [Source](http://justinbois.github.io/bootcamp/2016/lessons/l26_random_number_generation.html)
#
# To demonstrate that random number generation is deterministic, I will seed the random number generator
# +
# Seed the RNG
np.random.seed(25)
# Generate random numbers
np.random.random(size=5)
# +
# Re-seed the RNG
np.random.seed(25)
# Generate random numbers
np.random.random(size=5)
# -
# The random numbers are exactly the same. If I use a different seed, the outcome would be with different random numbers.
# # Conclusion
#
# Simple random sample advantages include ease of use and accuracy of representation. According to my the research I read there is no easier method to extract a research sample from a larger population than simple random sampling.
#
# The probability distributions are a common way to describe, and possibly predict, the probability of an event. The probability is zero for an impossible event and one for an event which is certain to occur. It's an important concept for making forecasts and risk assessments. These events could be anything from the number of cars passing through a certain point on a road ( I always see them wires on the road and know I now what they are used for and how they use this data) to number of calls a call centre gets per minute.
#
# To conlude, I found this assignement very interesting in relation to how different types of distributions work and how to perform random sampling.
|
numpy.random.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] toc="true"
# <h1>Table of Contents<span class="tocSkip"></span></h1>
# <div class="toc"><ul class="toc-item"><li><span><a href="#Building-an-Image-Classifier-with-Differential-Privacy" data-toc-modified-id="Building-an-Image-Classifier-with-Differential-Privacy-1">Building an Image Classifier with Differential Privacy</a></span><ul class="toc-item"><li><span><a href="#Overview" data-toc-modified-id="Overview-1.1">Overview</a></span></li><li><span><a href="#Hyper-parameters" data-toc-modified-id="Hyper-parameters-1.2">Hyper-parameters</a></span></li><li><span><a href="#Data" data-toc-modified-id="Data-1.3">Data</a></span></li><li><span><a href="#Model" data-toc-modified-id="Model-1.4">Model</a></span></li><li><span><a href="#Prepare-for-Training" data-toc-modified-id="Prepare-for-Training-1.5">Prepare for Training</a></span></li><li><span><a href="#Train-the-network" data-toc-modified-id="Train-the-network-1.6">Train the network</a></span></li><li><span><a href="#Test-the-network-on-test-data" data-toc-modified-id="Test-the-network-on-test-data-1.7">Test the network on test data</a></span></li><li><span><a href="#Tips-and-Tricks" data-toc-modified-id="Tips-and-Tricks-1.8">Tips and Tricks</a></span></li><li><span><a href="#Private-Model-vs-Non-Private-Model-Performance" data-toc-modified-id="Private-Model-vs-Non-Private-Model-Performance-1.9">Private Model vs Non-Private Model Performance</a></span></li></ul></li></ul></div>
# -
# # Building an Image Classifier with Differential Privacy
# ## Overview
#
# In this tutorial we will learn to do the following:
# 1. Learn about privacy specific hyper-parameters related to DP-SGD
# 2. Learn about ModelInspector, incompatible layers, and use model rewriting utility.
# 3. Train a differentially private ResNet18 for image classification.
# ## Hyper-parameters
# To train a model with Opacus there are three privacy-specific hyper-parameters that must be tuned for better performance:
#
# * Max Grad Norm: The maximum L2 norm of per-sample gradients before they are aggregated by the averaging step.
# * Noise Multiplier: The amount of noise sampled and added to the average of the gradients in a batch.
# * Delta: The target δ of the (ϵ,δ)-differential privacy guarantee. Generally, it should be set to be less than the inverse of the size of the training dataset. In this tutorial, it is set to $10^{−5}$ as the CIFAR10 dataset has 50,000 training points.
#
# We use the hyper-parameter values below to obtain results in the last section:
# +
MAX_GRAD_NORM = 1.2
NOISE_MULTIPLIER = .38
DELTA = 1e-5
LR = 1e-3
NUM_WORKERS = 2
# -
# There's another constraint we should be mindful of—memory. To balance peak memory requirement, which is proportional to `batch_size^2`, and training performance, we use virtual batches. With virtual batches we can separate physical steps (gradient computation) and logical steps (noise addition and parameter updates): use larger batches for training, while keeping memory footprint low. Below we will specify two constants:
BATCH_SIZE = 128
VIRTUAL_BATCH_SIZE = 512
# ## Data
# Now, let's load the CIFAR10 dataset. We don't use data augmentation here because, in our experiments, we found that data augmentation lowers utility when training with DP.
# +
import torch
import torchvision
import torchvision.transforms as transforms
# These values, specific to the CIFAR10 dataset, are assumed to be known.
# If necessary, they can be computed with modest privacy budget.
CIFAR10_MEAN = (0.4914, 0.4822, 0.4465)
CIFAR10_STD_DEV = (0.2023, 0.1994, 0.2010)
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize(CIFAR10_MEAN, CIFAR10_STD_DEV),
])
# -
# Using torchvision datasets, we can load CIFAR10 and transform the PILImage images to Tensors of normalized range [-1, 1]
# +
from torchvision.datasets import CIFAR10
DATA_ROOT = '../cifar10'
train_dataset = CIFAR10(
root=DATA_ROOT, train=True, download=True, transform=transform)
train_loader = torch.utils.data.DataLoader(
train_dataset,
batch_size=BATCH_SIZE,
shuffle=True,
num_workers=NUM_WORKERS,
)
test_dataset = CIFAR10(
root=DATA_ROOT, train=False, download=True, transform=transform)
test_loader = torch.utils.data.DataLoader(
test_dataset,
batch_size=BATCH_SIZE,
shuffle=False,
num_workers=NUM_WORKERS,
)
# -
# ## Model
# +
from torchvision import models
model = models.resnet18(num_classes=10)
# -
# Now, let’s check if the model is compatible with Opacus. Opacus does not support all type of Pytorch layers. To check if your model is compatible with the privacy engine, we have provided a util class to validate your model.
# If you run these commands, you will get the following error:
# +
from opacus.dp_model_inspector import DPModelInspector
inspector = DPModelInspector()
inspector.validate(model)
# -
# Let us modify the model to work with Opacus. From the output above, you can see that the BatchNorm layers are not supported because they compute the mean and variance across the batch, creating a dependency between samples in a batch, a privacy violation. One way to modify our model is to replace all the BatchNorm layers with [GroupNorm](https://arxiv.org/pdf/1803.08494.pdf) using the `convert_batchnorm_modules` util function.
# +
from opacus.utils import module_modification
model = module_modification.convert_batchnorm_modules(model)
inspector = DPModelInspector()
print(f"Is the model valid? {inspector.validate(model)}")
# -
# For maximal speed, we can check if CUDA is available and supported by the PyTorch installation. If GPU is available, set the `device` variable to your CUDA-compatible device. We can then transfer the neural network onto that device.
# +
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model = model.to(device)
# -
# We then define our optimizer and loss function. Opacus’ privacy engine can attach to any (first-order) optimizer. You can use your favorite—Adam, Adagrad, RMSprop—as long as it has an implementation derived from [torch.optim.Optimizer](https://pytorch.org/docs/stable/optim.html). In this tutorial, we're going to use [RMSprop](https://pytorch.org/docs/stable/optim.html).
# +
import torch.nn as nn
import torch.optim as optim
criterion = nn.CrossEntropyLoss()
optimizer = optim.RMSprop(model.parameters(), lr=LR)
# -
# ## Prepare for Training
# We will define a util function to calculate accuracy
def accuracy(preds, labels):
return (preds == labels).mean()
# We now attach the privacy engine initialized with the privacy hyperparameters defined earlier. There’s also the enigmatic-looking parameter `alphas`, which we won’t touch for the time being.
# +
from opacus import PrivacyEngine
print(f"Using sigma={NOISE_MULTIPLIER} and C={MAX_GRAD_NORM}")
privacy_engine = PrivacyEngine(
model,
batch_size=VIRTUAL_BATCH_SIZE,
sample_size=len(train_dataset),
alphas=[1 + x / 10.0 for x in range(1, 100)] + list(range(12, 64)),
noise_multiplier=NOISE_MULTIPLIER,
max_grad_norm=MAX_GRAD_NORM,
)
privacy_engine.attach(optimizer)
# -
# We will then define our train function. This function will train the model for one epoch.
assert VIRTUAL_BATCH_SIZE % BATCH_SIZE == 0 # VIRTUAL_BATCH_SIZE should be divisible by BATCH_SIZE
virtual_batch_rate = int(VIRTUAL_BATCH_SIZE / BATCH_SIZE)
# +
import numpy as np
def train(model, train_loader, optimizer, epoch, device):
model.train()
criterion = nn.CrossEntropyLoss()
losses = []
top1_acc = []
for i, (images, target) in enumerate(train_loader):
optimizer.zero_grad()
images = images.to(device)
target = target.to(device)
# compute output
output = model(images)
loss = criterion(output, target)
preds = np.argmax(output.detach().cpu().numpy(), axis=1)
labels = target.detach().cpu().numpy()
# measure accuracy and record loss
acc = accuracy(preds, labels)
losses.append(loss.item())
top1_acc.append(acc)
loss.backward()
# take a real optimizer step after N_VIRTUAL_STEP steps t
if ((i + 1) % virtual_batch_rate == 0) or ((i + 1) == len(train_loader)):
optimizer.step()
else:
optimizer.virtual_step() # take a virtual step
if i % 200 == 0:
epsilon, best_alpha = optimizer.privacy_engine.get_privacy_spent(DELTA)
print(
f"\tTrain Epoch: {epoch} \t"
f"Loss: {np.mean(losses):.6f} "
f"Acc@1: {np.mean(top1_acc) * 100:.6f} "
f"(ε = {epsilon:.2f}, δ = {DELTA})"
)
# -
# Next, we will define our test function to validate our model on our test dataset.
def test(model, test_loader, device):
model.eval()
criterion = nn.CrossEntropyLoss()
losses = []
top1_acc = []
with torch.no_grad():
for images, target in test_loader:
images = images.to(device)
target = target.to(device)
output = model(images)
loss = criterion(output, target)
preds = np.argmax(output.detach().cpu().numpy(), axis=1)
labels = target.detach().cpu().numpy()
acc = accuracy(preds, labels)
losses.append(loss.item())
top1_acc.append(acc)
top1_avg = np.mean(top1_acc)
print(
f"\tTest set:"
f"Loss: {np.mean(losses):.6f} "
f"Acc: {top1_avg * 100:.6f} "
)
return np.mean(top1_acc)
# ## Train the network
# +
from tqdm import tqdm_notebook
for epoch in tqdm_notebook(range(20), desc="Epoch", unit="epoch"):
train(model, train_loader, optimizer, epoch + 1, device)
# -
# ## Test the network on test data
top1_acc = test(model, test_loader, device)
# ## Tips and Tricks
# 1. Generally speaking, differentially private training is enough of a regularizer by itself. Adding any more regularization (such as dropouts or data augmentation) is unnecessary and typically hurts performance.
# 2. Tuning MAX_GRAD_NORM is very important. Start with a low noise multiplier like .1, this should give comparable performance to a non-private model. Then do a grid search for the optimal MAX_GRAD_NORM value. The grid can be in the range [.1, 10]
# ## Private Model vs Non-Private Model Performance
# Now let us compare how our private model compares with the non-private ResNet18.
#
# We trained a non-private ResNet18 model for 20 epochs using the same hyper-parameters as above and with BatchNorm replaced with GroupNorm. The results of that training and the training that is discussed in this tutorial are summarized in the table below:
# | Model | Top 1 Accuracy (%) | ϵ |
# |----------------|--------------------|---|
# | ResNet | 76 | ∞ |
# | Private ResNet | 56.61 | 53.54 |
|
tutorials/building_image_classifier.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: analysis
# language: python
# name: analysis
# ---
# # Masks generation
#
# The porpuses of this notebook is to show how to generate ocean masks for different regions. It uses functions genBasinMasks.
from mom6_tools.m6plot import xyplot
from mom6_tools.m6toolbox import genBasinMasks
from mom6_tools.MOM6grid import MOM6grid
from mom6_tools.DiagsCase import DiagsCase
import yaml
import numpy
import xarray as xr
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore")
# %matplotlib inline
# Read in the yaml file
diag_config_yml_path = "diag_config.yml"
diag_config_yml = yaml.load(open(diag_config_yml_path,'r'), Loader=yaml.Loader)
# Create the case instance
dcase = DiagsCase(diag_config_yml['Case'])
RUNDIR = dcase.get_value('RUNDIR')
print('Run directory is:', RUNDIR)
print('Casename is:', dcase.casename)
stream = True
# Load mom6 grid
grd = dcase.grid
depth = grd.depth_ocean
# remote Nan's, otherwise genBasinMasks won't work
depth[numpy.isnan(depth)] = 0.0
# ### Create masks for different regions
basin_code = genBasinMasks(grd.geolon, grd.geolat, depth)
# ### Check code number for each region defined
vals = numpy.unique(basin_code)
for v in vals:
dummy = numpy.zeros(basin_code.shape)
dummy[basin_code == v] = v
dummy = numpy.ma.masked_where(depth == 0., dummy)
plt.figure(figsize=(12,8))
xyplot(dummy, grd.geolon, grd.geolat,title='Code = '+str(v))
# reload codes as dataarray
basin_code = genBasinMasks(grd.geolon, grd.geolat, depth, xda=True)
# Noticed that point [391, 434] does not belong to any of the masks generated. This is okay but let see where this point is located:
plt.figure(figsize=(12,8))
xyplot(basin_code[0,:].values, grd.geolon, grd.geolat)
plt.plot(grd.geolon[434,391], grd.geolat[434,391],'xr', ms=10);
# ### Now, let's plot the masking for all the regions:
for r in range(len(basin_code.region)):
#plt.figure(figsize=(12,8))
xyplot((basin_code[0,:]+basin_code[r,:]*2).values, grd.geolon, grd.geolat,
title=str(basin_code['region'][r].values))
|
docs/source/examples/region_masks.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Link Checker
# This program checks all of the links on the Columbia Basin Water Hub. It is based upon the "Broke_links_v1", which in turn was a variation of code from "hackerdam" at
# https://gist.github.com/hackerdem/2872d7f994d192188970408980267e6e
#
# It prints out the links and their status. The Water Hub has some coding that is not "utf-8" so the program throws excepton and prints them below the coding.
#
# Feb 14, 2021 T.V. Columbia Analytic Technologies (Colana, or CAT ) .-.- .- -
# +
from bs4 import BeautifulSoup,SoupStrainer
import urllib.request
import colorama,re,queue,threading
from colorama import Fore
from urllib.parse import *
class check_link():
def __init__(self,address):
self.address=address
def check(self,address):
try:
req=urllib.request.Request(url=address)
resp=urllib.request.urlopen(req)
if resp.status in [400,404,403,408,409,501,502,503]:
f.write("Broken: "+resp.status+"-"+resp.reason+"-->"+address+"\n")
else: f.write("Link OK in-->"+address +"\n")
except Exception as e:
f.write("{}-{}".format(e,address) + "\n")
pass
def pattern_adjust(a):
try:
if re.match('^#' ,a):return 0
r=urlsplit(a)
if r.scheme=='' and (r.netloc!='' or r.path!=''):
d=urlunsplit(r)
if re.match('^//' ,d):
m= re.search('(?<=//)\S+', d)
d=m.group(0)
m="https://"+d
return m
elif r.scheme=='' and r.netloc=='':
return address+a
else:return a
except Exception as e:
pass
def extract_link(address):
tags= {'a':'href', 'img':'src', 'script':'src', 'link':'href' }
for key,value in iter(tags.items()):
try:
headers={"User-Agent": "Mozilla/5.0"}
res=urllib.request.urlopen(urllib.request.Request(url=address, headers=headers))
response=res.read().decode('utf-8') #needs improvement
for link in BeautifulSoup(response,"html.parser",parse_only=SoupStrainer(key)):
if link.has_attr(value) and address in link[value]: # address in link[value] to keep testing the target site only
p=pattern_adjust(link[value]) # checks that the called link is legitimate
if p!=0 and str(p)!='None':
newcheck=check_link(p)
newcheck.check(p)
if p not in hyperlinks:
hyperlinks.add(p)
if website.split('.')[1] in p:#needs improvement
if not website.endswith(('.png','.jpeg','.js','jpg')):
q.put(p)
except Exception as e:
print("exception-", e , address)
def threader():
while True:
value=q.get()
result=extract_link(value)
q.task_done()
import time
secondsSinceEpoch = time.time()
timeObj = time.localtime(secondsSinceEpoch)
stamp = 'Run on: %d/%d/%d %d:%d:%d' % (
timeObj.tm_mday, timeObj.tm_mon, timeObj.tm_year, timeObj.tm_hour, timeObj.tm_min, timeObj.tm_sec)
target_url = "https://waterhub.livinglakescanada.ca/"
def write_header():
f.write ("Columbia Analytic Technologies" + "\n" + "Report on link status" + "\n" )
f.write (target_url + "\n")
f.write (stamp + "\n" +"\n")
f = open("C:/Desktop/Link_Report.txt", "a")
write_header()
if __name__=="__main__":
colorama.init()
q=queue.Queue()
global hyperlinks,website,f
hyperlinks=set()
website = target_url
for x in range(30):
t=threading.Thread(target=threader)
t.deamon=True
t.start()
q.put(website.strip())
q.join()
f.close()
print ("\n"+"All links checked. 'Link_Report.txt' saved on desktop. ")
|
python/Link_Checker_cat-v2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 1.0.2
# language: julia
# name: julia-1.0
# ---
using Random, Printf
using Winston
# +
p = FramedPlot(aspect_ratio=1,xrange=(-10,110),yrange=(-10,110));
n = 21;
x = collect(range(0.0, length=n, stop=100.0));
# Create a set of random variates
yA = 10.0*randn(n) .+ 40.0;
yB = x .+ 5.0*randn(n);
# +
# Set labels and symbol styles
a = Points(x, yA, kind="circle");
setattr(a,label="'a' points");
b = Points(x, yB);
setattr(b,label="'b' points");
style(b, kind="filled circle");
# Plot a line which 'fits' through the yB points
# and add a legend in the top LHS part of the graph
s = Slope(1, (0,0), kind="dotted");
setattr(s, label="slope");
lg = Legend(.1, .9, Any[a,b,s] );
add(p, s, a, b, lg);
# -
display(p)
|
Chp08/Notebooks/WInston.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import sys
# ! whoami
print(sys.executable)
print(sys.version)
print(sys.version_info)
# tested on aws lightsail instance 21 July 2020 using python38 kernel spec
# # Hypothesis Testing
# In this notebook we continue with hypothesis testing, but examine larger datasets but using mostly the same themes.
#
# Also, we will reinforce the concept of accessing data files from a web server.
# The webroot for the subsequent examples/exercises is `http://atomickitty.ddns.net/documents/JupyterOrion/MyJupyterNotebooks/41A-HypothesisTests/`
#
# ## Example 1 : Do construction activities impact stormwater solids metrics?
#
# ### Background
# The Clean Water Act (CWA) prohibits storm water discharge from construction sites
# that disturb 5 or more acres, unless authorized by a National Pollutant Discharge
# Elimination System (NPDES) permit. Permittees must provide a site description,
# identify sources of contaminants that will affect storm water, identify appropriate
# measures to reduce pollutants in stormwater discharges, and implement these measures.
# The appropriate measures are further divided into four classes: erosion and
# sediment control, stabilization practices, structural practices, and storm water management.
# Collectively the site description and accompanying measures are known as
# the facility’s Storm Water Pollution Prevention Plan (SW3P).
# The permit contains no specific performance measures for construction activities,
# but states that ”EPA anticipates that storm water management will be able to
# provide for the removal of at least 80% of the total suspended solids (TSS).” The
# rules also note ”TSS can be used as an indicator parameter to characterize the
# control of other pollutants, including heavy metals, oxygen demanding pollutants,
# and nutrients commonly found in stormwater discharges”; therefore, solids control is
# critical to the success of any SW3P.
# Although the NPDES permit requires SW3Ps to be in-place, it does not require
# any performance measures as to the effectiveness of the controls with respect to
# construction activities. The reason for the exclusion was to reduce costs associated
# with monitoring storm water discharges, but unfortunately the exclusion also makes
# it difficult for a permittee to assess the effectiveness of the controls implemented at
# their site. Assessing the effectiveness of controls will aid the permittee concerned
# with selecting the most cost effective SW3P.
#
# ### Problem Statement
# The files SOLIDS.PRE.TXT and SOLIDS.DUR.TXT contain observations of cumulative
# rainfall, total solids, and total suspended solids collected from a construction
# site on Nasa Road 1 in Harris County. The data in the file SOLIDS.PRE.TXT was
# collected `before` construction began, and the data in the file SOLIDS.DUR.TXT were
# collected `during` the construction activity.
#
# The first few lines of the `SOLIDS.PRE.TXT` file is displayed below. The first column
# is the date that the observation was made, the second column the total solids (by standard methods),
# the third column is is the total suspended solids (also by standard methods), and the last column is the cumulative
# rainfall for that storm.
#
# DATE TS.PRE TSS.PRE RAIN.PRE
# 03/27/97 408.5 111 1
# 03/31/97 524.5 205.5 0.52
# 04/04/97 171.5 249 0.95
# 04/07/97 436.5 65 0.55
# 04/11/97 627 510.5 2.19
# 04/18/97 412.5 93 0.2
# ...
#
# The first few lines of the `SOLIDS.DUR.TXT` file is displayed below. The first column
# is the date that the observation was made, the second column is the cumulative
# rainfall for that storm, the third column is the total solids (by standard methods),
# and the last column is the total suspended solids (also by standard methods).
#
# DATE RAIN.DUR TS.DUR TSS.DUR
# 7/9/1997 1.59 3014 2871.5
# 7/21/1997 0.53 1137 602
# 8/1/1997 0.74 2362.5 2515
# 8/4/1997 0.11 395.5 130
# 8/9/1997 0.27 278.5 36.5
# 8/25/1997 0.69 506.5 320.5
# 9/11/1997 1.06 2829.5 3071.5
# ...
# Our task is to analyze these two data sets and decide if construction activities impact stormwater quality in terms of solids measures.
#
# Some broad questions to keep in mind as we proceede:
#
# Which summary statistics are relevant?
# Are the data approximately normal?
# Are the data homoscedastic?
# Do the two construction phases represent approximately the same rainfall conditions?
# Assuming the observations are upstream of any water quality control feature, what amount of solids load needs to be captured to preserve pre-construction loading to the environment?
#
# These data are not time series (there was sufficient time between site visits that you can safely assume each storm was independent.
#
# The first step is to acquire the data and structure a data model - notice how the two files contain similar data, but the rainfall column is in different order, we need to deal with this probably for the beginning.
#
# ### Acquire the Data from the server
import requests # Module to process http/https requests
remote_webroot="http://atomickitty.ddns.net/documents/JupyterOrion/MyJupyterNotebooks/41A-HypothesisTests/" # set the webroot
remote_url=remote_webroot+"solids.pre.txt"
rget = requests.get(remote_url, allow_redirects=True) # get the remote resource, follow imbedded links
open('solids.pre.txt','wb').write(rget.content) # extract from the remote the contents, assign to a local file same name
remote_url=remote_webroot+"solids.dur.txt"
rget = requests.get(remote_url, allow_redirects=True) # get the remote resource, follow imbedded links
open('solids.dur.txt','wb').write(rget.content) # extract from the remote the contents, assign to a local file same name
# ! ls -la # execute local bash command to show file strtucture
# Examine the files, see if we can understand their structure
import pandas as pd # Module to process dataframes (not absolutely needed but somewhat easier than using primatives, and gives graphing tools)
precon = pd.read_table("solids.pre.txt") # Read the file as a table assign to a dataframe
precon.plot.box()
durcon = pd.read_table("solids.dur.txt") # Read the file as a table assign to a dataframe
durcon.plot.box()
# Here we see that the scales of the two data sets are quite different, but first lets reorder the columns so the two dataframes have the same structure.
# + active=""
# durcon = durcon[['TS.DUR','TSS.DUR','RAIN.DUR']] # super sneaky!
# durcon.plot.box()
# -
precon['RAIN.PRE'].describe()
durcon['RAIN.DUR'].describe()
# If we look at the summary statistics, we might conclude there is more rainfall during construction, which could bias our interpretation, a box plot of just rainfall might be useful, as would hypothesis tests.
precon['RAIN.PRE'].plot.box()
durcon['RAIN.DUR'].plot.box()
# Hard to tell from the plots, they look a little different, but are they? Lets apply some hypothesis tests
from scipy.stats import mannwhitneyu # import a useful non-parametric test
stat, p = mannwhitneyu(precon['RAIN.PRE'],durcon['RAIN.DUR'])
print('statistic=%.3f, p-value at rejection =%.3f' % (stat, p))
if p > 0.05:
print('Probably the same distribution')
else:
print('Probably different distributions')
from scipy import stats
results = stats.ttest_ind(precon['RAIN.PRE'], durcon['RAIN.DUR'])
print('statistic=%.3f, p-value at rejection =%.3f ' % (results[0], results[1]))
if p > 0.05:
print('Probably the same distribution')
else:
print('Probably different distributions')
# From these two tests (the data are NOT paired) we conclude that the two sets of data originate from the same distribution.
# Thus the question "Do the two construction phases represent approximately the same rainfall conditions?" can be safely answered in the affirmative.
#
# Continuing, lets ask the same about total solids, first plots
precon['TS.PRE'].plot.box()
durcon['TS.DUR'].plot.box()
# Look at the difference in scales, the during construction phase, is about 5 to 10 times greater.
# But lets apply some tests to formalize our interpretation.
stat, p = mannwhitneyu(precon['TS.PRE'],durcon['TS.DUR'])
print('statistic=%.3f, p-value at rejection =%.3f' % (stat, p))
if p > 0.05:
print('Probably the same distribution')
else:
print('Probably different distributions')
# +
results = stats.ttest_ind(precon['TS.PRE'], durcon['TS.DUR'])
print('statistic=%.3f, p-value at rejection =%.3f ' % (results[0], results[1]))
if p > 0.05:
print('Probably the same distribution')
else:
print('Probably different distributions')
# -
# Both these tests indicate that the data derive from distirbutions with different measures of central tendency (means). Lets now ask the question about normality, we will apply a test called `normaltest`. This function tests a null hypothesis that a sample comes from a normal distribution. It is based on D’Agostino and Pearson’s test that combines skew and kurtosis to produce an omnibus test of normality. We will likely get a warning because our sample size is pretty small.
#
# #### References
#
# <NAME>. (1971), “An omnibus test of normality for moderate and large sample size”, Biometrika, 58, 341-348
#
# <NAME>. and <NAME>. (1973), “Tests for departure from normality”, Biometrika, 60, 613-622
#
stat, p = stats.normaltest(precon['TS.PRE'])
print('statistic=%.3f, p-value at rejection =%.3f' % (stat, p))
if p > 0.05:
print('Probably normal distributed')
else:
print('Probably Not-normal distributed')
stat, p = stats.normaltest(durcon['TS.DUR'])
print('statistic=%.3f, p-value at rejection =%.3f' % (stat, p))
if p > 0.05:
print('Probably normal distributed')
else:
print('Probably Not-normal distributed')
# Our next question is "Are the data homoscedastic?" which sort of requires us to look up the meaning of "homoscedastic."
# It refers to the variance of the two data samples, are the variances the same or not. From the box plots we see some differences but here we are asking if the differences are statistically significant.
#
# ### Bartlett's Test (for homoscedastic)
#
# A simple (to implement) test is Bartlett's Pear test.
# Bartlett’s test tests the null hypothesis that all input samples are from populations with equal variances (https://www.itl.nist.gov/div898/handbook/eda/section3/eda357.htm).
# For samples from significantly non-normal populations, Levene’s test `levene`_ is more robust (https://www.itl.nist.gov/div898/handbook/eda/section3/eda35a.htm).
#
# Here we will try both, bearing in mind that the Shirley and Levene test is more preferred for Happy Days distributed samples.
stat, p = stats.bartlett(precon['TS.PRE'],durcon['TS.DUR'])
print('statistic=%.3f, p-value at rejection =%.3f' % (stat, p))
if p > 0.05:
print('Probably homoscedastic')
else:
print('Probably heteroscedastic')
stat, p = stats.levene(precon['TS.PRE'],durcon['TS.DUR'])
print('statistic=%.3f, p-value at rejection =%.3f' % (stat, p))
if p > 0.05:
print('Probably homoscedastic')
else:
print('Probably heteroscedastic')
# While these produce contradictory results, recall we already know the samples depart from normality so we would favor the Levene test.
# At this point we have answered most of the questions, except for the solids management question - which is left as an exercise. To summarize:
#
# Are the data approximately normal? `No` based on `stats.normaltest()`
#
# Are the data homoscedastic? `No` based on `stats.levene(,)`
#
# Do the two construction phases represent approximately the same rainfall conditions? `Yes` based on `mannwhitneyu()` or T-tests
#
# ### Exercise Set 1:
# 1) Do the total suspended solids measures exhibit the same behavior as the total solids in the example. (Do the analysis!)
#
# 2) Assuming the observations are upstream of any water quality control feature, what amount of solids load needs to be captured to preserve pre-construction loading to the environment?
#
# <hr>
# # Example 2: Treaty Terms for the Colorado River
#
# ## Background
#
# The Colorado river originates in the Rocky mountains and has contributing tributaries
# and/or flows through the states of Wyoming, Colorado, Utah, Nevada, Arizona,
# and California.
# Prior to dams the river used to actually run to the ocean and at one
# time in history actually had commerce by river boats.
# In the late 1800’s and early 1900’s the river and its tributaries were dammed and diverted.
# Around the 1920’sa legal document called the Colorado River Compact was developed.
# A Compact is similar to a treaty, except the parties to the treaty are states (essentially the individual states have entered into the treaty with the United States and Mexico).
# The Colorado River Compact divides the Colorado River into Upper and Lower Basins with the division being at Lee Ferry on the Colorado River one mile below the Paria River in Arizona.
# The Lower Basin states are Arizona, California, and Nevada, with small portions of New Mexico and Utah that are tributary to the Colorado River below Lee Ferry. The Upper Basin states are Colorado, New Mexico, Utah, and Wyoming, with a small portion of Arizona tributary to the Colorado River above Lee Ferry.
#
# Article III of the Compact apportions the waters of the Colorado River to the Upper
# and Lower Basins as follows:
# The Compact apportions the right to exclusive beneficial consumptive use of 7.5
# million acre-feet of water per year from the ”Colorado River System” in perpetuity
# to the Upper Basin and the Lower Basin.
# The Compact allows an additional 1.0 million acre-feet per year of increased beneficial
# consumptive use to the Lower Basin.
# It provides water for Mexico pursuant to treaty. Water must first come from any
# surplus over the waters allocated to the states in Article III(a) and (b). If that
# surplus is insufficient, then the burden of that deficiency shall be shared equally by
# the Upper and Lower Basins.
# The Compact provides that the Upper Basin states will not cause the flow of the
# river at Lee Ferry, Arizona to be depleted below an aggregate of 75 million acrefeet
# for any period of ten consecutive years beginning with the ratification of the
# Compact.
# It provides that the Upper Basin states will not withhold water and the states of the
# Lower Basin shall not require delivery of water which cannot reasonably be applied
# to domestic and agricultural uses.
# ## Problem Statement
#
# The file named COLORADO.TXT contains annual natural flows volumes in the upper
# Colorado river basin from 1906 to present. These flows are historical reconstruction
# at approximately the same location as the current USGS gage 09380000. The
# location is approximately above (upstream of) Lee Ferry, hence the data represent
# the flows out of the upper basin.
# The data are in two columns, the first is the water year, the second column is
# cumulative discharge for the year in units of acre-feet.
#
# YEAR ANNUAL.VOLUME
# 1906 18550021
# 1907 21201694
# 1908 12218817
# 1909 22356301
# 1910 14650616
# ...
# Prepare an analysis of the data to support or refute the provisions of the Compact.
# You can assume that the data from 1906 to 1927 (the original Compact was ratified
# in 1922, many additional Compacts have been signed since all trying to reapportion
# water in the river basin witout violating the original agreement) were available to the
# authors of the Colorado River Compact, analyze this period of data and decide if the
# allocations to the lower basin are realistic (8.5 million acre-feet-per year) assuming
# the upper basin allocation is removed. Consumptive use means that the water may
# not return to the basin. The data are ’natural’ flows and the upper basin allocations
# are not removed in the data. Also, as in the previous problem, these data are timeseries
# and serial correlation is anticipated.
#
# Estimate the probability based on the the 20-year period that the lower basin allocation
# will not be met if upper basin allocation is satisfied. Estimate the probability
# that the allocation will not be met using the entire data set if the upper basin allocation
# is satisfied.
#
# Next assume that lower basin is satisfied first (this is the historical result of the
# original and subsequent treaties). Estimate the probability that the upper basin
# allocation will not be met. Determine an upper basin allocation that will be met
# 95% of the time. Again use the 20 year initial record, then the entire record.
#
# After these exploratory analyses decide if the basin allocations reasonable in the
# context of the flows that actually occured after the Compact was in effect? That
# is was the initial 20 year period sufficiently different from the later data that the
# Compact authors made decisions based on unusually high or low flows?
remote_webroot="http://atomickitty.ddns.net/documents/JupyterOrion/MyJupyterNotebooks/41A-HypothesisTests/" # set the webroot
remote_url=remote_webroot+"colorado.txt"
rget = requests.get(remote_url, allow_redirects=True) # get the remote resource, follow imbedded links
open('colorado.txt','wb').write(rget.content) # extract from the remote the contents, assign to a local file same name
colorado_df = pd.read_table("colorado.txt") # Read the file as a table assign to a dataframe
colorado_df.plot.line(x='YEAR', y='ANNUAL.VOLUME')
colorado_df.describe()
# We can kind of use the description to answer our questions.
# Estimate the probability based on the the 20-year period that the lower basin allocation will not be met if upper basin allocation is satisfied
#
# First filter the data
junkdf = colorado_df[colorado_df['YEAR'] <= 1927] # screen by year
junkdf.plot.line(x='YEAR', y='ANNUAL.VOLUME') # plot the first 22 years
junkdf.describe()
# Then observe that the minimum is 12 million, so the upper basin's 7.5 million is satisfied all 22 years (yay for the upstreamers!)
# If the downstreamers get their allocation the total in the river needs to be 15 million, so the question is what fraction of observations is less than 15 million, that fraction is an estimate of the probability downstreamers won't get their water.
result1 = junkdf.count()
result2 = junkdf[junkdf['ANNUAL.VOLUME'] < 15.0E6].count()
print ('Probability Downstreamers Wont Get their Agua =%.3f' % (result2[0]/result1[0]))
# The fraction is about 1/3; so 33% of the time, downstreamers won't get their water!
# Estimate the probability that the allocation will not be met using the entire data set if the upper basin allocation is satisfied.
# Here we use the same logic and scripts but dont need the date filter
result1 = colorado_df.count()
result2 = colorado_df[colorado_df['ANNUAL.VOLUME'] < 15.0E6].count()
print ("Probability Downstreamers Wont Get their Agua =%.3f " % (result2[0]/result1[0]))
# So the downstreamers wont get water 1/2 the time.
#
# Next assume that lower basin is satisfied first (this is the historical result of the original and subsequent treaties).
# Determine an upper basin allocation that will be met 95% of the time.
#
# Again use the 22 year initial record, then the entire record.
result1 = junkdf.count()
result2 = junkdf[junkdf['ANNUAL.VOLUME'] > 12.5e6].count()
print ('Probability Uptreamers Will Get their Agua based on 22 years =%.3f' % (result2[0]/result1[0]))
print ('Allocation Upstream =%.3f' % (12.5e6 - 7.5e6))
result1 = colorado_df.count()
result2 = colorado_df[colorado_df['ANNUAL.VOLUME'] > 8.5e6].count()
print ('Probability Uptreamers Will Get their Agua based on 98 years =%.3f' % (result2[0]/result1[0]))
print ('Allocation Upstream =%.3f' % (8.5e6 - 7.5e6))
# So based on 22 years of record, 5 million acre feet allocation would be satisfied 95% of the time.
# Using the entire record, only 1 million acre feet was available for the upstream - interestingly that same extra 1 million already available to the downstreamers.
#
# Not a favorable contract for Upstreamers and Mexico, the big error was the choice of absolute volumes; flow fractions would have made more sense and still kept lawyers busy.
#
# One observation in https://en.wikipedia.org/wiki/Cadillac_Desert notes that the base years were unusually wet - we can assess that claim using our hypothesis testing tools. First we will check for normality
newjunkdf = colorado_df[colorado_df['YEAR'] > 1927] # screen by year
stat, p = stats.normaltest(junkdf['ANNUAL.VOLUME'])
print('statistic=%.3f, p-value at rejection =%.3f' % (stat, p))
if p > 0.05:
print('Probably normal distributed')
else:
print('Probably Not-normal distributed')
stat, p = stats.normaltest(newjunkdf['ANNUAL.VOLUME'])
print('statistic=%.3f, p-value at rejection =%.3f' % (stat, p))
if p > 0.05:
print('Probably normal distributed')
else:
print('Probably Not-normal distributed')
# So the first portion of the data seem non-normal, the later quite normal, likely a consequence of moderate sample size (80-ish) and a bounded physical process (infinite discharge makes no sense, less then zero also undefined). Lets ask <NAME> Laverne what they think about variance.
stat, p = stats.levene(junkdf['ANNUAL.VOLUME'],newjunkdf['ANNUAL.VOLUME'])
print('statistic=%.3f, p-value at rejection =%.3f' % (stat, p))
if p > 0.05:
print('Probably homoscedastic')
else:
print('Probably heteroscedastic')
# So we have non-static variance, from the plots it looks to be increasing with respect to time, a quick check
oldvar = (junkdf['ANNUAL.VOLUME'].std())**2
newvar = (newjunkdf['ANNUAL.VOLUME'].std())**2
print('Variance first 22 years =%.3e' % oldvar)
print('Variance last 86 years =%.3e' % newvar)
# So the variance increased in the more reçent years, lets check means
oldmean = (junkdf['ANNUAL.VOLUME'].mean())
newmean = (newjunkdf['ANNUAL.VOLUME'].mean())
print('Mean first 22 years =%.3e' % oldmean)
print('Mean last 86 years =%.3e' % newmean)
# So there is evidence that the early years were wetter, by about 3 million acre feet. Lets examine if the difference is significant using our hypothesis testing tools.
stat, p = mannwhitneyu(junkdf['ANNUAL.VOLUME'],newjunkdf['ANNUAL.VOLUME'])
print('statistic=%.3f, p-value at rejection =%.3f' % (stat, p))
if p > 0.05:
print('Probably the same distribution')
else:
print('Probably different distributions')
# Based on the Mann-Whitney test the statement in Cadillac Desert is defendible, the early years are indeed different (wetter) with a small p-value, so its likely the difference is not random.
#
# ### Exercise
# If you were to rewrite the Compact provisions today, assuming that the original
# intent was to divide the water between upper and lower basin in a 46% 54% split,
# what annual allocations would you recomend as ’firm’ water at 90% reliability?
#
# <hr>
# # Example 3 Is a stinky bayou explained by water quality?
# ## Background
#
# Country Club Bayou, formerly <NAME>, is located in southeast Houston.
# The bayou drains from east to west connecting to Brays Bayou. The upper portion of the
# bayou is conveyed in a concrete channel that was initially placed in the early 1900’s. The
# lower portion of the bayou from the Hughes Street railroad bridge to the confluence with
# Braes Bayou is open, unlined channel.
#
# Pollution of the bayou has been problematic for at least a dozen years. Currently
# suspected high nutrient loading somewhere in the covered portion of the bayou
# contributes to observed low dissolved oxygen values, a septic `odor`, and septic (black)
# color. The out-fall from the covered portion of the bayou to the open portion is just
# upstream of the Hughes Street Bridge. Samples collected at the bridge by the City of
# Houston Health Department confirm these historical observations.
#
# At times the water at the out-fall just upstream of the Hughes Street Bridge has not meet
# state water quality standards for unclassified waters. Unclassified waters are waters
# which are not specifically listed in Appendices A or D of §307.10 of Title:30, Part 1,
# Chapter 307 of the Texas Administrative Code.
#
# The table lists some of the relevant standards.
# <table>
# <tr><td>Parameter</td><td> Value</td><td> Remarks</td></tr>
# <tr><td>Dissolved Oxygen</td><td> 2.0 mg/L - 24 hr. average </td><td> </td></tr>
# <tr><td> </td><td> 1.5 mg/L - absolute minimum </td><td> </td></tr>
# <tr><td> </td><td> 3.0 mg/L - proposed (circa 1998) </td><td> </td></tr>
# <tr><td> Sulfate</td><td> 65 mg/L - proposed (circa 1998) </td><td> </td></tr>
# <tr><td> pH</td><td> 6.5-9.0 - proposed (circa 1998) </td><td> </td></tr>
# <tr><td> Fecal Coliform</td><td> 200 cfu/100mL </td><td> Contact recreation </td></tr>
# <tr><td> </td><td> 2000 cfu/100mL </td><td> Non-contact recreation </td></tr>
# <tr><td> Temperature</td><td> 4oF above ambient</td><td> Fall, Winter, Spring</td></tr>
# <tr><td> </td><td> 1.5oF above ambient</td><td> Summer</td></tr>
# </table>
# These values are proposed for Segment 1014 (Buffalo Bayou above tidal) for contact
# recreation and limited aquatic life use.
#
# See: (http://www.tnrcc.state.tx.us/water/quality/standards/revisions.html)
#
# The figure below is a map of the area with storm and sanitary sewer systems drawn onto the map (the study pre-dates affordable GIS)
#
# 
#
# The current land-use in the area ranges includes residential, light-industrial, and several
# manufacturing facilities. The covered portion of the storm sewer system is owned
# by the City of Houston, while the open portion appears to be privately owned except for
# the portion through Wortham Park (COH). There are no known discharge permits issued
# by any authority for discharge into Country Club Bayou.
#
# The figure below shows sample locations were water quality samples were collected
#
# 
#
# For this example, the data from the Hughes Street location are examined.
# The data are stored in the file named HUGHES_STREET.txt and look like:
#
# MM DD YY pH T_degC DO_ppm NH3_ppm Odor
# 11 1 1999 6.63 22.5 4.54 0.63 0
# 5 28 1998 7.3 23.2 1.7 0.54 0
# 6 3 1998 7.2 24.1 1.2 0.31 0
# 6 8 1998 7.1 24.8 1 3.96 0
# 6 15 1998 7.2 25 2.9 0.57 0
# 6 26 1998 7.3 27.2 3.1 1.29 0
# 6 29 1998 7.7 26.2 7.9 0.28 0
# 7 8 1998 6.5 26.2 0.28 0.21 0
# 7 20 1998 6.5 28 8.1 0.32 0
# ...
# 7 15 1999 7.08 27.5 3.19 0.52 0
# 5 12 1998 7 21.6 1.41 0.66 1
# 5 21 1998 7.2 23.9 1.2 1.23 1
# 5 27 1998 6.9 23.6 1.1 0.36 1
# 6 11 1998 7 24.9 1.7 2.5 1
# ...
#
# ## Problem Statement
#
# The simple question for this example: Are the water quality measures different when the field notes report the classification variable "Odor" as "1"?
# As before, first lets get the data
remote_webroot="http://atomickitty.ddns.net/documents/JupyterOrion/MyJupyterNotebooks/41A-HypothesisTests/" # set the webroot
remote_url=remote_webroot+"HUGHES_STREET.txt"
rget = requests.get(remote_url, allow_redirects=True) # get the remote resource, follow imbedded links
open('HUGHES_STREET.txt','wb').write(rget.content) # extract from the remote the contents, assign to a local file same name
ccbayou = pd.read_table("HUGHES_STREET.txt") # Read the file as a table assign to a dataframe
ccbayou.describe()
# Lets look at some plots, after filtering the dataframe
yummydf = ccbayou[ccbayou['Odor'] == 0]
stinkydf = ccbayou[ccbayou['Odor'] == 1]
yummydf['DO_ppm'].plot.box()
stinkydf['DO_ppm'].plot.box()
# Not much from a plot, in general if we look at descriptions we will observe lower DO and higher NH3 for the cases where odor is reported. These data are good candidate for hypothesis testing, first check for normality (if yes then we will T-test)
# +
print('Testing on DO_ppm')
stat, p = stats.normaltest(stinkydf['DO_ppm'])
print('statistic=%.3f, p-value at rejection =%.3f' % (stat, p))
if p > 0.05:
print('Probably normal distributed')
else:
print('Probably Not-normal distributed')
stat, p = stats.normaltest(yummydf['DO_ppm'])
print('statistic=%.3f, p-value at rejection =%.3f' % (stat, p))
if p > 0.05:
print('Probably normal distributed')
else:
print('Probably Not-normal distributed')
print('Testing on NH3_ppm')
stat, p = stats.normaltest(stinkydf['NH3_ppm'])
print('statistic=%.3f, p-value at rejection =%.3f' % (stat, p))
if p > 0.05:
print('Probably normal distributed')
else:
print('Probably Not-normal distributed')
stat, p = stats.normaltest(yummydf['NH3_ppm'])
print('statistic=%.3f, p-value at rejection =%.3f' % (stat, p))
if p > 0.05:
print('Probably normal distributed')
else:
print('Probably Not-normal distributed')
# -
# So pretty much non-normal, hence we will rely on Mann-Whitney
print('Testing on DO_ppm')
stat, p = mannwhitneyu(yummydf['DO_ppm'],stinkydf['DO_ppm'])
print('statistic=%.3f, p-value at rejection =%.3f' % (stat, p))
if p > 0.05:
print('Probably the same distribution')
else:
print('Probably different distributions')
print('Testing on NH3_ppm')
stat, p = mannwhitneyu(yummydf['NH3_ppm'],stinkydf['NH3_ppm'])
print('statistic=%.3f, p-value at rejection =%.3f' % (stat, p))
if p > 0.05:
print('Probably the same distribution')
else:
print('Probably different distributions')
# These tests suggest that DO and NH3 play a role in the observation of Odor
print('Average DO no-odor =%.3f' % yummydf['DO_ppm'].mean())
print('Average DO odor =%.3f' % stinkydf['DO_ppm'].mean())
print('Average NH3 no-odor =%.3f' % yummydf['NH3_ppm'].mean())
print('Average NH3 odor =%.3f' % stinkydf['NH3_ppm'].mean())
# ## Exercise
#
# Are these observations homoscedastic?
# ## References
# <NAME>., <NAME>., <NAME>., <NAME>., <NAME>. 2000.
# ``Investigation and Demonstration of Intervention Strategies to Improve Water Quality on Country Club Bayou.'' Final Report to Houston Wastewater Program, Texas Natural Resources Conservation Commission, City of Houston, and the Environmental Institute of Houston
#
# http://atomickitty.ddns.net/documents/resumes/MyWebPapers/project_reports/ccbayou_report/
sortedDOyum = yummydf.sort_values(by=['DO_ppm'])
sortedDOstk = stinkydf.sort_values(by=['DO_ppm'])
sortedDOyum.head()
sDOy = sortedDOyum['DO_ppm']
sDOy.describe()
relfreq = [(x+1)/36 for x in range(35) ]
sDOy['DO_ppm'].plot.line(x=relfreq,y='DO_ppm')
|
1-Lessons/Lesson15/Lab15/lab15-development/Lab15-Part1-FullNarrative.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="WTY7kA7DOzpV"
# # Mount Drive
# + colab={"base_uri": "https://localhost:8080/"} id="4-7JU3Q7q_XT" outputId="908b61be-c291-4313-e724-e909351f16b9"
from google.colab import drive
drive.mount('/content/drive')
# + colab={"base_uri": "https://localhost:8080/"} id="DqqXI7Izk65p" outputId="490a6b78-2dd9-4f19-9eab-b35044f76cbd"
# !pip install -U -q PyDrive
# !pip install httplib2==0.15.0
import os
from pydrive.auth import GoogleAuth
from pydrive.drive import GoogleDrive
from pydrive.files import GoogleDriveFileList
from google.colab import auth
from oauth2client.client import GoogleCredentials
from getpass import getpass
import urllib
# 1. Authenticate and create the PyDrive client.
auth.authenticate_user()
gauth = GoogleAuth()
gauth.credentials = GoogleCredentials.get_application_default()
drive = GoogleDrive(gauth)
# Cloning PAL_2021 to access modules.
# Need password to access private repo.
if 'CLIPPER' not in os.listdir():
cmd_string = 'git clone https://github.com/PAL-ML/CLIPPER.git'
os.system(cmd_string)
# + [markdown] id="RGlVnbugxFK2"
# # Installation
# + [markdown] id="gmgIrfT8hDNE"
# ## Install multi label metrics dependencies
# + colab={"base_uri": "https://localhost:8080/"} id="b6xXPAFbe6Gp" outputId="9bfbd423-f468-4cf5-cc4f-2262608ef95d"
# ! pip install scikit-learn==0.24
# + [markdown] id="3rKe3HqM523g"
# ## Install CLIP dependencies
# + id="poS-WNDixIhY"
# import subprocess
# CUDA_version = [s for s in subprocess.check_output(["nvcc", "--version"]).decode("UTF-8").split(", ") if s.startswith("release")][0].split(" ")[-1]
# print("CUDA version:", CUDA_version)
# if CUDA_version == "10.0":
# torch_version_suffix = "+cu100"
# elif CUDA_version == "10.1":
# torch_version_suffix = "+cu101"
# elif CUDA_version == "10.2":
# torch_version_suffix = ""
# else:
# torch_version_suffix = "+cu110"
# + id="uA-69W8M59nA"
# # ! pip install torch==1.7.1{torch_version_suffix} torchvision==0.8.2{torch_version_suffix} -f https://download.pytorch.org/whl/torch_stable.html ftfy regex
# + id="sYwBZS1N6A3d"
# # ! pip install ftfy regex
# # ! wget https://openaipublic.azureedge.net/clip/bpe_simple_vocab_16e6.txt.gz -O bpe_simple_vocab_16e6.txt.gz
# + id="9oIcNBYB8lz3"
# # !pip install git+https://github.com/Sri-vatsa/CLIP # using this fork because of visualization capabilities
# + [markdown] id="OLU-gp7n8__E"
# ## Install clustering dependencies
# + id="6TLg9ozo9Hvc"
# !pip -q install umap-learn>=0.3.7
# + [markdown] id="9z1WQnXdLHy2"
# ## Install dataset manager dependencies
# + colab={"base_uri": "https://localhost:8080/"} id="J1vvMx7_LLSp" outputId="fba1dd7b-532a-4f1c-a4d9-9d9f2af2a645"
# !pip install wget
# + [markdown] id="NzsubsEm72rr"
# # Imports
# + colab={"base_uri": "https://localhost:8080/"} id="KZI62a6G74kw" outputId="e274796b-866b-4d46-c185-676615dedc4d"
# ML Libraries
import tensorflow as tf
import tensorflow_hub as hub
import torch
import torch.nn as nn
import torchvision.models as models
import torchvision.transforms as transforms
import keras
# Data processing
import PIL
import base64
import imageio
import pandas as pd
import numpy as np
import json
from PIL import Image
import cv2
from sklearn.feature_extraction.image import extract_patches_2d
# Plotting
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib.patches as patches
from IPython.core.display import display, HTML
from matplotlib import cm
import matplotlib.image as mpimg
# Models
# import clip
# Datasets
import tensorflow_datasets as tfds
# Clustering
# import umap
from sklearn import metrics
from sklearn.cluster import KMeans
#from yellowbrick.cluster import KElbowVisualizer
# Misc
import progressbar
import logging
from abc import ABC, abstractmethod
import time
import urllib.request
import os
from sklearn.metrics import jaccard_score, hamming_loss, accuracy_score, f1_score
from sklearn.preprocessing import MultiLabelBinarizer
# Modules
# from CLIPPER.code.ExperimentModules import embedding_models
from CLIPPER.code.ExperimentModules.dataset_manager import DatasetManager
from CLIPPER.code.ExperimentModules.weight_imprinting_classifier import WeightImprintingClassifier
from CLIPPER.code.ExperimentModules import simclr_data_augmentations
from CLIPPER.code.ExperimentModules.utils import (save_npy, load_npy,
get_folder_id,
create_expt_dir,
save_to_drive,
load_all_from_drive_folder,
download_file_by_name,
delete_file_by_name)
logging.getLogger('googleapicliet.discovery_cache').setLevel(logging.ERROR)
# + [markdown] id="zU_gxQ0KbwMh"
# # Initialization & Constants
# + [markdown] id="ND-Q6dDoYmDu"
# ## Dataset details
# + colab={"base_uri": "https://localhost:8080/"} id="bih5tBPdbx3u" outputId="18240d68-a1be-4564-f2a7-7e198f015d6b"
folder_name = "UCF101-Embeddings-28-02-21"
# Change parentid to match that of experiments root folder in gdrive
parentid = '1bK72W-Um20EQDEyChNhNJthUNbmoSEjD'
# Filepaths
train_labels_filename = "train_labels.npz"
val_labels_filename = "val_labels.npz"
train_embeddings_filename_suffix = "_embeddings_train.npz"
val_embeddings_filename_suffix = "_embeddings_val.npz"
# Initialize sepcific experiment folder in drive
folderid = create_expt_dir(drive, parentid, folder_name)
# + [markdown] id="GTHwQiOvljNU"
# ## Few shot learning parameters
# + id="HbRNiKZKlmQP"
num_ways = 5 # [5, 20]
num_shot = 5 # [5, 1]
num_eval = 15 # [5, 10, 15, 19]
num_episodes = 100
shuffle = False
# + [markdown] id="UxTa8MVsvQCN"
# # Load data
# + colab={"base_uri": "https://localhost:8080/"} id="n6S124Jfwuu5" outputId="75d82128-3416-49dd-dac7-068c7265649a"
def get_ndarray_from_drive(drive, folderid, filename):
download_file_by_name(drive, folderid, filename)
return np.load(filename)['data']
val_labels = get_ndarray_from_drive(drive, folderid, val_labels_filename)
# + [markdown] id="iLbRqaYxzbr7"
# # Create label dictionary
# + colab={"base_uri": "https://localhost:8080/"} id="Emz85fNX0Vif" outputId="40141d76-7526-471c-ed78-6625ca93b65e"
unique_labels = np.unique(val_labels)
print(len(unique_labels))
# + id="0TubS-RLzeVM"
label_dictionary = {la:[] for la in unique_labels}
for i in range(len(val_labels)):
la = val_labels[i]
label_dictionary[la].append(i)
# + [markdown] id="xP6ftkDCvKul"
# # Weight Imprinting models on train data embeddings
# + [markdown] id="fJIGo_R86GQi"
# ## Function definitions
# + id="QZ-BvKBH6LuI"
def calculate_single_label_accuracy(pred, y, label_mapping):
x = 0
for i, p in enumerate(pred):
pred_label = label_mapping[p]
if pred_label == y[i]:
x += 1
x = x/(i+1)
return x
# + id="pv68q8TH6tvG"
def start_progress_bar(bar_len):
widgets = [
' [',
progressbar.Timer(format= 'elapsed time: %(elapsed)s'),
'] ',
progressbar.Bar('*'),' (',
progressbar.ETA(), ') ',
]
pbar = progressbar.ProgressBar(
max_value=bar_len, widgets=widgets
).start()
return pbar
# + id="mUpPZ6ti6IEp"
def run_evaluations(
embeddings,
train_indices,
eval_indices,
wi_y,
eval_y,
num_episodes,
num_ways,
verbose=True,
metrics=["accuracy", "c_f1"]
):
accuracies = []
f1_scores = []
if verbose:
pbar = start_progress_bar(num_episodes)
for i in range(num_episodes):
wi_x = embeddings[train_indices[i]]
wi_x = WeightImprintingClassifier.preprocess_input(wi_x)
eval_x = embeddings[eval_indices[i]]
eval_x = WeightImprintingClassifier.preprocess_input(eval_x)
wi_weights, label_mapping = WeightImprintingClassifier.get_imprinting_weights(
wi_x, wi_y[i], False
)
wi_parameters = {
"num_classes": num_ways,
"input_dims": wi_x.shape[-1],
"scale": False,
"dense_layer_weights": wi_weights
}
wi_cls = WeightImprintingClassifier(wi_parameters)
# Evaluate the weight imprinting model
metric_vals = wi_cls.evaluate_single_label_metrics(eval_x, eval_y[i], label_mapping, metrics=metrics)
if "accuracy" in metrics:
accuracies.append(metric_vals["accuracy"])
if "c_f1" in metrics:
f1_scores.append(metric_vals["c_f1"])
del wi_x
del eval_x
del wi_cls
if verbose:
pbar.update(i+1)
metric_arrays = []
if "accuracy" in metrics:
metric_arrays.append(accuracies)
if "c_f1" in metrics:
metric_arrays.append(f1_scores)
return metric_arrays
# + [markdown] id="j2XrPKY9EJeG"
# ## Picking indices
# + colab={"base_uri": "https://localhost:8080/"} id="8_S_4DanEJeH" outputId="49a8616a-7235-430a-a11e-7f69c87856fe"
eval_indices = []
train_indices = []
wi_y = []
eval_y = []
label_dictionary = {la:label_dictionary[la] for la in label_dictionary if len(label_dictionary[la]) >= (num_shot+num_eval)}
unique_labels = list(label_dictionary.keys())
pbar = start_progress_bar(num_episodes)
for s in range(num_episodes):
# Setting random seed for replicability
np.random.seed(s)
_train_indices = []
_eval_indices = []
selected_labels = np.random.choice(unique_labels, size=num_ways, replace=False)
for la in selected_labels:
la_indices = label_dictionary[la]
select = np.random.choice(la_indices, size = num_shot+num_eval, replace=False)
tr_idx = list(select[:num_shot])
ev_idx = list(select[num_shot:])
_train_indices = _train_indices + tr_idx
_eval_indices = _eval_indices + ev_idx
if shuffle:
np.random.shuffle(_train_indices)
np.random.shuffle(_eval_indices)
train_indices.append(_train_indices)
eval_indices.append(_eval_indices)
_wi_y = val_labels[_train_indices]
_eval_y = val_labels[_eval_indices]
wi_y.append(_wi_y)
eval_y.append(_eval_y)
pbar.update(s+1)
# + [markdown] id="cOdSfodivGga"
# ## Inception V3
# + colab={"base_uri": "https://localhost:8080/"} id="WO5MzYeWzKBr" outputId="c4167f3f-8311-4649-e2df-63d86f8d489c"
# Load numpy data from drive
inceptionv3_embeddings_val_fn = "inceptionv3" + val_embeddings_filename_suffix
inceptionv3_embeddings_val = get_ndarray_from_drive(drive, folderid, inceptionv3_embeddings_val_fn)
# + colab={"base_uri": "https://localhost:8080/"} id="Dd3YWzRDadcj" outputId="1b7389e2-7324-42db-8ecd-4f5043d0cec4"
inceptionv3_accuracies, inceptionv3_f1_scores = run_evaluations(
inceptionv3_embeddings_val,
train_indices,
eval_indices,
wi_y,
eval_y,
num_episodes,
num_ways
)
# + colab={"base_uri": "https://localhost:8080/"} id="-MEo_xCIwo7U" outputId="2bb6384d-297b-465a-f0a9-09f1deb8f10d"
inceptionv3_mean_accuracy = np.mean(inceptionv3_accuracies)
print("Inceptionv3 Mean accuracy: ", inceptionv3_mean_accuracy)
inceptionv3_mean_f1_score = np.mean(inceptionv3_f1_scores)
print("Inceptionv3 Mean f1 score: ", inceptionv3_mean_f1_score)
# + [markdown] id="8kKBQlF6C2pM"
# ## Resnet 50
# + colab={"base_uri": "https://localhost:8080/"} id="Exo-5cHDC2pO" outputId="9df593a1-3c8b-4ef1-d74f-3309f447bc60"
resnet50_embeddings_val_fn = "resnet50" + val_embeddings_filename_suffix
resnet50_embeddings_val = get_ndarray_from_drive(drive, folderid, resnet50_embeddings_val_fn)
# + colab={"base_uri": "https://localhost:8080/"} id="4CKCz5S4a5HC" outputId="cda37c91-5f07-4a90-da88-d7ec814d22ec"
resnet50_accuracies, resnet50_f1_scores = run_evaluations(
resnet50_embeddings_val,
train_indices,
eval_indices,
wi_y,
eval_y,
num_episodes,
num_ways
)
# + colab={"base_uri": "https://localhost:8080/"} id="UQcPvZEK3vS2" outputId="2a64c82f-c74b-4abf-d92d-d0321694a49e"
resnet50_mean_accuracy = np.mean(resnet50_accuracies)
print("Resnet 50 Mean accuracy: ", resnet50_mean_accuracy)
resnet50_mean_f1_score = np.mean(resnet50_f1_scores)
print("Resnet 50 Mean f1 score: ", resnet50_mean_f1_score)
# + [markdown] id="3WfqxT8TC3sN"
# ## MoCo Resnet
# + colab={"base_uri": "https://localhost:8080/"} id="kf9XU2CUC3sN" outputId="5b4fc2e5-fad6-4c4a-9e44-45210752cbe0"
moco_resnet50_embeddings_val_fn = "moco_resnet50" + val_embeddings_filename_suffix
moco_resnet50_embeddings_val = get_ndarray_from_drive(drive, folderid, moco_resnet50_embeddings_val_fn)
# + colab={"base_uri": "https://localhost:8080/"} id="KnMT_X6La_oi" outputId="baaa4972-9c24-495b-9f4f-6c412d31bb62"
moco_resnet50_accuracies, moco_resnet50_f1_scores = run_evaluations(
moco_resnet50_embeddings_val,
train_indices,
eval_indices,
wi_y,
eval_y,
num_episodes,
num_ways
)
# + colab={"base_uri": "https://localhost:8080/"} id="Ep29BAUw4Ry4" outputId="6fbf804a-cfe1-4ea5-d187-85310ae0e303"
moco_resnet50_mean_accuracy = np.mean(moco_resnet50_accuracies)
print("Moco Resnet Mean accuracy: ", moco_resnet50_mean_accuracy)
moco_resnet50_mean_f1_score = np.mean(moco_resnet50_f1_scores)
print("Moco Resnet Mean f1 score: ", moco_resnet50_mean_f1_score)
# + [markdown] id="GpDsLlZgC4ZS"
# ## PCL Resnet
# + colab={"base_uri": "https://localhost:8080/"} id="OV9b5GHVC4ZS" outputId="47e50f7c-3a40-46fc-9706-fd8f2d68adeb"
pcl_resnet50_embeddings_val_fn = "pcl_resnet50" + val_embeddings_filename_suffix
pcl_resnet50_embeddings_val = get_ndarray_from_drive(drive, folderid, pcl_resnet50_embeddings_val_fn)
# + colab={"base_uri": "https://localhost:8080/"} id="DRwM2RTzbF67" outputId="8e030776-0707-45f3-923b-2059ff2a1c85"
pcl_resnet50_accuracies, pcl_resnet50_f1_scores = run_evaluations(
pcl_resnet50_embeddings_val,
train_indices,
eval_indices,
wi_y,
eval_y,
num_episodes,
num_ways
)
# + colab={"base_uri": "https://localhost:8080/"} id="5Q_fXQ864lik" outputId="dc36d67c-1104-4c90-c5ee-26130306d85f"
pcl_resnet50_mean_accuracy = np.mean(pcl_resnet50_accuracies)
print("PCL Resnet Mean accuracy: ", pcl_resnet50_mean_accuracy)
pcl_resnet50_mean_f1_score = np.mean(pcl_resnet50_f1_scores)
print("PCL Resnet Mean f1 score: ", pcl_resnet50_mean_f1_score)
# + [markdown] id="XRktKMM1FBQj"
# ## SwAV Resnet
# + colab={"base_uri": "https://localhost:8080/"} id="-PVlxnZ_FBQl" outputId="2f6ec58f-69fe-4c39-9a36-dd42a9031edb"
swav_resnet50_embeddings_val_fn = "swav_resnet50" + val_embeddings_filename_suffix
swav_resnet50_embeddings_val = get_ndarray_from_drive(drive, folderid, swav_resnet50_embeddings_val_fn)
# + colab={"base_uri": "https://localhost:8080/"} id="RTpsQPbobKxU" outputId="405030a5-bc6d-433d-f3e1-02a02854c766"
swav_resnet50_accuracies, swav_resnet50_f1_scores = run_evaluations(
swav_resnet50_embeddings_val,
train_indices,
eval_indices,
wi_y,
eval_y,
num_episodes,
num_ways
)
# + id="TXPWqOW55LRX" colab={"base_uri": "https://localhost:8080/"} outputId="295d139c-908f-447d-f813-3aff1901fd70"
swav_resnet50_mean_accuracy = np.mean(swav_resnet50_accuracies)
print("Swav Resnet Mean accuracy: ", swav_resnet50_mean_accuracy)
swav_resnet50_mean_f1_score = np.mean(swav_resnet50_f1_scores)
print("Swav Resnet Mean f1 score: ", swav_resnet50_mean_f1_score)
# + [markdown] id="eUuQyU_pFBy5"
# ## SimCLR
# + id="xEBOCPwlFBy6" colab={"base_uri": "https://localhost:8080/"} outputId="c94584dc-848e-4f7a-f432-ccec5b2a1d79"
simclr_embeddings_val_fn = "simclr" + val_embeddings_filename_suffix
simclr_embeddings_val = get_ndarray_from_drive(drive, folderid, simclr_embeddings_val_fn)
# + colab={"base_uri": "https://localhost:8080/"} id="v8dhTS5NbPd_" outputId="86d006d0-2701-4191-f8de-da899a60ceef"
simclr_accuracies, simclr_f1_scores = run_evaluations(
simclr_embeddings_val,
train_indices,
eval_indices,
wi_y,
eval_y,
num_episodes,
num_ways
)
# + id="rsGJt2GS5wu7" colab={"base_uri": "https://localhost:8080/"} outputId="0ff4a6de-4933-446a-dc4f-13d1e201d652"
simclr_mean_accuracy = np.mean(simclr_accuracies)
print("Simclr Mean accuracy: ", simclr_mean_accuracy)
simclr_mean_f1_score = np.mean(simclr_f1_scores)
print("Simclr Mean f1 score: ", simclr_mean_f1_score)
# + [markdown] id="J9TjD20ZF--3"
# ## VGG16
# + id="D_nT_W7eF--5" colab={"base_uri": "https://localhost:8080/"} outputId="cbdf0fbd-e505-4d21-f69c-5f31b74433b3"
vgg16_embeddings_val_fn = "vgg16" + val_embeddings_filename_suffix
vgg16_embeddings_val = get_ndarray_from_drive(drive, folderid, vgg16_embeddings_val_fn)
# + colab={"base_uri": "https://localhost:8080/"} id="3AxhZos3bUhZ" outputId="4ff399b2-c5ac-4b45-f30f-7fb5a88670c1"
vgg16_accuracies, vgg16_f1_scores = run_evaluations(
vgg16_embeddings_val,
train_indices,
eval_indices,
wi_y,
eval_y,
num_episodes,
num_ways
)
# + id="VB1ONpxC7UJF" colab={"base_uri": "https://localhost:8080/"} outputId="9f572c91-9a82-4b91-cb4d-4e20bd1244d7"
vgg16_mean_accuracy = np.mean(vgg16_accuracies)
print("VGG16 Mean accuracy: ", vgg16_mean_accuracy)
vgg16_mean_f1_score = np.mean(vgg16_f1_scores)
print("VGG16 Mean f1 score: ", vgg16_mean_f1_score)
# + [markdown] id="M9dYlVFDF_vs"
# ## CLIP
# + id="2y6RpvnEF_vs" colab={"base_uri": "https://localhost:8080/"} outputId="3660339c-0347-481d-9577-6b03d605fe13"
clip_embeddings_val_fn = "clip" + val_embeddings_filename_suffix
clip_embeddings_val = get_ndarray_from_drive(drive, folderid, clip_embeddings_val_fn)
# + id="AKJB9NiPbdo7" colab={"base_uri": "https://localhost:8080/"} outputId="0feb31e2-4d15-40dc-85e4-df0fa45420b8"
clip_accuracies, clip_f1_scores = run_evaluations(
clip_embeddings_val,
train_indices,
eval_indices,
wi_y,
eval_y,
num_episodes,
num_ways
)
# + colab={"base_uri": "https://localhost:8080/"} id="PDVdzHOH8Lf7" outputId="0bd004fe-32df-4c17-a8fa-83daec9f15ce"
clip_mean_accuracy = np.mean(clip_accuracies)
print("CLIP Mean accuracy: ", clip_mean_accuracy)
clip_mean_f1_score = np.mean(clip_f1_scores)
print("CLIP Mean f1 score: ", clip_mean_f1_score)
# + [markdown] id="Tn0jXMft8yHQ"
# # Conclusion
# + id="Is2QJads_ON_"
mean_accuracy_dict={
inceptionv3_mean_accuracy: "Inception V3",
resnet50_mean_accuracy: "Resnet 50",
moco_resnet50_mean_accuracy: "MoCo Resnet 50",
pcl_resnet50_mean_accuracy: "PCL Resnet 50",
swav_resnet50_mean_accuracy: "SwAV Resnet 50",
simclr_mean_accuracy: "SimCLR",
vgg16_mean_accuracy: "VGG 16",
clip_mean_accuracy: "CLIP"
}
acc_vals = sorted(list(mean_accuracy_dict.keys()), reverse=True)
# + id="tTwZaIPBDkc7"
mean_f1_score_dict={
inceptionv3_mean_f1_score: "Inception V3",
resnet50_mean_f1_score: "Resnet 50",
moco_resnet50_mean_f1_score: "MoCo Resnet 50",
pcl_resnet50_mean_f1_score: "PCL Resnet 50",
swav_resnet50_mean_f1_score: "SwAV Resnet 50",
simclr_mean_f1_score: "SimCLR",
vgg16_mean_f1_score: "VGG 16",
clip_mean_f1_score: "CLIP"
}
f1_vals = sorted(list(mean_f1_score_dict.keys()), reverse=True)
# + colab={"base_uri": "https://localhost:8080/"} id="rVc0H-s_F0M1" outputId="6816dd50-9020-46ff-8983-cd72482bf19d"
print("All accuracies for {} way {} shot classification on UCF101 with {} random episodes- ".format(
num_ways, num_shot, num_episodes
))
for val in acc_vals:
print(mean_accuracy_dict[val], ": ", val)
# + id="Kf7RFuo0K6-h" colab={"base_uri": "https://localhost:8080/"} outputId="853756b9-c84f-48b1-b7e6-d0deb821025f"
print("All f1 scores for {} way {} shot classification on Omniglot with {} random episodes- ".format(
num_ways, num_shot, num_episodes
))
for val in f1_vals:
print(mean_f1_score_dict[val], ": ", val)
|
notebooks/WeightImprintingSoftmaxBase_AllModels/WeightImprintingSoftmaxBase_AllModels_UCF101.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <img src="http://xarray.pydata.org/en/stable/_static/dataset-diagram-logo.png" align="right" width="30%">
#
# # Introduction to Dask
#
# In this lesson, we discuss cover the basics of Dask. Our learning goals are as
# follows. By the end of the lesson, we will be able to:
#
# - Identify and describe Dask Collections (Array, DataFrame) and Schedulers
# - Work with Dask Array's in much the same way you would work with a NumPy array
# - Understand some of the tradeoffs surounding chunk size, chunk shape, and
# computational overhead
# - Deploy a local Dask Distributed Cluster and access the diagnostics dashboard
#
# ## Table of contents
#
# 1. [**What-is-Dask?**](#What-is-Dask?)
# 1. [**Dask Collections**](#Dask-Collections)
# 1. [**Parallelism using the dask.distributed scheduler**](#Parallelism-using-the-dask.distributed-scheduler)
# 1. [**Profiling & Diagnostics using the Dask Dashboard**](#Profiling-&-Diagnostics-using-the-Dask-Dashboard)
# 1. [**Distributed Dask clusters for HPC and Cloud environments**](#Distributed-Dask-clusters-for-HPC-and-Cloud-environments)
#
# <img src="http://dask.readthedocs.io/en/latest/_images/dask_horizontal.svg"
# width="30%"
# align=right
# alt="Dask logo">
#
# ## What is Dask?
#
# Dask is a flexible parallel computing library for analytic computing. Dask
# provides dynamic parallel task scheduling and high-level big-data collections
# like `dask.array` and `dask.dataframe`, and an extensive suite of deployment
# options. Dask's documentation can be found here:
# https://docs.dask.org/en/latest/
#
# <img src="https://docs.dask.org/en/latest/_images/dask-overview.svg"
# width="75%"
# align=center
# alt="Dask overview">
#
# ## Quick setup
#
# For the purposes of this notebook, we'll use a Dask Cluster to manage
# computations. The next cell sets up a simple LocalCluster. We'll cover Dask
# schedulers and clusters later on in this notebook.
#
# +
from dask.distributed import Client
client = Client()
client
# -
# <p>👆</p> Click the Dashboard link above.
#
# ## Dask Collections
#
# Dask includes 3 main collections:
#
# - [Dask Array](https://docs.dask.org/en/latest/array.html): Parallel NumPy
# arrays
# - [Dask DataFrame](https://docs.dask.org/en/latest/dataframe.html): Parallel
# Pandas DataFrames
# - [Dask Bag](https://docs.dask.org/en/latest/bag.html): Parallel Python Lists
#
# Xarray primarily interfaces with the Dask Array collection so we'll skip the
# others for now. You can find out more about Dask's user interfaces
# [here](https://docs.dask.org/en/latest/user-interfaces.html).
#
# ## Dask Arrays
#
# Dask Array implements a subset of the NumPy ndarray interface using blocked
# algorithms, cutting up the large array into many small arrays. This lets us
# compute on arrays larger than memory using multiple cores. We coordinate these
# blocked algorithms using Dask graphs. Dask Array's are also _lazy_, meaning that
# they do not evaluate until you explicitly ask for a result using the `compute`
# method.
#
# If we want to create a NumPy array of all ones, we do it like this:
#
# +
import numpy as np
shape = (1000, 4000)
ones_np = np.ones(shape)
ones_np
# -
# This array contains exactly 32 MB of data:
#
print("%.1f MB" % (ones_np.nbytes / 1e6))
# Now let's create the same array using Dask's array interface.
#
# +
import dask.array as da
ones = da.ones(shape)
ones
# -
# This works, but we didn't tell Dask how to split up (or chunk) the array, so it
# is not optimized for parallel computation.
#
# A crucal difference with Dask is that we must specify the `chunks` argument.
# "Chunks" describes how the array is split up over many sub-arrays.
#
# 
# _source:
# [Dask Array Documentation](http://dask.pydata.org/en/latest/array-overview.html)_
#
# There are
# [several ways to specify chunks](http://dask.pydata.org/en/latest/array-creation.html#chunks).
# In this lecture, we will use a block shape.
#
chunk_shape = (1000, 1000)
ones = da.ones(shape, chunks=chunk_shape)
ones
# Notice that we just see a symbolic represetnation of the array, including its
# shape, dtype, and chunksize. No data has been generated yet. When we call
# `.compute()` on a Dask array, the computation is trigger and the dask array
# becomes a numpy array.
#
ones.compute()
# In order to understand what happened when we called `.compute()`, we can
# visualize the Dask _graph_, the symbolic operations that make up the array
#
ones.visualize()
# Our array has four chunks. To generate it, Dask calls `np.ones` four times and
# then concatenates this together into one array.
#
# Rather than immediately loading a Dask array (which puts all the data into RAM),
# it is more common to reduce the data somehow. For example:
#
sum_of_ones = ones.sum()
sum_of_ones.visualize()
# ### Exercise
#
# Modify the chunk size (or shape) in the `ones` array and visualize how the task
# graph changes.
#
# +
# your code here
# -
# Here we see Dask's strategy for finding the sum. This simple example illustrates
# the beauty of Dask: it automatically designs an algorithm appropriate for custom
# operations with big data.
#
# If we make our operation more complex, the graph gets more complex.
#
fancy_calculation = (ones * ones[::-1, ::-1]).mean()
fancy_calculation.visualize()
# ### A Bigger Calculation
#
# The examples above were toy examples; the data (32 MB) is probably not big
# enough to warrant the use of Dask.
#
# We can make it a lot bigger!
#
bigshape = (200000, 4000)
big_ones = da.ones(bigshape, chunks=chunk_shape)
big_ones
print("%.1f MB" % (big_ones.nbytes / 1e6))
# This dataset is 6.4 GB, rather than 32 MB! This is probably close to or greater
# than the amount of available RAM than you have in your computer. Nevertheless,
# Dask has no problem working on it.
#
# _Do not try to `.visualize()` this array!_
#
# When doing a big calculation, dask also has some tools to help us understand
# what is happening under the hood. Let's watch the dashboard again as we do a
# bigger computation.
#
# +
big_calc = (big_ones * big_ones[::-1, ::-1]).mean()
result = big_calc.compute()
result
# -
# ### Reduction
#
# All the usual numpy methods work on dask arrays. You can also apply numpy
# function directly to a dask array, and it will stay lazy.
#
big_ones_reduce = (np.cos(big_ones) ** 2).mean(axis=1)
big_ones_reduce
# Plotting also triggers computation, since we need the actual values
#
# %matplotlib inline
from matplotlib import pyplot as plt
plt.plot(big_ones_reduce)
# ## Parallelism using the dask.distributed scheduler
#
# In the [first cell](#Quick-setup) of this notebook, we started a local Dask
# Cluster and Client. We skipped past some important details there that we'll
# unpack now.
#
# ### Dask Schedulers
#
# The Dask _Schedulers_ orchestrate the tasks in the Task Graphs so that they can
# be run in parallel. _How_ they run in parallel, though, is determined by which
# _Scheduler_ you choose.
#
# There are 3 _local_ schedulers:
#
# - **Single-Thread Local:** For debugging, profiling, and diagnosing issues
# - **Multi-threaded:** Using the Python built-in `threading` package (the default
# for all Dask operations except `Bags`)
# - **Multi-process:** Using the Python built-in `multiprocessing` package (the
# default for Dask `Bags`)
#
# and 1 _distributed_ scheduler, which we will talk about later:
#
# - **Distributed:** Using the `dask.distributed` module (which uses `tornado` for
# communication over TCP). The distributed scheduler uses a `Cluster` to manage
# communication between the scheduler and the "workers". This is described in
# the next section.
#
# ### Distributed Clusters (http://distributed.dask.org/)
#
# - `LocalCluster` - Creates a `Cluster` that can be executed locally. Each
# `Cluster` includes a `Scheduler` and `Worker`s.
# - `Client` - Connects to and drives computation on a distributed `Cluster`
#
# ## Profiling & Diagnostics using the Dask Dashboard
#
# You'll recall from above, that we opened a url to the Dask Dashboard:
#
client
# The dashboard the Dask distributed scheduler provides a an incredibly valuable
# tool for gaining insights into the performance of your computation and the
# cluster as a whole. In the dashboard, you'll see a number of tags:
#
# - _Status_: Overview of the current state of the scheduler, including the active
# task stream, progress, memory per worker, and the number of tasks per worker.
# - _Workers_: The workers tab allows you to track cpu and memory use per worker.
# - _System_: Live tracking of system resources like cpu, memory, bandwidth, and
# open file descriptors
# - _Profile_: Fine-grained statistical profiling
# - _Info_: Worker status and logs.
#
# Another useful diagnostic tool is Dask's static performance report. This allows
# you to save a report, including the task stream, worker profiles, etc. for all
# or a specific part of a workflow. Below is an example of how you would create
# such a report:
#
# +
from dask.distributed import performance_report
with performance_report(filename="dask-report.html"):
big_calc.compute()
# -
# ### Exercise
#
# Again, let's modify the chunk size in `big_ones` (aim for ~100mb). How does the
# _Performance Report_ change with a larger chunk size?
#
# +
# your code here
with performance_report(filename="dask-report-large-chunk.html"):
big_calc.compute()
# -
# ## Distributed Dask clusters for HPC and Cloud environments
#
# Dask can be deployed on distributed infrastructure, such as a an HPC system or a
# cloud computing system. There is a growing ecosystem of Dask deployment projects
# that faciliate easy deployment and scaling of Dask clusters on a wide variety of
# computing systems.
#
# ### HPC
#
# #### Dask Jobqueue (https://jobqueue.dask.org/)
#
# - `dask_jobqueue.PBSCluster`
# - `dask_jobqueue.SlurmCluster`
# - `dask_jobqueue.LSFCluster`
# - etc.
#
# #### Dask MPI (https://mpi.dask.org/)
#
# - `dask_mpi.initialize`
#
# ### Cloud
#
# #### Dask Kubernetes (https://kubernetes.dask.org/)
#
# - `dask_kubernetes.KubeCluster`
#
# #### Dask Cloud Provider (https://cloudprovider.dask.org)
#
# - `dask_cloudprovider.FargateCluster`
# - `dask_cloudprovider.ECSCluster`
# - `dask_cloudprovider.ECSCluster`
#
# #### Dask Gateway (https://gateway.dask.org/)
#
# - `dask_gateway.GatewayCluster`
#
# ---
#
# _Note: Pieces of this notebook comes from the following sources:_
#
# - https://github.com/pangeo-data/pangeo-tutorial
# - https://github.com/rabernat/research_computing
# - https://github.com/dask/dask-examples
#
|
scipy-tutorial/05_intro_to_dask.ipynb
|
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 1.0.3
# language: julia
# name: julia-1.0
# ---
# +
using PyPlot
using DSP
using QuadGK
include("../src/num.jl")
include("../src/phy.jl")
using .num
using .physics
# -
const t = 0.5
U = 5.9
T = 0.
const nωn = 2^12
const nω = 2^12
const Nd = 20
ωrange = [-16.0,16.0]
const zeroplus = 0.01
const itermax = 200
const tol = 0.01
const mix = 0.50;
kB = 8.617333262145e-5;
# +
ω = range(ωrange[1],length=nω,stop=ωrange[2])
ω = convert(Array{Float64},ω);
β = 1. / kB / T
ωn = π .* (2 .* collect(1:nωn) .+ 1) ./ β;
# -
@time D0ω = baredos.("cubic",t,ω);
# +
function ipt_solver(Aw, nf, U)
Ap = Aw[:,1] .* nf
Am = Aw[:,2] .* nf
App = conv_same(Ap,Ap)
Appp = conv_same(Am, App)
return -π .* U^2 .* (Appp + Appp[end:-1:1])
return -π .* U^2 .* (AAB + BBA)
end
function ipt_selfcons(ω,dos,t,U,T,itermax,nω,zeroplus,mix,tol)
gloc = zeros(ComplexF64,nω,2)
g0 = zeros(ComplexF64,nω,2)
isi = zeros(Float64,nω,2)
hsi = zeros(Float64,nω,2)
A0 = zeros(Float64,nω,2)
Σ2 = zeros(ComplexF64,nω,2)
magnet = 0.0
dω = ω[2] - ω[1]
nf = fermi.(ω,T)
η = zeroplus
α = mix
ρe = dos[1:4:nω]
w = ω[1:4:nω]
Σ1 = U .* [0.9 -0.9]
for i = 1:nω
ζ_up = zeta(ω[i] - Σ1[1],η)
ζ_down = zeta(ω[i] - Σ1[2],η)
intg = ρe ./ (ζ_up*ζ_down .- w.^2.)
sum = trapz(w,intg)
gloc[i,1] = sum * ζ_down
gloc[i,2] = sum * ζ_up
end
for iter = 1:itermax
gloc_old = deepcopy(gloc)
ncalc = zeros(Float64,length(gloc[1,:]))
@fastmath @inbounds for i in 1:2
ncalc[i] = -1/π .* trapz(ω,imag(gloc[:,i]) .* nf)
end
Σ1[1] = U .* (ncalc[2] - sum(ncalc)/2)
Σ1[2] = U .* (ncalc[1] - sum(ncalc)/2)
magnet = (ncalc[2] - ncalc[1]) / sum(ncalc)
g0[:,1] = 1. ./ (ω .+ im*η .- t^2 .* gloc_old[:,2])
g0[:,2] = 1. ./ (ω .+ im*η .- t^2 .* gloc_old[:,1])
for i = 1:2 A0[:,i] = -imag(g0[:,i]) ./ π end
for i = 1:2
isi[:,i] = ipt_solver(A0,nf,U) * dω * dω
isi[:,i] = 0.5 .* (isi[:,i] + isi[end:-1:1,i])
hsi[:,i] = -imag.(Util.hilbert(isi[:,i]))
end
Σ2 = hsi .+ im .* isi
for i = 1:nω
ζ_up = zeta(ω[i] - Σ1[1] .- Σ2[i,1],η)
ζ_down = zeta(ω[i] - Σ1[2] .- Σ2[i,2],η)
intg = ρe ./ (ζ_up*ζ_down .- w.^2.)
sum = trapz(w,intg)
gloc[i,1] = sum * ζ_down
gloc[i,2] = sum * ζ_up
end
convg, error = convergent(gloc_old,gloc,ω,nω,tol)
if convg == false
gloc = mixing(gloc_old,gloc,mix)
elseif iter == itermax
println("Convergent is not achieved. Try Lower Mixings or Higher Iterations")
break
elseif convg == true
println("Convergent is achieved for U = $U, and T = $T K")
break
end
end
return gloc,Σ2,magnet
end;
# +
T = 150.
Us = [1.0, 1.5, 2.0, 2.5, 4.0, 4.5]
Us = convert(Array{Float64},Us)
glocU = zeros(ComplexF64,nω,2,length(Us))
Σ2U = zeros(ComplexF64,nω,2,length(Us))
magnetU = zeros(Float64,length(Us))
for (iU,U) in enumerate(Us)
glocU[:,:,iU],Σ2U[:,:,iU],magnetU[iU] = ipt_selfcons(ω,D0ω,t,U,T,itermax,nω,zeroplus,mix,tol);
end
# +
plt.figure(figsize=(10,4))
color = ["#0A7CC9","#0AC9AF","#0AC97C","#0AC94A","#0AC910","#63C90A"]
dashtype = ["-","-","--","-.",":"]
for (iU,U) in enumerate(Us)
plt.plot(ω,-imag(sum(glocU[:,:,iU],dims=2)) .+ 1.4*(iU - 1),color=color[iU],linewidth=0.8)
plt.text(3.4,(iU-1)* 1.4 + 0.1,"U = $U eV",fontsize=8)
plt.fill_between(ω,vec(-imag(sum(glocU[:,:,iU],dims=2)).+ (iU-1)*1.4),(iU-1)*1.4,alpha=0.7,color=color[iU])
end
plt.xlim(-4.5,4.5)
plt.ylim(0,8.8)
plt.xlabel("ω",fontsize=14)
plt.ylabel("D(ω)",fontsize=14)
plt.show()
plt.savefig("evolUDOS_IPT_AF.pdf",format="pdf")
# +
dashtype = ["-","--",":","-.","--",":"]
Us = [1.0, 1.5, 2.0, 2.5, 4.0, 4.5]
plt.figure(figsize=(12,4))
plt.subplot(1,3,1)
for iU in 1:2
plt.plot(ω,imag(sum(Σ2U[:,:,iU],dims=2)),dashtype[iU],label="U = $(Us[iU])")
end
plt.ylim(-2,0)
plt.xlim(-3,3)
plt.ylabel("Im Σ2",fontsize=12)
plt.xlabel("ω")
plt.legend()
plt.subplot(1,3,2)
for iU in 3:4
plt.plot(ω,imag(sum(Σ2U[:,:,iU],dims=2)),dashtype[iU-2],label="U = $(Us[iU])")
end
plt.ylim(-0.8,0)
plt.xlim(-6,6)
plt.xlabel("ω")
plt.legend()
plt.subplot(1,3,3)
for iU in 5:6
plt.plot(ω,imag(sum(Σ2U[:,:,iU],dims=2)),dashtype[iU-4],label="U = $(Us[iU])")
end
plt.ylim(-250,0)
plt.xlim(-0.5,0.5)
plt.xlabel("ω")
plt.legend()
plt.show()
plt.savefig("evolUΣ2_IPT_AF.pdf",format="pdf")
# +
Σ1 = U * magnetU[3]
plt.figure(figsize=(8,7)
)
plt.subplot(3,1,1)
plt.plot(ω,-imag(sum(glocU[:,:,3],dims=2)),color="grey",linewidth=0.8,label="total")
plt.plot(ω,-imag(glocU[:,1,3]),"--",label="n↑")
plt.plot(ω,-imag(glocU[:,2,3]),"--",label="n↓")
plt.xlim(-3,3)
plt.ylim(0,4)
plt.ylabel("D(ω)",fontsize=14)
plt.legend()
plt.subplot(3,1,2)
plt.plot(ω,imag(sum(Σ2U[:,:,3],dims=2)),color="grey",linewidth=0.8,label="total")
plt.plot(ω,imag(Σ2U[:,1,3]),"--",label="total")
plt.plot(ω,imag(Σ2U[:,2,3]),"--",label="total")
plt.ylabel("Im Σ",fontsize=14)
plt.subplot(3,1,3)
plt.plot(ω,real(sum(Σ2U[:,:,3],dims=2)),color="grey",linewidth=0.8,label="total")
plt.plot(ω,Σ1 .+ real(Σ2U[:,1,3]),"--",label="total")
plt.plot(ω,-Σ1 .+ real(Σ2U[:,2,3]),"--",label="total")
plt.xlabel("ω (eV)",fontsize=14)
plt.ylabel("Re Σ",fontsize=14)
plt.show()
plt.savefig("dosupdown_IPT_AF.pdf",format="pdf")
# +
U = 1.8
Ts = [200., 250., 300., 400., 600., 800., 1000.,]
Ts = convert(Array{Float64},Ts)
glocT = zeros(ComplexF64,nω,2,length(Ts))
Σ2T = zeros(ComplexF64,nω,2,length(Ts))
magnetT = zeros(Float64,length(Ts))
for (iT,T) in enumerate(Ts)
glocT[:,:,iT],Σ2T[:,:,iT],magnetT[iT] = ipt_selfcons(ω,D0ω,t,U,T,itermax,nω,zeroplus,mix,tol);
end
# +
plt.figure(figsize=(10,5))
color = ["#0A7CC9","#0AAFC9","#0AC9AF","#0AC97C","#0AC94A","#0AC910","#63C90A"]
dashtype = ["-","--","-.",":"]
for (iT,T) in enumerate(Ts)
plt.plot(ω,-imag(sum(glocT[:,:,iT],dims=2)) .+ 1.6*(iT - 1),color=color[iT],linewidth=0.8)
plt.text(3.4,(iT-1)*1.6 + 0.1,"T = $T K",fontsize=8)
plt.fill_between(ω,vec(-imag(sum(glocT[:,:,iT],dims=2)).+ (iT-1)*1.6),(iT-1)*1.6,alpha=0.7,color=color[iT])
end
plt.xlim(-4.5,4.5)
plt.ylim(0,11.4)
plt.xlabel("ω",fontsize=14)
plt.ylabel("D(ω)",fontsize=14)
plt.show()
plt.savefig("evolTDOS_IPT_AF.pdf",format="pdf")
# +
dashtype = ["-","--",":","-.","--",":"]
Ts = [200., 250., 300., 400., 600., 800., 1000.,]
plt.figure(figsize=(10,5))
plt.subplot(1,2,1)
for iT in 1:2
plt.plot(ω,imag(sum(Σ2T[:,:,iT],dims=2)),dashtype[iT],label="T = $(Ts[iT]) K")
end
plt.ylim(-2,0)
plt.xlim(-3,3)
plt.ylabel("Im Σ2",fontsize=12)
plt.xlabel("ω")
plt.legend()
plt.subplot(1,2,2)
for iT in 3:6
plt.plot(ω,imag(sum(Σ2T[:,:,iT],dims=2)),dashtype[iT-2],label="T = $(Ts[iT]) K")
end
plt.ylim(-3.5,0)
plt.xlim(-3,3)
plt.xlabel("ω")
plt.legend()
plt.show()
plt.savefig("evolTΣ2_IPT_AF.pdf",format="pdf")
# +
T = 100.
Us = range(0.8,length=20,step=0.3)
Us = convert(Array{Float64},Us)
magnetUs = zeros(Float64,length(Us))
for (iU,U) in enumerate(Us)
_,_,magnetUs[iU] = ipt_selfcons(ω,D0ω,t,U,T,itermax,nω,zeroplus,mix,tol);
end
# +
U = 2.0
Ts = range(0.0,length=20,stop = 500.)
Ts = convert(Array{Float64},Ts)
glocTs = zeros(ComplexF64,nω,2,length(Ts))
magnetTs = zeros(Float64,length(Ts))
for (iT,T) in enumerate(Ts)
_,_,magnetTs[iT] = ipt_selfcons(ω,D0ω,t,U,T,itermax,nω,zeroplus,mix,tol);
end
# +
plt.figure(figsize=(11,5))
plt.subplot(1,2,1)
plt.plot(Us,magnetUs,"-o")
plt.ylabel("Sublattice Magnetization",fontsize=12)
plt.xlabel("U (eV)",fontsize=14)
plt.subplot(1,2,2)
plt.plot(Ts,magnetTs,"-o")
plt.xlabel("T (K)",fontsize=14)
plt.show()
plt.savefig("magnetization_IPT_AF.pdf",format="pdf")
# -
|
nb/IPT - antiferromagnetic.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="llBtQyMWKmao"
# ## Predicting surface location using fluorescent beads
# + [markdown] id="IJ4jJKxHKxrt"
# Fluorescent beads on a clean coverslip were imaged with confocal laser scanning microscope. Their 3D position have been determined using 3D Gaussian fit. Given their radius, this is enough information to uncover coverslip surface position beneath them. However, bead radius has a wide variation. In this file, we learn how to correct for bead size using various parameters that 3D Gaussian fit spits out and an independent measurment of actual coverslip surface position.
# + [markdown] id="yUxnIqt34ZM7"
# ### Prepare data
# + id="_J59TKKWEMaw" outputId="79ec45b2-ec39-4b00-ab40-859db1925949" colab={"base_uri": "https://localhost:8080/", "height": 35}
# Use seaborn for pairplot
# !pip install -q seaborn
# Use some functions from tensorflow_docs
# !pip install -q git+https://github.com/tensorflow/docs
import pathlib
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
import tensorflow_docs as tfdocs
import tensorflow_docs.plots
import tensorflow_docs.modeling
# + [markdown] id="-w2OSzan20M6"
# #### Download and save data
# + id="yFGRjIAD25sT" outputId="69cac1d4-deeb-48b0-d6ee-6465b1638d6b" colab={"base_uri": "https://localhost:8080/", "height": 181}
# !git clone https://github.com/masterika/Fluorescence_BSVC.git
import os
# Root directory of the project
ROOT_DIR = os.getcwd()
os.chdir('Fluorescence_BSVC/Datasets')
# !unzip coverslip.zip # Results in creating a folder named "bacteria"
bacteria_dataset_path = os.path.join(os.getcwd(), "bacteria")
training_set = pd.read_csv("training.csv")
test_set = pd.read_csv("test.csv")
os.chdir(ROOT_DIR) # go back to root directory
# + [markdown] id="XgkXaOTv3gOr"
# #### Inspect data
# + id="VHkEB41p3d2k" outputId="afa81349-c8a9-4339-f4f8-ee0762fc0b9f" colab={"base_uri": "https://localhost:8080/", "height": 198}
training_set.head()
# + [markdown] id="20SJL5W2GS9e"
# Column contents are as follows:
# - x, y, and z: three dimensional position of fluorescent bead's center, 3D Gaussian fit result
# - stdx, stdy and stdz: gaussian spread (standard deviation) of fluorescent bead intensity in x, y and z directions respectively, fit result
# - prop: one of the fit coefficients, overal intensity indicator
# - const: Offset, fit coefficient
# - volume: number of voxels comprising bead
# - area: number of pixels surrounding the bead
# - dif: the label. Relative z position of bead's center to coverslip surface obtained by substracting coverslip position in bead's vicinity from bead's z position. This uses an independent measurement of coverslip surface position
#
# With 3D Gaussian fit: $$ const+prop\times e^\frac{(x-x_{av})^2}{2stdx^2}e^\frac{(y-y_{av})^2}{2stdy^2}e^\frac{(z-z_{av})^2}{2stdz^2}$$
# + id="UoJ8ATMnEs4X" outputId="e6ea6743-b871-4e8f-ce30-947784ad2a0d" colab={"base_uri": "https://localhost:8080/", "height": 921}
sns.pairplot(training_set[["dif","stdz","stdx","volume","prop"]], diag_kind="kde")
# + [markdown] id="kT1dWduTDipI"
# #### Separate labels from data
# + id="OHhSzodeDoWV"
LABEL = "dif"
training_labels = training_set.pop(LABEL)
test_labels = test_set.pop(LABEL)
# + [markdown] id="VKoemt1S3rab"
# #### Normalize data
# + id="3ghbhqeUEjOx"
training_set_n=(training_set-training_set.mean())/training_set.std()
test_set_n=(test_set-training_set.mean())/training_set.std()
# labels are already pretty close to 0-1 range, so we don't normilize them.
# + [markdown] id="VM20tC4w4gOW"
# ### Models
# + id="HpXonQzNMCn9"
FEATURES = ["stdz","stdx","volume","prop","stdy","area","const"] # set of meaniningful features for dif prediction. stdz feature does most of the job, but rest help.
# + [markdown] id="uGKL3dw963yd"
# #### Based on pair-plots above, dif seems to be approximately linear in features. Therefore, first let's see how the most intuitive, linear model will do
# + id="sZjRb36m60Yw"
def build_linear_model():
model = keras.Sequential([
layers.Dense(1)
])
optimizer = tf.keras.optimizers.Adam(0.001)
model.compile(loss='mse',
optimizer=optimizer,
metrics=['mae'])
return model
# + [markdown] id="XJn47lKK7ja4"
# #### Looking closer, plots seem consistently a bit curved. Let's see if neural networks can detect these subtle dependencies and improve precision
# + id="-Q4wUNRfF0Z1"
def build_neural_network():
model = keras.Sequential([
layers.Dense(6, activation='relu'),
layers.Dense(1)
])
optimizer = tf.keras.optimizers.Adam(0.001)
model.compile(loss='mse',
optimizer=optimizer,
metrics=['mae'])
return model
# + [markdown] id="gkFdURPE3w-e"
# ### Training with linear model
# + id="ffdzWy81LGMn" outputId="567e2c4c-a3c2-4aed-a6a2-647a31b2fd65" colab={"base_uri": "https://localhost:8080/", "height": 346}
model = build_linear_model()
EPOCHS = 2000
early_stop = keras.callbacks.EarlyStopping(monitor='val_loss', patience=10) # stop training whenever validation set stops showing improvement
early_history = model.fit(training_set_n[FEATURES], training_labels,
epochs=EPOCHS, validation_split = 0.3, verbose=0,
callbacks=[early_stop, tfdocs.modeling.EpochDots()])
# + [markdown] id="q1QhVUxG6ps8"
# #### Determining error
# + id="-A0cZpv9LzeA" outputId="d410febe-058e-4946-dfb9-be98d5a3bb07" colab={"base_uri": "https://localhost:8080/", "height": 297}
plotter = tfdocs.plots.HistoryPlotter(smoothing_std=2)
plotter.plot({'Early Stopping': early_history}, metric = "mae")
plt.ylabel('MAE [\u03BCm]')
# + id="oUWPoMVPMAIc" outputId="13bb7ae6-1f04-4637-ea5e-713103d2e0bf" colab={"base_uri": "https://localhost:8080/", "height": 54}
loss, mae = model.evaluate(test_set_n[FEATURES], test_labels, verbose=2)
print("Testing set Mean Abs Error: {:5.2f} \u03BCm".format(mae))
# + [markdown] id="cyLCHwsY7JmR"
# #### Prediction
# + id="iN-_6lJUOBmA" outputId="bee8375c-860f-41f9-9e63-dfaffd03965d" colab={"base_uri": "https://localhost:8080/", "height": 279}
test_predictions = model.predict(test_set_n[FEATURES]).flatten() # using test set to make predictions
a = plt.axes(aspect='equal')
plt.scatter(test_labels, test_predictions)
plt.xlabel('True Values [\u03BCm]')
plt.ylabel('Predictions [\u03BCm]')
lims = [0, 1.5]
plt.xlim(lims)
plt.ylim(lims)
_ = plt.plot(lims, lims)
# + id="vqMaIoxkPbD7" outputId="c538a3b2-fcdf-4454-ce49-0b157263ecbb" colab={"base_uri": "https://localhost:8080/", "height": 279}
error =[a_i - b_i for a_i, b_i in zip(test_predictions, test_labels)]
plt.hist(error, bins = 20, range = [-0.4,0.4])
plt.xlabel("Prediction Error [\u03BCm]")
_ = plt.ylabel("Count")
# + [markdown] id="eC_GsCGm77ce"
# ##### Eliminating obvious outliers in test set if any
# + id="gcLS2o9QPtQ3"
# Simple anomaly detection function
# Takes a list of numbers and a threshold value. Removes any number that is a threshold times standard deviation away from the mean from the list
thresh = 3 # should be adjusted for different test data size
def delouts(mylist,thresh):
num = 1
while (num !=0 ):
num = 0;
std = np.std(mylist)
mean = np.mean(mylist)
for val in mylist:
if (np.abs(mean-val)>thresh*std):
mylist.remove(val)
num = 1;
# + id="leTK4UgyPzB7" outputId="5f190d3c-97d6-4a55-e2e0-9c1a6f7a8968" colab={"base_uri": "https://localhost:8080/", "height": 72}
print("Error before removing outliers (linear model): "+str(round(np.std(error),3))+" [\u03BCm]")
delouts(error,thresh)
print("Error after removing outliers (if any): "+str(round(np.std(error),3))+" [\u03BCm]")
print("Error before correcting for size: "+str(round(np.std(test_labels),3))+" [\u03BCm]")
# + [markdown] id="6lh5nCFf8uxb"
# ### Training with neural network
# + id="slsAk5OS8jGu" outputId="8f6aa888-c9a1-429a-8794-354ef9f505cf" colab={"base_uri": "https://localhost:8080/", "height": 346}
model = build_neural_network()
EPOCHS = 2000
early_stop = keras.callbacks.EarlyStopping(monitor='val_loss', patience=10) # stop training whenever validation set stops showing improvement
early_history = model.fit(training_set_n[FEATURES], training_labels,
epochs=EPOCHS, validation_split = 0.3, verbose=0,
callbacks=[early_stop, tfdocs.modeling.EpochDots()])
# + [markdown] id="sIR2z6S384Mb"
# #### Determining error
# + id="jRDJSSYN87UW" outputId="341205cb-d6de-41dc-ecdc-be7bd6f84101" colab={"base_uri": "https://localhost:8080/", "height": 298}
plotter = tfdocs.plots.HistoryPlotter(smoothing_std=2)
plotter.plot({'Early Stopping': early_history}, metric = "mae")
plt.ylabel('MAE [\u03BCm]')
# + id="mVMsdETF9MSc" outputId="b4b166ee-878c-405a-c67f-90c41b1923ea" colab={"base_uri": "https://localhost:8080/", "height": 54}
loss, mae = model.evaluate(test_set_n[FEATURES], test_labels, verbose=2)
print("Testing set Mean Abs Error: {:5.2f} \u03BCm".format(mae))
# + [markdown] id="BhGDZQ2c9NFs"
# #### Prediction
# + id="nNCXgg6d9UHs" outputId="768e8dce-240c-4537-ef15-85600f04fb35" colab={"base_uri": "https://localhost:8080/", "height": 279}
test_predictions = model.predict(test_set_n[FEATURES]).flatten() # using test set to make predictions
a = plt.axes(aspect='equal')
plt.scatter(test_labels, test_predictions)
plt.xlabel('True Values [\u03BCm]')
plt.ylabel('Predictions [\u03BCm]')
lims = [0, 1.5]
plt.xlim(lims)
plt.ylim(lims)
_ = plt.plot(lims, lims)
# + id="6EIyFgoo9Yej" outputId="bf5a3220-b8f9-42be-f4b0-993431cebfee" colab={"base_uri": "https://localhost:8080/", "height": 279}
error =[a_i - b_i for a_i, b_i in zip(test_predictions, test_labels)]
plt.hist(error, bins = 20, range = [-0.4,0.4])
plt.xlabel("Prediction Error [\u03BCm]")
_ = plt.ylabel("Count")
# + [markdown] id="uhqNY1D99gZc"
# ##### Eliminating obvious outliers in test set if any
# + id="3JxIQqXx9jpc" outputId="63345d19-e770-49fa-db75-e59cb5202b24" colab={"base_uri": "https://localhost:8080/", "height": 72}
print("Error before removing outliers (neural network): "+str(round(np.std(error),3))+" [\u03BCm]")
delouts(error,thresh)
print("Error after removing outliers (if any): "+str(round(np.std(error),3))+" [\u03BCm]")
print("Error before correcting for size: "+str(round(np.std(test_labels),3))+" [\u03BCm]")
# + [markdown] id="PijjHpJR98z-"
# ### Summary
# + [markdown] id="UTupIzOY-DsU"
# We have improved the precision of detecting surface using fluorescent beads by capturing the variation of in bead size. Both, linear model and neural network improve the precision by factor three, neural networks performing slightly better. As the relationship looks linear for the big range of the parameter values, it is possible that neural networks will only show significant improvement if the data size is really big.
|
Keras_Regression_on_beads.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/archananair17/Python-Class-1/blob/main/Untitled3.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="aO4X2zIYHvW7"
import pandas as pd
# + id="1QQZ1ZVNKJnS"
df=pd.read_csv("/content/Supermarket_sales.csv")
# + colab={"base_uri": "https://localhost:8080/", "height": 661} id="oNPd2FU0Ma3I" outputId="595ceb3c-cb0b-4642-8a83-224f503cf57c"
df
# + colab={"base_uri": "https://localhost:8080/", "height": 357} id="YXkZ3kdAMcDL" outputId="1d0dc066-7247-4cac-df80-3838abbfceed"
df.head()
# + colab={"base_uri": "https://localhost:8080/", "height": 357} id="G5f7R5IbTefw" outputId="895e695a-a49d-4412-f950-95c6cd410768"
df.tail()
# + colab={"base_uri": "https://localhost:8080/", "height": 36} id="aSCDWz3NUdgX" outputId="f73e8e60-1919-4ea5-f2bc-015c9550f6cf"
df.loc[0,"City"]
# + colab={"base_uri": "https://localhost:8080/", "height": 36} id="z2A3Au4DVDdz" outputId="c2266737-dd35-498d-c936-99d1dcac98a3"
df.loc[500,"City"]
# + colab={"base_uri": "https://localhost:8080/", "height": 36} id="RghnHJBUV7YW" outputId="916f54a2-10f0-421e-af86-83a8eafa7694"
df.loc[999,"Productline"]
# + colab={"base_uri": "https://localhost:8080/", "height": 36} id="68QhJJPRWYLv" outputId="8f9b5e4f-64f4-4be7-c164-d2101267d1ff"
df.loc[649,"Payment"]
# + colab={"base_uri": "https://localhost:8080/", "height": 36} id="MBo_obmeWhRv" outputId="4259d07a-17a5-46f2-9471-a8acb34b1deb"
df.loc[648,"Payment"]
# + colab={"base_uri": "https://localhost:8080/"} id="slFuOI8NW-rF" outputId="d4761041-91de-4d38-a14d-38f379a2eac4"
new_data=[len(df)]
for x in range(500):
new_data.append(df.loc[x,"City"])
new_data
# + colab={"base_uri": "https://localhost:8080/", "height": 609} id="F4X7AH02YD_2" outputId="4ebe6a5a-b817-47ac-d3cb-b14306d3cfb0"
df.plot(figsize=(15,10))
# + colab={"base_uri": "https://localhost:8080/", "height": 609} id="hZQPAwgsaSdG" outputId="bdf7b45a-6d9b-4404-a716-583f44125e58"
df.Unitprice.plot(figsize=(15,10))
# + colab={"base_uri": "https://localhost:8080/", "height": 609} id="HMW3XUD2a20B" outputId="ae1d67ff-c024-4c6f-e8be-abadd845a5fc"
df.Quantity.plot(figsize=(15,10))
# + colab={"base_uri": "https://localhost:8080/", "height": 282} id="eGIhURVkbiT2" outputId="1b0e3473-ede1-40eb-c1e6-d166b59da67a"
df.Payment.hist()
# + colab={"base_uri": "https://localhost:8080/", "height": 282} id="hx22099Tb0gz" outputId="24feef39-2d98-4fb0-ed8f-5b0d824b7896"
df.Gender.hist()
# + colab={"base_uri": "https://localhost:8080/", "height": 265} id="kMMir9E6cURV" outputId="e3fd9a99-db46-4e37-8397-22c0a3416074"
import matplotlib.pyplot as plt
plt.hist(df["Tax"])
plt.show()
# + id="R7W76XI5dS_J"
|
Untitled3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Summarising the mean and the variance
#
# For this example we are going use the LFI module to infer the unknown mean, $\mu$, and variance, $\Sigma$, of $n_{\bf d}=10$ data points of a 1D random Gaussian field, ${\bf d}=\{d_i\sim\mathcal{N}(\mu,\Sigma)|i\in[1, n_{\bf d}]\}$. This is an interesting problem since we know the likelihood analytically, but it is non-Gaussian
# $$\mathcal{L}({\bf d}|\mu,\Sigma) = \prod_i^{n_{\bf d}}\frac{1}{\sqrt{2\pi|\Sigma|}}\exp\left[-\frac{1}{2}\frac{(d_i-\mu)^2}{\Sigma}\right]$$
# +
import numpy as np
import tensorflow as tf
import matplotlib as mpl
import matplotlib.pyplot as plt
import tensorflow as tf
import imnn_tf
from imnn_tf.lfi import GaussianApproximation, \
ApproximateBayesianComputation, PopulationMonteCarlo
from make_data import GenerateGaussianNoise
from make_data import GenerateGaussianNoise
from make_data import AnalyticLikelihood
import tensorflow_probability as tfp
tfd = tfp.distributions
print("IMNN {}\nTensorFlow {}\nTensorFlow Probability {}\nnumpy {}\nmatplotlib {}".format(
imnn_tf.__version__, tf.__version__, tfp.__version__, np.__version__, mpl.__version__))
# -
#
# Lets observe some data generated from a Gaussian distribution with a mean, $\mu=3$, and a variance $\Sigma=2$ - we're going to generate the data from seed 37 (for no particular reason). Once this is generated we're going to forget that we ever knew this. Simulations from this model can be made using
# +
generator = GenerateGaussianNoise()
θ_target = np.array([3., 2.])[np.newaxis, :]
target_data = generator.simulator(
parameters=θ_target,
seed=37,
simulator_args={"input_shape": generator.input_shape})
generator.plot_data(target_data, label="Observed data")
# -
# ## Inferring the mean and variance
#
# In the `AnalyticLikelihood` module we have routines for calculating the exact likelihood for this problem.
#
# For the inference we start by defining our prior as a uniform distribution. This distribution can be a TensorFlow Probability distribution for simplicity. We are going to choose the prior to be uniform from -10 to 10 for the mean and 0 to 10 for the variance.
#
# $$p(\mu,\Sigma)=\textrm{Uniform}\left[\textrm{lower}=(-10, 0),\textrm{upper}=(10,10)\right]$$
prior = tfd.Blockwise([tfd.Uniform(-10., 10.),
tfd.Uniform(0.1, 10.)])
AL = AnalyticLikelihood(
parameters=2,
data=target_data,
prior=prior,
generator=generator,
labels=[r"$\mu$", r"$\Sigma$"])
# As well as knowing the likelihood for this problem, we also know what sufficient statistics describe the mean and variance of the data - they are the mean and the variance
# $$\frac{1}{n_{\bf d}}\sum_i^{n_{\bf d}}d_i = \mu\textrm{ and }\frac{1}{n_{\bf d}-1}\sum_i^{n_{\bf d}}(d_i-\mu)^2=\Sigma$$
# What makes this an interesting problem for the IMNN is the fact that the sufficient statistic for the variance is non-linear, i.e. it is a sum of the square of the data, and so linear methods like MOPED would be lossy in terms of information.
#
# We can calculate the statistics of observed data (generated from a Gaussian distribution with mean and variance of $\mu=3$ and $\Sigma=2$)
print("Mean and variance of observed data = {}".format(
AL.get_estimate(target_data)))
# We might want to know how likely it is that any particular parameters of the Gaussian model are given that we have observed this data. This is given by the posterior distribution
# $$\mathcal{P}(\mu,\Sigma|{\bf d})\propto\mathcal{L}({\bf d}|\mu,\Sigma)p(\mu, \Sigma)$$
# For example, let's say we want to know how likely it is that this data came from a model with some fiducial parameters $\mu^\textrm{fid}=0$ and $\Sigma^\textrm{fid}=1$.
θ_fid = np.array([0., 1.])
# We can evaluate the analytic likelihood, weighted by the prior
print("log P(𝜇=0,Σ=1|d) ∝ {}".format(
AL.log_posterior(grid=θ_fid)))
ax = AL.plot(
gridsize=(1000, 1000),
figsize=(7, 7),
color="C0",
label="Analytic posterior")
# In the `LFI` submodule there are a handful of functions which allow us to do likelihood-free inference (LFI). The first order approximation is the Gaussian approximation to the likelihood.
GA = GaussianApproximation(
target_data=target_data,
prior=prior,
Fisher=AL.Fisher(θ_fid),
get_estimate=AL.get_estimate,
labels=[r"$\mu$", r"$\Sigma$"])
# We can calculate the Fisher information by taking the negative second derivative of the likelihood taking the expectation by inserting the relations for the sufficient statistics and examining at the fiducial parameter values
# $${\bf F}_{\alpha\beta} = -\left.\left(\begin{array}{cc}\displaystyle-\frac{n_{\bf d}}{\Sigma}&0\\0&\displaystyle-\frac{n_{\bf d}}{2\Sigma^2}\end{array}\right)\right|_{\textrm{fiducial}}.$$
# The inverse Fisher information describes the Cramer-Rao bound, i.e. the minimum variance of a Gaussian approximation of the likelihood about the fiducial parameter values. We can therefore use the Fisher information to make an approximation to posterior. The inverse Fisher can be view using
GA.plot_Fisher(figsize=(5, 5));
fig, ax = plt.subplots(2, 2, figsize=(7, 7))
AL.plot(
gridsize=(1000, 1000),
ax=ax,
figsize=(7, 7),
color="C0",
label="Analytic posterior");
GA.plot(
gridsize=(1000, 1000),
ax=ax,
color="C2",
label="Gaussian approximation");
# ## Approximate Bayesian computation
# We can also do approximate Bayesian computation using the mean and variance as sufficient statistics describing the data. The ABC draws parameter values from the prior and makes simulations at these points. These simulations are then summarised, i.e. we find the mean and variance of the simulations in this case, and then the distance between these estimates and the estimate of the target data can be calculated. Estimates within some small ϵ-ball around the target estimate are approximately samples from the posterior. Note that the larger the value of ϵ, the worse the approximation to the posterior.
ABC = ApproximateBayesianComputation(
target_data=target_data,
prior=prior,
Fisher=AL.Fisher(θ_fid),
get_estimate=AL.get_estimate,
simulator=lambda x : generator.simulator(
x, None, {"input_shape": generator.input_shape}),
labels=[r"$\mu$", r"$\Sigma$"])
# We can call the ABC directly, for (say) 100000 draws using
# ```python
# ABC(draws=100000, at_once=True, save_sims="simulations/sims")
# ```
# This triggers the production of `draws=100000` simulations with parameters sampled from the prior. By default, `at_once=True` and so the simulations are returned at once and processed parallelly - if the estimator cannot deal with the all the simulations in parallel then we need to set `at_once=False`. All of the simulations will be saved in a `simulations` directory (which should be premade) under the same `sims`. If you don't want to save the simulations then `save_sims=None` is default. The `ABC()` call returns parameters, estimates, differences from the target and distances from the target, but they are also available as attributes
# ```python
# ABC.parameters
# #(100000, 2)
# ABC.estimates
# #(100000, 2)
# ABC.differences
# #(100000, 1, 2)
# ABC.distances
# #(100000, 1)
# ```
#
# This runs the ABC, but doesn't define the accepted or rejected samples. To run the acceptance and rejection within a distance of `ϵ=1` we can run
# ```python
# ABC.accept_reject(ϵ=1)
# ```
# This makes available the accepted and rejected parameters, and statistics
# ```python
# ABC.num_draws
# # () = 100000
# ABC.num_accepted
# # (1) = 311
# ABC.num_rejected
# # (1) = 99689
# ABC.accepted_parameters
# # (1, 311, 2)
# ABC.accepted_estimates
# # (1, 311, 2)
# ABC.accepted_differences
# # (1, 311, 2)
# ABC.accepted_distances
# # (1, 311)
# ABC.rejected_parameters
# # (1, 99689, 2)
# ABC.rejected_estimates
# # (1, 99689, 2)
# ABC.rejected_differences
# # (1, 99689, 2)
# ABC.rejected_distances
# # (1, 99689)
# ```
#
# If we want to continue the ABC we can just call it again. However it can be useful to have a known number of samples (say `accepted=2000` samples) within a chosen ϵ-ball (say `ϵ=1`). This will iteratively run the ABC until 2000 samples are within an ϵ of 1 of the target. We can do as many or as few simulations at once as we like. In our case we will use `min_draws=10000`. We can use the same `ABC` arguments (`at_once` and `save_sims`) to process the simulations sequentially or not and to save the simulations. This method is run using
# ```python
# ABC.get_min_accepted(ϵ=1, accepted=2000, min_draws=10000)
# ```
# The posterior can then be obtained (as a histogram) using
# ```python
# ABC.posterior()
# ```
# where the number of `bins` and `ranges` can be passed if necessary. Note that we can also pass `ϵ`, `accepted`, `draws` (`draws` takes the place of `min_draws` if `accepted` is not `None`) and any of the other arguments directely to `ABC.posterior()`, so that the posterior is calculated without needing to run `ABC()`, `ABC.accept_reject()` or `ABC.get_min_accepted()` first.
#
# We can plot the posterior directly using
# ```python
# ABC.plot()
# ```
# which can also take `ϵ`, `accepted`, `draws`, as well as `bins` and `ranges` and `matplotlib` related arguments. This includes a Gaussian `smoothing` parameter which can smoothen out the histogram, at the expense of widening the approximate posterior.
#
# Finally, the estimates and parameters can be plotted using
# ```python
# ABC.scatter_plot(rejected=0.01)
# ```
# where we can set the fraction of the rejected points to be plotted using the `rejection` argument. This is useful because the number of rejected points tends to be orders of magnitude higher than the accepted points in ABC. We can avoid plotting the rejected samples at all using `rejected=0` or `rejected=None`. `ABC.scatter_plot()`, like `ABC.plot()`, can be passed `ABC` arguments to perform the ABC on first call, and `matplotlib` arguments. By default the parameter values are plotted on the x-axis and the estimates on the y-axis, but we can plot estimates on both axes (to look for degeneracies in the estimator) by passing `axes="estimate_estimate"` or the parameters on both axes (to look at the sampling of the prior) using `axes="parameter_parameter"`.
#
# The ABC can be reset back to default by running
# ```python
# ABC.reset()
# ```
#
# It is also possible to run the ABC with saved simulations. To do so imagine we have an array of parameter values `saved_parameters` with shape `saved_parameters.shape -> (100000, 2)` and corresponding simulations `saved_simulations` with shape `saved_simulations.shape -> (100000, 10)` (correctly aligned with `saved_parameters`, then we can call
# ```python
# ABC = LFI.ApproximateBayesianComputation(
# target_data=target_data,
# prior=prior,
# Fisher=AL.Fisher(θ_fid),
# get_estimate=AL.get_estimate,
# simulator=lambda _ : saved_simulations)
# ABC(draws=saved_parameters, predrawn=True)
# ABC.accept_reject(ϵ=1.)
# ```
ax = AL.plot(
gridsize=(1000, 1000),
figsize=(7, 7),
color="C0",
label="Analytic posterior");
GA.plot(
gridsize=(1000, 1000),
ax=ax,
color="C2",
label="Gaussian approximation");
ABC.plot(
ϵ=1.,
accepted=2000,
draws=10000,
ax=ax,
color="C1",
label="ABC posterior at ϵ={}".format(1),
bins=50);
ABC.scatter_plot(axes="parameter_estimate", rejected=0.01);
ABC.scatter_plot(axes="estimate_estimate", rejected=0.01);
ABC.scatter_plot(axes="parameter_parameter", rejected=0.01);
# ## Population Monte Carlo
#
# Whilst we can obtain approximate posteriors using ABC, the rejection rate is very high because we sample always from the prior. Population Monte Carlo (PMC) uses statistics of the population of samples to propose new parameter values, so each new simulation is more likely to be accepted. This prevents us needing to define an ϵ parameter to define the acceptance distance. Instead we start with a population from the prior and iteratively move samples inwards. Once it becomes difficult to move the population any more, i.e. the number of attempts to accept a parameter becomes very large, then the distribution is seen to be a stable approximation to the posterior.
#
# The whole module works very similarly to `ABC` with a few changes in arguments.
PMC = PopulationMonteCarlo(
target_data=target_data,
prior=prior,
Fisher=AL.Fisher(θ_fid),
get_estimate=AL.get_estimate,
simulator=lambda x : generator.simulator(
x, None, {"input_shape": generator.input_shape}),
labels=[r"$\mu$", r"$\Sigma$"])
# We can call the PMC directly for a population of 2000 samples using
# ```python
# PMC(draws=2000, initial_draws=5000, criterion=0.1, percentile=75, at_once=True, save_sims="simulations/sims")
# ```
# This performs ABC on 5000 samples, and selects a population from the 2000 samples closest to the target. This population is then moved towards the target until it takes 10 times as many simulations to be rejected as are accepted. We chose to move the outer 25% of samples all at once, rather than just the furthest simulation at a time, i.e. the stable population is defined by the 75th percentile. This can be more efficient for some distributions and less efficient for others. Setting `percentile=None` moves only the furthest sample.
#
# Similar to the ABC, by default, `at_once=True` and so the simulations are returned at once and processed parallelly - if the estimator cannot deal with the all the simulations in parallel then we need to set `at_once=False`. All of the simulations will be saved in a `simulations` directory (which should be premade) under the same `sims`. If you don't want to save the simulations then `save_sims=None` is default. The saving is not yet tested for the PMC. The `PMC()` call returns parameters, estimates, differences from the target and distances from the target, but they are also available as attributes
# ```python
# PMC.parameters
# #(1, 2000, 2)
# PMC.estimates
# #(1, 2000, 2)
# PMC.differences
# #(1, 2000, 2)
# PMC.distances
# #(1, 2000)
# PMC.num_draws
# #(1) = 112949
# ```
# Note that here `PMC.num_draws` does not include the `initial_draws`.
#
# The posterior can then be obtained (as a histogram) using
# ```python
# PMC.posterior()
# ```
# where the number of `bins` and `ranges` can be passed if necessary. Note that we can also pass `draws`, `initial_draws`, `criterion` and `percentile` and any of the other arguments directely to `PMC.posterior()`, so that the posterior is calculated without needing to run `PMC()` first.
#
# We can plot the posterior directly using
# ```python
# PMC.plot()
# ```
# which can also take `draws`, `initial_draws`, `criterion`, `percentile`, as well as `bins` and `ranges` and `matplotlib` related arguments. This includes a Gaussian `smoothing` parameter which can smoothen out the histogram, at the expense of widening the approximate posterior.
#
# Finally, the estimates and parameters can be plotted using
# ```python
# ABC.scatter_plot()
# ```
# Since there are no rejected points in the PMC, there is no `rejected` argument unlike for the ABC. `PMC.scatter_plot()`, like `PMC.plot()`, can be passed `PMC` arguments to perform the PMC on first call, and `matplotlib` arguments. By default the parameter values are plotted on the x-axis and the estimates on the y-axis, but we can plot estimates on both axes (to look for degeneracies in the estimator) by passing `axes="estimate_estimate"` or the parameters on both axes (to look at the sampling of the prior) using `axes="parameter_parameter"`.
#
# The PMC can be reset back to default by running
# ```python
# PMC.reset()
# ```
ax = AL.plot(
gridsize=(1000, 1000),
figsize=(7, 7),
color="C0",
label="Analytic posterior");
GA.plot(
gridsize=(1000, 1000),
ax=ax,
color="C2",
label="Gaussian approximation");
ABC.plot(
ax=ax,
color="C1",
label="ABC posterior at ϵ={}".format(1),
bins=50)
PMC.plot(
draws=2000,
initial_draws=5000,
criterion=0.1,
percentile=75,
ax=ax,
color="C3",
label="PMC posterior",
bins=50);
PMC.scatter_plot(axes="parameter_estimate")
PMC.scatter_plot(axes="estimate_estimate")
PMC.scatter_plot(axes="parameter_parameter")
|
examples/LFI - Mean and variance inference.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 1.4.1
# language: julia
# name: julia-1.4
# ---
# + [markdown] slideshow={"slide_type": "slide"}
# ## Getting Started With Julia
# -
# ### Starting Julia REPL
# + slideshow={"slide_type": "fragment"}
julia
# + [markdown] slideshow={"slide_type": "slide"}
# ### Getting Documents for Julia Functions
# -
?
# + [markdown] slideshow={"slide_type": "slide"}
# ### Switching to Package Manager REPL
# -
] # To enter. To return to Julia's REPL, just use backspace
# + [markdown] slideshow={"slide_type": "slide"}
# ### Shell Commands Inside Julia REPL
# -
;
# + [markdown] slideshow={"slide_type": "slide"}
# ### Print
# -
println("Hello dear Julia learner!")
# + [markdown] slideshow={"slide_type": "slide"}
# ### Exit Julia REPL
# -
exit()
|
Notebooks/getting_started.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Session 16: Word Embeddings using the Word2Vec skip-gram model
#
# ------------------------------------------------------
# *Introduction to Data Science & Machine Learning*
#
# *<NAME> <EMAIL>*
#
# ------------------------------------------------------
#
# The goal of this notebook is to train a Word2Vec skip-gram model over a data base of plain tex [Text8](http://mattmahoney.net/dc/textdata).
#
# This is a personal wrap-up of all the material provided by [Google's Deep Learning course on Udacity](https://www.udacity.com/course/deep-learning--ud730), so all credit goes to them.
#
# The following [link](http://mccormickml.com/2016/04/19/word2vec-tutorial-the-skip-gram-model/) gives a very simple explanation of the model. Check also the following video.
# +
from IPython.display import YouTubeVideo
YouTubeVideo('xMwx2A_o5r4')
# +
# These are all the modules we'll be using later. Make sure you can import them
# before proceeding further.
# %matplotlib inline
from __future__ import print_function
import collections
import math
import numpy as np
import os
import random
import tensorflow as tf
import zipfile
from matplotlib import pylab
from six.moves import range
from six.moves.urllib.request import urlretrieve
from sklearn.manifold import TSNE
#Here I provide some text preprocessing functions
import preprocessing
# +
# Lets check what version of tensorflow we have installed. The provided scripts should run with tf 1.0 and above
print(tf.__version__)
# -
# We will use the plain text database from this [link](http://mattmahoney.net/dc/textdata.html)
filename = './text8.zip'
# Read the data into a string
words = preprocessing.read_data(filename)
print('Data size %d' % len(words))
type(words)
print(words[0:20])
# Build the dictionary and replace rare unfrequent words with UNK token.
# +
vocabulary_size = 50000
data, count, dictionary, reverse_dictionary = preprocessing.build_dataset(vocabulary_size,words)
print('Most common words (+UNK)', count[:5])
print('Sample data', data[:10])
del words # Hint to reduce memory.
# -
# Let's display the internal variables to better understand their structure:
print(data[:10])
print(count[:10])
print(list(dictionary.items())[:10])
print(list(reverse_dictionary.items())[:10])
print('The index of the word dictionary is %d\n' %(dictionary['crafty']))
print('The word corresponding to the index 875 is %s\n' %(reverse_dictionary[875]))
# ## Generating training batches
# The function 'preprocessing.generate_batch' generates training batchs for the skip-gram model.
#
#
# <img src="Fig1.png" width="600" height="400">
#
# Figure borrowed from this [post](http://mccormickml.com/2016/04/19/word2vec-tutorial-the-skip-gram-model/).
# +
data_index = 0
"""Generate a batch of data for training.
Args:
batch_size: Number of samples to generate in the batch.
skip_window:# How many words to consider left and right.
How many words to consider around the target word, left and right.
With skip_window=2, in the sentence above for "consider" we'll
build the window [words, to, consider, around, the].
num_skips: How many times to reuse an input to generate a label.
For skip-gram, we map target word to adjacent words in the window
around it. This parameter says how many adjacent word mappings to
add to the batch for each target word. Naturally it can't be more
than skip_window * 2.
Returns:
batch, labels - ndarrays with IDs.
batch: Row vector of size batch_size containing target words.
labels:
Column vector of size batch_size containing a randomly selected
adjacent word for every target word in 'batch'.
"""
print('data:', [reverse_dictionary[di] for di in data[:32]])
for num_skips, skip_window in [(2, 4)]:
data_index = 0
batch, labels = preprocessing.generate_batch(data, data_index, batch_size=16, num_skips=num_skips, skip_window=skip_window)
print('\nwith num_skips = %d and skip_window = %d:' % (num_skips, skip_window))
print(' batch:', [reverse_dictionary[bi] for bi in batch])
print(' labels:', [reverse_dictionary[li] for li in labels.reshape(16)])
# -
# ## Using the above data set, now we train a skip-gram model!
# The following [link](http://mccormickml.com/2016/04/19/word2vec-tutorial-the-skip-gram-model/) gives a very simple explanation of the model. The following figures are borrowed from that post.
#
# <img src="Fig2.png" width="600" height="400">
#
# <img src="Fig3.png" width="600" height="400">
# +
batch_size = 32
embedding_size = 128 # Dimension of the embedding vector.
skip_window = 1 # How many words to consider left and right.
num_skips = 2 # How many times to reuse an input to generate a label.
# We pick a random validation set to sample nearest neighbors. here we limit the
# validation samples to the words that have a low numeric ID, which by
# construction are also the most frequent.
valid_size = 32 # Random set of words to evaluate similarity on.
valid_window = 200 # Only pick samples in the head of the distribution.
valid_examples = np.array(random.sample(range(valid_window), valid_size))
num_sampled = 64 # Number of negative examples to sample.
graph = tf.Graph()
with graph.as_default(), tf.device('/cpu:0'):
# Input data.
train_dataset = tf.placeholder(tf.int32, shape=[batch_size])
train_labels = tf.placeholder(tf.int32, shape=[batch_size, 1])
valid_dataset = tf.constant(valid_examples, dtype=tf.int32)
# Variables.
embeddings = tf.Variable(tf.random_uniform([vocabulary_size, embedding_size], -1.0, 1.0))
softmax_weights = tf.Variable(
tf.truncated_normal([vocabulary_size, embedding_size],stddev=1.0 / math.sqrt(embedding_size)))
softmax_biases = tf.Variable(tf.zeros([vocabulary_size]))
# Model.
# Look up embeddings for inputs. YOU DON'T NEED THE ONE HOT ENCODING FOR THE INPUT!!!!
embed = tf.nn.embedding_lookup(embeddings, train_dataset)
# Compute the softmax loss, using a sample of the negative labels each time.
loss = tf.reduce_mean(tf.nn.sampled_softmax_loss(softmax_weights, softmax_biases, train_labels,
embed, num_sampled, vocabulary_size))
# Optimizer.
optimizer = tf.train.AdagradOptimizer(1.0).minimize(loss)
# Compute the similarity between minibatch examples and all embeddings.
# We use the cosine distance:
norm = tf.sqrt(tf.reduce_sum(tf.square(embeddings), 1, keep_dims=True))
normalized_embeddings = embeddings / norm
valid_embeddings = tf.nn.embedding_lookup(normalized_embeddings, valid_dataset)
similarity = tf.matmul(valid_embeddings, tf.transpose(normalized_embeddings))
# +
num_steps = 100001
data_index = 0
with tf.Session(graph=graph) as session:
tf.global_variables_initializer().run()
print('Initialized')
average_loss = 0
for step in range(num_steps):
batch_data, batch_labels = preprocessing.generate_batch(data,data_index,batch_size, num_skips, skip_window)
data_index = (data_index + batch_size) % len(data)
feed_dict = {train_dataset : batch_data, train_labels : batch_labels}
_, l = session.run([optimizer, loss], feed_dict=feed_dict)
average_loss += l
if step % 2000 == 0:
if step > 0:
average_loss = average_loss / 2000
# The average loss is an estimate of the loss over the last 2000 batches.
print('Average loss at step %d: %f' % (step, average_loss))
average_loss = 0
# note that this is expensive (~20% slowdown if computed every 500 steps)
if step % 25000 == 0:
sim = similarity.eval()
for i in range(valid_size):
valid_word = reverse_dictionary[valid_examples[i]]
top_k = 8 # number of nearest neighbors
nearest = (-sim[i, :]).argsort()[1:top_k+1]
log = 'Nearest to %s:' % valid_word
for k in range(top_k):
close_word = reverse_dictionary[nearest[k]]
log = '%s %s,' % (log, close_word)
print(log)
final_embeddings = normalized_embeddings.eval()
# -
# This is what an embedding looks like:
print(final_embeddings[2,:])
# The embeddings have unit norm!
print(np.sum(np.square(final_embeddings[40000,:])))
# Now we project the emmbeding vectors into a 2-dimensional space using [TSNE](https://lvdmaaten.github.io/publications/papers/JMLR_2008.pdf)
#
# We use the [TSNE sklearn implementation](https://lvdmaaten.github.io/publications/papers/JMLR_2008.pdf)
# +
num_points = 200
tsne = TSNE(perplexity=30, n_components=2, init='pca', n_iter=500)
two_d_embeddings = tsne.fit_transform(final_embeddings[1:num_points+1, :])
# -
# Lets visualize the result
# +
def plot(embeddings, labels):
assert embeddings.shape[0] >= len(labels), 'More labels than embeddings'
pylab.figure(figsize=(15,15)) # in inches
for i, label in enumerate(labels):
x, y = embeddings[i,:]
pylab.scatter(x, y)
pylab.annotate(label, xy=(x, y), xytext=(5, 2), textcoords='offset points',ha='right', va='bottom')
pylab.show()
words = [reverse_dictionary[i] for i in range(1, num_points+1)]
plot(two_d_embeddings, words)
# -
|
Notebooks/Session 16 Word Embeddings/Session_16_Word_Embbeddings_Word2Vec.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
import hail as hl
hl.init(app_name="QC")
mt_path = "file:///directflow/ClinicalGenomicsPipeline/dev/2021-02-04-PIPELINE-1885-All-Hail/EricData/Glucoma/gvcf_WES.combined.VQSR.filtered.VEP.final.mt/"
mt = hl.read_matrix_table(mt_path)
mt_GT = mt.transmute_entries(GT = hl.experimental.lgt_to_gt(mt.LGT, mt.LA))
mt_GT = hl.split_multi_hts(mt_GT)
mt_GT = hl.sample_qc(mt_GT)
mt_GT = hl.variant_qc(mt_GT)
impute_sex_mt = hl.impute_sex(mt_GT.GT)
impute_sex_mt.describe()
final_mt = mt_GT.annotate_cols(impute_sex = impute_sex_mt[mt_GT.s])
output_path = "file:///directflow/ClinicalGenomicsPipeline/dev/2021-02-04-PIPELINE-1885-All-Hail/EricData/Glucoma/gvcf_WES.combined.VQSR.filtered.VEP.QC.sex.final.mt/"
final_mt.write(output_path,overwrite=True)
tmp_mt = mt_GT.annotate_cols(**impute_sex_mt[mt_GT.s])
final_mt.describe()
tmp_mt = final_mt.drop(final_mt.gvcf_info)
hl.export_vcf(tmp_mt, 'file:///directflow/ClinicalGenomicsPipeline/dev/2021-02-04-PIPELINE-1885-All-Hail/EricData/Glucoma/gvcf_WES.combined.VQSR.filtered.VEP.QC.sex.final.vcf')
|
notebooks/transmute_QC.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
filename='img1&2.csv'
df=pd.read_csv(filename, sep=' ')
lst=list(df.iloc[:,0])
ls1=[]
ls2=[]
for i in lst:
if 'img1' in i:
ls1.append(i)
else:
ls2.append(i)
len(ls1)
df.iloc[701,:]
df1=df.iloc[:702,:]
df1
df2=df.iloc[702:,:]
df2
exp_df1=df1.to_csv(r'dataset/img1.csv', index=None, sep=' ', header=True)
exp_df2=df2.to_csv(r'dataset/img2.csv', index=None, sep=' ', header=True)
|
sep.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:learn_pytorch]
# language: python
# name: conda-env-learn_pytorch-py
# ---
from google.cloud import vision
from google.cloud.vision import types
import io
from PIL import Image, ImageDraw
from enum import Enum
import os
import uuid
import glob
import time
# +
# make sure you have "data" directory in parallel to "notebooks". Create "input" directory under
# "data" directory and copy sample image file.
# application creates "output" programmatically.
# ----+/notebooks
# ----+/data
# ----------+/input
base_dir = '/Users/kd/Workspace/python/github/handwriting-recognition'
data_dir = 'data'
input_data_dir = 'input'
output_data_dir = 'output'
output_extracted_tables_dir = 'tables'
output_extracted_boxes_dir = 'boxes'
output_extracted_letters_dir = 'letters'
input_filename = 'sample_input_02.jpg'
# +
# utility function
def create_directory(path):
try:
os.mkdir(path)
return True
except FileExistsError as fe_error:
return True
except OSError as error:
print(error)
return False
# read files present in a directory
def read_directory_files(path, pattern='*'):
files = [f for f in glob.glob(os.path.join(path, pattern))]
return files
def get_subdirectories(path):
return [f.path for f in os.scandir(output_boxes_dir) if f.is_dir() ]
def show_img(img):
plt.axis('off')
plt.figure(figsize=(10,10))
plt.imshow(img);
# -
def ocr_from_google_vision(client, filepath):
with io.open(filepath, 'rb') as image_file1:
content = image_file1.read()
content_image = types.Image(content=content)
response = client.document_text_detection(image=content_image)
document = response.full_text_annotation
return document.text
# +
# program initialization
img_filename = os.path.join(base_dir, data_dir, input_data_dir, input_filename)
print("input filename : [%s]" % (img_filename))
processing_basedir = os.path.join(base_dir, data_dir, output_data_dir, os.path.splitext(input_filename)[0])
print("processing dir: [%s]" % (processing_basedir))
output_tables_dir = os.path.join(processing_basedir, output_extracted_tables_dir)
print("tables dir: [%s]" % (output_tables_dir))
output_boxes_dir = os.path.join(processing_basedir, output_extracted_boxes_dir)
print("boxes dir: [%s]" % (output_boxes_dir))
output_letters_dir = os.path.join(processing_basedir, output_extracted_letters_dir)
print("letters: [%s]" % (output_letters_dir))
# +
client = vision.ImageAnnotatorClient()
boxes_dirs = get_subdirectories(output_boxes_dir)
gvision_output = []
for boxes_dir in boxes_dirs:
boxes_files = read_directory_files(boxes_dir)
for file in boxes_files:
text = ocr_from_google_vision(client, file)
gvision_output.append([os.path.basename(boxes_dir), os.path.basename(file), text.strip('\n')])
print("table: [%s], boxes: [%s], text: [%s]" % (os.path.basename(boxes_dir), os.path.basename(file), text.strip('\n')))
time.sleep(1)
# -
gvision_output
|
notebooks/vision_ocr_model.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Try to use gpu
# ## 1 Import package
import numpy
import minpy.numpy
import cupy
import pandas
import matplotlib.pyplot as plt
import random
from scipy.io import loadmat
from scipy.optimize import minimize
from sklearn.preprocessing import OneHotEncoder
from scipy.special import expit
# ## 2 Choose whether to use gpu
np = numpy # Only use cpu
# ## 3 Determine the network structure
# +
num_units = 5 # the CNN ' size
in_size = 20 # input size is (20, 20)
k_size = 5 # the filtter size is (5, 5)
c_size = in_size - k_size + 1 # the convolution result's size is (16, 16)
pf_size = 2 # the pooling fillters' size is (2, 2)
p_size = c_size // pf_size # the pooling results' size is (8, 8)
output_size = 10
weights_size = (k_size * k_size + 1 +# w and b of convolution layer
p_size * p_size * output_size) * num_units + output_size # w of output layer
params = (np.random.random(size=weights_size) - 0.5) * 0.25 # all weights
params.shape
# -
# ## 4 Initializate data set
# +
data = loadmat("ex4data1.mat")
X = data["X"]
m = X.shape[0]
X = X.reshape((m, in_size, in_size))
y = data["y"]
training_set_scale = 0.7
tr_m = int(m * training_set_scale)
tr_X = np.array(X[:tr_m])
ts_m = m - tr_m
ts_X = np.array(X[tr_m:])
onehot_encoder = OneHotEncoder(sparse=False, categories="auto")
y_onehot = onehot_encoder.fit_transform(y)
tr_y = np.array(y_onehot[:tr_m]).reshape((tr_m, output_size, 1))
ts_y = np.array(y[tr_m:])
tr_X.shape, tr_y.shape, ts_X.shape, ts_y.shape
# -
# ## 5 Initializate weights
weights = (np.random.random(size=weights_size) - 0.5) * 0.25
weights.shape
# ## 6 Encode and decode weights
def encode(theta1, theta2, b1, b2):
return np.concatenate((theta1.ravel(), theta2.ravel(), b1.ravel(), b2.ravel()))
def decode(weights, num_units, k_size, p_size, output_size):
theta1 = weights[:num_units*k_size*k_size].reshape((num_units, k_size, k_size))
theta2 = weights[num_units*k_size*k_size:-output_size-num_units].reshape((num_units, p_size, p_size, output_size))
b1 = weights[-output_size-num_units:-output_size].reshape((num_units, 1))
b2 = weights[-output_size:].reshape((output_size, 1))
return theta1, theta2, b1, b2
theta1, theta2, b1, b2 = decode(weights, num_units, k_size, p_size, output_size)
theta1.shape, b1.shape, theta2.shape, b2.shape
encode(theta1, b1, theta2, b2).shape
theta1.size + b1.size + theta2.size + b2.size
# ## 7 Convolution
def convolution(X, w, k_size, c_size):
res = np.zeros((c_size, c_size))
for i in range(c_size):
for j in range(c_size):
res[i,j] = np.sum(w * X[i:i+k_size,j:j+k_size])
return res # (16, 16)
# ## 8 Pooling
def maxPooling(conv, c_size, pf_size, p_size):
res = np.zeros((p_size, p_size))
grad = np.zeros((c_size, c_size))
for i in range(0, c_size, pf_size):
for j in range(0, c_size, pf_size):
res[i//pf_size,j//pf_size] = np.max(conv[i:i+pf_size,j:j+pf_size])
idx = np.argmax(conv[i:i+pf_size,j:j+pf_size])
grad[i+idx//pf_size,j+idx%pf_size] = 1
return res, grad
#res, grad = maxPooling(a, crow, ccol, pfrow, pfcol, prow, pcol)
a = np.array([i for i in range(36)]).reshape((6,6))
b = np.array([[1, 1, 1], [1, 1, 1], [1, 1, 1]])
c = convolution(a, b, 3, 4)
res, grad = maxPooling(c, 4, 2, 2)
# ## 9 Sigmod
sigmod = expit
# ## 10 Forward propagate
def forwardPropagate(X, theta1, b1, theta2, b2, num_units, k_size,
c_size, p_size, output_size):
a1 = X # (20, 20)
z2 = np.zeros((num_units, c_size, c_size)) # (5, 16, 16)
a2 = z2.copy() # (5, 16, 16)
pooling_grad = z2.copy() # (5, 16, 16)
a3 = np.zeros((num_units, p_size, p_size)) # (5, 8, 8)
z4 = np.zeros((output_size, 1)) # (10, 1)
a4 = z4.copy() # (10, 1)
for i in range(num_units):
z2[i] = convolution(X, theta1[i], k_size, c_size) + b1[i] # (16, 16)
a2 = sigmod(z2) # (5, 16, 16)
for i in range(num_units):
a3[i], pooling_grad[i] = maxPooling(a2[i], c_size, pf_size, p_size)
temp_theta2 = theta2.reshape((output_size, num_units * p_size * p_size)) # (10, 5*8*8)
temp_a3 = a3.reshape((num_units * p_size * p_size, 1)) #(5*8*8, 1)
z4 = temp_theta2 @ temp_a3 + b2# (10, 1)
a4 = sigmod(z4)
return a1, z2, a2, pooling_grad, a3, z4, a4
a = forwardPropagate(X[0], theta1, b1, theta2, b2, num_units, k_size,
c_size, p_size, output_size)
def cost(weights, X, num_units, k_size,
c_size, p_size, output_size, lam=0.):
theta1, theta2, b1, b2 = decode(weights, num_units, k_size, p_size, output_size)
m = X.shape[0]
J = 0.
for i in range(m):
a1, z2, a2, pooling_grad, a3, z4, a4 = forwardPropagate(X[0], theta1, b1, theta2, b2,
num_units, k_size, c_size, p_size, output_size)
first_term = y[i] * np.log(a4)
second_term = (1 - y[i]) * np.log(1 - a4)
J += -np.sum(first_term + second_term)
J /= m
J += (float(lam) / (2 * m)) * \
(np.sum(theta1 **2) + np.sum(theta2 ** 2))
return J
a = cost(weights, tr_X[:1], num_units, k_size,
c_size, p_size, output_size)
a
# %%time
a = forwardPropagate(X[0], theta1, b1, theta2, b2, num_units, k_size,
c_size, p_size, output_size)
for i in a:
print(i.shape)
# +
def tencode(theta1, theta2, b1, b2):
return np.concatenate((theta1.flatten(), theta2.flatten(), b1.flatten(), b2.flatten()))
def tdecode(params, krow, kcol, hrow, hcol, num_units, output_size):
theta1 = params[: krow * kcol * num_units].reshape((num_units, krow, kcol)) # (5, 5, 5)
theta2 = params[krow * kcol * num_units:
krow * kcol * num_units +
hrow * hcol * output_size * num_units].reshape((num_units, output_size, hrow, hcol)) # (5, 10, 8,8)
b1 = params[-num_units - output_size: - output_size].reshape((num_units, 1))
b2 = params[-output_size:].reshape((output_size, 1))
return theta1, theta2, b1, b2
tt1, tt2, tb1, tb2 = tdecode(weights,k_size, k_size, p_size, p_size, num_units, output_size)
tt1.shape, tt2.shape, tb1.shape, tb2.shape
# +
def tconvolution(Xi, kernal, xrow, xcol, krow, kcol, rrow, rcol): #(20, 20) (5, 5)
xrow, xcol = Xi.shape
krow, kcol = kernal.shape
rrow, rcol = xrow - krow + 1, xcol - kcol + 1
res = np.zeros((rrow, rcol))
for i in range(rrow):
for j in range(rcol):
res[i][j] = np.sum(Xi[i:i+krow, j:j+kcol] * kernal)
return res # (16, 16)
def tmaxPooling(conv):
# use 2*2 pooling
row, col = conv.shape
res = np.zeros((row // 2, col // 2))
pooling_grad = np.zeros(conv.shape)
for i in range(0, row, 2):
for j in range(0, col, 2):
m = conv[i, j]
mr, mc = i, j
for p in range(i, i + 2):
for q in range(j, j + 2):
if conv[p, q] > m:
m = conv[p, q]
mr, mc = p, q
res[i // 2, j // 2] = m
pooling_grad[mr, mc] = 1
return res, pooling_grad
def tforwardPropagate(Xi, theta1, theta2, b1, b2, num_units, inrow, incol, krow,
kcol, conrow, concol, hrow, hcol):
a1 = Xi.reshape(inrow, incol) # (20, 20)
z2 = np.zeros((num_units, conrow, concol)) # (5, 16, 16)
a2 = np.zeros((num_units, conrow, concol)) # (5, 16, 16)
pooling_grad = np.zeros((num_units, conrow, concol)) # (5, 16, 16)
a3 = np.zeros((num_units, hrow, hcol)) # (5, 8, 8) z3 = a3
z4 = np.zeros((output_size, 1)) # (10, 1)
a4 = np.zeros((output_size, 1)) # (10, 1)
for i in range(num_units):
z2[i] = tconvolution(a1, theta1[i], inrow, incol, krow,
kcol, conrow, concol) + b1[i] # (16, 16)
a2[i] = sigmod(z2[i]) # (16, 16)
a3[i], pooling_grad[i] = tmaxPooling(a2[i]) # (8, 8) (16, 16)
for j in range(output_size):
z4[j] += np.sum(a3[i] * theta2[i,j])
for i in range(output_size):
z4[i] += b2[i]
a4 = sigmod(z4)
return a1, z2, a2, pooling_grad, a3, z4, a4
b = tforwardPropagate(X[0], tt1, tt2, tb1, tb2, num_units, in_size, in_size, k_size, k_size, c_size, c_size, p_size, p_size)
# -
a[5] == b[5]
b[5]
# ## 11 Predict
def predict(X, theta1, b1, theta2, b2, num_units, krow, kcol,
crow, ccol, prow, pcol, output_size):
*t, h = forwardPropagate(X, theta1, b1, theta2, b2, num_units, krow, kcol,
crow, ccol, prow, pcol, output_size)
return np.argmax(h) + 1
# ## 12 Comupte accuracy
def computeAccuracy(X, y, theta1, b1, theta2, b2, num_units, krow, kcol,
crow, ccol, prow, pcol, output_size):
m = X.shape[0]
correct = 0
for i in range(m):
ans = predict(X[i], theta1, b1, theta2, b2, num_units, krow, kcol,
crow, ccol, prow, pcol, output_size)
correct += ans == y[i]
return f"m:{m} correct:{correct} accuracy:{100 * correct / m}%"
#computeAccuracy(X, y, theta1, b1, theta2, b2, num_units, krow, kcol,
# crow, ccol, prow, pcol, output_size)
# ### The accuracy in all data
# %%time
computeAccuracy(X, y, theta1, b1, theta2, b2, num_units, krow, kcol,
crow, ccol, prow, pcol, output_size)
# ## 13 Sigmod gradient
def sigmodGradient(z):
t = expit(z)
return t * (1 - t)
# ## 14 Backpropagation
def backPropagate(weights, X, num_units, k_size,
c_size, pf_size, p_size, output_size, lam=0.):
m = X.shape[0]
theta1, theta2, b1, b2 = decode(weights, num_units,
k_size, p_size, output_size)
J = 0.
theta1_grad = np.zeros(theta1.shape) # (5, 5, 5)
b1_grad = np.zeros(b1.shape) # (5, 1)
theta2_grad = np.zeros(theta2.shape) # (5, 8, 10, 10)
b2_grad = np.zeros(b2.shape) # (10, 1)
for i in range(m):
a1, z2, a2, pooling_grad, a3, z4, a4 = forwardPropagate(X[i],
theta1, b1, theta2, b2, num_units, k_size,
c_size, p_size, output_size)
J += -np.sum(y[i] * np.log(a4) +
(1 - y[i]) * np.log(1 - a4)) # cost
print(J)
dt2 = a4 - y[i] # (10, 1)
b2_grad += dt2 # (10, 1)
temp_dt2 = dt2.reshape((1, output_size)) # (1, 10)
temp_grad = a3.reshape((num_units * p_size * p_size, 1)) * temp_dt2 # (5*8*8, 10)
theta2_grad += temp_grad.reshape((num_units, p_size, p_size, output_size))
temp = theta2.reshape((num_units * p_size * p_size, output_size
)) @ dt2
temp = temp.reshape((num_units, p_size, p_size))
temp2 = np.zeros((num_units, c_size, c_size)) # (5, 16, 16)
for j in range(num_units): #
for p in range(0, c_size, pf_size):
for q in range(0, c_size, pf_size):
temp2[j,p:p+pf_size,q:q+pf_size] = temp[j,p//pf_size,q//pf_size]
dt1 = temp2 * pooling_grad * z2 * (1 - z2) # (5, 16, 16)
for j in range(num_units):
b1_grad[j] = np.sum(dt1[j])
for p in range(k_size):
for q in range(k_size):
theta1_grad[j,p,q] += np.sum(dt1[j] * a1[p:p+c_size,q:q+c_size])
J /= m
theta1_grad /= m
b1_grad /= m
theta2_grad /=m
b2_grad /= m
#Regulation
J += (float(lam) / (2 * m)) * (np.sum(theta1 ** 2) + np.sum(theta2 ** 2))
theta1_grad += theta1 * lam / m
theta2_grad += theta2 * lam / m
return J, encode(theta1, b1, theta2, b2)
J, grad = backPropagate(weights,tr_X[:1], num_units, k_size,
c_size, pf_size, p_size, output_size)
J
# ## 15 Gradient checking
def checkGradient(weights, X, num_units, k_size,
c_size, pf_size, p_size, output_size, lam=0.):
eps = 1e-4
n = len(weights)
J, grad = backPropagate(weights, X, num_units, k_size,
c_size, pf_size, p_size, output_size)
print(J)
for i in range(10):
x = random.randint(0, n - 1)
epsvec = np.zeros(n)
epsvec[x] = eps
cost_high, t = backPropagate(weights + epsvec, X, num_units, k_size,
c_size, pf_size, p_size, output_size)
cost_low, t = backPropagate(weights - epsvec, X, num_units, k_size,
c_size, pf_size, p_size, output_size)
num_grad = (cost_high - cost_low) / (2 * eps)
print(f"Element:{x} Num grad = {num_grad} BP grad = {grad[x]}")
# %%time
checkGradient(weights, X[:1], num_units, k_size,
c_size, pf_size, p_size, output_size, 1.)
a = np.array([1, 2, 3, 4])
b = np.ones((1, 4))
a * b
# !curl www.google.com
|
StudyNotesOfML/4. Backforward /Optimize the training of CNN .ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Basic regression with Tensorflow
# Learning how tensorflow works starting with simple linear regression
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
# %matplotlib inline
# ## Settings
learning_rate = .001
epochs = 400
data_set_size = 50
batch_size = 10
test_set_size = 20
print_every = 50
num_batches = data_set_size/batch_size
assert data_set_size%batch_size == 0, "The data_set_size must be evely divisible by the batch_size"
# ## Generate some data
def getY(x):
return .125*x+np.random.randn(x.shape[0])*.125 +2
# +
# simple linear relationship
train_x = np.ones((data_set_size,2))
train_x[:,1:] = np.linspace(-10,10,data_set_size)[:,np.newaxis]
train_y = getY(train_x[:,1])
test_x = np.ones((test_set_size,2))
test_x[:,1:] = np.linspace(-10,10,test_set_size)[:,np.newaxis]
test_y = getY(test_x[:,1])
# -
plt.figure()
plt.plot(train_x[:,1],train_y,'ro',label='Training Data')
plt.plot(test_x[:,1],test_y,'bo',label='Testing Data')
plt.legend()
# Make the tensorflow placeholders
X = tf.placeholder(tf.float32, shape = [batch_size,2])
Y = tf.placeholder(tf.float32, shape = [batch_size])
# setup model weights
W = tf.Variable(np.random.randn(2,1).astype(np.float32),name='weight')
# +
# make the model
yhat = tf.matmul(X,W)
y_error = tf.subtract(yhat,Y)
cost = tf.reduce_sum(tf.divide(tf.pow(y_error,2),2*batch_size))
# -
# set up the optimizer
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)
init = tf.global_variables_initializer()
# utility function to compute a batch
# can compute over the optimizer or cost and return the cost if needed
def computeBatch(solveFor):
x = 0
for batch in xrange(num_batches):
batch_start = batch*batch_size
batch_end = batch_start + batch_size
temp = sess.run(solveFor, feed_dict={X:train_x[batch_start:batch_end,:],Y:train_y[batch_start:batch_end]})
if type(temp) is not type(None):
x += temp
return x
# +
costs = np.array([])
with tf.Session() as sess:
sess.run(init)
for epoch in xrange(epochs+1):
computeBatch(optimizer)
if epoch % print_every == 0:
c = computeBatch(cost)
costs = np.append(costs,c)
print('epoch: {}\t cost: {:.2e}'.format(epoch, computeBatch(cost)))
W_finished = sess.run(W)
plt.figure()
plt.plot(np.linspace(0,epochs,epochs/print_every+1),costs)
plt.title('Cost')
plt.xlabel('Epoch Number')
plt.ylabel('Cost')
plt.figure()
plt.plot(np.log(np.linspace(0,epochs,epochs/print_every+1)),np.log(costs))
plt.title('Log Cost')
plt.xlabel('log(Epoch Number)')
plt.ylabel('log(Cost)')
# -
# Compute the resulting line for the test set
pred_y = np.dot(test_x,W_finished)
plt.plot(train_x[:,1],train_y,'ro',label='Training Data')
plt.plot(test_x[:,1],test_y,'bo',label='Testing Data')
plt.plot(test_x[:,1],pred_y,label='Line of Best Fit (Test)')
plt.title('Resulting Model')
plt.xlabel('x-data')
plt.ylabel('y-data')
plt.legend()
print W_finished
|
Linear Regression.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
#XVFB will be launched if you run on a server
import os
if type(os.environ.get("DISPLAY")) is not str or len(os.environ.get("DISPLAY"))==0:
# !bash ../xvfb start
# %env DISPLAY=:1
# # Digging deeper: approximate crossentropy with neural nets
#
# 
#
# In this section we will train a neural network policy for continuous state space game
# +
import gym
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
env = gym.make("CartPole-v0").env #if you see "<classname> has no attribute .env", remove .env or update gym
env.reset()
n_actions = env.action_space.n
plt.imshow(env.render("rgb_array"))
# -
#create agent
from sklearn.neural_network import MLPClassifier
agent = MLPClassifier(hidden_layer_sizes=(20,20),
activation='tanh',
warm_start=True, #keep progress between .fit(...) calls
max_iter=1 #make only 1 iteration on each .fit(...)
)
#initialize agent to the dimension of state an amount of actions
agent.fit([env.reset()]*n_actions, list(range(n_actions)));
def generate_session(t_max=1000):
states,actions = [],[]
total_reward = 0
s = env.reset()
for t in range(t_max):
# a vector of action probabilities in current state
probs = agent.predict_proba([s])[0]
a = <sample action with such probabilities>
new_s, r, done, info = env.step(a)
#record sessions like you did before
states.append(s)
actions.append(a)
total_reward += r
s = new_s
if done: break
return states, actions, total_reward
# ### CEM steps
# Deep CEM uses exactly the same strategy as the regular CEM, so you can copy your function code from previous notebook.
#
# The only difference is that now each observation is not a number but a float32 vector.
def select_elites(states_batch,actions_batch,rewards_batch,percentile=50):
"""
Select states and actions from games that have rewards >= percentile
:param states_batch: list of lists of states, states_batch[session_i][t]
:param actions_batch: list of lists of actions, actions_batch[session_i][t]
:param rewards_batch: list of rewards, rewards_batch[session_i][t]
:returns: elite_states,elite_actions, both 1D lists of states and respective actions from elite sessions
Please return elite states and actions in their original order
[i.e. sorted by session number and timestep within session]
If you're confused, see examples below. Please don't assume that states are integers (they'll get different later).
"""
reward_threshold = <Compute minimum reward for elite sessions. Hint: use np.percentile>
elite_states = <your code here>
elite_actions = <your code here>
return elite_states, elite_actions
# # Training loop
# Generate sessions, select N best and fit to those.
# +
from IPython.display import clear_output
def show_progress(batch_rewards, log, percentile, reward_range=[-990,+10]):
"""
A convenience function that displays training progress.
No cool math here, just charts.
"""
mean_reward, threshold = np.mean(batch_rewards), np.percentile(batch_rewards, percentile)
log.append([mean_reward, threshold])
clear_output(True)
print("mean reward = %.3f, threshold=%.3f"%(mean_reward, threshold))
plt.figure(figsize=[8,4])
plt.subplot(1,2,1)
plt.plot(list(zip(*log))[0], label='Mean rewards')
plt.plot(list(zip(*log))[1], label='Reward thresholds')
plt.legend()
plt.grid()
plt.subplot(1,2,2)
plt.hist(batch_rewards, range=reward_range);
plt.vlines([np.percentile(batch_rewards, percentile)], [0], [100], label="percentile", color='red')
plt.legend()
plt.grid()
plt.show()
# +
n_sessions = 100
percentile = 70
log = []
for i in range(100):
#generate new sessions
sessions = [<generate a list of n_sessions new sessions>]
batch_states,batch_actions,batch_rewards = map(np.array, zip(*sessions))
elite_states, elite_actions = <select elite actions just like before>
<fit agent to predict elite_actions(y) from elite_states(X)>
show_progress(batch_rewards, log, percentile, reward_range=[0,np.max(batch_rewards)])
if np.mean(batch_rewards)> 190:
print("You Win! You may stop training now via KeyboardInterrupt.")
# -
# # Results
#record sessions
import gym.wrappers
env = gym.wrappers.Monitor(gym.make("CartPole-v0"), directory="videos", force=True)
sessions = [generate_session() for _ in range(100)]
env.close()
# +
#show video
from IPython.display import HTML
import os
video_names = list(filter(lambda s:s.endswith(".mp4"), os.listdir("./videos/")))
HTML("""
<video width="640" height="480" controls>
<source src="{}" type="video/mp4">
</video>
""".format("./videos/"+video_names[-1])) #this may or may not be _last_ video. Try other indices
# -
# ### Now what?
#
# By this moment you should have got enough score on [CartPole-v0](https://gym.openai.com/envs/CartPole-v0) to consider it solved (see the link). It's time to upload the result and get to something harder.
#
# _if you have any trouble with CartPole-v0 and feel stuck, take a look at the forums_
#
# * Pick one of environments: MountainCar-v0 or LunarLander-v2.
# * For MountainCar, get average reward of __at least -150__
# * For LunarLander, get average reward of __at least +50__
#
# See the tips section below, it's kinda important.
# __Note:__ If your agent is below the target score, you'll still get most of the points depending on the result, so don't be afraid to submit it.
#
#
# * Bonus quest: Devise a way to speed up training at least 2x against the default version
# * Obvious improvement: use [joblib](https://www.google.com/search?client=ubuntu&channel=fs&q=joblib&ie=utf-8&oe=utf-8)
# * Try re-using samples from 3-5 last iterations when computing threshold and training
# * Experiment with amount of training iterations and learning rate of the neural network (see params)
#
#
# ### Tips & tricks
# * Gym page: [mountaincar](https://gym.openai.com/envs/MountainCar-v0), [lunarlander](https://gym.openai.com/envs/LunarLander-v2)
# * Sessions for MountainCar may last for 10k+ ticks. Make sure ```t_max``` param is at least 10k.
# * Also it may be a good idea to cut rewards via ">" and not ">=". If 90% of your sessions get reward of -10k and 20% are better, than if you use percentile 20% as threshold, R >= threshold __fails cut off bad sessions__ whule R > threshold works alright.
# * _issue with gym_: Some versions of gym limit game time by 200 ticks. This will prevent cem training in most cases. Make sure your agent is able to play for the specified __t_max__, and if it isn't, try `env = gym.make("MountainCar-v0").env` or otherwise get rid of TimeLimit wrapper.
# * If you use old _swig_ lib for LunarLander-v2, you may get an error. See this [issue](https://github.com/openai/gym/issues/100) for solution.
# * If it won't train it's a good idea to plot reward distribution and record sessions: they may give you some clue. If they don't, call course staff :)
# * 20-neuron network is probably not enough, feel free to experiment.
# * __Please upload the results to openai gym and send links to all submissions in the e-mail__
# ### Submit to Coursera
from submit import submit_mountain_car
submit_mountain_car(generate_session, <EMAIL>, <TOKEN>)
|
week1_intro/deep_crossentropy_method.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # SUBSTITUCION
# Implemente un programa que implemente un cifrado de sustitución, como se indica a continuación.
# <img src='./img/ejercicio2.PNG'>
# <!-- "C:\Users\gdelgadr\Desktop\JoinProcess\PYTHON-FUNDAMENTOS-JOINPROCESS\Modulo1\Ejercicios\img\ejercicio1.PNG" -->
# ## ANTECEDENTES
# En un cifrado de sustitución, “ciframos” (es decir, ocultamos de forma reversible) un mensaje reemplazando cada letra por otra. Para ello utilizamos una clave : en este caso, un mapeo de cada una de las letras del alfabeto a la letra a la que debe corresponder cuando lo cifremos. Para "descifrar" el mensaje, el receptor del mensaje necesitaría conocer la clave, de modo que pueda revertir el proceso: traducir el texto cifrado (generalmente llamado texto cifrado ) al mensaje original (generalmente llamado texto plano ).
# Una clave, por ejemplo, podría ser la cadena <b>NQXPOMAFTRHLZGECYJIUWSKDVB</b>. Esta clave de 26 caracteres significa que <b>A</b> (la primera letra del alfabeto) debe convertirse en <b>N</b> (el primer carácter de la clave), <b>B</b> (la segunda letra del alfabeto) debe convertirse en <b>Q</b> (el segundo carácter de la clave) y así sucesivamente.
# Un mensaje como <b>HELLO</b>, entonces, sería encriptado como <b>FOLLE</b>, reemplazando cada una de las letras según el mapeo determinado por la clave.
# Escriba un programa llamado <b>substitution</b> que le permita cifrar mensajes usando un cifrado de sustitución. En el momento en que el usuario ejecuta el programa, debe decidir, proporcionando un argumento de línea de comandos, cuál debe ser la clave en el mensaje secreto que proporcionará en tiempo de ejecución.
#
#
# A continuación se muestran algunos ejemplos de cómo podría funcionar el programa. Por ejemplo, si el usuario ingresa una clave de <code>YTNSHKVEFXRBAUQZCLWDMIPGJO</code> y un texto sin formato de <code>HELLO</code>:
# ### Ejemplo1
# <code>python substitution.py YTNSHKVEFXRBAUQZCLWDMIPGJO <code>
# <code>plaintext: HELLO<code>
# <code>ciphertext: EHBBQ<code>
# Así es como el programa podría funcionar si el usuario proporciona una clave <code>VCHPRZGJNTLSKFBDQWAXEUYMOI</code> y un texto sin formato de <code>hello, world</code>:
# ### Ejemplo2
# <code>python substitution.py VCHPRZGJNTLSKFBDQWAXEUYMOI <code>
# plaintext: hello, world
# ciphertext: jrssb, ybwsp
# Observe que ni la coma ni el espacio fueron sustituidos por el cifrado. ¡Sustituya únicamente caracteres alfabéticos! Observe también que se ha conservado el caso del mensaje original. Las letras minúsculas permanecen en minúsculas y las letras mayúsculas permanecen en mayúsculas.
#
# No importa si los caracteres de la clave en sí son mayúsculas o minúsculas. Una clave de <code>VCHPRZGJNTLSKFBDQWAXEUYMOI</code> es funcionalmente idéntica a una clave de <code>vchprzgjntlskfbdqwaxeuymoi</code>(tal cual, para el caso <code>VcHpRzGjNtLsKfBdQwAxEuYmOi</code>).
#
# ¿Y si un usuario no proporciona una clave válida?
# <code>python substitution.py ABC
# Key must contain 26 characters.
# Para todos los casos en que no se proporcione una clave válida el programa debe concluir con algún mensaje de error
# ## ESPECIFICACIONES
# Diseñe e implemente un programa, <code>substitution</code> que encripta mensajes usando un cifrado de sustitución.
#
# - Implemente su programa en un archivo llamado <code>substitution.py</code>.
# - Su programa debe aceptar un único argumento de línea de comandos, la clave que se utilizará para la sustitución. La clave en sí no debe distinguir entre mayúsculas y minúsculas, por lo que si algún carácter de la clave está en mayúsculas o minúsculas no debería afectar el comportamiento de su programa.
# - Si su programa se ejecuta sin ningún argumento de línea de comando o con más de un argumento de línea de comando, su programa debe imprimir un mensaje de error de su elección (con <code>print</code>) y retornar un valor de <code>1</code>(que tiende a significar un error) inmediatamente.
# - Si la clave no es válida (por ejemplo, al no contener 26 caracteres, contener cualquier carácter que no sea un carácter alfabético o no contener cada letra exactamente una vez), su programa debe imprimir un mensaje de error de su elección (con <code>print</code>) y retornar un valor de <code>1</code>(que tiende a significar un error) inmediatamente.
# - Su programa debe generar <code>plaintext:</code> (sin una nueva línea) y luego solicitar al usuario un texto plano (usando <code>input</code>).
# - Su programa debe generar <code>ciphertext:</code>(sin una nueva línea) seguido por el texto cifrado correspondiente del texto sin formato, con cada carácter alfabético en el texto sin formato sustituido por el carácter correspondiente en el texto cifrado; Los caracteres no alfabéticos deben imprimirse sin cambios.
# - Su programa debe preservar el uso de mayúsculas y minúsculas: las letras en mayúscula deben permanecer en mayúsculas; las letras minúsculas deben permanecer en minúsculas.
#
# - Después de generar texto cifrado, debe imprimir una nueva línea con el valor de <code>0</code> (el cual implica ejecución exitosa).
# ## Pruebas
# Asegúrese de probar su código para cada uno de los siguientes.
#
# - Ejecute su programa como python sustitucion.py, para cada uno de los ejemplos dados en esta página
# - Otras pruebas se realizarán durante la clase
import string
# +
alfabeto = string.ascii_uppercase
clave = '<KEY>'
clave = clave.upper()
# -
# leemos plaintext
plaintext = input('introduzca palabra a encriptar: ')
# +
ciphertext = ''
for letra in plaintext:
# algoritmo transformacion
index_alfa = alfabeto.find(letra.upper()) # posicion de letra en alfabeto
if index_alfa >= 0:
if letra.isupper():
letra = clave[index_alfa] # transformo letra segun indice encontrado
else:
letra = clave[index_alfa].lower()
# Completando 'ciphertext' : 'a' + 'b'
ciphertext += letra
ciphertext
# -
# ### pruebas
'jrssb, ybwsp'
letra = 'd'
letra
letra.isupper()
# algortimo transformacion
letra = ','
letra.upper()
index_alfa = alfabeto.find(letra.upper())
index_alfa
clave[index_alfa]
letra in alfabeto
alfabeto[3]
import string
alfabeto = string.ascii_uppercase
clave = '<KEY>'
plaintext = input('introduzca palabra a encriptar: ')
# +
ciphertext = ''
for p in plaintext:
print(p)
# -
p.isupper()
vl_ciphert=""
for i in vl_plaint:
if i.isalpha():
if i.islower():
vl_ciphert+= vl_clave[string.ascii_lowercase.index(i)].lower()
else:
vl_ciphert+= vl_clave[string.ascii_uppercase.index(i)]
else:
vl_ciphert+=i
|
Modulo1/Ejercicios/Problema2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# **Chapter 11 – Deep Learning**
# _This notebook contains all the sample code and solutions to the exercises in chapter 11._
# # Setup
# First, let's make sure this notebook works well in both python 2 and 3, import a few common modules, ensure MatplotLib plots figures inline and prepare a function to save the figures:
# +
# To support both python 2 and python 3
from __future__ import division, print_function, unicode_literals
# Common imports
import numpy as np
import os
# to make this notebook's output stable across runs
def reset_graph(seed=42):
tf.reset_default_graph()
tf.set_random_seed(seed)
np.random.seed(seed)
# To plot pretty figures
# %matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
# Where to save the figures
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "deep"
def save_fig(fig_id, tight_layout=True):
path = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID, fig_id + ".png")
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format='png', dpi=300)
# -
# # Vanishing/Exploding Gradients Problem
def logit(z):
return 1 / (1 + np.exp(-z))
# +
z = np.linspace(-5, 5, 200)
plt.plot([-5, 5], [0, 0], 'k-')
plt.plot([-5, 5], [1, 1], 'k--')
plt.plot([0, 0], [-0.2, 1.2], 'k-')
plt.plot([-5, 5], [-3/4, 7/4], 'g--')
plt.plot(z, logit(z), "b-", linewidth=2)
props = dict(facecolor='black', shrink=0.1)
plt.annotate('Saturating', xytext=(3.5, 0.7), xy=(5, 1), arrowprops=props, fontsize=14, ha="center")
plt.annotate('Saturating', xytext=(-3.5, 0.3), xy=(-5, 0), arrowprops=props, fontsize=14, ha="center")
plt.annotate('Linear', xytext=(2, 0.2), xy=(0, 0.5), arrowprops=props, fontsize=14, ha="center")
plt.grid(True)
plt.title("Sigmoid activation function", fontsize=14)
plt.axis([-5, 5, -0.2, 1.2])
save_fig("sigmoid_saturation_plot")
plt.show()
# -
# ## Xavier and He Initialization
# Note: the book uses `tensorflow.contrib.layers.fully_connected()` rather than `tf.layers.dense()` (which did not exist when this chapter was written). It is now preferable to use `tf.layers.dense()`, because anything in the contrib module may change or be deleted without notice. The `dense()` function is almost identical to the `fully_connected()` function. The main differences relevant to this chapter are:
# * several parameters are renamed: `scope` becomes `name`, `activation_fn` becomes `activation` (and similarly the `_fn` suffix is removed from other parameters such as `normalizer_fn`), `weights_initializer` becomes `kernel_initializer`, etc.
# * the default `activation` is now `None` rather than `tf.nn.relu`.
# * it does not support `tensorflow.contrib.framework.arg_scope()` (introduced later in chapter 11).
# * it does not support regularizer params (introduced later in chapter 11).
import tensorflow as tf
# +
reset_graph()
n_inputs = 28 * 28 # MNIST
n_hidden1 = 300
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
# -
he_init = tf.contrib.layers.variance_scaling_initializer()
hidden1 = tf.layers.dense(X, n_hidden1, activation=tf.nn.relu,
kernel_initializer=he_init, name="hidden1")
# ## Nonsaturating Activation Functions
# ### Leaky ReLU
def leaky_relu(z, alpha=0.01):
return np.maximum(alpha*z, z)
# +
plt.plot(z, leaky_relu(z, 0.05), "b-", linewidth=2)
plt.plot([-5, 5], [0, 0], 'k-')
plt.plot([0, 0], [-0.5, 4.2], 'k-')
plt.grid(True)
props = dict(facecolor='black', shrink=0.1)
plt.annotate('Leak', xytext=(-3.5, 0.5), xy=(-5, -0.2), arrowprops=props, fontsize=14, ha="center")
plt.title("Leaky ReLU activation function", fontsize=14)
plt.axis([-5, 5, -0.5, 4.2])
save_fig("leaky_relu_plot")
plt.show()
# -
# Implementing Leaky ReLU in TensorFlow:
# +
reset_graph()
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
# +
def leaky_relu(z, name=None):
return tf.maximum(0.01 * z, z, name=name)
hidden1 = tf.layers.dense(X, n_hidden1, activation=leaky_relu, name="hidden1")
# -
# Let's train a neural network on MNIST using the Leaky ReLU. First let's create the graph:
# +
reset_graph()
n_inputs = 28 * 28 # MNIST
n_hidden1 = 300
n_hidden2 = 100
n_outputs = 10
# -
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int64, shape=(None), name="y")
with tf.name_scope("dnn"):
hidden1 = tf.layers.dense(X, n_hidden1, activation=leaky_relu, name="hidden1")
hidden2 = tf.layers.dense(hidden1, n_hidden2, activation=leaky_relu, name="hidden2")
logits = tf.layers.dense(hidden2, n_outputs, name="outputs")
with tf.name_scope("loss"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
# +
learning_rate = 0.01
with tf.name_scope("train"):
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
training_op = optimizer.minimize(loss)
# -
with tf.name_scope("eval"):
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
init = tf.global_variables_initializer()
saver = tf.train.Saver()
# Let's load the data:
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/")
# +
n_epochs = 40
batch_size = 50
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for iteration in range(mnist.train.num_examples // batch_size):
X_batch, y_batch = mnist.train.next_batch(batch_size)
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
if epoch % 5 == 0:
acc_train = accuracy.eval(feed_dict={X: X_batch, y: y_batch})
acc_test = accuracy.eval(feed_dict={X: mnist.validation.images, y: mnist.validation.labels})
print(epoch, "Batch accuracy:", acc_train, "Validation accuracy:", acc_test)
save_path = saver.save(sess, "./my_model_final.ckpt")
# -
# ### ELU
def elu(z, alpha=1):
return np.where(z < 0, alpha * (np.exp(z) - 1), z)
# +
plt.plot(z, elu(z), "b-", linewidth=2)
plt.plot([-5, 5], [0, 0], 'k-')
plt.plot([-5, 5], [-1, -1], 'k--')
plt.plot([0, 0], [-2.2, 3.2], 'k-')
plt.grid(True)
plt.title(r"ELU activation function ($\alpha=1$)", fontsize=14)
plt.axis([-5, 5, -2.2, 3.2])
save_fig("elu_plot")
plt.show()
# -
# Implementing ELU in TensorFlow is trivial, just specify the activation function when building each layer:
# +
reset_graph()
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
# -
hidden1 = tf.layers.dense(X, n_hidden1, activation=tf.nn.elu, name="hidden1")
# ### SELU
# This activation function was proposed in this [great paper](https://arxiv.org/pdf/1706.02515.pdf) by <NAME>, <NAME> and <NAME>, published in June 2017 (I will definitely add it to the book). It outperforms the other activation functions very significantly for deep neural networks, so you should really try it out.
def selu(z,
scale=1.0507009873554804934193349852946,
alpha=1.6732632423543772848170429916717):
return scale * elu(z, alpha)
# +
plt.plot(z, selu(z), "b-", linewidth=2)
plt.plot([-5, 5], [0, 0], 'k-')
plt.plot([-5, 5], [-1.758, -1.758], 'k--')
plt.plot([0, 0], [-2.2, 3.2], 'k-')
plt.grid(True)
plt.title(r"SELU activation function", fontsize=14)
plt.axis([-5, 5, -2.2, 3.2])
save_fig("selu_plot")
plt.show()
# -
# With this activation function, even a 100 layer deep neural network preserves roughly mean 0 and standard deviation 1 across all layers, avoiding the exploding/vanishing gradients problem:
np.random.seed(42)
Z = np.random.normal(size=(500, 100))
for layer in range(100):
W = np.random.normal(size=(100, 100), scale=np.sqrt(1/100))
Z = selu(np.dot(Z, W))
means = np.mean(Z, axis=1)
stds = np.std(Z, axis=1)
if layer % 10 == 0:
print("Layer {}: {:.2f} < mean < {:.2f}, {:.2f} < std deviation < {:.2f}".format(
layer, means.min(), means.max(), stds.min(), stds.max()))
# Here's a TensorFlow implementation (there will almost certainly be a `tf.nn.selu()` function in future TensorFlow versions):
def selu(z,
scale=1.0507009873554804934193349852946,
alpha=1.6732632423543772848170429916717):
return scale * tf.where(z >= 0.0, z, alpha * tf.nn.elu(z))
# SELUs can also be combined with dropout, check out [this implementation](https://github.com/bioinf-jku/SNNs/blob/master/selu.py) by the Institute of Bioinformatics, J<NAME> University Linz.
# Let's create a neural net for MNIST using the SELU activation function:
# +
reset_graph()
n_inputs = 28 * 28 # MNIST
n_hidden1 = 300
n_hidden2 = 100
n_outputs = 10
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int64, shape=(None), name="y")
with tf.name_scope("dnn"):
hidden1 = tf.layers.dense(X, n_hidden1, activation=selu, name="hidden1")
hidden2 = tf.layers.dense(hidden1, n_hidden2, activation=selu, name="hidden2")
logits = tf.layers.dense(hidden2, n_outputs, name="outputs")
with tf.name_scope("loss"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
learning_rate = 0.01
with tf.name_scope("train"):
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
training_op = optimizer.minimize(loss)
with tf.name_scope("eval"):
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
init = tf.global_variables_initializer()
saver = tf.train.Saver()
n_epochs = 40
batch_size = 50
# -
# Now let's train it. Do not forget to scale the inputs to mean 0 and standard deviation 1:
# +
means = mnist.train.images.mean(axis=0, keepdims=True)
stds = mnist.train.images.std(axis=0, keepdims=True) + 1e-10
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for iteration in range(mnist.train.num_examples // batch_size):
X_batch, y_batch = mnist.train.next_batch(batch_size)
X_batch_scaled = (X_batch - means) / stds
sess.run(training_op, feed_dict={X: X_batch_scaled, y: y_batch})
if epoch % 5 == 0:
acc_train = accuracy.eval(feed_dict={X: X_batch_scaled, y: y_batch})
X_val_scaled = (mnist.validation.images - means) / stds
acc_test = accuracy.eval(feed_dict={X: X_val_scaled, y: mnist.validation.labels})
print(epoch, "Batch accuracy:", acc_train, "Validation accuracy:", acc_test)
save_path = saver.save(sess, "./my_model_final_selu.ckpt")
# -
# # Batch Normalization
# Note: the book uses `tensorflow.contrib.layers.batch_norm()` rather than `tf.layers.batch_normalization()` (which did not exist when this chapter was written). It is now preferable to use `tf.layers.batch_normalization()`, because anything in the contrib module may change or be deleted without notice. Instead of using the `batch_norm()` function as a regularizer parameter to the `fully_connected()` function, we now use `batch_normalization()` and we explicitly create a distinct layer. The parameters are a bit different, in particular:
# * `decay` is renamed to `momentum`,
# * `is_training` is renamed to `training`,
# * `updates_collections` is removed: the update operations needed by batch normalization are added to the `UPDATE_OPS` collection and you need to explicity run these operations during training (see the execution phase below),
# * we don't need to specify `scale=True`, as that is the default.
#
# Also note that in order to run batch norm just _before_ each hidden layer's activation function, we apply the ELU activation function manually, right after the batch norm layer.
#
# Note: since the `tf.layers.dense()` function is incompatible with `tf.contrib.layers.arg_scope()` (which is used in the book), we now use python's `functools.partial()` function instead. It makes it easy to create a `my_dense_layer()` function that just calls `tf.layers.dense()` with the desired parameters automatically set (unless they are overridden when calling `my_dense_layer()`). As you can see, the code remains very similar.
# +
reset_graph()
import tensorflow as tf
n_inputs = 28 * 28
n_hidden1 = 300
n_hidden2 = 100
n_outputs = 10
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
training = tf.placeholder_with_default(False, shape=(), name='training')
hidden1 = tf.layers.dense(X, n_hidden1, name="hidden1")
bn1 = tf.layers.batch_normalization(hidden1, training=training, momentum=0.9)
bn1_act = tf.nn.elu(bn1)
hidden2 = tf.layers.dense(bn1_act, n_hidden2, name="hidden2")
bn2 = tf.layers.batch_normalization(hidden2, training=training, momentum=0.9)
bn2_act = tf.nn.elu(bn2)
logits_before_bn = tf.layers.dense(bn2_act, n_outputs, name="outputs")
logits = tf.layers.batch_normalization(logits_before_bn, training=training,
momentum=0.9)
# +
reset_graph()
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
training = tf.placeholder_with_default(False, shape=(), name='training')
# -
# To avoid repeating the same parameters over and over again, we can use Python's `partial()` function:
# +
from functools import partial
my_batch_norm_layer = partial(tf.layers.batch_normalization,
training=training, momentum=0.9)
hidden1 = tf.layers.dense(X, n_hidden1, name="hidden1")
bn1 = my_batch_norm_layer(hidden1)
bn1_act = tf.nn.elu(bn1)
hidden2 = tf.layers.dense(bn1_act, n_hidden2, name="hidden2")
bn2 = my_batch_norm_layer(hidden2)
bn2_act = tf.nn.elu(bn2)
logits_before_bn = tf.layers.dense(bn2_act, n_outputs, name="outputs")
logits = my_batch_norm_layer(logits_before_bn)
# -
# Let's build a neural net for MNIST, using the ELU activation function and Batch Normalization at each layer:
# +
reset_graph()
batch_norm_momentum = 0.9
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int64, shape=(None), name="y")
training = tf.placeholder_with_default(False, shape=(), name='training')
with tf.name_scope("dnn"):
he_init = tf.contrib.layers.variance_scaling_initializer()
my_batch_norm_layer = partial(
tf.layers.batch_normalization,
training=training,
momentum=batch_norm_momentum)
my_dense_layer = partial(
tf.layers.dense,
kernel_initializer=he_init)
hidden1 = my_dense_layer(X, n_hidden1, name="hidden1")
bn1 = tf.nn.elu(my_batch_norm_layer(hidden1))
hidden2 = my_dense_layer(bn1, n_hidden2, name="hidden2")
bn2 = tf.nn.elu(my_batch_norm_layer(hidden2))
logits_before_bn = my_dense_layer(bn2, n_outputs, name="outputs")
logits = my_batch_norm_layer(logits_before_bn)
with tf.name_scope("loss"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
with tf.name_scope("train"):
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
training_op = optimizer.minimize(loss)
with tf.name_scope("eval"):
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
init = tf.global_variables_initializer()
saver = tf.train.Saver()
# -
# Note: since we are using `tf.layers.batch_normalization()` rather than `tf.contrib.layers.batch_norm()` (as in the book), we need to explicitly run the extra update operations needed by batch normalization (`sess.run([training_op, extra_update_ops],...`).
n_epochs = 20
batch_size = 200
# +
extra_update_ops = tf.get_collection(tf.GraphKeys.UPDATE_OPS)
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for iteration in range(mnist.train.num_examples // batch_size):
X_batch, y_batch = mnist.train.next_batch(batch_size)
sess.run([training_op, extra_update_ops],
feed_dict={training: True, X: X_batch, y: y_batch})
accuracy_val = accuracy.eval(feed_dict={X: mnist.test.images,
y: mnist.test.labels})
print(epoch, "Test accuracy:", accuracy_val)
save_path = saver.save(sess, "./my_model_final.ckpt")
# -
# What!? That's not a great accuracy for MNIST. Of course, if you train for longer it will get much better accuracy, but with such a shallow network, Batch Norm and ELU are unlikely to have very positive impact: they shine mostly for much deeper nets.
# Note that you could also make the training operation depend on the update operations:
#
# ```python
# with tf.name_scope("train"):
# optimizer = tf.train.GradientDescentOptimizer(learning_rate)
# extra_update_ops = tf.get_collection(tf.GraphKeys.UPDATE_OPS)
# with tf.control_dependencies(extra_update_ops):
# training_op = optimizer.minimize(loss)
# ```
#
# This way, you would just have to evaluate the `training_op` during training, TensorFlow would automatically run the update operations as well:
#
# ```python
# sess.run(training_op, feed_dict={training: True, X: X_batch, y: y_batch})
# ```
# One more thing: notice that the list of trainable variables is shorter than the list of all global variables. This is because the moving averages are non-trainable variables. If you want to reuse a pretrained neural network (see below), you must not forget these non-trainable variables.
[v.name for v in tf.trainable_variables()]
[v.name for v in tf.global_variables()]
# ## Gradient Clipping
# Let's create a simple neural net for MNIST and add gradient clipping. The first part is the same as earlier (except we added a few more layers to demonstrate reusing pretrained models, see below):
# +
reset_graph()
n_inputs = 28 * 28 # MNIST
n_hidden1 = 300
n_hidden2 = 50
n_hidden3 = 50
n_hidden4 = 50
n_hidden5 = 50
n_outputs = 10
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int64, shape=(None), name="y")
with tf.name_scope("dnn"):
hidden1 = tf.layers.dense(X, n_hidden1, activation=tf.nn.relu, name="hidden1")
hidden2 = tf.layers.dense(hidden1, n_hidden2, activation=tf.nn.relu, name="hidden2")
hidden3 = tf.layers.dense(hidden2, n_hidden3, activation=tf.nn.relu, name="hidden3")
hidden4 = tf.layers.dense(hidden3, n_hidden4, activation=tf.nn.relu, name="hidden4")
hidden5 = tf.layers.dense(hidden4, n_hidden5, activation=tf.nn.relu, name="hidden5")
logits = tf.layers.dense(hidden5, n_outputs, name="outputs")
with tf.name_scope("loss"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
# -
learning_rate = 0.01
# Now we apply gradient clipping. For this, we need to get the gradients, use the `clip_by_value()` function to clip them, then apply them:
# +
threshold = 1.0
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
grads_and_vars = optimizer.compute_gradients(loss)
capped_gvs = [(tf.clip_by_value(grad, -threshold, threshold), var)
for grad, var in grads_and_vars]
training_op = optimizer.apply_gradients(capped_gvs)
# -
# The rest is the same as usual:
with tf.name_scope("eval"):
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32), name="accuracy")
init = tf.global_variables_initializer()
saver = tf.train.Saver()
n_epochs = 20
batch_size = 200
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for iteration in range(mnist.train.num_examples // batch_size):
X_batch, y_batch = mnist.train.next_batch(batch_size)
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
accuracy_val = accuracy.eval(feed_dict={X: mnist.test.images,
y: mnist.test.labels})
print(epoch, "Test accuracy:", accuracy_val)
save_path = saver.save(sess, "./my_model_final.ckpt")
# ## Reusing Pretrained Layers
# ## Reusing a TensorFlow Model
# First you need to load the graph's structure. The `import_meta_graph()` function does just that, loading the graph's operations into the default graph, and returning a `Saver` that you can then use to restore the model's state. Note that by default, a `Saver` saves the structure of the graph into a `.meta` file, so that's the file you should load:
reset_graph()
saver = tf.train.import_meta_graph("./my_model_final.ckpt.meta")
# Next you need to get a handle on all the operations you will need for training. If you don't know the graph's structure, you can list all the operations:
for op in tf.get_default_graph().get_operations():
print(op.name)
# Oops, that's a lot of operations! It's much easier to use TensorBoard to visualize the graph. The following hack will allow you to visualize the graph within Jupyter (if it does not work with your browser, you will need to use a `FileWriter` to save the graph and then visualize it in TensorBoard):
# +
from IPython.display import clear_output, Image, display, HTML
def strip_consts(graph_def, max_const_size=32):
"""Strip large constant values from graph_def."""
strip_def = tf.GraphDef()
for n0 in graph_def.node:
n = strip_def.node.add()
n.MergeFrom(n0)
if n.op == 'Const':
tensor = n.attr['value'].tensor
size = len(tensor.tensor_content)
if size > max_const_size:
tensor.tensor_content = b"<stripped %d bytes>"%size
return strip_def
def show_graph(graph_def, max_const_size=32):
"""Visualize TensorFlow graph."""
if hasattr(graph_def, 'as_graph_def'):
graph_def = graph_def.as_graph_def()
strip_def = strip_consts(graph_def, max_const_size=max_const_size)
code = """
<script>
function load() {{
document.getElementById("{id}").pbtxt = {data};
}}
</script>
<link rel="import" href="https://tensorboard.appspot.com/tf-graph-basic.build.html" onload=load()>
<div style="height:600px">
<tf-graph-basic id="{id}"></tf-graph-basic>
</div>
""".format(data=repr(str(strip_def)), id='graph'+str(np.random.rand()))
iframe = """
<iframe seamless style="width:1200px;height:620px;border:0" srcdoc="{}"></iframe>
""".format(code.replace('"', '"'))
display(HTML(iframe))
# -
show_graph(tf.get_default_graph())
# Once you know which operations you need, you can get a handle on them using the graph's `get_operation_by_name()` or `get_tensor_by_name()` methods:
# +
X = tf.get_default_graph().get_tensor_by_name("X:0")
y = tf.get_default_graph().get_tensor_by_name("y:0")
accuracy = tf.get_default_graph().get_tensor_by_name("eval/accuracy:0")
training_op = tf.get_default_graph().get_operation_by_name("GradientDescent")
# -
# If you are the author of the original model, you could make things easier for people who will reuse your model by giving operations very clear names and documenting them. Another approach is to create a collection containing all the important operations that people will want to get a handle on:
for op in (X, y, accuracy, training_op):
tf.add_to_collection("my_important_ops", op)
# This way people who reuse your model will be able to simply write:
X, y, accuracy, training_op = tf.get_collection("my_important_ops")
# Now you can start a session, restore the model's state and continue training on your data:
with tf.Session() as sess:
saver.restore(sess, "./my_model_final.ckpt")
# continue training the model...
# Actually, let's test this for real!
with tf.Session() as sess:
saver.restore(sess, "./my_model_final.ckpt")
for epoch in range(n_epochs):
for iteration in range(mnist.train.num_examples // batch_size):
X_batch, y_batch = mnist.train.next_batch(batch_size)
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
accuracy_val = accuracy.eval(feed_dict={X: mnist.test.images,
y: mnist.test.labels})
print(epoch, "Test accuracy:", accuracy_val)
save_path = saver.save(sess, "./my_new_model_final.ckpt")
# Alternatively, if you have access to the Python code that built the original graph, you can use it instead of `import_meta_graph()`:
# +
reset_graph()
n_inputs = 28 * 28 # MNIST
n_hidden1 = 300
n_hidden2 = 50
n_hidden3 = 50
n_hidden4 = 50
n_outputs = 10
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int64, shape=(None), name="y")
with tf.name_scope("dnn"):
hidden1 = tf.layers.dense(X, n_hidden1, activation=tf.nn.relu, name="hidden1")
hidden2 = tf.layers.dense(hidden1, n_hidden2, activation=tf.nn.relu, name="hidden2")
hidden3 = tf.layers.dense(hidden2, n_hidden3, activation=tf.nn.relu, name="hidden3")
hidden4 = tf.layers.dense(hidden3, n_hidden4, activation=tf.nn.relu, name="hidden4")
hidden5 = tf.layers.dense(hidden4, n_hidden5, activation=tf.nn.relu, name="hidden5")
logits = tf.layers.dense(hidden5, n_outputs, name="outputs")
with tf.name_scope("loss"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
with tf.name_scope("eval"):
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32), name="accuracy")
learning_rate = 0.01
threshold = 1.0
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
grads_and_vars = optimizer.compute_gradients(loss)
capped_gvs = [(tf.clip_by_value(grad, -threshold, threshold), var)
for grad, var in grads_and_vars]
training_op = optimizer.apply_gradients(capped_gvs)
init = tf.global_variables_initializer()
saver = tf.train.Saver()
# -
# And continue training:
with tf.Session() as sess:
saver.restore(sess, "./my_model_final.ckpt")
for epoch in range(n_epochs):
for iteration in range(mnist.train.num_examples // batch_size):
X_batch, y_batch = mnist.train.next_batch(batch_size)
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
accuracy_val = accuracy.eval(feed_dict={X: mnist.test.images,
y: mnist.test.labels})
print(epoch, "Test accuracy:", accuracy_val)
save_path = saver.save(sess, "./my_new_model_final.ckpt")
# In general you will want to reuse only the lower layers. If you are using `import_meta_graph()` it will load the whole graph, but you can simply ignore the parts you do not need. In this example, we add a new 4th hidden layer on top of the pretrained 3rd layer (ignoring the old 4th hidden layer). We also build a new output layer, the loss for this new output, and a new optimizer to minimize it. We also need another saver to save the whole graph (containing both the entire old graph plus the new operations), and an initialization operation to initialize all the new variables:
# +
reset_graph()
n_hidden4 = 20 # new layer
n_outputs = 10 # new layer
saver = tf.train.import_meta_graph("./my_model_final.ckpt.meta")
X = tf.get_default_graph().get_tensor_by_name("X:0")
y = tf.get_default_graph().get_tensor_by_name("y:0")
hidden3 = tf.get_default_graph().get_tensor_by_name("dnn/hidden4/Relu:0")
new_hidden4 = tf.layers.dense(hidden3, n_hidden4, activation=tf.nn.relu, name="new_hidden4")
new_logits = tf.layers.dense(new_hidden4, n_outputs, name="new_outputs")
with tf.name_scope("new_loss"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=new_logits)
loss = tf.reduce_mean(xentropy, name="loss")
with tf.name_scope("new_eval"):
correct = tf.nn.in_top_k(new_logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32), name="accuracy")
with tf.name_scope("new_train"):
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
training_op = optimizer.minimize(loss)
init = tf.global_variables_initializer()
new_saver = tf.train.Saver()
# -
# And we can train this new model:
with tf.Session() as sess:
init.run()
saver.restore(sess, "./my_model_final.ckpt")
for epoch in range(n_epochs):
for iteration in range(mnist.train.num_examples // batch_size):
X_batch, y_batch = mnist.train.next_batch(batch_size)
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
accuracy_val = accuracy.eval(feed_dict={X: mnist.test.images,
y: mnist.test.labels})
print(epoch, "Test accuracy:", accuracy_val)
save_path = new_saver.save(sess, "./my_new_model_final.ckpt")
# If you have access to the Python code that built the original graph, you can just reuse the parts you need and drop the rest:
# +
reset_graph()
n_inputs = 28 * 28 # MNIST
n_hidden1 = 300 # reused
n_hidden2 = 50 # reused
n_hidden3 = 50 # reused
n_hidden4 = 20 # new!
n_outputs = 10 # new!
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int64, shape=(None), name="y")
with tf.name_scope("dnn"):
hidden1 = tf.layers.dense(X, n_hidden1, activation=tf.nn.relu, name="hidden1") # reused
hidden2 = tf.layers.dense(hidden1, n_hidden2, activation=tf.nn.relu, name="hidden2") # reused
hidden3 = tf.layers.dense(hidden2, n_hidden3, activation=tf.nn.relu, name="hidden3") # reused
hidden4 = tf.layers.dense(hidden3, n_hidden4, activation=tf.nn.relu, name="hidden4") # new!
logits = tf.layers.dense(hidden4, n_outputs, name="outputs") # new!
with tf.name_scope("loss"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
with tf.name_scope("eval"):
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32), name="accuracy")
with tf.name_scope("train"):
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
training_op = optimizer.minimize(loss)
# -
# However, you must create one `Saver` to restore the pretrained model (giving it the list of variables to restore, or else it will complain that the graphs don't match), and another `Saver` to save the new model, once it is trained:
# +
reuse_vars = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES,
scope="hidden[123]") # regular expression
reuse_vars_dict = dict([(var.op.name, var) for var in reuse_vars])
restore_saver = tf.train.Saver(reuse_vars_dict) # to restore layers 1-3
init = tf.global_variables_initializer()
saver = tf.train.Saver()
with tf.Session() as sess:
init.run()
restore_saver.restore(sess, "./my_model_final.ckpt")
for epoch in range(n_epochs): # not shown in the book
for iteration in range(mnist.train.num_examples // batch_size): # not shown
X_batch, y_batch = mnist.train.next_batch(batch_size) # not shown
sess.run(training_op, feed_dict={X: X_batch, y: y_batch}) # not shown
accuracy_val = accuracy.eval(feed_dict={X: mnist.test.images, # not shown
y: mnist.test.labels}) # not shown
print(epoch, "Test accuracy:", accuracy_val) # not shown
save_path = saver.save(sess, "./my_new_model_final.ckpt")
# -
# ## Reusing Models from Other Frameworks
# In this example, for each variable we want to reuse, we find its initializer's assignment operation, and we get its second input, which corresponds to the initialization value. When we run the initializer, we replace the initialization values with the ones we want, using a `feed_dict`:
# +
reset_graph()
n_inputs = 2
n_hidden1 = 3
# +
original_w = [[1., 2., 3.], [4., 5., 6.]] # Load the weights from the other framework
original_b = [7., 8., 9.] # Load the biases from the other framework
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
hidden1 = tf.layers.dense(X, n_hidden1, activation=tf.nn.relu, name="hidden1")
# [...] Build the rest of the model
# Get a handle on the assignment nodes for the hidden1 variables
graph = tf.get_default_graph()
assign_kernel = graph.get_operation_by_name("hidden1/kernel/Assign")
assign_bias = graph.get_operation_by_name("hidden1/bias/Assign")
init_kernel = assign_kernel.inputs[1]
init_bias = assign_bias.inputs[1]
init = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init, feed_dict={init_kernel: original_w, init_bias: original_b})
# [...] Train the model on your new task
print(hidden1.eval(feed_dict={X: [[10.0, 11.0]]})) # not shown in the book
# -
# Note: the weights variable created by the `tf.layers.dense()` function is called `"kernel"` (instead of `"weights"` when using the `tf.contrib.layers.fully_connected()`, as in the book), and the biases variable is called `bias` instead of `biases`.
# Another approach (initially used in the book) would be to create dedicated assignment nodes and dedicated placeholders. This is more verbose and less efficient, but you may find this more explicit:
# +
reset_graph()
n_inputs = 2
n_hidden1 = 3
original_w = [[1., 2., 3.], [4., 5., 6.]] # Load the weights from the other framework
original_b = [7., 8., 9.] # Load the biases from the other framework
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
hidden1 = tf.layers.dense(X, n_hidden1, activation=tf.nn.relu, name="hidden1")
# [...] Build the rest of the model
# Get a handle on the variables of layer hidden1
with tf.variable_scope("", default_name="", reuse=True): # root scope
hidden1_weights = tf.get_variable("hidden1/kernel")
hidden1_biases = tf.get_variable("hidden1/bias")
# Create dedicated placeholders and assignment nodes
original_weights = tf.placeholder(tf.float32, shape=(n_inputs, n_hidden1))
original_biases = tf.placeholder(tf.float32, shape=n_hidden1)
assign_hidden1_weights = tf.assign(hidden1_weights, original_weights)
assign_hidden1_biases = tf.assign(hidden1_biases, original_biases)
init = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
sess.run(assign_hidden1_weights, feed_dict={original_weights: original_w})
sess.run(assign_hidden1_biases, feed_dict={original_biases: original_b})
# [...] Train the model on your new task
print(hidden1.eval(feed_dict={X: [[10.0, 11.0]]}))
# -
# Note that we could also get a handle on the variables using `get_collection()` and specifying the `scope`:
tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope="hidden1")
# Or we could use the graph's `get_tensor_by_name()` method:
tf.get_default_graph().get_tensor_by_name("hidden1/kernel:0")
tf.get_default_graph().get_tensor_by_name("hidden1/bias:0")
# ### Freezing the Lower Layers
# +
reset_graph()
n_inputs = 28 * 28 # MNIST
n_hidden1 = 300 # reused
n_hidden2 = 50 # reused
n_hidden3 = 50 # reused
n_hidden4 = 20 # new!
n_outputs = 10 # new!
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int64, shape=(None), name="y")
with tf.name_scope("dnn"):
hidden1 = tf.layers.dense(X, n_hidden1, activation=tf.nn.relu, name="hidden1") # reused
hidden2 = tf.layers.dense(hidden1, n_hidden2, activation=tf.nn.relu, name="hidden2") # reused
hidden3 = tf.layers.dense(hidden2, n_hidden3, activation=tf.nn.relu, name="hidden3") # reused
hidden4 = tf.layers.dense(hidden3, n_hidden4, activation=tf.nn.relu, name="hidden4") # new!
logits = tf.layers.dense(hidden4, n_outputs, name="outputs") # new!
with tf.name_scope("loss"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
with tf.name_scope("eval"):
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32), name="accuracy")
# -
with tf.name_scope("train"): # not shown in the book
optimizer = tf.train.GradientDescentOptimizer(learning_rate) # not shown
train_vars = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES,
scope="hidden[34]|outputs")
training_op = optimizer.minimize(loss, var_list=train_vars)
init = tf.global_variables_initializer()
new_saver = tf.train.Saver()
# +
reuse_vars = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES,
scope="hidden[123]") # regular expression
reuse_vars_dict = dict([(var.op.name, var) for var in reuse_vars])
restore_saver = tf.train.Saver(reuse_vars_dict) # to restore layers 1-3
init = tf.global_variables_initializer()
saver = tf.train.Saver()
with tf.Session() as sess:
init.run()
restore_saver.restore(sess, "./my_model_final.ckpt")
for epoch in range(n_epochs):
for iteration in range(mnist.train.num_examples // batch_size):
X_batch, y_batch = mnist.train.next_batch(batch_size)
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
accuracy_val = accuracy.eval(feed_dict={X: mnist.test.images,
y: mnist.test.labels})
print(epoch, "Test accuracy:", accuracy_val)
save_path = saver.save(sess, "./my_new_model_final.ckpt")
# +
reset_graph()
n_inputs = 28 * 28 # MNIST
n_hidden1 = 300 # reused
n_hidden2 = 50 # reused
n_hidden3 = 50 # reused
n_hidden4 = 20 # new!
n_outputs = 10 # new!
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int64, shape=(None), name="y")
# -
with tf.name_scope("dnn"):
hidden1 = tf.layers.dense(X, n_hidden1, activation=tf.nn.relu,
name="hidden1") # reused frozen
hidden2 = tf.layers.dense(hidden1, n_hidden2, activation=tf.nn.relu,
name="hidden2") # reused frozen
hidden2_stop = tf.stop_gradient(hidden2)
hidden3 = tf.layers.dense(hidden2_stop, n_hidden3, activation=tf.nn.relu,
name="hidden3") # reused, not frozen
hidden4 = tf.layers.dense(hidden3, n_hidden4, activation=tf.nn.relu,
name="hidden4") # new!
logits = tf.layers.dense(hidden4, n_outputs, name="outputs") # new!
# +
with tf.name_scope("loss"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
with tf.name_scope("eval"):
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32), name="accuracy")
with tf.name_scope("train"):
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
training_op = optimizer.minimize(loss)
# -
# The training code is exactly the same as earlier:
# +
reuse_vars = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES,
scope="hidden[123]") # regular expression
reuse_vars_dict = dict([(var.op.name, var) for var in reuse_vars])
restore_saver = tf.train.Saver(reuse_vars_dict) # to restore layers 1-3
init = tf.global_variables_initializer()
saver = tf.train.Saver()
with tf.Session() as sess:
init.run()
restore_saver.restore(sess, "./my_model_final.ckpt")
for epoch in range(n_epochs):
for iteration in range(mnist.train.num_examples // batch_size):
X_batch, y_batch = mnist.train.next_batch(batch_size)
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
accuracy_val = accuracy.eval(feed_dict={X: mnist.test.images,
y: mnist.test.labels})
print(epoch, "Test accuracy:", accuracy_val)
save_path = saver.save(sess, "./my_new_model_final.ckpt")
# -
# ### Caching the Frozen Layers
# +
reset_graph()
n_inputs = 28 * 28 # MNIST
n_hidden1 = 300 # reused
n_hidden2 = 50 # reused
n_hidden3 = 50 # reused
n_hidden4 = 20 # new!
n_outputs = 10 # new!
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int64, shape=(None), name="y")
with tf.name_scope("dnn"):
hidden1 = tf.layers.dense(X, n_hidden1, activation=tf.nn.relu,
name="hidden1") # reused frozen
hidden2 = tf.layers.dense(hidden1, n_hidden2, activation=tf.nn.relu,
name="hidden2") # reused frozen & cached
hidden2_stop = tf.stop_gradient(hidden2)
hidden3 = tf.layers.dense(hidden2_stop, n_hidden3, activation=tf.nn.relu,
name="hidden3") # reused, not frozen
hidden4 = tf.layers.dense(hidden3, n_hidden4, activation=tf.nn.relu,
name="hidden4") # new!
logits = tf.layers.dense(hidden4, n_outputs, name="outputs") # new!
with tf.name_scope("loss"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
with tf.name_scope("eval"):
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32), name="accuracy")
with tf.name_scope("train"):
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
training_op = optimizer.minimize(loss)
# +
reuse_vars = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES,
scope="hidden[123]") # regular expression
reuse_vars_dict = dict([(var.op.name, var) for var in reuse_vars])
restore_saver = tf.train.Saver(reuse_vars_dict) # to restore layers 1-3
init = tf.global_variables_initializer()
saver = tf.train.Saver()
# +
import numpy as np
n_batches = mnist.train.num_examples // batch_size
with tf.Session() as sess:
init.run()
restore_saver.restore(sess, "./my_model_final.ckpt")
h2_cache = sess.run(hidden2, feed_dict={X: mnist.train.images})
h2_cache_test = sess.run(hidden2, feed_dict={X: mnist.test.images}) # not shown in the book
for epoch in range(n_epochs):
shuffled_idx = np.random.permutation(mnist.train.num_examples)
hidden2_batches = np.array_split(h2_cache[shuffled_idx], n_batches)
y_batches = np.array_split(mnist.train.labels[shuffled_idx], n_batches)
for hidden2_batch, y_batch in zip(hidden2_batches, y_batches):
sess.run(training_op, feed_dict={hidden2:hidden2_batch, y:y_batch})
accuracy_val = accuracy.eval(feed_dict={hidden2: h2_cache_test, # not shown
y: mnist.test.labels}) # not shown
print(epoch, "Test accuracy:", accuracy_val) # not shown
save_path = saver.save(sess, "./my_new_model_final.ckpt")
# -
# # Faster Optimizers
# ## Momentum optimization
optimizer = tf.train.MomentumOptimizer(learning_rate=learning_rate,
momentum=0.9)
# ## Nesterov Accelerated Gradient
optimizer = tf.train.MomentumOptimizer(learning_rate=learning_rate,
momentum=0.9, use_nesterov=True)
# ## AdaGrad
optimizer = tf.train.AdagradOptimizer(learning_rate=learning_rate)
# ## RMSProp
optimizer = tf.train.RMSPropOptimizer(learning_rate=learning_rate,
momentum=0.9, decay=0.9, epsilon=1e-10)
# ## Adam Optimization
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
# ## Learning Rate Scheduling
# +
reset_graph()
n_inputs = 28 * 28 # MNIST
n_hidden1 = 300
n_hidden2 = 50
n_outputs = 10
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int64, shape=(None), name="y")
with tf.name_scope("dnn"):
hidden1 = tf.layers.dense(X, n_hidden1, activation=tf.nn.relu, name="hidden1")
hidden2 = tf.layers.dense(hidden1, n_hidden2, activation=tf.nn.relu, name="hidden2")
logits = tf.layers.dense(hidden2, n_outputs, name="outputs")
with tf.name_scope("loss"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
with tf.name_scope("eval"):
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32), name="accuracy")
# -
with tf.name_scope("train"): # not shown in the book
initial_learning_rate = 0.1
decay_steps = 10000
decay_rate = 1/10
global_step = tf.Variable(0, trainable=False, name="global_step")
learning_rate = tf.train.exponential_decay(initial_learning_rate, global_step,
decay_steps, decay_rate)
optimizer = tf.train.MomentumOptimizer(learning_rate, momentum=0.9)
training_op = optimizer.minimize(loss, global_step=global_step)
init = tf.global_variables_initializer()
saver = tf.train.Saver()
# +
n_epochs = 5
batch_size = 50
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for iteration in range(mnist.train.num_examples // batch_size):
X_batch, y_batch = mnist.train.next_batch(batch_size)
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
accuracy_val = accuracy.eval(feed_dict={X: mnist.test.images,
y: mnist.test.labels})
print(epoch, "Test accuracy:", accuracy_val)
save_path = saver.save(sess, "./my_model_final.ckpt")
# -
# # Avoiding Overfitting Through Regularization
# ## $\ell_1$ and $\ell_2$ regularization
# Let's implement $\ell_1$ regularization manually. First, we create the model, as usual (with just one hidden layer this time, for simplicity):
# +
reset_graph()
n_inputs = 28 * 28 # MNIST
n_hidden1 = 300
n_outputs = 10
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int64, shape=(None), name="y")
with tf.name_scope("dnn"):
hidden1 = tf.layers.dense(X, n_hidden1, activation=tf.nn.relu, name="hidden1")
logits = tf.layers.dense(hidden1, n_outputs, name="outputs")
# -
# Next, we get a handle on the layer weights, and we compute the total loss, which is equal to the sum of the usual cross entropy loss and the $\ell_1$ loss (i.e., the absolute values of the weights):
# +
W1 = tf.get_default_graph().get_tensor_by_name("hidden1/kernel:0")
W2 = tf.get_default_graph().get_tensor_by_name("outputs/kernel:0")
scale = 0.001 # l1 regularization hyperparameter
with tf.name_scope("loss"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y,
logits=logits)
base_loss = tf.reduce_mean(xentropy, name="avg_xentropy")
reg_losses = tf.reduce_sum(tf.abs(W1)) + tf.reduce_sum(tf.abs(W2))
loss = tf.add(base_loss, scale * reg_losses, name="loss")
# -
# The rest is just as usual:
# +
with tf.name_scope("eval"):
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32), name="accuracy")
learning_rate = 0.01
with tf.name_scope("train"):
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
training_op = optimizer.minimize(loss)
init = tf.global_variables_initializer()
saver = tf.train.Saver()
# +
n_epochs = 20
batch_size = 200
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for iteration in range(mnist.train.num_examples // batch_size):
X_batch, y_batch = mnist.train.next_batch(batch_size)
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
accuracy_val = accuracy.eval(feed_dict={X: mnist.test.images,
y: mnist.test.labels})
print(epoch, "Test accuracy:", accuracy_val)
save_path = saver.save(sess, "./my_model_final.ckpt")
# -
# Alternatively, we can pass a regularization function to the `tf.layers.dense()` function, which will use it to create operations that will compute the regularization loss, and it adds these operations to the collection of regularization losses. The beginning is the same as above:
# +
reset_graph()
n_inputs = 28 * 28 # MNIST
n_hidden1 = 300
n_hidden2 = 50
n_outputs = 10
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int64, shape=(None), name="y")
# -
# Next, we will use Python's `partial()` function to avoid repeating the same arguments over and over again. Note that we set the `kernel_regularizer` argument:
scale = 0.001
# +
my_dense_layer = partial(
tf.layers.dense, activation=tf.nn.relu,
kernel_regularizer=tf.contrib.layers.l1_regularizer(scale))
with tf.name_scope("dnn"):
hidden1 = my_dense_layer(X, n_hidden1, name="hidden1")
hidden2 = my_dense_layer(hidden1, n_hidden2, name="hidden2")
logits = my_dense_layer(hidden2, n_outputs, activation=None,
name="outputs")
# -
# Next we must add the regularization losses to the base loss:
with tf.name_scope("loss"): # not shown in the book
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits( # not shown
labels=y, logits=logits) # not shown
base_loss = tf.reduce_mean(xentropy, name="avg_xentropy") # not shown
reg_losses = tf.get_collection(tf.GraphKeys.REGULARIZATION_LOSSES)
loss = tf.add_n([base_loss] + reg_losses, name="loss")
# And the rest is the same as usual:
# +
with tf.name_scope("eval"):
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32), name="accuracy")
learning_rate = 0.01
with tf.name_scope("train"):
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
training_op = optimizer.minimize(loss)
init = tf.global_variables_initializer()
saver = tf.train.Saver()
# +
n_epochs = 20
batch_size = 200
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for iteration in range(mnist.train.num_examples // batch_size):
X_batch, y_batch = mnist.train.next_batch(batch_size)
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
accuracy_val = accuracy.eval(feed_dict={X: mnist.test.images,
y: mnist.test.labels})
print(epoch, "Test accuracy:", accuracy_val)
save_path = saver.save(sess, "./my_model_final.ckpt")
# -
# ## Dropout
# Note: the book uses `tf.contrib.layers.dropout()` rather than `tf.layers.dropout()` (which did not exist when this chapter was written). It is now preferable to use `tf.layers.dropout()`, because anything in the contrib module may change or be deleted without notice. The `tf.layers.dropout()` function is almost identical to the `tf.contrib.layers.dropout()` function, except for a few minor differences. Most importantly:
# * you must specify the dropout rate (`rate`) rather than the keep probability (`keep_prob`), where `rate` is simply equal to `1 - keep_prob`,
# * the `is_training` parameter is renamed to `training`.
# +
reset_graph()
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int64, shape=(None), name="y")
# +
training = tf.placeholder_with_default(False, shape=(), name='training')
dropout_rate = 0.5 # == 1 - keep_prob
X_drop = tf.layers.dropout(X, dropout_rate, training=training)
with tf.name_scope("dnn"):
hidden1 = tf.layers.dense(X_drop, n_hidden1, activation=tf.nn.relu,
name="hidden1")
hidden1_drop = tf.layers.dropout(hidden1, dropout_rate, training=training)
hidden2 = tf.layers.dense(hidden1_drop, n_hidden2, activation=tf.nn.relu,
name="hidden2")
hidden2_drop = tf.layers.dropout(hidden2, dropout_rate, training=training)
logits = tf.layers.dense(hidden2_drop, n_outputs, name="outputs")
# +
with tf.name_scope("loss"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
with tf.name_scope("train"):
optimizer = tf.train.MomentumOptimizer(learning_rate, momentum=0.9)
training_op = optimizer.minimize(loss)
with tf.name_scope("eval"):
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
init = tf.global_variables_initializer()
saver = tf.train.Saver()
# +
n_epochs = 20
batch_size = 50
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for iteration in range(mnist.train.num_examples // batch_size):
X_batch, y_batch = mnist.train.next_batch(batch_size)
sess.run(training_op, feed_dict={training: True, X: X_batch, y: y_batch})
acc_test = accuracy.eval(feed_dict={X: mnist.test.images, y: mnist.test.labels})
print(epoch, "Test accuracy:", acc_test)
save_path = saver.save(sess, "./my_model_final.ckpt")
# -
# ## Max norm
# Let's go back to a plain and simple neural net for MNIST with just 2 hidden layers:
# +
reset_graph()
n_inputs = 28 * 28
n_hidden1 = 300
n_hidden2 = 50
n_outputs = 10
learning_rate = 0.01
momentum = 0.9
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int64, shape=(None), name="y")
with tf.name_scope("dnn"):
hidden1 = tf.layers.dense(X, n_hidden1, activation=tf.nn.relu, name="hidden1")
hidden2 = tf.layers.dense(hidden1, n_hidden2, activation=tf.nn.relu, name="hidden2")
logits = tf.layers.dense(hidden2, n_outputs, name="outputs")
with tf.name_scope("loss"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
with tf.name_scope("train"):
optimizer = tf.train.MomentumOptimizer(learning_rate, momentum)
training_op = optimizer.minimize(loss)
with tf.name_scope("eval"):
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
# -
# Next, let's get a handle on the first hidden layer's weight and create an operation that will compute the clipped weights using the `clip_by_norm()` function. Then we create an assignment operation to assign the clipped weights to the weights variable:
threshold = 1.0
weights = tf.get_default_graph().get_tensor_by_name("hidden1/kernel:0")
clipped_weights = tf.clip_by_norm(weights, clip_norm=threshold, axes=1)
clip_weights = tf.assign(weights, clipped_weights)
# We can do this as well for the second hidden layer:
weights2 = tf.get_default_graph().get_tensor_by_name("hidden2/kernel:0")
clipped_weights2 = tf.clip_by_norm(weights2, clip_norm=threshold, axes=1)
clip_weights2 = tf.assign(weights2, clipped_weights2)
# Let's add an initializer and a saver:
init = tf.global_variables_initializer()
saver = tf.train.Saver()
# And now we can train the model. It's pretty much as usual, except that right after running the `training_op`, we run the `clip_weights` and `clip_weights2` operations:
n_epochs = 20
batch_size = 50
with tf.Session() as sess: # not shown in the book
init.run() # not shown
for epoch in range(n_epochs): # not shown
for iteration in range(mnist.train.num_examples // batch_size): # not shown
X_batch, y_batch = mnist.train.next_batch(batch_size) # not shown
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
clip_weights.eval()
clip_weights2.eval() # not shown
acc_test = accuracy.eval(feed_dict={X: mnist.test.images, # not shown
y: mnist.test.labels}) # not shown
print(epoch, "Test accuracy:", acc_test) # not shown
save_path = saver.save(sess, "./my_model_final.ckpt") # not shown
# The implementation above is straightforward and it works fine, but it is a bit messy. A better approach is to define a `max_norm_regularizer()` function:
def max_norm_regularizer(threshold, axes=1, name="max_norm",
collection="max_norm"):
def max_norm(weights):
clipped = tf.clip_by_norm(weights, clip_norm=threshold, axes=axes)
clip_weights = tf.assign(weights, clipped, name=name)
tf.add_to_collection(collection, clip_weights)
return None # there is no regularization loss term
return max_norm
# Then you can call this function to get a max norm regularizer (with the threshold you want). When you create a hidden layer, you can pass this regularizer to the `kernel_regularizer` argument:
# +
reset_graph()
n_inputs = 28 * 28
n_hidden1 = 300
n_hidden2 = 50
n_outputs = 10
learning_rate = 0.01
momentum = 0.9
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int64, shape=(None), name="y")
# +
max_norm_reg = max_norm_regularizer(threshold=1.0)
with tf.name_scope("dnn"):
hidden1 = tf.layers.dense(X, n_hidden1, activation=tf.nn.relu,
kernel_regularizer=max_norm_reg, name="hidden1")
hidden2 = tf.layers.dense(hidden1, n_hidden2, activation=tf.nn.relu,
kernel_regularizer=max_norm_reg, name="hidden2")
logits = tf.layers.dense(hidden2, n_outputs, name="outputs")
# +
with tf.name_scope("loss"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
with tf.name_scope("train"):
optimizer = tf.train.MomentumOptimizer(learning_rate, momentum)
training_op = optimizer.minimize(loss)
with tf.name_scope("eval"):
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
init = tf.global_variables_initializer()
saver = tf.train.Saver()
# -
# Training is as usual, except you must run the weights clipping operations after each training operation:
n_epochs = 20
batch_size = 50
# +
clip_all_weights = tf.get_collection("max_norm")
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for iteration in range(mnist.train.num_examples // batch_size):
X_batch, y_batch = mnist.train.next_batch(batch_size)
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
sess.run(clip_all_weights)
acc_test = accuracy.eval(feed_dict={X: mnist.test.images, # not shown in the book
y: mnist.test.labels}) # not shown
print(epoch, "Test accuracy:", acc_test) # not shown
save_path = saver.save(sess, "./my_model_final.ckpt") # not shown
# -
# # Exercise solutions
# ## 1. to 7.
# See appendix A.
# ## 8. Deep Learning
# ### 8.1.
# _Exercise: Build a DNN with five hidden layers of 100 neurons each, He initialization, and the ELU activation function._
# We will need similar DNNs in the next exercises, so let's create a function to build this DNN:
# +
he_init = tf.contrib.layers.variance_scaling_initializer()
def dnn(inputs, n_hidden_layers=5, n_neurons=100, name=None,
activation=tf.nn.elu, initializer=he_init):
with tf.variable_scope(name, "dnn"):
for layer in range(n_hidden_layers):
inputs = tf.layers.dense(inputs, n_neurons, activation=activation,
kernel_initializer=initializer,
name="hidden%d" % (layer + 1))
return inputs
# +
n_inputs = 28 * 28 # MNIST
n_outputs = 5
reset_graph()
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int64, shape=(None), name="y")
dnn_outputs = dnn(X)
logits = tf.layers.dense(dnn_outputs, n_outputs, kernel_initializer=he_init, name="logits")
Y_proba = tf.nn.softmax(logits, name="Y_proba")
# -
# ### 8.2.
# _Exercise: Using Adam optimization and early stopping, try training it on MNIST but only on digits 0 to 4, as we will use transfer learning for digits 5 to 9 in the next exercise. You will need a softmax output layer with five neurons, and as always make sure to save checkpoints at regular intervals and save the final model so you can reuse it later._
# Let's complete the graph with the cost function, the training op, and all the other usual components:
# +
learning_rate = 0.01
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
optimizer = tf.train.AdamOptimizer(learning_rate)
training_op = optimizer.minimize(loss, name="training_op")
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32), name="accuracy")
init = tf.global_variables_initializer()
saver = tf.train.Saver()
# -
# Let's fetch the MNIST dataset:
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/")
# Now let's create the training set, validation and test set (we need the validation set to implement early stopping):
X_train1 = mnist.train.images[mnist.train.labels < 5]
y_train1 = mnist.train.labels[mnist.train.labels < 5]
X_valid1 = mnist.validation.images[mnist.validation.labels < 5]
y_valid1 = mnist.validation.labels[mnist.validation.labels < 5]
X_test1 = mnist.test.images[mnist.test.labels < 5]
y_test1 = mnist.test.labels[mnist.test.labels < 5]
# +
n_epochs = 1000
batch_size = 20
max_checks_without_progress = 20
checks_without_progress = 0
best_loss = np.infty
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
rnd_idx = np.random.permutation(len(X_train1))
for rnd_indices in np.array_split(rnd_idx, len(X_train1) // batch_size):
X_batch, y_batch = X_train1[rnd_indices], y_train1[rnd_indices]
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
loss_val, acc_val = sess.run([loss, accuracy], feed_dict={X: X_valid1, y: y_valid1})
if loss_val < best_loss:
save_path = saver.save(sess, "./my_mnist_model_0_to_4.ckpt")
best_loss = loss_val
checks_without_progress = 0
else:
checks_without_progress += 1
if checks_without_progress > max_checks_without_progress:
print("Early stopping!")
break
print("{}\tValidation loss: {:.6f}\tBest loss: {:.6f}\tAccuracy: {:.2f}%".format(
epoch, loss_val, best_loss, acc_val * 100))
with tf.Session() as sess:
saver.restore(sess, "./my_mnist_model_0_to_4.ckpt")
acc_test = accuracy.eval(feed_dict={X: X_test1, y: y_test1})
print("Final test accuracy: {:.2f}%".format(acc_test * 100))
# -
# We get 98.05% accuracy on the test set. That's not too bad, but let's see if we can do better by tuning the hyperparameters.
# ### 8.3.
# _Exercise: Tune the hyperparameters using cross-validation and see what precision you can achieve._
# Let's create a `DNNClassifier` class, compatible with Scikit-Learn's `RandomizedSearchCV` class, to perform hyperparameter tuning. Here are the key points of this implementation:
# * the `__init__()` method (constructor) does nothing more than create instance variables for each of the hyperparameters.
# * the `fit()` method creates the graph, starts a session and trains the model:
# * it calls the `_build_graph()` method to build the graph (much lile the graph we defined earlier). Once this method is done creating the graph, it saves all the important operations as instance variables for easy access by other methods.
# * the `_dnn()` method builds the hidden layers, just like the `dnn()` function above, but also with support for batch normalization and dropout (for the next exercises).
# * if the `fit()` method is given a validation set (`X_valid` and `y_valid`), then it implements early stopping. This implementation does not save the best model to disk, but rather to memory: it uses the `_get_model_params()` method to get all the graph's variables and their values, and the `_restore_model_params()` method to restore the variable values (of the best model found). This trick helps speed up training.
# * After the `fit()` method has finished training the model, it keeps the session open so that predictions can be made quickly, without having to save a model to disk and restore it for every prediction. You can close the session by calling the `close_session()` method.
# * the `predict_proba()` method uses the trained model to predict the class probabilities.
# * the `predict()` method calls `predict_proba()` and returns the class with the highest probability, for each instance.
# +
from sklearn.base import BaseEstimator, ClassifierMixin
from sklearn.exceptions import NotFittedError
class DNNClassifier(BaseEstimator, ClassifierMixin):
def __init__(self, n_hidden_layers=5, n_neurons=100, optimizer_class=tf.train.AdamOptimizer,
learning_rate=0.01, batch_size=20, activation=tf.nn.elu, initializer=he_init,
batch_norm_momentum=None, dropout_rate=None, random_state=None):
"""Initialize the DNNClassifier by simply storing all the hyperparameters."""
self.n_hidden_layers = n_hidden_layers
self.n_neurons = n_neurons
self.optimizer_class = optimizer_class
self.learning_rate = learning_rate
self.batch_size = batch_size
self.activation = activation
self.initializer = initializer
self.batch_norm_momentum = batch_norm_momentum
self.dropout_rate = dropout_rate
self.random_state = random_state
self._session = None
def _dnn(self, inputs):
"""Build the hidden layers, with support for batch normalization and dropout."""
for layer in range(self.n_hidden_layers):
if self.dropout_rate:
inputs = tf.layers.dropout(inputs, self.dropout_rate, training=self._training)
inputs = tf.layers.dense(inputs, self.n_neurons,
kernel_initializer=self.initializer,
name="hidden%d" % (layer + 1))
if self.batch_norm_momentum:
inputs = tf.layers.batch_normalization(inputs, momentum=self.batch_norm_momentum,
training=self._training)
inputs = self.activation(inputs, name="hidden%d_out" % (layer + 1))
return inputs
def _build_graph(self, n_inputs, n_outputs):
"""Build the same model as earlier"""
if self.random_state is not None:
tf.set_random_seed(self.random_state)
np.random.seed(self.random_state)
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int32, shape=(None), name="y")
if self.batch_norm_momentum or self.dropout_rate:
self._training = tf.placeholder_with_default(False, shape=(), name='training')
else:
self._training = None
dnn_outputs = self._dnn(X)
logits = tf.layers.dense(dnn_outputs, n_outputs, kernel_initializer=he_init, name="logits")
Y_proba = tf.nn.softmax(logits, name="Y_proba")
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y,
logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
optimizer = self.optimizer_class(learning_rate=self.learning_rate)
training_op = optimizer.minimize(loss)
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32), name="accuracy")
init = tf.global_variables_initializer()
saver = tf.train.Saver()
# Make the important operations available easily through instance variables
self._X, self._y = X, y
self._Y_proba, self._loss = Y_proba, loss
self._training_op, self._accuracy = training_op, accuracy
self._init, self._saver = init, saver
def close_session(self):
if self._session:
self._session.close()
def _get_model_params(self):
"""Get all variable values (used for early stopping, faster than saving to disk)"""
with self._graph.as_default():
gvars = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES)
return {gvar.op.name: value for gvar, value in zip(gvars, self._session.run(gvars))}
def _restore_model_params(self, model_params):
"""Set all variables to the given values (for early stopping, faster than loading from disk)"""
gvar_names = list(model_params.keys())
assign_ops = {gvar_name: self._graph.get_operation_by_name(gvar_name + "/Assign")
for gvar_name in gvar_names}
init_values = {gvar_name: assign_op.inputs[1] for gvar_name, assign_op in assign_ops.items()}
feed_dict = {init_values[gvar_name]: model_params[gvar_name] for gvar_name in gvar_names}
self._session.run(assign_ops, feed_dict=feed_dict)
def fit(self, X, y, n_epochs=100, X_valid=None, y_valid=None):
"""Fit the model to the training set. If X_valid and y_valid are provided, use early stopping."""
self.close_session()
# infer n_inputs and n_outputs from the training set.
n_inputs = X.shape[1]
self.classes_ = np.unique(y)
n_outputs = len(self.classes_)
# Translate the labels vector to a vector of sorted class indices, containing
# integers from 0 to n_outputs - 1.
# For example, if y is equal to [8, 8, 9, 5, 7, 6, 6, 6], then the sorted class
# labels (self.classes_) will be equal to [5, 6, 7, 8, 9], and the labels vector
# will be translated to [3, 3, 4, 0, 2, 1, 1, 1]
self.class_to_index_ = {label: index
for index, label in enumerate(self.classes_)}
y = np.array([self.class_to_index_[label]
for label in y], dtype=np.int32)
self._graph = tf.Graph()
with self._graph.as_default():
self._build_graph(n_inputs, n_outputs)
# extra ops for batch normalization
extra_update_ops = tf.get_collection(tf.GraphKeys.UPDATE_OPS)
# needed in case of early stopping
max_checks_without_progress = 20
checks_without_progress = 0
best_loss = np.infty
best_params = None
# Now train the model!
self._session = tf.Session(graph=self._graph)
with self._session.as_default() as sess:
self._init.run()
for epoch in range(n_epochs):
rnd_idx = np.random.permutation(len(X))
for rnd_indices in np.array_split(rnd_idx, len(X) // self.batch_size):
X_batch, y_batch = X[rnd_indices], y[rnd_indices]
feed_dict = {self._X: X_batch, self._y: y_batch}
if self._training is not None:
feed_dict[self._training] = True
sess.run(self._training_op, feed_dict=feed_dict)
if extra_update_ops:
sess.run(extra_update_ops, feed_dict=feed_dict)
if X_valid is not None and y_valid is not None:
loss_val, acc_val = sess.run([self._loss, self._accuracy],
feed_dict={self._X: X_valid,
self._y: y_valid})
if loss_val < best_loss:
best_params = self._get_model_params()
best_loss = loss_val
checks_without_progress = 0
else:
checks_without_progress += 1
print("{}\tValidation loss: {:.6f}\tBest loss: {:.6f}\tAccuracy: {:.2f}%".format(
epoch, loss_val, best_loss, acc_val * 100))
if checks_without_progress > max_checks_without_progress:
print("Early stopping!")
break
else:
loss_train, acc_train = sess.run([self._loss, self._accuracy],
feed_dict={self._X: X_batch,
self._y: y_batch})
print("{}\tLast training batch loss: {:.6f}\tAccuracy: {:.2f}%".format(
epoch, loss_train, acc_train * 100))
# If we used early stopping then rollback to the best model found
if best_params:
self._restore_model_params(best_params)
return self
def predict_proba(self, X):
if not self._session:
raise NotFittedError("This %s instance is not fitted yet" % self.__class__.__name__)
with self._session.as_default() as sess:
return self._Y_proba.eval(feed_dict={self._X: X})
def predict(self, X):
class_indices = np.argmax(self.predict_proba(X), axis=1)
return np.array([[self.classes_[class_index]]
for class_index in class_indices], np.int32)
def save(self, path):
self._saver.save(self._session, path)
# -
# Let's see if we get the exact same accuracy as earlier using this class (without dropout or batch norm):
dnn_clf = DNNClassifier(random_state=42)
dnn_clf.fit(X_train1, y_train1, n_epochs=1000, X_valid=X_valid1, y_valid=y_valid1)
# The model is trained, let's see if it gets the same accuracy as earlier:
# +
from sklearn.metrics import accuracy_score
y_pred = dnn_clf.predict(X_test1)
accuracy_score(y_test1, y_pred)
# -
# Yep! Working fine. Now we can use Scikit-Learn's `RandomizedSearchCV` class to search for better hyperparameters (this may take over an hour, depending on your system):
# +
from sklearn.model_selection import RandomizedSearchCV
def leaky_relu(alpha=0.01):
def parametrized_leaky_relu(z, name=None):
return tf.maximum(alpha * z, z, name=name)
return parametrized_leaky_relu
param_distribs = {
"n_neurons": [10, 30, 50, 70, 90, 100, 120, 140, 160],
"batch_size": [10, 50, 100, 500],
"learning_rate": [0.01, 0.02, 0.05, 0.1],
"activation": [tf.nn.relu, tf.nn.elu, leaky_relu(alpha=0.01), leaky_relu(alpha=0.1)],
# you could also try exploring different numbers of hidden layers, different optimizers, etc.
#"n_hidden_layers": [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
#"optimizer_class": [tf.train.AdamOptimizer, partial(tf.train.MomentumOptimizer, momentum=0.95)],
}
rnd_search = RandomizedSearchCV(DNNClassifier(random_state=42), param_distribs, n_iter=50,
fit_params={"X_valid": X_valid1, "y_valid": y_valid1, "n_epochs": 1000},
random_state=42, verbose=2)
rnd_search.fit(X_train1, y_train1)
# -
rnd_search.best_params_
y_pred = rnd_search.predict(X_test1)
accuracy_score(y_test1, y_pred)
# Wonderful! Tuning the hyperparameters got us up to 99.32% accuracy! It may not sound like a great improvement to go from 98.05% to 99.32% accuracy, but consider the error rate: it went from roughly 2% to 0.7%. That's a 65% reduction of the number of errors this model will produce!
# It's a good idea to save this model:
rnd_search.best_estimator_.save("./my_best_mnist_model_0_to_4")
# ### 8.4.
# _Exercise: Now try adding Batch Normalization and compare the learning curves: is it converging faster than before? Does it produce a better model?_
# Let's train the best model found, once again, to see how fast it converges (alternatively, you could tweak the code above to make it write summaries for TensorBoard, so you can visualize the learning curve):
dnn_clf = DNNClassifier(activation=leaky_relu(alpha=0.1), batch_size=500, learning_rate=0.01,
n_neurons=140, random_state=42)
dnn_clf.fit(X_train1, y_train1, n_epochs=1000, X_valid=X_valid1, y_valid=y_valid1)
# The best loss is reached at epoch 19, but it was already within 10% of that result at epoch 9.
# Let's check that we do indeed get 99.32% accuracy on the test set:
y_pred = dnn_clf.predict(X_test1)
accuracy_score(y_test1, y_pred)
# Good, now let's use the exact same model, but this time with batch normalization:
dnn_clf_bn = DNNClassifier(activation=leaky_relu(alpha=0.1), batch_size=500, learning_rate=0.01,
n_neurons=90, random_state=42,
batch_norm_momentum=0.95)
dnn_clf_bn.fit(X_train1, y_train1, n_epochs=1000, X_valid=X_valid1, y_valid=y_valid1)
# The best params are reached during epoch 48, that's actually a slower convergence than earlier. Let's check the accuracy:
y_pred = dnn_clf_bn.predict(X_test1)
accuracy_score(y_test1, y_pred)
# Well, batch normalization did not improve accuracy. Let's see if we can find a good set of hyperparameters that will work well with batch normalization:
# +
from sklearn.model_selection import RandomizedSearchCV
param_distribs = {
"n_neurons": [10, 30, 50, 70, 90, 100, 120, 140, 160],
"batch_size": [10, 50, 100, 500],
"learning_rate": [0.01, 0.02, 0.05, 0.1],
"activation": [tf.nn.relu, tf.nn.elu, leaky_relu(alpha=0.01), leaky_relu(alpha=0.1)],
# you could also try exploring different numbers of hidden layers, different optimizers, etc.
#"n_hidden_layers": [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
#"optimizer_class": [tf.train.AdamOptimizer, partial(tf.train.MomentumOptimizer, momentum=0.95)],
"batch_norm_momentum": [0.9, 0.95, 0.98, 0.99, 0.999],
}
rnd_search_bn = RandomizedSearchCV(DNNClassifier(random_state=42), param_distribs, n_iter=50,
fit_params={"X_valid": X_valid1, "y_valid": y_valid1, "n_epochs": 1000},
random_state=42, verbose=2)
rnd_search_bn.fit(X_train1, y_train1)
# -
rnd_search_bn.best_params_
y_pred = rnd_search_bn.predict(X_test1)
accuracy_score(y_test1, y_pred)
# Slightly better than earlier: 99.4% vs 99.3%. Let's see if dropout can do better.
# ### 8.5.
# _Exercise: is the model overfitting the training set? Try adding dropout to every layer and try again. Does it help?_
# Let's go back to the best model we trained earlier and see how it performs on the training set:
y_pred = dnn_clf.predict(X_train1)
accuracy_score(y_train1, y_pred)
# The model performs significantly better on the training set than on the test set (99.91% vs 99.32%), which means it is overfitting the training set. A bit of regularization may help. Let's try adding dropout with a 50% dropout rate:
dnn_clf_dropout = DNNClassifier(activation=leaky_relu(alpha=0.1), batch_size=500, learning_rate=0.01,
n_neurons=90, random_state=42,
dropout_rate=0.5)
dnn_clf_dropout.fit(X_train1, y_train1, n_epochs=1000, X_valid=X_valid1, y_valid=y_valid1)
# The best params are reached during epoch 23. Dropout somewhat slowed down convergence.
# Let's check the accuracy:
y_pred = dnn_clf_dropout.predict(X_test1)
accuracy_score(y_test1, y_pred)
# We are out of luck, dropout does not seem to help either. Let's try tuning the hyperparameters, perhaps we can squeeze a bit more performance out of this model:
# +
from sklearn.model_selection import RandomizedSearchCV
param_distribs = {
"n_neurons": [10, 30, 50, 70, 90, 100, 120, 140, 160],
"batch_size": [10, 50, 100, 500],
"learning_rate": [0.01, 0.02, 0.05, 0.1],
"activation": [tf.nn.relu, tf.nn.elu, leaky_relu(alpha=0.01), leaky_relu(alpha=0.1)],
# you could also try exploring different numbers of hidden layers, different optimizers, etc.
#"n_hidden_layers": [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
#"optimizer_class": [tf.train.AdamOptimizer, partial(tf.train.MomentumOptimizer, momentum=0.95)],
"dropout_rate": [0.2, 0.3, 0.4, 0.5, 0.6],
}
rnd_search_dropout = RandomizedSearchCV(DNNClassifier(random_state=42), param_distribs, n_iter=50,
fit_params={"X_valid": X_valid1, "y_valid": y_valid1, "n_epochs": 1000},
random_state=42, verbose=2)
rnd_search_dropout.fit(X_train1, y_train1)
# -
rnd_search_dropout.best_params_
y_pred = rnd_search_dropout.predict(X_test1)
accuracy_score(y_test1, y_pred)
# Oh well, dropout did not improve the model. Better luck next time! :)
# But that's okay, we have ourselves a nice DNN that achieves 99.40% accuracy on the test set using Batch Normalization, or 99.32% without BN. Let's see if some of this expertise on digits 0 to 4 can be transferred to the task of classifying digits 5 to 9. For the sake of simplicity we will reuse the DNN without BN, since it is almost as good.
# ## 9. Transfer learning
# ### 9.1.
# _Exercise: create a new DNN that reuses all the pretrained hidden layers of the previous model, freezes them, and replaces the softmax output layer with a new one._
# Let's load the best model's graph and get a handle on all the important operations we will need. Note that instead of creating a new softmax output layer, we will just reuse the existing one (since it has the same number of outputs as the existing one). We will reinitialize its parameters before training.
# +
reset_graph()
restore_saver = tf.train.import_meta_graph("./my_best_mnist_model_0_to_4.meta")
X = tf.get_default_graph().get_tensor_by_name("X:0")
y = tf.get_default_graph().get_tensor_by_name("y:0")
loss = tf.get_default_graph().get_tensor_by_name("loss:0")
Y_proba = tf.get_default_graph().get_tensor_by_name("Y_proba:0")
logits = Y_proba.op.inputs[0]
accuracy = tf.get_default_graph().get_tensor_by_name("accuracy:0")
# -
# To freeze the lower layers, we will exclude their variables from the optimizer's list of trainable variables, keeping only the output layer's trainable variables:
# +
learning_rate = 0.01
output_layer_vars = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope="logits")
optimizer = tf.train.AdamOptimizer(learning_rate, name="Adam2")
training_op = optimizer.minimize(loss, var_list=output_layer_vars)
# +
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32), name="accuracy")
init = tf.global_variables_initializer()
five_frozen_saver = tf.train.Saver()
# -
# ### 9.2.
# _Exercise: train this new DNN on digits 5 to 9, using only 100 images per digit, and time how long it takes. Despite this small number of examples, can you achieve high precision?_
# Let's create the training, validation and test sets. We need to subtract 5 from the labels because TensorFlow expects integers from 0 to `n_classes-1`.
X_train2_full = mnist.train.images[mnist.train.labels >= 5]
y_train2_full = mnist.train.labels[mnist.train.labels >= 5] - 5
X_valid2_full = mnist.validation.images[mnist.validation.labels >= 5]
y_valid2_full = mnist.validation.labels[mnist.validation.labels >= 5] - 5
X_test2 = mnist.test.images[mnist.test.labels >= 5]
y_test2 = mnist.test.labels[mnist.test.labels >= 5] - 5
# Also, for the purpose of this exercise, we want to keep only 100 instances per class in the training set (and let's keep only 30 instances per class in the validation set). Let's create a small function to do that:
def sample_n_instances_per_class(X, y, n=100):
Xs, ys = [], []
for label in np.unique(y):
idx = (y == label)
Xc = X[idx][:n]
yc = y[idx][:n]
Xs.append(Xc)
ys.append(yc)
return np.concatenate(Xs), np.concatenate(ys)
X_train2, y_train2 = sample_n_instances_per_class(X_train2_full, y_train2_full, n=100)
X_valid2, y_valid2 = sample_n_instances_per_class(X_valid2_full, y_valid2_full, n=30)
# Now let's train the model. This is the same training code as earlier, using early stopping, except for the initialization: we first initialize all the variables, then we restore the best model trained earlier (on digits 0 to 4), and finally we reinitialize the output layer variables.
# +
import time
n_epochs = 1000
batch_size = 20
max_checks_without_progress = 20
checks_without_progress = 0
best_loss = np.infty
with tf.Session() as sess:
init.run()
restore_saver.restore(sess, "./my_best_mnist_model_0_to_4")
for var in output_layer_vars:
var.initializer.run()
t0 = time.time()
for epoch in range(n_epochs):
rnd_idx = np.random.permutation(len(X_train2))
for rnd_indices in np.array_split(rnd_idx, len(X_train2) // batch_size):
X_batch, y_batch = X_train2[rnd_indices], y_train2[rnd_indices]
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
loss_val, acc_val = sess.run([loss, accuracy], feed_dict={X: X_valid2, y: y_valid2})
if loss_val < best_loss:
save_path = five_frozen_saver.save(sess, "./my_mnist_model_5_to_9_five_frozen")
best_loss = loss_val
checks_without_progress = 0
else:
checks_without_progress += 1
if checks_without_progress > max_checks_without_progress:
print("Early stopping!")
break
print("{}\tValidation loss: {:.6f}\tBest loss: {:.6f}\tAccuracy: {:.2f}%".format(
epoch, loss_val, best_loss, acc_val * 100))
t1 = time.time()
print("Total training time: {:.1f}s".format(t1 - t0))
with tf.Session() as sess:
five_frozen_saver.restore(sess, "./my_mnist_model_5_to_9_five_frozen")
acc_test = accuracy.eval(feed_dict={X: X_test2, y: y_test2})
print("Final test accuracy: {:.2f}%".format(acc_test * 100))
# -
# Well that's not a great accuracy, is it? Of course with such a tiny training set, and with only one layer to tweak, we should not expect miracles.
# ### 9.3.
# _Exercise: try caching the frozen layers, and train the model again: how much faster is it now?_
# Let's start by getting a handle on the output of the last frozen layer:
hidden5_out = tf.get_default_graph().get_tensor_by_name("hidden5_out:0")
# Now let's train the model using roughly the same code as earlier. The difference is that we compute the output of the top frozen layer at the beginning (both for the training set and the validation set), and we cache it. This makes training roughly 1.5 to 3 times faster in this example (this may vary greatly, depending on your system):
# +
import time
n_epochs = 1000
batch_size = 20
max_checks_without_progress = 20
checks_without_progress = 0
best_loss = np.infty
with tf.Session() as sess:
init.run()
restore_saver.restore(sess, "./my_best_mnist_model_0_to_4")
for var in output_layer_vars:
var.initializer.run()
t0 = time.time()
hidden5_train = hidden5_out.eval(feed_dict={X: X_train2, y: y_train2})
hidden5_valid = hidden5_out.eval(feed_dict={X: X_valid2, y: y_valid2})
for epoch in range(n_epochs):
rnd_idx = np.random.permutation(len(X_train2))
for rnd_indices in np.array_split(rnd_idx, len(X_train2) // batch_size):
h5_batch, y_batch = hidden5_train[rnd_indices], y_train2[rnd_indices]
sess.run(training_op, feed_dict={hidden5_out: h5_batch, y: y_batch})
loss_val, acc_val = sess.run([loss, accuracy], feed_dict={hidden5_out: hidden5_valid, y: y_valid2})
if loss_val < best_loss:
save_path = five_frozen_saver.save(sess, "./my_mnist_model_5_to_9_five_frozen")
best_loss = loss_val
checks_without_progress = 0
else:
checks_without_progress += 1
if checks_without_progress > max_checks_without_progress:
print("Early stopping!")
break
print("{}\tValidation loss: {:.6f}\tBest loss: {:.6f}\tAccuracy: {:.2f}%".format(
epoch, loss_val, best_loss, acc_val * 100))
t1 = time.time()
print("Total training time: {:.1f}s".format(t1 - t0))
with tf.Session() as sess:
five_frozen_saver.restore(sess, "./my_mnist_model_5_to_9_five_frozen")
acc_test = accuracy.eval(feed_dict={X: X_test2, y: y_test2})
print("Final test accuracy: {:.2f}%".format(acc_test * 100))
# -
# ### 9.4.
# _Exercise: try again reusing just four hidden layers instead of five. Can you achieve a higher precision?_
# Let's load the best model again, but this time we will create a new softmax output layer on top of the 4th hidden layer:
# +
reset_graph()
n_outputs = 5
restore_saver = tf.train.import_meta_graph("./my_best_mnist_model_0_to_4.meta")
X = tf.get_default_graph().get_tensor_by_name("X:0")
y = tf.get_default_graph().get_tensor_by_name("y:0")
hidden4_out = tf.get_default_graph().get_tensor_by_name("hidden4_out:0")
logits = tf.layers.dense(hidden4_out, n_outputs, kernel_initializer=he_init, name="new_logits")
Y_proba = tf.nn.softmax(logits)
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(xentropy)
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32), name="accuracy")
# -
# And now let's create the training operation. We want to freeze all the layers except for the new output layer:
# +
learning_rate = 0.01
output_layer_vars = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope="new_logits")
optimizer = tf.train.AdamOptimizer(learning_rate, name="Adam2")
training_op = optimizer.minimize(loss, var_list=output_layer_vars)
init = tf.global_variables_initializer()
four_frozen_saver = tf.train.Saver()
# -
# And once again we train the model with the same code as earlier. Note: we could of course write a function once and use it multiple times, rather than copying almost the same training code over and over again, but as we keep tweaking the code slightly, the function would need multiple arguments and `if` statements, and it would have to be at the beginning of the notebook, where it would not make much sense to readers. In short it would be very confusing, so we're better off with copy & paste.
# +
n_epochs = 1000
batch_size = 20
max_checks_without_progress = 20
checks_without_progress = 0
best_loss = np.infty
with tf.Session() as sess:
init.run()
restore_saver.restore(sess, "./my_best_mnist_model_0_to_4")
for epoch in range(n_epochs):
rnd_idx = np.random.permutation(len(X_train2))
for rnd_indices in np.array_split(rnd_idx, len(X_train2) // batch_size):
X_batch, y_batch = X_train2[rnd_indices], y_train2[rnd_indices]
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
loss_val, acc_val = sess.run([loss, accuracy], feed_dict={X: X_valid2, y: y_valid2})
if loss_val < best_loss:
save_path = four_frozen_saver.save(sess, "./my_mnist_model_5_to_9_four_frozen")
best_loss = loss_val
checks_without_progress = 0
else:
checks_without_progress += 1
if checks_without_progress > max_checks_without_progress:
print("Early stopping!")
break
print("{}\tValidation loss: {:.6f}\tBest loss: {:.6f}\tAccuracy: {:.2f}%".format(
epoch, loss_val, best_loss, acc_val * 100))
with tf.Session() as sess:
four_frozen_saver.restore(sess, "./my_mnist_model_5_to_9_four_frozen")
acc_test = accuracy.eval(feed_dict={X: X_test2, y: y_test2})
print("Final test accuracy: {:.2f}%".format(acc_test * 100))
# -
# Still not fantastic, but much better.
# ### 9.5.
# _Exercise: now unfreeze the top two hidden layers and continue training: can you get the model to perform even better?_
# +
learning_rate = 0.01
unfrozen_vars = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope="hidden[34]|new_logits")
optimizer = tf.train.AdamOptimizer(learning_rate, name="Adam3")
training_op = optimizer.minimize(loss, var_list=unfrozen_vars)
init = tf.global_variables_initializer()
two_frozen_saver = tf.train.Saver()
# +
n_epochs = 1000
batch_size = 20
max_checks_without_progress = 20
checks_without_progress = 0
best_loss = np.infty
with tf.Session() as sess:
init.run()
four_frozen_saver.restore(sess, "./my_mnist_model_5_to_9_four_frozen")
for epoch in range(n_epochs):
rnd_idx = np.random.permutation(len(X_train2))
for rnd_indices in np.array_split(rnd_idx, len(X_train2) // batch_size):
X_batch, y_batch = X_train2[rnd_indices], y_train2[rnd_indices]
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
loss_val, acc_val = sess.run([loss, accuracy], feed_dict={X: X_valid2, y: y_valid2})
if loss_val < best_loss:
save_path = two_frozen_saver.save(sess, "./my_mnist_model_5_to_9_two_frozen")
best_loss = loss_val
checks_without_progress = 0
else:
checks_without_progress += 1
if checks_without_progress > max_checks_without_progress:
print("Early stopping!")
break
print("{}\tValidation loss: {:.6f}\tBest loss: {:.6f}\tAccuracy: {:.2f}%".format(
epoch, loss_val, best_loss, acc_val * 100))
with tf.Session() as sess:
two_frozen_saver.restore(sess, "./my_mnist_model_5_to_9_two_frozen")
acc_test = accuracy.eval(feed_dict={X: X_test2, y: y_test2})
print("Final test accuracy: {:.2f}%".format(acc_test * 100))
# -
# Let's check what accuracy we can get by unfreezing all layers:
# +
learning_rate = 0.01
optimizer = tf.train.AdamOptimizer(learning_rate, name="Adam4")
training_op = optimizer.minimize(loss)
init = tf.global_variables_initializer()
no_frozen_saver = tf.train.Saver()
# +
n_epochs = 1000
batch_size = 20
max_checks_without_progress = 20
checks_without_progress = 0
best_loss = np.infty
with tf.Session() as sess:
init.run()
two_frozen_saver.restore(sess, "./my_mnist_model_5_to_9_two_frozen")
for epoch in range(n_epochs):
rnd_idx = np.random.permutation(len(X_train2))
for rnd_indices in np.array_split(rnd_idx, len(X_train2) // batch_size):
X_batch, y_batch = X_train2[rnd_indices], y_train2[rnd_indices]
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
loss_val, acc_val = sess.run([loss, accuracy], feed_dict={X: X_valid2, y: y_valid2})
if loss_val < best_loss:
save_path = no_frozen_saver.save(sess, "./my_mnist_model_5_to_9_no_frozen")
best_loss = loss_val
checks_without_progress = 0
else:
checks_without_progress += 1
if checks_without_progress > max_checks_without_progress:
print("Early stopping!")
break
print("{}\tValidation loss: {:.6f}\tBest loss: {:.6f}\tAccuracy: {:.2f}%".format(
epoch, loss_val, best_loss, acc_val * 100))
with tf.Session() as sess:
no_frozen_saver.restore(sess, "./my_mnist_model_5_to_9_no_frozen")
acc_test = accuracy.eval(feed_dict={X: X_test2, y: y_test2})
print("Final test accuracy: {:.2f}%".format(acc_test * 100))
# -
# Let's compare that to a DNN trained from scratch:
dnn_clf_5_to_9 = DNNClassifier(n_hidden_layers=4, random_state=42)
dnn_clf_5_to_9.fit(X_train2, y_train2, n_epochs=1000, X_valid=X_valid2, y_valid=y_valid2)
y_pred = dnn_clf_5_to_9.predict(X_test2)
accuracy_score(y_test2, y_pred)
# Meh. How disappointing! ;) Transfer learning did not help much (if at all) in this task. At least we tried... Fortunately, the next exercise will get better results.
# ## 10. Pretraining on an auxiliary task
# In this exercise you will build a DNN that compares two MNIST digit images and predicts whether they represent the same digit or not. Then you will reuse the lower layers of this network to train an MNIST classifier using very little training data.
# ### 10.1.
# Exercise: _Start by building two DNNs (let's call them DNN A and B), both similar to the one you built earlier but without the output layer: each DNN should have five hidden layers of 100 neurons each, He initialization, and ELU activation. Next, add one more hidden layer with 10 units on top of both DNNs. You should use TensorFlow's `concat()` function with `axis=1` to concatenate the outputs of both DNNs along the horizontal axis, then feed the result to the hidden layer. Finally, add an output layer with a single neuron using the logistic activation function._
# **Warning**! There was an error in the book for this exercise: there was no instruction to add a top hidden layer. Without it, the neural network generally fails to start learning. If you have the latest version of the book, this error has been fixed.
# You could have two input placeholders, `X1` and `X2`, one for the images that should be fed to the first DNN, and the other for the images that should be fed to the second DNN. It would work fine. However, another option is to have a single input placeholder to hold both sets of images (each row will hold a pair of images), and use `tf.unstack()` to split this tensor into two separate tensors, like this:
# +
n_inputs = 28 * 28 # MNIST
reset_graph()
X = tf.placeholder(tf.float32, shape=(None, 2, n_inputs), name="X")
X1, X2 = tf.unstack(X, axis=1)
# -
# We also need the labels placeholder. Each label will be 0 if the images represent different digits, or 1 if they represent the same digit:
y = tf.placeholder(tf.int32, shape=[None, 1])
# Now let's feed these inputs through two separate DNNs:
dnn1 = dnn(X1, name="DNN_A")
dnn2 = dnn(X2, name="DNN_B")
# And let's concatenate their outputs:
dnn_outputs = tf.concat([dnn1, dnn2], axis=1)
# Each DNN outputs 100 activations (per instance), so the shape is `[None, 100]`:
dnn1.shape
dnn2.shape
# And of course the concatenated outputs have a shape of `[None, 200]`:
dnn_outputs.shape
# Now lets add an extra hidden layer with just 10 neurons, and the output layer, with a single neuron:
hidden = tf.layers.dense(dnn_outputs, units=10, activation=tf.nn.elu, kernel_initializer=he_init)
logits = tf.layers.dense(hidden, units=1, kernel_initializer=he_init)
y_proba = tf.nn.sigmoid(logits)
# The whole network predicts `1` if `y_proba >= 0.5` (i.e. the network predicts that the images represent the same digit), or `0` otherwise. We compute instead `logits >= 0`, which is equivalent but faster to compute:
y_pred = tf.cast(tf.greater_equal(logits, 0), tf.int32)
# Now let's add the cost function:
y_as_float = tf.cast(y, tf.float32)
xentropy = tf.nn.sigmoid_cross_entropy_with_logits(labels=y_as_float, logits=logits)
loss = tf.reduce_mean(xentropy)
# And we can now create the training operation using an optimizer:
# +
learning_rate = 0.01
momentum = 0.95
optimizer = tf.train.MomentumOptimizer(learning_rate, momentum, use_nesterov=True)
training_op = optimizer.minimize(loss)
# -
# We will want to measure our classifier's accuracy.
y_pred_correct = tf.equal(y_pred, y)
accuracy = tf.reduce_mean(tf.cast(y_pred_correct, tf.float32))
# And the usual `init` and `saver`:
init = tf.global_variables_initializer()
saver = tf.train.Saver()
# ### 10.2.
# _Exercise: split the MNIST training set in two sets: split #1 should containing 55,000 images, and split #2 should contain contain 5,000 images. Create a function that generates a training batch where each instance is a pair of MNIST images picked from split #1. Half of the training instances should be pairs of images that belong to the same class, while the other half should be images from different classes. For each pair, the training label should be 0 if the images are from the same class, or 1 if they are from different classes._
# The MNIST dataset returned by TensorFlow's `input_data()` function is already split into 3 parts: a training set (55,000 instances), a validation set (5,000 instances) and a test set (10,000 instances). Let's use the first set to generate the training set composed image pairs, and we will use the second set for the second phase of the exercise (to train a regular MNIST classifier). We will use the third set as the test set for both phases.
# +
X_train1 = mnist.train.images
y_train1 = mnist.train.labels
X_train2 = mnist.validation.images
y_train2 = mnist.validation.labels
X_test = mnist.test.images
y_test = mnist.test.labels
# -
# Let's write a function that generates pairs of images: 50% representing the same digit, and 50% representing different digits. There are many ways to implement this. In this implementation, we first decide how many "same" pairs (i.e. pairs of images representing the same digit) we will generate, and how many "different" pairs (i.e. pairs of images representing different digits). We could just use `batch_size // 2` but we want to handle the case where it is odd (granted, that might be overkill!). Then we generate random pairs and we pick the right number of "same" pairs, then we generate the right number of "different" pairs. Finally we shuffle the batch and return it:
def generate_batch(images, labels, batch_size):
size1 = batch_size // 2
size2 = batch_size - size1
if size1 != size2 and np.random.rand() > 0.5:
size1, size2 = size2, size1
X = []
y = []
while len(X) < size1:
rnd_idx1, rnd_idx2 = np.random.randint(0, len(images), 2)
if rnd_idx1 != rnd_idx2 and labels[rnd_idx1] == labels[rnd_idx2]:
X.append(np.array([images[rnd_idx1], images[rnd_idx2]]))
y.append([1])
while len(X) < batch_size:
rnd_idx1, rnd_idx2 = np.random.randint(0, len(images), 2)
if labels[rnd_idx1] != labels[rnd_idx2]:
X.append(np.array([images[rnd_idx1], images[rnd_idx2]]))
y.append([0])
rnd_indices = np.random.permutation(batch_size)
return np.array(X)[rnd_indices], np.array(y)[rnd_indices]
# Let's test it to generate a small batch of 5 image pairs:
batch_size = 5
X_batch, y_batch = generate_batch(X_train1, y_train1, batch_size)
# Each row in `X_batch` contains a pair of images:
X_batch.shape, X_batch.dtype
# Let's look at these pairs:
plt.figure(figsize=(3, 3 * batch_size))
plt.subplot(121)
plt.imshow(X_batch[:,0].reshape(28 * batch_size, 28), cmap="binary", interpolation="nearest")
plt.axis('off')
plt.subplot(122)
plt.imshow(X_batch[:,1].reshape(28 * batch_size, 28), cmap="binary", interpolation="nearest")
plt.axis('off')
plt.show()
# And let's look at the labels (0 means "different", 1 means "same"):
y_batch
# Perfect!
# ### 10.3.
# _Exercise: train the DNN on this training set. For each image pair, you can simultaneously feed the first image to DNN A and the second image to DNN B. The whole network will gradually learn to tell whether two images belong to the same class or not._
# Let's generate a test set composed of many pairs of images pulled from the MNIST test set:
X_test1, y_test1 = generate_batch(X_test, y_test, batch_size=len(X_test))
# And now, let's train the model. There's really nothing special about this step, except for the fact that we need a fairly large `batch_size`, otherwise the model fails to learn anything and ends up with an accuracy of 50%:
# +
n_epochs = 100
batch_size = 500
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for iteration in range(mnist.train.num_examples // batch_size):
X_batch, y_batch = generate_batch(X_train1, y_train1, batch_size)
loss_val, _ = sess.run([loss, training_op], feed_dict={X: X_batch, y: y_batch})
print(epoch, "Train loss:", loss_val)
if epoch % 5 == 0:
acc_test = accuracy.eval(feed_dict={X: X_test1, y: y_test1})
print(epoch, "Test accuracy:", acc_test)
save_path = saver.save(sess, "./my_digit_comparison_model.ckpt")
# -
# All right, we reach 97.6% accuracy on this digit comparison task. That's not too bad, this model knows a thing or two about comparing handwritten digits!
#
# Let's see if some of that knowledge can be useful for the regular MNIST classification task.
# ### 10.4.
# _Exercise: now create a new DNN by reusing and freezing the hidden layers of DNN A and adding a softmax output layer on top with 10 neurons. Train this network on split #2 and see if you can achieve high performance despite having only 500 images per class._
# Let's create the model, it is pretty straightforward. There are many ways to freeze the lower layers, as explained in the book. In this example, we chose to use the `tf.stop_gradient()` function. Note that we need one `Saver` to restore the pretrained DNN A, and another `Saver` to save the final model:
# +
reset_graph()
n_inputs = 28 * 28 # MNIST
n_outputs = 10
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int32, shape=(None), name="y")
dnn_outputs = dnn(X, name="DNN_A")
frozen_outputs = tf.stop_gradient(dnn_outputs)
logits = tf.layers.dense(dnn_outputs, n_outputs, kernel_initializer=he_init)
Y_proba = tf.nn.softmax(logits)
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
optimizer = tf.train.MomentumOptimizer(learning_rate, momentum, use_nesterov=True)
training_op = optimizer.minimize(loss)
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
init = tf.global_variables_initializer()
dnn_A_vars = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope="DNN_A")
restore_saver = tf.train.Saver(var_list={var.op.name: var for var in dnn_A_vars})
saver = tf.train.Saver()
# -
# Now on to training! We first initialize all variables (including the variables in the new output layer), then we restore the pretrained DNN A. Next, we just train the model on the small MNIST dataset (containing just 5,000 images):
# +
n_epochs = 100
batch_size = 50
with tf.Session() as sess:
init.run()
restore_saver.restore(sess, "./my_digit_comparison_model.ckpt")
for epoch in range(n_epochs):
rnd_idx = np.random.permutation(len(X_train2))
for rnd_indices in np.array_split(rnd_idx, len(X_train2) // batch_size):
X_batch, y_batch = X_train2[rnd_indices], y_train2[rnd_indices]
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
if epoch % 10 == 0:
acc_test = accuracy.eval(feed_dict={X: X_test, y: y_test})
print(epoch, "Test accuracy:", acc_test)
save_path = saver.save(sess, "./my_mnist_model_final.ckpt")
# -
# Well, 96.7% accuracy, that's not the best MNIST model we have trained so far, but recall that we are only using a small training set (just 500 images per digit). Let's compare this result with the same DNN trained from scratch, without using transfer learning:
# +
reset_graph()
n_inputs = 28 * 28 # MNIST
n_outputs = 10
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int32, shape=(None), name="y")
dnn_outputs = dnn(X, name="DNN_A")
logits = tf.layers.dense(dnn_outputs, n_outputs, kernel_initializer=he_init)
Y_proba = tf.nn.softmax(logits)
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
optimizer = tf.train.MomentumOptimizer(learning_rate, momentum, use_nesterov=True)
training_op = optimizer.minimize(loss)
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
init = tf.global_variables_initializer()
dnn_A_vars = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope="DNN_A")
restore_saver = tf.train.Saver(var_list={var.op.name: var for var in dnn_A_vars})
saver = tf.train.Saver()
# +
n_epochs = 150
batch_size = 50
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
rnd_idx = np.random.permutation(len(X_train2))
for rnd_indices in np.array_split(rnd_idx, len(X_train2) // batch_size):
X_batch, y_batch = X_train2[rnd_indices], y_train2[rnd_indices]
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
if epoch % 10 == 0:
acc_test = accuracy.eval(feed_dict={X: X_test, y: y_test})
print(epoch, "Test accuracy:", acc_test)
save_path = saver.save(sess, "./my_mnist_model_final.ckpt")
# -
# Only 94.8% accuracy... So transfer learning helped us reduce the error rate from 5.2% to 3.3% (that's over 36% error reduction). Moreover, the model using transfer learning reached over 96% accuracy in less than 10 epochs.
#
# Bottom line: transfer learning does not always work (as we saw in exercise 9), but when it does it can make a big difference. So try it out!
|
11_deep_learning.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # x.grad demystified
#
# > "An introduction to automatic differentiation with PyTorch and computing a gradient field"
#
# - toc: false
# - branch: master
# - badges: true
# - comments: true
# - categories: [neural networks]
# - image: images/Covers/2021_05_19.png
# - hide: false
# - search_exclude: true
# - metadata_key1: metadata_value1
# - metadata_key2: metadata_value2
#
# The key algorithm of neural networks is back-propagation which applies the chain rule to compute derivatives of a function. In PyTorch, assuming you have defined a function, say `f = sin(x)`, you would compute its gradient by calling `f.backward()` followed by `x.grad`. The gradient is a function but `x.grad` returns values, so it was not immediately obvious to me what was happening.
#
# To remind you, the gradient of scalar function $f(x,y,z)$ is a vector field defined by:
#
#
# $
# \nabla f = \begin{bmatrix}
# \frac{d f}{d x} \\
# \frac{d f}{d y} \\
# \frac{d f}{d z} \\
# \end{bmatrix}
# $
#
# You can sample this vector field at a given position say $(X,Y,Z)$.
#
#
# $
# \nabla f(X,Y,Z) = \begin{bmatrix}
# \frac{d f(X,Y,Z)}{d x} \\
# \frac{d f(X,Y,Z)}{d y} \\
# \frac{d f(X,Y,Z)}{d z} \\
# \end{bmatrix}
# $
#
# It turns out that calling `f.backward()` computes the function $\nabla f$. When calling `x.grad`, PyTorch treats the tensor `x` as the axis $x$ and its values as the positions $X$. Thus, `x.grad` returns $\frac{d f(X,Y,Z)}{d x}$.
#
# To illustrate this concept, let's compute the gradient of a scalar function of one or two variables.
# imports
import torch
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.size'] = 15
plt.rcParams['figure.figsize'] = [8,8]
# # Function of one variable
#
# First, we define a tensor `X` that stores positions $X$ along axis $x$, and a tensor `F` that stores the values of function $f(x)=sin(x)$ evaluated at positions $X$. Because the `backward()` function works only on scalar values we sum the values of `F` before calling backward. This operation does not affect the derivatives.
n = 100
X = torch.linspace(.0,2.*np.pi,n, requires_grad=True)
F = torch.sin(X)
F.sum().backward()
# Now we visualize the function (red line) and its gradient (black arrows). The gradient is computed by calling `X.grad`.
# +
r = 8 # sample rate for the gradient
with torch.no_grad():
plt.plot(X,F,'-r',lw=1,zorder=-1)
plt.quiver(X[::r],F[::r],np.ones(n)[::r],X.grad[::r],color='k')
plt.axis('scaled')
plt.xlabel('$x$')
_ =plt.ylabel('$f(x)$')
# -
# # Function of two variables
#
# We now define two 2D tensors, `X` and `Y` to store coordinates $(X,Y)$ in the space $(x,y)$. `F` stores the results of function $f(x,y)=sin(x)*cos(y)$ evaluated at positions $(X,Y)$.
X, Y = np.meshgrid(np.linspace(.0,2.*np.pi,n),np.linspace(.0,2.*np.pi,n))
X = torch.from_numpy(X.T)
Y = torch.from_numpy(Y.T)
X.requires_grad = True
Y.requires_grad = True
F = torch.sin(X)*torch.cos(Y)
F.sum().backward()
# In two dimensions the gradient is a vector field that can be represented using a quiverplot. The scalar function $f$ is represented as a heatmap. We calculate the components of the gradient vector at each of locations stored in `(X,Y)` by calling `X.grad` and `Y.grad`.
r = 5
with torch.no_grad():
plt.imshow(F,
extent=[x.item() for x in [X[0,0], X[-1,0], Y[0,0], Y[0,-1]]],
cmap='inferno')
plt.colorbar(label='f(x,y)')
plt.quiver(X[::r,::r],Y[::r,::r],X.grad[::r,::r], Y.grad[::r,::r])
plt.xlabel('$x$')
_ = plt.ylabel('$y$')
# # Conclusion
#
# PyTorch's automatic differentiation is a very neat tool that allows you to easily compute gradient fields. The function `f.backward()` computes the gradient function itself while calling, `x.grad` computes the derivative of the function $f(x)$ with respect to variable $x$ at the location stored in tensor `x`. This functionality can be used to easily compute gradient vector fields in an arbtrary number of dimensions.
|
_notebooks/2021-05-19-PyTorch-gradient.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from nltk.corpus import wordnet as wn
wn.synset('think.v.01').frame_ids()
for lemma in wn.synset('think.v.01').lemmas():
print(lemma, lemma.frame_ids())
print(" | ".join(lemma.frame_strings()))
wn.synset('stretch.v.02').frame_ids()
for lemma in wn.synset('stretch.v.02').lemmas():
print(lemma, lemma.frame_ids())
print(" | ".join(lemma.frame_strings()))
print(wn.synsets('犬', lang='jpn'))
print(wn.synsets('hund', lang='dan'))
words=['grøn', 'hvid', 'blå', 'øl']
for word in words:
print(wn.synsets(word, lang='dan'))
words=['red', 'green', 'blue', 'beer']
for word in words:
print(wn.synsets(word, lang='eng'))
cla='merchandise.n.01'
c=wn.synset(cla)
for c_c in list(c.closure(hyper)):
print(c_c.lemma_names('eng'))
c=wn.synset('red.n.01')
c.name()
c=wn.synset('red.n.01')
for c_c in list(c.closure(hyper)):
print(c_c.lemma_names('jpn'))
c=wn.synset('red.n.01')
for c_c in list(c.closure(hyper)):
print(c_c.lemma_names('fra'))
c=wn.synset('red.n.01')
for c_c in list(c.closure(hyper)):
print(c_c.name(), c_c.lemma_names('eng'), c_c.lemma_names('cmn'))
def desc(synset):
c=wn.synset(synset)
# keys=[c.name(), c.lemma_names('eng'), c.lemma_names('cmn')]
keys=[]
for c_c in [c]+list(c.closure(hyper)):
print(c_c.name(), c_c.lemma_names('eng'), c_c.lemma_names('cmn'))
keys.extend(c_c.lemma_names('eng'))
keys.extend(c_c.lemma_names('cmn'))
print(keys)
desc('dog.n.01')
desc('sweater.n.01')
c=wn.synset('blue.n.01')
keys=[]
for c_c in list(c.closure(hyper)):
print(c_c.name(), c_c.lemma_names('eng'), c_c.lemma_names('cmn'))
keys.extend(c_c.lemma_names('eng'))
keys.extend(c_c.lemma_names('cmn'))
print(keys)
c=wn.synset('blue.n.01')
print(c.lemma_names('fra'))
for c_c in list(c.closure(hyper)):
print(c_c.lemma_names('fra'))
langs=wn.langs()
print('total langs', len(langs))
c=wn.synset('blue.n.01')
for idx in range(len(langs)):
print(idx, langs[idx], c.lemma_names(langs[idx]))
c=wn.synset('red.n.01')
for idx in range(len(langs)):
print(idx, langs[idx], c.lemma_names(langs[idx]))
print(wn.synsets('six', lang='eng'))
print(wn.synsets('product', lang='eng'))
print(wn.synsets('good', lang='eng'))
print(wn.synsets('virtual', lang='eng'))
# print(wn.synsets('virtual_object', lang='eng'))
c=wn.synset('six.n.01')
for idx in range(len(langs)):
print(idx, langs[idx], c.lemma_names(langs[idx]))
# import sagas
# loc=sagas.locales.get_locale('ja')
import sagas.nlu.locales as locales
loc=locales.get_locale('ja')
print(wn.synsets('犬', lang=loc))
print(wn.synsets('猫', lang='cmn'))
c=wn.synset('cat.n.01')
hypo = lambda s: s.hyponyms()
hyper = lambda s: s.hypernyms()
list(c.closure(hypo))
list(c.closure(hyper))
c.lemma_names('jpn')
c.hypernyms()
c=wn.synset('cat.n.01')
for c_c in list(c.closure(hyper)):
print(c_c.lemma_names('jpn'))
c=wn.synset('cat.n.01')
for c_c in list(c.closure(hyper)):
print(c_c.lemma_names('cmn'))
c=wn.synset('cat.n.01')
for c_c in list(c.closure(hypo)):
print(c_c.name(), c_c.lemma_names('cmn'), c_c.lemma_names('eng'), c_c.lemma_names('fra'))
for c_c in list(c.closure(hyper)):
print(c_c.lemma_names('fra'))
good = wn.synset('good.a.01')
good.lemmas()[0].antonyms()
words=['红色','绿色','蓝', '紫']
for w in words:
print(wn.synsets(w, lang='cmn'))
c = wn.synset('purple.s.01')
for lemma in c.lemmas():
print(lemma, lemma.frame_ids())
hypo = lambda s: s.hyponyms()
list(c.closure(hypo))
wn.synsets('筛选', lang='cmn')
wn.synsets('找出', lang='cmn')
select = wn.synsets(u'选择', lang='cmn')[0]
selectn3= wn.synsets(u'找出', lang='cmn')[0]
print(select.path_similarity(selectn3))
selectn1 = wn.synsets(u'选出', lang='cmn')[0]
print(select.path_similarity(selectn1))
selectn2 = wn.synsets(u'选', lang='cmn')[0]
print(select.path_similarity(selectn2))
# ## Similarity
# synset1.path_similarity(synset2): Return a score denoting how similar two word senses are, based on the shortest path that connects the senses in the is-a (hypernym/hypnoym) taxonomy. The score is in the range 0 to 1. By default, there is now a fake root node added to verbs so for cases where previously a path could not be found---and None was returned---it should return a value. The old behavior can be achieved by setting simulate_root to be False. A score of 1 represents identity i.e. comparing a sense with itself will return 1.
>>> dog = wn.synset('dog.n.01')
>>> cat = wn.synset('cat.n.01')
>>> hit = wn.synset('hit.v.01')
>>> slap = wn.synset('slap.v.01')
>>> dog.path_similarity(cat) # doctest: +ELLIPSIS
>>> hit.path_similarity(slap) # doctest: +ELLIPSIS
# Iterate over all the noun synsets:
for synset in list(wn.all_synsets('n'))[:10]:
print(synset)
wn.synsets('dog') # doctest: +ELLIPSIS
wn.synsets('dog', pos='v')
# Walk through the synsets looking at their hypernyms:
synset=wn.synsets('dog', pos='v')[0]
print(synset, synset.hypernyms())
wn.synsets('yellow', pos='a')
wn.synsets('yellow', pos=['n','a'])
wn.synsets('amarelo', lang='por', pos='a')
rs=wn.synsets('amarelo', lang='por', pos=None)
for r in rs:
print(r.pos(), r)
from nltk.corpus import sentiwordnet as swn
breakdown = swn.senti_synset('breakdown.n.03')
print(breakdown)
breakdown.pos_score()
breakdown.neg_score()
breakdown.obj_score()
list(swn.senti_synsets('slow'))
happy = swn.senti_synsets('happy', 'a')
happy
all = swn.all_senti_synsets()
# ### synset1.res_similarity(synset2, ic):
# Resnik Similarity: Return a score denoting how similar two word senses are, based on the Information Content (IC) of the Least Common Subsumer (most specific ancestor node). Note that for any similarity measure that uses information content, the result is dependent on the corpus used to generate the information content and the specifics of how the information content was created.
#
>>> from nltk.corpus import genesis
>>> genesis_ic = wn.ic(genesis, False, 0.0)
>>> dog = wn.synset('dog.n.01')
>>> cat = wn.synset('cat.n.01')
>>> hit = wn.synset('hit.v.01')
>>> slap = wn.synset('slap.v.01')
>>> dog.res_similarity(cat, genesis_ic) # doctest: +ELLIPSIS
|
notebook/procs-nltk-verb-frames.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Sensing Matrix Diagonalization
# In this tutorial, we will demonstration the use of `kontrol.SensingMatrix` class to diagonalize a pair of coupled sensors.
#
# Here, suppose we have two displacements $x_1$ and $x_2$, and we have sensing readouts $s_1$ and $s_2$.
# We kicked the system and let it resonates. $x_1$ is a damped oscillation at $1\ \mathrm{Hz}$ and $x_2$ is a damped oscillation at $3\ \mathrm{Hz}$. We hard code sensing coupling $s_1 = x_1 + 0.1x_2$ and $s_2 = -0.2x_1 + x_2$.
# For simplicity, let's assume that these sesning readouts are obtained using an initial sensing matrix of $\mathbf{C}_\mathrm{sensing, initial}=\begin{bmatrix}1&0\\0&1\end{bmatrix}$.
#
# We will estimate the coupling ratios from the spectra of $s_1$ and $s_2$, and let's see if we can recover a sensing matrix $\mathbf{C}_\mathrm{sensing}$ such that $\left[x_1,\,x_2\right]^T=\mathbf{C}_\mathrm{sensing}\left[s_1,\,s_2\right]^T$.
# +
import numpy as np
import matplotlib.pyplot as plt
fs = 1024
t_ini = 0
t_end = 100
t = np.linspace(0, 100, (t_end-t_ini)*fs)
np.random.seed(123)
x_1_phase = np.random.uniform(0, np.pi)
x_2_phase = np.random.uniform(0, np.pi)
x_1 = np.real(1.5 * np.exp((-0.1+(2*np.pi*1)*1j) * t + x_1_phase*1j))
x_2 = np.real(3 * np.exp((-0.2+(2*np.pi*3)*1j) * t + x_2_phase*1j))
s_1 = x_1 + 0.1*x_2
s_2 = -0.2*x_1 + x_2
# +
plt.rcParams.update({"font.size": 14})
plt.figure(figsize=(15,5))
plt.subplot(121)
plt.plot(t, x_1, label="$x_1$")
plt.plot(t,x_2, label="$x_2$")
plt.ylabel("Amplitude")
plt.xlabel("time [s]")
plt.legend(loc=0)
plt.subplot(122)
plt.plot(t, s_1, label="$s_1$")
plt.plot(t, s_2, label="$s_2$")
plt.ylabel("Amplitude")
plt.xlabel("time [s]")
plt.legend(loc=0)
# -
# Now, let's obtain various spectra of the sensor readouts, like how we would use diaggui to obtain spectral densities and transfer functions.
# +
import scipy.signal
fs = 1/(t[1]-t[0])
f, psd_s_1 = scipy.signal.welch(s_1, fs=fs, nperseg=int(len(s_1)/5))
f, psd_s_2 = scipy.signal.welch(s_2, fs=fs, nperseg=int(len(s_2)/5))
f, csd_s_12 = scipy.signal.csd(s_1, s_2, fs=fs, nperseg=int(len(s_1)/5))
mask = f>0
f = f[mask]
psd_s_1 = psd_s_1[mask]
psd_s_2 = psd_s_2[mask]
csd_s_12 = csd_s_12[mask]
# +
plt.figure(figsize=(15, 10))
plt.subplot(221)
plt.loglog(f, abs(csd_s_12/psd_s_2), label="Transfer function $|s_1/s_2|$")
plt.loglog(f, abs(csd_s_12/psd_s_1), label="Transfer function $|s_2/s_1|$")
plt.ylabel("Amplitude")
plt.xlabel("Frequency [Hz]")
plt.legend(loc=0)
plt.grid(which="both")
plt.subplot(222)
plt.loglog(f, psd_s_1, label="$s_1$")
plt.loglog(f, psd_s_2, label="$s_2$")
plt.ylabel("Power spectral density [1/Hz]")
plt.xlabel("Frequency [Hz]")
plt.legend(loc=0)
plt.grid(which="both")
plt.subplot(223)
plt.semilogx(f, np.angle(csd_s_12/psd_s_2), label=r"Transfer function $\angle\left(s_1/s_2\right)$")
plt.semilogx(f, np.angle(csd_s_12/psd_s_1), label=r"Transfer function $\angle\left(s_2/s_1\right)$")
plt.ylabel("Phase [rad]")
plt.xlabel("Frequency [Hz]")
plt.legend(loc=0)
plt.grid(which="both")
# -
# Now, we know that the resonance frequencies are at 1 Hz and 3 Hz, so we can safely assume that these frequencies are purely $x_1$ and $x_2$ motion respectively. We see that the transfer functions $s_1/s_2$ and $s_2/s_1$ have flat response at these frequencies. These correspond to coupling ratios $s_1/x_2$ (at 3 Hz) and $s_2/x_1$ (at 3 Hz). From the phase response, we see that the phase between $x_2$ and $s_1$ is 0, and that between $x_1$ and $s_2$ is at $-\pi$, this correspond to a minus sign in the coupling ratio. Let's inspect further.
# f_1hz = f[(f>0.9) & (f<1.1)]
# f_3hz = f[(f>2.9) & (f<3.1)]
print(r"Coupling ratio $s_1/x_2$", np.mean(abs(csd_s_12/psd_s_2)[(f>2.9) & (f<3.1)]))
print(r"Coupling ratio $s_2/x_1$", np.mean(abs(csd_s_12/psd_s_1)[(f>0.9) & (f<1.1)]))
print(r"Phase $s_1/x_2$", np.angle(csd_s_12/psd_s_2)[(f>2.9) & (f<3.1)])
print(r"Phase $s_2/x_1$", np.angle(csd_s_12/psd_s_1)[(f>0.9) & (f<1.1)])
# Indeed, we find coupling ratios 0.100013 and -0.199978.
#
# Now, we assume the follow:
#
# $\mathbf{C}_\mathrm{coupling}\left[x_1,\,x_2\right]^T=\mathbf{C}_\mathrm{sensing, initial}\left[s_1,\,s_2\right]^T$, so the coupling matrix $\mathbf{C}_\mathrm{coupling}$ is $\begin{bmatrix}1&0.100013\\-0.199978&1\end{bmatrix}$.
#
# And now let's use `kontrol.SensingMatrix` to compute a new sensing matrix.
# +
import kontrol
c_sensing_initial = np.array([[1, 0], [0, 1]])
c_coupling = np.array([[1, 0.100013], [-0.199978, 1]])
sensing_matrix = kontrol.SensingMatrix(matrix=c_sensing_initial, coupling_matrix=c_coupling)
## Alternatively,
## sensing_matrix = kontrol.SensingMatrix(matrix=c_sensing_initial)
## sensing_matrix.coupling_matrix = c_coupling
## Now diagonalize
c_sensing = sensing_matrix.diagonalize()
## Alternatively
## c_sensing = sensing_matrix.diagonalize(coupling_matrix=c_coupling)
print(c_sensing)
# -
# Now let's test the new matrix.
#
# We compute the new sensing readout $\left[s_{1,\mathrm{new}},\,s_{2,\mathrm{new}}\right]^T = \mathbf{C}_\mathrm{sensing}\left[s_1,\,s_2\right]^T$, and then compute the power spectral densities and compare it with the old ones.
# +
s_new = c_sensing @ np.array([s_1, s_2])
s_1_new = s_new[0]
s_2_new = s_new[1]
f, psd_s_1_new = scipy.signal.welch(s_1_new, fs=fs, nperseg=int(len(s_1_new)/5))
f, psd_s_2_new = scipy.signal.welch(s_2_new, fs=fs, nperseg=int(len(s_2_new)/5))
f, csd_s_12_new = scipy.signal.csd(s_1_new, s_2_new, fs=fs, nperseg=int(len(s_1_new)/5))
mask = f>0
f = f[mask]
psd_s_1_new = psd_s_1_new[mask]
psd_s_2_new = psd_s_2_new[mask]
csd_s_12_new = csd_s_12_new[mask]
# +
plt.figure(figsize=(15, 5))
plt.subplot(121)
plt.loglog(f, psd_s_1, label="$s_1$ before")
plt.loglog(f, psd_s_1_new, label="$s_1$ diagonalized")
plt.ylabel("Power spectral density [1/Hz]")
plt.xlabel("Frequency [Hz]")
plt.legend(loc=0)
plt.grid(which="both")
plt.subplot(122)
plt.loglog(f, psd_s_2, label="$s_2$ before")
plt.loglog(f, psd_s_2_new, label="$s_2$ diagonalized")
plt.ylabel("Power spectral density [1/Hz]")
plt.xlabel("Frequency [Hz]")
plt.legend(loc=0)
plt.grid(which="both")
# -
# As we can see, the couplings have been reduced by many many orders of magnitudes, while the diagonal readout remains the same.
# By the way. `kontrol.SensingMatrix` class inherit `numpy.ndarray`, so you can do any numpy array operation on it.
# For example,
sensing_matrix + np.random.random(np.shape(sensing_matrix))
|
docs/source/tutorials/sensing_matrix_diagonalization.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/PacktPublishing/Modern-Computer-Vision-with-PyTorch/blob/master/Chapter04/CNN_on_FashionMNIST.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="lKXHmN72oSr-"
from torchvision import datasets
import torch
data_folder = '/content/' # This can be any directory you want to download FMNIST to
fmnist = datasets.FashionMNIST(data_folder, download=True, train=True)
# + id="8quMVIspoXAc"
tr_images = fmnist.data
tr_targets = fmnist.targets
# + id="pCybp42UoYfD"
val_fmnist = datasets.FashionMNIST(data_folder, download=True, train=False)
val_images = val_fmnist.data
val_targets = val_fmnist.targets
# + id="_wf7B5v_oZpV"
import matplotlib.pyplot as plt
# %matplotlib inline
import numpy as np
from torch.utils.data import Dataset, DataLoader
import torch
import torch.nn as nn
device = 'cuda' if torch.cuda.is_available() else 'cpu'
# + id="DeG0gLx4oavL"
class FMNISTDataset(Dataset):
def __init__(self, x, y):
x = x.float()/255
x = x.view(-1,1,28,28)
self.x, self.y = x, y
def __getitem__(self, ix):
x, y = self.x[ix], self.y[ix]
return x.to(device), y.to(device)
def __len__(self):
return len(self.x)
from torch.optim import SGD, Adam
def get_model():
model = nn.Sequential(
nn.Conv2d(1, 64, kernel_size=3),
nn.MaxPool2d(2),
nn.ReLU(),
nn.Conv2d(64, 128, kernel_size=3),
nn.MaxPool2d(2),
nn.ReLU(),
nn.Flatten(),
nn.Linear(3200, 256),
nn.ReLU(),
nn.Linear(256, 10)
).to(device)
loss_fn = nn.CrossEntropyLoss()
optimizer = Adam(model.parameters(), lr=1e-3)
return model, loss_fn, optimizer
def train_batch(x, y, model, opt, loss_fn):
prediction = model(x)
batch_loss = loss_fn(prediction, y)
batch_loss.backward()
optimizer.step()
optimizer.zero_grad()
return batch_loss.item()
@torch.no_grad()
def accuracy(x, y, model):
model.eval()
prediction = model(x)
max_values, argmaxes = prediction.max(-1)
is_correct = argmaxes == y
return is_correct.cpu().numpy().tolist()
# + id="-VxMySqHoyUc"
def get_data():
train = FMNISTDataset(tr_images, tr_targets)
trn_dl = DataLoader(train, batch_size=32, shuffle=True)
val = FMNISTDataset(val_images, val_targets)
val_dl = DataLoader(val, batch_size=len(val_images), shuffle=True)
return trn_dl, val_dl
# + id="MKIE_sjtpRP6"
@torch.no_grad()
def val_loss(x, y, model):
model.eval()
prediction = model(x)
val_loss = loss_fn(prediction, y)
return val_loss.item()
# + id="r2hKhLHQpSqx"
trn_dl, val_dl = get_data()
model, loss_fn, optimizer = get_model()
# + id="WQmmjw70pUe9" colab={"base_uri": "https://localhost:8080/"} outputId="e8836519-77c7-4b75-f009-d7fd3cd03e14"
# !pip install torch_summary
from torchsummary import summary
model, loss_fn, optimizer = get_model()
summary(model, torch.zeros(1,1,28,28));
# + id="97CcIWOBpXuw" colab={"base_uri": "https://localhost:8080/"} outputId="8b16304b-81dd-4a4b-ea15-bab0508a8cc2"
train_losses, train_accuracies = [], []
val_losses, val_accuracies = [], []
for epoch in range(5):
print(epoch)
train_epoch_losses, train_epoch_accuracies = [], []
for ix, batch in enumerate(iter(trn_dl)):
x, y = batch
batch_loss = train_batch(x, y, model, optimizer, loss_fn)
train_epoch_losses.append(batch_loss)
train_epoch_loss = np.array(train_epoch_losses).mean()
for ix, batch in enumerate(iter(trn_dl)):
x, y = batch
is_correct = accuracy(x, y, model)
train_epoch_accuracies.extend(is_correct)
train_epoch_accuracy = np.mean(train_epoch_accuracies)
for ix, batch in enumerate(iter(val_dl)):
x, y = batch
val_is_correct = accuracy(x, y, model)
validation_loss = val_loss(x, y, model)
val_epoch_accuracy = np.mean(val_is_correct)
train_losses.append(train_epoch_loss)
train_accuracies.append(train_epoch_accuracy)
val_losses.append(validation_loss)
val_accuracies.append(val_epoch_accuracy)
# + id="l9N0n1k0paJx" colab={"base_uri": "https://localhost:8080/", "height": 337} outputId="2b7a2e49-476c-45b5-f57c-9327eb98a662"
epochs = np.arange(5)+1
import matplotlib.ticker as mtick
import matplotlib.pyplot as plt
import matplotlib.ticker as mticker
# %matplotlib inline
plt.subplot(211)
plt.plot(epochs, train_losses, 'bo', label='Training loss')
plt.plot(epochs, val_losses, 'r', label='Validation loss')
plt.gca().xaxis.set_major_locator(mticker.MultipleLocator(1))
plt.title('Training and validation loss with CNN')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.grid('off')
plt.show()
plt.subplot(212)
plt.plot(epochs, train_accuracies, 'bo', label='Training accuracy')
plt.plot(epochs, val_accuracies, 'r', label='Validation accuracy')
plt.gca().xaxis.set_major_locator(mticker.MultipleLocator(1))
plt.title('Training and validation accuracy with CNN')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
#plt.ylim(0.8,1)
plt.gca().set_yticklabels(['{:.0f}%'.format(x*100) for x in plt.gca().get_yticks()])
plt.legend()
plt.grid('off')
plt.show()
# + id="CeIvkLO8p3ou" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="adc7a483-310d-4b72-8ab4-7ddc713603d3"
preds = []
ix = 24300
for px in range(-5,6):
img = tr_images[ix]/255.
img = img.view(28, 28)
img2 = np.roll(img, px, axis=1)
img3 = torch.Tensor(img2).view(-1,1,28,28).to(device)
np_output = model(img3).cpu().detach().numpy()
pred = np.exp(np_output)/np.sum(np.exp(np_output))
preds.append(pred)
plt.imshow(img2)
plt.title(fmnist.classes[pred[0].argmax()])
plt.show()
# + id="n-YPXmWxqon7" colab={"base_uri": "https://localhost:8080/"} outputId="8b0df65f-2ee9-4343-fc6b-5dc0f639df14"
np.array(preds).shape
# + id="Xnz-eFGTp4G8" colab={"base_uri": "https://localhost:8080/", "height": 625} outputId="71714277-f31b-4ebf-fd55-a03984dff7ea"
import seaborn as sns
fig, ax = plt.subplots(1,1, figsize=(12,10))
plt.title('Probability of each class for various translations')
sns.heatmap(np.array(preds).reshape(11,10), annot=True, ax=ax, fmt='.2f', xticklabels=fmnist.classes, yticklabels=[str(i)+str(' pixels') for i in range(-5,6)], cmap='gray')
# + id="JTsjWPuyqNNU"
|
Chapter04/32_CNN_on_FashionMNIST.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/vgaurav3011/EIP-3.0-/blob/master/Week%205/Misclassification_of_images.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="4f3Ar-5yBPcH" colab_type="code" colab={}
import tensorflow as tf
# + id="iyYek6_0B7Pi" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 52} outputId="dbf18f24-9fe8-43c3-8361-7d0cb4923625"
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
# + id="SCfF_e63B78m" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="e5b13edb-521d-4f77-cda4-8277069d1a8d"
print(x_train.shape, y_train.shape, x_test.shape, y_test.shape)
# + id="nZeOBR_eDKoU" colab_type="code" colab={}
import matplotlib.pyplot as plt
def plot_img(i):
# plot the image and the target for sample i
plt.imshow(x_train[i])
plt.title(y_train[i])
plt.axis('off')
# + id="lKP0ZSCrHf7R" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 281} outputId="d066ba0b-231f-4a70-a9c2-310bfdcb88b4"
plot_img(2)
# + id="Ige-Lm4-IC7M" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 807} outputId="f147d0a5-58e3-4c9e-c7bd-022423fbb2fd"
plt.hist(x_train[0])
# + id="qIyomisVIGCZ" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 790} outputId="9454a1ba-1f36-4e51-e4be-a6105e4e1a83"
import numpy as np
x_train = x_train/255.
plt.hist(x_train[0])
# + id="l6LeTm3xIKQU" colab_type="code" colab={}
x_test = x_test/255.
# + id="T2MsG-w3INbx" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="96aeb719-f312-4c0c-d8d1-b6319063a65e"
y_train[0]
# + id="VYD7dAxTIPw6" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="06735d04-7207-4fe7-f684-8239b95a86f6"
from keras.utils import np_utils
y_train = np_utils.to_categorical(y_train, 10)
y_test = np_utils.to_categorical(y_test, 10)
print(y_train[0])
# + id="59S4EIrSITGs" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 286} outputId="4ab66382-6294-4f78-98df-a624e56814ef"
import numpy as np
import seaborn as sns
# building the image of a zero:
zero = np.array([[0,0,0,1,0,0,0,0],
[0,1,2,3,2,1,0,0],
[0,4,3,1,3,2,0,0],
[1,5,2,0,0,5,1,0],
[2,4,0,0,0,6,2,0],
[1,3,0,0,0,4,1,0],
[0,2,3,2,1,3,0,0],
[0,0,3,4,3,1,0,0]])
sns.heatmap(zero, annot=True)
# + id="1TVlSmSxIwRR" colab_type="code" colab={}
from skimage.util import view_as_blocks
pooling_window_shape = (2,2)
view = view_as_blocks(zero, pooling_window_shape)
flatten_view = view.reshape(view.shape[0], view.shape[1], -1)
mean_view = np.mean(flatten_view, axis=2)
max_view = np.max(flatten_view, axis=2)
# + id="T3ZS_0cII1DJ" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 286} outputId="d8c1ecd2-0abf-45f2-9bce-cdf796b9d679"
sns.heatmap(max_view, annot=True)
# + id="mkQ7gPnrI3Sx" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 286} outputId="a1627554-835c-47cd-e9ae-c1cf9833e4c2"
sns.heatmap(mean_view, annot=True)
# + id="m1tOKAUWI5wg" colab_type="code" colab={}
from keras import models
from keras import layers
# + id="oATFMeSMJE6v" colab_type="code" colab={}
model = models.Sequential()
model.add( layers.Conv2D(10, 4, input_shape=(28,28,1), activation='relu') )
model.add( layers.Conv2D(10, 4, input_shape=(28,28,1), activation='relu') )
model.add( layers.Conv2D(10, 4, input_shape=(28,28,1), activation='relu') )
model.add( layers.Conv2D(10, 4, input_shape=(28,28,1), activation='relu') )
model.add( layers.Conv2D(10, 4, input_shape=(28,28,1), activation='relu') )
# + id="LxBr37knJH-0" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 312} outputId="4991be29-e747-4500-8f63-d0e08b571e99"
model.summary()
# + id="8XGPqaQYJLaD" colab_type="code" colab={}
model.add( layers.Flatten() )
model.add( layers.Dense(100, activation='relu') )
# + id="r6POf6n-JUWm" colab_type="code" colab={}
model.add( layers.Dense(10, activation='softmax') )
# + id="oyvE8yL5JfaT" colab_type="code" colab={}
from keras.optimizers import RMSprop
# + id="9rXnjRFvJqw4" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 72} outputId="e75de1d5-9a53-4a37-97e9-75ba649ced70"
model.compile(loss='categorical_crossentropy',
optimizer=RMSprop(lr=0.001),
metrics=['acc'])
# + id="ldj5FCAcJt87" colab_type="code" colab={}
kx_train = x_train.reshape(len(x_train),28,28,1)
kx_test = x_test.reshape(len(x_test),28,28,1)
# + id="8QmRii11Jx4r" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 382} outputId="56489635-44fd-4bc5-81d6-4136bf6fd8aa"
history = model.fit(kx_train, y_train, validation_data=(kx_test,y_test),
batch_size=512, epochs=10)
# + id="faHYap75J0Q3" colab_type="code" colab={}
def plot_accuracy(history, miny=None):
acc = history.history['acc']
test_acc = history.history['val_acc']
epochs = range(len(acc))
plt.plot(epochs, acc)
plt.plot(epochs, test_acc)
if miny:
plt.ylim(miny, 1.0)
plt.title('accuracy')
plt.figure()
# + id="4evWbKliJ6Ga" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 298} outputId="b7e2b4a2-ffec-4fd3-b1ad-ca8b8844d283"
plot_accuracy(history, miny=0.95)
# + id="RlFWBmCHKPc4" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 52} outputId="20b4ea8c-867d-4166-8cb2-16059f4d848b"
preds = model.predict(kx_test)
pred_digits = np.argmax(preds, axis=1)
y_digits = np.argmax(y_test, axis=1)
print(pred_digits)
print(y_digits)
# + id="WIBYPdSFKfDq" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="471901c7-1f39-4868-fd61-94d8c1a45e0f"
mispred_img = x_test[pred_digits!=y_digits]
mispred_true = y_digits[pred_digits!=y_digits]
mispred_pred = pred_digits[pred_digits!=y_digits]
print('number of misclassified digits:', mispred_img.shape[0])
# + id="H0bHcaxSKh9I" colab_type="code" colab={}
def plot_img_results(array, true, pred, i, n=1):
# plot the image and the target for sample i
ncols = 5
nrows = n/ncols + 1
fig = plt.figure( figsize=(ncols*1.5, nrows*1.5), dpi=90)
for j in range(n):
index = j+i
plt.subplot(nrows,ncols, j+1)
plt.imshow(array[index])
plt.title('true: {} pred: {}'.format(true[index], pred[index]))
plt.axis('off')
# + id="DvtD2-CZKk4y" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="ef03619b-5748-49bb-e870-b7df0d31a456"
plot_img_results(mispred_img, mispred_true, mispred_pred, 0, len(mispred_img))
|
Week 5/Misclassification_of_images.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# ---
# # 多尺度目标检测
#
# 在[“锚框”](anchor.md)一节中,我们在实验中以输入图像的每个像素为中心生成多个锚框。这些锚框是对输入图像不同区域的采样。然而,如果以图像每个像素为中心都生成锚框,很容易生成过多锚框而造成计算量过大。举个例子,假设输入图像的高和宽分别为561和728像素,如果以每个像素为中心生成5个不同形状的锚框,那么一张图像上则需要标注并预测两百多万个锚框($561 \times 728 \times 5$)。
#
# 减少锚框个数并不难。一个简单的方法是在输入图像中均匀采样一小部分像素,并以采样的像素为中心生成锚框。此外,在不同尺度下,我们可以生成不同数量和不同大小的锚框。值得注意的是,较小目标比较大目标在图像上出现位置的可能性更多。举个简单的例子:形状为$1 \times 1$、$1 \times 2$和$2 \times 2$的目标在形状为$2 \times 2$的图像上可能出现的位置分别有4、2和1种。因此,当使用较小锚框来检测较小目标时,我们可以采样较多的区域;而当使用较大锚框来检测较大目标时,我们可以采样较少的区域。
#
# 为了演示如何多尺度生成锚框,我们先读取一张图像。它的高和宽分别为561和728像素。
# + attributes={"classes": [], "id": "", "n": "1"}
# %matplotlib inline
import d2lzh as d2l
from mxnet import contrib, image, nd
img = image.imread('../img/catdog.jpg')
h, w = img.shape[0:2]
h, w
# -
# 我们在[“二维卷积层”](../chapter_convolutional-neural-networks/conv-layer.md)一节中将卷积神经网络的二维数组输出称为特征图。
# 我们可以通过定义特征图的形状来确定任一图像上均匀采样的锚框中心。
#
# 下面定义`display_anchors`函数。我们在特征图`fmap`上以每个单元(像素)为中心生成锚框`anchors`。由于锚框`anchors`中$x$和$y$轴的坐标值分别已除以特征图`fmap`的宽和高,这些值域在0和1之间的值表达了锚框在特征图中的相对位置。由于锚框`anchors`的中心遍布特征图`fmap`上的所有单元,`anchors`的中心在任一图像的空间相对位置一定是均匀分布的。具体来说,当特征图的宽和高分别设为`fmap_w`和`fmap_h`时,该函数将在任一图像上均匀采样`fmap_h`行`fmap_w`列个像素,并分别以它们为中心生成大小为`s`(假设列表`s`长度为1)的不同宽高比(`ratios`)的锚框。
# + attributes={"classes": [], "id": "", "n": "2"}
d2l.set_figsize()
def display_anchors(fmap_w, fmap_h, s):
fmap = nd.zeros((1, 10, fmap_w, fmap_h)) # 前两维的取值不影响输出结果
anchors = contrib.nd.MultiBoxPrior(fmap, sizes=s, ratios=[1, 2, 0.5])
bbox_scale = nd.array((w, h, w, h))
d2l.show_bboxes(d2l.plt.imshow(img.asnumpy()).axes,
anchors[0] * bbox_scale)
# -
# 我们先关注小目标的检测。为了在显示时更容易分辨,这里令不同中心的锚框不重合:设锚框大小为0.15,特征图的高和宽分别为4。可以看出,图像上4行4列的锚框中心分布均匀。
# + attributes={"classes": [], "id": "", "n": "3"}
display_anchors(fmap_w=4, fmap_h=4, s=[0.15])
# -
# 我们将特征图的高和宽分别减半,并用更大的锚框检测更大的目标。当锚框大小设0.4时,有些锚框的区域有重合。
# + attributes={"classes": [], "id": "", "n": "4"}
display_anchors(fmap_w=2, fmap_h=2, s=[0.4])
# -
# 最后,我们将特征图的高和宽进一步减半至1,并将锚框大小增至0.8。此时锚框中心即图像中心。
# + attributes={"classes": [], "id": "", "n": "5"}
display_anchors(fmap_w=1, fmap_h=1, s=[0.8])
# -
# 既然我们已在多个尺度上生成了不同大小的锚框,相应地,我们需要在不同尺度下检测不同大小的目标。下面我们来介绍一种基于卷积神经网络的方法。
#
# 在某个尺度下,假设我们依据$c_i$张形状为$h \times w$的特征图生成$h \times w$组不同中心的锚框,且每组的锚框个数为$a$。例如在刚才实验的第一个尺度下,我们依据10(通道数)张形状为$4 \times 4$的特征图生成了16组不同中心的锚框,且每组含3个锚框。
# 接下来,依据真实边界框的类别和位置,每个锚框将被标注类别和偏移量。在当前的尺度下,目标检测模型需要根据输入图像预测$h \times w$组不同中心的锚框的类别和偏移量。
#
# 假设这里的$c_i$张特征图为卷积神经网络根据输入图像做前向计算所得的中间输出。既然每张特征图上都有$h \times w$个不同的空间位置,那么相同空间位置可以看作含有$c_i$个单元。
# 根据[“二维卷积层”](../chapter_convolutional-neural-networks/conv-layer.md)一节中感受野的定义,特征图在相同空间位置的$c_i$个单元在输入图像上的感受野相同,并表征了同一感受野内的输入图像信息。
# 因此,我们可以将特征图在相同空间位置的$c_i$个单元变换为以该位置为中心生成的$a$个锚框的类别和偏移量。
# 不难发现,本质上,我们用输入图像在某个感受野区域内的信息来预测输入图像上与该区域位置相近的锚框的类别和偏移量。
#
# 当不同层的特征图在输入图像上分别拥有不同大小的感受野时,它们将分别用来检测不同大小的目标。例如,我们可以通过设计网络,令较接近输出层的特征图中每个单元拥有更广阔的感受野,从而检测输入图像中更大尺寸的目标。
#
# 我们将在后面的小节具体实现一个多尺度目标检测的模型。
#
#
# ## 小结
#
# * 我们可以在多个尺度下生成不同数量不同大小的锚框,从而在多个尺度下检测不同大小的目标。
# * 特征图的形状能确定任一图像上均匀采样的锚框中心。
# * 我们用输入图像在某个感受野区域内的信息来预测输入图像上与该区域相近的锚框的类别和偏移量。
#
#
# ## 练习
#
# * 给定一张输入图像,设特征图变量的形状为$1 \times c_i \times h \times w$,其中$c_i, h, w$分别为特征图的个数、高和宽。你能想到哪些将该变量变换为锚框的类别和偏移量的方法?输出的形状分别是什么?
#
#
# ## 扫码直达[讨论区](https://discuss.gluon.ai/t/topic/8859)
#
# 
|
chapter_computer-vision/multiscale-object-detection.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# - NVIDIA GeForce GTX 1060 6GB
# - Pytorch 1.4.0
# - model EfficientNet-B3
# - image size 128x128
# - batch size 64
# - 0-folds
# - 10 epochs
# - augmentation rotate 4.5
# - optimizer over 9000
# - one cycle learning rate
# +
# %reload_ext autoreload
# %autoreload 2
# %matplotlib inline
import os
import gc
import cv2
import numpy as np
from numpy import random
import pandas as pd
import matplotlib.pyplot as plt
from pathlib import Path
from tqdm.notebook import tqdm
import torch
import warnings
warnings.filterwarnings("ignore")
from crop_resize import read_feathers
# +
model_name = 'efficientnet-b3'
pretrained_model_name = './20200308_fold0_no_aug_0-1/efficientnet-b3_29.pth'
image_size = 128
batch_size = 64
random_state = 2020
n_epochs = 20
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
print(device)
in_dir = Path('../input/bengaliai-cv19')
feather_dir = Path('../input/bengaliai-cv19-feather')
out_dir = Path('./20200311_cutmix')
# +
def seed_everything(seed):
random.seed(seed)
os.environ['PYTHONHASHSEED'] = str(seed)
np.random.seed(seed)
torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = True
SEED = 2020
seed_everything(SEED)
# -
# <a id="images"></a>
# # Images
filenames = [feather_dir/f'train_image_data_1x{image_size}x{image_size}_{i}.feather' for i in range(4)]
images = read_feathers(filenames, image_size)
print(images.shape)
# <a id="labels"></a>
# # Labels
train_label = pd.read_csv(in_dir/'train.csv')
labels = train_label[['grapheme_root', 'vowel_diacritic', 'consonant_diacritic']].values
print(labels.shape)
# <a id="dataset"></a>
# # Dataset
# +
from torch.utils.data import Dataset
class GraphemeDataset(Dataset):
def __init__(self, images, labels=None, transform=None):
self.images = images
self.labels = labels
self.transform = transform
self.train = labels is not None
def __len__(self):
return len(self.images)
def __getitem__(self, idx):
image = self.images[idx]
image = image / image.max()
if self.transform:
image_size = image.shape[1]
image = self.transform(image=image[0])['image']
image = image.reshape(-1, image_size, image_size)
if self.train:
label = self.labels[idx]
return image, label[0], label[1], label[2]
else:
return image
# -
train_dataset = GraphemeDataset(images, labels)
print(len(train_dataset))
# <a id="visualize"></a>
# # Visualize
nrow, ncol = 2, 6
fig, axes = plt.subplots(nrow, ncol, figsize=(12, 3))
axes = axes.flatten()
for i, ax in enumerate(axes):
image, label1, label2, label3 = train_dataset[i]
ax.imshow(image[0], cmap='Greys')
ax.set_title(f'label: {label1, label2, label3}')
plt.tight_layout()
plt.show()
# <a id="dataloader"></a>
# # DataLoader
# +
from torch.utils.data import DataLoader
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
print('train loader length', len(train_loader))
# -
# <a id="cutmix"></a>
# # Cutmix
# +
from mix_augmentations import cutmix
testloader = iter(train_loader)
inputs, labels1, labels2, labels3 = testloader.next()
mixed_data, _, _, _, _ = cutmix(inputs, labels1, labels2, labels3, 1.0)
nrow, ncol = 2, 6
fig, axes = plt.subplots(nrow, ncol, figsize=(12, 3))
axes = axes.flatten()
for i, ax in enumerate(axes):
ax.imshow(mixed_data[i][0], cmap='Greys')
ax.set_title(f'label: {labels1[i].item(), labels2[i].item(), labels3[i].item()}')
plt.tight_layout()
plt.show()
# -
# <a id="model"></a>
# # Model
# +
from my_efficientnet_pytorch import EfficientNet
model = EfficientNet.from_pretrained(model_name, in_channels=1).to(device)
model.load_state_dict(torch.load(pretrained_model_name))
# -
# <a id="optimizer"></a>
# # Optimizer
# +
from optimizer.ralamb import Ralamb
from optimizer.lookahead import Lookahead
def Over9000(params, alpha=0.5, k=6, *args, **kwargs):
ralamb = Ralamb(params, *args, **kwargs)
return Lookahead(ralamb, alpha, k)
# +
optimizer =Over9000(model.parameters(), lr=2e-3, weight_decay=1e-3)
scheduler = torch.optim.lr_scheduler.OneCycleLR(optimizer, max_lr=1e-2, total_steps=None, epochs=n_epochs,
steps_per_epoch=len(train_loader), pct_start=0.0, anneal_strategy='cos',
cycle_momentum=True, base_momentum=0.85, max_momentum=0.95, div_factor=100.0)
# -
# <a id="loss"></a>
# # loss
# +
from torch import nn
from mix_augmentations import mixup_criterion
criterion = nn.CrossEntropyLoss()
# -
# <a id="metrics"></a>
# # Metrics
from metrics import macro_recall_multi
from mix_augmentations import mix_recall_multi
# <a id="train"></a>
# # Train
# +
history = pd.DataFrame()
for epoch in range(n_epochs):
# --- training start ---
torch.cuda.empty_cache()
gc.collect()
running_loss1, running_loss2, running_loss3 = 0.0, 0.0, 0.0
running_acc1, running_acc2, running_acc3 = 0.0, 0.0, 0.0
running_recall = 0.0
train_loss1, train_loss2, train_loss3 = 0.0, 0.0, 0.0
train_acc1, train_acc2, train_acc3 = 0.0, 0.0, 0.0
train_loss, train_acc, train_recall = 0.0, 0.0, 0.0
model.train()
# training loop
for idx, (inputs, labels1, labels2, labels3) in tqdm(enumerate(train_loader), total=len(train_loader)):
# to GPU
inputs, labels1, labels2, labels3 = inputs.float().to(device), labels1.to(device), labels2.to(device), labels3.to(device)
if np.random.rand() <= 0.5:
# cutmix
mixed_inputs, sh_labels1, sh_labels2, sh_labels3, lam = cutmix(inputs, labels1, labels2, labels3, 1.0)
# to GPU
mixed_inputs = mixed_inputs.float().to(device)
sh_labels1, sh_labels2, sh_labels3 = sh_labels1.to(device), sh_labels2.to(device), sh_labels3.to(device)
# zero the parameter gradients
optimizer.zero_grad()
# forward (on GPU)
outputs1, outputs2, outputs3 = model(mixed_inputs)
# loss
loss1 = lam * criterion(outputs1, labels1) + (1 - lam) * criterion(outputs1, sh_labels1)
loss2 = lam * criterion(outputs2, labels2) + (1 - lam) * criterion(outputs2, sh_labels2)
loss3 = lam * criterion(outputs3, labels3) + (1 - lam) * criterion(outputs3, sh_labels3)
running_loss1 += loss1.item()
running_loss2 += loss2.item()
running_loss3 += loss3.item()
# accuracy
running_acc1 += lam * (outputs1.argmax(1)==labels1).float().mean() + (1 - lam) * (outputs1.argmax(1)==sh_labels1).float().mean()
running_acc2 += lam * (outputs2.argmax(1)==labels2).float().mean() + (1 - lam) * (outputs2.argmax(1)==sh_labels2).float().mean()
running_acc3 += lam * (outputs3.argmax(1)==labels3).float().mean() + (1 - lam) * (outputs3.argmax(1)==sh_labels3).float().mean()
# recall
running_recall += mix_recall_multi(outputs1, labels1, sh_labels1, outputs2, labels2, sh_labels2, outputs3, labels3, sh_labels3, lam)
# backward (on GPU)
(0.8 * loss1 + 0.1 * loss2 + 0.1 * loss3).backward()
else:
# zero the parameter gradients
optimizer.zero_grad()
# forward (on GPU)
outputs1, outputs2, outputs3 = model(inputs)
# loss
loss1 = criterion(outputs1, labels1)
loss2 = criterion(outputs2, labels2)
loss3 = criterion(outputs3, labels3)
running_loss1 += loss1.item()
running_loss2 += loss2.item()
running_loss3 += loss3.item()
# accuracy
running_acc1 += (outputs1.argmax(1)==labels1).float().mean()
running_acc2 += (outputs2.argmax(1)==labels2).float().mean()
running_acc3 += (outputs3.argmax(1)==labels3).float().mean()
# recall
running_recall += macro_recall_multi(outputs1, labels1, outputs2, labels2, outputs3, labels3)
# backward (on GPU)
(0.8 * loss1 + 0.1 * loss2 + 0.1 * loss3).backward()
# optimize
optimizer.step()
scheduler.step()
# loss, accuracy, recall
train_loss1 = running_loss1 / len(train_loader)
train_loss2 = running_loss2 / len(train_loader)
train_loss3 = running_loss3 / len(train_loader)
train_loss = 0.5 * train_loss1 + 0.25 * train_loss2 + 0.25 * train_loss3
train_acc1 = running_acc1 / len(train_loader)
train_acc2 = running_acc2 / len(train_loader)
train_acc3 = running_acc3 / len(train_loader)
train_acc = (train_acc1 + train_acc2 + train_acc3) / 3
train_recall = running_recall / len(train_loader)
# log
print('train epoch : {}'.format(epoch))
print('loss : {:.4f}, loss1 : {:.4f}, loss2 : {:.4f}, loss3 : {:.4f}'.format(train_loss, train_loss1, train_loss2, train_loss3))
print('acc : {:.4f}, acc1 : {:.4f}, acc2 : {:.4f}, acc3 : {:.4f}'.format(train_acc, train_acc1, train_acc2, train_acc3))
print('recall : {:.4f}'.format(train_recall))
# history
history.loc[epoch, 'train/loss'] = train_loss
history.loc[epoch, 'train/loss1'] = train_loss1
history.loc[epoch, 'train/loss2'] = train_loss2
history.loc[epoch, 'train/loss3'] = train_loss3
history.loc[epoch, 'train/acc'] = train_acc.cpu().numpy()
history.loc[epoch, 'train/acc1'] = train_acc1.cpu().numpy()
history.loc[epoch, 'train/acc2'] = train_acc2.cpu().numpy()
history.loc[epoch, 'train/acc3'] = train_acc3.cpu().numpy()
history.loc[epoch, 'train/recall'] = train_recall
history.loc[epoch, 'lr'] = scheduler.get_lr()[0]
torch.save(model.state_dict(), out_dir/f'{model_name}_{epoch}.pth')
history.to_csv(out_dir/'history.csv')
# -
history
# <a id="inference"></a>
# # Inference
# +
from crop_resize import read_parquets
height = 137
width = 236
image_size = 128
filenames = [in_dir/f'test_image_data_{i}.parquet' for i in range(4)]
images = read_parquets(filenames, width, height, image_size)
test_dataset = GraphemeDataset(images)
test_loader = torch.utils.data.DataLoader(test_dataset, batch_size=1, shuffle=False)
# +
row_id = []
target = []
model.eval()
with torch.no_grad():
for idx, inputs in tqdm(enumerate(test_loader), total=len(test_loader)):
inputs = inputs.float().cuda()
outputs1, outputs2, outputs3 = model(inputs)
p1 = outputs1.argmax(-1).view(-1).cpu()
p2 = outputs2.argmax(-1).view(-1).cpu()
p3 = outputs3.argmax(-1).view(-1).cpu()
row_id += [f'Test_{idx}_grapheme_root', f'Test_{idx}_vowel_diacritic', f'Test_{idx}_consonant_diacritic']
target += [p1.item(), p2.item(), p3.item()]
sub_df = pd.DataFrame({'row_id': row_id, 'target': target})
sub_df.to_csv(out_dir/'submission.csv', index=False)
sub_df
# -
exit()
|
2019/bengaliai-cv19/20200311_train_effnet-b3_cutmix.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import scanpy.api as sc
import numpy as np
import pandas as pd
import bbknn
import time
sc.settings.verbosity = 3 # verbosity: errors (0), warnings (1), info (2), hints (3)
# -
# Perform the actual BBKNN with faiss benchmark. Import the PCA, create a batch vector matching what was in R, run the same BBKNN function, except with faiss. When done, write the times out in the same manner as well.
# +
faiss_time = []
for i in np.arange(10,19):
pca = np.load('pca'+str(i)+'.npy')
batch = ['a']*2**i + ['b']*2**i
t1 = time.time()
bbknn.bbknn_pca_matrix(pca=pca,batch_list=batch,approx=False)
t2 = time.time()
faiss_time.append(t2-t1)
with open('benchmark-times/faiss.txt','w') as fid:
fid.writelines([str(i)+'\n' for i in faiss_time])
# -
# Time for plotting. Use the scanpy plot configuration as it's nice.
# +
import matplotlib.pyplot as plt
sc.settings.set_figure_params(dpi=80) # low dpi (dots per inch) yields small inline figures
# -
# Read in the run times from the files created along the way.
times = {}
for alg in ['annoy','bbknn','cca','faiss','harmony','mnn','scanorama']:
times[alg] = pd.read_table('benchmark-times/'+alg+'.txt',header=None).values
# +
fig = plt.figure(figsize=(6,4))
ax = plt.subplot(111)
plt.plot(2**np.arange(11,20),times['bbknn'])
plt.plot(2**np.arange(11,20),times['annoy'])
plt.plot(2**np.arange(11,20),times['faiss'])
plt.plot(2**np.arange(11,20),times['harmony'])
plt.plot(2**np.arange(11,16),times['scanorama'])
plt.plot(2**np.arange(11,16),times['cca'])
plt.plot(2**np.arange(11,16),times['mnn'])
ax.set_xscale('log', basex=2)
ax.set_yscale('log', basey=10)
plt.xlabel('Total cells in dataset')
plt.ylabel('Run time (seconds)')
box = ax.get_position()
ax.set_position([box.x0, box.y0, box.width * 0.8, box.height])
ax.legend(['BBKNN (cKDTree)','BBKNN (annoy)','BBKNN (faiss)',
'Harmony','Scanorama','RunCCA','mnnCorrect'], loc='center left', bbox_to_anchor=(1, 0.5))
plt.show()
|
examples/benchmark2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python2.7
# language: python
# name: python2.7
# ---
import keras
from keras.models import load_model
import coremltools
import PIL
import requests
from io import BytesIO
import json
keras_model = load_model('zoo/09.3 retrained pet recognizer.h5')
class_labels = json.load(open('zoo/09.3 pet_labels.json'))
coreml_model = coremltools.converters.keras.convert(keras_model,
image_input_names="input_1",
input_names='input_1',
class_labels=class_labels,
is_bgr=True,
image_scale=1/255.)
coreml_model.save('zoo/PetRecognizer3.mlmodel')
img_url = 'https://upload.wikimedia.org/wikipedia/commons/9/93/Golden_Retriever_Carlos_%2810581910556%29.jpg'
response = requests.get(img_url)
img = PIL.Image.open(BytesIO(response.content))
img
dir(coreml_model)
dir(coreml_model.input_description)
class_labels
|
16.3 Prepare model for iOS.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python (deepcell)
# language: python
# name: deepcell
# ---
# # Fully Convolutional Interior/Edge Segmentation for 2D Data
#
# ---
#
# Classifies each pixel as either Cell Edge, Cell Interior, or Background.
#
# There are 2 different Cell Edge classes (Cell-Cell Boundary and Cell-Background Boundary)
# +
import os
import errno
import numpy as np
import deepcell
# -
# ### Load the training data
# +
# Download the data (saves to ~/.keras/datasets)
filename = 'HeLa_S3.npz'
(X_train, y_train), (X_test, y_test) = deepcell.datasets.hela_s3.load_data(filename)
print('X.shape: {}\ny.shape: {}'.format(X_train.shape, y_train.shape))
# -
# ### Set up filepath constants
# +
# the path to the data file is currently required for `train_model_()` functions
# NOTE: Change DATA_DIR if you are not using `deepcell.datasets`
DATA_DIR = os.path.expanduser(os.path.join('~', '.keras', 'datasets'))
DATA_FILE = os.path.join(DATA_DIR, filename)
# confirm the data file is available
assert os.path.isfile(DATA_FILE)
# -
print(DATA_FILE)
# +
# Set up other required filepaths
# If the data file is in a subdirectory, mirror it in MODEL_DIR and LOG_DIR
PREFIX = os.path.relpath(os.path.dirname(DATA_FILE), DATA_DIR)
ROOT_DIR = '/home/ebouilhol/Document/caltech' # TODO: Change this! Usually a mounted volume
MODEL_DIR = os.path.abspath(os.path.join(ROOT_DIR, 'models', PREFIX))
LOG_DIR = os.path.abspath(os.path.join(ROOT_DIR, 'logs', PREFIX))
# create directories if they do not exist
for d in (MODEL_DIR, LOG_DIR):
try:
os.makedirs(d)
except OSError as exc: # Guard against race condition
if exc.errno != errno.EEXIST:
raise
# -
# ### Set up training parameters
# +
from tensorflow.keras.optimizers import SGD
from deepcell.utils.train_utils import rate_scheduler
fgbg_model_name = 'conv_fgbg_model'
conv_model_name = 'conv_edgeseg_model'
n_epoch = 3 # Number of training epochs
test_size = .10 # % of data saved as test
norm_method = 'std' # data normalization
receptive_field = 61 # should be adjusted for the scale of the data
optimizer = SGD(lr=0.01, decay=1e-6, momentum=0.9, nesterov=True)
lr_sched = rate_scheduler(lr=0.01, decay=0.99)
# FC training settings
n_skips = 3 # number of skip-connections (only for FC training)
batch_size = 1 # FC training uses 1 image per batch
# Transformation settings
transform = 'deepcell'
dilation_radius = 1 # change dilation radius for edge dilation
n_features = 4 # (cell-background edge, cell-cell edge, cell interior, background)
# -
# ### First, create a foreground/background separation model
#
# #### Instantiate the fgbg model
# +
from deepcell import model_zoo
fgbg_model = model_zoo.bn_feature_net_skip_2D(
n_features=2, # segmentation mask (is_cell, is_not_cell)
receptive_field=receptive_field,
n_skips=n_skips,
n_conv_filters=32,
n_dense_filters=128,
input_shape=tuple(X_train.shape[1:]),
last_only=False)
# -
# #### Train the model fgbg model
# +
from deepcell.training import train_model_conv
fgbg_model = train_model_conv(
model=fgbg_model,
dataset=DATA_FILE, # full path to npz file
model_name=fgbg_model_name,
test_size=test_size,
optimizer=optimizer,
n_epoch=n_epoch,
batch_size=batch_size,
transform='fgbg',
model_dir=MODEL_DIR,
log_dir=LOG_DIR,
lr_sched=lr_sched,
rotation_range=180,
flip=True,
shear=False,
zoom_range=(0.8, 1.2))
# -
# ### Next, Create a model for the edge/interior segmentation
#
# #### Instantiate the segmentation transform model
# +
from deepcell import model_zoo
conv_model = model_zoo.bn_feature_net_skip_2D(
fgbg_model=fgbg_model,
receptive_field=receptive_field,
n_skips=n_skips,
n_features=n_features,
norm_method=norm_method,
n_conv_filters=32,
n_dense_filters=128,
last_only=False,
input_shape=tuple(X_train.shape[1:]))
# -
# #### Train the segmentation transform model
# +
from deepcell.training import train_model_conv
conv_model = train_model_conv(
model=conv_model,
dataset=DATA_FILE, # full path to npz file
model_name=conv_model_name,
test_size=test_size,
transform=transform,
dilation_radius=dilation_radius,
optimizer=optimizer,
batch_size=batch_size,
n_epoch=n_epoch,
log_dir=LOG_DIR,
model_dir=MODEL_DIR,
lr_sched=lr_sched,
rotation_range=180,
flip=True,
shear=False,
zoom_range=(0.8, 1.2))
# -
# ### Run the model
#
# #### Make predictions on test data
# +
test_images = conv_model.predict(X_test)[-1]
test_images_fgbg = fgbg_model.predict(X_test)[-1]
print('watershed transform shape:', test_images.shape)
print('segmentation mask shape:', test_images_fgbg.shape)
# -
# #### Post-processing
# +
# threshold the foreground/background
# and remove back ground from edge transform
threshold = 0.9
fg_thresh = test_images_fgbg[..., 1] > threshold
fg_thresh = np.expand_dims(fg_thresh, axis=-1)
test_images_post_fgbg = test_images * fg_thresh
# +
# Label interior predictions
from skimage.measure import label
from skimage import morphology
labeled_images = []
for i in range(test_images_post_fgbg.shape[0]):
interior = test_images_post_fgbg[i, ..., 2] > .2
labeled_image = label(interior)
labeled_image = morphology.remove_small_objects(
labeled_image, min_size=50, connectivity=1)
labeled_images.append(labeled_image)
labeled_images = np.array(labeled_images)
labeled_images = np.expand_dims(labeled_images, axis=-1)
print('labeled_images shape:', labeled_images.shape)
# +
import matplotlib.pyplot as plt
index = np.random.randint(low=0, high=X_test.shape[0])
print('Image number:', index)
fig, axes = plt.subplots(ncols=3, nrows=2, figsize=(15, 15), sharex=True, sharey=True)
ax = axes.ravel()
ax[0].imshow(X_test[index, ..., 0])
ax[0].set_title('Source Image')
ax[1].imshow(test_images_fgbg[index, ..., 1])
ax[1].set_title('Segmentation Prediction')
ax[2].imshow(fg_thresh[index, ..., 0], cmap='jet')
ax[2].set_title('FGBG Threshold {}%'.format(threshold * 100))
ax[3].imshow(test_images[index, ..., 0] + test_images[index, ..., 1], cmap='jet')
ax[3].set_title('Edge Prediction')
ax[4].imshow(test_images[index, ..., 2], cmap='jet')
ax[4].set_title('Interior Prediction')
ax[5].imshow(labeled_images[index, ..., 0], cmap='jet')
ax[5].set_title('Instance Segmentation')
fig.tight_layout()
plt.show()
# -
|
scripts/deepcell/Interior-Edge Segmentation 2D Fully Convolutional.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="7d3Tf3AXkKwz"
# # Exploring the Composition of the Dataset
# The notebook explores the composition of the dataset to get a better understanding of the number of measurements and identify potential class imbalances.
#
#
# -
# Plot graphs inline
# %matplotlib inline
# + [markdown] colab_type="text" id="pJdeqo2c_zZI"
# ## Notebook Setup
# + colab={} colab_type="code" id="h-6B7f68kJlc"
import os
# CoLab
if os.getcwd() == '/content':
from google.colab import drive
drive.mount('/content/gdrive')
BASE_PATH = '/content/gdrive/My Drive/Level-4-Project/'
os.chdir('gdrive/My Drive/Level-4-Project/')
# Laptop
elif os.getcwd() == 'D:\\Google Drive\\Level-4-Project\\notebooks':
BASE_PATH = "D:/Google Drive/Level-4-Project/"
# GPU cluster
else:
BASE_PATH = "/export/home/2192793m/Level-4-Project/"
RAW_PATH = BASE_PATH + 'data/raw/'
RESULTS_PATH = BASE_PATH + "results/dataset_composition_analysis/"
if not os.path.exists(RESULTS_PATH):
os.makedirs(RESULTS_PATH)
# + colab={} colab_type="code" id="PmGlJWMpkJlo"
import pandas as pd
import matplotlib.pyplot as plt
# + colab={} colab_type="code" id="jENpKKCcvscE"
SAVE_GRAPHS = False # Set to true to allow overriding of graphs
# + [markdown] colab_type="text" id="klVUBneIyAiT"
# The following cell contains functions to be applied to every row in a particular column of the dataframe.
# + colab={} colab_type="code" id="TWXeNXTUvscI"
def find_label(movement):
"""
Convert movement description to one word label
:param movement: movement description from experiment notes
:type movement: str
:return: one word label
:rtype: str
"""
if movement == "Walking":
return "walking"
if movement == "Moving arm faster towards radar, slower away":
return "pushing"
if movement == "Sitting and standing":
return "sitting"
if movement == "Moving arm slower towards radar, faster away":
return "pulling"
if movement == "Circling arm forwards":
return "circling"
if movement == "Clapping":
return "clapping"
if movement == "Bending to pick up and back up":
return "bending"
def identify_angle(angle):
"""
Strips " deg" from input
For example:
"0 deg" would return "0"
:param angle: angle in format "0 deg"
:type angle: str
:return: angle
:rtype: str
"""
return angle.split()[0]
def is_on_place(angle):
"""
Identifies if measurement has "on place" flag for it's aspect angle
:param angle: angle in format "0 deg"
:type angle: str
:return: if angle measurement is "on place"
:rtype: bool
"""
if len(angle.split()) > 2:
return True
return False
def assign_user_label(name):
"""
Takes in subjects name and returns a letter to represent that subject
:param name:
:type name: str
:return: Letter to represent subject
:rtype: str
"""
if name == "Aleksandar":
return "A"
if name == "Francesco":
return "B"
if name == "Nadezhda":
return "C"
if name == "Leila":
return "D"
if name == "Hadi":
return "E"
if name == "Ivelina":
return "F"
# -
# Load in the data labels and convert columns to suitable formats
# + colab={} colab_type="code" id="bLv3Yv6xkJl0"
df_labels = pd.read_csv(RAW_PATH + 'Labels.csv')
df_labels.rename(columns={'dataset ID': 'dataset_id'}, inplace=True)
df_labels["label"] = df_labels.movement.apply(find_label)
df_labels["user_label"] = df_labels.person.apply(assign_user_label)
df_labels["aspect_angle"] = df_labels.angle.apply(identify_angle)
df_labels["on_place"] = df_labels.angle.apply(is_on_place)
# + [markdown] colab_type="text" id="kvLJcKLgLEd6"
# ## The Dataset
# + colab={"base_uri": "https://localhost:8080/", "height": 1895} colab_type="code" executionInfo={"elapsed": 488, "status": "ok", "timestamp": 1546962279123, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/-24hiGmdxZDE/AAAAAAAAAAI/AAAAAAAAL_I/RW7nqM11LkM/s64/photo.jpg", "userId": "06804410358976473893"}, "user_tz": 0} id="IVQABSrsIpOV" outputId="c96ff7bb-152a-4416-f361-86341457f097"
df_labels[['dataset_id', 'label', 'user_label', 'aspect_angle']]
# + [markdown] colab_type="text" id="U8UbpQ_ALI2C"
# ## Measurements per Subject
# Includes measurements from different aspect angles
# + colab={"base_uri": "https://localhost:8080/", "height": 390} colab_type="code" executionInfo={"elapsed": 546, "status": "ok", "timestamp": 1546962800151, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/-24hiGmdxZDE/AAAAAAAAAAI/AAAAAAAAL_I/RW7nqM11LkM/s64/photo.jpg", "userId": "06804410358976473893"}, "user_tz": 0} id="3NiHfZx6JnxP" outputId="5174aa5a-c8f1-4955-efad-fb2fe0ca0406"
df_labels.groupby(['user_label'])['dataset_id'].count().plot(kind='bar', zorder=3)
plt.title("Number of Measurements per Subject")
plt.xlabel("Subject")
plt.ylabel("Number of Measurements")
plt.grid(axis='y', zorder=0)
plt.xticks(rotation=0)
if SAVE_GRAPHS:
plt.savefig(RESULTS_PATH + "measurements_per_subject.pdf", format='pdf')
plt.show()
# + [markdown] colab_type="text" id="lEFTia0JLNFo"
# ## Measurements per Action
# Includes measurements from different aspect angles
# + colab={"base_uri": "https://localhost:8080/", "height": 420} colab_type="code" executionInfo={"elapsed": 538, "status": "ok", "timestamp": 1546962804917, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/-24hiGmdxZDE/AAAAAAAAAAI/AAAAAAAAL_I/RW7nqM11LkM/s64/photo.jpg", "userId": "06804410358976473893"}, "user_tz": 0} id="VKBBnLTZKUSL" outputId="8afb3977-a3f9-4d1f-aac2-91b77a5f5a85"
df_labels.groupby(['label'])['dataset_id'].count().plot(kind='bar', zorder=3)
plt.title("Number of Measurements per Action")
plt.xlabel("Action")
plt.ylabel("Number of Measurements")
plt.grid(axis='y', zorder=0)
if SAVE_GRAPHS:
plt.savefig(RESULTS_PATH + "measurements_per_action.pdf", format='pdf')
plt.show()
# + [markdown] colab_type="text" id="saMDt8GfLPyg"
# ## Measurements per Aspect Angle (Degrees)
# + colab={"base_uri": "https://localhost:8080/", "height": 393} colab_type="code" executionInfo={"elapsed": 595, "status": "ok", "timestamp": 1546962828099, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/-24hiGmdxZDE/AAAAAAAAAAI/AAAAAAAAL_I/RW7nqM11LkM/s64/photo.jpg", "userId": "06804410358976473893"}, "user_tz": 0} id="1O6_Kf0VKy2Q" outputId="a3cb06fb-b6ac-4174-8cea-be60731f64cd"
df_labels.groupby(['aspect_angle'])['dataset_id'].count().plot(kind='bar', zorder=3)
plt.title("Number of Measurements per Aspect Angle")
plt.xlabel("Aspect Angle (°)")
plt.ylabel("Number of Measurements")
plt.grid(axis='y', zorder=0)
plt.xticks(rotation=0)
if SAVE_GRAPHS:
plt.savefig(RESULTS_PATH + "measurements_per_aspect_angle.pdf", format='pdf')
plt.show()
# + [markdown] colab_type="text" id="QKZhI_AELkeU"
# ## Measurements per Subject and Aspect Angle
# It appears that users C, D, E and F only have data for zero degrees
# + colab={"base_uri": "https://localhost:8080/", "height": 412} colab_type="code" executionInfo={"elapsed": 713, "status": "ok", "timestamp": 1546964110891, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/-24hiGmdxZDE/AAAAAAAAAAI/AAAAAAAAL_I/RW7nqM11LkM/s64/photo.jpg", "userId": "06804410358976473893"}, "user_tz": 0} id="9jbtAhgvLjbS" outputId="83ad64e7-d2bc-4a71-85cb-8a74c0d6ba3e"
df_labels.groupby(['user_label', 'aspect_angle'])['dataset_id'].count().plot(kind='bar', zorder=3)
plt.title("Number of Measurements per Subject")
plt.xlabel("Subject + Aspect Angle (°)")
plt.ylabel("Number of Measurements")
plt.grid(axis='y', zorder=0)
if SAVE_GRAPHS:
plt.savefig(RESULTS_PATH + "measurements_per_subject_and_aspect_angle.pdf", format='pdf')
plt.show()
# + [markdown] colab_type="text" id="BZvhXupTvsc2"
# ## Subject Comparison for 0° Aspect Angle
# + colab={} colab_type="code" id="fkUHVsBRvsc3"
zero_degrees = df_labels.loc[df_labels["aspect_angle"] == '0']
# + colab={} colab_type="code" id="JS3gpEmNvsc6" outputId="0236152f-2520-47c2-e4b6-dabd367c12ce"
zero_degrees.groupby(['user_label'])['dataset_id'].count().plot(kind='bar', zorder=3)
plt.title("Number of Measurements per Subject for 0° Aspect Angle ")
plt.xlabel("Subject")
plt.ylabel("Number of Measurements")
plt.xticks(rotation=0)
plt.grid(axis='y', zorder=0)
if SAVE_GRAPHS:
plt.savefig(RESULTS_PATH + "measurements_per_subject_at_0_aspect_angle.pdf", format='pdf')
plt.show()
# + colab={} colab_type="code" id="Px-y_-u0vsdA" outputId="dc814adf-9225-42b2-c13d-7a5276d5f70c"
zero_degrees.groupby(['user_label', 'label'])['dataset_id'].count().plot(kind='bar', zorder=3)
plt.title("Number of Measurements per Subject for 0° Aspect Angle ")
plt.xlabel("Subject")
plt.ylabel("Number of Measurements")
plt.xticks(rotation=90)
plt.grid(axis='y', zorder=0)
if SAVE_GRAPHS:
plt.savefig(RESULTS_PATH + "measurements_per_subject_at_0_aspect_angle.pdf", format='pdf')
plt.tight_layout()
plt.show()
# + [markdown] colab_type="text" id="PmnYdJz2MKWY"
# ## Analysis of Test Subject C
# Classes are balanced
# + colab={} colab_type="code" id="8cTXgkalNBIv"
user_c = df_labels.loc[df_labels["user_label"] == "C", :]
# + colab={"base_uri": "https://localhost:8080/", "height": 420} colab_type="code" executionInfo={"elapsed": 506, "status": "ok", "timestamp": 1546964168967, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/-24hiGmdxZDE/AAAAAAAAAAI/AAAAAAAAL_I/RW7nqM11LkM/s64/photo.jpg", "userId": "06804410358976473893"}, "user_tz": 0} id="fYuQDeoVMja9" outputId="f7f09a01-0604-4757-ef32-3cc0319f8368"
user_c.groupby(['label'])['dataset_id'].count().plot(kind='bar', zorder=3)
plt.title("Action Distribution for Subject C")
plt.xlabel("Action")
plt.ylabel("Number of Measurements")
plt.grid(axis='y', zorder=0)
plt.yticks([1, 2])
if SAVE_GRAPHS:
plt.savefig(RESULTS_PATH + "subject_c_action_distribution.pdf", format='pdf')
plt.show()
# + colab={} colab_type="code" id="JqatsK8oP1r0"
|
notebooks/01_dataset_composition_analysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# # !wget https://f000.backblazeb2.com/file/malay-dataset/voxceleb/vox2_test_aac.zip
# # !unzip vox2_test_aac.zip
# +
# # !wget https://www.robots.ox.ac.uk/~vgg/data/voxceleb/meta/vox2_meta.csv
# +
from glob import glob
files = glob('aac/**/*.m4a', recursive = True)
len(files)
# -
# !mkdir voxceleb-wav
import mp
from tqdm import tqdm
from pydub import AudioSegment
def loop(args):
files = args[0]
index = args[1]
for file in tqdm(files):
audio = AudioSegment.from_file(file)
new_file = file.replace('dev', 'wav').replace('/', '-').replace('.m4a', '.wav')
new_file = f'voxceleb-wav/{new_file}'
audio.set_frame_rate(16000).set_channels(1).export(new_file, format="wav")
r = mp.multiprocessing(files, loop, cores = 100, returned = False)
# !du -hs voxceleb-wav
# !tar -cf voxceleb2-test-wav.tar voxceleb-wav
from b2sdk.v1 import *
info = InMemoryAccountInfo()
b2_api = B2Api(info)
application_key_id = b2_application_key_id
application_key = b2_application_key
b2_api.authorize_account("production", application_key_id, application_key)
file_info = {'how': 'good-file'}
b2_bucket = b2_api.get_bucket_by_name('malay-dataset')
file = 'voxceleb2-test-wav.tar'
outPutname = 'voxceleb/voxceleb2-test-wav.tar'
b2_bucket.upload_local_file(
local_file=file,
file_name=outPutname,
file_infos=file_info,
)
|
data/voxceleb/download-voxceleb2-testset.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from IPython.core.display import HTML
with open('style.css', 'r') as file:
css = file.read()
HTML(css)
# # The $3 \times 3$ Sliding Puzzle
# <img src="8-puzzle.png">
# The picture above shows an instance of the $3 \times 3$
# <a href="https://en.wikipedia.org/wiki/Sliding_puzzle">sliding puzzle</a>:
# There is a board of size $3 \times 3$ with 8 tiles on it. These tiles are numbered with digits from the set $\{1,\cdots, 8\}$. As the the $3 \times 3$ board has an area of $9$ but there are only $8$ tiles, there is an empty square on the board. Tiles adjacent to the empty square can be moved into the square, thereby emptying the space that was previously occupied by theses tiles. The goal of the $3 \times 3$ puzzle is to transform the state shown on the left of the picture above into the state shown on the right.
#
# In order to get an idea of the sliding puzzle, you can play it online at <a href="http://mypuzzle.org/sliding">http://mypuzzle.org/sliding</a>.
# ## Utilities to Display the Solution
# We use a different color for each tile.
Colors = ['white', 'lightblue', 'pink', 'magenta',
'orange', 'red', 'yellow', 'lightgreen', 'salmon'
]
def get_style(n):
return 'background-color: ' + Colors[n] + ';">'
CSS_Table = { 'border' : '2px solid darkblue',
'border-style': 'double',
'border-width': '4px'
}
CSS_TD = { 'border' : '2px solid black',
'border-style': 'groove',
'border-width': '8px',
'padding' : '15px',
'font-size' : '150%',
}
def css_style(Dictionary):
result = ''
for k, v in Dictionary.items():
result += k + ':' + v + ';'
return result
# The function `state_to_html` displays a given state as an `Html` tabel.
def state_to_html(State):
result = '<table style="' + css_style(CSS_Table) + '">\n'
for row in State:
result += '<tr>'
for number in row:
result += '<td style="' + css_style(CSS_TD)
if number > 0:
result += get_style(number) + str(number)
else:
result += get_style(number)
result += '</td>'
result += '</tr>\n'
result += '</table>'
return result
# Given a non-empty set `S`, the function `arb` returns an arbitrary element of `S`.
# The set `S` is left unchanged.
def arb(S):
for x in S:
return x
# %run Breadth-First-Fast.ipynb
# ## Problem Specific Code
# We will represent states as tuples of tuples. For example, the start state that is shown in the picture at the beginnning of this notebook is represented as follows:
start = ((8, 0, 6),
(5, 4, 7),
(2, 3, 1)
)
# Note that the empty tile is represented by the digit $0$.
# **Exercise 1**: Define the goal state below.
goal = ((0, 1, 2),
(3, 4, 5),
(6, 7, 8)
)
# **Exercise 2:**
# The function $\texttt{findZero}(S)$ takes a state $S$ and returns a pair $(r, c)$ that specifies the row and the column of the blank in the state $S$. For example, we should have:
# $$ \texttt{findZero}(\texttt{start}) = (0, 1) \quad\mbox{and}\quad
# \texttt{findZero}(\texttt{goal}) = (0, 0)
# $$
def findZero(State):
for i in range(len(State)):
for j in range(len(State[i])):
if State[i][j] == 0:
return (i, j)
findZero(start)
findZero(goal)
# We have to represent states as tuples of tuples in order to be able to insert them into sets. However, as tuples are immutable, we need to be able to convert them to lists in order to change them. The function $\texttt{listOfLists}(S)$ takes a state $S$ and transforms it into a list of lists.
def listOfLists(S):
'Transform a tuple of tuples into a list of lists.'
return [ [x for x in row] for row in S ]
listOfLists(start)
# As lists can not be inserted into sets, we also need a function that takes a list of list and transforms it back into a tuple of tuple.
def tupleOfTuples(S):
'Transform a list of lists into a tuple of tuples.'
return tuple(tuple(x for x in row) for row in S)
tupleOfTuples([[8, 0, 6], [5, 4, 7], [2, 3, 1]])
# **Exercise 3**: Implement a function $\texttt{moveUp}(S, r, c)$ that computes the state that results from moving the tile below the blank space **up** in state $S$. The variables $r$ and $c$ specify the location of the *row* and *column* of the blank tile. Therefore we have $S[r][c] = 0$.
#
# In your implementation you may assume that there is indeed a tile below the blank space, i.e. we have $r < 2$.
def moveUp(S, r, c):
SasList = listOfLists(S)
'Move the tile below the blank up.'
"your code here"
SasList[r][c] = S[r+1][c]
SasList[r+1][c] = 0
return tupleOfTuples(SasList)
HTML(state_to_html(start))
HTML(state_to_html(moveUp(start, 0, 1)))
# **Exercise 4**: Implement a function $\texttt{moveDown}(S, r, c)$ that computes the state that results from moving the tile below the blank space **down** in state $S$. The variables $r$ and $c$ specify the location of the *row* and *column* of the blank tile. Therefore we have $S[r][c] = 0$.
#
# In your implementation you may assume that there is indeed a tile above the blank space, i.e. we have $r > 0$.
def moveDown(S, r, c):
SasList = listOfLists(S)
'Move the tile below the blank up.'
"your code here"
SasList[r][c] = S[r-1][c]
SasList[r-1][c] = 0
return tupleOfTuples(SasList)
HTML(state_to_html(moveUp(start, 0, 1)))
# **Exercise 5:**
# Similarly to the previous exercise, implement functions $\texttt{moveRight}(S, r, c)$ and $\texttt{moveLeft}(S, r, c)$.
def moveRight(S, r, c):
SasList = listOfLists(S)
'Move the tile below the blank up.'
"your code here"
SasList[r][c] = S[r][c-1]
SasList[r][c-1] = 0
return tupleOfTuples(SasList)
HTML(state_to_html(moveRight(start, 0, 1)))
def moveLeft(S, r, c):
'Move the tile right of the blank to the left.'
"your code here"
SasList = listOfLists(S)
'Move the tile below the blank up.'
"your code here"
SasList[r][c] = S[r][c+1]
SasList[r][c+1] = 0
return tupleOfTuples(SasList)
HTML(state_to_html(moveLeft(start, 0, 1)))
# **Exercise 6:**. Implement a function $\texttt{nextStates}(S)$ that takes a state $S$ representet as a tuple of tuple and that computes the set of states that are reachable from $S$ in one step. Remember to use the previously defined functions `findZero`, `moveUp`, $\cdots$, `moveLeft`. However, when you do use the function `moveUp`, then you should also check that it is possible to move a tile up.
def nextStates(State):
'Compute the set of states reachable in one step from the state S.'
"your code here"
zero = findZero(State)
possibleStates = set()
if zero[0] != 2:
possibleStates.add(moveUp(State, zero[0], zero[1]))
if zero[0] != 0:
possibleStates.add(moveDown(State, zero[0], zero[1]))
if zero[1] != 0:
possibleStates.add(moveRight(State, zero[0], zero[1]))
if zero[1] != 2:
possibleStates.add(moveLeft(State, zero[0], zero[1]))
#possibleStates = { moveUp(State, zero[0], zero[1]), moveDown(State, zero[0], zero[1]), moveRight(State, zero[0], zero[1]), moveLeft(State, zero[0], zero[1]) }
#return { x for x in possibleStates if x != State }
return possibleStates
nextStates(start)
# The computation of the relation `R` might take about 10 seconds. The reason is that `R` contains $967,680$ different pairs.
# The following computation takes about 3 seconds on my desktop computer, which has an 3,4 GHz Quad-Core Intel Core i5 (7500) Prozessor.
# %%time
Path = search(nextStates, start, goal)
# The tuple Path that is a solution to the sliding problem has a length of **32**. If your path is shorter, then you have to inspect it carefully to identify the problem. In order to do this, use the function <tt>printPath</tt> that is implemented at the bottom of this notebook.
len(Path)
# Print the solution via `HTML` tables.
for State in Path:
display(HTML(state_to_html(State)))
|
Python/Exercises/Blatt-06-Gruppenloesung.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# !date
# # Merfish 10x comparison
# +
import anndata
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import matplotlib.patches as mpatches
import scanpy as scanp
from scipy.stats import ks_2samp, ttest_ind
from scipy.sparse import csr_matrix
from sklearn.decomposition import TruncatedSVD
from sklearn.manifold import TSNE
from umap import UMAP
from sklearn.cluster import KMeans
from sklearn.metrics import adjusted_rand_score
from sklearn.preprocessing import LabelEncoder
from sklearn.neighbors import NeighborhoodComponentsAnalysis
from matplotlib import cm
from scipy.spatial import ConvexHull
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import normalize
import warnings
warnings.filterwarnings('ignore')
fsize=20
plt.rcParams.update({'font.size': fsize})
# %config InlineBackend.figure_format = 'retina'
# -
mfish = anndata.read_h5ad("../cell_ranger_annotation/merfish.h5ad")
tenx = anndata.read_h5ad("../cell_ranger_annotation/10xv3_gene.h5ad")
tenx
tenx = tenx[:,tenx.var.gene_short_name.isin(mfish.var.index)]
tenx.var.index = tenx.var.gene_short_name.values
tenx.obs.subclass_label.value_counts()
mfish.obs.subclass.value_counts()
# # Process
from sklearn.preprocessing import normalize
tenx.layers["X"] = tenx.X
tenx.layers["norm"] = normalize(tenx.X, norm='l1', axis=1)*1000000
tenx.layers["log1p"] = csr_matrix(np.log1p(tenx.layers["norm"]))
from sklearn.preprocessing import scale
# %%time
mat = tenx.layers["log1p"].todense()
mtx = scale(mat, axis=0, with_mean=True, with_std=True, copy=True)
tenx.X = mtx
del mat
# # Cluster comparisons
tenx = tenx[:,tenx.var.sort_index().index]
mfish = mfish[:,mfish.var.sort_index().index]
tenx.var.head()
mfish.var.head()
# +
unique_map = {
"L5_IT" : "L5 IT",
"L6_CT" : "L6 CT",
"L6b" : "L6b",
"Vip" : "Vip",
"Pvalb" : "Pvalb",
"L2/3_IT" : "L2/3 IT",
"L6_IT" : "L6 IT",
"Sst" : "Sst",
"Lamp5" : "Lamp5",
"L56_NP" : "L5/6 NP",
"Sncg" : "Sncg",
"SMC" : "SMC",
"L5_PT" : "L5 PT", # Check
"Endothelial" : "Endo",
"Astrocytes" : "Astro",
"VLMC" : "VLMC",
"L6_IT_Car3" : "L6 IT Car3"}
inv_map = {v: k for k, v in unique_map.items()}
# +
def split_by_target(mat, targets, target, axis=0):
"""
Split the rows of mat by the proper assignment
mat = ndarray
targets, length is equal to number of components (axis=0) or features (axis=1)
target is a singular element from unique(assignments/features)
"""
if axis==0 and len(targets) != mat.shape[axis]: return -1
if axis==1 and len(targets) != mat.shape[axis]: return -1
mask = targets == target
if axis==0:
t_mat = mat[mask] # target matrix
c_mat = mat[~mask] # complement matrix
elif axis==1:
t_mat = mat[:, mask] # target matrix
c_mat = mat[:, ~mask] # complement matrix
return (t_mat, c_mat)
def group_mtx_by_cluster(mtx, components, features, s2t, source_id="cell_id", target_id="subclass_label", by="components"):
"""
mtx: ndarray components by features
components: labels for rows of mtx
features: labels for columns of mtx
s2t: pandas dataframe mapping source (features or components) to a
targets features(components) to group by
target_id: column name in s2t to group by
"""
if target_id not in s2t.columns: return -1
ncomp = components.shape[0]
nfeat = features.shape[0]
ntarget = s2t[target_id].nunique()
if by =="features":
source = features
elif by =="components":
source = components
# Map the source to an index
source2idx = dict(zip(source, range(len(source))))
# Map the target to a list of source indices
target2idx = (s2t.groupby(target_id)[source_id].apply(lambda x: [source2idx[i] for i in x])).to_dict()
# array of unique targets
unique = s2t[target_id].unique().astype(str)
nuniq = unique.shape[0]
X = np.zeros((nuniq, mtx.shape[1]))
for tidx, t in enumerate(unique):
# Grab the matrix indices corresponding to columns and source columns to group by
source_indices = target2idx[t]
#print(source_indices)
# breaks generality
sub_mtx = mtx[source_indices,:].mean(axis=0) # Sum on source indicies
X[tidx,:] = sub_mtx # place summed vector in new matrix
# Return matrix that is grouped by
return (X, components, unique)
# -
tenx = tenx[tenx.obs.subclass_label!="Low Quality"]
mfish.obs["tenx_subclass"] = mfish.obs["subclass"].apply(lambda x: unique_map.get(x, "None"))
mfish = mfish[mfish.obs.tenx_subclass != "None"]
mfish_mat = mfish.X
mfish_ass = mfish.obs.tenx_subclass.values
tenx_mat = tenx.X
tenx_ass = tenx.obs.subclass_label.values
tenx
# +
features = mfish.var.index.values
unique = np.intersect1d(np.unique(mfish_ass), np.unique(tenx_ass))
# -
def nd(arr):
return np.asarray(arr).reshape(-1)
from scipy import stats
# +
# %%time
r2 = []
tenx_x = []
mfish_x = []
for uidx, u in enumerate(unique):
mfish_t_mat, _ = split_by_target(mfish_mat, mfish_ass, u)
tenx_t_mat, _ = split_by_target(tenx_mat, tenx_ass, u)
mf = np.asarray(mfish_t_mat.mean(axis=0)).reshape(-1)
t = np.asarray(tenx_t_mat.mean(axis=0)).reshape(-1)
tenx_x.append(t)
mfish_x.append(mf)
r, p = stats.pearsonr(mf, t)
r2.append(r)
print("[{} of {}] {:,.2f}: {}".format(uidx+1, unique.shape[0],r, u) )
# -
cluster_cmap = {
"Astro": (0.38823529411764707, 0.4745098039215686, 0.2235294117647059 ), # 637939,
"Endo" : (0.5490196078431373, 0.6352941176470588, 0.3215686274509804 ), # 8ca252,
"SMC" : (0.7098039215686275, 0.8117647058823529, 0.4196078431372549 ), # b5cf6b,
"VLMC" : (0.807843137254902, 0.8588235294117647, 0.611764705882353 ), # cedb9c,
"Low Quality" : (0,0,0),
"L2/3 IT" : (0.9921568627450981, 0.6823529411764706, 0.4196078431372549 ), # fdae6b
"L5 PT" : (0.9921568627450981, 0.8156862745098039, 0.6352941176470588 ), # fdd0a2
"L5 IT" : (0.5176470588235295, 0.23529411764705882, 0.2235294117647059 ), # 843c39
"L5/6 NP": "#D43F3A",
"L6 CT" : (0.8392156862745098, 0.3803921568627451, 0.4196078431372549 ), # d6616b
"L6 IT" : (0.9058823529411765, 0.5882352941176471, 0.611764705882353 ), # e7969c
"L6b" : (1.0, 0.4980392156862745, 0.054901960784313725), # ff7f0e
"L6 IT Car3" : (1.0, 0.7333333333333333, 0.47058823529411764 ), # ffbb78
"Lamp5" : (0.19215686274509805, 0.5098039215686274, 0.7411764705882353 ), # 3182bd # blues
"Sncg" : (0.4196078431372549, 0.6823529411764706, 0.8392156862745098 ), # 6baed6
"Vip" : (0.6196078431372549, 0.792156862745098, 0.8823529411764706 ), # 9ecae1
"Sst" : (0.7764705882352941, 0.8588235294117647, 0.9372549019607843 ), # c6dbef
"Pvalb":(0.7372549019607844, 0.7411764705882353, 0.8627450980392157 ), # bcbddc
}
tenx_size = tenx.obs["subclass_label"].value_counts()[unique]
# +
fig, ax = plt.subplots(figsize=(10,7))
x = tenx_size
y = r2
for i, txt in enumerate(unique):
ax.annotate(i, (x[i], y[i]))
ax.scatter(x[i], y[i], label="{}: {}".format(i, txt), color=cluster_cmap[txt])
ax.set_ylim((0, 1))
ax.set_xscale("log")
ax.set_xlabel("Number of 10xv3 cells")
ax.set_ylabel("Pearson correlation")
ax.legend(fontsize=15,loc='center left', bbox_to_anchor=(1, 0.5), markerscale=3)
ax.set_title("MERFISH v. 10xv3 gene subclass correlation")
plt.savefig("./figures/merfish_10x_gene_subclass_size.png", bbox_inches='tight', dpi=300)
plt.show()
# -
def trim_axs(axs, N):
"""little helper to massage the axs list to have correct length..."""
axs = axs.flat
for ax in axs[N:]:
ax.remove()
return axs[:N]
# +
fig, ax = plt.subplots(figsize=(15,15), ncols=4, nrows=5)
fig.subplots_adjust(hspace=0, wspace=0)
axs = trim_axs(ax, len(unique))
fig.suptitle('MERFISH v. 10xv3 gene subclass correlation', y=0.9)
#fig.subplots_adjust(top=1)
for cidx, (ax, c) in enumerate(zip(axs, unique)):
x = tenx_x[cidx]
y = mfish_x[cidx]
ax.scatter(x, y, label="{}: {:,}".format(c, tenx_size[cidx]), color="k", alpha=0.1)
slope, intercept, r_value, p_value, std_err = stats.linregress(x, y)
minx = min(x)
maxx = max(x)
x = np.linspace(minx, maxx, 10)
y = slope*x+intercept
ax.plot(x, y, label="corr : {:,.2f}".format(r_value**2), color="red", linewidth=3)
ax.legend(fontsize=15)
ax.xaxis.set_ticklabels([])
ax.yaxis.set_ticklabels([])
ax.set_axis_off()
fig.text(0.5, 0.1, '10xv3 scaled $log(TPM+1)$', ha='center', va='center', fontsize=30)
fig.text(0.1, 0.5, 'MERFISH scaled $log(CPM+1)$', ha='center', va='center', rotation='vertical', fontsize=30)
plt.savefig("./figures/merfish_10x_gene_subclass_correlation_scatter.png", bbox_inches='tight',dpi=300)
plt.show()
# -
tenx[tenx.obs.subclass_label=="L5 IT"].obs.cluster_label.value_counts()
mfish[mfish.obs.subclass=="L5_IT"].obs.label.value_counts()
mfish
|
analysis/biorxiv_1/merfish_v_10x.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (Data Science)
# language: python
# name: python3__SAGEMAKER_INTERNAL__arn:aws:sagemaker:us-west-2:236514542706:image/datascience-1.0
# ---
# ## Visualize and upload dataset to Amazon S3
# ### Import packages
import boto3
import sagemaker
import pandas as pd
import matplotlib.pyplot as plt
# ### Create a sagemaker_session
# +
boto_session = boto3.Session()
sagemaker_boto_client = boto_session.client('sagemaker')
sagemaker_session = sagemaker.session.Session(
boto_session=boto_session,
sagemaker_client=sagemaker_boto_client)
# -
# ### Use the default Amazon S3 bucket for dataset and results
# +
default_bucket = sagemaker_session.default_bucket() # Alternatively you can use your custom bucket here.
prefix = 'sagemaker-tutorial' # use this prefix to store all files pertaining to this workshop.
data_prefix = prefix + '/data'
# -
# ### Visualize the dataset
local_data_dir = './data'
df = pd.read_excel('./data/default_of_credit_card.xls', header=1)
df.head()
print(f'Total number of missing values in the data: {df.isnull().sum().sum()}')
# plot the bar graph customer gender
df['SEX'].value_counts(normalize=True).plot.bar()
plt.xticks([0,1], ['Male', 'Female'])
# plot the age distribution
plt.hist(df['AGE'], bins=30)
plt.xlabel('Clients Age Distribution')
# +
df.to_csv('./data/dataset_unchanged.csv', index=False)
response = sagemaker_session.upload_data(f'{local_data_dir}/dataset_unchanged.csv',
bucket=default_bucket,
key_prefix=data_prefix)
print(response)
|
notebooks/1_upload_dataset_for_autopilot.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: atoz
# language: python
# name: atoz
# ---
# # "E is for Exploratory Data Analysis: Numeric Data"
# > What is Exploratory Data Analysis (EDA), why is it done, and how do we do it in Python?
#
# - toc: false
# - badges: True
# - comments: true
# - categories: [E]
# - hide: False
# - image: images/e-is-for-eda/abstract-blackboard-bulb-chalk.jpg
# ## _What is **Exploratory Data Analysis(EDA)**?_
# EDA is the process of getting to know our data primarily through simple visualizations before fitting a model. As Wickham and Grolemund state, EDA is more an attitude than a scripted list of steps which must be carried out{% fn 1 %}.
# ## _Why is it done?_
# Two main reasons:
#
# 1. If we collected the data ourselves to solve a problem, we need to determine whether our data is sufficient for solving that problem.
#
# 2. If we didn't collect the data ourselves, we need to have a basic understanding of the type, quantity, quality, and possible relationships between the features in our data.
#
# ## _How do we do it in Python?_
#
# While I could use a toy data set, like in my [last post](https://educatorsrlearners.github.io/an-a-z-of-machine-learning/algorithm/2020/05/26/d-is-for-decision-tree.html), after seeing seeing tweets like this:
#
# > twitter: https://twitter.com/drob/status/1021233822392881152
#
#
#
# and listening to [<NAME>](https://twitter.com/hugobowne) on [DataFramed](https://www.datacamp.com/community/podcast) bemoan the over use of the [Iris](https://archive.ics.uci.edu/ml/datasets/iris) and [*Titanic*](https://www.openml.org/d/40945) datasets, I'm feeling inspired to use my own data :grin:
#
# As always, I'll follow the steps outlined in [_Hands-on Machine Learning with Scikit-Learn, Keras & TensorFlow_](https://github.com/ageron/handson-ml/blob/master/ml-project-checklist.md)
#
# ### Step 1: Frame the Problem
# "Given a set of features, can we determine how old someone needs to be to read a book?"
#
# ### Step 2: Get the Data
# To answer the question above, I sourced labeled data by scraping [Common Sense Media's Book Reviews](https://www.commonsensemedia.org/book-reviews) using `BeautifulSoup` and then wrote the data to a csv.{% fn 2 %}
#
# 
#
# Now that we have our data lets move on to...
#
# ### Step 3: Explore the Data to Gain Insights (i.e. EDA)
# As always, import the essential libraries, then load the data.
#hide
import warnings; warnings.simplefilter('ignore')
# +
#For data manipulation
import pandas as pd
import numpy as np
#For visualization
import seaborn as sns
import matplotlib.pyplot as plt
import missingno as msno
url = 'https://raw.githubusercontent.com/educatorsRlearners/book-maturity/master/csv/book_info_complete.csv'
df = pd.read_csv(url)
# -
# Time to start asking and answering some basic questions:
#
# - How much data do we have?
df.shape
# OK, so we have 23 features and one target as well as 5,816 observations.
#
# *Why do we have fewer than in the screenshot above?*
#
# Because Common Sense Media is constantly adding new reviews to their website, meaning they've added nearly 100 books to their site since I completed my project at the end of March 2020.
#
# - What type of data do we have?
df.info()
# Looks like a mix of strings and floats.
#
# Lets take a closer look.
df.head().T
# The picture is coming into focus. Again, since I collected the data, I know that the target is `csm_rating` which is the minimum age Common Sense Media (CSM) says a reader should be for the given book.
#
# Also, we have essentially three types of features:
# - Numeric
# - `par_rating` : Ratings of the book by parents
# - `kids_rating` : Ratings of the book by children
# - :dart:`csm_rating` : Ratings of the books by Common Sense Media
# - `Number of pages` : Length of the book
# - `Publisher's recommended age(s)`: Self explanatory
#
#
# - Date
# - `Publication date` : When the book was published
# - `Last updated`: When the book's information was updated
#
# with all other features being text.
#
# To make inspecting a little easier, lets clean those column names. {% fn 3 %}
df.columns
df.columns = df.columns.str.strip().str.lower().str.replace(' ', '_').str.replace('(', '').str.replace(')', '')
df.columns
# Much better.
#
# Given the number and variety of features, I'll focus on the numeric features in this post and analyze the text features in a part II.
#
# Therefore, lets subset the data frame work with only the features of interest.
numeric = ['par_rating', 'kids_rating', 'csm_rating', 'number_of_pages', "publisher's_recommended_ages"]
df_numeric = df[numeric]
df_numeric.head()
# :thumbsdown: `publisher's_recommended_ages` is a range instead of a single value.
# :thumbsdown: It's the wrong data type (i.e., non-numeric)
df_numeric.dtypes
# :thumbsup: We can fix both of those issues.
#
# Given that we only care about the minimum age, we can:
# - split the string on the hyphen
# - keep only the first value since that will be the minimum age recommended by the publisher
# - convert the column to `numeric`
# +
#Create a column with the minimum age
df_numeric['pub_rating'] = df.loc[:, "publisher\'s_recommended_ages"].str.split("-", n=1, expand=True)[0]
#Set the column as numeric
df_numeric.loc[:, 'pub_rating'] = pd.to_numeric(df_numeric['pub_rating'])
# -
df_numeric.head().T
# Now we can drop the unnecessary column.
df_numeric = df_numeric.drop(columns="publisher's_recommended_ages")
df_numeric.head().T
# Everything is in order so lets dig in and start by
#
# ### Inspecting the target
df_numeric.loc[:, 'csm_rating'].describe()
# Good news! We do not have any missing values for our target! Also, we can see the lowest recommended age for a book is 2 years old, which has to be a picture book, while the highest is 17.
#
# All useful info, but what does our target look like?
df_numeric.loc[:, 'csm_rating'].plot(kind= "hist",
bins=range(2,18),
figsize=(24,10),
xticks=range(2,18),
fontsize=16);
# Hmmm. Two thoughts:
#
# First, the distribution is multimodal so when we split the data into`train-test-validate` splits, we'll need to do a [stratified random sample](https://www.investopedia.com/terms/stratified_random_sampling.asp#:~:text=Stratified%20random%20sampling%20is%20a,as%20income%20or%20educational%20attainment.). Also, the book recommendations seem to fall into one of three categories: really young readers, (e.g., 5 years old), tweens, and teens or older.
#
# :bulb: Given this distribution, we could simplify our task from predicting an exact age and instead predict an age group. Something to keep in mind for future research.
#
# Moving on.
# #### Missing Values
# Looking back at the output from `df.info()`, its obvious that several features have missing values but let's visualize it to make it clear.
msno.bar(df_numeric);
# Good News!
# - There are fewer than 50 missing values for `number_of_pages`
#
# Bad News!
# - `pub_rating` is missing a thousand values
# - Nearly half of the `kids_rating` are missing
# - More than half of the `par_rating` are missing.
#
# When we get to the cleaning/feature engineering stage, we'll have to decide whether it's better to drop or [impute](https://en.wikipedia.org/wiki/Imputation_(statistics)) the missing values. However, before we do that, lets see visualize the data to get a better feel for it.
df_numeric['kids_rating'].plot(kind= "hist",
bins=range(2,18),
figsize=(24,10),
xticks=range(2,18),
fontsize=16);
# Hmmm. Looks like the children who wrote the bulk of the reviews think the books they reviewed were suitable for children between the ages of 8 and 14.
#
# What about the parent's ratings?
df_numeric['par_rating'].plot(kind= "hist",
bins=range(2,18),
figsize=(24,10),
xticks=range(2,18),
fontsize=16);
# Same shape as the kids but a little less pronounced?
#
# Finally, let's find out what the publishers think.
df_numeric['pub_rating'].plot(kind= "hist",
bins=range(2,18),
figsize=(24,10),
xticks=range(2,18),
fontsize=16);
# This looks promising. Let's compare it to our target `csm_rating`.
df_numeric.loc[:, ['pub_rating','csm_rating']].hist(bins=range(2,18),
figsize=(20,10));
# :thinking: While not identical by any means, both distributions have the same multimodal shape.
#
# Lets see how well our features correlate.
# +
#Create the correlation matrix
corr = df_numeric.corr()
#Generate a mask to over the upper-right side of the matrix
mask = np.zeros_like(corr)
mask[np.triu_indices_from(mask)] = True
#Plot the heatmap with correlations
with sns.axes_style("white"):
f, ax = plt.subplots(figsize=(8, 6))
ax = sns.heatmap(corr, mask=mask, annot=True, square=True)
# -
# :thinking: The `pub_rating` is nearly a proxy for the target.
#
# :thinking: The parents and kids ratings correlate more strongly with the target than they do with each other.
#
# Looks like we're going to have to impute those missing values after all.
# ### What about potential outliers?
#
# A final step in EDA is to search for potential outliers which are values significantly different from the norm.
#
# Our dataset could contain outliers for a couple of reasons:
# - data is miskeyed in, (e.g., someone types "100" instead of "10")
# - the observation genuinely is significantly different from the norm {% fn 4 %}
#
# The good news is that I chose to scrape Common Sense Media's book reviews because I felt confident in their ratings based on my knowledge of the domain and, given the professionalism of the organization, we can be fairly certain of the veracity of the data.
#
# However, the old maxim of "Trust, but verify" exists for a reason.
#
# This post is already much longer than I had planned so I won't go through all the numeric features, nor the multiple ways of [identifying outliers](https://statisticsbyjim.com/basics/outliers/), but a really simple one to plot the relationships between features so lets investigate the relationship between ratings and book length.
df_numeric.plot.scatter(x='number_of_pages',
y="csm_rating",
figsize=(24,10),
fontsize=16);
# We have spotted our first probable outliers: it is inconceivable for a ~400 page book to be meant for a two or three year old, right?
df.query('csm_rating < 6 & number_of_pages > 300')[['title','description']]
# Well so much for that idea :grin:
#
# To quote the [AI Guru](https://ai-guru.de/), instead of simply relying on printouts and plots, you "should always look at your *bleeping* data."
# ## Summary
#
# This post turned out to be part one of what will likely be at least three posts: EDA for:
# - :ballot_box_with_check: numeric data
# - :black_square_button: categorical data
# - :black_square_button: images (book covers)
#
# Going forward, my key points to remember are:
#
# ### Does the shape of the data make sense?
# Based on my problem statement, I do not need normally distributed data. However, based on the question I'm trying to solve, I might expect the data to fit a certain distribution.
#
#
# ### Similarly, are the values what I expect?
# What would have happened if the only ratings I had were for 4 year olds? Clearly, I would have made a mistake somewhere along the line and would have to go back and fix it.
#
# Also, I have to ask if the data makes sense or if I have outliers.
#
# ### What's missing?
# There will always be missing values. How many and in which features is going to drive a lot of feature engineering questions.
#
# Speaking of which...
#
# ### Are all the features I want present?
# The numeric features I have are pretty complete, but what would happen if I combined the `par_rating` with the `kids_rating` to create a new feature? Would the two features combined be more valuable than either one on its own? Only one way to find out :smile:
#
# Happy coding!
# #### Footnotes
# {{ '[Chapter 7: Exploratory Data Analysis in *R for Data Science* by <NAME> & <NAME>](https://r4ds.had.co.nz/exploratory-data-analysis.html)' | fndetail: 1 }}
# {{ 'You can find the code [here](https://github.com/educatorsRlearners/book-maturity/blob/master/00_get_search_pages.ipynb)' | fndetail: 2 }}
# {{ 'Big *Thank You* to [<NAME>](https://medium.com/@chaimgluck1/working-with-pandas-fixing-messy-column-names-42a54a6659cd) for providing this tip' | fndetail: 3 }}
# {{ '[Yao Ming really was 2 meters tall when he was 13](http://www.chinadaily.com.cn/sports/2007-03/01/content_817159.htm#:~:text=When%20Yao%20was%20four%20years,was%20already%20above%20two%20meters.)' | fndetail: 4 }}
|
_notebooks/2020-06-15-e-is-for-eda.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Session 1.2: Programming
#
# So you know the basics of individual instructions and that a program is just a series of instructions. But the real strength of programming isn't just running (or executing) one instruction after another. Based on how the expressions evaluate, the program can decide to skip instructions, repeat them, or choose one of several instructions to run. In fact, you almost never want your programs to start from the first line of code and simply execute every line, straight to the end. _Control flow statements_ can decide which Python instructions to execute under which conditions.
# ## Conditional Statements
# ### Boolean values and Comparison Operators
#
# _Boolean_ data type has only two values: `True` and `False`.
#
# _Comparison operators_ (`==`, `!=`, `<`, `>`, `<=`, `>=`) compare two values and evaluate down to a single Boolean value.
#@solution
34 != 43
# The `==` and `!=` operators can actually work with values of any data type
#@solution
'hello' == 'Hello'
#@solution
True != False
#@solution
34 == '34'
# <div class="alert alert-block alert-info">
# Why the expresion in a previous cell is `False`?
# </div>
# The `<`, `>`, `<=`, and `>=` operators, on the other hand, work always properly only with integer and floating-point values.
myAge = 29
print("myAge == 10 is", myAge == 10, ", but myAge >= 10 is", myAge >= 10)
#@solution
'24' > '8'
#@solution
'big' > 'small'
# ### Boolean Operators
#
# The three Boolean operators (`and`, `or`, and `not`) are used to compare Boolean values. Like comparison operators, they evaluate these expressions down to a Boolean value. Since the comparison operators evaluate to Boolean values, you can use them in expressions with the Boolean operators.
#@solution
print(True and True)
print(True and False)
print(True or False)
#@solution
print(2 + 2 == 4)
print(2 + 2 == 3 or 2 + 2 == 4)
# +
#@solution
x = 3
y = 4
x == 3 or y == 4
# -
2 + 2 == 4 and not 2 + 2 != 5 and 2 * 2 != 2 + 2
# <div class="alert alert-block alert-info">
# Modify the previous cell to make it `True`. Use brackets `(` `)` to make it readable.
# </div>
#@solution
# one solution migth be:
(2 + 2 == 4) and (not 2 + 2 == 5) and (2 * 3 != 2 + 2)
# ## Flow Control Statements
# ### *if-elif-else* Statements
# The most common type of control flow statement is the `if` statement. An `if` _statement's clause_ will execute if the statement's condition is `True`. The _clause_ is skipped if the condition is `False`. The `else` _clause_ is executed only when the `if` statement's condition is `False`. While only one of the `if` or `else` clauses will execute, you may have a case where you want one of many possible clauses to execute. The `elif` statement is an “else if” statement that always follows an `if` or another `elif` statement. It provides another condition that is checked only if all of the previous conditions were `False`.
# +
#@solution
print("Type a number")
num = int(input())
if num > 0:
print(str(num), "is a positive number")
if num == 0:
print("It is a zero")
if num < 0:
print(str(num), "is a negative number")
# +
#@solution
print("Type a number")
name = str(input())
name1 = "Anna"
name2 = "Jack"
if name == name1:
print("I know {}!".format(name))
elif name == name2:
print("I know {}!".format(name))
else:
print("I don't know {}! Sorry.".format(name))
# -
# ### *for* loop
#
# I hope it was a little bit annoying to type all 5 number and repeat execution of code by yourself. This is where loops are used. If you want to execute a block of code only a certain number of times, you can do this with a `for` loop statement.
#@solution
for x in [1,-2,0.3]: # iteration over list
print(x)
#@solution
for i in [0,-5,1000,-0.5,28.9]:
if i > 0:
print(str(i), "is a positive number")
elif i == 0:
print("It is a zero")
else:
print(str(i), "is a negative number")
# Or you can ask to type a value 5 times using `range()` function.
#@solution
for i in range(5):
print("Type a number")
num = float(input())
if num > 0:
print(str(num), "is a positive number")
elif num == 0:
print("It is a zero")
else:
print(str(num), "is a negative number")
# The `range()` function can also be called with two or three arguments. The first two arguments will be the start and stop values, and the third will be the step argument. The step is the amount that the variable is increased by after each iteration.
#@solution
for i in range(7, -2, -2):
print(i)
#@solution
for i, x in enumerate("Some text."): # use enumerate() to get index
print(i, x)
# ### *while* loop with *break* and *continue*
# In the `while` loop, the condition is always checked at the start of each iteration (that is, each time the loop is executed). If the condition is `True`, then the clause is executed, and afterward, the condition is checked again. The first time the condition is found to be `False`, the `while` clause is skipped. If the execution reaches a `break` statement, it immediately exits the `while` loop's clause. When the program execution reaches a `continue` statement, the program execution immediately jumps back to the start of the loop and reevaluates the loop's condition. (This is also what happens when the execution reaches the end of the loop.) Note: You can use `break` and `continue` statements inside `for` loops as well.
# +
# This is a guess the number game.
import random
secretNumber = random.randint(1, 10)
print('I am thinking of a number between 1 and 10.')
# Infinite Loop
guessesTaken = 1
while True:
print('Take a guess.')
guess = int(input())
if guess < secretNumber:
print('Your guess is too low.')
elif guess > secretNumber:
print('Your guess is too high.')
else:
break # This condition is the correct guess!
guessesTaken += 1
if guess == secretNumber:
print('Good job! You guessed my number in ' + str(guessesTaken) + ' guesses!')
else:
print('Nope. The number I was thinking of was ' + str(secretNumber))
# -
# To stop the infinite loop you would have to interrupt the kernel (a button with black square).
# <div class="alert alert-block alert-info">
# Modify an example above using `for` loop and allow a user maximum 5 attempt s to guess a number:
# </div>
# +
#@solution
secretNumber = random.randint(1, 10)
print('I am thinking of a number between 1 and 10.')
# Infinite Loop
guessesTaken = 1
for i in range(5):
print('Take a guess.')
guess = int(input())
if guess < secretNumber:
print('Your guess is too low.')
elif guess > secretNumber:
print('Your guess is too high.')
else:
break # This condition is the correct guess!
guessesTaken += 1
if guess == secretNumber:
print('Good job! You guessed my number in ' + str(guessesTaken) + ' guesses!')
else:
print('Nope. The number I was thinking of was ' + str(secretNumber))
# -
# ##### Non-Primitive Data Structures
# Non-primitive types don't just store a value, but rather a collection of values in various formats.
#
# ### Arrays
#
# First off, arrays in Python are a compact way of collecting basic data types, all the entries in an array must be of the same data type. However, arrays are not all that popular in Python and not a build in type, unlike the other programming languages. To work with them you would need to `import` additional libraries.
#
# In general, when people talk of arrays in Python, they are actually referring to `lists`. However, there is a fundamental difference between them and you will see this later, when we will work with `numpy` library. First we will consider, what is `list`.
# ### Lists
#
# A `list` is a value that contains multiple values in an ordered sequence. These are mutable, which means that you can change their content without changing their identity. You can recognize lists by their square brackets `[` and `]` that hold elements, separated by a comma `,`. Lists are built into Python: you do not need to invoke them separately.
#@solution
my_list = [1,2,3,4,5,6,7,8,9]
x = [] # Empty list
type(x)
# The *my_list* variable is still assigned only one value: the `list` value. But the `list` value itself contains other values. The value `[]` is an empty list that contains no values
# Whenever we want to access an element of a list we can do so by typing the list name and the index of the element in square brackets. Index starts at zero.
#@solution
my_list[0] # indexing returns the item
#@solution
my_list[100]
# Indexing of list can be used to get certain elements in various ways. Here are some examples:
# +
#@solution
print(my_list[0]) # first element
print(my_list[-1]) # last element
print(my_list[:4]) # the first four list elements
print(my_list[-4:]) # the last four list elements
print(my_list[1:4]) # list slice of elements from index 1 to (not including) index 4
print(my_list[::2]) # every second element
print(my_list[::]) # all elements
print(my_list[::-1]) # all elements in reversed order
# -
# <div class="alert alert-block alert-info">
# Try to get __[1,3,5]__ from my_list as output.
# </div>
#@solution
my_list[::2][:3]
# This should remind you of a `strings` examples. `Lists` and `strings` have many common properties, such as indexing and slicing operations.
# By using the index elements of a list can be altered.
#@solution
my_list[4] = 3004
my_list
# `Lists` can also contain other `list` values. The values in these lists of lists can be accessed using multiple indexes.
spam = [['cat', 'bat'], [10, 20, 30, 40, 50]]
spam
#@solution
spam[1][3]
# <div class="alert alert-block alert-info">
# Try to use print `['cat', 'bat']` and `[20, 30, 40]` (use a list slice), then change `30` to `3000`.
# </div>
# `Lists` can be concatenated using `+` and replicated with `*`. You can determine whether a value is or isn't in a list with the `in` and `not in` operators.
#@solution
my_list2 = [1, 2, 3]
my_list3 = my_list2 + ['A', 'B', 'C']
my_list3
#@solution
my_list4 = my_list2 * 3
my_list4
#@solution
'A' in my_list3
#@solution
'A' in my_list4
#@solution
'A' not in my_list2
# Python provides many more methods to manipulate and work with `lists`. Adding new items to a list, removing some items from a list, sorting or reversing a list are common list manipulations. Try some of them in action (use help if you are not sure how some of the functions work):
spam = ['cat', 'dog', 'bat']
spam.append('moose')
spam
spam.insert(1, 'chicken')
spam
spam.extend(['bat', 'horse'])
spam
help(spam.extend)
# <div class="alert alert-block alert-info">
# Type `spam.` and press `Tab`. You will see, which other functions are avaliable to `list`. Try some of them below and get `help()` if you don't know how to use them.
# </div>
# #### Referencing
#
# One important distinction between simple variables and list is when you assign a list to a variable, you are actually assigning a list _reference_ to the variable. A _reference_ is a value that points to some bit of data, and a list reference is a value that points to a list. Here is some code that will make this distinction easier to understand:
# simple variables
spam = 42
cheese = spam
spam = 100
print("spam: ", spam)
print("cheese: ", cheese)
# list variables
spam = [0, 1, 2, 3, 4, 5]
cheese = spam
#@solution
cheese[1] = 'Hello!'
print("spam: ", spam)
print("cheese: ", cheese)
# This might look odd to you. The code changed only the `cheese` list, but it seems that both the `cheese` and `spam` lists have changed. When you create the first list, you assign a reference to it in the `spam` variable. But the line `cheese = spam` copies only the list reference in `spam` to `cheese`, not the list value itself. This means the values stored in `spam` and `cheese` now both refer to the same list. There is only one underlying list because the list itself was never actually copied. So when you modify the first element of `cheese`, you are modifying the same list that `spam` refers to.
#
# It might sound complicated, but it's important to know to prevent errors in the future. Remember, if you want a copy of a `list` you cannot just assign it to new variable, you need to use the next options:
spam = [0, 1, 2, 3, 4, 5]
#@solution
cheese = spam[:]
cheese[1] = 'Hello!'
print("spam: ", spam)
print("cheese: ", cheese)
#@solution
cheese = list(spam)
cheese[1] = 'World!'
print("spam: ", spam)
print("cheese: ", cheese)
#@solution
import copy
spam = [0, 1, 2, 3, 4, 5]
cheese = copy.copy(spam)
cheese[1] = 'Hello again!'
print("spam: ", spam)
print("cheese: ", cheese)
# ### Tuples
#
# `Tuples` are another standard sequence data type. The difference between `tuples` and `list` is that tuples are _immutable_, which means once defined you cannot delete, add or edit any values inside it. `Tuples` are typed with parentheses, `(` and `)`, instead of square brackets, `[` and `]`.
#@solution
eggs = ('hello', 42, 0.5)
eggs[1:3]
#@solution
eggs[1] = 99
# If you need an ordered sequence of values that never changes, use a `tuple`. A second benefit of using `tuples` instead of `lists` is that, because they are immutable and their contents don’t change, Python can implement some optimizations that make code using `tuples` slightly faster than code using `lists`. Converting a `tuple` to a `list` is handy if you need a mutable version of a tuple value.
#@solution
tuple(['cat', 'dog', 5])
#@solution
list(('cat', 'dog', 5))
# But notice a difference between the next two cases:
print("Type of ('hello',) is", type(('hello',)), "and of ('hello') is ", type(('hello')))
#@solution
list(('hello',))
#@solution
list(('hello'))
# ### Sets
#
# `Sets` are a collection of distinct (unique) objects. These are useful to create lists that only hold unique values in the dataset. It is an unordered collection but a mutable one, this is very helpful when going through a huge dataset. `Set` objects also support mathematical operations like union `|`, intersection `&`, difference `-`, and symmetric difference `^`.
#
# Curly braces, `{` and`}` or the `set()` function can be used to create sets. Note: to create an empty set you have to use `set()`, not `{}`; the latter creates an empty __dictionary__, a data structure that we discuss in the next section.
#@solution
basket = {'apple', 'orange', 'apple', 'pear', 'orange', 'banana'}
print(basket)
#@solution
'orange' in basket
# Demonstrate set operations on unique letters from two words
a = set('abracadabra')
b = set('alacazam')
a # unique letters in a
#@solution
print(a - b) # letters in a but not in b
print(a | b) # letters in a or b or both
print(a & b) # letters in both a and b
print(a ^ b) # letters in a or b but not both
random_protein_sequences = ['HVHHE', 'RPTKT', 'RPTKT', 'KMPFI', 'PCRTR', 'HVHHE', 'KRPGP',
'DTGTN', 'FDTGW', 'HVHHE', 'HVHHE', 'VDCPF', 'MTDQC', 'THHMI',
'KRPGP', 'KMPFI', 'HVHHE', 'KRPGP', 'KRPGP']
# <div class="alert alert-block alert-info">
# Print only unique elements from the `random_protein_sequences`. Make two versions: with and without using `set`. Hint: for a version without `set` you would need to create an additional list, which contain all already seen elements and use `for`, `if` and `not in` statments.
# </div>
# +
# version 1: with set
# version 2: without set
seen_elements = []
for ...:
# +
#@solution
# version 1: with set
print(set(random_protein_sequences))
# version 2: without set
seen_elements = []
for protein_seq in random_protein_sequences:
if not protein_seq in seen_elements:
seen_elements.append(protein_seq)
print(protein_seq)
# -
# ### Dictionaries
#
# `Dictionaries` are exactly what you need if you want to implement something similar to a telephone book. None of the data structures that you have seen before are suitable for a telephone book.
#
# Like a `list`, a `dictionary` is a collection of many values. Unlike `lists`, which are indexed by a range of numbers, `dictionaries` are indexed by _keys_, indexes for dictionaries can use many different data types, not just integers. It is best to think of a dictionary as an unordered set of `key: value` pairs, with the requirement that the keys are _unique_ (within one dictionary). A pair of braces creates an empty dictionary: `{`,`}`.
#First we define the dictionary.
ages = {'Andi':88, 'Emily':6, 'Petra':24,
'Lewis':19}
#@solution
#Add a couple of names to the dictionary
ages['Sue'] = 23
ages['Peter'] = 19
ages['Andrew'] = 78
ages['Karren'] = 45
# +
# make a check, who is in a dictionary and if there is noone with this name, we will add them
print("Please, type a name")
name_in = str(input())
if name_in in ages:
print (name_in, " is in the dictionary and is", ages[name_in], "years old")
else:
print (name_in, " is not in the dictionary. Would you like to add ", name_in, "? (y/n)")
answer = str(input())
if answer == 'y':
print("Please type an age of ", name_in, ":")
age_in = int(input())
ages[name_in] = age_in
# -
#@solution
print ("The following people are in the dictionary:")
print (ages.keys())
#@solution
#You could use this function to put all the key names in a list:
keys = ages.keys()
keys
#@solution
#You can also get a list of all the values in a dictionary.
#You use the values() function:
print ("People are aged the following:", \
ages.values())
#Put it in a list:
values = ages.values()
# +
#@solution
#You can sort lists, with the sort() function
#It will sort all values in a list
#alphabetically, numerically, etc...
#You can't sort dictionaries -
#they are in no particular order
print(keys)
print(sorted(keys))
print(values)
print(sorted(values))
#You can find the number of entries
#with the len() function:
print("The dictionary has", len(ages), "entries in it")
# -
# <div class="alert alert-block alert-info">
# A year has passed. Icrease an age of all people in the dictionary by 1. Use the code below.
# </div>
for key, value in my_dictionary.items(): # iteration over dictionary
print(key, value)
# +
#@solution
for key, value in ages.items(): # iteration over dictionary
ages[key] = value + 1
print(ages)
# -
|
02_Programming_solutions.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # 简介
# ## 属性 attributes
# 属性是与对象绑定的一组数据,可以只读,只写,或者读写,使用时不加括号,例如:
f = file("new_file", 'w')
# 显示模式属性:
f.mode
# 是否关闭:
f.closed
# `mode` 是只读属性,所以这样会报错:
f.mode = 'r'
# 获取属性不需要加括号:
f.mode()
# ## 方法 method
# 方法是与属性绑定的一组函数,需要使用括号,作用于对象本身:
f.write('Hi.\n')
f.seek(0)
f.write('Hola!\n')
f.close()
# !rm new_file
# ## 使用 OPP 的原因
# - 构建自己的类型来模拟真实世界的对象
# - 处理抽象对象
# - 容易复用和扩展
# - 理解其他 OPP 代码
# - GUI 通常使用 OPP 规则编写
# - ...
|
lijin-THU:notes-python/08-object-oriented-programming/08.01-oop-introduction.ipynb
|
# ---
# jupyter:
# jupytext:
# formats: py:light
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:AKSDeploymentPytorch]
# language: python
# name: conda-env-AKSDeploymentPytorch-py
# ---
# # Test web application locally
#
# This notebook pulls some images and tests them against the local web app running inside the Docker container we made previously.
import matplotlib.pyplot as plt
import numpy as np
from testing_utilities import to_img, img_url_to_json, plot_predictions
import requests
from dotenv import get_key, find_dotenv
# %matplotlib inline
env_path = find_dotenv(raise_error_if_not_found=True)
image_name = get_key(env_path, "docker_login") + "/" + get_key(env_path, "image_repo")
image_name
# Run the Docker conatainer in the background and open port 80. Notice we are using nvidia-docker and not docker command.
# + active="ipynb" magic_args="--bg -s \"$image_name\"" language="bash"
# nvidia-docker run -p 80:80 $1
# -
# Wait a few seconds for the application to spin up and then check that everything works.
# !curl 'http://0.0.0.0:80/'
# !curl 'http://0.0.0.0:80/version' #reports pytorch version
# Pull an image of a Lynx to test our local web app with.
IMAGEURL = "https://upload.wikimedia.org/wikipedia/commons/thumb/6/68/Lynx_lynx_poing.jpg/220px-Lynx_lynx_poing.jpg"
plt.imshow(to_img(IMAGEURL))
jsonimg = img_url_to_json(IMAGEURL)
jsonimg[:100]
headers = {"content-type": "application/json"}
# %time r = requests.post('http://0.0.0.0:80/score', data=jsonimg, headers=headers)
print(r)
r.json()
# Let's try a few more images.
images = (
"https://upload.wikimedia.org/wikipedia/commons/thumb/6/68/Lynx_lynx_poing.jpg/220px-Lynx_lynx_poing.jpg",
"https://upload.wikimedia.org/wikipedia/commons/3/3a/Roadster_2.5_windmills_trimmed.jpg",
"https://upload.wikimedia.org/wikipedia/commons/thumb/e/e6/Harmony_of_the_Seas_%28ship%2C_2016%29_001.jpg/1920px-Harmony_of_the_Seas_%28ship%2C_2016%29_001.jpg",
"http://yourshot.nationalgeographic.com/u/ss/fQYSUbVfts-T7pS2VP2wnKyN8wxywmXtY0-FwsgxpiZv_E9ZfPsNV5B0ER8-bOdruvNfMD5EbP4SznWz4PYn/",
"https://cdn.arstechnica.net/wp-content/uploads/2012/04/bohol_tarsier_wiki-4f88309-intro.jpg",
"http://i.telegraph.co.uk/multimedia/archive/03233/BIRDS-ROBIN_3233998b.jpg",
)
url = "http://0.0.0.0:80/score"
results = [
requests.post(url, data=img_url_to_json(img), headers=headers) for img in images
]
plot_predictions(images, results)
# Next let's quickly check what the request response performance is for the locally running Docker container.
image_data = list(map(img_url_to_json, images)) # Retrieve the images and data
timer_results = list()
for img in image_data:
# res=%timeit -r 1 -o -q requests.post(url, data=img, headers=headers)
timer_results.append(res.best)
timer_results
print("Average time taken: {0:4.2f} ms".format(10 ** 3 * np.mean(timer_results)))
# + active="ipynb"
# !docker stop $(docker ps -q)
# -
# We can now [deploy our web application on AKS](04_DeployOnAKS.ipynb).
|
Pytorch/03_TestLocally.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Ahmad Task 18 - Motor Control
# ### Introduction to modeling and simulation of human movement
# https://github.com/BMClab/bmc/blob/master/courses/ModSim2018.md
# Implement a simulation of the ankle joint model using the parameters from Thelen (2003) and Elias (2014)
import numpy as np
import pandas as pd
import scipy.signal
# %matplotlib notebook
import matplotlib.pyplot as plt
import math
from Muscle import Muscle
# +
Lslack = 2.4*0.09 # tendon slack length
Lce_o = 0.09 # optimal muscle fiber length
Fmax = 1400 #maximal isometric DF force
alpha = 7*math.pi/180 # DF muscle fiber pennation angle
dt = 0.001
# -
dorsiflexor = Muscle(Lce_o=Lce_o, Fmax=Fmax, Lslack=Lslack, alpha=alpha, dt = dt)
soleus = Muscle(Lce_o=0.049, Fmax=8050, Lslack=0.289, alpha=25*np.pi/180, dt = dt)
soleus.Fmax
# ### Muscle properties
# Parameters from Nigg & Herzog (2006).
Umax = 0.04 # SEE strain at Fmax
width = 0.63 # Max relative length change of CE
# Activation dynamics parameters
a = 1
u = 1 #Initial conditional for Brain's activation
#b = .25*10#*Lce_o
# ## Subject's anthropometrics
# Parameters obtained experimentally or from Winter's book.
M = 75 #total body mass (kg)
Lseg = 0.26 #segment length (m)
m = 1*M #foot mass (kg)
g = 9.81 #acceleration of gravity (m/s2)
hcm = 0.85 #distance from ankle joint to center of mass (m)
I = (4/3)*m*hcm**2 #moment of inertia
legAng = math.pi/2 #angle of the leg with horizontal (90 deg)
As_TA = np.array([30.6, -7.44e-2, -1.41e-4, 2.42e-6, 1.5e-8]) / 100 # at [m] instead of [cm]
# Coefs for moment arm for ankle angle
Bs_TA = np.array([4.3, 1.66e-2, -3.89e-4, -4.45e-6, -4.34e-8]) / 100 # at [m] instead of [cm]
As_SOL = np.array([32.3, 7.22e-2, -2.24e-4, -3.15e-6, 9.27e-9]) / 100 # at [m] instead of [cm]
Bs_SOL = np.array([-4.1, 2.57e-2, 5.45e-4, -2.22e-6, -5.5e-9]) / 100 # at [m] instead of [cm]
# ### Initial conditions
phi = 5*np.pi/180
phid = 0 #zero velocity
Lm0 = 0.306 #initial total lenght of the muscle
dorsiflexor.Lnorm_ce = 1
soleus.Lnorm_ce = 1
t0 = 0 #Initial time
tf = 30 #Final Time
dt=0.001
# +
t = np.arange(t0,tf,dt) # time array
# preallocating
F = np.empty((t.shape[0],2))
phivec = np.empty(t.shape)
Fkpe = np.empty(t.shape)
FiberLen = np.empty((t.shape[0],2))
TendonLen = np.empty(t.shape)
a_dynamics = np.empty((t.shape[0],2))
Moment = np.empty(t.shape)
# -
# ## Simulation - Series
def momentArmDF(phi):
'''
Calculate the tibialis anterior moment arm according to Elias et al (2014)
Input:
phi: Ankle joint angle in radians
Output:
Rarm: TA moment arm
'''
# Consider neutral ankle position as zero degrees
phi = phi*180/np.pi # converting to degrees
Rf = 4.3 + 1.66E-2*phi + -3.89E-4*phi**2 + -4.45E-6*phi**3 + -4.34E-8*phi**4
Rf = Rf/100 # converting to meters
return Rf
def ComputeTotalLengthSizeTA(phi):
'''
Calculate TA MTU length size according to Elias et al (2014)
Input:
phi: ankle angle
'''
phi = phi*180/math.pi # converting to degrees
Lm = 30.6 + -7.44E-2*phi + -1.41E-4*phi**2 + 2.42E-6*phi**3 + 1.5E-8*phi**4
Lm = Lm/100
return Lm
def ComputeMomentJoint(Rf_TA, Fnorm_tendon_TA, Fmax_TA, Rf_SOL, Fnorm_tendon_SOL, Fmax_SOL, m, g, phi):
'''
Inputs:
RF = Moment arm
Fnorm_tendon = Normalized tendon force
m = Segment Mass
g = Acelleration of gravity
Fmax= maximal isometric force
Output:
M = Total moment with respect to joint
'''
M = (-0.65*m*g*hcm*phi +Rf_TA*Fnorm_tendon_TA*Fmax_TA
+ Rf_SOL*Fnorm_tendon_SOL*Fmax_SOL + m*g*hcm*np.sin(phi))
return M
def ComputeAngularAcelerationJoint(M, I):
'''
Inputs:
M = Total moment with respect to joint
I = Moment of Inertia
Output:
phidd= angular aceleration of the joint
'''
phidd = M/I
return phidd
def computeMomentArmJoint(theta, Bs):
# theta - joint angle (degrees)
# Bs - coeficients for the polinomio
auxBmultp = np.empty(Bs.shape);
for i in range (len(Bs)):
auxBmultp[i] = Bs[i] * (theta**i)
Rf = sum(auxBmultp)
return Rf
def ComputeTotalLenghtSize(theta, As):
# theta = joint angle(degrees)
# As - coeficients for the polinomio
auxAmultp = np.empty(As.shape);
for i in range (len(As)):
auxAmultp[i] = As[i] * (theta**i)
Lm = sum(auxAmultp)
return Lm
# +
Lce_TA_ref = 0.086
Lce_SOL_ref = 0.037
noise=0.1*np.random.randn(len(t))*1/dt * 0
[b,a] = scipy.signal.butter(2,40.0/(1/dt/2))
#filtNoise = scipy.signal.filtfilt(b,a,noise)
filtNoise = noise
phiRef=5*np.pi/180
Kp_TA=1000
Kd_TA=50
Kp_SOL=1000
Kd_SOL=50
for i in range (len(t)):
Lm_TA = ComputeTotalLenghtSize(phi*180/np.pi, As_TA)
Rf_TA = computeMomentArmJoint(phi*180/np.pi, Bs_TA)
Lm_SOL = ComputeTotalLenghtSize(phi*180/np.pi, As_SOL)
Rf_SOL = computeMomentArmJoint(phi*180/np.pi, Bs_SOL)
##################################################################
# e = phiRef - phi
# if e>0:
# U_TA, U_SOL = max(min(1, Kp*e-Kd*phid), 0.01), 0.01
# else:
# U_TA, U_SOL = 0.01, max(min(1, -Kp*e+Kd*phid), 0.01)
e_TA = Lce_TA_ref - dorsiflexor.Lnorm_ce*dorsiflexor.Lce_o
if e_TA > 0:
U_TA = 0.01
else:
U_TA = max(min(1, -Kp_TA*e_TA+Kd_TA*dorsiflexor.Lnorm_cedot*dorsiflexor.Lce_o), 0.01)
e_SOL = Lce_SOL_ref - soleus.Lnorm_ce*soleus.Lce_o
if e_SOL > 0:
U_SOL = 0.01
else:
U_SOL = max(min(1, -Kp_SOL*e_SOL+Kd_SOL*soleus.Lnorm_cedot*soleus.Lce_o), 0.01)
##############################################################
dorsiflexor.updateMuscle(Lm=Lm_TA, u=U_TA)
soleus.updateMuscle(Lm=Lm_SOL, u=U_SOL)
#####################################################################
#Compute MomentJoint
M = ComputeMomentJoint(Rf_TA,dorsiflexor.Fnorm_tendon,
dorsiflexor.Fmax,
Rf_SOL, soleus.Fnorm_tendon,
soleus.Fmax,
m,g,phi)
#Compute Angular Aceleration Joint
torqueWithNoise = M + filtNoise[i]
phidd = ComputeAngularAcelerationJoint (torqueWithNoise,I)
# Euler integration steps
phid= phid + dt*phidd
phi = phi + dt*phid
phideg= (phi*180)/math.pi #convert joint angle from radians to degree
# Store variables in vectors
F[i,0] = dorsiflexor.Fnorm_tendon*dorsiflexor.Fmax
F[i,1] = soleus.Fnorm_tendon*soleus.Fmax
Fkpe[i] = dorsiflexor.Fnorm_kpe*dorsiflexor.Fmax
FiberLen[i,0] = dorsiflexor.Lnorm_ce*dorsiflexor.Lce_o
FiberLen[i,1] = soleus.Lnorm_ce*soleus.Lce_o
TendonLen[i] = dorsiflexor.Lnorm_see*dorsiflexor.Lce_o
a_dynamics[i,0] = dorsiflexor.a
a_dynamics[i,1] = soleus.a
phivec[i] = phideg
Moment[i] = M
# -
# ## Plots
# +
fig, ax = plt.subplots(1, 1, figsize=(6,3))
ax.plot(t,a_dynamics[:,1],c='blue', label='SOL')
ax.plot(t,a_dynamics[:,0],c='red', label='TA')
plt.grid()
plt.xlabel('time (s)')
plt.ylabel('Activation signal')
plt.legend(loc='best')
plt.tight_layout()
plt.show()
# +
fig, ax = plt.subplots(1, 1, figsize=(6,3))
ax.plot(t, Moment)
plt.grid()
plt.xlabel('time (s)')
plt.ylabel('joint moment')
plt.tight_layout()
plt.show()
# +
fig, ax = plt.subplots(1, 1, figsize=(6,3))
ax.plot(t, F[:,1], c='red')
plt.grid()
plt.xlabel('time (s)')
plt.ylabel('Force (N)')
plt.tight_layout()
plt.show()
# +
fig, ax = plt.subplots(1, 1, figsize=(6,3))
ax.plot(t,phivec,c='red')
plt.grid()
plt.xlabel('time (s)')
plt.ylabel('Joint angle (deg)')
plt.show()
# +
fig, ax = plt.subplots(1, 1, figsize=(6,3))
ax.plot(t,FiberLen, label = 'fiber')
ax.plot(t,TendonLen, label = 'tendon')
plt.grid()
plt.xlabel('time (s)')
plt.ylabel('Length (m)')
ax.legend(loc='best')
plt.tight_layout()
plt.show()
fig, ax = plt.subplots(1, 3, figsize=(6,3), sharex=True, sharey=True)
ax[0].plot(t,FiberLen[:,0], label = 'fiber')
ax[1].plot(t,TendonLen, label = 'tendon')
ax[2].plot(t,FiberLen[:, 0] + TendonLen, label = 'muscle (tendon + fiber)')
ax[1].set_xlabel('time (s)')
ax[0].set_ylabel('Length (m)')
ax[0].legend(loc='best')
ax[1].legend(loc='best')
ax[2].legend(loc='best')
plt.tight_layout()
plt.show()
# +
fig, ax = plt.subplots(1, 1, figsize=(6,3))
ax.plot(t,Moment,c='red')
plt.grid()
plt.xlabel('time (s)')
plt.ylabel('Moment (Nm)')
plt.tight_layout()
plt.show()
# +
fig, ax = plt.subplots(1, 1, figsize=(6,3))
ax.plot(t,filtNoise*dt,c='red')
plt.grid()
plt.xlabel('time (s)')
plt.ylabel('Noise (Nm)')
plt.tight_layout()
plt.show()
# +
fig, ax = plt.subplots(1, 1, figsize=(6,3))
ax.plot(t,FiberLen[:,0],c='red', label='TA')
ax.plot(t,FiberLen[:,1],c='blue', label='SOL')
plt.grid()
plt.xlabel('time (s)')
plt.ylabel('Fiber Length (m)')
plt.legend(loc='best')
plt.tight_layout()
plt.show()
# -
|
courses/modsim2018/ahmadhassan/Ahmad_Task18.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# + tags=["hide_output"]
import arviz as az
import numpy as np
import pymc as pm
from pymc.math import log, dot
import pandas as pd
# %load_ext lab_black
# %load_ext watermark
# -
# # Arrhythmia
#
# A logistic regression example.
#
# Adapted from [unit 7: arrhythmia.odc](https://raw.githubusercontent.com/areding/6420-pymc/main/original_examples/Codes4Unit7/arrhythmia.odc).
#
# Data can be found [here](https://raw.githubusercontent.com/areding/6420-pymc/main/data/arrhythmia.csv).
#
# Associated lecture video: Unit 7 Lesson 15
# ## Problem statement
#
# Patients who undergo Coronary Artery Bypass Graft Surgery (CABG) have an approximate 19-40% chance of developing atrial fibrillation (AF). AF can lead to blood clots forming causing greater in-hospital mortality, strokes, and longer hospital stays. While this can be prevented with drugs, it is very expensive and sometimes dangerous if not warranted. Ideally, several risk factors which would indicate an increased risk of developing AF in this population could save lives and money by indicating which patients need pharmacological intervention. Researchers began collecting data from CABG patients during their hospital stay such as demographics like age and sex, as well as heart rate, cholesterol, operation time, etc.. Then, the researchers recorded which patients developed AF during their hospital stay. Researchers now want to find those pieces of data which indicate high risk of AF. In the past, indicators like age, hypertension, and body surface area (BSA) have been good indicators, though these alone have not produced a satisfactory solution.
#
# Fibrillation occurs when the heart muscle begins a quivering motion instead of a normal, healthy pumping rhythm. Fibrillation can affect the atrium (atrial fibrillation) or the ventricle (ventricular fibrillation); ventricular fibrillation is imminently life threatening.
#
# Atrial fibrillation is the quivering, chaotic motion in the upper chambers of the heart, known as the atria. Atrial fibrillation is often due to serious underlying medical conditions, and should be evaluated by a physician. It is not typically a medical emergency.
#
# Ventricular fibrillation occurs in the ventricles (lower chambers) of the heart; it is always a medical emergency. If left untreated, ventricular fibrillation (VF, or V-fib) can lead to death within minutes. When a heart goes into V-fib, effective pumping of the blood stops. V-fib is considered a form of cardiac arrest, and an individual suffering from it will not survive unless cardiopulmonary resuscitation (CPR) and defibrillation are provided immediately.
#
# DATA Arrhythmia
# - Y = Fibrillation
# - X1 = Age
# - X2 = Aortic Cross Clamp Time
# - X3 = Cardiopulmonary Bypass Time:
# - Bypass of the heart and lungs as, for example, in open heart surgery. Blood returning to the heart is diverted through a heart-lung machine (a pump-oxygenator) before returning it to the arterial circulation. The machine does the work both of the heart (pump blood) and the lungs (supply oxygen to red blood cells).
# - X4 = ICU Time (Intensive Care Unit)
# - X5 = Avg Heart Rate
# - X6 = Left Ventricle Ejection Fraction
# - X7 = Hypertension
# - X8 = Gender [1 -Female; 0-Male]
# - X9 = Diabetis
# - X10 = Previous MI
data_df = pd.read_csv("../data/arrhythmia.csv")
data_df.info()
X = data_df.iloc[:, 1:].to_numpy()
# add intercept column to X
X_aug = np.concatenate((np.ones((X.shape[0], 1)), X), axis=1)
y = data_df["Fibrillation"].to_numpy()
# + tags=["hide_output"]
with pm.Model() as m:
X_data = pm.Data("X_data", X_aug)
y_data = pm.Data("y_data", y)
betas = pm.Normal("beta", mu=0, tau=0.001, shape=X.shape[1] + 1)
p = dot(X_data, betas)
lik = pm.Bernoulli("y", logit_p=p, observed=y_data)
trace = pm.sample(
10000,
chains=4,
tune=500,
cores=4,
random_seed=1,
)
# -
az.summary(trace, hdi_prob=0.95)
# %watermark --iversions -v
|
unit7/glm-arrhythmia.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 1. Importing the libraries.
#importing modules
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
import seaborn as sns
import warnings
warnings.filterwarnings('ignore')
#importing the arff module
from scipy.io import arff
# # 2. Importing and Organizing the data.
#loading the dataset
dataset_1 = arff.loadarff('./data/1year.arff')
dataset_2 = arff.loadarff('./data/2year.arff')
dataset_3 = arff.loadarff('./data/3year.arff')
dataset_4 = arff.loadarff('./data/4year.arff')
dataset_5 = arff.loadarff('./data/5year.arff')
# +
#coverting the data into a dataframe
#Training dataset
df1 = pd.DataFrame(dataset_1[0])
df2 = pd.DataFrame(dataset_2[0])
df3 = pd.DataFrame(dataset_3[0])
df5 = pd.DataFrame(dataset_5[0])
Tr_df = pd.concat([df1,df2,df3,df5],axis = 0)
# -
#Testing dataset
Ts_df = pd.DataFrame(dataset_4[0])
#to convert the features to float
Tr_df.astype(float)
Ts_df.astype(float)
# +
#converting class labels to int
Tr_df['class'].replace(b'0',0,inplace=True)
Tr_df['class'].replace(b'1',1,inplace=True)
Ts_df['class'].replace(b'0',0,inplace=True)
Ts_df['class'].replace(b'1',1,inplace=True)
# -
#checking the datatype of the class
Tr_df['class'].dtype
Ts_df['class'].dtype
# # 3. Data analysis and Data preprocessing.
# ## i. Missing data analysis
#Checking missing values according to the features
Tr_df.isna().sum()
Ts_df.isna().sum()
# Note: From the above output, it shows that each attribute or feature consist of some missing values.
#The barplot shows that the Attr21 and Attr37 have more missing values
plt.figure(figsize=(25,7))
plt.xticks(rotation=45)
sns.set_theme(style='ticks')
sns.barplot(x = Tr_df.columns, y = Tr_df.isna().sum().values)
plt.figure(figsize=(25,7))
plt.xticks(rotation=45)
sns.set_theme(style='ticks')
sns.barplot(x = Ts_df.columns, y = Ts_df.isna().sum().values)
#Plotting the missing values with the displot showing the missing values as true and non missing as false
sns.displot(data=Tr_df.isna().melt(value_name='missing'),y='variable',hue='missing',height=20)
#Plotting the missing values with the displot showing the missing values as true and non missing as false
sns.displot(data=Ts_df.isna().melt(value_name='missing'),y='variable',hue='missing',height=20)
# Note: Here two attributes Attr20 and Attr37 have more missing values and mostly the Attr37 which has more missing values than the filled values.
# ## ii. Data Imputation.
# +
#Iterating through the columns and calculating the mean, then filling the mean in null vales place
for feature in Tr_df.columns:
m=Tr_df[feature].mean()
Tr_df[feature].fillna(m,inplace=True)
for feature in Ts_df.columns:
m=Ts_df[feature].mean()
Ts_df[feature].fillna(m,inplace=True)
# -
# Below, you can see that there are no null values as those values are filled by the mean attribute values of each attribute
#checking if there are any null values
Tr_df.isna().any().sum()
#checking if there are any null values
Ts_df.isna().any().sum()
# +
#sns.countplot(Tr_df['class'])
# -
sns.countplot(Ts_df['class'])
# The above plots shows taht there is an imbalance in the data and now, we SMOTE for oversampling of the data.
# ## iii. Dealing of imbalanced data
#installing the imbalanced learn package
# !pip3 install imblearn
#importing imblearn package
import imblearn
dir(imblearn)
#importing the SMOTE module from the imbalanced learn package
from imblearn.over_sampling import SMOTE
sm = SMOTE()
#Allocating the target class feature to the variable y and dropping the column class in the X variable for training data
y_train = Tr_df[['class']]
X_train = Tr_df.drop(columns = ['class'])
#Allocating the target class feature to the variable y and dropping the column class in the X variable for training data
y_test = Ts_df[['class']]
X_test = Ts_df.drop(columns = ['class'])
#Oversampling the data
X_train_res, y_train_res = sm.fit_resample(X_train,y_train)
X_train_res.shape
y_train_res.shape
X_test_res, y_test_res = sm.fit_resample(X_test,y_test)
sns.countplot(y_train_res['class'])
sns.countplot(y_test_res['class'])
# From the above it's obvious that the oversampling is done successfully with the help of SMOTE as the there are equal number of true and false in the bankruptcy.
final_train_df = pd.concat([X_train_res,y_train_res],axis=1)
final_test_df = pd.concat([X_test_res,y_test_res],axis=1)
final_train_df.to_csv('Train.csv')
final_test_df.to_csv('Test.csv')
|
sumair_EDA.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # ETL Pipeline Preparation
# Follow the instructions below to help you create your ETL pipeline.
# ### 1. Import libraries and load datasets.
# - Import Python libraries
# - Load `messages.csv` into a dataframe and inspect the first few lines.
# - Load `categories.csv` into a dataframe and inspect the first few lines.
# import libraries
import pandas as pd
from sqlalchemy import create_engine
# load messages dataset
messages = pd.read_csv('messages.csv')
messages.head()
# load categories dataset
categories = pd.read_csv('categories.csv')
categories.head()
# ### 2. Merge datasets.
# - Merge the messages and categories datasets using the common id
# - Assign this combined dataset to `df`, which will be cleaned in the following steps
# merge datasets
df = pd.merge(messages, categories, on='id')
df.head()
# ### 3. Split `categories` into separate category columns.
# - Split the values in the `categories` column on the `;` character so that each value becomes a separate column. You'll find [this method](https://pandas.pydata.org/pandas-docs/version/0.23/generated/pandas.Series.str.split.html) very helpful! Make sure to set `expand=True`.
# - Use the first row of categories dataframe to create column names for the categories data.
# - Rename columns of `categories` with new column names.
# create a dataframe of the 36 individual category columns
categories = pd.Series(df['categories']).str.split(';', expand=True)
categories.head()
# +
# select the first row of the categories dataframe
row = categories.iloc[0,:]
# use this row to extract a list of new column names for categories.
# one way is to apply a lambda function that takes everything
# up to the second to last character of each string with slicing
category_colnames = []
for entry in row:
category_colnames.append(entry[:-2])
print(category_colnames)
# -
# rename the columns of `categories`
categories.columns = category_colnames
categories.head()
# ### 4. Convert category values to just numbers 0 or 1.
# - Iterate through the category columns in df to keep only the last character of each string (the 1 or 0). For example, `related-0` becomes `0`, `related-1` becomes `1`. Convert the string to a numeric value.
# - You can perform [normal string actions on Pandas Series](https://pandas.pydata.org/pandas-docs/stable/text.html#indexing-with-str), like indexing, by including `.str` after the Series. You may need to first convert the Series to be of type string, which you can do with `astype(str)`.
for column in categories:
# set each value to be the last character of the string
categories[column] = categories[column].str[-1]
# convert column from string to numeric
categories[column] = categories[column].astype(int)
categories.head()
# ### 5. Replace `categories` column in `df` with new category columns.
# - Drop the categories column from the df dataframe since it is no longer needed.
# - Concatenate df and categories data frames.
# +
# drop the original categories column from `df`
df.drop('categories', inplace=True, axis=1)
df.head()
# -
# concatenate the original dataframe with the new `categories` dataframe
df = pd.concat([df, categories], axis=1)
df.head()
# ### 6. Remove duplicates.
# - Check how many duplicates are in this dataset.
# - Drop the duplicates.
# - Confirm duplicates were removed.
# check number of duplicates
print('Number of duplicated rows: {} out of {} samples'.format(df.duplicated().sum(),df.shape[0]))
# drop duplicates
df = df.drop_duplicates()
# check number of duplicates
print('Number of duplicated rows: {} out of {} samples'.format(df.duplicated().sum(),df.shape[0]))
# ### 7. Save the clean dataset into an sqlite database.
# You can do this with pandas [`to_sql` method](https://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.to_sql.html) combined with the SQLAlchemy library. Remember to import SQLAlchemy's `create_engine` in the first cell of this notebook to use it below.
engine = create_engine('sqlite:///InsertDatabaseName.db')
df.to_sql('DisasterTable', engine, index=False)
# ### 8. Use this notebook to complete `etl_pipeline.py`
# Use the template file attached in the Resources folder to write a script that runs the steps above to create a database based on new datasets specified by the user. Alternatively, you can complete `etl_pipeline.py` in the classroom on the `Project Workspace IDE` coming later.
|
ETL Pipeline Preparation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# ## Tutorial on how to implement periodic boundaries
# This tutorial will show how to implement Periodic boundary conditions (where particles that leave the domain on one side enter again on the other side) can be implemented in Parcels
# The idea in Parcels is to do two things:
# 1) Extend the fieldset with a small 'halo'
# 2) Add a periodic boundary kernel to the `.execute`
# We'll start by importing the relevant modules
# %matplotlib inline
from parcels import FieldSet, ParticleSet, JITParticle, plotTrajectoriesFile
from parcels import AdvectionRK4
from datetime import timedelta as delta
import math
# We import the Peninsula fieldset; note that we need to set `allow_time_extrapolation` because the Peninsula fieldset has only one time snapshot.
fieldset = FieldSet.from_parcels('Peninsula_data/peninsula', allow_time_extrapolation=True)
# Extending the fieldset with a halo is very simply done using the `add_periodic_halo()` method. Halos can be added either in the zonal direction, the meridional direction, or both, by setting `zonal` and/or `meridional` to `True`.
#
# But before we apply the halo, we first define two new fieldset constants `halo_east` and `halo_west`. They store the original zonal extend of the grid (so *before* adding the halo) and will be used later in the `periodicBC` kernel.
#
# ***Note that some hydrodynamic data, such as the global ORCA grid used in NEMO, already has a halo.*** In these cases, **do not** extent the fieldset with the halo but only add the periodic boundary kernel, where you use the explicit values for halo_east and halo_west
# +
fieldset.add_constant('halo_west', fieldset.U.grid.lon[0])
fieldset.add_constant('halo_east', fieldset.U.grid.lon[-1])
fieldset.add_periodic_halo(zonal=True)
# -
# The other item we need is a custom Kernel that can move the particle from one side of the domain to the other.
def periodicBC(particle, fieldset, time):
if particle.lon < fieldset.halo_west:
particle.lon += fieldset.halo_east - fieldset.halo_west
elif particle.lon > fieldset.halo_east:
particle.lon -= fieldset.halo_east - fieldset.halo_west
# Now define a particle set and execute it as usual
pset = ParticleSet.from_line(fieldset, pclass=JITParticle,
size=10, start=(20e3, 3e3), finish=(20e3, 45e3))
output_file = pset.ParticleFile(name="PeriodicParticle", outputdt=delta(hours=1))
pset.execute(AdvectionRK4 + pset.Kernel(periodicBC),
runtime=delta(hours=24), dt=delta(minutes=5),
output_file=output_file)
# And finally plot the particle trajectories
plotTrajectoriesFile('PeriodicParticle.nc');
# We can see that the particles start at 0.7E, move eastward, and once they hit the boundary at 0.895428E, they jump to the other side of the domain (the horizontal lines). So we have periodic boundary conditions!
# *As a note, one may ask why we need the halo. Why can't we use simply the `PeriodicBC` kernel? This is because, if the particle is close to the edge of the fieldset (but still in it), `AdvectionRK4` will need to interpolate velocities that may lay outside the fieldset domain. With the halo, we make sure `AdvectionRK4` can access these values.*
|
parcels/parcels/examples/tutorial_periodic_boundaries.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Comparing Data with Syngine Synthetics using ObsPy
#
# ### *Demo by <NAME>, May 2018*
#
# Useful links:
# - [Obspy Documentation](https://docs.obspy.org/)
# - [Syngine Documentation](http://ds.iris.edu/ds/products/syngine/)
#
#
# Contents:
# - [Part 1: Viewing Seismograms from the Hawaii Earthquake](#Part 1)
# - [Part 2: Practical Example 1: *Tuning Deconvolution Parameters*](#Part 2)
# - [Part 3: Practical Example 2: *Testing for apparent shear-wave splitting*](#Part 3)
#
# <a id='Part 1'></a>
#
#
# ## Part 1: Viewing Seismograms from the Hawaii Earthquake
#
#
# ### Step 1: Get event catalog from USGS
#
# - query events from May 1-6, 2018 with Mw >= 5.7
# - plot events on the map
# +
# %matplotlib inline
from obspy.clients.fdsn.client import Client
from obspy import UTCDateTime
client = Client('USGS')
starttime = UTCDateTime(2018,5,1)
endtime = UTCDateTime(2018,5,7)
minmagnitude = 5.7
cat = client.get_events(starttime=starttime, endtime=endtime, minmagnitude=minmagnitude)
_ = cat.plot()
# -
# ### Step 2: Set signal processing workflow
# - trim edges
# - rotate to ZNE (requires inventory, an obspy class that contains station response info)
# - rotate to RT (requires back_azimuth)
# - detrend and bandpass filter
# - resample
def process_signal(st0, inv, baz):
st1=st0.copy()
#trim by 5 sec
t1=st1[0].stats.starttime+5
t2=st1[0].stats.endtime-5
st1.trim(t1,t2)
st1.rotate('->ZNE',inventory=inv)
st1.rotate('NE->RT',back_azimuth=baz)
st1.detrend()
st1.filter('bandpass', freqmin = 0.005, freqmax =1./10., corners=4, zerophase=True)
st1.resample(5)
return(st1)
# ### Step 3: Get waveforms for Hawaii earthquake
# - download data from IRIS
# - remove response
# - process
# - plot
# +
from obspy.geodetics import gps2dist_azimuth
evt = cat[1]
etime, elat, elon = evt.preferred_origin().time, evt.preferred_origin().latitude, evt.preferred_origin().longitude
client = Client("IRIS")
network = 'IU'
station = 'HRV'
inv=client.get_stations(
starttime=etime,endtime=etime+3600,
level = "channel", channel="BH*", network=network, station=station)
sta = inv[0][0]
delm, az, baz = gps2dist_azimuth(elat, elon, sta.latitude, sta.longitude)
t1=etime
t2=etime+3600
client = Client('IRIS')
st0=client.get_waveforms(network,station,'00','BH?', t1, t2, attach_response=True)
pre_filt = (0.005, 0.01, 5.0, 10.0)
st0.remove_response(output='DISP', pre_filt=pre_filt)
st1=process_signal(st0, inv = inv, baz = baz)
st1.plot()
# -
# ### Step 4: Get synthetics for Hawaii earthquake
# - Manually input source parameters from [USGS Event Page](https://earthquake.usgs.gov/earthquakes/eventpage/us1000dyad#moment-tensor)
# - process
# - plot
# +
from numpy import arange
from obspy.clients.syngine import Client
elat = evt.preferred_origin().latitude
elon = evt.preferred_origin().longitude
edepth = evt.preferred_origin().depth
etime = evt.preferred_origin().time
strike = 240
dip = 20
rake= 114
M0 = 2.736e+19
stis = Client().get_waveforms(model="iasp91_2s",
sourcelatitude = elat, sourcelongitude = elon,
sourcedepthinmeters = edepth,
units='displacement',
receiverlatitude = sta.latitude,
receiverlongitude = sta.longitude,
sourcedoublecouple = [strike, dip, rake, M0],
origintime = etime)
stis1=process_signal(stis, inv, baz)
stis1.plot()
# -
# ### Step 5: Compare and plot
# +
from matplotlib import pylab as plt
def get_index(st,comp):
for itr, tr in enumerate(st):
if comp in tr.stats.channel:
return itr
fig=plt.figure(1,figsize=(15,15))
for iplt, comp in enumerate(['Z', 'R', 'T']):
icomp1 = get_index(st1,comp)
icomp2 = get_index(stis1,comp)
def plot_trace(trace, color):
times = arange(len(trace.data)) * trace.stats.delta
plt.plot(times,trace.data,color,label=trace.stats.channel)
plt.subplot(3,1,iplt+1)
plot_trace(st1 [icomp1],'k')
plot_trace(stis1[icomp2],'r')
plt.legend(loc=3)
plt.ylabel('Displacement')
plt.xlabel('Time (s)')
# -
# ### Other Steps to Consider
# - Convolve traces with source time function
#
#
#
#
#
#
#
#
# <a id='Part 2'></a>
# ## Practical Example 1: *Tuning Deconvolution Parameters*
# +
from obspy.taup import TauPyModel
model = TauPyModel('ak135')
arrivals = model.get_travel_times(source_depth_in_km=edepth/1000.0, distance_in_degree=delm/1000./111.11, phase_list = 'S')
assert arrivals[0].phase.name == 'S'
timeS = arrivals[0].time
stis.filter('bandpass', freqmin = 1./50.0, freqmax =1./4., corners=4, zerophase=True)
stis2 = stis.copy().rotate('ZNE->LQT', back_azimuth=baz, inclination = arrivals[0].incident_angle)
stis2.trim(etime+timeS-50, etime+timeS+50).plot()
# +
from etmtm import ETMTM
from scipy.signal import tukey
import warnings
warnings.filterwarnings('ignore')
fig = plt.figure(1,figsize=(5,10))
plt.style.use('ggplot')
for pctage in [0.25,0.85]:
assert 'L' in stis2[0].stats.channel
assert 'Q' in stis2[1].stats.channel
P = stis2.copy()[1].data
D = stis2.copy()[0].data
dt = stis2[0].stats.delta
#Indeces to mask out
i1 = int(len(P) * (pctage)/2)
i2 = int(len(P) - i1)
P[:i1]=0.0
P[i2:]=0.0
P[i1:i2]= P[i1:i2] * tukey(len(P[i1:i2]))
TB = 1.5
NT = 2
Poverlap = 0.99
win_len = 100
#times, RF = ETMTM(P,D,TB,NT,dt, tag='data', nalphas=20, Poverlap=0.99, win_len=70)
times, RF = ETMTM(P,D,TB,NT,dt, tag='data', nalphas=20, Poverlap=Poverlap, win_len=win_len)
_, RFnorm = ETMTM(P,P,TB,NT,dt, tag='data', nalphas=20, Poverlap=Poverlap, win_len=win_len)
norm = max(abs(RFnorm))
plt.subplot(111)
plt.plot(RF/norm,times,lw=2, label = '%d pct' % (pctage*100) )
plt.ylabel('Time (s)')
plt.xlabel('RF Amplitude')
plt.xlim(-0.12,0.12)
fig.add_axes([1.2,0.6,1.0,0.3])
tmp = arange(len(P))*dt - 50
def plot_wvfrm(wvfrm,label):
plt.plot(tmp,wvfrm)
plt.ticklabel_format(style='sci', axis='y', scilimits=(0,0))
plt.ylabel('Displacement')
plt.xlabel('Time (s)')
plt.title(label)
plot_wvfrm(P,'Parent')
fig.add_axes([1.2,0.15,1.0,0.3])
plot_wvfrm(D,'Daughter')
plt.subplot(111)
_ = plt.legend(title = 'Parent Mask', loc=4)
# -
# ### _Take Away: Complicated processing workflows can be fine-tuned and validated with syngine synthetics!_
# <a id='Part 3'></a>
#
#
#
#
# ## Practical Example 2: *Testing for apparent shear-wave splitting*
#
# - bandpass filter
# - take derivative to get velocity waveforms
# - trim +/- 30 s around S
# +
stis3 = stis.copy()
stis3.filter('bandpass', freqmin = 1./50.0, freqmax =1./8., corners=4, zerophase=True).differentiate()
stis3.trim(etime+timeS-20, etime+timeS+20).plot()
# -
# ### Now plot S particle motion
plt.figure(1,figsize=(7,7))
plt.plot(stis3[2].data,stis3[1].data, lw = 3)
plt.xlabel('East')
plt.ylabel('North')
boxlim=max([max(abs(stis3[2].data)), max(abs(stis3[1].data))])*1.1
ax=plt.gca()
ax.set_ylim(-boxlim,+boxlim)
ax.set_xlim(-boxlim,+boxlim)
# ### Try to linearize particle motion by applying rotations and time shifts
# +
from calculate_split import calculate_split
from numpy import pi
plt.figure(1,figsize=(7,7))
ax=plt.subplot(111)
degrad = pi / 180.0
calculate_split(stis3[1], stis3[2], az*degrad, plot=True, ax=ax)
for label in ax.get_xticklabels():
label.set_fontsize(16)
for label in ax.get_yticklabels():
label.set_fontsize(16)
plt.ylabel('Splitting Direction', fontsize=12)
plt.xlabel('Split Time (s)', fontsize = 12)
# -
# ### _This is clearly not a null pattern, but it is unlikely that an analyst would record this as a well-constrained split due to the large error contour._
#
# ### _To illustrate a better example of apparent splitting in syngine synthetics, see below._
#
# 
# ### _Take Away: Syngine synthetics empower scientists to check results and test ideas with relative ease._
|
Compare_Data_and_Synthetics.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# %matplotlib inline
import pickle
import numpy as np
import matplotlib.pyplot as plt
from pathlib import Path
from multiprocessing import Process
from Behavior_Cloning_ModelWithDAgger import BCModelWithDAgger
# -
data_path = Path('./expert_data/')
def load_data_from_pickle(envname):
file_path = data_path / (envname + '.pkl')
with open(file_path.resolve(), 'rb') as f:
data = pickle.load(f)
return data
envs = ['Hopper-v2', 'Ant-v2', 'HalfCheetah-v2', 'Humanoid-v2', 'Reacher-v2', 'Walker2d-v2']
min_loss = 1e-5
def estimateModel(env_name, training_epoch=5000):
print('estimating %s...' % env_name)
data = load_data_from_pickle(env_name)
train_inputs = data['observations']
train_outputs = data['actions']
train_outputs = np.reshape(train_outputs, (train_outputs.shape[0], train_outputs.shape[2]))
print('estimate env %s' % env_name)
print('train_inputs shape is: ', train_inputs.shape)
print('train_outputs shape is: ', train_outputs.shape)
model_params = {
'env_name': env_name,
'input_dim': train_inputs.shape[1],
'output_dim': train_outputs.shape[1],
'learning_rate': 5e-4,
'batch_size': 256
}
model = BCModelWithDAgger(**model_params)
model.build()
epochs = []
losses = []
mean_returns = []
std_returns = []
for epoch in range(training_epoch + 1):
batch = model.generate_batch(train_inputs, train_outputs)
loss = model.train_on_batch(*batch)
if loss < min_loss:
break
if epoch % 20 == 0:
returns = model.evaluate_reward()
epochs.append(epoch)
losses.append(loss)
mean_returns.append(np.mean(returns))
std_returns.append(np.std(returns))
if epoch % 10 == 0:
train_inputs, train_outputs = model.DAgger(train_inputs, train_outputs)
with open('%s_train_dagger.pkl' % env_name, 'wb') as f:
data = {
'epochs': epochs,
'losses': losses,
'mean_returns': mean_returns,
'std_returns': std_returns
}
pickle.dump(data, f)
print('estimating %s...finished' % env_name)
# +
# estimate all model
training_epoch = 400
pros = []
for env_name in envs:
process = Process(target=estimateModel, args=(env_name, training_epoch))
# estimateModel(env_name, training_epoch)
process.start()
pros.append(process)
for p in pros:
p.join()
# -
data = {}
data_old = {}
for env_name in envs:
with open('%s_train_dagger.pkl' % env_name, 'rb') as f:
data[env_name] = pickle.load(f)
with open('%s_train.pkl' % env_name, 'rb') as f:
data_old[env_name] = pickle.load(f)
# +
# plot all data
plt.figure(figsize=(20,20))
for idx in range(len(envs)):
env_name = envs[idx]
plt.subplot(len(envs), 3, (idx) * 3 + 1)
plt.title('%s loss' % env_name)
plt.plot(data[env_name]['epochs'], data[env_name]['losses'], 'r', label='dagger')
plt.plot(data_old[env_name]['epochs'], data_old[env_name]['losses'], 'b', label='old')
plt.legend()
plt.tight_layout()
plt.subplot(len(envs), 3, (idx) * 3 + 2)
plt.title('%s mean_returns' % env_name)
plt.plot(data[env_name]['epochs'], data[env_name]['mean_returns'], 'r', label='dagger')
plt.plot(data_old[env_name]['epochs'], data_old[env_name]['mean_returns'], 'b', label='old')
plt.legend()
plt.tight_layout()
plt.subplot(len(envs), 3, (idx) * 3 + 3)
plt.title('%s std_returns' % env_name)
plt.plot(data[env_name]['epochs'], data[env_name]['std_returns'], 'r', label='dagger')
plt.plot(data_old[env_name]['epochs'], data_old[env_name]['std_returns'], 'b', label='old')
plt.legend()
plt.tight_layout()
# -
|
hw1/Dagger.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:metis] *
# language: python
# name: conda-env-metis-py
# ---
# This document outlines the process for importing data and basic data cleaning that I followed for this project. Initial cleaning examples are done on a smaller dataframe to save processing time.
#
# ## Importing data into my database
#
# #### Importing the MTA Turnstile data:
#
# Step 1: Run `python get_mta_turnstiles.py "(19|20|21|22)"` in terminal to get the turnstile data.
#
# I wanted all of the data from 2019-2021 in my database, so I included 22 in the regex to make sure I got everything from 2021 (since the last few days of 2021 were included in the first upload in 2022). I could have been more specific here, but this worked for my purposes.
#
# #### Importing the MTA Fare data:
#
# Note: due to formatting differences in the MTA Fare data, I had to modify the get_mta.py file and split it into get_mta_fares.py and get_mta_fares_old.py.
#
# Step 1: Run `python get_mta_fares_new.py "(20|21|22)"` to get the bulk of the new format of MTA fare data.
#
# Step 2: Run `python get_mta_fares_old.py "19"` to get the remaining MTA fare data for 2019.
#
# #### Importing the MTA Turnstiles Remote-Complex Lookup:
#
# I found a hand-built resource from <NAME> that matches MTA station data found at `http://web.mta.info/developers/data/nyct/subway/Stations.csv` to the fields in the turnstile dataset.
reset -fs
# +
import pandas as pd
import datetime as dt
import sqlite3
from sqlalchemy import create_engine
engine = create_engine('sqlite:///database/mta_data.db')
# -
remote_lookup_df = pd.read_csv('database/mta_remote_lookup.csv')
remote_lookup_df.columns = [column.strip().upper() for column in remote_lookup_df.columns]
remote_lookup_df.head()
# strip whitespace from entries - just to be on the safe side
lookup = (['REMOTE',
'BOOTH',
'COMPLEX_ID',
'STATION',
'LINE_NAME',
'DIVISION'])
(remote_lookup_df[lookup].str.strip() for column in lookup)
remote_lookup_df.head()
remote_lookup_df.COMPLEX_ID
remote_lookup_df['REMOTE'] = remote_lookup_df['REMOTE'].astype(object)
remote_lookup_df['BOOTH'] = remote_lookup_df['BOOTH'].astype(object)
remote_lookup_df['COMPLEX_ID'] = remote_lookup_df['COMPLEX_ID'].astype(object)
remote_lookup_df['STATION'] = remote_lookup_df['STATION'].astype(object)
remote_lookup_df['LINE_NAME'] = remote_lookup_df['LINE_NAME'].astype(object)
remote_lookup_df['DIVISION'] = remote_lookup_df['DIVISION'].astype(object)
remote_lookup_df.REMOTE
# +
#remote_lookup_df.to_sql('remote_lookup',engine)
# -
# ## Processing Fare Data
#
# In order to get one table containing all fare types, including discontinued ones, I ran this:
fare_data_df = pd.read_sql('''SELECT [REMOTE], [STATION], [START_DATE], [END_DATE], [FF], [SEN/DIS],
[7-D AFAS UNL], [30-D AFAS/RMF UNL], [JOINT RR TKT], [7-D UNL], [30-D UNL],
[14-D RFM UNL], [1-D UNL], [14-D UNL], [7D-XBUS PASS], [TCMC], [RF 2 TRIP],
[RR UNL NO TRADE], [TCMC ANNUAL MC], [MR EZPAY EXP], [MR EZPAY UNL],
[PATH 2-T], [AIRTRAIN FF], [AIRTRAIN 30-D], [AIRTRAIN 10-T],
[AIRTRAIN MTHLY], [STUDENTS], [NICE 2-T], [CUNY-120],[CUNY-60],
'0' as [FF VALUE], '0' as [FF 7-DAY], '0' as [FF 30-DAY]
FROM mta_fare_data_old
UNION ALL
SELECT [REMOTE], [STATION], [START_DATE], [END_DATE], [FF], [SEN/DIS],
[7-D AFAS UNL], [30-D AFAS/RMF UNL], [JOINT RR TKT], [7-D UNL], [30-D UNL],
'0' as [14-D RFM UNL], '0' as [1-D UNL], '0' as [14-D UNL],
[7D-XBUS PASS], [TCMC], [RF 2 TRIP], [RR UNL NO TRADE], [TCMC ANNUAL MC],
[MR EZPAY EXP], [MR EZPAY UNL], [PATH 2-T], [AIRTRAIN FF], [AIRTRAIN 30-D],
[AIRTRAIN 10-T], [AIRTRAIN MTHLY], [STUDENTS], [NICE 2-T], [CUNY-120], [CUNY-60],
[FF VALUE], [FF 7-DAY], [FF 30-DAY]
FROM mta_fare_data_new;''', engine)
fare_data_df.head()
# Note that this query creates new columns in each of the tables to match the missing fare types from the other and sets the values to zero. The UNION ALL command is used to combine into one table. The SQL query is pretty clunky, but it gets the job done. I then strip the trailing whitespace from the entries in the STATION column and add the table to my database:
fare_data_df['STATION'] = fare_data_df['STATION'].str.strip()
fare_data_df.columns
#fare_data_df.to_sql('fare_data_total',engine)
fare_data_df.shape
# +
# remove bus data
#bus = ['R553', 'R554', 'R555', 'R556', 'R557', 'R558', 'R559', 'R560', 'R561', 'R562', 'R563', 'R564', 'R565', 'R566', 'R567', 'R568', 'R569', 'R573', 'R574', 'R575']
#fare_data_df = fare_data_df[(fare_data_df.REMOTE != [remove])]
#fare_data_df = fare_data_df[~fare_data_df.REMOTE.isin(bus)]
#fare_data_df.shape
# -
# Then I insert the values from the `remote_lookup_df` into the `fare_data_df` for ease of reference:
fare_data_df.rename(columns={'STATION': 'STOP'}, inplace=True)
fare_data_df.shape
# +
#fare_data_df.insert(1,'BOOTH',0)
#fare_data_df.insert(2,'COMPLEX_ID',0)
#fare_data_df.insert(3,'STATION',0)
#fare_data_df.insert(5,'LINE_NAME',0)
#fare_data_df.insert(6,'DIVISION',0)
#fare_data_df.shape
# -
fare_data_df = fare_data_df.merge(remote_lookup_df,on='REMOTE',how="left")
fare_data_df.columns
# ### Computing Commuter Percentage
#
# I want to know the percentage of likely commuter traffic for each station in this dataset. First I sum the total swipes across all categories:
fare_data_df['TOTAL'] = fare_data_df.iloc[:,4:33].sum(axis=1)
fare_data_df['TOTAL']
# Now I want to sum only those columns that I want to use as proxy for commuters. I look at the MTA Field Descriptions on the Fare Data page and compare them to the columns in `fare_data_df`:
fare_data_df.columns
# Field Description for the columns:\
# FF = full fare\
# SEN/DIS = senior citizen/disabled\
# 7-D AFAS UNL = 7-day unlimited ADA farecard access system\
# 30-D AFAS/RFM UNL = 30-day unlimited ADA farecard access system/reduced fare media\
# JOINT RR TKT = Joint railroad ticket\
# 7-D UNL = 7-day unlimited\
# 30-D UNL = 30-day unlimited\
# 14-D RFM UNL = 14-day reduced fare media unlimited\
# 1-D UNL = one day unlimited\
# 14-D UNL = 14-day unlimited\
# 7D-XBUS PASS = 7-day express bus pass\
# TCMC = Transit check metrocard\
# RF 2 TRIP = reduced fare 2 trip\
# RR UNL NO TRADE = Railroad unlimited no trade\
# TCMC ANNUAL MC = Transit check annual metrocard\
# MR EZPAY EXP = Mail and Ride EZ-pay express\
# MR EZPAY UNL = Mail and Ride EZ-pay unlimited\
# PATH 2-T = PATH train 2-trip\
# AIRTRAIN FF = Airtrain full fare\
# AIRTRAIN 30-D = Airtrain 30-day\
# AIRTRAIN 10-T = Airtrain 10-trip\
# AIRTRAIN MTHLY = Airtrain monthly\
# STUDENTS = School-age students (non-college)\
# NICE 2-T = ?? two-trip card\
# CUNY-120 = CUNY community college 120-day\
# CUNY-60 = CUNY community college 60-day\
# FF VALUE = Fair fares NYC (half price for low-income NYC residents)\
# FF 7-DAY = Fair Fares 7-Day\
# FF 30-DAY = Fair Fares 30-Day
#
# Based on the field descriptions for the columns, I create a new COMMUTERS column, which includes all student, ADA, and fare reductions for high-value trips or long durations (14-day, monthly, annual).
#
# I don't include EZ-pay, bus or rail/train cards except for the Airtrain 30-day, 10-trip and monthly cards. (Those cards are likely used by airport workers.)
#
# I also exclude full fare and one- and two-day unlimited cards, as those are more likely used by visitors.
commuters = (['SEN/DIS',
'7-D AFAS UNL',
'30-D AFAS/RMF UNL',
'7-D UNL',
'30-D UNL',
'14-D RFM UNL',
'14-D UNL',
'TCMC',
'TCMC ANNUAL MC',
'AIRTRAIN 30-D',
'AIRTRAIN 10-T',
'AIRTRAIN MTHLY',
'STUDENTS',
'CUNY-120',
'CUNY-60',
'FF VALUE',
'FF 7-DAY',
'FF 30-DAY'])
fare_data_df['COMMUTERS'] = fare_data_df[commuters].sum(axis=1)
fare_data_df['COMMUTERS']
fare_data_df.sort_values(['START_DATE'], inplace = True)
fare_data_df.head()
# ### Visualizing the commuter percentage at a station
#
# Now I take a look at the commuter percentage for one station, to get a visual sense of the pattern from 2019-2021.
commuters_df = (fare_data_df
.groupby(['BOOTH', 'STATION', 'END_DATE', 'TOTAL', 'COMMUTERS'],as_index=False)
.TOTAL.first())
commuters_df.shape
# To get the station totals, I need to aggregate:
# +
station_weekly_totals = (commuters_df
.groupby(['STATION', 'END_DATE'])
[['COMMUTERS', 'TOTAL']].sum().reset_index())
station_weekly_totals.shape
# -
# I then divide the COMMUTERS column by the TOTAL column to get the percentage of likely commuters:
station_weekly_totals['COMMUTER_PERCENT'] = (station_weekly_totals['COMMUTERS']
.div(station_weekly_totals['TOTAL']).multiply(100))
station_weekly_totals.shape
# Now I can plot a station's total swipes and likely commuter percentage over 2019-2021:
# +
# data
commuters_times_sq = (station_weekly_totals[station_weekly_totals['STATION'] ==
'42 ST-TIMES SQ'].copy()) #using mask to segment df
# plot
fig = (px.line(commuters_times_sq,
x='END_DATE',
y=commuters_times_sq.columns[2:4],
hover_data=['COMMUTER_PERCENT']))
# Change the layout
fig.update_layout(title_text='MTA Ridership at Times Square from 2019-2021',
legend=dict(
title=None))
fig.show()
# -
# ## Turnstile Data Cleaning
#
# To save processing time, I've run a `processing.py` python script on the full dataset from 2019-2021. Below are examples of the methods and functions run on smaller sets of the data. I essentially followed the process outlined in the pair programming exercises.
turnstiles_df = pd.read_sql('SELECT * FROM mta_turnstile_data WHERE [DATE] LIKE "12/%/2019"', engine)
turnstiles_df.head()
# +
# Create a single datetime column
import datetime
turnstiles_df['DATE_TIME'] = pd.to_datetime(turnstiles_df.DATE + ' ' + turnstiles_df.TIME,
format='%m/%d/%Y %H:%M:%S')
# -
# Get rid of the duplicate entries
turnstiles_df.sort_values(['C/A', 'UNIT', 'SCP', 'STATION', 'DATE_TIME'],
inplace=True, ascending=False)
turnstiles_df.drop_duplicates(subset=['C/A', 'UNIT', 'SCP', 'STATION', 'DATE_TIME'], inplace=True)
# get maximum entries per day per turnstile
turnstiles_daily = (turnstiles_df
.groupby(['C/A', 'UNIT', 'SCP', 'STATION', 'DATE'],as_index=False)
.ENTRIES.first())
turnstiles_daily.head()
# get total entries per day per turnstile
turnstiles_daily[['PREV_DATE', 'PREV_ENTRIES']] = (turnstiles_daily
.groupby(['C/A', 'UNIT', 'SCP', 'STATION'])[['DATE', 'ENTRIES']]
.shift(1))
turnstiles_daily.head()
# Drop the rows for the earliest date in the df
turnstiles_daily.dropna(subset=['PREV_DATE'], axis=0, inplace=True)
turnstiles_daily.head()
# for the `get_daily_counts` function, I set the `max counter` value to 20000:
# +
def get_daily_counts(row, max_counter):
counter = row['ENTRIES'] - row['PREV_ENTRIES']
if counter < 0:
counter = -counter # adjust for "reverse" counter
if counter > max_counter:
# Maybe counter was reset, so it may make sense to take the minimum
print(f"ENTRIES: {row['ENTRIES']} <-- {row['PREV_ENTRIES']}")
counter = min(row['ENTRIES'], row['PREV_ENTRIES'])
if counter > max_counter:
# If we still get a counter that is too big, set to zero
return 0
return counter
turnstiles_daily['DAILY_ENTRIES'] = turnstiles_daily.apply(get_daily_counts, axis=1, max_counter=20000)
# +
#turnstiles_daily.to_sql('mta_turnstiles_daily', engine)
# -
# ## MTA Visualizations
#Read in the data for turnstiles
turnstiles_2019 = pd.read_sql('SELECT * FROM mta_turnstiles_daily WHERE [DATE] LIKE "%/2019"', engine)
turnstiles_2021 = pd.read_sql('SELECT * FROM mta_turnstiles_daily WHERE [DATE] LIKE "%/2021"', engine)
# #### Creating a daily count of entries by station for 2019 and 2021:
station_daily_2019 = turnstiles_2019.groupby(['STATION', 'DATE'])[['DAILY_ENTRIES']].sum().reset_index()
station_daily_2021 = turnstiles_2021.groupby(['STATION', 'DATE'])[['DAILY_ENTRIES']].sum().reset_index()
station_daily_2019.head(20)
station_daily_2021.head()
# #### Sorting by the largest daily entries to get the highest-traffic stations:
# +
station_totals_2019 = (station_daily_2019.groupby('STATION')['DAILY_ENTRIES'].sum()
.reset_index()
.sort_values('DAILY_ENTRIES', ascending=False))
station_totals_2019.head()
# +
station_totals_2021 = (station_daily_2021.groupby('STATION')['DAILY_ENTRIES'].sum()
.reset_index()
.sort_values('DAILY_ENTRIES', ascending=False))
station_totals_2021.head()
# -
# #### Computing the percentage with respect to 2019 traffic for 2021:
# +
station_totals_2021['CHANGE'] = (station_totals_2021['DAILY_ENTRIES']
.div(station_totals_2019['DAILY_ENTRIES']))
#station_totals_2021['CHANGE'] = station_totals_2021['CHANGE'].abs()
station_totals_2021.head()
# -
# #### Adding a `2019_ENTRIES` column to the dataframe, and sorting by percentage of 2019 traffic:
#
# I created the `smallest_change_2021` dataframe in order to select the top 200 stations out of the list of stations that have retained the most traffic from pre-pandemic levels.
station_totals_2021['2019_ENTRIES'] = station_totals_2019['DAILY_ENTRIES']
smallest_change_2021 = station_totals_2021.reset_index().sort_values(by=['CHANGE'], ascending = False).head(200)
smallest_change_2021.head()
# #### Finding the stations from the previous list that have the largest total entries:
#
# In order to get that sweet spot between total volume and retained volume. I want to be able to recommend a selection of ten stations that the city health department should choose for their newest COVID testing and vaccination stations, so I want high volume but also high traffic retention (which implies larger commuter/local usage).
largest_sorted_2021 = smallest_change_2021.reset_index().sort_values(by=['DAILY_ENTRIES', 'CHANGE'], ascending = False).head(50)
largest_sorted_2021.head(10)
# #### EXAMPLE: plotting the highest traffic stations from 2019 relative to their 2021 traffic:
# +
top_stations=station_totals_2021['station'][:10]
fig = go.Figure(data=[
go.Bar(name='2019 Entries',
marker_color='dimgrey',
opacity=0.9,
x=top_stations,
y=station_totals_2021['2019_entries'][:10]),
go.Bar(name='2021 Entries',
marker_color='firebrick',
opacity=0.9,
x=top_stations,
y=station_totals_2021['daily_entries'][:10])
])
# Change the layout
fig.update_layout(title_text='MTA Usage Pre-Pandemic vs. 2021',
barmode='group',
hovermode='x unified',
xaxis_tickangle=75,
template="simple_white")
fig.show()
# -
# #### By comparison, my analysis shows much higher traffic retention outside of Manhattan
# +
top_stations=largest_sorted_2021['station'][:10]
fig = go.Figure(data=[
go.Bar(name='2019 Entries',
marker_color='dimgrey',
opacity=0.9,
x=top_stations,
y=largest_sorted_2021['2019_entries'][:10]),
go.Bar(name='2021 Entries',
marker_color='firebrick',
opacity=0.9,
x=top_stations,
y=largest_sorted_2021['daily_entries'][:10])
])
# Change the layout
fig.update_layout(title_text='MTA Usage Pre-Pandemic vs. 2021',
barmode='group',
hovermode='x unified',
xaxis_tickangle=75,
template="simple_white")
fig.show()
|
MTA EDA Process.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # pandas
#
# It is powerful python data analysis toolkit for reading , filtering, manipulating, visulalizing and exporting data
# ___________________________
# why pandas?
#
# reading different varieties of data
# functions
# plotting data for visualization
# __________________________
# #reading CSV files in py
#
# +
#importing pandas lib
import pandas as pd
# +
#reading the csv file
data=pd.read_csv('C:/Users/DELL/Downloads/read_csv/data.csv')
data.head()# to check
# +
#reading excel file
data1=pd.read_excel('C:/Users/DELL/Downloads/read_csv/data.xlsx')
data1.head()
# + active=""
# #dataframe: is similar to excel workbook tabluar datasheet
# we need to convert the data set into dataframe, import the pandas also and read the dataset
# -
data.shape#dimensions of dataframe rows*cols
data.head()#first top 5 rows
data.tail()# bottom 5
data.head(100)# top 100=n no's, similarily with bottom
data.columns #col names
data["Sex"] #selecting single column
data[["Sex","Fare"]] #multiple cols
# +
#selecting rows by their positionns
data.iloc[:5] # 0 to 4= 5
# +
#selecting rows by their positionns
data.iloc[:,:2] #[rows : rows , cols : cols]
data.iloc[5:10,2:5]
# -
data[data["Fare"]>=100]
data.shape[0]#rows
data.shape[1]#cols
data.head()
data.shape
data.iloc[25:26,3:4]
data.head()
# # Predictive Modelling
#
# making use of past data and other attributes ,predict the future using this data.
#
# types:
#
# supervised( regression[continuous], classification[discrete])
# unsupervised( clustering, segementation)
#
# stages:
#
# 1.Problem defination
# (identify the prob and represent in mathematical form)
#
# 2.all possible hypothesis
#
# 3.data collection
# (to prove or disprove the hypothesis)
#
# 4.data exploration and transformation
#
# (reading the data: raw data reading
# variable identification:
# identify the predictor and targe
# univariate analysis:
# bar plots/histograms to check the distributions
# bivariate analysis:
# btw two varibles
# missing value treatment:
# mean mode median
# outlier treatment:
# outlier is an observaion that appears far away and diverges from an overall pattern in a sample
# variable transformation )
#
# 5.Predictive model
#
# 6.model implementation
#
# +
#variable indentification
#categorical = stored as object
#continuous = as int/float
data.dtypes#identifies
# -
# # univariate analysis
#
#
# 1 explore one variable at a time
#
# 2 summarize the variable
#
# 3 reuslts
#
#
#
#
#
#
describe()
help()
data.dftypes
import pandas as pd
data=pd.read_csv('C:/Users/DELL/Downloads/read_csv/data.csv')
data.head()
data.dtypes
# # univariate analysis of continuous variables
#
# +
#desctibe function
data.describe()#o/p only the continuous variables
# +
#plotting a AGE variable
data['Age'].plot.hist()
# +
#box plot
data['Age'].plot.box()
# -
# # univariate analysis for categorical variables
# +
#creating frequency table for categorical variable Sex
data.dtypes
data['Sex'].value_counts()
# +
#creating percentage from frequency
data['Sex'].value_counts()/len(data['Sex'])
# +
#creating a bar plot using the frequencies
data['Sex'].value_counts().plot.bar()
# +
#creating a bar plot using the percentages
(data['Sex'].value_counts()/len(data['Sex'])).plot.bar()
# -
# # Bivariate analysis
#
#
# To see wether the two variables are associated with each other
#
# 1.continuous-continuous (scattet plot)
#
# 2.categorical-continuous(bar graph)
#
# 3.categorical-categorical( frequency plot)(chi sq test)
#
# histogram is used to plot single variable
# # 1
# +
# fare increase in with increase with age
data.plot.scatter('Age','Fare')
# +
#correlation
data.corr()
# -
data['Fare'].corr(data['Pclass'])
# # 2
# +
#mean age of males is different from mean age of females
#bar plot
data.groupby('Sex')['Age'].mean()
# -
data.groupby('Sex')['Age'].mean().plot.bar()
# +
# ttest to see whther both are different
#import ttest
from scipy.stats import ttest_ind
# -
m=data[data['Sex']=='male']
f=data[data['Sex']=='female']
# +
# ttest doesnt support the missing values
#so we omit the missinf vaules using the 3rd para
ttest_ind(m['Age'],f['Age'],nan_policy='omit')
#for the difference to be stastically between 2 groups the pvalue should be less than 0.05
#hence mean age of male and female is stastically different
# -
# # 3
# +
#are females more likely to be survived?
#survived?, sex?
#creating a two way table
pd.crosstab(data['Sex'],data['Survived'])
# +
#chi sq contingency test
from scipy.stats import chi2_contingency
# +
# i/p the previous table
chi2_contingency(pd.crosstab(data['Sex'],data['Survived']))
# +
#Missing values
import pandas as pd
data=pd.read_csv('C:/Users/DELL/Downloads/read_csv/data.csv')
data.head()
data.dtypes
data.shape
# -
data.describe()
#only works fot the continuous variables, if there are missing elements in categorical variables it doesnt help out
# +
#identifying the missing data in both
data.isnull()
# +
#adds up all the missing values
data.isnull().sum()
# +
#dropping all the rows of missing values
#this removes a row even if contains a single null value
data.dropna().isnull().sum()
# +
#removes the rows if all of them are null
#if axis=0== rows axis=1==cols
data.dropna(how='all').shape
# +
#dropping columns
data.dropna(axis=1).shape
data.dropna(axis=1,how='all').shape
# +
#filling missing values with zeros in all na
data.fillna(0)
# +
# as the 'age' is continous var , we can fill the missing values with mean median mode
data['Age'].fillna(data['Age'].mean())
# +
#outlier 1.univariate outliers 2.bivariate outliers
import pandas as pd
import matplotlib.pyplot as plt
# %matplotlib inline
import numpy as np
# -
data=pd.read_csv('C:/Users/DELL/Downloads/read_csv/data.csv')
data.head()
# +
# 1.univariate outliers
#box plot
data['Age'].plot.box()
# +
# 2.bivariate outliers
data.plot.scatter('Age','Fare')
# +
# removing outlier from the dataset
# with limiting the Fare var
df=data[data['Fare']<300]
# -
df.plot.scatter('Age','Fare')
# +
# replacing outliers in age with the mean age value
#loc[rows,cols]
df.loc[df['Age']>65,'Age']=np.mean(df['Age'])
# -
df['Age'].plot.box()
# +
#Variable transformation
# is used to tranfer the non linnear relationship into linear
#also used for creating symmetric distribution from skewed
df['Age'].plot.hist()# right skewed
# +
# 1.log transformation
np.log(df['Age']).plot.hist()
#became extreme left skewes , no use
# +
# 2.square transformation (positive ones)
np.sqrt(df['Age']).plot.hist()
# +
# 3.cubic transformation
np.power(df['Age'],1/3).plot.hist()
#left skewed , its ok with square
# -
# 4.binning
bins=[0,15,80]
group=['children','adult']
df['type']=pd.cut(df['Age'],bins,labels=group)
df['type'].frequency_table
# +
# model buliding
# alg selection-->traning model-->Prediction
#if dependant var(y)-->supervised learning-->continuous(y)-->regression
#(n)-->classification
#(n)-->clustering
# -
# # Problem: Data Exploration
#
# +
#import the lib and data
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
df=pd.read_csv('C:/Users/DELL/Desktop/chennai_house_price_prediction.csv')
df.shape
# +
#data exploration
#use describe function to checck the count,mean,std,
df.describe()#only continuous var
df.describe(include='all')#both continuous and categorical
# +
#check for the missing values
df.isnull().sum()
# +
#checking the data types of each variable
df.dtypes
# +
#univariate analysis
##target var
df['SALES_PRICE'].plot.hist(bins=50)
plt.xlabel('Sales')
#seems to be right skewed
# -
(df['SALES_PRICE'].loc[df['SALES_PRICE']<10000000]).plot.hist(bins=50)
df['INT_SQFT'].plot.hist(bins=50)
# +
#value counts
df['N_BEDROOM'].value_counts()
# -
df['N_BEDROOM'].value_counts()/len(df)*100
df['N_ROOM'].value_counts()
#bar plot
df['N_BEDROOM'].value_counts().plot.bar()
df['AREA'].value_counts().plot(kind='bar')
# # Data manipulation
#
#
# +
#dropping the duplicates
df.drop_duplicates()
#if both the rows are same, deletes one
# +
#drop rows with missing values
df.dropna(axis=1, how='any')
df.dropna(axis=0, how='any')
#this actually loss in infomartion, instead we fill them
# +
#filling the missing values( fillna() function)
df['N_BEDROOM'].fillna(value=(df['N_BEDROOM'].mode()[0]),inplace=True)
#inplace=True, which means the change will be reflected in dataframe
# -
df.loc[df['N_BATHROOM'].isnull()==True]
for i in range(0,len(df)):
if pd.isnull(df['N_BATHROOM'][i])==True:
if (df['N_BEDROOM'][i]==1.0):
df['N_BATHROOM'][i]=1.0
else:
df['N_BATHROOM'][i]=2.0
df[['QS_ROOMS','QS_BATHROOM','QS_BEDROOM','QS_OVERALL']].head()
# +
#finding the average of their ratings using temp var
temp=(df['QS_ROOMS']+df['QS_BATHROOM']+df['QS_BEDROOM'])/3
pd.concat([df['QS_ROOMS'],df['QS_BATHROOM'],df['QS_BEDROOM'],temp],axis=1).head(10)
# -
df.loc[df['QS_OVERALL'].isnull()==True].shape
#.shpe gives the count, here isnull count
# +
#to fill them we use
def fill_na(x):
return ((x['QS_ROOMS']+x['QS_BATHROOM']+x['QS_BEDROOM'])/3)
# +
#.apply() fucntion
df['QS_OVERALL']=df.apply(lambda x: fill_na(x) if pd.isnull(x['QS_OVERALL']) else x['QS_OVERALL'], axis=1)
# -
df.isnull().sum()
# +
#datatypes
df.dtypes
# +
#changing the datatype of a variable using astype()
#var name: datatype type
df = df.astype({'N_BEDROOM': 'object'})
df = df.astype({'N_ROOM':'object'})
df = df.astype({'N_BATHROOM':'object'})
#or
df = df.astype({'N_BEDROOM': 'object','N_ROOM':'object','N_BATHROOM':'object'})
df.dtypes
# +
#replacing the categories
temp=['AREA','N_BEDROOM','N_BATHROOM','N_ROOM','SALE_COND','PARK_FACIL','BUILDTYPE','UTILITY_AVAIL','STREET','MZZONE']
for i in temp:
print('*************** Value count in',i,'****************')
print(df[i].value_counts())
print('_________________________________________')
# +
#area, sale cond, park fac, buildtype, uitlity avail, street---need to be corrected
#by using the replace()
# -
df['AREA'].replace({'Chrompt':'Chrompet','Chormpet':'Chrompet','Chrmpet':'Chrompet','TNagar':'T Nagar','Adyr':'Adyar','KKNagar':'KK Nagar','Ana Nagar':'<NAME>','Ann Nagar':'<NAME>ar','Karapakam':'Karapakkam','Velchery':'Velachery'},inplace=True)
df['AREA'].value_counts()
df['SALE_COND'].replace({'Adj Land':'AdjLand','Partiall':'Partial','PartiaLl':'Partial','Ab Normal':'AbNormal'},inplace=True)
df['SALE_COND'].value_counts()
df['PARK_FACIL'].replace({'Noo':'No'}, inplace=True)
df['PARK_FACIL'].value_counts()
df['BUILDTYPE'].replace({'Comercial':'Commerical','Commerical':'Commercial','Other':'Others'}, inplace=True)
df['BUILDTYPE'].value_counts()
df['UTILITY_AVAIL'].replace({'NoSewr':'NoSewr','AllPub':'All Pub'},inplace=True)
df['UTILITY_AVAIL'].value_counts()
df['STREET'].replace({'Pavd':'Paved','NoAccess':'No Access'},inplace=True)
df['STREET'].value_counts()
# ## bivariate anaysis
df.columns
#hypothesis
# sales price should inc with in in interior sq feet
# sales price would depend on the area where house is loc
# higher the no of rooms, bathrooms in the house more should be the price
# +
#interior area and sales price(target)
df.plot.scatter('INT_SQFT','SALES_PRICE')#linear relationship
# -
fig, ax =plt.subplots()
colors = {'Commercial':'red','House':'blue','Others':'green'}
ax.scatter(df['INT_SQFT'] , df['SALES_PRICE'] , c = df['BUILDTYPE'].apply(lambda x: colors[x]))
plt.show()
# +
#sale price of house wrt no of bedrooms and bathrooms
df.pivot_table(values='SALES_PRICE',index='N_BEDROOM', columns='N_BATHROOM', aggfunc='median')
# +
#QS_OVERALL and sales price
df.plot.scatter('QS_OVERALL','SALES_PRICE')
# +
ax=plt.figure().add_subplot(111)
ax.set_title('Quality score for houses')
bp=ax.boxplot([df['QS_OVERALL'], df['QS_BEDROOM'], df['QS_ROOMS'], df['QS_BATHROOM']])
# -
df['QS_OVERALL'].plot.box()
# +
# sale price based on building type
df.groupby('BUILDTYPE').SALES_PRICE.median()
# -
temp_df = df.loc[(df['BUILDTYPE']=='Commercial')&(df['AREA']=='Anna Nagar')]
temp_df["SALES_PRICE"].plot.hist(bins=50)
temp_df = df.loc[(df['BUILDTYPE']=='House')&(df['AREA']=='Anna Nagar')]
temp_df["SALES_PRICE"].plot.hist(bins=50)
# +
#building type and parking facility
temp=df.groupby(['BUILDTYPE','PARK_FACIL']).SALES_PRICE.median()
temp.plot.bar()
# +
#area wise price of houses
t1=df.pivot_table(values='SALES_PRICE',index='AREA',aggfunc='median')
# -
t1.plot.bar()
# Preparing the dataset
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
df=pd.read_csv('C:/Users/DELL/Desktop/train_bm.csv')
df.shape
df.head()
df.isnull().sum()
# +
#shuffling and creating train and test set
from sklearn.utils import shuffle
data = shuffle(df, random_state=42)
div=int(data.shape[0]/4)
train=data.loc[:3*div+1, :]
test=data.loc[div+1 :]
train.shape
# +
#simple mean (mean of item outlet sales)
#storing simple mean in an new col in hte test set as 'simple mean'
test['simple_mean']=train['Item_Outlet_Sales'].mean()
# +
#cal mean absolute error
#simple_mean_error=smr
from sklearn.metrics import mean_absolute_error as mae
smr = mae(test['Item_Outlet_Sales'], test['simple_mean'])
smr
# +
#mean item outlet sales wrt outlet type
out_type = pd.pivot_table(train, values='Item_Outlet_Sales',index=['Outlet_Type'], aggfunc=np.mean)
out_type
# +
#initializing new col to zero
test['Out_type_mean']=0
#for every unique entry in outlet identifier
for i in train['Outlet_Type'].unique():
#assign the mean value corrresponding to unique entry
test['Out_type_mean'][test['Outlet_Type'] == str(i)] = train['Item_Outlet_Sales'][train['Outlet_Type'] == str(i)].mean()
# +
#caluculating mean absolute error
out_type_error = mae(test['Item_Outlet_Sales'], test['Out_type_mean'])
out_type_error
# -
|
ML introduction.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.8.12 64-bit (''base'': conda)'
# language: python
# name: python3
# ---
import pandas as pd
import random
# +
data_yelp = pd.read_table('yelp_labelled.txt')
data_amazon = pd.read_table('amazon_cells_labelled.txt')
data_imdb = pd.read_table('imdb_labelled.txt')
# Joining the tables
combined_col= [data_amazon,data_imdb,data_yelp]
# To observe how the data in each individual dataset is structured
print(data_amazon.columns)
# +
# In order to add headers for columns in each dataset
for colname in combined_col:
colname.columns = ["Review","Label"]
for colname in combined_col:
print(colname.columns)
# +
# In order to recognize which dataset belonged to which company, a 'Company' column is added as a key
company = [ "Amazon", "imdb", "yelp"]
comb_data = pd.concat(combined_col,keys = company)
# +
# Exploring the structure of the new data frame
print(comb_data.shape)
comb_data.head()
# +
comb_data.to_csv("Sentiment_Analysis_Dataset")
print(comb_data.columns)
print(comb_data.isnull().sum())
# +
import spacy
import en_core_web_sm
from spacy.lang.en.stop_words import STOP_WORDS
nlp = en_core_web_sm.load()
#nlp = spacy.load('en_core_web_sm')
# To build a list of stop words for filtering
stopwords = list(STOP_WORDS)
print(stopwords)
# -
import string
punctuations = string.punctuation
# Creating a Spacy Parser
from spacy.lang.en import English
parser = English()
def my_tokenizer(sentence):
mytokens = parser(sentence)
mytokens = [ word.lemma_.lower().strip() if word.lemma_ != "-PRON-" else word.lower_ for word in mytokens ]
mytokens = [ word for word in mytokens if word not in stopwords and word not in punctuations ]
return mytokens
# ML Packages
from sklearn.feature_extraction.text import CountVectorizer,TfidfVectorizer
from sklearn.metrics import accuracy_score
from sklearn.base import TransformerMixin
from sklearn.pipeline import Pipeline
from sklearn.svm import LinearSVC
# +
#Custom transformer using spaCy
class predictors(TransformerMixin):
def transform(self, X, **transform_params):
return [clean_text(text) for text in X]
def fit(self, X, y, **fit_params):
return self
def get_params(self, deep=True):
return {}
# Basic function to clean the text
def clean_text(text):
return text.strip().lower()
# -
# Vectorization
vectorizer = CountVectorizer(tokenizer=my_tokenizer,ngram_range=(1,1))
classifier = LinearSVC()
tfvectorizer = TfidfVectorizer(tokenizer=my_tokenizer)
# Splitting Data Set
from sklearn.model_selection import train_test_split
import tensorflow as tf
import tensorflow_datasets as tfds
ds = tfds.load('amazon_us_reviews', split='train', shuffle_files=True)
tfds.as_dataframe(ds.take(4), ds)
# +
# Features and Labels
X = comb_data['Review']
ylabels = comb_data['Label']
X_train, X_test, y_train, y_test = train_test_split(X, ylabels, test_size=0.2, random_state=42)
# +
# Create the pipeline to clean, tokenize, vectorize, and classify using"Count Vectorizor"
pipe_countvect = Pipeline([("cleaner", predictors()),
('vectorizer', vectorizer),
('classifier', classifier)])
# Fit our data
pipe_countvect.fit(X_train,y_train)
# Predicting with a test dataset
sample_prediction = pipe_countvect.predict(X_test)
# Prediction Results
# 1 = Positive review
# 0 = Negative review
for (sample,pred) in zip(X_test,sample_prediction):
print(sample,"Prediction=>",pred)
# Accuracy
print("Accuracy: ",pipe_countvect.score(X_test,y_test))
print("Accuracy: ",pipe_countvect.score(X_test,sample_prediction))
# Accuracy
print("Accuracy: ",pipe_countvect.score(X_train,y_train))
# -
# Another random review
pipe_countvect.predict(["This was a great movie"])
example = ["I do enjoy my job",
"What a poor product!,I will have to get a new one",
"I feel amazing!"]
pipe_countvect.predict(example)
#reviews = pd.read_csv('../csv/reviews_clean.csv').dropna()
reviews = pd.read_csv('../csv/reviews_translated.csv').dropna()
reviews.isna().value_counts()
review_train = random.sample(list(reviews['review']), 20)
for text in review_train:
print(text)
print(pipe_countvect.predict([text]))
print("------")
sentiment = pipe_countvect.predict(reviews['review'])
reviews['sentiment'] = sentiment
#reviews.to_csv('../csv/reviews_clean.csv', index=False)
reviews.to_csv('../csv/reviews_translated.csv', index=False)
|
reviews/sentimentanalysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## 简单的 Numpy Broadcasting
# Broadcasting(广播) 解决的是不同形状的矩阵(或者向量)之间的运算问题。
#
# 在代数运算中,不同形状的矩阵(或者向量)之间无法进行基本运算,但是在Numpy中,只要满足一般规则,这个运算的允许的。
import numpy as np
# #### 向量和一个数字相加
#
# ```
# a = [a1, a2, a3]
# b
#
# c = a + b
# c = [a1 + b, a2 + b, a3 + b]
# ```
a = np.array([1, 2, 3])
b = 2
a + b
# #### 二维数组和一个数字相加
#
# ```
# A = [[a11, a12, a13],
# [a21, a22, a23]]
# b
#
# C = A + b
# C = [[a11 + b, a12 + b, a13 + b],
# [a21 + b, a22 + b, a23 + b]]
# ```
A = np.array([[1, 2, 3],
[1, 2, 3]])
b = 2
C = A + b
C
# #### 二维数组和一维数组相加
#
# ```
# A = [[a11, a12, a13],
# [a21, a22, a23]]
# b = [b1, b2, b3]
#
# C = A + b
# C = [[a11 + b1, a12 + b2, a13 + b3],
# [a21 + b1, a22 + b2, a23 + b3]]
# ```
A = np.array([[1, 2, 3],
[1, 2, 3]])
b = np.array([1, 2, 3])
C = A + b
C
# ### Broadcasting的基本原则
#
# 整体而言,两个不同形状的矩阵(或者向量)进行基本运算,看两个矩阵(或者向量)的倒序维数。如果**倒序维数是一致的**,则“小矩阵”经过复制扩展,和“大矩阵”进行基本运算。
#
# 比如:
#
# ```
# A.shape = (2 x 3) -> A.shape = (2 x 3)
# b.shape = (3) -> b.shape = (1 x 3)
#
# A.shape = (2 x 3) -> A.shape = (2 x 3)
# b.shape = (1) -> b.shape = (1 x 1)
# ```
#
# 但是,在以下例子中,b无法broadcasting后和A进行运算
#
# ```
# A.shape = (2 x 3)
# b.shape = (1 x 2)
# ```
A = np.array([[1, 2, 3],
[1, 2, 3]])
b = np.array([1, 2]).reshape(-1,1)
C = A + b
C
|
03-Jupyter-Notebook-Numpy-and-Matplotlib/Optional-02-Numpy-Broadcasting/Optional-02-Numpy-Broadcasting.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: deep_env
# language: python
# name: deep_env
# ---
from keras.models import Sequential, save_model, load_model
from keras.layers import Dense, Dropout
from keras.optimizers import RMSprop
from keras.datasets import mnist
from keras.utils import np_utils
from keras.callbacks import ModelCheckpoint
from sklearn.metrics import confusion_matrix
# +
# Hyper parameters
batch_size = 128
epoch = 5
# Parameters for MNIST dataset
num_classes = 10
# Parameters for MLP
prob_drop_input = 0.2 # drop probability for dropout @ input layer
prob_drop_hidden = 0.5 # drop probability for dropout @ fc layer
# -
# Load MNIST dataset
(X_train, y_train), (X_test, y_test) = mnist.load_data()
X_train = X_train.reshape(60000, 784)
X_test = X_test.reshape(10000, 784)
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255
Y_Train = np_utils.to_categorical(y_train, num_classes)
Y_Test = np_utils.to_categorical(y_test, num_classes)
#MLP
model = Sequential()
model.add(Dense(output_dim=625, input_dim=784, init='normal', activation='relu'))
model.add(Dropout(prob_drop_input))
model.add(Dense(output_dim=625, input_dim=625, init='normal', activation='relu'))
model.add(Dropout(prob_drop_hidden))
model.add(Dense(output_dim=10, input_dim=625, init='normal', activation='softmax'))
model.compile(optimizer=RMSprop(lr=0.001, rho=0.9), loss='categorical_crossentropy', metrics=['accuracy'])
model.summary()
#Entrenar y guardar el entrenamiento
save_model(model, '../save/models')
checkpoint = ModelCheckpoint(filepath='../save/weights/weights.epoch.hdf5', verbose=0)
history = model.fit(X_train,Y_Train, epochs=epoch,
batch_size=batch_size, callbacks=[checkpoint],
validation_data=(X_test,Y_Test))
#Evalución
evaluation = model.evaluate(X_test, Y_Test)
print('Loss=',evaluation[0])
print('Accuracy=',evaluation[1])
# Predicting the Test set results
y_pred = model.predict(X_test)
y_pred = (y_pred > 0.5)
# Creating the Confusion Matrix
cm = confusion_matrix(Y_Test.argmax(axis=1), y_pred.argmax(axis=1))
print (cm)
#Restaurar el modeloya guardado
loaded_model = load_model('../save/models')
loaded_model.load_weights('../save/weights/weights.epoch.hdf5')
loaded_model.summary()
evaluation_loaded = loaded_model.evaluate(X_test, Y_Test)
print('Loss=',evaluation_loaded[0])
print('Accuracy=',evaluation_loaded[1])
# +
import numpy as np
import matplotlib.pyplot as plt #for plotting
# %matplotlib inline
test_im = X_test[4:5]
print(test_im)
plt.imshow(test_im.reshape(28,28), cmap='viridis', interpolation='none')
print(loaded_model.predict(X_test[4:5]))
# -
|
notebooks/10-Save-Restore-NN.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Ch `02`: Concept `01`
# ## Defining tensors
# Import TensorFlow and Numpy:
import tensorflow as tf
import numpy as np
# Now, define a 2x2 matrix in different ways:
# +
m1 = [[1.0, 2.0],
[3.0, 4.0]]
m2 = np.array([[1.0, 2.0],
[3.0, 4.0]], dtype=np.float32)
m3 = tf.constant([[1.0, 2.0],
[3.0, 4.0]])
# -
# Let's see what happens when we print them:
print(type(m1))
print(type(m2))
print(type(m3))
# So, that's what we're dealing with. Interesting.
#
# By the way, there's a function called `convert_to_tensor(...)` that does exactly what you might expect.
#
# Let's use it to create tensor objects out of various types:
t1 = tf.convert_to_tensor(m1, dtype=tf.float32)
t2 = tf.convert_to_tensor(m2, dtype=tf.float32)
t3 = tf.convert_to_tensor(m3, dtype=tf.float32)
# Ok, ok! Time for the reveal:
print(type(t1))
print(type(t2))
print(type(t3))
test complete; Gopal
|
tests/tf/tf-basics/Concept01_defining_tensors.ipynb
|