code
stringlengths 38
801k
| repo_path
stringlengths 6
263
|
|---|---|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
sns.set(style="white", color_codes=True)
floresta = pd.read_csv("floresta.csv")
floresta.dtypes
grupo1 = sns.barplot(x = 'Grupo 1', y = 'Grupo 1', data=floresta)
grupo1.set_ylim(0.0,35.0)
plt.savefig('grupo1-bar.png')
grupo2 = sns.barplot(x = 'Grupo 2', y = 'Grupo 2', data=floresta)
grupo2.set_ylim(0.0,35.0)
plt.savefig('grupo2-bar.png')
grupo3 = sns.barplot(x = 'Grupo 3', y = 'Grupo 3', data=floresta)
grupo3.set_ylim(0.0,35.0)
plt.savefig('grupo3-bar.png')
# +
sns.pointplot(x="Grupo 2", y="Grupo 2", color = 'red', data=floresta)
sns.pointplot(x="Grupo 3", y="Grupo 3", color = 'yellow', data=floresta)
pointp = sns.pointplot(x="Grupo 1", y="Grupo 1", color = 'green', data=floresta)
pointp.set(xlabel='', ylabel='Número de árvores')
#plt.show()
plt.savefig('comparação.png')
# -
|
2.1 - Describe distributions with numbers/script_florestas.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# !wget https://nlp.stanford.edu/sentiment/trainDevTestTrees_PTB.zip
# !unzip trainDevTestTrees_PTB.zip
# +
import nltk
a = nltk.corpus.BracketParseCorpusReader("trees", "(train|dev|test)\.txt")
text = {}
labels = {}
keys = ['train', 'dev', 'test']
for k in keys :
text[k] = [x.leaves() for x in a.parsed_sents(k+'.txt') if x.label() != '2']
labels[k] = [int(x.label()) for x in a.parsed_sents(k+'.txt') if x.label() != '2']
print(len(text[k]))
import spacy
nlp = spacy.load('en', disable=['parser', 'tagger', 'ner'])
import re
def tokenize(text) :
text = " ".join(text)
text = text.replace("-LRB-", '')
text = text.replace("-RRB-", " ")
text = re.sub(r'\W', ' ', text)
text = re.sub(r'\s+', ' ', text)
text = text.strip()
tokens = " ".join([t.text.lower() for t in nlp(text)])
return tokens
for k in keys :
text[k] = [tokenize(t) for t in text[k]]
labels[k] = [1 if x >= 3 else 0 for x in labels[k]]
# +
import pandas as pd
df_texts = []
df_labels = []
df_exp_split = []
for k in keys :
df_texts += text[k]
df_labels += labels[k]
df_exp_split += [k]*len(text[k])
data = pd.DataFrame({'text' : df_texts, 'label' : df_labels, 'exp_split' : df_exp_split})
# +
import json
from tqdm import tqdm
import os
os.makedirs('data/', exist_ok=True)
for key in ['train', 'dev', 'test'] :
data_key = data[data.exp_split == key].to_dict(orient='records')
data_key = [{'document' : x['text'], 'label' : x['label']} for x in tqdm(data_key)]
f = open('data/' + key + '.jsonl', 'w')
f.write('\n'.join([json.dumps(line) for line in data_key]))
f.close()
# -
import json
for key in ['train', 'dev', 'test'] :
data_key = [json.loads(line) for line in open('data/' + key + '.jsonl')]
for i, d in enumerate(data_key) :
d['annotation_id'] = key + '_' + str(i)
f = open('data/' + key + '.jsonl', 'w')
f.write('\n'.join([json.dumps(line) for line in data_key]))
f.close()
|
Datasets/SST/Process.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.6
# language: python
# name: python36
# ---
# # How To: Provisioning Data Science Virtual Machine (DSVM)
#
# __Notebook Version:__ 1.0<br>
# __Python Version:__ Python 3.6 (including Python 3.6 - AzureML)<br>
# __Required Packages:__ azure 4.0.0, azure-cli-profile 2.1.4<br>
# __Platforms Supported:__<br>
# - Azure Notebooks Free Compute
# - Azure Notebooks DSVM
# __Data Source Required:__<br>
# - no
#
# ### Description
# The sample notebook shows how to provision a Azure DSVM as an alternate computing resource for hosting Azure Notebooks.
#
# Azure Notebooks provides Free Compute as the default computing resource, which is free of charge. However, sometimes you do want to have a powerful computing environment, and you don't want to go through Direct Compute route which requires JupyterHub installation on Linux machines, then Data Science Virtual Machine (DSVM) becomes a vital choice.
#
# You may reference <a href='https://docs.microsoft.com/en-us/azure/notebooks/configure-manage-azure-notebooks-projects' target='_blank'>this article</a> for details. In a nutshell, you need to select Linux VM with Ubuntu flavor. And keep in mind that on Azure DSVM, if you want to use Python 3.6 which is required by Azure Sentinel notebooks, you need to <font color=red> select Python 3.6 - AzureML.</font>
# ## Table of Contents
#
# 1. How to create a new DSVM
# 2. How to use DSVM
# 3. Things to know about using DSVM
# ## 1. How to create a new DSVM
# only run once
# !pip install --upgrade Azure-Sentinel-Utilities
# please enter your tenant domain below, for Microsoft, using: microsoft.onmicrosoft.com
# !az login --tenant ''
# +
# User Input for creating a new DSVM
vm_size = 'Standard_DS3_v2'
# replace [[your_subcription_id]] with 'real subscription id'
# !az account set --subscription [[your_subcription_id]]
# -
# replace all [[your_stuff]] with 'real values'
# !az group deployment create \
# --resource-group [[your_subcription_id]] \
# --template-uri https://raw.githubusercontent.com/Azure/DataScienceVM/master/Scripts/CreateDSVM/Ubuntu/azuredeploy.json \
# --parameters \
# '{ \
# "$schema": "https://schema.management.azure.com/schemas/2015-01-01/deploymentParameters.json#",\
# "contentVersion": "1.0.0.0",\
# "parameters": {\
# "adminUsername": { "value" : "[[your_admin_id]]"},\
# "adminPassword": { "value" : "[[<PASSWORD>]]"},\
# "vmName": { "value" : "[[vm_name]]"},\
# "vmSize": { "value" : "Standard_DS3_v2"}\
# }\
# }'
# *** Please go to the project page to select the VM that you just created as your new computing platform (Run on ...) to continue ...
# ## 2. How to use DSVM
#
# 1. Now that you have a DSVM, when you login to https://notebooks.azure.com, you can see you DSVM on the drop down list under Free Compute and Direct Compute.<br>
# <br>
# 2. Of course you will select DSVM, it will ask you to validate your JIT credentials.<br>
# <br>
# 3. Once you pick a notebook to run, you may encounter the following warning:<br>
# <br>
# As you may see, [Python 3.6 - AzureML] is the correct answer.
#
# ## 3. Things to know about using DSVM
#
# 1. The most important thing to know about Azure Notebooks on DSVM is that: Azure Notebooks project home directory is not mounted on the DSVM. So any references to Azure Notebooks folders / files will incur File/folder not found exception. In other words, each ipynb notebook need to be independent of other files.
# 2. There are work-around solutions:<br>
# a. Data files can be stored on Azure Blob storage and <a href='https://github.com/Azure/azure-storage-fuse' target='_blank'>blobfufe</a><br>
# b. Python files can be added to the notebook by using the Jupyter magic, you can find an example here: <a href='https://github.com/Microsoft/connect-petdetector/blob/master/setup.ipynb' target='_blank'>%%writefile</a><br>
# c. Configuration files are a bit more complicated. Using our Azure Sentinel config.json as an example, it is generated when you import Azure Sentinel Jupyter project from GitHub repo through Azure portal. The configuration JSON is Azure Log Analytics workspace specific file, so you clone one project for one Log Analytics workspace. You can find the config.json file at the root of the project home directory. <a href='https://orion-zhaozp.notebooks.azure.com/j/notebooks/Notebooks/Get%20Start.ipynb' target='_blank'>Get Start.jpynb</a> section 1 demonstrates how to set the configuration settings manually.
|
Notebooks/HowTos/Provisioning DSVM.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import pickle
import os
from scipy.stats import norm
# Plotting
import matplotlib.pyplot as plt
def rlba(v = np.array([1, 1]),
A = 1,
b = 1.5,
s = 0.1,
n_samples = 1000):
rts = np.zeros((n_samples, 1))
choices = np.zeros((n_samples, 1))
n_choices = len(v)
for i in range(n_samples):
d = np.array([-0.1]*n_choices)
while np.max(d) < 0:
k = np.random.uniform(low = 0, high = A, size = n_choices)
d = np.random.normal(loc = v, scale = s)
tmp_rt = (b - k) / d
rts[i] = np.min(tmp_rt)
choices[i] = np.argmin(tmp_rt)
# Create some dics
v_dict = {}
for i in range(n_choices):
v_dict['v_' + str(i)] = v[i]
return (rts, choices, {**v_dict,
'A': A,
'b': b,
's': s,
'delta_t': 0,
'max_t': 1000,
'n_samples': n_samples,
'simulator': 'lba',
'boundary_fun_type': 'none',
'possible_choices': [i for i in range(n_choices)]})
# +
def dlba(rt = 0.5,
choice = 0,
v = np.array([1, 1]),
A = 1,
b = 1.5,
s = 0.1,
return_log = True):
n_choices = len(v)
l_f_t = 0
# if len(s) == 1:
# s = np.array([s[0]] * n_choices)
for i in range(n_choices):
if i == choice:
tmp = flba(rt = rt, A = A, b = b, v = v[i], s = s)
if tmp < 1e-29:
tmp = 1e-29
l_f_t += np.log(tmp)
else:
tmp = Flba(rt = rt, A = A, b = b, v = v[i], s = s)
# numerical robustness catches
if tmp < 1e-29:
tmp = 1e-29
if tmp > (1.0 - 1e-29):
tmp = (1.0 - 1e-29)
l_f_t += np.log(1.0 - tmp)
if return_log:
return l_f_t
else:
return np.exp(l_f_t)
# -
def Flba(rt = 0.5,
v = 1,
A = 1,
b = 1.5,
s = 0.1):
return (1 + ((1 / A) * ((b - A - (rt * v)) * norm.cdf((b - A - (rt * v)) / (rt * s))) - \
(b - (rt * v)) * norm.cdf((b - (rt * v)) / (rt * s)) + \
(rt * s) * (norm.pdf((b - A - (rt * v)) / (rt * s)) - norm.pdf((b - (rt * v)) / (rt * s)))))
def flba(rt = 0.5,
v = 1,
A = 1,
b = 1.5,
s = 0.1):
return ((1 / A) * ( (-v) * norm.cdf((b - A - (rt * v)) / (rt * s)) + \
s * norm.pdf((b - A - (rt * v)) / (rt * s)) + \
v * norm.cdf((b - (rt * v)) / (rt * s)) + \
(-s) * norm.pdf((b - (rt * v)) / (rt * s)) ))
out = rlba(n_samples = 20000, v = np.array([1.5, 1]), b = 1.5, A = 1)
out[0][out[1] == 0] = out[0][out[1] == 0] * -1
import pickle
out = pickle.load(open('/media/data_cifs/afengler/tmp/lba_8085c794bf7a11e9b003530bce13c5b4.pickle', 'rb'))
out[0][out[1] == 0] = out[0][out[1] == 0] * (-1)
plt.hist(out[0], bins = 50, density = True, alpha = 0.3)
plt.plot(-my_grid, np.exp(f_test_vals[:, 0]), color = 'green')
plt.plot(my_grid, np.exp(f_test_vals[:, 1]), color = 'green')
my_grid = np.linspace(0.01, 2.0, 1000)
f_test_vals = np.zeros((len(my_grid),2))
for c in range(2):
cnt = 0
for i in my_grid:
f_test_vals[cnt, c] = clba.dlba(rt = i, choice = c, v = np.array([1.1, 1]), ndt = 0.4)
cnt += 1
[i for i in range(4)]
out
#import lba
import lba
import clba
import numpy as np
import pickle
import os
import kde_training_utilities as kde_utils
import kde_class as kdec
# #%%timeit -n 1 -r 5
out_p = lba.rlba(v = np.array([1.1657, 1.118401]),
A = 0.852575,
b = 1.860735,
s = 0.170644,
n_samples = 1000)
# #%%timeit -n 1 -r 5
out_c = clba.rlba(v = np.array([1.1, 1]),
A = 1.0,
b = 1.5,
s = 0.1,
ndt = 0.4,
n_samples = 2500)
# +
out_c[0][out_c[1] == 0] = out_c[0][out_c[1] == 0] * (-1)
#out_p[0][out_p[1] == 0] = out_p[0][out_p[1] == 0] * (-1)
plt.hist(out_c[0], bins = 50, density = True, alpha = 0.3, color = 'red')
plt.plot(my_grid, np.exp(f_test_vals[:, 1]))
plt.plot(-my_grid, np.exp(f_test_vals[:, 0]))
#plt.hist(out_p[0], bins = 50, density = True, alpha = 0.3, color = 'black')
# -
my_lbakde = kdec.logkde(out)
os.listdir('/media/data_cifs/afengler/data/kde/lba/base_simulations_20000')[0]
kde_out = my_lbakde.kde_sample()
np.max(kde_out[0])
out_p
np.random.uniform(low = 0, high = 0)
a = [1]
rts = np.random.normal(size = 1000) + 2
choices = np.random.choice(2, size = 1000)
# %%timeit -n 1 -r 5
print(clba.batch_dlba2(rt = np.squeeze(out_c[0]), choice = np.squeeze(out_c[1]), v = np.array([1, 1]), ndt = 0.6))
# #%%timeit -n 1 -r 5
tmp = 0
for i in range(len(out_c[0])):
tmp += clba.dlba(rt = out_c[0][i], choice = out_c[1][i], ndt = 0.6)
#if i % 100 == 0:
#print(i)
print(tmp)
A = 1
b = 1.5
v = np.array([1, 1])
s = 0.1
rt = np.squeeze(out_c[0])
eps = 1e-16
tmp = np.zeros((2, len(rt), 2))
tmp[0, :, 0] = clba.flba(rt = rt, A = A, b = b, v = v[0], s = s)
tmp[0, tmp[0, :, 0] < eps, 0] = np.log(eps)
tmp[0, :, 1] = clba.flba(rt = rt, A = A, b = b, v = v[1], s = s)
tmp[0, tmp[0, :, 1] < eps, 1] = np.log(eps)
tmp[1, :, 0] = 1 - clba.Flba(rt = rt, A = A, b = b, v = v[1], s = s)
tmp[1, tmp[1, : , 0] < eps, 0] = np.log(eps)
tmp[1, :, 1] = 1 - clba.Flba(rt = rt, A = A, b = b, v = v[0], s = s)
tmp[1, tmp[1, : , 1] < eps, 1] = np.log(eps)
tmp = tmp[0, :, :] + tmp [1, :, :]
tmp[rt <= 0, :] = np.log(np.sqrt(eps))
np.min(tmp)
np.log(0.000000000000000000000000000000001)
|
lba_scripts/.ipynb_checkpoints/lba_tests_2-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Create a simulator that reports the machine's sensor values
#
# We don't have a real machine to monitor, so let's simulate one.
# For this we need a few components:
#
# * a machine that keeps running (M1)
# * a sensor attached to that machine (S1)
# * an API that we can query from our application (M-API)
#
# # Tasks
#
# 1. Run the code below
# 2. Query the machine using your web browser
# 3. Try to run different configurations and see if this changes your output
# # The machine and it's sensor
# +
import numpy as np
from threading import Thread
from datetime import datetime as dt
from time import sleep
# Configuration 1: working ok, intermittent failure
shape, scale = 1., .1
# Configuration 2: fail more often
# shape, scale = 5., .1
# Configuration 3: constantly failing
# shape, scale = 10., .1
# sensor buffer
size = 1000
STATE = [(None, 0)] * size
def sensor():
global STATE
rnd = np.random.default_rng()
while True:
data = rnd.gamma(shape, scale, size)
for i, value in enumerate(data):
record = (dt.now().isoformat(), value)
STATE = STATE[1:] + [record]
sleep(.1)
def machine():
# we use a Thread to run the machine "in the background"
t = Thread(target=sensor)
t.start()
# -
# # The sensor API
#
# The sensor API is very simple
#
# * `http://localhost:5000/query/10` reports the latest 10 sensor values
# * `http://localhost:5000/query/100` reports the latest 100 sensor values
# * it can report at most `size=1000` values (we could change this)
# +
from flask import Flask
def create_app():
app = Flask("factory")
@app.route("/query/<int:records>")
def data(records):
values = STATE[-records:]
return { 'values': values }
return app
machine()
app = create_app()
app.run()
|
baseline/predmaint/machine-simulator.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import uproot
import uproot_methods
import awkward
import matplotlib.pyplot as plt
import numpy as np
# +
G3 = uproot.open("/home/physicist/results/zjets_pt170.root")["T"]
g3 = G3.arrays(['gen_pt', 'gen_eta', 'gen_phi', 'gen_m',
'gen_id', 'gen_status',
'gen_mother1', 'gen_mother2',
'gen_daughter1', 'gen_daughter2',
'gen_col', 'jet_pt', 'jet_eta', 'jet_phi', 'jet_m', 'nJet', 'jet_ic', 'jet_nc'])
gen_pt = g3[b'gen_pt']
gen_eta = g3[b'gen_eta']
gen_phi = g3[b'gen_phi']
gen_m = g3[b'gen_m']
gen_id = g3[b'gen_id']
gen_status = g3[b'gen_status']
##### Jets
jet_pt = g3[b'jet_pt']
jet_eta = g3[b'jet_eta']
jet_phi = g3[b'jet_phi']
jet_m = g3[b'jet_m']
jet_ic = g3[b'jet_ic']
jet_nc = g3[b'jet_nc']
nJet = g3[b'nJet']
# -
particles = uproot_methods.TLorentzVectorArray.from_ptetaphim(gen_pt, gen_eta, gen_phi, gen_m)
jet3 = uproot_methods.TLorentzVectorArray.from_ptetaphim(jet_pt, jet_eta, jet_phi, jet_m)
isz = abs(gen_id) == 23
ishard = abs(gen_status) == 62
selected = isz & ishard
zbosons = particles[ selected ]
jets_pt = jet3.pt
jet_imaxpt = jets_pt.argmax()
leadingjets = jet3[jet_imaxpt]
print(len(leadingjets) , " -----", len(zbosons))
zjets_plot = leadingjets.cross(zbosons)
sum = zjets_plot.i0 + zjets_plot.i1
# +
arr = []
f = 0
for i in range(81):
arr.append(f)
f += 50
# -
plt.hist(x= sum.mass.flatten(), bins=arr, log=True, density=True, color = "blue")
|
Invariant mass for jets_pt170.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# %matplotlib inline
# %load_ext autoreload
# %autoreload 2
import os
import sys
import copy
import warnings
import cProfile
from time import time
from astropy.stats import sigma_clip
from astropy.table import Table, Column, vstack
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patches
from asap import io
from asap import smf
from asap import config
from asap import fitting
from asap import ensemble
from asap import plotting
from asap.parameters import AsapParams
from asap.likelihood import ln_likelihood, ln_probability
from asap.predictions import (predict_mstar_basic, predict_smf, predict_mhalo,
predict_dsigma_profiles, make_model_predictions)
plt.rc('text', usetex=True)
# -
# ## Corner and traceplot of the model
#
# * This is the default `A.S.A.P` model
# * Three stages burn-in with 256 walkers using the "Snooker" moves, each stage has 200 steps.
# * Using the walker position with the best likelihood as initial positions for the next stage.
# * Final sampling process has 400 steps.
# * **SMF**: use the covariance matrix of SMFs
# * **DeltaSigma** profiles: fit the radius between 0.05 to 25 Mpc.
# - Including all data points
# +
test_dir = '../model'
# The configuration file
config_file = os.path.join(test_dir, 'asap_test_4.yaml')
# The results from the 3-stage burn-in results
burnin_file_1 = os.path.join(test_dir, 'asap_test_4_burnin_1.npz')
burnin_file_2 = os.path.join(test_dir, 'asap_test_4_burnin_2.npz')
burnin_file_3 = os.path.join(test_dir, 'asap_test_4_burnin_3.npz')
# The results of the final sampling process
result_file = os.path.join(test_dir, 'asap_test_4_sample.npz')
# Initialize the model, load the data
cfg, params, obs_data, um_data = fitting.initial_model(config_file, verbose=True)
# Load the burn-in results
(mod_burnin_samples_1,
mod_burnin_chains_1,
mod_burnin_lnprob_1,
mod_burnin_best_1, _, _) = io.load_npz_results(burnin_file_1)
(mod_burnin_samples_2,
mod_burnin_chains_2,
mod_burnin_lnprob_2,
mod_burnin_best_2, _, _) = io.load_npz_results(burnin_file_2)
(mod_burnin_samples_3,
mod_burnin_chains_3,
mod_burnin_lnprob_3,
mod_burnin_best_3, _, _) = io.load_npz_results(burnin_file_3)
mod_burnin_chains = np.concatenate([
mod_burnin_chains_1, mod_burnin_chains_2, mod_burnin_chains_3], axis=1)
# Load in the final sampling results
(mod_result_samples,
mod_result_chains,
mod_result_lnprob,
mod_result_best, _, _) = io.load_npz_results(result_file)
print(np.nanmax(mod_burnin_lnprob_1), mod_burnin_best_1)
print(np.nanmax(mod_burnin_lnprob_2), mod_burnin_best_2)
print(np.nanmax(mod_burnin_lnprob_3), mod_burnin_best_3)
print(np.nanmax(mod_result_lnprob), mod_result_best)
# -
# ### Corner plot
# +
params_label = [r'$a$', r'$b$', r'$c$', r'$d$',
r'$f_{\rm ins}$', r'$A_{\rm exs}$', r'$B_{\rm exs}$']
params_range = [(0.594, 0.615), (11.831, 11.854),
(0.059, 0.180), (-0.01, 0.119),
(0.64, 0.695),
(-0.21, -0.15), (0.02, 0.096)]
title_fmt = '.3f'
mod_corner = plotting.plot_mcmc_corner(
mod_result_samples, params_label, truths=mod_result_best, truth_color='skyblue',
**{'title_fmt': title_fmt, 'plot_datapoints': False})
# -
# ### Trace plot
mod_trace = plotting.plot_mcmc_trace(
mod_result_chains, params_label,
mcmc_best=mod_result_best, mcmc_burnin=mod_burnin_chains,
burnin_alpha=0.15, trace_alpha=0.12)
# ### Quick checks of the SMFs
# +
# Predict the stellar mass in inner and outer apertures
logms_inn, logms_tot, sig_logms, mask_use = predict_mstar_basic(
um_data['um_mock'], mod_result_best, min_logms=10.6,
logmh_col=cfg['um']['logmh_col'], min_scatter=cfg['um']['min_scatter'],
pivot=cfg['um']['pivot_logmh'])
# Predict the SMFs and DeltaSigma profiles
um_smf_tot, um_smf_inn, um_dsigma = make_model_predictions(
mod_result_best, cfg, obs_data, um_data, verbose=True)
# Check the likelihood for SMF and DeltaSigma profiles
lnlike_smf, lnlike_dsigma = ln_likelihood(
mod_result_best, cfg, obs_data, um_data, sep_return=True)
print("# ln(Likelihood) for SMFs : %8.4f" % lnlike_smf)
print("# ln(Likelihood) for DSigma : %8.4f" % lnlike_dsigma)
# +
um_smf_tot_all = smf.get_smf_bootstrap(logms_tot, cfg['um']['volume'],
10, 10.9, 12.4, n_boots=1)
mod_smf_plot = plotting.plot_mtot_minn_smf(
obs_data['smf_tot'], obs_data['smf_inn'], obs_data['mtot'], obs_data['minn'],
um_smf_tot, um_smf_inn, logms_tot, logms_inn, obs_smf_full=obs_data['smf_full'],
um_smf_tot_all=um_smf_tot_all, not_table=True)
# -
# ### Save the figures
# +
mod_corner.savefig('fig/fig3_corner_model_4.pdf', dpi=120)
mod_trace.savefig('fig/fig3_trace_model_4.png', dpi=120)
mod_smf_plot.savefig('fig/fig3_smf_model_4.png', dpi=120)
|
note/fig3_model_4.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Exercise 17
#
import pandas as pd
train_df = pd.read_csv('14_mashable_train_df.csv', index_col=0)
train_df.head()
train_df.shape
X = train_df.drop(['url', 'Popular'], axis=1)
y = train_df['Popular']
# train/test split
from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1)
# # Exercice 17.1 (2 points)
#
# Estimate 600 bagged samples
#
# Estimate the following set of classifiers:
#
# * 100 Decision Trees where max_depth=None
# * 100 Decision Trees where max_depth=2
# * 100 Decision Trees using an under-sampled dataset where max_depth=None
# * 100 Decision Trees using an under-sampled dataset where max_depth=2
# * 100 GaussianNB
# * 100 GaussianNB using an under-sampled dataset
#
# **note:** the under-sampled set is estimated from the bagged samples, i.e., each under-sampled set is different
# # Exercice 17.2
#
# Ensemble using majority voting
#
# Evaluate using the following metrics:
# * Accuracy
# * F1-Score
# * F_Beta-Score (Beta=2)
# # Exercice 17.3
#
# Estimate te probability as %models that predict positive
#
# Modify the probability threshold and select the one that maximizes the fbeta_score
# # Exercice 17.4 (2 points)
#
# Ensemble using Weighted Voting
#
# Calculate the weight using the oob error
# # Exercice 17.5
#
# Estimate te probability of the weighted voting
#
# Modify the probability threshold and select the one that maximizes the fbeta_score
# # Exercice 17.6 (2 points)
#
# Estimate a logistic regression using as input the estimated classifiers
#
# Modify the probability threshold such that maximizes the fbeta_score
# # Exercice 17.7 (2 points)
#
# Estimate a AdaBoostClassifier and a GradientBoostingClassifier using the training and an under-sampled set
# # Bonus: Exercice 18.8 (4 points)
#
# Estimate 3 ensembles of the 600 models
# * Average the probabilities
# * Average the weighted probabilities
# * Learn a logistic regression using the probabilities
#
# For each select the threshold that maximizes the fbeta_score
|
exercises/17_ensemble_bagging&boosting.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <img src="../img/logo_amds.png" alt="Logo" style="width: 128px;"/>
#
# # AmsterdamUMCdb - Freely Accessible ICU Database
#
# version 1.0.1 January 2020
# Copyright © 2003-2020 Amsterdam UMC - Amsterdam Medical Data Science
# + [markdown] azdata_cell_guid="4a40ac09-522e-41f3-991b-d42bf3f5ec7d"
# # <a id='procedureorderitems'></a>procedureorderitems table
# The *procedureorderitems* table contains all orders for procedures and tasks, such drawing blood, perfforminroutine ICU nursing care and scoring. Please note that many of these tasks will lead to a result or observation, that can be found in the [freetextitems](freetextitems.ipynb#freetextitems), [listitems](listitems.ipynb#listitems) or [numericitems](numericitems.ipynb#numericitems) tables, depending on the type of documentation required. All items have an associated admissionid from the [admissions](admissions.ipynb#admissions) table.
#
# ## Fields
#
# |Name|Type|Description|
# |:---|:---|:---|
# |admissionid|integer|links the items with the admissionid in the [admissions](admissions.ipynb#admissions) table|
# |orderid|integer|unique number identifiying this order
# |ordercategoryid|integer|id of procedure category
# |[ordercategoryname](#ordercategoryname)|string|name of procedure category
# |itemid|integer|id of procedure name
# |[item](#item)|string|procedure name
# |registeredat|integer|time the result was stored in the database, expressed as milliseconds since the first ICU admission.
# |[registeredby](#registeredby)|string|user group that entered the result, e.g. nurses, physicians, etc.
# -
# # Example Python and SQL scripts
# ## Imports
# +
# %matplotlib inline
import amsterdamumcdb
import psycopg2
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
import matplotlib as mpl
import io
from IPython.display import display, HTML, Markdown
# -
# ## Display settings
# +
#matplotlib settings for image size
#needs to be in a different cell from %matplotlib inline
plt.style.use('seaborn-darkgrid')
plt.rcParams["figure.dpi"] = 288
plt.rcParams["figure.figsize"] = [8, 6]
plt.rcParams["font.size"] = 12
pd.options.display.max_columns = None
pd.options.display.max_rows = None
pd.options.display.max_colwidth = 1000
# -
# ## Connection settings
# +
#Modify config.ini in the root folder of the repository to change the settings to connect to your postgreSQL database
import configparser
import os
config = configparser.ConfigParser()
if os.path.isfile('../config.ini'):
config.read('../config.ini')
else:
config.read('../config.SAMPLE.ini')
#Open a connection to the postgres database:
con = psycopg2.connect(database=config['psycopg2']['database'],
user=config['psycopg2']['username'], password=config['psycopg2']['password'],
host=config['psycopg2']['host'], port=config['psycopg2']['port'])
con.set_client_encoding('WIN1252') #Uses code page for Dutch accented characters.
con.set_session(autocommit=True)
cursor = con.cursor()
cursor.execute('SET SCHEMA \'amsterdamumcdb\''); #set search_path to amsterdamumcdb schema
# -
# ## Overview of all fields
# + azdata_cell_guid="af0db8dd-df4e-4305-b2ac-f10e8fefe9b4"
sql = """
SELECT * FROM procedureorderitems
"""
display(Markdown("``` mysql\n" + sql + "\n```"))
df = pd.read_sql(sql,con)
df.head(10)
# -
df.describe()
# ## <a id='orderid'></a>orderid
sql = """
SELECT COUNT(*) AS "Number of unique observations" FROM (
SELECT DISTINCT orderid
FROM procedureorderitems
) as unique_items_table
"""
display(Markdown("``` mysql\n" + sql + "\n```"))
df = pd.read_sql(sql,con)
df
# +
sql = """
SELECT COUNT(admissionid) AS "procedures per admission"
FROM procedureorderitems
GROUP BY admissionid
"""
display(Markdown("``` mysql\n" + sql + "\n```"))
df = pd.read_sql(sql,con)
#plot the data
data = df['procedures per admission']
amsterdamumcdb.outliers_histogram(data, bins=32).show()
# -
# ## <a id='item'></a>item
sql = """
SELECT item, COUNT(item) AS "number of observations", itemid
FROM procedureorderitems
GROUP BY item, itemid
ORDER BY "number of observations" DESC
"""
import matplotlib as mpl
display(Markdown("``` mysql\n" + sql + "\n```"))
df = pd.read_sql(sql,con)
df.head(10)
# ## <a id='ordercategoryname'></a>ordercategoryname
sql = """
SELECT ordercategoryname AS "Order Category", COUNT(ordercategoryname) AS "Number of tasks", ordercategoryid
FROM procedureorderitems
GROUP BY ordercategoryname, ordercategoryid
ORDER BY "Number of tasks" DESC
"""
import matplotlib as mpl
display(Markdown("``` mysql\n" + sql + "\n```"))
df = pd.read_sql(sql,con)
cm = plt.get_cmap('RdPu')
color_step = int(-255/len(df.index))
ax = df.plot.bar(x=df.columns[0],y=df.columns[1], legend=False,color=cm(range(255,1,color_step)))
ax.set(ylabel=df.columns[1])
ax.yaxis.set_major_formatter(mpl.ticker.StrMethodFormatter('{x:,.0f}'))
# # registeredby
# Most documentation of the tasks was performed by either the intensive care (IC) or medium care (MC) nurses
sql = """
SELECT registeredby AS "User group", COUNT(registeredby) AS "Number of tasks"
FROM procedureorderitems
GROUP BY registeredby
ORDER BY "Number of tasks" DESC
"""
import matplotlib as mpl
display(Markdown("``` mysql\n" + sql + "\n```"))
df = pd.read_sql(sql,con)
cm = plt.get_cmap('RdPu')
color_step = int(-255/len(df.index))
ax = df.plot.bar(x=df.columns[0],y=df.columns[1], legend=False,color=cm(range(255,1,color_step)))
ax.set(ylabel=df.columns[1])
ax.yaxis.set_major_formatter(mpl.ticker.StrMethodFormatter('{x:,.0f}'))
|
tables/procedureorderitems.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: TensorFlow-GPU-1.14
# language: python
# name: tf-gpu
# ---
# +
# System libraries
from time import time
import numpy as np
import random
# Custom libraries
import dl_utils as utils
import datasets
# Helper libraries
from tensorflow.keras.callbacks import EarlyStopping
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
from matplotlib import colors
# %matplotlib inline
# +
tfw = 'v1'
if tfw == 'v1':
print("TF v1 behaviour enabled")
import tensorflow.compat.v1 as tf
# Enable tf v1 behavior as in v2 a lot have changed
tf.disable_v2_behavior()
else:
print("TF v2 behaviour enabled")
import tensorflow as tf
print("Tensorflow version",tf.__version__)
# -
X, Y = datasets.data_spiral(10000,40)
# +
plt.figure(figsize=(5, 5), dpi=75)
colormap = colors.ListedColormap(["#f59322", "#e8eaeb", "#0877bd"])
x_min, x_max = -6, 6 # grid x bounds
y_min, y_max = -6, 6 # grid y bounds
plt.scatter(X[:,0],X[:,1],edgecolors='k', s=50, c=Y, cmap=colormap)
# -
X_train, X_test, y_train, y_test = train_test_split(X,Y,test_size=0.33)
# +
plt.figure(figsize=(5, 5), dpi=75)
colormap = colors.ListedColormap(["#f59322", "#e8eaeb", "#0877bd"])
x_min, x_max = -6, 6 # grid x bounds
y_min, y_max = -6, 6 # grid y bounds
plt.scatter(X_train[:,0],X_train[:,1], edgecolors='k', s=50, cmap=colormap,label='train')
plt.scatter(X_test[:,0],X_test[:,1], edgecolors='k', s=50, cmap=colormap, label='test')
plt.legend()
# -
## Build NN - Hyperparameters ##
epochs = 40
lr = 0.001
def create_model():
model = tf.keras.Sequential()
# Input Layers
model.add(tf.keras.layers.Dense(8,input_dim=2,activation='relu'))
model.add(tf.keras.layers.Dense(8,activation='relu'))
model.add(tf.keras.layers.Dense(8,activation='relu'))
model.add(tf.keras.layers.Dense(8,activation='relu'))
# Output Layer
model.add(tf.keras.layers.Dense(2,activation='softmax'))
# Compile model
model.compile(loss='sparse_categorical_crossentropy',
optimizer=tf.keras.optimizers.Adam(lr),
metrics=['accuracy'])
return model
model = create_model()
# +
# Define a callback
callback = EarlyStopping(monitor='val_loss', patience=4, mode='min')
model_train = time()
results = model.fit(X_train,y_train,
batch_size=64,
epochs=epochs,
callbacks=[callback],
validation_data=(X_test,y_test),
verbose=2
)
keras_train = time() - model_train
print('Model training time %.1f sec' % keras_train)
# +
print("Evaluating on train set...")
(loss, accuracy) = model.evaluate(X_train, y_train.T, verbose=0)
print("loss={:.4f}, accuracy: {:.2f}%".format(loss,accuracy * 100))
print("Evaluating on test set...")
(loss, accuracy) = model.evaluate(X_test, y_test.T, verbose=0)
print("loss={:.4f}, accuracy: {:.2f}%".format(loss,accuracy * 100))
# +
plt.figure(figsize=(5, 5), dpi=75)
colormap = colors.ListedColormap(["#f59322", "#e8eaeb", "#0877bd"])
# Create a grid of points to predict
x, _, xx, yy = datasets.grid_points()
# Grid predictions
z_preds = model.predict(x)
# Test predictions
predictions = model.predict(X_test)
z_preds = np.argmax(z_preds,axis=1)
plt.scatter(X_test[:,0],X_test[:,1], c=predictions[:,1], edgecolors='k', s=50, cmap=colormap)
plt.contourf(xx,yy,z_preds.reshape(xx.shape), cmap=colormap, alpha=0.4)
# -
# ## Implementation with TF 1.14
tf.logging.set_verbosity(tf.logging.INFO)
logdir = './logs'
class NeuralNet:
def __init__(self, n_X = 1000, noise_X = 0, session_type='cpu'):
self.lr = 0.001
self.verbose = 0
self.batch_size = 64
self.n_X = n_X
self.noise_X = noise_X
tf.reset_default_graph()
if session_type == 'cpu':
self.sess = tf.Session()
else:
self.sess = tf
def get_data(self):
# Fetch dataset
X,Y = datasets.data_spiral(self.n_X,self.noise_X)
# Fetch test set - grid points
X_test, y_test, _, _ = datasets.grid_points()
# Split dataset for train and validation
X_train, self.X_valid, y_train, y_valid = train_test_split(X,Y,test_size=0.33)
self.valid_len = len(self.X_valid)
print("Train size", X_train.shape)
print("Valid size", self.X_valid.shape)
print("Test size", X_test.shape)
try:
assert(X_train.shape[1] == X_test.shape[1])
except AssertionError as e:
raise( AssertionError( "Dataset input size is not equal. %s"%e ) )
with tf.name_scope('data'):
# Define placeholders for test set, since eval() is used
x_test_pl = tf.placeholder(dtype = X_test.dtype,shape = X_test.shape)
y_test_pl = tf.placeholder(dtype = y_test.dtype,shape = y_test.shape)
# Create tensorflow compatible dataset with tf.data api (no placeholders)
train_data = tf.data.Dataset.from_tensor_slices((X_train,y_train)).batch(self.batch_size,drop_remainder=True)
valid_data = tf.data.Dataset.from_tensor_slices((self.X_valid,y_valid)).batch(self.batch_size,drop_remainder=False)
test_data = tf.data.Dataset.from_tensor_slices((X_test,y_test)).batch(self.batch_size,drop_remainder=False)
## Define Iterators
self.iterator = tf.data.Iterator.from_structure(train_data.output_types,
train_data.output_shapes)
self.train_init_op = self.iterator.make_initializer(train_data)
self.valid_init_op = self.iterator.make_initializer(valid_data)
self.test_init_op = self.iterator.make_initializer(test_data)
# Create test feed dict for inference
self.test_feed_dict = {x_test_pl: X_test,
y_test_pl: y_test}
# Take the next sample-label for the infered set into the computational Graph
self.sample, self.labels = self.iterator.get_next()
#self.sample = tf.reshape(self.sample,[-1,1])
self.labels = tf.one_hot(self.labels,depth=2,name='y1h')
#self.labels = tf.reshape(self.labels,[-1,1])
self.labels = tf.cast(self.labels,tf.float32)
self.sample = tf.cast(self.sample,tf.float32)
def model(self):
'''
Build model architecture using functional API
'''
with tf.name_scope('architecture'):
l1 = tf.layers.Dense(8,
activation=tf.nn.relu,
kernel_initializer=tf.keras.initializers.glorot_normal(),
name="hidden_1")(self.sample)
l2 = tf.layers.Dense(8,
activation=tf.nn.relu,
name="hidden_2")(l1)
l3 = tf.layers.Dense(8,
activation=tf.nn.relu,
name="hidden_2")(l2)
l4 = tf.layers.Dense(8,
activation=tf.nn.relu,
name="hidden_2")(l3)
self.logits = tf.layers.Dense(2,
activation=tf.nn.softmax,
name="output")(l4)
#self.logits = tf.transpose(self.logits)
def loss(self):
'''
Compute loss of the model
'''
with tf.name_scope('loss'):
#entropy = tf.keras.losses.binary_crossentropy(self.labels,self.logits,from_logits=True)
#entropy = tf.nn.sigmoid_cross_entropy_with_logits(labels=self.labels, logits=self.logits)
entropy = tf.nn.softmax_cross_entropy_with_logits(labels=self.labels, logits=self.logits)
self.loss = tf.reduce_mean(entropy,axis=0, name='loss')
tf.summary.scalar('loss',self.loss)
print("Labels shape:", self.labels.shape)
print("Logits shape:", self.logits.shape)
def optimize(self):
'''
Define Optimizer method to minimize loss
'''
with tf.name_scope('optimize'):
self.opt = tf.train.AdamOptimizer(self.lr).minimize(self.loss)
#self.opt = tf.train.GradientDescentOptimizer(self.lr).minimize(self.loss)
def evaluate(self):
'''
Compute predictions and accuracy in a batch
'''
with tf.name_scope('predict'):
#self.preds = tf.nn.sigmoid(self.logits)
#self.preds = tf.nn.softmax(self.logits)
#preds = tf.cast(preds > 0.5, tf.int64)
self.predictions = tf.nn.sigmoid(self.logits)
self.correct_preds = tf.equal(tf.argmax(self.predictions, -1), tf.argmax(self.labels, 1))
self.accuracy = tf.reduce_mean(tf.cast(self.correct_preds, tf.float32))
tf.summary.scalar('accuracy',self.accuracy)
def build(self):
'''
Build the computation graph
'''
self.get_data()
self.model()
self.loss()
self.optimize()
self.evaluate()
def train_predict(self, epochs):
'''
Train and evaluate model
:param epochs: number of epochs
:return: predictions
'''
merged = tf.summary.merge_all()
writer = tf.summary.FileWriter(logdir + '/graphs', tf.get_default_graph())
train_writer = tf.summary.FileWriter(logdir + '/train', self.sess.graph)
test_writer = tf.summary.FileWriter(logdir + '/test')
self.sess.run(tf.global_variables_initializer())
print("Start training process...")
for epoch in range(epochs):
self.sess.run(self.train_init_op)
total_loss = 0
n_batches = 0
sum_train_acc = 0
try:
while True:
summary, _ , loss, train_acc = self.sess.run([merged,self.opt,self.loss,self.accuracy])
total_loss += loss
sum_train_acc += train_acc
n_batches += self.batch_size
train_writer.add_summary(summary, epoch)
except tf.errors.OutOfRangeError:
pass
if epoch % 20 == 0:
print("Epoch: {}, Average loss: {:.4f}, Train Accuracy: {:.2f}%".format(
epoch,
total_loss/n_batches,
#(sum_train_acc/n_batches)*100))
train_acc))
train_writer.close()
## Evaluation ##
print("\nEvaluating...")
self.sess.run(self.valid_init_op)
sum_acc = 0
sum_loss = 0
sum_preds = []
try:
while True:
summary, batch_val_loss, batch_val_acc, preds = self.sess.run([merged,
self.loss,
self.accuracy,
self.predictions])
sum_loss += batch_val_loss
sum_acc += batch_val_acc
sum_preds.append(preds)
test_writer.add_summary(summary, epoch)
except tf.errors.OutOfRangeError:
pass
test_writer.close()
writer.close()
print("Average Validation loss: {:.4f}, Validation Accuracy: {:.2f}%".format(
sum_loss/self.valid_len,
#(sum_acc/self.valid_len)*100))
batch_val_acc))
return np.concatenate(sum_preds)
def test_plot(self,predictions):
'''
Infer test set to the trained model and plot predictions
:param predictions: array of predicted labels
:return: None
'''
## Test Set ##
self.sess.run(self.test_init_op)
z_preds = []
try:
while True:
z = self.predictions.eval(session = self.sess,feed_dict=self.test_feed_dict)
z_preds.append(z)
except tf.errors.OutOfRangeError:
pass
plt.figure(figsize=(5, 5), dpi=75)
colormap = colors.ListedColormap(["#f59322", "#e8eaeb", "#0877bd"])
_,_,xx,yy = datasets.grid_points()
z_preds = np.concatenate(z_preds)
z_preds = np.argmax(z_preds,axis=1)
plt.scatter(self.X_valid[:,0],self.X_valid[:,1], c=predictions[:,1], edgecolors='k', s=50, cmap=colormap)
plt.contourf(xx,yy,z_preds.reshape(xx.shape), cmap=colormap, alpha=0.4)
nn = NeuralNet(n_X=10000, noise_X=50)
nn.build()
model_train = time()
predictions = nn.train_predict(30)
print('Model train & evaluation time: %.1f sec' % (time() - model_train))
nn.test_plot(predictions)
# %load_ext tensorboard
# %tensorboard --logdir logs/ --port 1111
|
fcNN/tf_fcNN.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Handwritten Number Recognition with TFLearn and MNIST
# **This script is based on the exercise from udacity deep learning course**
# Import Numpy, TensorFlow, TFLearn, and MNIST data
import numpy as np
import tensorflow as tf
import tflearn
import tflearn.datasets.mnist as mnist
# Retrieve the training and test data
trainX, trainY, testX, testY = mnist.load_data(one_hot=True)
# ## Visualize the training data
# +
# Visualizing the data
import matplotlib.pyplot as plt
# %matplotlib inline
# Function for displaying a training image by it's index in the MNIST set
def show_digit(index):
label = trainY[index].argmax(axis=0)
# Reshape 784 array into 28x28 image
image = trainX[index].reshape([28,28])
plt.title('Training data, index: %d, Label: %d' % (index, label))
plt.imshow(image, cmap='gray_r')
plt.show()
# Display the first (index 0) training image
show_digit(0)
# -
# Define the neural network
def build_model():
# This resets all parameters and variables, leave this here
tf.reset_default_graph()
# input
net = tflearn.input_data([None, trainX.shape[1]])
# hidden
net = tflearn.fully_connected(net, 200, activation='ReLU')
# output
net = tflearn.fully_connected(net, 10, activation='softmax')
net = tflearn.regression(net,
optimizer='sgd',
learning_rate=0.01,
loss='categorical_crossentropy')
# This model assumes that your network is named "net"
model = tflearn.DNN(net)
return model
# Build the model
model = build_model()
# ### training
model.fit(trainX, trainY, validation_set=0.1, show_metric=True, batch_size=128, n_epoch=20)
# ### testing
# +
# Compare the labels that our model predicts with the actual labels
predictions = (np.array(model.predict(testX))[:,0] >= 0.5).astype(np.int_)
# Calculate the accuracy, which is the percentage of times the predicated labels matched the actual labels
test_accuracy = np.mean(predictions == testY[:,0], axis=0)
# Print out the result
print("Test accuracy: ", test_accuracy)
|
mnist_tflearn_default.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="4Prtukx5IOqh" papermill={} tags=[]
# # Notion - Explore API
# <a href="https://app.naas.ai/user-redirect/naas/downloader?url=https://raw.githubusercontent.com/jupyter-naas/awesome-notebooks/master/Notion/Notion_Explore_API.ipynb" target="_parent"><img src="https://img.shields.io/badge/-Open%20in%20Naas-success?labelColor=000000&logo=data:image/svg+xml;base64,PD94bWwgdmVyc2lvbj0iMS4wIiBlbmNvZGluZz0iVVRGLTgiPz4KPHN2ZyB3aWR0aD0iMTAyNHB4IiBoZWlnaHQ9IjEwMjRweCIgdmlld0JveD0iMCAwIDEwMjQgMTAyNCIgeG1sbnM9Imh0dHA6Ly93d3cudzMub3JnLzIwMDAvc3ZnIiB4bWxuczp4bGluaz0iaHR0cDovL3d3dy53My5vcmcvMTk5OS94bGluayIgdmVyc2lvbj0iMS4xIj4KIDwhLS0gR2VuZXJhdGVkIGJ5IFBpeGVsbWF0b3IgUHJvIDIuMC41IC0tPgogPGRlZnM+CiAgPHRleHQgaWQ9InN0cmluZyIgdHJhbnNmb3JtPSJtYXRyaXgoMS4wIDAuMCAwLjAgMS4wIDIyOC4wIDU0LjUpIiBmb250LWZhbWlseT<KEY>a>
# + [markdown] id="3zx-PjZ7N_UM" papermill={} tags=[]
# This notebook is an exploration of what you can do with the Notion's API.
#
# Resources:
# - Notion official documentation : https://developers.notion.com/
# - Youtube video (not official) : https://www.youtube.com/watch?v=sdn1HgxLwEg
# + [markdown] id="g02ao4cOR9Sl" papermill={} tags=[]
# # Input
# + id="RfMUE4p_R_Xp" papermill={} tags=[]
import requests
import pandas as pd
import json
# + [markdown] id="7noja8QcOHqD" papermill={} tags=[]
# ## Setting up Notion connections
# + [markdown] id="ODiJSP8WOMg2" papermill={} tags=[]
# 1. Create a page or a database on Notion.
# 2. Create an integration in your workspace.
# 3. Share your page or database to this integration.
#
# More explanation on how to do this here: https://developers.notion.com/docs/getting-started
# + id="ogm5MuphHwTW" papermill={} tags=[]
DATABASE_ID_TEST = "a296bd16b7284bc494aa91f50ad64d30" #https://www.notion.so/a296bd16b7284bc494aa91f50ad64d30?v=d37af84a3a6744fb957002073a267c44
PAGE_ID = "e2e8b31737174dbe86b9ae65f9b8eb9c" #click on Page and Get ID : https://www.notion.so/Mary-Meeks-2d822179eb59451e91e83086cdd74e5c
INTEGRATION_TOKEN = "<KEY>"
# + id="t2DzgcnhOHJ9" papermill={} tags=[]
NOTION_DB_URL = "https://api.notion.com/v1/databases/"
NOTION_PAGE_URL = "https://api.notion.com/v1/pages/"
NOTION_PAGE_CONTENT = "https://api.notion.com/v1/blocks/"
# + [markdown] id="ibDVAp6yRdd2" papermill={} tags=[]
# # Model
#
# + [markdown] id="ffGcyDQfPe8S" papermill={} tags=[]
# ## Get database properties
# + [markdown] id="uDBaydsEejek" papermill={} tags=[]
# More information here: https://developers.notion.com/reference/get-database
# + colab={"base_uri": "https://localhost:8080/"} id="jVW4IxjjJTn6" outputId="6110774d-6f42-4b40-d199-243753ad3ac2" papermill={} tags=[]
database_url = NOTION_DB_URL + DATABASE_ID_TEST
response = requests.get(database_url, headers={"Authorization": f"{INTEGRATION_TOKEN}"})
print (response.json())
# + [markdown] id="BLhbVoiuJQhe" papermill={} tags=[]
# More information here: https://developers.notion.com/reference/post-database-query
# + colab={"base_uri": "https://localhost:8080/"} id="vfzmGRbNRc7v" outputId="c9b3f70b-c7d2-4f06-d19f-e2d80adb0d31" papermill={} tags=[]
database_url = NOTION_DB_URL + DATABASE_ID_TEST + "/query"
query = {"filter": {"property": "High Priority", "checkbox": {"equals": True}}}
query = {"filter": {"property": "Cost of next trip", "number": {"greater_than_or_equal_to": 0.5}}}
headers = {"Authorization": f"{INTEGRATION_TOKEN}", "Notion-Version": "2021-05-13"}
response = requests.post(database_url, headers=headers, data=query)
print((response.json()['results']))
# + id="fUuczYrVN_Dt" papermill={} tags=[]
df_structure = pd.DataFrame.from_dict(response.json()['results'])
# + colab={"base_uri": "https://localhost:8080/", "height": 306} id="uYpIdw_lg00-" outputId="e7a3b964-0991-41b4-aae2-e2e5cb1422fb" papermill={} tags=[]
print("The size of the df is", df_structure.shape)
df_structure.head()
# + [markdown] id="jEbLAaebiuv6" papermill={} tags=[]
# ⚠️ Notion's API allows us to retrieve a maximum of 100 records. So if your base is bigger than 100 records it will only retrieve the 100 last edited ones.
#
# ⚠️ If your database has some relation to some other databases, think to share the linked databases with the integration aswell.
#
# As we can see the content of the Notion table is in the properties column. We will now extract it and see what it contains.
#
# The column properties contain a dictionary for each Notion record. We will exctract each of these disctionnaries and create a new dataFrame.
# + id="oIhSkVC2NxVz" papermill={} tags=[]
list_dict = []
for index, row in df_structure.iterrows():
list_dict.append(row['properties'])
temp_df = pd.DataFrame.from_dict(list_dict)
# + id="oQndDQl2AYsQ" papermill={} tags=[]
# Get the columns name in a list to use them later
columns = temp_df.columns.values.tolist()
# + colab={"base_uri": "https://localhost:8080/", "height": 374} id="tHRmy0uVjtaz" outputId="4d8ae852-7355-48d9-eafe-b2c08ecd61c5" papermill={} tags=[]
temp_df.head()
# + [markdown] id="8DkO7rkVnW1o" papermill={} tags=[]
# As we can see, each of the properties contains another dict of the information.
#
# Let's see how the dictionnary containing the data is structured.
# + colab={"base_uri": "https://localhost:8080/"} id="IWJDXyNxnFi0" outputId="bd068c93-6309-4eae-fdd5-cdd157a9bd7f" papermill={} tags=[]
for index, value in temp_df.iloc[2].items():
print(value)
# + colab={"base_uri": "https://localhost:8080/"} id="02_kmQPGip2P" outputId="f6de0174-a209-4e85-fe9c-2e8469fc385c" papermill={} tags=[]
pd.DataFrame.from_dict(list_dict).iloc[0]['Name']
# + [markdown] id="bujC9LaMpHx9" papermill={} tags=[]
# Let's create a small function to extract the data.
#
# All the properties contain an id and a type. The type will then be used to find the original information of the property.
#
# Sometimes, the data will be contained directly as a string, sometimes it will be a dict sometimes it will be a list of dict.
# + [markdown] id="YCAWDxKeJLTg" papermill={} tags=[]
# ## Query database
# + id="mJn95qB4r1qK" papermill={} tags=[]
def extract_name_or_plaintext(dictionnary):
# Given a dictionnary it will output the string of the key name or plain_text
if 'name' in dictionnary.keys():
return dictionnary['name']
elif 'plain_text' in dictionnary.keys():
return dictionnary['plain_text']
else:
return ''
def extract_date(dictionnary):
# For the moment we extract only the starting date of a date field
# Example {'id': 'prop_1', 'type': 'date', 'date': {'start': '2018-03-21', 'end': None}}
# Input : {'start': '2018-03-21', 'end': None}
return dictionnary['start']
# + id="hmaNLTjGpoMP" papermill={} tags=[]
def extract_data(element):
# input: a dictionnary of a notion property
# Exemple: {'id': 'W#4k', 'type': 'select', 'select': {'id': 'b305bd26-****-****-****-c78e2034db8f', 'name': 'Client', 'color': 'green'}}
# output: the string containing the information of the dict. (Client in the exemple)
if type(element) is dict:
dict_type = element['type']
informations = element[dict_type]
if dict_type == 'date':
informations = extract_date(informations)
elif type(informations) is dict:
informations = extract_name_or_plaintext(informations)
elif type(informations) is list:
informations_temp = ''
for element_of_informations_list in informations:
informations_temp += extract_name_or_plaintext(element_of_informations_list) + ", "
informations = informations_temp[:-2]
return informations
else:
return ''
# + id="oEREoIVSqjVL" papermill={} tags=[]
all_list = []
for i in range (temp_df.shape[0]):
temp_list = []
for index, value in temp_df.iloc[i].items():
temp_list.append(extract_data(value))
all_list.append(temp_list)
df_content = pd.DataFrame.from_records(all_list, columns = columns)
# + [markdown] papermill={} tags=[]
# ### Get only visible headers
# + colab={"base_uri": "https://localhost:8080/", "height": 204} id="8_A6C24l_DTZ" outputId="77cee2a8-bb71-49c4-d549-90e327f830ee" papermill={} tags=[]
df_content.head()
# + [markdown] papermill={} tags=[]
# ### Get full headers
# + id="XbuojdEbaGJy" papermill={} tags=[]
df_full = pd.concat([df_structure, df_content], axis=1)
# + id="rXi2iLQe_Va4" papermill={} tags=[]
df_full
# + [markdown] id="dTvDx-KljGzc" papermill={} tags=[]
# ## Get page properties
# + [markdown] id="EcqaPkgCFc-H" papermill={} tags=[]
# There is two different API calls to interact with a page.
#
# * **Get a page** will give us a page properties: https://developers.notion.com/reference/get-page
#
# * **Get block children** will give us the page content: https://developers.notion.com/reference/get-block-children
#
# + colab={"base_uri": "https://localhost:8080/"} id="DlWfZSVTQwoa" outputId="7a34a305-dc18-43a5-d9ed-4ddb58be13fa" papermill={} tags=[]
page_url = NOTION_PAGE_URL + PAGE_ID
response = requests.get(page_url, headers={"Authorization": f"{INTEGRATION_TOKEN}", "Notion-Version": "2021-05-13"})
print (response.json())
# + [markdown] id="8omlCdOD-Eao" papermill={} tags=[]
# ## Retrieve a page content
# + colab={"base_uri": "https://localhost:8080/"} id="PDsY77eX-Nj9" outputId="7ce4128b-3463-4a77-f297-65782504dbb6" papermill={} tags=[]
page_url = NOTION_PAGE_CONTENT + PAGE_ID + "/children"
headers = {"Authorization": f"{INTEGRATION_TOKEN}", "Notion-Version": "2021-05-13"}
response = requests.get(page_url, headers=headers)
print(response.json())
# + [markdown] id="FjG63wCMMVyE" papermill={} tags=[]
# Some types are accessible. But some other types are unsupported and cannot be read through the API.
#
# Some unsupported types :
# * image
# * bookmarked link
# * other page (it has an unsupported type but it will be readable through its page id)
# + [markdown] id="bnwPTUNxjukY" papermill={} tags=[]
# ## Create a record
# + colab={"base_uri": "https://localhost:8080/"} id="LcvVoyfHkfhR" outputId="e0c8e62e-5536-470c-8780-5a2e7a73d48d" papermill={} tags=[]
page_url = NOTION_PAGE_URL
page_id = DATABASE_ID_TEST
# Surprisingly in this case you need to add "Content-Type": "application/json"
# If not you will an error 400: body failed validation: body.parent should be defined, instead was 'undefined'.
headers = {"Authorization": f"{INTEGRATION_TOKEN}", "Notion-Version": "2021-05-13", "Content-Type": "application/json"}
name = {"title":[{"text":{"content":"Added via API NAAS"}}]}
company = {"rich_text": [{"text": {"content": "Test Company"}}]}
status = {"select": {"name": "Lost"}}
est_value = {"number": 10000 }
header = {"object": "block",
"type": "heading_2",
"heading_2": {
"text": [{ "type": "text", "text": { "content": "Naas API test" } }]
}
}
paragraph = {"object": "block",
"type": "paragraph",
"paragraph": {
"text": [
{
"type": "text",
"text": {
"content": "Notebooks as a service for data geeks. Naas notebooks enable you to script faster with low-code formulas & templates. Automate all your tasks in minutes..",
}
}
]
}
}
to_do = {"object": "block",
"type": "to_do",
"to_do": {
"text": [
{
"type": "text",
"text": {
"content": "Automate all your tasks in minutes..",
}
},
{
"type": "text",
"text": {
"content": "Script faster",
}
}
]
}
}
# + [markdown] papermill={} tags=[]
# # Output
# + [markdown] papermill={} tags=[]
# ### Setup object to post
# + papermill={} tags=[]
myobj = {
"parent": {"database_id": page_id},
"properties":
{
"Name":name,
"Company": company,
"Status": status,
"Estimated Value": est_value
},
"children":[header, paragraph,to_do]
}
# + [markdown] papermill={} tags=[]
# ### Post record
# + papermill={} tags=[]
data = json.dumps(myobj)
response = requests.post(page_url, headers=headers, data=data)
if 'status' in response.json().keys():
if response.json()['status'] != 200:
print ("Error:", response.json()['message'])
elif 'object' in response.json().keys():
print("✅ Your data was added to Notion")
print(response.json())
|
Notion/Notion_Explore_API.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Homework 1
# *This notebook includes both coding and written questions. Please hand in this notebook file with all the outputs and your answers to the written questions.*
#
# This assignment covers linear filters, convolution and correlation.
# +
# Setup
import numpy as np
import matplotlib.pyplot as plt
from time import time
from skimage import io
from __future__ import print_function
# %matplotlib inline
plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
# for auto-reloading extenrnal modules
# %load_ext autoreload
# %autoreload 2
# -
# ## Part 1: Convolutions
# ### 1.1 Commutative Property (10 points)
# Recall that the convolution of an image $f:\mathbb{R}^2\rightarrow \mathbb{R}$ and a kernel $h:\mathbb{R}^2\rightarrow\mathbb{R}$ is defined as follows:
# $$(f*h)[m,n]=\sum_{i=-\infty}^\infty\sum_{j=-\infty}^\infty f[i,j]\cdot h[m-i,n-j]$$
#
# Or equivalently,
# \begin{align}
# (f*h)[m,n] &= \sum_{i=-\infty}^\infty\sum_{j=-\infty}^\infty h[i,j]\cdot f[m-i,n-j]\\
# &= (h*f)[m,n]
# \end{align}
#
# Show that this is true (i.e. prove that the convolution operator is commutative: $f*h = h*f$).
# **Your Answer:** *Write your solution in this markdown cell. Please write your equations in [LaTex equations](http://jupyter-notebook.readthedocs.io/en/latest/examples/Notebook/Typesetting%20Equations.html).*
# ### 1.2 Shift Invariance (10 points)
# Let $f$ be a function $\mathbb{R}^2\rightarrow\mathbb{R}$. Consider a system $f\xrightarrow{s}g$, where $g=(f*h)$ with some kernel $h:\mathbb{R}^2\rightarrow\mathbb{R}$. Also consider functions $f'(m,n) = f(m-m_0, n-n_0)$ and $g'(m,n) = g(m-m_0, n-n_0)$.
#
# Show that $S$ defined by any kernel $h$ is a Shift Invariant system by showing that $g' = (f'*h)$.
# **Your Answer:** *Write your solution in this markdown cell. Please write your equations in [LaTex equations](http://jupyter-notebook.readthedocs.io/en/latest/examples/Notebook/Typesetting%20Equations.html).*
# ### 1.3 Implementation (30 points)
#
# In this section, you will implement two versions of convolution:
# - `conv_nested`
# - `conv_fast`
#
# First, run the code cell below to load the image to work with.
# +
# Open image as grayscale
img = io.imread('dog.jpg', as_grey=True)
# Show image
plt.imshow(img)
plt.axis('off')
plt.title("Isn't he cute?")
plt.show()
# -
# Now, implement the function **`conv_nested`** in **`filters.py`**. This is a naive implementation of convolution which uses 4 nested for-loops. It takes an image $f$ and a kernel $h$ as inputs and outputs the convolved image $(f*h)$ that has the same shape as the input image. This implementation should take a few seconds to run.
#
# *- Hint: It may be easier to implement $(h*f)$*
# We'll first test your `conv_nested` function on a simple input.
# +
from filters import conv_nested
# Simple convolution kernel.
kernel = np.array(
[
[1,0,1],
[0,0,0],
[1,0,0]
])
# Create a test image: a white square in the middle
test_img = np.zeros((9, 9))
test_img[3:6, 3:6] = 1
# Run your conv_nested function on the test image
test_output = conv_nested(test_img, kernel)
# Build the expected output
expected_output = np.zeros((9, 9))
expected_output[2:7, 2:7] = 1
expected_output[5:, 5:] = 0
expected_output[4, 2:5] = 2
expected_output[2:5, 4] = 2
expected_output[4, 4] = 3
# Plot the test image
plt.subplot(1,3,1)
plt.imshow(test_img)
plt.title('Test image')
plt.axis('off')
# Plot your convolved image
plt.subplot(1,3,2)
plt.imshow(test_output)
plt.title('Convolution')
plt.axis('off')
# Plot the exepected output
plt.subplot(1,3,3)
plt.imshow(expected_output)
plt.title('Exepected output')
plt.axis('off')
plt.show()
# Test if the output matches expected output
assert np.max(test_output - expected_output) < 1e-10, "Your solution is not correct."
# -
# Now let's test your `conv_nested` function on a real image.
# +
from filters import conv_nested
# Simple convolution kernel.
# Feel free to change the kernel to see different outputs.
kernel = np.array(
[
[1,0,-1],
[2,0,-2],
[1,0,-1]
])
out = conv_nested(img, kernel)
# Plot original image
plt.subplot(2,2,1)
plt.imshow(img)
plt.title('Original')
plt.axis('off')
# Plot your convolved image
plt.subplot(2,2,3)
plt.imshow(out)
plt.title('Convolution')
plt.axis('off')
# Plot what you should get
solution_img = io.imread('convoluted_dog.jpg', as_grey=True)
plt.subplot(2,2,4)
plt.imshow(solution_img)
plt.title('What you should get')
plt.axis('off')
plt.show()
# -
# Let us implement a more efficient version of convolution using array operations in numpy. As shown in the lecture, a convolution can be considered as a sliding window that computes sum of the pixel values weighted by the flipped kernel. The faster version will i) zero-pad an image, ii) flip the kernel horizontally and vertically, and iii) compute weighted sum of the neighborhood at each pixel.
#
# First, implement the function **`zero_pad`** in **`filters.py`**.
#
# +
from filters import zero_pad
pad_width = 20 # width of the padding on the left and right
pad_height = 40 # height of the padding on the top and bottom
padded_img = zero_pad(img, pad_height, pad_width)
# Plot your padded dog
plt.subplot(1,2,1)
plt.imshow(padded_img)
plt.title('Padded dog')
plt.axis('off')
# Plot what you should get
solution_img = io.imread('padded_dog.jpg', as_grey=True)
plt.subplot(1,2,2)
plt.imshow(solution_img)
plt.title('What you should get')
plt.axis('off')
plt.show()
# -
# Next, complete the function **`conv_fast`** in **`filters.py`** using `zero_pad`. Run the code below to compare the outputs by the two implementations. `conv_fast` should run significantly faster than `conv_nested`.
# Depending on your implementation and computer, `conv_nested` should take a few seconds and `conv_fast` should be around 5 times faster.
# +
from filters import conv_fast
t0 = time()
out_fast = conv_fast(img, kernel)
t1 = time()
out_nested = conv_nested(img, kernel)
t2 = time()
# Compare the running time of the two implementations
print("conv_nested: took %f seconds." % (t2 - t1))
print("conv_fast: took %f seconds." % (t1 - t0))
# Plot conv_nested output
plt.subplot(1,2,1)
plt.imshow(out_nested)
plt.title('conv_nested')
plt.axis('off')
# Plot conv_fast output
plt.subplot(1,2,2)
plt.imshow(out_fast)
plt.title('conv_fast')
plt.axis('off')
# Make sure that the two outputs are the same
if not (np.max(out_fast - out_nested) < 1e-10):
print("Different outputs! Check your implementation.")
# -
# ### Extra Credit 1 (10 points)
# Devise a faster version of convolution and implement **`conv_faster`** in **`filters.py`**. You will earn extra credit only if the `conv_faster` runs faster (by a fair margin) than `conv_fast` **and** outputs the same result.
# +
from filters import conv_faster
t0 = time()
out_fast = conv_fast(img, kernel)
t1 = time()
out_faster = conv_faster(img, kernel)
t2 = time()
# Compare the running time of the two implementations
print("conv_fast: took %f seconds." % (t1 - t0))
print("conv_faster: took %f seconds." % (t2 - t1))
# Plot conv_nested output
plt.subplot(1,2,1)
plt.imshow(out_fast)
plt.title('conv_fast')
plt.axis('off')
# Plot conv_fast output
plt.subplot(1,2,2)
plt.imshow(out_faster)
plt.title('conv_faster')
plt.axis('off')
# Make sure that the two outputs are the same
if not (np.max(out_fast - out_faster) < 1e-10):
print("Different outputs! Check your implementation.")
# -
# ---
# ## Part 2: Cross-correlation
#
# Cross-correlation of two 2D signals $f$ and $g$ is defined as follows:
# $$(f\star{g})[m,n]=\sum_{i=-\infty}^\infty\sum_{j=-\infty}^\infty f[i,j]\cdot g[i-m,j-n]$$
# ### 2.1 Template Matching with Cross-correlation (12 points)
# Suppose that you are a clerk at a grocery store. One of your responsibilites is to check the shelves periodically and stock them up whenever there are sold-out items. You got tired of this laborious task and decided to build a computer vision system that keeps track of the items on the shelf.
#
# Luckily, you have learned in CS131 that cross-correlation can be used for template matching: a template $g$ is multiplied with regions of a larger image $f$ to measure how similar each region is to the template.
#
# The template of a product (`template.jpg`) and the image of shelf (`shelf.jpg`) is provided. We will use cross-correlation to find the product in the shelf.
#
# Implement **`cross_correlation`** function in **`filters.py`** and run the code below.
#
# *- Hint: you may use the `conv_fast` function you implemented in the previous question.*
# +
from filters import cross_correlation
# Load template and image in grayscale
img = io.imread('shelf.jpg')
img_grey = io.imread('shelf.jpg', as_grey=True)
temp = io.imread('template.jpg')
temp_grey = io.imread('template.jpg', as_grey=True)
# Perform cross-correlation between the image and the template
out = cross_correlation(img_grey, temp_grey)
# Find the location with maximum similarity
y,x = (np.unravel_index(out.argmax(), out.shape))
# Display product template
plt.figure(figsize=(25,20))
plt.subplot(3, 1, 1)
plt.imshow(temp)
plt.title('Template')
plt.axis('off')
# Display cross-correlation output
plt.subplot(3, 1, 2)
plt.imshow(out)
plt.title('Cross-correlation (white means more correlated)')
plt.axis('off')
# Display image
plt.subplot(3, 1, 3)
plt.imshow(img)
plt.title('Result (blue marker on the detected location)')
plt.axis('off')
# Draw marker at detected location
plt.plot(x, y, 'bx', ms=40, mew=10)
plt.show()
# -
# #### Interpretation
# How does the output of cross-correlation filter look? Was it able to detect the product correctly? Explain what problems there might be with using a raw template as a filter.
# **Your Answer:** *Write your solution in this markdown cell.*
# ---
# ### 2.2 Zero-mean cross-correlation (6 points)
# A solution to this problem is to subtract the mean value of the template so that it has zero mean.
#
# Implement **`zero_mean_cross_correlation`** function in **`filters.py`** and run the code below.
# +
from filters import zero_mean_cross_correlation
# Perform cross-correlation between the image and the template
out = zero_mean_cross_correlation(img_grey, temp_grey)
# Find the location with maximum similarity
y,x = (np.unravel_index(out.argmax(), out.shape))
# Display product template
plt.figure(figsize=(30,20))
plt.subplot(3, 1, 1)
plt.imshow(temp)
plt.title('Template')
plt.axis('off')
# Display cross-correlation output
plt.subplot(3, 1, 2)
plt.imshow(out)
plt.title('Cross-correlation (white means more correlated)')
plt.axis('off')
# Display image
plt.subplot(3, 1, 3)
plt.imshow(img)
plt.title('Result (blue marker on the detected location)')
plt.axis('off')
# Draw marker at detcted location
plt.plot(x, y, 'bx', ms=40, mew=10)
plt.show()
# -
# You can also determine whether the product is present with appropriate scaling and thresholding.
# +
def check_product_on_shelf(shelf, product):
out = zero_mean_cross_correlation(shelf, product)
# Scale output by the size of the template
out = out / float(product.shape[0]*product.shape[1])
# Threshold output (this is arbitrary, you would need to tune the threshold for a real application)
out = out > 0.025
if np.sum(out) > 0:
print('The product is on the shelf')
else:
print('The product is not on the shelf')
# Load image of the shelf without the product
img2 = io.imread('shelf_soldout.jpg')
img2_grey = io.imread('shelf_soldout.jpg', as_grey=True)
plt.imshow(img)
plt.axis('off')
plt.show()
check_product_on_shelf(img_grey, temp_grey)
plt.imshow(img2)
plt.axis('off')
plt.show()
check_product_on_shelf(img2_grey, temp_grey)
# -
# ---
# ### 2.3 Normalized Cross-correlation (12 points)
# One day the light near the shelf goes out and the product tracker starts to malfunction. The `zero_mean_cross_correlation` is not robust to change in lighting condition. The code below demonstrates this.
# +
from filters import normalized_cross_correlation
# Load image
img = io.imread('shelf_dark.jpg')
img_grey = io.imread('shelf_dark.jpg', as_grey=True)
# Perform cross-correlation between the image and the template
out = zero_mean_cross_correlation(img_grey, temp_grey)
# Find the location with maximum similarity
y,x = (np.unravel_index(out.argmax(), out.shape))
# Display image
plt.imshow(img)
plt.title('Result (red marker on the detected location)')
plt.axis('off')
# Draw marker at detcted location
plt.plot(x, y, 'rx', ms=25, mew=5)
plt.show()
# -
# A solution is to normalize the pixels of the image and template at every step before comparing them. This is called **normalized cross-correlation**.
#
# The mathematical definition for normalized cross-correlation of $f$ and template $g$ is:
# $$(f\star{g})[m,n]=\sum_{i,j} \frac{f[i,j]-\overline{f_{m,n}}}{\sigma_{f_{m,n}}} \cdot \frac{g[i-m,j-n]-\overline{g}}{\sigma_g}$$
#
# where:
# - $f_{m,n}$ is the patch image at position $(m,n)$
# - $\overline{f_{m,n}}$ is the mean of the patch image $f_{m,n}$
# - $\sigma_{f_{m,n}}$ is the standard deviation of the patch image $f_{m,n}$
# - $\overline{g}$ is the mean of the template $g$
# - $\sigma_g$ is the standard deviation of the template $g$
#
# Implement **`normalized_cross_correlation`** function in **`filters.py`** and run the code below.
# +
from filters import normalized_cross_correlation
# Perform normalized cross-correlation between the image and the template
out = normalized_cross_correlation(img_grey, temp_grey)
# Find the location with maximum similarity
y,x = (np.unravel_index(out.argmax(), out.shape))
# Display image
plt.imshow(img)
plt.title('Result (red marker on the detected location)')
plt.axis('off')
# Draw marker at detcted location
plt.plot(x, y, 'rx', ms=25, mew=5)
plt.show()
# -
# ## Part 3: Separable Filters
# ### 3.1 Theory (10 points)
# Consider an $M_1\times{N_1}$ image $I$ and an $M_2\times{N_2}$ filter $F$. A filter $F$ is **separable** if it can be written as a product of two 1D filters: $F=F_1F_2$.
#
# For example,
# $$F=
# \begin{bmatrix}
# 1 & -1 \\
# 1 & -1
# \end{bmatrix}
# $$
# can be written as a matrix product of
# $$F_1=
# \begin{bmatrix}
# 1 \\
# 1
# \end{bmatrix},
# F_2=
# \begin{bmatrix}
# 1 & -1
# \end{bmatrix}
# $$
# Therefore $F$ is a separable filter.
#
# Prove that for any separable filter $F=F_1F_2$,
# $$I*F=(I*F_1)*F_2$$
# **Your Answer:** *Write your solution in this markdown cell. Please write your equations in [LaTex equations](http://jupyter-notebook.readthedocs.io/en/latest/examples/Notebook/Typesetting%20Equations.html).*
# ### 3.2 Complexity comparison (10 points)
# Consider an $M_1\times{N_1}$ image $I$ and an $M_2\times{N_2}$ filter $F$ that is separable (i.e. $F=F_1F_2$).
#
# (i) How many multiplication operations do you need to do a direct 2D convolution (i.e. $I*F$)?<br>
# (ii) How many multiplication operations do you need to do 1D convolutions on rows and columns (i.e. $(I*F_1)*F_2$)?<br>
# (iii) Use Big-O notation to argue which one is more efficient in general: direct 2D convolution or two successive 1D convolutions?
# **Your Answer:** *Write your solution in this markdown cell. Please write your equations in [LaTex equations](http://jupyter-notebook.readthedocs.io/en/latest/examples/Notebook/Typesetting%20Equations.html).*
# Now, we will empirically compare the running time of a separable 2D convolution and its equivalent two 1D convolutions. The Gaussian kernel, widely used for blurring images, is one example of a separable filter. Run the code below to see its effect.
# +
# Load image
img = io.imread('dog.jpg', as_grey=True)
# 5x5 Gaussian blur
kernel = np.array(
[
[1,4,6,4,1],
[4,16,24,16,4],
[6,24,36,24,6],
[4,16,24,16,4],
[1,4,6,4,1]
])
t0 = time()
out = conv_nested(img, kernel)
t1 = time()
t_normal = t1 - t0
# Plot original image
plt.subplot(1,2,1)
plt.imshow(img)
plt.title('Original')
plt.axis('off')
# Plot convolved image
plt.subplot(1,2,2)
plt.imshow(out)
plt.title('Blurred')
plt.axis('off')
plt.show()
# -
# In the below code cell, define the two 1D arrays (`k1` and `k2`) whose product is equal to the Gaussian kernel.
# +
# The kernel can be written as outer product of two 1D filters
k1 = None # shape (5, 1)
k2 = None # shape (1, 5)
### YOUR CODE HERE
pass
### END YOUR CODE
# Check if kernel is product of k1 and k2
if not np.all(k1 * k2 == kernel):
print('k1 * k2 is not equal to kernel')
assert k1.shape == (5, 1), "k1 should have shape (5, 1)"
assert k2.shape == (1, 5), "k2 should have shape (1, 5)"
# -
# We now apply the two versions of convolution to the same image, and compare their running time. Note that the outputs of the two convolutions must be the same.
# +
# Perform two convolutions using k1 and k2
t0 = time()
out_separable = conv_nested(img, k1)
out_separable = conv_nested(out_separable, k2)
t1 = time()
t_separable = t1 - t0
# Plot normal convolution image
plt.subplot(1,2,1)
plt.imshow(out)
plt.title('Normal convolution')
plt.axis('off')
# Plot separable convolution image
plt.subplot(1,2,2)
plt.imshow(out_separable)
plt.title('Separable convolution')
plt.axis('off')
plt.show()
print("Normal convolution: took %f seconds." % (t_normal))
print("Separable convolution: took %f seconds." % (t_separable))
# -
# Check if the two outputs are equal
assert np.max(out_separable - out) < 1e-10
|
hw1_release/.ipynb_checkpoints/hw1-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import ipywidgets as widgets
import time
from ipywidgets import interact, fixed
# Wygenerowac tablice N punktow (x,y)
np.random.seed(46)
def secret_fun(x):
return x * np.sin(x/2) + np.log(x) * np.cos(x**3) + 30 *np.random.rand()
# return x * np.random.rand() + np.random.rand()
# +
X = np.linspace(1, 100, 30)
Y = np.array([secret_fun(x) for x in X])
more_X = np.linspace(1, 100, 300)
more_Y = np.array([secret_fun(x) for x in more_X])
plt.scatter(X, Y)
plt.plot(more_X, more_Y, color='red')
plt.show()
# -
src_df = pd.DataFrame({'x': X, 'y':Y})
src_df.to_csv('secret_fun.csv', index=False)
# Uzyc funkcji gsl do interpolacji wielomianowej dla tych punktow - uzyc gsl_interp_polynomial. Narysowac jego wykres.
gsl_interp_df = pd.read_csv('gsl_interp.csv')
list(gsl_interp_df)
plt.scatter(X, Y)
plt.plot(gsl_interp_df['x'], gsl_interp_df['y'], color='red')
plt.plot(more_X, more_Y, color='green')
plt.show()
# Napisac wlasny program generujacy dane (recznie - bez korzystania z gsl) do narysowania wykresu wielomianu interpolujacego metoda Lagrange'a dla tych punktow w wybranym przedziale. Postarac sie zaprojektowac API podobnie do GSL - osobna funkcja init oraz eval Narysowac wykres.
def interpolation_nodes(XY, nodes_num):
all_points_no = XY.shape[0]
assert(nodes_num <= all_points_no)
nodes = np.array([XY[round(i*(all_points_no / nodes_num))] for i in range(nodes_num)])
nodes[nodes_num - 1] = XY[all_points_no - 1]
return nodes
# TODO vectorization
def lagrange_poly(X, Y, nodes_num=None):
nodes_num = len(X) if nodes_num is None else nodes_num
XY = np.c_[X,Y]
nodes = interpolation_nodes(XY, nodes_num)
def basis(m, j):
if m == j:
return lambda x: 1
return lambda x: (x - nodes[m][0] ) / (nodes[j][0] - nodes[m][0])
def result(x):
s = 0
for j in range(len(nodes)):
l = nodes[j][1]
for m in range(len(nodes)):
l *= basis(m, j)(x)
s += l
return s
return result, nodes
def demonstrate_lagrange(max_X, interp_nodes_no):
X = np.linspace(1, max_X, 30)
more_X = np.linspace(1, max_X, 300)
Y = np.array([secret_fun(x) for x in X])
poly, nodes = lagrange_poly(X, Y, nodes_num=interp_nodes_no)
more_Y_interp = poly(more_X)
more_Y = np.array([secret_fun(x) for x in more_X])
plt.scatter(X, Y, color='blue')
plt.scatter([n[0] for n in nodes], [n[1] for n in nodes], color='red')
plt.plot(more_X, more_Y_interp, color='red')
plt.plot(more_X, more_Y, color='green')
plt.show()
interact(demonstrate_lagrange,
max_X=widgets.IntSlider(min=1, max=1000, value=100),
interp_nodes_no=widgets.IntSlider(min=1, max=30, value=30)
)
# Zrobic to samo metoda Newtona. Porownac wszystkie 3 wyniki na jednym wykresie.
def newton_poly(X, Y):
XY = np.c_[X,Y]
cache = [[None for j in range(len(XY))] for i in range(len(XY))]
def div_difference(i, j):
assert(i <= j)
if(i == j):
return XY[i][1]
if cache[i][j] is None:
cache[i][j] = (div_difference(i + 1, j) - div_difference(i, j-1)) / (XY[j][0] - XY[i][0])
return cache[i][j]
def mul_up_to(i):
def result(x):
r = 1
for j in range(i):
r *= (x - XY[j][0])
return r
return result
A = np.array([div_difference(0,j) for j in range(len(XY))])
def result(x):
muls = np.array([mul_up_to(i)(x) for i in range(len(XY))])
return (A * muls).sum()
return result
def demonstrate_newton(max_X):
X = np.linspace(1, max_X, 30)
more_X = np.linspace(1, max_X, 300)
Y = np.array([secret_fun(x) for x in X])
poly = newton_poly(X, Y)
more_Y_interp = [poly(x) for x in more_X]
plt.scatter(X, Y, color='blue')
plt.plot(more_X, more_Y_interp, color='red')
plt.show()
interact(demonstrate_newton,
max_X=widgets.IntSlider(min=1, max=1000, value=100, step=10)
)
def demonstrate_all(max_X,lagrange_interp_nodes_no):
X = np.linspace(1, max_X, 30)
more_X = np.linspace(1, max_X, 300)
Y = np.array([secret_fun(x) for x in X])
lagrange_p, nodes = lagrange_poly(X, Y, nodes_num=lagrange_interp_nodes_no)
lagrange_Y_interp = np.array([lagrange_p(x) for x in more_X])
newton_p = newton_poly(X, Y)
newton_Y_interp = np.array([newton_p(x) for x in more_X])
plt.scatter(X, Y, color='blue')
plt.scatter([n[0] for n in nodes], [n[1] for n in nodes], color='red')
plt.plot(gsl_interp_df['x'], gsl_interp_df['y'], color='green')
plt.plot(more_X, newton_Y_interp, color='orange')
plt.plot(more_X, lagrange_Y_interp, color='red')
print((newton_Y_interp - lagrange_Y_interp).sum())
plt.show()
interact(demonstrate_all,
max_X=widgets.IntSlider(min=1, max=1000, value=100),
lagrange_interp_nodes_no=widgets.IntSlider(min=1, max=30, value=30)
)
# Porownac metody poprzez pomiar czasu wykonania dla zmiennej ilosci wezlow interpolacji. Dokonac pomiaru 10 razy i policzyc wartosc srednia oraz oszacowac blad pomiaru za pomoca odchylenia standardowego. Narysowac wykresy w R.
def interp_create_time(poly_generator, nodes_count, max_X=1000):
X = np.linspace(1, max_X, nodes_count)
Y = np.array([secret_fun(x) for x in X])
t_0 = time.time()
poly = poly_generator(X, Y)
t_1 = time.time()
return poly, t_1 - t_0
def interp_perform_time(poly, max_X=1000):
more_X = np.linspace(1, max_X, max_X)
t_0 = time.time()
interp = np.array([poly(x) for x in more_X])
t_1 = time.time()
return t_1 - t_0
def performance(generator, max_nodes, is_lagrange=False, repeats=10):
nodes_counts = []
creation_times = []
performance_times = []
for nodes_count in range(1, max_nodes):
for r in range(repeats):
poly, creation_time = interp_create_time(generator, nodes_count)
if is_lagrange:
poly = poly[0]
interp_time = interp_perform_time(poly)
nodes_counts.append(nodes_count)
creation_times.append(creation_time)
performance_times.append(interp_time)
return nodes_counts, creation_times, performance_times
max_nodes = 30
l_counts, l_creation, l_performance = performance(lagrange_poly, max_nodes, True)
n_counts, n_creation, n_performance = performance(newton_poly, max_nodes)
plt.scatter(l_counts, l_creation, color='red')
plt.scatter(l_counts, n_creation, color='blue')
plt.title('interpolation generation time')
plt.show()
plt.scatter(l_counts, l_performance, color='red')
plt.scatter(l_counts, n_performance, color='blue')
plt.title()
plt.show()
# +
def summarize_df(df):
return df.groupby('node_count', as_index=False).agg(
{
'creation': ["mean", "std"],
'evaluation': ["mean", "std"]
})
l_results_df = summarize_df(pd.DataFrame({
'node_count': l_counts,
'creation': l_creation,
'evaluation': l_performance
}))
n_results_df = summarize_df(pd.DataFrame({
'node_count': n_counts,
'creation': n_creation,
'evaluation': n_performance
}))
l_results_df
# +
plt.errorbar(l_results_df['node_count'],
l_results_df['creation']['mean'],
l_results_df['creation']['std'],
marker='.',
color='b',
ecolor='black'
)
plt.errorbar(n_results_df['node_count'],
n_results_df['creation']['mean'],
n_results_df['creation']['std'],
marker='.',
color='r',
ecolor='black'
)
plt.title('interpolation evaluation time')
plt.show()
# +
plt.errorbar(l_results_df['node_count'],
l_results_df['evaluation']['mean'],
l_results_df['evaluation']['std'],
marker='.',
color='b',
ecolor='black'
)
plt.errorbar(n_results_df['node_count'],
n_results_df['evaluation']['mean'],
n_results_df['evaluation']['std'],
marker='.',
color='r',
ecolor='black'
)
plt.title('interpolation evaluation time')
plt.show()
# -
# Poeksperymentowac z innymi typami interpolacji gsl (cspline, akima), zmierzyc czasy, narysowac wykresy i porownac z wykresami interpolacji wielomianowej. Zaobserwowac, gdzie wystepuje efekt Rungego.
# +
from scipy import interpolate
def demonstrate_cspline(max_X, interp_nodes):
X = np.linspace(1, max_X, interp_nodes)
Y = secret_fun(X)
more_X = np.linspace(1, max_X, max_X)
tck = interpolate.splrep(X, Y, s=0)
more_Y_interp = interpolate.splev(more_X, tck, der=0)
more_Y = secret_fun(more_X)
plt.scatter(X, Y, color='blue')
plt.plot(more_X, more_Y_interp, color='red')
plt.plot(more_X, more_Y, color='green')
plt.show()
# -
interact(demonstrate_cspline,
max_X=widgets.IntSlider(min=1, max=1000, value=100, step=10),
interp_nodes=widgets.IntSlider(min=1, max=100, value=30)
)
def demonstrate_akima(max_X, interp_nodes):
X = np.linspace(1, max_X, interp_nodes)
Y = secret_fun(X)
more_X = np.linspace(1, max_X, max_X)
interpolator = interpolate.Akima1DInterpolator(X, Y)
more_Y_interp = interpolator(more_X)
more_Y = secret_fun(more_X)
plt.scatter(X, Y, color='blue')
plt.plot(more_X, more_Y_interp, color='red')
plt.plot(more_X, more_Y, color='green')
plt.show()
interact(demonstrate_cspline,
max_X=widgets.IntSlider(min=1, max=1000, value=100, step=10),
interp_nodes=widgets.IntSlider(min=1, max=100, value=30)
)
|
lab5/lab5.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import numpy as np
from matplotlib import pyplot as plt
from math import sqrt
import skimage
import os
import math
import scipy.ndimage as snd
import cv2
os.chdir("/home/wrenchking/Desktop/Image_Analysis/Week_5/data")
# image1=skimage.io.imread("noise_free_circles.png").astype(np.int)
# Im = skimage.color.rgb2gray(image1)
# image2=skimage.io.imread("noisy_circles.png").astype(np.int)
# Im2 = skimage.color.rgb2gray(image2)
# hist = cv2.calcHist([img],[0],None,[256],[0,256])
# hist,bins = np.histogram(img.ravel(),256,[0,256])
# plt.hist(img.ravel(),256,[0,256]); plt.show()
from skimage import io
from skimage import color
img = io.imread('noise_free_circles.png')
img2=io.imread("noisy_circles.png")
print("img "+str(img.ravel()))
print("img2 "+str(img2.ravel()))
plt.figure()
bin_counts, bin_edges, patches = plt.hist(img.ravel())
plt.figure()
bin_counts2, bin_edges2, patches2 = plt.hist(img2.ravel(),bins=60)
# +
D = skimage.io.imread("noisy_circles.png").astype(np.int);
S = [1, 2, 3]
def Hist(D, S):
D = 1
f, ax = plt.subplots(1,2, figsize=(10,4))
ax[0].imshow(D, cmap='gray');
ax[1].hist(D.ravel(), bins=60, range=[0,256], rwidth=0.8, color='k');
# +
def thing(image,seg,other,stuff):
classVals=np.unique(seg.ravel())
#points needs to be numpy array
#gives energy sum for a set of points as a class
def oneClique(mean,points):
return np.sum((points-mean)**2)
def twoClique(points):
y,x=points.shape
counting=np.zeros((y,x))
for i in range(-1,2):
for j in range(-1,2):
tmp = points[1:y-1,1:x-1] > points[1+j:y-1+j,1+i:x-1+i]
counting[1:y-1,1:x-1] += tmp.astype(float)
return np.sum(counting)/2
|
Week 5 Exercises.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Profile Intel® oneAPI Deep Neural Network Library (oneDNN) Samples by using Verobse Mode and JIT DUMP inspection
#
# ## Learning Objectives
# In this module the developer will:
# * Learn how to use Verbose Mode to profile oneDNN samples on CPU & GPU
# * Learn how to inspect JIT Dump to profile oneDNN samples on CPU
# This module shows the elapsed time percentage over different oneDNN primitives
# <img src="images/cpu.JPG" style="float:left" width=600>
#
# This module also shows the elapsed time percentage over different oneDNN JIT or GPU kernels
# <img src="images/cpu_jit.JPG" style="float:left" width=400>
# <img src="images/gpu_kernel.JPG" style="float:right" width=400>
# ***
# # Verbose Mode Exercise
#
#
# ## prerequisites
# ***
# ### Step 1: Prepare the build/run environment
# oneDNN has four different configurations inside the Intel oneAPI toolkits. Each configuration is in a different folder under the oneDNN installation path, and each configuration supports a different compiler or threading library
#
# Set the installation path of your oneAPI toolkit
# ignore all warning messages
import warnings
warnings.filterwarnings('ignore')
# default path: /opt/intel/oneapi
# %env ONEAPI_INSTALL=/opt/intel/oneapi
import os
if os.path.isdir(os.environ['ONEAPI_INSTALL']) == False:
print("ERROR! wrong oneAPI installation path")
# !printf '%s\n' $ONEAPI_INSTALL/dnnl/latest/cpu_*
# As you can see, there are four different folders under the oneDNN installation path, and each of those configurations supports different features. This tutorial will use the dpcpp configuration to showcase the verbose log for both CPU and GPU.
# Create a lab folder for this exercise.
# !rm -rf lab;mkdir -p lab
# Install required python packages.
# !pip3 install -r requirements.txt
# Get current platform information for this exercise.
from profiling.profile_utils import PlatformUtils
plat_utils = PlatformUtils()
plat_utils.dump_platform_info()
# ### Step 2: Preparing the samples code
#
# This exercise uses the cnn_inference_f32.cpp example from oneDNN installation path.
#
# The section below will copy the cnn_inference_f32.cpp file into the lab folder.
# This section also copies the required header files and CMake file into the lab folder.
# !cp $ONEAPI_INSTALL/dnnl/latest/cpu_dpcpp_gpu_dpcpp/examples/cnn_inference_f32.cpp lab/
# !cp $ONEAPI_INSTALL/dnnl/latest/cpu_dpcpp_gpu_dpcpp/examples/example_utils.hpp lab/
# !cp $ONEAPI_INSTALL/dnnl/latest/cpu_dpcpp_gpu_dpcpp/examples/example_utils.h lab/
# !cp $ONEAPI_INSTALL/dnnl/latest/cpu_dpcpp_gpu_dpcpp/examples/CMakeLists.txt lab/
# ### Step 3: Build and Run with the oneAPI DPC++ Compiler
# One of the oneDNN configurations supports the oneAPI DPC++ compiler, and it can run on different architectures by using DPC++.
# The following section shows you how to build with DPC++ and run on different architectures.
# #### Script - build.sh
# The script **build.sh** encapsulates the compiler **dpcpp** command and flags that will generate the exectuable.
# To enable use of the DPC++ compiler and the related SYCL runtime, some definitions must be passed as cmake arguments.
# Here are the related cmake arguments for the DPC++ configuration:
#
# -DCMAKE_C_COMPILER=clang -DCMAKE_CXX_COMPILER=dpcpp -DDNNL_CPU_RUNTIME=SYCL -DDNNL_GPU_RUNTIME=SYCL
# %%writefile build.sh
# #!/bin/bash
source $ONEAPI_INSTALL/setvars.sh --force> /dev/null 2>&1
export EXAMPLE_ROOT=./lab/
# mkdir dpcpp
# cd dpcpp
cmake .. -DCMAKE_C_COMPILER=clang -DCMAKE_CXX_COMPILER=dpcpp -DDNNL_CPU_RUNTIME=SYCL -DDNNL_GPU_RUNTIME=SYCL
make cnn-inference-f32-cpp
# Once you achieve an all-clear from your compilation, you execute your program on the DevCloud or a local machine.
#
# #### Script - run.sh
# The script **run.sh** encapsulates the program for submission to the job queue for execution.
# By default, the built program uses CPU as the execution engine, but the user can switch to GPU by specifying the input argument "gpu".
# The user can refer to run.sh below to run cnn-inference-f32-cpp on both CPU and GPU.
# %%writefile run.sh
# #!/bin/bash
source $ONEAPI_INSTALL/setvars.sh --force > /dev/null 2>&1
# echo "########## Executing the run"
# enable verbose log
export DNNL_VERBOSE=0
./dpcpp/out/cnn-inference-f32-cpp cpu
./dpcpp/out/cnn-inference-f32-cpp gpu
# echo "########## Done with the run"
#
# #### OPTIONAL : replace $ONEAPI_INSTALL with set value in both build.sh and run.sh
# > NOTE : this step is mandatory if you run the notebook on DevCloud
from profiling.profile_utils import FileUtils
file_utils = FileUtils()
file_utils.replace_string_in_file('build.sh','$ONEAPI_INSTALL', os.environ['ONEAPI_INSTALL'] )
file_utils.replace_string_in_file('run.sh','$ONEAPI_INSTALL', os.environ['ONEAPI_INSTALL'] )
#
# #### Submitting **build.sh** and **run.sh** to the job queue
# Now we can submit **build.sh** and **run.sh** to the job queue.
# ##### NOTE - it is possible to execute any of the build and run commands in local environments.
# To enable users to run their scripts either on the Intel DevCloud or in local environments, this and subsequent training checks for the existence of the job submission command **qsub**. If the check fails, it is assumed that build/run will be local.
# ! rm -rf dpcpp;chmod 755 q; chmod 755 build.sh; chmod 755 run.sh;if [ -x "$(command -v qsub)" ]; then ./q build.sh; ./q run.sh; else ./build.sh; ./run.sh; fi
#
# ## Enable Verbose Mode
# ***
# In this section, we enable verbose mode on the built sample from the previous section, and users can see different results from CPU and GPU.
# Refer to the [link](https://oneapi-src.github.io/oneDNN/dev_guide_verbose.html) for detailed verbose mode information
# When the feature is enabled at build-time, you can use the DNNL_VERBOSE environment variable to turn verbose mode on and control the level of verbosity.
#
# |Environment variable|Value|Description|
# |:-----|:----|:-----|
# |DNNL_VERBOSE| 0 |no verbose output (default)|
# ||1|primitive information at execution|
# ||2|primitive information at creation and execution|
#
# prepare run.sh and enable DNNL_VERBOSE as 2
# +
# %%writefile run.sh
# #!/bin/bash
source $ONEAPI_INSTALL/setvars.sh --force > /dev/null 2>&1
# echo "########## Executing the run"
# enable verbose log
export DNNL_VERBOSE=2
./dpcpp/out/cnn-inference-f32-cpp cpu >>log_cpu_f32_vb2.csv 2>&1
./dpcpp/out/cnn-inference-f32-cpp gpu >>log_gpu_f32_vb2.csv 2>&1
# echo "########## Done with the run"
# -
#
# #### OPTIONAL : replace $ONEAPI_INSTALL with set value in run.sh
# > NOTE : this step is mandatory if you run the notebook on DevCloud
from profiling.profile_utils import FileUtils
file_utils = FileUtils()
file_utils.replace_string_in_file('run.sh','$ONEAPI_INSTALL', os.environ['ONEAPI_INSTALL'] )
#
# #### Submitting **run.sh** to the job queue
# Now we can submit **run.sh** to the job queue.
# ##### NOTE - it is possible to execute any of the build and run commands in local environments.
# To enable users to run their scripts either on the Intel DevCloud or in local environments, this and subsequent training checks for the existence of the job submission command **qsub**. If the check fails, it is assumed that build/run will be local.
# ! chmod 755 run.sh;if [ -x "$(command -v qsub)" ]; then ./q run.sh; else ./run.sh; fi
# ## Analyze Verbose Logs
# ***
#
# ### Step 1: List out all oneDNN verbose logs
# users should see two verbose logs listed in the table below.
#
# |Log File Name | Description |
# |:-----|:----|
# |log_cpu_f32_vb2.csv| log for cpu run |
# |log_cpu_f32_vb2.csv| log for gpu run|
# +
import os
filenames= os.listdir (".")
result = []
keyword = ".csv"
for filename in filenames:
#if os.path.isdir(os.path.join(os.path.abspath("."), filename)):
if filename.find(keyword) != -1:
result.append(filename)
result.sort()
index =0
for folder in result:
print(" %d : %s " %(index, folder))
index+=1
# -
# ### Step 2: Pick a verbose log by putting its index value below
# Users can pick either cpu or gpu log for analysis.
# Once users finish Step 2 to Step 8 for one log file, they can go back to step 2 and select another log file for analysis.
FdIndex=0
# #### OPTIONAL: browse the content of selected verbose log.
logfile = result[FdIndex]
with open(logfile) as f:
log = f.read()
print(log)
# ### Step 3: Parse verbose log and get the data back
logfile = result[FdIndex]
print(logfile)
from profiling.profile_utils import oneDNNUtils, oneDNNLog
onednn = oneDNNUtils()
log1 = oneDNNLog()
log1.load_log(logfile)
data = log1.data
exec_data = log1.exec_data
# ### Step 4: Time breakdown for exec type
# The exec type includes exec and create.
#
# |exec type | Description |
# |:-----|:----|
# |exec | Time for primitives exection. Better to spend most of time on primitives execution. |
# |create| Time for primitives creation. Primitives creation happens once. Better to spend less time on primitive creation. |
onednn.breakdown(data,"exec","time")
# ### Step 5: Time breakdown for primitives type
# The primitives type includes convolution, reorder, sum, etc.
# For this simple convolution net example, convolution and inner product primitives are expected to spend most of time.
# However, the exact time percentage of different primitivies may vary among different architectures.
# Users can easily identify top hotpots of primitives executions with this time breakdown.
onednn.breakdown(exec_data,"type","time")
# ### Step 6: Time breakdown for JIT kernel type
# oneDNN uses just-in-time compilation (JIT) to generate optimal code for some functions based on input parameters and instruction set supported by the system.
# Therefore, users can see different JIT kernel type among different CPU and GPU architectures.
# For example, users can see avx_core_vnni JIT kernel if the workload uses VNNI instruction on Cascake Lake platform.
# Users can also see different OCL kernels among different Intel GPU generations.
# Moreover, users can identify the top hotspots of JIT kernel executions with this time breakdown.
#
onednn.breakdown(exec_data,"jit","time")
# ### Step 7: Time breakdown for algorithm type
# oneDNN also supports different algorithms.
# Users can identify the top hotspots of algorthm executions with this time breakdown.
onednn.breakdown(exec_data,"alg","time")
# ### Step 8: Time breakdown for architecture type
# The supported architectures include CPU and GPU.
# For this simple net sample, we don't split computation among CPU and GPU,
# so users should see either 100% CPU time or 100% GPU time.
onednn.breakdown(data,"arch","time")
# ***
# ## Inspecting JIT Code
#
# In this section, we dump JIT code on the built sample from the previous section, and users can see different results from CPU.
# Refer to the [link](https://oneapi-src.github.io/oneDNN/dev_guide_inspecting_jit.html) for detailed JIT Dump information
# When the feature is enabled at build-time, you can use the DNNL_JIT_DUMP environment variable to inspect JIT code.
#
# |Environment variable|Value|Description|
# |:-----|:----|:-----|
# |DNNL_JIT_DUMP | 0 |JIT dump is disabled (default)|
# ||any other value|JIT dump is enabled|
#
#
# #### Step 1: Prepare run.sh and enable DNNL_JIT_DUMP as 1
# %%writefile run.sh
# #!/bin/bash
source $ONEAPI_INSTALL/setvars.sh --force > /dev/null 2>&1
# echo "########## Executing the run"
# disable verbose log
export DNNL_VERBOSE=0
# enable JIT Dump
export DNNL_JIT_DUMP=1
./dpcpp/out/cnn-inference-f32-cpp cpu
# echo "########## Done with the run"
#
# #### OPTIONAL : replace $ONEAPI_INSTALL with set value in run.sh
# > NOTE : this step is mandatory if you run the notebook on DevCloud
from profiling.profile_utils import FileUtils
file_utils = FileUtils()
file_utils.replace_string_in_file('run.sh','$ONEAPI_INSTALL', os.environ['ONEAPI_INSTALL'] )
#
# #### Step 2: Submitting **run.sh** to the job queue
# Now we can submit **run.sh** to the job queue.
# ! chmod 755 run.sh;if [ -x "$(command -v qsub)" ]; then ./q run.sh; else ./run.sh; fi
# #### Step 3: Move all JIT Dump files into the jitdump folder
# !mkdir jitdump;mv *.bin jitdump
# #### Step 4: List out all oneDNN JIT Dump files
# +
import os
filenames= os.listdir ("jitdump")
result = []
keyword = ".bin"
for filename in filenames:
#if os.path.isdir(os.path.join(os.path.abspath("."), filename)):
if filename.find(keyword) != -1:
result.append(filename)
result.sort()
index =0
for folder in result:
print(" %d : %s " %(index, folder))
index+=1
# -
# #### Step 5: Pick a JIT Dump file by putting its index value below
FdIndex=0
# #### Step 6: export JIT Dump file to environment variable JITFILE
logfile = result[FdIndex]
os.environ["JITFILE"] = logfile
# #### Step 7: disassembler JIT Dump file to view the code
#
# > NOTE: If the oneDNN sample uses VNNI instruction, users should be able to see "vpdpbusd" instruction from the JIT Dump file
#
# > NOTE: If the oneDNN sample uses BF16 instruction, users should see usage of vdpbf16ps or vcvtne2ps2bf16 in the JIT dump file.
#
# > NOTE: For disassembler vdpbf16ps and vcvtne2ps2bf16 instructions, users must use objdump with v2.34 or above.
# !objdump -D -b binary -mi386:x86-64 jitdump/$JITFILE
# ***
# # Summary
# In this lab the developer learned the following:
# * how to use Verbose Mode to profile different oneDNN samples on CPU and GPU
# * how to inspect JIT Dump to profile oneDNN samples on CPU
#
|
Libraries/oneDNN/tutorials/tutorial_verbose_jitdump.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# +
# Using the pcap https://mrncciew.files.wordpress.com/2014/08/wpa2-psk-final.zip for testing
from binascii import a2b_hex, b2a_hex, a2b_qp
from pbkdf2 import PBKDF2
import hmac
from hashlib import sha1
import struct
from Crypto.Cipher import AES
# -
def PRF512(key,A,B):
blen = 64
R = ''
for i in range(0,4):
hmacsha1 = hmac.new(key,A+B+chr(i),sha1)
R = R+hmacsha1.digest()
return R[:blen]
def frame_type(packet):
header_two_bytes = struct.unpack("h", (packet[0:2]))[0]
fc_type = bin(header_two_bytes)[-8:][4:6]
if fc_type == "10":
return "data"
else:
return None
# +
def compute_pairwise_master_key(preshared_key, ssid):
return PBKDF2(preshared_key, ssid, 4096).read(32)
def compute_message_integrity_check(pairwise_transient_key,data):
return hmac.new(pairwise_transient_key[0:16],data,sha1).digest()[0:16]
def compute_pairwise_transient_key(pairwise_master_key, A, B):
return PRF512(pairwise_master_key, A, B)
# +
ssid = "TEST1"
preshared_key = "Cisco123Cisco123"
# From message 2 in handshake QoS data for 802.11, packet 95 in example pcap
message_2_data = "88012c0064a0e7af474e001bd458e61a64a0e7af474e10000600aaaa03000000888e0203007502010a00100000000000000000605e85a79cfafdb0eaa050683f97be1b66def7bc652057316871c273c5ae477f00000000000000000000000000000000000000000000000000000000000000009189cdf188548e73cd37d57852660588001630140100000fac040100000fac040100000fac022800"
message_2_data = a2b_hex(message_2_data)
message_intgrity_code = message_2_data[115:131]
data = message_2_data[34:115] + "\x00"*16 + message_2_data[131:]
# +
# authenticator nonce found in message 1 of handshake, packet 93 in example
a_nonce = a2b_hex("126ace64c1a644d27b84e039263b633bc374e3299d7d45e1c42544054805bfe5")
# supplicant nonce found in message 2 of handshake, packet 95 in example
s_nonce = a2b_hex("605e85a79cfafdb0eaa050683f97be1b66def7bc652057316871c273c5ae477f")
mac_access_point = a2b_hex("64a0e7af474e")
mac_client = a2b_hex("001bd458e61a")
A = "Pairwise key expansion" + '\x00'
B = min(mac_access_point,mac_client)+max(mac_access_point,mac_client)+min(a_nonce,s_nonce)+max(a_nonce,s_nonce)
# -
pairwise_master_key = compute_pairwise_master_key(preshared_key, ssid)
pairwise_transient_key = compute_pairwise_transient_key(pairwise_master_key, A, B)
mic = compute_message_integrity_check(pairwise_transient_key,data)
# See the mic for packet 95
print b2a_hex(mic) == "9189cdf188548e73cd37d57852660588"
key_confirmation_key = pairwise_transient_key[0:16]
key_encryption_key = pairwise_transient_key[16:16*2]
temporal_key = pairwise_transient_key[16 * 2:(16 * 2) + 16]
mic_authenticator_tx = pairwise_transient_key[16 * 3:(16 * 3) + 8]
mic_authenticator_rx = pairwise_transient_key[(16 * 3) + 8:(16 * 3) + 8 + 8]
packet_103_encrypted_total_packet = "88512c0064a0e7af474e001bd458e61a64a0e7af474e1000000001000020000000003d833a329d1d0ccc0372742ab1031986151713a0c160a6035752c214ce42bebdaefad728edf8a728e013fb3939046e0823753aa4339f953c197d49e10a1e1aa2d19175bcf61e81867af5c8024a3d29ebce166e4401ea6994"
packet_103_encrypted_total_packet = a2b_hex(packet_103_encrypted_total_packet)
packet_103_encrypted_data = packet_103_encrypted_total_packet[34:34+84]
ccmp_header = packet_103_encrypted_total_packet[26:26 + 8]
ieee80211_header = packet_103_encrypted_total_packet[0:26]
source_address = packet_103_encrypted_total_packet[10:16]
# +
PN5 = ccmp_header[7]
PN4 = ccmp_header[6]
PN3 = ccmp_header[5]
PN2 = ccmp_header[4]
PN1 = ccmp_header[1]
PN0 = ccmp_header[0]
last_part_of_nonce = PN5 + PN4 + PN3 + PN2 + PN1 + PN0
flag = a2b_hex('01')
qos_priorty = a2b_hex('00')
# -
nonce_ = qos_priorty + source_address + last_part_of_nonce
IV = flag + nonce_
class WPA2Counter(object):
def __init__(self, secret):
self.secret = secret
self.current = 1
def counter(self):
count = a2b_hex(struct.pack('>h', self.current).encode('hex'))
i = self.secret + count
self.current += 1
return i
counter = WPA2Counter(IV)
crypto = AES.new(temporal_key, AES.MODE_CTR, counter=counter.counter)
test = packet_103_encrypted_data[0:-8]
crypto.decrypt(test).encode('hex')
|
80211_Crypto.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # One run full walkthrough
# * Do the full walkthrough on the large data set
# * Refactor the source code and bring it to individual scripts
# * Ensure a full run with one click
# + [markdown] heading_collapsed=true
# ## 1 Update the data
# + code_folding=[0] heading_collapsed=true hidden=true
# %load /media/sem/HDD/Home_Programming/Git/ads_covid-19-sem/src/data/get_data.py
import subprocess
import os
import pandas as pd
import numpy as np
from datetime import datetime
import requests
import json
def get_johns_hopkins():
''' Get data by a git pull request, the source code has to be pulled first
Result is stored in the predifined csv structure
'''
git_pull = subprocess.Popen( "/usr/bin/git pull" ,
cwd = os.path.dirname( '/media/sem/HDD/Home_Programming/Git/ads_covid-19-sem/data/raw/COVID-19/' ),
shell = True,
stdout = subprocess.PIPE,
stderr = subprocess.PIPE )
(out, error) = git_pull.communicate()
print("Error : " + str(error))
print("out : " + str(out))
def get_current_data_germany():
''' Get current data from germany, attention API endpoint not too stable
Result data frame is stored as pd.DataFrame
'''
# 16 states
#data=requests.get('https://services7.arcgis.com/mOBPykOjAyBO2ZKk/arcgis/rest/services/Coronaf%C3%A4lle_in_den_Bundesl%C3%A4ndern/FeatureServer/0/query?where=1%3D1&outFields=*&outSR=4326&f=json')
# 400 regions / Landkreise
data=requests.get('https://services7.arcgis.com/mOBPykOjAyBO2ZKk/arcgis/rest/services/RKI_Landkreisdaten/FeatureServer/0/query?where=1%3D1&outFields=*&outSR=4326&f=json')
json_object=json.loads(data.content)
full_list=[]
for pos,each_dict in enumerate (json_object['features'][:]):
full_list.append(each_dict['attributes'])
pd_full_list=pd.DataFrame(full_list)
pd_full_list.to_csv('/media/sem/HDD/Home_Programming/Git/ads_covid-19-sem/data/raw/NPGEO/GER_state_data.csv',sep=';')
print(' Number of regions rows: '+str(pd_full_list.shape[0]))
if __name__ == '__main__':
get_johns_hopkins()
get_current_data_germany()
# + [markdown] heading_collapsed=true
# ## 2 Process Pipeline
# + code_folding=[0] hidden=true
# %load /media/sem/HDD/Home_Programming/Git/ads_covid-19-sem/src/data/process_JH_data.py
import pandas as pd
import numpy as np
from datetime import datetime
def store_relational_JH_data():
''' Transformes the COVID data in a relational data set
'''
data_path='/media/sem/HDD/Home_Programming/Git/ads_covid-19-sem/data/raw/COVID-19/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_confirmed_global.csv'
pd_raw=pd.read_csv(data_path)
pd_data_base=pd_raw.rename(columns={'Country/Region':'country',
'Province/State':'state'})
pd_data_base['state']=pd_data_base['state'].fillna('no')
pd_data_base=pd_data_base.drop(['Lat','Long'],axis=1)
pd_relational_model=pd_data_base.set_index(['state','country']) .T .stack(level=[0,1]) .reset_index() .rename(columns={'level_0':'date',
0:'confirmed'},
)
pd_relational_model['date']=pd_relational_model.date.astype('datetime64[ns]')
pd_relational_model.to_csv('/media/sem/HDD/Home_Programming/Git/ads_covid-19-sem/data/processed/COVID_relational_confirmed.csv',sep=';',index=False)
print(' Number of rows stored: '+str(pd_relational_model.shape[0]))
if __name__ == '__main__':
store_relational_JH_data()
# -
# ## 3 Filter and Doubling Rate Calculation
# + code_folding=[0]
# %load /media/sem/HDD/Home_Programming/Git/ads_covid-19-sem/src/features/build_features.py
import numpy as np
from sklearn import linear_model
reg = linear_model.LinearRegression(fit_intercept=True)
import pandas as pd
from scipy import signal
def get_doubling_time_via_regression(in_array):
''' Use a linear regression to approximate the doubling rate
Parameters:
----------
in_array : pandas.series
Returns:
----------
Doubling rate: double
'''
y = np.array(in_array)
X = np.arange(-1,2).reshape(-1, 1)
assert len(in_array)==3
reg.fit(X,y)
intercept=reg.intercept_
slope=reg.coef_
return intercept/slope
def savgol_filter(df_input,column='confirmed',window=5):
''' Savgol Filter which can be used in groupby apply function (data structure kept)
parameters:
----------
df_input : pandas.series
column : str
window : int
used data points to calculate the filter result
Returns:
----------
df_result: pd.DataFrame
the index of the df_input has to be preserved in result
'''
degree=1
df_result=df_input
filter_in=df_input[column].fillna(0) # attention with the neutral element here
result=signal.savgol_filter(np.array(filter_in),
window, # window size used for filtering
1)
df_result[column+'_filtered']=result
return df_result
def rolling_reg(df_input,col='confirmed'):
''' Rolling Regression to approximate the doubling time'
Parameters:
----------
df_input: pd.DataFrame
col: str
defines the used column
Returns:
----------
result: pd.DataFrame
'''
days_back=3
result=df_input[col].rolling(
window=days_back,
min_periods=days_back).apply(get_doubling_time_via_regression,raw=False)
return result
def calc_filtered_data(df_input,filter_on='confirmed'):
''' Calculate savgol filter and return merged data frame
Parameters:
----------
df_input: pd.DataFrame
filter_on: str
defines the used column
Returns:
----------
df_output: pd.DataFrame
the result will be joined as a new column on the input data frame
'''
must_contain=set(['state','country',filter_on])
assert must_contain.issubset(set(df_input.columns)), ' Erro in calc_filtered_data not all columns in data frame'
pd_filtered_result=df_input[['state','country',filter_on]].groupby(['state','country']).apply(savgol_filter).reset_index()
df_output=pd.merge(df_input,pd_filtered_result[['index',filter_on+'_filtered']],on=['index'],how='left')
return df_output
def calc_doubling_rate(df_input,filter_on='confirmed'):
''' Calculate approximated doubling rate and return merged data frame
Parameters:
----------
df_input: pd.DataFrame
filter_on: str
defines the used column
Returns:
----------
df_output: pd.DataFrame
the result will be joined as a new column on the input data frame
'''
must_contain=set(['state','country',filter_on])
assert must_contain.issubset(set(df_input.columns)), ' Erro in calc_filtered_data not all columns in data frame'
pd_DR_result= df_input.groupby(['state','country']).apply(rolling_reg,filter_on).reset_index()
pd_DR_result=pd_DR_result.rename(columns={filter_on:filter_on+'_DR',
'level_2':'index'})
df_output=pd.merge(df_input,pd_DR_result[['index',filter_on+'_DR']],on=['index'],how='left')
return df_output
if __name__ == '__main__':
test_data_reg=np.array([2,4,6])
result=get_doubling_time_via_regression(test_data_reg)
print('the test slope is: '+str(result))
pd_JH_data=pd.read_csv('../data/processed/COVID_relational_confirmed.csv',sep=';',parse_dates=[0])
pd_JH_data=pd_JH_data.sort_values('date',ascending=True).reset_index().copy()
pd_result_larg=calc_filtered_data(pd_JH_data)
pd_result_larg=calc_doubling_rate(pd_result_larg)
pd_result_larg=calc_doubling_rate(pd_result_larg,'confirmed_filtered')
print(pd_result_larg.head())
# -
# ## 4 Visual Board
# + code_folding=[0]
# %load /media/sem/HDD/Home_Programming/Git/ads_covid-19-sem/src/visualization/visualize-Copy1.py
import pandas as pd
import numpy as np
import dash
dash.__version__
import dash_core_components as dcc
import dash_html_components as html
from dash.dependencies import Input, Output,State
import plotly.graph_objects as go
import os
print(os.getcwd())
df_input_large=pd.read_csv('../data/processed/COVID_final_set.csv',sep=';')
fig = go.Figure()
app = dash.Dash()
app.layout = html.Div([
dcc.Markdown('''
# Applied Data Science on COVID-19 data
Goal of the project is to teach data science by applying a cross industry standard process,
it covers the full walkthrough of: automated data gathering, data transformations,
filtering and machine learning to approximating the doubling time, and
(static) deployment of responsive dashboard.
'''),
dcc.Markdown('''
## Multi-Select Country for visualization
'''),
dcc.Dropdown(
id='country_drop_down',
options=[ {'label': each,'value':each} for each in df_input_large['country'].unique()],
value=['US', 'Germany','Italy'], # which are pre-selected
multi=True
),
dcc.Markdown('''
## Select Timeline of confirmed COVID-19 cases or the approximated doubling time
'''),
dcc.Dropdown(
id='doubling_time',
options=[
{'label': 'Timeline Confirmed ', 'value': 'confirmed'},
{'label': 'Timeline Confirmed Filtered', 'value': 'confirmed_filtered'},
{'label': 'Timeline Doubling Rate', 'value': 'doubling_rate'},
{'label': 'Timeline Doubling Rate Filtered', 'value': 'doubling_rate_filtered'},
],
value='confirmed',
multi=False
),
dcc.Graph(figure=fig, id='main_window_slope')
])
@app.callback(
Output('main_window_slope', 'figure'),
[Input('country_drop_down', 'value'),
Input('doubling_time', 'value')])
def update_figure(country_list,show_doubling):
if 'doubling_rate' in show_doubling:
my_yaxis={'type':"log",
'title':'Approximated doubling rate over 3 days (larger numbers are better #stayathome)'
}
else:
my_yaxis={'type':"log",
'title':'Confirmed infected people (source johns hopkins csse, log-scale)'
}
traces = []
for each in country_list:
df_plot=df_input_large[df_input_large['country']==each]
if show_doubling=='doubling_rate_filtered':
df_plot=df_plot[['state','country','confirmed','confirmed_filtered','doubling_rate','doubling_rate_filtered','date']].groupby(['country','date']).agg(np.mean).reset_index()
else:
df_plot=df_plot[['state','country','confirmed','confirmed_filtered','doubling_rate','doubling_rate_filtered','date']].groupby(['country','date']).agg(np.sum).reset_index()
#print(show_doubling)
traces.append(dict(x=df_plot.date,
y=df_plot[show_doubling],
mode='markers+lines',
opacity=0.9,
name=each
)
)
return {
'data': traces,
'layout': dict (
width=1280,
height=720,
xaxis={'title':'Timeline',
'tickangle':-45,
'nticks':20,
'tickfont':dict(size=14,color="#7f7f7f"),
},
yaxis=my_yaxis
)
}
if __name__ == '__main__':
app.run_server(debug=True, use_reloader=False)
# -
|
notebooks/Evaluation_Walk_through.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: matan_env
# language: python
# name: matan_env
# ---
# +
import torch
import hydra
from train import train
from dataset_temp import MyDataset
from models.base_model import MyModel
from torch.utils.data import DataLoader
from utils import main_utils, train_utils#, data_loader
from utils.train_logger import TrainLogger
from omegaconf import DictConfig, OmegaConf
import os
import pickle
import h5py
import time
import torch
import torch.nn as nn
from tqdm import tqdm
from utils.types import Scores, Metrics
from utils.train_utils import TrainParams
from utils.train_logger import TrainLogger
from abc import ABCMeta
# from nets.fc import FCNet
import torch
from torch import nn, Tensor
import itertools as it
from torch.nn.utils.rnn import pack_padded_sequence
import torch.nn.init as init
import torch.nn.functional as F
# %matplotlib inline
# %load_ext autoreload
# %autoreload 2
# -
ans = torch.rand(64,20)
print(ans)
zeros = torch.zeros(ans.shape[1])
max_values, predicted_index = ans.max(dim=1, keepdim=True)
for i in range(ans.shape[0]):
ans[i] = torch.where(ans[i]==max_values[i], ans[i], zeros)
print(ans[0])
# +
"""
Example for a simple model
"""
#POOLINGS = {"avg": nn.AvgPool2d, "max": nn.MaxPool2d}
class ResidualBlock(nn.Module):
"""
"""
def __init__(
self,
in_channels: int,
channels: list,
kernel_sizes: list,
batchnorm=False,
dropout=0.0,
activation_type: str = "relu",
activation_params: dict = {},
**kwargs,
):
super().__init__()
assert channels and kernel_sizes
assert len(channels) == len(kernel_sizes)
assert all(map(lambda x: x % 2 == 1, kernel_sizes))
"""if activation_type not in ACTIVATIONS:
raise ValueError("Unsupported activation type")"""
self.main_path, self.shortcut_path = None, None
main_layers = []
shortcut_layers = []
# - extract number of conv layers
N = len(channels)
# - first conv layer
main_layers.append(
nn.Conv2d(
in_channels,
channels[0],
kernel_size= kernel_sizes[0],
padding=(int((kernel_sizes[0]-1)/2),
int((kernel_sizes[0]-1)/2)), bias=True))
if dropout !=0:
main_layers.append(torch.nn.Dropout2d(p=dropout))
if batchnorm == True:
main_layers.append(torch.nn.BatchNorm2d(channels[0], eps=1e-05, momentum=0.1, affine=True, track_running_stats=True))
main_layers.append(nn.ReLU(inplace=True))
#middle layers
for i in range(1,N-1):
main_layers.append(
nn.Conv2d(
channels[i-1],
channels[i],
kernel_size= kernel_sizes[i],
padding=(int((kernel_sizes[i]-1)/2),
int((kernel_sizes[i]-1)/2)), bias=True))
if dropout !=0:
main_layers.append(torch.nn.Dropout2d(p=dropout))
if batchnorm == True:
main_layers.append(torch.nn.BatchNorm2d(channels[i], eps=1e-05, momentum=0.1, affine=True, track_running_stats=True))
if (i%2 == 1):
main_layers.append(nn.ReLU(inplace=True))
if N > 1:
main_layers.append(
nn.Conv2d(
channels[N-2],
channels[N-1],
kernel_size= kernel_sizes[N-1],
padding=(int((kernel_sizes[N-1]-1)/2),
int((kernel_sizes[N-1]-1)/2)), bias=True))
if (in_channels != channels[N-1]):
shortcut_layers.append(nn.Conv2d (in_channels, channels[N-1], kernel_size= 1, bias=False))
self.main_path = nn.Sequential(*main_layers)
self.shortcut_path = nn.Sequential(*shortcut_layers)
def forward(self, x):
out = self.main_path(x)
out = out + self.shortcut_path(x)
relu = torch.nn.ReLU()
out = relu(out)
return out
class ResNetClassifier(nn.Module):
def __init__(
self,
in_size,
channels,
pool_every,
# hidden_dims,
activation_type: str = "relu",
activation_params: dict = {},
pooling_type: str = "max",
pooling_params: dict = {},
batchnorm=False,
dropout=0.0,
**kwargs,
):
"""
See arguments of ConvClassifier & ResidualBlock.
"""
super().__init__()
self.batchnorm = batchnorm
self.dropout = dropout
self.conv_params=dict(kernel_size=3, stride=1, padding=1)
self.in_size = in_size
self.channels = channels
self.pool_every = pool_every
self.activation_type = activation_type
self.activation_params = activation_params
self.pooling_type = pooling_type
self.pooling_params = pooling_params
self.feature_extractor = self._make_feature_extractor()
def _make_feature_extractor(self):
in_channels, in_h, in_w, = tuple(self.in_size)
layers = []
self.output_dim = 2048
# - extract number of conv layers
N = len(self.channels)
#1st layer
temp_in_channels = in_channels
temp_channels = []
temp_kernel_sizes = []
layers.append(nn.Conv2d(3, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3), bias=False))
layers.append(torch.nn.BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True))
layers.append(nn.ReLU(inplace=True))
layers.append(nn.MaxPool2d(kernel_size=3, stride=2, padding=1, dilation=1, ceil_mode=False))
#middle layers
for i in range(1,N):
temp_channels.append(self.channels[i-1])
temp_kernel_sizes.append(3)
if ((i % self.pool_every)==0 and i!=0):
layers.append(
ResidualBlock(
in_channels=temp_in_channels,
channels=temp_channels,
kernel_sizes=temp_kernel_sizes,
batchnorm= self.batchnorm,
dropout= self.dropout,
activation_type= self.activation_type))
temp_in_channels = self.channels[i-1]
temp_channels = []
temp_kernel_sizes = []
#layers.append(nn.AvgPool2d(self.pooling_params['kernel_size']))
temp_channels.append(self.channels[N-1])
temp_kernel_sizes.append(3)
layers.append(ResidualBlock(
in_channels=temp_in_channels,
channels=temp_channels,
kernel_sizes=temp_kernel_sizes,
batchnorm= self.batchnorm,
dropout= self.dropout,
activation_type= self.activation_type))
if ((N % self.pool_every)==0):
# layers.append(nn.AvgPool2d(self.pooling_params['kernel_size']))
layers.append(torch.nn.AdaptiveAvgPool2d(output_size=(1, 1))) ########################################################
layers.append(nn.Linear(1000, self.output_dim, bias=True))
# add to go to 1x1
#layers.append(nn.AvgPool2d(2))
#layers.append(nn.AvgPool2d(15))
seq = nn.Sequential(*layers)
return seq
def forward(self, x):
out = self.feature_extractor(x)
batch_size = out.shape[0]
out = out.view(batch_size,-1,1,1)
#shortcut = self.shortcut_path(x)
#print("shortcut.shape = ", shortcut.shape)
#print("out.shape = ", out.shape)
#out = out + shortcut
#out = out.view(batch_size,-1,1,1)
#relu = torch.nn.ReLU()
#out = relu(out)
return out
class TextProcessor(nn.Module):
def __init__(self, embedding_tokens, embedding_features, lstm_features, drop=0.0):
super(TextProcessor, self).__init__()
self.embedding = nn.Embedding(embedding_tokens, embedding_features, padding_idx=0)
self.drop = nn.Dropout(drop)
self.tanh = nn.Tanh()
self.lstm = nn.LSTM(input_size=embedding_features,
hidden_size=lstm_features,
num_layers=1)
self.features = lstm_features
self._init_lstm(self.lstm.weight_ih_l0)
self._init_lstm(self.lstm.weight_hh_l0)
self.lstm.bias_ih_l0.data.zero_()
self.lstm.bias_hh_l0.data.zero_()
init.xavier_uniform(self.embedding.weight)
def _init_lstm(self, weight):
for w in weight.chunk(4, 0):
init.xavier_uniform(w)
def forward(self, ques, q_len):
embedded = self.embedding(ques)
tanhed = self.tanh(self.drop(embedded))
packed = pack_padded_sequence(tanhed, q_len, batch_first=True, enforce_sorted=False)
_, (_, c) = self.lstm(packed)
return c.squeeze(0)
class Attention(nn.Module):
def __init__(self, v_features, q_features, mid_features, glimpses, drop=0.0):
super(Attention, self).__init__()
self.v_conv = nn.Conv2d(v_features, mid_features, 1, bias=False) # let self.lin take care of bias
self.q_lin = nn.Linear(q_features, mid_features)
self.x_conv = nn.Conv2d(mid_features, glimpses, 1)
self.drop = nn.Dropout(drop)
self.relu = nn.ReLU(inplace=True)
def forward(self, img, ques):
ques = self.q_lin(self.drop(ques))
img = self.v_conv(self.drop(img))
ques = tile_2d_over_nd(ques, img)
x = self.relu(img + ques)
x = self.x_conv(self.drop(x))
return x
def apply_attention(input, attention):
""" Apply any number of attention maps over the input. """
n, c = input.size()[:2]
glimpses = attention.size(1)
# flatten the spatial dims into the third dim, since we don't need to care about how they are arranged
input = input.view(n, 1, c, -1) # [n, 1, c, s]
attention = attention.view(n, glimpses, -1)
attention = F.softmax(attention, dim=-1).unsqueeze(2) # [n, g, 1, s]
weighted = attention * input # [n, g, v, s]
weighted_mean = weighted.sum(dim=-1) # [n, g, v]
return weighted_mean.view(n, -1)
def tile_2d_over_nd(feature_vector, feature_map):
""" Repeat the same feature vector over all spatial positions of a given feature map.
The feature vector should have the same batch size and number of features as the feature map.
"""
n, c = feature_vector.size()
spatial_size = feature_map.dim() - 2
tiled = feature_vector.view(n, c, *([1] * spatial_size)).expand_as(feature_map)
return tiled
class ImageNet(nn.Module):
def __init__(self, output_dim):
super(ImageNet, self).__init__()
from torchvision import models
self.model = models.resnet34(pretrained=False)
self.fc = nn.Linear(1000, output_dim, bias=True)
def forward(self, image_tensor):
x = self.model(image_tensor)
x = self.fc(x)
return F.normalize(x, dim=1, p=2)
class MyModel(nn.Module, metaclass=ABCMeta):
"""
Example for a simple model
"""
#def __init__(self,):# input_dim: int = 50, num_hid: int = 256, output_dim: int = 2, dropout: float = 0.2):
def __init__(
self, image_in_size=((3,224,224)), img_encoder_out_classes=1024, img_encoder_channels=[32, 128, 512, 1024],
img_encoder_batchnorm=True, img_encoder_dropout=0.5, text_embedding_tokens=15193, text_embedding_features=100,
text_lstm_features=512, text_dropout=0.5, attention_mid_features=128, attention_glimpses=2, attention_dropout=0.5,
classifier_dropout=0.5, classifier_mid_features=128,classifier_out_classes=2410
):
super(MyModel, self).__init__()
self.image_in_size=image_in_size
self.img_encoder_out_classes=img_encoder_out_classes
self.img_encoder_channels=img_encoder_channels
self.img_encoder_batchnorm=img_encoder_batchnorm
self.img_encoder_dropout=img_encoder_dropout
self.text_embedding_tokens=text_embedding_tokens
self.text_embedding_features=text_embedding_features
self.text_lstm_features=text_lstm_features
self.text_dropout=text_dropout
self.attention_mid_features=attention_mid_features
self.attention_glimpses=attention_glimpses
self.attention_dropout=attention_dropout
self.classifier_dropout=classifier_dropout
self.classifier_mid_features=classifier_mid_features
self.classifier_out_classes=classifier_out_classes
self.img_encoder = ResNetClassifier(
in_size=image_in_size,
channels=img_encoder_channels,
pool_every=8,
activation_type='relu',
activation_params=dict(),
pooling_type='avg',
pooling_params=dict(kernel_size=3),
batchnorm=img_encoder_batchnorm,
dropout=img_encoder_dropout,
)
self.text = TextProcessor(
embedding_tokens=text_embedding_tokens,
embedding_features=text_embedding_features, #300,
lstm_features=text_lstm_features,
drop=text_dropout,
)
self.attention = Attention(
v_features=img_encoder_out_classes,#2048,
q_features=text_lstm_features,
mid_features=attention_mid_features,
glimpses=attention_glimpses,
drop=attention_dropout,
)
self.classifier = nn.Sequential(
nn.Dropout(classifier_dropout),
nn.Linear(2 * img_encoder_out_classes + text_lstm_features, classifier_mid_features), #(2*2048+1024,256)
nn.ReLU(),
nn.Dropout(classifier_dropout),
nn.Linear(classifier_mid_features, classifier_out_classes),
)
# self.img_encoder = ConvClassifier(**test_params)
#self.IP = ImageNet(2048)
def forward(self, x) -> Tensor:
temp_img = x[0]
batch_size = temp_img.shape[0]
#img = self.img_encoder(temp_img)
img = self.IP(temp_img)
img = img.view((batch_size, self.img_encoder_out_classes, 1, 1))
print("img.shape = ",img.shape)
ques = x[1]
q_len = x[2]
ques = self.text(ques, list(q_len.data))
a = self.attention(img, ques)
img = apply_attention(img, a)
combined = torch.cat([img, ques], dim=1)
answer = self.classifier(combined)
#answer = self.softmax(combined)
return answer
# +
# main:
# experiment_name_prefix: my_exp
# seed: 1
# num_workers: 6
# parallel: True
# gpus_to_use: 0,1
# trains: False
# paths:
# train: 'data/train.pkl'
# validation: 'data/validation.pkl'
# logs: 'logs/'
# train_images: '../../../datashare/train2014'
# train_qeustions: '../../../datashare/v2_OpenEnded_mscoco_train2014_questions.json'
# train_answers: '../../../datashare/v2_mscoco_train2014_annotations.json'
# val_images: '../../../datashare/val2014'
# val_qeustions: '../../../datashare/v2_OpenEnded_mscoco_val2014_questions.json'
# val_answers: '../../../datashare/v2_mscoco_val2014_annotations.json'
num_epochs = 50
grad_clip = 0.0
dropout = 0.2
num_hid = 20
batch_size = 64
save_model = True
img_encoder_out_classes = 2048
img_encoder_batchnorm = True
img_encoder_dropout = 0
text_embedding_tokens = 15193
text_embedding_features = 300
text_lstm_features = 1024
text_dropout = 0.4
attention_mid_features = 512
attention_glimpses = 2
attention_dropout = 0.5
classifier_dropout = 0.5
classifier_mid_features = 512
classifier_out_classes = 2410
# lr:
# lr_value: 5e-4
# lr_decay: 5
# lr_gamma: 0.1
# lr_step_size: 100000
# -
# Init model
image_in_size_input = ((3,224,224))
img_encoder_channels_input = [64, 64, 64, 64, 64, 64, 64, 64,
128, 128, 128, 128, 128, 128, 128, 128,
256, 256, 256, 256, 256, 256, 256, 256, 256, 256, 256,
512, 512, 512, 512, 512]#, 1024]
model = MyModel(image_in_size=image_in_size_input,
img_encoder_out_classes=img_encoder_out_classes,
img_encoder_channels=img_encoder_channels_input,
img_encoder_batchnorm=img_encoder_batchnorm,
img_encoder_dropout=img_encoder_dropout,
text_embedding_tokens=text_embedding_tokens,
text_embedding_features=text_embedding_features,
text_lstm_features=text_lstm_features,
text_dropout=text_dropout,
attention_mid_features=attention_mid_features,
attention_glimpses=attention_glimpses,
attention_dropout=attention_dropout,
classifier_dropout=classifier_dropout,
classifier_mid_features=classifier_mid_features,
classifier_out_classes=classifier_out_classes
)
print(model.size)
(IP): ImageNet(
(model): ResNet(
(conv1): Conv2d(3, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3), bias=False)
(bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(maxpool): MaxPool2d(kernel_size=3, stride=2, padding=1, dilation=1, ceil_mode=False)
(layer1): Sequential(
(0): BasicBlock(
(conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(1): BasicBlock(
(conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(2): BasicBlock(
(conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(layer2): Sequential(
(0): BasicBlock(
(conv1): Conv2d(64, 128, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(downsample): Sequential(
(0): Conv2d(64, 128, kernel_size=(1, 1), stride=(2, 2), bias=False)
(1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(1): BasicBlock(
(conv1): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(2): BasicBlock(
(conv1): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(3): BasicBlock(
(conv1): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(layer3): Sequential(
(0): BasicBlock(
(conv1): Conv2d(128, 256, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(downsample): Sequential(
(0): Conv2d(128, 256, kernel_size=(1, 1), stride=(2, 2), bias=False)
(1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(1): BasicBlock(
(conv1): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(2): BasicBlock(
(conv1): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(3): BasicBlock(
(conv1): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(4): BasicBlock(
(conv1): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(5): BasicBlock(
(conv1): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(layer4): Sequential(
(0): BasicBlock(
(conv1): Conv2d(256, 512, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(downsample): Sequential(
(0): Conv2d(256, 512, kernel_size=(1, 1), stride=(2, 2), bias=False)
(1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(1): BasicBlock(
(conv1): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(2): BasicBlock(
(conv1): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(avgpool): AdaptiveAvgPool2d(output_size=(1, 1))
(fc): Linear(in_features=512, out_features=1000, bias=True)
)
with open("../data/trainval_ans2label.pkl", "rb") as f:
unpickler = pickle.Unpickler(f)
# if file is not empty scores will be equal
# to the value unpickled
dict_answers = unpickler.load()
number_of_answers_per_question = len(dict_answers)
number_of_answers_per_question
import torch
temp = torch.ones(64,1073)
temp
print(matan.shape)
print(temp.shape)
matan = temp.sum(dim=1)
for i in range(len(matan)):
temp[i] = temp[i]/matan[i]
temp
|
.ipynb_checkpoints/playground-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Matplotlib
# Matplotlib is a Matplotlib is an amazing visualization library in Python for 2D plots of arrays. Matplotlib is a multi-platform data visualization library built on NumPy arrays and designed to work with the broader SciPy stack. It was introduced by <NAME> in the year 2002.
#
# One of the greatest benefits of visualization is that it allows us visual access to huge amounts of data in easily digestible visuals. Matplotlib consists of several plots like line, bar, scatter, histogram etc.
#
# comprehensive library for creating static, animated, and interactive visualizations in Python.
#
# # Importing Matplotlib
import matplotlib.pyplot as plt
# # Basic plots in Matplotlib :
#
# Matplotlib comes with a wide variety of plots. Plots helps to understand trends, patterns, and to make correlations. They’re typically instruments for reasoning about quantitative information. Some of the sample plots are covered here.
#
# ## Line plot
x=[0,1,2,3,4]
y=[0,2,4,6,8]
#plt.plot(x,y,label='2x',color='red',linewidth=2,linestyle='-',marker='o',markersize=10,markeredgecolor='blue')
plt.plot(x,y,'bo-',label='2x',linewidth=2)#,markeredgecolor='blue')
plt.title('My First Graph',fontdict={'fontname':'Comic Sans MS','fontsize':20})
plt.xlabel('X-Axis',fontdict={'fontname':'Arial','fontsize':10}) #Naming x axis
plt.ylabel('Y-Axis',fontdict={'fontname':'Arial','fontsize':10}) #Naming y axis
#plt.xticks([0,1,2,3,4,5]) #Scale of x axis
#plt.yticks([0,2,4,6,8,10]) #Scale of y axis
import numpy as np
x2=np.arange(0,4,0.5)
plt.plot(x2,x2**2,'ro-',label='x^2')
plt.legend() #To show the label
#plt.grid(True) #to apply grid
plt.show()
# ## Bar plot
labels=['A','B','C']
values=[1,4,2]
bars=plt.bar(labels,values)
#To get some pattern
bars[0].set_hatch('/')
bars[1].set_hatch('o')
bars[2].set_hatch('*')
plt.show()
# ## Histogram
# +
# Y-axis values
y = [10, 5, 8, 4, 2]
# Function to plot histogram
plt.hist(y)
# Function to show the plot
plt.show()
# -
# ## Scatter Plot
# +
# x-axis values
x = [5, 2, 9, 4, 7, 4, 3, 6, 7]
# Y-axis values
y = [10, 5, 8, 4, 2, 4, 6, 2, 9]
# Function to plot scatter
plt.scatter(x, y)
# function to show the plot
plt.show()
# -
# ## Pie Chart
#
label=['C++','Java','Python']
values=[25,35,40]
plt.pie(values,labels=label)
plt.show()
# # 3D Plotting with Matplotlib
# We will be creating an empty canvas at first. After that, we will be defining the axes of our 3D plot where we define that the projection of the plot will be in “3D” format. This helps us to create the 3D empty axes figure in the canvas. After this, if we show the plot using plt.show()
# +
# importing numpy package from
# python library
import numpy as np
# importing matplotlib.pyplot package from
# python
import matplotlib.pyplot as plt
# Creating an empty figure
# or plot
fig = plt.figure()
# Defining the axes as a
# 3D axes so that we can plot 3D
# data into it.
ax = plt.axes(projection="3d")
# Showing the above plot
plt.show()
# -
# # Plotting 3D graph
# We will be taking a simple curve in our 3D plot. Along with that, we will be plotting a range of points that have X-coordinate, Y-coordinate as well as Z-coordinate.
# +
# importing numpy package
import numpy as np
# importing matplotlib package
import matplotlib.pyplot as plt
# importing mplot3d from
# mpl_toolkits
from mpl_toolkits import mplot3d
# creating an empty canvas
fig = plt.figure()
# defining the axes with the projection
# as 3D so as to plot 3D graphs
ax = plt.axes(projection="3d")
# creating a wide range of points x,y,z
x=[0,1,2,3,4,5,6]
y=[0,1,4,9,16,25,36]
z=[0,1,4,9,16,25,36]
# plotting a 3D line graph with X-coordinate,
# Y-coordinate and Z-coordinate respectvely
ax.plot3D(x, y, z, 'red')
# plotting a scatter plot with X-coordinate,
# Y-coordinate and Z-coordinate respectvely
# and defining the points color as cividis
# and defining c as z which basically is a
# defination of 2D array in which rows are RGB
#or RGBA
ax.scatter3D(x, y, z, c=z, cmap='cividis');
# Showing the above plot
plt.show()
# -
# # 3D plotting using figure.gca()
# We will be creating a sine curve and a cosine curve with the values of x and y ranging from -5 to 5 with a gap of 1
# +
# importing matplotlib.pyplot from
# python
import matplotlib.pyplot as plt
# importing numpy package from
# python
import numpy as np
# creating a range of values for
# x,y,x1,y1 from -5 to 5 with
# a space of 1 between the elements
x = np.arange(-5,5,1)
y = np.arange(-5,5,1)
# creating a range of values for
# x,y,x1,y1 from -5 to 5 with
# a space of 0.6 between the elements
x1= np.arange(-5,5,0.6)
y1= np.arange(-5,5,0.6)
# Creating a mesh grid with x ,y and x1,
# y1 which creates an n-dimentional
# array
x, y = np.meshgrid(x, y)
x1,y1= np.meshgrid(x1,y1)
# Creating a sine function with the
# range of values from the meshgrid
z = np.sin(x * np.pi/2 )
# Creating a cosine function with the
# range of values from the meshgrid
z1= np.cos(x1* np.pi/2)
# Creating an empty figure for
# 3D plotting
fig = plt.figure()
# using fig.gca, we are creating a 3D
# projection plot in the empty figure
ax = fig.gca(projection="3d")
# Creating a wireframe plot with the x,y and
# z-coordinates respectively along with the
# color as red
surf = ax.plot_wireframe(x, y, z, color="red")
# Creating a wireframe plot with the points
# x1,y1,z1 along with the plot line as green
surf1 =ax.plot_wireframe(x1, y1, z1, color="green")
#showing the above plot
plt.show()
# -
# # Creating two 3D graphs in a single figure
# +
#importing matplotlib.pyplot from
# python
import matplotlib.pyplot as plt
# importing numpy package from python
import numpy as np
# creating an empty figure for plotting
fig = plt.figure()
# defining a sub-plot with 1x2 axis and defining
# it as first plot with projection as 3D
ax = fig.add_subplot(1, 2, 1, projection='3d')
# creating a range of 12 elements in both
# X and Y
X = np.arange(12)
Y = np.linspace(12, 1)
# Creating a mesh grid of X and Y
X, Y = np.meshgrid(X, Y)
# Creating an expression X and Y and
# storing it in Z
Z = X*2+Y*3;
# Creating a wireframe plot with the 3 sets of
# values X,Y and Z
ax.plot_wireframe(X, Y, Z)
# Creating my second subplot with 1x2 axis and defining
# it as the second plot with projection as 3D
ax = fig.add_subplot(1, 2, 2, projection='3d')
# defining a set of points for X,Y and Z
X1 = [1,2,1,4,3,2,7,5,9]
Y1 = [8,2,7,4,3,6,1,8,9]
Z1 = [1,2,4,7,9,6,7,6,9]
# Plotting 3 points X1,Y1,Z1 with
# color as green
ax.plot(X1, Y1, Z1,color='green')
# Showing the above plot
plt.show()
# -
# # Key 3D Plots using Matplotlib:
#
# ### Here we will create a surface plot and a tri-surface plot
# +
#importing matplotlib.pyplot from
# python
import matplotlib.pyplot as plt
# importing numpy package from python
import numpy as np
# creating an empty figure for plotting
fig = plt.figure()
# defining a sub-plot with 1x2 axis and defining
# it as first plot with projection as 3D
ax = fig.add_subplot(1, 2, 1, projection='3d')
# creating a range of values for
# x1,y1 from -1 to 1 with
# a space of 0.1 between the elements so that
# we can create a single curve in the plot
x1= np.arange(-1,1,0.1)
y1= np.arange(-1,1,0.1)
# Creating a mesh grid with x ,y and x1,
# y1 which creates an n-dimentional
# array
x1,y1= np.meshgrid(x1,y1)
# Creating a cosine function with the
# range of values from the meshgrid
z1= np.cos(x1* np.pi/2)
# Creating a wireframe plot with the points
# x1,y1,z1 along with the plot line as red
ax.plot_surface(x1, y1, z1, color="red")
# Creating my second subplot with 1x2 axis and defining
# it as the second plot with projection as 3D
ax = fig.add_subplot(1, 2, 2, projection='3d')
# defining a set of points for X1,Y1 and Z1
X1 = [1,2,1,4,3,2,7,5,9]
Y1 = [8,2,7,4,3,6,1,8,9]
Z1 = [1,2,4,7,9,6,7,6,9]
# Plotting 3 points X1,Y1,Z1 with
# color as purple
ax.plot_trisurf(X1, Y1, Z1,color='purple')
# Showing the above plot
plt.show()
# -
# ### Here, we will be looking at contour and filled contour plots
# +
# importing axes3d from mpl_toolkits.mplot
# module in python
from mpl_toolkits.mplot3d import axes3d
# importing matplotlib package from python
import matplotlib.pyplot as plt
#importing numpy package from
# python library
import numpy as np
# Creating an empty figure
fig = plt.figure()
# Creating a subplot where we are
# defining the projection as 3D projection
ax = fig.add_subplot(1,2,1, projection='3d')
# Creating a set of testing data using
# get_test_data from axes3d module in
# python. It creates a set of nD arrays
# for each of the variables X,Y,Z
X, Y, Z = axes3d.get_test_data(0.07)
#Plotting the contour plot with the
# following range of nD arrays
plot = ax.contour(X, Y, Z)
# Adding a second subplot in our figure with
# the projection as a 3D projection
ax=fig.add_subplot(1,2,2,projection='3d')
# Adding a range of values to the variables X1,Y1
X1=[1,2,3,4,5,6,7]
Y1=[1,2,3,4,5,6,7]
# Creating a meshgrid of X1 and Y1
X1, Y1 = np.meshgrid(X1,Y1)
# Creating an expression for Z1 with the
# help of X1 and Y1
Z1=(X1+4)*5+(Y1-5)/2
# Creating a contour plot
plot2 = ax.contourf(X1, Y1, Z1)
# Showing the above plot
plt.show()
# -
# ### Here, we will be exploring a polygon plot
# In this plot, we will be plotting a continuous set of points at different axes points of z
# +
# import Axes3D from mpl_toolkits.mplot3d
# from python
from mpl_toolkits.mplot3d import Axes3D
# importing PolyCollection from
# matplotlib.collections module
from matplotlib.collections import PolyCollection
#importing matplotlib.pyplot from
# python
import matplotlib.pyplot as plt
# importing numpy package from
# python
import numpy as np
# Creating an empty figure
fig = plt.figure()
# Creating a 3D projection using
# fig.gca
ax = fig.gca(projection='3d')
# Creating a wide range of elements
# using numpy package from python
xs = np.arange(0, 1, 0.1)
# Creating an empty list
verts = []
# Creating a range of values on
# Z-Axis
zs = [0.0, 0.2, 0.4, 0.6,0.8]
# Looping through all the values in zs
# and creating random values in ys using
# np.random.rand() which creates a range of
# elements in ys and we are appending each of them
# inside verts[]
for z in zs:
ys = np.random.rand(len(xs))
verts.append(list(zip(xs, ys)))
# using polycollection, we are providing a
# series of vertices to poly so as to
# plot our required plot
poly = PolyCollection(verts)
# Using add_collection3d, we are plotting
# ur required ploygon plot where we define
# zs with the range of values we defined in our
# list zs and also the zdir as Y-Axis
ax.add_collection3d(poly,zs=zs,zdir='y')
# Showing the required plot
plt.show()
# -
# ### Here, we will be learning about the quiver plot
# A quiver plot helps us to plot a 3d field of arrows in order to define the specified points.
# +
# import axes3d from mpl_toolkits.mplot3d
from mpl_toolkits.mplot3d import axes3d
# import matplotlib.pyplot from python
import matplotlib.pyplot as plt
# import numoy from python
import numpy as np
# Creating an empty figure
# to plot a 3D graph
fig = plt.figure()
# Creating a 3Dprojection for
# our 3D plots using fig.gca
ax = fig.gca(projection='3d')
# Creating a meshgrid for the range
# of values in X,Y,Z
x, y, z = np.meshgrid([1,2,5,2,4,8,3,3,1],[6,4,3,1,6,2,7,8,2],[1,2,5,2,4,8,3,3,1])
# Creating expressions for u,v,w
# with the help of x,y and z
# which will form the direction vectors
u = x*2+y*3+z*3
v = (x+3)*(y+5)*(z+7)
w = x+y+z
# Creating a quiver plot with length of the direction
# vector length as 0.2 ad normalise as true
ax.quiver(x, y, z, u, v, w, length=0.2, normalize=True)
#showing the above plot
plt.show()
# -
# ### 2D data to be plotted in 3D plots
# Here, we will be taking a set of 2D points to be plotted in a specific axis in our 3D plot because we cannot plot a 2D point in a 3D plane with all the coordinates. So a specific axis needs to be defined for plotting the 2D points.
# +
# importing numpy package
import numpy as np
# importing matplotlib package
import matplotlib.pyplot as plt
# Creating an empty canvas(figure)
fig = plt.figure()
# Using the gca function, we are defining
# the current axes as a 3D projection
ax = fig.gca(projection='3d')
# Labelling X-Axis
ax.set_xlabel('X-Axis')
# Labelling Y-Axis
ax.set_ylabel('Y-Axis')
# Labelling Z-Axis
ax.set_zlabel('Z-Axis')
# Creating 10 values for X
x = [1,1.2,1.4,1.6,1.8,2.0,2.2,2.4,2.6,2.8]
# Creating 10 values for Y
y = [1,1.2,1.4,1.6,1.8,2.0,2.2,2.4,2.6,2.8]
# Creating 10 random values for Y
z=[1,2,4,5,6,7,8,9,10,11]
# zdir='z' fixes all the points to zs=0 and
# (x,y) points are ploted in the x-y axis
# of the graph
ax.plot(x, y, zs=0, zdir='z')
# zdir='y' fixes all the points to zs=0 and
# (x,y) points are ploted in the x-z axis of the
# graph
ax.plot(x, y, zs=0, zdir='y')
# Showing the above plot
plt.show()
# -
|
Matplotlib Basics.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# #Inaugural project
#
# #Group: Anders&Frederik
#
# #Group members: <NAME>, rjv586. <NAME>, zpw586.
# #Question 1
#
# We first assign the parameters their values and define the utility function and the budget constraint.
import numpy as np
from scipy import optimize
# autoreload modules when c""" """ode is run
# %load_ext autoreload
# %autoreload 2
# +
#1.1. Defining globals
m = 1 #cash-on-hand
v = 10 #scales the disutility of labor
e = 0.3 #Frisch elasticity of labor supply
k = 0.4 #cut-off for the top labor income bracket
t0 = 0.4 #standard labor income tax
t1 = 0.1 #top bracket labor income tax
w = 1 #wage is assumed exogenous for now
#1.2. Defining utility
def utility(l,c,e,v):
u = np.log(c) - v*l**(1 + 1/e)/(1 + 1/e)
return u
#1.3. Defining budget constraint
def bc(m,w,l,t0,t1,k):
budget = m + w*l - w*l*t0 - t1*max((w*l - k),0)
return budget
# -
# We then define the budget constraint where we substitute c* into x using that c* = x. The objective function "utility" returns the negative value of the utility given a level of consumption- and a labor supply. This function returns a negative function as scipy optimize.minimize_scalar minimizes why minimizing a negative function is equivalent to maximizing.
#1.4. Substituting c into budget constraint as c*=x; creating a function l*(l)
def c_sub(l,w,e,v,t0,t1,k):
c = bc(m,w,l,t0,t1,k)
return -utility(l,c,e,v)
# We then define out optimiser "opt" using scipy optimize; the function "opt" uses c as a function of l to maximize labor supply given the parameter values using the bounds of (0,1) to the labor supply. The function returns a list of optimal labour supply values from the parameters (floats).
# Subsequently, we plug the optimal labor supply into the budget constraint to determine the optimal consumption. Ultimally, we plug the optimal labor supply and -consumption into the "utility" to obtain the maximized level of utility.
#1.5. Finding the l that optimizes l*
def optimizer(w,e,v,t0,t1,k,m):
sol = optimize.minimize_scalar(
c_sub, method = 'bounded',
bounds=(0,1),
args = (w,e,v,t0,t1,k))
lstar = sol.x
cstar = bc(m,w,lstar,t0,t1,k)
ustar = utility(lstar,cstar,e,v)
return [lstar,cstar,ustar]
# This function solves the consumer maximization problem.
# #Question 2
#
# We plot the optimal labor supply and -consumption as functions of the wage rate. Consequently, we import pyplot from matplotlib. We create a vector of 10.000 evenly spaced wage rates of a specificed interval between 0.5 and 1.5 using np.linspace. For each of these vector values, we need an optimal level of labor supply and -consumption. Accordingly, we use a for-loop with enumerate to create such values into two vectors; one for optimal labor supply and one for optimal consumption. Lastly, we create a plot using the wage rate vector and the two vectors of optimal labor supply and -consumption.
# +
import matplotlib.pyplot as plt
import random
plt.style.use('seaborn-poster')
np.random.seed(7)
#2.1. Defining population size and storage vectors
N = 10000
w_vec = np.linspace(0.5, 1.5, N)
l_vec = np.empty(N)
c_vec = np.empty(N)
#2.2. For every i in w_i, we get l_i* and c_i*
for i,w in enumerate(w_vec):
cord = optimizer(w, e, v, t0, t1, k, m)
l_vec[i] = cord[0]
c_vec[i] = cord[1]
#2.3. Choosing figure size
fig = plt.figure(figsize=(12,5))
#2.3.1 Plotting optimal labor supply again wage using the defined vectors
ax_left = fig.add_subplot(1,2,1)
ax_left.plot(w_vec,l_vec)
ax_left.set_title('Optimal labour supply given wage')
ax_left.set_xlabel('$w$')
ax_left.set_ylabel('$l^\star$')
ax_left.grid(True)
#2.3.2. Plotting optimal consumption again wage using the defined vectors
ax_right = fig.add_subplot(1,2,2)
ax_right.plot(w_vec,c_vec)
ax_right.set_title('Optimal consumption given wage')
ax_right.set_xlabel('$w$')
ax_right.set_ylabel('$c^\star$')
ax_right.grid(True)
plt.show
# -
# We see that a labor supply is increasing and the kink happens at the cutoff tax-rate. Consumption is increasing with a similair kink.
# #Question 3
#
# We calculate the total tax revenue. However, firstly, we need to draw a vector of invidual wages: $w_i ~ U((0.5), (1.5))$ with a population of 10.000. From this distribution, we would need the optimal labor supply and consumption per individual, $i$. We apply the optimizer-function "opt" to return the tax payment for each indiviual given the optimal labor supply and -consumption.
# +
#3.1. Drawing 10.000 random wage rates from a uniform distribution in the interval (0.5, 1.5)
np.random.seed(7)
Wage_draw = np.random.uniform(0.5,1.5,size=10000)
def Total_tax(PopWageVector,e,v,t0,t1,k,m):
#3.2. Returning an array of individual tax payments
N=len(PopWageVector)
pop_taxes=np.zeros((N))
#3.2 For each wage rate, return the optimal labor supply by using the optimizer function
for i,w in enumerate(PopWageVector):
the_optimum=optimizer(w,e,v,t0,t1,k,m)
opt_labor=the_optimum[0]
#3.2.1. Returning tax payment given the optimal labor supply
pop_taxes[i]=t0*w*opt_labor+t1*max(w*opt_labor-k,0)
#3.3. Summating over all tax payments
Total_tax=sum(pop_taxes)
return Total_tax
#3.4. Calling total tax revenue using the array of randomly drawn wages
Total_tax0 = Total_tax(Wage_draw,e,v,t0,t1,k,m)
print(f'The total tax revenue is {Total_tax0:.1f}')
# -
#
# #Question 4
#
# Changing the Frisch elasticity to 0.1 and watching the revenue rise as it is now more optimal to supply more labor for a given wage rate.
# +
#4.1. Defining new Frisch elasticity
e_new = 0.1
#4.2. Calling total tax revenue using the array of randomly drawn wages with the new Frisch elasticity
Tax_new = Total_tax(Wage_draw,e_new,v,t0,t1,k,m)
#4.3. Printing the result
print(f'The total tax revenue is {Tax_new:.1f}')
# -
# #Question 5
# We define a new optimizer to the purpose of finding the tax rates and cutoff income that maximizes tax revenue.
# +
#5.1. Defining tax function to be optimized
def tax_to_be_opt(taxes,Wages_pop,e,v,m):
t0 = taxes[0]
t1 = taxes[1]
k = taxes[2]
return -Total_tax(Wages_pop,e,v,t0,t1,k,m)
#5.2. Defining the 't_opt' function and finding the tax maximizing values of the vector 'taxes'.
def t_opt(Wages_pop,e,v,m):
# 5.2.1. Calling optimizer
initial_guess = [0.785,0.055,0.470]
sol = optimize.minimize(
tax_to_be_opt,
initial_guess,
method='Nelder-Mead',
args=(Wages_pop,e,v,m))
[t0star,t1star,kstar] = sol.x
#5.2.2 Printing the solution
print(f'Optimal lower tax rate is {t0star:.3f}')
print(f'Optimal upper tax rate is {t1star:.3f}')
print(f'Optimal k income is {kstar:.3f}')
return t0star,t1star,kstar
print('Optimal taxes and estimated total tax revenue')
t0star,t1star,kstar=t_opt(Wage_draw,e,v,m)
Total_tax_pop = Total_tax(Wage_draw,e,v,t0star,t1star,kstar,m)
print(f'Estimated total tax revenue is {Total_tax_pop:.2f}')
# -
# #Conclusion
# In this assignment we have found the optimal consumption and labor supply given certain parameter values, tax levels and wages, including the fact that both consumption and labour supply is increasing in the level of wages. In regards to the tax revenue we find that it is decreasing in the Frisch elasticity of labour supply since the revenue is larger in (4) than (3). In (5) we find that is is possible for the politician to increase the lower tax rate substantially, while the upper taxrate should be decreased in order to maximize the tax revenue.
|
inauguralproject/inauguralproject.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
# %matplotlib tk
# +
data = pd.read_csv("/home/adarsh/Files/Github/Sensor-Analytics/Module-6/data/Combined Cycle Power Plant Dataset/CCPP/Folds5x2_pp_set1.csv")
data.head()
# +
data
fig, ax = plt.subplots()
ax.plot(data['AT'], data['PE'], '.')
ax.set_xlabel('AMBIENT TEMPERATURE')
ax.set_ylabel('POWER GENERATED')
plt.grid()
plt.tight_layout()
plt.show()
# +
data
fig, ax = plt.subplots(5,5)
keys = data.keys()
for i in range(len(keys)):
for j in range(len(keys)):
ax[i][j].plot(data[keys[i]], data[keys[j]], '.')
ax[i][j].set_xlabel(keys[i])
ax[i][j].set_ylabel(keys[j])
plt.grid()
plt.show()
# +
import seaborn as sns
correlation_mat = data.corr()
sns.heatmap(correlation_mat, annot = True)
plt.show()
|
Module-6/All Lessons.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="6ScvUZ5psPuk" colab_type="text"
# **Important: This notebook will only work with fastai-0.7.x. Do not try to run any fastai-1.x code from this path in the repository because it will load fastai-0.7.x**
# + [markdown] id="kB8aHwpIsPum" colab_type="text"
# # Intro to Random Forests
# + [markdown] id="Q5gydRw3sPun" colab_type="text"
# ## About this course
# + [markdown] id="ApodvqTksPuo" colab_type="text"
# ### Teaching approach
# + [markdown] id="cPvWZMWZsPuo" colab_type="text"
# This course is being taught by <NAME>, and was developed by Jeremy along with <NAME>. Rachel has been dealing with a life-threatening illness so will not be teaching as originally planned this year.
#
# Jeremy has worked in a number of different areas - feel free to ask about anything that he might be able to help you with at any time, even if not directly related to the current topic:
#
# - Management consultant (McKinsey; AT Kearney)
# - Self-funded startup entrepreneur (Fastmail: first consumer synchronized email; Optimal Decisions: first optimized insurance pricing)
# - VC-funded startup entrepreneur: (Kaggle; Enlitic: first deep-learning medical company)
# + [markdown] id="xt2kO2tssPup" colab_type="text"
# I'll be using a *top-down* teaching method, which is different from how most math courses operate. Typically, in a *bottom-up* approach, you first learn all the separate components you will be using, and then you gradually build them up into more complex structures. The problems with this are that students often lose motivation, don't have a sense of the "big picture", and don't know what they'll need.
#
# If you took the fast.ai deep learning course, that is what we used. You can hear more about my teaching philosophy [in this blog post](http://www.fast.ai/2016/10/08/teaching-philosophy/) or [in this talk](https://vimeo.com/214233053).
#
# Harvard Professor <NAME> has a book, [Making Learning Whole](https://www.amazon.com/Making-Learning-Whole-Principles-Transform/dp/0470633719) in which he uses baseball as an analogy. We don't require kids to memorize all the rules of baseball and understand all the technical details before we let them play the game. Rather, they start playing with a just general sense of it, and then gradually learn more rules/details as time goes on.
#
# All that to say, don't worry if you don't understand everything at first! You're not supposed to. We will start using some "black boxes" such as random forests that haven't yet been explained in detail, and then we'll dig into the lower level details later.
#
# To start, focus on what things DO, not what they ARE.
# + [markdown] id="kv00vg6RsPuq" colab_type="text"
# ### Your practice
# + [markdown] id="0LRx6AQcsPur" colab_type="text"
# People learn by:
# 1. **doing** (coding and building)
# 2. **explaining** what they've learned (by writing or helping others)
#
# Therefore, we suggest that you practice these skills on Kaggle by:
# 1. Entering competitions (*doing*)
# 2. Creating Kaggle kernels (*explaining*)
#
# It's OK if you don't get good competition ranks or any kernel votes at first - that's totally normal! Just try to keep improving every day, and you'll see the results over time.
# + [markdown] id="3zmVEwTEsPur" colab_type="text"
# To get better at technical writing, study the top ranked Kaggle kernels from past competitions, and read posts from well-regarded technical bloggers. Some good role models include:
#
# - [<NAME>](http://nbviewer.jupyter.org/url/norvig.com/ipython/ProbabilityParadox.ipynb) (more [here](http://norvig.com/ipython/))
# - [<NAME>](https://smerity.com/articles/2017/deepcoder_and_ai_hype.html)
# - [<NAME>](https://codewords.recurse.com/issues/five/why-do-neural-networks-think-a-panda-is-a-vulture) (more [here](https://jvns.ca/blog/2014/08/12/what-happens-if-you-write-a-tcp-stack-in-python/))
# - [<NAME>](http://blog.juliaferraioli.com/2016/02/exploring-world-using-vision-twilio.html)
# - [<NAME>](http://blog.echen.me/2014/10/07/moving-beyond-ctr-better-recommendations-through-human-evaluation/)
# - [<NAME>](https://blog.slavv.com/picking-an-optimizer-for-style-transfer-86e7b8cba84b) (fast.ai student)
# - [<NAME>](https://hackernoon.com/non-artistic-style-transfer-or-how-to-draw-kanye-using-captain-picards-face-c4a50256b814) (fast.ai and USF MSAN student)
# + [markdown] id="zFQXX2z7sPus" colab_type="text"
# ### Books
# + [markdown] id="3cQ2bPiSsPus" colab_type="text"
# The more familiarity you have with numeric programming in Python, the better. If you're looking to improve in this area, we strongly suggest <NAME>'s [Python for Data Analysis, 2nd ed](https://www.amazon.com/Python-Data-Analysis-Wrangling-IPython/dp/1491957662/ref=asap_bc?ie=UTF8).
#
# For machine learning with Python, we recommend:
#
# - [Introduction to Machine Learning with Python](https://www.amazon.com/Introduction-Machine-Learning-Andreas-Mueller/dp/1449369413): From one of the scikit-learn authors, which is the main library we'll be using
# - [Python Machine Learning: Machine Learning and Deep Learning with Python, scikit-learn, and TensorFlow, 2nd Edition](https://www.amazon.com/Python-Machine-Learning-scikit-learn-TensorFlow/dp/1787125939/ref=dp_ob_title_bk): New version of a very successful book. A lot of the new material however covers deep learning in Tensorflow, which isn't relevant to this course
# - [Hands-On Machine Learning with Scikit-Learn and TensorFlow](https://www.amazon.com/Hands-Machine-Learning-Scikit-Learn-TensorFlow/dp/1491962291/ref=pd_lpo_sbs_14_t_0?_encoding=UTF8&psc=1&refRID=MBV2QMFH3EZ6B3YBY40K)
#
# + [markdown] id="XLu5rccwsPut" colab_type="text"
# ### Syllabus in brief
# + [markdown] id="n8IIfsUnsPuu" colab_type="text"
# Depending on time and class interests, we'll cover something like (not necessarily in this order):
#
# - Train vs test
# - Effective validation set construction
# - Trees and ensembles
# - Creating random forests
# - Interpreting random forests
# - What is ML? Why do we use it?
# - What makes a good ML project?
# - Structured vs unstructured data
# - Examples of failures/mistakes
# - Feature engineering
# - Domain specific - dates, URLs, text
# - Embeddings / latent factors
# - Regularized models trained with SGD
# - GLMs, Elasticnet, etc (NB: see what James covered)
# - Basic neural nets
# - PyTorch
# - Broadcasting, Matrix Multiplication
# - Training loop, backpropagation
# - KNN
# - CV / bootstrap (Diabetes data set?)
# - Ethical considerations
# + [markdown] id="t4c7SDstsPuu" colab_type="text"
# Skip:
#
# - Dimensionality reduction
# - Interactions
# - Monitoring training
# - Collaborative filtering
# - Momentum and LR annealing
#
# + id="EP4ZD-YjtF6l" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="27357f54-ce3d-4173-dbaa-4a6c13296472"
# !pip install fastai==0.7.0
# !pip install torchtext==0.2.3
# + [markdown] id="zB6k4GV5sPuv" colab_type="text"
# ## Imports
# + id="vNM1d29BsPuw" colab_type="code" colab={}
# %load_ext autoreload
# %autoreload 2
# %matplotlib inline
# + id="4KM42OEAsPuz" colab_type="code" colab={}
from fastai.imports import *
from fastai.structured import *
from pandas_summary import DataFrameSummary
from sklearn.ensemble import RandomForestRegressor, RandomForestClassifier
from IPython.display import display
from sklearn import metrics
# + id="LK2N0szesPu3" colab_type="code" colab={}
PATH = "data/bulldozers/"
# + id="lua9iWPusPu5" colab_type="code" colab={} outputId="fdf5f199-56c3-44e8-c9fe-27f9ca74b4ae"
# !ls {PATH}
# + [markdown] id="XtVdWR59sPu8" colab_type="text"
# # Introduction to *Blue Book for Bulldozers*
# + [markdown] id="cg7EMXYBsPu9" colab_type="text"
# ## About...
# + [markdown] id="uKkUUaAdsPu-" colab_type="text"
# ### ...our teaching
# + [markdown] id="9VdC9yoMsPu-" colab_type="text"
# At fast.ai we have a distinctive [teaching philosophy](http://www.fast.ai/2016/10/08/teaching-philosophy/) of ["the whole game"](https://www.amazon.com/Making-Learning-Whole-Principles-Transform/dp/0470633719/ref=sr_1_1?ie=UTF8&qid=1505094653). This is different from how most traditional math & technical courses are taught, where you have to learn all the individual elements before you can combine them (Harvard professor <NAME> call this *elementitis*), but it is similar to how topics like *driving* and *baseball* are taught. That is, you can start driving without [knowing how an internal combustion engine works](https://medium.com/towards-data-science/thoughts-after-taking-the-deeplearning-ai-courses-8568f132153), and children begin playing baseball before they learn all the formal rules.
# + [markdown] id="2gCtpJaSsPu_" colab_type="text"
# ### ...our approach to machine learning
# + [markdown] id="X3qGxDtqsPvA" colab_type="text"
# Most machine learning courses will throw at you dozens of different algorithms, with a brief technical description of the math behind them, and maybe a toy example. You're left confused by the enormous range of techniques shown and have little practical understanding of how to apply them.
#
# The good news is that modern machine learning can be distilled down to a couple of key techniques that are of very wide applicability. Recent studies have shown that the vast majority of datasets can be best modeled with just two methods:
#
# - *Ensembles of decision trees* (i.e. Random Forests and Gradient Boosting Machines), mainly for structured data (such as you might find in a database table at most companies)
# - *Multi-layered neural networks learnt with SGD* (i.e. shallow and/or deep learning), mainly for unstructured data (such as audio, vision, and natural language)
#
# In this course we'll be doing a deep dive into random forests, and simple models learnt with SGD. You'll be learning about gradient boosting and deep learning in part 2.
# + [markdown] id="YQ9-0DQAsPvA" colab_type="text"
# ### ...this dataset
# + [markdown] id="FpsnfPyPsPvC" colab_type="text"
# We will be looking at the Blue Book for Bulldozers Kaggle Competition: "The goal of the contest is to predict the sale price of a particular piece of heavy equiment at auction based on it's usage, equipment type, and configuration. The data is sourced from auction result postings and includes information on usage and equipment configurations."
#
# This is a very common type of dataset and prediciton problem, and similar to what you may see in your project or workplace.
# + [markdown] id="KUJJT-szsPvC" colab_type="text"
# ### ...Kaggle Competitions
# + [markdown] id="315DBWKGsPvE" colab_type="text"
# Kaggle is an awesome resource for aspiring data scientists or anyone looking to improve their machine learning skills. There is nothing like being able to get hands-on practice and receiving real-time feedback to help you improve your skills.
#
# Kaggle provides:
#
# 1. Interesting data sets
# 2. Feedback on how you're doing
# 3. A leader board to see what's good, what's possible, and what's state-of-art.
# 4. Blog posts by winning contestants share useful tips and techniques.
# + [markdown] id="biIVAlZtsPvE" colab_type="text"
# ## The data
# + [markdown] id="WQwNFkLgsPvF" colab_type="text"
# ### Look at the data
# + [markdown] id="889JB3TvsPvF" colab_type="text"
# Kaggle provides info about some of the fields of our dataset; on the [Kaggle Data info](https://www.kaggle.com/c/bluebook-for-bulldozers/data) page they say the following:
#
# For this competition, you are predicting the sale price of bulldozers sold at auctions. The data for this competition is split into three parts:
#
# - **Train.csv** is the training set, which contains data through the end of 2011.
# - **Valid.csv** is the validation set, which contains data from January 1, 2012 - April 30, 2012. You make predictions on this set throughout the majority of the competition. Your score on this set is used to create the public leaderboard.
# - **Test.csv** is the test set, which won't be released until the last week of the competition. It contains data from May 1, 2012 - November 2012. Your score on the test set determines your final rank for the competition.
#
# The key fields are in train.csv are:
#
# - SalesID: the unique identifier of the sale
# - MachineID: the unique identifier of a machine. A machine can be sold multiple times
# - saleprice: what the machine sold for at auction (only provided in train.csv)
# - saledate: the date of the sale
# + [markdown] id="SjiKY1busPvG" colab_type="text"
# *Question*
#
# What stands out to you from the above description? What needs to be true of our training and validation sets?
# + id="dblehUSPsPvH" colab_type="code" colab={}
df_raw = pd.read_csv(f'{PATH}Train.csv', low_memory=False,
parse_dates=["saledate"])
# + [markdown] id="aCKitDMlsPvK" colab_type="text"
# In any sort of data science work, it's **important to look at your data**, to make sure you understand the format, how it's stored, what type of values it holds, etc. Even if you've read descriptions about your data, the actual data may not be what you expect.
# + id="4Of7yAHbsPvK" colab_type="code" colab={}
def display_all(df):
with pd.option_context("display.max_rows", 1000, "display.max_columns", 1000):
display(df)
# + id="0OTmtOUKsPvM" colab_type="code" colab={} outputId="8ef18f5b-bb96-4084-cad0-32bf29d4e546"
display_all(df_raw.tail().T)
# + id="pzNHj-F2sPvP" colab_type="code" colab={} outputId="d85cdac8-8c98-4b7d-8d6a-745db66eb03d"
display_all(df_raw.describe(include='all').T)
# + [markdown] id="m1UbWBXKsPvR" colab_type="text"
# It's important to note what metric is being used for a project. Generally, selecting the metric(s) is an important part of the project setup. However, in this case Kaggle tells us what metric to use: RMSLE (root mean squared log error) between the actual and predicted auction prices. Therefore we take the log of the prices, so that RMSE will give us what we need.
# + id="xGUtb8t1sPvS" colab_type="code" colab={}
df_raw.SalePrice = np.log(df_raw.SalePrice)
# + [markdown] id="OMNNFI9DsPvU" colab_type="text"
# ### Initial processing
# + id="bP6X5rUisPvV" colab_type="code" colab={} outputId="da41ed4b-716e-4fea-d0f7-0a130c63ce62"
m = RandomForestRegressor(n_jobs=-1)
# The following code is supposed to fail due to string values in the input data
m.fit(df_raw.drop('SalePrice', axis=1), df_raw.SalePrice)
# + [markdown] id="SKZrZt0hsPvY" colab_type="text"
# This dataset contains a mix of **continuous** and **categorical** variables.
#
# The following method extracts particular date fields from a complete datetime for the purpose of constructing categoricals. You should always consider this feature extraction step when working with date-time. Without expanding your date-time into these additional fields, you can't capture any trend/cyclical behavior as a function of time at any of these granularities.
# + id="xffjvTXWsPva" colab_type="code" colab={} outputId="6311bf0b-0453-4b9f-8ecf-d36ca7efac0a"
add_datepart(df_raw, 'saledate')
df_raw.saleYear.head()
# + [markdown] id="wlIP_xwwsPvd" colab_type="text"
# The categorical variables are currently stored as strings, which is inefficient, and doesn't provide the numeric coding required for a random forest. Therefore we call `train_cats` to convert strings to pandas categories.
# + id="AXZeyAMesPve" colab_type="code" colab={}
train_cats(df_raw)
# + [markdown] id="zz4okc1psPvi" colab_type="text"
# We can specify the order to use for categorical variables if we wish:
# + id="LQjtAQPosPvj" colab_type="code" colab={} outputId="de417d62-22bc-49f8-ef7a-16601e0161ad"
df_raw.UsageBand.cat.categories
# + id="Ja4FLLnPsPvl" colab_type="code" colab={}
df_raw.UsageBand.cat.set_categories(['High', 'Medium', 'Low'], ordered=True, inplace=True)
# + [markdown] id="diRkx7ErsPvn" colab_type="text"
# Normally, pandas will continue displaying the text categories, while treating them as numerical data internally. Optionally, we can replace the text categories with numbers, which will make this variable non-categorical, like so:.
# + id="UDunhljHsPvo" colab_type="code" colab={}
df_raw.UsageBand = df_raw.UsageBand.cat.codes
# + [markdown] id="WErqelvssPvq" colab_type="text"
# We're still not quite done - for instance we have lots of missing values, which we can't pass directly to a random forest.
# + id="ysNVUHYvsPvq" colab_type="code" colab={} outputId="18a54483-7ca5-4e9b-8640-1ae0d715ac46"
display_all(df_raw.isnull().sum().sort_index()/len(df_raw))
# + [markdown] id="Ng_WJaLJsPvs" colab_type="text"
# But let's save this file for now, since it's already in format can we be stored and accessed efficiently.
# + id="0lVMcWx0sPvt" colab_type="code" colab={}
os.makedirs('tmp', exist_ok=True)
df_raw.to_feather('tmp/bulldozers-raw')
# + [markdown] id="onP8XwLusPvv" colab_type="text"
# ### Pre-processing
# + [markdown] id="q7LHfmvasPvv" colab_type="text"
# In the future we can simply read it from this fast format.
# + id="jnB1Nb0RsPvw" colab_type="code" colab={}
df_raw = pd.read_feather('tmp/bulldozers-raw')
# + [markdown] id="rP_u8JWKsPv0" colab_type="text"
# We'll replace categories with their numeric codes, handle missing continuous values, and split the dependent variable into a separate variable.
# + id="Q4IxQJD6sPv1" colab_type="code" colab={}
df, y, nas = proc_df(df_raw, 'SalePrice')
# + [markdown] id="hgRMAguSsPv3" colab_type="text"
# We now have something we can pass to a random forest!
# + id="Av7gF6UPsPv3" colab_type="code" colab={} outputId="08a5bdb4-e053-4a80-bf2c-c0dc4c557122"
m = RandomForestRegressor(n_jobs=-1)
m.fit(df, y)
m.score(df,y)
# + [markdown] id="W6xaWwpOsPv6" colab_type="text"
# In statistics, the coefficient of determination, denoted R2 or r2 and pronounced "R squared", is the proportion of the variance in the dependent variable that is predictable from the independent variable(s). https://en.wikipedia.org/wiki/Coefficient_of_determination
# + [markdown] id="rnO70uPqsPv7" colab_type="text"
# Wow, an r^2 of 0.98 - that's great, right? Well, perhaps not...
#
# Possibly **the most important idea** in machine learning is that of having separate training & validation data sets. As motivation, suppose you don't divide up your data, but instead use all of it. And suppose you have lots of parameters:
#
# <img src="https://github.com/nlauchande/fastai/blob/master/courses/ml1/images/overfitting2.png?raw=1" alt="" style="width: 70%"/>
# <center>
# [Underfitting and Overfitting](https://datascience.stackexchange.com/questions/361/when-is-a-model-underfitted)
# </center>
#
# The error for the pictured data points is lowest for the model on the far right (the blue curve passes through the red points almost perfectly), yet it's not the best choice. Why is that? If you were to gather some new data points, they most likely would not be on that curve in the graph on the right, but would be closer to the curve in the middle graph.
#
# This illustrates how using all our data can lead to **overfitting**. A validation set helps diagnose this problem.
# + id="0hScmrWosPv7" colab_type="code" colab={} outputId="ddea5432-1e71-4970-9d91-7594bb703910"
def split_vals(a,n): return a[:n].copy(), a[n:].copy()
n_valid = 12000 # same as Kaggle's test set size
n_trn = len(df)-n_valid
raw_train, raw_valid = split_vals(df_raw, n_trn)
X_train, X_valid = split_vals(df, n_trn)
y_train, y_valid = split_vals(y, n_trn)
X_train.shape, y_train.shape, X_valid.shape
# + [markdown] id="4tHxq-K4sPv9" colab_type="text"
# # Random Forests
# + [markdown] id="f4wQBAe-sPv-" colab_type="text"
# ## Base model
# + [markdown] id="hVQbyDRQsPv_" colab_type="text"
# Let's try our model again, this time with separate training and validation sets.
# + id="Y-yHasDQsPwA" colab_type="code" colab={}
def rmse(x,y): return math.sqrt(((x-y)**2).mean())
def print_score(m):
res = [rmse(m.predict(X_train), y_train), rmse(m.predict(X_valid), y_valid),
m.score(X_train, y_train), m.score(X_valid, y_valid)]
if hasattr(m, 'oob_score_'): res.append(m.oob_score_)
print(res)
# + id="A26sA8ZrsPwC" colab_type="code" colab={} outputId="81f55c5d-20f0-46f0-86cc-f1121b755243"
m = RandomForestRegressor(n_jobs=-1)
# %time m.fit(X_train, y_train)
print_score(m)
# + [markdown] id="ibMm65aLsPwE" colab_type="text"
# An r^2 in the high-80's isn't bad at all (and the RMSLE puts us around rank 100 of 470 on the Kaggle leaderboard), but we can see from the validation set score that we're over-fitting badly. To understand this issue, let's simplify things down to a single small tree.
# + [markdown] id="VJJAlJPDsPwF" colab_type="text"
# ## Speeding things up
# + id="QTdTCFU4sPwF" colab_type="code" colab={}
df_trn, y_trn, nas = proc_df(df_raw, 'SalePrice', subset=30000, na_dict=nas)
X_train, _ = split_vals(df_trn, 20000)
y_train, _ = split_vals(y_trn, 20000)
# + id="DiV0Jvq9sPwH" colab_type="code" colab={} outputId="7a0abc8f-7d14-4edd-a8f9-5184545e6e33"
m = RandomForestRegressor(n_jobs=-1)
# %time m.fit(X_train, y_train)
print_score(m)
# + [markdown] id="_6LtibkVsPwI" colab_type="text"
# ## Single tree
# + id="8Qq-oqWpsPwJ" colab_type="code" colab={} outputId="741823e3-130a-48cb-cb40-4ec4bd9ab55c"
m = RandomForestRegressor(n_estimators=1, max_depth=3, bootstrap=False, n_jobs=-1)
m.fit(X_train, y_train)
print_score(m)
# + id="dDiR7eoMsPwM" colab_type="code" colab={} outputId="e52e51ff-eb10-4d6e-da99-abf146b43180"
draw_tree(m.estimators_[0], df_trn, precision=3)
# + [markdown] id="nU1HN3NosPwQ" colab_type="text"
# Let's see what happens if we create a bigger tree.
# + id="N-rnP7tXsPwS" colab_type="code" colab={} outputId="9f226eab-30e2-4cf2-a97d-ecd2f9d97877"
m = RandomForestRegressor(n_estimators=1, bootstrap=False, n_jobs=-1)
m.fit(X_train, y_train)
print_score(m)
# + [markdown] id="xNRBoPAEsPwU" colab_type="text"
# The training set result looks great! But the validation set is worse than our original model. This is why we need to use *bagging* of multiple trees to get more generalizable results.
# + [markdown] id="bF9bhRQhsPwV" colab_type="text"
# ## Bagging
# + [markdown] id="mrUR9dyasPwV" colab_type="text"
# ### Intro to bagging
# + [markdown] id="Yd3667GesPwW" colab_type="text"
# To learn about bagging in random forests, let's start with our basic model again.
# + id="tpy8u0zYsPwW" colab_type="code" colab={} outputId="9460e77f-4ee5-4ff5-ef91-f51563535d3b"
m = RandomForestRegressor(n_jobs=-1)
m.fit(X_train, y_train)
print_score(m)
# + [markdown] id="awWVn5DqsPwX" colab_type="text"
# We'll grab the predictions for each individual tree, and look at one example.
# + id="XgwVUISxsPwY" colab_type="code" colab={} outputId="3cad9711-6199-4d07-c792-2a6a4cb1ea0b"
preds = np.stack([t.predict(X_valid) for t in m.estimators_])
preds[:,0], np.mean(preds[:,0]), y_valid[0]
# + id="0TYgIhA-sPwZ" colab_type="code" colab={} outputId="b0b1e070-0aa1-4e37-c361-04df1b38d479"
preds.shape
# + id="7g3vWYSrsPwc" colab_type="code" colab={} outputId="d76c2bbe-1d96-450a-b533-9c2727d0b876"
plt.plot([metrics.r2_score(y_valid, np.mean(preds[:i+1], axis=0)) for i in range(10)]);
# + [markdown] id="liiboEKvsPwe" colab_type="text"
# The shape of this curve suggests that adding more trees isn't going to help us much. Let's check. (Compare this to our original model on a sample)
# + id="BB08I29ksPwg" colab_type="code" colab={} outputId="a7698f0c-82c4-4c03-92db-ed9f7608003b"
m = RandomForestRegressor(n_estimators=20, n_jobs=-1)
m.fit(X_train, y_train)
print_score(m)
# + id="1FTqYy0jsPwi" colab_type="code" colab={} outputId="cb17a56c-22e7-4159-8c17-7d28828a939e"
m = RandomForestRegressor(n_estimators=40, n_jobs=-1)
m.fit(X_train, y_train)
print_score(m)
# + id="jRrsMwCisPwk" colab_type="code" colab={} outputId="57f79136-7198-49aa-97a9-3453efa128d7"
m = RandomForestRegressor(n_estimators=80, n_jobs=-1)
m.fit(X_train, y_train)
print_score(m)
# + [markdown] id="4hSky39TsPwm" colab_type="text"
# ### Out-of-bag (OOB) score
# + [markdown] id="-n6olc-ZsPwm" colab_type="text"
# Is our validation set worse than our training set because we're over-fitting, or because the validation set is for a different time period, or a bit of both? With the existing information we've shown, we can't tell. However, random forests have a very clever trick called *out-of-bag (OOB) error* which can handle this (and more!)
#
# The idea is to calculate error on the training set, but only include the trees in the calculation of a row's error where that row was *not* included in training that tree. This allows us to see whether the model is over-fitting, without needing a separate validation set.
#
# This also has the benefit of allowing us to see whether our model generalizes, even if we only have a small amount of data so want to avoid separating some out to create a validation set.
#
# This is as simple as adding one more parameter to our model constructor. We print the OOB error last in our `print_score` function below.
# + id="pzEhs5YNsPwm" colab_type="code" colab={} outputId="943c28ac-e644-411e-b497-8abac5f58050"
m = RandomForestRegressor(n_estimators=40, n_jobs=-1, oob_score=True)
m.fit(X_train, y_train)
print_score(m)
# + [markdown] id="dIAMPGTHsPwp" colab_type="text"
# This shows that our validation set time difference is making an impact, as is model over-fitting.
# + [markdown] id="bzu0r-PcsPwq" colab_type="text"
# ## Reducing over-fitting
# + [markdown] id="ZF_JOfsIsPwq" colab_type="text"
# ### Subsampling
# + [markdown] id="ttabbZ2msPwq" colab_type="text"
# It turns out that one of the easiest ways to avoid over-fitting is also one of the best ways to speed up analysis: *subsampling*. Let's return to using our full dataset, so that we can demonstrate the impact of this technique.
# + id="rTTajsp8sPwr" colab_type="code" colab={}
df_trn, y_trn, nas = proc_df(df_raw, 'SalePrice')
X_train, X_valid = split_vals(df_trn, n_trn)
y_train, y_valid = split_vals(y_trn, n_trn)
# + [markdown] id="oswjyviisPwt" colab_type="text"
# The basic idea is this: rather than limit the total amount of data that our model can access, let's instead limit it to a *different* random subset per tree. That way, given enough trees, the model can still see *all* the data, but for each individual tree it'll be just as fast as if we had cut down our dataset as before.
# + id="LVGbWVtOsPwt" colab_type="code" colab={}
set_rf_samples(20000)
# + id="zVQnJuTgsPwv" colab_type="code" colab={} outputId="24a13394-855d-4305-9e40-090a85d77ecc"
m = RandomForestRegressor(n_jobs=-1, oob_score=True)
# %time m.fit(X_train, y_train)
print_score(m)
# + [markdown] id="NJXVP6gpsPwy" colab_type="text"
# Since each additional tree allows the model to see more data, this approach can make additional trees more useful.
# + id="T3nd3rxFsPwz" colab_type="code" colab={} outputId="abb5f1e2-6d14-48ff-a7ff-8ff6247da8e5"
m = RandomForestRegressor(n_estimators=40, n_jobs=-1, oob_score=True)
m.fit(X_train, y_train)
print_score(m)
# + [markdown] id="pfZBPfBOsPw0" colab_type="text"
# ### Tree building parameters
# + [markdown] id="3llMoG22sPw1" colab_type="text"
# We revert to using a full bootstrap sample in order to show the impact of other over-fitting avoidance methods.
# + id="t8N5s_TdsPw1" colab_type="code" colab={}
reset_rf_samples()
# + [markdown] id="dQbpfRkusPw3" colab_type="text"
# Let's get a baseline for this full set to compare to.
# + id="qsryel3TsPw3" colab_type="code" colab={}
def dectree_max_depth(tree):
children_left = tree.children_left
children_right = tree.children_right
def walk(node_id):
if (children_left[node_id] != children_right[node_id]):
left_max = 1 + walk(children_left[node_id])
right_max = 1 + walk(children_right[node_id])
return max(left_max, right_max)
else: # leaf
return 1
root_node_id = 0
return walk(root_node_id)
# + id="1dOh_3-UsPw4" colab_type="code" colab={} outputId="086ac38c-6c06-48bf-c1f4-3d9abcc392e5"
m = RandomForestRegressor(n_estimators=40, n_jobs=-1, oob_score=True)
m.fit(X_train, y_train)
print_score(m)
# + id="2YhetoP7sPw7" colab_type="code" colab={}
t=m.estimators_[0].tree_
# + id="-CI1fEt9sPxB" colab_type="code" colab={} outputId="562301da-2220-49ea-f8cd-f51c5db3cb50"
dectree_max_depth(t)
# + id="AAODDWRHsPxD" colab_type="code" colab={} outputId="076511bc-0d9d-4151-c770-b112b8bcfa0e"
m = RandomForestRegressor(n_estimators=40, min_samples_leaf=5, n_jobs=-1, oob_score=True)
m.fit(X_train, y_train)
print_score(m)
# + id="95acFWXOsPxG" colab_type="code" colab={}
t=m.estimators_[0].tree_
# + id="FgJyqhZ9sPxH" colab_type="code" colab={} outputId="528ac304-7300-48c1-daca-27132e7bb3a3"
dectree_max_depth(t)
# + [markdown] id="i5H3cJdksPxI" colab_type="text"
# Another way to reduce over-fitting is to grow our trees less deeply. We do this by specifying (with `min_samples_leaf`) that we require some minimum number of rows in every leaf node. This has two benefits:
#
# - There are less decision rules for each leaf node; simpler models should generalize better
# - The predictions are made by averaging more rows in the leaf node, resulting in less volatility
# + id="bgtqdX3fsPxJ" colab_type="code" colab={} outputId="fdc07db0-7d15-4acf-a1a4-358e67bfe74a"
m = RandomForestRegressor(n_estimators=40, min_samples_leaf=3, n_jobs=-1, oob_score=True)
m.fit(X_train, y_train)
print_score(m)
# + [markdown] id="TwNFrqU_sPxK" colab_type="text"
# We can also increase the amount of variation amongst the trees by not only use a sample of rows for each tree, but to also using a sample of *columns* for each *split*. We do this by specifying `max_features`, which is the proportion of features to randomly select from at each split.
# + [markdown] id="LO7xzi2HsPxK" colab_type="text"
# - None
# - 0.5
# - 'sqrt'
# + [markdown] id="AtseVT5UsPxL" colab_type="text"
# - 1, 3, 5, 10, 25, 100
# + id="U1_3JsvhsPxL" colab_type="code" colab={} outputId="1f34dec8-54b4-4861-ac48-ddfe31cb988c"
m = RandomForestRegressor(n_estimators=40, min_samples_leaf=3, max_features=0.5, n_jobs=-1, oob_score=True)
m.fit(X_train, y_train)
print_score(m)
# + [markdown] id="TIEJiAb9sPxM" colab_type="text"
# We can't compare our results directly with the Kaggle competition, since it used a different validation set (and we can no longer to submit to this competition) - but we can at least see that we're getting similar results to the winners based on the dataset we have.
#
# The sklearn docs [show an example](http://scikit-learn.org/stable/auto_examples/ensemble/plot_ensemble_oob.html) of different `max_features` methods with increasing numbers of trees - as you see, using a subset of features on each split requires using more trees, but results in better models:
# 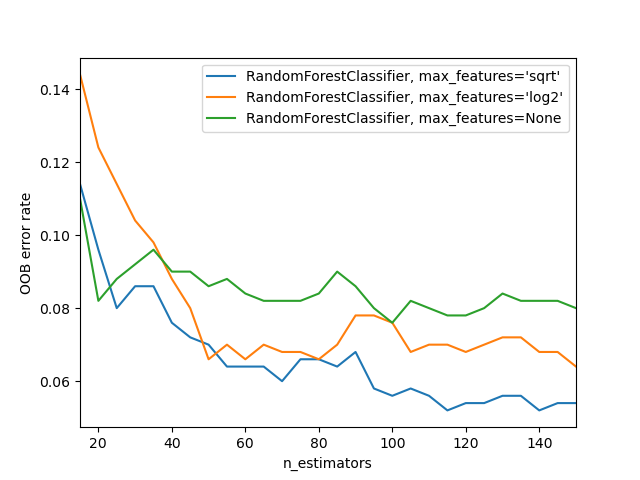
|
courses/ml1/lesson1-rf.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# ----------
# WORK IN PROGRESS
|
weather_forecast/gwd/notebooks/get-started.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# # Error Handling
#
# The code in this notebook helps with handling errors. Normally, an error in notebook code causes the execution of the code to stop; while an infinite loop in notebook code causes the notebook to run without end. This notebook provides two classes to help address these concerns.
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# **Prerequisites**
#
# * This notebook needs some understanding on advanced concepts in Python, notably
# * classes
# * the Python `with` statement
# * tracing
# * measuring time
# * exceptions
# -
# ## Synopsis
#
# <!-- Automatically generated. Do not edit. -->
#
#
#
# The `ExpectError` class allows you to catch and report exceptions, yet resume execution. This is useful in notebooks, as they would normally interrupt execution as soon as an exception is raised. Its typical usage is in conjunction with a `with` clause:
#
# ```python
# with ExpectError():
# x = 1 / 0
# ```
# ```python
# => Traceback (most recent call last):
# File "<ipython-input-14-264328004f25>", line 2, in <module>
# x = 1 / 0
# ZeroDivisionError: division by zero (expected)
#
# ```
# The `ExpectTimeout` class allows you to interrupt execution after the specified time. This is useful for interrupting code that might otherwise run forever.
#
# ```python
# with ExpectTimeout(5):
# long_running_test()
# ```
# ```python
# => Start
# 0 seconds have passed
# 1 seconds have passed
# 2 seconds have passed
# 3 seconds have passed
#
# Traceback (most recent call last):
# File "<ipython-input-15-7e5136e65261>", line 2, in <module>
# long_running_test()
# File "<ipython-input-11-8d0f8e53f106>", line 5, in long_running_test
# print(i, "seconds have passed")
# File "<ipython-input-11-8d0f8e53f106>", line 5, in long_running_test
# print(i, "seconds have passed")
# File "<ipython-input-10-a28a583f0630>", line 16, in check_time
# raise TimeoutError
# TimeoutError (expected)
#
# ```
# The exception and the associated traceback are printed as error messages. If you do not want that,
# use these keyword options:
#
# * `print_traceback` (default True) can be set to `False` to avoid the traceback being printed
# * `mute` (default False) can be set to `True` to completely avoid any output.
#
#
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# ## Catching Errors
#
# The class `ExpectError` allows to express that some code produces an exception. A typical usage looks as follows:
#
# ```Python
# from ExpectError import ExpectError
#
# with ExpectError():
# function_that_is_supposed_to_fail()
# ```
#
# If an exception occurs, it is printed on standard error; yet, execution continues.
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "skip"}
import fuzzingbook_utils
# + button=false new_sheet=false run_control={"read_only": false}
import traceback
import sys
# + button=false new_sheet=false run_control={"read_only": false}
class ExpectError(object):
def __init__(self, print_traceback=True, mute=False):
self.print_traceback = print_traceback
self.mute = mute
# Begin of `with` block
def __enter__(self):
return self
# End of `with` block
def __exit__(self, exc_type, exc_value, tb):
if exc_type is None:
# No exception
return
# An exception occurred
if self.print_traceback:
lines = ''.join(
traceback.format_exception(
exc_type,
exc_value,
tb)).strip()
else:
lines = traceback.format_exception_only(
exc_type, exc_value)[-1].strip()
if not self.mute:
print(lines, "(expected)", file=sys.stderr)
return True # Ignore it
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# Here's an example:
# + button=false new_sheet=false run_control={"read_only": false}
def fail_test():
# Trigger an exception
x = 1 / 0
# + button=false new_sheet=false run_control={"read_only": false}
with ExpectError():
fail_test()
# + button=false new_sheet=false run_control={"read_only": false}
with ExpectError(print_traceback=False):
fail_test()
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# ## Catching Timeouts
#
# The class `ExpectTimeout(seconds)` allows to express that some code may run for a long or infinite time; execution is thus interrupted after `seconds` seconds. A typical usage looks as follows:
#
# ```Python
# from ExpectError import ExpectTimeout
#
# with ExpectTimeout(2) as t:
# function_that_is_supposed_to_hang()
# ```
#
# If an exception occurs, it is printed on standard error (as with `ExpectError`); yet, execution continues.
#
# Should there be a need to cancel the timeout within the `with` block, `t.cancel()` will do the trick.
#
# The implementation uses `sys.settrace()`, as this seems to be the most portable way to implement timeouts. It is not very efficient, though. Also, it only works on individual lines of Python code and will not interrupt a long-running system function.
# + button=false new_sheet=false run_control={"read_only": false}
import sys
import time
# + button=false new_sheet=false run_control={"read_only": false}
try:
# Should be defined in Python 3
x = TimeoutError
except:
# For Python 2
class TimeoutError(Exception):
def __init__(self, value="Timeout"):
self.value = value
def __str__(self):
return repr(self.value)
# + button=false new_sheet=false run_control={"read_only": false}
class ExpectTimeout(object):
def __init__(self, seconds, print_traceback=True, mute=False):
self.seconds_before_timeout = seconds
self.original_trace_function = None
self.end_time = None
self.print_traceback = print_traceback
self.mute = mute
# Tracing function
def check_time(self, frame, event, arg):
if self.original_trace_function is not None:
self.original_trace_function(frame, event, arg)
current_time = time.time()
if current_time >= self.end_time:
raise TimeoutError
return self.check_time
# Begin of `with` block
def __enter__(self):
start_time = time.time()
self.end_time = start_time + self.seconds_before_timeout
self.original_trace_function = sys.gettrace()
sys.settrace(self.check_time)
return self
# End of `with` block
def __exit__(self, exc_type, exc_value, tb):
self.cancel()
if exc_type is None:
return
# An exception occurred
if self.print_traceback:
lines = ''.join(
traceback.format_exception(
exc_type,
exc_value,
tb)).strip()
else:
lines = traceback.format_exception_only(
exc_type, exc_value)[-1].strip()
if not self.mute:
print(lines, "(expected)", file=sys.stderr)
return True # Ignore it
def cancel(self):
sys.settrace(self.original_trace_function)
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# Here's an example:
# + button=false new_sheet=false run_control={"read_only": false}
def long_running_test():
print("Start")
for i in range(10):
time.sleep(1)
print(i, "seconds have passed")
print("End")
# + button=false new_sheet=false run_control={"read_only": false}
with ExpectTimeout(5, print_traceback=False):
long_running_test()
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# Note that it is possible to nest multiple timeouts.
# + button=false new_sheet=false run_control={"read_only": false}
with ExpectTimeout(5):
with ExpectTimeout(3):
long_running_test()
long_running_test()
# + [markdown] button=false new_sheet=false run_control={"read_only": false}
# That's it, folks – enjoy!
# -
# ## Synopsis
#
# The `ExpectError` class allows you to catch and report exceptions, yet resume execution. This is useful in notebooks, as they would normally interrupt execution as soon as an exception is raised. Its typical usage is in conjunction with a `with` clause:
with ExpectError():
x = 1 / 0
# The `ExpectTimeout` class allows you to interrupt execution after the specified time. This is useful for interrupting code that might otherwise run forever.
with ExpectTimeout(5):
long_running_test()
# The exception and the associated traceback are printed as error messages. If you do not want that,
# use these keyword options:
#
# * `print_traceback` (default True) can be set to `False` to avoid the traceback being printed
# * `mute` (default False) can be set to `True` to completely avoid any output.
|
notebooks/ExpectError.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
import numpy as np
np
lst = [[1,2,3,9],[4,5,6,9],[7,8,9,9]]
type(lst)
np_array = np.array(lst)
np_array
np_array.shape
np_array = np.reshape(np_array,(4,3))
np_array
np_array.shape
np.zeros((13,30), dtype = float)
np.ones((13,30), dtype = float)
# +
rand = np.random.randint(0,200)
print(rand)
# -
np.linspace(2,10,7)
np.mean(np.linspace(2,10,7))
np.sqrt(np.linspace(2,10,7))
array = np.linspace(2,10,7)
array
array + 2
array - 2
array * 2
array / 2
lst = [1,2,3]
# +
temp_lst = []
for i in lst:
temp = i + 2
temp_lst.append(temp)
# -
temp_lst
|
Module 1/Numpy.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: librosa_env
# language: python
# name: librosa_env
# ---
from os.path import dirname, join as pjoin
from scipy.io import wavfile
import scipy.io
from scipy.fft import fft, ifft, fftfreq, rfft, rfftfreq
import matplotlib.pyplot as plt
import IPython.display as ipd
import numpy as np
import pylab
import scipy.signal as signal
# +
sr, y = wavfile.read("janela.wav")
print(f"number of channels = {y.shape[1]}")
a, b = (2, 5) # start and stop in seconds
a = a*44100
b = b*44100
yshape = y[a:b, 0].shape[0]
y = y[a:b, 0]
length = yshape / sr
print(f"length = {length} sec")
x = np.linspace(0., length, yshape)
plt.plot(x, y, label="Left channel")
plt.legend()
plt.xlabel("Time [s]")
plt.ylabel("Amplitude")
plt.show()
ipd.Audio(y, rate=sr)
# +
# Number of samples in normalized_tone
N = yshape #sr * duration
yf = rfft(y)
xf = rfftfreq(N, 1 / sr)
yfa = 20*np.log10(np.abs(yf))
print(yfa.min(), yfa.max())
fs = 10e3
plt.figure(figsize=(14, 5))
plt.plot(xf, yfa) # magnitude spectrum
plt.xlabel('Frequency (Hz)')
plt.plot(xf, np.abs(yf))
plt.show()
f, Pwelch_spec = signal.welch(y, fs, scaling='spectrum')
plt.semilogy(f, Pwelch_spec)
plt.xlabel('frequency [Hz]')
plt.ylabel('PSD')
plt.grid()
plt.show()
# +
# normalized_sample = np.int16((np.abs(yf) / np.abs(yf).max()) * 32767)
# -
n = y.size
samplespace = 1
freqs = rfftfreq(n, d=samplespace)
print(freqs.min(), freqs.max())
# +
yfa = 20*np.log10(np.abs(yf))
threshold = 200
idx = np.argwhere(yfa>threshold)
freq = freqs[idx]
freq_in_herz = abs(freq * sr)
freq_list = []
for freq1, freq2 in zip(freq_in_herz, freq_in_herz[1:]):
if (freq2 - freq1) >= 1:
print("Frequency in hertz: ", freq1[0])
freq_list.append(freq1[0])
# -
plt.plot(xf, yfa)
plt.show()
plt.plot(xf, yfa)
for i, (a, b) in enumerate(zip(xf, yfa)):
if b >= threshold:
b2 = abs(freqs[i]*sr)
if b2 in freq_list:
plt.text(a, b, str(b2))
print("h")
|
a_rua_dos_cataventos/components/analysis/backup_analysis/fft_analysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <img align="left" src="https://ithaka-labs.s3.amazonaws.com/static-files/images/tdm/tdmdocs/CC_BY.png"><br />
#
# Created by [<NAME>](http://nkelber.com) and Ted Lawless for [JSTOR Labs](https://labs.jstor.org/) under [Creative Commons CC BY License](https://creativecommons.org/licenses/by/4.0/)<br />
# For questions/comments/improvements, email <EMAIL>.<br />
# ___
# **Pandas I**
#
# **Description:** This notebook describes how to:
# * Create a Pandas Series or DataFrame
# * Accessing data rows, columns, elements using `.loc` and `.iloc`
# * Creating filters using boolean operators
# * Changing data in rows, columns, and elements
#
# This is the first notebook in a series on learning to use Pandas.
#
# **Use Case:** For Learners (Detailed explanation, not ideal for researchers)
#
# **Difficulty:** Intermediate
#
# **Knowledge Required:**
# * Python Basics ([Start Python Basics I](./python-basics-1.ipynb))
#
# **Knowledge Recommended:**
# * [Working with Dataset Files](./working-with-dataset-files.ipynb)
#
# **Completion Time:** 75 minutes
#
# **Data Format:** CSV (.csv)
#
# **Libraries Used:** Pandas
#
# **Research Pipeline:** None
# ___
# # When to use Pandas
# Pandas is a Python data analysis and manipulation library. When it comes to viewing and manipulating data, most people are familiar with commercial spreadsheet software, such as Microsoft Excel or Google Sheets. While spreadsheet software and Pandas can accomplish similar tasks, each has significant advantages depending on the use-case.
#
# **Advantages of Spreadsheet Software**
# * Point and click
# * Easier to learn
# * Great for small datasets (<10,000 rows)
# * Better for browsing data
#
# **Advantages of Pandas**
# * More powerful data manipulation with Python
# * Can work with large datasets (millions of rows)
# * Faster for complicated manipulations
# * Better for cleaning and/or pre-processing data
# * Can automate workflows in a larger data pipeline
#
# In short, spreadsheet software is better for browsing small datasets and making moderate adjustments. Pandas is better for automating data cleaning processes that require large or complex data manipulation.
#
# Pandas can interpret a wide variety of data sources, including Excel files, CSV files, and Python objects like lists and dictionaries. Pandas converts these into two fundamental objects:
#
# * Data Series- a single column of data
# * DataFrame- a table of data containing multiple columns and rows
# # Pandas Series
#
# We can think of a Series as a single column of data. A DataFrame then is made by combining Series objects side-by-side into a table that has both height and width. Let's create a Series based on this data about the world's ten most-populated countries [according to Wikipedia](https://en.wikipedia.org/wiki/List_of_countries_and_dependencies_by_population).
#
# |Population (in millions)|
# |---|
# |1,404|
# |1,366|
# |330|
# |269|
# |220|
# |211|
# |206|
# |169|
# |146|
# |127|
#
# We can put the population data into a Series.
# import pandas, `as pd` allows us to shorten typing `pandas` to `pd` for each
import pandas as pd
# +
# Create a data series in Pandas
worldpop = pd.Series([1404, 1366, 330, 269, 220, 211, 206, 169, 146, 127])
# Give our series a name
worldpop.name = 'World Population (In Millions)'
print(worldpop)
# -
# Underneath the Series is a `dtype` which describes the way the data is stored in the Series. Here we see `int64`, denoting the data is a 64-bit integer.
#
# ## `.iloc[]` Integer Location Selection
#
# To the left of each Series is an index number. This index number is very similar to a Python list index; it can help us reference a particular row for data retrieval. Also, like a Python list, the index to a Series begins with 0. We can retrieve individual elements in a Series using the `.iloc` attribute, which stands for "integer location."
# Return the 4th element in our series
worldpop.iloc[3]
# Return a slice of elements in our series
# This slice will not include element 4
worldpop.iloc[2:4]
# By default, our Series has a numerical index like a Python list, but it would be much easier to use if our Series had names like a Python dictionary. We can
#
# It is cumbersome to remember the index number for each country, so we can instead give each row an index with names.
# +
# Rename the index to use names instead of numerical indexes
worldpop.index = [
'China',
'India',
'United States',
'Indonesia',
'Pakistan',
'Brazil',
'Nigeria',
'Bangladesh',
'Russia',
'Mexico'
]
worldpop
# -
# ## `.loc[]` Location Selection
# Now we can also reference each element by its index name, very similar to how we can supply a key to a dictionary to get a value. We use the `.loc` attribute.
# Return the series value for Nigeria
worldpop.loc['Nigeria']
# Return a series value for Indonesia and Mexico
worldpop.loc[['Indonesia', 'Mexico']]
# Return a slice from Nigeria to Russia
# This slice will include the final element!
worldpop.loc['Nigeria':'Russia']
# A Series is like an ordered dictionary. In fact, we can create a Series out of a list (where the index will automatically be numerical starting at 0) or a dictionary (where the keys are the index).
# +
# Creating a Series from a dictionary
# Based on most populous cities in the world according to Wikipedia
worldcitiespop = pd.Series({
'Tokyo': 37,
'Delhi': 28,
'Shanghai': 25,
'São Paulo': 21,
'Mexico City': 21,
'Cairo': 20,
'Mumbai': 19,
'Beijing': 19,
'Dhaka': 19,
'Osaka': 19,
}, name='World City Populations (In Millions)')
#Return the series
worldcitiespop
# -
# ## Boolean Expressions
#
# We have seen already how we can select a particular value in a series by using an index name or number. We can also select particular values using Boolean expressions. An expression will evaluate to a Truth Table.
# Which countries have populations greater than 200 million?
worldpop > 200
# Instead of evaluating to a Truth Table, we can also evaluate to a smaller series.
# +
# Evaluate worldpop for `worldpop > 200`
worldpop.loc[worldpop > 200]
# If we wanted to save this to a new series variable
#new_series = worldpop[worldpop > 200]
# -
# Pandas uses `|` to represent `or` operations. It uses `&` to represent `and` operations. We can also use `~` for negation.
#
# |Pandas Operator|Boolean|Requires|
# |---|---|---|
# |&|and|All required to `True`|
# |\||or|If any are `True`|
# |~|not|The opposite|
worldpop.loc[(worldpop > 500) | (worldpop < 250)]
# ## Modifying a Series
#
# We can use an initialization statement to change a value in our Series.
# Change the population of China to 1500
worldpop.loc['China'] = 1500
print(worldpop)
# Change the population of several countries based on an expression
worldpop.loc[worldpop < 300] = 25
worldpop
# ## Summary of Pandas Series
#
# * A Series is a single column of data that may contain a Name and Index
# * Use `.iloc` to select a row by index number
# * Use `.loc` to select a row by index name
# * Use an initialization statement to change values
# * Boolean operators include & (and), | (or), ~ (negation)
# # Pandas DataFrame
#
# If a Series is like a column of data, a DataFrame is like a table connecting multiple columns together. DataFrames can contain thousands or millions of rows and columns. When working with DataFrames, we are usually using a dataset that has been compiled by someone else. Often the data will be in the form of a CSV or Excel file.
# +
import pandas as pd
# Create a DataFrame `df` from the CSV file 'sample2.csv'
df = pd.read_csv('data/sample2.csv', index_col='Username')
# -
# ## Exploring DataFrame Contents
# Now that we have a DataFrame called `df`, we need to learn a little more about its contents. The first step is usually to explore the DataFrame's attributes. Attributes are properties of the dataset (not functions), so they do not have parentheses `()` after them.
#
# |Attribute|Reveals|
# |---|---|
# |.shape| The number of rows and columns|
# |.info| The shape plus the first and last 5 rows|
# |.columns| The name of each column|
# |.rows| The name of each row|
# Use `.shape` to find rows and columns in the DataFrame
df.shape
# Use `.info` to find the shape plus the first and last five rows of the DataFrame
df.info
# Use `.columns` to find the name of each column (if they are named)
df.columns
# We can use `.index` attribute to discover the name for each row in our DataFrame. We set the index column to `Username`, but `Identifier` would also make sense. If no column is chosen, a numeric index is created starting at 0.
# Use `.index` to list the rows of our DataFrame
df.index
# ## Preview with `.head()` and `.tail()`
# We can also use the `.head()` and `.tail` methods to get a preview of our DataFrame.
# Use `.head()` to see the first five lines
# Pass an integer into .head() to see a different number of lines
df.head()
# Use `.tail()` to see the last five lines
# Pass an integer into .tail() to see a different number lines
df.tail()
# ### Display More Rows or Columns
# By default, Pandas limits the number of rows and columns to display. If desired, we can increase or decrease the number to display. If your DataFrame has limited number of rows or columns, you may wish to show all of them.
# +
# Show all columns
# Set `None` to an integer to show a set number
pd.set_option('display.max_columns', None)
# Show all rows
# Set `None` to an integer to show a set number
# Be careful if your dataset is thousands of lines long!
pd.set_option('display.max_rows', None)
# -
# ## Change Column Names
# If we wanted to change the column names, one option is to modify the original data file. We can also change the column names in the DataFrame.
# Updating all column names at once
df.columns = ['email', 'Identifier', 'First name', 'Last name']
df
# Updating a single column name
df.rename(columns={'email': 'Login email'}, inplace=True)
df
# ## Reset the Index
#
# When we created the dataframe, we used the `index_col` attribute to set the index column to the `Username` column.
#
# ```df = pd.read_csv('data/sample2.csv', index_col='Username')```
#
# We could reset the index to a numerical index starting at 0 using the `.reset_index()` method.
# Reset the Index for the DataFrame to integers
# creating a new column
# Passing a `inplace=True` makes the change immediately
df.reset_index()
# For many operations that will alter a DataFrame, such as `.reset_index`, the changes will be previewed unless a `inplace=True` parameter is passed. This allows users to preview changes to the data before implementing them in a permanent fashion. Of course, you should always work on a copy of your data in case a manipulation goes awry.
# Confirm index has not been changed
df
# Make the change to reset the index
df.reset_index(inplace=True)
# Print the index, now changed
df
# Change the index back to `Username`
df.set_index('Username', inplace=True)
df
# ## Sorting the Index
#
# We can sort the index by using `sort_index()`.
# Sort the DataFrame by ascending order
df.sort_index()
# Sort by descending order
df.sort_index(ascending=False)
# ## `.loc[]` and `.iloc[]` Selection
#
# Like Series, DataFrames can use the `.iloc[]` and `.loc[]` methods for selection. To select a particular element, we need to supply a row *and* a column.
#
# View our DataFrame for reference
df
# Return the value for the specified row and column
df.iloc[6, 3]
# Return the value for the specified row and column
df.loc['booker12', '<NAME>']
# Select an entire row
df.loc['redtree333', :]
# Technically, we could also use: `df.loc['redtree333']` for the same result, but including the `, :` makes our row and column selections explicit, where the `:` is basically a slice that includes the whole column. Using a `:` is required if we want to select an entire column using `.loc[]` since the row selection comes before the column selection.
# Select an entire column
df.loc[:, 'Login email']
# Of course, we can use the `:` to make a slice using `.loc[]` or `.loc`.
# Slicing rows and columns using `.iloc`
df.iloc[0:3, 1:4]
# **Note that `.iloc[]` slicing is not inclusive of the final value, similar to a Python list**. On the other hand, `.loc[]` slicing *is* inclusive. The reason for this difference is that it would make the code confusing since we would need to include whatever name is *after* the name we want to include.
# Slicing rows and columns using `.loc`
df.loc['booker12':'french999', 'Login email':'<NAME>']
# ## Boolean Expressions
# We can also use Boolean expressions to select based on the contents of the elements. We can use these expressions to create filters for selecting particular rows or columns.
#
# |Pandas Operator|Boolean|Requires|
# |---|---|---|
# |&|and|All required to `True`|
# |\||or|If any are `True`|
# |~|not|The opposite|
#
df
# Return a Truth Table for the `Identifier` column
# Where the Identifier is more than 4000
df.loc[:, 'Identifier'] > 4000
# +
# Preview every row where the Identifier is more than 4000
id_filter = (df.loc[:, 'Identifier'] > 4000)
df.loc[id_filter, :]
# Alternatively, the whole expression can be written out
# But this can be a little more difficult to read
# In this case, it is a good idea to include parentheses
# To make clear the row filter is one expression
#df.loc[(df.loc[:, 'Identifier'] > 4000), :]
# -
# Preview every row with Last name not "Smith"
name_filter = df.loc[:, 'Last name'] == 'Smith'
df.loc[name_filter, :]
# Select the row with `First Name` of Jamie
# And last name of `Smith`
name_filter = (df.loc[:, 'Last name'] == 'Smith') & (df.loc[:, 'First name'] == 'Jamie')
df.loc[name_filter, :]
# +
# Find every row with Last Name not `Smith`
name_filter = (df.loc[:, 'Last name'] == 'Smith')
df.loc[~name_filter, :]
# Or alternatively
#name_filter = (df.loc[:, 'Last name'] != 'Smith')
#df.loc[name_filter, :]
# -
# ## Modifying a DataFrame
#
# A single element can be changed with an initialization statement.
# Change a value using `.loc[]`
df.loc['jenkins46', 'First name'] = 'Mark'
df
# We can also use filters for more powerful manipulation.
# Create a string filter that checks for email addresses containing
# 'example.com'. For missing (na) elements, output `False` instead of NaN.
email_filt = df['Login email'].str.contains('example.com', na=False)
email_filt
# Re-Initialize `df` without the users with no email address
df = df[email_filt]
df
# ## Dropping Rows Without Data
# There is also a `.dropna()` method specifically for dropping rows without data
# Recreate the DataFrame `df` from the CSV file 'sample2.csv'
df = pd.read_csv('data/sample2.csv', index_col='Username')
df # Confirm the NaN fields have returned
# Remove all rows without a `Login email` using `.dropna()`
df = df.dropna(subset=['Login email'])
df # Confirm the fields were dropped
# ## Summary of Pandas DataFrames
#
# * A DataFrame has multiple rows and columns
# * Use attributes along with `.head()` and `.tail()` to explore the DataFrame
# * Use `.iloc` and `.loc` to select an column, row, or element
# * Use `inplace=True` to confirm certain manipulations
# * Filters and Boolean Operators can be powerful selectors
# * Use an initialization statement to change one or many elements
# * Drop rows without data using the `.dropna()` method
|
pandas-1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# 1) With "<NAME>" and "<NAME>" there are a lot of "Lil" musicians. Do a search and print a list of 50 that are playable in the USA (or the country of your choice), along with their popularity score. <br />
# +
import requests
response = requests.get('https://api.spotify.com/v1/search?query=artist:lil&type=artist&market=us&limit=50')
data = response.json()
artists = data['artists']['items']
for artist in artists:
print(artist['name'], artist['popularity'])
# -
# 2) What genres are most represented in the search results? Edit your previous printout to also display a list of their genres in the format "GENRE_1, GENRE_2, GENRE_3". If there are no genres, print "No genres listed". <br />
for artist in artists:
if not artist['genres']:
print(artist['name'], artist['popularity'], 'No genres listed')
else:
print(artist['name'], artist['popularity'], ', '.join(artist['genres']))
# +
genre_list = []
for artist in artists:
for genre in artist['genres']:
genre_list.append(genre)
sorted_genre = sorted(genre_list)
genre_list_number = range(len(sorted_genre))
genre_count = 0
for number in genre_list_number:
if not sorted_genre[number] == sorted_genre[number - 1]:
print((sorted_genre[number]), genre_list.count(sorted_genre[number]))
if genre_count < genre_list.count(sorted_genre[number]):
genre_count = genre_list.count(sorted_genre[number])
freq_genre = sorted_genre[number]
print('')
print('With', genre_count, 'artists,', freq_genre, 'is the most represented in search results.')
# -
numbers = [72, 3, 0, 72, 34, 72, 3]
# Tip: "how to join a list Python" might be a helpful search <br />
# 3) Use a for loop to determine who BESIDES <NAME> has the highest popularity rating. Is it the same artist who has the largest number of followers? <br />
# +
highest_pop = 0
for artist in artists:
if artist['name'] != '<NAME>' and highest_pop < artist['popularity']:
highest_pop = artist['popularity']
highest_pop_artist = artist['name']
print(highest_pop_artist, 'is the second-most-popular artist with \"Lil\" in his/her name.')
most_followers = 0
for artist in artists:
if most_followers < artist['followers']['total']:
most_followers = artist['followers']['total']
most_followers_artist = artist['name']
print(most_followers_artist, 'has', most_followers, 'followers.')
if highest_pop_artist == most_followers_artist:
print('The second-most-popular \'Lil\' artist is also the one with the most followers.')
else:
print('The second-most-popular \'Lil\' artist and the one with the most followers are different people.')
# -
# 4) Print a list of Lil's that are more popular than <NAME>. <br />
for artist in artists:
if artist['name'] == '<NAME>':
more_popular = artist['popularity']
for artist in artists:
if more_popular < artist ['popularity']:
print(artist['name'], 'is more popular than <NAME> with a popularity score of', artist['popularity'])
# 5) Pick two of your favorite Lils to fight it out, and use their IDs to print out their top tracks. <br />
# +
wayne_id = '55Aa2cqylxrFIXC767Z865'
wayne_response = requests.get('https://api.spotify.com/v1/artists/' + wayne_id + '/top-tracks?country=us')
wayne_data = wayne_response.json()
print('<NAME>\'s top tracks:')
wayne_tracks = wayne_data['tracks']
for track in wayne_tracks:
print(track['name'])
print('')
kim_id = '5tth2a3v0sWwV1C7bApBdX'
kim_response = requests.get('https://api.spotify.com/v1/artists/' + kim_id + '/top-tracks?country=us')
kim_data = kim_response.json()
print('<NAME>\'s top tracks:')
kim_tracks = kim_data['tracks']
for track in kim_tracks:
print(track['name'])
# -
# Tip: You're going to be making two separate requests, be sure you DO NOT save them into the same variable. <br />
# 6) Will the world explode if a musicians swears? Get an average popularity for their explicit songs vs. their non-explicit songs. How many minutes of explicit songs do they have? Non-explicit? <br />
# +
print('<NAME>\'s explicit top tracks:')
ew_total_pop = 0
ew_total_tracks = 0
ew_playtime = 0
for track in wayne_tracks:
if track['explicit']:
ew_total_pop = ew_total_pop + track['popularity']
ew_total_tracks = ew_total_tracks + 1
ew_playtime = ew_playtime + track['duration_ms']/60000
if ew_total_tracks == 0:
print('There are no explicit tracks.')
else:
print('The average popularity is', ew_total_pop / ew_total_tracks)
print('He has', ew_playtime, 'minutes of explicit music in his top tracks.')
print('')
print('<NAME>\'s non-explicit top tracks:')
nw_total_pop = 0
nw_total_tracks = 0
nw_playtime = 0
for track in wayne_tracks:
if not track['explicit']:
nw_total_pop = nw_total_pop + track ['popularity']
nw_total_tracks = nw_total_tracks + 1
nw_playtime = nw_playtime + track['duration_ms']/60000
if nw_total_tracks == 0:
print('There are no non-explicit tracks.')
else:
print('The average popularity is', nw_total_pop / nw_total_tracks)
print('He has', nw_playtime, 'minutes of non-explicit music in his top tracks.')
print('')
print('<NAME>\'s explicit top tracks:')
ek_total_pop = 0
ek_total_tracks = 0
ek_playtime = 0
for track in kim_tracks:
if track['explicit']:
ek_total_pop = ek_total_pop + track ['popularity']
ek_total_tracks = ek_total_tracks + 1
ek_playtime = ek_playtime + track['duration_ms']/60000
if ek_total_tracks == 0:
print('There are no explicit tracks.')
else:
print('The average popularity is', ek_total_pop / ek_total_tracks)
print('She has', ek_playtime, 'minutes of explicit music in her top tracks.')
print('')
print('<NAME>\'s non-explicit top tracks:')
nk_total_pop = 0
nk_total_tracks = 0
nk_playtime = 0
for track in kim_tracks:
if not track['explicit']:
nk_total_pop = nk_total_pop + track ['popularity']
nk_total_tracks = nk_total_tracks + 1
nk_playtime = nk_playtime + track['duration_ms']/60000
if nk_total_tracks == 0:
print('There are no non-explicit tracks.')
else:
print('The average popularity is', nk_total_pop / nk_total_tracks)
print('She has', nk_playtime, 'minutes of non-explicit music in her top tracks.')
# -
# 7) Since we're talking about Lils, what about Biggies? How many total "Biggie" artists are there? How many total "Lil"s? If you made 1 request every 5 seconds, how long would it take to download information on all the Lils vs the Biggies? <br />
# +
biggie_response = requests.get('https://api.spotify.com/v1/search?query=artist:biggie&type=artist&market=us&limit=50')
biggie_data = biggie_response.json()
biggie_artists = biggie_data['artists']['items']
total_biggies = 0
for artist in biggie_artists:
total_biggies = total_biggies + 1
print('There are', total_biggies, 'Biggies on Spotify.')
print('It would take', total_biggies * 5, 'seconds to request all of the Biggies if you were requesting one every five seconds.')
print('')
# -
pages = range(90)
total_lils = 0
for page in pages:
lil_response = requests.get('https://api.spotify.com/v1/search?query=artist:lil&type=artist&market=us&limit=50&offset=' + str(page * 50))
lil_data = lil_response.json()
lil_artists = lil_data['artists']['items']
for artist in lil_artists:
total_lils = total_lils + 1
print('There are', total_lils, 'Lils on Spotify.')
print('It would take', round(total_lils / 12), 'minutes to request all of the Lils if you were requesting one every five seconds.')
# 8) Out of the top 50 "Lil"s and the top 50 "Biggie"s, who is more popular on average? <br />
biggie_total_pop = 0
for artist in biggie_artists:
biggie_total_pop = biggie_total_pop + artist['popularity']
biggie_avg_pop = biggie_total_pop / 50
lil_response_pg1 = requests.get('https://api.spotify.com/v1/search?query=artist:lil&type=artist&market=us&limit=50')
lil_data_pg1 = lil_response_pg1.json()
lil_artists_pg1 = lil_data_pg1['artists']['items']
lil_total_pop = 0
for artist in lil_artists_pg1:
lil_total_pop = lil_total_pop + artist['popularity']
lil_avg_pop = lil_total_pop / 50
if biggie_avg_pop > lil_avg_pop:
print('The top 50 biggies are more popular.')
elif biggie_avg_pop < lil_avg_pop:
print('The top 50 lils are more popular.')
else:
print('They are equally popular.')
|
05/.ipynb_checkpoints/Spotify-API-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Necessary imports
# +
import numpy as np
import matplotlib.pyplot as plt
from dojo.dimred import LinearDiscriminantAnalysis, PrincipalComponentAnalysis
from dojo.preprocessing import LabelEncoder
from sklearn.datasets import load_iris
# %matplotlib inline
# -
# ## Loading data
# +
iris = load_iris()
data = np.column_stack((iris["data"], iris["target"]))
np.random.shuffle(data)
X, y = data[:, :-1], data[:, -1]
y = LabelEncoder().fit_transform(y)
# -
# ## Building the model and transforming the data
# +
lda = LinearDiscriminantAnalysis(n_components=2)
pca = PrincipalComponentAnalysis(n_components=2)
X_lda = lda.fit_transform(X, y)
X_pca = pca.fit_transform(X)
# -
# ## Visualize
label_dict = {
0: "setosa",
1: "versicolor",
2: "virginica"
}
def plot_lda():
for label,marker,color in zip(
range(3),('^', 's', 'o'),('blue', 'red', 'green')):
plt.scatter(x=X_lda[:,0].real[y == label],
y=X_lda[:,1].real[y == label],
marker=marker,
color=color,
alpha=0.5,
label=label_dict[label]
)
plt.xlabel('LD1')
plt.ylabel('LD2')
leg = plt.legend(loc='upper right', fancybox=True)
leg.get_frame().set_alpha(0.5)
plt.title('LDA: Iris projection onto the first 2 linear discriminants')
plt.grid()
plt.show()
def plot_pca():
for label,marker,color in zip(
range(3),('^', 's', 'o'),('blue', 'red', 'green')):
plt.scatter(x=X_pca[:,0].real[y == label],
y=X_pca[:,1].real[y == label],
marker=marker,
color=color,
alpha=0.5,
label=label_dict[label]
)
plt.xlabel('PC1')
plt.ylabel('PC2')
leg = plt.legend(loc='upper right', fancybox=True)
leg.get_frame().set_alpha(0.5)
plt.title('PCA: Iris projection onto the first 2 principal components')
plt.grid()
plt.show()
plot_lda()
plot_pca()
|
examples/PCA-LDA comparison.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="ni9VMY1GIYlK"
# # Ejercicio 1. Transfer Learning con VGG16
#
# Ejercicio 1 del tutorial de Transfer Learning.
#
# GPT2: Diseño y Gestión de Proyectos en Data Science II.
# [Máster en Data Science y Big Data](http://masterds.es/) de la [Universidad de Sevilla](http://www.us.es).
#
# 25/06/2020. Profesor: [<NAME>](http://www.cs.us.es/~mdelamor)
#
# Este ejercicio puede ayudar a mejorar las habilidades con Keras. Para ello se propone emplear el modelo VGG16, el cual es más sencillo y que ya habéis visto en clase (o accediendo [aquí](https://github.com/fsancho/DL/blob/master/4.%20Redes%20Convolucionales/4.3.%20CNN%20Preentrenadas.ipynb)).
# + [markdown] colab_type="text" id="_jBmnvUlIYlO"
# ## 1. Importación de librerías y funciones auxiliares <a class="anchor" id="transferimp"></a>
# + id="y1r3-5CbamCL" colab_type="code" colab={}
# Antes de nada, si estás en Google Colab, evalúa esta celda:
import os
work_dir = "/content/TL-tutorial/"
if os.getcwd() != work_dir:
# !git clone https://github.com/miguelamda/TL-tutorial.git
os.chdir(work_dir)
# + colab_type="code" id="RvEmFXz-IYlP" colab={}
# %matplotlib inline
import matplotlib.pyplot as plt
import PIL
import tensorflow as tf
import numpy as np
import os
# + [markdown] colab_type="text" id="7QO-LQbbIYlb"
# A continuación la importación de la API de Keras. Como **primer ejercicio**, busca como se llama la función que carga el modelo VGG16, e importala en la celda siguiente.
# + colab_type="code" id="yFQhw0KuIYlc" colab={"base_uri": "https://localhost:8080/", "height": 52} outputId="16e3dcd6-1eb4-4354-bacd-ce1793db22b9"
from tensorflow import keras
from keras.models import Model, Sequential
from keras.layers import Dense, Flatten, Dropout
from keras.preprocessing.image import ImageDataGenerator
from keras.optimizers import Adam, RMSprop
# Importa a continuación la función que carga el modelo VGG16
from keras.applications import VGG16
from keras.applications.vgg16 import preprocess_input, decode_predictions
tf.__version__
# + [markdown] colab_type="text" id="QRUx2exEIYlg"
# Vamos a usar las mismas funciones auxiliares que en el tutorial, las tienes a continuación, todas en una sola celda para definirlas más rápido.
# + colab_type="code" id="uO5HEcP5IYd6" colab={}
def path_join(dirname, filenames):
return [os.path.join(dirname, filename) for filename in filenames]
def plot_images(images, cls_true, cls_pred=None, smooth=True):
assert len(images) == len(cls_true)
# Crea una figura con sub-gráficas.
fig, axes = plt.subplots(3, 3)
# Ajusta el espacio vertical.
if cls_pred is None:
hspace = 0.3
else:
hspace = 0.6
fig.subplots_adjust(hspace=hspace, wspace=0.3)
# Tipo de interpolación.
if smooth:
interpolation = 'spline16'
else:
interpolation = 'nearest'
for i, ax in enumerate(axes.flat):
# Puede haber menos de 9 imágenes, nos aseguramos que no falle.
if i < len(images):
# Dibuja imagen.
ax.imshow(images[i],
interpolation=interpolation)
# Number de la true class.
cls_true_name = class_names[cls_true[i]]
# Muestra clases predichas y verdaderas.
if cls_pred is None:
xlabel = "True: {0}".format(cls_true_name)
else:
# Nombre de la clase predicha.
cls_pred_name = class_names[cls_pred[i]]
xlabel = "True: {0}\nPred: {1}".format(cls_true_name, cls_pred_name)
# Muestra las clases con la etiqueta en el eje x.
ax.set_xlabel(xlabel)
# Elimina ticks en la gráfica.
ax.set_xticks([])
ax.set_yticks([])
# Asegurar que la gráfica se muestra correctamente con gráficos múltiples
# en una sola celda Notebook.
plt.show()
# Importa una función de sklearn para calcular la matriz de confusión.
from sklearn.metrics import confusion_matrix
def print_confusion_matrix(cls_pred):
# cls_pred es un array del número de la clase predicha para
# todas las imágenes del conjunto de test.
# Obtiene la matriz de confusión usando sklearn.
cm = confusion_matrix(y_true=cls_test, # True class para el conjunto de test.
y_pred=cls_pred) # Predicted class.
print("Matriz de confusión:")
# Imprime la matriz de confusión como texto.
print(cm)
# Imprime los nombres de clases para facilitar la referencia.
for i, class_name in enumerate(class_names):
print("({0}) {1}".format(i, class_name))
def plot_example_errors(cls_pred):
# cls_pred es un array del número de la clase predicha para
# todas las imágenes en el conjunto de test.
# Array booleano indicando si la clase predicha es incorrecta.
incorrect = (cls_pred != cls_test)
# Obtiene las rutas de ficheros para las imágenes que son clasificadas incorrectamente.
image_paths = np.array(image_paths_test)[incorrect]
# Carga las primeras 9 imágenes.
images = load_images(image_paths=image_paths[0:9])
# Obtiene las clases predichas para esas imágenes.
cls_pred = cls_pred[incorrect]
# Obtiene las clases de verdad para esas imágenes.
cls_true = cls_test[incorrect]
# Muestra las 9 imágenes que hemos cargado y sus correspondientes clases.
# Tenemos solo 9 imágenes, por lo que no hace falta dividirlas otra vez.
plot_images(images=images,
cls_true=cls_true[0:9],
cls_pred=cls_pred[0:9])
def example_errors(model=None):
# El generador de datos de Keras para el conjunto de test se debe resetear
# antes del procesamiento. Esto es porque el generador va a iterar
# infintamente y mantendrá un índice interno en el dataset.
# Por tanto, se podrá comenzar por el medio del conjunto de test si no lo
# reseteamos primero. Esto imposibilita encajar las clases predichas con
# las imágenes de entrada. Si reseteamos el generador, entonces siempre
# compienza por el comienzo, así que sabemos exáctamente qué imágenes
# de entrada se están usando.
if model is None:
model = new_model
generator_test.reset()
# Predecir las clases para todas las imágenes del conjunto de test.
y_pred = model.predict_generator(generator_test,
steps=steps_test)
# Convertir las clases predichas de arrays a enteros.
cls_pred = np.argmax(y_pred,axis=1)
# Muestra los ejemplos de imágenes mal clasificados.
plot_example_errors(cls_pred)
# Muestra la matriz de confusión.
print_confusion_matrix(cls_pred)
def load_images(image_paths):
# Carga las imágenes de disco.
images = [plt.imread(path) for path in image_paths]
# Convierte a un array de numpy y lo devuelve.
return np.asarray(images)
def plot_training_history(history):
# Obtiene la precisión de clasificación y el valor de pérdida para el
# conjunto de entrenamiento.
acc = history.history['categorical_accuracy']
loss = history.history['loss']
# También para el conjunto de validación (solo usamos el del conjunto de test).
val_acc = history.history['val_categorical_accuracy']
val_loss = history.history['val_loss']
# Muestra el valor del accuracy y pérdida para el conjunto de entrenamiento.
plt.plot(acc, linestyle='-', color='b', label='Training Acc.')
plt.plot(loss, 'o', color='b', label='Training Loss')
# Muestra el del conjunto de test.
plt.plot(val_acc, linestyle='--', color='r', label='Test Acc.')
plt.plot(val_loss, 'o', color='r', label='Test Loss')
# Muestra el título y la leyenda.
plt.title('Training and Test Accuracy')
plt.legend()
# Se asegura de mostrar la gráfica correctamente.
plt.show()
# + [markdown] colab_type="text" id="ExBplxfMIYlm"
# ## 2. El Modelo Pre-Entrenado: VGG16
#
# Lo siguiente crea una instancia del modelo VGG16 pre-entrenado usando la API de [Keras](https://keras.io/). Esto descarga automáticamente los archivos necesarios si no los tiene ya.
#
# El modelo VGG16 contiene una parte convolucional y una parte completamente conectada (o densa) que se utiliza para la clasificación. Si `include_top=True` entonces se descarga todo el modelo VGG16 que tiene unos 528 MB. Si `include_top=False` entonces sólo se descarga la parte convolucional del modelo VGG16, que es de sólo 57 MB. Descaragaremos esta última versión.
# + [markdown] colab_type="text" id="x_jS1EYVIYlo"
# 
# + colab_type="code" id="w0TMoN3RIYlp" colab={}
vggmodel = VGG16(include_top=True)
# + [markdown] colab_type="text" id="saAfmzgGIYlt"
# ## 3. El Dataset: Knifey-Spoony
#
# Carga el dataset tal y como se vió en el tutorial. A continuación las líneas de código.
# + id="lBEvDoALGPrR" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 104} outputId="2ac2bd7b-80d3-464e-e093-5408aba29218"
# Carga el dataset empleando el fichero kinfey.py
import knifey
# Descarga el dataset, si no se ha descargado ya
knifey.maybe_download_and_extract()
# Adapta la estructura de carpetas para Keras
knifey.copy_files()
# Define las rutas a los directorios de train y test
train_dir = knifey.train_dir
test_dir = knifey.test_dir
# + [markdown] colab_type="text" id="BTWfUl-ZIYlt"
# ## 4. El Canal de Entrada
#
# Para definir el pipeline de entrada para el modelo, primero necesitamos saber la forma de los tensores esperados como entrada por el modelo VGG16 pre-entrenado. En este caso, ¿qué forma tienen las imágenes de entrada?
# + colab_type="code" id="uCCzzSLEIYlu" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="8df7edf8-5489-4926-e7d1-43c4dc97f9b3"
input_shape = vggmodel.layers[0].output_shape[1:3]
input_shape
# + [markdown] colab_type="text" id="IZVb4TpsIYlw"
# Define a continuación un *generador de datos* que haga aumentado mediante transformaciones aleatorias. Para VGG16, es necesario tan solo reescalar los píxeles a 1.0/255, así que no hace falta usar la función de preprocesamiento de entrada.
# + colab_type="code" id="mHxjWS03IYlx" colab={}
datagen_train = ImageDataGenerator(
rescale=1./255, # En VGG16 el preprocesamiento es tan solo esta normalización
rotation_range=180,
width_shift_range=0.1,
height_shift_range=0.1,
shear_range=0.1,
zoom_range=[0.9, 1.5],
horizontal_flip=True,
vertical_flip=True,
fill_mode='nearest')
datagen_test = ImageDataGenerator(rescale=1./255)
# + [markdown] colab_type="text" id="B3JX5692IYl0"
# Debido a que el modelo VGG16 es muy grande, el tamaño del batch no puede ser demasiado grande.
# + colab_type="code" id="ZL3O-p5LIYl1" colab={}
batch_size = 20
# + [markdown] colab_type="text" id="_7cmwiLlIYl5"
# Podemos guardar las imágenes transformadas aleatoriamente durante el entrenamiento, para comprobar si han sido demasiado distorsionadas, por lo que tendríamos que ajustar los parámetros del generador de datos anterior.
# + colab_type="code" id="B6PWMMyaIYl5" colab={}
if True:
save_to_dir = None
else:
save_to_dir='augmented_images/'
# + [markdown] colab_type="text" id="UN_KAovWIYl-"
# Ahora creamos el generador de datos real que leerá los archivos del disco, redimensionará las imágenes y devolverá un lote aleatorio.
# + colab_type="code" id="9503pHv7IYl-" colab={"base_uri": "https://localhost:8080/", "height": 52} outputId="6ca998e3-f302-4953-84a0-97b81d0f641c"
generator_train = datagen_train.flow_from_directory(directory=train_dir,
target_size=input_shape,
batch_size=batch_size,
shuffle=True,
save_to_dir=save_to_dir)
generator_test = datagen_test.flow_from_directory(directory=test_dir,
target_size=input_shape,
batch_size=batch_size,
shuffle=False)
# + [markdown] colab_type="text" id="-CxntulPIYmB"
# Debido a que nuestro conjunto de pruebas contiene 530 imágenes y el tamaño del batch está configurado en 20, el número de pasos es 26,5 para un procesamiento completo del conjunto de pruebas.
# + colab_type="code" id="GxPlmen3IYmC" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="933c2850-fa7d-41de-b82e-d26891bf8a10"
steps_test = generator_test.n / batch_size
steps_test
# + [markdown] colab_type="text" id="ITl4WRVAIYmG"
# ## 5. Clases del Conjunto de Datos
# + [markdown] id="P6UgVdEf2QYM" colab_type="text"
# Obtengamos las rutas de los ficheros para todas las imágenes en los conjuntos de entrenamiento y de pruebas. Nos vendrá bien para las funciones auxiliares para visualizar ejemplos del conjunto de entrenamiento y de test.
# + id="X7azD7md2TFR" colab_type="code" colab={}
image_paths_train = path_join(train_dir, generator_train.filenames)
image_paths_test = path_join(test_dir, generator_test.filenames)
# + [markdown] colab_type="text" id="mDZYmV9WIYmP"
# Obtengamos las clasificaciones reales (el número correspondiente) de cada imagen en los conjuntos de training y test.
# + colab_type="code" id="0NBjj7-8IYmP" colab={}
cls_train = generator_train.classes
cls_test = generator_test.classes
# + [markdown] colab_type="text" id="FUOuHCXEIYmV"
# Obtengamos los nombres correspondientes de las clases del dataset y el número de ellos.
# + colab_type="code" id="pKG8i_F_IYmV" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="e14849d4-bf6e-4659-af38-0f4506971ff0"
class_names = list(generator_train.class_indices.keys())
num_classes = generator_train.num_classes
num_classes
# + [markdown] colab_type="text" id="pKAI0ppRIYmb"
# Dado que el conjunto de datos Knifey-Spoony está bastante desequilibrado porque tiene pocas imágenes de tenedores, más imágenes de cuchillos y muchas más imágenes de cucharas. Así que vamos a calcular **pesos** que equilibrarán adecuadamente el conjunto de datos.
# + colab_type="code" id="AEtH-2iYIYmb" colab={}
from sklearn.utils.class_weight import compute_class_weight
class_weight = compute_class_weight(class_weight='balanced',
classes=np.unique(cls_train),
y=cls_train)
# + [markdown] colab_type="text" id="EeU-Oh9RIYmd"
# ## 6. Transfer Learning
#
# Primero imprimimos un resumen del modelo VGG16 para poder ver los nombres y tipos de sus capas, así como las formas de los tensores que fluyen entre las capas.
# + colab_type="code" id="2UnlAnpaIYme" colab={"base_uri": "https://localhost:8080/", "height": 953} outputId="9f145287-c6ee-4f51-b854-b2a3f4befec8"
vggmodel.summary()
# + [markdown] colab_type="text" id="6FTqKHLEIYmm"
# En este ejercicio vamos a extraer la parte convolucional de forma personalizada, es decir, desde la entrada hasta una capa deseada (de esta forma podrás hacer transfer learning desde otras capas). Comprueba como difiere esto a como lo habéis hecho en clase anteriormente (o [aquí](https://github.com/fsancho/DL/blob/master/4.%20Redes%20Convolucionales/4.3.%20CNN%20Preentrenadas.ipynb)).
#
# Podemos ver que la última capa convolucional se llama 'block5_pool', y podemos usar Keras para obtener una referencia a dicha capa.
# + colab_type="code" id="i6jBeo8EIYmn" colab={}
transfer_layer = vggmodel.get_layer('block5_pool')
# + [markdown] colab_type="text" id="Y5s6usqHIYmu"
# Nos referiremos a esta capa como la Capa de Transferencia (**Transfer Layer**), puesto que su salida será re-enrutada a nuestra nueva red neuronal completamente conectada que hará la clasificación final sobre el Knifey-Spoony dataset.
#
# La salida de la capa de transferencia tiene la siguiente forma:
# + colab_type="code" id="i5Lip8PPIYmv" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="d63f7b69-d1f2-43d6-f238-26fb7a7ca324"
transfer_layer.output
# + [markdown] colab_type="text" id="9cWI7ePHIYmy"
# Es muy sencillo crear un nuevo modelo usando la API de Keras. Primero tomamos la parte del modelo VGG16 desde su capa de entrada hasta la salida de la capa de transferencia. Podemos llamarlo el modelo convolucional, porque consiste en todas las capas convolucionales del modelo VGG16.
# + colab_type="code" id="d_7qDWHrIYmy" colab={}
conv_model = Model(inputs=vggmodel.input,
outputs=transfer_layer.output)
# + [markdown] colab_type="text" id="jPuxlkH5IYm2"
# Podemos entonces usar Keras para construir un modelo nuevo encima de este.
# + colab_type="code" id="lBsCg7JpIYm3" colab={}
# Creamos un nuevo modelo Secuencial de Keras
nuevo_modelo = Sequential()
# Añadimos la parte convolucional del modelo VGG16 de arriba
nuevo_modelo.add(conv_model)
# Aplanamos la salida del modelo VGG16 dado que ésta viene
# de una capa convolucional.
nuevo_modelo.add(Flatten())
# Añade una capa densa (es decir, totalmente conectada o fully-connected).
# Esto es para combinar las características que el modelo VGG16 ha
# reconocido en la imagen. Usa como función de activación ReLu.
nuevo_modelo.add(Dense(1024, activation='relu'))
# Añade una capa dropout el cual prevendrá el sobreajuste y mejorará
# la capacidad de generalización en datos desconocidos (es decir, el
# conjunto de test). Usa un ratio de 0.5
nuevo_modelo.add(Dropout(0.5))
# Añade la capa final para la clasificación real, usando softmax.
nuevo_modelo.add(Dense(num_classes, activation='softmax'))
# + [markdown] colab_type="text" id="dt3OZNzqIYm5"
# Utilizamos el optimizador Adam con una tasa de aprendizaje bastante baja de 1e-5. La tasa de aprendizaje podría ser mayor, pero si se intenta entrenar más capas del modelo original VGG16, entonces la velocidad de aprendizaje debería ser bastante baja, de lo contrario los pesos preentrenados del modelo VGG16 se distorsionarán y no podrá aprender.
# + colab_type="code" id="sJRnpx1jIYm6" colab={}
optimizer = Adam(learning_rate=1e-5)
# + [markdown] colab_type="text" id="-57CuXcEIYm8"
# Tenemos 3 clases en el Knifey-Spoony dataset, por lo que Keras necesita usar una **función de pérdida** (loss function).
# + colab_type="code" id="VakMjiDlIYm8" colab={}
loss = 'categorical_crossentropy'
# + [markdown] colab_type="text" id="w8BJ_RATIYm_"
# La única **métrica de rendimiento** en la que estamos interesados es en la precisión de clasificación (clasiffication accuracy).
# + colab_type="code" id="eWL9wENYIYm_" colab={}
metrics = ['categorical_accuracy']
# + [markdown] colab_type="text" id="-KaJjO4CIYnC"
# Función auxiliar para imprimir si la capa en el modelo VGG16 debe ser entrenada.
# + colab_type="code" id="QH-TU1-2IYnD" colab={"base_uri": "https://localhost:8080/", "height": 347} outputId="c3becd1d-c8d2-4cb6-93a5-b54abea08a69"
def print_layer_trainable():
for layer in conv_model.layers:
print("{0}:\t{1}".format(layer.trainable, layer.name))
print_layer_trainable()
# + [markdown] colab_type="text" id="V9P6HBDBIYnH"
# Por defecto, todas las capas del modelo VGG16 son entrenables.
# + [markdown] colab_type="text" id="wCOodbuvIYnI"
# En transfer learning estamos inicialmente interesados tan solo en reusar el modelo VGG16 tal cual, como un **extractor de características**, por lo que deshabilitaremos el entrenamiento en todas sus capas.
# + colab_type="code" id="BwlonlTlIYnJ" colab={}
conv_model.trainable = False
# + colab_type="code" id="OjBmyocjIYnN" colab={}
for layer in conv_model.layers:
layer.trainable = False
# + colab_type="code" id="46B8BRI9IYnQ" colab={"base_uri": "https://localhost:8080/", "height": 347} outputId="9f3bad42-1325-4418-aae2-906335fd15b1"
print_layer_trainable()
# + [markdown] colab_type="text" id="3g4uPwR8IYnS"
# Una vez que hayamos cambiado si las capas del modelos son entrenables, necesitamos compilarlo para que los cambios surtan efecto.
# + colab_type="code" id="_fdf_8STIYnT" colab={}
nuevo_modelo.compile(optimizer=optimizer, loss=loss, metrics=metrics)
# + [markdown] colab_type="text" id="iask_euDIYnd"
# A continuación entrenamos el nuevo modelo, lo que se hace con tan solo una llamada a una función en la API de Keras. Definimos 20 épocas y 100 pasos por época (ya que tenemos batches de 20).
# + colab_type="code" id="Y9Tby_mUIYne" colab={"base_uri": "https://localhost:8080/", "height": 731} outputId="c4e5efc9-892f-4354-ea47-be5806e0d7af"
epochs = 20
steps_per_epoch = 100
history = nuevo_modelo.fit_generator(generator=generator_train,
epochs=epochs,
steps_per_epoch=steps_per_epoch,
class_weight=class_weight,
validation_data=generator_test,
validation_steps=steps_test)
# + [markdown] colab_type="text" id="WqKzBQnmIYno"
# Mostremos la gráfica de evolución de las métricas.
# + colab_type="code" id="gPM9vkanIYnq" colab={"base_uri": "https://localhost:8080/", "height": 281} outputId="24f1c00e-ac24-4380-999f-8192e2e2c11b"
plot_training_history(history)
# + [markdown] colab_type="text" id="qqe72_2bIYnw"
# Después del entrenamiento también podemos evaluar el rendimiento del nuevo modelo en el conjunto de pruebas usando una sola llamada de función en la API de Keras.
# + colab_type="code" id="u9Kb2mkyIYnw" colab={}
result = nuevo_modelo.evaluate_generator(generator_test, steps=steps_test)
# + colab_type="code" id="hU1ltSOOIYn0" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="ab571454-3916-40d4-e634-eec459be56ae"
print("Test-set classification accuracy: {0:.2%}".format(result[1]))
# + [markdown] colab_type="text" id="fU1zeX9VIYn2"
# Podemos representar algunos ejemplos de imágenes mal clasificadas del conjunto de pruebas.
# + colab_type="code" id="Yzv7ra1xIYn2" colab={"base_uri": "https://localhost:8080/", "height": 395} outputId="0e1e1742-de83-4a73-9e73-ac6360a32fc4"
example_errors(model=nuevo_modelo)
# + [markdown] colab_type="text" id="mc4q8J-ZIYn4"
# ### 7. Fine-Tuning
#
# Podemos tratar de afinar suavemente algunas de las capas más profundas del modelo VGG16 también. A esto lo llamamos "Ajuste fino", o **Fine Tuning**.
#
# No está claro si Keras usa el booleano `trainable` en cada capa del modelo original VGG16 o si es anulado por el booleano `trainable` en la'meta-capa' que llamamos `conv_layer`. Así que habilitaremos el booleano `trainable` tanto para `conv_layer` como para todas las capas relevantes en el modelo original VGG16.
# + colab_type="code" id="-T2HZwcfIYn5" colab={}
conv_model.trainable = True
# + [markdown] colab_type="text" id="4AIFavVsIYn7"
# Queremos entrenar las últimas dos capas convolucionales, es decir, cuyos nombres contienen 'block5' o 'block4'.
# + colab_type="code" id="LmNYiVoqIYn7" colab={}
for layer in conv_model.layers:
# Booleano de si la capa es entrenable
trainable = ('block5' in layer.name or 'block4' in layer.name)
# Ajusta el booleano de la capa
layer.trainable = trainable
# + [markdown] colab_type="text" id="LhxqtJ7pIYn8"
# Podemos comprobar que esto ha actualizado el booleano `trainable` para las capas relevantes.
# + colab_type="code" id="OMVFTd4nIYn8" colab={"base_uri": "https://localhost:8080/", "height": 347} outputId="a347cff8-5bf4-427b-bc4d-9c15a2fa02f3"
print_layer_trainable()
# + [markdown] colab_type="text" id="j93hktLdIYn-"
# Usaremos el optimizador Adam con un bajo factor de aprendizaje bajo para el ajuste fino, 1e-7.
# + colab_type="code" id="s_r2O5iHIYn-" colab={}
optimizer_fine = Adam(lr=1e-7)
# + [markdown] colab_type="text" id="Ibmrb2bSIYoD"
# Dado que hemos definido un nuevo optimizador y hemos cambiado los booleanos `trainable` para muchas de las capas en el modelo, necesitamos recompilarlo para que los cambios hagan efecto.
# + colab_type="code" id="R9wcT5iGIYoE" colab={}
nuevo_modelo.compile(optimizer=optimizer_fine, loss=loss, metrics=metrics)
# + [markdown] colab_type="text" id="EaVRbGXZIYoH"
# Continuamos por tanto con el entrenamiento por donde lo dejamos anteriormente, ahora aplicando fine-tuning al modelo VGG16 y el nuevo clasificador. Sigamos con 20 épocas.
# + colab_type="code" id="Qk0huhXRIYoH" colab={"base_uri": "https://localhost:8080/", "height": 731} outputId="6345e13a-08c3-4bac-c23f-883bcb0e86f5"
history = nuevo_modelo.fit_generator(generator=generator_train,
epochs=epochs,
steps_per_epoch=steps_per_epoch,
class_weight=class_weight,
validation_data=generator_test,
validation_steps=steps_test)
# + [markdown] colab_type="text" id="qkBfoISEIYoJ"
# Luego podemos mostrar gráficamente los valores de pérdida y precisión de la clasificación a partir del entrenamiento.
# + colab_type="code" id="qRR60KjoIYoJ" colab={"base_uri": "https://localhost:8080/", "height": 281} outputId="28fd789f-f4cc-47bf-a7be-b11fdc6d4aa4"
plot_training_history(history)
# + colab_type="code" id="Vj7i1NkNIYoM" colab={}
result = nuevo_modelo.evaluate_generator(generator_test, steps=steps_test)
# + colab_type="code" id="ZI9aWsCsIYoO" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="80c88750-c778-462e-8715-4c4940197942"
print("Test-set classification accuracy: {0:.2%}".format(result[1]))
# + [markdown] colab_type="text" id="zCt4vpP6IYoP"
# Podemos volver a mostrar algunos ejemplos de imágenes mal clasificadas, y también podemos ver en la matriz de confusión que el modelo sigue teniendo problemas para clasificar correctamente los tenedores.
# + colab_type="code" id="JOohX753IYoQ" colab={"base_uri": "https://localhost:8080/", "height": 395} outputId="93ab01d7-c41c-455e-9278-a0fa8b30d036"
example_errors(model=nuevo_modelo)
# + [markdown] id="6O-QAjuHGPs-" colab_type="text"
# ## License (MIT)
#
# Based on the TensorFlow tutorials by [<NAME>](http://www.hvass-labs.org/)
# / [GitHub](https://github.com/Hvass-Labs/TensorFlow-Tutorials) / [Videos on YouTube](https://www.youtube.com/playlist?list=PL9Hr9sNUjfsmEu1ZniY0XpHSzl5uihcXZ)
#
# Copyright (c) 2016-2017 by [<NAME>](http://www.hvass-labs.org/)
#
# Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
|
soluciones/TransferLearning-ejercicio1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ***Feature extract***
# import some library and load the data
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
df=pd.read_csv('model_df.csv')
df.head()
df.describe()
#Sort the data
df.sort_values(['bookingID','second'],inplace=True)
# +
#Calculate the degree of the phone
df['roll'] = np.arctan2(df['acceleration_y'],df['acceleration_z']) * 180/np.pi
df['pitch'] = np.arctan(-df['acceleration_x']/np.sqrt((df['acceleration_y']**2)+(df['acceleration_z']**2))) * 180/ np.pi
df['compAngleX'] = 0.98 * (df['roll'] + df['gyro_x']) + 0.02 * df['roll']
df['compAngleY'] = 0.98 * (df['pitch'] + df['gyro_x']) + 0.02 * df['pitch']
# -
# *Calculate feature*
df['Bearing_diff']=df['Bearing'].diff()
df.loc[df['second']==0,['Bearing_diff']]= 0
df['Speed_diff']=df['Speed'].diff()
df.loc[df['second']==0,['Speed_diff']]= 0
df['distance'] = df['Speed'] * df['second'].diff()
df['distance'][df['second'] == 0] = 0
df.head()
#Visualize a random trip:
trip1 = df[df['bookingID'] == 1]
trip1.head()
trip1.sort_values('second',inplace=True)
plt.figure(figsize=(25,1))
sns.lineplot(data=trip1,x='second',y='compAngleX')
sns.lineplot(data=trip1,x='second',y='compAngleY')
plt.figure(figsize=(25,1))
sns.lineplot(data=trip1,x='second',y='Speed')
plt.figure(figsize=(25,1))
sns.lineplot(data=trip1,x='second',y='Bearing')
trip2 = df[df['bookingID'] == 1073741824054]
trip2.head()
plt.figure(figsize=(25,1))
sns.lineplot(data=trip2,x='second',y='compAngleX')
sns.lineplot(data=trip2,x='second',y='compAngleY')
plt.figure(figsize=(25,1))
sns.lineplot(data=trip2,x='second',y='Speed')
plt.figure(figsize=(25,1))
sns.lineplot(data=trip2,x='second',y='Bearing')
df['bookingID'].unique()
# Group the data by trip:
def quantile_25(x):
return x.quantile(0.25)
def quantile_5(x):
return x.quantile(0.5)
def quantile_75(x):
return x.quantile(0.75)
def quantile_8(x):
return x.quantile(0.8)
def quantile_9(x):
return x.quantile(0.9)
def triptime(x):
return x.max()
model_df_1 = df.pivot_table(index='bookingID',values = ['distance'], aggfunc=sum)
model_df_2 = df.pivot_table(index='bookingID',values = ['second'], aggfunc=max)
model_df_3 = df.pivot_table(index='bookingID',values=['Speed','Bearing','compAngleX','compAngleY','Bearing_diff','Speed_diff'],aggfunc=[quantile_25,quantile_5,quantile_75,quantile_8,quantile_9])
model_df_4 = df.pivot_table(index='bookingID',values=['Speed','Bearing','compAngleX','compAngleY','Bearing_diff','Speed_diff'],aggfunc=[np.mean,np.std,np.min,np.max])
model_df = model_df_1.join([model_df_2,model_df_3,model_df_4])
model_df.head()
# Save the grouped data
model_df.to_csv('feature_extracted.csv')
|
Feature_extract.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Visualizing Data Using Matplotlib
#
# Knowing how to load data is of limited use if we don't know how to look at the data.
# Thankfully, there is **Matplotlib**!
#
# Matplotlib is a multiplatform data visualization library built on NumPy arrays—see, We
# promised you NumPy would show up again. It was conceived by <NAME> in 2002,
# originally designed as a patch to IPython to enable interactive MATLAB-style plotting from
# the command line. In more recent years, newer and shinier tools have popped up to
# eventually replace Matplotlib (such as `ggplot` and `ggvis` in the R language), but
# Matplotlib remains essential as a well-tested, cross-platform graphics engine.
# ## Importing matplotlib
#
# You might be in luck again: if you followed the advice outlined in the previous chapter and
# installed the Python Anaconda stack, you already have Matplotlib installed and are ready
# to go. Otherwise, you might want to visit http://matplotlib.org for installation
# instructions.
#
# Just as we used <tt>np</tt> shorthand for NumPy, we will use some standard shorthands for the Matplotlib imports:
import matplotlib as mpl
import matplotlib.pyplot as plt
# The <tt>plt</tt> interface is what we will use most often, as we shall see throughout the book.
# ## Producing a simple plot
#
# Without further ado, let's create our first plot.
#
# Let's say we want to produce a simple line plot of the sine function, <tt>sin(x)</tt>. We want the function to be evaluated at all points on the x axis where $0 \leq x < 10$. We will use NumPy's <tt>linspace</tt> function to create a linear spacing on the x axis, from x values 0 to 10, and a total of 100 sampling points:
import numpy as np
x = np.linspace(0, 10, 100)
# We can evaluate the sine function at all points `x` using NumPy's `sin` function, and visualize the result by calling `plt`'s `plot` function:
plt.plot(x, np.sin(x))
# Did you try it yourself? What happened? Did anything show up?
# In order for the plot to show up, we need to add some IPython magic commands. There are two options:
# - <tt>%matplotlib notebook</tt> will lead to interactive plots
# - <tt>%matplotlib inline</tt> will lead to static images of your plots
#
# Check page 37 in the book to find out how to plot from a`.py` script or from within IPython.
# In this book, we will generally opt for the inline option:
# %matplotlib inline
# Now let's try this again:
plt.plot(x, np.sin(x))
# If you want to save the figure for later, you have the option to do so directly from within the Jupyter Notebook:
plt.savefig('figures/02.03-sine.png')
|
Chapter02/02.03-Visualizing-Data-Using-Matplotlib.ipynb
|
// -*- coding: utf-8 -*-
// ---
// jupyter:
// jupytext:
// text_representation:
// extension: .fs
// format_name: light
// format_version: '1.5'
// jupytext_version: 1.14.4
// kernelspec:
// display_name: .NET (F#)
// language: F#
// name: .net-fsharp
// ---
// + dotnet_interactive={"language": "fsharp"}
#r "nuget: MathNet.Numerics.FSharp, 4.15.0"
open MathNet.Numerics.LinearAlgebra
// -
// # Итерационные методы решения линейных систем.
// ## Варинат 9
// + dotnet_interactive={"language": "fsharp"}
let a = matrix [
[12.78572; 1.534675; -3.947418]
[1.534675; 9.709232; 0.918435]
[-3.947418; 0.918435; 7.703946]
]
let b = vector [9.60565; 7.30777; 4.21575]
// + dotnet_interactive={"language": "fsharp"}
let accurateSolution = a.Solve b
printfn "Точное решение СЛАУ: %A" accurateSolution
// -
// **Задание 2.** Преобразовать исходную систему к системе вида x = H * x + g, где H = E − D^(−1) * A, g = D^(−1) * b. Здесь D - диагональная матрица, у которой на диагонали находятся диагональные элементы матрицы A. Вычислить ||H||∞.
// + dotnet_interactive={"language": "fsharp"}
let transform (matrix: Matrix<float>) (freeVector: Vector<float>) =
let n = matrix.RowCount
// H = E - D^(-1) * A
let h = DenseMatrix.init n n (fun i j -> if i = j then 0. else - matrix.[i, j] / matrix.[i, i])
// g = D ^ (-1) * b
let g = DenseVector.init n (fun i -> freeVector.[i] / matrix.[i, i])
h, g
// + dotnet_interactive={"language": "fsharp"}
let (h, g) = transform a b
printfn "Матрица H = %O" h
printfn "Вектор g = %O" g
printfn "||H||_inf = %f" <| h.InfinityNorm()
// + [markdown] dotnet_interactive={"language": "fsharp"}
// **Задание 3.** Найти априорную оценку того k, при котором ||x∗ − xk||∞ < ε, ε = 0.001
// + dotnet_interactive={"language": "fsharp"}
let epsilon = 0.001
let calculatePrioriEstimation (h: Matrix<float>) (g: Vector<float>) (firstEstiomation: Vector<float>) iterationsCount =
h.InfinityNorm() ** (float iterationsCount) * firstEstiomation.InfinityNorm() +
h.InfinityNorm() ** (float iterationsCount) / (1. - h.InfinityNorm()) * g.InfinityNorm()
let getIterationsCount accuracy (h: Matrix<float>) (g: Vector<float>) (firstEstiomation: Vector<float>) =
let mutable iterationsCount = 1
while calculatePrioriEstimation h g firstEstiomation iterationsCount >= accuracy do
iterationsCount <- iterationsCount + 1
int iterationsCount
// + dotnet_interactive={"language": "fsharp"}
let firstEstimation = DenseVector.zero<float> h.RowCount
let approximateIterationCount = getIterationsCount epsilon h g firstEstimation
let prioriEstimation = calculatePrioriEstimation h g firstEstimation approximateIterationCount
printfn "Для получения решения с априорной оценкой %f (< %f) необходимо %i итераций"
<| prioriEstimation
<| epsilon
<| approximateIterationCount
// -
// **Задание 4.** Вычислить решение методом простой итерации с точностью ε = 0.001. Сравнить требуемое фактическое число итераций с априорным значением k. Вывести фактическую погрешность, апостериорную оценку, априорную оценку. Уточнить последнее приближение по Люстернику. Вывести его фактическую погрешность.
// + dotnet_interactive={"language": "fsharp"}
let getMaxEigenValue (matrix: Matrix<float>) =
matrix.Evd().EigenValues.AbsoluteMaximum().Magnitude
// Достаточное условие сходимости: ||H|| < 1
// Необходимое и достаточное условие сходимости: ρ(H) < 1
let solveIterative accuracy (h: Matrix<float>) (g: Vector<float>) step =
let mutable previousEstimation = firstEstimation
let mutable currentEstimation: Vector<float> = step h g previousEstimation
let mutable iterationCount = 1
let calculatePosteriorEstimation (previousEstimation: Vector<float>) (currentEstimation: Vector<float>) =
h.InfinityNorm() / (1. - h.InfinityNorm()) * (currentEstimation - previousEstimation).InfinityNorm()
while calculatePosteriorEstimation previousEstimation currentEstimation >= accuracy do
previousEstimation <- currentEstimation
currentEstimation <- step h g currentEstimation
iterationCount <- iterationCount + 1
let optimizeLusternik (previousEstimation: Vector<float>) (currentEstimation: Vector<float>) =
let maxEigen = getMaxEigenValue h
if maxEigen > 1. then
currentEstimation
else
previousEstimation + (1. / (1. - maxEigen)) * (currentEstimation - previousEstimation)
currentEstimation,
{|
FactIterationCount = iterationCount
PosteriorEstimation = calculatePosteriorEstimation previousEstimation currentEstimation
LusternikOptimization = optimizeLusternik previousEstimation currentEstimation
|}
// + dotnet_interactive={"language": "fsharp"}
let solveSimpleIteration accuracy (h: Matrix<float>) (g: Vector<float>) =
solveIterative accuracy h g <| fun (h: Matrix<float>) (g: Vector<float>) (previousX: Vector<float>) ->
h * previousX + g
// + dotnet_interactive={"language": "fsharp"}
let (solutionSimpleIteration, infoSimpleIteration) = solveSimpleIteration epsilon h g
printfn "Решение системы методом простой итерации: %O" solutionSimpleIteration
printfn "Априорное число итераций: %O" approximateIterationCount
printfn "Фактическое число итераций: %O" infoSimpleIteration.FactIterationCount
printfn "Фактическая погрешность решения: %O" <| (solutionSimpleIteration - accurateSolution).InfinityNorm()
printfn "Априорная оценка решения: %O" prioriEstimation
printfn "Апостериорная оценка решения: %O" infoSimpleIteration.PosteriorEstimation
printfn "Решение с уточнением по Люстернику: %O" infoSimpleIteration.LusternikOptimization
printfn "Фактическая погрешность решения по Люстернику: %O" <| (infoSimpleIteration.LusternikOptimization - accurateSolution).InfinityNorm()
// -
// **Задание 5.** Вычислить решение систем методом Зейделя с точностью ε = 0.001.
// + dotnet_interactive={"language": "fsharp"}
let solveSeidel accuracy (h: Matrix<float>) (g: Vector<float>) =
solveIterative accuracy h g <| fun (h: Matrix<float>) (g: Vector<float>) (previousX: Vector<float>) ->
let x = DenseVector.zero<float> previousX.Count
for i = 0 to x.Count - 1 do
x.[i] <- h.[i, *] * x.[0 .. i - 1].ToColumnMatrix().Stack(previousX.[i .. x.Count - 1].ToColumnMatrix()).Column(0) + g.[i]
x
// + dotnet_interactive={"language": "fsharp"}
let (solutionSeidel, infoSeidel) = solveSeidel epsilon h g
printfn "Решение системы методом простой итерации: %O" solutionSeidel
printfn "Априорное число итераций: %O" approximateIterationCount
printfn "Фактическое число итераций: %O" infoSeidel.FactIterationCount
printfn "Фактическая погрешность решения: %O" <| (solutionSeidel - accurateSolution).InfinityNorm()
printfn "Априорная оценка решения: %O" prioriEstimation
printfn "Апостериорная оценка решения: %O" infoSeidel.PosteriorEstimation
printfn "Решение с уточнением по Люстернику: %O" infoSeidel.LusternikOptimization
printfn "Фактическая погрешность решения по Люстернику: %O" <| (infoSeidel.LusternikOptimization - accurateSolution).InfinityNorm()
// -
// **Задание 7.** Получить решение системы Ax = b методом верхней релаксации с точностью ε = 0.001. В качестве критерия использовать фактическую погрешность.
// + dotnet_interactive={"language": "fsharp"}
// Метод будет сходиться, если матрица самосопряженная, положительно-определенная и кроме того 0 < q < 2.
let solveUpperRelaxation accuracy (h: Matrix<float>) (g: Vector<float>) =
let q = 2. / (1. + sqrt (1. - (getMaxEigenValue h) ** 2.))
solveIterative accuracy h g <| fun (h: Matrix<float>) (g: Vector<float>) (previousX: Vector<float>) ->
let x = DenseVector.zero<float> previousX.Count
for i = 0 to x.Count - 1 do
x.[i] <-
previousX.[i] +
q * (h.[i, 0 .. i - 1] * x.[0 .. i - 1] +
h.[i, i + 1 .. x.Count - 1] * previousX.[i + 1 .. x.Count - 1] -
previousX.[i] + g.[i])
x
// + dotnet_interactive={"language": "fsharp"}
let (solutionUpperRelaxation, infoUpperRelaxation) = solveUpperRelaxation epsilon h g
printfn "Решение системы методом простой итерации: %O" solutionUpperRelaxation
printfn "Априорное число итераций: %O" approximateIterationCount
printfn "Фактическое число итераций: %O" infoUpperRelaxation.FactIterationCount
printfn "Фактическая погрешность решения: %O" <| (solutionUpperRelaxation - accurateSolution).InfinityNorm()
printfn "Априорная оценка решения: %O" prioriEstimation
printfn "Апостериорная оценка решения: %O" infoUpperRelaxation.PosteriorEstimation
printfn "Решение с уточнением по Люстернику: %O" infoUpperRelaxation.LusternikOptimization
printfn "Фактическая погрешность решения по Люстернику: %O" <| (infoUpperRelaxation.LusternikOptimization - accurateSolution).InfinityNorm()
|
notebooks/Lab2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:uncluster]
# language: python
# name: conda-env-uncluster-py
# ---
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('apw-notebook')
# %matplotlib inline
from scipy.integrate import quad
from scipy.special import gamma, gammainc, gammaln
from scipy.interpolate import interp1d
true_a,true_r_s = 0.65463, 15.
# +
def ln_einasto(r, a, r_s):
lnC1 = np.log(a) - np.log(r_s) - gammaln(1/a)
return -(r/r_s)**a + lnC1
def ln_gaussian(x, mu, std):
return -0.5*(x-mu)**2/std**2 - np.log(std) - 0.5*np.log(2*np.pi)
# -
r_grid = np.logspace(-1, 3., 1024)
cdf = np.array([quad(lambda *args: np.exp(ln_einasto(*args)), 0, rr, args=(true_a, true_r_s))[0]
for rr in r_grid])
plt.semilogx(r_grid, ln_einasto(r_grid, true_a, true_r_s))
cdf_func = interp1d(cdf, r_grid)
# sample some true distances that follow the profile
n_data = 128
uu = np.random.uniform(cdf.min(), cdf.max(), size=n_data)
true_r = cdf_func(uu)
d_err = true_r * 0.1 # 10% distance error
d = np.random.normal(true_r, d_err)
bins = np.logspace(-1, 2.5, 18)
plt.hist(true_r, bins=bins, alpha=0.4)
plt.hist(d, bins=bins, alpha=0.4)
plt.xscale('log')
# +
def ln_integrand(r, a, r_s, d, d_err):
return ln_einasto(r, a, r_s) + ln_gaussian(r, d, d_err)
def integrand(r, a, r_s, d, d_err):
return np.exp(ln_integrand(r, a, r_s, d, d_err))
# -
# check normalizations
for i in range(8):
_a = np.random.uniform(0.3, 0.9)
_rs = np.random.uniform(5., 25.)
_d = np.random.uniform(0, 250.)
val,_ = quad(integrand, 0, np.inf, args=(_a, _rs, _d, 0.2*_d), epsabs=1E-13)
# val,_ = quad(lambda *args: np.exp(ln_einasto(*args)), 0, np.inf,
# args=(_a, _rs), epsabs=1E-13)
# val,_ = quad(lambda *args: np.exp(ln_gaussian(*args)), 0, np.inf,
# args=(_d, _d*0.2), epsabs=1E-13)
print(val)
def marg_ln_likelihood(p, ds, d_errs):
a, r_s = p
ln_l = 0.
for d,d_err in zip(ds, d_errs):
val,err = quad(integrand, 0, np.inf, args=(a, r_s, d, d_err), epsabs=1E-13)
if np.abs(err/val) > 0.1:
# print(d, d_err)
# print(val, err)
# raise ValueError("fail")
return -np.inf
ln_l += np.log(val)
return ln_l
quad(integrand, 0, np.inf, args=(val, true_r_s, 208.007536811, 18.0238195762), epsabs=1E-13)
vals = np.linspace(0.5, 0.9, 128)
lls = np.zeros_like(vals)
for i,val in enumerate(vals):
lls[i] = marg_ln_likelihood([val, true_r_s], d, d_err)
fig,axes = plt.subplots(1, 2, figsize=(12,4))
axes[0].plot(vals[lls<0], lls[lls<0])
axes[1].plot(vals[lls<0], np.exp(lls[lls<0]-lls[lls<0].max()))
|
notebooks/Einasto gcs.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Quantitative analysis
# +
import csv
import itertools
import matplotlib.pyplot as plt
import mysql.connector
import numpy as np
import pandas as pd
import pickle
import seaborn as sb
from scipy.cluster.hierarchy import linkage, to_tree, fcluster
user = 'xxxx' # fill in MySQL user
password = '<PASSWORD>' # fill in MySQL pw
db = 'xxxx' # fill in MySQL database name
socket = '/x/x/x/x.sock' # fill in MySQL unix socket
# -
# ## Data
# ### Wrangle accessions
# +
cnx = mysql.connector.connect(user=user, password=password, database=db, unix_socket=socket)
cursor = cnx.cursor()
cursor.execute("SELECT DISTINCT(UniProt_ID), type, type_evidence, type_probability FROM UniProt;")
up_acc = []
types = []
type_evidence = []
type_probability = []
for i in cursor:
up_acc.append(i[0])
types.append(i[1])
type_evidence.append(i[2])
type_probability.append(i[3])
tmp = {'type' : types, 'type_evidence' : type_evidence, 'type_probability' : type_probability}
main_table = pd.DataFrame(tmp, index=up_acc)
#main_table
# +
### check and set confidence level threshold for protein typing
sb.distplot(list(main_table.drop([i for i in main_table.index if main_table.loc[i, 'type_evidence'] != 'ML prediction']).type_probability),
bins=50)
plt.xlim([50, 100])
plt.axvline(74, c='r')
endolysins = [i for i in main_table.index if main_table.loc[i, 'type'] == 'endolysin' and main_table.loc[i, 'type_probability'] >= 75]
vals = [i for i in main_table.index if main_table.loc[i, 'type'] == 'VAL' and main_table.loc[i, 'type_probability'] >= 75]
unclass = [i for i in main_table.index if i not in endolysins and i not in vals]
print('PhaLP includes', len(endolysins), 'endolysins,', len(vals), 'VALs and', len(unclass),
'uncertainly classified phage lytic proteins.')
# + active=""
# ### to write out endolysin accessions
# df = pd.DataFrame(data={"endo_accs": endolysins})
# df.to_csv("75certain_endolysin_accs.csv", sep=',',index=False)
# -
# Endolysins and VALs used for analyses will consist of the proteins that have been called as such with a certainty of at least 75%.
# +
### VALs vs endolysins
cnx = mysql.connector.connect(user=user, password=password, database=db, unix_socket=socket)
cursor = cnx.cursor()
cursor.execute("SELECT ur.protein_sequence, up.UniProt_ID FROM UniProt as up JOIN UniRef as ur WHERE up.UniRef_ID = ur.UniRef_ID;")
endolysin_seqs = []
val_seqs = []
acc2seq = {}
for i in cursor:
if i[1] in endolysins:
endolysin_seqs.append(i[0])
elif i[1] in vals:
val_seqs.append(i[0])
acc2seq[i[1]] = i[0]
print("There are", len(set(acc2seq.values())), "unique AA sequences in total.")
print("There are", len(set(val_seqs)), "unique VAL sequences. These are on average",
int(np.median([len(i) for i in val_seqs])), "AAs long.")
print("There are", len(set(endolysin_seqs)), "unique endolysin sequences. These are on average",
int(np.median([len(i) for i in endolysin_seqs])), "AAs long.")
# -
# ### Wrangle domains
domains = pd.read_csv("domains/custom_domain_clusters.csv", sep=',', index_col="accession",
usecols=['accession', 'abbreviation', 'class', 'sub'])
# +
cbds = []
pgas = []
pgaps = []
pgps = []
pggs = []
pgms = []
pgmts = []
pglts = []
misc = []
sorted_doms = []
for i in domains.index:
if domains.loc[i]['class'] == 'CBD' and domains.loc[i]['abbreviation'] not in sorted_doms:
cbds.append(domains.loc[i]['abbreviation'])
sorted_doms.append(domains.loc[i]['abbreviation'])
elif domains.loc[i]['class'] == 'EAD' and domains.loc[i]['abbreviation'] not in sorted_doms:
if domains.loc[i]['sub'] == 'A':
pgas.append(domains.loc[i]['abbreviation'])
sorted_doms.append(domains.loc[i]['abbreviation'])
elif domains.loc[i]['sub'] == 'A+P':
pgaps.append(domains.loc[i]['abbreviation'])
sorted_doms.append(domains.loc[i]['abbreviation'])
elif domains.loc[i]['sub'] == 'P':
pgps.append(domains.loc[i]['abbreviation'])
sorted_doms.append(domains.loc[i]['abbreviation'])
elif domains.loc[i]['sub'] == 'G':
pggs.append(domains.loc[i]['abbreviation'])
sorted_doms.append(domains.loc[i]['abbreviation'])
elif domains.loc[i]['sub'] == 'M':
pgms.append(domains.loc[i]['abbreviation'])
sorted_doms.append(domains.loc[i]['abbreviation'])
elif domains.loc[i]['sub'] == 'M+T':
pgmts.append(domains.loc[i]['abbreviation'])
sorted_doms.append(domains.loc[i]['abbreviation'])
elif domains.loc[i]['sub'] == 'T':
pglts.append(domains.loc[i]['abbreviation'])
sorted_doms.append(domains.loc[i]['abbreviation'])
elif domains.loc[i]['class'] == 'MISC' and domains.loc[i]['abbreviation'] not in sorted_doms:
misc.append(domains.loc[i]['abbreviation'])
sorted_doms.append(domains.loc[i]['abbreviation'])
amidases = pgas + pgaps
peptidases = pgaps + pgps
muramidases = pgms + pgmts
lts = pgmts + pglts
eads = pgas + pgaps + pgps + pggs + pgms + pgmts + pglts
# -
### Load in architectures
domains_per_entry = {}
with open('simplified_architectures.csv', mode='r') as file:
reader = csv.reader(file)
for row in reader:
domains_per_entry[row[0]] = [i for idx, i in enumerate(row) if idx != 0 and i != '']
print(len(set(itertools.chain.from_iterable(domains_per_entry.values()))), 'distinct domains across', len(list(domains_per_entry.keys())), 'entries.')
lens = [len(v) for v in domains_per_entry.values()]
print('On average', round(np.mean(lens), 2), 'domains found per entry, with a max of', max(lens))
print('{} entries do not have any domains linked to them.'.format(len([i for i in up_acc if i not in list(domains_per_entry.keys())])))
# +
endo_archs = {k:v for k, v in domains_per_entry.items() if k in endolysins}
endo_doms = set(itertools.chain.from_iterable(endo_archs.values()))
val_archs = {k:v for k, v in domains_per_entry.items() if k in vals}
val_doms = set(itertools.chain.from_iterable(val_archs.values()))
uncl_archs = {k:v for k, v in domains_per_entry.items() if k in unclass}
uncl_doms = set(itertools.chain.from_iterable(uncl_archs.values()))
print('ALL:', len(cbds), "unique CBDs,", len(eads), "unique EADs and", len(misc), "unique miscs.")
print('Endolysins:', len([i for i in endo_doms if i in cbds]), "unique CBDs,",
len([i for i in endo_doms if i in eads]), "unique EADs and",
len([i for i in endo_doms if i in misc]), "unique miscs.")
print('VALs:', len([i for i in val_doms if i in cbds]), "unique CBDs,",
len([i for i in val_doms if i in eads]), "unique EADs and",
len([i for i in val_doms if i in misc]), "unique miscs.")
print('Unclassifieds:', len([i for i in uncl_doms if i in cbds]), "unique CBDs,",
len([i for i in uncl_doms if i in eads]), "unique EADs and",
len([i for i in uncl_doms if i in misc]), "unique miscs.")
# -
# ### Wrangle hosts
# +
### get annotation
cnx = mysql.connector.connect(user=user, password=password, database=db, unix_socket=socket)
cursor.execute("SELECT DISTINCT lineage_phylum, lineage_class, lineage_order, lineage_family, lineage_genus FROM hosts;")
host = pd.DataFrame(index=np.arange(0, 1000), columns=["Phylum", "Class", "Order", "Family", "Genus"])
for idx, i in enumerate(cursor):
host.iloc[idx]["Phylum"] = i[0]
host.iloc[idx]["Class"] = i[1]
host.iloc[idx]["Order"] = i[2]
host.iloc[idx]["Family"] = i[3]
host.iloc[idx]["Genus"] = i[4]
host["Gramtype"] = '~'
to_remove = []
for i in host.index:
if host.loc[i]['Order'] in ['Synechococcales', 'Nostocales', 'Oscillatoriales', 'Chroococcales']:
host.loc[i]['Class'] = 'Cyanophyceae'
elif host.loc[i]['Genus'] == 'Plesiomonas':
host.loc[i]['Family'] = 'Enterobacteriaceae'
elif host.loc[i]['Genus'] == 'Exiguobacterium':
host.loc[i]['Family'] = 'Bacillaceae'
elif host.iloc[i]["Family"] == 'Thermoanaerobacterales Family III. Incertae Sedis':
host.iloc[i]["Family"] = 'Thermoanaerobacterales 3'
### remove unknowns
if all(host.iloc[i].isna()):
to_remove.append(i)
elif pd.isna(host.iloc[i]["Genus"]):
to_remove.append(i)
### gram annotation
if host.loc[i]["Phylum"] in ['Actinobacteria', 'Firmicutes']:
if host.loc[i]["Family"] != 'Mycobacteriaceae':
host.loc[i]["Gramtype"] = '+'
elif host.loc[i]["Phylum"] in ['Proteobacteria', 'Bacteroidetes', 'Cyanobacteria',
'Spirochaetes', 'Fusobacteria', 'Deinococcus-Thermus']:
host.loc[i]["Gramtype"] = '-'
host = host.fillna('Unknown')
host = host.drop(to_remove, axis=0)
### sort genera
gpos = host[host.Gramtype == '+'].sort_values(by=['Phylum', 'Class', 'Order', 'Family'])
gneg = host[host.Gramtype == '-'].sort_values(by=['Phylum', 'Class', 'Order', 'Family'])
gamb = host[host.Gramtype == '~'].sort_values(by=['Phylum', 'Class', 'Order', 'Family'])
sorted_genera = list(pd.concat([gpos, gamb, gneg]).Genus)
# +
### Get hosts for each entry
host_per_entry = {}
for i in list(domains_per_entry.keys()):
host_per_entry[i] = []
cnx = mysql.connector.connect(user=user, password=password, database=db, unix_socket=socket)
cursor = cnx.cursor()
query = "SELECT h.lineage_genus FROM UniProt as up JOIN link_phage_host as l JOIN hosts as h WHERE up.UniProt_ID = '" + i + "' AND up.phages_ID = l.phages_ID AND l.hosts_ID = h.hosts_ID;"
cursor.execute(query)
tmp = []
for j in cursor:
tmp.append(j[0])
host_per_entry[i] = [k for k in set(tmp) if k != None]
#remove none values
filtered = {k: v for k, v in host_per_entry.items() if None not in v and len(v) != 0}
host_per_entry.clear()
host_per_entry.update(filtered)
print("Amount of accessions with (at least one) host genus linked: ")
print(len(host_per_entry))
lens = [len(v) for v in host_per_entry.values()]
print('On average', round(np.mean(lens), 1), 'host found per entry, with a max of', max(lens))
print('Total of', len(list(set(itertools.chain.from_iterable(host_per_entry.values())))), 'distinct host genera.')
# -
# ### Wrangle phages
# +
### Get annotation
phage_per_entry = {}
for i in list(domains_per_entry.keys()):
phage_per_entry[i] = []
cnx = mysql.connector.connect(user=user, password=password, database=db, unix_socket=socket)
cursor = cnx.cursor()
query = "SELECT p.lineage_family FROM UniProt as up JOIN phages as p WHERE up.UniProt_ID = '" + i + "' AND up.phages_ID = p.phages_ID;"
cursor.execute(query)
tmp = []
for j in cursor:
tmp.append(j[0])
phage_per_entry[i] = [k for k in set(tmp) if k != None]
if len(phage_per_entry[i]) == 0:
phage_per_entry[i] = 'Unknown'
else:
phage_per_entry[i] = phage_per_entry[i][0]
### sort
sorted_phage_fams = ['Ackermannviridae', 'Herelleviridae', 'Myoviridae', 'Podoviridae', 'Siphoviridae', 'Microviridae', 'Tectiviridae']
# -
# ## General figures
# +
### globular proteins
print(round(len([i for i in lens if i == 1])/len(up_acc)*100, 2), "% of entries only contain a single domain (n = {})".format(len([i for i in lens if i == 1])))
print(len([list(domains_per_entry.values())[idx] for idx,i in enumerate(lens) if i == 1 and list(domains_per_entry.values())[idx][0] in cbds])/len(up_acc)*100, "% of entries only contain a CBD (n = {})".format(len([list(domains_per_entry.values())[idx] for idx,i in enumerate(lens) if i == 1 and list(domains_per_entry.values())[idx][0] in cbds])))
print(len([list(domains_per_entry.values())[idx] for idx,i in enumerate(lens) if i == 1 and list(domains_per_entry.values())[idx][0] in eads])/len(up_acc)*100, "% of entries only contain an EAD (n = {}).".format(len([list(domains_per_entry.values())[idx] for idx,i in enumerate(lens) if i == 1 and list(domains_per_entry.values())[idx][0] in eads])))
print(len([list(domains_per_entry.values())[idx] for idx,i in enumerate(lens) if i == 1 and list(domains_per_entry.values())[idx][0] in cbds])/len([i for i in lens if i == 1])*100, "% of globular proteins only contain a CBD.")
print(len([list(domains_per_entry.values())[idx] for idx,i in enumerate(lens) if i == 1 and list(domains_per_entry.values())[idx][0] in misc])/len([i for i in lens if i == 1])*100, "% of globular proteins contain an misc.")
print('For endolysins specifically, these figures are:')
print('- globular:', round(len([1 for v in endo_archs.values() if len(v) == 1])/len(endolysins)*100, 2), "% (n = {})".format(len([1 for v in endo_archs.values() if len(v) == 1])))
print('- EAD-only:', round(len([1 for v in endo_archs.values() if len(v) == 1 and v[0] in eads])/len(endolysins)*100, 2), "% (n = {})".format(len([1 for v in endo_archs.values() if len(v) == 1 and v[0] in eads])))
print('- CBD-only:', round(len([1 for v in endo_archs.values() if len(v) == 1 and v[0] in cbds])/len(endolysins)*100, 2), "% (n = {})".format(len([1 for v in endo_archs.values() if len(v) == 1 and v[0] in cbds])))
print('For VALs specifically, these figures are:')
print('- globular:', round(len([1 for v in val_archs.values() if len(v) == 1])/len(vals)*100, 2), "% (n = {})".format(len([1 for v in val_archs.values() if len(v) == 1])))
print('- EAD-only:', round(len([1 for v in val_archs.values() if len(v) == 1 and v[0] in eads])/len(vals)*100, 2), "% (n = {})".format(len([1 for v in val_archs.values() if len(v) == 1 and v[0] in eads])))
print('- CBD-only:', round(len([1 for v in val_archs.values() if len(v) == 1 and v[0] in cbds])/len(vals)*100, 2), "% (n = {})".format(len([1 for v in val_archs.values() if len(v) == 1 and v[0] in cbds])))
# +
### modular proteins
print(round(len([i for i in lens if i > 1])/len(up_acc)*100, 2), "% of entries contain more than one domain (n = {})".format(len([i for i in lens if i > 1])))
print(len([idx for idx,i in enumerate(lens) if i > 1 and set(list(domains_per_entry.values())[idx]).issubset(set(eads))])/len(up_acc)*100, "% of entries are eads-only, modular proteins (n = {}).".format(len([idx for idx,i in enumerate(lens) if i > 1 and set(list(domains_per_entry.values())[idx]).issubset(set(eads))])))
print(len([idx for idx,i in enumerate(lens) if i > 1 and set(list(domains_per_entry.values())[idx]).issubset(set(cbds))])/len(up_acc)*100, "% of modular are cbds-only, modular proteins (n = {}).".format(len([idx for idx,i in enumerate(lens) if i > 1 and set(list(domains_per_entry.values())[idx]).issubset(set(cbds))])))
# +
### proteins without CBDs
c = 0
for i in domains_per_entry:
if len([j for j in domains_per_entry[i] if j in cbds]) == 0:
c += 1
print(c/len(up_acc)*100, "% of entries don't have CBDs (n = {}).".format(c))
# +
### multiple CBDs
c = 0
n_repeats = []
for i in domains_per_entry:
if len([j for j in domains_per_entry[i] if j in cbds]) > 1:
c += 1
if len(set([j for j in domains_per_entry[i] if j in cbds])) == 1:
n_repeats.append(len([j for j in domains_per_entry[i] if j in cbds]))
print(c/len(up_acc)*100, "% of entries have multiple CBDs (n = {}).".format(c))
print(len(n_repeats)/len(up_acc)*100, "% of entries have repeated CBDs (n = {}).".format(len(n_repeats)))
print("CBD-repeats occur in lengths of", min(n_repeats), "to", max(n_repeats),"times.")
# +
### multiple EADs
c = 0
n_repeats = []
for i in domains_per_entry:
if len([j for j in domains_per_entry[i] if j in eads]) > 1:
c += 1
if len(set([j for j in domains_per_entry[i] if j in eads])) == 1:
n_repeats.append(len([j for j in domains_per_entry[i] if j in eads]))
print(c/len(up_acc)*100, "% of entries have multiple EADs (n = {}).".format(c))
print(len(n_repeats)/len(up_acc)*100, "% of entries have repeated EADs (n = {}).".format(len(n_repeats)))
#print("EAD-repeats occur in lengths of", min(n_repeats), "to", max(n_repeats),"times.")
# -
### CBDs in VALs
val_cbds = []
val_with_cbds = []
for i in val_archs:
if len([j for j in val_archs[i] if j in cbds]) > 0:
val_with_cbds.append(i)
val_cbds.append([j for j in val_archs[i] if j in cbds])
print((len(val_cbds)/len(val_archs))*100, "% percent of VALs contain CBDs.")
print(set(itertools.chain.from_iterable(val_cbds)))
print(len(val_with_cbds))
# +
### VAL composition vs endolysin composition
endolysin_arch = {i:domains_per_entry[i] for i in endolysins if i in domains_per_entry}
val_arch = {i:domains_per_entry[i] for i in vals if i in domains_per_entry}
doms_endo = set(itertools.chain.from_iterable(endolysin_arch.values()))
doms_val = set(itertools.chain.from_iterable(val_arch.values()))
doms_unann = set(itertools.chain.from_iterable(domains_per_entry.values())) - doms_endo - doms_val
doms_both = set(itertools.chain.from_iterable(endolysin_arch.values())).intersection(set(itertools.chain.from_iterable(val_arch.values())))
print("There are", len(doms_endo), "different domains in endolysins.")
print("There are", len(doms_val), "different domains in VALs.")
print(len(doms_both), "domains occur in both endolysins and VALs. Hence", len(doms_endo) - len(doms_both), "and",
len(doms_val) - len(doms_both), "are unique to endolysins and VALs, respectively, with",
len(doms_unann), "occurring only in unannotated proteins.")
# -
### Occurrence of each domain cluster
dom_occ = np.zeros((len(sorted_doms)))
for i in domains_per_entry:
for j in domains_per_entry[i]:
dom_occ[sorted_doms.index(j)] += 1
#list(dom_occ)
### Occurrence of each domain cluster in endolysins
dom_end_occ = np.zeros((len(sorted_doms)))
for i in domains_per_entry:
if i in endolysins:
for j in domains_per_entry[i]:
dom_end_occ[sorted_doms.index(j)] += 1
#list(dom_end_occ)
### C-terminal CBDs
cc = 0
cct = 0
for i in domains_per_entry:
if len([j for j in domains_per_entry[i] if j in cbds]) != 0:
cc += 1
if domains_per_entry[i][-1] in cbds:
cct += 1
print("When CBDs are present, they are C-terminal in", cct/cc * 100, "% of instances.")
# +
### N-terminals
mnt = 0
ennt = 0
ent = 0
cv = 0
for i in vals:
cv += 1
if i in domains_per_entry:
if domains_per_entry[i][0] in misc:
mnt += 1
if len(domains_per_entry[i]) > 1:
if domains_per_entry[i][1] in eads:
ennt += 1
elif domains_per_entry[i][0] in eads:
ent += 1
print("In VALs, miscs are are N-terminal in", mnt/cv * 100, "%(n =", mnt, ") of instances,")
print("followed by an EAD in", ennt/mnt * 100, "% (n =", ennt, ")of instances.")
print("EADs are N-terminal in VALs in", ent/cv * 100, "% (n =", ent,").")
ent = 0
ce = 0
for i in endolysins:
if i in domains_per_entry:
ce += 1
if domains_per_entry[i][0] in eads:
ent += 1
print("In endolysins, EADs are are N-terminal in", ent/ce * 100, "% (n =", ent,") of instances.")
# +
c = 0
cc = 0
ec = 0
nc = 0
for i in domains_per_entry:
rep = False
cbd_rep = False
ead_rep = False
misc_rep = False
for jdx in range(len(domains_per_entry[i])-1):
if domains_per_entry[i][jdx] == domains_per_entry[i][jdx+1]:
rep = True
if domains_per_entry[i][jdx] in cbds:
cbd_rep = True
elif domains_per_entry[i][jdx] in eads:
ead_rep = True
#print(domains_per_entry[i][jdx])
elif domains_per_entry[i][jdx] in misc:
misc_rep = True
if rep == True:
c += 1
if cbd_rep == True:
cc += 1
if ead_rep == True:
ec += 1
if misc_rep == True:
nc += 1
print(c/len(domains_per_entry)*100, "% (n =", c, ") of architectures have repeats.")
print(cc/len(domains_per_entry)*100, "% (n =", cc, ") of architectures have CBD repeats.")
print(ec/len(domains_per_entry)*100, "% (n =", ec, ") of architectures have EAD repeats.")
print(nc/len(domains_per_entry)*100, "% (n =", nc, ") of architectures have misc repeats.")
# -
# ### Host-related figures
# +
### likelihood of CBDs
cbd_containing_gpos = 0
cbd_containing_gneg = 0
gpos_known = len([k for k in host_per_entry if set(host_per_entry[k]).intersection(set(gpos.Genus))])
gneg_known = len([k for k in host_per_entry if set(host_per_entry[k]).intersection(set(gneg.Genus))])
for k in host_per_entry:
if set(host_per_entry[k]).intersection(set(gpos.Genus)):
if len(set(domains_per_entry[k]).intersection(set(cbds))) > 0:
cbd_containing_gpos += 1
elif set(host_per_entry[k]).intersection(set(gneg.Genus)):
if len(set(domains_per_entry[k]).intersection(set(cbds))) > 0:
cbd_containing_gneg += 1
print('The likelihood of a G+ targeting protein containing a CBD is {}%'.format(round(cbd_containing_gpos/gpos_known * 100, 2)))
print('The likelihood of a G- targeting protein containing a CBD is {}%'.format(round(cbd_containing_gneg/gneg_known * 100, 2)))
# -
### highest diversity of CBDs
all_hosts = list(set(itertools.chain.from_iterable(host_per_entry.values())))
highest_c = 0
highest_g = False
for i in all_hosts:
linked_cbds = []
for j in domains_per_entry:
if j in host_per_entry:
if i in host_per_entry[j]:
linked_cbds.extend(list(set(domains_per_entry[j]).intersection(cbds)))
if len(set(linked_cbds)) > highest_c:
highest_c = len(set(linked_cbds))
highest_g = [i]
elif len(set(linked_cbds)) == highest_c:
if not highest_g:
highest_g = [i]
else:
highest_g.append(i)
print(highest_g, 'have the highest number of linked CBDs:', highest_c)
### unique CBDs
unique_cbd_accs = [i for i in domains_per_entry if 'LysM' in domains_per_entry[i]]
unique_cbd_hosts = []
for i in unique_cbd_accs:
if i in host_per_entry:
unique_cbd_hosts.extend(host_per_entry[i])
print(set(unique_cbd_hosts))
### modular G- lysins
gramneg_accs = [i for i in host_per_entry if len(set(host_per_entry[i]).intersection(set(gneg.Genus))) != 0]
gramnneg_cbds = []
for i in gramneg_accs:
if i in domains_per_entry:
if len(set(domains_per_entry[i]).intersection(set(cbds))) != 0:
gramnneg_cbds.extend(list(set(domains_per_entry[i]).intersection(set(cbds))))
print(np.unique(gramnneg_cbds, return_counts=True))
# ## Host-specific evolution of phage lytic proteins by recombination
# ### With various
### Set properties
heatmap_rows = sorted_genera + ['All G+', 'All G-'] + sorted_phage_fams
sorted_doms = cbds + eads + misc
heatmap_cols = sorted_doms + ['All CBDs', 'All N-acetylmuramoyl-L-alanine amidases',
'All peptidases', 'All N-acetyl-β-D-muramidases', 'All lytic transglycosylases']
### Calculate fraction of accessions for a certain host that has a specific domain
genus_specific_entries = []
domain_genus_quant = np.zeros((len(heatmap_rows), len(heatmap_cols)))
for idx, i in enumerate(heatmap_rows):
if i == 'All G+':
G_pos = set(gpos.Genus)
entries_host = [k for k in host_per_entry if set(host_per_entry[k]).intersection(G_pos)]
genus_specific_entries.append(len(entries_host))
print("amount of positive entries: ")
print(len(entries_host))
elif i == 'All G-':
G_neg = set(gneg.Genus)
entries_host = [k for k in host_per_entry if set(host_per_entry[k]).intersection(G_neg)]
genus_specific_entries.append(len(entries_host))
print("amount of negative entries: ")
print(len(entries_host))
elif i in sorted_phage_fams:
entries_host = [k for k in phage_per_entry if phage_per_entry[k] == i]
genus_specific_entries.append(len(entries_host))
else:
entries_host = [k for k in host_per_entry if i in host_per_entry[k]] #entries that have this host
genus_specific_entries.append(len(entries_host))
for jdx, j in enumerate(heatmap_cols):
if j == 'All CBDs': #entries that have this host & a binding domain
CBDs = set(cbds)
entries_host_dom = [l for l in entries_host if CBDs.intersection(set(domains_per_entry[l]))]
elif j == 'All N-acetylmuramoyl-L-alanine amidases': #entries that have this host & an amidase
entries_host_dom = [l for l in entries_host if set(amidases).intersection(set(domains_per_entry[l]))]
elif j == 'All peptidases': #entries that have this host & a peptidase
entries_host_dom = [l for l in entries_host if set(peptidases).intersection(set(domains_per_entry[l]))]
elif j == 'All N-acetyl-β-D-muramidases': #entries that have this host & a muramidase/lysozyme
entries_host_dom = [l for l in entries_host if set(muramidases).intersection(set(domains_per_entry[l]))]
elif j == 'All lytic transglycosylases': #entries that have this host & a lytic transglycosylase
entries_host_dom = [l for l in entries_host if set(lts).intersection(set(domains_per_entry[l]))]
else:
entries_host_dom = [l for l in entries_host if j in domains_per_entry[l]] #entries that have this host & domain
domain_genus_quant[idx, jdx] = len(entries_host_dom)/len(entries_host) #calculate fraction
# +
### Create heatmap
plt.figure(figsize=(9, 8))
sb.set(font_scale = 0.3)
plt.tight_layout()
sb.heatmap(pd.DataFrame(domain_genus_quant, index=heatmap_rows, columns=heatmap_cols), cmap='Blues',
xticklabels=True, yticklabels=True)
plt.axhline(len(gpos), xmin = -0.1, ls='-', lw=1, c='k') #G+ vs G~
plt.text(-19, len(gpos)/2 + 1, "G+", fontsize=12)
plt.axhline(len(gpos)+len(gamb), ls='-', lw=1, c='k') #G~ vs G-
plt.text(-19, len(gpos)+(len(gamb)/2) + 1.3, "G~", fontsize=12)
plt.text(-19, len(gpos)+len(gamb)+(len(gneg)/2) + 1, "G-", fontsize=12)
plt.axhline(len(gpos)+len(gamb)+len(gneg), ls='-', lw=1, c='k') #G- vs summary
plt.axhline(len(gpos)+len(gamb)+len(gneg)+2, ls='-', lw=1, c='k') #summary vs phage fams
plt.text(-18, len(gpos)+len(gamb)+len(gneg) + (len(sorted_phage_fams)/2) + 2, "Phage", fontsize=10)
plt.text(-19, len(gpos)+len(gamb)+len(gneg) + (len(sorted_phage_fams)/2) + 5, "families", fontsize=10)
plt.axhline(list(pd.concat([gpos, gamb, gneg]).Phylum).index('Firmicutes'), ls='--', lw=0.3, c='k')
plt.axhline(list(pd.concat([gpos, gamb, gneg]).Phylum).index('Cyanobacteria'), ls='--', lw=0.3, c='k')
plt.axhline(list(pd.concat([gpos, gamb, gneg]).Phylum).index('Deinococcus-Thermus'), ls='--', lw=0.3, c='k')
plt.axhline(list(pd.concat([gpos, gamb, gneg]).Phylum).index('Fusobacteria'), ls='--', lw=0.3, c='k')
plt.axhline(list(pd.concat([gpos, gamb, gneg]).Phylum).index('Proteobacteria'), ls='--', lw=0.3, c='k')
plt.axhline(list(pd.concat([gpos, gamb, gneg]).Phylum).index('Spirochaetes'), ls='--', lw=0.3, c='k')
plt.axhline(heatmap_rows.index('Microviridae'), ls='--', lw=0.3, c='k')
plt.text((len(cbds)/2)-3, -6, "CBDs", fontsize=12)
plt.axvline(len(cbds), ls='-', lw=1, c='k') #CBDs vs EADs
plt.text(len(cbds) + (len(eads)/2)-3, -6, "EADs", fontsize=12)
plt.axvline(len(cbds)+len(eads), ls='-', lw=1, c='k') #EADs vs misc
plt.text(len(cbds)+len(eads) + (len(misc)/2)-5, -6, "Miscellaneous", fontsize=12)
plt.axvline(len(cbds)+len(eads)+len(misc), ls='-', lw=1, c='k') #EADs vs misc
plt.text(len(cbds)+(len(pgas)/2)-1, -2, "(A)", fontsize=6)
plt.axvline(len(cbds)+len(pgas), ls='--', lw=0.5, c='k') #PGAs vs PGAPs
plt.text(len(cbds)+len(pgas)+(len(pgaps)/2)-1, -2, "(B)", fontsize=6)
plt.axvline(len(cbds)+len(pgas)+len(pgaps), ls='--', lw=0.5, c='k') #PGAPs vs PGPs
plt.text(len(cbds)+len(pgas)+len(pgaps)+(len(pgps)/2)-1, -2, "(C)", fontsize=6)
plt.axvline(len(cbds)+len(pgas)+len(pgaps)+len(pgps), ls='--', lw=0.5, c='k') #PGPs vs PGGs
plt.text(len(cbds)+len(pgas)+len(pgaps)+len(pgps)+(len(pggs)/2)-1, -2, "(D)", fontsize=6)
plt.axvline(len(cbds)+len(pgas)+len(pgaps)+len(pgps)+len(pggs), ls='--', lw=0.5, c='k') #PGGs vs PGMs
plt.text(len(cbds)+len(pgas)+len(pgaps)+len(pgps)+len(pggs)+(len(pgms)/2)-1, -2, "(E)", fontsize=6)
plt.axvline(len(cbds)+len(pgas)+len(pgaps)+len(pgps)+len(pggs)+len(pgms), ls='--', lw=0.5, c='k') #PGMs vs PGMTs
plt.text(len(cbds)+len(pgas)+len(pgaps)+len(pgps)+len(pggs)+len(pgms)+(len(pgmts)/2)-1, -2, "(F)", fontsize=6)
plt.axvline(len(cbds)+len(pgas)+len(pgaps)+len(pgps)+len(pggs)+len(pgms)+len(pgmts), ls='--', lw=0.5, c='k') #PGMs vs PGMTs
plt.text(len(cbds)+len(pgas)+len(pgaps)+len(pgps)+len(pggs)+len(pgms)+len(pgmts)+(len(pglts)/2)-1, -2, "(G)", fontsize=6)
### add genus_counts
plt.text(len(heatmap_cols)+1, -6, "#", fontsize=10)
for idx, i in enumerate(genus_specific_entries):
plt.text(len(heatmap_cols)+1, idx+0.9, i, fontsize=3)
plt.savefig('S3 Fig.png', format='png', dpi=600, tight_layout=True)
plt.show()
# -
# ### Without various
### Set properties
heatmap_rows = sorted_genera + ['All G+', 'All G-'] + sorted_phage_fams
sorted_doms_wo = cbds + eads
heatmap_cols_wo = sorted_doms_wo + ['All CBDs', 'All N-acetylmuramoyl-L-alanine amidases',
'All peptidases', 'All N-acetyl-β-D-muramidases', 'All lytic transglycosylases']
### Calculate fraction of accessions for a certain host that has a specific domain
genus_specific_entries = []
domain_genus_quant_wo = np.zeros((len(heatmap_rows), len(heatmap_cols_wo)))
for idx, i in enumerate(heatmap_rows):
if i == 'All G+':
G_pos = set(gpos.Genus)
entries_host = [k for k in host_per_entry if set(host_per_entry[k]).intersection(G_pos)]
genus_specific_entries.append(len(entries_host))
print("amount of positive entries: ")
print(len(entries_host))
elif i == 'All G-':
G_neg = set(gneg.Genus)
entries_host = [k for k in host_per_entry if set(host_per_entry[k]).intersection(G_neg)]
genus_specific_entries.append(len(entries_host))
print("amount of negative entries: ")
print(len(entries_host))
elif i in sorted_phage_fams:
entries_host = [k for k in phage_per_entry if phage_per_entry[k] == i]
genus_specific_entries.append(len(entries_host))
else:
entries_host = [k for k in host_per_entry if i in host_per_entry[k]] #entries that have this host
genus_specific_entries.append(len(entries_host))
for jdx, j in enumerate(heatmap_cols_wo):
if j == 'All CBDs': #entries that have this host & a binding domain
CBDs = set(cbds)
entries_host_dom = [l for l in entries_host if CBDs.intersection(set(domains_per_entry[l]))]
elif j == 'All N-acetylmuramoyl-L-alanine amidases': #entries that have this host & an amidase
entries_host_dom = [l for l in entries_host if set(amidases).intersection(set(domains_per_entry[l]))]
elif j == 'All peptidases': #entries that have this host & a peptidase
entries_host_dom = [l for l in entries_host if set(peptidases).intersection(set(domains_per_entry[l]))]
elif j == 'All N-acetyl-β-D-muramidases': #entries that have this host & a muramidase/lysozyme
entries_host_dom = [l for l in entries_host if set(muramidases).intersection(set(domains_per_entry[l]))]
elif j == 'All lytic transglycosylases': #entries that have this host & a lytic transglycosylase
entries_host_dom = [l for l in entries_host if set(lts).intersection(set(domains_per_entry[l]))]
else:
entries_host_dom = [l for l in entries_host if j in domains_per_entry[l]] #entries that have this host & domain
domain_genus_quant_wo[idx, jdx] = len(entries_host_dom)/len(entries_host) #calculate fraction
# +
pos_entries = set([k for k in host_per_entry if set(host_per_entry[k]).intersection(set(gpos.Genus))])
neg_entries = set([k for k in host_per_entry if set(host_per_entry[k]).intersection(set(gneg.Genus))])
amb_entries = set([k for k in host_per_entry if set(host_per_entry[k]).intersection(set(gamb.Genus))])
print('Overlap in Gram-positive and Gram-negative hosts by the following entries:')
print(pos_entries.intersection(neg_entries))
print('Overlap in Gram-positive and Gram-ambiguous hosts by the following entries:')
print(pos_entries.intersection(amb_entries))
print('Overlap in Gram-negative and Gram-ambiguous hosts by the following entries:')
print(neg_entries.intersection(amb_entries))
# +
### Create heatmap
plt.figure(figsize=(8, 9))
sb.set(font_scale = 0.3)
plt.tight_layout()
sb.heatmap(pd.DataFrame(domain_genus_quant_wo, index=heatmap_rows, columns=heatmap_cols_wo), cmap='Blues',
xticklabels=True, yticklabels=True)
plt.axhline(len(gpos), xmin = -0.1, ls='-', lw=1, c='k') #G+ vs G~
plt.text(-8.2, len(gpos)/2 + 1, "G+", fontsize=12)
plt.axhline(len(gpos)+len(gamb), ls='-', lw=1, c='k') #G~ vs G-
plt.text(-8.2, len(gpos)+(len(gamb)/2) + 1.3, "G~", fontsize=12)
plt.text(-8.2, len(gpos)+len(gamb)+(len(gneg)/2) + 1, "G-", fontsize=12)
plt.axhline(len(gpos)+len(gamb)+len(gneg), ls='-', lw=1, c='k') #G- vs summary
plt.axhline(len(gpos)+len(gamb)+len(gneg)+2, ls='-', lw=1, c='k') #summary vs phage fams
plt.text(-8.4, len(gpos)+len(gamb)+len(gneg) + (len(sorted_phage_fams)/2) + 2, "Phage", fontsize=10)
plt.text(-8.75, len(gpos)+len(gamb)+len(gneg) + (len(sorted_phage_fams)/2) + 5, "families", fontsize=10)
plt.axhline(list(pd.concat([gpos, gamb, gneg]).Phylum).index('Firmicutes'), ls='--', lw=0.3, c='k')
plt.axhline(list(pd.concat([gpos, gamb, gneg]).Phylum).index('Cyanobacteria'), ls='--', lw=0.3, c='k')
plt.axhline(list(pd.concat([gpos, gamb, gneg]).Phylum).index('Deinococcus-Thermus'), ls='--', lw=0.3, c='k')
plt.axhline(list(pd.concat([gpos, gamb, gneg]).Phylum).index('Fusobacteria'), ls='--', lw=0.3, c='k')
plt.axhline(list(pd.concat([gpos, gamb, gneg]).Phylum).index('Proteobacteria'), ls='--', lw=0.3, c='k')
plt.axhline(list(pd.concat([gpos, gamb, gneg]).Phylum).index('Spirochaetes'), ls='--', lw=0.3, c='k')
plt.axhline(heatmap_rows.index('Microviridae'), ls='--', lw=0.3, c='k')
plt.text((len(cbds)/2)-2, -6, "CBDs", fontsize=12)
plt.axvline(len(cbds), ls='-', lw=1, c='k') #CBDs vs EADs
plt.text(len(cbds) + (len(eads)/2)-2, -6, "EADs", fontsize=12)
plt.axvline(len(cbds)+len(eads), ls='-', lw=1, c='k') #EADs vs summary
plt.text(len(cbds)+(len(pgas)/2)-0.5, -2, "(A)", fontsize=6)
plt.axvline(len(cbds)+len(pgas), ls='--', lw=0.5, c='k') #PGAs vs PGAPs
plt.text(len(cbds)+len(pgas)+(len(pgaps)/2)-0.5, -2, "(B)", fontsize=6)
plt.axvline(len(cbds)+len(pgas)+len(pgaps), ls='--', lw=0.5, c='k') #PGAPs vs PGPs
plt.text(len(cbds)+len(pgas)+len(pgaps)+(len(pgps)/2)-0.5, -2, "(C)", fontsize=6)
plt.axvline(len(cbds)+len(pgas)+len(pgaps)+len(pgps), ls='--', lw=0.5, c='k') #PGPs vs PGGs
plt.text(len(cbds)+len(pgas)+len(pgaps)+len(pgps)+(len(pggs)/2)-0.5, -2, "(D)", fontsize=6)
plt.axvline(len(cbds)+len(pgas)+len(pgaps)+len(pgps)+len(pggs), ls='--', lw=0.5, c='k') #PGGs vs PGMs
plt.text(len(cbds)+len(pgas)+len(pgaps)+len(pgps)+len(pggs)+(len(pgms)/2)-0.5, -2, "(E)", fontsize=6)
plt.axvline(len(cbds)+len(pgas)+len(pgaps)+len(pgps)+len(pggs)+len(pgms), ls='--', lw=0.5, c='k') #PGMs vs PGMTs
plt.text(len(cbds)+len(pgas)+len(pgaps)+len(pgps)+len(pggs)+len(pgms)+(len(pgmts)/2)-0.5, -2, "(F)", fontsize=6)
plt.axvline(len(cbds)+len(pgas)+len(pgaps)+len(pgps)+len(pggs)+len(pgms)+len(pgmts), ls='--', lw=0.5, c='k') #PGMs vs PGMTs
plt.text(len(cbds)+len(pgas)+len(pgaps)+len(pgps)+len(pggs)+len(pgms)+len(pgmts)+(len(pglts)/2)-0.5, -2, "(G)", fontsize=6)
### add genus_counts
plt.text(len(heatmap_cols_wo)+1, -6, "#", fontsize=10)
for idx, i in enumerate(genus_specific_entries):
plt.text(len(heatmap_cols_wo)+1, idx+0.9, i, fontsize=3)
plt.savefig('figure_6.png', format='png', dpi=600, tight_layout=True)
plt.show()
# -
# ## Host - Domain quantification
# ### With various
### Set properties
heatmap_cols = sorted_genera + ['ALL G+', 'ALL G-'] + sorted_phage_fams
heatmap_rows = sorted_doms + ['All CBDs', 'All N-acetylmuramoyl-L-alanine amidases', 'All peptidases', 'All N-acetyl-β-D-muramidases', 'All lytic transglycosylases']
### calculate fraction of accessions for a certain domain that has a specific host
domain_specific_entries = []
genus_domain_quant = np.zeros((len(heatmap_rows), len(heatmap_cols)))
for idx, i in enumerate(heatmap_rows):
if i == 'All CBDs': #entries that have this host & a binding domain
entries_dom = [l for l in domains_per_entry if set(cbds).intersection(set(domains_per_entry[l]))]
domain_specific_entries.append(len(entries_dom))
elif i == 'All N-acetylmuramoyl-L-alanine amidases': #entries that have this host & an amidase
entries_dom = [l for l in domains_per_entry if set(amidases).intersection(set(domains_per_entry[l]))]
domain_specific_entries.append(len(entries_dom))
elif i == 'All peptidases': #entries that have this host & a peptidase
entries_dom = [l for l in domains_per_entry if set(peptidases).intersection(set(domains_per_entry[l]))]
domain_specific_entries.append(len(entries_dom))
elif i == 'All N-acetyl-β-D-muramidases': #entries that have this host & a muramidase/lysozyme
entries_dom = [l for l in domains_per_entry if set(muramidases).intersection(set(domains_per_entry[l]))]
domain_specific_entries.append(len(entries_dom))
elif i == 'All lytic transglycosylases': #entries that have this host & a lytic transglycosylase
entries_dom = [l for l in domains_per_entry if set(lts).intersection(set(domains_per_entry[l]))]
domain_specific_entries.append(len(entries_dom))
else:
entries_dom = [l for l in domains_per_entry if i in domains_per_entry[l]]
domain_specific_entries.append(len(entries_dom))
for jdx, j in enumerate(heatmap_cols):
entries_dom_known_host = list(set(entries_dom).intersection(set(host_per_entry.keys())))
if j == 'ALL G+':
G_pos = set(gpos.Genus)
entries_dom_host = [k for k in entries_dom_known_host if G_pos.intersection(set(host_per_entry[k]))]
elif j == 'ALL G-':
G_neg = set(gneg.Genus)
entries_dom_host = [k for k in entries_dom_known_host if G_neg.intersection(set(host_per_entry[k]))]
elif j in sorted_phage_fams:
entries_dom_host = set([k for k in phage_per_entry if phage_per_entry[k] == j]).intersection(set(entries_dom))
else:
entries_dom_host = [k for k in entries_dom_known_host if j in host_per_entry[k]]
genus_domain_quant[idx, jdx] = len(entries_dom_host)/len(entries_dom) #calculate fraction
# +
### create heatmap
plt.figure(figsize=(9, 8))
sb.set(font_scale = 0.3)
plt.tight_layout()
sb.heatmap(pd.DataFrame(genus_domain_quant, index=heatmap_rows, columns=heatmap_cols), cmap='OrRd',
xticklabels=True, yticklabels=True)
plt.axvline(len(gpos), ls='-', lw=1, c='k') #G+ vs G~
plt.text(len(gpos)/2-3, -2, "G+", fontsize=12)
plt.axvline(len(gpos)+len(gamb), ls='-', lw=1, c='k') #G~ vs G-
plt.text(len(gpos)+(len(gamb)/2)-3, -2, "G~", fontsize=12)
plt.text(len(gpos)+len(gamb)+(len(gneg)/2)-3, -2, "G-", fontsize=12)
plt.axvline(len(gpos)+len(gamb)+len(gneg), ls='-', lw=1, c='k') #G- vs summary
plt.axvline(len(gpos)+len(gamb)+len(gneg)+2, ls='-', lw=1, c='k') #summary vs phage fams
plt.text(len(gpos)+len(gamb)+len(gneg) + (len(sorted_phage_fams)/2)-5, -4, "Phage", fontsize=8)
plt.text(len(gpos)+len(gamb)+len(gneg) + (len(sorted_phage_fams)/2)-6, -2, "families", fontsize=8)
plt.axvline(list(pd.concat([gpos, gamb, gneg]).Phylum).index('Firmicutes'), ls='--', lw=0.3, c='k')
plt.axvline(list(pd.concat([gpos, gamb, gneg]).Phylum).index('Cyanobacteria'), ls='--', lw=0.3, c='k')
plt.axvline(list(pd.concat([gpos, gamb, gneg]).Phylum).index('Bacteroidetes'), ls='--', lw=0.3, c='k')
plt.axvline(list(pd.concat([gpos, gamb, gneg]).Phylum).index('Fusobacteria'), ls='--', lw=0.3, c='k')
plt.axvline(list(pd.concat([gpos, gamb, gneg]).Phylum).index('Proteobacteria'), ls='--', lw=0.3, c='k')
plt.axvline(heatmap_cols.index('Microviridae'), ls='--', lw=0.3, c='k')
plt.text(-30, (len(cbds)/2)+1, "CBDs", fontsize=12)
plt.axhline(len(cbds), ls='-', lw=1, c='k') #CBDs vs EADs
plt.text(-30, len(cbds) + (len(eads)/2)+1, "EADs", fontsize=12)
plt.axhline(len(cbds)+len(eads), ls='-', lw=1, c='k') #EADs vs misc
plt.text(-30, len(cbds)+len(eads) + (len(misc)/2)-0.5, "Misc.", fontsize=12)
plt.axhline(len(cbds)+len(eads)+len(misc), ls='-', lw=1, c='k') #EADs vs misc
plt.text(-4, len(cbds)+(len(pgas)/2)+0.5, "(A)", fontsize=6)
plt.axhline(len(cbds)+len(pgas), ls='--', lw=0.5, c='k') #PGAs vs PGAPs
plt.text(-4, len(cbds)+len(pgas)+(len(pgaps)/2)+0.5, "(B)", fontsize=6)
plt.axhline(len(cbds)+len(pgas)+len(pgaps), ls='--', lw=0.5, c='k') #PGAPs vs PGPs
plt.text(-4, len(cbds)+len(pgas)+len(pgaps)+(len(pgps)/2)+0.5, "(C)", fontsize=6)
plt.axhline(len(cbds)+len(pgas)+len(pgaps)+len(pgps), ls='--', lw=0.5, c='k') #PGPs vs PGGs
plt.text(-4, len(cbds)+len(pgas)+len(pgaps)+len(pgps)+(len(pggs)/2)+0.5, "(D)", fontsize=6)
plt.axhline(len(cbds)+len(pgas)+len(pgaps)+len(pgps)+len(pggs), ls='--', lw=0.5, c='k') #PGGs vs PGMs
plt.text(-4, len(cbds)+len(pgas)+len(pgaps)+len(pgps)+len(pggs)+(len(pgms)/2)+0.5, "(E)", fontsize=6)
plt.axhline(len(cbds)+len(pgas)+len(pgaps)+len(pgps)+len(pggs)+len(pgms), ls='--', lw=0.5, c='k') #PGMs vs PGMTs
plt.text(-4, len(cbds)+len(pgas)+len(pgaps)+len(pgps)+len(pggs)+len(pgms)+(len(pgmts)/2)+0.5, "(F)", fontsize=6)
plt.axhline(len(cbds)+len(pgas)+len(pgaps)+len(pgps)+len(pggs)+len(pgms)+len(pgmts), ls='--', lw=0.5, c='k') #PGMs vs PGMTs
plt.text(-4, len(cbds)+len(pgas)+len(pgaps)+len(pgps)+len(pggs)+len(pgms)+len(pgmts)+(len(pglts)/2)+0.5, "(G)", fontsize=6)
### add domain_counts
plt.text(len(heatmap_cols)+1, -2, "#", fontsize=12)
for idx, i in enumerate(domain_specific_entries):
plt.text(len(heatmap_cols)+1, idx+0.8, i, fontsize=3)
plt.savefig('S4 Fig.png', format='png', dpi=600)
plt.show()
# -
# ### Without various
### Set properties
heatmap_cols = sorted_genera + ['ALL G+', 'ALL G-'] + sorted_phage_fams
heatmap_rows_wo = sorted_doms_wo + ['All CBDs', 'All N-acetylmuramoyl-L-alanine amidases', 'All peptidases', 'All N-acetyl-β-D-muramidases', 'All lytic transglycosylases']
### calculate fraction of accessions for a certain domain that has a specific host
domain_specific_entries = []
genus_domain_quant_wo = np.zeros((len(heatmap_rows_wo), len(heatmap_cols)))
for idx, i in enumerate(heatmap_rows_wo):
if i == 'All CBDs': #entries that have this host & a binding domain
entries_dom = [l for l in domains_per_entry if set(cbds).intersection(set(domains_per_entry[l]))]
domain_specific_entries.append(len(entries_dom))
elif i == 'All N-acetylmuramoyl-L-alanine amidases': #entries that have this host & an amidase
entries_dom = [l for l in domains_per_entry if set(amidases).intersection(set(domains_per_entry[l]))]
domain_specific_entries.append(len(entries_dom))
elif i == 'All peptidases': #entries that have this host & a peptidase
entries_dom = [l for l in domains_per_entry if set(peptidases).intersection(set(domains_per_entry[l]))]
domain_specific_entries.append(len(entries_dom))
elif i == 'All N-acetyl-β-D-muramidases': #entries that have this host & a muramidase/lysozyme
entries_dom = [l for l in domains_per_entry if set(muramidases).intersection(set(domains_per_entry[l]))]
domain_specific_entries.append(len(entries_dom))
elif i == 'All lytic transglycosylases': #entries that have this host & a lytic transglycosylase
entries_dom = [l for l in domains_per_entry if set(lts).intersection(set(domains_per_entry[l]))]
domain_specific_entries.append(len(entries_dom))
else:
entries_dom = [l for l in domains_per_entry if i in domains_per_entry[l]]
domain_specific_entries.append(len(entries_dom))
for jdx, j in enumerate(heatmap_cols):
entries_dom_known_host = list(set(entries_dom).intersection(set(host_per_entry.keys())))
if j == 'ALL G+':
G_pos = set(gpos.Genus)
entries_dom_host = [k for k in entries_dom_known_host if G_pos.intersection(set(host_per_entry[k]))]
elif j == 'ALL G-':
G_neg = set(gneg.Genus)
entries_dom_host = [k for k in entries_dom_known_host if G_neg.intersection(set(host_per_entry[k]))]
elif j in sorted_phage_fams:
entries_dom_host = set([k for k in phage_per_entry if phage_per_entry[k] == j]).intersection(set(entries_dom))
else:
entries_dom_host = [k for k in entries_dom_known_host if j in host_per_entry[k]]
genus_domain_quant_wo[idx, jdx] = len(entries_dom_host)/len(entries_dom) #calculate fraction
# +
### create heatmap
plt.figure(figsize=(12, 5))
sb.set(font_scale = 0.3)
plt.tight_layout()
sb.heatmap(pd.DataFrame(genus_domain_quant_wo, index=heatmap_rows_wo, columns=heatmap_cols), cmap='OrRd',
xticklabels=True, yticklabels=True)
plt.axvline(len(gpos), ls='-', lw=1, c='k') #G+ vs G~
plt.text(len(gpos)/2-3, -1, "G+", fontsize=12)
plt.axvline(len(gpos)+len(gamb), ls='-', lw=1, c='k') #G~ vs G-
plt.text(len(gpos)+(len(gamb)/2)-2, -1, "G~", fontsize=12)
plt.text(len(gpos)+len(gamb)+(len(gneg)/2)-2, -1, "G-", fontsize=12)
plt.axvline(len(gpos)+len(gamb)+len(gneg), ls='-', lw=1, c='k') #G- vs summary
plt.axvline(len(gpos)+len(gamb)+len(gneg)+2, ls='-', lw=1, c='k') #summary vs phage fams
plt.text(len(gpos)+len(gamb)+len(gneg) + (len(sorted_phage_fams)/2)-3, -3, "Phage", fontsize=8)
plt.text(len(gpos)+len(gamb)+len(gneg) + (len(sorted_phage_fams)/2)-4, -1, "families", fontsize=8)
plt.axvline(list(pd.concat([gpos, gamb, gneg]).Phylum).index('Firmicutes'), ls='--', lw=0.3, c='k')
plt.axvline(list(pd.concat([gpos, gamb, gneg]).Phylum).index('Cyanobacteria'), ls='--', lw=0.3, c='k')
plt.axvline(list(pd.concat([gpos, gamb, gneg]).Phylum).index('Bacteroidetes'), ls='--', lw=0.3, c='k')
plt.axvline(list(pd.concat([gpos, gamb, gneg]).Phylum).index('Fusobacteria'), ls='--', lw=0.3, c='k')
plt.axvline(list(pd.concat([gpos, gamb, gneg]).Phylum).index('Proteobacteria'), ls='--', lw=0.3, c='k')
plt.axvline(heatmap_cols.index('Microviridae'), ls='--', lw=0.3, c='k')
plt.text(-20, (len(cbds)/2)+1, "CBDs", fontsize=12)
plt.axhline(len(cbds), ls='-', lw=1, c='k') #CBDs vs EADs
plt.text(-20, len(cbds) + (len(eads)/2)+1, "EADs", fontsize=12)
plt.axhline(len(cbds)+len(eads), ls='-', lw=1, c='k') #EADs vs summary
plt.text(-3, len(cbds)+(len(pgas)/2)+0.5, "(A)", fontsize=6)
plt.axhline(len(cbds)+len(pgas), ls='--', lw=0.5, c='k') #PGAs vs PGAPs
plt.text(-3, len(cbds)+len(pgas)+(len(pgaps)/2)+0.5, "(B)", fontsize=6)
plt.axhline(len(cbds)+len(pgas)+len(pgaps), ls='--', lw=0.5, c='k') #PGAPs vs PGPs
plt.text(-3, len(cbds)+len(pgas)+len(pgaps)+(len(pgps)/2)+0.5, "(C)", fontsize=6)
plt.axhline(len(cbds)+len(pgas)+len(pgaps)+len(pgps), ls='--', lw=0.5, c='k') #PGPs vs PGGs
plt.text(-3, len(cbds)+len(pgas)+len(pgaps)+len(pgps)+(len(pggs)/2)+0.5, "(D)", fontsize=6)
plt.axhline(len(cbds)+len(pgas)+len(pgaps)+len(pgps)+len(pggs), ls='--', lw=0.5, c='k') #PGGs vs PGMs
plt.text(-3, len(cbds)+len(pgas)+len(pgaps)+len(pgps)+len(pggs)+(len(pgms)/2)+0.5, "(E)", fontsize=6)
plt.axhline(len(cbds)+len(pgas)+len(pgaps)+len(pgps)+len(pggs)+len(pgms), ls='--', lw=0.5, c='k') #PGMs vs PGMTs
plt.text(-3, len(cbds)+len(pgas)+len(pgaps)+len(pgps)+len(pggs)+len(pgms)+(len(pgmts)/2)+0.5, "(F)", fontsize=6)
plt.axhline(len(cbds)+len(pgas)+len(pgaps)+len(pgps)+len(pggs)+len(pgms)+len(pgmts), ls='--', lw=0.5, c='k') #PGMs vs PGMTs
plt.text(-3, len(cbds)+len(pgas)+len(pgaps)+len(pgps)+len(pggs)+len(pgms)+len(pgmts)+(len(pglts)/2)+0.5, "(G)", fontsize=6)
### add domain_counts
plt.text(len(heatmap_cols)+1, -2, "#", fontsize=12)
for idx, i in enumerate(domain_specific_entries):
plt.text(len(heatmap_cols)+1, idx+0.8, i, fontsize=3)
plt.savefig('S2 Fig.png', format='png', dpi=600)
plt.show()
# -
|
quantitative-analysis/quant_analysis.ipynb
|
# +
# Illustrate benefits of centering data
# for reducing correlation between slope and intercept for 1d regression
# Based on
# https://github.com/aloctavodia/BAP/blob/master/code/Chp3/03_Modeling%20with%20Linear%20Regressions.ipynb
try:
import pymc3 as pm
except:
# %pip install pymc3
import pymc3 as pm
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
try:
import arviz as az
except:
# %pip install arviz
import arviz as az
import probml_utils as pml
import os
np.random.seed(1)
N = 100
alpha_real = 2.5
beta_real = 0.9
noiseSD = 0.5
eps_real = np.random.normal(0, noiseSD, size=N)
x = np.random.normal(10, 1, N) # centered on 10
y_real = alpha_real + beta_real * x
y = y_real + eps_real
# save untransformed data for later
x_orig = x
y_orig = y
_, ax = plt.subplots(1, 2, figsize=(8, 4))
ax[0].plot(x, y, "C0.")
ax[0].set_xlabel("x")
ax[0].set_ylabel("y", rotation=0)
ax[0].plot(x, y_real, "k")
az.plot_kde(y, ax=ax[1])
ax[1].set_xlabel("y")
plt.tight_layout()
# Fit posterior with MCMC instead of analytically (for simplicity and flexibility)
# This is the same as BAP code, except we fix the noise variance to a constant.
with pm.Model() as model_g:
w0 = pm.Normal("w0", mu=0, sd=10)
w1 = pm.Normal("w1", mu=0, sd=1)
# ϵ = pm.HalfCauchy('ϵ', 5)
mu = pm.Deterministic("mu", w0 + w1 * x)
# y_pred = pm.Normal('y_pred', mu=μ, sd=ϵ, observed=y)
y_pred = pm.Normal("y_pred", mu=mu, sd=noiseSD, observed=y)
trace_g = pm.sample(1000, cores=1, chains=2)
az.plot_trace(trace_g, var_names=["w0", "w1"])
az.plot_pair(trace_g, var_names=["w0", "w1"], plot_kwargs={"alpha": 0.1})
pml.savefig("linreg_2d_bayes_post_noncentered_data.pdf")
plt.show()
# To reduce the correlation between alpha and beta, we can center the data
x = x_orig - x_orig.mean()
# or standardize the data
# x = (x - x.mean())/x.std()
# y = (y - y.mean())/y.std()
with pm.Model() as model_g_centered:
w0 = pm.Normal("w0", mu=0, sd=10)
w1 = pm.Normal("w1", mu=0, sd=1)
# ϵ = pm.HalfCauchy('ϵ', 5)
mu = pm.Deterministic("mu", w0 + w1 * x)
# y_pred = pm.Normal('y_pred', mu=μ, sd=ϵ, observed=y)
y_pred = pm.Normal("y_pred", mu=mu, sd=noiseSD, observed=y)
trace_g_centered = pm.sample(1000, cores=1, chains=2)
az.plot_pair(trace_g_centered, var_names=["w0", "w1"], plot_kwargs={"alpha": 0.1})
pml.savefig("linreg_2d_bayes_post_centered_data.pdf")
plt.show()
|
notebooks/book1/11/linreg_2d_bayes_centering_pymc3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Multivariate Time Series
# In this notebook, we show examples of how multivariate time series can be created and used in darts.
# fix python path if working locally
from utils import fix_pythonpath_if_working_locally
fix_pythonpath_if_working_locally()
# +
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from darts import TimeSeries
from darts.models.tcn_model import TCNModel
from darts.preprocessing import ScalerWrapper
from darts.metrics import r2_score
import darts.utils.timeseries_generation as tg
# -
# Let's start by creating two univariate TimeSeries instances and combining them to form a multivariate one using the TimeSeries.stack method.
series_a = tg.sine_timeseries(length=50)
series_b = tg.linear_timeseries(length=50)
series_ab = series_a.stack(series_b)
series_ab.plot()
# Any individual 'component' of a multivariate TimeSeries instance can be retrieved using the TimeSeries.univariate_component method which takes a 0-indexed integer as an argument.
series_ab.univariate_component(0).plot()
# In the following we will use real-world univariate data and see how we can expand upon it by creating multivariate TimeSeries objects.
# Read data:
df = pd.read_csv('AirPassengers.csv', delimiter=",")
ts = TimeSeries.from_dataframe(df, 'Month', ['#Passengers'])
ts.plot()
# Any univariate or multivariate TimeSeries instance can easily be augmented by additional components that are based on the datetime index. Any integer-valued attribute of pd.DatetimeIndex can be added, such as the number of the month, as shown below. Before plotting, the data is normalized so that all features are on the same scale.
series_with_month = ts.add_datetime_attribute('month')
ScalerWrapper().fit_transform(series_with_month).plot()
# Similarly, we can add a binary time series which indicates whether the current point on the time index represents a holiday in a specific country. Since the above time series is monthly, we shall use the artificial time series from before as an example.
series_with_holidays = series_a.add_holidays('US')
ScalerWrapper().fit_transform(series_with_holidays).plot()
# Now, how can we make use of such augmentations of TimeSeries instances? To see where it can help, let's look at the performance of a TCN forecasting model on the above air passengers data set. First let's fit the TCN model on the univariate series for 200 epochs and predict 13 steps into the future.
# +
# Create training and validation sets:
train, val = ts.split_after(pd.Timestamp('19580801'))
transformer = ScalerWrapper()
train_transformed = transformer.fit_transform(train)
val_transformed = transformer.transform(val)
ts_transformed = transformer.transform(ts)
# Create TCNModel instance
my_model = TCNModel(
n_epochs=300,
input_length=15,
output_length=13,
dropout=0.1,
dilation_base=2,
weight_norm=True,
kernel_size=4,
num_filters=3,
random_state=0
)
# Fit model
my_model.fit(train_transformed, val_training_series=val_transformed, verbose=True)
# Evaluate model
def eval_model(model):
pred_series = model.predict(13, True)
plt.figure(figsize=(8,5))
ts_transformed.univariate_component(0).plot(label='actual')
pred_series.plot(label='forecast')
plt.title('R2: {}'.format(r2_score(val_transformed.univariate_component(0), pred_series.slice_intersect(val_transformed))))
plt.legend();
eval_model(my_model)
# -
# Limited to 20 epochs, we do not get a very good performance. Let's try the same thing but with an enhanced series that contains information about the month. Here, we also pass the second positional argument to the 'add_datetime_attribute' method which refers to whether the datetime attribute should be encoded in a one-hot fashion or not. Note that for predictions of multivariate TimeSeries instances, the maximum number of steps that can be predicted into the future is equal to TorchForecastingModel.output_length.
# +
# Create training and validation sets:
ts_enhanced = ts.add_datetime_attribute('month', True)
train, val = ts_enhanced.split_after(pd.Timestamp('19580801'))
transformer = ScalerWrapper()
train_transformed = transformer.fit_transform(train)
val_transformed = transformer.transform(val)
ts_transformed = transformer.transform(ts_enhanced)
# Create TCNModel instance
my_model = TCNModel(
input_size=13,
n_epochs=300,
input_length=15,
output_length=13,
dropout=0.1,
dilation_base=2,
weight_norm=True,
kernel_size=4,
num_filters=3,
random_state=0
)
# Fit model
my_model.fit(
target_series=train_transformed['0'],
training_series=train_transformed,
val_target_series=val_transformed['0'],
val_training_series=val_transformed,
verbose=True
)
#Evaluate model
eval_model(my_model)
# -
# We can see that with this limited number of training epochs, we get a better performance out of the model that uses the multivariate series as input.
|
examples/multivariate-examples.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import time
import numpy as np
import h5py
import matplotlib.pyplot as plt
import scipy
import pandas as pd
from sklearn import preprocessing
from sklearn.metrics import accuracy_score
import tensorflow as tf
df1 = pd.read_csv("/home/udit/Documents/cognet/train.csv")
X_train=np.array(df1.iloc[:,1:]).T
X_train = X_train/255
#X_train = preprocessing.normalize(X_train)
Y_train = np.array(df1.iloc[:,0])
#Y_train = preprocessing.normalize(Y_train)
df2 = pd.read_csv("/home/udit/Documents/cognet/test.csv")
X_test = np.array(df2.iloc[:,:]).T
X_test = X_test/255
#X_test = preprocessing.normalize(X_test)
Y_test = np.array(df1.iloc[30000:,0])
#print(X_train.shape)
m = Y_train.shape[0]
#print(m)
#Y_train = (Y_train.reshape(m,1))
#Y_test = (Y_test.reshape(Y_test.shape[0],1))
print(X_train.shape)
print(Y_train.shape)
print(X_test.shape)
print(Y_test.shape)
def sigmoid(z):
x = tf.placeholder(tf.float32,name='z')
sigmoid = tf.sigmoid(x)
sess = tf.Session()
result = sess.run(sigmoid,feed_dict={x:z})
sess.close()
return result;
print ("sigmoid(0) = " + str(sigmoid(0)))
print ("sigmoid(12) = " + str(sigmoid(12)))
def one_hot_matrix(labels, C):
C = tf.constant(C,name = 'C')
one_hot_matrix = tf.one_hot(labels,C,axis=1)
sess = tf.Session()
one_hot = sess.run(one_hot_matrix)
sess.close()
return one_hot;
# +
labels = np.array([1,2,3,0,2,1])
one_hot = one_hot_matrix(labels, C = 10)
#print ("one_hot = " + str(one_hot))
Y_train = one_hot_matrix(Y_train, C = 10)
Y_test = one_hot_matrix(Y_test, C = 10)
print(X_train.shape)
print(Y_train.shape)
print(X_test.shape)
print(Y_test.shape)
# -
Y_train = Y_train.T
Y_test = Y_test.T
print(Y_train.shape)
print(Y_test.shape)
def ones(shape):
ones = tf.ones(shape)
sess = tf.Session()
ones = sess.run(ones,feed_dict={})
sess.close()
return ones
print ("ones = " + str(ones([3])))
def create_placeholder(n_x,n_y):
X = tf.placeholder(tf.float32,name = 'n_x')
Y = tf.placeholder(tf.float32,name = 'n_y')
return X,Y
X, Y = create_placeholder(X_train.shape[0],X_train.shape[1])
print ("X = " + str(X))
print ("Y = " + str(Y))
def initialise_parameters():
W1 = tf.get_variable("W1",[40,784],initializer= tf.contrib.layers.xavier_initializer(seed = 1))
b1 = tf.get_variable("b1",[40,1],initializer= tf.zeros_initializer())
W2 = tf.get_variable("W2",[20,40],initializer= tf.contrib.layers.xavier_initializer(seed = 1))
b2 = tf.get_variable("b2",[20,1],initializer= tf.zeros_initializer())
W3 = tf.get_variable("W3",[10,20],initializer= tf.contrib.layers.xavier_initializer(seed = 1))
b3 = tf.get_variable("b3",[10,1],initializer= tf.zeros_initializer())
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2,
"W3": W3,
"b3": b3}
return parameters
tf.reset_default_graph()
with tf.Session() as sess:
parameters = initialise_parameters()
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
def forward_prop(X,parameters):
W1 = parameters['W1']
b1 = parameters['b1']
W2 = parameters['W2']
b2 = parameters['b2']
W3 = parameters['W3']
b3 = parameters['b3']
Z1 =tf.add(tf.matmul(W1,X),b1)
A1 = tf.nn.relu(Z1)
Z2 =tf.add(tf.matmul(W2,A1),b2)
A2 =tf.nn.relu(Z2)
Z3 = tf.add(tf.matmul(W3,A2),b3)
return Z3
# +
tf.reset_default_graph()
with tf.Session() as sess:
X, Y = create_placeholder(784, 10)
parameters = initialise_parameters()
Z3 = forward_prop(X, parameters)
print("Z3 = " + str(Z3))
# -
def compute_cost(Z3,Y):
logits = tf.transpose(Z3)
labels = tf.transpose(Y)
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits = logits, labels = labels))
return cost;
# +
tf.reset_default_graph()
with tf.Session() as sess:
X, Y = create_placeholder(784, 10)
parameters = initialise_parameters()
Z3 = forward_prop(X, parameters)
cost = compute_cost(Z3, Y)
print("cost = " + str(cost))
# +
def model( X_train, Y_train, X_test, Y_test, learning_rate=0.05, num_of_iterations=1500, print_cost=True):
tf.set_random_seed(1)
(n_x,m) = X_train.shape
n_y = Y_train.shape[0]
costs = []
X, Y = tf.placeholder(tf.float32,name="n_x"),tf.placeholder(tf.float32,name="n_y") #X = 784 and Y = 10
parameters = initialise_parameters() #initialising parameters
Z3 = forward_prop(X,parameters) #forward prop
cost = compute_cost(Z3,Y) #computing cost
optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(cost)
init = tf.global_variables_initializer()
seed=0
with tf.Session() as sess:
sess.run(init)
for i in range(num_of_iterations):
iter_cost = 0.
num = m
seed = seed + 1
(minibatch_X, minibatch_Y) = X_train, Y_train
_ , minibatch_cost = sess.run([optimizer, cost], feed_dict={X: minibatch_X, Y: minibatch_Y})
iter_cost += minibatch_cost / num
if print_cost == True and i % 100 == 0:
print ("Cost after iteration %i: %f" % (i, iter_cost))
costs.append(iter_cost)
if print_cost == True and i % 5 == 0:
costs.append(iter_cost)
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
parameters = sess.run(parameters)
print ("Parameters have been trained!")
correct_prediction = tf.equal(tf.argmax(Z3), tf.argmax(Y))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
print ("Train Accuracy:", accuracy.eval({X: X_train, Y: Y_train}))
#print ("Test Accuracy:", accuracy.eval({X: X_test, Y: Y_test}))
return parameters
# -
tf.reset_default_graph()
parameters = model(X_train, Y_train, X_test, Y_test)
# +
X_test, y_pred = create_placeholder(784, 10)
y_pred = forward_prop(X_test, parameters)
with open('/home/udit/Documents/cognet/submission.csv', 'w') as out_file:
out_file.write('ImageId,Label\n')
for img_id, guess_label in enumerate(np.argmax(y_pred,1),1):
out_file.write('%d,%d\n' % (img_id, guess_label))
# -
|
mnist-tf.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Detect indices of sequential data identical to a value
#
# > <NAME>
# > [Laboratory of Biomechanics and Motor Control](http://demotu.org/](http://demotu.org/)
# > Federal University of ABC, Brazil
# The function `detect_seq.py` from Python module `detecta` detects initial and final indices of sequential data identical to parameter `value` in `x`.
# Use parameter `min_seq` to set the minimum number of sequential values to detect.
#
# The signature of `detect_seq.py` is:
#
# ```python
# idx = detect_seq(x, value=np.nan, index=False, min_seq=1, max_alert=0, show=False, ax=None)
# ```
# ## Installation
#
# ```bash
# pip install detecta
# ```
#
# Or
#
# ```bash
# conda install -c duartexyz detecta
# ```
# +
import numpy as np
# %matplotlib inline
from detecta import detect_seq
# -
help(detect_seq)
x = [1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0]
detect_seq(x, 0)
detect_seq(x, 0, index=True)
detect_seq(x, 0, index=True, min_seq=2)
detect_seq(x, 10)
detect_seq(x, 10, index=True)
detect_seq(x, 1, index=True, min_seq=2, show=True)
detect_seq(x, 1, index=False, min_seq=1, show=True)
detect_seq(x, 0, index=True, min_seq=2, show=True)
detect_seq(x, 0, index=True, max_alert=2)
x = [1, 2, np.nan, np.nan, 5, 4, 5, np.nan, 2, 1, 2]
detect_seq(x, np.nan, index=True, max_alert=2, show=True)
|
notebooks/detect_seq.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] _cell_guid="b90d37c0-fdef-47a0-af20-fbc6a8b93b0a" _uuid="8ee475a9b992ffb91daa2e7970f041cf5fdd82e9"
# **[Machine Learning Course Home Page](https://kaggle.com/learn/machine-learning).**
#
# ---
#
# # Introduction
#
# Decision trees leave you with a difficult decision. A deep tree with lots of leaves will overfit because each prediction is coming from historical data from only the few houses at its leaf. But a shallow tree with few leaves will perform poorly because it fails to capture as many distinctions in the raw data.
#
# Even today's most sophisticated modeling techniques face this tension between underfitting and overfitting. But, many models have clever ideas that can lead to better performance. We'll look at the **random forest** as an example.
#
# The random forest uses many trees, and it makes a prediction by averaging the predictions of each component tree. It generally has much better predictive accuracy than a single decision tree and it works well with default parameters. If you keep modeling, you can learn more models with even better performance, but many of those are sensitive to getting the right parameters.
#
# # Example
#
# You've already seen the code to load the data a few times. At the end of data-loading, we have the following variables:
# - train_X
# - val_X
# - train_y
# - val_y
# + _cell_guid="676bc8b4-c4ab-4da9-a5fc-16e30f6772a4" _kg_hide-input=true _kg_hide-output=true _uuid="9a6efd7b10678776a5d7525cf3a61e52545859fe"
import pandas as pd
# Load data
melbourne_file_path = '../input/melbourne-housing-snapshot/melb_data.csv'
melbourne_data = pd.read_csv(melbourne_file_path)
# Filter rows with missing values
melbourne_data = melbourne_data.dropna(axis=0)
# Choose target and features
y = melbourne_data.Price
melbourne_features = ['Rooms', 'Bathroom', 'Landsize', 'BuildingArea',
'YearBuilt', 'Lattitude', 'Longtitude']
X = melbourne_data[melbourne_features]
from sklearn.model_selection import train_test_split
# split data into training and validation data, for both features and target
# The split is based on a random number generator. Supplying a numeric value to
# the random_state argument guarantees we get the same split every time we
# run this script.
train_X, val_X, train_y, val_y = train_test_split(X, y,random_state = 0)
# + [markdown] _cell_guid="0f39ad40-06d7-47f1-b18a-aa787228fabc" _uuid="49d7b53d2639a3f31145baf072758586f9677dc6"
# We build a random forest model similarly to how we built a decision tree in scikit-learn - this time using the `RandomForestRegressor` class instead of `DecisionTreeRegressor`.
# + _cell_guid="172cccfa-69ba-42ab-96ba-dad4949eb980" _uuid="be7bbd4c1ede885ddf5515d767e168adbadb7253"
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_absolute_error
forest_model = RandomForestRegressor(random_state=1)
forest_model.fit(train_X, train_y)
melb_preds = forest_model.predict(val_X)
print(mean_absolute_error(val_y, melb_preds))
# + [markdown] _cell_guid="35438077-159b-437b-84af-d4a54f64dc69" _uuid="120d7969e1bc5e4baaca6b17cc112f0eb1467e7d"
# # Conclusion
# There is likely room for further improvement, but this is a big improvement over the best decision tree error of 250,000. There are parameters which allow you to change the performance of the Random Forest much as we changed the maximum depth of the single decision tree. But one of the best features of Random Forest models is that they generally work reasonably even without this tuning.
#
# You'll soon learn the XGBoost model, which provides better performance when tuned well with the right parameters (but which requires some skill to get the right model parameters).
#
# # Your Turn
# Try **[using a Random Forest model](https://www.kaggle.com/kernels/fork/1259186)** yourself and see how much it improves your model.
#
#
# ---
# **[Course Home Page](https://www.kaggle.com/learn/machine-learning)**
#
|
learntools/machine_learning/nbs/tut6.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/PacktPublishing/Hands-On-Computer-Vision-with-PyTorch/blob/master/Chapter05/Implementing_VGG16_for_image_classification.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="X1mQ8Y9ERCpa"
import torchvision
import torch.nn as nn
import torch
import torch.nn.functional as F
from torchvision import transforms,models,datasets
import matplotlib.pyplot as plt
from PIL import Image
import numpy as np
from torch import optim
device = 'cuda' if torch.cuda.is_available() else 'cpu'
import cv2, glob, numpy as np, pandas as pd
import matplotlib.pyplot as plt
from glob import glob
import torchvision.transforms as transforms
from torch.utils.data import DataLoader, Dataset
# + id="CQcFhpxVRNev" outputId="87230d9b-ab1d-4b8e-ab5f-f2b0a916c338" colab={"resources": {"http://localhost:8080/nbextensions/google.colab/files.js": {"data": "<KEY>", "ok": true, "headers": [["content-type", "application/javascript"]], "status": 200, "status_text": ""}}, "base_uri": "https://localhost:8080/", "height": 91}
# !pip install -q kaggle
from google.colab import files
files.upload()
# !mkdir -p ~/.kaggle
# !cp kaggle.json ~/.kaggle/
# !ls ~/.kaggle
# !chmod 600 /root/.kaggle/kaggle.json
# + id="FAYvATjiRPep"
# !kaggle datasets download -d tongpython/cat-and-dog
# !unzip cat-and-dog.zip
# + id="nCvdJ9U-RWb3"
train_data_dir = 'training_set/training_set'
test_data_dir = 'test_set/test_set'
# + id="NDfNnADpRYAV"
class CatsDogs(Dataset):
def __init__(self, folder):
cats = glob(folder+'/cats/*.jpg')
dogs = glob(folder+'/dogs/*.jpg')
self.fpaths = cats[:500] + dogs[:500]
self.normalize = transforms.Normalize(mean=[0.485, 0.456, 0.406],std=[0.229, 0.224, 0.225])
from random import shuffle, seed; seed(10); shuffle(self.fpaths)
self.targets = [fpath.split('/')[-1].startswith('dog') for fpath in self.fpaths]
def __len__(self): return len(self.fpaths)
def __getitem__(self, ix):
f = self.fpaths[ix]
target = self.targets[ix]
im = (cv2.imread(f)[:,:,::-1])
im = cv2.resize(im, (224,224))
im = torch.tensor(im/255)
im = im.permute(2,0,1)
im = self.normalize(im)
return im.float().to(device), torch.tensor([target]).float().to(device)
# + id="-90fyHONRah5"
data = CatsDogs(train_data_dir)
# + id="4VvoZixHRcNM" outputId="3cc48845-a8b7-432e-cc4a-1e64eab13e58" colab={"base_uri": "https://localhost:8080/", "height": 305}
im, label = data[200]
plt.imshow(im.permute(1,2,0).cpu())
print(label)
# + id="JwhHv9VYRfhj"
def get_model():
model = models.vgg16(pretrained=True)
for param in model.parameters():
param.requires_grad = False
model.avgpool = nn.AdaptiveAvgPool2d(output_size=(1,1))
model.classifier = nn.Sequential(nn.Flatten(),
nn.Linear(512, 128),
nn.ReLU(),
nn.Dropout(0.2),
nn.Linear(128, 1),
nn.Sigmoid())
loss_fn = nn.BCELoss()
optimizer = torch.optim.Adam(model.parameters(), lr= 1e-3)
return model.to(device), loss_fn, optimizer
# + id="WEodSA2URqK8" outputId="6b602eff-94f6-4013-bde2-531571b75349" colab={"base_uri": "https://localhost:8080/", "height": 1000}
# !pip install torch_summary
from torchsummary import summary
model, criterion, optimizer = get_model()
summary(model, torch.zeros(1,3,224,224))
# + id="wRSbFt3BRr5B"
def train_batch(x, y, model, opt, loss_fn):
model.train()
prediction = model(x)
batch_loss = loss_fn(prediction, y)
batch_loss.backward()
optimizer.step()
optimizer.zero_grad()
return batch_loss.item()
# + id="Fp2yASc_RuO2"
@torch.no_grad()
def accuracy(x, y, model):
model.eval()
prediction = model(x)
is_correct = (prediction > 0.5) == y
return is_correct.cpu().numpy().tolist()
# + id="tbOeDzCPSVfj"
def get_data():
train = CatsDogs(train_data_dir)
trn_dl = DataLoader(train, batch_size=32, shuffle=True, drop_last = True)
val = CatsDogs(test_data_dir)
val_dl = DataLoader(val, batch_size=32, shuffle=True, drop_last = True)
return trn_dl, val_dl
# + id="hz7QoetLSXNI"
trn_dl, val_dl = get_data()
model, loss_fn, optimizer = get_model()
# + id="X_vtpUGRSYvZ" outputId="342455c8-4da3-49c4-cec3-62b1e04aeb60" colab={"base_uri": "https://localhost:8080/", "height": 108}
train_losses, train_accuracies = [], []
val_accuracies = []
for epoch in range(5):
print(f" epoch {epoch + 1}/5")
train_epoch_losses, train_epoch_accuracies = [], []
val_epoch_accuracies = []
for ix, batch in enumerate(iter(trn_dl)):
x, y = batch
batch_loss = train_batch(x, y, model, optimizer, loss_fn)
train_epoch_losses.append(batch_loss)
train_epoch_loss = np.array(train_epoch_losses).mean()
for ix, batch in enumerate(iter(trn_dl)):
x, y = batch
is_correct = accuracy(x, y, model)
train_epoch_accuracies.extend(is_correct)
train_epoch_accuracy = np.mean(train_epoch_accuracies)
for ix, batch in enumerate(iter(val_dl)):
x, y = batch
val_is_correct = accuracy(x, y, model)
val_epoch_accuracies.extend(val_is_correct)
val_epoch_accuracy = np.mean(val_epoch_accuracies)
train_losses.append(train_epoch_loss)
train_accuracies.append(train_epoch_accuracy)
val_accuracies.append(val_epoch_accuracy)
# + id="5aFfpJGZSb5v" outputId="017f433d-0176-4144-b2a3-42d883f28fa3" colab={"base_uri": "https://localhost:8080/", "height": 310}
epochs = np.arange(5)+1
import matplotlib.ticker as mtick
import matplotlib.pyplot as plt
import matplotlib.ticker as mticker
# %matplotlib inline
plt.plot(epochs, train_accuracies, 'bo', label='Training accuracy')
plt.plot(epochs, val_accuracies, 'r', label='Validation accuracy')
plt.gca().xaxis.set_major_locator(mticker.MultipleLocator(1))
plt.title('Training and validation accuracy with VGG16 \nand 1K training data points')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.ylim(0.95,1)
plt.gca().set_yticklabels(['{:.0f}%'.format(x*100) for x in plt.gca().get_yticks()])
plt.legend()
plt.grid('off')
plt.show()
# + id="jc88Ywn8TA67"
|
Chapter05/Implementing_VGG16_for_image_classification.ipynb
|
/ -*- coding: utf-8 -*-
/ ---
/ jupyter:
/ jupytext:
/ text_representation:
/ extension: .q
/ format_name: light
/ format_version: '1.5'
/ jupytext_version: 1.14.4
/ ---
/ + [markdown] colab_type="text" id="copyright-notice"
/ #### Copyright 2017 Google LLC.
/ + cellView="both" colab={"autoexec": {"startup": false, "wait_interval": 0}} colab_type="code" id="copyright-notice2"
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
/ + [markdown] colab_type="text" id="rHLcriKWLRe4"
/ # Pandas 간단 소개
/ + [markdown] colab_type="text" id="QvJBqX8_Bctk"
/ **학습 목표:**
/ * *pandas* 라이브러리의 `DataFrame` 및 `Series` 데이터 구조에 관한 소개 확인하기
/ * `DataFrame` 및 `Series` 내의 데이터 액세스 및 조작
/ * *pandas* `DataFrame`으로 CSV 데이터 가져오기
/ * `DataFrame`의 색인을 다시 생성하여 데이터 셔플
/ + [markdown] colab_type="text" id="TIFJ83ZTBctl"
/ [*Pandas*](http://Pandas.pydata.org/)는 열 중심 데이터 분석 API입니다. 입력 데이터를 처리하고 분석하는 데 효과적인 도구이며, 여러 ML 프레임워크에서도 *Pandas* 데이터 구조를 입력으로 지원합니다.
/ *Pandas* API를 전체적으로 소개하려면 길어지겠지만 중요한 개념은 꽤 간단하므로 아래에서 소개하도록 하겠습니다. 전체 내용을 참조할 수 있도록 [*Pandas* 문서 사이트](http://pandas.pydata.org/pandas-docs/stable/index.html)에서 광범위한 문서와 여러 가이드를 제공하고 있습니다.
/ + [markdown] colab_type="text" id="s_JOISVgmn9v"
/ ## 기본 개념
/
/ 다음 행은 *Pandas* API를 가져와서 API 버전을 출력합니다.
/ + colab={"autoexec": {"startup": false, "wait_interval": 0}} colab_type="code" id="aSRYu62xUi3g"
import pandas as pd
pd.__version__
/ + [markdown] colab_type="text" id="daQreKXIUslr"
/ *Pandas*의 기본 데이터 구조는 두 가지 클래스로 구현됩니다.
/
/ * **`DataFrame`**은 행 및 이름 지정된 열이 포함된 관계형 데이터 테이블이라고 생각할 수 있습니다.
/ * **`Series`**는 하나의 열입니다. `DataFrame`에는 하나 이상의 `Series`와 각 `Series`의 이름이 포함됩니다.
/
/ 데이터 프레임은 데이터 조작에 일반적으로 사용하는 추상화입니다. [Spark](https://spark.apache.org/) 및 [R](https://www.r-project.org/about.html)에 유사한 구현이 존재합니다.
/ + [markdown] colab_type="text" id="fjnAk1xcU0yc"
/ `Series`를 만드는 한 가지 방법은 `Series` 객체를 만드는 것입니다. 예를 들면 다음과 같습니다.
/ + colab={"autoexec": {"startup": false, "wait_interval": 0}} colab_type="code" id="DFZ42Uq7UFDj"
pd.Series(['San Francisco', 'San Jose', 'Sacramento'])
/ + [markdown] colab_type="text" id="U5ouUp1cU6pC"
/ `DataFrame` 객체는 `string` 열 이름과 매핑되는 'dict'를 각각의 `Series`에 전달하여 만들 수 있습니다. `Series`의 길이가 일치하지 않는 경우, 누락된 값은 특수 [NA/NaN](http://pandas.pydata.org/pandas-docs/stable/missing_data.html) 값으로 채워집니다. 예를 들면 다음과 같습니다.
/ + colab={"autoexec": {"startup": false, "wait_interval": 0}} colab_type="code" id="avgr6GfiUh8t"
city_names = pd.Series(['San Francisco', 'San Jose', 'Sacramento'])
population = pd.Series([852469, 1015785, 485199])
pd.DataFrame({ 'City name': city_names, 'Population': population })
/ + [markdown] colab_type="text" id="oa5wfZT7VHJl"
/ 하지만 대부분의 경우 전체 파일을 `DataFrame`으로 로드합니다. 다음 예는 캘리포니아 부동산 데이터가 있는 파일을 로드합니다. 다음 셀을 실행하여 데이터에 로드하고 기능 정의를 만들어 보세요.
/ + colab={"autoexec": {"startup": false, "wait_interval": 0}} colab_type="code" id="av6RYOraVG1V"
california_housing_dataframe = pd.read_csv("https://storage.googleapis.com/mledu-datasets/california_housing_train.csv", sep=",")
california_housing_dataframe.describe()
/ + [markdown] colab_type="text" id="WrkBjfz5kEQu"
/ 위의 예에서는 `DataFrame.describe`를 사용하여 `DataFrame`에 관한 흥미로운 통계를 보여줍니다. 또 다른 유용한 함수는 `DataFrame.head`로, `DataFrame` 레코드 중 처음 몇 개만 표시합니다.
/ + colab={"autoexec": {"startup": false, "wait_interval": 0}} colab_type="code" id="s3ND3bgOkB5k"
california_housing_dataframe.head()
/ + [markdown] colab_type="text" id="w9-Es5Y6laGd"
/ *Pandas*의 또 다른 강력한 기능은 그래핑입니다. 예를 들어 `DataFrame.hist`를 사용하면 한 열에서 값의 분포를 빠르게 검토할 수 있습니다.
/ + colab={"autoexec": {"startup": false, "wait_interval": 0}} colab_type="code" id="nqndFVXVlbPN"
california_housing_dataframe.hist('housing_median_age')
/ + [markdown] colab_type="text" id="XtYZ7114n3b-"
/ ## 데이터 액세스
/
/ 익숙한 Python dict/list 작업을 사용하여 `DataFrame` 데이터에 액세스할 수 있습니다.
/ + colab={"autoexec": {"startup": false, "wait_interval": 0}} colab_type="code" id="_TFm7-looBFF"
cities = pd.DataFrame({ 'City name': city_names, 'Population': population })
print type(cities['City name'])
cities['City name']
/ + colab={"autoexec": {"startup": false, "wait_interval": 0}} colab_type="code" id="V5L6xacLoxyv"
print type(cities['City name'][1])
cities['City name'][1]
/ + colab={"autoexec": {"startup": false, "wait_interval": 0}} colab_type="code" id="gcYX1tBPugZl"
print type(cities[0:2])
cities[0:2]
/ + [markdown] colab_type="text" id="65g1ZdGVjXsQ"
/ 또한 *Pandas*는 고급 [색인 생성 및 선택](http://Pandas.pydata.org/Pandas-docs/stable/indexing.html) 기능을 위한 풍부한 API를 제공합니다. 이 내용은 너무 광범위하므로 여기에서 다루지 않습니다.
/ + [markdown] colab_type="text" id="RM1iaD-ka3Y1"
/ ## 데이터 조작
/
/ Python의 기본 산술 연산을 `Series`에 적용할 수도 있습니다. 예를 들면 다음과 같습니다.
/ + colab={"autoexec": {"startup": false, "wait_interval": 0}} colab_type="code" id="XWmyCFJ5bOv-"
population / 1000.
/ + [markdown] colab_type="text" id="TQzIVnbnmWGM"
/ [NumPy](http://www.numpy.org/)는 유명한 계산과학 툴킷입니다. *Pandas* `Series`는 대부분의 NumPy 함수에 인수로 사용할 수 있습니다.
/ + colab={"autoexec": {"startup": false, "wait_interval": 0}} colab_type="code" id="ko6pLK6JmkYP"
import numpy as np
np.log(population)
/ + [markdown] colab_type="text" id="xmxFuQmurr6d"
/ 더 복잡한 단일 열 변환에는 `Series.apply`를 사용할 수 있습니다. Python [map 함수](https://docs.python.org/2/library/functions.html#map)처럼,
/ `Series.apply`는 인수로 [lambda 함수](https://docs.python.org/2/tutorial/controlflow.html#lambda-expressions)를 허용하며, 이는 각 값에 적용됩니다.
/
/ 아래의 예에서는 `인구`가 백만 명을 초과하는지 나타내는 새 `Series`를 만듭니다.
/ + colab={"autoexec": {"startup": false, "wait_interval": 0}} colab_type="code" id="Fc1DvPAbstjI"
population.apply(lambda val: val > 1000000)
/ + [markdown] colab_type="text" id="ZeYYLoV9b9fB"
/
/ `DataFrames` 수정 역시 간단합니다. 예를 들어 다음 코드는 기존 `DataFrame`에 두 개의 `Series`를 추가합니다.
/ + colab={"autoexec": {"startup": false, "wait_interval": 0}} colab_type="code" id="0gCEX99Hb8LR"
cities['Area square miles'] = pd.Series([46.87, 176.53, 97.92])
cities['Population density'] = cities['Population'] / cities['Area square miles']
cities
/ + [markdown] colab_type="text" id="6qh63m-ayb-c"
/ ## 실습 #1
/
/ 다음 두 명제 *모두* True인 경우에만 True인 새 부울 열을 추가하여 `도시` 테이블을 수정합니다.
/
/ * 도시 이름은 성인의 이름을 본따서 지었다.
/ * 도시 면적이 130제곱킬로미터보다 넓다.
/
/ **참고:** 부울 `Series`는 기존 부울 연산자가 아닌 비트 연산자를 사용하여 결합할 수 있습니다. 예를 들어 *logical and*를 실행할 때 `and` 대신 `&`를 사용합니다.
/
/ **참고:** 스페인어에서 "San"은 "성인"의 의미입니다.
/ + colab={"autoexec": {"startup": false, "wait_interval": 0}} colab_type="code" id="zCOn8ftSyddH"
# Your code here
/ + [markdown] colab_type="text" id="YHIWvc9Ms-Ll"
/ ### 해결 방법
/
/ 해결 방법을 보려면 아래를 클릭하세요.
/ + colab={"autoexec": {"startup": false, "wait_interval": 0}} colab_type="code" id="T5OlrqtdtCIb"
cities['Is wide and has saint name'] = (cities['Area square miles'] > 50) & cities['City name'].apply(lambda name: name.startswith('San'))
cities
/ + [markdown] colab_type="text" id="f-xAOJeMiXFB"
/ ## 색인
/ `Series`와 `DataFrame` 객체 모두 식별자 값을 각 `Series` 항목이나 `DataFrame` 행에 할당하는 `index` 속성을 정의합니다.
/
/ 기본적으로 생성 시 *Pandas*는 소스 데이터의 순서를 나타내는 색인 값을 할당합니다. 생성된 이후 색인 값은 고정됩니다. 즉, 데이터의 순서가 재정렬될 때 변하지 않습니다.
/ + colab={"autoexec": {"startup": false, "wait_interval": 0}} colab_type="code" id="2684gsWNinq9"
city_names.index
/ + colab={"autoexec": {"startup": false, "wait_interval": 0}} colab_type="code" id="F_qPe2TBjfWd"
cities.index
/ + [markdown] colab_type="text" id="hp2oWY9Slo_h"
/ `DataFrame.reindex`를 호출하여 수동으로 행의 순서를 재정렬합니다. 예를 들어 다음은 도시 이름을 기준으로 분류하는 것과 효과가 같습니다.
/ + colab={"autoexec": {"startup": false, "wait_interval": 0}} colab_type="code" id="sN0zUzSAj-U1"
cities.reindex([2, 0, 1])
/ + [markdown] colab_type="text" id="-GQFz8NZuS06"
/ 색인 재생성은 `DataFrame`을 섞기(임의 설정하기) 위한 좋은 방법입니다. 아래의 예에서는 배열처럼 된 색인을 NumPy의 `random.permutation` 함수에 전달하여 값을 섞습니다. 이렇게 섞인 배열로 `reindex`를 호출하면 `DataFrame` 행도 같은 방식으로 섞입니다.
/ 다음 셀을 여러 번 실행해 보세요.
/ + colab={"autoexec": {"startup": false, "wait_interval": 0}} colab_type="code" id="mF8GC0k8uYhz"
cities.reindex(np.random.permutation(cities.index))
/ + [markdown] colab_type="text" id="fSso35fQmGKb"
/ 자세한 정보는 [색인 문서](http://pandas.pydata.org/pandas-docs/stable/indexing.html#index-objects)를 참조하세요.
/ + [markdown] colab_type="text" id="8UngIdVhz8C0"
/ ## 실습 #2
/
/ `reindex` 메서드는 원래 `DataFrame`의 색인 값에 없는 색인 값을 허용합니다. 메서드를 실행해보고 이런 값을 사용하면 어떤 결과가 나오는지 확인해보세요. 왜 이런 값이 허용된다고 생각하나요?
/ + colab={"autoexec": {"startup": false, "wait_interval": 0}} colab_type="code" id="PN55GrDX0jzO"
# Your code here
/ + [markdown] colab_type="text" id="TJffr5_Jwqvd"
/ ### 해결 방법
/
/ 해결 방법을 보려면 아래를 클릭하세요.
/ + [markdown] colab_type="text" id="8oSvi2QWwuDH"
/ `reindex` 입력 배열에 원래 `DataFrame` 색인 값에 없는 값을 포함하면 `reindex`가 이 \'누락된\' 색인에 새 행을 추가하고 모든 해당 열을 `NaN` 값으로 채웁니다.
/ + colab={"autoexec": {"startup": false, "wait_interval": 0}} colab_type="code" id="yBdkucKCwy4x"
cities.reindex([0, 4, 5, 2])
/ + [markdown] colab_type="text" id="2l82PhPbwz7g"
/ 색인은 보통 실제 데이터에서 가져온 문자열이기 때문에 이 동작이 바람직합니다([*Pandas* 색인 재생성 문서](http://Pandas.pydata.org/Pandas-docs/stable/generated/Pandas.DataFrame.reindex.html)에서 색인 값이 브라우저 이름인 예제 참조).
/
/ 이 경우 \'누락된\' 색인을 허용하면 외부 목록을 사용하여 쉽게 색인을 다시 생성할 수 있으므로, 입력 처리에 대해 걱정하지 않아도 됩니다.
|
ml/cc/prework/ko/intro_to_pandas.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Basic draftsim analysis (by <NAME> and <NAME>)
# +
import pandas as pd
import numpy as np
import csv
import json
import itertools
import matplotlib.pyplot as plt
import seaborn as sns
import time
import sklearn.manifold as skm
# +
from Arseny.draftsim_utils_ab import *
# A set of useful utils: fixName(name), getName(card), isLegendary(card), getCardColor(card)
# where 'card' is a line in mtgJSON
# -
# Change the set abbrevation below to work with a different set:
# Alternatives: XLN, DOM, M19, GRN, RNA, WAR
setName = 'M19'
# +
#mtgJSON = json.load(open('Allsets.json'))
with open('../data/Allsets.json', 'r',encoding='utf-8') as json_data:
mtgJSON = json.load(json_data)
jsonSubset = mtgJSON[setName]['cards']
if setName=='XLN':
jsonSubset = jsonSubset+ mtgJSON['RIX']['cards']
# -
thisSet = {getName(card) : card for card in jsonSubset} # dict with names as indices for cards, for all cards in set
dict((k.lower(), v) for k, v in thisSet.items()) # Lowercase the keys
cardlist = list(thisSet.keys()) # List of card names (strings)
# Change the addresses below if you store data ini a different folder locally:
# +
dataFileNames = {
'XLN': '../2018-02-23 Two days data XLN.csv',
'DOM': '../2018-04-16 Dominiaria initial data-2.csv',
'M19': '../data/m19_2.csv',
'GRN': '../2018-10-05 GRN Draft Data 1.csv',
'RNA': '../2019-01-22 RNA merged.csv',
'WAR': '../2019-04-29 WAR prerelease leadup.csv'
}
draftData = pd.read_csv(dataFileNames[setName],
names = ['format', 'human', 'bot1', 'bot2', 'bot3', 'bot4', 'bot5', 'bot6', 'bot7'])
draftData.head()
# +
# If you want to see a full record for any single card
# next(iter(thisSet.values()))
# +
# Prepare for the main loop:
# Initialize all vars to collect data
# We use basic arrays rather than numpy as they are ~10% faster
cardpicks = {cardName : [] for cardName in cardlist} # Pick order
nCards = len(cardlist)
pairs = [[0 for i in range(nCards)] for j in range(nCards)] # Cards that were drafted together
freq = [0]*nCards
guilds = [[0 for i in range(5)] for j in range(5)]
# -
# Main loop (may take up to 10 minutes to run)
# +
draftCount = 0
player = 'human' # normally should be: "human", but can also be "bot1" or any other bot
ticTime = time.time()
for pile in draftData[player]:#[0:500]:
pile = fixName(pile)
pile = pile.lower()
pile = pile.split(',')
draftCount = draftCount+1 # For debugging
colorCount = [0,0,0,0,0,0,0]
for i in range(len(pile)):
try:
colorCount[getCardColor(thisSet[pile[i]])] += 1 # Count card colors within this pile only
freq[cardlist.index(pile[i])] += 1 # Total times this card was drafted
for j in range(i):
indi = cardlist.index(pile[i])
indj = cardlist.index(pile[j])
if indi>indj:
pairs[indi][indj] += 1 # For now, only fill the left half of the matrix
else:
pairs[indj][indi] += 1
if i<14:
cardpicks[pile[i]].append(i+1) # For ratings, we only look at the 1st booster as God knows what happens after
except KeyError as e:
print(pile)
print(draftCount)
raise
color1 = np.argmax(colorCount) # Most common color in this pile (excluding multicolors, which is suboptimal)
colorCount[color1] = 0
color2 = np.argmax(colorCount)
if color1>1 and color2>1: # Let's pretend that artifact-only and gold-only decks don't exist
guilds[color1-2][color2-2] += 1
print("Time elapsed: ", time.time() - ticTime)
print("Total drafts analyzed: ", draftCount)
# -
pairs = np.array(pairs)
freq = np.array(freq)
guilds = np.array(guilds)
# plt.imshow(pairs, cmap="Greys")
plt.imshow(pairs, cmap="Greys");
# +
nDrafts = draftCount
prob = pairs*1.0 # Make a copy, and also make symmetric
for i in range(nCards):
for j in range(i+1):
if freq[i]>0 and freq[j]>0:
prob[i,j] = prob[i,j]/float(freq[i])/float(freq[j])*nDrafts
prob[j,i] = prob[i,j]
dist = (1-0.99*prob/prob.max())
plt.imshow(dist, cmap="Greys");
# -
# Debugging: a list of cards that weren't drafted, but are in the db
for i in range(nCards):
if freq[i]==0:
print(cardlist[i])
del cardpicks[cardlist[i]] # Remove undrafted cards from the dictionary
# +
# Remove missing cards from other arrays
# (I make copies of both arrays for some reason, just in case)
dist2 = dist.copy()
dist2 = dist2[freq>0,:]
dist2 = dist2[:,freq>0] # For some reason if I try to subset both rows and columns together, it outputs something stupid
plt.imshow(dist2, cmap="Greys");
freq2 = freq[freq>0]
# +
fit = skm.locally_linear_embedding(dist2, n_components=2, n_neighbors=len(freq2)-1)
fit = fit[0] # For some reason it returns a tuple
#embedding = MDS(n_components=2, dissimilarity='precomputed', max_iter=1000, eps=0.0001)
#fit = embedding.fit_transform(dist2)
# +
df = pd.DataFrame({
'avg' : [np.mean(cardpicks[card]) for card in cardpicks],
'var' : [np.var(cardpicks[card]) for card in cardpicks],
'count' : [len(cardpicks[card]) for card in cardpicks],
'color' : [getCardColor(thisSet[card]) for card in cardpicks],
'rarity': [thisSet[card]['rarity'] for card in cardpicks],
'legendary' : [1 if isLegendary(thisSet[card]) else 0 for card in cardpicks],
'x' : fit[:,0],
'y' : fit[:,1],
'freq': freq2[:]
}, list(cardpicks.keys()))
# Now some torturous attempt to use proper color names, while retaining their sequence
colorName = {0:"C", 1:"Multi", 2:"W", 3:"U", 4:"B", 5:"R", 6:"G"}
df['color'] = df.color.map(colorName)
from pandas.api.types import CategoricalDtype
ctype = CategoricalDtype(categories=["C","Multi","W","U","B","R","G"],ordered=True)
df['color'] = df['color'].astype(ctype)
df.head()
# +
# #%matplotlib inline
myPal = sns.xkcd_palette(["grey","lavender","gold","deep blue","black","red","green"])
s = sns.relplot(data=df,x="x",y="y",hue="color",palette=myPal)
s.fig.set_size_inches(7,6)
sns.set_style("white")
s.despine(left=True,bottom=True)
s.set(xticklabels=[],yticklabels=[],xlabel='',ylabel='');
# +
# Save the data.
# Note, it saves to gitHub-visible folder, not to hidden 'data' folder:
df.to_csv('bots/bots_data/basic_data_'+setName+'.csv', index_label="name")
np.savetxt('bots/bots_data/distances_'+setName+'.csv', dist2, delimiter=",")
# -
ax = sns.heatmap(guilds/np.sum(guilds), annot=True, fmt="2.0%", cmap="YlGnBu", annot_kws={"size": 12})
ax.set_aspect('equal')
ax.figure.set_size_inches(7,5)
ax.set_xticklabels(["W","U","B","R","G"]); # suppress output, or it returns something
ax.set_yticklabels(["W","U","B","R","G"]);
# +
# Symmetric version for symmetric people
guilds_sim = guilds + guilds.transpose()
guilds_sim = np.triu(guilds_sim).transpose()
ax = sns.heatmap(guilds_sim/np.sum(guilds_sim), annot=True, fmt="2.0%", cmap="YlGnBu", annot_kws={"size": 12})
ax.set_aspect('equal')
ax.figure.set_size_inches(7,5)
ax.set_xticklabels(["W","U","B","R","G"]); # suppress output, or it returns something
ax.set_yticklabels(["W","U","B","R","G"]);
# -
# Top picks:
df.sort_values(by=['avg'], ascending=True).head(12)
# Top controversial cards (without correction for 'intrinsic controversy')
df.sort_values(by=['var'], ascending=False).head(12)
|
basic_analysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
#A veces necesitamos medir el taamñoa de un vector, llamada norma, recibe de entrada un vector y ese vector asocia un numeor, puede ser cero o mas grande.
#Para Mlearning se mide, sirve apra saber el error qu eestamos cometiendo.
# %matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# +
v1 = np.array([2,7])
v2 = np.array([3,5])
print(v1)
print(v2)
# -
v1v2 = v1+v2
print(v1v2)
np.linalg.norm(v1v2)
# +
# norma(v1v2) <= norma (v1) + norma(v2)
norma_v1 = np.linalg.norm(v1)
norma_v2 = np.linalg.norm(v2)
norma_v1v2 = np.linalg.norm(v1v2)
print(norma_v1v2 <= (norma_v1 + norma_v2))
# -
print(norma_v1+norma_v2)
# +
v1 = np.array([0,0,2,7])
v2 = np.array([0,0,3,5])
v1_aux = np.array([v1[2],v1[3],v2[2],v2[3]])
v1v2 = np.array([0,0,5,12])
# +
plt.quiver([v1[0], v1_aux[0], v1v2[0]],
[v1[1], v1_aux[1], v1v2[1]],
[v1[2], v1_aux[2], v1v2[2]],
[v1[3], v1_aux[3], v1v2[3]],
angles = 'xy', scale_units = 'xy', scale = 1,
color = sns.color_palette()
)
plt.xlim(-0.5, 6)
plt.ylim(-0.5, 15)
# -
|
NoteBooks/Curso de Algebra lineal con Python/fundamentos-algebra-lineal-master/06 - Normas/01 - Que es una norma y su uso.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: tensorflow22
# language: python
# name: tensorflow22
# ---
# + [markdown] colab_type="text" id="SbkD92kfzL1A"
# ### Accessing content in your drive
#
# + [markdown] colab_type="text" id="6LoYGJSRTw6W"
# ### Navigate to the location of folder ###
# + colab={} colab_type="code" executionInfo={"elapsed": 1157, "status": "ok", "timestamp": 1595183195390, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "03063971511613622677"}, "user_tz": -330} id="IoYIoChl7RNa"
import os
os.chdir('../../src/Enviroments/ExternalEnv/RPNet')
# + [markdown] colab_type="text" id="Vv5Zk4iWzGwI"
# ### Importing required modules
# + colab={} colab_type="code" executionInfo={"elapsed": 1555, "status": "ok", "timestamp": 1595183202693, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "03063971511613622677"}, "user_tz": -330} id="5KS-9VEirZ7X"
### Importing basic libraries
import scipy.io
import numpy as np
import torch
from scipy import signal
from tqdm import tqdm_notebook as tqdm
from matplotlib import pyplot as plt
import random
import pandas as pd
import scipy
import pickle
import sklearn
from sklearn.preprocessing import MinMaxScaler
import warnings
import math
import csv
from tqdm.notebook import tqdm
from scipy.signal import butter, lfilter, lfilter_zi
from pylab import plot, show, title, xlabel, ylabel, subplot
### Importing torch related libraries
from torch.utils.data import DataLoader
from torch.utils.data import TensorDataset
import torch.nn as nn
import torch.functional as F
from torch.autograd import Variable
import torch.optim as optim
from torch.optim import lr_scheduler
import datetime
### Importing Custom Libraries
from network import IncUNet
# + [markdown] colab_type="text" id="KLloorhcT50Y"
# # Preprocessing #
# + [markdown] colab_type="text" id="APNa7e1tyCiH"
# ### Navigate to the folder containing the model and data
# + colab={} colab_type="code" executionInfo={"elapsed": 1278, "status": "ok", "timestamp": 1595178230901, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "03063971511613622677"}, "user_tz": -330} id="5FbsPEjixAP3"
data_path = "../../../../Data/CPSC_2019/train/data"
reference_path = "../../../../Data/CPSC_2019/train/ref"
# + [markdown] colab_type="text" id="skbXk1ZyrZ8A"
# ### Loading from the Mat file
# + colab={} colab_type="code" executionInfo={"elapsed": 1189, "status": "ok", "timestamp": 1595178708359, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "03063971511613622677"}, "user_tz": -330} id="LRIBLoABrZ8B"
count = 0
patient_info = []
for files in sorted(os.listdir(data_path)):
count += 1
patient_info.append(scipy.io.loadmat(os.path.join(data_path,files)))
# if count == 20:
# break
# + colab={} colab_type="code" executionInfo={"elapsed": 1023, "status": "ok", "timestamp": 1595178709559, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "03063971511613622677"}, "user_tz": -330} id="PnRei9_kCLCU"
count = 0
patient_reference = []
for files in sorted(os.listdir(reference_path)):
count += 1
patient_reference.append(scipy.io.loadmat(os.path.join(reference_path,files)))
# if count == 20:
# break
### Entire thing can be run in a single line
### patient_reference = [scipy.io.loadmat(os.path.join(reference_path,files)) for files in tqdm(sorted(os.listdir(reference_path)))]
# + colab={"base_uri": "https://localhost:8080/", "height": 51} colab_type="code" executionInfo={"elapsed": 1131, "status": "ok", "timestamp": 1595178712341, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "03063971511613622677"}, "user_tz": -330} id="o-tPH98uCfRn" outputId="8fa4e1f5-6ecf-4e5c-b51e-0bdf543000dc"
print(len(patient_info))
print(len(patient_reference))
# + [markdown] colab_type="text" id="qKSRXHtYrZ8V"
# ### To obtain the patient's ECG Record ###
# + colab={"base_uri": "https://localhost:8080/", "height": 83, "referenced_widgets": ["<KEY>", "<KEY>", "<KEY>", "2d859fb9e6304a149dd04847f2c00616", "<KEY>", "60def240f2294eb0bead3c27b78a814e", "<KEY>", "053c08f89b80490e93ae6cc0484707f7"]} colab_type="code" executionInfo={"elapsed": 1166, "status": "ok", "timestamp": 1595178719689, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "03063971511613622677"}, "user_tz": -330} id="XgCliWQnrZ8W" outputId="7faba977-b0ad-43cb-fd5a-0170be41fbac"
patient_ecg = np.asarray( [patient_info[i]['ecg'] for i in (range(0,len(patient_info)))] )
print("Shape of the ECG record",patient_ecg.shape)
patient_ecg = patient_ecg[:,:,0]
# + [markdown] colab_type="text" id="XwXZQlLlrZ8d"
#
# ### Normalizing Patient ECG
# + colab={} colab_type="code" executionInfo={"elapsed": 1192, "status": "ok", "timestamp": 1595179044244, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "03063971511613622677"}, "user_tz": -330} id="ECtjCKc64yT2"
scaler = sklearn.preprocessing.StandardScaler()
patient_ecg = scaler.fit_transform(patient_ecg.transpose()).transpose()
# + [markdown] colab_type="text" id="SufdQRuWrZ86"
# ### To obtain the Reference Value ###
# + colab={} colab_type="code" executionInfo={"elapsed": 1155, "status": "ok", "timestamp": 1595179071308, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "03063971511613622677"}, "user_tz": -330} id="DnkVkiwUrZ87"
patient_ref = []
for j in range(0,len(patient_reference)):
if(patient_reference[j]['R_peak'].shape[0] == 1):
patient_ref.append(patient_reference[j]['R_peak'][0].ravel().astype(np.float16))
else:
patient_ref.append(patient_reference[j]['R_peak'].ravel().astype(np.float16))
# + [markdown] colab_type="text" id="PGD4O5ARrZ9J"
# ### Determining no of QRS complexes in windows
# + colab={} colab_type="code" executionInfo={"elapsed": 1142, "status": "ok", "timestamp": 1595179101396, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "03063971511613622677"}, "user_tz": -330} id="rTLI6rzerZ9L"
count = np.zeros((5,1))
for i in range(len(patient_ref)-64):
if(len(patient_ref[i]) <= 10):
count[0] += 1
elif (len(patient_ref[i]) > 10 and len(patient_ref[i]) <= 20):
count[1] += 1
elif (len(patient_ref[i]) > 20 and len(patient_ref[i]) <= 30):
count[2] += 1
elif (len(patient_ref[i])>30 and len(patient_ref[i])<=40):
count[3] += 1
elif (len(patient_ref[i])>40 and len(patient_ref[i])<=50):
count[4] += 1
# + [markdown] colab_type="text" id="6sUvjfCArZ9s"
# ### Distance Transform- Obtaining ground truth
# + colab={"base_uri": "https://localhost:8080/", "height": 66, "referenced_widgets": ["c8f9b9b525e44dfdbd675713220a210f", "d326d4e62ea341c78d09b126ecec0315", "cf1cf687acd4494685d963c6867d87e3", "862ecdffe598460c8705b4c05159e551", "776ef00e70ef4e1ab7dd7c4a0e0b009e", "f40f9fee85a1420591f055e31ab3a820", "79f82bfc4d8247bf97708bb800aa00ec", "e20e7078af6245808d479ecf6b9adc10"]} colab_type="code" executionInfo={"elapsed": 1213, "status": "ok", "timestamp": 1595179201252, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "03063971511613622677"}, "user_tz": -330} id="IpLHCDiqrZ9s" outputId="31d3a75b-c86f-42fb-e532-ae986e495a67"
distance_transform = []
for i in (range(len(patient_ref))):
prev_qrs = patient_ref[i][0]
next_qrs = patient_ref[i][1]
dist_tran = np.zeros(patient_ecg.shape[1])
beat_count = 1
for j in range(len(dist_tran)):
threshold = (prev_qrs + next_qrs)/2
if(j < threshold):
dist_tran[j] = int(abs(j - prev_qrs))/250
elif(j >= threshold):
dist_tran[j] = int(abs(j - next_qrs))/250
if(j == next_qrs and beat_count != len(patient_ref[i])-1): ## -2 instead of -1 because we are incrementing the beat in the loop
beat_count += 1
prev_qrs = next_qrs
next_qrs = patient_ref[i][beat_count]
distance_transform.append(dist_tran)
distance_transform = np.asarray(distance_transform)
scaler = MinMaxScaler(feature_range = (0,1))
distance_transform = np.transpose(scaler.fit_transform(distance_transform.transpose()))
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" executionInfo={"elapsed": 1221, "status": "ok", "timestamp": 1595179206158, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "03063971511613622677"}, "user_tz": -330} id="FRBHobjMrZ90" outputId="cbf035ba-0a61-4901-8238-e88790b82610"
dist_transform = torch.Tensor(distance_transform)
dist_transform = dist_transform.view(dist_transform.shape[0],1,dist_transform.shape[1])
print(dist_transform.shape)
# + colab={} colab_type="code" id="FLUbT5Uk2o5c"
BATCH_SIZE = 64
patient_ecg_t = torch.from_numpy(patient_ecg).float()
patient_ecg_train = patient_ecg_t[:1936,:]
patient_ecg_train = patient_ecg_train.view((patient_ecg_train.shape[0],1,patient_ecg_train.shape[1]))
dist_transform_train = dist_transform[:1936,0,:]
dist_transform_train = dist_transform_train.view(dist_transform_train.shape[0],1,dist_transform_train.shape[1])
print("Shape of input:",patient_ecg_train.shape)
print("Shape of ground truth:",dist_transform_train.shape)
patient_ecg_tl = TensorDataset(patient_ecg_train,dist_transform_train)
trainloader = DataLoader(patient_ecg_tl, batch_size=BATCH_SIZE, shuffle = True)
patient_ecg_t_test = patient_ecg_t[1936:,:]
patient_ecg_t_test = patient_ecg_t_test.view((patient_ecg_t_test.shape[0],1,patient_ecg_t_test.shape[1]))
dist_transform_test = dist_transform[1936:,:]
print("Shape of input:",patient_ecg_t_test.shape)
print("Shape of ground truth:",dist_transform_test.shape)
patient_ecg_tl_test = TensorDataset(patient_ecg_t_test,dist_transform_test)
testloader = DataLoader(patient_ecg_tl_test, batch_size=BATCH_SIZE)
torch.save(patient_ecg_train, 'train.pt')
torch.save(patient_ecg_t_test, 'test.pt')
torch.save(dist_transform_train, 'dist_transform_train.pt')
torch.save(dist_transform_test, 'dist_transform_test.pt')
# + [markdown] colab_type="text" id="AUQ447F1rZ-I"
# # Train and Evaluate #
# + [markdown] colab_type="text" id="MMn9e3pcrZ-J"
# ### Hyperparameters and Related parameters
# + colab={} colab_type="code" executionInfo={"elapsed": 1212, "status": "ok", "timestamp": 1595183209430, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "03063971511613622677"}, "user_tz": -330} id="dPfIA-lOrZ-K"
BATCH_SIZE=64
C,H,W = 1,1,5000
learn_rate = 0.05
num_epochs = 480
# + [markdown] colab_type="text" id="EOMdQQOmy4Ap"
# ### Loading data via the pt files
# + colab={} colab_type="code" executionInfo={"elapsed": 1124, "status": "ok", "timestamp": 1595183212561, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "03063971511613622677"}, "user_tz": -330} id="FgDMzUZ8y2b_"
patient_ecg_train = torch.load('train.pt')
dist_transform_train = torch.load('dist_transform_train.pt')
patient_ecg_test = torch.load('test.pt')
dist_transform_test = torch.load('dist_transform_test.pt')
patient_ecg_train_td = TensorDataset(patient_ecg_train, dist_transform_train)
trainloader = DataLoader(patient_ecg_train_td, batch_size=BATCH_SIZE, shuffle = True)
patient_ecg_test_td = TensorDataset(patient_ecg_test, dist_transform_test)
testloader = DataLoader(patient_ecg_test_td, batch_size=BATCH_SIZE)
# + [markdown] colab_type="text" id="t0Px41-pAFFF"
# ### Visualizing using Matplotlib
# + colab={"base_uri": "https://localhost:8080/", "height": 282} colab_type="code" executionInfo={"elapsed": 1484, "status": "ok", "timestamp": 1595183482793, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "03063971511613622677"}, "user_tz": -330} id="6F93ayksAEja" outputId="a1254dac-1c95-4ca8-b767-2bac2699e11d"
record_no = 18
plt.plot(patient_ecg_train[record_no,0,:].numpy())
plt.plot(dist_transform_train[record_no,0,:].numpy())
# + [markdown] colab_type="text" id="GcC1nSeW2VVd"
# ### Ensuring deterministicity through Random seeding
#
# + colab={} colab_type="code" executionInfo={"elapsed": 1129, "status": "ok", "timestamp": 1595183223109, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "03063971511613622677"}, "user_tz": -330} id="cXDLjoNl2UhR"
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False
manualSeed = 4
random.seed(manualSeed)
torch.manual_seed(manualSeed)
if torch.cuda.is_available():
torch.cuda.manual_seed(manualSeed)
# + [markdown] colab_type="text" id="W4jG7ivprZ-y"
# ### Setting the optimizer and Loss function
# + colab={} colab_type="code" executionInfo={"elapsed": 3973, "status": "ok", "timestamp": 1595183232895, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "03063971511613622677"}, "user_tz": -330} id="OfQNokSUrZ-z"
model = IncUNet(in_shape = (C,H,W))
model.cuda()
optimizer = optim.Adam(model.parameters(), lr = learn_rate)# Try out weight decay ,
scheduler = optim.lr_scheduler.MultiStepLR(optimizer, milestones=[90,190,450], gamma=0.1)
criterion = nn.SmoothL1Loss()
# + [markdown] colab_type="text" id="Wbe1kLYCrZ-4"
# ### Initializing Tensorboard ###
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" executionInfo={"elapsed": 1125, "status": "ok", "timestamp": 1595183237345, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "03063971511613622677"}, "user_tz": -330} id="FSuCJ988rZ-5" outputId="f0e34b44-4fc8-474b-bb63-92726e4e5209"
### Using datetime to capture date time and write details into a text file
date_time = str(datetime.datetime.now())
date = date_time[:10]
start_time = date_time[11:19]
model_path = "saved_model/" + date + "__" + start_time + "/"
if not(os.path.exists('saved_model')):
os.mkdir('saved_model')
os.mkdir(model_path)
log_file = './' + model_path + 'logfile.txt'
log_data = open(log_file,'w+')
settings = ' The Settings of the model are: Epoch:%d, LR:%f, BATCH_SIZE:%d Seed:%d\n'%(num_epochs,learn_rate,BATCH_SIZE,manualSeed)
log_data.write(settings)
# + [markdown] colab_type="text" id="e-Hf-yCxrZ_T"
# ### Training ###
# + colab={"base_uri": "https://localhost:8080/", "height": 1000, "referenced_widgets": ["613e3121a6954bc3ad6b304792d6ffc0", "33161a85b3ed48c280c15ecec72dc407", "969aa4977b3544649e81b9fc40478fb2", "bc729aea834f47548f564012920e96ed", "06c419d4a11744ae883efa3eb3dde16d", "db4c7d1f4bf1463caca66524d719e050", "95b89a795924443d9f921ecd2b265a5d", "314dfc662be24750a30d953044d894f9"]} colab_type="code" executionInfo={"elapsed": 139249, "status": "error", "timestamp": 1595183380345, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "03063971511613622677"}, "user_tz": -330} id="vnDKw-rkrZ_a" jupyter={"outputs_hidden": true} outputId="898f1473-4360-4f5e-8d47-8bc4e312ea00"
epoch_loss = []
min_test_loss = 1000 ### Set a very high number
best_epoch = 0
for epoch in (range(num_epochs)):
print ('-'*40)
model.train()
print ('Epoch {}/{}'.format(epoch+1,num_epochs))
print ('-'*10)
net_loss = 0
for step,(x,y) in enumerate(trainloader):
print("Step no: {}/{}".format(step+1, len(trainloader)))
x,y = x.cuda(),y.cuda()
y_predict = model(x)
### Loss computation and Optimization ###
loss = criterion(y,y_predict)
optimizer.zero_grad()
loss.backward()
optimizer.step()
net_loss += loss
net_loss = net_loss/ (step + 1)
### Logging ###
settings = "\nEpoch:{},Loss:{}".format(epoch,net_loss)
log_data.write(settings)
if(epoch == num_epochs - 1):
log_data.close()
print("Net loss is:", net_loss)
epoch_loss.append(net_loss.data)
scheduler.step()
### Evaluation and saving best model ###
if epoch % 10 == 0:
print ('-'*40)
print("..........Evaluation..........")
print("Epoch No is:", epoch)
model.eval()
with torch.no_grad():
net_test_loss = 0
for step,(x,y) in enumerate(testloader): ### Use trainloader for AK2-11 ###
x,y = Variable(x.cuda()),Variable(y.cuda())
y_predict_test = model(x)
test_loss = criterion(y_predict_test,y)
net_test_loss += test_loss
net_test_loss /= step + 1
### Saving the best model based on the Minimum Loss
if net_test_loss < min_test_loss:
min_test_loss = net_test_loss
best_epoch = epoch
print("..........Saving the model..........")
torch.save(model.state_dict(),model_path+'Epoch'+str(epoch)+'.pt')
print("base model in epoch: ", best_epoch)
# + [markdown] colab_type="text" id="UYrjL8Cs4uO5"
# ### Evaluation
#
#
# -
plt.plot(epoch_loss)
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" executionInfo={"elapsed": 1500, "status": "ok", "timestamp": 1595183439808, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "03063971511613622677"}, "user_tz": -330} id="XjS8FQb3LsUE" outputId="fc9688d9-f843-4ea5-c5a2-2fe16819aad2"
best_model_path = model_path+'Epoch160.pt'
print(best_model_path)
SAVED_MODEL_PATH = "model_1.pt"
# model.load_state_dict(torch.load(SAVED_MODEL_PATH))
model.load_state_dict(torch.load(best_model_path))
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" executionInfo={"elapsed": 2590, "status": "ok", "timestamp": 1595183443906, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "03063971511613622677"}, "user_tz": -330} id="XL_8udoWxoPA" outputId="72f7e0e0-6e09-41ab-9886-d082391a40e7"
model.eval()
y_pred_array = []
ecg = []
with torch.no_grad():
net_test_loss = 0
for step,(x,y) in enumerate(testloader):
x,y = x.cuda(),y.cuda()
y_predict_test = model(x)
test_loss = criterion(y_predict_test,y)
net_test_loss += test_loss
print('Step: {}, Loss: {} '.format(step,net_test_loss))
ecg.append(x.cpu().numpy())
y_pred_array.append(y_predict_test[:,0,:].cpu().numpy())
# + [markdown] colab_type="text" id="AfTPsVFTPQd4"
# ### Post Processing ###
# + colab={} colab_type="code" executionInfo={"elapsed": 1107, "status": "ok", "timestamp": 1595183448608, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "03063971511613622677"}, "user_tz": -330} id="lM0Z2Z0JLfwe"
batch_no = 0
y_pred_array = np.asarray(y_pred_array[batch_no])
ecg = np.asarray(ecg[batch_no])[:,0,:]
peak_locs = []
for i in range(y_pred_array.shape[0]):
peak_locs.append(scipy.signal.find_peaks(-y_pred_array[i,:],distance = 90,height = -0.2,prominence = 0.035)[0])
### Getting the amplitude values at valley location.
y_roll_valleys = []
y = []
for j in range(len(peak_locs)):
y = [ecg[j,i] for i in peak_locs[j]]
y_roll_valleys.append(y)
# + [markdown] colab_type="text" id="Ed84FVtSPs09"
# ### Plotting output ###
# + colab={"base_uri": "https://localhost:8080/", "height": 282} colab_type="code" executionInfo={"elapsed": 1358, "status": "ok", "timestamp": 1595183453995, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "03063971511613622677"}, "user_tz": -330} id="x1hsN7CcPIGU" outputId="d9e3329e-2b6f-43ca-f2a0-e6fb6a264021"
record_no = 10
plt.plot(ecg[record_no,:])
plt.scatter(peak_locs[record_no], y_roll_valleys[record_no])
# -
y_predict_test.shape,y.shape
nn.SmoothL1Loss(reduction='none')(y_predict_test,y).shape
loss = torch.mean(torch.abs(y_predict_test-y),axis=2).cpu().numpy()
loss.mean(),loss.min(),loss.max()
import pandas as pd
pd.DataFrame(loss).describe()
plt.boxplot(loss)
|
notebook/RPNet_keras/train_CPSC.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 3 Pre-processing and Modelling<a id='4_Pre-Processing_and_Training_Data'></a>
# ## 3.1 Contents<a id='3.1_Contents'></a>
# * [3 Pre-Processing and Training Data](#3_Pre-Processing_and_Training_Data)
# * [3.1 Contents](#3.1_Contents)
# * [3.2 Introduction](#3.2_Introduction)
# * [3.3 Imports](#3.3_Imports)
# * [3.4 Load data](#3.3_Load_Data)
# * [3.5 Pre-Processing Data](#3.5_set_the_index)
# * [3.6 Build the Base Model](#3.6_Build_Model)
# * [3.6.1 Model Architecture](#3.6.1_Model_Architecture)
# * [3.7 Define a Callback Object](#3.7_Define_Callback)
# * [3.8 The Model with the Adam Optimizer](#3.8_Adam_Optimizer)
# * [3.8.1 Hyperparameter search using RandomSearch](#3.8.1_Hyperparameter_RandomSearch)
# * [3.8.2 Learning Curves](#3.8.2_Learning_Curve)
# * [3.8.3 Model Performance](#3.8.3_Model_Performance)
# * [3.9 The Model with the SGD Optimizer](#3.9_SGD_Optimizer)
# * [3.9.1 Hyperparameter search using RandomSearch](#3.9.1_Hyperparameter_RandomSearch)
# * [3.9.2 Learning Curves](#3.9.2_Learning_Curve)
# * [3.9.3 Model Performance](#3.9.3_Model_Performance)
# * [3.10 The Model with the AdaGrad Optimizer](#3.10_Adagrad_Optimizer)
# * [3.10.1 Hyperparameter search using RandomSearch](#3.10.1_Hyperparameter_RandomSearch)
# * [3.10.2 Learning Curves](#3.10.2_Learning_Curve)
# * [3.10.3 Model Performance](#3.10.3_Model_Performance)
# * [3.11 Final Model Selection](#3.11_final_model_selection)
#
# ## 3.2 Introduction<a id='3.2_Introduction'></a>
# In preceding notebooks, we transformed data from one "raw" data form into another format in order to to make it more appropriate and valuable for our analysis. In this step we will do the followings:
#
# * Data Pre-Processing
# * Build Models With Different Optimizers
# * Compare the performance of the models
# * Pick the Best of the Models
#
#
# ## 3.3 Imports<a id='3.3_Imports'></a>
# +
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import os
import random
import missingno as msno
import warnings
warnings.filterwarnings(action='ignore')
#from library.sb_utils import save_file
from sklearn.preprocessing import LabelBinarizer
import tensorflow as tf
from tensorflow import keras
import tensorflow_hub as hub
from PIL import Image
from keras_tuner import RandomSearch
from keras_tuner.engine.hyperparameters import HyperParameters
from tensorflow.keras.preprocessing.image import ImageDataGenerator
from keras.models import Sequential
from keras.layers import Dense, Conv2D , MaxPool2D , Flatten , Dropout , BatchNormalization
from keras.callbacks import ReduceLROnPlateau
from sklearn.metrics import accuracy_score,confusion_matrix
from keras.callbacks import ReduceLROnPlateau
from sklearn import __version__ as sklearn_version
from sklearn.decomposition import PCA
from sklearn.preprocessing import scale
from sklearn.model_selection import train_test_split, cross_validate, GridSearchCV, learning_curve
from sklearn.preprocessing import StandardScaler, MinMaxScaler
from sklearn.metrics import r2_score,accuracy_score, mean_squared_error, mean_absolute_error, precision_recall_fscore_support
from sklearn import metrics
from sklearn.metrics import roc_auc_score
from sklearn.pipeline import make_pipeline
from sklearn.metrics import classification_report
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn import metrics
# %matplotlib inline
# -
# ## 3.4 Load data<a id='3.4_Load_Data'></a>
df_train = pd.read_csv('sign_mnist_train.csv')
df_test = pd.read_csv('sign_mnist_test.csv')
df_train.head()
df_train.info()
df_test.head()
df_test.info()
# ## 3.5 Data Pre-Processing<a id='3.5_Data_Pre-Processing'></a>
# We take the following data pre-processing steps in our project:
#
# * Analyzing the labels and making sure that dataset is balanced.
# * Converting arrays to images (tensors).
# * Performing one hot encoding for the labels.
# * Augmenting the data
y_train=df_train['label']
y_test=df_test['label']
label_binarizer = LabelBinarizer()
y_train = label_binarizer.fit_transform(y_train)
y_test = label_binarizer.fit_transform(y_test)
y_train
X_train=df_train.drop(columns=['label']).values
X_test=df_test.drop(columns=['label']).values
X_train
X_train.shape
X_train = X_train / 255
X_test = X_test / 255
X_train = X_train.reshape(-1,28,28,1)
X_test = X_test.reshape(-1,28,28,1)
X_train.shape
# +
random_10, ax = plt.subplots(2,5)
random_10.set_size_inches(10, 10)
for i in range(2):
for j in range(5):
ax[i,j].imshow(X_train[random.randint(0, 27445)].reshape(28, 28) , cmap = "gray")
plt.tight_layout()
# -
# +
data_augmented = ImageDataGenerator(
featurewise_center=False,
samplewise_center=False,
featurewise_std_normalization=False,
samplewise_std_normalization=False,
zca_whitening=False,
rotation_range=10, # Randomly rotates images in 10 degrees
zoom_range = 0.1, # Randomly zoom images by %10
width_shift_range=0.1, # Randomly shift images horizontally
height_shift_range=0.1, # Randomly shift images vertically
horizontal_flip=False,
vertical_flip=False)
data_augmented.fit(X_train)
# -
# ## 3.6 Build the Base Model<a id='3.6_Build_Model'></a>
# We build a CNN model to classify images. We have the following in our model:
#
# * Conv2D layers with activation function "relu":
# * In the first and the last conv2D layer we set strides=1 and padding="same" which means the input and output will have the same size and the filter will shift by one.
#
# * Batch normalization - to normalize the inputs of each layer in order to fight the internal covariate shift problem.
#
# * Max Pooling with 2×2 pixels applied with a stride of 2 pixels - to calculate the maximum value for each patch of the feature map. This will also reduce the size of each feature map by a factor of 2.
#
# * Droupout, a regularization technique - to prevent neural networks from overfitting.
#
# * Flatten layer - to convert the input data into a long vector in order to pass the input through the artificial neural network to be processed further.
#
# * Dense layers - to connect the neurons of the layer to every neuron of its preceding layer.
model = Sequential()
model.add(Conv2D(75 , (3,3) , strides = 1 , padding = 'same' , activation = 'relu' , input_shape = (28,28,1)))
model.add(BatchNormalization())
model.add(MaxPool2D((2,2) , strides = 2 , padding = 'same'))
model.add(Conv2D(50 , (3,3) , strides = 1 , padding = 'same' , activation = 'relu'))
model.add(Dropout(0.2))
model.add(BatchNormalization())
model.add(MaxPool2D((2,2) , strides = 2 , padding = 'same'))
model.add(Conv2D(25 , (3,3) , strides = 1 , padding = 'same' , activation = 'relu'))
model.add(BatchNormalization())
model.add(MaxPool2D((2,2) , strides = 2 , padding = 'same'))
model.add(Flatten())
model.add(Dense(units = 512 , activation = 'relu'))
model.add(Dropout(0.3))
model.add(Dense(units = 24 , activation = 'softmax'))
model.compile(loss = 'categorical_crossentropy' , metrics = ['accuracy'])
#model.summary()
# ## 3.6.1 Model Architecture<a id='3.6.1_Model_Architecture'></a>
# Next, we convert the model to dot format and save it to a file.
tf.keras.utils.plot_model(
model,
to_file="model.png",
show_shapes=True,
show_layer_names=True,
)
# ## 3.7 Define a Callback Object<a id='3.7_Define_Callback'></a>
# Models often benefit from reducing the learning rate by a factor of 5-10 once learning stagnates. We will define a callback object that performs actions at various stages of training in order to monitor a quantity and if no improvement is seen for a 'patience' number of epochs, the learning rate is reduced (see below for the details).
reduce_learning_rate = ReduceLROnPlateau(monitor='val_loss', factor=0.5,
patience=3, verbose=1, min_lr=0.00001)
# We try out multiple optimizers when we compile our model to determine the optimizer with the best performance. We try the following optimizers:
#
# * adam
# * SGD
# * AdaGrad
Optimizer1 = keras.optimizers.Adam()
Optimizer2 = keras.optimizers.SGD()
Optimizer3 = keras.optimizers.Adagrad()
# ## 3.8 Model with Optimizer Adam<a id='3.8_Adam_Optimizer'></a>
# In this section we use our base model with optimizer Adam.
def build_model(hp):
model = Sequential()
model.add(Conv2D(75 , (3,3) , strides = 1 , padding = 'same' , activation = 'relu' , input_shape = (28,28,1)))
model.add(BatchNormalization())
model.add(MaxPool2D((2,2) , strides = 2 , padding = 'same'))
model.add(Conv2D(50 , (3,3) , strides = 1 , padding = 'same' , activation = 'relu'))
model.add(Dropout(0.2))
model.add(BatchNormalization())
model.add(MaxPool2D((2,2) , strides = 2 , padding = 'same'))
model.add(Conv2D(25 , (3,3) , strides = 1 , padding = 'same' , activation = 'relu'))
model.add(BatchNormalization())
model.add(MaxPool2D((2,2) , strides = 2 , padding = 'same'))
model.add(Flatten())
model.add(Dense(units = 512 , activation = 'relu'))
model.add(Dropout(0.3))
model.add(Dense(units = 24 , activation = 'softmax'))
model.compile(optimizer = Optimizer1, loss = 'categorical_crossentropy' , metrics = ['accuracy'])
return model
# ## 3.8.1 Hyperparameter Search using RandomSearch<a id='3.8.1_Hyperparameter_RandomSearch'></a>
# Next, we will tune some of the hyperparameters using `keras-tuner`.
tuner_search=RandomSearch(build_model,
objective='val_accuracy', directory='output1', max_trials=5)
tuner_search.search(X_train,y_train, batch_size = 128,
epochs=10, validation_data = (X_test, y_test))
# We extract the best model from `tuner_search` object.
model_best=tuner_search.get_best_models(num_models=1)[0] #this will give us the best tuned model
tuner_search.results_summary()
# Next, we fit the best model to the augmented data.
# +
model_best_optimizer1 = model_best.fit(data_augmented.flow(X_train,y_train, batch_size = 128) ,epochs = 15 ,
validation_data = (X_test, y_test), callbacks=[reduce_learning_rate])
# -
# ## 3.8.2 Learning Curves<a id='3.8.2_Learning_Curve'></a>
# We visualize the performance of the best model with respect to each epoch.
# +
epochs = [i for i in range(15)]
fig , ax = plt.subplots(1,2)
train_accuracy = model_best_optimizer1.history['accuracy']
train_loss = model_best_optimizer1.history['loss']
validation_accuracy = model_best_optimizer1.history['val_accuracy']
validation_loss = model_best_optimizer1.history['val_loss']
fig.set_size_inches(18,5)
ax[0].plot(epochs , train_accuracy , 'bo-' , label = 'Training Accuracy')
ax[0].plot(epochs , validation_accuracy , 'go-' , label = 'Testing Accuracy')
ax[0].set_title('Training and Testing Accuracy with Optimizer Adam')
ax[0].legend()
ax[0].set_xlabel("Epochs")
ax[0].set_ylabel("Accuracy")
ax[1].plot(epochs , train_loss , 'b-o' , label = 'Training Loss')
ax[1].plot(epochs , validation_loss , 'g-o' , label = 'Testing Loss')
ax[1].set_title('Training and Testing Loss with Optimizer Adam')
ax[1].legend()
ax[1].set_xlabel("Epochs")
ax[1].set_ylabel("Loss")
plt.show()
# -
# ## 3.8.3 Model Performance<a id='3.8.3_Model_Performance'></a>
# We assess the performance of the model with adam optimizer in this section.
rounded_predictions = model_best.predict_classes(X_test, batch_size=128, verbose=1)
rounded_labels=np.argmax(y_test, axis=1)
classes = ["Class " + str(i) for i in range(25) if i != 9]
print('-----------------------------------------------------------')
print("Accuracy_test:",metrics.accuracy_score(rounded_labels, rounded_predictions))
print('-----------------------------------------------------------')
print(classification_report(rounded_labels, rounded_predictions, target_names = classes))
cm = confusion_matrix(rounded_labels,rounded_predictions)
cm[:3]
# ## 3.9 Model with SGD Optimizer<a id='3.9_SGD_Optimizer'></a>
# In this section we use our base model with optimizer SGD.
def build_model(hp):
model = Sequential()
model.add(Conv2D(75 , (3,3) , strides = 1 , padding = 'same' , activation = 'relu' , input_shape = (28,28,1)))
model.add(BatchNormalization())
model.add(MaxPool2D((2,2) , strides = 2 , padding = 'same'))
model.add(Conv2D(50 , (3,3) , strides = 1 , padding = 'same' , activation = 'relu'))
model.add(Dropout(0.2))
model.add(BatchNormalization())
model.add(MaxPool2D((2,2) , strides = 2 , padding = 'same'))
model.add(Conv2D(25 , (3,3) , strides = 1 , padding = 'same' , activation = 'relu'))
model.add(BatchNormalization())
model.add(MaxPool2D((2,2) , strides = 2 , padding = 'same'))
model.add(Flatten())
model.add(Dense(units = 512 , activation = 'relu'))
model.add(Dropout(0.3))
model.add(Dense(units = 24 , activation = 'softmax'))
model.compile(optimizer = Optimizer2, loss = 'categorical_crossentropy' , metrics = ['accuracy'])
return model
# ## 3.9.1 Hyperparameter Search using RandomSearch<a id='3.9.1_Hyperparameter_RandomSearch'></a>
# Here, the hyperparameter are tuned using `keras-tuner`.
tuner_search=RandomSearch(build_model,
objective='val_accuracy', directory='output2', max_trials=5)
tuner_search.search(X_train,y_train, batch_size = 128,
epochs=10, validation_data = (X_test, y_test))
# We use `get_best_models()` of `tuner_search` to select the best model.
model_best=tuner_search.get_best_models(num_models=1)[0] #this will give us the best tuned model
# +
model_best_optimizer2 = model_best.fit(data_augmented.flow(X_train,y_train, batch_size = 128) ,epochs = 15 , validation_data = (X_test, y_test))
# -
# ## 3.9.2 Learning Curves<a id='3.9.2_Learning_Curve'></a>
# In the next cell we plot the performance of the best model on the training data as well as the testing data.
# +
epochs = [i for i in range(15)]
fig , ax = plt.subplots(1,2)
train_accuracy = model_best_optimizer2.history['accuracy']
train_loss = model_best_optimizer2.history['loss']
validation_accuracy = model_best_optimizer2.history['val_accuracy']
validation_loss = model_best_optimizer2.history['val_loss']
fig.set_size_inches(18,5)
ax[0].plot(epochs , train_accuracy , 'bo-' , label = 'Training Accuracy')
ax[0].plot(epochs , validation_accuracy , 'go-' , label = 'Testing Accuracy')
ax[0].set_title('Training and Testing Accuracy with Optimizer SGD')
ax[0].legend()
ax[0].set_xlabel("Epochs")
ax[0].set_ylabel("Accuracy")
ax[1].plot(epochs , train_loss , 'b-o' , label = 'Training Loss')
ax[1].plot(epochs , validation_loss , 'g-o' , label = 'Testing Loss')
ax[1].set_title('Training and Testing Loss with Optimizer SGD')
ax[1].legend()
ax[1].set_xlabel("Epochs")
ax[1].set_ylabel("Loss")
plt.show()
# -
# ## 3.9.3 Model Performance<a id='3.9.3_Model_Performance'></a>
# We evaluate the performance of the model with SGD optimizer.
rounded_predictions = model_best.predict_classes(X_test, batch_size=128, verbose=1)
rounded_labels=np.argmax(y_test, axis=1)
classes = ["Class " + str(i) for i in range(25) if i != 9]
print('-----------------------------------------------------------')
print("Accuracy_test:",metrics.accuracy_score(rounded_labels, rounded_predictions))
print('-----------------------------------------------------------')
print(classification_report(rounded_labels, rounded_predictions, target_names = classes))
cm = confusion_matrix(rounded_labels,rounded_predictions)
cm[:3]
# ## 3.10 Model with AdaGrad Optimizer<a id='3.10_Adagrad_Optimizer'></a>
# In this section we use our base model with optimizer AdaGrad.
def build_model(hp):
model = Sequential()
model.add(Conv2D(75 , (3,3) , strides = 1 , padding = 'same' , activation = 'relu' , input_shape = (28,28,1)))
model.add(BatchNormalization())
model.add(MaxPool2D((2,2) , strides = 2 , padding = 'same'))
model.add(Conv2D(50 , (3,3) , strides = 1 , padding = 'same' , activation = 'relu'))
model.add(Dropout(0.2))
model.add(BatchNormalization())
model.add(MaxPool2D((2,2) , strides = 2 , padding = 'same'))
model.add(Conv2D(25 , (3,3) , strides = 1 , padding = 'same' , activation = 'relu'))
model.add(BatchNormalization())
model.add(MaxPool2D((2,2) , strides = 2 , padding = 'same'))
model.add(Flatten())
model.add(Dense(units = 512 , activation = 'relu'))
model.add(Dropout(0.3))
model.add(Dense(units = 24 , activation = 'softmax'))
model.compile(optimizer = Optimizer3, loss = 'categorical_crossentropy' , metrics = ['accuracy'])
return model
# ## 3.10.1 Hyperparameter Search using RandomSearch<a id='3.10.1_Hyperparameter_RandomSearch'></a>
# The hyperparameters are tuned using `keras-tuner`.
tuner_search=RandomSearch(build_model,
objective='val_accuracy', directory='output3', max_trials=5)
# +
tuner_search.search(X_train,y_train, batch_size = 128,
epochs=10, validation_data = (X_test, y_test))
# -
model_best=tuner_search.get_best_models(num_models=1)[0] #this will give us the best tuned model
# +
model_best_optimizer3=model_best.fit(data_augmented.flow(X_train,y_train, batch_size = 128) ,epochs = 15 , validation_data = (X_test, y_test))
# -
# ## 3.10.2 Learning Curve<a id='3.10.2_Learning_Curve'></a>
# We visualize the performance of the model with AdaGrad optimizer with respect to each epoch.
# +
epochs = [i for i in range(15)]
fig , ax = plt.subplots(1,2)
train_accuracy = model_best_optimizer3.history['accuracy']
train_loss = model_best_optimizer3.history['loss']
validation_accuracy = model_best_optimizer3.history['val_accuracy']
validation_loss = model_best_optimizer3.history['val_loss']
fig.set_size_inches(18,5)
ax[0].plot(epochs , train_accuracy , 'bo-' , label = 'Training Accuracy')
ax[0].plot(epochs , validation_accuracy , 'go-' , label = 'Testing Accuracy')
ax[0].set_title('Training and Testing Accuracy with Optimizer AdaGrad')
ax[0].legend()
ax[0].set_xlabel("Epochs")
ax[0].set_ylabel("Accuracy")
ax[1].plot(epochs , train_loss , 'b-o' , label = 'Training Loss')
ax[1].plot(epochs , validation_loss , 'g-o' , label = 'Testing Loss')
ax[1].set_title('Training and Testing Loss with Optimizer AdaGrad')
ax[1].legend()
ax[1].set_xlabel("Epochs")
ax[1].set_ylabel("Loss")
plt.show()
# -
# ## 3.10.3 Model Performance<a id='3.10.3_Model_Performance'></a>
# In this section, we evaluate our last model.
rounded_predictions = model_best.predict_classes(X_test, batch_size=128, verbose=1)
rounded_labels=np.argmax(y_test, axis=1)
classes = ["Class " + str(i) for i in range(25) if i != 9]
print('-----------------------------------------------------------')
print("Accuracy_test:",metrics.accuracy_score(rounded_labels, rounded_predictions))
print('-----------------------------------------------------------')
print(classification_report(rounded_labels, rounded_predictions, target_names = classes))
cm = confusion_matrix(rounded_labels,rounded_predictions)
cm[:3]
# ## 3.11 Final Model Selection<a id='3.11_final_model_selection'></a>
# #### After analyzing multiple models, we observe the following:
#
# * The model with AdaGrad optimizer has approximately 94% accuracy score. This is the lowest score among the 3 models we have tried.
# * The model with SGD optimizer has approximately 97% accuracy score. This is the second best score we get.
# * The model with Adam optimizer has approximately 99% accuracy score which is the best. This model also has the highest score for precision, recall and f1 across all classes.
#
# Thereby, we pick the tuned model with Adam optimizer.
|
Pre-processing and Modelling/03_preprocessing_and_modeling.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="fND9fMxuSCsi"
# Task 2 - Sentiment Classifier & Transfer Learning (10 points)
# Imports
#
#
# + id="T3MIG5VsqDLf"
# Imports
import torch
torch.manual_seed(10)
from torch.autograd import Variable
import pandas as pd
import numpy as np
import sklearn as sk
import re
import itertools
import warnings
warnings.filterwarnings("ignore")
from matplotlib import pyplot as plt
import nltk
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
# + colab={"base_uri": "https://localhost:8080/"} id="HQbN9otHM-SU" outputId="09746c8e-a90b-4648-9d31-5b7e8891dca1"
from google.colab import drive
drive.mount('/content/drive')
import sys
sys.path.append('/content/drive/MyDrive/Colab Notebooks')
# + id="M0o7a4qkNg6h"
import modelinput
# + [markdown] id="O1qPhGs82b-O"
# 2.2.1 Get the data (0.5 points)
#
# + colab={"resources": {"http://localhost:8080/nbextensions/google.colab/files.js": {"data": "<KEY>", "ok": true, "headers": [["content-type", "application/javascript"]], "status": 200, "status_text": ""}}, "base_uri": "https://localhost:8080/", "height": 75} id="veCv7VsAowag" outputId="f0125025-053b-4408-ecd6-094da79e0731"
from google.colab import files
upload = files.upload()
data = pd.read_csv("bengali_hatespeech.csv",sep=',')
data1 = data.iloc[0:19000,:]
# + id="-zCtLO8p5au_"
#Split off a part of the Bengali corpus such that it roughly equals the Hindi corpus in size and distribution of classes
from sklearn.model_selection import train_test_split
x, y = data1['sentence'], data1['hate']
X_TRAIN,x_test,Y_TRAIN,y_test=train_test_split(x,y,train_size=0.25,random_state=123)
X_TRAIN = X_TRAIN.values #roughtly the same number of sentences
Y_TRAIN = Y_TRAIN.values #roughtly the same number of labels
result = pd.value_counts(Y_TRAIN)
#print(Y_TRAIN)
# + id="HnpVZczLFEc9" colab={"base_uri": "https://localhost:8080/"} outputId="a8ab5c57-fedd-4129-d519-e9e661ebf676"
# using a small development set
x_train_dev=X_TRAIN[1900:3000]
y_train = Y_TRAIN[1900:3000]
result = pd.value_counts(y_train)
print(result)
print(len(x_train_dev))
# + [markdown] id="NX2DCfm0JhXg"
# 2.2.2clean the data
# + colab={"resources": {"http://localhost:8080/nbextensions/google.colab/files.js": {"data": "<KEY>", "ok": true, "headers": [["content-type", "application/javascript"]], "status": 200, "status_text": ""}}, "base_uri": "https://localhost:8080/", "height": 75} id="12UrwLSLEPVt" outputId="8bde8662-27f0-42be-e7a9-5ec1b00751cd"
#clean the data
uploaded = files.upload()
stopwords = pd.read_csv('stopwords-bn.txt',header=None)
def clean_the_data(data):
new_list=[]
punc=r'''!()-[]{};:'"\,<>./?@#$%^&*_“~'''
stop_words=stopwords[0].tolist()
for i in range(0,len(data)):
# Punctuations removal
new=' '.join(word for word in data[i].split() if word[0] not in punc)
new = ' '.join(re.sub("(\w+:\/\/\S+)", " ", new).split())
new = ' '.join(re.sub(r"\b\d+\b", " ", new).split())
new = ' '.join(re.sub("[\.\,\!\?\:\;\-\=\#\%\…\\u200d\।।]", " ", new).split())
new = ' '.join(re.sub("[\U0001F600-\U0001F64F]"," ",new).split()) # emotions
new = ' '.join(re.sub("[\U0001F300-\U0001F5FF]"," ",new).split()) # symbols & pictographs
new = ' '.join(re.sub("[\U0001F680-\U0001F6FF]"," ",new).split()) # transport & map symbols
new = ' '.join(re.sub("[\U0001F1E0-\U0001F1FF]"," ",new).split()) # flags (iOS)
new = ' '.join(re.sub("[\U00002702-\U000027B0]"," ",new).split())
new = ' '.join(re.sub("[\U000024C2-\U0001F251]"," ",new).split())
new = ' '.join(re.sub("[\U00001F92C]"," ",new).split())
# Converting into lowercase
new= new.lower()
# Removing stop words
new=' '.join(word for word in new.split() if word not in stop_words)
# Appending to the text list
new_list.append(new)
return new_list
new_list = clean_the_data(x_train_dev)
#print(new_list)
# + colab={"base_uri": "https://localhost:8080/"} id="1JHzrXoNIWtT" outputId="f595a72d-8fb1-4ac6-da5a-eaee61f09c19"
nltk.download('punkt')
# + id="IDFtdqfIIYmw"
# Tokenizes each sentence by implementing the nltk tool
new_list_new = [nltk.tokenize.word_tokenize(x) for x in new_list]
#print(new_list_new[0])
# + [markdown] id="CEJRGjxcJqtd"
# 2.2.3Build the vocabulary
# + id="EH9HqPb7jAbi"
V=modelinput.vocabulary(new_list_new)
#print(V)
# + [markdown] id="AFmpRB1PNtqx"
# returns one-hot encoding
# + id="7-LXbE2bN3yt"
def word_to_one_hot(word):
words = V.keys()
str_to_int = dict((c, i) for i, c in enumerate(words))
integer_encoded = [str_to_int[string] for string in [word]]
# one hot encode
onehot_encoded = []
for value in integer_encoded:
letter = [0 for _ in range(len(V))]
letter[value] = 1
onehot_encoded.append(letter)
#onehot_encoded.long()
return onehot_encoded
pass
# + [markdown] id="dyPGZt1URdkw"
# 2.2.4Subsampling
# + id="o2_4s9mURc0q"
Words = {}
i=0
for s in range(len(new_list_new)):
n=new_list_new[s]
for y in range(len(n)):
w=new_list_new[s][y]
Words[w] = i
i+=1
y+=1
s+=1
W2=list(Words)
def sampling_prob(word):
frac = W2.count(word)/len(W2)
prob = (np.sqrt(frac/0.000001) + 1) * (0.000001/frac)
return prob
pass
# + [markdown] id="ZSKzWbWlXHAb"
# 2.2.5Skip-Grams
# + id="FT8AiU5eXFyL"
#from bndatapro import get_target_context
def get_target_context(sentence):
word_lists=[]
for i in range(len(sentence)):
w=sentence[i]
p_sample = sampling_prob(w)
threshold = np.random.random()
#print(threshold)
if p_sample > threshold:
# the word is kept
for n in range(2):
# look back
if (i-n-1)>=0:
word_lists.append([w] + [sentence[i-n-1]])
# look forward
if (i+n+1)<len(sentence):
word_lists.append([w]+[sentence[i+n+1]])
else:
# the word is dropped
i+=1
return word_lists
pass
# + [markdown] id="9v5XjmO3X1mt"
# 2.2.6Hyperparameters
# + id="YRYaiilEXwUq" colab={"base_uri": "https://localhost:8080/"} outputId="0ce458d7-6d96-4747-daa7-c825811fdccc"
# Set hyperparameters
window_size = 2
embedding_size = 64
vocabulary_size=len(V)
print(len(V))
# More hyperparameters
learning_rate = 0.05
epochs = 20
# + id="vVkEI2cLSQG0"
from modelss import Word2Vec
# + [markdown] id="EQ8YNLGFYWaA"
# 2.2.7 Word2Vec model
# + id="MmAkeW2wSZsj"
net = modelinput.Word2Vec(embed_size=embedding_size, vocab_size=vocabulary_size)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
net = net.to(device)
W1 = net.input.weight
W2 = net.output.weight
# + [markdown] id="xE3ZW3osZNS4"
# 2.2.8loss function and optimizer
# + id="zzrBKuWxYT2q"
optimizer = torch.optim.SGD(net.parameters(), lr=learning_rate)
criterion = nn.CrossEntropyLoss()
# + [markdown] id="w8NY0_AZmyXP"
# 2.2.9training model
# + colab={"base_uri": "https://localhost:8080/"} id="34eGdvHtZLmR" outputId="09100ff1-9bba-4f45-a924-447f14a7f33d"
# load initial weights
window_size = 2
embedding_size = 64
losses = [torch.tensor(1., device=device)]
#losses.append(1)
losses_mean=np.mean([tensor.cpu() for tensor in losses])
def train():
print("Training started")
train()
for epo in range(epochs):
#while losses_mean> 0.006:
losses_mean=np.mean([tensor.cpu() for tensor in losses])
#mean = torch.mean(torch.stack(losses))
#mean = mean.to(device)
print("Loss: ", losses_mean)
net.train()
for i in range(len(new_list_new)):
# Define train procedure
# step1:Skip-Grams
sentence = new_list_new[i]
idx_pairs = get_target_context(sentence)
for target, context in idx_pairs:
# step2:target one-hot encoding
X = word_to_one_hot(target)
X = torch.tensor(X)
x1 = X[0]
x1 = x1.to(device)
#print(x1)
# step3:Word2Vec
y =net.forward(x1)
Y = word_to_one_hot(context)
Y = Y[0]
y_ture = torch.tensor(Y)
y_ture = y_ture.to(device)
# step4:loss
loss = criterion(y,y_ture)
#print(loss)
losses.append(loss.data)
losses.pop(0)
optimizer.zero_grad()
loss.backward()
optimizer.step()
# step5:Backprop to update model parameters
print("Training finished")
# + id="T5r4kwATm5rR"
Weight3=[]
for i in range(len(V)-1):
weight3=[]
w=W1[i]
for y in range(embedding_size):
wei=w[y].item()
weight3.append(wei)
Weight3.append(weight3)
V2 = dict(zip(V, Weight3))
# + colab={"base_uri": "https://localhost:8080/"} id="uBRDKXXlm9hU" outputId="652c78e2-2b7e-433a-fd2d-c9269cb933ed"
sentence_padding =[]
pad_idx = 0
padding_standard = max(new_list_new, key=len,default='')
#padding the sentence to the same length
for i in range(len(new_list_new)):
temp_sentence = list()
temp = new_list_new[i]
while len(temp) < len(padding_standard):
temp.insert(len(temp), pad_idx)
sentence_padding.append(temp)
#make sentences to the same size matrix using word embedding expression
sentence_train=[]
for i in range(len(sentence_padding)):
temp_sentence = list()
temp = new_list_new[i]
for word in temp:
if word in V2.keys():
temp_sentence.append(V2[word])
else:
temp_sentence.append(np.zeros(embedding_size))
sentence_train.append(temp_sentence)
print(np.shape(sentence_train))
# + id="QHriSHLZnBSx"
sentence_train3=torch.tensor(sentence_train)
# + [markdown] id="ofKWY_L6BP6O"
# We create an instance of our CNN class.
# + id="C6JikZ1znMAP"
from modelinput import CNN
EMBEDDING_DIM = embedding_size
N_FILTERS = 100
FILTER_SIZES = [2,3,4]
OUTPUT_DIM = 1
DROPOUT = 0.5
model = CNN(EMBEDDING_DIM, N_FILTERS, FILTER_SIZES, OUTPUT_DIM, DROPOUT)
# + [markdown] id="WRe4U2MWBt8B"
# Train the Model : The method of training is same as the previous one. We can initialize the values of optimizer and criterion (loss function).
# + id="Jxd1bLkynTkd"
optimizer1 = optim.Adam(model.parameters())
criterion1 = nn.BCEWithLogitsLoss()
model = model.to(device)
criterion1 = criterion1.to(device)
# + [markdown] id="8calTXccnxTt"
# Apply the old classifer to the new data and print accuracy: We import a package called 'binary_accuracy' to calculate the accuracy. It returns accuracy per batch. For instance if 7/10 are correct repsonses, the output will be 0.7. Further, we define a function "evaluate(model)" for training our model.
# + id="TMqO473XnYwN" colab={"base_uri": "https://localhost:8080/"} outputId="03bea454-2be4-4d1d-b62c-004e91962afe"
from modelinput import binary_accuracy
sentence_train3=sentence_train3.to(device,dtype=torch.float)
Y_train = torch.tensor(y_train).to(device)
def evaluate(model):
epoch_loss = 0
epoch_acc = 0
model.eval()
predictions = model(sentence_train3).squeeze(1)
loss = criterion1(predictions, Y_train.float())
acc = binary_accuracy(predictions, Y_train)
epoch_loss += loss.item()
epoch_acc += acc.item()
return epoch_loss, epoch_acc
model.load_state_dict(torch.load('/content/CNNweight.pt'))
test_loss, test_acc = evaluate(model)
print(f'Test Loss: {test_loss:.3f} | Test Acc: {test_acc*100:.2f}%')
# + [markdown] id="T8MW7hFjuH90"
# retrain the model and print new accuracy
# + id="5wfAeCxOnvQE" colab={"base_uri": "https://localhost:8080/"} outputId="4b96e7c3-6010-4dc6-df22-8c27f56f61d5"
N_EPOCHS = 20
sentence_train3=sentence_train3.to(device,dtype=torch.float)
#train_iterator = iter(sentence_train1)
#best_valid_loss = float('inf')
Y_train = torch.tensor(y_train).to(device)
for epoch in range(N_EPOCHS):
epoch_loss = 0
epoch_acc = 0
model.train()
optimizer1.zero_grad()
predictions = model.forward(sentence_train3).squeeze(1)
loss1 = criterion1(predictions, Y_train.float())
acc = binary_accuracy(predictions, Y_train)
loss1.backward()
optimizer1.step()
epoch_loss += loss1.item()
epoch_acc += acc.item()
print(f'\tTrain Loss: {loss1:.3f} | Train Acc: {acc*100:.2f}%')
# + [markdown] id="w-8MgMNwUUCe"
# Transformer model
# + id="1EtF3YmuOBJO"
import torch.nn as nn
import copy
def clones(module, N):
"Produce N identical layers."
return nn.ModuleList([copy.deepcopy(module) for _ in range(N)])
# + id="W79Re4TgOEbF"
import math,copy
#doing the position encoding first
def positionalencoding1d(d_model, length):
if d_model % 2 != 0:
raise ValueError("Cannot use sin/cos positional encoding with "
"odd dim (got dim={:d})".format(d_model))
pe = torch.zeros(length, d_model)
position = torch.arange(0, length).unsqueeze(1)
div_term = torch.exp((torch.arange(0, d_model, 2, dtype=torch.float) *
-(math.log(10000.0) / d_model)))
pe[:, 0::2] = torch.sin(position.float() * div_term)
pe[:, 1::2] = torch.cos(position.float() * div_term)
return pe
posit = positionalencoding1d(64,219) # the shape of one padding sentence
posit = torch.tensor(posit,device=device)
AttInput=torch.empty(np.shape(sentence_train3))
for i in range(len(sentence_train3)):
tar =sentence_train3[i]
AttInput[i]= tar+posit
Input = AttInput[0:100,]
# + colab={"base_uri": "https://localhost:8080/"} id="t3fvgBYaOHVP" outputId="a2f04551-b5b9-4e73-da14-a6aa1ca6b01e"
torch.cuda.empty_cache()
SRC_VOCAB=1
N_CLASS=1
D_MODEL=embedding_size
D_FF=1024
N = 6
H=8
DROP_OUT=0.1
model2 = modelinput.make_model(SRC_VOCAB,N,D_MODEL,D_FF,H,DROP_OUT, N_CLASS)
model2 = model2.to(device)
lr=0.005
criterion2 = nn.CrossEntropyLoss()
optimizer2 = torch.optim.Adam(model2.parameters(),lr)
N_EPOCHS = 10
for epoch in range(N_EPOCHS):
epoch_loss2 = 0
epoch_acc2 = 0
optimizer2.zero_grad()
x = Input.to(device)
y = torch.tensor(y_train[0:100], dtype=torch.long, device=device)
y = y.unsqueeze(1)
output = model2(x, None)
loss2 = criterion2(output,y)
loss2.backward()
optimizer2.step()
epoch_loss2 += loss2.item()
print(f'\tTrain Loss: {loss2:.3f}')
|
Bengali.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: torch
# language: python
# name: torch
# ---
# # references
# 1. https://www.kaggle.com/columbia2131/device-eda-interpolate-by-removing-device-en-ja
# # Load Libraries
# +
import numpy as np
import pandas as pd
from glob import glob
import os
import matplotlib.pyplot as plt
from tqdm.notebook import tqdm
from pathlib import Path
import plotly.express as px
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.utils.data import TensorDataset, DataLoader
from sklearn.model_selection import train_test_split
# -
device = torch.device('cuda:0' if torch.cuda.is_available() else "cpu")
print(device)
notebookName = 'Baseline'
PATH = Path(f"./models/{notebookName}")
if os.path.isdir(PATH):
dir_list = os.listdir(PATH)
num_files = 0
while True:
if os.path.isfile(str(PATH / f"{num_files}")):
print(num_files)
num_files += 1
else:
break
else:
os.mkdir(PATH)
num_files = 0
num_files
# +
RANDOM_STATE = 42
lr = 0.005
batch_size = 4
EPOCH_NUM = 1000
torch.manual_seed(RANDOM_STATE)
experience_name = f"{num_files}"
checkpoint_name = "check_point"
model_name = str("model - " + experience_name)
param_name = str("param - " + experience_name)
result_name = str("result - " + experience_name)
dummy_path = str(PATH / f"{num_files}")
checkpoint_path = str(PATH / f"{checkpoint_name}.pth")
model_path = str(PATH / f"{model_name}.pth")
param_path = str(PATH / f"{param_name}.pth")
result_path = str(PATH / f"{result_name}.csv")
model_path, param_path, result_path
# -
# # Useful Functions
def calc_haversine(lat1, lon1, lat2, lon2):
dlat = (lat2 - lat1) % 360
dlon = (lon2 - lon1) % 360
dlat, dlon = map(np.radians, [dlat, dlon])
a = np.sin(dlat / 2.0)**2 + np.cos(lat1) * np.cos(lat2) * np.sin(dlon / 2.0)**2
c = 2 * np.arcsin(a ** 0.5)
c = c + np.isnan(c) * ((a > 1) * np.pi/2 + (a < -1) * (-1 * np.pi / 2))
dist = 6_367_000 * c
return dist
def check_score(input_df: pd.DataFrame) -> pd.DataFrame:
output_df = input_df.copy()
output_df['meter'] = input_df.apply(
lambda r: calc_haversine(
r.latDeg, r.lngDeg, r.t_latDeg, r.t_lngDeg
),
axis=1
)
meter_score = output_df['meter'].mean()
print(f'error meter: {meter_score}')
scores = []
for phone in output_df['phone'].unique():
_index = output_df['phone']==phone
p_50 = np.percentile(output_df.loc[_index, 'meter'], 50)
p_95 = np.percentile(output_df.loc[_index, 'meter'], 95)
scores.append(p_50)
scores.append(p_95)
score = sum(scores) / len(scores)
print(f'score: {score}')
return output_df, meter_score , score
def check_score_np(predict:torch.Tensor, target:torch.Tensor):
m = []
predict = predict.detach().numpy()
target = target.detach().numpy()
for i in range(predict.shape[0]):
temp = calc_haversine(predict[i,0], predict[i,1], target[i,0], target[i,1])
m.append(temp)
m = np.array(m)
score = (np.percentile(m, 50) + np.percentile(m, 95))/2
return score
# # Load Datasets
data_dir = Path("../input/google-smartphone-decimeter-challenge")
df_train = pd.read_pickle(str(data_dir / "gsdc_train.pkl.gzip"))
# check score
df_train, default_loss, default_meas = check_score(df_train)
# # Feature Engineering
# ## Simple view, what is in data frame.
print(df_train.shape)
df_train.head()
for c in df_train.columns:
print(c)
print(df_train[c].describe())
print()
for col in df_train.columns:
print(col)
df_train[['latDeg', 'lngDeg', 'heightAboveWgs84EllipsoidM',
'xSatVelMps', 'ySatVelMps', 'zSatVelMps',
'xSatPosM', 'ySatPosM', 'zSatPosM',
'UncalGyroXRadPerSec', 'UncalGyroYRadPerSec', 'UncalGyroZRadPerSec',
'DriftXRadPerSec' , 'DriftYRadPerSec', 'DriftZRadPerSec',
'UncalMagXMicroT', 'UncalMagYMicroT', 'UncalMagZMicroT',
'UncalAccelXMps2', 'UncalAccelYMps2', 'UncalAccelZMps2']].info()
df_train = df_train.fillna(method = 'pad')
df_train = df_train.fillna(0)
df_train[['latDeg', 'lngDeg', 'heightAboveWgs84EllipsoidM',
'xSatVelMps', 'ySatVelMps', 'zSatVelMps',
'xSatPosM', 'ySatPosM', 'zSatPosM',
'UncalGyroXRadPerSec', 'UncalGyroYRadPerSec', 'UncalGyroZRadPerSec',
'DriftXRadPerSec' , 'DriftYRadPerSec', 'DriftZRadPerSec',
'UncalMagXMicroT', 'UncalMagYMicroT', 'UncalMagZMicroT',
'UncalAccelXMps2', 'UncalAccelYMps2', 'UncalAccelZMps2']].describe()
# +
def data_slice_by_phone(df:pd.DataFrame,
xCols = ['latDeg', 'lngDeg', 'heightAboveWgs84EllipsoidM'],
yCols = ['t_latDeg', 't_lngDeg', 't_heightAboveWgs84EllipsoidM', 'speedMps', 'courseDegree']):
indexCols = ['collectionName', 'phoneName', 'millisSinceGpsEpoch']
indx = []
data = []
true = []
for i, phone in enumerate(df['phone'].unique()):
temp = df[df['phone'] == phone]
indx.append(temp[indexCols])
data.append(temp[xCols])
true.append(temp[yCols])
return indx, data, true
def data_merge_by_index(df:pd.DataFrame, index:pd.DataFrame, src:pd.DataFrame, srcCols = ['latDeg', 'lngDeg', 'heightAboveWgs84EllipsoidM']):
indexCols = ['collectionName', 'phoneName', 'millisSinceGpsEpoch']
output = df.copy()
listFrame = []
for i in range(len(index)):
idxFrame = index[i]
srcFrame = src[i]
temp = pd.concat([idxFrame, srcFrame], axis = 1)
listFrame.append(temp)
dataFrame = pd.concat(listFrame, axis = 0)
output = output.merge(dataFrame,
on=["collectionName", "phoneName", "millisSinceGpsEpoch"])
return output
features = ['latDeg', 'lngDeg', 'heightAboveWgs84EllipsoidM',
'xSatVelMps', 'ySatVelMps', 'zSatVelMps',
'xSatPosM', 'ySatPosM', 'zSatPosM',
'UncalGyroXRadPerSec', 'UncalGyroYRadPerSec', 'UncalGyroZRadPerSec',
'DriftXRadPerSec' , 'DriftYRadPerSec', 'DriftZRadPerSec',
'UncalMagXMicroT', 'UncalMagYMicroT', 'UncalMagZMicroT',
'UncalAccelXMps2', 'UncalAccelYMps2', 'UncalAccelZMps2']
labels = ['t_latDeg', 't_lngDeg', 't_heightAboveWgs84EllipsoidM', 'speedMps', 'courseDegree']
idxFrame, dataFrame, trueFrame = data_slice_by_phone(df_train, xCols=features, yCols = labels)
# data_merge_by_index(df_train[["collectionName", "phoneName", "millisSinceGpsEpoch"]], idxFrame, dataFrame)
# -
# # Check!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
# slide window 기반은 때려치고, 데이터프레임에서 직접 읽어오는 방식으로 변경할 필요가 있음
# collectionName, phoneName기반으로 데이터를 잘라서 시계열 데이터처럼 쓸 예정 우선적으로 필요한 것은 lstm으로 돌려보기(baseline을 그렇게 하자!)
# # Modeling
# +
# build model
class ConvBlock(nn.Module):
def __init__(self, input_features, output_features, kernel_size = 3):
super().__init__()
self.convK = nn.Conv1d(input_features, output_features, kernel_size = kernel_size, padding = kernel_size//2)
self.conv = nn.Conv1d(input_features, output_features, 1)
self.bn = nn.BatchNorm1d(output_features)
def forward(self, inputs):
x = self.convK(inputs)
inputs = self.conv(inputs)
x = self.bn(x)
x = F.relu(x)
outputs = x + inputs
return outputs
class BigConv(nn.Module):
def __init__(self, input_size, output_size):
super().__init__()
self.conv1 = ConvBlock(input_size, 2*input_size)
self.conv2 = ConvBlock(2*input_size, 4*input_size)
self.conv3 = ConvBlock(4*input_size, 4*input_size)
self.conv4 = ConvBlock(4*input_size, 4*input_size)
self.conv5 = ConvBlock(4*input_size, output_size)
def forward(self, x):
x = self.conv1(x)
x = self.conv2(x)
x = self.conv3(x)
x = self.conv4(x)
x = self.conv5(x)
return x
class ConvolutionNetwork(nn.Module):
def __init__(self, input_size, output_size):
super().__init__()
# self.conv = nn.Conv1d(input_size, output_size, 1)
self.conv1 = BigConv(input_size, 64)
self.conv2 = BigConv(64, 64)
self.conv3 = BigConv(64, 64)
self.conv4 = BigConv(64, output_size)
# self.lstm = nn.LSTM(input_size = 512 + output_size, hidden_size = output_size, num_layers = 3, dropout = 0.3)
def forward(self, x):
# x1 = self.conv(x)
x = self.conv1(x)
x = self.conv2(x)
x = self.conv3(x)
x = self.conv4(x)
# x = torch.cat([x1, x], axis = 1)
# x, hidden = self.lstm(x)
return x
model = ConvolutionNetwork(len(features), len(labels))
model.to(device)
# loss_func = nn.SmoothL1Loss()
loss_func = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr = lr)
scheduler = optim.lr_scheduler.LambdaLR(optimizer=optimizer,
lr_lambda=lambda epoch: 0.90 ** epoch,
last_epoch=-1,
verbose=True)
# -
class CustomDataloader(torch.utils.data.Dataset):
def __init__(self, data, true = None):
self.data = data
self.true = true
self.len = len(data)
def __len__(self):
return self.len
def __shuffle__(self):
index = np.array(range(self.len), dtype = 'int')
index = np.random.permutation(index)
data = []
true = []
for i in range(self.len):
data.append(self.data[index[i]])
true.append(self.true[index[i]])
self.data = data
self.true = true
def __getitem__(self, idx):
data = self.data[idx]
if self.true is None:
true = []
else:
true = self.true[idx]
data = torch.Tensor(np.expand_dims(np.array(data), 0)).transpose(2, 1)
true = torch.Tensor(np.expand_dims(np.array(true), 0)).transpose(2, 1)
return data, true
# +
Xtrain, Xtest, ytrain, ytest = train_test_split(dataFrame, trueFrame, test_size = 1/10)
loader_train = CustomDataloader(Xtrain, ytrain)
loader_test = CustomDataloader(Xtest, ytest)
# -
def train(epoch):
model.train() # 신경망을 학습 모드로 전환
# 데이터로더에서 미니배치를 하나씩 꺼내 학습을 수행
predict = []
ground = []
loader_train.__shuffle__()
for data, targets in loader_train:
data = data.to(device)
targets = targets.to(device)
optimizer.zero_grad() # 경사를 0으로 초기화
outputs = model(data) # 데이터를 입력하고 출력을 계산
loss = loss_func(outputs, targets) # 출력과 훈련 데이터 정답 간의 오차를 계산
loss.backward() # 오차를 역전파 계산
optimizer.step() # 역전파 계산한 값으로 가중치를 수정
predict.append(outputs.squeeze(dim = 0).transpose(1,0))
ground.append(targets.squeeze(dim = 0).transpose(1,0))
scheduler.step()
# 정확도 출력
predict = torch.cat(predict,axis = 0)
ground = torch.cat(ground,axis = 0)
loss = loss_func(predict, ground)
meas = check_score_np(predict.to('cpu'), ground.to('cpu'))
return loss, meas
def test():
model.eval() # 신경망을 추론 모드로 전환
# 데이터로더에서 미니배치를 하나씩 꺼내 추론을 수행
predict = []
ground = []
with torch.no_grad(): # 추론 과정에는 미분이 필요없음
for data, targets in loader_test:
data = data.to(device)
targets = targets.to(device)
outputs = model(data) # 데이터를 입력하고 출력을 계산
predict.append(outputs.squeeze(dim = 0).transpose(1,0))
ground.append(targets.squeeze(dim = 0).transpose(1,0))
# 정확도 출력
predict = torch.cat(predict,axis = 0)
ground = torch.cat(ground,axis = 0)
loss = loss_func(predict, ground)
meas = check_score_np(predict.to('cpu'), ground.to('cpu'))
return loss, meas
test()
# +
history = []
train_loss, train_meas = 0,0
test_loss, test_meas = 0,0
check_meas = np.inf
check_loss = np.inf
check_epoch = 0
for epoch in range(EPOCH_NUM+1):
if epoch != 0:
train_loss, train_meas = train(epoch)
test_loss, test_meas = test()
history.append({'epoch':epoch, 'train_loss':train_loss, 'train_meas':train_meas, 'test_loss':test_loss, 'test_meas':test_meas})
if (test_meas < check_meas):
print("")
print(f"/***CHECK_POINT***/ ")
print(f"TRAIN - {train_loss}, {train_meas}")
print(f"TEST - {test_loss}, {test_meas}")
print("")
check_meas = test_meas
check_loss = test_loss
check_epoch = epoch
torch.save(model.state_dict(), checkpoint_path)
print(f"/*** EPOCH : {epoch}/{EPOCH_NUM} ***/")
print(f"TRAIN - {train_loss}, {train_meas}")
print(f"TEST - {test_loss}, {test_meas}")
print("")
df_history = pd.DataFrame(history)
# +
df_history = pd.DataFrame(history)
fig, axes = plt.subplots(2,1,figsize = (8,12))
axes[0].plot(df_history['epoch'], df_history['train_loss'])
axes[0].plot(df_history['epoch'], df_history['test_loss'])
axes[0].axvline(x = check_epoch, ymin = 0, ymax = df_history['test_loss'].max(), color = 'r')
axes[0].axhline(y = default_loss, xmin = 0, xmax = df_history['epoch'].max(), color = 'k')
axes[1].plot(df_history['epoch'], df_history['train_meas'])
axes[1].plot(df_history['epoch'], df_history['test_meas'])
axes[1].axvline(x = check_epoch, ymin = 0, ymax = df_history['test_meas'].max(), color = 'r')
axes[1].axhline(y = default_meas, xmin = 0, xmax = df_history['epoch'].max(), color = 'k')
# -
del X_train, X_test, y_train, y_test
# # Submission
# +
df_test = pd.read_pickle(str(data_dir / "gsdc_test.pkl.gzip"))
print(df_test.shape)
df_test.head()
# -
model.load_state_dict(torch.load(checkpoint_path))
torch.save(model.state_dict(), model_path)
# Load submission sample
submission = pd.read_csv(str(data_dir / "sample_submission.csv"))
print(submission.shape)
model = SimpleNetwork(X.shape[1] * X.shape[2], y.shape[1])
model = model.to(device)
model.load_state_dict(torch.load(model_path))
# +
X, _ = extract_features(df_test, train = False)
X = torch.Tensor(X)
loader_test = DataLoader(X, batch_size = batch_size, shuffle = False)
# +
model.eval() # 신경망을 추론 모드로 전환
# 데이터로더에서 미니배치를 하나씩 꺼내 추론을 수행
predict = []
with torch.no_grad(): # 추론 과정에는 미분이 필요없음
for data in loader_test:
data = data.to(device)
outputs = model(data) # 데이터를 입력하고 출력을 계산
predict.append(outputs)
predict = torch.cat(predict, axis = 0).to('cpu')
# -
predict.shape
print(submission.shape)
submission.columns
submission['latDeg'] = predict[:,1]
submission['lngDeg'] = predict[:,2]
submission.to_csv(f"./models/{notebookName}/{num_files} - result.csv", index = False)
pd.DataFrame([]).to_csv(dummy_path)
|
Research/GoogleSmartPhone/code/.ipynb_checkpoints/Baseline-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: torch
# language: python
# name: torch
# ---
# ### This notebook provides some examples of use of topological distillation methods.
# +
from model import Base_model, FTD, HTD
from utils import train_dataset, test_dataset, evaluate, print_result, read_settings
from run import run_base, run_FTD, run_HTD
from copy import deepcopy
import time
import torch
import torch.utils.data as data
import torch.optim as optim
import random
import numpy as np
import matplotlib.pyplot as plt
# -
# ## 0. Loading Dataset & Setting hyperparameters
# The hyperparameters need to be determined considering dataset, base model, capacity gap, and a selected layer for distillation.
# We use BPR as the base model and CiteULike for the dataset.
# +
random.seed(0)
np.random.seed(0)
torch.manual_seed(0)
# Setup
## gpu setting
gpu = torch.device('cuda:0')
## Hyperparameters for Training
lr, batch_size = 0.001, 1024
reg = 0.001
## Load dataset
user_num, item_num = 5220, 25182
train_R, train_interactions, valid_R, test_R = read_settings()
train_dataset = train_dataset(user_num, item_num, train_R, train_interactions)
test_dataset = test_dataset(user_num, item_num, valid_R, test_R)
train_loader = data.DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
run_dict = {'train_loader':train_loader, 'test_dataset':test_dataset, 'lr':lr, 'reg':reg, 'gpu':gpu, \
'max_epoch': 100, 'eval_period':10, 'lmbda_TD': 0.001, 'alpha':0.5}
# -
# ## 1. Generating Teacher Model
Teacher = Base_model(user_num, item_num, dim=200, gpu=gpu).to(gpu)
Teacher_history = run_base(run_dict, Teacher)
# ## 2. Guiding Student Model via Topology Distillation
# +
history_dict = {}
Teacher_user_emb, Teacher_item_emb = Teacher.get_embedding()
for student_dim in [10, 20, 100, 200]:
history_dict[student_dim] = []
# Student
model = Base_model(user_num, item_num, dim=student_dim, gpu=gpu).to(gpu)
Student_history = run_base(run_dict, model)
history_dict[student_dim].append(Student_history[:])
# FTD
model = FTD(user_num, item_num, Teacher_user_emb, Teacher_item_emb, gpu=gpu, student_dim=student_dim).to(gpu)
FTD_history = run_FTD(run_dict, model)
history_dict[student_dim].append(FTD_history[:])
# HTD
model = HTD(user_num, item_num, Teacher_user_emb, Teacher_item_emb, gpu=gpu, student_dim=student_dim, K=30, choice='second').to(gpu)
HTD_history = run_HTD(run_dict, model)
history_dict[student_dim].append(HTD_history[:])
# -
# ## Results
# ### A. Model size = 0.05, 0.1
# When the capacity of the student model is highly limited, the student model learns best with HTD.
# +
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(15, 5))
for idx, student_dim in enumerate([10, 20]):
axes[idx].plot([i for i in range(0, 101, 10)], Teacher_history, label='Teacher', marker='o')
axes[idx].plot([i for i in range(0, 101, 10)], history_dict[student_dim][0], label='Student', marker='o')
axes[idx].plot([i for i in range(0, 101, 10)], history_dict[student_dim][1], label='FTD', marker='o')
axes[idx].plot([i for i in range(0, 101, 10)], history_dict[student_dim][2], label='HTD', marker='o')
axes[idx].legend(loc=4, fontsize=17)
axes[idx].tick_params(axis="x", labelsize=15.9)
axes[idx].tick_params(axis="y", labelsize=18)
axes[idx].set_title('Model size: ' + str(student_dim / 200), fontsize=20)
axes[idx].set_xlabel('Epoch', fontsize=20)
axes[idx].set_ylabel('Recall@50', fontsize=20)
# -
# ### B. Model size = 0.5, 1.0
# As the capacity gap between the teacher model and student model decreases, the student model takes more benefits from FTD.
# +
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(15, 5))
for idx, student_dim in enumerate([100, 200]):
axes[idx].plot([i for i in range(0, 101, 10)], Teacher_history, label='Teacher', marker='o')
axes[idx].plot([i for i in range(0, 101, 10)], history_dict[student_dim][0], label='Student', marker='o')
axes[idx].plot([i for i in range(0, 101, 10)], history_dict[student_dim][1], label='FTD', marker='o')
axes[idx].plot([i for i in range(0, 101, 10)], history_dict[student_dim][2], label='HTD', marker='o')
axes[idx].legend(loc=4, fontsize=17)
axes[idx].tick_params(axis="x", labelsize=15.9)
axes[idx].tick_params(axis="y", labelsize=18)
axes[idx].set_title('Model size: ' + str(student_dim / 200), fontsize=20)
axes[idx].set_xlabel('Epoch', fontsize=20)
axes[idx].set_ylabel('Recall@50', fontsize=20)
# -
|
modeling-component-layer/relational-modeling-component/Topology_Distillation/Guide to using topology distillation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import pandas as pd
import sys
sys.path.append('../analysis/')
from csv_to_pandas import dictionary_of_dataframes
import matplotlib.pyplot as plt
# %matplotlib inline
# -
df_dict = dictionary_of_dataframes()
key_list = list(df_dict.keys() )
key_list
total = df_dict['total']
total.plot(legend = False)
total.head(5)
|
app/jupyter/wavelet_transformation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# + [markdown] tags=[]
# ## _Reco. Track Evaluation_
#
# - evaluate track reconstruction of GNN
# - we have reconstructed tracks from _`trkx_from_gnn.py`_ (see its code breakdown in _`trkx_from_gnn.ipynb`_)
#
#
# This is code breakdown of _`eval_reco_trkx.py`_ by using the similar script from _`gnn4itk/scripts/eval_reco_trkx.py`_
# -
import glob, os, sys, yaml
import numpy as np
import scipy as sp
import pandas as pd
import matplotlib.pyplot as plt
# %matplotlib inline
import torch
import time
from sklearn.cluster import DBSCAN
from multiprocessing import Pool
from functools import partial
# select a device
device = 'cuda' if torch.cuda.is_available() else 'cpu'
from LightningModules.Processing import SttTorchDataReader
# ### _(1) Tracks from GNN_
#
# * from _`tracks_from_gnn.py`_
reco_track_path = "run/trkx_from_gnn"
reco_trkx_reader = SttTorchDataReader(reco_track_path)
# what are the events?
reco_trkx_reader.all_evtids[:10]
# fetch a single event
reco_trkx_data = reco_trkx_reader(900)
reco_trkx_data.head()
# filter missed hits
reco_trkx_data.query("track_id==-1").head()
# number of reco tracks
np.unique(reco_trkx_data.track_id.values)
# renaming
reconstructed = reco_trkx_data
# ### _(2) Track Evaluation_
#
# - _Fixing `eval_reco_trkx.py`_
# arguments for script: args = parser.parse_args()
max_evts = 100
force = True
num_workers = 8
outname = "run/trkx_reco_eval"
outdir = os.path.dirname(os.path.abspath(outname))
os.makedirs(outdir, exist_ok=True)
# * Read raw CSV files to get truth information
# * But I have torch-geometric data from the GNN stage
# fetch `raw` data
raw_tracks_path="run/gnn_evaluation/test"
raw_trkx_reader = SttTorchDataReader(raw_tracks_path)
n_tot_files = reco_trkx_reader.nevts
all_evtids = reco_trkx_reader.all_evtids
max_evts = max_evts if max_evts > 0 and max_evts <= n_tot_files else n_tot_files
raw_trkx_reader.all_evtids[:10]
raw_trkx_data = raw_trkx_reader(900)
# +
# particles: ['particle_id', 'pt', 'eta', 'radius', 'vz'] where radius = sqrt(vx**2 + vy**2) and and ['vx', 'vy', 'vz'] are the production vertex
# +
# raw_trkx_data
# raw_trkx_data.hid.numpy()
# raw_trkx_data.pid.int().numpy()
# -
raw_trkx_data
# reco: ['hit_id', 'track_id']
reco_trkx_data.head()
# truth: ['hit_id', 'particle_id']
truth = pd.DataFrame({'hit_id': raw_trkx_data.hid.numpy(), 'particle_id': raw_trkx_data.pid.int().numpy()}, columns=['hit_id', 'particle_id'])
truth.head()
np.unique(truth.particle_id.values)
# particles: ['particle_id', 'pt', 'eta', 'radius', 'vz']
particles = pd.DataFrame({'particle_id': raw_trkx_data.pid.int().numpy(), 'pt': raw_trkx_data.pt.numpy()}, columns=['particle_id', 'pt'])
particles.drop_duplicates(subset=['particle_id']).shape
np.unique(particles.particle_id.values)
# ### Current Torch Geometric Data I have
#
# ```
# Data(x=[158, 3], pid=[158], layers=[158], event_file='/home/adeak977/current/3_deeptrkx/stttrkx-hsf/train_all/event0000000900', hid=[158], pt=[158], modulewise_true_edges=[2, 148], layerwise_true_edges=[2, 153], edge_index=[2, 946], y_pid=[946], scores=[1892])
# ```
#
# ### What I have in my torch-geometric data after GNNBuilder?
#
# 1. x,y coordinates
# 2. hit_id (hid)
# 3. particle_id (pid)
# 4. pt
# 5. scores, etc
#
# ### What I don't have in my torch-geometric data after GNNBuilder?
#
# 1. eta
# 2. radius
# 3. vz
#
#
# Can get `eta, radius, vz` if one re-process an event directly from **CSV** (similar to **ACTSCSVReader**) and add these variable in addition to what I already have.
# + active=""
# # What we need for evaluate_reco_tracks()
#
# """
# truth: a dataframe with columns of ['hit_id', 'particle_id']
# reconstructed: a dataframe with columns of ['hit_id', 'track_id']
# particles: a dataframe with columns of
# ['particle_id', 'pt', 'eta', 'radius', 'vz'].
# where radius = sqrt(vx**2 + vy**2) and
# ['vx', 'vy', 'vz'] are the production vertex of the particle
# min_hits_truth: minimum number of hits for truth tracks
# min_hits_reco: minimum number of hits for reconstructed tracks
# """
# -
# ### `evaluate_reco_tracks(truth_data, reco_data, particles)`
truth.head()
reconstructed.head()
particles.head()
min_hits_truth=7
min_hits_reco=5
min_pt=0.
frac_reco_matched=0.5
frac_truth_matched=0.5
# just in case particle_id == 0 included in truth.
if 'particle_id' in truth.columns:
truth = truth[truth.particle_id > 0]
reconstructed.describe()
# get number of spacepoints in each reconstructed tracks
n_reco_hits = reconstructed.track_id.value_counts(sort=False)\
.reset_index().rename(
columns={"index":"track_id", "track_id": "n_reco_hits"})
n_reco_hits.head(11)
# only tracks with a minimum number of spacepoints are considered
n_reco_hits = n_reco_hits[n_reco_hits.n_reco_hits >= min_hits_reco]
reconstructed = reconstructed[reconstructed.track_id.isin(n_reco_hits.track_id.values)]
reconstructed.describe()
particles.describe()
# get number of spacepoints in each particle
hits = truth.merge(particles, on='particle_id', how='left')
n_true_hits = hits.particle_id.value_counts(sort=False).reset_index().rename(
columns={"index":"particle_id", "particle_id": "n_true_hits"})
hits.describe()
n_true_hits.describe()
# only particles leaves at least min_hits_truth spacepoints
# and with pT >= min_pt are considered.
particles = particles.merge(n_true_hits, on=['particle_id'], how='left')
is_trackable = particles.n_true_hits >= min_hits_truth
# event has 3 columnes [track_id, particle_id, hit_id]
event = pd.merge(reconstructed, truth, on=['hit_id'], how='left')
event.head()
# +
# n_common_hits and n_shared should be exactly the same
# for a specific track id and particle id
# +
# Each track_id will be assigned to multiple particles.
# To determine which particle the track candidate is matched to,
# we use the particle id that yields a maximum value of n_common_hits / n_reco_hits,
# which means the majority of the spacepoints associated with the reconstructed
# track candidate comes from that true track.
# However, the other way may not be true.
# -
reco_matching = event.groupby(['track_id', 'particle_id']).size()\
.reset_index().rename(columns={0:"n_common_hits"})
reco_matching.head(15)
# Each particle will be assigned to multiple reconstructed tracks
truth_matching = event.groupby(['particle_id', 'track_id']).size()\
.reset_index().rename(columns={0:"n_shared"})
truth_matching.head(15)
# +
# add number of hits to each of the maching dataframe
reco_matching = reco_matching.merge(n_reco_hits, on=['track_id'], how='left')
truth_matching = truth_matching.merge(n_true_hits, on=['particle_id'], how='left')
# calculate matching fraction
reco_matching = reco_matching.assign(
purity_reco=np.true_divide(reco_matching.n_common_hits, reco_matching.n_reco_hits))
truth_matching = truth_matching.assign(
purity_true = np.true_divide(truth_matching.n_shared, truth_matching.n_true_hits))
# -
# select the best match
reco_matching['purity_reco_max'] = reco_matching.groupby(
"track_id")['purity_reco'].transform(max)
truth_matching['purity_true_max'] = truth_matching.groupby(
"track_id")['purity_true'].transform(max)
|
eda/trkx_reco_eval.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: qiskit_env_march2022
# language: python
# name: qiskit_env_march2022
# ---
# # qiskit_alt
#
# This python package provides a thin wrapper around some features of Qiskit that have been (re-)implemented in Julia and provides a Python interface. The input and output of the Python interface are the same as the input and output to Python qiskit. At present, we have prepared two high level demonstrations
#
# * Performing the Jordan-Wigner transform from a Fermionic operator to a Pauli operator.
#
# * Computing the Fermionic operator from integrals computed by `pyscf`.
#
# In both cases, we will see that the `qiskit_alt` implementation is much more performant.
#
# We have also prepared some lower-level demonstrations of performance gains
#
# * Converting an operator from the computational basis to the Pauli basis.
#
# * Creating a `SparsePauliOp` from a list of strings
# The Python package has been installed in a virtual environment created with `python -m venv ./env`. The Julia packages have been installed in a local environment in the standard way, via a spec in `Project.toml` file.
#
# When we import the package `qiskit_alt`, the Julia environment is also activated.
# There are two options for communcating with Julia: `PyCall.jl/pyjulia` and `PythonCall.jl/juliacall`.
# Here we use the second by passing `calljulia="juliacall"` when initializing.
import qiskit_alt
qiskit_alt.project.ensure_init(calljulia="juliacall", compile=False)
# We assume that no one is familiar with Julia, much less with `juliacall`, the package we use to call Julia from Python. So, we inject a bit of tutorial.
#
# The default `Module` in Julia `Main` is available. You can think of it as a namespace. And, as always, objects from the `Module` `Base` have been imported into `Main`.
#
# As an example of how `juliacall` works, we create an `Array` of `Float64` zeros on the Julia side. On the Python side, they are dispalyed as they would in Julia.
julia = qiskit_alt.project.julia
Main = julia.Main
julia.Main.zeros(3)
# However, we can see that the Julia `Vector` is in fact wrapped in a Python class.
type(julia.Main.zeros(3))
# There are several ways to call Julia from Python and vice versa, and to specifiy features such as the copying vs. sharing semantics. We won't go into much of this in this demo.
# ## Electronic structure
#
# Part of a workflow for, say, VQE involves using qiskit-nature to do the following:
# * Get a description of a model Hamiltonian from the package `pyscf` by passing it a description of the geometry of a molecule.
# * Convert that description of a Hamiltonian to a qiskit-native Fermionic operator.
# * Convert the Fermionic operator to a qubit operator expressed in the Pauli basis.
#
# The last step above may be done in several ways, one of which is known as the Jordan-Wigner transform. It is this step that we will benchmark here.
# ### qiskit-nature
#
# First, we see how this is done in qiskit-nature. We need to specify the geometry of the molecule and the
# [basis set](https://en.wikipedia.org/wiki/Basis_set_(chemistry)). We choose `sto3g`, one of the smallest, simplest, basis sets.
# +
from qiskit_nature.drivers import UnitsType, Molecule
from qiskit_nature.drivers.second_quantization import ElectronicStructureDriverType, ElectronicStructureMoleculeDriver
# Specify the geometry of the H_2 molecule
geometry = [['H', [0., 0., 0.]],
['H', [0., 0., 0.735]]]
basis = 'sto3g'
# -
# Then, we compute the fermionic Hamiltonian like this.
# +
molecule = Molecule(geometry=geometry,
charge=0, multiplicity=1)
driver = ElectronicStructureMoleculeDriver(molecule, basis=basis, driver_type=ElectronicStructureDriverType.PYSCF)
from qiskit_nature.problems.second_quantization import ElectronicStructureProblem
from qiskit_nature.converters.second_quantization import QubitConverter
from qiskit_nature.mappers.second_quantization import JordanWignerMapper
es_problem = ElectronicStructureProblem(driver)
second_q_op = es_problem.second_q_ops()
fermionic_hamiltonian = second_q_op[0]
# -
# The Jordan-Wigner transform is performed like this.
qubit_converter = QubitConverter(mapper=JordanWignerMapper())
nature_qubit_op = qubit_converter.convert(fermionic_hamiltonian)
nature_qubit_op.primitive
# ### qiskit_alt
#
# The only high-level code in `qiskit_alt` was written to support this demo. So doing the JW-transform is less verbose.
import qiskit_alt.electronic_structure
fermi_op = qiskit_alt.electronic_structure.fermionic_hamiltonian(geometry, basis)
pauli_op = qiskit_alt.electronic_structure.jordan_wigner(fermi_op)
pauli_op.simplify() # The Julia Pauli operators use a different sorting convention; we sort again for comparison.
# Note that the constant term differs. The qiskit-nature version ignores the nuclear-repulsion term. I need to open an issue about whether and how to handle it.
# ### Benchmarking
#
# Computing the Hamiltonian for a larger molecule or a larger basis set takes more time and produces a Hamiltonian with more factors and terms. Here we compare the performance of `qiskit_alt` and `qiskit-nature` on combinations of $\text{H}_2$ and $\text{H}_2\text{O}$ molecules for several basis sets.
# First we benchmark qiskit-nature, and record the times in `nature_times`.
# %run ../bench/jordan_wigner_nature_time.py
nature_times
# Next we benchmark qiskit_alt, and record the times in `alt_times`.
# %run ../bench/jordan_wigner_alt_time.py
alt_times
# We compare the relative performance.
[t_nature / t_qk_alt for t_nature, t_qk_alt in zip(nature_times, alt_times)]
# We see that
# * qiskit_alt is at least ten times faster
# * The relative performance increases as the problem in some sense gets larger.
#
# In fact, another problem, not shown here, finishes in 18s with qiskit_alt and in 5730s in qiskit-nature.
# In this case, `qiskit_alt` is 320 times faster than `qiskit-nature`. I don't have an idea about the origin of this scaling.
# ### Computing the Fermonic operator
#
# Computing the Fermionic operator from the output of `pyscf` is also much more efficient in `qiskit_alt`.
# We benchmark qiskit-nature computing the fermionic Hamiltonian
# %run ../bench/fermionic_nature_time.py
nature_times
# We benchmark qiskit_alt computing the fermionic Hamiltonian.
# %run ../bench/fermionic_alt_time.py
alt_times
# We compare the relative performance.
[t_nature / t_qk_alt for t_nature, t_qk_alt in zip(nature_times, alt_times)]
# We see again that, as the problem size increases, `qiskit_alt` is increasingly more performant.
# ## Discussion
#
# The Julia implemenation consists of these packages
#
# * [`QuantumOps.jl`](https://github.com/Qiskit-Extensions/QuantumOps.jl) implementing Fermionic and Pauli operators and calculations using them.
#
# * [`ElectronicStructure.jl`](https://github.com/Qiskit-Extensions/ElectronicStructure.jl) provides an interface to electronic structure packages.
#
# * [`ElectronicStructurePySCF.jl`](https://github.com/Qiskit-Extensions/ElectronicStructurePySCF.jl) provides an interface to `pyscf`
#
# * [`QiskitQuantumInfo.jl`](https://github.com/Qiskit-Extensions/QiskitQuantumInfo.jl) provides data structures that mirror Python Qiskit data structures. These are used as intermedidate structures for converting from `QuantumOps` and `ElectronicStructure` to Python Qiskit. In the future these might be used directly for calculations.
#
#
# The Python interface is a Python package `qiskit_alt`. This could contain a mixture of Julia and Python code. Or all the Julia code might be moved to the Julia packages.
#
# ### Implementation
#
# In the examples above, the following happens.
#
# * Julia code calls `pyscf` and stores the results in Julia data structures.
#
# * These data are used to construct a Fermionic operator as a data structure defined in `QuantumOps`.
#
# * The Jordan-Wigner transform, implemented in `QuantumOps` is used to compute a Pauli operator.
#
# * The Pauli operator (as a structure in `QuantumOps`) is converted to a Qiskit-like operator defined in `QiskitQuantumInfo.jl`.
#
# * The operator defined in `QiskitQuantumInfo.jl` is sent to Python and converted to numpy arrays, which are then used to construct native Qiskit types. The conversion to numpy arrays is provided by `pyjulia`.
#
# ### Complexity, dynamism
#
# * It is worth noting that operators in `QuantumOps` are *not* highly optimized implementations. In fact, much of the code for the two types of operators is shared, they inherit from a parent class. There are other implementations of Pauli operators in Julia that are much more efficient for instance in [`QuantumClifford.jl`](https://github.com/Krastanov/QuantumClifford.jl).
#
# * [Issue](https://github.com/Qiskit-Extensions/QuantumOps.jl/issues/17) for improving performance of Jordan-Wigner in `QuantumOps`.
# * Precompute one and two-body terms
# * Use @threads
#
# # More demos
#
# Here are some smaller scale demonstrations.
#
# ## Converting a matrix to the Pauli basis
#
# Here we convert a matrix representing an operator in the computational basis to the Pauli basis.
# In this case, `qiskit_alt` is much more performant than `qiskit.quantum_info`.
# This is how it is done in `QuantumOps`.
from qiskit_alt.pauli_operators import QuantumOps, PauliSum_to_SparsePauliOp
import numpy as np
m = np.random.rand(2**3, 2**3) # 3-qubit operator
m = Main.convert(Main.Matrix, m) # Convert PythonCall.PyArray to a native Julia type
pauli_sum = QuantumOps.PauliSum(m) # This is a wrapped Julia object
PauliSum_to_SparsePauliOp(pauli_sum) # Convert to qiskit.quantum_info.SparsePauliOp
# When using `pyjulia`, the `numpy` matrix is automatically converted to a Julia `Matrix`.
# But, here, we are using `juliacall`. In this case the `numpy` matrix is wrapped in `PythonCall.PyArray`, a subtype of `AbstractMatrix` that is particular to `juliacall`. It supports iteration in Julia, but the iterator calls python. The performance in this case is much worse. For this reason, we convert it to a matrix of Julia floats via
# `m = Main.convert(Main.Matrix, m)`
# We run benchmarks of conversion of matrices to the Pauli basis.
# %run ../bench/from_matrix_quantum_info.py
# %run ../bench/from_matrix_alt.py
# Here are the ratios of the times for `qiskit.quantum_info` to those for `qiskit_alt`.
[t_pyqk / t_qk_alt for t_pyqk, t_qk_alt in zip(pyqk_times, qk_alt_times)]
# Again, the performance gain increases with the problem size.
# ## Creating a `SparsePauliOp` from a list of strings
#
#
# Here, we create a `SparsePauliOp` from a list of `n` strings, each with `k` single-Pauli factors, and simplify the result.
# First, using `qiskit.quantum_info`
# %run ../bench/pauli_from_list_qinfo.py
# Now, using `qiskit_alt`
# %run ../bench/pauli_from_list_alt.py
# The results were written to lists `quantum_info_times` and `qkalt_times`. We compare the performance:
[x / y for x,y in zip(quantum_info_times, qkalt_times)]
# We see that the performance improvement in `qiskit_alt` is significant, but does not increase with the number of terms `n`. Further benchmarks show that the time required to convert the strings from Python to Julia takes all the time.
#
# We see this in the following.
# These last magics (below this version table) are not defined for `juliacall`, so we skip them.
import qiskit.tools.jupyter
d = qiskit.__qiskit_version__._version_dict
d['qiskit_alt'] = qiskit_alt.__version__
# %qiskit_version_table
# +
# # %load_ext julia.magic
# -
# Generate `1000` ten-qubit Pauli strings.
# +
# # %julia using Random: randstring
# #%julia pauli_strings = [randstring("IXYZ", 10) for _ in 1:1000]
# None;
# -
# Benchmark converting these to a `QuantumOps.PauliSum`. Note that as the sums are always sorted.
# +
# # %julia import Pkg; Pkg.add("BenchmarkTools")
# #%julia using BenchmarkTools: @btime
# #%julia @btime QuantumOps.PauliSum($pauli_strings)
#None;
# -
# Check that we are actually getting the right result.
# +
# #%julia pauli_sum = QuantumOps.PauliSum(pauli_strings);
# #%julia println(length(pauli_sum))
# #%julia println(pauli_sum[1])
# +
#6.9 * 2.29 / .343 # Ratio of time to construct PauliSum via qiskit_alt to time in pure Julia
# -
# So the pure Julia code is `46` times faster than the qiskit.quantum_info.
# **But, the `qiskit.quantum_info` is also extracting a possible phase !**
|
demos/qiskit_alt_demo_jc.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Purchase Prediction through Ads by People in a Social Network using
# - ### Logistic Regression
# - ### K-Nearest Neighbors (K-NN)
# - ### Support Vector Machine (SVM)
# - ### Kernel SVM
# - ### Naive Bayes Classifier
# - ### Decision Tree Classifier
# - ### Random Forest Classifier
# # LOGISTIC REGRESSION
# ### Importing the libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# ### Importing the dataset
data = pd.read_csv('Purchases_Through_Ads.csv')
data.head()
# ### User ID is unique for each customer, so we drop User ID
X = data.iloc[:, [2, 3]].values
y = data.iloc[:, 4].values
# ### Splitting the dataset into Training & Test set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)
# ### Feature Scaling
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
# ### Fitting Logistic Regression to the dataset
from sklearn.linear_model import LogisticRegression
logreg = LogisticRegression(random_state = 0)
logreg.fit(X_train, y_train)
# ### Predicting the Test set using our model
y_pred = logreg.predict(X_test)
y_pred
# ### Confusion Matrix
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
cm
# ### Accuracy
logreg.score(X_test,y_test)
# ## Accuracy is 89 %
# ### Visualising the Training set results
from matplotlib.colors import ListedColormap
X_set, y_set = X_train, y_train
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, logreg.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Logistic Regression (Training set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
# ### Visualising the Test set results
from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, logreg.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Logistic Regression (Test set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
# # --------------------------------------------------------------------------------------------------------
# # K-Nearest Neighbors (K-NN)
# ### Importing the dataset
data = pd.read_csv('Purchases_Through_Ads.csv')
data.head()
# ### User ID is unique for each customer, so we drop User ID
X = data.iloc[:, [2, 3]].values
y = data.iloc[:, 4].values
# ### Splitting the dataset into Training & Test set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)
# ### Feature Scaling
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
# ### Fitting K-NN to the dataset
from sklearn.neighbors import KNeighborsClassifier
classifier = KNeighborsClassifier(n_neighbors = 5, p = 2)
classifier.fit(X_train, y_train)
# ### Predicting the Test set using our model
y_pred = classifier.predict(X_test)
y_pred
# ### Confusion Matrix
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
cm
# ### Accuracy
classifier.score(X_test,y_test)
# ## Accuracy is 93 %
# ### Visualising the Training set results
from matplotlib.colors import ListedColormap
X_set, y_set = X_train, y_train
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('K-NN (Training set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
# ### Visualising the Test set results
from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('K-NN (Test set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
# # --------------------------------------------------------------------------------------------------------
# # Support Vector Machine (SVM)
# ### Importing the dataset
data = pd.read_csv('Purchases_Through_Ads.csv')
data.head()
# ### User ID is unique for each customer, so we drop User ID
X = data.iloc[:, [2, 3]].values
y = data.iloc[:, 4].values
# ### Splitting the dataset into Training & Test set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)
# ### Feature Scaling
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
# ### Fitting SVM to the dataset
from sklearn.svm import SVC
classifier = SVC(kernel = 'linear', random_state = 0)
classifier.fit(X_train, y_train)
# ### Predicting the Test set using our model
y_pred = classifier.predict(X_test)
y_pred
# ### Confusion Matrix
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
cm
# ### Accuracy
classifier.score(X_test,y_test)
# ## Accuracy is 90 %
# ### Visualising the Training set results
from matplotlib.colors import ListedColormap
X_set, y_set = X_train, y_train
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('SVM (Training set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
# ### Visualising the Test set results
from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('SVM (Test set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
# # --------------------------------------------------------------------------------------------------------
# # Kernel SVM
# ### Importing the dataset
data = pd.read_csv('Purchases_Through_Ads.csv')
data.head()
# ### User ID is unique for each customer, so we drop User ID
X = data.iloc[:, [2, 3]].values
y = data.iloc[:, 4].values
# ### Splitting the dataset into Training & Test set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)
# ### Feature Scaling
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
# ### Fitting Kernel SVM to the dataset
from sklearn.svm import SVC
classifier = SVC(kernel = 'rbf', random_state = 0)
classifier.fit(X_train, y_train)
# ### Predicting the Test set using our model
y_pred = classifier.predict(X_test)
y_pred
# ### Confusion Matrix
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
cm
# ### Accuracy
classifier.score(X_test,y_test)
# ## Accuracy is 93 %
# ### Visualising the Training set results
from matplotlib.colors import ListedColormap
X_set, y_set = X_train, y_train
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Kernel SVM (Training set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
# ### Visualising the Test set results
from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Kernel SVM (Test set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
# # --------------------------------------------------------------------------------------------------------
# # Naive Bayes
# ### Importing the dataset
data = pd.read_csv('Purchases_Through_Ads.csv')
data.head()
# ### User ID is unique for each customer, so we drop User ID
X = data.iloc[:, [2, 3]].values
y = data.iloc[:, 4].values
# ### Splitting the dataset into Training & Test set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)
# ### Feature Scaling
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
# ### Fitting Naive Bayes Classifier to the dataset
from sklearn.naive_bayes import GaussianNB
classifier = GaussianNB()
classifier.fit(X_train, y_train)
# ### Predicting the Test set using our model
y_pred = classifier.predict(X_test)
y_pred
# ### Confusion Matrix
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
cm
# ### Accuracy
classifier.score(X_test,y_test)
# ## Accuracy is 90 %
# ### Visualising the Training set results
from matplotlib.colors import ListedColormap
X_set, y_set = X_train, y_train
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Naive Bayes (Training set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
# ### Visualising the Test set results
from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Naive Bayes (Test set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
# # --------------------------------------------------------------------------------------------------------
# # Decision Tree Classification
# ### Importing the dataset
data = pd.read_csv('Purchases_Through_Ads.csv')
data.head()
# ### User ID is unique for each customer, so we drop User ID
X = data.iloc[:, [2, 3]].values
y = data.iloc[:, 4].values
# ### Splitting the dataset into Training & Test set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)
# ### Feature Scaling
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
# ### Fitting Decision Tree Classifier to the dataset
from sklearn.tree import DecisionTreeClassifier
classifier = DecisionTreeClassifier(criterion = 'entropy', random_state = 0)
classifier.fit(X_train, y_train)
# ### Predicting the Test set using our model
y_pred = classifier.predict(X_test)
y_pred
# ### Confusion Matrix
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
cm
# ### Accuracy
classifier.score(X_test,y_test)
# ## Accuracy is 91 %
# ### Visualising the Training set results
from matplotlib.colors import ListedColormap
X_set, y_set = X_train, y_train
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Decision Tree Classification (Training set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
# ### Visualising the Test set results
from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Decision Tree Classification (Test set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
# # --------------------------------------------------------------------------------------------------------
# # Random Forest Classification
# ### Importing the dataset
data = pd.read_csv('Purchases_Through_Ads.csv')
data.head()
# ### User ID is unique for each customer, so we drop User ID
X = data.iloc[:, [2, 3]].values
y = data.iloc[:, 4].values
# ### Splitting the dataset into Training & Test set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)
# ### Feature Scaling
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
# ### Fitting Random Forest Classifier to the dataset
from sklearn.ensemble import RandomForestClassifier
classifier = RandomForestClassifier(n_estimators = 10, criterion = 'entropy', random_state = 0)
classifier.fit(X_train, y_train)
# ### Predicting the Test set using our model
y_pred = classifier.predict(X_test)
y_pred
# ### Confusion Matrix
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
cm
# ### Accuracy
classifier.score(X_test,y_test)
# ## Accuracy is 91 %
# ### Visualising the Training set results
from matplotlib.colors import ListedColormap
X_set, y_set = X_train, y_train
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Random Forest Classification (Training set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
# ### Visualising the Test set results
from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Random Forest Classification (Test set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
# # --------------------------------------------------------------------------------------------------------
|
Purchase Prediction through Ads by People in a Social Network.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Create user minibatch sources
#
# In order to make use of CNTK’s (distributed) training functionality, one has to provide input data as an instance of [MinibatchSource](https://cntk.ai/pythondocs/cntk.io.html#cntk.io.MinibatchSource). In CNTK, there are a variety of means to provide minibatch sources:
#
# - (**best**) convert data to the formats of built-in data readers - they support rich functionality of randomization/packing with high performance (see [How to feed data](https://github.com/Microsoft/CNTK/blob/master/Manual/Manual_How_to_feed_data.ipynb) and [cntk.io](https://cntk.ai/pythondocs/cntk.io.html))
# - (**preferred**) if it is hard to convert the data and the data can fit in memory, please use [MinibatchSourceFromData](https://cntk.ai/pythondocs/cntk.io.html?highlight=minibatchsourcefromdata#cntk.io.MinibatchSourceFromData),
# - if the data does not fit in memory and you want a fine grained control over how minibatch is created, then implementing the abstract [UserMinibatchSource](https://cntk.ai/pythondocs/cntk.io.html#cntk.io.UserMinibatchSource) interface is the option.
#
# This manual explains the last approach: How to create user minibatch source in Python.
#
#
# ## User minibatch sources
#
# A minibatch source is responsible for providing:
#
# 1. meta-information regarding the data, such as *storage format*, *data type*, *shape of elements*,
# 2. batches of data, and
# 3. auxiliary information for advanced features, such as checkpoint state of the current data access position so that interrupted learning processes can be restored from the data position where the processes were interrupted.
#
# Correspondingly, a minibatch source API needs to implement the following $4$ methods (see [UserMinibatchSource](https://cntk.ai/pythondocs/cntk.io.html?highlight=userminibatch#cntk.io.UserMinibatchSource) for details):
#
# 1. **stream_infos()**: Returns a list of StreamInformation instances. Each piece of stream information contains the meta information regarding a stream of the data: e.g. storage format, data type, shape of elements (see [StreamInformation](https://cntk.ai/pythondocs/cntk.io.html#cntk.io.StreamInformation) for details)
# 2. **next_minibatch(num_samples, number_of_workers, worker_rank, device=None)**: Returns next minibatch of data of the specified nature as specified by given parameters:
# * num_samples: the number of samples that are being requested
# * num_of_workders: the number of workers in a distributed training session; if it is not in a distributed training setting, this number is always 1
# * worker_rank: the number which identifies the specific worker who requests this minibatch in the distributed training setting; if this is not a distributed training session, the worker rank is always 0 (the first worker)
# * device: a device descriptor specifying which device the minibatch data should be copied to, e.g. cntk.device.cpu() or cntk.device.gpu(device_id) (see [DeviceDescriptor](https://cntk.ai/pythondocs/cntk.device.html#cntk.device.DeviceDescriptor) for details)
# 3. **get_checkpoint_state()**: Returns a dictionary which describe the current state of the minibatch source
# 4. **restore_from_checkpoint(state)**: Sets the state of the minibatch source according to a checkint state object. This allows a minibatch source restoring data feeding from position where the checkpoint was saved. Note that *state* is the dictionary returned by get_checkpoint_state().
#
#
# Now let's go through th implementation of these $4$ methods step by step.
#
# ## User minibatch source step by step
# In the following example, we will detail the steps on how to implement the [UserMinibatchSource](https://cntk.ai/pythondocs/cntk.io.html#cntk.io.UserMinibatchSource) interface.
# First, let's import the necessary packages:
import numpy as np
import cntk as C
from cntk.io import UserMinibatchSource, StreamInformation, MinibatchData
# Secondly, let's assume that we have a data set in the following tab seperated text format:
# * The first column is the sequence ID: e.g. 0 is the ID for sequecne 0; and 1 is the ID for sequence 1.
# * The second column starts with symbol "|". It is the feature named 'x' which is a sparse representation for the words in our training data.
# * The third column again starts with symbol "|". It is our lable named 'y' which is the one-hot representation of label.
#
# In the fllowing, our toy data set contains 4 sequences:
sample_data = r'''0 |x 560:1 |y 1 0 0 0 0
0 |x 0:1
0 |x 0:1
1 |x 560:1 |y 0 1 0 0 0
1 |x 0:1
1 |x 0:1
1 |x 424:1
2 |x 160:1 |y 0 0 1 0 0
2 |x 5:1
2 |x 6:1
3 |x 460:1 |y 0 0 0 1 0
3 |x 3:1
3 |x 3:1
3 |x 425:1
'''
# ### Inherit *UserMinibatchSource* to create your user minibatch class:
#
# To implement our example user minibatch source, we first prepare the data access and its meta information:
#
# 1. Parse the text formatted data into an intermediate representation so that we can access the data by their sequence indices:
# ```
# features = self.data[seq_idx]['features']
# labels = self.data[seq_idx]['labels']
# ```
# This is done by create a private method ``_prepare_data()`` in the example below. We ommit the implementation detail of text format parsing here as the detail is irrelevant to the understanding of the UserMinibatchSource interface. However, the parsing mechanims should be able to keep track of where the current data access point is so that the data feeding process can be restored at any point. In the example, we are tracking the sequence index.
#
# 2. Define the meta information of the data: e.g.
# ```
# self.fsi = StreamInformation("features", 0, 'sparse', np.float32, (self.f_dim,))
# self.lsi = StreamInformation("labels", 1, 'dense', np.float32, (self.l_dim,))
# ```
# The self.fsi and self.lsi define the meta information (see [StreamInformation](https://cntk.ai/pythondocs/cntk.io.html#cntk.io.StreamInformation) for definition ) regarding the features and labels respectively. For example, ``StreamInformation("features", 0, 'sparse', np.float32, (self.f_dim,))`` specifies that :
#
# >a) the "feature" data stream is indentified by ID $0$ (it is required that every data stream is identified by a unique ID),
#
# >b) it is sparse,
#
# >c) its data type is ``np.float32``, and
#
# >d) its dimension is ``(self.f_dim, )``.
#
# 3. Set the initial states of the data source. For example, set the next sequence index to the beginning:
# ```
# self.next_seq_idx = 0
# ```
#
# 4. Finally, create your minibatch class based on **UserMinibatchSource** and put the above data access preparation steps in its constructor:
# ```python
# class MyMultiWorkerDataSource(UserMinibatchSource):
# def __init__(self, f_dim, l_dim):
# self.f_dim, self.l_dim = f_dim, l_dim
# self._prepare_data()
# #setting the state
# self.fsi = StreamInformation("features", 0, 'sparse', np.float32, (self.f_dim,))
# self.lsi = StreamInformation("labels", 1, 'dense', np.float32, (self.l_dim,))
# self.sequences = sorted(self.data)
# self.next_seq_idx = 0
# super(MyMultiWorkerDataSource, self).__init__()
# ```
# Do not forget to call the super class' constructor: ``super(MyMultiWorkerDataSource, self)`` **init()** function.
# ### Override *stream_infos()* method to provide meta-informatoin of data:
#
# After the preparation is done by the constructor, we can implement *stream_infos()* simply by returning the list of stream information instances:
# ```python
# def stream_infos(self):
# return [self.fsi, self.lsi]
# ```
# With this method implemented, the underlying minibatch source framework will able to refer to the meta information by names "featuers" and "labels".
# ### Override *next_minibatch()* method to provide data
# Let us first review the function signature of the next_minibatch method:
# ```python
# def next_minibatch(self, num_samples, number_of_workers, worker_rank, device)
# ```
# This method is invoked by the outer CNTK learning loops with four parameters:
# * the nubmer of samples needed,
# * number of workers,
# * worker rank (i.e. worker ID), and
# * the device on which the data should be copied to.
#
# In other words, it is the user minibatch source's responsibility to understand these parameters and provide minibatch data accordingly. The minibatch source need to ensure that
# * the returned minibatch contains the specified number of samples or less,
# * the returned minbiatch contains only the data that are supposed to be assigned to the specified worker (identified by the worker_rank) - it is the user minibanch's responsisbility to ensure that the data load of these workers are balanced in certain manner, and
# * the data are ready in the specified device (e.g. CPU or GPU).
#
# To make the underlying requirement stand out, in the example below we implemented a private function *_prepare_nextbatch()* to encapsulate details:
# ```python
# def _prepare_nextbatch(self, num_samples, number_of_workers, worker_rank):
# # details....
# return features, f_sample_count, labels, l_sample_count, sweep_end
# ```
# This function ensure that *features* and *labels* contains the *num_samples* of samples or less. The sample counts are also returned as *f_sample_count* and *l_sample_count* respectively. Note that different data streams might contain different number of samples. In addition, *sweep_end* tells whether this minibatch is at the end of a sweep of the whole data set.
#
# To define user minibatch source that can be used with distributed learners, e.g. BlockMomentum. We will need to use number_of_workers to cut the data into slices and then return the slices depending on which worker_rank requested the next minibatch. In this private function, we implement a naive logic to distribute the data to the specific worker by skipping sequences if its sequence index modulo the number of workers does not equal to the worker rank:
# ```python
# if (seq_id % number_of_workers) != worker_rank:
# continue
# ```
# This is only for demonstration purpose. In practice, the distribution of data to workers should be based on a more efficient mechanism: e.g. based on how costly the specific worker can access the specific subset of data and the randomization mechanism.
#
# After the data is prepared, we need to convert them into the values that CNTK operators can operate on efficiently. This is done by create various types of cntk.Value instances:
# ```python
# feature_data = C.Value.one_hot(batch=features, num_classes=self.f_dim, device = device)
# label_data = C.Value(batch=np.asarray(labels, dtype=np.float32), device = device)
# ```
# In this example, the feature data are of a special type of sparse data which are created through the [cntk.Value.one_hot](https://cntk.ai/pythondocs/cntk.core.html?highlight=one_hot#cntk.core.Value.one_hot) function --- an element within a sequence is a one-hot vector. The label data are of a type of dense data which are created through the [cntk.Value](https://cntk.ai/pythondocs/cntk.core.html?highlight=value#cntk.core.Value) constructor. Note that in these CNTK value constructors, we explicitly specify on which device these values should be constructed. Reall that the *device* parameter is provided by the outher learning loops.
#
# Finally, we need to create [MinibatchData](https://cntk.ai/pythondocs/cntk.io.html?highlight=minibatchdata#cntk.io.MinibatchData) instances and return them in a dictionary with the corresponding [StreamInformation](https://cntk.ai/pythondocs/cntk.io.html#cntk.io.StreamInformation) instances as keys:
# ```python
# res = {
# self.fsi: MinibatchData(feature_data, num_seq, feature_sample_count, sweep_end),
# self.lsi: MinibatchData(label_data, num_seq, label_sample_count, sweep_end)}
# return res
# ```
# The constructor of *MinibatchData* takes 1) the data that are already in the form [cntk.Value](https://cntk.ai/pythondocs/cntk.core.html?highlight=value#cntk.core.Value): i.e. feature_data and label_data here, 2) the number of sequences in the minibatch, 3) the number of samples, and 4) whether it is at the end of a sweep of the whole data set.
#
# All together, we've implemented our *next_minibatch()* method to provide minibatches of data of specified properties for the outer learning loops to consume.
# ### Override *get_checkpoint_state()* and *restore_from_checkpoint()* methods to provide checkpoint state and restore from it
#
# Firstly, we need to define the state of our user minibatch so that the data feeding process can be restored from the exact point where it was stopped. In our simple example, we just need to know to next sequence index to restore the data feeding process by the following *get* and *restore* checkpoints methods:
# ```python
# def get_checkpoint_state(self):
# return {'next_seq_idx': self.next_seq_idx}
# ```
# ```python
# def restore_from_checkpoint(self, state):
# self.next_seq_idx = state['next_seq_idx']
# ```
# It is easy to see that a checkpoint state is a dictionary from string keys to the corresponding state variable value objects. In this example, it is the next sequence index.
# ### The complete user minibatch example
#
# All together we have our complete user minibatch implementation as follows:
class MyMultiWorkerDataSource(UserMinibatchSource):
def __init__(self, f_dim, l_dim):
self.f_dim, self.l_dim = f_dim, l_dim
self._prepare_data()
#setting the state
self.fsi = StreamInformation("features", 0, 'sparse', np.float32, (self.f_dim,))
self.lsi = StreamInformation("labels", 1, 'dense', np.float32, (self.l_dim,))
self.sequences = sorted(self.data)
self.next_seq_idx = 0
super(MyMultiWorkerDataSource, self).__init__()
def _prepare_data(self):
"""
Parse the text and load the data into self.data.
self.data is of the following structure:
sequence id -> "features" -> list of features
and
sequence id -> "labels" -> label
"""
self.data = {}
for line in sample_data.split('\n'):
line = line.strip()
if not line:
continue
seq_id, data = line.split('|', 1)
data = data.split("|")
seq_id = int(seq_id.strip())
if seq_id not in self.data:
self.data[seq_id] = {'features': []}
# Processing features - expecting one per line.
features = data[0].split(" ")
vocab_idx = int(features[1].split(":")[0])
self.data[seq_id]['features'].append(vocab_idx)
# Process label, if exists
if len(data) == 2:
labels = np.asarray([data[1].split(" ")[1:]], dtype=np.float32)
self.data[seq_id]['labels'] = labels
def _prepare_nextbatch(self, num_samples, number_of_workers, worker_rank):
features = []
labels = []
sweep_end = False
f_sample_count = l_sample_count = 0
while max(f_sample_count, l_sample_count) < num_samples:
if self.next_seq_idx == len(self.sequences):
sweep_end = True
self.next_seq_idx = 0
seq_id = self.sequences[self.sequences[self.next_seq_idx]]
#Based on the worker rank, determines whether to add this
#data in the batch: If the sequences doesn't belong to this
#worker, skip it. In practice, this should be based on more
#efficient mechanism: e.g. based on the location of the worker
#and the data location
if (seq_id % number_of_workers) != worker_rank:
continue
feature_data = self.data[seq_id]['features']
label_data = self.data[seq_id]['labels']
if (features or labels) and \
max(f_sample_count+len(feature_data), \
l_sample_count+len(label_data)) > num_samples:
break
f_sample_count += len(feature_data)
features.append(feature_data)
l_sample_count += len(label_data)
labels.append(label_data)
self.next_seq_idx += 1
return features, f_sample_count, labels, l_sample_count, sweep_end
def stream_infos(self):
"""
Override the stream_infos method of the base UserMinibatchSource class
to provide stream meta information.
"""
return [self.fsi, self.lsi]
def next_minibatch(self, num_samples, number_of_workers, worker_rank, device):
"""
Override the next_minibatch method of the base UserMinibatchSource class
to provide minibatch data.
"""
features, feature_sample_count, \
labels, label_sample_count, sweep_end = self._prepare_nextbatch(num_samples,
number_of_workers,
worker_rank)
feature_data = C.Value.one_hot(batch=features, num_classes=self.f_dim, device = device)
label_data = C.Value(batch=np.asarray(labels, dtype=np.float32), device = device)
num_seq = len(features)
res = {
self.fsi: MinibatchData(feature_data, num_seq, feature_sample_count, sweep_end),
self.lsi: MinibatchData(label_data, num_seq, label_sample_count, sweep_end)
}
return res
def get_checkpoint_state(self):
return {'next_seq_idx': self.next_seq_idx}
def restore_from_checkpoint(self, state):
self.next_seq_idx = state['next_seq_idx']
# Note that in this example, for simplicity we load the whole data set into the memory. In practice, the minibatch source should depend on the data source state (e.g. the mapping between the requesting next batch data and its logical/physical location in the data storage) to load (or pre-load) the data at the point (or right before) they are requested.
#
# ### Using the user minibatch data source in training sessions with distributed learners
# The implemented minitbatch source can then be used wherever a MinibatchSource instance is accepted. For example,
# +
input_dim = 1000
num_output_classes = 5
# instantiating the user minibatch source
mbs = MyMultiWorkerDataSource( input_dim, num_output_classes)
feature = C.sequence.input_variable(shape=(input_dim,))
label = C.input_variable(shape=(num_output_classes,))
# setting up the model
rnn = C.layers.Recurrence(C.layers.LSTM(20), go_backwards=False)(feature)
end = C.sequence.last(rnn)
z = C.layers.Dense(num_output_classes)(end)
loss = C.cross_entropy_with_softmax(z, label)
errs = C.classification_error(z, label)
local_learner = C.sgd(z.parameters,
C.learning_parameter_schedule_per_sample(0.5))
dist_learner = C.distributed.data_parallel_distributed_learner(local_learner)
# and train
trainer = C.Trainer(z, (loss, errs),
[dist_learner],
[C.logging.ProgressPrinter(tag='Training', num_epochs=10)])
input_map = {
feature: mbs.fsi,
label: mbs.lsi
}
session = C.training_session(
trainer = trainer,
mb_source = mbs,
model_inputs_to_streams = input_map,
mb_size = 7,
max_samples = 80,
progress_frequency = 20
)
session.train()
#finalize the distributed learning
C.distributed.Communicator.finalize()
# -
# ## User minibatch sources in restricted scenarios
#
# In certain simplified scenarios, we might not want to implement a minibatch source with full functionality.
#
# * If parallel data learning is not reqired, we can omit the logic of distributing data to workers. Set number_of_workers = 1 and worker_rank = 0 when overriding the *next_minibatch()* method.
#
# * If checkpoint restoration is not require, we can omit implementing the two checkpoint related methods: *get_checkpoint_state()* and *restore_from_checkpoint()*.
#
|
Manual/Manual_How_to_create_user_minibatch_sources.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.8.12 64-bit (''pytorch_m1'': conda)'
# language: python
# name: python3812jvsc74a57bd06542be600deb830c4bce82ce8a12106e8b76a038cf3920d451d7fa959f745ece
# ---
# # 1. Run these commands in Terminal
conda activate pytorch_m1
# cd /Users/jasle1/Desktop/MDSI/ADSI/AT_2
#
# +
# Download the cookiecutter data science template to load to github
cookiecutter -c v1 https://github.com/drivendata/cookiecutter-data-science
# follow the prompts and template will be downloaded as a folder
# -
# # 2. Upload the folder onto github repository
# cd /Users/jasle1/Desktop/MDSI/ADSI/AT_2/adsi_at2
git init
git remote add origin https://github.com/JKaur1992/adsi_at2.git
git add .
git commit -m "first commit"
git push --set-upstream origin master
# +
# Push changes to Github
# -
|
notebooks/Kaur_Jasleen-13368028_AT2_git-setup.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Sandbox help documentation
#
# The Digital Earth Africa Sandbox, by default, will load several folders containing helpful notebooks and source code. They are essential to the Sandbox's operation, so do not delete or move any of the files.
#
# The Beginner's Guide notebooks cover similar material to the explanations and exercises in this workshop series. However, they also provides more in-depth detail on how to perform data extraction and analysis. The Beginner's Guide notebooks, along with the 'frequently used code' notebooks, are a great reference tool.
#
# This section provides a summary of these folders and their contents. It also contains some recommended but **not compulsory** activities that will help increase your familiarity with Digital Earth Africa and the Sandbox.
#
# For tips on how to access files and folders in the Sandbox, check out the section on [navigating the Sandbox](./session_1/03_navigate_the_sandbox.ipynb).
#
# For a review on how to execute code in a notebook, see this section on [running a notebook](./session_1/04_running_a_notebook.ipynb).
# ## Beginner's Guide - start here
#
# <img align="middle" src="./_static/other_information/sandbox-beginners-guide.PNG" alt="Beginners Guide folder" width="300">
#
# The **Beginners_guide** folder contains step-by-step tutorials to help you become more familiar with the Digital Earth Africa Sandbox. The tutorials contain background information and context, as well as code and data examples and explanations. The guide covers a range of basic Sandbox functions, including how to load data and plot it.
#
# If you are still unclear on the scope and focus of Digital Earth Africa and the Sandbox, this is also a great place to read more about it and see some hands-on demonstrations of Earth observation data at work.
#
# The notebooks are numbered in progress order; start at `01_Jupyter_notebooks.ipynb`. There are no prerequisites to be able to complete this notebook.
#
# **Suggested activity:** Read and follow examples in the Beginner's Guide notebooks, starting with `01_Jupyter_notebooks.ipynb`. This can be done interactively (recommended), as detailed in [running a notebook](./session_1/04_running_a_notebook.ipynb). Open the file and from the horizontal menu bar select **Kernel -> Restart Kernel and Clear All Outputs**, then follow instructions in the notebook.
#
# Take your time — it is not necessary to review all of the notebooks in one sitting. If you are new to Python coding, there will be a fair amount of content. Some of it will be covered in subsequent sessions of this workshop series.
# ## Frequently used code
#
# <img align="middle" src="./_static/other_information/sandbox-freq-used-code.PNG" alt="Frequently used code folder" width="300">
#
# The **Frequently_used_code** folder contains a series of notebooks that demonstrate code snippets doing useful and common functions. For example, want to calculate the Normalised Difference Vegetation Index (NDVI)? You could set up your own formula — but it would be faster and easier to use the NDVI function as shown in `Calculating_band_indices.ipynb`. How about drawing a contour line between water and land? Check out `Contour_extraction.ipynb`. There are many useful tips and tricks in the **Frequently_used_code** folder.
#
# It is helpful to know what is in this folder, so you can draw upon the code if you need to do something similar when writing your own notebooks.
#
# **Suggested activity:** Read all the titles of the notebooks in the folder. Open `Masking_data.ipynb` and run through its contents by selecting **Kernel -> Restart Kernel and Clear All Outputs** and then executing cells as you go.
# ## Real world examples
#
# <img align="middle" src="./_static/other_information/sandbox-real-world-examples.PNG" alt="Real world examples folder" width="300">
#
# The analytical power of the Sandbox is shown in the folder **Real_world_examples**. This folder contains multiple notebooks which cater to 'real world' use cases, from monitoring crop health to detecting water.
#
# The code in these notebooks is more complex, but it is exciting to see what Digital Earth Africa can do.
#
# **Suggested activity:** Pick a notebook that interests you and run through it.
# ## Datasets
#
# <img align="middle" src="./_static/other_information/sandbox-datasets.PNG" alt="Datasets folder" width="300">
#
# The notebooks in the Sandbox are all based on Earth observation data available to Digital Earth Africa. These datasets are explained in individual notebooks in the **Datasets** folder. Each notebook contains background information about the dataset and examples of use.
#
# Some of the datasets are based directly on satellite measurements. For example, information on the Landsat and Sentinel satellite datasets can be found in their respective notebooks:
#
# * `Landsat_Surface_Reflectance.ipynb`
# * `Sentinel-1.ipynb`
# * `Sentinel-2.ipynb`
#
# Other datasets refer to derived products which have been created to show a particular environmental feature. These include:
#
# * `Fractional_Cover.ipynb`
# * `Water_Observations_from_Space.ipynb`
#
# More dataset notebooks are added to this folder as the Digital Earth Africa collection expands. Use the notebooks in this folder to familiarise yourself with the available data and products.
#
# **Suggested activity:** Run through the notebook on Sentinel-2 data, `Sentinel-2.ipynb`.
# ## Help! I deleted a file...
#
# See the [Frequently asked questions](./Frequently_asked_questions.ipynb) section on restoring pre-loaded notebooks.
|
docs/help_documentation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # a) By using Logistic Regression Algorithm
# # Part A: Data Preprocessing
# # Step1 : importing the libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# # step2: import data set
dataset=pd.read_csv('Logistic Data.csv')
dataset
# # step3: to create feature matrix and dependent variable vector
a=dataset.iloc[:,:-1].values
b=dataset.iloc[:,-1].values
a
b
# # step4: replace the missing data
from sklearn.impute import SimpleImputer
imputer=SimpleImputer(missing_values=np.nan,strategy='mean')
imputer.fit(a[:,:])
a[:,:]=imputer.transform(a[:,:])
a
b
# # Step5: Encoding(not required)
# # step6 : spiliting of data set into training and testing set
from sklearn.model_selection import train_test_split
atrain,atest,btrain,btest=train_test_split(a,b,test_size=0.2,random_state=1)
atrain
# # step7 : Feature scaling
from sklearn.preprocessing import StandardScaler
sc=StandardScaler()
atrain=sc.fit_transform(atrain)
atest=sc.fit_transform(atest)
atrain
# # Part B: build my first linear model
# # step 1: training the classification model
from sklearn.linear_model import LogisticRegression
LoR=LogisticRegression(random_state=0)
LoR.fit(atrain,btrain)
# # step 2: testing the linear model
bestimated=LoR.predict(atest)
print(np.concatenate((bestimated.reshape(len(bestimated),1),btest.reshape(len(btest),1)),1))
# # step C: performance matrix
from sklearn.metrics import confusion_matrix,accuracy_score,precision_score
cm=confusion_matrix(btest,bestimated)
print(cm)
print(accuracy_score(btest,bestimated))
print(precision_score(btest,bestimated))
np.mean((True,True,False))
error_rate=[]
for i in range(1,30):
KC=KNeighborsClassifier(n_neighbors=i)
KC.fit(atrain,btrain)
bpred_i=KC.predict(atest)
error_rate.append(np.mean(bpred_i!=btest))
plt.plot(range(1,30),error_rate,marker='o',markerfacecolor='red',markersize=5)
plt.xlabel('K value')
plt.ylabel('Error rate')
# # b) By using KNN Algorithm
# # Part A: Data Preprocessing
# # Step1 : importing the libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# # step2: import data set
dataset=pd.read_csv('Logistic Data.csv')
dataset
# # step3: to create feature matrix and dependent variable vector
a=dataset.iloc[:,:-1].values
b=dataset.iloc[:,-1].values
a
b
# # step4: replace the missing data
from sklearn.impute import SimpleImputer
imputer=SimpleImputer(missing_values=np.nan,strategy='mean')
imputer.fit(a[:,:])
a[:,:]=imputer.transform(a[:,:])
a
# # Step5: Encoding(not required)
# # step6 : spiliting of data set into training and testing set
from sklearn.model_selection import train_test_split
atrain,atest,btrain,btest=train_test_split(a,b,test_size=0.2,random_state=1)
atrain
# # step7 : Feature scaling
from sklearn.preprocessing import StandardScaler
sc=StandardScaler()
atrain=sc.fit_transform(atrain)
atest=sc.fit_transform(atest)
atrain
# # Part B: build my KNN classification model
# # step 1: training the classification model
from sklearn.neighbors import KNeighborsClassifier
KC=KNeighborsClassifier(n_neighbors=7,weights='uniform',p=2)
KC.fit(atrain,btrain)
# # step 2: testing the linear model
bestimated=KC.predict(atest)
# # step C: performance matrix
from sklearn.metrics import confusion_matrix,accuracy_score,precision_score
cm=confusion_matrix(btest,bestimated)
print(cm)
print(accuracy_score(btest,bestimated))
print(precision_score(btest,bestimated))
np.mean((True,True,False))
error_rate=[]
for i in range(1,30):
KC=KNeighborsClassifier(n_neighbors=i)
KC.fit(atrain,btrain)
bpred_i=KC.predict(atest)
error_rate.append(np.mean(bpred_i!=btest))
plt.plot(range(1,30),error_rate,marker='o',markerfacecolor='red',markersize=5)
plt.xlabel('K value')
plt.ylabel('Error rate')
|
Project 2/.ipynb_checkpoints/PROJECT 2-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Implementing the Gradient Descent Algorithm
# ##### _Written by <NAME>_
# In this lab, we'll implement the basic functions of the Gradient Descent algorithm to find the boundary in a small dataset. First, we'll start with some functions that will help us plot and visualize the data.
# +
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
#Some helper functions for plotting and drawing lines
def plot_points(X, y):
admitted = X[np.argwhere(y==1)]
rejected = X[np.argwhere(y==0)]
plt.scatter([s[0][0] for s in rejected], [s[0][1] for s in rejected], s = 25, color = 'blue', edgecolor = 'k')
plt.scatter([s[0][0] for s in admitted], [s[0][1] for s in admitted], s = 25, color = 'red', edgecolor = 'k')
def display(m, b, color='g--'):
plt.xlim(-0.05,1.05)
plt.ylim(-0.05,1.05)
x = np.arange(-10, 10, 0.1)
plt.plot(x, m*x+b, color)
# -
# ## Reading and plotting the data
data = pd.read_csv('data.csv', header=None)
X = np.array(data[[0, 1]])
y = np.array(data[2])
plot_points(X, y)
plt.show()
# print(data)
# ## TODO: Implementing the basic functions
# Here is your turn to shine. Implement the following formulas, as explained in the text.
# - Sigmoid activation function
#
# $$\sigma(x) = \frac{1}{1+e^{-x}}$$
#
# - Output (prediction) formula
#
# $$\hat{y} = \sigma(w_1 x_1 + w_2 x_2 + b)$$
#
# - Error function
#
# $$Error(y, \hat{y}) = - y \log(\hat{y}) - (1-y) \log(1-\hat{y})$$
#
# - The function that updates the weights
#
# $$ w_i \longrightarrow w_i + \alpha (y - \hat{y}) x_i$$
#
# $$ b \longrightarrow b + \alpha (y - \hat{y})$$
# +
# Implement the following functions
# Activation (sigmoid) function
def sigmoid(x):
# print(x)
return 1/(1+np.exp(-x))
# Output (prediction) formula
def output_formula(features, weights, bias):
return sigmoid(np.dot(features, weights)+bias)
# Error (log-loss) formula
def error_formula(y, output):
return -y*np.log(output)-(1-y)*np.log(1-output)
# Gradient descent step
def update_weights(x, y, weights, bias, learnrate):
# learnrate=learnrate*1/len(x)
for i in range(0, len(x)):
weights[i] = weights[i] + learnrate * \
(y-output_formula(x, weights, bias))*x[i]
bias = bias+learnrate*(y-output_formula(x, weights, bias))
return weights, bias
# -
# ## Training function
# This function will help us iterate the gradient descent algorithm through all the data, for a number of epochs. It will also plot the data, and some of the boundary lines obtained as we run the algorithm.
# +
np.random.seed(44)
epochs = 100
learnrate = 0.01
def train(features, targets, epochs, learnrate, graph_lines=False):
errors = []
n_records, n_features = features.shape
last_loss = None
weights = np.random.normal(scale=1 / n_features**.5, size=n_features)
bias = 0
for e in range(epochs):
del_w = np.zeros(weights.shape)
for x, y in zip(features, targets):
output = output_formula(x, weights, bias)
error = error_formula(y, output)
weights, bias = update_weights(x, y, weights, bias, learnrate)
# Printing out the log-loss error on the training set
out = output_formula(features, weights, bias)
loss = np.mean(error_formula(targets, out))
errors.append(loss)
if e % (epochs / 10) == 0:
print("\n========== Epoch", e, "==========")
if last_loss and last_loss < loss:
print("Train loss: ", loss, " WARNING - Loss Increasing")
else:
print("Train loss: ", loss)
last_loss = loss
predictions = out > 0.5
accuracy = np.mean(predictions == targets)
print("Accuracy: ", accuracy)
if graph_lines and e % (epochs / 100) == 0:
display(-weights[0]/weights[1], -bias/weights[1])
# Plotting the solution boundary
plt.title("Solution boundary")
display(-weights[0]/weights[1], -bias/weights[1], 'black')
# Plotting the data
plot_points(features, targets)
plt.show()
# Plotting the error
plt.title("Error Plot")
plt.xlabel('Number of epochs')
plt.ylabel('Error')
plt.plot(errors)
plt.show()
# -
# ## Time to train the algorithm!
# When we run the function, we'll obtain the following:
# - 10 updates with the current training loss and accuracy
# - A plot of the data and some of the boundary lines obtained. The final one is in black. Notice how the lines get closer and closer to the best fit, as we go through more epochs.
# - A plot of the error function. Notice how it decreases as we go through more epochs.
train(X, y, epochs, learnrate, True)
|
Gradient Descent/.ipynb_checkpoints/GradientDescent-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# default_exp deck
from nbdev import *
# # Deck
# > Playing Cards
#export
from deck_of_cards.card import Card
#export
class Deck:
"""Represents a deck of cards.
Attributes:
cards: list of Card objects.
"""
def __init__(self):
"""Initializes the Deck with 52 cards.
"""
self.cards = []
for suit in range(4):
for rank in range(1, 14):
card = Card(suit, rank)
self.cards.append(card)
def __str__(self):
"""Returns a string representation of the deck.
"""
res = []
for card in self.cards:
res.append(str(card))
return '\n'.join(res)
def add_card(self, card):
"""Adds a card to the deck.
card: Card
"""
self.cards.append(card)
def remove_card(self, card):
"""Removes a card from the deck or raises exception if it is not there.
card: Card
"""
self.cards.remove(card)
def pop_card(self, i=-1):
"""Removes and returns a card from the deck.
i: index of the card to pop; by default, pops the last card.
"""
return self.cards.pop(i)
def shuffle(self):
"""Shuffles the cards in this deck."""
random.shuffle(self.cards)
def sort(self):
"""Sorts the cards in ascending order."""
self.cards.sort()
def move_cards(self, hand, num):
"""Moves the given number of cards from the deck into the Hand.
hand: destination Hand object
num: integer number of cards to move
"""
for i in range(num):
hand.add_card(self.pop_card())
# A Deck of cards is a collection of `Card` objects:
deck = Deck()
assert isinstance(deck.pop_card(), Card)
show_doc(Deck.remove_card)
# If we remove a card from the Deck we can verify that it no longer exists:
# +
card23 = Card(2, 3)
deck.remove_card(card23)
assert card23 not in deck.cards
# -
# However, another card that we haven't removed, such as the `10 of hearts` will still be in the Deck of cards because we haven't removed it:
c = Card(2,10)
assert c in deck.cards
c
|
01_deck.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# %load_ext autoreload
# %autoreload 2
# %matplotlib inline
# -
#export
from exp.nb_06 import *
# ## ConvNet
# Let's get the data and training interface from where we left in the last notebook.
# +
x_train,y_train,x_valid,y_valid = get_data()
x_train,x_valid = normalize_to(x_train,x_valid)
train_ds,valid_ds = Dataset(x_train, y_train),Dataset(x_valid, y_valid)
nh,bs = 50,512
c = y_train.max().item()+1
loss_func = F.cross_entropy
data = DataBunch(*get_dls(train_ds, valid_ds, bs), c)
# -
mnist_view = view_tfm(1,28,28)
cbfs = [Recorder,
partial(AvgStatsCallback,accuracy),
CudaCallback,
partial(BatchTransformXCallback, mnist_view)]
nfs = [8,16,32,64,64]
learn,run = get_learn_run(nfs, data, 0.4, conv_layer, cbs=cbfs)
# %time run.fit(2, learn)
# ## Batchnorm
# ### Custom
# Let's start by building our own `BatchNorm` layer from scratch.
class BatchNorm(nn.Module):
def __init__(self, nf, mom=0.1, eps=1e-5):
super().__init__()
# NB: pytorch bn mom is opposite of what you'd expect
self.mom,self.eps = mom,eps
self.mults = nn.Parameter(torch.ones (nf,1,1))
self.adds = nn.Parameter(torch.zeros(nf,1,1))
self.register_buffer('vars', torch.ones(1,nf,1,1))
self.register_buffer('means', torch.zeros(1,nf,1,1))
def update_stats(self, x):
m = x.mean((0,2,3), keepdim=True)
v = x.var ((0,2,3), keepdim=True)
self.means.lerp_(m, self.mom)
self.vars.lerp_ (v, self.mom)
return m,v
def forward(self, x):
if self.training:
with torch.no_grad(): m,v = self.update_stats(x)
else: m,v = self.means,self.vars
x = (x-m) / (v+self.eps).sqrt()
return x*self.mults + self.adds
def conv_layer(ni, nf, ks=3, stride=2, bn=True, **kwargs):
# No bias needed if using bn
layers = [nn.Conv2d(ni, nf, ks, padding=ks//2, stride=stride, bias=not bn),
GeneralRelu(**kwargs)]
if bn: layers.append(BatchNorm(nf))
return nn.Sequential(*layers)
# +
#export
def init_cnn_(m, f):
if isinstance(m, nn.Conv2d):
f(m.weight, a=0.1)
if getattr(m, 'bias', None) is not None: m.bias.data.zero_()
for l in m.children(): init_cnn_(l, f)
def init_cnn(m, uniform=False):
f = init.kaiming_uniform_ if uniform else init.kaiming_normal_
init_cnn_(m, f)
def get_learn_run(nfs, data, lr, layer, cbs=None, opt_func=None, uniform=False, **kwargs):
model = get_cnn_model(data, nfs, layer, **kwargs)
init_cnn(model, uniform=uniform)
return get_runner(model, data, lr=lr, cbs=cbs, opt_func=opt_func)
# -
# We can then use it in training and see how it helps keep the activations means to 0 and the std to 1.
learn,run = get_learn_run(nfs, data, 1., conv_layer, cbs=cbfs)
with Hooks(learn.model, append_stats) as hooks:
run.fit(1, learn)
fig,(ax0,ax1) = plt.subplots(1,2, figsize=(10,4))
for h in hooks[:-1]:
ms,ss = h.stats
ax0.plot(ms[:10])
ax1.plot(ss[:10])
h.remove()
plt.legend(range(6));
fig,(ax0,ax1) = plt.subplots(1,2, figsize=(10,4))
for h in hooks[:-1]:
ms,ss = h.stats
ax0.plot(ms)
ax1.plot(ss)
learn,run = get_learn_run(nfs, data, 1.0, conv_layer, cbs=cbfs)
# %time run.fit(3, learn)
# ### Builtin batchnorm
#export
def conv_layer(ni, nf, ks=3, stride=2, bn=True, **kwargs):
layers = [nn.Conv2d(ni, nf, ks, padding=ks//2, stride=stride, bias=not bn),
GeneralRelu(**kwargs)]
if bn: layers.append(nn.BatchNorm2d(nf, eps=1e-5, momentum=0.1))
return nn.Sequential(*layers)
learn,run = get_learn_run(nfs, data, 1., conv_layer, cbs=cbfs)
# %time run.fit(3, learn)
# ### With scheduler
# Now let's add the usual warm-up/annealing.
sched = combine_scheds([0.3, 0.7], [sched_lin(0.6, 2.), sched_lin(2., 0.1)])
learn,run = get_learn_run(nfs, data, 0.9, conv_layer, cbs=cbfs
+[partial(ParamScheduler,'lr', sched)])
run.fit(8, learn)
# ## More norms
# ### Layer norm
# From [the paper](https://arxiv.org/abs/1607.06450): "*batch normalization cannot be applied to online learning tasks or to extremely large distributed models where the minibatches have to be small*".
# General equation for a norm layer with learnable affine:
#
# $$y = \frac{x - \mathrm{E}[x]}{ \sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \beta$$
#
# The difference with BatchNorm is
# 1. we don't keep a moving average
# 2. we don't average over the batches dimension but over the hidden dimension, so it's independent of the batch size
class LayerNorm(ScriptModule):
__constants__ = ['eps']
def __init__(self, eps=1e-5):
super().__init__()
self.eps = eps
self.mult = nn.Parameter(tensor(1.))
self.add = nn.Parameter(tensor(0.))
def forward(self, x):
m = x.mean((1,2,3), keepdim=True)
v = x.std ((1,2,3), keepdim=True)
x = (x-m) / ((v+self.eps).sqrt())
return x*self.mult + self.add
def conv_ln(ni, nf, ks=3, stride=2, bn=True, **kwargs):
layers = [nn.Conv2d(ni, nf, ks, padding=ks//2, stride=stride, bias=True),
GeneralRelu(**kwargs)]
if bn: layers.append(LayerNorm())
return nn.Sequential(*layers)
learn,run = get_learn_run(nfs, data, 0.8, conv_ln, cbs=cbfs)
# %time run.fit(3, learn)
# *Thought experiment*: can this distinguish foggy days from sunny days (assuming you're using it before the first conv)?
# ### Instance norm
# From [the paper](https://arxiv.org/abs/1607.08022):
# The key difference between **contrast** and batch normalization is that the latter applies the normalization to a whole batch of images instead for single ones:
#
# \begin{equation}\label{eq:bnorm}
# y_{tijk} = \frac{x_{tijk} - \mu_{i}}{\sqrt{\sigma_i^2 + \epsilon}},
# \quad
# \mu_i = \frac{1}{HWT}\sum_{t=1}^T\sum_{l=1}^W \sum_{m=1}^H x_{tilm},
# \quad
# \sigma_i^2 = \frac{1}{HWT}\sum_{t=1}^T\sum_{l=1}^W \sum_{m=1}^H (x_{tilm} - mu_i)^2.
# \end{equation}
#
# In order to combine the effects of instance-specific normalization and batch normalization, we propose to replace the latter by the *instance normalization* (also known as *contrast normalization*) layer:
#
# \begin{equation}\label{eq:inorm}
# y_{tijk} = \frac{x_{tijk} - \mu_{ti}}{\sqrt{\sigma_{ti}^2 + \epsilon}},
# \quad
# \mu_{ti} = \frac{1}{HW}\sum_{l=1}^W \sum_{m=1}^H x_{tilm},
# \quad
# \sigma_{ti}^2 = \frac{1}{HW}\sum_{l=1}^W \sum_{m=1}^H (x_{tilm} - mu_{ti})^2.
# \end{equation}
class InstanceNorm(nn.Module):
__constants__ = ['eps']
def __init__(self, nf, eps=1e-0):
super().__init__()
self.eps = eps
self.mults = nn.Parameter(torch.ones (nf,1,1))
self.adds = nn.Parameter(torch.zeros(nf,1,1))
def forward(self, x):
m = x.mean((2,3), keepdim=True)
v = x.std ((2,3), keepdim=True)
res = (x-m) / ((v+self.eps).sqrt())
return res*self.mults + self.adds
def conv_in(ni, nf, ks=3, stride=2, bn=True, **kwargs):
layers = [nn.Conv2d(ni, nf, ks, padding=ks//2, stride=stride, bias=True),
GeneralRelu(**kwargs)]
if bn: layers.append(InstanceNorm(nf))
return nn.Sequential(*layers)
learn,run = get_learn_run(nfs, data, 0.1, conv_in, cbs=cbfs)
# %time run.fit(3, learn)
# *Question*: why can't this classify anything?
# Lost in all those norms? The authors from the [group norm paper](https://arxiv.org/pdf/1803.08494.pdf) have you covered:
#
# 
# ### Group norm
# *From the PyTorch docs:*
# `GroupNorm(num_groups, num_channels, eps=1e-5, affine=True)`
#
# The input channels are separated into `num_groups` groups, each containing
# ``num_channels / num_groups`` channels. The mean and standard-deviation are calculated
# separately over the each group. $\gamma$ and $\beta$ are learnable
# per-channel affine transform parameter vectorss of size `num_channels` if
# `affine` is ``True``.
#
# This layer uses statistics computed from input data in both training and
# evaluation modes.
#
# Args:
# - num_groups (int): number of groups to separate the channels into
# - num_channels (int): number of channels expected in input
# - eps: a value added to the denominator for numerical stability. Default: 1e-5
# - affine: a boolean value that when set to ``True``, this module
# has learnable per-channel affine parameters initialized to ones (for weights)
# and zeros (for biases). Default: ``True``.
#
# Shape:
# - Input: `(N, num_channels, *)`
# - Output: `(N, num_channels, *)` (same shape as input)
#
# Examples::
#
# >>> input = torch.randn(20, 6, 10, 10)
# >>> # Separate 6 channels into 3 groups
# >>> m = nn.GroupNorm(3, 6)
# >>> # Separate 6 channels into 6 groups (equivalent with InstanceNorm)
# >>> m = nn.GroupNorm(6, 6)
# >>> # Put all 6 channels into a single group (equivalent with LayerNorm)
# >>> m = nn.GroupNorm(1, 6)
# >>> # Activating the module
# >>> output = m(input)
# ## Fix small batch sizes
# ### What's the problem?
# When we compute the statistics (mean and std) for a BatchNorm Layer on a small batch, it is possible that we get a standard deviation very close to 0. because there aren't many samples (the variance of one thing is 0. since it's equal to its mean).
data = DataBunch(*get_dls(train_ds, valid_ds, 2), c)
def conv_layer(ni, nf, ks=3, stride=2, bn=True, **kwargs):
layers = [nn.Conv2d(ni, nf, ks, padding=ks//2, stride=stride, bias=not bn),
GeneralRelu(**kwargs)]
if bn: layers.append(nn.BatchNorm2d(nf, eps=1e-5, momentum=0.1))
return nn.Sequential(*layers)
learn,run = get_learn_run(nfs, data, 0.4, conv_layer, cbs=cbfs)
# %time run.fit(1, learn)
# ### Running Batch Norm
# To solve this problem we introduce a Running BatchNorm that uses smoother running mean and variance for the mean and std.
class RunningBatchNorm(nn.Module):
def __init__(self, nf, mom=0.1, eps=1e-5):
super().__init__()
self.mom,self.eps = mom,eps
self.mults = nn.Parameter(torch.ones (nf,1,1))
self.adds = nn.Parameter(torch.zeros(nf,1,1))
self.register_buffer('sums', torch.zeros(1,nf,1,1))
self.register_buffer('sqrs', torch.zeros(1,nf,1,1))
self.register_buffer('batch', tensor(0.))
self.register_buffer('count', tensor(0.))
self.register_buffer('step', tensor(0.))
self.register_buffer('dbias', tensor(0.))
def update_stats(self, x):
bs,nc,*_ = x.shape
self.sums.detach_()
self.sqrs.detach_()
dims = (0,2,3)
s = x.sum(dims, keepdim=True)
ss = (x*x).sum(dims, keepdim=True)
c = self.count.new_tensor(x.numel()/nc)
self.mom1 = self.dbias.new_tensor(1 - (1-self.mom)**bs)
self.sums.lerp_(s, self.mom1)
self.sqrs.lerp_(ss, self.mom1)
self.count.lerp_(c, self.mom1)
self.dbias.lerp_(self.mom1, self.mom1)
self.batch += bs
self.step += 1
def forward(self, x):
if self.training: self.update_stats(x)
sums = self.sums
sqrs = self.sqrs
c = self.count
if self.step<100:
sums = sums / self.dbias
sqrs = sqrs / self.dbias
c = c / self.dbias
means = sums/c
vars = (sqrs/c).sub_(means*means)
if bool(self.batch < 20): vars.clamp_min_(0.01)
x = (x-means).div_((vars.add_(self.eps)).sqrt())
return x.mul_(self.mults).add_(self.adds)
def conv_rbn(ni, nf, ks=3, stride=2, bn=True, **kwargs):
layers = [nn.Conv2d(ni, nf, ks, padding=ks//2, stride=stride, bias=not bn),
GeneralRelu(**kwargs)]
if bn: layers.append(RunningBatchNorm(nf))
return nn.Sequential(*layers)
learn,run = get_learn_run(nfs, data, 0.4, conv_rbn, cbs=cbfs)
# %time run.fit(1, learn)
# This solves the small batch size issue!
# ### What can we do in a single epoch?
# Now let's see with a decent batch size what result we can get.
data = DataBunch(*get_dls(train_ds, valid_ds, 32), c)
learn,run = get_learn_run(nfs, data, 0.9, conv_rbn, cbs=cbfs
+[partial(ParamScheduler,'lr', sched_lin(1., 0.2))])
# %time run.fit(1, learn)
# ## Export
nb_auto_export()
|
dev_course/dl2/07_batchnorm.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Example: Growth Rates
#
# The relationship between two measurements of the same quantity taken at different times is often expressed as a *growth rate*. For example, the United States federal government [employed](http://www.bls.gov/opub/mlr/2013/article/industry-employment-and-output-projections-to-2022.htm) 2,766,000 people in 2002 and 2,814,000 people in 2012. To compute a growth rate, we must first decide which value to treat as the `initial` amount. For values over time, the earlier value is a natural choice. Then, we divide the difference between the `changed` and `initial` amount by the `initial` amount.
initial = 2766000
changed = 2814000
(changed - initial) / initial
# It is also typical to subtract one from the ratio of the two measurements, which yields the same value.
(changed/initial) - 1
# This value is the growth rate over 10 years. A useful property of growth rates is that they don't change even if the values are expressed in different units. So, for example, we can express the same relationship between thousands of people in 2002 and 2012.
initial = 2766
changed = 2814
(changed/initial) - 1
# In 10 years, the number of employees of the US Federal Government has increased by only 1.74%. In that time, the total expenditures of the US Federal Government increased from \$2.37 trillion to \$3.38 trillion in 2012.
initial = 2.37
changed = 3.38
(changed/initial) - 1
# A 42.6% increase in the federal budget is much larger than the 1.74% increase in federal employees. In fact, the number of federal employees has grown much more slowly than the population of the United States, which increased 9.21% in the same time period from 287.6 million people in 2002 to 314.1 million in 2012.
initial = 287.6
changed = 314.1
(changed/initial) - 1
# A growth rate can be negative, representing a decrease in some value. For example, the number of manufacturing jobs in the US decreased from 15.3 million in 2002 to 11.9 million in 2012, a -22.2% growth rate.
initial = 15.3
changed = 11.9
(changed/initial) - 1
# An annual growth rate is a growth rate of some quantity over a single year. An annual growth rate of 0.035, accumulated each year for 10 years, gives a much larger ten-year growth rate of 0.41 (or 41%).
1.035 * 1.035 * 1.035 * 1.035 * 1.035 * 1.035 * 1.035 * 1.035 * 1.035 * 1.035 - 1
# This same computation can be expressed using names and exponents.
annual_growth_rate = 0.035
ten_year_growth_rate = (1 + annual_growth_rate) ** 10 - 1
ten_year_growth_rate
# Likewise, a ten-year growth rate can be used to compute an equivalent annual growth rate. Below, `t` is the number of years that have passed between measurements. The following computes the annual growth rate of federal expenditures over the last 10 years.
initial = 2.37
changed = 3.38
t = 10
(changed/initial) ** (1/t) - 1
# The total growth over 10 years is equivalent to a 3.6% increase each year.
# In summary, a growth rate `g` is used to describe the relative size of an `initial` amount and a `changed` amount after some amount of time `t`. To compute $changed$, apply the growth rate `g` repeatedly, `t` times using exponentiation.
#
# `initial * (1 + g) ** t`
#
# To compute `g`, raise the total growth to the power of `1/t` and subtract one.
#
# `(changed/initial) ** (1/t) - 1`
|
Mathematics/Statistics/Statistics and Probability Python Notebooks/Computational and Inferential Thinking - The Foundations of Data Science (book)/Notebooks - by chapter/3. programming-in-python/3.2.1a Growth.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Snail and well
#
# A snail falls at the bottom of a 125 cm well. Each day the snail rises 30 cm. But at night, while sleeping, slides 20 cm because the walls are wet. How many days does it take to escape from the well?
#
# TIP: http://puzzles.nigelcoldwell.co.uk/sixtytwo.htm
# ## Solución
# +
# Assign problem data to variables with representative names
# well height, daily advance, night retreat, accumulated distance
# Assign 0 to the variable that represents the solution
well_height=125
daily_advance=30
night_retreat=20
acc_distance=0
days =0
# Write the code that solves the problem
while acc_distance <= well_height:
acc_distance =acc_distance + daily_advance
days += 1
if acc_distance < well_height:
acc_distance = acc_distance - night_retreat
# Print the result with print('Days =', days)
print('Days =', days)
# -
# ## Goals
#
# 1. Treatment of variables
# 2. Use of loop **while**
# 3. Use of conditional **if-else**
# 4. Print in console
# ## Bonus
# The distance traveled by the snail is now defined by a list.
# ```
# advance_cm = [30, 21, 33, 77, 44, 45, 23, 45, 12, 34, 55]
# ```
# How long does it take to raise the well?
#
# What is its maximum displacement in one day? And its minimum?
#
# What is its average speed during the day?
#
# What is the standard deviation of its displacement during the day?
# +
# Assign problem data to variables with representative names
# well height, daily advance, night retreat, accumulated distance
import math
well_height = 125
daily_advance = 30
night_retreat = 20
acc_distance = 0
days = 0
advance_cm = [30, 21, 33, 77, 44, 45, 23, 45, 12, 34, 55]
x = 0
daily_dis = []
numerator_lst = []
y = 0
# Assign 0 to the variable that represents the solution
# Write the code that solves the problem
while acc_distance < well_height:
acc_distance =acc_distance + advance_cm[x]
days += 1
if acc_distance < well_height:
acc_distance = acc_distance - night_retreat
daily_dis.append(advance_cm[x]-night_retreat)
x += 1
# Print the result with print('Days =', days)
print('Days =', days)
# What is its maximum displacement in a day? And its minimum?
print("Maximum displacement in a day =", max(daily_dis))
print("Minimum displacement in a day =", min(daily_dis))
# What is its average progress?
avg_speed = sum(daily_dis)/len(daily_dis)
print("Avarage speed during the day =", avg_speed )
# What is the standard deviation of your displacement during the day?
while y < len(daily_dis):
numerator_lst.append((daily_dis[y]-avg_speed)**2)
y += 1
numerator = sum(numerator_lst)
denominator = len(daily_dis) - 1
stan_diviation = math.sqrt(numerator/denominator)
print ("the standard deviation of your displacement =", stan_diviation)
# -
|
snail-and-well/snail-and-well.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.8.8 64-bit (''base'': conda)'
# name: python3
# ---
# + [markdown] id="YckoFp3Zvm7E"
# # NYC OpenData: Data Set Lister
# This script lists all the data sets given by a NYC OpenData URL. (The script scrapes the website successfully as of September 27, 2021.)
# -
# ## Installing and Loading Libraries
# !pip install beautifulsoup4
# !pip install esprima
import json
import re
import requests
import time
import esprima
from datetime import datetime, timezone
from functools import partial
from itertools import dropwhile
from os.path import isfile
from random import randint
from urllib.parse import urljoin
from bs4 import BeautifulSoup, Tag
# ## Settings and Functions
# + id="ub8rvxXfvRsN" cellView="form"
#@title Settings
url = "https://data.cityofnewyork.us/browse?Dataset-Information_Agency=Department+of+Education+%28DOE%29&sortBy=alpha&utf8=%E2%9C%93" #@param {type:"string"}
#@markdown When providing the `url`, note that by default, the search results
#@markdown are ordered by “relevance” which will likely cause the order of the
#@markdown results to change while parsing multiple search result pages.
#@markdown Consequently, it’s possible to parse all of the pages in the set and
#@markdown still not have *all* of the search results. Use a sort order like
#@markdown “alphabetical” for more stable results.
cache = "cache.json" #@param {type:"string"}
use_cache = "Yes" #@param ["Yes", "No"]
#@markdown The `use_cache` setting above only affects getting search results.
#@markdown Activating the setting means the provided `url` will *not* be used if
#@markdown the cache file exists.
# A regular expression to match all whitespace except line breaks
whitespace_re = re.compile(r'[^\S\r\n]+', re.DOTALL)
# A regular expression to match “# results”
results_count_re = re.compile(r'(\d+)\s+Results|(1)\s+Result', re.IGNORECASE)
# Loads a JSON a file
def load_from_cache(path):
with open(path, 'r') as cache_file:
return json.load(cache_file)
# Gets the first item in a subscriptable object or None
def first(iterable):
return next(iter(iterable), None)
# Gets the first non-null item in a subscriptable object or None
def first_nonnull(iterable):
return first(dropwhile(lambda item: item is None, iterable))
# Removes excess whitespace inside and out
def strip(value):
return whitespace_re.sub(' ', value.strip())
# Converts UNIX time to an ISO format string
def unix_time_to_iso(timestamp):
return datetime.fromtimestamp(timestamp, timezone.utc).isoformat()
# Scrapes the supplied NYC OpenData *browse* url for items
def get_data_sets(url, data_sets={}):
delay_factor = 1 # This delay factor will increase exponentially on errors.
sleep = lambda: time.sleep(randint(2, 4) * delay_factor)
print(f'Getting search results from {url}...')
try:
page_data_sets, next_url, last_url, expected_length = parse_results_page(url)
page_data_sets.update(data_sets) # Data sets already in the collection
data_sets = page_data_sets # override the freshly extracted ones.
print(f'Expecting a total of {expected_length} search results...')
sleep()
while next_url:
print(f'Getting additional search results from {next_url}...')
try:
url = next_url
page_data_sets, next_url, new_last_url, new_expected_length \
= parse_results_page(next_url)
page_data_sets.update(data_sets) # Data sets already in the collection
data_sets = page_data_sets # override the freshly extracted ones.
if expected_length != new_expected_length:
print(f'The number of search results provided by the server changed '
f'from {expected_length} to {new_expected_length}!')
expected_length = new_expected_length
if next_url:
delay_factor = max(1, delay_factor // 2)
sleep() # Take it nice and easy; the server will be angry otherwise.
elif last_url and last_url != url:
print(f'last_url = {last_url}, url = {url}')
print('The server returned unexpected results. Could not extract a '
'link to the next search results page. The returned results may'
' not be complete.')
except Exception as e:
print(f'An error occured while getting additional search results: {e}')
print('The returned results may not be complete.')
delay_factor = min(1800, delay_factor * 2)
sleep()
print(f'Finished extracting {len(data_sets)} search results.')
if len(data_sets) != expected_length:
print(f'The number of search results extracted did not match the expected'
f' number of results ({expected_length}).')
return data_sets
except Exception as e:
print(f'An error occured while getting the search results: {e}')
# Loads and parses the results page, returning the items and the next page’s url
def parse_results_page(url):
make_full_url = lambda relative_url: urljoin(url, relative_url) \
if relative_url \
else None
response = requests.get(url)
response.raise_for_status() # Raises an error if the request is not successful
soup = BeautifulSoup(response.text) # Parses the raw HTML into a structure
data_sets = {result_element.get('data-view-id'):
element_to_dict(result_element)
for result_element
in soup.select('.browse2-result')}
next_url = make_full_url(extract_next_url(soup))
last_url = make_full_url(extract_last_url(soup))
expected_length = extract_expected_length(soup)
return (data_sets, next_url, last_url, expected_length)
# Extracts information about each result into a dictionary
def element_to_dict(element):
def get_element(selector):
return first(element.select(selector))
def get_link(selector):
element = get_element(selector)
if element:
return element.get('href')
def get_text(selector):
element = get_element(selector)
if element:
return strip(element.text)
timestamp = get_element('.browse2-result-timestamp-value > '
+ '[data-rawdatetime]') \
.get('data-rawdatetime')
return {'name': get_text('.browse2-result-name-link'),
'link': get_link('.browse2-result-name-link'),
'category': get_text('.browse2-result-category'),
'type': get_text('.browse2-result-type-name'),
'description': get_text('.browse2-result-description'),
'tags': [*map(Tag.get_text, element.select('.browse2-result-topic'))],
'updated': unix_time_to_iso(int(timestamp)),
'apiDocLink': get_link('.browse2-result-api-link')}
# Adds details to each item by modifying its dictionary in-place
def get_details(data_sets):
delay_factor = 1 # This delay factor will increase exponentially on errors.
sleep = lambda: time.sleep(randint(2, 4) * delay_factor)
for id in data_sets:
data_set = data_sets[id]
if 'dataDownloads' in data_set or \
'attachments' in data_set or \
'columns' in data_set:
continue # Skip items with any of those keys already.
try:
data_set_name = data_set['name']
details_url = data_set['link']
print(f'Getting details for {data_set_name} from {details_url}...')
sleep() # Take it nice and easy; the server will be angry otherwise.
data_set_information, initial_state = parse_details_page(details_url)
data_downloads = extract_data_downloads(url, data_set_information)
attachments = extract_attachments(url, initial_state)
agency = extract_agency(initial_state)
columns = extract_column_schema(initial_state)
update_frequency = extract_update_frequency(initial_state)
data_sets[id]['agency'] = agency
data_sets[id]['attachments'] = attachments
data_sets[id]['columns'] = columns
data_sets[id]['dataDownloads'] = data_downloads
data_sets[id]['updateFrequency'] = update_frequency
delay_factor = max(1, delay_factor // 2)
except ValueError as e:
print(f'\tAn error occured while getting the details: {e}')
delay_factor = min(300, delay_factor * 2)
# Extracts the data downloads information associated with the item
def extract_data_downloads(url_base, data_set_information):
if data_set_information and data_set_information['distribution']:
return [{'contentUrl': data_download['contentUrl'],
'encodingFormat': data_download['encodingFormat']}
for data_download
in data_set_information['distribution']
if data_download['@type'] == 'DataDownload']
# Extracts the attachments information associated with the item
def extract_attachments(url_base, initial_state):
if initial_state and \
initial_state['view'] and \
initial_state['view']['attachments']:
return {attachment['name']: urljoin(url_base, attachment['href'])
for attachment
in initial_state['view']['attachments']}
# Extracts the column schema information associated with the item
def extract_column_schema(initial_state):
if initial_state and \
initial_state['view'] and \
initial_state['view']['columns']:
return [{'name': column['fieldName'], # TODO: Refactor this statement; it’s getting complicated.
'type': column['dataTypeName'],
'humanName': column['name'],
'nullCount': get_value(column, 'cachedContents', 'null'),
'nonNullCount': get_value(column, 'cachedContents', 'non_null'),
'largest': get_value(column, 'cachedContents', 'largest'),
'average': get_value(column, 'cachedContents', 'average'),
'smallest': get_value(column, 'cachedContents', 'smallest'),
'topValues': [*map(lambda _: _['item'],
get_value(column, 'cachedContents', 'top') or [])] or \
None}
for column
in sorted(initial_state['view']['columns'],
key=lambda _: int(_['position']))]
# Tries to extract the data set’s agency using one of two ways
def extract_agency(initial_state):
try:
result = get_value(initial_state,
'view',
'metadata',
'custom_fields',
'Dataset Information',
'Agency')
if result is None:
result = get_value(initial_state,
'view',
'coreView',
'metadata',
'custom_fields',
'Dataset Information',
'Agency')
return result
except TypeError:
return None
# Tries to extract the data set’s update frequency using one of two ways
def extract_update_frequency(initial_state):
try:
result = get_value(initial_state,
'view',
'metadata',
'custom_fields',
'Update',
'Update Frequency')
if result is None:
result = get_value(initial_state,
'view',
'coreView',
'metadata',
'custom_fields',
'Update',
'Update Frequency')
return result
except TypeError:
return None
# Gets a value given the keys and indices to it
def get_value(object, *path_components, default=None):
if path_components:
try:
return get_value(object[path_components[0]],
*path_components[1:],
default=default)
except (IndexError, KeyError):
return default
return object
# Digs into the item’s page to extract additional details
def parse_details_page(url):
response = requests.get(url)
response.raise_for_status()
soup = BeautifulSoup(response.text)
data_set_information = None # The information about the data set embedded in the page
json_objects = extract_inline_json(soup)
for json_object in json_objects:
if json_object and json_object['@type'] == 'Dataset': # Found the information!
data_set_information = json_object
break
initial_state = None # The embedded information that the page uses to initialize its tables
scripts = extract_inline_javascript(soup)
for script in scripts:
try:
ast = esprima.parseScript(script, {'range': True}) # Guards against not-JavaScript
if ast.type == 'Program' and \
ast.sourceType == 'script' and \
len(ast.body) == 1 and \
ast.body[0].type == 'VariableDeclaration' and \
len(ast.body[0].declarations) == 1: # Found the script with a single variable declaration
declaration = ast.body[0].declarations[0]
if declaration.type == 'VariableDeclarator' and \
declaration.id.type == 'Identifier' and \
declaration.id.name == 'initialState' and \
declaration.init.type == 'ObjectExpression': # Found the initial state!
json_start, json_end = declaration.init.range
initial_state = json.loads(script[json_start:json_end])
break
except Exception as e:
pass # Ignore the “script” if parsing it throws an exception.
return (data_set_information, initial_state)
# Loads all of the inline JSON found in the page’s script tags
def extract_inline_json(soup):
return [json.loads(element.string)
for element
in soup.select('script[type="application/ld+json"]')
if element.string]
# Loads all of the inline JavaScript found in the page’s script tags
def extract_inline_javascript(soup):
return [element.string
for element
in soup.select('script')
if element.string]
# Gets the URL of the next results page
def extract_next_url(soup):
element = soup.select('a.nextLink')
if element:
return element[0].get('href')
# Gets the URL of the last results page
def extract_last_url(soup):
element = soup.select('a.lastLink')
if element:
return element[0].get('href')
# Gets the number of search results to expect
def extract_expected_length(soup):
element = first(soup.select('.browse2-mobile-filter-result-count'))
return int(first_nonnull(first(map(re.Match.groups,
filter(None,
map(results_count_re.match,
element.stripped_strings))))))
# + [markdown] id="4FiTW1vjXoPZ"
# ## Parsing the Search Results
# The code below extracts the data from the first search results page and all subsequent pages until it cannot find a link to the next page. For each page, it looks for the search result elements and maps each one to a dictionary. The dictionary schema is as follows:
# * **name** (string): the name of the item
# * **link** (string): the link to the page with more information about the item
# * **category** (string): the category of the item (e.g., *Education*)
# * **type** (string): the type of the item (e.g., *Dataset*)
# * **description** (string): a description of the item
# * **tags** (list of strings): a set of tags associated with the item
# * **updated** (string): the timestamp which this item was last updated
# * **apiDocLink** (string): a link to the API documentation (which might possibly be used to extract more metadata about the item)
# + id="v8PPw6lnwOO-" colab={"base_uri": "https://localhost:8080/"} outputId="22cb392b-f1fe-46ab-d093-0932d816224a"
data_sets = load_from_cache(cache) if use_cache == 'Yes' and isfile(cache) else get_data_sets(url)
# + [markdown] id="U8nQnEB4K0Pr"
# ## Getting the Data Set Details
# The code below extracts additional information about the items using the links to the items’ pages. It adds the following keys if the information is available:
# * **columns**: a list of columns and their properties
# * **name** (string): the name of the column
# * **humanName** (string): a human-friendly name for the column
# * **type** (string): the column type (one of: `calendar_date`, `checkbox`, `location`, `number`, `point`, `text`, or `url`)
# * **nullCount** (number): the count of null values for the column
# * **nonNullCount** (number): the count of non-null values for the column
# * **largest**: the largest value for the column
# * **smallest**: the smallest value for the column
# * **top** (list): a list of the top values for the column
# * **attachments**: a list of downloadable files—most often spreadsheets or PDFs—that describe the data in more detail
# * **dataDownloads**: a list of downloadable files containing all of the data in different formats
#
# In the case where download of data set details is interrupted, the code will attempt to resume progress. Simply, it checks each dictionary entry for the existence of the above keys. If those don’t exist, it tries to retrieve them and amends the dictionary. Existing keys will not be updated.
# + id="2-2QbHRsMS4W"
get_details(data_sets)
# + [markdown] id="bnTGn10FSikm"
# ## Caching Data
# The code below will save a copy of the data to storage for loading and processing by other scripts. The file name is defined in the settings above.
# + id="UZz_9mslTlNi"
with open(cache, 'w') as cache_file:
json.dump(data_sets, cache_file, indent=2, sort_keys=True)
|
NYC_OpenData_Data_Set_Lister.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + id="YfIk2es3hJEd"
import tensorflow as tf
import os
import time
from matplotlib import pyplot as plt
from IPython import display
import tensorflow_datasets as tfds
# + id="2CbTEt448b4R"
BUFFER_SIZE = 400
EPOCHS = 100
LAMBDA = 100
DATASET = 'seg'
BATCH_SIZE = 32
IMG_WIDTH = 128
IMG_HEIGHT = 128
patch_size = 8
num_patches = (IMG_HEIGHT // patch_size) ** 2
projection_dim = 64
embed_dim = 64
num_heads = 2
ff_dim = 32
assert IMG_WIDTH == IMG_HEIGHT, "image width and image height must have same dims"
tf.config.run_functions_eagerly(False)
# + colab={"base_uri": "https://localhost:8080/", "height": 347, "referenced_widgets": ["e6d3b16d24cd4468b68af5be44eeaa46", "8fd55e55c24e48afb223ff8b7422a546", "954933d3187645c6bd191289c122a6b5", "1c7b1be085354daa90f7491366bf3f26", "84132b5022db442183e409973de11d67", "f60bacd17c604608a7fd80a06a305bdf", "112fde1fafb042c7abe870a471f69cb4", "<KEY>", "<KEY>", "5c6312228c08467186d56dba16c4028c", "642dffa8e9374234bbce51d29e75c7ea", "<KEY>", "e292c1f1791e4b349a931400f52e980c", "<KEY>", "<KEY>", "605b204e45bb401e97270eba6eceb351", "<KEY>", "<KEY>", "<KEY>", "d8118a57a2814d19b2fde27d2452c84e", "<KEY>", "<KEY>", "a625ba1ffcc340c5a4f042be0b4877c3", "5695c6a28a5e47008227462f5ade5c9b", "83c9ad4ed8bb4aa9804a23a330da4d8c", "2d19d5c44a0348768a9ff242aa199119", "<KEY>", "<KEY>", "231b5248ecd746d0939739f6a42db75e", "<KEY>", "<KEY>", "6abe70e78dce42a091dca068f5af4696", "2c75ae91013c455e8cedafddcd12052f", "<KEY>", "c11d62582c59442e9cf388a6fbacaad7", "<KEY>", "5979ebdad11f4f6f941b32ba4a509416", "<KEY>", "7e7891071f7c4f5e87d876da643a3045", "12aae5a01c5a462e999735d848d3e354", "1612ca06675349d4b76e5378a129eefb", "<KEY>", "<KEY>", "<KEY>", "bd9ea3399660446897f60580a39588f2", "<KEY>", "<KEY>", "<KEY>", "600a3e8becc84abeadc682bae8db52d5", "97c62988c2e1454db66b33ab880f08d1", "<KEY>", "<KEY>", "<KEY>", "6ba3d098f19b4919a06ecca5b3763596", "<KEY>", "<KEY>"]} id="Kn-k8kTXuAlv" outputId="6cc83593-137e-429a-e2ef-060e8d07d41a"
dataset, info = tfds.load('oxford_iiit_pet:3.*.*', with_info=True)
# + id="aO9ZAGH5K3SY"
def normalize(input_image, input_mask):
input_image = tf.cast(input_image, tf.float32) / 255.0
input_mask -= 1
return input_image, input_mask
# + id="4OLHMpsQ5aOv"
@tf.function
def load_image_train(datapoint):
input_image = tf.image.resize(datapoint['image'], (128, 128))
input_mask = tf.image.resize(datapoint['segmentation_mask'], (128, 128))
if tf.random.uniform(()) > 0.5:
input_image = tf.image.flip_left_right(input_image)
input_mask = tf.image.flip_left_right(input_mask)
input_image, input_mask = normalize(input_image, input_mask)
return input_image, input_mask
# + id="rwwYQpu9FzDu"
def load_image_test(datapoint):
input_image = tf.image.resize(datapoint['image'], (128, 128))
input_mask = tf.image.resize(datapoint['segmentation_mask'], (128, 128))
input_image, input_mask = normalize(input_image, input_mask)
return input_image, input_mask
# + colab={"base_uri": "https://localhost:8080/"} id="Yn3IwqhiIszt" outputId="e52589a1-2d3a-42c8-ec89-7a08e27b9538"
TRAIN_LENGTH = info.splits['train'].num_examples
STEPS_PER_EPOCH = TRAIN_LENGTH // BATCH_SIZE
# + id="muhR2cgbLKWW"
train = dataset['train'].map(load_image_train, num_parallel_calls=tf.data.AUTOTUNE)
test = dataset['test'].map(load_image_test)
# + id="fVQOjcPVLrUc"
train_dataset = train.cache().shuffle(BUFFER_SIZE).batch(BATCH_SIZE).repeat()
train_dataset = train_dataset.prefetch(buffer_size=tf.data.AUTOTUNE)
test_dataset = test.batch(BATCH_SIZE)
# + id="n0OGdi6D92kM"
def display(display_list):
plt.figure(figsize=(15, 15))
title = ['Input Image', 'True Mask', 'Predicted Mask']
for i in range(len(display_list)):
plt.subplot(1, len(display_list), i+1)
plt.title(title[i])
plt.imshow(tf.keras.preprocessing.image.array_to_img(display_list[i]))
plt.axis('off')
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 427} id="tyaP4hLJ8b4W" outputId="ba14a1a1-ecc9-4fe1-f512-10e0793cd921"
for image, mask in train.take(1):
sample_image, sample_mask = image, mask
display([sample_image, sample_mask])
# + id="VB3Z6D_zKSru"
def create_mask(pred_mask):
pred_mask = tf.argmax(pred_mask, axis=-1)
pred_mask = pred_mask[..., tf.newaxis]
return pred_mask[0]
# + id="SQHmYSmk8b4b"
def show_predictions(dataset=None, num=1):
if dataset:
for image, mask in dataset.take(num):
pred_mask = generator.predict(image)
display([image[0], mask[0], create_mask(pred_mask)])
else:
display([sample_image, sample_mask,
create_mask(generator.predict(sample_image[tf.newaxis, ...]))])
# + id="AWSBM-ckAZZL"
class Patches(tf.keras.layers.Layer):
def __init__(self, patch_size):
super(Patches, self).__init__()
self.patch_size = patch_size
def call(self, images):
batch_size = tf.shape(images)[0]
patches = tf.image.extract_patches(
images=images,
sizes=[1, self.patch_size, self.patch_size, 1],
strides=[1, self.patch_size, self.patch_size, 1],
rates=[1, 1, 1, 1],
padding="SAME",
)
patch_dims = patches.shape[-1]
patches = tf.reshape(patches, [batch_size, -1, patch_dims])
return patches
# + id="mXT2GyxTAZWq"
class PatchEncoder(tf.keras.layers.Layer):
def __init__(self, num_patches, projection_dim):
super(PatchEncoder, self).__init__()
self.num_patches = num_patches
self.projection = layers.Dense(units=projection_dim)
self.position_embedding = layers.Embedding(
input_dim=num_patches, output_dim=projection_dim
)
def call(self, patch):
positions = tf.range(start=0, limit=self.num_patches, delta=1)
encoded = self.projection(patch) + self.position_embedding(positions)
return encoded
# + id="EsRN0b3qAdWz"
class TransformerBlock(tf.keras.layers.Layer):
def __init__(self, embed_dim, num_heads, ff_dim, rate=0.1):
super(TransformerBlock, self).__init__()
self.att = layers.MultiHeadAttention(num_heads=num_heads, key_dim=embed_dim)
self.ffn = tf.keras.Sequential(
[layers.Dense(ff_dim, activation="relu"), layers.Dense(embed_dim),]
)
self.layernorm1 = layers.LayerNormalization(epsilon=1e-6)
self.layernorm2 = layers.LayerNormalization(epsilon=1e-6)
self.dropout1 = layers.Dropout(rate)
self.dropout2 = layers.Dropout(rate)
def call(self, inputs, training):
attn_output = self.att(inputs, inputs)
attn_output = self.dropout1(attn_output, training=training)
out1 = self.layernorm1(inputs + attn_output)
ffn_output = self.ffn(out1)
ffn_output = self.dropout2(ffn_output, training=training)
return self.layernorm2(out1 + ffn_output)
# + id="h9GZYWlkAsBn"
from tensorflow import Tensor
from tensorflow.keras.layers import Input, Conv2D, ReLU, BatchNormalization,\
Add, AveragePooling2D, Flatten, Dense
from tensorflow.keras.models import Model
def relu_bn(inputs: Tensor) -> Tensor:
relu = ReLU()(inputs)
bn = BatchNormalization()(relu)
return bn
def residual_block(x: Tensor, downsample: bool, filters: int, kernel_size: int = 3) -> Tensor:
y = Conv2D(kernel_size=kernel_size,
strides= (1 if not downsample else 2),
filters=filters,
padding="same")(x)
y = relu_bn(y)
y = Conv2D(kernel_size=kernel_size,
strides=1,
filters=filters,
padding="same")(y)
if downsample:
x = Conv2D(kernel_size=1,
strides=2,
filters=filters,
padding="same")(x)
out = Add()([x, y])
out = relu_bn(out)
return out
# + id="lFPI4Nu-8b4q"
from tensorflow.keras import layers
def Generator():
inputs = layers.Input(shape=(128, 128, 3))
patches = Patches(patch_size)(inputs)
encoded_patches = PatchEncoder(num_patches, projection_dim)(patches)
x = TransformerBlock(64, num_heads, ff_dim)(encoded_patches)
x = TransformerBlock(64, num_heads, ff_dim)(x)
x = TransformerBlock(64, num_heads, ff_dim)(x)
x = TransformerBlock(64, num_heads, ff_dim)(x)
x = layers.Reshape((8, 8, 256))(x)
x = layers.Conv2DTranspose(512, (5, 5), strides=(2, 2), padding='same', use_bias=False)(x)
x = layers.BatchNormalization()(x)
x = layers.LeakyReLU()(x)
x = residual_block(x, downsample=False, filters=512)
x = layers.Conv2DTranspose(256, (5, 5), strides=(2, 2), padding='same', use_bias=False)(x)
x = layers.BatchNormalization()(x)
x = layers.LeakyReLU()(x)
x = residual_block(x, downsample=False, filters=256)
x = layers.Conv2DTranspose(64, (5, 5), strides=(2, 2), padding='same', use_bias=False)(x)
x = layers.BatchNormalization()(x)
x = layers.LeakyReLU()(x)
x = residual_block(x, downsample=False, filters=64)
x = layers.Conv2DTranspose(32, (5, 5), strides=(2, 2), padding='same', use_bias=False)(x)
x = layers.BatchNormalization()(x)
x = layers.LeakyReLU()(x)
x = residual_block(x, downsample=False, filters=32)
x = layers.Conv2D(3, (3, 3), strides=(1, 1), padding='same', use_bias=False, activation='tanh')(x)
return tf.keras.Model(inputs=inputs, outputs=x)
# + colab={"base_uri": "https://localhost:8080/"} id="dIbRPFzjmV85" outputId="5216d85f-f401-4657-d41e-233f9be51233"
generator = Generator()
tf.keras.utils.plot_model(generator, show_shapes=True, dpi=64)
generator.summary()
# + id="o58eGY46eiPQ"
class DisplayCallback(tf.keras.callbacks.Callback):
def on_epoch_end(self, epoch, logs=None):
clear_output(wait=True)
show_predictions()
print ('\nSample Prediction after epoch {}\n'.format(epoch+1))
# + id="5nfPDmCNemKf"
generator.compile(optimizer='adam',
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=['accuracy'])
# + colab={"base_uri": "https://localhost:8080/"} id="LyA03ie2dUAS" outputId="0639a42b-4a8a-4603-9998-7c1409f1c71c"
EPOCHS = 200
VAL_SUBSPLITS = 5
VALIDATION_STEPS = info.splits['test'].num_examples//BATCH_SIZE//VAL_SUBSPLITS
model_history = generator.fit(train_dataset, epochs=EPOCHS,
steps_per_epoch=STEPS_PER_EPOCH,
validation_steps=VALIDATION_STEPS,
validation_data=test_dataset)
# + colab={"base_uri": "https://localhost:8080/", "height": 293} id="U1N1_obwtdQH" outputId="20004ed9-8789-4c37-962c-629d0bfd9946"
show_predictions(train_dataset)
# + id="NiTrkKItvZHE"
generator.save_weights('seg-gen-weights.h5')
# -
generator.load_weights('weights/seg-gen-weights (5).h5')
for inp, tar in train_dataset:
break
plt.imshow(generator(inp)[0])
import numpy as np
plt.imsave('pred1.png', np.array(create_mask(generator(inp))).astype(np.float32).reshape(128, 128))
plt.imshow(inp[0])
import numpy as np
plt.imsave('tar1.png', np.array(inp[0]).astype(np.float32).reshape(128, 128, 3))
|
VIT/notebooks/image-segmentation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Golden Cross / Death Cross S&P 500 index (^GSPC)
#
# 1. sma50>sma200, buy
# 2. sma50<sma200, sell your long position.
# +
import datetime
import matplotlib.pyplot as plt
import pandas as pd
from talib.abstract import *
import pinkfish as pf
# Format price data
pd.options.display.float_format = '{:0.2f}'.format
# %matplotlib inline
# -
# Set size of inline plots
'''note: rcParams can't be in same cell as import matplotlib
or %matplotlib inline
%matplotlib notebook: will lead to interactive plots embedded within
the notebook, you can zoom and resize the figure
%matplotlib inline: only draw static images in the notebook
'''
plt.rcParams["figure.figsize"] = (10, 7)
# Some global data
# +
symbol = '^GSPC'
#symbol = 'SPY'
capital = 10000
start = datetime.datetime(1900, 1, 1)
#start = datetime.datetime(*pf.SP500_BEGIN)
end = datetime.datetime.now()
use_adj=True
# -
# Prepare timeseries
# +
# Fetch and select timeseries.
ts = pf.fetch_timeseries(symbol,)
ts = pf.select_tradeperiod(ts, start, end, use_adj=use_adj)
# Add technical indicator: day sma regime filter.
ts['regime'] = \
pf.CROSSOVER(ts, timeperiod_fast=50, timeperiod_slow=200)
# Finalize the time series before implementing trading strategy.
ts, start = pf.finalize_timeseries(ts, start)
# Create Trade Log (tlog); Create Daily Balance (dbal).
tlog = pf.TradeLog(symbol)
dbal = pf.DailyBal()
# -
# Algo: Buy when 50 day ma crosses above 200 day ma. Sell when 50 day ma crosses below 200 day ma.
# +
pf.TradeLog.cash = capital
for i, row in enumerate(ts.itertuples()):
date = row.Index.to_pydatetime()
high = row.high; low = row.low; close = row.close;
end_flag = pf.is_last_row(ts, i)
# Buy
# Note ts['regime'][i-1] is regime for previous day
# We want to buy only on the day of a moving average crossover
# i.e. yesteraday regime is negative, today it is positive
if tlog.shares == 0:
if row.regime > 0 and ts['regime'][i-1] < 0:
tlog.buy(date, close)
# Sell
else:
if row.regime < 0 or end_flag:
tlog.sell(date, close)
# record daily balance
dbal.append(date, high, low, close)
# -
# Retrieve logs
tlog = tlog.get_log()
dbal = dbal.get_log(tlog)
# Generate strategy stats - display all available stats
stats = pf.stats(ts, tlog, dbal, capital)
pf.print_full(stats)
# Benchmark: Run, retrieve logs, generate stats
benchmark = pf.Benchmark(symbol, capital, start, end, use_adj=use_adj)
benchmark.run()
# Plot Equity Curves: Strategy vs Benchmark
pf.plot_equity_curve(dbal, benchmark=benchmark.dbal)
# Plot Trades
pf.plot_trades(dbal, benchmark=benchmark.dbal)
# Strategy vs Benchmark
df = pf.summary(stats, benchmark.stats, metrics=pf.currency_metrics)
df
# +
extras = ('avg_month',)
df = pf.plot_bar_graph(stats, benchmark.stats, extras=extras)
df
# -
|
examples/050.golden-cross/strategy.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Data Vizualization
# !pip install matplotlib
import matplotlib.pyplot as plt
import numpy as np
# # Line plot
x = np.arange(10)
y1=x**2
y2=2*x+3
print(x)
print(y1)
print(y2)
plt.plot(x,y1,c='g')
plt.show()
plt.plot(x,y2,c='r')
plt.show()
themes = plt.style.available
print(themes)
plt.style.use("seaborn")
plt.plot(x,y1,c='g')
plt.plot(x,y2,c='r')
plt.show()
plt.plot(x,y1,c='g')
plt.plot(x,y2,c='r')
plt.xlabel("x")
plt.ylabel("f(x)")
plt.plot(x,y1,c='g',label='f1',marker='o')
plt.plot(x,y2,c='r',label='f2',linestyle='dashed',marker='*')
plt.xlabel("x")
plt.ylabel("f(x)")
plt.legend()
plt.show()
# +
# plt.plot?
# -
prices = np.array([1,2,3,4])**2
print(prices)
plt.plot(prices,marker='o')
plt.show()
# # Scatter Plots
plt.scatter(x,y1)
plt.scatter(x,y2)
plt.show()
plt.figure(figsize=(2,2))
plt.scatter(x,y1,c='g',label='f1',marker='o')
plt.scatter(x,y2,c='r',label='f2',linestyle='dashed',marker='*')
plt.xlabel("x")
plt.ylabel("f(x)")
plt.legend()
plt.title('scatter plot')
plt.show()
# # Bar Graph
# +
# plt.bar?
# -
plt.bar([0,1,2],[10,20,50])
plt.show()
plt.bar([0,1,2],[10,20,50])
plt.bar([0,1,2],[20,10,40])
plt.show()
x = np.array([0,1,2])*2
plt.bar(x,[10,20,50],width=0.5)
plt.bar(x+0.5,[20,10,40],width=0.5)
plt.show()
plt.style.use("dark_background")
x = np.array([0,1,2])*2
plt.bar(x,[10,20,30],width=0.5,label="curr year",tick_label=["gold","plat","silver"],color='blue')
plt.bar(x+0.5,[20,10,20],width=0.5,label="next year",color='red')
plt.xlabel('x')
plt.ylabel('y')
plt.ylim(0,40)
plt.xlim(-2,5)
plt.legend()
plt.show()
# # pie chart
# +
# plt.pie?
# -
plt.style.use("seaborn")
sub= "maths","chem","phy","eng"
weight=[20,10,15,5]
plt.pie(weight,labels=sub,explode=(0,0,0.1,0),autopct='%1.1f%%',shadow=True)
plt.title('bar graph')
plt.show()
# # histogram
xsn = np.random.randn(100)
sigma=5
u=70
x=np.round(xsn*sigma+u)
x2= np.round(xsn*5+40)
print(x)
plt.style.use("seaborn")
plt.hist(x,alpha=0.8)
plt.hist(x2,alpha=0.6)
plt.xlim(0,100)
plt.show()
# # Data vizualization Challenge
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
df = pd.read_csv('')
df.head(n=10)
df.columns
titles= list(df.get('movie_title'))
print(titles[:5])
print(titles[0][-1])
# +
freq_titles={}
for title in titles:
length = len(title)
if freq_titles.get(length) is None:
freq_title[length]=1
else:
freq_title[length]+=1
# -
print(freq_titles)
x=np.array(list(freq_titles.keys()))
y=np.array(list(freq_titles.values()))
plt.scatter(x,y)
plt.xlabel("movie length")
plt.ylabel("freq count")
plt.title('Movies')
plt.show()
|
Data-Vizualization/Untitled.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Using data collected from Google playstore for data analysis
#
#
# This project is an analysis of the data set collected on Kaggle by <NAME>, and can be viewed on this website https://www.kaggle.com/lava18/google-play-store-apps.
#
# There are two datasets: one which includes:
# - the name of the Apps,
# - their category,
# - number of reviews,
# - the size of the App,
# - number if intalls,
# - type of app and price,
# - the content rating,
# - genre,
# - the last time it was updated,
# - current version and android version.
#
# the second data set contains:
# - App
# - Translated_Review Sentiment
# - Sentiment_Polarity
# - Sentiment_Subjectivity
#
# I will be using the python libraries numpy, pandas, matplotlib and seaborn to clean and prepare the data to create graphs and answer five questions using the techniques I have gained from [the course](http://zerotopandas.com).
#
# As a first step, let's upload our Jupyter notebook to [Jovian.ml](https://jovian.ml).
project_name = "Play_Store_Data_Analysis "
# ## Data Preparation and Cleaning
#
# There is quite a bit of information in these files which will be merged at some point. However, though I will keep them (more for asthetics than true usefulness), I feel that the most useful columns will be the App, Category, App, Rating, Reviews, Size, Installs, Price, Content Rating and Genres column from the googleplaystore csv and the App, Sentiment, Sentiment_Polarity and Sentiment_Subjectivity columns in the googleplaystore_user_reviews csv. Let's begin by:
#
# - importing the files,
# - the shape,
# - null values
# - data frame (playStore_df) info and
# - a sample of the playStore_df data
#
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
import seaborn as sns
# %matplotlib inline
playStore_df = pd.read_csv('googleplaystore.csv')
playStoreReviews_df = pd.read_csv('googleplaystore_user_reviews.csv')
playStore_df
playStoreReviews_df
print(playStore_df.shape)
print(playStoreReviews_df.shape)
playStore_df.info()
playStore_df.columns
playStoreReviews_df.columns
irregular_df = playStore_df[playStore_df['Genres']=='February 11, 2018']
irregular_df
playStore_df.isnull().values.any()
playStore_df.isnull().sum().sum()
playStore_df.info()
playStore_df.sample(frac=0.1, replace=True, random_state=1)
# # Exploratory Analysis and Visualization
#
# From the info returned about the data types, we can see that a few columns such as Reviews, Size, Installs and Price are not of type float or int so we will need to convert those columns. We also noticed there was an irreguglar row which may need to be removed.
#
# So for this section, we will:
#
# - investigate the irregular row,
# - find out how many different genres there are,
# - alter and convert columns so they can be used for calculations and
# - Create a few graphs
#
# Let's continue!
playStore_df.describe()
irregular_df
# Remove irregular_df data as the Genre for it does not make any sense - it's a date!
playStore_df = playStore_df[playStore_df['Rating']< 5]
playStore_df.describe()
# We can see that the number of rows has been reduced by one so the drop has been successful. Next we can look on the types of data we have for each column.
typesofGenres = playStore_df['Genres'].unique()
typesofGenres
numberOfGenres = playStore_df['Genres'].nunique()
numberOfGenres
# We have removed the irregular row and checked the number of Genres. Now let's change the dtaa types of a few columns.
playStore_df.info()
# This isn't very helpful as though Ratings has a data type of float, this does not hold true for the Size, Reviews, Price or even Installs data columns. Therefore, I will need to change them to be able to make use of the data provided. The main issue is to remove the M,k and other additional characters which are hindering the size values being converted into floats.
pd.set_option('mode.chained_assignment', None)
playStore_df['Reviews'] = playStore_df['Reviews'].str.replace('M','')
pd.set_option('mode.chained_assignment', None)
playStore_df['Rating'] = pd.to_numeric(playStore_df.Rating, errors='coerce')
pd.set_option('mode.chained_assignment', None)
playStore_df['Reviews'] = playStore_df['Reviews'].astype('float')
playStore_df['Size']
playStore_df['Size'] = playStore_df['Size'].replace({'M': '','Varies with device':'0','k':''}, regex=True)
playStore_df['Size'] = playStore_df['Size'].str.replace('+','').str.replace(',','')
pd.set_option('mode.chained_assignment', None)
playStore_df['Size'] = playStore_df['Size'].astype('float32')
pd.set_option('mode.chained_assignment', None)
playStore_df['Size']
# Now that that Size column has been convered into the float data type, the same process must be carried out for the other columns - Price and Installs
playStore_df['Price']
# Looking at the strings that will be replaced in the Price column, we can see that another error has been made as the column contains the value 'Everyone' which is not numeric. This most likely belongs to the Content Rating column. Instead of removing this row entirely, I will convert it's value to zero instead (mainly for ease but also based on the number of zeroes that are already in the column).
playStore_df['Price'] = playStore_df['Price'].str.replace('$','').str.replace('Everyone','0')
playStore_df['Price'] = playStore_df['Price'].astype('float')
playStore_df['Price']
# There doesn't appear to be any other value apart from zero for this column, but in order to be sure but I know that not to be true as I have seen the CSV file in excel and seen other values. To ensure this, I will see what the sum of the Price column is.
playStore_df['Price'].sum()
# As mentioned before I will now remove commas and + signs and and replace with '' and remove and replace word 'Free' with 0 so that column can be converted into an integer column
playStore_df['Installs'] = playStore_df['Installs'].str.replace('+','').str.replace(',','').str.replace('Free','0')
playStore_df['Installs'] = playStore_df['Installs'].astype('int')
playStore_df.describe()
playStore_df.drop(playStore_df[playStore_df.Rating > 10].index, inplace=True)
playStore_df.drop(playStore_df[playStore_df.Reviews < 500].index, inplace=True)
# Let's get a picture of the top 10 apps in the data collected, looking at the difference between the top rated App and the app at the bottom of the list. The table should be minimised but include the App (so we can see the name), Review (for a comparison of the reviewsd to the rating) and of course the Rating columns.
toprating_df = playStore_df.sort_values('Rating', ascending=False).head(10)[['App','Reviews','Rating']].head(10)
toprating_df
playStore_df['Reviews per thousand'] = playStore_df.Reviews/1000
toprating_df = playStore_df.sort_values('Rating', ascending=False).head(10)[['App','Reviews','Rating','Reviews per thousand']].head(10)
toprating_df
# +
sns.set_style('darkgrid')
matplotlib.rcParams['font.size'] = 14
matplotlib.rcParams['figure.figsize'] = (9, 5)
# +
plt.figure(figsize=(18,9))
plt.xticks(rotation=85)
labels = ['Ratings','Reviews']
plt.title('Top Rated App')
plt.bar(toprating_df['App'],toprating_df['Rating'])
plt.bar(toprating_df['App'],toprating_df['Reviews per thousand'], alpha=0.8)
plt.legend(labels = labels)
# -
# There appears to be a larger number of content rating's compared to other. It would be interesting to see which rating has the highest count, and put these calues into a pie chart.
topThirtyContent = playStore_df['Content Rating'].value_counts()
topThirtyContent
# +
explode = (0,0.1,0.2,0.3,0.4,0.8)
labels = topThirtyContent.index
plt.figure(figsize=(21,10))
plt.title('Content rating of apps')
plt.pie(topThirtyContent, autopct='%1.1f%%', startangle=180, shadow=True, labeldistance=None,
rotatelabels=True, explode=explode);
plt.legend(labels, loc='upper right')
# -
newplayStore = playStore_df.sort_values('Reviews', ascending=False)[['App','Installs','Reviews','Rating','Genres']]
newplayStore = newplayStore.drop_duplicates(['App']).head(20)
newplayStore
# +
plt.figure(figsize=(12, 6))
plt.title("Number of Apps that recieved rating.")
plt.xlabel('Ratings for App')
plt.ylabel('Ratings given to apps for App')
plt.hist(newplayStore.Rating, color='purple');
# -
# We are now going to merge the two data frames to create one data frame - merged_df
merged_df = playStore_df.merge(playStoreReviews_df, on="App")
merged_df
# Though there are only three types of sentimental values, it would be interesting to view the number of setiments that were positive.
merged_df['Sentiment'].value_counts()
# We can also compare the highest rated cateogrys to a sample set to see if there are any distinct and concerning differences. The comparison will be made using barplots.
highest_rated_category = merged_df.sort_values('Rating',ascending=False)[['App','Category','Rating']]
highest_rated_category = highest_rated_category.drop_duplicates(['App'])
new_highest_rated_category = highest_rated_category.head(15)
new_highest_rated_category
# +
plt.figure(figsize=(24, 14))
plt.title('Top rated category')
plt.xticks(rotation=10)
plt.ylabel('Rating')
sns.barplot(data=new_highest_rated_category,y='App',x='Rating', hue='Category', palette="Greens_d",dodge=False);
# -
sample_df = merged_df.sample(n=18, replace=True, random_state=1)
highest_rated_category1 = sample_df.sort_values('Rating',ascending=False).head(15)[['App','Category','Rating']]
highest_rated_category1
# +
plt.figure(figsize=(24, 14))
plt.title('Top rated category')
plt.xticks(rotation=10)
plt.ylabel('Rating')
sns.barplot(data=highest_rated_category1,y='App',x='Rating', hue='Category', palette="Blues_d",dodge=False);
# -
# Though there appears to be more range in variety in values in the sample barplot, there does not appear any drastic differences. The data appears to be satisfactory.
# # Asking and Answering Questions
#
# We've already gained some insight about the data but now we are going to asks 5 specific questions about the data we have and also answer them. Here we go...
# ## Question 1
# Is there a realtionship between customers being happy with the app, and the app being free?
reviewAndSentiment = merged_df.sort_values('Sentiment_Polarity', ascending=False)[['Sentiment_Polarity','Price','Sentiment','Rating']].head(15)
reviewAndSentiment
reviewAndSentiment['SentimentValue'] = reviewAndSentiment['Sentiment'].str.replace('Positive','1')
reviewAndSentiment['SentimentValue'] = reviewAndSentiment['SentimentValue'].astype('float')
reviewAndSentiment
reviewAndSentiment['Sentiment_Polarity']= reviewAndSentiment['Sentiment_Polarity'].astype('float')
reviewAndSentiment.corr()
# While it can be observed that a high sentiment polarity also saw a postive sentiment and sentiment value there does not appear to be a correlation between these two things. However, the ratings appear to be favourable, with the lowest rating being 3.9.
# ## Question 2
# What is the difference in sentiment polarity in the most popular genre compared to the least popular genre?
most_popular_game = merged_df['Genres'].value_counts()
most_popular_game
# The most popular genre is Sports and the least popular genre includes a number of genres. let us obtain all of the lowest genres
lowest_genres = most_popular_game[most_popular_game < 41]
lowest_genres
sentiment_pop1 = merged_df[merged_df.Genres=='Sports'][['App','Genres','Sentiment_Polarity']]
sentiment_pop1 = sentiment_pop1.drop_duplicates(['App'])
sentiment_pop1
sentiment1 = sentiment_pop1['Sentiment_Polarity'].mean()
sentiment1
for i in lowest_genres.index:
sentiment_pop2 = merged_df[merged_df.Genres== i][['App','Sentiment_Polarity']]
sentiment_pop2 = sentiment_pop2.drop_duplicates(['App'])
print(sentiment_pop2)
# The output printed above provides a check list of all the rows that should be used in calculation of the lowest genres and their mean sentiment polarity.
sentiment_pop2 = merged_df[merged_df.Genres.isin(lowest_genres.index)][['App','Genres','Sentiment_Polarity']]
sentiment_pop2= sentiment_pop2.drop_duplicates(['App'])
sentiment_pop2
sentiment2 = sentiment_pop2['Sentiment_Polarity'].mean()
sentiment2
difference = sentiment1 - sentiment2
difference
# So the difference in sentiment polarity is 0.06591827598140731 which is a small value.
# # Question 3
# Which category had the highest Rating and highest number of reviews.
highest_df = merged_df.sort_values('Rating', ascending= False)
highest_df = highest_df.drop_duplicates(['App']).head(15)
highest_df
highest_rating_and_reviews = highest_df.sort_values('Reviews', ascending=False)
highest_rating_and_reviews
# +
plt.figure(figsize=(12, 12))
plt.xticks(rotation = 90)
sns.barplot(data = highest_rating_and_reviews, y = highest_rating_and_reviews['Reviews'],x=highest_rating_and_reviews['App'])
plt.title("15 highest rated apps with in order of highest number of reviews ");
plt.xlabel('App Name')
plt.ylabel('No. of Reviews (per million)')
# -
# The top 15 apps were first sorted by their ratings and then by the number of reviews, to show the App with the highest rating and number of reviews. In this case, this app is Amino: Communities and Chats. Interestingly, this app is a social app, not a sports app which was the most popular genre.
# # Question 4
# Which category had the most apps that had to be paid for?
apps = merged_df[merged_df['Price']>0]
apps = apps.drop_duplicates(['App'])
apps
most_paid_category = apps['Category'].value_counts()
most_paid_category
highest_paid_category = apps.sort_values('Price', ascending = False) [['App','Category','Rating','Reviews','Installs','Genres','Price']]
highest_paid_category
# Of the apps that had to be paid for, they only came from three categories:
#
# - PERSONALIZATION which appeared 3 times,
# - GAME which appeared 3 times,
# - MEDICAL which appeared 2 times,
# - FAMILY which appeared 2 times,
# - SPORTS which appeared once,
# - PHOTOGRAPHY which appeared once,
#
# The top categories were Personalization and Game, however, as a little addition, I wanted to find out which item had the highest price and compare it to the number of installs, reviews and ratings.
# ## Question 5
# What were the general sentiments of the 20 most installed apps. Compare to a random sample.
# +
sentiments_most_installed = merged_df.sort_values('Installs',ascending=False)[['App','Translated_Review','Sentiment']]
sentiments_most_installed = sentiments_most_installed.drop_duplicates(['App'])
sentiments_most_installed = sentiments_most_installed.head(20)
sentiments_most_installed
# -
sentiments_most_installed_count = sentiments_most_installed['Sentiment'].value_counts()
sentiments_most_installed_count
# +
explode = (0.0,0.3,0.4)
labels = sentiments_most_installed_count.index
colors = ['#66b3ff','#99ff99','#ffcc99']
plt.figure(figsize=(21,10))
plt.title('Sentiments of the top 20 most installed apps')
plt.pie(sentiments_most_installed_count, autopct='%1.0f%%', startangle=180, shadow=True, labeldistance=None,
rotatelabels=True, explode=explode, colors= colors);
plt.legend(labels, loc='upper right')
# +
sentiments_sample = merged_df.sort_values('Installs',ascending=False)[['App','Translated_Review','Sentiment']]
sentiments_sample = sentiments_most_installed.drop_duplicates(['App'])
sentiments_sample = sentiments_most_installed.sample(frac=0.94, replace=True, random_state=1)
sentiments_sample
# -
sentiments_sample_count = sentiments_sample['Sentiment'].value_counts()
sentiments_sample_count
# +
explode = (0.0,0.3)
labels = sentiments_sample_count.index
colors = ['#99ff99','#ffcc99']
plt.figure(figsize=(21,10))
plt.title('Sentiments of 20 apps from sample')
plt.pie(sentiments_sample_count, autopct='%1.0f%%', startangle=180, shadow=True, labeldistance=None,
rotatelabels=True, explode=explode, colors= colors);
plt.legend(labels, loc='upper right')
# -
# The general sentiments of the top 20 apps are not as high in percentage as the sample but have similar results: in both charts, the highest sentiment is Postive. However, while there is no output for negative in the sample chart, this was the second highest value for the top twenty installe apps.
# ## Inferences and Conclusion
#
# Now we have completed the questions, we can make some inferences.
# There are number of inferences we can make from the data:
#
# - there are 115 genres of Apps
#
# - there are 6 Content ratings, the most popular being 'Everyone'
#
# - the app with the most reviews is Facebook
#
# - the highest rated category was 'AUTO_AND_VEHICLES'
#
# - while positive sentiment seemed to also show good sentiment polarity and rating score, there is no definite correlation
#
# - the difference in sentiment polarity in the most popular genre compared to the least popular genre was small
#
# - while there was only one outright popular genre, there were several for the least popular genres.
#
# - The category that had the highest Rating and highest number of reviews was the socail cateogory, with the app Amino: Communities and Chats.
#
# - Of the apps that had to be paid for, there were two top categories:
#
# PERSONALIZATION which appeared 3 times,
# GAME which appeared 3 times,
#
# The top categories were Personalization and Game, however, as an addition, I wanted to find out which item had the highest price and compare it to the number of installs, reviews and ratings.
#
# - The general sentiments of the top 20 apps are not as high in percentage as the sample but have similar results: in both charts, the highest sentiment is Postive.
#
# ## References and Future Work
#
# - https://www.kaggle.com/lava18/google-play-store-apps
# - https://datacarpentry.org/python-ecology-lesson/03-index-slice-subset/index.html
# - https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.Series.str.replace.html?highlight=replace#pandas.Series.str.replace
# - https://jovian.ml/learn/data-analysis-with-python-zero-to-pandas/lesson/lesson-4-analyzing-tabular-data-with-pandas
# - https://jovian.ml/learn/data-analysis-with-python-zero-to-pandas/lesson/lesson-6-exploratory-data-analysis-a-case-study
|
dataProject.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import rlssm
import pandas as pd
import os
# #### Import the data of a single subject
# +
par_path = os.path.abspath(os.path.join(os.getcwd(), os.pardir))
data_path = os.path.join(par_path, 'data/data_experiment.csv')
data = pd.read_csv(data_path, index_col=0)
data = data[data.participant == 20].reset_index(drop=True)
data['block_label'] += 1
data.head()
# -
# #### Initialise the model
model = rlssm.RLModel_2A(hierarchical_levels = 1)
model.family, model.model_label, model.hierarchical_levels
model.increasing_sensitivity, model.separate_learning_rates
# #### Fit
# +
# sampling parameters
n_iter = 1000
n_chains = 2
n_thin = 1
# learning parameters
K = 4 # n options
initial_value_learning = 27.5 # intitial value (Q0)
# bayesian model
alpha_pos_priors = {'mu':0, 'sd':1}
# -
model_fit = model.fit(
data,
K,
initial_value_learning,
alpha_pos_priors = alpha_pos_priors,
thin = n_thin,
iter = n_iter,
chains = n_chains,
verbose = False)
model_fit.to_pickle()
# #### get Rhat
model_fit.rhat.describe()
model_fit.rhat.head()
# #### get wAIC
model_fit.waic
# ### Posteriors
model_fit.samples
model_fit.trial_samples
import seaborn as sns
sns.set(context = "talk",
style = "white",
palette = "husl",
rc={'figure.figsize':(15, 8)})
model_fit.plot_posteriors(height=5, show_intervals="HDI", alpha_intervals=.05);
model_fit.plot_posteriors(height=5, show_intervals="BCI", alpha_intervals=.1, clip=(0, 1));
# ### Posterior predictives
# #### Ungrouped
# +
pp = model_fit.get_posterior_predictives_df(n_posterior_predictives=500)
pp
# +
pp_summary = model_fit.get_posterior_predictives_summary(n_posterior_predictives=500)
pp_summary
# +
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1, 1, figsize=(10, 8))
model_fit.plot_mean_posterior_predictives(n_posterior_predictives=500, ax=ax, show_intervals='HDI')
ax.set_ylabel('Density')
ax.set_xlabel('Mean accuracy')
sns.despine()
# -
# #### Grouped
# +
import numpy as np
data['choice_pair'] = 'AB'
data.loc[(data.cor_option == 3) & (data.inc_option == 1), 'choice_pair'] = 'AC'
data.loc[(data.cor_option == 4) & (data.inc_option == 2), 'choice_pair'] = 'BD'
data.loc[(data.cor_option == 4) & (data.inc_option == 3), 'choice_pair'] = 'CD'
data['block_bins'] = pd.cut(data.trial_block, 8, labels=np.arange(1, 9))
data.head()
# -
model_fit.get_grouped_posterior_predictives_summary(grouping_vars=['block_label', 'block_bins', 'choice_pair'], n_posterior_predictives=500)
# +
import matplotlib.pyplot as plt
fig, axes = plt.subplots(1, 2, figsize=(20,8))
model_fit.plot_mean_grouped_posterior_predictives(grouping_vars=['block_bins'], n_posterior_predictives=500, ax=axes[0])
model_fit.plot_mean_grouped_posterior_predictives(grouping_vars=['block_bins', 'choice_pair'], n_posterior_predictives=500, ax=axes[1])
sns.despine()
# -
# ### Get last values for eventual further sampling
sv = model_fit.last_values
sv
|
tests/notebooks/RL_2A_fitting.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="WFYuAxS2hcu6"
# **Consider the following Python dictionary data and Python list labels:**
#
# data = {'birds': ['Cranes', 'Cranes', 'plovers', 'spoonbills', 'spoonbills', 'Cranes', 'plovers', 'Cranes', 'spoonbills', 'spoonbills'],
# 'age': [3.5, 4, 1.5, np.nan, 6, 3, 5.5, np.nan, 8, 4],
# 'visits': [2, 4, 3, 4, 3, 4, 2, 2, 3, 2],
# 'priority': ['yes', 'yes', 'no', 'yes', 'no', 'no', 'no', 'yes', 'no', 'no']}
#
# labels = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j']
#
# + [markdown] colab_type="text" id="KaY8jRX3hcu9"
# **1. Create a DataFrame birds from this dictionary data which has the index labels.**
# + colab={} colab_type="code" id="AWrM74tnhcu_"
import numpy as np
import pandas as pd
labels = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j']
data = {'birds': ['Cranes', 'Cranes', 'plovers', 'spoonbills', 'spoonbills', 'Cranes', 'plovers', 'Cranes', 'spoonbills', 'spoonbills'], 'age': [3.5, 4, 1.5, np.nan, 6, 3, 5.5, np.nan, 8, 4], 'visits': [2, 4, 3, 4, 3, 4, 2, 2, 3, 2], 'priority': ['yes', 'yes', 'no', 'yes', 'no', 'no', 'no', 'yes', 'no', 'no']}
birds=pd.DataFrame.from_dict(data)
birds
# + [markdown] colab_type="text" id="31bQ4H55hcvG"
# **2. Display a summary of the basic information about birds DataFrame and its data.**
# + colab={} colab_type="code" id="PT7e5BiThcvI"
birds.describe()
# + [markdown] colab_type="text" id="ppsyynzjhcvN"
# **3. Print the first 2 rows of the birds dataframe **
# + colab={} colab_type="code" id="mJtG2ES9hcvQ"
birds.head(2)
# + [markdown] colab_type="text" id="331CiAQDhcvW"
# **4. Print all the rows with only 'birds' and 'age' columns from the dataframe**
# + colab={} colab_type="code" id="eJm1icJhhcvY"
birds[['age','birds']]
# + [markdown] colab_type="text" id="33v_rzNyhcvf"
# **5. select [2, 3, 7] rows and in columns ['birds', 'age', 'visits']**
# + colab={} colab_type="code" id="ia5weqCOhcvh"
birds.iloc[[2,3,7],[0,1,3]]
# + [markdown] colab_type="text" id="uulxo5y-hcvo"
# **6. select the rows where the number of visits is less than 4**
# + colab={} colab_type="code" id="<KEY>"
birds.loc[birds['visits']<4]
# + [markdown] colab_type="text" id="sB8icEBVhcvy"
# **7. select the rows with columns ['birds', 'visits'] where the age is missing i.e NaN**
# + colab={} colab_type="code" id="dHoZ2z2ghcv2"
birds.loc[birds['age'].isna(),['birds','visits']]
# + [markdown] colab_type="text" id="sgiIkh1Ghcv-"
# **8. Select the rows where the birds is a Cranes and the age is less than 4**
# + colab={} colab_type="code" id="4of7A8gehcwC"
birds.loc[(birds['birds']=='Cranes') & (birds['age']<4),:]
# + [markdown] colab_type="text" id="IZrFrd1AhcwH"
# **9. Select the rows the age is between 2 and 4(inclusive)**
# + colab={} colab_type="code" id="Ij6co9oJhcwT"
birds.loc[(birds['age']>=2) & (birds['age']<=4),:]
# + [markdown] colab_type="text" id="KvV1eyyehcwX"
# **10. Find the total number of visits of the bird Cranes**
# + colab={} colab_type="code" id="y5NyL569hcwY"
birds.loc[birds['birds']=='Cranes','visits'].sum()
# + [markdown] colab_type="text" id="S-1B7oDehcwf"
# **11. Calculate the mean age for each different birds in dataframe.**
# + colab={} colab_type="code" id="ljKjf7nyhcwg"
birds.groupby('birds').mean().loc[:,'age']
# + [markdown] colab_type="text" id="B5HIznnMhcwl"
# **12. Append a new row 'k' to dataframe with your choice of values for each column. Then delete that row to return the original DataFrame.**
# + colab={} colab_type="code" id="GDDd9mXEhcwm"
birds.loc[len(birds)]=[7,"Cranes",'No',12]
birds
birds.drop(birds.index[[len(birds)-1]],inplace=True)
birds
#birds.drop(birds.index[0])
# -
# + [markdown] colab_type="text" id="_cLx6xLahcwq"
# **13. Find the number of each type of birds in dataframe (Counts)**
# + colab={} colab_type="code" id="aTHV8JJMhcws"
birds.groupby(['birds']).count().loc[:,'age']
# + [markdown] colab_type="text" id="-SJ6OYuYhcww"
# **14. Sort dataframe (birds) first by the values in the 'age' in decending order, then by the value in the 'visits' column in ascending order.**
# + colab={} colab_type="code" id="1oeqEqBjhcwy"
birds.sort_values(by=['age','visits'],ascending=[False,True])
# + [markdown] colab_type="text" id="JaKj7ZQUhcw7"
# **15. Replace the priority column values with'yes' should be 1 and 'no' should be 0**
# + colab={} colab_type="code" id="AJAPYiIHhcw9"
#birds['priority']=birds['priority'].map({'no':0,'yes':1})
#not sure why this didn't work
'''ref: https://stackoverflow.com/questions/23307301/replacing-column-values-in-a-pandas-dataframe'''
birds.loc[birds['priority']=='no','priority']=0
birds.loc[birds['priority']=='yes','priority']=1
birds
# + [markdown] colab_type="text" id="E2EFmujbhcxA"
# **16. In the 'birds' column, change the 'Cranes' entries to 'trumpeters'.**
# + colab={} colab_type="code" id="Bi29Cc6lhcxC"
birds.loc[birds['birds']=='Cranes','birds']='trumpeters'
birds
# -
|
suny.sn1@gmail.com_op1.2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] tags=["remove_cell"]
# # Solving linear systems of equations using HHL and its Qiskit implementation
# -
# In this tutorial, we introduce the HHL algorithm, derive the circuit, and implement it using Qiskit. We show how to run the HHL on a simulator and on a five qubit device.
# + [markdown] tags=["contents"]
# ## Contents
# 1. [Introduction](#introduction)
# 2. [The HHL algorithm](#hhlalg)
# 1. [Some mathematical background](#mathbackground)
# 2. [Description of the HHL](#hhldescription)
# 3. [Quantum Phase Estimation (QPE) within HHL](#qpe)
# 4. [Non-exact QPE](#qpe2)
# 3. [Example 1: 4-qubit HHL](#example1)
# 4. [Qiskit Implementation](#implementation)
# 1. [Running HHL on a simulator: general method](#implementationsim)
# 2. [Running HHL on a real quantum device: optimised example](#implementationdev)
# 5. [Problems](#problems)
# 6. [References](#references)
# -
# ## 1. Introduction <a id='introduction'></a>
#
# Systems of linear equations arise naturally in many real-life applications in a wide range of areas, such as in the solution of Partial Differential Equations, the calibration of financial models, fluid simulation or numerical field calculation. The problem can be defined as, given a matrix $A\in\mathbb{C}^{N\times N}$ and a vector $\vec{b}\in\mathbb{C}^{N}$, find $\vec{x}\in\mathbb{C}^{N}$ satisfying $A\vec{x}=\vec{b}$
#
# For example, take $N=2$,
#
# $$A = \begin{pmatrix}1 & -1/3\\-1/3 & 1 \end{pmatrix},\quad \vec{x}=\begin{pmatrix} x_{1}\\ x_{2}\end{pmatrix}\quad \text{and} \quad \vec{b}=\begin{pmatrix}1 \\ 0\end{pmatrix}$$
#
# Then the problem can also be written as find $x_{1}, x_{2}\in\mathbb{C}$ such that
# $$\begin{cases}x_{1} - \frac{x_{2}}{3} = 1 \\ -\frac{x_{1}}{3} + x_{2} = 0\end{cases} $$
#
# A system of linear equations is called $s$-sparse if $A$ has at most $s$ non-zero entries per row or column. Solving an $s$-sparse system of size $N$ with a classical computer requires $\mathcal{ O }(Ns\kappa\log(1/\epsilon))$ running time using the conjugate gradient method <sup>[1](#conjgrad)</sup>. Here $\kappa$ denotes the condition number of the system and $\epsilon$ the accuracy of the approximation.
#
# The HHL is a quantum algorithm to estimate a function of the solution with running time complexity of $\mathcal{ O }(\log(N)s^{2}\kappa^{2}/\epsilon)$<sup>[2](#hhl)</sup> when $A$ is a Hermitian matrix under the assumptions of efficient oracles for loading the data, Hamiltonian simulation and computing a function of the solution. This is an exponential speed up in the size of the system, however one crucial remark to keep in mind is that the classical algorithm returns the full solution, while the HHL can only approximate functions of the solution vector.
# ## 2. The HHL algorithm<a id='hhlalg'></a>
#
# ### A. Some mathematical background<a id='mathbackground'></a>
# The first step towards solving a system of linear equations with a quantum computer is to encode the problem in the quantum language. By rescaling the system, we can assume $\vec{b}$ and $\vec{x}$ to be normalised and map them to the respective quantum states $|b\rangle$ and $|x\rangle$. Usually the mapping used is such that $i^{th}$ component of $\vec{b}$ (resp. $\vec{x}$) corresponds to the amplitude of the $i^{th}$ basis state of the quantum state $|b\rangle$ (resp. $|x\rangle$). From now on, we will focus on the rescaled problem
#
# $$ A|x\rangle=|b\rangle$$
#
# Since $A$ is Hermitian, it has a spectral decomposition
# $$
# A=\sum_{j=0}^{N-1}\lambda_{j}|u_{j}\rangle\langle u_{j}|,\quad \lambda_{j}\in\mathbb{ R }
# $$
# where $|u_{j}\rangle$ is the $j^{th}$ eigenvector of $A$ with respective eigenvalue $\lambda_{j}$. Then,
# $$
# A^{-1}=\sum_{j=0}^{N-1}\lambda_{j}^{-1}|u_{j}\rangle\langle u_{j}|
# $$
# and the right hand side of the system can be written in the eigenbasis of $A$ as
# $$
# |b\rangle=\sum_{j=0}^{N-1}b_{j}|u_{j}\rangle,\quad b_{j}\in\mathbb{ C }
# $$
# It is useful to keep in mind that the goal of the HHL is to exit the algorithm with the readout register in the state
# $$
# |x\rangle=A^{-1}|b\rangle=\sum_{j=0}^{N-1}\lambda_{j}^{-1}b_{j}|u_{j}\rangle
# $$
# Note that here we already have an implicit normalisation constant since we are talking about a quantum state.
# ### B. Description of the HHL algorithm <a id='hhldescription'></a>
#
# The algorithm uses three quantum registers, all of them set to $|0\rangle $ at the beginning of the algorithm. One register, which we will denote with the subindex $n_{l}$, is used to store a binary representation of the eigenvalues of $A$. A second register, denoted by $n_{b}$, contains the vector solution, and from now on $N=2^{n_{b}}$. There is an extra register, for the auxiliary qubits. These are qubits used as intermediate steps in the individual computations but will be ignored in the following description since they are set to $|0\rangle $ at the beginning of each computation and restored back to the $|0\rangle $ state at the end of the individual operation.
#
# The following is an outline of the HHL algorithm with a high-level drawing of the corresponding circuit. For simplicity all computations are assumed to be exact in the ensuing description, and a more detailed explanation of the non-exact case is given in Section [2.D.](#qpe2).
#
# <img src="images/hhlcircuit.png" width = "75%" height = "75%">
#
# 1. Load the data $|b\rangle\in\mathbb{ C }^{N}$. That is, perform the transformation
#
# $$ |0\rangle _{n_{b}} \mapsto |b\rangle _{n_{b}} $$
#
# 2. Apply Quantum Phase Estimation (QPE) with
#
# $$
# U = e ^ { i A t } := \sum _{j=0}^{N-1}e ^ { i \lambda _ { j } t } |u_{j}\rangle\langle u_{j}|
# $$
#
# The quantum state of the register expressed in the eigenbasis of $A$ is now
#
# $$
# \sum_{j=0}^{N-1} b _ { j } |\lambda _ {j }\rangle_{n_{l}} |u_{j}\rangle_{n_{b}}
# $$
#
# where $|\lambda _ {j }\rangle_{n_{l}}$ is the $n_{l}$-bit binary representation of $\lambda _ {j }$.
#
# 3. Add an auxiliary qubit and apply a rotation conditioned on $|\lambda_{ j }\rangle$,
#
# $$
# \sum_{j=0}^{N-1} b _ { j } |\lambda _ { j }\rangle_{n_{l}}|u_{j}\rangle_{n_{b}} \left( \sqrt { 1 - \frac { C^{2} } { \lambda _ { j } ^ { 2 } } } |0\rangle + \frac { C } { \lambda _ { j } } |1\rangle \right)
# $$
#
# where $C$ is a normalisation constant, and, as expressed in the current form above, should be less than the smallest eigenvalue $\lambda_{min}$ in magnitude, i.e., $|C| < \lambda_{min}$.
#
# 4. Apply QPE$^{\dagger}$. Ignoring possible errors from QPE, this results in
#
# $$
# \sum_{j=0}^{N-1} b _ { j } |0\rangle_{n_{l}}|u_{j}\rangle_{n_{b}} \left( \sqrt { 1 - \frac {C^{2} } { \lambda _ { j } ^ { 2 } } } |0\rangle + \frac { C } { \lambda _ { j } } |1\rangle \right)
# $$
#
# 5. Measure the auxiliary qubit in the computational basis. If the outcome is $1$, the register is in the post-measurement state
#
# $$
# \left( \sqrt { \frac { 1 } { \sum_{j=0}^{N-1} \left| b _ { j } \right| ^ { 2 } / \left| \lambda _ { j } \right| ^ { 2 } } } \right) \sum _{j=0}^{N-1} \frac{b _ { j }}{\lambda _ { j }} |0\rangle_{n_{l}}|u_{j}\rangle_{n_{b}}
# $$
#
# which up to a normalisation factor corresponds to the solution.
#
# 6. Apply an observable $M$ to calculate $F(x):=\langle x|M|x\rangle$.
#
# ### C. Quantum Phase Estimation (QPE) within HHL <a id='qpe'></a>
#
# Quantum Phase Estimation is described in more detail in Chapter 3. However, since this quantum procedure is at the core of the HHL algorithm, we recall here the definition. Roughly speaking, it is a quantum algorithm which, given a unitary $U$ with eigenvector $|\psi\rangle_{m}$ and eigenvalue $e^{2\pi i\theta}$, finds $\theta$. We can formally define this as follows.
#
# **Definition:** Let $U\in\mathbb{ C }^{2^{m}\times 2^{m}}$ be unitary and let $|\psi\rangle_{m}\in\mathbb{ C }^{2^{m}}$ be one of its eigenvectors with respective eigenvalue $e^{2\pi i\theta}$. The **Quantum Phase Estimation** algorithm, abbreviated **QPE**, takes as inputs the unitary gate for $U$ and the state $|0\rangle_{n}|\psi\rangle_{m}$ and returns the state $|\tilde{\theta}\rangle_{n}|\psi\rangle_{m}$. Here $\tilde{\theta}$ denotes a binary approximation to $2^{n}\theta$ and the $n$ subscript denotes it has been truncated to $n$ digits.
# $$
# \operatorname { QPE } ( U , |0\rangle_{n}|\psi\rangle_{m} ) = |\tilde{\theta}\rangle_{n}|\psi\rangle_{m}
# $$
#
# For the HHL we will use QPE with $U = e ^ { i A t }$, where $A$ is the matrix associated to the system we want to solve. In this case,
# $$
# e ^ { i A t } = \sum_{j=0}^{N-1}e^{i\lambda_{j}t}|u_{j}\rangle\langle u_{j}|
# $$
# Then, for the eigenvector $|u_{j}\rangle_{n_{b}}$, which has eigenvalue $e ^ { i \lambda _ { j } t }$, QPE will output $|\tilde{\lambda }_ { j }\rangle_{n_{l}}|u_{j}\rangle_{n_{b}}$. Where $\tilde{\lambda }_ { j }$ represents an $n_{l}$-bit binary approximation to $2^{n_l}\frac{\lambda_ { j }t}{2\pi}$. Therefore, if each $\lambda_{j}$ can be exactly represented with $n_{l}$ bits,
# $$
# \operatorname { QPE } ( e ^ { i A t } , \sum_{j=0}^{N-1}b_{j}|0\rangle_{n_{l}}|u_{j}\rangle_{n_{b}} ) = \sum_{j=0}^{N-1}b_{j}|\lambda_{j}\rangle_{n_{l}}|u_{j}\rangle_{n_{b}}
# $$
# ### D. Non-exact QPE <a id='qpe2'></a>
#
# In reality, the quantum state of the register after applying QPE to the initial state is
# $$
# \sum _ { j=0 }^{N-1} b _ { j } \left( \sum _ { l = 0 } ^ { 2 ^ { n_{l} } - 1 } \alpha _ { l | j } |l\rangle_{n_{l}} \right)|u_{j}\rangle_{n_{b}}
# $$
# where
# $$
# \alpha _ { l | j } = \frac { 1 } { 2 ^ { n_{l} } } \sum _ { k = 0 } ^ { 2^{n_{l}}- 1 } \left( e ^ { 2 \pi i \left( \frac { \lambda _ { j } t } { 2 \pi } - \frac { l } { 2 ^ { n_{l} } } \right) } \right) ^ { k }
# $$
#
# Denote by $\tilde{\lambda_{j}}$ the best $n_{l}$-bit approximation to $\lambda_{j}$, $1\leq j\leq N$. Then we can relabel the $n_{l}$-register so that $\alpha _ { l | j }$ denotes the amplitude of $|l + \tilde { \lambda } _ { j } \rangle_{n_{l}}$. So now,
# $$
# \alpha _ { l | j } : = \frac { 1 } { 2 ^ { n_{l}} } \sum _ { k = 0 } ^ { 2 ^ { n_{l} } - 1 } \left( e ^ { 2 \pi i \left( \frac { \lambda _ { j } t } { 2 \pi } - \frac { l + \tilde { \lambda } _ { j } } { 2 ^ { n_{l} } } \right) } \right) ^ { k }
# $$
# If each $\frac { \lambda _ { j } t } { 2 \pi }$ can be represented exactly with $n_{l}$ binary bits, then $\frac { \lambda _ { j } t } { 2 \pi }=\frac { \tilde { \lambda } _ { j } } { 2 ^ { n_{l} } }$ $\forall j$. Therefore in this case $\forall j$, $1\leq j \leq N$, it holds that $\alpha _ { 0 | j } = 1$ and $\alpha _ { l | j } = 0 \quad \forall l \neq 0$. Only in this case we can write that the state of the register after QPE is
# $$
# \sum_{j=0}^{N-1} b _ { j } |\lambda _ {j }\rangle_{n_{l}} |u_{j}\rangle_{n_{b}}
# $$
# Otherwise, $|\alpha _ { l | j }|$ is large if and only if $\frac { \lambda _ { j } t } { 2 \pi } \approx \frac { l + \tilde { \lambda } _ { j } } { 2 ^ { n_{l} } }$ and the state of the register is
# $$
# \sum _ { j=0 }^{N-1} \sum _ { l = 0 } ^ { 2 ^ { n_{l} } - 1 } \alpha _ { l | j } b _ { j }|l\rangle_{n_{l}} |u_{j}\rangle_{n_{b}}
# $$
# ## 3. Example: 4-qubit HHL<a id='example1'></a>
#
# Let's take the small example from the introduction to illustrate the algorithm. That is,
# $$A = \begin{pmatrix}1 & -1/3\\-1/3 & 1 \end{pmatrix}\quad \text{and} \quad |b\rangle=\begin{pmatrix}1 \\ 0\end{pmatrix}$$
#
# We will use $n_{b}=1$ qubit to represent $|b\rangle$, and later the solution $|x\rangle$, $n_{l}=2$ qubits to store the binary representation of the eigenvalues and $1$ auxiliary qubit to store whether the conditioned rotation, hence the algorithm, was successful.
#
# For the purpose of illustrating the algorithm, we will cheat a bit and calculate the eigenvalues of $A$ to be able to choose $t$ to obtain an exact binary representation of the rescaled eigenvalues in the $n_{l}$-register. However, keep in mind that for the HHL algorithm implementation one does not need previous knowledge of the eigenvalues. Having said that, a short calculation will give
# $$\lambda_{1} = 2/3\quad\text{and}\quad\lambda_{2}=4/3$$
#
# Recall from the previous section that the QPE will output an $n_{l}$-bit ($2$-bit in this case) binary approximation to $\frac{\lambda_ { j }t}{2\pi}$. Therefore, if we set
# $$t=2\pi\cdot \frac{3}{8}$$
# the QPE will give a $2$-bit binary approximation to
# $$\frac{\lambda_ { 1 }t}{2\pi} = 1/4\quad\text{and}\quad\frac{\lambda_ { 2 }t}{2\pi}=1/2$$
# which is, respectively,
# $$|01\rangle_{n_{l}}\quad\text{and}\quad|10\rangle_{n_{l}}$$
#
# The eigenvectors are, respectively,
# $$|u_{1}\rangle=\begin{pmatrix}1 \\ -1\end{pmatrix}\quad\text{and}\quad|u_{2}\rangle=\begin{pmatrix}1 \\ 1\end{pmatrix}$$
# Again, keep in mind that one does not need to compute the eigenvectors for the HHL implementation. In fact, a general Hermitian matrix $A$ of dimension $N$ can have up to $N$ different eigenvalues, therefore calculating them would take $\mathcal{O}(N)$ time and the quantum advantage would be lost.
#
# We can then write $|b\rangle$ in the eigenbasis of $A$ as
# $$|b\rangle _{n_{b}}=\sum_{j=1}^{2}\frac{1}{\sqrt{2}}|u_{j}\rangle _{n_{b}}$$
#
# Now we are ready to go through the different steps of the HHL algorithm.
#
# 1. State preparation in this example is trivial since $|b\rangle=|0\rangle$.
# 2. Applying QPE will yield
# $$
# \frac{1}{\sqrt{2}}|01\rangle|u_{1}\rangle + \frac{1}{\sqrt{2}}|10\rangle|u_{2}\rangle
# $$
# 3. Conditioned rotation with $C=1/8$ that is less than the smallest (rescaled) eigenvalue of $\frac {1} {4}$. Note, the contant $C$ here needs to be chosen such that it is less than the smallest (rescaled) eigenvalue of $\frac {1} {4}$ but as large as possible so that when the auxiliary qubit is measured, the probabilit of it being in the state $|1>$ is large.
# $$\frac{1}{\sqrt{2}}|01\rangle|u_{1}\rangle\left( \sqrt { 1 - \frac { (1/8)^{2} } {(1/4)^{2} } } |0\rangle + \frac { 1/8 } { 1/4 } |1\rangle \right) + \frac{1}{\sqrt{2}}|10\rangle|u_{2}\rangle\left( \sqrt { 1 - \frac { (1/8)^{2} } {(1/2)^{2} } } |0\rangle + \frac { 1/8 } { 1/2 } |1\rangle \right)
# $$
# $$
# =\frac{1}{\sqrt{2}}|01\rangle|u_{1}\rangle\left( \sqrt { 1 - \frac { 1 } {4 } } |0\rangle + \frac { 1 } { 2 } |1\rangle \right) + \frac{1}{\sqrt{2}}|10\rangle|u_{2}\rangle\left( \sqrt { 1 - \frac { 1 } {16 } } |0\rangle + \frac { 1 } { 4 } |1\rangle \right)
# $$
# 4. After applying QPE$^{\dagger}$ the quantum computer is in the state
# $$
# \frac{1}{\sqrt{2}}|00\rangle|u_{1}\rangle\left( \sqrt { 1 - \frac { 1 } {4 } } |0\rangle + \frac { 1 } { 2 } |1\rangle \right) + \frac{1}{\sqrt{2}}|00\rangle|u_{2}\rangle\left( \sqrt { 1 - \frac { 1 } {16 } } |0\rangle + \frac { 1 } { 4 } |1\rangle \right)
# $$
# 5. On outcome $1$ when measuring the auxiliary qubit, the state is
# $$
# \frac{\frac{1}{\sqrt{2}}|00\rangle|u_{1}\rangle\frac { 1 } { 2 } |1\rangle + \frac{1}{\sqrt{2}}|00\rangle|u_{2}\rangle\frac { 1 } { 4 } |1\rangle}{\sqrt{5/32}}
# $$
# A quick calculation shows that
# $$
# \frac{\frac{1}{2\sqrt{2}}|u_{1}\rangle+ \frac{1}{4\sqrt{2}}|u_{2}\rangle}{\sqrt{5/32}} = \frac{|x\rangle}{||x||}
# $$
# 6. Without using extra gates, we can compute the norm of $|x\rangle$: it is the probability of measuring $1$ in the auxiliary qubit from the previous step.
# $$
# P(|1\rangle) = \left(\frac{1}{2\sqrt{2}}\right)^{2} + \left(\frac{1}{4\sqrt{2}}\right)^{2} = \frac{5}{32} = ||x||^{2}
# $$
#
#
# ## 4. Qiskit Implementation<a id='implementation'></a>
# Now that we have analytically solved the problem from the example we are going to use it to illustrate how to run the HHL on a quantum simulator and on the real hardware. For the quantum simulator, Qiskit Aqua already provides an implementation of the HHL algorithm requiring the matrix $A$ and $|b\rangle$ as basic inputs. The main advantage is that it can take a general Hermitian matrix and an arbitrary initial state as inputs. This means that the algorithm is designed for a general purpose and does not optimise the circuit for a particular problem, which is problematic if the goal is to run the circuit on the existing real hardware. At the time of writing, the existing quantum computers are noisy and can only run small circuits. Therefore, in Section [4.B.](#implementationdev) we will see an optimised circuit that can be used for a class of problems to which our example belongs and mention the existing procedures to deal with noise in quantum computers.
# ## A. Running HHL on a simulator: general method<a id='implementationsim'></a>
# To run the HHL algorithm provided by Qiskit Aqua we just need to import the right modules and set the parameters as follows. In the worked out example we set the time of the Hamiltonian simulation to $t=2\pi\cdot \frac{3}{8}$, however we will run the simulation without setting this parameter to show that knowledge of the eigenvalues is not required. Nonetheless, if the matrix has some structure it might be possible to obtain information about the eigenvalues and use it to choose a suitable $t$ and improve the accuracy of the solution returned by the HHL. As an exercise to see this, run the algorithm setting the time to $t=2\pi\cdot \frac{3}{8}$. If done correctly, the fidelity of the solution should be $1$.
from qiskit import Aer, transpile, assemble
from qiskit.circuit.library import QFT
from qiskit.aqua import QuantumInstance, aqua_globals
from qiskit.quantum_info import state_fidelity
from qiskit.aqua.algorithms import HHL, NumPyLSsolver
from qiskit.aqua.components.eigs import EigsQPE
from qiskit.aqua.components.reciprocals import LookupRotation
from qiskit.aqua.operators import MatrixOperator
from qiskit.aqua.components.initial_states import Custom
import numpy as np
def create_eigs(matrix, num_auxiliary, num_time_slices, negative_evals):
ne_qfts = [None, None]
if negative_evals:
num_auxiliary += 1
ne_qfts = [QFT(num_auxiliary - 1), QFT(num_auxiliary - 1).inverse()]
return EigsQPE(MatrixOperator(matrix=matrix),
QFT(num_auxiliary).inverse(),
num_time_slices=num_time_slices,
num_ancillae=num_auxiliary,
expansion_mode='suzuki',
expansion_order=2,
evo_time=None, # This is t, can set to: np.pi*3/4
negative_evals=negative_evals,
ne_qfts=ne_qfts)
# The following function will be used to calculate the fidelity of solution returned by the HHL algorithm.
def fidelity(hhl, ref):
solution_hhl_normed = hhl / np.linalg.norm(hhl)
solution_ref_normed = ref / np.linalg.norm(ref)
fidelity = state_fidelity(solution_hhl_normed, solution_ref_normed)
print("Fidelity:\t\t %f" % fidelity)
matrix = [[1, -1/3], [-1/3, 1]]
vector = [1, 0]
# +
orig_size = len(vector)
matrix, vector, truncate_powerdim, truncate_hermitian = HHL.matrix_resize(matrix, vector)
# Initialize eigenvalue finding module
eigs = create_eigs(matrix, 3, 50, False)
num_q, num_a = eigs.get_register_sizes()
# Initialize initial state module
init_state = Custom(num_q, state_vector=vector)
# Initialize reciprocal rotation module
reci = LookupRotation(negative_evals=eigs._negative_evals, evo_time=eigs._evo_time)
algo = HHL(matrix, vector, truncate_powerdim, truncate_hermitian, eigs,
init_state, reci, num_q, num_a, orig_size)
# -
# The reason to choose $t=2\pi\cdot \frac{3}{8}$ was so that the rescaled eigenvalues could be represented exactly with $2$ binary digits. Since now this is not the case, the representation will be approximate, hence QPE not exact and the returned solution will be an approximation.
# +
result = algo.run(QuantumInstance(Aer.get_backend('statevector_simulator')))
print("Solution:\t\t", np.round(result['solution'], 5))
result_ref = NumPyLSsolver(matrix, vector).run()
print("Classical Solution:\t", np.round(result_ref['solution'], 5))
print("Probability:\t\t %f" % result['probability_result'])
fidelity(result['solution'], result_ref['solution'])
# -
# We can print the resources used by the algorithm. The depth is the maximum number of gates applied to a single qubit, while the width is defined as the number of qubits required. We will also print the number of CNOTs since this number together with the width gives a good idea of whether running the circuit on current real hardware is feasible.
print("circuit_width:\t", result['circuit_info']['width'])
print("circuit_depth:\t", result['circuit_info']['depth'])
print("CNOT gates:\t", result['circuit_info']['operations']['cx'])
# ## B. Running HHL on a real quantum device: optimised example<a id='implementationdev'></a>
# In the previous section we ran the standard algorithm provided in Qiskit and saw that it uses $7$ qubits, has a depth of ~$100$ gates and requires a total of $54$ CNOT gates. These numbers are not feasible for the current available hardware, therefore we need to decrease these quantities. In particular, the goal will be to reduce the number of CNOTs by a factor of $5$ since they have worse fidelity than single-qubit gates. Furthermore, we can reduce the number of qubits to $4$ as was the original statement of the problem: the Qiskit method was written for a general problem and that is why it requires $3$ additional auxiliary qubits.
#
# However, solely decreasing the number of gates and qubits will not give a good approximation to the solution on real hardware. This is because there are two sources of errors: those that occur during the run of the circuit and readout errors.
#
# Qiskit provides a module to mitigate the readout errors by individually preparing and measuring all basis states, a detailed treatment on the topic can be found in the paper by Dewes et al.<sup>[3](#readouterr)</sup> To deal with the errors occurring during the run of the circuit, Richardson extrapolation can be used to calculate the error to the zero limit by running the circuit three times, each replacing each CNOT gate by $1$, $3$ and $5$ CNOTs respectively<sup>[4](#richardson)</sup>. The idea is that theoretically the three circuits should produce the same result, but in real hardware adding CNOTs means amplifying the error. Since we know that we have obtained results with an amplified error, and we can estimate by how much the error was amplified in each case, we can recombine the quantities to obtain a new result that is a closer approximation to the analytic solution than any of the previous obtained values.
#
# Below we give the optimised circuit that can be used for any problem of the form
# $$A = \begin{pmatrix}a & b\\b & a \end{pmatrix}\quad \text{and} \quad |b\rangle=\begin{pmatrix}\cos(\theta) \\ \sin(\theta)\end{pmatrix},\quad a,b,\theta\in\mathbb{R}$$
#
# The following optimisation was extracted from a work on the HHL for tridiagonal symmetric matrices<sup>[[5]](#tridi)</sup>, this particular circuit was derived with the aid of the UniversalQCompiler software<sup>[[6]](#qcompiler)</sup>.
#
# +
from qiskit import QuantumRegister, QuantumCircuit
import numpy as np
t = 2 # This is not optimal; As an exercise, set this to the
# value that will get the best results. See section 8 for solution.
nqubits = 4 # Total number of qubits
nb = 1 # Number of qubits representing the solution
nl = 2 # Number of qubits representing the eigenvalues
theta = 0 # Angle defining |b>
a = 1 # Matrix diagonal
b = -1/3 # Matrix off-diagonal
# Initialise the quantum and classical registers
qr = QuantumRegister(nqubits)
# Create a Quantum Circuit
qc = QuantumCircuit(qr)
qrb = qr[0:nb]
qrl = qr[nb:nb+nl]
qra = qr[nb+nl:nb+nl+1]
# State preparation.
qc.ry(2*theta, qrb[0])
# QPE with e^{iAt}
for qu in qrl:
qc.h(qu)
qc.p(a*t, qrl[0])
qc.p(a*t*2, qrl[1])
qc.u(b*t, -np.pi/2, np.pi/2, qrb[0])
# Controlled e^{iAt} on \lambda_{1}:
params=b*t
qc.p(np.pi/2,qrb[0])
qc.cx(qrl[0],qrb[0])
qc.ry(params,qrb[0])
qc.cx(qrl[0],qrb[0])
qc.ry(-params,qrb[0])
qc.p(3*np.pi/2,qrb[0])
# Controlled e^{2iAt} on \lambda_{2}:
params = b*t*2
qc.p(np.pi/2,qrb[0])
qc.cx(qrl[1],qrb[0])
qc.ry(params,qrb[0])
qc.cx(qrl[1],qrb[0])
qc.ry(-params,qrb[0])
qc.p(3*np.pi/2,qrb[0])
# Inverse QFT
qc.h(qrl[1])
qc.rz(-np.pi/4,qrl[1])
qc.cx(qrl[0],qrl[1])
qc.rz(np.pi/4,qrl[1])
qc.cx(qrl[0],qrl[1])
qc.rz(-np.pi/4,qrl[0])
qc.h(qrl[0])
# Eigenvalue rotation
t1=(-np.pi +np.pi/3 - 2*np.arcsin(1/3))/4
t2=(-np.pi -np.pi/3 + 2*np.arcsin(1/3))/4
t3=(np.pi -np.pi/3 - 2*np.arcsin(1/3))/4
t4=(np.pi +np.pi/3 + 2*np.arcsin(1/3))/4
qc.cx(qrl[1],qra[0])
qc.ry(t1,qra[0])
qc.cx(qrl[0],qra[0])
qc.ry(t2,qra[0])
qc.cx(qrl[1],qra[0])
qc.ry(t3,qra[0])
qc.cx(qrl[0],qra[0])
qc.ry(t4,qra[0])
qc.measure_all()
print("Depth: %i" % qc.depth())
print("CNOTS: %i" % qc.count_ops()['cx'])
qc.draw(fold=-1)
# -
# The code below takes as inputs our circuit, the real hardware backend and the set of qubits we want to use, and returns and instance that can be run on the specified device. Creating the circuits with $3$ and $5$ CNOTs is the same but calling the transpile method with the right quantum circuit.
#
# Real hardware devices need to be recalibrated regularly, and the fidelity of a specific qubit or gate can change over time. Furthermore, different chips have different connectivities. If we try to run a circuit that performs a two-qubit gate between two qubits that are not connected on the specified device, the transpiler will add SWAP gates. Therefore it is good practice to check with the IBM Quantum Experience webpage<sup>[[7]](#qexperience)</sup> before running the following code and choose a set of qubits with the right connectivity and lowest error rates at the given time.
# + tags=["uses-hardware"]
from qiskit import execute, BasicAer, ClassicalRegister, IBMQ
from qiskit.compiler import transpile
from qiskit.ignis.mitigation.measurement import (complete_meas_cal, # Measurement error mitigation functions
CompleteMeasFitter,
MeasurementFilter)
provider = IBMQ.load_account()
backend = provider.get_backend('ibmqx2') # calibrate using real hardware
layout = [2,3,0,4]
chip_qubits = 5
# Transpiled circuit for the real hardware
qc_qa_cx = transpile(qc, backend=backend, initial_layout=layout)
# -
# The next step is to create the extra circuits used to mitigate the readout errors<sup>[[3]](#readouterr)</sup>.
# + tags=["uses-hardware"]
meas_cals, state_labels = complete_meas_cal(qubit_list=layout, qr=QuantumRegister(chip_qubits))
qcs = meas_cals + [qc_qa_cx]
qobj = assemble(qcs, shots=10)
job = backend.run(qobj)
# -
# The following plot<sup>[[5]](#tridi)</sup>, shows the results from running the circuit above on real hardware for $10$ different initial states. The $x$-axis represents the angle $\theta$ defining the initial state in each case. The results where obtained after mitigating the readout error and then extrapolating the errors arising during the run of the circuit from the results with the circuits with $1$, $3$ and $5$ CNOTs.
#
# <img src="images/norm_public.png">
#
# Compare to the results without error mitigation nor extrapolation from the CNOTs<sup>[5](#tridi)</sup>.
#
# <img src="images/noerrmit_public.png">
# ## 8. Problems<a id='problems'></a>
# 1. Run the algorithm 'evo_time': $2\pi(3/8)$. The fidelity should now be $1$.
#
# ##### Real hardware:
#
# 1. Set the time parameter for the optimised example.
#
# <details>
# <summary> Solution (Click to expand)</summary>
# t = 2.344915690192344
#
# The best result is to set it so that the smallest eigenvalue can be represented exactly, since it's inverse will have the largest contribution in the solution
# </details>
#
# 2. Create transpiled circuits for $3$ and $5$ CNOTs from a given circuit 'qc'. When creating the circuits you will have to add barriers so that these consecutive CNOT gates do not get cancelled when using the transpile() method.
# 3. Run your circuits on the real hardware and apply a quadratic fit to the results to obtain the extrapolated value.
# ## 9. References<a id='references'></a>
# 1. <NAME>. An Introduction to the Conjugate Gradient Method Without the Agonizing Pain. Technical Report CMU-CS-94-125, School of Computer Science, Carnegie Mellon University, Pittsburgh, Pennsylvania, March 1994.<a id='conjgrad'></a>
# 2. <NAME>, <NAME>, and <NAME>, “Quantum algorithm for linear systems of equations,” Phys. Rev. Lett. 103.15 (2009), p. 150502.<a id='hhl'></a>
# 3. <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, and <NAME>, “Characterization of a two-transmon processor with individual single-shot qubit readout,” Phys. Rev. Lett. 108, 057002 (2012). <a id='readouterr'></a>
# 4. <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, and <NAME>, “Option Pricing using Quantum Computers,” arXiv:1905.02666 . <a id='richardson'></a>
# 5. <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, and <NAME>, “Enhancing Quantum Linear System Algorithm by Richardson Extrapolation,” (to be included).<a id='tridi'></a>
# 6. <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, “Introduction to UniversalQCompiler,” arXiv:1904.01072 .<a id='qcompiler'></a>
# 7. https://quantum-computing.ibm.com/ .<a id='qexperience'></a>
# 8. <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, "Qiskit Aqua: Solving linear systems of equations with the HHL algorithm" https://github.com/Qiskit/qiskit-tutorials/blob/master/legacy_tutorials/aqua/linear_systems_of_equations.ipynb
|
notebooks/ch-applications/hhl_tutorial.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="1BTuotdozuJU"
# importing Required libraries
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
from tqdm import tqdm
from torchsummary import summary
# + [markdown] id="kDQ4CzYk0Qcj"
# # Structure-1 (Same as given Notebook)
# + id="9zgxo3oFz76G"
class Net(nn.Module): # image siE in mnist is 1x28x28
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 32, 3, padding=1)
self.conv2 = nn.Conv2d(32, 64, 3, padding=1)
self.pool1 = nn.MaxPool2d(2, 2)
self.conv3 = nn.Conv2d(64, 128, 3, padding=1)
self.conv4 = nn.Conv2d(128, 256, 3, padding=1)
self.pool2 = nn.MaxPool2d(2, 2)
self.conv5 = nn.Conv2d(256, 512, 3)
self.conv6 = nn.Conv2d(512, 1024, 3)
self.conv7 = nn.Conv2d(1024, 10, 3)
def forward(self, x):
x = self.pool1(F.relu(self.conv2(F.relu(self.conv1(x))))) # 1 convolutional block
x = self.pool2(F.relu(self.conv4(F.relu(self.conv3(x)))))
x = F.relu(self.conv6(F.relu(self.conv5(x))))
x = F.relu(self.conv7(x))
x = x.view(-1, 10)
return F.log_softmax(x)
# + colab={"base_uri": "https://localhost:8080/"} id="SJJXxP3L0eXk" outputId="76d8c8eb-0914-4271-ed78-af770f9d36f5"
# Checking that cuda is available or not
torch.cuda.is_available()
# + colab={"base_uri": "https://localhost:8080/"} id="4tpgXZ870j96" outputId="4f90dd2e-25e4-4e02-92a6-84c993a38876"
use_cuda = torch.cuda.is_available()
device = torch.device("cuda" if use_cuda else "cpu")
model = Net().to(device)
summary(model, input_size=(1, 28, 28))
# + colab={"base_uri": "https://localhost:8080/"} id="lh4eXrOl0pwY" outputId="58e854ec-79a6-451a-db04-cc9b8bf12f17"
torch.manual_seed(1)
batch_size = 128
kwargs = {'num_workers': 1, 'pin_memory': True} if use_cuda else {}
train_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data', train=True, download=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=batch_size, shuffle=True, **kwargs)
test_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data', train=False, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=batch_size, shuffle=True, **kwargs)
# + id="zHmOVYPn0tiC"
def train(model, device, train_loader, optimizer, epoch):
model.train()
pbar = tqdm(train_loader)
for batch_idx, (data, target) in enumerate(pbar):
data, target = data.to(device), target.to(device)
optimizer.zero_grad()
output = model(data)
loss = F.nll_loss(output, target)
loss.backward()
optimizer.step()
pbar.set_description(desc= f'loss={loss.item()} batch_id={batch_idx}')
def test(model, device, test_loader):
model.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for data, target in test_loader:
data, target = data.to(device), target.to(device)
output = model(data)
test_loss += F.nll_loss(output, target, reduction='sum').item() # sum up batch loss
pred = output.argmax(dim=1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(target.view_as(pred)).sum().item()
test_loss /= len(test_loader.dataset)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
# + colab={"base_uri": "https://localhost:8080/"} id="s3KI1yIy0v0z" outputId="51cb76ac-62ed-4455-fb9e-48c52b10a3b9"
model = Net().to(device)
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
for epoch in range(1, 2):
train(model, device, train_loader, optimizer, epoch)
test(model, device, test_loader)
# + id="2-U5pPF70xji"
# + [markdown] id="LtKkDGHV2qUh"
# # Structure-2 (Except structure all are same)
# + id="oLQLefj420a7"
class Net(nn.Module): # image siE in mnist is 1x28x28
## Without max pooling, use kernels with different shapes and randomly increase as well as decreasing the filter size.
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 32, 3, padding=1) # 32x28x28.
self.conv2 = nn.Conv2d(32, 64, 3, padding=1) # 64x28x28.
#self.pool1 = nn.MaxPool2d(2, 2) # Cancelling the maxpool part.
self.conv3 = nn.Conv2d(64, 128, 3, padding=1) # 128x28x28.
self.conv4 = nn.Conv2d(128, 256, 3, padding=1) # 256x28x28.
#self.pool2 = nn.MaxPool2d(2, 2)
self.conv5 = nn.Conv2d(256, 512, 3) # 512x26x26
self.conv6 = nn.Conv2d(512, 1024, 5) # 1024x22x22
self.conv7 = nn.Conv2d(1024, 2048, 7) # 2048x16x16
self.conv8 = nn.Conv2d(2048, 512, 3) # 512x14x14
self.conv9 = nn.Conv2d(512, 1024, 7) # 1024x8x8
self.conv10 = nn.Conv2d(1024, 2048, 5) # 2048x4x4
self.conv11 = nn.Conv2d(2048, 1024, 3) # 1024x2x2
self.conv12 = nn.Conv2d(1024, 10, 2) # 10x1x1
def forward(self, x):
x = F.relu(self.conv2(F.relu(self.conv1(x)))) # 1 convolutional block, self.pool1(
x = F.relu(self.conv4(F.relu(self.conv3(x)))) #self.pool2(
x = F.relu(self.conv6(F.relu(self.conv5(x))))
x = F.relu(self.conv8(F.relu(self.conv7(x))))
x = F.relu(self.conv10(F.relu(self.conv9(x))))
x = F.relu(self.conv12(F.relu(self.conv11(x))))
x = x.view(-1, 10)
return F.log_softmax(x)
# + colab={"base_uri": "https://localhost:8080/"} id="t9Bac8-O3cBW" outputId="d0feece0-f6e8-464d-a885-a3f1cbc73eda"
# Checking that cuda is available or not
torch.cuda.is_available()
# + colab={"base_uri": "https://localhost:8080/"} id="Q7VhreJS3b9y" outputId="ede5a327-3749-443c-f262-9b5bbb1a7ae9"
use_cuda = torch.cuda.is_available()
device = torch.device("cuda" if use_cuda else "cpu")
model = Net().to(device)
summary(model, input_size=(1, 28, 28))
# + id="HXnS4L6e3b2O"
torch.manual_seed(1)
batch_size = 128
kwargs = {'num_workers': 1, 'pin_memory': True} if use_cuda else {}
train_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data', train=True, download=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=batch_size, shuffle=True, **kwargs)
test_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data', train=False, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=batch_size, shuffle=True, **kwargs)
# + id="n9bBa8FD3byw"
def train(model, device, train_loader, optimizer, epoch):
model.train()
pbar = tqdm(train_loader)
for batch_idx, (data, target) in enumerate(pbar):
data, target = data.to(device), target.to(device)
optimizer.zero_grad()
output = model(data)
loss = F.nll_loss(output, target)
loss.backward()
optimizer.step()
pbar.set_description(desc= f'loss={loss.item()} batch_id={batch_idx}')
def test(model, device, test_loader):
model.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for data, target in test_loader:
data, target = data.to(device), target.to(device)
output = model(data)
test_loss += F.nll_loss(output, target, reduction='sum').item() # sum up batch loss
pred = output.argmax(dim=1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(target.view_as(pred)).sum().item()
test_loss /= len(test_loader.dataset)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
# + colab={"base_uri": "https://localhost:8080/"} id="fQocos563npg" outputId="9d708655-44f0-4b73-a62a-ee36a8076ecd"
model = Net().to(device)
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9) ## It is taking more and moere time to train. I think because of the
## filters dimension as i chnaged them randomly and lot of number of channels such as 2048, 1024.
## I decrease them and also increase them in a random manner.
## The next reason may be i did not use the maxpooling and use the kernels randomly
## Such as 3x3, 5x5, 7x7. As kernels are high in dimension with high number of filters,
## this will be the reason for taking so much time to train.
''' it is taking --> "2h 1m 7s" to train and give the prediction. The accuracy is also
decrease.'''
for epoch in range(1, 2):
train(model, device, train_loader, optimizer, epoch)
test(model, device, test_loader)
# + id="blWzY4VeCEUd"
# + [markdown] id="yVhkJ7D5CEuO"
# # Structure-3
# + id="hAI6RWBN3nl6"
class Net(nn.Module): # image siE in mnist is 1x28x28
# More maxpooling and more padding.
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 32, 3, padding=1) ## 32x28x28
self.conv2 = nn.Conv2d(32, 64, 3, padding=1) ## 64x28x28
self.pool1 = nn.MaxPool2d(2, 2) ## 64x14x14
self.conv3 = nn.Conv2d(64, 128, 3, padding=1) ## 128x14x14
self.conv4 = nn.Conv2d(128, 256, 3, padding=1) ## 256x14x14
self.pool2 = nn.MaxPool2d(4, 2) ## 256x6x6
self.conv5 = nn.Conv2d(256, 512, 3, padding=1) ## 512x6x6
self.conv6 = nn.Conv2d(512, 1024, 3, padding = 1) ## 1024x6x6
#self.pool3 = nn.MaxPool2d(2, 2) ## 1024x5x5
self.conv7 = nn.Conv2d(1024, 512, 3, padding = 1) ## 512x6x6
self.pool3 = nn.MaxPool2d(2, 1) ## 512x5x5
self.conv8 = nn.Conv2d(512, 1024, 3) ## 1024x3x3
self.conv9 = nn.Conv2d(1024, 10, 3) ## 10x1x1
def forward(self, x):
x = self.pool1(F.relu(self.conv2(F.relu(self.conv1(x))))) # 1 convolutional block
x = self.pool2(F.relu(self.conv4(F.relu(self.conv3(x)))))
x = F.relu(self.conv6(F.relu(self.conv5(x))))
x = self.pool3(F.relu(self.conv7(x)))
x = F.relu(self.conv9(F.relu(self.conv8(x))))
x = x.view(-1, 10)
return F.log_softmax(x)
# + colab={"base_uri": "https://localhost:8080/"} id="RvttrjvvPxXP" outputId="2b7dd8cf-129d-46a9-e32c-8425b6beb20a"
# Checking that cuda is available or not
torch.cuda.is_available()
# + colab={"base_uri": "https://localhost:8080/"} id="S013zwrIPyXg" outputId="f7b7bc6b-1105-433b-d157-736fd096f3c2"
use_cuda = torch.cuda.is_available()
device = torch.device("cuda" if use_cuda else "cpu")
model = Net().to(device)
summary(model, input_size=(1, 28, 28))
# + id="cdX1Fph-PyUM"
torch.manual_seed(1)
batch_size = 128
kwargs = {'num_workers': 1, 'pin_memory': True} if use_cuda else {}
train_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data', train=True, download=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=batch_size, shuffle=True, **kwargs)
test_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data', train=False, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=batch_size, shuffle=True, **kwargs)
# + id="CU9Wt01XPySb"
def train(model, device, train_loader, optimizer, epoch):
model.train()
pbar = tqdm(train_loader)
for batch_idx, (data, target) in enumerate(pbar):
data, target = data.to(device), target.to(device)
optimizer.zero_grad()
output = model(data)
loss = F.nll_loss(output, target)
loss.backward()
optimizer.step()
pbar.set_description(desc= f'loss={loss.item()} batch_id={batch_idx}')
def test(model, device, test_loader):
model.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for data, target in test_loader:
data, target = data.to(device), target.to(device)
output = model(data)
test_loss += F.nll_loss(output, target, reduction='sum').item() # sum up batch loss
pred = output.argmax(dim=1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(target.view_as(pred)).sum().item()
test_loss /= len(test_loader.dataset)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
# + colab={"base_uri": "https://localhost:8080/"} id="_n_kq2OvPyQQ" outputId="92e91bb3-67af-4117-c263-a40e5865d69f"
model = Net().to(device)
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
for epoch in range(1, 2):
train(model, device, train_loader, optimizer, epoch)
test(model, device, test_loader)
# + id="tw3tKDpFPyOA"
# + id="hhCoJ51iPxT2"
# + [markdown] id="jVLK2SBkQARr"
# # Structure - 4
# + id="J1qZ5uubQC3C"
class Net(nn.Module): # image siE in mnist is 1x28x28
# More maxpooling, bigger kernel size as well as padding size
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 32, 7, padding=3) ## 32x28x28
self.conv2 = nn.Conv2d(32, 64, 7, padding=3) ## 64x28x28
self.pool1 = nn.MaxPool2d(2, 2) ## 64x14x14
self.conv3 = nn.Conv2d(64, 128, 3, padding=1) ## 128x14x14
self.conv4 = nn.Conv2d(128, 256, 7, padding=3) ## 256x14x14
self.pool2 = nn.MaxPool2d(4, 2) ## 256x6x6
self.conv5 = nn.Conv2d(256, 512, 3, padding=1) ## 512x6x6
self.conv6 = nn.Conv2d(512, 1024, 3, padding=1) ## 1024x6x6
self.pool3 = nn.MaxPool2d(2, 2) ## 1024x3x3
self.conv7 = nn.Conv2d(1024, 10, 3) ## 10x1x1
def forward(self, x):
x = self.pool1(F.relu(self.conv2(F.relu(self.conv1(x))))) # 1 convolutional block
x = self.pool2(F.relu(self.conv4(F.relu(self.conv3(x)))))
x = self.pool3(F.relu(self.conv6(F.relu(self.conv5(x)))))
x = F.relu(self.conv7(x))
x = x.view(-1, 10)
return F.log_softmax(x)
# + colab={"base_uri": "https://localhost:8080/"} id="qeZsVHnJYuFv" outputId="aad45652-2bc8-4728-e230-53fecb0d33de"
# Checking that cuda is available or not
torch.cuda.is_available()
# + colab={"base_uri": "https://localhost:8080/"} id="Nbheefu0YuCf" outputId="afd18975-dddd-4d84-eda6-e573cefc6cbf"
use_cuda = torch.cuda.is_available()
device = torch.device("cuda" if use_cuda else "cpu")
model = Net().to(device)
summary(model, input_size=(1, 28, 28))
# + id="l5DONl5NYuA-"
torch.manual_seed(1)
batch_size = 128
kwargs = {'num_workers': 1, 'pin_memory': True} if use_cuda else {}
train_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data', train=True, download=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=batch_size, shuffle=True, **kwargs)
test_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data', train=False, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=batch_size, shuffle=True, **kwargs)
# + id="8aj_dKdQYt-C"
def train(model, device, train_loader, optimizer, epoch):
model.train()
pbar = tqdm(train_loader)
for batch_idx, (data, target) in enumerate(pbar):
data, target = data.to(device), target.to(device)
optimizer.zero_grad()
output = model(data)
loss = F.nll_loss(output, target)
loss.backward()
optimizer.step()
pbar.set_description(desc= f'loss={loss.item()} batch_id={batch_idx}')
def test(model, device, test_loader):
model.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for data, target in test_loader:
data, target = data.to(device), target.to(device)
output = model(data)
test_loss += F.nll_loss(output, target, reduction='sum').item() # sum up batch loss
pred = output.argmax(dim=1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(target.view_as(pred)).sum().item()
test_loss /= len(test_loader.dataset)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
# + colab={"base_uri": "https://localhost:8080/"} id="V8hP61gRYt75" outputId="3d06e79e-cf02-4f57-de96-c6bbeb434bc4"
model = Net().to(device)
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
for epoch in range(1, 2):
train(model, device, train_loader, optimizer, epoch)
test(model, device, test_loader)
# + id="CDQgmqybYt5x"
# + id="TdnQ3l5DYtz9"
|
Mrinal/assignments/Packt_Mrinal_Shahi_Neural_Network_Structure.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.6
# language: python
# name: python36
# ---
# # Multiple Correspondence Analysis with Central Asian Countries and Organizations
#
# by <NAME>, D.ENG.
#
# December 20, 2018
#
# Uses the MCA technique to identify similarities in multilateral diplomacy of Central Asian countries based on their participation in political economic organizations.
import numpy as np
import pandas as pd
import mca
df = pd.read_excel('correspond.xlsx', skiprows=0, index_col=0, header=0)
df.head()
x_dummy = mca.dummy(df)
mca_ben = mca.MCA(x_dummy)
src_index = (['OSCE']*2 +
['Eurasian Economic Union']*2 +
['Eurasian customs union']*2 +
['Commonwealth of Independent States Free Trade Area']*2+
['Shainghai Cooperation Organizatin']*2+
['Collective Security Treaty Organization']*2+
['parternship for peace']*2+
['Asia-Pacific Economic Cooperation']*2+
['Eurasian Economic Union.1']*2+
['Individual action plan (NATO)']*2+
['commonwealth of indipendent states']*2+
['Economic Cooperation Organization']*2
)
yn = ['y','n']; val_index = yn*len(df.columns)
col_index = pd.MultiIndex.from_arrays([src_index, val_index],
names=['source', 'value'])
table1 = pd.DataFrame(data=x_dummy.values, index=x_dummy.index, columns=col_index)
table1
mca_ben
# +
ncols = 24
mca_ben = mca.MCA(x_dummy, ncols=ncols)
mca_ind = mca.MCA(x_dummy, ncols=ncols, benzecri=False)
print(mca.MCA.__doc__)
# +
data = {'Zλ': pd.Series(mca_ben.L),
'τZ': mca_ben.expl_var(greenacre=False, N=4)}
# 'Indicator Matrix', 'Benzecri Correction', 'Greenacre Correction'
columns = ['Iλ', 'τI', 'Zλ', 'τZ', 'cλ', 'τc']
table2 = pd.DataFrame(data=data, columns=columns).fillna(0)
table2.index += 1
table2.loc['Σ'] = table2.sum()
table2.index.name = 'Factor'
table2
# -
data = np.array([mca_ben.L[:2],
mca_ben.expl_var(greenacre=True, N=2) * 100]).T
df = pd.DataFrame(data=data, columns=['cλ','%c'], index=range(1,3))
df
# +
fs, cos, cont = 'Factor score','Squared cosines', 'Contributions x 1000'
table3 = pd.DataFrame(columns=x_dummy.index, index=pd.MultiIndex
.from_product([[fs, cos, cont], range(1, 3)]))
table3.loc[fs, :] = mca_ben.fs_r(N=2).T
table3.loc[cos, :] = mca_ben.cos_r(N=2).T
table3.loc[cont, :] = mca_ben.cont_r(N=2).T * 1000
np.round(table3.astype(float), 2)
# +
# %matplotlib inline
import matplotlib.pyplot as plt
points = table3.loc[fs].values
labels = table3.columns.values
plt.figure()
plt.margins(0.1)
plt.axhline(0, color='gray')
plt.axvline(0, color='gray')
plt.xlabel('Factor 1')
plt.ylabel('Factor 2')
plt.scatter(*points, s=120, marker='o', c='r', alpha=.5, linewidths=0)
for label, x, y in zip(labels, *points):
plt.annotate(label, xy=(x, y), xytext=(x + .03, y + .03))
plt.show()
# -
|
MCA-using organization.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: s3
# language: python
# name: s3
# ---
# +
from IPython.display import HTML
def yt(url, width=500, height=None):
"""
Function to embed a youtube movie in a notebook
"""
if height is None:
height = (9/16*width)
url = url.replace("youtu.be", 'youtube.com/embed')
embed_code = """
<iframe
width="{0}"
height="{1}"
src="{2}"
frameborder="0"
allowfullscreen>
</iframe>
""".format(width, height, url)
return HTML(embed_code)
# -
# # Topic 06 - Deep Learning
#
# Deep learning is the particular AI technique that will power our self-driving car.
# + [markdown] toc-hr-collapsed=true
# # Introduction
#
# This is just a basic machine learning algorithm. However, if we manage to understand this thoroughly, it offers a straight path to understand, at least conceptually, deep learning. Deep learning models can get quite complex, but this complexity is mainly a consequence of their composite nature. The fundamental building block is actually rather simple, and logistic regression offers a good opportunity to understand these fundamentals.
# +
# imports
import numpy as np # as always
import matplotlib.pyplot as plt
import cv2
import os
from os.path import dirname
# %matplotlib inline
# +
redo_preprocessing = False
# dirstuff
this_dir = os.getcwd()
root_dir = dirname(this_dir)
data_dir = os.path.join(root_dir, 'resc', 'data', 'step-01', 'cats-vs-cars')
train_dir, test_dir = os.path.join(data_dir, 'train'), os.path.join(data_dir, 'test')
pp_dir = os.path.join(root_dir, 'resc', 'data', 'step-02')
# get filenames
fns_train = [os.path.join(train_dir, f) for f in os.listdir(train_dir)]
fns_test = [os.path.join(test_dir, f) for f in os.listdir(test_dir)]
fns_train.sort()
fns_test.sort()
train_array_fn = os.path.join(pp_dir, 'train.npy')
test_array_fn = os.path.join(pp_dir, 'test.npy')
# label data
labels_train = np.array([fn.find('car-')>0 for fn in fns_train], dtype=int)
labels_test = np.array([fn.find('car-')>0 for fn in fns_test], dtype=int)
# Preprocess
if redo_preprocessing:
nb_pix = 64
nb_channels = 3
train = np.zeros((len(fns_train), nb_pix, nb_pix, nb_channels))
test = np.zeros((len(fns_test), nb_pix, nb_pix, nb_channels))
for idx, fn in enumerate(fns_train):
img = cv2.imread(fn)
img = img/255.
res = cv2.resize(img, dsize=(64, 64))
res = res[:,:,[2,1,0]]
train[idx, :, :, :] = res
for idx, fn in enumerate(fns_test):
img = cv2.imread(fn)
img = img/255.
res = cv2.resize(img, dsize=(64, 64))
res = res[:,:,[2,1,0]]
test[idx, :, :, :] = res
np.save(train_array_fn, train)
np.save(test_array_fn, test)
# -
train_set_x_orig, train_set_y = np.load(train_array_fn), labels_train
test_set_x_orig, test_set_y = np.load(test_array_fn), labels_test
# +
# Let us look at a single picture
# Example of a picture
index = 198
plt.imshow(train_set_x_orig[index])
msg = """
The label is: {}, so it's a {}
""".format(train_set_y[index], 'car' if train_set_y[index] else 'cat')
print(msg)
# -
train_set_y
# ## Exercise
#
# Make sure you understand how the preprocessing code above -more or less- works. Basically, using some libraries it takes `jpg` in and arrays out.
# ## Exercise
#
# It is always important, especially when dealing with linear algebra based algorithms, to make sure you are well aware of the dimensionality of your problem.
#
# Verify the dimensions of all your input data.
# +
# code your solution here
nb_train = None
nb_test = None
dimension_of_image = None
nb_channels=None
# Message that prints our outputs. Make sure you understand how this works.
msg = """
The size of the training set: {}
The size of the test set: {}
The dimensions of the iamges: {}
The number of channels: {}
""".format(nb_train, nb_test, dimension_of_image, nb_channels)
print(msg)
# -
# ## Exercise - Reshape
#
# Reshape the input arrays. We don't want a tensor as input. We are just going to handle it as one big vector. That's inconvenient for us as humans, but our algorithm in this case would not care.
# +
# code solution here.
train_set_x = np.zeros((2000))
train_set_y = np.zeros((2000))
test_set_x = np.zeros((2000))
test_set_y = np.zeros((2000))
# -
# + [markdown] toc-hr-collapsed=false
# # Building blocks of the algorithm
#
# Our algorithm has a few parts.
#
# 1. We need to initialize all the datastructures.
# 2. Forward propagation
# 3. Compute the Loss function
# 4. Backward propagation
#
#
# **Mathematical expression of the algorithm**:
#
# For one input vector $\vec{i}$
#
# For one example $x^{(i)}$:
# $$z^{(i)} = w^T x^{(i)} + b \tag{1}$$
# $$\hat{y}^{(i)} = a^{(i)} = sigmoid(z^{(i)})\tag{2}$$
# $$ \mathcal{L}(a^{(i)}, y^{(i)}) = - y^{(i)} \log(a^{(i)}) - (1-y^{(i)} ) \log(1-a^{(i)})\tag{3}$$
#
# The cost is then computed by summing over all training examples:
# $$ J = \frac{1}{m} \sum_{i=1}^m \mathcal{L}(a^{(i)}, y^{(i)})\tag{6}$$
# -
# Take one input vector $\vec{i}$, and desired output $y$
#
# The neuron computes basically a matrix multiplication;
#
# $$
# z = W \dot \vec{i} + b \\
# a = sigmoid(z) \\
#
# \mathcal{L} = -a \cdot log(y) - (1-y) \cdot log(1-a)
# $$
#
# + [markdown] toc-hr-collapsed=true
# ## Helper functions
# -
# ### Exercise
#
# Implement the sigmoid function. This converts any scaler into a value between 0 and 1.m
def sigmoid(z):
"""
Compute the sigmoid of z
Arguments:
z -- A scalar or numpy array of any size.
Return:
s -- sigmoid(z)
"""
s = 1/(1+np.exp(-z))
return s
# ## Initialize
#
# Initialize the weights and the bias parameters. This basically means constructing arrays of correct dimensionality.
# +
def initialize_weights(input_dimension):
"""
The weights are a vector (or matrix, depending how you look at it) with shape (input_dimension, 1)
"""
w = None
return w
def initialize_bias(input_dimension):
w = None
return w
# -
# ## Forward propagation
#
# The first step is to take inputs, and propagete them forward through your very tiny network, as to get a first try at the solution.
def forward_propagation(w, b, X):
nb_examples = Y.shape[1]
# compute activation here
A = None
return A
# ## Loss
#
# $\mathcal{L}(O, O')$
#
# Now we need to compute how much this deviates from what we actually wanted. For some funky mathematical reasons, we cannot simply take the difference, but we need something that is called the log-loss.
#
# The formula of log-loss is this;
#
# $$
# \mathcal{L} = \frac{1}{m} \Sigma (Y \cdot log(A) - (1-Y) \cdot log(1-A))
# $$
def compute_loss(A, Y):
"""
Compute the log-loss function.
"""
nb_examples = Y.shape[1]
# compute loss
return np.squeeze(loss)
# ## Backward propagation
#
# Now we know three things:
# - inputs
# - desired outputs
# - our outputs
#
# Now, we are interested in how we need to change the parameters of our model in order to improve our performance. For this, we want to know how the loss function **changes** when we change the parameters.
#
# We only have a single sample of the loss function, so we want to know how much the loss function changes at **one single point**. Notice the simalirity with our discussion of derivatives.
#
# If think back of motion, we first defined speed as the distance travelled over a certain time interval. In this case, we were interested in how the distance **changes** when we change the time. When we wanted to know this change at **one single moment in time**, we could not longer rely on these intervals. But, we solved that problem by making the interval super, super, super small. To be precise, we looked at;
#
# $$
# \text{lim}_{\Delta t \rightarrow 0} \frac{\Delta s(t)}{\Delta t} = \frac{d}{dt} s(t)
# $$
#
# which we then started calling the **derivative of s**. Of course, the change of distance per time is just the **velocity**.
#
# Now, the only thing to understand is that derivatives are more than a tool for calculating velocities. They quantify change. And moreover, they quantify change at single points, something that is impossible without this *limit-trick*! Now, in Machine Learning, we find ourselves in a situation where we literally need exactly that: *quantify the change of the cost function, when the parameters vary*. Hence, we shall use derivatives again!
#
# If we know how the loss function changes with respect to the paramters, we can change the parameters to get a better model. How does this work? Simple! Again think of the distance-time-velocity example. The distance plays the role of the cost. The goal is to minimize the distance. There are three possible scenariosIf my velocity is positive, I know I am increasing the distance.
#
#
# **Formulas**
# Here are the two formulas you will be using:
#
# $$ \frac{\partial \mathcal{L}}{\partial w} = \frac{1}{m}X(A-Y)^T\tag{7}$$
# $$ \frac{\partial \mathcal{L}}{\partial b} = \frac{1}{m} \sum_{i=1}^m (a^{(i)}-y^{(i)})\tag{8}$$
def backward_propagation(A, X, Y):
"""
This step could also simply be called differentation. But OK,
in neural network land this is called backpropagation, or backprop.
Just remember it is just derivation.
"""
# write the formula for the loss with regard to w
dw = None
# write the formula for the loss with regard to b
db = None
return dw, db
# ## Putting it all together
#
# Group your forward propagation, cost computation and backward propagation together in one easy function.
def single_attempt_plus_what_to_try_next(w, b, X, Y):
# Use the model (forward propagation)
A = None
# See how well it did
loss = None
# Figure out how to improve
dw, db = None
return dw, db, loss
# ## Improving the model
#
# Of course, now we now all about the derivatives and how they can tell us where to go.
#
# Once again, think of the analogy of the motion of a car. If the speed at time $t=t_0$ is negative, than we know that at a later time, let's call that $t=t_1$, we'll be closer to the origin, which is where we'd like to end up. And if the speed is positive, we should just do the reverse. The point is surprisingly simple; if you know the derivative, you something about the *motion* of your system. So, you know where to look to find a _time_ where you were closer to the origin. The amazing thing of the derivative is that information about change can be learned from observing just a single point! As if you could look at a normal picture and still could tell how everything is moving.
#
# So, what now? Now that we know (thanks to the derivatives!) where in parameter space to look next, we should *update our parameter accordingly!*. So, let's do that.
def improve_model(w, b, dw, db, learning_rate):
# Adapt the weights
w = None
# Adapt the bias
b = None
return w, b
# ## Train (fit)
#
# One iteration is not enough, we need to this entire thing over and over again.m
def train_model(X, Y, nb_iterations, learning_rate):
# Init
input_dimension = X.shape[0]
w = # Init weight
b = # Init bias
losses = []
for i in range(nb_iterations):
# Forward propagation
A = None
# Compute loss
loss = None
# Backward propagation/backprop/derivation
dw, db = None
# Improve model
w, b = None
# Track the losses to verify we are, in fact, learning
if i % 100 == 0:
losses.append(loss)
return w, b, dw, db, losses
# ## Test (predict)
#
# Now, use our model. _In principle_, this is just forward propagation, but we need to convert our outputs to binary outputs.
def predict(w, b, X):
# Init
input_dimension = X.shape[0]
Y_pred = np.zeros(input_dimension)
# Forward propagation
A = None
# Conversion to 0 (cat) or 1 (car)
Y_pred = None
# Reshape to (1 x input_dimension) matrix
Y_pred = Y_pred.reshape(1, -1)
assert Y_pred.shape == (1, input_dimension) # Assert statements warn when something is off
return Y_prediction
# + [markdown] toc-hr-collapsed=true
# # Bringing it all back home
#
# Now, we do the entire task.
# -
# ## Training
#
# First we learn, on the training data.
# +
# parameters
X_train = train_set_x
Y_train = train_set_y
nb_iterations = 1000
learning_rate = 5 * 10**(-3)
# actual training
w, b, dw, db, losses = train_model(X_train,
Y_train,
nb_iterations,
learning_rate)
# +
# Performance on training set
Y_pred_train = predict(w, b, X_train)
100 - np.mean(np.abs(Y_pred_train - Y_train)) * 100
# -
# ## Testing
# +
X_test = test_set_x
Y_test = test_set_y
# Performance on training set
Y_pred_test = predict(w, b, X_test)
100 - np.mean(np.abs(Y_pred_test - Y_test)) * 100
# -
# ### Closer look
#
# Example of a picture that was wrongly classified.
index = 1
plt.imshow(test_set_x_flatten[:,index].reshape((num_px, num_px, 3)))
print ("y = " + str(test_set_y[0,index]) + ", you predicted that it is a \"" + classes[d["Y_prediction_test"][0,index]].decode("utf-8") + "\" picture.")
# ### Loss-plot
#
# In this way we can literally check that we are learning!
# Plot learning curve (with costs)
costs = np.squeeze(d['costs'])
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(d["learning_rate"]))
plt.show()
# ### Closer look at learning rates
# +
learning_rates = [0.01, 0.001, 0.0001]
models = {}
for i in learning_rates:
print ("learning rate is: " + str(i))
models[str(i)] = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 1500, learning_rate = i, print_cost = False)
print ('\n' + "-------------------------------------------------------" + '\n')
for i in learning_rates:
plt.plot(np.squeeze(models[str(i)]["costs"]), label= str(models[str(i)]["learning_rate"]))
plt.ylabel('cost')
plt.xlabel('iterations (hundreds)')
legend = plt.legend(loc='upper center', shadow=True)
frame = legend.get_frame()
frame.set_facecolor('0.90')
plt.show()
|
note/06 - Deep Learning-Exercise.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from gurobipy import * # import the optimize solver Gurobi
number_of_year = 25 # Set the index j for total number of year
number_of_month = 12 # Set the index i for total number of year
m = Model() # Import and create the model
# Set the input Parameter:
actual_amount = 850000 # The house original price
end_payment = 50000 # Ending payment/Balloon payment
monthly_rate = 0.05 / 12 # Monthly interest rate
yearly_increase = 1.05 # Yearly increase in monthly payments
# Set the Variable list: Monthly payment for year 1
# Set the variable to continuous number
x1 = m.addVar(vtype=GRB.CONTINUOUS, name='x1')
# Caculate monthly payment for year j
x = [0] * 25
for j in range(number_of_year):
if j >= 1:
x[j] = yearly_increase * x[j - 1]
else:
x[j] = x1
# Caculate ending balance after month i
Q = []
for j in range(number_of_year):
for i in range(number_of_month):
if j == i == 0:
start_amount = actual_amount
else:
start_amount = Q[-1]
Q.append(start_amount*(1 + monthly_rate) - x[j])
# Set the Minimize Obijective: Total Revenue
m.setObjective( x1 , GRB.MINIMIZE)
# Set Non Negative month payment
c1 = m.addConstr(x1 >= 0)
# Amount remaining after balloon payment should be fully repaid after 25 years
c2 = m.addConstr(Q[-1] - end_payment == 0)
# Run the optimize solver
m.optimize()
# Get the Optimal Solution for X
m.printAttr('X')
# Get the monthly payment for each year
x = [0] * 25
for j in range(number_of_year):
if j >= 1:
x[j] = yearly_increase * x[j - 1]
else:
x[j] = m.X[0]
print('Monthly payment for %d year:'%(j + 1), round(x[j], 2))
# Get the ending balance after month i
Q = []
for j in range(number_of_year):
print('Ending balance amount of %d year is '%(j+1))
for i in range(number_of_month):
if j == i == 0:
start_amount = actual_amount
else:
start_amount = Q[-1]
Q.append(start_amount*(1 + monthly_rate) - x[j])
print(' %d month : '%(i+1), round((start_amount*(1 + monthly_rate) - x[j]), 2))
|
assets/python/Ex20[Loan]_s.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Jigsaw Unintended Bias in Toxicity Classification, EDA + DL (Keras LSTM)
#
# ## Detect toxicity across a diverse range of conversations
#
# 
# [image source](https://storage.googleapis.com/kaggle-media/competitions/jigsaw/003-avatar.png)
#
# In this competition, you’re challenged to build a multi-headed model that’s capable of detecting different types of of toxicity like threats, obscenity, insults, and identity-based hate better than Perspective’s current models. You’ll be using a dataset of comments from Wikipedia’s talk page edits. Improvements to the current model will hopefully help online discussion become more productive and respectful.
#
# ## *Kernel in progress, is continuously being updated and extended*
# + _uuid="8f2839f25d086af736a60e9eeb907d3b93b6e0e5" _cell_guid="b1076dfc-b9ad-4769-8c92-a6c4dae69d19"
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
import os
print(os.listdir("../input"))
from sklearn import metrics
from tqdm import tqdm
tqdm.pandas()
import matplotlib.pyplot as plt
import seaborn as sns
plt.style.use('fivethirtyeight')
from keras.preprocessing.text import Tokenizer
from keras.preprocessing import text, sequence
from keras.models import load_model
import keras
from keras.models import Sequential
from keras.layers import Dense, Input, LSTM, Embedding, Dropout, SpatialDropout1D, Activation, Conv1D
from keras.layers import Bidirectional, GlobalMaxPool1D, MaxPooling1D, Flatten, GlobalMaxPooling1D
from keras.callbacks import ModelCheckpoint
from keras.callbacks import EarlyStopping
from sklearn.model_selection import train_test_split
import gc
# Any results you write to the current directory are saved as output.
# + _cell_guid="79c7e3d0-c299-4dcb-8224-4455121ee9b0" _uuid="d629ff2d2480ee46fbb7e2d37f6b5fab8052498a"
TEXT_COL = 'comment_text'
EMB_PATH = '../input/fasttext-crawl-300d-2m/crawl-300d-2M.vec'
train_df = pd.read_csv('../input/jigsaw-unintended-bias-in-toxicity-classification/train.csv', index_col='id')
test_df = pd.read_csv('../input/jigsaw-unintended-bias-in-toxicity-classification/test.csv', index_col='id')
# -
train_df.head()
train_df.shape
train_df.describe()
train_df.isna().sum()
# ## EDA
train_df.columns
train_df.target.plot.hist()
# Since for evaluation, the test set examples with target >= 0.5 will be considered to be in the positive class (toxic). The same notion will be applied here; The target from the train set will be transformed as bescribed above.
train_df.target = np.where(train_df.target> 0.5, 1, 0)
print(train_df.target.value_counts())
sns.countplot(train_df.target)
# #### Rating Univariate analysis
# Converting the character feature 'rating' which takes 2 values; approved and rejected into 1 and 0 respectively.
#train_df['rating'].value_counts()
train_df['rating'] = np.where(train_df['rating'] == "approved", 1, 0)
train_df['rating'].value_counts()
sns.countplot(train_df['rating'])
# +
features = ['severe_toxicity', 'obscene',
'identity_attack', 'insult', 'threat', 'asian', 'atheist', 'bisexual',
'black', 'buddhist', 'christian', 'female', 'heterosexual', 'hindu',
'homosexual_gay_or_lesbian', 'intellectual_or_learning_disability',
'jewish', 'latino', 'male', 'muslim', 'other_disability',
'other_gender', 'other_race_or_ethnicity', 'other_religion',
'other_sexual_orientation', 'physical_disability',
'psychiatric_or_mental_illness', 'transgender', 'white', 'rating', 'funny', 'wow',
'sad', 'likes', 'disagree', 'sexual_explicit',
'identity_annotator_count', 'toxicity_annotator_count']
toxicity_features = ["severe_toxicity", "obscene", "threat", "insult", "identity_attack", "sexual_explicit"]
identity_features = ["male", "female", "transgender", "other_gender", "heterosexual", "homosexual_gay_or_lesbian",
"bisexual", "other_sexual_orientation", "christian", "jewish", "muslim", "hindu", "buddhist",
"atheist", "other_religion", "black", "white", "asian", "latino", "other_race_or_ethnicity",
"physical_disability", "intellectual_or_learning_disability", "psychiatric_or_mental_illness", "other_disability"]
metadata_features = ["rating", "funny", "wow", "sad", "likes", "disagree", "toxicity_annotator_count", "identity_annotator_count"]
# -
train_df[features].head()
print('Distributions columns')
plt.figure(figsize=(20, 150))
for i, col in enumerate(toxicity_features):
plt.subplot(40, 4, i + 1)
plt.hist(train_df[col])
plt.title(col)
plt.tight_layout()
print('Distributions columns')
plt.figure(figsize=(20, 150))
for i, col in enumerate(identity_features):
plt.subplot(40, 4, i + 1)
plt.hist(train_df[col])
plt.title(col)
plt.tight_layout()
print('Distributions columns')
plt.figure(figsize=(20, 150))
for i, col in enumerate(metadata_features):
plt.subplot(40, 4, i + 1)
plt.hist(train_df[col])
plt.title(col)
plt.tight_layout()
print('Distributions columns')
plt.figure(figsize=(20, 150))
for i, col in enumerate(toxicity_features):
plt.subplot(40, 4, i + 1)
plt.hist(train_df[col])
plt.hist(train_df[train_df["target"] == 0][col], alpha=0.5, label='0', color='b')
plt.hist(train_df[train_df["target"] == 1][col], alpha=0.5, label='1', color='r')
plt.title(col)
plt.tight_layout()
print('Distributions columns')
plt.figure(figsize=(20, 150))
for i, col in enumerate(identity_features):
plt.subplot(40, 4, i + 1)
plt.hist(train_df[col])
plt.hist(train_df[train_df["target"] == 0][col], alpha=0.5, label='0', color='b')
plt.hist(train_df[train_df["target"] == 1][col], alpha=0.5, label='1', color='r')
plt.title(col)
plt.tight_layout()
print('Distributions columns')
plt.figure(figsize=(20, 150))
for i, col in enumerate(metadata_features):
plt.subplot(40, 4, i + 1)
plt.hist(train_df[col])
plt.hist(train_df[train_df["target"] == 0][col], alpha=0.5, label='0', color='b')
plt.hist(train_df[train_df["target"] == 1][col], alpha=0.5, label='1', color='r')
plt.title(col)
plt.tight_layout()
plt.close();
gc.collect();
train_data = train_df["comment_text"]
label_data = train_df["target"]
test_data = test_df["comment_text"]
train_data.shape, label_data.shape, test_data.shape
tokenizer = text.Tokenizer()
tokenizer.fit_on_texts(list(train_data) + list(test_data))
train_data = tokenizer.texts_to_sequences(train_df['comment_text'])
test_data = tokenizer.texts_to_sequences(test_df['comment_text'])
# +
MAX_LEN = 200
train_data = sequence.pad_sequences(train_data, maxlen=MAX_LEN)
test_data = sequence.pad_sequences(test_data, maxlen=MAX_LEN)
xtrain, xvalid, ytrain, yvalid = train_test_split(train_data, label_data, stratify=train_df.target, random_state=42, test_size=0.2, shuffle=True)
# -
max_features = len(tokenizer.word_index) + 1
max_features
# +
embedding_path1 = "../input/fasttext-crawl-300d-2m/crawl-300d-2M.vec"
#embedding_path2 = "../input/glove840b300dtxt/glove.840B.300d.txt"
embed_size = 300
def get_coefs(word,*arr):
return word, np.asarray(arr, dtype='float32')
def build_matrix(embedding_path, tokenizer):
embedding_index = dict(get_coefs(*o.strip().split(" ")) for o in open(embedding_path))
word_index = tokenizer.word_index
nb_words = min(max_features, len(word_index))
embedding_matrix = np.zeros((nb_words + 1, embed_size))
for word, i in word_index.items():
if i >= max_features:
continue
embedding_vector = embedding_index.get(word)
if embedding_vector is not None:
embedding_matrix[i] = embedding_vector
return embedding_matrix
embedding_matrix = build_matrix(embedding_path1, tokenizer)
# -
del train_data;
del train_df;
del test_df;
del tokenizer;
gc.collect();
def plot_history(history):
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
x = range(1, len(acc) + 1)
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(x, acc, 'b', label='Training acc')
plt.plot(x, val_acc, 'r', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(x, loss, 'b', label='Training loss')
plt.plot(x, val_loss, 'r', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
# +
NUM_HIDDEN = 256
EMB_SIZE = 300
LABEL_SIZE = 1
MAX_FEATURES = max_features
DROP_OUT_RATE = 0.2
DENSE_ACTIVATION = "sigmoid"
NUM_EPOCH = 5
conv_size = 128
BATCH_SIZE = 512
LOSS_FUNC = "binary_crossentropy"
OPTIMIZER_FUNC = "adam"
METRICS = ["accuracy"]
from numpy.random import seed
seed(42)
from tensorflow import set_random_seed
set_random_seed(42)
model=Sequential()
model.add(Embedding(max_features, EMB_SIZE, weights=[embedding_matrix], trainable=False))
#model.add(keras.layers.Embedding(max_features, EMB_SIZE))
model.add(SpatialDropout1D(DROP_OUT_RATE))
model.add(LSTM(NUM_HIDDEN, return_sequences=True))
#model.add(Dropout(rate=DROP_OUT_RATE))
model.add(Conv1D(conv_size, 2, activation='relu', padding='same'))
model.add(MaxPooling1D(5, padding='same'))
model.add(Conv1D(conv_size, 3, activation='relu', padding='same'))
model.add(GlobalMaxPooling1D())
#model.add(Flatten())
model.add(Dense(LABEL_SIZE, activation=DENSE_ACTIVATION))
checkpointer = ModelCheckpoint(monitor='val_acc', mode='max', filepath='model.hdf5', verbose=2, save_best_only=True)
earlyStopping = EarlyStopping(monitor='val_acc', min_delta=0, patience=3, verbose=0, mode='max')
model.compile(loss=LOSS_FUNC, optimizer=OPTIMIZER_FUNC, metrics=METRICS)
history_lstm = model.fit(
xtrain,
ytrain,
batch_size = BATCH_SIZE,
epochs = NUM_EPOCH, callbacks=[checkpointer, earlyStopping],
validation_data=(xvalid, yvalid))
# -
plot_history(history_lstm)
# +
from sklearn.metrics import accuracy_score
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
from sklearn.metrics import f1_score
from sklearn.metrics import classification_report
y_pred_lstm = model.predict_classes(xvalid, verbose=1, batch_size = BATCH_SIZE)
print(classification_report(yvalid, y_pred_lstm))
print()
print("accuracy_score", accuracy_score(yvalid, y_pred_lstm))
print()
print("Weighted Averaged validation metrics")
print("precision_score", precision_score(yvalid, y_pred_lstm, average='weighted'))
print("recall_score", recall_score(yvalid, y_pred_lstm, average='weighted'))
print("f1_score", f1_score(yvalid, y_pred_lstm, average='weighted'))
print()
from sklearn.metrics import confusion_matrix
import scikitplot as skplt
sns.set(rc={'figure.figsize':(8,8)})
skplt.metrics.plot_confusion_matrix(yvalid, y_pred_lstm)
# +
submission_in = '../input/jigsaw-unintended-bias-in-toxicity-classification/sample_submission.csv'
result = model.predict(test_data, verbose=1, batch_size = BATCH_SIZE)
submission = pd.read_csv(submission_in, index_col='id')
submission['prediction'] = result
submission.reset_index(drop=False, inplace=True)
submission.to_csv('submission.csv',index=False)
|
Jigsaw Toxicity Classification EDA + DL Keras LSTM.ipynb
|
-- ---
-- jupyter:
-- jupytext:
-- text_representation:
-- extension: .hs
-- format_name: light
-- format_version: '1.5'
-- jupytext_version: 1.14.4
-- kernelspec:
-- display_name: Haskell
-- language: haskell
-- name: haskell
-- ---
:load KrapshDisplays KrapshDagDisplay
:extension DeriveGeneric
:extension FlexibleContexts
:extension OverloadedStrings
:extension GeneralizedNewtypeDeriving
:extension FlexibleInstances
:extension MultiParamTypeClasses
-- +
import Spark.Core.Dataset
import Spark.Core.Context
import Spark.Core.Column
import Spark.Core.ColumnFunctions
import Spark.Core.Functions
import Spark.Core.Row
import Spark.Core.Types
import Spark.Core.Try
import qualified Data.Vector as V
import qualified Data.Text as T
import GHC.Generics
-- -
myScaler :: Column ref Double -> Column ref Double
myScaler col =
let cnt = asDouble (countCol col)
m = sumCol col / cnt
centered = col .- m
stdDev = sumCol (centered * centered) / cnt
in centered ./ stdDev
:t myScaler
let ds = dataset [-1, 1] :: Dataset Double
let c = myScaler (asCol ds)
let ds2 = pack1 c
showGraph ds2
|
haskell/notebooks/.ipynb_checkpoints/06 Column operations-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: inf553
# language: python
# name: inf553
# ---
# ``` shell
# python3 bfr.py <input_path> <n_cluster> <out_file1> <out_file2>
# ```
import findspark
findspark.init()
import bfr
res = bfr.main()
DS, CS, RS, res_DS, res_CS, d, md_threshold = res
len(res_CS)
len(res_DS)
len(CS)
len(DS)
len(RS)
for k in CS:
print(k, CS[k][0])
for k in DS:
print(k, DS[k][0])
|
assignment/assignment5/python/bfr.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="view-in-github"
# <a href="https://colab.research.google.com/github/NeuromatchAcademy/course-content/blob/master/tutorials/W1D5_DimensionalityReduction/student/W1D5_Tutorial3.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] colab_type="text" id="a1pq-AcBBJ5L"
# # Neuromatch Academy: Week 1, Day 5, Tutorial 3
# # Dimensionality Reduction and reconstruction
#
# __Content creators:__ <NAME>, <NAME>
#
# __Content reviewers:__ <NAME>, <NAME>, <NAME>, <NAME>, <NAME>
# + [markdown] colab_type="text" id="_coTqnWnBo7V"
# ---
# # Tutorial Objectives
#
# In this notebook we'll learn to apply PCA for dimensionality reduction, using a classic dataset that is often used to benchmark machine learning algorithms: MNIST. We'll also learn how to use PCA for reconstruction and denoising.
#
# Overview:
# - Perform PCA on MNIST
# - Calculate the variance explained
# - Reconstruct data with different numbers of PCs
# - (Bonus) Examine denoising using PCA
#
# You can learn more about MNIST dataset [here](https://en.wikipedia.org/wiki/MNIST_database).
# + cellView="form" colab={"base_uri": "https://localhost:8080/", "height": 538} colab_type="code" id="o3An8t_BXkpj" outputId="2f77fc8f-8de1-40dc-c44b-03b5a0372e6c"
# @title Video 1: PCA for dimensionality reduction
from IPython.display import YouTubeVideo
video = YouTubeVideo(id="oO0bbInoO_0", width=854, height=480, fs=1)
print("Video available at https://youtube.com/watch?v=" + video.id)
video
# + [markdown] colab_type="text" id="Lvd-FYmlXyiH"
# ---
# # Setup
# Run these cells to get the tutorial started.
# + colab={} colab_type="code" id="ExhYAoZHv-8_"
# Imports
import numpy as np
import matplotlib.pyplot as plt
# + cellView="form" colab={} colab_type="code" id="4GcQOmtlBb8V"
# @title Figure Settings
import ipywidgets as widgets # interactive display
# %config InlineBackend.figure_format = 'retina'
plt.style.use("https://raw.githubusercontent.com/NeuromatchAcademy/course-content/master/nma.mplstyle")
# + cellView="form" colab={} colab_type="code" id="LFts1a8oflAC"
# @title Helper Functions
def plot_variance_explained(variance_explained):
"""
Plots eigenvalues.
Args:
variance_explained (numpy array of floats) : Vector of variance explained
for each PC
Returns:
Nothing.
"""
plt.figure()
plt.plot(np.arange(1, len(variance_explained) + 1), variance_explained,
'--k')
plt.xlabel('Number of components')
plt.ylabel('Variance explained')
plt.show()
def plot_MNIST_reconstruction(X, X_reconstructed):
"""
Plots 9 images in the MNIST dataset side-by-side with the reconstructed
images.
Args:
X (numpy array of floats) : Data matrix each column
corresponds to a different
random variable
X_reconstructed (numpy array of floats) : Data matrix each column
corresponds to a different
random variable
Returns:
Nothing.
"""
plt.figure()
ax = plt.subplot(121)
k = 0
for k1 in range(3):
for k2 in range(3):
k = k + 1
plt.imshow(np.reshape(X[k, :], (28, 28)),
extent=[(k1 + 1) * 28, k1 * 28, (k2 + 1) * 28, k2 * 28],
vmin=0, vmax=255)
plt.xlim((3 * 28, 0))
plt.ylim((3 * 28, 0))
plt.tick_params(axis='both', which='both', bottom=False, top=False,
labelbottom=False)
ax.set_xticks([])
ax.set_yticks([])
plt.title('Data')
plt.clim([0, 250])
ax = plt.subplot(122)
k = 0
for k1 in range(3):
for k2 in range(3):
k = k + 1
plt.imshow(np.reshape(np.real(X_reconstructed[k, :]), (28, 28)),
extent=[(k1 + 1) * 28, k1 * 28, (k2 + 1) * 28, k2 * 28],
vmin=0, vmax=255)
plt.xlim((3 * 28, 0))
plt.ylim((3 * 28, 0))
plt.tick_params(axis='both', which='both', bottom=False, top=False,
labelbottom=False)
ax.set_xticks([])
ax.set_yticks([])
plt.clim([0, 250])
plt.title('Reconstructed')
plt.tight_layout()
def plot_MNIST_sample(X):
"""
Plots 9 images in the MNIST dataset.
Args:
X (numpy array of floats) : Data matrix each column corresponds to a
different random variable
Returns:
Nothing.
"""
fig, ax = plt.subplots()
k = 0
for k1 in range(3):
for k2 in range(3):
k = k + 1
plt.imshow(np.reshape(X[k, :], (28, 28)),
extent=[(k1 + 1) * 28, k1 * 28, (k2+1) * 28, k2 * 28],
vmin=0, vmax=255)
plt.xlim((3 * 28, 0))
plt.ylim((3 * 28, 0))
plt.tick_params(axis='both', which='both', bottom=False, top=False,
labelbottom=False)
plt.clim([0, 250])
ax.set_xticks([])
ax.set_yticks([])
plt.show()
def plot_MNIST_weights(weights):
"""
Visualize PCA basis vector weights for MNIST. Red = positive weights,
blue = negative weights, white = zero weight.
Args:
weights (numpy array of floats) : PCA basis vector
Returns:
Nothing.
"""
fig, ax = plt.subplots()
cmap = plt.cm.get_cmap('seismic')
plt.imshow(np.real(np.reshape(weights, (28, 28))), cmap=cmap)
plt.tick_params(axis='both', which='both', bottom=False, top=False,
labelbottom=False)
plt.clim(-.15, .15)
plt.colorbar(ticks=[-.15, -.1, -.05, 0, .05, .1, .15])
ax.set_xticks([])
ax.set_yticks([])
plt.show()
def add_noise(X, frac_noisy_pixels):
"""
Randomly corrupts a fraction of the pixels by setting them to random values.
Args:
X (numpy array of floats) : Data matrix
frac_noisy_pixels (scalar) : Fraction of noisy pixels
Returns:
(numpy array of floats) : Data matrix + noise
"""
X_noisy = np.reshape(X, (X.shape[0] * X.shape[1]))
N_noise_ixs = int(X_noisy.shape[0] * frac_noisy_pixels)
noise_ixs = np.random.choice(X_noisy.shape[0], size=N_noise_ixs,
replace=False)
X_noisy[noise_ixs] = np.random.uniform(0, 255, noise_ixs.shape)
X_noisy = np.reshape(X_noisy, (X.shape[0], X.shape[1]))
return X_noisy
def change_of_basis(X, W):
"""
Projects data onto a new basis.
Args:
X (numpy array of floats) : Data matrix each column corresponding to a
different random variable
W (numpy array of floats) : new orthonormal basis columns correspond to
basis vectors
Returns:
(numpy array of floats) : Data matrix expressed in new basis
"""
Y = np.matmul(X, W)
return Y
def get_sample_cov_matrix(X):
"""
Returns the sample covariance matrix of data X.
Args:
X (numpy array of floats) : Data matrix each column corresponds to a
different random variable
Returns:
(numpy array of floats) : Covariance matrix
"""
X = X - np.mean(X, 0)
cov_matrix = 1 / X.shape[0] * np.matmul(X.T, X)
return cov_matrix
def sort_evals_descending(evals, evectors):
"""
Sorts eigenvalues and eigenvectors in decreasing order. Also aligns first two
eigenvectors to be in first two quadrants (if 2D).
Args:
evals (numpy array of floats) : Vector of eigenvalues
evectors (numpy array of floats) : Corresponding matrix of eigenvectors
each column corresponds to a different
eigenvalue
Returns:
(numpy array of floats) : Vector of eigenvalues after sorting
(numpy array of floats) : Matrix of eigenvectors after sorting
"""
index = np.flip(np.argsort(evals))
evals = evals[index]
evectors = evectors[:, index]
if evals.shape[0] == 2:
if np.arccos(np.matmul(evectors[:, 0],
1 / np.sqrt(2) * np.array([1, 1]))) > np.pi / 2:
evectors[:, 0] = -evectors[:, 0]
if np.arccos(np.matmul(evectors[:, 1],
1 / np.sqrt(2)*np.array([-1, 1]))) > np.pi / 2:
evectors[:, 1] = -evectors[:, 1]
return evals, evectors
def pca(X):
"""
Performs PCA on multivariate data. Eigenvalues are sorted in decreasing order
Args:
X (numpy array of floats) : Data matrix each column corresponds to a
different random variable
Returns:
(numpy array of floats) : Data projected onto the new basis
(numpy array of floats) : Vector of eigenvalues
(numpy array of floats) : Corresponding matrix of eigenvectors
"""
X = X - np.mean(X, 0)
cov_matrix = get_sample_cov_matrix(X)
evals, evectors = np.linalg.eigh(cov_matrix)
evals, evectors = sort_evals_descending(evals, evectors)
score = change_of_basis(X, evectors)
return score, evectors, evals
def plot_eigenvalues(evals, limit=True):
"""
Plots eigenvalues.
Args:
(numpy array of floats) : Vector of eigenvalues
Returns:
Nothing.
"""
plt.figure()
plt.plot(np.arange(1, len(evals) + 1), evals, 'o-k')
plt.xlabel('Component')
plt.ylabel('Eigenvalue')
plt.title('Scree plot')
if limit:
plt.show()
# + [markdown] colab_type="text" id="7jFNyCJ5ChXQ"
# ---
# # Section 1: Perform PCA on MNIST
#
# The MNIST dataset consists of a 70,000 images of individual handwritten digits. Each image is a 28x28 pixel grayscale image. For convenience, each 28x28 pixel image is often unravelled into a single 784 (=28*28) element vector, so that the whole dataset is represented as a 70,000 x 784 matrix. Each row represents a different image, and each column represents a different pixel.
#
# Enter the following cell to load the MNIST dataset and plot the first nine images.
# + colab={"base_uri": "https://localhost:8080/", "height": 430} colab_type="code" id="f4TNMebrBDSQ" outputId="84d48910-cec2-4938-a852-b86c9684d6e8"
from sklearn.datasets import fetch_openml
mnist = fetch_openml(name='mnist_784')
X = mnist.data
plot_MNIST_sample(X)
# + [markdown] colab_type="text" id="L590FVgkXrTV"
# The MNIST dataset has an extrinsic dimensionality of 784, much higher than the 2-dimensional examples used in the previous tutorials! To make sense of this data, we'll use dimensionality reduction. But first, we need to determine the intrinsic dimensionality $K$ of the data. One way to do this is to look for an "elbow" in the scree plot, to determine which eigenvalues are signficant.
# + [markdown] colab_type="text" id="OxtBZtgXHIAT"
# ## Exercise 1: Scree plot of MNIST
#
# In this exercise you will examine the scree plot in the MNIST dataset.
#
# **Steps:**
# - Perform PCA on the dataset and examine the scree plot.
# - When do the eigenvalues appear (by eye) to reach zero? (**Hint:** use `plt.xlim` to zoom into a section of the plot).
#
# + colab={"base_uri": "https://localhost:8080/", "height": 446} colab_type="code" id="3kiAFD9KOG8F" outputId="81b75f6c-cce7-444b-a03a-42520a2d6ad8"
help(pca)
help(plot_eigenvalues)
# + colab={} colab_type="code" id="7zgeszJSHVr9"
#################################################
## TO DO for students: perform PCA and plot the eigenvalues
#################################################
# perform PCA
score, evectors, evals = pca(X)
# plot the eigenvalues
plot_eigenvalues(evals, limit=False)
plt.xlim((0,100)) # limit x-axis up to 100 for zooming
# + [markdown] colab={"base_uri": "https://localhost:8080/", "height": 430} colab_type="text" id="HAM5vUWJBpiJ" outputId="f5f51657-5200-4c21-895e-dfdb9df13964"
# [*Click for solution*](https://github.com/NeuromatchAcademy/course-content/tree/master//tutorials/W1D5_DimensionalityReduction/solutions/W1D5_Tutorial3_Solution_a876e927.py)
#
# *Example output:*
#
# <img alt='Solution hint' align='left' width=558 height=414 src=https://raw.githubusercontent.com/NeuromatchAcademy/course-content/master/tutorials/W1D5_DimensionalityReduction/static/W1D5_Tutorial3_Solution_a876e927_0.png>
#
#
# + [markdown] colab_type="text" id="ccOz9ePZPGMz"
# ---
# # Section 2: Calculate the variance explained
#
# The scree plot suggests that most of the eigenvalues are near zero, with fewer than 100 having large values. Another common way to determine the intrinsic dimensionality is by considering the variance explained. This can be examined with a cumulative plot of the fraction of the total variance explained by the top $K$ components, i.e.,
#
# \begin{equation}
# \text{var explained} = \frac{\sum_{i=1}^K \lambda_i}{\sum_{i=1}^N \lambda_i}
# \end{equation}
#
# The intrinsic dimensionality is often quantified by the $K$ necessary to explain a large proportion of the total variance of the data (often a defined threshold, e.g., 90%).
# + [markdown] colab_type="text" id="1W30pzQPIwZ0"
# ## Exercise 2: Plot the explained variance
#
# In this exercise you will plot the explained variance.
#
# **Steps:**
# - Fill in the function below to calculate the fraction variance explained as a function of the number of principal componenets. **Hint:** use `np.cumsum`.
# - Plot the variance explained using `plot_variance_explained`.
#
# **Questions:**
# - How many principal components are required to explain 90% of the variance?
# - How does the intrinsic dimensionality of this dataset compare to its extrinsic dimensionality?
#
# + colab={"base_uri": "https://localhost:8080/", "height": 223} colab_type="code" id="XnQt-y4_WwVp" outputId="91624394-32ad-4355-88ac-df7e4ea527f8"
help(plot_variance_explained)
# + colab={} colab_type="code" id="FEVRB7fCVcOR"
def get_variance_explained(evals):
"""
Calculates variance explained from the eigenvalues.
Args:
evals (numpy array of floats) : Vector of eigenvalues
Returns:
(numpy array of floats) : Vector of variance explained
"""
#################################################
## TO DO for students: calculate the explained variance using the equation
## from Section 2.
# Comment once you've filled in the function
# raise NotImplementedError("Student excercise: calculate explaine variance!")
#################################################
# cumulatively sum the eigenvalues
csum = np.cumsum(evals)
# normalize by the sum of eigenvalues
variance_explained = csum/sum(evals)
return variance_explained
#################################################
## TO DO for students: call the function and plot the variance explained
#################################################
# calculate the variance explained
variance_explained = get_variance_explained(evals)
# Uncomment to plot the variance explained
plot_variance_explained(variance_explained)
# + [markdown] colab={"base_uri": "https://localhost:8080/", "height": 433} colab_type="text" id="7HhFNTajH55u" outputId="dd0a99c6-5691-4449-9da6-a2ae82d388ac"
# [*Click for solution*](https://github.com/NeuromatchAcademy/course-content/tree/master//tutorials/W1D5_DimensionalityReduction/solutions/W1D5_Tutorial3_Solution_0f5f51b9.py)
#
# *Example output:*
#
# <img alt='Solution hint' align='left' width=560 height=416 src=https://raw.githubusercontent.com/NeuromatchAcademy/course-content/master/tutorials/W1D5_DimensionalityReduction/static/W1D5_Tutorial3_Solution_0f5f51b9_0.png>
#
#
# + [markdown] colab_type="text" id="8lVO2rHv0kDi"
# ---
# # Section 3: Reconstruct data with different numbers of PCs
#
# + [markdown] colab_type="text" id="dhA1ioJJlrtw"
# Now we have seen that the top 100 or so principal components of the data can explain most of the variance. We can use this fact to perform *dimensionality reduction*, i.e., by storing the data using only 100 components rather than the samples of all 784 pixels. Remarkably, we will be able to reconstruct much of the structure of the data using only the top 100 components. To see this, recall that to perform PCA we projected the data $\bf X$ onto the eigenvectors of the covariance matrix:
# \begin{equation}
# \bf S = X W
# \end{equation}
# Since $\bf W$ is an orthogonal matrix, ${\bf W}^{-1} = {\bf W}^T$. So by multiplying by ${\bf W}^T$ on each side we can rewrite this equation as
# \begin{equation}
# {\bf X = S W}^T.
# \end{equation}
# This now gives us a way to reconstruct the data matrix from the scores and loadings. To reconstruct the data from a low-dimensional approximation, we just have to truncate these matrices. Let's call ${\bf S}_{1:K}$ and ${\bf W}_{1:K}$ as keeping only the first $K$ columns of this matrix. Then our reconstruction is:
# \begin{equation}
# {\bf \hat X = S}_{1:K} ({\bf W}_{1:K})^T.
# \end{equation}
#
# + [markdown] colab_type="text" id="Ls8Lm1wM6laH"
# ## Exercise 3: Data reconstruction
#
# Fill in the function below to reconstruct the data using different numbers of principal components.
#
# **Steps:**
#
# * Fill in the following function to reconstruct the data based on the weights and scores. Don't forget to add the mean!
# * Make sure your function works by reconstructing the data with all $K=784$ components. The two images should look identical.
# + colab={"base_uri": "https://localhost:8080/", "height": 309} colab_type="code" id="mozpTVpMniYw" outputId="e5b1505a-b5fa-4b28-fe24-3fe234f47759"
help(plot_MNIST_reconstruction)
# + colab={} colab_type="code" id="YS1c_mSLIdMu"
def reconstruct_data(score, evectors, X_mean, K):
"""
Reconstruct the data based on the top K components.
Args:
score (numpy array of floats) : Score matrix
evectors (numpy array of floats) : Matrix of eigenvectors
X_mean (numpy array of floats) : Vector corresponding to data mean
K (scalar) : Number of components to include
Returns:
(numpy array of floats) : Matrix of reconstructed data
"""
#################################################
## TO DO for students: Reconstruct the original data in X_reconstructed
# Comment once you've filled in the function
# raise NotImplementedError("Student excercise: reconstructing data function!")
#################################################
# Reconstruct the data from the score and eigenvectors
# Don't forget to add the mean!!
X_reconstructed = score[:,:K]@evectors[:,:K].T+X_mean
return X_reconstructed
K = 784
#################################################
## TO DO for students: Calculate the mean and call the function, then plot
## the original and the recostructed data
#################################################
# Reconstruct the data based on all components
X_mean = X.mean(axis=0)
X_reconstructed = reconstruct_data(score,evectors,X_mean,100)
# Plot the data and reconstruction
plot_MNIST_reconstruction(X, X_reconstructed)
# + [markdown] colab={"base_uri": "https://localhost:8080/", "height": 303} colab_type="text" id="P5q8yvs6TJAA" outputId="49767e58-b3d1-47d6-f16f-d101571859b0"
# [*Click for solution*](https://github.com/NeuromatchAcademy/course-content/tree/master//tutorials/W1D5_DimensionalityReduction/solutions/W1D5_Tutorial3_Solution_e3395916.py)
#
# *Example output:*
#
# <img alt='Solution hint' align='left' width=557 height=289 src=https://raw.githubusercontent.com/NeuromatchAcademy/course-content/master/tutorials/W1D5_DimensionalityReduction/static/W1D5_Tutorial3_Solution_e3395916_0.png>
#
#
# + [markdown] colab_type="text" id="aHxJHV4BrRHi"
# ## Interactive Demo: Reconstruct the data matrix using different numbers of PCs
#
# Now run the code below and experiment with the slider to reconstruct the data matrix using different numbers of principal components.
#
# **Steps**
# * How many principal components are necessary to reconstruct the numbers (by eye)? How does this relate to the intrinsic dimensionality of the data?
# * Do you see any information in the data with only a single principal component?
# + cellView="form" colab={"base_uri": "https://localhost:8080/", "height": 341, "referenced_widgets": ["c315b4dd891b4fa2a41f5ff44c790bb0", "398ca35357eb45628de71dd13deffb0e", "7f038a81c3ac4ba89503373d82bb7a24", "9c29a3dcc56e4316af3f76e3502e12df", "7293e4d4d9154a7a949753c2cec2ad25", "82edc9bc68c04be19ef1b601b542a1f7", "e9d62b17a2414176bf7f815c6d995cf7"]} colab_type="code" id="_ZGFzhXqlvmM" outputId="b66b14c6-9887-45fa-bd19-1d6f531a91b8"
# @title
# @markdown Make sure you execute this cell to enable the widget!
def refresh(K=100):
X_reconstructed = reconstruct_data(score, evectors, X_mean, K)
plot_MNIST_reconstruction(X, X_reconstructed)
plt.title('Reconstructed, K={}'.format(K))
_ = widgets.interact(refresh, K=(1, 784, 10))
# + [markdown] colab_type="text" id="bnmqJqd3nue7"
# ## Exercise 4: Visualization of the weights
#
# Next, let's take a closer look at the first principal component by visualizing its corresponding weights.
#
# **Steps:**
#
# * Enter `plot_MNIST_weights` to visualize the weights of the first basis vector.
# * What structure do you see? Which pixels have a strong positive weighting? Which have a strong negative weighting? What kinds of images would this basis vector differentiate?
# * Try visualizing the second and third basis vectors. Do you see any structure? What about the 100th basis vector? 500th? 700th?
# + colab={"base_uri": "https://localhost:8080/", "height": 223} colab_type="code" id="ZghlYuowoaAn" outputId="a547f0e5-0ff9-4488-932d-56801f73d0f1"
help(plot_MNIST_weights)
# + colab={} colab_type="code" id="W7BkraA4IDR9"
#################################################
## TO DO for students: plot the weights calling the plot_MNIST_weights function
#################################################
# Plot the weights of the first principal component
plot_MNIST_weights(evectors[:,3])
# + [markdown] colab={"base_uri": "https://localhost:8080/", "height": 433} colab_type="text" id="OPYX_kK9nvBn" outputId="6f3085b8-0f6f-4b87-df7c-ea653f3f5557"
# [*Click for solution*](https://github.com/NeuromatchAcademy/course-content/tree/master//tutorials/W1D5_DimensionalityReduction/solutions/W1D5_Tutorial3_Solution_f358e413.py)
#
# *Example output:*
#
# <img alt='Solution hint' align='left' width=499 height=416 src=https://raw.githubusercontent.com/NeuromatchAcademy/course-content/master/tutorials/W1D5_DimensionalityReduction/static/W1D5_Tutorial3_Solution_f358e413_0.png>
#
#
# + [markdown] colab_type="text" id="xTHjnpZV43mU"
# ---
# # Summary
# * In this tutorial, we learned how to use PCA for dimensionality reduction by selecting the top principal components. This can be useful as the intrinsic dimensionality ($K$) is often less than the extrinsic dimensionality ($N$) in neural data. $K$ can be inferred by choosing the number of eigenvalues necessary to capture some fraction of the variance.
# * We also learned how to reconstruct an approximation of the original data using the top $K$ principal components. In fact, an alternate formulation of PCA is to find the $K$ dimensional space that minimizes the reconstruction error.
# * Noise tends to inflate the apparent intrinsic dimensionality, however the higher components reflect noise rather than new structure in the data. PCA can be used for denoising data by removing noisy higher components.
# * In MNIST, the weights corresponding to the first principal component appear to discriminate between a 0 and 1. We will discuss the implications of this for data visualization in the following tutorial.
# + [markdown] colab_type="text" id="4o207yNk0c-I"
# ---
# # Bonus: Examine denoising using PCA
#
# In this lecture, we saw that PCA finds an optimal low-dimensional basis to minimize the reconstruction error. Because of this property, PCA can be useful for denoising corrupted samples of the data.
# + [markdown] colab_type="text" id="X4dD9tPdgDW5"
# ## Exercise 5: Add noise to the data
# In this exercise you will add salt-and-pepper noise to the original data and see how that affects the eigenvalues.
#
# **Steps:**
# - Use the function `add_noise` to add noise to 20% of the pixels.
# - Then, perform PCA and plot the variance explained. How many principal components are required to explain 90% of the variance? How does this compare to the original data?
#
# + colab={"base_uri": "https://localhost:8080/", "height": 223} colab_type="code" id="2E16UTYWemHT" outputId="94a57348-702d-4cdd-b5c7-007a9efec513"
help(add_noise)
# + colab={} colab_type="code" id="dFEaRM-giCRl"
###################################################################
# Insert your code here to:
# Add noise to the data
# Plot noise-corrupted data
# Perform PCA on the noisy data
# Calculate and plot the variance explained
###################################################################
np.random.seed(2020) # set random seed
X_noisy = add_noise(X,0.1)
score_noisy, evectors_noisy, evals_noisy = pca(X_noisy)
variance_explained_noisy = get_variance_explained(evals_noisy)
plot_MNIST_sample(X_noisy)
plot_variance_explained(variance_explained_noisy)
# + [markdown] colab={"base_uri": "https://localhost:8080/", "height": 849} colab_type="text" id="wVWrn-mn5m4w" outputId="61914c0b-e037-47ac-fda6-9bb03edb9b32"
# [*Click for solution*](https://github.com/NeuromatchAcademy/course-content/tree/master//tutorials/W1D5_DimensionalityReduction/solutions/W1D5_Tutorial3_Solution_d4a41b8c.py)
#
# *Example output:*
#
# <img alt='Solution hint' align='left' width=424 height=416 src=https://raw.githubusercontent.com/NeuromatchAcademy/course-content/master/tutorials/W1D5_DimensionalityReduction/static/W1D5_Tutorial3_Solution_d4a41b8c_0.png>
#
# <img alt='Solution hint' align='left' width=560 height=416 src=https://raw.githubusercontent.com/NeuromatchAcademy/course-content/master/tutorials/W1D5_DimensionalityReduction/static/W1D5_Tutorial3_Solution_d4a41b8c_1.png>
#
#
# + [markdown] colab_type="text" id="wWojBrz2xbjC"
# ## Exercise 6: Denoising
#
# Next, use PCA to perform denoising by projecting the noise-corrupted data onto the basis vectors found from the original dataset. By taking the top K components of this projection, we can reduce noise in dimensions orthogonal to the K-dimensional latent space.
#
# **Steps:**
# - Subtract the mean of the noise-corrupted data.
# - Project the data onto the basis found with the original dataset (`evectors`, not `evectors_noisy`) and take the top $K$ components.
# - Reconstruct the data as normal, using the top 50 components.
# - Play around with the amount of noise and K to build intuition.
#
# + colab={} colab_type="code" id="j7ZORGDJihuH"
###################################################################
# Insert your code here to:
# Subtract the mean of the noise-corrupted data
# Project onto the original basis vectors evectors
# Reconstruct the data using the top 50 components
# Plot the result
###################################################################
X_noisy_mean = X_noisy.mean(axis=0)
X_reconstructed = reconstruct_data(score_noisy,evectors_noisy,X_mean,100)
plot_MNIST_reconstruction(X_noisy, X_reconstructed)
# + [markdown] colab={"base_uri": "https://localhost:8080/", "height": 303} colab_type="text" id="KB5QiPn-3Pag" outputId="fec7e91c-91de-4e02-ee89-23bfc4903bd9"
# [*Click for solution*](https://github.com/NeuromatchAcademy/course-content/tree/master//tutorials/W1D5_DimensionalityReduction/solutions/W1D5_Tutorial3_Solution_e3ee8262.py)
#
# *Example output:*
#
# <img alt='Solution hint' align='left' width=557 height=289 src=https://raw.githubusercontent.com/NeuromatchAcademy/course-content/master/tutorials/W1D5_DimensionalityReduction/static/W1D5_Tutorial3_Solution_e3ee8262_0.png>
#
#
|
tutorials/W1D5_DimensionalityReduction/student/W1D5_Tutorial3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Matrix Plots
#
# Matrix plots allow you to plot data as color-encoded matrices and can also be used to indicate clusters within the data (later in the machine learning section we will learn how to formally cluster data).
#
# Let's begin by exploring seaborn's heatmap and clutermap:
import seaborn as sns
# %matplotlib inline
flights = sns.load_dataset('flights')
tips = sns.load_dataset('tips')
tips.head()
flights.head()
# ## Heatmap
#
# In order for a heatmap to work properly, your data should already be in a matrix form, the sns.heatmap function basically just colors it in for you. For example:
tips.head()
# Matrix form for correlation data
tips.corr()
sns.heatmap(tips.corr())
sns.heatmap(tips.corr(),cmap='coolwarm',annot=True)
# Or for the flights data:
flights.pivot_table(values='passengers',index='month',columns='year')
pvflights = flights.pivot_table(values='passengers',index='month',columns='year')
sns.heatmap(pvflights)
sns.heatmap(pvflights,cmap='magma',linecolor='white',linewidths=1)
# ## clustermap
#
# The clustermap uses hierarchal clustering to produce a clustered version of the heatmap. For example:
sns.clustermap(pvflights)
# Notice now how the years and months are no longer in order, instead they are grouped by similarity in value (passenger count). That means we can begin to infer things from this plot, such as August and July being similar (makes sense, since they are both summer travel months)
# More options to get the information a little clearer like normalization
sns.clustermap(pvflights,cmap='coolwarm',standard_scale=1)
# # Great Job!
|
data-visualization/seaborn/3_matrix_plots.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/ChristopherMajor/DS-Unit-2-Linear-Models/blob/master/module2-regression-2/Christopher_Major_LS_DS_212_assignment.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="u9Ep_wdc1HWE" colab_type="text"
# Lambda School Data Science
#
# *Unit 2, Sprint 1, Module 2*
#
# ---
# + [markdown] colab_type="text" id="7IXUfiQ2UKj6"
# # Regression 2
#
# ## Assignment
#
# You'll continue to **predict how much it costs to rent an apartment in NYC,** using the dataset from renthop.com.
#
# - [ ] Do train/test split. Use data from April & May 2016 to train. Use data from June 2016 to test.
# - [ ] Engineer at least two new features. (See below for explanation & ideas.)
# - [ ] Fit a linear regression model with at least two features.
# - [ ] Get the model's coefficients and intercept.
# - [ ] Get regression metrics RMSE, MAE, and $R^2$, for both the train and test data.
# - [ ] What's the best test MAE you can get? Share your score and features used with your cohort on Slack!
# - [ ] As always, commit your notebook to your fork of the GitHub repo.
#
#
# #### [Feature Engineering](https://en.wikipedia.org/wiki/Feature_engineering)
#
# > "Some machine learning projects succeed and some fail. What makes the difference? Easily the most important factor is the features used." — <NAME>, ["A Few Useful Things to Know about Machine Learning"](https://homes.cs.washington.edu/~pedrod/papers/cacm12.pdf)
#
# > "Coming up with features is difficult, time-consuming, requires expert knowledge. 'Applied machine learning' is basically feature engineering." — <NAME>, [Machine Learning and AI via Brain simulations](https://forum.stanford.edu/events/2011/2011slides/plenary/2011plenaryNg.pdf)
#
# > Feature engineering is the process of using domain knowledge of the data to create features that make machine learning algorithms work.
#
# #### Feature Ideas
# - Does the apartment have a description?
# - How long is the description?
# - How many total perks does each apartment have?
# - Are cats _or_ dogs allowed?
# - Are cats _and_ dogs allowed?
# - Total number of rooms (beds + baths)
# - Ratio of beds to baths
# - What's the neighborhood, based on address or latitude & longitude?
#
# ## Stretch Goals
# - [ ] If you want more math, skim [_An Introduction to Statistical Learning_](http://faculty.marshall.usc.edu/gareth-james/ISL/ISLR%20Seventh%20Printing.pdf), Chapter 3.1, Simple Linear Regression, & Chapter 3.2, Multiple Linear Regression
# - [ ] If you want more introduction, watch [<NAME>, Statistics 101: Simple Linear Regression](https://www.youtube.com/watch?v=ZkjP5RJLQF4)
# (20 minutes, over 1 million views)
# - [ ] Add your own stretch goal(s) !
# + colab_type="code" id="o9eSnDYhUGD7" colab={}
# %%capture
import sys
# If you're on Colab:
if 'google.colab' in sys.modules:
DATA_PATH = 'https://raw.githubusercontent.com/LambdaSchool/DS-Unit-2-Applied-Modeling/master/data/'
# !pip install category_encoders==2.*
# If you're working locally:
else:
DATA_PATH = '../data/'
# Ignore this Numpy warning when using Plotly Express:
# FutureWarning: Method .ptp is deprecated and will be removed in a future version. Use numpy.ptp instead.
import warnings
warnings.filterwarnings(action='ignore', category=FutureWarning, module='numpy')
# + colab_type="code" id="cvrw-T3bZOuW" colab={}
import numpy as np
import pandas as pd
# Read New York City apartment rental listing data
df = pd.read_csv(DATA_PATH+'apartments/renthop-nyc.csv')
assert df.shape == (49352, 34)
# Remove the most extreme 1% prices,
# the most extreme .1% latitudes, &
# the most extreme .1% longitudes
df = df[(df['price'] >= np.percentile(df['price'], 0.5)) &
(df['price'] <= np.percentile(df['price'], 99.5)) &
(df['latitude'] >= np.percentile(df['latitude'], 0.05)) &
(df['latitude'] < np.percentile(df['latitude'], 99.95)) &
(df['longitude'] >= np.percentile(df['longitude'], 0.05)) &
(df['longitude'] <= np.percentile(df['longitude'], 99.95))]
# + id="y3JqM4LY2BAp" colab_type="code" outputId="87c791b3-a944-49ac-bb6e-a1e9c400f2c1" colab={"base_uri": "https://localhost:8080/", "height": 126}
df['created'].tail()
# + id="KFvUmQ-43rkh" colab_type="code" colab={}
#make created column dt format
df['created']= pd.to_datetime(df['created'], infer_datetime_format=True)
#making new column with just month value
df['month'] = df['created'].dt.month
# + id="mWTHLlT49zXT" colab_type="code" outputId="32e99147-e678-48a8-b65f-2c3a22ae4a1c" colab={"base_uri": "https://localhost:8080/", "height": 235}
df['month']
# + id="OvoLhBHl91k4" colab_type="code" colab={}
#set conditions for training data to include only april and may
condition = ((df['month'] == 4)|
(df['month'] == 5))
train = df[condition]
# + id="hpter4SjBXeO" colab_type="code" outputId="f89cf778-4667-4847-bf45-684a954bf524" colab={"base_uri": "https://localhost:8080/", "height": 181}
#making sure only april and may are in data
train['month'].describe()
# + id="gkRFNTRoDjDI" colab_type="code" outputId="a13fee86-70e3-4867-bb70-defa727045eb" colab={"base_uri": "https://localhost:8080/", "height": 181}
#setting up test set
condition2 = (df['month']==6)
test=df[condition2]
test['month'].describe()
# + id="9UICvyWfEL9g" colab_type="code" outputId="d6437eec-6e07-491b-88d1-5ee6c8e7d7cc" colab={"base_uri": "https://localhost:8080/", "height": 35}
train.shape, test.shape
# + id="SFSnClZOJg4F" colab_type="code" colab={}
from sklearn.linear_model import LinearRegression
# + id="Bqdt5exFJ2Fk" colab_type="code" outputId="54628517-10c3-4f92-9563-a88364248d11" colab={"base_uri": "https://localhost:8080/", "height": 512}
model = LinearRegression()
df.head()
# + id="Jaeb_2k5MFaI" colab_type="code" colab={}
import pandas as pd
import plotly.express as px
# + id="ykUhmZj3J8el" colab_type="code" colab={}
#arrange y target vectors
target= 'price'
y_train = train[target]
y_test = test[target]
# + id="iX8V9ylAKqVS" colab_type="code" colab={}
#arrange X features matrices
features = ['latitude',
'longitude']
X_train = train[features]
X_test = test[features]
# + id="mBp_T44fL-AE" colab_type="code" colab={}
# px.scatter_3d(train,
# x='latitude',
# y='longitude',
# z='price',
# title='Apartment Prices in NY from May to April 2016')
#this for some reason crashed my notebook. i ran the 3dscatter in lecture notebook it worked fine.
#but after this one crashed its not showing up either idk.
# + id="am8G4elcMugk" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="f8dbb114-4802-45c3-fd2a-305ed7852497"
#fit model and calculate mae for training data
from sklearn.metrics import mean_absolute_error
model.fit(X_train, y_train)
y_pred=model.predict(X_train)
mae=mean_absolute_error(y_train, y_pred)
print(mae)
# + id="DwC6zYy1PbNm" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="ccbdd589-fa32-42c5-d3ae-58644fe253d4"
#trying model on test data
y_pred = model.predict(X_test)
mae=mean_absolute_error(y_test, y_pred)
print(f'Test Error: {mae:.2f} Dollars')
# + id="ZFxV0gSkP7t7" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="b1cc0a25-36a4-4666-b492-8f88a5bd8a47"
#model coefficient and intercepts.
model.intercept_, model.coef_
#hard to interpret because the latitudes are negative as well.
#i think higher north it adds to value, then moving west increases values too.
# + id="EimR8lnTQaby" colab_type="code" colab={}
import numpy as np
from sklearn.metrics import mean_squared_error, r2_score
# + id="0EUFGAsiT9hw" colab_type="code" colab={}
def squared_errors(df, features,target,m,b):
#make predictions
x=df[features]
y=df[target]
y_pred = m*x+b
#print regression metrics
mse=mean_squared_error(y, y_pred)
rmse=np.sqrt(mse)
mae=mean_absolute_error(y ,y_pred)
r2=r2_score(y, y_pred)
print('Mean Squared Error', mse)
print('Root Mean Squared Error:', rmse)
print('Mean Absolute Error', mae)
print('R^2:', r2)
# + id="h1B_SAz3WDvJ" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 90} outputId="56aba3cc-d439-4470-9c7a-ec86b2f8f54c"
#finding squared errors for training data set
features= ['dogs_allowed']
squared_errors(train, features, target, m=0, b=y_train.mean())
# + id="4onz-Fa1Wq8Y" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 90} outputId="cb4a83b3-4b4e-4737-d2de-298b9066bfce"
#error for test data
squared_errors(test, features, target, m=0, b=y_test.mean())
# + id="nygSEUIEdTkI" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 90} outputId="b316f5fb-07f6-49a4-925b-1f22b0c08a19"
#trying other m and b values
squared_errors(test, features, target, m=2000, b=y_test.mean())
# + id="CQvluAr8d8Rl" colab_type="code" colab={}
|
module2-regression-2/Christopher_Major_LS_DS_212_assignment.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# + [markdown] state="normal"
# # Python Language Intro (Part 1)
# + [markdown] state="normal"
# ## Agenda
#
# 1. Language overview
# 2. White space sensitivity
# 3. Basic Types and Operations
# 4. Statements & Control Structures
# 5. Functions
# 6. OOP (Classes, Methods, etc.)
# 7. Immutable Sequence Types (Strings, Ranges, Tuples)
# 8. Mutable data structures: Lists, Sets, Dictionaries
# + [markdown] state="normal"
# ## 1. Language overview
#
# Note: this is *not* a language course! Though I'll cover the important bits of the language (and standard library) that are relevant to class material, I expect you to master the language on your own time.
#
# Python ...
#
# - is *interpreted*
# - is *dynamically-typed* (vs. statically typed)
# - is *automatically memory-managed*
# - supports *procedural*, *object-oriented*, *imperative* and *functional* programming paradigms
# - is designed (mostly) by one man: <NAME> (aka “benevolent dictator”), and therefore has a fairly *opinionated* design
# - has a single reference implementation (CPython)
# - version 3 (the most recent version) is *not backwards-compatible* with version 2, though the latter is still widely used
# - has an interesting programming philosophy: "There should be one — and preferably only one — obvious way to do it." (a.k.a. the "Pythonic" way) — see [The Zen of Python](https://www.python.org/dev/peps/pep-0020/)
# + state="normal"
# by default, only the result of the last expression in a cell is displayed after evaluation.
# the following forces display of *all* self-standing expressions in a cell.
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
# + [markdown] state="normal"
# ## 2. White Space Sensitivity
# + [markdown] state="normal"
# Python has no beginning/end block markers! Blocks must be correctly indented (4 spaces is the convention) to delineate them.
# + state="normal"
if True:
print('In if-clause')
else:
print('In else-clause')
# + state="normal"
for x in range(5):
print('In for loop body')
# + state="normal"
def foo():
print('In function definition')
# -
foo()
# + [markdown] state="normal"
# ## 3. Basic Types and Operations
# + [markdown] state="normal"
# In Python, variables do not have types. *Values* have types (though they are not explicitly declared). A variable can be assigned different types of values over its lifetime.
# + state="normal"
a = 2 # starts out an integer
print(type(a)) # the `type` function tells us the type of a value
a = 1.5
print(type(a))
a = 'hello'
print(type(a))
# + [markdown] state="normal"
# Note that all the types reported are *classes*. I.e., even types we are accustomed to thinking of as "primitives" (e.g., integers in Java) are actually instances of classes. **All values in Python are objects!**
#
# There is no dichotomy between "primitive" and "reference" types in Python. **All variables in Python store references to objects.**
# + [markdown] state="normal"
# ### Numbers
# + state="normal"
# int: integers, unlimited precision
1
500
-123456789
6598293784982739874982734
# + state="normal"
# basic operations
1 + 2
1 - 2
2 * 3
2 * 3 + 2 * 4
2 / 5
2 ** 3 # exponentiation
abs(-25)
# + state="normal"
# modulus (remainder) and integer division
10 % 3
10 // 3
# + state="normal"
# floating point is based on the IEEE double-precision standard (limit to precision!)
2.5
-3.14159265358924352345
1.000000000000000000000001
# + state="normal"
# mixed arithmetic "widens" ints to floats
3 * 2.5
1 / 0.3
# + [markdown] state="normal"
# ### Booleans
# + state="normal"
True
False
# + state="normal"
not True
# + state="normal"
True and True
False and True
True and False
False and False
# + state="normal"
True or True
False or True
True or False
False or False
# + state="normal"
# relational operators
1 == 1
1 != 2
1 < 2
1 <= 1
1 > 0
1 >= 1
1.0 == 1
1.0000000000000000001 == 1
type(1) == type(1.0)
# + state="normal"
# object identity (reference) testing
x = 1000
y = 1000
x == x
x is x
x is not x
# + state="normal"
x == y
x is y
x is not y
# + state="normal"
# but Python caches small integers! so ...
x = 5
y = 5
x == y
x is y
# + [markdown] state="normal"
# ### Strings
# + state="normal"
# whatever strings you want
'hello world!'
"hello world!"
# + state="normal"
# convenient for strings with quotes:
print('she said, "how are you?"')
print("that's right!")
# + state="normal"
'hello' + ' ' + 'world'
'thinking... ' * 3
'*' * 80
# + [markdown] state="normal"
# Strings are an example of a *sequence* type; https://docs.python.org/3.5/library/stdtypes.html#typesseq
#
# Other sequence types are: *ranges*, *tuples* (both also immutable), and *lists* (mutable).
#
# All immutable sequences support the [common sequence operations](https://docs.python.org/3/library/stdtypes.html#common-sequence-operations), and mutable sequences additionally support the [mutable sequence operations](https://docs.python.org/3/library/stdtypes.html#mutable-sequence-types)
# + state="normal"
# indexing
greeting = 'hello there'
greeting[0]
greeting[6]
len(greeting)
greeting[len(greeting)-1]
# + state="normal"
# negative indexes
greeting[-1]
greeting[-2]
greeting[-len(greeting)]
# + state="normal"
# "slices"
greeting[0:11]
greeting[0:5]
greeting[6:11]
# + state="normal"
# default slice ranges
greeting[:11]
greeting[6:]
greeting[:]
# + state="normal"
# slice "steps"
greeting[::2]
greeting[::3]
greeting[6:11:2]
# + state="normal"
# negative steps
greeting[::-1]
# + state="normal"
# other sequence ops
greeting
greeting.count('e')
greeting.index('e')
greeting.index('e', 2)
'e' in greeting
'z' not in greeting
min(greeting)
max(greeting)
# + [markdown] state="normal"
# Strings also support a large number of [type-specific methods](https://docs.python.org/3/library/stdtypes.html#string-methods).
# + [markdown] state="normal"
# ### Type "Conversions"
# + [markdown] state="normal"
# Constructors for most built-in types exist that create values of those types from other types:
# + state="normal"
# making ints
int('123')
int(12.5)
int(True)
# floats
float('123.123')
# strings
str(123)
# + [markdown] state="normal"
# ### Operators/Functions as syntactic sugar for special methods
# + state="normal"
5 + 6
(5).__add__(6)
# + state="normal"
class MyInt(int):
def __add__(self, other):
return self * other
# + state="normal"
a = MyInt(5)
b = MyInt(6)
a + b
# + state="normal"
abs(-2.8)
(-2.8).__abs__()
# + state="normal"
'hello' + ' ' + 'world'
'hello'.__add__(' ').__add__('world')
# + [markdown] state="normal"
# ### `None`
# + [markdown] state="normal"
# **`None`** is like "null" in other languages
# + state="normal"
# often use as a default, initial, or "sentinel" value
x = None
# + [markdown] state="normal"
# note: notebooks do not display the result of expressions that evaluate to None
# + state="normal"
None
# + state="normal"
a = None
b = 100
c = None
a
b
c
# + [markdown] state="normal"
# some functions return `None`, so when we call them, there is no "Out" cell
# + state="normal"
print('Hello')
# + [markdown] state="normal"
# ### "Truthiness"
# + [markdown] state="normal"
# All objects in Python can be evaluated in a Boolean context (e.g., as the condition for an `if` statement). Values for most types act as `True`, but some act (conveniently, usually) as `False`.
# + state="normal"
if True: # try numbers, strings, other values here
print('tests as True')
else:
print('tests as False')
# + [markdown] state="normal"
# What tests as `False`?
|
CS331/Lect 01 Python Fundamentals.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# evolution-strategies
#
# Copyright (c) 2019 <NAME>
#
# Permission is hereby granted, free of charge, to any person obtaining a copy
# of this software and associated documentation files (the "Software"), to deal
# in the Software without restriction, including without limitation the rights
# to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
# copies of the Software, and to permit persons to whom the Software is
# furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in
# all copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
# AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
# OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN
# THE SOFTWARE.
#
# evolution-strategies includes:
#
# evolution-strategies-starter
# Copyright (c) 2016 OpenAI (http://openai.com)
#
# Permission is hereby granted, free of charge, to any person obtaining a copy
# of this software and associated documentation files (the "Software"), to deal
# in the Software without restriction, including without limitation the rights
# to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
# copies of the Software, and to permit persons to whom the Software is
# furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in
# all copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
# AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
# OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN
# THE SOFTWARE.
# # Using evolution strategies to train PyBullet Environments
#
# ## Introduction
#
# This Jupyter Notebook is based on the [paper](https://arxiv.org/abs/1703.03864), [blog article](https://openai.com/blog/evolution-strategies/) and [implementation](https://github.com/openai/evolution-strategies-starter) of OpenAI on the topic of using an evolution strategy algorithm for a typical reinforcement learning task.
#
# My implementation summarizes their implementation, by simplifying, refactoring and organizing the code into this Jupyter notebook which can be used to test the algorithm. One can tweak the hyperparameters, change the environment which shall be trained or even expand the implementation to support for example Atari environments.
#
# I recommend reading the paper or at least the article before trying out the notebook. Also depending on the environment the training can be very computationally intense (for example training the Humanoid), so if you want to try out the harder ones I recommend using a highly parallelizable machine, i.e. a machine with a high number of cores/threads which can use multiple processes simultaneously.
#
# ## Algorithm overview
#
# This section gives a brief overview over the algorithm. First of all we need to define what this implementation is going to do. The Roboschool is a group of environments in the [OpenAi Gym](https://gym.openai.com/), a program to test the behavior of machine learning algorithms on _real world_ problems. Since the Roboschool has been deprecated, we use the drop-in replacement, PyBullet. In our case, we want to train different robotic environments using an evolutionary algorithm which belongs to the class of natural evolution strategies. We therefore define a neural net with a configurable number of hidden layers, where the input dimension equals the observation space of the environment and the dimension of the output layer equals the dimension of the action space of the environment. This neural net is also called policy or in this implementation also referred to as a model. Therefore we train our policy to output the best possible action sequence given an observation sequence. Now, how do we train this policy? Training an evolutionary strategy consists of a cycle which is repeated over and over. First, an initial weight vector is randomly generated. In our context this weight vector is equal to the weights of our policy. Then we perturb the vector with gaussian noise. The number of perturbations is called the population size. What we now have is a population of slightly different weight vectors compared with the weight vector we started. Each one of these vectors will then be evaluated by first updating our policy with the weights and then run the environment using the policy. When this is done for the whole population, we calculate a gradient ascent step in the direction of steepest ascent. In our case, where we are dealing with natural evolution strategies, we calculate the step with the natural gradient. This is done by approximating this gradient using Monte Carlo estimates.
#
# So lets say we have our initial weight vector $\theta$, a population size $n$, random perturbations $\epsilon_i$, $0 \leq i \leq n$, learning rate $\alpha$, noise standard deviation $\sigma$ and a fitness Function $F(\cdot)$. We then calculate the resulting weight vector like this:
# $\theta_{t+1} = \theta_{t} + \alpha \frac{1}{n \sigma} \sum \limits_{i=0}^n F(\theta_{t} + \epsilon_i)$
#
#
# This gives us the weight vector for the next cycle which we will then, again, perturb a number of times (depending on the population size). A cycle in the context of evolutionary strategies is called a generation.
#
# One might ask himself now what this fitness function is in the context of robotic simulations. When initializing such an environment one can call the `step` function on the environment with an array in the shape of the action space (in our case this would be the output of the policy). The environment then evaluates the provided action based on the current observation and other parameters in the environment and outputs a reward. This is done for either a fixed number of timesteps (some environments have a maximum of timesteps defined) or stops, when the action resulted in a state where the environment is `done`, for example when the `Humanoid` environment falls over and touches the surface. The rewards get summed up for every timestep which forms the reward for one action.
#
# ## Setup
#
# Before starting any computation we need to configure the training and define some methods and objects we will use later on.
#
# ### Imports
#
# Note that TensorFlow does not get imported here. We will only import it inside of a function which runs in another process. This is due to the fact that when importing TensorFlow a session is created in the background which will interefere with our models which we run in subprocesses. When importing the package only inside a function and then running these functions inside of subprocesses, every process has its own TensorFlow session and they therefore don't interfere with each other.
# + pycharm={"is_executing": false}
import csv
import datetime
import errno
import json
import os
import pandas as pd
import time
from collections import namedtuple, OrderedDict
import ctypes
import distutils.dir_util
import multiprocessing
import numpy as np
import gym
import pybullet_envs
from utils.config_values import ConfigValues, LogColumnHeaders
from utils.es_utils import validate_config_objects, parse_generation_number
from utils.es_errors import InvalidTrainingError
# -
# ### Directory for storing the training
#
# For evaluating the trained data we need to define a directory where we want to store the trained policies, as well as the log file to record the results of every generation.
#
# Depending on your disk space you may not want to save every model, but for an indepth evaluation this is necessary. During training there will be so called _evaluation runs_ which will not add noise but test the currently trained policy to give insight on training. But since it relies on probability the number of evaluation runs will not be equal through generations. An additional Jupyter Notebook with the prefix **-visualization** can be used after training to load all saved weight files and evaluate them a given number of times.
#
# If you want to change the location change the variable `main_directory` to a directory where the user which runs this notebook has write permissions. If it does not exist the program will create it. The default location is a `training_runs` folder which is created in the working directory.
#
# When starting the master a subfolder is created inside `main_directory` where the the current progress of a training is stored.
# + pycharm={"is_executing": false}
def mkdir_p(path):
try:
os.makedirs(path)
except OSError as exc:
if exc.errno == errno.EEXIST and os.path.isdir(path):
pass
else:
raise
main_directory = "/home/jovyan/work/evolution-strategies/training_runs/".format(os.getpid())
try:
mkdir_p(main_directory)
except PermissionError:
print("The user running this notebook has no permission to create this folder. Please provide a path to a folder"
+ " with write permissions.")
# + [markdown] pycharm={"name": "#%% md\n"}
# ### Configuration, Task and Result Classes
#
# Using `namedtuple` from the `collections` package from python allows us to quickly create small classes with different attributes, which is ideal for quickly accessing different attributes during training as well as saving the configurations to a file.
#
# Each attribute will be explained in a bit, where objects of these classes are created and their parameters are set. The definition of these classes is stored in the `utils/config_objects.py` file.
# +
from utils.config_objects import Config, Optimizations, ModelStructure
Task = namedtuple('Task', [
'theta', 'ob_mean', 'ob_std', 'task_id'])
Result = namedtuple('Result', [
'noise_inds','returns', 'signreturns', 'lengths',
'eval_return', 'eval_length',
'ob_sum', 'ob_sumsq', 'ob_count',
'task_id',
'times_predict'
])
# -
# ### Configuration
#
# #### Optimizations object
#
# First we start with the optimizations for the training, since other parameters are only used when the respective optimization is activated.
#
# All values can only be either `True` or `False`. The term _activated_ means the value is set to `True` in this context.
#
# When `mirrored_sampling` is activated, sampled noise gets used twice: One time it will get added to the parameter vector and the result gets evaluated and the other time it gets subtracted from the parameter vector and the result will be evaluated.
#
# `fitness_shaping` processes the rewards by applying a rank transformation.
#
# `weight_decay` slighty changes the parameter vector.
#
# `discretize_actions` can be used to bin the actions. This means that you can provide a number of uniformely shaped bins in which the output of the model will be put. For some environments this can encourage exploration behavior.
#
# `gradient_optimizer` will use a gradient optimizer for the computed gradient, for example the `Adam` optimizer.
#
# `observation_normalization` When turned on, before an observation gets feeded into the neural network it will be subtracted by the observation mean and divided with the observation standard deviation. The observation mean and standard deviation get constantly updated on training based on the configured probability.
# + pycharm={"is_executing": false}
optimizations = Optimizations(
mirrored_sampling=True,
fitness_shaping=True,
weight_decay=True,
discretize_actions=False,
gradient_optimizer=True,
observation_normalization=True,
divide_by_stdev=False
)
# + [markdown] pycharm={"name": "#%% md\n"}
# #### Config object
#
# The config object will serve us as a general configuration for the training.
#
# First of all it defines the `env_id` which has to be a valid ID for a `PyBullet` environment, for example `AntBulletEnv-v0`. A complete list can be found [here](https://github.com/bulletphysics/bullet3/blob/master/examples/pybullet/gym/pybullet_envs/__init__.py).
#
# `env_seed` is the random seed used by the environment. Choosing a random seed will make the environment deterministic (assuming the seed is chosen again).
#
# `population_size` defines the number of perturbations per generation.
#
# `timesteps_per_gen` defines the minimum number of timesteps which shall be processed during a generation.
#
# `num_workers` defines the amount of parallel processes to be created during calculation and must be larger than 0. By default this value is the output of `os.cpu_count()` which allows the program to use the maximum amount of computational power in terms of the provided hardware.
#
# `learning_rate` defines how much the estimated gradient influences the next generation and must be larger than 0 for the training to work. If the gradient optimizer is activated this value is not used. Instead, `step_size` in the model structure is the corresponding value.
#
# `noise_stdev` is the standard devation for the noise and should be larger than 0. It cannot be equal to 0 since if it would be at some point there could then be a division by zero. Other than that it would not benefit training.
#
# `snapshot_freq` describes the frequency in which generations shall be saved to a `.h5` file. For example a snapshot frequency of 5 would save every fifth generation to a file. Setting it to 0 disables snapshotting.
#
# `return_proc_mode` translates to return processing mode and describes how the calculated rewards for a generation shall be processed. By default this is `centered_rank` which will calculate the ranks of the rewards. This option is only used when also activating the `fitness_shaping` optimization. One can choose between the three enums `RETURN_PROC_MODE_CR`, `RETURN_PROC_MODE_SIGN` and `RETURN_PROC_MODE_CR_SIGN` from the ConfigValues class. Please use the values of the enum because the enums themselves cannot be saved in the JSON format when saving the configuration objects to disk.
#
# `calc_obstat_prob` is the probability of saving the observations during a rollout (evaluating the fitness of a policy) and updating the observation mean and standard deviation. These values are used to normalize the input of a model which helps a neural network to generalize faster. The parameter is only used in combination with the `observation_normalization` optimization. Must be greater than 0 when using the optimization since otherwise it would waste performance while not normalizing.
#
# `l2coeff` is the coefficient which is used for weight decay to deform the parameter vector.
#
# `eval_prob` is the probability of inserting an evaluation run. This is useful for training to quickly monitor the reward mean, reward standard deviation and length mean of the current generation. The value must be greater or equal 0 (equal 0 turns of the evaluation runs).
#
# Below the configuration we create an environment with the configured ID and check if it is valid.
# + pycharm={"is_executing": false, "name": "#%%\n"}
config = Config(
env_id="AntBulletEnv-v0",
env_seed=None,
population_size=500,
timesteps_per_gen=10000,
num_workers=os.cpu_count(),
learning_rate=0.01,
noise_stdev=0.02,
snapshot_freq=1,
return_proc_mode=ConfigValues.RETURN_PROC_MODE_CR.value,
calc_obstat_prob=0.01,
l2coeff=0.005,
eval_prob=0.003
)
# -
# #### ModelStructure object
#
# The ModelStructure object defines the overall structure of the neural network.
#
# `ac_noise_std` is the standard deviation for the noise which is added during training. Adding noise shall generalize the training. It must be greater than 0, or equal to 0 for no noise.
#
# When using the `discretize_actions` optimizations, `ac_bins` defines into how much uniformely spaced bins the actions shall be put. For example if the possible action values range from -1 to 1 and one defines 5 action bins the model will output values from $\{-1, -0.5, 0, 0.5, 1\}$. If you use the optimization the number of bins must be greater than 0.
#
# `hidden_dims` define the number of hidden layers and their dimensions. It must be a list of positive Integers.
#
# `nonlin_type` defines the activation function for the hidden layers. Can be `tanh`, `relu`, `lrelu` or `elu` for the hyperbolic tangent, rectified linear, leaky ReLU and the exponential linear. If something else is defined `tanh` will be picked.
#
# `optimizer` is only used when the `gradient_optimizer` optimization is turned on. It can be the value of the `OPTIMIZER_ADAM` enum for the Adam optimizer or the `OPTIMIZER_SGD` enum value for the SGD Optimizer. Defining anything other will result in an error. The enums are stored in the `ConfigValues` class.
#
# `optimizer_args` is only used when the `gradient_optimizer` optimization is turned on. This will be feeded into the constructor of the optimizer. For the Adam and SGD optimizer one must specify the `stepsize` but can also specify other optimizer specific attributes. Please check the constructor signature for the names. If you specify something else than stepsize be careful, this does not get checked for errors.
# + pycharm={"is_executing": false, "name": "#%%\n"}
model_structure = ModelStructure(
ac_noise_std=0.01,
ac_bins=5,
hidden_dims=[256, 256],
nonlin_type='tanh',
optimizer=ConfigValues.OPTIMIZER_ADAM.value,
optimizer_args={
'stepsize': config.learning_rate
}
)
# -
# #### Validating the Values for the configurations
#
# By running the next cell the values selected for the configuration objects get validated. If they are for example of a wrong type, an InvalidTrainingError is raised. Normally the error message should indicate which value is wrong so one can fix it.
_, _, _ = validate_config_objects(optimizations, model_structure, config)
# #### Task class
#
# During training the master will enqueue a new Task object per generation. The workers will then take the latest task, compute it and push a result object on a queue. In the following table the attributes of a task object are explained in depth.
#
# | Attribute | Explanation |
# | :---------|:------------|
# | `theta` | The one-dimensional parameter vector of this task, i.e. the current generation|
# | `ob_mean` | When observation normalization is used this is the current mean of the observed observation |
# | `ob_std` | When observation normalization is used this is the current standard deviation of the observed observation|
# | `task_id` | The ID of this Task, which equals the generation number |
#
#
# #### Result class
#
# An object of the Result class will define a computed task by the workers. This can either be an evaluation task, where no noise gets added and the policy will simply be evaluated on the environment or a regular task. This means that the noise gets sampled, added (and subtracted when mirrored sampling is used) and evaluated. The following table gives a more detailed information on each attribute.
#
# | Attribute | Explanation |
# | :---------------------|:--------------|
# | `noise_inds` | A numpy array with the indices of the used noise|
# | `returns` | A numpy array with the rewards. When mirrored sampling is used this list is two dimensional| |`signreturns` | The sum of the signs of the rewards. When mirrored sampling is used this list is two dimensional| |`lengths` | A numpy array with the sum of the timesteps. When mirrored sampling is used this list is two dimensional|
# | `eval_return` | np.nan if this was not an evaluation task, otherwise a numpy array with the reward of the evaluation|
# | `eval_length`|np.nan if this was not an evaluation task, otherwise a numpy array with the timesteps of the evaluation| |`ob_sum` | If observation normalization is used this contains the sum of the tracked observations |
# | `ob_sumsq` | If observation normalization is used this contains the squared sum of the tracked observations |
# | `ob_count` | If observation normalization is used this contains the amount of tracked observations|
# | `task_id` | The ID of the task that has been calculated|
# | `times_predict` | A list of time measurements, where each value is the time how long a prediciton with the Keras model needs|
# ### Saving the configuration
#
# When this method is called the specified configuration gets saved to `save_directory`, so when training is done one can reproduce the training with the exact parameters.
# + pycharm={"is_executing": false}
def save_configuration(save_directory):
with open(os.path.join(save_directory, 'config.json'), 'w', encoding='utf-8') as f:
chained_dict = OrderedDict([
('config', config._asdict()),
('model_structure', model_structure._asdict()),
('optimizations', optimizations._asdict())])
json.dump(chained_dict, f, ensure_ascii=False, indent=4)
# + [markdown] pycharm={"name": "#%% md\n"}
# ## Function, Variable and Class definitions
#
#
# + [markdown] pycharm={"name": "#%% md\n"}
# ### Using Keras for the models
#
# The original implementation from OpenAI used chained TensorFlow operations to construct the model. This notebook however, uses Keras (which is integrated into TensorFlow) as a high-level API to construct `Model` objects. These objects are, in our case, chained layers which will represent our neural network.
#
# Also, note that all imports of TensorFlow need to be inside function definitions and these functions can only be called inside subprocesses. This is needed since importing TensorFlow automatically starts a background session which would be inherited to then started subprocesses. Therefore each worker would have the same TensorFlow session which would interfere with their respective models. Another noteworthy finding is that when creating Keras models in a loop there will be a memory leak when one does not clear the session. This will be adressed in the `run_worker` method.
#
# In the following cell the method `create_model` creates and returns a Keras model as defined with the configurations. It needs to have the `ob_space` and `ac_space` variable set to the observation space and action space of the used environment in training, because they define the input and output dimension.
#
# After adding an input layer the method will add the custom `ObservationNormalizationLayer` if the `observation_normalization` optimization is turned on. This layer uses the method parameters `ob_mean` and `ob_std` to normalize the input $o$ with this equation $\frac{o - \text{ob_mean}}{\text{ob_std}}$ and clip the values to $[-5, 5]$.
#
# Next, depending on the dimension and number of hidden layers defined in the configuration these hidden layers get added as Dense layers.
#
# As a last step the output layer gets added. If the `discretize_actions` optimization is turned the number of chosen bins will be used to add an extra Dense layer. This Dense layer has an input shape of $\text{num_bins} \cdot \text{adim}$ to enable the custom `DiscretizeActionsUniformLayer` to reshape the input to $[-1, \text{adim}, \text{num_bins}]$. From there it pics the argument with the maximum value from the third dimension. This essentially means that it will pick `adim` maximum values from the bins. As a last step the picked values get transformed into the $[\text{alow}, \text{ahigh}]$ interval, which for the PyBullet environments is typically $[-1, 1]$.
#
# If `discretize_actions` optimization is not used a simple Dense Layer with the action dimension serves as output layer.
#
# All weights use the custom defined `Normc_initializer` to initialize their weights. This is copied from the OpenAI implementation, since initializing them differently can lead to a large minus reward when starting the training. With this custom layer one can specify the standard deviation for the random variables. For all layers `std=1.0` is used, except for the output layer and the layer before the `DiscretizeActionsUniformLayer`, where `std=0.01` is set.
# A low standard deviation in the output layer leads to a more stable result.
#
# The implementation of the custom layers and the custom initializer are located in `utils/es_custom_layers.py` if you want to take a look at it. This is convenient since for the loading of the models we need the implementations of these classes and to avoid duplicate code they are stored in a seperate file.
#
# When `initial_weights` is provided these weights get set as the weights of the model. They need to be in the correct shape for the model.
# + pycharm={"is_executing": false, "name": "#%%\n"}
def create_model(ac_space, ob_space, initial_weights=None, model_name="model", ob_mean=None, ob_std=None):
import tensorflow as tf
from utils.es_custom_layers import Normc_initializer, ObservationNormalizationLayer, DiscretizeActionsUniformLayer
nonlin = tf.nn.tanh
if model_structure.nonlin_type == 'relu':
nonlin = tf.nn.relu
elif model_structure.nonlin_type == 'lrelu':
nonlin = tf.nn.leaky_relu
elif model_structure.nonlin_type == 'elu':
nonlin = tf.nn.leaky_relu
# Policy network
input_layer = x = tf.keras.Input(ob_space.shape, dtype=tf.float32)
if ob_mean is not None and ob_std is not None and optimizations.observation_normalization:
if ob_std.all() != 0:
x = ObservationNormalizationLayer(ob_mean, ob_std)(x)
for hd in model_structure.hidden_dims:
x = tf.keras.layers.Dense(
hd, activation=nonlin,
kernel_initializer=Normc_initializer(std=1.0),
bias_initializer=tf.initializers.zeros())(x)
# Action dimension and the lowest and highest possible values for an action
adim, ahigh, alow = ac_space.shape[0], ac_space.high, ac_space.low
if optimizations.discretize_actions:
num_ac_bins = int(model_structure.ac_bins)
x = tf.keras.layers.Dense(
adim * num_ac_bins,
kernel_initializer=Normc_initializer(std=0.01),
bias_initializer=tf.initializers.zeros())(x)
a = DiscretizeActionsUniformLayer(num_ac_bins, adim, ahigh, alow)(x)
else:
a = tf.keras.layers.Dense(
adim,
kernel_initializer=Normc_initializer(std=0.01),
bias_initializer=tf.initializers.zeros())(x)
model = tf.keras.Model(inputs=input_layer, outputs=a, name=model_name)
if initial_weights is not None:
set_from_flat(model, initial_weights)
return model
# -
# ### The RunningStat class
#
# This class is used for tracking the observations during training. It is only used in combination with the `observation_normalization` optimization. When used, the master holds an object of this class and updates the `sum`, `sumsq` and `count` attributes with the values computed by the masters. Then when the master puts out a new task it provides the current `ob_mean` and `ob_std` with the two methods `mean` and `std` which will be provided to the workers.
#
# The workers simply track the observations by appending the observation for each step in the environment to a list, calculate the sums, add them to their own RunningStat object and send them to the master inside a `Result` object.
# + pycharm={"is_executing": false}
class RunningStat(object):
def __init__(self, shape, eps):
self.sum = np.zeros(shape, dtype=np.float32)
self.sumsq = np.full(shape, eps, dtype=np.float32)
self.count = eps
def save(self, save_file):
# leading underscore in sum to distinct with 'sum' keyword
np.savez(save_file, _sum=self.sum, sumsq=self.sumsq, count=self.count)
def load(self, save_file):
self.data = None
try:
self.data = np.load(save_file, allow_pickle=True)
except IOError:
print("{} cannot be found or is not a file. Initializing observation normalization with default values.".format(save_file))
except KeyError:
print("The file {} is corrupted or not created by this program. Initializing observation normalization with default values.".format(save_file))
else:
try:
_sum = self.data["_sum"]
sumsq = self.data["sumsq"]
count = float(self.data["count"])
except KeyError:
print("{} does not provide enough data to initialize the observation normalization. Using default values".format(save_file))
except TypeError:
print("The data from {} does not match or is corrupted. Using default values".format(save_file))
else:
self.sum = _sum
self.sumsq = sumsq
self.count = count
def increment(self, s, ssq, c):
self.sum += s
self.sumsq += ssq
self.count += c
@property
def mean(self):
return self.sum / self.count
@property
def std(self):
return np.sqrt(np.maximum(self.sumsq / self.count - np.square(self.mean), 1e-2))
# -
# ### Specifiying the number of paramters
#
# For the Optimizer classes we need the total amount of parameters in our models. For this we define the `get_initial_weights` methods, which will create us a normal model, prints its layout and returns the random weights.
# Remember this needs to be done in a subprocess to avoid creating a TensorFlow session in the main process. So we call a `multiprocessing` `Pool` which allows us to spawn a subprocess and return the weights. In addition, the model structure is printed out.
#
# We then calculate the number of parameters from our weight vector $\theta$. The weight vector is also important for later, because it will be the starting weight vector for our training.
# + pycharm={"is_executing": false}
def get_initial_weights(ac_space, ob_space, ob_mean=None, ob_std=None, model_file_path=None):
model = None
if model_file_path:
from utils.es_utils import load_model
model = load_model(model_file_path)
# Extra if is needed because one could not initialize from a directory and then the warning message would be printed everytime
if model is None:
print("Could not initalize a model from {}. Creating a new one.".format(model_file_path))
if model is None:
model = create_model(ac_space, ob_space, ob_mean=ob_mean, ob_std=ob_std)
# Print out the model
model.summary()
return model.get_weights()
def initialize_parameter_vector(ac_space, ob_space, model_file_path=None):
with multiprocessing.Pool(1) as pool:
if optimizations.observation_normalization:
ob_stat = RunningStat(
ob_space.shape,
eps=1e-2 # eps to prevent dividing by zero at the beginning when computing mean/stdev
)
theta = pool.apply(func=get_initial_weights, args=(ac_space, ob_space, ob_stat.mean, ob_stat.std, model_file_path))
else:
theta = pool.apply(func=get_initial_weights, args=(ac_space, ob_space, None, None, model_file_path))
return theta, sum(np.prod(v.shape) for v in theta)
# -
# ### Optimization: Using a neural network optimizer
#
# These optimizer are copied from the implementation from OpenAI. They are also implemented in Keras but need a loss function to work which we do not have when using neuroevolution.
#
# One must provide the `stepsize` attribute for both optimizers and can customize the other ones. It is recommended to leave them as is.
#
# Of course these classes do only get used when the `gradient_optimizer` optimization is active.
# + pycharm={"is_executing": false}
class Optimizer(object):
def __init__(self, num_params):
self.dim = num_params
self.t = 0
self.data = None
def update(self, theta, globalg):
self.t += 1
step = self._compute_step(globalg)
ratio = np.linalg.norm(step) / np.linalg.norm(theta)
theta_new = theta + step
return theta_new, ratio
def save(self, save_file, **kwargs):
np.savez(save_file, **kwargs, t=self.t, dim=self.dim)
def load(self, save_file):
self.data = None
try:
self.data = np.load(save_file, allow_pickle=True)
except IOError:
print("{} cannot be found or is not a file. Initializing optimizer with default values.".format(save_file))
except KeyError:
print("The file {} is corrupted or not created by this program. Initializing the optimizer with default values.".format(save_file))
else:
try:
t = int(self.data["t"])
dim = int(self.data["dim"])
except KeyError:
print("{} does not provide enough data to initialize the optimizer. Using default values".format(save_file))
except TypeError:
print("The data from {} does not match or is corrupted. Using default values".format(save_file))
else:
self.t = t
self.dim = dim
def _compute_step(self, globalg):
raise NotImplementedError
class SGD(Optimizer):
def __init__(self, num_params, stepsize, momentum=0.9):
Optimizer.__init__(self, num_params)
self.v = np.zeros(self.dim, dtype=np.float32)
self.stepsize, self.momentum = stepsize, momentum
def save(self, save_file, **kwargs):
super().save(save_file, stepsize=self.stepsize, momentum=self.momentum, v=self.v)
def load(self, save_file):
super.load(save_file)
if self.data is not None:
try:
stepsize = float(self.data["stepsize"])
momentum = float(self.data["momentum"])
v = self.data["v"]
assert isinstance(v, np.ndarray)
assert v.size == self.dim
except KeyError:
print("{} does not provide enough data to initialize the optimizer. Using default values".format(save_file))
except TypeError or AssertionError:
# Either assertion error or cast failed. Same error message for both
print("The data from {} does not match or is corrupted. Using default values".format(save_file))
else:
self.stepsize = stepsize
self.momentum = momentum
self.v = v
def _compute_step(self, globalg):
self.v = self.momentum * self.v + (1. - self.momentum) * globalg
step = -self.stepsize * self.v
return step
class Adam(Optimizer):
def __init__(self, num_params, stepsize, beta1=0.9, beta2=0.999, epsilon=1e-08):
Optimizer.__init__(self, num_params)
self.stepsize = stepsize
self.beta1 = beta1
self.beta2 = beta2
self.epsilon = epsilon
self.m = np.zeros(self.dim, dtype=np.float32)
self.v = np.zeros(self.dim, dtype=np.float32)
def save(self, save_file, **kwargs):
super().save(save_file, stepsize=self.stepsize, beta1=self.beta1, beta2=self.beta2, epsilon=self.epsilon, m=self.m, v=self.v)
def load(self, save_file):
super().load(save_file)
if self.data is not None:
try:
stepsize = float(self.data["stepsize"])
beta1 = float(self.data["beta1"])
beta2 = float(self.data["beta2"])
epsilon = float(self.data["epsilon"])
m = self.data["m"]
v = self.data["v"]
assert self.m.size == self.dim and self.v.size == self.dim
assert isinstance(m, np.ndarray)
assert isinstance(v, np.ndarray)
except KeyError:
print("{} does not provide enough data to initialize the optimizer. Using default values".format(save_file))
except TypeError or AssertionError:
# Either assertion error or cast failed. Same error message for both
print("The data from {} does not match or is corrupted. Using default values".format(save_file))
else:
self.stepsize = stepsize
self.beta1 = beta1
self.beta2 = beta2
self.epsilon = epsilon
self.m = m
self.v = v
def _compute_step(self, globalg):
a = self.stepsize * np.sqrt(1 - self.beta2 ** self.t) / (1 - self.beta1 ** self.t)
self.m = self.beta1 * self.m + (1 - self.beta1) * globalg
self.v = self.beta2 * self.v + (1 - self.beta2) * (globalg * globalg)
step = -a * self.m / (np.sqrt(self.v) + self.epsilon)
return step
# + [markdown] pycharm={"name": "#%% md\n"}
# ### Shared Noise
#
# To perturb the parameter vector we need noise to sample from. This class provides this noise to the master and the workers. It creates a multiprocessing array, which is stored in shared memory so every spawned process can access it. The array is then filled with samples from the standard normal distribution with the specified `seed`. As a default value `count` is set to $250 \cdot 10^6$ which will sample 2GB of random numbers.
# + pycharm={"is_executing": false, "name": "#%%\n"}
class SharedNoiseTable(object):
def __init__(self, seed=123):
self.seed = seed
count = 250000000
print('Sampling {} random numbers with seed {}'.format(count, self.seed))
# Instantiate an array of C float datatype with size count
self._shared_mem = multiprocessing.Array(ctypes.c_float, count)
# Convert to numpy array
self.noise = np.ctypeslib.as_array(self._shared_mem.get_obj())
assert self.noise.dtype == np.float32
self.noise[:] = np.random.RandomState(seed).randn(count)
print('Sampled {} bytes'.format(self.noise.size * 4))
def get(self, i, dim):
return self.noise[i:i + dim]
def sample_index(self, stream, dim):
return stream.randint(0, len(self.noise) - dim + 1)
# + [markdown] pycharm={"name": "#%% md\n"}
# ### Reshape the parameter vector
#
# Depending on our model structure the weight vector has a specific shape. To easily add or subtract noise, we define the `get_flat` and `set_from_flat` methods which will allow us to reshape the vector.
#
# `get_flat` as the name suggests flattens the given vector.
#
# `set_from_flat` serves two purposes. First it reshapes the one-dimensional array `theta` to the shape the model needs and then it sets the reshaped vector as the weight vector for the given `model`.
# + pycharm={"is_executing": false, "name": "#%%\n"}
def get_flat(theta):
return np.concatenate([np.reshape(v, [-1]) for v in theta], 0)
def set_from_flat(model, theta):
old_theta = model.get_weights()
shapes = [v.shape for v in old_theta]
total_size = theta.size
start = 0
reshapes = []
for (shape, v) in zip(shapes, theta):
size = int(np.prod(shape))
reshapes.append(np.reshape(theta[start:start+size], shape))
start += size
assert start == total_size
model.set_weights(reshapes)
# + [markdown] pycharm={"name": "#%% md\n"}
# ### The rollout function
#
# This function will connect our model with our environment. In `utils/es_utils.py` you can find the implementation of the function.
#
# Each environment in the OpenAI Gym has some functions with which it can be controlled. `env.reset()` resets the environment to the starting position and returns the initial observation. It must be called before doing anything else. `env.step(action)` does one timestep in the environment with the provided action vector and returns four values. First the observation, which represents the state of the environment after our action. Second, the reward for our action. Third, the boolean value `done` which is `True` when the environment reached a state where the environment is finished, for example after the maximum number of timesteps. The fourth value is `info` which gives additional information, but is not used here since for the two PyBullet environments `HumanoidBulletEnv-v0` and `AntBulletEnv-v0`, `info` is just an empty set (This should also be the case for the other robotic environments of PyBullet). Other than that the additional information would require a problem specific handling which we want to avoid when using black-box optimization.
# `env.render()` renders the environment and opens a window where one can see how the environment is performing instead of looking on only numbers. In training this is not done. When you want to view your progress you can use the additional Jupyter Notebook where you can load the latest model and visualize it.
#
# The way `rollout` works is that after resetting the environment and getting the first observation, it creates a loop for the maximum number of timesteps in the environment, mostly this is $1000$ timesteps. In this loop the act function is called with the observation `ob`, the model which is currently used and the perhabs provided `random_stream` which adds action noise to help generalize the model. Based on the model the action is predicted and returned which can then be used for a step in the environment. Lastly, the reward of this step gets saved to a list and the timestep counter `t` gets incremented. If the `save_obs` parameter is `True` every observation gets added to a list and returned later on to calculate the mean and standard deviation of the observation space.
# -
from utils.es_utils import rollout
# ### Collect the observations, if needed
#
# Now, we will define one last method before we go into how the workers operate. `rollout_and_update_ob_stat` is a helper function to do a rollout and collect the observation statistics. If the `observation_normalization` optimization is active, a random number is sampled. If this number is lower than `config.calc_obstat_prob` the rollout is started with the parameter `save_obs` set to `True`. This simply saves every observation after each step in the rollout and returns them as a NumPy array. The `task_ob_stat` then gets incremented with the values of this array. `task_ob_stat` is a RunningStat object created by the worker to keep track of the observation statistics. If the random number is greater or equal to `config.calc_obstat_prob` therew will be a standard rollout where the observations do not get collected.
#
# + pycharm={"is_executing": false}
def rollout_and_update_ob_stat(env, model, rs, task_ob_stat):
if optimizations.observation_normalization and config.calc_obstat_prob != 0 and rs.rand() < config.calc_obstat_prob:
try:
rollout_rews, rollout_len, times_predict, obs = rollout(
env, model, save_obs=True, random_stream=rs)
except AssertionError:
raise
task_ob_stat.increment(obs.sum(axis=0), np.square(obs).sum(axis=0), len(obs))
else:
try:
rollout_rews, rollout_len, times_predict = rollout(env, model, random_stream=rs)
except AssertionError:
raise
return rollout_rews, rollout_len, times_predict
# + [markdown] pycharm={"name": "#%% md\n"}
# ## Using a master-worker architecture
#
# ### The workers
#
# In the next cell we will define the `run_worker` method. As the name suggests this method will be executed by the worker processes. The way this works is that in the master a number of subprocesses is started using the `multiprocessing` package. Each subprocess will run the `run_worker` function with the given parameters `task_list`, `result_queue` and `num_params`. The workers get the latest task from the task list, compute it and push their result on the queue, where the master pulls the results from the queue as long as the configured population size did not exceed yet.
#
# In a more detailed manner, the worker function starts by importing `TensorFlow`, as well as `Keras`. Then the worker runs an infinite loop, where at the beginning the worker gets the last entry in the `task_list`. If a task with the same `task_id` is cached, the cached version will be used. If not the cache gets updated with the newest task and a new model is created. This is needed, since every new task has potentially a new observation mean and standard deviation and they need to be given when creating a model. An important step here is to know that Keras uses a TensorFlow session in the background for their computation. When one creates models in a loop this session gets filled up with new data which reduces the performance of a prediction, as well as it causes a memory leak. Therefore we need to call `clear_session` on the Keras backend which will destroy the current session and starts a new one. To improve performance we then need to set this new session to one with a defined configuration where we set `inter_op_parallelism_threads` and `intra_op_parallelism_threads` both to 1. These allow to use a Thread pool to compute TensorFlow operations, but since we already implemented parallel processing with our master-worker architectur adding another layer of multithreading just creates more overhead and hinders performance.
# Now the worker has the task and the model and can start computing. First it samples a random number. If this number is lower than `config.eval_prob` it will do an evaluation run. This simply takes the current parameter vector, which is `theta` in the task, and performs a rollout without adding noise. This gives insight into the different generations when starting the training. The result object will then consist of only `eval_return` which is the sum of the returned rewards, and `eval_length` which is the number of timesteps for this evaluation episode. Also `task_id` is added to the result for the master to check for outdated tasks (This will be explained when we get to the master).
# If the random number is greater or equal to `config.eval_prob`, the task will be calculated with noise. First, `task_ob_stat`, a RunningStat object is created to track the observations. Then we sample a noise vector from our SharedNoiseTable object `noise`, with dimension `num_params`. Then the weights of the model get updated with `set_from_flat` where define the new weigths as theta plus the noise vector. Then we call `rollout_and_update_ob_stat` which will do a rollout and potentially save the observations as previously discussed. If we also use `mirrored_sampling`, we set the weights to theta minus the noise vector and, again, do a rollout. We then send back the computation in a Result object which is pushed on the `result_queue`.
# + pycharm={"is_executing": false, "name": "#%%\n"}
def run_worker(task_list, result_queue, stop_work, noise, num_params):
from tensorflow.keras import backend as K
import tensorflow as tf
print("PID {}: Started worker".format(os.getpid()))
assert isinstance(noise, SharedNoiseTable)
# Setup
env = gym.make(config.env_id)
# First reset of a PyBullet environment is different to all next ones, see: https://github.com/bulletphysics/bullet3/issues/2596
# Therefore we have to reset one time before we actually use the environment
env.reset()
env.seed(config.env_seed)
# Random stream used for adding noise to the actions as well as deciding if the observation statistics shall be
# updated
rs = np.random.RandomState()
wait_time = 1
cached_task = None
cached_task_id = -1
model = None
while not bool(stop_work.value):
# Get the latest Task from the Manger list
try:
task = task_list[-1]
except IndexError:
if wait_time > 100:
print("The task list does not get tasks, something went wrong in the Master. Aborting.")
break
print("Task list is empty, waiting {} seconds before trying again".format(wait_time))
wait_time *= 2
time.sleep(wait_time)
continue
assert isinstance(task, Task)
task_id = task.task_id
assert isinstance(task_id, int)
if task_id != cached_task_id:
cached_task = task
cached_task_id = task_id
K.clear_session()
# Threading pools set to 1 since we are parallelizing using multiprocessing and larger pools would decrease performance
tf.compat.v1.keras.backend.set_session(tf.compat.v1.Session(config=tf.compat.v1.ConfigProto(inter_op_parallelism_threads=1, intra_op_parallelism_threads=1)))
model = create_model(
env.action_space,
env.observation_space,
initial_weights=cached_task.theta,
model_name=str(os.getpid()),
ob_mean=cached_task.ob_mean,
ob_std=cached_task.ob_std)
if rs.rand() < config.eval_prob:
# Evaluation sample
set_from_flat(model, cached_task.theta)
try:
eval_rews, eval_length, times_predict = rollout(env, model)
except AssertionError:
result_queue.put(None)
return
result_queue.put(Result(
noise_inds=None,
returns=None,
signreturns=None,
lengths=None,
eval_return=eval_rews.sum(),
eval_length=eval_length,
ob_sum=None,
ob_sumsq=None,
ob_count=None,
task_id=cached_task_id,
times_predict=times_predict
))
else:
task_ob_stat = RunningStat(env.observation_space.shape, eps=0.) # eps=0 because we're incrementing only
noise_inds, returns, signreturns, lengths = [], [], [], []
times_predict = []
while not noise_inds:
# Noise sample
noise_idx = noise.sample_index(rs, num_params)
epsilon = config.noise_stdev * noise.get(noise_idx, num_params)
# Evaluate the sampled noise
set_from_flat(model, cached_task.theta + epsilon)
try:
rews_pos, len_pos, times_predict_pos = rollout_and_update_ob_stat(env,
model,
rs=rs,
task_ob_stat=task_ob_stat)
except AssertionError:
result_queue.put(None)
return
# Gather results
noise_inds.append(noise_idx)
returns.append([rews_pos.sum()])
signreturns.append([np.sign(rews_pos).sum()])
lengths.append([len_pos])
times_predict += times_predict_pos
# Mirrored sampling also evaluates the noise by subtracting it
if optimizations.mirrored_sampling:
set_from_flat(model, cached_task.theta - epsilon)
try:
rews_neg, len_neg, times_predict_neg = rollout_and_update_ob_stat(env,
model,
rs=rs,
task_ob_stat=task_ob_stat)
except AssertionError:
result_queue.put(None)
return
returns[-1].append(rews_neg.sum())
signreturns[-1].append(np.sign(rews_neg).sum())
lengths[-1].append(len_neg)
times_predict += times_predict_neg
result_queue.put(Result(
noise_inds=np.array(noise_inds),
returns=np.array(returns, dtype=np.float32),
signreturns=np.array(signreturns, dtype=np.float32),
lengths=np.array(lengths, dtype=np.int32),
eval_return=None,
eval_length=None,
ob_sum=None if task_ob_stat.count == 0 else task_ob_stat.sum,
ob_sumsq=None if task_ob_stat.count == 0 else task_ob_stat.sumsq,
ob_count=task_ob_stat.count,
task_id=cached_task_id,
times_predict=times_predict
))
# -
# ### Supporting functions for the master
#
# #### Batched dot product
#
# A computationally intense part of the algorithm is the calculation of this sum: $\sum \limits_{i=0}^n F_i \epsilon_i$. It is the rewards, weighted by the used noise vector. For a large population, meaning a large $n$, this can get slow, but we use the following technique from the OpenAI implementation. The `weights` and `vecs` paramters get divided into smaller `groups` and then the dot product is calculated on these groups. Each grouped dot product is then simply summed which results in the result.
# + pycharm={"is_executing": false, "name": "#%%\n"}
def itergroups(items, group_size):
assert group_size >= 1
group = []
for x in items:
group.append(x)
if len(group) == group_size:
yield tuple(group)
del group[:]
if group:
yield tuple(group)
def batched_weighted_sum(weights, vecs, batch_size):
total = 0.
num_items_summed = 0
for batch_weights, batch_vecs in zip(itergroups(weights, batch_size), itergroups(vecs, batch_size)):
assert len(batch_weights) == len(batch_vecs) <= batch_size
total += np.dot(np.asarray(batch_weights, dtype=np.float32), np.asarray(batch_vecs, dtype=np.float32))
num_items_summed += len(batch_weights)
return total, num_items_summed
# -
# #### Optimization: Fitness shaping with a rank transformation
#
# One possible optimization which has not yet been discussed is rank transformation. What this does is, it transforms the range of rewards the master gets from the workers for a generation into ranks. So instead of having float numbers as rewards we get integer values in the $[0, len(x)]$ interval as our rewards. `compute_centered_ranks` therefore reshapes the paramter `x`, which in our case will be a one-dimensional reward array when no mirrored sampling is used and two-dimensional otherwise, and then invokes `compute_ranks` on it. This method sorts the input by the argument and sets the interval as the values. Back in the original method the returned array gets reshaped as it was and returned.
# + pycharm={"is_executing": false}
def compute_ranks(x):
"""
Returns ranks in [0, len(x))
Note: This is different from scipy.stats.rankdata, which returns ranks in [1, len(x)].
"""
assert x.ndim == 1
ranks = np.empty(len(x), dtype=int)
ranks[x.argsort()] = np.arange(len(x))
return ranks
def compute_centered_ranks(x):
y = compute_ranks(x.ravel()).reshape(x.shape).astype(np.float32)
y /= (x.size - 1)
y -= .5
return y
# -
# When the function is called with a valid `save_path` the model gets saved to this path as a `.h5` file, including the current weights as well as the structure of the model. Normally, this allows to easily load the model based on the file without providing additional information. Here on the other hand, one must provide the custom classes `Normc_initializer`, `ObservationNormalizationLayer` and `DiscretizeActionsUniformLayer` when loading a saved model, since Keras does not have the implementation of these classes when the model gets loaded. An example and also visualizing the trained data can be found in another Jupyter Notebook, called `evolution-strategies-evaluation.ipynb`.
# + pycharm={"is_executing": false}
def save_model(save_directory, stop_work, save_tasks_queue, ac_space, ob_space):
import tensorflow as tf
from tensorflow.keras import backend as K
print("PID {}: Started saving process".format(os.getpid()))
while not bool(stop_work.value):
save_task = save_tasks_queue.get()
assert isinstance(save_task, Task)
# We are creating models in a loop therefore we need to clear the session to avoid build up
K.clear_session()
model = create_model(
ac_space,
ob_space,
initial_weights=save_task.theta,
model_name=config.env_id + "_Generation_" + str(save_task.task_id),
ob_mean=save_task.ob_mean,
ob_std=save_task.ob_std)
model.save(os.path.join(save_directory, "snapshot_{:05d}.h5".format(save_task.task_id)))
save_tasks_queue.task_done()
# + [markdown] pycharm={"name": "#%% md\n"}
# ### The Master
#
# In the following cell the master and thus the training gets started. After the initial setup an infinite loop is started where in every iteration a new task, representing a new generation, gets pushed onto the task queue. The workers which have been started before the loop, pick up the new task and compute their results, which then, in turn, get enqueued onto the result queue. From their the master picks up results as long as the population size has not been exceeded. Then depending on the optimizations the results get processed and the parameter vector for the new generation is calculated. After logging the weights of the current model may get saved and then a new generation is started. This continues until one stops the kernel, or if you want you can change the infinite loop to a predefined length.
#
# #### Setup
#
# Preferably this notebook would be run in order and start the master cell one time to start the training. But since one may want to start the training again with different optimizations we need to create a subdirectory every time we start the training to avoid duplicating log and weight files.
#
# Note that if you alter the configuration files you of course need to restart that cell to _activate_ these settings. But the best way to restart a training is to restart the kernel and clear the output which resets this notebook. Remember that you sample a rather large noise object (approximately 1GB) of memory which resides does not get freed immediately after aborting the computation.
#
# After creating the noise object which is used by the master and all workers, we create the `task_list` as a list of a `Manager` object. The manager automatically shares the data between processes and handles access to it. For the `result_queue` we use a `multiprocessing.Queue` object. Like the list from the manger this queue object allows for access between processes but when one accesses an item of this queue with `get()` the item also gets removed from the queue. Each worker is a `multiprocessing.Process` which get the queue and list as parameter. Then they get started and compute in their infinite loop as previously discussed.
#
# If we use `observation_normalization` the `ob_stat` object is used to track the mean and standard deviation throughout the training. As a last setup step we define the headrow of our logging file which we save as a comma separated value file.
#
# #### Training
#
# The training starts by appending a new task to the task list. `theta` is the current parameter vector, which in the first generation is just the randomly initiated vector when creating a model. It is reshaped to be one-dimensional with the size `num_params` to easily add or subtract noise. After putting out the task we need to collect the results by the workers. In the while loop we iterate until `num_episodes_popped` exceed our configured population size. Inside the loop we first pop a result from the queue with `result_queue.get()`. This function blocks until an item is returned. Then we need to differentiate between two cases. First, the returned result is an evaluation result and second, the result is a job where noise was added. For the evaluation result we increase the `episodes_so_far` counter which counts exactly what its name says and add the timesteps of the evaluation to `timesteps_so_far`. Then we compare the `task_id` of the result and the task_id which is currently gathered by the master. If they match we have a valid evaluation for this task and we collect the reward of this evaluation and its timestep length to `eval_returns` and `eval_lengths`. For the second case we also increase `episodes_so_far` and `timesteps_so_far` depending on the number of episodes in the result object. Then again we compare the task id's. If they match, we append the result to the `curr_task_results` list and increase our `num_episodes_popped` counter, which remember is our exit condition for the while loop. If we use observation normalization we also increase the values in the `ob_stat` object. On the other hand if the task id's do not match we increase the `num_results_skipped` counter by one. Later on we can then calculate the fraction of skipped results.
#
# After the while loop whe have the results for this generation in `curr_task_results`. We then concatenate the noise indices, rewards and lengths of the results in `noise_inds`, `returns` and `lengths`. If we do fitness shaping we process the rewards with our method of computing the ranks. Then we calculate the dot product and divide by the number of episodes. If we use a gradient-based optimizer, like for example Adam, we input our gradient into it and get the updated `theta` back. Without an optimizer we devide by the standard deviation and multiply the learning rate, as described in the paper, to get our new parameter vector.
#
# Now we log the results of this generation to our csv file and if we snapshot the policy in this generation we create a model with our new theta as initial weights and store them to disk. This is done in a subprocess to avoid an inflicting TensorFlow session.
# + pycharm={"is_executing": false, "name": "#%%\n"}
def run_master(max_timesteps=np.inf, random_seed=123, init_from_directory=None):
# Set the save directory and save the configurations
save_directory = os.path.join(main_directory, time.strftime('%Y_%m_%d-%Hh_%Mm_%Ss', time.localtime(time.time())))
mkdir_p(save_directory)
# Save the configuration files. They could be overwritten when a valid init_from_directory is provided
save_configuration(save_directory)
with open(os.path.join(save_directory, "random_seed.txt"), 'w') as f:
f.write("{}".format(random_seed))
noise = SharedNoiseTable(random_seed)
if max_timesteps is None:
# Convenient to check for None, since users could easily forget to use np.inf
max_timesteps=np.inf
else:
assert max_timesteps > 0
model_file = None
ob_normalization_file = None
optimizer_file = None
log = None
if init_from_directory is not None:
from utils.es_utils import index_training_folder
try:
training_run = index_training_folder(init_from_directory)
except InvalidTrainingError:
print("Could not resume the training from {}. Starting a new one.".format(init_from_directory))
else:
global optimizations, model_structure, config
optimizations, model_structure, config, model_file, ob_normalization_file, optimizer_file = training_run.get_training_state(generation=-1)
log = training_run.log
# Copy all the files from the init directory to the new directory
distutils.dir_util.copy_tree(init_from_directory, save_directory)
print("Resuming training from {} in a new directory.".format(init_from_directory))
env = gym.make(config.env_id)
# Only used with observation_normalization optimization
ob_stat = RunningStat(
env.observation_space.shape,
eps=1e-2 # eps to prevent dividing by zero at the beginning when computing mean/stdev
)
if optimizations.observation_normalization and ob_normalization_file is not None:
ob_stat.load(ob_normalization_file)
theta, num_params = initialize_parameter_vector(env.action_space, env.observation_space, model_file)
theta = get_flat(theta)
if optimizations.gradient_optimizer:
if model_structure.optimizer == ConfigValues.OPTIMIZER_ADAM.value:
optimizer = Adam(int(num_params), **model_structure.optimizer_args)
elif model_structure.optimizer == ConfigValues.OPTIMIZER_SGD.value:
optimizer = SGD(int(num_params), **model_structure.optimizer_args)
else:
raise NotImplementedError
if optimizer_file is not None:
# A previous state of the optimizer was given, restore it
optimizer.load(optimizer_file)
# Setup and starting for the parallel work
manager = multiprocessing.Manager()
task_list = manager.list()
result_queue = multiprocessing.Queue()
save_tasks_queue = multiprocessing.JoinableQueue()
stop_work = multiprocessing.Value('i', 0, lock=False)
# Start workers
workers = []
for _ in range(config.num_workers):
worker = multiprocessing.Process(target=run_worker, args=(task_list, result_queue, stop_work, noise, num_params))
workers.append(worker)
worker.start()
save_process = multiprocessing.Process(target=save_model, args=(save_directory, stop_work, save_tasks_queue, env.action_space, env.observation_space))
save_process.start()
# Logging variables
episodes_so_far = 0
timesteps_so_far = 0
generations = 0
tstart = time.time()
if log is not None:
# Increase generations by one to avoid redoing an already finished generation
if model_file:
last_completed_generation = parse_generation_number(model_file)
generations = last_completed_generation + 1
else:
last_completed_generation = -1
generations = int(log[LogColumnHeaders.GEN.value].iloc[last_completed_generation]) + 1
episodes_so_far = int(log[LogColumnHeaders.EPS_SO_FAR.value].iloc[last_completed_generation])
timesteps_so_far = int(log[LogColumnHeaders.TIMESTEPS_SO_FAR.value].iloc[last_completed_generation])
# The new max_timesteps are for this new TrainingRun, therefore it is necessary to shift the value accordingly
max_timesteps += timesteps_so_far
# The last entry in the log for the time is in seconds but the program uses the epoch value to calculate the timings, therefore we need to shift again
tstart = datetime.datetime.now() - datetime.timedelta(seconds=log[LogColumnHeaders.TIME_ELAPSED.value].iloc[last_completed_generation])
# Convert to time since epoch
tstart = tstart.timestamp()
generation_log = OrderedDict()
generation_log_file = os.path.join(save_directory, "log.csv")
fieldnames = [field.value for field in LogColumnHeaders]
if log is None:
with open(generation_log_file, "w", newline="") as csvfile:
writer = csv.DictWriter(csvfile, fieldnames=fieldnames)
writer.writeheader()
else:
# We have initialized from another TrainingRun and are starting at a certain generation.
# Therefore we have to drop the rest of the columns if there are any
with open(generation_log_file, "r", newline="") as csvfile:
reader = csv.DictReader(csvfile)
rows_to_keep = list(reader)[:generations]
with open(generation_log_file, "w") as csvfile:
writer = csv.DictWriter(csvfile, fieldnames=fieldnames)
writer.writeheader()
for row in rows_to_keep:
writer.writerow(row)
while timesteps_so_far < max_timesteps:
step_tstart = time.time()
task_list.append(Task(
theta=theta,
ob_mean=ob_stat.mean if optimizations.observation_normalization else None,
ob_std=ob_stat.std if optimizations.observation_normalization else None,
task_id=generations
))
print("---------------- Generation: {}----------------".format(generations))
assert theta.dtype == np.float32
curr_task_results, eval_returns, eval_lengths = [], [], []
num_results_skipped, num_episodes_popped, num_timesteps_popped, ob_count_this_gen = 0, 0, 0, 0
times_predict = []
stop_training = False
print("PID {}: Waiting for results".format(os.getpid()))
while num_episodes_popped < config.population_size or num_timesteps_popped < config.timesteps_per_gen:
result = result_queue.get()
if result is None:
print("Stopping training. The model produced non finite numbers inside the action vector. Try a"
+ " different configuration.")
stop_training = True
break
assert isinstance(result, Result)
task_id = result.task_id
assert isinstance(task_id, int)
assert (result.eval_return is None) == (result.eval_length is None)
if result.eval_length is not None:
# The result was an evaluation job therefore do not collect the result only the evaluation
if task_id == generations:
eval_returns.append(result.eval_return)
eval_lengths.append(result.eval_length)
times_predict += result.times_predict
else:
assert result.noise_inds.ndim == 1 and result.returns.dtype == np.float32
if optimizations.mirrored_sampling:
assert result.returns.shape == result.lengths.shape == (len(result.noise_inds), 2)
else:
assert result.returns.shape == result.lengths.shape == (len(result.noise_inds), 1)
if task_id == generations:
curr_task_results.append(result)
# Update counts
result_num_eps = result.lengths.size
result_num_timesteps = result.lengths.sum()
episodes_so_far += result_num_eps
timesteps_so_far += result_num_timesteps
num_episodes_popped += result_num_eps
num_timesteps_popped += result_num_timesteps
# Update observation stats if the optimization is used
if optimizations.observation_normalization and result.ob_count > 0:
ob_stat.increment(result.ob_sum, result.ob_sumsq, result.ob_count)
ob_count_this_gen += result.ob_count
times_predict += result.times_predict
else:
num_results_skipped += 1
if stop_training:
break
print("Gathered results")
# Compute skip fraction
frac_results_skipped = num_results_skipped / (num_results_skipped + len(curr_task_results))
if num_results_skipped > 0:
print("Skipped {} out of date results ({:.2f}%)".format(
num_results_skipped, 100. * frac_results_skipped))
# Assemble results
noise_inds = np.concatenate([r.noise_inds for r in curr_task_results])
returns = np.concatenate([r.returns for r in curr_task_results])
lengths = np.concatenate([r.lengths for r in curr_task_results])
assert noise_inds.shape[0] == returns.shape[0] == lengths.shape[0]
# If fitness shaping is turned on rank the results
if optimizations.fitness_shaping:
if config.return_proc_mode == ConfigValues.RETURN_PROC_MODE_CR.value:
proc_returns = compute_centered_ranks(returns)
# sign and centered_sign_rank are obviously only useful in combination with mirrored sampling
elif config.return_proc_mode == ConfigValues.RETURN_PROC_MODE_SIGN.value:
proc_returns = np.concatenate([r.signreturns for r in curr_task_results])
elif config.return_proc_mode == ConfigValues.RETURN_PROC_MODE_CR_SIGN.value:
proc_returns = compute_centered_ranks(np.concatenate([r.signreturns for r in curr_task_results]))
else:
# Throw error to indicate the false input instead of silently pass on.
# This should have been already catched in the configuration section, so this here is a misconfiguration.
raise NotImplementedError
else:
proc_returns = returns
# Mirrored sampling returns a 2D numpy array therefore we need to preprocess it accordingly
if optimizations.mirrored_sampling:
# Calculates the difference between the rewards sampled with the positive and negative noise
proc_returns = proc_returns[:, 0] - proc_returns[:, 1]
else:
proc_returns = proc_returns.ravel()
# Calculate the approximated gradient with a batch variant which saves time on large vectors
g, count = batched_weighted_sum(
proc_returns,
(noise.get(idx, num_params) for idx in noise_inds),
batch_size=500
)
assert g.shape == (num_params,) and g.dtype == np.float32 and count == len(noise_inds)
# Update with the approximated gradient
g /= returns.size
if optimizations.divide_by_stdev:
g /= config.noise_stdev
if optimizations.gradient_optimizer:
step = -g
if optimizations.weight_decay:
step += config.l2coeff * theta
theta, _ = optimizer.update(theta, step)
else:
step = g * config.learning_rate
if optimizations.weight_decay:
step *= config.l2coeff
theta += step
step_tend = time.time()
# Log the generation and print to stdout
generation_log[LogColumnHeaders.GEN.value] = generations
generation_log[LogColumnHeaders.GEN_REW_MEAN.value] = returns.mean()
generation_log[LogColumnHeaders.GEN_REW_STD.value] = returns.std()
generation_log[LogColumnHeaders.GEN_LEN_MEAN.value] = lengths.mean()
generation_log[LogColumnHeaders.EVAL_GEN_REW_MEAN.value] = np.nan if not eval_returns else np.mean(eval_returns)
generation_log[LogColumnHeaders.EVAL_GEN_REW_STD.value] = np.nan if not eval_returns else np.std(eval_returns)
generation_log[LogColumnHeaders.EVAL_GEN_LEN_MEAN.value] = np.nan if not eval_lengths else np.mean(eval_lengths)
generation_log[LogColumnHeaders.EVAL_GEN_COUNT.value] = len(eval_returns)
generation_log[LogColumnHeaders.EPS_THIS_GEN.value] = lengths.size
generation_log[LogColumnHeaders.EPS_SO_FAR.value] = episodes_so_far
generation_log[LogColumnHeaders.TIMESTEPS_THIS_GEN.value] = lengths.sum()
generation_log[LogColumnHeaders.TIMESTEPS_SO_FAR.value] = timesteps_so_far
generation_log[LogColumnHeaders.UNIQUE_WORKERS.value] = config.num_workers
generation_log[LogColumnHeaders.RESULTS_SKIPPED_FRAC.value] = frac_results_skipped
generation_log[LogColumnHeaders.OBS_COUNT.value] = ob_count_this_gen
generation_log[LogColumnHeaders.TIME_ELAPSED_THIS_GEN.value] = step_tend - step_tstart
generation_log[LogColumnHeaders.TIME_ELAPSED.value] = step_tend - tstart
generation_log[LogColumnHeaders.TIME_PREDICT_MIN.value] = np.amin(times_predict)
generation_log[LogColumnHeaders.TIME_PREDICT_MAX.value] = np.amax(times_predict)
generation_log[LogColumnHeaders.TIME_PREDICT_MEAN.value] = np.mean(times_predict)
generation_log[LogColumnHeaders.TIME_PREDICT_COUNT.value] = len(times_predict)
for key, value in generation_log.items():
print(f'{key:25} {value}')
# Append the log the csv file
with open(generation_log_file, 'a', newline='') as csvfile:
writer = csv.DictWriter(csvfile, fieldnames=fieldnames)
writer.writerow(generation_log)
# Note that the model is created with a custom layer and custom initializer, and therefore needs these two
# custom classes if one wants to load a saved model
if config.snapshot_freq != 0 and generations % config.snapshot_freq == 0:
# Save model
save_tasks_queue.put(Task(
theta=theta,
ob_mean=ob_stat.mean if optimizations.observation_normalization else None,
ob_std=ob_stat.std if optimizations.observation_normalization else None,
task_id=generations
))
# Save optimizer
if optimizations.gradient_optimizer:
optimizer.save(os.path.join(save_directory, "optimizer_{:05d}.npz".format(generations)))
# Save observation normalization
if optimizations.observation_normalization:
ob_stat.save(os.path.join(save_directory, "ob_normalization_{:05d}.npz".format(generations)))
print("Saved training state in generation {} to {}".format(generations, save_directory))
generations += 1
# Quit the multiprocessing data structures and processes
stop_work.value = 1
result_queue.close()
for w in workers:
# Workers are blocking on empty queues and cannot be joined. When attempted they will try to join forever
# Therefore we terminate the process. This is not crucial since we already saved everything for the last
# generation.
w.terminate()
# Save tasks queue is a joinable queue, therefore we can gracefully join the queue
save_tasks_queue.join()
save_tasks_queue.close()
# Like the worker processes a join would result in an indefinite block, since save_tasks_queue is closed and all
# save jobs have been processed we can terminate the process
save_process.terminate()
# -
run_master(max_timesteps=None, random_seed=123, init_from_directory=None)
|
evolution-strategies.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Self-Driving Car Engineer Nanodegree
#
# ## Deep Learning
#
# ## Project: Build a Traffic Sign Recognition Classifier
#
# In this notebook, a template is provided for you to implement your functionality in stages, which is required to successfully complete this project. If additional code is required that cannot be included in the notebook, be sure that the Python code is successfully imported and included in your submission if necessary.
#
# > **Note**: Once you have completed all of the code implementations, you need to finalize your work by exporting the iPython Notebook as an HTML document. Before exporting the notebook to html, all of the code cells need to have been run so that reviewers can see the final implementation and output. You can then export the notebook by using the menu above and navigating to \n",
# "**File -> Download as -> HTML (.html)**. Include the finished document along with this notebook as your submission.
#
# In addition to implementing code, there is a writeup to complete. The writeup should be completed in a separate file, which can be either a markdown file or a pdf document. There is a [write up template](https://github.com/udacity/CarND-Traffic-Sign-Classifier-Project/blob/master/writeup_template.md) that can be used to guide the writing process. Completing the code template and writeup template will cover all of the [rubric points](https://review.udacity.com/#!/rubrics/481/view) for this project.
#
# The [rubric](https://review.udacity.com/#!/rubrics/481/view) contains "Stand Out Suggestions" for enhancing the project beyond the minimum requirements. The stand out suggestions are optional. If you decide to pursue the "stand out suggestions", you can include the code in this Ipython notebook and also discuss the results in the writeup file.
#
#
# >**Note:** Code and Markdown cells can be executed using the **Shift + Enter** keyboard shortcut. In addition, Markdown cells can be edited by typically double-clicking the cell to enter edit mode.
# ---
# ## Step 0: Load The Data
# +
# Load pickled data
import pickle
import csv
# TODO: Fill this in based on where you saved the training and testing data
training_file = '../data/train.p'
validation_file = '../data/valid.p'
testing_file = '../data/test.p'
with open(training_file, mode='rb') as f:
train = pickle.load(f)
with open(validation_file, mode='rb') as f:
valid = pickle.load(f)
with open(testing_file, mode='rb') as f:
test = pickle.load(f)
X_train, y_train = train['features'], train['labels']
X_valid, y_valid = valid['features'], valid['labels']
X_test, y_test = test['features'], test['labels']
with open('signnames.csv', mode='r') as infile:
reader = csv.reader(infile)
signdict = {rows[0]:rows[1] for rows in reader}
# -
# ---
#
# ## Step 1: Dataset Summary & Exploration
#
# The pickled data is a dictionary with 4 key/value pairs:
#
# - `'features'` is a 4D array containing raw pixel data of the traffic sign images, (num examples, width, height, channels).
# - `'labels'` is a 1D array containing the label/class id of the traffic sign. The file `signnames.csv` contains id -> name mappings for each id.
# - `'sizes'` is a list containing tuples, (width, height) representing the original width and height the image.
# - `'coords'` is a list containing tuples, (x1, y1, x2, y2) representing coordinates of a bounding box around the sign in the image. **THESE COORDINATES ASSUME THE ORIGINAL IMAGE. THE PICKLED DATA CONTAINS RESIZED VERSIONS (32 by 32) OF THESE IMAGES**
#
# Complete the basic data summary below. Use python, numpy and/or pandas methods to calculate the data summary rather than hard coding the results. For example, the [pandas shape method](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.shape.html) might be useful for calculating some of the summary results.
# ### Provide a Basic Summary of the Data Set Using Python, Numpy and/or Pandas
# +
import numpy as np
import matplotlib.pyplot as plt
### Replace each question mark with the appropriate value.
### Use python, pandas or numpy methods rather than hard coding the results
# TODO: Number of training examples
n_train = X_train.shape[0]
# TODO: Number of validation examples
n_validation = X_valid.shape[0]
# TODO: Number of testing examples.
n_test = X_test.shape[0]
# TODO: What's the shape of an traffic sign image?
image_shape = X_valid[-1].shape
# TODO: How many unique classes/labels there are in the dataset.
n_classes = len(np.unique(y_train))
print("Number of training examples =", n_train)
print("Number of testing examples =", n_test)
print("Image data shape =", image_shape)
print("Number of classes =", n_classes)
# -
# ### Include an exploratory visualization of the dataset
# Visualize the German Traffic Signs Dataset using the pickled file(s). This is open ended, suggestions include: plotting traffic sign images, plotting the count of each sign, etc.
#
# The [Matplotlib](http://matplotlib.org/) [examples](http://matplotlib.org/examples/index.html) and [gallery](http://matplotlib.org/gallery.html) pages are a great resource for doing visualizations in Python.
#
# **NOTE:** It's recommended you start with something simple first. If you wish to do more, come back to it after you've completed the rest of the sections. It can be interesting to look at the distribution of classes in the training, validation and test set. Is the distribution the same? Are there more examples of some classes than others?
# +
### Data exploration visualization code goes here.
### Feel free to use as many code cells as needed.
import matplotlib.pyplot as plt
import random
from textwrap import wrap
# Visualizations will be shown in the notebook.
# %matplotlib inline
examples = []
for i in range(18):
examples.append(random.randrange(0,n_train-1))
fig, axes = plt.subplots(3, 6, figsize=(12, 6),
subplot_kw={'xticks': [], 'yticks': []})
fig.subplots_adjust(hspace=0.3, wspace=0.05)
plt.rcParams['font.size'] = 8
for ax, ex in zip(axes.flat, examples):
ax.imshow(X_train[ex])
ax.set_title("\n".join(wrap(signdict[str(train['labels'][ex])],25)))
plt.show()
# -
plt.hist(y_train, bins=n_classes)
plt.show()
number_of_most_common_class=np.amax(np.histogram(y_train,range(0,n_classes+1))[0])
# +
import Automold as am
import random
from scipy import ndarray
import skimage as sk
from skimage import transform
from skimage import util
import cv2
def random_jitter_and_rotation(image: ndarray):
# Store height and width of the image
height, width = image.shape[:2]
random_degree = random.uniform(-20, 20)
image_center = tuple(np.array(image.shape[1::-1]) / 2)
rot_mat = cv2.getRotationMatrix2D(image_center, random_degree, 1.0)
image = cv2.warpAffine(image, rot_mat, (width, height), flags=cv2.INTER_LINEAR)
T = np.float32([[1, 0, random.randint(-2,2)], [0, 1, random.randint(-2,2)]])
# We use warpAffine to transform
# the image using the matrix, T
return cv2.warpAffine(image, T, (width, height))
def generate_n_random_image_permutations(image_array_to_sample_from: ndarray, n):
sample_size=image_array_to_sample_from.shape[0]
new_images = np.zeros((n,)+X_train.shape[1:], dtype=np.uint8)
for i in range(0,n):
sample_image = image_array_to_sample_from[random.randint(0,sample_size-1)]
#plt.imshow(sample_image)
#plt.show()
generated_image = random_jitter_and_rotation(sample_image)
if random.randint(0,1)>0:
generated_image = am.add_shadow(generated_image)
#generated_image = am.add_speed(generated_image)
#plt.imshow(generated_image)
#plt.show()
new_images[i] = generated_image
return new_images
hist_of_num_samples_each_class = np.histogram(y_train,range(0,n_classes+1))
DESIRED_NUMBER_OF_IMAGES_FOR_EACH_CLASS = 2500
for c in range(0,len(hist_of_num_samples_each_class[0])):
print("Class:" + str(hist_of_num_samples_each_class[1][c]) + " - " + str(hist_of_num_samples_each_class[0][c]))
samples_in_class = hist_of_num_samples_each_class[0][c]
number_of_samples_to_generate = DESIRED_NUMBER_OF_IMAGES_FOR_EACH_CLASS - samples_in_class
print("Samples to generate:" + str(number_of_samples_to_generate))
indices_of_existing_sample_images = np.argwhere(y_train==c)
#print(indexes_of_existing_sample_images)
images_for_class = np.take(X_train,indices_of_existing_sample_images,axis=0).reshape((samples_in_class,) + X_train.shape[1:])
#print(images_for_class.shape)
#plt.imshow(images_for_class[0])
#plt.show()
if(number_of_samples_to_generate>0):
generated_images = generate_n_random_image_permutations(images_for_class,number_of_samples_to_generate)
"""fig, axes = plt.subplots(3, 6, figsize=(12, 6), subplot_kw={'xticks': [], 'yticks': []})
fig.subplots_adjust(hspace=0.3, wspace=0.05)
plt.rcParams['font.size'] = 8
for ax, ex in zip(axes.flat, range(0,18)):
ax.imshow(generated_images[ex,:,:])"""
#plt.imshow(generated_images[-1])
#plt.show()
X_train = np.concatenate((X_train,generated_images),axis=0)
y_train = np.concatenate((y_train,np.full((number_of_samples_to_generate),c)))
plt.hist(y_train, bins=n_classes)
plt.show()
# -
print(X_train.shape)
print(y_train.shape)
# ----
#
# ## Step 2: Design and Test a Model Architecture
#
# Design and implement a deep learning model that learns to recognize traffic signs. Train and test your model on the [German Traffic Sign Dataset](http://benchmark.ini.rub.de/?section=gtsrb&subsection=dataset).
#
# The LeNet-5 implementation shown in the [classroom](https://classroom.udacity.com/nanodegrees/nd013/parts/fbf77062-5703-404e-b60c-95b78b2f3f9e/modules/6df7ae49-c61c-4bb2-a23e-6527e69209ec/lessons/601ae704-1035-4287-8b11-e2c2716217ad/concepts/d4aca031-508f-4e0b-b493-e7b706120f81) at the end of the CNN lesson is a solid starting point. You'll have to change the number of classes and possibly the preprocessing, but aside from that it's plug and play!
#
# With the LeNet-5 solution from the lecture, you should expect a validation set accuracy of about 0.89. To meet specifications, the validation set accuracy will need to be at least 0.93. It is possible to get an even higher accuracy, but 0.93 is the minimum for a successful project submission.
#
# There are various aspects to consider when thinking about this problem:
#
# - Neural network architecture (is the network over or underfitting?)
# - Play around preprocessing techniques (normalization, rgb to grayscale, etc)
# - Number of examples per label (some have more than others).
# - Generate fake data.
#
# Here is an example of a [published baseline model on this problem](http://yann.lecun.com/exdb/publis/pdf/sermanet-ijcnn-11.pdf). It's not required to be familiar with the approach used in the paper but, it's good practice to try to read papers like these.
# ### Pre-process the Data Set (normalization, grayscale, etc.)
# Minimally, the image data should be normalized so that the data has mean zero and equal variance. For image data, `(pixel - 128)/ 128` is a quick way to approximately normalize the data and can be used in this project.
#
# Other pre-processing steps are optional. You can try different techniques to see if it improves performance.
#
# Use the code cell (or multiple code cells, if necessary) to implement the first step of your project.
# +
### Preprocess the data here. It is required to normalize the data. Other preprocessing steps could include
### converting to grayscale, etc.
### Feel free to use as many code cells as needed.
import tensorflow as tf
import cv2
number_of_channels = 3
def preprocess(input):
output = np.zeros(input.shape[0:3] + (number_of_channels,))
for i in range(input.shape[0]):
#print("pre mean: " + str(np.mean(input[i])))
#input[i] = (input[i] - np.mean(input[i])) // np.std(input[i])
yuv = cv2.cvtColor(input[i], cv2.COLOR_RGB2YUV)
y_float = yuv[:,:,0].astype(np.float32) / 255.0
blur = cv2.GaussianBlur(y_float, (0, 0), sigmaX=2, sigmaY=2)
num = y_float - blur
blur = cv2.GaussianBlur(num*num, (0, 0), sigmaX=2, sigmaY=2)
den = cv2.pow(blur, 0.5)
y = num / den
y_norm = cv2.normalize(y, dst=y, alpha=0.0, beta=1.0, norm_type=cv2.NORM_MINMAX)
hue = cv2.cvtColor(input[i], cv2.COLOR_RGB2HSV)[:,:,0] #note inversion of rgb prior to conversion
red = np.minimum(hue, 180-hue)/20 #center around red
red = np.exp(-red*red) - 0.5
#hue = cv2.cvtColor(input[i], cv2.COLOR_RGB2HSV)[:,:,0]
blue = (hue - 105)/20 #center around blue
blue = np.exp(-blue*blue) - 0.5
output[i,:,:,0] = y_norm
#output[i,:,:,1] = (yuv[:,:,1] - np.mean(yuv[:,:,1])) / np.std(yuv[:,:,1])
output[i,:,:,1] = red
#output[i,:,:,1] = (yuv[:,:,2] - np.mean(yuv[:,:,2])) / np.std(yuv[:,:,2])
output[i,:,:,2] = blue
#output[i] = input[i]
#print("post mean: " + str(np.mean(input[i])))
return output
# -
X_train_norm = preprocess(X_train)
X_valid_norm = preprocess(X_valid)
X_test_norm = preprocess(X_test)
# +
for i in range(18):
examples.append(random.randrange(0,n_train-1))
fig, axes = plt.subplots(3, 6, figsize=(12, 6),
subplot_kw={'xticks': [], 'yticks': []})
fig.subplots_adjust(hspace=0.3, wspace=0.05)
plt.rcParams['font.size'] = 8
for ax, ex in zip(axes.flat, examples):
ax.imshow(X_train_norm[ex,:,:,0], cmap=plt.get_cmap('gray'))
ax.set_title("\n".join(wrap(signdict[str(train['labels'][ex])],25)))
plt.show()
# +
fig, axes = plt.subplots(3, 6, figsize=(12, 6),
subplot_kw={'xticks': [], 'yticks': []})
fig.subplots_adjust(hspace=0.3, wspace=0.05)
plt.rcParams['font.size'] = 8
for ax, ex in zip(axes.flat, examples):
ax.imshow(X_train_norm[ex,:,:,1], cmap=plt.get_cmap('gray'))
ax.set_title("\n".join(wrap(signdict[str(train['labels'][ex])],25)))
plt.show()
# +
for i in range(18):
examples.append(random.randrange(0,n_train-1))
fig, axes = plt.subplots(3, 6, figsize=(12, 6),
subplot_kw={'xticks': [], 'yticks': []})
fig.subplots_adjust(hspace=0.3, wspace=0.05)
plt.rcParams['font.size'] = 8
for ax, ex in zip(axes.flat, examples):
ax.imshow(X_train_norm[ex,:,:,2], cmap=plt.get_cmap('gray'))
ax.set_title("\n".join(wrap(signdict[str(train['labels'][ex])],25)))
plt.show()
# -
# ### Model Architecture
# +
### Define your architecture here.
### Feel free to use as many code cells as needed.
from tensorflow.contrib.layers import flatten
#Not used
def LeNet(x):
# Arguments used for tf.truncated_normal, randomly defines variables for the weights and biases for each layer
mu = 0
sigma = 0.1
# Layer 1: Convolutional. Input = 32x32x3. Output = 28x28x6.
conv1_W = tf.Variable(tf.truncated_normal(shape=(5, 5, number_of_channels, 6), mean = mu, stddev = sigma))
conv1_b = tf.Variable(tf.zeros(6,dtype=tf.float32))
conv1 = tf.nn.conv2d(x, conv1_W, strides=[1, 1, 1, 1], padding='VALID') + conv1_b
# Activation.
conv1 = tf.nn.relu(conv1)
# Pooling. Input = 28x28x6. Output = 14x14x6.
conv1 = tf.nn.max_pool(conv1, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='VALID')
# Layer 2: Convolutional. Output = 10x10x16.
conv2_W = tf.Variable(tf.truncated_normal(shape=(5, 5, 6, 16), mean = mu, stddev = sigma))
conv2_b = tf.Variable(tf.zeros(16))
conv2 = tf.nn.conv2d(conv1, conv2_W, strides=[1, 1, 1, 1], padding='VALID') + conv2_b
# Activation.
conv2 = tf.nn.relu(conv2)
# Pooling. Input = 10x10x16. Output = 5x5x16.
conv2 = tf.nn.max_pool(conv2, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='VALID')
# Flatten. Input = 5x5x16. Output = 400.
fc0 = flatten(conv2)
# Layer 3: Fully Connected. Input = 400. Output = 120.
fc1_W = tf.Variable(tf.truncated_normal(shape=(400, 120), mean = mu, stddev = sigma))
fc1_b = tf.Variable(tf.zeros(120))
fc1 = tf.matmul(fc0, fc1_W) + fc1_b
# Activation.
fc1 = tf.nn.relu(fc1)
# Layer 4: Fully Connected. Input = 120. Output = 84.
fc2_W = tf.Variable(tf.truncated_normal(shape=(120, 84), mean = mu, stddev = sigma))
fc2_b = tf.Variable(tf.zeros(84))
fc2 = tf.matmul(fc1, fc2_W) + fc2_b
# Activation.
fc2 = tf.nn.relu(fc2)
# Layer 5: Fully Connected. Input = 84. Output = 43.
fc3_W = tf.Variable(tf.truncated_normal(shape=(84, 43), mean = mu, stddev = sigma))
fc3_b = tf.Variable(tf.zeros(43))
logits = tf.matmul(fc2, fc3_W) + fc3_b
return logits
def sermanet(x):
# Arguments used for tf.truncated_normal, randomly defines variables for the weights and biases for each layer
mu = 0
sigma = 0.1
# Layer 1: Convolutional. Input = 32x32x1. Output = 28x28x100.
conv1_W = tf.Variable(tf.truncated_normal(shape=(5, 5, 1, 100), mean = mu, stddev = sigma))
conv1_b = tf.Variable(tf.zeros(100,dtype=tf.float32))
conv1 = tf.nn.conv2d(x, conv1_W, strides=[1, 1, 1, 1], padding='VALID') + conv1_b
# Activation.
conv1 = tf.nn.relu(conv1)
# Pooling. Input = 28x28x100. Output = 14x14x100.
conv1 = tf.nn.max_pool(conv1, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='VALID')
# Layer 2: Convolutional. Output = 10x10x200.
conv2_W = tf.Variable(tf.truncated_normal(shape=(5, 5, 100, 200), mean = mu, stddev = sigma))
conv2_b = tf.Variable(tf.zeros(200))
conv2 = tf.nn.conv2d(conv1, conv2_W, strides=[1, 1, 1, 1], padding='VALID') + conv2_b
# Activation.
conv2 = tf.nn.relu(conv2)
# Pooling. Input = 10x10x200. Output = 5x5x200.
conv2 = tf.nn.max_pool(conv2, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='VALID')
# Flatten. Input = 5x5x200 + 14x14x100. Output = 24600.
fc0 = tf.concat((flatten(conv1),flatten(conv2)), axis=1)
# Layer 3: Fully Connected. Input = 24600. Output = 43.
fc1_W = tf.Variable(tf.truncated_normal(shape=(24600, 43), mean = mu, stddev = sigma))
fc1_b = tf.Variable(tf.zeros(43))
return tf.matmul(fc0, fc1_W) + fc1_b
# -
# ### Train, Validate and Test the Model
# A validation set can be used to assess how well the model is performing. A low accuracy on the training and validation
# sets imply underfitting. A high accuracy on the training set but low accuracy on the validation set implies overfitting.
# +
from sklearn.utils import shuffle
import tensorflow as tf
### Train your model here.
### Calculate and report the accuracy on the training and validation set.
### Once a final model architecture is selected,
### the accuracy on the test set should be calculated and reported as well.
### Feel free to use as many code cells as needed.
EPOCHS = 10
BATCH_SIZE = 32
x = tf.placeholder(tf.float32, (None, 32, 32, 1))
y = tf.placeholder(tf.int32, (None))
one_hot_y = tf.one_hot(y, 43)
rate = 0.001
logits = sermanet(x)
cross_entropy = tf.nn.softmax_cross_entropy_with_logits(labels=one_hot_y, logits=logits)
loss_operation = tf.reduce_mean(cross_entropy)
optimizer = tf.train.AdamOptimizer(learning_rate = rate)
training_operation = optimizer.minimize(loss_operation)
prediction_operation = tf.argmax(logits, 1)
correct_prediction = tf.equal(tf.argmax(logits, 1), tf.argmax(one_hot_y, 1))
accuracy_operation = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
saver = tf.train.Saver()
def evaluate(X_data, y_data):
num_examples = len(X_data)
total_accuracy = 0
sess = tf.get_default_session()
for offset in range(0, num_examples, BATCH_SIZE):
batch_x, batch_y = X_data[offset:offset+BATCH_SIZE], y_data[offset:offset+BATCH_SIZE]
accuracy = sess.run(accuracy_operation, feed_dict={x: batch_x, y: batch_y})
total_accuracy += (accuracy * len(batch_x))
return total_accuracy / num_examples
# +
X_train_norm = np.reshape(X_train_norm[:,:,:,0],X_train_norm.shape[0:3]+(1,))
X_valid_norm = np.reshape(X_valid_norm[:,:,:,0],X_valid_norm.shape[0:3]+(1,))
X_test_norm = np.reshape(X_test_norm[:,:,:,0],X_test_norm.shape[0:3]+(1,))
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
num_examples = len(X_train_norm)
last_validation_accuracy = 0.0
print("Training...")
print()
for i in range(EPOCHS):
X_train_norm, y_train = shuffle(X_train_norm, y_train)
for offset in range(0, num_examples, BATCH_SIZE):
end = offset + BATCH_SIZE
batch_x, batch_y = X_train_norm[offset:end], y_train[offset:end]
sess.run(training_operation, feed_dict={x: batch_x, y: batch_y})
training_accuracy = evaluate(X_train_norm, y_train)
validation_accuracy = evaluate(X_valid_norm, y_valid)
print("EPOCH {} ...".format(i+1))
print("Training Accuracy = {:.3f}".format(training_accuracy))
print("Validation Accuracy = {:.3f}".format(validation_accuracy))
print()
if(validation_accuracy-last_validation_accuracy < 0):
#reduce learning rate if no convergence
rate = rate/3
print("No improvement in accuracy - reducing learning rate to = {:.5f}".format(rate))
last_validation_accuracy = validation_accuracy
test_accuracy = evaluate(X_test_norm, y_test)
print("Test accuracy = {:.3f}".format(test_accuracy))
saver.save(sess, './sermanet')
print("Model saved")
# -
# ---
#
# ## Step 3: Test a Model on New Images
#
# To give yourself more insight into how your model is working, download at least five pictures of German traffic signs from the web and use your model to predict the traffic sign type.
#
# You may find `signnames.csv` useful as it contains mappings from the class id (integer) to the actual sign name.
# ### Load and Output the Images
# +
### Load the images and plot them here.
### Feel free to use as many code cells as needed.
import os
import matplotlib.image as mpimg
import numpy as np
import matplotlib.pyplot as plt
from textwrap import wrap
import math
example_images = []
example_images_labels = []
example_dir = "./example_images_from_the_web/"
# Loop over each file in the example directory
for file in os.listdir(example_dir):
filename = os.fsdecode(file)
if filename.endswith(".jpeg") or filename.endswith(".png") or filename.endswith(".jpg"):
image = cv2.imread(os.path.join(example_dir, filename))
#if image.shape[2]==4:
image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
dim = (28,28)
image = cv2.resize(image, dim, interpolation = cv2.INTER_AREA)
image = np.pad(image, ((2,2),(2,2),(0,0)), 'constant')
example_images.append(image)
example_images_labels.append(int(filename.split(".")[0]))
example_images = np.asarray(example_images)
fig, axes = plt.subplots(math.ceil(len(example_images)/5), 5, figsize=(12, 6),
subplot_kw={'xticks': [], 'yticks': []})
fig.subplots_adjust(hspace=0.3, wspace=0.05)
plt.rcParams['font.size'] = 8
for ax, ex in zip(axes.flat, range(0,example_images.shape[0])):
ax.imshow(example_images[ex])
ax.set_title("\n".join(wrap(signdict[str(example_images_labels[ex])],15)))
# -
# ### Predict the Sign Type for Each Image
# +
### Run the predictions here and use the model to output the prediction for each image.
### Make sure to pre-process the images with the same pre-processing pipeline used earlier.
### Feel free to use as many code cells as needed.
example_images_norm = preprocess(np.asarray(example_images))[:,:,:,0]
example_images_norm = np.reshape(example_images_norm,example_images_norm.shape[0:3]+(1,))
sess = tf.Session()
saver = tf.train.Saver()
saver.restore(sess, './sermanet')
logit = sess.run(logits, feed_dict={x: example_images_norm})
# -
# ### Analyze Performance
# +
### Calculate the accuracy for these 5 new images.
### For example, if the model predicted 1 out of 5 signs correctly, it's 20% accurate on these new images.
accuracy = sess.run(accuracy_operation, feed_dict={x: example_images_norm, y: example_images_labels})
print(accuracy)
# -
# ### Output Top 5 Softmax Probabilities For Each Image Found on the Web
# For each of the new images, print out the model's softmax probabilities to show the **certainty** of the model's predictions (limit the output to the top 5 probabilities for each image). [`tf.nn.top_k`](https://www.tensorflow.org/versions/r0.12/api_docs/python/nn.html#top_k) could prove helpful here.
#
# The example below demonstrates how tf.nn.top_k can be used to find the top k predictions for each image.
#
# `tf.nn.top_k` will return the values and indices (class ids) of the top k predictions. So if k=3, for each sign, it'll return the 3 largest probabilities (out of a possible 43) and the correspoding class ids.
#
# Take this numpy array as an example. The values in the array represent predictions. The array contains softmax probabilities for five candidate images with six possible classes. `tf.nn.top_k` is used to choose the three classes with the highest probability:
#
# ```
# # (5, 6) array
# a = np.array([[ 0.24879643, 0.07032244, 0.12641572, 0.34763842, 0.07893497,
# 0.12789202],
# [ 0.28086119, 0.27569815, 0.08594638, 0.0178669 , 0.18063401,
# 0.15899337],
# [ 0.26076848, 0.23664738, 0.08020603, 0.07001922, 0.1134371 ,
# 0.23892179],
# [ 0.11943333, 0.29198961, 0.02605103, 0.26234032, 0.1351348 ,
# 0.16505091],
# [ 0.09561176, 0.34396535, 0.0643941 , 0.16240774, 0.24206137,
# 0.09155967]])
# ```
#
# Running it through `sess.run(tf.nn.top_k(tf.constant(a), k=3))` produces:
#
# ```
# TopKV2(values=array([[ 0.34763842, 0.24879643, 0.12789202],
# [ 0.28086119, 0.27569815, 0.18063401],
# [ 0.26076848, 0.23892179, 0.23664738],
# [ 0.29198961, 0.26234032, 0.16505091],
# [ 0.34396535, 0.24206137, 0.16240774]]), indices=array([[3, 0, 5],
# [0, 1, 4],
# [0, 5, 1],
# [1, 3, 5],
# [1, 4, 3]], dtype=int32))
# ```
#
# Looking just at the first row we get `[ 0.34763842, 0.24879643, 0.12789202]`, you can confirm these are the 3 largest probabilities in `a`. You'll also notice `[3, 0, 5]` are the corresponding indices.
# +
### Print out the top five softmax probabilities for the predictions on the German traffic sign images found on the web.
### Feel free to use as many code cells as needed.
probabilities = sess.run(tf.nn.softmax(logit))
top5 = sess.run(tf.nn.top_k(probabilities, k=5))
title_text = []
for ex in range(0,len(top5[1])):
title_text.append("True: " + signdict[str(example_images_labels[ex])][:18] + (signdict[str(example_images_labels[ex])][18:] and "..") + "\n")
for prob in range(0,5):
title_text[ex] = title_text[ex] + signdict[str(top5[1][ex][prob])][:18] + (signdict[str(top5[1][ex][prob])][17:] and "..") + ": " + "{0:.2f}".format(top5[0][ex][prob]) + "\n"
fig, axes = plt.subplots(math.ceil(len(example_images)/5), 5, figsize=(12, 6),
subplot_kw={'xticks': [], 'yticks': []})
for ax, ex in zip(axes.flat, range(0,example_images_norm.shape[0])):
ax.imshow(example_images[ex,:,:])
ax.set_title(title_text[ex])
#print(title_text[ex])
fig.subplots_adjust(hspace=1)
plt.show()
# +
if X_test_norm.shape[1:4] != (32,32,1):
X_test_norm = np.reshape(X_test_norm[:,:,:,0],X_test_norm.shape[0:3]+(1,))
prediction = sess.run(prediction_operation, feed_dict={x: X_test_norm, y: y_test})
correct = sess.run(correct_prediction, feed_dict={x: X_test_norm, y: y_test})
incorrect_images = []
incorrect_images_norm = []
incorrect_images_labels = []
for i in range(0,len(correct)):
if not correct[i]:
incorrect_images_norm.append(X_test_norm[i])
incorrect_images.append(X_test[i])
incorrect_images_labels.append(y_test[i])
incorrect_images = np.asarray(incorrect_images)
incorrect_images_norm = np.asarray(incorrect_images_norm)
logit = sess.run(logits, feed_dict={x: incorrect_images_norm})
probabilities = sess.run(tf.nn.softmax(logit))
top5 = sess.run(tf.nn.top_k(probabilities, k=5))
title_text = []
for ex in range(0,len(top5[1])):
title_text.append("True: " + signdict[str(incorrect_images_labels[ex])][:18] + (signdict[str(incorrect_images_labels[ex])][18:] and "..") + "\n")
for prob in range(0,5):
title_text[ex] = title_text[ex] + signdict[str(top5[1][ex][prob])][:18] + (signdict[str(top5[1][ex][prob])][17:] and "..") + ": " + "{0:.2f}".format(top5[0][ex][prob]) + "\n"
fig, axes = plt.subplots(3, 5, figsize=(12, 12),
subplot_kw={'xticks': [], 'yticks': []})
for ax, ex in zip(axes.flat, range(0,15)):
#ax.imshow(incorrect_images_norm[ex,:,:,0],cmap=plt.get_cmap('gray'))
ax.imshow(incorrect_images[ex,:,:])
ax.set_title(title_text[ex])
#print(title_text[ex])
fig.subplots_adjust(hspace=1)
plt.show()
# +
from sklearn import metrics
true = []
pred = []
for i in range(0,len(y_test)):
true.append( signdict[str(y_test[i])] )
pred.append( signdict[str(prediction[i])] )
labels = ["Speed limit (20km/h)",
"Speed limit (30km/h)",
"Speed limit (50km/h)",
"Speed limit (60km/h)",
"Speed limit (70km/h)",
"Speed limit (80km/h)",
"End of speed limit (80km/h)",
"Speed limit (100km/h)",
"Speed limit (120km/h)",
"No passing",
"No passing for vehicles over 3.5 metric tons",
"Right-of-way at the next intersection",
"Priority road",
"Yield",
"Stop",
"No vehicles",
"Vehicles over 3.5 metric tons prohibited",
"No entry",
"General caution",
"Dangerous curve to the left",
"Dangerous curve to the right",
"Double curve",
"Bumpy road",
"Slippery road",
"Road narrows on the right",
"Road work",
"Traffic signals",
"Pedestrians",
"Children crossing",
"Bicycles crossing",
"Beware of ice/snow",
"Wild animals crossing",
"End of all speed and passing limits",
"Turn right ahead",
"Turn left ahead",
"Ahead only",
"Go straight or right",
"Go straight or left",
"Keep right",
"Keep left",
"Roundabout mandatory",
"End of no passing",
"End of no passing by vehicles over 3.5 metric tons"]
confusion_matrix = metrics.confusion_matrix(true, pred,labels=labels)
print(confusion_matrix)
np.savetxt("confusion.csv", confusion_matrix, delimiter=",")
# Print the precision and recall, among other metrics
print(metrics.classification_report(true, pred, labels=labels, digits=3))
# -
# ### Project Writeup
#
# Once you have completed the code implementation, document your results in a project writeup using this [template](https://github.com/udacity/CarND-Traffic-Sign-Classifier-Project/blob/master/writeup_template.md) as a guide. The writeup can be in a markdown or pdf file.
# > **Note**: Once you have completed all of the code implementations and successfully answered each question above, you may finalize your work by exporting the iPython Notebook as an HTML document. You can do this by using the menu above and navigating to \n",
# "**File -> Download as -> HTML (.html)**. Include the finished document along with this notebook as your submission.
# ---
#
# ## Step 4 (Optional): Visualize the Neural Network's State with Test Images
#
# This Section is not required to complete but acts as an additional excersise for understaning the output of a neural network's weights. While neural networks can be a great learning device they are often referred to as a black box. We can understand what the weights of a neural network look like better by plotting their feature maps. After successfully training your neural network you can see what it's feature maps look like by plotting the output of the network's weight layers in response to a test stimuli image. From these plotted feature maps, it's possible to see what characteristics of an image the network finds interesting. For a sign, maybe the inner network feature maps react with high activation to the sign's boundary outline or to the contrast in the sign's painted symbol.
#
# Provided for you below is the function code that allows you to get the visualization output of any tensorflow weight layer you want. The inputs to the function should be a stimuli image, one used during training or a new one you provided, and then the tensorflow variable name that represents the layer's state during the training process, for instance if you wanted to see what the [LeNet lab's](https://classroom.udacity.com/nanodegrees/nd013/parts/fbf77062-5703-404e-b60c-95b78b2f3f9e/modules/6df7ae49-c61c-4bb2-a23e-6527e69209ec/lessons/601ae704-1035-4287-8b11-e2c2716217ad/concepts/d4aca031-508f-4e0b-b493-e7b706120f81) feature maps looked like for it's second convolutional layer you could enter conv2 as the tf_activation variable.
#
# For an example of what feature map outputs look like, check out NVIDIA's results in their paper [End-to-End Deep Learning for Self-Driving Cars](https://devblogs.nvidia.com/parallelforall/deep-learning-self-driving-cars/) in the section Visualization of internal CNN State. NVIDIA was able to show that their network's inner weights had high activations to road boundary lines by comparing feature maps from an image with a clear path to one without. Try experimenting with a similar test to show that your trained network's weights are looking for interesting features, whether it's looking at differences in feature maps from images with or without a sign, or even what feature maps look like in a trained network vs a completely untrained one on the same sign image.
#
# <figure>
# <img src="visualize_cnn.png" width="380" alt="Combined Image" />
# <figcaption>
# <p></p>
# <p style="text-align: center;"> Your output should look something like this (above)</p>
# </figcaption>
# </figure>
# <p></p>
#
# +
### Visualize your network's feature maps here.
### Feel free to use as many code cells as needed.
# image_input: the test image being fed into the network to produce the feature maps
# tf_activation: should be a tf variable name used during your training procedure that represents the calculated state of a specific weight layer
# activation_min/max: can be used to view the activation contrast in more detail, by default matplot sets min and max to the actual min and max values of the output
# plt_num: used to plot out multiple different weight feature map sets on the same block, just extend the plt number for each new feature map entry
def outputFeatureMap(image_input, tf_activation, activation_min=-1, activation_max=-1 ,plt_num=1):
# Here make sure to preprocess your image_input in a way your network expects
# with size, normalization, ect if needed
# image_input =
# Note: x should be the same name as your network's tensorflow data placeholder variable
# If you get an error tf_activation is not defined it may be having trouble accessing the variable from inside a function
activation = tf_activation.eval(session=sess,feed_dict={x : image_input})
featuremaps = activation.shape[3]
plt.figure(plt_num, figsize=(15,15))
for featuremap in range(featuremaps):
plt.subplot(6,8, featuremap+1) # sets the number of feature maps to show on each row and column
plt.title('FeatureMap ' + str(featuremap)) # displays the feature map number
if activation_min != -1 & activation_max != -1:
plt.imshow(activation[0,:,:, featuremap], interpolation="nearest", vmin =activation_min, vmax=activation_max, cmap="gray")
elif activation_max != -1:
plt.imshow(activation[0,:,:, featuremap], interpolation="nearest", vmax=activation_max, cmap="gray")
elif activation_min !=-1:
plt.imshow(activation[0,:,:, featuremap], interpolation="nearest", vmin=activation_min, cmap="gray")
else:
plt.imshow(activation[0,:,:, featuremap], interpolation="nearest", cmap="gray")
# +
from IPython.display import display, Markdown
with open('writeup.md', 'r') as fh:
content = fh.read()
display(Markdown(content))
# -
|
Traffic_Sign_Classifier.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/piyushjain220/TSAI/blob/main/NLP/Session7/Sentiment_Analysis_using_LSTM_RNN.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + colab={"base_uri": "https://localhost:8080/"} id="ZcC6LphTBiJ5" outputId="29fb0412-8850-492e-e445-3c75dbec0868"
from google.colab import drive
drive.mount('/content/drive')
# + id="MwT29I7gBv43"
# # mkdir drive/MyDrive/data
# + colab={"base_uri": "https://localhost:8080/"} id="5bAp0ullBz1R" outputId="f8422a41-9503-44af-f65a-553a5d1b8b83"
# cd drive/MyDrive/data
# + colab={"base_uri": "https://localhost:8080/"} id="8JjKWnurB9Hd" outputId="a60ffa44-8561-44d0-b84e-4a801942a4c8"
# # %%shell
# wget http://nlp.stanford.edu/~socherr/stanfordSentimentTreebank.zip
# + colab={"base_uri": "https://localhost:8080/"} id="mwU3nvk1CcEm" outputId="8244c003-1965-47fe-d51d-517cfe0737ed"
# %%shell
unzip stanfordSentimentTreebank.zip
# + colab={"base_uri": "https://localhost:8080/"} id="WWwKpp3ND1HQ" outputId="06427b34-ced5-4c46-a6ba-44ea5b3be464"
# cd ../../..
# + id="g3vZmvoBEDRo"
DATA_DIR = 'drive/MyDrive/data/stanfordSentimentTreebank'
# + colab={"base_uri": "https://localhost:8080/", "height": 35} id="cARmxH9uEMOq" outputId="a0435665-2dec-4144-a444-28accc5a44c4"
import os
os.path.join(DATA_DIR, 'datasetSentences.txt')
# + id="Mab8vlOzD_ZD"
import pandas as pd
datasetSentences = pd.read_csv(os.path.join(DATA_DIR, 'datasetSentences.txt'), sep='\t')
# + colab={"base_uri": "https://localhost:8080/", "height": 199} id="V99KSbmGEz9F" outputId="f2229db2-2d46-46b7-be7a-cbaccb499c62"
datasetSplit = pd.read_csv(os.path.join(DATA_DIR, 'datasetSplit.txt'), sep=',')
datasetSplit.head()
# + id="IXNLjc79E43w"
splitset_label = {1:'train',2:'test',3:'dev'}
# + colab={"base_uri": "https://localhost:8080/"} id="GLYPm3jNFZ3I" outputId="ea0885a9-1e8c-4aaa-aebd-bf89eefdf9b6"
datasetSentences.shape, datasetSplit.shape
# + colab={"base_uri": "https://localhost:8080/"} id="DejZAqa7Ft1M" outputId="124a68a5-6c29-4bdd-e238-b8f4807d0045"
datasetSentences.columns, datasetSplit.columns
# + id="dDLG7aTQFjN9"
merged_dataset = datasetSentences.merge(datasetSplit, on='sentence_index')
# + colab={"base_uri": "https://localhost:8080/"} id="3f081TGGF5YB" outputId="b53255fa-4c7f-42a6-e7b7-0e940605f746"
merged_dataset.shape
# + colab={"base_uri": "https://localhost:8080/", "height": 199} id="4IkHkGSoF6lT" outputId="d3c76ffd-4677-4c2b-fc2f-728effa19fc3"
merged_dataset.head()
# + [markdown] id="H09DzWKJGdS1"
# add sentiment label to the merged_dataset
# + id="l2pgIqfSFqTG"
# read sentiment_labels text
sentiment_label = pd.read_csv(os.path.join(DATA_DIR, "sentiment_labels.txt"),sep='|')
# + colab={"base_uri": "https://localhost:8080/"} id="vEpSD526PzO9" outputId="f091c542-232a-4b43-ef90-c63e9558f7a5"
sentiment_label.shape
# + colab={"base_uri": "https://localhost:8080/", "height": 199} id="T8roF9RPJZIq" outputId="0b41ee60-b426-42ae-e5b7-fcc1323d5dfe"
sentiment_label.head()
# + colab={"base_uri": "https://localhost:8080/", "height": 199} id="zqFd9X9NJa0g" outputId="124cf138-c03f-479b-f829-3a56006d2d80"
dictionary = pd.read_csv(os.path.join(DATA_DIR, "dictionary.txt"), sep='|',header=None)
dictionary.head()
# + id="4v7pQ8i6QZ5W"
dictionary.columns = ['phrases', 'phrase_id']
# + colab={"base_uri": "https://localhost:8080/", "height": 199} id="W3WW78JxQg67" outputId="69e32001-17d4-451b-cd20-e8e099f03074"
dictionary.head()
# + colab={"base_uri": "https://localhost:8080/"} id="v3d6j-ZvNy1H" outputId="35daee0b-f9fb-4d1f-a1ea-efd2cdc86cf8"
dictionary.shape
# + colab={"base_uri": "https://localhost:8080/", "height": 216} id="BwHlgAr0N1OX" outputId="3e615645-ab3c-486d-dcb8-ec3335bf792d"
org_txt =pd.read_csv(os.path.join(DATA_DIR, "original_rt_snippets.txt"), sep='\t')
org_txt.head()
# + id="ckvczFh3OAkU"
dataset_with_phrase_id = merged_dataset.merge(dictionary, left_on='sentence', right_on ='phrases', how='left')
# + colab={"base_uri": "https://localhost:8080/", "height": 199} id="taV9hE1mSVV1" outputId="40e25b80-f491-476b-fbd8-e6d6eb29128c"
sentiment_label.head()
# + id="0D18v2uNRbPP"
ads = dataset_with_phrase_id.merge(sentiment_label, left_on='phrase_id', right_on='phrase ids', how='left')
# + colab={"base_uri": "https://localhost:8080/"} id="DjRc3daSRZJp" outputId="b486f429-3f6d-450d-d7e2-e03f559ed57b"
ads.shape
# + colab={"base_uri": "https://localhost:8080/"} id="bAxgBj51SoQ8" outputId="bbf59f23-ad9d-4edf-85a3-9903a0398909"
ads.columns
# + id="Q0cLe0Q6Spu4"
# ads.drop(['phrases', 'phrase ids'], axis=1, inplace=True)
ads['labels'] = [(1 if 0 <=i <=0.2 else (2 if 0.2<i<=0.4 else (3 if 0.4 <i<=0.6 else (4 if 0.6 <i<=0.8 else 5)))) for i in ads['sentiment values'] ]
ads.rename(columns={'sentence':'tweets'}, inplace=True)
# + colab={"base_uri": "https://localhost:8080/"} id="XUttwLXkSN2h" outputId="263ae155-7b60-4929-bbe7-42177750b5bf"
nltk.download('wordnet')
# + colab={"base_uri": "https://localhost:8080/"} id="4zt39ZRdcEUh" outputId="01b97506-3d8e-4fed-acfd-6cc0a8194ee0"
# DATA Augmentation approaches
from nltk.corpus import stopwords
from nltk import word_tokenize
import nltk
import random
from nltk.corpus import wordnet
nltk.download('stopwords')
nltk.download('punkt')
nltk.download('wordnet')
stoplist = set(stopwords.words('english'))
stop = stopwords.words('english')
import string
punct = list(string.punctuation)
punct.remove("-")
punct.append(" ")
def get_synonyms(word):
if word.lower() in stop:
return [word], [1]
synonyms = set()
for syn in wordnet.synsets(word):
for l in syn.lemmas():
synonym = l.name().replace("_", " ").replace("-", " ").lower()
synonym = "".join([char for char in synonym if char in ' qwertyuiopasdfghjklzxcvbnm'])
synonyms.add(synonym)
if word not in synonyms:
synonyms.add(word)
n = len(synonyms)
if n == 1:
word_ = "".join(list(filter(lambda x: x not in punct, word)))
if word_.lower() in stop:
return [word, word_], [0.5, 0.5]
for syn in wordnet.synsets(word_):
for l in syn.lemmas():
synonym = l.name().replace("_", " ").replace("-", " ").lower()
synonym = "".join([char for char in synonym if char in ' qwertyuiopasdfghjklzxcvbnm'])
synonyms.add(synonym)
if word_ not in synonyms:
synonyms.add(word_)
n = len(synonyms)
if n == 1:
probabilities = [1]
else:
probabilities = [0.5 if w==word else 0.5/(n-1) for w in synonyms]
return list(synonyms), probabilities
def new_row(row, n_samples=1):
text = row['text']
new_rows = [row]
for i in range(n_samples):
row2 = row
new_words = []
for word in text.split():
syns, prob = get_synonyms(word)
selected_word = np.random.choice(syns, p=prob, replace=True)
if type(row['keyword']) == str:
if word != selected_word and word in row['keyword']:
row2['keyword'] = row2['keyword'].replace(word, selected_word)
new_words.append(selected_word)
new_text = " ".join(new_words)
row2['text'] = new_text
new_rows.append(row2)
new_rows = pd.concat(new_rows, axis=1).transpose().drop_duplicates(subset=['text'], inplace=False, ignore_index=True)
new_rows = new_rows.loc[new_rows['text'].apply(len)<150]
return new_rows
def remove_stopwords(text):
return [word for word in word_tokenize(text) if not word in stoplist]
def random_swap(sentence, n=5):
length = range(len(sentence))
for _ in range(n):
idx1, idx2 = random.sample(length, 2)
sentence[idx1], sentence[idx2] = sentence[idx2], sentence[idx1]
return sentence
def random_insertion(sentence, n):
words = remove_stopwords(sentence)
for _ in range(n):
new_synonym = get_synonyms(random.choice(words))
sentence.insert(randrange(len(sentence)+1), new_synonym)
return sentence
# + colab={"base_uri": "https://localhost:8080/"} id="2jkyZNMdaInz" outputId="e23cf0ce-04dc-4dba-9082-69e49b3ec5d4"
x, y = get_synonyms('happy')
x, y
# + id="kVDYYELezOGQ"
final_df = ads[['tweets','labels', 'splitset_label']].copy()
# + colab={"base_uri": "https://localhost:8080/"} id="31Hbt7jHztUb" outputId="ac88aa17-40d2-49f2-fe43-ccc3064b06bc"
final_df.shape
# + id="Yt-hopwlS_tM"
train_df, test_df, dev_df = [groups for name, groups in final_df.groupby('splitset_label')]
# + id="HEnvtEIXeqP9"
train_df.reset_index(drop=True, inplace=True)
test_df.reset_index(drop=True, inplace=True)
dev_df.reset_index(drop=True, inplace=True)
train_df['tweets'] = train_df['tweets'].apply(lambda x:clean_text(x))
# + id="A6yK1K4BUS4C"
train_df['tweets'] = train_df['tweets'].apply(lambda x:clean_text(x))
# + colab={"base_uri": "https://localhost:8080/", "height": 199} id="peTbGQiVe6_Y" outputId="262f9d9c-ee5b-4543-9735-365a9620155b"
train_df.head()
# + colab={"base_uri": "https://localhost:8080/"} id="1mqudfNV5KsJ" outputId="f6b8f7c9-933c-4112-d1aa-395b6f4c36d2"
# experimenting with one, random_insertion
ran_swapped_tweets = random_swap(train_df['tweets'], 5)
new_df = pd.DataFrame()
new_df['tweets'] = ran_swapped_tweets
new_df['labels'] = train_df['labels']
#new_df taken from below
new_df['splitset_label'] = train_df['splitset_label']
# + colab={"base_uri": "https://localhost:8080/"} id="JDDLna9r5ctI" outputId="a2fab9af-2802-44e2-dc6f-ea596ce35bbb"
train_df.shape, new_df.shape
# + id="LzJRVkZB5WKs"
augmented_train_df = pd.concat([train_df[['tweets','labels','splitset_label']], new_df], ignore_index=True)
# + colab={"base_uri": "https://localhost:8080/"} id="np7EP26Y5q11" outputId="63af4bcc-bdd0-448a-d3dc-c732600e710d"
print("train_data count", augmented_train_df.labels.value_counts(), augmented_train_df.shape)
# + id="120S2jlMTgzH"
def clean_text(x):
x = str(x)
for punct in "/-'":
x = x.replace(punct, ' ')
for punct in '&':
x = x.replace(punct, f' {punct} ')
for punct in '?!.,"#$%\'()*+-/:;<=>@[\\]^_`{|}~' + '“”’':
x = x.replace(punct, '')
return x
# + id="iVAxbdkYTjos"
# #!pip install nlpaug
import nlpaug.augmenter.word as naw
#aug = naw.BackTranslationAug()
# + id="75s9xIY3U1Be"
# Synonym Augmentation
# + id="Ax6HtxtpWmzL"
# + id="BKPRAlgPZKaF"
augmented_synonyms = [aug.augment(i,num_thread=32) for i in train_df['tweets']]
# + id="w57ul1gWT4Zd"
# aug = naw.SynonymAug()
augment_synonyms_df = pd.DataFrame()
augment_synonyms_df['tweets'] = augmented_synonyms
augment_synonyms_df['labels'] = train_df['labels']
#new_df taken from below
augment_synonyms_df['splitset_label'] = train_df['splitset_label']
# + id="dbiEGcR8VuOW"
augmented_train_df = pd.concat([augmented_train_df, augment_synonyms_df], ignore_index=True)
# + id="6BPa7AUAYH3D"
augmented_train_df.to_csv("drive/MyDrive/data/augmented_data.csv")
# + colab={"base_uri": "https://localhost:8080/"} id="-h-Wa-EwaXoL" outputId="44819418-16af-49ef-e69d-69befbd2999e"
print("completed")
# + id="9wEcgAQCUyhX"
# BackTranslate Augmentation
# + colab={"base_uri": "https://localhost:8080/", "height": 683} id="3MihuWHdUxmy" outputId="44b201d3-abf5-4ee4-f24f-4da6871a3f30"
aug = naw.BackTranslationAug()
# + id="XKnH8boZUv_W"
augment_bt_df = pd.DataFrame()
augment_bt_df['tweets'] = train_df['tweets'].apply(lambda x:aug.augment(x))
augment_bt_df['labels'] = train_df['labels']
#new_df taken from below
augment_bt_df['splitset_label'] = train_df['splitset_label']
# + id="PC52Kgt9Und7"
augmented_train_df = pd.concat([augmented_train_df, augment_bt_df], ignore_index=True)
# + [markdown] id="tp5IzBGsPGHs"
# ## Dataset Preview
#
# Your first step to deep learning in NLP. We will be mostly using PyTorch. Just like torchvision, PyTorch provides an official library, torchtext, for handling text-processing pipelines.
#
# We will be using previous session tweet dataset. Let's just preview the dataset.
# + [markdown] id="XJ6o_79ISSVb"
# ## Defining Fields
# + [markdown] id="e63g08ijOrf7"
# Now we shall be defining LABEL as a LabelField, which is a subclass of Field that sets sequen tial to False (as it’s our numerical category class). TWEET is a standard Field object, where we have decided to use the spaCy tokenizer and convert all the text to lower‐ case.
# + id="qk8IP4SK1Lrp" colab={"base_uri": "https://localhost:8080/"} outputId="6f3c88a3-2719-4926-9c9a-a200b85086ed"
# Import Library
import random
import torch, torchtext
from torchtext import data
# Manual Seed
SEED = 43
torch.manual_seed(SEED)
# + id="u6bKQax2Mf_U"
Tweet = data.Field(sequential = True, tokenize = 'spacy', batch_first =True, include_lengths=True)
Label = data.LabelField(tokenize ='spacy', is_target=True, batch_first =True, sequential =False)
# + [markdown] id="mX-lYIe_O7Vy"
# Having defined those fields, we now need to produce a list that maps them onto the list of rows that are in the CSV:
# + id="VawdWq36O6td"
fields = [('tweets', Tweet),('labels',Label)]
# + [markdown] id="ZbtZ-Ph2P1xL"
# Armed with our declared fields, lets convert from pandas to list to torchtext. We could also use TabularDataset to apply that definition to the CSV directly but showing an alternative approach too.
# + colab={"base_uri": "https://localhost:8080/", "height": 199} id="T6ZqZXZmdXAT" outputId="b08ef617-50c8-4f6f-aa63-bd2d3583503b"
final_df.head()
# + id="PtMLDAB4hrRa"
df = final_df[['tweets','labels']].copy()
train_df = augmented_train_df.copy()
# + id="znPlfj7Ii7fJ"
train_example = [data.Example.fromlist([train_df.tweets[i],train_df.labels[i]], fields) for i in range(train_df.shape[0])]
test_example = [data.Example.fromlist([test_df.tweets[i],test_df.labels[i]], fields) for i in range(test_df.shape[0])]
valid_example = [data.Example.fromlist([dev_df.tweets[i],dev_df.labels[i]], fields) for i in range(dev_df.shape[0])]
# + id="cNALGws_jkY5"
train = data.Dataset(train_example, fields)
valid = data.Dataset(valid_example, fields)
test = data.Dataset(test_example, fields)
# + id="ykvsCGQMR6UD" colab={"base_uri": "https://localhost:8080/"} outputId="e8c72fac-7066-49ef-f3c9-fb3187da67d6"
(len(train), len(valid), len(test))
# + [markdown] id="kix8P2IKSBaV"
# An example from the dataset:
# + id="dUpEOQruR9JL" colab={"base_uri": "https://localhost:8080/"} outputId="13cf1b4b-26df-4731-c7a1-782ef71c58cd"
vars(train.examples[10])
# + [markdown] id="AKdllP3FST4N"
# ## Building Vocabulary
# + [markdown] id="SuvWQ-SpSmSz"
# At this point we would have built a one-hot encoding of each word that is present in the dataset—a rather tedious process. Thankfully, torchtext will do this for us, and will also allow a max_size parameter to be passed in to limit the vocabu‐ lary to the most common words. This is normally done to prevent the construction of a huge, memory-hungry model. We don’t want our GPUs too overwhelmed, after all.
#
# Let’s limit the vocabulary to a maximum of 5000 words in our training set:
#
# + colab={"base_uri": "https://localhost:8080/"} id="sE6oZZitkQdY" outputId="169122cb-d777-4df9-f23d-ac141d07ab09"
# !ls drive/MyDrive/data/.vector_cache
# + id="wwQYN7rfhM_W"
glove_path = "drive/MyDrive/data/.vector_cache"
# + id="mx955u93SGeY"
MAX_VOCAB_SIZE = 25_000
Tweet.build_vocab(train,
max_size = MAX_VOCAB_SIZE,
vectors = "glove.6B.100d",
unk_init = torch.Tensor.normal_)
Label.build_vocab(train)
# + [markdown] id="xvyEeEjXTGhX"
# By default, torchtext will add two more special tokens, <unk> for unknown words and <pad>, a padding token that will be used to pad all our text to roughly the same size to help with efficient batching on the GPU.
# + id="rA3tIESdcJdN" colab={"base_uri": "https://localhost:8080/"} outputId="c186094c-df70-4109-97ac-073d6e5819c9"
print('Size of input vocab : ', len(Tweet.vocab))
print('Size of label vocab : ', len(Label.vocab))
print('Top 10 words appreared repeatedly :', list(Tweet.vocab.freqs.most_common(10)))
print('Labels : ', Label.vocab.stoi)
# + [markdown] id="rwjD2-ebTeUX"
# **Lots of stopwords!!**
# + [markdown] id="sLWW221gTpNs"
# Now we need to create a data loader to feed into our training loop. Torchtext provides the BucketIterator method that will produce what it calls a Batch, which is almost, but not quite, like the data loader we used on images.
# + [markdown] id="EQqMhMoDUDmn"
# But at first declare the device we are using.
# + id="Zfo2QhGJUK4l"
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# + colab={"base_uri": "https://localhost:8080/"} id="PThKHdDHkEF_" outputId="a8534ca5-2aba-4194-9425-8220fd6a8f66"
device
# + id="qEhirtf6qzaR"
batch_size = 64
# + id="zK2ORoqdTNsM"
train_iterator, valid_iterator = data.BucketIterator.splits((train, valid), batch_size = batch_size,
sort_key = lambda x: len(x.tweets),
sort_within_batch=True, device = device)
# + id="SKbTs3JA1AVC"
train_iterator, test_iterator = data.BucketIterator.splits((train, test), batch_size = batch_size,
sort_key = lambda x: len(x.tweets),
sort_within_batch=True, device = device)
# + [markdown] id="Gg7gTFQO4fby"
# Save the vocabulary for later use
# + id="niE9Cc6-2bD_"
import os, pickle
with open('tokenizer.pkl', 'wb') as tokens:
pickle.dump(Tweet.vocab.stoi, tokens)
# + [markdown] id="1AbsQwqkVyAy"
# ## Defining Our Model
# + [markdown] id="E4PED4HJWH4t"
# We use the Embedding and LSTM modules in PyTorch to build a simple model for classifying tweets.
#
# In this model we create three layers.
# 1. First, the words in our tweets are pushed into an Embedding layer, which we have established as a 300-dimensional vector embedding.
# 2. That’s then fed into a 2 stacked-LSTMs with 100 hidden features (again, we’re compressing down from the 300-dimensional input like we did with images). We are using 2 LSTMs for using the dropout.
# 3. Finally, the output of the LSTM (the final hidden state after processing the incoming tweet) is pushed through a standard fully connected layer with three outputs to correspond to our three possible classes (negative, positive, or neutral).
# + id="43pVRccMT0bT"
import torch.nn as nn
import torch.nn.functional as F
class classifier(nn.Module):
# Define all the layers used in model
def __init__(self, vocab_size, embedding_dim, hidden_dim, output_dim, n_layers, dropout, pad_idx, bidirectional=False):
super().__init__()
self.bidirectional = bidirectional
# Embedding layer
self.embedding = nn.Embedding(vocab_size, embedding_dim, padding_idx = pad_idx)
# LSTM layer
self.encoder = nn.LSTM(embedding_dim,
hidden_dim,
num_layers=n_layers,
dropout=dropout,
bidirectional=bidirectional,
batch_first=True)
# try using nn.GRU or nn.RNN here and compare their performances
# try bidirectional and compare their performances
# Dense layer
self.dropout = nn.Dropout(dropout)
scaling_factor = 2 if bidirectional else 1
self.fc = nn.Linear(hidden_dim*scaling_factor, output_dim)
def forward(self, text, text_lengths):
# text = [batch size, sent_length]
embedded = self.dropout(self.embedding(text))
# embedded = [batch size, sent_len, emb dim]
# packed sequence
packed_embedded = nn.utils.rnn.pack_padded_sequence(embedded, text_lengths.cpu(), batch_first=True)
packed_output, (hidden, cell) = self.encoder(packed_embedded)
#hidden = [batch size, num layers * num directions,hid dim]
#cell = [batch size, num layers * num directions,hid dim]
# Hidden = [batch size, hid dim * num directions]
if self.bidirectional:
hidden = self.dropout(torch.cat((hidden[-2,:,:], hidden[-1,:,:]), dim = 1))
else:
hidden = self.dropout(hidden)
hidden = hidden[0]
dense_outputs = self.fc(hidden)
# Final activation function softmax
output = F.softmax(dense_outputs, dim=1)
return output
# + id="rwBoGE_X_Fl8"
# Define hyperparameters
size_of_vocab = len(Tweet.vocab)
embedding_dim = 100
num_hidden_nodes = 256
num_output_nodes = 5
num_layers = 2
dropout = 0.5
bidirectional=True
PAD_IDX = Tweet.vocab.stoi[Tweet.pad_token]
# Instantiate the model
model = classifier(size_of_vocab, embedding_dim, num_hidden_nodes, num_output_nodes, num_layers, dropout = dropout, pad_idx=PAD_IDX, bidirectional=bidirectional)
# + id="UH2QHkRJq-6o"
PAD_IDX = Tweet.vocab.stoi[Tweet.pad_token]
UNK_IDX = Tweet.vocab.stoi[Tweet.unk_token]
model.embedding.weight.data[UNK_IDX] = torch.zeros(embedding_dim)
model.embedding.weight.data[PAD_IDX] = torch.zeros(embedding_dim)
# + id="O-pOMqzJ3eTv" colab={"base_uri": "https://localhost:8080/"} outputId="8b8b5d29-f003-4c7b-9a7e-db3c75e2617e"
print(model)
#No. of trianable parameters
def count_parameters(model):
return sum(p.numel() for p in model.parameters() if p.requires_grad)
print(f'The model has {count_parameters(model):,} trainable parameters')
# + [markdown] id="eXajorf5Xz7t"
# ## Model Training and Evaluation
# + [markdown] id="PrE9RpMtZ1Vs"
# First define the optimizer and loss functions
# + id="-u86JWdlXvu5"
import torch.optim as optim
# define optimizer and loss
# lr=0.005
# lr = 2e-4
lr = 1e-3
optimizer = optim.Adam(model.parameters(), lr=lr)
criterion = nn.CrossEntropyLoss()
# criterion = nn.BCELoss()
# define metric
def binary_accuracy(preds, y):
#round predictions to the closest integer
_, predictions = torch.max(preds, 1)
correct = (predictions == y).float()
acc = correct.sum() / len(correct)
return acc
def categorical_accuracy(preds, y):
"""
Returns accuracy per batch, i.e. if you get 8/10 right, this returns 0.8, NOT 8
"""
_, predictions = torch.max(preds, 1)
correct = (predictions == y).float()
acc = correct.sum() / len(correct)
return acc
# push to cuda if available
model = model.to(device)
criterion = criterion.to(device)
# + [markdown] id="3VCJtNb3Zt8w"
# The main thing to be aware of in this new training loop is that we have to reference `batch.tweets` and `batch.labels` to get the particular fields we’re interested in; they don’t fall out quite as nicely from the enumerator as they do in torchvision.
# + [markdown] id="2WjEPLKsAiS_"
# **Training Loop**
# + id="HDWNnGK3Y5oJ"
def train(model, iterator, optimizer, criterion):
# initialize every epoch
epoch_loss = 0
epoch_acc = 0
# set the model in training phase
model.train()
for batch in iterator:
# resets the gradients after every batch
optimizer.zero_grad()
# retrieve text and no. of words
tweet, tweet_lengths = batch.tweets
# convert to 1D tensor
predictions = model(tweet, tweet_lengths).squeeze()
# compute the loss
loss = criterion(predictions, batch.labels)
# compute the binary accuracy
#acc = binary_accuracy(predictions, batch.labels)
acc = categorical_accuracy(predictions, batch.labels)
# backpropage the loss and compute the gradients
loss.backward()
# update the weights
optimizer.step()
# loss and accuracy
epoch_loss += loss.item()
epoch_acc += acc.item()
return epoch_loss / len(iterator), epoch_acc / len(iterator)
# + [markdown] id="CZcHhkkvAsCt"
# **Evaluation Loop**
# + id="zHEe-zSVAriL"
def evaluate(model, iterator, criterion):
# initialize every epoch
epoch_loss = 0
epoch_acc = 0
# deactivating dropout layers
model.eval()
# deactivates autograd
with torch.no_grad():
for batch in iterator:
# retrieve text and no. of words
tweet, tweet_lengths = batch.tweets
# convert to 1d tensor
predictions = model(tweet, tweet_lengths).squeeze()
# compute loss and accuracy
loss = criterion(predictions, batch.labels)
# acc = binary_accuracy(predictions, batch.labels)
acc = categorical_accuracy(predictions, batch.labels)
# keep track of loss and accuracy
epoch_loss += loss.item()
epoch_acc += acc.item()
return epoch_loss / len(iterator), epoch_acc / len(iterator)
# + [markdown] id="L6LJFW7HaJoV"
# **Let's Train and Evaluate**
# + id="tq330XlnaEU9" colab={"base_uri": "https://localhost:8080/"} outputId="175cbdfe-1d53-4092-a5ef-7f3796657814"
N_EPOCHS = 20
best_valid_loss = float('inf')
for epoch in range(N_EPOCHS):
# train the model
train_loss, train_acc = train(model, train_iterator, optimizer, criterion)
# evaluate the model
valid_loss, valid_acc = evaluate(model, valid_iterator, criterion)
# save the best model
if valid_loss < best_valid_loss:
best_valid_loss = valid_loss
torch.save(model.state_dict(), 'saved_weights.pt')
print(f'\tTrain Loss: {train_loss:.3f} | Train Acc: {train_acc*100:.2f}%')
print(f'\t Val. Loss: {valid_loss:.3f} | Val. Acc: {valid_acc*100:.2f}% \n')
# + [markdown] id="LZgzB0ZkHVTI"
# ## Model Testing
# + colab={"base_uri": "https://localhost:8080/"} id="uR7Qo22YndW1" outputId="08b9120b-41d0-40df-d829-8ad9aafa2a70"
model.load_state_dict(torch.load('saved_weights.pt'))
test_loss, test_acc = evaluate(model, test_iterator, criterion)
print(f'Test Loss: {test_loss:.3f} | Test Acc: {test_acc*100:.2f}%')
# + id="xeuB1vYnnkbI"
path = './sentiment_analysis_saved_weights_1.pt'
# + id="aZZfnWo0abRx"
#load weights and tokenizer
path = './sentiment_analysis_saved_weights_1.pt'
# path='./saved_weights.pt'
model.load_state_dict(torch.load(path));
model.eval();
tokenizer_file = open('./tokenizer.pkl', 'rb')
tokenizer = pickle.load(tokenizer_file)
#inference
import spacy
nlp = spacy.load('en')
def classify_tweet(tweet):
# labels: very negative, negative, neutral, positive, very positive
categories = {1: "very negative", 2:"negative", 3:"neutral", 4:'positive', 5: 'very positive'}
# tokenize the tweet
tokenized = [tok.text for tok in nlp.tokenizer(tweet)]
# convert to integer sequence using predefined tokenizer dictionary
indexed = [tokenizer[t] for t in tokenized]
# compute no. of words
length = [len(indexed)]
# convert to tensor
tensor = torch.LongTensor(indexed).to(device)
# reshape in form of batch, no. of words
tensor = tensor.unsqueeze(1).T
# convert to tensor
length_tensor = torch.LongTensor(length)
# Get the model prediction
prediction = model(tensor, length_tensor)
_, pred = torch.max(prediction, 1)
return categories[pred.item()]
# + id="yTkHLEipIlM9" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="8bfc18f6-b1c7-4f81-fc82-a74da34281c1"
classify_tweet("A valid explanation for why Trump won't let women on the golf course.")
# + [markdown] id="WVjCuKK_LVEF"
# ## Discussion on Data Augmentation Techniques
#
# You might wonder exactly how you can augment text data. After all, you can’t really flip it horizontally as you can an image! :D
#
# In contrast to data augmentation in images, augmentation techniques on data is very specific to final product you are building. As its general usage on any type of textual data doesn't provides a significant performance boost, that's why unlike torchvision, torchtext doesn’t offer a augmentation pipeline. Due to powerful models as transformers, augmentation tecnhiques are not so preferred now-a-days. But its better to know about some techniques with text that will provide your model with a little more information for training.
#
# ### Synonym Replacement
#
# First, you could replace words in the sentence with synonyms, like so:
#
# The dog slept on the mat
#
# could become
#
# The dog slept on the rug
#
# Aside from the dog's insistence that a rug is much softer than a mat, the meaning of the sentence hasn’t changed. But mat and rug will be mapped to different indices in the vocabulary, so the model will learn that the two sentences map to the same label, and hopefully that there’s a connection between those two words, as everything else in the sentences is the same.
# + [markdown] id="T_uEfWJpL6Nq"
# ### Random Insertion
# A random insertion technique looks at a sentence and then randomly inserts synonyms of existing non-stopwords into the sentence n times. Assuming you have a way of getting a synonym of a word and a way of eliminating stopwords (common words such as and, it, the, etc.), shown, but not implemented, in this function via get_synonyms() and get_stopwords(), an implementation of this would be as follows:
#
# + id="7Alm5D7WIvAC"
def random_insertion(sentence, n):
words = remove_stopwords(sentence)
for _ in range(n):
new_synonym = get_synonyms(random.choice(words))
sentence.insert(randrange(len(sentence)+1), new_synonym)
return sentence
# + [markdown] id="gqLWzwJ3Mm8h"
# ## Random Deletion
# As the name suggests, random deletion deletes words from a sentence. Given a probability parameter p, it will go through the sentence and decide whether to delete a word or not based on that random probability. Consider of it as pixel dropouts while treating images.
# + id="-7Dz7JJfMqyC"
def random_deletion(words, p=0.5):
if len(words) == 1: # return if single word
return words
remaining = list(filter(lambda x: random.uniform(0,1) > p,words))
if len(remaining) == 0: # if not left, sample a random word
return [random.choice(words)]
else:
return remaining
# + [markdown] id="zOIbi5WzO5OU"
# ### Random Swap
# The random swap augmentation takes a sentence and then swaps words within it n times, with each iteration working on the previously swapped sentence. Here we sample two random numbers based on the length of the sentence, and then just keep swapping until we hit n.
# + id="LnkbG15HO3Yj"
def random_swap(sentence, n=5):
length = range(len(sentence))
for _ in range(n):
idx1, idx2 = random.sample(length, 2)
sentence[idx1], sentence[idx2] = sentence[idx2], sentence[idx1]
return sentence
# + [markdown] id="599NpwfMR5Vm"
# For more on this please go through this [paper](https://arxiv.org/pdf/1901.11196.pdf).
# + [markdown] id="a5aeKuNCRGip"
# ### Back Translation
#
# Another popular approach for augmenting text datasets is back translation. This involves translating a sentence from our target language into one or more other languages and then translating all of them back to the original language. We can use the Python library googletrans for this purpose.
# + id="pHhNBbYrRXNy"
import random
import googletrans
import googletrans.Translator
translator = Translator()
sentence = ['The dog slept on the rug']
available_langs = list(googletrans.LANGUAGES.keys())
trans_lang = random.choice(available_langs)
print(f"Translating to {googletrans.LANGUAGES[trans_lang]}")
translations = translator.translate(sentence, dest=trans_lang)
t_text = [t.text for t in translations]
print(t_text)
translations_en_random = translator.translate(t_text, src=trans_lang, dest='en')
en_text = [t.text for t in translations_en_random]
print(en_text)
|
NLP/Session7/Sentiment_Analysis_using_LSTM_RNN.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Feature Extraction I
# +
import os
import numpy as np
import pandas as pd
import scipy as sp
import scipy.signal
import scipy.stats
import activity_classifier_utils
# -
# Load the data
fs = 256
data = activity_classifier_utils.LoadWristPPGDataset()
# ### Features
# Time Domain:
# * mean
# * std
# * 5, 10, 15, 20, 25 percentile
# * cross-correlation of all pairs of channels
# * total energy
#
# Frequency Domain:
# * dominant frequency
# * fraction of energy in each 1Hz bin from 0 to 6 Hz
# * spectral entropy of each channel - i'll do
# Low-pass filter at 12 Hz
def LowpassFilter(signal, fs):
b, a = sp.signal.butter(3, 12, btype='lowpass', fs=fs)
return sp.signal.filtfilt(b, a, signal)
# Compute Features
def Featurize(accx, accy, accz, fs):
"""A partial featurization of the accelerometer signal.
Args:
accx: (np.array) x-channel of the accelerometer.
accy: (np.array) y-channel of the accelerometer.
accz: (np.array) z-channel of the accelerometer.
fs: (number) the sampling rate of the accelerometer
Returns:
n-tuple of accelerometer features
"""
accx = LowpassFilter(accx, fs)
accy = LowpassFilter(accy, fs)
accz = LowpassFilter(accz, fs)
# The mean of the x-channel
mn_x = None
# The standard deviation of the x-channel
std_x = None
# The 5th percentile of the x-channel
p5_x = None
# The pearson correlation coefficient between the x and y channels
corr_xy = None
# The total AC energy of the x-axis
energy_x = np.sum(np.square(accx - np.mean(accx)))
# Take an FFT of the signal. If the signal is too short, 0-pad it so we have at least 2046 points in the FFT.
fft_len = max(len(accx), 2046)
# Create an array of frequency bins
fft_freqs = np.fft.rfftfreq(fft_len, 1 / fs)
# Take an FFT of the centered signal
fft_x = np.fft.rfft(accx - np.mean(accx), fft_len)
# The frequency with the most power between 0.25 and 12 Hz
dominant_frequency_x = None
# The fraction of energy between 2 and 3 Hz in the x-channel
spectral_energy_x = np.square(np.abs(fft_x))
energy_23_x = np.sum(spectral_energy_x[(fft_freqs >= 2) & (fft_freqs <= 3)]) / np.sum(spectral_energy_x)
return (mn_x,
std_x,
p5_x,
corr_xy,
energy_x,
dominant_frequency_x,
energy_23_x)
# ## Check The Code
# Extract a 10 second window of the DataFrame
seg = data[0][2].iloc[:fs * 10]
accx = seg.accx.values
accy = seg.accy.values
accz = seg.accz.values
Featurize(accx, accy, accz, fs)
|
AI-for-Healthcare/wearable-data/lesson 4/2_feature_extraction.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Convolution Neural Network with K-Fold
#
# Convolution Neural Networks or CNN or Convnets are the current state of the art for most computer vision tasks.
#
# This notebook will aply k-fold with a very simple CNN architecture.
# +
# Import libraries and ignore warnings
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
import numpy as np
np.random.seed(2)
from sklearn.model_selection import StratifiedKFold
from sklearn.metrics import classification_report
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import OneHotEncoder, LabelEncoder
#from sklearn.metrics import confusion_matrix
from keras import models
from keras import layers
from keras import optimizers
from keras.preprocessing.image import ImageDataGenerator
from keras.callbacks import ReduceLROnPlateau, EarlyStopping
from keras.preprocessing import image
import os
from PIL import Image
# -
# # Data
#
# The first step is to import images and store their **pixel** values in a dataframe. This will allow us to create 10 fold by using the index of the rows.
#
# We will also **shuffle** the dataframe because the first 200 images are smilling and next 200 images are neutral.
# +
# Read the annotations file that contains the label and the image file name
labels = pd.read_csv('./SMILE_Dataset/annotations.csv', header=None, names=['fname','label'])
# Shuffle data
labels = labels.sample(frac=1).reset_index()
# Use a list comprehension to loop over image file names and import one by one and store pixel values
x = np.array([image.img_to_array(image.load_img('./SMILE_Dataset/all/'+fname, target_size=(128, 128))) for fname in labels['fname']])
# Because the names are strings, the neural network only takes in numerical formats so we will one-hot encode the label
label_encoder = LabelEncoder()
integer_encoded = label_encoder.fit_transform(labels['label'])
y = integer_encoded
# -
# Now we have two variables.
#
# x: all of the values for our images
# y: all of the labels (0:1)
#
# Now we have finished working with the data. Let's define an architecture for our CNN.
#
# # Model
#
# Here I defined a function that will be called when we loop over our 10 folds. This is just to keep the code cleaner later on.
def build_model():
model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(128, 128, 3)))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
# Switched 24 to 128, got 96.75 with 128.
model.add(layers.Conv2D(128, (3, 3), activation='relu'))
#model.add(layers.Dropout(0.05)) # added small dropout to help with overfitting - not good
# Added following but overfitting
#model.add(layers.MaxPooling2D((2, 2)))
#model.add(layers.Conv2D(128, (3, 3), activation='relu'))
#model.add(layers.MaxPooling2D((2, 2)))
# Feed to a densily connected layer for prediction
model.add(layers.Flatten())
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy',
optimizer=optimizers.RMSprop(lr=0.001, rho=0.9, epsilon=1e-08, decay=0.0),
metrics=['acc'])
return model
# # K-Fold
# +
# All classification reports will be added here. When we are done we can average the f1 scores
reports = []
# Apply stratified K-fold ith 10 splits. Stratified means the same distribution of classes than the whole dataset
# In this case, 50-50
kf = StratifiedKFold(n_splits=2)
# Just for printing purposes
id = 1
for train_index, test_index in kf.split(x,y):
print('Kfold iteration {}/10'.format(id))
print('Total images: {} ---- Train images: {} ---- Test images: {}'.format(len(x),len(train_index),len(test_index)))
id += 1
X_train, X_test = x[train_index], x[test_index]
y_train, y_test = y[train_index], y[test_index]
#model = build_model()
model = loaded_model
datagen = ImageDataGenerator(rescale=1./255,
rotation_range=10, # randomly rotate images in the range (degrees, 0 to 180)
width_shift_range=0.1, # randomly shift images horizontally (fraction of total width)
height_shift_range=0.1,
shear_range=0.1,
zoom_range=0.1)
datagen.fit(X_train)
# Secret sauce to get 3-5 % accuracy more
# Adjust the learning rate over time. (Like we saw in class!)
# The learning rate determines the size of the steps taken during the gradient descent process.
learning_rate_reduction = ReduceLROnPlateau(monitor='val_acc',
patience=3,
verbose=1,
factor=0.5,
min_lr=0.00001)
# Used to prevent overfitting.
# es = EarlyStopping(monitor='val_loss', mode='min', verbose=1, patience=50)
history = model.fit_generator(datagen.flow(X_train, y_train, batch_size = 20), epochs = 20,
validation_data = (X_test,y_test), steps_per_epoch=len(X_train) / 20,
callbacks=[learning_rate_reduction])
y_pred = model.predict(X_test)
y_pred = [np.round(p[0]) for p in y_pred]
print(classification_report(y_test, y_pred))
reports.append(classification_report(y_test, y_pred,output_dict=True))
# -
model.save('my_model.h5')
# +
# We loop over all reports (1 per fold) and then compute the average of all weighted f1 scores
final_f1_score = np.mean([rep['weighted avg']['f1-score'] for rep in reports])
print('Final F1-Score is: {}%'.format(np.round(final_f1_score*100,2)))
# -
model.load_model('my_model.h5')
from keras.models import model_from_json
# serialize model to JSON
model_json = model.to_json()
with open("model.json", "w") as json_file:
json_file.write(model_json)
# serialize weights to HDF5
model.save_weights("model.h5")
print("Saved model to disk")
# load json and create model
json_file = open('model.json', 'r')
loaded_model_json = json_file.read()
json_file.close()
loaded_model = model_from_json(loaded_model_json)
# load weights into new model
loaded_model.load_weights("model.h5")
print("Loaded model from disk")
# remove the last 2 dense FC layers and freeze it
loaded_model.pop()
loaded_model.pop()
loaded_model.summary()
for layer in loaded_model.layers[:3]:
layer.trainable = False
loaded_model.summary()
# +
loaded_model.add(layers.Dense(32, activation='relu'))
loaded_model.add(layers.Dense(1, activation='sigmoid'))
loaded_model.compile(loss='binary_crossentropy',
optimizer=optimizers.RMSprop(lr=0.001, rho=0.9, epsilon=1e-08, decay=0.0),
metrics=['acc'])
# -
loaded_model.summary()
|
trash/transfer learning fer cnn.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# %qtconsole
import napari
viewer = napari.Viewer()
from napari.plugins import NapariPluginManager
plugin_manager = NapariPluginManager()
# +
import napari_j
plugin_manager.register(napari_j, name="napari-J")
# -
import yaml
with open('./naparij.yml', 'r') as file:
params = yaml.load(file, Loader=yaml.FullLoader)
params
connection_params = params['connection']
connection_params['jvm_path']
m
|
Untitled.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Lab 3: Tables
#
# Welcome to lab 3! This week, we'll learn about *tables*, which let us work with multiple arrays of data about the same things. Tables are described in [Chapter 6](https://www.inferentialthinking.com/chapters/06/Tables) of the text.
#
# First, set up the tests and imports by running the cell below.
# +
import numpy as np
from datascience import *
# These lines load the tests.
from client.api.notebook import Notebook
ok = Notebook('lab03.ok')
_ = ok.auth(inline=True)
# -
# ## 1. Introduction
#
# For a collection of things in the world, an array is useful for describing a single attribute of each thing. For example, among the collection of US States, an array could describe the land area of each state. Tables extend this idea by describing multiple attributes for each element of a collection.
#
# In most data science applications, we have data about many entities, but we also have several kinds of data about each entity.
#
# For example, in the cell below we have two arrays. The first one contains the world population in each year by the US Census Bureau, and the second contains the years themselves (in order, so the first elements in the population and the years arrays correspond).
population_amounts = Table.read_table("world_population.csv").column("Population")
years = np.arange(1950, 2015+1)
print("Population column:", population_amounts)
print("Years column:", years)
# Suppose we want to answer this question:
#
# > When did the world population cross 6 billion?
#
# You could technically answer this question just from staring at the arrays, but it's a bit convoluted, since you would have to count the position where the population first crossed 6 billion, then find the corresponding element in the years array. In cases like these, it might be easier to put the data into a *`Table`*, a 2-dimensional type of dataset.
#
# The expression below:
#
# - creates an empty table using the expression `Table()`,
# - adds two columns by calling `with_columns` with four arguments,
# - assigns the result to the name `population`, and finally
# - evaluates `population` so that we can see the table.
#
# The strings `"Year"` and `"Population"` are column labels that we have chosen. The names `population_amounts` and `years` were assigned above to two arrays of the same length. The function `with_columns` (you can find the documentation [here](http://data8.org/datascience/tables.html)) takes in alternating strings (to represent column labels) and arrays (representing the data in those columns), which are all separated by commas.
population = Table().with_columns(
"Population", population_amounts,
"Year", years
)
population
# Now the data are all together in a single table! It's much easier to parse this data,if you need to know what the population was in 1959, for example, you can tell from a single glance. We'll revisit this table later.
# ## 2. Creating Tables
#
# **Question 2.1.** In the cell below, we've created 2 arrays. Using the steps above, create a table called `top_10_movies` that has two columns called "Rating" and "Name", which hold `top_10_movie_ratings` and `top_10_movie_names` respectively.
# +
top_10_movie_ratings = make_array(9.2, 9.2, 9., 8.9, 8.9, 8.9, 8.9, 8.9, 8.9, 8.8)
top_10_movie_names = make_array(
'The Shawshank Redemption (1994)',
'The Godfather (1972)',
'The Godfather: Part II (1974)',
'Pulp Fiction (1994)',
"Schindler's List (1993)",
'The Lord of the Rings: The Return of the King (2003)',
'12 Angry Men (1957)',
'The Dark Knight (2008)',
'Il buono, il brutto, il cattivo (1966)',
'The Lord of the Rings: The Fellowship of the Ring (2001)')
top_10_movies = Table().with_columns("Rating", "Name")
# We've put this next line here so your table will get printed out when you
# run this cell.
top_10_movies
# -
_ = ok.grade('q2_1')
# #### Loading a table from a file
# In most cases, we aren't going to go through the trouble of typing in all the data manually. Instead, we can use our `Table` functions.
#
# `Table.read_table` takes one argument, a path to a data file (a string) and returns a table. There are many formats for data files, but CSV ("comma-separated values") is the most common.
# Below is an example on how to use ``Table.read_table``. The file ``imdb_2015.csv`` contains a table of information about the 250 highest-rated movies on IMDb in 2015. The following code loads it as a table called ``imdb2015``.
imdb2015 = Table().read_table("data/imdb_2015.csv")
imdb2015
# Notice the part about "... (240 rows omitted)." This table is big enough that only a few of its rows are displayed, but the others are still there. 10 are shown, so there are 250 movies total.
#
# Where did `imdb_2015.csv` come from? Take a look at [the data folder in the lab](./data). You should see a file called `imdb_2015.csv`.
#
# Open up the `imdb_2015.csv` file in that folder and look at the format. What do you notice? The `.csv` filename ending says that this file is in the [CSV (comma-separated value) format](http://edoceo.com/utilitas/csv-file-format).
# Now do the following exercise accoding to the example above.
# **Question 2.2.** The file `imdb_2019.csv` contains a table of information about the 250 highest-rated movies on IMDb. Load it as a table called `imdb2019`.
imdb2019 = ...
imdb2019
_ = ok.grade('q2_2')
# ## 3. Using lists
#
# A *list* is another Python sequence type, similar to an array. It's different than an array because the values it contains can all have different types. A single list can contain `int` values, `float` values, and strings. Elements in a list can even be other lists. A list is created by giving a name to the list of values enclosed in square brackets and separated by commas. For example, `values_with_different_types = ['data', 8, ['lab', 3]]`
#
# Lists can be useful when working with tables because they can describe the contents of one row in a table, which often corresponds to a sequence of values with different types. A list of lists can be used to describe multiple rows.
#
# Each column in a table is a collection of values with the same type (an array). If you create a table column from a list, it will automatically be converted to an array. A row, on the other hand, mixes types.
#
# Next, let's use lists to store your favorite pokemons in a table!
# Run this cell to recreate the table
my_pokemons = Table().with_columns(
'Index', make_array(7, 39, 60),
'Name', make_array('squirtle', 'jigglypuff', 'poliwag')
)
my_pokemons
# **Question 3.1.** Create a list that describes a new fourth row of this table. The details can be whatever you want, but the list must contain two values: the index of the pokemon in the Pokedex (an `int` value) and the name of the pokemon (a string). How about the "pikachu"? Its index is 25. Or select your favourite pokemons [here](https://pokemondb.net/pokedex/all)!
new_pokemon = ...
new_pokemon
_ = ok.grade('q3_1')
# **Question 3.2.** Now let's assemble your team for [pokemon battles](https://bulbapedia.bulbagarden.net/wiki/Pok%C3%A9mon_battle)! Complete the cell below to create a table of six pokemons (`six_pokemons`). For this purpose, first create a table `four_pokemons` that includes `new_pokemon` list as the fourth row to table `my_pokemons`. Then create a table `six_pokemons` from `four_pokemons` by including `other_pokemons` list as later rows.
#
#
# _Hint_: You can use `with_row` to create a new table with one extra row by passing a list of values and `with_rows` to create a table with multiple extra rows by passing a list of lists of values.
# +
# Use the method .with_row(...) to create a new table that includes new_pokemon
four_pokemons = ...
# Use the method .with_rows(...) to create a table that
# includes four_pokemons followed by other_pokemons
other_pokemons = [[94, 'gengar'], [130, 'gyarados']]
six_pokemons = ...
six_pokemons
# -
_ = ok.grade('q3_2')
# ## 4. Analyzing datasets
# With just a few table methods, we can answer some interesting questions about the IMDb2015 dataset.
#
# If we want just the ratings of the movies, we can get an array that contains the data in that column:
imdb2015.column("Rating")
# The value of that expression is an array, exactly the same kind of thing you'd get if you typed in `make_array(8.4, 8.3, 8.3, [etc])`.
#
# **Question 4.1.** Find the rating of the highest-rated movie in the dataset in 2015.
#
# *Hint:* Think back to the functions you've learned about for working with arrays of numbers. Ask for help if you can't remember one that's useful for this.
highest_rating = ...
highest_rating
_ = ok.grade('q4_1')
# That's not very useful, though. You'd probably want to know the *name* of the movie whose rating you found! To do that, we can sort the entire table by rating, which ensures that the ratings and titles will stay together.
imdb2015.sort("Rating")
# Well, that actually doesn't help much, either -- we sorted the movies from lowest -> highest ratings. To look at the highest-rated movies, sort in reverse order:
imdb2015.sort("Rating", descending=True)
# (The `descending=True` bit is called an *optional argument*. It has a default value of `False`, so when you explicitly tell the function `descending=True`, then the function will sort in descending order.)
#
# So there are actually 2 highest-rated movies in the dataset: *The Shawshank Redemption* and *The Godfather*.
#
# Some details about sort:
#
# 1. The first argument to `sort` is the name of a column to sort by.
# 2. If the column has strings in it, `sort` will sort alphabetically; if the column has numbers, it will sort numerically.
# 3. The value of `imdb2015.sort("Rating")` is a *copy of `imdb2015`*; the `imdb2015` table doesn't get modified. For example, if we called `imdb2015.sort("Rating")`, then running `imdb2015` by itself would still return the unsorted table.
# 4. Rows always stick together when a table is sorted. It wouldn't make sense to sort just one column and leave the other columns alone. For example, in this case, if we sorted just the "Rating" column, the movies would all end up with the wrong ratings.
#
# **Question 4.2.** Create a version of `imdb2015` that's sorted chronologically, with the earliest movies first. Call it `imdb2015_by_year`.
imdb2015_by_year = ...
imdb2015_by_year
_ = ok.grade('q4_2')
# **Question 4.3.** What's the title of the earliest movie in the dataset in 2015? You could just look this up from the output of the previous cell. Instead, write Python code to find out.
#
# *Hint:* Starting with `imdb2015_by_year`, extract the Title column to get an array, then use `item` to get its first item.
earliest_movie_title = ...
earliest_movie_title
_ = ok.grade('q4_3')
# **Question 4.4.** What's the title of the earliest movie in the dataset in 2019? Write python code to find out. Store the name of the movie in `earliest_movie_title_2019`.
# +
# Replace the ellipsis with your code below.
...
earliest_movie_title_2019 = ...
earliest_movie_title_2019
# -
_ = ok.grade('q4_4')
# **Optional Question** Let's compare the 10 most highly rated movies in `imdb2015` and `imdb2019`. What's added and what's removed? Also, one movie's name is updated; can you spot it? Write your code in the cell below, and replace the ellipsis with your answers in the cell below the next cell.
# Write your code here
...
# ...
# ## 5. Finding pieces of a dataset
# Suppose you're interested in movies from the 1940s. Sorting the table by year doesn't help you, because the 1940s are in the middle of the dataset.
#
# Instead, we use the table method `where`.
forties = imdb2015.where('Decade', are.equal_to(1940))
forties
# Ignore the syntax for the moment. Instead, try to read that line like this:
#
# > Assign the name **`forties`** to a table whose rows are the rows in the **`imdb2015`** table **`where`** the **`'Decade'`**s **`are` `equal` `to` `1940`**.
#
# **Question 5.1.** Compute the average rating of movies from the 1940s in `imdb2015`.
#
# *Hint:* The function `np.average` computes the average of an array of numbers.
# +
average_rating_in_forties = np.average(forties.column('Rating'))
average_rating_in_forties
imdb2015.column('Rating').mean()
# -
_ = ok.grade('q5_1')
# Now let's dive into the details a bit more. `where` takes 2 arguments:
#
# 1. The name of a column. `where` finds rows where that column's values meet some criterion.
# 2. Something that describes the criterion that the column needs to meet, called a predicate.
#
# To create our predicate, we called the function `are.equal_to` with the value we wanted, 1940. We'll see other predicates soon.
#
# `where` returns a table that's a copy of the original table, but with only the rows that meet the given predicate.
#
# **Question 5.2.** Create a table called `ninety_nine` containing the movies that came out in the year 1999 in `imdb2015`. Use `where`.
ninety_nine = ...
ninety_nine
_ = ok.grade('q5_2')
# So far we've only been finding where a column is *exactly* equal to a certain value. However, there are many other predicates. Here are a few:
#
# |Predicate|Example|Result|
# |-|-|-|
# |`are.equal_to`|`are.equal_to(50)`|Find rows with values equal to 50|
# |`are.not_equal_to`|`are.not_equal_to(50)`|Find rows with values not equal to 50|
# |`are.above`|`are.above(50)`|Find rows with values above (and not equal to) 50|
# |`are.above_or_equal_to`|`are.above_or_equal_to(50)`|Find rows with values above 50 or equal to 50|
# |`are.below`|`are.below(50)`|Find rows with values below 50|
# |`are.between`|`are.between(2, 10)`|Find rows with values above or equal to 2 and below 10|
#
#
# **Question 5.3.** Using `where` and one of the predicates from the table above, find all the movies with a rating higher than 8.5 in `imdb2015`. Put their data in a table called `really_highly_rated`.
# Note: `TableName.labels` will return a list of the names of all the columns in a Table.
really_highly_rated = ...
really_highly_rated
_ = ok.grade('q5_3')
# **Question 5.4.** Find the average rating for movies released in the 20th century and the average rating for movies released in the 21st century for the movies in `imdb2015`.
#
# *Hint*: Think of the steps you need to do (take the average, find the ratings, find movies released in 20th/21st centuries), and try to put them in an order that makes sense. Confused about the definition of a century? For example, 18th century includes 1700 up to 1799, but not 1800.
average_20th_century_rating = ...
average_21st_century_rating = ...
print("Average 20th century rating:", average_20th_century_rating)
print("Average 21st century rating:", average_21st_century_rating)
_ = ok.grade('q5_4')
# The property `num_rows` tells you how many rows are in a table. (A "property" is just a method that doesn't need to be called by adding parentheses.)
num_movies_in_dataset = imdb2015.num_rows
num_movies_in_dataset
# **Question 5.5.** Use `num_rows` (and arithmetic) to find the *proportion* of movies in `imdb2015` that were released in the 20th century, and the proportion from the 21st century.
#
# *Hint:* The *proportion* of movies released in the 20th century is the *number* of movies released in the 20th century, divided by the *total number* of movies.
proportion_in_20th_century = ...
proportion_in_21st_century = ...
print("Proportion in 20th century:", proportion_in_20th_century)
print("Proportion in 21st century:", proportion_in_21st_century)
_ = ok.grade('q5_5')
# **Question 5.6.** Here's a challenge: Find the number of movies that came out in *even* years in `imdb2015`.
#
# *Hint 1:* The operator `%` computes the remainder when dividing by a number. So `5 % 2` is 1 and `6 % 2` is 0. A number is even if the remainder is 0 when you divide by 2.
#
# *Hint 2:* `%` can be used on arrays, operating elementwise like `+` or `*`. So `make_array(5, 6, 7) % 2` is `array([1, 0, 1])`.
#
# *Hint 3:* Create a column called "Year Remainder" that's the remainder when each movie's release year is divided by 2. Make a copy of `imdb2015` that includes that column. Then use `where` to find rows where that new column is equal to 0. Then use `num_rows` to count the number of such rows.
# + for_assignment_type="student"
num_even_year_movies = ...
num_even_year_movies
# -
_ = ok.grade('q5_6')
# **Question 5.7.** Check out the `population` table from the introduction to this lab. Compute the year when the world population first went above 6 billion.
year_population_crossed_6_billion = ...
year_population_crossed_6_billion
_ = ok.grade('q5_7')
# ## 6. Miscellanea
# There are a few more table methods you'll need to fill out your toolbox. The first 3 have to do with manipulating the columns in a table.
#
# The table `farmers_markets.csv` contains data on farmers' markets in the United States. Each row represents one such market.
#
# **Question 6.1.** Load the dataset into a table. Call it `farmers_markets`.
farmers_markets = Table().read_table("farmers_markets.csv")
farmers_markets
_ = ok.grade('q6_1')
# You'll notice that it has a large number of columns in it!
#
# ### `num_columns`
#
# **Question 6.2.** The table property `num_columns` (example call: `tbl.num_columns`) produces the number of columns in a table. Use it to find the number of columns in our farmers' markets dataset.
num_farmers_markets_columns = ...
print("The table has", num_farmers_markets_columns, "columns in it!")
_ = ok.grade('q6_2')
# Most of the columns are about particular products -- whether the market sells tofu, pet food, etc. If we're not interested in that stuff, it just makes the table difficult to read. This comes up more than you might think.
#
# ### `select`
#
# In such situations, we can use the table method `select` to pare down the columns of a table. It takes any number of arguments. Each should be the name or index of a column in the table. It returns a new table with only those columns in it.
#
# For example, the value of `imdb2015.select("Year", "Decade")` is a table with only the years and decades of each movie in `imdb2015`.
#
# **Question 6.3.** Use `select` to create a table with only the name, city, state, latitude ('y'), and longitude ('x') of each market. Call that new table `farmers_markets_locations`.
farmers_markets_locations = ...
farmers_markets_locations
_ = ok.grade('q6_3')
# ### `select` is not `column`!
#
# The method `select` is **definitely not** the same as the method `column`.
#
# `farmers_markets.column('y')` is an *array* of the latitudes of all the markets. `farmers_markets.select('y')` is a table that happens to contain only 1 column, the latitudes of all the markets.
#
# **Question 6.4.** Below, we tried using the function `np.average` to find the average latitude ('y') and average longitude ('x') of the farmers' markets in the table, but we screwed something up. Run the cell to see the (somewhat inscrutable) error message that results from calling `np.average` on a table. Then, fix our code.
# + for_assignment_type="student"
average_latitude = np.average(farmers_markets.select('y'))
average_longitude = np.average(farmers_markets.select('x'))
print("The average of US farmers' markets' coordinates is located at (", average_latitude, ",", average_longitude, ")")
# -
_ = ok.grade('q6_4')
# ### `drop`
#
# `drop` serves the same purpose as `select`, but it takes away the columns you list instead of the ones you don't list, leaving all the rest of the columns.
#
# **Question 6.5.** Suppose you just didn't want the "FMID" or "updateTime" columns in `farmers_markets`. Create a table that's a copy of `farmers_markets` but doesn't include those columns. Call that table `farmers_markets_without_fmid`.
farmers_markets_without_fmid = ...
farmers_markets_without_fmid
_ = ok.grade('q6_5')
# #### `take`
# Let's find the 5 northernmost farmers' markets in the US. You already know how to sort by latitude ('y'), but we haven't seen how to get the first 5 rows of a table. That's what `take` is for.
#
# The table method `take` takes as its argument an array of numbers. Each number should be the index of a row in the table. It returns a new table with only those rows.
#
# Most often you'll want to use `take` in conjunction with `np.arange` to take the first few rows of a table.
#
# **Question 6.6.** Make a table of the 5 northernmost farmers' markets in `farmers_markets_locations`. Call it `northern_markets`. (It should include the same columns as `farmers_markets_locations`.
northern_markets = ...
northern_markets
_ = ok.grade('q6_6')
# **Question 6.7.** Make a table of the farmers' markets in Santa Barbara, California. (It should include the same columns as `farmers_markets_locations`.)
sb_markets = ...
sb_markets
_ = ok.grade('q6_7')
# Recognize any of them?
# ## 7. Summary
#
# For your reference, here's a table of all the functions and methods we saw in this lab.
#
# |Name|Example|Purpose|
# |-|-|-|
# |`Table`|`Table()`|Create an empty table, usually to extend with data|
# |`Table.read_table`|`Table.read_table("my_data.csv")`|Create a table from a data file|
# |`with_columns`|`tbl = Table().with_columns("N", np.arange(5), "2*N", np.arange(0, 10, 2))`|Create a copy of a table with more columns|
# |`column`|`tbl.column("N")`|Create an array containing the elements of a column|
# |`sort`|`tbl.sort("N")`|Create a copy of a table sorted by the values in a column|
# |`where`|`tbl.where("N", are.above(2))`|Create a copy of a table with only the rows that match some *predicate*|
# |`num_rows`|`tbl.num_rows`|Compute the number of rows in a table|
# |`num_columns`|`tbl.num_columns`|Compute the number of columns in a table|
# |`select`|`tbl.select("N")`|Create a copy of a table with only some of the columns|
# |`drop`|`tbl.drop("2*N")`|Create a copy of a table without some of the columns|
# |`take`|`tbl.take(np.arange(0, 6, 2))`|Create a copy of the table with only the rows whose indices are in the given array|
#
# <br/>
#
# Alright! You're finished with lab 3! Be sure to...
# - **run all the tests** (the next cell has a shortcut for that),
# - **Save and Checkpoint** from the `File` menu,
# - **run the last cell to submit your work**,
#
# For your convenience, you can run this cell to run all the tests at once!
import os
_ = [ok.grade(q[:-3]) for q in os.listdir("tests") if q.startswith('q')]
_ = ok.submit()
|
lab03/lab03.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/jacobpad/DS-Unit-2-Kaggle-Challenge/blob/master/module4-classification-metrics/LS_DS_224.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] colab_type="text" id="EZyiOteN16cD"
# Lambda School Data Science
#
# *Unit 2, Sprint 2, Module 4*
#
# ---
# + [markdown] colab_type="text" id="KMI2k-oBsS08"
# # Classification Metrics
#
# - get and interpret the **confusion matrix** for classification models
# - use classification metrics: **precision, recall**
# - understand the relationships between precision, recall, **thresholds, and predicted probabilities**, to help **make decisions and allocate budgets**
# - Get **ROC AUC** (Receiver Operating Characteristic, Area Under the Curve)
# + [markdown] colab_type="text" id="rU7RuVcjWdcp"
# ### Setup
#
# Run the code cell below. You can work locally (follow the [local setup instructions](https://lambdaschool.github.io/ds/unit2/local/)) or on Colab.
#
# Libraries
#
# - category_encoders
# - ipywidgets
# - matplotlib
# - numpy
# - pandas
# - scikit-learn
# - seaborn
# + colab_type="code" id="OpFoag9QoTgA" colab={}
# %%capture
import sys
# If you're on Colab:
if 'google.colab' in sys.modules:
DATA_PATH = 'https://raw.githubusercontent.com/LambdaSchool/DS-Unit-2-Kaggle-Challenge/master/data/'
# !pip install category_encoders==2.*
# If you're working locally:
else:
DATA_PATH = '../data/'
# + [markdown] colab_type="text" id="EfhziD2Wn_iO"
# # Get and interpret the confusion matrix for classification models
# + [markdown] id="sg1daUtcWAnN" colab_type="text"
# ## Overview
# + [markdown] colab_type="text" id="xZNCHldPn_iL"
# First, load the Tanzania Waterpumps data and fit a model. (This code isn't new, we've seen it all before.)
# + colab_type="code" id="t8Cjxzrwn_iL" outputId="c7f1fa9e-5f65-4092-c2dc-5ef432e49c56" colab={"base_uri": "https://localhost:8080/", "height": 34}
# %matplotlib inline
import category_encoders as ce
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn.impute import SimpleImputer
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
from sklearn.ensemble import RandomForestClassifier
def wrangle(X):
"""Wrangles train, validate, and test sets in the same way"""
X = X.copy()
# Convert date_recorded to datetime
X['date_recorded'] = pd.to_datetime(X['date_recorded'], infer_datetime_format=True)
# Extract components from date_recorded, then drop the original column
X['year_recorded'] = X['date_recorded'].dt.year
X['month_recorded'] = X['date_recorded'].dt.month
X['day_recorded'] = X['date_recorded'].dt.day
X = X.drop(columns='date_recorded')
# Engineer feature: how many years from construction_year to date_recorded
X['years'] = X['year_recorded'] - X['construction_year']
# Drop recorded_by (never varies) and id (always varies, random)
unusable_variance = ['recorded_by', 'id']
X = X.drop(columns=unusable_variance)
# Drop duplicate columns
duplicate_columns = ['quantity_group']
X = X.drop(columns=duplicate_columns)
# About 3% of the time, latitude has small values near zero,
# outside Tanzania, so we'll treat these like null values
X['latitude'] = X['latitude'].replace(-2e-08, np.nan)
# When columns have zeros and shouldn't, they are like null values
cols_with_zeros = ['construction_year', 'longitude', 'latitude', 'gps_height', 'population']
for col in cols_with_zeros:
X[col] = X[col].replace(0, np.nan)
return X
# Merge train_features.csv & train_labels.csv
train = pd.merge(pd.read_csv(DATA_PATH+'waterpumps/train_features.csv'),
pd.read_csv(DATA_PATH+'waterpumps/train_labels.csv'))
# Read test_features.csv & sample_submission.csv
test = pd.read_csv(DATA_PATH+'waterpumps/test_features.csv')
sample_submission = pd.read_csv(DATA_PATH+'waterpumps/sample_submission.csv')
# Split train into train & val. Make val the same size as test.
target = 'status_group'
train, val = train_test_split(train, test_size=len(test),
stratify=train[target], random_state=42)
# Wrangle train, validate, and test sets in the same way
train = wrangle(train)
val = wrangle(val)
test = wrangle(test)
# Arrange data into X features matrix and y target vector
X_train = train.drop(columns=target)
y_train = train[target]
X_val = val.drop(columns=target)
y_val = val[target]
X_test = test
# Make pipeline!
pipeline = make_pipeline(
ce.OrdinalEncoder(),
SimpleImputer(strategy='mean'),
RandomForestClassifier(n_estimators=100, random_state=42, n_jobs=-1)
)
# Fit on train, score on val
pipeline.fit(X_train, y_train)
y_pred = pipeline.predict(X_val)
print('Validation Accuracy', accuracy_score(y_val, y_pred))
# + [markdown] id="nMbLXEKHWAnU" colab_type="text"
# ## Follow Along
#
# Scikit-learn added a [**`plot_confusion_matrix`**](https://scikit-learn.org/stable/modules/generated/sklearn.metrics.plot_confusion_matrix.html) function in version 0.22!
# + colab_type="code" id="2MSWehj9n_iO" outputId="1cfc5d0a-eefc-47f7-9279-7d82f1829038" colab={"base_uri": "https://localhost:8080/", "height": 34}
# Check scikit-learn version
import sklearn
sklearn.__version__
# + id="K3jhDMw5X6Px" colab_type="code" colab={}
from sklearn.metrics import plot_confusion_matrix
# + id="8tci-hTQX9XZ" colab_type="code" outputId="ab9d360c-0618-4c49-e999-0322e1c94c82" colab={"base_uri": "https://localhost:8080/", "height": 389}
plot_confusion_matrix(pipeline, X_val, y_val, values_format='.0f', xticks_rotation='vertical');
# + [markdown] colab_type="text" id="fP6FGBGUn_iQ"
# #### How many correct predictions were made?
# + colab_type="code" id="wRSaYRPWn_iR" outputId="caa788d4-ee13-4313-f550-aca3c05dab74" colab={"base_uri": "https://localhost:8080/", "height": 34}
correct_predictions = 7005 + 332 + 4351
correct_predictions
# + [markdown] colab_type="text" id="-q-3R7Ean_iT"
# #### How many total predictions were made?
# + colab_type="code" id="vLAQL05fn_iT" outputId="a6ba4a91-4514-4e84-9f75-c46b366546bd" colab={"base_uri": "https://localhost:8080/", "height": 34}
total_predictions = 7005 + 171 + 622 + 555 + 332 + 156 + 1098 + 68 + 4351
total_predictions
# + [markdown] colab_type="text" id="K1yQ_jYPn_iV"
# #### What was the classification accuracy?
# + colab_type="code" id="fskAC6SYn_iW" outputId="a49413d2-8323-4511-f0cf-28a55ccfcce4" colab={"base_uri": "https://localhost:8080/", "height": 34}
correct_predictions / total_predictions
# + id="7MX2-0djcBxI" colab_type="code" outputId="5e9a1a8e-8774-4a79-8428-882cec7e035d" colab={"base_uri": "https://localhost:8080/", "height": 34}
accuracy_score(y_val, y_pred)
# + id="eFEmUPTXcEeY" colab_type="code" outputId="d32518c7-4fd2-4e3b-cadf-3f0b2042ecca" colab={"base_uri": "https://localhost:8080/", "height": 34}
sum(y_pred == y_val) / len(y_pred)
# + [markdown] colab_type="text" id="EqFgEm3tn_iY"
# # Use classification metrics: precision, recall
# + [markdown] id="aN9ZsaqKWAni" colab_type="text"
# ## Overview
#
# [Scikit-Learn User Guide — Classification Report](https://scikit-learn.org/stable/modules/model_evaluation.html#classification-report)
# + colab_type="code" id="mGv7OLL4n_iY" outputId="9875f813-f6b6-4300-8fb5-92d966425456" colab={"base_uri": "https://localhost:8080/", "height": 185}
from sklearn.metrics import classification_report
print(classification_report(y_val, y_pred))
# + [markdown] colab_type="text" id="Z1U7HdC6n_ia"
# #### Wikipedia, [Precision and recall](https://en.wikipedia.org/wiki/Precision_and_recall)
#
# > Both precision and recall are based on an understanding and measure of relevance.
#
# > Suppose a computer program for recognizing dogs in photographs identifies 8 dogs in a picture containing 12 dogs and some cats. Of the 8 identified as dogs, 5 actually are dogs (true positives), while the rest are cats (false positives). The program's precision is 5/8 while its recall is 5/12.
#
# > High precision means that an algorithm returned substantially more relevant results than irrelevant ones, while high recall means that an algorithm returned most of the relevant results.
#
# <img src="https://upload.wikimedia.org/wikipedia/commons/thumb/2/26/Precisionrecall.svg/700px-Precisionrecall.svg.png" width="400">
# + [markdown] id="dF_Oj0kTWAnm" colab_type="text"
# ## Follow Along
# + [markdown] colab_type="text" id="50R-Xhwdn_ie"
# #### [We can get precision & recall from the confusion matrix](https://en.wikipedia.org/wiki/Precision_and_recall#Definition_(classification_context))
# + colab_type="code" id="eIta6Vwsn_if" outputId="588fd8f3-b73c-4ff7-b210-7a02132ba79a" colab={"base_uri": "https://localhost:8080/", "height": 389}
cm = plot_confusion_matrix(pipeline, X_val, y_val, values_format='.0f', xticks_rotation='vertical')
cm;
# + [markdown] colab_type="text" id="iY2rfzA4n_ih"
# #### How many correct predictions of "non functional"?
# + colab_type="code" id="O-anLkCin_ii" colab={}
correct_predictions_nonfunctional = 4351
# + [markdown] colab_type="text" id="pYM6f99cn_ij"
# #### How many total predictions of "non functional"?
# + colab_type="code" id="_qCiA8j2n_ik" colab={}
total_predictions_nonfunctional = 4351 + 156 + 622
# + [markdown] colab_type="text" id="mXNuZ_Rnn_il"
# #### What's the precision for "non functional"?
# + colab_type="code" id="X1f7VsyXn_im" outputId="d61126a5-57b1-4956-a432-a7a9bb41c11c" colab={"base_uri": "https://localhost:8080/", "height": 34}
correct_predictions_nonfunctional / total_predictions_nonfunctional
# + id="c8XrxddYj9ob" colab_type="code" outputId="1aa07b0e-6af9-4b44-a861-5462f47aadc6" colab={"base_uri": "https://localhost:8080/", "height": 185}
print(classification_report(y_val, y_pred))
# + [markdown] colab_type="text" id="ci4QguAkn_in"
# #### How many actual "non functional" waterpumps?
# + colab_type="code" id="FlqxNhlYn_io" colab={}
actual_nonfunctional = 1098 + 68 + 4351
# + [markdown] colab_type="text" id="9IY-vC-hn_iq"
# #### What's the recall for "non functional"?
# + colab_type="code" id="4U3v8lPP4KbP" outputId="1033af92-cca5-48da-dc9e-737ef2fd2ce6" colab={"base_uri": "https://localhost:8080/", "height": 34}
correct_predictions_nonfunctional / actual_nonfunctional
# + [markdown] colab_type="text" id="ObVED_ugn_is"
# # Understand the relationships between precision, recall, thresholds, and predicted probabilities, to help make decisions and allocate budgets
# + [markdown] id="QjCddOORWAn5" colab_type="text"
# ## Overview
# + [markdown] colab_type="text" id="kBcQQJ2kn_is"
# ### Imagine this scenario...
#
# Suppose there are over 14,000 waterpumps that you _do_ have some information about, but you _don't_ know whether they are currently functional, or functional but need repair, or non-functional.
# + colab_type="code" id="jEEy86CHn_it" outputId="d0a9dcd6-2104-4cf6-82be-a65c11c12431" colab={"base_uri": "https://localhost:8080/", "height": 34}
len(test)
# + [markdown] colab_type="text" id="3az2llAAn_iu"
# **You have the time and resources to go to just 2,000 waterpumps for proactive maintenance.** You want to predict, which 2,000 are most likely non-functional or in need of repair, to help you triage and prioritize your waterpump inspections.
#
# You have historical inspection data for over 59,000 other waterpumps, which you'll use to fit your predictive model.
# + colab_type="code" id="pEWc2zt2n_iv" outputId="37194161-f5c1-4654-edd3-d20b50186959" colab={"base_uri": "https://localhost:8080/", "height": 34}
len(train) + len(val)
# + [markdown] colab_type="text" id="L2LiGJLin_ix"
# Based on this historical data, if you randomly chose waterpumps to inspect, then about 46% of the waterpumps would need repairs, and 54% would not need repairs.
# + colab_type="code" id="JliDXTp5n_iy" outputId="75fe6d90-46b3-4e1c-c344-8b4d2758c8f7" colab={"base_uri": "https://localhost:8080/", "height": 84}
y_train.value_counts(normalize=True)
# + colab_type="code" id="0dP7fjQJeQEX" outputId="b449498c-55bb-46ef-cff5-3cd1b80ac69b" colab={"base_uri": "https://localhost:8080/", "height": 34}
2000 * 0.46
# + [markdown] colab_type="text" id="dLnJ7Fnan_i1"
# **Can you do better than random at prioritizing inspections?**
# + [markdown] colab_type="text" id="sIh2Xj8fn_i3"
# In this scenario, we should define our target differently. We want to identify which waterpumps are non-functional _or_ are functional but needs repair:
# + colab_type="code" id="7naqusI0n_i4" outputId="46a57f0c-c27c-46e6-c5c6-1ba910bf98b5" colab={"base_uri": "https://localhost:8080/", "height": 67}
y_train = y_train != 'functional'
y_val = y_val != 'functional'
y_train.value_counts(normalize=True)
# + [markdown] colab_type="text" id="P1UR1t8Zn_i6"
# We already made our validation set the same size as our test set.
# + colab_type="code" id="CHHIplB7n_i8" outputId="60c4c0ec-cb00-4e97-f03e-381e030e7ce9" colab={"base_uri": "https://localhost:8080/", "height": 34}
len(val) == len(test)
# + [markdown] colab_type="text" id="g41DA70rn_i9"
# We can refit our model, using the redefined target.
#
# Then make predictions for the validation set.
# + colab_type="code" id="VXL0LaXQn_i-" colab={}
pipeline.fit(X_train, y_train)
y_pred = pipeline.predict(X_val)
# + [markdown] id="ZBFoVpVFWAoN" colab_type="text"
# ## Follow Along
# + [markdown] colab_type="text" id="qISPzM43n_jA"
# #### Look at the confusion matrix:
# + colab_type="code" id="y72fakpmn_jB" outputId="3071a6ae-1a6a-44be-ceeb-c2141bd1df2f" colab={"base_uri": "https://localhost:8080/", "height": 295}
plot_confusion_matrix(pipeline, X_val, y_val, values_format='.0f', xticks_rotation='vertical');
# + [markdown] colab_type="text" id="M30BXR6Rn_jC"
# #### How many total predictions of "True" ("non functional" or "functional needs repair") ?
# + colab_type="code" id="4IeTJFo8n_jD" outputId="62e344d7-3c44-4409-aa0a-a13b0282ff6c" colab={"base_uri": "https://localhost:8080/", "height": 34}
5032 + 977
# + [markdown] colab_type="text" id="1aZSdskSn_jF"
# ### We don't have "budget" to take action on all these predictions
#
# - But we can get predicted probabilities, to rank the predictions.
# - Then change the threshold, to change the number of positive predictions, based on our budget.
# + [markdown] colab_type="text" id="rXkfXDDZn_jF"
# ### Get predicted probabilities and plot the distribution
# + colab_type="code" id="jwfe7j7W_jTp" outputId="ec448602-6851-40f6-8efa-67f4f1f8152b" colab={"base_uri": "https://localhost:8080/", "height": 34}
# Discrete predictions look like this...
pipeline.predict(X_val)
# + id="D9nblZTlq5hk" colab_type="code" outputId="2c1b2052-1424-4561-9644-c3a4eca848a7" colab={"base_uri": "https://localhost:8080/", "height": 134}
# Predicted probabilities look like this...
pipeline.predict_proba(X_val)
# + id="l8GwYmqPrq9W" colab_type="code" outputId="b966b7cb-0459-49c7-b133-1794f651b7c7" colab={"base_uri": "https://localhost:8080/", "height": 34}
# Predicted probabilities *for the positive class* ...
pipeline.predict_proba(X_val)[:, 1]
# + id="_-ibudaysEYW" colab_type="code" outputId="b8533823-add5-47f4-8eee-c5e726636cd5" colab={"base_uri": "https://localhost:8080/", "height": 34}
# Make predicted probabilities into discrete predictions,
# using a "threshold"
threshold = 0.50
pipeline.predict_proba(X_val)[:, 1] > threshold
# + id="KMqMOIkasdre" colab_type="code" outputId="29d11e20-f9a9-4dc4-dc5c-de9fff06cca7" colab={"base_uri": "https://localhost:8080/", "height": 265}
import seaborn as sns
y_pred_proba = pipeline.predict_proba(X_val)[:, 1]
sns.distplot(y_pred_proba);
# + [markdown] colab_type="text" id="eD6pRFKOn_jH"
# ### Change the threshold
# + id="3UKX9vygtf0Q" colab_type="code" colab={}
y_pred_proba = pipeline.predict_proba(X_val)[:, 1]
# + colab_type="code" id="SjOhH0BMB55A" outputId="0e1c878b-e171-40e3-9291-cfde1939c5d9" colab={"base_uri": "https://localhost:8080/", "height": 315}
threshold = 0.92
y_pred = y_pred_proba > threshold
ax = sns.distplot(y_pred_proba)
ax.axvline(threshold, color='red')
pd.Series(y_pred).value_counts()
# + id="N_q8Ywustw1l" colab_type="code" outputId="4f96ffb3-b41d-4d0f-d088-090109631dd2" colab={"base_uri": "https://localhost:8080/", "height": 696, "referenced_widgets": ["63da0508b8144031b11b06fd98f4331d", "19806b30f4aa46129fe7c343405e5315", "5bbfff5596c44df3b991a0e106b4e9d2", "2a3856c1cc834ef589d679e23e8b4cdd", "65d251225a2d4481be01f34b64d97f79", "c5bcc06b823b48e3bb8d8a025a40e712"]}
from ipywidgets import interact, fixed
import seaborn as sns
from sklearn.metrics import confusion_matrix
from sklearn.utils.multiclass import unique_labels
def my_confusion_matrix(y_true, y_pred):
labels = unique_labels(y_true)
columns = [f'Predicted {label}' for label in labels]
index = [f'Actual {label}' for label in labels]
table = pd.DataFrame(confusion_matrix(y_true, y_pred),
columns=columns, index=index)
return sns.heatmap(table, annot=True, fmt='d', cmap='viridis')
def set_threshold(y_true, y_pred_proba, threshold=0.5):
y_pred = y_pred_proba > threshold
ax = sns.distplot(y_pred_proba)
ax.axvline(threshold, color='red')
plt.show()
print(classification_report(y_true, y_pred))
my_confusion_matrix(y_true, y_pred)
interact(set_threshold,
y_true=fixed(y_val),
y_pred_proba=fixed(y_pred_proba),
threshold=(0, 1, 0.02));
# + [markdown] id="lDGCJz3cWAoZ" colab_type="text"
# ### Or, get exactly 2,000 positive predictions
# + [markdown] id="DXZ9hEhTWAoa" colab_type="text"
# Identify the 2,000 waterpumps in the validation set with highest predicted probabilities.
# + id="IZ0YgYTjWAob" colab_type="code" outputId="783001ca-fd31-4ea4-bb03-10c18a69bd87" colab={"base_uri": "https://localhost:8080/", "height": 402}
results = pd.DataFrame({'y_val': y_val, 'y_pred_proba': y_pred_proba})
results
# + id="DTbOVIGxvPh1" colab_type="code" colab={}
top2000 = results.sort_values(by='y_pred_proba', ascending=False)[:2000]
# + [markdown] id="mkyCf4_5WAod" colab_type="text"
# Most of these top 2,000 waterpumps will be relevant recommendations, meaning `y_val==True`, meaning the waterpump is non-functional or needs repairs.
#
# Some of these top 2,000 waterpumps will be irrelevant recommendations, meaning `y_val==False`, meaning the waterpump is functional and does not need repairs.
#
# Let's look at a random sample of 50 out of these top 2,000:
# + id="SC3pAOcsWAod" colab_type="code" outputId="144e1ca0-b68f-4b3d-87bc-37e7f78e239b" colab={"base_uri": "https://localhost:8080/", "height": 1000}
top2000.sample(n=50)
# + [markdown] id="RwnOsDcOWAoh" colab_type="text"
# So how many of our recommendations were relevant? ...
# + id="fjZIaSg7WAoh" colab_type="code" outputId="92cd849c-47bf-436c-ec21-0d0e293bfa20" colab={"base_uri": "https://localhost:8080/", "height": 50}
trips = 2000
print(f'Basseline: {trips * 0.46} waterpump repairs in {trips} trips')
relevant_recommendations = top2000['y_val'].sum()
print(f'With model: Predict {relevant_recommendations} waterpump repairs in {trips} trips')
# + [markdown] id="jhOpDn7bWAoj" colab_type="text"
# What's the precision for this subset of 2,000 predictions?
# + id="L30Z8-9YWAok" colab_type="code" outputId="28e508d0-b67c-42f5-f3c0-e27cadd871ab" colab={"base_uri": "https://localhost:8080/", "height": 34}
precision_at_k_2000 = relevant_recommendations / trips
print('Precision @ k=2000', precision_at_k_2000)
# + [markdown] colab_type="text" id="top80m_Gn_jI"
# ### In this scenario ...
#
# Accuracy _isn't_ the best metric!
#
# Instead, change the threshold, to change the number of positive predictions, based on the budget. (You have the time and resources to go to just 2,000 waterpumps for proactive maintenance.)
#
# Then, evaluate with the precision for "non functional"/"functional needs repair".
#
# This is conceptually like **Precision@K**, where k=2,000.
#
# Read more here: [Recall and Precision at k for Recommender Systems: Detailed Explanation with examples](https://medium.com/@m_n_malaeb/recall-and-precision-at-k-for-recommender-systems-618483226c54)
#
# > Precision at k is the proportion of recommended items in the top-k set that are relevant
#
# > Mathematically precision@k is defined as: `Precision@k = (# of recommended items @k that are relevant) / (# of recommended items @k)`
#
# > In the context of recommendation systems we are most likely interested in recommending top-N items to the user. So it makes more sense to compute precision and recall metrics in the first N items instead of all the items. Thus the notion of precision and recall at k where k is a user definable integer that is set by the user to match the top-N recommendations objective.
#
# We asked, can you do better than random at prioritizing inspections?
#
# If we had randomly chosen waterpumps to inspect, we estimate that only 920 waterpumps would be repaired after 2,000 maintenance visits. (46%)
#
# But using our predictive model, in the validation set, we succesfully identified over 1,900 waterpumps in need of repair!
#
# So we will use this predictive model with the dataset of over 14,000 waterpumps that we _do_ have some information about, but we _don't_ know whether they are currently functional, or functional but need repair, or non-functional.
#
# We will predict which 2,000 are most likely non-functional or in need of repair.
#
# We estimate that approximately 1,900 waterpumps will be repaired after these 2,000 maintenance visits.
#
# So we're confident that our predictive model will help triage and prioritize waterpump inspections.
# + [markdown] id="jxKAvCAtWAon" colab_type="text"
# ### But ...
#
# This metric (~1,900 waterpumps repaired after 2,000 maintenance visits) is specific for _one_ classification problem and _one_ possible trade-off.
#
# Can we get an evaluation metric that is generic for _all_ classification problems and _all_ possible trade-offs?
#
# Yes — the most common such metric is **ROC AUC.**
# + [markdown] id="TQ8SNJ1aWAon" colab_type="text"
# ## Get ROC AUC (Receiver Operating Characteristic, Area Under the Curve)
#
# [Wikipedia explains,](https://en.wikipedia.org/wiki/Receiver_operating_characteristic) "A receiver operating characteristic curve, or ROC curve, is a graphical plot that illustrates the diagnostic ability of a binary classifier system as its discrimination threshold is varied. **The ROC curve is created by plotting the true positive rate (TPR) against the false positive rate (FPR) at various threshold settings.**"
#
# ROC AUC is the area under the ROC curve. [It can be interpreted](https://stats.stackexchange.com/questions/132777/what-does-auc-stand-for-and-what-is-it) as "the expectation that a uniformly drawn random positive is ranked before a uniformly drawn random negative."
#
# ROC AUC measures **how well a classifier ranks predicted probabilities.** So, when you get your classifier’s ROC AUC score, you need to **use predicted probabilities, not discrete predictions.**
#
# ROC AUC ranges **from 0 to 1.** Higher is better. A naive majority class **baseline** will have an ROC AUC score of **0.5.**
#
# #### Scikit-Learn docs
# - [User Guide: Receiver operating characteristic (ROC)](https://scikit-learn.org/stable/modules/model_evaluation.html#receiver-operating-characteristic-roc)
# - [sklearn.metrics.roc_curve](https://scikit-learn.org/stable/modules/generated/sklearn.metrics.roc_curve.html)
# - [sklearn.metrics.roc_auc_score](https://scikit-learn.org/stable/modules/generated/sklearn.metrics.roc_auc_score.html)
#
# #### More links
# - [ROC curves and Area Under the Curve explained](https://www.dataschool.io/roc-curves-and-auc-explained/)
# - [The philosophical argument for using ROC curves](https://lukeoakdenrayner.wordpress.com/2018/01/07/the-philosophical-argument-for-using-roc-curves/)
# + id="bRS-JTHNWAoo" colab_type="code" colab={}
# "The ROC curve is created by plotting the true positive rate (TPR)
# against the false positive rate (FPR)
# at various threshold settings."
# Use scikit-learn to calculate TPR & FPR at various thresholds
from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y_val, y_pred_proba)
# + id="vDZysu2xWAos" colab_type="code" outputId="b2461f33-520b-4be7-dee8-7b4ac54d267f" colab={"base_uri": "https://localhost:8080/", "height": 402}
# See the results in a table
pd.DataFrame({
'False Positive Rate': fpr,
'True Positive Rate': tpr,
'Threshold': thresholds
})
# + id="fBxgkKKXWAov" colab_type="code" outputId="8a829c2f-43c0-419e-bab4-421b6df05004" colab={"base_uri": "https://localhost:8080/", "height": 295}
# See the results on a plot.
# This is the "Receiver Operating Characteristic" curve
plt.scatter(fpr, tpr)
plt.title('ROC curve')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate');
# + id="MpRRVxZNWAox" colab_type="code" outputId="432eb842-0a57-4d4d-d0a6-964cc6fd32db" colab={"base_uri": "https://localhost:8080/", "height": 34}
# Use scikit-learn to calculate the area under the curve.
from sklearn.metrics import roc_auc_score
roc_auc_score(y_val, y_pred_proba)
# + [markdown] id="8Qr_hoKHWAo0" colab_type="text"
# **Recap:** ROC AUC measures how well a classifier ranks predicted probabilities. So, when you get your classifier’s ROC AUC score, you need to use predicted probabilities, not discrete predictions.
#
# Your code may look something like this:
#
# ```python
# from sklearn.metrics import roc_auc_score
# y_pred_proba = model.predict_proba(X_test_transformed)[:, -1] # Probability for last class
# print('Test ROC AUC:', roc_auc_score(y_test, y_pred_proba))
# ```
#
# ROC AUC ranges from 0 to 1. Higher is better. A naive majority class baseline will have an ROC AUC score of 0.5.
|
module4-classification-metrics/LS_DS_224.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %load_ext autoreload
# %autoreload 2
# %cd /home/aditya/git/kaggle_pneumonia
# %env PROJECT_PATH = /home/aditya/git/kaggle_pneumonia
# %matplotlib inline
import seaborn as sns
import pandas as pd
import numpy as np
import pydicom
from PIL import Image
import multiprocessing as mp
from tqdm import tqdm_notebook as tqdm
# +
from __future__ import print_function, division
import os
import torch
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from torch.utils.data import Dataset, DataLoader
from torchvision import transforms, utils
# Ignore warnings
import warnings
warnings.filterwarnings("ignore")
# -
import torch.nn as nn
import torch.nn.functional as F
# +
import torch.optim as optim
import torchvision
from sklearn.model_selection import train_test_split
from utils.envs import *
from utils.data_load import *
from utils.lr_finder import lr_plot, lr_find
from utils.common import get_batch_info
from utils.checkpoint import save_checkpoint, load_cp_model, load_cp_optim
from utils.logger import logger
from model.arch.header import Header
from model.arch.pneunetv1 import PneuNetv1
from model.dataset import Single_Pneumonia_Dataset, Single_Pneumonia_Dataset_Test
from model.criterion import LabelBoundBoxCriterion
from model.train import train_step, fit_model
from model.validation import validate_model
from model.test import predict_model
from model.optim import CLR
# -
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
train_label_df = pd.read_csv(train_label_repo)
train_label_df['area'] = train_label_df.width * train_label_df.height
single_label_df = train_label_df.sort_values('area', ascending = False).drop_duplicates('patientId').sort_index().reset_index(drop = True).copy()
single_label_df.fillna(0, inplace = True)
train_idx = np.arange(len(single_label_df))
dev_idx, val_idx = train_test_split(train_idx, test_size = 0.20)
dev_df = single_label_df.iloc[dev_idx,:].reset_index(drop = True)
val_df = single_label_df.iloc[val_idx,:].reset_index(drop = True)
dev_dataset = Single_Pneumonia_Dataset(dev_df, train_dcm_path, device)
val_dataset = Single_Pneumonia_Dataset(val_df, train_dcm_path, device)
test_dataset = Single_Pneumonia_Dataset_Test(test_dcm_path, device)
dev_dataloader = DataLoader(dev_dataset, batch_size = 32, shuffle = True)
val_dataloader = DataLoader(val_dataset, batch_size = 32)
test_dataloader = DataLoader(test_dataset, batch_size = 32)
preload_model = torchvision.models.densenet121(pretrained=True).to(device)
header_model = Header(1024, 5, [1000, 1000, 128], 0.5).to(device)
n_epoch = 51
model = PneuNetv1(preload_model, header_model).to(device)
optimizer = optim.Adam(model.parameters(), lr=0.0001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0, amsgrad=False)
criterion = LabelBoundBoxCriterion(alpha = 0.5).to(device)
n_obs, batch_size, n_batch_per_epoch = get_batch_info(dev_dataloader)
clr = CLR(optimizer, n_epoch, n_batch_per_epoch, 0.1, 1., 0.95, 0.85, 2)
callbacks = [clr]
# +
#lrfind_model, lrfind_callbacks = lr_find(model, val_dataloader, criterion, min_lr = 1e-2, max_lr = 1)
#lr_plot(lrfind_callbacks[0], lrfind_callbacks[1])
# -
model, callbacks = fit_model(model = model, n_epoch = n_epoch, dev_dataloader = dev_dataloader, optimizer = optimizer, criterion = criterion, callbacks = callbacks, val_dataloader = val_dataloader)
# +
#save_checkpoint(0, model, optimizer, True)
#load_cp_model(model ,'/home/aditya/git/kaggle_pneumonia/output/model_checkpoint/md_model.pth')
#load_cp_optim(optimizer, '/home/aditya/git/kaggle_pneumonia/output/model_checkpoint/md_optim.pth')
# -
validate_model(model, criterion, val_dataloader)
df_predict = predict_model(model, test_dataloader)
df_predict
|
notebooks/dev_notebooks/run_notebook.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: geo-sprint
# language: python
# name: geo-sprint
# ---
# # Horizontally-layered media ray-tracing
#
# 2D traveltimes from 1D model.
# Computations are based on the offset-traveltime parametric equations:
# $$ \Large
# \begin{cases}
# x = - \sum_{i=1}^{N} z_i \frac{d q_i}{dp} \\
# t = \sum_{i=1}^{N} x_i p + z_i q_i
# \end{cases}
# $$
# where $x,t$ is the one-way offset-traveltime pair for a stack of $N$ layers for a given horizontal slowness $p$,
# $\mathbf{p_i} = (p,q_i)$ is the slowness vector in $i$-th layer,
# $z_i$ is the thickness of the $i$-th layer.
#
# Vertical slowness in $i$-th layer is given by
# $$
# q_i = \sqrt{\frac{1}{v_i^2} - p^2},
# $$
# where $v_i$ is the wave velocity in $i$-th layer. Choosing $v_p$ or $v_s$, one get the corresponding traveltimes.
#
# In order to get the converted waves, down-going ray is that of the P-wave, and up-going is that of the S-wave. Snell's law is honored by keeping $p$ constant for a given ray.
#
# TODO:
# 1. Get reflectivities implemented (RT-coefficients at each interface)
# 2. Geometrical spreading
# 3. Convolution with a wavelet to get a synthetic shot gather
# 4. Implemnt post-critical reflections
import bruges as b
import numpy as np
import matplotlib as mlp
import matplotlib.pyplot as plt
import scipy.interpolate as scpi
# %matplotlib inline
def vertical_slowness(p, v):
svec = np.tile(1 / v**2,(p.size,1)).T
pvec = np.tile(- p**2,(v.size,1))
q = np.sqrt(svec + pvec)
dq = - p * (q)**(-1)
return q, dq
def max_slowness(v):
p = 1/np.max(v)
return p
def traveltimes(vp, vs, dz_layers, x_rec, n_iter = 3):
n_offsets = x_rec.size
X = np.zeros((vp.size,x_rec.size))
Xi = np.zeros((vp.size,x_rec.size))
T = np.zeros((vp.size,x_rec.size))
Ti = np.zeros((vp.size,x_rec.size))
XPS = np.zeros((vp.size,x_rec.size))
TPS = np.zeros((vp.size,x_rec.size))
XPSi = np.zeros((vp.size,x_rec.size))
TPSi = np.zeros((vp.size,x_rec.size))
for i in range(vp.size):
vpi = vp[:i+1]
vsi = vs[:i+1]
dzi = dz_layers[:i+1]
pmax = max_slowness(vpi) * .9999
pvec = np.linspace(0,pmax,n_offsets)
for j in range(n_iter):
qA, dqA = vertical_slowness(pvec,vpi)
# P-wave
x = - (dzi * dqA.T).T
t = x * pvec + (qA.T * dzi).T
x_total = 2* np.sum(x, axis=0)
t_total = 2* np.sum(t, axis=0)
# PS-wave
qAS, dqAS = vertical_slowness(pvec,vsi)
xS = - (dzi * dqAS.T).T
tS = xS * pvec + (qAS.T * dzi).T
xPS_total = x_total/2 + np.sum(xS, axis=0)
tPS_total = t_total/2 + np.sum(tS, axis=0)
x_reg = np.linspace(0,np.max(x_total),n_offsets)
xPS_reg = np.linspace(0,np.max(xPS_total),n_offsets)
pvec = scpi.interp1d(x_total, pvec, kind='slinear')(x_reg)
if np.max(x_rec) <= np.max(x_reg) and np.max(x_rec) <= np.max(xPS_reg):
tint = scpi.interp1d(x_reg, t_total, kind='cubic')(x_rec)
tPSint = scpi.interp1d(xPS_total, tPS_total, kind='cubic')(x_rec)
xi = x_rec;
xPSi = x_rec;
elif np.max(x_rec) < np.max(x_reg) and np.max(x_rec) > np.max(xPS_reg):
print("maximum PS offset is smaller than desired")
tint = scpi.interp1d(x_reg, t_total, kind='cubic')(x_rec)
tPSint = scpi.interp1d(xPS_total, tPS_total, kind='cubic')(xPS_reg)
xi = x_rec;
xPSi = xPS_reg;
elif np.max(x_rec) > np.max(x_reg) and np.max(x_rec) > np.max(xPS_reg):
print("maximum PP and PS offsets are smaller than desired")
tint = scpi.interp1d(x_reg, t_total, kind='cubic')(x_reg)
tPSint = scpi.interp1d(xPS_total, tPS_total, kind='cubic')(xPS_reg)
xi = x_reg;
xPSi = xPS_reg;
X[i,:] = x_reg
T[i,:] = t_total
Xi[i,:] = xi
Ti[i,:] = tint
XPS[i,:] = xPS_total
TPS[i,:] = tPS_total
XPSi[i,:] = xPSi
TPSi[i,:] = tPSint
return X, T, Xi, Ti, XPS, TPS, XPSi, TPSi
# arrays of interval velocities and density
vp = np.array([1600, 2000, 2500, 2400, 2600, 2500])
vs = np.array([400, 1000, 1250, 1400, 2000, 1900])
#rho = np.array([1200, 2300, 2100, 2500, 3000, 3600])
dz = (.75 * np.random.random_sample((vp.size,)) + .25) * 1000
z_total = np.sum(dz)
x_rec = np.arange(0,z_total*4,25)
x, t, xi, ti, xPS, tPS, xPSi, tPSi = traveltimes(vp, vs, dz, x_rec)
# +
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 5))
ax1.plot(x.T,t.T,'o',xi.T,ti.T,'.')
ax1.set_xlim(0,np.max(x_rec))
ax1.set_ylim(0,np.max(ti)*1.1)
ax1.set_title('PP reflected waves traveltimes')
ax1.set_xlabel('offset (m)')
ax1.set_ylabel('time (s)')
ax1.grid(True)
ax2.plot(xPS.T,tPS.T,'o',xPSi.T,tPSi.T,'.')
ax2.set_xlim(0,np.max(x_rec))
ax2.set_ylim(0,np.max(tPSi)*1.1)
ax2.set_title('PS converted waves traveltimes')
ax2.set_xlabel('offset (m)')
ax2.set_ylabel('time (s)')
ax2.grid(True)
# -
|
dev/Ray-tracing.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: conda_python3
# language: python
# name: conda_python3
# ---
# ## Inside Account A
# This account demonstrates how to access feature groups owned by Account B & C from within Account A. <br>
# <b>Note:</b> Run this notebook, if you had allowed this access by granting ACLs to Account A when creating feature groups in Account B and C. Notebooks x and y grant ACLs, ensure they are run.
# #### Imports
import awswrangler as wr
import boto3
# #### Essentials
region = boto3.Session().region_name
s3_client = boto3.client('s3', region_name=region)
bucket = 'sagemaker-feature-store-account-a'
offline_feature_store_s3_uri = f's3://{bucket}/'
offline_feature_store_s3_uri
# #### Validate if we can access feature groups created by Account B from here (Account A)
account_id = '149456328460' # account ID of account B
feature_group_name = 'employees'
feature_group_s3_prefix = f'{account_id}/sagemaker/{region}/offline-store/{feature_group_name}/data'
feature_group_s3_prefix
offline_store_contents = None
objects = s3_client.list_objects(Bucket=bucket, Prefix=feature_group_s3_prefix)
if 'Contents' in objects and len(objects['Contents']) > 1:
offline_store_contents = objects['Contents']
offline_store_contents
s3_prefix = '/'.join(offline_store_contents[0]['Key'].split('/')[:-5])
s3_uri = f's3://{bucket}/{s3_prefix}'
s3_uri
df = wr.s3.read_parquet(path=s3_uri)
df
# #### Validate if we can access feature groups created by Account C from here (Account A)
account_id = '105242341581' # account ID of account C
feature_group_name = 'employees'
feature_group_s3_prefix = f'{account_id}/sagemaker/{region}/offline-store/{feature_group_name}/data'
feature_group_s3_prefix
offline_store_contents = None
objects = s3_client.list_objects(Bucket=bucket, Prefix=feature_group_s3_prefix)
if 'Contents' in objects and len(objects['Contents']) > 1:
offline_store_contents = objects['Contents']
offline_store_contents
s3_prefix = '/'.join(offline_store_contents[0]['Key'].split('/')[:-5])
s3_uri = f's3://{bucket}/{s3_prefix}'
s3_uri
df = wr.s3.read_parquet(path=s3_uri)
df
|
pattern-2/account-a/access-b-and-c.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import torch
import torchvision
from UNet import*
from loader import *
from training import *
# ## Visualization of the road segmentation
# ### 1. Load pretrained model
checkpoint_path = r'C:\Users\<NAME>\Documents\GitHub\ML_road_seg\code\Unet_64_epoch_99_0875.pt'
net = UNet( n_channels = 3, n_classes = 1, n_filters = 64)
epoch = load_from_checkpoint(checkpoint_path, net, optimizer = None, scheduler = None, verbose = True)
# ### 2. Load test images
test_dir = r'C:\Users\<NAME>\Documents\GitHub\ML_road_seg\test_set_images'
test_set = TestDataset(test_dir, num_imgs=50, to_numpy=False)
sample = test_set.__getitem__(10)
Tensor2PIL = torchvision.transforms.ToPILImage(mode='RGB')
img = Tensor2PIL(sample["image"])
plt.imshow(img)
plt.show()
# ### 3. Make prediction and visualize the result
# +
def predict_mask(img, model):
if len(img.size()) < 4:
img = torch.unsqueeze(img, dim=0)
mask_pred = net(img)
pred = torch.sigmoid(mask_pred)
pred = (pred > 0.5).float()
pred = torch.squeeze(pred).numpy()
return pred
pred = predict_mask(sample["image"], net)
plt.imshow(pred,cmap='jet')
plt.colorbar()
#plt.savefig(fname='mask_30', dpi=600 )
# -
#plt.figure(figsize = (8,8))
plt.imshow(img)
plt.imshow(pred,cmap='jet', interpolation='none', alpha=0.25)
#plt.axis('off')
plt.show()
#plt.savefig(fname='test_30', dpi=1200)
|
visualization.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernel_info:
# name: python3
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %matplotlib inline
from matplotlib import style
style.use('fivethirtyeight')
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import datetime as dt
# # Reflect Tables into SQLAlchemy ORM
# Python SQL toolkit and Object Relational Mapper
import sqlalchemy
from sqlalchemy.ext.automap import automap_base
from sqlalchemy.orm import Session
from sqlalchemy import create_engine, func
engine = create_engine("sqlite:///Resources/hawaii.sqlite")
# reflect an existing database into a new model
Base = automap_base()
# reflect the tables
Base.prepare(engine, reflect=True)
# We can view all of the classes that automap found
Base.classes.keys()
# Save references to each table
Measurement = Base.classes.measurement
Station = Base.classes.station
# Create our session (link) from Python to the DB
session = Session(engine)
# # Exploratory Climate Analysis
# +
# Design a query to retrieve the last 12 months of precipitation data and plot the results
# Extract dates from August 2016 to August 2017.
# Calculate the date 1 year ago from the last data point in the database
last_date = "2017-08-23"
# Perform a query to retrieve the data and precipitation scores
#select prcp, date
#from hawaii_measurements
#where date > '8-23-16'
query_results = session.query(Measurement.date, Measurement.prcp).filter(Measurement.date>'2016-08-23').all()
# Save the query results as a Pandas DataFrame and set the index to the date column
prcp_df = pd.DataFrame(query_results)
prcp_df
# Sort the dataframe by date
prcp_df.sort_values("date", inplace=True)
# Use Pandas Plotting with Matplotlib to plot the data
prcp_df.plot(x = "date", rot=45)
# -
# Use Pandas to calcualte the summary statistics for the precipitation data
prcp_df.describe()
# Design a query to show how many stations are available in this dataset?
session.query(func.count(Station.station)).all()
# What are the most active stations? (i.e. what stations have the most rows)?
# List the stations and the counts in descending order.
session.query(Measurement.station, func.count(Measurement.station)).\
group_by(Measurement.station).order_by(func.count(Measurement.station).desc()).all()
# Using the station id from the previous query, calculate the lowest temperature recorded,
# highest temperature recorded, and average temperature of the most active station?
session.query(func.min(Measurement.tobs), func.max(Measurement.tobs), func.avg(Measurement.tobs)).\
filter(Measurement.station == 'USC00519281').all()
# +
# Choose the station with the highest number of temperature observations.
# Query the last 12 months of temperature observation data for this station and plot the results as a histogram.
import datetime as dt
from pandas.plotting import table
prev_year = dt.date(2017, 8, 23) - dt.timedelta(days=365)
results = session.query(Measurement.tobs).\
filter(Measurement.station == 'USC00519281').\
filter(Measurement.date >= prev_year).all()
prcp_df = pd.DataFrame(results, columns=['tobs'])
prcp_df.plot.hist(bins=12)
plt.tight_layout()
# -
# 
# +
# This function called `calc_temps` will accept start date and end date in the format '%Y-%m-%d'
# and return the minimum, average, and maximum temperatures for that range of dates
def calc_temps(start_date, end_date):
"""TMIN, TAVG, and TMAX for a list of dates.
Args:
start_date (string): A date string in the format %Y-%m-%d
end_date (string): A date string in the format %Y-%m-%d
Returns:
TMIN, TAVE, and TMAX
"""
return session.query(func.min(Measurement.tobs), func.avg(Measurement.tobs), func.max(Measurement.tobs)).\
filter(Measurement.date >= start_date).filter(Measurement.date <= end_date).all()
# function usage example
print(calc_temps('2012-02-28', '2012-03-05'))
# +
# Use your previous function `calc_temps` to calculate the tmin, tavg, and tmax
# for your trip using the previous year's data for those same dates.
import datetime as dt
prev_year_start = dt.date(2018,1,1) - dt.timedelta(days=365)
prev_year_end = dt.date(2018,1,7) - dt.timedelta(days=365)
tmin, tavg, tmax = calc_temps(prev_year_start.strftime("%Y-%m-%d"), prev_year_end.strftime("%Y-%m-%d"))[0]
print(tmin, tavg, tmax)
# +
# Plot the results from your previous query as a bar chart.
# Use "Trip Avg Temp" as your Title
# Use the average temperature for the y value
# Use the peak-to-peak (tmax-tmin) value as the y error bar (yerr)
fig, ax = plt.subplots(figsize=plt.figaspect(2.))
xpos = 1
yerr = tmax - tmin
bar = ax.bar(xpos, tmax, yerr=yerr, alpha=0.5, color='coral', align='center')
ax.set(xticks=range(xpos), xticklabels="a", title= 'Trip Avg. Temp', ylabel="Temp(F)")
ax.margins(.2,.2)
fig.tight_layout()
fig.show()
# +
# Calculate the total amount of rainfall per weather station for your trip dates using the previous year's matching dates.
# Sort this in descending order by precipitation amount and list the station, name, latitude, longitude, and elevation
start_date = '2012-01-01'
end_date = '2012-01-07'
sel = [Station.station, Station.name, Station.latitude,
Station.longitude, Station.elevation, func.sum(Measurement.prcp)]
results = session.query(*sel).\
filter(Measurement.station == Station.station).\
filter(Measurement.date >= start_date).\
filter(Measurement.date <= end_date).\
group_by(Station.name).order_by(func.sum(Measurement.prcp).desc()).all()
print(results)
# -
# ## Optional Challenge Assignment
from sqlalchemy import extract
june_temps = session.query(Measurement).filter(extract('month', Measurement.date == 6))
june_temp_list = [temp.tobs for temp in june_temps]
print(np.mean(june_temp_list))
dec_temps = session.query(Measurement).filter(extract('month', Measurement.date == 12))
dec_temp_list = [temp.tobs for temp in dec_temps]
print(np.mean(dec_temp_list))
from scipy import stats
stats.ttest_ind(june_temp_list, dec_temp_list)
# +
# Create a query that will calculate the daily normals
# (i.e. the averages for tmin, tmax, and tavg for all historic data matching a specific month and day)
def daily_normals(date):
"""Daily Normals.
Args:
date (str): A date string in the format '%m-%d'
Returns:
A list of tuples containing the daily normals, tmin, tavg, and tmax
"""
sel = [func.min(Measurement.tobs), func.avg(Measurement.tobs), func.max(Measurement.tobs)]
return session.query(*sel).filter(func.strftime("%m-%d", Measurement.date) == date).all()
daily_normals("01-01")
# -
# +
# calculate the daily normals for your trip
# push each tuple of calculations into a list called `normals`
# Set the start and end date of the trip
trip_start = '2018-01-01'
trip_end = '2018-01-07'
# Use the start and end date to create a range of dates
trip_dates = pd.date_range(trip_start, trip_end, freq='D')
# Stip off the year and save a list of %m-%d strings
trip_month_day = trip_dates.strftime('%m-%d')
# Loop through the list of %m-%d strings and calculate the normals for each date
normals = []
for date in trip_month_day:
normals.append(*daily_normals(date))
normals
# -
# Load the previous query results into a Pandas DataFrame and add the `trip_dates` range as the `date` index
df = pd.DataFrame(normals, columns=['tmin', 'tvag', 'tmax'])
df['date'] = trip_dates
df.set_index(['date'], inplace=True)
df.head()
# Plot the daily normals as an area plot with `stacked=False`
df.plot(kind='area', stacked=False, x_compat=True, alpha=.2)
plt.tight_layout()
|
SQLAlchemy_Challenge/climate_starter.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier
import seaborn as sns
from sklearn.feature_selection import f_classif
from sklearn.model_selection import cross_val_score
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
import sklearn.naive_bayes as nb
dataset = pd.read_csv('dataset/diabetes.csv')
dataset.shape
# ## Data Preprocessing
dataset.describe()
cols =['Glucose','BloodPressure','SkinThickness','Insulin','BMI','Age', "DiabetesPedigreeFunction"]
d = dataset.copy()
d[cols] = d[cols].replace({'0':np.nan, 0:np.nan})
d.isnull().sum()
# Drop Insulin and Skin Thickness columns due to lots of missing values. We also dropped the Pregnancies column to generalize the model for males and females and replaced missing values in the remaining columns with their medians.
dataset.drop("Insulin",axis=1,inplace=True)
dataset.drop("SkinThickness",axis=1,inplace=True)
dataset.drop("Pregnancies",axis=1,inplace=True)
dataset.loc[dataset.Glucose == 0,'Glucose'] = dataset["Glucose"].median()
dataset.loc[dataset.BloodPressure == 0,'BloodPressure'] = dataset["BloodPressure"].median()
dataset.loc[dataset.BMI == 0,'BMI'] = dataset["BMI"].median()
sns.set_theme(style="whitegrid")
fig, ax = plt.subplots(figsize=(24,24), nrows=1, ncols=5)
sns.boxplot(data=dataset, y="Glucose", ax=ax[0], color='red')
sns.boxplot(data=dataset, y="BloodPressure", ax=ax[1], color='red')
sns.boxplot(data=dataset, y="Age", ax=ax[2], color='red')
sns.boxplot(data=dataset, y="BMI", ax=ax[3], color='red')
sns.boxplot(data=dataset, y="DiabetesPedigreeFunction", ax=ax[4], color='red')
# We used analysis of variance (ANOVA) to test the dispersion of each feature with respect to the outcome. All values had significant p-values.
f,p = f_classif(dataset.iloc[:,:-1],dataset.iloc[:,-1])
print(f)
print(p)
# Plot the distribution of all features
pd.plotting.scatter_matrix(dataset.iloc[:,:], c=dataset.iloc[:,-1].replace({0:"red",1:"green"}), alpha=0.5, figsize=(20,20))
plt.show()
# Plot the correlation matrix. There were no highly correlated features.
hm = sns.heatmap(dataset.iloc[:,:-1].corr(), annot = True)
hm.set(title = "Correlation matrix")
plt.show()
# Scale the data then train using different models.
# +
X_train, X_test, y_train, y_test = train_test_split(dataset.iloc[:,:-1].values,dataset.iloc[:,-1].values,test_size=0.2,random_state=0)
log = make_pipeline(StandardScaler(),LogisticRegression(random_state = 0))
log_score = cross_val_score(log, X_train, y_train, cv=5)
DT = make_pipeline(StandardScaler(), DecisionTreeClassifier(criterion = 'entropy', random_state = 0))
DT_score = cross_val_score(DT, X_train, y_train, cv=5)
SV = make_pipeline(StandardScaler(),SVC(kernel = 'linear', random_state = 0))
SV_score = cross_val_score(SV, X_train, y_train, cv=5)
NB = make_pipeline(StandardScaler(),nb.GaussianNB())
NB_score = cross_val_score(SV, X_train, y_train, cv=5)
print("Logistic Regression cross validation mean",log_score.mean())
print("Decision Tree cross validation mean: ",DT_score.mean())
print("Support Vector cross validation mean: ",SV_score.mean())
print("Naive Bayes cross validation mean",NB_score.mean())
y_log = log.fit(X_train,y_train).predict(X_test)
y_DT = DT.fit(X_train,y_train).predict(X_test)
y_SV = SV.fit(X_train,y_train).predict(X_test)
y_NB = NB.fit(X_train,y_train).predict(X_test)
# -
def discretize(dataset):
datasetcopy=dataset.copy()
datasetcopy.loc[datasetcopy.Age <= 30,'Age'] = 1
datasetcopy.loc[(datasetcopy.Age >30) & (datasetcopy.Age <= 40),'Age'] = 2
datasetcopy.loc[(datasetcopy.Age >40) & (datasetcopy.Age <= 50),'Age'] = 3
datasetcopy.loc[(datasetcopy.Age >50) & (datasetcopy.Age <= 60),'Age'] = 4
datasetcopy.loc[datasetcopy.Age > 60,'Age'] = 5
datasetcopy.loc[datasetcopy.Glucose <= 60,'Glucose'] = 1
datasetcopy.loc[(datasetcopy.Glucose >60) & (datasetcopy.Glucose <= 80),'Glucose'] = 2
datasetcopy.loc[(datasetcopy.Glucose >80) & (datasetcopy.Glucose <= 140),'Glucose'] = 3
datasetcopy.loc[(datasetcopy.Glucose >140) & (datasetcopy.Glucose <= 180),'Glucose'] = 4
datasetcopy.loc[datasetcopy.Glucose > 180,'Glucose'] = 5
datasetcopy.loc[datasetcopy.BloodPressure <= 60,'BloodPressure'] = 1
datasetcopy.loc[(datasetcopy.BloodPressure >60) & (datasetcopy.BloodPressure <= 75),'BloodPressure'] = 2
datasetcopy.loc[(datasetcopy.BloodPressure >75) & (datasetcopy.BloodPressure <= 90),'BloodPressure'] = 3
datasetcopy.loc[(datasetcopy.BloodPressure >90) & (datasetcopy.BloodPressure <= 100),'BloodPressure'] = 4
datasetcopy.loc[datasetcopy.BloodPressure > 100,'BloodPressure'] = 5
datasetcopy.loc[datasetcopy.BMI < 19,'BMI'] = 1
datasetcopy.loc[(datasetcopy.BMI >= 19) & (datasetcopy.BMI <= 24),'BMI'] = 2
datasetcopy.loc[(datasetcopy.BMI >24) & (datasetcopy.BMI <= 30),'BMI'] = 3
datasetcopy.loc[(datasetcopy.BMI >30) & (datasetcopy.BMI <= 40),'BMI'] = 4
datasetcopy.loc[datasetcopy.BMI > 40,'BMI'] = 5
return datasetcopy
# Discretize the dataset into 5 bins
# +
discretized_dataset = discretize(dataset)
X_train_discrete, X_test_discrete, y_train_discrete, y_test_discrete = train_test_split(discretized_dataset.iloc[:,:-1].values,discretized_dataset.iloc[:,-1].values,test_size=0.2,random_state=0)
log = LogisticRegression(random_state = 0)
log_score = cross_val_score(log, X_train, y_train, cv=5)
DT = DecisionTreeClassifier(criterion = 'entropy', random_state = 0)
DT_score = cross_val_score(DT, X_train, y_train, cv=5)
SV = SVC(kernel = 'linear', random_state = 0)
SV_score = cross_val_score(SV, X_train, y_train, cv=5)
NB = nb.GaussianNB()
NB_score = cross_val_score(SV, X_train, y_train, cv=5)
print("Logistic Regression cross validation mean",log_score.mean())
print("Decision Tree cross validation mean: ",DT_score.mean())
print("Support Vector cross validation mean: ",SV_score.mean())
print("Naive Bayes cross validation mean",NB_score.mean())
y_log_discrete = log.fit(X_train,y_train).predict(X_test)
y_DT_discrete = DT.fit(X_train,y_train).predict(X_test)
y_SV_discrete = SV.fit(X_train,y_train).predict(X_test)
y_NB_discrete= NB.fit(X_train,y_train).predict(X_test)
# -
pd.DataFrame({
"Discrete": [accuracy_score(y_test_discrete,y_SV_discrete),accuracy_score(y_test_discrete,y_DT_discrete),accuracy_score(y_test_discrete,y_log_discrete),accuracy_score(y_test_discrete,y_NB_discrete)],
"Continuous": [accuracy_score(y_test,y_DT),accuracy_score(y_test,y_DT),accuracy_score(y_test,y_log),accuracy_score(y_test,y_NB)]
}, index= ["Support Vector Classifier","Decision Tree","Logistic Regression","Naive Bayes"])
|
main.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import pandas as pd
import numpy as np
# import seaborn as sns
# import matplotlib.pyplot as plt
import os
from sklearn.model_selection import train_test_split
from sklearn.metrics import roc_curve, roc_auc_score
# plt.style.use('seaborn-colorblind')
# # %matplotlib inline
#from feature_cleaning import rare_values as ra
# -
# ## Load Dataset
# +
use_cols = [
'Pclass', 'Sex', 'Age', 'Fare', 'SibSp',
'Survived'
]
data = pd.read_csv('./data/titanic.csv', usecols=use_cols)
# -
data.head(3)
# Note that we include target variable in the X_train
# because we need it to supervise our discretization
# this is not the standard way of using train-test-split
X_train, X_test, y_train, y_test = train_test_split(data, data.Survived, test_size=0.3,
random_state=0)
X_train.shape, X_test.shape
# ## Polynomial Expansion
#
# generate a new feature set consisting of all polynomial combinations of the features with degree less than or equal to the specified degree
# create polynomial combinations of feature 'Pclass','SibSp' with degree 2
from sklearn.preprocessing import PolynomialFeatures
pf = PolynomialFeatures(degree=2,include_bias=False).fit(X_train[['Pclass','SibSp']])
tmp = pf.transform(X_train[['Pclass','SibSp']])
X_train_copy = pd.DataFrame(tmp,columns=pf.get_feature_names(['Pclass','SibSp']))
print(X_train_copy.head(6))
# ## Feature Learning by Trees
# GBDT derived feature + LR
# +
from sklearn.ensemble import GradientBoostingClassifier,RandomForestClassifier
from sklearn.preprocessing import OneHotEncoder
gbdt = GradientBoostingClassifier(n_estimators=20)
one_hot = OneHotEncoder()
X_train = X_train[[ 'Pclass', 'Age', 'Fare', 'SibSp']].fillna(0)
X_test = X_test[[ 'Pclass', 'Age', 'Fare', 'SibSp']].fillna(0)
gbdt.fit(X_train, y_train)
X_leaf_index = gbdt.apply(X_train)[:, :, 0] # apply return the node index on each tree
print("sample's belonging node of each base tree \n'",X_leaf_index)
# fit one-hot encoder
one_hot.fit(X_leaf_index)
X_one_hot = one_hot.transform(X_leaf_index)
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(solver='lbfgs', max_iter=1000)
lr.fit(X_one_hot,y_train)
y_pred = lr.predict_proba(
one_hot.transform(gbdt.apply(X_test)[:, :, 0]))[:,1]
fpr_grd_lm, tpr_grd_lm, _ = roc_curve(y_test, y_pred)
print("AUC for GBDT derived feature + LR:", roc_auc_score(y_test, y_pred))
# -
# ## Feature Learning by Trees
# RandomForest derived feature + LR
# +
rf = RandomForestClassifier(n_estimators=20)
one_hot = OneHotEncoder()
X_train = X_train[[ 'Pclass', 'Age', 'Fare', 'SibSp']].fillna(0)
X_test = X_test[[ 'Pclass', 'Age', 'Fare', 'SibSp']].fillna(0)
rf.fit(X_train, y_train)
X_leaf_index = rf.apply(X_train) # apply return the node index on each tree
print("sample's belonging node of each base tree \n'",X_leaf_index)
# fit one-hot encoder
one_hot.fit(X_leaf_index)
X_one_hot = one_hot.transform(X_leaf_index)
lr = LogisticRegression(solver='lbfgs', max_iter=1000)
lr.fit(X_one_hot,y_train)
y_pred = lr.predict_proba(
one_hot.transform(rf.apply(X_test)))[:,1]
fpr_grd_lm, tpr_grd_lm, _ = roc_curve(y_test, y_pred)
print("AUC for RandomForest derived feature + LR:", roc_auc_score(y_test, y_pred))
# -
# ## Feature Learning by Trees
# GBDT derived feature + Raw feature +LR
# +
from scipy.sparse import hstack
X_train_ext = hstack([one_hot.transform(gbdt.apply(X_train)[:, :, 0]), X_train])
X_test_ext = hstack([one_hot.transform(gbdt.apply(X_test)[:, :, 0]), X_test])
lr = LogisticRegression(solver='lbfgs', max_iter=1000)
lr.fit(X_train_ext,y_train)
y_pred = lr.predict_proba(X_test_ext)[:,1]
fpr_grd_lm, tpr_grd_lm, _ = roc_curve(y_test, y_pred)
print("AUC for GBDT derived feature + Raw feature +LR:", roc_auc_score(y_test, y_pred))
# -
# ## Feature Learning by Trees
# RandomForest derived feature + Raw feature +LR
X_train_ext = hstack([one_hot.transform(rf.apply(X_train)), X_train])
X_test_ext = hstack([one_hot.transform(rf.apply(X_test)), X_test])
lr = LogisticRegression(solver='lbfgs', max_iter=1000)
lr.fit(X_train_ext,y_train)
y_pred = lr.predict_proba(X_test_ext)[:,1]
fpr_grd_lm, tpr_grd_lm, _ = roc_curve(y_test, y_pred)
print("AUC for RandomForest derived feature + Raw feature + LR:", roc_auc_score(y_test, y_pred))
# ## Feature Learning by Trees
# Use only Raw Feature + LR
lr = LogisticRegression(solver='lbfgs', max_iter=1000)
lr.fit(X_train,y_train)
y_pred = lr.predict_proba(X_test)[:,1]
fpr_grd_lm, tpr_grd_lm, _ = roc_curve(y_test, y_pred)
print("AUC for RandomForest derived feature + LR:", roc_auc_score(y_test, y_pred))
# ## Feature Learning by Trees
#
# Use only Raw Feature + GBDT
# +
gbdt = GradientBoostingClassifier(n_estimators=20)
X_train = X_train[[ 'Pclass', 'Age', 'Fare', 'SibSp']].fillna(0)
X_test = X_test[[ 'Pclass', 'Age', 'Fare', 'SibSp']].fillna(0)
gbdt.fit(X_train, y_train)
y_pred = gbdt.predict_proba(X_test)[:,1]
fpr_grd_lm, tpr_grd_lm, _ = roc_curve(y_test, y_pred)
print("AUC for Raw feature + GBDT:", roc_auc_score(y_test, y_pred))
# -
# ## Feature Learning by Trees
#
# Use only Raw Feature + RF
#
# +
rf = RandomForestClassifier(n_estimators=20)
X_train = X_train[[ 'Pclass', 'Age', 'Fare', 'SibSp']].fillna(0)
X_test = X_test[[ 'Pclass', 'Age', 'Fare', 'SibSp']].fillna(0)
rf.fit(X_train, y_train)
y_pred = rf.predict_proba(X_test)[:,1]
fpr_grd_lm, tpr_grd_lm, _ = roc_curve(y_test, y_pred)
print("AUC for Raw feature + RF:", roc_auc_score(y_test, y_pred))
# -
# #### Without tuning, we can see GBDT derived feature + LR get the best result
|
feature-engineering-and-data-transformations/using-toy-exmaples/3.5_Demo_Feature_Generation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# example of training an conditional gan on the fashion mnist dataset
from numpy import expand_dims
from numpy import zeros
from numpy import ones
from numpy.random import randn
from numpy.random import randint
from keras.datasets.fashion_mnist import load_data
from keras.optimizers import Adam
from keras.models import Model
from keras.layers import Input
from keras.layers import Dense
from keras.layers import Reshape
from keras.layers import Flatten
from keras.layers import Conv2D
from keras.layers import Conv2DTranspose
from keras.layers import LeakyReLU
from keras.layers import Dropout
from keras.layers import Embedding
from keras.layers import Concatenate
# define the standalone discriminator model
def define_discriminator(in_shape=(28,28,1), n_classes=10):
# label input
in_label = Input(shape=(1,))
# embedding for categorical input
li = Embedding(n_classes, 50)(in_label)
# scale up to image dimensions with linear activation
n_nodes = in_shape[0] * in_shape[1]
li = Dense(n_nodes)(li)
# reshape to additional channel
li = Reshape((in_shape[0], in_shape[1], 1))(li)
# image input
in_image = Input(shape=in_shape)
# concat label as a channel
merge = Concatenate()([in_image, li])
# downsample
fe = Conv2D(128, (3,3), strides=(2,2), padding='same')(merge)
fe = LeakyReLU(alpha=0.2)(fe)
# downsample
fe = Conv2D(128, (3,3), strides=(2,2), padding='same')(fe)
fe = LeakyReLU(alpha=0.2)(fe)
# flatten feature maps
fe = Flatten()(fe)
# dropout
fe = Dropout(0.4)(fe)
# output
out_layer = Dense(1, activation='sigmoid')(fe)
# define model
model = Model([in_image, in_label], out_layer)
# compile model
opt = Adam(lr=0.0002, beta_1=0.5)
model.compile(loss='binary_crossentropy', optimizer=opt, metrics=['accuracy'])
return model
# +
model=define_discriminator()
model.summary()
# -
from keras.utlis.vis_utlis import plot_model
plot_model(model, to_file='model_plot.png', show_shapes=True, show_layer_names=True)
# define the standalone generator model
def define_generator(latent_dim, n_classes=10):
# label input
in_label = Input(shape=(1,))
# embedding for categorical input
li = Embedding(n_classes, 50)(in_label)
# linear multiplication
n_nodes = 7 * 7
li = Dense(n_nodes)(li)
# reshape to additional channel
li = Reshape((7, 7, 1))(li)
# image generator input
in_lat = Input(shape=(latent_dim,))
# foundation for 7x7 image
n_nodes = 128 * 7 * 7
gen = Dense(n_nodes)(in_lat)
gen = LeakyReLU(alpha=0.2)(gen)
gen = Reshape((7, 7, 128))(gen)
# merge image gen and label input
merge = Concatenate()([gen, li])
# upsample to 14x14
gen = Conv2DTranspose(128, (4,4), strides=(2,2), padding='same')(merge)
gen = LeakyReLU(alpha=0.2)(gen)
# upsample to 28x28
gen = Conv2DTranspose(128, (4,4), strides=(2,2), padding='same')(gen)
gen = LeakyReLU(alpha=0.2)(gen)
# output
out_layer = Conv2D(1, (7,7), activation='tanh', padding='same')(gen)
# define model
model = Model([in_lat, in_label], out_layer)
return model
model=define_generator(100,10)
model.summary()
plot_model(model, to_file='model_plot.png', show_shapes=True, show_layer_names=True)
# define the combined generator and discriminator model, for updating the generator
def define_gan(g_model, d_model):
# make weights in the discriminator not trainable
d_model.trainable = False
# get noise and label inputs from generator model
gen_noise, gen_label = g_model.input
# get image output from the generator model
gen_output = g_model.output
# connect image output and label input from generator as inputs to discriminator
gan_output = d_model([gen_output, gen_label])
# define gan model as taking noise and label and outputting a classification
model = Model([gen_noise, gen_label], gan_output)
# compile model
opt = Adam(lr=0.0002, beta_1=0.5)
model.compile(loss='binary_crossentropy', optimizer=opt)
return model
model=define_gan(define_generator(100,10),define_discriminator())
model.summary()
plot_model(model, to_file='model_plot.png', show_shapes=True, show_layer_names=True)
# load fashion mnist images
def load_real_samples():
# load dataset
(trainX, trainy), (_, _) = load_data()
# expand to 3d, e.g. add channels
X = expand_dims(trainX, axis=-1)
# convert from ints to floats
X = X.astype('float32')
# scale from [0,255] to [-1,1]
X = (X - 127.5) / 127.5
return [X, trainy]
# # select real samples
def generate_real_samples(dataset, n_samples):
# split into images and labels
images, labels = dataset
# choose random instances
ix = randint(0, images.shape[0], n_samples)
# select images and labels
X, labels = images[ix], labels[ix]
# generate class labels
y = ones((n_samples, 1))
return [X, labels], y
# load image data
dataset = load_real_samples()
generate_real_samples(dataset,1)[0]
# +
# generate points in latent space as input for the generator
def generate_latent_points(latent_dim, n_samples, n_classes=10):
# generate points in the latent space
x_input = randn(latent_dim * n_samples)
# reshape into a batch of inputs for the network
z_input = x_input.reshape(n_samples, latent_dim)
# generate labels
labels = randint(0, n_classes, n_samples)
return [z_input, labels]
# -
# use the generator to generate n fake examples, with class labels
def generate_fake_samples(generator, latent_dim, n_samples):
# generate points in latent space
z_input, labels_input = generate_latent_points(latent_dim, n_samples)
# predict outputs
images = generator.predict([z_input, labels_input])
# create class labels
y = zeros((n_samples, 1))
return [images, labels_input], y
# +
# train the generator and discriminator
def train(g_model, d_model, gan_model, dataset, latent_dim, n_epochs=5, n_batch=128):
bat_per_epo = int(dataset[0].shape[0] / n_batch)
half_batch = int(n_batch / 2)
# manually enumerate epochs
for i in range(n_epochs):
# enumerate batches over the training set
for j in range(bat_per_epo):
# get randomly selected 'real' samples
[X_real, labels_real], y_real = generate_real_samples(dataset, half_batch)
# update discriminator model weights
d_loss1, _ = d_model.train_on_batch([X_real, labels_real], y_real)
# generate 'fake' examples
[X_fake, labels], y_fake = generate_fake_samples(g_model, latent_dim, half_batch)
# update discriminator model weights
d_loss2, _ = d_model.train_on_batch([X_fake, labels], y_fake)
# prepare points in latent space as input for the generator
[z_input, labels_input] = generate_latent_points(latent_dim, n_batch)
# create inverted labels for the fake samples
y_gan = ones((n_batch, 1))
# update the generator via the discriminator's error
g_loss = gan_model.train_on_batch([z_input, labels_input], y_gan)
# summarize loss on this batch
print('>%d, %d/%d, d1=%.3f, d2=%.3f g=%.3f' %
(i+1, j+1, bat_per_epo, d_loss1, d_loss2, g_loss))
# save the generator model
g_model.save('cgan_generator.h5')
# size of the latent space
latent_dim = 100
# create the discriminator
d_model = define_discriminator()
# create the generator
g_model = define_generator(latent_dim)
# create the gan
gan_model = define_gan(g_model, d_model)
# load image data
dataset = load_real_samples()
# train model
train(g_model, d_model, gan_model, dataset, latent_dim)
# +
# example of loading the generator model and generating images
from numpy import asarray
from numpy.random import randn
from numpy.random import randint
from keras.models import load_model
from matplotlib import pyplot
# generate points in latent space as input for the generator
def generate_latent_points(latent_dim, n_samples, n_classes=10):
# generate points in the latent space
x_input = randn(latent_dim * n_samples)
# reshape into a batch of inputs for the network
z_input = x_input.reshape(n_samples, latent_dim)
# generate labels
labels = randint(0, n_classes, n_samples)
return [z_input, labels]
# create and save a plot of generated images
def save_plot(examples, n):
# plot images
for i in range(n * n):
# define subplot
pyplot.subplot(n, n, 1 + i)
# turn off axis
pyplot.axis('off')
# plot raw pixel data
pyplot.imshow(examples[i, :, :, 0], cmap='gray_r')
pyplot.show()
# load model
model = load_model('cgan_generator.h5')
# generate images
latent_points, labels = generate_latent_points(100, 100)
# specify labels
labels = asarray([x for _ in range(10) for x in range(10)])
# generate images
X = model.predict([latent_points, labels])
# scale from [-1,1] to [0,1]
X = (X + 1) / 2.0
# plot the result
save_plot(X, 10)
# -
g_model.load_weights('cgan_generator.h5')
# +
# example of loading the generator model and generating images
from numpy import asarray
from numpy.random import randn
from numpy.random import randint
from keras.models import load_model
from matplotlib import pyplot
# generate points in latent space as input for the generator
def generate_latent_points(latent_dim, n_samples, n_classes=10):
# generate points in the latent space
x_input = randn(latent_dim * n_samples)
# reshape into a batch of inputs for the network
z_input = x_input.reshape(n_samples, latent_dim)
# generate labels
labels = randint(0, n_classes, n_samples)
return [z_input, labels]
# create and save a plot of generated images
def save_plot(examples, n):
# plot images
for i in range(n * n):
# define subplot
pyplot.subplot(n, n, 1 + i)
# turn off axis
pyplot.axis('off')
# plot raw pixel data
pyplot.imshow(examples[i, :, :, 0], cmap='gray_r')
pyplot.show()
# load model
#model = load_model('cgan_generator.h5')
model= g_model
# generate images
latent_points, labels = generate_latent_points(100, 100)
# specify labels
labels = asarray([x for _ in range(10) for x in range(10)])
# generate images
X = model.predict([latent_points, labels])
# scale from [-1,1] to [0,1]
X = (X + 1) / 2.0
# plot the result
save_plot(X, 10)
# -
latent_points.shape
labels
a=randn(10*100*5)
a=a.reshape(50,100)
a.shape
b=randint(0, 5, len(a))
b=b.reshape(50,1)
p=g_model.predict([a,b])
# scale from [-1,1] to [0,1]
p = (p + 1) / 2.0
# plot the result
save_plot(p, 5)
|
CGAN.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Microsim Analysis
#
# Does some analysis of the outputs from the [microsim_model.py](./microsim_model.py).
# ## Initialisation
# +
# Import libraries
import pandas as pd
import pickle
from typing import List
import os
import glob
import matplotlib.pyplot as plt
from pathlib import Path
from tqdm import tqdm # For a progress bar
#sys.path.append("microsim")
#from microsim.microsim_model import Microsim
# Set directories
base_dir = str(Path(os.getcwd()).parent) # Get main RAMP-UA directory (should be parent to this file)
data_dir = os.path.join(base_dir, "data")
results_dir = os.path.join(data_dir, "output")
if base_dir.split("/")[-1] != "RAMP-UA":
raise Exception(f"The base directory should point to the main 'RAMP-UA' directory,"
f"but it points to {base_dir}")
# -
# ## Read data
#
# Each time the model is run it outputs data into a new sub-directory under [../data/output/](../data/output) numbered incrementally. E.g.:
# - `data/output/0`
# - `data/output/1`
# - `...`
#
# The following variables specify which directories to read the data from
START_DIRECTORY = 0
END_DIRECTORY = 9
# Now read the data:
def read_data(results_dir, start_directory=None, end_directory=None):
"""
Read all the available output files stored in subdirectories of `results_dir`. Results directories
should be numbered incrementally.
Optionally provide `start_directory` and `end_directory` to only select results directories within
those.
:param results_dir: The directory to look in for results
:param start_directory: Optinal directory to start reading from
:param end_directory: Optinal directory to start reading to
:return: a dictionary with the results. Structured as follows:
dict:
-> 4 (the name of the model results subdirectory)
-> Retail (dataframe showing locations for the activity)
-> SecondarySchool
-> Individuals
-> PrimarySchool
-> Work
-> Home
-> 9
-> ...
"""
# Get all the subdirectories in the results directory
all_dirs = [ d for d in glob.glob(os.path.join(results_dir,"*")) if os.path.isdir(d)]
# Now get those inbetween start and end (inclusive)
selected_dirs = []
if start_directory is None and end_directory is None:
selected_dirs = all_dirs
else:
for d in all_dirs:
if start_directory <= int(d.split('/')[-1]) <= end_directory:
selected_dirs.append(d)
print("Reading results from directories:\n", "\n".join(selected_dirs), flush=True)
# Read the results in each of those directories. Use a dict. Each item will be another dict that
# stores the results of one model run (i.e. one subdiectory).
results_dict = dict()
for d in tqdm(selected_dirs, desc="Reading directories"):
model_name = d.split('/')[-1] # Name of the model run (e.g. '2')
model_results = dict() # results for this model run
for filename in glob.glob(os.path.join(d,"*")):
#print(filename)
if filename.split("/")[-1] == "m0.pickle": # Special case: whole model object is stored
# Not actually reading the full model yet
pass
elif filename.endswith(".pickle"): # In all other cases just dataframes are stored
with open(filename, 'rb') as f:
df_name = filename.split("/")[-1].replace(".pickle","") # Name of the file (e.g. 'Work')
df = pickle.load(f) # The dataframe stored in the file
model_results[df_name] = df
else: # Other files (e.g. csv files) can be ignored
pass
# Store this model in the main dictionary
results_dict[model_name] = model_results
assert len(results_dict) == len(selected_dirs)
return results_dict
res = read_data(results_dir, 3, 9)
print(f"Read results from {len(res)} models")
# ## Disease status
#
# A graph of disease statuses over time ...
# _Just working with one model at the moment, in future should work with many results_
# +
# Just get the first result
m = res[next(iter(res.keys()))]
individuals = m['Individuals'] # Dataframe of the individuals
individuals
# -
# ## Locations
#
# Some analysis/visualisation of the locations ...
retail = m['Retail']
homes = m['Home']
# Where an individual goes *shopping*:
# +
_id = 2
individuals.loc[_id]
shops_they_visit = retail.loc[retail.ID.isin(list(individuals.loc[_id, "Retail_Venues"]))]
shops_they_visit[:,]
# -
# Where an individual lives:
home = homes.loc[homes.ID.isin(list(individuals.loc[_id, "Home_Venues"]))]
home
# Who else lives there
home_id = home.ID.values[0]
individuals.loc[individuals.Home_Venues.apply(lambda x: home_id in x ) ]
|
microsim/microsim_analysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # ML Pipeline Preparation
# Follow the instructions below to help you create your ML pipeline.
# ### 1. Import libraries and load data from database.
# - Import Python libraries
# - Load dataset from database with [`read_sql_table`](https://pandas.pydata.org/pandas-docs/stable/generated/pandas.read_sql_table.html)
# - Define feature and target variables X and Y
# +
# import libraries
from sqlalchemy import create_engine
import re
import nltk
nltk.download(['stopwords', 'punkt', 'wordnet'])
import pickle
import numpy as np
import pandas as pd
from nltk.corpus import stopwords
from sklearn.pipeline import Pipeline
from nltk.tokenize import word_tokenize
from nltk.stem import WordNetLemmatizer
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import GridSearchCV
from sklearn.ensemble import RandomForestClassifier, AdaBoostClassifier
from sklearn.multioutput import MultiOutputClassifier
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import CountVectorizer, TfidfTransformer
# + code_folding=[]
# read in file
engine = create_engine('sqlite:///disaster.db')
df = pd.read_sql_table('disaster', engine)
X = df['message']
y = df.iloc[:, 4:]
# -
# ### 2. Write a tokenization function to process your text data
def tokenize(text):
# Define common paras
stop_words = stopwords.words("english")
lemmatizer = WordNetLemmatizer()
# Normalize and remove punctuation
text = re.sub(r'[^a-zA-Z0-9]', '', text.lower())
# Tokenize text
text = word_tokenize(text)
# Lemmatize and remove stop words
tokens = [lemmatizer.lemmatize(word) for word in text if word not in stop_words]
# return tokens
return tokens
# ### 3. Build a machine learning pipeline
# This machine pipeline should take in the `message` column as input and output classification results on the other 36 categories in the dataset. You may find the [MultiOutputClassifier](http://scikit-learn.org/stable/modules/generated/sklearn.multioutput.MultiOutputClassifier.html) helpful for predicting multiple target variables.
pipeline = Pipeline([
('vect', CountVectorizer(tokenizer=tokenize)),
('tfidf', TfidfTransformer()),
('mutclf', MultiOutputClassifier(RandomForestClassifier(), n_jobs=-1))])
# ### 4. Train pipeline
# - Split data into train and test sets
# - Train pipeline
# +
# Split train & test data
X_train, X_test, y_train, y_test = train_test_split(X, y)
# Train pipeline
pipeline.fit(X_train, y_train)
# -
# ### 5. Test your model
# Report the f1 score, precision and recall for each output category of the dataset. You can do this by iterating through the columns and calling sklearn's `classification_report` on each.
# Predict use the trained model
y_pred = pipeline.predict(X_test)
# Report Model Effectiveness
for i, col in enumerate(y_test.columns):
target_names = ['class 0', 'class 1', 'class 2']
print(classification_report(y_test[col].tolist(), list(y_pred[:, i]), target_names=target_names))
# ### 6. Improve your model
# Use grid search to find better parameters.
# +
parameters = {
'vect__ngram_range': ((1, 1), (1, 2)),
'vect__max_df': (0.5, 0.75, 1.0),
'vect__max_features': (None, 5000, 10000),
'tfidf__use_idf': (True, False)}
cv = GridSearchCV(pipeline, param_grid=parameters)
cv.fit(X_train, y_train)
y_pred = cv.predict(X_test)
# -
# ### 7. Test your model
# Show the accuracy, precision, and recall of the tuned model.
#
# Since this project focuses on code quality, process, and pipelines, there is no minimum performance metric needed to pass. However, make sure to fine tune your models for accuracy, precision and recall to make your project stand out - especially for your portfolio!
# Report New Model Effectiveness
for i, col in enumerate(y_test.columns):
target_names = ['class 0', 'class 1', 'class 2']
print(classification_report(y_test[col].tolist(), list(y_pred[:, i]), target_names=target_names))
# ### 8. Try improving your model further. Here are a few ideas:
# * try other machine learning algorithms
# * add other features besides the TF-IDF
pipeline2 = Pipeline([
('vect', CountVectorizer(tokenizer=tokenize)),
('tfidf', TfidfTransformer()),
('mutclf', MultiOutputClassifier(AdaBoostClassifier(), n_jobs=-1))])
# ### 9. Export your model as a pickle file
# Save CV Model
with open('model.pickle', 'wb') as file:
pickle.dump(cv, file)
# ### 10. Use this notebook to complete `train.py`
# Use the template file attached in the Resources folder to write a script that runs the steps above to create a database and export a model based on a new dataset specified by the user.
|
ML Pipeline Preparation.ipynb
|