code
stringlengths 38
801k
| repo_path
stringlengths 6
263
|
|---|---|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.7.0 ('ineuronMLclass')
# language: python
# name: python3
# ---
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
df = pd.read_csv(r'C:\Users\kushal\Desktop\Modular_aprr\modular\ML_live_class\data\Advertising.csv')
df.head()
x = df.drop(['sales'], axis=1)
x
y = df['sales']
y
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
poly_conv = PolynomialFeatures(degree=3, include_bias=False)
final_model = LinearRegression
poly_conv.fit(x)
poly_features = poly_conv.transform(x)
poly_features.shape
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(poly_features, y, test_size=0.33, random_state=101)
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(x_train)
scaler_x_train = scaler.transform(x_train)
scaler_x_test = scaler.transform(x_test)
x_train[0]
scaler_x_train[0]
from sklearn.linear_model import Ridge
ridge_model = Ridge(alpha = 10)
ridge_model.fit(x_train, y_train)
test_predictions = ridge_model.predict(x_test)
from sklearn.metrics import mean_absolute_error, mean_squared_error
MAE = mean_absolute_error(y_test, test_predictions)
RMSE = np.sqrt(mean_squared_error(y_test,test_predictions))
MAE
RMSE
|
Regularisation/regularization_aprroach.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import sklearn
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# -
# ## The Titanic dataset
#
# Source: https://www.kaggle.com/francksylla/titanic-machine-learning-from-disaster
titanic_df = pd.read_csv('datasets/titanic_train.csv')
titanic_df.head(10)
# + [markdown] heading_collapsed=true
# ### Exploratory Data Analysis
# + hidden=true
titanic_df.shape
# + hidden=true
titanic_df.drop(['PassengerId', 'Name', 'Ticket', 'Cabin'], 'columns', inplace=True)
titanic_df.head()
# + hidden=true
titanic_df[titanic_df.isnull().any(axis=1)].count()
# + hidden=true
titanic_df = titanic_df.dropna()
# + hidden=true
titanic_df.shape
# + hidden=true
titanic_df.describe()
# + [markdown] heading_collapsed=true
# ### Visualizing relationships
# + hidden=true
fig, ax = plt.subplots(figsize=(12, 8))
plt.scatter(titanic_df['Age'], titanic_df['Survived'])
plt.xlabel('Age')
plt.ylabel('Survived')
# + hidden=true
fig, ax = plt.subplots(figsize=(12, 8))
plt.scatter(titanic_df['Fare'], titanic_df['Survived'])
plt.xlabel('Fare')
plt.ylabel('Survived')
# + hidden=true
pd.crosstab(titanic_df['Sex'], titanic_df['Survived'])
# + hidden=true
pd.crosstab(titanic_df['Pclass'], titanic_df['Survived'])
# + hidden=true
titanic_data_corr = titanic_df.corr()
titanic_data_corr
# + hidden=true
fig, ax = plt.subplots(figsize=(12, 10))
sns.heatmap(titanic_data_corr, annot=True)
# + [markdown] heading_collapsed=true
# ### Data Wrangling
# + hidden=true
from sklearn import preprocessing
label_encoding = preprocessing.LabelEncoder()
titanic_df['Sex'] = label_encoding.fit_transform(titanic_df['Sex'].astype(str))
titanic_df.head()
# + hidden=true
label_encoding.classes_
# + [markdown] hidden=true
# #### C = Cherbourg, Q = Queenstown, S = Southampton
# + hidden=true
titanic_df = pd.get_dummies(titanic_df, columns=['Embarked'])
titanic_df.head()
# + hidden=true
titanic_df = titanic_df.sample(frac=1).reset_index(drop=True)
titanic_df.head()
# + [markdown] heading_collapsed=true
# ### Binary Classification Logistic Regression
# + hidden=true
from sklearn.model_selection import train_test_split
X = titanic_df.drop('Survived', axis=1)
Y = titanic_df['Survived']
x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=0.2)
# + hidden=true
x_train.shape, y_train.shape
# + hidden=true
x_test.shape, y_test.shape
# + [markdown] hidden=true
# https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html
# + hidden=true
from sklearn.linear_model import LogisticRegression
logistic_model = LogisticRegression(penalty='l2', C=1.0, solver='liblinear')
logistic_model.fit(x_train, y_train)
# + hidden=true
y_pred = logistic_model.predict(x_test)
# + hidden=true
pred_results = pd.DataFrame({'y_test': y_test,'y_pred': y_pred})
pred_results.head()
# + hidden=true
# Confusion matrix
titanic_crosstab = pd.crosstab(pred_results.y_pred, pred_results.y_test)
titanic_crosstab
# + hidden=true
TP = titanic_crosstab[1][1]
TN = titanic_crosstab[0][0]
FP = titanic_crosstab[0][1]
FN = titanic_crosstab[1][0]
# + hidden=true
accuracy_score_verified = (TP + TN) / (TP + FP + TN + FN)
accuracy_score_verified
# + hidden=true
precision_score_survived = TP / (TP + FP)
precision_score_survived
# + hidden=true
recall_score_survived = TP / (TP + FN)
recall_score_survived
# + [markdown] hidden=true
# For computing Precision-recall score, we need to specify an averaging method to determine how the precision and recall scores for different labels should be weighted
#
# * https://scikit-learn.org/stable/modules/generated/sklearn.metrics.precision_score.html
# * https://scikit-learn.org/stable/modules/generated/sklearn.metrics.recall_score.html
# + hidden=true
from sklearn.metrics import accuracy_score
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
# + hidden=true
acc = accuracy_score(y_test, y_pred)
prec = precision_score(y_test, y_pred)
recall = recall_score(y_test, y_pred)
print("accuracy_score : ", acc)
print("precision_score : ", prec)
print("recall_score : ", recall)
# + [markdown] heading_collapsed=true
# ### Multiple Classification Models
# + hidden=true
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
from sklearn.linear_model import SGDClassifier
from sklearn.svm import LinearSVC
from sklearn.neighbors import RadiusNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import confusion_matrix
from IPython.display import display
# + hidden=true
FEATURES = list(titanic_df.columns[1:])
FEATURES
# + hidden=true
# To store results of various Classifiers
result_dict = {}
# + hidden=true
def summarize_classification(y_test, y_pred):
acc = accuracy_score(y_test, y_pred, normalize=True)
num_acc = accuracy_score(y_test, y_pred, normalize=False)
prec = precision_score(y_test, y_pred)
recall = recall_score(y_test, y_pred)
return {'accuracy': acc,
'precision': prec,
'recall':recall,
'accuracy_count':num_acc}
# + hidden=true
def build_model(classifier_fn, name_of_y_col, names_of_x_cols, dataset, test_frac=0.2):
print('Classification: ', classifier_fn)
X = dataset[names_of_x_cols]
Y = dataset[name_of_y_col]
x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=test_frac)
model = classifier_fn.fit(x_train, y_train)
y_pred = model.predict(x_test)
y_pred_train = model.predict(x_train)
pred_results = pd.DataFrame({'y_test': y_test,
'y_pred': y_pred})
model_crosstab = pd.crosstab(pred_results.y_pred, pred_results.y_test)
print('\nConfusion_matrix:')
display(model_crosstab)
train_summary = summarize_classification(y_train, y_pred_train)
print('\nTraining data',train_summary)
test_summary = summarize_classification(y_test, y_pred)
print('\nTesting data',test_summary)
return {'training': train_summary,
'test': test_summary,
'confusion_matrix': model_crosstab}
# + hidden=true
result_dict['logistic'] = build_model(LogisticRegression(solver='liblinear'),
'Survived',FEATURES,titanic_df)
# + hidden=true
result_dict['linear_discriminant'] = build_model(LinearDiscriminantAnalysis(solver='svd'),
'Survived',FEATURES,titanic_df)
# + hidden=true
result_dict['quadratic_discriminant'] = build_model(QuadraticDiscriminantAnalysis(),
'Survived',FEATURES,titanic_df)
# + hidden=true
result_dict['sgd'] = build_model(SGDClassifier(max_iter=1000, tol=1e-3),
'Survived',FEATURES,titanic_df)
# + hidden=true
# SVC with a linear kernel
# dual=False when number of samples > number of features
result_dict['linear_svc'] = build_model(LinearSVC(C=1.0, max_iter=1000, tol=1e-3, dual=False),
'Survived',FEATURES,titanic_df)
# + hidden=true
result_dict['radius_neighbors'] = build_model(RadiusNeighborsClassifier(radius=40.0),
'Survived',FEATURES,titanic_df)
# + hidden=true
# max_depth = None, then nodes are expanded until all leaves are pure
# or until all leaves contain less than min_samples_split samples
# max_features = None -- (then max_features=n_features), auto -- (then max_features=sqrt(n_features)),
# sqrt -- (then max_features=sqrt(n_features)), log2 -- (then max_features=log2(n_features))
result_dict['decision_tree'] = build_model(DecisionTreeClassifier(max_depth=None, max_features=None),
'Survived',FEATURES,titanic_df)
# + hidden=true
result_dict['naive_bayes'] = build_model(GaussianNB(priors=None),
'Survived',FEATURES,titanic_df)
# + cell_style="split" hidden=true
training_result=[]
for key in result_dict:
training_result.append(pd.DataFrame(result_dict[key]['training'],index=[key]))
training_result=pd.concat(training_result)
display(training_result)
# + cell_style="split" hidden=true
testing_result=[]
for key in result_dict:
testing_result.append(pd.DataFrame(result_dict[key]['test'],index=[key]))
testing_result=pd.concat(testing_result)
display(testing_result)
# + [markdown] heading_collapsed=true
# ### Hyperparameter Tuning With GridSearch
# + [markdown] heading_collapsed=true hidden=true
# #### GridSearchCV on DecisionTreeClassifier
# + hidden=true
from sklearn.model_selection import GridSearchCV
parameters = {'max_depth': [2, 4, 5, 7, 9, 10]}
grid_search = GridSearchCV(DecisionTreeClassifier(), parameters, cv=3, return_train_score=True)
grid_search.fit(x_train, y_train)
grid_search.best_params_
# + hidden=true
grid_results=pd.DataFrame(list(zip(grid_search.cv_results_['params'],grid_search.cv_results_['mean_test_score'],grid_search.cv_results_['rank_test_score'])),columns=['Params','Mean_test_score','Rank_test_score'])
grid_results.set_index('Rank_test_score',inplace=True)
grid_results.sort_index()
# + hidden=true
decision_tree_model = DecisionTreeClassifier(max_depth = grid_search.best_params_['max_depth'])
decision_tree_model.fit(x_train, y_train)
# + hidden=true
y_pred = decision_tree_model.predict(x_test)
# + hidden=true
summarize_classification(y_test, y_pred)
# + [markdown] heading_collapsed=true hidden=true
# #### GridSearchCV on LogisticRegression
# + hidden=true
parameters = {'penalty': ['l1', 'l2'],
'C': [0.1, 0.4, 0.8, 1, 2, 5]}
grid_search = GridSearchCV(LogisticRegression(solver='liblinear'), parameters, cv=3, return_train_score=True)
grid_search.fit(x_train, y_train)
grid_search.best_params_
# + hidden=true
grid_results=pd.DataFrame(list(zip(grid_search.cv_results_['params'],grid_search.cv_results_['mean_test_score'],grid_search.cv_results_['rank_test_score'])),columns=['Params','Mean_test_score','Rank_test_score'])
grid_results.set_index('Rank_test_score',inplace=True)
grid_results.sort_index()
# + hidden=true
logistic_model = LogisticRegression(solver='liblinear', penalty=grid_search.best_params_['penalty'],
C=grid_search.best_params_['C'])
logistic_model.fit(x_train, y_train)
# + hidden=true
y_pred = logistic_model.predict(x_test)
# + hidden=true
summarize_classification(y_test, y_pred)
# + hidden=true
|
05. The Titanic Dataset.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="uiaQXkVfYr_F"
import numpy as np
import cv2
import pandas as pd
import matplotlib.pyplot as plt
from skimage.color import rgb2lab, lab2rgb
from moviepy.editor import *
import os
import random
import sys
import tensorflow as tf
from tensorflow.keras.layers import *
from tensorflow.keras.models import *
import tensorflow.keras.backend as K
from tensorflow.keras.preprocessing import image
# + id="YYY85hG_iRE3"
cam = cv2.VideoCapture("/content/sample.mp4")
video = VideoFileClip("/content/sample.mp4")
# + id="GwiXhfGvjK7c" outputId="9070acc0-1bd2-4a40-d55f-65b99d2d66b2" colab={"base_uri": "https://localhost:8080/", "height": 1000}
currentframe = 0
audio = video.audio
while(True):
frame_Array = []
ret,frame = cam.read()
if ret:
frame = cv2.resize(frame, (256, 256), interpolation = cv2.INTER_NEAREST)
reconstructed_model = tf.keras.models.load_model("/content/Autoencoder100.hdf5")
img_color = []
img = image.img_to_array(frame, dtype=np.uint8)
img_color.append(img)
img_color = np.array(img_color, dtype=float)
img_color = rgb2lab(img_color/255.0)[:,:,:,0]
img_color = img_color.reshape(img_color.shape+(1,))
output = reconstructed_model.predict(img_color)
output = output*128
result = np.zeros((256, 256, 3))
result[:,:,0] = img_color[0][:,:,0]
result[:,:,1:] = output[0]
result = cv2.resize(result,(1280,720))
frame_Array.append(result)
currentframe += 1
else:
break
# + id="2sMmSHK4ohx4" outputId="f05d8a1d-01be-4de6-cbd8-122b9ed10e9e" colab={"base_uri": "https://localhost:8080/", "height": 229}
out = cv2.VideoWriter('output.mp4',cv2.VideoWriter_fourcc(*'DIVX'), 30, (1024,720))
for i in range(len(frame_Array)):
out.write(frame_Array[i])
cam.release()
cv2.destroyAllWindows()
videoclip = VideoFileClip("output.mp4")
videoclip.audio = audio
videoclip.write_videofile("output.mp4")
|
ImageColorization/VideoColorizationAlpha.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
data = pd.read_csv('titanic.csv')
data.head()
data.columns
data.drop(['PassengerId','Name', 'SibSp', 'Parch', 'Ticket', 'Cabin', 'Embarked'], axis=1, inplace=True)
data.head()
target = data.Survived
target.head()
features = data.drop('Survived', axis=1)
features.head()
dummies = pd.get_dummies(features.Sex)
dummies.head()
features = pd.concat([features, dummies], axis=1)
features.head()
features.drop('Sex',axis=1,inplace=True)
features.head()
features.columns[features.isna().any()]
features.Age[:10]
# Mean imputation
features.Age = features.Age.fillna(features.Age.mean())
features.head(10)
X_train, X_test, y_train, y_test = train_test_split(features, target,test_size=0.2)
model = GaussianNB()
model.fit(X_train, y_train)
model.score(X_test, y_test)
print (y_test[:20])
model.predict(X_test[:10])
model.score(X_test[:10],y_test[:10])
|
Supervised/Classification/NaiveBayes/Naive_Bayes_Classifier.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### POLISCI 88 FA 21
# ### Lab #: The role of self-interest in elite bargaining
# #### Due Date: X
# ### The Ultimatum Game
# Previous studies have shown that humans typically reject low offers in bargaining games, even when doing so goes against their material self-interest.
#
# In these “ultimatum games”, a proposer makes an offer to a responder for how to divide a fixed prize. A responder then decides whether to accept or reject the offer.
#
# If it is accepted, both players divide the prize as agreed.
#
# If it is rejected, both players receive nothing. If both players are completely rational and selfish—an assumption that is widely used by social scientists in formal models of inter- national bargaining —then proposers will offer almost nothing to responders, an offer that rational responders nonetheless accept because something is better than nothing.
#
# Note: The ultimatum game in the research paper we will look at for the lab assignment provides instruction to both elite and college subjects. If you would like to read through the game instructions as an example of the "ultimatum games" referenced above you can refer to page 4 [here](https://www.pnas.org/content/pnas/suppl/2014/12/11/1409885111.DCSupplemental/pnas.1409885111.sapp.pdf). It is not required to read the document to complete the lab assignemnt.
# ### Elites and Undergraduates
# In this lab assignment we will reproduce results from [this](https://faculty.ucmerced.edu/bleveck/assets/pdfs/role_of_self_interest_in_elite_bargaining.pdf) research article published by Leveck et. al.
#
# The study uses a unique sample set of 102 policy and business elites with an average of 21 years of international diplomacy or political strategy experience, compared with undergraduates and the general public, to explore whether elites are more or less likely to reject "low" offers when playing a standard ultimatum game.
#
# We will replicate Figure 1 to display the population differences in elites and undergraduates.
# 
# Run the following cell to import the libraries we will explore in this lab assignment.
# import the required libraries
import pandas as pd
import numpy as np
from numpy import median
import seaborn as sns
from matplotlib import pyplot as plt
# ### Comparing the Sample Data
# We will first compare the elite and college samples and find some important differences.
# Read in the `.csv` file `pnas.elite.turk.data_1.csv` into a pandas dataframe with the name `behavior`. The [documentation](https://pandas.pydata.org/docs/reference/api/pandas.read_csv.html) is particularly helpful for the first step.
#
# `pnas.elite.turk.data_1.csv` is the data used to compare the elite sample to n- other convenience sample of 1,007 subjects recruited for the online labor market Amazon Mechanical Turk (mTurk).
# read a csv file
behavior=pd.read_csv("dataverse_files/pnas.elite.turk.data_1.csv")
behavior
# The relevant columns you will you to create your replication are `demand`, `propose`, and `elite`.
#
# `demand` - minimum amount subject would accept in the ultimatum game. This is their "demand"
#
# `propose` - what the subject offered in the ultimatum game.
#
# `elite` - 1 if elite subject 0 if undergraduate
# Fig. 1A will show the mean offer and demand in both our elite and college sample.
# #### Question 1.a
#
# Create a barplot using [`sns.barplot(...)`](https://seaborn.pydata.org/generated/seaborn.barplot.html) of the population difference in mean offer for our elite and undergraduate sample. The bars should be sample means/ proportions.
#
# Do not forget to include a meaningful title and label both axes.
# bar plot using hue attribute
# for colouring out points
# according to the subject type
ax=sns.barplot(x="elite", y="propose", hue="elite", data=behavior, estimator=np.mean) #propose
ax.set(xlabel="Ultimatum Bargaining Behavior", ylabel="Mean", title="Propose");
# Create a barplot using `sns.barplot(...)` of the population difference in mean demand for our elite and undergraduate sample. The bars should be sample means/ proportions.
#
# Do not forget to include a meaningful title and label both axes.
ax=sns.barplot(x="elite", y="demand", hue="elite", data=behavior, estimator=np.mean) #demand
ax.set(xlabel="Ultimatum Bargaining Behavior", ylabel="Mean", title="Demand");
# Discuss how the mean offer and demand in both our elite and college sample compare. What do your observations suggest about the role rejecting low offers play in bargaining intuitions? How does this compare to the widely held assumption that experience with decision making leads elites to become more self-interested and rational?
# ### More Traits With More Barplots
# Can we explain the difference in bargaining between elites and college students based on other traits? Fig. 1B shows the mean number of patient choices for college students and elites.
# Read in the `.csv` file `elite.ug.lk.patience.dists.csv` into a pandas dataframe with the name `reason`.
#
# `elite.ug.lk.patience.dists.csv`is the main data used to compare elites and undergraduates on the ultimatum game.
reason=pd.read_csv("dataverse_files/elite.ug.lk.patience.dists.csv")
reason
# Variables:
#
# `levelk` - subject's measured level-k reasoning from 0 to 2
#
# `patience` - subject's measured patience from 0 to 20
#
# `elite` - 1 if elite subject 0 if undergraduate
#
# `L0` - 1 if measured as level-0 reasoner
#
# `L1` - 1 if measured as level-1 reasoner
#
# `L2`- 1 if measured as level-2 reasoner
# #### Question 1.b
#
# Create a barplot using `sns.barplot(...)` of the population difference in mean number of patient choices for our elite and undergraduate sample. The bars should be sample means/ proportions.
#
# Do not forget to label both axes.
ax=sns.barplot(x="elite", y="patience", hue="elite", data=reason)
ax.set(xlabel="Subject Type", ylabel="Mean # of Patient Choices");
# Do elites or undergraduates make more patient choices? What does this suggest about the value they make on future outcomes?
# Fig. 1C shows the estimated level of strategic learning for elites and college students.
# #### Question 1.c
#
# Create a barplot using `sns.barplot(...)` of the population difference in level-k reasoning for level-0 reasoner in our elite and undergraduate sample. The bars should be sample means/ proportions.
ax=sns.barplot(x="elite", y="L0", hue="elite", data=reason)
ax.set(xlabel="Estimated Level of Strategic Reasoning", ylabel="Proportion of Population", title="K=0");
# Create a barplot of the population difference in level-k reasoning for level-1 reasoner in our elite and undergraduate sample. The bars should be sample means/ proportions.
ax=sns.barplot(x="elite", y="L1", hue="elite", data=reason)
ax.set(xlabel="Estimated Level of Strategic Reasoning", ylabel="Proportion of Population", title="K=1");
# Create a barplot of the population difference in level-k reasoning for level-2 reasoner in our elite and undergraduate sample. The bars should be sample means/ proportions.
ax=sns.barplot(x="elite", y="L2", hue="elite", data=reason)
ax.set(xlabel="Estimated Level of Strategic Reasoning", ylabel="Proportion of Population", title="K=2");
# Are elites more or less likely to respond randomly to the task (k=0) and by how much? Are elites more or less likely to iterate once in their reasoning (k=1) and by how much? Are elites more or less likely to iterate twice in their reasoning (k=2) and by how much?
# Is this level of strategic reasoning among elites consistent with their tendency to make higher demands than college students? Support your answer using your answer to the previous questions.
|
lab/leveck/.ipynb_checkpoints/leveck_student-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# !wget https://resources.lendingclub.com/LoanStats_2019Q1.csv.zip
# !wget https://resources.lendingclub.com/LoanStats_2019Q2.csv.zip
# !wget https://resources.lendingclub.com/LoanStats_2019Q3.csv.zip
# !wget https://resources.lendingclub.com/LoanStats_2019Q4.csv.zip
# !wget https://resources.lendingclub.com/LoanStats_2020Q1.csv.zip
import numpy as np
import pandas as pd
from pathlib import Path
from collections import Counter
from sklearn.model_selection import train_test_split
# +
columns = [
"loan_amnt", "int_rate", "installment", "home_ownership", "annual_inc",
"verification_status", "pymnt_plan", "dti", "delinq_2yrs",
"inq_last_6mths", "open_acc", "pub_rec", "revol_bal", "total_acc",
"initial_list_status", "out_prncp", "out_prncp_inv", "total_pymnt",
"total_pymnt_inv", "total_rec_prncp", "total_rec_int",
"total_rec_late_fee", "recoveries", "collection_recovery_fee",
"last_pymnt_amnt", "collections_12_mths_ex_med", "policy_code",
"application_type", "acc_now_delinq", "tot_coll_amt", "tot_cur_bal",
"open_acc_6m", "open_act_il", "open_il_12m", "open_il_24m",
"mths_since_rcnt_il", "total_bal_il", "il_util", "open_rv_12m",
"open_rv_24m", "max_bal_bc", "all_util", "total_rev_hi_lim", "inq_fi",
"total_cu_tl", "inq_last_12m", "acc_open_past_24mths", "avg_cur_bal",
"bc_open_to_buy", "bc_util", "chargeoff_within_12_mths", "delinq_amnt",
"mo_sin_old_il_acct", "mo_sin_old_rev_tl_op", "mo_sin_rcnt_rev_tl_op",
"mo_sin_rcnt_tl", "mort_acc", "mths_since_recent_bc",
"mths_since_recent_inq", "num_accts_ever_120_pd", "num_actv_bc_tl",
"num_actv_rev_tl", "num_bc_sats", "num_bc_tl", "num_il_tl",
"num_op_rev_tl", "num_rev_accts", "num_rev_tl_bal_gt_0", "num_sats",
"num_tl_120dpd_2m", "num_tl_30dpd", "num_tl_90g_dpd_24m",
"num_tl_op_past_12m", "pct_tl_nvr_dlq", "percent_bc_gt_75",
"pub_rec_bankruptcies", "tax_liens", "tot_hi_cred_lim",
"total_bal_ex_mort", "total_bc_limit", "total_il_high_credit_limit",
"hardship_flag", "debt_settlement_flag",
"loan_status"
]
target = "loan_status"
# +
# Load the data
df1 = pd.read_csv(Path('../Generator/LoanStats_2019Q1.csv.zip'), skiprows=1)[:-2]
df2 = pd.read_csv(Path('../Generator/LoanStats_2019Q2.csv.zip'), skiprows=1)[:-2]
df3 = pd.read_csv(Path('../Generator/LoanStats_2019Q3.csv.zip'), skiprows=1)[:-2]
df4 = pd.read_csv(Path('../Generator/LoanStats_2019Q4.csv.zip'), skiprows=1)[:-2]
df = pd.concat([df1, df2, df3, df4]).loc[:, columns].copy()
# Drop the null columns where all values are null
df = df.dropna(axis='columns', how='all')
# Drop the null rows
df = df.dropna()
# Remove the `Issued` loan status
issued_mask = df['loan_status'] != 'Issued'
df = df.loc[issued_mask]
# convert interest rate to numerical
df['int_rate'] = df['int_rate'].str.replace('%', '')
df['int_rate'] = df['int_rate'].astype('float') / 100
# Convert the target column values to low_risk and high_risk based on their values
x = {'Current': 'low_risk'}
df = df.replace(x)
x = dict.fromkeys(['Late (31-120 days)', 'Late (16-30 days)', 'Default', 'In Grace Period'], 'high_risk')
df = df.replace(x)
low_risk_rows = df[df[target] == 'low_risk']
high_risk_rows = df[df[target] == 'high_risk']
#df = pd.concat([low_risk_rows, high_risk_rows.sample(n=len(low_risk_rows), replace=True)])
df = pd.concat([low_risk_rows.sample(n=len(high_risk_rows), random_state=42), high_risk_rows])
df = df.reset_index(drop=True)
df = df.rename({target:'target'}, axis="columns")
df
# -
df.to_csv('2019loans.csv', index=False)
# +
# Load the data
validate_df = pd.read_csv(Path('../Generator/LoanStats_2020Q1.csv.zip'), skiprows=1)[:-2]
validate_df = validate_df.loc[:, columns].copy()
# Drop the null columns where all values are null
validate_df = validate_df.dropna(axis='columns', how='all')
# Drop the null rows
validate_df = validate_df.dropna()
# Remove the `Issued` loan status
issued_mask = validate_df[target] != 'Issued'
validate_df = validate_df.loc[issued_mask]
# convert interest rate to numerical
validate_df['int_rate'] = validate_df['int_rate'].str.replace('%', '')
validate_df['int_rate'] = validate_df['int_rate'].astype('float') / 100
# Convert the target column values to low_risk and high_risk based on their values
x = dict.fromkeys(['Current', 'Fully Paid'], 'low_risk')
validate_df = validate_df.replace(x)
x = dict.fromkeys(['Late (31-120 days)', 'Late (16-30 days)', 'Default', 'In Grace Period', 'Charged Off'], 'high_risk')
validate_df = validate_df.replace(x)
low_risk_rows = validate_df[validate_df[target] == 'low_risk']
high_risk_rows = validate_df[validate_df[target] == 'high_risk']
validate_df = pd.concat([low_risk_rows.sample(n=len(high_risk_rows), random_state=37), high_risk_rows])
validate_df = validate_df.reset_index(drop=True)
validate_df = validate_df.rename({target:'target'}, axis="columns")
validate_df
# -
validate_df.to_csv('2020Q1loans.csv', index=False)
|
Resources/Generator/GenerateData.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.5
# language: python
# name: python3.5
# ---
# # Lomb-Scargle Example Dataset
# ## The Data
#
# For simplicity, we download the data here and save locally
# +
import pandas as pd
def get_LINEAR_lightcurve(lcid):
from astroML.datasets import fetch_LINEAR_sample
LINEAR_sample = fetch_LINEAR_sample()
data = pd.DataFrame(LINEAR_sample[lcid],
columns=['t', 'mag', 'magerr'])
data.to_csv('LINEAR_{0}.csv'.format(lcid), index=False)
# Uncomment to download the data
# get_LINEAR_lightcurve(lcid=11375941)
# -
data = pd.read_csv('LINEAR_11375941.csv')
data.head()
data.shape
(data.t.max() - data.t.min()) / 365.
# ## Visualizing the Data
# +
# %matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
plt.style.use('seaborn-whitegrid')
# +
fig, ax = plt.subplots(figsize=(8, 3))
ax.errorbar(data.t, data.mag, data.magerr,
fmt='.k', ecolor='gray', capsize=0)
ax.set(xlabel='time (MJD)',
ylabel='magnitude',
title='LINEAR object 11375941')
ax.invert_yaxis()
fig.savefig('fig01_LINEAR_data.pdf');
# +
from astropy.timeseries import LombScargle
ls = LombScargle(data.t, data.mag, data.magerr)
frequency, power = ls.autopower(nyquist_factor=500,
minimum_frequency=0.2)
period_days = 1. / frequency
period_hours = period_days * 24
# +
best_period = period_days[np.argmax(power)]
phase = (data.t / best_period) % 1
print("Best period: {0:.2f} hours".format(24 * best_period))
# +
fig, ax = plt.subplots(1, 2, figsize=(8, 3))
# PSD has a _LOT_ of elements. Rasterize it so it can be displayed as PDF
ax[0].plot(period_days, power, '-k', rasterized=True)
ax[0].set(xlim=(0, 2.5), ylim=(0, 0.8),
xlabel='Period (days)',
ylabel='Lomb-Scargle Power',
title='Lomb-Scargle Periodogram')
ax[1].errorbar(phase, data.mag, data.magerr,
fmt='.k', ecolor='gray', capsize=0)
ax[1].set(xlabel='phase',
ylabel='magnitude',
title='Phased Data')
ax[1].invert_yaxis()
ax[1].text(0.02, 0.03, "Period = {0:.2f} hours".format(24 * best_period),
transform=ax[1].transAxes)
inset = fig.add_axes([0.25, 0.6, 0.2, 0.25])
inset.plot(period_hours, power, '-k', rasterized=True)
inset.xaxis.set_major_locator(plt.MultipleLocator(1))
inset.yaxis.set_major_locator(plt.MultipleLocator(0.2))
inset.set(xlim=(1, 5),
xlabel='Period (hours)',
ylabel='power')
fig.savefig('fig02_LINEAR_PSD.pdf');
# -
# ## Peak Precision
#
# Estimate peak precision by plotting the Bayesian periodogram peak and fitting a Gaussian to the peak (for simplicity, just do it by-eye):
# +
f, P = ls.autopower(nyquist_factor=500,
minimum_frequency=9.3,
maximum_frequency=9.31,
samples_per_peak=20,
normalization='psd')
P = np.exp(P)
P /= P.max()
h = 24. / f
plt.plot(h, P, '-k')
plt.fill(h, np.exp(-0.5 * (h - 2.58014) ** 2 / 0.00004 ** 2), color='gray', alpha=0.3)
plt.xlim(2.58, 2.5803)
# -
# Looks like $2.58023 \pm 0.00006$ hours
# +
fig, ax = plt.subplots(figsize=(10, 3))
phase_model = np.linspace(-0.5, 1.5, 100)
best_frequency = frequency[np.argmax(power)]
mag_model = ls.model(phase_model / best_frequency, best_frequency)
for offset in [-1, 0, 1]:
ax.errorbar(phase + offset, data.mag, data.magerr, fmt='.',
color='gray', ecolor='lightgray', capsize=0);
ax.plot(phase_model, mag_model, '-k', lw=2)
ax.set(xlim=(-0.5, 1.5),
xlabel='phase',
ylabel='mag')
ax.invert_yaxis()
fig.savefig('fig18_ls_model.pdf')
# +
period_hours_bad = np.linspace(1, 6, 10001)
frequency_bad = 24 / period_hours_bad
power_bad = ls.power(frequency_bad)
mask = (period_hours > 1) & (period_hours < 6)
fig, ax = plt.subplots(figsize=(10, 3))
ax.plot(period_hours[mask], power[mask], '-', color='lightgray',
rasterized=True, label='Well-motivated frequency grid')
ax.plot(period_hours_bad, power_bad, '-k',
rasterized=True, label='10,000 equally-spaced periods')
ax.grid(False)
ax.legend()
ax.set(xlabel='period (hours)',
ylabel='Lomb-Scargle Power',
title='LINEAR object 11375941')
fig.savefig('fig19_LINEAR_coarse_grid.pdf')
# -
# ## Required Grid Spacing
# !head LINEAR_11375941.csv
# +
n_digits = 6
f_ny = 0.5 * 10 ** n_digits
T = (data.t.max() - data.t.min())
n_o = 5
delta_f = 1. / n_o / T
print("f_ny =", f_ny)
print("T =", T)
print("n_grid =", f_ny / delta_f)
|
figures/LINEAR_Example.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ___
#
# <a href='http://www.pieriandata.com'> <img src='../Pierian_Data_Logo.png' /></a>
# ___
# # Operations
#
# There are lots of operations with pandas that will be really useful to you, but don't fall into any distinct category. Let's show them here in this lecture:
import pandas as pd
df = pd.DataFrame({'col1':[1,2,3,4],'col2':[444,555,666,444],'col3':['abc','def','ghi','xyz']})
df.head()
# ### Info on Unique Values
df['col2'].unique()
df['col2'].nunique()
df['col2'].value_counts()
# ### Selecting Data
#Select from DataFrame using criteria from multiple columns
newdf = df[(df['col1']>2) & (df['col2']==444)]
newdf
# ### Applying Functions
def times2(x):
return x*2
df['col1'].apply(times2)
df['col2'].apply(lambda x: x*2)
df['col3'].apply(len)
df['col1'].sum()
# ** Permanently Removing a Column**
del df['col1']
# or df.drop('col1, axis = 1, inplace=True)
df
# ** Get column and index names: **
df.columns
df.index
# ** Sorting and Ordering a DataFrame:**
df
df.sort_values(by='col2') #inplace=False by default
# ** Find Null Values or Check for Null Values**
df.isnull()
# Drop rows with NaN Values
df.dropna()
# ** Filling in NaN values with something else: **
import numpy as np
df = pd.DataFrame({'col1':[1,2,3,np.nan],
'col2':[np.nan,555,666,444],
'col3':['abc','def','ghi','xyz']})
df.head()
df.fillna('FILL')
# +
data = {'A':['foo','foo','foo','bar','bar','bar'],
'B':['one','one','two','two','one','one'],
'C':['x','y','x','y','x','y'],
'D':[1,3,2,5,4,1]}
df = pd.DataFrame(data)
# -
df
df.pivot_table(values='D',index=['A', 'B'],columns=['C'])
# # Great Job!
|
1 MyPractice/Refactored_Py_DS_ML_Bootcamp-master/03-Python-for-Data-Analysis-Pandas/07-Operations.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Averaging Blur
import cv2
from matplotlib import pyplot as plot
import numpy as nm
img =cv2.imread("butterfly.jfif")
gray_image=cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
plot.imshow(img)
plot.title("Original Image")
averaging_blur_img=cv2.blur(gray_image,(6,6))
plot.imshow(averaging_blur_img)
plot.title("Sobel Image X-Direction")
|
ImageSmoothing/Averaging_smoothing.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.7.3 64-bit
# language: python
# name: python37364bite72acbb0cda24fc4847ed421ff53abec
# ---
# # 1.1.3. Recursion
# ## Learning Objectives
#
# * [Divide-and-conquer or decrease-and-conquer](#divide)
# * [Examples of real-life problems that are recursive in nature](#real)
# * [Recursive steps vs base case](#step)
# * [Recursion vs Iteration](#rec-iter)
# <a id='divide'></a>
# ## Divide-and-conquer or decrease-and-conquer
# Algorithmically: a way to design solutions to problems by **divide-and-conquer** or **decrease-and-conquer**. “Divide and conquer” algorithm solve a hard problem by breaking it into a set of subproblems such that:
# * sub-problems are easier to solve than the original
# * solutions of the sub-problems can be combined to solve the original
#
# Semantically: a programming technique where a function calls itself
# * in programming, goal is to NOT have infinite recursion
# * must have 1 or more base cases that are easy to solve
# * must solve the same problem on some other input with the goal of simplifying the larger problem input
# Have you ever done this before? Open your browser right now and type "recursion" on Google. Did you notice the **“Did you mean: recursion”** message? Uhm yes, but what does it mean really? Go further, click on that message. It will appear again. Click again. There it is again. Click… ENOUGH!
# <br>
# <img src="images/google.png" style="display: block; margin-left:auto; margin-right:auto; width:50%"/> <br>
#
#
# **Recursion** is the process of repeating items in a self-similar way.
# * A recursive function is a function that calls itself within its definition.
# * This can be hard to get your head around at first, but think of it as a breaking a big problem down into doing a small problem many times over.
# * This means that a complex problem can be made increasingly simpler by repeatedly doing a simpler and simpler and simpler form of the same problem with each repetition.
# * However, we must provide a 'simplest form' of the function where the function stops, otherwise it will repeat forever and throw an error.
# * We call this 'simplest form' a base case.
# * This is best illustrated with an example:
# +
# Function that takes in as input the starting number to countdown from
def countdown(n):
# base case: this is where the function will eventually stop
if n == 0:
print(0)
# here we reduce the problem into a simpler version
else:
# we print the countdown number
print(n)
# we repeat the function with the next smallest number
countdown(n-1)
countdown(5)
# -
# <a id='real'></a>
# ## Examples of real-life problems that are recursive in nature
# Here are some examples from our daily life:
# <br>**DNA**
# <br>
# <img src="images/dna.jpg" style="display: block; margin-left:auto; margin-right:auto; width:30%"/> <br>
#
#
# ([Source](https://qph.fs.quoracdn.net/main-qimg-905203aa42ecfa447e613c1dee2e3b4e-c))<br>
#
# **Romanesco broccoli**: its pattern has been modeled as a recursive helical arrangement of cones.
# <br>
# <img src="images/rom.jpg" style="display: block; margin-left:auto; margin-right:auto; width:30%"/> <br>
#
#
# ([Source](https://qph.fs.quoracdn.net/main-qimg-2d3fccb284d0e185d9d20b8d0268bb32-c))<br>
#
# **Russian dolls**
# <br>
# <img src="images/rus.jpg" style="display: block; margin-left:auto; margin-right:auto; width:30%"/> <br>
#
#
# ([Source](http://pythonpracticeprojects.com/real-world-recursion.html))<br>
#
# <a id='step'></a>
# ## Recursive steps vs base case
# **recursive step**
# * think how to reduce problem to a simpler/smaller version of same problem
#
# **base case**
# * keep reducing problem until reach a simple case that can be solved directly
# * when b = 1, a*b = a
#
# You can see recursive step and base case part in the multiplication example shown below:
# <br>
# <img src="images/recu.png" style="display: block; margin-left:auto; margin-right:auto; width:30%"/> <br>
#
# ([Source](https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-0001-introduction-to-computer-science-and-programming-in-python-fall-2016/lecture-slides-code/MIT6_0001F16_Lec6.pdf))<br>
#
#
# * In a base case, we compute the result immediately given the inputs to the function call.
# * In a recursive step, we compute the result with the help of one or more recursive calls to this same function, but with the inputs somehow reduced in size or complexity, closer to a base case.
# As a code break, let's see if you can write your very own, first recursive function to take one input to the power of the other. Remembering that:
# - $a^{b} = a \times a \times a \times ... \times a $: b times
# +
## It's coding time!!!
# -
# <a id='rec-iter'></a>
# ## Recursion vs Iteration
# * looping constructs (while and for loops) lead to iterative algorithms
# * can capture computation in a set of state variables that update on each iteration through loop
#
# A program is called __recursive__ when an entity calls itself. A program is called __iterative__ when there is a loop (or repetition). Example: Program to find the factorial of a number. Remember that the factorial of a number $x$, denoted as $x!$, is given by:
# - $x!$ = $x \times (x-1) \times (x-2) \times ... \times 2 \times 1 = x \times (x-1)!$
# - e.g.
# - $3! = 3 \times 2 \times 1 = 6$
# - $4! = 4 \times 3 \times 2 \times 1 = 4 \times 3! = 24$
# +
# ----- Recursion -----
# method to find factorial of given number
def factorialUsingRecursion(n):
# base case
if (n == 0):
return 1;
# recursion call
return n * factorialUsingRecursion(n - 1);
# ----- Iteration -----
# Method to find the factorial of a given number
def factorialUsingIteration(n):
res = 1;
# using iteration
for i in range(2, n + 1):
res *= i;
return res;
# Driver method
num = 5;
print("Factorial of",num,"using Recursion is:",
factorialUsingRecursion(5));
print("Factorial of",num,"using Iteration is:",
factorialUsingIteration(5));
# This code is contributed by mits
# -
# <br>
# <img src="images/rec_it.png" style="display: block; margin-left:auto; margin-right:auto; width:40%"/> <br>
#
# ([Source](https://www.geeksforgeeks.org/difference-between-recursion-and-iteration/))<br>
#
# ## Summary
# * Recursion is the process of repeating items in a self-similar way.
# * “Divide and conquer” algorithm solve a hard problem by breaking it into a set of subproblems
# * A program is called recursive when an entity calls itself.
# * A program is call iterative when there is a loop (or repetition).
# * Base case is to keep reducing problem until reach a simple case that can be solved directly
# * In a recursive step, we compute the result with the help of one or more recursive calls to this same function.
# ## Exercise:
#
# ### Question 1
# Write a Python program to solve the Fibonacci sequence using recursion. For more info about Fibonacci: https://en.wikipedia.org/wiki/Fibonacci_number
# - Takes in an integer, $n$, as input representing the number of the term in the sequence you would like to calculate
# - Returns the $n^{th}$ term of the Fibonacci sequence
# ### Question 2
# Write a recursive Python function that has a
# parameter representing a list of integers and returns the maximum
# stored in the list. Thinking recursively, the maximum is either the
# first value in the list or the maximum of the rest of the list,
# whichever is larger. If the list only has 1 integer, then its maximum
# is this single value, naturally.
#
# * Helpful Python syntax:
# If A is a list of integers, and you want to set the list B to all of the
# integers in A except the first one, you can write
#
# B = A[1:len(A)]
#
# (This sets B to the integers in A starting at index 1 and ending at
# index len(A)-1, the last index. The integer in the first position of A
# at index 0 is not included.)
#
#
# The function will:
# - Take in a list of numbers as an input argument
# - Return the maximum value from the input list
|
English/8. Recursion.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Futures
#
# Try out a moving average crossover strategy on futures. One at a time and summarize the results
# +
import pandas as pd
import matplotlib.pyplot as plt
import datetime
from talib.abstract import *
import pinkfish as pf
import strategy
#pd.set_option('display.max_rows', None)
pd.set_option('display.max_columns', None)
# format price data
pd.options.display.float_format = '{:0.2f}'.format
# %matplotlib inline
# -
# set size of inline plots
'''note: rcParams can't be in same cell as import matplotlib
or %matplotlib inline
%matplotlib notebook: will lead to interactive plots embedded within
the notebook, you can zoom and resize the figure
%matplotlib inline: only draw static images in the notebook
'''
plt.rcParams["figure.figsize"] = (10, 7)
# Investment Universe:
#
# Futures contracts cover these main asset classes:
# - Currencies
# - Energies
# - Financials
# - Grains
# - Indices
# - Meats
# - Metals
# - Softs
# ### FUTURES
# https://www.barchart.com/futures/contract-specifications/currencies
# +
# symbol: (description, multiplier)
currencies = {
'DX=F': ('U.S. Dollar Index', 1000),
'BTC=F': ('Bitcoin Futures', 5),
'6B=F': ('British Pound', 62500),
'6C=F': ('Canadian Dollar', 100000),
'6J=F': ('Japanese Yen', 125000),
'6S=F': ('Swiss Franc', 125000),
'6E=F': ('Euro FX', 125000),
'6A=F': ('Australian Dollar', 100000),
'6M=F': ('Mexican Peso', 500000),
'6N=F': ('New Zealand Dollar', 100000),
'6Z=F': ('South African Rand', 500000),
'6L=F': ('Brazilian Real', 100000),
'6R=F': ('Russian Ruble', 500000)
}
energies = {
'CL=F': ('Crude Oil West Texas Intermediate', 1000),
'HO=F': ('New York Harbor ULSD', 42000),
'RB=F': ('Gasoline Blendstock New York Harbor [RBOB]', 42000),
'NG=F': ('Natural Gas', 10000),
#'BZ=F': ('Brent Crude Oil Financial Futures', 1000),
'EH=F': ('Ethanol', 29000)
}
financials = {
'ZB=F': ('U.S. Treasury Bond Futures', 1000),
'UB=F': ('Ultra Treasury Bond', 1000),
'ZN=F': ('10-Year Treasury-Note', 1000),
'TN=F': ('Ultra 10-Year Treasury-Note', 1000),
'ZF=F': ('5-Year Treasury-Note', 1000),
'ZT=F': ('2-Year Treasury-Note', 2000),
'ZQ=F': ('30-Day Fed Funds', 2000),
#'GE=F': ('EuroDollar', 2500)
}
grains = {
'ZC=F': ('Corn', 50),
'ZS=F': ('Soybean', 50),
'ZM=F': ('Soybean Meal', 1000),
'ZL=F': ('Soybean Oil', 600),
'ZW=F': ('Chicago Soft Red Winter Wheat', 50),
'KE=F': ('KC Hard Red Winter Wheat', 50),
'ZO=F': ('Oats', 50),
#'ZR=F': ('Rough Rice', 2000),
'ZS=F': ('Rapeseed Canola', 20)
}
indices = {
'ES=F': ('E-Mini S&P 500 Index', 50),
'NQ=F': ('E-Mini Nasdaq 100', 20),
'YM=F': ('E-Mini Dow Jones Industrial Averagen', 5),
'RTY=F': ('E-Mini Russell 2000 Index', 50),
#'VI=F': ('CBOE Volatilty Index VIX Futures', 1000),
#'GD=F': ('GSCI - Goldman Sachs Commodity Index', 250)
}
meats = {
'LE=F': ('Live Cattle', 400),
'GF=F': ('Feeder Cattle', 500),
'HE=F': ('Lean Hogs', 400),
#'KM=F': ('Pork Cutout', 400),
'DC=F': ('Milk Class III', 2000)
}
metals = {
'GC=F': ('Gold 100-oz', 100),
'SI=F': ('Silver 5,000-oz', 5000),
'HG=F': ('High Grade Copper', 25000),
'PL=F': ('Platinum', 50),
'PA=F': ('Palladium', 100),
}
softs = {
'CT=F': ('Cotton #2', 500),
#'OJ=F': ('Orange Juice [FCOJ-A]', 150),
'KC=F': ('Coffee C Arabica', 375),
'SB=F': ('Sugar #11', 1120),
'CC=F': ('Cocoa', 10),
'LBS=F': ('Lumber', 110),
'SF=F': ('Sugar #16', 1120)
}
merged = {**currencies, **energies, **financials, **grains,
**indices, **meats, **metals, **softs}
# -
# Globals
# +
symbols = list(softs)
#symbols = ['ES=F', 'GC=F', 'CL=F']
capital = 100000
start = datetime.datetime(1900, 1, 1)
end = datetime.datetime.now()
# set options
stop_loss_pct = 0/100
margin = 1
sma_fast = 10
sma_slow = 100
percent_band = 0/100
enable_shorts = True
# -
# Run Strategy
strategies = pd.Series(dtype=object)
for symbol in symbols:
print("{0}".format(symbol), end=" ")
strategies[symbol] = strategy.Strategy(symbol, capital, start, end)
# set options
strategies[symbol].stop_loss_pct = stop_loss_pct
strategies[symbol].margin = margin
strategies[symbol].multiplier = merged[symbol][1]
strategies[symbol].timeperiod_fast = sma_fast
strategies[symbol].timeperiod_slow = sma_slow
strategies[symbol].percent_band = percent_band
strategies[symbol].enable_shorts = enable_shorts
#run
strategies[symbol].run()
#get logs
_, strategies[symbol].tlog, strategies[symbol].dbal = strategies[symbol].get_logs()
strategies[symbol].stats = strategies[symbol].get_stats()
#strategies[symbol].tlog.head(50)
# Summarize results
# +
metrics = ('start',
'annual_return_rate',
'max_closed_out_drawdown',
'sharpe_ratio',
'sortino_ratio',
'monthly_std',
'annual_std',
'pct_time_in_market',
'total_num_trades',
'pct_profitable_trades',
'avg_points',
'ending_balance')
df = strategy.summary(strategies, metrics)
pd.set_option('display.max_columns', len(df.columns))
df
# -
# averages
avg_annual_return_rate = df.loc['annual_return_rate'].mean()
avg_sharpe_ratio = df.loc['sharpe_ratio'].mean()
print('avg_annual_return_rate: {}'.format(avg_annual_return_rate))
print('avg_sharpe_ratio: {}'.format(avg_sharpe_ratio))
|
examples/futures-forex-crypto/futures.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] deletable=true editable=true
# * [Excercise 5.8. Racetrack](#Excercise-5.8.-Racetrack)
# + [markdown] deletable=true editable=true
# ## Excercise 5.8. Racetrack
# + deletable=true editable=true
from collections import namedtuple, defaultdict
import random
import numpy as np
from tqdm import tqdm
# %matplotlib inline
import matplotlib.pyplot as plt
# -
# ### Define Racetracks
# + [markdown] deletable=true editable=true
# Track definitions were copied from https://github.com/jkillingsworth/ReinforcementLearning/blob/master/chapter05/Racetrack/Track.fs
# + deletable=true editable=true
MAX_SPEED = 4
N_ACTIONS = 3 # number of actions along x and y: 0, 1, -1
# + deletable=true editable=true
track1 = """
XXXXXXXXXXXXXF
XXXXXXXXXXXXXXF
XXXXXXXXXXXXXXF
XXXXXXXXXXXXXXXF
XXXXXXXXXXXXXXXXF
XXXXXXXXXXXXXXXXF
XXXXXXXXXX
XXXXXXXXX
XXXXXXXXX
XXXXXXXXX
XXXXXXXXX
XXXXXXXXX
XXXXXXXXX
XXXXXXXXX
XXXXXXXX
XXXXXXXX
XXXXXXXX
XXXXXXXX
XXXXXXXX
XXXXXXXX
XXXXXXXX
XXXXXXXX
XXXXXXX
XXXXXXX
XXXXXXX
XXXXXXX
XXXXXXX
XXXXXXX
XXXXXXX
XXXXXX
XXXXXX
SSSSSS
"""
# + deletable=true editable=true
track2 = """
XXXXXXXXXXXXXXXF
XXXXXXXXXXXXXXXXXXF
XXXXXXXXXXXXXXXXXXXF
XXXXXXXXXXXXXXXXXXXXF
XXXXXXXXXXXXXXXXXXXXF
XXXXXXXXXXXXXXXXXXXXF
XXXXXXXXXXXXXXXXXXXXF
XXXXXXXXXXXXXXXXXXXF
XXXXXXXXXXXXXXXXXXF
XXXXXXXXXXXXXXXX
XXXXXXXXXXXXX
XXXXXXXXXXXX
XXXXXXXXXX
XXXXXXXXX
XXXXXXXXXX
XXXXXXXXXXX
XXXXXXXXXXXX
XXXXXXXXXXXXX
XXXXXXXXXXXXXX
XXXXXXXXXXXXXXX
XXXXXXXXXXXXXXXX
XXXXXXXXXXXXXXXXX
XXXXXXXXXXXXXXXXXX
XXXXXXXXXXXXXXXXXXX
XXXXXXXXXXXXXXXXXXXX
XXXXXXXXXXXXXXXXXXXXX
XXXXXXXXXXXXXXXXXXXXXX
XXXXXXXXXXXXXXXXXXXXXXX
XXXXXXXXXXXXXXXXXXXXXXX
SSSSSSSSSSSSSSSSSSSSSSS
"""
# + deletable=true editable=true
State = namedtuple('State', ['x', 'y', 'vx', 'vy']) # current position and speed
Action = namedtuple('Action', ['ax', 'ay']) # acceleration along each component
Transition = namedtuple('Transition', ['state1',
'action',
'reward',
'state2'])
# -
# ### Create Racetrack environment
# + deletable=true editable=true
class Racetrack(object):
def __init__(self, track_str):
rows = track_str.split('\n')
rows = rows[1:-1] # remove first and last rows
rows = rows[::-1] # flip vertically so [0,0] corresponds to bottom left corner
cells = map(list, rows) # convert rows of strings to rows of chars
self._track = np.array(list(cells))
self._state = None
# define all possible actions
self.actions = []
for ax in [-1, 0, 1]:
for ay in [-1, 0, 1]:
self.actions.append(Action(ax, ay))
def _track_cell(self, x, y):
max_y = self._track.shape[0] - 1
max_x = self._track.shape[1] - 1
if x < 0 or x > max_x:
return ' '
if y < 0 or y > max_y:
return ' '
return self._track[y, x]
def _is_on_track(self, state):
assert state.vx <= MAX_SPEED
assert state.vx >= 0
assert state.vy <= MAX_SPEED
assert state.vy >= 0
return self._track_cell(state.x, state.y) != ' '
def _has_finished(self, state):
return self._track_cell(state.x, state.y) == 'F'
def _transition(self, state, action):
# update speed
vx2 = state.vx + action.ax
vy2 = state.vy + action.ay
vx2 = np.clip(vx2, 0, MAX_SPEED)
vy2 = np.clip(vy2, 0, MAX_SPEED)
# keep the speed constant if both components are zero
if vx2 == 0 and vy2 == 0:
vx2, vy2 = state.vx, state.vy
# advance car position
x2 = state.x + vx2
y2 = state.y + vy2
# # additional random move
# if random.random() > 0.5:
# if random.random() > 0.5:
# x2 += 1 # move right
# else:
# y2 += 1 # move forward
collision_y = collision_x = False
# check and fix collisions along 'x'
while True:
s2 = State(x2, state.y, vx2, vy2)
if self._is_on_track(s2):
break
collision_x = True
x2 -= 1
vx2 = 1
assert x2 >= 0
# check and fix collision along 'y'
while True:
s2 = State(x2, y2, vx2, vy2)
if self._is_on_track(s2):
break
collision_y = True
y2 -= 1
vy2 = 1
assert y2 >= 0
if collision_y or collision_x:
r = -5
else:
r = -1
if state.x == x2 and state.y == y2:
# the car did not move
if collision_y:
x2 += 1
elif collision_x:
y2 += 1
else:
assert False, 'the car has to move'
s2 = State(x2, y2, vx2, vy2)
assert self._is_on_track(s2)
term = self._has_finished(s2)
if term:
r = 0
return r, s2, term
def reset(self):
max_x = self._track.shape[1]
while True:
x = random.randint(0, max_x)
vx = random.choice([0, 1])
vy = random.choice([0, 1])
if vx == 0 and vy == 0:
continue
s = State(x=x, y=0, vx=vx, vy=vy)
if self._is_on_track(s):
break
self._state = s
return s
def step(self, action):
r, s2, term = self._transition(self._state, action)
self._state = s2
return s2, r, term, _
def track_as_np(self):
_track = self._track
track_np = np.zeros_like(_track, dtype=int)
track_np[_track == 'S'] = 1
track_np[_track == 'X'] = 2
track_np[_track == 'F'] = 3
return track_np
# -
# ### Off-Policy Monte Carlo Control
# + deletable=true editable=true
class OffPolicyMC(object):
def __init__(self, env, gamma=0.99):
self.env = env
self._policy = {}
self._Q = defaultdict(lambda: defaultdict(int)) # Q[s][a]
self._C = defaultdict(lambda: defaultdict(int)) # C[s][a]
self.gamma = gamma
def generate_episode(self, policy):
s = env.reset()
trajectory = []
while True:
a = policy(s)
s2, r, term, _ = self.env.step(a)
t = Transition(s, a, r, s2)
trajectory.append(t)
if term:
break
s = s2
return trajectory
def random_policy(self, state):
return random.choice(self.env.actions)
def greedy_policy(self, state):
if state in self._Q:
return max(self._Q[state], key=self._Q[state].get)
else:
return self.random_policy(state)
def optimize(self, n_iter):
myu = 1 / len(self.env.actions) # probability of action under random policy
for _ in tqdm(range(n_iter)):
traj = self.generate_episode(self.random_policy)
G = 0
W = 1
for tr in reversed(traj):
s, a, r = tr.state1, tr.action, tr.reward
G = self.gamma * G + r
self._C[s][a] += W
self._Q[s][a] = self._Q[s][a] + W / self._C[s][a] * (G - self._Q[s][a])
a_greedy = max(self._Q[s], key=self._Q[s].get)
if a_greedy != a:
break
W = W * 1 / myu
# -
# ### Solve Racetrack MDP
# + deletable=true editable=true
env = Racetrack(track2)
mc = OffPolicyMC(env)
# + deletable=true editable=true
mc.optimize(5000000)
# -
# ### Visualize trajectories for the greedy policy
# + deletable=true editable=true
plt.imshow(env.track_as_np())
plt.gca().invert_yaxis()
trajectory = mc.generate_episode(mc.greedy_policy)
for t in trajectory:
plt.plot(t.state2.x, t.state2.y, '.r')
rewards = map(lambda t: t.reward, trajectory)
print('return', sum(rewards))
# +
plt.imshow(env.track_as_np())
plt.gca().invert_yaxis()
trajectory = mc.generate_episode(mc.greedy_policy)
for t in trajectory:
plt.plot(t.state2.x, t.state2.y, '.r')
rewards = map(lambda t: t.reward, trajectory)
print('return', sum(rewards))
# +
plt.imshow(env.track_as_np())
plt.gca().invert_yaxis()
trajectory = mc.generate_episode(mc.greedy_policy)
for t in trajectory:
plt.plot(t.state2.x, t.state2.y, '.r')
rewards = map(lambda t: t.reward, trajectory)
print('return', sum(rewards))
# -
# Note that at the last position before the finish line the car tries to go off the track. The way the game rules are defined it does not get penalized as long as it crosses the finish line.
# ### Visualize optimal value function
np.full_like
# +
V_xy = np.full_like(env.track_as_np(), -np.inf,dtype=float)
Q_max = defaultdict(list)
for s, actions in mc._Q.items():
Q_max[s.y, s.x].append(max(mc._Q[s].values()))
for pos, vals in Q_max.items():
V_xy[pos] = np.mean(vals)
# -
plt.imshow(V_xy)
plt.colorbar()
plt.gca().invert_yaxis()
# ### Check action-state coverage by Monte Carlo
# + deletable=true editable=true
# count all possible car positions
n_start_positions = (env._track == 'S').sum()
n_track_positions = (env._track == 'X').sum()
n_start_positions, n_track_positions
# -
# count all possible states, each state is car's position and speed
n_possible_states = n_start_positions * 3 + n_track_positions * (MAX_SPEED * MAX_SPEED - 1)
n_sampled_states = len(mc._Q)
print('n_possible_states = ', n_possible_states)
print('n_sampled_states = ', n_sampled_states)
print('n_sampled_states / n_possible_states = %d%%'
% round(n_sampled_states/n_possible_states * 100))
n_possible_state_actions = n_possible_states * len(env.actions)
n_sampled_state_actions = sum(map(lambda v: len(v), mc._Q.values()))
print('n_possible_state_actions = ', n_possible_state_actions)
print('n_sampled_state_actions = ', n_sampled_state_actions)
print('n_sampled_state_actions / n_possible_state_actions = %d%%'
% round(n_sampled_state_actions/n_possible_state_actions * 100))
|
ch05.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# ## Q1. What is the percentage of Male Players in the Winter Olympics
# ## Q2. Number of Gold Medals wins in entire Winter Olympics
# ## Q3. Which country is having most numbers of Medals
# ## Q4. Which country is having most numbers of Gold Medals
# ## Q5. Which sport is having most number of Gold Medals
# ## Q6. Top 5 Disciplines in terms of Medals
# ## Q7. Top 5 Disciplines in terms of Bronze Medals
# ## Q8. How many players has won atleast one medal in Winter Olympics
|
Data Analysis Assignment/Winter Olympics Analysis - Assignment.ipynb
|
// ---
// jupyter:
// jupytext:
// text_representation:
// extension: .groovy
// format_name: light
// format_version: '1.5'
// jupytext_version: 1.14.4
// kernelspec:
// display_name: Groovy
// language: groovy
// name: groovy
// ---
// ## Gaussian Op
// +
//load ImageJ
// %classpath config resolver scijava.public https://maven.scijava.org/content/groups/public
// %classpath add mvn net.imagej imagej 2.0.0-rc-67
//create ImageJ object
ij = new net.imagej.ImageJ()
// -
// This `Op` performs a [Gaussian blur](https://en.wikipedia.org/wiki/Gaussian_blur) on any image. This is how the `Op` is called:
ij.op().help("gauss")
// Note the parameters here:
//
// * `RandomAccessibleInterval out`: the (optional) output image
// * `RandomAccessibleInterval in`: the input image
// * `double[] sigmas`/`double sigma`: the sigma or array of sigmas used in the Gaussian. If you choose an array the array must be as long in length as the number of dimensions of the input image, and if you do not want to perform a Gaussian in a particular dimension set the value for that dimension to `0`. If you choose the single value that value will be applied in all dimensions.
// * `OutOfBoundsFactory outOfBounds`: an **optional** parameter that tells the `Op` how to populate the values outside of the image `Interval` when performing the convolution. Since this parameter is optional we will not deal with it in this notebook.
//
// Let's get an image to blur:
// +
input = ij.scifio().datasetIO().open("http://imagej.net/images/clown.png")
ij.notebook().display(input)
// -
// Now that we have our image all we have to do is declare our sigma array and then run the Gaussian:
// +
sigmas = [8, 8, 0]
output = ij.op().run("filter.gauss", input, sigmas)
ij.notebook().display(output)
|
notebooks/1-Using-ImageJ/Ops/filter/gauss.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <img src="images/usm.jpg" width="480" height="240" align="left"/>
# # MAT281 - Laboratorios N°01
#
# ## Objetivos del laboratorio
#
# * Reforzar conceptos básicos de regresión lineal.
# ## Contenidos
#
# * [Problema 01](#p1)
#
# <a id='p1'></a>
# ## I.- Problema 01
#
#
# <img src="https://upload.wikimedia.org/wikipedia/commons/thumb/b/b6/Anscombe.svg/1200px-Anscombe.svg.png" width="360" height="360" align="center"/>
#
#
# El **cuarteto de Anscombe** comprende cuatro conjuntos de datos que tienen las mismas propiedades estadísticas, pero que evidentemente son distintas al inspeccionar sus gráficos respectivos.
#
# Cada conjunto consiste de once puntos (x, y) y fueron construidos por el estadístico <NAME>. El cuarteto es una demostración de la importancia de mirar gráficamente un conjunto de datos antes de analizarlos.
# +
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# %matplotlib inline
sns.set_palette("deep", desat=.6)
sns.set(rc={'figure.figsize':(11.7,8.27)})
# -
# cargar datos
df = pd.read_csv(os.path.join("data","anscombe.csv"), sep=",")
df.head()
# Basado en la información presentada responda las siguientes preguntas:
#
# 1. Gráfique mediante un gráfico tipo **scatter** cada grupo. A simple vista, ¿ los grupos son muy distintos entre si?.
# 2. Realice un resumen de las medidas estadísticas más significativas ocuapando el comando **describe** para cada grupo. Interprete.
# 3. Realice un ajuste lineal para cada grupo. Además, grafique los resultados de la regresión lineal para cada grupo. Interprete.
# 4. Calcule los resultados de las métricas para cada grupo. Interprete.
# 5. Es claro que el ajuste lineal para algunos grupos no es el correcto. Existen varias formas de solucionar este problema (eliminar outliers, otros modelos, etc.). Identifique una estrategia para que el modelo de regresión lineal ajuste de mejor manera e implemente otros modelos en los casos que encuentre necesario.
# # Parte1
grupos=df.groupby('grupo')
plt.figure(figsize=(15,6))
g1=plt.subplot(2,2,1)
g2=plt.subplot(2,2,2)
g3=plt.subplot(2,2,3)
g4=plt.subplot(2,2,4)
sns.scatterplot(x='x', y='y', data=grupos.get_group('Grupo_1'), ax=g1)
sns.scatterplot(x='x', y='y', data=grupos.get_group('Grupo_2'), ax=g2)
sns.scatterplot(x='x', y='y', data=grupos.get_group('Grupo_3'), ax=g3)
sns.scatterplot(x='x', y='y', data=grupos.get_group('Grupo_4'), ax=g4)
# Los grupos son MUY distintos entre si, de hecho algunos no tienen comportamiento lineal.
# # Parte 2
df.groupby(['grupo']).describe()
# # Parte 3
from sklearn import datasets
from sklearn.model_selection import train_test_split
# +
grupos=df.groupby('grupo') # categorizo por grupo
X1=grupos.get_group('Grupo_1')[['x']] #Genero un nuevo dataframe solo del grupo1, con los valores de la columna x
X2=grupos.get_group('Grupo_2')[['x']] #Genero un nuevo dataframe solo del grupo2, con los valores de la columna x
X3=grupos.get_group('Grupo_3')[['x']] #Genero un nuevo dataframe solo del grupo3, con los valores de la columna x
X4=grupos.get_group('Grupo_4')[['x']] #Genero un nuevo dataframe solo del grupo4, con los valores de la columna x
y1=grupos.get_group('Grupo_1')['y'] #Genero una nueva serie solo del grupo1, con los valores de la columna y
y2=grupos.get_group('Grupo_2')['y'] #Genero una nueva serie solo del grupo2, con los valores de la columna y
y3=grupos.get_group('Grupo_3')['y'] #Genero una nueva serie solo del grupo3, con los valores de la columna y
y4=grupos.get_group('Grupo_4')['y'] #Genero una nueva serie solo del grupo4, con los valores de la columna y
#Separo los conjuntos anteriores en partes de prueba y testeo
X1_train, X1_test, y1_train, y1_test = train_test_split(X1, y1, test_size=0.3, random_state=77)
X2_train, X2_test, y2_train, y2_test = train_test_split(X2, y2, test_size=0.3, random_state=77)
X3_train, X3_test, y3_train, y3_test = train_test_split(X3, y3, test_size=0.3, random_state=77)
X4_train, X4_test, y4_train, y4_test = train_test_split(X4, y4, test_size=0.3, random_state=77)
# importando el modelo de regresión lineal
from sklearn.linear_model import LinearRegression
model_rl1 = LinearRegression() # Creando el modelo.
model_rl2 = LinearRegression() # Creando el modelo.
model_rl3 = LinearRegression() # Creando el modelo.
model_rl4 = LinearRegression() # Creando el modelo.
# ajustando el modelo
model_rl1.fit(X1_train, y1_train)
model_rl2.fit(X2_train, y2_train)
model_rl3.fit(X3_train, y3_train)
model_rl4.fit(X4_train, y4_train)
# Lista de coeficientes B para cada X_train de grupo 1
beta1_0 = round(model_rl1.intercept_,4)
beta1_1 = round(model_rl1.coef_[0],4)
print(f"El mejor ajuste lineal para el grupo 1 viene dado por la recta: \n\n \
f(x) = {beta1_0} + {beta1_1}*x")
# Lista de coeficientes B para cada X_train de grupo 2
beta2_0 = round(model_rl2.intercept_,4)
beta2_1 = round(model_rl2.coef_[0],4)
print(f"El mejor ajuste lineal para el grupo 2 viene dado por la recta: \n\n \
f(x) = {beta2_0} + {beta2_1}*x")
# Lista de coeficientes B para cada X_train de grupo 3
beta3_0 = round(model_rl3.intercept_,4)
beta3_1 = round(model_rl3.coef_[0],4)
print(f"El mejor ajuste lineal para el grupo 3 viene dado por la recta: \n\n \
f(x) = {beta3_0} + {beta3_1}*x")
# Lista de coeficientes B para cada X_train de grupo 4
beta4_0 = round(model_rl4.intercept_,4)
beta4_1 = round(model_rl4.coef_[0],4)
print(f"El mejor ajuste lineal para el grupo 4 viene dado por la recta: \n\n \
f(x) = {beta4_0} + {beta4_1}*x")
# +
# graficos con seaborn grafico 1
plt.figure(figsize=(15,10))
g1=plt.subplot(2,2,1)
g2=plt.subplot(2,2,2)
g3=plt.subplot(2,2,3)
g4=plt.subplot(2,2,4)
x_range = np.arange(0,22,0.1)
df_plot1 = pd.DataFrame({'x':x_range,
'y':[beta1_0 + beta1_1*n for n in x_range]})
df1 = pd.concat([X1_train,y1_train],axis=1)
grafico1A=sns.scatterplot(x='x', y='y', data=df1, ax=g1)
grafico1B=sns.lineplot(x='x', y='y', data=df_plot1,ax=g1,color="green")
grafico1A.set(xlabel='x',ylabel='y')
plt.xlabel('x')
plt.ylabel('y')
# graficos con seaborn grafico 2
df_plot2 = pd.DataFrame({'x':x_range,
'y':[beta2_0 + beta2_1*n for n in x_range]})
df2 = pd.concat([X2_train,y2_train],axis=1)
grafico2A=sns.scatterplot(x='x', y='y', data=df2, ax=g2)
grafico2B=sns.lineplot(x='x', y='y', data=df_plot2,ax=g2,color="green")
grafico2A.set(xlabel='x',ylabel='y')
plt.xlabel('x')
plt.ylabel('y')
# graficos con seaborn grafico 3
df_plot3 = pd.DataFrame({'x':x_range,
'y':[beta3_0 + beta3_1*n for n in x_range]})
df3 = pd.concat([X3_train,y3_train],axis=1)
grafico3A=sns.scatterplot(x='x', y='y', data=df3, ax=g3)
grafico3B=sns.lineplot(x='x', y='y', data=df_plot3,ax=g3,color="green")
grafico3A.set(xlabel='x',ylabel='y')
plt.xlabel('x')
plt.ylabel('y')
# graficos con seaborn grafico 4
df_plot4 = pd.DataFrame({'x':x_range,
'y':[beta4_0 + beta4_1*n for n in x_range]})
df4 = pd.concat([X4_train,y4_train],axis=1)
grafico4A=sns.scatterplot(x='x', y='y', data=df4, ax=g4)
grafico4B=sns.lineplot(x='x', y='y', data=df_plot4,ax=g4,color="green")
grafico4A.set(xlabel='x',ylabel='y')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
# -
# # Parte 4
# +
from metrics_regression import *
from sklearn.metrics import r2_score
# Grupo1
#Genero un dataframe con los valores de prueba con X e y
df_temp1 = pd.DataFrame(
{
'y':y1_test,
'yhat': model_rl1.predict(X1_test)
}
)
#Genero metricas a partir de mis datos de testeo con mi modelo lineal encontrado en la sección anterior
df_metrics1 = summary_metrics(df_temp1)
df_metrics1['r2'] = round(r2_score(y1_test, model_rl1.predict(X1_test)),4)
print('\nMetricas para el regresor grupo1:\n')
print(df_metrics1)
# Grupo2
#Genero un dataframe con los valores de prueba con X e y
df_temp2 = pd.DataFrame(
{
'y':y2_test,
'yhat': model_rl2.predict(X2_test)
}
)
#Genero metricas a partir de mis datos de testeo con mi modelo lineal encontrado en la sección anterior
df_metrics2 = summary_metrics(df_temp2)
df_metrics2['r2'] = round(r2_score(y2_test, model_rl2.predict(X2_test)),4)
print('\nMetricas para el regresor grupo2:\n')
print(df_metrics2)
# Grupo3
#Genero un dataframe con los valores de prueba con X e y
df_temp3 = pd.DataFrame(
{
'y':y3_test,
'yhat': model_rl3.predict(X3_test)
}
)
#Genero metricas a partir de mis datos de testeo con mi modelo lineal encontrado en la sección anterior
df_metrics3 = summary_metrics(df_temp3)
df_metrics3['r2'] = round(r2_score(y3_test, model_rl3.predict(X3_test)),4)
print('\nMetricas para el regresor grupo3:\n')
print(df_metrics3)
# Grupo4
#Genero un dataframe con los valores de prueba con X e y
df_temp4 = pd.DataFrame(
{
'y':y4_test,
'yhat': model_rl4.predict(X4_test)
}
)
#Genero metricas a partir de mis datos de testeo con mi modelo lineal encontrado en la sección anterior
df_metrics4 = summary_metrics(df_temp4)
df_metrics4['r2'] = round(r2_score(y4_test, model_rl4.predict(X4_test)),4)
print('\nMetricas para el regresor grupo4:\n')
print(df_metrics4)
# -
# Se puede apreciar que para cada grupo hay un indice bajo de error para cada metrica excepto par r cuadrado, el cual solo es medianamente preciso para el grupo 1, y para el resto es bastante malo al acercarse mucho al valor cero, en especial destaca el grupo 4 que tiene coeficiente r cuadrado negativo lo que nos indica que el ajuste no tiene ningun sentido respecto a los datos entregados, esto nos dice que el grupo 4 probablemente tenga otro tipo de comportamiento que no es lineal.
# # Parte 5
# Es claro que para el grupo 1 el ajuste es bueno ya que r cuadrado se aproxima a 1,
# por otro lado para el resto de grupos se debe cambiar el modelo que se esta usando.
# Grupo2: Se debe ocupar una regresion polinomica de grado 2, ya que es claro con ver los datos en el grafico que ese es su comportamiento
# Grupo3: Se debe eliminar el dato anomalo que esta causando problemas.
# Grupo4: Se deben invertir los ejes y eliminar el dato anomalo, para que así se tenga una buena aproximación lineal.
|
labs/C2_machine_learning/02_analisis_supervisado_regresion/laboratorio_07.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/ralsouza/kaggle_used_cars/blob/master/src/04_Kaggle_Analysis_4.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="lQ1ynFgBvD3c" colab_type="text"
# # Analysis #4
# + id="9nROWv07uu9d" colab_type="code" colab={}
# Imports
import os
import subprocess
import stat
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from datetime import datetime
sns.set(style="white")
# %matplotlib inline
# + id="C9wmJmqfvHy5" colab_type="code" colab={}
# Dataset
clean_data_path = "drive/My Drive/datasets/autos.csv"
df = pd.read_csv(clean_data_path,encoding="latin-1")
# + id="t8nBAWcXvLV9" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 394} outputId="78504d69-8a0e-464c-a667-3af6c55df90d"
df.head()
# + [markdown] id="1f1C7wL6vfVY" colab_type="text"
# ### Média de preço por marca e por veículo
# + id="e52u4T0Evy7r" colab_type="code" colab={}
# Calcule a média de preço por marca e por veículo
trial = pd.DataFrame()
for b in list(df["brand"].unique()):
for v in list(df["vehicleType"].unique()):
z = df[(df["brand"] == b) & (df["vehicleType"] == v)]["price"].mean()
trial = trial.append(pd.DataFrame({'brand':b , 'vehicleType':v , 'avgPrice':z}, index=[0]))
trial = trial.reset_index()
del trial["index"]
trial["avgPrice"].fillna(0,inplace=True)
trial["avgPrice"].isnull().value_counts()
trial["avgPrice"] = trial["avgPrice"].astype(int)
# + id="1I0Tw6Wxy4HO" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 204} outputId="bc4bf8ba-4762-4a80-c32b-9843cad4dbd6"
trial.head()
# + [markdown] id="Gt0HPuqXzbUO" colab_type="text"
# ### Preço médio de um veículo por marca, bem como tipo de veículo
# + id="l0X3S9QczdPu" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="591622cb-b332-4992-a2ae-a3aa84df0003"
tri = trial.pivot("brand","vehicleType", "avgPrice")
fig, ax = plt.subplots(figsize=(15,20))
sns.heatmap(tri,linewidths=1,cmap="YlGnBu",annot=True, ax=ax, fmt="d")
ax.set_title("Heatmap - Preço médio de um veículo por marca e tipo de veículo",fontdict={'size':20})
ax.xaxis.set_label_text("Tipo de Veículo",fontdict= {'size':20})
ax.yaxis.set_label_text("Marca",fontdict= {'size':20})
plt.show()
|
src/04_Kaggle_Analysis_4.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from pyvista import examples
import pyvista as pv
import numpy as np
surface = examples.download_foot_bones()
surface
dir(surface)
# +
voxels = pv.voxelize(surface,density=surface.length/200)
p = pv.Plotter()
p.add_mesh(voxels,color=True,show_edges=True,opacity=0.5)
p.add_mesh(surface,color="lightblue",opacity=0.5)
cpos = [(7.656346967151718, -9.802071079151158, -11.021236183314311),
(0.2224512272564101, -0.4594554282112895, 0.5549738359311297),
(-0.6279216753504941, -0.7513057097368635, 0.20311105371647392)]
p.show(cpos=cpos)
# -
dir(voxels)
|
python/tlbm/stl_utils/Foot_bones.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.6
# language: python
# name: python36
# ---
# 
# Copyright (c) Microsoft Corporation. All rights reserved.
#
# Licensed under the MIT License.
# # Logging
#
# _**This notebook showcases various ways to use the Azure Machine Learning service run logging APIs, and view the results in the Azure portal.**_
#
# ---
# ---
#
# ## Table of Contents
#
# 1. [Introduction](#Introduction)
# 1. [Setup](#Setup)
# 1. Validate Azure ML SDK installation
# 1. Initialize workspace
# 1. Set experiment
# 1. [Logging](#Logging)
# 1. Starting a run
# 1. Viewing a run in the portal
# 1. Viewing the experiment in the portal
# 1. Logging metrics
# 1. Logging string metrics
# 1. Logging numeric metrics
# 1. Logging vectors
# 1. Logging tables
# 1. Uploading files
# 1. [Analyzing results](#Analyzing-results)
# 1. Tagging a run
# 1. [Next steps](#Next-steps)
#
# ## Introduction
#
# Logging metrics from runs in your experiments allows you to track results from one run to another, determining trends in your outputs and understand how your inputs correspond to your model and script performance. Azure Machine Learning services (AzureML) allows you to track various types of metrics including images and arbitrary files in order to understand, analyze, and audit your experimental progress.
#
# Typically you should log all parameters for your experiment and all numerical and string outputs of your experiment. This will allow you to analyze the performance of your experiments across multiple runs, correlate inputs to outputs, and filter runs based on interesting criteria.
#
# The experiment's Run History report page automatically creates a report that can be customized to show the KPI's, charts, and column sets that are interesting to you.
#
# |  |  |
# |:--:|:--:|
# | *Run Details* | *Run History* |
#
# ---
#
# ## Setup
#
# If you are using an Azure Machine Learning Notebook VM, you are all set. Otherwise, go through the [configuration](../../../configuration.ipynb) Notebook first if you haven't already to establish your connection to the AzureML Workspace. Also make sure you have tqdm and matplotlib installed in the current kernel.
#
# ```
# (myenv) $ conda install -y tqdm matplotlib
# ```
# ### Validate Azure ML SDK installation and get version number for debugging purposes
# + tags=["install"]
from azureml.core import Experiment, Workspace, Run
import azureml.core
import numpy as np
from tqdm import tqdm
# Check core SDK version number
print("This notebook was created using SDK version 1.11.0, you are currently running version", azureml.core.VERSION)
# -
# ### Initialize workspace
#
# Initialize a workspace object from persisted configuration.
# + tags=["create workspace"]
ws = Workspace.from_config()
print('Workspace name: ' + ws.name,
'Azure region: ' + ws.location,
'Subscription id: ' + ws.subscription_id,
'Resource group: ' + ws.resource_group, sep='\n')
# -
# ### Set experiment
# Create a new experiment (or get the one with the specified name). An *experiment* is a container for an arbitrary set of *runs*.
experiment = Experiment(workspace=ws, name='logging-api-test')
# ---
#
# ## Logging
# In this section we will explore the various logging mechanisms.
#
# ### Starting a run
#
# A *run* is a singular experimental trial. In this notebook we will create a run directly on the experiment by calling `run = exp.start_logging()`. If you were experimenting by submitting a script file as an experiment using ``experiment.submit()``, you would call `run = Run.get_context()` in your script to access the run context of your code. In either case, the logging methods on the returned run object work the same.
#
# This cell also stores the run id for use later in this notebook. The run_id is not necessary for logging.
# +
# start logging for the run
run = experiment.start_logging()
# access the run id for use later
run_id = run.id
# change the scale factor on different runs to see how you can compare multiple runs
scale_factor = 2
# change the category on different runs to see how to organize data in reports
category = 'Red'
# -
# #### Viewing a run in the Portal
# Once a run is started you can see the run in the portal by simply typing ``run``. Clicking on the "Link to Portal" link will take you to the Run Details page that shows the metrics you have logged and other run properties. You can refresh this page after each logging statement to see the updated results.
run
# ### Viewing an experiment in the portal
# You can also view an experiement similarly by typing `experiment`. The portal link will take you to the experiment's Run History page that shows all runs and allows you to analyze trends across multiple runs.
experiment
# ## Logging metrics
# Metrics are visible in the run details page in the AzureML portal and also can be analyzed in experiment reports. The run details page looks as below and contains tabs for Details, Outputs, Logs, and Snapshot.
# * The Details page displays attributes about the run, plus logged metrics and images. Metrics that are vectors appear as charts.
# * The Outputs page contains any files, such as models, you uploaded into the "outputs" directory from your run into storage. If you place files in the "outputs" directory locally, the files are automatically uploaded on your behald when the run is completed.
# * The Logs page allows you to view any log files created by your run. Logging runs created in notebooks typically do not generate log files.
# * The Snapshot page contains a snapshot of the directory specified in the ''start_logging'' statement, plus the notebook at the time of the ''start_logging'' call. This snapshot and notebook can be downloaded from the Run Details page to continue or reproduce an experiment.
#
# ### Logging string metrics
# The following cell logs a string metric. A string metric is simply a string value associated with a name. A string metric String metrics are useful for labelling runs and to organize your data. Typically you should log all string parameters as metrics for later analysis - even information such as paths can help to understand how individual experiements perform differently.
#
# String metrics can be used in the following ways:
# * Plot in hitograms
# * Group by indicators for numerical plots
# * Filtering runs
#
# String metrics appear in the **Tracked Metrics** section of the Run Details page and can be added as a column in Run History reports.
# log a string metric
run.log(name='Category', value=category)
# ### Logging numerical metrics
# The following cell logs some numerical metrics. Numerical metrics can include metrics such as AUC or MSE. You should log any parameter or significant output measure in order to understand trends across multiple experiments. Numerical metrics appear in the **Tracked Metrics** section of the Run Details page, and can be used in charts or KPI's in experiment Run History reports.
# log numerical values
run.log(name="scale factor", value = scale_factor)
run.log(name='Magic Number', value=42 * scale_factor)
# ### Logging vectors
# Vectors are good for recording information such as loss curves. You can log a vector by creating a list of numbers, calling ``log_list()`` and supplying a name and the list, or by repeatedly logging a value using the same name.
#
# Vectors are presented in Run Details as a chart, and are directly comparable in experiment reports when placed in a chart.
#
# **Note:** vectors logged into the run are expected to be relatively small. Logging very large vectors into Azure ML can result in reduced performance. If you need to store large amounts of data associated with the run, you can write the data to file that will be uploaded.
# +
fibonacci_values = [0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89]
scaled_values = (i * scale_factor for i in fibonacci_values)
# Log a list of values. Note this will generate a single-variable line chart.
run.log_list(name='Fibonacci', value=scaled_values)
for i in tqdm(range(-10, 10)):
# log a metric value repeatedly, this will generate a single-variable line chart.
run.log(name='Sigmoid', value=1 / (1 + np.exp(-i)))
# -
# ### Logging tables
# Tables are good for recording related sets of information such as accuracy tables, confusion matrices, etc.
# You can log a table in two ways:
# * Create a dictionary of lists where each list represents a column in the table and call ``log_table()``
# * Repeatedly call ``log_row()`` providing the same table name with a consistent set of named args as the column values
#
# Tables are presented in Run Details as a chart using the first two columns of the table
#
# **Note:** tables logged into the run are expected to be relatively small. Logging very large tables into Azure ML can result in reduced performance. If you need to store large amounts of data associated with the run, you can write the data to file that will be uploaded.
# +
# create a dictionary to hold a table of values
sines = {}
sines['angle'] = []
sines['sine'] = []
for i in tqdm(range(-10, 10)):
angle = i / 2.0 * scale_factor
# log a 2 (or more) values as a metric repeatedly. This will generate a 2-variable line chart if you have 2 numerical columns.
run.log_row(name='Cosine Wave', angle=angle, cos=np.cos(angle))
sines['angle'].append(angle)
sines['sine'].append(np.sin(angle))
# log a dictionary as a table, this will generate a 2-variable chart if you have 2 numerical columns
run.log_table(name='Sine Wave', value=sines)
# -
# ### Logging images
# You can directly log _matplotlib_ plots and arbitrary images to your run record. This code logs a _matplotlib_ pyplot object. Images show up in the run details page in the Azure ML Portal.
# +
# %matplotlib inline
# Create a plot
import matplotlib.pyplot as plt
angle = np.linspace(-3, 3, 50) * scale_factor
plt.plot(angle,np.tanh(angle), label='tanh')
plt.legend(fontsize=12)
plt.title('Hyperbolic Tangent', fontsize=16)
plt.grid(True)
# Log the plot to the run. To log an arbitrary image, use the form run.log_image(name, path='./image_path.png')
run.log_image(name='Hyperbolic Tangent', plot=plt)
# -
# ### Uploading files
#
# Files can also be uploaded explicitly and stored as artifacts along with the run record. These files are also visible in the *Outputs* tab of the Run Details page.
#
# +
file_name = 'outputs/myfile.txt'
with open(file_name, "w") as f:
f.write('This is an output file that will be uploaded.\n')
# Upload the file explicitly into artifacts
run.upload_file(name = file_name, path_or_stream = file_name)
# -
# ### Completing the run
#
# Calling `run.complete()` marks the run as completed and triggers the output file collection. If for any reason you need to indicate the run failed or simply need to cancel the run you can call `run.fail()` or `run.cancel()`.
run.complete()
# ---
#
# ## Analyzing results
# You can refresh the run in the Azure portal to see all of your results. In many cases you will want to analyze runs that were performed previously to inspect the contents or compare results. Runs can be fetched from their parent Experiment object using the ``Run()`` constructor or the ``experiment.get_runs()`` method.
fetched_run = Run(experiment, run_id)
fetched_run
# Call ``run.get_metrics()`` to retrieve all the metrics from a run.
fetched_run.get_metrics()
# Call ``run.get_metrics(name = <metric name>)`` to retrieve a metric value by name. Retrieving a single metric can be faster, especially if the run contains many metrics.
fetched_run.get_metrics(name = "scale factor")
# See the files uploaded for this run by calling ``run.get_file_names()``
fetched_run.get_file_names()
# Once you know the file names in a run, you can download the files using the ``run.download_file()`` method
# +
import os
os.makedirs('files', exist_ok=True)
for f in run.get_file_names():
dest = os.path.join('files', f.split('/')[-1])
print('Downloading file {} to {}...'.format(f, dest))
fetched_run.download_file(f, dest)
# -
# ### Tagging a run
# Often when you analyze the results of a run, you may need to tag that run with important personal or external information. You can add a tag to a run using the ``run.tag()`` method. AzureML supports valueless and valued tags.
# +
fetched_run.tag("My Favorite Run")
fetched_run.tag("Competition Rank", 1)
fetched_run.get_tags()
# -
# ## Next steps
# To experiment more with logging and to understand how metrics can be visualized, go back to the *Start a run* section, try changing the category and scale_factor values and going through the notebook several times. Play with the KPI, charting, and column selection options on the experiment's Run History reports page to see how the various metrics can be combined and visualized.
#
# After learning about all of the logging options, go to the [train on remote vm](..\train-on-remote-vm\train-on-remote-vm.ipynb) notebook and experiment with logging from remote compute contexts.
|
how-to-use-azureml/track-and-monitor-experiments/logging-api/logging-api.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Data Preparation
# +
# Load the "autoreload" extension
# %load_ext autoreload
# always reload modules marked with "%aimport"
# %autoreload 1
# +
import os
import sys
import pandas as pd
# add the 'src' directory as one where we can import modules
src_dir = os.path.join(os.getcwd(), os.pardir,'src')
sys.path.append(src_dir)
# -
print(src_dir)
# # Definiton of an epiweek :
#
# Epiweeks use the U.S. definition. That is, the first epiweek each year is the week, starting on a Sunday, containing January 4.
# ref : [epiweek](http://www.cmmcp.org/epiweek.htm)
# +
## Testing Delphi epidata
# import my method from the source code
# #%aimport data.delphi_epidata
#from data.delphi_epidata import Epidata
# -
# Fetch State data from 2010 to 2015 in the US
import pandas as pd
# %aimport data.clean_data
from data.clean_data import get_states
#from data.clean_data import get_ilinet_data
#from data.clean_data import get_fluview_data
filepath = '/Users/bbuildman/Documents/Developer/GitHub/001-BB-DL-ILI/src/labels/states.txt'
# %pinfo
states = get_states()
start = 2010
end = 2015
print(states)
from ulmo.ncdc import gsod
stations = {}
for state in states:
stations[state] = gsod.get_stations(country="US",state= state, start=2010, end=2015)
print("number of states {}".format(len(stations)))
# %store stations
len(stations)
# +
clim_states ={}
for state in states:
s_weather = []
for station in stations[state]:
s_weather.append(gsod.get_data(station_codes=station, start=2010, end=2015))
clim_states[state] = s_weather
print("number of station {} in the state : {}".format(len(clim_states[state]), state ))
# -
# %store clim_states
len(clim_states)
clim_states
|
notebooks/0.0-BB-CLIMATE-DATA-2017-12-04.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# +
import pandas as pd
from pathlib import Path
import fastbook
from fastbook import *
from fastai.tabular.all import *
# -
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
Path.cwd()
DATA_PATH = Path.cwd()/'data'
train_df = pd.read_csv(DATA_PATH/'train_data.csv')
test_df = pd.read_csv(DATA_PATH/'test_data.csv')
df = pd.read_csv(DATA_PATH/'full_data.csv')
train_idx = np.array(range(len(train_df))).tolist()
test_idx = np.array(range(len(test_df)))
test_idx = (test_idx + train_idx[-1] + 1).tolist()
cont = list(df.columns)[1:-1]
cat = list(df.columns)[0:1]
dep_var = list(df.columns)[-1]
procs = [Categorify]
dls = TabularDataLoaders.from_df(df, DATA_PATH, procs=procs, cat_names=cat, cont_names=cont,
y_names=dep_var, valid_idx=test_idx, bs=64, device=device)
# + tags=[]
learn = tabular_learner(dls, layers=[400, 100], y_range=(20, 90), loss_func=mae)
# + tags=[]
lr = learn.lr_find().valley
# + tags=[]
learn.fit_one_cycle(10, lr)
#400->100
# -
learn.show_results()
mae(*learn.get_preds())
learn.save(DATA_PATH.parent/'models'/'fastai400_100')
# + tags=[]
learn.fit_one_cycle(20, lr)
#400->200->200->100
#wd=0.1
# + tags=[]
learn.fit_one_cycle(20, lr)
#200->100
|
notebooks/FastAI_Model.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Piecewise Affine Transforms
import numpy as np
from menpo.transform import PiecewiseAffine
# We build a `PiecewiseAffine` by supplying two sets of points and a shared triangle list
# +
from menpo.shape import TriMesh, PointCloud
a = np.array([[0, 0], [1, 0], [0, 1], [1, 1],
[-0.5, -0.7], [0.8, -0.4], [0.9, -2.1]])
b = np.array([[0,0], [2, 0], [-1, 3], [2, 6],
[-1.0, -0.01], [1.0, -0.4], [0.8, -1.6]])
tl = np.array([[0,2,1], [1,3,2]])
src = TriMesh(a, tl)
src_points = PointCloud(a)
tgt = PointCloud(b)
pwa = PiecewiseAffine(src_points, tgt)
# -
# Lets make a random 5000 point `PointCloud` in the unit square and view it
# %matplotlib inline
# points_s = PointCloud(np.random.rand(10000).reshape([-1,2]))
points_f = PointCloud(np.random.rand(10000).reshape([-1,2]))
points_f.view()
# Now lets see the effect having warped
t_points_f = pwa.apply(points_f);
t_points_f.view()
test = np.array([[0.1,0.1], [0.7, 0.9],
[0.2,0.3], [0.5, 0.6]])
pwa.index_alpha_beta(test)
|
menpo/Transforms/Piecewise_Affine.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/LilySu/DS-Unit-2-Sprint-4-Practicing-Understanding/blob/master/LS_DS_241_Hyperparameter_Optimization_Assignment.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="TCZaoClzRU9P" colab_type="code" colab={}
#Using a good validation set can prevent this.
#You can check if your validation set is any good by seeing if your model
#has similar scores on it to compared with on the Kaggle test set.
# + [markdown] colab_type="text" id="O67uhlT4MExK"
# _Lambda School Data Science — Practicing & Understanding Predictive Modeling_
#
# # Hyperparameter Optimization
# + [markdown] colab_type="text" id="VE4rfZd4NUGA"
# Today we'll use this process:
#
# ## "A universal workflow of machine learning"
#
# _Excerpt from <NAME>, [Deep Learning with Python](https://github.com/fchollet/deep-learning-with-python-notebooks/blob/master/README.md), Chapter 4: Fundamentals of machine learning_
#
# **1. Define the problem at hand and the data on which you’ll train.** Collect this data, or annotate it with labels if need be.
#
# **2. Choose how you’ll measure success on your problem.** Which metrics will you monitor on your validation data?
#
# **3. Determine your evaluation protocol:** hold-out validation? K-fold validation? Which portion of the data should you use for validation?
#
# **4. Develop a first model that does better than a basic baseline:** a model with statistical power.
#
# **5. Develop a model that overfits.** The universal tension in machine learning is between optimization and generalization; the ideal model is one that stands right at the border between underfitting and overfitting; between undercapacity and overcapacity. To figure out where this border lies, first you must cross it.
#
# **6. Regularize your model and tune its hyperparameters, based on performance on the validation data.** Repeatedly modify your model, train it, evaluate on your validation data (not the test data, at this point), modify it again, and repeat, until the model is as good as it can get.
#
# **Iterate on feature engineering: add new features, or remove features that don’t seem to be informative.**
#
# Once you’ve developed a satisfactory model configuration, you can **train your final production model on all the available data (training and validation) and evaluate it one last time on the test set.**
#
# + [markdown] colab_type="text" id="3kt6bzEcOIaa"
# ## 1. Define the problem at hand and the data on which you'll train
# + [markdown] colab_type="text" id="di16k7vpRg67"
# We'll apply the workflow to a [project from _Python Data Science Handbook_](https://jakevdp.github.io/PythonDataScienceHandbook/05.06-linear-regression.html#Example:-Predicting-Bicycle-Traffic) by <NAME>:
#
# > **Predicting Bicycle Traffic**
#
# > As an example, let's take a look at whether we can predict the number of bicycle trips across Seattle's Fremont Bridge based on weather, season, and other factors.
#
# > We will join the bike data with another dataset, and try to determine the extent to which weather and seasonal factors—temperature, precipitation, and daylight hours—affect the volume of bicycle traffic through this corridor. Fortunately, the NOAA makes available their daily [weather station data](http://www.ncdc.noaa.gov/cdo-web/search?datasetid=GHCND) (I used station ID USW00024233) and we can easily use Pandas to join the two data sources.
#
# > Let's start by loading the two datasets, indexing by date:
# + [markdown] colab_type="text" id="19dpb_d0R1A6"
# So this is a regression problem, not a classification problem. We'll define the target, choose an evaluation metric, and choose models that are appropriate for regression problems.
#
#
#
# + [markdown] colab_type="text" id="os1zruXQ30KM"
# ### Download data
# + colab_type="code" id="5XVu-HSeMDtV" outputId="1fdb87c0-5aef-4d34-e30a-d619531bba29" colab={"base_uri": "https://localhost:8080/", "height": 71}
# !curl -o FremontBridge.csv https://data.seattle.gov/api/views/65db-xm6k/rows.csv?accessType=DOWNLOAD
# + colab_type="code" id="sih_7mTzMdfr" outputId="63cf6444-5a1b-4cef-f029-42f73ace1ee0" colab={"base_uri": "https://localhost:8080/", "height": 214}
# !wget https://raw.githubusercontent.com/jakevdp/PythonDataScienceHandbook/master/notebooks/data/BicycleWeather.csv
# + [markdown] colab_type="text" id="9GYm74kD34OQ"
# ### Load data
# + colab_type="code" id="BfQ7gE28MNdF" colab={}
# Modified from cells 15, 16, and 20, at
# https://jakevdp.github.io/PythonDataScienceHandbook/05.06-linear-regression.html#Example:-Predicting-Bicycle-Traffic
import pandas as pd
# Download and join data into a dataframe
def load():
fremont_bridge = 'https://data.seattle.gov/api/views/65db-xm6k/rows.csv?accessType=DOWNLOAD'
bicycle_weather = 'https://raw.githubusercontent.com/jakevdp/PythonDataScienceHandbook/master/notebooks/data/BicycleWeather.csv'
counts = pd.read_csv(fremont_bridge, index_col='Date', parse_dates=True,
infer_datetime_format=True)
weather = pd.read_csv(bicycle_weather, index_col='DATE', parse_dates=True,
infer_datetime_format=True)
daily = counts.resample('d').sum()
daily['Total'] = daily.sum(axis=1)
daily = daily[['Total']] # remove other columns
weather_columns = ['PRCP', 'SNOW', 'SNWD', 'TMAX', 'TMIN', 'AWND']
daily = daily.join(weather[weather_columns], how='inner')
# Make a feature for yesterday's total
daily['Total_yesterday'] = daily.Total.shift(1)
daily = daily.drop(index=daily.index[0])
return daily
daily = load()
# + id="QznSxqvjWThH" colab_type="code" outputId="199030a9-bab5-44af-83f7-90d09f8e5aef" colab={"base_uri": "https://localhost:8080/", "height": 294}
daily.head().T
# + id="0VJnqNOnwSCp" colab_type="code" colab={}
#choose evaluation metric, and models
# + [markdown] colab_type="text" id="VVB3g4704An5"
# ### First fast look at the data
# - What's the shape?
# - What's the date range?
# - What's the target and the features?
# + id="HNbIspCbyLy-" colab_type="code" outputId="e1a82788-699e-47a3-abf3-d3468c472ad2" colab={"base_uri": "https://localhost:8080/", "height": 35}
daily.shape
# + id="zwZzFlDvyReB" colab_type="code" outputId="46b34245-5de9-427e-dd38-0b5a7b7e93a3" colab={"base_uri": "https://localhost:8080/", "height": 202}
daily.tail()
# + id="8ScRNK4pyYfw" colab_type="code" outputId="eaf0f2aa-faaf-428f-91e2-ed1cb7744129" colab={"base_uri": "https://localhost:8080/", "height": 250}
daily.info()
# + [markdown] colab_type="text" id="XgMvCsaWJR7Q"
# Target
# - Total : Daily total number of bicycle trips across Seattle's Fremont Bridge
#
# Features
# - Date (index) : from 2012-10-04 to 2015-09-01 in index
# - Total_yesterday : Total trips yesterday
# - PRCP : Precipitation (1/10 mm)
# - SNOW : Snowfall (1/10 mm)
# - SNWD : Snow depth (1/10 mm)
# - TMAX : Maximum temperature (1/10 Celsius)
# - TMIN : Minimum temperature (1/10 Celsius)
# - AWND : Average daily wind speed (1/10 meters per second)
# + [markdown] colab_type="text" id="lenL-przSYCo"
# 2. Choose how you’ll measure success on your problem.
#
# Which metrics will you monitor on your validation data?
#
# This is a regression problem, so we need to choose a regression [metric](https://scikit-learn.org/stable/modules/model_evaluation.html#common-cases-predefined-values).
#
#
#
# I'll choose mean absolute error.
#
#
# + colab_type="code" id="1TqbomapSyRP" colab={}
from sklearn.metrics import mean_absolute_error
#regression problem, we choose regression metric
#on average, how many bike passengers pass the tremont bridge
# + id="3157h4iKzG-2" colab_type="code" colab={}
#we want hyperparameter optimization.
#these last 100 days, we'll hold those out, with slice notation
# + id="RaqPEHaXzTwR" colab_type="code" outputId="7119181e-8d0a-4071-8d9f-2e363aec72cb" colab={"base_uri": "https://localhost:8080/", "height": 35}
#out of time test
train = daily[:-100]#everything but the last 100 days
test = daily[-100:]#last 100 days
train.shape, test.shape
# + id="b920hEnhznPE" colab_type="code" colab={}
#to predict the future, we can rewind time to 100 days ago
#then predict for past 100 days with the next 100 days
# it is a more difficult test than a random set, worse test scores, but maybe more realistic
# + id="Ehy2kpRSzXUi" colab_type="code" outputId="40879937-2f94-4728-a493-263ddd0562e1" colab={"base_uri": "https://localhost:8080/", "height": 35}
X_train = train.drop(columns='Total')
y_train = train['Total']
X_test = test.drop(columns='Total')
y_test = test['Total']
X_train.shape, y_train.shape, X_test.shape, y_test.shape
# + [markdown] colab_type="text" id="IRHrB3rsS5hF"
# 3. Determine your evaluation protocol
#
# We're doing model selection, hyperparameter optimization, and performance estimation. So generally we have two ideal [options](https://sebastianraschka.com/images/blog/2018/model-evaluation-selection-part4/model-eval-conclusions.jpg) to choose from:
#
# - 3-way holdout method (train/validation/test split)
# - Cross-validation with independent test set
#
# I'll choose cross-validation with independent test set. Scikit-learn makes cross-validation convenient for us!
#
# Specifically, I will use random shuffled cross validation to train and validate, but I will hold out an "out-of-time" test set, from the last 100 days of data:
#
#
#
#
# + colab_type="code" id="A3xo6HgbPMFm" colab={}
# TODO
# + [markdown] colab_type="text" id="vH6IsORQTvTU"
# 4. Develop a first model that does better than a basic baseline
# + [markdown] colab_type="text" id="DJBs2nQkj7oB"
# ### Look at the target's distribution and descriptive stats
# + colab_type="code" id="P5peakv9Zs71" outputId="c758e83c-c3a6-46a0-ce2d-ec6aaa2d307c" colab={"base_uri": "https://localhost:8080/", "height": 283}
# TODO
# %matplotlib inline
import seaborn as sns
sns.distplot(y_train);
#if gives negative number, poisson and other models
# + id="a3CguYXi0ZZB" colab_type="code" colab={}
#if this were to have an extremem right skew, we might do a log linear
#poisson if I want it to be positive
# + id="yx6F0J2oAxWK" colab_type="code" outputId="f731bda8-6f52-4fd4-9f5c-19c2c3389f6e" colab={"base_uri": "https://localhost:8080/", "height": 178}
y_train.describe()
# + [markdown] colab_type="text" id="fEjxxgV9kExY"
# ### Basic baseline 1
# + colab_type="code" id="6GepKdQjYcEP" outputId="247fb1b3-99ad-4aa3-cdd1-7191944a384a" colab={"base_uri": "https://localhost:8080/", "height": 35}
y_pred = [y_train.median()] * len(y_train)# a variety of baselines work
mean_absolute_error(y_train, y_pred)
#if I always predicted the median number of bicyclists per day, then I would be off 972 days
# + [markdown] colab_type="text" id="tN2I_F3FkIHb"
# ### Basic baseline 2
# + colab_type="code" id="ZW8bhZFtTunV" outputId="5037ab20-2705-4195-a835-bdc41ff4071a" colab={"base_uri": "https://localhost:8080/", "height": 202}
X_train.head()
# + id="hb8F3n741yRN" colab_type="code" outputId="22d86d77-7859-40e2-dc85-67d8599923c1" colab={"base_uri": "https://localhost:8080/", "height": 125}
y_train.head()
# + id="kXwLm5nC1x7d" colab_type="code" outputId="c1b8a1ad-3203-45bd-a3b4-d102c368b15f" colab={"base_uri": "https://localhost:8080/", "height": 35}
y_pred = X_train['Total_yesterday']#we're going to predict if today is the same as yesterday
mean_absolute_error(y_train,y_pred)#we're going to be off this many days
# + [markdown] colab_type="text" id="Ggf3VpxwkJ0T"
# ### First model that does better than a basic baseline
# + [markdown] colab_type="text" id="KfaqL1Ezer2-"
# https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.cross_validate.html
# + id="6_EE9ee42N2c" colab_type="code" colab={}
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_validate# returns dictionary on test scores in test set
#estimator itself
#scoring is none on default
#return dictionary of validation scores on test and train scores
# + id="7TTl0XIo2eBy" colab_type="code" colab={}
#neg_mean_absolute_error doesn't maximize, like other scikitlearn functions
#regularly mean absolute error would return a smaller number,
#but by taking a negative mean absolute error, we can flip it for a bigger number
# + colab_type="code" id="OeBtU68skfW-" colab={}
scores = cross_validate(LinearRegression(), X_train, y_train,
scoring = 'neg_mean_absolute_error', cv = 3,#higher numbers may have more variance, could be 5 or 7, computational time increases
return_train_score = True, return_estimator = True)#we return training scores as well as test score. We can put the dictionary this outputs into a dataframe
# + id="VoW_vfHzEVKE" colab_type="code" outputId="6e6a5716-7072-4224-f5d6-7726c9869c1d" colab={"base_uri": "https://localhost:8080/", "height": 141}
pd.DataFrame(scores)
#-mean absolute error optimizing for scikitlearn
#most scikit learn scores tries to maximize scores, when taking the negative, then the lower the mean absolute error fits, lower
#Neg_mean_abs_error optimizes for closer to zero. where 0= good.
# + id="sqVITZdX28Pl" colab_type="code" colab={}
#We see above that for 3-fold validation, each time we get a different test score from training score
# + id="kWJxbflKE-VO" colab_type="code" outputId="7f3e5569-1a3b-4c31-8267-8e35bcb1dca9" colab={"base_uri": "https://localhost:8080/", "height": 35}
-scores['test_score'].mean()#like multiplying by negative one
#we're off by 600 bicyclists per day
# + id="kk3xWLvM4IfF" colab_type="code" outputId="3fd1e649-f987-4283-e9de-4dfa3e511ac2" colab={"base_uri": "https://localhost:8080/", "height": 35}
scores['estimator'][0]
# + id="1h6fGxUwFVti" colab_type="code" outputId="89b23d29-b6ac-4303-92a2-cda0743dceec" colab={"base_uri": "https://localhost:8080/", "height": 35}
type(scores['estimator'][0])#so I can get out the intercept and coefficents from this model
# + id="J2nCGksiFf83" colab_type="code" outputId="c8feea0b-685f-4423-f071-6e390abfbedf" colab={"base_uri": "https://localhost:8080/", "height": 53}
scores['estimator'][0].coef_
# + id="CflHX_3X4T9a" colab_type="code" outputId="6a9b01cc-5010-41e8-d72c-48c5d897c2ed" colab={"base_uri": "https://localhost:8080/", "height": 35}
scores['estimator'][0].intercept_
# + id="J0gmf3flFjfP" colab_type="code" outputId="d29cfb9d-6e4f-40a8-b8f5-9e664a1d217a" colab={"base_uri": "https://localhost:8080/", "height": 608}
for i, model in enumerate(scores['estimator']):#loop over scores dictionary
#enumerate iterates if I want the thing itself and also some index number
#for each score, we have an linear regression model and i, an integer
coefficients = model.coef_
intercept = model.intercept_
feature_names = X_train.columns
#get their intercept
#get their column name
print(f'Model form cross-validation fold #{i}')
print('Intercept', intercept)
print(pd.Series(coefficients, feature_names).to_string())
print('\n')
#we split training data into a, b and c
#fold #0: train a and b and tested on c, what are intercepts and coefficients
#fold #1: train a and c
#fold #2: train b and c
# + id="fzxaRH7j5b0L" colab_type="code" colab={}
#analogous to stats models at the 95% confidence interval - having a high p value for this coef so we do not reject the null hypothesis
#that the coefficient's value might be zero, we're not sure if it is positive or negative
# + id="KBToNKw8G2Lv" colab_type="code" colab={}
#univariate linear regression
# linear regression plus other models should be better, at 607 a day compared to other scores
# + id="zMhqNOsW6NfN" colab_type="code" colab={}
#with no additional features, no feature engineering done
#It's like saying we have X_train['Total_yesterday'] as the feature, where intercept is zero
#and coefficient of 1, so 1 multiplied by ['Total_yesterday'] + 0, which is nothing,
#So a model that uses this useless feature plus another feature should outperform it
# + [markdown] colab_type="text" id="fg1YI4X8n9nI"
# ## 5. Develop a model that overfits.
#
# "The universal tension in machine learning is between optimization and generalization; the ideal model is one that stands right at the border between underfitting and overfitting; between undercapacity and overcapacity. To figure out where this border lies, first you must cross it." —Chollet
# + [markdown] colab_type="text" id="lodd6UPOoy89"
# <img src="https://jakevdp.github.io/PythonDataScienceHandbook/figures/05.03-validation-curve.png">
#
# Diagram Source: https://jakevdp.github.io/PythonDataScienceHandbook/05.03-hyperparameters-and-model-validation.html#Validation-curves-in-Scikit-Learn
# + [markdown] colab_type="text" id="xj82P0VdwYlh"
# ### Random Forest?
#
# https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestRegressor.html
# + id="PRM5bVgr67S9" colab_type="code" colab={}
#With a more complex model, your training score should keep improving
#Yet your validation score could decrease with model complexity until it gets overfit
# + id="Xv-RWS4l7O1e" colab_type="code" colab={}
#Your training score should provide a ceiling for your validation score
# + colab_type="code" id="_yYXpk99C4cM" outputId="da08ddcc-408b-4c23-c318-7a38060e8807" colab={"base_uri": "https://localhost:8080/", "height": 141}
# Random Forest Regressor - this is a regressor problem
from sklearn. ensemble import RandomForestRegressor
model = RandomForestRegressor(n_estimators=100, max_depth=None, n_jobs=-1)#Instantiating Random Forest Regressor Object
#this model should pick up non-linear, non-monotonic and interactions between features.
#With these features this is the best that can be done without feature engineering and hyperparameter tuning
scores = cross_validate(model, X_train, y_train,#doing cross validation with random forest
scoring='neg_mean_absolute_error',
cv=3, return_train_score=True,
return_estimator=True)
pd.DataFrame(scores)
#random forest not performing as well as linear regression
# + id="z-Mn33G-NbM1" colab_type="code" outputId="d15c34f1-9321-4ebf-f395-9bae91c429f7" colab={"base_uri": "https://localhost:8080/", "height": 35}
-scores['test_score'].mean()
# + id="qfIhRgpGLlIe" colab_type="code" outputId="afe89f5f-94b4-4381-c546-6fd43171d950" colab={"base_uri": "https://localhost:8080/", "height": 248}
# TODO
from xgboost import XGBRegressor
model = XGBRegressor(n_estimators=50)
scores = cross_validate(model, X_train, y_train,
scoring='neg_mean_absolute_error',
cv=3, return_train_score=True,
return_estimator=True)
pd.DataFrame(scores)
#random forest not performing as well as linear regression
# + id="VzQ-IX2uN1pE" colab_type="code" outputId="bec9e0b8-7dd4-4cce-ddc6-0a2af31477a0" colab={"base_uri": "https://localhost:8080/", "height": 35}
-scores['test_score'].mean()
# + [markdown] colab_type="text" id="_ryO1hVKr-6f"
# ### Validation Curve
#
# https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.validation_curve.html
#
# > Validation curve. Determine training and test scores for varying parameter values. This is similar to grid search with one parameter.
# + id="3bKiU7068Ecg" colab_type="code" outputId="4b1330e5-eda2-4396-9acb-13b2dcbf574d" colab={"base_uri": "https://localhost:8080/", "height": 35}
-scores['test_score'].mean()
# + colab_type="code" id="apKk4vKiwgtM" outputId="bf3faa86-51f2-4559-9f52-477112ad54bb" colab={"base_uri": "https://localhost:8080/", "height": 283}
# Modified from cell 13 at
# https://jakevdp.github.io/PythonDataScienceHandbook/05.03-hyperparameters-and-model-validation.html#Validation-curves-in-Scikit-Learn
# %matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import validation_curve#allows for any given model a variety of parameter values
model = RandomForestRegressor(n_estimators=100)
depth = [2, 3, 4, 5, 6]#try a variety of parameters for model
train_score, val_score = validation_curve(
model, X_train, y_train,
param_name='max_depth', param_range=depth,
scoring='neg_mean_absolute_error', cv=3)
plt.plot(depth, np.median(train_score, 1), color='blue', label='training score')
plt.plot(depth, np.median(val_score, 1), color='red', label='validation score')
plt.legend(loc='best')
plt.xlabel('depth');
#like training with max-depth 2, train with 3, 4 etc
# + id="3iy-njNQ8e_O" colab_type="code" colab={}
#It is possible and recommended to search the hyperparameter space for the best cross validation score
#GridSearchCV will exhaustively consider all parameter combinations
#RandomizedSearchCV can sample a given number of subjects
# + [markdown] colab_type="text" id="DQoMvZ7-yCAQ"
# ### `RandomizedSearchCV`
#
# https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.RandomizedSearchCV.html
#
# https://scikit-learn.org/stable/modules/grid_search.html
# + colab_type="code" id="bk_dX_mByKm7" outputId="01530d40-bdaa-4905-a6fb-5ed4a6e1a2ea" colab={"base_uri": "https://localhost:8080/", "height": 1486}
# recommended to search with highest validation score, gridsearch will exhaustively consider all parameters
#Gridsearch may take a long time, to get an incrementally better score
# RandomizedSearch CV can sample a given number of candidates
from sklearn.model_selection import RandomizedSearchCV
param_distributions = {#What is the distribution of values that we'll try
'n_estimators': [100, 200],#Do exactly one hundred or two hundred
'max_depth': [4, 5],
'criterion': ['mse', 'mae']#Mean Squared Error, Mean Absolute Error, we try both and see what does the best.
}#I can try different options for my pipeline
#in real world, you will have more parameter values
gridsearch = RandomizedSearchCV(
RandomForestRegressor(n_jobs=-1, random_state=42),#parameters, what are the estimators we are using
param_distributions=param_distributions,
n_iter = 8,#if that took too long, can try like 4, tradeoff of runtime to optimization of solution
#We have 2 n_estimators, multiply by 2 max depth, multiplied by criterion - 8 will exhaustively use all which will equal GridSearchCV
#grid search would take too long, Randomized Search is faster
#at 8 iterations, this equals grid search
cv=3,
scoring='neg_mean_absolute_error',
verbose=10,#operate where it's at, because it might take too long
return_train_score=True
)
gridsearch.fit(X_train, y_train)
#n_iter trades off runtime vs quality of solution
#criterion measure quality of split using mean squared error or mean absolute error, not going to make a huge difference
# + id="-iGSpdqi_xly" colab_type="code" outputId="5bdb4360-38b1-4f93-9e9e-09646d62e9a8" colab={"base_uri": "https://localhost:8080/", "height": 895}
gridsearch.cv_results_
# + id="4JdVs19SQ7i7" colab_type="code" outputId="7b09e260-15f5-4b61-a701-3a340154a1ce" colab={"base_uri": "https://localhost:8080/", "height": 168}
results = pd.DataFrame(gridsearch.cv_results_)
print(f'Best result from search of {len(results)} parameter combinations')
results.sort_values(by='rank_test_score').head(1)#spits out 8 rows
#randomized search cv, we have to look at parameters
# + id="rr3BCDvKWhIM" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="c3f6baae-6283-4156-c6de-1cf8b113a9ac"
-gridsearch.best_score_
# + id="PhN92ZFyAJ8H" colab_type="code" outputId="c59f3887-325e-4888-9d17-b983f4badb59" colab={"base_uri": "https://localhost:8080/", "height": 35}
type(gridsearch.best_estimator_)
# + id="UzNsYkkdRwC4" colab_type="code" outputId="c7abd95a-d121-496b-8941-f53f0e952d20" colab={"base_uri": "https://localhost:8080/", "height": 142}
gridsearch.best_estimator_
# gridsearch.best_estimator_.predict_proba
# + id="KUR-tAkISNO2" colab_type="code" colab={}
#It's important to develop a model that overfits, otherwise it is not working
#Deep learning is less feature engineering, more architecture
# + id="FRCsCSHIBURt" colab_type="code" colab={}
#deep learning can memorize noise, so if you are not able to overfit, something is wrong
#in deep learning there is more emphasis on regularization and tuning of hyperparameters
# + id="MhHFoXY8BtU5" colab_type="code" colab={}
#get to the basic baseline first, then emphasize feature engineering
# + [markdown] colab_type="text" id="ZW5HfYtU0GW2"
# FEATURE ENGINEERING!
# + [markdown] colab_type="text" id="0ms-eoOHFvPG"
# <NAME> demonstrates this feature engineering:
# https://jakevdp.github.io/PythonDataScienceHandbook/05.06-linear-regression.html#Example:-Predicting-Bicycle-Traffic
# He has some awesome examples
# + colab_type="code" id="sEwME8wR3A5g" colab={}
import numpy as np
from datetime import date, datetime, timedelta
# Modified from code cells 17-21 at
# https://jakevdp.github.io/PythonDataScienceHandbook/05.06-linear-regression.html#Example:-Predicting-Bicycle-Traffic
def jake_wrangle(X):
X = X.copy()
# patterns of use generally vary from day to day;
# let's add binary columns that indicate the day of the week:
days = ['Mon', 'Tue', 'Wed', 'Thu', 'Fri', 'Sat', 'Sun']#manual one hot encoding
for i, day in enumerate(days):
X[day] = (X.index.dayofweek == i).astype(float)
X['IsWeekday'] = X['Mon']+X['Tue']+X['Wed']+X['Thu']+X['Fri'] == 1#--------------------Is Weekday?
# we might expect riders to behave differently on holidays;
# let's add an indicator of this as well:
# from pandas.tseries.holiday import USFederalHolidayCalendar
# cal = USFederalHolidayCalendar()
# holidays = cal.holidays('2012', '2016')
# X = X.join(pd.Series(1, index=holidays, name='holiday'))
# X['holiday'].fillna(0, inplace=True)
# We also might suspect that the hours of daylight would affect
# how many people ride; let's use the standard astronomical calculation
# to add this information:
def hours_of_daylight(date, axis=23.44, latitude=47.61):
"""Compute the hours of daylight for the given date"""
days = (date - pd.datetime(2000, 12, 21)).days
m = (1. - np.tan(np.radians(latitude))
* np.tan(np.radians(axis) * np.cos(days * 2 * np.pi / 365.25)))
return 24. * np.degrees(np.arccos(1 - np.clip(m, 0, 2))) / 180.
# DOY = X.index.values
# DOY = pd.to_datetime(DOY)
# Y = DOY.year
# M = DOY.month
# D = DOY.date
# Winter = X.loc[datetime.date(year=Y,month=12,day=21):datetime.date(year=Y,month=3,day=19)]
# X['IsWinter'] = DOY in Winter
X['Month'] = X.index.month
X['Day'] = X.index.day
X['IsWinter'] = ((X['Month'] == 3) & (X['Day'] < 21)) & ((X['Month'] == 12) & (X['Day'] >= 21)) & (X['Month'] <= 2) #--------------------Is from 12/22 - 3/21?
X['NearPopRidership'] = (X['Month'] == 5) & (abs(X['Day'] - 14) < 5)
X['daylight_hrs'] = list(map(hours_of_daylight, X.index))
# temperatures are in 1/10 deg C; convert to C
X['TMIN'] /= 10
X['TMINear13'] = abs(X['TMIN'] - 13) < 3#--------------------Is below 45F?
X['TMAX'] /= 10
X['TMAXNear28'] = abs(X['TMAX'] - 28) < 3#--------------------Is above 90F?
X['daylight_hrsNear15'] = abs(X['daylight_hrs'] - 15) < 3
# We can also calcuate the average temperature.
X['Temp (C)'] = 0.5 * (X['TMIN'] + X['TMAX'])
# precip is in 1/10 mm; convert to inches
X['PRCP'] /= 254
X['PrecipitationAboveHalfin'] = X['PRCP'] > 0.5#--------------------Is above .5 in?
# In addition to the inches of precipitation, let's add a flag that
# indicates whether a day is dry (has zero precipitation):
X['dry day'] = (X['PRCP'] == 0).astype(int)#binary flag of whether a day is dry or not
#wind speed is in 1/10 meters per second, convert to miles per hour
X['AWND'] *= .2237
X['WindAbove8mph'] = X['AWND'] > 8
# Let's add a counter that increases from day 1, and measures how many
# years have passed. This will let us measure any observed annual increase
# or decrease in daily crossings:
X['annual'] = (X.index - X.index[0]).days / 365.
X['AvgPast6DayCount'] = (X['Total_yesterday'].shift(1) + X['Total_yesterday'].shift(2) + X['Total_yesterday'].shift(3) + X['Total_yesterday'].shift(4) + X['Total_yesterday'].shift(5) + X['Total_yesterday'].shift(6))/6#--------------------Avg 3 Past Day Count
X['AvgPast6DayTempMin'] = (X['TMIN'].shift(1) + X['TMIN'].shift(2) + X['TMIN'].shift(3) + X['TMIN'].shift(4) + X['TMIN'].shift(5) + X['TMIN'].shift(6))/6#--------------------Avg Past 3 Day Temp
X['AvgPast6DayTempMax'] = (X['TMAX'].shift(1) + X['TMAX'].shift(2) + X['TMAX'].shift(3) + X['TMIN'].shift(4) + X['TMIN'].shift(5) + X['TMIN'].shift(6))/6#--------------------Avg Past 3 Day Temp
NewDFNearestTmax = X.iloc[(X['TMAX']-1).abs().argsort()[:20]]
X['Avg3PastDayMAXTemp'] = NewDFNearestTmax['TMAX'].mean()#--------------------Nearest Temperature Max
X['Avg3PastDayMAXCount'] = NewDFNearestTmax['AvgPast6DayCount'].mean()#--------------------Nearest Temperature Max
NewDFNearestTmax = X.iloc[(X['TMIN']-1).abs().argsort()[:20]]
X['Avg3PastDayMINTemp'] = NewDFNearestTmax['TMIN'].mean()#--------------------Nearest Temperature Max
X['Avg3PastDayMINCount'] = NewDFNearestTmax['AvgPast6DayCount'].mean()#--------------------Nearest Temperature Max
# X.index - timedelta(2)
# X['AvgLast3Days'] = X.iloc['Total_yesterday',['GetDayBeforeYesName']]
return X
X_train = jake_wrangle(X_train)
# + id="ZhQqgtlJIkwP" colab_type="code" outputId="532b9100-d3f5-4f6c-bdba-e2357089773b" colab={"base_uri": "https://localhost:8080/", "height": 1141}
X_train.tail(10).T
# + id="vwiGmwRv_oeE" colab_type="code" outputId="3df33682-929a-4705-ca4b-08c4f1aac359" colab={"base_uri": "https://localhost:8080/", "height": 1124}
# X_train['Total_yesterday'].max
maxval = X_train.loc[X_train['Total_yesterday'].idxmax()]
maxval.to_frame()
# df.loc[df['Value'].idxmax()]
# + id="2d6SaaqXHqd2" colab_type="code" outputId="0b112144-c147-4aad-8ad9-1e9a19a5880b" colab={"base_uri": "https://localhost:8080/", "height": 89}
# X_train.nlargest(3, X_train.Total_yesterday)
X_train.apply(lambda s: s.abs()).max().nlargest(3)
# + id="DenYRZbmJkTU" colab_type="code" outputId="0fcdab69-9e8e-4516-e888-2c52ccef08c4" colab={"base_uri": "https://localhost:8080/", "height": 564}
X_train.sort_values(by = 'Total_yesterday', ascending = False)[:10]
# + id="F1Mp79p5dMC4" colab_type="code" outputId="c47a0d11-35af-4e10-d204-ba3f1c808180" colab={"base_uri": "https://localhost:8080/", "height": 662}
X_train.dtypes
# + id="IzTll3Sob646" colab_type="code" outputId="671b8733-3e85-4350-dfeb-88ed3b76f063" colab={"base_uri": "https://localhost:8080/", "height": 314}
X_train.describe()
# + id="dzSYmbWwfoEt" colab_type="code" outputId="d0e1ff61-afab-4623-f686-d3c1b7e034ee" colab={"base_uri": "https://localhost:8080/", "height": 268}
X_train_num = X_train.select_dtypes(include=['float64', 'int64'])
Riderbymonth = X_train_num.groupby('Month')['Total_yesterday'].mean()
Riderbymonth
# + id="ybW4mGnqjoP8" colab_type="code" outputId="b6abb5e3-9840-4e9c-a80a-fe5ca180eb43" colab={"base_uri": "https://localhost:8080/", "height": 301}
Riderbymonth.plot()
# + id="h5Bh7xSdj3hx" colab_type="code" outputId="e55a7443-d6cc-4f92-91ed-0e9257e1f454" colab={"base_uri": "https://localhost:8080/", "height": 301}
windbymonth = X_train_num.groupby('AWND')['Total_yesterday'].mean()
windbymonth.plot()
# + id="Hxbp-1vAkf6j" colab_type="code" outputId="2f97b078-edc7-4366-9346-455b16be02fe" colab={"base_uri": "https://localhost:8080/", "height": 302}
lightbymonth = X_train_num.groupby('daylight_hrs')['Total_yesterday'].mean()
lightbymonth.plot()
# + id="0AQl4jVdlAzq" colab_type="code" outputId="b32205b3-881c-45a2-c297-eb437944e362" colab={"base_uri": "https://localhost:8080/", "height": 301}
Tbymonth = X_train_num.groupby('Temp (C)')['Total_yesterday'].mean()
Tbymonth.plot()
# + id="Wv3IvQdiqQ7g" colab_type="code" colab={}
# sns.pairplot(X_train)
# + id="yZtKjwQeIUw7" colab_type="code" outputId="73bc7caf-cfd4-4f51-ad71-47a800a34704" colab={"base_uri": "https://localhost:8080/", "height": 268}
grouped = X_train.groupby(["Month"])
grouped['Total_yesterday'].agg(np.mean)
# x=pd.DataFrame(X_train.reset_index()).T
# for i in x.columns:
# df1row = pd.DataFrame(x.nlargest(3, i).index.tolist(), index=['top1','top2','top3']).T
# rslt = pd.concat([rslt, df1row], axis=0)
# print(rslt)
# + id="N5PyebIj_ob7" colab_type="code" outputId="b08244b5-551a-4053-e997-5c068c37719d" colab={"base_uri": "https://localhost:8080/", "height": 662}
# X_train.apply(X_train['Total_yesterday']).sort_values()
X_train.loc[X_train['Total_yesterday'].idxmax()]
# X_train.groupby("Total_yesterday").apply(lambda X_train:X_train.Total_yesterday(X_train.value.argmax()))
# + id="AKxB8_b87rTP" colab_type="code" colab={}
X_train = X_train.fillna(X_train.mean())
# + id="WpS5J56S98aZ" colab_type="code" colab={}
# X_train = X_train.dropna()
# + id="jopLTqFDIkuU" colab_type="code" colab={}
# import datetime
# DOY = X_train.index.values
# DOY = pd.to_datetime(DOY)
# Y = DOY.year
# X_train.loc[datetime.date(year=Y,month=12,day=21):datetime.date(year=Y,month=3,day=19)]
# + id="YP9WneSRKwyN" colab_type="code" outputId="33325939-8098-4970-c786-91b66541c7cb" colab={"base_uri": "https://localhost:8080/", "height": 35}
NewDFNearestTmax = X_train.iloc[(X_train['TMAX']-1).abs().argsort()[:3]]
NewDFNearestTmax['TMAX'].mean()
# + id="FfdscVk2W74W" colab_type="code" colab={}
# X_train['d'] = X_train.index.values
# + id="rPQFZ6JCXEd6" colab_type="code" colab={}
# import datetime
# DOY = X_train.index.values
# DOY = pd.to_datetime(DOY)
# Y = DOY.year
# X_train[(X_train['d']>datetime.date(Y,1,1)) & (X_train['d']<datetime.date(Y,3,1))]
# + id="dkJFTh7L2PI1" colab_type="code" colab={}
X_train['year'] = X_train.index.year
# + id="L8W9QlCF2cVM" colab_type="code" colab={}
X_train['month'] = X_train.index.month
# + id="u_dRxXSN2y9w" colab_type="code" outputId="0ed27510-d4ff-4a00-83b9-c14fe82a3fb2" colab={"base_uri": "https://localhost:8080/", "height": 229}
X_train.head(3)
# + id="8kefvvKr2OYR" colab_type="code" colab={}
# pd.cut(orders_with_hour_of_day['order_hour_of_day'],bins=24)
# + id="cgI7xPSEfO_m" colab_type="code" outputId="7f7f4d86-4593-4aa6-f72e-168f6d638322" colab={"base_uri": "https://localhost:8080/", "height": 160}
X_train.index - timedelta(1)
# + id="R7_I-KRGfK_v" colab_type="code" outputId="1e444cfd-e276-4565-b827-3533601a98ca" colab={"base_uri": "https://localhost:8080/", "height": 35}
type(X_train.index)
# + id="jAu5noWjhNxH" colab_type="code" colab={}
# springsol =
# test = X_train[X_train.index.to_pydatetime() < datetime.datetime(2015,3,21)]
# test
# + id="gjF8lTRfnc4i" colab_type="code" colab={}
# X_train.index.values.strftime("%Y")
# + id="TCvk75Tsnc15" colab_type="code" colab={}
# uniqueyear = X_train.index.year.unique()
# for eachyear in uniqueyear:
# fo
# test = X_train[X_train.index.to_pydatetime() < datetime.datetime(i,3,21)]
# + id="SCexCvJGrstA" colab_type="code" outputId="8913e5aa-8ea9-4fb1-8e20-fbcc96e915f0" colab={"base_uri": "https://localhost:8080/", "height": 35}
test.shape
# + id="Xor3MgjvjZpx" colab_type="code" colab={}
# X_train['r'] = X_train[X_train.index.to_pydatetime() < datetime.datetime(2015,1,1)]
# + id="NEbKn4gWhjEq" colab_type="code" colab={}
X_train['r'] = X_train.index.month < 3
X_train['r'] = X_train.index.month > 12
# + id="ptpLMjwKk5fx" colab_type="code" colab={}
# s = X_train.index.values
# X_tr = s.pd.to_datetime()
# + id="6hE0aFsJiFIL" colab_type="code" colab={}
# |X_train.head(1)
# + id="1bAKH_iucv5N" colab_type="code" colab={}
# X_train = pd.Timestamp.now()
# X_train.to_pydatetime()
# X_train.year
# + id="XQwYdVirdP1n" colab_type="code" colab={}
# import calendar
# import datetime
# X_train['AdjustedDateToEndOfMonth'] = X_train['d'].map(
# lambda x: datetime.datetime(
# x.year,
# x.month,
# max(calendar.monthcalendar(x.year, x.month)[-1][:5])
# )
# )
# + id="7nSboGwIdsfU" colab_type="code" colab={}
# X_train['nn'] = pd.DatetimeIndex(X_train).year
# X_train.head()
# + id="ZWl5VkN8bu6l" colab_type="code" colab={}
# X_train['t'] = X_train.index.values in New
# + [markdown] colab_type="text" id="dDGkAv813Wtj"
#
# Linear Regression (with new features)
# + colab_type="code" id="cj3HTM6p5F1A" outputId="9594bb3a-a528-4753-d3ce-6e8803e329f3" colab={"base_uri": "https://localhost:8080/", "height": 141}
scores = cross_validate(LinearRegression(),X_train, y_train,
scoring='neg_mean_absolute_error', cv=3,
return_train_score=True, return_estimator=True)
pd.DataFrame(scores)
#with feature engineering, we cut the error in half
#a good prediction usually involves feature engineering and a complex model type
# + id="J4WT1mPzUo6o" colab_type="code" outputId="5e0116f4-62a5-42ba-8b31-1c54c3f6972a" colab={"base_uri": "https://localhost:8080/", "height": 35}
-scores['test_score'].mean()
# + id="YJpQG0AvF-MW" colab_type="code" outputId="a8ad5554-977a-4652-a0e5-4453262ee60b" colab={"base_uri": "https://localhost:8080/", "height": 1774}
from xgboost import XGBRegressor
model = XGBRegressor(n_estimators=100)
param_distributions = {
'n_estimators': [100,125,150],#iterable
'max_depth' : [4,5],
'criterion' : ['mae']
}
#My X_train has changed with different features
gridsearch2 = RandomizedSearchCV(
XGBRegressor(n_jobs=-1, random_state=42),
param_distributions=param_distributions,
n_iter = 100,
cv=3,
scoring='neg_mean_absolute_error',
verbose=10,
return_train_score=True
)
gridsearch2.fit(X_train, y_train)
pd.DataFrame(scores)
# + id="BMqh_hveYLE0" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="cc998e32-64b2-485a-afc6-5e733fdeb790"
-gridsearch2.best_score_
# + id="7mofK1s9nYyv" colab_type="code" outputId="3e36c90d-bb9a-4d5e-b4b4-83e4bf3c49b3" colab={"base_uri": "https://localhost:8080/", "height": 287}
plt.plot(depth, np.median(train_score, 1), color='blue', label='training score')
plt.plot(depth, np.median(val_score, 1), color='red', label='validation score')
plt.legend(loc='best')
# + id="253edK6aGWvk" colab_type="code" outputId="4b869b63-fadb-4679-e767-6f4e8c290933" colab={"base_uri": "https://localhost:8080/", "height": 141}
pd.DataFrame(scores)
# + [markdown] colab_type="text" id="b6zxN2xB3bX_"
# ### Random Forest (with new features)
# + id="JgN7WhJuFalM" colab_type="code" outputId="32ba378e-f413-4801-ddb6-172c2ad4ef28" colab={"base_uri": "https://localhost:8080/", "height": 287}
# %matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import validation_curve
model = RandomForestRegressor(n_estimators=200)
depth = [2, 3, 4, 5, 6]#try a range of values for these parameters
train_score, val_score = validation_curve(
model, X_train, y_train,
param_name='max_depth', param_range=depth,
scoring='neg_mean_absolute_error', cv=3)
plt.plot(depth, np.median(train_score, 1), color='blue', label='training score')
plt.plot(depth, np.median(val_score, 1), color='red', label='validation score')
plt.legend(loc='best')
# + id="spGTEfBAFai4" colab_type="code" outputId="6100199b-005a-409b-9dd7-2b96b401fec3" colab={"base_uri": "https://localhost:8080/", "height": 141}
pd.DataFrame(scores)
# + colab_type="code" id="3sWUDZIz1-kk" outputId="020292b7-6fdf-4f71-b057-19d38fd386bc" colab={"base_uri": "https://localhost:8080/", "height": 1112}
param_distributions = {
'n_estimators': [50,100],#iterable
'max_depth' : [4,5],
'criterion' : ['mae']
}
#My X_train has changed with different features
gridsearch = RandomizedSearchCV(
RandomForestRegressor(n_jobs=-1, random_state=42),
param_distributions=param_distributions,
n_iter = 10,
cv=3,
scoring='neg_mean_absolute_error',
verbose=10,
return_train_score=True
)
gridsearch.fit(X_train, y_train)
# + id="xS6UUdH_pLRn" colab_type="code" outputId="7ec77f27-6cf3-469c-905c-74f7b2a730e8" colab={"base_uri": "https://localhost:8080/", "height": 396}
pd.DataFrame(gridsearch.cv_results_)
# + id="nekIZkOYrcYi" colab_type="code" outputId="08ee56f8-08fe-40a1-a23a-ffe10aa005b6" colab={"base_uri": "https://localhost:8080/", "height": 141}
pd.DataFrame(scores)
# + id="EVGdblCSt-4G" colab_type="code" colab={}
# importances = pd.Series(search.best_estimator_.feature_importances_,X_train.columns)
# plt.figure(figsize=(5,10))
# importances.sort_values().plot.barh(color='grey');
# + id="nUHB0Zj0Xq0V" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="b22073a7-d774-4e61-9503-32914ac5dc85"
-gridsearch.best_score_
# + [markdown] colab_type="text" id="edpJ87A8A8sd"
#
# ### Feature engineering, explained by <NAME>
#
# > _Feature engineering_ is the process of using your own knowledge about the data and about the machine learning algorithm at hand to make the algorithm work better by applying hardcoded (nonlearned) transformations to the data before it goes into the model. In many cases, it isn’t reasonable to expect a machine-learning model to be able to learn from completely arbitrary data. The data needs to be presented to the model in a way that will make the model’s job easier.
#
# > Let’s look at an intuitive example. Suppose you’re trying to develop a model that can take as input an image of a clock and can output the time of day.
#
# > If you choose to use the raw pixels of the image as input data, then you have a difficult machine-learning problem on your hands. You’ll need a convolutional neural network to solve it, and you’ll have to expend quite a bit of computational resources to train the network.
#
# > But if you already understand the problem at a high level (you understand how humans read time on a clock face), then you can come up with much better input features for a machine-learning algorithm: for instance, write a Python script to follow the black pixels of the clock hands and output the (x, y) coordinates of the tip of each hand. Then a simple machine-learning algorithm can learn to associate these coordinates with the appropriate time of day.
#
# > You can go even further: do a coordinate change, and express the (x, y) coordinates as polar coordinates with regard to the center of the image. Your input will become the angle theta of each clock hand. At this point, your features are making the problem so easy that no machine learning is required; a simple rounding operation and dictionary lookup are enough to recover the approximate time of day.
#
# > That’s the essence of feature engineering: making a problem easier by expressing it in a simpler way. It usually requires understanding the problem in depth.
#
# > Before convolutional neural networks became successful on the MNIST digit-classification problem, solutions were typically based on hardcoded features such as the number of loops in a digit image, the height of each digit in an image, a histogram of pixel values, and so on.
#
# > Neural networks are capable of automatically extracting useful features from raw data. Does this mean you don’t have to worry about feature engineering as long as you’re using deep neural networks? No, for two reasons:
#
# > - Good features still allow you to solve problems more elegantly while using fewer resources. For instance, it would be ridiculous to solve the problem of reading a clock face using a convolutional neural network.
# > - Good features let you solve a problem with far less data. The ability of deep-learning models to learn features on their own relies on having lots of training data available; if you have only a few samples, then the information value in their features becomes critical.
#
# + id="AQGoWlNYV9u4" colab_type="code" colab={}
#encoded values ie 999, -999
#best_estimator = .predict
# + [markdown] colab_type="text" id="oux-dd-5FD6p"
# ASSIGNMENT
#
# **1.** Complete the notebook cells that were originally commented **`TODO`**.
#
# **2.** Then, focus on feature engineering to improve your cross validation scores. Collaborate with your cohort on Slack. You could start with the ideas [Jake VanderPlas suggests:](https://jakevdp.github.io/PythonDataScienceHandbook/05.06-linear-regression.html#Example:-Predicting-Bicycle-Traffic)
#
# > Our model is almost certainly missing some relevant information. For example, nonlinear effects (such as effects of precipitation and cold temperature) and nonlinear trends within each variable (such as disinclination to ride at very cold and very hot temperatures) cannot be accounted for in this model. Additionally, we have thrown away some of the finer-grained information (such as the difference between a rainy morning and a rainy afternoon), and we have ignored correlations between days (such as the possible effect of a rainy Tuesday on Wednesday's numbers, or the effect of an unexpected sunny day after a streak of rainy days). These are all potentially interesting effects, and you now have the tools to begin exploring them if you wish!
#
# **3.** Experiment with the Categorical Encoding notebook.
#
# **4.** At the end of the day, take the last step in the "universal workflow of machine learning" — "You can train your final production model on all the available data (training and validation) and evaluate it one last time on the test set."
#
# See the [`RandomizedSearchCV`](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.RandomizedSearchCV.html) documentation for the `refit` parameter, `best_estimator_` attribute, and `predict` method:
#
# > **refit : boolean, or string, default=True**
#
# > Refit an estimator using the best found parameters on the whole dataset.
#
# > The refitted estimator is made available at the `best_estimator_` attribute and permits using `predict` directly on this `GridSearchCV` instance.
#
# ### STRETCH
#
# **A.** Apply this lesson other datasets you've worked with, like Ames Housing, Bank Marketing, or others.
#
# **B.** In additon to `RandomizedSearchCV`, scikit-learn has [`GridSearchCV`](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.GridSearchCV.html). Another library called scikit-optimize has [`BayesSearchCV`](https://scikit-optimize.github.io/notebooks/sklearn-gridsearchcv-replacement.html). Experiment with these alternatives.
#
# **C.** _[Introduction to Machine Learning with Python](http://shop.oreilly.com/product/0636920030515.do)_ discusses options for "Grid-Searching Which Model To Use" in Chapter 6:
#
# > You can even go further in combining GridSearchCV and Pipeline: it is also possible to search over the actual steps being performed in the pipeline (say whether to use StandardScaler or MinMaxScaler). This leads to an even bigger search space and should be considered carefully. Trying all possible solutions is usually not a viable machine learning strategy. However, here is an example comparing a RandomForestClassifier and an SVC ...
#
# The example is shown in [the accompanying notebook](https://github.com/amueller/introduction_to_ml_with_python/blob/master/06-algorithm-chains-and-pipelines.ipynb), code cells 35-37. Could you apply this concept to your own pipelines?
# + id="2_FxInLrFDWb" colab_type="code" colab={}
|
LS_DS_241_Hyperparameter_Optimization_Assignment.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + colab={"base_uri": "https://localhost:8080/", "height": 394} colab_type="code" id="4EFZCuqpuWfe" outputId="cf1b034a-1487-432c-ea00-f69270a671fe"
# !pip install hdf5storage
# !git clone https://github.com/adityajn105/brain-tumor-segmentation-unet
# !bash download_data.sh
# !python mat_to_numpy.py brain_tumor_dataset/
# +
# !python mat_to_numpy.py brain_tumor_dataset/
# -
# !pip install hdf5storage
# !python mat_to_numpy.py brain_tumor_dataset/
# + colab={"base_uri": "https://localhost:8080/", "height": 68} colab_type="code" id="m453oM2Zj1BA" outputId="b1f6502d-69ca-42eb-d4e6-313f6c16b0ab"
import os
import numpy as np
import matplotlib.pyplot as plt
import cv2
integer_to_class = {'1': 'meningioma (1)', '2': 'glioma (2)', '3': 'pituitary tumor (3)'}
##Load images, labels, masks
labels = np.load('brain_tumor_dataset/labels.npy')
images = np.clip( (np.load('brain_tumor_dataset/images.npy')/12728),0,1)
masks = np.load('brain_tumor_dataset/masks.npy')*1
print(labels.shape)
print(images.shape)
print(masks.shape)
# + colab={"base_uri": "https://localhost:8080/", "height": 51} colab_type="code" id="oTxNHKzPXFTK" outputId="3d2f0d27-bc80-4f13-ee76-d1695a186583"
from skimage.transform import resize
img_size_ori = 512
img_size_target = 128
images = np.expand_dims(images,axis=-1)
masks = np.expand_dims(masks,axis=-1)
def downsample(img):
if img_size_ori == img_size_target:
return img
return resize(img, (img_size_target, img_size_target), mode='constant', preserve_range=True,)
def upsample(img):
if img_size_ori == img_size_target:
return img
return resize(img, (img_size_ori, img_size_ori), mode='constant', preserve_range=True)
images = np.array([ downsample(image) for image in images ])
masks = (np.array([ downsample(mask) for mask in masks ])>0)*1
print(images.shape)
print(masks.shape)
# + colab={"base_uri": "https://localhost:8080/", "height": 286} colab_type="code" id="EISjQccNpyv9" outputId="2f507cba-fc17-40a3-cf26-cf2447b1af6c"
classes, counts = np.unique(labels,return_counts=True)
plt.bar(classes,counts,tick_label=list(integer_to_class.values()))
print(counts)
# + colab={"base_uri": "https://localhost:8080/", "height": 336} colab_type="code" id="c30PtaQIquAA" outputId="4c0f9c69-d054-4ba2-f88b-a70198e297ca"
plt.figure(figsize=(12, 5))
for i, idx in enumerate(np.random.randint(images.shape[0], size=18), start=1):
plt.subplot(3, 6, i)
plt.imshow( np.squeeze(images[idx],axis=-1), cmap='gray')
plt.imshow( np.squeeze(np.ones_like(masks[idx])-masks[idx],axis=-1), alpha=0.5, cmap='Set1')
plt.title(integer_to_class[str(labels[idx])])
plt.axis('off')
# + [markdown] colab_type="text" id="tKAr7g_t5rgd"
# ### Train Image and its mask which is to be predicted
# + colab={"base_uri": "https://localhost:8080/", "height": 336} colab_type="code" id="axj-fH992zom" outputId="0910e1f2-a373-4692-8eb6-6fda1e09e13f"
plt.figure(figsize=(12, 5))
i=1
for idx in np.random.randint( images.shape[0], size=9):
plt.subplot(3,6,i);i+=1
plt.imshow( np.squeeze(images[idx],axis=-1))
plt.title("Train Image")
plt.axis('off')
plt.subplot(3,6,i);i+=1
plt.imshow( np.squeeze(masks[idx],axis=-1))
plt.title("Train Mask")
plt.axis('off')
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="4q1ICWtBBroq" outputId="10108f99-03d7-41db-9f75-5f6998a16656"
from sklearn.model_selection import train_test_split
import gc
X,X_v,Y,Y_v = train_test_split( images,masks,test_size=0.2,stratify=labels)
del images
del masks
del labels
gc.collect()
X.shape,X_v.shape
# + [markdown] colab_type="text" id="nzKAQI-V7zah"
# ### Augmentation
# -
# !pip install keras
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="NCHv4pjX5CSd" outputId="da94819a-e5b1-49c8-fa1b-582b993b1d91"
X = np.append( X, [ np.fliplr(x) for x in X], axis=0 )
Y = np.append( Y, [ np.fliplr(y) for y in Y], axis=0 )
X.shape,Y.shape
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="Zrf28ZDQAvjJ" outputId="63b8d0e8-f856-488c-bdb0-ab2442eea752"
from keras.preprocessing.image import ImageDataGenerator
train_datagen = ImageDataGenerator(brightness_range=(0.9,1.1),
zoom_range=[.9,1.1],
fill_mode='nearest')
val_datagen = ImageDataGenerator()
# + [markdown] colab_type="text" id="9acZGpnYDNw1"
# ### Defining Dice Loss
# Dice = 2|A∩B|/|A|+|B|
# + colab={} colab_type="code" id="7hlqTp52C6J4"
from keras.losses import binary_crossentropy
from keras import backend as K
import tensorflow as tf
def dice_loss(y_true, y_pred):
smooth = 1.
y_true_f = K.flatten(y_true)
y_pred_f = K.flatten(y_pred)
intersection = y_true_f * y_pred_f
score = (2. * K.sum(intersection) + smooth) / (K.sum(y_true_f) + K.sum(y_pred_f) + smooth)
return 1. - score
### bce_dice_loss = binary_crossentropy_loss + dice_loss
def bce_dice_loss(y_true, y_pred):
return binary_crossentropy(y_true, y_pred) + dice_loss(y_true, y_pred)
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} colab_type="code" id="IbjruP71DV9n" outputId="3ba540a5-33ae-4a43-d706-13b002874294"
from keras.layers import Conv2D, MaxPooling2D, Conv2DTranspose, concatenate, Dropout, Input, BatchNormalization
from keras import optimizers
from keras.models import Model
IMG_DIM = (128,128,1)
def conv2d_block( input_tensor, n_filters, kernel_size = (3,3), name="contraction"):
"Add 2 conv layer"
x = Conv2D(filters=n_filters, kernel_size=kernel_size, kernel_initializer='he_normal',
padding='same',activation="relu", name=name+'_1')(input_tensor)
x = Conv2D(filters=n_filters, kernel_size=kernel_size, kernel_initializer='he_normal',
padding='same',activation="relu",name=name+'_2')(x)
return x
inp = Input( shape=IMG_DIM )
d1 = conv2d_block( inp, 64, name="contraction_1")
p1 = MaxPooling2D( pool_size=(2,2), strides=(2,2))(d1)
p1 = BatchNormalization(momentum=0.8)(p1)
p1 = Dropout(0.1)(p1)
d2 = conv2d_block( p1, 128, name="contraction_2_1" )
p2 = MaxPooling2D(pool_size=(2,2), strides=(2,2) )(d2)
p2 = BatchNormalization(momentum=0.8)(p2)
p2 = Dropout(0.1)(p2)
d3 = conv2d_block( p2, 256, name="contraction_3_1")
p3 = MaxPooling2D(pool_size=(2,2), strides=(2,2) )(d3)
p3 = BatchNormalization(momentum=0.8)(p3)
p3 = Dropout(0.1)(p3)
d4 = conv2d_block(p3,512, name="contraction_4_1")
p4 = MaxPooling2D(pool_size=(2,2), strides=(2,2) )(d4)
p4 = BatchNormalization(momentum=0.8)(p4)
p4 = Dropout(0.1)(p4)
d5 = conv2d_block(p4,512, name="contraction_5_1")
u1 = Conv2DTranspose(512, (3, 3), strides = (2, 2), padding = 'same')(d5)
u1 = concatenate([u1,d4])
u1 = Dropout(0.1)(u1)
c1 = conv2d_block(u1, 512, name="expansion_1")
u2 = Conv2DTranspose(256, (3, 3), strides = (2, 2), padding = 'same')(c1)
u2 = concatenate([u2,d3])
u2 = Dropout(0.1)(u2)
c2 = conv2d_block(u2, 256, name="expansion_2")
u3 = Conv2DTranspose(128, (3, 3), strides = (2, 2), padding = 'same')(c2)
u3 = concatenate([u3,d2])
u3 = Dropout(0.1)(u3)
c3 = conv2d_block(u3, 128, name="expansion_3")
u4 = Conv2DTranspose(64, (3, 3), strides = (2, 2), padding = 'same')(c3)
u4 = concatenate([u4,d1])
u4 = Dropout(0.1)(u4)
c4 = conv2d_block(u4,64, name="expansion_4")
out = Conv2D(1, (1,1), name="output", activation='sigmoid')(c4)
unet = Model( inp, out )
unet.summary()
# + [markdown] colab_type="text" id="fuQfiXzAMTp0"
# ### Defining IOU metric and compile Model
# + colab={"base_uri": "https://localhost:8080/", "height": 343} colab_type="code" id="O7RmzPp6FLiJ" outputId="f0eb6155-a73d-40e7-aa08-854524435833"
def get_iou_vector(A, B):
t = A>0
p = B>0
intersection = np.logical_and(t,p)
union = np.logical_or(t,p)
iou = (np.sum(intersection) + 1e-10 )/ (np.sum(union) + 1e-10)
return iou
def iou_metric(label, pred):
return tf.py_func(get_iou_vector, [label, pred>0.5], tf.float64)
unet.compile(optimizer=optimizers.Adam(lr=1e-3),
loss=bce_dice_loss, metrics=['accuracy',iou_metric])
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} colab_type="code" id="llR10XboMXGI" outputId="cca57f6b-3647-4562-b851-32cb12b2959b"
from keras.callbacks import ModelCheckpoint, EarlyStopping, ReduceLROnPlateau
from sklearn.preprocessing import LabelEncoder
from keras.models import load_model
model_checkpoint = ModelCheckpoint('model_best_checkpoint.h5', save_best_only=True,
monitor='val_loss', mode='min', verbose=1)
early_stopping = EarlyStopping(monitor='val_loss', patience=10, mode='min')
reduceLR = ReduceLROnPlateau(patience=4, verbose=2, monitor='val_loss',min_lr=1e-4, mode='min')
callback_list = [early_stopping, reduceLR, model_checkpoint]
train_generator = train_datagen.flow(X, Y, batch_size=32)
val_generator = val_datagen.flow(X_v, Y_v, batch_size=32)
hist = unet.fit(X,Y,batch_size=32,epochs=100,
validation_data=(X_v,Y_v),verbose=1,callbacks= callback_list)
unet = load_model('model_best_checkpoint.h5', custom_objects={'bce_dice_loss': bce_dice_loss,'iou_metric':iou_metric}) #or compile = False
# + colab={"base_uri": "https://localhost:8080/", "height": 308} colab_type="code" id="vBgb-raTKt2N" outputId="52348e29-77fa-474f-a33d-63f1c92e8840"
f, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(16, 4))
t = f.suptitle('Unet Performance in Segmenting Tumors', fontsize=12)
f.subplots_adjust(top=0.85, wspace=0.3)
epoch_list = hist.epoch
ax1.plot(epoch_list, hist.history['accuracy'], label='Train Accuracy')
ax1.plot(epoch_list, hist.history['val_accuracy'], label='Validation Accuracy')
ax1.set_xticks(np.arange(0, epoch_list[-1], 5))
ax1.set_ylabel('Accuracy Value');ax1.set_xlabel('Epoch');ax1.set_title('Accuracy')
ax1.legend(loc="best");ax1.grid(color='gray', linestyle='-', linewidth=0.5)
ax2.plot(epoch_list, hist.history['loss'], label='Train Loss')
ax2.plot(epoch_list, hist.history['val_loss'], label='Validation Loss')
ax2.set_xticks(np.arange(0, epoch_list[-1], 5))
ax2.set_ylabel('Loss Value');ax2.set_xlabel('Epoch');ax2.set_title('Loss')
ax2.legend(loc="best");ax2.grid(color='gray', linestyle='-', linewidth=0.5)
ax3.plot(epoch_list, hist.history['iou_metric'], label='Train IOU metric')
ax3.plot(epoch_list, hist.history['val_iou_metric'], label='Validation IOU metric')
ax3.set_xticks(np.arange(0, epoch_list[-1], 5))
ax3.set_ylabel('IOU metric');ax3.set_xlabel('Epoch');ax3.set_title('IOU metric')
ax3.legend(loc="best");ax3.grid(color='gray', linestyle='-', linewidth=0.5)
# + colab={} colab_type="code" id="YRh0Q4KbnXm6"
# + colab={} colab_type="code" id="GsgHta1LjI_T"
# src: https://www.kaggle.com/aglotero/another-iou-metric
def get_iou_vector(A, B):
t = A>0
p = B>0
intersection = np.logical_and(t,p)
union = np.logical_or(t,p)
iou = (np.sum(intersection) + 1e-10 )/ (np.sum(union) + 1e-10)
return iou
def getIOUCurve(mask_org,predicted):
thresholds = np.linspace(0, 1, 100)
ious = np.array([get_iou_vector(mask_org, predicted > threshold) for threshold in thresholds])
thres_best_index = np.argmax(ious[9:-10]) + 9
iou_best = ious[thres_best_index]
thres_best = thresholds[thres_best_index]
return thresholds,ious,iou_best,thres_best
# + colab={"base_uri": "https://localhost:8080/", "height": 325} colab_type="code" id="VxaQOEY7jKdy" outputId="bb0f00c7-ced8-4184-b867-7e7c56adcc02"
f, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
t = f.suptitle('Unet Performance', fontsize=12)
f.subplots_adjust(top=0.85, wspace=0.3)
th, ious, iou_best, th_best = getIOUCurve(Y_v,unet.predict(X_v))
ax1.plot(th, ious,label="For Validation")
ax1.plot(th_best, iou_best, "xr", label="Best threshold")
ax1.set_ylabel('IOU');ax1.set_xlabel('Threshold')
ax1.set_title("Threshold vs IoU ({}, {})".format(th_best, iou_best))
th, ious, iou_best, th_best = getIOUCurve(Y,unet.predict(X))
ax2.plot(th, ious, label="For Training")
ax2.plot(th_best, iou_best, "xr", label="Best threshold")
ax2.set_ylabel('IOU');ax1.set_xlabel('Threshold')
ax2.set_title("Threshold vs IoU ({}, {})".format(th_best, iou_best))
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} colab_type="code" id="n3-iDU-aMAtq" outputId="e3b6bac3-ff86-4269-e464-e2e141299219"
THRESHOLD = 0.2
predicted_mask = (unet.predict(X_v)>THRESHOLD)*1
plt.figure(figsize=(8,30))
i=1;total=10
temp = np.ones_like( Y_v[0] )
for idx in np.random.randint(0,high=X_v.shape[0],size=total):
plt.subplot(total,3,i);i+=1
plt.imshow( np.squeeze(X_v[idx],axis=-1), cmap='gray' )
plt.title("MRI Image");plt.axis('off')
plt.subplot(total,3,i);i+=1
plt.imshow( np.squeeze(X_v[idx],axis=-1), cmap='gray' )
plt.imshow( np.squeeze(temp - Y_v[idx],axis=-1), alpha=0.2, cmap='Set1' )
plt.title("Original Mask");plt.axis('off')
plt.subplot(total,3,i);i+=1
plt.imshow( np.squeeze(X_v[idx],axis=-1), cmap='gray' )
plt.imshow( np.squeeze(temp - predicted_mask[idx],axis=-1), alpha=0.2, cmap='Set1' )
plt.title("Predicted Mask");plt.axis('off')
# + colab={} colab_type="code" id="6wo4TH2wqal6"
|
brain_tumor_segmentation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import os
import matplotlib.pyplot as plt
import numpy as np
import pickle
import colorsys
datadir = "../../../../data/EnergyHack/Хакатон-2021/"
files = os.listdir(datadir)
# +
features_dict = {
"Гроза" : 0,
"Риск животные и птиц" : 1,
"Ветер" : 2,
# "Природа прочее" : 3,
# "Перегрев" : 4,
"Гололед" : 5,
"Пожары, перегрев" : 4,
# "Природные пожары" : 4,
"Падение деревьев" : 2,
# "Взрыв, загорание, пожар" : 4,
"Погодные явления" : 3,
"Разрушение фундамента": 6,
# "Гололёдообразование" : 5,
"Паводок" : 7,
"Поломка" :8
#"Воздействие повторяющихся стихийных явлений" : 3,
}
ft_ids = {v:k for k,v in features_dict.items()}
with open("features_dict.pkl","wb") as f:
pickle.dump(features_dict,f)
# -
proc_folder = "processed/"
files_proc = os.listdir(proc_folder)
print(files_proc)
avarii1 = pd.read_csv(proc_folder+'Аварии_Причины_САЦ_2020_xlsx_Аварии_2020output.csv', names=["data","oblast","why",0,1,2,3,4,5,6,7],
delimiter=",")
avarii2 = pd.read_csv(proc_folder+'Аварии_погода_САЦ_2020_xlsx_Аварии_2020_Природныеoutput.csv', names=["data","oblast","why","desc","whereloc",0,1,2,3,4,5,6],
delimiter=",")
#avarii1.whereloc.value_counts()
def _get_colors(num_colors):
colors=[]
for i in np.arange(0., 1, 1/(num_colors-1)):
hue = (i+1)/(num_colors+1)
lightness = (i+1)/(num_colors+1) #* 10)/100.
saturation = (i+1)/(num_colors+1) #* 10)/100.
colors.append(colorsys.hsv_to_rgb(i*2, (int(i*num_colors)%3)*0.7+0.3, (int(i*num_colors)%2)*0.3+0.7))
return colors
with open("colors.pkl","wb") as f:
pickle.dump(_get_colors(10),f)
avarii1.shape #, avarii2.shape
import colorsys
max_i = 1
for i in np.arange(0., max_i, max_i/5):
print(colorsys.hsv_to_rgb(6*i, 50, 50))
avarii1.reset_index(inplace=True)
avarii1["date_dt"] = pd.to_datetime(avarii1.data)
avarii1["oblast"] = avarii1["oblast"].str.replace("г. ",""
).str.replace(" - кузбасс",""
).str.replace("",""
).str.replace (" (татарстан)",""
).str.replace (" - чувашия",""
).str.replace ("","").str.lower()
#avarii1.set_index("oblast",inplace=True)
avarii1["причина"] = ""
for i in list(ft_ids.keys())[:-1]:
avarii1.loc[avarii1[i]>0,"причина"] += ft_ids[i] + " "
avarii1
with open("avarii1.pkl","wb") as f:
pickle.dump(avarii1,f)
avarii1
# + tags=[]
import json
with open("Regions.json","r") as f:
reg_j = json.load(f)
#reg_j
# -
3
# +
# #Following is the example to send HTML content as an e-mail. Try it once −
# # #!/usr/bin/python
# import smtplib
# message = """From: From Person <<EMAIL>>
# To: To Person <<EMAIL>>
# MIME-Version: 1.0
# Content-type: text/html
# Subject: SMTP HTML e-mail test
# This is an e-mail message to be sent in HTML format
# <b>This is HTML message.</b>
# <h1>This is headline.</h1>
# """
# sender = '<EMAIL>'
# receivers = ['<EMAIL>']
# try:
# smtpObj = smtplib.SMTP('localhost')
# smtpObj.sendmail(sender, receivers, message)
# print "Successfully sent email"
# except SMTPException:
# print "Error: unable to send email"
# -
1
avarii1.index
oblast_list = [c.lower().replace("г. ",""
).replace(" - кузбасс",""
).replace("",""
).replace (" (татарстан)",""
).replace (" - чувашия",""
).replace ("","")
for c in avarii1.oblast.unique() if "," not in c and "/" not in c]
with open("oblast_list.pkl","wb") as f:
pickle.dump(oblast_list,f)
oblast_list
avarii1.head(6)
# +
goroda_coord = pd.read_csv(proc_folder+"goroda_coord.csv")
oblast_coords = pd.DataFrame(goroda_coord.loc[goroda_coord.groupby("region").population.idxmax()])
oblast_coords["region"] = oblast_coords["region"].str.lower()
oblast_coords.region.unique()
# +
import pickle
test_df = pd.DataFrame(index=oblast_list)
test_df["lat"] = oblast_coords.set_index("region")["latitude_dd"]
test_df["lon"] = oblast_coords.set_index("region")["longitude_dd"]
test_df["risk8"] = 0
for k,v in list(ft_ids.items())[:-1]:
test_df["risk"+str(k)]=np.random.rand(test_df.shape[0])/2
test_df["risk8"] += (1-test_df["risk8"])* test_df["risk"+str(k)]
with open("test_df.pkl","wb") as f:
pickle.dump(test_df,f)
test_df
# -
test_df
# +
# pds = {}
# for file in files:
# print(file)
# pds[file]=pd.read_excel(datadir+file)
# +
# with open("pds.pkl","wb") as f:
# pickle.dump(pds,f)
# -
with open("pds.pkl","rb") as f:
pds = pickle.load(f)
pds.keys()
# +
pozhars = pds['Пожары_2020.xlsx']
pozhars["oblast"] = pozhars["Субъект"].str.lower().str.replace("обл\.","область").str.replace("а.о.","автономный округ")
pozhars["date"] = pd.to_datetime(pozhars["ACQ_DATE"].astype(str).str.replace("Северо-Енисейский р-н","2020-06-22").astype(str))
pozhars["date"].min(),pozhars["date"].max()
# + tags=[]
datas = [date for date in pd.date_range(start='6/22/2020', end='12/1/2020',freq="1D") for i in range(len(avarii1["oblast"].unique()))]
obls = [obl for i in range(len(pd.date_range(start='6/22/2020', end='12/1/2020',freq="1D"))) for obl in avarii1["oblast"].unique() ]
dat_obl = pd.DataFrame({"data":datas,"oblast":obls})
pozhar_ind=4
dat_obl["month"]=dat_obl.apply(lambda x: x[0].month,axis=1)
dat_obl["target"+str(pozhar_ind)]=dat_obl.apply(lambda x: min(60,(avarii1[(avarii1.oblast==x[1])&(avarii1.date_dt>=x[0])&(~avarii1[pozhar_ind].isna())].date_dt.min()-x[0]).days),axis=1)
dat_obl["prev"+str(pozhar_ind)]=dat_obl.apply(lambda x: (avarii1[(avarii1.oblast==x[1])&(avarii1.date_dt<=x[0])&(~avarii1[pozhar_ind].isna())].date_dt.max()-x[0]).days,axis=1)
# + tags=[]
dat_obl["prev_pozhar"+str(pozhar_ind)]=dat_obl.apply(lambda x: (pozhars[(pozhars.oblast==x[1])&(pozhars.date<=x[0])].date.max()-x[0]).days,axis=1)
# + tags=[]
pozhar_ind=4
dat_obl["prev_pozhar"+str(pozhar_ind)].fillna(-180,inplace=True)
dat_obl["prev"+str(pozhar_ind)].fillna(-180,inplace=True)
dat_obl
# + tags=[]
from datetime import timedelta
dat_obl["total_pozhar"+str(pozhar_ind)]=dat_obl.apply(lambda x: (pozhars[(pozhars.oblast==x[1])&(pozhars.date<=x[0])&(pozhars.date>=x[0]-timedelta(days=7))]).shape[0],axis=1)
dat_obl.head(2)
# + tags=[]
with open("dat_obl.pkl","wb") as f:
pickle.dump(dat_obl,f)
# + tags=[]
4
# -
with open("dat_obl.pkl","rb") as f:
dat_obl = pickle.load(f)
import sklearn
from sklearn import model_selection, metrics
X_train, X_test,y_train,y_test = model_selection.train_test_split(dat_obl[["oblast","prev4","month",
"prev_pozhar4","total_pozhar4"]],dat_obl["target4"], test_size=0.2,shuffle=True)
y_train.shape
import lightgbm, catboost
lgb = catboost.CatBoostRegressor(cat_features=["oblast"], n_estimators=2000) #LGBMRegressor()
lgb.fit(X_train,y_train, eval_set=(X_test,y_test),early_stopping_rounds=10, verbose=0 )
metrics.mean_absolute_error(y_test,lgb.predict(X_test))
#only pozhaer 4.179 with pozhar 3.99
import math
math.sqrt(metrics.mean_squared_error(y_test,lgb.predict(X_test)))
# +
import importlib
import predictor
importlib.reload(predictor)
from datetime import timedelta
import predictor
#from predictor import Predictor
pr = predictor.Predictor(avarii1, test_df,dat_obl=dat_obl, lgbs={"4":lgb})
te=pr.got_prediction(pd.to_datetime("2020-10-06"),1,"москва",4)
# with open("predictor.pkl","wb") as f:
# pickle.dump(pr,f)
# pr.got_dataset(pd.to_datetime("2020-10-06"),where=oblast_list,length=10)
te
# -
lgb.predict(te)
oblast_coords[oblast_coords.region.str.contains("югр")]
df_test = pd.DataFrame()
# +
import pickle
# open("pogoda.pkl", "rb") as f:
pogoda = pds[groupbygoda
# -
files
pds[-1]
# # ft_ids.items()
np.random.rand(100)
# +
pogoda["datetime_d"] = pd.to_datetime(pogoda["datetime_d"])
with open("pogoda.pkl", "wb") as f:
pickle.dump(pds[0],f)
# +
import pydeck as pdk
UK_ACCIDENTS_DATA = 'https://raw.githubusercontent.com/visgl/deck.gl-data/master/examples/3d-heatmap/heatmap-data.csv'
df = pd.read_csv(UK_ACCIDENTS_DATA)
# -
df["lat"] = 51
df.iloc[0]
# +
pogoda["lng"] = pogoda.lon
def_date= pd.to_datetime('2020-07-01 00:00:00')
pogoda["check"] = pogoda["winddirection"].apply(lambda x: random.randint(0,255))
check_df = pogoda[(pogoda.datetime_d == def_date)&(pogoda.lon<60)&(pogoda.lat<60)&(pogoda.lon>40)&(pogoda.lat>40)]
# -
df[:10]
import numpy as np
import colorsys
def _get_colors(num_colors):
colors=[]
for i in np.arange(0., 360., 360. / num_colors):
hue = i/360.
lightness = (50 + np.random.rand() * 10)/100.
saturation = (90 + np.random.rand() * 10)/100.
colors.append(colorsys.hls_to_rgb(hue, lightness, saturation))
return colors
_get_colors(5)[0][0]
# +
def color_funct(x):
with open("tttt.txt","w") as f:
f.write(str(x))
return [155,0,144,255]
"""
ColumnLayer
===========
Real estate values for select properties in Taipei. Data is from 2012-2013.
The height of a column indicates increasing price per unit area, and the color indicates distance from a subway stop.
The real estate valuation data set from UC Irvine's Machine Learning repository, viewable here:
https://archive.ics.uci.edu/ml/datasets/Real+estate+valuation+data+set
"""
import pandas as pd
import pydeck as pdk
DATA_URL = "https://raw.githubusercontent.com/ajduberstein/geo_datasets/master/housing.csv"
df = pd.read_csv(DATA_URL)
df = check_df
view = pdk.data_utils.compute_view(df[["lng", "lat"]])
view.pitch = 75
view.bearing = 60
view_state = pdk.ViewState(
longitude=47.415,
latitude=46.2323,
zoom=6,
min_zoom=5,
max_zoom=15,
pitch=40.5,
bearing=-27.36)
column_layer = pdk.Layer(
"ColumnLayer",
data=df,
get_position=["lng", "lat"],
get_elevation=["temperature"],
elevation_scale=1000,
radius=20000,
get_fill_color= ["check",0,0],
pickable=True#,
# auto_highlight=True,
)
tooltip = {
"html": "<b>{mrt_distance}</b> meters away from an MRT station, costs <b>{price_per_unit_area}</b> NTD/sqm",
"style": {"background": "grey", "color": "white", "font-family": '"Helvetica Neue", Arial', "z-index": "10000"},
}
r = pdk.Deck(
column_layer,
initial_view_state=view,
#tooltip=tooltip,
#map_provider="mapbox",
map_style=pdk.map_styles.LIGHT
#pdk.map_styles.SATELLITE,
)
r.to_html("column_layer.html")
# -
f = lambda x=0: 1
# +
"""
ColumnLayer
===========
Real estate values for select properties in Taipei. Data is from 2012-2013.
The height of a column indicates increasing price per unit area, and the color indicates distance from a subway stop.
The real estate valuation data set from UC Irvine's Machine Learning repository, viewable here:
https://archive.ics.uci.edu/ml/datasets/Real+estate+valuation+data+set
"""
import pandas as pd
import pydeck as pdk
DATA_URL = "https://raw.githubusercontent.com/ajduberstein/geo_datasets/master/housing.csv"
df = pd.read_csv(DATA_URL)
view = pdk.data_utils.compute_view(df[["lng", "lat"]])
view.pitch = 75
view.bearing = 60
column_layer = pdk.Layer(
"ColumnLayer",
data=df,
get_position=["lng", "lat"],
get_elevation="price_per_unit_area",
elevation_scale=100,
radius=50,
get_fill_color=["mrt_distance * 10", "mrt_distance", "mrt_distance * 10", 140],
pickable=True,
auto_highlight=True,
)
# Set the viewport location
view_state = pdk.ViewState(
longitude=-1.415,
latitude=52.2323,
zoom=6,
min_zoom=5,
max_zoom=15,
pitch=40.5,
bearing=-27.36)
tooltip = {
"html": "<b>{mrt_distance}</b> meters away from an MRT station, costs <b>{price_per_unit_area}</b> NTD/sqm",
"style": {"background": "grey", "color": "white", "font-family": '"Helvetica Neue", Arial', "z-index": "10000"},
}
r = pdk.Deck(
column_layer,
initial_view_state=view,
# tooltip=tooltip,
#map_provider="mapbox",
map_style=pdk.map_styles.LIGHT,
)
res = r.to_html("column_layer.html")
# + tags=[]
r.to_html().data
# +
import pydeck as pdk
UK_ACCIDENTS_DATA = 'https://raw.githubusercontent.com/visgl/deck.gl-data/master/examples/3d-heatmap/heatmap-data.csv'
layer = pdk.Layer(
'HexagonLayer', # `type` positional argument is here
UK_ACCIDENTS_DATA,
get_position=['lng', 'lat'],
auto_highlight=True,
elevation_scale=50,
pickable=True,
elevation_range=[0, 3000],
extruded=True,
coverage=1)
# Set the viewport location
view_state = pdk.ViewState(
longitude=-1.415,
latitude=52.2323,
zoom=6,
min_zoom=5,
max_zoom=15,
pitch=40.5,
bearing=-27.36)
f = 0
def filter_by_viewport(c):
global f
f=c
print(str(c))
# Combined all of it and render a viewport
r = pdk.Deck(layers=[layer], initial_view_state=view_state)
r.deck_widget.on_click(filter_by_viewport)
r.to_html('hexagon-example.html')
# -
f
# +
from ipywidgets import HTML
text = HTML(value='Move the viewport')
layer = pdk.Layer(
'ScatterplotLayer',
df,
pickable=True,
get_position=['lng', 'lat'],
get_fill_color=[255, 0, 0],
get_radius=100
)
r = pdk.Deck(layer, initial_view_state= pdk.data_utils.compute_view(df))
def filter_by_bbox(row, west_lng, east_lng, north_lat, south_lat):
return west_lng < row['lng'] < east_lng and south_lat < row['lat'] < north_lat
def filter_by_viewport(widget_instance, payload):
try:
west_lng, north_lat = payload['data']['nw']
east_lng, south_lat = payload['data']['se']
filtered_df = df[df.apply(lambda row: filter_by_bbox(row, west_lng, east_lng, north_lat, south_lat), axis=1)]
text.value = 'Points in viewport: %s' % int(filtered_df.count()['lng'])
except Exception as e:
text.value = 'Error: %s' % e
r.deck_widget.on_click(filter_by_viewport)
display(text)
r.show()
# -
# !pip install
|
Energy_sandbox.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
from scipy.io import loadmat
import numpy as np
from nltk.tokenize import word_tokenize
from nltk import pos_tag
from nltk.corpus import stopwords
from nltk.stem import WordNetLemmatizer
from sklearn.preprocessing import LabelEncoder
from collections import defaultdict
from nltk.corpus import wordnet as wn
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn import model_selection, naive_bayes, svm
from sklearn.metrics import accuracy_score
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
import seaborn as sns
from utilities import remove_empty_tweets
# +
train_data_path = 'cleaned_data/cleaned_train_data_for_subtask1.csv'
test_data_path = 'cleaned_data/cleaned_test_data_for_subtask1.csv'
#read files.
train_data = pd.read_csv(train_data_path)
test_data = pd.read_csv(test_data_path)
print("Train set:"% train_data.columns, train_data.shape, len(train_data))
print("Test set:"% test_data.columns, test_data.shape, len(test_data))
# +
train_data = remove_empty_tweets(train_data, "#2_tweet_clean_V1")
test = remove_empty_tweets(test_data, "#2_tweet_clean_V1")
train_data.head()
# -
#prepare train and test data.
X_train = train_data['#2_tweet_clean_V1'].tolist()
y_train = train_data['#classes_id'].tolist()
X_test = test_data['#2_tweet_clean_V1'].tolist()
y_test = test_data['#classes_id'].tolist()
# +
x_train, x_valid, y_train, y_valid = model_selection.train_test_split(train_data['#2_tweet_clean_V1'],train_data['#classes_id'],test_size=0.3, random_state=42)
print(len(x_train),len(x_valid))
# +
#Create vocabulary
Tfidf_vect = TfidfVectorizer(max_features=5000, ngram_range=(1,3), stop_words=STOPWORDS)
Tfidf_vect.fit(train_data['#2_tweet_clean_V1'])
Train_X_Tfidf = Tfidf_vect.transform(x_train)
Test_X_Tfidf = Tfidf_vect.transform(x_valid)
print(Tfidf_vect.vocabulary_)
# -
test_X_Tfidf = Tfidf_vect.transform(X_test)
print(test_X_Tfidf)
# # Radial Basis Function (RBF) kernel
# +
import timeit
start = timeit.default_timer()
SVM = svm.SVC(C=1.0, kernel='rbf', degree=3, gamma=2)
SVM.fit(Train_X_Tfidf,y_train)
stop = timeit.default_timer()
print('Train time: ', stop - start)
# predict the labels on validation dataset
predictions_SVM_valid = SVM.predict(Test_X_Tfidf)
# Use accuracy_score function to get the accuracy
print("SVM Accuracy Score -> ",accuracy_score(predictions_SVM_valid, y_valid)*100)
# +
predictions_SVM = SVM.predict(test_X_Tfidf)
print(classification_report(predictions_SVM, y_test))
# -
# # Quadratic (poly) kernel
# +
startquad = timeit.default_timer()
SVMquad = svm.SVC(C=1.0, kernel='poly', degree=3, gamma=2)
SVMquad.fit(Train_X_Tfidf,y_train)
stopquad = timeit.default_timer()
print('Train time: ', stopquad - startquad)
# predict the labels on validation dataset
predictions_SVMquad = SVMquad.predict(Test_X_Tfidf)
# Use accuracy_score function to get the accuracy
print("SVM Accuracy Score -> ",accuracy_score(predictions_SVMquad, y_valid)*100)
# +
predictions_SVMquad_test = SVMquad.predict(test_X_Tfidf)
print(classification_report(predictions_SVMquad_test, y_test))
# -
print(classification_report(predictions_SVMquad, y_valid))
# # Linear kernel
# +
startlin = timeit.default_timer()
SVMlin = svm.SVC(C=1.0, kernel='linear', degree=3, gamma=2)
SVMlin.fit(Train_X_Tfidf,y_train)
stoplin = timeit.default_timer()
print('Train time: ', stoplin - startlin)
# predict the labels on validation dataset
predictions_SVMlin = SVMlin.predict(Test_X_Tfidf)
# Use accuracy_score function to get the accuracy
print("SVM Accuracy Score -> ",accuracy_score(predictions_SVMlin, y_valid)*100)
# +
predictions_SVMlin_test = SVMlin.predict(test_X_Tfidf)
print(classification_report(predictions_SVMlin_test, y_test))
# -
print(classification_report(predictions_SVMlin, y_valid))
# # Sigmoid kernel
# +
startsig = timeit.default_timer()
SVMsig = svm.SVC(C=1.0, kernel='sigmoid', degree=3, gamma=2)
SVMsig.fit(Train_X_Tfidf,y_train)
stopsig = timeit.default_timer()
print('Train time: ', stopsig - startsig)
# predict the labels on validation dataset
predictions_SVMsig = SVMsig.predict(Test_X_Tfidf)
# Use accuracy_score function to get the accuracy
print("SVM Accuracy Score -> ",accuracy_score(predictions_SVMsig, y_valid)*100)
# -
print(classification_report(predictions_SVMsig, y_valid))
|
SVM.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # SKLEARN PIEPLINES
# ---
# Materials prepared, or collected and modified by:
# __<NAME>__, www.SimpleAI.ch
#
# ## CONTENT
# * My Infopages
# * Code examples
#
# ## SOURCE MATERIALS
# links to source materials, and additional readings, were added to text or code in each section directly.
# 
# 
# ## CODE EXAMPLES:
# ---
# +
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import matplotlib as mpl
from sklearn.datasets import load_breast_cancer
from sklearn import neighbors, preprocessing
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.datasets import make_classification # creates simple data egxample
# -
# #### import my helper functions
from src.utils.ml_model_metrics import plot_confusion_matrix # creates annotated heatmap for confusion matrix
# ### Step 1. create example data
# +
X, y = make_classification(
n_samples=1000,
n_features=20,
n_informative=10,
n_redundant=2,
n_repeated=0,
n_classes=4,
n_clusters_per_class=2
)
print(f'X shape: {X.shape}')
print(f'y shape: {y.shape}')
# are classes balanced
print("target:\n",pd.Series(y).value_counts())
# -
# ### create simple classyficaiton model
# +
# split to train/test
X_tr, X_te, y_tr, y_te = train_test_split(
X, y, train_size=0.7, random_state=0)
# scale input data
scaler = preprocessing.StandardScaler().fit(X_tr)
X_tr = scaler.transform(X_tr)
X_te = scaler.transform(X_te)
# Create classifier & train it
clf = neighbors.KNeighborsClassifier(n_neighbors=2)
clf.fit(X_tr, y_tr)
# predict test values and check summary
y_pred = clf.predict(X_te)
# +
# Function, ..............................
def show_results(model, y_tr, y_te):
'helper funtion to examine classyficaiotn results'
print(f'train_acc: {accuracy_score(y_tr, model.predict(X_tr))}')
print(f'test_acc: {accuracy_score(y_te, model.predict(X_te))}')
plot_confusion_matrix(X_te, y_te, model,
with_perc=True, cmap="coolwarm", figsize=(5,4))
# create confusion matrix, with % of predicted classes in each row
show_results(clf, y_tr, y_te)
# -
# ### Use Pipeline Function to find best k-value
# __Pipeline function__ is used to encapsulate multiple steps with pipeline
# https://scikit-learn.org/stable/modules/generated/sklearn.pipeline.Pipeline.html
# +
from sklearn.pipeline import Pipeline
# each step requires a name, and a function
pipe = Pipeline([
('scaler', preprocessing.StandardScaler()),
('knn',neighbors.KNeighborsClassifier(n_neighbors=5))
])
# test different k values
results = []
for k in list(range(2,30)):
# set k in the pipeline
pipe.set_params(knn__n_neighbors=k)
pipe.fit(X_tr, y_tr)
# collect the results
results.append({
'k':k,
'train_acc': accuracy_score(y_tr, pipe.predict(X_tr)),
'test_acc': accuracy_score(y_te, pipe.predict(X_te))
})
# convert the results to pd.dataframe & plot them
gs = pd.DataFrame(results)
# plot results
plt.style.use("ggplot")
plt.plot(gs.loc[:,'k'], gs.loc[:,'train_acc'], label="train acc")
plt.plot(gs.loc[:,'k'], gs.loc[:,'test_acc'], label="test acc")
plt.xlabel("k")
plt.ylabel("accuracy")
plt.legend()
plt.show()
# -
# retrain model with bext k-value and plot the results with test data
# +
# find best k, and show confusion matrix
best_k = gs.sort_values(by="test_acc", ascending=False).k.iloc[0]
# retrain the model with bst_k
pipe.set_params(knn__n_neighbors=best_k)
pipe.fit(X_tr, y_tr)
# create confusion matrix, with % of predicted classes in each row
show_results(clf, y_tr, y_te)
# -
# #### check parameters in pipeline
# +
# to see parameters at each step
pipe.get_params()
# returns: {'memory': None,
#. 'steps': [( ...
# basic text info
pipe.named_steps
# returns: {'scaler': StandardScaler(), 'knn': KNeighborsClassifier()}
# visualize the pipeline
from sklearn import set_config
set_config(display="diagram"); pipe
# beatiful visualizations (HTML)
# -
# #### disable the step, remove, etc..
# +
# retrain the model with bst_k
pipe.set_params(scaler=None)
pipe.fit(X_tr, y_tr)
# create confusion matrix, with % of predicted classes in each row
show_results(pipe, y_tr, y_te)
# -
pipe.get_params()
# ### Use ParameterGrid to search fro optimal comabination of Hyperparameters
# ---
# +
from sklearn.model_selection import ParameterGrid
# create a basic grid and tun it.
''' important,
if you use None, or eg standardscaller,
the object must be provided in the list
'''
grid = ParameterGrid({
'scaler':[None, preprocessing.StandardScaler()],
'knn__n_neighbors': list(range(2,8))
})
# you may also create unique comabinations,
# ...ie groups of hyperparameters that are not mixed with each other
'''each group must be in separate dct'''
grid = (
{'scaler':[None], # even one param must be in a list
'knn__n_neighbors': list(range(2,4))
},
{'scaler':[preprocessing.StandardScaler()],
'knn__n_neighbors': list(range(5,6))
}
)
list(ParameterGrid(grid))
# -
# we can access all elements in a parameter grid as in the list,
# here is example, of simple funciton that I am using to store the results
def my_grid_search(pipe, grid):
# test different k values
results = []
for params in grid:
# set k in the pipeline
pipe.set_params(**params)
pipe.fit(X_tr, y_tr)
# collect the results
results.append({
**params,
'train_acc': accuracy_score(y_tr, pipe.predict(X_tr)),
'test_acc': accuracy_score(y_te, pipe.predict(X_te))
})
# convert the results to pd.dataframe & list top 5
gs = pd.DataFrame(results)
print(gs.sort_values(by='test_acc', ascending=False).head())
# Finally run it on an example:
# +
# create sklearn pipeline with the classifier
pipe = Pipeline([
('scaler', None), # you must add that step, otherwise it may be a problem,
('knn',neighbors.KNeighborsClassifier(n_neighbors=5))
])
# define parameter grid
grid = ParameterGrid({
'scaler':[None, preprocessing.StandardScaler()],
'knn__n_neighbors': list(range(2,8))
})
# find best hyperparameters
my_grid_search(pipe, grid)
# -
# ### make_pipeline vs pipeline functions & applying custom transformers
# * make_pipeline
# * creates the same type of objects as Pipleine() functio
# * gives names for each step automatically,
# * very usefull for preprocessing functions,
# * I use it, often to create smaller pipelines for data transfomers,
# * eg I create a transfomer and later provide it into the final pipeline created with Pipeline() function
#
#
# 
# #### example
# +
from sklearn.preprocessing import FunctionTransformer # creates custom transfomers
from sklearn.pipeline import make_pipeline # like pipeline function, but give step names automatically,
from sklearn.preprocessing import OneHotEncoder, StandardScaler, KBinsDiscretizer # skleanr transformers,
from sklearn.compose import ColumnTransformer # allows using different transformers to different columns
# create custom transformer
log_scale_transformer = make_pipeline(
FunctionTransformer(np.abs, validate=False), # see below
FunctionTransformer(np.log1p, validate=False), # creates runtime warning if negative data are used
StandardScaler()
)
# use ColumnTransformer to create data preprocessor
'''we can aplly different tranfomers to different columns
- give unique names for each transformer
- passthrough - keyword, nothing is done with that column
- column names are always provided as LIST
'''
data_preprocessor = ColumnTransformer(
transformers=[
("passthrough_numeric", "passthrough", list(range(1,10))),
("log_scaled_numeric", log_scale_transformer, [0]),
("binned_numeric", KBinsDiscretizer(n_bins=10, encode="ordinal"), [11, 12]), # is encode="onehot", all bins are in different columns, Caution, it does not drop 1 column 1
],
remainder="drop", # what to do with other columns? TWO OPTION {‘drop’, ‘passthrough’}, if drop, these are removed.
)
transformed_data = data_preprocessor.fit_transform(X_tr)
transformed_data.shape
# -
# #### now lest try to run it,
# +
# create sklearn pipeline with the classifier
pipe = Pipeline([
('data_preprocessor', data_preprocessor), # you must add that step, otherwise it may be a problem,
('knn',neighbors.KNeighborsClassifier(n_neighbors=5))
])
pipe.fit(X_tr, y_tr)
# visualize the pipeline
from sklearn import set_config
set_config(display="diagram"); pipe
# +
# just to see how did i channged the accuracy
# define parameter grid
grid = ParameterGrid({
'knn__n_neighbors': list(range(2,8))
})
# find best hyperparameters
my_grid_search(pipe, grid)
# -
# ### cross-validation with Scikit-learn
# ---
#
# __INTRODUCTION__
# * Scikit-learn allows implementing several strategies for cross-validation https://scikit-learn.org/stable/modules/cross_validation.html
# * Important:
# * it is important to not use test data to learn, on estimator, but also on scaling, feature selection etc...
# * skleanr funcitons such as Pipeline, make_pipeline, or crossvalidation help you with that
#
# __KEY FUNCTIONS__
# * train_test_split
# * fast method t generate one test/train set split,
# * with random shuffle of rowns in the df,
# * not very usefull, for tuning hyperparameters (eg. alpha, and c), because data in train/test sets, may affect the results,
#
#
# * __cross_validate__
# - used in code examples below,
# - allows specifying multiple metrics for evaluation.
# - allows using different Cross validation iterators
# - returns a dict containing
# * fit-times,
# * scores, for test data,
# * optionally: training scores with fitted estimators
# - The multiple metrics can be specified either as a list, tuple or set of predefined scorer names;
# > from sklearn.metrics import recall_score
# > scoring = ['precision_macro', 'recall_macro']
# > clf = svm.SVC(kernel='linear', C=1, random_state=0)
# > scores = cross_validate(clf, X, y, scoring=scoring)
# > sorted(scores.keys())
# > ['fit_time', 'score_time', 'test_precision_macro', 'test_recall_macro']
# > scores['test_recall_macro']
# > array([0.96..., 1. ..., 0.96..., 0.96..., 1. ])
#
#
# __CV Iteratoors__
# * __KFold__
# - divides all the samples in k groups of samples, called folds
# - if k=n, this is equivalent to the Leave One Out strategy
# - The prediction function is learned using k-1 folds, and the fold left out is used for test.
# > from sklearn.model_selection import KFold
# > kfold = KFold(n_splits=3, shuffle=True, random_state=0)
#
# * __ShuffleSplit__
# - creates, n different train/tests sets, by shuffling the data,
# - equalivalent to applying ntimes train_test_split()
# - Samples are first shuffled and then split into a pair of train and test sets
# - It is possible to control the randomness for reproducibility of the results by explicitly seeding the random_state pseudo random number generator
#
# __STRATIFIED CV__
# * __Stratified k-fold__
# - default iterator in cross_validate function,
# - type of k-fold which returns stratified folds:
# * ie. each set contains approximately the same percentage of samples of each target class as the complete set.
# - default iterator in cross_validate function,
# > from sklearn.model_selection import StratifiedKFold
# > skf = StratifiedKFold(n_splits=3)
#
# * __StratifiedShuffleSplit__
# - type of ShuffleSplit, which returns stratified splits,
#
# __Other types__
# * __RepeatedKFold__
# - repeats K-Fold n times, producing different splits in each repetition
# > from sklearn.model_selection import RepeatedKFold
# > random_state = 12883823
# > rkf = RepeatedKFold(n_splits=2, n_repeats=2, random_state=random_state)
#
# * __Leave One Out (LOO)__
# - Each learning set is created by taking all the samples except one
# - the test set being the sample left out,
# - __Pros:__ do not waste much data, almostz all are uzsed for traning,
# - __Cons:__
# * test rersults have high varinace in accuracy,
# * models, constructed from almost all data are virtally identical,
# * As a general rule, most authors, and empirical evidence, suggest that 5- or 10- fold cross validation should be preferred to LOO.
# > from sklearn.model_selection import LeaveOneOut
# > loo = LeaveOneOut()
#
# * __Leave P Out (LPO)__
# - creates all the possible training/test sets by removing p samples from the complete set.
# > from sklearn.model_selection import LeavePOut
# > lpo = LeavePOut(p=2)
# ### example 1. Cross-validation with KFold, & cross_validate
# +
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_validate
# Create k-fold object
''' remember to shuffle the data,
by default shuffle = False
'''
kfold = KFold(n_splits=3, shuffle=True, random_state=0)
# create simple pipeline
pipe = make_pipeline(
StandardScaler(),
neighbors.KNeighborsClassifier()
)
# Apply cross-validation to find optimal hypeparameters,
# Option 1 - Use custom kfold obj
scores = cross_validate(
pipe, # model,
X, y, # inpiut data,
cv=kfold, # cross vakldation object,
return_train_score=True
)
scores
# {'fit_time': array([0.00321221, 0.00180292, 0.0014317 ]),
# 'score_time': array([0.02344394, 0.01779819, 0.01449227]),
# 'test_score': array([0.64371257, 0.66366366, 0.65165165]),
# 'train_score': array([0.78528529, 0.76161919, 0.7856072 ])}
"""
'fit_time', - time to fit the estimator,
'score_time', - time to evaluate the est...
'test_score', - perfomrmance of the (k-1) parts used to train the est..
'train_score' - performance on the remaning "validation set"
"""
# .. (option 2) Use build-in k-fold cross validation,
''' by default it uses stratified k-fold strategy,
that ensures that categories are eqally mixed and represented, in each class
'''
scores = cross_validate(
pipe, # model,
X, y, # inpiut data,
cv=3, # JUST GIVE AND INT WITH K CLASSES,
# . most often used varinats are 3, 5 and 10!
return_train_score=True
)
"""
Important Issue;
large difference in accuracy, between train and test sets
- by default k-fold splits, data without shuffling,
in our case, data were organized by species, thus,
part of the data was never seen by the the model, and test accuracy
may be much lower then the acc of the train sets,
""";
# +
# evaluate results
print('Tr mean: {:.3f} std: {:.3f}'.format(
np.mean(scores['train_score']), np.std(scores['train_score'])))
print('Te mean: {:.3f} std: {:.3f}'.format(
np.mean(scores['test_score']), np.std(scores['test_score'])))
# -
# #### you can add custom set of metrics to cross_validate function
# https://scikit-learn.org/stable/modules/grid_search.html#multimetric-grid-search
# +
from sklearn.metrics import recall_score
scoring = ['precision_macro', 'recall_macro', 'accuracy']
scores = cross_validate(
pipe, # model,
X, y, # inpiut data,
cv=kfold, # cross vakldation object,
return_train_score=True,
scoring=scoring
)
scores
# -
# #### other types of CV strategy - examples
# +
"""
ShuffleSplit
--------------
- creates, n different train/tests sets, ny shuffling the data,
- equalivalent to applying ntimes train_test_split()
"""
from sklearn.model_selection import ShuffleSplit
cv_type = ShuffleSplit(
n_splits=10,
test_size=20,
random_state=0
)
# -
# ### GridSearchCV
# ---
# - used similarly to model.fit(X,y)
# - returns, both, the model and the results, in fitted object
# - https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.GridSearchCV.html#sklearn.model_selection.GridSearchCV
#
# +
from sklearn.model_selection import GridSearchCV
# create pipeline
pipe = Pipeline([
('scaler', None), # you must add that step, otherwise it may be a problem,
('knn',neighbors.KNeighborsClassifier(n_neighbors=5))
])
# define parameter grid; dct with lists
grid = {'knn__n_neighbors': list(range(2,8))}
# Create k-fold object
kfold = KFold(n_splits=3, shuffle=True, random_state=0)
# set scoring methods
scoring = ['precision_macro', 'recall_macro', 'accuracy']
# create GridSearchCV object
grid_cv = GridSearchCV(
estimator=pipe, param_grid=grid, cv=kfold,
return_train_score=True, n_jobs=-1
)
# fit, the model & tune parameters,
grid_cv.fit(X,y)
# see the model, as pipe
grid_cv
# -
# #### chec the best model
# +
# youi may make prediciotns
y_te_predicted = grid_cv.predict(X_te)
# get the "best" model
best_model = grid_cv.best_estimator_
y_te_predicted_best = best_model.predict(X_te)
# examing hyperarameters, and score from the best model
best_score = grid_cv.best_score_
best_model_params = grid_cv.best_params_
print(best_score)
print(best_model_params)
# -
# #### examine the process of gridsearch
# +
# you may see available scores here, per split,
sorted(gridcv_results.cv_results_.keys())
#. ['mean_fit_time',
#. 'mean_score_time',
#. 'mean_test_score',
#. 'mean_train_score' ...
# you may call all of them,
'''caution params are in dct,
and if saved as txt, file, they will be hard to reload
'''
df_res = pd.DataFrame(gridcv_results.cv_results_)
df_res.head(3)
# +
# here is what you can do to add params as separate columns
df_res = pd.concat([
df_res,
pd.DataFrame(df_res.params.to_list())
], axis=1)
df_res.head(2)
# k values were added as the last column called knn__n_neighbors
# other parameters will be treated in the same way
# +
# Function, ........................................................
def plot_model_results(ax, params, means, sd, label=""):
'''creates a lne plot, and fill between lines on provided axis object
. params; used as labels on x-axis
. means; y-axis values
. sd; values used to create fillin area, ±1/2sd abouve each mean
. label; labels for a line plotted
'''
# create the plot
x_axis = np.arange(params.size)
ax.plot(x_axis,means,linewidth=3, label=label)
ax.fill_between( x_axis, means-sd/2, means+sd/2, alpha=0.4)
# add x-tick labels
ax.set_xticks(x_axis)
ax.set_xticklabels(params.tolist(), rotation=0, fontsize=10)
# set default style and create a figure
mpl.rcParams.update(mpl.rcParamsDefault)
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(3,3))
# plot test scores
plot_model_results(ax=ax,params=df_res.knn__n_neighbors,
means=df_res.mean_test_score, sd=df_res.std_test_score, label="test"
)
# plot train scores
plot_model_results(ax=ax,params=df_res.knn__n_neighbors,
means=df_res.mean_train_score, sd=df_res.std_train_score, label="train"
)
# add labels
ax.set(xlabel="k", ylabel="accuracy")
ax.legend()
# plint info and show the plot
print(f"best score: {best_score}")
print(f"best model params: {best_model_params}")
plt.show();
|
MachineLearning_code_examples/Sklearn_pipelines.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <img src="http://hilpisch.com/tpq_logo.png" alt="The Python Quants" width="35%" align="right" border="0"><br>
# # Python for Finance (2nd ed.)
#
# **Mastering Data-Driven Finance**
#
# © Dr. <NAME> | The Python Quants GmbH
#
# <img src="http://hilpisch.com/images/py4fi_2nd_shadow.png" width="300px" align="left">
# # Data Analysis with pandas
# ## pandas Basics
# ### First Steps with DataFrame Class
# + uuid="eda2a742-134d-4d47-8b30-557b846b9bb3"
import pandas as pd
# -
df = pd.DataFrame([10, 20, 30, 40],
columns=['numbers'],
index=['a', 'b', 'c', 'd'])
# + uuid="f3be2d89-829a-49b2-96fc-07c475db1e3f"
df
# + uuid="47b70a7b-710f-4c40-9a70-b09db7af1a12"
df.index
# + uuid="a36c6695-520d-4df1-a6fa-5f8362af37a3"
df.columns
# + uuid="c93aed37-21de-429d-86ed-9849e4c3e23c"
df.loc['c']
# + uuid="8c7c2f69-3673-40d9-a568-0471c629810d"
df.loc[['a', 'd']]
# + uuid="c3ce0cc3-26e8-4256-ab8c-9a2d4b181633"
df.iloc[1:3]
# + uuid="94b1d846-63df-49f4-8a7f-8fed03e5f4fa"
df.sum()
# + uuid="4e73eb4f-352d-4527-b0c5-4f3a6e7eb354"
df.apply(lambda x: x ** 2)
# + uuid="75206a83-0154-4be2-88d0-7a82a190fda1"
df ** 2
# -
df['floats'] = (1.5, 2.5, 3.5, 4.5)
# + uuid="49a2633a-b3c0-4d00-a227-e0ff4a8cf81d"
df
# + uuid="c49b9aea-417a-4c2b-8e27-0e8771a77c87"
df['floats']
# -
df['names'] = pd.DataFrame(['Yves', 'Sandra', 'Lilli', 'Henry'],
index=['d', 'a', 'b', 'c'])
# + uuid="aa892c41-6637-45ed-876b-6a70285e4c0b"
df
# + uuid="584ac18c-161f-4c7b-8ff1-1cd406fb8437"
df.append({'numbers': 100, 'floats': 5.75, 'names': 'Jil'},
ignore_index=True)
# -
df = df.append(pd.DataFrame({'numbers': 100, 'floats': 5.75,
'names': 'Jil'}, index=['y',]))
# + uuid="9068cd04-c6ff-4d0c-bd52-cf04cd89a0e9"
df
# -
df = df.append(pd.DataFrame({'names': 'Liz'}, index=['z',]), sort=False)
# + uuid="9068cd04-c6ff-4d0c-bd52-cf04cd89a0e9"
df
# -
df.dtypes
# + uuid="3e863c7f-7875-4911-997b-6e48123dc1e5"
df[['numbers', 'floats']].mean()
# + uuid="c52173a0-485d-4eb2-b6b4-407d1ff2c30e"
df[['numbers', 'floats']].std()
# -
# ### Second Steps with DataFrame Class
import numpy as np
np.random.seed(100)
a = np.random.standard_normal((9, 4))
# + uuid="d6f56a00-91e6-4221-a1ec-6093f416d1be"
a
# -
df = pd.DataFrame(a)
# + uuid="450bd14d-7668-4f3f-a863-966f13562818"
df
# -
df.columns = ['No1', 'No2', 'No3', 'No4']
# + uuid="968395a4-12bc-46d2-b486-6c767abce366"
df
# + uuid="68e8d73f-93d3-47ac-a656-1edbdebcd1ff"
df['No2'].mean()
# -
dates = pd.date_range('2019-1-1', periods=9, freq='M')
# + uuid="a80e1e88-d211-4ee4-a6d3-90403a7739a8"
dates
# -
df.index = dates
# + uuid="d8fef9ed-25ca-4ae0-bd0c-026d340a903b"
df
# + uuid="bcc38d60-3e1c-49bb-b883-ea7564c136b4"
df.values
# + uuid="bcc38d60-3e1c-49bb-b883-ea7564c136b4"
np.array(df)
# -
# ## Basic Analytics
df.info()
# + uuid="125980cc-91ec-4ab4-9a4a-cfd772dd1254"
df.describe()
# + uuid="f760ea25-c64c-4e70-9f91-b72701d919ce"
df.sum()
# + uuid="3dd9bd77-eb80-46cb-87f3-62c053a8e223"
df.mean()
# + uuid="3dd9bd77-eb80-46cb-87f3-62c053a8e223"
df.mean(axis=0)
# -
df.mean(axis=1)
# + uuid="8e167ea8-09b7-4585-8cac-28fe20eefe66"
df.cumsum()
# -
np.mean(df)
# raises warning
np.log(df)
# + uuid="9dfc1e40-c030-4a9c-9e3a-ff28c64a93df"
np.sqrt(abs(df))
# + uuid="a540362b-50d7-4ef0-89ba-0b6ee38033f6"
np.sqrt(abs(df)).sum()
# -
100 * df + 100
# ## Basic Visualization
from pylab import plt, mpl
plt.style.use('seaborn')
mpl.rcParams['font.family'] = 'serif'
# %matplotlib inline
# + uuid="4b1834ec-9f9b-41d6-8d06-f2efc8433dc4"
df.cumsum().plot(lw=2.0, figsize=(10, 6));
# plt.savefig('../../images/ch05/pd_plot_01.png')
# + uuid="4b1834ec-9f9b-41d6-8d06-f2efc8433dc4"
df.plot.bar(figsize=(10, 6), rot=30);
# df.plot(kind='bar', figsize=(10, 6))
# plt.savefig('../../images/ch05/pd_plot_02.png')
# -
# ## Series Class
# + uuid="e86f82d1-5934-42d3-a986-f01bc829adaa"
type(df)
# -
S = pd.Series(np.linspace(0, 15, 7), name='series')
S
type(S)
s = df['No1']
s
# + uuid="ca241ef9-5359-4c89-bc92-be6346cb3959"
type(s)
# -
s.mean()
# + uuid="b3d4cc90-e499-459c-88a5-011fde80d864"
s.plot(lw=2.0, figsize=(10, 6));
# plt.savefig('../../images/ch05/pd_plot_03.png')
# -
# ## GroupBy Operations
# + uuid="4bc106dd-9590-4566-bc70-d410517c8223"
df['Quarter'] = ['Q1', 'Q1', 'Q1', 'Q2', 'Q2',
'Q2', 'Q3', 'Q3', 'Q3']
df
# -
groups = df.groupby('Quarter')
# + uuid="a871b95e-5946-4b09-b8dc-bc9503d2ff14"
groups.size()
# + uuid="804e567f-6b74-4405-a10e-d19d914655e7"
groups.mean()
# + uuid="7eb45e5c-b86f-4464-afd9-d5a3665e0f8e"
groups.max()
# -
groups.aggregate([min, max]).round(2)
# + uuid="542cf99a-bbf8-447e-9643-d6887ac74be7"
df['Odd_Even'] = ['Odd', 'Even', 'Odd', 'Even', 'Odd', 'Even',
'Odd', 'Even', 'Odd']
# + uuid="f5144c9f-ff37-4e35-9417-e39debdcd45b"
groups = df.groupby(['Quarter', 'Odd_Even'])
# + uuid="06904508-dbf1-431f-a3a2-681f29f03c51"
groups.size()
# + uuid="b8471956-40fc-4203-a54a-aaa45f5a3c00"
groups[['No1', 'No4']].aggregate([sum, np.mean])
# -
# ## Complex Selection
data = np.random.standard_normal((10, 2))
df = pd.DataFrame(data, columns=['x', 'y'])
df.info()
df.head()
df.tail()
df['x'] > 0.5
(df['x'] > 0) & (df['y'] < 0)
(df['x'] > 0) | (df['y'] < 0)
df[df['x'] > 0]
df.query('x > 0')
df[(df['x'] > 0) & (df['y'] < 0)]
df.query('x > 0 & y < 0')
df[(df.x > 0) | (df.y < 0)]
df > 0
df[df > 0]
# ## Concatenation, Joining and Merging
df1 = pd.DataFrame(['100', '200', '300', '400'],
index=['a', 'b', 'c', 'd'],
columns=['A',])
df1
df2 = pd.DataFrame(['200', '150', '50'],
index=['f', 'b', 'd'],
columns=['B',])
# + slideshow={"slide_type": "-"}
df2
# -
# #### Concatenation
df1.append(df2, sort=False)
df1.append(df2, ignore_index=True, sort=False)
pd.concat((df1, df2), sort=False)
pd.concat((df1, df2), ignore_index=True, sort=False)
# #### Joining
df1.join(df2)
df2.join(df1)
df1.join(df2, how='left')
df1.join(df2, how='right')
df1.join(df2, how='inner')
df1.join(df2, how='outer')
df = pd.DataFrame()
df['A'] = df1['A']
df
df['B'] = df2
df
df = pd.DataFrame({'A': df1['A'], 'B': df2['B']})
df
# #### Merging
c = pd.Series([250, 150, 50], index=['b', 'd', 'c'])
df1['C'] = c
df2['C'] = c
df1
df2
pd.merge(df1, df2)
pd.merge(df1, df2, on='C')
pd.merge(df1, df2, how='outer')
pd.merge(df1, df2, left_on='A', right_on='B')
pd.merge(df1, df2, left_on='A', right_on='B', how='outer')
pd.merge(df1, df2, left_index=True, right_index=True)
pd.merge(df1, df2, on='C', left_index=True)
pd.merge(df1, df2, on='C', right_index=True)
pd.merge(df1, df2, on='C', left_index=True, right_index=True)
# ## Performance Aspects
data = np.random.standard_normal((1000000, 2))
data.nbytes
df = pd.DataFrame(data, columns=['x', 'y'])
df.info()
# %time res = df['x'] + df['y']
res[:3]
# %time res = df.sum(axis=1)
res[:3]
# %time res = df.values.sum(axis=1)
res[:3]
# %time res = np.sum(df, axis=1)
res[:3]
# %time res = np.sum(df.values, axis=1)
res[:3]
# %time res = df.eval('x + y')
res[:3]
# %time res = df.apply(lambda row: row['x'] + row['y'], axis=1)
res[:3]
# <img src="http://hilpisch.com/tpq_logo.png" alt="The Python Quants" width="35%" align="right" border="0"><br>
#
# <a href="http://tpq.io" target="_blank">http://tpq.io</a> | <a href="http://twitter.com/dyjh" target="_blank">@dyjh</a> | <a href="mailto:<EMAIL>"><EMAIL></a>
|
code/ch05/05_pandas.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + init_cell=true
# %matplotlib inline
# %load_ext iminizinc
import asyncio
from IPython.display import HTML
import ipywidgets as widgets
from ipywidgets import interact, interactive
from problems import nqueens, us_map_coloring
from draw_utils import draw_nqueens, draw_us_map
from slide_utils import SlideController
from backtracking_search import nqueens_backtracking
from utils import autoupdate_cells
# + init_cell=true
HTML('<script src="http://d3js.org/d3.v3.min.js" charset="utf-8"></script>')
# -
# # Constraint Programming
# ## Introduction
# Constraints naturally arise in a variety of interactions and fields of study such as game theory, social studies, operations research, engineering, and artificial intelligence. A constraint refers to the relationship between the state of objects, such as the constraint that the three angles of a triangle must sum to 180 degrees. Note that this constraint has not precisely stated each angle's value and still allows some flexibility. Said another way, the triangle constraint restricts the values that the three variables (each angle) can take, thus providing information that will be useful in finding values for the three angles.
#
# Another example of a constrained problem comes from the recently-aired hit TV series *Buddies*, where a group of five (mostly mutual) friends would like to sit at a table with three chairs in specific arrangements at different times, but have requirements as to who they will and will not sit with.
#
# Another example comes from scheduling: at the university level, there is a large number of classes that must be scheduled in various classrooms such that no professor or classroom is double booked. Further, there are some constraints on which classes can be scheduled for the same time, as some students will need to be registered for both.
#
# Computers can be employed to solve these types of problems, but in general these tasks are computationally intractable and cannot be solved efficiently in all cases with a single algorithm \cite{Dechter2003}. However, by formalizing these types of problems in a constraint processing framework, we can identify classes of problems that can be solved using efficient algorithms.
#
# Below, we discuss generally the three core concepts in constraint programming: **modeling**, **inference**, and **search**. Modeling is an important step that can greatly affect the ability to efficiently solve constrained problems and inference (e.g., constraint propagation) and search are solution methods. Basic constraint propagation and state-space search are building blocks that state of the art solvers incorporate.
#
# ### Modeling
#
# A **constraint satisfaction problem** (CSP) is formalized by a *constraint network*, which is the triple $\mathcal{R} = \langle X,D,C\rangle$, where
# - $X = \{x_i\}_{i=1}^n$ is the set of $n$ variables
# - $D = \{D_i\}_{i=1}^n$ is the set of variable domains, where the domain of variable $x_k$ is $D_k$
# - $C = \{C_i\}_{i=1}^m$ is the set of constraints on the values that each $x_i$ can take on. Specifically,
# - Each constraint $C_i = \langle S_i,R_i\rangle$ specifies allowed variable assignments.
# - $S_i \subset X$ contains the variables involved in the constraint, called the *scope* of the constraint.
# - $R_i$ is the constraint's *relation* and represents the simultaneous legal value assignments of variables in the associated scope.
# - For example, if the scope of the first constraint is $S_1 = \{x_3, x_8\}$, then the relation $R_1$ is a subset of the Cartesian product of those variables' domains: $R_1 \subset D_3 \times D_8$, and an element of the relation $R_1$ could be written as a 2-tuple $(a,b)\in R_1$.
#
# Each variable in a CSP can be assigned a value from its domain. A **complete assignment** is one in which every variable is assigned and a **solution** to a CSP is a consistent (or legal w.r.t. the constraints) complete assignment.
#
# Note that for a CSP model, *any* consistent complete assignment of the variables (i.e., where all constraints are satisfied) constitutes a valid solution; however, this assignment may not be the "best" solution. Notions of optimality can be captured by introducing an objective function which is used to find a valid solution with the lowest cost. This is referred to as a **constraint *optimization* problem** (COP). We will refer generally to CSPs with the understanding that a CSP can easily become a COP by introducing a heuristic.
#
# In this notebook, we will restrict ourselves to CSPs that can be modeled as having **discrete, finite domains**. This helps us to manage the complexity of the constraints so that we can clearly discuss the different aspects of CSPs. Other variations exist such as having discrete but *infinite* domains, where constraints can no longer be enumerated as combinations of values but must be expressed as either linear or nonlinear inequality constraints, such as $T_1 + d_1 \leq T_2$. Therefore, infinite domains require a different constraint language and special algorithms only exist for linear constraints. Additionally, the domain of a CSP may be continuous. With this change, CSPs become mathematical programming problems which are often studied in operations research or optimization theory, for example.
#
# ### Modeling as a Graph
#
# In a general CSP, the *arity* of each constraint (i.e., the number of variables involved) is arbitrary. We can have unary constraints on a single variable, binary constraints between two variables, or $n$-ary constraints between $n$ variables. However, having more than binary constraints adds complexity to the algorithms for solving CSPs. It can be shown that every finite-domain constraint can be reduced to a set of binary constraints by adding enough auxiliary variables \cite{AIMA}. Therefore, since we are only discussing CSPs with finite domains, we will assume that the CSPs we are working with have only unary and binary constraints, meaning that each constraint scope has at most two variables.
#
# An important view of a binary constraint network that defines a CSP is as a graph, $\langle\mathcal{V},\mathcal{E}\rangle$. In particular, each vertex corresponds to a variable, $\mathcal{V} = X$, and the edges of the graph $\mathcal{E}$ correspond to various constraints between variables. Since we are only working with binary and unary constraint networks, it is easy to visualize a graph corresponding to a CSP. For constraint networks with more than binary constraints, the constraints must be represented with a hypergraph, where hypernodes are inserted that connect three or more variables together in a constraint.
#
# For example, consider a CSP $\mathcal{R}$ with the following definition
# \begin{align}
# X &= \{x_1, x_2, x_3\} \\
# D &= \{D_1, D_2, D_3\},\ \text{where}\; D_1 = \{0,5\},\ D_2 = \{1,2,3\},\ D_3 = \{7\} \\
# C &= \{C_1, C_2, C_3\},
# \end{align}
# where
# \begin{align}
# C_1 &= \langle S_1, R_1 \rangle = \langle \{x_1\}, \{5\} \rangle \\
# C_2 &= \langle S_2, R_2 \rangle = \langle \{x_1, x_2\}, \{(0, 1), (0,3), (5,1)\} \rangle \\
# C_3 &= \langle S_3, R_3 \rangle = \langle \{x_2, x_3\}, \{(1, 7), (2, 7)\} \rangle.
# \end{align}
# The graphical model of this CSP is shown below.
#
# <img src="images/example_graph.png" width="35%" align="center"/>
#
#
# ### Solving
#
# The goal of formalizing a CSP as a constraint network model is to efficiently solve it using computational algorithms and tools. **Constraint programming** (CP) is a powerful tool to solve combinatorial constraint problems and is the study of computational systems based on constraints. Once the problem has been modeled as a formal CSP, a variety of computable algorithms could be used to find a solution that satisfies all constraints.
#
# In general, there are two methods used to solve a CSP: search or inference. In previous 16.410/413 problems, **state-space search** was used to find the best path through some sort of graph or tree structure. Likewise, state-space search could be used to find a valid "path" through the CSP that satisfies each of the local constraints and is therefore a valid global solution. However, this approach would quickly become intractable as the number of variables and the size of each of their domains increase.
#
# In light of this, the second solution method becomes more attractive. **Constraint propagation**, a specific type of inference, is used to reduce the number of legal values from a variable's domain by pruning values that would violate the constraints of the given variable. By making a variable locally consistent with its constraints, the domain of adjacent variables may potentially be further reduced as a result of missing values in the pairwise constraint of the two variables. In this way, by making the first variable consistent with its constraints, the constraints of neighboring variables can be re-evaluated, causing a further reduction of domains through the propagation of constraints. These ideas will later be formalized as $k$-consistency.
#
# Constraint propagation may be combined with search, using the pros of both methods simultaneously. Alternatively, constraint propagation may be performed as a pre-processing pruning step so that search has a smaller state space to search over. Sometimes, constraint propagation is all that is required and a solution can be found without a search step at all.
#
# After giving examples of modeling CSPs, this notebook will explore a variety of solution methods based on constraint propagation and search.
# ---
# ## Problem Models
#
# Given a constrained problem, it is desirable to identify an appropriate constraint network model $\mathcal{R} = \langle X,D,C\rangle$ that can be used to find its solution. Modeling for CSPs is an important step that can dramatically affect the difficulty in enumerating the associated constraints or efficiency of finding a solution.
#
# Using the general ideas and formalisms from the previous section, we consider two puzzle problems and model them as CSPs in the following sections.
#
# ### N-Queens
#
# The N-Queens problem (depicted below for 4 queens) is a well-know puzzle among computer scientists and will be used as a recurring example throughout this notebook. The problem statement is as follows: given any integer $N$, the goal is to place $N$ queens on an $N\times N$ chessboard satisfying the constraint that no two queens threaten each other. A queen can threaten any other queen that is on the same row, column, or diagonal.
#
# Example n-queens
draw_nqueens(nqueens(4))
# Now let's try to understand the problem formally.
#
# #### Attempt 1
#
# To illustrate the effect of modeling, we first consider a (poor) model for the N-Queens constraint problem, given by the following definitions:
# \begin{align}
# X &= \{x_i\}_{i=1}^{N^2} && \text{(Chessboard positions)} \\
# D &= \{D_i\}_{i=1}^{N^2},\ \text{where}\; D_i = \{0, 1,2,\dots,N\} && \text{(Empty or the $k^\text{th}$ queen)}
# \end{align}
#
# Without considering constraints, the size of the state space (i.e., the number of assignments) is an enormous $(N+1)^{N^2}$. For only $N=4$ queens, this becomes $5^{16} \approx 153$ billion states that could potentially be searched.
#
# Expressing the constraints of this problem in terms of the variables and their domains also poses a challenge. Because of the way we have modeled this problem, there are six primary constraints to satisfy:
# 1. Exactly $N$ chess squares shall be filled (i.e., there are only $N$ queens and all of them must be used)
# 1. The $k^\text{th}$ queen, ($1\le k\le N$) shall only be used once.
# 1. No queens share a column
# 1. No queens share a row
# 1. No queens share a positive diagonal (i.e., a diagonal from bottom left to top right)
# 1. No queens share a negative diagonal (i.e., a diagonal from top left to bottom right)
#
# To express these constraints mathematically, we first let $Y\triangleq\{1\le i\le N^2|x_i\in X,x_i\ne 0\}$ be the set of chess square numbers that are non-empty and $Z \triangleq \{x\in X|x\ne 0\}$ be the set of queens in those chess squares (unordered). With pointers back to which constraint they satisfy, the expressions are:
# \begin{align}
# |Z| = |Y| &= N && (C1) \\
# z_i-z_j &\ne 0 && (C2) \\
# |y_i-y_j| &\ne N && (C3) \\
# \left\lfloor\frac{y_i-1}{N}\right\rfloor &\ne \left\lfloor\frac{y_j-1}{N}\right\rfloor && (C4) \\
# |y_i-y_j| &\ne (N-1) && (C5) \\
# |y_i-y_j| &\ne (N+1), && (C6)
# \end{align}
# where $z_i, z_j\in Z$ and $y_i,y_j\in Y, \forall i\ne j$, and applying $|\cdot|$ to a set is the set's cardinality (i.e., size) and applied to a scalar is the absolute value. Additionally, we use $\lfloor\cdot\rfloor$ as the floor operator. Notice how we are able to express all the constraints as pairwise (binary).
#
# We can count the number of constraints in this model as a function of $N$. In each pairwise constraint (C2)-(C6), there are $N$ choose $2$ pairs. Since we have 5 different types of pairwise constraints, we have that the number of constraints, $\Gamma$, is
# \begin{equation}
# \Gamma(N) = 5 {N \choose 2} + 1 = \frac{5N!}{2!(N-2)!} + 1,
# \end{equation}
# where the plus one comes from the single constraint for (C1). Thus, $\Gamma(N=4) = 31$.
#
# Examining the size of the state space in this model, we see the infeasibility of simply performing a state-space search and then performing a goal test that encodes the problem constraints. This motivates the idea of efficiently using constraints either before or during our solution search, which we will explore in the following sections.
#
# #### Attempt 2
#
# Motivated by the desire to do less work in searching and writing constraints, we consider another model of the N-Queens problem. We wish to decrease the size of the state space and number and difficulty of writing the constraints. Good modeling involves cleverly choosing variables and their semantics so that constraints are implicitly encoded, requiring less explicit constraints.
#
# We can achieve this by encoding the following assumptions:
# 1. assume one queen per column;
# 1. an assignment determines which row the $i^\text{th}$ queen should be in.
#
# With this understanding, we can write the constraint network as
# \begin{align}
# X &= \{x_i\}_{i=1}^{N} && \text{(Queen $i$ in the $i^\text{th}$ column)} \\
# D &= \{D_i\}_{i=1}^{N},\ \text{where}\; D_i = \{1,2,\dots,N\} && \text{(The row in which the $i^\text{th}$ queen should be placed)}.
# \end{align}
#
# Now considering the size of the state space without constraints, we see that this intelligent encoding reduces the size to only $N^N$ assignments.
#
# Writing down the constraints is also easier for this model. In fact, we only need to address constraints (C4)-(C6) from above, as (C1)-(C3) are taken care of by intelligently choosing our variables and their domains. The expressions, $\forall x_i,x_j\in X, i\ne j$, are
# \begin{align}
# x_i &\ne x_j && \text{(C4)} \\
# |x_i-x_j| &\ne |i-j|. && \text{(C5, C6)}
# \end{align}
#
# With this reformulation, the number of constraints is
# \begin{equation}
# \Gamma(N) = 2 {N \choose 2} = \frac{N!}{(N-2)!}.
# \end{equation}
# Thus $\Gamma(N=4) = 12$.
#
# We have successfully modeled the N-Queens problem with a reduced state space and with only two pairwise constraints. Both of these properties will allow the solvers discussed next to more efficiently find solutions to this CSP.
# ### Map Coloring
#
# Map coloring is another classic example of a CSP. Consider the map of Australia shown below (from \cite{AIMA}). The goal is to assign a color to Australia's seven territories such that no neighboring regions share the same color. We are further constrained by only being able to use three colors (e.g., <span style="color:red;font-weight:bold">R</span>, <span style="color:green;font-weight:bold">G</span>, <span style="color:blue;font-weight:bold">B</span>). Next to the map is the constraint graph representation of this specific map-coloring problem.
#
# <table width="70%">
# <tr>
# <td><img src="images/mapcoloring_map.png" align="center"/></td>
# <td><img src="images/mapcoloring_graph.png" align="center"/></td>
# </tr>
# </table>
#
# The constraint network model $\mathcal{R}=\langle X,D,C \rangle$ for the general map-coloring problem with $N$ regions and $M$ colors is defined as:
# \begin{align}
# X &= \{x_i\}_{i=1}^N && \text{(Each region)} \\
# D &= \{D_i\}_{i=1}^N,\ \text{where}\; D_i = \{c_j\}_{j=1}^M, && \text{(Available colors)}
# \end{align}
# and the constraints are encoded as
# \begin{align}
# \forall x_i\in X: x_i &\ne n_j,\ \forall n_j\in\mathcal{N}(x_i), && \text{(Each region cannot have the same color as any of its neighbors)}
# \end{align}
# where the neighborhood of the region $x_i$ is defined as the set $\mathcal{N}(x_i) = \{x_j\in X| A_{ij}=1,i\ne j, \forall j\}$. The matrix $A\in\mathbb{Z}_{\ge 0}^{N\times N}$ is called the *adjacency matrix* of a graph with $N$ vertices and represents the variables that a given variable is connected to by constraints (i.e., edges). The notation $A_{mn}$ indexes into the matrix by row $m$ and column $n$.
#
# We will use the map coloring problem as a COP example later on.
# ### First MiniZinc model
#
# We are now ready to solve our first CPS problem! Let us now introduce [MiniZinc](https://www.minizinc.org/), a **high-level**, **solver-independent** language to express constraint programming problems and solve them. It has a large library of constraints already encoded that we can exploit to encode our problem.
#
# A very useful constraint is `alldifferent(array[int] of var int: x)`, which is one of the most studied and used constraint in constraint programming. As the name suggest it takes an array of variables and constrains them to take different values.
#
# Let's focus on the N-Queens problem as formulated in attempt 2. The reader can notice that we can write (C1), (C2) and (C3) leveraging the `alldifferent` constraint. As result we get the following model.
# +
# %%minizinc
include "globals.mzn";
int: n = 4;
array[1..n] of var 1..n: queens;
constraint all_different(queens);
constraint all_different([queens[i]+i | i in 1..n]);
constraint all_different([queens[i]-i | i in 1..n]);
solve satisfy;
# -
# Here we are asking MiniZinc to solve find any feasible solution (`solve satisfy`) given the constraints.
#
# With high-level languages is easy to describe and solve a CSP. The solver at the same time abstract away the complexity of the search process. Let's now focus on how a CSP is actually solved.
# ---
# ## Constraint Propagation Methods
#
# As previously mentioned, the domain size of a CSP can be dramatically reduced by removing values from variable domains that would violate the relevant constraints. This idea is called **local consistency**. By representing a CSP as a binary constraint graph, making a graph locally consistent amounts to visiting the $i^\text{th}$ node and for each of the values in the domain $D_i$, removing the values of neighboring domains that would cause an illegal assignment.
#
# A great example of the power of constraint propagation is seen in Sudoku puzzles. Simple puzzles are designed to be solved by constraint propagation alone. By enforcing local consistency throughout simple formulations of Sudoku common in newspapers, the unique solution is found without the need for search.
#
# While there are multiple forms of consistency, we will forgo a discussion of node consistency (single node), path consistency (3 nodes), and generally **$k$-consistency** ($k$ nodes) to focus on arc consistency.
#
# ### Arc Consistency
#
# The most well-known notion of local consistency is **arc consistency**, where the key idea is to remove values of variable domains that can never satisfy a specified constraint. The arc $\langle x_i, x_j \rangle$ between two variables $x_i$ and $x_j$ is said to be arc consistent if $\langle x_i, x_j \rangle$ and $\langle x_j, x_i \rangle$ are *directed* arc consistent.
#
# The arc $\langle x_i, x_j \rangle$ is **directed arc consistent** (from $x_i$ to $x_j$) if $\forall a_i \in D_i \;
# \exists a_j \in D_j$ s.t. $\langle a_i, a_j \rangle \in C_{ij}$. The notation $C_{ij}$ represents a constraint between variables $x_i$ and $x_j$ with a relation on their domains $D_i, D_j$. In other words, we write a constraint $\langle \{x_i, x_j\}, R \rangle$ as $C_{ij} = R$, where $R\subset D_i\times D_j$.
#
# As an example, consider the following simple constraint network:
# \begin{align}
# X &= \{x_1, x_2\} \\
# D &= \{D_1, D_2\},\ \text{where}\; D_1=\{1,3,5,7\}, D_2=\{2,4,6,8\} \\
# C &= \{C_{12}\},
# \end{align}
# where $C_{12} = \{(1,2),(3,8),(7,4)\}$ lists legal assignment relationships between $x_1$ and $x_2$.
#
# To make $\langle x_1, x_2 \rangle$ directed arc consistent, we would remove the values from $D_1$ that could never satisfy the constraint $C_{12}$. The original domains are shown on the left, while the directed arc consistent graph is shown on the right. Note that 6 is not removed from $D_2$ because directed arc consistency only considers consistency in one direction.
#
# <table width="70%">
# <tr style="background-color:white">
# <td><img src="images/directedac_1a.png" align="center"/></td>
# <td><img src="images/directedac_1b.png" align="center"/></td>
# </tr>
# </table>
#
# Similarly, we can make $\langle x_2, x_1 \rangle$ directed arc consistent by removing 6 from $D_2$. This results in an arc consistent graph, shown below.
#
# <img src="images/example_ac.png" width="35%"/>
#
# #### Sound but Incomplete
# By making a CSP arc consistent, we are guaranteed that solutions to the CSP will be found in the reduced domain of the arc consistent CSP. However, we are not guaranteed that any arbitrary assignment of variables from the reduced domain will offer a valid CSP solution. In other words, arc consistency is sound (all solutions are arc-consistent solutions) but incomplete (not all arc-consistent solutions are valid solutions).
#
# ### Algorithms
#
# To achieve arc consistency in a graph, we can formalize the ideas that we discussed above about removing values from domains that will never participate in a legal constraint. Two widespread algorithms are considered, known `AC-1` and `AC-3`, which are the first and third versions described by Mackworth in \cite{Mackworth1977}.
#
# In this section, we give the pseudocode for these algorithms and a discussion of their complexities and trade offs.
#
# #### The `REVISE` Algorithm
#
# First, we formalize the procedure of achieving local consistency via the `REVISE` procedure, which is an algorithm that enforces directed arc consistency on a subnetwork. This is the algorithm that we used in the toy example above with $x_1$ and $x_2$.
#
# ```vhdl
# 1 procedure REVISE(xi,xj)
# 2 for each ai in Di
# 3 if there is no aj in Dj such that (ai,aj) is consistent,
# 4 delete ai from Di
# 5 end if
# 6 end for
# 7 end
# ```
#
# ##### Complexity Analysis
#
# The complexity of `REVISE` is $O(k^2)$, where $k$ bounds the domain size, i.e., $k=\max_i|D_i|$. The $k^2$ comes from the fact that there is a double `for loop`---the outer loop is on line 2 and the inner loop is on line 3.
#
# #### The `AC-1` Algorithm
#
# A first pass of enforcing arc consistency on an entire constraint network would be to revise each variable domain in a brute-force manner. This is the objective of the following `AC-1` procedure, which takes a CSP definition $\mathcal{R}=\langle X, D, C\rangle$ as input.
#
# ```vhdl
# 1 procedure AC1(csp)
# 2 loop
# 3 for each cij in C
# 4 REVISE(xi, xj)
# 5 REVISE(xj, xi)
# 6 end for
# 7 until no domain is changed
# 8 end
# ```
#
# If after the `AC-1` procedure is run any of the variable domains are empty, then we conclude that the network has no solution. Otherwise, we are guaranteed an arc-consistent network.
#
# ##### Complexity Analysis
#
# Let $k$ bound the domain size as before and let $n=|X|$ be the number of variables and $e=|C|$ be the number of constraints. One cycle through all of the constraints (lines 3-6) takes $O(2\,e\,O_\text{REVISE}) = O(ek^2)$. In the worst case, only a single domain is changed in one cycle. In this case, the maximum number of repeats (line 7) will be the total number of values, $nk$. Therefore, the worst-case complexity of the `AC-1` procedure is $O(enk^3)$.
#
# #### The `AC-3` Algorithm
#
# Clearly, `AC-1` is straightforward to implement and generates an arc-consistent network, but at great expense. The question we must ask ourselves when using any brute-force method is: Can we do better?
#
# A key observation about `AC-1` is that it processes all constraints even if only a single domain was reduced. This is unnecessary because changes in a domain typically only affect a local subgraph around the node in question.
#
# The `AC-3` procedure is an improved version that maintains a queue of ordered pairs of variables that participate in a constraint (see lines 2-4). Each arc that is processed is removed from the queue (line 6). If the domain of the arc tail $x_i$ is revised, arcs that have $x_i$ as the head will need to be re-evaluated and are added back to the queue (lines 8-10).
#
# ```vhdl
# 1 procedure AC3(csp)
# 2 for each cij in C do
# 3 Q ← Q ∪ {<xi,xj>, <xj,xi>};
# 4 end for
# 5 while Q is not empty
# 6 select and delete any arc (xi,xj) from Q
# 7 REVISE(xi,xj)
# 8 if REVISE(xi,xj) caused a change in Di
# 9 Q ← Q ∪ {<xk,xi> | k ≠ i, k ≠ j, ∀k }
# 10 end if
# 11 end while
# 12 end
# ```
#
# ##### Complexity Analysis
#
# Using the same notation as before, the time complexity of `AC-3` is computed as follows. Building the initial `Q` is $O(e)$. We know that `REVISE` is $O(k^2)$ (line 7). This algorithm processes constraints at most $2k$ times since each time it is reintroduced into the queue (line 9), the domain of one of its associated variables has just been revised by at least one value, and there are at most $2k$ values. Therefore, the total time complexity of `AC-3` is $O(ek^3)$.
#
# Note that the optimal algorithm has complexity $O(ek^2)$ since the worst case of merely verifying the arc consistency of a network requires $ek^2$ operations. There is an `AC-4` algorithm that achieves this performance by not using `REVISE` as a block box, but by exploiting the structures at the constraint level \cite{Dechter2003}.
# ### Example
#
# Using our efficient CSP model (Attempt 2) from the previous section, consider the following 4-Queens problem, with the chessboard shown to the left and the corresponding constraint graph representation to the right. We have already placed the first queen in the first row, $x_1=1$.
#
# <table width="70%">
# <tr>
# <td><img src="images/4queens_board_x1.png" align="center" width="60%" /></td>
# <td><img src="images/4queens_graph_x1.png" align="center"/></td>
# </tr>
# </table>
#
# We would like to use the `AC-3` algorithm to propagate constraints and eliminate inconsistent values in the domains of variables $x_2$, $x_3$ and $x_4$. Intuitively, we already know which values are inconsistent with our constraints (shown with $\times$ in the chessboard above). Follow the slides below to walk through the `AC-3` algorithm.
ac3_slides = SlideController('images/4queens_slide%02d.png', 8)
# Note how in this example, the efficiencies of `AC-3` were unnecessary. In fact, a single pass of `AC-2` would have achieved the same result. Although this was the case for this specific instance, by adding arcs back to the queue to by examined, `AC-3` is more computationally efficient in general.
# ---
# ## Search Methods
#
# In the previous 4-Queens example, constraint propagation via `AC-3` was not enough to find a satisfying complete assignment to the CSP. In fact, if `AC-3` had been applied to the empty 4-Queens chessboard, no domains would have been pruned because all variables were already arc consistent. In these cases, we must assign the next variable a value by *guessing and testing*.
#
# This trial and error method of guessing a variable and testing if it is consistent is formalized in **search methods** for solving CSPs. As mentioned previously, a simple state-space search would be intractable as the number of variables and their domains increase. However, we will first examine state-space search in more detail and then move to a more clever search algorithm called backtrack search (BT) that checks consistency along the way.
#
# ### Generic Search for CSPs
#
# As we have studied before, a generic search problem can be specified by the following four elements: (1) state space, (2) initial states, (3) operator, and (4) goal test. In a CSP, consider the following definitions of these elements:
# - state space
# - partial assignment to variables at the current iteration of the search
# - initial state
# - no assignment
# - operator
# - add a new assignment to any unassigned variable, e.g., $x_i = a$, where $a\in D_i$.
# - child extends parent assignments with new
# - goal test
# - all variables are assigned
# - all constraints are satisfied
#
# ### Making Search More Efficient for CSPs
#
# The inefficiency of using the generic state-space search approaches we have previously employed is caused by the size of the state space. Recall that a simple state-space search (using either breadth-first search or depth-first search) has worst case performance of $O(b^d)$, where $b$ is the branching factor and $d$ is the search depth, as illustrated below (from 16.410/413, Lecture 3).
#
# <img src="images/L3_16.413_treedefs.png" width="70%" />
#
# In the above formulation of generic state-space search of CSPs, note that the branching factor is calculated as the sum of the maximum domain size $k$ for all variables $n$, i.e., $b = nk$. The search depth of a CSP is exactly $n$, because all variables must be assigned to be considered a solution. Therefore, the performance is exponential in the number of variables, $O([nk]^n)$.
#
# This analysis fails to recognize that there are only $k^n$ possible complete assignments of the CSP. That is because the property of **commutativity** is ignored in the above formulation of CSP state-space search. CSPs are commutative because the order in which partial assignments are made do not affect the outcome. Therefore, by restricting the choice of assignment to a single variable at each node in the search tree, the runtime performance becomes only $O(k^n)$.
#
# By combining this property with the idea that **extensions to inconsistent partial assignments are always inconsistent**, backtracking search shows how checking consistency after each assignment enables a more efficient CSP search.
#
# <!--
# With a better understanding of how expensive it can become to solve interesting problems with a simple state-space search, we are motivated to find a better searching algorithm. Two factors that contribute to the size of a search space are (1) variable ordering, and (2) consistency level.
# We have already seen from the `AC-3` example on 4-Queens how enforcing arc-consistency on a network can result in the pruning of variable domains. This clearly reduces the search space of the CSP resulting in better performance from a search algorithm. Therefore, we will focus our discussion on the effects of **variable ordering**.
# -->
# ### Backtracking Search
#
# Backtracking (BT) search is based on depth-first search to choose values for one variable at a time, but it backtracks whenever there are no legal values left to assign. The state space is searched by extending the current partial solution with an assignment to unassigned variables. Starting with the first variable, the algorithm assigns a provisional value to each subsequent variable, checking value consistency along the way. If the algorithm encounters a variable for which no domain value is consistent with the previous assignments, a *dead-end* occurs. At this point, the search *backtracks* and the variable preceding the dead-end assignment is changed and the search continues. The algorithm returns when a solution is found, or when the search is exhausted with no solution.
#
# #### Algorithm
#
# The following recursive algorithm performs a backtracking search on a given CSP. The recursion base case occurs on line 3, which indicates the halting condition of the algorithm.
#
# ```vhdl
# 1 procedure backtrack(csp)
# 2 if csp.assignment is complete and feasible then
# 3 return assignment ; recursion base case
# 4 end if
# 5 var ← csp.get_unassigned_var()
# 6 for next value in csp.var_domain(var)
# 7 original_domain = csp.assign(var, value)
# 8 if csp.assignment is feasible then
# 9 result ← backtrack(csp)
# 10 if result ≠ failure then
# 11 return result
# 12 end if
# 13 csp.restore_domain(original_domain)
# 14 end if
# 15 csp.unassign(var, value)
# 16 return failure
# 17 end
# ```
#
# #### Example
#
# We can apply the backtrack search algorithm to the N-Queens problem. Note that this simple version of the algorithm makes finding a solution tractable for a handful of queens, but there are other improvements that can be made that are discussed in the following section.
queens, exec_time = nqueens_backtracking(4)
draw_nqueens([queens.assignment])
print("Solution found in %0.4f seconds" % exec_time)
# ### Branch and Bound
#
# Suppose we would like to find the *best* solution (in some sense) to the CSP. This amounts to solving the associated constraint optimization problem (COP), where our constraint network is now a 4-tuple, $\langle X, D_X, C, f \rangle$, where $X\in D_X$, $C: D_X \to \{\operatorname{True},\operatorname{False}\}$ and $f: D_x\to\mathbb{R}$ is a cost function. We would like to find the variable assignments $X$ that solve
# \begin{array}{ll@{}ll}
# \text{minimize} & f(X) &\\
# \text{subject to}& C(X) &
# \end{array}
#
# By adding a cost function $f(X)$, we turn a CSP into a COP, and we can use the **branch and bound algorithm** to find the solution with the lowest cost.
#
# To find a solution of a COP we could surely explore the whole tree and then pick the leaves with the smallest cost value. However, one may want to integrate the optimization process into the search process allowing to **prune** even if no inconsistency has been detected yet.
#
# The main idea behind branch and bound is the following: if the best solution so far has cost $c$, this is a _lower bound_ for all other possible solutions. So, if a partial solution has led to costs of $x$ (cost so far) and the best we can achieve for all other cost components is $y$ with $x + y < c$, then we do not need to continue in this branch.
#
# Of course every time we prune a subtree we are implicitly making the search faster compared with full exploration. Therefore with a small overhead in the algorithm, we can improve (in the average case) the runtime.
#
# #### Algorithm
#
# ```vhdl
# 1 procedure BranchAndBound(cop)
# 2 i ← 1; ai ← {} ; initialize variable counter and assignments
# 3 a_inc ← {}; f_inc ← ∞ ; initialize incumbent assignment and cost
# 4 Di´ ← Di ; copy domain of first variable
# 5 while 1 ≤ i ≤ n+1
# 6 if i = n+1 ; "unfathomed" consistent assignment
# 7 f_inc ← f(ai) and a_inc ← ai ; updated incumbent
# 8 i ← i - 2
# 9 else
# 10 instantiate xi ← SelectValueBB(f_inc) ; Add to assignments ai; update Di
# 11 if xi is null ; if no value was returned,
# 12 i ← i - 1 ; then backtrack
# 13 else
# 14 i ← i + 1 ; else step forward and
# 15 Di´ ← Di ; copy domain of next variable.
# 16 end if
# 17 end if
# 18 end while
# 19 return incumbent X_inc and f_inc ; Assignments exhausted, return incumbent
# 20 end
# ```
# <br><br>
# ```vhdl
# 1 procedure SelectValueBB(f_inc)
# 2 while Di´ ≠ ∅
# 3 select an arbitrary element a ∈ Di´ and remove a from Di´
# 4 ai ← ai ∪ {xi = a}
# 5 if consistent(ai) and b(ai) < f_inc
# 6 return a;
# 7 end if
# 8 end while ; no consistent value
# 9 return null
# 10 end
# ```
#
# #### Example
#
# Now let's revive our discussion on the map coloring problem. Imagine that we work at a company that wishes to print a colored map of the United States, so they need to choose a color for each state. Let's also imagine that the available colors are:
colors = [
'red',
'green',
'blue',
'#6f2da8', #Grape
'#ffbf00', #Amber
'#01796f', #Pine
'#813f0b', #Clay
'#ff2000', #yellow
'#ff66cc', #pink
'#d21f3c' #raspberry
]
# The CEO asks the engineering department (they have one of course) to find a color assignment that satisfies the constraints as specified above in _Map Coloring_ and they arrive at the following solution:
map_colors, num_colors = us_map_coloring(colors)
draw_us_map(map_colors)
# Unfortunately, management is never happy and they complain that {{ num_colors }} colors are really too many. Can we do better? Yes, by adding an objective function $f$ that gives a cost proportional to the number of used colors, we can minimize $f$. This results in the following solution:
map_colors, opt_num_colors = us_map_coloring(colors, optimize=True)
draw_us_map(map_colors)
# Fortunately we saved {{ num_colors - opt_num_colors }} color, well done!
# ---
# ## Extended Methods
#
# The methods discussed in this section arise from viewing a CSP from different perspectives and from a combination of constraint propagation and search methods.
#
# ### BT Search with Forward Checking (BT-FC)
#
# By interleaving inference from constraint propagation and search, we can obtain much more efficient solutions. A well-known way of doing this is by adding an arc consistency step to the backtracking algorithm. The result is called **forward checking**, which allows us to run search on graphs that have not already been pre-processed into arc consistent CSPs.
#
# #### Algorithm
#
# **Main Idea**: Maintain n domain copies for resetting, one for each search level i.
#
# ```vhdl
# 1 procedure BTwithFC(csp)
# 2 Di´ ← Di for 1 ≤ i ≤ n ; copy all domains
# 3 i ← 1; ai = {} ; init variable counter, assignments
# 4 while 1 ≤ i ≤ n
# 5 instantiate xi ← SelectValueFC() ; add to assignments, making ai
# 6 if xi is null ; if no value was returned
# 7 reset each Dk´ for k>i to
# 8 its value before xi
# 9 was last instantiated
# 10 i ← i - 1 ; backtrack
# 11 else
# 12 i ← i + 1 ; step forward
# 13 end if
# 14 end while
# 15 if i = 0
# 16 return "inconsistent"
# 17 else
# 18 return ai ; the instantiated values of {xi, ..., xn}
# 19 end
# ```
#
# ```vhdl
# 1 procedure SelectValueFC()
# 2 while Di´ ≠ ∅
# 3 select an arbitrary element a ∈ Di´ and remove a from Di´
# 4 for all k, i < k ≤ n
# 5 for all values b ∈ Dk´
# 6 if not consistent(a_{i-1}, xi=a, xk=b)
# 7 remove b from Dk´
# 8 end if
# 9 end for
# 10 if Dk´ = ∅ ; xi=a leads to a dead-end: do not select a
# 11 reset each Dk´, i<k≤n to its value before a was selected
# 12 else
# 13 return a
# 14 end if
# 15 end for
# 16 end while
# 17 return null
# 18 end
# ```
# #### Example
#
# The example code below runs a backtracking search with forward checking on the N-Queens problem. For the same value of $N$, note how a solution can be found much faster than without forward checking.
queens, exec_time = nqueens_backtracking(4, with_forward_checking=True)
draw_nqueens([queens.assignment])
print("Solution found in %0.4f seconds" % exec_time)
# ### BT-FC with Dynamic Variable and Value Ordering
#
# Traditional backtracking as it was introduced above uses a fixed ordering over variables and values. However, it is often better to choose ordering dynamically as the search proceeds. The idea is as follows. At each node during the search, choose:
# - the most constrained variable; picking the variable with the fewest legal variables in its domain will minimize the branching factor,
# - the least constraining value; choosing a value that rules out the smallest number of values of variables connected to the chosen variable via constraints will leave most options for finding a satisfying assignment.
#
# These two ordering heuristics cause the algorithm to choose the variable that fails first and the value that fails last. This helps minimize the search space by pruning larger parts of the tree early on.
#
# #### Example
#
# The example code below demonstrates BT-FC with dynamic variable ordering using the most-constrained-variable heurestic. The run time cost of finding a solution to the N-Queens problem is lower than both BT and BT-FC, allowing the problem to be solved for even higher $N$.
queens, exec_time = nqueens_backtracking(4, with_forward_checking=True, var_ordering='smallest_domain')
draw_nqueens([queens.assignment])
print("Solution found in %0.4f seconds" % exec_time)
# ### Adaptive Consistency: Bucket Elimination
#
# Another method of solving constraint problems entails eliminating constraints through bucket elimination. This method can be understood through the lens of Gaussian elimination, where equations (i.e., constraints) are added and then extra variables are eliminated. More formally, these operations can be thought of from the perspective of relations as **join** and **project** operations.
#
# Bucket elimination uses the join and projection operations on the set of constraints in order to transform a constraint graph into a single variable. After solving for that variable, other constraints are solved for by back substitution just as you would in an algebraic system in Gaussian elimination.
#
# Using the map coloring problem where an `AllDiff` constraint exists between each neighboring variables, the join and project operators are explained. The constraint graph for the map coloring problem is shown below.
#
# <img src="images/search_mapcoloring.png" width="40%" />
#
# #### The Join Operator
#
# The map coloring CSP can be trivially solved using the join operation on the constraints, which is defined as the consistent Cartesian product of the constraint relations.
#
# Written as tables, the relations of each constraint $C_{12}$, $C_{23}$, and $C_{13}$ are
#
# <table>
# <tr><th style="text-align:center">$C_{12}$</th><th style="text-align:center">$C_{23}$</th><th style="text-align:center">$C_{13}$</th></tr>
# <tr><td>
#
# |$V_1$|$V_2$|
# |-----|-----|
# | R | G |
# | G | R |
# | B | R |
# | B | G |
#
# </td><td>
#
# |$V_2$|$V_3$|
# |-----|-----|
# | R | G |
#
# </td><td>
#
# |$V_1$|$V_3$|
# |-----|-----|
# | R | G |
# | B | G |
#
# </td></tr>
# </table>
#
# These constraint relation tables are then joined together as
#
# <table>
# <tr><th style="text-align:center">$C_{12}\Join C_{23}$</th><th style="text-align:center">$C_{13}$</th></tr>
# <tr><td>
#
# |$V_1$|$V_2$|$V_3$|
# |-----|-----|-----|
# | G | R | G |
# | B | R | G |
#
# </td><td>
#
# |$V_1$|$V_3$|
# |-----|-----|
# | R | G |
# | B | G |
#
# </td></tr>
# </table>
#
# <table>
# <tr><th style="text-align:center;width:140px">$C_{12}\Join C_{23}\Join C_{13}$</th></tr>
# <tr><td>
#
# |$V_1$|$V_2$|$V_3$|
# |-----|-----|-----|
# | B | R | G |
#
# </td></tr>
# </table>
#
# #### The Projection Operator
#
# The projection operator is akin to the elimination step in Gaussian elimination and is useful for shrinking the size of the constraints. After joining all the constraints in the above example, we can project out all constraints except for one to obtain the value of that variable.
#
# For example, the projection of $C_{12}\Join C_{23}\Join C_{13}$ onto $C_1$ is
#
# <table>
# <tr><th style="text-align:center;width:180px">$C_2 = \Pi_2 (C_{12}\Join C_{23}\Join C_{13})$</th></tr>
# <tr><td>
#
# |$V_1$|
# |-----|
# | B |
#
# </td></tr>
# </table>
# ---
# # Symmetries
#
# <img src="images/escher_2.jpg" align="center"/>
# <div style="text-align: right"> <NAME> </div>
#
#
# ## Introduction
#
# A CSP often exhibits some symmetries, which are mappings that preserve satisfiability of the CSP. Symmetries are particularly disadvantageous when we are looking for **all possible solutions** of a CSP, since search can revisit equivalent states over and over again.
#
# \begin{definition} \label{def:symmetry}
# (Symmetry). For any CSP instance $P = \langle X, D, C \rangle$, a solution symmetry of $P$ is a permutation of the set $X\times D$ that preserves the set of solutions to $P$.
# \end{definition}
#
# In other words, a solution symmetry is a bijective mapping defined on the set of possible variable-value pairs of a CSP that maps solutions to solutions.
#
# ### Why is symmetry important?
#
# A principal reason for identifying CSP symmetries is to **reduce search efforts** by not exploring assignments that are symmetrically equivalent to assignments considered elsewhere in the search. In other words, if a problem has a lot of symmetric solutions of a small subset of non-symmetric solutions, the search tree is bigger and if we are looking for all those solutions, the search process is forced to visit all the symmetric solutions of the big search tree. Alternatively, if we can prune-out the subtree containing symmetric solutions, the search effort will reduce drastically.
# ### Case Study: symmetries in N-Queens problem
#
# We have already seen the N-Queens problem. Let us see all the solutions of a $4 \times 4$ chessboard.
#
queens = nqueens(4)
draw_nqueens(queens, all_solutions=True)
# There are exactly 2 solutions.
#
# It's easy to notice the two are the same solution if we flip (or rotate) the chessboard.
#
# ### Interactive examples
#
# All the following code snippets are a refinement of the original N-Queens problem where we modify the problem to reduce the number of symmetries. Feel free to explore how the number of solutions to the N-Queens problem changes when we change symmetry breaking strategy and $N$.
#
# You can use the following slider to change $N$, than press the button `Update cells...` to quickly update the results of the models.
n = 5
def update_n(x):
global n
n = x
interact(update_n , x=widgets.IntSlider(value=n, min=1,max=12,step=1, description='Queens:'));
## Update all cells dependent from the slider with the following button
button = widgets.Button(description="Update cells...")
display(button)
button.on_click(autoupdate_cells)
# + [markdown] autoupdate=true
# ## Avoid symmetries
#
# ### Adding Constraints Before Search
#
# In practice, symmetry in CSPs is usually identified by applying human insight: the programmer sees that some transformation would translate a hypothetical solution into another hypothetical solution. Then, the programmer can try to formalize some constraint that preserves solutions but removes some of the symmetries.
#
# For $N$ = {{n}} the N-Queens problem has {{ len(nqueens(n)) }} solutions. One naive way to remove some of the symmetric solutions is to restrict the position for some of the queens, for example, we can say that the first queen should be on the top half of the chess board by imposing an additional constraint like
#
# ```
# constraint queens[0] <= n div 2;
# ```
#
# This constraint should remove approximately half of the symmetries. Let's try the new model!
# + autoupdate=true
# %%minizinc --all-solutions --statistics -m bind
include "globals.mzn";
int: n;
array[0..n-1] of var 0..n-1: queens;
constraint all_different(queens);
constraint all_different([queens[i]+i | i in 0..n-1]);
constraint all_different([queens[i]-i | i in 0..n-1]);
constraint queens[0] <= n div 2;
solve satisfy;
# -
# If you play with $N$ you will notice that for $N=4$ all solutions are retained. However, For $N>4$ symmetric solutions will begin to be pruned out.
#
# This approach is fine and if done correctly it can greatly reduce the search space. However, this additional constraint can lose solutions if done incorrectly.
#
# To address the problem in a better way we need some formal tool.
# ### Chessboard symmetries
#
# Looking at the chessboard, we notice that it has eight geometric symmetries---one for each geometric transformation. In particular they are:
#
# - identity (no-reflections) $id$ (we always include the identity)
# - horizontal reflection $r_x$
# - vertical reflection $r_y$
# - reflections along the two diagonal axes ($r_{d_1}$ and $r_{d_2}$)
# - rotations through $90$°, $180$° and $270$° ($r_{90}$, $r_{180}$, $r_{270}$)
#
# If we label the sixteen squares of a $4 \times 4$ chessboard with the numbers 1 to 16, we can graphically see how symmetries move cells.
#
# <img src="images/4x4_symm.png" width="80%" align="center"/>
#
# Now it's easy to see that a symmetry is a **permutation** that acts on a point: for example, if a queen is at $(2,1)$ (which correspondes to element $2$ in $id$), under the mapping $r_{90}$, it moves to $(4,2)$.
#
# One useful form to write a permutation is in _Cauchy form_, for example for $r_{90}$
#
# \begin{equation}
# r_{90} : \left( \begin{array} { c c c c c c c c c }
# 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16\\
# 13 & 9 & 5 & 1 & 14 & 10 & 6 & 2 & 15 & 11 & 7 & 3 & 16 & 12 & 8 & 4
# \end{array} \right)
# \end{equation}
#
# What this notation says is that an element in position $i$ in the top row, is moved to the corresponding position of the bottom row. For example $1$ → $13$, $2$ → $9$, $3$ → $5$ and so on.
#
# This form will help us compactly write constraints to remove unwanted permutations.
# ### The Lex-Leader Method
#
# Puget proved that whenever a CSP has symmetry that can be expressed as permutations of the variables, it is possible to find a _reduced form_ with the symmetries eliminated by adding constraints to the original problem \cite{Puget2003}. Puget found such a reduction for three simple constraint problems and showed that this reduced CSP could be solved more efficiently than in its original form.
#
# The intuition is rather simple: for each equivalence class of solutions (permutation), we predefine one to be the **canonical solution**. We achieve this by choosing a static variable ordering and imposing the **lexicographic order** for each permutation. This method is called **lex-leader**.
#
# For example, let us consider a problem where we have three variables $x_1$, $x_2$, and $x_3$ subject to the `alldifferent` constraint and domain {A,B,C}. This problem has $3!$ solutions, where $3!-1$ are symmetric solutions. Let's say that our canonical solution is `ABC`, and we want to prevent `ACB` from being a solution, the lex-leader method would impose the following additional constraint:
#
# $$ x_1\,x_2\,x_3 \preceq_{\text{lex}} x_1\,x_3\,x_2. $$
#
# In fact, if $x = (\text{A},\text{C},\text{B})$ the constraint is not satisfied, written as
#
# $$ \text{A}\text{C}\text{B}\,\, \npreceq_{\text{lex}} \text{A}\text{B}\text{C}. $$
#
# Adding constraints like this for all $3!$ permutations will remove all symmetric solutions, leaving exactly one solution (`ABC`). All other solutions can be recovered by applying each symmetry.
#
# In general, if we have a permutation $\pi$ that generates a symmetric solution that we wish to remove, we would impose an additional constraint, usually expressed as
#
# $$ x_1 \ldots x_k \preceq_{\text{lex}} x_{\pi (1)} \ldots x_{\pi (k)}, $$
#
# where $\pi(i)$ is the index of the variable after the permutation.
# Unfortunately, for the N-Queens problem formulated as we have seen, this technique does not immediately apply, because some of its symmetries cannot be described as permutations of the `queens` array.
#
# The trick to overcoming this limitation is to express the N-Queens problem in terms of Boolean variables for each square of the chessboard that model whether it contains a queen or not (i.e., Attempt 1 from above). Now all the symmetries can be modeled as permutations of this array using Cauchy form.
#
# Since the main constraints of the N-Queens problem are much easier to express with the integer `queens` array, we use both models together connecting them using _channeling constraints_.
# + autoupdate=true
# %%minizinc --all-solutions --statistics -m bind
include "globals.mzn";
int: n;
array[0..n-1,0..n-1] of var bool: qb;
array[0..n-1] of var 0..n-1: q;
constraint all_different(q);
constraint all_different([q[i]+i | i in 0..n-1]);
constraint all_different([q[i]-i | i in 0..n-1]);
constraint % Channeling constraint
forall (i,j in 0..n-1) ( qb[i,j] <-> (q[i]=j) );
constraint % Lexicographic symmetry breaking constraints
lex_lesseq(array1d(qb), [ qb[j,i] | i in reverse(0..n-1), j in 0..n-1 ]) /\ % r_{90}
lex_lesseq(array1d(qb), [ qb[i,j] | i,j in reverse(0..n-1) ]) /\ % r_{180}
lex_lesseq(array1d(qb), [ qb[j,i] | i in 0..n-1, j in reverse(0..n-1) ]) /\ % r_{270}
lex_lesseq(array1d(qb), [ qb[i,j] | i in reverse(0..n-1), j in 0..n-1 ]) /\ % r_{x}
lex_lesseq(array1d(qb), [ qb[i,j] | i in 0..n-1, j in reverse(0..n-1) ]) /\ % r_{y}
lex_lesseq(array1d(qb), [ qb[j,i] | i,j in 0..n-1 ]) /\ % r_{d_1}
lex_lesseq(array1d(qb), [ qb[j,i] | i,j in reverse(0..n-1) ]); % r_{d_2}
solve satisfy;
# -
# In this model the constraint `lex_lesseq(array_1, array_2)` implements the lexicographic operator $\preceq_{\text{lex }}$ between `array_1` and `array_2`. Notice that `array_2` represent the permutation fo each of the geometric symmetry of the chessboard (except the identity).
#
# Using the lex-leader method we reduced the number of solutions but we also added a lot of constraints...
# ### Double-Lex
#
# When dealing with a matrix of decision variables, we often have that any permutation of the rows (or columns) of a solution is also a solution. This class of symmetries is called _row and column symmetries_.
#
# We can certainly use the lex-leader method to break all symmetries, but in an $n \times m$ matrix with rows and column symmetry we would add $n!m!$ constraints. Adding so many constraints can be counter-productive.
#
# When breaking all symmetries proves too difficult, it is often possible to achieve good results by breaking a smaller
# set of symmetries. One method to do this for row and column symmetries is **double-lex** (Flener et al. 2002). The idea is to impose the ordering on the rows and on the columns **independently**. This produces only $n + m − 2$ symmetry breaking constraints.
#
# One example where the double-lex can be applied is the problem seen during the course assignments: _Buddies_. In that problem, we could permute each element on each row (i.e., seat assignment) independently while preserving the same solution. Similarly, we could also permute each column independently (i.e., swap the 20-minute segments). This is a typical case where the double-lex is effective and cheap to implement.
#
# <div class="alert alert-block alert-info">
# The double-lex method is not applicable to the N-Queens problem, because not all column (or row) permutations preserve the solution.
# </div>
# ## Symmetry breaking constraints
#
# ### Soundness and completeness
#
# Two important properties of symmetry breaking constraints are **soundness** and **completeness**, a set of symmetry breaking constraints
# - is **sound** if and only if it leaves at least one solution in each symmetry class
# - is **complete** if and only if it leaves at most one solution in each symmetry class
#
# All the approaches we used so far in the N-Queens problem are sound and complete since they leave at least one solution in the only symmetry class available (geometric symmetries). Other problems might have different symmetry classes and it is very important that constraints added to remove a given symmetry don't remove desirable solutions from the problem.
#
#
# ### Intractability of Breaking Symmetry
#
# It is worth mentioning that lex-leader requires one constraint for each element of the group.
# In the case of a matrix with $m$ rows and $n$ columns, rows and column symmetry, this is $m!n!$, which is impractical in general. Therefore there are many cases where lex-leader is applicable but impractical.
#
# \begin{theorem} \label{theo:simple_ordering_NP}
# (Walsh 2011) Given any _simple_ ordering, there exists a symmetry group such that deciding if an assignment is smallest in its symmetry class according to this ordering is NP-hard.
# \end{theorem}
#
# In other words, Walsh proved that breaking symmetry completely by adding constraints to eliminate symmetric solutions is computationally intractable in general. More specifically, he proves that given any simple variable ordering, deciding if an assignment is the smallest in its symmetry class is NP-hard.
#
# An alternative to full symmetry breaking is to break some symmetry by using just a subset of the lex-leader constraints, for example, the double-lex.
#
# \begin{theorem} \label{theo:lex2_NP}
# (Katsirelos, Narodytska, and Walsh 2010) Propagating the double-lex constraint is NP-hard.
# \end{theorem}
#
# In other words, this theorem states that there is no efficient algorithm to restrict variable domain after an assignment.
#
# Since symmetry breaking appears intractable in general, a major research direction is to identify special cases where the symmetry group is more tractable in practice.
# ## Reducing the Set of Symmetry Breaking Constraints
#
# Lex-leader constraints can be simplified to remove redundancies. For example, imagine having the following lexicographic constraint:
#
# $$ x_1\,x_2\,x_3\,x_4\,x_5,\,x_6 \preceq_{\text{lex}}x_1\,x_3\,x_2\,x_4\,x_6,x_5. $$
#
# We can remove the first and fourth variables from each tuple, since clearly $x_1 = x_1$ and $x_4 = x_4$, obtaining
#
# $$ x_2\,x_3\,x_5,\,x_6 \preceq_{\text{lex}}x_3\,x_2\,x_6,x_5. $$
#
# But we can also notice that if $x_2 < x_3$ the constraint is satisfied no matter the other values, and otherwise we have $x_2 = x_3$ to satisfy the constraint. In other words, if the second variables in the tuples are relevant, they must be equal. Similarly for $x_5$ and $x_6$. Thus, the constraint is equivalent to
#
# $$ x_2\,x_5\preceq_{\text{lex}}x_3\,x_5. $$
#
# Since $\preceq_{\text{lex}}$ is transitive we can go further, treating the constraints as a set and not just individually. This would help us to reduce the size of the constraint even more.
#
# Unfortunately, the approach outlined here does not get around the fundamental problem of the exponential number of symmetries. However, the approach does illustrate how the set of constraints can be simplified, and we will see in the next section a particular case where the results are quite dramatic.
#
# ### Lex constraint decomposition
#
# We can decompose the lex constraint of the form $x_1\ldots x_2 \preceq_{\text{lex }} y_1\ldots y_2$ to a conjunction of clauses like
# $$ \left(x_1 = y_1 \right),\ldots,\left(x_k = y_k\right)\rightarrow x_{k+1}\leq y_{k+1} $$
# We call clauses of this form lex implications.
#
# In practice many lex-implications are redundant \cite{Codish2018}. Given this observation, we can ask ourselves the direct question: how many lex implications are required to express a complete symmetry break?
# ### Reduce implications
#
# In a recent paper \cite{Codish2018}, the authors develop a method to find a complete and compact set of symmetry breaking constraints. Basically, the algorithm iterates over the set of lex implications, and checks for each of them if they are redundant.
#
# Define $\phi$ to be the set of constraints expressed as a Boolean formula, and $\psi$ to be the set of lex implications used to break the symmetries in the solution space defined by $\phi$.
#
# Given these two sets, the idea behind the reduction is quite intuitive: remove one clause from the formula, and check if there is a solution which would be forbidden by this clause. If this is not the case, the clause is redundant and can be removed.
#
# We note that the number of clauses which can actually be removed depends on the order in which clauses are checked, thus the reduction splits in two phases:
#
# - The first phase is shown in Algorithm 1. We rank the clauses by checking if a clause $c\in\phi$ is redundant. If so, we compute a subset $\psi\subseteq\varphi^\prime$ of clauses which makes $c$ redundant, and increase the ranking of all clauses within this set.
#
# The rationale is that removing these clauses is more likely make other clauses no longer redundant, and so increase the size of the final symmetry break.
#
# <img src="images/reduce_alg_1.png" width="80%" align="center"/>
#
# - The second stage is shown in Algorithm 2. We sort the clauses by ranking, so clauses which were frequently the cause of redundancy appear as late as possible. Then remove the clauses if there is not a solution which would be forbidden.
#
# <img src="images/reduce_alg_2.png" width="80%" align="center"/>
#
# This approach can be applied to any lexicographic-based ordering.
# ### Example
#
# In their paper \cite{Codish2018} show some result of their method applied to a generic matrix model
#
# <table>
# <tr>
# <th>n</th>
# <th colspan="2">Double-Lex</th>
# <th colspan="2">All Permutations</th>
# </tr>
# <tr>
# <td></td>
# <td>Original</td>
# <td>Reduced</td>
# <td>Original</td>
# <td>Reduced</td>
# </tr>
# <tr>
# <td>3</td>
# <td>12</td>
# <td>12</td>
# <td>48</td>
# <td>13</td>
# </tr>
# <tr>
# <td>4</td>
# <td>24</td>
# <td>24</td>
# <td>312</td>
# <td>32</td>
# </tr>
# <tr>
# <td>5</td>
# <td>40</td>
# <td>40</td>
# <td>2440</td>
# <td>71</td>
# </tr>
# <tr>
# <td>6</td>
# <td>60</td>
# <td>60</td>
# <td>21660</td>
# <td>148</td>
# </tr>
# <tr>
# <td>7</td>
# <td>84</td>
# <td>84</td>
# <td>211764</td>
# <td>310</td>
# </tr>
# </table>
#
#
# It is interesting to note that with the complete symmetry break it is possible to reduce the number of implications quite drastically but double-lex has no redundant implications.
# ### Conclusion
#
# Removing redundant clauses can be costly due to the use of a SAT solver. However, if an instance of the same size needs to be solved several times but with different values it can greatly improve the search time since the reduction can be done offline just once.
# # References
#
# (<a id="cit-Dechter2003" href="#call-Dechter2003">Dechter, 2003</a>) <NAME>, ``_Constraint Processing_'', 2003.
#
# (<a id="cit-AIMA" href="#call-AIMA">Russell and Norvig, 2003</a>) <NAME> and <NAME>, ``_Artificial Intelligence: A Modern Approach_'', 2003.
#
# (<a id="cit-Mackworth1977" href="#call-Mackworth1977">Mackworth, 1977</a>) <NAME>., ``_Consistency in Networks of Relations_'', Artif. Intell., vol. 8, number 1, pp. 99--118, 1977. [online](http://dx.doi.org/10.1016/0004-3702(77)90007-8)
#
# (<a id="cit-Puget2003" href="#call-Puget2003">Puget, 1993</a>) <NAME>, ``_On the satisfiability of symmetrical constrained satisfaction problems_'', Methodologies for Intelligent Systems, 1993.
#
# (<a id="cit-Codish2018" href="#call-Codish2018">Codish, Ehlers <em>et al.</em>, 2018</a>) <NAME>, <NAME>, <NAME> <em>et al.</em>, ``_Breaking Symmetries with Lex Implications_'', FLOPS, 2018.
#
#
|
source/ConstraintProgramming.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # MNIST Example for MLP with momentum and batchnorm
#
# The purpose of this demo is to help you learn about neural networks and explore how changing the architecture of a neural network impacts the performance of the network.
#
# You are free to change model acrhitecture, add depth or select any other hidden layers sizes.
#
# If you have any suggestions or find errors, please, don't be hesitate to text me up @ <EMAIL>
#
import mlp
import activation as ac
import loss
from random import randint
import mnist
import numpy as np
import time
from matplotlib import pyplot as plt
import os
import glob
# #### Initializing parameters
#
# #### Download MNIST data
# If MNIST dataset doesn't exist in "data" folder, it will be downloaded from
# http://deeplearning.net/data/mnist/mnist.pkl.gz
# +
np.random.seed(11785)
#initialize neural parameters
learning_rate = 0.004
momentum = 0.996
num_bn_layers= 1
mini_batch_size = 10
epochs = 5
# random weight init
def weight_init(x, y):
return np.random.randn(x, y)
# zero bias init
def bias_init(x):
return np.zeros((1, x))
# initialize training, validation and testing data
train, val, test = mnist.load_mnist()
# -
# #### Creating multi-layer perceptron class
net = mlp.MLP(784, 10, [64, 32], [ac.Sigmoid(), ac.Sigmoid(), ac.Sigmoid()], weight_init, bias_init, loss.SoftmaxCrossEntropy(), learning_rate, momentum, num_bn_layers)
# #### Display MNIST data
# If MNIST dataset doesn't exist in "data" folder, it will be downloaded from
# http://deeplearning.net/data/mnist/mnist.pkl.gz
m = train[0].shape[0]
for i in range(36):
ax = plt.subplot(6, 6, i+1)
ax.axis('off')
x_draw = train[0][randint(0, m)]
x_draw = np.reshape(x_draw, (-1, 28))
plt.imshow(x_draw, cmap='Greys')
# #### Training MLP
# %%time
[training_losses, training_errors, validation_losses, validation_errors] = net.get_training_stats(mnist.load_mnist(), epochs, mini_batch_size)
# #### Training loss
plt.plot(training_losses)
plt.title('training losses')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['training'], loc='best')
plt.show()
# #### Validation accuracy curve
plt.plot(net.validation_acc)
plt.title('validation accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['validation acc'], loc='best')
plt.show()
#save the model
net.save()
# #### Loading last trained model
# +
path = os.path.join(os.curdir, 'models/*')
files = sorted(
glob.iglob(path), key=os.path.getctime, reverse=True)
#load latest model
print(files[0])
net.load(files[0])
# -
# #### Let's check accuracy according to the test samples
#testing neural network
test_acc = net.validate(test) * 100.0
print("Test Accuracy: " + str(test_acc) + "%")
|
demo.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # EventVestor: Earnings Calendar
#
# In this notebook, we'll take a look at EventVestor's *Earnings Calendar* dataset, available on the [Quantopian Store](https://www.quantopian.com/store). This dataset spans January 01, 2007 through the current day, and documents the quarterly earnings releases calendar indicating date and time of reporting.
#
# ## Notebook Contents
#
# There are two ways to access the data and you'll find both of them listed below. Just click on the section you'd like to read through.
#
# - <a href='#interactive'><strong>Interactive overview</strong></a>: This is only available on Research and uses blaze to give you access to large amounts of data. Recommended for exploration and plotting.
# - <a href='#pipeline'><strong>Pipeline overview</strong></a>: Data is made available through pipeline which is available on both the Research & Backtesting environment. Recommended for custom factor development and moving back & forth between research/backtesting.
#
# ### Free samples and limits
# One key caveat: we limit the number of results returned from any given expression to 10,000 to protect against runaway memory usage. To be clear, you have access to all the data server side. We are limiting the size of the responses back from Blaze.
#
# There is a *free* version of this dataset as well as a paid one. The free sample includes data until 2 months prior to the current date.
#
# To access the most up-to-date values for this data set for trading a live algorithm (as with other partner sets), you need to purchase acess to the full set.
#
# With preamble in place, let's get started:
#
# <a id='interactive'></a>
# #Interactive Overview
# ### Accessing the data with Blaze and Interactive on Research
# Partner datasets are available on Quantopian Research through an API service known as [Blaze](http://blaze.pydata.org). Blaze provides the Quantopian user with a convenient interface to access very large datasets, in an interactive, generic manner.
#
# Blaze provides an important function for accessing these datasets. Some of these sets are many millions of records. Bringing that data directly into Quantopian Research directly just is not viable. So Blaze allows us to provide a simple querying interface and shift the burden over to the server side.
#
# It is common to use Blaze to reduce your dataset in size, convert it over to Pandas and then to use Pandas for further computation, manipulation and visualization.
#
# Helpful links:
# * [Query building for Blaze](http://blaze.readthedocs.io/en/latest/queries.html)
# * [Pandas-to-Blaze dictionary](http://blaze.readthedocs.io/en/latest/rosetta-pandas.html)
# * [SQL-to-Blaze dictionary](http://blaze.readthedocs.io/en/latest/rosetta-sql.html).
#
# Once you've limited the size of your Blaze object, you can convert it to a Pandas DataFrames using:
# > `from odo import odo`
# > `odo(expr, pandas.DataFrame)`
#
#
# ###To see how this data can be used in your algorithm, search for the `Pipeline Overview` section of this notebook or head straight to <a href='#pipeline'>Pipeline Overview</a>
# +
# import the dataset
from quantopian.interactive.data.eventvestor import earnings_calendar as dataset
# or if you want to import the free dataset, use:
# from quantopian.data.eventvestor import earnings_calendar_free
# import data operations
from odo import odo
# import other libraries we will use
import pandas as pd
import matplotlib.pyplot as plt
# -
# Let's use blaze to understand the data a bit using Blaze dshape()
dataset.dshape
# And how many rows are there?
# N.B. we're using a Blaze function to do this, not len()
dataset.count()
# Let's see what the data looks like. We'll grab the first three rows.
dataset[:3]
# Let's go over the columns:
# - **event_id**: the unique identifier for this event.
# - **asof_date**: EventVestor's timestamp of event capture.
# - **trade_date**: for event announcements made before trading ends, trade_date is the same as event_date. For announcements issued after market close, trade_date is next market open day.
# - **symbol**: stock ticker symbol of the affected company.
# - **event_type**: this should always be *Earnings Calendar*.
# - **event_headline**: a brief description of the event
# - **event_phase**: the inclusion of this field is likely an error on the part of the data vendor. We're currently attempting to resolve this.
# - **calendar_date**: proposed earnings reporting date
# - **calendar_time**: earnings release time: *before/after market hours*, or *other*.
# - **event_rating**: this is always 1. The meaning of this is uncertain.
# - **timestamp**: this is our timestamp on when we registered the data.
# - **sid**: the equity's unique identifier. Use this instead of the symbol.
#
# We've done much of the data processing for you. Fields like `timestamp` and `sid` are standardized across all our Store Datasets, so the datasets are easy to combine. We have standardized the `sid` across all our equity databases.
#
# We can select columns and rows with ease. Below, we'll fetch all of Apple's entries from 2012.
# get apple's sid first
aapl_sid = symbols('AAPL').sid
aapl_earnings = earnings_calendar[('2011-12-31' < earnings_calendar['asof_date']) & (earnings_calendar['asof_date'] <'2013-01-01') & (earnings_calendar.sid==aapl_sid)]
# When displaying a Blaze Data Object, the printout is automatically truncated to ten rows.
aapl_earnings.sort('asof_date')
# Finally, suppose we want a DataFrame of all earnings calendar releases in February 2012, but we only want the event_headline and the calendar_time.
# manipulate with Blaze first:
feb_2012 = earnings_calendar[(earnings_calendar['asof_date'] < '2012-03-01')&('2012-02-01' <= earnings_calendar['asof_date'])]
# now that we've got a much smaller object, we can convert it to a pandas DataFrame
feb_df = odo(feb_2012, pd.DataFrame)
reduced = feb_df[['event_headline','calendar_time']]
# When printed: pandas DataFrames display the head(30) and tail(30) rows, and truncate the middle.
reduced
# <a id='pipeline'></a>
#
# #Pipeline Overview
#
# ### Accessing the data in your algorithms & research
# The only method for accessing partner data within algorithms running on Quantopian is via the pipeline API. Different data sets work differently but in the case of this data, you can add this data to your pipeline as follows:
#
# Import the data set here
# > `from quantopian.pipeline.data.eventvestor import EarningsCalendar`
#
# Then in intialize() you could do something simple like adding the raw value of one of the fields to your pipeline:
# > `pipe.add(EarningsCalendar.previous_announcement.latest, 'previous_announcement')`
# Import necessary Pipeline modules
from quantopian.pipeline import Pipeline
from quantopian.research import run_pipeline
from quantopian.pipeline.factors import AverageDollarVolume
# +
# For use in your algorithms
# Using the full dataset in your pipeline algo
from quantopian.pipeline.data.eventvestor import EarningsCalendar
# To use built-in Pipeline factors for this dataset
from quantopian.pipeline.factors.eventvestor import (
BusinessDaysUntilNextEarnings,
BusinessDaysSincePreviousEarnings
)
# -
# Now that we've imported the data, let's take a look at which fields are available for each dataset.
#
# You'll find the dataset, the available fields, and the datatypes for each of those fields.
# +
print "Here are the list of available fields per dataset:"
print "---------------------------------------------------\n"
def _print_fields(dataset):
print "Dataset: %s\n" % dataset.__name__
print "Fields:"
for field in list(dataset.columns):
print "%s - %s" % (field.name, field.dtype)
print "\n"
for data in (EarningsCalendar,):
_print_fields(data)
print "---------------------------------------------------\n"
# -
# Now that we know what fields we have access to, let's see what this data looks like when we run it through Pipeline.
#
#
# This is constructed the same way as you would in the backtester. For more information on using Pipeline in Research view this thread:
# https://www.quantopian.com/posts/pipeline-in-research-build-test-and-visualize-your-factors-and-filters
# +
# Let's see what this data looks like when we run it through Pipeline
# This is constructed the same way as you would in the backtester. For more information
# on using Pipeline in Research view this thread:
# https://www.quantopian.com/posts/pipeline-in-research-build-test-and-visualize-your-factors-and-filters
pipe = Pipeline()
pipe.add(EarningsCalendar.previous_announcement.latest, 'previous_announcement')
pipe.add(EarningsCalendar.next_announcement.latest, 'next_announcement')
pipe.add(BusinessDaysSincePreviousEarnings(), "business_days_since")
# +
# Setting some basic liquidity strings (just for good habit)
dollar_volume = AverageDollarVolume(window_length=20)
top_1000_most_liquid = dollar_volume.rank(ascending=False) < 1000
pipe.set_screen(top_1000_most_liquid & EarningsCalendar.previous_announcement.latest.notnull())
# -
# The show_graph() method of pipeline objects produces a graph to show how it is being calculated.
pipe.show_graph(format='png')
# run_pipeline will show the output of your pipeline
pipe_output = run_pipeline(pipe, start_date='2013-11-01', end_date='2013-11-25')
pipe_output
# Taking what we've seen from above, let's see how we'd move that into the backtester.
# +
# This section is only importable in the backtester
from quantopian.algorithm import attach_pipeline, pipeline_output
# General pipeline imports
from quantopian.pipeline import Pipeline
from quantopian.pipeline.factors import AverageDollarVolume
# Import the datasets available
# For use in your algorithms
# Using the full dataset in your pipeline algo
from quantopian.pipeline.data.eventvestor import EarningsCalendar
# To use built-in Pipeline factors for this dataset
from quantopian.pipeline.factors.eventvestor import (
BusinessDaysUntilNextEarnings,
BusinessDaysSincePreviousEarnings
)
def make_pipeline():
# Create our pipeline
pipe = Pipeline()
# Screen out penny stocks and low liquidity securities.
dollar_volume = AverageDollarVolume(window_length=20)
is_liquid = dollar_volume.rank(ascending=False) < 1000
# Create the mask that we will use for our percentile methods.
base_universe = (is_liquid)
# Add pipeline factors
pipe.add(EarningsCalendar.previous_announcement.latest, 'previous_announcement')
pipe.add(EarningsCalendar.next_announcement.latest, 'next_announcement')
pipe.add(BusinessDaysSincePreviousEarnings(), "business_days_since")
# Set our pipeline screens
pipe.set_screen(is_liquid)
return pipe
def initialize(context):
attach_pipeline(make_pipeline(), "pipeline")
def before_trading_start(context, data):
results = pipeline_output('pipeline')
# -
# Now you can take that and begin to use it as a building block for your algorithms, for more examples on how to do that you can visit our <a href='https://www.quantopian.com/posts/pipeline-factor-library-for-data'>data pipeline factor library</a>
|
docs/memo/notebooks/data/eventvestor.earnings_calendar/notebook.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # THIRD PROJECT
# ## Exploring the USA's milk imports and exports in the whole of 2020
# A country's economy depends, sometimes heavily, on its exports and imports. The United Nations Comtrade database provides data on global trade. It will be used to analyse the USA's imports and exports of milk and cream in 2020:
#
# How much does the US export and import and is the balance positive (more exports than imports)?
# Which are the main trading partners, i.e. from/to which countries does the US import/export the most?
# Which are the regular customers, i.e. which countries buy milk from the US every month?
# Which countries does the US both import from and export to?
# #### GETTING THE DATASET
# The data is obtained from the United Nations Comtrade website, by selecting the following configuration:
#
# Type of Product:
# goods
# Frequency:
# monthly
# Periods:
# January to May of 2020
# Reporter: United States
# Partners: all
# Flows: imports and exports
# HS (as reported) commodity codes: 0401 (Milk and cream, neither concentrated nor sweetened) and 0402 (Milk and cream, concentrated or sweetened)
#
# Clicking on 'Preview' results in a message that the data exceeds 500 rows. Data was downloaded using the Download CSV button and the download file renamed appropriately.
# +
import warnings
warnings.simplefilter('ignore', FutureWarning)
import pandas as pd
from pandas import *
# %matplotlib inline
# -
LOCATION = 'comtrade_milk_usa_all_of_2020.csv'
#LOCATION.head(2)
# The data can also be downloaded directly from Comtrade using the "View API Call" URL, modified in two ways:
#
# max=500 is increased to max=5000 to make sure all data is loaded,
# &fmt=csv is added at the end to obtain the data in CSV format.
# +
#http://comtrade.un.org/api/get?max=5000&type=C&freq=M&px=HS&ps=2020&r=842&p=all&rg=1%2C2&cc=0401%2C0402&fmt=csv
# -
milk = read_csv(LOCATION, dtype={'Commodity Code':str})
milk.tail(2)
# +
def milkType(code):
if code == '401': # neither concentrated nor sweetened
return 'unprocessed'
if code == '402': # concentrated or sweetened
return 'processed'
return 'unknown'
COMMODITY = 'Milk and cream'
milk[COMMODITY] = milk['Commodity Code'].apply(milkType)
MONTH = 'Period'
PARTNER = 'Partner'
FLOW = 'Trade Flow'
VALUE = 'Trade Value (US$)'
headings = [MONTH, PARTNER, FLOW, COMMODITY, VALUE]
milk = milk[headings]
milk.head()
# -
# The data contains the total imports and exports per month, under the 'World' partner. Those rows are removed to keep only the per-country data.
milk = milk[milk[PARTNER] != 'World']
milk.head()
milk_world = milk[milk['Partner'] == 'World']
milk.head()
# Total trade flow
# To answer the first question, 'how much does USA export and import and is the balance positive (more exports than imports)?', the dataframe is split into two groups: exports from the USA and imports into the USA. The trade values within each group are summed up to get the total trading.
grouped = milk.groupby([FLOW])
grouped[VALUE].aggregate(sum)
# This shows a trade surplus of over 100 million dollars.
# ### Main trade partners
# To address the second question, 'Which are the main trading partners, i.e. from/to which countries does USA import/export the most?', the dataframe is split by country instead, and then each group aggregated for the total trade value. This is done separately for imports and exports. The result is sorted in descending order so that the main partners are at the top
imports = milk[milk[FLOW] == 'Imports']
grouped = imports.groupby([PARTNER])
print('The USA imports from', len(grouped), 'countries.')
print('The 5 biggest exporters to USA are:')
totalImports = grouped[VALUE].aggregate(sum).sort_values(inplace=False,ascending=False)
totalImports.head()
milk_imports = milk[milk['Trade Flow'] == 'Imports']
milk_countries_imports = milk[milk['Trade Flow'] == 'Imports']
milk_world_imports=milk_world[milk_world['Trade Flow'] == 'Imports']
# The export values can be plotted as a bar chart, making differences between countries easier to see.
totalImports.head(10).plot(kind='barh',grid=False)
exports = milk[milk[FLOW] == 'Exports']
grouped = exports.groupby([PARTNER])
print('USA exports to', len(grouped), 'countries.')
print('The 5 biggest importers from the USA are:')
grouped[VALUE].aggregate(sum).sort_values(ascending=False,inplace=False).head()
# Regular importers
# Given that there are two commodities, the third question, 'Which are the regular customers, i.e. which countries buy milk from the UK every month?', is meant in the sense that a regular customer imports both commodities every month. This means that if the exports dataframe is grouped by country, each group has exactly ten rows (two commodities bought each of the five months). To see the countries, only the first month of one commodity has to be listed, as by definition it's the same countries every month and for the other commodity.
# +
def buysEveryMonth(group):
return len(group) == 10
grouped = exports.groupby([PARTNER])
regular = grouped.filter(buysEveryMonth)
regular[(regular[MONTH] == 202001) & (regular[COMMODITY] == 'processed')]
# -
# Just over 75% of the total USA exports are due to these regular customers.
regular[VALUE].sum() / exports[VALUE].sum()
# Bi-directional trade
# To address the fourth question, 'Which countries does USA both import from and export to?', a pivot table is used to list the total export and import value for each country.
countries = pivot_table(milk, index=[PARTNER], columns=[FLOW],
values=VALUE, aggfunc=sum)
countries.head()
# Removing the rows with a missing value will result in only those countries with bi-directional trade flow with the USA.
countries.dropna()
# Conclusions
# The milk and cream trade of the UK from January to May 2015 was analysed in terms of which countries the UK mostly depends on for income (exports) and goods (imports). Over the period, the UK had a trade surplus of over 100 million US dollars.
#
# Ireland is the main partner, but it imported from the UK almost the triple in value than it exported to the UK.
#
# The UK exported to over 100 countries during the period, but only imported from 21 countries, the main ones (top five by trade value) being geographically close. China and Hong Kong are the main importers that are not also main exporters.
#
# The UK is heavily dependent on its regular customers, the 16 countries that buy all types of milk and cream every month. They contribute three quarters of the total export value.
#
# The UK has bi-directional trade (i.e. both exports and imports) with 20 countries, although for some the trade value (in US dollars) is suspiciously low, which raises questions about the data's accuracy.
|
Funmilayo Aina WT-21-091/Week 5 Assessment/PROJECT_2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# 
#
# # Predicting Retail Spending with Automated Feature Engineering in Featuretools
#
# In this notebook, we will implement an automated feature engineering solution with [Featuretools](https://docs.featuretools.com/#minute-quick-start) for a set of online retail purchases. The dataset (available from the [UCI machine learning repository](https://archive.ics.uci.edu/ml/datasets/online+retail#)) is a series of time-stamped purchases and does not come with any labels, so we'll have to make our own prediction problem. After defining the problem, we can use automated feature engineering to build a set of features that are used for training a predictive model.
#
# This set of retail spending data is great practice both for defining our own prediction problem (known as [prediction engineering](http://ieeexplore.ieee.org/document/7796929/)), and for using some of the time-based capabilities of Featuretools, notably cutoff times. Whenever we have time-series data, we need to be extra careful to not "leak labels" or use information from the future to predict a past event. Usually, when we're doing manual feature engineering, this can be an issue and often, a system will work well in development but utterly fail when deployed because it was trained on invalid data. Fortunately, Featuretools will take care of the time issue for us, creating a rich set of features that obey the time restrictions.
#
# ## Roadmap
#
# Following is an outline for this notebook:
#
# 1. Read in data, inspect, and clean
# 2. Develop a prediction problem
# * Create a dataframe of labels - what we want to predict, and cutoff times - the point that all data must come before for predicting a label
# 3. Create an entityset and add entities
# * Normalize the original table to develop new tables
# * These new tables can be used for making features
# 4. Run deep feature sythesis on the entityset to make features
# * Use the cutoff times to make features using valid data for each label
# 5. Use the features to train a machine learning model
# * Measure performance of the model relative to an informed baseline
# 6. Tune deep feature synthesis
# * Specify custom primitives
# * Adjust maximum depth of features
# * Re-evaluate model
#
# This problem is a great display of both the time and feature-creation capabilities of Featuretools. Also, we'll be able to use custom primitives to expand on our domain knowledge. Doing this problem by hand and ensuring we use only valid data for each label is a daunting task (as can be seen in the Manual Retail Spending notebook)!
# +
# Data manipulation
import pandas as pd
import numpy as np
# Visualization
import matplotlib.pyplot as plt
import seaborn as sns
plt.style.use('fivethirtyeight')
# %matplotlib inline
# Automated feature engineering
import featuretools as ft
# Machine learning
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import Imputer, MinMaxScaler
from sklearn.metrics import precision_score, recall_score, f1_score, roc_auc_score, precision_recall_curve, roc_curve
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.ensemble import RandomForestClassifier
# -
# ### Load in Raw Data
#
# The raw data is a collection of purchases from an online retailer collected in 2010-2011. Each row in the original data represents one product that was purchased with multiple purchases forming an order. There are a few issues with the data that will need to be addressed (as with most real-world datasets)!
#
# This code loads in the data from an s3 bucket, converts the price in Pounds to dollars (based on the exchange rate on May 31, 2011), subsets the data to 2011, and creates a column representing the total of the purchase. The original data description can be found on [the UCI Machine Learning Repository.](https://archive.ics.uci.edu/ml/datasets/online+retail#)
# +
csv_s3 = "s3://featurelabs-static/online-retail-logs.csv"
data = pd.read_csv(csv_s3, parse_dates=["order_date"])
# Convert to dollars
data['price'] = data['price'] * 1.65
data['total'] = data['price'] * data['quantity']
# Restrict data to 2011
data = data[data['order_date'].dt.year == 2011]
data.head()
# -
# ## Data Cleaning
#
# There are a few issues we need to address with the data. First, we'll drop the duplicated rows, then we'll drop any rows that contain a `nan`. Finally, we can add a `Boolean` column indicating whether or not an order is a cancellation.
# +
# drop the duplicates
data = data.drop_duplicates()
# drop rows with null customer id
data = data.dropna(axis=0)
data['cancelled'] = data['order_id'].str.startswith('C')
data['cancelled'].value_counts().plot.bar(figsize = (6, 5));
plt.title('Cancelled Purchases Breakdown');
# -
# All of the cancelled orders have negative quantities which mean that they cancel out with the corresponding purchase. We'll leave in the cancelled purchases, because if our goal (defined later in the prediction problem) is to predict the total amount purchased by a customer, we'll need to take into account their cancelled orders.
data.describe()
# We can see that most total purchase prices are less than \$50 (this is for a one item). The negative numbers represent cancelled orders. We can plot the purchase total by country (limited to only positive amounts and less than \$1000) to see if there are differences between countries.
plt.figure(figsize = (20, 6))
sns.boxplot(x = 'country', y = 'total', data = data[(data['total'] > 0) & (data['total'] < 1000)]);
plt.title("Total Purchase Amount by Country");
plt.xticks(rotation = 90);
plt.figure(figsize = (20, 6))
sns.boxplot(x = 'country', y = 'quantity', data = data[(data['total'] > 0) & (data['total'] < 1000)]);
plt.title("Purchased Quantity by Country");
plt.xticks(rotation = 90);
# Both the purchase total and the quantity are heavily skewed. This occurs often in real-world data and means this might be difficult as a regression problem (predict the actual spending amount). We might want to frame the problem as classification because the large purchase totals could throw off a machine learning algorithm. Our other option would be to remove the outliers, but given that these are probably legitimate, that does not seem like a responsible choice!
#
# ### Skewness of Data
#
# To see the extent of how skewed the data is, we can use an [Empirical Cumulative Distribution Function (ECDF) plot](https://www.itl.nist.gov/div898/software/dataplot/refman1/auxillar/ecdfplot.htm).
def ecdf(data):
x = np.sort(data)
y = np.arange(1, len(x) + 1) / len(x)
return x, y
# +
plt.figure(figsize = (14, 4))
# Total
plt.subplot(121)
x, y = ecdf(data.loc[data['total'] > 0, 'total'])
plt.plot(x, y, marker = '.')
plt.xlabel('Total'); plt.ylabel('Percentile'); plt.title('ECDF of Purchase Total');
# Quantity
plt.subplot(122)
x, y = ecdf(data.loc[data['total'] > 0, 'quantity'])
plt.plot(x, y, marker = '.')
plt.xlabel('Quantity'); plt.ylabel('Percentile'); plt.title('ECDF of Purchase Quantity');
# -
# The majority of total purchases are less than \$20, but there a number of outliers. Rather than using a regression problem, we therefore might want to try classifying customers based on their spending per month.
# # Prediction Problem
#
# The goal of machine learning is to predict some quantity (regression) or a label (classification). Our data exploration showed that regression might not be the best approach because of the extreme outliers, so instead we can make the problem classification.
#
# With this dataset, there are an _unlimited number of prediction problems_ because there are no labels (unlike in many machine learning competitions). Choosing a worthwhile quantity to predict therefore becomes critical. In most real-world situations, we could use a domain expert to frame a problem based on what they know is important in the field, and then it's our objective to make a set of labels and features based on that problem. This is known as prediction engineering.
#
# We'll frame the problem as predicting whether or not a customer will spend more than \$500 in the next month. This could be useful to a business because it will let them market more effectively to those customers who are likely to spend more. Moreover, an online retailer could advertise differently to customers based on their predicted class of spending.
#
# Instead of picking just a single month for predictions, we can use each customer as a label multiple times. In other words, we not only predict whether a given customer will spend more than \$500 in May, but we also ask the same question in June, July, and so on. The thing to note is that for each month, we _can't use data from the future_ to predict the class of spending. Each month we can use information from _any previous month_ which means that our predictions should get more accurate as we advance further in time through the data since we'll be able to use more information. Each label for a customer therefore has a different set of features because there is more or less data available to us depending on the month. Doing this by hand is very tedious and error-prone, but we'll see how Featuretools is able to handle the times associated with each label using cutoff times.
#
# ## Making Labels
#
# The function below takes in a start date and an end date (which we set to 30 days apart) and generates a dataframe of the labels, which depends on how much the customer spent in the period and the threshold. Our threshold will be \$500 for this prediction problem.
#
# For customers who appear in the data prior to the start date but then do have a purchase in between the start and end date, we set their total to 0. If we simply did not include them in the labels, then that would be cheating since we have no way of knowing ahead of time that they will not spend anything in the next month.
def make_retail_cutoffs_total(start_date, end_date, threshold = 500):
# Find customers who exist before start date
customer_pool = data[data['order_date'] < start_date]['customer_id'].unique()
tmp = pd.DataFrame({'customer_id': customer_pool})
# For customers in the customer pool, find their sum between the start and end date
totals = data[data['customer_id'].isin(customer_pool) &
(data['order_date'] > start_date) &
(data['order_date']<end_date)
].groupby('customer_id')['total'].sum().reset_index()
# Merge with all the customer ids to record all customers who existed before start date
totals = totals.merge(tmp, on = 'customer_id', how = 'right')
# Set the total for any customer who did not have a purchase in the timeframe equal to 0
totals['total'] = totals['total'].fillna(0)
# Label is based on the threshold
totals['label'] = (totals['total'] > threshold).astype(int)
# The cutoff time is the start date
totals['cutoff_time'] = pd.to_datetime(start_date)
totals = totals[['customer_id', 'cutoff_time', 'total', 'label']]
return totals
may_spending = make_retail_cutoffs_total(pd.datetime(2011, 5, 1), pd.datetime(2011, 6, 1))
may_spending.head()
# For each customer who appeared in the data before May, we have a label for them for the month of May which is the sum of their spending in May converted to a binary label. When we make features for these labels, we can only use data from _before May_. The `cutoff_time` represents the point at which any data we use must come before and the `label` is based on our threshold of \$500.
may_spending['label'].value_counts().plot.bar();
plt.title('Label Distribution for May');
# This is an imbalanced classification problem which means that we probably don't want to use accuracy as our metric.
#
# ### Metrics
#
# Instead of accuracy, we can measure performance in terms of:
#
# 1. Precision: the percentage of customers predicted to spend more than \$500 that actually did
# 2. Recall: the percentage of customers that actually spent more than \$500 that were correctly identified
# 3. F1 score: the harmonic mean of precision and recall
# 4. Receiver Operating Characterisic Area Under the Curve (ROC AUC): a 0 to 1 measure (with 1 being optimal) that measures the performance of a model across a range of thresholds
#
# We'll have to establish a baseline for these metrics (which will be a little later) so we know whether machine learning is useful for this task.
#
# Next we'll go ahead and make labels for the rest of the year. Keep in mind that this will generate one label for each customer for each month. We're used to thinking of a single label per customer, but since we have the data, we might as well use each customer as a training example as many times as possible (as long as we use valid data each time). A greater number of training observations should increase the predictive power of our model.
march_spending = make_retail_cutoffs_total('2011-03-01', '2011-04-01', 500)
april_spending = make_retail_cutoffs_total('2011-04-01', '2011-05-01', 500)
june_spending = make_retail_cutoffs_total('2011-06-01', '2011-07-01', 500)
july_spending = make_retail_cutoffs_total('2011-07-01', '2011-08-01', 500)
august_spending = make_retail_cutoffs_total('2011-08-01', '2011-09-01', 500)
september_spending = make_retail_cutoffs_total('2011-09-01', '2011-10-01', 500)
october_spending = make_retail_cutoffs_total('2011-10-01', '2011-11-01', 500)
november_spending = make_retail_cutoffs_total('2011-11-01', '2011-12-01', 500)
december_spending = make_retail_cutoffs_total('2011-12-01', '2012-01-01', 500)
labels = pd.concat([march_spending, april_spending, may_spending, june_spending, july_spending, august_spending,
september_spending, october_spending, november_spending, december_spending], axis = 0)
labels.to_csv('../input/labels.csv')
labels.describe()
# We have roughly 28,000 labels with ~17% of them positive. The total is very skewed, with several customers recording negative total for some months (they had more cancellations than purchases). By framing this as a classification problem, we don't have to worry about the outlying purchase totals throwing off our model.
#
# Just to examine the data, we can plot the total spending distribution by month (with negative totals removed).
# +
plot_labels = labels.copy()
plot_labels['month'] = plot_labels['cutoff_time'].dt.month
plt.figure(figsize = (12, 6))
sns.boxplot(x = 'month', y = 'total',
data = plot_labels[(plot_labels['total'] > 0) & (plot_labels['total'] < 1000)]);
plt.title('Customer Spending Distribution by Month');
# -
# Let's zoom in to one customer to make sure we understand the labels.
labels.loc[labels['customer_id'] == 12347]
labels.loc[labels['customer_id'] == 12347].set_index('cutoff_time')['total'].plot(figsize = (6, 4), linewidth = 3)
plt.xlabel('Date', size = 16);
plt.ylabel('Spending', size = 16);
plt.title('Monthly Spending for Customer', size = 20);
plt.xticks(size = 16); plt.yticks(size = 16);
# One customer, 8 different labels. It seems like it might be difficult to predict this customer's spending given her fluctuating total spending! We'll have to see if Featuretools is up to the task.
# We now have our prediction problem all set. The next step is to start making features we can use in a machine learning model.
#
# # Featuretools Implementation
#
# The first step in Featuretools is to create an `EntitySet` which will hold all of our data and the relationships between the multiple tables (which we'll create shortly). Initially we'll add the entire `data` as an `entity` to the set. Since data has a `time_index`, we'll add that and specify the variable type of the product description.
#
# The `time_index` represents the first time the information in that row is known. When we build features, Featuretools will use this `time_index` to filter data based on the cutoff time of the label. We can't use any purchases from after the cutoff time of the label to make features for that label.
# +
es = ft.EntitySet(id="Online Retail Logs")
# Add the entire data table as an entity
es.entity_from_dataframe("purchases",
dataframe=data,
index="purchases_index",
time_index = 'order_date',
variable_types = {'description': ft.variable_types.Text})
es['purchases']
# -
# ### Normalizing Entities
#
# In order to create new tables out of the original table, we can normalize this `entity`. This creates new tables by creating a unique row for every variable that we pass in, such as the customer or the product.
#
# The code below creates a new entity for the `products` where each row contains one product and the columns describe the product.
# +
# create a new "products" entity
es.normalize_entity(new_entity_id="products",
base_entity_id="purchases",
index="product_id",
additional_variables=["description"])
es['products'].df.head()
# -
# The `first_purchases_time` is automatically created because the `purchases` table has a time index. This represents the first time the product appears in the purchase data. Again, Featuretools will filter data from this table for each label so that we only build valid features.
#
# We can use this table to create new features; the products table is a parent of the `purchases` table with the linking variable `product_id`. For each product in `products`, there can be multiple purchases of that product in `purchases`.
#
# ### Additional Tables
#
# We'll repeat the process to create tables for both the `customers` and the `orders`. `normalize_entity` automatically creates the relationships and time index so we don't have to do that ourselves. If we want to include any other additional variables in the table, we can pass those in. These variables must be unique to the object that we are normalizing for. As an example, each order comes from one country, so we can include that as additional variables when creating the `orders` table. However, the description is not unique to an order, so that should not be a variable that appears in the orders table.
es['purchases']
# +
# create a new "customers" entity based on the orders entity
es.normalize_entity(new_entity_id="customers",
base_entity_id="purchases",
index="customer_id")
# create a new "orders" entity
es.normalize_entity(new_entity_id="orders",
base_entity_id="purchases",
index="order_id",
additional_variables=["country", 'cancelled'])
es
# -
# # Deep Feature Synthesis
#
# Now that our `EntitySet` is defined with the proper relationships between tables, we can perform [deep feature synthesis](http://www.jmaxkanter.com/static/papers/DSAA_DSM_2015.pdf) to generate 100s or 1000s of features. We can theoretically make features for any entity, but since our objective is to classify customer spending, we'll make features for each customer for each month.
#
# ## Using cutoff times
#
# To ensure the features are valid for the customer and the month, we'll pass in the labels dataframe that has the cutoff time for each customer for each month. Featuretools will make one row for each customer for each month, with the features for each month derived only from data prior to the cutoff time. This is an _extremely useful method_ because it means we don't have to worry about using invalid data to make features. For example, if we were doing this by hand, it would be very easy to create features that use information from the future to make features for the labels, which is not allowed. One issue when we have the entire dataset is that _we have access to all the data_ and must prevent ourselves from using it when building training features since _when our model is deployed, it won't have access to data from the future_ and we want our models to do well in deployment.
#
# The requirements of the cutoff time dataframe are that the first column contains the ids corresponding to the index of the target entity, and the second column must have the cutoff times. Featuretools then takes care of the rest, for each month making features only using valid data.
#
# The following call will generate features for each customer, resulting in a `feature_matrix` where each row consists of one customer for one month corresponding to a label and each column is one feature.
# +
feature_matrix, feature_names = ft.dfs(entityset=es, target_entity='customers',
cutoff_time = labels, verbose = 2,
cutoff_time_in_index = True,
chunk_size = len(labels), n_jobs = -1,
max_depth = 1)
feature_matrix.head()
# -
# We will want to drop the `total` and `label` columns before training because these were passed through from the `cutoff_time` data (this happens a little later). We also can remove the `MODE` of the order id and product id. These should not be used for creating features since they are index variables.
feature_matrix = feature_matrix.drop(columns = ['MODE(purchases.order_id)', 'MODE(purchases.product_id)'])
feature_matrix.shape
# Initially we did not generate very many features because we limited the `max_depth` to 1. This means that only 1 aggregation will be stacked at a time. Let's take a look at some of the features. First, we'll zoom back in to a single one of the customers.
feature_matrix.loc[12347, :].sample(10, axis = 1)
# We see that as we get deeper into the year, the numbers change for this customer because we are using more information to build the features. We would expect our predictions to get more accurate with time because we are incorporating more information. However, it's also possible that customer behavior changes over time and therefore using all the previous data might not acutally be useful.
# +
# feature_matrix.reset_index(inplace = True)
feature_matrix.groupby('time')['COUNT(purchases)'].mean().plot();
plt.title('Average Monthly Count of Purchases');
plt.ylabel('Purchases Per Customer');
# -
# This shows that as we progress through time, we have more purchases per customer to use for prediction.
feature_matrix.groupby('time')['SUM(purchases.quantity)'].mean().plot();
plt.title('Average Monthly Sum of Purchased Products');
plt.ylabel('Total Purchased Products Per Customer');
# Naturally, as we include more information, our forecasts should improve in accuracy. Therefore, if we are predicting purchase in November, we would expect better performance than predicting purchases in June.
# ## Correlations
#
# As a first approximation of useful features, we can see if there are any significant correlations between the features and the `total`. We'll one-hot encode the categorical features first.
feature_matrix = pd.get_dummies(feature_matrix).reset_index()
feature_matrix.shape
corrs = feature_matrix.corr().sort_values('total')
corrs['total'].head()
corrs['total'].dropna().tail()
# A few of the features have a moderate positive correlation with the `total` (ignoring the `label` for now). The number and total of the purchases is clearly related to the total spending! Keep in mind that the features are built using only data from before the cutoff time.
g = sns.FacetGrid(feature_matrix[(feature_matrix['SUM(purchases.total)'] > 0) & (feature_matrix['SUM(purchases.total)'] < 1000)],
hue = 'label', size = 4, aspect = 3)
g.map(sns.kdeplot, 'SUM(purchases.total)')
g.add_legend();
plt.title('Distribution of Purchases Total by Label');
# The sum of purchase totals prior to the month of the label is clearly higher for those customers who then went on to spend more than \$500 in the next month. We would expect this to be a useful feature in modeling.
feature_matrix['month'] = feature_matrix['time'].dt.month
sns.violinplot(x = 'month', y = 'NUM_UNIQUE(purchases.order_id)', hue = 'label', figsize = (24, 6),
data = feature_matrix[(feature_matrix['SUM(purchases.total)'] > 0) & (feature_matrix['SUM(purchases.total)'] < 1000)])
plt.title('Number of Unique Purchases by Label');
# ## Preliminary modeling
#
# We can now directly use this feature matrix for training and making predictions with a machine learning model. We'll predict one month at a time, each time training on all the previous observations. The testing features for each testing label are built using all data prior to the month of the testing label.
#
# ### Model
#
# For a model, we will use the `RandomForestClassifier` as implemented in Scikit-Learn. We'll keep most of the hyperparameters at the default values but increase the number of trees to 1000. This is not an optimized model but should allow us to tell whether or not our solution is better than a baseline estimate.
model = RandomForestClassifier(n_estimators = 1000,
random_state = 50,
n_jobs = -1)
# The function below trains and tests for a single month. We pass in the month, and the training data is subsetted to label - observation pairs from before the month, while the testing data comes from the month. This ensures that when making predictions for one month, we're only using data from before than month.
def predict_month(month, feature_matrix, return_probs = False):
"""Train and test a machine learning model using a feature set
for one month. Testing labels are from the month."""
feature_matrix['month'] = feature_matrix['time'].dt.month
# Subset labels
test_labels = feature_matrix.loc[feature_matrix['month'] == month, 'label']
train_labels = feature_matrix.loc[feature_matrix['month'] < month, 'label']
# Features
X_train = feature_matrix[feature_matrix['time'].dt.month < month].drop(columns = ['customer_id', 'time',
'month', 'label', 'total'])
X_test = feature_matrix[feature_matrix['time'].dt.month == month].drop(columns = ['customer_id', 'time',
'month', 'label', 'total'])
feature_names = list(X_train.columns)
# Impute and scale features
pipeline = Pipeline([('imputer', Imputer(strategy = 'median')),
('scaler', MinMaxScaler())])
# Fit and transform training data
X_train = pipeline.fit_transform(X_train)
X_test = pipeline.transform(X_test)
# Labels
y_train = np.array(train_labels).reshape((-1, ))
y_test = np.array(test_labels).reshape((-1, ))
print('Training on {} observations.'.format(len(X_train)))
print('Testing on {} observations.\n'.format(len(X_test)))
# Train
model.fit(X_train, y_train)
# Make predictions
predictions = model.predict(X_test)
probs = model.predict_proba(X_test)[:, 1]
# Calculate metrics
p = precision_score(y_test, predictions)
r = recall_score(y_test, predictions)
f = f1_score(y_test, predictions)
auc = roc_auc_score(y_test, probs)
print(f'Precision: {round(p, 5)}')
print(f'Recall: {round(r, 5)}')
print(f'F1 Score: {round(f, 5)}')
print(f'ROC AUC: {round(auc, 5)}')
# Feature importances
fi = pd.DataFrame({'feature': feature_names, 'importance': model.feature_importances_})
if return_probs:
return fi, probs
return fi
june_fi = predict_month(6, feature_matrix)
# We can plot the feature importances using a utility function. These should allow us to see what the model considers useful information for predicting spending.
# +
from utils import plot_feature_importances
norm_june_fi = plot_feature_importances(june_fi)
# -
# The most important features are those that are most correlated with the total. This should give us confidence that our machine learning model is learning the important relationships and that the Featuretools features are useful for the problem. If we want to predict future spending next month, the best indicators are the customer's total spending to date and the total number of their purchases to date.
# # Comparison to Baseline
#
# We calculated metrics for our model, but it's possible that these numbers are no better than we might have done by guessing. One question we have to ask is how do those numbers compare to an informed baseline? If our model can't beat a simple baseline, then we might want to question our approach or even if machine learning is applicable to the problem.
#
# For an informed baseline, let's use the amount the customer spent in the past month to predict how much they will spend in the next month. We can try this for July 2011. For the probability (used for the ROC AUC), we'll divide the previous month's total by the threhold (so a spending of 0 corresponds to 0 probability) and then clip any values to 1.
# +
labels['month'] = labels['cutoff_time'].dt.month
july_labels = labels[labels['month'] == 7]
june_labels = labels[labels['month'] == 6]
july_labels = july_labels.rename(columns = {'total': 'july_total'})
june_labels = june_labels.rename(columns = {'total': 'june_total'})
# Merge the current month with the previous
july_labels = july_labels.merge(june_labels[['customer_id', 'june_total']], on = 'customer_id', how = 'left')
july_labels['june_total'] = july_labels['june_total'].fillna(0)
july_labels['predicted_label'] = (july_labels['june_total'] > 500).astype(int)
july_labels['probability'] = july_labels['june_total'] / 500
# Set probabilities greater than 1 equal to 1
july_labels.loc[july_labels['probability'] > 1, 'probability'] = 1
july_labels.sample(10, random_state=50)
# -
# To test whether this is reasonable, we can find the correlation between the previous months total and the current months total.
july_labels['july_total'].corr(july_labels['june_total'])
# There is a moderate correlation between spending from one month to the next.
sns.lmplot('june_total', 'july_total', data = july_labels, fit_reg = False)
plt.title('July vs June Spending');
# Let's look at the four performance metrics.
print('Precision: {:.5f}.'.format(precision_score(july_labels['label'], july_labels['predicted_label'])))
print('Recall: {:.5f}.'.format(recall_score(july_labels['label'], july_labels['predicted_label'])))
print('F1 Score: {:.5f}.'.format(f1_score(july_labels['label'], july_labels['predicted_label'])))
print('ROC AUC Score: {:.5f}.'.format(roc_auc_score(july_labels['label'], july_labels['probability'])))
# We can now compare this performance to that from the model.
july_fi, july_probs = predict_month(7, feature_matrix, True)
# For a classifier, the most important metric is the ROC AUC because that accounts for performance across all possible thresholds. We can adjust the threshold to maximize the Recall/Precision/F1 Score depending on our preferences.
#
# To make sure that our model is really outperforming the baseline, we can plot the Receiver Operating Characteristic Curve for the two sets of predictions.
# +
# Calculate false positive rates and true positive rates
base_fpr, base_tpr, _ = roc_curve(july_labels['label'], july_labels['probability'])
model_fpr, model_tpr, _ = roc_curve(feature_matrix[feature_matrix['month'] == 7]['label'], july_probs)
plt.figure(figsize = (8, 6))
plt.rcParams['font.size'] = 16
# Plot both curves
plt.plot(base_fpr, base_tpr, 'b', label = 'baseline')
plt.plot(model_fpr, model_tpr, 'r', label = 'model')
plt.legend();
plt.xlabel('False Positive Rate'); plt.ylabel('True Positive Rate'); plt.title('ROC Curves');
# -
# __Based on the metrics and this plot, we can say that our model does indeed outperform the informed baseline guess.__ Machine learning, and the features from Featuretools, yield us a better solution than using a decent approximation.
#
# __If we were an online retailer currently using an informed guess for advertising, machine learning could make our advertising campaigns more efficient.__
#
# Let's take all of the code for comparing the baseline to the model and put it in a single function. First we need to calculate the informed baseline in a function.
def informed_baseline(month_number, threshold = 500):
"""Calculate an informed baseline for a given month.
The informed baseline is guessing the previous month's spending
for the next month. The probability is assessed by dividing
the previous month's total by the threshold and setting
any values greater than 1 to 1."""
# Subset to the months
month = labels[labels['month'] == month_number]
previous_month = labels[labels['month'] == (month_number - 1)]
previous_month = previous_month.rename(columns = {'total': 'previous_total'})
# Merge the current month with the previous month
month = month.merge(previous_month[['customer_id', 'previous_total']], on = 'customer_id', how = 'left')
# For customers who had no spending in the previous month, set their spending to 0
month['previous_total'] = month['previous_total'].fillna(0)
# Calculate a probability based on the previous months spending and the threshold
month['probability'] = month['previous_total'] / threshold
# Set probabilities greater than 1 equal to 1
month.loc[month['probability'] > 1, 'probability'] = 1
# Make the predicted label
month['prediction'] = (month['previous_total'] > threshold).astype(int)
# Calculate metrics
print('Precision: {:.5f}.'.format(precision_score(month['label'], month['prediction'])))
print('Recall: {:.5f}.'.format(recall_score(month['label'], month['prediction'])))
print('F1 Score: {:.5f}.'.format(f1_score(month['label'], month['prediction'])))
print('ROC AUC Score: {:.5f}.'.format(roc_auc_score(month['label'], month['probability'])))
return month
# The next function compares a machine learning model trained on a set of features to the informed baseline.
def compare(month, feature_matrix):
"""Compare machine learning model to baseline performance.
Computes statistics and shows ROC curve."""
print('Baseline Performance')
baseline = informed_baseline(month)
print('\nModel Performance')
fi, probs = predict_month(month, feature_matrix, return_probs=True)
# Calculate false positive rates and true positive rates
base_fpr, base_tpr, _ = roc_curve(baseline['label'], baseline['probability'])
model_fpr, model_tpr, _ = roc_curve(feature_matrix[feature_matrix['month'] == month]['label'], probs)
plt.figure(figsize = (8, 6))
plt.rcParams['font.size'] = 16
# Plot both curves
plt.plot(base_fpr, base_tpr, 'b', label = 'baseline')
plt.plot(model_fpr, model_tpr, 'r', label = 'model')
plt.legend();
plt.xlabel('False Positive Rate'); plt.ylabel('True Positive Rate'); plt.title('ROC Curves');
compare(6, feature_matrix)
# We clearly see our model outpeforming the baseline. In practice, we would optimize the model threshold for Precision/Recall/F1 Score.
#
# Let's test December, when theoretically our model should do the best because it is training on the most data.
compare(12, feature_matrix)
# We get a slightly better ROC AUC. It's possible that the data does not stay consistent over the couse of the year so using more data might not necessarily create a better model. In other words, consumer behavior can shift (potentially due to seasonality) so the older data might not be relevant.
# # Tuning Deep Feature Synthesis
#
# We saw that even a basic implementation of Featuretools can yield a set of useful features. Next, we want to ask if we can achieve better performance by generating a richer set of features. We can expand the capabilities of Featuretools by specifying the primitives we use, increasing the maximum depth of stacked features, writing our own custom primitives, identifying interesting values, and using seed features. For an explanation of all these concepts, refer to the [Featuretools documentation.](https://docs.featuretools.com/guides/tuning_dfs.html) In this notebook we'll stick to custom primitives and using more primitives, but there are still other options for building better predictive models!
#
# In the code cell below, we again use Featuretools but this time specify a few more primitives and increase the maximum depth. This might create some unnecessary features, but we can then use feature selection to remove them. Having too many features is a better problem than having too few!
labels = labels.reset_index(drop = True)
feature_matrix, feature_names = ft.dfs(entityset=es, target_entity='customers',
agg_primitives = ['std', 'max', 'min', 'mode',
'mean', 'skew', 'last', 'avg_time_between'],
trans_primitives = ['cum_sum', 'cum_mean', 'day',
'month', 'hour', 'weekend'],
n_jobs = -1, chunk_size = 100, max_depth = 2,
cutoff_time = labels, cutoff_time_in_index = True,
verbose = 1)
feature_matrix.head()
# Before we can use these features for modeling, we need to one-hot encode them. Because some of the features are built from the id variables, one-hot encoding them will create far too many features. We'll have to be careful about increasing the number of columns too greatly. First let's look at the `object` type columns.
feature_matrix.loc[:, feature_matrix.dtypes == 'object'].columns
# We'll remove the `order_id` and `product_id` derived columns. One-hot encoding the countries will not add too many columns since there are a limited number of countries.
feature_matrix.drop(columns = ['MODE(purchases.order_id)', 'MODE(purchases.product_id)',
'LAST(purchases.order_id)', 'LAST(purchases.product_id)'], inplace = True)
feature_matrix = pd.get_dummies(feature_matrix).reset_index()
feature_matrix.shape
# Now we can use these features to build a machine learning model and compare to the baseline.
labels = labels.sort_values(['cutoff_time', 'customer_id'])
feature_matrix['time'] = list(labels['cutoff_time'])
compare(12, feature_matrix)
# The performance is siginficant;y better than with the default primitives. Let's look at the most important features.
december_fi = predict_month(12, feature_matrix)
norm_fi = plot_feature_importances(december_fi)
# The most important features all have to do with `cum_sum`. Intuitively, this makes sense: tracking the total amount that a customer has purchased thus far seems like an effective method for predicting how much they will spend in the next month. Moreover, this is not necessarily a feature we would build by hand, or if it is, we probably would not stack other operations on this feature such as standard deviations and cumulative sums.
#
# ## Feature Selection
#
# At this point, we might want to apply some feature selection to our `feature_matrix`. It's likely that many of the features are highly correlated which can have a negative impact on model performance.
#
# The following call removes:
#
# * Any features with more than 90% missing values
# * Any features with only a single unique value
# * One out of every pair of columns with a correlation greater than 0.9.
# +
from utils import feature_selection
# %load_ext autoreload
# %autoreload 2
# -
feature_matrix_selection = feature_selection(feature_matrix.drop(columns = ['time', 'customer_id']))
# +
feature_matrix_selection['time'] = feature_matrix['time']
feature_matrix_selection['customer_id'] = feature_matrix['customer_id']
december_fi = predict_month(12, feature_matrix_selection)
norm_fi = plot_feature_importances(december_fi)
# -
# Feature selection did not significantly improve our model performance.
# ## Custom Primitives
#
# We saw that an informed baseline guess just using the previous month's total yielded a decent solution (although worse than machine learning). Therefore, we might want to consider using this as a feature in our model. To build this feature (which will actually find the total of any numeric column for the previous month) we can write a custom primitive.
#
# __Custom primitives__ allow us to expand on the capabilities of Featuretools by writing functions that use our domain knowledge. __Featuretools will stack custom primitives allowing us to effectively amplify any previous experience we have with the problem.__
from featuretools.primitives import make_agg_primitive
# This primitive is an aggregation and will take in a `numeric` column, a `datetime`, and the `time` (representing `cutoff_time`) and return the sum of the `numeric` column for the month prior to the cutoff time. An aggregation primitive works across tables using the relationships between tables and returns a single number for all the children of a single parent instance.
#
# One thing to note is that this custom primitive uses the cutoff time which we specify by using the `time` keyword argument. The function only finds totals in the single month prior to the cutoff time.
def total_previous_month(numeric, datetime, time):
"""Return total of `numeric` column in the month prior to `time`."""
df = pd.DataFrame({'value': numeric, 'time': datetime})
previous_month = time.month - 1
# Handle January
if previous_month == 0:
previous_month = 12
previous_year = time.year - 1
# Filter data
df = df[(df['time'].dt.month == previous_month) & (df['time'].dt.year == previous_year)]
else:
df = df[df['time'].dt.month == previous_month]
# Sum up total
total = df['value'].sum()
return total
# We need to specify the input and output types of the primitive as well as that it `uses_calc_time` which means it needs the cutoff time.
total_previous = make_agg_primitive(total_previous_month, input_types = [ft.variable_types.Numeric,
ft.variable_types.Datetime],
return_type = ft.variable_types.Numeric,
uses_calc_time = True)
# Since we already have a decent set of features, we don't want to have to recalculate all of them. Therefore we'll just calculate the custom primitives and then join these to the existing feature matrix.
feature_matrix_custom, feature_names_custom = ft.dfs(entityset=es, target_entity='customers',
cutoff_time = labels,
cutoff_time_in_index = True,
agg_primitives = [total_previous],
trans_primitives = [], chunk_size = len(labels),
verbose = 1, n_jobs = 4)
feature_matrix_custom.drop(columns = ['total', 'label', 'month'], inplace = True)
feature_matrix_custom.reset_index(inplace = True)
# We can merge pandas dataframes using keys. Here we'll want to merge the features on the customer and the time (which is the cutoff time).
feature_matrix_new_selection = feature_matrix_selection.merge(feature_matrix_custom, on = ['customer_id', 'time'],
how = 'left')
december_fi = predict_month(12, feature_matrix_new_selection)
norm_fi = plot_feature_importances(december_fi)
# The custom primitives did not improve the performance of the model significantly. Nonetheless, using custom primitives is one of many ways that we can encode domain knowledge into a set of featuretools features and expand the capabilities of this library. Furthermore, a custom primitive that we write for one problem can be applied to any problem. This "data-agnosticism" is one of the [primary ideas behind Deep Feature Synthesis](http://www.jmaxkanter.com/static/papers/DSAA_DSM_2015.pdf) since many operations can be applied to any dataset.
#
# We can do one final test on this set of features to make sure that it performs better than the baseline across different months of the data.
compare(5, feature_matrix_new_selection)
compare(8, feature_matrix_new_selection)
# Feel free to check all of the months! It's clear that featuretools and machine learning is able to outperform the baseline for this problem. Even without concentrating on the model, we were able to perform significantly better than a well-informed guess. With some minor hyperparameter tuning (using random search) we could achieve even better performance. We'll not implement any hyperparameter tuning here, but usually it delivers a small performance gain relative to feature engineering (as can be seen in the other two projects in this repository.)
# ## Precision Recall Curve
#
# Our model was using a default threshold of 0.5 to make predictions. We can use the precision recall curve to identify the ideal threshold for our model. For example, we may care more about identifying customers who will spend more than \$500 than about false positive so we choose a threshold that results in high recall but low precision. Conversely, we may want to limit false positives even if that means missing some potential high-spending customers so we would try for a higher level of precision. The ideal threshold for a classifier will depend on the problem.
#
# We use the ROC AUC to compare models across a range of thresholds, so we know which model is strictly better, but then we can use a precision recall curve to adjust the threshold for our business needs. This is usually a process done with the help of domain experts and validated in cross validation (or on a separate validation set of data).
def precision_recall(month, feature_matrix):
"Show the precision vs recall curve for a month"
# Find the probability
fi, probs = predict_month(month, feature_matrix,
return_probs = True)
# Calculate metrics across thresholds
precision, recall, t = precision_recall_curve(labels.loc[labels['cutoff_time'].dt.month == month, 'label'],
probs)
# Plot the curve
plt.step(recall, precision, color='b', alpha=0.5,
where='post')
# Fill in the curve
plt.fill_between(recall, precision, step='post', alpha=0.5,
color='b')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.ylim([0.0, 1.05])
plt.xlim([0.0, 1.0])
plt.title("Precision vs. Recall Curve"); plt.show();
precision_recall(12, feature_matrix_selection)
precision_recall(10, feature_matrix_selection)
# Depending on what we want to maximize for, we can use these plots to select the appropriate threshold. If we want a recall around 80%, then we would have to accept a precision of near 40%. Conversely, a precision of 80% would result in a recall closer to 25%.
# Below we generate probabilities for each month to plot the ROC curve compared to both the baseline and manual engineered features. The graphs can be seen in the conclusions section. The code used to make the graphs is included in the Manual Retail Spending notebook.
# +
# %%capture
# Record probabilities for each month
for month in range(4, 13):
_, probs = predict_month(month, feature_matrix_new_selection, return_probs = True)
temp_df = pd.DataFrame({'Automated': probs, 'month': month})
if month == 4:
probs_df = temp_df.copy()
else:
probs_df = probs_df.append(temp_df)
# -
probs_df.head()
probs_df['label'] = list(feature_matrix_new_selection[feature_matrix_new_selection['month'] > 3]['label'])
probs_df.to_csv('../input/auto_probs.csv')
# # Conclusions
#
# In this notebook we saw that Featuretools automated feature engineering in a machine learning pipeline results in better prediction of future customer behavior than an informed baseline guess. There are many advantages to using Featuretools in a time-series problem with multiple tables of data such as we often encouter in real life. Following are the key takeaways:
#
# 1. Featuretools creates a rich set of relevant features from a set of related tables
# * These features can deliver effective machine learning model performance
# 2. Featuretools handles the issue of filtering data in a time-series problem
# * Cutoff times for each label filter data
# * All features for each label use only valid data
# 3. Even using the default settings for Featuretools, we can create an effective machine learning model
# * The featuretools and random forest classifier outperformed an informed guess in terms of ROC AUC and F1 score
# 4. We can build upon the capabilities of featuretools using custom primitives
# * There are other methods for improving featuretools we didn't even cover!
# * The model improved with more features up to a point (more feature selection would help)
# * Changing the max depth and number of primitives can create more useful and interpretable features
#
# __When I tried manual feature engineering for this problem, I spent significantly more time than with Featuretools and yet was barely able to develop a model better than the baseline.__ Part of the issue was that I couldn't figure out how to use valid data and even when I could, managing the time aspect of the problem proved difficult leading to a poor model. Presented below are the ROC AUC comparison between manual and automated feature engineering.
#
# 
#
# Maybe this inabilitity to achieve success with manual feature engineering speaks to my limitations as a data scientist, but why not use a method such as featuretools if it exists and can make our job much simpler? Data science is about using the right methods to get the job done as efficiently as possible, and for the retail dataset, that method is Featuretools in a predictive modeling pipeline. The implementation with automated feature engineering is faster, safer, and just as interpretable as any manual engineering work and delivers an effect machine learning model.
|
Retail Spending/notebooks/Automated Retail Spending.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Refactor: Wine Quality Analysis
# In this exercise, you'll refactor code that analyzes a wine quality dataset taken from the UCI Machine Learning Repository [here](https://archive.ics.uci.edu/ml/datasets/wine+quality). Each row contains data on a wine sample, including several physicochemical properties gathered from tests, as well as a quality rating evaluated by wine experts.
#
# The code in this notebook first renames the columns of the dataset and then calculates some statistics on how some features may be related to quality ratings. Can you refactor this code to make it more clean and modular?
import pandas as pd
df = pd.read_csv('winequality-red.csv', sep=';')
df.head()
# ### Renaming Columns
# You want to replace the spaces in the column labels with underscores to be able to reference columns with dot notation. Here's one way you could've done it.
df.columns = [label.replace(' ', '_') for label in df.columns]
df.head()
# ### Analyzing Features
# Now that your columns are ready, you want to see how different features of this dataset relate to the quality rating of the wine. A very simple way you could do this is by observing the mean quality rating for the top and bottom half of each feature. The code below does this for four features. It looks pretty repetitive right now. Can you make this more concise?
#
# You might challenge yourself to figure out how to make this code more efficient! But you don't need to worry too much about efficiency right now - we will cover that more in the next section.
def numeric_to_buckets(df, column_name):
median = df[column_name].median()
for i, val in enumerate(df[column_name]):
if val >= median:
df.loc[i, column_name] = 'high'
else:
df.loc[i, column_name] = 'low'
for feature in df.columns[:-1]:
numeric_to_buckets(df, feature)
print(df.groupby(feature).quality.mean(), '\n')
|
Software Engineering Practices Part I/refactor_wine_quality.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from BurstCube.bcSim import simFiles
sfs = simFiles('config.yaml')
import numpy as np
energies = np.empty([len(sfs.sims)])
for i, S in enumerate(sfs.sims):
energies[i] = S.energy
print(S.energy)
area = sfs.calculateAeff(useEres=False, sigma=2.0)
print(area)
sfs.sims
sfs.calculateAeff()
# +
#Extracted the elements from the area array
aeff = sfs.calculateAeff()
gEres = list(aeff['aeff_eres'])
bEres = list(aeff['aeff_eres_modfrac'])
Area = list(aeff['aeff'])
azimuth = list(aeff['az'])
# +
#plotting area against energy with GBM data
from BurstCube.plotSim import plotAeffvsEnergy
fig = plotAeffvsEnergy(energies, Area, gEres, bEres, az=0, ze=15, plotGBM=True)
# plt.savefig('plotEnergy.png', dpi=300)
# -
|
lepalmer/plotData/f_test_energy/Aeff vs. Energy Plot.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 1.5 Command Line Interface (CLI)
#
# The following section demonstrates how to use the **signac** command line interface (CLI).
# The CLI allows you to interact with your data space without python, which may be advantageous in various situations, e.g., for scripting or data exploration.
#
# You will find that for many of the functions introduced earlier there is an equivalent CLI command.
#
# The CLI is accessed via the top-level ``signac`` command.
# You can get help about the various functions with the `-h` or `--help` argument.
# + language="bash"
# signac --help
# -
# To interact with a project on the command line, the current working directory needs to be within or below the project's root directory.
# Let's start by reseting the designated project root directory for this section of the tutorial.
% rm -rf projects/tutorial/cli
% mkdir -p projects/tutorial/cli
# Next we switch the current working directory to the project root directory.
% cd projects/tutorial/cli
# Then we initialize the project.
# + language="bash"
# signac init TutorialCLIProject
# -
# We can verify the project configuration using the `signac project` command.
# + language="bash"
# signac project
# signac project --workspace
# -
# We access a job by providing the state point on the command line in JSON format †).
#
# †) *The JSON format requires double quotes for keys.*
# + language="bash"
# signac job '{"kT": 1.0, "p": 1.0, "N": 1000}'
# -
# By default this will print the associated *job id* to STDOUT.
# Instead of the *job id*, we can also get the path to the job's workspace.
# + language="bash"
# signac job '{"kT": 1.0, "p": 1.0, "N": 1000}' --workspace
# -
# Please not, that obtaining the path in this way does not necessarily mean that the path exists.
# However, we can initialize the job and create the workspace using the `-c` or `--create` argument.
# + language="bash"
# signac job '{"kT": 1.0, "p": 1.0, "N": 1000}' --create
# -
# We can use the `signac statepoint` command to get the statepoint associated with the *initialized* job.
# + language="bash"
# signac statepoint ee617ad585a90809947709a7a45dda9a
# -
# Usually we will not provide statepoints on the command line, but read them from a file.
# Let's create a statepoint file with one statepoint:
# + language="bash"
# echo '{"kT": 1.0, "p": 0.1, "N": 1000}' > statepoint.txt
# cat statepoint.txt
# -
# We can pipe the content of this file into the **signac** CLI to get the corresponding *job id*.
# + language="bash"
# cat statepoint.txt | signac job
# -
# We will reproduce the ideal gas project from section 1.1 to generate some data for the following examples.
# +
import signac
def V_idg(N, p, kT):
return N * kT / p
project = signac.get_project()
for p in 0.1, 1.0, 10.0:
sp = {'p': p, 'kT': 1.0, 'N': 1000}
job = project.open_job(sp)
job.document['V'] = V_idg(**sp)
# -
# We can use the `signac find` command to find all jobs within our project's workspace.
# + language="bash"
# signac find
# -
# Just like with `project.find_jobs()` we can provide a filter argument to find a subset of jobs matching the given filter.
# Here we get all jobs with a pressure of 0.1:
# + language="bash"
# signac find '{"p": 0.1}'
# -
# In this example, that is of course only one job.
#
# Similarly, we can also filter based on information in the job document. Here, we find all jobs that have a volume corresponding to a pressure of 1 (volume = 1000*1/1 = 1000).
# + language="bash"
# signac find --doc-filter '{"V": 1000.0}'
# -
# Once again, this only returns one job in this case.
#
# We can pipe `signac find` results into `signac statepoint` with `xargs` to resolve the statepoints.
# + language="bash"
# signac find | xargs signac statepoint
# -
# You will have noticed that each time we execute a *find* operation the data space is indexed anew.
#
# This is no problem for small data spaces, however especially for larger data spaces, where the indexing process may be substantially expensive it's advantageous to cache the index in a file.
# + language="bash"
# signac project --index > index.txt
# -
# This index file can be used in conjunction with all functions that require a data space index, for example `signac find`:
# + language="bash"
# signac find -i index.txt '{"p": 0.1}'
# -
# Or for instance when creating a linked view.
# + language="bash"
# signac view -i index.txt ./view
# -
# The `signac view` command works exactly like `project.create_linked_view` such that the `./view` directory now contains a linked view to the job workspaces.
# %ls view
# This concludes the first chapter of the tutorial.
# The next chapter introduces a few more advanced topics.
#
# [Return to index](index.ipynb)
|
notebooks/signac_105_Command_Line_Interface.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Visualisation of many initial condition for 3d ODE
# +
import k3d
import numpy as np
points_number = 11200
positions = 100 * np.random.random_sample((points_number,3)).astype(np.float32) - 50
colors = np.random.randint(0, 0x777777, points_number).astype(np.uint32)
plot = k3d.plot()
p = k3d.points(positions, colors, point_size=1)
plot += p
sigma=10.0
beta=8./3
rho=28.0
def lorenz_deriv(X, sigma=sigma, beta=beta, rho=rho):
"""Compute the time-derivative of a Lorenz system."""
x, y, z = X.T
return np.vstack([sigma * (y - x), x * (rho - z) - y, x * y - beta * z]).T
# +
X = p.positions
colors = p.colors
m = (X[:,0]-.5*X[:,1])>0
colors = np.random.randint(0, 0x777777, points_number).astype(np.uint32)
colors[m]=1
colors[~m]=0xff0000
p.colors = colors
# -
plot.display()
# +
plot.camera_auto_fit = False
plot.grid_auto_fit = False
X = p.positions
for i in range(1000):
X = X + lorenz_deriv(X, sigma=sigma, beta=beta, rho=rho)*0.005
if i%1==0 and i>0:
p.positions = X[::1,:]
p.positions = X
# -
# %time X = X + lorenz_deriv(X, sigma=sigma, beta=beta, rho=rho)*0.005
# %time p.positions = X
# %time p.positions = X[::10,:]
p.point_size =1
|
Lorenz_system.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="McvjJuNeZNxh"
# # Train a Cats-vs-dogs Recognizer with CNN model
# + id="dn-6c02VmqiN" executionInfo={"status": "ok", "timestamp": 1613404771699, "user_tz": 300, "elapsed": 1634, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17684077615557436866"}}
import os
import zipfile
import random
import shutil
import tensorflow as tf
from tensorflow.keras.optimizers import RMSprop
from tensorflow.keras.preprocessing.image import ImageDataGenerator
from shutil import copyfile
from os import getcwd
# + [markdown] id="3bonYpoRYSt3"
# ## Download
#
# If the URL for download doesn't work, visit https://www.microsoft.com/en-us/download/confirmation.aspx?id=54765 and right click on the 'Download Manually' link to get a new URL to the dataset.
# + id="YdNknoRQYBJ6"
# !wget --no-check-certificate \
# "https://download.microsoft.com/download/3/E/1/3E1C3F21-ECDB-4869-8368-6DEBA77B919F/kagglecatsanddogs_3367a.zip" \
# -O "/tmp/cats-and-dogs.zip"
# + [markdown] id="ww7AdybZhl1z"
# ## Preprocessing
# First, create a directory "tmp/PetImages" containing subdirectories called 'Cat' and 'Dog'.
#
# Next, create folder "tmp/cats-v-dogs" and split data for training and testing with the ratio of 90-10, since the data size is more than 10,000.
# + id="5RlAXFwhapKH" executionInfo={"status": "ok", "timestamp": 1613404784850, "user_tz": 300, "elapsed": 8523, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17684077615557436866"}}
local_zip = '/tmp/cats-and-dogs.zip'
zip_ref = zipfile.ZipFile(local_zip, 'r')
zip_ref.extractall('/tmp')
zip_ref.close()
print(len(os.listdir('/tmp/PetImages/Cat/')))
print(len(os.listdir('/tmp/PetImages/Dog/')))
# + id="F-QkLjxpmyK2" executionInfo={"status": "ok", "timestamp": 1613405191860, "user_tz": 300, "elapsed": 227, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17684077615557436866"}}
try:
os.mkdir("/tmp/cats-v-dogs")
os.mkdir("/tmp/cats-v-dogs/training")
os.mkdir("/tmp/cats-v-dogs/training/cats")
os.mkdir("/tmp/cats-v-dogs/training/dogs")
os.mkdir("/tmp/cats-v-dogs/testing")
os.mkdir("/tmp/cats-v-dogs/testing/cats")
os.mkdir("/tmp/cats-v-dogs/testing/dogs")
except OSError:
pass
# + colab={"base_uri": "https://localhost:8080/"} id="MCqGfp1wgqkT" executionInfo={"status": "ok", "timestamp": 1613406328864, "user_tz": 300, "elapsed": 3487, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17684077615557436866"}} outputId="53c39d10-7a01-440b-eba7-dab1f4e24573"
def split_data(SOURCE, TRAINING, TESTING, SPLIT_SIZE):
files = []
for filename in os.listdir(SOURCE):
file = SOURCE + filename
if os.path.getsize(file) > 0:
files.append(filename)
else:
print(filename + " is zero length, so ignoring.")
training_length = int(len(files) * SPLIT_SIZE)
testing_length = int(len(files) - training_length)
shuffled_set = random.sample(files, len(files))
training_set = shuffled_set[0:training_length]
testing_set = shuffled_set[-testing_length:]
for filename in training_set:
this_file = SOURCE + filename
destination = TRAINING + filename
copyfile(this_file, destination)
for filename in testing_set:
this_file = SOURCE + filename
destination = TESTING + filename
copyfile(this_file, destination)
CAT_SOURCE_DIR = "/tmp/PetImages/Cat/"
TRAINING_CATS_DIR = "/tmp/cats-v-dogs/training/cats/"
TESTING_CATS_DIR = "/tmp/cats-v-dogs/testing/cats/"
DOG_SOURCE_DIR = "/tmp/PetImages/Dog/"
TRAINING_DOGS_DIR = "/tmp/cats-v-dogs/training/dogs/"
TESTING_DOGS_DIR = "/tmp/cats-v-dogs/testing/dogs/"
split_size = .9
split_data(CAT_SOURCE_DIR, TRAINING_CATS_DIR, TESTING_CATS_DIR, split_size)
split_data(DOG_SOURCE_DIR, TRAINING_DOGS_DIR, TESTING_DOGS_DIR, split_size)
# Expected Output:
# 666.jpg is zero length, so ignoring.
# 11702.jpg is zero length, so ignoring.
# + colab={"base_uri": "https://localhost:8080/"} id="luthalB76ufC" executionInfo={"status": "ok", "timestamp": 1613406505780, "user_tz": 300, "elapsed": 209, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17684077615557436866"}} outputId="3300ee65-fc09-447c-d49f-114b26cfeff6"
print(len(os.listdir('/tmp/cats-v-dogs/training/cats/')))
print(len(os.listdir('/tmp/cats-v-dogs/training/dogs/')))
print(len(os.listdir('/tmp/cats-v-dogs/testing/cats/')))
print(len(os.listdir('/tmp/cats-v-dogs/testing/dogs/')))
# Expected Output:
# 11250
# 11250
# 1250
# 1250
# + [markdown] id="LpvhIPezi5cf"
# ## Definition
# + id="-BQrav4anTmj" executionInfo={"status": "ok", "timestamp": 1613428109605, "user_tz": 300, "elapsed": 310, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17684077615557436866"}}
model = tf.keras.models.Sequential([
tf.keras.layers.Conv2D(16, (3,3), activation='relu', input_shape=(150, 150, 3)),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(32, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(64, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(512, activation='relu'),
tf.keras.layers.Dense(1, activation='sigmoid')
])
model.compile(optimizer=RMSprop(lr=0.001), loss='binary_crossentropy', metrics=['acc'])
# + colab={"base_uri": "https://localhost:8080/"} id="AcCO6RWIFayv" executionInfo={"status": "ok", "timestamp": 1613433798334, "user_tz": 300, "elapsed": 240, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17684077615557436866"}} outputId="659ed553-4cd8-44c1-dc0f-7f999215a46a"
model.summary()
# + colab={"base_uri": "https://localhost:8080/"} id="HOSfCg2SmMa4" executionInfo={"status": "ok", "timestamp": 1613428110093, "user_tz": 300, "elapsed": 789, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17684077615557436866"}} outputId="692cb1ad-ff12-45fd-8ebe-568bf097a8eb"
TRAINING_DIR = "/tmp/cats-v-dogs/training/"
train_datagen = ImageDataGenerator(rescale=1.0/255.)
train_generator = train_datagen.flow_from_directory(TRAINING_DIR,
batch_size=250,
class_mode='binary',
target_size=(150, 150))
VALIDATION_DIR = "/tmp/cats-v-dogs/testing/"
validation_datagen = ImageDataGenerator(rescale=1.0/255.)
validation_generator = validation_datagen.flow_from_directory(VALIDATION_DIR,
batch_size=250,
class_mode='binary',
target_size=(150, 150))
# Expected Output:
# Found 22498 images belonging to 2 classes.
# Found 2500 images belonging to 2 classes.
# + [markdown] id="VzlqR9WHrAgB"
# ## Training
# + colab={"base_uri": "https://localhost:8080/"} id="mu41FydqnCt1" executionInfo={"status": "ok", "timestamp": 1613420197061, "user_tz": 300, "elapsed": 2555037, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17684077615557436866"}} outputId="faec500c-8b44-40a5-e924-8efe4bf115ed"
history = model.fit(train_generator,
epochs=40,
steps_per_epoch=90,
validation_data=validation_generator,
validation_steps=6)
# + [markdown] id="Cj5WYBqCrSjJ"
# ## Performance
# + colab={"base_uri": "https://localhost:8080/", "height": 582} id="BUzYCINqrRe0" executionInfo={"status": "ok", "timestamp": 1613420242288, "user_tz": 300, "elapsed": 620, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17684077615557436866"}} outputId="a9cd6ba9-5caf-4adc-a2b0-5ae2ce169c14"
# %matplotlib inline
import matplotlib.image as mpimg
import matplotlib.pyplot as plt
#-----------------------------------------------------------
# Retrieve a list of list results on training and test data
# sets for each training epoch
#-----------------------------------------------------------
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc)) # Get number of epochs
#------------------------------------------------
# Plot training and validation accuracy per epoch
#------------------------------------------------
plt.plot ( epochs, acc, label='Training accuracy' )
plt.plot ( epochs, val_acc, label='Validation accuracy' )
plt.title ('Training and validation accuracy')
plt.legend(loc=0)
plt.figure()
#------------------------------------------------
# Plot training and validation loss per epoch
#------------------------------------------------
plt.plot ( epochs, loss, label='Training loss')
plt.plot ( epochs, val_loss, label='Validation loss')
plt.title ('Training and validation loss' )
plt.legend(loc=0)
plt.figure()
# + [markdown] id="ethGY6_zvV5k"
# ## Overfitting
#
# Note with a large dataset of diversity, Data Augmentation won't help much. In stead, we use "Dropout" to improve the Validation accuracy from 82% to 85%.
# + id="KNhamIqq8dhK" executionInfo={"status": "ok", "timestamp": 1613431167363, "user_tz": 300, "elapsed": 255, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17684077615557436866"}}
model = tf.keras.models.Sequential([
tf.keras.layers.Conv2D(16, (3,3), activation='relu', input_shape=(150, 150, 3)),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(32, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(64, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Flatten(),
tf.keras.layers.Dropout(0.65),
tf.keras.layers.Dense(512, activation='relu'),
tf.keras.layers.Dense(1, activation='sigmoid')
])
model.compile(optimizer=RMSprop(lr=0.001), loss='binary_crossentropy', metrics=['acc'])
# + colab={"base_uri": "https://localhost:8080/"} id="pkl9zaCQ-BoM" executionInfo={"status": "ok", "timestamp": 1613433751868, "user_tz": 300, "elapsed": 2565413, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17684077615557436866"}} outputId="9bc7cc62-cf06-4b5a-b014-911c3813aeeb"
history = model.fit(train_generator,
epochs=40,
steps_per_epoch=90,
validation_data=validation_generator,
validation_steps=6)
# + colab={"base_uri": "https://localhost:8080/", "height": 582} id="13znaj0l8F5O" executionInfo={"status": "ok", "timestamp": 1613433819260, "user_tz": 300, "elapsed": 547, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17684077615557436866"}} outputId="945a518f-60aa-4733-ef2c-08b1873c4131"
# %matplotlib inline
import matplotlib.image as mpimg
import matplotlib.pyplot as plt
#-----------------------------------------------------------
# Retrieve a list of list results on training and test data
# sets for each training epoch
#-----------------------------------------------------------
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc)) # Get number of epochs
#------------------------------------------------
# Plot training and validation accuracy per epoch
#------------------------------------------------
plt.plot ( epochs, acc, label='Training accuracy' )
plt.plot ( epochs, val_acc, label='Validation accuracy' )
plt.title ('Training and validation accuracy')
plt.legend(loc=0)
plt.figure()
#------------------------------------------------
# Plot training and validation loss per epoch
#------------------------------------------------
plt.plot ( epochs, loss, label='Training loss')
plt.plot ( epochs, val_loss, label='Validation loss')
plt.title ('Training and validation loss' )
plt.legend(loc=0)
plt.figure()
# + [markdown] id="YnEsX6Ak4imA"
# ## Visualization
# + colab={"base_uri": "https://localhost:8080/"} id="WES0Z45L59Ai" executionInfo={"status": "ok", "timestamp": 1613430720556, "user_tz": 300, "elapsed": 198, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17684077615557436866"}} outputId="11bc2bc0-6238-4307-bed8-351034c757bf"
train_cats_dir = TRAINING_CATS_DIR
train_dogs_dir = TRAINING_DOGS_DIR
train_cat_fnames = os.listdir( train_cats_dir )
train_dog_fnames = os.listdir( train_dogs_dir )
print(train_cat_fnames[:10])
print(train_dog_fnames[:10])
# + colab={"base_uri": "https://localhost:8080/", "height": 421} id="A-NGjEyD4Lh_" executionInfo={"status": "ok", "timestamp": 1613430939274, "user_tz": 300, "elapsed": 1568, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17684077615557436866"}} outputId="9e879364-389e-4b3e-9a8d-c3cc1c04c502"
import numpy as np
import random
from tensorflow.keras.preprocessing.image import img_to_array, load_img
# Let's define a new Model that will take an image as input, and will output
# intermediate representations for all layers in the previous model after
# the first.
successive_outputs = [layer.output for layer in model.layers[1:]]
#visualization_model = Model(img_input, successive_outputs)
visualization_model = tf.keras.models.Model(inputs = model.input, outputs = successive_outputs)
# Let's prepare a random input image of a cat or dog from the training set.
cat_img_files = [os.path.join(train_cats_dir, f) for f in train_cat_fnames]
dog_img_files = [os.path.join(train_dogs_dir, f) for f in train_dog_fnames]
img_path = random.choice(cat_img_files + dog_img_files)
img = load_img(img_path, target_size=(150, 150)) # this is a PIL image
x = img_to_array(img) # Numpy array with shape (150, 150, 3)
x = x.reshape((1,) + x.shape) # Numpy array with shape (1, 150, 150, 3)
# Rescale by 1/255
x /= 255.0
# Let's run our image through our network, thus obtaining all
# intermediate representations for this image.
successive_feature_maps = visualization_model.predict(x)
# These are the names of the layers, so can have them as part of our plot
layer_names = [layer.name for layer in model.layers]
# -----------------------------------------------------------------------
# Now let's display our representations
# -----------------------------------------------------------------------
for layer_name, feature_map in zip(layer_names, successive_feature_maps):
if len(feature_map.shape) == 4:
#-------------------------------------------
# Just do this for the conv / maxpool layers, not the fully-connected layers
#-------------------------------------------
n_features = feature_map.shape[-1] # number of features in the feature map
size = feature_map.shape[ 1] # feature map shape (1, size, size, n_features)
# We will tile our images in this matrix
display_grid = np.zeros((size, size * n_features))
#-------------------------------------------------
# Postprocess the feature to be visually palatable
#-------------------------------------------------
for i in range(n_features):
x = feature_map[0, :, :, i]
x -= x.mean()
x /= x.std ()
x *= 64
x += 128
x = np.clip(x, 0, 255).astype('uint8')
display_grid[:, i * size : (i + 1) * size] = x # Tile each filter into a horizontal grid
#-----------------
# Display the grid
#-----------------
scale = 20. / n_features
plt.figure( figsize=(scale * n_features, scale) )
plt.title ( layer_name )
plt.grid ( False )
plt.imshow( display_grid, aspect='auto', cmap='viridis' )
# + [markdown] id="4pLUTDP0r1zw"
# ## Prediction
# + id="Sy9536M4rr1r"
# Upload an image here and have it classified without crashing
import numpy as np
from google.colab import files
from keras.preprocessing import image
uploaded = files.upload()
for fn in uploaded.keys():
# predicting images
path = '/content/' + fn
img = image.load_img(path, target_size=(150, 150))
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
images = np.vstack([x])
classes = model.predict(images, batch_size=10)
print(classes[0])
if classes[0]>0.5:
print(fn + " is a dog")
else:
print(fn + " is a cat")
|
Convolutional-Image-Recognition.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
import numpy
import matplotlib.pyplot
# %matplotlib inline
data = numpy.loadtxt (fname = 'data/weather-01.csv', delimiter =',')
# +
fig = matplotlib.pyplot.figure (figsize= (10.0, 3.0))
# create placeholders for plots
subplot1 = fig.add_subplot (1, 3, 1)
subplot2 = fig.add_subplot (1, 3, 2)
subplot3 = fig.add_subplot (1, 3, 3)
subplot1.set_ylabel('average')
subplot1.plot(numpy.mean(data, axis = 0))
subplot2.set_ylabel('max')
subplot2.plot(numpy.max(data, axis = 0))
subplot3.set_ylabel('min')
subplot3.plot(numpy.min(data, axis = 0))
fig.tight_layout()
matplotlib.pyplot.show
# -
# # LOOPS
word = 'notebook'
print(word[4])
for char in word:
print(char)
# ## Get a list of all filenames from disk
import glob
print (glob.glob('data/weather*.csv')) # generates a list, single dimension container for data
# ## Putting it all together
# +
filenames = sorted(glob.glob('data/weather*.csv')) # sorted gets data sets in right order
#filenames = filenames[0:3]
for f in filenames:
print (f)
data = numpy.loadtxt(fname=f, delimiter =',')
if numpy.max (data, axis = 0)[0] and numpy.max(data, axis = 0)[20] ==20:
print ("Suspicious looking maximum")
elif numpy.sum(numpy.min(data, axis = 0)) ==0:
print ("Minima to zero")
else:
print ("Data looks OK")
fig = matplotlib.pyplot.figure (figsize= (10.0, 3.0))
subplot1 = fig.add_subplot (1, 3, 1)
subplot2 = fig.add_subplot (1, 3, 2)
subplot3 = fig.add_subplot (1, 3, 3)
subplot1.set_ylabel('average')
subplot1.plot(numpy.mean(data, axis = 0))
subplot2.set_ylabel('max')
subplot2.plot(numpy.max(data, axis = 0))
subplot3.set_ylabel('min')
subplot3.plot(numpy.min(data, axis = 0))
fig.tight_layout()
matplotlib.pyplot.show()
# -
# ## Making decisions
num = 107
if num > 100:
print("Greater")
print("Done")
else:
print ("Not greater")
print ("Done")
num = -3
if num > 0:
print(num, "is positive")
elif num == 0:
print (num, "is zero")
else:
print (num, "is negative")
num = 107 + 33 + 222
for inte in num:
if num > 100:
print("Greater")
print("Done")
else:
print ("Not greater")
print ("Done")
# ## Functions
def fahr_to_kelvin(temp):
return ((temp - 32) * (5/9) + 273.15)
fahr_to_kelvin(44)
print('Freezing point of water: ', fahr_to_kelvin(32))
print('Boiling point of water: ', fahr_to_kelvin(212))
def analyse (filename):
""" Displays the mean, maxima and minimum value for each weather station.
Creates a figure of three subplots, showing values for mean, maxima and minimum value with axis = 0,
y axis labels, and a tight layout.
"""
data = numpy.loadtxt(fname=filename, delimiter =',')
fig = matplotlib.pyplot.figure (figsize= (10.0, 3.0))
subplot1 = fig.add_subplot (1, 3, 1)
subplot2 = fig.add_subplot (1, 3, 2)
subplot3 = fig.add_subplot (1, 3, 3)
subplot1.set_ylabel('average')
subplot1.plot(numpy.mean(data, axis = 0))
subplot2.set_ylabel('max')
subplot2.plot(numpy.max(data, axis = 0))
subplot3.set_ylabel('min')
subplot3.plot(numpy.min(data, axis = 0))
fig.tight_layout()
matplotlib.pyplot.show()
def detect_problems (filename):
"""Some of our temperature files have problems, check for these
This function reads a file(filename argument) and reports on odd looking maxima,
and minima that add up to zero. This seems to happen when the sensors break.
The function does not return any data.
"""
data = numpy.loadtxt(fname=filename, delimiter =',')
if numpy.max (data, axis = 0)[0] and numpy.max(data, axis = 0)[20] ==20:
print ("Suspicious looking maximum")
elif numpy.sum(numpy.min(data, axis = 0)) ==0:
print ("Minima to zero")
else:
print ("Data looks OK")
for f in filenames [0:5]:
print(f)
analyse(f)
detect_problems(f)
# how to we write help documentation for our own functions?
help(detect_problems)
help(detect_problems)
help(analyse)
|
02-plots-and-subplots.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Ensembl genes table extraction EDA
#
# This notebook is useful for development as well as exploratory data analysis on the extracted tables.
# It is currently automically executed and saved as part of exports using `papermill`.
# %load_ext autoreload
# %autoreload 2
import pandas as pd
from ensembl_genes import ensembl_genes
# + tags=["parameters"]
# parameters cell
species = "human"
release = "104"
# -
ensg = ensembl_genes.Ensembl_Gene_Queries(release=release, species=species)
ensg.connection_url
database = ensg.database
database
# ## Extract data
# ## gene attrib counts
ensg.run_query("gene_attrib_counts").head(15)
# ## genes
ensg.gene_df.head()
# clone-based genes no longer get a symbol and are filled with the stable ID
# https://www.ensembl.info/2021/03/15/retirement-of-clone-based-gene-names/
ensg.gene_df.query("gene_symbol == ensembl_gene_id").head(2)
# which external database the gene symbol derives from versus the ensembl source
pd.crosstab(
ensg.gene_df.ensembl_source,
ensg.gene_df.gene_symbol_source_db.fillna("missing (clone-based)"),
margins=True,
)
ensg.gene_df.coord_system.value_counts().head(10)
ensg.gene_df.gene_biotype.value_counts().head(10)
ensg.gene_df.seq_region_exc_type.value_counts(dropna=False)
ensg.gene_df.mhc.value_counts()
len(ensg.gene_df)
# ## alternative gene alleles
#
# Related:
#
# - [OTP: Origin of genes_with_non_reference_ensembl_ids.tsv](https://github.com/opentargets/platform/issues/702)
# - [biostars: map between different assemblies of one ensembl release](https://www.biostars.org/p/143956/)
# - using `attrib_type.code = "non_ref"` for `primary_assembly` doesn't appear to return any results
ensg.alt_allele_df.head()
# looks like non_ref isn't set for human genes
query = '''
SELECT *
FROM gene_attrib
LEFT JOIN attrib_type
ON gene_attrib.attrib_type_id = attrib_type.attrib_type_id
WHERE attrib_type.code = "non_ref"
LIMIT 5
'''
pd.read_sql(sql=query, con=ensg.connection_url)
ensg.alt_allele_df.alt_allele_attrib.value_counts()
ensg.alt_allele_df.query("is_representative_gene").representative_gene_method.value_counts()
ensg.gene_df.query("ensembl_gene_id != ensembl_representative_gene_id").head(2)
# # replaced ID converter
#
# A single `old_stable_id` can map to multiple `new_stable_id`. For example, `ENSG00000152006`
#
# https://uswest.ensembl.org/Homo_sapiens/Tools/IDMapper/Results?tl=AzhM62SpkvdiLC4H-6808613
#
# Requested ID | Matched ID(s) | Releases
# -- | -- | --
# ENSG00000152006 | ENSG00000196273 | 26: ENSG00000196273.1
# ENSG00000152006 | ENSG00000197016 | 26: ENSG00000197016.1
# ENSG00000152006 | ENSG00000196239 | 26: ENSG00000196239.1
ensg.old_to_new_df.head(2)
# some ensembl genes replaced by many new ensembl genes
ensg.old_to_new_df.old_ensembl_gene_id.value_counts().head(2)
# example
ensg._update_ensembl_gene("ENSG00000152006")
ensg.old_to_newest_df.head(2)
len(ensg.old_to_newest_df)
ensg.old_to_newest_df.is_current.value_counts()
# ## omni-updater
#
# The omni-updater dataset is designed to convert ensembl gene IDs from input data to the current, representative ensembl_gene_ids for this ensembl release. It assumes:
#
# - users want to update outdated genes with their replacements
# - users want a dataset of representative genes only, and want to convert alternative alleles to representative genes
#
# An inner join of a dataset with `update_df` on `input_ensembl_gene_id` will do the following:
#
# - produce output ensembl_gene_ids that are current and representatives
# - update outdated genes with their current identifiers. Outdated genes with no current replacement will be removed by the inner join.
# - update alternative gene alleles with their representatives
# - genes that are already represenative and current will map to themselves
ensg.update_df.head(2)
ensg.update_df.sort_values("input_maps_to_n_genes", ascending=False).head(2)
ensg.update_df.sort_values("n_inputs_map_to_gene", ascending=False).head(2)
(ensg.update_df.input_maps_to_n_genes == 1).mean()
ensg.update_df.query("ensembl_gene_id == 'ENSG00000256263'")
print(
f"The omni-updater contains {len(ensg.update_df):,} rows for mapping "
f"{ensg.update_df.input_ensembl_gene_id.nunique():,} input genes to "
f"{ensg.update_df.ensembl_gene_id.nunique():,} current, representative genes."
)
# https://useast.ensembl.org/Homo_sapiens/Tools/IDMapper/Results?tl=P45VLMbogubpI0QA-6815464
ensg.update_df.query("input_ensembl_gene_id == 'ENSG00000201456'").head(3)
# ## cross-refrences (xrefs)
ensg.xref_df.head()
# datasets where there are ensembl_gene_id-xref_source-xref_accession pairs might not be distinct
xref_dup_df = ensg.xref_df[ensg.xref_df.duplicated(subset=["ensembl_gene_id", "xref_source", "xref_accession"], keep=False)]
xref_dup_df.xref_source.value_counts()
# xref sources versus info_types
pd.crosstab(ensg.xref_df.xref_source, ensg.xref_df.xref_info_type, margins=True)
# ## Gene Ontology xrefs
ensg.xref_go_df.head(3)
# GO terms for CCR5
# compare to http://useast.ensembl.org/Homo_sapiens/Gene/Ontologies/molecular_function?g=ENSG00000160791
sorted(ensg.xref_go_df.query("ensembl_gene_id == 'ENSG00000160791'").go_label)
# ## lrg xrefs
ensg.xref_lrg_df.head(2)
len(ensg.xref_lrg_df)
# ### ncbigene xrefs
ensg.xref_ncbigene_df.head()
# ensembl gene mapped to by multiple ncbigenes
ensg.xref_ncbigene_df.ensembl_representative_gene_id.value_counts().head(3)
len(ensg.xref_ncbigene_df), ensg.xref_ncbigene_df.ensembl_representative_gene_id.duplicated().sum()
# ncbigene mapped to by multiple ensembl genes, likely due to alt gene alleles
ensg.xref_ncbigene_df.ncbigene_id.value_counts().head(3)
len(ensg.xref_ncbigene_df), ensg.xref_ncbigene_df.ncbigene_id.duplicated().sum()
# +
# ensg.xref_ncbigene_df.query("ensembl_representative_gene_id == 'ENSG00000231500'")
# ensg.xref_ncbigene_df.query("ncbigene_id == '51206'")
# -
repr_ensembl_gene_ids = set(ensg.gene_df.ensembl_representative_gene_id)
len(repr_ensembl_gene_ids)
# many of these genes should probably be alternative alleles rather than representative
ensg.gene_df.query("not primary_assembly and ensembl_gene_id==ensembl_representative_gene_id")
|
ensembl_genes/notebooks/ensembl_genes_eda.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="CazISR8X_HUG"
# # Multiple Linear Regression
# + [markdown] colab_type="text" id="pOyqYHTk_Q57"
# ## Importing the libraries
# + colab={} colab_type="code" id="T_YHJjnD_Tja"
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# + [markdown] colab_type="text" id="vgC61-ah_WIz"
# ## Importing the dataset
# + colab={} colab_type="code" id="UrxyEKGn_ez7"
dataset = pd.read_csv('50_Startups.csv')
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, -1].values
# + colab={"base_uri": "https://localhost:8080/", "height": 857} colab_type="code" executionInfo={"elapsed": 552, "status": "ok", "timestamp": 1586353652778, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEuXdT7eQweUmRPW8_laJuPggSK6hfvpl5a6WBaA=s64", "userId": "15047218817161520419"}, "user_tz": -240} id="GOB3QhV9B5kD" outputId="4a05377a-2db2-43fc-b824-a0710448baee"
print(X)
# + [markdown] colab_type="text" id="VadrvE7s_lS9"
# ## Encoding categorical data
# + colab={} colab_type="code" id="wV3fD1mbAvsh"
from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import OneHotEncoder
ct = ColumnTransformer(transformers=[('encoder', OneHotEncoder(), [3])], remainder='passthrough')
X = np.array(ct.fit_transform(X))
# + colab={"base_uri": "https://localhost:8080/", "height": 857} colab_type="code" executionInfo={"elapsed": 616, "status": "ok", "timestamp": 1586353657759, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEuXdT7eQweUmRPW8_laJuPggSK6hfvpl5a6WBaA=s64", "userId": "15047218817161520419"}, "user_tz": -240} id="4ym3HdYeCGYG" outputId="ce09e670-cf06-4a1c-f5b0-89422aae0496"
print(X)
# + [markdown] colab_type="text" id="WemVnqgeA70k"
# ## Splitting the dataset into the Training set and Test set
# + colab={} colab_type="code" id="Kb_v_ae-A-20"
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0)
# + [markdown] colab_type="text" id="k-McZVsQBINc"
# ## Training the Multiple Linear Regression model on the Training set
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" executionInfo={"elapsed": 757, "status": "ok", "timestamp": 1586353664008, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEuXdT7eQweUmRPW8_laJuPggSK6hfvpl5a6WBaA=s64", "userId": "15047218817161520419"}, "user_tz": -240} id="ywPjx0L1BMiD" outputId="099836bc-4d85-4b4f-a488-093faf02e8cb"
from sklearn.linear_model import LinearRegression
regressor = LinearRegression()
regressor.fit(X_train, y_train)
# + [markdown] colab_type="text" id="xNkXL1YQBiBT"
# ## Predicting the Test set results
# + colab={"base_uri": "https://localhost:8080/", "height": 185} colab_type="code" executionInfo={"elapsed": 951, "status": "ok", "timestamp": 1586353666678, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhEuXdT7eQweUmRPW8_laJuPggSK6hfvpl5a6WBaA=s64", "userId": "15047218817161520419"}, "user_tz": -240} id="TQKmwvtdBkyb" outputId="493436bf-a4ae-4374-ca16-0b0c25d19457"
y_pred = regressor.predict(X_test)
np.set_printoptions(precision=2)
print(np.concatenate((y_pred.reshape(len(y_pred),1), y_test.reshape(len(y_test),1)),1))
|
Foundations_of_strategic_business_analytics/Week_2/Factors_leading_to_events__recitals/linear_regression/multiple_linear_regression.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import sys
sys.path.append('../python_packages_static/')
import pyemu
import os
import matplotlib.pyplot as plt
# ## run NOPTMAX=0 to get residuals, then load and reweight like we were doing for Monte Carlo. But, also set up standard deviation column for noise on observations for the ensembles
# ### NOTE: Make sure `run_ensemble` is set appropriately - If `run_ensemble` is set to `True`, local runs are performed. If `run_ensemble` set to `False`results from the journal article are used.
run_ensemble=False
# +
if run_ensemble==True:
input_dir = '../noptmax0_testing/' # read the pst file from here and get residuals
else:
input_dir = '../output/noptmax0/' # read the pst file from here and get residuals
output_dir = '../run_data' # write out the new run file here
pst_root = 'never_iES_noptmax0' # the PST root we are reading in from
ies_noise_obs_file = 'never_ies_0.noise_lt_obs.pst' # Name of the PST file to write out as the start of iES
# -
# ### read in the PEST control file
pst = pyemu.Pst(os.path.join(input_dir,'{}.pst'.format(pst_root)))
# ### make a quick pie chart showing the current distribution of the observation groups in the objective function
pst.plot(kind='phi_pie')
# ### we can use `pyemu` functionality to assign new weights that adjust and honor whatever balance we seek
new_proportions = pst.phi_components.copy()
new_proportions
# ### here we assign proportions (that sum to 1.0) to the various groups. We want to retain the same total Phi so we multiply our proportions by the total Phi
new_proportions['flux'] = 0.3*pst.phi
new_proportions['head'] = 0.2*pst.phi
new_proportions['land_surface'] = 0.5*pst.phi
new_proportions['budget'] = 0
new_proportions
# ### using the `phi_components` dictionary, making a copy of it, and reassigning values, we can update the PST object using the `adjust_weights` function
pst.adjust_weights(obsgrp_dict=new_proportions)
pst.observation_data
pst.plot(kind='phi_pie')
# +
# set some values for pestpp-ies
if run_ensemble == True:
pst.pestpp_options["ies_num_reals"] = 20
else:
pst.pestpp_options["ies_num_reals"] = 500
pst.pestpp_options["ies_bad_phi_sigma"] = 2.5
pst.pestpp_options["overdue_giveup_fac"] = 4
pst.pestpp_options["ies_save_rescov"] = True
pst.pestpp_options["ies_no_noise"] = True
pst.pestpp_options["ies_drop_conflicts"] = False
pst.pestpp_options["ies_pdc_sigma_distance"] = 3.0
pst.pestpp_options['ies_autoadaloc']=True
pst.pestpp_options['ies_num_threads']=4
pst.pestpp_options['ies_lambda_mults']=(0.1,1.0,10.0,100.0)
pst.pestpp_options['lambda_scale_fac'] = (0.75,0.9,1.0,1.1)
pst.pestpp_options['ies_subset_size']=10
# set SVD for some regularization
pst.svd_data.maxsing = 250
# -
# check number of realizations
pst.pestpp_options["ies_num_reals"]
# ### we want to use the observations in the `land_surface` group as inequality observations (e.g. unweighted unless needed to enforce "less than" condition). By naming the groups starting with "less_than" PESTPP-IES will interpret them as such
pst.observation_data.loc[pst.observation_data.obgnme=='land_surface', 'obgnme'] = 'less_than_land_surface' # rename for less than inequality
pst.observation_data
# # Add standard deviation column for observations to control noise realizations
# ### make a "standard_deviation" column in the pst observation_data dataframe. This will inform PESTPP-IES to use these value for sampling in generating the observation noise on the ensembles.
#
# Start out with a value of -9999 that we can use as a test to make sure we set a value for every observation group.
obs = pst.observation_data
obs['standard_deviation'] = -9999
# ### now we set some subjective standard deviation values that we assert are more appropriate than the straight up weights.
obs.loc[obs.obsnme=='q_1436500'].obsval/(3.33*3)
obs.loc[obs.obsnme=='q_1366650'].obsval/30
obs.loc[obs.obsnme=='q_1436500', 'standard_deviation'] = obs.loc[obs.obsnme=='q_1436500'].obsval/(3.33*3)
obs.loc[obs.obsnme=='q_1366650', 'standard_deviation'] = obs.loc[obs.obsnme=='q_1366650'].obsval/(10.*3)
obs.loc[obs.obgnme=='head', 'standard_deviation'] = 5/3 # 5 is the range, div by 3 for the range
obs.loc[obs.obgnme=='less_than_land_surface', 'standard_deviation'] = 10/3
obs.loc[obs.obgnme=='budget', 'standard_deviation'] = 9999
# ### use an `assert` statment to make sure we set obs to have a standard deviation not -9999
assert pst.observation_data.standard_deviation.min()>0
pst.observation_data
# ### Write out an updated parameter summary XLS file
parsum = pst.write_par_summary_table('../report_materials/initial_iES_parsum.xlsx', report_in_linear_space=True)
parsum
# ### Now set `NOPTMAX=10` and write out the PEST control file. Note - to use the standard deviation column requires writing out in the new `version=2` format. In this format, the parameter and observation data sections are written to external files. This is not backward compatible with older version of PEST, but enables this new capability. Filenames for the external files will be identified in the PST file.
pst.control_data.noptmax = 10
pst.pestpp_options["ies_no_noise"] = False
pst.write(os.path.join(output_dir, ies_noise_obs_file), version=2)
# ## If `run_ensemble=True` the cell below will run a local `never_ies_0.noise_lt_obs.pst` iES history-matching run
# * simillar process as in notebooks 1.0, 1.3, and 2.0
# * using the number of realizations per iteration specified by `pst.pestpp_options["ies_num_reals"]`
# * will run in parallel locally using the number of cores specified below by `num_workers`
# * creates a new directory called `"../master_ies/"` which is a copy of run_data
# * while running function generates worker directories that are removed when run is complete
# * results moved to `"../run_data/"`
if run_ensemble==True:
# set some variables for starting a group of PEST++ workers on the local machine
# MAKE SURE THAT PESTPP-IES and MF6 executables are in your system path or are in '../run_data'
num_workers = 5 # number of local workers -- VERY IMPORTANT, DO NOT MAKE TOO BIG
if sys.platform == 'win32':
pst_exe = 'pestpp-ies.exe'
else:
pst_exe = 'pestpp-ies'
template_ws = '../run_data' # template_directory
m_d = '../master_ies'
pyemu.os_utils.start_workers(worker_dir=template_ws,
exe_rel_path=pst_exe,
pst_rel_path=ies_noise_obs_file,
num_workers=num_workers,
master_dir=m_d
)
if run_ensemble==True:
# move results into run_data and clean up
move_result_files = glob.glob(os.path.join(m_d, 'prior_mc_wide*'))
move_result_files = [f for f in move_result_files if 'pst' not in f]
[shutil.copy(os.path.join(m_d, file), output_dir) for file in move_result_files]
# Remove master dir.
shutil.rmtree(m_d)
|
notebooks_workflow_complete/3.1_prepare_for_iES_reweight_objective_function.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + slideshow={"slide_type": "skip"} tags=["hide_input"]
# IPython magic
from IPython.display import Image, HTML
# Suppress warnings
import warnings
warnings.filterwarnings("ignore")
# Data directory
DATADIR='../../../data/loans'
# + [markdown] slideshow={"slide_type": "slide"} tags=["hide_input"]
# # Predicting loan default using automated data wrangling
# + [markdown] slideshow={"slide_type": "skip"}
# We will use the example of predicting loan default to practically walk you through a textbook data science problem and show how to use getML for automating the most tedious parts of the process and developing a production-ready solution in just a few hours - still beating most other models.
#
# More concretely, you will use the getML Python API in order to
#
# 1. [Approach a real world dataset](#data-preparation)
# 2. [Train a single Multirel Model](#training-a-multirel-model)
# 3. [Perform a Hyperparameter optimization](#hyperparameter-optimization)
# 4. [Access the trained features](#extracting-features)
#
# If you wish to follow along the code sections in this tutorial, you can do so by downloading and installing [getML](https://getml.com/product). It's free.
# + [markdown] slideshow={"slide_type": "skip"}
# **Introduction**
#
# This tutorial features a use case from the financial sector. We will use getML in order to predict loan default. A loan is the lending of money to companies or individuals. Banks grant loans in exchange for the promise of repayment. Loan default is defined as the failure to meet this legal obligation, for example when a home buyer fails to make a mortgage payment. It is essential for a bank to estimate the risk it carries when granting loans to potentially non-performing customers.
#
# The analysis is based on the [financial](https://relational.fit.cvut.cz/dataset/Financial) dataset from the [the CTU Prague Relational Learning Repository](https://arxiv.org/abs/1511.03086). It contains information about 606 successful and 76 not successful loans and consists of 8 tables:
# + slideshow={"slide_type": "slide"} tags=["hide_input"]
Image(filename="dataset_jupyter.png")
# + [markdown] slideshow={"slide_type": "skip"}
# The `loan` table contains information about the loans granted by the bank, such as the date of creation, the amount, and the planned duration of the loan. It also contains the `status` of the loan. This is the target variable that we will predict in this analysis. The `loan` table is connected to the table `account` via the column `account_id`.
#
# The `account` table contains further information about the accounts associated with each loan. Static characteristics such as the date of creation are contained in `account` and dynamic characteristics such as debited payments and balances are contained in `order` and `trans`. The table `client` includes characteristics of the account owners. Clients and accounts are related via the table `disp`. The `card` table describes credit card services the bank offers to its clients and is related to a certain account also via the table `disp`. The table `district` contains publicly available information such as the unemployment rate about the districts a certain account or client is related to. More information about the dataset can be found [here](https://sorry.vse.cz/~berka/challenge/pkdd1999/berka.htm).
#
# In the following, we will further explore the data and prepare a data model to be used for the analysis with getML. As usual, we start with setting a project.
# + slideshow={"slide_type": "slide"}
import getml
getml.engine.set_project('loans')
# + [markdown] slideshow={"slide_type": "skip"}
# Since the data sets from the CTU Prague Relational Learning Repository are available from a MariaDB database, we use getML's data base connector to directly load the data into the getML engine.
# + slideshow={"slide_type": "subslide"}
getml.database.connect_mysql(
host="relational.fit.cvut.cz",
port=3306,
dbname="financial",
user="guest",
password="<PASSWORD>",
time_formats=['%Y/%m/%d']
)
loan = getml.data.DataFrame.from_db('loan', name='loan')
account = getml.data.DataFrame.from_db('account', name='account')
order = getml.data.DataFrame.from_db('order', name='order')
trans = getml.data.DataFrame.from_db('trans', name='trans')
card = getml.data.DataFrame.from_db('card', name='card')
client = getml.data.DataFrame.from_db('client', name='client')
disp = getml.data.DataFrame.from_db('disp', name='disp')
district = getml.data.DataFrame.from_db('district', name='district')
# + [markdown] slideshow={"slide_type": "skip"}
# ## Data preparation
#
# We will have a closer look at the tables from the financial dataset and setup the data model. Note that a convenient way to explore the data frames we just loaded into the getML engine is to have a look at them in the [getML monitor](https://docs.getml.com/latest/user_guide/getml_suite/monitor/monitor.html). We recommend to check what is going on there in parallel to this tutorial.
# + [markdown] slideshow={"slide_type": "skip"}
# ### Setting roles
#
# In order to tell getML feature engineering algorithms how to treat the columns of each Data Frame we need to set its *role*. For more information about roles, check out the [user guide](https://docs.getml.com/latest/user_guide/annotating_data/annotating_data.html#roles). The loan table looks like this:
# + slideshow={"slide_type": "slide"} tags=["hide_input"]
display(HTML(loan.to_pandas().to_html(max_rows=10, border=0)))
# + [markdown] slideshow={"slide_type": "fragment"}
# The `status` column is our target variable. It contains 4 different categories:
#
# * A means that the contract finished, no problems,
# * B means that the contract finished, loan not paid,
# * C means that contract is running, OK so far,
# * D means that the contract is running, but the client has already missed at least one payment
#
# Before assigning it the role `target` we need to transform it to a numerical variable. We will consider A and C a successful loan and B and D a default.
# + slideshow={"slide_type": "subslide"}
default = ((loan['status'] == 'B') | (loan['status'] == 'D'))
loan.add(default, name='default', role='target')
print(loan['default'].sum())
# + [markdown] slideshow={"slide_type": "fragment"}
# The data set contains 76 defaulted loans out of 681 data points in total, which corresponds to roughly 10%.
# + [markdown] slideshow={"slide_type": "subslide"}
# Next, we assign roles to the remaining columns in `loan`
#
# * **join_key**: loan_id, account_id
# * **time_stamp**: date
# * **numerical**: amount, duration, payments
#
# Note that the column `status`, which obviously contains a data leak, will not be considered by getML since we do not assign it a role.
# + slideshow={"slide_type": "fragment"}
loan.set_role(["account_id", "loan_id"], getml.data.roles.join_key)
loan.set_role(["date"], getml.data.roles.time_stamp)
loan.set_role(["amount", "duration", "payments"], getml.data.roles.numerical)
# + [markdown] slideshow={"slide_type": "slide"}
# The `account` table looks like this:
# + slideshow={"slide_type": "fragment"} tags=["hide_input"]
display(HTML(account.to_pandas().to_html(max_rows=10, border=0)))
# + slideshow={"slide_type": "subslide"}
print(account['frequency'].count_distinct())
# + [markdown] slideshow={"slide_type": "fragment"}
# Frequency is a categorial variable with 3 distinct categories, so we add it to the data model. Accordingly, we set the **time_stamp** and **join_key** columns for `account`.
# + slideshow={"slide_type": "fragment"}
account.set_role(["account_id", "district_id"], getml.data.roles.join_key)
account.set_role(["date"], getml.data.roles.time_stamp)
account.set_role(["frequency"], getml.data.roles.categorical)
# + [markdown] slideshow={"slide_type": "slide"}
# ### Population table
#
# Let's have a closer look at the relation between `loans` and `account`:
# + slideshow={"slide_type": "fragment"}
print(loan['account_id'].count_distinct())
print(account['account_id'].count_distinct())
# + [markdown] slideshow={"slide_type": "skip"}
# The join key `account_id` has no duplicated value neither in `loan` nor in `account`. That means, each row in `loan` is associated with exactly one row in `account`. This is called a one-to-one relation.
#
# It does not make sense to let getML's feature engineering algorithms try to find aggregations over the accounts associated with each loan (because there is only one). So we perform the join operation between both tables before feeding them into getML. This is part of the definition of the data model and is generally recommended for one-to-one or many-to-one relations. The resulting table will be the population table of our analysis.
# + slideshow={"slide_type": "subslide"}
population = loan.join(
name='population',
other=account,
how='left',
join_key='account_id',
other_cols=[
account['district_id'],
account['frequency'],
account['date'].alias('date_account')
]
)
# + slideshow={"slide_type": "subslide"} tags=["hide_input"]
display(HTML(population.to_pandas().to_html(max_rows=20, border=0)))
# + [markdown] slideshow={"slide_type": "slide"}
# We also randomly split the data into a training and a validation set. We use 70% of the data set for training and the rest for testing.
# + slideshow={"slide_type": "fragment"}
split = 0.7
population_train = population.where('population_train', population.random() < split)
population_test = population.where('population_test', population.random() >= split)
# + [markdown] slideshow={"slide_type": "slide"}
# ### Peripheral tables
# + [markdown] slideshow={"slide_type": "skip"}
# The next step is to check the join relations between the population table and the remaining peripheral tables. We start by considering `order` and `trans` since the are both joined via `account_id` and do not have any further relationships with other tables. We check if any of the rows in `population` has a one-to-many relationship with `order` (or `trans`). If it is the case, we cannot perform the join relation directly but pass the peripheral table to getML's feature engieering algorithms in order to let them find the right aggregation operations to create the best features.
# + slideshow={"slide_type": "subslide"}
import numpy as np
account_ids = population['account_id'].to_numpy()
for peri_ in [order, trans]:
print(peri_.name)
unique, counts = np.unique(peri_['account_id'].to_numpy(), return_counts=True)
for acc_ in account_ids:
idx = np.where(unique == float(acc_))[0]
if counts[idx] > 1:
print("-> has one-to-many")
break
# + [markdown] slideshow={"slide_type": "skip"}
# Consequently, we keep both `order` and `trans` as part of our relational data model and assign the columns in both tables appropriate roles. Before assigning a column the role categorical we make sure that the number of distinct categories is not too large.
# + slideshow={"slide_type": "subslide"}
print('order')
order.set_role(["account_id"], getml.data.roles.join_key)
order.set_role(["amount"], getml.data.roles.numerical)
for col_ in ["bank_to", "k_symbol", "account_to"]:
unique_cat = len(np.unique(order[col_].to_numpy()))
print("Distinct categories in {}: {}".format(col_, unique_cat))
if unique_cat <= 20:
order.set_role([col_], getml.data.roles.categorical)
print('trans')
trans.set_role(["account_id", "trans_id"], getml.data.roles.join_key)
trans.set_role(["date"], getml.data.roles.time_stamp)
trans.set_role(["amount", "balance"], getml.data.roles.numerical)
for col_ in ["type", "k_symbol", "bank","operation", "account"]:
unique_cat = len(np.unique(trans[col_].to_numpy()))
print("Distinct categories in {}: {}".format(col_, unique_cat))
if unique_cat <= 20:
trans.set_role([col_], getml.data.roles.categorical)
# + [markdown] slideshow={"slide_type": "slide"}
# ### Setting units
# + [markdown] slideshow={"slide_type": "skip"}
# At this point, we stop adding peripheral tables to our data model and see how far we can get with only the two tables `trans` and `order`. However, there is one more thing we can do: We can also to tell the engine about the _unit_ for each column. Columns with the same unit will be directly compared during the feature engineering process. For more information, check out the [user guide](https://docs.getml.com/latest/user_guide/annotating_data/annotating_data.html#units).
# + slideshow={"slide_type": "fragment"}
loan.set_unit(["amount"], 'money')
order.set_unit(["amount"], 'money')
trans.set_unit(["amount", "balance"], 'money')
# + [markdown] slideshow={"slide_type": "slide"}
# ### Data model
#
# Now, we can formally define the data model. This is done using [Placeholders](https://docs.getml.com/latest/user_guide/data_model/data_model.html#placeholders). We can create these placeholder directly from the DataFrames.
# + slideshow={"slide_type": "fragment"}
population_placeholder = population.to_placeholder()
order_placeholder = order.to_placeholder()
trans_placeholder = trans.to_placeholder()
# + [markdown] slideshow={"slide_type": "skip"}
# These placeholders are then joined together in order to define the data model we will then turn over to the engine.
# + slideshow={"slide_type": "fragment"}
population_placeholder.join(order_placeholder,
join_key="account_id")
population_placeholder.join(trans_placeholder,
join_key="account_id",
time_stamp="date")
# + [markdown] slideshow={"slide_type": "slide"}
# The final data model looks like this
# + slideshow={"slide_type": "fragment"} tags=["hide_input"]
Image(filename="dataset2_jupyter.png")
# + [markdown] slideshow={"slide_type": "slide"}
# ## Training a Multirel Model
# + [markdown] slideshow={"slide_type": "skip"}
# After having prepared the dataset we can dive into the actual analysis. This is the point where getML sets in with automated feature engineering and model training. We will train a [Multirel](https://docs.getml.com/latest/user_guide/feature_engineering/feature_engineering.html#multirel) Model in order to predict the target column `default`. We will start with the default settings and take care of the hyperparameter optimization later on. Input to the model are a feature selector and a predictor. We will use XGBoost for both in this tutorial.
# + slideshow={"slide_type": "subslide"}
feature_selector = getml.predictors.XGBoostClassifier(
reg_lambda=500
)
predictor = getml.predictors.XGBoostClassifier(
reg_lambda=500
)
# + [markdown] slideshow={"slide_type": "subslide"}
# We also need to provied the placeholders defined above. Now we are ready to instantiate the MultirelModel.
# + slideshow={"slide_type": "fragment"}
agg_ = getml.models.aggregations
model = getml.models.MultirelModel(
aggregation=[
agg_.Avg,
agg_.Count,
agg_.Max,
agg_.Median,
agg_.Min,
agg_.Sum,
agg_.Var
],
num_features=30,
population=population_placeholder,
peripheral=[order_placeholder, trans_placeholder],
loss_function=getml.models.loss_functions.CrossEntropyLoss(),
feature_selector=feature_selector,
predictor=predictor,
seed=1706
).send()
# + [markdown] slideshow={"slide_type": "subslide"}
# The next step is to fit the model using the training data set.
# + slideshow={"slide_type": "fragment"}
model = model.fit(
population_table=population_train,
peripheral_tables=[order, trans]
)
# + [markdown] slideshow={"slide_type": "subslide"}
# The training time of the model is below one minute. Let's look at how well the model performs on the validation dataset.
# + slideshow={"slide_type": "fragment"}
in_sample = model.score(
population_table=population_train,
peripheral_tables=[order, trans]
)
out_of_sample = model.score(
population_table=population_test,
peripheral_tables=[order, trans]
)
print("In sample accuracy: {:.2f}\nIn sample AUC: {:.2f}\nOut of sample accuracy: {:.2f}\nOut of sample AUC: {:.2f}".format(
in_sample['accuracy'][0], in_sample['auc'][0], out_of_sample['accuracy'][0], out_of_sample['auc'][0]))
# + [markdown] slideshow={"slide_type": "skip"}
# This is already a promising result but we can try to do better by performing a hyperparameter optimization.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Hyperparameter optimization
# + [markdown] slideshow={"slide_type": "skip"}
# We will perform a hyperparamter optimization to improve the out-of-sample accuracy. We will do this using a latin hypercube search.
# + slideshow={"slide_type": "subslide"}
param_space = dict(
grid_factor = [1.0, 16.0],
max_length = [1, 10],
num_features = [10, 100],
regularization = [0.0, 0.01],
share_aggregations = [0.01, 0.3],
share_selected_features = [0.1, 1.0],
shrinkage = [0.01, 0.4],
predictor_n_estimators = [100, 400],
predictor_max_depth = [3, 15],
predictor_reg_lambda = [0.0, 1000.0]
)
latin_search = getml.hyperopt.LatinHypercubeSearch(
model=model,
param_space=param_space,
# n_iter=30,
# Set n_iter to a smaller value in order to make the notebook finish quickly
n_iter=2,
seed=1706
)
latin_search.fit(
population_table_training=population_train,
population_table_validation=population_test,
peripheral_tables=[order, trans],
)
# + slideshow={"slide_type": "subslide"}
scores = latin_search.get_scores()
best_model_name = max(scores, key=lambda key: scores[key]['auc'])
print("Out of sample accuracy: {:.2f}".format(scores[best_model_name]['accuracy'][0]))
print("AUC: {:.2f}".format(scores[best_model_name]['auc'][0]))
# + [markdown] slideshow={"slide_type": "fragment"}
# The hyperparameter optimization has improved the in sample accuracy and AUC. These results will get even better when performing a more thorough hyperparameter optimization.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Extracting Features
# + [markdown] slideshow={"slide_type": "skip"}
# So far, we have trained a MultirelModel and conducted a hyperparameter optimization. But what actually happened behind the scenes? In order to gain insight into the features the MultirelModel has construced, we will look at the in SQL code of the constructed features. This information is available in the getML monitor or by calling `to_sql` on a getML model. The feature with the highest importance looks like this:
# + [markdown] slideshow={"slide_type": "subslide"}
# ```sql
# CREATE TABLE FEATURE_2 AS
# SELECT MEDIAN( t1.date_account - t2.date ) AS feature_2,
# t1.account_id,
# t1.date
# FROM (
# SELECT *,
# ROW_NUMBER() OVER ( ORDER BY account_id, date ASC ) AS rownum
# FROM population
# ) t1
# LEFT JOIN trans t2
# ON t1.account_id = t2.account_id
# WHERE (
# ( t2.balance > 390.000000 AND t2.balance > 159331.000000 AND t1.date - t2.date <= 28.142857 )
# OR ( t2.balance > 390.000000 AND t2.balance <= 159331.000000 AND t1.amount > 464288.000000 )
# OR ( t2.balance <= 390.000000 AND t1.date_account - t2.date <= -148.000000 )
# ) AND t2.date <= t1.date
# GROUP BY t1.rownum,
# t1.account_id,
# t1.date;
# ```
# + [markdown] slideshow={"slide_type": "fragment"}
# This is a typical example of a feature generated by MultirelModel. You can see the logic behind the aggregation, but its also clear that it would have been impossible to come up with the specific values by hand or using brute force approaches.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Results
#
# We are able to predict loan default in the example dataset with an accuracy of over 95% and a very good AUC. With this result getML is in the top 1% of [published](https://relational.fit.cvut.cz/dataset/Financial) solutions on this problem. The training time for the initial model was less than one minute. Altogether, this project can easily be completed within one day.
#
# You can use this tutorial as starting point for your own analysis or head over the other tutorials and the [user guide](https://docs.getml.com) if you want to learn more about the functionality getML offers. Please [contact us](https://get.ml/contact/lets-talk) to give us feedback about this tutorial or general inquiries.
#
# You can also [download getML for free](https://getml.com/product).
|
python/projects/loans/loans.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# # Facies classification using Convolutional Neural Networks #
# ## Team StoDIG - Statoil Deep-learning Interest Group ##
# ### _[<NAME>](https://no.linkedin.com/in/david-wade-79918023), [<NAME>](https://www.linkedin.com/in/john-thurmond-098b774) & [<NAME>](https://www.linkedin.com/in/eskil-k-dahl-87a94679)_###
# In this python notebook we propose a facies classification model, building on the simple Neural Network solution proposed by LA_Team in order to outperform the prediction model proposed in the [predicting facies from well logs challenge](https://github.com/seg/2016-ml-contest).
#
# Given the limited size of the training data set, Deep Learning is not likely to exceed the accuracy of results from refined Machine Learning techniques (such as Gradient Boosted Trees). However, we chose to use the opportunity to advance our understanding of Deep Learning network design, and have enjoyed participating in the contest. With a substantially larger training set and perhaps more facies ambiguity, Deep Learning could be a preferred approach to this sort of problem.
#
#
# We use three key innovations:
# - Inserting a convolutional layer as the first layer in the Neural Network
# - Initializing the weights of this layer to detect gradients and extrema
# - Adding Dropout regularization to prevent overfitting
#
# Since our submission #2 we have:
# - Added the distance to the next NM_M transition as a feature (thanks to geoLEARN where we spotted this)
# - Removed Recruit F9 from training
#
# ... and since our submission #3 we have:
# - Included training/predicting on the Formation categories
# - Made our facies plot better, including demonstrating our confidence in each prediction
# ## Problem Modeling
# ----
#
# The dataset we will use comes from a class excercise from The University of Kansas on [Neural Networks and Fuzzy Systems](http://www.people.ku.edu/~gbohling/EECS833/). This exercise is based on a consortium project to use machine learning techniques to create a reservoir model of the largest gas fields in North America, the Hugoton and Panoma Fields. For more info on the origin of the data, see [<NAME> (2003)](http://www.kgs.ku.edu/PRS/publication/2003/ofr2003-50.pdf) and [Dubois et al. (2007)](http://dx.doi.org/10.1016/j.cageo.2006.08.011).
#
# The dataset we will use is log data from nine wells that have been labeled with a facies type based on oberservation of core. We will use this log data to train a classifier to predict facies types.
#
# This data is from the Council Grove gas reservoir in Southwest Kansas. The Panoma Council Grove Field is predominantly a carbonate gas reservoir encompassing 2700 square miles in Southwestern Kansas. This dataset is from nine wells (with 4149 examples), consisting of a set of seven predictor variables and a rock facies (class) for each example vector and validation (test) data (830 examples from two wells) having the same seven predictor variables in the feature vector. Facies are based on examination of cores from nine wells taken vertically at half-foot intervals. Predictor variables include five from wireline log measurements and two geologic constraining variables that are derived from geologic knowledge. These are essentially continuous variables sampled at a half-foot sample rate.
#
# The seven predictor variables are:
# * Five wire line log curves include [gamma ray](http://petrowiki.org/Gamma_ray_logs) (GR), [resistivity logging](http://petrowiki.org/Resistivity_and_spontaneous_%28SP%29_logging) (ILD_log10),
# [photoelectric effect](http://www.glossary.oilfield.slb.com/en/Terms/p/photoelectric_effect.aspx) (PE), [neutron-density porosity difference and average neutron-density porosity](http://petrowiki.org/Neutron_porosity_logs) (DeltaPHI and PHIND). Note, some wells do not have PE.
# * Two geologic constraining variables: nonmarine-marine indicator (NM_M) and relative position (RELPOS)
#
# The nine discrete facies (classes of rocks) are:
# 1. Nonmarine sandstone
# 2. Nonmarine coarse siltstone
# 3. Nonmarine fine siltstone
# 4. Marine siltstone and shale
# 5. Mudstone (limestone)
# 6. Wackestone (limestone)
# 7. Dolomite
# 8. Packstone-grainstone (limestone)
# 9. Phylloid-algal bafflestone (limestone)
#
# These facies aren't discrete, and gradually blend into one another. Some have neighboring facies that are rather close. Mislabeling within these neighboring facies can be expected to occur. The following table lists the facies, their abbreviated labels and their approximate neighbors.
#
# Facies |Label| Adjacent Facies
# :---: | :---: |:--:
# 1 |SS| 2
# 2 |CSiS| 1,3
# 3 |FSiS| 2
# 4 |SiSh| 5
# 5 |MS| 4,6
# 6 |WS| 5,7
# 7 |D| 6,8
# 8 |PS| 6,7,9
# 9 |BS| 7,8
# ## Setup
# ---
#
# Check we have all the libraries we need, and import the modules we require. Note that we have used the Theano backend for Keras, and to achieve a reasonable training time we have used an NVidia K20 GPU.
# + language="sh"
# pip install pandas
# pip install scikit-learn
# pip install keras
# pip install sklearn
# -
from __future__ import print_function
import time
import numpy as np
# %matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.colors as colors
from mpl_toolkits.axes_grid1 import make_axes_locatable
from keras.preprocessing import sequence
from keras.models import Model, Sequential
from keras.constraints import maxnorm, nonneg
from keras.optimizers import SGD, Adam, Adamax, Nadam
from keras.regularizers import l2, activity_l2
from keras.layers import Input, Dense, Dropout, Activation, Convolution1D, Cropping1D, Cropping2D, Permute, Flatten, MaxPooling1D, merge
from keras.wrappers.scikit_learn import KerasClassifier
from keras.utils import np_utils
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import KFold , StratifiedKFold
from classification_utilities import display_cm, display_adj_cm
from sklearn.metrics import confusion_matrix, f1_score
from sklearn import preprocessing
from sklearn.model_selection import GridSearchCV
# ## Data ingest
# ---
# We load the training and testing data to preprocess it for further analysis, filling the missing data values in the PE field with zero and proceeding to normalize the data that will be fed into our model. We now incorporate the Imputation from <NAME> via LA_Team's Submission 5.
# +
data = pd.read_csv('train_test_data.csv')
# Set 'Well Name' and 'Formation' fields as categories
data['Well Name'] = data['Well Name'].astype('category')
data['Formation'] = data['Formation'].astype('category')
def coding(col, codeDict):
colCoded = pd.Series(col, copy=True)
for key, value in codeDict.items():
colCoded.replace(key, value, inplace=True)
return colCoded
data['Formation_coded'] = coding(data['Formation'], {'A1 LM':1,'A1 SH':2,'B1 LM':3,'B1 SH':4,'B2 LM':5,'B2 SH':6,'B3 LM':7,'B3 SH':8,'B4 LM':9,'B4 SH':10,'B5 LM':11,'B5 SH':12,'C LM':13,'C SH':14})
formation = data['Formation_coded'].values[:,np.newaxis]
# Parameters
feature_names = ['Depth', 'GR', 'ILD_log10', 'DeltaPHI', 'PHIND', 'PE', 'NM_M', 'RELPOS']
facies_labels = ['SS', 'CSiS', 'FSiS', 'SiSh', 'MS','WS', 'D','PS', 'BS']
facies_colors = ['#F4D03F', '#F5B041','#DC7633','#6E2C00', '#1B4F72','#2E86C1', '#AED6F1', '#A569BD', '#196F3D']
well_names_test = ['SHRIMPLIN', '<NAME>', 'SHANKLE', '<NAME>', '<NAME>', '<NAME>', 'NOLAN', 'Recruit F9', 'NEWBY', '<NAME>']
well_names_validate = ['STUART', 'CRAWFORD']
data_vectors = data[feature_names].values
correct_facies_labels = data['Facies'].values
nm_m = data['NM_M'].values
nm_m_dist = np.zeros((nm_m.shape[0],1), dtype=int)
for i in range(nm_m.shape[0]):
count=1
while (i+count<nm_m.shape[0]-1 and nm_m[i+count] == nm_m[i]):
count = count+1
nm_m_dist[i] = count
nm_m_dist.reshape(nm_m_dist.shape[0],1)
well_labels = data[['Well Name', 'Facies']].values
depth = data['Depth'].values
# Fill missing values and normalize for 'PE' field
imp = preprocessing.Imputer(missing_values='NaN', strategy='mean', axis=0)
imp.fit(data_vectors)
data_vectors = imp.transform(data_vectors)
data_vectors = np.hstack([data_vectors, nm_m_dist, formation])
scaler = preprocessing.StandardScaler().fit(data_vectors)
scaled_features = scaler.transform(data_vectors)
data_out = np.hstack([well_labels, scaled_features])
# -
# Split data into training data and blind data, and output as Numpy arrays
# +
def preprocess(data_out):
data = data_out
X = data[0:4149,0:12]
y = np.concatenate((data[0:4149,0].reshape(4149,1), np_utils.to_categorical(correct_facies_labels[0:4149]-1)), axis=1)
X_test = data[4149:,0:12]
return X, y, X_test
X_train_in, y_train, X_test_in = preprocess(data_out)
print(X_train_in.shape)
# -
# ## Data Augmentation
# ---
#
# We expand the input data to be acted on by the convolutional layer.
# +
conv_domain = 11
# Reproducibility
np.random.seed(7)
# Load data
def expand_dims(input):
r = int((conv_domain-1)/2)
l = input.shape[0]
n_input_vars = input.shape[1]
output = np.zeros((l, conv_domain, n_input_vars))
for i in range(l):
for j in range(conv_domain):
for k in range(n_input_vars):
output[i,j,k] = input[min(i+j-r,l-1),k]
return output
X_train = np.empty((0,conv_domain,10), dtype=float)
X_test = np.empty((0,conv_domain,10), dtype=float)
y_select = np.empty((0,9), dtype=int)
well_names_train = ['SHRIMPLIN', '<NAME>', 'SHANKLE', '<NAME>', '<NAME>', '<NAME>', 'NOLAN', 'NEWBY', '<NAME>']
for wellId in well_names_train:
X_train_subset = X_train_in[X_train_in[:, 0] == wellId][:,2:12]
X_train_subset = expand_dims(X_train_subset)
X_train = np.concatenate((X_train,X_train_subset),axis=0)
y_select = np.concatenate((y_select, y_train[y_train[:, 0] == wellId][:,1:11]), axis=0)
for wellId in well_names_validate:
X_test_subset = X_test_in[X_test_in[:, 0] == wellId][:,2:12]
X_test_subset = expand_dims(X_test_subset)
X_test = np.concatenate((X_test,X_test_subset),axis=0)
y_train = y_select
print(X_train.shape)
print(X_test.shape)
print(y_select.shape)
# -
# ### Convolutional Neural Network
# #### We build a CNN with the following layers (no longer using Sequential() model):
#
# - Dropout layer on input
# - One 1D convolutional layer (7-point radius)
# - One 1D cropping layer (just take actual log-value of interest)
# - Series of Merge layers re-adding result of cropping layer plus Dropout & Fully-Connected layers
#
# #### Instead of running CNN with gradient features added, we initialize the Convolutional layer weights to achieve this
# - This allows the CNN to reject them, adjust them or turn them into something else if required
# +
# Set parameters
input_dim = 10
output_dim = 9
n_per_batch = 128
epochs = 100
crop_factor = int(conv_domain/2)
filters_per_log = 11
n_convolutions = input_dim*filters_per_log
starting_weights = [np.zeros((conv_domain, 1, input_dim, n_convolutions)), np.ones((n_convolutions))]
norm_factor=float(conv_domain)*2.0
for i in range(input_dim):
for j in range(conv_domain):
starting_weights[0][j, 0, i, i*filters_per_log+0] = j/norm_factor
starting_weights[0][j, 0, i, i*filters_per_log+1] = j/norm_factor
starting_weights[0][j, 0, i, i*filters_per_log+2] = (conv_domain-j)/norm_factor
starting_weights[0][j, 0, i, i*filters_per_log+3] = (conv_domain-j)/norm_factor
starting_weights[0][j, 0, i, i*filters_per_log+4] = (2*abs(crop_factor-j))/norm_factor
starting_weights[0][j, 0, i, i*filters_per_log+5] = (conv_domain-2*abs(crop_factor-j))/norm_factor
starting_weights[0][j, 0, i, i*filters_per_log+6] = 0.25
starting_weights[0][j, 0, i, i*filters_per_log+7] = 0.5 if (j%2 == 0) else 0.25
starting_weights[0][j, 0, i, i*filters_per_log+8] = 0.25 if (j%2 == 0) else 0.5
starting_weights[0][j, 0, i, i*filters_per_log+9] = 0.5 if (j%4 == 0) else 0.25
starting_weights[0][j, 0, i, i*filters_per_log+10] = 0.25 if (j%4 == 0) else 0.5
def dnn_model(init_dropout_rate=0.5, main_dropout_rate=0.5,
hidden_dim_1=24, hidden_dim_2=40,
max_norm=10, nb_conv=n_convolutions):
# Define the model
inputs = Input(shape=(conv_domain,input_dim,))
inputs_dropout = Dropout(init_dropout_rate)(inputs)
x1 = Convolution1D(nb_conv, conv_domain, border_mode='valid', weights=starting_weights, activation='tanh', input_shape=(conv_domain,input_dim), input_length=input_dim, W_constraint=nonneg())(inputs_dropout)
x1 = Flatten()(x1)
xn = Cropping1D(cropping=(crop_factor,crop_factor))(inputs_dropout)
xn = Flatten()(xn)
xA = merge([x1, xn], mode='concat')
xA = Dropout(main_dropout_rate)(xA)
xA = Dense(hidden_dim_1, init='uniform', activation='relu', W_constraint=maxnorm(max_norm))(xA)
x = merge([xA, xn], mode='concat')
x = Dropout(main_dropout_rate)(x)
x = Dense(hidden_dim_2, init='uniform', activation='relu', W_constraint=maxnorm(max_norm))(x)
predictions = Dense(output_dim, init='uniform', activation='softmax')(x)
model = Model(input=inputs, output=predictions)
optimizerNadam = Nadam(lr=0.002, beta_1=0.9, beta_2=0.999, epsilon=1e-08, schedule_decay=0.004)
model.compile(loss='categorical_crossentropy', optimizer=optimizerNadam, metrics=['accuracy'])
return model
# Load the model
t0 = time.time()
model_dnn = dnn_model()
model_dnn.summary()
t1 = time.time()
print("Load time = %d" % (t1-t0) )
def plot_weights(n_convs_disp=input_dim):
layerID=2
print(model_dnn.layers[layerID].get_weights()[0].shape)
print(model_dnn.layers[layerID].get_weights()[1].shape)
fig, ax = plt.subplots(figsize=(12,10))
for i in range(n_convs_disp):
plt.subplot(input_dim,1,i+1)
plt.imshow(model_dnn.layers[layerID].get_weights()[0][:,0,i,:], interpolation='none')
plt.show()
plot_weights(1)
# -
# #### We train the CNN and evaluate it on precision/recall.
# +
#Train model
t0 = time.time()
model_dnn.fit(X_train, y_train, batch_size=n_per_batch, nb_epoch=epochs, verbose=2)
t1 = time.time()
print("Train time = %d seconds" % (t1-t0) )
# Predict Values on Training set
t0 = time.time()
y_predicted = model_dnn.predict( X_train , batch_size=n_per_batch, verbose=2)
t1 = time.time()
print("Test time = %d seconds" % (t1-t0) )
# Print Report
# Format output [0 - 8 ]
y_ = np.zeros((len(y_train),1))
for i in range(len(y_train)):
y_[i] = np.argmax(y_train[i])
y_predicted_ = np.zeros((len(y_predicted), 1))
for i in range(len(y_predicted)):
y_predicted_[i] = np.argmax( y_predicted[i] )
# Confusion Matrix
conf = confusion_matrix(y_, y_predicted_)
def accuracy(conf):
total_correct = 0.
nb_classes = conf.shape[0]
for i in np.arange(0,nb_classes):
total_correct += conf[i][i]
acc = total_correct/sum(sum(conf))
return acc
adjacent_facies = np.array([[1], [0,2], [1], [4], [3,5], [4,6,7], [5,7], [5,6,8], [6,7]])
def accuracy_adjacent(conf, adjacent_facies):
nb_classes = conf.shape[0]
total_correct = 0.
for i in np.arange(0,nb_classes):
total_correct += conf[i][i]
for j in adjacent_facies[i]:
total_correct += conf[i][j]
return total_correct / sum(sum(conf))
# Print Results
print ("\nModel Report")
print ("-Accuracy: %.6f" % ( accuracy(conf) ))
print ("-Adjacent Accuracy: %.6f" % ( accuracy_adjacent(conf, adjacent_facies) ))
print ("\nConfusion Matrix")
display_cm(conf, facies_labels, display_metrics=True, hide_zeros=True)
# -
# #### We display the learned 1D convolution kernels
plot_weights()
# #### In order to avoid overfitting, we evaluate our model by running a 5-fold stratified cross-validation routine.
# +
# Cross Validation
def cross_validate():
t0 = time.time()
estimator = KerasClassifier(build_fn=dnn_model, nb_epoch=epochs, batch_size=n_per_batch, verbose=0)
skf = StratifiedKFold(n_splits=5, shuffle=True)
results_dnn = cross_val_score(estimator, X_train, y_train, cv= skf.get_n_splits(X_train, y_train))
t1 = time.time()
print("Cross Validation time = %d" % (t1-t0) )
print(' Cross Validation Results')
print( results_dnn )
print(np.mean(results_dnn))
cross_validate()
# -
# ## Prediction
# ---
# To predict the STUART and CRAWFORD blind wells we do the following:
# #### Set up a plotting function to display the logs & facies.
# +
# 1=sandstone 2=c_siltstone 3=f_siltstone
# 4=marine_silt_shale 5=mudstone 6=wackestone 7=dolomite
# 8=packstone 9=bafflestone
facies_colors = ['#F4D03F', '#F5B041','#DC7633','#6E2C00', '#1B4F72','#2E86C1', '#AED6F1', '#A569BD', '#196F3D']
#facies_color_map is a dictionary that maps facies labels
#to their respective colors
facies_color_map = {}
for ind, label in enumerate(facies_labels):
facies_color_map[label] = facies_colors[ind]
def label_facies(row, labels):
return labels[ row['Facies'] -1]
def make_facies_log_plot(logs, facies_colors, y_test=None, wellId=None):
#make sure logs are sorted by depth
logs = logs.sort_values(by='Depth')
cmap_facies = colors.ListedColormap(
facies_colors[0:len(facies_colors)], 'indexed')
ztop=logs.Depth.min(); zbot=logs.Depth.max()
facies = np.zeros(2*(int(zbot-ztop)+1))
shift = 0
depth = ztop
for i in range(logs.Depth.count()-1):
while (depth < logs.Depth.values[i] + 0.25 and depth < zbot+0.25):
if (i<logs.Depth.count()-1):
new = logs['Facies'].values[i]
facies[shift] = new
depth += 0.5
shift += 1
facies = facies[0:facies.shape[0]-1]
cluster=np.repeat(np.expand_dims(facies,1), 100, 1)
f, ax = plt.subplots(nrows=1, ncols=8, gridspec_kw={'width_ratios':[1,1,1,1,1,1,2,2]}, figsize=(10, 12))
ax[0].plot(logs.GR, logs.Depth, '-g')
ax[1].plot(logs.ILD_log10, logs.Depth, '-')
ax[2].plot(logs.DeltaPHI, logs.Depth, '-', color='0.5')
ax[3].plot(logs.PHIND, logs.Depth, '-', color='r')
ax[4].plot(logs.PE, logs.Depth, '-', color='black')
ax[5].plot(logs.NM_M, logs.Depth, '-', color='black')
if (y_test is not None):
for i in range(9):
if (wellId == 'STUART'):
ax[6].plot(y_test[0:474,i], logs.Depth, color=facies_colors[i], lw=1.5)
else:
ax[6].plot(y_test[474:,i], logs.Depth, color=facies_colors[i], lw=1.5)
im=ax[7].imshow(cluster, interpolation='none', aspect='auto',
cmap=cmap_facies,vmin=1,vmax=9)
divider = make_axes_locatable(ax[7])
cax = divider.append_axes("right", size="20%", pad=0.05)
cbar=plt.colorbar(im, cax=cax)
cbar.set_label((17*' ').join([' SS ', 'CSiS', 'FSiS',
'SiSh', ' MS ', ' WS ', ' D ',
' PS ', ' BS ']))
cbar.set_ticks(range(0,1)); cbar.set_ticklabels('')
for i in range(len(ax)-1):
ax[i].set_ylim(ztop,zbot)
ax[i].invert_yaxis()
ax[i].grid()
ax[i].locator_params(axis='x', nbins=5)
ax[0].set_xlabel("GR")
ax[0].set_xlim(logs.GR.min(),logs.GR.max())
ax[1].set_xlabel("ILD_log10")
ax[1].set_xlim(logs.ILD_log10.min(),logs.ILD_log10.max())
ax[2].set_xlabel("DeltaPHI")
ax[2].set_xlim(logs.DeltaPHI.min(),logs.DeltaPHI.max())
ax[3].set_xlabel("PHIND")
ax[3].set_xlim(logs.PHIND.min(),logs.PHIND.max())
ax[4].set_xlabel("PE")
ax[4].set_xlim(logs.PE.min(),logs.PE.max())
ax[5].set_xlabel("NM_M")
ax[5].set_xlim(logs.NM_M.min()-1.,logs.NM_M.max()+1.)
ax[6].set_xlabel("Facies Prob")
ax[6].set_xlim(0.0,1.0)
ax[7].set_xlabel('Facies')
ax[0].set_yticklabels([]);
ax[1].set_yticklabels([]); ax[2].set_yticklabels([]); ax[3].set_yticklabels([])
ax[4].set_yticklabels([]); ax[5].set_yticklabels([])
ax[6].set_xticklabels([]); ax[7].set_xticklabels([]);
f.suptitle('Well: %s'%logs.iloc[0]['Well Name'], fontsize=14,y=0.94)
# -
# #### Run the model on the blind data
# - Output a CSV
# - Plot the wells in the notebook
# +
# DNN model Prediction
y_test = model_dnn.predict( X_test , batch_size=n_per_batch, verbose=0)
predictions_dnn = np.zeros((len(y_test),1))
for i in range(len(y_test)):
predictions_dnn[i] = np.argmax(y_test[i]) + 1
predictions_dnn = predictions_dnn.astype(int)
# Store results
train_data = pd.read_csv('train_test_data.csv')
test_data = pd.read_csv('../validation_data_nofacies.csv')
test_data['Facies'] = predictions_dnn
test_data.to_csv('Prediction_StoDIG_3.csv')
for wellId in well_names_validate:
make_facies_log_plot( test_data[test_data['Well Name'] == wellId], facies_colors=facies_colors, y_test=y_test, wellId=wellId)
#for wellId in well_names_test:
# make_facies_log_plot( train_data[train_data['Well Name'] == wellId], facies_colors=facies_colors)
|
StoDIG/Facies_classification_StoDIG_4.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %matplotlib inline
#
# # Layer Images
#
#
# Layer images above one another using alpha blending
#
# +
import matplotlib.pyplot as plt
import numpy as np
def func3(x, y):
return (1 - x / 2 + x**5 + y**3) * np.exp(-(x**2 + y**2))
# make these smaller to increase the resolution
dx, dy = 0.05, 0.05
x = np.arange(-3.0, 3.0, dx)
y = np.arange(-3.0, 3.0, dy)
X, Y = np.meshgrid(x, y)
# when layering multiple images, the images need to have the same
# extent. This does not mean they need to have the same shape, but
# they both need to render to the same coordinate system determined by
# xmin, xmax, ymin, ymax. Note if you use different interpolations
# for the images their apparent extent could be different due to
# interpolation edge effects
extent = np.min(x), np.max(x), np.min(y), np.max(y)
fig = plt.figure(frameon=False)
Z1 = np.add.outer(range(8), range(8)) % 2 # chessboard
im1 = plt.imshow(Z1, cmap=plt.cm.gray, interpolation='nearest',
extent=extent)
Z2 = func3(X, Y)
im2 = plt.imshow(Z2, cmap=plt.cm.viridis, alpha=.9, interpolation='bilinear',
extent=extent)
plt.show()
# -
# ------------
#
# References
# """"""""""
#
# The use of the following functions and methods is shown
# in this example:
#
#
import matplotlib
matplotlib.axes.Axes.imshow
matplotlib.pyplot.imshow
|
matplotlib/gallery_jupyter/images_contours_and_fields/layer_images.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from scipy.optimize import minimize
import numpy as np
import matplotlib.pyplot as plt
import scipy as sp
from scipy.fftpack import fft as spfft
import os
f_sample = 500
sampling_factor = 10000
SaveFFTFig = True
SaveDir = 'Results/Exp2/FFT/'
if not os.path.exists(SaveDir):
os.makedirs(SaveDir)
# # Load data
# ## Experiment 2
Exp2_data_file = 'OptMagData/Exp2/20190406/20190406/AxionWeel000.0500.flt.csv'
Exp2_data = np.loadtxt(Exp2_data_file,delimiter= '\t')
Exp2_time = Exp2_data[:,0]
Exp2_AW_Z = Exp2_data[:,1]
Exp2_AW_X = -Exp2_data[:,2]
Exp2_AV_X = Exp2_data[:,3]
Exp2_AV_Z = Exp2_data[:,4]
plt.figure(figsize = (17,4));plt.plot(Exp2_time,Exp2_AW_X)
# +
## Full useable range
Exp2_Freq = [0.1,0.5, 1, 3, 5]
Exp2_Start_Time = [ 20,150,280,365,440]
Exp2_Stop_Time = [ 140,260,334,427,500]
Exp2_AW_X_FFT = {}
Exp2_AW_Z_FFT = {}
Exp2_AV_X_FFT = {}
Exp2_AV_Z_FFT = {}
Exp2_Freq_FFT = {}
for ii in range(len(Exp2_Freq)):
# loop_nu = Freq[ii]
key = Exp2_Freq[ii]
f_new_sample = sampling_factor*key
if f_new_sample >f_sample:
n_skips = 1
f_new_sample = f_sample
else:
n_skips = int(np.ceil(f_sample/f_new_sample))
# Cut up data
arraybool = (Exp2_time>Exp2_Start_Time[ii] )& (Exp2_time<Exp2_Stop_Time[ii])
Time_Full_Sample = Exp2_time[arraybool]
AW_X_Full = 1e-12*Exp2_AW_X[arraybool]
AW_Z_Full = 1e-12*Exp2_AW_Z[arraybool]
AV_X_Full = 1e-12*Exp2_AV_X[arraybool]
AV_Z_Full = 1e-12*Exp2_AV_Z[arraybool]
# FFT
TimeArrayLength = len(Time_Full_Sample)
Exp2_AW_X_FFT[key] = (np.fft.rfft(AW_X_Full)/TimeArrayLength)
Exp2_AW_Z_FFT[key] = (np.fft.rfft(AW_Z_Full)/TimeArrayLength)
Exp2_AV_X_FFT[key] = (np.fft.rfft(AV_X_Full)/TimeArrayLength)
Exp2_AV_Z_FFT[key] = (np.fft.rfft(AV_Z_Full)/TimeArrayLength)
Exp2_Freq_FFT[key] = f_new_sample/TimeArrayLength*np.arange(1,int(TimeArrayLength/2)+2,1)
# +
# nu = 5
# print(Exp1_Time_cut[nu].shape)
# print(Exp1_Freq_FFT[nu].shape)
# print(Exp1_X_FFT[nu].shape)
# plt.figure(figsize = (12,8))
bigplt_AW = plt.figure()
bigax_AW = bigplt_AW.add_axes([0, 0, 1, 1])
bigplt_AV = plt.figure()
bigax_AV = bigplt_AV.add_axes([0, 0, 1, 1])
for nu in Exp2_Freq:
Bmax_AW = max([max(1e12*abs(Exp2_AW_X_FFT[nu])),max(1e12*abs(Exp2_AW_Z_FFT[nu]))])
Bmax_AV = max([max(1e12*abs(Exp2_AV_X_FFT[nu])),max(1e12*abs(Exp2_AV_Z_FFT[nu]))])
indnu = (np.abs(Exp2_Freq_FFT[nu]-nu)<0.08*nu)
# print(indnu)
ind11nu = (np.abs(Exp2_Freq_FFT[nu]-11*nu)<0.08*nu)
Bmaxatnu_AW = max([1e12*abs(Exp2_AW_X_FFT[nu][indnu]).max(),1e12*abs(Exp2_AW_Z_FFT[nu][indnu]).max()])
Bmaxatnu_AV = max([1e12*abs(Exp2_AV_X_FFT[nu][indnu]).max(),1e12*abs(Exp2_AV_Z_FFT[nu][indnu]).max()])
Bmaxat11nu_AW = max([1e12*abs(Exp2_AW_X_FFT[nu][ind11nu]).max(),1e12*abs(Exp2_AW_Z_FFT[nu][ind11nu]).max()])
Bmaxat11nu_AV = max([1e12*abs(Exp2_AV_X_FFT[nu][ind11nu]).max(),1e12*abs(Exp2_AV_Z_FFT[nu][ind11nu]).max()])
figloop = plt.figure()
plt.loglog(Exp2_Freq_FFT[nu],1e12*abs(Exp2_AW_X_FFT[nu]), label = str(nu)+'Hz X',figure=figloop)
plt.loglog(Exp2_Freq_FFT[nu],1e12*abs(Exp2_AW_Z_FFT[nu]), label = str(nu)+'Hz Z',figure=figloop)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnetic Field (pT)')
plt.grid()
plt.grid(which = 'minor',linestyle = '--')
plt.annotate('$f_\mathrm{rot}$',xy = (nu,Bmaxatnu_AW),xytext=(nu,Bmax_AW),\
arrowprops=dict(color='limegreen',alpha=0.7,width = 3.5,headwidth=8, shrink=0.),\
horizontalalignment='center')
plt.annotate('$11f_\mathrm{rot}$',xy = (11*nu,Bmaxat11nu_AW),xytext=(11*nu,Bmax_AW),\
arrowprops=dict(color='fuchsia',alpha=0.5,width = 3.5,headwidth=8,shrink=0.),\
horizontalalignment='center')
plt.legend(loc='lower left')
if SaveFFTFig:
plt.savefig(SaveDir+'Exp2_AW_'+str(nu)+'Hz_FFT.png',bbox_inches = 'tight',dpi = 1000)
figloop = plt.figure()
plt.loglog(Exp2_Freq_FFT[nu],1e12*abs(Exp2_AV_X_FFT[nu]), label = str(nu)+'Hz X',figure=figloop)
plt.loglog(Exp2_Freq_FFT[nu],1e12*abs(Exp2_AV_Z_FFT[nu]), label = str(nu)+'Hz Z',figure=figloop)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnetic Field (pT)')
plt.grid()
plt.grid(which = 'minor',linestyle = '--')
plt.annotate('$f_\mathrm{rot}$',xy = (nu,Bmaxatnu_AV),xytext=(nu,Bmax_AV),\
arrowprops=dict(color='limegreen',alpha=0.7,width = 3.5,headwidth=8, shrink=0.),\
horizontalalignment='center')
plt.annotate('$11f_\mathrm{rot}$',xy = (11*nu,Bmaxat11nu_AV),xytext=(11*nu,Bmax_AV),\
arrowprops=dict(color='fuchsia',alpha=0.5,width = 3.5,headwidth=8,shrink=0.),\
horizontalalignment='center')
plt.legend(loc='lower left')
if SaveFFTFig:
plt.savefig(SaveDir+'Exp2_AV_'+str(nu)+'Hz_FFT.png',bbox_inches = 'tight',dpi = 1000)
bigax_AW.loglog(Exp2_Freq_FFT[nu],1e12*abs(Exp2_AW_X_FFT[nu]), label = str(nu)+'Hz X',figure=bigplt_AW)
bigax_AW.loglog(Exp2_Freq_FFT[nu],1e12*abs(Exp2_AW_Z_FFT[nu]), label = str(nu)+'Hz Z',figure=bigplt_AW)
bigax_AV.loglog(Exp2_Freq_FFT[nu],1e12*abs(Exp2_AV_X_FFT[nu]), label = str(nu)+'Hz X',figure=bigplt_AV)
bigax_AV.loglog(Exp2_Freq_FFT[nu],1e12*abs(Exp2_AV_Z_FFT[nu]), label = str(nu)+'Hz Z',figure=bigplt_AV)
bigax_AW.set_xlabel('Frequency (Hz)')
bigax_AW.set_ylabel('Magnetic Field (pT)')
bigax_AW.grid()
bigax_AW.grid(which = 'minor',linestyle = '--')
bigax_AW.legend(loc = 'lower left')
if SaveFFTFig:
bigplt_AW.savefig(SaveDir+'Exp2_AW_'+str('all')+'Hz_FFT.png',bbox_inches = 'tight',dpi = 1000)
bigax_AV.set_xlabel('Frequency (Hz)')
bigax_AV.set_ylabel('Magnetic Field (pT)')
bigax_AV.grid()
bigax_AV.grid(which = 'minor',linestyle = '--')
bigax_AV.legend(loc = 'lower left')
if SaveFFTFig:
bigplt_AV.savefig(SaveDir+'Exp2_AV_'+str('all')+'Hz_FFT.png',bbox_inches = 'tight',dpi = 1000)
# -
|
Code/.ipynb_checkpoints/FFT analysis-old-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## This script gets the statisctical informaiton about predictions
######### import packages
import pandas as pd
import numpy as np
import os
import glob
import torch
# Below, we start to run our script. Please note that the folders name in this script should be modified and set according to what model folders you have.
# +
if __name__ == '__main__':
#------------ set up parameters
layer_num = [2, 5, 10]
hidden_dim = [32]
# the directory of test results
# "DNN_Models/DNN_Regression/deepnn_results/test_results"
root_dir = os.path.join('../','src','DNN_Regression','deepnn_results','test_results')
# to save the statistical results
stat_info_dict = {'Layer_num':[],
'Hidden_dim':[],
'Trn_RMSE':[],
'Val_RMSE':[],
'Tst_RMSE':[],
'Pred_-12_RMSE':[],
'Pred_-12_mean':[],
'Pred_-12_std':[],
'Pred_-29_RMSE':[],
'Pred_-29_mean':[],
'Pred_-29_std':[],
'Pred_-41_RMSE':[],
'Pred_-41_mean':[],
'Pred_-41_std':[],
}
for cur_layer in layer_num:
for cur_hd in hidden_dim:
# predictions of training set
trn_pred_file = os.path.join(root_dir, 'train_prediction_L{}_H{}.csv'.format(cur_layer, cur_hd))
val_pred_file = os.path.join(root_dir, 'validation_prediction_L{}_H{}.csv'.format(cur_layer, cur_hd))
tst_pred_file = os.path.join(root_dir, 'hos_test_prediction_L{}_H{}.csv'.format(cur_layer, cur_hd))
rmse_file = os.path.join(root_dir, 'final_RMSE_L{}_H{}.csv'.format(cur_layer, cur_hd))
# read data to dataframe
trn_pred_df = pd.read_csv(trn_pred_file)
val_pred_df = pd.read_csv(val_pred_file)
tst_pred_df = pd.read_csv(tst_pred_file)
rmse_df = pd.read_csv(rmse_file)
trn_rmse = rmse_df[rmse_df['Type']=='Train_RMSE']['RMSE'].values[0]
val_rmse = rmse_df[rmse_df['Type']=='Validation_RMSE']['RMSE'].values[0]
tst_rmse = rmse_df[rmse_df['Type']=='Test_RMSE']['RMSE'].values[0]
held_out_positions = []
held_out_positions = tst_pred_df['Y_True'].unique()
print(held_out_positions)
# process each held_out positon:
temp_dict = {'-12':[], '-29':[], '-41':[]}
for cur_position in held_out_positions:
cur_pred_df = tst_pred_df[tst_pred_df['Y_True']==cur_position]
cur_Y_true = cur_pred_df['Y_True'].values
cur_Y_true = torch.from_numpy(cur_Y_true)
cur_Y_pred = cur_pred_df['Y_Prediction'].values
cur_Y_pred = torch.from_numpy(cur_Y_pred)
loss = torch.nn.MSELoss()
cur_mse = loss(cur_Y_pred, cur_Y_true)
cur_mse = torch.sqrt(cur_mse) #RMSE
cur_mse = cur_mse.item()
cur_pred_mean = cur_pred_df['Y_Prediction'].mean()
cur_pred_std = cur_pred_df['Y_Prediction'].std()
cur_position = str(cur_position).split('.')[0]
temp_dict[cur_position].append([cur_mse, cur_pred_mean, cur_pred_std])
stat_info_dict['Layer_num'].append(cur_layer)
stat_info_dict['Hidden_dim'].append(cur_hd)
stat_info_dict['Trn_RMSE'].append(trn_rmse)
stat_info_dict['Val_RMSE'].append(val_rmse)
stat_info_dict['Tst_RMSE'].append(tst_rmse)
stat_info_dict['Pred_-12_RMSE'].append(temp_dict['-12'][0][0])
stat_info_dict['Pred_-12_mean'].append(temp_dict['-12'][0][1])
stat_info_dict['Pred_-12_std'].append(temp_dict['-12'][0][2])
stat_info_dict['Pred_-29_RMSE'].append(temp_dict['-29'][0][0])
stat_info_dict['Pred_-29_mean'].append(temp_dict['-29'][0][1])
stat_info_dict['Pred_-29_std'].append(temp_dict['-29'][0][2])
stat_info_dict['Pred_-41_RMSE'].append(temp_dict['-41'][0][0])
stat_info_dict['Pred_-41_mean'].append(temp_dict['-41'][0][1])
stat_info_dict['Pred_-41_std'].append(temp_dict['-41'][0][2])
############# after finishing, let's save it
stat_info_df = pd.DataFrame.from_dict(stat_info_dict)
stat_info_file = 'stat_results/stat_info.csv'
if not os.path.exists('stat_results'):
os.makedirs('stat_results')
else:
pass
stat_info_df.to_csv(stat_info_file, index=False)
print('')
print('Congrats! The statistical information about predictions has been saved!')
# -
|
analysis/1_statistical_info.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# version 1.0.2
# # + 
# # **Introduction to Machine Learning with Apache Spark**
# ## **Predicting Movie Ratings**
# #### One of the most common uses of big data is to predict what users want. This allows Google to show you relevant ads, Amazon to recommend relevant products, and Netflix to recommend movies that you might like. This lab will demonstrate how we can use Apache Spark to recommend movies to a user. We will start with some basic techniques, and then use the [Spark MLlib][mllib] library's Alternating Least Squares method to make more sophisticated predictions.
# #### For this lab, we will use a subset dataset of 500,000 ratings we have included for you into your VM (and on Databricks) from the [movielens 10M stable benchmark rating dataset](http://grouplens.org/datasets/movielens/). However, the same code you write will work for the full dataset, or their latest dataset of 21 million ratings.
# #### In this lab:
# #### *Part 0*: Preliminaries
# #### *Part 1*: Basic Recommendations
# #### *Part 2*: Collaborative Filtering
# #### *Part 3*: Predictions for Yourself
# #### As mentioned during the first Learning Spark lab, think carefully before calling `collect()` on any datasets. When you are using a small dataset, calling `collect()` and then using Python to get a sense for the data locally (in the driver program) will work fine, but this will not work when you are using a large dataset that doesn't fit in memory on one machine. Solutions that call `collect()` and do local analysis that could have been done with Spark will likely fail in the autograder and not receive full credit.
# [mllib]: https://spark.apache.org/mllib/
# ### Code
# #### This assignment can be completed using basic Python and pySpark Transformations and Actions. Libraries other than math are not necessary. With the exception of the ML functions that we introduce in this assignment, you should be able to complete all parts of this homework using only the Spark functions you have used in prior lab exercises (although you are welcome to use more features of Spark if you like!).
# +
import sys
import os
from test_helper import Test
baseDir = os.path.join('data')
inputPath = os.path.join('cs100', 'lab4', 'small')
ratingsFilename = os.path.join(baseDir, inputPath, 'ratings.dat.gz')
moviesFilename = os.path.join(baseDir, inputPath, 'movies.dat')
# -
# ### **Part 0: Preliminaries**
# #### We read in each of the files and create an RDD consisting of parsed lines.
# #### Each line in the ratings dataset (`ratings.dat.gz`) is formatted as:
# #### `UserID::MovieID::Rating::Timestamp`
# #### Each line in the movies (`movies.dat`) dataset is formatted as:
# #### `MovieID::Title::Genres`
# #### The `Genres` field has the format
# #### `Genres1|Genres2|Genres3|...`
# #### The format of these files is uniform and simple, so we can use Python [`split()`](https://docs.python.org/2/library/stdtypes.html#str.split) to parse their lines.
# #### Parsing the two files yields two RDDS
# * #### For each line in the ratings dataset, we create a tuple of (UserID, MovieID, Rating). We drop the timestamp because we do not need it for this exercise.
# * #### For each line in the movies dataset, we create a tuple of (MovieID, Title). We drop the Genres because we do not need them for this exercise.
# +
numPartitions = 2
rawRatings = sc.textFile(ratingsFilename).repartition(numPartitions)
rawMovies = sc.textFile(moviesFilename)
def get_ratings_tuple(entry):
""" Parse a line in the ratings dataset
Args:
entry (str): a line in the ratings dataset in the form of UserID::MovieID::Rating::Timestamp
Returns:
tuple: (UserID, MovieID, Rating)
"""
items = entry.split('::')
return int(items[0]), int(items[1]), float(items[2])
def get_movie_tuple(entry):
""" Parse a line in the movies dataset
Args:
entry (str): a line in the movies dataset in the form of MovieID::Title::Genres
Returns:
tuple: (MovieID, Title)
"""
items = entry.split('::')
return int(items[0]), items[1]
ratingsRDD = rawRatings.map(get_ratings_tuple).cache()
moviesRDD = rawMovies.map(get_movie_tuple).cache()
ratingsCount = ratingsRDD.count()
moviesCount = moviesRDD.count()
print 'There are %s ratings and %s movies in the datasets' % (ratingsCount, moviesCount)
print 'Ratings: %s' % ratingsRDD.take(3)
print 'Movies: %s' % moviesRDD.take(3)
assert ratingsCount == 487650
assert moviesCount == 3883
assert moviesRDD.filter(lambda (id, title): title == 'Toy Story (1995)').count() == 1
assert (ratingsRDD.takeOrdered(1, key=lambda (user, movie, rating): movie)
== [(1, 1, 5.0)])
# -
# #### In this lab we will be examining subsets of the tuples we create (e.g., the top rated movies by users). Whenever we examine only a subset of a large dataset, there is the potential that the result will depend on the order we perform operations, such as joins, or how the data is partitioned across the workers. What we want to guarantee is that we always see the same results for a subset, independent of how we manipulate or store the data.
# #### We can do that by sorting before we examine a subset. You might think that the most obvious choice when dealing with an RDD of tuples would be to use the [`sortByKey()` method][sortbykey]. However this choice is problematic, as we can still end up with different results if the key is not unique.
# #### Note: It is important to use the [`unicode` type](https://docs.python.org/2/howto/unicode.html#the-unicode-type) instead of the `string` type as the titles are in unicode characters.
# #### Consider the following example, and note that while the sets are equal, the printed lists are usually in different order by value, *although they may randomly match up from time to time.*
# #### You can try running this multiple times. If the last assertion fails, don't worry about it: that was just the luck of the draw. And note that in some environments the results may be more deterministic.
# [sortbykey]: https://spark.apache.org/docs/latest/api/python/pyspark.html#pyspark.RDD.sortByKey
# +
tmp1 = [(1, u'alpha'), (2, u'alpha'), (2, u'beta'), (3, u'alpha'), (1, u'epsilon'), (1, u'delta')]
tmp2 = [(1, u'delta'), (2, u'alpha'), (2, u'beta'), (3, u'alpha'), (1, u'epsilon'), (1, u'alpha')]
oneRDD = sc.parallelize(tmp1)
twoRDD = sc.parallelize(tmp2)
oneSorted = oneRDD.sortByKey(True).collect()
twoSorted = twoRDD.sortByKey(True).collect()
print oneSorted
print twoSorted
assert set(oneSorted) == set(twoSorted) # Note that both lists have the same elements
assert twoSorted[0][0] < twoSorted.pop()[0] # Check that it is sorted by the keys
assert oneSorted[0:2] != twoSorted[0:2] # Note that the subset consisting of the first two elements does not match
# -
# #### Even though the two lists contain identical tuples, the difference in ordering *sometimes* yields a different ordering for the sorted RDD (try running the cell repeatedly and see if the results change or the assertion fails). If we only examined the first two elements of the RDD (e.g., using `take(2)`), then we would observe different answers - **that is a really bad outcome as we want identical input data to always yield identical output**. A better technique is to sort the RDD by *both the key and value*, which we can do by combining the key and value into a single string and then sorting on that string. Since the key is an integer and the value is a unicode string, we can use a function to combine them into a single unicode string (e.g., `unicode('%.3f' % key) + ' ' + value`) before sorting the RDD using [sortBy()][sortby].
# [sortby]: https://spark.apache.org/docs/latest/api/python/pyspark.html#pyspark.RDD.sortBy
# +
def sortFunction(tuple):
""" Construct the sort string (does not perform actual sorting)
Args:
tuple: (rating, MovieName)
Returns:
sortString: the value to sort with, 'rating MovieName'
"""
key = unicode('%.3f' % tuple[0])
value = tuple[1]
return (key + ' ' + value)
print oneRDD.sortBy(sortFunction, True).collect()
print twoRDD.sortBy(sortFunction, True).collect()
# -
# #### If we just want to look at the first few elements of the RDD in sorted order, we can use the [takeOrdered][takeordered] method with the `sortFunction` we defined.
# [takeordered]: https://spark.apache.org/docs/latest/api/python/pyspark.html#pyspark.RDD.takeOrdered
oneSorted1 = oneRDD.takeOrdered(oneRDD.count(),key=sortFunction)
twoSorted1 = twoRDD.takeOrdered(twoRDD.count(),key=sortFunction)
print 'one is %s' % oneSorted1
print 'two is %s' % twoSorted1
assert oneSorted1 == twoSorted1
# ### **Part 1: Basic Recommendations**
# #### One way to recommend movies is to always recommend the movies with the highest average rating. In this part, we will use Spark to find the name, number of ratings, and the average rating of the 20 movies with the highest average rating and more than 500 reviews. We want to filter our movies with high ratings but fewer than or equal to 500 reviews because movies with few reviews may not have broad appeal to everyone.
# #### **(1a) Number of Ratings and Average Ratings for a Movie**
# #### Using only Python, implement a helper function `getCountsAndAverages()` that takes a single tuple of (MovieID, (Rating1, Rating2, Rating3, ...)) and returns a tuple of (MovieID, (number of ratings, averageRating)). For example, given the tuple `(100, (10.0, 20.0, 30.0))`, your function should return `(100, (3, 20.0))`
# +
# TODO: Replace <FILL IN> with appropriate code
# First, implement a helper function `getCountsAndAverages` using only Python
def getCountsAndAverages(IDandRatingsTuple):
""" Calculate average rating
Args:
IDandRatingsTuple: a single tuple of (MovieID, (Rating1, Rating2, Rating3, ...))
Returns:
tuple: a tuple of (MovieID, (number of ratings, averageRating))
"""
aggr_result = (IDandRatingsTuple[0], (len(IDandRatingsTuple[1]), float(sum(IDandRatingsTuple[1])) / len(IDandRatingsTuple[1])))
return aggr_result
# +
# TEST Number of Ratings and Average Ratings for a Movie (1a)
Test.assertEquals(getCountsAndAverages((1, (1, 2, 3, 4))), (1, (4, 2.5)),
'incorrect getCountsAndAverages() with integer list')
Test.assertEquals(getCountsAndAverages((100, (10.0, 20.0, 30.0))), (100, (3, 20.0)),
'incorrect getCountsAndAverages() with float list')
Test.assertEquals(getCountsAndAverages((110, xrange(20))), (110, (20, 9.5)),
'incorrect getCountsAndAverages() with xrange')
# -
# #### **(1b) Movies with Highest Average Ratings**
# #### Now that we have a way to calculate the average ratings, we will use the `getCountsAndAverages()` helper function with Spark to determine movies with highest average ratings.
# #### The steps you should perform are:
# * #### Recall that the `ratingsRDD` contains tuples of the form (UserID, MovieID, Rating). From `ratingsRDD` create an RDD with tuples of the form (MovieID, Python iterable of Ratings for that MovieID). This transformation will yield an RDD of the form: `[(1, <pyspark.resultiterable.ResultIterable object at 0x7f16d50e7c90>), (2, <pyspark.resultiterable.ResultIterable object at 0x7f16d50e79d0>), (3, <pyspark.resultiterable.ResultIterable object at 0x7f16d50e7610>)]`. Note that you will only need to perform two Spark transformations to do this step.
# * #### Using `movieIDsWithRatingsRDD` and your `getCountsAndAverages()` helper function, compute the number of ratings and average rating for each movie to yield tuples of the form (MovieID, (number of ratings, average rating)). This transformation will yield an RDD of the form: `[(1, (993, 4.145015105740181)), (2, (332, 3.174698795180723)), (3, (299, 3.0468227424749164))]`. You can do this step with one Spark transformation
# * #### We want to see movie names, instead of movie IDs. To `moviesRDD`, apply RDD transformations that use `movieIDsWithAvgRatingsRDD` to get the movie names for `movieIDsWithAvgRatingsRDD`, yielding tuples of the form (average rating, movie name, number of ratings). This set of transformations will yield an RDD of the form: `[(1.0, u'Autopsy (Macchie Solari) (1975)', 1), (1.0, u'Better Living (1998)', 1), (1.0, u'Big Squeeze, The (1996)', 3)]`. You will need to do two Spark transformations to complete this step: first use the `moviesRDD` with `movieIDsWithAvgRatingsRDD` to create a new RDD with Movie names matched to Movie IDs, then convert that RDD into the form of (average rating, movie name, number of ratings). These transformations will yield an RDD that looks like: `[(3.6818181818181817, u'Happiest Millionaire, The (1967)', 22), (3.0468227424749164, u'Grumpier Old Men (1995)', 299), (2.882978723404255, u'Hocus Pocus (1993)', 94)]`
# +
# TODO: Replace <FILL IN> with appropriate code
# From ratingsRDD with tuples of (UserID, MovieID, Rating) create an RDD with tuples of
# the (MovieID, iterable of Ratings for that MovieID)
movieIDsWithRatingsRDD = (ratingsRDD
.map(lambda x:(x[1], x[2]))
.groupByKey())
print 'movieIDsWithRatingsRDD: %s\n' % movieIDsWithRatingsRDD.take(3)
# Using `movieIDsWithRatingsRDD`, compute the number of ratings and average rating for each movie to
# yield tuples of the form (MovieID, (number of ratings, average rating))
movieIDsWithAvgRatingsRDD = movieIDsWithRatingsRDD.map(getCountsAndAverages)
print 'movieIDsWithAvgRatingsRDD: %s\n' % movieIDsWithAvgRatingsRDD.take(3)
# To `movieIDsWithAvgRatingsRDD`, apply RDD transformations that use `moviesRDD` to get the movie
# names for `movieIDsWithAvgRatingsRDD`, yielding tuples of the form
# (average rating, movie name, number of ratings)
movieNameWithAvgRatingsRDD = (moviesRDD
.join(movieIDsWithAvgRatingsRDD).map(lambda x:(x[1][1][1], x[1][0], x[1][1][0])))
print 'movieNameWithAvgRatingsRDD: %s\n' % movieNameWithAvgRatingsRDD.take(3)
# +
# TEST Movies with Highest Average Ratings (1b)
Test.assertEquals(movieIDsWithRatingsRDD.count(), 3615,
'incorrect movieIDsWithRatingsRDD.count() (expected 3615)')
movieIDsWithRatingsTakeOrdered = movieIDsWithRatingsRDD.takeOrdered(3)
Test.assertTrue(movieIDsWithRatingsTakeOrdered[0][0] == 1 and
len(list(movieIDsWithRatingsTakeOrdered[0][1])) == 993,
'incorrect count of ratings for movieIDsWithRatingsTakeOrdered[0] (expected 993)')
Test.assertTrue(movieIDsWithRatingsTakeOrdered[1][0] == 2 and
len(list(movieIDsWithRatingsTakeOrdered[1][1])) == 332,
'incorrect count of ratings for movieIDsWithRatingsTakeOrdered[1] (expected 332)')
Test.assertTrue(movieIDsWithRatingsTakeOrdered[2][0] == 3 and
len(list(movieIDsWithRatingsTakeOrdered[2][1])) == 299,
'incorrect count of ratings for movieIDsWithRatingsTakeOrdered[2] (expected 299)')
Test.assertEquals(movieIDsWithAvgRatingsRDD.count(), 3615,
'incorrect movieIDsWithAvgRatingsRDD.count() (expected 3615)')
Test.assertEquals(movieIDsWithAvgRatingsRDD.takeOrdered(3),
[(1, (993, 4.145015105740181)), (2, (332, 3.174698795180723)),
(3, (299, 3.0468227424749164))],
'incorrect movieIDsWithAvgRatingsRDD.takeOrdered(3)')
Test.assertEquals(movieNameWithAvgRatingsRDD.count(), 3615,
'incorrect movieNameWithAvgRatingsRDD.count() (expected 3615)')
Test.assertEquals(movieNameWithAvgRatingsRDD.takeOrdered(3),
[(1.0, u'Autopsy (<NAME>) (1975)', 1), (1.0, u'Better Living (1998)', 1),
(1.0, u'Big Squeeze, The (1996)', 3)],
'incorrect movieNameWithAvgRatingsRDD.takeOrdered(3)')
# -
# #### **(1c) Movies with Highest Average Ratings and more than 500 reviews**
# #### Now that we have an RDD of the movies with highest averge ratings, we can use Spark to determine the 20 movies with highest average ratings and more than 500 reviews.
# #### Apply a single RDD transformation to `movieNameWithAvgRatingsRDD` to limit the results to movies with ratings from more than 500 people. We then use the `sortFunction()` helper function to sort by the average rating to get the movies in order of their rating (highest rating first). You will end up with an RDD of the form: `[(4.5349264705882355, u'<NAME>, The (1994)', 1088), (4.515798462852263, u"Schindler's List (1993)", 1171), (4.512893982808023, u'Godfather, The (1972)', 1047)]`
# +
# TODO: Replace <FILL IN> with appropriate code
# Apply an RDD transformation to `movieNameWithAvgRatingsRDD` to limit the results to movies with
# ratings from more than 500 people. We then use the `sortFunction()` helper function to sort by the
# average rating to get the movies in order of their rating (highest rating first)
movieLimitedAndSortedByRatingRDD = (movieNameWithAvgRatingsRDD
.filter(lambda x: (x[2] > 500))
.sortBy(sortFunction, False))
print 'Movies with highest ratings: %s' % movieLimitedAndSortedByRatingRDD.take(20)
# +
# TEST Movies with Highest Average Ratings and more than 500 Reviews (1c)
Test.assertEquals(movieLimitedAndSortedByRatingRDD.count(), 194,
'incorrect movieLimitedAndSortedByRatingRDD.count()')
Test.assertEquals(movieLimitedAndSortedByRatingRDD.take(20),
[(4.5349264705882355, u'Shawshank Redemption, The (1994)', 1088),
(4.515798462852263, u"Schindler's List (1993)", 1171),
(4.512893982808023, u'Godfather, The (1972)', 1047),
(4.510460251046025, u'Raiders of the Lost Ark (1981)', 1195),
(4.505415162454874, u'Usual Suspects, The (1995)', 831),
(4.457256461232604, u'Rear Window (1954)', 503),
(4.45468509984639, u'Dr. Strangelove or: How I Learned to Stop Worrying and Love the Bomb (1963)', 651),
(4.43953006219765, u'Star Wars: Episode IV - A New Hope (1977)', 1447),
(4.4, u'Sixth Sense, The (1999)', 1110), (4.394285714285714, u'North by Northwest (1959)', 700),
(4.379506641366224, u'Citizen Kane (1941)', 527), (4.375, u'Casablanca (1942)', 776),
(4.363975155279503, u'Godfather: Part II, The (1974)', 805),
(4.358816276202219, u"One Flew Over the Cuckoo's Nest (1975)", 811),
(4.358173076923077, u'Silence of the Lambs, The (1991)', 1248),
(4.335826477187734, u'Saving Private Ryan (1998)', 1337),
(4.326241134751773, u'Chinatown (1974)', 564),
(4.325383304940375, u'Life Is Beautiful (La Vita \ufffd bella) (1997)', 587),
(4.324110671936759, u'Monty Python and the Holy Grail (1974)', 759),
(4.3096, u'Matrix, The (1999)', 1250)], 'incorrect sortedByRatingRDD.take(20)')
# -
# #### Using a threshold on the number of reviews is one way to improve the recommendations, but there are many other good ways to improve quality. For example, you could weight ratings by the number of ratings.
# ## **Part 2: Collaborative Filtering**
# #### In this course, you have learned about many of the basic transformations and actions that Spark allows us to apply to distributed datasets. Spark also exposes some higher level functionality; in particular, Machine Learning using a component of Spark called [MLlib][mllib]. In this part, you will learn how to use MLlib to make personalized movie recommendations using the movie data we have been analyzing.
# #### We are going to use a technique called [collaborative filtering][collab]. Collaborative filtering is a method of making automatic predictions (filtering) about the interests of a user by collecting preferences or taste information from many users (collaborating). The underlying assumption of the collaborative filtering approach is that if a person A has the same opinion as a person B on an issue, A is more likely to have B's opinion on a different issue x than to have the opinion on x of a person chosen randomly. You can read more about collaborative filtering [here][collab2].
# #### The image below (from [Wikipedia][collab]) shows an example of predicting of the user's rating using collaborative filtering. At first, people rate different items (like videos, images, games). After that, the system is making predictions about a user's rating for an item, which the user has not rated yet. These predictions are built upon the existing ratings of other users, who have similar ratings with the active user. For instance, in the image below the system has made a prediction, that the active user will not like the video.
# 
# [mllib]: https://spark.apache.org/mllib/
# [collab]: https://en.wikipedia.org/?title=Collaborative_filtering
# [collab2]: http://recommender-systems.org/collaborative-filtering/
# #### For movie recommendations, we start with a matrix whose entries are movie ratings by users (shown in red in the diagram below). Each column represents a user (shown in green) and each row represents a particular movie (shown in blue).
# #### Since not all users have rated all movies, we do not know all of the entries in this matrix, which is precisely why we need collaborative filtering. For each user, we have ratings for only a subset of the movies. With collaborative filtering, the idea is to approximate the ratings matrix by factorizing it as the product of two matrices: one that describes properties of each user (shown in green), and one that describes properties of each movie (shown in blue).
# 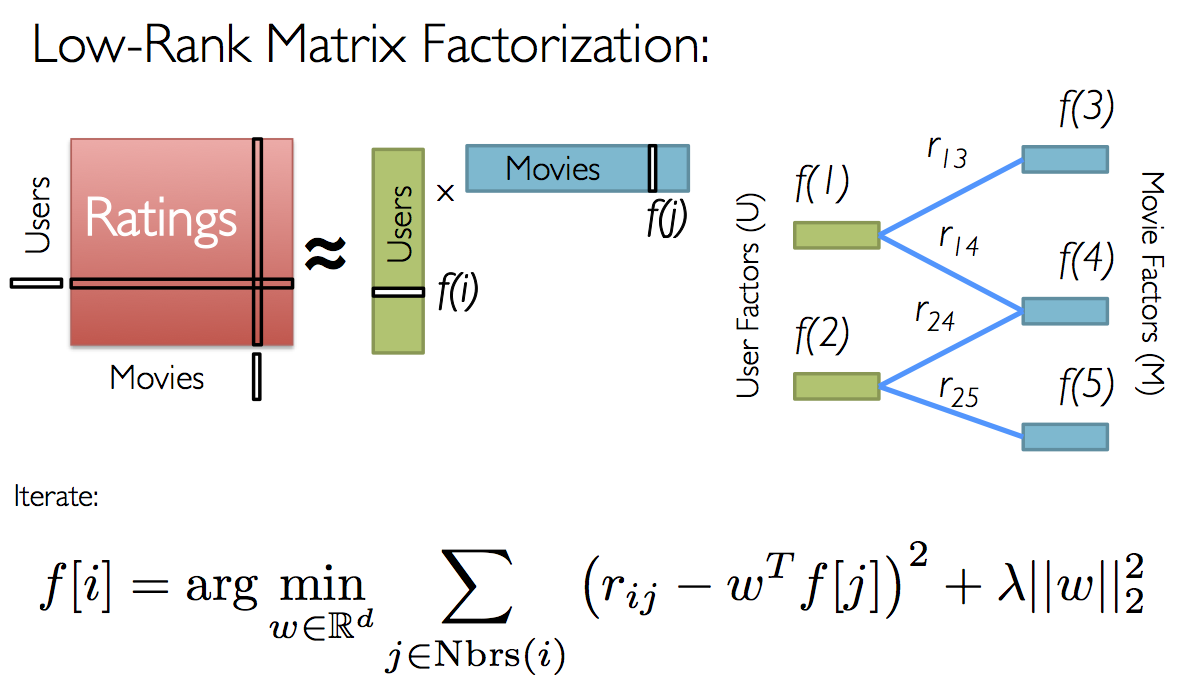
# #### We want to select these two matrices such that the error for the users/movie pairs where we know the correct ratings is minimized. The [Alternating Least Squares][als] algorithm does this by first randomly filling the users matrix with values and then optimizing the value of the movies such that the error is minimized. Then, it holds the movies matrix constrant and optimizes the value of the user's matrix. This alternation between which matrix to optimize is the reason for the "alternating" in the name.
# #### This optimization is what's being shown on the right in the image above. Given a fixed set of user factors (i.e., values in the users matrix), we use the known ratings to find the best values for the movie factors using the optimization written at the bottom of the figure. Then we "alternate" and pick the best user factors given fixed movie factors.
# #### For a simple example of what the users and movies matrices might look like, check out the [videos from Lecture 8][videos] or the [slides from Lecture 8][slides]
# [videos]: https://courses.edx.org/courses/BerkeleyX/CS100.1x/1T2015/courseware/00eb8b17939b4889a41a6d8d2f35db83/3bd3bba368be4102b40780550d3d8da6/
# [slides]: https://courses.edx.org/c4x/BerkeleyX/CS100.1x/asset/Week4Lec8.pdf
# [als]: https://en.wikiversity.org/wiki/Least-Squares_Method
# #### **(2a) Creating a Training Set**
# #### Before we jump into using machine learning, we need to break up the `ratingsRDD` dataset into three pieces:
# * #### A training set (RDD), which we will use to train models
# * #### A validation set (RDD), which we will use to choose the best model
# * #### A test set (RDD), which we will use for our experiments
# #### To randomly split the dataset into the multiple groups, we can use the pySpark [randomSplit()](https://spark.apache.org/docs/latest/api/python/pyspark.html#pyspark.RDD.randomSplit) transformation. `randomSplit()` takes a set of splits and and seed and returns multiple RDDs.
# +
trainingRDD, validationRDD, testRDD = ratingsRDD.randomSplit([6, 2, 2], seed=0L)
print 'Training: %s, validation: %s, test: %s\n' % (trainingRDD.count(),
validationRDD.count(),
testRDD.count())
print trainingRDD.take(3)
print validationRDD.take(3)
print testRDD.take(3)
assert trainingRDD.count() == 292716
assert validationRDD.count() == 96902
assert testRDD.count() == 98032
assert trainingRDD.filter(lambda t: t == (1, 914, 3.0)).count() == 1
assert trainingRDD.filter(lambda t: t == (1, 2355, 5.0)).count() == 1
assert trainingRDD.filter(lambda t: t == (1, 595, 5.0)).count() == 1
assert validationRDD.filter(lambda t: t == (1, 1287, 5.0)).count() == 1
assert validationRDD.filter(lambda t: t == (1, 594, 4.0)).count() == 1
assert validationRDD.filter(lambda t: t == (1, 1270, 5.0)).count() == 1
assert testRDD.filter(lambda t: t == (1, 1193, 5.0)).count() == 1
assert testRDD.filter(lambda t: t == (1, 2398, 4.0)).count() == 1
assert testRDD.filter(lambda t: t == (1, 1035, 5.0)).count() == 1
# -
# #### After splitting the dataset, your training set has about 293,000 entries and the validation and test sets each have about 97,000 entries (the exact number of entries in each dataset varies slightly due to the random nature of the `randomSplit()` transformation.
# #### **(2b) Root Mean Square Error (RMSE)**
# #### In the next part, you will generate a few different models, and will need a way to decide which model is best. We will use the [Root Mean Square Error](https://en.wikipedia.org/wiki/Root-mean-square_deviation) (RMSE) or Root Mean Square Deviation (RMSD) to compute the error of each model. RMSE is a frequently used measure of the differences between values (sample and population values) predicted by a model or an estimator and the values actually observed. The RMSD represents the sample standard deviation of the differences between predicted values and observed values. These individual differences are called residuals when the calculations are performed over the data sample that was used for estimation, and are called prediction errors when computed out-of-sample. The RMSE serves to aggregate the magnitudes of the errors in predictions for various times into a single measure of predictive power. RMSE is a good measure of accuracy, but only to compare forecasting errors of different models for a particular variable and not between variables, as it is scale-dependent.
# #### The RMSE is the square root of the average value of the square of `(actual rating - predicted rating)` for all users and movies for which we have the actual rating. Versions of Spark MLlib beginning with Spark 1.4 include a [RegressionMetrics](https://spark.apache.org/docs/latest/api/python/pyspark.mllib.html#pyspark.mllib.evaluation.RegressionMetrics) modiule that can be used to compute the RMSE. However, since we are using Spark 1.3.1, we will write our own function.
# #### Write a function to compute the sum of squared error given `predictedRDD` and `actualRDD` RDDs. Both RDDs consist of tuples of the form (UserID, MovieID, Rating)
# #### Given two ratings RDDs, *x* and *y* of size *n*, we define RSME as follows: $ RMSE = \sqrt{\frac{\sum_{i = 1}^{n} (x_i - y_i)^2}{n}}$
# #### To calculate RSME, the steps you should perform are:
# * #### Transform `predictedRDD` into the tuples of the form ((UserID, MovieID), Rating). For example, tuples like `[((1, 1), 5), ((1, 2), 3), ((1, 3), 4), ((2, 1), 3), ((2, 2), 2), ((2, 3), 4)]`. You can perform this step with a single Spark transformation.
# * #### Transform `actualRDD` into the tuples of the form ((UserID, MovieID), Rating). For example, tuples like `[((1, 2), 3), ((1, 3), 5), ((2, 1), 5), ((2, 2), 1)]`. You can perform this step with a single Spark transformation.
# * #### Using only RDD transformations (you only need to perform two transformations), compute the squared error for each *matching* entry (i.e., the same (UserID, MovieID) in each RDD) in the reformatted RDDs - do *not* use `collect()` to perform this step. Note that not every (UserID, MovieID) pair will appear in both RDDs - if a pair does not appear in both RDDs, then it does not contribute to the RMSE. You will end up with an RDD with entries of the form $ (x_i - y_i)^2$ You might want to check out Python's [math](https://docs.python.org/2/library/math.html) module to see how to compute these values
# * #### Using an RDD action (but **not** `collect()`), compute the total squared error: $ SE = \sum_{i = 1}^{n} (x_i - y_i)^2 $
# * #### Compute *n* by using an RDD action (but **not** `collect()`), to count the number of pairs for which you computed the total squared error
# * #### Using the total squared error and the number of pairs, compute the RSME. Make sure you compute this value as a [float](https://docs.python.org/2/library/stdtypes.html#numeric-types-int-float-long-complex).
# #### Note: Your solution must only use transformations and actions on RDDs. Do _not_ call `collect()` on either RDD.
# +
# TODO: Replace <FILL IN> with appropriate code
import math
def computeError(predictedRDD, actualRDD):
""" Compute the root mean squared error between predicted and actual
Args:
predictedRDD: predicted ratings for each movie and each user where each entry is in the form
(UserID, MovieID, Rating)
actualRDD: actual ratings where each entry is in the form (UserID, MovieID, Rating)
Returns:
RSME (float): computed RSME value
"""
# Transform predictedRDD into the tuples of the form ((UserID, MovieID), Rating)
predictedReformattedRDD = predictedRDD.map(lambda x: ((x[0], x[1]), x[2]))
# Transform actualRDD into the tuples of the form ((UserID, MovieID), Rating)
actualReformattedRDD = actualRDD.map(lambda x: ((x[0], x[1]), x[2]))
# Compute the squared error for each matching entry (i.e., the same (User ID, Movie ID) in each
# RDD) in the reformatted RDDs using RDD transformtions - do not use collect()
squaredErrorsRDD = (predictedReformattedRDD
.join(actualReformattedRDD)
.map(lambda x: (x, (x[1][0] - x[1][1])**2)))
# Compute the total squared error - do not use collect()
totalError = squaredErrorsRDD.values().sum()
# Count the number of entries for which you computed the total squared error
numRatings = squaredErrorsRDD.count()
# Using the total squared error and the number of entries, compute the RSME
return math.sqrt(float(totalError)/numRatings)
# sc.parallelize turns a Python list into a Spark RDD.
testPredicted = sc.parallelize([
(1, 1, 5),
(1, 2, 3),
(1, 3, 4),
(2, 1, 3),
(2, 2, 2),
(2, 3, 4)])
testActual = sc.parallelize([
(1, 2, 3),
(1, 3, 5),
(2, 1, 5),
(2, 2, 1)])
testPredicted2 = sc.parallelize([
(2, 2, 5),
(1, 2, 5)])
testError = computeError(testPredicted, testActual)
print 'Error for test dataset (should be 1.22474487139): %s' % testError
testError2 = computeError(testPredicted2, testActual)
print 'Error for test dataset2 (should be 3.16227766017): %s' % testError2
testError3 = computeError(testActual, testActual)
print 'Error for testActual dataset (should be 0.0): %s' % testError3
# -
# TEST Root Mean Square Error (2b)
Test.assertTrue(abs(testError - 1.22474487139) < 0.00000001,
'incorrect testError (expected 1.22474487139)')
Test.assertTrue(abs(testError2 - 3.16227766017) < 0.00000001,
'incorrect testError2 result (expected 3.16227766017)')
Test.assertTrue(abs(testError3 - 0.0) < 0.00000001,
'incorrect testActual result (expected 0.0)')
# #### **(2c) Using ALS.train()**
# #### In this part, we will use the MLlib implementation of Alternating Least Squares, [ALS.train()](https://spark.apache.org/docs/latest/api/python/pyspark.mllib.html#pyspark.mllib.recommendation.ALS). ALS takes a training dataset (RDD) and several parameters that control the model creation process. To determine the best values for the parameters, we will use ALS to train several models, and then we will select the best model and use the parameters from that model in the rest of this lab exercise.
# #### The process we will use for determining the best model is as follows:
# * #### Pick a set of model parameters. The most important parameter to `ALS.train()` is the *rank*, which is the number of rows in the Users matrix (green in the diagram above) or the number of columns in the Movies matrix (blue in the diagram above). (In general, a lower rank will mean higher error on the training dataset, but a high rank may lead to [overfitting](https://en.wikipedia.org/wiki/Overfitting).) We will train models with ranks of 4, 8, and 12 using the `trainingRDD` dataset.
# * #### Create a model using `ALS.train(trainingRDD, rank, seed=seed, iterations=iterations, lambda_=regularizationParameter)` with three parameters: an RDD consisting of tuples of the form (UserID, MovieID, rating) used to train the model, an integer rank (4, 8, or 12), a number of iterations to execute (we will use 5 for the `iterations` parameter), and a regularization coefficient (we will use 0.1 for the `regularizationParameter`).
# * #### For the prediction step, create an input RDD, `validationForPredictRDD`, consisting of (UserID, MovieID) pairs that you extract from `validationRDD`. You will end up with an RDD of the form: `[(1, 1287), (1, 594), (1, 1270)]`
# * #### Using the model and `validationForPredictRDD`, we can predict rating values by calling [model.predictAll()](https://spark.apache.org/docs/latest/api/python/pyspark.mllib.html#pyspark.mllib.recommendation.MatrixFactorizationModel.predictAll) with the `validationForPredictRDD` dataset, where `model` is the model we generated with ALS.train(). `predictAll` accepts an RDD with each entry in the format (userID, movieID) and outputs an RDD with each entry in the format (userID, movieID, rating).
# * #### Evaluate the quality of the model by using the `computeError()` function you wrote in part (2b) to compute the error between the predicted ratings and the actual ratings in `validationRDD`.
# #### Which rank produces the best model, based on the RMSE with the `validationRDD` dataset?
# #### Note: It is likely that this operation will take a noticeable amount of time (around a minute in our VM); you can observe its progress on the [Spark Web UI](http://localhost:4040). Probably most of the time will be spent running your `computeError()` function, since, unlike the Spark ALS implementation (and the Spark 1.4 [RegressionMetrics](https://spark.apache.org/docs/latest/api/python/pyspark.mllib.html#pyspark.mllib.evaluation.RegressionMetrics) module), this does not use a fast linear algebra library and needs to run some Python code for all 100k entries.
# +
# TODO: Replace <FILL IN> with appropriate code
from pyspark.mllib.recommendation import ALS
validationForPredictRDD = validationRDD.map(lambda x: (x[0], x[1]))
seed = 5L
iterations = 5
regularizationParameter = 0.1
ranks = [4, 8, 12]
errors = [0, 0, 0]
err = 0
tolerance = 0.03
minError = float('inf')
bestRank = -1
bestIteration = -1
for rank in ranks:
model = ALS.train(trainingRDD, rank, seed=seed, iterations=iterations,
lambda_=regularizationParameter)
predictedRatingsRDD = model.predictAll(validationForPredictRDD)
error = computeError(predictedRatingsRDD, validationRDD)
errors[err] = error
err += 1
print 'For rank %s the RMSE is %s' % (rank, error)
if error < minError:
minError = error
bestRank = rank
print 'The best model was trained with rank %s' % bestRank
# -
# TEST Using ALS.train (2c)
Test.assertEquals(trainingRDD.getNumPartitions(), 2,
'incorrect number of partitions for trainingRDD (expected 2)')
Test.assertEquals(validationForPredictRDD.count(), 96902,
'incorrect size for validationForPredictRDD (expected 96902)')
Test.assertEquals(validationForPredictRDD.filter(lambda t: t == (1, 1907)).count(), 1,
'incorrect content for validationForPredictRDD')
Test.assertTrue(abs(errors[0] - 0.883710109497) < tolerance, 'incorrect errors[0]')
Test.assertTrue(abs(errors[1] - 0.878486305621) < tolerance, 'incorrect errors[1]')
Test.assertTrue(abs(errors[2] - 0.876832795659) < tolerance, 'incorrect errors[2]')
# #### **(2d) Testing Your Model**
# #### So far, we used the `trainingRDD` and `validationRDD` datasets to select the best model. Since we used these two datasets to determine what model is best, we cannot use them to test how good the model is - otherwise we would be very vulnerable to [overfitting](https://en.wikipedia.org/wiki/Overfitting). To decide how good our model is, we need to use the `testRDD` dataset. We will use the `bestRank` you determined in part (2c) to create a model for predicting the ratings for the test dataset and then we will compute the RMSE.
# #### The steps you should perform are:
# * #### Train a model, using the `trainingRDD`, `bestRank` from part (2c), and the parameters you used in in part (2c): `seed=seed`, `iterations=iterations`, and `lambda_=regularizationParameter` - make sure you include **all** of the parameters.
# * #### For the prediction step, create an input RDD, `testForPredictingRDD`, consisting of (UserID, MovieID) pairs that you extract from `testRDD`. You will end up with an RDD of the form: `[(1, 1287), (1, 594), (1, 1270)]`
# * #### Use [myModel.predictAll()](https://spark.apache.org/docs/latest/api/python/pyspark.mllib.html#pyspark.mllib.recommendation.MatrixFactorizationModel.predictAll) to predict rating values for the test dataset.
# * #### For validation, use the `testRDD`and your `computeError` function to compute the RMSE between `testRDD` and the `predictedTestRDD` from the model.
# * #### Evaluate the quality of the model by using the `computeError()` function you wrote in part (2b) to compute the error between the predicted ratings and the actual ratings in `testRDD`.
# +
# TODO: Replace <FILL IN> with appropriate code
myModel = ALS.train(trainingRDD, bestRank, seed=seed, iterations=iterations, lambda_=regularizationParameter)
testForPredictingRDD = testRDD.map(lambda x: (x[0], x[1]))
predictedTestRDD = myModel.predictAll(testForPredictingRDD)
testRMSE = computeError(testRDD, predictedTestRDD)
print 'The model had a RMSE on the test set of %s' % testRMSE
# -
# TEST Testing Your Model (2d)
Test.assertTrue(abs(testRMSE - 0.87809838344) < tolerance, 'incorrect testRMSE')
# #### **(2e) Comparing Your Model**
# #### Looking at the RMSE for the results predicted by the model versus the values in the test set is one way to evalute the quality of our model. Another way to evaluate the model is to evaluate the error from a test set where every rating is the average rating for the training set.
# #### The steps you should perform are:
# * #### Use the `trainingRDD` to compute the average rating across all movies in that training dataset.
# * #### Use the average rating that you just determined and the `testRDD` to create an RDD with entries of the form (userID, movieID, average rating).
# * #### Use your `computeError` function to compute the RMSE between the `testRDD` validation RDD that you just created and the `testForAvgRDD`.
# +
# TODO: Replace <FILL IN> with appropriate code
trainingAvgRating = float(trainingRDD.map(lambda x: x[2]).sum()) / trainingRDD.count()
print 'The average rating for movies in the training set is %s' % trainingAvgRating
testForAvgRDD = testRDD.map(lambda x: (x[0], x[1], trainingAvgRating))
testAvgRMSE = computeError(testRDD, testForAvgRDD)
print 'The RMSE on the average set is %s' % testAvgRMSE
# -
# TEST Comparing Your Model (2e)
Test.assertTrue(abs(trainingAvgRating - 3.57409571052) < 0.000001,
'incorrect trainingAvgRating (expected 3.57409571052)')
Test.assertTrue(abs(testAvgRMSE - 1.12036693569) < 0.000001,
'incorrect testAvgRMSE (expected 1.12036693569)')
# #### You now have code to predict how users will rate movies!
# ## **Part 3: Predictions for Yourself**
# #### The ultimate goal of this lab exercise is to predict what movies to recommend to yourself. In order to do that, you will first need to add ratings for yourself to the `ratingsRDD` dataset.
# #### **(3a) Your Movie Ratings**
# #### To help you provide ratings for yourself, we have included the following code to list the names and movie IDs of the 50 highest-rated movies from `movieLimitedAndSortedByRatingRDD` which we created in part 1 the lab.
# +
print 'Most rated movies:'
print '(average rating, movie name, number of reviews)'
for ratingsTuple in movieLimitedAndSortedByRatingRDD.take(50):
print ratingsTuple
#a = moviesRDD.join(movieIDsWithAvgRatingsRDD).map(lambda x: (x[0], x[1][0], x[1][1][1], x[1][1][0])).filter(lambda x: (x[3] > 1000 )).filter(lambda x: (x[2] < 4 )).take(50)
#for i in a:
# print i
# -
# #### The user ID 0 is unassigned, so we will use it for your ratings. We set the variable `myUserID` to 0 for you. Next, create a new RDD `myRatingsRDD` with your ratings for at least 10 movie ratings. Each entry should be formatted as `(myUserID, movieID, rating)` (i.e., each entry should be formatted in the same way as `trainingRDD`). As in the original dataset, ratings should be between 1 and 5 (inclusive). If you have not seen at least 10 of these movies, you can increase the parameter passed to `take()` in the above cell until there are 10 movies that you have seen (or you can also guess what your rating would be for movies you have not seen).
# +
# TODO: Replace <FILL IN> with appropriate code
myUserID = 0
# Note that the movie IDs are the *last* number on each line. A common error was to use the number of ratings as the movie ID.
myRatedMovies = [
# The format of each line is (myUserID, movie ID, your rating)
# For example, to give the movie "Star Wars: Episode IV - A New Hope (1977)" a five rating, you would add the following line:
# (myUserID, 260, 5),
(myUserID, 2115, 4.5), # Indiana Jones and the Temple of Doom
(myUserID, 480, 4), # <NAME>
(myUserID, 1377, 3.8), # <NAME>
(myUserID, 648, 4), # Mission Impossible
(myUserID, 2571, 4.8), # Matrix
(myUserID, 1198, 5), # Raiders of the Lost Ark
(myUserID, 1580, 3.6), # Men In Black
(myUserID, 1219, 4.5), # Psycho
(myUserID, 589, 3.2), # Terminator 2
(myUserID, 1097, 4) # ET
]
myRatingsRDD = sc.parallelize(myRatedMovies)
print 'My movie ratings: %s' % myRatingsRDD.take(10)
# -
# #### **(3b) Add Your Movies to Training Dataset**
# #### Now that you have ratings for yourself, you need to add your ratings to the `training` dataset so that the model you train will incorporate your preferences. Spark's [union()](http://spark.apache.org/docs/latest/api/python/pyspark.rdd.RDD-class.html#union) transformation combines two RDDs; use `union()` to create a new training dataset that includes your ratings and the data in the original training dataset.
# +
# TODO: Replace <FILL IN> with appropriate code
trainingWithMyRatingsRDD = trainingRDD.union(myRatingsRDD)
print ('The training dataset now has %s more entries than the original training dataset' %
(trainingWithMyRatingsRDD.count() - trainingRDD.count()))
assert (trainingWithMyRatingsRDD.count() - trainingRDD.count()) == myRatingsRDD.count()
# -
# #### **(3c) Train a Model with Your Ratings**
# #### Now, train a model with your ratings added and the parameters you used in in part (2c): `bestRank`, `seed=seed`, `iterations=iterations`, and `lambda_=regularizationParameter` - make sure you include **all** of the parameters.
# TODO: Replace <FILL IN> with appropriate code
myRatingsModel = ALS.train(trainingWithMyRatingsRDD, bestRank, seed=seed, iterations=iterations, lambda_=regularizationParameter)
# #### **(3d) Check RMSE for the New Model with Your Ratings**
# #### Compute the RMSE for this new model on the test set.
# * #### For the prediction step, we reuse `testForPredictingRDD`, consisting of (UserID, MovieID) pairs that you extracted from `testRDD`. The RDD has the form: `[(1, 1287), (1, 594), (1, 1270)]`
# * #### Use `myRatingsModel.predictAll()` to predict rating values for the `testForPredictingRDD` test dataset, set this as `predictedTestMyRatingsRDD`
# * #### For validation, use the `testRDD`and your `computeError` function to compute the RMSE between `testRDD` and the `predictedTestMyRatingsRDD` from the model.
# TODO: Replace <FILL IN> with appropriate code
predictedTestMyRatingsRDD = myRatingsModel.predictAll(testForPredictingRDD)
testRMSEMyRatings = computeError(testRDD, predictedTestMyRatingsRDD)
print 'The model had a RMSE on the test set of %s' % testRMSEMyRatings
# #### **(3e) Predict Your Ratings**
# #### So far, we have only used the `predictAll` method to compute the error of the model. Here, use the `predictAll` to predict what ratings you would give to the movies that you did not already provide ratings for.
# #### The steps you should perform are:
# * #### Use the Python list `myRatedMovies` to transform the `moviesRDD` into an RDD with entries that are pairs of the form (myUserID, Movie ID) and that does not contain any movies that you have rated. This transformation will yield an RDD of the form: `[(0, 1), (0, 2), (0, 3), (0, 4)]`. Note that you can do this step with one RDD transformation.
# * #### For the prediction step, use the input RDD, `myUnratedMoviesRDD`, with myRatingsModel.predictAll() to predict your ratings for the movies.
# +
# TODO: Replace <FILL IN> with appropriate code
# Use the Python list myRatedMovies to transform the moviesRDD into an RDD with entries that are pairs of the form (myUserID, Movie ID) and that does not contain any movies that you have rated.
myUnratedMoviesRDD = (moviesRDD
.filter(lambda x: x[0] not in [x[1] for x in myRatedMovies])
.map(lambda x: (myUserID, x[0])))
# Use the input RDD, myUnratedMoviesRDD, with myRatingsModel.predictAll() to predict your ratings for the movies
predictedRatingsRDD = myRatingsModel.predictAll(myUnratedMoviesRDD)
# -
# #### **(3f) Predict Your Ratings**
# #### We have our predicted ratings. Now we can print out the 25 movies with the highest predicted ratings.
# #### The steps you should perform are:
# * #### From Parts (1b) and (1c), we know that we should look at movies with a reasonable number of reviews (e.g., more than 75 reviews). You can experiment with a lower threshold, but fewer ratings for a movie may yield higher prediction errors. Transform `movieIDsWithAvgRatingsRDD` from Part (1b), which has the form (MovieID, (number of ratings, average rating)), into an RDD of the form (MovieID, number of ratings): `[(2, 332), (4, 71), (6, 442)]`
# * #### We want to see movie names, instead of movie IDs. Transform `predictedRatingsRDD` into an RDD with entries that are pairs of the form (Movie ID, Predicted Rating): `[(3456, -0.5501005376936687), (1080, 1.5885892024487962), (320, -3.7952255522487865)]`
# * #### Use RDD transformations with `predictedRDD` and `movieCountsRDD` to yield an RDD with tuples of the form (Movie ID, (Predicted Rating, number of ratings)): `[(2050, (0.6694097486155939, 44)), (10, (5.29762541533513, 418)), (2060, (0.5055259373841172, 97))]`
# * #### Use RDD transformations with `predictedWithCountsRDD` and `moviesRDD` to yield an RDD with tuples of the form (Predicted Rating, Movie Name, number of ratings), _for movies with more than 75 ratings._ For example: `[(7.983121900375243, u'Under Siege (1992)'), (7.9769201864261285, u'Fifth Element, The (1997)')]`
# +
# TODO: Replace <FILL IN> with appropriate code
# Transform movieIDsWithAvgRatingsRDD from part (1b), which has the form (MovieID, (number of ratings, average rating)), into and RDD of the form (MovieID, number of ratings)
movieCountsRDD = movieIDsWithAvgRatingsRDD.map(lambda x: (x[0], x[1][0]))
# Transform predictedRatingsRDD into an RDD with entries that are pairs of the form (Movie ID, Predicted Rating)
predictedRDD = predictedRatingsRDD.map(lambda x: (x[1], x[2]))
# Use RDD transformations with predictedRDD and movieCountsRDD to yield an RDD with tuples of the form (Movie ID, (Predicted Rating, number of ratings))
predictedWithCountsRDD = (predictedRDD
.join(movieCountsRDD))
# Use RDD transformations with PredictedWithCountsRDD and moviesRDD to yield an RDD with tuples of the form (Predicted Rating, Movie Name, number of ratings), for movies with more than 75 ratings
ratingsWithNamesRDD = (predictedWithCountsRDD
.filter(lambda x: x[1][1] > 75)
.join(moviesRDD)
.map(lambda x: (x[1][0][0], x[1][1], x[1][0][1])))
predictedHighestRatedMovies = ratingsWithNamesRDD.takeOrdered(20, key=lambda x: -x[0])
print ('My highest rated movies as predicted (for movies with more than 75 reviews):\n%s' %
'\n'.join(map(str, predictedHighestRatedMovies)))
|
Week 5 - Introduction to Machine Learning with Apache Spark/lab4_machine_learning_student.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Tutorial on how to use Parcels on NEMO curvilinear grids
# Parcels also supports [curvilinear grids](https://www.nemo-ocean.eu/doc/node108.html) such as those used in the [NEMO models](https://www.nemo-ocean.eu/).
#
# We will be using the example data in the `NemoCurvilinear_data/` directory. These fields are a purely zonal flow on an aqua-planet (so zonal-velocity is 1 m/s and meridional-velocity is 0 m/s everywhere, and no land). However, because of the curvilinear grid, the `U` and `V` fields vary north of 20N.
from parcels import FieldSet, ParticleSet, JITParticle, ParticleFile, plotTrajectoriesFile
from parcels import AdvectionRK4
import numpy as np
from datetime import timedelta as delta
# %matplotlib inline
# We can create a `FieldSet` just like we do for normal grids.
# Note that NEMO is discretised on a C-grid. U and V velocities are not located on the same nodes (see https://www.nemo-ocean.eu/doc/node19.html ).
#
# ```
# __V1__
# | |
# U0 U1
# |__V0__|
# ```
#
# To interpolate U, V velocities on the C-grid, Parcels needs to read the f-nodes, which are located on the corners of the cells (for indexing details: https://www.nemo-ocean.eu/doc/img360.png ).
data_path = 'NemoCurvilinear_data/'
filenames = {'U': {'lon': data_path + 'mesh_mask.nc4',
'lat': data_path + 'mesh_mask.nc4',
'data': data_path + 'U_purely_zonal-ORCA025_grid_U.nc4'},
'V': {'lon': data_path + 'mesh_mask.nc4',
'lat': data_path + 'mesh_mask.nc4',
'data': data_path + 'V_purely_zonal-ORCA025_grid_V.nc4'}}
variables = {'U': 'U',
'V': 'V'}
dimensions = {'lon': 'glamf', 'lat': 'gphif', 'time': 'time_counter'}
field_set = FieldSet.from_nemo(filenames, variables, dimensions, allow_time_extrapolation=True)
# And we can plot the `U` field.
field_set.U.show()
# As you see above, the `U` field indeed is 1 m/s south of 20N, but varies with longitude and latitude north of that
#
# Now we can run particles as normal. Parcels will take care to rotate the `U` and `V` fields
# +
# Start 20 particles on a meridional line at 180W
npart = 20
lonp = -180 * np.ones(npart)
latp = [i for i in np.linspace(-70, 88, npart)]
# Create a periodic boundary condition kernel
def periodicBC(particle, fieldset, time):
if particle.lon > 180:
particle.lon -= 360
pset = ParticleSet.from_list(field_set, JITParticle, lon=lonp, lat=latp)
pfile = ParticleFile("nemo_particles", pset, outputdt=delta(days=1))
kernels = pset.Kernel(AdvectionRK4) + periodicBC
pset.execute(kernels, runtime=delta(days=50), dt=delta(hours=6),
output_file=pfile)
# -
# And then we can plot these trajectories. As expected, all trajectories go exactly zonal and due to the curvature of the earth, ones at higher latitude move more degrees eastward (even though the distance in km is equal for all particles)
pfile.export() # export the trajectory data to a netcdf file
plotTrajectoriesFile("nemo_particles.nc");
# ### Speeding up `ParticleSet` initialisation by efficiently finding particle start-locations on the `Grid`
# On a Curvilinear grid, determining the location of each `Particle` on the grid is more complicated and therefore takes longer than on a Rectilinear grid. Since Parcels version 2.2.2, a function is available on the `ParticleSet` class, that speeds up the look-up. After creating the `ParticleSet`, but before running the `ParticleSet.execute()`, simply call the function `ParticleSet.populate_indices()`. Note that this only works if you have the [`pykdtree`](https://anaconda.org/conda-forge/pykdtree) package installed, which is only included in the Parcels dependencies in version >= 2.2.2
pset = ParticleSet.from_list(field_set, JITParticle, lon=lonp, lat=latp)
pset.populate_indices()
|
parcels/examples/tutorial_nemo_curvilinear.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Fremont Bridge Bike Traffic Analysis
#
# ### <NAME>
# First, save data location URL so we can access anytime
# %matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('seaborn')
from jupyterworkflow.data import get_fremont_data
df = get_fremont_data()
df.resample('W').sum().plot()
ax = df.resample('D').sum().rolling(365).sum().plot()
ax.set_ylim(0, None); # sets y axis to 0 at bottom, and automatic at top
df.groupby(df.index.time).mean().plot()
pivoted = df.pivot_table('Total', index=df.index.time, columns=df.index.date)
pivoted.iloc[:5, :5]
pivoted.plot(legend=False, alpha=0.02);
|
Fremont_bridge_analysis/Bridge.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Capstone Project - The Battle of Neighborhoods (Week 2)
# ## Table of contents
# * [Introduction: Business Problem](#introduction)
# * [Data](#Data)
# * [Covid-19:India](#Covid19:India)
# * [Methodology](#Methodology)
# * [Analysis:Mumbai](#Analysis:Mumbai)
# * [Results and Discussion](#results)
# * [Conclusion](#Conclusion)
#
# ## Introduction: Business Problem <a name="introduction"></a>
# # <font face="Arial Black">COVID-19 </font>
# #### Last Update - 22/04/2020
# <b face="Arial">#StayHome,SaveLives</b>
# 
# The outbreak was identified in Wuhan, China, in December 2019, declared to be a Public Health Emergency of International Concern on 30 January 2020, and **recognized as a pandemic by the World Health Organization on 11 March 2020**. As of 16 April 2020, more than 2.1 million cases of COVID-19 have been reported in 210 countries and territories, resulting in more than 140,000 deaths. More than 532,000 people have recovered, although there may be a possibility of relapse or reinfection. The deaths per diagnosed cases varies significantly between countries
#
# Coronavirus disease (COVID-19) is an infectious disease caused by a newly discovered coronavirus. Most people who fall sick with COVID-19 will experience mild to moderate symptoms and recover without special treatment.
#
# Fortunately we are in times of social media and internet to keep us update with all the information, as social media has negative side to, with all fake news making rounds on social media which ill-informs manys
#
# So with this project it is my attempt to plot and visualize correct information from genuine sources to spread correct information.
#
# Scope of this project is to do **analysis & clustering** on COVID-19 zones in **Mumbai, Maharashtra, India(The most effected city in India)** & further Map testing labs/Hospitals(**Get information using foursquare**) for COVID-19 in mumbai
#
#
#
#
# # Data
# Based on definition of our problem, For COVID-19 following are the main data scores:
#
# * https://www.kaggle.com/sudalairajkumar/covid19-in-india
# * Information tracked on daily basis https://api.covid19india.org/data.jso
# * Number of Active Cases/Cured Cases/Deaths
# * Data for mumbai covid-19 cases is sourced from http://stopcoronavirus.mcgm.gov.in/ https://github.com/shasaankdave/Coursera_Capstone/blob/master/Containment_Zones_BMC_Mumbai.pdf
# * Details about mumbai Pincodes, Area,Borough(Called BMC Wards) are sourced from https://data.gov.in/resources/all-india-pincode-directory-along-contact-details & only mumbai's pincodes & details are extracted.
#
# We decided to use folium maps with latitude & longitude to display covid-19 zones, cluster & testing facilities
# Latitude & Longitude based on Pincodes of mumbai are obtained using **Google Maps API geocoding**
#
# **Details about COVID-19 testing labs in mumbai are collect as follows**
#
# * Testing Labs in mumbai are selected using https://www.kaggle.com/sudalairajkumar/covid19-in-india
#
# * Further Details about Hospitals/testing labs are got from **Foursquare API** using **categoryId parameter** in the request URL to select hostipal as venue category
# example venue categoryId for hospitals : “4bf58dd8d48988d196941735”
# Refer for more details : https://developer.foursquare.com/docs/build-with-foursquare/categories/
# ## Covid-19:India <a name="Covid19:India"></a>
#importing dependencies
import pandas as pd
import numpy as np
from geopy.geocoders import Nominatim
import folium
import matplotlib.cm as cm
import matplotlib.colors as colors
from geopy.geocoders import Nominatim
from sklearn.cluster import KMeans
# +
#Importing Dependencies
from IPython.core.display import HTML
import folium
import datetime
from datetime import datetime
import requests
from bs4 import BeautifulSoup
import lxml.html as lh
import re
import time
import psutil
import json
from PIL import Image
import os
from os import path
import matplotlib.pyplot as plt
import plotly.graph_objects as go
from pandas.plotting import register_matplotlib_converters
import plotly.express as px
from plotly.subplots import make_subplots
from IPython.display import display, Markdown, Latex
import matplotlib as plot
from matplotlib.pyplot import figure
import seaborn as sns
register_matplotlib_converters()
from IPython.display import Markdown
import plotly.offline as py
import plotly.express as px
dataset = pd.DataFrame()
# -
# # India's Neighbour with Corona :Timeline Visualization
# Visualization Credits: https://flo.uri.sh/story/258632/embed#slide-0
from IPython.core.display import HTML
HTML('''<div class="flourish-embed" data-src="story/258632" data-url="https://flo.uri.sh/story/258632/embed"><script src="https://public.flourish.studio/resources/embed.js"></script></div>''')
# ## Importing & Groupfy Data by States
# +
df = pd.read_csv('/mnt/d/Coursera_Capstone/covid19/Covid_data_srk/covid_19_india.csv')
data = df.copy()
data['Date'] = data['Date'].apply(pd.to_datetime)
data.drop(['Sno', 'Time'],axis=1,inplace=True)
# collect present data
from datetime import date
data_apr = data[data['Date'] > pd.Timestamp(date(2020,4,12))]
# prepaing data state wise
state_cases = data_apr.groupby('State/UnionTerritory')['Confirmed','Deaths','Cured'].max().reset_index()
state_cases['Active'] = state_cases['Confirmed'] - (state_cases['Deaths']- state_cases['Cured'])
state_cases["Death Rate (per 100)"] = np.round(100*state_cases["Deaths"]/state_cases["Confirmed"],2)
state_cases["Cure Rate (per 100)"] = np.round(100*state_cases["Cured"]/state_cases["Confirmed"],2)
# -
state_cases.head()
# ### Data Credits: https://api.covid19india.org/data.json
# Get COVID-19 Data Daily
testingHistory = pd.DataFrame()
testingNO = []
testedPos = []
timeStamp = []
indiaLiveJson = 'https://api.covid19india.org/data.json'
r = requests.get(indiaLiveJson)
indiaData = r.json()
indiaData
# ### Creating list for India State/UT
state_lst=state_cases['State/UnionTerritory'].unique().tolist()
# ### Get India State/UT Co-ordinates using GeoLocator Nominatim API
# +
#Get Statewise Location Co-ordinates using GeoCoder API
lat=[]
long=[]
state_val=[]
#address = 'Mumbai, india'
for state in state_cases['State/UnionTerritory']:
add= str(state) + ',india'
address = add
geolocator = Nominatim(user_agent="can_explorer")
location = geolocator.geocode(address,timeout=15)
latitude = lat.append(location.latitude)
longitude =long.append(location.longitude)
state_val.append(state)
print('The geograpical coordinate found for {}.'.format(add))
# +
map_india= pd.DataFrame({"States": state_val,
"Latitude": lat,
"Longitude": long,
"Confirmed":list(state_cases['Confirmed']),
"Recovered" :list(state_cases['Cured']),
"Deaths" :list(state_cases['Deaths'])})
map_india.head()
# -
# ### Get Location Co-Ordinates for India
address = ' India'
geolocator = Nominatim(user_agent="can_explorer")
location = geolocator.geocode(address,timeout=15)
latitude = location.latitude
longitude =location.longitude
print('The geograpical coordinate found for {} Lat: {} Long:{}'.format(address,latitude,longitude))
# ### Map India from co-ordinates: Circle Marker size based on number of confirmed cases in State
# +
#_map= folium.Map(location=[latitude, longitude], zoom_start=4)
covid_map_india=folium.Map(location=[23,80], tiles="Stamen Toner", zoom_start=4)
for lat, long, value, state in zip(map_india['Latitude'], map_india['Longitude'], map_india['Confirmed'], map_india['States']):
label = '{},{}'.format(state,value)
label = folium.Popup(label, parse_html=True)
folium.CircleMarker(
[lat, long],
#radius=5,
radius=(int((np.log(value+1.00001))))*3,
popup=label,
color='Red',
fill=True,
fill_color='#3186cc',
fill_opacity=0.7,
parse_html=False).add_to(covid_map_india)
covid_map_india
# -
display(Markdown("** STATE WISE CONFIRMED, DEATH AND CURED CASES of 2019-nCoV**"))
state_cases.sort_values('Confirmed', ascending= False).fillna(0).style.background_gradient(cmap='YlOrBr',subset=["Confirmed"])\
.background_gradient(cmap='Reds',subset=["Deaths"])\
.background_gradient(cmap='Greens',subset=["Cured"])\
.background_gradient(cmap='Blues',subset=["Active"])\
.background_gradient(cmap='Purples',subset=["Death Rate (per 100)"])\
.background_gradient(cmap='Greens',subset=["Cure Rate (per 100)"])
# # From Above Chart it is clear that Maharashtra State of India & Mumbai city in the state has Max. Cases, Hence our problem statement is based on Mumbai City
# # Top 5 States with Highest Confirmed cases & Deaths
india_grouped=map_india.groupby('States')['States','Confirmed','Recovered','Deaths'].sum().reset_index()
india_grouped.sort_values(by=['Confirmed','Recovered','Deaths'],inplace=True,ascending=False)
india_head=india_grouped.head()
india_head
# ### States with Most Number of cases
plt.plot(india_head['States'], india_head['Confirmed'], 'b--', label='Confirmed')
plt.plot(india_head['States'], india_head['Recovered'], 'g--', label='Recovered')
plt.plot(india_head['States'], india_head['Deaths'], 'r--', label='Deaths')
plt.grid()
plt.legend() # add legend based on line labels
plt.show()
# ### Cases to Death Ratio on Plot for all INDIA STATES/UT
# +
f, ax = plt.subplots(figsize=(15, 8))
data = state_cases[['State/UnionTerritory','Confirmed','Deaths']]
data.sort_values('Confirmed',ascending=False,inplace=True)
sns.set_color_codes("pastel")
sns.barplot(x="Confirmed", y="State/UnionTerritory", data=data,
label="Total", color="r")
sns.set_color_codes("muted")
sns.barplot(x="Deaths", y="State/UnionTerritory", data=data,
label="Deaths", color="g")
# Add a legend and informative axis label
ax.legend(ncol=2, loc="lower right", frameon=True)
ax.set(xlim=(0, 10000), ylabel="",
xlabel="Cases")
sns.despine(left=True, bottom=True)
plt.show()
# -
# # Let's Have Look at Relations Between Cases & Deaths
# ### COVID-19 Death History in INDIA
# ### <font face="Arial Black">COVID-19 India: Analysis, Visualization, And Comparison</font>
# #### Last Update - 23/04/2020
# 
india_data=df
india_count_grouped=india_data.groupby('Date')['Date','Confirmed','Deaths','Cured'].sum().reset_index()
india_count_grouped.columns
india_count_grouped.info()
#india_count_grouped['Date'] =pd.to_datetime(india_count_grouped['Date'])
#
#df['Date']=pd.to_datetime(df['Date'])
india_count_grouped['Date']=pd.to_datetime(india_count_grouped['Date'])
india_count_grouped.sort_values(by=['Date'], inplace=True)
india_count_grouped.head()
#india_count_grouped['Date']=pd.to_datetime(india_count_grouped['Date'].dt.strftime('%m/%d/%Y'))
india_count_grouped['Date'] = pd.to_datetime(india_count_grouped['Date'].dt.strftime('%d/%m/%Y'))
dg= india_count_grouped.groupby(pd.Grouper(key='Date', freq='1M')).sum()
dg.index = dg.index.strftime('%B')
dg
dg.plot(kind='line',x='Deaths',y='Confirmed',color='red')
#df.plot(kind='scatter',x='num_children',y='num_pets',color='red')
plt.show()
# # Linear Relationship between Cases & Deaths so Death Cases are Directly Proportional to Confirmed Cases
# ## From this ground work we know, maximum number of cases are in Maharastra state of india & Mumbai city, Hence we choose to do our capstone project on mumbai city for week 2.
# ## Methodology <a name="Methodology"></a>
# In this project we will direct our efforts on finding covid-19 zones in mumbai and further find details and plot folium maps for:
# * Covid-19 zones in Mumbai, India
# * Covid-19 testing facilities in the neighbourhood
# * Coivd-19 Clustered for mumbai neighbourhood.
#
#
# In first step with "**COVID-19:INDIA**" above we tried to analyse covid-19 situation in INDIA with bar plot, line plot & folium maps to get the top effected city, after analysis we found **Mumbai, Maharashtra, India** is the most effected city in india, Hence we selected Mumbai as our neighbourhood for this capstone project.
#
# In Second step we tried get data for hospitals/testing labs in mumbai from source & tried to get details using **foursquare API** and all information for latitude & longitude was obtained using **Geolocator API **
#
# In Third step we started with getting information regarding covid-19 zones in mumbai, information is sourced from mumbai municipal corportation website, other needed information regarding postal code was found from government of india site and to have a clear picture of cases in mumbai we grouped mumbai covid zones as per boroughs(Called Wards in Mumbai) and plotted covid zones in mumbai with bar plot & folium maps
#
# In fourth and final step we tried to cluster mumbai covid-19 zone using k-mean clustering, to have clear label on clustering we plot a folium maps for clusters color-coded by cluster numbers.
# ## Analysis:Mumbai <a name="Analysis:Mumbai"></a>
#Start with Postal code imports
mumbai_pincodes=pd.read_csv('./Mumbai_Data/Mumbai_Pincodes_latitude_longitude.csv')
mumbai_pincodes.head()
mumbai_pincodes.shape
#Read Covid-19 zones in Mumbai sourced from :http://stopcoronavirus.mcgm.gov.in/
# https://github.com/shasaankdave/Coursera_Capstone/blob/master/Containment_Zones_BMC_Mumbai.pdf
covid_zones_mumbai=pd.read_csv('./Mumbai_Data/Covid_Zones_Mumbai.csv')
covid_zones_mumbai.head()
#Merging Covid zones & mumbai pincode data to get covid zones latitude & Longitude
covid19_mumbai=covid_zones_mumbai.merge(mumbai_pincodes,how='left',on='Pincode',validate='m:1')
#Comprehensive dataset of covid-19 cases in mumbai uptill 18th April
#Source: http://stopcoronavirus.mcgm.gov.in/
covid19_mumbai.head()
# # Hospitals/testing Labs in Mumbai
#Looking at Testing labs from india's list & extract mumbai's data
testing_labs_india=pd.read_csv('./covid19/Covid_data_srk/ICMRTestingLabs.csv')
testing_labs_india.rename(columns={"pincode": "Pincode"},inplace=True)
mumbai_testing_labs=testing_labs_india.loc[testing_labs_india['city']== 'Mumbai']
mumbai_testing_labs.head()
#Map Mumbai's Testing labs with latitude & Longitude:Key{PinCode}
mumbai_labs_ll=mumbai_testing_labs.merge(mumbai_pincodes,how='left',on='Pincode',validate='m:1')
mumbai_labs_ll.head()
# # Found Latitude on Longitude reported Above as not correct.
# ## Hence Use GeoLocator API to get authentic Latitude & Longitude
# +
lat=[]
long=[]
pincd=[]
#address = 'Mumbai, india'
for pincode in mumbai_labs_ll['Pincode']:
add= str(pincode) + ',india'
address = add
geolocator = Nominatim(user_agent="can_explorer")
location = geolocator.geocode(address,timeout=15)
latitude = lat.append(location.latitude)
longitude =long.append(location.longitude)
pincd.append(pincode)
print('The geograpical coordinate found for {}.'.format(add))
# -
# ### Preprocessing Data before Mapping
# +
Mumbai_covid_labs = pd.DataFrame({"Pincode": pincd,
"Latitude": lat,
"Longitude": long})
Mumbai_covid_labs.head()
Mumbai_covid_labs.drop_duplicates('Pincode',inplace=True)
# -
mumbai_labs_final=mumbai_testing_labs.merge(Mumbai_covid_labs,how='left',on='Pincode',validate='m:1')
mumbai_labs_final.dropna(inplace=True)
mumbai_labs_final.head()
#Get Location co-ordinates for MUMBAI
address = ' Mumbai,India'
geolocator = Nominatim(user_agent="can_explorer")
location = geolocator.geocode(address,timeout=15)
latitude = location.latitude
longitude =location.longitude
print('The geograpical coordinate found for {} Lat: {} Long:{}'.format(address,latitude,longitude))
# ### Find Data for Hospitals using FourSquare Location API
# Category ID is used to find a particular type of veune in neighbourhood Refer https://developer.foursquare.com/docs/build-with-foursquare/categories/ for more details on venue category Ids Category Id for **Hospitals = 4bf58dd8d48988d196941735 **
# +
#FourSquare API Parameter SetUp
LIMIT = 100
CLIENT_ID = 'ZVLUP1PU41P2XVZN1R15EWMRBMOUU5MA3HTHOYKFKZTHWMYJ' # your Foursquare ID
CLIENT_SECRET = '<KEY>' # your Foursquare Secret
VERSION = '20180605' # Foursquare API version
CATEGORYID='4bf58dd8d48988d196941735' #venueid for hospitals
print('Your credentails:')
print('CLIENT_ID: ' + CLIENT_ID)
print('CLIENT_SECRET:' + CLIENT_SECRET)
lat='19.25023195'
lng='73.16017493'
radius=500
# -
# create the API request URL
radius=500
latitude=19.0025 #Mumbai
longitude=72.8421 #Mumbai
#for latitude,longitude in zip(mumbai_covid_clusters['Latitude'],mumbai_covid_clusters['Longitude']):
url = 'https://api.foursquare.com/v2/venues/search?categoryId={}&client_id={}&client_secret={}&v={}&ll={},{}&radius={}&limit={}'.format(CATEGORYID,CLIENT_ID, CLIENT_SECRET, VERSION, latitude, longitude, radius, LIMIT)
results = requests.get(url).json()["response"]#['groups'][0]['items']
#results = requests.get(url).json()
results
# +
#Plot Mumbai COVID testing Labs
mumbai_labs= folium.Map(location=[latitude, longitude], zoom_start=9)
for lat, lng, Pincode, lab,typeh in zip(mumbai_labs_final['Latitude'], mumbai_labs_final['Longitude'], mumbai_labs_final['Pincode'], mumbai_labs_final['lab'],mumbai_labs_final['type']):
label = '{}, {},{}'.format(Pincode,lab,typeh)
label = folium.Popup(label, parse_html=True)
if typeh =='Private Laboratory':
val='blue'
else:
val='green'
folium.CircleMarker(
[lat, lng],
radius=5,
popup=label,
color=val,
fill=True,
fill_color='#3186cc',
fill_opacity=0.7,
parse_html=False).add_to(mumbai_labs)
mumbai_labs
# -
# ### Green Points for Government testing labs & Blue for Non-Government Testing Labs
#
# ### Step 3: Mumbai COVID-19 Zones
#Get Data to Start with covid zones
covid19_zones=covid19_mumbai
covid19_zones.drop_duplicates('Pincode',inplace=True)
covid19_zones.shape
covid19_zones.head()
#Get Overview of effected Wards(boroughs) in Mumbai
zn=covid19_zones['Ward'].unique()
zn
# ### <font face="Arial Black">COVID-19 Mumbai Overview</font>
# **Image credit http://stopcoronavirus.mcgm.gov.in/ **
# #### Last Update - 23/04/2020
# 
# PreProcessing data for plotting:
covid19_zones
covid19_zones.dropna(subset=['Latitude', 'Longitude'],inplace=True)
# +
#Plot Mumbai City Covid-19 Zones on Map using folium
mumbai_19= folium.Map(location=[latitude, longitude], zoom_start=10)
x = np.arange(21)
ys = [i + x + (i*x)**2 for i in range(21)]
colors_array = cm.rainbow(np.linspace(0, 1, len(ys)))
rainbow = [colors.rgb2hex(i) for i in colors_array]
for lat, lng, Pincode,ward,address in zip(covid19_zones['Latitude'], covid19_zones['Longitude'], covid19_zones['Pincode'], covid19_zones['Ward'],covid19_zones['Address']):
label = '{}, {},{}'.format(Pincode,ward,address)
label = folium.Popup(label, parse_html=True)
folium.CircleMarker(
[lat, lng],
radius=5,
popup=label,
color='red',
fill=True,
fill_color='#3186cc',
fill_opacity=0.7,
parse_html=False).add_to(mumbai_19)
mumbai_19
# -
# ## South Mumbai is Mostly effected region
# Preprocessing for Wards
covid_mumbai_wards=covid_zones_mumbai
covid_mumbai_wards.shape
ward_group=covid_mumbai_wards.groupby('Ward')['Address'].count().reset_index()
ward_group.rename(columns={"Address": "Cases_Count"},inplace=True)
ward_group.columns
# ### Plot Ward-wise Counts : Bar Plot
# +
#Plotting Ward-wise Count:
f, ax = plt.subplots(figsize=(15, 8))
data = ward_group[['Ward','Cases_Count']]
data.sort_values('Ward',ascending=False,inplace=True)
sns.set_color_codes("pastel")
sns.barplot(x="Ward", y="Cases_Count", data=data,
label="Total", color="r")
# Add a legend and informative axis label
ax.legend(ncol=2, loc="lower right", frameon=True)
ax.set(xlim=(0, 10), ylabel="",
xlabel="Cases")
sns.despine(left=True, bottom=True)
plt.show()
# -
# # Step 4: Mumbai Clustering & Visualization
# ## Read_Data & Pre-processing
postal_cd=mumbai_pincodes
mum_postal_cd=postal_cd.loc[postal_cd['Region']== 'Mumbai']
mum_postal_cd.columns
mum_final=mum_postal_cd[['Pincode',' Area']]
mum_final.shape
zones=covid_zones_mumbai.groupby('Pincode')['Address'].count().reset_index()
zones.head()
zones.rename(columns={"Address": "Cases_Count"},inplace=True)
zones.columns
#Data Frame to be used for clustering
model_mum=mum_final.merge(zones,how='left',on='Pincode')
model_mum.head()
model_mum["Cases_Count"].fillna(0.0, inplace = True)
# Final DataFrame as clustering input
model_mum1=model_mum[['Pincode','Cases_Count']]
# ## K-Mean Clustering on COVID-19 zones in Mumbai
# +
kclusters = 3
clustering_covid_mumbai = model_mum1
# run k-means clustering
kmeans = KMeans(n_clusters=kclusters, random_state=0).fit(clustering_covid_mumbai)
# check cluster labels generated for each row in the dataframe
kmeans.labels_[0:80]
# -
# ### Pre-Processing For Plotting
pincd_lst=mum_postal_cd['Pincode'].unique().tolist()
covid_lat_lst=mum_postal_cd['Latitude'].tolist()
covid_long_lst=mum_postal_cd['Longitude'].tolist()
cluster_labels=kmeans.labels_[0:]
cluster_lst=cluster_labels.tolist()
#=cluster_labels
len(cluster_lst)
len(covid_long_lst)
len(covid_lat_lst)
len(pincd_lst)
mumbai_covid_clusters=pd.DataFrame({"Pincode": pincd_lst,
"Latitude": covid_lat_lst,
"Longitude":covid_long_lst,
"Cluster_label":cluster_lst,
})
mumbai_covid_clusters.head()
mumbai_clust=mumbai_covid_clusters.merge(covid_zones_mumbai,how='left',on='Pincode')
# +
#Finally Plotting Clusters for Mumbai Covid-19 Zone
map_clusters = folium.Map(location=[latitude, longitude],tiles="Stamen Toner", zoom_start=10)
# set color scheme for the clusters
x = np.arange(kclusters)
ys = [i + x + (i*x)**2 for i in range(kclusters)]
#colors_array = cm.rainbow(np.linspace(0, 1, len(ys)))
#rainbow = [colors.rgb2hex(i) for i in colors_array]
color_code = ['green','blue','red']
# add markers to the map
markers_colors = []
for lat, lon, poi, cluster in zip(mumbai_covid_clusters['Latitude'], mumbai_covid_clusters['Longitude'], mumbai_covid_clusters['Pincode'], mumbai_covid_clusters['Cluster_label']):
label = folium.Popup(str(poi) + ' Cluster ' + str(cluster), parse_html=True)
if cluster != 'Nan':
val=int(cluster)
folium.CircleMarker(
[lat, lon],
radius=5,
popup=label,
color=color_code[val],
fill=True,
fill_color=rainbow[val-1],
fill_opacity=0.7).add_to(map_clusters)
map_clusters
# -
# ## Results and Discussion <a name="Results"></a>
# ### Our Analysis show following are the insights:
# * Total Number of covid-19 cases in India : 27892
# * Total Number of covid-19 cases in mumbai: 5407 src: https://en.wikipedia.org/wiki/2020_coronavirus_pandemic_in_Maharashtra
# * Around 20% of totals india's cases are in mumbai with around 17 Hospitals/testing labs(3 Government/14 Non-Government Labs)
#
# **Tops 5 BMC Ward effected by COVID-19 from total 11 wards are:**
# * L Ward
# * PN Ward
# * S Ward
# * ME Ward
# * MW Ward
#
# Mumbai City is most populated city in india with population of **20,411,274** Source:https://worldpopulationreview.com/world-cities/mumbai-population/ , with very densily populated slums around and as **Mumbai** is epicenter for COVID-19 in india currently with around 20% cases of india's number, it is highly on the risk of getting into phase 3(Community transmission).
#
# Mumbai city has around 1000 diagnostic centre and only 17 are catering for COVID-19 which is very few in number & for such pandemic situation and for epicenter like mumbai testing facilities should be increased for quick assessment, rapid testing and stop the spread of virus.
# ## Conclusion <a name="Conclusion"></a>
# Purpose of this project was to start analysing COVID-19 situation in India & pickup the city which has the most number of corona positive cases, Further to put the analysis & visuzlation sourced from authentic sources to avoid fake information & inform people well.
#
# Mumbai was identified as epicenter city for current corona pandemic with around 20% share alone by this city for total number of case in india, further information about testing center was mapped with cases to know relation between number of cases vs testing labs.
#
# Based upon this analysis it was found that for common man testing facilities for COVID-19 in the city of mumbai should be increases looking at the current number.
#
# Finally I would say!!
# # STAY HOME #STAY SAFE
# # <font face="Arial Black">COVID-19 India Guidelines</font>
#
# <b face="Arial">#StayHome,SaveLives</b>
# 
# Image Source: greenpeace.org
|
IBM DS Coursera Capstone Project - The Battle of Neighborhoods (Week 2).ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # CS4487 - Tutorial 1: Introduction to Jupyter and Python
#
# Welcome to Jupyter (IPython Notebooks)! In this tutorial you will get familiar with the Jupyter computing environment, and also practice writing some small Python programs.
# # What's Jupyter Notebook?
# The Jupyter Notebook is an open-source web application that allows you to create and share documents that contain live code, equations, visualizations and narrative text. Jupyter Notebook is maintained by the people at [Project Jupyter](https://jupyter.org/).
#
# Jupyter Notebook is a spin-off project from the IPython project, which used to have an IPython Notebook project itself. The name, Jupyter, comes from the core supported programming languages that it supports: Julia, Python, and R. Jupyter ships with the IPython kernel, which allows you to write your programs in Python, but there are currently over 100 other kernels that we can also use.
# ## 1. Installation
# The Jupyter Notebook is not included with Python, so you need to install Python. We recommend [Anaconda](https://www.anaconda.com/), which is a free and open-source distribution of the Python and R programming languages for scientific computing (data science, machine learning applications, large-scale data processing, predictive analytics, etc), that aims to simplify package management and deployment.
#
# The Anaconda provides large selection of packages (Jupyter, Numpy, Panda, Conda, etc) and commercial support. It is an environment manager, which provides the facility to create different python environments, each with their own settings. In addition, Anaconda has its own installer tool called conda that you could use for installing a third-party package.
#
# Recommanded version: [Anaconda3-4.2.0](https://repo.continuum.io/archive/)
#
# Enter the terminal and run the command: jupyter notebook
# 
# ## 2. Basics
# Notebooks are organized by cells. Each cell can hold either Markdown formatted text or Python code.
# - To create a new cell, use the "Insert" Menu.
# - To cut, copy, delete, or move the cell, use the "Edit" Menu
# - To choose the cell type using the dropdown menu in the toolbar, or in the "Cell" -> "Cell Type" menu.
# - To "run" the cell, use the "Cell/Run" menu item, or push the "play" button on the toolbar.
#
# Here are some useful keyboard shortcuts:
# - [arrow keys] - move up or down cells
# - b - create new cell below current one
# - a - create new cell above current one
# - dd - delete current cell
# - m - change cell to Markdown (default is code)
# - [enter] - edit cell
# - [ctrl+enter] - render/run the current cell
# - [shift+enter] - render/run the current cell, and move to the next cell.
# **Tips**:
# - In the tutorial and assignment ipynb files, it is okay to make additional code cells in the file. This will allow you to work incrementally, and avoid re-running time-consuming code blocks.
# - This cell is holding Markdown formatted text. Here is a [Markdown cheatsheet](https://github.com/adam-p/markdown-here/wiki/Markdown-Cheatsheet).
# - use the `--notebook-dir=mydir` option to start the notebook in a particular directory.
# - Windows: create a shortcut to run `jupyter-notebook.exe --notebook-dir=%userprofile%`.
# # What is Python?
# - General-purpose high-level programming language
# - Design philosophy emphasizes programmer productivity and code readability
# - "executable pseudo-code"
# - Supports multiple programming paradigms
# - object-oriented, imperative, functional
# - Dynamic typing and automatic memory management
# ## 1. Introduction
# - Object-oriented: everything is an object
# - Clean: usually one way to do something, not a dozen
# - Easy-to-learn: learn in 1-2 days
# - Easy-to-read
# - Powerful: full-fledged programming language
# - Useful: rich expansion package
# ## 2. Python Basics
# - Formatting
# - case-sensitive
# - statements end in **newline** (not semicolon)
# - use semicolon for multiple statements in one line.
# - **indentation** for code blocks (after a colon).
print("Hello")
print("Hello"); print("World")
name = "Bob"
if name == "George":
print("Hi George")
else:
print("Who are you?")
# ### 2.1 Identifiers and Variables
print("Hello World!")
# The notebook remembers the current state of the environment. Thus, variables and functions that are executed will persist. Here is a variable. Run the cell to initialize the variable.
x = 100 # int variable
miles = 1000.0 # float variable
name = "John" # string
print(x)
print(miles)
print(name)
# Now try running the below cell several times. You will see the value of `x` increase each time you run it.
x += 1
print(x)
# To reset the environment, you need to restart the kernel by either: 1) using the "Kernel/Restart" menu; or 2) the "Refresh" button on the toolbar.
#
# If you restart the kernel and try to run the above cell, you will get an error because `x` is not defined yet.
#
# The outputs can also be cleared using "Cell/All output/Clear" menu item.
# ### 2.2 List
# +
list_tmp = [ 'runoob', 786 , 2.23, 'john', 70.2 ]
tinylist = [123, 'john']
print(list_tmp) # output whole list
print(list_tmp[0]) # print first element of list
print(list_tmp[1:3]) # print second to fourth element
print(list_tmp[2:]) # print third to end element
print(tinylist * 2) # print twice
print(list_tmp + tinylist) # print combination of list and tinylist
# -
# Creating lists of numbers
a = list(range(0,5))
print(a)
a.append('blah') # add item to end
print(a)
a.pop() # remove last item and return it
# - insert and delete
a.insert(0,42) # insert 42 at index 0
print(a)
del a[2] # delete item 2
print(a)
# ### 2.3 Tuples
# - Similar to a list
# - but immutable (read-only)
# - cannot change the contents (like a string constant)
# make some tuples
x = (1,2,'three')
print(x)
y = 4,5,6 # parentheses not needed!
print(y)
z = (1,) # tuple with 1 element (the trailing comma is required)
print(z)
# ### 2.4 String methods
# - Useful methods
"112211".count("11") # 2
"this.com".endswith(".com") # True
"wxyz".startswith("wx") # True
"abc".find("c") # finds first: 2
",".join(['a', 'b', 'c']) # join list: 'a,b,c'
"aba".replace("a", "d") # replace all: "dbd"
"a,b,c".split(',') # make list: ['a', 'b', 'c']
" abc ".strip() # "abc", also rstrip(), lstrip()
# - String formatting: automatically fill in type
"{} and {} and {}".format('string', 123, 1.6789)
# - String formatting: specify type (similar to C)
"{:d} and {:f} and {:0.2f}".format(False, 3, 1.234)
# ### 2.5 Dictionaries
# - Stores key-value pairs (associative array or hash table)
# - key can be a string, number, or tuple
mydict = {'name': 'john', 42: 'sales', ('hello', 'world'): 6734}
print(mydict)
# - Access
print(mydict['name']) # get value for key 'name'
mydict['name'] = 'jon' # change value for key 'name'
mydict[2] = 5 # insert a new key-value pair
print(mydict)
del mydict[2] # delete entry for key 2
print(mydict)
# - Other operations:
mydict.keys() # iterator of all keys (no random access)
list(mydict.keys()) # convert to a list for random access
mydict.values() # iterator of all values
mydict.items() # iterator of tuples (key, value)
'name' in mydict # check the presence of a key
# ### 2.6 Sets
# - A set is a collection of unique items
a=[1, 2, 2, 2, 4, 5, 5]
sA = set(a)
sA
# Set operations
sB = {4, 5, 6, 7}
print(sA - sB) # set difference
print (sA | sB) # set union
print (sA & sB) # set intersect
# ### 2.7 List Comprehension
# - Build a new list with a "for" loop
myList = [1, 2, 2, 2, 4, 5, 5]
myList4 = [4*item for item in myList] # multiply each item by 4
myList4
# equivalent code
myList4=[]
for item in myList:
myList4.append(4*item)
myList4
# can also use conditional to select items
[4*item*4 for item in myList if item>2]
# To import package
import math
print(math.log(4))
# ### 2.8 Operators
# operator| descriptor
# - | -
# + | add
# - | subtracte
# * | multiplicate
# / | divide
# % | mode
# ** | power
# +
a = 21
b = 10
c = 0
c = a + b
print("c = ", c)
c = a - b
print("c = ", c)
c = a * b
print("c = ", c)
c = a / b
print("c = ", c)
c = a % b
print("c = ", c)
a = 2
b = 3
c = a**b
print("c = ", c)
# -
# ### 2.9 Loop: while
#
# <img src="./while.gif">
a = 1
while a < 10:
print(a)
a+=2
# ### 2.10 Conditional statement
# <img src="./if_else.gif">
flag = False
name = 'luren'
if name == 'python': # Determine whether the variable is python
flag = True # Set the flag to true when the condition is true
print('welcome boss')
else:
print(name) # Output variable name when condition is not valid
# +
num = 9
if num >= 0 and num <= 10: # Determine whether the value is between 0 and 10
print('hello')
# hello
num = 10
if num < 0 or num > 10: # Determine whether the value is less than 0 or greater than 10
print('hello')
else:
print('undefine')
num = 8
# Determine whether the value is between 0 and 5 or between 10 and 15
if (num >= 0 and num <= 5) or (num >= 10 and num <= 15):
print('hello')
else:
print('undefine')
# -
# ### 2.11 Function
def functionname( parameters ):
function_suite
return [expression]
# +
def printme( str ):
print(str);
return;
printme("Use user-defined functions");
# -
# ### 2.12 Classes
# - Defining a class
# - `self` is a reference to the object instance (passed _implicitly_)
class MyList:
"class documentation string"
num = 0 # a class variable
def __init__(self, b): # constructor
self.x = [b] # an instance variable
MyList.num += 1 # modify class variable
def appendx(self, b): # a class method
self.x.append(b) # modify an instance variable
self.app = 1 # create new instance variable
# Using the class
c = MyList(0) # create an instance of MyList
print(c.x)
c.appendx(1) # c.x = [0, 1]
print(c.x)
c.appendx(2) # c.x = [0, 1, 2]
print(c.x)
print(MyList.num) # access class variable (same as c.num)
# ### 2.13 More on Classes
# - There are _no_ "private" members
# - everything is accessible
# - convention to indicate _private_:
# - `_variable` means private method or variable (but still accessible)
# - convention for _very private_:
# - `__variable` is not directly visible
# - actually it is renamed to `_classname__variable`
# - Instance variable rules
# - On _use_ via instance (`self.x`), scope search order is:
# - (1) instance, (2) class, (3) base classes
# - also the same for method lookup
# - On _assignment_ via instance (`self.x=...`):
# - always makes an instance variable
# - Class variables "default" for instance variables
# - _class_ variable: one copy _shared_ by all
# - _instance_ variable: each instance has its own
# ### 2.14 Inheritence
# - Child class inherits attributes from parents
class MyListAll(MyList):
def __init__(self, a): # overrides MyList
self.allx = [a]
MyList.__init__(self, a) # call base class constructor
def popx(self):
return self.x.pop()
def appendx(self, a): # overrides MyList
self.allx.append(a)
MyList.appendx(self, a) # "super" method call
# - Multiple inheritence
# - `class ChildClass(Parent1, Parent2, ...)`
# - calling method in parent
# - `super(ChildClass, self).method(args)`
# ### 2.15 Class methods & Built-in Attributes
# - Useful methods to override in class
# class MyList2:
# ...
# def __str__(self): # string representation
# ...
# def __cmp__(self, x): # object comparison
# ...
# def __del__(self): # destructor
# - Built-in attributes
print(c.__dict__) # Dictionary with the namespace.
print(c.__doc__) # Class documentation string
print(c.__module__) # Module which defines the class
print(MyList.__name__) # Class name
print(MyList.__bases__) # tuple of base classes
# ### 2.16 File Input/Ouput
# - Write a file
f = open("myfile.txt", "w")
f.write("blah\n")
f.writelines(['line1\n', 'line2\n', 'line3\n'])
f.close()
# - Read a whole file
f = open("myfile.txt", "r")
contents = f.read() # read the whole file as a string
f.close()
print(contents)
# - Read line or remaining lines
f = open("myfile.txt", 'r')
print(f.readline()) # read a single line.
print(f.readlines()) # read remaining lines in a list.
f.close()
# - Read line by line with a loop
f = open("myfile.txt", 'r')
for line in f:
print(line) # still contains newline char
# ### 2.17 Saving Objects with Pickle
# - Turns almost **any** Python **object** into a string representation for saving into a file.
import pickle # load the pickle library
mylist = MyList(0) # an object
file = open('alist.pickle', 'wb') # open file to save object (write bytes)
pickle.dump(mylist, file) # save the object using pickle
file.close() # close the file
# - Load object from file
file = open('alist.pickle', 'rb') # (read bytes)
mylist2 = pickle.load(file) # load pickled object from file
file.close()
print(mylist2)
print(mylist2.x)
# - cPickle is a faster version (1,000 times faster!)
# ### 2.18 Exception Handling
# - Catching an exception
# - `except` block catches exceptions
# - `else` block executes if no exception occurs
# - `finally` block always executes at end
try:
file = open('blah.pickle', 'r')
blah = pickle.load(file)
file.close()
except: # catch everything
print("No file!")
else: # executes if no exception occurred
print("No exception!")
finally:
print("Bye!") # always executes
# ### 2.19 Pandas
# - pandas is a Python library for data wrangling and analysis.
# - `Dataframe` is a table of entries (like an Excel spreadsheet).
# - each column does not need to be the same type
# - operations to modify and operate on the table
# setup pandas and display
import pandas as pd
# +
# read CSV file
df = pd.read_csv('mycsv.csv')
# print the dataframe
df
# -
# - select a column
df['Name']
# - query the table
# select Age greater than 30
df[df.Age > 30]
# - compute statistics
df.mean()
# ### 2.20 NumPy
# - Library for multidimensional arrays and 2D matrices
# - `ndarray` class for multidimensional arrays
# - elements are all the same type
# - aliased to `array`
from numpy import * # import all classes from numpy
a = arange(15)
a
b = a.reshape(3,5)
b
b.shape # get the shape (num rows x num columns)
b.ndim # get number of dimensions
b.size # get number of elements
b.dtype # get the element type
# ### 2.21 Array Creation
a = array([1, 2, 3, 4]) # use a list to initialize
a
b = array([[1.1,2,3], [4,5,6]]) # or list of lists
b
zeros( (3,4) ) # 3x4 array of zeros
ones( (2,4) ) # 2x4 array of ones
empty( (2,3) ) # create an array, but do not prepopulate it.
# contents are random
arange(0,5,0.5) # from 0 to 5 (exclusive), increment by 0.5
linspace(0,1,10) # 10 evenly-spaced numbers between 0 to 1 (inclusive)
logspace(-3,3,13) # 13 numbers evenly spaced in log-space between 1e-3 and 1e3
# ### 2.22 Array Indexing
# - One-dimensional arrays are indexed, sliced, and iterated similar to Python lists.
a = array([1,2,3,4,5])
a[2]
a[2:5] # index 2 through 4
a[0:5:2] # index 0 through 4, by 2
# iterating with loop
for i in a:
print(i)
# - For multi-dimensional arrays, each axis had an index.
# - indices are given using tuples (separated by commas)
a = array([[1, 2, 3], [4, 5, 6], [7,8,9]])
print(a)
a[0,1] # row 0, column 1
a[:,1] # all elements in column 1
a[0:2, 1:3] # sub array: rows 0-1, and columns 1-2
# - indexing with a boolean mask
a = array([3, 1, 2, 4])
m = array([True, False, False, True])
print("m =", m)
a[m] # select with a mask
# ### 2.23 Array Operations
# - operators are applied **elementwise**
a = array( [20,30,40,50] )
b = arange( 4 ) # [0 1 2 3]
a - b # element-wise subtraction
b**2 # element-wise exponentiation
10*sin(a) # element-wise product and sin
a < 35 # element-wise comparison
# - product operator (`*`) is **elementwise**
A = array( [[1,1],
[0,1]] )
B = array( [[2,0],
[3,4]] )
A*B # elementwise product
# - use `dot` function for matrix product
dot(A,B) # matrix product
# - compound assignment: `*=`, `+=`, `-=`
# - unary operators
a = array( [[1,2,3], [4, 5, 6]])
a.sum()
a.min()
a.max()
# - unary operators on each axis of array
a = array( [[1,2,3], [4, 5, 6]])
a.sum(axis=0) # sum over rows
a.sum(axis=1) # sum over column
# - Numpy provides functions for other operations (called universal functions)
# - `argmax`, `argmin`, `min`, `max`
# - `average`, `cov`, `std`, `mean`, `median`,
# - `ceil`, `floor`
# - `cumsum`, `cumprod`, `diff`, `sum`, `prod`
# - `inv`, `dot`, `trace`, `transpose`
# ### 2.24 Array Shape Manipulation
# - The shape of an array can be changed
a = array([[1,2,3], [4, 5, 6]])
print(a)
a.shape
a.ravel() # return flattened array (last index iterated first).
a.transpose() # return transposed array
a.reshape(3,2) # return reshaped array
a.resize(3,2) # change the shape directly
print(a)
# ### 2.25 Concatenating arrays
a = array([1, 2, 3])
b = array([4, 5, 6])
concatenate((a,b))
c_[a,b] # concatenate as column vectors
r_[a,b] # concatenate as row vectors
# +
# Stacking arrays
# -
a = array([[1, 1],
[1, 1]])
b = array([[2, 2],
[2, 2]])
vstack( (a,b) ) # stack vertically
hstack( (a,b) ) # stack horizontally
# ### 2.26 Copies and Views
# - When operating on arrays, data is sometimes copied and sometimes not.
# - _No copy is made for simple assignment._
# - **Be careful!**
a = array([1,2,3,4])
b = a # simple assignment (no copy made!)
b is a # yes, b references the same object
b[1] = -2 # changing b also changes a
a
# - View or shallow copy
# - different array objects can share the same data (called a view)
# - happens when slicing
c = a.view() # create a view of a
c is a # not the same object
c.base is a # but the data is owned by a
c.shape = 2,2 # change shape of c
c
a # but the shape of a is the same
# - Deep copy
d = a.copy() # create a complete copy of a (new data is created)
d is a # not the same object
d.base is a # not sharing the same data
# ### 2.27 Visualizing Data
# - Use matplotlib package to make plots and graphs
# - Works with Jupyter to show plots within the notebook
# setup matplotlib
# %matplotlib inline
# setup output image format (Chrome works best)
import IPython.core.display
IPython.core.display.set_matplotlib_formats("svg") # file format
import matplotlib.pyplot as plt
# - Each cell will start a new figure automatically.
# - Plots are made piece by piece.
x = linspace(0,2*pi,16)
y = sin(x)
plt.plot(x, y, 'bo-')
plt.grid(True)
plt.ylabel('y label')
plt.xlabel('x label')
plt.title('my title')
plt.show()
# - plot string specifies three things (e.g., `'bo-'`)
# - colors:
# - **b**lue, **r**ed, **g**reen, **m**agenta, **c**yan, **y**ellow, blac**k**, **w**hite
# - markers:
# - ”.” point
# - “o” circle
# - “v” triangle down
# - “^” triangle up
# - “<” triangle left
# - “>” triangle right
# - “8” octagon
# - “s” square
# - “p” pentagon
# - “*” star
# - “h” hexagon1
# - “+” plus
# - “x” x
# - “d” thin_diamond
# - line styles:
# - '-' solid line
# - '--' dashed line
# - '-.' dash-dotted line
# - ':' dotted lione
# ### 2.28 Python Tutorials
# - Python - https://docs.python.org/3/tutorial/
# - numpy - https://docs.scipy.org/doc/numpy-dev/user/quickstart.html
# - scikit-learn - http://scikit-learn.org/stable/tutorial/
# - matplotlib - http://matplotlib.org/users/pyplot_tutorial.html
# - pandas - https://pandas.pydata.org/pandas-docs/stable/tutorials.html
#
#
# ## 3. Python Program
# In the rest of the tutorial, you will write a small program to get familiar with Python.
#
# The goal of the program is to count the number of factors (_not including 1 and the number itself_) for each number between 2 and 100. For example, the number of factors of 2 is 0, and the number of factors for 4 is 1.
#
# Here are two variables to get you started, `xs` stores the numbers from 2 to 100, and `fs` will store the factors for each number in `xs`.
xs = range(2,101) # the number
fs = [] # store number of factors in this list
# Write the program in the cell below.
# +
# INSERT YOUR CODE HERE
# -
# Now we will make some plots using `xs` and `fs`. First, we need to initialize the matplotlib library.
# setup matplotlib display
# %matplotlib inline
import IPython.core.display # setup output image format
IPython.core.display.set_matplotlib_formats("svg")
import matplotlib.pyplot as plt # import matplotlib
# Write code to plot the number of factors (y-axis) vs the number (x-axis). Don't forget to label your axes!
# +
# INSERT YOUR CODE HERE
# -
# Next we will plot a histogram of the number of factors.
binedges = [i-0.5 for i in range(0,12)] # first get the edges of bins
plt.hist(fs, binedges, # histogram plot (data, bins)
facecolor='g', alpha=0.75, align='mid') # appearance options
plt.xlabel('Number of factors')
plt.ylabel('Count')
plt.title('Histogram of number of factors')
plt.axis([-0.5, 10.5, 0, 35]) # set the axis (xmin, xmax, ymin, ymax)
plt.grid(True)
# ## 4. Pickle
# Next you will practice using pickle to load data from the file "data1.pickle". The pickle is storing an ndarray object (numpy multi-dimensional array). Load the pickle file and save its contents into a variable called `mydata`.
#
# +
# INSERT YOUR CODE HERE
# -
# `mydata` is a 2-d array. Each row of the array is a "sample". Let's look at the shape of the array.
mydata.shape
# Inspecting the shape of the array, we see that there are 120 samples (rows). Each sample is a 2-dimensional vector (the number of columns).
# Finally, let's visualise the data with a plot. Treat the 1st dimension of the samples as the x-variable, and the 2nd dimension as the y-variable. In other words, plot the 1st column of the data vs. the 2nd column of the data.
# +
# INSERT YOUR CODE HERE
# -
# ## 5. Getting Help
#
# IPython has built-in help. Here are some useful commands:
# - `?` - introduction to IPython
# - `object?` - info/help about an object, class, or module
# - `object??` - even more details
# - `%quickref` - quick reference for IPython magic functions (%)
# - `%history` - show the history of the session
# - tab-completion - hit tab to use auto-completion
|
tutorial-1/Tutorial1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/Rdeandres/fight-churn/blob/master/Template_Data_Exploration.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="jBXtGnDmzJB5" colab_type="text"
# **Churn Analysis**
#
# *The goal is to perform a simple churn model in python. There is a first series of notebooks and then finetuning for automatization of model in production*
#
# *The Data and description of the data can be found here:
# https://www.kaggle.com/blastchar/telco-customer-churn*
# + [markdown] id="OO1jFkslzJB7" colab_type="text"
# # Setup
# + [markdown] id="SEuhKvL8zJB7" colab_type="text"
# Importing common moduls and making sure that we have the right Environment.
# + id="LVuAWEK3zJB8" colab_type="code" colab={}
# Python ≥3.5 is required
import sys
assert sys.version_info >= (3, 5)
# Scikit-Learn ≥0.20 is required
import sklearn
assert sklearn.__version__ >= "0.20"
# Common imports
import numpy as np
import pandas as pd
import os
# To plot pretty figures
# %matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
import seaborn as sns
sns.set()
# For modelling
# !pip install -q dython
from dython import nominal
from sklearn.impute import SimpleImputer
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
# Where to save the figures
#PROJECT_ROOT_DIR = "."
#CHAPTER_ID = "end_to_end_project"
#IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID)
#os.makedirs(IMAGES_PATH, exist_ok=True)
#def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
#path = os.path.join(IMAGES_PATH, fig_id + "." + fig_extension)
#print("Saving figure", fig_id)
#if tight_layout:
#plt.tight_layout()
#plt.savefig(path, format=fig_extension, dpi=resolution)
# Ignore useless warnings (see SciPy issue #5998)
import warnings
warnings.filterwarnings(action="ignore", message="^internal gelsd")
# + [markdown] id="vtnnCPiTzJCA" colab_type="text"
# # Get the data
# + id="cB1T3_GZzJCG" colab_type="code" colab={}
import pandas as pd
df = pd.read_csv('/content/telco-customer-churn.csv')
# + [markdown] id="E7cgnfip261x" colab_type="text"
# # Explore Data (DataViz + Insights)
# + [markdown] id="ZfbCikIX4FXx" colab_type="text"
#
#
# > Outliers
#
#
# + [markdown] id="6cUvm1Yb4Noy" colab_type="text"
#
#
# > Missing Values
#
#
#
#
#
#
# + [markdown] id="zX2KQVHb5IRB" colab_type="text"
# Summary Data: Aggregations and Visualizations
# + [markdown] id="yywMknDJ5Pzb" colab_type="text"
# Correlation and Crammer's V Analysis
# + [markdown] id="DanWMMF53Hc_" colab_type="text"
# # Prepare Data for Machine Learning Algorithms
# + [markdown] id="08HxS0sl5biJ" colab_type="text"
#
#
# > Dealing with Numeric Features
#
#
# + [markdown] id="KSSQxCWN5jj4" colab_type="text"
# Dealing With Categorial features
#
# > Bloc en retrait
#
#
# + [markdown] id="Omer_2Lr5p9T" colab_type="text"
#
#
# > Joining Tables
#
#
# + [markdown] id="o8gii65K5tjO" colab_type="text"
#
#
# > Test and Learning DataSet
#
#
# + [markdown] id="mGT5HfSE3PL0" colab_type="text"
# # Select and train baseline model
# + [markdown] id="hBRnhqIp3VT8" colab_type="text"
# # Fine tune Model
# + [markdown] id="2iRRFCln33EW" colab_type="text"
# # Additional Model
|
Template_Data_Exploration.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Preprocess the dataset and creating class labels into meta data
# Import libraries
import random
import csv
import cv2
import os
import shutil
from imutils import paths
def check_dir_exist(directory):
'''
Check for directory otherwise creates that directory
'''
if not os.path.exists(directory):
os.makedirs(directory)
Dataset_path = './Dataset' # Path to the dataset
# sorted list of directory
data_path_ = sorted(list(paths.list_images(Dataset_path)))
# split train and test data
random.shuffle(data_path_)
i = int(len(data_path_) * 0.75)
trainPaths = data_path_[:i]
testPaths = data_path_[i:]
datasets = [
("train", trainPaths, "train.csv"),
("test", testPaths, "test.csv")
]
# +
labels = []
for (dType, imagePaths, outputPath) in datasets:
# open the meta data file for writing
print("writing '{}' split...".format(dType))
f = open(outputPath, "w")
# loop over images
for imagePath in imagePaths:
# load the input image and resize it to a fixed size (64 x 64)
image = cv2.imread(imagePath)
image = cv2.resize(image, (64, 64))
# flatten pixel values
image = [str(x) for x in image.flatten()]
# Split label values from meta data
label = imagePath.split(os.path.sep)[-2]
labels.append(label)
f.write("{},{}\n".format(label, ",".join(image)))
# close the meta data file
f.close()
with open("class_labels.csv", "w") as f:
writer = csv.writer(f)
writer.writerow(labels)
|
1-pre_processing.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/obdegirmenci/colablend/blob/master/colablend.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="l7XaeFHvFqFU"
# # Check Hardware
# + id="uVpVp9PpFyy9"
# !nvidia-smi -q -i 0 | grep "Product Name"
# + [markdown] id="JhKyQE_C19a4"
# #Connect to Google Drive
# + [markdown] id="bN7GH5sr-Zb0"
# Specify your desired blender version and the path to your blend file within google drive.
# + id="KBF6fUHMqm-_"
from google.colab import drive
drive.mount('/gdrive', force_remount=True)
# + [markdown] id="l0YvORjcFnEh"
# # Settings
# + id="8dFNjYGTgNjR"
#@title # **Blender** Configuration { form-width: "35%" }
#@markdown ## *Use the form that has various setup options* <br>
#@markdown Please check the [latest](https://wiki.blender.org/wiki/Reference/Release_Notes/3.0/Corrective_Releases) version before beginning. [2.83 LTS](https://www.blender.org/download/lts/2-83/) & [2.93 LTS](https://www.blender.org/download/lts/2-89/)
#@markdown ## **Colab Definitions**
blender_version = '3.0.1' #@param ["2.83.19-LTS", "2.93.8-LTS", "3.0.1"] {allow-input: false}
blend_path = 'Blender/projects/' #@param {type: "string"}
output_path = 'Blender/projects/output/' #@param {type: "string"}
log_path = 'Blender/logs/log.txt' #@param {type: "string"}
root_path = '/gdrive/My Drive/' #@param {type: "string"}
#@markdown ---
#@markdown ## **Blender Preferences**
#@markdown ### Cycles Render Devices
UseGPU = True #@param {type:"boolean"}
UseCPU = True #@param {type:"boolean"}
#@markdown ---
#@markdown ## **Render Properties**
RenderEngine = 'CYCLES' #@param ["CYCLES"] {allow-input: false}
FeatureSet = 'SUPPORTED' #@param ["SUPPORTED", "EXPERIMENTAL"] {allow-input: false}
Device = 'GPU' #@param ["GPU", "CPU"] {allow-input: false}
#@markdown ---
#@markdown ### Sampling
MaxSamples = 400 #@param {type: "integer"}
# Light Paths
# TODO
#@markdown ---
#@markdown ### Performance
#@markdown #### Threads
ThreadsMode = 'AUTO' #@param ["AUTO"] {allow-input: false}
#@markdown #### Memory
UseAutoTile = True #@param {type: "boolean"}
TileSize = '256' #@param [16, 32, 64, 128, 256, 512] {allow-input: false}
#@markdown #### Acceleration Structure
UseSpatialSplits = True #@param {type: "boolean"}
#@markdown #### Final Render
PersistentData = False #@param {type: "boolean"}
#@markdown ---
#@markdown ## **Output Properties**
#@markdown ### Format
# Just basic formats. The others (like Blender's presets) can be added later after after aspect ratio definitions.
Resolution = '1920x1080' #@param ["640x360", "1280x720", "1920x1080", "2560x1440", "3840x2160"] {allow-input: false}
calcRes = Resolution.split('x')
ResolutionX = calcRes[0]
ResolutionY = calcRes[1]
Percentage = 100 #@param {type:"slider", min:25, max:200, step:25}
# Frame Range
# TODO
# Output
# TODO
#@markdown ### Post Processing
Compositing = True #@param {type: "boolean"}
#@markdown ## **Scene Properties**
#@markdown ### Scene
Camera = 'Camera.001' #@param {type: "string"}
#@markdown ---
# + [markdown] id="UUwwvaq5BxzN"
# Download, unpack and move Blender
# + id="OQ54OjLVjb26"
blender_mirrors = {'2.83.19-LTS': 'https://ftp.nluug.nl/pub/graphics/blender/release/Blender2.83/blender-2.83.19-linux-x64.tar.xz',
'2.93.8-LTS' : 'https://ftp.nluug.nl/pub/graphics/blender/release/Blender2.93/blender-2.93.8-linux-x64.tar.xz',
'3.0.1' : 'https://ftp.nluug.nl/pub/graphics/blender/release/Blender3.0/blender-3.0.1-linux-x64.tar.xz'}
isVerExist = blender_version in blender_mirrors
if isVerExist:
blender_url = blender_mirrors[blender_version]
# !mkdir $blender_version
# !wget -O '{blender_version}.tar.xz' -nc $blender_url
# !tar xf '{blender_version}.tar.xz' -C ./$blender_version --strip-components=1
else:
print ("Invalid Blender version. Please check the mirrors.")
# + [markdown] id="s3uIDMZLbYOE"
# This block is required as some weird behaviors with libtcmalloc appeared in the colab VM
# + id="h6vohA2q2BDF"
import os
os.environ["LD_PRELOAD"] = ""
# !apt update
# !apt remove libtcmalloc-minimal4
# !apt install libtcmalloc-minimal4
os.environ["LD_PRELOAD"] = "/usr/lib/x86_64-linux-gnu/libtcmalloc_minimal.so.4.3.0"
# !echo $LD_PRELOAD
# + id="RU3p_G4hDk97"
# !apt install libboost-all-dev
# !apt install libgl1-mesa-dev
# !apt install libglu1-mesa libsm-dev
# + [markdown] id="RazfUKL3vPd7"
# # Render Config
# Required for Blender to use the GPU as expected. In addition you can add custom properties to here.
#
# [Blender CLI Wiki](https://docs.blender.org/manual/en/latest/advanced/command_line/arguments.html)
# + id="E41P1QS9vYf8"
#Custom Properties
data = "import re\n"+\
"import bpy\n"+\
"scene = bpy.context.scene\n"+\
"scene.cycles.device = '"+str(Device)+"'\n"+\
"objects = bpy.data.objects\n"+\
"collections = bpy.context.view_layer.layer_collection\n"+\
"prefs = bpy.context.preferences\n"+\
"prefs.addons['cycles'].preferences.get_devices()\n"+\
"cprefs = prefs.addons['cycles'].preferences\n"+\
"print(cprefs)\n"+\
"# Attempt to set GPU device types if available\n"+\
"for compute_device_type in ('CUDA', 'OPENCL', 'NONE'):\n"+\
" try:\n"+\
" cprefs.compute_device_type = compute_device_type\n"+\
" print('Device found',compute_device_type)\n"+\
" break\n"+\
" except TypeError:\n"+\
" pass\n"+\
"for scene in bpy.data.scenes:\n"+\
" scene.cycles.feature_set = '"+str(FeatureSet)+"'\n"+\
" scene.cycles.samples = "+str(MaxSamples)+"\n"+\
" scene.render.threads_mode = '"+str(ThreadsMode)+"'\n"+\
" scene.cycles.use_auto_tile = "+str(UseAutoTile)+"\n"+\
" scene.cycles.tile_size = "+str(TileSize)+"\n"+\
" #scene.render.tile_x = "+str(TileSize)+"\n"+\
" #scene.render.tile_y = "+str(TileSize)+"\n"+\
" scene.cycles.debug_use_spatial_splits = "+str(UseSpatialSplits)+"\n"+\
" scene.render.use_persistent_data = "+str(PersistentData)+"\n"+\
" scene.render.resolution_x = "+str(ResolutionX)+"\n"+\
" scene.render.resolution_y = "+str(ResolutionY)+"\n"+\
" scene.render.resolution_percentage = "+str(Percentage)+"\n"+\
" #scene.render.use_compositing = "+str(Compositing)+"\n"+\
" scene.camera = objects['"+str(Camera)+"']\n"+\
"\n"+\
"# bpy.context.objects['Cube'].hide_render = True\n"+\
"# for collection in collections:\n"+\
"# collection['Volume'].hide_render = True\n"+\
"# bpy.ops.collection.objects_remove(collection='Volume')\n"+\
"\n"+\
"# Enable all CPU and GPU devices\n"+\
"for device in cprefs.devices:\n"+\
" if not re.match('intel', device.name, re.I):\n"+\
" print('Activating',device)\n"+\
" device.use = "+str(UseGPU)+"\n"+\
" else:\n"+\
" device.use = "+str(UseCPU)+"\n"
with open('setgpu.py', 'w') as f:
f.write(data)
# + [markdown] id="EVTxsg6J8E1A"
# #Render animation
#
# Use this if you want to render all Frames
#
# Use `-s` to speficy the start frame.
# eg: `-s 10`
#
# Use `-e` to speficy the end frame.
# eg: `-e 20`
#
# **THE ORDER IS IMPORTANT. BOTH `-s` AND `-e` MUST BE SPEFICIED BEFORE `-a`**
#
#
# + id="Fpk2w3yM8XqQ"
# !./$blender_version/blender -b -noaudio '{root_path}{blend_path}.blend' -P './setgpu.py' -E {RenderEngine} -o '{root_path}{output_path}' -a |& tee '{root_path}{log_path}'
# + [markdown] id="zMuGCuoX8o2x"
# #Render a frame
#
# Use to render a single frame.
# Specify the frame with `-f` *frame_number*
# + id="VFVx8omJCGBN"
# !./$blender_version/blender -b -noaudio '{root_path}{blend_path}' -P './setgpu.py' -E {RenderEngine} -o '{root_path}{output_path}' -f 1 |& tee '{root_path}{log_path}'
|
colablend.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # TP Optimisation II: A simple neural network
#
# ### Nom(s): <NAME>
# ### Prénom(s): <NAME>
# ### Groupe: B2
# ## Useful packages
import numpy as np
import random
import matplotlib.pyplot as plt
from sklearn.utils import shuffle
# ## Loading of the train and test data
# +
#
# Load train data
#
Xtrain = np.load('train-images.npy')
Xtrain = np.array([x.ravel()/255 for x in Xtrain])
Xtrain = Xtrain.reshape(Xtrain.shape[0],Xtrain.shape[1],1)
Ytrain = np.load('train-labels.npy')
targets_train = []
#
# Convert digits to 10x1 vectors
#
for lab in Ytrain:
v = np.zeros((10,1))
v[lab] = 1
targets_train+=[np.array(v)]
#
# Load test data
#
Xtest = np.load('t10k-images.npy')
Xtest = np.array([x.ravel()/255 for x in Xtest])
Xtest = Xtest.reshape(Xtest.shape[0],Xtest.shape[1],1)
Ytest = np.load('t10k-labels.npy')
targets_test = []
#
# Convert digits to 10x1 vectors
#
for lab in Ytest:
v = np.zeros((10,1))
v[lab]=1
targets_test+=[np.array(v)]
#
# Outputs
#
print('there are ',Xtrain.shape[0],'images in the train set')
print('there are ',Xtest.shape[0],'images in the test set')
# -
# ## Definition of the activation function
#
# The activation function defines the output of a node given a set of inputs. We use the <a href="https://en.wikipedia.org/wiki/Softmax_function">softmax</a> function defined by
#
# $$\sigma_{\alpha} : \mathbb{R}^p\rightarrow [0,1]^p, \quad \mbox{ s.t.} \quad[\sigma_{\alpha}(x)]_i=\frac{e^{x_i+\alpha_i}}{\displaystyle{\sum_{j=1}^{p}e^{x_j+\alpha_j}}}\quad \forall i=1:p. $$
#
#
# Nonlinear activation function
#
def softmax(x,alpha):
"""
Softmax unit activation function
x : Numpy array
alpha: scalar
"""
#
# TO DO
#
return value
#
# Example of a plot of the activation function
#
t = np.arange(-5,5,0.1)
alpha = 0. #np.arange(-50,50,1)
plt.figure(figsize=(10,10))
plt.plot(t,softmax(t,alpha))
plt.grid(True)
plt.show()
# ## Definition of a simple neural network
#
# We use a one-layer fully-connected neural network with the <a href="https://en.wikipedia.org/wiki/Softmax_function">softmax</a> activation function.
#
def NN(x,W):
"""
# One-layer fully connected neural network
# x: image, i.e. 784x1 vector (28x28)
# W: weight matrices of shape 10x784
"""
#
# TO DO: return pred (preticted probabilities)
#
return pred
# ## Definition of the loss function
#
# The loss function is the <a href="https://en.wikipedia.org/wiki/Cross_entropy">cross-entropy</a> defined by
#
# $$J(W)=-\sum_{i=1}^N p_i \log(q_i(W)),$$ where $N$ is the number of classes, $(p_i)_{i=1:N}$ are the probabilities of a data from the training set to belong to a class (0 or 1 because the labels are known), and $(q_i(W))_{i=1:N}$ are the predicted probabilities from the model
#
# $$\forall i=1:N, \quad q_i(W)=[\sigma_{\alpha}(Wx)]_i.$$
#
# Loss function = Cross-entropy
#
def cross_entropy(pred,target,x):
"""
pred: predicted probabilities (q(W))
target: probabilities (p)
x: image
"""
#
# TO DO: return ce,grad (cross_entropy, gradient of the cross-entropy)
#
return ce,grad
#
# Main function
#
def f(W,x,target):
"""
W: weights
target: probabilities (p)
x: image
"""
#
# TO DO: return ce, grad, pred (cross_entropy, gradient, predicted probabilities)
#
return ce,grad,pred
# +
#
# Test information on the gradient with calls of f
#
# Define weight matrices
W = np.random.rand(10,Xtrain.shape[1])
eps = 1e-8
d = np.random.rand(10,Xtrain.shape[1])
Wtilde = w+eps*d
# Retrieve the information on the gradients
res = (f(Wtilde,Xtrain[0],targets_train[0])[0]-f(W,Xtrain[0],targets_train[0])[0])/eps
print(res)
g = f(W,Xtrain[0],targets_train[0])[1]
print(g.T.dot(d.reshape(7840,1)))
# -
# ## Generating batches
#
# Function to create batches of samples to be used later in the training phase
#
def create_batches(x,bs):
"""
x : set to be considered (array)
bs: batch size (scalar)
"""
batches = []
ind = np.arange(x.shape[0])
random.shuffle(ind)
nbatch = ind.shape[0]//bs
rest = ind.shape[0]%bs
for n in range(nbatch):
batches +=[ind[bs*n:bs*(n+1)]]
# Put the remaining elements in a last batch
if rest !=0:
batches += [ind[-rest:]]
return batches
# ## Training of the neural network
# +
history = {}
eta = 1e-5 # learning rate
momentum = 0. # momemtum factor
N_EPOCHS = 10
BatchSizes = [10000,1024,256] # try different batch sizes for the analysis
for bs in BatchSizes:
#
# Sensitivity to the batch size to be investigated in the analysis
#
print('batch size=',bs)
history[bs]={'train loss':[],'train acc':[],'test loss':[0], 'test acc':[0]}
# Initialization of the weights
w = np.random.rand(10,Xtrain.shape[1])
for n in range(N_EPOCHS):
# Minimization of the loss function
Batches=create_batches(Xtrain,bs)
for batch in Batches:
# Loop on the batches
#
# TO DO
#
# Test accuracy at the end of each epoch
#
# TO DO
#
print('Epoch number :', n+1,'test accuracy:',history[bs]['test acc'][n+1],'test loss',history[bs]['test loss'][n+1])
print('\n')
# -
# ## Plots of the evolution of the loss function
for bs in BatchSizes:
n_batch = Xtrain.shape[0]//bs
if Xtrain.shape[0]%bs!=0:
n_batch+=1
E = [n_batch*n for n in np.arange(N_EPOCHS+1)]
Ep = [str(n) for n in np.arange(N_EPOCHS+1)]
plt.figure(figsize=(7,7))
plt.plot(history[bs]['train loss'],label = 'training loss')
plt.plot(E[1:],history[bs]['test loss'][1:],linewidth=2.5,label = 'test loss')
plt.xticks(E,Ep)
plt.xlabel('Epochs')
plt.ylabel('Loss Value')
#plt.ylim([0,np.max(history[bs]['test loss'])+2])
plt.grid(True)
plt.legend()
plt.title(f'model trained with a Batch size of {bs} samples and learning rate of {eta}')
plt.show()
# ## Plots of the evolution of the accuracy
for bs in BatchSizes:
print(bs)
n_batch = Xtrain.shape[0]//bs
if Xtrain.shape[0]%bs!=0:
n_batch+=1
print(n_batch)
E=[n_batch*n for n in np.arange(N_EPOCHS+1)]
Ep = [str(n) for n in np.arange(N_EPOCHS+1)]
plt.figure(figsize=(7,7))
plt.plot(history[bs]['train acc'] ,label = 'training acuracy')
plt.plot(E[1:],history[bs]['test acc'][1:],linewidth=2.5,label = 'test acuracy')
plt.xticks(E,Ep)
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.grid(True)
plt.title(f'model trained with a Batch size of {bs} samples and learning rate of {eta}')
plt.ylim([0,1])
plt.legend()
plt.show()
# ## Analysis of the results
#
# Please provide your comments on the sensitivity of the results to the parameters involved in the learning process (batch size, learning rate, momentum).
# ### Your comments:
|
2A/S8/UE Apprentissage Machine et optimisation/Optimisation 2/TP3/.ipynb_checkpoints/MNIST-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Customer Segmentation and Cohort Analysis
import numpy as np
import pandas as pd
data = pd.read_excel('/Users/khushal/Desktop/CustomerSegmentation/CSP3/Online-Retail.xlsx')
data.head()
# #### Assigning a Daily Acquisition Cohort
from datetime import datetime
def get_month(x):
return datetime(x.year,x.month,1)
data['InvoiceMonth'] = data['InvoiceDate'].apply(get_month)
grouping = data.groupby('CustomerID')['InvoiceMonth']
data['CohortMonth'] = grouping.transform('min')
data.head()
# #### Extract Integer Values From Data
def get_date_int(df,column):
year = df[column].dt.year
month = df[column].dt.month
day = df[column].dt.day
return year,month,day
# #### Assign Time Offset Value
# +
invoice_year,invoice_month, _ = get_date_int(data, 'InvoiceMonth')
cohort_year, cohort_month, _ = get_date_int(data, 'CohortMonth')
years_diff = invoice_year - cohort_year
months_diff = invoice_month - cohort_month
data['CohortIndex'] = years_diff * 12 + months_diff + 1
data
# -
# #### Count Monthly active customers from each cohort
grouping = data.groupby(['CohortMonth', 'CohortIndex'])
# Count number of customers in each group by applying pandas nunique() function
cohort_data = grouping['CustomerID'].apply(pd.Series.nunique)
# Reset the index and create pandas pivot with CohortMonth
cohort_data = cohort_data.reset_index()
cohort_counts = cohort_data.pivot(index = 'CohortMonth',
columns = 'CohortIndex',
values = 'CustomerID')
print(cohort_counts)
# #### Calculate Cohort Metrics
# #### We have assigned the cohorts and calculated the monthly offset for the metrics, now we will see how to calculate business metrics for these customer cohorts, We will start by using cohort counts table from above to calculate customer retention then we will calculate the average purchase quantity. The retention measures how many customers from each cohort have returned in the subsequent months.
# #### First Step : Select the First Column which is the total number of customers in the cohort
# #### Second Step: We will calculate the ratio of how many of these customers came back in the subsequent months which is the retention rate
#
# #### Note: You will see that the first month's retention - by defination will be 100% of all cohorts, This is because the number of active customers in the first month is actually the size of the cohort
# Calculate Rentention Rate
cohort_sizes = cohort_counts.iloc[:,0]
retention = cohort_counts.divide(cohort_sizes, axis = 0)
retention.round(3) * 100
# Calculate Average Quantity
grouping = data.groupby(['CohortMonth', 'CohortIndex'])
cohort_data = grouping['Quantity'].mean()
cohort_data = cohort_data.reset_index()
average_quantity = cohort_data.pivot(index = 'CohortMonth',
columns = 'CohortIndex',
values = 'Quantity')
average_quantity.round(1)
# #### HeatMap for Visualizing Cohort Analysis
retention.round(3) * 100
# +
import seaborn as sns
import matplotlib.pyplot as plt
plt.figure(figsize=(10,8))
plt.title('Retentation Rates')
sns.heatmap(data = retention,
annot = True,
fmt = '.0%',
vmin = 0.0,
vmax = 0.5,
cmap = 'BuGn')
plt.show()
# -
average_quantity.round(1)
plt.figure(figsize=(8,6))
plt.title('Average Spend by Monthly Cohorts')
sns.heatmap(data = average_quantity,
annot = True,
cmap = 'Blues')
# ## RFM Metrics
# ### RECENCY (R) - Which measures how recent was each customer's last purchase (Days since the last customer purchase)
# ### FREQUENCY (F) - Which measures how many purchases the customer has done in the last 12 months (Number of transactions in the last 12 months)
# ### MONETARY VALUE (M) - Which measures how much has the customer spent in the last 12 months (Total Spend in the last 12 months)
data['TotalSum'] = data['UnitPrice'] * data['Quantity']
data.head()
print ('Min:{};Max:{}'.format(min(data.InvoiceDate), max(data.InvoiceDate)))
# Creating a hypothetical snapshot_day data, by adding one day to the max invoice date
from datetime import datetime, date, time, timedelta
snapshot_date = max(data.InvoiceDate) + timedelta(days = 1)
snapshot_date
# +
# Aggregate date on a customer level
datamart = data.groupby(['CustomerID']).agg({
'InvoiceDate': lambda x : (snapshot_date - x.max()).days,
'InvoiceNo' : 'count',
'TotalSum' : 'sum'})
# Rename the columns for easier interpretation
datamart.rename(columns = {'InvoiceDate' : 'Recency',
'InvoiceNo' : 'Frequency',
'TotalSum' : 'Monetary Value'}, inplace=True)
datamart['Monetary Value'].round(1)
datamart.head()
# -
# This will assign label to most recent customer as 4 and least recent customer as 1
r_labels = range(4,0,-1)
r_quartiles = pd.qcut(datamart['Recency'], 4, labels = r_labels)
datamart = datamart.assign(R = r_quartiles.values)
datamart.head()
# +
# This will assign label to most frequent customer as 1 and least frequent customer as 4
# Also assign label most monetary value generating customer as 1 and least monetary value generating customer as 4
f_labels = range(1,5)
m_labels = range(1,5)
f_quartiles = pd.qcut(datamart['Frequency'], 4 , labels = f_labels)
m_quartiles = pd.qcut(datamart['Monetary Value'], 4, labels = m_labels)
datamart = datamart.assign(F = f_quartiles.values)
datamart = datamart.assign(M = m_quartiles.values)
datamart.head()
# -
# ### Build RFM Segment and RFM Score
#
# #### 1. Concatenate RFM quartile values to RFM_Segment
#
# #### 2. Sum RFM quartiles values to RFM_Score
# +
datamart = datamart[['Recency','Frequency','Monetary Value', 'R','F','M']]
def join_rfm(x):
return str(x['R']) + str(x['F']) + str(x['M'])
datamart['RFM_Segment'] = datamart.apply(join_rfm, axis = 1)
datamart['RFM_Score'] = datamart[['R','F','M']].sum(axis = 1)
datamart
# -
datamart.groupby('RFM_Segment').size().sort_values(ascending = False)[:10]
datamart[datamart['RFM_Segment']=='111'].head(15)
datamart.groupby('RFM_Score').agg(
{
'Recency' : 'mean',
'Frequency': 'mean',
'Monetary Value' : ['mean','count']
}
).round(1)
# ### To Understand data better lets group them in named segments
# +
def segment_me(df):
if df['RFM_Score'] >= 9:
return 'Gold'
elif (df['RFM_Score'] >= 5) and (df['RFM_Score'] < 9):
return 'Silver'
else:
return 'Bronze'
datamart['General_Segment'] = datamart.apply(segment_me, axis = 1)
datamart.groupby('General_Segment').agg(
{
'Recency' : 'mean',
'Frequency' : 'mean',
'Monetary Value' : ['mean', 'count']
}
).round(1)
# -
# ### Data Pre-processing for K-Means Clustering
# #### Exploring distribution of Recency and Frequency
# +
import seaborn as sns
from matplotlib import pyplot as plt
plt.subplot(2,1,1); sns.distplot(datamart['Recency'])
plt.subplot(2,1,2); sns.distplot(datamart['Frequency'])
plt.show()
# -
# #### Data Transformations to manage Skewness
### Logarithmic Transformation (Positive Values Only)
import numpy as np
frequency_log = np.log(datamart['Frequency'])
sns.distplot(frequency_log)
plt.show()
# ### NOTE
#
# #### Dealing with Negative Values
#
# #### 1. Adding a constant before log transformation
# #### 2. Cube Root transformation
datamart_rfm = datamart[['Recency','Frequency','Monetary Value','RFM_Score']]
datamart_rfm.head()
datamart_rfm.describe()
# #### Centering Variables with different means
# #### 1. K-means works well on variables with the same mean
# #### 2. Centering Variables is done by subracting average values from each observation.
datamart_centered = datamart_rfm - datamart_rfm.mean()
datamart_centered.describe().round(2)
# #### Scaling Variables with Different Variance
#
# #### 1. K-means works better on variables with the same variance and Standard Deviation.
#
# #### 2. Scaling variables is done by dividing them by standard deviation of each.
# Scaling the Values
datamart_scaled = datamart_rfm / datamart_rfm.std()
datamart_scaled.describe().round(2)
# #### Combining Centering and Scaling
#
# #### 1. Subract mean and divide by standard deviation manually
# #### 2. Or use a scaler from scikit-learn library (returns numpy.ndarray object)
### Using 2nd Method
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(datamart_rfm)
datamart_normalized = scaler.transform(datamart_rfm)
datamart_normalized = pd.DataFrame(data=datamart_normalized, index=datamart_rfm.index, columns=datamart_rfm.columns)
datamart_normalized.describe().round(2)
# print ('mean:', datamart_normalized.mean(axis = 0).round(2))
# print ('std:' , datamart_normalized.std(axis = 0).round(2))
# #### Sequence of Structuring Pre-processing steps
#
# #### 1. Unskew the data -- Log Transformation
# #### 2. Standardize to the same average values
# #### 3. Scale to the separate standard deviation
# #### 4. Store as a separate array to be used for clustering
# #### Visualizing the Normalized Data
# +
# ## Unskew the data with log transformation
# import numpy as np
# datamart_log = np.log(datamart_rfm)
# ## Normalize the variables with StandardScaler
# from sklearn.preprocessing import StandardScaler
# scaler = StandardScaler()
# scaler.fit(datamart_log)
# ## Store it separately for clustering
# datamart_normalized = scaler.transform(datamart_log)
# datamart_normalized = pd.DataFrame(data=datamart_normalized, index=datamart_rfm.index, columns=datamart_rfm.columns)
# datamart_normalized.describe()
# -
plt.subplot(3,1,1); sns.distplot(datamart_normalized['Recency'])
plt.subplot(3,1,2); sns.distplot(datamart_normalized['Frequency'])
plt.subplot(3,1,3); sns.distplot(datamart_normalized['Monetary Value'])
# ### K- means Clustering
# #### Methods to define the number of clusters
#
# #### 1. Visual Methods - elbow criterion
#
# * Plot the number of clusters against within-cluster sum of squared errors (SSE) - Sum of Squared distances from every data point to their cluster center.
# * Identify the "elbow" in the plot
# * Elbow- a point representing an "optimal" number of clusters
#
# #### 2. Mathematical Methods - Silhouette Coefficient
# #### 3. Experimentation and Interpretation
# +
# Way to choose the number of clusters
# Elbow Criterion Method
from sklearn.cluster import KMeans
import seaborn as sns
from matplotlib import pyplot as plt
# Fit KMeans and calculate SSE for each *k*
sse = {}
for k in range(1,11):
kmeans = KMeans(n_clusters = k, random_state = 1)
kmeans.fit(datamart_normalized)
sse[k] = kmeans.inertia_ # Sum of Squared distances to closest cluster center
# Plot SSE for each *k*
plt.title('The Elbow Method')
plt.xlabel('k');plt.ylabel('SSE')
sns.pointplot(x=list(sse.keys()), y=list(sse.values()))
plt.show()
# -
# #### The Way to look at it is try to find the point with the largest angle which is so-called elbow, in the above graph the largest angle is at k = 4
# ### Experimental Approach - analyze segments
# 2-cluster approach
# Import KMeans from sklearn library and initialize it as kmeans
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters = 2, random_state = 1)
# Compute k-means clustering on pre-processed data
kmeans.fit(datamart_normalized)
# Extract cluster labels from labels_ attribute
cluster_labels = kmeans.labels_
# Analyzing average RFM values of each cluster
# Create a cluster label column in the original DataFrame
datamart_rfm_k2 = datamart_rfm.assign(Cluster = cluster_labels)
# Calculate average RFM values and size for each cluster
datamart_rfm_k2.groupby(['Cluster']).agg({
'Recency':'mean',
'Frequency' : 'mean',
'Monetary Value' : ['mean', 'count']
}).round(0)
# #### The results above is a simple table where we see how these two segments differ from each other, It's clear that segment 0 has customers who have not been very recent, are much less frequent with their purchases and their monetary value is much lower than that of segment 1.
# 3 - Cluster Approach
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters = 3, random_state = 1)
kmeans.fit(datamart_normalized)
cluster_labels = kmeans.labels_
datamart_rfm_k3 = datamart_rfm.assign(Cluster = cluster_labels)
datamart_rfm_k3.groupby(['Cluster']).agg({
'Recency':'mean',
'Frequency':'mean',
'Monetary Value' : ['mean', 'count']
}).round(0)
# ### Profile and Interpret Segments
# #### Approach to build customer personas
#
# #### Summary statistics for each cluster e.g. average RFM values
# * We have already seen the approach where we assign the cluster label to the original dataset and then calculate average values of each cluster.
#
# #### Note: We have already this above in cell 48 and 49, as we can see there are some inherant differences between 2-segment and 3-segment solutions, while the former is simpler, the 3-segment solution gives more insights.
#
# #### Snake Plots (from Market Research)
#
# * Another approach is to use snake plots - a chart that visualizes RFM values between the segments.
# * Market Research technique to compare different segments.
# * Visual Representation of each segment attributes.
# * Need to first normalize data(center and scale).
# * Plot each cluster's average normalized values of each attribute on a line plot.
#
# #### Relative importance of cluster attributes compared to population
# Preparing data for snake plot
# Transform datamart_normalized as DataFrame and add a Cluster column
datamart_normalized = pd.DataFrame(datamart_normalized,
index = datamart_rfm.index,
columns = datamart_rfm.columns)
datamart_normalized['Cluster'] = datamart_rfm_k3['Cluster']
# Melt the data into a long format so RFM values and metric names are stored in 1 column each
datamart_melt = pd.melt(datamart_normalized.reset_index(),
id_vars = ['CustomerID', 'Cluster'],
value_vars = ['Recency','Frequency', 'Monetary Value'],
var_name = 'Attribute',
value_name = 'Value')
# Visualize the snake plot
plt.title('Snake Plot of Standardized Variables')
sns.lineplot(x='Attribute', y = 'Value', hue = 'Cluster', data = datamart_melt)
# #### Relative Importance of Segment Attributes
# * Useful technique to identify relative importance of each segment's attribute
# * Calculate average values of each cluster
cluster_avg = datamart_rfm_k3.groupby(['Cluster']).mean()
population_avg = datamart_rfm.mean()
relative_imp = cluster_avg / population_avg - 1
# Understanding the relative_imp using a heatmap
plt.figure(figsize=(8,2))
plt.title('Relative Importance of Attributes')
sns.heatmap(data = relative_imp,
annot = True,
fmt = '.2f',
cmap = 'RdYlGn')
plt.show()
# #### Analysis of above results
#
# * The further a ratio from 0, the more important that attribute is for a segment relative to the total population
#
# ## *************************************************** Project ****************************************************
# #### Implementation Summary of end-to-end segmentation solution
# #### Key Steps
# * Gather Data - You will use an updated data that has recency, frequency and monetary values from the previous lessons and an additional variable to make this more interesting.
# * Pre-process data the data to ensure k-means clustering works as expected.
# * Explore the data and decide on the number of clusters
# * Run k-means clustering.
# * Analyze and Visualize results
# #### We will not be using an additional dataset, this is taken from a different CSV file 'datamart_rfmt.csv' which is loaded below.
# #### New Dataset: Tenure, which means time since first transaction. It ultimately defines how long the customer has been with the company, since their first transaction.
datamart_rfmt = pd.read_csv('/Users/khushal/Desktop/CustomerSegmentation/CSP3/datamart_rfmt.csv')
datamart_rfmt.head()
# ### First Step -- Pre- Process the Data
# +
# Import StandardScaler
from sklearn.preprocessing import StandardScaler
# Apply log transformation
datamart_rfmt_log = np.log(datamart_rfmt)
# Initialize StandardScaler and fit it
scaler = StandardScaler(); scaler.fit(datamart_rfmt_log)
# Transform and store the scaled data as datamart_rfmt_normalized
datamart_rfmt_normalized = scaler.transform(datamart_rfmt_log)
# -
# ### Second Step: Calculate and plot sum of squared errors
# +
# Fit KMeans and calculate SSE for each k between 1 and 10
for k in range(1, 11):
# Initialize KMeans with k clusters and fit it
kmeans = KMeans(n_clusters= k , random_state=1).fit(datamart_rfmt_normalized)
# Assign sum of squared distances to k element of the sse dictionary
sse[k] = kmeans.inertia_
# Add the plot title, x and y axis labels
plt.title('The Elbow Method'); plt.xlabel('k'); plt.ylabel('SSE')
# Plot SSE values for each k stored as keys in the dictionary
sns.pointplot(x=list(sse.keys()), y=list(sse.values()))
plt.show()
# -
# ### Third Step: Since the elbow is at 4 so , Build a 4-Cluster solution
# +
# Import KMeans
from sklearn.cluster import KMeans
# Initialize KMeans
kmeans = KMeans(n_clusters = 4, random_state = 1)
# Fit k-means clustering on the normalized data set
kmeans.fit(datamart_rfmt_normalized)
# Extract cluster labels
cluster_labels = kmeans.labels_
# -
# ### Fourth Step : Analyze the Segments
# +
# Create a new DataFrame by adding a cluster label column to datamart_rfmt
datamart_rfmt_k4 = datamart_rfmt.assign(Cluster= cluster_labels)
# Group by cluster
grouped = datamart_rfmt_k4.groupby(['Cluster'])
# Calculate average RFMT values and segment sizes for each cluster
grouped.agg({
'Recency': 'mean',
'Frequency': 'mean',
'MonetaryValue': 'mean',
'Tenure': ['mean', 'count']
}).round(1)
# -
|
Customer Segmentation in Python 3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + pycharm={"name": "#%% #0: Importing libraries\n", "is_executing": false}
# Source: https://stackoverflow.com/questions/15091982/manipulating-the-numpy-random-exponential-distribution-in-python
import numpy as np
import matplotlib.pyplot as plt
# Solved: https://stackoverflow.com/questions/29045636/attributeerror-module-object-has-no-attribute-hist
# + pycharm={"name": "#%% #1: Generating n=20 random variables\n", "is_executing": false}
target = 250
beta = 1.0/target
# + pycharm={"name": "#%% #2: Plot the generated data \n", "is_executing": false}
Y = np.random.exponential(beta, 5000)
# plt.hist(Y, normed=True, bins=200,lw=0,alpha=.8)
plt.hist(Y, density=True, bins=200,lw=0,alpha=.8)
plt.plot([0,max(Y)],[target,target],'r--')
plt.ylim(0,target*1.1)
plt.show()
|
hw1/others/mle-test.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Unsupervised Learning
#
# In contrast to everything we've seen up till now, the data in these problems is **unlabeled**. This means that the metrics that we've used up till now (e.g. accuracy) won't be available to evaluate our models with. Furthermore, the loss functions we've seen also require labels. Unsupervised learning algorithms need to describe the hidden structure in the data.
#
# # Clustering
#
# [Clustering](https://en.wikipedia.org/wiki/Cluster_analysis) is an unsupervised learning problem, where the goal is to split the data into several groups called **clusters**.
#
# 
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
# As stated previously, in unsupervised problems the data **isn't** accompanied by labels. We don't even know **how many** groups our data belongs to.
#
# To illustrate how unsupervised algorithms cope with the challenge, we'll create an easy example consisting of 100 data points that can easily be split into two categories (of 50 points each). We'll attempt to create an algorithm that can identify the two groups and split the data accordingly.
# +
# CODE:
# --------------------------------------------
np.random.seed(55) # for reproducibility
p1 = np.random.rand(50,2) * 10 + 1 # 100 random numbers uniformly distributed in [1,11). these are stored in a 50x2 array.
p2 = np.random.rand(50,2) * 10 + 12 # 100 random numbers uniformly distributed in [12,22). these are stored in a 50x2 array.
points = np.concatenate([p1, p2]) # we merge the two into a 100x2 array
# the first column represents the feature x1, while the second represents x2
# subsequently the 30th row represents the two coordinates of the 30th sample
# PLOTTING:
# --------------------------------------------
ax = plt.subplot(111) # create a subplot to get access to the axes object
ax.scatter(points[:,0], points[:,1], c='#7f7f7f') # scatter the points and color them all as gray
# this is done to show that we don't know which
# categories the data can be split into
# Remove ticks from both axes
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
# Remove the spines from the figure
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
# Set labels and title
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.set_title('Data points randomly placed into two groups')
# -
# ## K-Means
#
# **[k-means](https://en.wikipedia.org/wiki/K-means_clustering)**, is probably the simplest clustering algorithm. Let's see how it works step by step.
#
# The most important hyperparameter is $k$, a number signifying the number of clusters the algorithm would attempt to group the data into. K-means represents clusters through points in space called **centroids**. Initially the centroids are **placed randomly**. Afterwards the distance of each centroid to every data point is computed. These points are **assigned** to the cluster with the closest centroid. Finally, for each cluster, the mean location of all its data points is calculated. Each cluster's centroid is moved to that location (this movement is also referred to as an **update**). The assignment and update stages are repeated until convergence.
#
# 
#
# In the above image:
#
# - (a): Data points
# - (b): Random initialization
# - (c): Initial assignment
# - (d): Initial centroid update
# - (e): Second assignment
# - (f): Second update
#
# The whole training procedure can also be viewed in the image below:
#
# 
#
# In order to better understand the algorithm, we'll attempt to create a simple k-means algorithm on our own. As previously stated, the only hyperparameter we need to define is $k$. The first step is to create $k$ centroids, randomly placed near the data points.
# +
# CODE:
# --------------------------------------------
np.random.seed(55) # for reproducibility
# Select the value of the hyperparameter k:
k = 2
# STEP 1:
# Randomly place two centroids in the same space as the data points
centroids = np.random.rand(k, 2) * 22
# PLOTTING:
# --------------------------------------------
colors = ['#1f77b4', '#ff7f0e'] # select colors for the two groups
ax = plt.subplot(111)
ax.scatter(points[:, 0], points[:, 1], c='#7f7f7f') # data points in gray
ax.scatter(centroids[:, 0], centroids[:, 1], color=colors, s=80) # centroids in orange and blue
# Aesthetic parameters:
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
# -
# In order to continue, we need a way to measure *how close* one point is to another, or in other words a *distance metric*. For this purpose, we will use probably the most common distance metric, [Euclidean distance](https://en.wikipedia.org/wiki/Euclidean_distance).
#
# The distance of two points $a$ and $b$ is calculated as follows:
#
# $$
# d \left( a, b \right) = \sqrt{ \left( a_x - b_x \right)^2 + \left( a_y - b_y \right)^2}
# $$
#
# Of course there are many more [distance metrics][1] we can use.
#
# [1]: https://en.wikipedia.org/wiki/Metric_(mathematics)
# +
# CODE:
# --------------------------------------------
def euclidean_distance(point1, point2):
"""
calculates the Euclidean distance between point1 and point2. these points need to be two-dimensional.
"""
return np.sqrt( (point1[0] - point2[0]) ** 2 + (point1[1] - point2[1]) ** 2 )
print('the distance from (5,2) to (2,5) is: ', euclidean_distance((5, 2), (2, 5)))
print('the distance from (3,3) to (3,3) is: ', euclidean_distance((3, 3), (3, 3)))
print('the distance from (1,12) to (12,15) is: ', euclidean_distance((1, 12), (12, 15)))
# -
# Tip: Alternatively we could use the built-in function [pdist](https://docs.scipy.org/doc/scipy-0.19.1/reference/generated/scipy.spatial.distance.pdist.html) from scipy.spatial.distance.
#
# The second step would be to calculate the distance from each point to every centroid. To do this, we'll use the previously defined function.
# +
# CODE:
# --------------------------------------------
def calc_distances(centroids, points):
"""
Calculates the Euclidean distance from each centroid to every point.
"""
distances = np.zeros((len(centroids), len(points))) # array with (k x N) dimensions, where we will store the distances
for i in range(len(centroids)):
for j in range(len(points)):
distances[i,j] = euclidean_distance(centroids[i], points[j])
return distances
# The above could also be written as:
# return np.reshape(np.array([euclidean_distance(centroids[i], points[j]) for i in range(len(centroids))
# for j in range(len(points))]), (len(centroids), len(points)))
print('first 10 distances from the first centroid:')
print(calc_distances(centroids, points)[0, :10])
print('...')
# -
# Afterwards, we'll use these distances to assign the data points into clusters (depending on which centroid they are closer to).
# +
# CODE:
# --------------------------------------------
def assign_cluster(centroids, points):
"""
Calculates the Euclidean distance from each centroid to every point. Assigns the points to clusters.
"""
distances = calc_distances(centroids, points)
return np.argmin(distances, axis=0)
print('Which cluster does each point belong to?')
print(assign_cluster(centroids, points))
# -
# Due to the distance metric we elected, the two groups are geometrically separated through their perpendicular bisector. The lines or planes that separate groups are called [decision boundaries](https://en.wikipedia.org/wiki/Decision_boundary).
#
# We'll proceed to draw this line.
# +
# PLOTTING:
# --------------------------------------------
# First, we'll calculate the perpendicular bisector's function
def generate_perp_bisector(centroids):
midpoint = ((centroids[0, 0] + centroids[1, 0]) / 2, (centroids[0, 1] + centroids[1, 1]) / 2) # the midpoint of the two centroids
slope = (centroids[1, 1] - centroids[0, 1]) / (centroids[1, 0] - centroids[0, 0]) # the angle of the line that connects the two centroids
perpendicular = -1/slope # its perpendicular
return lambda x: perpendicular * (x - midpoint[0]) + midpoint[1] # the function
perp_bisector = generate_perp_bisector(centroids)
# Color mapping
map_colors = {0:'#1f77b4', 1:'#ff7f0e'}
point_colors = [map_colors[i] for i in assign_cluster(centroids, points)]
# Range of values in the x axis
x_range = [points[:, 0].min(), points[:, 0].max()]
fig = plt.figure(figsize=(7, 5))
ax = plt.subplot(111)
# Scatter the points
ax.scatter(points[:, 0], points[:, 1], c=point_colors, s=50, lw=0, edgecolor='black', label='data points')
ax.scatter(centroids[:, 0], centroids[:, 1], c=colors, s=100, lw=1, edgecolor='black', label='centroids')
# Draw the decision boundary
ax.plot(x_range, [perp_bisector(x) for x in x_range], c='purple', label='decision boundary')
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('KMeans: Random Centroid Initialization')
ax.legend(loc='lower right', scatterpoints=3)
# -
# The third step involves computing the mean of all points of each class and update the corresponding centroid to that location.
# +
# CODE:
# --------------------------------------------
def update_centers(centroids, points):
clusters = assign_cluster(centroids, points) # assign points to clusters
new_centroids = np.zeros(centroids.shape) # array where the new positions will be stored
for i in range(len(centroids)):
cluster_points_idx = [j for j in range(len(clusters)) if clusters[j] == i] # finds the positions of the points that belong to cluster i
if cluster_points_idx: # if the centroid has any data points assigned to it, update its position
cluster_points = points[cluster_points_idx] # slice the relevant positions
new_centroids[i, 1] = cluster_points[:,1].sum() / len(cluster_points) # calculate the centroid's new position
new_centroids[i, 0] = cluster_points[:,0].sum() / len(cluster_points)
else: # if the centroid doesn't have any points we keep its old position
new_centroids[i, :] = centroids[i, :]
return new_centroids
# PLOTTING:
# --------------------------------------------
# Compute the new centroid positions and generate the decision boundary and the new assignments
new_centroids = update_centers(centroids, points)
new_boundary = generate_perp_bisector(new_centroids)
new_colors = [map_colors[i] for i in assign_cluster(new_centroids, points)]
# Create figure
fig = plt.figure(figsize=(6, 4))
ax = plt.subplot(111)
# Scatter the points
ax.scatter(points[:, 0], points[:, 1], c=new_colors, s=50, lw=0, edgecolor='black', label='data points')
ax.scatter(centroids[:, 0], centroids[:, 1], c=colors, s=100, lw=1, edgecolor='black', alpha=0.3, label='old centroids')
ax.scatter(new_centroids[:, 0], new_centroids[:, 1], c=colors, s=100, lw=1, edgecolor='black', label='new centroids')
# Draw the decision boundaries
ax.plot(x_range, [perp_bisector(x) for x in x_range], c='black', alpha=0.3, label='old boundary')
ax.plot(x_range, [new_boundary(x) for x in x_range], c='purple', label='new boundary')
# Draw the arrows
for i in range(k):
ax.arrow(centroids[i, 0], centroids[i, 1], new_centroids[i, 0] - centroids[i, 0], new_centroids[i, 1] - centroids[i, 1],
length_includes_head=True, head_width=0.5, color='black')
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('KMeans: Boundary changes after first centroid update')
ax.legend(loc='lower right', scatterpoints=3)
# -
# The second and third steps are repeated until convergence. An interactive tutorial to try out k-means for different data types and initial conditions is available [here](https://www.naftaliharris.com/blog/visualizing-k-means-clustering/).
#
# At this point, we'll attempt to create our own k-means class. For ease we'll try to model it to match the functionality of scikit-learn estimators, as closely as possible. The only hyperparameter, the class will accept, is the number of classes $k$. There will be two methods: `.fit()` which will initialize the centroids and handle the whole training procedure until convergence; and `.predict()` which will compute the distance between one or more points and the centroids and assign them accordingly.
class KMeans:
def __init__(self, k, term_distance=0.05, max_steps=50, seed=None):
self.k = k
self.seed = seed
self.history = []
# Termination conditions:
self.term_distance = term_distance # minimum allowed centroid update distance before termination
self.max_steps = max_steps # maximum number of epochs
def initialize(self, data):
# Place k centroids in random spots in the space defined by the date
np.random.seed(self.seed)
self.centroids = np.random.rand(self.k,2) * data.max()
self.history = [self.centroids] # holds a history of the centroids' previous locations
def calc_distances(self, points):
# Calculates the distances between the points and centroids
distances = np.zeros((len(self.centroids), len(points)))
for i in range(len(self.centroids)):
for j in range(len(points)):
distances[i,j] = self.euclidean_distance(self.centroids[i], points[j])
return distances
def assign_cluster(self, points):
# Compares the distances between the points ant the centroids and carries out the assignment
distances = self.calc_distances(points)
return np.argmin(distances, axis=0)
def update_centers(self, points):
# Calculates the new positions of the centroids
clusters = self.assign_cluster(points)
new_centroids = np.zeros(self.centroids.shape)
for i in range(len(self.centroids)):
cluster_points_idx = [j for j in range(len(clusters)) if clusters[j] == i]
if cluster_points_idx:
cluster_points = points[cluster_points_idx]
new_centroids[i, 1] = cluster_points[:,1].sum() / len(cluster_points)
new_centroids[i, 0] = cluster_points[:,0].sum() / len(cluster_points)
else:
new_centroids[i, :] = self.centroids[i, :]
return new_centroids
def fit(self, data):
# Undertakes the whole training procedure
# 1) initializes the centroids
# 2, 3) computes the distances and updates the centroids
# Repeats steps (2) and (3) until a termination condition is met
self.initialize(data)
self.previous_positions = [self.centroids]
step = 0
cluster_movement = [self.term_distance + 1] * self.k
while any([x > self.term_distance for x in cluster_movement]) and step < self.max_steps: # checks for both termination conditions
new_centroids = self.update_centers(data)
self.history.append(new_centroids) # store centroids past locations
cluster_movement = [self.euclidean_distance(new_centroids[i,:], self.centroids[i,:]) for i in range(self.k)]
self.centroids = new_centroids
self.previous_positions.append(self.centroids)
step += 1
def predict(self, points):
# Checks if points is an array with multiple points or a tuple with the coordinates of a single point
# and carries out the assignment. This could be done through the built in 'assign_cluster' method,
# but for reasons of clarity we elected to perform it manually.
if isinstance(points, np.ndarray):
if len(points.shape) == 2:
return [np.argmin([self.euclidean_distance(point, centroid) for centroid in self.centroids]) for point in points]
return np.argmin([self.euclidean_distance(points, self.centroids[i]) for i in range(self.k)])
def fit_predict(self, points):
# Runs the training phase and returns the assignment of the training data
self.fit(points)
return self.predict(points)
@staticmethod
def euclidean_distance(point1, point2):
# Computes the Euclidean distance between two points
return np.sqrt( (point1[0] - point2[0]) ** 2 + (point1[1] - point2[1]) ** 2 )
# Initially, we'll run a few iterations manually (without the use of `.fit()`) to check if it works correctly.
#
# First, let's initialize the $k$ centroids.
# +
# CODE:
# --------------------------------------------
km = KMeans(2, seed=13)
km.initialize(points)
# PLOTTING:
# --------------------------------------------
# Assign data points and generate decision boundary
point_colors = [map_colors[i] for i in km.predict(points)]
decision_boundary = generate_perp_bisector(km.centroids)
# Create figure
fig = plt.figure(figsize=(7, 5))
ax = plt.subplot(111)
# Scatter the points and draw the decision boundary
ax.scatter(points[:, 0], points[:, 1], c=point_colors, s=50, lw=0, edgecolor='black', label='data points')
ax.scatter(km.centroids[:, 0], km.centroids[:, 1], c=colors, s=100, lw=1, edgecolor='black', label='centroids')
ax.plot(x_range, [decision_boundary(x) for x in x_range], c='purple', label='new boundary')
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('KMeans: Boundary after initialization')
ax.legend(loc='upper left', scatterpoints=3)
# -
# Now, we'll run an iteration and update the centroids.
# +
# CODE:
# --------------------------------------------
old = km.centroids
km.centroids = new = km.update_centers(points)
# PLOTTING:
# --------------------------------------------
# Assign points and generate decision boundary
point_colors = [map_colors[i] for i in km.predict(points)]
new_boundary = generate_perp_bisector(new)
# Create figure
fig = plt.figure(figsize=(7, 5))
ax = plt.subplot(111)
# Scatter the points and draw the decision boundary
ax.scatter(points[:, 0], points[:, 1], c=point_colors, s=50, lw=0, edgecolor='black', label='data points')
ax.scatter(old[:, 0], old[:, 1], c=colors, s=100, lw=1, edgecolor='black', alpha=0.3, label='old centroids')
ax.scatter(new[:, 0], new[:, 1], c=colors, s=100, lw=1, edgecolor='black', label='new centroids')
ax.plot(x_range, [decision_boundary(x) for x in x_range], c='black', alpha=0.3, label='old boundary')
ax.plot(x_range, [new_boundary(x) for x in x_range], c='purple', label='new boundary')
# Draw arrows
for i in range(km.k):
plt.arrow(old[i, 0], old[i, 1], new[i, 0] - old[i, 0], new[i, 1] - old[i, 1],
length_includes_head=True, head_width=0.5, color='black')
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('KMeans: Boundary changes after first centroid update')
ax.legend(loc='upper left', scatterpoints=3)
# -
# One more iteration...
# +
# CODE:
# --------------------------------------------
old = km.centroids
new = km.update_centers(points)
# PLOTTING:
# --------------------------------------------
# Assign points and generate decision boundary
decision_boundary = new_boundary
point_colors = [map_colors[i] for i in km.predict(points)]
new_boundary = generate_perp_bisector(new)
# Create figure
fig = plt.figure(figsize=(7, 5))
ax = plt.subplot(111)
# Scatter the points and draw the decision boundary
ax.scatter(points[:, 0], points[:, 1], c=point_colors, s=50, lw=0, edgecolor='black', label='data points')
ax.scatter(old[:, 0], old[:, 1], c=colors, s=100, lw=1, edgecolor='black', alpha=0.3, label='old centroids')
ax.scatter(new[:, 0], new[:, 1], c=colors, s=100, lw=1, edgecolor='black', label='new centroids')
ax.plot(x_range, [decision_boundary(x) for x in x_range], c='black', alpha=0.3, label='old boundary')
ax.plot(x_range, [new_boundary(x) for x in x_range], c='purple', label='new boundary')
# Draw arrows
for i in range(km.k):
plt.arrow(old[i, 0], old[i, 1], new[i, 0] - old[i, 0], new[i, 1] - old[i, 1],
length_includes_head=True, head_width=0.5, color='black')
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('KMeans: Boundary changes after first centroid update')
ax.legend(loc='upper left', scatterpoints=3)
# -
# Now that we confirmed that the class' main functionality works we can try out the `.fit()` method, which handles the training procedure for as many iterations as necessary.
# +
# CODE:
# --------------------------------------------
km = KMeans(2, seed=44)
km.fit(points)
# PLOTTING:
# --------------------------------------------
# Assign points and generate decision boundary
point_colors = [map_colors[i] for i in km.predict(points)]
decision_boundary = generate_perp_bisector(km.centroids)
# Create figure
fig = plt.figure(figsize=(7, 5))
ax = plt.subplot(111)
# Scatter the points and draw the decision boundary
ax.scatter(points[:, 0], points[:, 1], c=point_colors, s=50, lw=0, edgecolor='black', label='data points')
ax.scatter(km.centroids[:, 0], km.centroids[:, 1], c=colors, s=100, lw=1, edgecolor='black', label='centroids')
ax.plot(x_range, [new_boundary(x) for x in x_range], c='purple', label='decision boundary')
# We'll use km.history to plot the centroids' previous locations
steps = len(km.history)
for s in range(steps-2): # the last position (where s==steps-1) is already drawn;
# we'll ignore the penultimate position for two reasons:
# 1) it represents the last iteration, where the centroid movement was minimal and
# 2) because the arrows must be 1 less than the points
ax.scatter(km.history[s][:, 0], km.history[s][:, 1], c=colors, s=100, alpha=1.0 / (steps-s))
for i in range(km.k):
ax.arrow(km.history[s][i, 0], km.history[s][i, 1], km.history[s + 1][i, 0] - km.history[s][i, 0],
km.history[s + 1][i, 1] - km.history[s][i, 1], length_includes_head=True, head_width=0.3,
color='black', alpha=1.0 / (steps - s))
# Draw one more time to register the label
ax.scatter(km.history[s][:, 0], km.history[s][:, 1], c=colors, s=100, alpha=1.0 / (steps-s), label='previous positions')
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('KMeans: Complete training')
ax.legend(loc='upper left', scatterpoints=3)
# -
# Once the system is trained, we can use `.predict()` to figure out which cluster a point belongs to.
print(' (0,0) belongs to cluster:', km.predict((0, 0)))
print(' (5,5) belongs to cluster:', km.predict((5, 5)))
print('(10,10) belongs to cluster:', km.predict((10, 10)))
print('(15,15) belongs to cluster:', km.predict((15, 15)))
print('(20,20) belongs to cluster:', km.predict((20, 20)))
print('(25,25) belongs to cluster:', km.predict((25, 25)))
# Now that we've covered the basics, let's dive into some more advanced concepts of unsupervised learning. Up till now we haven't given any thought on the selection of $k$. What would happen if we selected a larger value than was necessary?
# +
# CODE:
# --------------------------------------------
k = 5
km = KMeans(k, seed=13)
km.fit(points)
# PLOTTING:
# --------------------------------------------
# Create figure
fig = plt.figure(figsize=(7, 5))
ax = plt.subplot(111)
# For ease, from now on, we will allow matplotlib so select the colors on its own
ax.scatter(points[:, 0], points[:, 1], c=km.predict(points), s=50, lw=0, label='data points')
ax.scatter(km.centroids[:, 0], km.centroids[:, 1], c=range(k), s=100, lw=1, edgecolor='black', label='centroids')
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('KMeans: k={}'.format(k))
ax.legend(loc='upper left', scatterpoints=3)
# -
# Is this a worse solution to the problem than that with $k=2$? Is there a way to confirm this?
#
# What if we had a more complex problem where we wouldn't know what $k$ to use?
# +
# CODE:
# --------------------------------------------
np.random.seed(77)
# We'll create 4 groups of 50 points with centers in the positions (7,7), (7,17), (17,7) και (17,17)
# The points will be highly dispersed so the groups won't be clearly visible
lowb, highb, var = 2, 12, 10
p1 = np.random.rand(50, 2) * var + lowb
p2 = np.random.rand(50, 2) * var + highb
a = np.array([highb] * 50)
b = np.array([lowb] * 50)
c = np.zeros((50, 2))
c[:, 0], c[:, 1] = a, b
p3 = np.random.rand(50, 2) * var + c
c[:, 1], c[:, 0] = a, b
p4 = np.random.rand(50, 2) * var + c
points = np.concatenate([p1, p2, p3, p4])
# PLOTTING:
# --------------------------------------------
# Create figure
fig = plt.figure(figsize=(7, 5))
ax = plt.subplot(111)
# Scatter new points
ax.scatter(points[:, 0], points[:, 1], c='#7f7f7f')
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('Data Points'.format(k))
# -
# Select whichever value of $k$ you feel appropriate.
# +
# CODE:
# --------------------------------------------
k = int(input('Select value for k: '))
km = KMeans(k, seed=77)
km.fit(points)
# PLOTTING:
# --------------------------------------------
# Create figure
fig = plt.figure(figsize=(7, 5))
ax = plt.subplot(111)
# Scatter new points
ax.scatter(points[:, 0], points[:, 1], c=km.predict(points), lw=0, s=50)
ax.scatter(km.centroids[:, 0], km.centroids[:, 1], c=range(k), lw=1, edgecolor='black', s=100)
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('k-means clustering for k={}'.format(k))
# -
# We'll draw a few more for $k = {2, 3, 4, 5, 6, 7}$.
# +
# PLOTTING:
# --------------------------------------------
# Create 6 subplots
f, ax = plt.subplots(2, 3, figsize=(10, 5))
seed = 55
# k = 2
km = KMeans(2, seed=seed)
ax[0, 0].scatter(points[:, 0], points[:, 1], c=km.fit_predict(points), lw=0)
ax[0, 0].scatter(km.centroids[:, 0], km.centroids[:, 1], c=range(km.k), lw=1, edgecolor='black', s=80)
ax[0, 0].set_title('k = 2')
ax[0, 0].axis('off')
# k = 3
km = KMeans(3, seed=seed)
ax[0, 1].scatter(points[:, 0], points[:, 1], c=km.fit_predict(points), lw=0)
ax[0, 1].scatter(km.centroids[:, 0], km.centroids[:, 1], c=range(km.k), lw=1, edgecolor='black', s=80)
ax[0, 1].set_title('k = 3')
ax[0, 1].axis('off')
# k = 4
km = KMeans(4, seed=seed)
ax[0, 2].scatter(points[:, 0], points[:, 1], c=km.fit_predict(points), lw=0)
ax[0, 2].scatter(km.centroids[:, 0], km.centroids[:, 1], c=range(km.k), lw=1, edgecolor='black', s=80)
ax[0, 2].set_title('k = 4')
ax[0, 2].axis('off')
# k = 5
km = KMeans(5, seed=seed)
ax[1, 0].scatter(points[:, 0], points[:, 1], c=km.fit_predict(points), lw=0)
ax[1, 0].scatter(km.centroids[:, 0], km.centroids[:, 1], c=range(km.k), lw=1, edgecolor='black', s=80)
ax[1, 0].set_title('k = 5')
ax[1, 0].axis('off')
# k = 6
km = KMeans(6, seed=seed)
ax[1, 1].scatter(points[:, 0], points[:, 1], c=km.fit_predict(points), lw=0)
ax[1, 1].scatter(km.centroids[:, 0], km.centroids[:, 1], c=range(km.k), lw=1, edgecolor='black', s=80)
ax[1, 1].set_title('k = 6')
ax[1, 1].axis('off')
# k = 7
km = KMeans(7, seed=seed)
ax[1, 2].scatter(points[:, 0], points[:, 1], c=km.fit_predict(points), lw=0)
ax[1, 2].scatter(km.centroids[:, 0], km.centroids[:, 1], c=range(km.k), lw=1, edgecolor='black', s=80)
ax[1, 2].set_title('k = 7')
ax[1, 2].axis('off')
# -
# So, how should we select the value of $k$ in this task? Is there an objective way to measure whether or not one of the above results is better than the other?
#
# ## Clustering Evaluation
#
# In order to be able to select the value of $k$ that yields the best results, we first need a way to **objectively** evaluate the performance of a clustering algorithm.
#
# We can't use any of the metrics we described in previous tutorials (e.g. accuracy, precision, recall), as they compare the algorithm's predictions to the class labels. However, as stated previously, in unsupervised problems there aren't any labels accompanying the data. So how can we measure the performance of a clustering algorithm?
#
# One way involves comparing the relationships in the clustered data. The simplest metric we could think of is to compare the variance of the samples of each cluster.
#
# For the cluster $C$ this can be calculated through the following formula:
#
# $$
# I_C = \sum_{i \in C}{(x_i - \bar{x}_C)^2}
# $$
#
# where $x_i$ is an example that belongs to cluster $C$ with a centroid $\bar{x}_C$.
#
# The smaller the value of $I_C$, the less the variance in cluster $C$, meaning that the cluster is more "compact". Metrics like this are called **inertia**. To calculate the total inertia, we can just sum the inertia of each cluster.
#
# $$
# I = \sum_{C = 1}^k{I_C}
# $$
#
# Many times, this is be divided with the total variance of the data.
#
# From now on we will be using the [KMeans](http://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html) estimator from scikit-learn, which provides more features and is better optimized than our simpler implementation.
# +
# CODE:
# --------------------------------------------
from sklearn.cluster import KMeans
k = 5
km = KMeans(k, random_state=99)
km.fit(points)
# PLOTTING:
# --------------------------------------------
# Create figure
fig = plt.figure(figsize=(7, 5))
ax = plt.subplot(111)
# Scatter data points and centroids
ax.scatter(points[:, 0], points[:, 1], c=km.predict(points), lw=0, s=50)
ax.scatter(km.cluster_centers_[:, 0], km.cluster_centers_[:, 1], c=range(km.n_clusters), lw=1, edgecolor='black', s=100)
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('k-means for k={}\nInertia={:.2f}'.format(k, km.inertia_))
# -
# As stated previously, the lower the value of inertia the better. An initial thought would be to try to **minimize** this criterion. Let's run k-means with $k={2, ..., 100}$ to see which value minimizes the inertia.
# +
# CODE:
# --------------------------------------------
cluster_scores = []
for k in range(2, 101):
km = KMeans(k, random_state=77)
km.fit(points)
cluster_scores.append(km.inertia_)
# PLOTTING:
# --------------------------------------------
# Create figure
fig = plt.figure(figsize=(7, 5))
ax = plt.subplot(111)
# Plot total inertia for all values of k
ax.plot(range(2, 101), cluster_scores)
# Aesthetic parameters
ax.set_xlabel('k')
ax.set_ylabel('inertia')
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.yaxis.set_ticks_position('left')
ax.xaxis.set_ticks_position('bottom')
ax.set_title('Inertia for different values of k')
# -
# From the figure above, we can observe that as $k$ increases, the system's total inertia decreases. This makes sense because more clusters in the system, will result in each of them having only few examples, close to their centroid. This means that the total variance of the system will decrease, as the number of clusters ($k$) increases. Finally, when $k=N$ (where $N$ is the total number of examples) inertia will reach 0.
#
# Can inertia help us select the best $k$? Not directly.
#
# We can use an **empirical** criterion called the [elbow][1]. To use this, we simply draw the inertia curve and look for where it forms an "elbow".
#
# [1]: https://en.wikipedia.org/wiki/Elbow_method_(clustering)
# +
# PLOTTING:
# --------------------------------------------
# Create figure
fig = plt.figure(figsize=(6, 4))
ax = plt.subplot(111)
# Draw first 6 values of k
plt.plot(range(2,8), cluster_scores[:6])
plt.annotate("elbow", xy=(3, cluster_scores[1]), xytext=(5, 6000),arrowprops=dict(arrowstyle="->"))
plt.annotate("elbow", xy=(4, cluster_scores[2]), xytext=(5, 6000),arrowprops=dict(arrowstyle="->"))
plt.annotate("elbow", xy=(6, cluster_scores[4]), xytext=(5, 6000),arrowprops=dict(arrowstyle="->"))
# Aesthetic parameters
ax.set_xlabel('k')
ax.set_ylabel('inertia')
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.yaxis.set_ticks_position('left')
ax.xaxis.set_ticks_position('bottom')
ax.set_title('Elbow criterion')
# -
# In the figure above we could choose $k=3$, $k=4$ or $k=6$. This method however is **highly subjective** and even if we used an objective method of figuring out the "sharpest" elbow (e.g. looking at the curve's second derivative), it still wouldn't produce any objective results, as the criterion is empirical.
#
# In order to get an **objective** evaluation on our clustering method's performance we need to dive a bit deeper into [clustering evaluation](https://en.wikipedia.org/wiki/Cluster_analysis#Evaluation_and_assessment). There are two main categories here:
#
# - Extrinsic evaluation: Involves running the clustering algorithm in a supervised problem, where class labels are available. They are obviously not included during the training phase but are used for evaluation. However, this type of evaluation can't be applied to any truly unsupervised problems.
# - Intrinsic evaluation: Requires analyzing the structure of the clusters, much like inertia we saw previously.
#
# ### Intrinsic Clustering Evaluation
#
# These metrics analyze the structure of the clusters and try to produce better scores for solutions with more "compact" clusters. Inertia did this by measuring the variance within each cluster. The problem with inertia, was that it rewarded solutions with more clusters. We are now going to examine two metrics that reward solutions with fewer (more sparse) clusters:
#
# - [Dunn index](https://en.wikipedia.org/wiki/Dunn_index):
# This metric consists of two parts:
# - The nominator is a measure of the **distance between two clusters**. This could be the distance between their centroids, the distance between their closest points, etc.
# - The denominator is a measure of the **size of the largest cluster**. This could be the largest distance between a centroid and the most remote point assigned to it, the maximum distance between two points of the same cluster, etc.
#
#
#
# $$
# DI= \frac{ min \left( \delta \left( C_i, C_j \right) \right)}{ max \, \Delta_p }
# $$
#
# where $C_i, C_j$ are two random centroids, $ \left( C_i, C_j \right)$ is a measure of their distance and $\Delta_p$ in a measure of the size of cluster $p$, where $p \in [0,k]$.
#
# The larger Dunn index is, the better the solution. The denominator of this index deals with the size of the clusters. Solutions with smaller (or more "**compact**") clusters produce a smaller denominator, which increases the index's value. The nominator becomes larger the farther apart the clusters are, which rewards **sparse solutions** with fewer clusters.
#
# - [Silhouette coefficient][1]:
# Like Dunn, this metric two can be decomposed into two parts. For cluster $i$:
# - A measure of cluster **homogeneity** $a(i)$ (e.g. the mean distance of all points assigned to $i$, to its centroid).
# - A measure of cluster $i$'s **distance to its nearest cluster** $b(i)$ (e.g. the distance of their centroids, the distance of their nearest points etc.)
#
# The silhouette coefficient is defined for each cluster separately:
#
# $$
# s \left( i \right) = \frac{b \left( i \right) - a \left( i \right) }{max \left( a \left( i \right) , b \left( i \right) \right)}
# $$
#
# A small value of $a(i)$ means cluster $i$ is more "compact", while a large $b(i)$ means that $i$ is far away from its nearest cluster. It is apparent that larger values of the nominator are better. The denominator scales the index to $[-1, 1]$. The best score we can achieve is $s(i) \approx 1$ for $b(i) >> a(i)$.
#
# In order to evaluate our algorithm, we usually average the silhouette coefficients $s(i)$ for all the clusters.
#
# We'll now attempt to use the silhouette coefficient to figure out the best $k$ for our previous problem.
#
# [1]: https://en.wikipedia.org/wiki/Silhouette_(clustering)
# +
# CODE:
# --------------------------------------------
from sklearn.metrics import silhouette_score
silhouette_scores = []
for k in range(2, 101):
km = KMeans(k, random_state=77)
km.fit(points)
preds = km.predict(points)
silhouette_scores.append(silhouette_score(points, preds))
# PLOTTING:
# --------------------------------------------
# Find out the value of k which produced the best silhouette score
best_k = np.argmax(silhouette_scores) + 2 # +2 because range() begins from k=2
# Create figure
fig = plt.figure(figsize=(6, 4))
ax = plt.subplot(111)
# Draw figures
ax.plot(range(2, 101), silhouette_scores)
ax.scatter(best_k, silhouette_scores[best_k-2], color='#ff7f0e')
ax.annotate("best k", xy=(best_k, silhouette_scores[best_k-2]), xytext=(50, 0.39), arrowprops=dict(arrowstyle="->"))
# Aesthetic parameters
ax.set_xlabel('k')
ax.set_ylabel('silhouette score')
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.yaxis.set_ticks_position('left')
ax.xaxis.set_ticks_position('bottom')
ax.set_title('Silhouette scores for different values of k')
print('Maximum average silhouette score for k =', best_k)
# -
# Let's draw the clustering solution for $k=61$.
# +
# CODE:
# --------------------------------------------
km = KMeans(best_k, random_state=77)
preds = km.fit_predict(points)
# PLOTTING:
# --------------------------------------------
# Create figure
fig = plt.figure(figsize=(6, 4))
ax = plt.subplot(111)
# Draw assigned points
ax.scatter(points[:, 0], points[:, 1], c=preds, lw=0, label='data points')
ax.scatter(km.cluster_centers_[:, 0], km.cluster_centers_[:,1], c='#ff7f0e', s=50, lw=1, edgecolor='black', label='centroids')
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('k-means for k={}\nSilhouette score={:.2f}'.format(best_k, silhouette_scores[best_k-2]))
plt.legend(loc='upper left', scatterpoints=3)
# -
# This result, however, still might not be desirable due to the large number of clusters. In most applications it doesn't help us very much to cluster 200 points into 61 clusters. We could take that into account and add another restriction to our problem: only examine solutions with 20 or less clusters.
# +
# CODE:
# --------------------------------------------
good_k = np.argmax(silhouette_scores[:10]) + 2
km = KMeans(good_k, random_state=77)
preds = km.fit_predict(points)
# PLOTTING:
# --------------------------------------------
# Create figure
fig = plt.figure(figsize=(6, 4))
ax = plt.subplot(111)
# Draw assigned points
ax.scatter(points[:, 0], points[:, 1], c=preds, lw=0, label='data points')
ax.scatter(km.cluster_centers_[:, 0], km.cluster_centers_[:,1], c='#ff7f0e', s=80, lw=1, edgecolor='black', label='centroids')
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('k-means for k={}\nSilhouette score={:.2f}'.format(good_k, silhouette_scores[good_k-2]))
ax.legend(loc='upper left', scatterpoints=3)
print('A good value for k is: k =', good_k)
# -
# We can view where this solution's silhouette score ranks compared to the best solution.
# +
# PLOTTING:
# --------------------------------------------
# Create figure
fig = plt.figure(figsize=(6, 4))
ax = plt.subplot(111)
# Draw figure
ax.plot(range(2, 101), silhouette_scores)
ax.scatter([good_k, best_k], [silhouette_scores[good_k-2], silhouette_scores[best_k-2]], color='#ff7f0e')
ax.annotate("best k", xy=(best_k, silhouette_scores[best_k-2]), xytext=(50, 0.39), arrowprops=dict(arrowstyle="->"))
ax.annotate("good k", xy=(good_k, silhouette_scores[good_k-2]), xytext=(10, 0.43), arrowprops=dict(arrowstyle="->"))
# Aesthetic parameters
ax.set_xlabel('k')
ax.set_ylabel('silhouette score')
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.yaxis.set_ticks_position('left')
ax.xaxis.set_ticks_position('bottom')
ax.set_title('Silhouette scores for different values of k')
# -
# Now we normally would want to decide if the drop-off in the silhouette score is acceptable.
#
# We could also generate a list of candidate values of $k$ and select the best one manually.
# +
# PLOTTING:
# --------------------------------------------
# Create figure
fig = plt.figure(figsize=(6, 4))
ax = plt.subplot(111)
# Draw figure
topN = 3
ax.plot(range(2, 22), silhouette_scores[:20])
candidate_k = np.argpartition(silhouette_scores[:20], -topN)[-topN:]
ax.scatter([k+2 for k in candidate_k], [silhouette_scores[k] for k in candidate_k], color='#ff7f0e')
for k in candidate_k:
ax.annotate("candidate k", xy=(k+2, silhouette_scores[k]), xytext=(6, 0.38), arrowprops=dict(arrowstyle="->"))
print('For k = {:<2}, the average silhouette score is: {:.4f}.'.format(k+2, silhouette_scores[k]))
# Aesthetic parameters
ax.set_xlabel('k')
ax.set_ylabel('silhouette score')
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.yaxis.set_ticks_position('left')
ax.xaxis.set_ticks_position('bottom')
ax.set_title('Silhouette scores for different values of k')
# -
# It should be noted at this point that cluster evaluation is **highly subjective**. There is no such thing as the "best solution". In the example above one might have preferred the solution that produced the best silhouette score, while another a sparser solution with a worse score.
#
# Scikit-learn offers many [metrics](http://scikit-learn.org/stable/modules/classes.html#clustering-metrics) for cluster evaluation. We need to be careful, however, because some metrics are unfit for use for the selection of $k$.
#
# For example [Calinski-Harabaz](http://scikit-learn.org/stable/modules/generated/sklearn.metrics.calinski_harabaz_score.html):
#
# $$
# CH \left( i \right) = \frac{B \left( i \right) / \left( k - 1 \right) }{W \left( i \right) / \left( N - k \right)}
# $$
#
# where $N$ is the number of samples, $k$ is the number of clusters, $i$ is a cluster ($i \in \{1, ..., k \}$), $B \left( i \right)$ is an intra-cluster variance metric (e.g. the mean squared distance between the cluster centroids) and $W \left( i \right)$ is an inter-cluster variance metric (e.g. the mean squared distance between points of the same cluster).
# +
# CODE:
# --------------------------------------------
from sklearn.metrics import calinski_harabaz_score
ch_scores = []
for k in range(2, 101):
km = KMeans(k, random_state=77)
km.fit(points)
preds = km.predict(points)
ch_scores.append(calinski_harabaz_score(points, preds))
# PLOTTING:
# --------------------------------------------
# Find best score
ch_k = np.argmax(ch_scores) + 2
# Create figure
fig = plt.figure(figsize=(6, 4))
ax = plt.subplot(111)
# Draw figures
ax.plot(range(2, 101), ch_scores)
ax.scatter(ch_k, ch_scores[ch_k-2], color='#ff7f0e')
ax.annotate("best k", xy=(ch_k, ch_scores[ch_k-2]), xytext=(50, 450), arrowprops=dict(arrowstyle="->"))
# Aesthetic parameters
ax.set_xlabel('k')
ax.set_ylabel('Calinski-Harabaz score')
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.yaxis.set_ticks_position('left')
ax.xaxis.set_ticks_position('bottom')
ax.set_title('Calinski-Harabaz scores for different values of k')
print('Maximum Calinski-Harabaz score for k =', ch_k)
# -
# Note: For visualization purposes, in this tutorial, we've used only data with two dimensions. The same principles apply to data of any dimensionality.
#
# ## Bonus material
#
# ### Methods for the selection of **k**:
#
# [1](https://datasciencelab.wordpress.com/2013/12/27/finding-the-k-in-k-means-clustering/), [2](http://www.sthda.com/english/articles/29-cluster-validation-essentials/96-determining-the-optimal-number-of-clusters-3-must-know-methods/)
#
# ### Initialization
#
# Until now, we've initialized the algorithm by creating $k$ centroids and placing them randomly, in the same space as the data. The initialization of k-means is very important for optimal convergence. We'll illustrate this through an example.
# +
# CODE:
# --------------------------------------------
# We'll make 3 groups of 50 points each with centers in the positions (7,7), (17,7) and (17,17)
np.random.seed(77)
lowb, highb, var = 2, 12, 5
p1 = np.random.rand(50, 2) * var + lowb
p2 = np.random.rand(50, 2) * var + highb
a = np.array([highb] * 50)
b = np.array([lowb] * 50)
c = np.zeros((50, 2))
c[:, 0], c[:, 1] = a, b
p3 = np.random.rand(50, 2) * var + c
points = np.concatenate([p1, p2, p3])
# Place 3 centroids in the positions (0,20), (1,19) and (2,18)
centroids = np.array([[0, 20], [1, 19], [2, 18]])
# PLOTTING:
# --------------------------------------------
map_colors = {0: '#1f77b4', 1:'#ff7f0e', 2:'#e377c2'}
color_list = ['#1f77b4', '#ff7f0e', '#e377c2']
# Create figure
fig = plt.figure(figsize=(7, 5))
ax = plt.subplot(111)
# Draw figures
ax.scatter(points[:, 0], points[:, 1], lw=0, s=50, label='data points')
ax.scatter(centroids[:, 0], centroids[:, 1], c=color_list, s=100, lw=1, edgecolor='black', label='centroids')
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('KMeans: Centroid Initialization')
ax.legend(loc='upper right', scatterpoints=3)
# -
# There clearly are 3 groups of points and 3 centroids nearby. Normally, we would expect each centroid to claim one group. Let's run the first iteration to see how the centroids move.
# +
# CODE:
# --------------------------------------------
new_centroids = update_centers(centroids, points)
# PLOTTING:
# --------------------------------------------
colors = [map_colors[i] for i in assign_cluster(new_centroids, points)]
# Create figure
fig = plt.figure(figsize=(7, 5))
ax = plt.subplot(111)
# Draw figures
ax.scatter(points[:, 0], points[:, 1], c=colors, lw=0, s=50, label='data points')
ax.scatter(new_centroids[:, 0], new_centroids[:, 1], c=color_list, s=100, edgecolors='black', label='new centroids')
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('KMeans: First step')
ax.legend(loc='upper right', scatterpoints=3)
ax.arrow(centroids[2, 0], centroids[2, 1], new_centroids[2, 0] - centroids[2, 0], new_centroids[2, 1] - centroids[2, 1],
length_includes_head=True, head_width=0.5, color='black')
# -
# The first iteration updated one of the 3 centroids. Let's run one more...
# +
# CODE:
# --------------------------------------------
centroids = new_centroids
new_centroids = update_centers(centroids, points)
# PLOTTING:
# --------------------------------------------
colors = [map_colors[i] for i in assign_cluster(new_centroids, points)]
# Create figure
fig = plt.figure(figsize=(7, 5))
ax = plt.subplot(111)
# Draw figures
ax.scatter(points[:, 0], points[:, 1], c=colors, lw=0, s=50, label='data points')
ax.scatter(new_centroids[:, 0], new_centroids[:, 1], c=color_list, s=100, edgecolors='black', label='centroids')
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('KMeans: M step')
ax.legend(loc='upper right', scatterpoints=3)
# -
# We can run the cell above as many times as we want, the centroids won't move. The reason becomes apparent once we draw the decision boundary.
# +
# PLOTTING:
# --------------------------------------------
# Generate the decision boudary between the pink and the orange centroids
decision_boundary = generate_perp_bisector(centroids[1:, :])
# Find the range of values along the x axis
x_min = min([points[:, 0].min(), centroids[:, 0].min()])
x_max = max([points[:, 0].max(), centroids[:, 0].max()])
x_range = [x_min, x_max]
# Create figure
fig = plt.figure(figsize=(6, 4))
ax = plt.subplot(111)
# Draw figures
ax.scatter(points[:, 0], points[:, 1], c=colors, lw=0, s=50, label='data points')
ax.scatter(new_centroids[:, 0], new_centroids[:, 1], c=color_list, s=100, edgecolors='black', label='centroids')
ax.plot(x_range, decision_boundary(x_range), c='black', label='decision boundary')
# Aesthetic parameters
ax.set_xlabel('$x_1$', size=15)
ax.set_ylabel('$x_2$', size=15)
ax.tick_params(axis='both', which='both', bottom=False, left=False,
top=False, right=False, labelbottom=False, labelleft=False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_title('KMeans: Decision Boundary')
ax.legend(loc='upper right', scatterpoints=3)
# -
# Because all the data points have been assigned to one of the three clusters, the remaining two are impossible to update. This issue was caused by the bad initialization of the centroids. The best-known technique for initializing the centroids in k-means is called [K-means++](https://en.wikipedia.org/wiki/K-means%2B%2B).
#
# K-means++ is also the default method for initialization in scikit-learn's k-means estimator. Furthermore, scikit-learn by default runs the algorithm 10 times for different initial conditions and selects the solution that minimizes the total inertia of the system.
#
# ### Computational complexity
#
# The time complexity of the k-means algorithm is:
#
# $$
# O \left( k \cdot N \cdot d \cdot i \right)
# $$
#
# where
#
# - **k** is the number of clusters.
# - **N** is the number of examples.
# - **d** is the number of dimensions of each example.
# - **i** is the number of iterations until convergence.
#
# Because k-means typically converges after a few iterations, k-means is often considered to have "linear" complexity and in practice it is one of the **fastest** clustering algorithms. The issue with k-means it that it can easily fall into **local minima** (like we saw previously due to bad initialization). Using k-means++ initialization can add an additional complexity, but usually helps the algorithm to converge faster.
#
# ### Comparison to other clustering algorithms
#
# K-means is considered a **centroid-based hard clustering** algorithm.
#
# #### Hard vs soft clustering
#
# Clustering algorithms can be split into two main categories: **hard** and **soft (or fuzzy)** clustering algorithms. The first place each example in a separate group, while the second return a probability for each example to belong in a specific category.
#
# A **soft clustering** solution is depicted below:
# 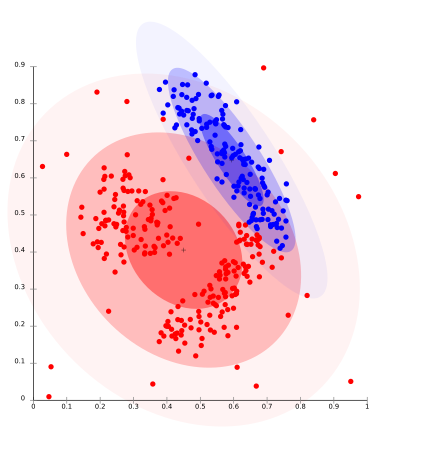
#
# An example of such an algorithm is the [Expectation-Maximization (ΕΜ)](https://en.wikipedia.org/wiki/Expectation%E2%80%93maximization_algorithm) algorithm.
#
# #### Hierarchical clustering
#
# These algorithms create a whole hierarchy of clusters. This way each example can belong to multiple clusters of different hierarchies.
#
# 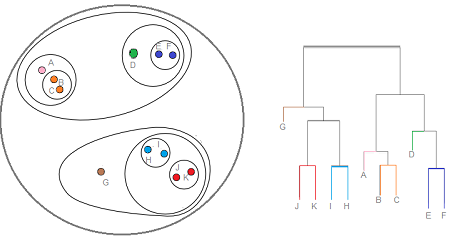
|
notebooks/26_clustering.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="hLEyhfMqmnrt"
# ## Colab JAX TPU Setup
# + colab={} colab_type="code" id="5CTEVmyKmkfp"
import jax.tools.colab_tpu
jax.tools.colab_tpu.setup_tpu()
# + [markdown] colab_type="text" id="ebUMqK9mGIDm"
# ## The basics: interactive NumPy on GPU and TPU
#
# ---
#
#
# + colab={} colab_type="code" id="27TqNtiQF97X"
import jax
import jax.numpy as jnp
from jax import random
key = random.PRNGKey(0)
# + colab={} colab_type="code" id="cRWoxSCNGU4o"
key, subkey = random.split(key)
x = random.normal(key, (5000, 5000))
print(x.shape)
print(x.dtype)
# + colab={} colab_type="code" id="diPllsvgGfSA"
y = jnp.dot(x, x)
print(y[0, 0])
# + colab={} colab_type="code" id="8-psauxnGiRk"
x
# + colab={} colab_type="code" id="-2FMQ8UeoTJ8"
import matplotlib.pyplot as plt
plt.plot(x[0])
# + colab={} colab_type="code" id="DRnwCKFuGk8P"
jnp.dot(x, x.T)
# + colab={} colab_type="code" id="z4VX5PkMHJIu"
print(jnp.dot(x, 2 * x)[[0, 2, 1, 0], ..., None, ::-1])
# + colab={} colab_type="code" id="ORZ9Odu85BCJ"
import numpy as np
x_cpu = np.array(x)
# %timeit -n 1 -r 1 np.dot(x_cpu, x_cpu)
# + colab={} colab_type="code" id="5BKh0eeAGvO5"
# %timeit -n 5 -r 5 jnp.dot(x, x).block_until_ready()
# + [markdown] colab_type="text" id="fm4Q2zpFHUAu"
# ## Automatic differentiation
# + colab={} colab_type="code" id="MCIQbyUYHWn1"
from jax import grad
# + colab={} colab_type="code" id="kfqZpKYsHo4j"
def f(x):
if x > 0:
return 2 * x ** 3
else:
return 3 * x
# + colab={} colab_type="code" id="K_26_odPHqLJ"
key = random.PRNGKey(0)
x = random.normal(key, ())
print(grad(f)(x))
print(grad(f)(-x))
# + colab={} colab_type="code" id="q5V3A6loHrhS"
print(grad(grad(f))(-x))
print(grad(grad(grad(f)))(-x))
# + colab={} colab_type="code" id="ba4WY4ArHv8I"
def predict(params, inputs):
for W, b in params:
outputs = jnp.dot(inputs, W) + b
inputs = jnp.tanh(outputs) # inputs to the next layer
return outputs # no activation on last layer
def loss(params, batch):
inputs, targets = batch
predictions = predict(params, inputs)
return jnp.sum((predictions - targets)**2)
def init_layer(key, n_in, n_out):
k1, k2 = random.split(key)
W = random.normal(k1, (n_in, n_out))
b = random.normal(k2, (n_out,))
return W, b
layer_sizes = [5, 2, 3]
key = random.PRNGKey(0)
key, *keys = random.split(key, len(layer_sizes))
params = list(map(init_layer, keys, layer_sizes[:-1], layer_sizes[1:]))
key, *keys = random.split(key, 3)
inputs = random.normal(keys[0], (8, 5))
targets = random.normal(keys[1], (8, 3))
batch = (inputs, targets)
# + colab={} colab_type="code" id="LiTBibJdHz4K"
print(loss(params, batch))
# + colab={} colab_type="code" id="a3KFpwH3H4Cl"
step_size = 1e-2
for _ in range(20):
grads = grad(loss)(params, batch)
params = [(W - step_size * dW, b - step_size * db)
for (W, b), (dW, db) in zip(params, grads)]
# + colab={} colab_type="code" id="YLltDr0GH7LX"
print(loss(params, batch))
# + [markdown] colab_type="text" id="bmxAPFC0I8b0"
# Other JAX autodiff highlights:
#
# * Forward- and reverse-mode, totally composable
# * Fast Jacobians and Hessians
# * Complex number support (holomorphic and non-holomorphic)
# * Jacobian pre-accumulation for elementwise operations (like `gelu`)
#
#
# For much more, see the [JAX Autodiff Cookbook (Part 1)](https://jax.readthedocs.io/en/latest/notebooks/autodiff_cookbook.html).
# + [markdown] colab_type="text" id="TRkxaVLJKNre"
# ## End-to-end compilation with XLA using `jit`
# + colab={} colab_type="code" id="bKo4rX9-KSW7"
from jax import jit
# + colab={} colab_type="code" id="94iIgZSfKWh8"
key = random.PRNGKey(0)
x = random.normal(key, (5000, 5000))
# + colab={} colab_type="code" id="Ybuz8Ag9KXMd"
def f(x):
y = x
for _ in range(10):
y = y - 0.1 * y + 3.
return y[:100, :100]
f(x)
# + colab={} colab_type="code" id="Y9dx5ifSKaGJ"
g = jit(f)
g(x)
# + colab={} colab_type="code" id="UtsS67BvKYkC"
# %timeit f(x).block_until_ready()
# + colab={} colab_type="code" id="-vfcaSo9KbvR"
# %timeit g(x).block_until_ready()
# + colab={} colab_type="code" id="E3BQF1_AKeLn"
grad(jit(grad(jit(grad(jnp.tanh)))))(1.0)
# + [markdown] colab_type="text" id="AvXl1WDPKjmV"
# ### Constraints that come with using `jit`
# + colab={} colab_type="code" id="mCtwRF18KnsE"
def f(x):
if x > 0:
return 2 * x ** 2
else:
return 3 * x
g = jit(f)
# + colab={} colab_type="code" id="_82tY-ZSKqv4"
f(2)
# + colab={} colab_type="code" id="TjSAFc-iKrcB"
try:
g(2)
except Exception as e:
print(e)
pass
# + colab={} colab_type="code" id="RhizP9pjKsug"
def f(x, n):
i = 0
while i < n:
x = x * x
i += 1
return x
g = jit(f)
# + colab={} colab_type="code" id="Wn6haTmUK-Q8"
f(jnp.array([1., 2., 3.]), 5)
# + colab={} colab_type="code" id="HwBy1I04K-81"
try:
g(jnp.array([1., 2., 3.]), 5)
except Exception as e:
print(e)
pass
# + colab={} colab_type="code" id="XmaTryZaK_3M"
g = jit(f, static_argnums=(1,))
# + colab={} colab_type="code" id="HcWjxVktV4fa"
g(jnp.array([1., 2., 3.]), 5)
# + [markdown] colab_type="text" id="0M_-pJe7LOcO"
# ## Vectorization with `vmap`
# + colab={} colab_type="code" id="8XIot_ndLRH1"
from jax import vmap
# + colab={} colab_type="code" id="tRvCZn2wBkXP"
print(vmap(lambda x: x**2)(jnp.arange(8)))
# + colab={} colab_type="code" id="icfsXizI_rkD"
from jax import make_jaxpr
make_jaxpr(jnp.dot)(jnp.ones(8), jnp.ones(8))
# + colab={} colab_type="code" id="uQm4cvAbA6M3"
make_jaxpr(vmap(jnp.dot))(jnp.ones((10, 8)), jnp.ones((10, 8)))
# + colab={} colab_type="code" id="NeiFfCHEBLsU"
make_jaxpr(vmap(vmap(jnp.dot)))(jnp.ones((10, 10, 8)), jnp.ones((10, 10, 8)))
# + colab={} colab_type="code" id="csX71fkSCZrp"
perex_grads = vmap(grad(loss), in_axes=(None, 0))
make_jaxpr(perex_grads)(params, batch)
# + [markdown] colab_type="text" id="Tmf1NT2Wqv5p"
# ## Parallel accelerators with pmap
# + colab={} colab_type="code" id="t6RRAFn1CEln"
jax.devices()
# + colab={} colab_type="code" id="tEK1I6Duqunw"
from jax import pmap
# + colab={} colab_type="code" id="S-iCNfeGqzkY"
y = pmap(lambda x: x ** 2)(jnp.arange(8))
print(y)
# + colab={} colab_type="code" id="xgutf5JPP3wi"
y
# + colab={} colab_type="code" id="xxShG3Tdq4Gj"
z = y / 2
print(z)
# + colab={} colab_type="code" id="uvDL2_bCq7kq"
import matplotlib.pyplot as plt
plt.plot(y)
# + colab={} colab_type="code" id="Xg76CmLYq_Q6"
keys = random.split(random.PRNGKey(0), 8)
mats = pmap(lambda key: random.normal(key, (5000, 5000)))(keys)
result = pmap(jnp.dot)(mats, mats)
print(pmap(jnp.mean)(result))
# + colab={} colab_type="code" id="jbw_hRx7rDzX"
timeit -n 5 -r 5 pmap(jnp.dot)(mats, mats).block_until_ready()
# + [markdown] colab_type="text" id="xf5N9ZRirJhL"
# ### Collective communication operations
# + colab={} colab_type="code" id="9i1PfxUvrThh"
from functools import partial
from jax.lax import psum
@partial(pmap, axis_name='i')
def normalize(x):
return x / psum(x, 'i')
print(normalize(jnp.arange(8.)))
# + colab={} colab_type="code" id="lnvwnlOFrVa-"
@partial(pmap, axis_name='rows')
@partial(pmap, axis_name='cols')
def f(x):
row_sum = psum(x, 'rows')
col_sum = psum(x, 'cols')
total_sum = psum(x, ('rows', 'cols'))
return row_sum, col_sum, total_sum
x = jnp.arange(8.).reshape((4, 2))
a, b, c = f(x)
print("input:\n", x)
print("row sum:\n", a)
print("col sum:\n", b)
print("total sum:\n", c)
# + [markdown] colab_type="text" id="f-FBsWeo1AXE"
# <img src="https://raw.githubusercontent.com/google/jax/main/cloud_tpu_colabs/images/nested_pmap.png" width="70%"/>
# + [markdown] colab_type="text" id="jC-KIMQ1q-lK"
# For more, see the [`pmap` cookbook](https://colab.research.google.com/github/google/jax/blob/main/cloud_tpu_colabs/Pmap_Cookbook.ipynb).
# + [markdown] colab_type="text" id="-A-oVDo6rdWA"
# ### Compose pmap with other transforms!
# + colab={} colab_type="code" id="WC_dMIN2rgTZ"
@pmap
def f(x):
y = jnp.sin(x)
@pmap
def g(z):
return jnp.cos(z) * jnp.tan(y.sum()) * jnp.tanh(x).sum()
return grad(lambda w: jnp.sum(g(w)))(x)
f(x)
# + colab={} colab_type="code" id="apuACjPWrixV"
grad(lambda x: jnp.sum(f(x)))(x)
# + [markdown] colab_type="text" id="WD9xtROsYX4i"
# ### Compose everything
# + colab={} colab_type="code" id="h65c9AQCWAyn"
from jax import jvp, vjp # forward and reverse-mode
curry = lambda f: partial(partial, f)
@curry
def jacfwd(fun, x):
pushfwd = partial(jvp, fun, (x,)) # jvp!
std_basis = jnp.eye(np.size(x)).reshape((-1,) + jnp.shape(x)),
y, jac_flat = vmap(pushfwd, out_axes=(None, -1))(std_basis) # vmap!
return jac_flat.reshape(jnp.shape(y) + jnp.shape(x))
@curry
def jacrev(fun, x):
y, pullback = vjp(fun, x) # vjp!
std_basis = jnp.eye(np.size(y)).reshape((-1,) + jnp.shape(y))
jac_flat, = vmap(pullback)(std_basis) # vmap!
return jac_flat.reshape(jnp.shape(y) + jnp.shape(x))
def hessian(fun):
return jit(jacfwd(jacrev(fun))) # jit!
# + colab={} colab_type="code" id="G9qDX84RWhW7"
input_hess = hessian(lambda inputs: loss(params, (inputs, targets)))
per_example_hess = pmap(input_hess) # pmap!
per_example_hess(inputs)
# + colab={} colab_type="code" id="u3ggM_WYZ8QC"
|
cloud_tpu_colabs/JAX_demo.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %config Completer.use_jedi = False
# +
from itertools import combinations_with_replacement
def factorize_natural_number(n, m):
"""
자연수 n, m을 입력받아서 n이 m개의 자연수들의 합으로 표현합니다.
-----------------------------------------------------
return
1. 경우의 수
2. 자연수들 쌍
"""
pairs = combinations_with_replacement(range(1, n), m)
result = [pair for pair in pairs if sum(pair) == n]
return len(result), result
# Example
num, result = factorize_natural_number(10, 4)
print("경우의 수: {}".format(num))
print("자연수들 쌍: {}".format(result))
|
FactorizeNaturalNumber.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import os
from scipy.io import wavfile
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from keras.layers import Conv2D, MaxPool2D, Flatten, LSTM
from keras.layers import Dropout, Dense, TimeDistributed
from keras.models import Sequential, load_model
from keras.utils import to_categorical
from sklearn.utils.class_weight import compute_class_weight
from tqdm import tqdm
import itertools
from python_speech_features import mfcc, logfbank
import librosa
from sklearn.metrics import confusion_matrix
import librosa
class Config:
def __init__(self, mode='conv', nfilt=26, nfeat=13, nfft=512, rate=16000):
self.mode = mode
self.nfilt = nfilt
self.nfeat = nfeat
self.nfft = nfft
self.rate = rate
self.step = int(rate/10)
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
def build_rand_feat():
X = []
y = []
_min, _max = float('inf'), -float('inf')
print('tqdm: ',n_samples)
for _ in tqdm(range(int(n_samples))):
rand_class = np.random.choice(class_dist.index, p = prob_dist)
file = np.random.choice(df[df.label==rand_class].index)
rate, wav = wavfile.read('clean_voice/'+file)
label = df.at[file, 'label']
rand_index = np.random.randint(0, wav.shape[0]-config.step)
sample = wav[rand_index:rand_index+config.step]
X_sample = mfcc(sample, rate, numcep=config.nfeat, nfilt=config.nfilt, nfft=config.nfft).T
_min = min(np.amin(X_sample), _min)
_max = max(np.amax(X_sample), _max)
X.append(X_sample if config.mode == 'conv' else X_sample.T)
y.append(classes.index(label))
X, y = np.array(X), np.array(y)
X = (X - _min) / (_max - _min)
if config.mode == 'conv':
X = X.reshape(X.shape[0], X.shape[1], X.shape[2], 1)
elif config.mode == 'time':
X = X.reshape(X.shape[0], X.shape[1], X.shape[2])
y = to_categorical(y, num_classes=8)
return X, y, _min, _max
def envelope(y, rate, threshold):
mask = []
y = pd.Series(y).apply(np.abs)
y_mean = y.rolling(window=int(rate/10), min_periods = 1, center = True).mean()
for mean in y_mean:
if mean > threshold:
mask.append(True)
else:
mask.append(False)
return mask
def calc_fft(y, rate):
n = len(y)
freq = np.fft.rfftfreq(n, d=1/rate)
Y = abs(np.fft.rfft(y)/n)
return(Y, freq)
def plot_signals(signals):
fig, axes = plt.subplots(nrows=2, ncols=4, sharex=False,
sharey=True, figsize=(20,5))
fig.suptitle('Time Series', size=16)
i = 0
for x in range(2):
for y in range(4):
axes[x,y].set_title(list(signals.keys())[i])
axes[x,y].plot(list(signals.values())[i])
axes[x,y].get_xaxis().set_visible(False)
axes[x,y].get_yaxis().set_visible(False)
i += 1
# +
df = pd.read_csv('voice_label.csv')
df.set_index('fname', inplace=True)
for f in df.index:
rate, signal = wavfile.read('clean_voice/'+f)
df.at[f, 'length'] = signal.shape[0]/rate
classes = list(np.unique(df.label))
class_dist = df.groupby(['label'])['length'].mean()
fig, ax = plt.subplots()
ax.set_title('class Distribution', y=1.08)
ax.pie(class_dist, labels = class_dist.index, autopct='%1.1f%%', shadow=False, startangle=90)
ax.axis('equal')
plt.show()
df.reset_index(inplace=True)
signals = {}
fft = {}
fbank = {}
mfccs = {}
for c in classes:
wav_file = df[df.label == c].iloc[0,0]
print(wav_file)
signal, rate = librosa.load('clean_voice/'+wav_file, sr=44100)
mask = envelope(signal, rate, 0.0005)
signal = signal[mask]
signals[c] = signal
fft[c] = calc_fft(signal, rate)
bank = logfbank(signal[:rate], rate, nfilt=26, nfft=1103).T
fbank[c] = bank
mel = mfcc(signal[:rate], rate, numcep = 13, nfilt=26, nfft = 1103).T
mfccs[c] = mel
plot_signals(signals)
plt.show()
# +
df = pd.read_csv('voice_label.csv')
df.set_index('fname', inplace=True) #danh so thu tu tung file
print(df.index[0])
for f in df.index:
rate, signal = wavfile.read('clean_voice/'+f) #tan so lay mau(rate=16000) va so mau moi file
df.at[f, 'length'] = signal.shape[0]/rate #tgian s
classes = list(np.unique(df.label))
print(classes)
class_dist = df.groupby(['label'])['length'].mean()
n_samples = 2*int(df['length'].sum())/0.1
print(n_samples)
prob_dist = class_dist/class_dist.sum()
choices = np.random.choice(class_dist.index, p = prob_dist)
fig, ax = plt.subplots()
ax.set_title('Class Distribution', y=1.08)
ax.pie(class_dist, labels=class_dist.index, autopct='%1.1f%%',
shadow=False, startangle=90)
ax.axis('equal')
plt.show()
config = Config(mode='conv')
# -
X, y, _min, _max = build_rand_feat()
y_flat = np.argmax(y, axis=1)
input_shape = (X.shape[1], X.shape[2], 1)
class_weight = compute_class_weight('balanced',np.unique(y_flat),y_flat)
print('class_weight: ',class_weight)
# print(list(X[0][0][0]))
# print(list(X[0][0][1]))
print(X.shape)
print(X)
print(X[0].dtype)
a = list(X[0])
# for i in X[0]:
# for j in X[0][X[0].index(i)]:
# print(j)
model = load_model('voice_conv.h5')
y_pred = model.predict(X)
print(y_pred.shape)
print(y_pred)
y0 = model.predict(X[0])
print(y0)
print(y_pred.shape)
cfm = confusion_matrix(np.argmax(y,axis=1), np.argmax(y_pred, axis=1))
np.set_printoptions(precision=2)
plt.figure()
class_names = ['ba', 'bay', 'bon', 'hai', 'mot', 'nam', 'sau', 'tam']
plot_confusion_matrix(cfm, classes=class_names, title='Confusion Matrix')
plt.show()
|
Test.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from splinter import Browser
from bs4 import BeautifulSoup as soup
# Path to chromedriver
# !which chromedriver
# Windows users
executable_path = {'executable_path': 'chromedriver.exe'}
browser = Browser('chrome', **executable_path, headless=False)
# Visit the Quotes to Scrape site
url = 'http://quotes.toscrape.com/'
browser.visit(url)
# Parse the HTML
html_parse = browser.html
parsed_soup = soup(html_parse, 'html.parser')
# +
# Scrape the Title
parse_title = parsed_soup.find('h2').text
parse_title
# +
# top_ten = parsed_soup.find('tag-item')
# top_ten
# scrape top ten tags
tag_box = parsed_soup.find('div', class_='tags-box')
# tag-box stores search results for div elements with tags-box class
# tag box
tags = tag_box.find_all('a', class_='tag')
tags
# # tags search within tag_box tweaked
for tag in tags:
word = tag.text
print(word)
# loops thru each tag with text only
# -
url = 'http://quotes.toscrape.com/'
browser.visit(url)
# +
for y in range (1,6): # through 6 pages
parse_html = browser.html # html object with parse_html assigned
soup_parsed = soup(parse_html, 'html.parser') #bs to parse html object
quotes = soup_parsed.find_all('span', class_ = 'text') #find quotes within span and specific class text
for quote in quotes:
print(f"page {y} of 6 --------") #separating the pages
print(f"{quote.text}") #prints each quote within a page
browser.links.find_by_partial_text('Next') #clicks next button thru splinter
# +
url = 'http://books.toscrape.com/'
browser.visit(url)
parsed_soup = soup(browser.html, 'html.parser')
bookcate = parsed_soup.find('ul', class_='nav nav-list').text
# bookList = bookcate.find_all()
# +
# skilldrill
bookcate = parsed_soup.find('ul', class_='nav nav-list').find('li').find_all('a')
for book in bookcate:
word = book.text
print(word)
# -
browser.quit()
|
Mars_Scraping/practice_scraping.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Simulating any compartmental model using the `Spp` class
#
# In the present notebook, we show how (most) compartmenal models can be simulated using the `pyross.deterministic.Spp` class. We allow users to specify any number of epidemiological classes, as well as any linear or infectious coupling between them.
# %matplotlib inline
import numpy as np
import pyross
import matplotlib.pyplot as plt
#from matplotlib import rc; rc('text', usetex=True)
# ### The SIR model
#
# Below you will find the model-specification dictionary for the SIR model with some constant injection into the S class:
# +
model_spec = {
"classes" : ["S", "I"],
"S" : {
"constant" : [ ["k"] ],
"infection" : [ ["I", "-beta"] ]
},
"I" : {
"linear" : [ ["I", "-gamma"] ],
"infection" : [ ["I", "beta"] ]
}
}
# -
# This corresponds to
#
# $$
# \begin{aligned}
# \dot{S}_i & = k - \beta \sum_j C_{ij} \frac{I_j}{N_j} S_i \\
# \dot{I}_i & = \beta \sum_j C_{ij} \frac{I_j}{N_j} S_i - \gamma I_i \\
# \dot{R}_i & = \gamma I_i
# \end{aligned}
# $$
#
# Let's go through each component of the model specification step-by-step:
#
# - The list `"classes" : ["S", "I", "R"]` defines the epidemiological
# classes of the model. <i>The order in which they are written are important</i>, as this ordering will have to be mainained if giving the initial conditions of the simulation as an array. Each model requires the presence of a susceptible class. This class
# will always be the first element of the list `classes`, regardless of whether it is labelled as `S` or not.
# - The dynamics of each class is defined by a key-value pair. Consider
#
# <br>
#
# ```json
# "E" : {
# "linear" : [ ["E", "-gammaE"] ],
# "infection" : [ ["I", "betaI"], ["A", "betaA"] ]
# },
# ```
#
# <br>
#
# - This reads out as:
# $$\dot{E}^\mu = -\gamma_E E^\mu + \beta_I \sum_\nu C^I_{\mu \nu} \frac{I^\nu}{N^\nu} S^\mu + \beta_A \sum_\nu C^A_{\mu \nu} \frac{A^\nu}{N^\nu} S^\mu.$$
# - The linear terms for each epidemic class is defined by the lists of lists:
#
# <br>
#
# ```json
# "linear" : [ ["E", "-gammaE"] ]
# ```
#
# <br>
#
# Eeach pair in `linear` corresponds to the linear coupling
# with the class and the coupling constant respectively. So
# `["E", "-gammaE"]` corresponds to the term $-\gamma_E E$ in
# the equation for $\dot{E}$. The minus sign in front of `gammaE`
# signifies that the negative of the coefficient should be used.
# - The infection terms are defined in a similar manner. Each pair
# in `infection` corresponds to the non-linear coupling with $S$
# and the coupling constant respectively. So `["I", "betaI"]`
# corresponds to the term $\beta_I \sum_\nu C^I_{\mu \nu} \frac{I^\nu}{N^\nu} S$.
# Next, we define the parameter values:
parameters = {
'beta' : 0.1,
'gamma' : 0.1,
'k' : 1,
}
# The initial conditions can be defined in either of two ways. They can either be defined using a dictionary, where for each model class we have a corresponding 1D array of length $M$ (where $M$ is the number of age-groups), or a numpy array. The numpy array must have dimensions $M \times (d-1)$, where $d$ is the number of model classes (so 3 for SIR, for example).
#
# If the initial conditions are provided as a dictionary, we are free to leave out one of the classes. In which case the initial conditions of the left out class will be inferred from the others.
# +
M = 3
Ni = 1000*np.ones(M)
N = np.sum(Ni)
# Initial conditions as an array
x0 = np.array([
999, 1000, 1000, # S
1, 0, 0, # I
])
# Or initial conditions as a dictionary
I0 = [10, 10, 10]
S0 = [n-20 for n in Ni]
x0 = {
'S' : S0,
'I' : I0
}
CM = np.array([
[1, 0.5, 0.1],
[0.5, 1, 0.5],
[0.1, 0.5, 1 ]
], dtype=float)
def contactMatrix(t):
return CM
# duration of simulation and data file
Tf = 160; Nf=Tf+1;
model = pyross.deterministic.Spp(model_spec, parameters, M, Ni)
# simulate model
data = model.simulate(x0, contactMatrix, Tf, Nf)
# +
# plot the data and obtain the epidemic curve
S = np.sum(model.model_class_data('S', data), axis=1)
I = np.sum(model.model_class_data('I', data), axis=1)
R = np.sum(model.model_class_data('R', data), axis=1)
t = data['t']
fig = plt.figure(num=None, figsize=(10, 8), dpi=80, facecolor='w', edgecolor='k')
plt.rcParams.update({'font.size': 22})
plt.fill_between(t, 0, S/N, color="#348ABD", alpha=0.3)
plt.plot(t, S, '-', color="#348ABD", label='$S$', lw=4)
plt.fill_between(t, 0, I/N, color='#A60628', alpha=0.3)
plt.plot(t, I, '-', color='#A60628', label='$I$', lw=4)
plt.fill_between(t, 0, R/N, color="dimgrey", alpha=0.3)
plt.plot(t, R, '-', color="dimgrey", label='$R$', lw=4)
plt.legend(fontsize=26); plt.grid()
plt.autoscale(enable=True, axis='x', tight=True)
plt.ylabel('Compartment value')
plt.xlabel('Days');
# -
# We can use `pyross.determinisitic.Spp.update_model_parameters` to change the parameters from what we set them initially:
# +
parameters = {
'beta' : 0.1,
'gamma' : 0.01,
'k':1
}
model.update_model_parameters(parameters)
# simulate model
data = model.simulate(x0, contactMatrix, Tf, Nf)
# +
# plot the data and obtain the epidemic curve
S = np.sum(model.model_class_data('S', data), axis=1)
I = np.sum(model.model_class_data('I', data), axis=1)
R = np.sum(model.model_class_data('R', data), axis=1)
t = data['t']
fig = plt.figure(num=None, figsize=(10, 8), dpi=80, facecolor='w', edgecolor='k')
plt.rcParams.update({'font.size': 22})
plt.fill_between(t, 0, S/N, color="#348ABD", alpha=0.3)
plt.plot(t, S/N, '-', color="#348ABD", label='$S$', lw=4)
plt.fill_between(t, 0, I/N, color='#A60628', alpha=0.3)
plt.plot(t, I/N, '-', color='#A60628', label='$I$', lw=4)
plt.fill_between(t, 0, R/N, color="dimgrey", alpha=0.3)
plt.plot(t, R/N, '-', color="dimgrey", label='$R$', lw=4)
plt.legend(fontsize=26); plt.grid()
plt.autoscale(enable=True, axis='x', tight=True)
plt.ylabel('Fraction of compartment value')
plt.xlabel('Days');
|
examples/deterministic/ex02-Spp.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Sentiment Analysis with an RNN
#
# In this notebook, you'll implement a recurrent neural network that performs sentiment analysis. Using an RNN rather than a feedfoward network is more accurate since we can include information about the *sequence* of words. Here we'll use a dataset of movie reviews, accompanied by labels.
#
# The architecture for this network is shown below.
#
# <img src="assets/network_diagram.png" width=400px>
#
# Here, we'll pass in words to an embedding layer. We need an embedding layer because we have tens of thousands of words, so we'll need a more efficient representation for our input data than one-hot encoded vectors. You should have seen this before from the word2vec lesson. You can actually train up an embedding with word2vec and use it here. But it's good enough to just have an embedding layer and let the network learn the embedding table on it's own.
#
# From the embedding layer, the new representations will be passed to LSTM cells. These will add recurrent connections to the network so we can include information about the sequence of words in the data. Finally, the LSTM cells will go to a sigmoid output layer here. We're using the sigmoid because we're trying to predict if this text has positive or negative sentiment. The output layer will just be a single unit then, with a sigmoid activation function.
#
# We don't care about the sigmoid outputs except for the very last one, we can ignore the rest. We'll calculate the cost from the output of the last step and the training label.
import numpy as np
import tensorflow as tf
with open('../sentiment-network/reviews.txt', 'r') as f:
reviews = f.read()
with open('../sentiment-network/labels.txt', 'r') as f:
labels = f.read()
reviews[:2000]
# ## Data preprocessing
#
# The first step when building a neural network model is getting your data into the proper form to feed into the network. Since we're using embedding layers, we'll need to encode each word with an integer. We'll also want to clean it up a bit.
#
# You can see an example of the reviews data above. We'll want to get rid of those periods. Also, you might notice that the reviews are delimited with newlines `\n`. To deal with those, I'm going to split the text into each review using `\n` as the delimiter. Then I can combined all the reviews back together into one big string.
#
# First, let's remove all punctuation. Then get all the text without the newlines and split it into individual words.
# +
from string import punctuation
all_text = ''.join([c for c in reviews if c not in punctuation])
reviews = all_text.split('\n')
all_text = ' '.join(reviews)
words = all_text.split()
# -
all_text[:2000]
words[:100]
# ### Encoding the words
#
# The embedding lookup requires that we pass in integers to our network. The easiest way to do this is to create dictionaries that map the words in the vocabulary to integers. Then we can convert each of our reviews into integers so they can be passed into the network.
#
# > **Exercise:** Now you're going to encode the words with integers. Build a dictionary that maps words to integers. Later we're going to pad our input vectors with zeros, so make sure the integers **start at 1, not 0**.
# > Also, convert the reviews to integers and store the reviews in a new list called `reviews_ints`.
# +
# Create your dictionary that maps vocab words to integers here
vocab_to_int =
# Convert the reviews to integers, same shape as reviews list, but with integers
reviews_ints =
# -
# ### Encoding the labels
#
# Our labels are "positive" or "negative". To use these labels in our network, we need to convert them to 0 and 1.
#
# > **Exercise:** Convert labels from `positive` and `negative` to 1 and 0, respectively.
# Convert labels to 1s and 0s for 'positive' and 'negative'
labels =
# If you built `labels` correctly, you should see the next output.
from collections import Counter
review_lens = Counter([len(x) for x in reviews_ints])
print("Zero-length reviews: {}".format(review_lens[0]))
print("Maximum review length: {}".format(max(review_lens)))
# Okay, a couple issues here. We seem to have one review with zero length. And, the maximum review length is way too many steps for our RNN. Let's truncate to 200 steps. For reviews shorter than 200, we'll pad with 0s. For reviews longer than 200, we can truncate them to the first 200 words.
#
# > **Exercise:** First, remove the review with zero length from the `reviews_ints` list.
# Filter out that review with 0 length
reviews_ints =
# > **Exercise:** Now, create an array `features` that contains the data we'll pass to the network. The data should come from `review_ints`, since we want to feed integers to the network. Each row should be 200 elements long. For reviews shorter than 200 words, left pad with 0s. That is, if the review is `['best', 'movie', 'ever']`, `[117, 18, 128]` as integers, the row will look like `[0, 0, 0, ..., 0, 117, 18, 128]`. For reviews longer than 200, use on the first 200 words as the feature vector.
#
# This isn't trivial and there are a bunch of ways to do this. But, if you're going to be building your own deep learning networks, you're going to have to get used to preparing your data.
#
#
seq_len = 200
features =
# If you build features correctly, it should look like that cell output below.
features[:10,:100]
# ## Training, Validation, Test
#
#
# With our data in nice shape, we'll split it into training, validation, and test sets.
#
# > **Exercise:** Create the training, validation, and test sets here. You'll need to create sets for the features and the labels, `train_x` and `train_y` for example. Define a split fraction, `split_frac` as the fraction of data to keep in the training set. Usually this is set to 0.8 or 0.9. The rest of the data will be split in half to create the validation and testing data.
# +
split_frac = 0.8
train_x, val_x =
train_y, val_y =
val_x, test_x =
val_y, test_y =
print("\t\t\tFeature Shapes:")
print("Train set: \t\t{}".format(train_x.shape),
"\nValidation set: \t{}".format(val_x.shape),
"\nTest set: \t\t{}".format(test_x.shape))
# -
# With train, validation, and text fractions of 0.8, 0.1, 0.1, the final shapes should look like:
# ```
# Feature Shapes:
# Train set: (20000, 200)
# Validation set: (2500, 200)
# Test set: (2500, 200)
# ```
# ## Build the graph
#
# Here, we'll build the graph. First up, defining the hyperparameters.
#
# * `lstm_size`: Number of units in the hidden layers in the LSTM cells. Usually larger is better performance wise. Common values are 128, 256, 512, etc.
# * `lstm_layers`: Number of LSTM layers in the network. I'd start with 1, then add more if I'm underfitting.
# * `batch_size`: The number of reviews to feed the network in one training pass. Typically this should be set as high as you can go without running out of memory.
# * `learning_rate`: Learning rate
lstm_size = 256
lstm_layers = 1
batch_size = 500
learning_rate = 0.001
# For the network itself, we'll be passing in our 200 element long review vectors. Each batch will be `batch_size` vectors. We'll also be using dropout on the LSTM layer, so we'll make a placeholder for the keep probability.
# > **Exercise:** Create the `inputs_`, `labels_`, and drop out `keep_prob` placeholders using `tf.placeholder`. `labels_` needs to be two-dimensional to work with some functions later. Since `keep_prob` is a scalar (a 0-dimensional tensor), you shouldn't provide a size to `tf.placeholder`.
# +
n_words = len(vocab_to_int) + 1 # Adding 1 because we use 0's for padding, dictionary started at 1
# Create the graph object
graph = tf.Graph()
# Add nodes to the graph
with graph.as_default():
inputs_ =
labels_ =
keep_prob =
# -
# ### Embedding
#
# Now we'll add an embedding layer. We need to do this because there are 74000 words in our vocabulary. It is massively inefficient to one-hot encode our classes here. You should remember dealing with this problem from the word2vec lesson. Instead of one-hot encoding, we can have an embedding layer and use that layer as a lookup table. You could train an embedding layer using word2vec, then load it here. But, it's fine to just make a new layer and let the network learn the weights.
#
# > **Exercise:** Create the embedding lookup matrix as a `tf.Variable`. Use that embedding matrix to get the embedded vectors to pass to the LSTM cell with [`tf.nn.embedding_lookup`](https://www.tensorflow.org/api_docs/python/tf/nn/embedding_lookup). This function takes the embedding matrix and an input tensor, such as the review vectors. Then, it'll return another tensor with the embedded vectors. So, if the embedding layer has 200 units, the function will return a tensor with size [batch_size, 200].
#
#
# +
# Size of the embedding vectors (number of units in the embedding layer)
embed_size = 300
with graph.as_default():
embedding =
embed =
# -
# ### LSTM cell
#
# <img src="assets/network_diagram.png" width=400px>
#
# Next, we'll create our LSTM cells to use in the recurrent network ([TensorFlow documentation](https://www.tensorflow.org/api_docs/python/tf/contrib/rnn)). Here we are just defining what the cells look like. This isn't actually building the graph, just defining the type of cells we want in our graph.
#
# To create a basic LSTM cell for the graph, you'll want to use `tf.contrib.rnn.BasicLSTMCell`. Looking at the function documentation:
#
# ```
# tf.contrib.rnn.BasicLSTMCell(num_units, forget_bias=1.0, input_size=None, state_is_tuple=True, activation=<function tanh at 0x109f1ef28>)
# ```
#
# you can see it takes a parameter called `num_units`, the number of units in the cell, called `lstm_size` in this code. So then, you can write something like
#
# ```
# lstm = tf.contrib.rnn.BasicLSTMCell(num_units)
# ```
#
# to create an LSTM cell with `num_units`. Next, you can add dropout to the cell with `tf.contrib.rnn.DropoutWrapper`. This just wraps the cell in another cell, but with dropout added to the inputs and/or outputs. It's a really convenient way to make your network better with almost no effort! So you'd do something like
#
# ```
# drop = tf.contrib.rnn.DropoutWrapper(cell, output_keep_prob=keep_prob)
# ```
#
# Most of the time, your network will have better performance with more layers. That's sort of the magic of deep learning, adding more layers allows the network to learn really complex relationships. Again, there is a simple way to create multiple layers of LSTM cells with `tf.contrib.rnn.MultiRNNCell`:
#
# ```
# cell = tf.contrib.rnn.MultiRNNCell([drop] * lstm_layers)
# ```
#
# Here, `[drop] * lstm_layers` creates a list of cells (`drop`) that is `lstm_layers` long. The `MultiRNNCell` wrapper builds this into multiple layers of RNN cells, one for each cell in the list.
#
# So the final cell you're using in the network is actually multiple (or just one) LSTM cells with dropout. But it all works the same from an architectural viewpoint, just a more complicated graph in the cell.
#
# > **Exercise:** Below, use `tf.contrib.rnn.BasicLSTMCell` to create an LSTM cell. Then, add drop out to it with `tf.contrib.rnn.DropoutWrapper`. Finally, create multiple LSTM layers with `tf.contrib.rnn.MultiRNNCell`.
#
# Here is [a tutorial on building RNNs](https://www.tensorflow.org/tutorials/recurrent) that will help you out.
#
with graph.as_default():
# Your basic LSTM cell
lstm =
# Add dropout to the cell
drop =
# Stack up multiple LSTM layers, for deep learning
cell =
# Getting an initial state of all zeros
initial_state = cell.zero_state(batch_size, tf.float32)
# ### RNN forward pass
#
# <img src="assets/network_diagram.png" width=400px>
#
# Now we need to actually run the data through the RNN nodes. You can use [`tf.nn.dynamic_rnn`](https://www.tensorflow.org/api_docs/python/tf/nn/dynamic_rnn) to do this. You'd pass in the RNN cell you created (our multiple layered LSTM `cell` for instance), and the inputs to the network.
#
# ```
# outputs, final_state = tf.nn.dynamic_rnn(cell, inputs, initial_state=initial_state)
# ```
#
# Above I created an initial state, `initial_state`, to pass to the RNN. This is the cell state that is passed between the hidden layers in successive time steps. `tf.nn.dynamic_rnn` takes care of most of the work for us. We pass in our cell and the input to the cell, then it does the unrolling and everything else for us. It returns outputs for each time step and the final_state of the hidden layer.
#
# > **Exercise:** Use `tf.nn.dynamic_rnn` to add the forward pass through the RNN. Remember that we're actually passing in vectors from the embedding layer, `embed`.
#
#
with graph.as_default():
outputs, final_state =
# ### Output
#
# We only care about the final output, we'll be using that as our sentiment prediction. So we need to grab the last output with `outputs[:, -1]`, the calculate the cost from that and `labels_`.
with graph.as_default():
predictions = tf.contrib.layers.fully_connected(outputs[:, -1], 1, activation_fn=tf.sigmoid)
cost = tf.losses.mean_squared_error(labels_, predictions)
optimizer = tf.train.AdamOptimizer(learning_rate).minimize(cost)
# ### Validation accuracy
#
# Here we can add a few nodes to calculate the accuracy which we'll use in the validation pass.
with graph.as_default():
correct_pred = tf.equal(tf.cast(tf.round(predictions), tf.int32), labels_)
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))
# ### Batching
#
# This is a simple function for returning batches from our data. First it removes data such that we only have full batches. Then it iterates through the `x` and `y` arrays and returns slices out of those arrays with size `[batch_size]`.
def get_batches(x, y, batch_size=100):
n_batches = len(x)//batch_size
x, y = x[:n_batches*batch_size], y[:n_batches*batch_size]
for ii in range(0, len(x), batch_size):
yield x[ii:ii+batch_size], y[ii:ii+batch_size]
# ## Training
#
# Below is the typical training code. If you want to do this yourself, feel free to delete all this code and implement it yourself. Before you run this, make sure the `checkpoints` directory exists.
# +
epochs = 10
with graph.as_default():
saver = tf.train.Saver()
with tf.Session(graph=graph) as sess:
sess.run(tf.global_variables_initializer())
iteration = 1
for e in range(epochs):
state = sess.run(initial_state)
for ii, (x, y) in enumerate(get_batches(train_x, train_y, batch_size), 1):
feed = {inputs_: x,
labels_: y[:, None],
keep_prob: 0.5,
initial_state: state}
loss, state, _ = sess.run([cost, final_state, optimizer], feed_dict=feed)
if iteration%5==0:
print("Epoch: {}/{}".format(e, epochs),
"Iteration: {}".format(iteration),
"Train loss: {:.3f}".format(loss))
if iteration%25==0:
val_acc = []
val_state = sess.run(cell.zero_state(batch_size, tf.float32))
for x, y in get_batches(val_x, val_y, batch_size):
feed = {inputs_: x,
labels_: y[:, None],
keep_prob: 1,
initial_state: val_state}
batch_acc, val_state = sess.run([accuracy, final_state], feed_dict=feed)
val_acc.append(batch_acc)
print("Val acc: {:.3f}".format(np.mean(val_acc)))
iteration +=1
saver.save(sess, "checkpoints/sentiment.ckpt")
# -
# ## Testing
test_acc = []
with tf.Session(graph=graph) as sess:
saver.restore(sess, tf.train.latest_checkpoint('checkpoints'))
test_state = sess.run(cell.zero_state(batch_size, tf.float32))
for ii, (x, y) in enumerate(get_batches(test_x, test_y, batch_size), 1):
feed = {inputs_: x,
labels_: y[:, None],
keep_prob: 1,
initial_state: test_state}
batch_acc, test_state = sess.run([accuracy, final_state], feed_dict=feed)
test_acc.append(batch_acc)
print("Test accuracy: {:.3f}".format(np.mean(test_acc)))
|
sentiment-rnn/Sentiment_RNN.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from typing import List
class Solution:
def prisonAfterNDays(self, cells: List[int], N: int) -> List[int]:
for _ in range(N):
res = cells[::]
res[0] = res[-1] = 0
for i in range(1, 7):
res[i] = (cells[i-1] ^ cells[i+1]) ^ 1
cells = res
return res
# -
# +
from typing import List
from collections import defaultdict
class Solution:
def prisonAfterNDays(self, cells: List[int], N: int) -> List[int]:
# 寻找循环节, 将 cells 转换为整形的形式
s_cells = [str(x) for x in cells]
int_s = int(''.join(s_cells), 2)
n2s = defaultdict(int)
s2n = defaultdict(int)
s2n[int_s] = 0
n2s[0] = int_s
start = None
for i in range(1, N+1):
s = ~((int_s >> 1) ^ (int_s << 1)) & 126
int_s = s
if int_s not in s2n:
s2n[int_s] = i
n2s[i] = int_s
else: # 出现循环节
start = s2n[int_s]
break
if start is None:
res = n2s[N]
else:
idx = start + (N - start) % (i - start)
res = n2s[idx]
res = bin(res)[2:]
return [0] * (8 - len(res)) + [int(x) for x in res]
# -
solution = Solution()
solution.prisonAfterNDays([0,0,0,1,1,0,1,0], 574)
a = ~(1 & 1)
print(bin(a))
# +
# print(bin(s), int_s, i)
# -
6 % 1
if circle and N % circle == 0:
res = n2s[1] if n2s[0] != n2s[1] else n2s[0]
else:
res = n2s[N] if not circle else n2s[N % circle]
res = bin(res)[2:]
return [0] * (8 - len(res)) + [int(x) for x in res]
|
Hash Table/0118/957. Prison Cells After N Days.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] deletable=true editable=true
# # selenium path 설정 ( chrome driver )
#
# - [chorome driver 다운](https://sites.google.com/a/chromium.org/chromedriver/downloads)
# - 다운로드한 파일을 finder에서 더블클릭하면 파일이 나옴
# - 그 후 terminal을 열어서 echo $PATH 입력
# - 환경변수 폴더가 나오는데, /usr/local/bin/으로 파일을 옮기면 됩니다!
# ~~~
# # # cd Downloads
# # # cp chromedriver /usr/local/bin/
# # # cd /usr/local/bin/
# ~~~
#
# - 확인해보면 이제 크롬으로도 셀레니움 사용 가능!
# + [markdown] deletable=true editable=true
# - phantomjs의 경우도 다운받아서 bin파일에 넣는 방법도 있고, 터미널에서 아래와 같이 입력해도됨
# ~~~
# brew install phantomjs
# ~~~
# + [markdown] deletable=true editable=true
# ## 최근 selenium을 사용하는 경우, 파이어폭스는 geckodriver를 설치해야함
#
# [gecko driver](https://github.com/mozilla/geckodriver/releases)
#
# 다운로드 후, /usr/local/bin/으로 옮기면 됩니다
# + [markdown] deletable=true editable=true
# # 윈도우
# 드라이버를 다운로드한 후, c:\windows\system32에 복붙하면 됩니다!!!
# -
|
python/selenium ( install chrome driver with mac ).ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # numpy & numexpr
# Load the required modules.
import numexpr as ne
import numpy as np
# numexpr can be used to speed up arithmetic operations on numpy arrays, and conserve memory when doing so by avoiding the creation of unnecessary intermediate arrays.
# Create some matrices to compute with.
a = np.random.uniform(0, 1, (1000, 1000))
b = np.random.uniform(0, 1, (1000, 1000))
c = np.random.uniform(0, 1, (1000, 1000))
# %timeit d = 3*a + b*c**3
# %timeit d = ne.evaluate('3*a + b*c**3')
# Under the hood, numexpr uses Intel VML (Vector Math Library) that is part of MKL if that is available, hence ensuring that the vector/matrix aritmethic is vectorized.
# numexpr also supports the `where` function to "mask" arrays according to boolean conditions on the elements.
# %timeit e = np.where(a > 0.5, 1, -1)
# %timeit e = ne.evaluate('where(a > 0.5, 1, -1)')
# Although this result is not very impressive, keep in mind that this output was generated on a single core machine. VML will automatically use multithreading to further parallelize vector/matrix arithmetic operations.
# **Important note:** numexpr supports only element-wise operations, except for accumulation using `sum` and `prod`.
|
Python/Numpy/numexpr.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.9.4 64-bit
# name: python394jvsc74a57bd0fc2b9b8e7ffc55491203f57f14c59c77deaf23810082ba77383500414caf9122
# ---
# Business Understanding:
# 1) How does age impact how frequently an individual learns a new language or framework?
# 2) How does country impact how frequently an individual learns a new language or framework?
# 3) How does education level impact how frequently an individual learns a new language or framework?
# 4) How does employment status impact how frequently an individual learns a new language or framework?
# 5) How does job satisfaction impact how frequently an individual learns a new language or framework?
# 6) How does number of years coding impact how frequently an individual learns a new language or framework?
import numpy as np
import pandas as pd
from IPython import display
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score, mean_squared_error
from collections import defaultdict
import general_functions as gf
# %matplotlib inline
# Gather (see data_prep.ipynb for Assess and Clean Data steps)
df = pd.read_csv(r'reduced_data.csv', sep = ',', error_bad_lines = False, index_col = False)
df_schem = pd.read_csv(r'reduced_data_schema.csv', sep = ',', error_bad_lines = False, index_col = False)
# Analyze: Begin Data Modeling/Evaluation
# Create list of responses to how frequently a user learns a new language
df = df.dropna(subset = ['NEWLearn'])
df['NEWLearn'] = df['NEWLearn'].astype(str)
learn_resp = list(df['NEWLearn'].unique())
learn_resp
# Create data frame of languages used sorted by total count
learn = df['NEWLearn'].value_counts().reset_index()
learn.rename(columns = {'index':'learning frequency','NEWLearn':'count'}, inplace = True)
learn_df = gf.total_count(learn,'learning frequency','count',learn_resp)
gf.bar_plotting(learn_df,'Frequency of Learning a New Language',plot = True)
# Analyze: Comparing Age to Frequency Learning a New Language Responses
def age_bins(age):
"""
FUNCTION: sort the given age in to the ocrrect age range (or bin)
INPUTS:
age - integer
OUTPUTS:
string describe the age bin the input was sorted in to
"""
if age < 10 :
return 'Under 10 Years'
elif age >= 10 and age < 20:
return '10-19 Years'
elif age >= 20 and age < 30:
return '20-29 Years'
elif age >= 30 and age < 40:
return '30-39 Years'
elif age >= 40 and age < 50:
return '40-49 Years'
elif age >= 50 and age < 60:
return '50-59 Years'
elif age >= 60 and age < 70:
return '60-69 Years'
elif age >= 70 and age < 80:
return '70-79 Years'
else:
return 'Over 80 Years'
age_df = df['Age'].apply(age_bins).value_counts().reset_index()
age_df.rename(columns = {'index':'age','Age':'count'}, inplace = True)
df['AgeRanges'] = df['Age'].apply(age_bins)
gf.bar_plotting(age_df,'Age-Learning a New Language',plot = True)
range_1 = gf.percentage_breakdown(df[df['AgeRanges'] == 'Under 10 Years'], learn_resp, 'NEWLearn', 'Under 10 Years')
range_2 = gf.percentage_breakdown(df[df['AgeRanges'] == '10-19 Years'], learn_resp, 'NEWLearn', '10-19 Years')
range_3 = gf.percentage_breakdown(df[df['AgeRanges'] == '20-29 Years'], learn_resp, 'NEWLearn', '20-29 Years')
range_4 = gf.percentage_breakdown(df[df['AgeRanges'] == '30-39 Years'], learn_resp, 'NEWLearn', '30-39 Years')
range_5 = gf.percentage_breakdown(df[df['AgeRanges'] == '40-49 Years'], learn_resp, 'NEWLearn', '40-49 Years')
range_6 = gf.percentage_breakdown(df[df['AgeRanges'] == '50-59 Years'], learn_resp, 'NEWLearn', '50-59 Years')
range_7 = gf.percentage_breakdown(df[df['AgeRanges'] == '60-69 Years'], learn_resp, 'NEWLearn', '60-69 Years')
range_8 = gf.percentage_breakdown(df[df['AgeRanges'] == '70-79 Years'], learn_resp, 'NEWLearn', '70-79 Years')
range_9 = gf.percentage_breakdown(df[df['AgeRanges'] == 'Over 80 Years'], learn_resp, 'NEWLearn', 'Over 80 Years')
list_of_ranges = [range_1, range_2, range_3, range_4, range_5, range_6, range_7, range_8, range_9]
top_age_resp = pd.DataFrame(columns = ['Age Range','Frequency Learning a New Language'])
top_age_resp = gf.add_top_per_cat(top_age_resp, list_of_ranges)
top_age_resp
# Visualize: Create a table comparing the percentage breakdown of frequency of learning a new language by age range and compare to the total breakdown
comp_df_2 = pd.merge(range_1, range_2, how = 'outer', left_index = True, right_index = True)
comp_df_2.columns = ['Under 10 Years', '10-19 Years']
for x in list_of_ranges[2:]:
comp_df_2[x.columns[0]] = x
comp_df_2['Total'] = gf.percentage_breakdown(df, learn_resp, 'NEWLearn', 'Total')
comp_df_2 = comp_df_2.sort_values(by = ['Total'], ascending = False)
comp_df_2 = comp_df_2.style.apply(lambda x: ['background: green' if v >= (1.5*x.iloc[-1])
else ('background: yellow' if v >= (1.25*x.iloc[-1])
else ('background: red' if v <= (0.75*x.iloc[-1])
else '')) for v in x], axis = 1)
comp_df_2
# Analyze: Comparing Countrty to Frequency Learning a New Language Responses
country_df = df['Country'].value_counts().reset_index()
country_df.rename(columns = {'index':'country','Country':'count'}, inplace = True)
country_df = country_df[:10]
gf.bar_plotting(country_df,'Country-Learning a New Language',plot=True)
country_resp = ['United States','India','Germany','United Kingdom','Canada','France','Brazil','Netherlands','Poland','Australia']
country_1 = gf.percentage_breakdown(df[df['Country'] == 'United States'], learn_resp, 'NEWLearn', 'United States')
country_2 = gf.percentage_breakdown(df[df['Country'] == 'India'], learn_resp, 'NEWLearn', 'India')
country_3 = gf.percentage_breakdown(df[df['Country'] == 'Germany'], learn_resp, 'NEWLearn', 'Germany')
country_4 = gf.percentage_breakdown(df[df['Country'] == 'United Kingdom'], learn_resp, 'NEWLearn', 'United Kingdom')
country_5 = gf.percentage_breakdown(df[df['Country'] == 'Canada'], learn_resp, 'NEWLearn', 'Canada')
country_6 = gf.percentage_breakdown(df[df['Country'] == 'France'], learn_resp, 'NEWLearn', 'France')
country_7 = gf.percentage_breakdown(df[df['Country'] == 'Brazil'], learn_resp, 'NEWLearn', 'Brazil')
country_8 = gf.percentage_breakdown(df[df['Country'] == 'Netherlands'], learn_resp, 'NEWLearn', 'Netherlands')
country_9 = gf.percentage_breakdown(df[df['Country'] == 'Poland'], learn_resp, 'NEWLearn', 'Poland')
country_10 = gf.percentage_breakdown(df[df['Country'] == 'Australia'], learn_resp, 'NEWLearn', 'Australia')
list_of_countries = [country_1, country_2, country_3, country_4, country_5, country_6, country_7, country_8, country_9, country_10]
top_country_resp = pd.DataFrame(columns = ['Country','Frequency Learning a New Language'])
top_country_resp = gf.add_top_per_cat(top_country_resp, list_of_countries)
top_country_resp
# Visualize: Create a table comparing the percentage breakdown of frequency of learning a new language by country and compare to the total breakdown
comp_df_3 = pd.merge(country_1, country_2, how = 'outer', left_index = True, right_index = True)
comp_df_3.columns = ['United States', 'India']
for x in list_of_countries[2:]:
comp_df_3[x.columns[0]] = x
comp_df_3['Total'] = gf.percentage_breakdown(df, learn_resp, 'NEWLearn', 'Total')
comp_df_3 = comp_df_3.sort_values(by = ['Total'], ascending = False)
comp_df_3 = comp_df_3.style.apply(lambda x: ['background: green' if v >= (1.5*x.iloc[-1])
else ('background: yellow' if v >= (1.25*x.iloc[-1])
else ('background: red' if v <= (0.75*x.iloc[-1])
else '')) for v in x], axis = 1)
comp_df_3
# Analyze: Comparing Education Level to Frequency Learning a New Language Responses
ed_level_resp = list(df['EdLevel'].unique())
ed_level_resp
ed_level_df = df['EdLevel'].value_counts().reset_index()
ed_level_df.rename(columns = {'index':'ed level','EdLevel':'count'}, inplace = True)
gf.bar_plotting(ed_level_df,'Education Level-Learning a New Language',plot = True)
level_1 = gf.percentage_breakdown(df[df['EdLevel'] == 'Bachelor’s degree (B.A., B.S., B.Eng., etc.)'], learn_resp, 'NEWLearn', 'Bachelor’s degree')
level_2 = gf.percentage_breakdown(df[df['EdLevel'] == 'Master’s degree (M.A., M.S., M.Eng., MBA, etc.)'], learn_resp, 'NEWLearn', 'Master’s degree')
level_3 = gf.percentage_breakdown(df[df['EdLevel'] == 'Some college/university study without earning a degree'], learn_resp, 'NEWLearn', 'Some College/University')
level_4 = gf.percentage_breakdown(df[df['EdLevel'] ==
'Secondary school (e.g. American high school, German Realschule or Gymnasium, etc.)'], learn_resp, 'NEWLearn', 'Secondary school')
level_5 = gf.percentage_breakdown(df[df['EdLevel'] == 'Associate degree (A.A., A.S., etc.)'], learn_resp, 'NEWLearn',
'Associate degree')
level_6 = gf.percentage_breakdown(df[df['EdLevel'] == 'Other doctoral degree (Ph.D., Ed.D., etc.)'], learn_resp, 'NEWLearn',
'Doctoral degree')
level_7 = gf.percentage_breakdown(df[df['EdLevel'] == 'Primary/elementary school'], learn_resp, 'NEWLearn',
'Primary/elementary school')
level_8 = gf.percentage_breakdown(df[df['EdLevel'] == 'Professional degree (JD, MD, etc.)'], learn_resp, 'NEWLearn',
'Professional degree')
level_9 = gf.percentage_breakdown(df[df['EdLevel'] == 'I never completed any formal education'], learn_resp, 'NEWLearn',
'No formal education')
list_of_ed_levels = [level_1, level_2, level_3, level_4, level_5, level_6, level_7, level_8, level_9]
top_ed_level_resp = pd.DataFrame(columns = ['EdLevel','Frequency Learning a New Language'])
top_ed_level_resp = gf.add_top_per_cat(top_ed_level_resp, list_of_ed_levels)
top_ed_level_resp
# Visualize: Create a table comparing the percentage breakdown of frequency of learning a new language by education level and compare to the total breakdown
comp_df_4 = pd.merge(level_1, level_2, how = 'outer', left_index = True, right_index = True)
comp_df_4.columns = ['Bachelor’s degree', 'Master’s degree']
for x in list_of_ed_levels[2:]:
comp_df_4[x.columns[0]] = x
comp_df_4['Total'] = gf.percentage_breakdown(df, learn_resp, 'NEWLearn', 'Total')
comp_df_4 = comp_df_4.sort_values(by = ['Total'], ascending = False)
comp_df_4 = comp_df_4.style.apply(lambda x: ['background: green' if v >= (1.5*x.iloc[-1])
else ('background: yellow' if v >= (1.25*x.iloc[-1])
else ('background: red' if v <= (0.75*x.iloc[-1])
else '')) for v in x], axis = 1)
comp_df_4
# Analyze: Comparing Employment Status to Frequency Learning a New Language Responses
employ_resp = list(df['Employment'].unique())
employ_resp
employment_df = df['Employment'].value_counts().reset_index()
employment_df.rename(columns = {'index':'employment','Employment':'count'}, inplace = True)
gf.bar_plotting(employment_df,'Employment-Learning a New Language',plot=True)
emp_stat_1 = gf.percentage_breakdown(df[df['Employment'] == 'Employed full-time'], learn_resp, 'NEWLearn', 'Employed full-time')
emp_stat_2 = gf.percentage_breakdown(df[df['Employment'] == 'Independent contractor, freelancer, or self-employed'], learn_resp, 'NEWLearn', 'Independent contractor, freelancer, or self-employed')
emp_stat_3 = gf.percentage_breakdown(df[df['Employment'] == 'Employed part-time'], learn_resp, 'NEWLearn', 'Employed part-time')
emp_stat_4 = gf.percentage_breakdown(df[df['Employment'] == 'Not employed, but looking for work'], learn_resp, 'NEWLearn',
'Not employed, but looking for work')
emp_stat_5 = gf.percentage_breakdown(df[df['Employment'] == 'Not employed, and not looking for work'], learn_resp, 'NEWLearn',
'Not employed, and not looking for work')
emp_stat_6 = gf.percentage_breakdown(df[df['Employment'] == 'Retired'], learn_resp, 'NEWLearn', 'Retired')
list_of_emp = [emp_stat_1, emp_stat_2, emp_stat_3, emp_stat_4, emp_stat_5, emp_stat_6]
top_employment_resp = pd.DataFrame(columns = ['Employment','Frequency of Learning a New Language'])
top_employment_resp = gf.add_top_per_cat(top_employment_resp, list_of_emp)
top_employment_resp
# Visualize: Create a table comparing the percentage breakdown of frequency of learning a new language by employment status and compare to the total breakdown
comp_df_5 = pd.merge(emp_stat_1, emp_stat_2, how = 'outer', left_index = True, right_index = True)
comp_df_5.columns = ['Employed full-time', 'Independent contractor, freelancer, or self-employed']
for x in list_of_emp[2:]:
comp_df_5[x.columns[0]] = x
comp_df_5['Total'] = gf.percentage_breakdown(df, learn_resp, 'NEWLearn', 'Total')
comp_df_5 = comp_df_5.sort_values(by = ['Total'], ascending = False)
comp_df_5 = comp_df_5.style.apply(lambda x: ['background: green' if v >= (1.5*x.iloc[-1])
else ('background: yellow' if v >= (1.25*x.iloc[-1])
else ('background: red' if v <= (0.75*x.iloc[-1])
else '')) for v in x], axis = 1)
comp_df_5
# Analyze: Comparing Job Satisfaction to Frequency Learning a New Language Responses
job_sat_resp = list(df['JobSat'].unique())
job_sat_resp
job_sat_df = df['JobSat'].value_counts().reset_index()
job_sat_df.rename(columns = {'index':'jobsat','JobSat':'count'}, inplace = True)
gf.bar_plotting(job_sat_df,'Job Satisfaction-Learning a New Language',plot = True)
job_sat_1 = gf.percentage_breakdown(df[df['JobSat'] == 'Very satisfied'], learn_resp, 'NEWLearn', 'Very satisfied')
job_sat_2 = gf.percentage_breakdown(df[df['JobSat'] == 'Slightly satisfied'], learn_resp, 'NEWLearn', 'Slightly satisfied')
job_sat_3 = gf.percentage_breakdown(df[df['JobSat'] == 'Slightly dissatisfied'], learn_resp, 'NEWLearn', 'Slightly dissatisfied')
job_sat_4 = gf.percentage_breakdown(df[df['JobSat'] == 'Neither satisfied nor dissatisfied'], learn_resp, 'NEWLearn',
'Neither satisfied nor dissatisfied')
job_sat_5 = gf.percentage_breakdown(df[df['JobSat'] == 'Very dissatisfied'], learn_resp, 'NEWLearn', 'Very dissatisfied')
list_of_job_sat = [job_sat_1, job_sat_2, job_sat_3, job_sat_4, job_sat_5]
top_job_sat_resp = pd.DataFrame(columns = ['JobSat','Frequency of Learning a New Language'])
top_job_sat_resp = gf.add_top_per_cat(top_job_sat_resp, list_of_job_sat)
top_job_sat_resp
# Visualize: Create a table comparing the percentage breakdown of frequency of learning a new language by job satisfaction and compare to the total breakdown
comp_df_6 = pd.merge(job_sat_1, job_sat_2, how = 'outer', left_index = True, right_index = True)
comp_df_6.columns = ['Very satisfied', 'Slightly satisfied']
for x in list_of_job_sat[2:]:
comp_df_6[x.columns[0]] = x
comp_df_6['Total'] = gf.percentage_breakdown(df, learn_resp, 'NEWLearn', 'Total')
comp_df_6 = comp_df_6.sort_values(by = ['Total'], ascending = False)
comp_df_6 = comp_df_6.style.apply(lambda x: ['background: green' if v >= (1.3*x.iloc[-1])
else ('background: yellow' if v >= (1.15*x.iloc[-1])
else ('background: red' if v <= (0.85*x.iloc[-1])
else '')) for v in x], axis = 1)
comp_df_6
# Analyze: Comparing Years of Coding to Frequency Learning a New Language Responses
def yr_bin(yrs):
"""
FUNCTION: sort the given years of coding in to the correct time range
INPUTS:
yrs - string describing number of years coding
OUTPUTS:
string describe the time range the input was sorted in to
"""
if yrs == 'Less than 1 year' :
return 'Less than 1 year'
elif yrs in ['1','2','3','4','5','6','7','8','9']:
return '1-9 Years'
elif yrs in ['10', '11', '12','13','14','15','16','17','18','19']:
return '10-19 Years'
elif yrs in ['20', '21', '22','23','24','25','26','27','28','29']:
return '20-29 Years'
elif yrs in ['30', '31', '32','33','34','35','36','37','38','39']:
return '30-39 Years'
elif yrs in ['40', '41', '42','43','44','45','46','47','48','49', '50']:
return '40-50 Years'
else:
return 'More than 50 years'
yr_code_df = df['YearsCode'].apply(yr_bin).value_counts().reset_index()
yr_code_df.rename(columns = {'index':'years code','YearsCode':'count'}, inplace = True)
df['YearsCode Ranges'] = df['YearsCode'].apply(yr_bin)
gf.bar_plotting(yr_code_df,'Years Coding-Learning a New Language',plot = True)
yr_1 = gf.percentage_breakdown(df[df['YearsCode Ranges'] == '1-9 Years'], learn_resp, 'NEWLearn', '1-9 Years')
yr_2 = gf.percentage_breakdown(df[df['YearsCode Ranges'] == '10-19 Years'], learn_resp, 'NEWLearn', '10-19 Years')
yr_3 = gf.percentage_breakdown(df[df['YearsCode Ranges'] == '20-29 Years'], learn_resp, 'NEWLearn', '20-29 Years')
yr_4 = gf.percentage_breakdown(df[df['YearsCode Ranges'] == '30-39 Years'], learn_resp, 'NEWLearn', '30-39 Years')
yr_5 = gf.percentage_breakdown(df[df['YearsCode Ranges'] == '40-50 Years'], learn_resp, 'NEWLearn', '40-50 Years')
yr_6 = gf.percentage_breakdown(df[df['YearsCode Ranges'] == 'More than 50 years'], learn_resp, 'NEWLearn', 'More than 50 years')
yr_7 = gf.percentage_breakdown(df[df['YearsCode Ranges'] == 'Less than 1 year'], learn_resp, 'NEWLearn', 'Less than 1 year')
list_of_yrs = [yr_1, yr_2, yr_3, yr_4, yr_5, yr_6, yr_7]
top_yrs_resp = pd.DataFrame(columns = ['YearCode Ranges','Frequency of Learning a New Language'])
top_yrs_resp = gf.add_top_per_cat(top_yrs_resp, list_of_yrs)
top_yrs_resp
# Visualize: Create a table comparing the percentage breakdown of frequency of learning a new language by years of coding and compare to the total breakdown
comp_df_7 = pd.merge(yr_1, yr_2, how = 'outer', left_index = True, right_index = True)
comp_df_7.columns = ['1-9 Years', '10-19 Years']
for x in list_of_yrs[2:]:
comp_df_7[x.columns[0]] = x
comp_df_7['Total'] = gf.percentage_breakdown(df, learn_resp, 'NEWLearn', 'Total')
comp_df_7 = comp_df_7.sort_values(by = ['Total'], ascending = False)
comp_df_7 = comp_df_7.style.apply(lambda x: ['background: green' if v >= (1.5*x.iloc[-1])
else ('background: yellow' if v >= (1.25*x.iloc[-1])
else ('background: red' if v <= (0.75*x.iloc[-1])
else '')) for v in x], axis = 1)
comp_df_7
|
language_learning.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="aHlV836QxSf8"
# # Handwritting Recognition
# + [markdown] id="dRjpWzW3xWO9"
# ### Importing models and dataset
# + id="5yPGJujQrnS6"
from tkinter import *
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import keras
from keras.layers import Dense,Dropout,Flatten
from keras.layers import Conv2D,MaxPooling2D,GRU
from keras.datasets import mnist
from keras.models import Sequential
from keras import backend as K
import tensorflow as tf
# + id="vmUjYkn2t9eB" colab={"base_uri": "https://localhost:8080/"} outputId="861b4880-9a5e-4104-bf96-24c6af4f5106"
(x_train,y_train),(x_test,y_test)=mnist.load_data()
# + colab={"base_uri": "https://localhost:8080/"} id="mVf2CWCVuuB1" outputId="9ada107f-352c-4ae3-aa13-01aaec18534b"
print(x_train.shape)
# + colab={"base_uri": "https://localhost:8080/"} id="WoalbB8Uu4jb" outputId="0bdbac8e-e987-4024-fe47-360b860b07a2"
print(y_train.shape)
# + colab={"base_uri": "https://localhost:8080/"} id="Q2pYgob2u7mv" outputId="7e2431f1-f356-4b82-8d90-fd7060b401ab"
x_train[:,1:2]
# + [markdown] id="O9FLi_kHxeG3"
# ### Preprocessing
# + id="DpQxlrDhvZkN"
x_train2 = x_train.reshape(x_train.shape[0],28,28,1)
x_test2 = x_test.reshape(x_test.shape[0],28,28,1)
# + id="dJ9rN1UuvuOu"
input = (28,28,1)
# + id="7Xri29YrxxWO"
y_train2 = keras.utils.to_categorical(y_train,10)
y_test2 = keras.utils.to_categorical(y_test,10)
# + id="TvOxmA2Ux97n"
x_train2 = x_train2.astype('float32')
x_test2 = x_test2.astype('float32')
# + id="vq3sTxKs1y3E"
x_train2 = x_train2/255
x_test2 = x_test2/255
# + colab={"base_uri": "https://localhost:8080/"} id="b1-54jW2yOvC" outputId="132c3399-fba5-479c-abec-998dbb5dc24a"
x_train2.shape
# + colab={"base_uri": "https://localhost:8080/"} id="_JU6wQq2yRvu" outputId="7629e67b-0952-4508-db36-a24c066fa8da"
x_test2.shape
# + colab={"base_uri": "https://localhost:8080/"} id="IquvDKvOyVwg" outputId="a740067a-72c7-4fbc-9538-7c077e6116e1"
y_train2.shape
# + colab={"base_uri": "https://localhost:8080/"} id="uAd25pxhyaLp" outputId="e10b1f0d-7b83-401a-d3b6-a332ab07032a"
y_test2.shape
# + [markdown] id="C4Y3YXFIxNY1"
# ## CNN
# + id="pBi59kndynSh"
bs = 64
e=10
num_classes = 10
# + colab={"base_uri": "https://localhost:8080/"} id="qX2M-jrgvww7" outputId="2d79d71d-159f-4468-cd93-88897967094b"
model = Sequential()
model.add(Conv2D(32,kernel_size=(3,3),padding='same',activation='relu',input_shape=input))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Conv2D(64,kernel_size=(3,3),padding='same',activation='relu'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Conv2D(64,kernel_size=(3,3),padding='same',activation='relu'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Flatten())
model.add(Dense(128,activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(128,activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes,activation='softmax'))
model.compile(optimizer='adam',loss='categorical_crossentropy',metrics=['accuracy'])
model.summary()
# + colab={"base_uri": "https://localhost:8080/"} id="ZIJnlRf02qYt" outputId="c248bae6-6731-4695-f740-7f688c9fe207"
history=model.fit(x_train2,y_train2,batch_size=bs,epochs=e,validation_data=(x_test2,y_test2))
# + colab={"base_uri": "https://localhost:8080/", "height": 265} id="B5Z-m0NLq69q" outputId="23f8d73c-2f6e-4eca-f2a6-d2ba9d068c88"
plt.plot(history.history['loss'], label='train')
plt.plot(history.history['val_loss'], label='test')
plt.legend()
plt.show()
# + colab={"base_uri": "https://localhost:8080/"} id="G-1cj_cwxkug" outputId="8d0e963a-e7dc-438b-8861-615a0cf9fff2"
s = model.evaluate (x_test2,y_test2)
s[0]=s[0]*100
s[1]=s[1]*100
print('Test loss:', s[0])
print('Test accuracy:', s[1])
# + id="XIs9renzxraI"
model.save('mnist_cnn.h5')
# + colab={"resources": {"http://localhost:8080/nbextensions/google.colab/files.js": {"data": "<KEY>", "ok": true, "headers": [["content-type", "application/javascript"]], "status": 200, "status_text": ""}}, "base_uri": "https://localhost:8080/", "height": 643} id="2eX8HeWITOjM" outputId="cd671bb0-0b26-452f-a9ed-900d836adc24"
from google.colab import files
from io import BytesIO
from PIL import Image
from keras.preprocessing.image import img_to_array
from keras.models import load_model
upload = files.upload()
im = Image.open(BytesIO(upload['7.png']))
m = load_model("mnist_cnn.h5")
plt.imshow(im)
plt.show()
img = im.resize((28,28))
img = img.convert('L')
img = np.array(img)
plt.imshow(img)
plt.show()
img = img.reshape(1, 28, 28, 1)
img = img / 255.0
result = m.predict(img)[0]
r = np.argmax(result)
r1 = np.max(result)
print(str(r))
print(str(int(r1*100)))
# + [markdown] id="NHxkP160xJqG"
# ## GRU
# + id="9gMQnfQYL2mI"
x_train1 = x_train.reshape(x_train.shape[0],28,x_train.shape[1])
x_test1 = x_test.reshape(x_test.shape[0],28,x_test.shape[1])
# + colab={"base_uri": "https://localhost:8080/"} id="StHg0MT2Omsz" outputId="b7c9a93e-1b83-4f8f-d799-fbb9025f16dd"
x_train1.shape
# + id="6LrikGbqNBRq"
y_train1 = y_train.reshape(y_train.shape[0],1,1)
y_test1 = y_test.reshape(y_test.shape[0],1,1)
# + colab={"base_uri": "https://localhost:8080/"} id="ojDPBhqAOpCo" outputId="25763365-2071-49f7-a071-b1556a288fca"
y_train1.shape
# + colab={"base_uri": "https://localhost:8080/"} id="n2f0LsNFKcQu" outputId="7ad1cdf0-a104-4177-8b14-40ce82d53117"
import warnings
warnings.filterwarnings("ignore")
epochs = 5
model1 = Sequential()
model1.add(GRU(units=50,return_sequences=True,input_shape=(x_train.shape[0],x_train.shape[1])))
model1.add(Dropout(0.3))
model1.add(GRU(units=5,return_sequences=True))
model1.add(Dropout(0.3))
model1.add(GRU(units=50,return_sequences=True))
model1.add(Dropout(0.3))
model1.add(GRU(units=50))
model1.add(Dropout(0.3))
model1.add(Dense(units=9))
model1.compile(optimizer='adam',loss='mse',metrics= ['accuracy'])
history=model1.fit(x_train1,y_train1, batch_size = 32, epochs = epochs,validation_data=(x_test1, y_test1))
# + colab={"base_uri": "https://localhost:8080/"} id="viKaYJiSTKof" outputId="b4f08886-0c47-40f5-9a04-27de59674782"
model1.summary()
# + colab={"base_uri": "https://localhost:8080/", "height": 265} id="qyIMEYLmq-9p" outputId="88ff1e99-f14a-4204-b1ce-28d175c1b3a3"
plt.plot(history.history['loss'], label='train')
plt.plot(history.history['val_loss'], label='test')
plt.legend()
plt.show()
# + colab={"base_uri": "https://localhost:8080/"} id="8cVAIwuSSGvo" outputId="ceb7b8e9-30b1-416a-f2a6-31215548809d"
s1 = model1.evaluate (x_test,y_test)
s1[0]=s1[0]*100
s1[1]=s1[1]*100
print('Test loss:', s1[0])
print('Test accuracy:', s1[1])
# + id="DAkA_uQlSlQj"
model1.save('mnist_gru.h5')
|
Handwritten_Digit_Classification.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Installing requirements
# ! export PATH='$PATH:/home/monga/.local/lib/python3.8/site-packages'
#import util
from psfdataset import PSFDataset, transforms
import torch
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import confusion_matrix, accuracy_score, ConfusionMatrixDisplay
from tqdm.notebook import tqdm, trange
import util_lip_data as util_lip
import custom_transforms as ctransform
from importlib import reload
# +
"""
script to compute the number
of jsons created for each
word. The output is a .csv
file where for each word the
number of jsons corresponding
to train, val, and test subsets
is mentioned
"""
import os
import json
import re
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
def get_rect_and_landmarks(rect, landmarks):
# converts and returns the face rectangle and landmarks
# in formats appropriate for the display function
x = rect["left"]
y = rect["top"]
w = rect["width"]
h = rect["height"]
if landmarks is not None:
temp_agg = list()
for i in range(len(landmarks)):
temp = list()
temp.append(landmarks["point-" + str(i+1)]["x"])
temp.append(landmarks["point-" + str(i+1)]["y"])
temp_agg.append(temp)
return (x, y, w, h), np.asarray(temp_agg)
else:
return (x, y, w, h), np.empty((0, 0))
def choose_the_largest_face(faces_list):
if len(faces_list) == 1:
return faces_list[0]
area_max = 0
area_max_id = 0
for i,face in enumerate(faces_list):
(face_rect,landmarks) = face
area = face_rect[2] * face_rect[3] # area = width * height
if area > area_max:
area_max = area
area_max_id = i
return faces_list[area_max_id]
def load_one_json_file(filename, isDebug=False):
# load the metadata and facial landmarks
face_rect_list = []
landmarks_list = []
with open(filename) as f:
video_data_dict = json.load(f)
# extract duration
if video_data_dict["metaData"] is not None:
duration = float(re.findall(r"[-+]?\d*\.\d+|\d+", video_data_dict["metaData"]["Duration"])[0])
if isDebug:
print("duration metadata: %.3f" % duration)
# extract frame information aggregated for all frames
agg_frame_data = video_data_dict["aggFrameInfo"] # list of frame-wise visual data
for frame_data in agg_frame_data:
n_faces = frame_data["numFaces"]
if isDebug:
print("frame index: %d number of faces: %d" % (frame_data["frameIndex"], n_faces))
if frame_data["facialAttributes"] is not None:# if so, the n_faces should > 0
faces_list = []
for attr in frame_data["facialAttributes"]:
face_idx = attr["faceIndex"]
face_rect, landmarks = get_rect_and_landmarks(attr["faceRectangle"],
attr["faceLandmarks"])
faces_list.append((face_rect, landmarks))
face_rect_chosen, landmarks_chosen = choose_the_largest_face(faces_list)
face_rect_list.append(face_rect_chosen)
landmarks_list.append(landmarks_chosen)
face_rect_array = np.array(face_rect_list)
landmarks_array = np.array(landmarks_list)
return face_rect_array, landmarks_array
i_data = "/cache/lrw/lipread_landmarks/dlib68_2d_sparse_json/lipread_mp4"
# or i_data = "/cache/lrw/lipread_landmarks/dlib68_2d_sparse_json_defects_not_one_face/lipread_mp4"
selected_n_classes = 10 # the max is 500
cnt = 0
data = dict()
for word in os.listdir(i_data):
if not word.startswith('.'):
cnt += 1
if cnt > selected_n_classes:
break
print(cnt,word)
splits = dict() # 'train' 'val' and 'test' sets
# print("analysing data for the word: '%s'" % word)
p = os.path.join(i_data, word)
for sub_dir in os.listdir(p):
if not sub_dir.startswith('.'):
# print(sub_dir)
p_sub = os.path.join(p, sub_dir)
for _, _, files in os.walk(p_sub):
samples_list = []
for filename in files:
if filename.endswith('.json'):
face_rect_array, landmarks_array = load_one_json_file(os.path.join(p_sub, filename))
lip_region = []
for j in range(len(landmarks_array)):
lip_region.append(landmarks_array[j][48:68])
samples_list.append(np.array(lip_region))
splits[sub_dir] = samples_list
data[word] = splits
print('-------------------------------')
print(data.keys()) # names of all the 'selected_n_classes' classes
print(data['THOUGHT'].keys()) # print the names of the 3 splits for the first class 'THOUGHT'
print(len(data['THOUGHT']['train'])) # print the number of train samples of the first class
print(data['THOUGHT']['train'][0].shape) # print the shape (29 frames, 68 landmarks, 2 coordinates) of the first training sample of the first class
print('-------------------------------')
# -
# # Step 0: Defining a LabelEncoder to transform text class to numberic class
encoder= LabelEncoder()
categories = list(data.keys())
encoder.fit(categories)
# # Step 1: Defining my custom Data loader from above 'data'. We only need to properly define iterators for train/test/validation sets
def generate_iterator(data, key = 'train', refLength = 29):
iter_list = []
x = 0
for word, keypointsOneWord in data.items():
keypointsList = keypointsOneWord[key]
num_of_samples = len(keypointsList)
## There are some sample whose length is smaller than 29. We need to either delete it,
## or extend it to 29 length for now. But this can be resolved if signature transform is introduced
for i in range(len(keypointsList)):
singleSample = keypointsList[i]
if len(singleSample) < refLength:
singleSample = np.array(list(singleSample) + [singleSample[-1]] * (refLength - len(singleSample)))
keypointsList[i] = singleSample
iter_list = iter_list + list(zip(keypointsList, np.array(list(encoder.transform([word])) * num_of_samples)))
return iter(iter_list)
iter_train = generate_iterator(data, key = 'train')
iter_test = generate_iterator(data, key = 'test')
iter_val = generate_iterator(data, key = 'val')
iiter_test = [x for x in iter_test]
iiter_train = [x for x in iter_train]
# # Step 2: Let's adapt the PSFDataset from human body movement
tr = transforms.Compose([
#transforms.spatial.Crop(),
# transforms.spatial.Normalize(),
# transforms.SpatioTemporalPath(),
# transforms.temporal.MultiDelayedTransformation(2),
transforms.temporal.DyadicPathSignatures(dyadic_levels=2,
signature_level=4)
])
# As first steps, no transforms are introduced yet.
# +
# We create new dictionaries identical to 'data' that contain the normalized landmarks without aumenting
#the training set
d_normalize = {} # normalized data set
for i in data:
d_normalize[i] = dict((k,ctransform.normalize_based_on_first_frame(v)) for k, v in data[i].items())
d_rotate = {} # rotated data set
for i in data:
d_rotate[i] = dict((k,ctransform.rotate(v)) for k, v in data[i].items())
d_normalize_rotate= {} # normalized and rotated data set
for i in d_normalize:
d_normalize_rotate[i] = dict((k,ctransform.rotate(v)) for k, v in d_normalize[i].items())
# +
# We create a new dictionary identical to 'data' that contains the normalized landmarks augmenting
#the training set
aug_data = ctransform.flip_train_augmentation(data)
d_normalize_a = {} #normalized data set
for i in data:
d_normalize_a[i] = dict((k,ctransform.normalize_based_on_first_frame(v)) for k, v in aug_data[i].items())
d_rotate_a = {} #rotated data set
for i in data:
d_rotate_a[i] = dict((k,ctransform.rotate(v)) for k, v in aug_data[i].items())
d_normalize_rotate_a= {} ## normalized and rotated data set
for i in d_normalize_a:
d_normalize_rotate_a[i] = dict((k,ctransform.rotate(v)) for k, v in d_normalize_a[i].items())
# -
# # Step 3: Train the model
model, outputs = ctransform.trainModelWithSpecificDataDict(dataDict = data, transforms = tr, EPOCHS = 20)
|
Full_Lip_region_original_data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
nb = [17, 1, 3, 16, 19, 0]
def compute(nb, n):
last = nb[-1]
d = {k: i + 1 for i, k in enumerate(nb[:-1])}
for i in range(len(nb) + 1, n + 1):
if last not in d:
tmp = 0
else:
tmp = i - 1 - d[last]
d[last] = i - 1
last = tmp
return last
# -
print(f"Answer part one: {compute(nb, 2020)}")
print(f"Answer part two: {compute(nb, 30_000_000)}")
|
day_15/Day 15 - Rambunctious Recitation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: conda-ml
# language: python
# name: conda-ml
# ---
# # Naive Bayes Spam Classifier
#
# Naive Bayes classifiers are a type of machine learning algorithm based applying [bayes theorem](https://en.wikipedia.org/wiki/Bayes%27_theorem) with strong (naive) independence assumptions between features. In short, a naive bayes classifier treats every features independent from each other, making inference very efficient. These types of classifiers are commonly used for spam detection.
#
# The TF-IDF Tabu list was inspired by this [kaggle post](https://www.kaggle.com/clydewang/a-naive-bayes-way-for-spam-classification/notebook), with some improvements such as using pandas functions to clean the entire dataset instead of loop through it, and creating a better train and test split of the data.
#
# ## Before we start...
#
# Let's quickly cover some of the basic definitions needed to understand our problem.
#
# ### Bayes Theorem
#
# Bayes Theorem describes the probability of an event, based on prior knowledge of conditions that might be related to the event. Bayes Theorem is considered "naive" because it assumes that the presence (or absence) of a particular feature of a class is unrelated to the presence (or absence) of any other feature. In other words, every feature is taken into account without considering the existence of another feature.
#
# Mathmatically, Bayes Theorem can be written as:
#
# $$
# P(A \mid B) = \frac{P(B \mid A) \, P(A)}{P(B)}
# $$
#
# Lets break this down:
# - $A$ and $B$ are considered seperate events, and the Probability of $B$ (ie $P(B)$) ≠ 0.
# - $P(A)$ and $P(B)$ are the probabilities of observing events $A$ and $B$ without regard to each other.
# - $ P(A \mid B) $ is the probability of observing event $A$ given that $B$ is true
# - $ P(B \mid A) $ is the probability of observing event $B$ given that $A$ is true
#
# When applying Bayes Theorem to spam classification, we can rewrite the problem statment as:
#
# $$
# P(\textrm{spam} \mid \textrm{w}1 \cap \textrm{w}2 \> \cap .. \cap \> \textrm{w}n) = \frac{P(\textrm{w}1 \cap \textrm{w}2 \> \cap \> .. \cap \> \textrm{w}n \mid \textrm{spam}) \, P(\textrm{spam})}{P(\textrm{w}1 \cap \textrm{w}2 \> \cap \> .. \cap \> \textrm{w}n)}
# $$
#
# Now, we have a message m that is made up of n number of words, or m = $ (w1 \cap w2 \cap .. \cap wn) $. We assume the occurence of any word wn is independent of all other words.
#
#
#
# ## 1. Environment Setup
# +
# Loads watermark extension and prints details about current platform
# %load_ext watermark
# %watermark -v -n -m -p numpy,scipy,sklearn,pandas,matplotlib
# autoreloads changes in imported files
# %load_ext autoreload
# %autoreload 2
# import packages
# %matplotlib inline
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import os
import re
from sklearn.naive_bayes import BernoulliNB
# Get project directory
PROJ_ROOT = os.path.abspath(os.path.join(os.pardir, os.pardir))
print(PROJ_ROOT)
import sys
# make sure matplotlib will display inline
# %matplotlib inline
# -
# ## 2. Read in Data
#
# We'll define a function that reads in our data and splits it into a training and test dataset.
# +
def read_data():
SMS_df = pd.read_csv(PROJ_ROOT +'/data/naive_bayes/raw/spam.csv',usecols=[0,1],encoding='latin-1')
SMS_df.columns=['label','content']
n = int(SMS_df.shape[0])
# split into training data and test data
return split_train_test(SMS_df)
def split_train_test(df, train_size=0.8):
""" Splits data into train and test dataframes. Defaults to 80 20 split if not specified"""
split_df = pd.DataFrame(np.random.randn(df.shape[0], 2))
msk = np.random.rand(len(df)) < train_size
train = df[msk]
test = df[~msk]
return train, test
# -
# ## 3. Generate a Tabu List
# A **tabu list** is a list of those significant indicators of spam SMS. Here we select TF-IDF as the principle of list generation.
#
# **Term Frequency Inverse Document Frequence (TF-IDF)** is a statistical representation of the most important words in a collection of documents, or collection of messages in our case. The TF-IDF value increases proportionally the more often a word is found in a document, and is offset by the number of times that word occurs in the collection.
#
# Term Frequency (TF) is the frequency of a word in a certain kind of document. If there is a article of 50 words with 2 'data' in it, then the TF of the 'data' is given by 2/50=0.01.
#
# However, there are some words of high frequency in English, like 'a', 'is', 'are', etc. We have to remove those words from our list. We'll use IDF (inverse document frequency) to acomplish this task. Inverse Document Frequency is the indicator to reflect how important a word is related to some certain topic. It is given by
#
# $$
# \textrm{IDF} = \log(\frac{\textrm{total articles number of articles}}{\textrm{total number of articles containing word w}})
# $$
#
# The more common a word is across all examples, the lower it's "importance" score will be. Each word gets assigned a score, which is it's Term Frequency x Inverse Document Frequency (TF(w) * IDF(w)).
#
# Here is the code:
# +
def generate_tabu_list(path, tabu_size=200,ignore=3):
"""
path = file name to use for exporting list
tabu_size = length of exported list (ie how many rows through dataframe that function will process)
ignore = minimum word length necessary to process word (ie ignore common short words like a, at, the, etc)
"""
train_df,_ = read_data()
spam_TF_dict = dict()
valid_TF_dict = dict()
IDF_dict = dict()
# ignore all other than letters.
# returns list of words downcased, removing punctuation and anything that is not a letter
train_df['cleaned_content'] = train_df.content.apply( lambda x: [i.lower() for i in re.findall('[A-Za-z]+', re.sub("'","",x))])
# # go through each word in the dataset and add it to a dict of
for i in range(train_df.shape[0]):
if train_df.iloc[i].label == 'spam':
for find in train_df.iloc[i].cleaned_content:
if len(find)<ignore: continue
try:
# if the current word is already in our spam dict, increment the value (ie number of
# occurences) by 1
spam_TF_dict[find] = spam_TF_dict[find] + 1
except:
# if the current word is not in our spam dict, add it, set the initial value to 1
# and add the word to our valid dict and set the value to 0
spam_TF_dict[find] = spam_TF_dict.get(find,1)
valid_TF_dict[find] = valid_TF_dict.get(find,0)
else:
for find in train_df.iloc[i].cleaned_content:
if len(find)<ignore: continue
try:
valid_TF_dict[find] = valid_TF_dict[find] + 1
except:
spam_TF_dict[find] = spam_TF_dict.get(find,0)
valid_TF_dict[find] = valid_TF_dict.get(find,1)
# basically just a list of each unique word
word_set = set()
for find in train_df.iloc[i].cleaned_content:
if len(find)<ignore: continue
if not(find in word_set):
try:
IDF_dict[find] = IDF_dict[find] + 1
except:
IDF_dict[find] = IDF_dict.get(find,1)
word_set.add(find)
word_df = pd.DataFrame(list(zip(valid_TF_dict.keys(),valid_TF_dict.values(),spam_TF_dict.values(),IDF_dict.values())))
word_df.columns = ['keyword','valid_TF','spam_TF','IDF']
word_df['valid_TF'] = word_df['valid_TF'].astype('float')/train_df[train_df['label']=='ham'].shape[0]
word_df['spam_TF'] = word_df['spam_TF'].astype('float')/train_df[train_df['label']=='spam'].shape[0]
word_df['IDF'] = np.log10(train_df.shape[0]/word_df['IDF'].astype('float'))
word_df['valid_TFIDF'] = word_df['valid_TF']*word_df['IDF']
word_df['spam_TFIDF'] = word_df['spam_TF']*word_df['IDF']
word_df['diff']=word_df['spam_TFIDF']-word_df['valid_TFIDF']
selected_spam_key = word_df.sort_values('diff',ascending=False)
print('>>>Generating Tabu List...\n Tabu List Size: {}\n File Name: {}\n The words shorter than {} are ignored by model\n'.format(tabu_size, path, ignore))
file = open(path,'w')
for word in selected_spam_key.head(tabu_size).keyword:
file.write(word+'\n')
file.close()
# -
# ## 4. Read Tabu List and Convert SMS
# Since the message is of variant length, it is not easy for the implementation of learning algorithm. So we define a Function above generating tabu list and storing them in the local file. And we can use this file to convert a SMS expressed in string to a vector of fixed length expressed in binary value.
#
# The idea is given like this: If we have a tabu list then we could find those word in the list and represent them by a index. Thus a string can be converted to an array of int. Further, we could define an array filled with zeros with the same length of tabu list. if this str contains the word in the tabu list, we could assign 1 to the corresponding element of the array representing 'message contains word w'. (tips: the query of python.dict is of constant time, much faster than python.list)
#
# By taking this step, we could convert our raw data of variant length into the numeric data of fixed length.
#
# These two function is given below:
# +
def read_tabu_list(path):
file = open(path,'r')
keyword_dict = dict()
i = 0
for line in file:
keyword_dict.update({line.strip():i})
i+=1
return keyword_dict
# create a numpy array of length tabu, ie the number of unique words
# go through each word passed in 'content' (content is a string of words)
# for each unique word in the string, find it's index in the numpy array,
# and set its value to '1' to show it exists
def convert_content(content, tabu):
m = len(tabu)
res = np.int_(np.zeros(m))
finds = re.findall('[A-Za-z]+', content)
for find in finds:
find=find.lower()
try:
i = tabu[find]
res[i]=1
except:
continue
return res
# -
# ## 5. Learning, Testing and Predicting
# After we generate our tabu list and those supporting functions, we are now well prepared for the learning part in this problem. And here we could use the library from sklearn.naive_bayes import BernoulliNB. It will help us train this model.
#
# Before this part, let review our data: our feature input X is a nm matrix, where X[i,j] = 1 means the sample #i contains the word j in the tabu list, and supervised label Y is a n1 vector where Y[i] = 1 representing for a spam and 0 for a ham.
#
# Let prepare the materials for the learning algorithm.
def learn():
global tabu, m
train,_ = read_data()
n = train.shape[0]
X = np.zeros((n,m)); Y=np.int_(train.label=='spam')
for i in range(n):
X[i,:] = convert_content(train.iloc[i].content, tabu)
NaiveBayes = BernoulliNB()
NaiveBayes.fit(X, Y)
Y_hat = NaiveBayes.predict(X)
print('>>>Learning...\n Learning Sample Size: {}\n Accuarcy (Training sample): {:.2f}%\n'.format(n,sum(np.int_(Y_hat==Y))*100./n))
return NaiveBayes
# The Function above returns a well trained Naive Bayes Model object, and we could use it to make prediction.
# +
def test(NaiveBayes):
global tabu, m
_,test = read_data()
n = test.shape[0]
X = np.zeros((n,m)); Y=np.int_(test.label=='spam')
for i in range(n):
X[i,:] = convert_content(test.iloc[i].content, tabu)
Y_hat = NaiveBayes.predict(X)
print ('>>>Cross Validation...\n Testing Sample Size: {}\n Accuarcy (Testing sample): {:.2f}%\n'.format(n,sum(np.int_(Y_hat==Y))*100./n))
return
def predictSMS(SMS):
global NaiveBayes, tabu, m
X = convert_content(SMS, tabu)
Y_hat = NaiveBayes.predict(X.reshape(1,-1))
if int(Y_hat) == 1:
print ('SPAM: {}'.format(SMS))
else:
print ('HAM: {}'.format(SMS))
# -
# ## 6. Overall Assembly
# After we define the every modules we need in this problem, we could integrate them into a whole part.
# +
print('UCI SMS SPAM CLASSIFICATION PROBLEM SET\n -- implemented by Bernoulli Naive Bayes Model\n')
tabu_file = PROJ_ROOT + '/data/naive_bayes/interim/tabu.txt' # user defined tabu file
tabu_size = 300 # how many features are used to classify spam
word_len_ignored = 3 # ignore those words shorter than this variable
# build a tabu list based on the training data
generate_tabu_list(tabu_file,tabu_size, word_len_ignored)
tabu = read_tabu_list(tabu_file)
m = len(tabu)
# train the Naive Bayes Model using training data
NaiveBayes=learn()
# Test Model using testing data
test(NaiveBayes)
print('>>>Testing')
# I select two messages from the test data here.
predictSMS('Ya very nice. . .be ready on thursday')
predictSMS('Had your mobile 10 mths? Update to the latest Camera/Video phones for FREE. KEEP UR SAME NUMBER, Get extra free mins/texts. Text YES for a call')
|
notebooks/naive_bayes/0001-Model-BUILD-Naive-Bayes-Spam-Classification.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.8.3 64-bit (''py383'': conda)'
# language: python
# name: python38364bitpy383conda2309aa976eb546f3b7675a3d2adb70e0
# ---
# #%%appyter init
from appyter import magic
magic.init(lambda _=globals: _())
# ### Hexagonal Canvas Creator from Enrichr Libraries
#
# This appyter creates a hexagonal canvas comparing your inputted gene list to a library selected from Enrichr (https://amp.pharm.mssm.edu/Enrichr/).
#
# The resulting figure will have each hexagon representing one gene set in the library you chose and they will be colored based on their similarity to your inputted gene set (the darker, the more similar). Hovering over a hexagon will tell you the gene set it represents as well as the jaccard similarity index of that set with the set you inputted.
import pandas as pd
import numpy as np
import json
import requests
import math
import matplotlib
import uuid
import urllib
import pickle
from textwrap import dedent
from IPython.core.display import display, HTML
from string import Template
from random import seed, randint
from operator import itemgetter
# +
# %%appyter hide_code
{% do SectionField(name='section0', title = 'Create a Canvas', subtitle = 'Create a hexagonal canvas comparing your inputted gene set to the gene sets of your chosen Enrichr library. The resulting figure will have each hexagon representing one gene set in the library you chose and they will be colored based on their similarity to your inputted gene set (the darker, the more similar).', img = 'enrichr-icon.png')%}
{% do SectionField(name='section1', title = '1. Submit Your Gene List', subtitle = 'Upload a text file containing your gene list -OR- copy and paste your gene list into the text box below (One gene per row).', img = 'enrichr-icon.png')%}
{% do SectionField(name='section2', title = '2. Choose Enrichr Library', subtitle = 'Select up to two Enrichr libraries for which you would like to create canvases.', img = 'enrichr-icon.png')%}
{% do SectionField(name='section3', title = '3. Color Options', subtitle = 'Choose a color for your chart and choose how many hexagons are colored (default is 10).', img = 'enrichr-icon.png')%}
{% do SectionField(name='section4', title = '4. Color Scaling (Optional)', subtitle = 'Enter a value by which to normalize the color scaling. If you are not trying to compare multiple canvases, it is best to leave this blank. The value you enter must be greater than or equal to all Jaccard indices. Every Jaccard index will be divided by this value, then the coloring will be scaling based on the divided index. This is useful if you want to compare multiple canvases of different libraries and want the brightness to be constant throughout the figures. Be sure to scale by the highest maximum of the figures you are trying to compare. Scaling values will be provided in the output along with your canvas.', img = 'enrichr-icon.png')%}
# -
# ### Input options
# +
# %%appyter code_eval
gene_list_filename = {{ FileField(name='gene_list_filename', label='Gene List File', default='', description='Upload your gene list as a text file (One gene per row).', section = 'section1') }}
gene_list_input = {{ TextField(name='gene_list_input', label='Gene List', default='', description='Paste your gene list (One gene per row).', section = 'section1') }}
all_libraries = {{ MultiChoiceField(name='enrichr_libraries', description='Select the Enrichr libraries you would like in your figure.', label='Enrichr libraries', default=[], section = 'section2',choices=[
'Transcription_Factor_PPIs',
'TRRUST_Transcription_Factors_2019',
'BioCarta_2016',
'HMS_LINCS_KinomeScan',
'HumanCyc_2016',
'huMAP',
'KEA_2015',
'KEGG_2019_Human',
'KEGG_2019_Mouse',
'NCI-Nature_2016',
'Panther_2016',
'Phosphatase_Substrates_from_DEPOD',
'SILAC_Phosphoproteomics',
'SubCell_BarCode',
'WikiPathways_2019_Human',
'GO_Cellular_Component_2018',
'GO_Molecular_Function_2018',
'Achilles_fitness_decrease',
'Achilles_fitness_increase',
'ClinVar_2019',
'dbGaP',
'LINCS_L1000_Ligand_Perturbations_down',
'LINCS_L1000_Ligand_Perturbations_up',
'MSigDB_Computational',
'MSigDB_Oncogenic_Signatures',
'OMIM_Disease',
'OMIM_Expanded',
'PheWeb_2019',
'UK_Biobank_GWAS_v1',
'VirusMINT',
'Tissue_Protein_Expression_from_Human_Proteome_Map',
'Data_Acquisition_Method_Most_Popular_Genes',
'Enrichr_Libraries_Most_Popular_Genes',
'Pfam_InterPro_Domains',
'Pfam_Domains_2019',
'BioCarta_2013'
'BioCarta_2015',
'HumanCyc_2015']) }}
color = '{{ ChoiceField(name='color', description='Select a color for your barchart.', label='Color', default='Purple', section = 'section3',choices=[
'Blue',
'Green',
'Orange',
'Purple',
'Red',
'Yellow',
'Pink']) }}'
num_hex_colored = '{{ ChoiceField(name='num_colored', description='Select the number of hexagons you want colored.', label='num_colored', default='10', section='section3', choices=[
'10',
'20']) }}'
scaling_factor = {{ TextField(name='scaling_factor', label='Scaling Factor', default='', description='Provide your color scaling factor here (optional).', section = 'section4') }}
# -
# ### Import gene list
# Import gene list as file or from text box file
# Will choose file upload over textbox if a file is given
if gene_list_filename != '':
open_gene_list_file = open(gene_list_filename,'r')
lines = open_gene_list_file.readlines()
genes = [x.strip().upper() for x in lines]
open_gene_list_file.close()
else:
genes = gene_list_input.split('\n')
genes = [x.strip().upper() for x in genes]
# +
# %%appyter code_eval
def library_processing(library_index):
# downloads library data
# library data is pre-annealed so the canvas will have the most similar gene sets closest together
raw_library_data = []
library_data = []
library_name = all_libraries[library_index]
with urllib.request.urlopen('https://raw.githubusercontent.com/skylar73/Enrichr-Library-Annealing/master/Annealed-Libraries/' + all_libraries[library_index] + '.txt') as f:
for line in f.readlines():
raw_library_data.append(line.decode('utf-8').split("\t\t"))
name = []
gene_list = []
for i in range(len(raw_library_data)):
name += [raw_library_data[i][0]]
raw_genes = raw_library_data[i][1].split('\t')
gene_list += [raw_genes[:-1]]
library_data = [list(a) for a in zip(name, gene_list)]
# raw_library_data: a 2D list where the first element is the name and the second element is a list of genes associated with that name
jaccard_indices = []
indices = []
for gene_set in library_data:
intersection = [value for value in gene_set[1] if value in genes]
index = len(intersection)/(len(gene_set[1]) + len(genes))
jaccard_indices += [[gene_set[0], index]]
indices += [round(index, 5)]
# determine the dimensions of the canvas
x_dimension = math.ceil(math.sqrt(len(indices)))
y_dimension = math.ceil(math.sqrt(len(indices)))
# zip name, gene_list, indices, and blank list for neighbor score then add dummy entries to the zipped list
num_hex = x_dimension*y_dimension
anneal_list = list(zip(name, gene_list, indices))
return anneal_list, x_dimension, y_dimension
# -
def unzip_list(anneal_list):
unzipped_list = zip(*anneal_list)
return list(unzipped_list)
# ### Process color choice
def get_color(anneal_list, cut_off_value, scaling_factor, x_dimension, y_dimension):
# Deal with cut_off_value (only color the most significant 10/20 hexagons)
if cut_off_value == 2.0:
sort_list = sorted(anneal_list, key=itemgetter(2), reverse=True)
cut_off_value = sort_list[int(num_hex_colored)-1][2]
r_value = 0
g_value = 0
b_value = 0
if color == 'Red':
r_value = 0.0
g_value = 0.8
b_value = 0.8
if color == 'Yellow':
r_value = 0.0
g_value = 0.3
b_value = 1.0
if color == 'Purple':
r_value = 0.5
g_value = 1.0
b_value = 0.0
if color == 'Pink':
r_value = 0.0
g_value = 1.0
b_value = 0.2
if color == 'Orange':
r_value = 0.0
g_value = 0.45
b_value = 1.0
if color == 'Green':
r_value = 1.0
g_value = 0.0
b_value = 1.0
if color == 'Blue':
r_value = 1.0
g_value = 0.9
b_value = 0.0
color_list = []
unzipped_anneal_list = unzip_list(anneal_list)
if scaling_factor == '':
max_index = max(unzipped_anneal_list[2])
else:
max_index = float(scaling_factor)
scaled_list = [i/max_index for i in unzipped_anneal_list[2]]
for i in range(x_dimension*y_dimension):
if i < len(unzipped_anneal_list[2]) and float(unzipped_anneal_list[2][i]) >= cut_off_value:
color_list += [matplotlib.colors.to_hex((1-scaled_list[i]*r_value,
1-scaled_list[i]*g_value, 1-scaled_list[i]*b_value))]
elif i < len(unzipped_anneal_list[2]):
color_list += [matplotlib.colors.to_hex((1-scaled_list[i],
1-scaled_list[i], 1-scaled_list[i]))]
else:
color_list += ["#FFFFFF"]
return color_list, max_index, cut_off_value
# ### Functions to create Canvas (uses Javascript's D3)
# +
def init_chart():
chart_id = 'mychart-' + str(uuid.uuid4())
display(HTML('<script src="/static/components/requirejs/require.js"></script>'))
display(HTML(Template(dedent('''
<script>
require.config({
paths: {
'd3': 'https://cdnjs.cloudflare.com/ajax/libs/d3/5.16.0/d3.min',
'd3-hexbin': 'https://d3js.org/d3-hexbin.v0.2.min',
},
shim: {
'd3-hexbin': ['d3']
}
})
// If we configure mychart via url, we can eliminate this define here
define($chart_id, ['d3', 'd3-hexbin'], function(d3, d3_hexbin) {
return function (figure_id, numA, numB, colorList, libraryList, indices) {
var margin = {top: 50, right: 20, bottom: 20, left: 50},
width = 850 - margin.left - margin.right,
height = 350 - margin.top - margin.bottom;
// append the svg object to the body of the page
var svG = d3.select('#' + figure_id)
.attr("width", width + margin.left + margin.right)
.attr("height", height + margin.top + margin.bottom)
.append("g")
.attr("transform", "translate(" + margin.left + "," + margin.top + ")");
//The number of columns and rows of the heatmap
var MapColumns = numA,
MapRows = numB;
//The maximum radius the hexagons can have to still fit the screen
var hexRadius = d3.min([width/((MapColumns + 0.5) * Math.sqrt(3)), height/((MapRows + 1/3) * 1.5)]);
//Calculate the center position of each hexagon
var points = [];
for (var i = 0; i < MapRows; i++) {
for (var j = 0; j < MapColumns; j++) {
var x = hexRadius * j * Math.sqrt(3)
//Offset each uneven row by half of a "hex-width" to the right
if(i%2 === 1) x += (hexRadius * Math.sqrt(3))/2
var y = hexRadius * i * 1.5
points.push([x,y])
}
}
//Set the hexagon radius
var hexbin = d3_hexbin.hexbin().radius(hexRadius);
svG.append("g")
.selectAll(".hexagon")
.data(hexbin(points))
.enter().append("path")
.attr("class", "hexagon")
.attr("d", function (d) {
return "M" + d.x + "," + d.y + hexbin.hexagon();
})
.attr("stroke", "black")
.attr("stroke-width", "1px")
.style("fill", function (d,i) { return colorList[i]; })
.on("mouseover", mover)
.on("mouseout", mout)
.append("svg:title")
.text(function(d,i) { return libraryList[i].concat(" ").concat(indices[i]); });
// Mouseover function
function mover(d) {
d3.select(this)
.transition().duration(10)
.style("fill-opacity", 0.3)
};
// Mouseout function
function mout(d) {
d3.select(this)
.transition().duration(10)
.style("fill-opacity", 1)
};
}
})
</script>
''')).substitute({ 'chart_id': repr(chart_id) })))
return chart_id
def Canvas(numA, numB, colorList, libraryList, indices):
chart_id = init_chart()
display(HTML(Template(dedent('''
<svg id=$figure_id></svg>
<script>
require([$chart_id], function(mychart) {
mychart($figure_id, $numA, $numB, $colorList, $libraryList, $indices)
})
</script>
''')).substitute({
'chart_id': repr(chart_id),
'figure_id': repr('fig-' + str(uuid.uuid4())),
'numA': repr(numA),
'numB': repr(numB),
'colorList': repr(colorList),
'libraryList': repr(libraryList),
'indices': repr(indices)
})))
# +
if len(all_libraries) == 1:
anneal_list, x_dimension, y_dimension = library_processing(0)
color_list, scaling_factor, cut_off_value = get_color(anneal_list, 2.0, scaling_factor, x_dimension, y_dimension)
unzipped_anneal_list = unzip_list(anneal_list)
print(all_libraries[0])
Canvas(x_dimension, y_dimension, color_list, list(unzipped_anneal_list[0]), list(unzipped_anneal_list[2]))
print("The color scaling factor for this canvas is: " + str(scaling_factor))
print("Gene sets with a similarity index less than " + str(cut_off_value) + " are not colored")
elif len(all_libraries) == 2:
# first library
anneal_list_1, x_dimension_1, y_dimension_1 = library_processing(0)
color_list_1, scaling_factor_1, cut_off_value_1 = get_color(anneal_list_1, 2.0, scaling_factor, x_dimension_1, y_dimension_1)
# second library
anneal_list_2, x_dimension_2, y_dimension_2 = library_processing(1)
color_list_2, scaling_factor_2, cut_off_value_2 = get_color(anneal_list_2, 2.0, scaling_factor, x_dimension_2, y_dimension_2)
if scaling_factor_1 > scaling_factor_2:
scaling_factor = scaling_factor_1
color_list_2, scaling_factor_2, cut_off_value_2 = get_color(anneal_list_2, 2.0, scaling_factor, x_dimension_2, y_dimension_2)
else:
scaling_factor = scaling_factor_2
color_list_1, scaling_factor_1, cut_off_value_1 = get_color(anneal_list_1, 2.0, scaling_factor, x_dimension_1, y_dimension_1)
unzipped_anneal_list_1 = unzip_list(anneal_list_1)
unzipped_anneal_list_2 = unzip_list(anneal_list_2)
print(all_libraries[0])
Canvas(x_dimension_1, y_dimension_1, color_list_1, list(unzipped_anneal_list_1[0]), list(unzipped_anneal_list_1[2]))
print(all_libraries[1])
Canvas(x_dimension_2, y_dimension_2, color_list_2, list(unzipped_anneal_list_2[0]), list(unzipped_anneal_list_2[2]))
print("The color scaling factor for these canvases are: " + str(scaling_factor))
print("For the first canvas, gene sets with a similarity index less than " + str(cut_off_value_1) + " are not colored")
print("For the second canvas, gene sets with a similarity index less than " + str(cut_off_value_2) + " are not colored")
|
appyters/Enrichr_Canvas_Appyter/Enrichr-Canvas-Appyter.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Study session 10 - data analysis
# ### BIOINF 575 - Fall 2020
# SOLUTION
# ____
#
# ### <font color = "red">Exercise</font>
#
# [ClinVar][1] is a freely accessible, public archive of reports of the relationships among human variations and phenotypes, with supporting evidence.
#
#
# The data you will be working with (`clinvar.vcf`). More information about the database can be found [here][3].
#
# From: https://ftp.ncbi.nlm.nih.gov/pub/clinvar/vcf_GRCh38/
#
# Download the file clinvar.vcf.gz
#
#
# ### The file format
# The beginning of every VCF file contains various sets of information:
# * Meta-information (details about the experiment or configuration) lines start with **`##`**
# * These lines are helpful in understanding specialized keys found in the `INFO` column. It is in these sections that one can find:
# * The description of the key
# * The data type of the values
# * The default value of the values
# * Header lines (column names) start with **`#`**
#
# From there on, each line is made up of tab (`\t`) separated values that make up eight (8) columns. Those columns are:
# 1. CHROM (chromosome)
# 2. POS (base pair position of the variant)
# 3. ID (identifier if applicable; `.` if not applicable/missing)
# 4. REF (reference base)
# 5. ALT (alternate base(s): comma (`,`) separated if applicable)
# 6. QUAL (Phred-scaled quality score; `.` if not applicable/missing)
# 7. FILTER (filter status; `.` if not applicable/missing)
# 8. INFO (any additional information about the variant)
# * Semi-colon (`;`) separated key-value pairs
# * Key-value pairs are equal sign (`=`) separated (key on the left, value on the right)
# * If a key has multiple values, the values are pipe (`|`) separated
#
# ---
# [1]: https://www.ncbi.nlm.nih.gov/clinvar/intro/
# [2]: https://samtools.github.io/hts-specs/VCFv4.3.pdf
# [3]: http://exac.broadinstitute.org
#
#
# We also have a file with the gene expression for 45h every three hours for breast cancer cells treated with a HER2 inhibitor, `GSE22955_small_gene_table.txt`.
# This is in the class_notebooks folder.
# https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE22955
# ### - Load the data from the 2 files in pandas dataframes
import numpy as np
import pandas as pd
variant_file_name = "clinvar.vcf"
expression_file_path = "../class_notebooks/GSE22955_small_gene_table.txt"
variant_data = pd.read_csv(variant_file_name, comment = "#", sep = "\t", header = None)
variant_data.columns = ("CHROM","POS","ID","REF","ALT","QUAL","FILTER","INFO")
variant_data
expression_data = pd.read_csv(expression_file_path, comment = "#", sep = "\t", index_col = 0)
expression_data
# ______
#
# #### - Select only 5 genes of interest from the expression data frame TP53, BARD1, BRCA1, MAPK1, CHEK2
important_genes = ("TP53", "BARD1", "BRCA1", "MAPK1", "CHEK2")
goi_data = expression_data.loc[important_genes,:]
goi_data
# #### - Plot the expression of these genes
goi_data.plot()
goi_data.T.plot()
# ______
#
# #### - Select only genes that have a standard dev > 0.7 and a change between hour 0 and hour 45 > 1.4 fold.
#
gene_sd = expression_data.std(axis = 1)
gene_sd
gene_sd > 0.7
sum(gene_sd > 0.7)
cond_sd = gene_sd > 0.7
gene_sd.name = "geneSD"
expression_data_sd = expression_data.join(gene_sd)
expression_data_sd[cond_sd]
expression_data[cond_sd]
# +
# log2(1/2) == -1 log2(2) == 1
gene_fold_change = expression_data.loc[:,"45"]/expression_data.loc[:,"0"]
cond_fold_change = abs(np.log2(gene_fold_change)) > np.log2(1.4)
# -
cond_fold_change
sum(cond_fold_change)
# expression_data_sd.drop(columns = "geneFC", inplace = True)
# +
gene_fold_change.name = "geneFC"
expression_data_sd = expression_data_sd.join(gene_fold_change)
expression_data_sd[cond_sd & cond_fold_change]
# -
1/0.619946
# #### - Plot the expression of these genes
selected_genes = expression_data[cond_sd & cond_fold_change]
selected_genes.T.plot()
# #### - From the VCF file identify the genes for each variant from the info column GENEINFO key
#
# +
def get_genes(info):
genes = set()
info_dict = {}
for info_elem in info.split(";"):
key, value = info_elem.split("=")
info_dict[key] = value
#print(info_dict)
if "GENEINFO" in info_dict:
for gene_pair in info_dict["GENEINFO"].split("|"):
gene_symbol, gene_id = gene_pair.split(":")
genes.add(gene_symbol)
return genes
# -
info_data = "ALLELEID=824438;CLNDISDB=MedGen:CN517202;CLNDN=not_provided;CLNHGVS=NC_000001.11:g.930188G>A;CLNREVSTAT=criteria_provided,_single_submitter;CLNSIG=Uncertain_significance;CLNVC=single_nucleotide_variant;CLNVCSO=SO:0001483;GENEINFO=SAMD11:148398|test_gene:1234;MC=SO:0001583|missense_variant;ORIGIN=1"
info_data
get_genes(info_data)
gene_data = variant_data.INFO.apply(get_genes)
gene_data
# #### - Select only the variants for our genes of interest:
important_genes = ("TP53", "BARD1", "BRCA1", "MAPK1", "CHEK2")
cond_genes = gene_data.apply(lambda gene_set: len(gene_set.intersection(set(important_genes))) > 0)
sum(cond_genes)
gene_data.name = "GenesSet"
variant_data_genes = variant_data.join(gene_data)
variant_data_genes.drop(columns = "INFO", inplace = True)
variant_data_genes[cond_genes]
variant_data_genes.info()
variant_data.info()
|
study_sessions/study_session10_data_analysis_solution1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.9.5 64-bit (''zebraket-cdl-hackathon-2021'': conda)'
# name: python3
# ---
import os
os.chdir('..') # Weird pathing hack
from services.classical_optimizers import binary_supplier_optimizer, discrete_profit_optimizer, binary_profit_optimizer
import pandas as pd
# Define some constants
budget = 100 # 100 dollars buget
# Fake data (TODO: implement this method in Data.py)
prices = (3.5, 3.4, 3.8, 6.1)
costs = (1.5, 1.4, 1.8, 2.1)
items = (f'item{i}' for i in range(len(prices)))
row_names = ['price', 'cost']
fake_data = pd.DataFrame([prices, costs], columns=items, index=row_names)
print('Here is our generated data: \n', fake_data)
# See the binary knapsack is working:
# Test the binary knapsack solution
binary_solution, binary_cost, binary_profit = binary_profit_optimizer(price_data=fake_data, budget=budget)
print('\n\nfound solution for BINARY knapsack: ', binary_cost, binary_profit)
print('result\n', binary_solution, '\n\n')
# But the discrete knapsack is working as far as I can tell, we just don't get the actual solution out, we only get the cost...
# Test the discrete knapsack
discrete_profit = discrete_profit_optimizer(price_data=fake_data, budget=budget)
print('found solution for DISCRETE knapsack: ', 'profit', discrete_profit)
# And for completness, here is the supplier optimization (i.e. the cover set problem)
universe = set(range(1, 11))
subsets = [set([1, 2, 3, 8, 9, 10]),
set([1, 2, 3, 4, 5]),
set([4, 5, 7]),
set([5, 6, 7]),
set([6, 7, 8, 9, 10])]
cover = binary_supplier_optimizer(universe, subsets)
print('\n\n', 'Found inventory optimization solution', cover)
|
ZebraKet/Alex test files/fix-classical-solutions.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] colab_type="text" id="wJcYs_ERTnnI"
# ##### Copyright 2018 The TensorFlow Authors.
# + cellView="form" colab={} colab_type="code" id="HMUDt0CiUJk9"
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# + [markdown] colab_type="text" id="77z2OchJTk0l"
# # Конвертируйте ваш существующий код в TensorFlow 2.0
#
# <table class="tfo-notebook-buttons" align="left">
# <td>
# <a target="_blank" href="https://www.tensorflow.org/guide/migration_guide">
# <img src="https://www.tensorflow.org/images/tf_logo_32px.png" />
# Посмотреть в TensorFlow.org</a>
# </td>
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/ru/guide/migration_guide.ipynb">
# <img src="https://www.tensorflow.org/images/colab_logo_32px.png" />
# Запустить в Google Colab</a>
# </td>
# <td>
# <a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/ru/guide/migration_guide.ipynb">
# <img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />
# Посмотреть исходники на GitHub</a>
# </td>
# </table>
# + [markdown] colab_type="text" id="C0V10enS1_WU"
# В TensorFlow 2.0 все еще возможно исполнить 1.X код без изменений (за исключением contrib):
#
# ```
# import tensorflow.compat.v1 as tf
# tf.disable_v2_behavior()
# ```
#
# Однако, это не дает вам воспользоваться преимуществами многих улучшений сделанных в TensorFlow 2.0. Это руководство поможет вам обновить ваш код, сделав его проще, производительнее и легче в поддержке.
#
# ## Скрипт автоматической конвертации
#
# Первым шагом вы можете попробовать запустить [скрипт обновления](./upgrade.md).
#
# Он выполнит начальный этап обновления вашего кода до TensorFlow 2.0. Но это не может сделать ваш код идиоматичным TensorFlowF 2.0. Ваш код все еще может использовать `tf.compat.v1` для доступа к плейсхолдерам, сессиям, коллекциям, и другой функциональности в стиле 1.x.
#
# ## Сделайте код 2.0-нативным
#
#
# В этом руководстве рассматриваются несколько примеров преобразования кода TensorFlow 1.x в TensorFlow 2.0. Эти изменения позволят вашему коду воспользоваться преимуществами оптимизации производительности и упрощенных вызовов API.
#
# В каждом случае паттерн следующий:
# + [markdown] colab_type="text" id="uP0O8Pc45LNs"
# ### 1. Заменить вызовы `tf.Session.run`
#
# Каждый вызов `tf.Session.run` нужо заменить функцией Python.
#
# * `feed_dict` и `tf.placeholder`s становятся аргументами функции.
# * `fetches` становится возвращаемым значением функции.
#
# Вы можете пройти пошагово и отладить функцию, используя стандартные инструменты Python, такие как `pdb`.
#
# Когда вы убедитесь, что функция работает, добавьте декоратор`tf.function` чтобы она работала эффективно в режиме графа. Смотри [Руководство Autograph](autograph.ipynb) чтобы узнать больше о том, как это работает.
# + [markdown] colab_type="text" id="jlBOqROL5NmN"
# ### 2. Используйте объекты python для отслеживания переменных и значений потерь
#
# Используйте `tf.Variable` вместо `tf.get_variable`.
#
# Каждый `variable_scope` может быть сконвертирован в объект Python. Как правило это будет что-то из:
#
# * `tf.keras.layers.Layer`
# * `tf.keras.Model`
# * `tf.Module`
#
# Если вам нужны свести списки переменных (как например `tf.Graph.get_collection(tf.GraphKeys.VARIABLES)`), используйте аттрибуты `.variables` и `.trainable_variables` объектов `Layer` и `Model`.
#
# Эти классы `Layer` и `Model` реализуют несколько других свойств которые устраняют необходимость глобальных коллекций.
#
# Смотри [руководства keras](keras.ipynb) для подробностей.
#
# Предупреждение: Многие символы `tf.compat.v1` неявно используют глобальные коллекции.
#
# + [markdown] colab_type="text" id="rGFhBzoF5FIq"
# ### 3. Обновите ваши обучающие циклы
#
# Используйте API наиболее высокого уровня который работает в вашем случае. Предпочтите `tf.keras.Model.fit` построению своего собственного обучающего цикла.
#
# Эти высокоуровневые функции управляют большим количеством низкоуровневых деталей которые могут быть легко упущены если вы пишете собственный обучающий цикл. Например, они автоматически собирают потери регуляризации и устанавливают аргумент `training = True` при вызове модели.
#
# ### 4. Обновите ваши конвейеры ввода данных
#
# Используйте наборы данных `tf.data` для входных данных. Эти объекты эффективны, выразительны и хорошо интегрированы с tensorflow.
#
# Их можно передать напрямую в метод `tf.keras.Model.fit`.
#
# ```
# model.fit(dataset, epochs=5)
# ```
#
# Их можно напрямую итерировать в стандартном Python:
#
# ```
# for example_batch, label_batch in dataset:
# break
# ```
#
# + [markdown] colab_type="text" id="X_ilfTGJ4Yml"
# ## Конвертация моделей
#
# ### Установка
# + colab={} colab_type="code" id="bad2N-Z115W1"
from __future__ import absolute_import, division, print_function, unicode_literals
# !pip install tensorflow==2.0.0-alpha0
import tensorflow as tf
import tensorflow_datasets as tfds
# + [markdown] colab_type="text" id="FB99sqHX2Q5m"
# ### Низкоуровневые переменные и исполнение оператора
#
# Примеры использования низкоуровневого API включают:
#
# * использование областей видимости переменных для управления повторным использованием
# * создание переменных с `tf.get_variable`.
# * явный доступ к коллекциям
# * неявный доступ к коллекциям с такими методами, как:
#
# * `tf.global_variables`
# * `tf.losses.get_regularization_loss`
#
# * использование `tf.placeholder` для установления входных данных графа
# * выполнение графа с `session.run`
# * ручная инициализация переменных
#
# + [markdown] colab_type="text" id="e582IjyF2eje"
# #### Перед конвертацией
#
# Здесь как могут выглядеть эти паттерны в коде использующем TensorFlow 1.x.
#
# ```python
# in_a = tf.placeholder(dtype=tf.float32, shape=(2))
# in_b = tf.placeholder(dtype=tf.float32, shape=(2))
#
# def forward(x):
# with tf.variable_scope("matmul", reuse=tf.AUTO_REUSE):
# W = tf.get_variable("W", initializer=tf.ones(shape=(2,2)),
# regularizer=tf.contrib.layers.l2_regularizer(0.04))
# b = tf.get_variable("b", initializer=tf.zeros(shape=(2)))
# return W * x + b
#
# out_a = forward(in_a)
# out_b = forward(in_b)
#
# reg_loss = tf.losses.get_regularization_loss(scope="matmul")
#
# with tf.Session() as sess:
# sess.run(tf.global_variables_initializer())
# outs = sess.run([out_a, out_b, reg_loss],
# feed_dict={in_a: [1, 0], in_b: [0, 1]})
#
# ```
# + [markdown] colab_type="text" id="QARwz4Xd2lc2"
# #### После конвертации
# + [markdown] colab_type="text" id="x0AVzBFRBPcU"
# В сконвертированном коде:
#
# * Переменные являются локальными объектами Python.
# * Функция `forward` все еще определяет вычисления.
# * Вызов `sess.run` заменен вызовом `forward`
# * Опциональный декоратор `tf.function` может быть добавлен для производительности.
# * Регуляризации вычисляются вручную без ссылок на глобальные коллекции.
# * **Нет сессий и плейсхолдеров.**
# + colab={} colab_type="code" id="lXEZoLMP2cWJ"
W = tf.Variable(tf.ones(shape=(2,2)), name="W")
b = tf.Variable(tf.zeros(shape=(2)), name="b")
@tf.function
def forward(x):
return W * x + b
out_a = forward([1,0])
print(out_a)
# + colab={} colab_type="code" id="YmE96A_1jZTg"
out_b = forward([0,1])
regularizer = tf.keras.regularizers.l2(0.04)
reg_loss = regularizer(W)
# + [markdown] colab_type="text" id="ycDxY9nL268-"
# ### Модели основанные на `tf.layers`
# + [markdown] colab_type="text" id="K-bIk7wL48U7"
# Модуль `tf.layers` используется для содержания layer-функций использующих `tf.variable_scope` для определения и переиспользования переменных.
# + [markdown] colab_type="text" id="8I_qKpT73KyM"
# #### До конвертации
# ```python
# def model(x, training, scope='model'):
# with tf.variable_scope(scope, reuse=tf.AUTO_REUSE):
# x = tf.layers.conv2d(x, 32, 3, activation=tf.nn.relu,
# kernel_regularizer=tf.contrib.layers.l2_regularizer(0.04))
# x = tf.layers.max_pooling2d(x, (2, 2), 1)
# x = tf.layers.flatten(x)
# x = tf.layers.dropout(x, 0.1, training=training)
# x = tf.layers.dense(x, 64, activation=tf.nn.relu)
# x = tf.layers.batch_normalization(x, training=training)
# x = tf.layers.dense(x, 10, activation=tf.nn.softmax)
# return x
#
# train_out = model(train_data, training=True)
# test_out = model(test_data, training=False)
# ```
# + [markdown] colab_type="text" id="b8_Ii7CQ3fK-"
# #### После конвертации
# + [markdown] colab_type="text" id="BsAseSMfB9XN"
# * Простой стек слоев аккуратно встраивается в `tf.keras.Sequential`. (Для более сложных моделей см. [пользовательские слои и модели](keras/custom_layers_and_models.ipynb), и [функциональный API](keras/functional.ipynb).)
# * Модель отслеживает переменные и потери регуляризации.
# * Преобразование взаимно-однозначно поскольку существует прямое отображение из `tf.layers` в `tf.keras.layers`.
#
# Большинство аргументов остались прежними. Но обратите внимание на различия:
#
# * Аргумент `training` передается моделью каждому слою при его запуске.
# * Первого аргумента исходной функции `model` (вводный `x`) больше нет. Это связано с тем, что слои объекта отделяют построение модели от вызова модели.
#
#
# Также заметьте что:
#
# * Если вы использовали регуляризаторы инициализаторов из `tf.contrib`, у них больше изменений аргументов чем у остальных.
# * Код больше не записывает в коллекции, так что функции наподобие `tf.losses.get_regularization_loss` больше не возращают эти значения, что может нарушить ваши циклы обучения.
# + colab={} colab_type="code" id="DLAPORrN3lct"
model = tf.keras.Sequential([
tf.keras.layers.Conv2D(32, 3, activation='relu',
kernel_regularizer=tf.keras.regularizers.l2(0.04),
input_shape=(28, 28, 1)),
tf.keras.layers.MaxPooling2D(),
tf.keras.layers.Flatten(),
tf.keras.layers.Dropout(0.1),
tf.keras.layers.Dense(64, activation='relu'),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Dense(10, activation='softmax')
])
train_data = tf.ones(shape=(1, 28, 28, 1))
test_data = tf.ones(shape=(1, 28, 28, 1))
# + colab={} colab_type="code" id="6nWh6IXvkMKv"
train_out = model(train_data, training=True)
print(train_out)
# + colab={} colab_type="code" id="YnAdIDLlj3go"
test_out = model(test_data, training=False)
print(test_out)
# + colab={} colab_type="code" id="sAgqwCJBMx_x"
# Здесь все обучаемые переменные.
len(model.trainable_variables)
# + colab={} colab_type="code" id="uX6knaYMNM8p"
# Здесь потери регуляризации.
model.losses
# + [markdown] colab_type="text" id="9moqw5E_4Cwl"
# ### Смесь переменных и tf.layers
#
# + [markdown] colab_type="text" id="80DEsImmq6VX"
# Существующий код часто смешивает низкоуровневые TF 1.x переменные и операции с высокоуровневыми `tf.layers`.
# + [markdown] colab_type="text" id="oZe9L6RR4OcP"
# #### До конвертации
# ```python
# def model(x, training, scope='model'):
# with tf.variable_scope(scope, reuse=tf.AUTO_REUSE):
# W = tf.get_variable(
# "W", dtype=tf.float32,
# initializer=tf.ones(shape=x.shape),
# regularizer=tf.contrib.layers.l2_regularizer(0.04),
# trainable=True)
# if training:
# x = x + W
# else:
# x = x + W * 0.5
# x = tf.layers.conv2d(x, 32, 3, activation=tf.nn.relu)
# x = tf.layers.max_pooling2d(x, (2, 2), 1)
# x = tf.layers.flatten(x)
# return x
#
# train_out = model(train_data, training=True)
# test_out = model(test_data, training=False)
# ```
# + [markdown] colab_type="text" id="y6ORX7cD4TkD"
# #### После конвертации
# + [markdown] colab_type="text" id="2BaRwog5CBpz"
# Для конвертации этого кода следуйте паттерну отображения слоев в слои как и в предыдущем примере.
#
# `tf.variable_scope` фактически является слоем сам по себе. Поэтому перепишите его как `tf.keras.layers.Layer`. См. [руководство](keras/custom_layers_and_models.ipynb) для подробностей.
#
# В общем паттерн следующий:
#
# * Собрать параметры слоев в `__init__`.
# * Создать переменные в `build`.
# * Выполнить вычисления в `call` и вернуть результат.
#
# `tf.variable_scope` по сути является собственным слоем. Поэтому перепишите его как `tf.keras.layers.Layer`. Смотрите [руководство](keras/custom_layers_and_models.ipynb) для деталей.
# + colab={} colab_type="code" id="YcCAjNuP4NVh"
# Создайте пользовательский слой для части модели
class CustomLayer(tf.keras.layers.Layer):
def __init__(self, *args, **kwargs):
super(CustomLayer, self).__init__(*args, **kwargs)
def build(self, input_shape):
self.w = self.add_weight(
shape=input_shape[1:],
dtype=tf.float32,
initializer=tf.keras.initializers.ones(),
regularizer=tf.keras.regularizers.l2(0.02),
trainable=True)
# Метод call будет иногда использоваться в режиме графа,
# training превратится в тензор
@tf.function
def call(self, inputs, training=None):
if training:
return inputs + self.w
else:
return inputs + self.w * 0.5
# + colab={} colab_type="code" id="dR_QO6_wBgMm"
custom_layer = CustomLayer()
print(custom_layer([1]).numpy())
print(custom_layer([1], training=True).numpy())
# + colab={} colab_type="code" id="VzqaIf4E42oY"
train_data = tf.ones(shape=(1, 28, 28, 1))
test_data = tf.ones(shape=(1, 28, 28, 1))
# Build the model including the custom layer
model = tf.keras.Sequential([
CustomLayer(input_shape=(28, 28, 1)),
tf.keras.layers.Conv2D(32, 3, activation='relu'),
tf.keras.layers.MaxPooling2D(),
tf.keras.layers.Flatten(),
])
train_out = model(train_data, training=True)
test_out = model(test_data, training=False)
# + [markdown] colab_type="text" id="dS5ed_jjOkvh"
# Некоторые вещи на заметку:
#
# * Подклассы моделей и слоев Keras нужно запускать и в v1 графах (без автоматического контроля зависимостей) и в режиме eager mode
# * Оберните `call()` в `tf.function()` чтобы получить autograph и автоматический контроль зависимостей
#
# * Не забудьте принять аргумент `training` в `call`.
# * Иногда это `tf.Tensor`
# * Иногда это булеан Python.
#
# * Создайте переменные модели в конструкторе или `def build()` используя `self.add_weight()`.
# * В `build` у вас есть доступ к размерности входных данных, так что создайте веса с совпадающими размерностями.
# * Использование `tf.keras.layers.Layer.add_weight` позволяет Keras отслеживать переменные и потери регуляризации.
#
# * Не храните `tf.Tensors` в своих объектах.
# * Они могут быть созданы либо в `tf.function` либо в контексте eager, и эти тензоры ведут себя по-другому.
# * Используйте `tf.Variable`s для состояния, их всегда можно использовать из обеих контекстов
# * `tf.Tensors` это только промежуточные значения.
# + [markdown] colab_type="text" id="ulaB1ymO4pw5"
# ### Замечание о Slim и contrib.layers
#
# Большое количество старого TensorFlow 1.x кода использует библиотеку [Slim](https://ai.googleblog.com/2016/08/tf-slim-high-level-library-to-define.html) которая входит в пакет TensorFlow 1.x в качестве `tf.contrib.layers`. В качестве модуля `contrib` она более не доступна в TensorFlow 2.0, даже в `tf.compat.v1`. Конвертация кода использовавшего Slim в TF 2.0 запутаннее чем конвертация репозиториев использующих `tf.layers`. Имеет смысл сперва сконвертировать ваш Slim код сперва в`tf.layers`, а затем конвертировать в Keras.
#
# * Уберите `arg_scopes`, все аргументы должны быть явными
# * Если вы используете их, поделите `normalizer_fn` и `activation_fn` каждый в свой собственный слой
# * Separable сверточные слои отображаются в один или более различных слоев Keras (по глубине, поточечно, и separable слои Keras)
# * Slim и `tf.layers` имеют разные имена аргументов и значения по умолчанию
# * Некоторые аргументы имеют разные размерности
# * Если вы используете предобученные модели Slim, попробуйте `tf.keras.applications` или [TFHub](https://tensorflow.orb/hub)
#
# Некоторые слои `tf.contrib` возможно не были перемещены в ядро TensorFlow, а вместо этого были перемещены в пакет [TF add-ons](https://github.com/tensorflow/addons).
#
# + [markdown] colab_type="text" id="1w72KrXm4yZR"
# ## Обучение
# + [markdown] colab_type="text" id="56PQxTgy2bpI"
# Существует много способов подачи данных в модели `tf.keras`. Они допускают генераторы Python и массивы Numpy в качестве входных данных.
#
# Рекомендуемы способ подачи данных в модель это - использовать пакет `tf.data`, который содержит набор высокопроизводительных классов для манипуляций с данными.
#
# Если вы все еще используете `tf.queue`, они поддерживаются только как структуры данных, а не как входные конвейеры.
# + [markdown] colab_type="text" id="m6htasZ7iBB4"
# ### Использование наборов данных
# + [markdown] colab_type="text" id="loTPH2Pz4_Oj"
# Пакет [TensorFlow Datasets](https://tensorflow.org/datasets) (`tfds`) содержит утилиты для загрузки предопределенных баз данных как объектов `tf.data.Dataset`.
#
# Например, загрузим MNISTdataset, используя `tfds`:
# + colab={} colab_type="code" id="BMgxaLH74_s-"
datasets, info = tfds.load(name='mnist', with_info=True, as_supervised=True)
mnist_train, mnist_test = datasets['train'], datasets['test']
# + [markdown] colab_type="text" id="hPJhEuvj5VfR"
# Затем приготовим данные для обучения:
#
# * Изменим размер каждого изображения.
# * Перемешаем порядок примеров.
# * Соберем batches изображений и меток.
#
# + colab={} colab_type="code" id="StBRHtJM2S7o"
BUFFER_SIZE = 10 # Используйте намного большее значение для настоящего кода.
BATCH_SIZE = 64
NUM_EPOCHS = 5
def scale(image, label):
image = tf.cast(image, tf.float32)
image /= 255
return image, label
# + [markdown] colab_type="text" id="SKq14zKKFAdv"
# Чтобы пример оставался коротким обрежем данные, чтобы он возвращал только 5 batches:
# + colab={} colab_type="code" id="_J-o4YjG2mkM"
train_data = mnist_train.map(scale).shuffle(BUFFER_SIZE).batch(BATCH_SIZE).take(5)
test_data = mnist_test.map(scale).batch(BATCH_SIZE).take(5)
STEPS_PER_EPOCH = 5
train_data = train_data.take(STEPS_PER_EPOCH)
test_data = test_data.take(STEPS_PER_EPOCH)
# + colab={} colab_type="code" id="XEqdkH54VM6c"
image_batch, label_batch = next(iter(train_data))
# + [markdown] colab_type="text" id="mSev7vZC5GJB"
# ### Использование обучающик циклов Keras
#
# Если вам не нужен низкоуровневый коноль процесса обучения модели, рекомендуется использовать встроенные в Keras методы `fit`, `evaluate` и `predict`. Эти методы обеспечивают единый интерфейс обучения модели независимо от реализации (sequential, functional или sub-classed).
#
# Преимущества этих методов включают:
#
# * Они допускают массивы Numpy, генераторы Python и `tf.data.Datasets`
# * Они применяют регуляризационные и активационные потери автоматически.
# * Они поддерживают `tf.distribute` [для обучения на нескольких устройствах](distribute_strategy.ipynb).
# * Они поддерживают произвольные вызываемые объекты как потери и метрики.
# * Они поддерживают коллбеки такие как `tf.keras.callbacks.TensorBoard` и пользовательские коллбеки.
# * Они производительны, автоматически используя графы TensorFlow.
#
# Приведем пример обучения модели с ипользованием `Dataset`. (Подробнее о том как это работает смотри [тьюториалы](../tutorials).)
# + colab={} colab_type="code" id="uzHFCzd45Rae"
model = tf.keras.Sequential([
tf.keras.layers.Conv2D(32, 3, activation='relu',
kernel_regularizer=tf.keras.regularizers.l2(0.02),
input_shape=(28, 28, 1)),
tf.keras.layers.MaxPooling2D(),
tf.keras.layers.Flatten(),
tf.keras.layers.Dropout(0.1),
tf.keras.layers.Dense(64, activation='relu'),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Dense(10, activation='softmax')
])
# Model is the full model w/o custom layers
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
model.fit(train_data, epochs=NUM_EPOCHS)
loss, acc = model.evaluate(test_data)
print("Loss {}, Accuracy {}".format(loss, acc))
# + [markdown] colab_type="text" id="akpeOb09YBhq"
# ### Напишите свой собственный цикл
#
# Если обучающий шаг модели Keras подходит вам, но вне шага вам нужет больший контроль, рассмотрите использование `tf.keras.model.train_on_batch` method, в вашем собтвенном цикле итерации данных.
#
# Запомните: Многие вещи могут быть реализованы как `tf.keras.Callback`.
#
# Этот метод имеет много преимуществ перед методами, упомянутыми в предыдущем разделе, но он дает пользователю контроль над внешним циклом.
#
# Вы также можете использовать `tf.keras.model.test_on_batch` или `tf.keras.Model.evaluate` чтобы проверить производительность во время обучения.
#
# Примечание: `train_on_batch` и `test_on_batch` по умолчанию возвращают потерю и метрики для одного batch. Если вы передаете `reset_metrics=False` они возвращают накопленные метрики и вы должны помнить своевременно сбрасывать накопители метрик. Таже помните, что некоторые метрики, такие как `AUC` требуют `reset_metrics=False` для корректного вычисления.
#
# Чтобы продолжить обучение вышеуказанной модели:
#
# + colab={} colab_type="code" id="eXr4CyJMtJJ6"
# Model это полная модель без пользовательских слоев
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
metrics_names = model.metrics_names
for epoch in range(NUM_EPOCHS):
#Reset the metric accumulators
model.reset_metrics()
for image_batch, label_batch in train_data:
result = model.train_on_batch(image_batch, label_batch)
print("train: ",
"{}: {:.3f}".format(metrics_names[0], result[0]),
"{}: {:.3f}".format(metrics_names[1], result[1]))
for image_batch, label_batch in test_data:
result = model.test_on_batch(image_batch, label_batch,
# return accumulated metrics
reset_metrics=False)
print("\neval: ",
"{}: {:.3f}".format(metrics_names[0], result[0]),
"{}: {:.3f}".format(metrics_names[1], result[1]))
# + [markdown] colab_type="text" id="LQTaHTuK5S5A"
# <p id="custom_loops"/>
#
# ### Настройте шаг обучения
#
# Если вам нужны большая гибкость и контроль, вы можете получить их реализовав собственный цикл обучения. Есть три шага:
#
# 1. Проитерируйте генератор Python или `tf.data.Dataset` чтобы получить пакеты примеров.
# 2. Используйте `tf.GradientTape` чтобы собрать градиенты.
# 3. Используйте `tf.keras.optimizer` чтобы применить обновления весов к переменным модели.
#
# Помните:
#
# * Всегда включайте аргумент `training` в метод `call` подклассов слоев и моделей.
# * Убедитесь что вызываете модель с корректно установленным аргументом `training`.
# * В зависимости от использования, переменные модели могут не существовать, пока модель не будет запущена на пакете данных.
# * Вам нужно вручную обрабатывать такие вещи, как потери регуляризации для модели.
#
# Обратите внимание на упрощения относительно v1:
#
# * Нет необходимости запускать инициализаторы переменных. Переменные инициализируются при создании.
# * Нет необходимости добавлять зависимости ручного управления. Даже в операциях `tf.function` действующих как в eager mode.
# + colab={} colab_type="code" id="gQooejfYlQeF"
model = tf.keras.Sequential([
tf.keras.layers.Conv2D(32, 3, activation='relu',
kernel_regularizer=tf.keras.regularizers.l2(0.02),
input_shape=(28, 28, 1)),
tf.keras.layers.MaxPooling2D(),
tf.keras.layers.Flatten(),
tf.keras.layers.Dropout(0.1),
tf.keras.layers.Dense(64, activation='relu'),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Dense(10, activation='softmax')
])
optimizer = tf.keras.optimizers.Adam(0.001)
loss_fn = tf.keras.losses.SparseCategoricalCrossentropy()
@tf.function
def train_step(inputs, labels):
with tf.GradientTape() as tape:
predictions = model(inputs, training=True)
regularization_loss = tf.math.add_n(model.losses)
pred_loss = loss_fn(labels, predictions)
total_loss = pred_loss + regularization_loss
gradients = tape.gradient(total_loss, model.trainable_variables)
optimizer.apply_gradients(zip(gradients, model.trainable_variables))
for epoch in range(NUM_EPOCHS):
for inputs, labels in train_data:
train_step(inputs, labels)
print("Finished epoch", epoch)
# + [markdown] colab_type="text" id="kS7WW5Z75ve3"
# ### Метрики в новом стиле
#
# В TensorFlow 2.0, метрики являются объектами. Метрики работают и eagerly и в `tf.function`. Объекты-метрики обладают следующими методами:
#
# * `update_state()` — добавить новые наблюдения
# * `result()` — получить текущий результат метрики при данных наблюдаемых значениях
# * `reset_states()` — очистить все наблюдения.
#
# Объект сам является вызываемым. Вызов обновляет состояние новыми наблюдениями, как и с `update_state`, и возвращает новый результат метрики
#
# Вам не нужно вручную инициализировать переменные метрики, и, поскольку у TensorFlow 2.0 автоматическое управление зависимостями, вам не нужно беспокоиться и об этом.
#
# В приведенном ниже коде используется метрика для отслеживания среднего значения потерь, наблюдаемых в пользовательском цикле обучения.
# + colab={} colab_type="code" id="HAbA0fKW58CH"
# Создайте метрики
loss_metric = tf.keras.metrics.Mean(name='train_loss')
accuracy_metric = tf.keras.metrics.SparseCategoricalAccuracy(name='train_accuracy')
@tf.function
def train_step(inputs, labels):
with tf.GradientTape() as tape:
predictions = model(inputs, training=True)
regularization_loss = tf.math.add_n(model.losses)
pred_loss = loss_fn(labels, predictions)
total_loss = pred_loss + regularization_loss
gradients = tape.gradient(total_loss, model.trainable_variables)
optimizer.apply_gradients(zip(gradients, model.trainable_variables))
# Обновите метрики
loss_metric.update_state(total_loss)
accuracy_metric.update_state(labels, predictions)
for epoch in range(NUM_EPOCHS):
# Сбросьте метрики
loss_metric.reset_states()
accuracy_metric.reset_states()
for inputs, labels in train_data:
train_step(inputs, labels)
# Получите результаты метрики
mean_loss = loss_metric.result()
mean_accuracy = accuracy_metric.result()
print('Epoch: ', epoch)
print(' loss: {:.3f}'.format(mean_loss))
print(' accuracy: {:.3f}'.format(mean_accuracy))
# + [markdown] colab_type="text" id="JmMLBKs66DeA"
# ## Сохранение и загрузка
#
# + [markdown] colab_type="text" id="5_QKn3Kl6TUu"
# ### Совместимость контрольных точек
#
# TensorFlow 2.0 использует [контрольные точки основанные на объектах](checkpoints.ipynb).
#
# Контрольные точки в старом стиле основанные на именах по-прежнему могут быть загружены, если вы осторожны с ними.
# В процессе конвертации кода могут измениться имена переменных, но есть обходные пути.
#
# Самый простой подход - согласовать имена новой модели с именами в контрольной точке.:
#
# * У переменных все еще есть аргумент `name` который вы можете установить.
# * Модели Keras также используют аргумент `name`, который они устанавливают в качестве префикса для своих переменных.
# * Функция `tf.name_scope` может использоваться для установки префиксов имен переменных. Это сильно отличается от `tf.variable_scope`. Он влияет только на имена и не отслеживает переменные и их переиспользование.
#
# Если это не работает для вашего случая, попробуйте функцию `tf.compat.v1.train.init_from_checkpoint`. Она принимает аргумент `assignment_map`, который определяет соответствие старых и новых имен.
#
# Примечание: В отличие от основанных на объектах контрольных точек, которые могут [отложить загрузку] (checkpoints.ipynb#loading_mechanics), основанные на именах контрольных точек требуют, чтобы при вызове функции были созданы все переменные. Некоторые модели откладывают создание переменных до тех пор, пока вы не вызовете `build` или не запустите модель на пакете данных.
# + [markdown] colab_type="text" id="_ONjobDD6Uur"
# ### Совместимость сохраненных моделей
#
# У совместимости для сохраненных моделей нет существенных проблем.
#
# * TensorFlow 1.x saved_models работают TensorFlow 2.0.
# * TensorFlow 2.0 saved_models даже загруженные работают в TensorFlow 1.x если все операции поддерживаются.
# + [markdown] colab_type="text" id="ewl9P3oZ6ZtR"
# ## Estimators
# + [markdown] colab_type="text" id="YprVP9g3l6eG"
# ### Обучение с оценщиками
#
# Оценщики поддерживаются TensorFlow 2.0.
#
# Когда вы используете оценщики, вы можете использовать `input_fn()`, `tf.estimator.TrainSpec`, и `tf.estimator.EvalSpec` из TensorFlow 1.x.
#
# Здесь пример использующий `input_fn` с train and evaluate specs.
# + [markdown] colab_type="text" id="N5kZeJsF8lS2"
# #### Создание input_fn и train/eval specs
# + colab={} colab_type="code" id="AOlXGO4J6jDh"
# Определим input_fn оценщика
def input_fn():
datasets, info = tfds.load(name='mnist', with_info=True, as_supervised=True)
mnist_train, mnist_test = datasets['train'], datasets['test']
BUFFER_SIZE = 10000
BATCH_SIZE = 64
def scale(image, label):
image = tf.cast(image, tf.float32)
image /= 255
return image, label[..., tf.newaxis]
train_data = mnist_train.map(scale).shuffle(BUFFER_SIZE).batch(BATCH_SIZE)
return train_data.repeat()
# Define train & eval specs
train_spec = tf.estimator.TrainSpec(input_fn=input_fn,
max_steps=STEPS_PER_EPOCH * NUM_EPOCHS)
eval_spec = tf.estimator.EvalSpec(input_fn=input_fn,
steps=STEPS_PER_EPOCH)
# + [markdown] colab_type="text" id="_o6J48Nj9H5c"
# ### Использование определения модели Keras
# + [markdown] colab_type="text" id="IXCQdhGq9SbB"
# Есть некоторые отличия в том, как построить ваши оценщики в TensorFlow 2.0.
#
# Мы рекомендуем вам определить модель используя Keras, потом используйте утилиту `tf.keras.model_to_estimator` для преобразования вашей модели в оценщика. Нижеприведенный код показывает как использовать эту утилиту когда создаешь и обучаешь оценщик.
# + colab={} colab_type="code" id="aelsClm3Cq4I"
def make_model():
return tf.keras.Sequential([
tf.keras.layers.Conv2D(32, 3, activation='relu',
kernel_regularizer=tf.keras.regularizers.l2(0.02),
input_shape=(28, 28, 1)),
tf.keras.layers.MaxPooling2D(),
tf.keras.layers.Flatten(),
tf.keras.layers.Dropout(0.1),
tf.keras.layers.Dense(64, activation='relu'),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Dense(10, activation='softmax')
])
# + colab={} colab_type="code" id="HJb6f8dtl6rr"
model = make_model()
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
estimator = tf.keras.estimator.model_to_estimator(
keras_model = model
)
tf.estimator.train_and_evaluate(estimator, train_spec, eval_spec)
# + [markdown] colab_type="text" id="-ptTxL1q6flL"
# ### Использование пользовательской `model_fn`
#
# Если у вас есть существующий пользовательский оценщик `model_fn`, который вам нужно поддерживать, вы можете конвертировать свой` model_fn` чтобы использовать модель Keras.
#
# Однако по соображениям совместимости пользовательский `model_fn` будет по-прежнему работать в стиле 1.x графа. Это означает, что нет будет eager execution и нет автоматического управления зависимостей.
#
# Использование моделей Keras в пользовательском `model_fn` аналогично использованию в пользовательском цикле обучения:
#
# * Установите фазу `training` соответствующе, основываясь на аргументе `mode`.
# * Явно передайте `trainable_variables` модели оптимизатору.
#
# Но есть важные различия отлосящиеся к [пользовательскому циклу](#custom_loop):
#
# * Вместо использования `model.losses` извлеките потери, используя` tf.keras.Model.get_losses_for`.
# * Извлеките обновления модели используя `tf.keras.Model.get_updates_for`
#
# Примечание: "Updates" это изменения которые необходимо применить к модели после каждого пакета. Например, скользящие средние среднего и дисперсии в слое `tf.keras.layers.BatchNormalization`.
#
# Следующий код создает оценщик из пользовательского `model_fn`, иллюстрируя все эти проблемы.
# + colab={} colab_type="code" id="iY16eZKW606-"
def my_model_fn(features, labels, mode):
model = make_model()
optimizer = tf.compat.v1.train.AdamOptimizer()
loss_fn = tf.keras.losses.SparseCategoricalCrossentropy()
training = (mode == tf.estimator.ModeKeys.TRAIN)
predictions = model(features, training=training)
reg_losses = model.get_losses_for(None) + model.get_losses_for(features)
total_loss = loss_fn(labels, predictions) + tf.math.add_n(reg_losses)
accuracy = tf.compat.v1.metrics.accuracy(labels=labels,
predictions=tf.math.argmax(predictions, axis=1),
name='acc_op')
update_ops = model.get_updates_for(None) + model.get_updates_for(features)
minimize_op = optimizer.minimize(
total_loss,
var_list=model.trainable_variables,
global_step=tf.compat.v1.train.get_or_create_global_step())
train_op = tf.group(minimize_op, update_ops)
return tf.estimator.EstimatorSpec(
mode=mode,
predictions=predictions,
loss=total_loss,
train_op=train_op, eval_metric_ops={'accuracy': accuracy})
# Создайте оценщик и обучите
estimator = tf.estimator.Estimator(model_fn=my_model_fn)
tf.estimator.train_and_evaluate(estimator, train_spec, eval_spec)
# + [markdown] colab_type="text" id="g1l6VnOTodfA"
# ### Готовые оценщики
#
# [Готовые оценщики](https://www.tensorflow.org/guide/premade_estimators) из семейств `tf.estimator.DNN*`, `tf.estimator.Linear*` и `tf.estimator.DNNLinearCombined*` все еще поддерживаются в TensorFlow 2.0 API, однако, некоторые аргументы изменились:
#
# 1. `input_layer_partitioner`: Убрано в 2.0.
# 2. `loss_reduction`: Обновлено до `tf.keras.losses.Reduction` вместо `tf.compat.v1.losses.Reduction`. Значение по умолчанию также изменилось и стало `tf.keras.losses.Reduction.SUM_OVER_BATCH_SIZE` вместо `tf.compat.v1.losses.Reduction.SUM`.
# 3. `optimizer`, `dnn_optimizer` и `linear_optimizer`: эти аргументы обновились до `tf.keras.optimizers` вместо `tf.compat.v1.train.Optimizer`.
#
# Для переноса вышеуказанных изменений:
# 1. Для `input_layer_partitioner` миграция не требуется поскольку [`Стратегия распределения`](https://www.tensorflow.org/guide/distribute_strategy) обработает это автоматически в TF 2.0.
# 2. Для `loss_reduction`, проверьте [`tf.keras.losses.Reduction`](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/keras/losses/Reduction) для поддерживаемых опций.
# 3. Для аргументов `optimizer` args, если вы не передаете аргумента `optimizer`, `dnn_optimizer` или `linear_optimizer`, или если вы укажете в своем коде аргумент `optimizer` как `string`, вам не нужно ничего менять. `tf.keras.optimizers` используются по умолчанию. Иначе, вам нужно обновить его от `tf.compat.v1.train.Optimizer` до соответсвующей [`tf.keras.optimizers`](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/keras/optimizers)
#
# #### Конвертер контрольных точек
# Миграция `optimizer` повредит контрольные точки в TF 1.x, так как` tf.keras.optimizer` генерирует другой набор переменных для сохранения в контрольных точках. Чтобы сделать контрольную пригодной к использованию после перехода на TF 2.0, пожалуйста, посмотрите инструмент конвертации контрольных точек для оптимизаторов, чтобы преобразовать контрольные точки из TF 1.x в TF 2.0. Преобразованные контрольные точки можно использовать для восстановления предварительно обученных моделей в TF 2.0.
# + [markdown] colab_type="text" id="dt8ct9XCFqls"
# ## TensorShape
#
# Этот класс был упрощен для хранения `int` вместо объектов `tf.compat.v1.Dimension`. Так что нет необходимости в вызове `.value()` чтобы получить `int`.
#
# Отдельные объекты `tf.compat.v1.Dimension` по-прежнему доступны из `tf.TensorShape.dims`.
# + [markdown] colab_type="text" id="x36cWcmM8Eu1"
#
#
# Следующее демонстрирует отличия TensorFlow 1.x и TensorFlow 2.0.
# + colab={} colab_type="code" id="PbpD-kHOZR4A"
# Создайте shape и выберите index
i = 0
shape = tf.TensorShape([16, None, 256])
shape
# + [markdown] colab_type="text" id="kDFck03neNy0"
# Если у вас есть это в TF 1.x:
#
# ```python
# value = shape[i].value
# ```
#
# Сделайте это в TF 2.0:
#
# + colab={} colab_type="code" id="KuR73QGEeNdH"
value = shape[i]
value
# + [markdown] colab_type="text" id="bPWPNKRiZmkd"
# Если у вас есть это в TF 1.x:
#
# ```python
# for dim in shape:
# value = dim.value
# print(value)
# ```
#
# TСделайте это в TF 2.0:
# + colab={} colab_type="code" id="y6s0vuuprJfc"
for value in shape:
print(value)
# + [markdown] colab_type="text" id="YpRgngu3Zw-A"
# Если у вас есть это в 1.x (Или используется любой другой метод размерности):
#
# ```python
# dim = shape[i]
# dim.assert_is_compatible_with(other_dim)
# ```
#
# Сделайте это в TF 2.0:
# + colab={} colab_type="code" id="LpViGEcUZDGX"
other_dim = 16
Dimension = tf.compat.v1.Dimension
if shape.rank is None:
dim = Dimension(None)
else:
dim = shape.dims[i]
dim.is_compatible_with(other_dim) # или любой другой метод размерности
# + colab={} colab_type="code" id="GaiGe36dOdZ_"
shape = tf.TensorShape(None)
if shape:
dim = shape.dims[i]
dim.is_compatible_with(other_dim) # или любой другой метод размерности
# + [markdown] colab_type="text" id="3kLLY0I3PI-l"
# Булево значение `tf.TensorShape` является `True` если ранг известен, `False` в противном случае.
# + colab={} colab_type="code" id="-Ow1ndKpOnJd"
print(bool(tf.TensorShape([]))) # Скаляр
print(bool(tf.TensorShape([0]))) # Вектор длины 0
print(bool(tf.TensorShape([1]))) # Вектор длины 1
print(bool(tf.TensorShape([None]))) # Вектор неизвестной длины
print(bool(tf.TensorShape([1, 10, 100]))) # 3D тензор
print(bool(tf.TensorShape([None, None, None]))) # 3D тензор с неизвестными размерностями
print()
print(bool(tf.TensorShape(None))) # Тензор неизвестного ранга.
# + [markdown] colab_type="text" id="lwswSCLT9g63"
# ## Другие поведенческие изменения
#
# В TensorFlow 2.0 есть несколько других поведенческих изменений, с которыми вы можете столкнуться.
#
#
# ### ResourceVariables
#
# TensorFlow 2.0 создает по умолчанию `ResourceVariables`, а не `RefVariables`.
#
# `ResourceVariables` закрыты для записи, и обеспечивают лучшие гарантии согласовенности.
#
# * Это может изменить поведение в граничных случаях.
# * Это может иногда создавать дополнительные копии и использовать большие объемы памяти
# * Это можно отключить, передав `use_resource = False` конструктору` tf.Variable`.
#
# ### Control Flow
#
# Реализация control flow была упрощена, поэтому в TensorFlow 2.0 создаются другие графы.
# + [markdown] colab_type="text" id="vKX6AdTAQhB-"
# ## Выводы
#
# Общий процесс следующий:
#
# 1. Запуститсе upgrade script.
# 2. Удалите символы contrib.
# 3. Переключите ваши модели в объектно ориентированный стиль (Keras).
# 4. Используйте циклы обучения и оценки `tf.keras` или `tf.estimator` там где вы можете.
# 5. Иначе используйте пользовательские циклы, но избегайте сессий и коллекций.
#
#
# Для преобразования кода в идиоматический TensorFlow 2.0 требуется небольшая работа, но каждое изменение приводит к:
#
# * Меньшему количеству строк кода.
# * Увеличившейся понятности и простоте.
# * К более легкой отладке.
#
#
|
site/ru/guide/migration_guide.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + _cell_guid="b1076dfc-b9ad-4769-8c92-a6c4dae69d19" _uuid="8f2839f25d086af736a60e9eeb907d3b93b6e0e5" papermill={"duration": 0.017239, "end_time": "2022-02-23T05:11:51.923067", "exception": false, "start_time": "2022-02-23T05:11:51.905828", "status": "completed"} tags=[]
def ad(a,b):
Y = a+b
return Y
def sq(a):
Y = a*a
return Y
# + papermill={"duration": 0.002439, "end_time": "2022-02-23T05:11:51.928955", "exception": false, "start_time": "2022-02-23T05:11:51.926516", "status": "completed"} tags=[]
|
add-function.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# HIDDEN
from datascience import *
import matplotlib
path_data = '../../../data/'
matplotlib.use('Agg', warn=False)
# %matplotlib inline
import matplotlib.pyplot as plots
plots.style.use('fivethirtyeight')
import numpy as np
# ### Applying a Function to a Column ###
#
# We have seen many examples of creating new columns of tables by applying functions to existing columns or to other arrays. All of those functions took arrays as their arguments. But frequently we will want to convert the entries in a column by a function that doesn't take an array as its argument. For example, it might take just one number as its argument, as in the function `cut_off_at_100` defined below.
def cut_off_at_100(x):
"""The smaller of x and 100"""
return min(x, 100)
cut_off_at_100(17)
cut_off_at_100(117)
cut_off_at_100(100)
# The function `cut_off_at_100` simply returns its argument if the argument is less than or equal to 100. But if the argument is greater than 100, it returns 100.
#
# In our earlier examples using Census data, we saw that the variable `AGE` had a value 100 that meant "100 years old or older". Cutting off ages at 100 in this manner is exactly what `cut_off_at_100` does.
#
# To use this function on many ages at once, we will have to be able to *refer* to the function itself, without actually calling it. Analogously, we might show a cake recipe to a chef and ask her to use it to bake 6 cakes. In that scenario, we are not using the recipe to bake any cakes ourselves; our role is merely to refer the chef to the recipe. Similarly, we can ask a table to call `cut_off_at_100` on 6 different numbers in a column.
# First, we create the table `ages` with a column for people and one for their ages. For example, person `C` is 52 years old.
ages = Table().with_columns(
'Person', make_array('A', 'B', 'C', 'D', 'E', 'F'),
'Age', make_array(17, 117, 52, 100, 6, 101)
)
ages
# ### `apply` ###
#
# To cut off each of the ages at 100, we will use the a new Table method. The `apply` method calls a function on each element of a column, forming a new array of return values. To indicate which function to call, just name it (without quotation marks or parentheses). The name of the column of input values is a string that must still appear within quotation marks.
ages.apply(cut_off_at_100, 'Age')
# What we have done here is `apply` the function `cut_off_at_100` to each value in the `Age` column of the table `ages`. The output is the array of corresponding return values of the function. For example, 17 stayed 17, 117 became 100, 52 stayed 52, and so on.
#
# This array, which has the same length as the original `Age` column of the `ages` table, can be used as the values in a new column called `Cut Off Age` alongside the existing `Person` and `Age` columns.
ages.with_column(
'Cut Off Age', ages.apply(cut_off_at_100, 'Age')
)
# ### Functions as Values ###
# We've seen that Python has many kinds of values. For example, `6` is a number value, `"cake"` is a text value, `Table()` is an empty table, and `ages` is a name for a table value (since we defined it above).
#
# In Python, every function, including `cut_off_at_100`, is also a value. It helps to think about recipes again. A recipe for cake is a real thing, distinct from cakes or ingredients, and you can give it a name like "Ani's cake recipe." When we defined `cut_off_at_100` with a `def` statement, we actually did two separate things: we created a function that cuts off numbers at 100, and we gave it the name `cut_off_at_100`.
#
# We can refer to any function by writing its name, without the parentheses or arguments necessary to actually call it. We did this when we called `apply` above. When we write a function's name by itself as the last line in a cell, Python produces a text representation of the function, just like it would print out a number or a string value.
cut_off_at_100
# Notice that we did not write `"cut_off_at_100"` with quotes (which is just a piece of text), or `cut_off_at_100()` (which is a function call, and an invalid one at that). We simply wrote `cut_off_at_100` to refer to the function.
#
# Just like we can define new names for other values, we can define new names for functions. For example, suppose we want to refer to our function as `cut_off` instead of `cut_off_at_100`. We can just write this:
cut_off = cut_off_at_100
# Now `cut_off` is a name for a function. It's the same function as `cut_off_at_100`, so the printed value is exactly the same.
cut_off
# Let us see another application of `apply`.
# ### Example: Prediction ###
#
# Data Science is often used to make predictions about the future. If we are trying to predict an outcome for a particular individual – for example, how she will respond to a treatment, or whether he will buy a product – it is natural to base the prediction on the outcomes of other similar individuals.
#
# <NAME>'s cousin [<NAME>](https://en.wikipedia.org/wiki/Francis_Galton) was a pioneer in using this idea to make predictions based on numerical data. He studied how physical characteristics are passed down from one generation to the next.
#
# The data below are Galton's carefully collected measurements on the heights of parents and their adult children. Each row corresponds to one adult child. The variables are a numerical code for the family, the heights (in inches) of the father and mother, a "midparent height" which is a weighted average [[1]](#footnotes) of the height of the two parents, the number of children in the family, as well as the child's birth rank (1 = oldest), gender, and height.
# Galton's data on heights of parents and their adult children
galton = Table.read_table(path_data + 'galton.csv')
galton
# A primary reason for collecting the data was to be able to predict the adult height of a child born to parents similar to those in the dataset. Let us try to do this, using midparent height as the variable on which to base our prediction. Thus midparent height is our *predictor* variable.
#
# The table `heights` consists of just the midparent heights and child's heights. The scatter plot of the two variables shows a positive association, as we would expect for these variables.
heights = galton.select(3, 7).relabeled(0, 'MidParent').relabeled(1, 'Child')
heights
heights.scatter(0)
# Now suppose Galton encountered a new couple, similar to those in his dataset, and wondered how tall their child would be. What would be a good way for him to go about predicting the child's height, given that the midparent height was, say, 68 inches?
#
# One reasonable approach would be to base the prediction on all the points that correspond to a midparent height of around 68 inches. The prediction equals the average child's height calculated from those points alone.
#
# Let's pretend we are Galton and execute this plan. For now we will just make a reasonable definition of what "around 68 inches" means, and work with that. Later in the course we will examine the consequences of such choices.
#
# We will take "close" to mean "within half an inch". The figure below shows all the points corresponding to a midparent height between 67.5 inches and 68.5 inches. These are all the points in the strip between the red lines. Each of these points corresponds to one child; our prediction of the height of the new couple's child is the average height of all the children in the strip. That's represented by the gold dot.
#
# Ignore the code, and just focus on understanding the mental process of arriving at that gold dot.
heights.scatter('MidParent')
_ = plots.plot([67.5, 67.5], [50, 85], color='red', lw=2)
_ = plots.plot([68.5, 68.5], [50, 85], color='red', lw=2)
_ = plots.scatter(68, 66.24, color='gold', s=40)
# In order to calculate exactly where the gold dot should be, we first need to indentify all the points in the strip. These correspond to the rows where `MidParent` is between 67.5 inches and 68.5 inches.
close_to_68 = heights.where('MidParent', are.between(67.5, 68.5))
close_to_68
# The predicted height of a child who has a midparent height of 68 inches is the average height of the children in these rows. That's 66.24 inches.
close_to_68.column('Child').mean()
# We now have a way to predict the height of a child given any value of the midparent height near those in our dataset. We can define a function `predict_child` that does this. The body of the function consists of the code in the two cells above, apart from choices of names.
def predict_child(mpht):
"""Predict the height of a child whose parents have a midparent height of mpht.
The prediction is the average height of the children whose midparent height is
in the range mpht plus or minus 0.5.
"""
close_points = heights.where('MidParent', are.between(mpht-0.5, mpht + 0.5))
return close_points.column('Child').mean()
# Given a midparent height of 68 inches, the function `predict_child` returns the same prediction (66.24 inches) as we got earlier. The advantage of defining the function is that we can easily change the value of the predictor and get a new prediction.
predict_child(68)
predict_child(74)
# How good are these predictions? We can get a sense of this by comparing the predictions with the data that we already have. To do this, we first apply the function `predict_child` to the column of `Midparent` heights, and collect the results in a new column called `Prediction`.
# +
# Apply predict_child to all the midparent heights
heights_with_predictions = heights.with_column(
'Prediction', heights.apply(predict_child, 'MidParent')
)
# -
heights_with_predictions
# To see where the predictions lie relative to the observed data, we can draw overlaid scatter plots with `MidParent` as the common horizontal axis.
heights_with_predictions.scatter('MidParent')
# The graph of gold dots is called a *graph of averages,* because each gold dot is the center of a vertical strip like the one we drew earlier. Each one provides a prediction of a child's height given the midparent height. For example, the scatter shows that for a midparent height of 72 inches, the predicted height of the child would be somewhere between 68 inches and 69 inches, and indeed `predict_child(72)` returns 68.5.
# Galton's calculations and visualizations were very similar to ours, except that he didn't have Python. He drew the graph of averages through the scatter diagram and noticed that it roughly followed a straight line. This straight line is now called the *regression line* and is one of the most common methods of making predictions. Galton's friend, the mathematician <NAME>, used these analyses to formalize the notion of *correlation*.
# This example, like the one about <NAME>'s analysis of cholera deaths, shows how some of the fundamental concepts of modern data science have roots going back more than a century. Galton's methods such as the one we have used here are precursors to *nearest neighbor* prediction methods that now have powerful applications in diverse settings. The modern field of *machine learning* includes the automation of such methods to make predictions based on vast and rapidly evolving datasets.
# <a id='footnotes'></a>
# ##### Footnotes
# [1] Galton multiplied the heights of all the women by 1.08 before taking the average height of the men and the women. For a discussion of this, see [Chance](http://chance.amstat.org/2013/09/1-pagano/), a magazine published by the American Statistical Association.
|
notebooks/08/1/Applying_a_Function_to_a_Column.ipynb
|
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .r
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: R
# language: R
# name: ir
# ---
# # Einlesen der Daten
# Schau Dir zunächst die CSV-Datei *salary.csv* im Verzeichnis *data* an. [Hier findest Du sie.](https://raw.githubusercontent.com/simonprewo/R-CSV-File-Example/master/data/salary.csv)
# Wir beginnen mit Einlesen der Daten per CSV:
mitarbeiter = read.csv("data/mitarbeiter.csv")
# # Anzeigen der Daten
print(mitarbeiter)
# # Durchschnittsgehalt berechnen
durchschnittsgehalt = mean(mitarbeiter$Jahresgehalt)
print(durchschnittsgehalt)
|
simple-r-read-csv-file-example.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="BX4onq55l8KK" colab={"base_uri": "https://localhost:8080/", "height": 204} outputId="1b879cc6-dfe4-4990-c35e-577b4ddb9b17"
import pandas as pd
import numpy as np
df = pd.read_csv('EnjoySport.csv',index_col=0)
df.head()
# + id="SjCwCJucoUaW"
def is_consistent(H,D):
for i,d in enumerate(D):
if H[i] != d and H[i] != '?':
return False
return True
def generalize_s(S,H):
if (S == np.array(['%','%','%','%','%','%'])).all():
return H
for i,h in enumerate(H):
if S[i] != h:
S[i] = '?'
return S
def specialize_g(G,S,H):
for i,h in enumerate(H):
if S[i] != h:
G[i][i] = S[i]
return G
# + colab={"base_uri": "https://localhost:8080/"} id="S02QHOiMoKYI" outputId="4f042d3c-ae4b-4b64-f3c3-7f5abc70f5dd"
concepts = np.array(df.iloc[:,:-1]).copy()
target = np.array(df.iloc[:,-1]).copy()
S = ['%','%','%','%','%','%']
G = [['?' for i in range(len(concepts[0]))] for j in range(len(concepts[0]))]
for i,h in enumerate(concepts):
if target[i] == 'Yes':
if not is_consistent(h,S):
S = generalize_s(S,h)
inconsistent_g = [i for i,s in enumerate(S) if s == '?']
for g in inconsistent_g:
G[g][g] = '?'
# print(S)
else:
for j,g in enumerate(G):
if is_consistent(g,h):
G = specialize_g(G,S,h)
# print(G)
filter_g = [i for i,g in enumerate(G) if g == ['?', '?', '?', '?', '?', '?']]
for i in filter_g:
G.remove(['?', '?', '?', '?', '?', '?'])
print(S)
print(G)
# + id="5i2rPE42o72-"
|
ipynb/P2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "slide"} tags=[]
# # Fuzzing with Generators
#
# In this chapter, we show how to extend grammars with _functions_ – pieces of code that get executed during grammar expansion, and that can generate, check, or change elements produced. Adding functions to a grammar allows for very versatile test generation, bringing together the best of grammar generation and programming.
# + slideshow={"slide_type": "skip"}
from bookutils import YouTubeVideo
YouTubeVideo('oeMxtboPD_s')
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
# **Prerequisites**
#
# * As this chapter deeply interacts with the techniques discussed in the [chapter on efficient grammar fuzzing](GrammarFuzzer.ipynb), a good understanding of the techniques is recommended.
# + [markdown] slideshow={"slide_type": "skip"}
# ## Synopsis
# <!-- Automatically generated. Do not edit. -->
#
# To [use the code provided in this chapter](Importing.ipynb), write
#
# ```python
# >>> from fuzzingbook.GeneratorGrammarFuzzer import <identifier>
# ```
#
# and then make use of the following features.
#
#
# This chapter introduces the ability to attach _functions_ to individual production rules:
#
# * A `pre` function is executed _before_ the expansion takes place. Its result (typically a string) can _replace_ the actual expansion.
# * A `post` function is executed _after_ the expansion has taken place. If it returns a string, the string replaces the expansion; it it returns `False`, it triggers a new expansion.
#
# Both functions can return `None` to not interfere with grammar production at all.
#
# To attach a function `F` to an individual expansion `S` in a grammar, replace `S` with a pair
#
# ```python
# (S, opts(pre=F)) # Set a function to be executed before expansion
# ```
# or
# ```python
# (S, opts(post=F)) # Set a function to be executed after expansion
# ```
#
# Here is an example, To take an area code from a list that is given programmatically, we can write:
#
# ```python
# >>> from Grammars import US_PHONE_GRAMMAR, extend_grammar, opts
# >>> def pick_area_code():
# >>> return random.choice(['555', '554', '553'])
# >>> PICKED_US_PHONE_GRAMMAR = extend_grammar(US_PHONE_GRAMMAR,
# >>> {
# >>> "<area>": [("<lead-digit><digit><digit>", opts(pre=pick_area_code))]
# >>> })
# ```
# A `GeneratorGrammarFuzzer` will extract and interpret these options. Here is an example:
#
# ```python
# >>> picked_us_phone_fuzzer = GeneratorGrammarFuzzer(PICKED_US_PHONE_GRAMMAR)
# >>> [picked_us_phone_fuzzer.fuzz() for i in range(5)]
# ['(553)200-6118',
# '(553)889-0205',
# '(555)317-0936',
# '(553)455-2577',
# '(553)263-8511']
# ```
# As you can see, the area codes now all stem from `pick_area_code()`. Such definitions allow to closely tie program code (such as `pick_area_code()`) to grammars.
#
# The `PGGCFuzzer` class incorporates all features from [the `GrammarFuzzer` class](GrammarFuzzer.ipynb) and its [coverage-based](GrammarCoverageFuzzer.ipynb), [probabilistic-based](ProbabilisticGrammarFuzzer.ipynb), and [generator-based](GeneratorGrammarFuzzer.ipynb) derivatives.
#
# 
#
#
# + [markdown] button=false new_sheet=true run_control={"read_only": false} slideshow={"slide_type": "slide"}
# ## Example: Test a Credit Card System
#
# Suppose you work with a shopping system that – among several other features – allows customers to pay with a credit card. Your task is to test the payment functionality.
# + [markdown] button=false new_sheet=true run_control={"read_only": false} slideshow={"slide_type": "fragment"}
# To make things simple, we will assume that we need only two pieces of data – a 16-digit credit card number and an amount to be charged. Both pieces can be easily generated with grammars, as in the following:
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "skip"}
import bookutils
# + slideshow={"slide_type": "skip"}
from typing import Callable, Set, List, Dict, Optional, Iterator, Any, Union, Tuple, cast
# + slideshow={"slide_type": "skip"}
from Fuzzer import Fuzzer
# + slideshow={"slide_type": "skip"}
from Grammars import EXPR_GRAMMAR, is_valid_grammar, is_nonterminal, extend_grammar
from Grammars import opts, exp_opt, exp_string, crange, Grammar, Expansion
# + slideshow={"slide_type": "skip"}
from GrammarFuzzer import DerivationTree
# + slideshow={"slide_type": "subslide"}
CHARGE_GRAMMAR: Grammar = {
"<start>": ["Charge <amount> to my credit card <credit-card-number>"],
"<amount>": ["$<float>"],
"<float>": ["<integer>.<digit><digit>"],
"<integer>": ["<digit>", "<integer><digit>"],
"<digit>": crange('0', '9'),
"<credit-card-number>": ["<digits>"],
"<digits>": ["<digit-block><digit-block><digit-block><digit-block>"],
"<digit-block>": ["<digit><digit><digit><digit>"],
}
# + slideshow={"slide_type": "fragment"}
assert is_valid_grammar(CHARGE_GRAMMAR)
# + [markdown] slideshow={"slide_type": "fragment"}
# All of this works neatly – we can generate arbitrary amounts and credit card numbers:
# + slideshow={"slide_type": "skip"}
from GrammarFuzzer import GrammarFuzzer, all_terminals
# + slideshow={"slide_type": "subslide"}
g = GrammarFuzzer(CHARGE_GRAMMAR)
[g.fuzz() for i in range(5)]
# + [markdown] slideshow={"slide_type": "subslide"}
# However, when actually testing our system with this data, we find two problems:
#
# 1. We'd like to test _specific_ amounts being charged – for instance, amounts that would excess the credit card limit.
# 2. We find that 9 out of 10 credit card numbers are rejected because of having an incorrect checksum. This is fine if we want to test rejection of credit card numbers – but if we want to test the actual functionality of processing a charge, we need _valid_ numbers.
# + [markdown] slideshow={"slide_type": "subslide"}
# We could go and ignore these issues; after all, eventually, it is only a matter of time until large amounts and valid numbers are generated. As it comes to the first concern, we could also address it by changing the grammar appropriately – say, to only produce charges that have at least six leading digits. However, generalizing this to arbitrary ranges of values will be cumbersome.
#
# The second concern, the checksums of credit card numbers, however, runs deeper – at least as far as grammars are concerned, is that a complex arithmetic operation like a checksum cannot be expressed in a grammar alone – at least not in the _context-free grammars_ we use here. (In principle, one _could_ do this in a _context–sensitive_ grammar, but specifying this would be no fun at all.) What we want is a mechanism that allows us to _attach programmatic computations_ to our grammars, bringing together the best of both worlds.
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "skip"} toc-hr-collapsed=true
# ## Attaching Functions to Expansions
# + [markdown] slideshow={"slide_type": "fragment"}
# The key idea of this chapter is to _extend_ grammars such that one can _attach Python functions_ to individual expansions. These functions can be executed
#
# 1. _before_ expansion, _replacing_ the element to be expanded by a computed value; or
# 2. _after_ expansion, _checking_ generated elements, and possibly also replacing them.
#
# In both cases, functions are specified using the `opts()` expansion mechanism introduced in the [chapter on grammars](Grammars.ipynb). They are thus tied to a specific expansion $e$ of a symbol $s$.
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Functions Called Before Expansion
#
# A function defined using the `pre` option is invoked _before_ expansion of $s$ into $e$. Its value _replaces_ the expansion $e$ to be produced. To generate a value for the credit card example, above, we could define a _pre-expansion_ generator function
# + slideshow={"slide_type": "skip"}
import random
# + slideshow={"slide_type": "fragment"}
def high_charge() -> float:
return random.randint(10000000, 90000000) / 100.0
# + [markdown] slideshow={"slide_type": "fragment"}
# With `opts()`, we could attach this function to the grammar:
# + slideshow={"slide_type": "fragment"}
CHARGE_GRAMMAR.update({
"<float>": [("<integer>.<digit><digit>", opts(pre=high_charge))],
})
# + [markdown] slideshow={"slide_type": "subslide"}
# with the intention that whenever `<float>` is expanded, the function `high_charge` would be invoked to generate a value for `<float>`. (The actual expansion in the grammar would still be present for fuzzers that ignore functions, such as `GrammarFuzzer`).
# + [markdown] slideshow={"slide_type": "fragment"}
# Since functions tied to a grammar are frequently very simple, we can also _inline_ them using a *lambda* expression. A _lambda expression_ is used for _anonymous_ functions that are limited in scope and functionality. Here's an example:
# + slideshow={"slide_type": "fragment"}
def apply_twice(function, x):
return function(function(x))
# + slideshow={"slide_type": "fragment"}
apply_twice(lambda x: x * x, 2)
# + [markdown] slideshow={"slide_type": "fragment"}
# Here, we don't have to give the `function` to be applied twice a name (say, `square()`); instead, we apply it inline within the invocation.
# + [markdown] slideshow={"slide_type": "fragment"}
# Using `lambda`, this is what our grammar looks like:
# + slideshow={"slide_type": "subslide"}
CHARGE_GRAMMAR.update({
"<float>": [("<integer>.<digit><digit>",
opts(pre=lambda: random.randint(10000000, 90000000) / 100.0))]
})
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Functions Called After Expansion
#
# A function defined using the `post` option is invoked _after_ expansion of $s$ into $e$, passing the expanded values of the symbols in $e$ as arguments. A post-expansion function can serve in two ways:
#
# 1. It can serve as a *constraint* or _filter_ on the expanded values, returning `True` if the expansion is valid, and `False` if not; if it returns `False`, another expansion is attempted.
# 2. It can also serve as a *repair*, returning a string value; like pre-expansion functions, the returned value replaces the expansion.
#
# For our credit card example, we can choose both ways. If we have a function `check_credit_card(s)` which returns `True` for a valid number `s` and `False` for invalid ones, we would go for the first option:
# + slideshow={"slide_type": "subslide"}
CHARGE_GRAMMAR.update({
"<credit-card-number>": [("<digits>", opts(post=lambda digits: check_credit_card(digits)))]
})
# + [markdown] slideshow={"slide_type": "fragment"}
# With such a filter, only valid credit cards will be produced. On average, it will still take 10 attempts for each time `check_credit_card()` is satisfied, but then, we do not have to recourse to the system under test.
# + [markdown] slideshow={"slide_type": "fragment"}
# If we have a function `fix_credit_card(s)` which changes the number such that the checksum is valid and returns the "fixed" number, we can make use of this one instead:
# + slideshow={"slide_type": "fragment"}
CHARGE_GRAMMAR.update({
"<credit-card-number>": [("<digits>", opts(post=lambda digits: fix_credit_card(digits)))]
})
# + [markdown] slideshow={"slide_type": "fragment"}
# Here, each number is generated only once and then repaired. This is very efficient.
# + [markdown] slideshow={"slide_type": "subslide"}
# The checksum function used for credit cards is the [Luhn algorithm](https://en.wikipedia.org/wiki/Luhn_algorithm), a simple yet effective formula.
# + slideshow={"slide_type": "fragment"}
def luhn_checksum(s: str) -> int:
"""Compute Luhn's check digit over a string of digits"""
LUHN_ODD_LOOKUP = (0, 2, 4, 6, 8, 1, 3, 5, 7,
9) # sum_of_digits (index * 2)
evens = sum(int(p) for p in s[-1::-2])
odds = sum(LUHN_ODD_LOOKUP[int(p)] for p in s[-2::-2])
return (evens + odds) % 10
# + slideshow={"slide_type": "fragment"}
def valid_luhn_checksum(s: str) -> bool:
"""Check whether the last digit is Luhn's checksum over the earlier digits"""
return luhn_checksum(s[:-1]) == int(s[-1])
# + slideshow={"slide_type": "subslide"}
def fix_luhn_checksum(s: str) -> str:
"""Return the given string of digits, with a fixed check digit"""
return s[:-1] + repr(luhn_checksum(s[:-1]))
# + slideshow={"slide_type": "fragment"}
luhn_checksum("123")
# + slideshow={"slide_type": "fragment"}
fix_luhn_checksum("123x")
# + [markdown] slideshow={"slide_type": "fragment"}
# We can make use of these functions in our credit card grammar:
# + slideshow={"slide_type": "fragment"}
check_credit_card: Callable[[str], bool] = valid_luhn_checksum
fix_credit_card: Callable[[str], str] = fix_luhn_checksum
# + slideshow={"slide_type": "fragment"}
fix_credit_card("1234567890123456")
# + [markdown] slideshow={"slide_type": "slide"}
# ## A Class for Integrating Constraints
# + [markdown] slideshow={"slide_type": "fragment"}
# While it is easy to specify functions, our grammar fuzzer will simply ignore them just as it ignores all extensions. It will issue a warning, though:
# + slideshow={"slide_type": "fragment"}
g = GrammarFuzzer(CHARGE_GRAMMAR)
g.fuzz()
# + [markdown] slideshow={"slide_type": "fragment"}
# We need to define a special fuzzer that actually invokes the given `pre` and `post` functions and acts accordingly. We name this a `GeneratorGrammarFuzzer`:
# + slideshow={"slide_type": "fragment"}
class GeneratorGrammarFuzzer(GrammarFuzzer):
def supported_opts(self) -> Set[str]:
return super().supported_opts() | {"pre", "post", "order"}
# + [markdown] slideshow={"slide_type": "fragment"}
# We define custom functions to access the `pre` and `post` options:
# + slideshow={"slide_type": "subslide"}
def exp_pre_expansion_function(expansion: Expansion) -> Optional[Callable]:
"""Return the specified pre-expansion function, or None if unspecified"""
return exp_opt(expansion, 'pre')
# + slideshow={"slide_type": "fragment"}
def exp_post_expansion_function(expansion: Expansion) -> Optional[Callable]:
"""Return the specified post-expansion function, or None if unspecified"""
return exp_opt(expansion, 'post')
# + [markdown] slideshow={"slide_type": "fragment"}
# The `order` attribute will be used [later in this chapter](#Ordering-Expansions).
# + [markdown] slideshow={"slide_type": "slide"} toc-hr-collapsed=true
# ## Generating Elements before Expansion
# + [markdown] slideshow={"slide_type": "fragment"}
# Our first task will be implementing the pre-expansion functions – that is, the function that would be invoked _before_ expansion to replace the value to be expanded. To this end, we hook into the `process_chosen_children()` method, which gets the selected children before expansion. We set it up such that it invokes the given `pre` function and applies its result on the children, possibly replacing them.
# + slideshow={"slide_type": "skip"}
import inspect
# + slideshow={"slide_type": "subslide"}
class GeneratorGrammarFuzzer(GeneratorGrammarFuzzer):
def process_chosen_children(self, children: List[DerivationTree],
expansion: Expansion) -> List[DerivationTree]:
function = exp_pre_expansion_function(expansion)
if function is None:
return children
assert callable(function)
if inspect.isgeneratorfunction(function):
# See "generators", below
result = self.run_generator(expansion, function)
else:
result = function()
if self.log:
print(repr(function) + "()", "=", repr(result))
return self.apply_result(result, children)
def run_generator(self, expansion: Expansion, function: Callable):
...
# + [markdown] slideshow={"slide_type": "subslide"}
# The method `apply_result()` takes the result from the pre-expansion function and applies it on the children. The exact effect depends on the type of the result:
#
# * A _string_ $s$ replaces the entire expansion with $s$.
# * A _list_ $[x_1, x_2, \dots, x_n]$ replaces the $i$-th symbol with $x_i$ for every $x_i$ that is not `None`. Specifying `None` as a list element $x_i$ is useful to leave that element unchanged. If $x_i$ is not a string, it is converted to a string.
# * A value of `None` is ignored. This is useful if one wants to simply call a function upon expansion, with no effect on the expanded strings.
# * _Boolean_ values are ignored. This is useful for post-expansion functions, discussed below.
# * All _other types_ are converted to strings, replacing the entire expansion.
# + slideshow={"slide_type": "subslide"}
class GeneratorGrammarFuzzer(GeneratorGrammarFuzzer):
def apply_result(self, result: Any,
children: List[DerivationTree]) -> List[DerivationTree]:
if isinstance(result, str):
children = [(result, [])]
elif isinstance(result, list):
symbol_indexes = [i for i, c in enumerate(children)
if is_nonterminal(c[0])]
for index, value in enumerate(result):
if value is not None:
child_index = symbol_indexes[index]
if not isinstance(value, str):
value = repr(value)
if self.log:
print(
"Replacing", all_terminals(
children[child_index]), "by", value)
# children[child_index] = (value, [])
child_symbol, _ = children[child_index]
children[child_index] = (child_symbol, [(value, [])])
elif result is None:
pass
elif isinstance(result, bool):
pass
else:
if self.log:
print("Replacing", "".join(
[all_terminals(c) for c in children]), "by", result)
children = [(repr(result), [])]
return children
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Example: Numeric Ranges
#
# With the above extensions, we have full support for pre-expansion functions. Using the augmented `CHARGE_GRAMMAR`, we find that the pre-expansion `lambda` function is actually used:
# + slideshow={"slide_type": "fragment"}
charge_fuzzer = GeneratorGrammarFuzzer(CHARGE_GRAMMAR)
charge_fuzzer.fuzz()
# + [markdown] slideshow={"slide_type": "fragment"}
# The log reveals a bit more details what happens when the pre-expansion function is called. We see that the expansion `<integer>.<digit><digit>` is directly replaced by the computed value:
# + slideshow={"slide_type": "subslide"}
amount_fuzzer = GeneratorGrammarFuzzer(
CHARGE_GRAMMAR, start_symbol="<amount>", log=True)
amount_fuzzer.fuzz()
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Example: More Numeric Ranges
#
# We can use such pre-expansion functions in other contexts, too. Suppose we want to generate arithmetic expressions in which each number is between 100 and 200. We can extend `EXPR_GRAMMAR` accordingly:
# + slideshow={"slide_type": "subslide"}
expr_100_200_grammar = extend_grammar(EXPR_GRAMMAR,
{
"<factor>": [
"+<factor>", "-<factor>", "(<expr>)",
# Generate only the integer part with a function;
# the fractional part comes from
# the grammar
("<integer>.<integer>", opts(
pre=lambda: [random.randint(100, 200), None])),
# Generate the entire integer
# from the function
("<integer>", opts(
pre=lambda: random.randint(100, 200))),
],
}
)
# + slideshow={"slide_type": "subslide"}
expr_100_200_fuzzer = GeneratorGrammarFuzzer(expr_100_200_grammar)
expr_100_200_fuzzer.fuzz()
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Support for Python Generators
#
# The Python language has its own concept of generator functions, which we of course want to support as well. A *generator function in Python* is a function that returns a so-called *iterator object* which we can iterate over, one value at a time.
# + [markdown] slideshow={"slide_type": "fragment"}
# To create a generator function in Python, one defines a normal function, using the `yield` statement instead of a `return` statement. While a `return` statement terminates the function, a `yield` statement pauses its execution, saving all of its state, to be resumed later for the next successive calls.
# + [markdown] slideshow={"slide_type": "fragment"}
# Here is an example of a generator function. When first invoked, `iterate()` yields the value 1, followed by 2, 3, and so on:
# + slideshow={"slide_type": "subslide"}
def iterate():
t = 0
while True:
t = t + 1
yield t
# + [markdown] slideshow={"slide_type": "fragment"}
# We can use `iterate` in a loop, just like the `range()` function (which also is a generator function):
# + slideshow={"slide_type": "fragment"}
for i in iterate():
if i > 10:
break
print(i, end=" ")
# + [markdown] slideshow={"slide_type": "fragment"}
# We can also use `iterate()` as a pre-expansion generator function, ensuring it will create one successive integer after another:
# + slideshow={"slide_type": "subslide"}
iterate_grammar = extend_grammar(EXPR_GRAMMAR,
{
"<factor>": [
"+<factor>", "-<factor>", "(<expr>)",
# "<integer>.<integer>",
# Generate one integer after another
# from the function
("<integer>", opts(pre=iterate)),
],
})
# + [markdown] slideshow={"slide_type": "subslide"}
# To support generators, our `process_chosen_children()` method, above, checks whether a function is a generator; if so, it invokes the `run_generator()` method. When `run_generator()` sees the function for the first time during a `fuzz_tree()` (or `fuzz()`) call, it invokes the function to create a generator object; this is saved in the `generators` attribute, and then called. Subsequent calls directly go to the generator, preserving state.
# + slideshow={"slide_type": "subslide"}
class GeneratorGrammarFuzzer(GeneratorGrammarFuzzer):
def fuzz_tree(self) -> DerivationTree:
self.reset_generators()
return super().fuzz_tree()
def reset_generators(self) -> None:
self.generators: Dict[str, Iterator] = {}
def run_generator(self, expansion: Expansion,
function: Callable) -> Iterator:
key = repr((expansion, function))
if key not in self.generators:
self.generators[key] = function()
generator = self.generators[key]
return next(generator)
# + [markdown] slideshow={"slide_type": "subslide"}
# Does this work? Let us run our fuzzer on the above grammar, using `iterator()`:
# + slideshow={"slide_type": "fragment"}
iterate_fuzzer = GeneratorGrammarFuzzer(iterate_grammar)
iterate_fuzzer.fuzz()
# + [markdown] slideshow={"slide_type": "fragment"}
# We see that the expression contains all integers starting with 1.
# + [markdown] slideshow={"slide_type": "fragment"}
# Instead of specifying our own Python generator function such as `iterate()`, we can also use one of the built-in Python generators such as `range()`. This will also generate integers starting with 1:
# + slideshow={"slide_type": "subslide"}
iterate_grammar = extend_grammar(EXPR_GRAMMAR,
{
"<factor>": [
"+<factor>", "-<factor>", "(<expr>)",
("<integer>", opts(pre=range(1, 1000))),
],
})
# + [markdown] slideshow={"slide_type": "fragment"}
# It is also possible to use Python list comprehensions, by adding their generator functions in parentheses:
# + slideshow={"slide_type": "subslide"}
iterate_grammar = extend_grammar(EXPR_GRAMMAR,
{
"<factor>": [
"+<factor>", "-<factor>", "(<expr>)",
("<integer>", opts(
pre=(x for x in range(1, 1000)))),
],
})
# + [markdown] slideshow={"slide_type": "fragment"}
# Note that both above grammars will actually cause the fuzzer to raise an exception when more than 1,000 integers are created, but you will find it very easy to fix this.
# + [markdown] slideshow={"slide_type": "fragment"}
# Finally, `yield` is actually an expression, not a statement, so it is also possible to have a `lambda` expression `yield` a value. If you find some reasonable use for this, let us know.
# + [markdown] slideshow={"slide_type": "slide"} toc-hr-collapsed=true
# ## Checking and Repairing Elements after Expansion
#
# Let us now turn to our second set of functions to be supported – namely, post-expansion functions. The simplest way of using them is to run them once the entire tree is generated, taking care of replacements as with `pre` functions. If one of them returns `False`, however, we start anew.
# + slideshow={"slide_type": "subslide"}
class GeneratorGrammarFuzzer(GeneratorGrammarFuzzer):
def fuzz_tree(self) -> DerivationTree:
while True:
tree = super().fuzz_tree()
(symbol, children) = tree
result, new_children = self.run_post_functions(tree)
if not isinstance(result, bool) or result:
return (symbol, new_children)
self.restart_expansion()
def restart_expansion(self) -> None:
# To be overloaded in subclasses
self.reset_generators()
# + [markdown] slideshow={"slide_type": "subslide"}
# The method `run_post_functions()` is applied recursively on all nodes of the derivation tree. For each node, it determines the expansion applied, and then runs the function associated with that expansion.
# + slideshow={"slide_type": "subslide"}
class GeneratorGrammarFuzzer(GeneratorGrammarFuzzer):
# Return True iff all constraints of grammar are satisfied in TREE
def run_post_functions(self, tree: DerivationTree,
depth: Union[int, float] = float("inf")) \
-> Tuple[bool, Optional[List[DerivationTree]]]:
symbol: str = tree[0]
children: List[DerivationTree] = cast(List[DerivationTree], tree[1])
if children == []:
return True, children # Terminal symbol
try:
expansion = self.find_expansion(tree)
except KeyError:
# Expansion (no longer) found - ignore
return True, children
result = True
function = exp_post_expansion_function(expansion)
if function is not None:
result = self.eval_function(tree, function)
if isinstance(result, bool) and not result:
if self.log:
print(
all_terminals(tree),
"did not satisfy",
symbol,
"constraint")
return False, children
children = self.apply_result(result, children)
if depth > 0:
for c in children:
result, _ = self.run_post_functions(c, depth - 1)
if isinstance(result, bool) and not result:
return False, children
return result, children
# + [markdown] slideshow={"slide_type": "subslide"}
# The helper method `find_expansion()` takes a subtree `tree` and determines the expansion from the grammar that was applied to create the children in `tree`.
# + slideshow={"slide_type": "subslide"}
class GeneratorGrammarFuzzer(GeneratorGrammarFuzzer):
def find_expansion(self, tree):
symbol, children = tree
applied_expansion = \
"".join([child_symbol for child_symbol, _ in children])
for expansion in self.grammar[symbol]:
if exp_string(expansion) == applied_expansion:
return expansion
raise KeyError(
symbol +
": did not find expansion " +
repr(applied_expansion))
# + [markdown] slideshow={"slide_type": "subslide"}
# The method `eval_function()` is the one that takes care of actually invoking the post-expansion function. It creates an argument list containing the expansions of all nonterminal children – that is, one argument for each symbol in the grammar expansion. It then calls the given function.
# + slideshow={"slide_type": "subslide"}
class GeneratorGrammarFuzzer(GeneratorGrammarFuzzer):
def eval_function(self, tree, function):
symbol, children = tree
assert callable(function)
args = []
for (symbol, exp) in children:
if exp != [] and exp is not None:
symbol_value = all_terminals((symbol, exp))
args.append(symbol_value)
result = function(*args)
if self.log:
print(repr(function) + repr(tuple(args)), "=", repr(result))
return result
# + [markdown] slideshow={"slide_type": "subslide"}
# Note that unlike pre-expansion functions, post-expansion functions typically process the values already produced, so we do not support Python generators here.
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Example: Negative Expressions
#
# Let us try out these post-expression functions on an example. Suppose we want to produce only arithmetic expressions that evaluate to a negative number – for instance, to feed such generated expressions into a compiler or some other external system. Doing so constructively with `pre` functions would be very difficult. Instead, we can define a constraint that checks for precisely this property, using the Python `eval()` function.
# + [markdown] slideshow={"slide_type": "subslide"}
# The Python `eval()` function takes a string and evaluates it according to Python rules. Since the syntax of our generated expressions is slightly different from Python, and since Python can raise arithmetic exceptions during evaluation, we need a means to handle such errors gracefully. The function `eval_with_exception()` wraps around `eval()`; if an exception occurs during evaluation, it returns False – which causes the production algorithm to produce another value.
# + slideshow={"slide_type": "skip"}
from ExpectError import ExpectError
# + slideshow={"slide_type": "fragment"}
def eval_with_exception(s):
# Use "mute=True" to suppress all messages
with ExpectError(print_traceback=False):
return eval(s)
return False
# + slideshow={"slide_type": "subslide"}
negative_expr_grammar = extend_grammar(EXPR_GRAMMAR,
{
"<start>": [("<expr>", opts(post=lambda s: eval_with_exception(s) < 0))]
}
)
assert is_valid_grammar(negative_expr_grammar)
# + slideshow={"slide_type": "fragment"}
negative_expr_fuzzer = GeneratorGrammarFuzzer(negative_expr_grammar)
expr = negative_expr_fuzzer.fuzz()
expr
# + [markdown] slideshow={"slide_type": "fragment"}
# The result is indeed negative:
# + slideshow={"slide_type": "subslide"}
eval(expr)
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Example: Matching XML Tags
#
# Post-expansion functions can not only be used to _check_ expansions, but also to repair them. To this end, we can have them return a string or a list of strings; just like pre-expansion functions, these strings would then replace the entire expansion or individual symbols.
# + [markdown] slideshow={"slide_type": "fragment"}
# As an example, consider *XML documents*, which are composed of text within matching _XML tags_. For instance, consider the following fragment in HTML, a subset of XML:
# + slideshow={"slide_type": "skip"}
from bookutils import HTML
# + slideshow={"slide_type": "fragment"}
HTML("<strong>A bold text</strong>")
# + [markdown] slideshow={"slide_type": "fragment"}
# This fragment consists of two HTML (XML) tags that surround the text; the tag name (`strong`) is present both in the opening (`<strong>`) as well as in the closing (`</strong>`) tag.
# + [markdown] slideshow={"slide_type": "subslide"}
# For a _finite_ set of tags (for instance, the HTML tags `<strong>`, `<head>`, `<body>`, `<form>`, and so on), we could define a context-free grammar that parses it; each pair of tags would make up an individual rule in the grammar. If the set of tags is _infinite_, though, as with general XML, we cannot define an appropriate grammar; that is because the constraint that the closing tag must match the opening tag is context-sensitive and thus does not fit context-free grammars.
# + [markdown] slideshow={"slide_type": "fragment"}
# (Incidentally, if the closing tag had the identifier _reversed_ (`</gnorts>`), then a context-free grammar could describe it. Make this a programming exercise.)
# + [markdown] slideshow={"slide_type": "fragment"}
# We can address this problem by introducing appropriate post-expansion functions that automatically make the closing tag match the opening tag. Let us start with a simple grammar for producing XML trees:
# + slideshow={"slide_type": "subslide"}
XML_GRAMMAR: Grammar = {
"<start>": ["<xml-tree>"],
"<xml-tree>": ["<<id>><xml-content></<id>>"],
"<xml-content>": ["Text", "<xml-tree>"],
"<id>": ["<letter>", "<id><letter>"],
"<letter>": crange('a', 'z')
}
# + slideshow={"slide_type": "fragment"}
assert is_valid_grammar(XML_GRAMMAR)
# + [markdown] slideshow={"slide_type": "fragment"}
# If we fuzz using this grammar, we get non-matching XML tags, as expected:
# + slideshow={"slide_type": "fragment"}
xml_fuzzer = GrammarFuzzer(XML_GRAMMAR)
xml_fuzzer.fuzz()
# + [markdown] slideshow={"slide_type": "fragment"}
# Setting up a post-expansion function that sets the second identifier to the string found in the first solves the problem:
# + slideshow={"slide_type": "subslide"}
XML_GRAMMAR.update({
"<xml-tree>": [("<<id>><xml-content></<id>>",
opts(post=lambda id1, content, id2: [None, None, id1])
)]
})
# + slideshow={"slide_type": "fragment"}
assert is_valid_grammar(XML_GRAMMAR)
# + slideshow={"slide_type": "fragment"}
xml_fuzzer = GeneratorGrammarFuzzer(XML_GRAMMAR)
xml_fuzzer.fuzz()
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Example: Checksums
#
# As our last example, let us consider the checksum problem from the introduction. With our newly defined repair mechanisms, we can now generate credit card numbers that are valid:
# + slideshow={"slide_type": "fragment"}
credit_card_fuzzer = GeneratorGrammarFuzzer(
CHARGE_GRAMMAR, start_symbol="<credit-card-number>")
credit_card_number = credit_card_fuzzer.fuzz()
credit_card_number
# + slideshow={"slide_type": "fragment"}
assert valid_luhn_checksum(credit_card_number)
# + [markdown] slideshow={"slide_type": "fragment"}
# The validity extends to the entire grammar:
# + slideshow={"slide_type": "fragment"}
charge_fuzzer = GeneratorGrammarFuzzer(CHARGE_GRAMMAR)
charge_fuzzer.fuzz()
# + [markdown] slideshow={"slide_type": "slide"}
# ## Local Checking and Repairing
#
# So far, we have always first generated an entire expression tree, only to check it later for validity. This can become expensive: If several elements are first generated only to find later that one of them is invalid, we spend a lot of time trying (randomly) to regenerate a matching input.
# + [markdown] slideshow={"slide_type": "fragment"}
# To demonstrate the issue, let us create an expression grammar in which all digits consist of zeros and ones. Rather than doing this constructively, though, we filter out all non-conforming expressions after the fact, using a `post` constraint:
# + slideshow={"slide_type": "subslide"}
binary_expr_grammar = extend_grammar(EXPR_GRAMMAR,
{
"<integer>": [("<digit><integer>", opts(post=lambda digit, _: digit in ["0", "1"])),
("<digit>", opts(post=lambda digit: digit in ["0", "1"]))]
}
)
# + slideshow={"slide_type": "fragment"}
assert is_valid_grammar(binary_expr_grammar)
# + [markdown] slideshow={"slide_type": "fragment"}
# This works, but is very slow; it can take several seconds before a matching expression is found.
# + slideshow={"slide_type": "fragment"}
binary_expr_fuzzer = GeneratorGrammarFuzzer(binary_expr_grammar)
binary_expr_fuzzer.fuzz()
# + [markdown] slideshow={"slide_type": "subslide"}
# We can address the problem by checking constraints not only for the final subtree, but also for partial subtrees as soon as they are complete. To this end, we extend the method `expand_tree_once()` such that it invokes the post-expansion function as soon as all symbols in a subtree are expanded.
# + slideshow={"slide_type": "fragment"}
class RestartExpansionException(Exception):
pass
# + slideshow={"slide_type": "subslide"}
class GeneratorGrammarFuzzer(GeneratorGrammarFuzzer):
def expand_tree_once(self, tree: DerivationTree) -> DerivationTree:
# Apply inherited method. This also calls `expand_tree_once()` on all
# subtrees.
new_tree: DerivationTree = super().expand_tree_once(tree)
(symbol, children) = new_tree
if all([exp_post_expansion_function(expansion)
is None for expansion in self.grammar[symbol]]):
# No constraints for this symbol
return new_tree
if self.any_possible_expansions(tree):
# Still expanding
return new_tree
return self.run_post_functions_locally(new_tree)
# + [markdown] slideshow={"slide_type": "subslide"}
# The main work takes place in the helper method `run_post_functions_locally()`. It runs the post-expansion function $f$ with `run_post_functions()` only on the current node by setting `depth` to zero, as any completed subtrees would have their post-expansion functions ran already. If $f$ returns `False`, `run_post_functions_locally()` returns an unexpanded symbol, such that the main driver can try another expansion. It does so for up to 10 times (configurable via a `replacement_attempts` parameter during construction); after that, it raises a `RestartExpansionException` to restart creating the tree from scratch.
# + slideshow={"slide_type": "subslide"}
class GeneratorGrammarFuzzer(GeneratorGrammarFuzzer):
def run_post_functions_locally(self, new_tree: DerivationTree) -> DerivationTree:
symbol, _ = new_tree
result, children = self.run_post_functions(new_tree, depth=0)
if not isinstance(result, bool) or result:
# No constraints, or constraint satisfied
# children = self.apply_result(result, children)
new_tree = (symbol, children)
return new_tree
# Replace tree by unexpanded symbol and try again
if self.log:
print(
all_terminals(new_tree),
"did not satisfy",
symbol,
"constraint")
if self.replacement_attempts_counter > 0:
if self.log:
print("Trying another expansion")
self.replacement_attempts_counter -= 1
return (symbol, None)
if self.log:
print("Starting from scratch")
raise RestartExpansionException
# + [markdown] slideshow={"slide_type": "subslide"}
# The class constructor method and `fuzz_tree()` are set up to handle the additional functionality:
# + slideshow={"slide_type": "subslide"}
class GeneratorGrammarFuzzer(GeneratorGrammarFuzzer):
def __init__(self, grammar: Grammar, replacement_attempts: int = 10,
**kwargs) -> None:
super().__init__(grammar, **kwargs)
self.replacement_attempts = replacement_attempts
def restart_expansion(self) -> None:
super().restart_expansion()
self.replacement_attempts_counter = self.replacement_attempts
def fuzz_tree(self) -> DerivationTree:
self.replacement_attempts_counter = self.replacement_attempts
while True:
try:
# This is fuzz_tree() as defined above
tree = super().fuzz_tree()
return tree
except RestartExpansionException:
self.restart_expansion()
# + slideshow={"slide_type": "subslide"}
binary_expr_fuzzer = GeneratorGrammarFuzzer(
binary_expr_grammar, replacement_attempts=100)
binary_expr_fuzzer.fuzz()
# + [markdown] slideshow={"slide_type": "slide"} tags=[]
# ## Definitions and Uses
#
# With the above generators and constraints, we can also address complex examples. The `VAR_GRAMMAR` grammar from [the chapter on parsers](Parser.ipynb) defines a number of variables as arithmetic expressions (which in turn can contain variables, too). Applying a simple `GrammarFuzzer` on the grammar produces plenty of identifiers, but each identifier has a unique name.
# + slideshow={"slide_type": "skip"}
import string
# + slideshow={"slide_type": "subslide"}
VAR_GRAMMAR: Grammar = {
'<start>': ['<statements>'],
'<statements>': ['<statement>;<statements>', '<statement>'],
'<statement>': ['<assignment>'],
'<assignment>': ['<identifier>=<expr>'],
'<identifier>': ['<word>'],
'<word>': ['<alpha><word>', '<alpha>'],
'<alpha>': list(string.ascii_letters),
'<expr>': ['<term>+<expr>', '<term>-<expr>', '<term>'],
'<term>': ['<factor>*<term>', '<factor>/<term>', '<factor>'],
'<factor>':
['+<factor>', '-<factor>', '(<expr>)', '<identifier>', '<number>'],
'<number>': ['<integer>.<integer>', '<integer>'],
'<integer>': ['<digit><integer>', '<digit>'],
'<digit>': crange('0', '9')
}
# + slideshow={"slide_type": "subslide"}
assert is_valid_grammar(VAR_GRAMMAR)
# + slideshow={"slide_type": "fragment"}
g = GrammarFuzzer(VAR_GRAMMAR)
for i in range(10):
print(g.fuzz())
# + [markdown] slideshow={"slide_type": "subslide"}
# What we'd like is that within expressions, only identifiers _previously defined_ should be used. To this end, we introduce a set of functions around a *symbol table*, which keeps track of all variables already defined.
# + slideshow={"slide_type": "fragment"}
SYMBOL_TABLE: Set[str] = set()
# + slideshow={"slide_type": "fragment"}
def define_id(id: str) -> None:
SYMBOL_TABLE.add(id)
# + slideshow={"slide_type": "fragment"}
def use_id() -> Union[bool, str]:
if len(SYMBOL_TABLE) == 0:
return False
id = random.choice(list(SYMBOL_TABLE))
return id
# + slideshow={"slide_type": "subslide"}
def clear_symbol_table() -> None:
global SYMBOL_TABLE
SYMBOL_TABLE = set()
# + [markdown] slideshow={"slide_type": "fragment"}
# To make use of the symbol table, we attach pre- and post-expansion functions to `VAR_GRAMMAR` that define and lookup identifiers from the symbol table. We name our extended grammar `CONSTRAINED_VAR_GRAMMAR`:
# + slideshow={"slide_type": "fragment"}
CONSTRAINED_VAR_GRAMMAR = extend_grammar(VAR_GRAMMAR)
# + [markdown] slideshow={"slide_type": "fragment"}
# First, we set up the grammar such that after each time an identifier is defined, we store its name in the symbol table:
# + slideshow={"slide_type": "fragment"}
CONSTRAINED_VAR_GRAMMAR = extend_grammar(CONSTRAINED_VAR_GRAMMAR, {
"<assignment>": [("<identifier>=<expr>",
opts(post=lambda id, expr: define_id(id)))]
})
# + [markdown] slideshow={"slide_type": "subslide"}
# Second, we make sure that when an identifier is generated, we pick it from the symbol table, too. (We use `post` here such that we can return `False` if no identifier is yet available, leading to another expansion being made.)
# + slideshow={"slide_type": "fragment"}
CONSTRAINED_VAR_GRAMMAR = extend_grammar(CONSTRAINED_VAR_GRAMMAR, {
"<factor>": ['+<factor>', '-<factor>', '(<expr>)',
("<identifier>", opts(post=lambda _: use_id())),
'<number>']
})
# + [markdown] slideshow={"slide_type": "fragment"}
# Finally, we clear the symbol table each time we (re)start an expansion. This is helpful as we may occasionally have to restart expansions.
# + slideshow={"slide_type": "fragment"}
CONSTRAINED_VAR_GRAMMAR = extend_grammar(CONSTRAINED_VAR_GRAMMAR, {
"<start>": [("<statements>", opts(pre=clear_symbol_table))]
})
# + slideshow={"slide_type": "fragment"}
assert is_valid_grammar(CONSTRAINED_VAR_GRAMMAR)
# + [markdown] slideshow={"slide_type": "subslide"}
# Fuzzing with this grammar ensures that each identifier used is actually defined:
# + slideshow={"slide_type": "subslide"}
var_grammar_fuzzer = GeneratorGrammarFuzzer(CONSTRAINED_VAR_GRAMMAR)
for i in range(10):
print(var_grammar_fuzzer.fuzz())
# + [markdown] slideshow={"slide_type": "slide"}
# ## Ordering Expansions
#
# While our previous def/use example ensures that each _used_ variable also is a _defined_ variable, it does not take care of the _order_ in which these definitions are made. In fact, it is possible that first, the term on the right hand side of a `;` expands, creating an entry in the symbol table, which is then later used in the expression on the left hand side. We can demonstrate this by actually evaluating the produced variable assignments in Python, using `exec()` to execute the sequence of assignments. (Little known fact: Python _does_ support `;` as statement separator.)
# + slideshow={"slide_type": "subslide"}
var_grammar_fuzzer = GeneratorGrammarFuzzer(CONSTRAINED_VAR_GRAMMAR)
with ExpectError():
for i in range(100):
s = var_grammar_fuzzer.fuzz()
try:
exec(s, {}, {})
except SyntaxError:
continue
except ZeroDivisionError:
continue
print(s)
# + [markdown] slideshow={"slide_type": "subslide"}
# To address this issue, we allow to explicitly specify an *ordering of expansions*. For our previous fuzzers, such an ordering was inconsequential, as eventually, all symbols would be expanded; if we have expansion functions with side effects, though, having control over the ordering in which expansions are made (and thus over the ordering in which the associated functions are called) can be important.
# + [markdown] slideshow={"slide_type": "fragment"}
# To specify orderings, we assign a special attribute `order` to individual expansions. This is a list with a number for each symbol in the expansion stating in which order the expansions are to be made, starting with the smallest one. As an example, the following rule specifies that the left hand side of a `;` separator should be expanded first:
# + slideshow={"slide_type": "fragment"}
CONSTRAINED_VAR_GRAMMAR = extend_grammar(CONSTRAINED_VAR_GRAMMAR, {
"<statements>": [("<statement>;<statements>", opts(order=[1, 2])),
"<statement>"]
})
# + [markdown] slideshow={"slide_type": "subslide"}
# Likewise, we want the definition of a variable to be produced only _after_ the expression is expanded, since otherwise, the expression might already refer to the defined variable:
# + slideshow={"slide_type": "fragment"}
CONSTRAINED_VAR_GRAMMAR = extend_grammar(CONSTRAINED_VAR_GRAMMAR, {
"<assignment>": [("<identifier>=<expr>", opts(post=lambda id, expr: define_id(id),
order=[2, 1]))],
})
# + [markdown] slideshow={"slide_type": "fragment"}
# The helper `exp_order()` allows us to retrieve the order:
# + slideshow={"slide_type": "fragment"}
def exp_order(expansion):
"""Return the specified expansion ordering, or None if unspecified"""
return exp_opt(expansion, 'order')
# + [markdown] slideshow={"slide_type": "subslide"}
# To control the ordering in which symbols are expanded, we hook into the method `choose_tree_expansion()`, which is specifically set for being extended in subclasses. It proceeds through the list `expandable_children` of expandable children to choose from and matches them with the nonterminal children from the expansion to determine their order number. The index `min_given_order` of the expandable child with the lowest order number is then returned, choosing this child for expansion.
# + slideshow={"slide_type": "subslide"}
class GeneratorGrammarFuzzer(GeneratorGrammarFuzzer):
def choose_tree_expansion(self, tree: DerivationTree,
expandable_children: List[DerivationTree]) \
-> int:
"""Return index of subtree in `expandable_children`
to be selected for expansion. Defaults to random."""
(symbol, tree_children) = tree
assert isinstance(tree_children, list)
if len(expandable_children) == 1:
# No choice
return super().choose_tree_expansion(tree, expandable_children)
expansion = self.find_expansion(tree)
given_order = exp_order(expansion)
if given_order is None:
# No order specified
return super().choose_tree_expansion(tree, expandable_children)
nonterminal_children = [c for c in tree_children if c[1] != []]
assert len(nonterminal_children) == len(given_order), \
"Order must have one element for each nonterminal"
# Find expandable child with lowest ordering
min_given_order = None
j = 0
for k, expandable_child in enumerate(expandable_children):
while j < len(
nonterminal_children) and expandable_child != nonterminal_children[j]:
j += 1
assert j < len(nonterminal_children), "Expandable child not found"
if self.log:
print("Expandable child #%d %s has order %d" %
(k, expandable_child[0], given_order[j]))
if min_given_order is None or given_order[j] < min_given_order:
min_given_order = k
assert min_given_order is not None
if self.log:
print("Returning expandable child #%d %s" %
(min_given_order, expandable_children[min_given_order][0]))
return min_given_order
# + [markdown] slideshow={"slide_type": "subslide"}
# With this, our fuzzer can now respect orderings, and all variables are properly defined:
# + slideshow={"slide_type": "subslide"}
var_grammar_fuzzer = GeneratorGrammarFuzzer(CONSTRAINED_VAR_GRAMMAR)
for i in range(100):
s = var_grammar_fuzzer.fuzz()
if i < 10:
print(s)
try:
exec(s, {}, {})
except SyntaxError:
continue
except ZeroDivisionError:
continue
# + [markdown] slideshow={"slide_type": "subslide"}
# Real programming languages not only have one global scope, but multiple local scopes, frequently nested. By carefully organizing global and local symbol tables, we can set up a grammar to handle all of these. However, when fuzzing compilers and interpreters, we typically focus on single functions, for which one single scope is enough to make most inputs valid.
# + [markdown] slideshow={"slide_type": "slide"}
# ## All Together
#
# Let us close this chapter by integrating our generator features with the other grammar features introduced earlier, in particular [coverage-driven fuzzing](GrammarCoverageFuzzer.ipynb) and [probabilistic grammar fuzzing](ProbabilisticGrammarFuzzer.ipynb).
# + [markdown] slideshow={"slide_type": "fragment"}
# The general idea to integrate the individual features is through *multiple inheritance*, which we already used for `ProbabilisticGrammarCoverageFuzzer`, introduced in the [exercises on probabilistic fuzzing](ProbabilisticGrammarFuzzer.ipynb).
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Generators and Probabilistic Fuzzing
#
# Probabilistic fuzzing integrates very easily with generators, as both extend `GrammarFuzzer` in different ways.
# + slideshow={"slide_type": "skip"}
from ProbabilisticGrammarFuzzer import ProbabilisticGrammarFuzzer # minor dependency
# + slideshow={"slide_type": "skip"}
from bookutils import inheritance_conflicts
# + slideshow={"slide_type": "fragment"}
inheritance_conflicts(ProbabilisticGrammarFuzzer, GeneratorGrammarFuzzer)
# + [markdown] slideshow={"slide_type": "fragment"}
# We have to implement `supported_opts()` as the merger of both superclasses. At the same time, we also set up the constructor such that it invokes both.
# + slideshow={"slide_type": "subslide"}
class ProbabilisticGeneratorGrammarFuzzer(GeneratorGrammarFuzzer,
ProbabilisticGrammarFuzzer):
"""Join the features of `GeneratorGrammarFuzzer`
and `ProbabilisticGrammarFuzzer`"""
def supported_opts(self) -> Set[str]:
return (super(GeneratorGrammarFuzzer, self).supported_opts() |
super(ProbabilisticGrammarFuzzer, self).supported_opts())
def __init__(self, grammar: Grammar, *, replacement_attempts: int = 10,
**kwargs):
"""Constructor.
`replacement_attempts` - see `GeneratorGrammarFuzzer` constructor.
All other keywords go into `ProbabilisticGrammarFuzzer`.
"""
super(GeneratorGrammarFuzzer, self).__init__(
grammar,
replacement_attempts=replacement_attempts)
super(ProbabilisticGrammarFuzzer, self).__init__(grammar, **kwargs)
# + [markdown] slideshow={"slide_type": "subslide"}
# Let us give our joint class a simple test, using probabilities to favor long identifiers:
# + slideshow={"slide_type": "fragment"}
CONSTRAINED_VAR_GRAMMAR.update({
'<word>': [('<alpha><word>', opts(prob=0.9)),
'<alpha>'],
})
# + slideshow={"slide_type": "fragment"}
pgg_fuzzer = ProbabilisticGeneratorGrammarFuzzer(CONSTRAINED_VAR_GRAMMAR)
pgg_fuzzer.supported_opts()
# + slideshow={"slide_type": "fragment"}
pgg_fuzzer.fuzz()
# + [markdown] slideshow={"slide_type": "slide"}
# # Generators and Grammar Coverage
#
# Fuzzing based on grammar coverage is a bigger challenge. Not so much for the methods overloaded in both; we can resolve these just as above.
# + slideshow={"slide_type": "skip"}
from ProbabilisticGrammarFuzzer import ProbabilisticGrammarCoverageFuzzer # minor dependency
# + slideshow={"slide_type": "skip"}
from GrammarCoverageFuzzer import GrammarCoverageFuzzer # minor dependency
# + slideshow={"slide_type": "fragment"}
inheritance_conflicts(ProbabilisticGrammarCoverageFuzzer,
GeneratorGrammarFuzzer)
# + slideshow={"slide_type": "skip"}
import copy
# + slideshow={"slide_type": "subslide"}
class ProbabilisticGeneratorGrammarCoverageFuzzer(GeneratorGrammarFuzzer,
ProbabilisticGrammarCoverageFuzzer):
"""Join the features of `GeneratorGrammarFuzzer`
and `ProbabilisticGrammarCoverageFuzzer`"""
def supported_opts(self) -> Set[str]:
return (super(GeneratorGrammarFuzzer, self).supported_opts() |
super(ProbabilisticGrammarCoverageFuzzer, self).supported_opts())
def __init__(self, grammar: Grammar, *,
replacement_attempts: int = 10, **kwargs) -> None:
"""Constructor.
`replacement_attempts` - see `GeneratorGrammarFuzzer` constructor.
All other keywords go into `ProbabilisticGrammarFuzzer`.
"""
super(GeneratorGrammarFuzzer, self).__init__(
grammar,
replacement_attempts)
super(ProbabilisticGrammarCoverageFuzzer, self).__init__(
grammar,
**kwargs)
# + [markdown] slideshow={"slide_type": "subslide"}
# The problem is that during expansion, we _may_ generate (and cover) expansions that we later drop (for instance, because a `post` function returns `False`). Hence, we have to _remove_ this coverage which is no longer present in the final production.
# + [markdown] slideshow={"slide_type": "fragment"}
# We resolve the problem by _rebuilding the coverage_ from the final tree after it is produced. To this end, we hook into the `fuzz_tree()` method. We have it save the original coverage before creating the tree, restoring it afterwards. Then we traverse the resulting tree, adding its coverage back again (`add_tree_coverage()`).
# + slideshow={"slide_type": "subslide"}
class ProbabilisticGeneratorGrammarCoverageFuzzer(
ProbabilisticGeneratorGrammarCoverageFuzzer):
def fuzz_tree(self) -> DerivationTree:
self.orig_covered_expansions = copy.deepcopy(self.covered_expansions)
tree = super().fuzz_tree()
self.covered_expansions = self.orig_covered_expansions
self.add_tree_coverage(tree)
return tree
def add_tree_coverage(self, tree: DerivationTree) -> None:
(symbol, children) = tree
assert isinstance(children, list)
if len(children) > 0:
flat_children: List[DerivationTree] = [
(child_symbol, None)
for (child_symbol, _) in children
]
self.add_coverage(symbol, flat_children)
for c in children:
self.add_tree_coverage(c)
# + [markdown] slideshow={"slide_type": "subslide"}
# As a final step, we ensure that if we do have to restart an expansion from scratch, we also restore the previous coverage such that we can start fully anew:
# + slideshow={"slide_type": "fragment"}
class ProbabilisticGeneratorGrammarCoverageFuzzer(
ProbabilisticGeneratorGrammarCoverageFuzzer):
def restart_expansion(self) -> None:
super().restart_expansion()
self.covered_expansions = self.orig_covered_expansions
# + [markdown] slideshow={"slide_type": "fragment"}
# Let us try this out. After we have produced a string, we should see its coverage in `expansion_coverage()`:
# + slideshow={"slide_type": "fragment"}
pggc_fuzzer = ProbabilisticGeneratorGrammarCoverageFuzzer(
CONSTRAINED_VAR_GRAMMAR)
pggc_fuzzer.fuzz()
# + slideshow={"slide_type": "subslide"}
pggc_fuzzer.expansion_coverage()
# + [markdown] slideshow={"slide_type": "subslide"}
# Fuzzing again would eventually cover all letters in identifiers:
# + slideshow={"slide_type": "fragment"}
[pggc_fuzzer.fuzz() for i in range(10)]
# + [markdown] slideshow={"slide_type": "subslide"}
# With `ProbabilisticGeneratorGrammarCoverageFuzzer`, we now have a grammar fuzzer that combines efficient grammar fuzzing with coverage, probabilities, and generator functions. The only thing that is missing is a shorter name. `PGGCFuzzer`, maybe?
# + slideshow={"slide_type": "fragment"}
class PGGCFuzzer(ProbabilisticGeneratorGrammarCoverageFuzzer):
"""The one grammar-based fuzzer that supports all fuzzingbook features"""
pass
# + [markdown] slideshow={"slide_type": "slide"}
# ## Synopsis
#
# This chapter introduces the ability to attach _functions_ to individual production rules:
#
# * A `pre` function is executed _before_ the expansion takes place. Its result (typically a string) can _replace_ the actual expansion.
# * A `post` function is executed _after_ the expansion has taken place. If it returns a string, the string replaces the expansion; it it returns `False`, it triggers a new expansion.
#
# Both functions can return `None` to not interfere with grammar production at all.
# + [markdown] slideshow={"slide_type": "subslide"}
# To attach a function `F` to an individual expansion `S` in a grammar, replace `S` with a pair
#
# ```python
# (S, opts(pre=F)) # Set a function to be executed before expansion
# ```
# or
# ```python
# (S, opts(post=F)) # Set a function to be executed after expansion
# ```
# + [markdown] slideshow={"slide_type": "fragment"}
# Here is an example, To take an area code from a list that is given programmatically, we can write:
# + slideshow={"slide_type": "skip"}
from Grammars import US_PHONE_GRAMMAR, extend_grammar, opts
# + slideshow={"slide_type": "subslide"}
def pick_area_code():
return random.choice(['555', '554', '553'])
# + slideshow={"slide_type": "fragment"}
PICKED_US_PHONE_GRAMMAR = extend_grammar(US_PHONE_GRAMMAR,
{
"<area>": [("<lead-digit><digit><digit>", opts(pre=pick_area_code))]
})
# + [markdown] slideshow={"slide_type": "fragment"}
# A `GeneratorGrammarFuzzer` will extract and interpret these options. Here is an example:
# + slideshow={"slide_type": "fragment"}
picked_us_phone_fuzzer = GeneratorGrammarFuzzer(PICKED_US_PHONE_GRAMMAR)
[picked_us_phone_fuzzer.fuzz() for i in range(5)]
# + [markdown] slideshow={"slide_type": "subslide"}
# As you can see, the area codes now all stem from `pick_area_code()`. Such definitions allow to closely tie program code (such as `pick_area_code()`) to grammars.
# + [markdown] slideshow={"slide_type": "fragment"}
# The `PGGCFuzzer` class incorporates all features from [the `GrammarFuzzer` class](GrammarFuzzer.ipynb) and its [coverage-based](GrammarCoverageFuzzer.ipynb), [probabilistic-based](ProbabilisticGrammarFuzzer.ipynb), and [generator-based](GeneratorGrammarFuzzer.ipynb) derivatives.
# + slideshow={"slide_type": "fragment"}
# ignore
from ClassDiagram import display_class_hierarchy
# + slideshow={"slide_type": "subslide"}
# ignore
display_class_hierarchy([PGGCFuzzer],
public_methods=[
Fuzzer.run,
Fuzzer.runs,
GrammarFuzzer.__init__,
GrammarFuzzer.fuzz,
GrammarFuzzer.fuzz_tree,
GeneratorGrammarFuzzer.__init__,
GeneratorGrammarFuzzer.fuzz_tree,
GrammarCoverageFuzzer.__init__,
ProbabilisticGrammarFuzzer.__init__,
ProbabilisticGrammarCoverageFuzzer.__init__,
ProbabilisticGeneratorGrammarCoverageFuzzer.__init__,
ProbabilisticGeneratorGrammarCoverageFuzzer.fuzz_tree,
PGGCFuzzer.__init__,
],
types={
'DerivationTree': DerivationTree,
'Expansion': Expansion,
'Grammar': Grammar
},
project='fuzzingbook')
# + [markdown] button=false new_sheet=true run_control={"read_only": false} slideshow={"slide_type": "slide"}
# ## Lessons Learned
#
# Functions attached to grammar expansions can serve
# * as _generators_ to efficiently produce a symbol expansion from a function;
# * as _constraints_ to check produced strings against (complex) validity conditions; and
# * as _repairs_ to apply changes to produced strings, such as checksums and identifiers.
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "slide"}
# ## Next Steps
#
# With this chapter, we have powerful grammars which we can use in a number of domains:
#
# * In the [chapter on fuzzing APIs](APIFuzzer.ipynb), we show how to produce complex data structures for testing, making use of `GeneratorGrammarFuzzer` features to combine grammars and generator functions.
# * In the [chapter on fuzzing User Interfaces](WebFuzzer.ipynb), we make use of `GeneratorGrammarFuzzer` to produce complex user interface inputs.
#
# + [markdown] slideshow={"slide_type": "slide"}
# ## Background
#
# For fuzzing APIs, generator functions are very common. In the [chapter on API fuzzing](APIFuzzer.ipynb), we show how to combine them with grammars for even richer test generation.
#
# The combination of generator functions and grammars is mostly possible because we define and make use of grammars in an all-Python environment. We are not aware of another grammar-based fuzzing system that exhibits similar features.
# + [markdown] button=false new_sheet=true run_control={"read_only": false} slideshow={"slide_type": "slide"}
# ## Exercises
#
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"} solution2="hidden" solution2_first=true
# ### Exercise 1: Tree Processing
#
# So far, our `pre` and `post` processing functions all accept and produce strings. In some circumstances, however, it can be useful to access the _derivation trees_ directly – for instance, to access and check some child element.
#
# Your task is to extend `GeneratorGrammarFuzzer` with pre- and post-processing functions that can accept and return derivation trees. To this end, proceed as follows:
#
# 1. Extend `GeneratorGrammarFuzzer` such that a function can return a derivation tree (a tuple) or a list of derivation trees, which would then replace subtrees in the same way as strings.
# 2. Extend `GeneratorGrammarFuzzer` with a `post_tree` attribute which takes a function just like `post`, except that its arguments would be derivation trees.
# + [markdown] slideshow={"slide_type": "skip"} solution2="hidden"
# **Solution.** Left to the reader at this point.
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"} solution="hidden" solution2="hidden" solution2_first=true solution_first=true
# ### Exercise 2: Attribute Grammars
#
# Set up a mechanism through which it is possible to attach arbitrary _attributes_ to individual elements in the derivation tree. Expansion functions could attach such attributes to individual symbols (say, by returning `opts()`), and also access attributes of symbols in later calls. Here is an example:
# + slideshow={"slide_type": "fragment"} solution2="hidden" solution2_first=true
ATTR_GRAMMAR = {
"<clause>": [("<xml-open>Text<xml-close>", opts(post=lambda x1, x2: [None, x1.name]))],
"<xml-open>": [("<<tag>>", opts(post=lambda tag: opts(name=...)))],
"<xml-close>": ["</<tag>>"]
}
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "skip"} solution="hidden" solution2="hidden"
# **Solution.** Left to the reader at this point.
|
docs/beta/notebooks/GeneratorGrammarFuzzer.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Environment (cie)
# language: ''
# name: cie
# ---
# # Figure. peQTN TSS Distances and Ciona Experiments
# +
import copy
import os
import cdpybio as cpb
import matplotlib.gridspec as gridspec
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
pd.options.mode.chained_assignment = None
import pybedtools as pbt
import scipy
import seaborn as sns
import cardipspy as cpy
import ciepy
# %matplotlib inline
dy_name = 'figure_peqtn_tss_distances_and_ciona_experiments'
import socket
if socket.gethostname() == 'fl-hn1' or socket.gethostname() == 'fl-hn2':
dy = os.path.join(ciepy.root, 'sandbox', 'tmp', dy_name)
cpy.makedir(dy)
pbt.set_tempdir(dy)
outdir = os.path.join(ciepy.root, 'output', dy_name)
cpy.makedir(outdir)
private_outdir = os.path.join(ciepy.root, 'private_output', dy_name)
cpy.makedir(private_outdir)
# -
sns.set_style('whitegrid')
pdfs = pd.read_table(os.path.join(ciepy.root, 'output', 'fine_mapping', 'tss_distance_kde.tsv'), index_col=0)
pdfs.columns = ['ChIA-PET interactions', 'Lead variants to TSS', 'peQTNs to TSS']
sns.set_palette(sns.color_palette("Dark2", 10))
# +
fig = plt.figure(figsize=(4, 3), dpi=300)
gs = gridspec.GridSpec(1, 1)
ax = fig.add_subplot(gs[0, 0])
ax.text(0, 0, 'Figure S2',
size=16, va='bottom')
ciepy.clean_axis(ax)
ax.set_xticks([])
ax.set_yticks([])
gs.tight_layout(fig, rect=[0, 0.85, 0.5, 1])
gs = gridspec.GridSpec(1, 1)
ax = fig.add_subplot(gs[0, 0])
ax = pdfs.plot(ax=ax)
ax.legend(fontsize=8, loc='upper left', fancybox=True, frameon=True)
for t in ax.get_xticklabels() + ax.get_yticklabels():
t.set_fontsize(8)
ax.set_xlabel('$\log_{10}$ distance in base pairs', fontsize=8)
ax.set_ylabel('Density', fontsize=8);
gs.tight_layout(fig, rect=[0, 0, 1, 0.9])
fig.savefig(os.path.join(outdir, 'peqtn_tss_distances.pdf'))
fig.savefig(os.path.join(outdir, 'peqtn_tss_distances.png'), dpi=300)
# -
allele = ['Ref', 'Alt', 'EV', 'Ref', 'Alt', 'EV',
'Ref', 'Alt', 'EV', 'Ref', 'Alt', 'EV',
'Ref', 'Alt', 'EV', 'Ref', 'Alt', 'EV',
'Ref', 'Alt', 'EV', 'Ref', 'Alt', 'EV',
'Ref', 'Alt', 'EV', 'Ref', 'Alt', 'EV',
'Ref', 'Alt', 'EV', 'Ref', 'Alt', 'EV',
'Ref', 'Alt', 'EV', 'Ref', 'Alt', 'EV',
]
construct = ['E1', 'E1', 'E1', 'E1', 'E1', 'E1',
'E2', 'E2', 'E2', 'E2', 'E2', 'E2',
'E4', 'E4', 'E4', 'E4', 'E4', 'E4',
'E5', 'E5', 'E5', 'E5', 'E5', 'E5',
'E5', 'E5', 'E5', 'E5', 'E5', 'E5',
'E8', 'E8', 'E8', 'E8', 'E8', 'E8',
'E8', 'E8', 'E8', 'E8', 'E8', 'E8',
]
repeat = ['Rep. 1', 'Rep. 1', 'Rep. 1', 'Rep. 2', 'Rep. 2', 'Rep. 2',
'Rep. 1', 'Rep. 1', 'Rep. 1', 'Rep. 2', 'Rep. 2', 'Rep. 2',
'Rep. 1', 'Rep. 1', 'Rep. 1', 'Rep. 2', 'Rep. 2', 'Rep. 2',
'Rep. 1', 'Rep. 1', 'Rep. 1', 'Rep. 2', 'Rep. 2', 'Rep. 2',
'Rep. 1', 'Rep. 1', 'Rep. 1', 'Rep. 2', 'Rep. 2', 'Rep. 2',
'Rep. 1', 'Rep. 1', 'Rep. 1', 'Rep. 2', 'Rep. 2', 'Rep. 2',
'Rep. 1', 'Rep. 1', 'Rep. 1', 'Rep. 2', 'Rep. 2', 'Rep. 2',
]
tissue = ['TM', 'TM', 'TM', 'TM', 'TM', 'TM',
'TM', 'TM', 'TM', 'TM', 'TM', 'TM',
'ED', 'ED', 'ED', 'ED', 'ED', 'ED',
'ED', 'ED', 'ED', 'ED', 'ED', 'ED',
'TM', 'TM', 'TM', 'TM', 'TM', 'TM',
'ED', 'ED', 'ED', 'ED', 'ED', 'ED',
'TM', 'TM', 'TM', 'TM', 'TM', 'TM',
]
percent = [7, 11, 4, 10, 8, 0,
6, 15, 4, 4, 20, 0,
17, 0, 0, 12, 0, 2,
4, 6.5, 0, 6, 4, 2,
10, 4, 4, 10, 8, 0,
22, 12, 0, 20, 6, 0,
26, 22, 4, 10, 14, 0
]
count = [7, 11, 4, 10, 8, 0,
6, 15, 4, 4, 20, 0,
17, 0, 0, 12, 0, 2,
2, 4, 0, 3, 2, 2,
5, 2, 4, 5, 4, 0,
11, 6, 0, 10, 3, 0,
13, 11, 4, 5, 7, 0
]
number = [100, 100, 100, 100, 100, 100,
100, 100, 100, 100, 100, 100,
100, 100, 100, 100, 100, 100,
50, 50, 100, 50, 50, 100,
50, 50, 100, 50, 50, 100,
50, 50, 50, 50, 50, 50,
50, 50, 50, 50, 50, 50,
]
diff = [False, False, False, False, False, False,
True, True, True, True, True, True,
True, True, True, True, True, True,
False, False, False, False, False, False,
False, False, False, False, False, False,
True, True, True, True, True, True,
False, False, False, False, False, False,
]
ciona_res = pd.DataFrame({'allele':allele, 'construct':construct,
'repeat':repeat, 'tissue':tissue,
'percent':percent, 'different':diff,
'count':count, 'number':number})
import scipy.stats as stats
# WORKING HERE: Are my counts correct? Can I do a stats test?
pvals = {}
for c in set(ciona_res.construct):
tdf = ciona_res[ciona_res.construct == c]
for t in set(tdf.tissue):
tdf2 = tdf[tdf.tissue == t]
ref_count = tdf2.ix[tdf2.allele == 'Ref', 'count'].sum()
alt_count = tdf2.ix[tdf2.allele == 'Alt', 'count'].sum()
n = tdf2.number.values[0]
s,p = stats.fisher_exact([[ref_count, alt_count], [n - ref_count, n - alt_count]])
pvals[c + ', ' + t] = p
pvals = pd.Series(pvals)
1.561699e-02
pvals[pvals < 0.05]
# +
fig = plt.figure(figsize=(6, 8), dpi=300)
gs = gridspec.GridSpec(1, 1)
ax = fig.add_subplot(gs[0, 0])
ax.text(0, 0, 'Figure S2',
size=16, va='bottom')
ciepy.clean_axis(ax)
ax.set_xticks([])
ax.set_yticks([])
gs.tight_layout(fig, rect=[0, 0.95, 0.5, 1])
gs = gridspec.GridSpec(1, 1)
ax = fig.add_subplot(gs[0, 0])
ax = pdfs.plot(ax=ax)
ax.legend(fontsize=8, loc='upper left', fancybox=True, frameon=True)
for t in ax.get_xticklabels() + ax.get_yticklabels():
t.set_fontsize(8)
ax.set_xlabel('$\log_{10}$ distance in base pairs', fontsize=8)
ax.set_ylabel('Density', fontsize=8);
gs.tight_layout(fig, rect=[0, 0.7, 1, 0.95])
# Constructs/tissues with expression differences
gs = gridspec.GridSpec(2, 2)
ax = fig.add_subplot(gs[0, 0])
tdf = ciona_res[ciona_res.construct == 'E2']
sns.barplot(x='allele', y='percent', hue='repeat', data=tdf)
for t in ax.get_xticklabels() + ax.get_yticklabels():
t.set_fontsize(7)
ax.set_ylabel('Percent embryos\nwith expression', fontsize=8)
ax.legend(fontsize=7, fancybox=True, frameon=True)
ax.set_xlabel('')
ax.set_title('region = E2, tissue = tail muscle', fontsize=8)
ymin, ymax = ax.get_ylim()
h = (ymax - ymin) * 0.1
ax.plot([0, 1], [ymax + 2*h, ymax + 2*h], color='k', linestyle='-', linewidth=1)
ax.plot([0, 0], [ymax + h, ymax + 2*h], color='k', linestyle='-', linewidth=1)
ax.plot([1, 1], [ymax + h, ymax + 2*h], color='k', linestyle='-', linewidth=1)
ax.text(0.5, ymax + 2*h, '$p < 10^{-3}$', ha='center', va='bottom')
ax.plot([0, 1], [ymax + 4*h, ymax + 4*h], color='k', linestyle='-', linewidth=1, alpha=0)
ax = fig.add_subplot(gs[0, 1])
tdf = ciona_res[ciona_res.construct == 'E4']
sns.barplot(x='allele', y='percent', hue='repeat', data=tdf)
for t in ax.get_xticklabels() + ax.get_yticklabels():
t.set_fontsize(7)
ax.set_ylabel('Percent embryos\nwith expression', fontsize=8)
ax.legend(fontsize=7, fancybox=True, frameon=True)
ax.set_xlabel('')
ax.set_title('region = E4, tissue = endoderm', fontsize=8)
ymin, ymax = ax.get_ylim()
h = (ymax - ymin) * 0.1
ax.plot([0, 1], [ymax + 2*h, ymax + 2*h], color='k', linestyle='-', linewidth=1)
ax.plot([0, 0], [ymax + h, ymax + 2*h], color='k', linestyle='-', linewidth=1)
ax.plot([1, 1], [ymax + h, ymax + 2*h], color='k', linestyle='-', linewidth=1)
ax.text(0.5, ymax + 2*h, '$p < 10^{-9}$', ha='center', va='bottom')
ax.plot([0, 1], [ymax + 4*h, ymax + 4*h], color='k', linestyle='-', linewidth=1, alpha=0)
ax = fig.add_subplot(gs[1, 0])
tdf = ciona_res[(ciona_res.construct == 'E8') & (ciona_res.tissue == 'ED')]
sns.barplot(x='allele', y='percent', hue='repeat', data=tdf)
for t in ax.get_xticklabels() + ax.get_yticklabels():
t.set_fontsize(7)
ax.set_ylabel('Percent embryos\nwith expression', fontsize=8)
ax.legend(fontsize=7, fancybox=True, frameon=True)
ax.set_xlabel('')
ax.set_title('region = E8, tissue = endoderm', fontsize=8)
ymin, ymax = ax.get_ylim()
h = (ymax - ymin) * 0.1
ax.plot([0, 1], [ymax + 2*h, ymax + 2*h], color='k', linestyle='-', linewidth=1)
ax.plot([0, 0], [ymax + h, ymax + 2*h], color='k', linestyle='-', linewidth=1)
ax.plot([1, 1], [ymax + h, ymax + 2*h], color='k', linestyle='-', linewidth=1)
ax.text(0.5, ymax + 2*h, '$p = 0.016$', ha='center', va='bottom')
ax.plot([0, 1], [ymax + 4*h, ymax + 4*h], color='k', linestyle='-', linewidth=1, alpha=0)
gs.tight_layout(fig, rect=[0, 0.35, 1, 0.7])
# Construct/tissues without expression differences
gs = gridspec.GridSpec(2, 2)
ax = fig.add_subplot(gs[0, 0])
tdf = ciona_res[ciona_res.construct == 'E1']
sns.barplot(x='allele', y='percent', hue='repeat', data=tdf)
for t in ax.get_xticklabels() + ax.get_yticklabels():
t.set_fontsize(7)
ax.set_ylabel('Percent embryos\nwith expression', fontsize=8)
ax.legend(fontsize=7, fancybox=True, frameon=True)
ax.set_xlabel('')
ax.set_title('region = E1, tissue = tail muscle', fontsize=8)
ax = fig.add_subplot(gs[0, 1])
tdf = ciona_res[(ciona_res.construct == 'E5') & (ciona_res.tissue == 'ED')]
sns.barplot(x='allele', y='percent', hue='repeat', data=tdf)
for t in ax.get_xticklabels() + ax.get_yticklabels():
t.set_fontsize(7)
ax.set_ylabel('Percent embryos\nwith expression', fontsize=8)
ax.legend(fontsize=7, fancybox=True, frameon=True)
ax.set_xlabel('')
ax.set_title('region = E5, tissue = endoderm', fontsize=8)
ax = fig.add_subplot(gs[1, 0])
tdf = ciona_res[(ciona_res.construct == 'E5') & (ciona_res.tissue == 'TM')]
sns.barplot(x='allele', y='percent', hue='repeat', data=tdf)
for t in ax.get_xticklabels() + ax.get_yticklabels():
t.set_fontsize(7)
ax.set_ylabel('Percent embryos\nwith expression', fontsize=8)
ax.legend(fontsize=7, fancybox=True, frameon=True)
ax.set_xlabel('')
ax.set_title('region = E5, tissue = tail muscle', fontsize=8)
ax = fig.add_subplot(gs[1, 1])
tdf = ciona_res[(ciona_res.construct == 'E8') & (ciona_res.tissue == 'TM')]
sns.barplot(x='allele', y='percent', hue='repeat', data=tdf)
for t in ax.get_xticklabels() + ax.get_yticklabels():
t.set_fontsize(7)
ax.set_ylabel('Percent embryos\nwith expression', fontsize=8)
ax.legend(fontsize=7, fancybox=True, frameon=True)
ax.set_xlabel('')
ax.set_title('region = E8, tissue = tail muscle', fontsize=8)
gs.tight_layout(fig, rect=[0, 0, 1, 0.35])
t = fig.text(0.005, 0.95, 'A', weight='bold',
size=12)
t = fig.text(0.005, 0.68, 'B', weight='bold',
size=12)
t = fig.text(0.005, 0.33, 'C', weight='bold',
size=12)
fig.savefig(os.path.join(outdir, 'peqtn_tss_distances_ciona.pdf'))
fig.savefig(os.path.join(outdir, 'peqtn_tss_distances_ciona.png'), dpi=300)
# +
fig = plt.figure(figsize=(6, 7.8), dpi=300)
gs = gridspec.GridSpec(1, 1)
ax = fig.add_subplot(gs[0, 0])
ax = pdfs.plot(ax=ax)
ax.legend(fontsize=8, loc='upper left', fancybox=True, frameon=True)
for t in ax.get_xticklabels() + ax.get_yticklabels():
t.set_fontsize(8)
ax.set_xlabel('$\log_{10}$ distance in base pairs', fontsize=8)
ax.set_ylabel('Density', fontsize=8);
gs.tight_layout(fig, rect=[0, 0.72, 1, 1])
# Constructs/tissues with expression differences
gs = gridspec.GridSpec(2, 2)
ax = fig.add_subplot(gs[0, 0])
tdf = ciona_res[ciona_res.construct == 'E2']
sns.barplot(x='allele', y='percent', hue='repeat', data=tdf)
for t in ax.get_xticklabels() + ax.get_yticklabels():
t.set_fontsize(7)
ax.set_ylabel('Percent embryos\nwith expression', fontsize=8)
ax.legend(fontsize=7, fancybox=True, frameon=True)
ax.set_xlabel('')
ax.set_title('region = E2, tissue = tail muscle', fontsize=8)
ymin, ymax = ax.get_ylim()
h = (ymax - ymin) * 0.1
ax.plot([0, 1], [ymax + 2*h, ymax + 2*h], color='k', linestyle='-', linewidth=1)
ax.plot([0, 0], [ymax + h, ymax + 2*h], color='k', linestyle='-', linewidth=1)
ax.plot([1, 1], [ymax + h, ymax + 2*h], color='k', linestyle='-', linewidth=1)
ax.text(0.5, ymax + 2*h, '$p < 10^{-3}$', ha='center', va='bottom')
ax.plot([0, 1], [ymax + 4*h, ymax + 4*h], color='k', linestyle='-', linewidth=1, alpha=0)
ax = fig.add_subplot(gs[0, 1])
tdf = ciona_res[ciona_res.construct == 'E4']
sns.barplot(x='allele', y='percent', hue='repeat', data=tdf)
for t in ax.get_xticklabels() + ax.get_yticklabels():
t.set_fontsize(7)
ax.set_ylabel('Percent embryos\nwith expression', fontsize=8)
ax.legend(fontsize=7, fancybox=True, frameon=True)
ax.set_xlabel('')
ax.set_title('region = E4, tissue = endoderm', fontsize=8)
ymin, ymax = ax.get_ylim()
h = (ymax - ymin) * 0.1
ax.plot([0, 1], [ymax + 2*h, ymax + 2*h], color='k', linestyle='-', linewidth=1)
ax.plot([0, 0], [ymax + h, ymax + 2*h], color='k', linestyle='-', linewidth=1)
ax.plot([1, 1], [ymax + h, ymax + 2*h], color='k', linestyle='-', linewidth=1)
ax.text(0.5, ymax + 2*h, '$p < 10^{-9}$', ha='center', va='bottom')
ax.plot([0, 1], [ymax + 4*h, ymax + 4*h], color='k', linestyle='-', linewidth=1, alpha=0)
ax = fig.add_subplot(gs[1, 0])
tdf = ciona_res[(ciona_res.construct == 'E8') & (ciona_res.tissue == 'ED')]
sns.barplot(x='allele', y='percent', hue='repeat', data=tdf)
for t in ax.get_xticklabels() + ax.get_yticklabels():
t.set_fontsize(7)
ax.set_ylabel('Percent embryos\nwith expression', fontsize=8)
ax.legend(fontsize=7, fancybox=True, frameon=True)
ax.set_xlabel('')
ax.set_title('region = E8, tissue = endoderm', fontsize=8)
ymin, ymax = ax.get_ylim()
h = (ymax - ymin) * 0.1
ax.plot([0, 1], [ymax + 2*h, ymax + 2*h], color='k', linestyle='-', linewidth=1)
ax.plot([0, 0], [ymax + h, ymax + 2*h], color='k', linestyle='-', linewidth=1)
ax.plot([1, 1], [ymax + h, ymax + 2*h], color='k', linestyle='-', linewidth=1)
ax.text(0.5, ymax + 2*h, '$p = 0.016$', ha='center', va='bottom')
ax.plot([0, 1], [ymax + 4*h, ymax + 4*h], color='k', linestyle='-', linewidth=1, alpha=0)
gs.tight_layout(fig, rect=[0, 0.36, 1, 0.72])
# Construct/tissues without expression differences
gs = gridspec.GridSpec(2, 2)
ax = fig.add_subplot(gs[0, 0])
tdf = ciona_res[ciona_res.construct == 'E1']
sns.barplot(x='allele', y='percent', hue='repeat', data=tdf)
for t in ax.get_xticklabels() + ax.get_yticklabels():
t.set_fontsize(7)
ax.set_ylabel('Percent embryos\nwith expression', fontsize=8)
ax.legend(fontsize=7, fancybox=True, frameon=True)
ax.set_xlabel('')
ax.set_title('region = E1, tissue = tail muscle', fontsize=8)
ax = fig.add_subplot(gs[0, 1])
tdf = ciona_res[(ciona_res.construct == 'E5') & (ciona_res.tissue == 'ED')]
sns.barplot(x='allele', y='percent', hue='repeat', data=tdf)
for t in ax.get_xticklabels() + ax.get_yticklabels():
t.set_fontsize(7)
ax.set_ylabel('Percent embryos\nwith expression', fontsize=8)
ax.legend(fontsize=7, fancybox=True, frameon=True)
ax.set_xlabel('')
ax.set_title('region = E5, tissue = endoderm', fontsize=8)
ax = fig.add_subplot(gs[1, 0])
tdf = ciona_res[(ciona_res.construct == 'E5') & (ciona_res.tissue == 'TM')]
sns.barplot(x='allele', y='percent', hue='repeat', data=tdf)
for t in ax.get_xticklabels() + ax.get_yticklabels():
t.set_fontsize(7)
ax.set_ylabel('Percent embryos\nwith expression', fontsize=8)
ax.legend(fontsize=7, fancybox=True, frameon=True)
ax.set_xlabel('')
ax.set_title('region = E5, tissue = tail muscle', fontsize=8)
ax = fig.add_subplot(gs[1, 1])
tdf = ciona_res[(ciona_res.construct == 'E8') & (ciona_res.tissue == 'TM')]
sns.barplot(x='allele', y='percent', hue='repeat', data=tdf)
for t in ax.get_xticklabels() + ax.get_yticklabels():
t.set_fontsize(7)
ax.set_ylabel('Percent embryos\nwith expression', fontsize=8)
ax.legend(fontsize=7, fancybox=True, frameon=True)
ax.set_xlabel('')
ax.set_title('region = E8, tissue = tail muscle', fontsize=8)
gs.tight_layout(fig, rect=[0, 0, 1, 0.36])
t = fig.text(0.005, 0.97, 'A', weight='bold',
size=12)
t = fig.text(0.005, 0.7, 'B', weight='bold',
size=12)
t = fig.text(0.005, 0.34, 'C', weight='bold',
size=12)
fig.savefig(os.path.join(outdir, 'peqtn_tss_distances_ciona.pdf'))
|
notebooks/Figure. peQTN TSS Distances and Ciona Experiments.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from sklearn.cluster import MeanShift, estimate_bandwidth
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import datetime
import math
import os
import sys
from numpy.fft import fft, ifft
import glob
# -
def remove_periodic(X, df_index, detrending=True, model='additive', frequency_threshold=0.1e12):
rad = np.array(X)
if detrending:
det_rad = rad - np.average(rad)
else:
det_rad = rad
det_rad_fft = fft(det_rad)
# Get the power spectrum
rad_ps = [np.abs(rd)**2 for rd in det_rad_fft]
clean_rad_fft = [det_rad_fft[i] if rad_ps[i] > frequency_threshold else 0
for i in range(len(det_rad_fft))]
rad_series_clean = ifft(clean_rad_fft)
rad_series_clean = [value.real for value in rad_series_clean]
if detrending:
rad_trends = rad_series_clean + np.average(rad)
else:
rad_trends = rad_series_clean
rad_clean_ts = pd.Series(rad_trends, index=df_index)
#rad_clean_ts[(rad_clean_ts.index.hour < 6) | (rad_clean_ts.index.hour > 20)] = 0
residual = rad - rad_clean_ts.values
clean = rad_clean_ts.values
return residual, clean
def load_data(path, resampling=None):
## some resampling options: 'H' - hourly, '15min' - 15 minutes, 'M' - montlhy
## more options at:
## http://benalexkeen.com/resampling-time-series-data-with-pandas/
allFiles = glob.iglob(path + "/**/*.txt", recursive=True)
frame = pd.DataFrame()
list_ = []
for file_ in allFiles:
#print("Reading: ",file_)
df = pd.read_csv(file_,index_col="datetime",parse_dates=['datetime'], header=0, sep=",")
if frame.columns is None :
frame.columns = df.columns
list_.append(df)
frame = pd.concat(list_)
if resampling is not None:
frame = frame.resample(resampling).mean()
frame = frame.fillna(method='ffill')
return frame
def create_spatio_temporal_data(nrel_df):
lat = [21.31236,21.31303,21.31357,21.31183,21.31042,21.31268,21.31451,21.31533,21.30812,21.31276,21.31281,21.30983,21.31141,21.31478,21.31179,21.31418,21.31034]
lon = [-158.08463,-158.08505,-158.08424,-158.08554,-158.0853,-158.08688,-158.08534,-158.087,-158.07935,-158.08389,-158.08163,-158.08249,-158.07947,-158.07785,-158.08678,-158.08685,-158.08675]
additional_info = pd.DataFrame({'station': df.columns, 'latitude': lat, 'longitude': lon })
ll = []
for ind, row in nrel_df.iterrows():
for col in nrel_df.columns:
lat = additional_info[(additional_info.station == col)].latitude.values[0]
lon = additional_info[(additional_info.station == col)].longitude.values[0]
irradiance = row[col]
ll.append([lat, lon, irradiance])
return pd.DataFrame(columns=['latitude','longitude','irradiance'], data=ll)
# +
path = '/Users/cseveriano/spatio-temporal-forecasting/data/processed/NREL/Oahu'
df = load_data(path)
# Corrigir ordem das colunas
df.columns = ['DHHL_3','DHHL_4', 'DHHL_5', 'DHHL_10', 'DHHL_11', 'DHHL_9', 'DHHL_2', 'DHHL_1', 'DHHL_1_Tilt', 'AP_6', 'AP_6_Tilt', 'AP_1', 'AP_3', 'AP_5', 'AP_4', 'AP_7', 'DHHL_6', 'DHHL_7', 'DHHL_8']
#inicio dos dados possui falhas na medicao
df = df.loc[df.index > '2010-03-20']
df.drop(['DHHL_1_Tilt', 'AP_6_Tilt'], axis=1, inplace=True)
# -
# ## Preparação bases de treinamento e testes
# +
clean_df = pd.DataFrame(columns=df.columns, index=df.index)
residual_df = pd.DataFrame(columns=df.columns, index=df.index)
for col in df.columns:
residual, clean = remove_periodic(df[col].tolist(), df.index, frequency_threshold=0.01e12)
clean_df[col] = clean.tolist()
residual_df[col] = residual.tolist()
# +
train_df = df[(df.index >= '2010-09-01') & (df.index <= '2011-09-01')]
train_clean_df = clean_df[(clean_df.index >= '2010-09-01') & (clean_df.index <= '2011-09-01')]
train_residual_df = residual_df[(residual_df.index >= '2010-09-01') & (residual_df.index <= '2011-09-01')]
test_df = df[(df.index >= '2010-08-05')& (df.index < '2010-08-06')]
test_clean_df = clean_df[(clean_df.index >= '2010-08-05')& (clean_df.index < '2010-08-06')]
test_residual_df = residual_df[(residual_df.index >= '2010-08-05')& (residual_df.index < '2010-08-06')]
# +
train_df.to_pickle("train_df.pkl")
train_clean_df.to_pickle("train_clean_df.pkl")
train_residual_df.to_pickle("train_residual_df.pkl")
test_df.to_pickle("test_df.pkl")
test_clean_df.to_pickle("test_clean_df.pkl")
test_residual_df.to_pickle("test_residual_df.pkl")
# +
# ms_df = create_spatio_temporal_data(train_residual_df)
# ms_df.to_pickle("cluster_df.pkl")
# -
ms_df = train_residual_df
ms_df.to_pickle("cluster_all_stations_df.pkl")
# +
#ms_df = pd.read_pickle("cluster_df.pkl")
# -
test_residual_df.to_pickle("test_cluster_all_stations_df.pkl")
# +
from sklearn import preprocessing
X = ms_df.values #returns a numpy array
min_max_scaler = preprocessing.MinMaxScaler()
X = min_max_scaler.fit_transform(X)
# -
# ## Mini-batch KMeans
#
from sklearn.cluster import MiniBatchKMeans
from sklearn.metrics import silhouette_samples, silhouette_score
np.arange(10,100,10)
# Busca de melhor valor k com base no Sillouette Coefficient
# +
batch_size = 1000
init_size = 1000
#range_n_clusters = np.arange(2,40)
range_n_clusters = np.arange(100,500,100)
print("Starting Loop")
results = []
for n_clusters in range_n_clusters:
# print("Starting Mini-batch")
clusterer = MiniBatchKMeans(init='k-means++', n_clusters=n_clusters, batch_size=batch_size, init_size=init_size,
n_init=1, verbose=False)
# print("Starting Fit predict")
cluster_labels = clusterer.fit_predict(X)
# The silhouette_score gives the average value for all the samples.
# This gives a perspective into the density and separation of the formed
# clusters
# print("Starting Silhouette")
silhouette_avg = silhouette_score(X, cluster_labels, sample_size=10000)
print("For n_clusters =", n_clusters,"The average silhouette_score is :", silhouette_avg)
results.append(silhouette_avg)
plt.plot(range_n_clusters,results)
# +
batch_size = 1000
init_size = 1000
#range_n_clusters = np.arange(2,40)
range_n_clusters = np.arange(2,100)
print("Starting Loop")
results = []
for n_clusters in range_n_clusters:
# print("Starting Mini-batch")
clusterer = MiniBatchKMeans(init='k-means++', n_clusters=n_clusters, batch_size=batch_size, init_size=3 * n_clusters,
n_init=1, verbose=False)
# print("Starting Fit predict")
cluster_labels = clusterer.fit_predict(X)
print("For n_clusters =", n_clusters,"The within-cluster variance is :", clusterer.inertia_)
results.append( clusterer.inertia_ )
plt.plot(range_n_clusters,results)
# -
print("Best value: ",max(results), "Number of clusters: ", range_n_clusters[np.argmax(results)])
# +
import matplotlib.cm as cm
n_clusters = 20
n_samples = 10000
# Create a subplot with 1 row and 2 columns
fig, ax1 = plt.subplots(1)
fig.set_size_inches(18, 7)
# The 1st subplot is the silhouette plot
ax1.set_xlim([-0.1, 1])
# The (n_clusters+1)*10 is for inserting blank space between silhouette
# plots of individual clusters, to demarcate them clearly.
ax1.set_ylim([0, n_samples + (n_clusters + 1) * 10])
# Initialize the clusterer with n_clusters value and a random generator
# seed of 10 for reproducibility.
clusterer = MiniBatchKMeans(init='k-means++', n_clusters=n_clusters, batch_size=batch_size, init_size=init_size,
n_init=1, verbose=False)
cluster_labels = clusterer.fit_predict(X)
# The silhouette_score gives the average value for all the samples.
# This gives a perspective into the density and separation of the formed
# clusters
silhouette_avg = silhouette_score(X, cluster_labels, sample_size=n_samples)
print("For n_clusters =", n_clusters,
"The average silhouette_score is :", silhouette_avg)
idx = np.random.choice(np.arange(len(X)), n_samples, replace=False)
x_sample = X[idx]
c_sample = cluster_labels[idx]
sample_silhouette_values = silhouette_samples(x_sample, c_sample)
y_lower = 10
for i in range(n_clusters):
# Aggregate the silhouette scores for samples belonging to
# cluster i, and sort them
ith_cluster_silhouette_values = sample_silhouette_values[c_sample == i]
ith_cluster_silhouette_values.sort()
size_cluster_i = ith_cluster_silhouette_values.shape[0]
y_upper = y_lower + size_cluster_i
color = cm.spectral(float(i) / n_clusters)
ax1.fill_betweenx(np.arange(y_lower, y_upper),
0, ith_cluster_silhouette_values,
facecolor=color, edgecolor=color, alpha=0.7)
# Label the silhouette plots with their cluster numbers at the middle
ax1.text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))
# Compute the new y_lower for next plot
y_lower = y_upper + 10 # 10 for the 0 samples
ax1.set_title("The silhouette plot for the various clusters.")
ax1.set_xlabel("The silhouette coefficient values")
ax1.set_ylabel("Cluster label")
# The vertical line for average silhouette score of all the values
ax1.axvline(x=silhouette_avg, color="red", linestyle="--")
ax1.set_yticks([]) # Clear the yaxis labels / ticks
ax1.set_xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])
plt.suptitle(("Silhouette analysis for KMeans clustering on sample data "
"with n_clusters = %d" % n_clusters),
fontsize=14, fontweight='bold')
plt.show()
# -
from scipy.stats import truncnorm
a, b = 0.1, 2
mean, var, skew, kurt = truncnorm.stats(a, b, moments='mvsk')
# +
fig, ax = plt.subplots(1, 1)
x = np.linspace(truncnorm.ppf(0.01, a, b), truncnorm.ppf(0.99, a, b), 100)
ax.plot(x, truncnorm.pdf(x, a, b),'r-', lw=5, alpha=0.6, label='truncnorm pdf')
# -
from pyFTS.common import Membership
fig, ax = plt.subplots(1, 1)
y = [Membership.gaussmf(xx,[mean,var]) for xx in x]
ax.plot(x, y,'r-', lw=5, alpha=0.6, label='truncnorm pdf')
a, b = (myclip_a - mean) / my_std, (myclip_b - my_mean) / my_std
max(x)
|
notebooks/180426 - Oahu MiniBatch.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # DAT210x - Programming with Python for DS
# ## Module5- Lab3
# +
import pandas as pd
from datetime import timedelta
import matplotlib.pyplot as plt
import matplotlib
from sklearn.cluster import KMeans
matplotlib.style.use('ggplot') # Look Pretty
# -
# A convenience function for you to use:
def clusterInfo(model):
print("Cluster Analysis Inertia: ", model.inertia_)
print('------------------------------------------')
for i in range(len(model.cluster_centers_)):
print("\n Cluster ", i)
print(" Centroid ", model.cluster_centers_[i])
print(" #Samples ", (model.labels_==i).sum()) # NumPy Power
# Find the cluster with the least # attached nodes
def clusterWithFewestSamples(model):
# Ensure there's at least on cluster...
minSamples = len(model.labels_)
minCluster = 0
for i in range(len(model.cluster_centers_)):
if minSamples > (model.labels_==i).sum():
minCluster = i
minSamples = (model.labels_==i).sum()
print("\n Cluster With Fewest Samples: ", minCluster)
return (model.labels_==minCluster)
# ### CDRs
# A [call detail record](https://en.wikipedia.org/wiki/Call_detail_record) (CDR) is a data record produced by a telephone exchange or other telecommunications equipment that documents the details of a telephone call or other telecommunications transaction (e.g., text message) that passes through that facility or device.
#
# The record contains various attributes of the call, such as time, duration, completion status, source number, and destination number. It is the automated equivalent of the paper toll tickets that were written and timed by operators for long-distance calls in a manual telephone exchange.
#
# The dataset we've curated for you contains call records for 10 people, tracked over the course of 3 years. Your job in this assignment is to find out where each of these people likely live and where they work at!
#
# Start by loading up the dataset and taking a peek at its `head` and `dtypes`. You can convert date-strings to real date-time objects using `pd.to_datetime`, and the times using `pd.to_timedelta`:
# +
# .. your code here ..
df = pd.read_csv('Datasets/CDR.csv')
print(df.head())
df.CallDate = pd.to_datetime(df.CallDate)
df.Duration = pd.to_timedelta(df.Duration)
df.CallTime = pd.to_timedelta(df.CallTime)
#print(df[(df.TowerLat ==32.9000009 ) & (df.TowerLon==-96.90951639)])
# -
# Create a unique list of the phone number values (people) stored in the `In` column of the dataset, and save them in a regular python list called `unique_numbers`. Manually check through `unique_numbers` to ensure the order the numbers appear is the same order they (uniquely) appear in your dataset:
# .. your code here ..
unique_numbers = list(df.In.unique())
print(unique_numbers)
# Using some domain expertise, your intuition should direct you to know that people are likely to behave differently on weekends vs on weekdays:
#
# #### On Weekends
# 1. People probably don't go into work
# 1. They probably sleep in late on Saturday
# 1. They probably run a bunch of random errands, since they couldn't during the week
# 1. They should be home, at least during the very late hours, e.g. 1-4 AM
#
# #### On Weekdays
# 1. People probably are at work during normal working hours
# 1. They probably are at home in the early morning and during the late night
# 1. They probably spend time commuting between work and home everyday
print("Examining person: ", 0)
# Create a slice called `user1` that filters to only include dataset records where the `In` feature (user phone number) is equal to the first number on your unique list above:
# .. your code here ..
user1 = df[(df.In == unique_numbers[0])]
# Alter your slice so that it includes only Weekday (Mon-Fri) values:
# .. your code here ..
user1 = user1[(user1.DOW != 'Sat') & (user1.DOW != 'Sun') ]
# The idea is that the call was placed before 5pm. From Midnight-730a, the user is probably sleeping and won't call / wake up to take a call. There should be a brief time in the morning during their commute to work, then they'll spend the entire day at work. So the assumption is that most of the time is spent either at work, or in 2nd, at home:
# .. your code here ..
user1 = user1[(user1.CallTime < "17:00:00")]
user1.DOW.unique()
# Plot the Cell Towers the user connected to
# +
# .. your code here ..
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(user1.TowerLon,user1.TowerLat, c='g', marker='o', alpha=0.2)
ax.set_title('Weekday Calls before 5PM')
# -
def doKMeans(data, num_clusters=0):
# TODO: Be sure to only feed in Lat and Lon coordinates to the KMeans algo, since none of the other
# data is suitable for your purposes. Since both Lat and Lon are (approximately) on the same scale,
# no feature scaling is required. Print out the centroid locations and add them onto your scatter
# plot. Use a distinguishable marker and color.
#
# Hint: Make sure you fit ONLY the coordinates, and in the CORRECT order (lat first). This is part
# of your domain expertise. Also, *YOU* need to create, initialize (and return) the variable named
# `model` here, which will be a SKLearn K-Means model for this to work:
# .. your code here ..
df1 = pd.concat([data.TowerLat, data.TowerLon], axis = 1)
kmean = KMeans(n_clusters = num_clusters)
labels = kmean.fit_predict(df1)
centroids = kmean.cluster_centers_
print(centroids)
model = kmean
ax.scatter(x=centroids[:,0], y=centroids[:,1], marker='x', c='red', alpha=0.5, linewidths=3, s=169)
return model
# Let's tun K-Means with `K=3` or `K=4`. There really should only be a two areas of concentration. If you notice multiple areas that are "hot" (multiple areas the user spends a lot of time at that are FAR apart from one another), then increase K=5, with the goal being that all centroids except two will sweep up the annoying outliers and not-home, not-work travel occasions. the other two will zero in on the user's approximate home location and work locations. Or rather the location of the cell tower closest to them.....
model = doKMeans(user1,3)
# Print out the mean `CallTime` value for the samples belonging to the cluster with the LEAST samples attached to it. If our logic is correct, the cluster with the MOST samples will be work. The cluster with the 2nd most samples will be home. And the `K=3` cluster with the least samples should be somewhere in between the two. What time, on average, is the user in between home and work, between the midnight and 5pm?
user1
len(midWayClusterIndices)
midWayClusterIndices = clusterWithFewestSamples(model)
midWaySamples = user1[midWayClusterIndices]
print(" Its Waypoint Time: ", midWaySamples.CallTime.mean())
# Let's visualize the results! First draw the X's for the clusters:
fig = plt.figure()
ax = fig.add_subplot(111)
centroids = model.cluster_centers_
ax.scatter(centroids[:,1], centroids[:,0], s=169, c='r', marker='x', alpha=0.8, linewidths=2)
ax.set_title('Weekday Calls Centroids')
plt.show()
|
Module5/Module5 - Lab3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Epidemiological models: Introduction
#
# This tutorial introduces the [pyro.contrib.epidemiology](http://docs.pyro.ai/en/latest/contrib.epidemiology.html) module, an epidemiological modeling language with a number of black box inference algorithms. This tutorial assumes the reader is already familiar with [modeling](http://pyro.ai/examples/intro_part_ii.html), [inference](http://pyro.ai/examples/intro_part_ii.html), and [distribution shapes](http://pyro.ai/examples/tensor_shapes.html).
#
# See also the following scripts:
#
# - [Epidemiological models: Univariate](http://pyro.ai/examples/epi_sir.html)
# - [Epidemiological models: Regional](http://pyro.ai/examples/epi_regional.html)
# - [Epidemiological inference via HMC](http://pyro.ai/examples/sir_hmc.html)
#
# #### Summary
#
# - To create a new model, inherit from the [CompartmentalModel](http://docs.pyro.ai/en/latest/contrib.epidemiology.html#pyro.contrib.epidemiology.compartmental.CompartmentalModel) base class.
# - Override methods [.global_model()](http://docs.pyro.ai/en/latest/contrib.epidemiology.html#pyro.contrib.epidemiology.compartmental.CompartmentalModel.global_model), [.initialize(params)](http://docs.pyro.ai/en/latest/contrib.epidemiology.html#pyro.contrib.epidemiology.compartmental.CompartmentalModel.initialize), and [.transition(params, state, t)](http://docs.pyro.ai/en/latest/contrib.epidemiology.html#pyro.contrib.epidemiology.compartmental.CompartmentalModel.transition).
# - Take care to support broadcasting and vectorized interpretation in those methods.
# - For single time series, set `population` to an integer.
# - For batched time series, let `population` be a vector, and use [self.region_plate](http://docs.pyro.ai/en/latest/contrib.epidemiology.html#pyro.contrib.epidemiology.compartmental.CompartmentalModel).
# - For models with complex inter-compartment flows, override the [.compute_flows()](http://docs.pyro.ai/en/latest/contrib.epidemiology.html#pyro.contrib.epidemiology.compartmental.CompartmentalModel.compute_flows) method.
# - Flows with loops (undirected or directed) are not currently supported.
# - To perform cheap approximate inference via SVI, call the [.fit_svi()](http://docs.pyro.ai/en/latest/contrib.epidemiology.html#pyro.contrib.epidemiology.compartmental.CompartmentalModel.fit_svi) method.
# - To perform more expensive inference via MCMC, call the [.fit_mcmc()](http://docs.pyro.ai/en/latest/contrib.epidemiology.html#pyro.contrib.epidemiology.compartmental.CompartmentalModel.fit_mcmc) method.
# - To stochastically predict latent and future variables, call the [.predict()](http://docs.pyro.ai/en/latest/contrib.epidemiology.html#pyro.contrib.epidemiology.compartmental.CompartmentalModel.predict) method.
#
# #### Table of contents
#
# - [Basic workflow](#Basic-workflow)
# - [Modeling](#Modeling)
# - [Generating data](#Generating-data)
# - [Inference](#Inference)
# - [Prediction](#Prediction)
# - [Forecasting](#Forecasting)
# - [Advanced modeling](#Advanced-modeling)
# - [Regional models](#Regional-models)
# - [Phylogenetic likelihoods](#Phylogenetic-likelihoods)
# - [Heterogeneous models](#Heterogeneous-models)
# - [Complex compartment flow](#Complex-compartment-flow)
# - [References](#References)
# +
import os
import matplotlib.pyplot as plt
import seaborn as sns
import torch
import pyro
import pyro.distributions as dist
from pyro.contrib.epidemiology import CompartmentalModel, binomial_dist, infection_dist
# %matplotlib inline
assert pyro.__version__.startswith('1.7.0')
torch.set_default_dtype(torch.double) # Required for MCMC inference.
smoke_test = ('CI' in os.environ)
# -
# ## Basic workflow <a class="anchor" id="Basic-workflow"></a>
#
# The [pyro.contrib.epidemiology](http://docs.pyro.ai/en/latest/contrib.epidemiology.html) module provides a modeling language for a class of stochastic discrete-time discrete-count compartmental models, together with a number of black box inference algorithms to perform joint inference on global parameters and latent variables. This modeling language is more restrictive than the full Pyro probabilistic programming language:
#
# - control flow must be static;
# - compartmental distributions are restricted to [binomial_dist()](http://docs.pyro.ai/en/latest/contrib.epidemiology.html#pyro.contrib.epidemiology.distributions.binomial_dist), [beta_binomial_dist()](http://docs.pyro.ai/en/latest/contrib.epidemiology.html#pyro.contrib.epidemiology.distributions.beta_binomial_dist), and [infection_dist()](http://docs.pyro.ai/en/latest/contrib.epidemiology.html#pyro.contrib.epidemiology.distributions.infection_dist);
# - plates are not allowed, except for the single optional [.region_plate](http://docs.pyro.ai/en/latest/contrib.epidemiology.html#pyro.contrib.epidemiology.compartmental.CompartmentalModel.region_plate);
# - all random variables must be either global or Markov and sampled at every time step, so e.g. time-windowed random variables are not supported;
# - models must support broadcasting and vectorization of time `t`.
#
# These restrictions allow inference algorithms to vectorize over the time dimension, leading to inference algorithms with per-iteration parallel complexity sublinear in length of the time axis. The restriction on distributions allows inference algorithms to approximate parts of the model as Gaussian via moment matching, further speeding up inference. Finally, because real data is so often overdispersed relative to Binomial idealizations, the three distribution helpers provide an [overdispersion](http://docs.pyro.ai/en/latest/contrib.epidemiology.html#pyro.contrib.epidemiology.distributions.binomial_dist) parameter calibrated so that in the large-population limit all distribution helpers converge to log-normal.
#
# Black box inference algorithms currently include: [SVI](http://docs.pyro.ai/en/latest/inference_algos.html#pyro.infer.svi.SVI) with a moment-matching approximation, and [NUTS](http://docs.pyro.ai/en/latest/mcmc.html#pyro.infer.mcmc.NUTS) either with a moment-matched approximation or with an exact auxiliary variable method detailed in the [SIR HMC tutorial](http://pyro.ai/examples/sir_hmc.html). All three algorithms initialize using [SMC](http://docs.pyro.ai/en/latest/inference_algos.html#pyro.infer.smcfilter.SMCFilter) and reparameterize time dependent variables using a fast [Haar wavelet](http://docs.pyro.ai/en/latest/infer.reparam.html#pyro.infer.reparam.haar.HaarReparam) transform. Default inference parameters are set for cheap approximate results; accurate results will require more steps and ideally comparison among different inference algorithms. We recommend that, when running MCMC inference, you use multiple chains, thus making it easier to diagnose mixing issues.
#
# While MCMC inference can be more accurate for a given model, SVI is much faster and thus allows richer model structure (e.g. incorporating neural networks) and more rapid [model iteration](https://www.annualreviews.org/doi/abs/10.1146/annurev-statistics-022513-115657?journalCode=statistics). We recommend starting model exploration using mean field SVI (via `.fit_svi(guide_rank=0)`), then optionally increasing accuracy using a low-rank multivariate normal guide (via `.fit_svi(guide_rank=None)`). For even more accurate posteriors you could then try moment-matched MCMC (via `.fit_mcmc(num_quant_bins=1)`), or the most accurate and most expensive enumerated MCMC (via `.fit_mcmc(num_quant_bins=4)`). We recommend that, when fitting models with neural networks, you train via `.fit_svi()`, then freeze the network (say by omitting a `pyro.module()` statement) before optionally running MCMC inference.
# ### Modeling <a class="anchor" id="Modeling"></a>
#
# The [pyro.contrib.epidemiology.models](http://docs.pyro.ai/en/latest/contrib.epidemiology.html#module-pyro.contrib.epidemiology.models) module provides a number of example models. While in principle these are reusable, we recommend forking and modifying these models for your task. Let's take a look at one of the simplest examples, [SimpleSIRModel](http://docs.pyro.ai/en/latest/contrib.epidemiology.html#pyro.contrib.epidemiology.models.SimpleSIRModel). This model derives from the [CompartmentalModel](http://docs.pyro.ai/en/latest/contrib.epidemiology.html#pyro.contrib.epidemiology.compartmental.CompartmentalModel) base class and overrides the three standard methods using familiar Pyro modeling code in each method.
#
# - [.global_model()](http://docs.pyro.ai/en/latest/contrib.epidemiology.html#pyro.contrib.epidemiology.compartmental.CompartmentalModel.global_model) samples global parameters and packs them into a single return value (here a tuple, but any structure is allowed). The return value is available as the `params` argument to the other two methods.
# - [.initialize(params)](http://docs.pyro.ai/en/latest/contrib.epidemiology.html#pyro.contrib.epidemiology.compartmental.CompartmentalModel.initialize) samples (or deterministically sets) initial values of time series, returning a dictionary mapping time series name to initial value.
# - [.transition(params, state, t)](http://docs.pyro.ai/en/latest/contrib.epidemiology.html#pyro.contrib.epidemiology.compartmental.CompartmentalModel.transition) inputs global `params`, the `state` at the previous time step, and the time index `t` (which may be a slice!). It then samples flows and updates the state dict.
class SimpleSIRModel(CompartmentalModel):
def __init__(self, population, recovery_time, data):
compartments = ("S", "I") # R is implicit.
duration = len(data)
super().__init__(compartments, duration, population)
assert isinstance(recovery_time, float)
assert recovery_time > 1
self.recovery_time = recovery_time
self.data = data
def global_model(self):
tau = self.recovery_time
R0 = pyro.sample("R0", dist.LogNormal(0., 1.))
rho = pyro.sample("rho", dist.Beta(100, 100))
return R0, tau, rho
def initialize(self, params):
# Start with a single infection.
return {"S": self.population - 1, "I": 1}
def transition(self, params, state, t):
R0, tau, rho = params
# Sample flows between compartments.
S2I = pyro.sample("S2I_{}".format(t),
infection_dist(individual_rate=R0 / tau,
num_susceptible=state["S"],
num_infectious=state["I"],
population=self.population))
I2R = pyro.sample("I2R_{}".format(t),
binomial_dist(state["I"], 1 / tau))
# Update compartments with flows.
state["S"] = state["S"] - S2I
state["I"] = state["I"] + S2I - I2R
# Condition on observations.
t_is_observed = isinstance(t, slice) or t < self.duration
pyro.sample("obs_{}".format(t),
binomial_dist(S2I, rho),
obs=self.data[t] if t_is_observed else None)
# Note that we've stored data in the model. These models have a scikit-learn like interface: we instantiate a model class with data, then call a `.fit_*()` method to train, then call `.predict()` on a trained model.
#
# Note also that we've taken special care so that `t` can be either an integer or a `slice`. Under the hood, `t` is an integer during SMC initialization, a `slice` during SVI or MCMC inference, and an integer again during prediction.
# ### Generating data <a class="anchor" id="Generating-data"></a>
#
# To check that our model generates plausible data, we can create a model with empty data and call the model's [.generate()](http://docs.pyro.ai/en/latest/contrib.epidemiology.html#pyro.contrib.epidemiology.compartmental.CompartmentalModel.generate) method. This method first calls, `.global_model()`, then calls `.initialize()`, then calls `.transition()` once per time step (based on the length of our empty data.
# +
population = 10000
recovery_time = 10.
empty_data = [None] * 90
model = SimpleSIRModel(population, recovery_time, empty_data)
# We'll repeatedly generate data until a desired number of infections is found.
pyro.set_rng_seed(20200709)
for attempt in range(100):
synth_data = model.generate({"R0": 2.0})
total_infections = synth_data["S2I"].sum().item()
if 4000 <= total_infections <= 6000:
break
print("Simulated {} infections after {} attempts".format(total_infections, 1 + attempt))
# -
# The generated data contains both global variables and time series, packed into tensors.
for key, value in sorted(synth_data.items()):
print("{}.shape = {}".format(key, tuple(value.shape)))
plt.figure(figsize=(8,4))
for name, value in sorted(synth_data.items()):
if value.dim():
plt.plot(value, label=name)
plt.xlim(0, len(empty_data) - 1)
plt.ylim(0.8, None)
plt.xlabel("time step")
plt.ylabel("individuals")
plt.yscale("log")
plt.legend(loc="best")
plt.title("Synthetic time series")
plt.tight_layout()
# ### Inference <a class="anchor" id="Inference"></a>
#
# Next let's recover estimates of the latent variables given only observations `obs`. To do this we'll create a new model instance from the synthetic observations.
obs = synth_data["obs"]
model = SimpleSIRModel(population, recovery_time, obs)
# The `CompartmentalModel` provides a number of inference algorithms. The cheapest and most scalable algorithm is SVI, avilable via the `.fit_svi()` method. This method returns a list of losses to help us diagnose convergence; the fitted parameters are stored in the model object.
# %%time
losses = model.fit_svi(num_steps=101 if smoke_test else 2001,
jit=True)
plt.figure(figsize=(8, 3))
plt.plot(losses)
plt.xlabel("SVI step")
plt.ylabel("loss")
plt.ylim(min(losses), max(losses[50:]));
# After inference, samples of latent variables are stored in the `.samples` attribute. These are primarily for internal use, and do not contain the full set of latent variables.
for key, value in sorted(model.samples.items()):
print("{}.shape = {}".format(key, tuple(value.shape)))
# ### Prediction <a class="anchor" id="Prediction"></a>
#
# After inference we can both examine latent variables and forecast forward using the [.predict()](http://docs.pyro.ai/en/latest/contrib.epidemiology.html#pyro.contrib.epidemiology.compartmental.CompartmentalModel.predict) method. First let's simply predict latent variables.
# %%time
samples = model.predict()
for key, value in sorted(samples.items()):
print("{}.shape = {}".format(key, tuple(value.shape)))
names = ["R0", "rho"]
fig, axes = plt.subplots(2, 1, figsize=(5, 5))
axes[0].set_title("Posterior estimates of global parameters")
for ax, name in zip(axes, names):
truth = synth_data[name]
sns.distplot(samples[name], ax=ax, label="posterior")
ax.axvline(truth, color="k", label="truth")
ax.set_xlabel(name)
ax.set_yticks(())
ax.legend(loc="best")
plt.tight_layout()
# Notice that while the inference recovers the basic reproductive number `R0`, it poorly estimates the response rate `rho` and underestimates its uncertainty. While perfect inference would provide better uncertainty estimates, the response rate is known to be difficult to recover from data. Ideally the model can either incorporate a narrower prior, either obtained by testing a random sample of the population, or by more accurate observations, e.g. counting deaths rather than confirmed infections.
# ### Forecasting <a class="anchor" id="Forecasting"></a>
#
# We can forecast forward by passing a `forecast` argument to the `.predict()` method, specifying the number of time steps ahead we'd like to forecast. The returned `sample` will contain time values during both the first observed time interval (here 90 days) and the forecasted window (say 30 days).
# %time
samples = model.predict(forecast=30)
# +
def plot_forecast(samples):
duration = len(empty_data)
forecast = samples["S"].size(-1) - duration
num_samples = len(samples["R0"])
time = torch.arange(duration + forecast)
S2I = samples["S2I"]
median = S2I.median(dim=0).values
p05 = S2I.kthvalue(int(round(0.5 + 0.05 * num_samples)), dim=0).values
p95 = S2I.kthvalue(int(round(0.5 + 0.95 * num_samples)), dim=0).values
plt.figure(figsize=(8, 4))
plt.fill_between(time, p05, p95, color="red", alpha=0.3, label="90% CI")
plt.plot(time, median, "r-", label="median")
plt.plot(time[:duration], obs, "k.", label="observed")
plt.plot(time[:duration], synth_data["S2I"], "k--", label="truth")
plt.axvline(duration - 0.5, color="gray", lw=1)
plt.xlim(0, len(time) - 1)
plt.ylim(0, None)
plt.xlabel("day after first infection")
plt.ylabel("new infections per day")
plt.title("New infections in population of {}".format(population))
plt.legend(loc="upper left")
plt.tight_layout()
plot_forecast(samples)
# -
# It looks like the mean field guide underestimates uncertainty. To improve uncertainty estimates we can instead try MCMC inference. In this simple model MCMC is only a small factor slower than SVI; in more complex models MCMC can be multiple orders of magnitude slower than SVI.
# %%time
model = SimpleSIRModel(population, recovery_time, obs)
mcmc = model.fit_mcmc(num_samples=4 if smoke_test else 400,
jit_compile=True)
samples = model.predict(forecast=30)
plot_forecast(samples)
# ## Advanced modeling <a class="anchor" id="Advanced-modeling"></a>
#
# So far we've seen how to create a simple univariate model, fit the model to data, and predict and forecast future data. Next let's consider more advanced modeling techniques:
#
# - [regional models](#Regional-models) that couple compartments among multiple aggregated regions;
# - [phylogenetic likelihoods](#Phylogenetic-likelihoods) to incorporate genetic sequencing data;
# - [heterogeneous models](#Heterogeneous-models) with time-varying latent variables; and
# - [Complex compartment flow](#Complex-compartment-flow) for models with non-linear transitions.
# ### Regional models <a class="anchor" id="Regional-models"></a>
#
# Epidemiology models vary in their level of detail. At the coarse-grained extreme are univariate aggregate models as we saw above. At the fine-grained extreme are network models where each individual's state is tracked and infections occur along edges of a sparse graph (`pyro.contrib.epidemiology` does not implement network models). We now consider an mid-level model where each of many regions (e.g. countries or zip codes) is tracked in aggregate, and infections occur both within regions and between pairs of regions. In Pyro we model multiple regions with a [plate](http://docs.pyro.ai/en/stable/primitives.html#pyro.primitives.plate). Pyro's [CompartmentalModel](http://docs.pyro.ai/en/latest/contrib.epidemiology.html#pyro.contrib.epidemiology.compartmental.CompartmentalModel) class does not support general `pyro.plate` syntax, but it does support a single special `self.region_plate` for regional models. This plate is available iff a `CompartmentalModel` is initialized with a vector `population`, and the size of the `region_plate` will be the length of the `population` vector.
#
# Let's take a look at the example [RegionalSIRModel](http://docs.pyro.ai/en/latest/contrib.epidemiology.html#pyro.contrib.epidemiology.models.RegionalSIRModel):
class RegionalSIRModel(CompartmentalModel):
def __init__(self, population, coupling, recovery_time, data):
duration = len(data)
num_regions, = population.shape
assert coupling.shape == (num_regions, num_regions)
assert (0 <= coupling).all()
assert (coupling <= 1).all()
assert isinstance(recovery_time, float)
assert recovery_time > 1
if isinstance(data, torch.Tensor):
# Data tensors should be oriented as (time, region).
assert data.shape == (duration, num_regions)
compartments = ("S", "I") # R is implicit.
# We create a regional model by passing a vector of populations.
super().__init__(compartments, duration, population, approximate=("I",))
self.coupling = coupling
self.recovery_time = recovery_time
self.data = data
def global_model(self):
# Assume recovery time is a known constant.
tau = self.recovery_time
# Assume reproductive number is unknown but homogeneous.
R0 = pyro.sample("R0", dist.LogNormal(0., 1.))
# Assume response rate is heterogeneous and model it with a
# hierarchical Gamma-Beta prior.
rho_c1 = pyro.sample("rho_c1", dist.Gamma(10, 1))
rho_c0 = pyro.sample("rho_c0", dist.Gamma(10, 1))
with self.region_plate:
rho = pyro.sample("rho", dist.Beta(rho_c1, rho_c0))
return R0, tau, rho
def initialize(self, params):
# Start with a single infection in region 0.
I = torch.zeros_like(self.population)
I[0] += 1
S = self.population - I
return {"S": S, "I": I}
def transition(self, params, state, t):
R0, tau, rho = params
# Account for infections from all regions. This uses approximate (point
# estimate) counts I_approx for infection from other regions, but uses
# the exact (enumerated) count I for infections from one's own region.
I_coupled = state["I_approx"] @ self.coupling
I_coupled = I_coupled + (state["I"] - state["I_approx"]) * self.coupling.diag()
I_coupled = I_coupled.clamp(min=0) # In case I_approx is negative.
pop_coupled = self.population @ self.coupling
with self.region_plate:
# Sample flows between compartments.
S2I = pyro.sample("S2I_{}".format(t),
infection_dist(individual_rate=R0 / tau,
num_susceptible=state["S"],
num_infectious=I_coupled,
population=pop_coupled))
I2R = pyro.sample("I2R_{}".format(t),
binomial_dist(state["I"], 1 / tau))
# Update compartments with flows.
state["S"] = state["S"] - S2I
state["I"] = state["I"] + S2I - I2R
# Condition on observations.
t_is_observed = isinstance(t, slice) or t < self.duration
pyro.sample("obs_{}".format(t),
binomial_dist(S2I, rho),
obs=self.data[t] if t_is_observed else None)
# The main differences from the earlier univariate model are that: we assume `population` is a vector of length `num_regions`, we sample all compartmental variables and some global variables inside the `region_plate`, and we compute coupled vectors `I_coupled` and `pop_coupled` of the effective number of infected individuals and population accounting for both intra-region and inter-region infections. Among global variables we have chosen for demonstration purposes to make `tau` a fixed single number, `R0` a single latent variable shared among all regions, and `rho` a local latent variable that can take a different value for each region. Note that while `rho` is not shared among regions, we have created a hierarchical model whereby `rho`'s parent variables are shared among regions. While some of our variables are region-global and some region-local, only the compartmental variables are both region-local and time-dependent; all other parameters are fixed for all time. See the [heterogeneous models](#Heterogeneous-models) section below for time-dependent latent variables.
#
# Note that Pyro's enumerated MCMC strategy (`.fit_mcmc()` with `num_quant_bins > 1`) requires extra logic to use a mean-field approximation across compartments: we pass `approximate=("I",)` to the constructor and force compartements to iteract via `state["I_approx"]` rather than `state["I"]`. This code is not required for SVI inference or for moment-matched MCMC inference (`.fit_mcmc()` with the default `num_quant_bins=0`).
#
# See the [Epidemiology: regional models](http://pyro.ai/examples/epi_regional.html) example for a demonstration of how to generate data, train, predict, and forecast with regional models.
# ### Phylogenetic likelihoods <a class="anchor" id="Phylogenetic-likelihoods"></a>
#
# Epidemiological parameters can be difficult to identify from aggregate observations alone. However some parameters like the superspreading parameter `k` can be more accurately identified by combining aggregate count data with viral phylogenetic trees reconstructed from viral genetic sequencing data [(Li et al. 2017)](#1). Pyro implements a [CoalescentRateLikelihood](http://docs.pyro.ai/en/latest/contrib.epidemiology.html#pyro.distributions.CoalescentRateLikelihood) class to compute a population likelihood `p(I|phylogeny)` given statistics of a phylogenetic tree (or a batch of tree samples). The statistics needed are exactly the times of each sampling event (i.e. when a viral genome was sequenced) and the times of genetic coalescent events in a binary phylogenetic tree; let us call these two vectors ``leaf_times`` and ``coal_times``, respectively, where ``len(leaf_times) == 1 + len(coal_times)`` for binary trees. Pyro provides a helper [bio_phylo_to_times()](http://docs.pyro.ai/en/latest/contrib.epidemiology.html#pyro.distributions.coalescent.bio_phylo_to_times) to extract these statistics from a [Bio.Phylo tree objects](https://biopython.readthedocs.io/en/latest/api/Bio.Phylo.BaseTree.html#Bio.Phylo.BaseTree.Clade); in turn [Bio.Phylo](https://biopython-tutorial.readthedocs.io/en/latest/notebooks/13%20-%20Phylogenetics%20with%20Bio.Phylo.html) can parse many file formats of phylogenetic trees.
#
# Let's take a look at the [SuperspreadingSEIRModel](http://docs.pyro.ai/en/latest/contrib.epidemiology.html#pyro.contrib.epidemiology.models.SuperspreadingSEIRModel) which includes a phylogenetic likelihood. We'll focus on the phylogenetic parts of the model:
#
# ```python
# class SuperspreadingSEIRModel(CompartmentalModel):
# def __init__(self, population, incubation_time, recovery_time, data, *,
# leaf_times=None, coal_times=None):
# compartments = ("S", "E", "I") # R is implicit.
# duration = len(data)
# super().__init__(compartments, duration, population)
# ...
# self.coal_likelihood = dist.CoalescentRateLikelihood(
# leaf_times, coal_times, duration)
# ...
#
# def transition(self, params, state, t):
# ...
# # Condition on observations.
# t_is_observed = isinstance(t, slice) or t < self.duration
# R = R0 * state["S"] / self.population
# coal_rate = R * (1. + 1. / k) / (tau_i * state["I"] + 1e-8)
# pyro.factor("coalescent_{}".format(t),
# self.coal_likelihood(coal_rate, t)
# if t_is_observed else torch.tensor(0.))
# ```
# We first constructed a ``CoalescentRateLikelihood`` object to be used throughout inference and prediction; this performs preprocessing work once so that it is cheap to evaluate ``self.coal_likelihood(...)``. Note that ``(leaf_times, coal_times)`` should be in units of time steps, the same time steps as the time index `t` and `duration`. Typically ``leaf_times`` are in ``[0, duration)``, but ``coal_times`` precede ``leaf_times`` (as points of common ancestry), and may be negative. The likelihood involves the coalescent rate ``coal_rate`` in a coalescent process; we can compute this from an epidemiological model. In this superspreading model ``coal_rate`` depends on the reproductive number ``R``, the superspreading parameter ``k``, the incubation time ``tau_i``, and the current number of infected individuals ``state["I"]`` [(Li et al. 2017)](#1).
# ### Heterogeneous models <a class="anchor" id="Heterogeneous-models"></a>
#
# Epidemiological parameters often vary in time, due to human interventions, changes in weather, and other external factors. We can model real-valued time-varying latent variables in ``CompartmentalModel`` by moving static latent variables from ``.global_model()`` to ``.initialize()`` and ``.transition()``. For example we can model a reproductive number under Brownian drift in log-space by initializing at a random ``R0`` and multiplying by a drifting factor, as in the [HeterogeneousSIRModel](http://docs.pyro.ai/en/latest/contrib.epidemiology.html#pyro.contrib.epidemiology.models.HeterogeneousSIRModel) example:
# ```python
# class HeterogeneousSIRModel(CompartmentalModel):
# ...
# def global_model(self):
# tau = self.recovery_time
# R0 = pyro.sample("R0", dist.LogNormal(0., 1.))
# rho = ...
# return R0, tau, rho
#
# def initialize(self, params):
# # Start with a single infection.
# # We also store the initial beta value in the state dict.
# return {"S": self.population - 1, "I": 1, "beta": torch.tensor(1.)}
#
# def transition(self, params, state, t):
# R0, tau, rho = params
# # Sample heterogeneous variables.
# # This assumes beta slowly drifts via Brownian motion in log space.
# beta = pyro.sample("beta_{}".format(t),
# dist.LogNormal(state["beta"].log(), 0.1))
# Rt = pyro.deterministic("Rt_{}".format(t), R0 * beta)
#
# # Sample flows between compartments.
# S2I = pyro.sample("S2I_{}".format(t),
# infection_dist(individual_rate=Rt / tau,
# num_susceptible=state["S"],
# num_infectious=state["I"],
# population=self.population))
# ...
# # Update compartments and heterogeneous variables.
# state["S"] = state["S"] - S2I
# state["I"] = state["I"] + S2I - I2R
# state["beta"] = beta # We store the latest beta value in the state dict.
# ...
# ```
# Here we deterministically initialize a scale factor ``beta = 1`` in ``.initialize()`` then let it drift via log-Brownian motion. We also need to update ``state["beta"]`` just as we update the compartmental variables. Now ``beta`` will be provided as a time series when we ``.predict()``. While we could have written ``Rt = R0 * beta``, we instead wrapped this computation in a ``pyro.deterministic`` thereby exposing ``Rt`` as another time series provided by ``.predict()``. Note that we could have instead sampled ``R0`` in ``.initialize()`` and let ``Rt`` drift directly, rather than introducing a scale factor ``beta``. However separating the two into a non-centered form improves geometry [(Betancourt and Girolami 2013)](#2).
#
# It is also easy to pass in time-varying covariates as tensors, in the same way we have passed in ``data`` to the constructors of all example models. To predict the effects of different causal interventions, you can pass in a covariate that is longer than ``duration``, run inference (looking only at the first ``[0,duration)`` entries), then mutate entries of the covariate after ``duration`` and generate different ``.predict()``ions.
# ### Complex compartment flow <a class="anchor" id="Complex-compartment-flow"></a>
#
# The [CompartmentalModel](http://docs.pyro.ai/en/latest/contrib.epidemiology.html#pyro.contrib.epidemiology.compartmental.CompartmentalModel) class assumes by default that the compartments are arranged linearly and terminate in an implicit terminal compartment named "R", for example S-I-R, S-E-I-R or boxcar models like S-E1-E2-I1-I2-I3-R. To describe other more complex flows between compartments, you can override the [.compute_flows()](http://docs.pyro.ai/en/latest/contrib.epidemiology.html#pyro.contrib.epidemiology.compartmental.CompartmentalModel.compute_flows) method. However currently there is no support for flows with undirected loops (e.g. S-I-S).
#
# Let's create a branching SIRD model with possible flows
# ```
# S → I → R
# ↘
# D
# ```
# As with other models, we'll keep the "R" state implicit (although we could equally keep the "D" state implicit and the "R" state explicit). In the ``.compute_flows()`` method, we'll input a pair of states and we'll need to compute three flow values: ``S2I``, ``I2R``, and ``I2D``.
# ```python
# class SIRDModel(CompartmentalModel):
# def __init__(self, population, data):
# compartments = ("S", "I", "D")
# duration = len(data)
# super().__init__(compartments, duration, population)
# self.data = data
#
# def compute_flows(self, prev, curr, t):
# S2I = prev["S"] - curr["S"] # S can only go in one direction.
# I2D = curr["D"] - prev["D"] # D can only have come from one direction.
# # Now by conservation at I, change + inflows + outflows = 0,
# # so we can solve for the single unknown I2R.
# I2R = prev["I"] - curr["I"] + S2I - I2D
# return {
# "S2I_{}".format(t): S2I,
# "I2D_{}".format(t): I2D,
# "I2R_{}".format(t): I2R,
# }
# ...
# def transition(self, params, state, t):
# ...
# # Sample flows between compartments.
# S2I = pyro.sample("S2I_{}".format(t), ...)
# I2D = pyro.sample("I2D_{}".format(t), ...)
# I2R = pyro.sample("I2R_{}".format(t), ...)
#
# # Update compartments with flows.
# state["S"] = state["S"] - S2I
# state["I"] = state["I"] + S2I - I2D - I2R
# state["D"] = state["D"] + I2D
# ...
# ```
# Note you can name the dict keys anything you want, as long as they match your sample statements in ``.transition()`` and you correctly reverse the flow computation in ``.transition()``. During inference Pyro will check that the ``.compute_flows()`` and ``.transition()`` computations agree. Take care to avoid in-place PyTorch operations, since these can modify the tensors rather than the dictionary:
# ```diff
# + state["S"] = state["S"] - S2I # Correct
# - state["S"] -= S2I # AVOID: may corrupt tensors
# ```
#
# For a slightly more complex example, take a look at the [SimpleSEIRDModel](http://docs.pyro.ai/en/latest/contrib.epidemiology.html#pyro.contrib.epidemiology.models.SimpleSEIRDModel).
# ## References
#
# 1. <a class="anchor" id="1"></a>
# <NAME>, <NAME>, <NAME> (2017)
# "Quantifying Transmission Heterogeneity Using Both Pathogen Phylogenies
# and Incidence Time Series"
# https://academic.oup.com/mbe/article/34/11/2982/3952784
# 2. <a class="anchor" id="2"></a>
# <NAME>, <NAME> (2013)
# "Hamiltonian Monte Carlo for Hierarchical Models"
# https://arxiv.org/abs/1312.0906
|
tutorial/source/epi_intro.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
import seaborn as sns
sns.set_style('whitegrid')
def clean_rpe():
pre = pd.read_csv('./data/rpe.csv',na_values=['None'])
df = pre
print('df shape is ', df.shape)
# traing
df.Training = df.Training.replace('Yes', 1)
df.Training = df.Training.replace('No', 0)
# dummies for SessionType
dummies= pd.get_dummies(df.SessionType, prefix='SessionType' )
for col in list((dummies)):
df.insert(4, col, dummies[col] )
# for numeric cols, replace nan with mean for each player
numeric_cols = [
'Duration',
'RPE',
'SessionLoad',
'DailyLoad',
'AcuteLoad',
'ChronicLoad',
'AcuteChronicRatio',
'ObjectiveRating',
'FocusRating']
for col in numeric_cols:
for player in set(df.PlayerID):
mean_ = (df[df.PlayerID == player][col].mean())
df.update( df[df.PlayerID == player][col].fillna(mean_))
# df[df.PlayerID == player][col] = df[df.PlayerID == player][col].replace(np.nan, mean_)
# dummies for BestOutOfMyself
dummies= pd.get_dummies(df.BestOutOfMyself, prefix='BestOutOfMyself' )
for col in list((dummies)):
df.insert(21, col, dummies[col] )
df = df.drop(columns = ['SessionType','BestOutOfMyself'])
df.head()
return df
df.groupby('PlayerID').describe()
numeric_cols = list(df.describe().columns)
plt.figure(figsize = (14,30))
for n, col in enumerate(numeric_cols):
ax = plt.subplot(5,2,n+1)
df[col].hist() #etc.
plt.title(col)
|
clean_data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="eVD2FatpQopm" colab_type="code" colab={}
import pandas as pd
# + id="tHhTp0lVQ0nO" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 498} outputId="a936c768-2503-4fe5-deba-bff034fd66ff"
# !pip install ctrl4ai
# + id="X1U6KZGTQ6Zq" colab_type="code" colab={}
from ctrl4ai import preprocessing
from ctrl4ai import automl
# + id="S6noQlExQ6xq" colab_type="code" colab={}
from ctrl4ai import datasets
# + id="az1JLz6xRHKQ" colab_type="code" colab={}
data = pd.read_csv('titanic_train.csv')
# + id="AL1BhaZhRhZt" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 197} outputId="691e2145-4a1e-4c13-cdb0-b305abadc254"
data.head()
# + id="lDRz7ldVRjB4" colab_type="code" colab={}
y = data['Fare']
# + id="Z-XJUas8Rjp1" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 850} outputId="01816fb2-f7f6-4c12-b1d1-2b3b62a094cb"
data1 = automl.preprocess(data,'supervised', target_variable='supervised', target_type='continuous',
define_continuous_cols=['Fare'])
# + id="Q9Dh5qBJSKcN" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 197} outputId="44c9d858-cc93-4940-c817-b2b06596bb02"
import pandas as pd
dataset = pd.read_csv('titanic_train.csv')
#deleting the columns and features with only NULL values or zero value
#to check the columns are categorical or not if it is categorical then print true
from ctrl4ai import helper
for i in dataset.columns:
if helper.check_categorical_col(dataset[i]) == True :
x['i'] = dum
dummy = pd.get_dummies( , drop_first = True)
df = pd.concat([dataset , dummy] ,axis=1)
df.head()
#in this code both numeric as well as strings are checked if they are categorical or not
# + id="cpb5Xn5QZUNH" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 197} outputId="25ca370b-0cc7-4121-a404-913e5606899f"
df.head()
# + id="miaVMz36Rjs5" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 197} outputId="77446805-9a23-4aad-ec8c-bff52c5425c4"
dataset.head()
# + id="6PLn0XCMdowB" colab_type="code" colab={}
# + id="cVdI8ea4do1F" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 197} outputId="fa2a7d87-d1e7-40cd-b0d6-3c4a6d13c097"
dummy = pd.get_dummies( dataset['Pclass'] , drop_first = True)
df = pd.concat([dataset , dummy] ,axis=1)
df.head()
# + id="bS350KUodo5q" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 230} outputId="a1a27950-2fed-4e57-eafd-13f2ce4c9dd2"
dataset['Pclass']
# + id="KuzL-uCAdo_C" colab_type="code" colab={}
# + id="IP6rrr01YtYA" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 230} outputId="be98739e-73bb-4ee8-d03a-af5ec9ee644a"
# for converting the catergorical variable of any dataset........
for i in dataset.columns :
if i :
pd.get_dummies(i , drop_first= True )
print(i)
|
dummy_variables_dynamic_code.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Bit serial computation - Multiplication
#
# The notebook illustrates how bit-serial multiplicaton of an operand `A` by an operand `B`, where the `A` operand is viewed at the bit level, can be treated as a tensor computation. This computation can be viewed as a tensor computation where the bit-level representation of `A` is achieved with a sparse fiber with a 1 at those coordinates that match the bit-positions with a 1 in the binary representation of the value. The operand `B` is simply represented as a scalar value. As a result this computation can be represented with the following Einsum:
#
# $$
# Z = A_j \times 2^j \times B
# $$
# ## Setup
#
# The first step is to set up the environment and create some tensors
# +
# Run boilerplate code to set up environment
# %run ../prelude.py --style=tree --animation=movie
# -
# ## Configure some tensors
# +
# Default value for the number of bits in the operand A
J = 8
tm = TensorMaker("dot product inputs")
tm.addTensor("A_J", rank_ids=["J"], shape=[J], density=0.5, interval=1, seed=0, color="blue")
tm.displayControls()
# -
# ## Create and display the tensors
# +
A_J = tm.makeTensor("A_J")
#
# Calculate binary value of A from bit-wise represenation
#
a_value = 0
for j, _ in A_J:
a_value += 2**j
B = Tensor(rank_ids=[], name="B", color="green")
b = B.getRoot()
b <<= 5
print(f"A_J (with value {a_value})")
displayTensor(A_J)
print("B")
displayTensor(B)
# -
# ## Create power array
#
# Although the original Einsum notation includes a multiplication by a value that is a function only of an index value (`2^j`), this code will express that as a multiplicaton by a value from a constant rank-1 tensor (`pow2`). In reality, this would probably be implemented directly in hardware (in this case as a **shift**).
# +
pow2 = Tensor(rank_ids=["J"], shape=[J], name="Pow2", color="lightblue")
pow2_j = pow2.getRoot()
for j, pow2_ref in pow2_j.iterShapeRef():
pow2_ref <<= 2 ** j
displayTensor(pow2)
# -
# ## Serial execution
#
# Observations:
#
# - Elapsed time is proportional to the occupancy of fiber in the `J` rank of `A_J`.
# +
z = Tensor(rank_ids=[], name="Product")
a_j = A_J.getRoot()
b_val = B.getRoot()
pow2_j = pow2.getRoot()
z_ref = z.getRoot()
canvas = createCanvas(A_J, B, pow2, z)
for j, (a_val, pow2_val) in a_j & pow2_j:
z_ref += (a_val * b_val) * pow2_val
canvas.addFrame((j,),(0,),(j,), (0,))
displayTensor(z)
displayCanvas(canvas)
# -
|
notebooks/bit-serial/bit-serial-multiplication.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Things to do to improve performance.
#
# So the first submission didn't score as well as the train set, not surprising!
#
# Lets try and;
#
# 1. Extract more of the text from the html, the body and title aren't enough it seems.
# 2. Over/undersample and see if I improve performance with either strategy.
# +
import numpy as np
import pandas as pd
import os
from bs4 import BeautifulSoup
import nltk
from nltk import wordpunct_tokenize
from nltk.stem.snowball import EnglishStemmer
from nltk.corpus import stopwords
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.decomposition import TruncatedSVD
from sklearn.pipeline import make_pipeline, make_union
from tpot.builtins import StackingEstimator
from sklearn.ensemble import ExtraTreesClassifier
from sklearn.model_selection import train_test_split
import tldextract
nltk.download('punkt')
nltk.download('stopwords')
stop_words = set(stopwords.words('english'))
data_dir = "../data/2018-08-10_AV_Innoplexus/"
#After we use get_text, use nltk's clean_html function.
def nltkPipe(soup_text):
#Convert to tokens
tokens = [x.lower() for x in wordpunct_tokenize(soup_text)]
text = nltk.Text(tokens)
#Get lowercase words. No single letters, and no stop words
words = [w.lower() for w in text if w.isalpha() and len(w) > 1 and w.lower() not in stop_words]
#Remove prefix/suffixes to cut down on vocab
stemmer = EnglishStemmer()
words_nostems = [stemmer.stem(w) for w in words]
return ', '.join(words_nostems)
def getTitleTokens(soup):
soup_title = soup.title
if soup_title != None:
soup_title_text = soup.title.get_text()
text_arr = nltkPipe(soup_title_text)
return text_arr
else:
return ''
def getBodyTokens(soup):
#Get the text body
soup_para = soup.find_all('p')
if soup_para != None:
soup_para_clean = ' '.join([x.get_text() for x in soup_para if x.span==None and x.a==None])
text_arr = nltkPipe(soup_para_clean)
return text_arr
else:
return ''
def getDomainTokens(domainstr):
domain_extracted = tldextract.extract(domainstr)#.domain
domain_tokens = nltkPipe(domain_extracted.domain+","+domain_extracted.suffix)
return domain_tokens
def getUrlTokens(url):
domain_split = url.rsplit('/')
if len(domain_split) > 1:
domain_split_elements = ' '.join(domain_split[1:])
domain_split_tokens = nltkPipe(domain_split_elements)
return domain_split_tokens
else:
return ''
def getDescriptionTokens(soup):
#Get the text body
soup_desc = soup.find_all('dl')
if soup_desc != None:
soup_desc_clean = ' '.join([x.get_text() for x in soup_desc])
text_arr = nltkPipe(soup_desc_clean)
return text_arr
else:
return ''
def getHeaderTokens(soup):
#Get the html header tokens
soup_heads = soup.find_all('header')
if soup_heads != None:
soup_heads_clean = ' '.join([x.get_text() for x in soup_heads])
text_arr = nltkPipe(soup_heads_clean)
return text_arr
else:
return ''
def getHeadTokens(soup):
#Get the html head tokens
soup_head = soup.find_all('head')
if soup_head != None:
soup_head_clean = ' '.join([x.get_text() for x in soup_head])
text_arr = nltkPipe(soup_head_clean)
return text_arr
else:
return ''
def getFontTokens(soup):
soup_font = soup.find_all('font')
if soup_font != None:
soup_font_clean = ' '.join([x.get_text() for x in soup_font])
text_arr = nltkPipe(soup_font_clean)
return text_arr
else:
return ''
def getTableTokens(soup):
soup_table = soup.find_all('table')
soup_table_headers = [[a for a in x.find_all('th')] for x in soup_table]
soup_table_cells = [[a for a in x.find_all('td')] for x in soup_table]
if soup_table != None:
soup_table_headers_clean = ' '.join([' '.join([a.get_text() for a in x]) for x in soup_table_headers])
soup_table_cells_clean = ' '.join([' '.join([a.get_text() for a in x]) for x in soup_table_cells])
text_arr = nltkPipe(soup_table_headers_clean+soup_table_cells_clean)
return text_arr
else:
return ''
def getHrefTokens(soup):
soup_href = soup.find_all('href')
if soup_href != None:
soup_href_clean = ' '.join([x.get_text() for x in soup_href])
text_arr = nltkPipe(soup_href_clean)
return text_arr
else:
return ''
def getListTokens(soup):
soup_list = soup.find_all('ol') + soup.find_all('ul')
if soup_list != None:
soup_list_items = [x.find_all('li') for x in soup_list]
soup_list_items_clean = ' '.join([' '.join([a.get_text() for a in x]) for x in soup_list_items])
text_arr = nltkPipe(soup_list_items_clean)
return text_arr
else:
return ''
def get_all_tokens(frame):
print("Parsing domain tokens...")
domain_tokens = frame['Domain'].apply(getDomainTokens)
print("Parsing url tokens...")
url_tokens = frame['Url'].apply(getUrlTokens)
print("Parsing soup...")
soup = frame['Html'].apply(lambda x: BeautifulSoup(x, 'html.parser'))
print("Getting title tokens...")
title_tokens = soup.apply(getTitleTokens)
print("Getting body tokens...")
body_tokens = soup.apply(getBodyTokens)
print("Getting description tokens...")
description_tokens = soup.apply(getDescriptionTokens)
print("Getting header tokens...")
header_tokens = soup.apply(getHeaderTokens)
print("Getting head-metadata tokens...")
head_tokens = soup.apply(getHeadTokens)
print("Getting font tokens...")
font_tokens = soup.apply(getFontTokens)
print("Getting table tokens...")
table_tokens = soup.apply(getTableTokens)
print("Getting href tokens...")
href_tokens = soup.apply(getHrefTokens)
print("Getting list tokens...")
list_tokens = soup.apply(getListTokens)
print("Done!")
return title_tokens + body_tokens + domain_tokens + url_tokens\
+ description_tokens + header_tokens + head_tokens + font_tokens +\
table_tokens + href_tokens + list_tokens
#Build the model
def get_html(in_df, out_file_name, chunk_size=5000, overwrite=False, test=False):
keep_cols = ["Webpage_id","Domain","Url","Tag"]
read_cols = ["Webpage_id","all_tokens","Tag"]
if test:
keep_cols = ["Webpage_id","Domain","Url"]
read_cols = ["Webpage_id","all_tokens"]
if os.path.isfile(data_dir+out_file_name)==False:
if test:
out_frame = pd.DataFrame(columns=["Webpage_id","all_tokens"])
else:
out_frame = pd.DataFrame(columns=["Webpage_id","Tag","all_tokens"])
out_frame.to_csv(data_dir+out_file_name,index=False)
else:
if overwrite:
if test:
out_frame = pd.DataFrame(columns=["Webpage_id","all_tokens"])
else:
out_frame = pd.DataFrame(columns=["Webpage_id","Tag","all_tokens"])
out_frame.to_csv(data_dir+out_file_name,index=False)
use_df = in_df[keep_cols]
html_reader_obj = pd.read_csv(data_dir+'html_data.csv',iterator=True, chunksize=chunk_size)
match_indices = use_df['Webpage_id'].values.tolist()
print("Getting tokens...")
print(len(match_indices),' indices left...')
while len(match_indices) > 0:
for chunk in html_reader_obj:
merge_df = pd.merge(use_df,chunk,how='inner',on='Webpage_id')
merge_df['all_tokens'] = get_all_tokens(merge_df)
merge_df.drop(['Html','Domain','Url'],axis=1,inplace=True)
merge_indices = merge_df['Webpage_id'].values.tolist()
match_indices = [x for x in match_indices if x not in merge_indices]
print(len(match_indices),' indices left...')
concat_frame = pd.read_csv(data_dir+out_file_name,usecols=read_cols)
return_frame = concat_frame.append(merge_df)[read_cols]
return_frame.to_csv(data_dir+out_file_name,index=False)
#frames.append(merge_df)
#Process HTMl for bags of words of the body and title.
#process_df = pd.concat(frames)
print("Done! You can get your file at\n"+data_dir+out_file_name)
def build_model():
"""Return the estimator and the object to transform the test data."""
train_df = pd.read_csv(data_dir+'train.csv')
tags = train_df['Tag']
#Get tokens
train_df = get_html(train_df)
#Fit_transform to tdfif matrix
print("Transforming to tdfif_matrix...")
train_df = vectorizer.fit_transform(train_df['all_tokens'])
#Prune unneeded features
print("Performing SVD...")
train_df = svd.fit_transform(train_df)
vector_features = vectorizer.get_feature_names()
eigen_features = [vector_features[i] for i in svd.components_[0].argsort()[::-1]][:500]
train_df = pd.DataFrame(train_df,columns=eigen_features)
train_df['Tag'] = tags
tags = train_df['Tag'].unique().tolist()
tags.sort()
tag_dict = {key: value for (key, value) in zip(tags,range(len(tags)))}
train_df['Tag_encoded'] = train_df['Tag'].map(tag_dict)
train_df = train_df.drop('Tag',axis=1)
#Build the model
print("Building the model...")
exported_pipeline = make_pipeline(
StackingEstimator(
estimator=ExtraTreesClassifier(
bootstrap=False, criterion="gini", max_features=0.2,
min_samples_leaf=11, min_samples_split=17, n_estimators=100)
),
ExtraTreesClassifier(
bootstrap=False, criterion="entropy", max_features=0.5,
min_samples_leaf=6, min_samples_split=9, n_estimators=100
)
)
x_cols = [x for x in train_df_svd.columns if x != "Tag_encoded"]
X_train, X_test, y_train, y_test = train_test_split(
train_df[x_cols],
train_df['Tag_encoded'],
test_size=0.33
)
print("Fitting the model...")
exported_pipeline.fit(X_train, y_train)
print("Done!")
return exported_pipeline, vectorizer, svd, tag_dict
def prep_test(vectorizer_obj, svd_obj):
"""Transform test dataset for predicting."""
print("Getting tokens from html...")
test_df = pd.read_csv(data_dir+'test.csv')
#Get the HTMl
test_df_tokens = get_html(test_df)
#Transform to tdfif matrix
print("Transforming to tfidf matrix...")
test_df_tdif = vectorizer_obj.transform(test_df_tokens['all_tokens'])
#Prune unneeded features
print("Performing SVD...")
test_svd_array = svd_obj.transform(test_df_tdif)
vector_features = vectorizer_obj.get_feature_names()
eigen_features = [vector_features[i] for i in svd_obj.components_[0].argsort()[::-1]][:500]
#Map to dataframe
test_df_svd = pd.DataFrame(test_svd_array,columns=eigen_features)
test_df_svd['Tag'] = test_df['Tag']
print("Done!")
return test_df_svd
def main():
#Get the model
print("Getting the model, transform objects and tag-dict...")
model, vectorizer_obj, svd_obj, tag_dict = build_model()
#Prep the test set
print("Prepping the test dataset...")
test_df = prep_test(vectorizer_obj, svd_obj)
print("Making predictions...")
predictions = model.predict(test_df)
print("Formatting predictions...")
print("Saving predictions for submission...")
return predictions
# -
# Lets try and extract more tokens. I want to extract tokens from; description, headings, highlights, special fonts, table and list elements.
#
# To do this I'll write an html reading script for a subset of rows to test my parser on. Then I'll incorporate into the get_html function and make sure I get all tokens to train on.
train_df = pd.read_csv(data_dir+'train.csv')
train_df.sample(5)
test_df = pd.read_csv(data_dir+'test.csv')
test_df.sample(5)
get_html(train_df,'train_df_all_tokens.csv')
get_html(test_df,'test_df_all_tokens.csv', test=True)
|
2018-08-10_AV_Innoplexus/07. Submission 02 - Test Token Extraction.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Dependencies
# +
# Initial imports
import pandas as pd
import matplotlib.pyplot as plt
from pathlib import Path
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.decomposition import PCA
from sklearn.manifold import TSNE
from sklearn.cluster import KMeans
import sklearn.preprocessing as preprocessing
# -
# # Data cleaning and Preparation
# +
# Read csv file
data = Path('Resources/crypto_data.csv')
cryptoData_df = pd.read_csv(data).copy()
# Drop Unnamed:0 column
cryptoData_df = cryptoData_df.drop(columns= 'Unnamed: 0')
# -
print(cryptoData_df.columns.tolist())
cryptoData_df.head()
# Filter data by IsTrading = True and then drop IsTrading column
cryptoData_df = cryptoData_df[cryptoData_df['IsTrading'] == True]
cryptoData_df = cryptoData_df.drop(columns='IsTrading')
cryptoData_df.head()
# Remove rows that has at least one NaN values
cryptoData_df.dropna(inplace=True)
cryptoData_df.isnull().sum()
print(f'Lenght of the dataframe: {len(cryptoData_df)}')
# Filter the data to only the cryptos that has been mined
cryptoData_df = cryptoData_df[cryptoData_df['TotalCoinsMined'] > 0]
print(f'Lenght of the dataframe after removing cryptos that have not been mined: {len(cryptoData_df)}')
# Remove CoinName and transform Algorithm and ProofType to numerical values
crypto_df = cryptoData_df.drop(columns='CoinName').copy()
cryptoDummies_df = pd.get_dummies(crypto_df, columns=['Algorithm', 'ProofType'])
print(f'Number of rows: {len(crypto_df)} and number of columns {len(crypto_df.columns.tolist())} for the cryptoData_df')
print(f'Number of rows: {len(cryptoDummies_df)} and number of columns {len(cryptoDummies_df.columns.tolist())} for the cryptoDummies_df')
# create scaler and Standardize the dataset
scaler = StandardScaler()
scaled_data = scaler.fit_transform(cryptoDummies_df)
# # Dimensionality Reduction
# +
# Initialize PCA model with 90% of the data
pca = PCA(n_components=0.9)
# Get principal components for the iris data.
scaled_pca = pca.fit_transform(scaled_data)
# -
# Create a dataframe with the iris data
pca_df = pd.DataFrame(data=scaled_pca, index=cryptoDummies_df.index)
pca_df
# Fetch features and how did it change
print(f'Number of features {len(cryptoDummies_df.columns.tolist())} for the cryptoDummies_df')
print(f'Number of features {len(pca_df.columns.tolist())} for the pca_df')
# Initialize t-SNE model
tsne = TSNE(learning_rate=200)
# Reduce dimensions
tsne_features = tsne.fit_transform(scaled_pca)
# Shape of the data set
tsne_features.shape
# +
# Create dataframe to visualize the clusters
tsne_df = pd.DataFrame(data=tsne_features, columns=['Principal Component 1','Principal Component 2'])
plt.figure(figsize=(10,6))
plt.scatter(tsne_df['Principal Component 1'], tsne_df['Principal Component 2'])
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.show()
# -
# There are at least 2 to 3 cluster after the tsne transformation
# # Cluster Analysis with k-Means
# +
inertia = []
k = list(range(1, 11))
# Calculate the inertia for the range of k values
for i in k:
km = KMeans(n_clusters=i, random_state=42)
km.fit(tsne_df)
inertia.append(km.inertia_)
# Create the Elbow Curve using hvPlot
elbow_data = {"k": k, "inertia": inertia}
df_elbow = pd.DataFrame(elbow_data)
df_elbow
# -
# Plot the elbow curve to find the best candidate(s) for k
plt.figure(figsize=(10,6))
plt.plot(df_elbow['k'], df_elbow['inertia'])
plt.xticks(range(1,11))
plt.xlabel('Number of clusters')
plt.ylabel('Inertia')
plt.title('Elbow curve for customer data')
plt.show()
def get_clusters(k, data):
# Initialize the K-Means model
model = KMeans(n_clusters=k, random_state=0)
# Train the model
model.fit(data)
# Predict clusters
predictions = model.predict(data)
# Create return DataFrame with predicted clusters
data["class"] = model.labels_
return data
clusters = get_clusters(4, tsne_df)
clusters
def show_clusters(df):
plt.figure(figsize=(10,6))
plt.scatter(df['Principal Component 1'], df['Principal Component 2'], c=df['class'])
plt.xlabel('p[1]')
plt.ylabel('p[2]')
plt.show()
show_clusters(clusters)
# #### From the graph, we can observe that the cryptos can be clustered into 4 different groups with 3 outliers. My recommendation would be to pick 2 cryptos from each cluster and monitore them to see which one perform the best. The ones that I would chose will be those with similar Total Coins Mined and Total Coin Supply. If there is a high demand with low coin supply, then the value of the crypto will skyrocket.
|
Unsupervised_ML.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python (lsl_eeg)
# language: python
# name: lsl_eeg
# ---
# +
import os
import pandas as pd
# -
# The following BMBF (left and right) recordings had `EventData` but no matching `ExperimentData`.
left = [
"0cadb84adb8c4d7e8dad99e93fd63c92",
"0cd501320bd841758f204e43ce00362f",
"267d95a19e8147eca7b2080ba596cba1",
"2e2ce16f18514b0080db2e9dfbd8d919",
"4159d09e5c524e8c85e1ac40796898e4",
"<KEY>",
"5caba490f12a49fd91013d09ff416e79",
"61a79ce907f14fd2b9e06bf69d420085",
"<KEY>",
"<KEY>",
"<KEY>",
"<KEY>",
"<KEY>",
"<KEY>",
"bd58ebe70fa44bafad76ecacca28f2b0",
"<KEY>",
"<KEY>",
"<KEY>",
"da26f4ead610421785f7fd0cda87dcfe",
"e7af7fc5e75c43809a96ae4e1f0e730e",
]
right = [
"0cd501320bd841758f204e43ce00362f",
"267d95a19e8147eca7b2080ba596cba1",
"2e2ce16f18514b0080db2e9dfbd8d919",
"4159d09e5c524e8c85e1ac40796898e4",
"<KEY>",
"<KEY>",
"<KEY>",
"<KEY>",
"bd58ebe70fa44bafad76ecacca28f2b0",
"c227fc73d82244de8a37f3592161a53e",
"c76ddcb99c9940ecaf8d7a0fbef6bdb2",
"c7ffb69015b94c819d131095ffd09568",
"da26f4ead610421785f7fd0cda87dcfe",
"e7af7fc5e75c43809a96ae4e1f0e730e",
]
# +
print(f"TOTAL left: {len(left)}")
print(f"TOTAL right: {len(right)}")
dup_left = []
for l in left:
if l in right:
print(f"Duplicated ID => {l}")
dup_left.append(l)
print(f"TOTAL left duplicated: {len(dup_left)}")
# +
print(f"TOTAL left: {len(left)}")
print(f"TOTAL right: {len(right)}")
dup_left = []
for r in right:
if r in left:
print(f"Duplicated ID => {r}")
dup_left.append(l)
print(f"TOTAL right duplicated: {len(dup_left)}")
# -
# Interestingly, 14 out of 20 `EventData` recording ids were generated on both left and right sides without matching `ExperimentData` recording.
# +
# get files to merge ids
path = "../data/ids"
files = os.listdir(path)
files
# +
df = pd.DataFrame()
# merge uids in one df
for f in files:
cur = pd.read_csv(f"{path}/{f}")
df = cur if df.index.size == 0 else df.append(cur)
df = df.sort_values("created")
display(df)
# -
# check for duplicates
duplicated = df[df["id"].duplicated() == True]
duplicated
# to be 100% sure
print(f"Length before duplicates check: {df.index.size}")
print(f"Length after duplicates check: {len(df.id.unique())}")
# There are no duplicates (uids)
df = df.set_index("id")
df
df.to_csv("../participants_full.csv")
|
checks/ids/unify_ids_checks_and_notes.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:dev_pydelmod]
# language: python
# name: conda-env-dev_pydelmod-py
# ---
import pydsm
from pydsm import postpro
# # Sample Notebook to show postprocessor usage
# ## Setup
# A setup consists of "Observed" and one or more "Models":
# * A study has a name and dssfile
# * A location has a name, a bpart and a description
# * A vartype has a name and units
#
# +
obs_study=postpro.Study('Observed','data/sample_obs.dss')
m1_study=postpro.Study('Model1','data/sample_model1.dss')
m2_study=postpro.Study('Model2','data/sample_model2.dss')
studies=[obs_study, m1_study, m2_study]
location=postpro.Location('RSAN018','RSAN018','Jersey Pt Station')
obs_location=postpro.Location('RSAN018','JER','Jersey Pt Station') # B part for observed is JER
vartype=postpro.VarType('EC','mmhos/cm')
# -
pp=[postpro.PostProcessor(study,location,vartype) for study in [m1_study,m2_study]]
pp=[postpro.PostProcessor(obs_study,obs_location,vartype)]+pp
# Customized processor for observed for merging and resampling to get it to uniform 15 min data
pp[0].do_resample_with_merge('15MIN')
pp[0].do_fill_in()
# pp[0].do_scale(-1) # If you want to scale the values as part of the post processing uncomment this line
for p in pp:
p.process()
p.store_processed()
# Show loading of a specific time window. Used in other places
p.load_processed('05OCT2013 0000 - 21OCT2013 0000')
p.df.index[0],p.df.index[-1]
|
examples/nbcalibplots/sample_calib_postpro.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import numpy as np
# +
def autolabel(ax, rects, xpos='center'):
"""
Attach a text label above each bar in *rects*, displaying its height.
*xpos* indicates which side to place the text w.r.t. the center of
the bar. It can be one of the following {'center', 'right', 'left'}.
"""
xpos = xpos.lower() # normalize the case of the parameter
ha = {'center': 'center', 'right': 'left', 'left': 'right'}
offset = {'center': 0.5, 'right': 0.57, 'left': 0.43} # x_txt = x + w*off
for rect in rects:
height = rect.get_height()
ax.text(rect.get_x() + rect.get_width()*offset[xpos], 1.01*height,
'{}'.format(height), ha=ha[xpos], va='bottom')
sns.set(style="darkgrid")
# +
std = pd.DataFrame({
'Amsterdam (NL)': [1.03, 0.61, 0.50, 2.37, 4.57],
'Poznań (PL)': [1.44, 1.20, 2.63, 4.06, 6.41],
'Jülich (DE)': [0.97, 2.12, 2.27, 3.53, 4.51],
})
df = pd.DataFrame({
'Amsterdam (NL)': [9.99, 11.98, 11.89, 14.59, 19.24],
'Poznań (PL)': [7.82, 8.97, 12.24, 14.44, 26.63],
'Jülich (DE)': [9.03, 12.50, 17.00, 16.98, 32.15],
'x': [20, 40, 80, 160, 320],
})
plt.plot('x', 'Jülich (DE)', data=df, marker='s', color='peru')
plt.fill_between(df['x'], df['Jülich (DE)'] - std['Jülich (DE)'], df['Jülich (DE)'] + std['Jülich (DE)'], color='k', alpha=.1)
plt.plot('x', 'Amsterdam (NL)', data=df, marker='s', color='orange')
plt.fill_between(df['x'], df['Amsterdam (NL)'] - std['Amsterdam (NL)'], df['Amsterdam (NL)'] + std['Amsterdam (NL)'], color='k', alpha=.1)
plt.plot('x', 'Poznań (PL)', data=df, marker='s', color='dodgerblue')
plt.fill_between(df['x'], df['Poznań (PL)'] - std['Poznań (PL)'], df['Poznań (PL)'] + std['Poznań (PL)'], color='k', alpha=.1)
plt.xlabel('Total size (in gigabytes)')
plt.ylabel('Time (in minutes)')
plt.xticks(df['x'])
plt.title('Time as a function of size')
plt.legend(loc='upper left')
plt.savefig('time-size-func.pdf')
plt.show()
# -
def autolabel_mins(ax, rects, xpos='center'):
xpos = xpos.lower() # normalize the case of the parameter
ha = {'center': 'center', 'right': 'left', 'left': 'right'}
offset = {'center': 0.5, 'right': 0.57, 'left': 0.43} # x_txt = x + w*off
for rect in rects:
height = rect.get_height()
seconds = round(height * 60)
m, s = divmod(seconds, 60)
h, m = divmod(m, 60)
ax.text(rect.get_x() + rect.get_width()*offset[xpos], 1.01*height, "%02d:%02d" % (m, s), ha=ha[xpos], va='bottom')
# +
objects = ('Jülich (DE)', 'Amsterdam (NL)', 'Poznań (PL)')
y_pos = np.arange(len(objects))
time = [8.19,5.19,7.53]
std = [4.64, 1.53, 2.56]
bars = plt.bar(y_pos, time, align='center', yerr=std, alpha=0.8)
bars[0].set_color('peru')
bars[1].set_color('orange')
bars[2].set_color('dodgerblue')
autolabel_mins(plt, bars, 'right')
plt.xticks(y_pos, objects)
plt.ylabel('Time (in minutes)')
plt.title('Estimated queuing/preparation time')
plt.savefig('queing-time.pdf')
plt.show()
# +
de_means, de_std = (96.3, 78.3, 90.5), (17.1, 3.1, 5.6)
nl_means, nl_std = (96.5, 241.5, 91.74), (0.7, 25.2, 1.8)
pl_means, pl_std = (21.1, 34.2, 120.04), (9.8, 6.2, 16.2)
fig, (ax, ax2) = plt.subplots(2, 1, sharex=True)
ind = np.arange(len(nl_means)) # the x locations for the groups
width = 0.4 # the width of the bars
rects1 = ax.bar(ind - width/2, de_means, width/2, yerr=de_std,
color='peru', label='Jülich (DE', alpha=0.8)
rects1 = ax2.bar(ind - width/2, de_means, width/2, yerr=de_std,
color='peru', label='Jülich (DE)', alpha=0.8)
rects2 = ax.bar(ind, nl_means, width /2, yerr=nl_std,
color='orange', label='Amsterdam (NL)', alpha=0.8)
rects2 = ax2.bar(ind, nl_means, width /2, yerr=nl_std,
color='orange', label='Amsterdam (NL)', alpha=0.8)
rects3 = ax.bar(ind + width/2, pl_means, width /2, yerr=pl_std,
color='dodgerblue', label='Poznań (PL)', alpha=0.8)
rects3 = ax2.bar(ind + width/2, pl_means, width /2, yerr=pl_std,
color='dodgerblue', label='Poznań (PL)', alpha=0.8)
# zoom-in / limit the view to different portions of the data
ax.set_ylim(200, 275) # outliers only
ax2.set_ylim(0, 150) # most of the data
ax.spines['bottom'].set_visible(False)
ax2.spines['top'].set_visible(False)
ax.xaxis.tick_top()
ax.tick_params(labeltop=False)
ax2.xaxis.tick_bottom()
# Add some text for labels, title and custom x-axis tick labels, etc.
ax.set_ylabel('Transfer speed (in MB/s)', y=0)
ax2.set_xlabel('Target location)')
ax.set_xticks(ind)
ax.set_xticklabels(('LRZ (DE)', 'LISA (NL)', 'CYF (PL)'))
ax.legend()
autolabel(ax2, rects1, "left")
autolabel(ax2, rects2[:1], "center")
autolabel(ax, rects2[1:2], "left")
autolabel(ax2, rects2[2:], "center")
autolabel(ax2, rects3, "right")
d = .01
kwargs = dict(transform=ax.transAxes, color='k', clip_on=False)
ax.plot((-d, +d), (-d, +d), **kwargs) # top-left diagonal
ax.plot((1 - d, 1 + d), (-d, +d), **kwargs) # top-right diagonal
kwargs.update(transform=ax2.transAxes) # switch to the bottom axes
ax2.plot((-d, +d), (1 - d, 1 + d), **kwargs) # bottom-left diagonal
ax2.plot((1 - d, 1 + d), (1 - d, 1 + d), **kwargs) # bottom-right diagonal
plt.title('Transfer speeds from LTA to HPCs', y=2.3)
plt.savefig('transfer-speeds.pdf')
plt.show()
# -
|
matplotlib/lofar-benchmark.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# name: python2
# ---
# + [markdown] colab_type="text" id="Ma19Ks2CTDbZ"
# ##### Copyright 2018 The TF-Agents Authors.
# + [markdown] colab_type="text" id="4_16bQF0anmE"
# ### Get Started
# <table class="tfo-notebook-buttons" align="left">
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/tensorflow/agents/blob/master/tf_agents/colabs/2_environments_tutorial.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
# </td>
# <td>
# <a target="_blank" href="https://github.com/tensorflow/agents/blob/master/tf_agents/colabs/2_environments_tutorial.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
# </td>
# </table>
#
# + colab={} colab_type="code" id="KKU2iY_7at8Y"
# Note: If you haven't installed tf-agents or gym yet, run:
# !pip install tf-agents-nightly
# !pip install tf-nightly
# !pip install 'gym==0.10.11'
# + [markdown] colab_type="text" id="6J5G3q-xa3Ag"
# ### Imports
# + colab={} colab_type="code" id="1ZAoFNwnRbKK"
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import abc
import tensorflow as tf
import numpy as np
from tf_agents.environments import py_environment
from tf_agents.environments import tf_environment
from tf_agents.environments import tf_py_environment
from tf_agents.environments import utils
from tf_agents.specs import array_spec
from tf_agents.environments import wrappers
from tf_agents.environments import suite_gym
from tf_agents.trajectories import time_step as ts
tf.compat.v1.enable_v2_behavior()
# + [markdown] colab_type="text" id="9h3B-YBHopJI"
# # Introduction
# + [markdown] colab_type="text" id="n9c6vCPGovOM"
# The goal of Reinforcement Learning (RL) is to design agents that learn by interacting with an environment. In the standard RL setting, the agent receives an observation at every time step and chooses an action. The action is applied to the environment and the environment returns a reward and and a new observation. The agent trains a policy to choose actions to maximize the sum of rewards, also known as return.
#
# In TF-Agents, environments can be implemented either in Python or TensorFlow. Python environments are usually easier to implement, understand or debug, but TensorFlow environments are more efficient and allow natural parallelization. The most common workflow is to implement an environment in Python and use one of our wrappers to automatically convert it into TensorFlow.
#
# Let us look at Python environments first. TensorFlow environments follow a very similar API.
# + [markdown] colab_type="text" id="x-y4p9i9UURn"
# # Python Environments
# + [markdown] colab_type="text" id="JPSwHONKMNv9"
# Python environments have a `step(action) -> next_time_step` method that applies an action to the environment, and returns the following information about the next step:
# 1. `observation`: This is the part of the environment state that the agent can observe to choose its actions at the next step.
# 2. `reward`: The agent is learning to maximize the sum of these rewards across multiple steps.
# 3. `step_type`: Interactions with the environment are usually part of a sequence/episode. e.g. multiple moves in a game of chess. step_type can be either `FIRST`, `MID` or `LAST` to indicate whether this time step is the first, intermediate or last step in a sequence.
# 4. `discount`: This is a float representing how much to weight the reward at the next time step relative to the reward at the current time step.
#
# These are grouped into a named tuple `TimeStep(step_type, reward, discount, observation)`.
#
# The interface that all python environments must implement is in `environments/py_environment.PyEnvironment`. The main methods are:
# + colab={} colab_type="code" id="GlD2Dd2vUTtg"
class PyEnvironment(object):
def reset(self):
"""Return initial_time_step."""
self._current_time_step = self._reset()
return self._current_time_step
def step(self, action):
"""Apply action and return new time_step."""
if self._current_time_step is None:
return self.reset()
self._current_time_step = self._step(action)
return self._current_time_step
def current_time_step(self):
return self._current_time_step
def time_step_spec(self):
"""Return time_step_spec."""
@abc.abstractmethod
def observation_spec(self):
"""Return observation_spec."""
@abc.abstractmethod
def action_spec(self):
"""Return action_spec."""
@abc.abstractmethod
def _reset(self):
"""Return initial_time_step."""
@abc.abstractmethod
def _step(self, action):
"""Apply action and return new time_step."""
self._current_time_step = self._step(action)
return self._current_time_step
# + [markdown] colab_type="text" id="zfF8koryiGPR"
# In addition to the `step()` method, environments also provide a `reset()` method that starts a new sequence and provides an initial `TimeStep`. It is not necessary to call the `reset` method explicitly. We assume that environments reset automatically, either when they get to the end of an episode or when step() is called the first time.
#
# Note that subclasses do not implement `step()` or `reset()` directly. They instead override the `_step()` and `_reset()` methods. The time steps returned from these methods will be cached and exposed through `current_time_step()`.
#
# The `observation_spec` and the `action_spec` methods return a nest of `(Bounded)ArraySpecs` that describe the name, shape, datatype and ranges of the observations and actions respectively.
#
# In TF-Agents we repeatedly refer to nests which are defined as any tree like structure composed of lists, tuples, named-tuples, or dictionaries. These can be arbitrarily composed to maintain structure of observations and actions. We have found this to be very useful for more complex environments where you have many observations and actions.
# + [markdown] colab_type="text" id="r63R-RbjcIRw"
# ## Using Standard Environments
#
# TF Agents has built-in wrappers for many standard environments like the OpenAI Gym, DeepMind-control and Atari, so that they follow our `py_environment.PyEnvironment` interface. These wrapped evironments can be easily loaded using our environment suites. Let's load the CartPole environment from the OpenAI gym and look at the action and time_step_spec.
# + colab={} colab_type="code" id="1kBPE5T-nb2-"
environment = suite_gym.load('CartPole-v0')
print('action_spec:', environment.action_spec())
print('time_step_spec.observation:', environment.time_step_spec().observation)
print('time_step_spec.step_type:', environment.time_step_spec().step_type)
print('time_step_spec.discount:', environment.time_step_spec().discount)
print('time_step_spec.reward:', environment.time_step_spec().reward)
# + [markdown] colab_type="text" id="vWXOC863Apo_"
# So we see that the environment expects actions of type `int64` in [0, 1] and returns `TimeSteps` where the observations are a `float32` vector of length 4 and discount factor is a `float32` in [0.0, 1.0]. Now, let's try to take a fixed action `(1,)` for a whole episode.
# + colab={} colab_type="code" id="AzIbOJ0-0y12"
action = 1
time_step = environment.reset()
print(time_step)
while not time_step.is_last():
time_step = environment.step(action)
print(time_step)
# + [markdown] colab_type="text" id="4xAbBl4_PMtA"
# ## Creating your own Python Environment
#
# For many clients, a common use case is to apply one of the standard agents (see agents/) in TF-Agents to their problem. To do this, they have to frame their problem as an environment. So let us look at how to implement an environment in Python.
#
# Let's say we want to train an agent to play the following (Black Jack inspired) card game:
#
# 1. The game is played using an infinite deck of cards numbered 1...10.
# 2. At every turn the agent can do 2 things: get a new random card, or stop the current round.
# 3. The goal is to get the sum of your cards as close to 21 as possible at the end of the round, without going over.
#
# An environment that represents the game could look like this:
#
# 1. Actions: We have 2 actions. Action 0: get a new card, and Action 1: terminate the current round.
# 2. Observations: Sum of the cards in the current round.
# 3. Reward: The objective is to get as close to 21 as possible without going over, so we can achieve this using the following reward at the end of the round:
# sum_of_cards - 21 if sum_of_cards <= 21, else -21
#
#
# + colab={} colab_type="code" id="9HD0cDykPL6I"
class CardGameEnv(py_environment.PyEnvironment):
def __init__(self):
self._action_spec = array_spec.BoundedArraySpec(
shape=(), dtype=np.int32, minimum=0, maximum=1, name='action')
self._observation_spec = array_spec.BoundedArraySpec(
shape=(1,), dtype=np.int32, minimum=0, name='observation')
self._state = 0
self._episode_ended = False
def action_spec(self):
return self._action_spec
def observation_spec(self):
return self._observation_spec
def _reset(self):
self._state = 0
self._episode_ended = False
return ts.restart(np.array([self._state], dtype=np.int32))
def _step(self, action):
if self._episode_ended:
# The last action ended the episode. Ignore the current action and start
# a new episode.
return self.reset()
# Make sure episodes don't go on forever.
if action == 1:
self._episode_ended = True
elif action == 0:
new_card = np.random.randint(1, 11)
self._state += new_card
else:
raise ValueError('`action` should be 0 or 1.')
if self._episode_ended or self._state >= 21:
reward = self._state - 21 if self._state <= 21 else -21
return ts.termination(np.array([self._state], dtype=np.int32), reward)
else:
return ts.transition(
np.array([self._state], dtype=np.int32), reward=0.0, discount=1.0)
# + [markdown] colab_type="text" id="LYEwyX7QsqeX"
# Let's make sure we did everything correctly defining the above environment. When creating your own environment you must make sure the observations and time_steps generated follow the correct shapes and types as defined in your specs. These are used to generate the TensorFlow graph and as such can create hard to debug problems if we get them wrong.
#
# To validate our environment we will use a random policy to generate actions and we will iterate over 5 episodes to make sure things are working as intended. An error is raised if we receive a time_step that does not follow the environment specs.
# + colab={} colab_type="code" id="6Hhm-5R7spVx"
environment = CardGameEnv()
utils.validate_py_environment(environment, episodes=5)
# + [markdown] colab_type="text" id="_36eM7MvkNOg"
# Now that we know the environment is working as intended, let's run this environment using a fixed policy: ask for 3 cards and then end the round.
# + colab={} colab_type="code" id="FILylafAkMEx"
get_new_card_action = 0
end_round_action = 1
environment = CardGameEnv()
time_step = environment.reset()
print(time_step)
cumulative_reward = time_step.reward
for _ in range(3):
time_step = environment.step(get_new_card_action)
print(time_step)
cumulative_reward += time_step.reward
time_step = environment.step(end_round_action)
print(time_step)
cumulative_reward += time_step.reward
print('Final Reward = ', cumulative_reward)
# + [markdown] colab_type="text" id="_vBLPN3ioyGx"
# ## Environment Wrappers
#
# An environment wrapper takes a python environment and returns a modified version of the environment. Both the original environment and the modified environment are instances of `py_environment.PyEnvironment`, and multiple wrappers can be chained together.
#
# Some common wrappers can be found in `environments/wrappers.py`. For example:
#
# 1. `ActionDiscretizeWrapper`: Converts a continuous action space to a discrete action space.
# 2. `RunStats`: Captures run statistics of the environment such as number of steps taken, number of episodes completed etc.
# 3. `TimeLimit`: Terminates the episode after a fixed number of steps.
#
#
#
#
# + [markdown] colab_type="text" id="_8aIybRdnFfb"
# ### Example 1: Action Discretize Wrapper
# + [markdown] colab_type="text" id="YIaxJRUpvfyc"
# InvertedPendulum is a PyBullet environment that accepts continuous actions in the range `[-1, 1]`. If we want to train a discrete action agent such as DQN on this environment, we have to discretize (quantize) the action space. This is exactly what the `ActionDiscretizeWrapper` does. Compare the `action_spec` before and after wrapping:
# + colab={} colab_type="code" id="AJxEoZ4HoyjR"
env = suite_gym.load('Pendulum-v0')
print('Action Spec:', env.action_spec())
discrete_action_env = wrappers.ActionDiscretizeWrapper(env, num_actions=5)
print('Discretized Action Spec:', discrete_action_env.action_spec())
# + [markdown] colab_type="text" id="njFjW8bmwTWJ"
#
# The wrapped `discrete_action_env` is an instance of `py_environment.PyEnvironment` and can be treated like a regular python environment.
#
#
# + [markdown] colab_type="text" id="8l5dwAhsP_F_"
# # TensorFlow Environments
# + [markdown] colab_type="text" id="iZG39AjBkTjr"
# The interface for TF environments is defined in `environments/tf_environment.TFEnvironment` and looks very similar to the Python environments. TF Environments differ from python envs in a couple of ways:
#
# * They generate tensor objects instead of arrays
# * TF environments add a batch dimension to the tensors generated when compared to the specs.
#
# Converting the python environments into TFEnvs allows tensorflow to parellalize operations. For example, one could define a `collect_experience_op` that collects data from the environment and adds to a `replay_buffer`, and a `train_op` that reads from the `replay_buffer` and trains the agent, and run them in parallel naturally in TensorFlow.
# + colab={} colab_type="code" id="WKBDDZqKTxsL"
class TFEnvironment(object):
def time_step_spec(self):
"""Describes the `TimeStep` tensors returned by `step()`."""
def observation_spec(self):
"""Defines the `TensorSpec` of observations provided by the environment."""
def action_spec(self):
"""Describes the TensorSpecs of the action expected by `step(action)`."""
def reset(self):
"""Returns the current `TimeStep` after resetting the Environment."""
return self._reset()
def current_time_step(self):
"""Returns the current `TimeStep`."""
return self._current_time_step()
def step(self, action):
"""Applies the action and returns the new `TimeStep`."""
return self._step(action)
@abc.abstractmethod
def _reset(self):
"""Returns the current `TimeStep` after resetting the Environment."""
@abc.abstractmethod
def _current_time_step(self):
"""Returns the current `TimeStep`."""
@abc.abstractmethod
def _step(self, action):
"""Applies the action and returns the new `TimeStep`."""
# + [markdown] colab_type="text" id="tFkBIA92ThWf"
# The `current_time_step()` method returns the current time_step and initializes the environment if needed.
#
# The `reset()` method forces a reset in the environment and returns the current_step.
#
# If the `action` doesn't depend on the previous `time_step` a `tf.control_dependency` is needed in `Graph` mode.
#
# For now, let us look at how `TFEnvironments` are created.
# + [markdown] colab_type="text" id="S6wS3AaLdVLT"
# ## Creating your own TensorFlow Environment
#
# This is more complicated than creating environments in Python, so we will not cover it in this colab. An example is available [here](https://github.com/tensorflow/agents/blob/master/tf_agents/environments/tf_environment_test.py). The more common use case is to implement your environment in Python and wrap it in TensorFlow using our `TFPyEnvironment` wrapper (see below).
# + [markdown] colab_type="text" id="V_Ny2lb-dU5R"
# ## Wrapping a Python Environment in TensorFlow
# + [markdown] colab_type="text" id="Lv4-UcurZ8nb"
# We can easily wrap any Python environment into a TensorFlow environment using the `TFPyEnvironment` wrapper.
# + colab={} colab_type="code" id="UYerqyNfnVRL"
env = suite_gym.load('CartPole-v0')
tf_env = tf_py_environment.TFPyEnvironment(env)
print(isinstance(tf_env, tf_environment.TFEnvironment))
print("TimeStep Specs:", tf_env.time_step_spec())
print("Action Specs:", tf_env.action_spec())
# + [markdown] colab_type="text" id="z3WFrnX9CNpC"
# Note the specs are now of type: `(Bounded)TensorSpec`.
# + [markdown] colab_type="text" id="vQPvC1ARYALj"
# ## Usage Examples
# + [markdown] colab_type="text" id="ov7EIrk8dKUU"
# ### Simple Example
# + colab={} colab_type="code" id="gdvFqUqbdB7u"
env = suite_gym.load('CartPole-v0')
tf_env = tf_py_environment.TFPyEnvironment(env)
# reset() creates the initial time_step after resetting the environment.
time_step = tf_env.reset()
num_steps = 3
transitions = []
reward = 0
for i in range(num_steps):
action = tf.constant([i % 2])
# applies the action and returns the new TimeStep.
next_time_step = tf_env.step(action)
transitions.append([time_step, action, next_time_step])
reward += next_time_step.reward
time_step = next_time_step
np_transitions = tf.nest.map_structure(lambda x: x.numpy(), transitions)
print('\n'.join(map(str, np_transitions)))
print('Total reward:', reward.numpy())
# + [markdown] colab_type="text" id="kWs48LNsdLnc"
# ### Whole Episodes
# + colab={} colab_type="code" id="t561kUXMk-KM"
env = suite_gym.load('CartPole-v0')
tf_env = tf_py_environment.TFPyEnvironment(env)
time_step = tf_env.reset()
rewards = []
steps = []
num_episodes = 5
for _ in range(num_episodes):
episode_reward = 0
episode_steps = 0
while not time_step.is_last():
action = tf.random_uniform([1], 0, 2, dtype=tf.int32)
time_step = tf_env.step(action)
episode_steps += 1
episode_reward += time_step.reward.numpy()
rewards.append(episode_reward)
steps.append(episode_steps)
time_step = tf_env.reset()
num_steps = np.sum(steps)
avg_length = np.mean(steps)
avg_reward = np.mean(rewards)
print('num_episodes:', num_episodes, 'num_steps:', num_steps)
print('avg_length', avg_length, 'avg_reward:', avg_reward)
|
tf_agents/colabs/2_environments_tutorial.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # TextAttack End-to-End
#
# This tutorial provides a broad end-to-end overview of training, evaluating, and attacking a model using TextAttack.
# [](https://colab.research.google.com/drive/1cBRUj2l0m8o81vJGGFgO-o_zDLj24M5Y?usp=sharing)
#
# [](https://github.com/QData/TextAttack/blob/master/docs/examples/1_Introduction_and_Transformations.ipynb)
# ## Training
#
# First, we're going to train a model. TextAttack integrates directly with [transformers](https://github.com/huggingface/transformers/) and [datasets](https://github.com/huggingface/datasets) to train any of the `transformers` pre-trained models on datasets from `datasets`.
#
# Let's use the SNLI textual entailment dataset: it's relatively short (in word count, at least), and showcases a lot of the features of `textattack train`. Let's take a look at the dataset using `textattack peek-dataset`:
# !textattack peek-dataset --dataset-from-huggingface snli
# The dataset looks good! It's not lowercased already, so we'll make sure our model is cased. Looks like there are some missing (-1) labels, so we need to filter those out. The longest input is 114 words, so we can cap our maximum sequence length (`--max-length`) at 128.
#
# We'll train [`distilbert-base-cased`](https://huggingface.co/transformers/model_doc/distilbert.html), since it's a relatively small model, and a good example of how we integrate with `transformers`.
#
# So we have our command:
#
# ```bash
# textattack train \ # Train a model with TextAttack
# --model distilbert-base-cased \ # Using distilbert, cased version, from `transformers`
# --dataset snli \ # On the SNLI dataset
# --max-length 128 \ # With a maximum sequence length of 128
# --batch-size 256 \ # And a batch size of 256
# --epochs 3 \ # For 3 epochs
# --allowed-labels 0 1 2 # And only allow labels 0, 1, 2 (filter out -1!)
# ```
#
# Now let's run it:
# !textattack train --model distilbert-base-cased --dataset snli --max-length 128 --batch-size 256 --epochs 3 --allowed-labels 0 1 2
# ## Evaluation
#
# We successfully fine-tuned `distilbert-base-cased` for 5 epochs. Now let's evaluate it using `textattack eval`. This is as simple as providing the path to the pretrained model to `--model`, along with the number of evaluation samples. `textattack eval` will automatically load the evaluation data from training:
# !textattack eval --num-examples 1000 --model /p/qdata/jm8wx/research/text_attacks/textattack/outputs/training/distilbert-base-cased-snli-2020-06-24-14:03/
# Awesome -- we were able to train a model up to 86.8% validation-set accuracy– with only a single command!
# ## Attack
#
# Finally, let's attack our pre-trained model. We can do this the same way as before (by providing the path to the pretrained model to `--model`). For our attack, let's use the "TextFooler" attack recipe, from the paper ["Is BERT Really Robust? A Strong Baseline for Natural Language Attack on Text Classification and Entailment" (Jin et al, 2019)](https://arxiv.org/abs/1907.11932). We can do this by passing `--recipe textfooler` to `textattack attack`.
#
# > *Warning*: We're printing out 1000 examples and, if the attack succeeds, their perturbations. The output of this command is going to be quite long!
#
# !textattack attack --recipe textfooler --num-examples 1000 --model /p/qdata/jm8wx/research/text_attacks/textattack/outputs/training/distilbert-base-cased-snli-2020-06-24-14:03/
# Looks like our model was 86.8% successful (makes sense - same evaluation set as `textattack eval`!), meaning that TextAttack attacked the model with 868 examples (since the attack won't run if an example is originally mispredicted). The attack success rate was 88.7%, meaning that TextFooler failed to find an adversarial example only 11.3% of the time.
#
#
# ## Conclusion
#
# That's all, folks! We've learned how to train, evaluate, and attack a model with TextAttack, using only three commands! 😀
|
docs/examples/0_End_to_End.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + pycharm={"is_executing": true}
import numpy as np
# + pycharm={"name": "#%%\n"}
small_counts = np.random.randint(0, 100, 20)
# + pycharm={"name": "#%%\n"}
np.floor_divide(small_counts, 10)
# + pycharm={"name": "#%%\n"}
large_counts = [296, 8286, 64011, 80, 3, 725, 867, 2215, 7689, 11495, 91897, 44, 28, 7971, 926, 122, 22222]
# + pycharm={"name": "#%%\n"}
np.floor(np.log10(large_counts))
|
2-3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# +
# -*- coding: utf-8 -*-
# segmentation.py
# this file is material part of of the dissertation 'Deep Learning for Emotion Recognition in Cartoons'
# [c] 2016-2017 <NAME>
import os
import cv2
import numpy as np
# -
# settings
videopath = './No Sound/'
exclusion = {
'.DS_Store'
}
# gets the import location for videos (dataset).
def get_dataset(videopath=videopath):
videos = os.listdir(os.path.dirname(videopath))
for item in videos:
if item in exclusion:
videos.remove(item)
return videos
# detect character by using a custom trained haar cascade for each character.
def detect(character, video, show_video=True):
cap = cv2.VideoCapture(videopath + video)
face_cascade = cv2.CascadeClassifier(character['cascade'])
results_path = os.path.join('results/' + "tom_or_jerry")
# make a folder in results for our recognised faces.
if not os.path.exists(results_path) and character['save'] == True:
os.mkdir(results_path)
while(1):
# grab a frame.
ret, frame = cap.read()
faces = None
if character['name'] == "Tom":
# detect faces in our image.
faces = face_cascade.detectMultiScale(frame,
scaleFactor=1.10,
minNeighbors=40,
minSize=(24, 24),
flags=cv2.cv.CV_HAAR_SCALE_IMAGE
)
else:
faces = face_cascade.detectMultiScale(frame,
scaleFactor=1.10,
minNeighbors=20,
minSize=(24, 24),
flags=cv2.cv.CV_HAAR_SCALE_IMAGE
)
# loop over detected faces.
for (x, y, w, h) in faces:
# setup region of interest (ROI) for the captured face.
roi = frame[y:y+h, x:x+w]
frame_number = str(int(cap.get(cv2.cv.CV_CAP_PROP_POS_FRAMES)))
# write detected face to disk.
if character['save'] == True:
cv2.imwrite(results_path + '/' + "tom_or_jerry" + '_frame_' + frame_number + '.png', roi)
if show_video is True:
# display detection box for visual purposes.
cv2.rectangle(frame, (x, y), (x+w, y+h), character['detect_color'], 2)
cv2.putText(frame, character['name'], (x, y - 10), cv2.FONT_HERSHEY_SIMPLEX, 0.55, (0, 255, 0), 2)
else:
print 'detected face @ frame ' + frame_number
if show_video is True:
# display our image.
try:
cv2.imshow('frame', frame)
except:
break
# quit or (next video) on esc.
esc = cv2.waitKey(30) & 0xff
if esc == 27:
break
# destroy & release resources.
cv2.destroyAllWindows()
cap.release()
# process all our videos.
def process(character):
videos = get_dataset()
print 'number of videos: ' + str(len(videos))
for video in enumerate(videos):
episode = video[1].split('- ')[1].split('(')[0].strip()
# dump frames and save to disk each character.
print 'attempting to detect ' + character['name'] + ' in \'' + episode + '\''
# detect our character.
detect(character, video[1], show_video=True)
# step 1: prepare our results folder.
if not os.path.exists('results'):
os.mkdir('results')
# step 2: process all our videos to detect Tom & Jerry.
characters = [
{
'name': "Tom",
'detect_color': (165, 91, 0),
'save': True,
'cascade': 'tom.xml'
},
{
'name': "Jerry",
'detect_color': (165, 100, 0),
'save': True,
'cascade': 'jerry.xml'
}
]
# process characters...
[process(character) for character in characters]
print 'done'
|
notebooks/segmentation_notebook.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="rVLSo4TR0aQU"
# # CIS 519 Homework 2: Linear Classifiers
#
# - Handed Out: October 5, 2020
# - Due: October 19, 2020 at 11:59pm.
#
# Although the solutions are my own, I consulted with the following people
# while working on this homework:
# <NAME>
#
# ## Preface
#
# - Feel free to talk to other members of the class in doing the homework. I am more concerned that you learn how to solve the problem than that you demonstrate that you solved it entirely on your own. You should, however, **write down your solution yourself**. Please include here the list of people you consulted with in the course of working on the homework:
#
# - While we encourage discussion within and outside the class, cheating and copying code is strictly not allowed. Copied code will result in the entire assignment being discarded at the very least.
#
# - Please use Piazza if you have questions about the homework. Also, please come to the TAs recitations and to the office hours.
#
# - The homework is due at 11:59 PM on the due date. We will be using Gradescope for collecting the homework assignments. You should have been automatically added to Gradescope. If not, please ask a TA for assistance. Post on Piazza and contact the TAs if you are having technical difficulties in submitting the assignment.
#
# - Here are some resources you will need for this assignment (https://www.seas.upenn.edu/~cis519/fall2020/assets/HW/HW2/hw2-materials.zip)
#
# + [markdown] id="ClICZP2npLtE"
# # Overview
#
# ### About Jupyter Notebooks
#
# In this homework assignment, we will use a Jupyter notebook to implement, analyze, and discuss ML classifiers.
# Knowing and being comfortable with Jupyter notebooks is a must in every data scientist, ML engineer, researcher, etc. They are widely used in industry and are a standard form of communication in ML by intertwining text and code to "tell a story". There are many resources that can introduce you to Jupyter notebooks (they are pretty easy to understand!), and if you still need help any of the TAs are more than willing to help.
#
# We will be using a local instance of Jupyter instead of Colab. You are of course free to use Colab, but you will need to understand how to hook your Colab instance with Google Drive to upload the datasets and to save images.
#
#
#
# ### About the Homework
#
# You will experiment with several different linear classifiers and analyze
# their performances in both real and synthetic datasets. The goal is to understand the differences and
# similarities between the algorithms and the impact that the dataset characteristics have on the
# algorithms' learning behaviors and performances.
#
# In total, there are seven different learning algorithms which you will implement.
# Six are variants of the Perceptron algorithm and the seventh is a support vector machine (SVM).
# The details of these models is described in Section 1.
#
#
# In order to evaluate the performances of these models, you will use several different datasets.
# The first two datasets are synthetic datasets that have features and labels that were programatically
# generated. They were generated using the same script but use different input parameters that produced
# sparse and dense variants. The second two datasets are for the task of named-entity recognition (NER),
# identifying the names of people, locations, and organizations within text.
# One comes from news text and the other from a corpus of emails.
# For these two datasets, you need to implement the feature extraction yourself.
# All of the datasets and feature extraction information are described in Section 2.
#
# Finally, you will run two sets of experiments, one on the synthetic data and one on the NER data.
# The first set will analyze how the amount of training data impacts model performance.
# The second will look at the consequences of having training and testing data that come from different domains.
# The details of the experiments are described in Section 3.
#
# ### Distribution of Points
#
# The homework has 4 sections for a total of 100 points + 10 extra credit points:
# - Section 0: Warmup (5 points)
# - Section 1: Linear Classifiers (30 points)
# - Section 2: Datasets (0 points, just text)
# - Section 3: Experiments (65 points)
# - Synthetic Experiment:
# - Parameter Tuning (10 points)
# - Learning Curves(10 points)
# - Final Test Accuracies (5 points)
# - Discussion Questions (5 points)
# - Noise Experiment (10 points **extra credit**)
# - NER Experiment:
# - Feature Extraction (25 points)
# - Final Test Accuracies (5 points)
# - $F_1$ Discussion Questions (5 points)
# + [markdown] id="u4gI2-Ygpr69"
# # Section 0: Warmup
# + [markdown] id="Ecz8xJo-ojUs"
# ###### Only For Colab
#
# If you want to complete this homework in Colab, you are more than welcome to.
# You will need a little bit more maneuvering since you will need to upload
# the files of hw2 to your Google Drive and run the following two cells:
# + colab={"base_uri": "https://localhost:8080/", "height": 33} executionInfo={"elapsed": 16579, "status": "ok", "timestamp": 1601838226119, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjKvzcGAASWuvxjrEp7uMipUJWbOgy2JiGGaHeOtg=s64", "userId": "11877295110173304666"}, "user_tz": 240} id="PUMTPLGG-3s2" outputId="9f08f1c8-19ed-4983-e733-5586d32d5649"
# Uncomment if you want to use Colab for this homework.
# from google.colab import drive
# drive.mount('/content/drive', force_remount=True)
# + colab={"base_uri": "https://localhost:8080/", "height": 33} executionInfo={"elapsed": 348, "status": "ok", "timestamp": 1601838234837, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjKvzcGAASWuvxjrEp7uMipUJWbOgy2JiGGaHeOtg=s64", "userId": "11877295110173304666"}, "user_tz": 240} id="eL4xKfSbop6z" outputId="d7f3736e-791d-466e-d836-c71d44d2e87d"
# Uncomment if you want to use Colab for this homework.
# # %cd /content/drive/My Drive/Colab Notebooks/YOUR_PATH_TO_HW_FOLDER
# + [markdown] id="cwXv78-V_wL_"
# ###### Python Version
#
# Python 3.6 or above is required for this homework. Make sure you have it installed.
# + id="T5ANvqaM_wMA"
# Let's check.
import sys
if sys.version_info[:2] < (3, 6):
raise Exception("You have Python version " + str(sys.version_info))
# + [markdown] id="y0fVHRxp0aQX"
# ## Imports and Helper Functions (5 points total)
# + [markdown] id="u2feRgjW0aQY"
# Let's import useful modules we will need throughout the homework
# as well as implement helper functions for our experiment. **Read and remember** what each function is doing, as you will probably need some of them down the line.
# + id="Ah78siKM0aQZ"
# Install necessary libraries for this homework. only need to run once i think
# %pip install sklearn
# %pip install matplotlib
# %pip install numpy
# + id="s4IV1W4y0aQg"
import json
import os
import numpy as np
import matplotlib.pylab as plt
from sklearn.feature_extraction import DictVectorizer
from sklearn.metrics import accuracy_score
DATASETS_PATH = "datasets/"
NER_PATH = os.path.join(DATASETS_PATH, 'ner')
SYNTHETIC_PATH = os.path.join(DATASETS_PATH, 'synthetic')
# + id="UdcTYi0w0aQl"
"""
Helper function that loads a synthetic dataset from the dataset root (e.g. "synthetic/sparse").
You should not need to edit this method.
"""
def load_synthetic_data(dataset_type):
def load_jsonl(file_path):
data = []
with open(file_path, 'r') as f:
for line in f:
data.append(json.loads(line))
return data
def load_txt(file_path):
data = []
with open(file_path, 'r') as f:
for line in f:
data.append(int(line.strip()))
return data
def convert_to_sparse(X):
sparse = []
for x in X:
data = {}
for i, value in enumerate(x):
if value != 0:
data[str(i)] = value
sparse.append(data)
return sparse
path = os.path.join(SYNTHETIC_PATH, dataset_type)
X_train = load_jsonl(os.path.join(path, 'train.X'))
X_dev = load_jsonl(os.path.join(path, 'dev.X'))
X_test = load_jsonl(os.path.join(path, 'test.X'))
num_features = len(X_train[0])
features = [str(i) for i in range(num_features)]
X_train = convert_to_sparse(X_train)
X_dev = convert_to_sparse(X_dev)
X_test = convert_to_sparse(X_test)
y_train = load_txt(os.path.join(path, 'train.y'))
y_dev = load_txt(os.path.join(path, 'dev.y'))
y_test = load_txt(os.path.join(path, 'test.y'))
return X_train, y_train, X_dev, y_dev, X_test, y_test, features
# + id="rYO0o0VB0aQp"
"""
Helper function that loads the NER data from a path (e.g. "ner/conll/train").
You should not need to edit this method.
"""
def load_ner_data(dataset=None, dataset_type=None):
# List of tuples for each sentence
data = []
path = os.path.join(os.path.join(NER_PATH, dataset), dataset_type)
for filename in os.listdir(path):
with open(os.path.join(path, filename), 'r') as file:
sentence = []
for line in file:
if line == '\n':
data.append(sentence)
sentence = []
else:
sentence.append(tuple(line.split()))
return data
# + id="YYpjru5b0aQu"
"""
A helper function that plots the relationship between number of examples
and accuracies for all the models.
You should not need to edit this method.
"""
def plot_learning_curves(
perceptron_accs,
winnow_accs,
adagrad_accs,
avg_perceptron_accs,
avg_winnow_accs,
avg_adagrad_accs,
svm_accs
):
"""
This function will plot the learning curve for the 7 different models.
Pass the accuracies as lists of length 11 where each item corresponds
to a point on the learning curve.
"""
accuracies = [
('perceptron', perceptron_accs),
('winnow', winnow_accs),
('adagrad', adagrad_accs),
('avg-perceptron', avg_perceptron_accs),
('avg-winnow', avg_winnow_accs),
('avg-adagrad', avg_adagrad_accs),
('svm', svm_accs)
]
x = [500, 1000, 1500, 2000, 2500, 3000, 3500, 4000, 4500, 5000, 10000]
plt.figure()
f, (ax, ax2) = plt.subplots(1, 2, sharey=True, facecolor='w')
for label, acc_list in accuracies:
assert len(acc_list) == 11
ax.plot(x, acc_list, label=label)
ax2.plot(x, acc_list, label=label)
ax.set_xlim(0, 5500)
ax2.set_xlim(9500, 10000)
ax2.set_xticks([10000])
# hide the spines between ax and ax2
ax.spines['right'].set_visible(False)
ax2.spines['left'].set_visible(False)
ax.yaxis.tick_left()
ax.tick_params(labelright='off')
ax2.yaxis.tick_right()
ax2.legend()
plt.show()
# + [markdown] id="sg9QfIak0aQz"
# ### F1 Score (5 points)
#
# For some part of the homework, you will use the F1 score instead of accuracy to evaluate how well a model does. The F1 score is computed as the harmonic mean of the precision and recall of the classifier. Precision measures the number of correctly identified positive results by the total number of positive results. Recall, on the other hand, measures the number of correctly identified positive results divided by the number of all samples that should have been identified as positive. More formally, we have that
#
# $$
# \begin{align}
# \text{Precision} &= \frac{TP}{TP + FP} \\
# \text{Recall} &= \frac{TP}{TP + FN}
# \end{align}
# $$
#
# where $TP$ is the number of true positives, $FP$ false positives and $FN$ false negatives. Combining these two we define F1 as
#
# $$
# \text{F1} = 2 \cdot \frac{\text{Precision} \cdot \text{Recall}}{\text{Precision} + \text{Recall}}
# $$
#
# You now need to implement the calculation of F1 yourself using the provided function header. It will be unit tested on Gradescope.
# + id="WnzC-Gce0aQ0"
def calculate_f1(y_gold, y_model):
"""
TODO: MODIFY
Computes the F1 of the model predictions using the
gold labels. Each of y_gold and y_model are lists with
labels 1 or -1. The function should return the F1
score as a number between 0 and 1.
"""
import numpy as np
diff = np.zeros(len(y_gold))
for i in range(len(y_gold)):
diff[i] = y_gold[i] - y_model[i]
TP = 0
FP = 0
FN = 0
for i in range(len(diff)):
if diff[i] == 0 and y_gold[i] == 1:
TP += 1
if diff[i] > 0:
FN += 1
if diff[i] < 0:
FP += 1
precision = TP / (TP + FP)
recall = TP / (TP + FN)
F1 = 2 * precision * recall / (precision + recall)
print('TP is',TP)
print('FP is',FP)
print('FN is',FN)
return F1
# + [markdown] id="_Pbt52HH0aQ7"
# Looking at the formula for the F1 score, what is the highest and lowest possible value?
# + id="jB4UrDGR0aQ8"
def highest_and_lowest_f1_score():
"""
TODO: MODIFY
Return the highest and lowest possible F1 score
(ie one line solution returning the theoretical max and min)
"""
maxscore = 1
minscore = 0
return maxscore, minscore
# + [markdown] id="FS0BO0AJ0aRA"
# # Section 1. Linear Classifiers (30 points total)
# + [markdown] id="ZM2eSe030aRB"
# This section details the seven different algorithms that you will use in the experiments. For each of the algorithms, we describe the initialization you should use to start training and the different parameter settings that you should use for the experiment on the synthetic datasets. Each of the update functions for the Perceptron, Winnow, and Perceptron with AdaGrad will be unittested on Gradescope, so please do not edit the function definitions.
# + [markdown] id="YahdyT4H0aRC"
# ### 1.1 Base Classifier
# + id="kRcseeXa0aRD"
class Classifier(object):
"""
DO NOT MODIFY
The Classifier class is the base class for all of the Perceptron-based
algorithms. Your class should override the "process_example" and
"predict_single" functions. Further, the averaged models should
override the "finalize" method, where the final parameter values
should be calculated.
You should not need to edit this class any further.
"""
ITERATIONS = 10
def train(self, X, y):
for iteration in range(self.ITERATIONS):
for x_i, y_i in zip(X, y):
self.process_example(x_i, y_i)
self.finalize()
def process_example(self, x, y):
"""
Makes a prediction using the current parameter values for
the features x and potentially updates the parameters based
on the gradient. Note "x" is a dictionary which maps from the feature
name to the feature value and y is either 1 or -1.
"""
raise NotImplementedError
def finalize(self):
"""Calculates the final parameter values for the averaged models."""
pass
def predict(self, X):
"""
Predicts labels for all of the input examples. You should not need
to override this method.
"""
return [self.predict_single(x) for x in X]
def predict_single(self, x):
"""
Predicts a label, 1 or -1, for the input example. "x" is a dictionary
which maps from the feature name to the feature value.
"""
raise NotImplementedError
# + [markdown] id="TzRKTNaK0aRH"
# ### 1.2 Basic Perceptron (2 points)
# + [markdown] id="xVvMIuX10aRI"
# We do this classifier for you, so enjoy the two free points and pay attention to the techniques and code written.
#
# #### 1.2.1 Description
#
# This is the basic version of the Perceptron Algorithm.
# In this version, an update will be performed on the example $(\textbf{x}, y)$ if $y(\mathbf{w}^\intercal \mathbf{x} + \theta) \leq 0$. The Perceptron needs to learn both the bias term $\theta$ and the weight vector $\mathbf{w}$ parameters.
# When the Perceptron makes a mistake on the example $(\textbf{x}, y)$, both $\mathbf{w}$ and $\theta$ need to be updated using the following update equations:
# $$
# \begin{align*}
# \mathbf{w}^\textrm{new} &\gets \mathbf{w} + \eta \cdot y \cdot \mathbf{x} \\
# \theta^\textrm{new} &\gets \theta + \eta \cdot y
# \end{align*}
# $$
# where $\eta$ is the learning rate.
#
# #### 1.2.2 Hyperparameters
#
# We set $\eta$ to 1, so there are no hyperparameters to tune.
#
# Note: If we assume that the order of the examples presented to the algorithm is fixed, we initialize $\mathbf{w} = \mathbf{0}$ and $\theta = 0$, and train both together, then the learning rate $\eta$ does not have any effect.
# In fact you can show that, if $\mathbf{w}_1$ and $\theta_1$ are the outputs of the Perceptron algorithm with learning rate $\eta_1$, then $\mathbf{w}_1/\eta_1$ and $\theta_1/\eta_1$ will be the result of the Perceptron with learning rate 1 (note that these two hyperplanes give identical predictions).
#
# #### 1.2.3 Initialization
#
# $\mathbf{w} = [0, 0, \dots, 0]$ and $\theta = 0$.
# + id="zotWbBvj0aRJ"
class Perceptron(Classifier):
"""
DO NOT MODIFY THIS CELL
The Perceptron model. Note how we are subclassing `Classifier`.
"""
def __init__(self, features):
"""
Initializes the parameters for the Perceptron model. "features"
is a list of all of the features of the model where each is
represented by a string.
"""
# NOTE: Do not change the names of these 3 data members because
# they are used in the unit tests
self.eta = 1
self.theta = 0
self.w = {feature: 0.0 for feature in features}
def process_example(self, x, y):
y_pred = self.predict_single(x)
if y != y_pred:
for feature, value in x.items():
self.w[feature] += self.eta * y * value
self.theta += self.eta * y
def predict_single(self, x):
score = 0
for feature, value in x.items():
score += self.w[feature] * value
score += self.theta
if score <= 0:
return -1
return 1
# + [markdown] id="kaiyRKjo0aRN"
# For the rest of the Perceptron-based algorithms, you will have to implement the corresponding class like we have done for `Perceptron`.
# Use the `Perceptron` class as a guide for how to implement the functions.
# + [markdown] id="pWiuhyOm0aRO"
# ### 1.3 Winnow (5 points)
# + [markdown] id="s9dx93VU0aRR"
# #### 1.3.1 Description
# The Winnow algorithm is a variant of the Perceptron algorithm with multiplicative updates. Since the algorithm requires that the target function is monotonic, you will only use it on the synthetic datasets.
#
# The Winnow algorithm only learns parameters $\mathbf{w}$.
# We will fix $\theta = -n$, where $n$ is the number of features.
# When the Winnow algorithm makes a mistake on the example $(\textbf{x}, y)$, the parameters are updated with the following equation:
# $$
# \begin{equation}
# w^\textrm{new}_i \gets w_i \cdot \alpha^{y \cdot x_i}
# \end{equation}
# $$
# where $w_i$ and $x_i$ are the $i$th components of the corresponding vectors.
# Here, $\alpha$ is a promotion/demotion hyperparameter.
#
# #### 1.3.2 Hyperparameters
#
# For the experiment, choose $\alpha \in \{1.1, 1.01, 1.005, 1.0005, 1.0001\}$.
#
# #### 1.3.3 Initialization
#
# $\mathbf{w} = [1, 1, \dots, 1]$ and $\theta = -n$ (constant).
# + id="g9pPUPTd0aRS"
class Winnow(Classifier):
def __init__(self, alpha, features):
# DO NOT change the names of these 3 data members because
# they are used in the unit tests
self.alpha = alpha
self.w = {feature: 1.0 for feature in features}
self.theta = -len(features)
def process_example(self, x, y):
""" TODO: IMPLEMENT"""
y_pred = self.predict_single(x)
if y != y_pred:
for feature, value in x.items():
self.w[feature] = self.w[feature] * pow(self.alpha,y*value)
def predict_single(self, x):
""" TODO: IMPLEMENT"""
score = 0
for feature, value in x.items():
score += self.w[feature] * value
score += self.theta
if score <= 0:
return -1
return 1
# + [markdown] id="--I-w3_U0aRX"
# ### 1.4 AdaGrad (10 points)
# + [markdown] id="d5AXEuKn0aRY"
# #### 1.4.1 Description
# AdaGrad is a variant of the Perceptron algorithm that adapts the learning rate for each parameter based on historical information.
# The idea is that frequently changing features get smaller learning rates and stable features higher ones.
#
# To derive the update equations for this model, we first need to start with the loss function.
# Instead of using the hinge loss with the elbow at 0 (like the basic Perceptron does), we will instead use the standard hinge loss with the elbow at 1:
#
# $$
# \begin{equation}
# \mathcal{L}(\mathbf{x}, y, \mathbf{w}, \theta) = \max\left\{0, 1 - y(\mathbf{w}^\intercal \mathbf{x} + \theta)\right\}
# \end{equation}
# $$
#
# Then, by taking the partial derivative of $\mathcal{L}$ with respect to $\mathbf{w}$ and $\theta$, we can derive the respective graidents (make sure you understand how you could derive these gradients on your own):
#
# $$
# \begin{align}
# \frac{\partial\mathcal{L}}{\partial\mathbf{w}} &=
# \begin{cases}
# \mathbf{0} & \text{if $y(\mathbf{w}^\intercal \mathbf{x} + \theta) > 1$} \\
# -y\cdot \mathbf{x} & \textrm{otherwise}
# \end{cases} \\
# \frac{\partial\mathcal{L}}{\partial\theta} &=
# \begin{cases}
# 0 & \text{if $y(\mathbf{w}^\intercal \mathbf{x} + \theta) > 1$} \\
# -y & \textrm{otherwise}
# \end{cases}
# \end{align}
# $$
#
# Then for each parameter, we will keep track of the sum of the parameters' squared gradients.
# In the following equations, the $k$ superscript refers to the $k$th non-zero gradient (i.e., the $k$th weight vector/misclassified example) and $t$ is the number of mistakes seen thus far.
#
# $$
# \begin{align}
# G^t_j &= \sum_{k=1}^t \left(\frac{\partial \mathcal{L}}{\partial w^k_j}\right)^2 \\
# H^t &= \sum_{k=1}^t \left(\frac{\partial \mathcal{L}}{\partial \theta^k}\right)^2
# \end{align}
# $$
#
# For example, on the 3rd mistake ($t = 3$), $G^3_j$ is the sum of the squares of the first three non-zero gradients ($\left(\frac{\partial \mathcal{L}}{\partial w^1_j}\right)^2$, $\left(\frac{\partial \mathcal{L}}{\partial w^2_j}\right)^2$, and $\left(\frac{\partial \mathcal{L}}{\partial w^3_j}\right)^2$).
# Then $\mathbf{G}^3$ is used to calculate the 4th value of the weight vector as follows.
# On example $(\mathbf{x}, y)$, if $y(\mathbf{w}^\intercal \mathbf{x} + \theta) \leq 1$, then the parameters are updated with the following equations:
#
# $$
# \begin{align}
# \mathbf{w}^{t+1} &\gets \mathbf{w}^t + \eta \cdot \frac{y \cdot \mathbf{x}}{\sqrt{\mathbf{G}^t}} \\
# \theta^{t+1} &\gets \theta^t + \eta \frac{y}{\sqrt{H^t}}
# \end{align}
# $$
#
# Note that, although we use the hinge loss with the elbow at 1 for training, you still make the prediction based on whether or not $y(\mathbf{w}^\intercal \mathbf{x} + \theta) \leq 0$ during testing.
#
# #### 1.4.2 Hyperparameters
#
# For the experiment, choose $\eta \in \{1.5, 0.25, 0.03, 0.005, 0.001\}$
#
# #### 1.4.3 Initialization
#
# $\mathbf{w} = [0, 0, \dots, 0]$ and $\theta = 0$.
# + id="w50RXTza0aRZ"
class AdaGrad(Classifier):
def __init__(self, eta, features):
# DO NOT change the names of these 3 data members because
# they are used in the unit tests
self.eta = eta
self.w = {feature: 0.0 for feature in features}
self.theta = 0
self.G = {feature: 1e-5 for feature in features} # 1e-5 prevents divide by 0 problems
self.H = 0
def process_example(self, x, y):
""" TODO: IMPLEMENT"""
import numpy as np
y_pred = self.predict_single(x)
dotpro = 0
if y != y_pred:
# calculate dot product
for feature, value in x.items():
dotpro += self.w[feature] * value
# update w
for feature, value in x.items():
if(y * (dotpro + self.theta) > 1):
dldw = 0
else:
dldw = -y * value
self.G[feature] += dldw ** 2
self.w[feature] += self.eta * y * value / np.sqrt(self.G[feature])
# update theta
if(y * (dotpro + self.theta) > 1):
dldtheta = 0
else:
dldtheta = -y
self.H += dldtheta ** 2
self.theta += self.eta * y / np.sqrt(self.H)
def predict_single(self, x):
""" TODO: IMPLEMENT"""
score = 0
for feature, value in x.items():
score += self.w[feature] * value
score += self.theta
if score <= 0:
return -1
return 1
# + [markdown] id="LmAio9O40aRd"
# ### 1.5 Averaged Models (15 points)
# + [markdown] id="lzPnbRJ60aRe"
# You will also implement the averaged version of the previous three algorithms.
#
# During the course of training, each of the above algorithms will have $K + 1$ different parameter settings for the $K$ different updates it will make during training.
# The regular implementation of these algorithms uses the parameter values after the $K$th update as the final ones.
# Instead, the averaged version use the weighted average of the $K + 1$ parameter values as the final parameter values.
# Let $m_k$ denote the number of correctly classified examples by the $k$th parameter values and $M$ the total number of correctly classified examples.
# The final parameter values are
#
# $$
# \begin{align}
# M &= \sum_{k=1}^{K+1} m_k \\
# \mathbf{w} &\gets \frac{1}{M} \sum_{k=1}^{K+1} m_k \cdot \mathbf{w}^k \\
# \theta &\gets \frac{1}{M} \sum_{k=1}^{K+1} m_k \cdot \theta^k \\
# \end{align}
# $$
#
# For each of the averaged versions of Perceptron, Winnow, and AdaGrad, use the same hyperparameters and initialization as before.
#
# #### 1.5.1 Implementation Note
# Implementing the averaged variants of these algorithms can be tricky.
# While the final parameter values are based on the sum of $K$ different vectors, there is no need to maintain *all* of these parameters.
# Instead, you should implement these algorithms by keeping only two vectors, one which maintains the cumulative sum and the current one.
#
# Additionally, there are two ways of keeping track of these two vectors.
# One is more straightforward but prohibitively slow.
# The second requires some algebra to derive but is significantly faster to run.
# Try to analyze how the final weight vector is a function of the intermediate updates and their corresponding weights.
# It should take less than a minute or two for ten iterations for any of the averaged algorithms.
# **You need to think about how to efficiently implement the averaged algorithms yourself.**
#
# Further, the implementation for Winnow is slightly more complicated than the other two, so if you consistently have low accuracy for the averaged Winnow, take a closer look at the derivation.
# +
class AveragedPerceptron(Classifier):
def __init__(self, features):
self.eta = 1
self.w = {feature: 0.0 for feature in features}
self.theta = 0
"""TODO: You will need to add data members here"""
self.M = 0
self.lastM = 0
self.weightedW = {feature: 0.0 for feature in features}
self.weightedT = 0
self.Mk = []
self.yvec = []
self.xvec = []
def process_example(self, x, y):
""" TODO: IMPLEMENT"""
y_pred = self.predict_single(x)
if y != y_pred:
self.weightedT += (self.M - self.lastM) * self.theta
# append variables for weighted W calculation
self.xvec.append(x)
self.yvec.append(y)
self.Mk.append(self.M - self.lastM)
# update weights
for feature, value in x.items():
self.w[feature] += self.eta * y * value
self.theta += self.eta * y
# reset lastM
self.lastM = self.M
else:
self.M += 1
def predict_single(self, x):
""" TODO: IMPLEMENT"""
score = 0
for feature, value in x.items():
score += self.w[feature] * value
score += self.theta
if score <= 0:
return -1
return 1
def finalize(self):
""" TODO: IMPLEMENT"""
self.M +=1
self.Msum = self.M
self.w = {feature: 0.0 for feature in features}
# sum up rebuild weight vectors from saved x,y,mk values by just summing
# 1/M * (m1+m2+...mk)*y*x and (mi) terms reduces m[i] every iteration
for i in range(len(self.yvec)):
for feature, value in self.xvec[i].items():
self.weightedW[feature] += 1/self.M * self.Msum * \
self.eta * self.yvec[i] * value
# self.w[feature] += 1/self.M * self.Msum * self.eta * self.yvec[i] * value
self.Msum -= self.Mk[i]
self.theta = 1/self.M * self.weightedT
self.w = self.weightedW
# +
# test the averaged perceptron model
X_train, y_train, X_dev, y_dev, X_test, y_test, features = load_synthetic_data('dense')
AvgPerceptron = AveragedPerceptron(features)
iteration = 10
for iter in range(iteration):
for i in range(len(X_train)):
AvgPerceptron.process_example(X_train[i],y_train[i])
AvgPerceptron.finalize()
count = 0
for i in range(len(X_dev)):
x = X_dev[i]
y = AvgPerceptron.predict_single(x)
if y_dev[i] == y:
count += 1
print(count/len(X_dev))
# + id="bv-kvuF30aRj"
class AveragedWinnow(Classifier):
def __init__(self, alpha, features):
self.alpha = alpha
self.w = {feature: 1.0 for feature in features}
self.theta = -len(features)
"""TODO: You will need to add data members here"""
self.M = 0
self.lastM = 0
self.weightedW = {feature: 1.0 for feature in features}
def process_example(self, x, y):
""" TODO: IMPLEMENT"""
y_pred = self.predict_single(x)
if y != y_pred:
for feature, value in x.items():
self.w[feature] = self.w[feature] * pow(self.alpha,y*value)
for feature in self.weightedW:
self.weightedW[feature] += (self.M - self.lastM) * self.w[feature]
# self.M += 1
self.lastM = self.M
else:
self.M +=1
def predict_single(self, x):
""" TODO: IMPLEMENT"""
score = 0
for feature, value in x.items():
score += self.w[feature] * value
score += self.theta
if score <= 0:
return -1
return 1
def finalize(self):
""" TODO: IMPLEMENT"""
self.M += 1
for feature in self.weightedW:
self.w[feature] = 1/self.M * self.weightedW[feature]
# +
# test the averaged Winnow model
X_train, y_train, X_dev, y_dev, X_test, y_test, features = load_synthetic_data('sparse')
iteration = 10
alpha = 1.1
AvgWinnow = AveragedWinnow(alpha,features)
AvgWinnow.train(X_train,y_train)
# AvgWinnow = Winnow(alpha,features)
# AvgWinnow.train(X_train,y_train)
count = 0
for i in range(len(X_dev)):
x = X_dev[i]
y = AvgWinnow.predict_single(x)
if y_dev[i] == y:
count += 1
print(count/len(X_dev))
# + id="L9xWrGHS0aRn"
class AveragedAdaGrad(Classifier):
def __init__(self, eta, features):
self.eta = eta
self.w = {feature: 0.0 for feature in features}
self.theta = 0
self.G = {feature: 1e-5 for feature in features}
self.H = 0
"""TODO: You will need to add data members here"""
self.M = 0
self.lastM = 0
self.weightedW = {feature: 1.0 for feature in features}
self.weightedT = 0
def process_example(self, x, y):
""" TODO: IMPLEMENT"""
import numpy as np
y_pred = self.predict_single(x)
dotpro = 0
if y != y_pred:
for feature in self.weightedW:
self.weightedW[feature] += (self.M - self.lastM) * self.w[feature]
self.weightedT += (self.M - self.lastM) * self.theta
# append variables for weighted W calculation
self.xvec.append(x)
self.yvec.append(y)
self.Mk.append(self.M - self.lastM)
# calculate dot product
for feature, value in x.items():
dotpro += self.w[feature] * value
# update w
for feature, value in x.items():
if(y * (dotpro + self.theta) > 1):
dldw = 0
else:
dldw = -y * value
self.G[feature] += dldw ** 2
self.w[feature] += self.eta * y * value / np.sqrt(self.G[feature])
# update theta
if(y * (dotpro + self.theta) > 1):
dldtheta = 0
else:
dldtheta = -y
self.H += dldtheta ** 2
self.theta += self.eta * y / np.sqrt(self.H)
self.lastM = self.M
else:
self.M += 1
def predict_single(self, x):
""" TODO: IMPLEMENT"""
score = 0
for feature, value in x.items():
score += self.w[feature] * value
score += self.theta
if score <= 0:
return -1
return 1
def finalize(self):
""" TODO: IMPLEMENT"""
self.M += 1
for feature in self.weightedW:
self.w[feature] = 1/self.M * self.weightedW[feature]
self.theta = 1/self.M * self.weightedT
# +
# test the averaged Adagrad model
X_train, y_train, X_dev, y_dev, X_test, y_test, features = load_synthetic_data('dense')
# 𝜂∈{1.5,0.25,0.03,0.005,0.001}
eta = 1.5
AvgAdaGrad = AveragedAdaGrad(eta,features)
AvgAdaGrad.train(X_train,y_train)
# OrigAdaGrad = AdaGrad(eta,features)
# OrigAdaGrad.train(X_train,y_train)
count = 0
for i in range(len(X_dev)):
x = X_dev[i]
y = AvgAdaGrad.predict_single(x)
if y_dev[i] == y:
count += 1
print(count/len(X_dev))
# + [markdown] id="kMi5gf710aRr"
# ### 1.6 Support Vector Machines
#
# Although we have not yet covered SVMs in class, you can still train them using the `sklearn` library.
# We will use a soft margin SVM for non-linearly separable data.
# You should use the `sklearn` implementation as follows:
# ```
# from sklearn.svm import LinearSVC
# classifier = LinearSVC(loss='hinge')
# classifier.fit(X, y)
# ```
#
# `sklearn` requires a different feature representation than what we use for the Perceptron models.
# The provided Python template code demonstrates how to convert to the require representation.
#
#
# Given training samples $S = \{(\mathbf{x}^1, y^1), (\mathbf{x}^2, y^2), \dots, (\mathbf{x}^m, y^m)\}$, the objective for the SVM is the following:
#
# $$
# \begin{equation}
# \min_{\mathbf{w}, b, \boldsymbol{\xi}} \frac{1}{2} \vert\vert \mathbf{w}\vert\vert^2_2 + C \sum_{i=1}^m \xi_i
# \end{equation}
# $$
#
# subject to the following constraints:
#
# $$
# \begin{align}
# y^i(\mathbf{w}^\intercal \mathbf{x}^i + b) \geq 1 - \xi_i \;\;&\textrm{for } i = 1, 2, \dots, m \\
# \xi_i \geq 0 \;\;& \textrm{for } i = 1, 2, \dots, m
# \end{align}
# $$
#
# -
class SVMClassifier(Classifier):
def __init__(self):
from sklearn.svm import LinearSVC
self.local_classifier = LinearSVC(loss = 'hinge')
self.vectorizer = DictVectorizer()
def trainSVM(self,X_train,y_train):
X_train_dict = self.vectorizer.fit_transform(X_train)
self.local_classifier.fit(X_train_dict,y_train)
def testSVM(self,X_test,y_test):
X_test_dict = self.vectorizer.transform(X_test)
return self.local_classifier.score(X_test_dict,y_test)
# + id="ys83AbV50aRt"
"""TODO: Create an SVM classifier"""
X_train, y_train, X_dev, y_dev, X_test, y_test, features = load_synthetic_data('dense')
# This is how you convert from the way we represent features in the
# Perceptron code to how you need to represent features for the SVM.
# You can then train with (X_train_dict, y_train) and test with
# (X_conll_test_dict, y_conll_test) and (X_enron_test_dict, y_enron_test)
vectorizer = DictVectorizer()
X_train_dict = vectorizer.fit_transform(X_train)
X_test_dict = vectorizer.transform(X_test)
from sklearn.svm import LinearSVC
classifier = LinearSVC(loss = 'hinge')
classifier.fit(X_train_dict,y_train)
classifier.score(X_test_dict,y_test)
# -
# + [markdown] id="HzmeTfF20aR0"
# # Section 2. Datasets
#
# In this section, we describe the synthetic and NER datasets that you will use for your experiments.
# For the NER datasets, there is also an explanation for the features which you need to extract from the data.
#
# ### 2.1 Synthetic Data
#
# #### 2.1.1 Introduction
#
# The synthetic datasets have features and labels which are automatically generated from a python script.
# Each instance will have $n$ binary features and are labeled according to a $l$-of-$m$-of-$n$ Boolean function.
# Specifically, there is a set of $m$ features such that an example if positive if and only if at least $l$ of these $m$ features are active.
# The set of $m$ features is the same for the dataset (i.e., it is not a separate set of $m$ features for each individual instance).
#
# We provide two versions of the synthetic dataset called sparse and dense.
# For both datasets, we set $l = 10$ and $m=20$.
# We set $n = 200$ for the sparse data and $n = 40$ for the dense data.
# Additionally, we add noise to the data as follows:
# With probability $0.05$ the label assigned by the function is changed and with probability $0.001$ each feature value is changed.
# Consequently, the data is not linearly separable.
#
# We have provided you with three data splits for both sparse and dense with 10,000 training, 2,000 development, and 2,000 testing examples.
# Section 3 describes the experiments that you need to run on these datasets.
#
# #### 2.1.2 Feature Representation
#
# The features of the synthetic data provided are vectors of 0s and 1s.
# Storing these large matrices requires lots of memory so we use a sparse representation that stores them as dictionaries instead.
# For example, the vector $[0,1,0,0,0,1]$ can be stored as `{"x2": 1,"x6": 1}` (using 1-based indexing).
# We have provided you with the code for parsing and converting the data to this format.
# You can use these for the all algorithms you develop except the SVM.
# Since you will be using the implementation of SVM from sklearn, you will need to provide a vector to it. You can use `sklearn.feature_extraction.DictVectorizer` for converting feature-value dictionaries to vectors.
#
# ### 2.2 NER Data
#
# In addition to the synthetic data, we have provided you two datasets for the task of named-entity recognition (NER).
# The goal is to identify whether strings in text represent names of people, organizations, or locations.
# An example instance looks like the following:
#
# ```
# [<NAME>] , currently a journalist in [LOC Argentina] , played with
# [PER del Bosque] in the final years of the seventies in
# [ORG Real Madrid] .
# ```
#
# In this problem, we will simplify the task to identifying whether a string is named entity or not (that is, you don't have to say which type of entity it is).
# For each token in the input, we will use the tag $\texttt{I}$ to denote that token is an entity and $\texttt{O}$ otherwise.
# For example, the full tagging for the above instace is as follows:
#
# ```
# [I Wolff] [O ,] [O currently] [a] [O journalist] [O in] [I Argentina]
# [O ,] [O played] [O with] [I del] [I Bosque] [O in] [O the] [O final]
# [O years] [O of] [O the] [O seventies] [O in] [I Real] [I Madrid] .
# ```
#
# Given a sentence $S = w_1, w_2, \dots, w_n$, you need to predict the `I`, `O` tag for each word in the sentence.
# That is, you will produce the sequence $Y = y_1, y_2, \dots, y_n$ where $y_i \in$ {`I`, `O`}.
#
# #### 2.2.1 Datasets: CoNLL and Enron
#
# We have provided two datasets, the CoNLL dataset which is text from news articles, and Enron, a corpus of emails.
# The files contain one word and one tag per line.
# For CoNLL, there are training, development, and testing files, whereas Enron only has a test dataset.
# There are 14,987 training sentences (204,567 words), 336 development sentences (3,779 words), and 303 testing sentences (3,880 words) in CoNLL.
# For Enron there are 368 sentences (11,852 words).
#
# **Please note that the CoNLL dataset is available only for the purposes of this assignment.
# It is copyrighted, and you are granted access because you are a Penn student, but please delete it when you are done with the homework.**
#
# #### 2.2.2 Feature Extraction
#
# The NER data is provided as raw text, and you are required to extract features for the classifier.
# In this assignment, we will only consider binary features based on the context of the word that is supposed to be tagged.
#
# Assume that there are $V$ unique words in the dataset and each word has been assigned a unique ID which is a number $\{1, 2, \dots, V\}$.
# Further, $w_{-k}$ and $w_{+k}$ indicate the $k$th word before and after the target word.
# The feature templates that you should use to generate features are as follows:
#
# | Template | Number of Features |
# |----------------------|--------------------|
# | $w_{-3}$ | $V$ |
# | $w_{-2}$ | $V$ |
# | $w_{-1}$ | $V$ |
# | $w_{+1}$ | $V$ |
# | $w_{+2}$ | $V$ |
# | $w_{+3}$ | $V$ |
# | $w_{-1}$ & $w_{-2}$ | $V \times V$ |
# | $w_{+1}$ \& $w_{+2}$ | $V \times V$ |
# | $w_{-1}$ \& $w_{+1}$ | $V \times V$ |
#
# Each feature template corresponds to a set of features that you will compute (similar to the features you generated in problem 2 from the first homework assignment).
# The $w_{-3}$ feature template corresponds to $V$ features where the $i$th feature is 1 if the third word to the left of the target word has ID $i$.
# The $w_{-1} \& w_{+1}$ feature template corresponds to $V \times V$ features where there is one feature for every unique pair words.
# For example, feature $(i - 1) \times V + j$ is a binary feature that is 1 if the word 1 to the left of the target has ID $i$ and the first word to the right of the target has ID $j$.
# In practice, you will not need to keep track of the feature IDs.
# Instead, each feature will be given a name such as "$w_{-1}=\textrm{the} \& w_{+1}=\textrm{cat}$".
#
# In total, all of the above feature templates correspond to a very large number of features.
# However, for each word, there will be exactly 9 features which are active (non-zero), so the feature vector is quite sparse.
# You will represent this as a dictionary which maps from the feature name to the value.
# In the provided Python template, we have implemented a couple of the features for you to demonstrate how to compute them and what the naming scheme should look like.
#
# In order to deal with the first two words and the last two words in a sentence, we will add special symbol "SSS" and "EEE" to the vocabulary to represent the words before the first word and the words after the last word.
# Notice that in the test data you may encounter a word that was not observed in training, and therefore is not in your dictionary.
# In this case, you cannot generate a feature for it, resulting in less than 7 active features in some of the test examples.
# + [markdown] id="RHHy_nGx0aR2"
# # Section 3. Experiments (65 points total)
# + [markdown] id="2PKCZQ9Z0aR3"
# You will run two sets of experiments, one using the synthetic data and one using the NER data.
#
# ### 3.1 Synthetic Experiment (30 + 10 extra credit points)
#
# This experiment will explore the impact that the amount of training data has on model performance.
# First, you will do hyperparameter tuning for Winnow and Perceptron with AdaGrad (both standard and averaged versions).
# Then you will generate learning curves that will plot the size of the training data against the performance.
# Finally, for each of the models trained on all of the training data, you will find the test score.
# You should use accuracy to compute the performance of the model.
#
# In summary, the experiment consists of three parts
# 1. Parameter Tuning
# 2. Learning Curves
# 3. Final Evaluation
#
# #### 3.1.1 Parameter Tuning (10 points)
#
# For both the Winnow and Perceptron with AdaGrad (standard and averaged), there are hyperparameters that you need to choose.
# (The same is true for SVM, but you should only use the default settings.)
# Similarly to cross-validation from Homework 1, we will estimate how well each model will do on the true test data using the development dataset (we will not run cross-validation), and choose the hyperparameter settings based on these results.
#
# For each hyperparameter value in Section 1, train a model using that value on the training data and compute the accuracy on the development dataset. Each model should be trained for 10 iterations (i.e., 10 passes over the entire dataset).
#
# TODO: Fill in the table with the best hyperparameter values and the corresponding validation accuracies.
# Repeat this for both the sparse and dense data.
# + [markdown] id="xdoFHNKp0aR4"
# # Winnow Sweep
#
# | $\alpha$ | Sparse | Dense |
# |----------|--------|-------|
# | 1.1 | 0.8935 | 0.8995 |
# | 1.01 | 0.9270 | 0.9215 |
# | 1.005 | 0.9195 | 0.9080 |
# | 1.0005 | 0.5630 | 0.8615 |
# | 1.0001 | 0.5205 | 0.6140 |
#
# ##### Averaged Winnow Sweep
#
# | $\alpha$ | Sparse | Dense |
# |----------|--------|-------|
# | 1.1 | 0.9390 | 0.9445 |
# | 1.01 | 0.8980 | 0.9335 |
# | 1.005 | 0.8405 | 0.9150 |
# | 1.0005 | 0.5255 | 0.6700 |
# | 1.0001 | 0.5095 | 0.5460 |
#
# ##### AdaGrad Sweep
#
# | $\eta$ | Sparse | Dense |
# |----------|--------|-------|
# | 1.5 | 0.8745 | 0.9325 |
# | 0.25 | 0.8745 | 0.9325 |
# | 0.03 | 0.8745 | 0.9325 |
# | 0.005 | 0.8745 | 0.9325 |
# | 0.001 | 0.8745 | 0.9325 |
#
# ##### Averaged AdaGrad Sweep
#
# | $\eta$ | Sparse | Dense |
# |----------|--------|-------|
# | 1.5 | 0.8935 | 0.9445 |
# | 0.25 | 0.8935 | 0.9445 |
# | 0.03 | 0.8935 | 0.9445 |
# | 0.005 | 0.8935 | 0.9445 |
# | 0.001 | 0.8935 | 0.9445 |
# + [markdown] id="sHZZ6U240aR6"
# #### 3.1.2 Learning Curves (10 points)
#
# Next, you will train all 7 models with different amounts of training data.
# For Winnow and Perceptron with AdaGrad (standard and averaged), use the best hyperparameters from the parameter tuning experiment.
#
# Each of the datasets contains 10,000 training examples.
# You will train each model 11 times on varying amounts of training data.
# The first 10 will increase by 500 examples: 500, 1k, 1.5k, 2k, ..., 5k.
# The 11th model should use all 10k examples.
# Each Perceptron-based model should be trained for 10 iterations (e.g., 10 passes over the total number of training examples available to that model).
# The SVM can be run until convergence with the default parameters.
#
# For each model, compute the accuracy on the development dataset and plot the results using the provided code.
# There should be a separate plot for the sparse and dense data.
#
# **Note** how we have included an image in markdown. You should do the same for both plots and include them in the output below by running your experiment, saving your plots to the images folder, and linking it to this cell.
#
# ##### Sparse Plot
#
# 
#
# ##### Dense Plot
#
# 
# +
# set up the learning curve variables and load the dataset
perceptron_accs = np.zeros(11)
winnow_accs = np.zeros(11)
adagrad_accs = np.zeros(11)
avg_perceptron_accs = np.zeros(11)
avg_winnow_accs = np.zeros(11)
avg_adagrad_accs = np.zeros(11)
svm_accs = np.zeros(11)
X_train, y_train, X_dev, y_dev, X_test, y_test, features = load_synthetic_data('sparse')
# -
# basic perceptron
for i in range(1,12):
X_train_i = X_train[0:(i*500)]
y_train_i = y_train[0:(i*500)]
if i == 11:
X_train_i = X_train
y_train_i = y_train
eta = 1.5
model = Perceptron(features)
model.train(X_train_i,y_train_i)
perceptron_accs[i-1] = compute_accuracy_313(X_dev,y_dev,model)
# averaged perceptron
for i in range(1,12):
X_train_i = X_train[0:(i*500)]
y_train_i = y_train[0:(i*500)]
if i == 11:
X_train_i = X_train
y_train_i = y_train
model = AveragedPerceptron(features)
model.train(X_train_i,y_train_i)
avg_perceptron_accs[i-1] = compute_accuracy_313(X_dev,y_dev,model)
# winnow
for i in range(1,12):
X_train_i = X_train[0:(i*500)]
y_train_i = y_train[0:(i*500)]
if i == 11:
X_train_i = X_train
y_train_i = y_train
alpha = 1.01
model = Winnow(alpha,features)
model.train(X_train_i,y_train_i)
winnow_accs[i-1] = compute_accuracy_313(X_dev,y_dev,model)
# averaged winnow
for i in range(1,12):
X_train_i = X_train[0:(i*500)]
y_train_i = y_train[0:(i*500)]
if i == 11:
X_train_i = X_train
y_train_i = y_train
alpha = 1.1
model = AveragedWinnow(alpha,features)
model.train(X_train_i,y_train_i)
avg_winnow_accs[i-1] = compute_accuracy_313(X_dev,y_dev,model)
# adagrad
for i in range(1,12):
X_train_i = X_train[0:(i*500)]
y_train_i = y_train[0:(i*500)]
if i == 11:
X_train_i = X_train
y_train_i = y_train
eta = 1.5
model = AdaGrad(eta,features)
model.train(X_train_i,y_train_i)
adagrad_accs[i-1] = compute_accuracy_313(X_dev,y_dev,model)
# averaged AdaGrad
for i in range(1,12):
X_train_i = X_train[0:(i*500)]
y_train_i = y_train[0:(i*500)]
if i == 11:
X_train_i = X_train
y_train_i = y_train
eta = 1.5
model = AveragedAdaGrad(eta,features)
model.train(X_train_i,y_train_i)
avg_adagrad_accs[i-1] = compute_accuracy_313(X_dev,y_dev,model)
# +
from sklearn.svm import LinearSVC
for i in range(1,12):
X_train_i = X_train[0:(i*500)]
y_train_i = y_train[0:(i*500)]
if i == 11:
X_train_i = X_train
y_train_i = y_train
vectorizer = DictVectorizer()
X_train_dict = vectorizer.fit_transform(X_train_i)
X_dev_dict = vectorizer.transform(X_dev)
classifier = LinearSVC(loss = 'hinge')
classifier.fit(X_train_dict,y_train_i)
svm_accs[i-1] = classifier.score(X_dev_dict,y_dev)
# +
plot_learning_curves(perceptron_accs,
winnow_accs,
adagrad_accs,
avg_perceptron_accs,
avg_winnow_accs,
avg_adagrad_accs,
svm_accs
)
# -
def compute_accuracy_313(X_dev,y_dev,classifier):
count = 0
for i in range(len(X_dev)):
x = X_dev[i]
y = classifier.predict_single(x)
if y_dev[i] == y:
count += 1
return (count/len(X_dev))
# + [markdown] id="2wHcZsGo0aR8"
# #### 3.1.3 Final Evaluation (5 points)
#
# Finally, for each of the 7 models, train the models on all of the training data and compute the test accuracy.
# For Winnow and Perceptron with AdaGrad, use the best hyperparameter settings you found.
# Report these accuracies in a table.
#
# We will run our models with [500, 1000, 1500, 2000, 2500, 3000, 3500, 4000, 4500, 5000, 10000] examples.
# + id="NCfmjoYw_wNQ"
sample_sizes = [500 * i for i in range(1, 11)] + [10_000]
# -
# + id="ZJJ9u_kf0aSB"
def run_synthetic_experiment(dataset_type='sparse'):
"""
TODO: IMPLEMENT
Runs the synthetic experiment on either the sparse or dense data
depending on the data path (e.g. "data/sparse" or "data/dense").
We have provided how to train the Perceptron on the training and
test on the testing data (the last part of the experiment). You need
to implement the hyperparameter sweep, the learning curves, and
predicting on the test dataset for the other models.
"""
X_train, y_train, X_dev, y_dev, X_test, y_test, features = load_synthetic_data(dataset_type)
# TODO: YOUR CODE HERE. Determine the best hyperparameters for the relevant models
# report the validation accuracy after training using the best hyper parameters
# i think i did all of these picked the best hyper parameters way above here near the hyper parameter tables
# TOOD: YOUR CODE HERE. Downsample the dataset to the number of desired training
# instances (e.g. 500, 1000), then train all of the models on the
# sampled dataset. Compute the accuracy and add the accuracies to
# the corresponding list. Use plot_learning_curves()
# I did all of these near where the plot is, separated into 7 or 8 cells. please refer to that.
# TODO: Train all 7 models on the training data and make predictions
# for test data
# We will show you how to do it for the basic Perceptron model.
classifier = Perceptron(features)
classifier.train(X_train, y_train)
y_pred = classifier.predict(X_test)
acc = accuracy_score(y_test, y_pred)
print(f"Perceptron's accuracy is {acc}")
# YOUR CODE HERE: Repeat for the other 6 models.
# Averaged Perceptron
classifier = AveragedPerceptron(features)
classifier.train(X_train, y_train)
y_pred = classifier.predict(X_test)
acc = accuracy_score(y_test, y_pred)
print(f"Averaged Perceptron's accuracy is {acc}")
# Winnow
alpha = 1.01
classifier = Winnow(alpha,features)
classifier.train(X_train, y_train)
y_pred = classifier.predict(X_test)
acc = accuracy_score(y_test, y_pred)
print(f"Winnow's accuracy is {acc}")
# Averaged Winnow
alpha = 1.1
classifier = AveragedWinnow(alpha,features)
classifier.train(X_train, y_train)
y_pred = classifier.predict(X_test)
acc = accuracy_score(y_test, y_pred)
print(f"Averged Winnow's accuracy is {acc}")
# Averaged Winnow
eta = 1.5
classifier = AdaGrad(eta,features)
classifier.train(X_train, y_train)
y_pred = classifier.predict(X_test)
acc = accuracy_score(y_test, y_pred)
print(f"AdaGrad's accuracy is {acc}")
# Averaged Winnow
eta = 1.5
classifier = AveragedAdaGrad(eta,features)
classifier.train(X_train, y_train)
y_pred = classifier.predict(X_test)
acc = accuracy_score(y_test, y_pred)
print(f"Averged AdaGrad's accuracy is {acc}")
vectorizer = DictVectorizer()
X_train_dict = vectorizer.fit_transform(X_train)
X_test_dict = vectorizer.transform(X_test)
classifier = LinearSVC(loss = 'hinge')
classifier.fit(X_train_dict,y_train)
acc = classifier.score(X_test_dict,y_test)
print(f"SVM's accuracy is {acc}")
# + id="Sz_oTWqC0aSE"
"""
Run the synthetic experiment on the sparse dataset. For reference,
"synthetic/sparse" is the path to where the data is located.
Note: This experiment takes substantial time (around 15 minutes),
so don't worry if it's taking a long time to finish.
"""
run_synthetic_experiment('sparse')
# + id="lXcorX8ndhRo"
"""
Run the synthetic experiment on the dense dataset. For reference,
"synthetic/dense" is the path to where the data is located.
Note: this experiment should take much less time.
"""
run_synthetic_experiment('dense')
# + [markdown] id="-2hLx_9Q0aSJ"
# ##### Questions (5 points)
#
# Answer the following questions:
#
# 1. Discuss the trends that you see when comparing the standard version of an algorithm to the averaged version (e.g., Winnow versus Averaged Winnow). Is there an observable trend?
#
# Typically averaged version of the algorithm has a slightly higher accuracy than the standard version, only 0.01~0.02 improvement but quite consistent. Averaged version also tends to converge a faster than regular version
#
#
# 2. We provided you with 10,000 training examples.
# Were all 10,000 necessary to achieve the best performance for each classifier?
# If not, how many were necessary? (Rough estimates, no exact numbers required)
#
# Not all were necessary. Looking at the learning rate graph, accuracy for both dense and sparse datasets plateau around 6000-7000 training examples for even the worst-performing algorithm. Winnow and averaged winnow converged around 2000 and 4000 examples respectively. For the best-performing algorithm, SVM, it converge to the highest accuracy with only about 1000 training examples. Other algorithm converged between 5000-7000 examples. Further examples did not provide any improvement over accuracy.
#
#
# 3. Report your Final Test Accuracies
#
#
#
# | Model | Sparse | Dense |
# |---------------------|--------|-------|
# | Perceptron | 0.7170 | 0.9205 |
# | Winnow | 0.9260 | 0.9255 |
# | AdaGrad | 0.8780 | 0.9325 |
# | Averaged Perceptron | 0.9135 | 0.9405 |
# | Averaged Winnow | 0.9360 | 0.9405 |
# | Averaged AdaGrad | 0.8840 | 0.9405 |
# | SVM | 0.9360 | 0.9405 |
#
#
# + [markdown] id="bPZtn5Fv0aSK"
# #### 3.1.5 Extra Credit (10 points)
#
# Included in the resources for this homework assignment is the code that we used to generate the synthetic data.
# We used a small amount of noise to create the dataset which you ran the experiments on.
# For extra credit, vary the amount of noise in either/both of the label and features.
# Then, plot the models' performances as a function of the amount of noise.
# Discuss your observations.
# + [markdown] id="0iW_koNXv79l"
# TODO: Extra Credit observations
# -
# I ran the experiment with varying random values using the code shown below. Key thing is the 100% random value means that I randomly switched len(y_train) amount of the y_train, but they could've been repeatedly flipped. In the figure below, we can see the perceptron and adagrad approaches 50% which is essentially guess randomly. However, winnow algorithm did not descend to that low of an accuracy because a wrong y_train for winnow means that the added weight goes from w^alpha*y*x to 1/w^alpha*y*x. While for perceptron and adagrad, a wrong y_train means altering the weight vector in the completely opposite direction. Therefore, winnow accuracy decreased but not to a meaningless value while adagrad and perceptron algorithms become obsolete with 100% noise. For some reason SVM did not change. I experiemnted with different ways to make noise but its accuracy end up being a step function not sure why.
# +
X_train, y_train, X_dev, y_dev, X_test, y_test, features = load_synthetic_data('dense')
noise = np.linspace(0,1,21)
ec_winnowacc = np.zeros(len(noise))
ec_perceptronacc = np.zeros(len(noise))
ec_adagradacc = np.zeros(len(noise))
ec_svmacc = np.zeros(len(noise))
for i in range(len(noise)):
X_train, y_train, X_dev, y_dev, X_test, y_test, features = load_synthetic_data('dense')
classifier = Perceptron(features)
num = int(len(y_train) * noise[i])
for j in range(num):
tempRand = np.random.randint(0,len(y_train))
y_train[tempRand] = -y_train[tempRand]
classifier.train(X_train, y_train)
y_pred = classifier.predict(X_test)
ec_perceptronacc[i] = accuracy_score(y_test, y_pred)
for i in range(len(noise)):
X_train, y_train, X_dev, y_dev, X_test, y_test, features = load_synthetic_data('dense')
classifier = Winnow(1.1,features)
num = int(len(y_train) * noise[i])
for j in range(num):
tempRand = np.random.randint(0,len(y_train))
y_train[tempRand] = -y_train[tempRand]
classifier.train(X_train, y_train)
y_pred = classifier.predict(X_test)
ec_winnowacc[i] = accuracy_score(y_test, y_pred)
for i in range(len(noise)):
X_train, y_train, X_dev, y_dev, X_test, y_test, features = load_synthetic_data('dense')
classifier = AdaGrad(1.5,features)
num = int(len(y_train) * noise[i])
for j in range(num):
tempRand = np.random.randint(0,len(y_train))
y_train[tempRand] = -y_train[tempRand]
classifier.train(X_train, y_train)
y_pred = classifier.predict(X_test)
ec_adagradacc[i] = accuracy_score(y_test, y_pred)
for i in range(len(noise)):
X_train, y_train, X_dev, y_dev, X_test, y_test, features = load_synthetic_data('dense')
num = int(len(y_train) * noise[i])
for j in range(num):
tempRand = np.random.randint(0,len(y_train))
y_train[tempRand] = -y_train[tempRand]
vectorizer = DictVectorizer()
X_train_dict = vectorizer.fit_transform(X_train)
X_test_dict = vectorizer.transform(X_test)
classifier = LinearSVC(loss = 'hinge')
classifier.fit(X_train_dict,y_train)
ec_svmacc[i] = classifier.score(X_test_dict,y_test)
# -
plot_EC_curves(ec_perceptronacc,ec_winnowacc,ec_adagradacc,ec_svmacc)
"""
A helper function that plots the relationship between number of examples
and accuracies for all the models.
You should not need to edit this method.
"""
def plot_EC_curves(
perceptron_accs,
winnow_accs,
adagrad_accs,
svm_accs
):
accuracies = [
('perceptron', perceptron_accs),
('winnow', winnow_accs),
('adagrad', adagrad_accs),
('svm', svm_accs)
]
x = np.linspace(0,1,21)
plt.figure()
# f, (ax, ax2) = plt.subplots(1, 2, sharey=True, facecolor='w')
for label, acc_list in accuracies:
assert len(acc_list) == 21
plt.plot(x, acc_list, label=label)
# ax2.plot(x, acc_list, label=label)
# plt.set_xlim(0,1)
# ax.set_xlim(0, 1)
# ax2.set_xlim(9500, 10000)
# ax2.set_xticks([10000])
# hide the spines between ax and ax2
# plt.spines['right'].set_visible(False)
# ax2.spines['left'].set_visible(False)
# ax.yaxis.tick_left()
# ax.tick_params(labelright='off')
# ax2.yaxis.tick_right()
# ax2.legend()
plt.legend()
plt.title('Extra Credit Noise Plot')
plt.show()
ec_winnowacc
# + [markdown] id="OMisGYXj0aSK"
# ### 3.2 NER Experiment: Welcome to the Real World (35 points)
#
# The experiment with the NER data will analyze how changing the domain of the training and testing data can impact the performance of a model.
#
# Instead of accuracy, you will use your $F_1$ score implementation in Section 0 to evaluate how well a model does.
# Recall measures how many of the actual entities the model successfully tagged as an entity.
#
# $$
# \begin{align}
# \textrm{Precision} &= \frac{\#\textrm{(Actually Entity & Model Predicted Entity)}}{\#\textrm{(Model Predicted Entity)}} \\
# \textrm{Recall} &= \frac{\#\textrm{(Actually Entity & Model Predicted Entity)}}{\#\textrm{(Actually Entity)}} \\
# \textrm{F}_1 &= 2 \cdot \frac{\textrm{Precision} \times \textrm{Recall}}{\textrm{Precision} + \textrm{Recall}}
# \end{align}
# $$
#
# For this experiment, you will only use the averaged basic Perceptron and SVM.
# Hence, no parameter tuning is necessary.
# Train both models on the CoNLL training data then compute the F$_1$ on the development and testing data of both CoNLL and Enron.
# Note that the model which is used to predict labels for Enron is trained on CoNLL data, not Enron data.
# Report the F$_1$ scores in a table.
#
# #### 3.2.1 Extracting NER Features (25 points)
#
# Reread Section 2.2.2 to understand how to extract the features required to train the models
# and translate it to the code below.
# + id="Y0gPdPmp0aSL"
def extract_ner_features_train(train):
"""
Extracts feature dictionaries and labels from the data in "train"
Additionally creates a list of all of the features which were created.
We have implemented the w-1 and w+1 features for you to show you how
to create them.
TODO: You should add your additional featurization code here.
(which might require adding and/or changing existing code)
"""
y = []
X = []
features = set()
for sentence in train:
padded = [('SSS', None)] + [('SSS', None)] + [('SSS', None)] + sentence[:]\
+ [('EEE', None)] + [('EEE', None)] + [('EEE', None)]
for i in range(3, len(padded) - 3):
y.append(1 if padded[i][1] == 'I' else -1)
feat1 = 'w-1=' + str(padded[i - 1][0])
feat2 = 'w+1=' + str(padded[i + 1][0])
feat3 = 'w-3=' + str(padded[i - 3][0])
feat4 = 'w-2=' + str(padded[i - 2][0])
feat5 = 'w+2=' + str(padded[i + 2][0])
feat6 = 'w+3=' + str(padded[i + 3][0])
feat7 = 'w-1&w-2=' + str(padded[i - 1][0] + str(padded[i - 2][0]))
feat8 = 'w+1&w+2=' + str(padded[i + 1][0] + str(padded[i + 2][0]))
feat9 = 'w-1&w+1=' + str(padded[i - 1][0] + str(padded[i + 1][0]))
feats = [feat1, feat2, feat3, feat4, feat5, feat6, feat7, feat8, feat9]
features.update(feats)
feats = {feature: 1 for feature in feats}
X.append(feats)
return features, X, y
# + [markdown] id="EQOz2fZ_0aSV"
# Now, repeat the process of extracting features from the test data.
# What is the difference between the code above and below?
# + id="TzqdP7oE0aSX"
def extract_features_dev_or_test(data, features):
"""
Extracts feature dictionaries and labels from "data". The only
features which should be computed are those in "features". You
should add your additional featurization code here.
TODO: You should add your additional featurization code here.
"""
y = []
X = []
for sentence in data:
padded = [('SSS', None)] + [('SSS', None)] + [('SSS', None)] + sentence[:]\
+ [('EEE', None)] + [('EEE', None)] + [('EEE', None)]
for i in range(3, len(padded) - 3):
y.append(1 if padded[i][1] == 'I' else -1)
feat1 = 'w-1=' + str(padded[i - 1][0])
feat2 = 'w+1=' + str(padded[i + 1][0])
feat3 = 'w-3=' + str(padded[i - 3][0])
feat4 = 'w-2=' + str(padded[i - 2][0])
feat5 = 'w+2=' + str(padded[i + 2][0])
feat6 = 'w+3=' + str(padded[i + 3][0])
feat7 = 'w-1&w-2=' + str(padded[i - 1][0] + str(padded[i - 2][0]))
feat8 = 'w+1&w+2=' + str(padded[i + 1][0] + str(padded[i + 2][0]))
feat9 = 'w-1&w+1=' + str(padded[i - 1][0] + str(padded[i + 1][0]))
feats = [feat1, feat2, feat3, feat4, feat5, feat6, feat7, feat8, feat9]
feats = {feature: 1 for feature in feats if feature in features}
X.append(feats)
return X, y
# + [markdown] id="Um-IG2cv0aSe"
# #### 3.2.2 Running the NER Experiment
#
# As stated previously, train both models on the CoNLL training data then compute the $F_1$ on the development and testing data of both CoNLL and Enron. Note that the model which is used to predict labels for Enron is trained on CoNLL data, not Enron data.
# + id="jxvboxmg0aSe"
def run_ner_experiment(data_path):
"""
Runs the NER experiment using the path to the ner data
(e.g. "ner" from the released resources). We have implemented
the standard Perceptron below. You should do the same for
the averaged version and the SVM.
The SVM requires transforming the features into a different
format. See the end of this function for how to do that.
"""
train = load_ner_data(dataset='conll', dataset_type='train')
conll_test = load_ner_data(dataset='conll', dataset_type='test')
enron_test = load_ner_data(dataset='enron', dataset_type='test')
features, X_train, y_train = extract_ner_features_train(train)
X_conll_test, y_conll_test = extract_features_dev_or_test(conll_test, features)
X_enron_test, y_enron_test = extract_features_dev_or_test(enron_test, features)
# TODO: We show you how to do this for Perceptron.
# You should do this for the Averaged Perceptron and SVM
classifier = Perceptron(features)
classifier.train(X_train, y_train)
y_pred = classifier.predict(X_conll_test)
conll_f1 = calculate_f1(y_conll_test, y_pred)
y_pred = classifier.predict(X_enron_test)
enron_f1 = calculate_f1(y_enron_test, y_pred)
print('Perceptron on NER')
print(' CoNLL', conll_f1)
print(' Enron', enron_f1)
print('Accuracy',accuracy_score(y_enron_test, y_pred))
# Averaged Perceptron
classifier = AveragedPerceptron(features)
classifier.train(X_train, y_train)
y_pred = classifier.predict(X_conll_test)
conll_f1 = calculate_f1(y_conll_test, y_pred)
y_pred = classifier.predict(X_enron_test)
enron_f1 = calculate_f1(y_enron_test, y_pred)
print('Averaged Perceptron on NER')
print(' CoNLL', conll_f1)
print(' Enron', enron_f1)
print('Accuracy',accuracy_score(y_enron_test, y_pred))
# SVM
# This is how you convert from the way we represent features in the
# Perceptron code to how you need to represent features for the SVM.
# You can then train with (X_train_dict, y_train) and test with
# (X_conll_test_dict, y_conll_test) and (X_enron_test_dict, y_enron_test)
vectorizer = DictVectorizer()
X_train_dict = vectorizer.fit_transform(X_train)
X_conll_test_dict = vectorizer.transform(X_conll_test)
X_enron_test_dict = vectorizer.transform(X_enron_test)
classifier = LinearSVC(loss = 'hinge')
classifier.fit(X_train_dict,y_train)
y_pred = classifier.predict(X_conll_test_dict)
conll_f1 = calculate_f1(y_conll_test,y_pred)
y_pred = classifier.predict(X_enron_test_dict)
enron_f1 = calculate_f1(y_enron_test, y_pred)
print('SVM on NER')
print(' CoNLL', conll_f1)
print(' Enron', enron_f1)
print('Accuracy',classifier.score(X_enron_test_dict,y_enron_test))
# + id="-yy6Y9320aSi"
# Run the NER experiment. "ner" is the path to where the data is located.
run_ner_experiment('ner')
# -
conll_test = load_ner_data(dataset='conll', dataset_type='test')
enron_test = load_ner_data(dataset='enron', dataset_type='test')
X_conll_test, y_conll_test = extract_features_dev_or_test(conll_test, features)
X_enron_test, y_enron_test = extract_features_dev_or_test(enron_test, features)
print(np.shape(y_conll_test))
print(np.shape(y_enron_test))
# + [markdown] id="qeElQnS_0aSw"
#
# ##### F1 Scores Table
# TODO: report your values:
#
# | Model | CoNLL Test F1 | Enron Test F1 |
# |---------------------|---------------|---------------|
# | Averaged Perceptron | 0.8131 | 0.2187 |
# | SVM | 0.8278 | 0.2412 |
# + [markdown] id="fpzm2yA20aSx"
# ##### Questions (5 points)
#
# Comment on the results:
# 1. Are the F$_1$ scores on CoNLL and Enron similar?
#
# No, F$_1$ scores on CoNLL and Enron are quite different. CoNLL has much higher ones than Enron.
#
#
# 2. If they are dissimilar, explain why you think the F$_1$ score increased/decreased on the Enron data.
#
# In CoNLL, TP is significantly higher than FN and FP. However, in Enron TP is lower than FN and FP which resulted in a much lower F1 score. I printed out the accuracy on Enron data which is very high (80~90 percent for both). And then I printed out the TP,FN,FP,TN (TN = total - TP - FN - FP) and found that true negative is an order of magnitude higher than all three other values. It seems like Enron has lots of true negative but algorithms have trouble identify the positive examples in Enron. It didn't have this problem with CoNLL.
#
# + [markdown] id="tKr_PXhO0aSy"
# ## Submission Instructions
#
# We will be using Gradescope to turn in both the Python code.
# You should have been automatically added to Gradescope.
# If you do not have access, please ask the TA staff on Piazza.
#
# There are three parts to the submission on Gradescope:
# * ipynb file: Submit this notebook (.ipynb). If you are using Google Colab, you will have to download it as an ipynb file.
# * PDF: This notebook saved as a PDF. We will use this to see the overall structure of your homework and code, and to check manual questions like the tables, plots, and your discussions. How should I convert this notebook to PDF, you may ask? There are a few ways, but for simplicity print the Jupyter notebook and _Save as PDF_.
# * Code: A `hw2.py` file. We will use this to unit test and automate grading some parts of the homework. We only need a few functions/classes from the whole notebook. In particular, to unit test we only need:
# - `calculate_f1`
# - `highest_and_lowest_f1_score`
# - `Perceptron`, `Winnow`, and `AdaGrad` classes.
#
# There are two ways to submit these pieces of code. You can either manually copy and paste these to a Python file,
# or you can use Jupyter's _Download as .py_, and delete all unnecessary code.
|
Homework2/hw2-materials/hw2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# %matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
# -
# # 100 gene
# +
nnet=5
nn=10
genie3pr, gpgeneLpr, gpgeneP2pr, grnboost2pr, leappr = np.zeros((nnet, nn)), np.zeros((nnet, nn)), np.zeros((nnet, nn)), np.zeros((nnet, nn)), np.zeros((nnet, nn))
genie3roc, gpgeneLroc, gpgeneP2roc, grnboost2roc, leaproc = np.zeros((nnet, nn)), np.zeros((nnet, nn)), np.zeros((nnet, nn)), np.zeros((nnet, nn)), np.zeros((nnet, nn))
with open('/home/linaiqi/Lab/data/gene/tmp/result_genie3_100gene.txt') as fin:
for l in fin:
v = l.strip().split()
# print(v)
genie3pr[int(v[2])-1, int(v[4])//100-1] = float(v[8])
genie3roc[int(v[2])-1, int(v[4])//100-1] = float(v[11])
genie3pr_mu, genie3pr_std = np.mean(genie3pr, axis=0), np.std(genie3pr, axis=0)
genie3roc_mu, genie3roc_std = np.mean(genie3roc, axis=0), np.std(genie3roc, axis=0)
with open('/home/linaiqi/Lab/data/gene/tmp/result_gpgeneL_100gene.txt') as fin:
for l in fin:
v = l.strip().split()
#print(v)
gpgeneLpr[int(v[2])-1, int(v[4])//100-1] = float(v[8])
gpgeneLroc[int(v[2])-1, int(v[4])//100-1] = float(v[11])
gpgeneLpr_mu, gpgeneLpr_std = np.mean(gpgeneLpr, axis=0), np.std(gpgeneLpr, axis=0)
gpgeneLroc_mu, gpgeneLroc_std = np.mean(gpgeneLroc, axis=0), np.std(gpgeneLroc, axis=0)
with open('/home/linaiqi/Lab/data/gene/tmp/result_gpgeneP2_100gene.txt') as fin:
for l in fin:
v = l.strip().split()
#print(v)
gpgeneP2pr[int(v[2])-1, int(v[4])//100-1] = float(v[8])
gpgeneP2roc[int(v[2])-1, int(v[4])//100-1] = float(v[11])
gpgeneP2pr_mu, gpgeneP2pr_std = np.mean(gpgeneP2pr, axis=0), np.std(gpgeneP2pr, axis=0)
gpgeneP2roc_mu, gpgeneP2roc_std = np.mean(gpgeneP2roc, axis=0), np.std(gpgeneP2roc, axis=0)
with open('/home/linaiqi/Lab/data/gene/tmp/result_grnboost2_100gene.txt') as fin:
for l in fin:
v = l.strip().split()
# print(v)
grnboost2pr[int(v[2])-1, int(v[4])//100-1] = float(v[8])
grnboost2roc[int(v[2])-1, int(v[4])//100-1] = float(v[11])
grnboost2pr_mu, grnboost2pr_std = np.mean(grnboost2pr, axis=0), np.std(grnboost2pr, axis=0)
grnboost2roc_mu, grnboost2roc_std = np.mean(grnboost2roc, axis=0), np.std(grnboost2roc, axis=0)
with open('/home/linaiqi/Lab/data/gene/tmp/result_leap_100gene.txt') as fin:
for l in fin:
v = l.strip().split()
# print(v)
leappr[int(v[2])-1, int(v[4])//100-1] = float(v[8])
leaproc[int(v[2])-1, int(v[4])//100-1] = float(v[11])
leappr_mu, leappr_std = np.mean(leappr, axis=0), np.std(leappr, axis=0)
leaproc_mu, leaproc_std = np.mean(leaproc, axis=0), np.std(leaproc, axis=0)
# +
xs=[int(100*(k+1)) for k in range(10)]
plt.figure()
plt.errorbar([x+5 for x in xs], gpgeneLpr_mu, gpgeneLpr_std, fmt='-', label='GPGene-linear', capsize=5)
plt.errorbar([x+0 for x in xs], gpgeneP2pr_mu, gpgeneP2pr_std, fmt='-', label='GPGene-poly2', capsize=5)
plt.errorbar([x-5 for x in xs], genie3pr_mu, genie3pr_std, fmt='-', label='GENIE3', capsize=5)
plt.errorbar([x+10 for x in xs], grnboost2pr_mu, grnboost2pr_std, fmt='-', label='GRNBoost2', capsize=5)
plt.errorbar([x-10 for x in xs], leappr_mu, leappr_std, fmt='-', label='LEAP', capsize=5)
plt.legend(); plt.grid(); plt.xlabel('# of training instances'); plt.ylabel('AUPR');
# -
plt.figure()
plt.errorbar([x+5 for x in xs], gpgeneLroc_mu, gpgeneLroc_std, fmt='-', label='GPGene-linear', capsize=5)
plt.errorbar([x+0 for x in xs], gpgeneP2roc_mu, gpgeneP2roc_std, fmt='-', label='GPGene-poly2', capsize=5)
plt.errorbar([x-5 for x in xs], genie3roc_mu, genie3roc_std, fmt='-', label='GENIE3', capsize=5)
plt.errorbar([x+10 for x in xs], grnboost2roc_mu, grnboost2roc_std, fmt='-', label='GRNBoost2', capsize=5)
plt.errorbar([x-10 for x in xs], leaproc_mu, leaproc_std, fmt='-', label='LEAP', capsize=5)
plt.legend(); plt.grid(); plt.xlabel('# of training instances'); plt.ylabel('AUROC');
|
draw_fig.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # What is the probability that an email be spam?
# Resource: [Link](https://github.com/Make-School-Courses/QL-1.1-Quantitative-Reasoning/blob/master/Notebooks/Conditional_Probability/Conditional_probability.ipynb)
#
# 
# ## We know an email is spam, what is the probability that password be a word in it? (What is the frequency of password in a spam email?)
# * Dictionary of spam where its key would be unique words in spam emails and the value shows the occurance of that word
spam_data = {
"password": 2,
"review": 1,
"send": 3,
"us": 3,
"your": 3,
"account": 1
}
# 
p_password_given_spam = float(spam_data['password']) / float(sum(spam_data.values()))
print(p_password_given_spam)
# # Activity: Do the above computation for each word by writing code
# +
spam = {}
ham = {}
spam_v = float(4)/float(6)
ham_v = float(2)/float(6)
def open_text(text, histogram):
full_text = text.split()
for word in full_text:
if word not in histogram:
histogram[word] = 1
else:
histogram[word] += 1
spam_texts = ['Send us your password', 'review us', 'Send your password', 'Send us your account']
ham_texts = ['Send us your review', 'review your password']
for text in spam_texts:
open_text(text, spam)
for text in ham_texts:
open_text(text, ham)
ls1 = []
ls2 = []
for i in spam:
# obtain the probability of each word by assuming the email is spam
p_word_given_spam = float(spam[i]) / float(sum(spam.values()))
# obtain the probability of each word by assuming the email is ham
p_word_given_ham = 0 if i not in ham else float(ham[i]) / float(sum(ham.values()))
p_word_in_email = float(p_word_given_spam * spam_v) + float(p_word_given_ham * ham_v)
# obtain the probability that for a seen word it belongs to spam email
p_word_is_in_spam = float(p_word_given_spam * spam_v) / float(p_word_in_email)
# obtain the probability that for a seen word it belongs to ham email
p_word_is_in_ham = float(p_word_given_ham * ham_v) / float(p_word_in_email)
print('WORD: {}\nProbability in spam: {}\nProbability in ham: {}\n'. format(i, p_word_is_in_spam, p_word_is_in_ham))
|
Ham_Spam.ipynb
|