problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
4. Variant 1.
The numbers $96, 28, 6, 20$ were written on the board. One of them was multiplied, another was divided, a third was increased, and a fourth was decreased by the same number. As a result, all the numbers became equal to one number. Which one?
|
Answer: 24.
Solution: Addition and multiplication increase numbers, while subtraction and division decrease them, so the two larger numbers have decreased, and the smaller ones have increased. Now let's consider the two middle numbers 20 and 28. It is clear that a number was subtracted from 28, and the same number was added to 20. There can be no other options, because if you add a number to 6 and multiply 20 by the same number, the numbers will not be equal. The numbers became equal, and $28-20=8$, so both became equal to the number 24. Note that $96: 24=4,28-24=4,20+4=24,6 \cdot 4=24$. Therefore, the required number is 24.
|
24
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Variant 1.
Petya wrote the numbers from 1 to 10 on cards and laid them out along the edge of a $3 \times 4$ rectangle. At first, one of the cards - with the number 7 - was opened (see the figure). When the other cards were opened, it turned out that the sum of the numbers in the top and bottom horizontal rows is the same and equals $A$. What is the largest possible value of the number $A$?
| $\circ$ | $\circ$ | $\circ$ | $\circ$ |
| :---: | :---: | :---: | :---: |
| 7 | | | $\circ$ |
| $\circ$ | $\circ$ | $\circ$ | $\circ$ |
|
Answer: 23.
Solution. Let $B$ be the last number in the second horizontal row. Since the sum of all numbers from 1 to 10 is 55, we have $2A + B + 7 = 55$ or $B = 48 - 2A$. It follows that $B$ is an even number. To make $A$ the largest, $B$ needs to be the smallest. The smallest even number among the given numbers is 2. Then $2A = 55 - 9$, so $A = 23$. We will show that an example of such an arrangement exists. Let the numbers in the first row be $10, 6, 4, 3$, and in the second row - $1, 5, 8, 9$.
|
23
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 7. Variant 1.
100 natural numbers are written in a circle. It is known that among any three consecutive numbers, there is an even number. What is the smallest number of even numbers that can be among the written numbers?
|
Answer: 34.
Solution. Consider any 3 consecutive numbers. Among them, there is an even number. Fix it, and divide the remaining 99 into 33 groups of 3 consecutive numbers. In each such group, there is at least one even number. Thus, the total number of even numbers is at least $1+33=34$. Such a situation is possible. Number the numbers in a circle. And the even numbers can be those with numbers $1,4,7, \ldots, 100$.
|
34
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.3. Grandma has two balls of wool: a large one and a small one. From the large one, she can knit either a sweater and three socks, or five identical caps. $A$ from the small one - either half a sweater, or two caps. (In both cases, all the wool will be used.) What is the maximum number of socks that Grandma can knit using both balls? Justify your answer.
|
# Solution:
Method 1. Half a sweater requires as much wool as 2 hats, so a sweater requires as much wool as 4 hats. Then 4 hats and 3 socks require as much wool as 5 hats. Therefore, one hat is equivalent to three socks. In total, 5 + 2 = 7 hats or 21 socks can be knitted.
Method 2. Let the amount of wool required for a sock, a hat, and a sweater be \( x, y, \) and \( z \) respectively (it doesn't matter in what units the unknowns are taken). Then the grandmother has \( 3x + z = 5y \) in the first ball and \( 0.5z = 2y \) in the second ball. We need to express the sum \( 5y + 2y \) in terms of \( x \). From the second equation, express \( z \) and substitute the result into the first: \( 3x + 4y = 5y \), from which \( y = 3x \). Then \( 5y + 2y = 7y = 21x \), that is, 21 socks can be knitted from all the wool.
Answer: 21 socks.
| in progress | points |
| :--- | :--- |
| Correct and fully justified answer | 7 points |
| The solution process is completely correct, but there are computational errors, possibly leading to an incorrect answer | 6 points |
| The problem condition is correctly written as a system of equations, but the further solution is incorrect or missing | 3 points |
| There are correct logically justified conclusions about the amounts of wool required for socks, sweaters, and hats, but they did not lead to an answer | 2 points |
| Correct answer without justification or with incorrect justification | 1 point |
| Incorrect answer without justification or with incorrect justification | 0 points |
|
21
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.5. Ten different natural numbers are such that the product of any five of them is even, and the sum of all ten is odd. What is the smallest possible sum of all these numbers? Justify your answer.
|
Solution: There cannot be more than four odd numbers (five odd numbers in a product give an odd number), and, moreover, their quantity must be odd. Therefore, there are either 3 or 1 odd numbers, and 7 or 9 even numbers, respectively. The sets with the smallest sum are 1, 3, 5, 2, 4, 6, 8, 10, 12, 14 and 1, 2, 4, 6, 8, 10, 12, 14, 16, 18, respectively. The latter set gives a larger sum, so the first one fits. The sum of the numbers in it is 51.
Answer: 51.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and fully justified answer | 7 points |
| Correct and justified set found, but the sum of its numbers is calculated incorrectly | 6 points |
| Proven that the number of odd numbers in the set is odd, but not all such cases are correctly investigated. | 3 points |
| The answer is correct, a set realizing this answer is provided, but the optimality of the provided example is not proven | 2 points |
| The correct set is indicated, but its optimality is not proven, and the sum of the numbers in the set is calculated with an error | 1 point |
| Answer without justification and/or incorrect answer | 0 points |
|
51
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. On the faces $BCD, ACD, ABD$, and $ABC$ of the tetrahedron $ABCD$, points $A_{1}, B_{1}, C_{1}$, and $D_{1}$ are marked, respectively. It is known that the lines $AA_{1}, BB_{1}, CC_{1}$, and $DD_{1}$ intersect at point $P$, and $\frac{AP}{A_{1}P}=\frac{BP}{B_{1}P}=\frac{CP}{C_{1}P}=\frac{DP}{D_{1}P}=r$. Find all possible values of $r$.
|
Solution. Let V be the volume* of tetrahedron ABCD. We introduce the consideration of the partition of the original tetrahedron ABCD into tetrahedra PBCD, PACD, PABD, and PABC. Then for the volumes of the specified tetrahedra, the following is true:
$$
V=V_{\mathrm{PBCD}}+V_{\mathrm{PACD}}+V_{\mathrm{PABD}}+V_{\mathrm{PABC}}
$$
Note that if $\mathrm{H}$ is the height of tetrahedron $\mathrm{ABCD}$, dropped from vertex A to the base BCD, and $\mathrm{h}$ is the height of tetrahedron PBCD, dropped from vertex P to the base BCD, then $\frac{H}{h}=\frac{A A_{1}}{A_{1} P}$. Due to this observation and the condition $r=\frac{A P}{A_{1} P}=\frac{B P}{B_{1} P}=\frac{C P}{C_{1} P}=\frac{D P}{D_{1} P}$, we have
$$
\frac{V}{V_{\mathrm{PBCD}}}=\frac{\mathrm{A} A_{1}}{A_{1} P}=\frac{A P+A_{1} P}{A_{1} P}=1+\frac{A P}{A_{1} P}=r+1
$$
Similar relations are valid for the other tetrahedra, so
$$
\frac{v}{V_{\mathrm{PBCD}}}=\frac{v}{V_{\mathrm{PACD}}}=\frac{v}{V_{\mathrm{PABD}}}=\frac{v}{V_{\mathrm{PABC}}}=r+1 \text { or }
$$
$V=(r+1) V_{\mathrm{PBCD}}=(r+1) V_{\mathrm{PACD}}=(r+1) V_{\mathrm{PABD}}=(r+1) V_{\mathrm{PABC}}$.
Then
$$
r+1=\frac{(r+1) V_{\mathrm{PBCD}}+(r+1) V_{\mathrm{PACD}}+(r+1) V_{\mathrm{PABD}}+(r+1) V_{\mathrm{PABC}}}{V_{\mathrm{PBCD}}+V_{\mathrm{PACD}}+V_{\mathrm{PABD}}+V_{\mathrm{PABC}}}
$$
or
$$
r+1=\frac{4 V}{V_{\mathrm{PBCD}}+V_{\mathrm{PACD}}+V_{\mathrm{PABD}}+V_{\mathrm{PABC}}}=\frac{4 V}{V}=4
$$
Thus, $r=3$.
*Note that for solving this problem, it is not necessary to know the formula for the volume of a tetrahedron. It is sufficient to introduce a conditional quantity $V=S h$, and use its additivity (a known fact from mathematics and physics courses).
## Recommendations for evaluating solutions.
A correct solution for a specific case - 2 points.
The partition of the original tetrahedron ABCD into tetrahedra PBCD, PACD, PABD, and PABC is presented, and relations of the form $\frac{V}{V_{\text {PBCD }}}=\frac{\mathrm{AA}_{1}}{A_{1} P}=\frac{A P+A_{1} P}{A_{1} P}=1+\frac{A P}{A_{1} P}=r+1$ are obtained - no less than 3 points.
Note that the problem can be solved using the vector method.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 7.1. (7 points)
Find the value of the expression
$$
\left(1+\frac{1}{2}\right)\left(1-\frac{1}{3}\right)\left(1+\frac{1}{4}\right)\left(1-\frac{1}{5}\right) \ldots\left(1+\frac{1}{2 m}\right)\left(1-\frac{1}{2 m+1}\right)
$$
|
Answer: 1.
Solution: Notice that
$$
\begin{array}{r}
\left(1+\frac{1}{2}\right)\left(1-\frac{1}{3}\right)=\frac{3}{2} \cdot \frac{2}{3}=1,\left(1+\frac{1}{4}\right)\left(1-\frac{1}{5}\right)=\frac{5}{4} \cdot \frac{4}{5}=1, \ldots \\
\left(1+\frac{1}{2 m}\right)\left(1-\frac{1}{2 m+1}\right)=\frac{2 m+1}{2 m} \cdot \frac{2 m}{2 m+1}=1
\end{array}
$$
Therefore, the value of the expression is 1.
#
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 7.2. (7 points)
Two pedestrians set out at dawn. Each walked at a constant speed. One walked from $A$ to $B$, the other from $B$ to $A$. They met at noon and, without stopping, arrived: one - in $B$ at 4 PM, and the other - in $A$ at 9 PM. At what hour was dawn that day?
|
Answer: at 6 o'clock.
Solution: Let $x$ be the number of hours from dawn to noon. The first pedestrian walked $x$ hours before noon and 4 after, the second - $x$ before noon and 9 after. Note that the ratio of times is equal to the ratio of the lengths of the paths before and after the meeting point, so $\frac{x}{4}=\frac{9}{x}$. From this proportion, we find that $x=6$.
Indeed, let the speed of the first pedestrian (walking from $A$ to $B$) be $V_{1}$, and the speed of the second pedestrian (walking from $B$ to $A$) be $V_{2}$. Then before the meeting point, the first pedestrian walked $V_{1} \cdot x$ hours, and the second $-V_{2} \cdot x$. After noon, the first pedestrian walked $V_{1} \cdot 4$, and the second $-V_{2} \cdot 9$. But after noon, the first pedestrian walked as much as the second did before noon. And vice versa, after noon, the second pedestrian walked as much as the first did before noon. We have:
$$
\begin{aligned}
& V_{1} \cdot x=V_{2} \cdot 9, \frac{V_{1}}{V_{2}}=\frac{9}{x} \\
& V_{1} \cdot 4=V_{2} \cdot x, \frac{V_{1}}{V_{2}}=\frac{x}{4}
\end{aligned}
$$
From this, $\frac{x}{4}=\frac{9}{x}$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 7.5. (7 points)
In a family, there are six children. Five of them are older than the youngest by 2, 6, 8, 12, and 14 years, respectively. How old is the youngest if the ages of all the children are prime numbers?
|
Answer: 5 years.
Solution. First, let's check the prime numbers less than six. It is obvious that the number we are looking for is odd. The number 3 does not satisfy the condition because $3+6=9-$ is not a prime number. The number 5 satisfies the condition because $5+2=7, 5+6=11, 5+8=13, 5+12=17, 5+14=19$, which means the ages of all the children are indeed prime numbers.
Let's prove that this answer is unique. For this, consider the remainders when the numbers added to the age of the youngest child are divided by 5: the remainder of 2 is 2, the remainder of 6 is 1, the remainder of 8 is 3, the remainder of 12 is 2, and the remainder of 14 is 4. Thus, all remainders from 1 to 4 are present. Therefore, if the age of the youngest child is not a multiple of five, adding a number with a remainder that complements it to five will result in a number that is a multiple of five and greater than five, which is a composite number.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The second term of an infinite decreasing geometric progression is 3. Find the smallest possible value of the sum $A$ of this progression, given that $A>0$.
|
Answer: 12.
Solution. Let the first term of the progression be $a$, and the common ratio be $q$. The sum of the progression $A$ is $\frac{a}{1-q}$. From the condition, we have $3=a q$, from which $a=3 / q$. Therefore, we need to find the minimum value of $A=\frac{3}{q(1-q)}$. Note that from the condition it follows: $0<q<1$. The number $A$ takes its minimum value when the denominator of the fraction $q(1-q)$ is maximized, but $\left(-q^{2}+q\right)$ has a maximum point at $q=1 / 2$, and the maximum value of $q(1-q)$ is $1 / 4$. Then the minimum possible value of $A=3 / 1 / 4=12$.
Comment. The sum $A$ is represented as a function of one variable - 3 points.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. A positive integer $N$ and $N^{2}$ end with the same sequence of digits $\overline{a b c d}$, where $a-$ is a non-zero digit. Find $\overline{a b c}$.
|
Answer: 937.
Solution. Let's represent the number $N$ as $10000 M+k$, where $k$ and $M$ are natural numbers, and $1000 \leq k \leq 9999$. Since $N$ and $N^{2}$ end with the same sequence of digits, the difference
$$
N^{2}-N=\left(10^{4} M+k\right)^{2}-\left(10^{4} M+k\right)=10^{4}\left(10^{4} M^{2}+2 M k-M\right)+k^{2}-k
$$
ends with $\overline{0000}$. Thus, $k^{2}-k=k(k-1)$ is divisible by $10000=2^{4} \cdot 5^{4}$. At the same time, the numbers $k$ and $k-1$ are coprime. Therefore, there are four possible cases:
1) if $k$ is divisible by $10^{4}$, then $k=0$;
2) if $k-1$ is divisible by $10^{4}$, then $k=1$;
3) if $k$ is divisible by $5^{4}$ and $k-1$ is divisible by $2^{4}$, then $k=625$;
4) if $k$ is divisible by $2^{4}$ and $k-1$ is divisible by $5^{4}$, then $k-1=625 m$ ( $m$ is a natural number), and $625 m+1$ is divisible by 16. Since $625 \equiv 1(\bmod 16), 15 \cdot 625 \equiv 15(\bmod 16)$, and $15 \cdot 625+1=9376$ is divisible by 16, then $k=9376$.
Thus, $\frac{\text { First three digits }}{a b c}=937$.
Comment. It is proven that $N^{2}-N$ is divisible by $2^{4} \cdot 5^{4}-1$ point, it is noted that the numbers $k$ and $k-1$ (or $N$ and $N-1$) are coprime - 1 point, it is established that the numbers $k$ and $k-1$ cannot simultaneously contain factors 2 and $5-1$ point, the correct answer is found - 2 points, it is proven that there are no other possibilities - 2 points. Points are summed up.
|
937
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.2. In the city of Perpendicularinsk, it was decided to build new multi-story houses (some of them may be single-story), but in such a way that the total number of floors would be 30. The city architect, Parallelnikov, proposed a project according to which, if after construction one climbs to the roof of each new house, counts the number of lower new houses, and adds up all these numbers, the resulting sum would be the largest possible. What is the indicated sum? How many houses, and of what height, are proposed to be built?
|
Solution: 1) We will show that the project does not involve building houses with more than two floors. Assume the opposite, that such houses are planned. Take the lowest of them and reduce it by one floor, building an additional one-story house as a result. The sum of the numbers in question will decrease by the number of new two-story houses (and only in the case where we reduced a three-story house) and increase by the number of new houses with 2 or more floors (due to the built one-story house). Therefore, the sum of the new project is greater. Contradiction. Thus, Parallelnikov proposes to build only one- and two-story houses.
2) Let the project involve building $x$ one-story houses and $y$ two-story houses. Then $x+2y=30$, and the sum will be equal to the product $xy$. We need to maximize the expression $y(30-2y)$ on the interval $[0; 15]$. The maximum is achieved at the vertex of the parabola, at the point $y=7.5$. Considering that $y$ is an integer, we get that the maximum value is achieved at $y=7$ or $y=8$ and is equal to 112. Accordingly, $x$ is either 16 or 14.
Answer: The sum is 112. The project involves building either 14 one-story and 8 two-story houses, or 16 one-story and 7 two-story houses.
| in progress | points |
| :--- | :--- |
| Correct justified answer | 7 points |
| One of the two sets of houses that make up the answer is "lost" in the correct solution process and/or the sum is determined incorrectly due to arithmetic errors | 6 points |
| It is proven that the project does not involve houses higher than three floors, but further reasoning is incorrect | 4 points |
| The case where all houses are one- or two-story is correctly analyzed, but it is not proven that the maximum is achieved precisely on such sets of houses | 3 points |
| Some statements about the properties of the optimal set of houses are proven, but they do not lead to a solution (for example, that there must be one-story houses, or that the heights of the houses go without gaps) | no more than 2 points |
| Both possible sets of houses are provided without any justification, and the required sum is correctly calculated | 2 points |
| The required sum is correctly indicated without justification, or one of the two examples on which this sum is achieved is provided | 1 point |
| Incorrect answer | 0 points |
|
112
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.6. The sheriff believes that if the number of bandits he catches on a certain day is a prime number, then he is lucky. On Monday and Tuesday, the sheriff was lucky, and starting from Wednesday, the number of bandits he caught was equal to the sum of the number from the day before yesterday and twice the number from yesterday. What is the maximum number of consecutive days the sheriff could have been lucky this week? Justify your answer.
|
Solution: Let's say the sheriff caught 7 bandits on Monday and 3 on Tuesday. Then on Wednesday, Thursday, and Friday, he caught 13, 29, and 71 bandits, respectively. All these numbers are prime, and the sheriff has been lucky for five days in a row.
We will show that the sheriff cannot be lucky for six days in a row. Note that by Wednesday, this number is no less than $2 \cdot 2 + 3 = 7$, and it only increases from there. Therefore, it is sufficient to show that on Wednesday, Thursday, Friday, or Saturday, there will be a day when the number of bandits caught is divisible by 3.
Assume the opposite, that on all these days, the number of bandits caught is not divisible by 3. In particular, the numbers of bandits caught on Wednesday and Thursday do not divide by 3; let's denote them as $A$ and $B$ respectively. Then the number of bandits caught on Friday is $A + 2B$. There are two possible situations.
1) The remainders of $A$ and $B$ when divided by 3 are the same. Then the number $A + 2B = A + B + B$ is the sum of three numbers with the same remainder when divided by 3, so it is divisible by 3. Contradiction.
2) The remainders of $A$ and $B$ when divided by 3 are different: one is 1, the other is 2. Then the number $A + B$ is divisible by 3, so the number $A + 2B = (A + B) + B$ has the same remainder when divided by 3 as the number $B$. Therefore, the numbers of bandits caught on Thursday and Friday have the same remainder when divided by 3. Reasoning as in point 1, we get that the number of bandits caught on Saturday is divisible by 3. Again, a contradiction. The proof is complete.
Answer: 5 days.
Note: The mathematical model of the problem is as follows: Given a sequence $\left\{a_{n}\right\}$ of natural numbers, for all natural $n$ satisfying the relation $a_{n} + 2a_{n+1} = a_{n+2}$. We need to determine the maximum number of consecutive terms in this sequence that can be prime numbers.
The key point in the solution is the assertion that among any four terms of this sequence, there is at least one that is divisible by 3. This fact can be proven in different ways, including by considering all remainders when dividing $a_{1}$ and $a_{2}$ by 3. Of course, the enumeration must be complete.
From the solution, it also follows that to get five consecutive prime numbers, one of the numbers $a_{1}$ or $a_{2}$ must be equal to 3.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and justified answer | 7 points |
| Justified that the sheriff cannot be lucky for 6 days in a row, but no justification that he can be lucky for 5 days in a row | 4 points |
| The idea of considering remainders when dividing by 3 (or any other number divisible by 3) | 2 points |
| Example where the sheriff is lucky for exactly 5 days without proof that a larger number is impossible | 1 point |
| Answer without justification or incorrect answer, as well as examples where the sheriff is lucky for fewer than 5 consecutive days | 0 points |
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.9. In the company, there are 100 children, some of whom are friends (friendship is always mutual). It is known that by selecting any child, the remaining 99 children can be divided into 33 groups of three such that in each group, all three are pairwise friends. Find the minimum possible number of pairs of friends.
(S. Berlov, N. Vlasova)
|
Answer: 198.
Solution: Let's translate the problem into the language of graphs, associating each child with a vertex and each friendship with an edge. Then we know that in this graph with 100 vertices, after removing any vertex, the remaining vertices can be divided into 33 triples such that the vertices in each triple are pairwise connected. We need to find the minimum possible number of edges in such a graph.
First, let's construct an example with exactly 198 edges. Divide 99 vertices, except for vertex $A$, into 33 groups of 3 vertices each. Connect the vertices pairwise within each triple; finally, connect $A$ to all other vertices. Then the conditions of the problem are satisfied: if $A$ is removed, the division into triples is already given, and if any other vertex $B$ is removed, in this division, it is sufficient to replace $B$ with $A$. In this described graph, there are a total of $33 \cdot 3 + 99 = 198$ edges.
It remains to prove that this number is the smallest.
We will call a graph on $3k+1$ vertices good if, after removing any vertex, the remaining $3k$ vertices can be divided into $k$ triples that are pairwise connected. We will prove by induction on $k$ that in a good graph on $3k+1$ vertices, there are at least $6k$ edges; for $k=33$, we will get the required estimate. The base case for $k=1$ is simple: since after removing any vertex, the remaining three are pairwise connected, any two vertices must be connected, so the number of edges is $C_{4}^{2}=6$.
Let's prove the inductive step. If from each vertex at least 4 edges come out, the total number of edges is not less than $(3k+1) \cdot 4 / 2 = 2(3k+1)$, which is even more than the required $6k$. Otherwise, there is a vertex $A$ connected to no more than three other vertices. If any vertex other than $A$ is removed, $A$ will end up in some triple, which means it is connected to at least two vertices. If one of these vertices is removed, $A$ will still have at least two adjacent vertices, so there were at least three. Thus, $A$ is connected to exactly three vertices $B, C$, and $D$. Then, when, for example, $B$ is removed, the vertices $A, C$, and $D$ form a triple, so $C$ and $D$ are connected; similarly, we get that $B$, $C$, and $D$ are pairwise connected.
Now, let's remove from our graph the vertices $A, B, C$, and $D$, and add one vertex $X$ connected to all those with whom at least one of the vertices $B, C$, and $D$ was connected. Note that in this case, the number of edges decreases by at least 6 (i.e., by the number of edges between $A, B, C$, and $D$). We will show that the resulting new graph is good; from this, the inductive step will follow, and then in the new graph, there will be at least $6(k-1)$ edges, which means in the original graph, there are at least $6(k-1) + 6 = 6k$ edges.
Suppose some vertex $Y \neq X$ is removed from the new graph. If it is removed from the original graph, the remaining vertices will be divided into triples; let's say, for definiteness, that vertex $A$ ends up in a triple with $B$ and $C$, and vertex $D$ in another triple. Then the new graph can be divided in the same way, placing vertex $X$ in the triple where vertex $D$ was. Finally, if vertex $X$ is removed from the new graph, the same operation can be performed, considering that vertex $D$ is removed from the original graph (then $A, B$, and $C$ will automatically end up in one triple). Thus, the inductive step is proven.
Remark. The provided example is not the only one. The reasoning in the second part of the solution essentially shows that many different optimal examples can be constructed in the following inductive manner. For $k=1$, take 4 vertices and connect all pairs with edges. When transitioning from $k$ to $k+1$, add three vertices $B, C, D$, connect them pairwise with each other, and also connect them all to some already existing vertex $A$.
In such an example, there will always be $6k$ edges, and it will satisfy the conditions of the problem.
Comment. Only the correct answer - 0 points.
Only an example with 198 pairs of friends is provided - 1 point.
Examples with more pairs of friends are not evaluated.
Only the proof that the number of pairs of friends is not less than $198-6$ points.
|
198
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. 9 knights and liars stood in a row. Each said that there is exactly one liar next to him. How many liars are there among them, if knights always tell the truth, and liars always lie?
|
Answer: 3 liars.
Sketch of the solution. Consider the partition of all into groups of people of the same type standing in a row, with people of different types in adjacent groups. In such a group, there can only be one liar. If there are at least two, the extreme liars tell the truth. There are no more than two knights in a group. If there are at least three, the middle knights lie. A group of two knights cannot stand at the edge, otherwise the edge knight lies. A group of one knight can only stand at the edge, otherwise, there are two liars around the knight, and he lies.
Based on these statements, we get that there are two possible arrangements: LRRRLRRRL and RLRRLRRRL. The first one is impossible, as there is a group of two knights at the edge.
Criteria: Answer without justification: 1 point.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Will Katya be able to write a ten-digit number on the board where all digits are different and all differences between two adjacent digits are different (when finding the difference, the larger is subtracted from the smaller)?
|
Answer: will be able to.
Example: 9081726354.
Criteria. 7 points for any correct example.
|
9081726354
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. There is a paper rectangle $3 \times 100$, divided into 300 cells $1 \times 1$. What is the maximum number of pairs consisting of one corner and one $2 \times 2$ square that can be cut out along the grid lines? (A corner is obtained from a $2 \times 2$ square by removing one of its corner cells).
|
Answer: 33.
Sketch of the solution. The square in the middle row occupies two cells, and the corner - at least one, so the pair occupies at least three cells in the middle row. If there are no fewer than 34 pairs, then they occupy at least $34 \times 3=102$ cells in the middle row, while there are only 100 there.
Example: we cut out 33 squares $3 \times 3$. From each $3 \times 3$ square, we cut out a $2 \times 2$ square and a corner.
Criteria. Answer only: 0 points.
|
33
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. Parallelogram $A B C D$ is such that $\angle B<90^{\circ}$ and $A B<B C$. Points $E$ and $F$ are chosen on the circle $\omega$ circumscribed around triangle $A B C$ such that the tangents to $\omega$ at these points pass through $D$. It turns out that $\angle E D A=\angle F D C$. Find the angle $A B C$.
(A. Yakubov)
|
Answer: $60^{\circ}$.
Solution. Let $\ell$ be the bisector of angle $E D F$. Since $D E$ and $D F$ are tangents to $\omega$, the line $\ell$ passes through the center $O$ of the circle $\omega$.
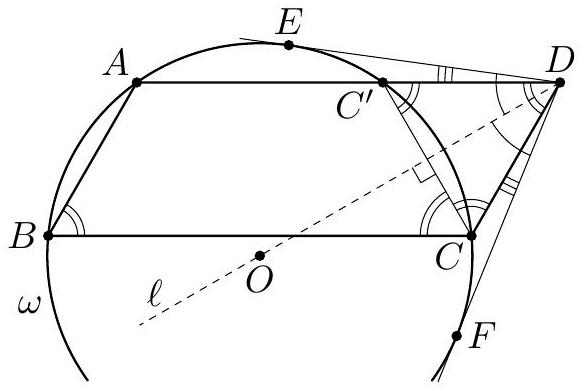
Fig. 3
Perform a reflection about $\ell$. Since $\angle E D A = \angle F D C$, the ray $D C$ will be mapped to the ray $D A$. Since $\ell$ passes through $O$, the circle $\omega$ will map to itself; hence, point $C$ will map to a point $C^{\prime}$ lying on $D A$ and on $\omega$. Since $A D \neq D C$, points $C^{\prime}$ and $A$ are distinct (see Fig. 3).
From the same reflection, we have $\angle D C C^{\prime} = \angle D C^{\prime} C$. Since points $A, B, C$, and $C^{\prime}$ lie on $\omega$, we have $\angle D C^{\prime} C = \angle A B C = \angle A D C$. Therefore, all three angles of triangle $D C C^{\prime}$ are equal, from which it follows that $\angle A B C = \angle C D C^{\prime} = 60^{\circ}$.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. Find the smallest integer $x$ that satisfies the inequality $\frac{100}{|x|}>x^{2}+1$.
|
Answer: -4.
If $|x| \geq 5$, then $\frac{100}{|x|} \leq \frac{100}{5}=20 \leq 17 = (-4)^{2} + 1$ we verify the correctness of the answer.
Comment. The correct answer without a rigorous justification up to 2 points. The inequality is solved, but the wrong answer is chosen 2 points.
|
-4
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. Two cars simultaneously departed from the same point and are driving in the same direction. One car was traveling at a speed of 50 km/h, the other at 40 km/h. Half an hour later, a third car departed from the same point and in the same direction, which overtook the first car one and a half hours later than the second car. Find the speed of the third car.
|
Answer: 60 km/h.
In half an hour, the first car will travel 25 km, and the second car will travel 20 km. Let $x$ be the speed of the third car. The time it takes for the third car to catch up with the first car is $\frac{25}{x-50}$, and the time to catch up with the second car is $\frac{20}{x-40}$. We get the equation $\frac{25}{x-50}-\frac{20}{x-40}=\frac{3}{2}$, and from it $x=60$.
Comment. Correctly formulated equation or system of equations corresponding to the problem - 2 points.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3. At a drama club rehearsal, 8 people gathered. Some of them (honest people) always tell the truth, while the others always lie. One of those present said: "There is not a single honest person here." The second said: "There is no more than one honest person here." The third said: "There is no more than two honest people here," and so on up to the eighth, who said: "There is no more than seven honest people here." How many honest people were there among those gathered?
|
3. The standard evaluation methodology for solutions is provided below.
| Points | Correctness (Incorrectness) of the Solution |
| :---: | :--- |
| 7 | Fully correct solution. |
| $6-7$ | Correct solution, but with minor flaws that do not significantly affect the solution. |
| $5-6$ | The solution is generally correct. However, it contains errors or omits cases that do not affect the logical reasoning. |
| $3-4$ | In cases where the solution to the problem is divided into two equally important parts—solution of one of the parts. |
| $2-3$ | Auxiliary statements that help in solving the problem have been proven. |
| $0-1$ | Individual cases have been considered in the absence of a solution. |
| 0 | The solution is incorrect, and there is no progress. |
| 0 | The solution is absent. |
It is important to note that any correct solution is awarded 7 points. Points should not be deducted for a solution being too long, or for a correct solution that differs from the one provided in the criteria or from other solutions known to the jury. At the same time, any solution, no matter how long, that does not contain useful progress should be awarded 0 points.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Two-headed and seven-headed dragons came to a meeting. At the very beginning of the meeting, one of the heads of one of the seven-headed dragons counted all the other heads. There were 25 of them. How many dragons in total came to the meeting?
|
Answer: 8 dragons. Solution. Subtract the 6 heads belonging to the seven-headed dragon from the 25 heads counted by the seven-headed dragon. 19 heads remain. The remaining dragons cannot all be two-headed (19 is an odd number). There can only be one more seven-headed dragon (if there were two, an odd number of heads would remain for the two-headed dragons. And for three seven-headed dragons, there would not be enough heads ($7 \cdot 3=21>19$)). Subtract the 7 heads of this single dragon from the 19 heads, and we get the total number of heads belonging to the two-headed dragons. Therefore, the number of two-headed dragons: (19 - 7) $: 2=6$. In total: $6+1+1=8$ dragons.
Grading criteria: Full solution - $\mathbf{7}$ points. Only answer - $\mathbf{2}$ points.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Vovodya is running on a circular track at a constant speed. There are two photographers standing at two points on the track. After the start, Vovodya was closer to the first photographer for 2 minutes, then closer to the second photographer for 3 minutes, and then closer to the first photographer again. How long did it take Vovodya to run the entire circle?
|
Solution. Let's divide both arcs of the circle between the photographers in half. The halves of the arcs adjacent to the second photographer make up half the distance. Vasya ran this half in 3 minutes, so he will run the entire circle in 6 minutes.
Answer: in 6 minutes.
Grading criteria: Full solution - 7 points. Only answer - $\mathbf{2}$ points.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.2. What is the minimum number of factors that need to be crossed out from the number $99!=1 \cdot 2 \cdot \ldots \cdot 99$ so that the product of the remaining factors ends in $2?$
|
Answer: 20 factors.
Solution. From the number 99! it is necessary to remove all factors that are multiples of 5, otherwise the product will end in 0. There are a total of 19 such factors (ending in 0 or 5).
The product of the remaining factors ends in 6. Indeed, since the product $1 \times 2 \cdot 3 \cdot 4 \cdot 6 \cdot 7 \cdot 8 \cdot 9$ ends in 6, then similar products in each subsequent decade also end in 6. Therefore, removing 19 factors is insufficient. But 20 is sufficient. If you remove another number ending in 3 or 8, the product of the numbers in the corresponding decade will end in 2. The product of this number and a number ending in 6 also ends in 2.
## Grading Criteria
+ correct answer and a fully justified solution
$\pm$ correct answer and a generally correct solution, but there are minor gaps in the justification
干 correct answer and a correct example, but it is not explained why the specified number of removed factors is the smallest
$\mp$ correct answer, but some of the numbers to be removed are incorrectly identified in the reasoning
干 correct approach to the solution, but an error was made that affected the answer
干 an estimate is provided without an example
- only the answer is provided
- the problem is not solved or is solved incorrectly
|
20
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. Does there exist a ten-digit number, divisible by 11, in which all digits from 0 to 9 appear?
|
Answer. Yes, for example, 9576843210.
Solution. Let's consider a possible way to find the required number. Note that a number is divisible by 11 if the difference between the sum of the digits in the odd positions and the sum of the digits in the even positions is divisible by 11. If we write all ten digits in descending order, that is, 9876543210, then this difference will be 5. If we swap 5 and 8, the first sum will increase by 3, and the second sum will decrease by 3, so their difference will become 11. Therefore, the number 9576843210 is divisible by 11.
Comment. Any correct number provided - 7 points.
|
9576843210
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. There are pan scales without weights and 11 visually identical coins, among which one may be counterfeit, and it is unknown whether it is lighter or heavier than the genuine coins (genuine coins have the same weight). How can you find at least 8 genuine coins in two weighings?
|
Solution. Let's divide the coins into three piles of three coins each. Compare pile 1 and pile 2, and then compare pile 2 and pile 3. If all three piles weigh the same, then all the coins in them are genuine, and we have found 9 genuine coins. Otherwise, one of the piles differs in weight from the others, and the counterfeit coin can only be in it. Then the genuine coins are in the other two piles plus the two remaining coins that we did not weigh.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. From the set of numbers $1,2,3,4, \ldots, 2021$, one number was removed, after which it turned out that the sum of the remaining numbers is divisible by 2022. Which number was removed?
|
Answer: 1011.
Solution. Let's write out the sum and perform grouping:
$1+2+3+\cdots+2019+2020+2021=(1+2021)+(2+2020)+$ $\cdots+(1012+1010)+1011$.
All the terms enclosed in parentheses are divisible by 2022. If we remove the last ungrouped term from the sum, the sum will be a multiple of 2022.
Comment. Answer only - 0 points.
|
1011
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. Petya came home from school today at $16:45$, looked at the clock and wondered: after what time will the hands of the clock be in the same position for the seventh time since he came home from school?
|
Answer: 435 minutes.
Solution. The speed of the minute hand is 12 divisions/hour (one division here refers to the distance between adjacent numbers on the clock face), and the hour hand is 1 division/hour. Before the seventh meeting of the minute and hour hands, the minute hand must first "lap" the hour hand 6 times, meaning it must complete 6 full circles of 12 divisions. Let's say after this, the hour hand travels $L$ divisions until the seventh meeting. The total distance traveled by the minute hand then consists of the 72 divisions found, plus the initial 7.75 divisions separating them (since the clock shows 4:45), and the final $L$ divisions. Equate the time of movement of the hour and minute hands:
$$
\frac{L}{1}=\frac{L+72+7.75}{12} \Leftrightarrow 12 L=L+79.75 \Leftrightarrow L=7.25
$$
The hour hand will travel 7.25 divisions, which corresponds to 7.25 hours, or 435 minutes.
|
435
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (7 points) There are apples in five boxes, with an equal number of apples in each. When 60 apples were taken out of each box, after that, the total number of apples left was the same as the number of apples that were originally in two boxes. How many apples were in each box?
Answer: 100.
|
Solution. In total, $60 \cdot 5=300$ apples were taken out, and this is equal to the number of apples that were in three boxes. Therefore, there were 100 apples in each box.
Criteria. Any correct solution: 7 points.
If it is not justified that there were 100 apples in each box, but it is verified that the condition is satisfied in this case: 4 points.
Correct answer without any explanation: 2 points.
|
100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (7 points) A gnome in shoes weighs 2 kg more than a gnome without shoes. If you put five identical gnomes in shoes and five such gnomes without shoes on the scales, the scales will show 330 kg. How much does a gnome in shoes weigh?
|
Answer: 34 kg.
Solution. Let's put boots on five gnomes, then the weight will increase by 10 kg. It turns out that ten gnomes in boots weigh 340 kg. Therefore, one gnome in boots weighs 34 kg.
Criteria. Correctly found the weight of a gnome in boots by any method: 7 points.
Correctly found the weight of a gnome without boots, but did not find (did not specify in the answer) the weight of a gnome in boots: 5 points.
Did not find the correct weight of a gnome either with boots or without boots: 0 points.
|
34
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. Two runners, starting simultaneously at constant speeds, run on a circular track in opposite directions. One of them runs the loop in 5 minutes, while the other takes 8 minutes. Find the number of different meeting points of the runners on the track, if they ran for at least an hour.
|
Answer: 13 points.
Solution.
Let the length of the track be $\mathrm{S}$ meters. Then the speeds of the runners are $\mathrm{S} / 5$ and S/8 meters per minute, respectively.
|
13
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. Three families of parallel lines have been drawn, with 10 lines in each. What is the maximum number of triangles they can cut out from the plane?
Answer: 150 triangles
#
|
# Solution.
Consider 100 nodes - the intersection points of lines in the first and second directions. Divide them into 10 sectors: the first sector - nodes lying on the first lines of the first and second
directions. The second sector - nodes lying on the second lines (excluding points lying in the first sector) and so on. Triangles with sides parallel to three fixed directions can have two orientations, and each of our 100 nodes can be the vertex of no more than one triangle of each orientation. Therefore, 10 lines in the third direction form no more than $2 \cdot 25$ triangles with the last five sectors, since these five sectors contain a total of 25 nodes.
Furthermore, note that each line in the third direction forms no more than one triangle of each orientation with nodes belonging to one sector. Therefore, the number of triangles with vertices in the nodes of the remaining five sectors will not exceed $10 \cdot 2 \cdot 5$.
In total, there are no more than $100+50=150$ triangles. An example with 150 triangles is shown in the figure.
|
150
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. A convex quadrilateral $ABCD$ is such that $\angle BAC = \angle BDA$ and $\angle BAD = \angle ADC = 60^{\circ}$. Find the length of $AD$, given that $AB = 14$ and $CD = 6$.
Answer: 20.
|
Solution. Extend $A B$ and $C D$ to intersect at point $P$. Since $\angle P A D = \angle A D P = 60^{\circ}$, triangle $A D P$ is equilateral. Next, we note that triangle $A P C$ is congruent to triangle $D A B$, because $A P = A B$, $\angle A P C = 60^{\circ} = \angle D A B$, and $\angle P A C = \angle A D B$ (Fig. 2). Therefore, $P C = A B = 14$, and $A D = P D = P C + C D = 14 + 6 = 20$.
Fig. 2: to the solution of problem 6
## Criteria
0 points. Only the correct answer without justification.
1 point. The additional construction to the equilateral triangle $A P D$ is present, but there is no further progress.
3 points. A pair of congruent triangles leading to the solution is found, but the solution is not completed.
4 points. The correct answer and justification are provided.
|
20
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. What is the sum of the digits of the number $A=10^{50}-10^{40}+10^{30}-10^{20}+10^{10}-1$?
|
# Answer: 270.
Solution. The number is the sum of three numbers: a number composed of 10 nines followed by 40 zeros, a number composed of 10 nines followed by 20 zeros, and finally, a number composed of 10 nines. All the nines fall on the zeros in the other addends, so there is no carry-over, and the answer is $90+90+90=270$.
Comment. Correct answer without justification - 2 points.
|
270
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. Find the largest natural number with all distinct digits such that the sum of any two of its digits is a prime number.
|
Answer: 520.
Solution: If the desired number is at least a four-digit number, then it either has three digits of the same parity or two pairs of digits of the same parity. In each of these cases, we get that two of the sums of the digits are even. Therefore, they must equal 2. The number 2 can be represented as the sum of different digits in only one way: $0+2$. A three-digit number that satisfies the condition is 520. We will show that there cannot be a larger number. A three-digit number has two digits of the same parity, and as we showed above, these digits can only be 0 and 2. The third digit must be odd. The digit 9 does not work: $9+0=9$ - a composite number. The digit 7 does not work: $7+2=9$. But the digit 5 works.
Comment: Correct answer without justification - 2 points. Proven that the number is no more than three digits - 2 points.
|
520
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. A round table was sat at by 10 people - liars and knights. Liars always lie, and knights always tell the truth. Each of them was given a coin. Then each of them passed their coin to one of their two neighbors. After that, each one said: “I have more coins than my right neighbor.” What is the maximum number of knights that could have been sitting at the table?
|
Answer: 6.
Solution: After the coins are passed, each person sitting at the table can have 0, 1, or 2 coins. Note that 3 knights cannot sit in a row. Indeed, let knights $A, B, C$ sit next to each other, with $B$ sitting to the right of $A$, $C$ to the right of $B$, and $D$ to the right of $C$. If $A$ has $x$ coins, $B$ has $y$ coins, $C$ has $z$ coins, and $D$ has $t$ coins, then the inequality $x > y > z > t$ would hold, which is impossible for the numbers 0, 1, 2. Therefore, among any 3 people sitting in a row, there is a liar. Choose any liar sitting at the table (such a person exists because there are 3 people sitting in a row), and divide the remaining people into 3 groups of 3 people each sitting next to each other. In each of these groups, there is a liar. Thus, there are at least $1 + 3 = 4$ liars at the table, and therefore no more than 6 knights. We will show that 6 knights could be sitting at the table. Suppose they are seated as follows: -K-K-L-L-K-K-L-K-K-L-. And the knights sitting next to each other exchange coins, while the liars give their coins to the people sitting to their right. Then the number of coins each person has will be -K(2)-K(1)-L(0)-L(1)-K(2)-K(1)-L(0)-K(2)-K(1)-L(0)-. And the knights will tell the truth, while the liars will lie.
Comment: It is proven that no more than 6 knights can sit at the table - 5 points. It is proven that 6 knights can sit at the table - 2 points.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. In the class, there are more than 20 but fewer than 30 students. In the class, those who attend the chess club are half the number of those who do not attend. And those who attend the checkers club are one-third the number of those who do not attend. How many students are in the class? Provide all possible answers and prove that there are no others.
|
Solution: Let $n$ be the number of students in the class who attend the chess club, then $2n$ students do not attend, and the total number of students in the class is $3n$, meaning the total number of students in the class is divisible by 3. Similarly, from the fact that the number of people attending the checkers club is three times less than those who do not attend, we get that the total number of students in the class is divisible by 4. The numbers 3 and 4 are coprime, so the total number of students in the class must also be divisible by 12. In the range from 20 to 30, there is only one such number: 24. It is easy to construct an example showing that a class can contain 24 students: in this case, 8 people attend the chess club, and 6 attend the checkers club.
Answer: 24 students.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and fully justified answer (an example that 24 students can be in the class is NOT REQUIRED) | 7 points |
| Proven that the total number of students in the class is divisible by both the number 3 and the number 4 | 5 points |
| Proven that the total number of students in the class is divisible by one of the numbers 3 or 4 with no further progress | 3 points |
| The correct answer is given, supported by an example, and the uniqueness is not proven | 1 point |
| Answer without justification and/or incorrect answer | 0 points |
|
24
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.3. On the island of knights and liars, each resident was asked about each of the others: is he a knight or a liar. In total, 42 answers of "knight" and 48 answers of "liar" were received. What is the maximum number of knights that could have been on the island? Justify your answer. (It is known that knights always tell the truth, while liars always lie.)
|
Solution: Each of the $n$ residents gave $n-1$ answers; in total, there were $n(n-1)$ answers, which, according to the problem, equals $42+48=90$. Hence, $n=10$, meaning there are 10 residents on the island. Let the number of knights be $x$, then the number of liars is $10-x$. Answers of "liar" arise in two cases: when a knight speaks about a liar (there are $x(10-x)$ such cases) and vice versa (the same number of cases). We have the equation $2 x(10-x)=48$, from which $x=6$ or $x=4$. Both options are possible.
Note: Instead of the equation $2 x(10-x)=48$, the equation $x(x-1)+(10-x)(9-x)=42$ (by the number of "knight" answers) or even an equation of the type $\frac{2 x(10-x)}{x(x-1)+(10-x)(9-x)}=\frac{48}{42}$ might arise. All of them are equally valid.
Answer: 6 knights.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and fully justified answer | 7 points |
| A correct approach to the solution resulted in an incorrect answer due to calculation errors | 6 points |
| A correct equation (system of equations) that fully describes the problem condition; this equation (system) is not solved | 4 points |
| The number of residents on the island is correctly found (in the absence of further progress) | 3 points |
| It is shown that the number of knights could have been 4 or 6 (at least one of these numbers) and it is not proven that there are no other options | 1 point |
| Answer without justification | 0 points |
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1 How many five-digit natural numbers are there that are divisible by 9, and for which the last digit is 2 more than the second last digit?
|
Answer: 800. Hint The second last digit (the tens digit) can be any from 0 to 7 (so that after adding two, the last digit makes sense). The third and second digits can be any (from 0 to 9). After choosing the specified three digits (the second, third, and fourth), the last digit is uniquely determined by the second last, and the first digit is uniquely determined by the other four under the condition of divisibility by 9 (note that the first digit cannot be 0, and all other digits $1,2, \ldots, 9$ give all possible remainders when divided by 9). In total, by the rule of product, we have $8 \cdot 10 \cdot 10=800$ numbers.
|
800
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. A tourist goes on a hike from $A$ to $B$ and back, and completes the entire journey in 3 hours and 41 minutes. The route from $A$ to $B$ first goes uphill, then on flat ground, and finally downhill. Over what distance does the road run on flat ground, if the tourist's speed is 4 km/h when climbing uphill, 5 km/h on flat ground, and 6 km/h when descending, and the distance $\mathrm{AB}$ is 9 km?
|
Solution. Let $x$ km of the path be on flat ground, then $9-x$ km of the path (uphill and downhill) the tourist travels twice, once (each of the ascent or descent) at a speed of 4 km/h, the other at a speed of 6 km/h, and spends $(9-x) / 4 + (9-x) / 6$ hours on this part. Since the tourist walks $2x / 5$ hours on flat ground, and the round trip takes 3 hours and 41 minutes, then $2x / 5 + (9-x) / 4 + (9-x) / 6 = 221 / 60$, from which $x=4$ km.
Answer: 4 km.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1-0. The number 111123445678 is written on the board, and several digits (not all) need to be erased to get a number that is a multiple of 5. In how many ways can this be done?
|
Answer: 60
Solution. The digits 6, 7, and 8 must be crossed out, and 5 must be kept (otherwise, the number will not be divisible by 5). Each digit before the five can be crossed out or not. There are two options for each of the digits 2 and 3 (cross out or not), three options for the digit 4 (do not cross out, cross out one, or cross out both), and five options for the ones (do not cross out any, cross out one, two, three, or all four). The deletions of different digits are independent events, so the obtained numbers should be multiplied: $5 \cdot 3 \cdot 2 \cdot 2=60$.
|
60
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2-0. The number $n$ is such that $8n$ is a 100-digit number, and $81n$ is a 102-digit number. What can the second digit from the beginning of $n$ be?
|
Answer: 2
Solution. Since $8 n10^{101}$ (equality here is obviously impossible), it means $n>123 \cdot 10^{97}$. Therefore, the second digit from the beginning of the number $n$ is 2.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4-0. Kisa and Busya came to the cafeteria during the break, where only muffins and doughnuts were sold, costing a whole number of rubles. Kisa bought 8 muffins and 3 doughnuts, spending less than 200 rubles, while Busya bought 4 muffins and 5 doughnuts, spending more than 150 rubles. Name the highest possible price of one muffin.
|
Answer: 19
Solution. Let the price of a cake be $k$, and the price of a bun be $p$ rubles. Then $8 k+3 p<150$. Multiplying the first inequality by 5, and the second by 3, we get $40 k+15 p<1000, -12 k-15 p<-450$. Adding these inequalities: $28 k<550$, from which, taking into account the integer nature, $k \leqslant 19$.
Note that the case $k=19, p=15$ satisfies all conditions.
|
19
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5-0. A certain quadratic trinomial $x^{2}-p x+q$ has integer roots $x_{1}$ and $x_{2}$. It turns out that the numbers $x_{1}$, $x_{2}$, and $q$ form a decreasing arithmetic progression. Find the sum of all possible values of $x_{2}$.
|
Answer: -5
Solution. By Vieta's theorem $q=x_{1} x_{2}$. Then $2 x_{2}=x_{1}+x_{1} x_{2}$, from which $x_{1}=\frac{2 x_{2}}{1+x_{2}}$. Since the roots are integers, $2 x_{2}$ is divisible by $1+x_{2}$. But $2+2 x_{2}$ is divisible by $1+x_{2}$, which means 2 is also divisible by $1+x_{2}$. Therefore, $x_{2}=-3,-2,0$ or 1. In these cases, $x_{1}$ takes the values $3,4,0$ and 1. Since $x_{2}<x_{1}$, only the first two options are suitable, from which the sum of possible values of $x_{2}$ is -5.
|
-5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7-0. The number $n$ has exactly six divisors (including 1 and itself). They were arranged in ascending order. It turned out that the third divisor is seven times greater than the second, and the fourth is 10 more than the third. What is $n$?
|
Answer: 2891
Solution. If $n$ has six divisors, then either $n=p^{5}$ or $n=p \cdot q^{2}$ (where $p$ and $q$ are prime numbers). In the first case, $p=7$ (since the third divisor is seven times the second), but then the second condition is not satisfied.
Therefore, $n$ has two prime divisors (one of which is squared), and one of the prime factors is 7. Let the smallest divisors of $n$ be $1, p, 7p$, and $7p+10$. If $p=7$, then $7p+10=59$, and we get the answer 2891. If $p<7$, then $p=2$ (then $7p+10=24$, and such a number has more than six divisors). If $p=3$, then $7p+10=31$, and if $p=5$, then $7p+10=45$. In each of these cases, $n$ has more than two prime divisors.
|
2891
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8-0. Once, King Shahryar said to Scheherazade: "Here is a paper circle with 1001 points on its boundary. Each night, you must cut the figure you have along a straight line containing any two of the marked points, keeping only one fragment and discarding the other. And make sure that the figure you keep is not a polygon, but a figure from which a polygon can be obtained by further cutting." On which night will Scheherazade, even with her most skillful actions, no longer be able to fulfill Shahryar's condition?
|
# Answer: 1999
Solution. First, let's describe the strategy that Scheherazade will use to meet Shahryar's conditions for 1998 nights. Initially, she will cut along the lines connecting adjacent vertices and discard the smaller part (let's call such a part a segment). She will do this for 1000 nights. After this, a 1001-gon with a segment attached to one of its sides will remain. After this, she will cut off triangles. After each such cut, the number of vertices decreases by 1 (and a segment is still attached to one of the sides), and after another 998 moves, a triangle with a segment will remain, after which there will be nothing left to cut according to the rules.
Similarly, it can be proven that Scheherazade has no strategy for more moves. With each move, Scheherazade discards either a segment or a vertex (or both). Eventually, a segment and at least three vertices must remain, which means that it is impossible to make more than 1998 cuts.
|
1999
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. A right triangle ABC is inscribed in a circle with hypotenuse AB. On the larger leg BC, a point D is taken such that AC = BD, and point E is the midpoint of the arc AB containing point C. Find the angle DEC.
|
3. Point $\mathrm{E}$ is the midpoint of arc $\mathrm{AB}$, so $\mathrm{AE}=\mathrm{BE}$. Moreover, the inscribed angles $\mathrm{CAE}$ and $\mathrm{EBC}$, which subtend the same arc, are equal. Also, by the given condition, $\mathrm{AC}=\mathrm{BD}$. Therefore, triangles $\mathrm{ACE}$ and $\mathrm{BDE}$ are congruent, from which it follows that $\angle \mathrm{CEA}=\angle \mathrm{BED}$. But then $\angle \mathrm{DEC}=\angle \mathrm{BEA}=90^{\circ}$, since $\angle \mathrm{BEA}=\angle \mathrm{BCA}$.
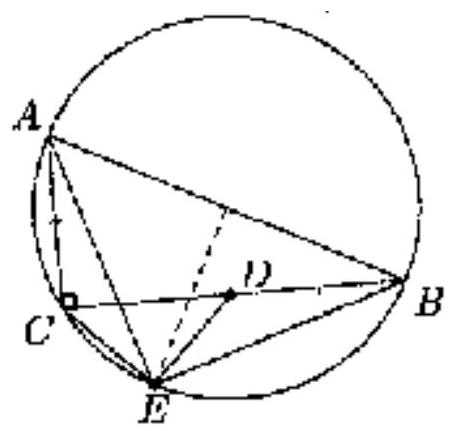
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. For numbers $a, b, c, d$, it is known that $a^{2}+b^{2}=1, c^{2}+d^{2}=1, a c+b d=0$. Calculate $a b+c d$.
|
4. Consider the equality: $(a c+b d)(a d+b c)=0$, since $a c+b d=0$.
We get $a^{2} c d+b^{2} c d+c^{2} a b+d^{2} a b=0$ or $\left(a^{2}+b^{2}\right) c d+\left(c^{2}+d^{2}\right) a b=0$.
Since $a^{2}+b^{2}=1$ and $c^{2}+d^{2}=1$ we obtain $a b+c d=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. There are 40 visually identical coins, among which 3 are counterfeit - they weigh the same and are lighter than the genuine ones (the genuine coins also weigh the same). How can you use three weighings on a balance scale without weights to select 16 genuine coins?
|
5. First solution: Divide all the coins into two parts of 20 coins each and weigh them. Since the number of counterfeit coins is odd, one of the piles will weigh more. This means that there is no more than one counterfeit coin in it. Divide it into two piles of 10 coins and weigh them. If the scales are in balance, then all 20 weighed coins are genuine. If one of the pans outweighs, then there are 10 genuine coins on that pan, and among the other 10 coins, there is exactly one counterfeit. Divide these 10 coins into three piles of 4, 4, and 2 coins. In the third weighing, compare the two piles of 4 coins. If they balance, then all 8 coins are genuine, and we have found 18 genuine coins. If one of the piles outweighs, then there are 4 genuine coins in it, the other pile contains the counterfeit coin, and the 2 set aside coins are genuine.
Second solution: Divide all the coins into five equal piles, each containing 8 coins, and number them. Place the 1st and 2nd piles on one pan of the scales, and the 3rd and 4th on the other. Consider the first case - the scales balance. Then either there is one counterfeit coin on each pan, or all the coins in the weighing are genuine. Then take and weigh the 1st and 2nd piles. If they balance, then all 16 coins are genuine. If one of the piles outweighs, then there are 8 genuine coins in it. In the third weighing, compare the 3rd and 4th piles and determine the next 8 genuine coins. Now consider the second case - the scales do not balance. Let's assume for definiteness that the 1st and 2nd piles outweigh, then there is no more than one counterfeit coin among them. In the second weighing, compare the 1st and 2nd piles. If they balance, then all 16 coins are genuine. If one of the piles outweighs, then there are 8 genuine coins in it, and exactly one counterfeit in the other. Consequently, there are exactly two counterfeit coins in the 3rd and 4th piles, and 8 genuine coins in the 5th pile. Thus, a total of 16 genuine coins have been found.
|
16
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the value of the expression $a^{3}+b^{3}+12 a b$, given that $a+b=4$.
|
1. $a^{3}+b^{3}+12 a b=(a+b)\left(a^{2}-a b+b^{2}\right)+12 a b=4\left(a^{2}-\right.$ $\left.a b+b^{2}\right)+12 a b=4 a^{2}+4 b^{2}+8 a b=4(a+b)^{2}=4 \cdot 16=64$
|
64
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The boy went to the shooting range with his father. The father bought him 10 bullets. Later, the father took away one bullet for each miss and gave one additional bullet for each hit. The son fired 55 times, after which he ran out of bullets. How many times did he hit the target?
|
2. Each time the boy hit the target, the number of bullets he had remained the same (he used one and received one from his father). Each time the boy missed, the number of bullets he had decreased by 2 (he used one and his father took one). This means that the son missed $10: 2=5$ times out of 55 shots, so he hit 55 - 5 $=50$ times.
|
50
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.5. How many solutions in integers \(x, y\) does the equation \(6 x^{2}+2 x y+y+x=2019\) have?
|
Answer. 4 solutions. Solution. Express $y$ from the given equation: $y=\frac{2019-6 x^{2}-x}{2 x+1}$. Dividing $6 x^{2}+x$ by $2 x+1$ with a remainder, we get $6 x^{2}+x=(3 x-1)(2 x+1)+1$. Thus, the expression for $y$ will take the form: $y=\frac{2019-(3 x-1)(2 x+1)-1}{2 x+1}=\frac{2018}{2 x+1}-3 x+1$. Therefore, for $y$ to be an integer, 2018 must be divisible by $2 x+1$. Since $2 x+1$ is an odd number, and 2018:2=1009 is a prime number, $2 x+1$ can take 4 values: $1, -1, 1009, -1009$. Then the corresponding values of $x$ and $y$ are: (0;2019), (-1;-2014), (504;-1509), (-505;1514).
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.2. From a square with a side of 10, a green square with a side of 2, a blue square, and a yellow rectangle were cut out (see figure). What is the perimeter of the remaining figure?
The perimeter of a figure is the sum of the lengths of all its sides.
|
Answer: 44.
Solution. We will sequentially cut out our figures from the initial square with a perimeter of 40.
- After cutting out the yellow rectangle, we get a figure with the same perimeter as the original square.
- Next, we cut off the blue square, and again we get a figure with the same perimeter.
- The last action is to cut off the green square, and the perimeter increases by twice the side of the green square, that is, by 4.
|
44
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.3. Irina did poorly in math at the beginning of the school year, so she had 3 threes and 2 twos in her journal. But in mid-October, she pulled herself together and started getting only fives. What is the minimum number of fives Irina needs to get so that her average grade is exactly 4?
|
Answer: 7.
Solution. Let Irina need to get $x$ fives. Then the sum of her grades will be $3 \cdot 3+2 \cdot 2+5 x=5 x+13$, and the number of grades $-3+2+x=x+5$.
We get the equation
$$
\begin{aligned}
(5 x+13) & :(x+5)=4 \\
5 x+13 & =4(x+5) \\
5 x+13 & =4 x+20 \\
x & =7
\end{aligned}
$$
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.5. On some trees in the magical forest, coins grow. The number of trees that do not grow any coins at all is twice as many as the trees that grow three coins. On three trees, two coins grow, on four trees - four coins, and no tree grows more than four coins. By how much is the total number of coins in the magical forest greater than the number of trees?
|
Answer: 15.
Solution. Let $x$ be the number of trees in the forest on which three coins grow, and on which one coin grows. Then in the forest, $2 x$ trees do not grow any coins at all.
Thus, the total number of coins is
$$
2 x \cdot 0+y \cdot 1+3 \cdot 2+x \cdot 3+4 \cdot 4=3 x+y+22
$$
and the total number of trees is
$$
2 x+y+3+x+4=3 x+y+7
$$
The first number is 15 more than the second.
|
15
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.6. In the zoo, there are red, yellow, and green parrots (there is at least one parrot of each of the listed colors; there are no parrots of other colors in the zoo). It is known that among any 10 parrots, there is definitely a red one, and among any 12 parrots, there is definitely a yellow one. What is the maximum number of parrots that can be in the zoo?
|
Answer: 19.
Solution. Let there be $x$ red, $y$ yellow, and $z$ green parrots in the zoo.
Since among any 10 parrots there is a red one, the number of non-red parrots does not exceed 9, that is, $y+z \leqslant 9$. By similar reasoning, we get that the number of non-yellow parrots does not exceed 11, that is, $x+z \leqslant 11$.
Thus,
$$
\begin{gathered}
x+y+2 z=(y+z)+(x+z) \leqslant 9+11=20 ; \\
x+y+z \leqslant 20-z \leqslant 19
\end{gathered}
$$
This means that the total number of parrots does not exceed 19. At the same time, there could have been 10 red, 8 yellow, and 1 green parrot in the zoo, that is, exactly 19 parrots.
|
19
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.8. A boastful fisherman says the same phrase every day: "Today I caught more perch than I did the day before yesterday (2 days ago), but less than I did 9 days ago." What is the maximum number of days in a row that he can tell the truth?
|
Answer: 8.
Solution. First, let's provide an example where he tells the truth for 8 days in a row. The numbers of perch he caught on consecutive days are indicated:
$$
2020202020202061 \underbrace{728394105}_{\text {truth }} \text {. }
$$
Now let's prove that he could not have told the truth for 9 days in a row. Suppose he did. Let's denote the truthful days as the 3rd, ..., 11th, the previous day as the 2nd, and the day before that as the 1st.
Then on the 10th day, he caught more than on the 8th, which is more than on the 6th, 4th, and 2nd. At the same time, on the 11th day, he caught less than on the 2nd, since it was exactly 9 days ago. Therefore, on the 11th day, he caught less than on the 10th.
On the other hand, on the 11th day, the fisherman caught more than on the 9th, which is more than on the 7th, 5th, 3rd, and 1st. At the same time, on the 10th day, he caught less than on the 1st. This means that on the 10th day, he caught less than on the 11th, which contradicts the previously obtained conclusion.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. Borya found the smallest prime number \( p \) such that \( 5 p^{2} + p^{3} \) is a square of some natural number. What number did Borya find?
|
Answer: 11.
Solution: Since $5 p^{2}+p^{3}=p^{2}(5+p)$, the original number is a perfect square if and only if the number $5+p$ is a perfect square. Since $p$ is a prime number, $p+5 \geq 7$. It is sufficient to verify that if $p+5=9$, then $p=4$ is not a prime; if $p+5=16$, then $p=11$ satisfies the condition, and this value of $p$ will be the smallest.
Note: The problem can also be solved by sequentially checking prime numbers starting from $p=2$. Criteria: Only the answer (including verification) - 0 points. Correct answer with a correct solution (including finding by checking all (!) primes $p$ up to 11) - 7 points. The problem is reduced to the fact that $(5+p)$ is a prime number, but not completed or further with an error - 3 points.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. In a convex quadrilateral $\mathrm{ABCD}$, the bisector of angle $\mathrm{B}$ passes through the midpoint of side $\mathrm{AD}$, and $\angle \mathrm{C}=\angle \mathrm{A}+\angle \mathrm{D}$. Find the angle $\mathrm{ACD}$.
|
Solution. Let $\mathrm{E}$ be the midpoint of side AD, and $\mathrm{F}$ be the intersection point of $\mathrm{BE}$ and AC. From the condition, we have: $\angle \mathrm{B}=360-2(\angle \mathrm{A}+\angle \mathrm{D})$, from which $\angle \mathrm{AEB}=180-\angle \mathrm{A}-\angle \mathrm{B} / 2=\angle \mathrm{D}$. Therefore, $\mathrm{BE} \| \mathrm{CD}$, and $\mathrm{EF}$ is the midline of triangle $\mathrm{ACD}$, meaning $\mathrm{AF}=\mathrm{FC}$. Thus, $\mathrm{BF}$
is the bisector and median of triangle $\mathrm{ABC}$, and therefore its altitude. Consequently, line $\mathrm{CD}$, parallel to $\mathrm{BF}$, is also perpendicular to $\mathrm{AC}$, from which the answer follows.
Answer. Angle ACC is 90.
Criteria. Only the answer: 0 points.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3. On the board, 100 pairwise distinct natural numbers $a_{1}, a_{2}, \ldots, a_{100}$ were written. Then, under each number $a_{i}$, a number $b_{i}$ was written, obtained by adding to $a_{i}$ the greatest common divisor of the remaining 99 original numbers. What is the smallest number of pairwise distinct numbers that can be among $b_{1}, b_{2}, \ldots, b_{100}$?
(S. Berlov)
|
# Answer. 99.
First solution. If we set $a_{100}=1$ and $a_{i}=2 i$ for $i=1,2, \ldots, 99$, then $b_{1}=b_{100}=3$, so there will be no more than 99 different numbers among the numbers $b_{i}$. It remains to prove that there will always be 99 different numbers among the numbers $b_{i}$.
Without loss of generality, we can assume that $a_{1}a_{j} \geqslant a_{i}+d_{i}=b_{i}$
$$
which implies $b_{i} \neq b_{j}$. Thus, we have established that $b_{j} \neq b_{i}$ when $i \neq k \neq j$. Therefore, all 99 numbers $b_{i}$ for $i \neq k$ are different.
Second solution. We will provide another proof that there are at least 99 different numbers among the numbers $b_{i}$. We will again use the notation $d_{i}$ from the previous solution; we will also assume that $a_{1}<\ldots<a_{100}$.
Let $c_{i}=a_{i+1}-a_{i}$. Suppose $c_{\ell}$ is the minimum of the numbers $c_{1}, c_{2}, \ldots, c_{99}$. We will show that if $i<j$ and $i \neq \ell+1 \neq j$, then the numbers $b_{i}$ and $b_{j}$ are different. This will again lead to the required result.
Assume that $i<j-1$. Then $i \leqslant 98$, and the numbers $a_{i+1}$ and $a_{i+2}$ are divisible by $d_{i}$. Therefore, $d_{i} \leqslant a_{i+2}-a_{i+1}<a_{j}-a_{i}$, which implies
$$
b_{i}=a_{i}+d_{i}<a_{i}+\left(a_{j}-a_{i}\right)=a_{j}<b_{j}
$$
Now suppose $j=i+1$. Then $i \neq \ell+1$ and $i \neq \ell$ (since $j \neq \ell+1$). Therefore, the numbers $a_{\ell}$ and $a_{\ell+1}$ are divisible by $d_{i}$. Hence, $d_{i} \leqslant$ $\leqslant a_{\ell+1}-a_{\ell}=c_{\ell} \leqslant c_{i}$, which leads to
$$
b_{i}=a_{i}+d_{i} \leqslant a_{i}+c_{i}=a_{i+1}=a_{j}<b_{j}
$$
Thus, in both cases, we have obtained that $b_{i}<b_{j}$, as required.
|
99
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 9.4. (7 points)
At a joint conference of the party of liars and the party of truth-tellers, 32 people were elected to the presidium and seated in four rows of eight. During the break, each member of the presidium claimed that among their neighbors there are representatives of both parties. It is known that liars always lie, and truth-tellers always tell the truth. What is the minimum number of liars in the presidium for the described situation to be possible? (Two members of the presidium are neighbors if one of them sits to the left, right, in front of, or behind the other).
|
Answer: with eight liars.
Solution: Divide all the seats in the presidium into eight groups as shown in the figure. If there are fewer than eight liars, then in one of these groups, only truth-tellers will be sitting, which is impossible. The contradiction obtained shows that there are no fewer than eight liars. The figure shows how eight liars can be seated in the presidium so that the condition of the problem is satisfied.
Comments. Without an example of seating the liars - 5 points.
#
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.5. A large rectangle consists of three identical squares and three identical small rectangles. The perimeter of the square is 24, and the perimeter of the small rectangle is 16. What is the perimeter of the large rectangle?
The perimeter of a figure is the sum of the lengths of all its sides.
|
Answer: 52.
Solution. All sides of a square are equal, and its perimeter is 24, so each side is $24: 4=6$. The perimeter of the rectangle is 16, and its two largest sides are each 6, so the two smallest sides are each $(16-6 \cdot 2): 2=2$. Then the entire large rectangle has dimensions $8 \times 18$, and its perimeter is $2 \cdot(8+18)=$ 52.
|
52
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.1. The set includes 8 weights: 5 identical round, 2 identical triangular, and one rectangular weight weighing 90 grams.
It is known that 1 round and 1 triangular weight balance 3 round weights. Additionally, 4 round weights and 1 triangular weight balance 1 triangular, 1 round, and 1 rectangular weight.
How much does the triangular weight weigh?
|
Answer: 60.
Solution. From the first weighing, it follows that 1 triangular weight balances 2 round weights.
From the second weighing, it follows that 3 round weights balance 1 rectangular weight, which weighs 90 grams. Therefore, a round weight weighs $90: 3=30$ grams, and a triangular weight weighs $30 \cdot 2=60$ grams.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.2. A jeweler has six boxes: two contain diamonds, two contain emeralds, and two contain rubies. On each box, it is written how many precious stones are inside.
It is known that the total number of rubies is 15 more than the total number of diamonds. How many emeralds are there in total in the boxes?

#
|
# Answer: 12.
Solution. The total number of rubies is no more than $13+8=21$, and the number of diamonds is no less than $2+4=6$. According to the condition, their quantities differ by 15. This is only possible if the rubies are in the boxes with 13 and 8 stones, and the diamonds are in the boxes with 2 and 4 stones. Then the emeralds are in the two remaining boxes, and there are a total of $5+7=12$.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.4. Seven boxes are arranged in a circle, each containing several coins. The diagram shows how many coins are in each box.
In one move, it is allowed to move one coin to a neighboring box. What is the minimum number of moves required to equalize the number of coins in all the boxes?
|
Answer: 22.
Solution. Note that there are a total of 91 coins, so after all moves, each box should have exactly 13 coins. At least 7 coins need to be moved from the box with 20 coins. Now consider the boxes adjacent to the box with 20 coins. Initially, they have a total of 25 coins, and at least 7 more coins will be transferred from the box with 20 coins. In the end, these two boxes should have a total of 26 coins, so at least \(25 + 7 - 26 = 6\) coins need to be moved from these boxes. Next, consider the boxes with 17 and 18 coins, from which at least 4 and 5 coins need to be moved, respectively. In total, there should be at least \(7 + 6 + 4 + 5 = 22\) moves.
Let's provide an example of how to equalize all the boxes in exactly 22 moves. From the box with 20 coins, we move 3 coins to the box with 10 (which then becomes 13), and 4 coins to the box with 15 (which then becomes 19). From the box that now has 19 coins, we move 6 coins to the box with 5 coins (which then becomes 11). From the box with 17 coins, we move 2 coins to the box with 11, and 2 coins to the box with 6 (which then becomes 8). Finally, we move 5 coins from the box with 18 coins to the box with 8 coins. In the end, each box has exactly 13 coins. It is easy to verify that exactly 22 moves were made.

|
22
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.4. Given a square $A B C D$. Point $L$ is on side $C D$ and point $K$ is on the extension of side $D A$ beyond point $A$ such that $\angle K B L=90^{\circ}$. Find the length of segment $L D$, if $K D=19$ and $C L=6$.
|
Answer: 7.
Solution. Since $A B C D$ is a square, then $A B=B C=C D=A D$.
Fig. 1: to the solution of problem 8.4
Notice that $\angle A B K=\angle C B L$, since they both complement $\angle A B L$ to $90^{\circ}$. Then the right triangles $A B K$ and $C B L$ are equal by the acute angle and the leg $A B=B C$ (Fig. 1). Therefore, $A K=C L=6$. Then
$$
L D=C D-C L=A D-C L=(K D-A K)-C L=K D-2 \cdot C L=19-2 \cdot 6=7
$$
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.5. There are 7 completely identical cubes, each of which has 1 dot marked on one face, 2 dots on another, ..., and 6 dots on the sixth face. Moreover, on any two opposite faces, the total number of dots is 7.
These 7 cubes were used to form the figure shown in the diagram, such that on each pair of glued faces, the same number of dots is marked. All dots were erased from all faces except nine, as shown in the diagram. What is the total number of dots that were initially marked on the surface of the figure?
|
Answer: 75.
Solution. There are 9 ways to cut off a "brick" consisting of two $1 \times 1 \times 1$ cubes from our figure. In each such "brick," there are two opposite faces $1 \times 1$, the distance between which is 2. Let's correspond these two faces to each other.
Consider one such pair of faces: on one of them, the dots were not erased, while on the other, they were erased. It is not difficult to understand that originally there were the same number of dots on these faces.
Let's calculate the total number of dots that were originally on all 9 pairs of faces. We get
$$
2 \cdot(1+1+6+2+2+5+3+3+4)=54
$$
There are 6 faces $1 \times 1$ left, about which we still know nothing. However, it can be noticed that they are divided into pairs according to the following principle: in one pair, there will be faces from one $1 \times 1 \times 1$ cube. In each such pair, the sum of the numbers was 7. Then we get that the number of dots on the surface of the figure originally was
$$
54+3 \cdot 7=75
$$
|
75
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.7. For quadrilateral $A B C D$, it is known that $\angle B A C=\angle C A D=60^{\circ}, A B+A D=$ $A C$. It is also known that $\angle A C D=23^{\circ}$. How many degrees does the angle $A B C$ measure?
|
Answer: 83.
Solution. Mark a point $K$ on the ray $AB$ such that $AK = AC$. Then the triangle $KAC$ is equilateral; in particular, $\angle AKC = 60^{\circ}$ and $KC = AC$. At the same time, $BK = AK - AB = AC - AB = AD$. This means that triangles $BKC$ and $DAC$ are equal by two sides and the angle $60^{\circ}$ between them (Fig. 2).
It remains to note that the angle $\angle ABC$ - the exterior angle of triangle $BKC$ - is equal to the exterior angle at vertex $D$ of triangle $DAC$, which is calculated as the sum of two interior angles: $60^{\circ} + 23^{\circ} = 83^{\circ}$.
|
83
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.5. On the base $AC$ of isosceles triangle $ABC (AB = BC)$, a point $M$ is marked. It is known that $AM = 7, MB = 3, \angle BMC = 60^\circ$. Find the length of segment $AC$.
|
Answer: 17.
Fig. 3: to the solution of problem 9.5
Solution. In the isosceles triangle \(ABC\), draw the height and median \(BH\) (Fig. 3). Note that in the right triangle \(BHM\), the angle at vertex \(B\) is \(30^\circ\), so \(HM = \frac{1}{2} BM = 1.5\). Then \(AC = 2AH = 2(AM + MH) = 2 \cdot (7 + 1.5) = 17\).
Fig. 4: to the solution of problem 9.5
Another solution. Mark a point \(K\) on \(MC\) such that \(\angle BKM = 60^\circ\) (Fig. 4; such a point lies exactly on the segment \(MC\) because \(\angle BCM = \angle BAM = \angle BMC - \angle ABM < 60^\circ\)). Note that in triangle \(BMK\), two angles are \(60^\circ\), so it is equilateral and \(BK = MK = BM = 3\). Also note that triangles \(ABM\) and \(CBK\) are equal because \(BC = AB\), \(\angle A = \angle C\), \(\angle AMB = \angle CKB = 120^\circ\) (therefore, \(\angle ABM = \angle CBK\)). Then \(CK = AM = 7\) and \(AC = AM + MK + KC = 7 + 3 + 7 = 17\).
|
17
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.8. On the side $CD$ of trapezoid $ABCD (AD \| BC)$, a point $M$ is marked. A perpendicular $AH$ is dropped from vertex $A$ to segment $BM$. It turns out that $AD = HD$. Find the length of segment $AD$, given that $BC = 16$, $CM = 8$, and $MD = 9$.
|
Answer: 18.
Solution. Let the lines $B M$ and $A D$ intersect at point $K$ (Fig. 5). Since $B C \| A D$, triangles $B C M$ and $K D M$ are similar by angles, from which we obtain $D K = B C \cdot \frac{D M}{C M} = 16 \cdot \frac{9}{8} = 18$.
Fig. 5: to the solution of problem 9.8
In the isosceles triangle $A D H$, draw the height and median $D S$. Then, in triangle $A H K$, the segment $D S$ passes through the midpoint of side $A H$ and is parallel to $H K$. Therefore, $D S$ is the midline of this triangle, and $A D = D K = 18$.
Remark. If in a right triangle a point on the hypotenuse is equidistant from two vertices of the triangle, then it is equidistant from all three vertices of the triangle.
## 10th Grade
|
18
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.3. On the side $AD$ of rectangle $ABCD$, a point $E$ is marked. On the segment $EC$, there is a point $M$ such that $AB = BM, AE = EM$. Find the length of side $BC$, given that $ED = 16, CD = 12$.

|
Answer: 20.
Solution. Note that triangles $A B E$ and $M B E$ are equal to each other by three sides. Then $\angle B M E=\angle B A E=90^{\circ}$.
Fig. 6: to the solution of problem 10.3
From the parallelism of $A D$ and $B C$, it follows that $\angle B C M=\angle C E D$ (Fig. 6). Therefore, right triangles $B C M$ and $C E D$ are equal by an acute angle and the leg $B M=A B=C D$. Using the Pythagorean theorem for triangle $C D E$, we conclude
$$
B C=C E=\sqrt{C D^{2}+E D^{2}}=\sqrt{12^{2}+16^{2}}=20
$$
|
20
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.6. In a convex quadrilateral $A B C D$, the midpoint of side $A D$ is marked as point $M$. Segments $B M$ and $A C$ intersect at point $O$. It is known that $\angle A B M=55^{\circ}, \angle A M B=$ $70^{\circ}, \angle B O C=80^{\circ}, \angle A D C=60^{\circ}$. How many degrees does the angle $B C A$ measure?
|
Answer: 35.
Solution. Since
$$
\angle B A M=180^{\circ}-\angle A B M-\angle A M B=180^{\circ}-55^{\circ}-70^{\circ}=55^{\circ}=\angle A B M
$$
triangle $A B M$ is isosceles, and $A M=B M$.
Notice that $\angle O A M=180^{\circ}-\angle A O M-\angle A M O=180^{\circ}-80^{\circ}-70^{\circ}=30^{\circ}$, so $\angle A C D=$ $180^{\circ}-\angle C A D-\angle A D C=180^{\circ}-30^{\circ}-60^{\circ}=90^{\circ}$.
Fig. 7: to the solution of problem 10.6
Draw segment $C M$ (Fig. 7). Since in a right triangle, the median to the hypotenuse is equal to half of it, we have $C M=D M=A M=B M$. Triangle $M C D$ is isosceles with an angle of $60^{\circ}$ at the base, so it is equilateral, and $\angle C M D=60^{\circ}$. Then $\angle B M C=180^{\circ}-\angle A M B-\angle C M D=180^{\circ}-70^{\circ}-60^{\circ}=50^{\circ}$. Since triangle $B M C$ is isosceles with vertex $M$, we have $\angle C B M=$ $\frac{1}{2}\left(180^{\circ}-\angle B M C\right)=\frac{1}{2}\left(180^{\circ}-50^{\circ}\right)=65^{\circ}$. Finally,
$$
\angle B C A=180^{\circ}-\angle C B M-\angle B O C=180^{\circ}-65^{\circ}-80^{\circ}=35^{\circ} \text {. }
$$
Remark. There are other solutions that use the fact that $A B C D$ is a cyclic quadrilateral with the center of the circumscribed circle $M$.
|
35
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.5. Quadrilateral $ABCD$ is inscribed in a circle. It is known that $BC=CD, \angle BCA=$ $64^{\circ}, \angle ACD=70^{\circ}$. A point $O$ is marked on segment $AC$ such that $\angle ADO=32^{\circ}$. How many degrees does the angle $BOC$ measure?
|
Answer: 58.
Solution. As is known, in a circle, inscribed angles subtended by equal chords are either equal or supplementary to $180^{\circ}$. Since $B C=C D$ and $\angle B A D<180^{\circ}$, we get that $\angle B A C=\angle D A C$.
Fig. 9: to the solution of problem 11.5
Since $\angle B D A=\angle B C A=64^{\circ}$, we get that $\angle B D O=\angle A D O=32^{\circ}$. Therefore, point $O$ lies on the two angle bisectors of triangle $A B D$, i.e., it is the point of intersection of the angle bisectors (Fig. 9). Then
$$
\angle B O C=\angle B A O+\angle A B O=\frac{\angle B A D+\angle A B D}{2}=\frac{180^{\circ}-\angle B D A}{2}=\frac{180^{\circ}-64^{\circ}}{2}=58^{\circ}
$$
Remark. The solution could also have been completed differently: since $O$ is the point of intersection of the angle bisectors of triangle $A B D$, by the trident lemma $C D=C B=C O$, from which $\angle C O B$ is easily found.
|
58
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. A unified control test in mathematics was conducted among all eleventh-graders in the school. As a result, 5/8 of the students received fives, 11/20 of the number of excellent students received fours, and the remaining three eleventh-graders did not come to the test due to illness. How many eleventh-graders are there in the school
|
Answer: 96.
The share of students who received fours is 55/160. The share of students who received fives and fours is $5 / 8 + 55 / 160 = 155 / 160$. Thus, the share of students who missed the exam is $5 / 160 = 1 / 32$. Let $N-$ be the number of eleventh graders, then from the condition $N / 32 = 3$ and $N = 96$.
|
96
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.2. For the angles of triangle $ABC$, it is known that $\sin A + \cos B = \sqrt{2}$ and $\cos A + \sin B = \sqrt{2}$. Find the measure of angle $C$.
|
Answer: $90^{\circ}$.
First method. Squaring both equalities and adding them. After transformations, we get $\sin (A+B)=1$, that is, $A+B=90^{\circ}$.
Second method. Adding the original equalities, we get $\sin \left(A+45^{\circ}\right)+\sin \left(B+45^{\circ}\right)=2$, from which $\sin \left(A+45^{\circ}\right)=\sin \left(B+45^{\circ}\right)=1$. Therefore, $A=B=45^{\circ}$. Hence, $C=90^{\circ}$.
|
90
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Two parks with a total area of 110 hectares are divided into the same number of plots, and in each park, the plots have the same area, but differ from those in the other park. If the first park were divided into plots of the same area as the second, it would result in 75 plots. If the second park were divided into plots of the same area as the first, it would result in 108 plots. Determine the area of each park.
|
2. Answer. 50 and 60 hectares. Solution. Let x be the area of the first park. According to the condition, we will construct a table (for the new division):
| Park | In the new division | | |
| :---: | :---: | :---: | :---: |
| | Area of the park | Number of plots | Area of the plot |
| First | x | 75 | x/75 |
| Second | $110-\mathrm{x}$ | 108 | $(110-\mathrm{x}) / 108$ |
Then for the original division, the following applies:
| Park | In the original division | | |
| :---: | :---: | :---: | :---: |
| | Area of the park | Number of plots | Area of the plot |
| First | $\mathrm{x}$ | $108 \mathrm{x} /(110-\mathrm{x})$ | $(110-\mathrm{x}) / 108$ |
| Second | $110-\mathrm{x}$ | $75(110-\mathrm{x}) / \mathrm{x}$ | $\mathrm{x} / 75$ |
According to the condition, $108 \mathrm{x} /(110-\mathrm{x})=75(110-\mathrm{x}) /$ x. From this, we find x=50.
Evaluation criteria. Correct solution - 7 points, correct solution but incorrect answer due to a calculation error - 5 points, correct model and equation - $\mathbf{3}$ points, in all other cases - $\mathbf{0}$ points.
|
50
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Given the functions $f(x)=x^{2}+4 x+3$ and $g(x)=x^{2}+2 x-1$. Find all integer solutions to the equation $f(g(f(x)))=g(f(g(x)))$.
|
4. Answer. $x=-2$. Solution. Let's represent the functions as $f(x)=x^{2}+4 x+3=(x+2)^{2}-1$ and $g(x)=x^{2}+2 x-1=(x+1)^{2}-2 . \quad$ Then $\quad f(g(x))=\left((x+1)^{2}-2+2\right)^{2}-1=(x+1)^{4}-1$, $g(f(x))=\left((x+2)^{2}-1+1\right)^{2}-2=(x+2)^{4}-2$. Performing similar operations, we get $g(f(g(x)))=(x+1)^{8}-2$ and $f(g(f(x)))=(x+2)^{8}-1$. Thus, the equation is
$$
\begin{gathered}
(x+1)^{8}-(x+2)^{8}=1 \\
\left((x+1)^{4}-(x+2)^{4}\right)\left((x+1)^{4}+(x+2)^{4}\right)=1
\end{gathered}
$$
Obviously, the second bracket can only be equal to 1, which means the first bracket is also equal to 1. This system has a unique solution $x=-2$.
Grading criteria. Correct solution - 7 points, all function compositions are correctly written but the solution is incomplete or incorrect - 2 points, the solution is incorrect or only the answer - $\mathbf{0}$ points.
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.3. Given a triangle $A B C$. It is known that $\angle B=60^{\circ}, \angle C=75^{\circ}$. On side $B C$ as the hypotenuse, an isosceles right triangle $B D C$ is constructed inside triangle $A B C$. What is the measure of angle $D A C$?
|
Answer: $30^{0}$.
Solution 1: From the problem statement, it follows that $\angle A=45^{0}$. Draw a circle with center $\mathrm{M}$ and radius $\mathrm{MB}=\mathrm{MC}$. Since $\angle \mathrm{BDC}=90^{\circ}$, the major arc BC is seen at an angle of $45^{0}$. Therefore, vertex A lies on this circle. This means that triangle ADC is isosceles, so $\angle \mathrm{DAC}=\angle \mathrm{DCA}=\angle \mathrm{BCA}-\angle \mathrm{DCB}=75^{\circ}-45^{\circ}=$ $30^{0}$.
Solution 2: Let $\mathrm{BC}=\mathrm{a}$, then from triangle ВМС: $D C=\frac{a}{\sqrt{2}}$. From triangle АВС using the sine rule, we get $\frac{B C}{\sin 45^{\circ}}=\frac{A C}{\sin 60^{\circ}}$, which means $A C=a \sqrt{\frac{3}{2}}$. Next, from triangle CDA using the cosine rule:
$$
A D^{2}=C D^{2}+C A^{2}-2 C D \cdot C A \cdot \cos D C A=\frac{a^{2}}{2}+\frac{3 a^{2}}{2}-2 \cdot \frac{a}{\sqrt{2}} \cdot a \cdot \sqrt{\frac{3}{2}} \cdot \frac{\sqrt{3}}{2}=\frac{a^{2}}{2}
$$
so $A D=\frac{a}{\sqrt{2}}$. Therefore, triangle ADC is isosceles. Further calculations are as in Solution 1.
## Criteria:
7 points - correct answer and a fully justified solution;
5 points - it is proven that triangle $\mathrm{ABC}$ is isosceles, but an arithmetic error is made in further calculations;
only answer - 0 points.
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3. Sasha chose a natural number $N>1$ and wrote down in ascending order all its natural divisors: $d_{1}<\ldots<d_{s}$ (so that $d_{1}=1$ and $d_{s}=N$). Then, for each pair of adjacent numbers, he calculated their greatest common divisor; the sum of the resulting $s-1$ numbers turned out to be $N-2$. What values could $N$ take?
(A. Kuznetsov)
|
Answer: $N=3$.
Solution. Note immediately that $d_{s+1-i}=N / d_{i}$ for all $i=$ $=1,2, \ldots, s$.
The number $d_{i+1}-d_{i}$ is divisible by the GCD $\left(d_{i}, d_{i+1}\right)$, so the GCD $\left(d_{i}, d_{i+1}\right) \leqslant d_{i+1}-d_{i}$. For $i=1, \ldots, s-1$, let $r_{i}=\left(d_{i+1}-d_{i}\right)-$ GCD $\left(d_{i}, d_{i+1}\right) \geqslant 0$. According to the condition,
$$
\left(d_{2}-d_{1}\right)+\left(d_{3}-d_{2}\right)+\ldots+\left(d_{s}-d_{s-1}\right)=d_{s}-d_{1}=N-1
$$
and
GCD $\left(d_{1}, d_{2}\right)+$ GCD $\left(d_{2}, d_{3}\right)+\ldots+$ GCD $\left(d_{s-1}, d_{s}\right)=N-2$.
Subtracting the second equation from the first, we get $r_{1}+\ldots+r_{s-1}=$ $=1$. This means that $r_{k}=1$ for some $k$, while all other $r_{i}$ are zero.
Thus, $1=\left(d_{k+1}-d_{k}\right)-$ GCD $\left(d_{k}, d_{k+1}\right)$. The right, and therefore the left side of this equation, is divisible by GCD $\left(d_{k}, d_{k+1}\right)$, so GCD $\left(d_{k}, d_{k+1}\right)=1$ and $d_{k+1}-d_{k}=2$. This is possible only if both numbers $d_{k}$ and $d_{k+1}$ are odd.
Since $d_{k}$ and $d_{k+1}$ are two consecutive divisors of the number $N$, then $\frac{N}{d_{k+1}}$ and $\frac{N}{d_{k}}$ are also two consecutive divisors of the number $N$. Therefore, if $\frac{N}{d_{k+1}}=d_{m}$, then $\frac{N}{d_{k}}=d_{m+1}$. In this case,
$$
\begin{aligned}
\operatorname{GCD}\left(d_{m}, d_{m+1}\right)= & \frac{N}{\operatorname{LCM}\left(d_{k}, d_{k+1}\right)}=\frac{N \cdot \operatorname{GCD}\left(d_{k}, d_{k+1}\right)}{d_{k} d_{k+1}}=1$, which is possible only when $k=m$ (and, consequently, $s=2 k)$.
Thus, $d_{k+1}=\frac{N}{d_{k}}$, meaning the number $N=d_{k} d_{k+1}$ is odd. But then $d_{s-1} \leqslant \frac{N}{3}$, from which GCD $\left(d_{s-1}, d_{s}\right) \leqslant d_{s-1} \leqslant \frac{N}{3}$. Therefore, $1 \geqslant r_{s-1} \geqslant \frac{2 N}{3}-\frac{N}{3}=\frac{N}{3}$, i.e., $N \leqslant 3$. Since $N>1$, we get the only possible value $N=3$, which, as is easy to verify, satisfies the condition.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Two-digit numbers are written on the board. Each number is composite, but any two numbers are coprime. What is the maximum number of numbers that can be written?
|
Answer: four numbers.
Solution. Evaluation. Since any two of the written numbers are coprime, each of the prime numbers 2, 3, 5, and 7 can appear in the factorization of no more than one of them. If there are five or more numbers on the board, then all prime factors in the factorization of some of them must be at least 11. But this composite number is at least 121. This contradicts the condition that all written numbers are two-digit. Therefore, there are no more than four numbers on the board.
Example. 25, 26, $33, 49$.
Other examples exist.
Grading criteria.
“+” - a complete and justified solution is provided
“ $\pm$ " - a correct estimate is provided, but the example is not given or is incorrect
"耳” - only the correct answer and correct example are provided
“-" - only the answer is provided
“-" - the problem is not solved or is solved incorrectly
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. The altitudes of an acute-angled, non-isosceles triangle \(ABC\) intersect at point \(H\). \(O\) is the center of the circumcircle of triangle \(BHC\). The center \(I\) of the inscribed circle of triangle \(ABC\) lies on the segment \(OA\). Find the angle \(BAC\).
|
Answer: $60^{\circ}$.
Solution. From the problem statement, it follows that point O lies at the intersection of the angle bisector of angle $A$ and the perpendicular bisector of side $BC$. Since these lines intersect on the circumcircle of triangle $ABC$, point O lies on this circle and is the midpoint of arc $BC$ (see Fig. 9.6a, b). Additionally, $\angle BHC = 180^{\circ} - \angle BAC$, since $H$ is the orthocenter of triangle $ABC$. We can reason in different ways from here.
First method. Let the angles of triangle $ABC$ be: $\angle A = \alpha, \angle B = \beta, \angle C = \gamma$. (see Fig. 9.6a) Then $\angle OCB = \angle OAB = \alpha / 2, \angle BHC = 90^{\circ} - \beta, \angle OCH = \angle OCB + \angle BHC = 90^{\circ} + \alpha / 2 - \beta$.
In triangle $OHC: OH = OC$ (radii of the same circle), so $\angle OHC = \angle OCH = 90^{\circ} + \alpha / 2 - \beta$. Similarly, $\angle OHB = \angle OBH = 90^{\circ} + \alpha / 2 - \gamma$. Therefore, $\angle BHC = \angle OHB + \angle OHC = 90^{\circ} + \alpha / 2 - \gamma + 90^{\circ} + \alpha / 2 - \beta = 180^{\circ} + \alpha - \gamma - \beta = 2\alpha$.
Since $\angle BHC = 180^{\circ} - \alpha$, we get the equation $2\alpha = 180^{\circ} - \alpha$, from which $\alpha = 60^{\circ}$.
Second method. We use the fact that the circumcircle of triangle $BHC$ is symmetric to the circumcircle of triangle $ABC$ with respect to line $BC$ (see Fig. 9.6b). Then the center $P$ of the circumcircle of triangle $ABC$ lies on arc $BHC$. Therefore, $\angle BHC = \angle BPC = 2 \angle BAC$. From $180^{\circ} - \angle BAC = 2 \angle BAC$, we get: $\angle BAC = 60^{\circ}$.
## Grading Criteria.
"+" - a complete and well-justified solution is provided
“$\pm$” - a generally correct solution with minor gaps in justification
"Ғ" - correct reasoning is provided, but there is an error in angle calculation leading to an incorrect answer
"Ғ" - it is proven that point O belongs to the circumcircle of triangle $ABC$, but there is no further progress
“-” - only the answer is provided
“-” - the problem is not solved or is solved incorrectly
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. Given two five-digit numbers without the digits 0 and 1 in their notation. The absolute value of their difference is a four-digit number \( S \). It is known that if each digit of one of the original numbers is decreased by 1, then the absolute value of the difference becomes 10002. What values can the number \( S \) take?
|
Answer: 1109.
Solution: Let $A$ and $B$ be the two given numbers, and $C$ be the number obtained from $B$ by decreasing each of its digits by 1, that is, $C = B - 11111$. If $A10000 > B - A$ (this number is four-digit), then $C > B$. This is a contradiction. Therefore, $A > C$. Also, the case $A > B$ is impossible (then $A - C = A - (B - 11111) = (A - B) + 11111 > 10002 = A - C)$. Thus, the only possible case is: $C < A < B$. And then $A - C = A - (B - 11111) = 10002$, that is, $A - B = -1109$. Hence, $S = |A - B| = B - A = 1109$.
Comment: The correct answer without justification - 0 points.
The correct answer obtained by considering an example -1 point.
The order of numbers $A, B, C$ (in the notation of the solution) is established - 3 points.
An extraneous solution is obtained - no more than 4 points for the problem.
Note: It is not necessary to provide examples of suitable numbers $A, B$, as it has been proven that only one answer is possible, and it follows from the condition that a suitable pair exists. Points are not deducted for the lack of such an example.
|
1109
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In volleyball competitions, where there are no ties, 5 teams participate. All teams played against each other. The team that took 1st place won all their matches, and the teams that took 2nd and 3rd place each won exactly two matches. In the case of equal points, the position is determined by the result of the match between the teams. How many victories did the team that took last place achieve? Determine who won against whom.
|
Solution. Let's denote a team by a point. If team A won against team B, we draw an arrow from A to B.
The number of outgoing arrows equals the number of wins. In total, 10 arrows can be drawn between five points, i.e., 10 matches were played. The first, second, and third teams won a total of 8 matches. This leaves 2 wins for the fourth and fifth teams. Since only the second and third teams won 2 matches each, the fourth and fifth teams won 1 match each. Since in the case of equal points, the higher position is determined by a win in the head-to-head match, the second team beat the third, and the fourth beat the fifth.

The third team won 2 matches, so it beat the fourth and fifth teams.
The fifth team won its only match against the second team.
One arrow remains.
Comment. A correct answer alone is worth 3 points. Subsequent points are awarded based on the completeness of the justification of the answer.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Little One gave a big box of candies to Karlson. Karlson ate all the candies in three days. On the first day, he ate 0.2 of the entire box and 16 more candies. On the second day, he ate -0.3 of the remainder and 20 more candies. On the third day, he ate -0.75 of the remainder and the last 30 candies. How many candies were in the box?
|
Solution. Let $x$ be the number of candies in the box. On the first day, $(0.2x + 16)$ candies were eaten; on the second and third days, $(0.8x - 16)$ candies were eaten. On the second day, $(0.3(0.8x - 16) + 20) = (0.24x + 15.2)$ candies were eaten; on the third day, $(0.56x - 31.2)$ candies remained. Since on the third day, 0.75 of the remainder and another 30 candies were eaten, the remainder will be 120 candies. We get the equation $0.56x - 31.2 = 120$, from which we find $x = 270$.
Answer: 270 candies.
|
270
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The figure "archer" on a grid board attacks along a ray - along cells upwards, downwards, to the right, or to the left (exactly one of the four directions; the directions for different archers are independent). What is the maximum number of non-attacking archers that can be placed on an $8 \times 8$ chessboard?
|
Solution. Answer: 28. We will prove that it is impossible to place more than 28 archers. Consider any arrangement with the maximum possible number of archers. Perform the following two operations sequentially:
1) turn those archers who are standing at the edge of the board so that they shoot "outward" (this will not "worsen" the situation, that is, no archers will start shooting at each other if they were not shooting at each other before);
2) move the archers who are not standing at the edge of the board in the direction of their shooting to the edge of the board. As a result, there will be no more than one archer in each boundary cell of the board. Moreover, no two archers will shoot at each other (since those who were standing at the edge, we turned "outward"). Therefore, the total number of archers will not exceed the number of boundary cells, that is, no more than 28.
Example with 28 archers: on the bottom row, 8 archers shoot downward; on the top row, 8 archers shoot upward; in the leftmost column on the 2nd to 7th rows, 6 archers shoot to the left; in the rightmost column on the 2nd to 7th rows, 6 archers shoot to the right.
Note: A solution based solely on "moving archers in the direction of their shooting to the edge of the table" cannot be considered fully correct. After all, with such an operation, two archers can claim the same boundary cell of the board!
|
28
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. In the parliament of the island state of Promenade-and-Tornado, only the indigenous inhabitants of the island can be elected, who are divided into knights and liars: knights always tell the truth, liars always lie. In the last convocation, 2020 deputies were elected to the parliament. At the first plenary session of the parliament, 1011 deputies stated: "If you don't count me, then among the other deputies - liars are more than half." How many liars are there in the parliament of this country?
|
Solution. Note that the statement was made by more than half of the deputies. If all those who made the statement are knights, then their statements turn out to be false; if all those who made the statement are liars, then their statements turn out to be true - both are impossible. Therefore, among those who made the statement, there was at least one knight and at least one liar. The knight who spoke told the truth, so there are no fewer than 1010 liars in the parliament; the liar who spoke told a lie, so among the rest, except for him, there are no more than 1009 liars, and with him - no more than 1010. Thus, there are no more than 1010 and no fewer than 1010 liars in the parliament, i.e., exactly 1010.
Answer: There are 1010 liars in the parliament.
|
1010
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. A trading organization wholesale purchased exotic fruits, the moisture content of which was $99\%$ of their mass. After delivering the fruits to the market, the moisture content dropped to $98\%$. By what percentage should the trading organization increase the retail price of the fruits (the price at which it will sell them to the public) compared to the wholesale price to at least cover the costs of purchasing the fruits?
|
Solution. In 100 kg of fresh fruits, there was 99 kg of water and 1 kg of solid mass. After drying, 1 kg of solid mass constituted $2 \%$ of the mass of 50 kg, i.e., every 100 kg of fresh fruits dried down to 50 kg, i.e., by half, and the retail price, compared to the wholesale price, should be increased by two times.
Answer: by $100 \%$.
|
100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4. Find the smallest natural number ending in the digit 6 (on the right) which, when this digit is moved to the beginning (to the left), increases exactly four times.
|
Solution. Multiplication "in column" is performed from the end, so we can start the process of multiplication by sequentially finding all the digits: *****6 ( $6 \times 4=24$ - "4 we write, 2 in mind" - the 4 written under the line is the 4th digit that stood before 6; by writing 4 in the top line before 6, we will continue the process until the 6 appears in the bottom line.
Answer: 153846.
|
153846
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. The following numbers are written on the wall: $1,3,4,6,8,9,11,12,16$. Four of these numbers were written by Vova, four numbers were written by Dima, and one number was simply the house number of the local police officer. The police officer found out that the sum of the numbers written by Vova is three times the sum of the numbers written by Dima. Calculate the house number.
|
Solution. The sum of all numbers on the wall is $1+3+4+6+8+9+11+12+16=70$. Let $n$ be the sum of the numbers written by Dima, then $3n$ is the sum of the numbers written by Vova, $4n$ is the sum of the numbers written by both, $70-4n-$ is the house number of the district police officer, which when divided by 4 leaves a remainder of 2. The only such number among those given is 6.
Answer: 6.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Masha left the house for school. A few minutes later, Vanya ran out of the same house to school. He overtook Masha at one-third of the way, and when he arrived at school, Masha still had half of the way left to go. How many times faster does Vanya run compared to how Masha walks?
|
Solution. At one third of the way, Masha and Vanya were at the same time. After that, Vanya ran $2 / 3$ of the way, while Masha walked $1 / 2 - 1 / 3 = 1 / 6$ of the way in the same time. This means that he runs $2 / 3$ : $1 / 6 = 4$ times more in the same amount of time than Masha.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. What is the smallest identical number of pencils that need to be placed in each of 6 boxes so that any 4 boxes contain pencils of any of the 26 pre-specified colors (there are enough pencils available)? Prove that fewer is impossible.
|
Solution. Let's assume that we have fewer than 3 pencils of some color. Then, if we take 4 boxes in which such pencils are not present (and such boxes can be found, since there are no more than $2 y x$ pencils of that color), the condition of the problem will not be met. This means that there are at least 3 pencils of each color, and the total number of pencils is no less than $26 * 3 = 78$. It remains to provide an example with 78. Let's put 13 pencils of colors $1, 2, 3, \ldots, 13$ (let's number the colors from 1 to 26) in the first, second, and third boxes. And in the fourth, fifth, and sixth boxes, put pencils of colors $14, 15, \ldots, 26$. Then, no matter which 4 boxes we take, we will definitely take pencils of all colors.
Comment. Only the correct answer - 1 point. Proved that there are no fewer than 78 pencils, but no example provided - 3 points. Provided an example with 78, but not proved that it cannot be less - 3 points.
|
78
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
1. Real numbers $a, b, c$ are such that $a+1 / b=9, b+1 / c=10$, $c+1 / a=11$. Find the value of the expression $a b c+1 /(a b c)$.
|
Answer: 960.
Sketch of the solution. By multiplying the equations, expanding the brackets, and grouping, we get: $a b c + 1/(a b c) + a + 1/b + b + 1/c + c + 1/a = 990$. From this, $a b c + 1/(a b c) = 990 - 9 - 10 - 11 = 960$.
|
960
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In a football tournament, 17 teams participate, and each team plays against each other exactly once. A team earns 3 points for a win. For a draw, 1 point is awarded. The losing team gets no points. What is the maximum number of teams that can accumulate exactly 10 points?
|
Answer: 11.
Sketch of the solution. Estimation. Let $n$ teams have scored exactly 10 points each. The total points include all points scored by these teams in matches against each other (at least 2) and possibly in matches against other teams: $10 n \geq 2(n-1) n / 2$. Hence, $n \leq 11$.
Example: All eleven teams played to a draw against each other and lost to the rest.
Criteria. Answer only, without justification: 1 point.
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Given three non-zero real numbers $a, b, c$ such that the equations: $a x^{2}+b x+c=0, b x^{2}+c x+a=0, c x^{2}+a x+b=0$ each have two roots. How many of the roots of these equations can be negative?
|
Answer: 2.
Sketch of the solution.
If the numbers $a, b, c$ are replaced by their opposites, then the "new" equations will have the same set of roots as the original ones. There are two possible cases: the numbers $a, b, c$ are of the same sign; among them, there are both positive and negative numbers.
First case. Due to the initial observation, we can assume that they are positive. And due to the cyclic symmetry of the coefficients of the equations, we can assume that $0<a \leq b, 0<a \leq c$. Multiplying these inequalities, we get $\mathrm{a}^{2} \leq \mathrm{bc}<4 \mathrm{bc}$. From this inequality, it follows that the discriminant of the equation $c x^{2}+a x+b=0$ is negative, and the equation has no roots. This case is impossible.
Second case. Due to the initial observation and the cyclic symmetry of the coefficients of the equations, we can assume that $0<a, 0<c, b<0$. From these inequalities, it follows that in the equations $b x^{2}+c x+a=0$, $c x^{2}+a x+b=0$, the product of the roots is negative, and thus exactly one root is negative. In the equation $a x^{2}+b x+c=0$, the product of the roots is positive and the sum is positive, meaning both roots are positive. In the end, we have two negative roots.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Several cells on a $14 \times 14$ board are marked. It is known that no two marked cells are in the same row and the same column, and also, that a knight can, starting from some marked cell, visit all marked cells in several jumps, visiting each exactly once. What is the maximum possible number of marked cells?
|
Answer: 13.
Since there is no more than one marked cell (field) in each row, there are no more than 14 marked cells. Suppose there are 14 marked cells. Number the rows and columns from 1 to 14 from bottom to top and from left to right, and color the cells in a checkerboard pattern, where the sum of the row and column numbers for white cells is odd, and for black cells, it is even. Let the path of the knight through the marked cells be $\left(\mathrm{x}_{1}, \mathrm{y}_{1}\right),\left(\mathrm{x}_{2}, \mathrm{y}_{2}\right),\left(\mathrm{x}_{3}, \mathrm{y}_{3}\right), \ldots,\left(\mathrm{x}_{14}, \mathrm{y}_{14}\right)$. Consider the sum $\left(\mathrm{x}_{1}+\mathrm{y}_{1}\right)+\left(\mathrm{x}_{2}+\mathrm{y}_{2}\right)+\left(\mathrm{x}_{3}+\mathrm{y}_{3}\right)+ \ldots+\left(\mathrm{x}_{14}+\mathrm{y}_{14}\right)$. Since the knight changes the color of the cell with each move, there will be seven odd terms in the sum, making it odd. On the other hand, the knight visits each row and column exactly once, so the sum is $2(1+2+3+\ldots+14)$ and is even. This is a contradiction.
An example for 13 marked cells is shown in the figure on the right.
Criteria. An example is provided, but there is no estimate: 2 points.
An estimate is made, but there is no example or it is incorrect: 4 points.
|
13
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 8.1. Can a cube be cut into 71 smaller cubes (of any non-zero size)?
|
Answer: Yes, it is possible.
Solution: Let's divide each edge of the cube in half and cut the cube into 8 smaller cubes. Now, take one of these smaller cubes and divide it into 8 even smaller cubes. One cube disappears, but 8 new ones appear, increasing the total number of parts by \(8-1=7\) to 15. Repeating this operation, we get \(15+7=22\), \(22+7=29\), \(29+7=36\), \(36+7=43\), \(43+7=50\), \(50+7=57\), \(57+7=64\), \(64+7=71\) parts.
Comment: A correct answer without justification (without providing an example) - 0 points. Justification in the form of any correct example - 7 points.
|
71
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. Two cyclists, Andrey and Boris, are riding at a constant and identical speed along a straight highway in the same direction, so that the distance between them remains constant. There is a turnoff to a village ahead. At some point in time, the distance from Andrey to the turnoff was equal to the square of the distance from Boris to the same turnoff. When each of them had traveled another 1 km, the distance from Andrey to the turnoff became three times the distance from Boris to the turnoff. What is the distance between the cyclists?
|
Answer: 2 or 0 km.
Solution: Let the first mentioned distances be $a$ and $b$, then $a=b^{2}$. When each of them had traveled another kilometer, the remaining distance to the turn was $a-1$ and $b-1$ km, respectively, so $a-1=3(b-1)$, which means $b^{2}-1=3(b-1),(b-1)(b+1)=3(b-1)$, from which $b=1$ or $b=2$. When $b=1$, we have $a=1$, so $a-b=0$. When $b=2$, we have $a=4$, so $a-b=2$.
Comment: A complete and justified solution - 7 points. Both equations are correctly set up, but the answer is not obtained - 3 points. The answer is found by selecting numbers that satisfy the condition, but it is not shown that other answers are impossible - 2 points, if only part of the answer is found by selection - 1 point. The solution is correctly started, but there is no significant progress - 1 point. Errors in transformations are made in an otherwise correct solution - deduct 2 points per error. Only the answer is provided - 0 points. The problem is not solved or is solved incorrectly - 0 points.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.3. In triangle $A B C$ with angle $C$ equal to $30^{\circ}$, median $A D$ is drawn. Angle $A D B$ is equal to $45^{\circ}$. Find angle $B A D$.
#
|
# Answer: $30^{\circ}$.
Solution. Draw the height $B H$ (see the figure). In the right triangle $B H C$, the leg $B H$ lies opposite the angle $30^{\circ}$, so $B H=\frac{B C}{2}=B D$. The angle $H B C$ is $180^{\circ}-90^{\circ}-30^{\circ}=60^{\circ}$. Triangle $B H D$ is isosceles with an angle of $60^{\circ}$, so it is equilateral, and $B H=B D=H D$. Let's find the angles of triangle $A D H$: $\angle A D H=60^{\circ}-45^{\circ}=15^{\circ} ; \quad \angle A H D=90^{\circ}+60^{\circ}=150^{\circ} ; \quad \angle D A H=$ $180^{\circ}-150^{\circ}-15^{\circ}=15^{\circ}$. Therefore, $A H=H D$. Then $A H=B H$, and
triangle $A B H$ is isosceles. Since it is a right triangle, $\angle B A H=45^{\circ}$. Then $\angle B A D=$ $\angle B A H-\angle D A H=45^{\circ}-15^{\circ}=30^{\circ}$.
Comment. A correct and justified solution - 7 points. A correct solution with some non-obvious and unexplained transitions - 5-6 points. If the solution is not completed, points are given for proving useful auxiliary statements - 2-3 points. Only the answer is provided - 0 points. The problem is not solved or solved incorrectly - 0 points.
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.4. It is known that for real numbers $a$ and $b$ the following equalities hold:
$$
a^{3}-3 a b^{2}=11, \quad b^{3}-3 a^{2} b=2
$$
What values can the expression $a^{2}+b^{2}$ take?
|
Answer: 5.
Solution. We have
$$
\left(a^{2}+b^{2}\right)^{3}=a^{6}+3 a^{4} b^{2}+3 a^{2} b^{4}+b^{6}=\left(a^{3}-3 a b^{2}\right)^{2}+\left(b^{3}-3 a^{2} b\right)^{2}=11^{2}+2^{2}=125
$$
From this, $a^{2}+b^{2}=5$.
Comment. A correct and justified solution - 7 points. The correct answer obtained based on a simple example satisfying the condition ( $a=-1, b=2$ ), but not proven that the same answer for other pairs - 3 points. Some progress - 2 points. The solution is started, but the progress is insignificant - 1 point. Only the answer is provided - 0 points. The problem is not solved or solved incorrectly - 0 points.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. What is the maximum number of members that can be in a sequence of non-zero integers, for which the sum of any seven consecutive numbers is positive, and the sum of any eleven consecutive numbers is negative?
|
Answer: 16.
Solution: Estimation. Assume there are no fewer than 17 numbers. Construct a table with 7 columns and 11 rows, in which the first 17 numbers are arranged.
| $a_{1}$ | $a_{2}$ | $a_{3}$ | $a_{4}$ | $a_{5}$ | $a_{6}$ | $a_{7}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $a_{2}$ | $a_{3}$ | $a_{4}$ | $a_{5}$ | $a_{6}$ | $a_{7}$ | $a_{8}$ |
| $a_{3}$ | $a_{4}$ | $a_{5}$ | $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ |
| $a_{4}$ | $a_{5}$ | $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ |
| $a_{5}$ | $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ |
| $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ |
| $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ | $a_{13}$ |
| $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ | $a_{13}$ | $a_{14}$ |
| $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ | $a_{13}$ | $a_{14}$ | $a_{15}$ |
| $a_{10}$ | $a_{11}$ | $a_{12}$ | $a_{13}$ | $a_{14}$ | $a_{15}$ | $a_{16}$ |
| $a_{11}$ | $a_{12}$ | $a_{13}$ | $a_{14}$ | $a_{15}$ | $a_{16}$ | $a_{17}$ |
Consider the sums by rows:
$$
a_{1}+\ldots+a_{7}, \ldots, \quad a_{2}+\ldots+a_{8}, \quad a_{11}+\ldots+a_{17}
$$
All these sums are positive, so the sum of all the numbers written is positive. But if we sum by columns, we get negative sums. The obtained contradiction shows that the number of numbers in the sequence must be less than 17.
Example: 16 numbers can be: $-5,-5,13,-5,-5,-5,13,-5,-5,13,-5,-5,-5,13,-5,-5$.
Comment: A fully justified solution - 7 points. Correct estimation - 5 points, a correct example constructed - 2 points, points are summed. The problem is not solved or solved incorrectly - 0 points.
|
16
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.