problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
Problem 11.3. In a football tournament, 15 teams participated, each playing against each other exactly once. For a win, 3 points were awarded, for a draw - 1 point, and for a loss - 0 points.
After the tournament ended, it turned out that some 6 teams scored at least $N$ points each. What is the greatest integer value that $N$ can take?
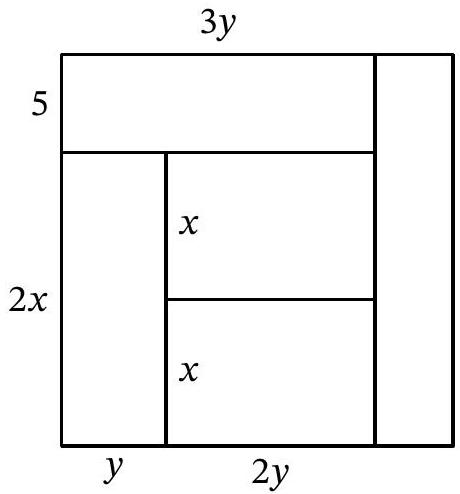
Fig. 13: to the solution of problem 11.2
#
|
# Answer: 34.
Solution. Let's call these 6 teams successful, and the remaining 9 teams unsuccessful. We will call a game between two successful teams an internal game, and a game between a successful and an unsuccessful team an external game.
First, note that for each game, the participating teams collectively earn no more than 3 points. Clearly, there were exactly $\frac{6 \cdot 5}{2}=15$ internal games, and only from these games did all successful teams collectively earn no more than $15 \cdot 3=45$ points. There were exactly $6 \cdot 9=54$ external games, and in each such game, a successful team earned no more than 3 points. Therefore, collectively, all successful teams earned no more than $54 \cdot 3=162$ points from external games. According to the problem, the successful teams collectively earned at least $6 \mathrm{~N}$ points, so we get the inequality $6 N \leqslant 45+162$. From this, it follows that $N \leqslant \frac{207}{6}<35$ and $N \leqslant 34$. Now let's provide an example for $N=34$. Number the teams from 1 to 15. We will show how teams from 1 to 6 can earn at least 34 points.
- Suppose each team from 1 to 6 won against each team from 7 to 15, then each team from 1 to 6 earned $9 \cdot 3=27$ points just from these games.
- Suppose the teams from 1 to 6 played among themselves as indicated in the following table (in each cell, the number of points is shown that the team from the corresponding row received in the game with the team from the corresponding column):
| | $\mathbf{1}$ | $\mathbf{2}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{5}$ | $\mathbf{6}$ |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| $\mathbf{1}$ | | 3 | 3 | 1 | 0 | 0 |
| $\mathbf{2}$ | 0 | | 3 | 3 | 1 | 0 |
| $\mathbf{3}$ | 0 | 0 | | 3 | 3 | 1 |
| $\mathbf{4}$ | 1 | 0 | 0 | | 3 | 3 |
| $\mathbf{5}$ | 3 | 1 | 0 | 0 | | 3 |
| $\mathbf{6}$ | 3 | 3 | 1 | 0 | 0 | |
- Suppose in each game between teams from 7 to 15, the team with the higher number won (the outcome of these games does not matter).
In total, teams from 1 to 6 earned at least $27+7=34$ points.
|
34
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.6. The quadratic trinomial $P(x)$ is such that $P(P(x))=x^{4}-2 x^{3}+4 x^{2}-3 x+4$. What can $P(8)$ be? List all possible options.
|
Answer: 58.
Solution. Let $P(x)=a x^{2}+b x+c$. Then $P(P(x))=a\left(a x^{2}+b x+c\right)^{2}+b\left(a x^{2}+b x+c\right)+c=$
$a\left(a^{2} x^{4}+2 a b x^{3}+\left(b^{2}+2 a c\right) x^{2}+2 b c x+c^{2}\right)+b\left(a x^{2}+b x+c\right)+c$. Therefore,
\[
\begin{aligned}
& x^{4}-2 x^{3}+4 x^{2}-3 x+4=P(P(x))= \\
& =a^{3} x^{4}+2 a^{2} b x^{3}+\left(a b^{2}+2 a^{2} c+a b\right) x^{2}+\left(2 a b c+b^{2}\right) x+\left(a c^{2}+b c+c\right)
\end{aligned}
\]
Equating the corresponding coefficients, we get the system of equations
\[
\left\{\begin{array}{l}
a^{3}=1 \\
2 a^{2} b=-2 \\
a b^{2}+2 a^{2} c+a b=4 \\
2 a b c+b^{2}=-3 \\
a c^{2}+b c+c=4
\end{array}\right.
\]
From the first equation, it immediately follows that $a=1$. Substituting $a=1$ into the second equation, we get $2 b=-2$, hence $b=-1$. Substituting $a=1$ and $b=-1$ into the third equation, we get $1+2 c-1=4$, hence $c=2$. It is clear that $a=1, b=-1, c=2$ is a solution to this system, so $P(x)=x^{2}-x+2$ and $P(8)=8^{2}-8+2=58$.
|
58
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.7. In a country, there are 110 cities. Between any two of them, there is either a road or there is not.
A motorist was in a certain city, from which there was exactly one road. After driving along this road, he arrived at a second city, from which there were already exactly two roads. Driving along one of them, he arrived at a third city, from which there were already exactly three roads, and so on. At some point, after driving along one of the roads, he arrived at the $N$-th city, from which there were already exactly $N$ roads. At this point, the motorist ended his journey. (For each $2 \leqslant k \leqslant N$, from the $k$-th city, there were exactly $k$ roads, including the one by which the motorist arrived in this city.)
What is the largest value that $N$ can take?
|
Answer: 107.
Solution. Let's number the cities in the order they are visited by the motorist: $1,2,3, \ldots, N$.
Suppose $N \geqslant 108$. From city 1, there is a road only to city 2, so from city 108, all roads lead to all 108 cities, except for 1 and 108. But then from city 2, there are at least three roads: to cities 1, 3, and 108. This is a contradiction, so $N \leqslant 107$.
Let's provide an example for $N=107$. Suppose the cities are numbered $1,2,3, \ldots, 109,110$. Let
- for all $1 \leqslant i \leqslant 54$, there is a road from city $i$ to city $i+1$;
- for all $56 \leqslant j \leqslant 107$, there are roads from city $j$ to all cities from 110 - $j$ to 110 inclusive, except for city $j$ itself;
- from city 55, there are roads to cities 109 and 110;
- there are no other roads in the country.
It is not difficult to verify that for all $1 \leqslant k \leqslant 107$, there are exactly $k$ roads from city $k$. The motorist could have driven through these cities.
|
107
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
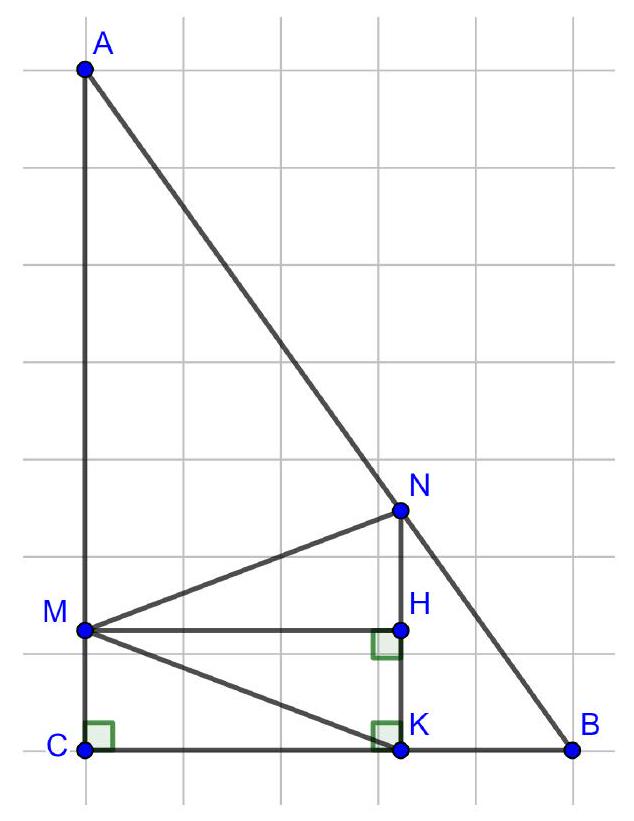
Problem 11.8. Given a parallelepiped $A B C D A_{1} B_{1} C_{1} D_{1}$. A point $X$ is chosen on the edge $A_{1} D_{1}$, and a point $Y$ is chosen on the edge $B C$. It is known that $A_{1} X=5, B Y=3, B_{1} C_{1}=14$. The plane $C_{1} X Y$ intersects the ray $D A$ at point $Z$. Find $D Z$.
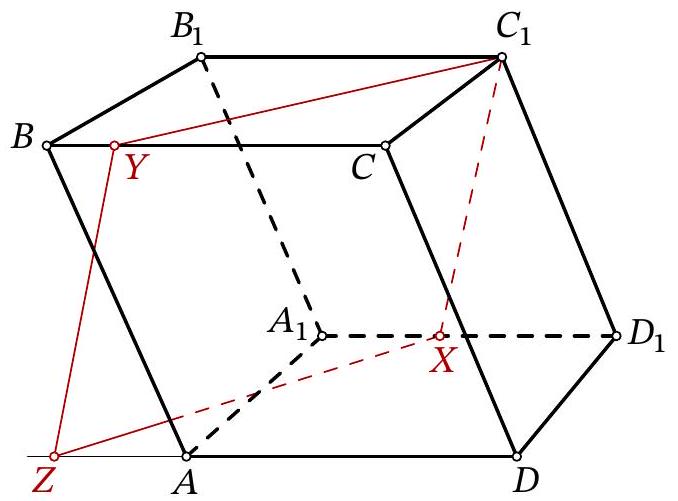
|
Answer: 20.
Solution. Lines $C_{1} Y$ and $Z X$ lie in parallel planes $B B_{1} C_{1} C$ and $A A_{1} D_{1} D$, so they do not intersect. Since these two lines also lie in the same plane $C_{1} X Z Y$, they are parallel. Similarly, lines $Y Z$ and $C_{1} X$ are parallel. Therefore, quadrilateral $C_{1} X Z Y$ is a parallelogram.
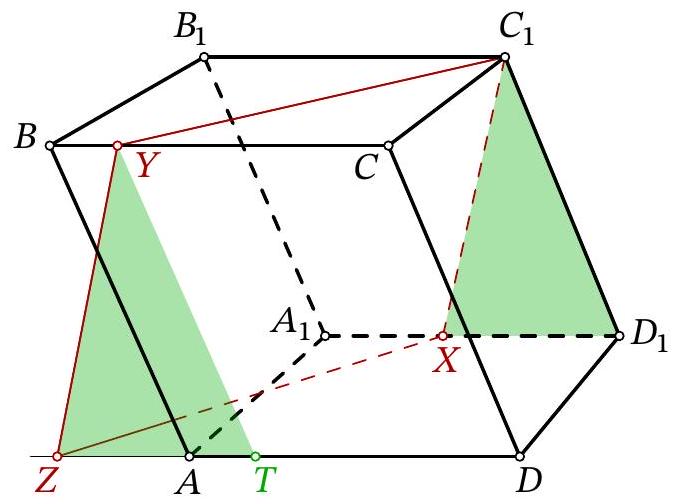
Fig. 15: to the solution of problem 11.8
Let us lay off segment $A T$ on $A D$, equal to $B Y$ (Fig. 15). Quadrilateral $B Y T A$ is a parallelogram, meaning segments $Y T, B A$, and $C_{1} D_{1}$ are parallel and equal. Additionally, segments $Y Z$ and $C_{1} X$ are parallel and equal; from the parallelism follows the equality of angles $Z Y T$ and $X C_{1} D_{1}$, which gives the equality of triangles $Z Y T$ and $X C_{1} D_{1}$.
Then
$$
\begin{aligned}
D Z & =Z T+A D-A T=X D_{1}+B_{1} C_{1}-B Y= \\
& =\left(A_{1} D_{1}-A_{1} X\right)+B_{1} C_{1}-B Y=(14-5)+14-3=20
\end{aligned}
$$
Another solution. As in the previous solution, we will use the fact that $C_{1} X Z Y$ is a parallelogram.
Consider the chain of vector equalities:
$$
\overrightarrow{D Z}=\overrightarrow{D C}+\overrightarrow{C Y}+\overrightarrow{Y Z}=\overrightarrow{D_{1} C_{1}}+\overrightarrow{C Y}+\overrightarrow{C_{1} X}=\overrightarrow{C Y}+\overrightarrow{D_{1} X}
$$
In the last part, all vectors are oriented the same as $\overrightarrow{D Z}$, so we can transition to the equality of segments and continue:
$$
D Z=C Y+D_{1} X=(C B-B Y)+\left(D_{1} A_{1}-A_{1} X\right)=2 B_{1} C_{1}-B Y-A_{1} X
$$
Substituting the lengths given in the condition, we get $D Z=2 \cdot 14-3-5=20$.
|
20
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.2. On the plate, there were 15 doughnuts. Karlson took three times more doughnuts than Little Man, and Little Man's dog Bibbo took three times fewer than Little Man. How many doughnuts are left on the plate? Explain your answer.
|
Answer: 2 doughnuts are left.
From the condition of the problem, it follows that Little One took three times as many doughnuts as Bimbo, and Karlson took three times as many doughnuts as Little One. We can reason in different ways from here.
First method. If Bimbo took one doughnut, then Little One took three doughnuts, and Karlson took nine doughnuts, so together they took $1+3+9=13$ doughnuts. Thus, two doughnuts are left on the plate.
If Bimbo had taken two doughnuts or more, then Little One would have taken six doughnuts or more, and Karlson would have taken 18 doughnuts or more, which is impossible.
Second method. Let Bimbo take $x$ doughnuts, then Little One took $3x$ doughnuts, and Karlson took $3 \cdot 3x = 9x$ doughnuts. Then together they took $x + 3x + 9x = 13x$ doughnuts. Since the number $13x$ must not exceed 15, the only possible natural value for $x$ is 1. Therefore, together they ate 13 doughnuts, and two doughnuts are left on the plate.
+ a complete and justified solution
$\pm$ the correct answer is provided, it is shown that it satisfies the condition, and there is a statement that it is the only one
$\pm$ the number of doughnuts each person ate is justified, but the explicit answer to the question is not provided
干 the correct answer is provided, it is shown that it satisfies the condition, but there is no mention of its uniqueness
干 only the correct answer is provided
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.5. Ladybugs gathered on a clearing. If a ladybug has 6 spots on its back, it always tells the truth, and if it has 4 spots, it always lies, and there were no other ladybugs on the clearing. The first ladybug said: "Each of us has the same number of spots on our backs." The second said: "Together, we have 30 spots on our backs." "No, together we have 26 spots on our backs," - the third one objected. "Exactly one of these three told the truth," - each of the other ladybugs stated. How many ladybugs gathered on the clearing?
|
Answer: 5 ladybugs.
If the first ladybug is telling the truth, then the second and third should also be telling the truth, as they should have the same number of spots as the first. However, the second and third ladybugs contradict each other, so at least one of them is lying, which means the first ladybug is also lying.
Assume that each of the first three ladybugs lied, then all the others lied as well, since none of these three told the truth. This means all the ladybugs are liars, so each ladybug should have four spots on its back. But in this case, it turns out that the first ladybug actually told the truth, which cannot be. Therefore, the first three ladybugs cannot lie simultaneously, so either the second or the third told the truth, and the other two are liars.
Thus, each of the other ladybugs told the truth.
Therefore, there are two ladybugs with 4 spots on their backs, and several ladybugs with 6 spots on their backs, and in total, the spots on the backs of all the ladybugs are either 30 or 26.
1) If there are 30 spots, then $30 - 2 \cdot 4 = 22$, which is not divisible by 6, so this case is impossible.
2) If there are 26 spots, then $(26 - 2 \cdot 4) : 6 = 3$. This means there are $2 + 3 = 5$ ladybugs on the meadow.
+ A complete and justified solution
$\pm$ Correctly and justifiedly determined who lied and who told the truth, but the answer is not found or is incorrect
$\mp$ Provided the correct answer and shown that it satisfies the condition
- Only the answer is provided
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (7 points) Cheburashka and Gena ate a cake. Cheburashka ate twice as slowly as Gena, but started eating a minute earlier. In the end, they each got an equal amount of cake. How long would it take Cheburashka to eat the cake alone?
|
Answer. In 4 minutes.
Solution.
First method. If Cheburashka eats twice as slowly as Gena, then to eat the same amount of cake as Gena, he needs twice as much time. This means that the time Cheburashka ate alone (1 minute) is half of the total time it took him to eat half the cake. Thus, he ate half the cake in 2 minutes, and the whole cake in 4 minutes.
Second method. Let Gena eat the whole cake in $x$ minutes, then Cheburashka needs $2x$ minutes for the whole cake. Each of them got half the cake, so Gena ate for $0.5x$ minutes, and Cheburashka for $x$ minutes. From the condition, it follows that $0.5x + 1 = x$, from which $x = 2$. Therefore, Cheburashka will eat the cake in $2 \cdot 2 = 4$ minutes.
## Grading criteria.
- Any complete correct solution - 7 points.
- The equation is correctly set up and solved, or correct reasoning is provided, but the answer is to a different question - 6 points.
- The solution considers a specific mass of the cake - 2 points.
- The equation is set up correctly but solved incorrectly - 2 points.
- The correct answer is provided, and it is verified that it satisfies the problem's condition - 1 point.
- Only the answer is provided - 0 points.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In an equilateral triangle $ABC$ with side length $a$, points $M, N, P, Q$ are positioned as shown in the figure. It is known that $MA + AN = PC + CQ = a$. Find the measure of angle $NOQ$.
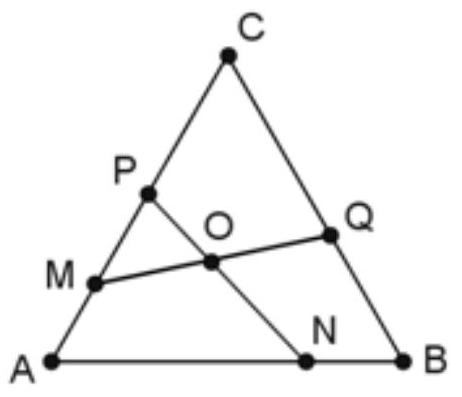
|
Answer: $60^{\circ}$
Solution. According to the problem, $A N=a-A M$, hence $A N=M C$. Similarly, $A P=Q C$. From these equalities and the equality $\angle A=\angle C=60^{\circ}$, it follows that $\triangle A N P=\triangle C M Q$. Therefore, $\angle A N P=\angle Q M C, \angle A P N=\angle M Q C$. By the theorem on the sum of angles in a triangle, $\angle A N P+\angle A P N=120^{\circ}$, so $\angle O M P+\angle O P M=120^{\circ}$, and thus $\angle M O P=60^{\circ}$. Angles $M O P$ and $N O Q$ are vertical, so $\angle N O Q=60^{\circ}$.
Grading criteria.
- Any complete and correct solution - 7 points.
- It is proven that triangles $A N P$ and $Q C M$ are equal, but there is no further progress or it is incorrect - 2 points.
- Only the answer is provided - 0 points.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
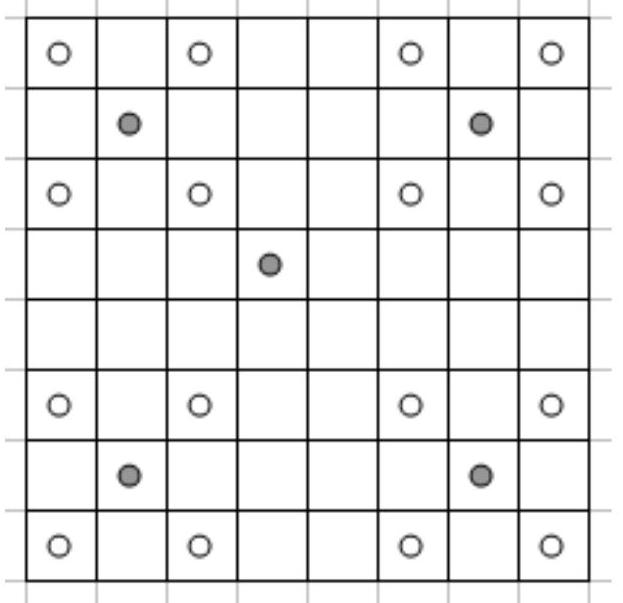
6. (7 points) On a chessboard, there were 21 kings. Each king was under attack by at least one of the others. After some kings were removed, no two of the remaining kings attack each other. What is the maximum number of kings that could remain?
a) Provide an example of the initial arrangement and mark the removed kings.
b) Prove that a greater number of kings could not remain.
|
Answer: b) 16.
Solution: Note that each king removed from the board could not have attacked more than 4 of the remaining ones (otherwise, some of the remaining ones would also attack each other). Therefore, the number of remaining kings cannot exceed the number of removed ones by more than 4 times, meaning it cannot be more than 16. An example is shown in the figure: gray marks the kings that need to be removed.
## Grading Criteria.
- Any complete and correct solution of both parts - 7 points.
- Only one part is correctly solved - 3 points
- Only the answer is provided - 0 points.
Maximum score for all completed tasks - 42.
|
16
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the sum $(1-2-3+4)+(5-6-7+8)+\ldots+(2009-2010-2011+2012)+$ (2013-2014-2015), all numbers that end in 0 were crossed out. Find the value of the resulting expression.
|
3. Answer: -3026. It is easy to see that in all parentheses except the last one, the sum is zero. Then the entire sum before cancellation was equal to -2016. At the same time, numbers that end in 0 and are divisible by 4 were included in it with a plus, while numbers that end in 0 and are not divisible by 4 were included with a minus. Therefore, to find the final answer, the first numbers should be subtracted, and the second ones should be added. Then the final sum is -2016 + $(20+40+60+\ldots+2000)-(10+30+50+\ldots+2010)=-2016+1000-2010=-3026$.
Criteria: full solution with explanation - 7 points. Correct calculations are provided, but comments are missing - 5 points. The sum is written correctly, but calculated with an error - 3 points. Only the answer - 0 points.
|
-3026
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. There are 10 red and 10 yellow apples with a total weight of 1 kg. It is known that the weights of any two apples of the same color differ by no more than 40 g. All apples were sequentially paired "red with yellow," with red apples chosen in non-decreasing order and yellow apples in non-increasing order (i.e., the heaviest red apple was paired with the lightest yellow apple, the second heaviest red apple with the lightest of the remaining yellow apples, and so on). What is the maximum possible weight of a pair?
|
6. Answer: 136 g. Solution Estimate. Note that the weights of the pairs also cannot differ by more than 40 g. Therefore, if the weight of the heaviest pair is more than 136 g, then the weight of each of the other nine pairs will be more than 96 g, but then the total weight of all apples will be more than 1 kg, which is impossible. Example. Let one red apple weigh 86 g, and the others weigh 46 g each, and each yellow apple weigh 50 g.
Criteria: full solution - 7 points. Only estimate or only example - 3 points. In other cases 0 points.
|
136
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. There are seven cards on the table. In one move, it is allowed to flip any five cards. What is the minimum number of moves required to flip all the cards?
|
9.1. Answer. 3 moves.
Obviously, one move is not enough. After two moves, there will be at least three cards that have been flipped twice, which means these cards will be in their original position.
Let's provide an example of flipping all the cards in three moves. Number the cards from 1 to 7 and flip cards numbered $1,2,3,4,5$ on the first move, $-1,3,4,5,6$ on the second move, and $-1,3,4,5,7$ on the third move.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. In the country, there are 20 cities. An airline wants to organize two-way flights between them so that from any city, it is possible to reach any other city with no more than $k$ transfers. At the same time, the number of air routes from any city should not exceed four. What is the smallest $k$ for which this is possible?
## 9th grade
## Second day
|
9.4. Answer. $k=2$.
Note that at least two transfers will be required. Indeed, from an arbitrary city $A$ without a transfer, one can reach no more than 4 cities, and with exactly one transfer - no more than $4 \cdot 3=12$ cities (since one of the flights from each of these cities leads back to $A$). Therefore, if using no more than one transfer, one can reach no more than 16 other cities from any city, but it is required
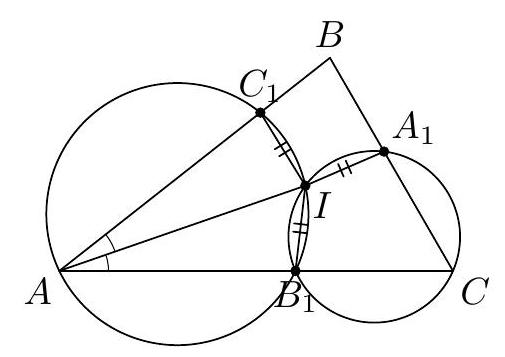
Fig. 4
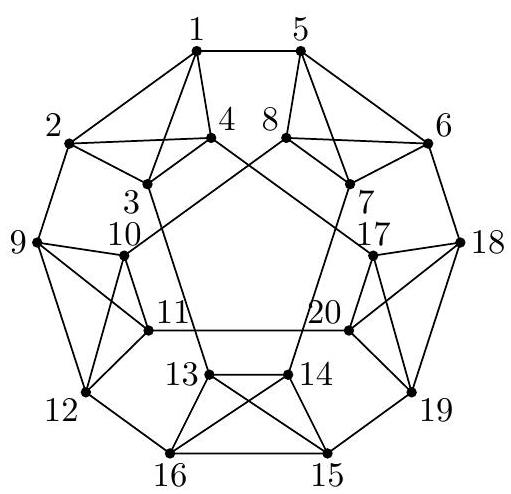
Fig. 5
- to reach 19. In Fig. 5, it is shown how flights can be organized so that there are no more than two transfers. The diagram is symmetric, so it is sufficient to show how to reach from the first city to any other. From it, without a transfer, one can reach cities $2,3,4,5$. Then with one transfer to cities $6,7,8$ (from 5), 9 (from 2), 13 (from 3), and 17 (from 4). And with two transfers - to cities 10, 11, 12 (from 9), to 14, 15, 16 (from 13), to $18,19,20$ (from 17).
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.8. A circle is circumscribed around triangle $A B C$. Let $A_{0}$ and $C_{0}$ be the midpoints of its arcs $B C$ and $A B$, not containing vertices $A$ and $C$. It turns out that the segment $A_{0} C_{0}$ is tangent to the circle inscribed in triangle $A B C$. Find the angle $B$.
|
9.8. Let the incircle of triangle $ABC$ be denoted by $\omega$, its center by $I$, and the points of tangency of $\omega$ with $AC$ and $A_0 C_0$ by $K$ and $L$ respectively. Then, in triangles $IKC$ and $ILA_0$, angles $IKC$ and $ILA_0$ are right angles (as angles between a radius and a tangent), and $IK = IL$, since both segments are radii of $\omega$ (see Fig. 6). Also, since points $A, I, A_0$ lie on the angle bisector of angle $A$, and points $C, I, C_0$ lie on the angle bisector of angle $C$, we have $\angle ICK = \angle C_0 CA = \angle C_0 A_0 A = \angle LA_0 I$.
Fig. 6 (since angles $\angle C_0 A_0 A$ and $\angle C_0 CA$ subtend the same arc of the circumcircle $C_0 A$). Therefore, right triangles $IKC$ and $ILA_0$ are congruent by a leg and an acute angle, hence $IA_0 = IC$, which means triangle $IA_0 C$ is
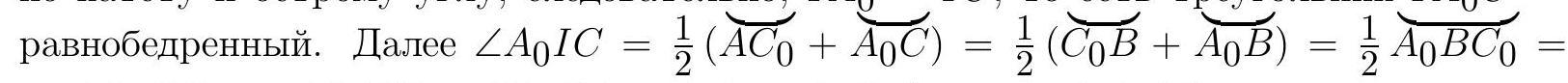
$=\angle A_0 CC_0 \Rightarrow \angle A_0 IC = \angle A_0 CI \Rightarrow A_0 I = A_0 C$. Thus, $\triangle A_0 IC$ is equilateral. Therefore, $\angle ABC = \angle AA_0 C = 60^\circ$.
Remark. If we consider an arbitrary triangle $ABC$ where $\angle B = 60^\circ$, then the segment $A_0 C_0$ is tangent to $\omega$. Indeed, by reversing all the arguments (taking $L$ as the projection of $I$ onto $A_0 C_0$), we obtain the congruence of triangles $IKC$ and $ILA_0$ by the hypotenuse and an acute angle, from which it follows that $IK = IL$, so $L$ lies on $\omega$, and therefore $A_0 C_0$ is tangent to $\omega$.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Triangle $A B C$ is equilateral. On side $A C$, point $M$ is marked, and on side $B C$, point $N$, such that $M C=B N=2 A M$. Segments $M B$ and $A N$ intersect at point $Q$. Find the angle $C Q B$.
#
|
# Answer: $90^{\circ}$.
## Solution:
Since $M C=B N$ and $A C=B C$, then $A M=A C-M C=B C-B N=N C$.
From the fact that $A M=N C, A B=A C$ and $\angle B A M=\angle C A N=60^{\circ}$, it follows that triangles $B A M$ and $A C N$ are congruent, so $\angle N A C=\angle M B A=\alpha$.
From triangle $A B M: \angle A M B$ (and it is also $\angle A M Q)=180^{\circ}-60^{\circ}-\alpha=120^{\circ}-\alpha$.
And from triangle $A Q M: \angle A Q M=180^{\circ}-\angle A M Q-\alpha=180^{\circ}-\left(120^{\circ}-\alpha\right)-\alpha=60^{\circ}$.
Then $\angle M Q N=120^{\circ}$, so $\angle M Q N+\angle M C N=180^{\circ}-$ from which it follows that quadrilateral $M Q N C$ is cyclic.
But then $\angle N Q C=\angle N M C$.
In triangle $N M C$, side $N C$ is half the length of side $M C$, and the angle between them is $60^{\circ}$, so this triangle is a right triangle with angles $90^{\circ}, 60^{\circ}, 30^{\circ}$. From this cyclic property: $\angle M Q C=\angle M N C=90^{\circ}$, then $\angle C Q B$ is also a right angle.
## Criteria:
If it is proven that $\angle M Q N=120^{\circ}$ or $\angle A Q M=60^{\circ}$ - award 2 points.
If this is not proven but used, award no more than 3 points for the solution.
Similarly for the equality $\angle M Q C=90^{\circ}$ (proven - award 2 points, not proven - award no more than 3 points for the solution).
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In the record of three two-digit numbers, there are no zeros, and in each of them, both digits are different. Their sum is 41. What could be their sum if the digits in them are swapped?
|
Answer: 113.
Solution. In all numbers, the tens digit is 1. Otherwise, the largest is at least 21, and the other two are at least 12. Their sum is no less than $12+12+21=44$, which is not equal to 41. The sum of the units digits is 11 (zeros are not allowed). Therefore, the sum with the digits rearranged is 113.
There are five possible sets of three numbers: $12,12,17$ or $12,13,16$, or 12, 14, 15 or 13, 13, 15 or 13, 14, 15. (This can justify the answer)
Criteria. Answer with one or two, three or four examples: 1 point.
Answer with five examples, but without proof that there are no others: 2 points.
## Full solution: 7 points.
|
113
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Each of the 5 brothers owns a plot of land. One day, they pooled their money, bought a neighbor's garden, and divided the new land equally among themselves. As a result, Andrey's plot increased by $10 \%$, Boris's plot - by $\frac{1}{15}$, Vladimir's plot - by $5 \%$, Grigory's plot - by $4 \%$, and Dmitry's plot - by $\frac{1}{30}$. By what percentage did the total area of their land increase as a result?
|
Answer: By $5 \%$.
Solution. Let A, B, V, G, D be the areas of the plots of each brother, respectively. Then, according to the problem, $\frac{1}{10} \mathrm{~A}=\frac{1}{15} \mathrm{~B}=\frac{1}{20} \mathrm{~V}=\frac{1}{25} \mathrm{~G}=\frac{1}{30} \mathrm{~D}$ (*). Denoting $\mathrm{A}=x$, we find: $\mathrm{B}=1.5 x, \mathrm{~V}=2 x, \mathrm{~G}=2.5 x$, D $=3 x$. Therefore, the total area of their plots was $10 x$, and increased by $\frac{1}{10} \mathrm{~A}=0.1 x$ for each, that is, by $0.5 x$ in total. Thus, the increase amounted to $\frac{0.5 x}{10 x} \cdot 100 \% = 5 \%$.
Comment. The relationship (*) is obtained - 2 points. The correct answer is obtained in the case of a particular example - 2 points. If arithmetic errors are made in the correct solution process, deduct $1-2$ points.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The participants of the Olympiad left 9 pens in the office. Among any four pens, at least two belong to the same owner. And among any five pens, no more than three belong to the same owner. How many students forgot their pens, and how many pens does each student have?
|
Answer. There are three students, each owning three pens.
Solution. No student owned more than three pens, as otherwise the condition "among any five pens, no more than three belonged to one owner" would not be met. There are a total of 9 pens, so there are no fewer than 3 students. On the other hand, among any four pens, there are two pens belonging to one student, so there are fewer than 4 students. Therefore, there are three students, and each forgot no more than three pens, with a total of 9 pens. This means each student forgot 3 pens.
Comment. A complete and justified solution - 7 points. Only proved that no student owned more than three pens - 1 point. Only proved that there are no fewer than 3 students - 2 points. Only proved that there are fewer than 4 students - 2 points. Proved that there are three students - 5 points. Provided the answer without justification or with incorrect justifications - 0 points.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
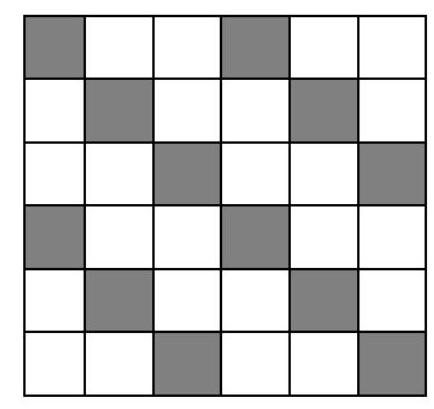
4. What is the minimum number of cells that need to be colored on a $6 \times 6$ board so that, for any placement (including rotations and flips) of a figure consisting of 4 cells in the shape of the letter $\Gamma$, there is at least one colored cell?
|
Answer: 12.
Solution: Consider a $2 \times 3$ rectangle. It is obvious that at least 2 cells need to be colored in it. Divide the $6 \times 6$ board into 6 rectangles of $2 \times 3$. In each, at least 2 cells need to be colored, so in total, at least 12 cells need to be colored. An example with 12 cells is shown on the right.
Comment: A correct example with 12 colored cells - 3 points. An estimate that fewer than 12 cells are not enough - 4 points. The estimate should not rely on an example. Reasoning such as: "in my example, it is impossible to reduce the number of colored cells" is not an estimate.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In triangle $A B C$, points $M$ and $N$ are the midpoints of sides $A C$ and $B C$ respectively. It is known that the point of intersection of the medians of triangle $A M N$ is the point of intersection of the altitudes of triangle $A B C$. Find the angle $A B C$.
|
Answer: $45^{\circ}$.
Solution. Triangles $E T N$ and $A T B$ are similar, therefore, $T N: T B=T E: T A=E N: A B=1: 4$. Therefore, $C T=1 / 2 B T$. Since $H$ is the intersection point of the medians of triangle $A M N$, $E H=1 / 3 A E=E T$. Therefore, $H T=1 / 2 A T$.
Thus, right triangles $C T H$ and $B T A$ are similar, and
$\square T C H=\square T B A$. But $C H$ is part of the height $C Q$ of triangle $A B C$, so these equal angles are acute angles
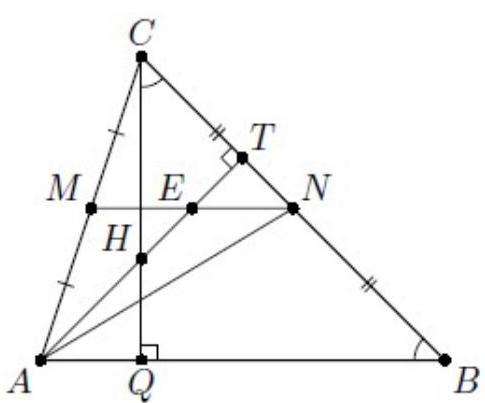
of the right triangle $C Q B$.
|
45
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
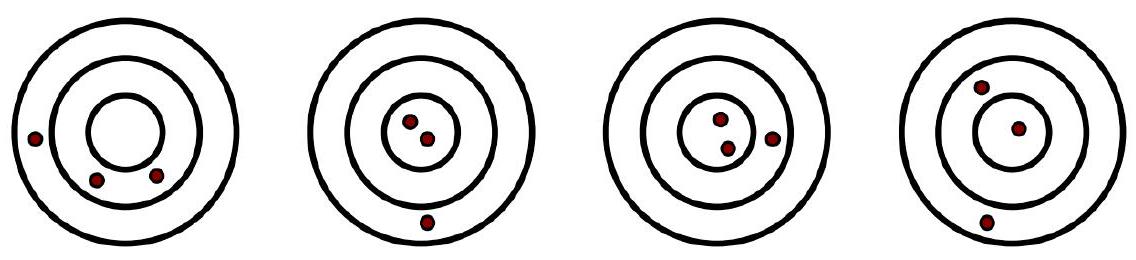
Problem 4.7. Denis threw darts at four identical dartboards: he threw exactly three darts at each board, where they landed is shown in the figure. On the first board, he scored 30 points, on the second - 38 points, on the third - 41 points. How many points did he score on the fourth board? (For hitting each specific zone - ring or central area - a certain number of points is awarded.)
|
Answer: 34.
Solution. "Add" the first two dart fields: we get 2 hits in the central field, 2 hits in the inner ring, 2 hits in the outer ring. Thus, the sum of points on the first and second fields is twice the number of points obtained for the fourth field.
From this, it is not difficult to get the answer
$$
(30+38): 2=34
$$
|
34
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.1. After a football match, the coach lined up the team as shown in the figure, and commanded: "Run to the locker room, those whose number is less than that of any of their neighbors." After several people ran away, he repeated his command. The coach continued until only one player was left. What is Igor's number, if it is known that after he ran away, 3 people remained in the line? (After each command, one or several players ran away, after which the line closed, and there were no empty spaces between the remaining players.)

|
Answer: 5.
Solution. It is clear that after the first command, the players left are $9,11,10,6,8,5,4,1$. After the second command, the players left are $11,10,8,5,4$. After the third - $11,10,8,5$. After the fourth - $11,10,8$. Therefore, Igor had the number 5.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
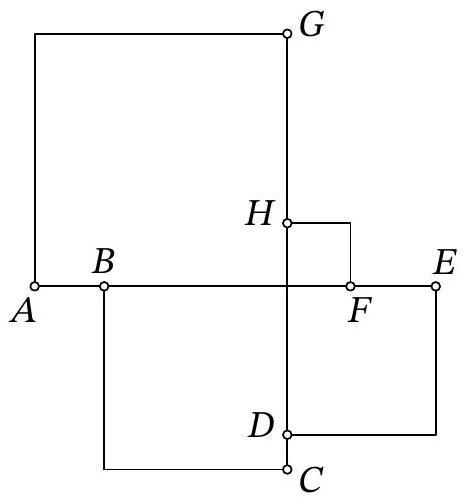
Problem 6.5. The figure shows 4 squares. It is known that the length of segment $A B$ is 11, the length of segment $F E$ is 13, and the length of segment $C D$ is 5. What is the length of segment $G H$?
|
Answer: 29.
Solution. The side of the largest square (with vertex $A$) is greater than the side of the second largest square (with vertex $C$) by the length of segment $A B$, which is 11. Similarly, the side of the second largest square is greater than the side of the third largest square (with vertex $E$) by the length of segment $C D$, which is 5. And its side is greater than the side of the smallest square by the length of segment $E F$, which is 13. In total, the side of the largest square is greater than the side of the smallest square by the length of segment $G H$, which is $11+5+13=29$.
|
29
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
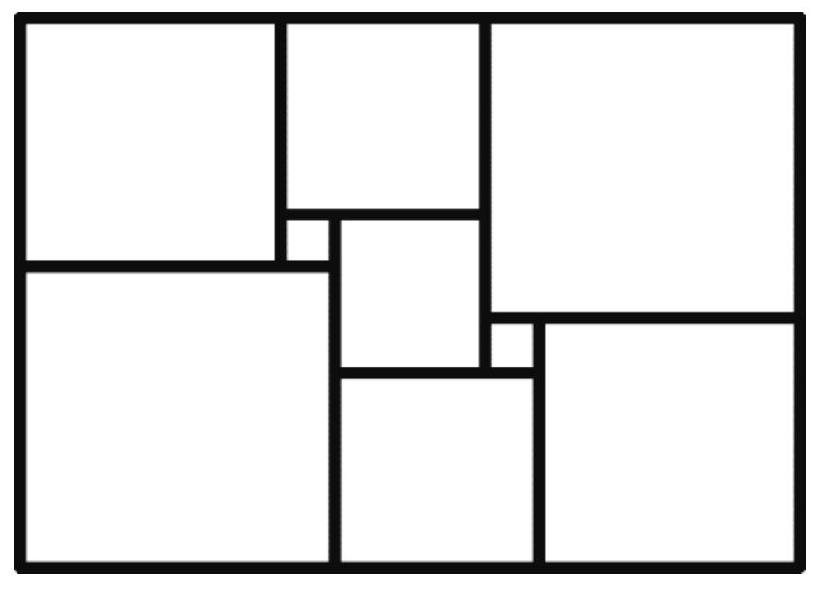
Problem 7.5. A rectangle was cut into nine squares, as shown in the figure. The lengths of the sides of the rectangle and all the squares are integers. What is the smallest value that the perimeter of the rectangle can take?
|
Answer: 52.
Solution. Inside the square, we will write the length of its side. Let the sides of the two squares be $a$ and $b$, and we will sequentially calculate the lengths of the sides of the squares.
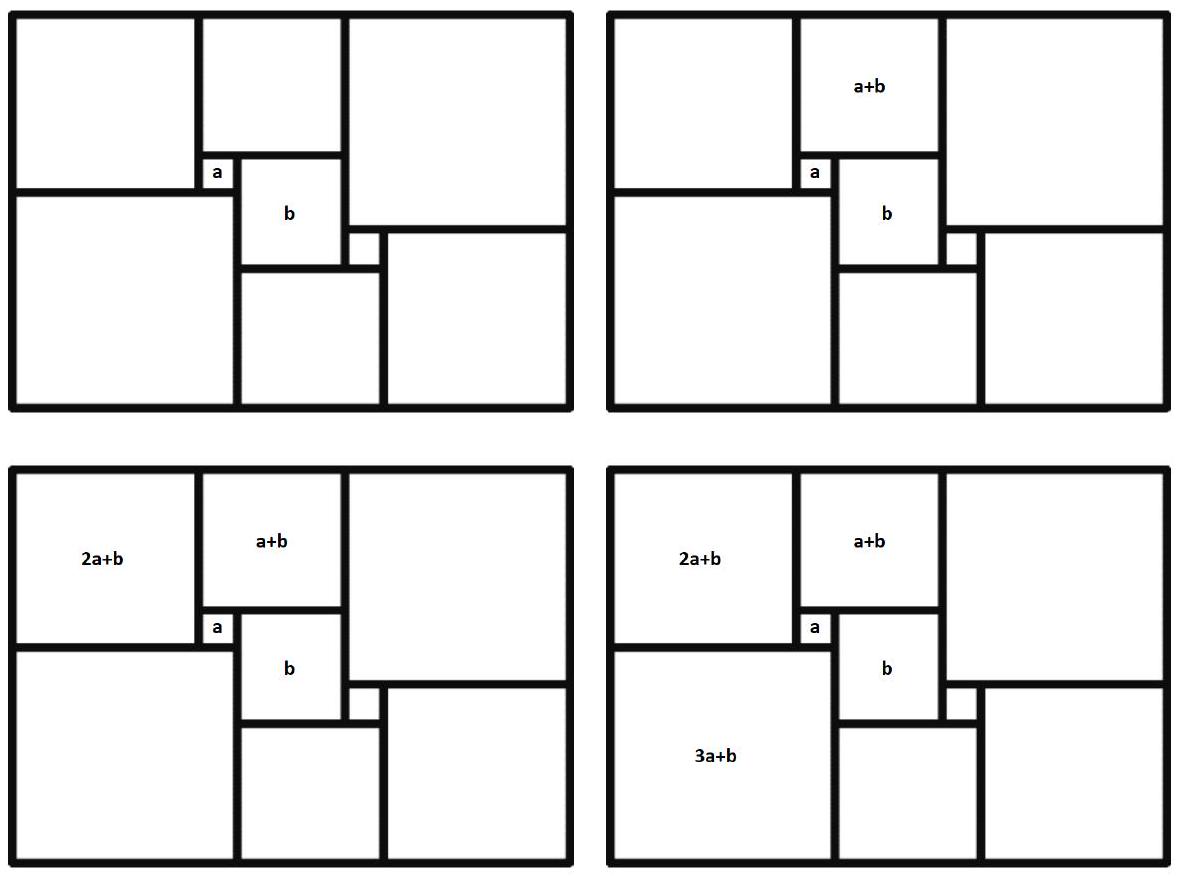

The sum of the lengths of the sides of the two squares adjacent to the left side of the rectangle is equal to the sum of the lengths of the sides of the two squares adjacent to the right side of the rectangle. We get the equation
$$
\begin{aligned}
(2 a+b)+(3 a+b) & =(12 a-2 b)+(8 a-b) \\
5 a+2 b & =20 a-3 b \\
b & =3 a
\end{aligned}
$$
Thus, to minimize the perimeter of the rectangle, we need to choose $a=1$, $b=3$. It is not difficult to check that with these values, the rectangle will have dimensions $11 \times 15$, and its perimeter will be 52.
|
52
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
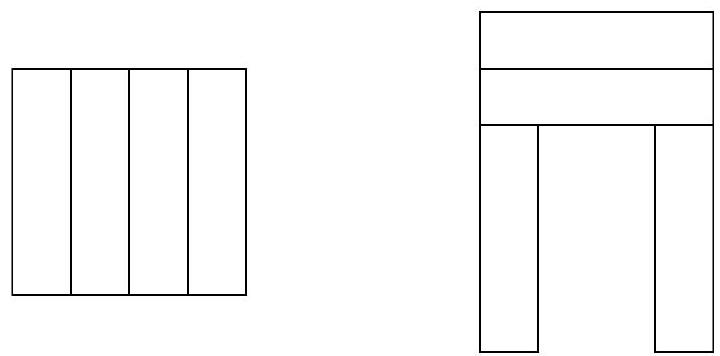
Problem 8.1. A square was cut into four equal rectangles, and from them, a large letter P was formed, as shown in the figure, with a perimeter of 56.
What is the perimeter of the original square
|
Answer: 32.
Solution. Let the width of the rectangle be $x$. From the first drawing, we understand that the length of the rectangle is four times its width, that is, it is equal to $4 x$. Now we can calculate the dimensions of the letter P.
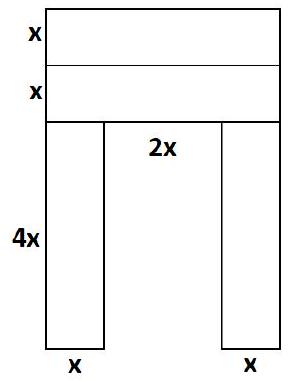
From this, we get the equation
$$
\begin{gathered}
28 x=56 \\
x=2
\end{gathered}
$$
The perimeter of the square is $16 x=32$.
|
32
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.2. The numbers from 1 to 9 were placed in the cells of a $3 \times 3$ table such that the sum of the numbers on one diagonal is 7, and on the other - 21. What is the sum of the numbers in the five shaded cells?
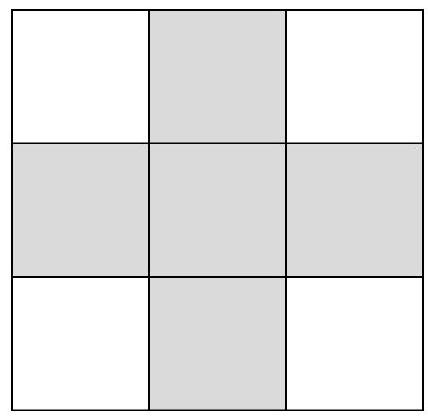
|
Answer: 25.
Solution. Note that 7 can be represented uniquely as the sum of numbers from 1 to 9 - this is $1+2+4=7$.
Let's look at the other diagonal with a sum of 21. The largest possible value of the sum in it is $9+8+4=21$ (since the number in the central cell is no more than 4). Therefore, it must contain the numbers $9,8,4$.
Thus, the number 4 is in the central cell, and the numbers 1, 2, 8, and 9 are at the corners. Now it is not difficult to find the sum of the numbers in the shaded cells: $3+4+5+6+7=25$.
|
25
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.6. For quadrilateral $ABCD$, it is known that $AB=BD, \angle ABD=\angle DBC, \angle BCD=90^{\circ}$. A point $E$ is marked on segment $BC$ such that $AD=DE$. What is the length of segment $BD$, if it is known that $BE=7, EC=5$?
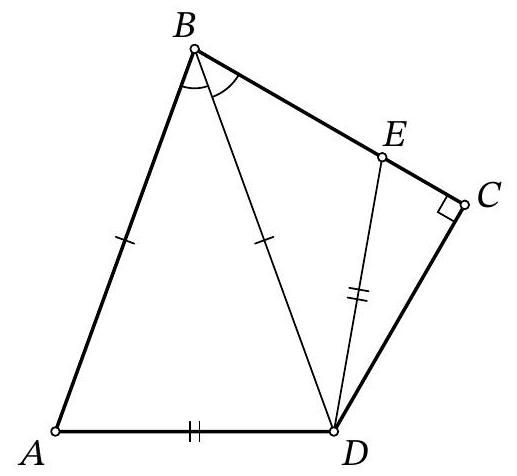
|
Answer: 17.
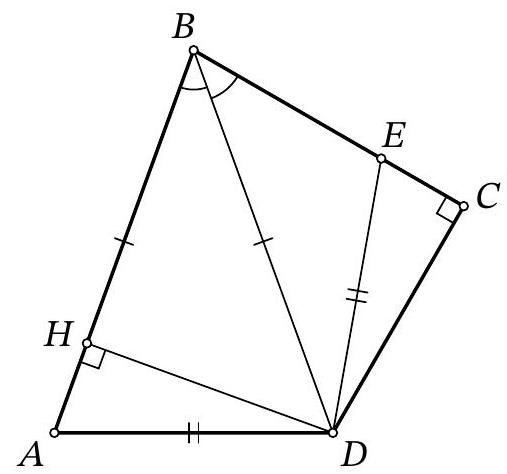
Fig. 3: to the solution of problem 8.6
Solution. In the isosceles triangle $ABD$, drop a perpendicular from point $D$, let $H$ be its foot (Fig. 3). Since this triangle is acute-angled ($\angle ABD = \angle CBD < 90^\circ$, $\left.\angle BAD = \angle ADB = \frac{180^\circ - \angle ABD}{2} < 90^\circ\right)$, point $H$ lies on the segment $AB$.
Notice that the right triangles $BDH$ and $BDC$ are equal by the common hypotenuse $BD$ and the acute angle at vertex $B$. Therefore, $BH = BC$ and $DH = CD$.
Now, notice that the right triangles $ADH$ and $EDC$ are also equal by the hypotenuse $AD = ED$ and the leg $DH = CD$. Therefore, $EC = AH$.
Thus, $BD = BA = BH + AH = BC + EC = (7 + 5) + 5 = 17$.
|
17
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.4. From left to right, intersecting squares with sides $12, 9, 7, 3$ are depicted respectively. By how much is the sum of the black areas greater than the sum of the gray areas?
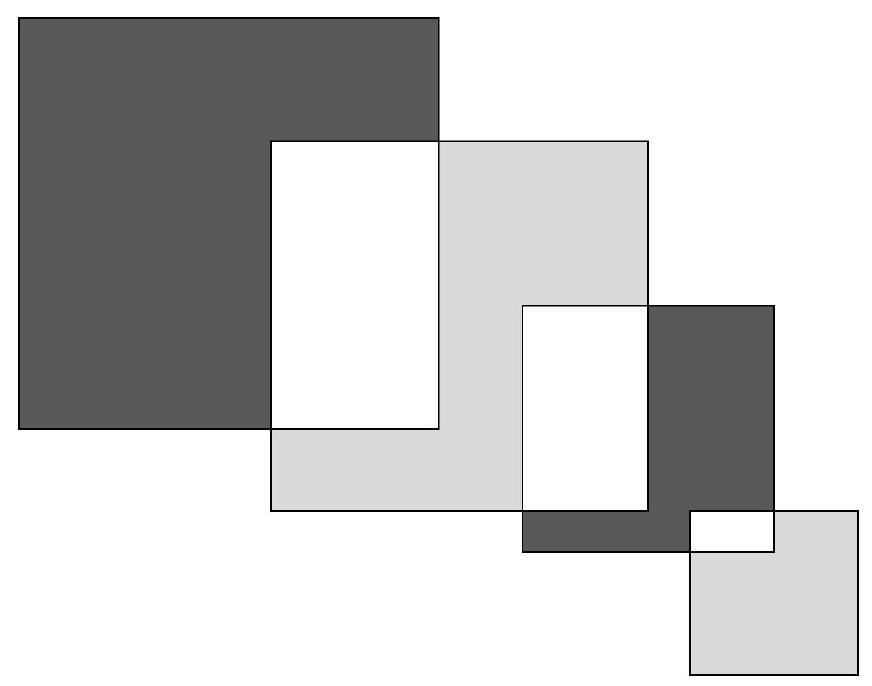
|
Answer: 103.
Solution. Let's denote the areas by $A, B, C, D, E, F, G$.
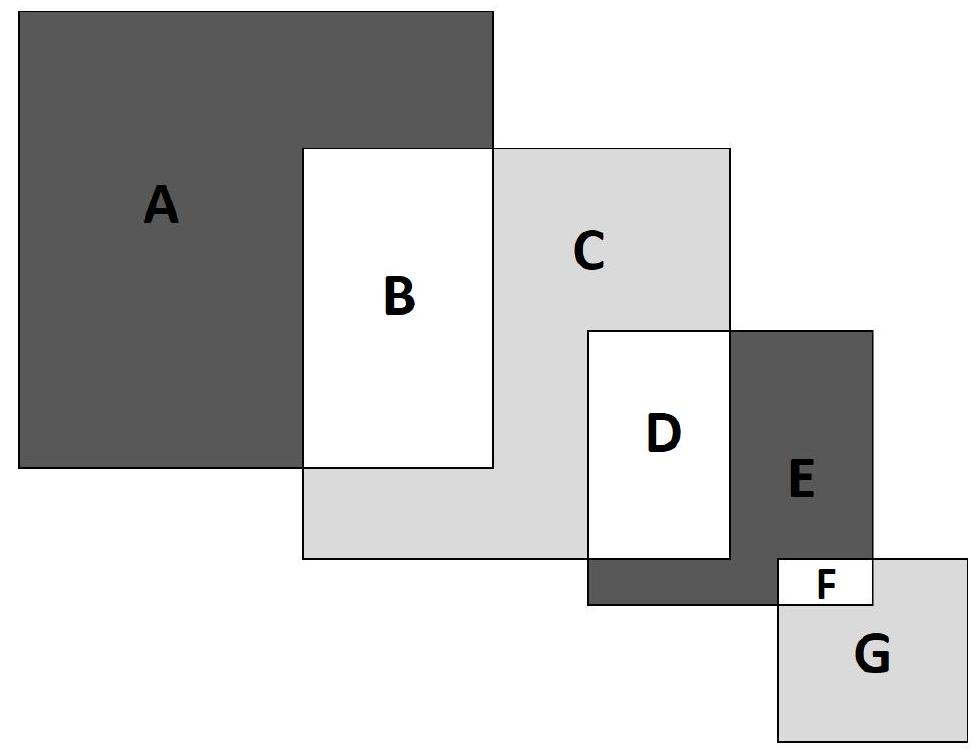
We will compute the desired difference in areas:
$$
\begin{aligned}
A+E-(C+G) & =A-C+E-G=A+B-B-C-D+D+E+F-F-G= \\
& =(A+B)-(B+C+D)+(D+E+F)-(F+G)= \\
& =12^{2}-9^{2}+7^{2}-3^{2}=103
\end{aligned}
$$
|
103
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.7. In triangle $ABC$, the bisector $AL$ is drawn. Points $E$ and $D$ are marked on segments $AB$ and $BL$ respectively such that $DL = LC$, $ED \parallel AC$. Find the length of segment $ED$, given that $AE = 15$, $AC = 12$.
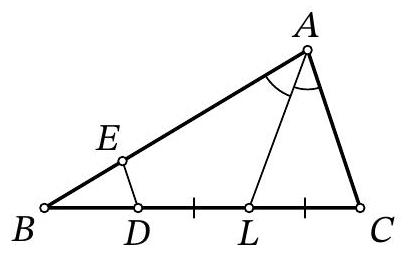
|
Answer: 3.
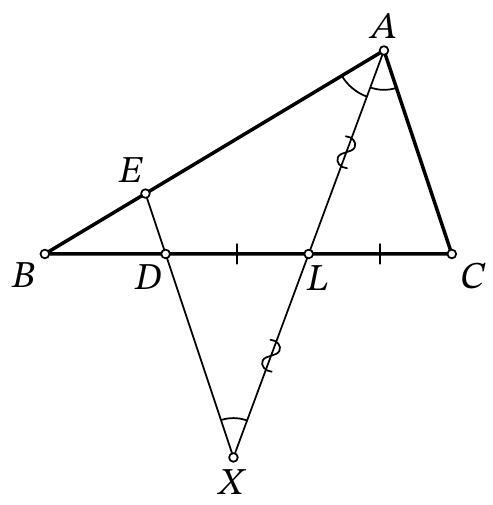
Fig. 5: to the solution of problem 9.7
Solution. On the ray $AL$ beyond point $L$, mark a point $X$ such that $XL = LA$ (Fig. 5). Since in the quadrilateral $ACXD$ the diagonals are bisected by their intersection point $L$, it is a parallelogram (in particular, $AC = DX$). Therefore, $DX \parallel AC$. Since $AC \parallel ED$ by the problem's condition, the points $X, D, E$ lie on the same line.
Since $AC \parallel EX$, then $\angle EAX = \angle CAX = \angle AXE$, i.e., triangle $AEX$ is isosceles, $EA = EX$. Then
$$
ED = EX - XD = EA - AC = 15 - 12 = 3
$$
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.1. In each cell of a $5 \times 5$ table, a natural number is written in invisible ink. It is known that the sum of all the numbers is 200, and the sum of three numbers located inside any $1 \times 3$ rectangle is 23. What is the central number in the table?
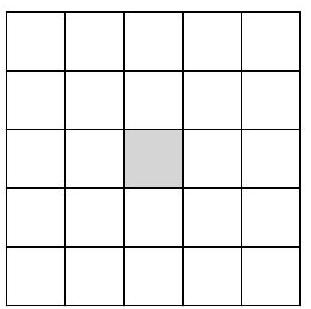
|
Answer: 16.
Solution. Divide the $5 \times 5$ square without the central cell into four $2 \times 3$ rectangles, and each of them into two $1 \times 3$ rectangles.
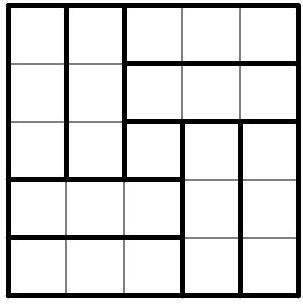
We get 8 rectangles $1 \times 3$, the sum of the numbers in each of which is 23. Since the sum of all the numbers is 200, we find the number in the central cell as $200 - 23 \cdot 8 = 16$.
|
16
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.8. Rectangle $ABCD$ is such that $AD = 2AB$. Point $M$ is the midpoint of side $AD$. Inside the rectangle, there is a point $K$ such that $\angle AMK = 80^{\circ}$ and ray $KD$ is the bisector of angle $MKC$. How many degrees does angle $KDA$ measure?
|
Answer: 35.
Solution. Let's start with the assumption that the quadrilateral KMDС is inscribed (several proofs of this fact will be proposed below).
Using the fact that in the inscribed quadrilateral $K M D C$ the sum of opposite angles is $180^{\circ}$, we get $\angle M K D=\frac{\angle M K C}{2}=\frac{180^{\circ}-\angle M D C}{2}=45^{\circ}$. The angle $A M K$ as an external angle for triangle $K D M$ is equal to the sum of angles $M K D$ and $K D A$, so the required angle КDA is $80^{\circ}-45^{\circ}=35^{\circ}$.
Fig. 8: to the solution of problem 10.8
Let's provide the first possible proof of the inscribed nature of quadrilateral KMDC. Consider triangle $M K C$ and its circumscribed circle. Note that point $D$ lies on the bisector of angle $M K C$, and is equidistant from vertices $M$ and $C$ (Fig. 8). However, the bisector of an angle of a non-isosceles triangle and the perpendicular bisector of its opposite side, as is known, intersect at the midpoint of the "smaller" arc of the circumscribed circle of the triangle. In other words, $D$ is the midpoint of the arc $M C$ of the circumscribed circle of triangle $M K C$, not containing point $K$. It should also be noted that $M K \neq K C$ (otherwise triangles $K M D$ and $K C D$ would be equal, but $\angle K M D>90^{\circ}>\angle K C D$ ).
Let's provide the second possible proof of the inscribed nature of quadrilateral KMDC. It will use the fourth criterion for the equality of triangles: if two sides and an angle not between them are equal in two triangles, then these triangles are either equal or the sum of the other two angles not between them is $180^{\circ}$. The fourth criterion is satisfied for triangles $M D K$ and $C D K (M D=D C, D K$ - common, $\angle M K D=\angle C K D)$. However, angles $K M D$ and $K C D$ are not equal (again, the first is obtuse, and the second is acute), so their sum is $180^{\circ}$, which are the opposite angles of quadrilateral KMDC. Therefore, it is inscribed.
## 11th grade
|
35
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
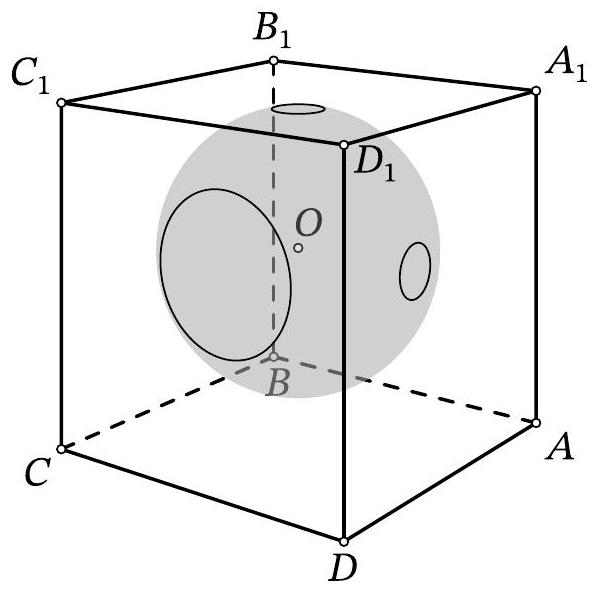
Problem 11.6. Inside the cube $A B C D A_{1} B_{1} C_{1} D_{1}$, there is the center $O$ of a sphere with radius 10. The sphere intersects the face $A A_{1} D_{1} D$ along a circle with radius 1, the face $A_{1} B_{1} C_{1} D_{1}$ along a circle with radius 1, and the face $C D D_{1} C_{1}$ along a circle with radius 3. Find the length of the segment $O D_{1}$.
|
Answer: 17.
Solution. Let $\omega$ be the circle that the sphere cuts out on the face $C D D_{1} C_{1}$. From point $O$
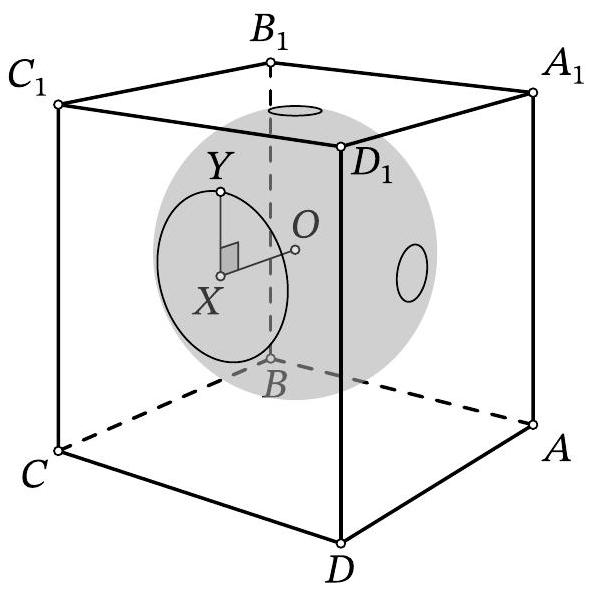
Fig. 10: to the solution of problem 11.6
drop a perpendicular $O X$ to this face, then point $X$ is the center of $\omega$ (point $O$ is equidistant from all points of $\omega$, so the projection of $O$ onto the plane of $\omega$ is also equidistant from them). Let $Y$ be an arbitrary point on $\omega$ (Fig. 10). Triangle $OXY$ is a right triangle; by the problem's condition, $X Y=3$ and $O Y=10$. By the Pythagorean theorem, we get $O X^{2}=10^{2}-3^{2}=91$.
Similarly, we find the squares of the distances from point $O$ to the planes $A_{1} B_{1} C_{1} D_{1}$ and $A D D_{1} A_{1}$, which are both equal to $10^{2}-1^{2}=99$.
By the spatial Pythagorean theorem, the square of the length of segment $O D_{1}$ is equal to the sum of the squares of the distances from point $O$ to the three faces containing point $D_{1}$. Therefore, $O D_{1}^{2}=$ $91+99+99=289$, from which $O D_{1}=17$.
|
17
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Variant 1.
Find the sum:
$$
(-2021)+(-2020)+(-2019)+\ldots+2023+2024
$$
|
Answer: 6069.
Solution. By pairing numbers that differ in sign, we get that in each such pair the sum is 0, and without pairs, the numbers left are $0, 2022, 2023, 2024$.
|
6069
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 2. Option 1.
In a certain three-digit number $N$, the last two digits were swapped and the resulting number was added to the original. The sum turned out to be a four-digit number starting with 173. Find the largest possible sum of the digits of the number $N$.
|
Answer: 20.
Solution: Let the original number be $\overline{a b c}$, and the last digit of the sum $\overline{a b c}+\overline{a c b}$ be $x$. Then, $100 a+10 b+c+100 a+10 c+b=200 a+11(c+b)=1730+x$. If $a1730+x$.
Therefore, $a=8$. Thus, $(800+10 b+c)+(800+10 c+b)=1730+x$, i.e., $11(b+c)=130+x$. From this, it follows that $x=2$ (among the numbers from 130 to 139, only 132 is divisible by 11). Therefore, $b+c=132 / 11=12$. Answer: $a+b+c=8+12=20$.
|
20
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 3. Option 1.
In the village, 7 people live. Some of them are liars who always lie, while the rest are knights (who always tell the truth). Each resident said whether each of the others is a knight or a liar. A total of 42 answers were received, and in 24 cases, a resident called a fellow villager a liar. What is the minimum number of knights that can live in the village?
|
Answer: 3.
Solution: The phrase "He is a knight" would be said by a knight about a knight and by a liar about a liar, while the phrase "He is a liar" would be said by a knight about a liar and by a liar about a knight. Therefore, in each pair of "knight-liar," the phrase "He is a liar" will be said twice. Since this phrase was said 24 times in total, there are 12 pairs of "knight-liar," from which we can determine that there are 3 knights and 4 liars, or vice versa.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Variant 1.
Given an equilateral triangle $A B C$ with an area of 210. Inside it, points for which vertex $A$ is neither the closest nor the farthest are painted red. What is the area of the painted part of the triangle?
|
Answer: 41.
Solution.
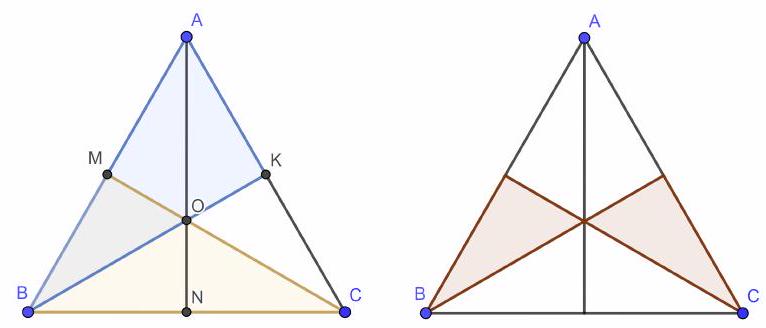
Consider a point $D$ for which vertex $B$ is the nearest, and vertex $C$ is the farthest. Let $M, N, K$ be the midpoints of sides $AB, BC$, and $AC$ respectively. $O$ is the point of intersection of the medians $AN, BK, CM$, which are also the perpendicular bisectors of the sides of the triangle. Since point $D$ is closer to $B$ than to $A$, $D$ lies on the sides or inside triangle $CMB$. Since point $D$ is closer to $A$ than to $C$, $D$ lies on the sides or inside triangle $ABK$. Therefore, point $D$ lies in the intersection of these triangles, i.e., in triangle $BOM$. Similarly, points for which vertex $B$ is the farthest and vertex $C$ is the nearest lie in triangle $COK$. Since $CO: OM = 2: 1$, the area of triangle $BOM$ is one-third of the area of triangle $CMB$, which is half the area of triangle $ABC$. Therefore, the area of triangle $BOM$ is $\frac{1}{6}$ of the area of triangle $ABC$. Applying similar reasoning to triangle $COK$, we finally get that the sum of the areas of triangles $BOM$ and $COK$ is $\frac{1}{6} + \frac{1}{6} = \frac{1}{3}$ of the area of triangle $ABC$, i.e., it is equal to 41.
|
41
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 2.
What is the smallest sum that nine consecutive natural numbers can have if this sum ends in 2050306?
|
Answer: 22050306.
Option 3.
What is the smallest sum that nine consecutive natural numbers can have if this sum ends in $1020156$?
Answer: 31020156.
|
31020156
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 6. Variant 1.
What is the largest root that the equation
$$
(x-a)(x-b)=(x-c)(x-d)
$$
can have if it is known that $a+d=b+c=2022$, and the numbers $a$ and $c$ are different?
|
Answer: 1011.
Solution. By expanding the brackets and combining like terms, we find $x=\frac{c d-a b}{c+d-a-b}$. Note that $c+d-a-b \neq 0$, because otherwise $c+d=a+b$, and considering the equality $a+d=b+c$, we would get $a=c$.
Considering that $d=2022-a, c=2022-b, x=\frac{2022^{2}-2022 a-2022 b}{2(2022-a-b)}=\frac{2022}{2}=1011$.
|
1011
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
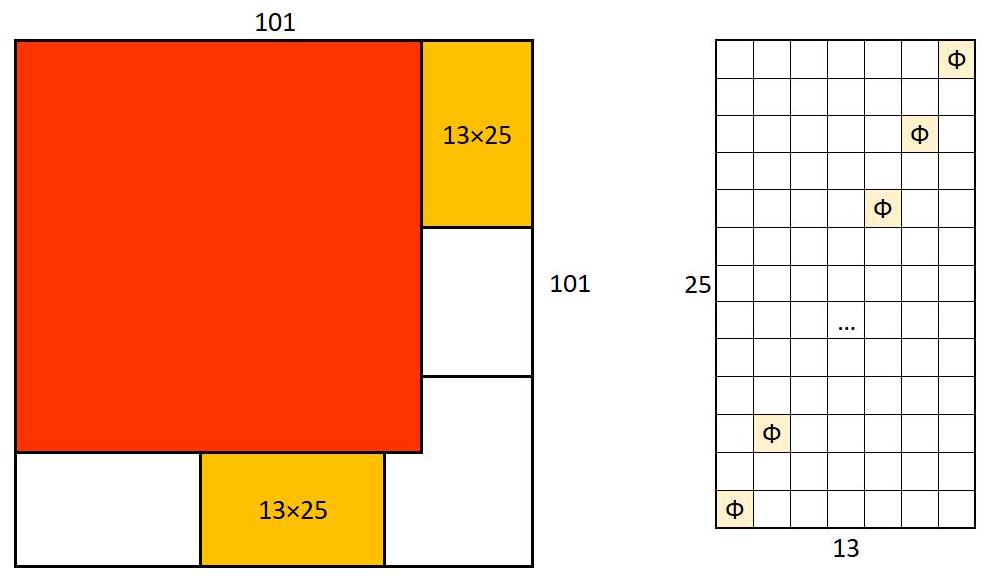
7. Variant 1.
In a $101 \times 101$ square, an $88 \times 88$ corner square is painted red. What is the maximum number of non-attacking queens that can be placed on the board without placing the figures on the red cells? A queen attacks along the horizontal, vertical, and diagonals of the square. Attacking through the painted cells is allowed.
|
Answer: 26.
Solution. Consider 13 horizontal and 13 vertical strips of size $1 \times 101$, not containing any red cells. Each of the queens stands on at least one of these strips, and no strip can contain more than one queen, so there are no more than 26 queens. To construct an example, consider two rectangles of size $13 \times 25$ (see the figure) and place the queens in each of them according to the scheme shown in the figure.
|
26
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Variant 1.
A line parallel to the leg $A C$ of the right triangle $A B C$ intersects the leg $B C$ at point $K$, and the hypotenuse $A B$ at point $N$. On the leg $A C$, a point $M$ is chosen such that $M K=M N$. Find the ratio $\frac{A M}{M C}$, if $\frac{B K}{B C}=14$.
|
Answer: 7.
Solution.
Drop the altitude $M H$ from point $M$ in the isosceles triangle $M N K$. Then $M H K C$ is a rectangle and $M C=K H=H N$. Let $M C=K H=H N=y$. Let $K B=x$, then $C K=C B-K B=4 x-x=3 x$. From the similarity of triangles $N K B$ and $A C B$, it follows that $\frac{A C}{C B}=\frac{N K}{K B}$. Therefore, $\frac{A C}{4 x}=\frac{2 y}{x}$. Hence, $A C=8 y$. We get that $\frac{A M}{M C}=\frac{8 x-x}{x}=7$.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task No. 1.1
## Condition:
Five friends - Masha, Nastya, Irina, Olya, and Anya - meet in the park every day after buying ice cream from the shop around the corner. One day, the girls had a conversation.
Irina: I was the first in line!
Olya: No one was after me.
Anya: Only one person was after me.
Masha: There were five people in front of me.
Nastya: I was standing next to Irina.
The girls are friends, so they don't lie to each other. How many people were between Masha and Nastya?
|
Answer: 3
Exact match of the answer - 1 point
## Solution.
From the statements of Irina and Olya, it is clear that they were first and last, respectively. Since there was only one person after Anya, it was Olya. Nastya stood next to Irina, but she could not have stood in front of her, so Nastya was second. This means that Masha stood somewhere between Nastya and Anya, and since there were five people in front of her, two of whom were Irina and Nastya, there were exactly three people between Masha and Nastya.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task No. 1.2
## Condition:
Five friends - Katya, Polina, Alyona, Lena, and Svetlana - meet in the park every day after buying ice cream from the shop around the corner. One day, the girls had a conversation.
Polina: I stood next to Alyona.
Alyona: I was the first in line!
Lena: No one was after me.
Katya: There were five people in front of me.
Svetlana: Only one person was after me.
The girls are friends, so they don't lie to each other. How many people were between Katya and Polina?
|
# Answer: 3
Exact match of the answer - 1 point
Solution by analogy with task №1.1
#
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 1.3
## Condition:
Five friends - Sasha, Yulia, Rita, Alina, and Natasha - meet in the park every day after buying ice cream from the little shop around the corner. One day, the girls had a conversation.
Sasha: There were five people in front of me.
Alina: There was no one after me.
Rita: I was the first in line!
Natasha: There was only one person after me.
Yulia: I was standing next to Rita.
The girls are friends, so they don't lie to each other. How many people were there between Sasha and Yulia?
|
Answer: 3
Exact match of the answer - 1 point
Solution by analogy with task №1.1
#
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task No. 1.4
## Condition:
Five friends - Kristina, Nadya, Marina, Liza, and Galia - meet in the park every day after buying ice cream from the shop around the corner. One day, the girls had a conversation.
Kristina: There were five people in front of me.
Marina: I was the first in line!
Liza: No one was behind me.
Nadya: I was standing next to Marina.
Galia: Only one person was behind me.
The girls are friends, so they don't lie to each other. How many people were between Kristina and Nadya?
|
# Answer: 3
Exact match of the answer - 1 point
Solution by analogy with task №1.1
#
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 2.1
## Condition:
Karlson and Little together weigh 10 kg more than Freken Bok, and Little and Freken Bok weigh 30 kg more than Karlson. How much does Little weigh? Give your answer in kilograms.
|
Answer: 20
Exact match of the answer -1 point
Solution.
Let's denote Carlson's mass by K, Freken Bok's mass by F, and Little One's mass by M. Then from the condition, it follows that $K+M=F+10$ and $M+F=K+30$. Adding these equations term by term, we get $K+2M+F=F+K+40$. From this, $M=20$.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task No. 3.1
## Condition:
Polina makes jewelry on order for a jewelry store. Each piece of jewelry consists of a chain, a stone, and a pendant. The chain can be silver, gold, or iron. Polina has stones - a diamond, an emerald, and a quartz - and pendants in the shape of a star, a sun, and a moon. Polina is only satisfied when three pieces of jewelry are laid out in a row from left to right on the display according to the following rules:
- There must be a piece of jewelry with a sun on an iron chain;
- Next to the piece of jewelry with a sun, there must be a gold and a silver piece of jewelry;
- The three pieces of jewelry in the row must have different stones, pendants, and chains.
How many ways are there to make Polina satisfied?
|
# Answer: 24
Exact match of the answer - 1 point
## Solution.
Notice that the iron ornament with the sun is definitely in the middle, as it must be between the gold and silver ornaments. For the first position, we can choose a silver or gold chain. After choosing a chain for the first position, the chain for the third position is uniquely determined. For the first position, we can choose the moon or the star. After choosing a pendant for the first position, the pendant for the third position is uniquely determined. The three stones can be arranged in six ways (one of three stones on the first position, one of the remaining two on the second position, and the remaining stone on the third position). There are four ways to correctly arrange the chains and pendants, and for each of these four ways, there are six ways to arrange the stones. In total, $2 * 2 * 6 = 24$.
#
|
24
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 3.2
## Condition:
Artyom makes watches for a jewelry store on order. Each watch consists of a bracelet and a dial. The bracelet can be leather, metal, or nylon. Artyom has round, square, and oval dials. Watches can be mechanical, quartz, or electronic.
Artyom is only satisfied when the watches are arranged in a row from left to right on the display according to the following rules:
- There must be mechanical watches with a round dial;
- Next to the watches with a round dial, there must be electronic watches to the right and quartz watches to the left;
- The three watches in the row must have different mechanisms, bracelets, and dials.
How many ways are there to make Artyom happy?
|
Answer: 12
Exact match of the answer -1 point
Solution by analogy with task №3.1
#
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 3.3
## Condition:
Alina makes phone cases on order for a tech store. Each case has a pattern and a charm.
The case can be silicone, leather, or plastic. Alina has charms in the shapes of a bear, a dinosaur, a raccoon, and a fairy, and she can draw the moon, the sun, and clouds on the case.
Alina is only satisfied when three cases are laid out in a row from left to right on the display according to the following rules:
- There must be a silicone case with a bear charm;
- Next to the case with the bear charm, there must be a leather case on the left and a plastic case on the right;
- The three cases in the row must have different materials, charms, and patterns.
How many ways are there to make Alina happy?
|
Answer: 36
Exact match of the answer - 1 point
Solution by analogy with task №3.1
#
|
36
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 3.4
## Condition:
Anton makes watches for a jewelry store on order. Each watch consists of a bracelet, a precious stone, and a clasp.
The bracelet can be silver, gold, or steel. Anton has precious stones: zircon, emerald, quartz, diamond, and agate, and clasps: classic, butterfly, and buckle. Anton is only satisfied when three watches are laid out in a row on the display according to the following rules:
- There must be steel watches with a classic clasp and a zircon stone
- Next to the watches with the classic clasp, there must be gold and silver watches;
- The three watches in a row must have different bracelets, precious stones, and clasps.
How many ways are there to make Anton happy?
|
Answer: 48
Exact match of the answer -1 point
Solution by analogy with task №3.1
#
|
48
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 6.1
## Condition:
Yasha and Grisha are playing a game: first, they take turns naming a number from 1 to 105 (Grisha names the number first, the numbers must be different). Then each counts the number of different rectangles with integer sides, the perimeter of which is equal to the named number. The one with the greater number of rectangles wins. What number should Grisha name to win? Rectangles that differ only by rotation are considered the same. For example, rectangles $2 \times 3$ and $3 \times 2$ are the same.
|
# Answer: 104
## Exact match of the answer -1 point
## Solution.
We will show that by naming the number 104, Grisha will win. Consider a rectangle with sides a and b. Its perimeter \( P = 2(a + b) \Rightarrow (a + b) = P / 2 \), then the length of the smaller side can take integer values from 1 to the integer part of the number \( P / 4 \), that is, for the chosen number \( P \), the number of different rectangles with such a perimeter and integer sides is equal to the integer part of the number \( P / 4 \). Note also that \( P \) is even, since it equals \( 2(a + b) \), where \( a \) and \( b \) are integers. For \( P = 104 \), the number of rectangles is 26. Yasha cannot name a number greater than 104, and for \( P \leq 102 \), the number of rectangles is no more than 25. Therefore, Grisha will definitely win.
|
104
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 6.2
## Condition:
Sasha and Misha are playing a game: first, they take turns naming a number from 1 to 213 (Misha names the first number, the numbers must be different). Then each counts the number of different rectangles with integer sides, the perimeter of which is equal to the named number. The winner is the one who has more rectangles. Rectangles that differ only by rotation are considered the same. For example, rectangles $2 \times 3$ and $3 \times 2$ are the same.
|
Answer: 212
Exact match of the answer -1 point
Solution by analogy with task №6.1
## Condition:
Oksana and Seryozha are playing a game: they take turns naming a number from 1 to 165 (Oksana goes first, the numbers must be different). Then each counts the number of different rectangles with integer sides whose perimeter is equal to the named number. The winner is the one who has more rectangles. What number should Oksana name to win? Rectangles that differ only by rotation are considered the same. For example, rectangles $2 \times 3$ and $3 \times 2$ are the same.
Answer: 164
Exact match of the answer -1 point
Solution by analogy with task №6.1
#
|
164
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 6.4
## Condition:
Dima and Vlad are playing a game: first, they take turns naming a number from 1 to 97 (Dima names the first number, the numbers must be different). Then each of them counts the number of different rectangles with integer sides, the perimeter of which is equal to the named number. The winner is the one who has more rectangles. Rectangles that differ only by rotation are considered the same. For example, rectangles $2 \times 3$ and $3 \times 2$ are the same.
What number should Dima name to win?
|
Answer: 96
Exact match of the answer -1 point
Solution by analogy with task №6.1
#
|
96
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Assignment No. 7.1
## Condition:
Professor Severus Snape has prepared three potions, each with a volume of 300 ml. The first potion makes the person who drinks it smart, the second makes them beautiful, and the third makes them strong. To ensure the potion works, one needs to drink at least 30 ml of it. Severus Snape was about to drink his potions when he was called to the headmaster's office and left, leaving the labeled potions in large jugs on his desk. Taking advantage of his absence, Harry, Hermione, and Ron approached the table with the potions and began to sample them.
Hermione was the first to try the potions: she approached the first jug with the potion of wisdom and drank half of it, then poured the remainder into the second jug with the potion of beauty, thoroughly mixed the contents, and drank half of it. Next, it was Harry's turn: he drank half of the third jug with the potion of strength, then poured the remainder into the second jug, thoroughly mixed everything in this jug, and drank half of it. Now all the contents were in the second jug, which fell to Ron. What percentage of the contents of this jug does he need to drink to ensure that each of the three potions will definitely affect him?
|
# Answer: 80
## Exact match of the answer -1 point
## Solution.
First, Hermione drinks $300 / 2=150$ ml of the wisdom potion, and then she pours 150 ml into the second jug, after which the second jug contains 150 ml of the wisdom potion and 300 ml of the beauty potion. When she drinks half of the contents of this jug, 75 ml of the wisdom potion and 150 ml of the beauty potion remain. Now it's Harry's turn. He drinks $300 / 2=150$ ml of the strength potion, and then he pours 150 ml into the second jug. There, it becomes 75 ml of the wisdom potion, 150 ml of the beauty potion, and 150 ml of the strength potion. When Harry drinks half of it, 37.5 ml of the wisdom potion, 75 ml of the beauty potion, and 75 ml of the strength potion remain. Now it's Ron's turn.
According to the problem, to make the potion effective, it is enough to drink at least 30 ml of it. Therefore, Ron needs to drink at least 30 ml of the wisdom potion. Since the wisdom potion is the least in quantity, if Ron drinks 30 ml of it, he will drink more than 30 ml of the other potions. This means he needs to drink a portion of the jug equal to 30 ml / 37.5 ml * $100 \% = 80 \%$.
|
80
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task No. 7.2
## Condition:
Professor Severus Snape has prepared three potions, each with a volume of 600 ml. The first potion makes the person who drinks it smart, the second makes them beautiful, and the third makes them strong. To ensure the potion works, one needs to drink at least 30 ml of it. Severus Snape was about to drink his potions when he was called to the headmaster's office and left, leaving the labeled potions in large jugs on his desk. Taking advantage of his absence, Harry, Hermione, and Ron approached the table with the potions and began to sample them.
Hermione was the first to try the potions: she approached the first jug with the potion of wisdom and drank half of it, then poured the remainder into the second jug with the potion of beauty, thoroughly mixed the contents, and drank half of it. Next, it was Harry's turn: he drank half of the third jug with the potion of strength, then poured the remainder into the second jug, thoroughly mixed everything in this jug, and drank half of it. Now all the contents were in the second jug, which was left for Ron. What percentage of the contents of this jug does Ron need to drink to ensure that each of the three potions will definitely affect him?
|
Answer: 40
Exact match of the answer -1 point
Solution by analogy with task №7.1
#
|
40
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 7.3
## Condition:
Potions teacher Severus Snape has prepared three potions, each with a volume of 400 ml. The first potion makes the person who drinks it smart, the second makes them beautiful, and the third makes them strong. To ensure the potion works, one needs to drink at least 30 ml of it. Severus Snape was about to drink his potions when he was called to the headmaster's office and left, leaving the labeled potions in large jugs on his desk. Taking advantage of his absence, Harry, Hermione, and Ron approached the table with the potions and began to sample them.
Hermione was the first to try the potions: she approached the first jug with the potion of wisdom and drank half of it, then poured the remainder into the second jug with the potion of beauty, thoroughly mixed the contents, and drank half of it. Next, it was Harry's turn: he drank half of the third jug with the potion of strength, then poured the remainder into the second jug, thoroughly mixed everything in this jug, and drank half of it. Now all the contents were in the second jug, which fell to Ron. What percentage of the contents of this jug does he need to drink to ensure that each of the three potions will definitely affect him?
|
Answer: 60
Exact match of the answer -1 point
Solution by analogy with task №7.1
#
|
60
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task No. 7.4
## Condition:
Professor Severus Snape has prepared three potions, each with a volume of 480 ml. The first potion makes the person who drinks it smart, the second makes them beautiful, and the third makes them strong. To ensure the potion works, one needs to drink at least 30 ml of it. Severus Snape was about to drink his potions when he was called to the headmaster's office and left, leaving the labeled potions in large jugs on his desk. Taking advantage of his absence, Harry, Hermione, and Ron approached the table with the potions and began to sample them.
Hermione was the first to try the potions: she approached the first jug with the potion of wisdom and drank half of it, then poured the remainder into the second jug with the potion of beauty, thoroughly mixed the contents, and drank half of it. Next, it was Harry's turn: he drank half of the third jug with the potion of strength, then poured the remainder into the second jug, thoroughly mixed everything in this jug, and drank half of it. Now all the contents were in the second jug, which was left for Ron. What percentage of the contents of this jug does Ron need to drink to ensure that each of the three potions will definitely affect him?
|
Answer: 50
Exact match of the answer -1 point
Solution by analogy with task №7.1
#
|
50
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Given a sequence $x_{n}$ such that $x_{1}=1, x_{2}=2, x_{n+2}=\left|x_{n+1}\right|-x_{n}$. Find $x_{2015}$.
|
5. Answer. ${ }^{x_{2015}}=0$.
We will show that the given sequence is periodic with a period of 9. Let's find
$x_{1}=1, x_{2}=2, x_{3}=1, x_{4}=-1, x_{5}=0, x_{6}=1, x_{7}=1, x_{8}=0, x_{9}=-1, x_{10}=1, x_{11}=2, \ldots$.
Since the sequence is completely determined by any two consecutive terms, we have obtained that 9 is the period of this sequence. This means that for any $k, r \in N$, the equality $x_{9 k+r}=x_{r}$ holds.
To find $x_{2015}$, we divide the number 2015 by 9 with a remainder: 2015=9$\cdot$223+8. Then $x_{2015}=x_{8}=0$.
## Evaluation Criteria and Organization of Work Checking
Mathematical Olympiad tasks are creative and allow for several different solutions. Additionally, partial progress in problems (for example, considering an important case, proving a lemma, finding an example, etc.) is evaluated. Thus, when calculating the final scores for a problem, the jury takes into account all these cases, as well as possible logical and arithmetic errors in the solutions.
The checking of works at the Mathematical Olympiad is carried out in two stages. In the first stage, the jury checks the works without assigning scores, using a so-called "plus-minus" system. The sign is assigned according to the table provided below. The preliminary evaluation in the "plus-minus" system may be slightly adjusted after discussing the criteria and classifying the cases.
| Correctness of Solution | |
| :---: | :--- |
| + | Complete correct solution |
| .+ | Correct solution. There are minor flaws that do not significantly affect the solution |
| $\pm$ | The solution is generally correct. However, the solution contains significant errors or cases are omitted, which do not affect the logical reasoning |
| $+/ 2$ | One of two (more complex) significant cases is correctly considered, or in a problem of the type "estimate + example," the estimate is correctly obtained |
| $\mp$ | Auxiliary statements that help in solving the problem are proven |
| .- | Important individual cases are considered in the absence of a solution |
| - | The solution is incorrect, and there is no progress |
| 0 | The solution is absent |
Sometimes the grade "++" is given to note a correct and elegant solution.
After the first stage of checking, the group of checkers for each problem, analyzing and generalizing the provided solutions, highlights various ways of solving, typical partial progress, and main errors. In accordance with the comparative analysis of different progress, a scale of evaluation criteria is developed.
In the second stage, final scores are assigned for each problem. According to the regulations for conducting school mathematical Olympiads, each problem is scored out of 7 points. The table below provides the scale for converting signs into points.
| Sign | + | .+ | $\pm$ | $+/ 2$ | $\mp$ | .- | - | 0 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| Points | 7 | $6-7$ | $5-6$ | 4 | $2-3$ | $0-1$ | 0 | 0 |
The maximum score for completing all tasks is 35.
It is important to note that any correct solution is scored 7 points. Points are not deducted for a solution being too long or for a solution that differs from the one provided in methodological developments or from other solutions known to the jury.
At the same time, any arbitrarily long text of a solution that does not contain useful progress is scored 0 points.
A traditional mistake made by students when solving proof problems is using the statement to be proven as an initial condition or the basis of the proof. For example, in a problem requiring proof that a triangle is isosceles, the proof begins with the words: "Let triangle $A B C$ be isosceles." Such "solutions" are scored 0 points due to a gross logical error.
Each work is evaluated and checked (rechecked) by at least two members of the jury.
After the preliminary results of the Olympiad work checking are published, Participants have the right to review their works, including informing about their disagreement with the assigned scores. In this case, the Chairman of the Olympiad Jury appoints a jury member to reconsider the work. The score for the work can be changed if the Participant's request for a score change is deemed justified. The score change is agreed upon with the Chairman of the Jury and entered into the final table.
A final table is created for each parallel based on the results of the Olympiad.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.3. Several different real numbers are written on the board. It is known that the sum of any three of them is rational, while the sum of any two of them is irrational. What is the largest number of numbers that can be written on the board? Justify your answer.
|
Solution: The set of three numbers $\sqrt{2}, \sqrt{3}, -\sqrt{2}-\sqrt{3}$, as is easily verified, satisfies the condition of the problem. We will show that no more than three numbers can be written on the board.
Assume the contrary, and let $a_{i} (i=\overline{1,4})$ be some four numbers from this set. Then the numbers $a_{1}+a_{2}+a_{3}$ and $a_{1}+a_{2}+a_{4}$ are rational, so the number $\left(a_{1}+a_{2}+a_{3}\right)-\left(a_{1}+a_{2}+a_{4}\right)=a_{3}-a_{4}$ is also rational. Similarly, the rationality of the number $a_{3}-a_{2}$ can be proven. Then the number $\left(a_{3}-a_{4}\right)+\left(a_{3}-a_{2}\right)-\left(a_{2}+a_{3}+a_{4}\right)=a_{3}$ is rational. The same can be shown for the rationality of all numbers $a_{i}$. But then the sum of any two of them is rational, which contradicts the condition of the problem.
Answer: Three numbers.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and justified answer | 7 points |
| There is a correct example of three numbers, but there are inaccuracies in the proof (which is basically correct) of its optimality | 5 points |
| Correct proof that 4 numbers cannot exist (in the absence of an example of 3 numbers) | 3 points |
| In a correct (in general) proof that 4 numbers cannot exist, there are inaccuracies and no example of 3 numbers | 2 points |
| An example of three numbers is given, but the proof of its optimality is missing | 1 point |
| Correct answer without justification (or with incorrect justification) | 0 points |
| Proof that there are fewer than 5 (or even more) numbers | not evaluated |
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.6. At the factory, there are exactly 217 women, among whom 17 are brunettes, and the remaining 200 are blondes. Before New Year's, all of them dyed their hair, and each of these women wrote in "VK" the surnames of exactly 200 women from the factory, whom they believed to be definitely blondes. Each of the brunettes correctly identified all the blondes, while each blonde could indicate anyone except herself. Prove that based on this data, it is possible to identify at least 13 blondes.
|
Solution: According to the problem, the correct list of all 200 blondes will be on "Vkontakte" exactly for 17 female workers at the plant: brunettes will write exactly this list, and a blonde will never write it, as otherwise she would have to include herself in it. Therefore, if a certain list appears not 17 times but any other number, it is incorrect and was written by a blonde. Remove all lists that appear exactly 17 times. There will be $217-17n$ lists left. $217-17n \geqslant 0$, so $n \leqslant 12$ (we remember that $n$ is a natural number). Then at least $217-12 \cdot 17=13$ lists remain, and we have identified at least 13 of their authors, who are blondes. Recommendations for checking:
| present in the work | points |
| :--- | :--- |
| Correct proof | 7 points |
| It is justified that the correct list of blondes appears exactly 17 times (without further progress) | 4 points |
| It is justified that the correct list of blondes appears at least 17 times (without further progress) | 2 points |
| There is only the idea of identifying blondes as the authors of incorrect lists | 1 point |
| Any ideas that do not lead to proof | not evaluated |
|
13
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.1. Denis thought of four different natural numbers. He claims that
- the product of the smallest and the largest numbers is 32;
- the product of the two remaining numbers is 14.
What is the sum of all four numbers?
|
Answer: 42.
Solution. There are two ways to represent the number 14 as the product of two numbers: $1 \cdot 14$ and $2 \cdot 7$; therefore, the second and third largest numbers are 1 and 14 or 2 and 7. The first case does not work for us, as 1 cannot be the second largest number. So, the second largest number is 2, and the third largest is 7.
Since our four numbers are distinct, the smallest (first by size) number is 1. Then the largest number is 32. From this, it is not difficult to find the sum of all the numbers.
|
42
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.4. On Monday, 5 people in the class received fives in math, on Tuesday, 8 people received fives, on Wednesday - 6 people, on Thursday - 4 people, on Friday - 9 people. No student received fives on two consecutive days. What is the minimum number of students that could have been in the class
|
Answer: 14.
Solution. Let's consider pairs of consecutive days.
- On Monday and Tuesday, 5s were received by $5+8=13$ people.
- On Tuesday and Wednesday, 5s were received by $8+6=14$ people.
- On Wednesday and Thursday, 5s were received by $6+4=10$ people.
- On Thursday and Friday, 5s were received by $4+9=13$ people.
Since no one could receive a 5 for two consecutive days, the number of students in the class is at least as large as the maximum of the obtained numbers. That is, there are at least 14 students in the class.
Let's provide an example of how fourteen students could receive 5s. We will number the children from 1 to 14.
- On Monday, 5s were received by students $10,11,12,13$ and 14.
- On Tuesday, 5s were received by students $1,2,3,4,5,6,7$ and 8.
- On Wednesday, 5s were received by students $9,10,11,12,13$ and 14.
- On Thursday, 5s were received by students $1,2,3$ and 4.
- On Friday, 5s were received by students $6,7,8,9,10,11,12,13$ and 14.
|
14
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.5. At a tribal council meeting, 60 people spoke in turn. Each of them said only one phrase. The first three speakers said the same thing: "I always tell the truth!" The next 57 speakers also said the same phrase: "Among the previous three speakers, exactly two told the truth." What is the maximum number of speakers who could have told the truth?
|
Answer: 45.
Solution. Note that among any four consecutive speakers, at least one lied (if the first three told the truth, then the fourth definitely lied). By dividing 60 people into 15 groups of four consecutive speakers, we get that at least 15 people lied, meaning no more than 45 people told the truth.
To construct an example, assume that the first three in each group of four (in the above division) tell the truth, while the fourth lies. It is easy to see that this situation meets the condition.
|
45
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.6. Points $D$ and $E$ are marked on sides $A C$ and $B C$ of triangle $A B C$ respectively. It is known that $A B=B D, \angle A B D=46^{\circ}, \angle D E C=90^{\circ}$. Find $\angle B D E$, if it is known that $2 D E=A D$.
|
Answer: $67^{\circ}$.
Solution. Draw the height $B M$ in triangle $A B D$. Since this triangle is isosceles, $M$ bisects $A D$ (Fig. 7.6). This means that $M D = A D / 2 = D E$.
Then the right triangles $B D M$ and $B D E$ are congruent by the leg ( $D M = D E$ ) and the hypotenuse ( $B D$ - common). From this, it is not difficult to find the required angle:
$$
\angle B D E = \angle B D A = \frac{180^{\circ} - \angle A B D}{2} = \frac{180^{\circ} - 46^{\circ}}{2} = 67^{\circ}
$$
Fig. 2: for the solution of problem 7.6
|
67
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.7. In the classroom, there are several single desks (no more than one person can sit at each desk; there are no other desks in the classroom). During the break, a quarter of the students went out into the corridor, and the number of people left in the classroom was equal to 4/7 of the total number of desks. How many desks are in the room if there are no more than 30?
|
Answer: 21.
Solution. Note that the number of remaining students is $\frac{3}{4}$ of the initial number, so it must be divisible by 3. Let's denote it by $3x$. Let $y$ be the number of desks. Then
$$
3 x=\frac{4}{7} y
$$
from which $21 x=4 y$. Since 4 and 21 are coprime, $y$ must be divisible by 21. From the problem's condition, we know that $y \leqslant 30$, so $y=21$.
|
21
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.8. Tanya and Vера are playing a game. Tanya has cards with numbers from 1 to 30. She arranges them in some order in a circle. For each pair of adjacent numbers, Vера calculates their difference, subtracting the smaller number from the larger one, and writes down the resulting 30 numbers in her notebook. After that, Vера gives Tanya a number of candies equal to the smallest number written in the notebook. Tanya arranges the cards so as to get as many candies as possible. What is the maximum number of candies she can get?
|
Answer: 14.
Solution. We will prove that Tanya cannot get 15 candies. Let's look at the card with the number 15. The number 15 differs from all the remaining numbers, except for the number 30, by no more than 14. Thus, at least one of the differences involving the number 15 will be no more than 14.
Let's provide an example of an arrangement where Tanya can get 14 candies. Arrange the numbers in a circle in the following order: $1,16,2,17,3,18, \ldots, 14,29,15,30$.
|
14
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Plot the graph of the function $y=(4 \sin 4 x-2 \cos 2 x+3)^{0.5}+(4 \cos 4 x+2 \cos 2 x+3)^{0.5}$.
|
Solution:
$\mathbf{y}=\sqrt{4 \sin ^{4} x-2 \cos 2 x+3}+\sqrt{4 \cos ^{4} x+2 \cos 2 x+3}$
$\mathrm{y}=\sqrt{4 \sin ^{4} x-2+4 \sin ^{2} x+3}+\sqrt{4 \cos ^{4} x+4 \cos ^{2} x-2+3}$
$\mathrm{y}=\sqrt{4 \sin ^{4} x+4 \sin ^{2} x+1}+\sqrt{4 \cos ^{4} x+4 \cos ^{2} x+1}$
$\mathrm{y}=2 \sin ^{2} x+1+2 \cos ^{2} x+1, \mathrm{y}=4$.
Answer: The graph of the function will be a straight line $y=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Find the smallest natural number $A$, which is divisible by $p$, ends in $\boldsymbol{p}$, and has the sum of its digits equal to $p$, given that $p$ is a prime number and is the cube of a natural number.
|
Solution. Let $2 \mathrm{p}+1=\mathrm{n}^{3}$. Then $(\mathrm{n}-1)\left(\mathrm{n}^{2}+n+1\right)=2 \mathrm{p}$. The number $2 \mathrm{p}$ can only have the following positive divisors: 1, 2, p, 2p. The number n is clearly odd, so n-1 is divisible by 2. The number $n^{2}+n+1$ is greater than 1, so $n-1=2, n^{2}+n+1=$ p. From this, $n=3, p=13$. The desired number A can be represented as $\mathrm{A}=\mathrm{B} \times 100+13$, where the number $\mathrm{B}$ is the number A without the last two digits. Since A is divisible by 13, then B is also divisible by 13. The sum of the digits of the number B is $13-(1+3)=9$, so B is divisible by 9, and since 9 and 13 are coprime, B is divisible by $9 \times 13=117$. The smallest such number is $B=117$, then $A=117 \times 100+13=11713$.
Answer: 11713.
|
11713
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The numbers from 1 to 25 (each exactly once) were placed in the cells of a $5 \times 5$ square such that the sum of the numbers in each row and each column is the same. A boy erased all the numbers except for four (see the picture). Find the number marked with a circle $\bigcirc$.
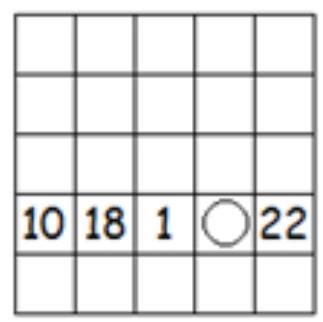
|
Solution. The sum of all numbers $1+2+3+\ldots+25=325$, so the sum of the numbers in one row is $325: 5=65$. Now let's find the unknown number $65-(10+18+1+22)=$ $65-51=14$. Answer: 14.
|
14
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In grandmother's garden, apples have ripened: Antonovka, Grushovka, and White Naliv. If there were three times as many Antonovka apples, the total number of apples would increase by $70 \%$. If there were three times as many Grushovka apples, it would increase by $50 \%$. By what percentage would the total number of apples change if there were three times as many White Naliv apples?
|
Solution. First method. If the quantity of each type of apple were three times as much, the total number of apples would increase by $200 \%$. Of this increase, $70 \%$ is due to Antonovka, and $50 \%$ is due to Grushovka. Therefore, the increase due to White Naliv would be $200 \%-70 \%-50 \%=80 \%$.
Second method. Since adding twice the amount of Antonovka results in a $70 \%$ increase, Antonovka makes up 0.35 of all apples. Similarly, Grushovka makes up 0.25 of all apples. Therefore, the share of White Naliv is 0.4. If you add 0.4 twice to a number, the number will increase by $80 \%$. Answer: $\mathbf{8 0 \%}$.
Comment: The reasoning is correct, but a computational error has been made - 5 points. Only the correct answer is provided or it is obtained by considering a specific example - 1 point.
|
80
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Three mryak are more expensive than five bryak by 10 rubles. And six mryak are more expensive than eight bryak by 31 rubles. By how many rubles are seven mryak more expensive than nine bryak
|
3. Answer: by 38 rubles. Solution. By adding 3 bryaks and myraks, we increase the price difference between myraks and bryaks by 21 rubles. This means that one myrak is 7 rubles more expensive than one bryak. Then seven myraks are more expensive than nine bryaks by $31+7=38$ rubles. Criteria: correct solution - 7 points. The reasoning is correct, but an arithmetic error is made - 5 points. It is established that a myrak is 7 rubles more expensive than a bryak, but the solution is not completed - 2 points.
|
38
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Two very small fleas are jumping on a large sheet of paper. The first jump of the fleas is along a straight line towards each other (their jumps may have different lengths). The first flea first jumps to the right, then up, then to the left, then down, then to the right again, and so on. Each jump is 1 cm longer than the previous one. The second flea first jumps to the left, then up, then to the right, then down, then to the left again, and so on. Each subsequent jump is also 1 cm longer than the previous one. After 100 jumps, the fleas are 3 meters apart. How far apart were the fleas initially?
|
4. Answer: 2 meters. Solution: Let's observe the first four jumps of the first flea: 2 cm more to the left than to the right, and 2 cm more down than up. That is, after four jumps, the first flea moves 2 cm to the left and 2 cm down. Therefore, after 100 jumps, it will move 50 cm to the left and 50 cm down. Similarly, the second flea will move 50 cm to the right and 50 cm down after 100 jumps. Since both fleas have moved down the same amount, the distance between them has increased by $50 \mathrm{~cm} + 50 \mathrm{~cm} = 100 \mathrm{~cm} = 1$ m. Therefore, the initial distance between them was 2 m. Criteria: correct solution - 7 points. Correct reasoning but with an arithmetic error - 5 points. Correct conclusion about the change in position of the flea after a series of four jumps, but no further progress - 2 points. In all other cases, 0 points.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. The first term of the sequence is 934. Each subsequent term is equal to the sum of the digits of the previous term, multiplied by 13. Find the 2013-th term of the sequence.
|
Answer: 130
Solution. Let's calculate the first few terms of the sequence. We get: $a_{1}=934 ; a_{2}=16 \times 13=208$; $a_{3}=10 \times 13=130 ; a_{4}=4 \times 13=52 ; a_{5}=7 \times 13=91 ; a_{6}=10 \times 13=130=a_{3}$. Since each subsequent number is calculated using only the previous number, the terms of the sequence will repeat with a period of 3. The number 2013 is divisible by three, so $a_{2013}=a_{3}=130$.
## Grading Criteria:
+ the correct answer and a fully justified solution are provided
$\pm$ the correct answer and generally correct reasoning are provided, with minor gaps or inaccuracies
干 the correct line of reasoning is provided, but a computational error is made
- only the answer is provided
|
130
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.3. Point $F$ is the midpoint of side $B C$ of square $A B C D$. A perpendicular $A E$ is drawn to segment $D F$. Find the angle $C E F$.
---
Translation provided as requested, maintaining the original format and line breaks.
|
Answer: $45^{\circ}$.
Solution. Let the line $A E$ intersect the side $C D$ of the square at point $M$ (see Fig. 10.3). Then triangles $A D M$ and $D C F$ are equal (by the leg and acute angle). Therefore, point $M$ is the midpoint of side $C D$. Then triangle $C F M$ is a right and isosceles triangle, so $\angle C M F=45^{\circ}$.
Since $\angle M E F=\angle M C F=90^{\circ}$, a circle can be circumscribed around quadrilateral $M C F E$. The inscribed angles $C E F$ and $C M F$ subtend the same arc of this circle, hence $\angle C E F=\angle C M F=45^{\circ}$.
There are also "computational" methods of solving, for example, using coordinates or vectors.
Evaluation criteria:
Fig. 10.3
+ a complete and justified solution is provided
- only the answer is provided
|
45
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.4. Find the maximum value of the expression $a+b+c+d-ab-bc-cd-da$, if each of the numbers $a, b, c$ and $d$ belongs to the interval $[0 ; 1]$.
|
Answer: 2.
Solution. The first method. The value 2 is achieved, for example, if $a=c=1, b=d=0$. We will prove that with the given values of the variables $a+b+c+d-ab-bc-cd-da \leqslant 2$.
Notice that $a+b+c+d-ab-bc-cd-da=(a+c)+(b+d)-(a+c)(b+d)$. Let $a+c=x, b+d=y$, then we need to prove that $x+y-xy \leqslant 2$, if $0 \leqslant x \leqslant 2$ and $0 \leqslant y \leqslant 2$.
Indeed, $x+y-xy=(x+y-xy-1)+1=(x-1)(1-y)+1$, where $-1 \leqslant x-1 \leqslant 1$ and $-1 \leqslant 1-y \leqslant 1$. Therefore, $(x-1)(1-y) \leqslant 1$, so $x+y-xy \leqslant 2$.
By introducing new variables, we can reason differently. Fix the variable $y$ and consider the function $f(x) = (1-y)x + y$, where $x \in [0; 2]$. Since it is linear, its maximum value is achieved at one of the endpoints of the interval $[0; 2]$. But $f(0) = y \leqslant 2$ and $f(2) = 2 - y \leqslant 2$, so for all $x \in [0; 2]$ the inequality $f(x) \leqslant 2$ holds.
The second method. The same idea of linearity can be used initially. The given expression can be considered a linear function of one of the variables if the other three variables are fixed.
For example, fix the values of the variables $b, c$, and $d$ and consider the function $f(a) = (1-b-d)a + b + c + d - bc - cd$, where $a \in [0; 1]$. Due to monotonicity, its maximum value is achieved at one of the endpoints of the interval $[0; 1]$. The same situation will arise for similarly defined linear functions of the variables $b$, $c$, and $d$.
Therefore, the maximum value of the original expression can only be achieved when the variables $a, b, c$, and $d$ take one of two values: 0 or 1. Considering the symmetry of the given expression, it is sufficient to check the following cases:
1) if $a=b=c=d=0$ or $a=b=c=d=1$, the value of the expression is 0;
2) if $a=b=c=0, d=1$ or $a=b=c=1, d=0$, the value of the expression is 1;
3) if $a=b=0, c=d=1$ or $a=b=1, c=d=0$, the value of the expression is 1;
4) if $a=c=0, b=d=1$ or $a=c=1, b=d=0$, the value of the expression is 2.
Thus, the maximum value of the given expression is 2.
## Grading Criteria:
+ The correct answer and a fully justified solution are provided
$\pm$ The correct answer and generally correct reasoning are provided, but there are minor gaps or inaccuracies (e.g., the estimate is proven, but an example is missing)
干 The correct line of reasoning is provided, but a computational error is made
$\mp$ The idea of linearity is present, but it is not fully developed
干 The correct answer is provided, and the values of the variables at which it can be achieved are indicated, but the estimate is not conducted
- Only the answer is provided
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.5. On side $AB$ of triangle $ABC$, point $K$ is marked, and on side $AC$, point $M$ is marked. Segments $BM$ and $CK$ intersect at point $P$. It turns out that angles $APB$, $BPC$, and $CPA$ are each $120^{\circ}$, and the area of quadrilateral $AKPM$ is equal to the area of triangle $BPC$. Find angle $BAC$.
|
Answer: $60^{\circ}$.
Solution. To both sides of the equality $S_{A K P M}=S_{B P C}$, add the area of triangle $B P K$ (see Fig. 10.5). We get that $S_{A B M}=S_{B C K}$. Therefore, $\frac{1}{2} B C \cdot B K \sin \angle B = \frac{1}{2} A B \cdot A M \sin \angle A$. Then $\frac{B K}{A M} = \frac{A B \sin \angle A}{B C \sin \angle B}$. From the Law of Sines: $\frac{\sin \angle A}{\sin \angle B} = \frac{B C}{A C}$, so $\frac{B K}{A M} = \frac{A B}{A C} \Leftrightarrow \frac{B K}{A B} = \frac{A M}{A C}$. Thus, points $K$ and $M$ divide segments $B A$ and $A C$ in the same ratio, counting from vertices $B$ and $A$ respectively, that is, $\frac{B K}{K A} = \frac{A M}{M C}$ (*).
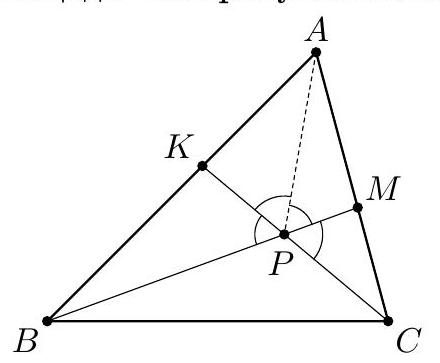
Fig. 10.5
Notice now that $\angle B P K = \angle K P A = \angle A P M = \angle M P C = 60^{\circ}$ (angles adjacent to the given angles of $120^{\circ}$). Therefore, $P K$ and $P M$ are the angle bisectors of triangles $A P B$ and $A P C$ respectively. By the property of the angle bisector of a triangle, we get: $\frac{B K}{K A} = \frac{B P}{P A}$ and $\frac{A M}{M C} = \frac{A P}{P C}$. Then, taking into account the equality (*), we get that $\frac{B P}{P A} = \frac{A P}{P C}$.
Moreover, $\angle B P A = \angle A P C = 120^{\circ}$. Thus, triangles $B P A$ and $A P C$ are similar (by two sides and the angle between them). Therefore, $\angle P A C = \angle P B A$. Hence, $\angle B A C = \angle B A P + \angle P A C = \angle B A P + \angle P B A = 180^{\circ} - 120^{\circ} = 60^{\circ}$.
## Grading Criteria:
## + a complete and justified solution 干 only that points K and M divide the sides in the same ratio - only the answer is provided
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. There was a whole number of cheese heads on the kitchen. At night, rats came and ate 10 heads, and everyone ate equally. Several rats got stomachaches from overeating. The remaining seven rats the next night finished off the remaining cheese, but each rat could eat only half as much cheese as the night before. How much cheese was there in the kitchen initially?
|
Solution. Let there be $k$ rats in total $(k>7)$, then each rat ate $\frac{10}{k}$ pieces of cheese on the first night. On the second night, each rat ate half as much, that is, $\frac{5}{k}$ pieces. Then seven rats ate $\frac{35}{k}$ pieces. This is an integer. The only divisor of the number 35 that exceeds 7 is the number 35 itself. Therefore, $\frac{35}{k}=1$, and there were $10+1=$ 11 pieces of cheese in the warehouse before the rat invasion. Answer: 11.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In an equilateral triangle, 3 points were marked on each side so that they divide the side into 4 equal segments. These points and the vertices of the triangle were painted. How many isosceles triangles exist with vertices at the painted points?
|
# Answer. 20
Solution. Let the vertices of the triangle be denoted as A, B, C. Suppose points M, N (M closer to A) are taken on side AB, points P, Q (P closer to A) on side AC, and points K, L (K closer to B) on side BC. Then the following cases are possible for isosceles triangles with the vertex at point A: ABC, AKL, APM, AQN. For the vertex at point B: BNK, BPQ, BML. For the vertex at point C: CQL, CPK, CMN. Another 8 cases arise without using the vertices of the original triangle: MQK, PLM, and 6 triangles, two sides of which are equal to $1 / 3$ of the side of the original triangle: MNK, etc. In total, there are 20 cases.
Criteria. All cases found - 7 points. Number of cases of one type found - 1 point, two types - 3 points.
|
20
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1 From a three-digit number $A$, which does not contain zeros in its notation, a two-digit number $B$ was obtained by writing the sum of the first two digits instead of them (for example, the number 243 turns into 63). Find $A$ if it is known that $A=3 B$.
|
Answer: 135.
Solution: The last digit of the numbers $B$ and $A=3B$ is the same, so this digit is 5. Moreover, $A$ is divisible by 3, which means $B$ is also divisible by 3 (the sums of the digits are the same). Therefore, $B$ is one of the numbers $15, 45, 75$. By checking, we find that the number $B=45$ satisfies the condition.
Comment: A correct answer without justification - 2 points.
|
135
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. On a line, there are blue and red points, with no fewer than 5 red points. It is known that on any segment with endpoints at red points, containing a red point inside, there are at least 4 blue points. And on any segment with endpoints at blue points, containing 3 blue points inside, there are at least 2 red points. What is the maximum number of blue points that can be on a segment with endpoints at red points, not containing other red points?
|
Answer: 4.
Solution: Note that on a segment with endpoints at red points, not containing other red points, there cannot be 5 blue points. Indeed, in this case, between the outermost blue points, there would be 3 blue points, which means there would be at least 2 more red points. Therefore, on such a segment, there are no more than 4 blue points.
We will show that 4 blue points can lie on a segment with endpoints at red points, not containing other red points. Suppose the points are arranged on a line in the following order: 2 red - 4 blue - 2 red - 4 blue - 2 red. Then all conditions are satisfied, and there is a segment with 4 blue points.
Comment: It is proven that there are no more than 4 blue points between neighboring red points - 4 points.
A correct example with 4 blue points is provided - 3 points.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. In the castle, there are 9 identical square rooms, forming a $3 \times 3$ square. Nine people, consisting of liars and knights (liars always lie, knights always tell the truth), each occupied one of these rooms. Each of these 9 people said: "At least one of the neighboring rooms to mine is occupied by a liar." What is the maximum number of knights that could be among these 9 people? Rooms are considered neighboring if they share a common wall.
|
Answer: 6 knights.
Solution: Note that each knight must have at least one neighbor who is a liar. We will show that there must be at least 3 liars (thus showing that there are no more than 6 knights). Suppose there are no more than 2 liars, then there will be a "vertical row" of rooms where only knights live. But then each of these knights must have a neighbor who is a liar (and these neighbors are different). Therefore, there must be at least 3 liars.
The diagram below shows how 6 knights and 3 liars could be accommodated.
| $\mathrm{P}$ | L | $\mathrm{P}$ |
| :--- | :--- | :--- |
| $\mathrm{P}$ | $\mathrm{P}$ | L |
| L | $\mathrm{P}$ | $\mathrm{P}$ |
Comment: A correct answer without justification - 0 points.
Example of accommodating 3 liars and 6 knights - 2 points.
Proven that there are no more than 6 knights - 5 points.
Note 1: In the example, the liars should not be neighbors.
Note 2: There are other examples.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.1. The lines containing the bisectors of the exterior angles of a triangle with angles of 42 and 59 degrees intersected pairwise and formed a new triangle. Find the degree measure of its largest angle.
|
Answer: 69
Solution. Let the vertices of the given triangle be $A, B, C$, and its angles be $\alpha, \beta$, and $\gamma$, respectively. Additionally, let $A_{1}, B_{1}$, and $C_{1}$ be the points of intersection of the external angle bisectors of angles $B$ and $C$, $A$ and $C$, and $A$ and $B$, respectively. Then, $\angle B_{1} A C = \angle C_{1} A B = \left(180^{\circ} - \alpha\right) / 2 = 90^{\circ} - \alpha / 2$. Similarly, $\angle B_{1} C A = 90^{\circ} - \gamma / 2$. From the sum of the angles in triangle $B_{1} A C$, we find $\angle A B_{1} C = 180^{\circ} - \left(90^{\circ} - \alpha / 2\right) - \left(90^{\circ} - \gamma / 2\right) = \alpha / 2 + \gamma / 2$. Therefore, the angles of triangle $A_{1} B_{1} C_{1}$ are the half-sums of the angles of triangle $A B C$. Clearly, to obtain the largest angle of triangle $A_{1} B_{1} C_{1}$, we need to take the half-sum of the two largest angles of triangle $A B C$. The angles of $A B C$ are $42^{\circ}, 59^{\circ}$, and $79^{\circ}$, so the largest half-sum is $69^{\circ}$.
|
69
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.1. For what largest $k$ can we assert that in any coloring of $k$ cells in black in a white $7 \times 7$ square, there will necessarily remain a completely white $3 \times 3$ square with sides along the grid lines?
|
Answer: 3
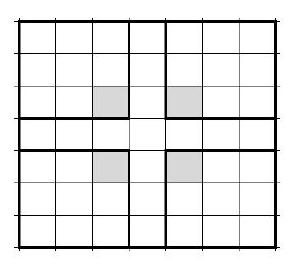
Solution. Let's highlight four $3 \times 3$ squares that are adjacent to the corners of the $7 \times 7$ square. These squares do not overlap, so if no more than three cells are shaded, at least one of these $3 \times 3$ squares will remain entirely white. If, however, we shade 4 cells, marked in gray on the diagram, then no white $3 \times 3$ square will remain.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.1. A pedestrian left point $A$ for point $B$. At the same time, a cyclist left point $B$ for point $A$. After one hour, the pedestrian was three times farther from the cyclist than from point $A$. Another 30 minutes later, they met, after which both continued their journey. How many hours did it take the pedestrian to travel from $A$ to $B$?
|
Answer: 9
Solution. Let the distance from $A$ to $B$ be 1 km, the pedestrian moves at a speed of $x$ km/h, and the cyclist at $y$ km/h. Then in one hour, the pedestrian has walked $x$ km, the cyclist has traveled $y$ km, and the distance between them is $1-x-y$, which should be three times $x$. Therefore, $3 x=1-x-y, y=1-4 x$. In the next half hour, they will together cover $1-x-y$ km. Since their closing speed is $x+y$, we get the equation $\frac{1}{2}(x+y)=1-x-y$, from which $x+y=\frac{2}{3}$. Substituting $y=1-4 x$ into the last equation: $1-3 x=\frac{2}{3}, x=\frac{1}{9}$. Therefore, it will take the pedestrian 9 hours to travel the distance from $A$ to $B$.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1. Petya wrote a natural number $A$ on the board. If it is multiplied by 8, the result is the square of a natural number. How many three-digit numbers $B$ exist such that $A \cdot B$ is also a square of a natural number?
|
# Answer: 15
Solution. If $8 A$ is the square of a natural number, then any prime number greater than 2 must appear in $A$ with an even exponent, and the number 2 must appear with an odd exponent. Therefore, in $B$, any prime number greater than 2 must also appear with an even exponent, and the number 2 must appear with an odd exponent, meaning $B$ must be of the form $2 x^{2}$. Consequently, we need to find the number of such $x$ for which $2 x^{2}$ is a three-digit number. In other words, $1000 > 2 x^{2} \geqslant 100, 500 > x^{2} \geqslant 50$. Suitable values for $x$ range from 8 to 22, and there are $22-7=15$ such values.
|
15
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. How many six-digit numbers exist that consist only of the digits 1 and 2, given that each of them appears?
|
Answer: 62
Solution. There are a total of $64=2^{6}$ six-digit numbers consisting of the digits 1 and 2, since there are 6 positions and for each position, there are two options to place a digit. However, two numbers - the one consisting only of ones and the one consisting only of twos - do not satisfy the condition, so 62 numbers remain.
|
62
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. Coins come in denominations of 50 kopecks, 1 ruble, 2 rubles, 5 rubles, 10 rubles. $V$ has several coins in his wallet. It is known that no matter which 20 coins are taken out of the wallet, there will be at least one 1-ruble coin, at least one 2-ruble coin, and at least one 5-ruble coin. What is the maximum number of coins in the wallet for this to be possible?
|
Answer: 28
Solution. Example: 9 coins of 1 ruble, 9 coins of 2 rubles, 9 coins of 5 rubles, and 1 coin of 10 rubles. Note that the wallet contains a total of $9+9+1=19$ coins that are not 1 ruble, so among any 20 coins, there will definitely be a 1-ruble coin. Similarly, this can be verified for all other denominations.
Estimate: Suppose there are $x$ coins in the wallet. Since the number of coins not worth 1 ruble is no more than 19 (otherwise, there would be 20 coins without a 1-ruble coin), the number of 1-ruble coins must be at least $x-19$. Similarly for 2-ruble and 5-ruble coins. Therefore, the total number of coins is at least $3(x-19)$. We get the inequality $x \geqslant 3 x-57$, from which $57 \geqslant 2 x, 28.5 \geqslant x$. Since $x$ is an integer, it does not exceed 28.
|
28
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. The real number a is such that $2a - 1/a = 3$. What is the value of $16a^4 + 1/a^4$?
|
Answer: 161
Solution. Squaring the equality from the condition, we get $4 a^{2}-4+1 / a^{2}=9$, that is, $4 a^{2}+1 / a^{2}=13$. Squaring again, we obtain $16 a^{4}+8+1 / a^{4}=169$. Therefore, $16 a^{4}+1 / a^{4}=161$.
|
161
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8-1. Kolya made a figure from four identical blocks as shown in the picture. What is the surface area of this figure? Express your answer in square centimeters.
|
Answer: 64.
Solution. The surface area of one block is 18 cm². Out of this area, 2 cm² is "lost" at the joints with other blocks, leaving a total area of $18-2=16$ cm². Since there are 4 blocks, the answer is $4 \cdot 16=64$ cm².
|
64
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8-2. On a distant planet in the mangrove forests, there lives a population of frogs. The number of frogs born each year is one more than the difference between the number of frogs born in the previous two years (the larger number minus the smaller number).
For example, if 5 frogs were born last year and 2 in the year before, then 4 frogs will be born this year; if 3 frogs were born last year and 10 in the year before, then 8 frogs will be born this year.
In 2020, 2 frogs were born, and in 2021, 9. In which nearest year will only 1 frog be born for the first time?
|
Answer: 2033.
Solution: This is a fairly simple problem where the only thing you need to do is correctly understand the condition and apply it the necessary number of times. The ability to correctly understand the condition is an important skill in solving problems!
By applying the algorithm described in the condition, we get that the number of frogs born on the planet is $2 \rightarrow 9 \rightarrow 8 \rightarrow 2 \rightarrow 7 \rightarrow 6 \rightarrow 2 \rightarrow 5 \rightarrow 4 \rightarrow 2 \rightarrow 3 \rightarrow 2 \rightarrow 2 \rightarrow 1$, which means that 12 more years need to pass starting from 2021, hence the answer is 2033.
|
2033
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8-3. Olya bought three gifts and packed them in three rectangular boxes: blue, red, and green. She tried to place these gifts in different ways: one on the table, and two on top of each other on the floor. Some distances are given in the diagram. Find the height of the table $h$. Express your answer in centimeters.
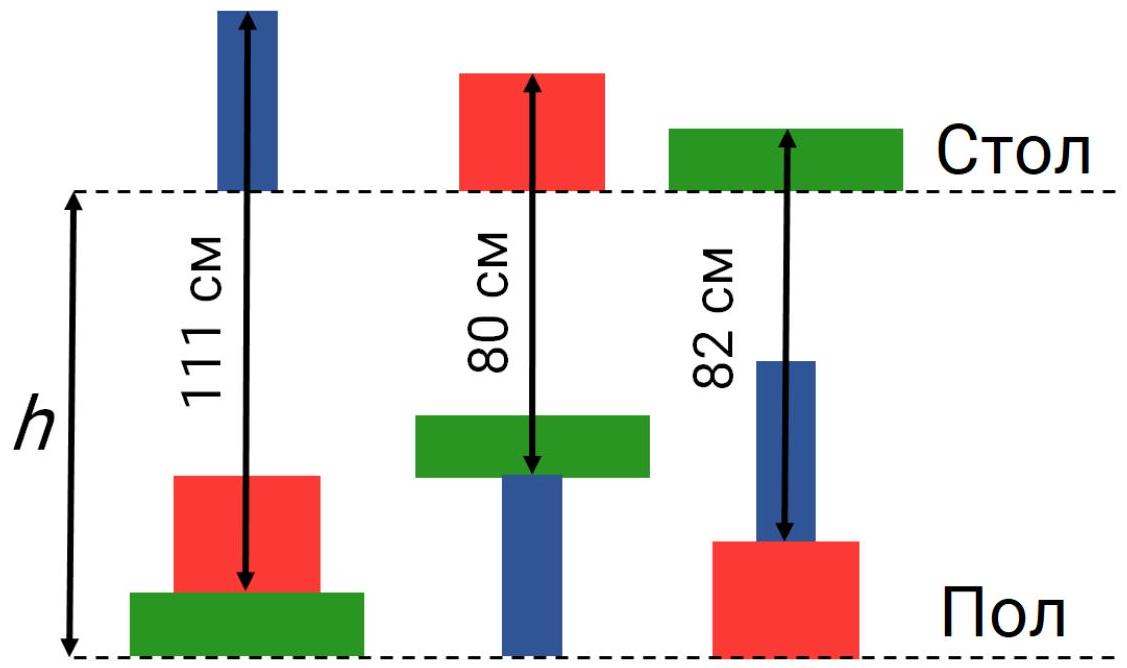
|
Answer: 91.
Solution: Let the height of the blue rectangle be $b$, the height of the red rectangle be $r$, and the height of the green rectangle be $g$. Then, according to the condition, $h+b-g=111, h+r-b=80, h+g-r=82$. Adding all these equations, we get $3h=273$, from which $h=91$.
|
91
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8-4. There are 50 parking spaces on a car park, numbered from 1 to 50. Currently, all parking spaces are empty. Two cars, a black one and a pink one, have arrived at the parking lot. How many ways are there to park these cars such that there is at least one empty parking space between them?
If the black and pink cars switch places, this is considered a new way.
|
Answer: 2352.
Solution I. Carefully consider the cases of the placement of the black car. If it parks in spot number 1 or 50, the pink car can park in any of the 48 spots (numbered from 3 to 50 or from 1 to 48, respectively). If the black car parks in a spot numbered from 2 to 49, the pink car has only 47 options (all except the spot of the black car and the two adjacent spots). In total, there are $2 \cdot 48 + 48 \cdot 47 = 2352$ options.
Solution II. Count the number of options as a difference: from the total number of possible ways to arrange the two cars, subtract the "extra" - the number of ways in which they are adjacent.
In total, we have 50 $\cdot$ 49 options: for each of the 50 ways to choose a spot for the black car, there are 49 ways to choose a spot for the pink car. The number of options where the cars are adjacent is $49 \cdot 2$: for each of the 49 ways to choose two adjacent parking spots, there are 2 ways to park the cars.
Thus, the answer is $50 \cdot 49 - 49 \cdot 2 = 2352$.
|
2352
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8-6. In a kindergarten, 150 children are standing in a circle. Each child is looking at the teacher standing in the center of the circle. Some children are wearing blue jackets, and the rest are wearing red ones. There are 12 children in blue jackets whose left neighbor is in a red jacket. How many children have a left neighbor wearing a jacket of the same color?
|
Answer: 126.
Solution I. Let each of the children say whether the color of their jacket is the same as that of the child to their left. We need to find out how many children will say "The same."
Let's find out how many children said "Different." Note that if we go around the circle, the jacket colors of such children alternate. Indeed, if someone has a red jacket and their left neighbor has a blue one, then further on, there are several (possibly one) children in blue jackets until someone says that their left neighbor has a red jacket. Similarly, if someone has a blue jacket and their left neighbor has a red one. Therefore, among the children who said "Different," there are an equal number of children in red and blue jackets. According to the problem, there are 12 children in red jackets. Thus, the total number of children who said "Different" is twice as many, i.e., 24. Therefore, the answer is $150 - 2 \cdot 12 = 126$.
Solution II. We know that 12 children in blue jackets have a neighbor to their left dressed in a red jacket. This means that in the circle, there are 12 pairs of adjacent children, where the right one is in a red jacket and the left one is in a blue jacket. We will denote such pairs as BK. What do we need to find? We need to find the number of pairs of adjacent children whose jackets are of the same color, i.e., pairs RR and BB.
The main observation for this solution is as follows: the total number of pairs BK and BB equals simply the number of children in blue jackets, since each of them has some neighbor to their right. If this neighbor is in a red jacket, we count them in pairs BK, and if they are in a blue jacket, we count them in pairs BB. So, let the total number of children in blue jackets be $s$. There are 12 pairs BK, so there are $s - 12$ pairs BB.
Similarly, the total number of pairs BK and RR equals the number of children in red jackets. The number of children in red jackets is $150 - s$, and there are 12 pairs BK, so there are $138 - s$ pairs RR. Therefore, the total number of pairs BB and RR is $(s - 12) + (138 - s) = 126$.
|
126
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8-8. The numbers $a, b$, and $c$ (not necessarily integers) are such that
$$
a+b+c=0 \quad \text { and } \quad \frac{a}{b}+\frac{b}{c}+\frac{c}{a}=100
$$
What is $\frac{b}{a}+\frac{c}{b}+\frac{a}{c}$ ?
|
Answer: -103.
Solution. We have
$$
100=\frac{a}{b}+\frac{b}{c}+\frac{c}{a}=\frac{-b-c}{b}+\frac{-a-c}{c}+\frac{-a-b}{a}=-3-\left(\frac{c}{b}+\frac{a}{c}+\frac{b}{a}\right)
$$
from which $\frac{b}{a}+\frac{c}{b}+\frac{a}{c}=-103$.
## Variants of tasks
|
-103
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.4. We will call a natural number interesting if it is the product of exactly two (distinct or equal) prime numbers. What is the greatest number of consecutive numbers, all of which are interesting
|
Solution. One of four consecutive numbers is divisible by 4. However, among the numbers divisible by 4, only the number 4 itself is interesting. But the numbers 3 and 5 are not interesting, so four consecutive interesting numbers do not exist. An example of three consecutive interesting numbers: $33,34,35$. Answer: three.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Given a rectangular grid of size 1 x 60. In how many ways can it be cut into grid rectangles of size 1 x 3 and 1 x 4?
|
3. Answer: 45665.
Solution. Let $x$ be the number of rectangles of size 1 x $3, y$ be the number of rectangles of size $1 \times 4$. Then $3 x+4 y=60$, where $x, y$ are non-negative integers. The value $\mathrm{x}=\frac{60-4 \mathrm{y}}{3}=20-\frac{4 \mathrm{y}}{3}$ is an integer if $\mathrm{y}=3 \mathrm{t}(\mathrm{t} \in \mathrm{Z})$, hence $\mathrm{x}=20 \cdot 4 \mathrm{t} \cdot(0 \leq t \leq 5)$. In the end, we get 6 solutions to the equation $3 x+4 y=60$:
$(20 ; 0),(16 ; 3),(12 ; 6),(8 ; 9),(4 ; 12),(0 ; 15)$. The number of ways to cut the given rectangle into $x$ rectangles of size 1 x 3 and $y$ rectangles of size 1 x 4 is $\mathrm{C}^{0}_{20}+\mathrm{C}^{3}_{19}+\mathrm{C}^{6}_{18}+\mathrm{C}^{9}_{17}+\mathrm{C}^{12}_{16}+\mathrm{C}^{15}_{15}=1+969+18564+24310+1820+1=45665$ ways.
|
45665
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On the board, there are 2010 non-zero numbers $\mathrm{a}_{1}$, $\mathrm{a}_{2}, \ldots \mathrm{a}_{2010}$ and the products of all pairs of adjacent numbers: $\mathrm{a}_{1} \cdot \mathrm{a}_{2}, \mathrm{a}_{2} \cdot \mathrm{a}_{3}, \ldots \mathrm{a}_{2009} \cdot \mathrm{a}_{2010}$. What is the maximum number of negative numbers that can be among the 4019 numbers?
|
4. Answer: 3014.
Solution. Consider the triples of numbers ( $\left.\mathrm{a}_{1}, \mathrm{a}_{2}, \mathrm{a}_{1} \cdot \mathrm{a}_{2}\right)$ ), ( $\left.\mathrm{a}_{3}, \mathrm{a}_{4}, \mathrm{a}_{3} \cdot \mathrm{a}_{4}\right), \ldots,\left(\mathrm{a}_{2009}, \mathrm{a}_{2010}, \mathrm{a}_{2009} \cdot \mathrm{a}_{2010}\right)$ ).
The product of the numbers in each triple is positive (as the product of squares of two non-zero numbers). Therefore, among the numbers in each triple, there is at least one positive number (the product of three negative numbers is negative). The specified triples of numbers do not overlap, so among the numbers written on the board, there are at least 1005 positive numbers. We will show that it is possible to choose such 2010 initial numbers that there will be 1005 positive numbers on the board. For this, we will make all the numbers with odd indices (a total of 1005) positive, and those with even indices negative. Then each product will be negative (as the product of two numbers with different signs), and the positive numbers will be only the 1005 initial numbers with odd indices. Therefore, the maximum number of negative numbers on the board will be 4019 $-1005=3014$.
|
3014
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.2. Several married couples came to the New Year's Eve party, each of whom had from 1 to 10 children. Santa Claus chose one child, one mother, and one father from three different families and took them for a ride in his sleigh. It turned out that he had exactly 3630 ways to choose the required trio of people. How many children could there be in total at this party?
(S. Volchonkov)
|
Answer: 33.
Solution: Let there be $p$ married couples and $d$ children at the party (from the condition, $d \leqslant 10 p$). Then each child was part of $(p-1)(p-2)$ trios: a mother could be chosen from one of the $p-1$ married couples, and with a fixed choice of mother, a father could be chosen from one of the $p-2$ remaining couples. Therefore, the total number of trios is $d \cdot(p-1)(p-2)=3630$. Since $d \leqslant 10 p$, we get $3630 \leqslant 10 p^{3}$, that is, $p^{3} \geqslant 363>7^{3}$. Thus, $p \geqslant 8$.
Next, the number $3630=2 \cdot 3 \cdot 5 \cdot 11^{2}$ has two divisors $p-1$ and $p-2$, differing by 1. If one of these divisors is divisible by 11, then the other gives a remainder of 1 or 10 when divided by 11. Then it is coprime with 11, and thus divides $2 \cdot 3 \cdot 5=30$ and is at least 10. It is easy to see that this divisor can only be 10; then $p-2=10, p-1=11$ and $d=3630 / 110=33$.
If, however, neither of the numbers $p-2$ and $p-1$ is divisible by 11, then the number $2 \cdot 3 \cdot 5=30$ is divisible by their product; this contradicts the fact that $p \geqslant 8$.
Comment: The equality $d(p-1)(p-2)=3630$ was justified - 4 points.
|
33
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. The part of the graph of a linear function located in the second coordinate quadrant, together with the coordinate axes, forms a triangle. By what factor will its area change if the slope of the function is doubled and the y-intercept is halved?
|
Answer: It will decrease by eight times.
Solution. Let the original linear function be defined by the equation $y=k x+b$. From the condition of the problem, it follows that $k>0$ and $b>0$ (see Fig. 8.2). The points of intersection of its graph with the axes are: $A(0 ; b)$ and $B\left(-\frac{b}{k} ; 0\right)$. Since the triangle $A O B$ cut off by it is a right triangle, its area is $\frac{1}{2} O A \cdot O B=\frac{1}{2} b \cdot \frac{b}{k}=\frac{b^{2}}{2 k}$.
After the specified change in coefficients, the function becomes $y=2 k x+0.5 b$. Its graph intersects the coordinate axes at points $\mathrm{C}\left(0 ; \frac{b}{2}\right)$ and $D\left(-\frac{b}{4 k} ; 0\right)$. The area of the right triangle COD is $\frac{1}{2} O C \cdot O D=\frac{1}{2} \cdot \frac{b}{2} \cdot \frac{b}{4 k}=$ $\frac{b^{2}}{16 k}$. Therefore, the area will decrease by $\frac{b^{2}}{2 k}: \frac{b^{2}}{16 k}=8$ times.
Grading Criteria. «+» A complete and well-reasoned solution is provided «士» A generally correct reasoning is provided, containing minor gaps or inaccuracies that did not affect the answer
«Ғ» Correct reasoning, but computational errors were made
«Ғ» Only the correct answer is provided or the answer was obtained by considering a specific example
«-» The problem is not solved or is solved incorrectly
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.3. The height $CH$, dropped from the vertex of the right angle of triangle $ABC$, bisects the bisector $BL$ of this triangle. Find the angle $BAC$.
---
The provided text has been translated from Russian to English, maintaining the original formatting and structure.
|
Answer: $30^{\circ}$.
Solution. Let $C H$ and $B L$ intersect at point $K$ (see Fig. 8.3). Then $C K$ is the median of the right triangle $B C L$, drawn to the hypotenuse, so $C K = 0.5 B L = B K$. Therefore, $\angle K C B = \angle K B C = \angle K B H$. Since the sum of these three angles is $90^{\circ}$ (from triangle $CBH$),
each of them is $30^{\circ}$. Consequently, $\angle C B A = 60^{\circ}, \angle B A C = 30^{\circ}$.
Grading Criteria.
「+」 A complete and well-reasoned solution is provided
「亡」 A generally correct reasoning is provided, containing minor gaps or inaccuracies that do not affect the answer
「Ғ」 It is proven that $CK = 0.5BL$, but further reasoning contains errors or is missing
「-」 Only the answer is provided
「-」 The problem is not solved or is solved incorrectly
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.4. On the Island of Liars and Knights, a circular arrangement is called correct if each person standing in the circle can say that among their two neighbors, there is a representative of their tribe. Once, 2019 natives formed a correct circular arrangement. A liar approached them and said: "Now we can also form a correct circular arrangement together." How many knights could there have been in the initial arrangement?
|
Answer: 1346.
Solution. We will prove that a correct arrangement in a circle is possible if and only if the number of knights is at least twice the number of liars.
Indeed, from the problem's condition, it follows that in such an arrangement, each liar has two knights as neighbors, and among the neighbors of any knight, there is at least one knight. Therefore, the correct arrangement should look like this: a group of knights, a liar, a group of knights, a liar, and so on (with at least two knights in each group). This means that in such an arrangement, the number of knights is at least twice the number of liars.
In the reverse direction: if the number of knights is at least twice the number of liars, then we can make an arrangement of the form RRKRRK..., and place any remaining knights (if they exist) between any two knights. Thus, if this condition is met, a correct arrangement is possible.
Let \( P \) be the number of knights and \( L \) be the number of liars in the correct arrangement specified in the problem, then \( P \geq 2L \). The liar who arrived told a lie, so together with him, a correct arrangement is impossible, hence \( P \leq 2L + 1 \). Therefore, \( P = 2L \) or \( P = 2L + 1 \). In the first case, in the initial arrangement, \( 2019 \cdot \frac{2}{3} = 1346 \) knights, and the second case is impossible because the number \( (2019 - 1) \cdot \frac{2}{3} \) would not be an integer.
Evaluation criteria.
«+» A complete and justified solution is provided.
«士» A generally correct reasoning is provided, containing minor gaps or inaccuracies (for example, only the necessary condition for the existence of a correct arrangement is proven or a computational error is made at the end).
«Ғ» The answer is obtained based on the assumption that the number of knights is twice the number of liars, but this is not proven.
«-» Only the answer is provided.
«-» The problem is not solved or is solved incorrectly.
|
1346
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.