problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
1. (7 points) The graphs of the functions $y=k x+b$ and $y=b x+k$ intersect. Find the abscissa of the point of intersection.
#
|
# Solution.
Method 1. The desired abscissa is the solution to the equation $k x + b = b x + k$. This equation can be reduced to $(k - b) x = k - b$. Since the given graphs intersect (do not coincide), $k \neq b$, so $x = 1$.
Method 2. Notice that $x = 1$ is a solution to the problem, because when $x = 1$, both given linear functions take the same value $y = k + b$. Since their graphs intersect, meaning these lines have exactly one common point, there are no other solutions.
Answer. $x = 1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.4. On a circle, $2 N$ points are marked ($N$ is a natural number). It is known that through any point inside the circle, no more than two chords with endpoints at the marked points pass. We will call a matching a set of $N$ chords with endpoints at the marked points such that each marked point is the endpoint of exactly one of these chords. We will call a matching even if the number of points where its chords intersect is even, and odd otherwise. Find the difference between the number of even and odd matchings.
(V. Shmarov)
|
Answer. 1.
First solution. We will prove by induction on $N$ that there is one more even matching than odd. For $N=1$, the statement is obvious: there is only one matching, and it is even. Now we will prove the statement for $2N$ points, assuming it is true for $2(N-1)$ points. Let the marked points be $A_{1}, A_{2}, \ldots, A_{2N}$ in the order of traversal of the circle clockwise.
Lemma. Suppose a chord $A_{1}A_{i}$ is involved in the matching. Then for even $i$, it intersects an even number of chords, and for odd $i$, an odd number.
Proof. Let the chord $A_{1}A_{i}$ intersect exactly $k$ chords. Consider the points $A_{2}, \ldots, A_{i-1}$; exactly $k$ of them are the endpoints of chords intersecting $A_{1}A_{i}$ (one endpoint of each chord). The remaining $i-2-k$ points are paired with points connected by chords that do not intersect $A_{1}A_{i}$. Thus, the number $i-2-k$ is even, meaning that the numbers $i$ and $k$ have the same parity. The lemma is proved.
Now we will divide all matchings into $2N-1$ groups $\Pi_{2}, \ldots, \Pi_{2N}$: the group $\Pi_{i}$ will contain those matchings in which point $A_{1}$ is connected to $A_{i}$. Now, remove the chord $A_{1}A_{i}$ from each matching in $\Pi_{i}$; we will get all possible matchings on the remaining $2N-2$ points. By the induction hypothesis, among them, there is one more even matching than odd. At the same time, if $i$ is even, then according to the lemma, the parity of the matching does not change when removed, and if $i$ is odd, it changes. Thus, in each of the $N$ sets $\Pi_{2}, \ldots, \Pi_{2N}$, there is one more even matching than odd, and in each of the $N-1$ sets $\Pi_{3}, \ldots, \Pi_{2N-1}$, there is one more odd than even. In total, there are more even matchings than odd by $N-(N-1)=1$, which is what we needed to prove.
Second solution. We will provide another proof of the induction step.
Let the marked points be $A_{1}, \ldots, A_{2N}$. Consider all matchings in which $A_{2N-1}$ and $A_{2N}$ are connected by a chord. This chord does not intersect any other. Thus, by removing it from each of the considered matchings, we will get all matchings on the points $A_{1}, \ldots, A_{2N-2}$, and the parity of each of them will be preserved. By the induction hypothesis, among our matchings, there is one more even than odd.
To complete the proof, it is sufficient to show that among all other matchings, there are equally many even and odd. Consider any of them; suppose it contains chords $A_{2N-1}A_{i}$ and $A_{2N}A_{k}$. Now, "swap" the points $A_{2N-1}$ and $A_{2N}$, that is, replace the chords with $A_{2N}A_{i}$ and $A_{2N-1}A_{k}$. In this case, if the original chord intersected with some of the others, then the new chord will also intersect with it. On the other hand, if the chords $A_{2N-1}A_{i}$ and $A_{2N}A_{k}$ did not intersect, then the new chords will intersect, and vice versa. Thus, to each remaining even matching, we have associated an odd one, and vice versa; different matchings, obviously, correspond to different ones. Therefore, there are equally many remaining even and odd matchings, which is what we needed to prove.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.6. Petya chose a natural number $a>1$ and wrote down fifteen numbers $1+a, 1+a^{2}, 1+a^{3}, \ldots, 1+a^{15}$ on the board. Then he erased several numbers so that any two remaining numbers are coprime. What is the maximum number of numbers that could remain on the board?
(O. Podlipsky)
|
# Answer. 4 numbers.
Solution. First, we will show that there cannot be more than four such numbers. Note that if $k$ is odd, then the number $1+a^{n k}=1^{k}+\left(a^{n}\right)^{k}$ is divisible by $1+a^{n}$. Next, each of the numbers $1,2, \ldots, 15$ has one of the forms $k, 2 k, 4 k, 8 k$, where $k$ is odd. Thus, each of the numbers $1+a, 1+a^{2}, 1+a^{3}, \ldots, 1+a^{15}$ is divisible by either $1+a$, or $1+a^{2}$, or $1+a^{4}$, or $1+a^{8}$. Therefore, if we take at least five numbers, then among them there will be two that are divisible by the same number greater than 1; hence, they will not be coprime. Thus, there cannot be more than four remaining numbers.
It remains to show that four numbers could remain. Indeed, if $a=2$, then we can leave the numbers $1+2=3$, $1+2^{2}=5$, $1+2^{4}=17$, and $1+2^{8}=257$. All of them are pairwise coprime.
Remark. It can be shown that for any even $a$, the numbers $1+a, 1+a^{2}, 1+a^{4}, 1+a^{8}$ will be pairwise coprime.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.3. In triangle $A B C$, the median $A M$ is perpendicular to the bisector $B D$. Find the perimeter of the triangle, given that $A B=1$, and the lengths of all sides are integers.
|
Answer: 5.
Solution. Let $O$ be the point of intersection of the median $A M$ and the bisector $B D$. Triangles $A B O$ and $M B O$ are congruent (by the common side $B O$ and the two adjacent angles). Therefore, $A B = B M = 1$ and $C M = 1$, since $A M$ is a median. Thus, $A B = 1, B C = 2$. By the triangle inequality, $A C = B C - A B = 1$, and since the length of $A C$ is given to be an integer, $A C = 2$. Therefore, the perimeter of the triangle is 5.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. Given a $5 \times 5$ square grid of cells. In one move, you can write a number in any cell, equal to the number of cells adjacent to it by side that already contain numbers. After 25 moves, each cell will contain a number. Prove that the value of the sum of all the resulting numbers does not depend on the order in which the cells are filled.
|
Solution. Consider all unit segments that are common sides for two cells. There are exactly forty such segments - 20 vertical and 20 horizontal. If a segment separates two filled cells, we will say that it is "painted." Note that when we write a number in a cell, it indicates the number of segments that were not painted before filling this cell, but are now painted. When we start summing, all 40 segments are painted, so the sum of the numbers will always be equal to 40.
|
40
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the smallest natural number $n$ such that the sum of the digits of each of the numbers $n$ and $n+1$ is divisible by 17.
|
Answer: 8899.
Solution. If $n$ does not end in 9, then the sums of the digits of the numbers $n$ and $n+1$ differ by 1 and cannot both be divisible by 17. Let $n=\overline{m 99 \ldots 9}$, where the end consists of $k$ nines, and the number $m$ has a sum of digits $s$ and does not end in 9. Then the sum of the digits of the number $n$ is $s+9k$, and the sum of the digits of the number $n+1$ is clearly $s+1$. According to the condition, these two sums are divisible by 17, in particular, the number $s+1$ is a multiple of 17 $\Longrightarrow s \geqslant 16$. The smallest number $m$ that does not end in 9 and has a sum of digits of 16 is 88.
Next, the number $s+9k=(s+1)+(9k-1)$ is divisible by 17. Since the first term is divisible by 17, the number $9k-1$ is also a multiple of 17. The smallest value of $k$ that satisfies this condition is 2, that is, $n=8899$. The sums of the digits of each of the numbers $n$ and $n+1$ are divisible by 17.
Criteria. It is proven that the sought number ends in the digit $9-1$ point. Correct answer -2 points. It is proven that the sum of the digits, different from 9, is not less than 16 - another 2 points. It is proven that there are exactly two nines - another 2 points. Full solution -7 points.
|
8899
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In the Rhind Papyrus (Ancient Egypt), among other information, there are decompositions of fractions into the sum of fractions with a numerator of 1, for example,
$\frac{2}{73}=\frac{1}{60}+\frac{1}{219}+\frac{1}{292}+\frac{1}{x}$
One of the denominators here is replaced by the letter $x$. Find this denominator.
|
# Solution:
First, find $\stackrel{1}{-.}$ from the equation:
$\frac{2}{73}=\frac{1}{60}+\frac{1}{219}+\frac{1}{292}+\frac{1}{x}$
$\frac{2}{73}-\frac{1}{219}-\frac{1}{292}-\frac{1}{60}=\frac{1}{x}$
$\frac{2}{73}-\frac{1}{73 \cdot 3}-\frac{1}{73 \cdot 4}-\frac{1}{60}=\frac{1}{x}$
$\frac{2 \cdot 3 \cdot 4-4-3}{73 \cdot 3 \cdot 4}-\frac{1}{60}=\frac{1}{x}$
$\frac{17}{73 \cdot 3 \cdot 4}-\frac{1}{5 \cdot 3 \cdot 4}=\frac{1}{x}$
$\frac{17 \cdot 5-73}{73 \cdot 3 \cdot 4 \cdot 5}=\frac{1}{x}$
$\frac{12}{73 \cdot 3 \cdot 4 \cdot 5}=\frac{1}{x}$
$\frac{1}{73 \cdot 5}=\frac{1}{x}$
$\frac{1}{365}=\frac{1}{x}$
Thus, $x=365$.
Answer: $x=365$.
|
365
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. At a certain moment, Anna measured the angle between the hour and minute hands of her clock. Exactly one hour later, she measured the angle between the hands again. The angle turned out to be the same. What could this angle be? (Consider all cases).
#
|
# Solution:
After 1 hour, the minute hand remains in its place. During this time, the hour hand has turned $30^{\circ}$. Since the angle has not changed, the minute hand must be dividing one of the
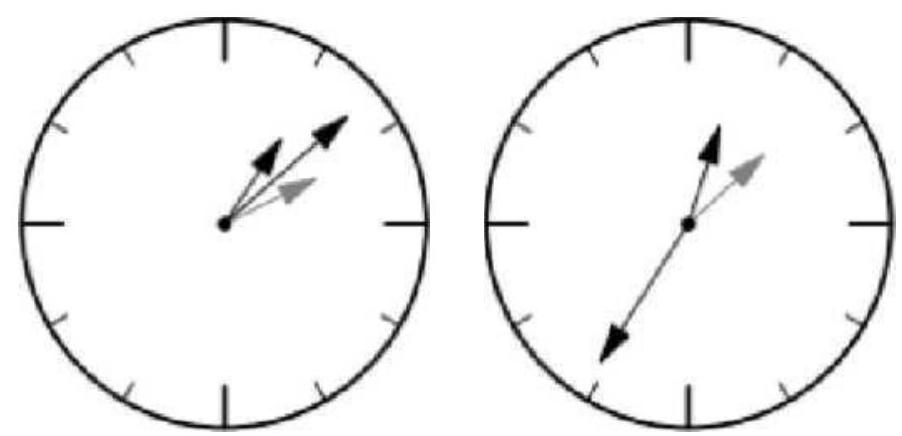
angles between the positions of the hour hand (additional angle in $\left.330^{\circ}\right)$.
This means that either the hour hand was at $15^{\circ}$ earlier, or $165^{\circ}$ later.
Answer: $15^{\circ}$ or $165^{\circ}$.
|
15
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. It is known that the quadratic trinomials $x^{2}+p x+q$ and $x^{2}+q x+p$
have different real roots. Consider all possible pairwise products of the roots of the first quadratic trinomial with the roots of the second (there are four such products in total). Prove that the sum of the reciprocals of these products does not depend on $p$ and $q$.
|
Let $x_{1}, x_{2}$ be the roots of the first quadratic polynomial and $x_{3}, x_{4}$, then we need to prove that $\frac{1}{x_{1} x_{3}}+\frac{1}{x_{1} x_{4}}+\frac{1}{x_{2} x_{3}}+\frac{1}{x_{2} x_{4}}$ does not depend on $p$ and $q$. Transform the given expression:
$\frac{1}{x_{1} x_{3}}+\frac{1}{x_{1} x_{4}}+\frac{1}{x_{2} x_{3}}+\frac{1}{x_{2} x_{4}}=\frac{1}{x_{1}}\left(\frac{1}{x_{3}}+\frac{1}{x_{4}}\right)+\frac{1}{x_{2}}\left(\frac{1}{x_{3}}+\frac{1}{x_{4}}\right)=$
$=\left(\frac{1}{x_{1}}+\frac{1}{x_{2}}\right)\left(\frac{1}{x_{3}}+\frac{1}{x_{4}}\right)=\left(\frac{x_{1}+x_{2}}{x_{1} x_{2}}\right)\left(\frac{x_{3}+x_{4}}{x_{3} x_{4}}\right)$
By Vieta's formulas, we have: $\left\{\begin{array}{c}x_{1}+x_{2}=-p \\ x_{1} x_{2}=q\end{array}\right.$ and $\left\{\begin{array}{c}x_{3}+x_{4}=-q \\ x_{3} x_{4}=p\end{array}\right.$
Then $\frac{1}{x_{1} x_{3}}+\frac{1}{x_{1} x_{4}}+\frac{1}{x_{2} x_{3}}+\frac{1}{x_{2} x_{4}}=\frac{-p(-q)}{q p}=1$.
|
1
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3. Solve the equation in integers $x^{4}-2 y^{4}-4 z^{4}-8 t^{4}=0$.
## Answer: $x=y=z=t=0$
|
Note that $x$ is even. Let $x=2x_{1}$, then we get
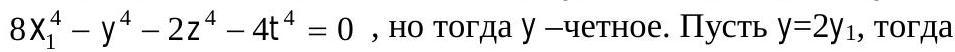
$4x_{1}^{4}-8y_{1}^{4}-z^{4}-2t^{4}=0$. Therefore, $z=2z_{1}$ and $2x_{1}^{4}-4y_{1}^{4}-8z_{1}^{4}-t^{4}=0$. Similarly, $t=2t_{1}$ and $x_{1}^{4}-2y_{1}^{4}-4z_{1}^{4}-8t_{1}^{4}=0$ we obtain the original equation, but for variables $x_{1}, y_{1}, z_{1}, t_{1}$, so we can repeat the same reasoning and so on. We get that each variable is divisible by any power of 2. Therefore, $x=y=z=t=0$.
## Recommendations for checking
1) Noted that $x$ is even - 1 point.
2) Using correct reasoning, the equation
$x_{1}^{4}-2y_{1}^{4}-4z_{1}^{4}-8t_{1}^{4}=0$, where $x=2x_{1}, y=2y_{1}, z=2z_{1}, t=2t_{1}$, but no corresponding conclusion - 4 points.
3) Only the answer is provided without proof that there are no other solutions - 0 points.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On the table lie three balls, touching each other pairwise. The radii of the balls form a geometric progression with a common ratio $q \neq 1$. The radius of the middle one is 2012. Find the ratio of the sum of the squares of the sides of the triangle formed by the points of contact of the balls with the table to the sum of the sides of the triangle formed by the centers of the balls.
Answer: 4024
|
Let the radius of the smaller of the balls be $r$, then the radii of the others are $r q=2012$ and $r^{2}$, and the points of contact of the balls with the table are denoted as $A, B, C$ respectively. Consider the section of two balls by a plane perpendicular to the table and passing through the centers of these balls (see the figure, for the two smaller balls in size). Then for the balls shown in the figure, we get that $O A=r, O_{1} B=r q$ and $0 O_{1}=r+r q$. Further, $O_{1} D=0{ }_{1} D-D C=0{ }_{1} B-O A=r(q-1)$. From $\triangle O O_{1} D$ by the Pythagorean theorem, we get that $O D=2 r \sqrt{q}=A B$. Similarly, considering the remaining pairs of balls, we get that $A C=2 r q, B C=2 r q \sqrt{q}$, then the desired value is $\frac{4 r^{2} q+4 r^{2} q^{2}+4 r^{2} q^{3}}{r(1+q)+r\left(q+q^{2}\right)+r\left(1+q^{2}\right)}=2 r q=2 \cdot 2012=4024$
Recommendations for checking: 2 points for calculating all sides of the triangle formed by the points of contact of the balls.
|
4024
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A natural number has a digit sum of 2013. The next number has a smaller digit sum and is not divisible by 4. What is the digit sum of the next natural number.
|
Answer: 2005.
Solution. The sum of the digits of the next number decreases only if it ends in nine.
It cannot end in two or more nines, as the next number would end in two zeros and be divisible by 4.
Therefore, the 9 is replaced by 0, but the tens digit increases by 1. The sum of the digits of the next number is 2013-9+1=2005.
## Grading Criteria.
Answer without justification: 0 points.
Failure to explain that there is only one nine: 4 points.
|
2005
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the number of all seven-digit natural numbers for which the digits in the decimal representation are in strictly increasing order up to the middle, and then in strictly decreasing order. For example, the number 1358620 would fit.
#
|
# Solution.
If the middle digit of a seven-digit number is 4 (it cannot be less), the number of desired numbers can be obtained by erasing one digit to the right of the " " "middle digit of the final number" in the number 12343210. There are 4 such numbers.
If the middle digit of a seven-digit number is 5, the number of desired numbers can be obtained by erasing one digit to the left of the "5" - the middle digit of the final number - and two digits to the right in the number 1234543210. There are $C_{4}^{1} C_{5}^{2}=4 \cdot 10$ such variants.
Similarly, if the middle digit of a seven-digit number is 6, the number of "suitable" ones is $C_{5}^{2} C_{6}^{3}=10 \cdot 20$.
For a middle digit of 7, there will be $C_{6}^{3} C_{7}^{4}=20 \cdot 35$ such numerical variants.
For 8 and 9, we will get, respectively, $C_{7}^{4} C_{8}^{5}=35 \cdot 56$ and $C_{8}^{5} C_{9}^{6}=56 \cdot 84$.
In total $4+4 \cdot 10+10 \cdot 20+20 \cdot 35+35 \cdot 56+56 \cdot 84=$
$$
=4 \cdot 11+20 \cdot(10+35)+56 \cdot(84+35)=7608 . \text { Answer: } 7608 .
$$
Recommendations for checking.
Guessed solution: 0 points.
|
7608
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Solve the following equation for positive $x$.
$$
x^{2014} + 2014^{2013} = x^{2013} + 2014^{2014}
$$
|
Answer: 2014.
Solution. Rewrite the equation in the following form $x^{2013}(x-1)=2014^{2013}(2014-1)$. The solution is $x=2014$. Since the function on the left, for $x>1$ this function is increasing, as the product of two positive increasing functions, the intersection with a constant function can be no more than one and one is already defined.
## Grading Criteria.
The solution is guessed: 0 points.
|
2014
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. It is known that in the pyramid $A B C D$ with vertex $D$, the sum $\angle A B D+\angle D B C=\pi$. Find the length of the segment $D L$, where $L$ is the base of the bisector $B L$ of triangle $A B C$, if it is known that
$$
A B=9, B C=6, A C=5, D B=1 .
$$
|
Answer: 7.
Solution. Let point $M$ lie on the line, outside the segment $B C$, beyond point $B$. From the condition, we have the equality of angles $\angle A B D=\angle D B M$. Then the projection of line $B D$ onto the plane $A B C$ is the bisector $B K$ of angle $A B M$. The bisectors $B K$ and $B L$ are perpendicular, as the bisectors of the internal and external angles. Also, line $B L$ is perpendicular to the height of the pyramid $D H$. Therefore, $B L \perp D B K$ and, consequently, $B L \perp D B$, and triangle $L B D$ is a right triangle with $\angle B=\pi / 2$. Similarly, consider the case when point $M$ is beyond point $C$. From the ratio $C L / L A=B C / B A=2 / 3$, we find that $L C=2, A L=3$. Since $B L^{2}=A B \cdot B C-A L \cdot L C$, then $B L^{2}=48$. By the Pythagorean theorem, we get $D L^{2}=D B^{2}+B L^{2}=49$. Answer: 7.
## Grading Criteria.
Guessed the solution: 0 points.
Found the length of the bisector: 1 point.
Determined that triangle $L B D$ is a right triangle: 4 points.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 9.2 (7 points)
In a bag, there are 70 balls that differ only in color: 20 red, 20 blue, 20 yellow, and the rest are black and white.
What is the minimum number of balls that need to be drawn from the bag, without seeing them, to ensure that among them there are at least 10 balls of the same color?
|
# Solution:
By drawing 37 balls, we risk getting 9 red, 9 blue, and 9 yellow balls, and we won't have ten balls of one color. If we draw 38 balls, the total number of red, blue, and yellow balls among them will be at least 28, and the number of balls of one of these colors will be at least ten (since $28 > 3 \cdot 9$).
| Criteria | Points |
| :--- | :---: |
| Complete solution | 7 |
| Answer without justification | 1 |
| Incorrect answer | 0 |
Answer: 38 balls
|
38
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 9.3 (7 points)
$H$ is the point of intersection of the altitudes of an acute-angled triangle $ABC$. It is known that $HC = BA$. Find the angle $ACB$.
#
|
# Solution:
Let $\mathrm{D}$ be the foot of the altitude dropped from vertex A to side BC. Angles НСВ and DAB are equal as acute angles with mutually perpendicular sides. Therefore, $\triangle \mathrm{CHD}=\Delta \mathrm{ABD}$ (by hypotenuse and acute angle). Hence, $=\mathrm{AD}$, i.e., triangle $\mathrm{ACD}$ is isosceles and right-angled, so $\angle \mathrm{ACB}=45^{\circ}$.
| Criteria | Points |
| :--- | :---: |
| Complete solution | 7 |
| Proved $\triangle \mathrm{CHD}=\triangle \mathrm{ABD}$ | 5 |
| Proved $\angle \mathrm{HCB}=\angle \mathrm{DAB}$ | 3 |
| Correct answer without justification | 1 |
Answer: $\angle A C B=45^{\circ}$
#
|
45
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 9.4 (7 points)
A palindrome is a number, letter combination, word, or text that reads the same in both directions. How much time in a day do palindromes appear on the clock display, if the clock shows time from 00.00.00 to 23.59.59?
|
# Solution:
If the digits on the display are ab.cd.mn, then $\mathrm{a}=0,1,2,0 \leq \mathrm{b} \leq 9,0 \leq \mathrm{c} \leq 5,0 \leq \mathrm{d} \leq 9,0 \leq \mathrm{m} \leq 5$, $0 \leq \mathrm{n} \leq 9$. Therefore, if $\mathrm{a}=\mathrm{n}, \mathrm{b}=\mathrm{m}, \mathrm{c}=\mathrm{d}$, then the symmetric number on the display is uniquely determined by the digits $\mathrm{a}, \mathrm{b}$, and $\mathrm{c}$, where $\mathrm{a}=0,1,2 ; 0 \leq \mathrm{b} \leq 5 ; 0 \leq \mathrm{c} \leq 5$. If $\mathrm{a}=0$ or 1, then $\mathrm{b}$ and $\mathrm{c}$ can be any digits from 0 to 5, the number of such sets of numbers is $2 \cdot 6 \cdot 6=72$. If $\mathrm{a}=2$, then $\mathrm{b}=0,1,2,3 ; 0 \leq \mathrm{c} \leq 5$, the number of such sets is $4 \cdot 6=24$. In total, $72+24=96$ sets of numbers, each of which is displayed for 1 second.
| Criteria | Points |
| :--- | :---: |
| Complete solution | 7 |
| Correct approach with arithmetic error | 5 |
| Correctly specified numerical ranges for $\mathrm{a}, \mathrm{b}, \mathrm{c}$. | 3 |
| Correct answer without justification | 1 |
## Answer: 96 seconds
|
96
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 9.5 (7 points)
In a store, there are buttons of six colors. What is the smallest number of buttons that need to be bought so that they can be sewn in a row, such that for any two different colors in the row, there are two adjacent buttons of these colors?
|
# Solution:
From the condition, it follows that for each fixed color A, a button of this color must appear in a pair with a button of each of the other 5 colors. In a row, a button has no more than two neighbors, so a button of color A must appear at least 3 times. The same applies to each other color. Thus, there should be no less than $3 \cdot 6=18$ buttons. Here is one example of the desired arrangement of buttons: 123456246325164135 (the colors are denoted by digits).
| Criteria | Points |
| :--- | :---: |
| Complete solution | 7 |
| Estimating the number of buttons without an example | 4 |
| Example without estimating the number | 3 |
| Incorrect solution | 0 |
## Answer: 18 buttons
|
18
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.4. From sticks of the same length, a row of 800 hexagons was laid out as shown in the figure. How many sticks were used in total?
Answer, option 1. 5001.
Answer, option 2. 2501.
Answer, option 3. 3001.
Answer, option 4. 4001.
|
Solution option 1. In the first hexagon, there are 6 sticks. Building each subsequent hexagon adds 5 sticks. In total, it will be $6+5 \cdot 999=5001$ sticks.
|
5001
|
Geometry
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
4.4. In a $3 \times 4$ rectangle, natural numbers $1,2,3, \ldots, 12$ were written, each exactly once. The table had the property that in each column, the sum of the top two numbers was twice the bottom number. Over time, some numbers were erased. Find all possible numbers that could have been written in place of $\star$.
| 6 | | | |
| :--- | :--- | :--- | :--- |
| 4 | | | |
| | 8 | 11 | $\star$ |
Answer, variant 1. 11.
Answer, variant 2. 8.
Answer, variant 3. 11.
Answer, variant 4. 2.
|
Solution 1. According to the condition, the number 2 is written in the bottom-left cell. The sum of the two unknown numbers in the second column is 10, and in the third column, it is 16. Therefore, the sum of the numbers in the first three columns is $6+15+24$, and the sum of all numbers in the table is $1+2+\ldots+12=78$. Thus, the sum of the numbers in the fourth column is $78-6-15-24=33$. From the condition, it follows that the number at $\star$ is one-third of 33, which is 11.
Remark. The arrangement of numbers described in the condition is indeed possible. For example, such an arrangement:
| 1 | 6 | 9 | 10 |
| :--- | :--- | :--- | :--- |
| 3 | 4 | 7 | 12 |
| 2 | 5 | 8 | 11 |
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.4. 10 children stood in a circle. Each thought of an integer and told it to their clockwise neighbor. Then each loudly announced the sum of their number and the number of the counterclockwise neighbor. The first said "10", the next clockwise - "9", the next clockwise - "8", and so on, the ninth said "2". What number did the remaining child say?
Answer, option 1.5.
Answer, option 2. 9.
Answer, option 3. 14.
Answer, option 4. 6.
|
Solution option 1. The sum of all ten thought-of numbers will be obtained if we add what the first child said to what the third, fifth, seventh, and ninth children said. Similarly, we add what the second, fourth, sixth, eighth, and tenth children said. Again, we get the sum of all ten thought-of numbers, so the equation $1+3+5+7+9=2+4+6+8+x$ must hold, where $x$ is the number named by the tenth child. From this, $x=5$.
Remark. Where was the condition that the numbers thought of are integers used? Nowhere. The solution works for non-integer numbers as well.
|
5
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
7.4. In isosceles triangle $ABC$, the base $AC$ is equal to $x$, and the lateral side is 12. On the ray $AC$, point $D$ is marked such that $AD=24$. A perpendicular $DE$ is dropped from point $D$ to line $AB$. Find $x$ if it is known that $BE=6$.
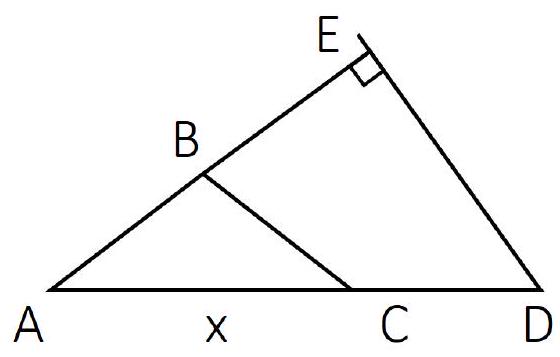
Answer, option 1. 13.
Answer, option 2. 17.
Answer, option 3. 14.
Answer, option 4. 18.
|
Solution Option 1. In triangle $A E D$, the angle at vertex $E$ is a right angle. In a right triangle, it is often useful to draw the median from the vertex of the right angle. If $E M$ is the median, then it is equal to half the hypotenuse $A D$, that is, $E M=M A=M D=10$.
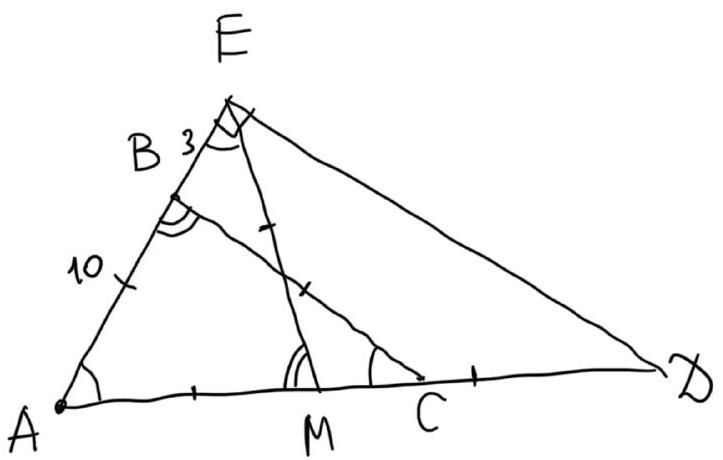
Consider the isosceles triangles $A M E$ and $A B C$. Their lateral sides are equal to 10, and the angles at the base in each of them are equal to the angle $B A C$. Therefore, the angles at the vertices in these triangles are also equal, and thus the triangles themselves are equal by the first criterion. Consequently, $A C=A E=A B+B E=13$.
|
13
|
Geometry
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
# Task 9.1
For which natural numbers $n$ is the expression $n^{2}-4 n+11$ a square of a natural number?
## Number of points 7
|
Answer:
for $n=5$
## Solution
Let $n^{2}-4 n+11=t^{2}$.
Note that $n^{2}-4 n+4=(n-2)^{2}$ is also the square of some integer $r=n-2$, which is less than $t$.
We get that $t^{2}-r^{2}=(t+r)(t-r)=7$.
The numbers $(t+r)$ and $(t-r)$ are natural and the first is greater than the second.
Thus, $(t+r)=7$, and $(t-r)=1$.
Solving this system, we get $t=4, r=3$, which gives $n=5$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 9.4
On the sides $B C$ and $C D$ of the square $A B C D$, points $M$ and $K$ are marked such that $\angle B A M = \angle C K M = 30^{\circ}$. Find the angle $A K D$.
## Number of points 7
#
|
# Answer:
$75^{\circ}$
## Solution
## First Solution
If we find angle $A K D$, it is only present in triangle $A K D$, and we do not know another angle in this triangle.
All the information in the problem is above line $A K$. Therefore, we need to move upwards.
And we need to find angle $A K M$. Triangle $A K M$ is also not a good one; it is unlikely to expect properties of equilateral or even isosceles triangles from it. Therefore, we extend angle $A K M$ to another triangle: we extend $K M$.
It will intersect $A B$ at some point $P$. In this triangle, we immediately note that angle $P$ is $30^{\circ}$. Therefore, triangle $A P M$ is isosceles. Let's try to express the lengths of the sides of triangle $A K P$. For this, we denote the side of the square as $a$. Then triangles $P B M$ and $A B M$ are equal, so $A P = 2a$. Next, $P M = A M = 2 B M$ (the leg opposite the $30^{\circ}$ angle is half the hypotenuse) and $M K = 2 M C$.
Then $P K = 2(B M + M C) = 2a$. As expected, triangle $A P K$ is isosceles, angle $K$ in it is $75^{\circ}$, and the required angle is $75^{\circ}$.
## Second Solution
$K A$ turned out to be the bisector of angle $M K D$. $M A$ is the bisector of angle $B M K$. These are the external angles of triangle $M K C$. It remains to see that $A C$ is the bisector of the internal angle $C$ of this triangle. Therefore, point $A$ is the excenter of triangle $M C K$. We draw the diagonal $A C$ in the square. Then point $A$ is the intersection of the bisectors of the internal angle $C$ of triangle $M C K$ and the external angle $M$ of the same triangle. That is, point $A$ is the excenter of this triangle. Consequently, the line passing through the third vertex of this triangle and point $A$ will also be the bisector of the external angle $K$ of this triangle. Again, we get the same $75^{\circ}$.
#
|
75
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In a beach soccer tournament, 17 teams participate, and each team plays against each other exactly once. Teams are awarded 3 points for a win in regular time, 2 points for a win in extra time, and 1 point for a win on penalties. The losing team does not receive any points. What is the maximum number of teams that can accumulate exactly 5 points?
|
Answer: 11.
Sketch of the solution. Estimation. Let $n$ teams have scored exactly 5 points each. The total points include all points scored by these teams in matches against each other (at least 1) and possibly in matches against other teams: $5 n \geq(n-1) n / 2$. Hence, $n \leq 11$.
Example: Place eleven teams in a circle, and let each team win against the five teams following them in a clockwise direction by penalty. The remaining teams lost to them.
Criteria. Example without estimation: 2 points. Estimation without example: 4 points.
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. Find the number of roots of the equation
$$
|x|+|x+1|+\ldots+|x+2018|=x^{2}+2018 x-2019
$$
(V. Dubinskaya)
|
Answer: 2.
Solution. For $x \in(-2019,1)$ there are no roots, since on the given interval the left side is non-negative, while the right side is negative.
For $x \in[1, \infty)$ all absolute values are resolved with a positive sign, so the equation will take the form $g(x)=0$, where $g(x)=x^{2}-x-2009+(1+2+\ldots+2018)$. Since $g(1)<0$, this quadratic equation has a single root on the interval $[1, \infty)$.
Since the graphs of the functions on the left and right sides are symmetric with respect to the line $x=-1009$ (i.e., $f(x)=f(-2018-x)$), there are as many roots on the interval $(-\infty,-2019]$ as there are on the interval $[1,+\infty)$, i.e., exactly one root. In total, the given equation has two roots.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. Initially, there are 111 pieces of clay of the same mass on the table. In one operation, you can choose several groups with the same number of pieces and in each group, combine all the clay into one piece. What is the minimum number of operations required to get exactly 11 pieces, any two of which have different masses?
(I. Bogdanov)
|
Answer. In two operations.
Solution. Let the mass of one original piece be 1. If in the first operation there are $k$ pieces in each group, then after it each piece will have a mass of 1 or $k$; therefore, it is impossible to obtain eleven pieces of different masses in one operation.
We will show that the required result can be achieved in two operations. In the first operation, select 37 groups of 2 pieces each; after the operation, there will be 37 pieces with masses of 1 and 2. In the second operation, select 9 groups of 8 pieces each: in the $i$-th group $(1 \leqslant i \leqslant 9)$ there will be $i-1$ pieces of mass 2 and $9-i$ pieces of mass 1. Then two pieces of masses 1 and 2 will remain unused, and from the $i$-th group a piece of mass $9-i+2(i-1)=7+i$ will be obtained. Thus, 11 pieces with masses $1,2,8,9, \ldots, 16$ will be obtained, as required.
Remark. It can be shown that the method presented is the only possible one.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. The younger brother takes 25 minutes to reach school, while the older brother takes 15 minutes to walk the same route. How many minutes after the younger brother leaves home will the older brother catch up to him if he leaves 8 minutes later?
|
Answer. in 17 minutes. Solution. See problem 7.1
|
17
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.3. In triangle $A B C$, side $A C$ is the largest. Points $M$ and $N$ on side $A C$ are such that $A M=A B$ and $C N=C B$. It is known that angle $N B M$ is three times smaller than angle $A B C$. Find $\angle A B C$.
|
Answer: $108^{\circ}$. Solution: Let $\angle N B M=x$. Then $\angle A B M+\angle N B C=\angle A B C+\angle N B M=4 x . \quad$ On the other hand, $\angle A B M+\angle N B C=\angle B M N+\angle B N M=180^{\circ}-\angle N B M=180^{\circ}-x$. Therefore, we have the equation $4 x=180^{\circ}-x$. Thus, $5 x=180^{\circ}, x=36^{\circ}$ and $\angle A B C=3 x=108^{\circ}$.
|
108
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4-1. Katya attached a square with a perimeter of 40 cm to a square with a perimeter of 100 cm as shown in the figure. What is the perimeter of the resulting figure in centimeters?
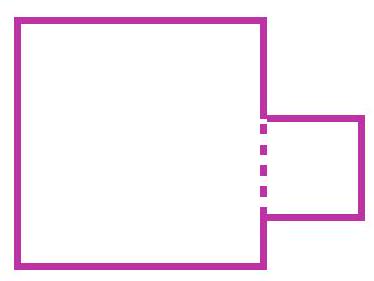
|
Answer: 120.
Solution: If we add the perimeters of the two squares, we get $100+40=140$ cm. This is more than the perimeter of the resulting figure by twice the side of the smaller square. The side of the smaller square is $40: 4=10$ cm. Therefore, the answer is $140-20=120$ cm.
|
120
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5-1. A square with a side of 100 was cut into two equal rectangles. They were placed next to each other as shown in the figure. Find the perimeter of the resulting figure.
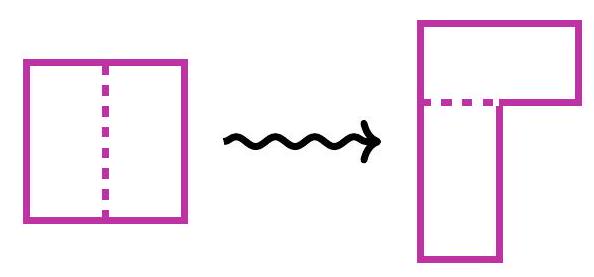
|
Answer: 500.
Solution. The perimeter of the figure consists of 3 segments of length 100 and 4 segments of length 50. Therefore, the length of the perimeter is
$$
3 \cdot 100 + 4 \cdot 50 = 500
$$
|
500
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5-5. Along a straight alley, 400 lamps are placed at equal intervals, numbered in order from 1 to 400. At the same time, from different ends of the alley, Alla and Boris started walking towards each other at different constant speeds (Alla from the first lamp, Boris from the four hundredth). When Alla was at the 55th lamp, Boris was at the 321st lamp. At which lamp will their meeting occur? If the meeting occurs between two lamps, indicate the smaller number of these two.
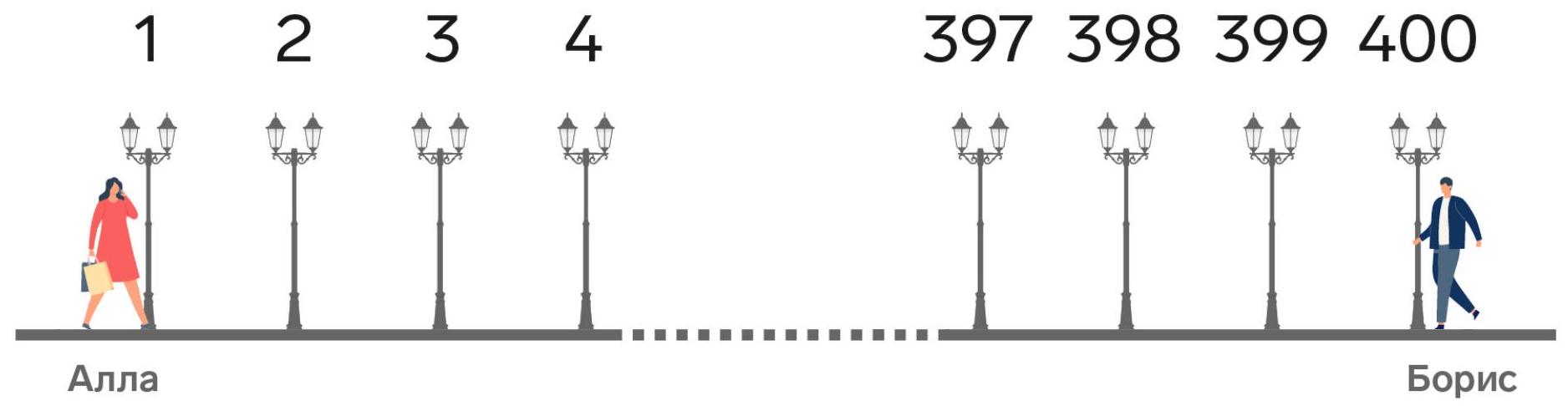
|
Answer. At the 163rd lamppost.
Solution. There are a total of 399 intervals between the lampposts. According to the condition, while Allа walks 54 intervals, Boris walks 79 intervals. Note that $54+79=133$, which is exactly three times less than the length of the alley. Therefore, Allа should walk three times more to the meeting point than to the 55th lamppost, i.e., $54 \cdot 3=162$ intervals. And she will be at the 163rd lamppost.
|
163
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5-6. A rectangular table of size $x$ cm $\times 80$ cm is covered with identical sheets of paper of size 5 cm $\times 8$ cm. The first sheet touches the bottom left corner, and each subsequent sheet is placed one centimeter higher and one centimeter to the right of the previous one. The last sheet touches the top right corner. What is the length $x$ in centimeters?
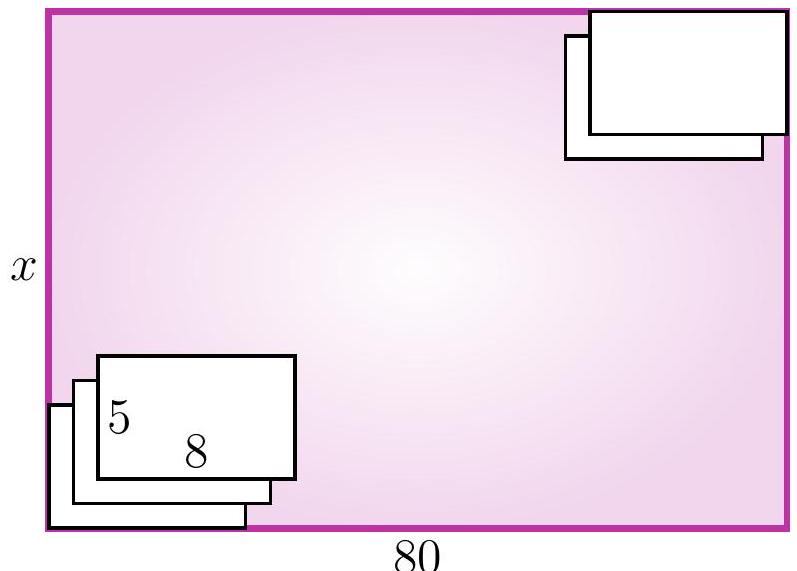
|
Answer: 77.
Solution I. Let's say we have placed another sheet of paper. Let's look at the height and width of the rectangle for which it will be in the upper right corner.
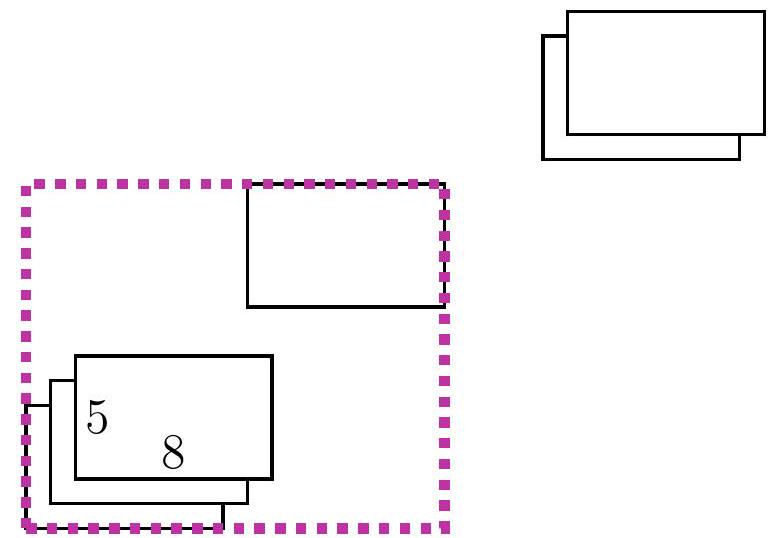
We will call such a rectangle the current one. Notice that for each new current rectangle, both the width and the height are 1 cm larger than the previous one. Initially, when there was only one sheet of paper, the width of the large rectangle was 8 cm, and at the end, it was 80 cm. Thus, a total of $(80-8): 1=72$ sheets of paper were added. The height of the current rectangle also increased by $72 \cdot 1$ cm, initially it was 5, so $x=5+72=77$.
Solution II. As in the first solution, let's look at the length and width of the current rectangles. Again, notice that for each new current rectangle, both the length and the width are 1 cm larger than the previous one. However, we will draw a different conclusion: specifically, the difference between the width and the height of the current rectangle is always the same! (Such a value that does not change during a certain process is called an invariant.) Since initially the width was 3 cm greater than the height, i.e., $8-5=3$ cm, at the end it should also be 3 cm greater, so the answer is $x=80-3=77$ cm.
|
77
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8-1. Two rectangles $8 \times 10$ and $12 \times 9$ are overlaid as shown in the figure. The area of the black part is 37. What is the area of the gray part? If necessary, round the answer to 0.01 or write the answer as a common fraction.
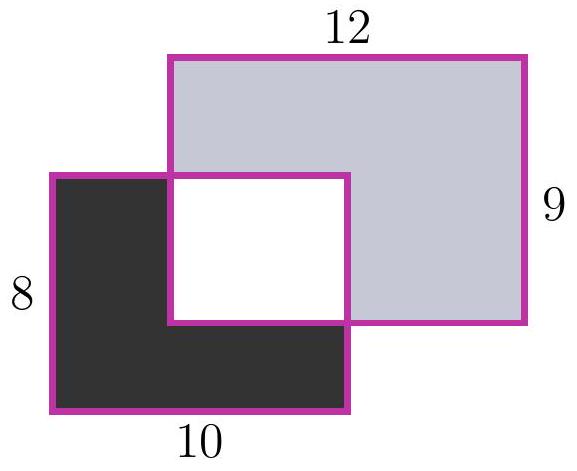
|
Answer: 65.
Solution. The area of the white part is $8 \cdot 10-37=43$, so the area of the gray part is $12 \cdot 9-43=65$
|
65
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8-2. In square $A B C D$, a segment $C E$ is drawn such that the angles shown in the diagram are $7 \alpha$ and $8 \alpha$. Find the value of angle $\alpha$ in degrees. If necessary, round the answer to 0.01 or write the answer as a common fraction.
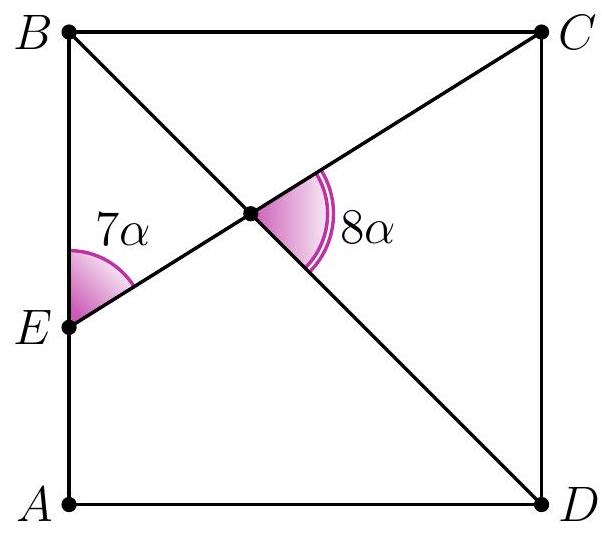
|
Answer: $9^{\circ}$.
Solution. In triangle $D F E$, the angles are $7 \alpha, 8 \alpha$ and $45^{\circ}$.
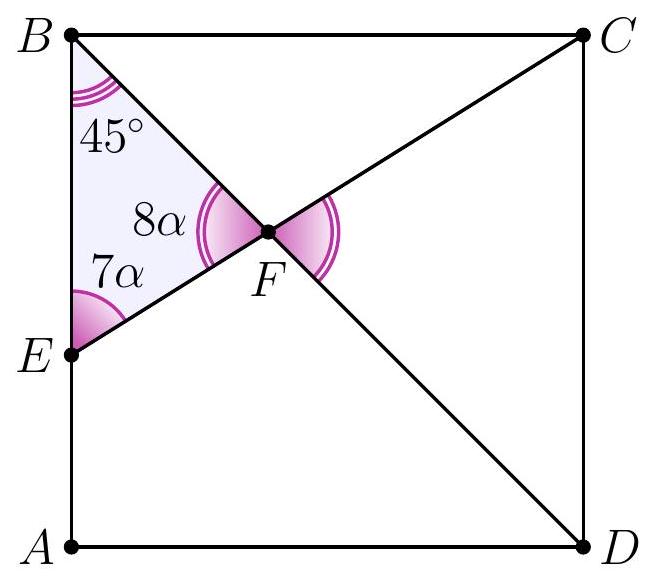
Since the sum of the angles in triangle $D F E$ is $180^{\circ}$, we have $7 \alpha + 8 \alpha + 45^{\circ} = 180^{\circ}$, from which $\alpha = \frac{1}{15} \cdot 135^{\circ} = 9^{\circ}$.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9-1. Segment $P Q$ is divided into several smaller segments. On each of them, a square is constructed (see figure).
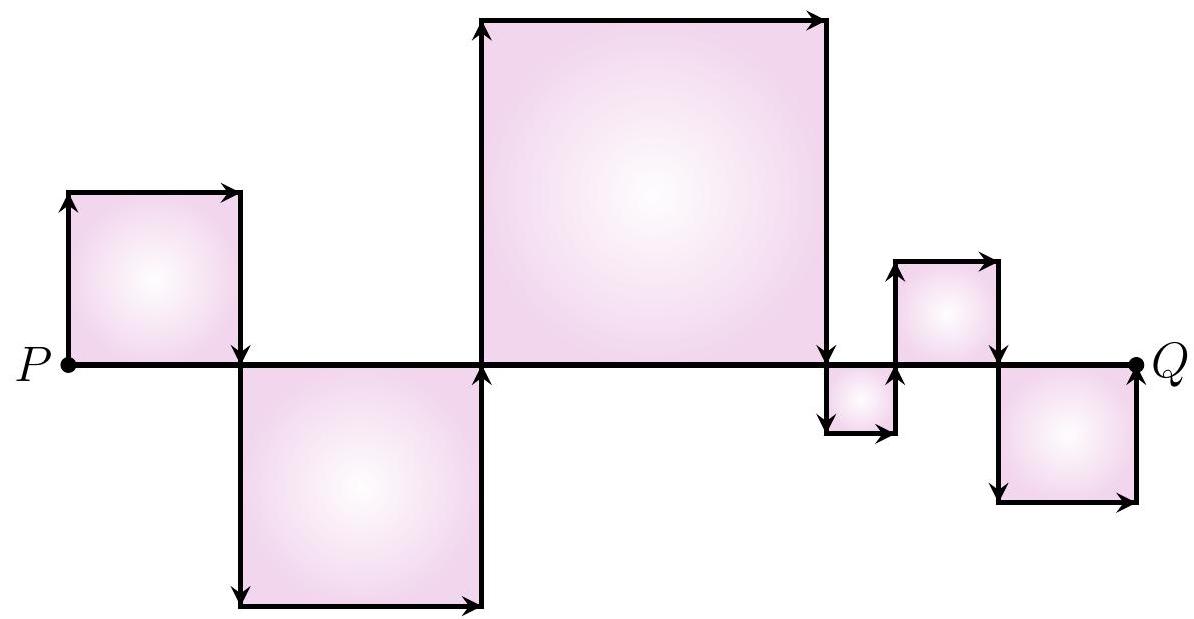
What is the length of the path along the arrows if the length of segment $P Q$ is 73? If necessary, round the answer to 0.01 or write the answer as a common fraction.
|
Answer: 219.
Solution. Note that in each square, instead of going along one side, we go along three sides. Therefore, the length of the path along the arrows is 3 times the length of the path along the segment, hence the answer $73 \cdot 3=219$.
|
219
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem №2
In an $8 \times 8$ frame that is 2 cells wide (see figure), there are a total of 48 cells.
How many cells are in a $254 \times 254$ frame that is 2 cells wide?
|
Answer: 2016.
## Solution
First method. Cut the frame into four identical rectangles as shown in the figure. The width of the rectangles is equal to the width of the frame, i.e., 2 cells. The length of each
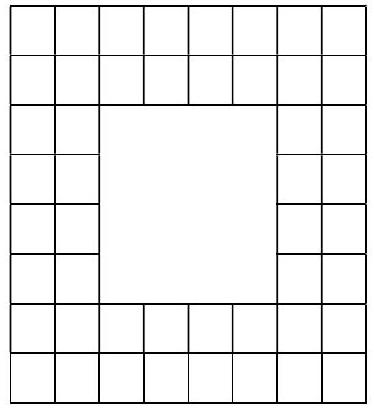
rectangle is 2 less than the side of the frame: $254-2=252$ cells. Then the area of one rectangle is $2 \cdot 252=504$. Therefore, the total number of cells in the frame is $4 \cdot 504=2016$.

Second method. The area of the frame can be obtained by subtracting the area of the inner square from the area of the large square $254 \times 254$. The side of the inner square is 4 cells less than the side of the large square. Therefore, the area of the frame is $254^{2}-250^{2}=(254-250)(254+250)=2016$.
Note. If the side of the frame is denoted by $n$, it can be proven (for example, by the methods described above) that its area will be $(8n - 16)$ cells.
## Grading Criteria.
- Any complete correct solution - 7 points.
- Correct approach, but an arithmetic error was made - 3 points.
- Correct reasoning, but an error was made in estimating the dimensions (for example, in the second method, it is incorrectly assumed that the side of the inner square is 2 cells less than the large one) - 2 points.
- Only the correct answer - 1 point.
|
2016
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem №4
Two ferries simultaneously depart from opposite banks of a river and cross it perpendicularly to the banks. The speeds of the ferries are constant but not equal. The ferries meet at a distance of 720 meters from one bank, after which they continue their journey. On the return trip, they meet 400 meters from the other bank. What is the width of the river?
|
Answer: $1760 \mathrm{M}$
## Solution.
The total distance traveled by the ferries by the time of their first meeting is equal to the width of the river, and the distance traveled by the time of their second meeting is three times the width of the river. Therefore, by the time of the second meeting, each ferry has traveled three times the distance it traveled by the time of the first meeting. Since one of the ferries traveled 720 meters by the time of the first meeting, it traveled a distance of $720 \cdot 3=2160$ meters by the time of the second meeting. By this time, it had traveled a distance equal to the width of the river plus an additional 400 meters. Therefore, the width of the river is $2160-400=1760$ meters.
#
|
1760
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
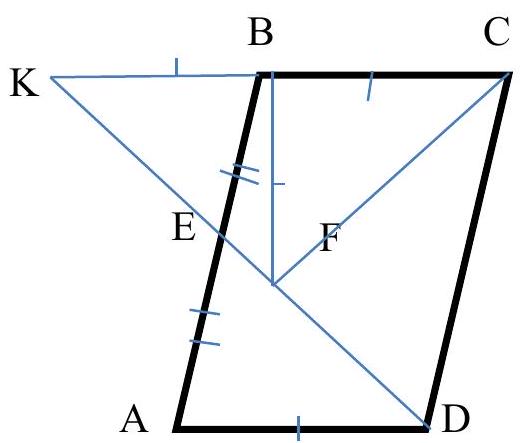
# Problem №5
Point $E$ is the midpoint of side $A B$ of parallelogram $A B C D$. On segment $D E$, there is a point $F$ such that $A D = B F$. Find the measure of angle $C F D$.
|
Answer: $90^{\circ}$
Solution
Extend $\mathrm{DE}$ to intersect line $\mathrm{BC}$ at point $\mathrm{K}$ (see figure).
Since $\mathrm{BK} \| \mathrm{AD}$, then $\angle \mathrm{KBE}=\angle \mathrm{DAE}$.
Moreover, $\angle \mathrm{KEB}=\angle \mathrm{DEA}$ and $\mathrm{AE}=\mathrm{BE}$, thus triangles $\mathrm{BKE}$ and $\mathrm{ADE}$ are equal. Therefore, $\mathrm{BK}=\mathrm{AD}=\mathrm{BC}$. Thus, in triangle CFK, the median FB is equal to half the side to which it is drawn, so this triangle is a right triangle with a right angle at $\mathrm{F}$. Consequently, angle CFD is also a right angle.
## Grading Criteria.
「+」A correct and justified solution is provided
「土」A generally correct reasoning is provided, containing minor gaps or inaccuracies
「-」Only the answer is provided
「-」The problem is not solved or is solved incorrectly
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Four princesses each thought of a two-digit number, and Ivan thought of a four-digit number. After they wrote their numbers in a row in some order, the result was 132040530321. Find Ivan's number.
|
Solution. Let's go through the options. Option 1320 is not suitable because the remaining part of the long number is divided into fragments of two adjacent digits: 40, 53, 03, 21, and the fragment 03 is impossible, as it is not a two-digit number. Option 3204 is impossible due to the invalid fragment 05 (or the fragment 1 from a single digit). Option 2040 results in the impossible fragment 03. Option 0405 is not an option - it is a three-digit number. Option 4053 results in the impossible fragment 03. Option 0530 is impossible. Option 5303 is the only possible one, as option 3032 leads to a fragment of one digit 1.
Answer. 5303.
## CONDITION
|
5303
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. There are more than 30 people in the class, but less than 40. Any boy is friends with three girls, and any girl is friends with five boys. How many people are in the class
|
Solution. Let $\mathrm{m}$ be the number of boys, $\mathrm{d}$ be the number of girls, and $\mathrm{r}$ be the number of friendly pairs "boy-girl". According to the problem, $\mathrm{r}=3 \mathrm{~m}$ and $\mathrm{r}=5 \mathrm{~d}$. Therefore, $\mathrm{r}$ is divisible by 3 and 5, and thus by 15: $\mathrm{r}=15 \mathrm{k}$. Then $\mathrm{m}=5 \mathrm{k}, \mathrm{d}=3 \mathrm{k}$, and the total number of students is $\mathrm{m}+\mathrm{d}=8 \mathrm{k}$, which means it is divisible by 8. The only number between 30 and 40 that is a multiple of 8 is 32.
Answer: 32.
|
32
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. Little kids were eating candies. Each one ate 11 candies less than all the others together, but still more than one candy. How many candies were eaten in total?
|
Answer: 33 candies.
Solution: Let $S$ be the total number of candies eaten by the children. If one of the children ate $a$ candies, then according to the condition, all the others ate $a+11$ candies, and thus all together ate $S=a+(a+11)=2a+11$ candies. This reasoning is valid for each child, so all the children ate the same number of candies: $a=(S-11)/2$ each.
Now let $N$ be the number of children. Then the condition can be written as $a=a \cdot (N-1)-11$, from which $11=a \cdot (N-2)$. The number 11 is prime, so one of the factors is 1, and the other is 11. But by the condition $a>1$, so $a=11, N-2=1$. Thus, $N=3$, and a total of $S=a \cdot N=33$ candies were eaten.
|
33
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. The number 49 is written on the board. In one move, it is allowed to either double the number or erase its last digit. Is it possible to get the number 50 in several moves?
|
Answer: Yes.
Solution: The number 50 can be obtained by doubling 25, and 25 can be obtained by erasing the last digit of the number 256, which is a power of two. Thus, the necessary chain of transformations can look like this: $49 \rightarrow 4 \rightarrow 8 \rightarrow 16 \rightarrow 32 \rightarrow 64 \rightarrow 128 \rightarrow 256 \rightarrow 25 \rightarrow 50$.
There are other solutions as well.
|
50
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.3. Given an acute-angled triangle $A B C$. Point $M$ is the intersection point of its altitudes. Find the angle $A$, if it is known that $A M=B C$.
---
The text has been translated while preserving the original formatting and line breaks.
|
83. Given an acute-angled triangle $A B C$. Point $M$ is the intersection point of its altitudes. Find the angle $A$, if it is known that $A M=B C$.
Answer: $45^{\circ}$. Hint Let $\mathrm{K}$ be the foot of the altitude from point В. We will prove that triangles АМ К and BKC are equal. Indeed, we have right triangles, in which $\angle \mathrm{MAK}=\angle \mathrm{CBK}=90^{\circ}-\angle \mathrm{C}$ and, by condition, $A M=B C$. Then, from the equality of the triangles, it follows that $A K=B K$, and therefore, in the right triangle $A B K$, the legs are equal. Therefore, $\angle A=45^{\circ}$.
|
45
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 3. The numbers $2^{2021}$ and $5^{2021}$ are written one after another. How many digits are written in total?
#
|
# Solution
Let the number $2^{2021}$ have $\mathrm{k}$ digits, and the number $5^{2021}$ have $\mathrm{m}$ digits, then the number of digits in the desired number is $\mathrm{k}+\mathrm{m}$. $10^{k-1}<2^{2021}<10^{k}, 10^{m-1}<5^{2021}<10^{m}$, therefore, $10^{k+m-2}<$ $10^{2021}<10^{m+k}$ and $\mathrm{k}+\mathrm{m}=2022$.
## Evaluation Criteria
The solution includes intermediate estimates that allow reaching the required estimate - from 13 points depending on the progress in the solution.
An incorrect answer due to a logical error - from 1-4 points depending on the progress in the solution.
An incorrect answer due to a computational error - 5 points.
A correct result obtained with justification - 7 points.
|
2022
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Solve the inequality $\sqrt{2 x^{2}-8 x+6}+\sqrt{4 x-x^{2}-3}<x-1$
|
Note that all solutions to the original inequality exist if the expressions under the square roots are non-negative. These inequalities are simultaneously satisfied only under the condition $x^{2}-4 x+3=0$. This equation has two roots, 1 and 3. Checking shows that the original inequality has a unique solution 3.
Answer: 3.
#
|
3
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. At first, there were natural numbers, from 1 to 2021. And they were all white. Then the underachiever Borya painted every third number blue. Then the top student Vova came and painted every fifth number red. How many numbers remained white? (7 points)
#
|
# Solution
Borya repainted the numbers divisible by 3, a total of [2021:3]=673 numbers. Vova repainted [2021:5]=404 numbers. 673+404=1077. However, numbers divisible by 15 were counted twice. [2021:15]=134. Therefore, the number of white numbers remaining is 2021-1077+134=1078.
Answer: 1078 white numbers
| criteria | points |
| :--- | :---: |
| 1. correct solution | 7 |
| 2. Not accounted for numbers divisible by 15 being counted twice. | 4 |
| 3. For each arithmetic error | 1 |
|
1078
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.2. Doctor Vaccinov and Doctor Injectionov vaccinated all the residents of the village of Covido. Vaccinov thought: if I had given 40% more vaccinations, then Injectionov's share would have decreased by 60%. And how would Injectionov's share change if Vaccinov had given 50% more vaccinations? (7 points)
#
|
# Solution
$40 \%$ of the injections given by Privevkin equals $60 \%$ of the number of injections given by Ukolkin, so Privevkin gave 1.5 times more injections. Therefore, an increase in Privevkin's share by $n \%$ would decrease Ukolkin's share by $1.5 n \%$.
Answer: It would decrease by $75 \%$.
| criteria | points |
| :--- | :---: |
| 1. correct solution | 7 |
| 2. Found that Privevkin gave 1.5 times more injections | 3 |
| 3. unjustified correct answer | 0 |
|
75
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.5. Solve the equation $2021 x^{2021}-2021+x=\sqrt[2021]{2022-2021 x}$. (7 points)
#
|
# Solution
The function $f(x)=2021x^{2021}-2021+x$ is increasing, while the function $g(x)=\sqrt[2021]{2022-2021x}$ is decreasing. Therefore, the equation $f(x)=g(x)$ has no more than one root. However, it is obvious that $f(1)=g(1)$.
Answer: $x=1$.
| criteria | points |
| :--- | :---: |
| correct solution | 7 |
| Proven that there is no more than one root. | 4 |
| Root found, but not proven that there are no other roots | 2 |
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. Four non-zero numbers are written on the board, and the sum of any three of them is less than the fourth number. What is the smallest number of negative numbers that can be written on the board? Justify your answer.
|
Solution: Let the numbers on the board be $a \geqslant b \geqslant c \geqslant d$. The condition of the problem is equivalent to the inequality $a+b+c < d$ for optimality | 7 points |
| There is a proof that there are no fewer than three negative numbers (in the absence of an example with three numbers) | 3 points |
| An example of a set with three negative numbers is provided (in the absence of a proof of its optimality) | 1 point |
| Correct answer without justification (or with incorrect justification) | 0 points |
| Examples of sets with four negative numbers | not evaluated |
|
3
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. At the exchange office, only the following operations can be performed:
1) exchange 2 gold coins for three silver coins and one copper coin;
2) exchange 5 silver coins for three gold coins and one copper coin.
Nikolai had only silver coins. After several visits to the exchange office, he had fewer silver coins, no gold coins appeared, but he got 50 copper coins. By how much did the number of silver coins decrease for Nikolai? Justify your answer. Note that exchanging money at the bank is not an equivalent operation, meaning that with each exchange, the purchasing power of the coins Nikolai had slightly decreased.
|
Solution: As a result of each operation, Nikolai acquires exactly 1 copper coin, which means there were exactly 50 operations in total. Of these, some (let's say \(a\)) were of the first type, and the rest \(50-a\) were of the second type. On operations of the first type, Nikolai spent \(2a\) gold coins, and on operations of the second type, he earned \(3(50-a)\) gold coins. Since he has no gold coins left, \(2a = 3(50-a)\), from which \(a = 30\). This means that on operations of the first type, Nikolai received \(30 \cdot 3 = 90\) silver coins, and on operations of the second type, he lost \((50-30) \cdot 5 = 100\) such coins. Thus, the number of silver coins decreased by \(100 - 90 = 10\) coins.
Answer: By 10 coins.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and justified answer | 7 points |
| Correct solution path, but the answer is incorrect due to arithmetic errors | 6 points |
| Correctly and justifiedly found the number of operations of one type (either the first or the second) | 5 points |
| Proven that the ratio of the number of operations of the 1st and 2nd types is 3:2 AND/OR the total number of operations of both types is justified | 3 points |
| The problem is correctly solved under the assumption of equal value of all exchanges (the general case is not investigated) | 2 points |
| A specific example of exchanges is provided, showing that the answer 10 is possible, but its uniqueness is not justified | 1 point |
| Correct answer without justification (with incorrect justification) | |
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. On an $8 \times 8$ chessboard, tokens are placed according to the following rule. Initially, the board is empty. A move consists of placing a token on any free square. With this move, exactly one of the tokens that ends up adjacent to it is removed from the board (if there is such an adjacent token). What is the maximum number of tokens that can be placed on the board, considering the specified rule? Adjacent squares are those that are nearest horizontally, vertically, and diagonally. Solution.
The number of tokens on the board can be increased by one only when a new token is placed on a completely free square, i.e., a square all of whose adjacent squares are free of tokens.
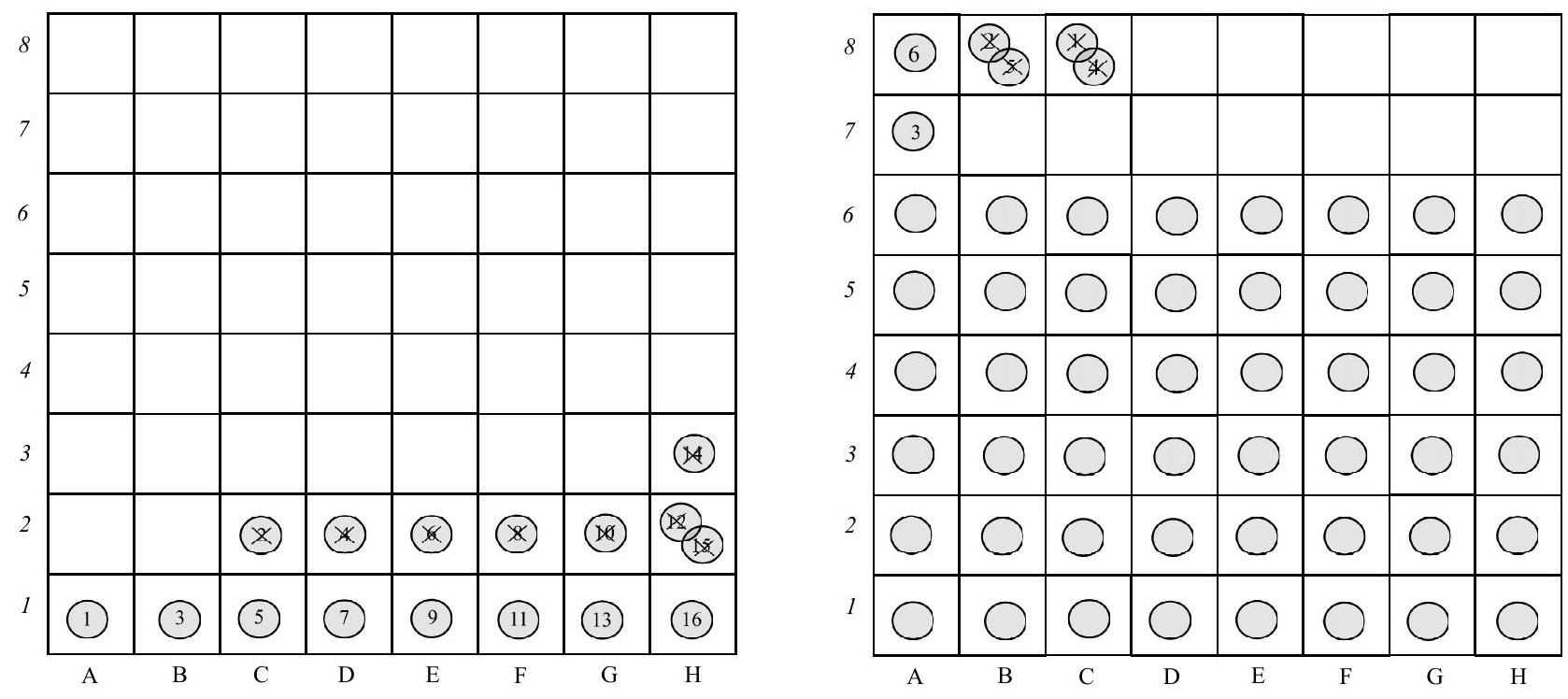
Let's highlight one horizontal row A1-H1, see the figure. We can fill this row with tokens from left to right. To do this, we will place the tokens in sequence, as shown in the figure. The numbers in circles indicate the sequence of placing the tokens. A crossed-out number means removing a token when placing an adjacent one. When filling the bottom row, each subsequent token removes the previous one from the board, so placing a token with an odd number in the row A1-H1 removes the previous even-numbered token from the row A2-H2. To place a token on the H1 field, we first need to place token number 14 on the H3 field, then token number 15 on the H2 field, removing the previous one. Finally, we can place token number 16 on the corner field H1, removing token number 15 from the board.
Next, we can fill all the horizontal rows up to A6-H6 in a similar manner. Rows A7-F7 and A8-F8 will have to be filled differently, as there are not enough free squares above them. The order of filling the two vertical squares A7 and A8 is shown in the second figure. To fill them, we need to start twice from the C8 field. This way, we will reach the F7 and F8 fields. We cannot move further to the right, as there is no free field except for the H8 field. We can place a token on this field and, if we wish to fill the G8 field, remove the token from the H8 field. Thus, we have shown how to fill the board with 61 tokens. There are other sequences of placements and other final arrangements of 61 tokens.
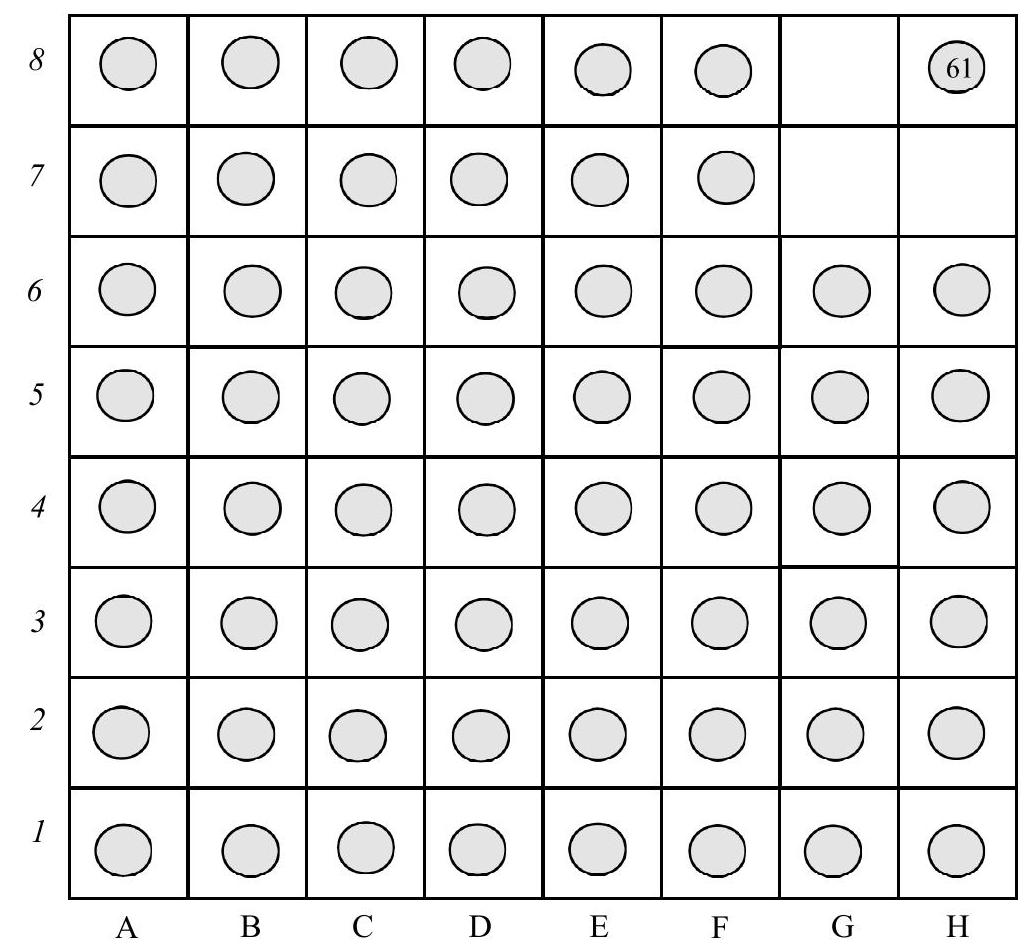
It remains to prove that it is impossible to place 62 tokens. Suppose 61 tokens are placed on the board. The three free squares do not allow us to select one that does not have any adjacent occupied squares. The minimum number of sides of a free square that can adjoin another free square is two, in the corner of the board. Therefore, the minimum necessary number of free neighbors is three, taking into account the diagonally adjacent square, see the figure.
|
Answer: No more than 61 chips can be placed.
|
61
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In a certain country, there are 47 cities. Each city has a bus station from which buses run to other cities in the country and possibly abroad. A traveler studied the schedule and determined the number of internal bus routes departing from each city. It turned out that if the city of Lake is not considered, then for each of the remaining 46 cities, the number of internal routes departing from it differs from the number of routes departing from other cities. Find out how many cities in the country have direct bus connections with the city of Lake.
The number of internal bus routes for a given city is the number of cities in its own country that can be reached from the given city by a direct bus, without transfers. The routes are symmetric: if you can travel from city $A$ to city $B$, then you can also travel from city $B$ to city $A$.
|
Solution.
Note that external lines are not considered in this problem.
There are a total of 47 variants of the number of internal lines - from 0 to 46. Note that the existence of a city with 46 lines excludes the existence of a city with 0 lines and vice versa.
Suppose there is a city with 46 lines. Then the smallest number of lines leading out of one city is one, and all numbers from 1 to 46 are encountered without gaps (cities excluding Lake City - 46). The city with one bus line cannot be connected to Lake City, as its only line must lead to the city with 46 lines (otherwise, the 46th pair would not be found). We have organized the pair 1-46. Now consider the city with 45 lines. We will match it with the city with two lines. Note that the city with two lines cannot be connected to Lake City. Continuing this reasoning, we will organize pairs 3-44, 4-43, and so on, up to the pair 23-24. The city with the smaller number of lines in each pair is not connected to Lake City. Note that Lake City does not enter these pairs, as a connection with Lake City is necessary for a larger number of lines in each pair. Thus, all cities are divided into pairs, and each number of lines from 1 to 46 occurs exactly once. Since in each pair exactly one city is connected to Lake City, Lake City is connected to 23 cities, the number of pairs.
Suppose the maximum number of lines is 45. Then there is a city with 0 lines (buses from it go only abroad), and all numbers from 0 to 45 are encountered without gaps (cities excluding Lake City - 46). Again, we will form pairs 0-45, 1-44, and so on to 22-23. Similarly to the previous case, in the pair 0-45, the first city is not connected to Lake City, while the second is connected (otherwise, it would not be possible to get 45 lines from it). In the pair 1-44, the city with one line is not connected to Lake City (its connection is occupied by the line to the city with 44 lines), while the city with 44 lines is connected to Lake City to reach the required number of lines. Further, in the pair 2-43, the city with two lines is not connected to Lake City (its connection is occupied by lines to the cities with 44 and 43 lines), while the city with 43 lines is connected to Lake City to reach the required number of lines. We have 23 pairs. Lake City is connected to exactly one city in each pair, so it is connected to 23 cities.
Answer. Lake City is connected to 23 cities.
|
23
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Find all natural numbers $n \geq 2$ such that $20^{n}+19^{n}$ is divisible by $20^{n-2}+19^{n-2}$.
|
Solution.
Consider the expression
$$
20^{n}+19^{n}-19^{2} \cdot\left(20^{n-2}+19^{n-2}\right)
$$
By the condition, it is divisible by $20^{n-2}+19^{n-2}$. On the other hand,
$$
20^{n}+19^{n}-19^{2} \cdot\left(20^{n-2}+19^{n-2}\right)=20^{n-2}\left(20^{2}-19^{2}\right)=20^{n-2} \cdot 39
$$
Note that $20^{n-2}$ and $20^{n-2}+19^{n-2}$ are coprime, since no prime divisor of $20^{n-2}$ is a divisor of $19^{n-2}$, and the expressions $20^{n-2}$ and $20^{n-2}+19^{n-2}$ do not have
common prime divisors. Therefore, in the product $20^{n-2} \cdot 39$, only the second factor can be divisible by $20^{n-2}+19^{n-2}$. For $n-2>1$, the expression $20^{n-2}+19^{n-2}$ exceeds 39, so it cannot be its divisor. It remains to check by substitution $n=2,3$.
For $n=2$, $20^{0}+19^{0}=2$, the odd number $20^{2}+19^{2}=761$ is not divisible by 2. For $n=3$, $20^{1}+19^{1}=39,20^{3}+19^{3}=39 \cdot\left(20^{2}-20 \cdot 19+19^{2}\right)$ is divisible by $20^{1}+19^{1}=39$. Answer. $n=3$.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. The teacher suggested that his students - Kolya and Seryozha - solve the same number of problems during the lesson. After some time from the start of the lesson, it turned out that Kolya had solved a third of what Seryozha had left to solve, and Seryozha had left to solve half of what he had already completed. Seryozha calculated that if he continued solving problems at the same speed, he would manage to solve all the problems by the end of the lesson. By what factor does Kolya need to increase his problem-solving speed to solve all the problems by the end of the lesson?
|
# 8.1. Answer: 16.
Solution. Let Tanya have solved x problems, then she has $\frac{x}{2}$ problems left to solve.
Let $\mathrm{t}_{1}$ be the time interval after which Tanya and Kolya evaluated the shares of solved and remaining problems, and $\mathrm{t}_{2}$ be the remaining time. Since Tanya's problem-solving speed is constant, then $\mathrm{t}_{2}=\mathrm{t}_{1} \cdot \frac{1}{2}$, i.e., $\frac{t_{1}}{t_{2}}=2$.
Then Kolya solved $\frac{1}{3} \cdot \frac{x}{2}=\frac{x}{6}$ problems, and he has $x+\frac{x}{2}-\frac{x}{6}=\frac{8 x}{6}=\frac{4}{3}$ x problems left to solve.
His speed was $\frac{\mathrm{x}}{6 t_{1}}$, and it should become $\frac{4 \mathrm{x}}{3 t_{2}}$.
The ratio of the speeds is $\frac{4 x \cdot 6 t_{1}}{3 t_{2} \cdot x}=\frac{8 t_{1}}{t_{2}}=16$.
|
16
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. At a round table, 10 people are sitting, some of them are knights, and the rest are liars (knights always tell the truth, while liars always lie). It is known that among them, there is at least one knight and at least one liar. What is the maximum number of people sitting at the table who can say: "Both of my neighbors are knights"? (A false statement is one that is at least partially not true.)
#
|
# Answer. 9.
Solution. Note that all 10 could not have said such a phrase. Since at the table there is both a knight and a liar, there will be a liar and a knight sitting next to each other. But then this knight does not have both neighbors as knights. If, however, at the table there are 9 liars and 1 knight, then each of these 9 liars could say the phrase "Both of my neighbors are knights," since each liar has a liar among their neighbors.
Comment. It has been proven that all 10 people could not have said the required phrase - 4 points.
It has been shown that with a certain seating arrangement, 9 people could have said the required phrase - 3 points.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.3. What is the minimum number of L-shaped corners consisting of 3 cells that need to be painted in a $5 \times 5$ square so that no more L-shaped corners can be painted? (Painted L-shaped corners should not overlap.)
|
Answer: 4.
Solution: Let the cells of a $5 \times 5$ square be painted in such a way that no more corners can be painted. Consider the 4 corners marked in Fig. 7. Since none of these corners can be painted, at least one cell in each of these corners must be painted. Note that one corner cannot paint cells of two marked corners. Therefore, at least 4 corners must be painted.

Fig. 7
Fig. 8
Fig. 8 shows how to paint 4 corners so that no more corners can be painted.
Comment: It is proven that the number of painted corners is not less than $4-4$ points.
A correct example with 4 painted corners is drawn 3 points.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.4. We will call a number greater than 25 semi-prime if it is the sum of some two different prime numbers. What is the maximum number of consecutive natural numbers that can be semi-prime
|
Answer: 5.
Solution: Note that an odd semiprime number can only be the sum of two and an odd prime number.
We will show that three consecutive odd numbers $2n+1$, $2n+3$, and $2n+5$, greater than 25, cannot all be semiprimes simultaneously. Assuming the contrary, we get that the numbers $2n-1$, $2n+1$, and $2n+3$ are prime, and all are greater than 3. But one of these three numbers is divisible by 3. Contradiction.
Note that among any six consecutive numbers, there are three consecutive odd numbers; therefore, there cannot be more than five consecutive semiprime numbers. Five consecutive numbers can be semiprimes; for example, $30=17+13, 31=29+2, 32=19+13, 33=31+2$, $34=23+11$.
Remark: There are other examples.
Comment: It is proven that there cannot be more than 5 consecutive semiprime numbers (greater than 25) - 4 points.
An example of 5 consecutive semiprime numbers (greater than 25) is provided - 3 points.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.8. In the vertices of a regular 100-gon, 100 chips numbered $1, 2, \ldots, 100$ were placed, in exactly that order clockwise. In one move, it is allowed to swap two adjacent chips if their numbers differ by no more than $k$. For what smallest $k$ can a series of such moves result in a configuration where each chip is shifted one position clockwise relative to its initial position?
(S. Berlov)
|
# Answer. 50.
Solution. Example. The chip 50 is sequentially exchanged 99 times with the next one counterclockwise. We get the required arrangement.
There are several ways to prove the estimate, below we provide two of them.
The first way. Suppose that for some $k<50$ the required arrangement is obtained.
At any moment, we consider the arc from chip 100 to chip 1 clockwise to be painted. Since chips 100 and 1 cannot be swapped in one move, each specific chip $m$ $(2 \leqslant m \leqslant 99)$ could only enter the painted arc or leave the painted arc by swapping with one of the chips 1 or 100.
Since initially and at the end, chip $m$ was not on the painted arc, it made an equal number of entries onto the painted arc and exits from the painted arc. For $m \leqslant 50$, chip $m$ could not swap with chip 100, so it could only enter or exit by swapping with chip 1. Upon entry, chip 1 moves 1 position clockwise, and upon exit - 1 position counterclockwise. We conduct similar reasoning for chips $m \geqslant 51$, which cannot swap with chip 1.
Thus, chips 1 and 100 will make an equal number of moves clockwise and counterclockwise, so they will remain in their positions. Contradiction.
The second way. We will count the shifts of the chips relative to their initial position, with a shift clockwise being counted as positive and a shift counterclockwise as negative. Then, when two chips are swapped, +1 is added to the shift of one of them, and -1 to the other. Therefore, the sum of the shifts after the operations will be 0.
We reason by contradiction: suppose that for $k<50$ each chip $i$ is finally shifted one position clockwise, i.e., its shift is $1+100 t_{i}$ (here $t_{i}$ is the integer "number of rotations" clockwise, in particular, if $t_{i}<0$, chip $i$ made $\left|t_{i}\right|$ rotations counterclockwise). Then the total shift of all 100 chips is $100\left(t_{1}+t_{2}+\ldots+t_{100}\right)+100$. Since it must equal 0, we have $t_{1}+t_{2}+\ldots+t_{100}=-1$.
Since $k<50$, chips with numbers $i$ and $j$, where $j \geqslant i+50$, could not swap places, so their shifts at any moment are definitely less than 100 apart, meaning the "number of rotations" $t_{i}$ and $t_{j}$ are equal for $j \geqslant i+50$. Hence, $t_{1}=t_{51}$, $t_{2}=t_{52}, \ldots, t_{50}=t_{100}$. Then the sum $t_{1}+t_{2}+\ldots+t_{100}=2\left(t_{1}+\right.$ $\left.+t_{2}+\ldots+t_{50}\right)$ is even, and thus not equal to -1. Contradiction.
Remark 1. The last reasoning can be modified as follows.
From this, $t_{1}=t_{51}, t_{1}=t_{52}, \ldots, t_{1}=t_{100}, t_{2}=t_{100}, t_{3}=t_{100}$, $\ldots, t_{50}=t_{100}$, thus all $t_{i}$ are equal to $t_{1}$. Then $t_{1}+t_{2}+$ $+\ldots+t_{100}=100 t_{1} \neq-1$.
Remark 2. The proof can be completed by contradiction in another way, replacing the last paragraph of the solution with the following reasoning.
We will paint chips red for which $t_{i} \geqslant 0$, and blue for which $t_{i}<0$. Clearly, at some point, a blue and a red chip must swap, since the difference in their shifts is at least 100. Since $k<50$, the pair of chips 1 and 51
- are the same color, similarly pairs of chips 1 and $52, \ldots, 1$ and 100, 2 and 100, 3 and $100, \ldots, 50$ and $100-$ are the same color. Thus, all chips are the same color. We know that $t_{1}+t_{2}+\ldots+t_{100}=-1$, so among the numbers $t_{1}, \ldots, t_{100}$ there are both non-negative and negative ones, i.e., there are both red and blue chips - contradiction.
Comment. Only the correct answer -0 points.
Points for the example and the estimate are summed.
A correct example is provided -2 points.
There is a complete proof of the estimate - 5 points.
In the absence of a complete proof of the estimate, the following progress is evaluated (points for progress (1) are not summed with points for progress (2a), (2b), (2c), points for progress ( $2 \mathrm{a}),(2 \mathrm{~b}),(2 \mathrm{c})$ are summed):
(1) The idea of tracking the membership of chips to the arc 100-1 (or the relative position of the triplet of chips $1, m, 100)-2$ points.
(2a) shifts are considered and it is shown that the sum of shifts is $0-1$ point.
(2b) in the assumption that the chips are finally shifted 1 position clockwise, an equation for the sum of "number of rotations" is written -1 point.
(2c) it is shown that chips with different "number of rotations" or with "number of rotations" of different signs must have swapped places at some point -1 point.
|
50
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.4. Point $E$ is the midpoint of side $A B$ of parallelogram $A B C D$. On segment $D E$, there is a point $F$ such that $A D = B F$. Find the measure of angle $C F D$.
|
Answer: $90^{\circ}$.
Solution. Extend $D E$ to intersect line $B C$ at point $K$ (see Fig. 8.4). Since $B K \| A D$, then $\angle K B E = \angle D A E$. Moreover, $\angle K E B = \angle D E A$ and $A E = B E$, therefore, triangles $B K E$ and $A D E$ are equal. Thus, $B K = A D = B C$.
Therefore, in triangle $CFK$, the median $F B$ is equal to half the side to which it is drawn, so this triangle is a right triangle with a right angle at $F$. Consequently, angle $CFD$ is also a right angle.
Grading Criteria.
「+」 A correct and well-reasoned solution is provided
「±」 A generally correct reasoning is provided, containing minor gaps or inaccuracies
「-」 Only the answer is provided
「-」 The problem is not solved or is solved incorrectly
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. Kuzya cut a convex paper 67-gon along a straight line into two polygons, then similarly cut one of the two resulting polygons, then one of the three resulting ones, and so on. In the end, he got eight $n$-gons. Find all possible values of $n$.
|
Answer: $n=11$.
Solution. A straight-line cut can be of three types: from side to side, from a vertex to a side, and from a vertex to a vertex. Therefore, after one cut, the total number of sides of the polygons increases by 4, 3, or 2, respectively. Kuzya made 7 cuts, so the number of sides added is at least 14 but no more than 28. Therefore, the total number of sides of the eight $n$-gons is between 81 and 95. Among the integers in this range, only the number 88 is divisible by 8 without a remainder, so $n=88 \div 8=11$.
Grading Criteria.
“+” A complete and well-reasoned solution is provided
“土” A generally correct reasoning is provided, but it contains minor gaps or inaccuracies (for example, it is not explained how the total number of sides changes in each of the three cases)
“干” The correct answer is obtained, but not all cases are considered
“干” The correct answer is provided and it is only verified that it satisfies the condition, but there is no proof of the absence of other answers
“-” Only the answer is provided
“-” The problem is not solved or is solved incorrectly
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.6. A triangle is divided into triangular cells as shown in the figure. A natural number is written in each cell. For each side of the triangle, there are four layers parallel to this side, containing seven, five, three, and one cell, respectively. It turns out that the sum of the numbers in each of these twelve layers is a prime number. What is the smallest possible sum of all the written numbers?
|
Answer: 22.
Solution. Example. In each of the three corner cells, we write the number 3, and in each of the others, we write the number 1. Then the sum of the written numbers is $3 \cdot 3 + 13 \cdot 1 = 22$, and the sums of the numbers in the layers are: 11, 5, 3, and 3, respectively.
Estimation. Any corner cell is a separate layer, so each such cell must contain at least the number 2. Consider, for example, the other horizontal layers. In the two layers below the corner cell, we can place numbers with the minimum sums: 1-1-1 and 1-1-1-1-1. Then, in the bottom layer, the arrangement with the minimum sum is: $2+1$ $+1+1+1+1+2=9$, but this is not a prime number. The nearest prime number greater than nine is 11. Therefore, the sum of all numbers is no less than $2+3+5+11=21$.
However, this sum is not achievable, as when considering four layers along the other sides of the original triangle, we find that 2 must be added to each layer of seven cells. Consequently, 22 is the smallest possible sum.
Grading Criteria.
“+” A complete and well-reasoned solution is provided
“土” A generally correct reasoning is provided, containing minor gaps or inaccuracies
“干” The correct answer and example are provided, but the estimation is missing
“-” Only the answer is provided
“-” The problem is not solved or is solved incorrectly
|
22
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 4.2. Find the smallest number in which all digits are different, and the sum of all digits is 32.
|
Answer: 26789.
Solution. For a four-digit number with different digits, the maximum possible sum of digits is $9+8+7+6=30<32$, so the number we need must be at least five digits.
We will try to make the first digit as small as possible. It is clear that it is no less than 2. We will place 2 in the first position. The sum of the remaining four digits is 30, which can only be obtained as $9+8+7+6$. We place the smallest of these digits, 6, in the second position, the next largest digit, 7, in the third position, 8 in the fourth, and 9 in the fifth.
|
26789
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.3. Zhenya drew a square with a side of 3 cm, and then erased one of these sides. A figure in the shape of the letter "P" was obtained. The teacher asked Zhenya to place dots along this letter "P", starting from the edge, so that the next dot was 1 cm away from the previous one, as shown in the picture, and then count how many dots he got. He got 10 dots.
Then the teacher decided to complicate the task and asked to count the number of dots, but for the letter "P" obtained in the same way from a square with a side of 10 cm. How many dots will Zhenya have this time?
|
Answer: 31.
Solution. Along each of the three sides of the letter "П", there will be 11 points. At the same time, the "corner" points are located on two sides, so if 11 is multiplied by 3, the "corner" points will be counted twice. Therefore, the total number of points is $11 \cdot 3-2=31$.
|
31
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.4. Lev Alex decided to count the stripes on Marty the zebra (black and white stripes alternate). It turned out that there is one more black stripe than white ones. Alex also noticed that all white stripes are of the same width, while black stripes can be wide or narrow, and there are 7 more white stripes than wide black ones. How many narrow black stripes does Marty have?
|
# Answer: 8.
Solution. First, let's look only at the wide black stripes. There are 7 fewer of them than white ones. If we add the narrow black stripes to the wide black ones, we get all the black stripes, which are 1 more than the white ones. Therefore, to find the number of narrow black stripes, we need to first "compensate" for the 7 white stripes - the number by which the white ones were greater, and then add one more. This gives us $7+1=8$.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.5. Hooligan Dima laid out a structure in the shape of a $3 \times 5$ rectangle using 38 wooden toothpicks. Then he simultaneously set fire to two adjacent corners of this rectangle, marked in the diagram.
It is known that one toothpick burns for 10 seconds. How many seconds will it take for the entire structure to burn?
(Fire spreads along the toothpicks at a constant speed. The fire continues to spread from each burned toothpick to all adjacent unburned toothpicks.)

|
Answer: 65.
Solution. In the picture below, for each "node", the point where the toothpicks connect, the time in seconds it takes for the fire to reach it is indicated. It will take the fire another 5 seconds to reach the middle of the middle toothpick in the top horizontal row (marked in the picture).
|
65
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 011011010011.
Information has emerged that this encoding has been deciphered, as a result of which the agent will have to use a backup encoding. In it, the letter A is replaced by 21, the letter B by 122, and the letter V by 1. What code will this message receive in the new encoding?
|
Answer: 211221121.
Solution. Let's look at the right end of the code. Two ones at the end can only come from the letter A: 011011010011.
Next, we look at the rightmost digit of those we haven't figured out yet, from which letter it came. The digit 0 at the end is only present in B: 011011010011.
Similarly, the previous letter is also B: 011011010011.
Now the "undeciphered" rightmost digit is 1. Before it stands a 0. This can only come from the letter B: 011011010011.
The "undeciphered" digits on the right are two ones. This can only come from A:
The message obtained is ABBBA, which when encoded anew gives 211221121.
A B BB A
|
211221121
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.2. Several people were seated around a round table such that the distances between adjacent people are the same. One of them was given a sign with the number 1, and then everyone was given signs with numbers 2, 3, and so on, in a clockwise direction.
The person with the sign numbered 31 noticed that the distance from them to the person with the sign numbered 7 is the same as the distance to the person with the sign numbered 14. How many people in total sat at the table?
|
Answer: 41.
Solution. For such a situation to be possible, people from the 31st to the 14th need to be counted in a circle in the direction of decreasing numbers, and from the 31st to the 7th - in a circle in the direction of increasing numbers.
There are 16 people sitting between the 31st and the 14th. Therefore, there are also 16 people between the 31st and the 7th. Among them, 6 have numbers from 1 to 6, so the remaining $16-6=10$ people are those with numbers from the 32nd. The largest number is 41.
|
41
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.4. The school principal, the caretaker, and the parent committee, failing to agree with each other, each bought a carpet for the school auditorium, which is $10 \times 10$. After thinking about what to do, they decided to place all three carpets as shown in the picture: the first carpet $6 \times 8$ - in one corner, the second carpet $6 \times 6$ - in the opposite corner, and the third carpet $5 \times 7$ - in one of the remaining corners (all dimensions are in meters).
Find the area of the part of the hall covered by carpets in three layers (give the answer in square meters).
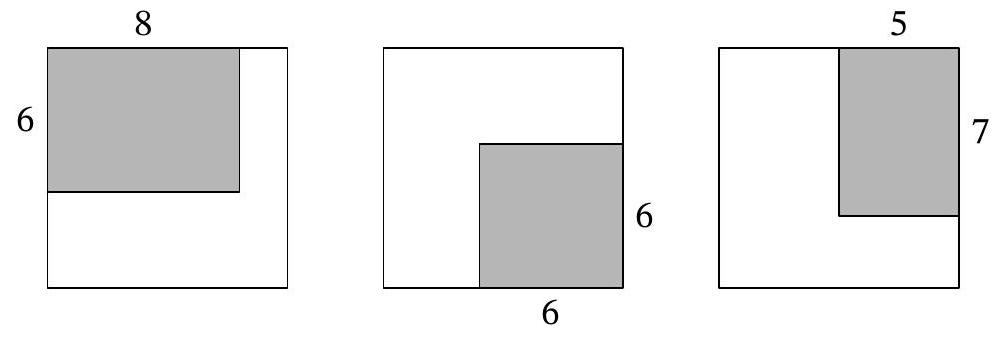
|
Answer: 6.
Solution. We will measure all dimensions in meters and the area in square meters.
Let's look at the overlap of the second and third carpets. This will be a rectangle $5 \times 3$ (5 along the horizontal, 3 along the vertical), adjacent to the right side of the square room, 4 units from the top side, and 3 units from the bottom side.
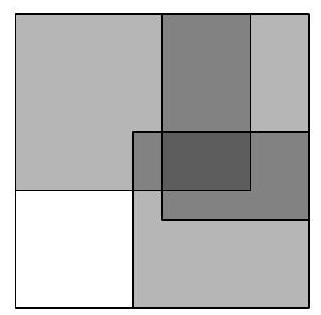
The first carpet intersects this rectangle horizontally between the 5th and 8th meters from the left side of the square room, and vertically between the 4th and 6th meters from the top side. In the end, this results in a rectangle $2 \times 3$, the area of which is 6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.6. Several stones are arranged in 5 piles. It is known that
- in the fifth pile, there are six times more stones than in the third;
- in the second pile, there are twice as many stones as in the third and fifth combined;
- in the first pile, there are three times fewer stones than in the fifth, and ten fewer than in the fourth;
- in the fourth pile, there are half as many stones as in the second.
How many stones are there in total in these five piles?
|
Answer: 60.
Solution. Let's denote the number of stones in the third pile as a rectangle. Then, since there are 6 times more stones in the fifth pile, this can be represented as 6 rectangles. In the second pile, the number of stones is twice the sum of the third and fifth piles, which is $(1+6) \cdot 2=14$ rectangles. In the first pile, there are three times fewer stones than in the fifth pile, which is $6: 3=2$ rectangles. In the fourth pile, there are two times fewer stones than in the second pile, which is $14: 2=7$ rectangles.
It is also known that there are 10 fewer stones in the first pile than in the fourth pile. Therefore, 5 rectangles correspond to 10 stones. This means 1 rectangle = 2 stones.
In total, $2+14+1+7+6=30$ rectangles. This is $30 \cdot 2=60$ stones.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.8. Inside a large triangle with a perimeter of 120, several segments were drawn, dividing it into nine smaller triangles, as shown in the figure. It turned out that the perimeters of all nine small triangles are equal to each other. What can they be equal to? List all possible options.
The perimeter of a figure is the sum of the lengths of all its sides.
|
Answer: 40.
Solution. Let's add the perimeters of the six small triangles marked in gray in the following figure:
From the obtained value, subtract the perimeters of the other three small white triangles. Since the perimeters of the small triangles are equal, on one side, we get three times the perimeter of a small triangle. On the other side, in this sum, there will only be segments that make up the perimeter of the large triangle, which is 120. Therefore, the perimeter of a small triangle is $120: 3=40$.
## 6th grade
|
40
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.1. Five consecutive natural numbers are written in a row. The sum of the three smallest of them is 60. What is the sum of the three largest?
|
Answer: 66.
Solution. The fifth number is 4 more than the first, and the fourth is 2 more than the second. Then the sum of the three largest numbers is $2+4=6$ more than the sum of the three smallest, and it is equal to $60+6=66$.
|
66
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.6. On an island, there live knights who always tell the truth, and liars who always lie. One day, 65 inhabitants of the island gathered for a meeting. Each of them, in turn, made the statement: "Among the previously made statements, there are exactly 20 fewer true statements than false ones." How many knights were at this meeting?
|
Answer: 23.
Solution. The first 20 people are liars, because before them, there were no more than 19 statements made, which means there cannot be exactly 20 fewer true statements than false ones.
Next, the 21st person tells the truth (since before him, there were exactly 20 false statements), so he is a knight. Then the 22nd person lies (before him, there were 20 false and 1 true statement), so he is a liar. Next, the 23rd person tells the truth (the number of false statements is again 20 more than the number of true ones), so the 23rd is a knight, and so on.
Among the people starting from the 21st, those with odd numbers are knights, and those with even numbers are liars. Among the numbers from 21 to 65 inclusive, there are exactly 23 odd numbers, so there were exactly 23 knights at the meeting.
|
23
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.7. Anya places pebbles on the sand. First, she placed one stone, then added pebbles to form a pentagon, then made a larger outer pentagon with pebbles, then another outer pentagon, and so on, as shown in the picture. The number of stones she had arranged on the first four pictures: 1, 5, 12, and 22. If she continues to create such pictures, how many stones will be on the 10th picture?
-
|
Answer: 145.
Solution. On the second picture, there are 5 stones. To get the third picture from it, you need to add three segments with three stones on each. The corner stones will be counted twice, so the total number of stones in the third picture will be $5+3 \cdot 3-2=12$.
To get the fourth picture from the third, you need to add three segments with four stones on each. The corner stones will be counted twice, so the total number of stones will be $12+3 \cdot 4-2=22$.
Similarly, we will calculate the number of stones on each of the remaining pictures:
on the 5th: $22+3 \cdot 5-2=35$;
on the 6th: $\quad 35+3 \cdot 6-2=51$;
on the 7th: $51+3 \cdot 7-2=70$;
on the 8th: $\quad 70+3 \cdot 8-2=92$;
on the 9th: $92+3 \cdot 9-2=117$
on the 10th: ~ 117+3 \cdot 10-2=145$.
|
145
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.1. Sasha and Vanya are playing a game. Sasha asks Vanya questions. If Vanya answers correctly, Sasha gives him 7 candies. If Vanya answers incorrectly, he gives Sasha 3 candies. After Sasha asked 50 questions, it turned out that each of them had as many candies as they had at the beginning. How many questions did Vanya answer correctly?
|
Answer: 15.
Solution. Let Vanya answer correctly to $x$ questions, then he answered incorrectly to $50-x$ questions. This means that during the game, Vanya received $7 x$ candies and gave away $3(50-x)$ candies. Since the total number of candies for both boys did not change after the game, we get $7 x=3(50-x)$. Solving this, we find $x=15$.
Remark. The same answer could have been obtained by understanding that to "balance the candies," Vanya should "compensate" every 3 correct answers with 7 incorrect ones.
|
15
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.3. Numbers were placed in the cells of a square such that the sums of the numbers in each vertical, horizontal, and each diagonal of three cells are equal. Then some numbers were hidden. What is the sum of the numbers in the two shaded cells?
| 16 | | |
| :--- | :--- | :--- |
| | | 10 |
| 8 | | 12 |
|
Answer: 34.
Solution. Let $a$ be the number in the top right cell, and $b$ be the number in the central cell. The sum of the diagonal containing the number 8 and the sum of the numbers in the right column have a common term $a$, so $8+b=10+12$, from which $b=14$. The sums of the three numbers along both diagonals have a common number $b$, so $16+12=8+a$, from which $a=20$. Therefore, $a+b=20+14=34$.
Remark. The other numbers can also be placed to verify that the problem's condition is correct:
| 16 | 6 | 20 |
| :---: | :---: | :---: |
| 18 | 14 | 10 |
| 8 | 22 | 12 |
|
34
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.4. Masha and Olya bought many identical pens for the new school year at the store. It is known that one pen costs an integer number of rubles, more than 10. Masha bought pens for exactly 357 rubles, and Olya - for exactly 441 rubles. How many pens did they buy in total?
|
Answer: 38.
Solution. Let the pen cost $r$ rubles. Then the numbers 357 and 441 are divisible by $d$. Since the greatest common divisor of the numbers $357=3 \cdot 7 \cdot 17$ and $441=3^{2} \cdot 7^{2}$ is $3 \cdot 7$, then 21 is also divisible by $r$. Since $r>10$, then $r=21$. Therefore, the total number of pens bought is $\frac{357}{21}+\frac{441}{21}=17+21=38$.
|
38
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.5. In each room of the hotel, no more than 3 people can be accommodated. The hotel manager knows that a group of 100 football fans, who support three different teams, will soon arrive. In one room, only men or only women can be accommodated; also, fans of different teams cannot be accommodated together. How many rooms need to be reserved to definitely accommodate all the fans?
|
Answer: 37.
Solution. All fans are divided into six groups: men/women, supporting the first team; men/women, supporting the second team; men/women, supporting the third team. Only people from the same group can be housed in one room. We divide the number of people in each of the six groups by 3 with a remainder. If the remainder in any group is 1, we will house one person from that group in a separate room. If the remainder is 2, we will house any two people from that group in a separate room. Now, in each group, the number of unaccommodated fans is divisible by 3.
After we have accommodated the remainders of each group, some number of unaccommodated people remain. This total number is no more than 100 and no less than 88 (since the sum of all six remainders is no more than $6 \cdot 2=12$, and $100-12=88$). This number is divisible by 3, so it is equal to one of the values $90, 93, 96, 99$ (and all corresponding people can be accommodated in rooms of three). Let's consider several cases.
- If 90 people remain, they need $90: 3=30$ rooms, and the remaining 10 people from the 6 groups will definitely fit into 6 rooms. In total, no more than 36 rooms are needed.
- If 93 people remain, they need $93: 3=31$ rooms, and the remaining 7 people from the 6 groups will definitely fit into 6 rooms. In total, no more than 37 rooms are needed.
- If 96 people remain, they need $96: 3=32$ rooms, and the remaining 4 people will definitely fit into 4 rooms. In total, no more than 36 rooms are needed.
- If 99 people remain, they need $99: 3=33$ rooms, and the remaining one person will definitely fit into 1 room. In total, no more than 34 rooms are needed.
Thus, 37 rooms are definitely enough.
We will also provide an example where at least 37 rooms are necessary. Suppose the distribution of people among the six groups is such: $20, 16, 16, 16, 16, 16$. For the group of 20 people, at least 7 rooms are needed, and for each of the others, at least 6 rooms are needed. In total, at least $7+6 \cdot 5=37$ rooms are needed.
|
37
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.7. The numbers from 1 to 200 were arranged in a random order on a circle such that the distances between adjacent numbers on the circle are the same.
For any number, the following is true: if you consider 99 numbers standing clockwise from it and 99 numbers standing counterclockwise from it, there will be an equal number of numbers that are smaller than it in both groups. Which number stands opposite the number 113?
|
Answer: 114.
Solution. Consider the number 2. Less than it is only the number 1. Since it is unique, it cannot be in any of the groups relative to the number 2. Therefore, 1 must be opposite 2.
Consider the number 4. The numbers less than it are three in number - an odd count. This means that one of them should not be in any of the groups relative to the number 4, i.e., it should be opposite. Since 1 and 2 are already standing opposite each other, 3 is opposite 4.
Continuing similar reasoning further, we get that opposite any even number stands an odd number that is one less than it. Thus, opposite the number 114 stands the number 113. And vice versa: opposite 113 stands 114.
|
114
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.2. In the chat of students from one of the schools, a vote was held: "On which day to hold the disco: October 22 or October 29?"
The graph shows how the votes were distributed an hour after the start of the voting.
Then, 80 more people participated in the voting, voting only for October 22. After that, the voting ended. The final distribution of votes is also shown on the graph.
How many people participated in the voting?
|
Answer: 260.
Solution. Let $x$ be the number of people who voted an hour after the start. From the left chart, it is clear that $0.35 x$ people voted for October 22, and $-0.65 x$ people voted for October 29.
In total, $x+80$ people voted, of which $45\%$ voted for October 29. Since there are still $0.65 x$ of them, we get the equation
$0.65 x=0.45(x+80)$, from which we find $x=180$. Therefore, a total of $180+80=260$ people participated in the voting.
|
260
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.3. In the class, there are 29 students: some are excellent students and some are troublemakers. Excellent students always tell the truth, while troublemakers always lie.
All students in this class sat around a round table.
- Several students said: “There is exactly one troublemaker next to me.”
- All other students said: “There are exactly two troublemakers next to me.”
What is the minimum number of troublemakers that can be in the class?
|
Answer: 10.
Solution. If there were three straight-A students in a row, the middle one would definitely lie. Therefore, among any three consecutive people, there must be at least one troublemaker.
Choose an arbitrary troublemaker. Assign this person the number 29, and number all the people following them clockwise from 1 to 28. Since in each of the non-overlapping groups $(1,2,3),(4,5,6), \ldots,(25,26,27),(29)$ there is at least one troublemaker, there must be at least $\frac{27}{3}+1=10$ troublemakers in total.
Note also that there could have been exactly 10 troublemakers. Again, numbering the people clockwise from 1 to 29, let the students with numbers $3,6,9,12,15,18,21,24$, 27, 29 be the troublemakers, and the students with all other numbers be straight-A students. In this case, all straight-A students except the one with number 28 said the first phrase, while the student with number 28 and all the troublemakers said the second phrase. It is easy to see that all the conditions of the problem are satisfied.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.4. Points $D$ and $E$ are marked on sides $A C$ and $B C$ of triangle $A B C$ respectively, such that $A D=E C$. It turns out that $B D=E D, \angle B D C=\angle D E B$. Find the length of segment $A C$, given that $A B=7$ and $B E=2$.
|
Answer: 12.
Solution. Note that triangles $D E C$ and $B D A$ are equal. Indeed, $D E=B D, E C=$ $D A$ and $\angle D E C=180^{\circ}-\angle B E D=180^{\circ}-\angle B D C=\angle B D A$. From this, it follows that $D C=A B=7$ and $\angle D C E=\angle B A D$ (Fig. 3). From the equality of these angles, it follows that triangle $A B C$ is isosceles, $7=A B=B C=2+E C$, from which we get $5=E C=A D$ and $A C=A D+D C=5+7=12$.
Fig. 3: to the solution of problem 8.4
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.5. The numbers $1, 2, 3, \ldots, 235$ were written on a board. Petya erased some of them. It turned out that among the remaining numbers, no number is divisible by the difference of any two others. What is the maximum number of numbers that could remain on the board?
|
Answer: 118.
Solution. 118 odd numbers could remain on the board: none of them is divisible by the difference of any two others, because this difference is even.
Suppose at least 119 numbers could remain. Consider 118 sets: 117 pairs $(1,2)$, $(3,4),(5,6), \ldots,(233,234)$ and one number 235. By the Pigeonhole Principle, in one of these sets, at least two numbers remained. This means that among the remaining numbers, there will be two consecutive numbers, but then their difference, equal to 1, is a divisor of any other remaining number. Contradiction.
|
118
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.7. The figure shows two equal triangles: $A B C$ and $E B D$. It turns out that $\angle D A E = \angle D E A = 37^{\circ}$. Find the angle $B A C$.
|
Answer: 7.
Fig. 4: to the solution of problem 8.7
Solution. Draw segments $A D$ and $A E$ (Fig. 4). Since $\angle D A E=\angle D E A=37^{\circ}$, triangle $A D E$ is isosceles, $A D=D E$.
Notice that triangle $A B D$ is equal to triangle $E B D$ by three sides: $B D$ is a common side, $A D=D E, A B=B E$ from the equality of triangles $A B C$ and $E B D$. Then $\angle D A B=$ $\angle B E D=\angle B A C$ and $\angle A B D=\angle D B E=\angle A B E=\frac{1}{3} \cdot 360^{\circ}=120^{\circ}$.
Since $A B=B E$, triangle $A B E$ is isosceles with an angle of $120^{\circ}$, so $\angle B A E=\frac{1}{2}\left(180^{\circ}-120^{\circ}\right)=30^{\circ}$. Therefore,
$$
\angle B A C=\angle D A B=\angle D A E-\angle B A E=37^{\circ}-30^{\circ}=7^{\circ}
$$
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.8. In how many ways can all natural numbers from 1 to 200 be painted in red and blue so that the sum of any two different numbers of the same color is never equal to a power of two?
|
Answer: 256.
## Solution.
Lemma. If the sum of two natural numbers is a power of two, then the powers of 2 in the prime factorizations of these two numbers are the same.
Proof of the lemma. Let the sum of the numbers $a=2^{\alpha} \cdot a_{1}$ and $b=2^{\beta} \cdot b_{1}$, where $a_{1}$ and $b_{1}$ are odd, be $2^{n}$. Since $2^{n}=a+b>a \geqslant 2^{\alpha}$, then $n>\alpha$. Suppose that $\alpha$ and $\beta$ are different, without loss of generality, $\alpha>\beta$. Then $b=2^{\beta} \cdot b_{1}=2^{n}-2^{\alpha} \cdot a_{1}=2^{\alpha}\left(2^{n-\alpha}-a_{1}\right)$ is divisible by $2^{\alpha}$. But $\beta<\alpha$, a contradiction. The lemma is proved.
We call a two-color coloring of a set $M$ good if the sum of any two different numbers of the same color from the set $M$ is not a power of two. We call a two-color coloring of a sequence $x_{1} \leqslant x_{2} \ldots \leqslant x_{t}$ alternating if any two adjacent numbers in this sequence are painted in different colors.
Consider 8 sets of numbers, each having the same power of 2 in their prime factorization:
$$
M_{0}=\{1,3,5, \ldots, 199\}, M_{1}=\{2,6,10, \ldots, 198\}, M_{2}=\{4,12,20, \ldots, 196\}, \ldots, M_{7}=\{128\}
$$
We will prove that for each of these 8 sets, there exist exactly two good colorings, both of which are alternating. Since numbers from different sets do not add up to a power of two (this follows from the lemma), we will get that the total number of good colorings of the numbers $1,2, \ldots, 200$ is exactly $2^{8}=256$.
Consider $M_{k}=\left\{2^{k}, 3 \cdot 2^{k}, 5 \cdot 2^{k}, \ldots\right\}$. Consider the set of numbers $M_{k}^{*}$, which contains all the numbers of the set $M_{k}$ divided by $2^{k}$. Obviously, any good coloring of the set $M_{k}$ corresponds to exactly one good coloring of the set $M_{k}^{*}$ (if the sum of two numbers was a power of two, then the sum of these numbers divided by $2^{k}$ will also be a power of two, and vice versa). It is sufficient to prove that for $M_{k}^{*}$ there exist exactly two good colorings, both of which are alternating.
Obviously, $M_{k}^{*}$ consists of several of the first odd natural numbers (possibly one). Without loss of generality, the number 1 in it is red. Since $1+3=2^{2}$, the number 3 is blue. Since $5+3=7+1=2^{3}$, the number 5 is red, and the number 7 is blue. This can be continued: if the coloring of the odd numbers from 1 to $2^{s}-1$ is alternating, then the coloring of the odd numbers from $2^{s}+1$ to $2^{s+1}-1$ is also alternating (since $\left.\left(2^{s}+1\right)+\left(2^{s}-1\right)=\left(2^{s}+3\right)+\left(2^{s}-3\right)=\ldots=\left(2^{s+1}-1\right)+1=2^{s+1}\right)$. At the same time, the numbers $2^{s}-1$ and $2^{s}+1$ are painted in different colors, so the coloring of the numbers from 1 to $2^{s+1}-1$ is also alternating. Thus, if the number 1 is red, then the coloring is uniquely determined, and it is alternating. Obviously, if the number 1 is blue, then the coloring is also uniquely determined, and it is also alternating. It is also clear that alternating colorings work: in them, any two different numbers of the same color are odd and have the same remainder when divided by 4, so their sum is greater than 2 and does not divide by 4, hence it is not a power of two. There are no other colorings.
Another solution. If the sum of two different numbers is a power of two, we will call the smaller of them the parent of the larger one. We will prove that powers of two have no parents, and all other numbers have exactly one parent.
Indeed, consider a number $x$ in the range $2^{k-1} \leqslant x<2^{k}$ for some $k \geqslant 0$. Let one of its parents be some number $y<x$. Then $2^{k-1} \leqslant x<$
$x+y<2 x<2^{k+1}$, from which $x+y=2^{k}$ (this must be some power of two). Therefore, the parent $y=2^{k}-x$ for $x \neq 2^{k-1}$ is uniquely determined (and for $x=2^{k-1}$ we get $y=x$, which is impossible). On the other hand, it is clear that if $x \neq 2^{k-1}$, then $2^{k}-x$ is indeed a parent of the number $x\left(2^{k}-x \leqslant 2^{k}-2^{k-1}=2^{k-1}<x\right.$ and $\left.2^{k}-x+x=2^{k}\right)$.
Now we will show that any coloring of the powers of two can be uniquely continued to a coloring of the entire given set of numbers. Suppose all powers of two from our set are already painted red or blue. We will start going through the other numbers in ascending order $(3,5,6, \ldots)$; when we reach the next number, it will have a parent, and it will already be painted. Therefore, we can paint the current number in the only possible way - in the color opposite to the color of its parent. This way we will paint all the numbers.
The resulting coloring will satisfy the condition, since in any pair of numbers that add up to a power of two, the larger number will be painted in the color opposite to the color of its parent, i.e., the smaller number of the pair.
Therefore, the number of ways to color the given range in the required manner coincides with the number of ways to color the powers of two from the range arbitrarily. Since we have 8 powers of two (from $2^{0}$ to $2^{7}$), the number of ways is exactly $2^{8}$.
## 9th grade
|
256
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.1. On an island, there live red, yellow, green, and blue chameleons.
- On a cloudy day, either one red chameleon changes its color to yellow, or one green chameleon changes its color to blue.
- On a sunny day, either one red chameleon changes its color to green, or one yellow chameleon changes its color to blue.
In September, there were 18 sunny and 12 cloudy days. As a result, the number of yellow chameleons increased by 5. By how much did the number of green chameleons increase?
|
Answer: 11.
Solution. Let $A$ be the number of green chameleons on the island, and $B$ be the number of yellow chameleons. Consider the quantity $A-B$. Note that each cloudy day it decreases by 1, and each sunny day it increases by 1. Since there were $18-12=6$ more sunny days than cloudy days in September, the quantity $A-B$ increased by 6 over this period. Since $B$ increased by 5, $A$ must have increased by $5+6=11$.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.2. Denis has cards with numbers from 1 to 50. How many ways are there to choose two cards such that the difference between the numbers on the cards is 11, and the product is divisible by 5?
The order of the selected cards does not matter: for example, the way to choose cards with numbers 5 and 16, and the way to choose cards with numbers 16 and 5 - this is the same way.
|
Answer: 15.
Solution. For the product to be divisible by 5, it is necessary and sufficient that one of the factors is divisible by 5. Let $n$ be the chosen number divisible by 5, then its pair should be $n-11$ or $n+11$, and both chosen numbers must be natural numbers. Clearly, for $n=5,10,40,45,50$ there is only one way to choose a pair, while for $n=15,20,25,30,35$ there are exactly two ways to choose a pair. In total, $5 \cdot 1+5 \cdot 2=15$ ways.
|
15
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.3. Traders Andrey and Boris bought 60 bags of potatoes each from the same farmer. All the bags cost the same.
Andrey sold all his bags, increasing their price by $100 \%$. Boris first increased the price by $60 \%$, and after selling 15 bags, increased the price by another $40 \%$ and sold the remaining 45 bags.
It turned out that Boris earned 1200 rubles more than Andrey. How many rubles did one bag of potatoes cost from the farmer?
|
Answer: 250.
Solution. Let the bag cost the farmer $x$ rubles. Andrei and Boris spent the same amount on buying 60 bags.
From the condition, it follows that Andrei sold 60 bags for $2 x$ rubles each, i.e., he received $60 \cdot 2 x$ rubles. Boris, on the other hand, sold 15 bags at a price of $1.6 x$ rubles and then sold 45 bags at a price of $1.6 x \cdot 1.4$ rubles. We get the equation
$$
2 x \cdot 60 + 1200 = 15 \cdot 1.6 x + 45 \cdot 1.6 x \cdot 1.4
$$
Solving it, we find $x=250$.
|
250
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.4. A line $\ell$ is drawn through vertex $A$ of rectangle $ABCD$, as shown in the figure. Perpendiculars $BX$ and $DY$ are dropped from points $B$ and $D$ to line $\ell$. Find the length of segment $XY$, given that $BX=4$, $DY=10$, and $BC=2AB$.
|
Answer: 13.
Fig. 5: to the solution of problem 9.4
Solution. Note that since $\angle Y A D=90^{\circ}-\angle X A B$ (Fig. 5), right triangles $X A B$ and $Y D A$ are similar by the acute angle $\angle Y A D=\angle X B A$. The similarity coefficient is the ratio $A B: A D$, which is $\frac{1}{2}$. From this, we get $X A=\frac{1}{2} D Y=5$ and $A Y=2 B X=8$, which in total gives $X Y=13$.
Fig. 6: to the solution of problem 9.4
Another solution. Let $M$ be the midpoint of segment $A D$, then $A M=M D=\frac{A D}{2}=\frac{B C}{2}=A B$ (Fig. 6). Drop a perpendicular from $M$ to $M H$ on line $\ell$. Since in triangle $A D Y$ the segment $M H$ passes through the midpoint of side $A D$ and is parallel to side $D Y$, it is the midline, $A H=H Y$ and $M H=\frac{D Y}{2}=\frac{10}{2}=5$.
Note that $\angle A B X=90^{\circ}-\angle B A X=90^{\circ}-\left(180-90^{\circ}-\angle M A H\right)=\angle M A H$. Then right triangles $A B X$ and $M A H$ are equal by hypotenuse $A B=A M$ and acute angle $\angle A B X=\angle M A H$. From this, it follows that $A X=M H=5$ and $A H=B X=4$.
Thus, $X Y=A X+A H+H Y=5+4+4=13$.
|
13
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.6. In triangle $ABC$, the angles $\angle B=30^{\circ}$ and $\angle A=90^{\circ}$ are known. On side $AC$, point $K$ is marked, and on side $BC$, points $L$ and $M$ are marked such that $KL=KM$ (point $L$ lies on segment $BM$).
Find the length of segment $LM$, if it is known that $AK=4$, $BL=31$, and $MC=3$.
|
Answer: 14.
Solution. In the solution, we will use several times the fact that in a right-angled triangle with an angle of $30^{\circ}$, the leg opposite this angle is half the hypotenuse. Drop the height $K H$ from the isosceles triangle $K M L$ to the base (Fig. 7). Since this height is also a median, then $M H=H L=x$. In the right-angled triangle $C K H$ we have $\angle C K H=90^{\circ}-\angle C=\angle A=30^{\circ}$, so $K C=2 \cdot C H=2 \cdot(C M+M H)=$ $2 \cdot(3+x)=6+2 x$. In the right-angled triangle $A B C$ we have $\angle A=30^{\circ}$, so $B C=2 \cdot A C$. Setting up and solving the corresponding equation $31+2 x+3=2 \cdot(4+6+2 x)$, we find $x=7$. Then $L M=2 x=2 \cdot 7=14$.
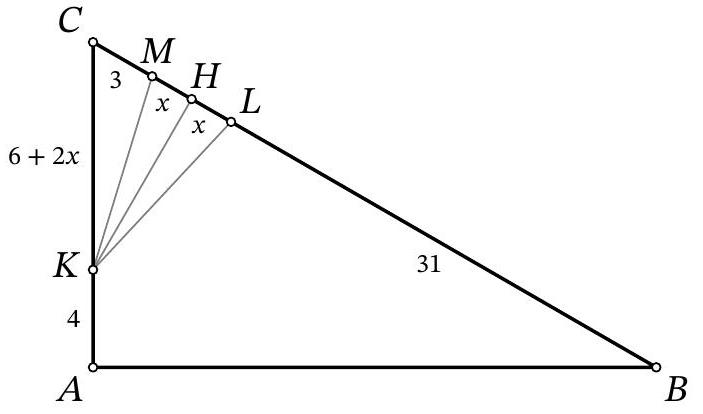
Fig. 7: to the solution of problem 9.6
|
14
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.8. Integers $n$ and $m$ satisfy the inequalities $3 n - m \leq 26$, $3 m - 2 n < 46$. What can $2 n + m$ be? List all possible options.
|
Answer: 36.
Solution. Since the numbers $m$ and $n$ are integers, the values of the expressions in the condition $3 n-m$, $n+m$, $3 m-2 n$ are also integers. Then
$$
\left\{\begin{array}{l}
3 n-m \leqslant 4 \\
n+m \geqslant 27 \\
3 m-2 n \leqslant 45
\end{array}\right.
$$
By adding three times the first inequality to the third, we get $7 n \leqslant 57$, from which $n \leqslant 8$. By adding twice the first inequality to three times the third, we get $7 m \leqslant 143$, from which $m \leqslant 20$.
Thus, $n \leqslant 8, m \leqslant 20$, and $n+m \geqslant 27$. This is possible in only three cases.
- Suppose $n=7, m=20$. Then the condition $3 m-2 n \leqslant 45$ is not satisfied.
- Suppose $n=8, m=19$. Then the condition $3 n-m \leqslant 4$ is not satisfied.
- Suppose $n=8, m=20$. It is easy to see that all conditions are satisfied in this case. Therefore, $2 n+m=2 \cdot 8+20=36$.
Another solution. Let's represent the given inequalities as regions on the coordinate plane Omn, as shown in Fig. 8. Each inequality corresponds to a certain half-plane. For example, the inequality $3 n-m<5$ is the half-plane located below the line $3 n-m=5$.
The intersection of these half-planes is a triangle, inside which lies one integer point $m=20, n=8$ (points on the boundary of the triangle do not work, as the inequalities are strict), from which we immediately get the unique answer $2 n+m=36$.
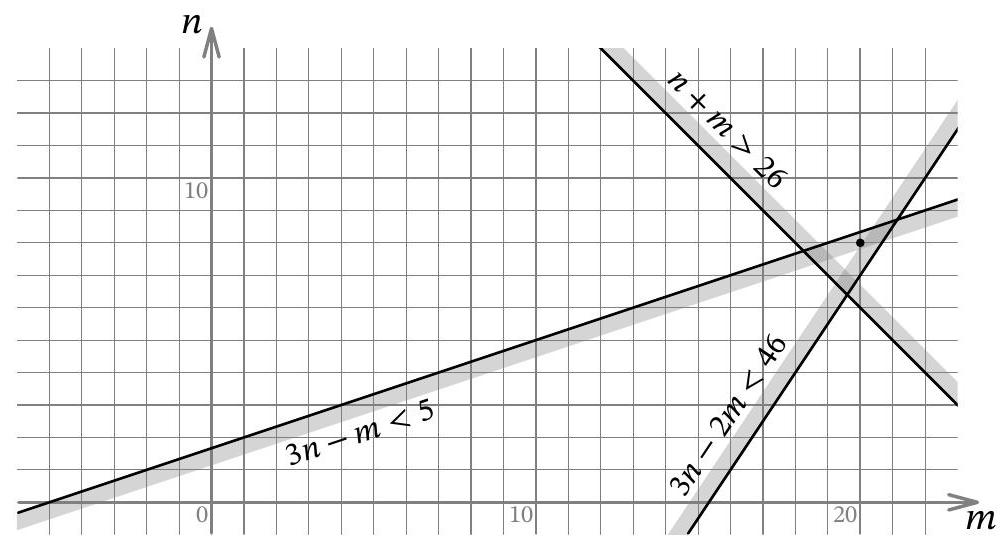
Fig. 8: to the solution of problem 9.8
## 10th grade
|
36
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 10.1. Find the largest 12-digit number $N$ that satisfies the following two conditions:
- In the decimal representation of the number $N$, there are six digits «4» and six digits «7»;
- In the decimal representation of the number $N$, no four consecutive digits form the number «7444».
|
Answer: 777744744744.
Solution. It is clear that the number 777744744744 meets the condition of the problem.
Suppose there exists a larger number, then it must start with four sevens. In this number, we select the largest number of consecutive fours, let there be $k$ of them. If $k \geqslant 3$, then by selecting among these $k$ fours the three leftmost ones, as well as the seven to the left of them, we get a segment of digits "7444," which is a contradiction.
Therefore, $k \leqslant 2$. In the last eight digits of the number, there must be six fours. Since no three consecutive digits can all be fours, the last eight digits are uniquely determined: they are 44744744. But the corresponding number 777744744744 we have already found.
|
777744744744
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.2. Points $A, B, C, D, E, F, G$ are located clockwise on a circle, as shown in the figure. It is known that $A E$ is the diameter of the circle. Also, it is known that $\angle A B F=81^{\circ}, \angle E D G=76^{\circ}$. How many degrees does the angle $F C G$ measure?
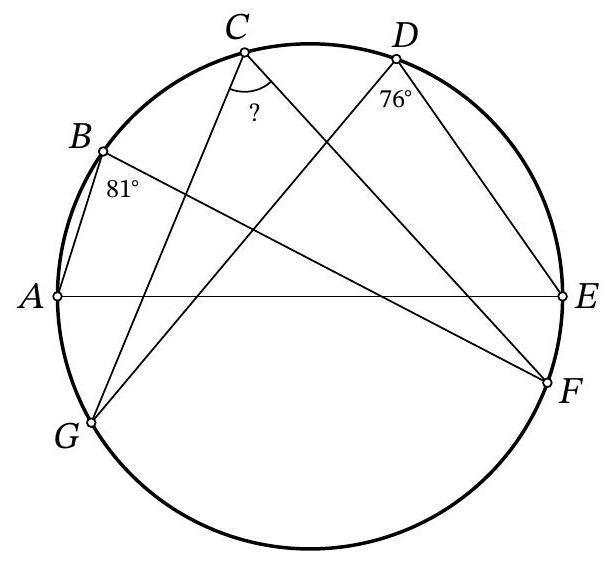
|
Answer: 67.
Solution. Since inscribed angles subtended by the same arc are equal, then $\angle A C F=$ $\angle A B F=81^{\circ}$ and $\angle E C G=\angle E D G=76^{\circ}$. Since a right angle is subtended by the diameter,
$$
\angle F C G=\angle A C F+\angle E C G-\angle A C E=81^{\circ}+76^{\circ}-90^{\circ}=67^{\circ}
$$
|
67
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.3. Lёsha cut a cube $n \times n \times n$ into 153 smaller cubes. Moreover, all the cubes, except one, have an edge length of 1. Find $n$.
|
Answer: 6.
Solution. Let the remaining cube have an edge of $s$. Obviously, the numbers $n$ and $s$ are natural, and $n>s$.
The difference in the volumes of the cubes with edges $n$ and $s$ is equal to the total volume of the unit cubes. Therefore, $n^{3}-s^{3}=152$.
Since $n^{3}>152>5^{3}$, then $n>5$. Note that $n=6$ satisfies the equation above, corresponding to $s=4$, since $6^{3}-4^{3}=152$. However, $n=7$ does not satisfy the equation, as the number $7^{3}-152=191$ is not a perfect cube. Neither do all $n \geqslant 8$ satisfy the equation, since otherwise
$$
152=n^{3}-s^{3} \geqslant n^{3}-(n-1)^{3}=3 n^{2}-3 n+1=3 n(n-1)+1 \geqslant 3 \cdot 8 \cdot 7+1>152
$$
Clearly, the only possible value of $n=6$ is valid: a cube $6 \times 6 \times 6$ can be cut into a cube $4 \times 4 \times 4$ and 152 unit cubes $1 \times 1 \times 1$.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 10.5. Vika has 60 cards with numbers from 1 to 60. She wants to divide all the cards into pairs so that the modulus of the difference of the numbers in all pairs is the same. How many ways are there to do this?
|
# Answer: 8.
Solution. Let $d$ be the absolute difference between the numbers. It is clear that the number $d$ is a natural number.
It is clear that the number 1 must be paired with $d+1$, the number 2 must be paired with $d+2, \ldots$, the number $d$ must be paired with $2d$. Therefore, the first $2d$ natural numbers are paired with each other.
Considering the number $2d+1$, we get that it must be paired with $3d+1$, the number $2d+2$ must be paired with $3d+2, \ldots$, the number $3d$ must be paired with $4d$. Therefore, the next $2d$ natural numbers are also paired with each other.
Continuing in this manner, we get that the set of all numbers $\{1,2, \ldots, 60\}$ should be divided into non-overlapping groups of $2d$ numbers (which in turn are divided into $d$ pairs). Therefore, 60 is divisible by $2d$, which is equivalent to 30 being divisible by $d$. The number 30 has exactly 8 natural divisors: $1,2,3,5,6,10,15,30$. It is clear that all of them are suitable, as each number $d$ among them corresponds to $\frac{30}{d}$ groups of the form $\{2kd+1,2kd+2, \ldots, 4kd\}$, which are obviously divided into pairs with the absolute difference $d$.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.7. The graph of the function $f(x)=\frac{1}{12} x^{2}+a x+b$ intersects the $O x$ axis at points $A$ and $C$, and the $O y$ axis at point $B$, as shown in the figure. It turned out that for the point $T$ with coordinates $(3 ; 3)$, the condition $T A=T B=T C$ is satisfied. Find $b$.
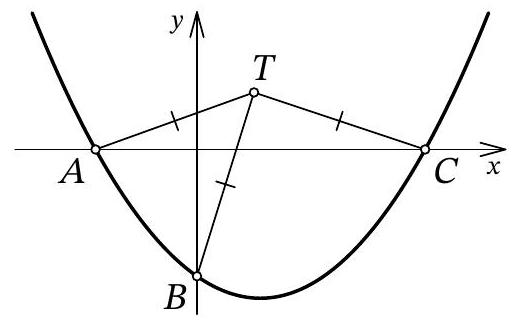
|
Answer: -6.
Fig. 11: to the solution of problem 10.7
Solution. Let point $A$ have coordinates $\left(x_{1} ; 0\right)$, and point $C$ have coordinates $\left(x_{2} ; 0\right)$. From the condition, it is clear that $x_{1} < 0$ and $x_{2} > 0$. Since $x_{1}$ and $x_{2}$ are the roots of the quadratic trinomial $f(x)$, by Vieta's theorem, we have $x_{1} \cdot x_{2} = 12b$, from which we get $b = \frac{x_{1} \cdot x_{2}}{12} < 0$.
Let $H$ be the point with coordinates $(3 ; 0)$ (Fig. 11). Clearly, in the isosceles triangle $A T C$, the segment $T H$ is the height, and therefore it is also the median. Thus, $3 - x_{1} = A H = H C = x_{2} - 3$, from which we get $x_{1} = 6 - x_{2}$.
Let $M$ be the point with coordinates $(0, 3)$. Since $T H = T M = 3$ and $T A = T B$, the right triangles $A T H$ and $B T M$ are equal by the leg and hypotenuse. Therefore, $3 - x_{1} = H A = M B = 3 - b$, that is, $x_{1} = b = \frac{x_{1} \cdot x_{2}}{12}$ (by Vieta's theorem), from which we find $x_{2} = 12$. Finally, $x_{1} = 6 - x_{2} = 6 - 12 = -6$ and $b = x_{1} = -6$.
Another solution. As in the previous solution, let the abscissas of points $A$ and $C$ be $x_{1}$ and $x_{2}$, respectively; we will also use the fact that point $B$ has coordinates $(0 ; b)$. Immediately, we understand that $O A = |x_{1}| = -x_{1}$, $O C = |x_{2}| = x_{2}$, and $O B = |b| = -b$.
Let's find the second intersection of the circle with the y-axis, let this be point $D$ with coordinates $(0 ; d)$ (Fig. 12). The chords $A C$ and $B D$ of the circle intersect at the origin $O$; from the properties of the circle, we know that $O A \cdot O C = O B \cdot O D$. We get $-x_{1} \cdot x_{2} = -b \cdot d$, from which, replacing $x_{1} \cdot x_{2}$ with $12b$ by Vieta's theorem, we get $d = 12$.
Fig. 12: to the solution of problem 10.7
It remains to note that triangle $BTD$ is isosceles, and the midpoint of its base, point $M$, has coordinates $(0 ; 3)$. Reflecting point $D(0 ; 12)$ relative to it, we get $B(0 ; -6)$.
|
-6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.8. For what least natural $a$ does the numerical interval ( $a, 3 a$ ) contain exactly 50 perfect squares?
|
Answer: 4486.
Solution. Let's choose the largest natural $n$ such that $n^{2} \leqslant a$. Then
$$
n^{2} \leqslant a\frac{49}{\sqrt{3}-1}=\frac{49(\sqrt{3}+1)}{2}>\frac{49(1.7+1)}{2}>\frac{132}{2}=66
$$
From the fact that $n+1>66$, it follows that $n \geqslant 66$ and $a \geqslant 66^{2}$.
If on the corresponding interval for $n=66$, $\left[66^{2} ; 67^{2}\right)$, there are suitable values of $a$, then the smallest of them will be the answer to the problem. In this case, the conditions $66^{2}=4356 \leqslant a<4489=67^{2}$ must be satisfied. Additionally, the conditions $13456=116^{2}<3 a \leqslant 117^{2}=13689$ must be satisfied, which are equivalent to $4485 \frac{1}{3}<a \leqslant 4563$. Clearly, the smallest $a$ that fits all these conditions is $a=4486$. It fits: on the corresponding interval $(a ; 3 a)$, there are only perfect squares $67^{2}, 68^{2}, \ldots, 116^{2}$, and there are exactly 50 of them.
## 11th Grade
|
4486
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 11.1. The product of nine consecutive natural numbers is divisible by 1111. What is the smallest possible value that the arithmetic mean of these nine numbers can take?
|
Answer: 97.
Solution. Let these nine numbers be $-n, n+1, \ldots, n+8$ for some natural number $n$. It is clear that their arithmetic mean is $n+4$.
For the product to be divisible by $1111=11 \cdot 101$, it is necessary and sufficient that at least one of the factors is divisible by 11, and at least one of the factors is divisible by 101. Therefore, one of the nine numbers must be at least 101, so $n+8 \geqslant 101$ and $n+4 \geqslant 97$. It is also clear that for the nine numbers $93,94, \ldots, 101$, the value $n+4=97$ is achieved, since 99 is divisible by 11, and 101 is divisible by 101.
|
97
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.2. A square was cut into five rectangles of equal area, as shown in the figure. The width of one of the rectangles is 5. Find the area of the square.
|
Answer: 400.
Solution. The central rectangle and the rectangle below it have a common horizontal side, and their areas are equal. Therefore, the vertical sides of these rectangles are equal, let's denote them as $x$ (Fig. 13). The vertical side of the lower left rectangle is $2x$, and we will denote its horizontal side as $y$. Since its area $2xy$ is the same as the area of the central rectangle, the horizontal side of the central rectangle is $2y$. Then the horizontal side of the upper left rectangle is $3y$, and its area $3y \cdot 5 = 15y$ should be equal to $2xy$, from which we find $x=7.5$. Then the side of the entire square is $5+2x=5+2 \cdot 7.5=20$, and its area is $20^2=400$.
|
400
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.