problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
Problem 8.7. The figure shows two equal triangles: $A B C$ and $E B D$. It turns out that $\angle D A E = \angle D E A = 37^{\circ}$. Find the angle $B A C$.
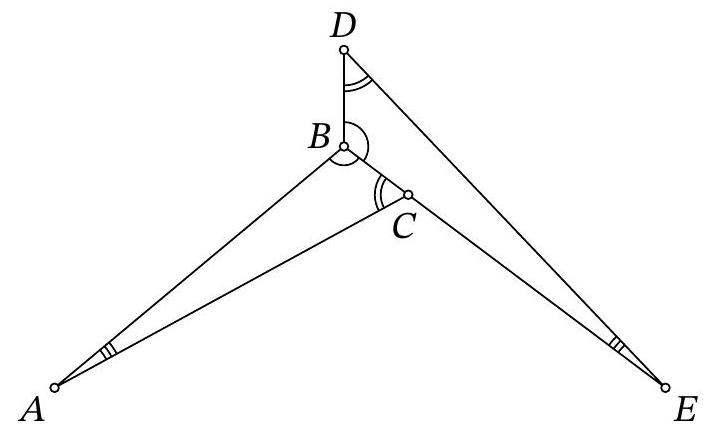
|
Answer: 7.
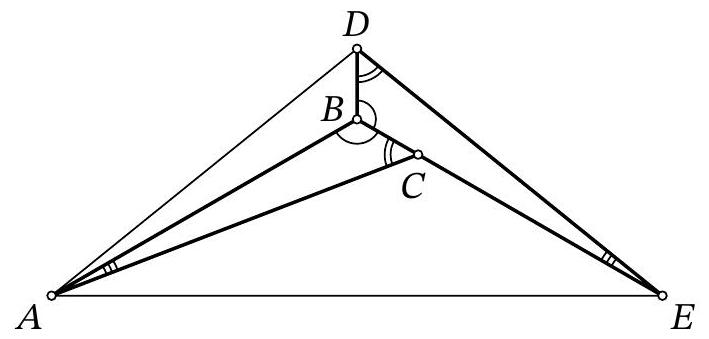
Fig. 4: to the solution of problem 8.7
Solution. Draw segments $A D$ and $A E$ (Fig. 4). Since $\angle D A E=\angle D E A=37^{\circ}$, triangle $A D E$ is isosceles, $A D=D E$.
Notice that triangle $A B D$ is equal to triangle $E B D$ by three sides: $B D$ is a common side, $A D=D E, A B=B E$ from the equality of triangles $A B C$ and $E B D$. Then $\angle D A B=$ $\angle B E D=\angle B A C$ and $\angle A B D=\angle D B E=\angle A B E=\frac{1}{3} \cdot 360^{\circ}=120^{\circ}$.
Since $A B=B E$, triangle $A B E$ is isosceles with an angle of $120^{\circ}$, so $\angle B A E=\frac{1}{2}\left(180^{\circ}-120^{\circ}\right)=30^{\circ}$. Therefore,
$$
\angle B A C=\angle D A B=\angle D A E-\angle B A E=37^{\circ}-30^{\circ}=7^{\circ}
$$
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
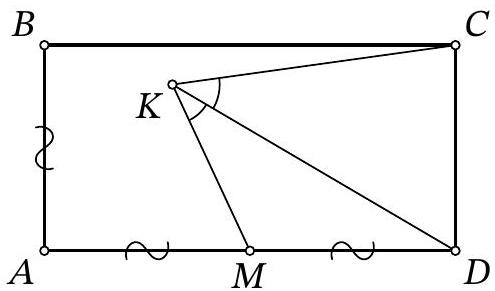
Problem 9.4. A line $\ell$ is drawn through vertex $A$ of rectangle $ABCD$, as shown in the figure. Perpendiculars $BX$ and $DY$ are dropped from points $B$ and $D$ to line $\ell$. Find the length of segment $XY$, given that $BX=4$, $DY=10$, and $BC=2AB$.
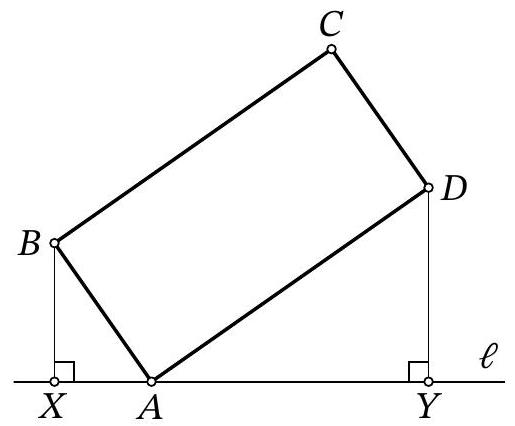
|
Answer: 13.
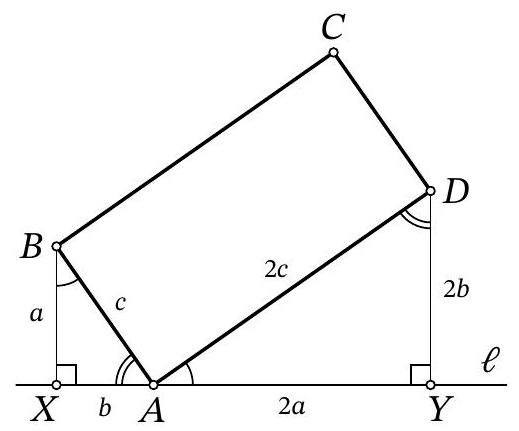
Fig. 5: to the solution of problem 9.4
Solution. Note that since $\angle Y A D=90^{\circ}-\angle X A B$ (Fig. 5), right triangles $X A B$ and $Y D A$ are similar by the acute angle $\angle Y A D=\angle X B A$. The similarity ratio is the ratio $A B: A D$, which is $\frac{1}{2}$. From this, we get $X A=\frac{1}{2} D Y=5$ and $A Y=2 B X=8$, which in total gives $X Y=13$.
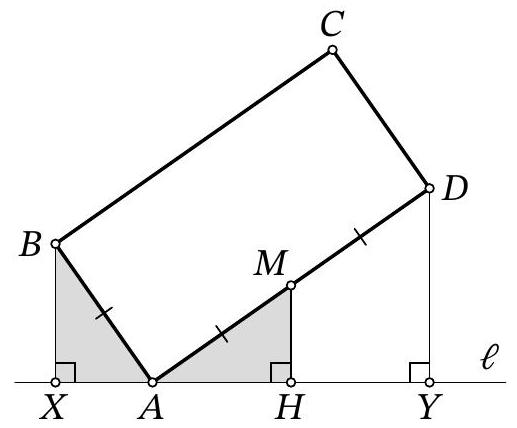
Fig. 6: to the solution of problem 9.4
Another solution. Let $M$ be the midpoint of segment $A D$, then $A M=M D=\frac{A D}{2}=\frac{B C}{2}=A B$ (Fig. 6). Drop a perpendicular from $M$ to $M H$ on line $\ell$. Since in triangle $A D Y$ the segment $M H$ passes through the midpoint of side $A D$ and is parallel to side $D Y$, it is the midline, $A H=H Y$ and $M H=\frac{D Y}{2}=\frac{10}{2}=5$.
Note that $\angle A B X=90^{\circ}-\angle B A X=90^{\circ}-\left(180-90^{\circ}-\angle M A H\right)=\angle M A H$. Then right triangles $A B X$ and $M A H$ are equal by hypotenuse $A B=A M$ and acute angle $\angle A B X=\angle M A H$. From this, it follows that $A X=M H=5$ and $A H=B X=4$.
Thus, $X Y=A X+A H+H Y=5+4+4=13$.
|
13
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.6. In triangle $A B C$, the angles $\angle B=30^{\circ}$ and $\angle A=90^{\circ}$ are known. On side $A C$, point $K$ is marked, and on side $B C$, points $L$ and $M$ are marked such that $K L=K M$ (point $L$ lies on segment $B M$).
Find the length of segment $L M$, if it is known that $A K=4, B L=31, M C=3$.
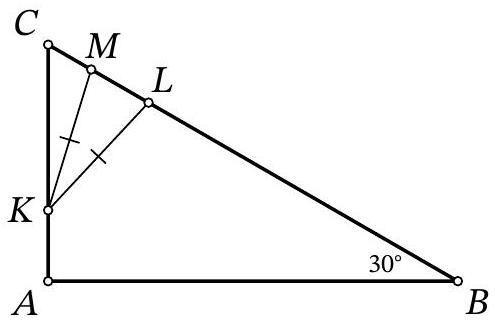
|
Answer: 14.
Solution. In the solution, we will use several times the fact that in a right-angled triangle with an angle of $30^{\circ}$, the leg opposite this angle is half the hypotenuse. Drop the height $K H$ from the isosceles triangle $K M L$ to the base (Fig. 7). Since this height is also a median, then $M H=H L=x$. In the right-angled triangle $C K H$ we have $\angle C K H=90^{\circ}-\angle C=\angle A=30^{\circ}$, so $K C=2 \cdot C H=2 \cdot(C M+M H)=$ $2 \cdot(3+x)=6+2 x$. In the right-angled triangle $A B C$ we have $\angle A=30^{\circ}$, so $B C=2 \cdot A C$. Setting up and solving the corresponding equation $31+2 x+3=2 \cdot(4+6+2 x)$, we find $x=7$. Then $L M=2 x=2 \cdot 7=14$.
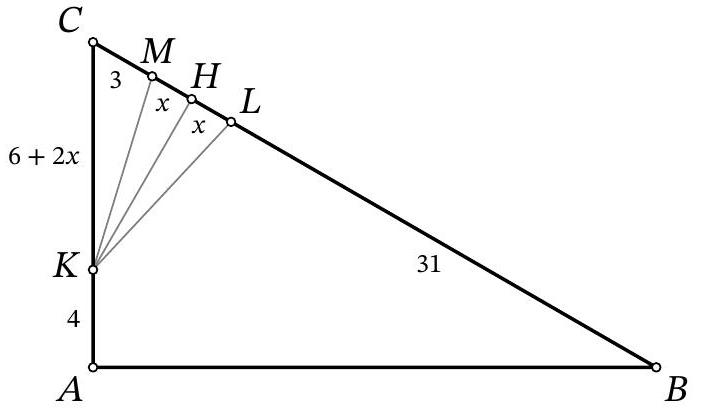
Fig. 7: to the solution of problem 9.6
|
14
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.2. Points $A, B, C, D, E, F, G$ are located clockwise on a circle, as shown in the figure. It is known that $A E$ is the diameter of the circle. Also, it is known that $\angle A B F=81^{\circ}, \angle E D G=76^{\circ}$. How many degrees does the angle $F C G$ measure?
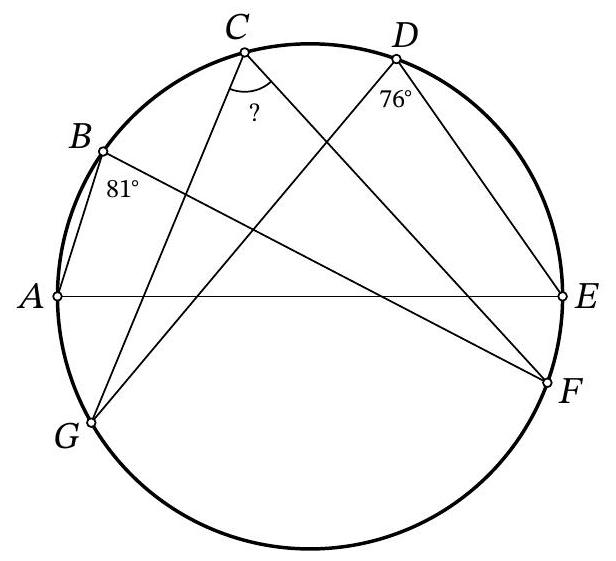
|
Answer: 67.
Solution. Since inscribed angles subtended by the same arc are equal, then $\angle A C F=$ $\angle A B F=81^{\circ}$ and $\angle E C G=\angle E D G=76^{\circ}$. Since a right angle is subtended by the diameter,
$$
\angle F C G=\angle A C F+\angle E C G-\angle A C E=81^{\circ}+76^{\circ}-90^{\circ}=67^{\circ}
$$
|
67
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.7. The graph of the function $f(x)=\frac{1}{12} x^{2}+a x+b$ intersects the $O x$ axis at points $A$ and $C$, and the $O y$ axis at point $B$, as shown in the figure. It turned out that for the point $T$ with coordinates $(3 ; 3)$, the condition $T A=T B=T C$ is satisfied. Find $b$.
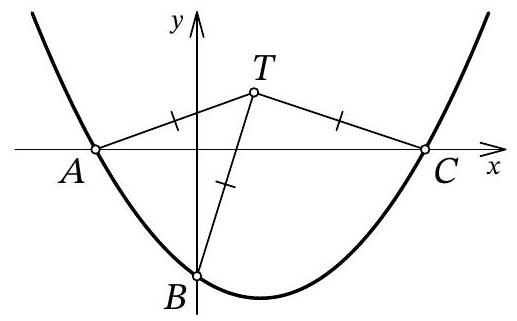
|
Answer: -6.
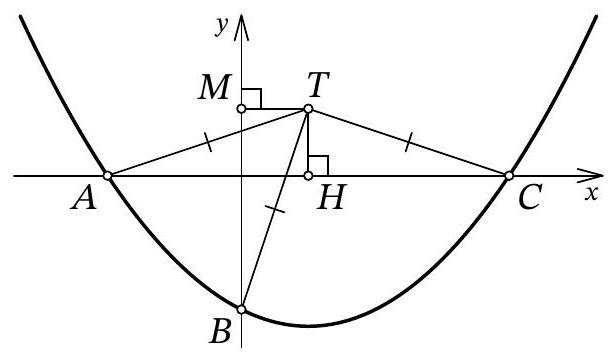
Fig. 11: to the solution of problem 10.7
Solution. Let point $A$ have coordinates $\left(x_{1} ; 0\right)$, and point $C$ have coordinates $\left(x_{2} ; 0\right)$. From the condition, it is clear that $x_{1} < 0$ and $x_{2} > 0$. Since $x_{1}$ and $x_{2}$ are the roots of the quadratic trinomial $f(x)$, by Vieta's theorem, we have $x_{1} \cdot x_{2} = 12b$, from which we get $b = \frac{x_{1} \cdot x_{2}}{12} < 0$.
Let $H$ be the point with coordinates $(3 ; 0)$ (Fig. 11). Clearly, in the isosceles triangle $A T C$, the segment $T H$ is the height, and therefore it is also the median. Thus, $3 - x_{1} = A H = H C = x_{2} - 3$, from which we get $x_{1} = 6 - x_{2}$.
Let $M$ be the point with coordinates $(0, 3)$. Since $T H = T M = 3$ and $T A = T B$, the right triangles $A T H$ and $B T M$ are equal by the leg and hypotenuse. Therefore, $3 - x_{1} = H A = M B = 3 - b$, that is, $x_{1} = b = \frac{x_{1} \cdot x_{2}}{12}$ (by Vieta's theorem), from which we find $x_{2} = 12$. Finally, $x_{1} = 6 - x_{2} = 6 - 12 = -6$ and $b = x_{1} = -6$.
Another solution. As in the previous solution, let the abscissas of points $A$ and $C$ be $x_{1}$ and $x_{2}$, respectively; we will also use the fact that point $B$ has coordinates $(0 ; b)$. Immediately, we understand that $O A = |x_{1}| = -x_{1}$, $O C = |x_{2}| = x_{2}$, and $O B = |b| = -b$.
Let's find the second intersection of the circle with the y-axis, let this be point $D$ with coordinates $(0 ; d)$ (Fig. 12). The chords $A C$ and $B D$ of the circle intersect at the origin $O$; from the properties of the circle, we know that $O A \cdot O C = O B \cdot O D$. We get $-x_{1} \cdot x_{2} = -b \cdot d$, from which, replacing $x_{1} \cdot x_{2}$ with $12b$ by Vieta's theorem, we get $d = 12$.
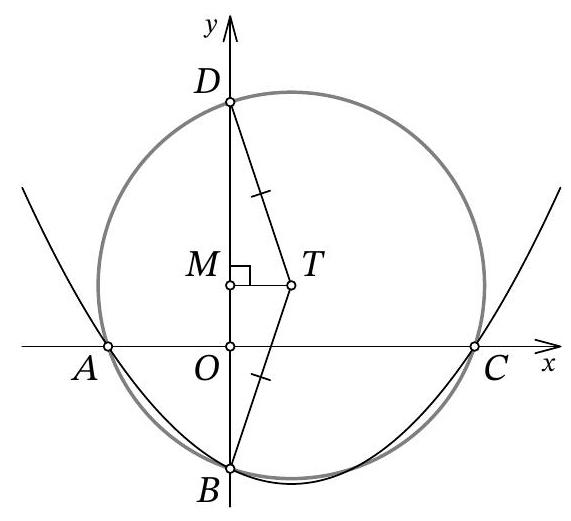
Fig. 12: to the solution of problem 10.7
It remains to note that triangle $BTD$ is isosceles, and the midpoint of its base, point $M$, has coordinates $(0 ; 3)$. Reflecting point $D(0 ; 12)$ relative to it, we get $B(0 ; -6)$.
|
-6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.2. A square was cut into five rectangles of equal area, as shown in the figure. The width of one of the rectangles is 5. Find the area of the square.
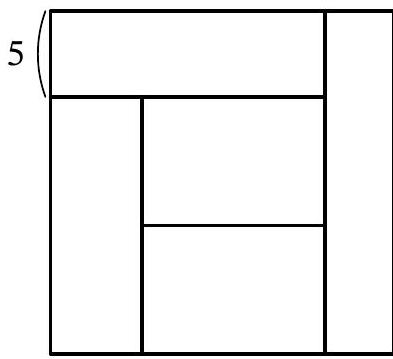
|
Answer: 400.
Solution. The central rectangle and the rectangle below it have a common horizontal side, and their areas are equal. Therefore, the vertical sides of these rectangles are equal, let's denote them by $x$ (Fig. 13). The vertical side of the lower left rectangle is $2x$, and we will denote its horizontal side by $y$. Since its area $2xy$ is the same as the area of the central rectangle, the horizontal side of the central rectangle is $2y$. Then the horizontal side of the upper left rectangle is $3y$, and its area $3y \cdot 5 = 15y$ should be equal to $2xy$, from which we find $x=7.5$. Then the side of the entire square is $5+2x=5+2 \cdot 7.5=20$, and its area is $20^2=400$.
|
400
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.3. In a football tournament, 15 teams participated, each playing against each other exactly once. For a win, 3 points were awarded, for a draw - 1 point, and for a loss - 0 points.
After the tournament ended, it turned out that some 6 teams scored at least $N$ points each. What is the greatest integer value that $N$ can take?
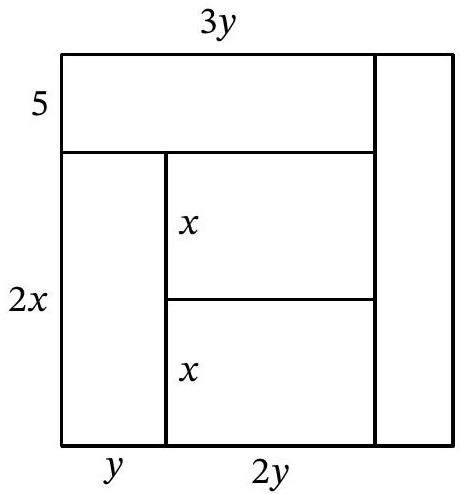
Fig. 13: to the solution of problem 11.2
#
|
# Answer: 34.
Solution. Let's call these 6 teams successful, and the remaining 9 teams unsuccessful. We will call a game between two successful teams an internal game, and a game between a successful and an unsuccessful team an external game.
First, note that for each game, the participating teams collectively earn no more than 3 points. Clearly, there were exactly $\frac{6 \cdot 5}{2}=15$ internal games, and only from these games did all successful teams collectively earn no more than $15 \cdot 3=45$ points. There were exactly $6 \cdot 9=54$ external games, and in each such game, a successful team earned no more than 3 points. Therefore, collectively, all successful teams earned no more than $54 \cdot 3=162$ points from external games. According to the problem, the successful teams collectively earned at least $6 \mathrm{~N}$ points, so we get the inequality $6 N \leqslant 45+162$. From this, it follows that $N \leqslant \frac{207}{6}<35$ and $N \leqslant 34$. Now let's provide an example for $N=34$. Number the teams from 1 to 15. We will show how teams from 1 to 6 can earn at least 34 points.
- Suppose each team from 1 to 6 won against each team from 7 to 15, then each team from 1 to 6 earned $9 \cdot 3=27$ points just from these games.
- Suppose the teams from 1 to 6 played among themselves as indicated in the following table (in each cell, the number of points is shown that the team from the corresponding row received in the game with the team from the corresponding column):
| | $\mathbf{1}$ | $\mathbf{2}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{5}$ | $\mathbf{6}$ |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| $\mathbf{1}$ | | 3 | 3 | 1 | 0 | 0 |
| $\mathbf{2}$ | 0 | | 3 | 3 | 1 | 0 |
| $\mathbf{3}$ | 0 | 0 | | 3 | 3 | 1 |
| $\mathbf{4}$ | 1 | 0 | 0 | | 3 | 3 |
| $\mathbf{5}$ | 3 | 1 | 0 | 0 | | 3 |
| $\mathbf{6}$ | 3 | 3 | 1 | 0 | 0 | |
- Suppose in each game between teams from 7 to 15, the team with the higher number won (the outcome of these games does not matter).
In total, teams from 1 to 6 earned at least $27+7=34$ points.
|
34
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.8. Given a parallelepiped $A B C D A_{1} B_{1} C_{1} D_{1}$. A point $X$ is chosen on the edge $A_{1} D_{1}$, and a point $Y$ is chosen on the edge $B C$. It is known that $A_{1} X=5, B Y=3, B_{1} C_{1}=14$. The plane $C_{1} X Y$ intersects the ray $D A$ at point $Z$. Find $D Z$.
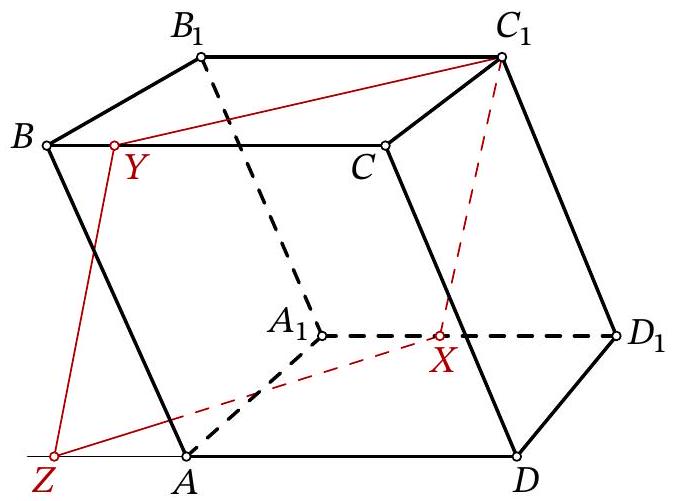
|
Answer: 20.
Solution. Lines $C_{1} Y$ and $Z X$ lie in parallel planes $B B_{1} C_{1} C$ and $A A_{1} D_{1} D$, so they do not intersect. Since these two lines also lie in the same plane $C_{1} X Z Y$, they are parallel. Similarly, lines $Y Z$ and $C_{1} X$ are parallel. Therefore, quadrilateral $C_{1} X Z Y$ is a parallelogram.

Fig. 15: to the solution of problem 11.8
Let us lay off segment $A T$ on $A D$, equal to $B Y$ (Fig. 15). Quadrilateral $B Y T A$ is a parallelogram, meaning segments $Y T, B A$, and $C_{1} D_{1}$ are parallel and equal. Additionally, segments $Y Z$ and $C_{1} X$ are parallel and equal; from the parallelism follows the equality of angles $Z Y T$ and $X C_{1} D_{1}$, which gives the equality of triangles $Z Y T$ and $X C_{1} D_{1}$.
Then
$$
\begin{aligned}
D Z & =Z T+A D-A T=X D_{1}+B_{1} C_{1}-B Y= \\
& =\left(A_{1} D_{1}-A_{1} X\right)+B_{1} C_{1}-B Y=(14-5)+14-3=20
\end{aligned}
$$
Another solution. As in the previous solution, we will use the fact that $C_{1} X Z Y$ is a parallelogram.
Consider the chain of vector equalities:
$$
\overrightarrow{D Z}=\overrightarrow{D C}+\overrightarrow{C Y}+\overrightarrow{Y Z}=\overrightarrow{D_{1} C_{1}}+\overrightarrow{C Y}+\overrightarrow{C_{1} X}=\overrightarrow{C Y}+\overrightarrow{D_{1} X}
$$
In the last part, all vectors are oriented the same as $\overrightarrow{D Z}$, so we can transition to the equality of segments and continue:
$$
D Z=C Y+D_{1} X=(C B-B Y)+\left(D_{1} A_{1}-A_{1} X\right)=2 B_{1} C_{1}-B Y-A_{1} X
$$
Substituting the lengths given in the condition, we get $D Z=2 \cdot 14-3-5=20$.
|
20
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The first two digits of a four-digit number are either each less than 5 or each greater than 5. The same can be said about the last two digits. How many such numbers are there?
|
Answer: 1476.
## Solution:
If the first 2 digits are less than 5, this gives $4 \cdot 5=20$ options, and if they are greater than 5, it gives $4 \cdot 4=16$ options.
If the last 2 digits are less than 5, this gives $5 \cdot 5=25$ options, and if they are greater than 5, it gives $4 \cdot 4=16$ options.
Total options: $(20+16) \cdot(25+16)=1476$.
## Instructions for Checking:
Answer without justification - 0 points. Penalty for calculation errors - 2-3 points.
|
1476
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. The year 2009 has the property that by rearranging its digits, it is impossible to form a smaller four-digit number (numbers do not start with zero). In which year will this property reoccur for the first time?
(I. V. Raskina)
|
Answer: in 2022.
Solution. In 2010, 2011, ..., 2019, and in 2021, the year number contains a one, and if it is moved to the first position, the number will definitely decrease. The number 2020 can be reduced to 2002. However, the number 2022 cannot be decreased by rearranging the digits.
## Comment.
3 points. For the answer without justification.
|
2022
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. What angle do the clock hands form at 12:20?
|
Answer: $110^{\circ}$.
Solution. At 12:00, the clock hands coincide. After this, in 20 minutes, the minute hand travels $1 / 3$ of the circumference, i.e., it describes an angle of $120^{\circ}$. The hour hand moves 12 times slower than the minute hand (since it describes one circle in 12 hours). Therefore, in 20 minutes, it will describe an angle of $120^{\circ}: 12=10^{\circ}$ and will form an angle of $120^{\circ}-10^{\circ}=110^{\circ}$ with the minute hand.
|
110
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. Grandfather is 31 times older than his grandson. In how many years will he be 7 times older than his grandson, given that the grandfather is more than 50 but less than 90 years old?
|
Answer: In 8 years.
Solution: Grandfather's age is divisible by 31. But the only such number greater than 50 and less than 90 is 62. Therefore, the grandfather is 62 years old, and the grandson is 2 years old. In x years, the grandfather will be x+62 years old, and the grandson will be x+2 years old. If at that time he will be 7 times older than the grandson, then x+62=7(x+2), from which x=8.
Comment: It is written that the grandfather's age is 62 years - 3 points.
Internet resources: http://www.problems.ru, https://olimpiada.ru.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Solve the equation $\left(x^{2}-|x|-2\right)^{2}+\sqrt{|2 x+1|-3}=0$.
|
# Solution
Since each term of the original equation is non-negative, the equation can have solutions if and only if both terms are equal to zero. We obtain the equivalent system of equations
$$
\left\{\begin{array}{l}
x^{2}-|x|-2=0 \\
|2 x+1|-3=0
\end{array}\right.
$$
The solution to this system is $x=-2$.
## Criteria
The equivalent system is formulated and justified, but solved incorrectly - 4 points. The equivalent system is formulated and solved, but not justified - 5 points.
The equivalent system is formulated, but not justified and solved with an error - 3 points.
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.5. A square plot of 14 by 14 cells needs to be paved with rectangular tiles of size $1 \times 4$. The tiles can only be laid along the grid (not diagonally), and the tiles cannot be broken. What is the maximum number of tiles required? Will there be any uncovered area left?
|
# Solution:
Evaluation. The total number of cells on the plot is $14 \times 14=196$. Dividing by the number of cells in one tile, 196:4 = 49. Therefore, the number of tiles that can be cut from the $14 \times 14$ plot is no more than 49.
We will color the cells of the plot in 4 colors, as shown in the diagram. Clearly, each rectangle of size $1 \times 4$ will contain one cell of each of the four colors. There are 49 cells of color 1, 50 cells of color 2, 49 cells of color 3, and only 48 cells of color 4. Therefore, no more than 48 tiles can be laid, and 4 cells will remain uncovered.
| 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 |
| 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 |
| 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 |
| 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 |
| 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 |
| 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 |
| 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 |
| 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 |
| 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 |
| 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 |
| 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 |
| 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 |
| 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 |
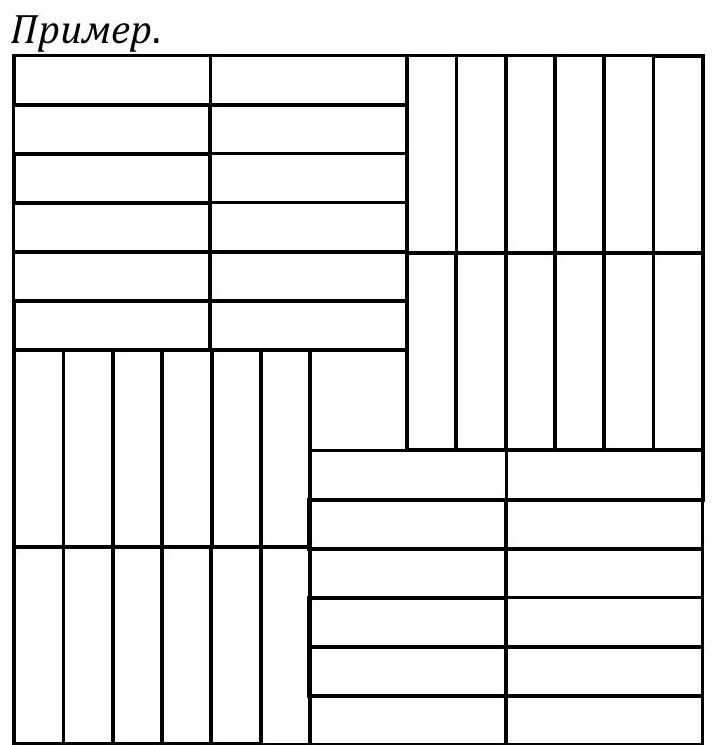
Criteria: Only the answer - 0 points. Only the evaluation - 5 points. Only the example - 2 points. 7 points should be given if both the evaluation and the example are present.
|
48
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. A $3 \times 3$ table was filled with prime numbers. It turned out that the sum of the numbers in any two adjacent cells is a prime number. What is the maximum number of different numbers that can be in the table? Provide an example and prove that there cannot be more different numbers.
Fill the $3 \times 3$ table with prime numbers such that the sum of the numbers in any two adjacent cells is a prime number. Determine the maximum number of different prime numbers that can be used and provide an example. Prove that it is not possible to use more different prime numbers.
|
3. Answer: 6.
Example:
| 5 | 2 | 29 | |
| :---: | :---: | :---: | :---: |
| 2 | 3 | 2 | |
| 11 | 2 | 17 | |
| | -2 | | 0 |

We will prove that it cannot be more. Divide the cells of the table into 4 pairs of adjacent cells and one central cell. In each pair of adjacent cells, the sum of the numbers is a prime number. But the sum of two odd primes is an even number greater than two and, therefore, composite. Thus, in each pair, there must be a number 2. Therefore, there must be at least four 2s. The different numbers can be the five remaining and the 2, meaning there are no more than 6 different numbers.
## Grading Criteria.
Only the correct example is provided: 3 points.
Proved that there are at least four 2s, 6 different numbers, but no example: 4 points.
It can also be proved by coloring the board in a checkerboard pattern and explaining that on each color, the numbers have the same parity.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Six numbers are written in a row on the board. It is known that each number, starting from the third, is equal to the product of the two preceding numbers, and the fifth number is equal to 108. Find the product of all six numbers in this row.
|
4. Answer: 136048896.
Solution. Let the first number be $x$, and the second number be $y$. Then the third number is $xy$.
The fourth number is $xy^2$. The fifth number is $x^2 y^3 = 108$. The sixth number is $x^3 y^3$.
The product of all six numbers is $x^8 y^{12} = (x^2 y^3)^4 = 108^4 = 136048896$.
## Grading Criteria.
A specific case is considered - a sequence where the first number is 2 and the second number is 3: 1 point.
Comment. Other sequences also work, for example, a sequence with the first number (-2) and the second number 3.
The answer $108^4$ is derived correctly but not calculated or calculated incorrectly: 6 points.
|
136048896
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In Grandfather Frost's bag, there are chocolate and jelly candies, a total of 2023 pieces. Chocolate candies make up 75% of the jelly candies. How many chocolate candies are in Grandfather Frost's bag?
|
Answer: 867. Solution. Chocolate candies make up 3/4 of the quantity of jelly candies. Then the total number of candies is 7/4 of jelly candies. Therefore, the number of jelly candies is 2023×4:7=1156, and the number of chocolate candies is 2023-1156=867.
Grading criteria. A correct and justified solution - 7 points. One arithmetic error is made, but the correct sequence of all steps is present - 5 points. In all other cases - 0 points.
|
867
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. What is the greatest length of an arithmetic progression of natural numbers
$a_{1}, a_{2}, \ldots, a_{n}$ with a difference of 2, in which for all $k=1,2 \ldots, n$ all numbers $a_{k}^{2}+1$ are prime
|
Solution.
All members of the progression must be even numbers. Consider the remainders when divided by 5. Since the common difference of the arithmetic progression is 2, the remainders in the progression will appear in the order
$\ldots 2,4,1,3,0,2,4,1,3,0, \ldots$ This means that among the terms of the progression, there will be numbers of the form $a_{k}=5 t+2$ and $a_{k}=5 t+3\left(t-\right.$ natural). For these numbers, we calculate $a_{k}^{2}+1=$ $25 t^{2}+20 t+5$ and $a_{k}^{2}+1=25 t^{2}+30 t+10$. We have found that the specified terms of the progression $a_{k}=5 t+2$ and $a_{k}=5 t+3$ yield expressions $a_{k}^{2}+1$ that are divisible by 5 and are not prime. The longest set of terms in the arithmetic progression that does not contain numbers of the form $a_{k}=5 t+2$ and $a_{k}=5 t+3$ consists of two numbers. Therefore, the number of consecutive terms of the progression that meet our criteria cannot exceed two. The only case where a sequence of three numbers can be obtained is by including the number 5 in $a_{k}^{2}+1$. Indeed, the numbers $2,4,6$ form an arithmetic progression and yield the corresponding sequence of prime numbers 5, 17, 37. Answer. $n=3$.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A $10 \times 10$ square was cut into 17 rectangles, each with both side lengths greater than 1. What is the smallest number of squares that could be among these rectangles? Provide an example of such a cutting.
|
Answer: one square.
Solution. Suppose that among the rectangles, there is not a single square. Let $a$ and $b$ be the sides of an arbitrary rectangle, with $a > b$. Since the integer $b$ is greater than 1, then $b \geqslant 2$, and thus $a \geqslant 3$. Therefore, the area of each such rectangle $a \times b$ is at least $2 \cdot 3 = 6$ cells. However, then 17 rectangles should occupy at least $17 \cdot 6 = 102$ cells, while the original square $10 \times 10$ has only 100 cells.
In Figure 1, an example of cutting the $10 \times 10$ square into 17 rectangles, among which there is exactly one square, is provided.
Criteria. Only the answer - 0 points. Proved that the area of each non-square rectangle is at least 6 cells - 1 point. Proved,
Fig. 1 that among the rectangles there is a square - another 3 points. Correct example of cutting - another 3 points. Full solution - 7 points.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The diagonals of quadrilateral $A B C D$ intersect at point $O$. It is known that $A B=B C=$ $=C D, A O=8$ and $\angle B O C=120^{\circ}$. What is $D O ?$
|
Answer: $D O=8$.
Solution. Mark a point $E$ on the line $A C$ such that triangle $B O E$ is equilateral (Fig. 2). We will prove the equality of triangles $B A E$ and $B C O$. Indeed, since $A B=B C$, triangle $A B C$ is isosceles, and thus $\angle B A C=\angle B C A$. Additionally, note another pair of equal angles $\angle A E B=\angle B O C=120^{\circ}$. Therefore, triangles $B A E$ and $B C O$ are equal by one side and two angles, hence $A E=C O$ and $A O=A E+E O=C O+B O$.
If we mark a point $F$ on the line $B D$ such that triangle $C O F$ is equilateral, then by similar reasoning we get $D O=B O+C O$. Therefore, it follows that $D O=A O=8$.
Fig. 2
Criteria. Only the answer - 0 points. Correct additional construction related to the equilateral triangle - 2 points. The equality $A O=C O+B O$ or its equivalent $D O=B O+C O$ is established - 4 points. Complete solution - 7 points.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A seagull is being fed from a moving boat. A piece of bread is thrown down, the seagull takes 3 seconds to pick up the piece from the sea surface, and then it takes 12 seconds to catch up with the boat. Upon entering the bay, the boat reduces its speed by half. How much time will it now take the seagull to catch up with the boat after picking up the piece of bread?
Om vem: 2 seconds.
|
Solution. Let the speed of the seagull relative to the boat be $x$ (m/s). Then in 12 seconds, it flies $12 x$ (m). The boat covers this distance in 3 seconds, so its speed is $4 x$ (m/s), and the speed of the seagull is $5 x$ (m/s). In the bay, the boat's speed becomes $2 x$ (m/s). In 3 seconds, it travels $6 x$ (m). The speed of the seagull relative to the boat is now $5 x - 2 x = 3 x$ (m/s). Therefore, it will take her 2 seconds to catch up with the boat.
Criteria. If the solution is incorrect - 0 points.
Only the correct answer - 0 points.
If the reasoning is correct and there is a computational error - 3 points. If the solution is correct - 7 points.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
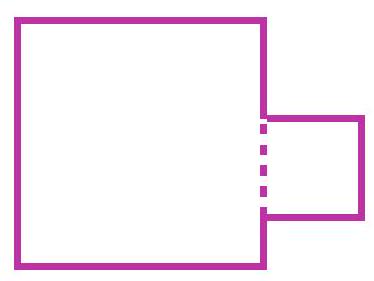
4-1. Katya attached a square with a perimeter of 40 cm to a square with a perimeter of 100 cm as shown in the figure. What is the perimeter of the resulting figure in centimeters?
|
Answer: 120.
Solution: If we add the perimeters of the two squares, we get $100+40=140$ cm. This is more than the perimeter of the resulting figure by twice the side of the smaller square. The side of the smaller square is $40: 4=10$ cm. Therefore, the answer is $140-20=120$ cm.
|
120
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
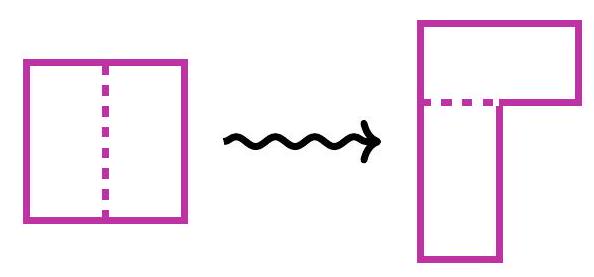
5-1. A square with a side of 100 was cut into two equal rectangles. They were placed next to each other as shown in the figure. Find the perimeter of the resulting figure.
|
Answer: 500.
Solution. The perimeter of the figure consists of 3 segments of length 100 and 4 segments of length 50. Therefore, the length of the perimeter is
$$
3 \cdot 100 + 4 \cdot 50 = 500
$$
|
500
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
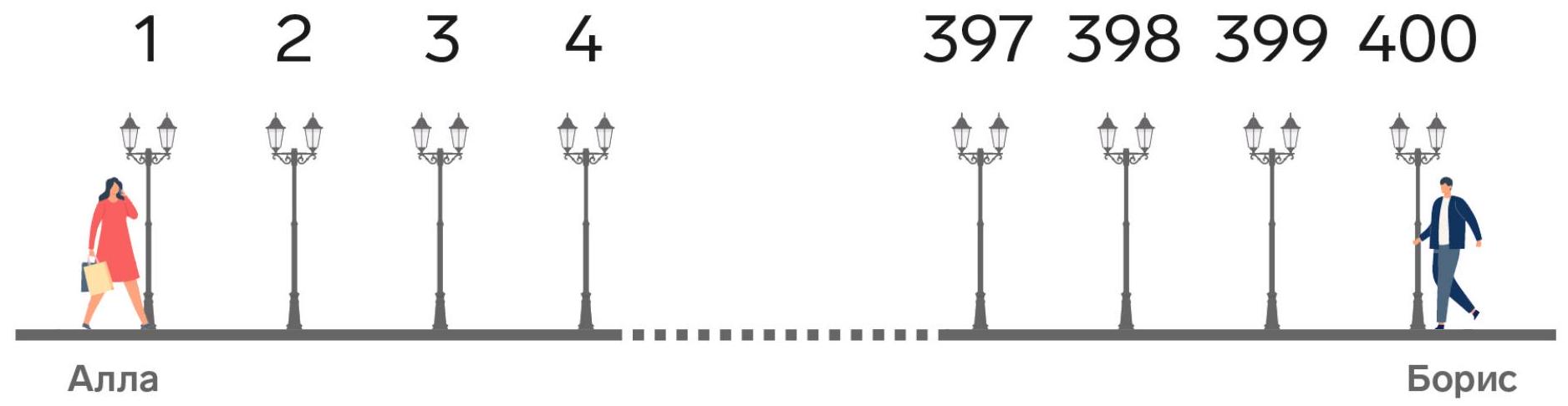
5-5. Along a straight alley, 400 lamps are placed at equal intervals, numbered in order from 1 to 400. At the same time, from different ends of the alley, Alla and Boris started walking towards each other at different constant speeds (Alla from the first lamp, Boris from the four hundredth). When Alla was at the 55th lamp, Boris was at the 321st lamp. At which lamp will their meeting occur? If the meeting occurs between two lamps, indicate the smaller number of these two.
|
Answer. At the 163rd lamppost.
Solution. There are a total of 399 intervals between the lampposts. According to the condition, while Allа walks 54 intervals, Boris walks 79 intervals. Note that $54+79=133$, which is exactly three times less than the length of the alley. Therefore, Allа should walk three times more to the meeting point than to the 55th lamppost, i.e., $54 \cdot 3=162$ intervals. And she will be at the 163rd lamppost.
|
163
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5-6. On a rectangular table of size $x$ cm $\times 80$ cm, identical sheets of paper of size 5 cm $\times 8$ cm are placed. The first sheet touches the bottom left corner, and each subsequent sheet is placed one centimeter higher and one centimeter to the right of the previous one. The last sheet touches the top right corner. What is the length $x$ in centimeters?
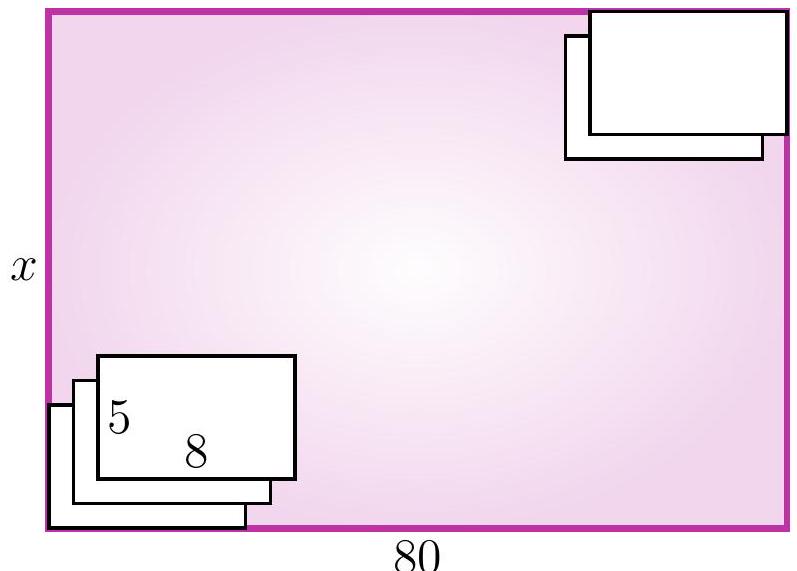
|
Answer: 77.
Solution I. Let's say we have placed another sheet of paper. Let's look at the height and width of the rectangle for which it will be in the upper right corner.
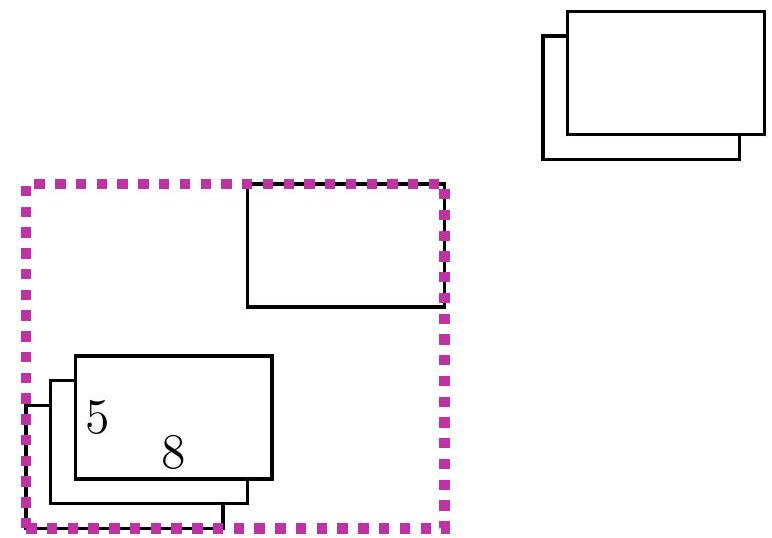
Let's call such a rectangle the current one. Notice that for each new current rectangle, both the width and the height are 1 cm larger than the previous one. Initially, when there was only one sheet of paper, the width of the large rectangle was 8 cm, and at the end, it was 80 cm. Thus, a total of $(80-8): 1=72$ sheets of paper were added. The height of the current rectangle also increased by $72 \cdot 1$ cm, initially it was 5 cm, so $x=5+72=77$.
Solution II. As in the first solution, let's look at the length and width of the current rectangles. Again, notice that for each new current rectangle, both the length and the width are 1 cm larger than the previous one. However, we will draw a different conclusion: specifically, the difference between the width and the height of the current rectangle is always the same! (Such a value that does not change during a certain process is called an invariant.) Since initially the width was 3 cm greater than the height, i.e., $8-5=3$ cm, at the end it should also be 3 cm greater, so the answer is $x=80-3=77$ cm.
|
77
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8-1. Two rectangles $8 \times 10$ and $12 \times 9$ are overlaid as shown in the figure. The area of the black part is 37. What is the area of the gray part? If necessary, round the answer to 0.01 or write the answer as a common fraction.
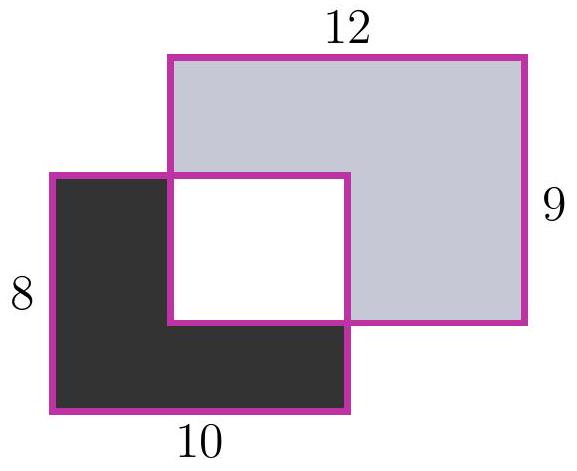
|
Answer: 65.
Solution. The area of the white part is $8 \cdot 10-37=43$, so the area of the gray part is $12 \cdot 9-43=65$
|
65
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8-2. In square $A B C D$, a segment $C E$ is drawn such that the angles shown in the diagram are $7 \alpha$ and $8 \alpha$. Find the value of angle $\alpha$ in degrees. If necessary, round the answer to 0.01 or write the answer as a common fraction.
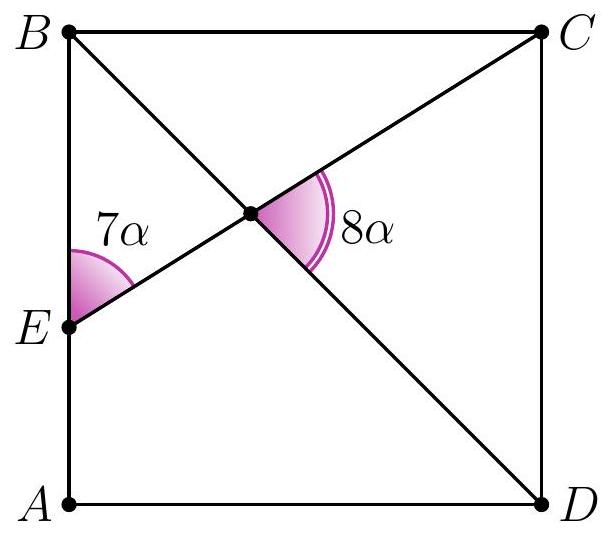
|
Answer: $9^{\circ}$.
Solution. In triangle $D F E$, the angles are $7 \alpha, 8 \alpha$ and $45^{\circ}$.
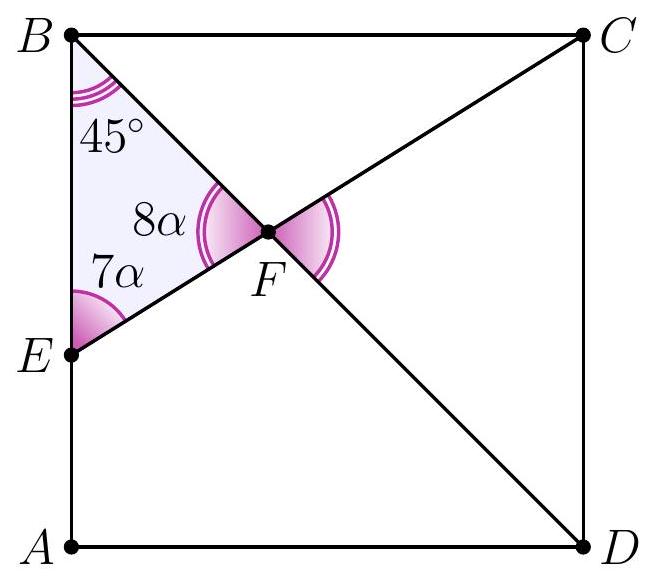
Since the sum of the angles in triangle $D F E$ is $180^{\circ}$, we have $7 \alpha + 8 \alpha + 45^{\circ} = 180^{\circ}$, from which $\alpha = \frac{1}{15} \cdot 135^{\circ} = 9^{\circ}$.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9-1. Segment $P Q$ is divided into several smaller segments. On each of them, a square is constructed (see figure).
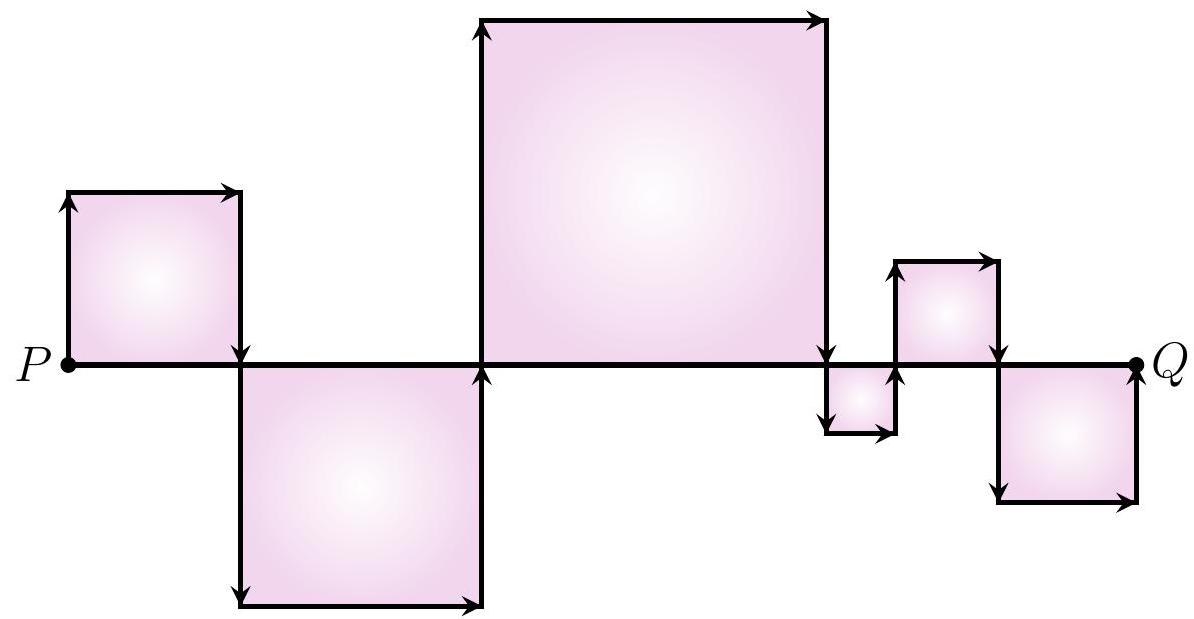
What is the length of the path along the arrows if the length of segment $P Q$ is 73? If necessary, round the answer to 0.01 or write the answer as a common fraction.
|
Answer: 219.
Solution. Note that in each square, instead of going along one side, we go along three sides. Therefore, the length of the path along the arrows is 3 times the length of the path along the segment, hence the answer $73 \cdot 3=219$.
|
219
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.8. A numismatist has 100 coins that look identical. He knows that among them, 30 are genuine and 70 are counterfeit. Moreover, he knows that the weights of all genuine coins are the same, while the weights of all counterfeit coins are different, and any counterfeit coin is heavier than a genuine one; however, the exact weights of the coins are unknown. There are balance scales without weights, on which it is possible to compare the weights of two groups consisting of the same number of coins in one weighing. What is the minimum number of weighings on these scales that the numismatist can guarantee to find at least one genuine coin?
(C. Berlov, I. Bogdanov)
|
Answer: 70.
Solution: 1. We will show that the numismatist can find the genuine coin in 70 weighings. Stack all 100 coins in a pile. With each weighing, he will select two coins from the pile and compare them. If their weights are equal, then both coins are genuine, and the required coin is found. If not, then the heavier coin is counterfeit, and it can be discarded from the pile.
After 70 such weighings, if equality is never achieved, then 30 coins will remain in the pile, and all genuine coins will remain in the pile. Thus, in this case, the numismatist will even find all 30 genuine coins.
|
70
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.1. Twelve different natural numbers are written in a circle, one of which is 1. Any two adjacent numbers differ by either 10 or 7. What is the greatest value that the largest written number can take?
|
Answer: 58.
Solution. For convenience, let's number all the numbers in a circle clockwise, starting from the number 1: $a_{1}=1, a_{2}, \ldots, a_{12}$. Notice that for all $1 \leqslant i \leqslant 6$ we have
$$
\begin{gathered}
a_{i+1}-a_{1}=\left(a_{i+1}-a_{i}\right)+\left(a_{i}-a_{i-1}\right)+\ldots+\left(a_{2}-a_{1}\right) \leqslant 10 i \\
a_{13-i}-a_{1}=\left(a_{13-i}-a_{14-i}\right)+\ldots+\left(a_{12}-a_{1}\right) \leqslant 10 i
\end{gathered}
$$
therefore, $a_{7}$ does not exceed $1+6 \cdot 10=61$, and all other numbers do not exceed $1+5 \cdot 10=51$.
If $a_{7}=61$, then all differences $a_{2}-a_{1}, a_{3}-a_{2}, \ldots, a_{7}-a_{6}, a_{7}-a_{8}, a_{8}-a_{9}, \ldots, a_{12}-a_{1}$ are equal to 10, but then $a_{2}=a_{12}=11$, which is a contradiction. Therefore, $a_{7}<61$, which implies that $a_{7} \leqslant 1+5 \cdot 10+7=58$. Thus, the largest written number does not exceed 58.
It remains to check that the number 58 can indeed be present on the board. Let the numbers $1,11,21,31,41,51,58,48,38,28,18,8$ be written in a circle clockwise.
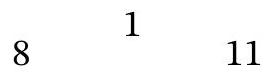
It is easy to see that all the conditions of the problem are satisfied.
|
58
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.2. Let $\alpha$ and $\beta$ be the real roots of the equation $x^{2}-x-2021=0$, with $\alpha>\beta$. Denote
$$
A=\alpha^{2}-2 \beta^{2}+2 \alpha \beta+3 \beta+7
$$
Find the greatest integer not exceeding $A$.
|
Answer: -6055.
Solution. By Vieta's theorem, we have $\alpha+\beta=1$ and $\alpha \beta=-2021$. Also, $\beta^{2}-\beta-2021=0$, since $\beta$ is a root of the equation. Therefore,
$A=\alpha^{2}-2 \beta^{2}+2 \alpha \beta+3 \beta+7=(\alpha+\beta)^{2}-3\left(\beta^{2}-\beta-2021\right)-6063+7=1^{2}-3 \cdot 0-6063+7=-6055$, so the answer to the problem is the number -6055.
The fact that $\alpha>\beta$ was not used.
|
-6055
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.3. Let $k_{1}$ be the smallest natural number that is a root of the equation
$$
\sin k^{\circ}=\sin 334 k^{\circ}
$$
(a) (2 points) Find $k_{1}$.
(b) (2 points) Find the smallest root of this equation that is a natural number greater than $k_{1}$.
|
# Answer:
(a) (2 points) 36.
(b) (2 points) 40.
Solution.
$$
0=\sin 334 k^{\circ}-\sin k^{\circ}=2 \sin \frac{333 k^{\circ}}{2} \cos \frac{335 k^{\circ}}{2}
$$
- Let $\sin \frac{333 k^{\circ}}{2}=0$. This is equivalent to $\frac{333 k}{2}=180 \mathrm{~m}$ for some integer $m$, that is, $333 k=360 m$ and $37 k=40 m$. Since $k$ is a natural number, $k$ must be divisible by 40, that is, $k \geqslant 40$. It is also clear that $k=40$ is a root (corresponding to $m=37$).
- Let $\cos \frac{335 k^{\circ}}{2}=0$. This is equivalent to $\frac{335 k}{2}=90+180 n$ for some integer $n$, that is, $335 k=360 n+180$ and $67 k=36(2 n+1)$. Since $k$ is a natural number, $k$ must be divisible by 36, that is, $k \geqslant 36$. It is also clear that $k=36$ is a root (corresponding to $m=33$). The next largest root in this series of solutions is greater than 40.
Thus, the smallest natural root of the original equation is 36, and the next largest is 40.
|
40
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.4. In a sports school, 55 people are training, each of whom is either a tennis player or a chess player. It is known that there are no four chess players who would have the same number of friends among the tennis players. What is the maximum number of chess players that can train in this school?
|
Answer: 42.
Solution. Let there be $a$ tennis players and $55-a$ chess players in the school. Each of the chess players has a number of tennis player friends that is no less than 0 and no more than $a$, meaning it can take on $a+1$ values. If there were more than $3(a+1)$ chess players, by the pigeonhole principle, there would be four of them with the same number of tennis player friends. Therefore, the number of chess players cannot exceed $3(a+1)$, leading to the inequality $55-a \leqslant 3(a+1)$. Solving this, we get $a \geqslant 13$, so $55-a \leqslant 55-13=42$.
Note also that there could have been exactly 42 chess players: for each integer $0 \leqslant k \leqslant 13$, let some three chess players have exactly $k$ arbitrary tennis player friends.
|
42
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.5. Points $A, B, C, D, E, F$ are arranged clockwise on a circle, as shown in the figure. Chords $A D$ and $C E$ intersect at point $X$ at a right angle, and chords $A D$ and $B F$ intersect at point $Y$.
It is known that $C X=12, X E=27, X Y=15, B Y=9, Y F=11$.
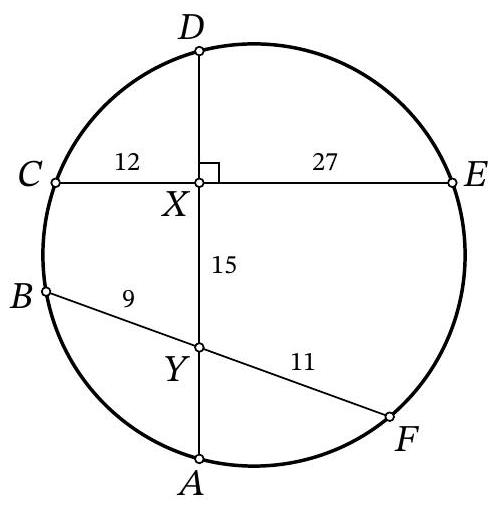
(a) (2 points) Find the length of segment $A D$.
(b) (2 points) Find the radius of the circle.
|
# Answer:
(a) (2 points) 36.
(b) (2 points) 19.5.
Solution. Let $A Y=a, X D=b$ (Fig. 8). We use the fact that the products of the segments of intersecting chords through a given point inside a circle are equal. This means that $324=12 \cdot 27=a(15+b)$ and $99=9 \cdot 11=b(a+15)$. Subtracting the second equation from the first, we get $225=15(a-b)$, which means $a-b=15$. Then $18^{2}=324=a(15+b)=(15+b)^{2}$, from which we obtain $18=15+b$ and $b=3$. Therefore, $a=18$ and $A D=a+15+b=3+15+18=36$. Thus, $A X=X D=18$. The center of the circle lies on the perpendicular bisector of the chord $A D$, that is, on the segment $C E$. Therefore, $C E$ is the diameter of the given circle, so its radius
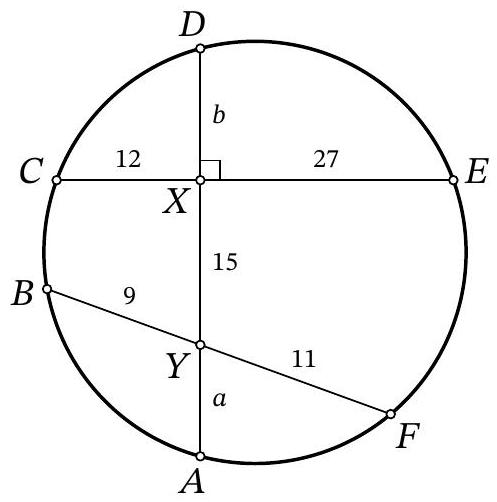
Fig. 8: to the solution of problem 11.5
is $\frac{1}{2} C E=\frac{1}{2}(12+27)=19.5$.
|
36
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.6. Given the set of numbers $\{-1,-2,-3, \ldots,-26\}$. On the board, all possible subsets of this set were written, each containing at least 2 numbers. For each written subset, the product of all numbers belonging to that subset was calculated. What is the sum of all these products?
|
Answer: 350.
Solution. Consider the expression $(1-1)(1-2)(1-3) \ldots(1-26)$, the value of which is 0. Expand this expression without combining like terms, resulting in the sum $1^{26}-1^{25}(1+2+3+\ldots+26)+S$. Notice that the sum $S$ coincides with the sum from the problem's condition. Therefore, it equals $0-1+(1+2+3+\ldots+26)=350$.
|
350
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.7. All vertices of a regular tetrahedron $ABCD$ are on the same side of the plane $\alpha$. It turns out that the projections of the vertices of the tetrahedron onto the plane $\alpha$ form the vertices of a certain square. Find the value of $AB^2$ if it is known that the distances from points $A$ and $B$ to the plane $\alpha$ are 17 and 21, respectively.
|
Answer: 32.
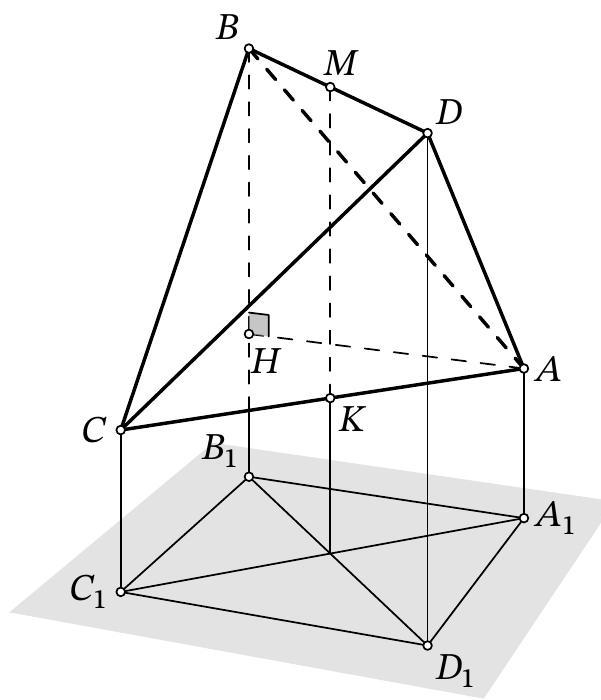
Fig. 9: to the solution of problem 11.7
Solution. Let $A_{1}, B_{1}, C_{1}, D_{1}$ be the projections of points $A, B, C, D$ onto the plane $\alpha$. Let $M$ be the midpoint of segment $B D$, and $K$ be the midpoint of segment $A C$ (Fig. 9). The projections of points $M$ and $K$ onto the plane $\alpha$ are the midpoints of segments $B_{1} D_{1}$ and $A_{1} C_{1}$, respectively, and thus coincide. Therefore, the line $M K$ is perpendicular to the plane $\alpha$. It is also perpendicular to the line $A C$ (the segments $A M$ and $C M$ are equal as medians of equal triangles $A B D$ and $C B D$, so the median $M K$ of the isosceles triangle $A M C$ is also its altitude), which means $A C \| \alpha$. Therefore, $A A_{1} C_{1} C$ is a rectangle and $A_{1} C_{1}=A C$.
Let the side of the square $A_{1} B_{1} C_{1} D_{1}$ be $x$, then by the Pythagorean theorem, $A_{1} C_{1}^{2}=2 x^{2}$. Drop a perpendicular $A H$ to the line $B B_{1}$. Clearly, $A A_{1} B_{1} H$ is a rectangle, so $A A_{1}=H B_{1}=17$ and $A H=A_{1} B_{1}=x$. Also, $B H=B B_{1}-H B_{1}=21-17=4$. By the Pythagorean theorem for triangle $A B H$, we have $A B^{2}=16+x^{2}$. Therefore,
$$
16+x^{2}=A B^{2}=A C^{2}=A_{1} C_{1}^{2}=2 x^{2}
$$
from which we find $x=4$. Then $A B^{2}=2 \cdot 4^{2}=32$.
|
32
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.8. In each cell of a strip $1 \times N$ there is either a plus or a minus. Vanya can perform the following operation: choose any three cells (not necessarily consecutive), one of which is exactly in the middle between the other two cells, and change the three signs in these cells to their opposites. A number $N$ is called positive if from an arrangement of $N$ minuses Vanya can, by such operations, obtain an arrangement of $N$ pluses.
Consider the numbers $3,4,5, \ldots, 1400$. How many of them are positive?
|
Answer: 1396.
Solution. We will prove that all the numbers under consideration are positive, except for 4 and 5. Then the answer to the problem will be $1398-2=1396$.
For each $N$, we will number the cells of the strip $1 \times N$ from left to right with numbers from 1 to $N$.
- Let $N=3$. By applying the operation to the cells with numbers $(1,2,3)$, we immediately obtain a configuration of all pluses.
- Let $N=6$. By applying the operations to the cells with numbers $(1,2,3)$ and to the cells with numbers $(4,5,6)$, we immediately obtain a configuration of all pluses.
- Let $N=7$. By applying the operations to the cells with numbers $(1,4,7)$, to the cells with numbers $(2,3,4)$, and to the cells with numbers $(4,5,6)$, we immediately obtain a configuration of all pluses.
- Let $N \geqslant 8$. By applying the operations to the cells with numbers $(N, N-1, N-2)$, to the cells with numbers $(N-3, N-4, N-5)$, and so on, we can achieve a configuration where pluses are in all cells of the strip, except possibly in cells with numbers 1 and 2. If there is a minus in cell number 2, apply the operations to the cells with numbers $(2,5,8)$, $(5,6,7)$, $(6,7,8)$, and we will get pluses in all cells from 2 to $N$ inclusive. If there is a minus in cell number 1, apply the operations to the cells with numbers $(1,4,7)$, $(4,5,6)$, $(5,6,7)$. Thus, we have achieved a configuration of all pluses.
- Let $N=4$. The operations can only be applied to the cells with numbers $(1,2,3)$ or $(2,3,4)$. Clearly, in this way, we can only obtain the configurations - - --, ,,,+++--++++--+ and it is impossible to obtain a configuration of all pluses.
- Let $N=5$. The operations can only be applied to the cells with numbers $(1,2,3)$, $(2,3,4)$, $(3,4,5)$, $(1,3,5)$. Note that in cells with numbers $2,3,5$, there is always an odd number of minuses, so it is impossible to obtain a configuration of all pluses.
|
1396
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.7. Denis threw darts at four identical dartboards: he threw exactly three darts at each board, where they landed is shown in the figure. On the first board, he scored 30 points, on the second - 38 points, on the third - 41 points. How many points did he score on the fourth board? (For hitting each specific zone - ring or central field - a certain number of points is awarded.)
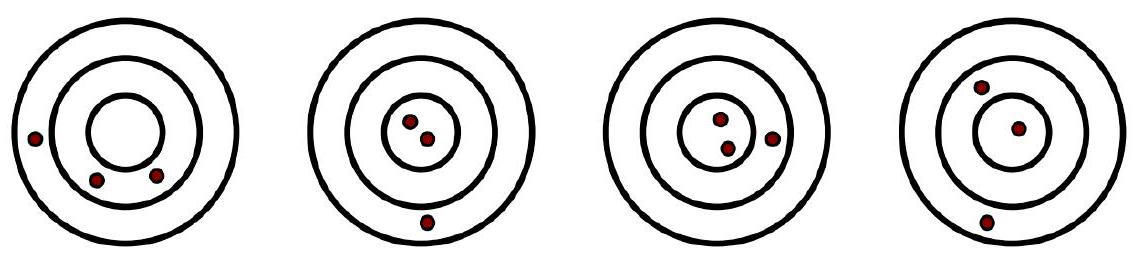
|
Answer: 34.
Solution. "Add" the first two dart fields: we get 2 hits in the central field, 2 hits in the inner ring, 2 hits in the outer ring. Thus, the sum of points on the first and second fields is twice the number of points obtained for the fourth field.
From this, it is not difficult to get the answer
$$
(30+38): 2=34
$$
|
34
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.1. After a football match, the coach lined up the team as shown in the figure, and commanded: "Run to the locker room, those whose number is less than that of any of their neighbors." After several people ran away, he repeated his command. The coach continued until only one player was left. What is Igor's number, if it is known that after he ran away, 3 people remained in the line? (After each command, one or several players ran away, after which the line closed, and there were no empty spaces between the remaining players.)

|
Answer: 5.
Solution. It is clear that after the first command, the players left are $9,11,10,6,8,5,4,1$. After the second command, the players left are $11,10,8,5,4$. After the third - $11,10,8,5$. After the fourth - $11,10,8$. Therefore, Igor had the number 5.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.5. The figure shows 4 squares. It is known that the length of segment $A B$ is 11, the length of segment $F E$ is 13, and the length of segment $C D$ is 5. What is the length of segment $G H$?
|
Answer: 29.
Solution. The side of the largest square (with vertex $A$) is greater than the side of the second largest square (with vertex $C$) by the length of segment $A B$, which is 11. Similarly, the side of the second largest square is greater than the side of the third largest square (with vertex $E$) by the length of segment $C D$, which is 5. And its side is greater than the side of the smallest square by the length of segment $E F$, which is 13. In total, the side of the largest square is greater than the side of the smallest square by the length of segment $G H$, which is $11+5+13=29$.
|
29
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
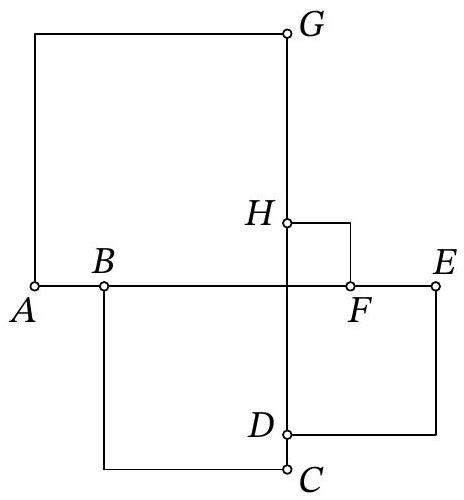
Problem 7.5. A rectangle was cut into nine squares, as shown in the figure. The lengths of the sides of the rectangle and all the squares are integers. What is the smallest value that the perimeter of the rectangle can take?
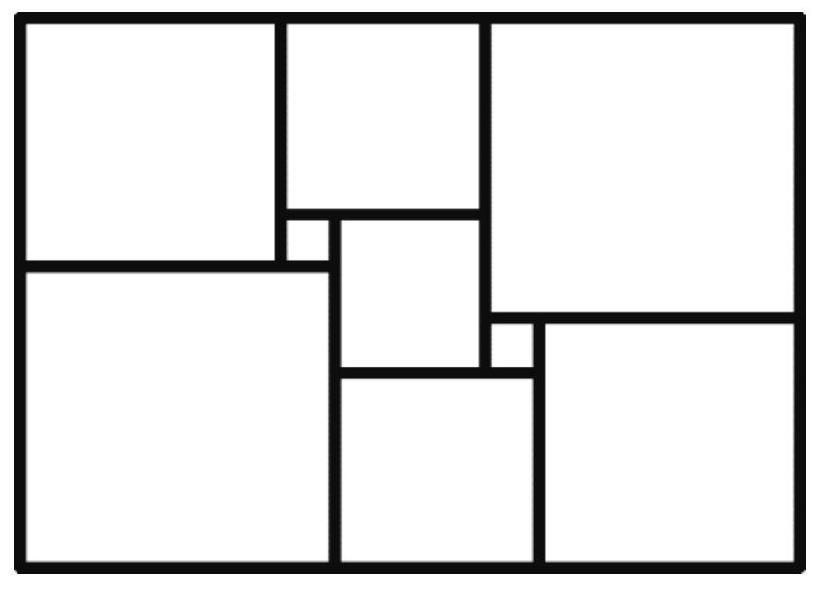
|
Answer: 52.
Solution. Inside the square, we will write the length of its side. Let the sides of the two squares be $a$ and $b$, and we will sequentially calculate the lengths of the sides of the squares.
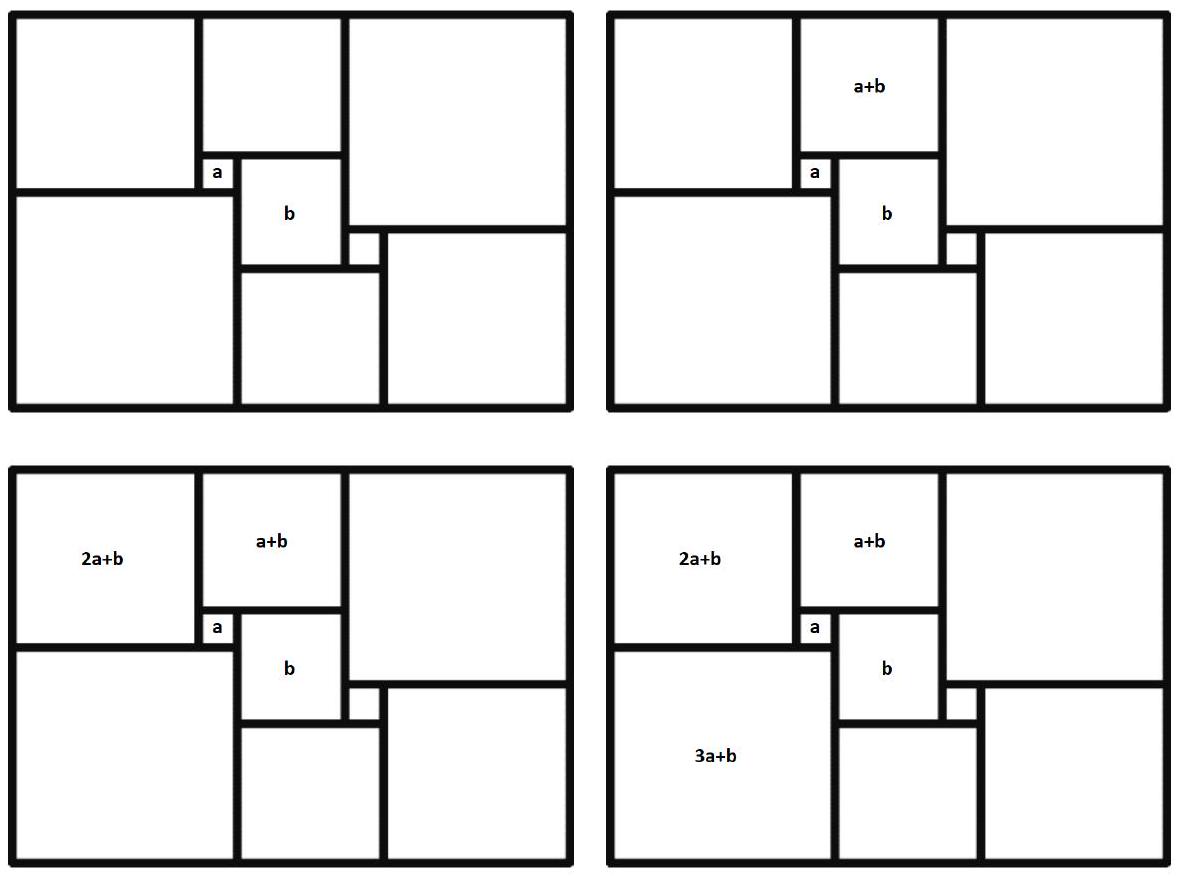
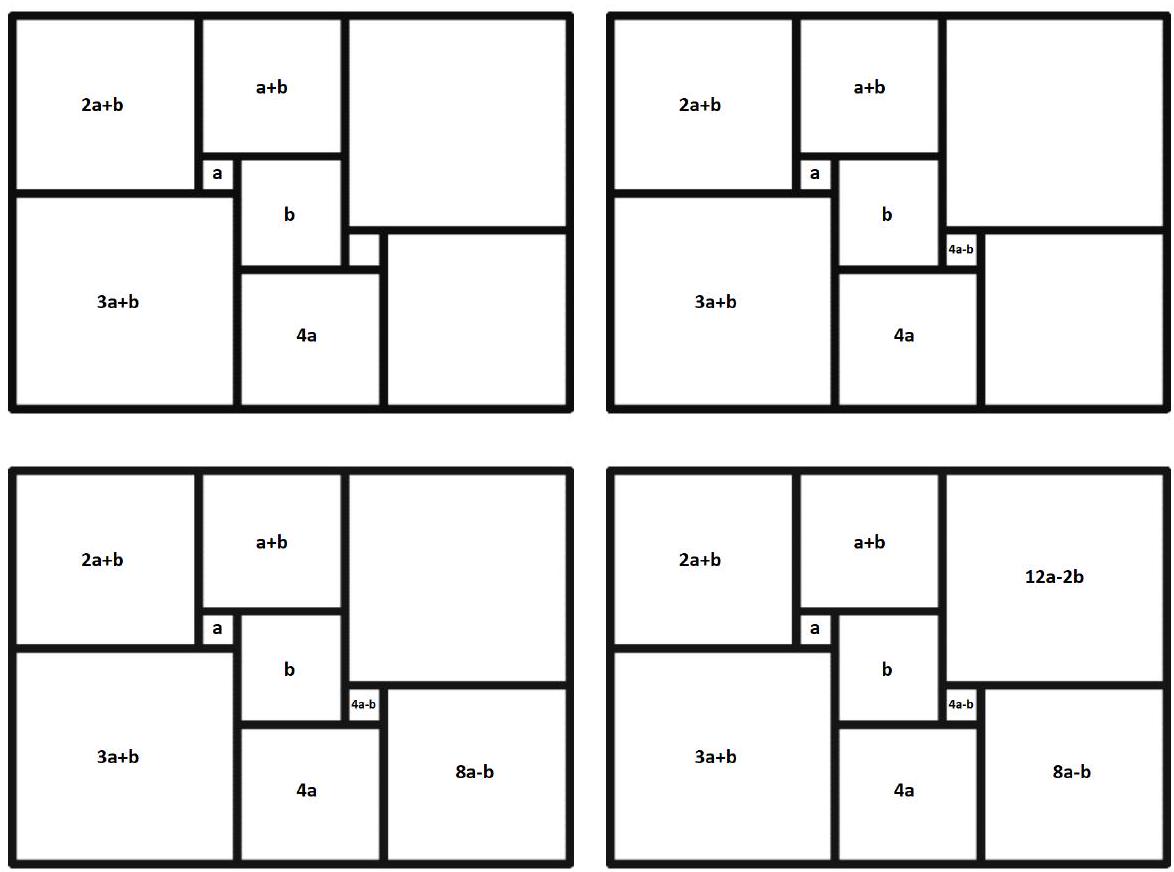
The sum of the lengths of the sides of the two squares adjacent to the left side of the rectangle is equal to the sum of the lengths of the sides of the two squares adjacent to the right side of the rectangle. We get the equation
$$
\begin{aligned}
(2 a+b)+(3 a+b) & =(12 a-2 b)+(8 a-b) \\
5 a+2 b & =20 a-3 b \\
b & =3 a
\end{aligned}
$$
Thus, to minimize the perimeter of the rectangle, we need to choose $a=1$, $b=3$. It is easy to check that with these values, the rectangle will have dimensions $11 \times 15$, and its perimeter will be 52.
|
52
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.1. A square was cut into four equal rectangles, and from them, a large letter P was formed, as shown in the figure, with a perimeter of 56.
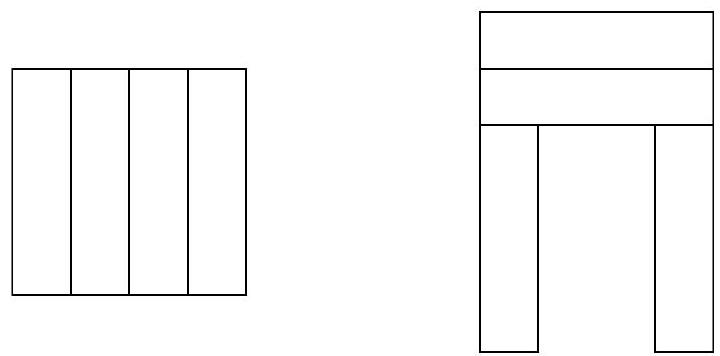
What is the perimeter of the original square
|
Answer: 32.
Solution. Let the width of the rectangle be $x$. From the first drawing, we understand that the length of the rectangle is four times its width, that is, it is equal to $4 x$. Now we can calculate the dimensions of the letter P.
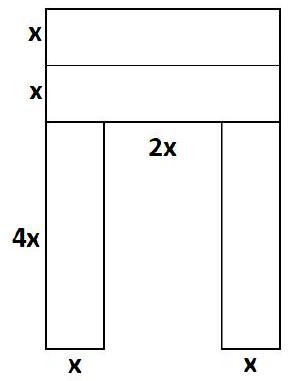
From this, we get the equation
$$
\begin{gathered}
28 x=56 \\
x=2
\end{gathered}
$$
The perimeter of the square is $16 x=32$.
|
32
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.2. The numbers from 1 to 9 were placed in the cells of a $3 \times 3$ table such that the sum of the numbers on one diagonal is 7, and on the other - 21. What is the sum of the numbers in the five shaded cells?
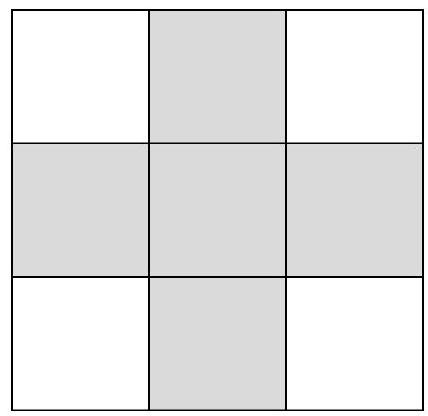
|
Answer: 25.
Solution. Note that 7 can be represented uniquely as the sum of numbers from 1 to 9 - this is $1+2+4=7$.
Let's look at the other diagonal with a sum of 21. The largest possible value of the sum in it is $9+8+4=21$ (since the number in the central cell is no more than 4). Therefore, it must contain the numbers $9,8,4$.
Thus, the number 4 is in the central cell, and the numbers 1, 2, 8, and 9 are at the corners. Now it is not difficult to find the sum of the numbers in the shaded cells: $3+4+5+6+7=25$.
|
25
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.6. For quadrilateral $ABCD$, it is known that $AB=BD, \angle ABD=\angle DBC, \angle BCD=90^{\circ}$. A point $E$ is marked on segment $BC$ such that $AD=DE$. What is the length of segment $BD$, if it is known that $BE=7, EC=5$?
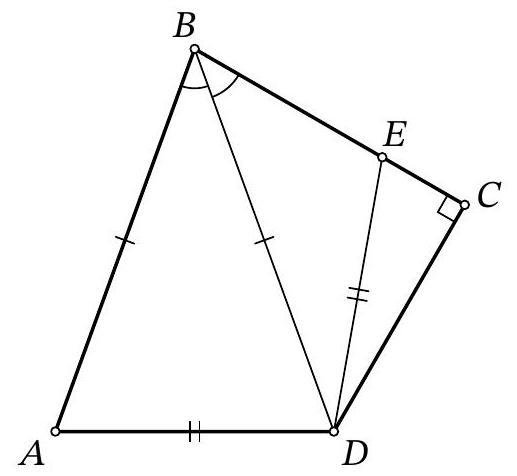
|
Answer: 17.
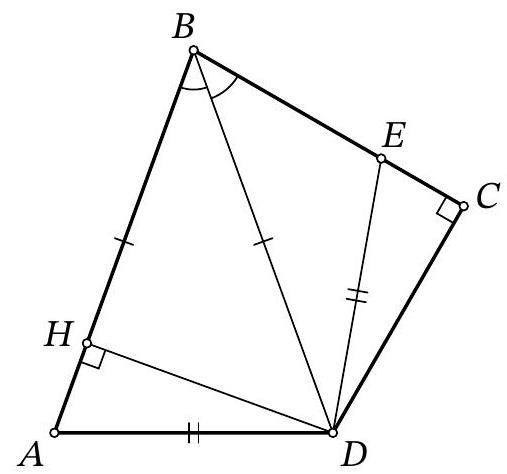
Fig. 3: to the solution of problem 8.6
Solution. In the isosceles triangle $ABD$, drop a perpendicular from point $D$, let $H$ be its foot (Fig. 3). Since this triangle is acute-angled ($\angle ABD = \angle CBD < 90^\circ$, $\left.\angle BAD = \angle ADB = \frac{180^\circ - \angle ABD}{2} < 90^\circ\right)$, point $H$ lies on the segment $AB$.
Notice that the right triangles $BDH$ and $BDC$ are equal by the common hypotenuse $BD$ and the acute angle at vertex $B$. Therefore, $BH = BC$ and $DH = CD$.
Now, notice that the right triangles $ADH$ and $EDC$ are also equal by the hypotenuse $AD = ED$ and the leg $DH = CD$. Therefore, $EC = AH$.
Thus, $BD = BA = BH + AH = BC + EC = (7 + 5) + 5 = 17$.
|
17
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.4. From left to right, intersecting squares with sides $12, 9, 7, 3$ are depicted respectively. By how much is the sum of the black areas greater than the sum of the gray areas?
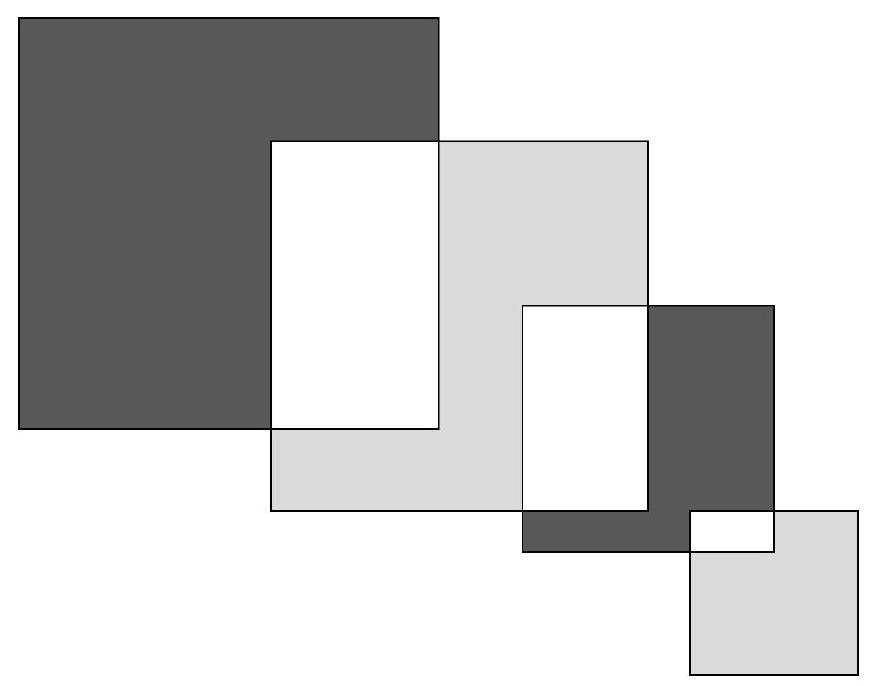
|
Answer: 103.
Solution. Let's denote the areas by $A, B, C, D, E, F, G$.
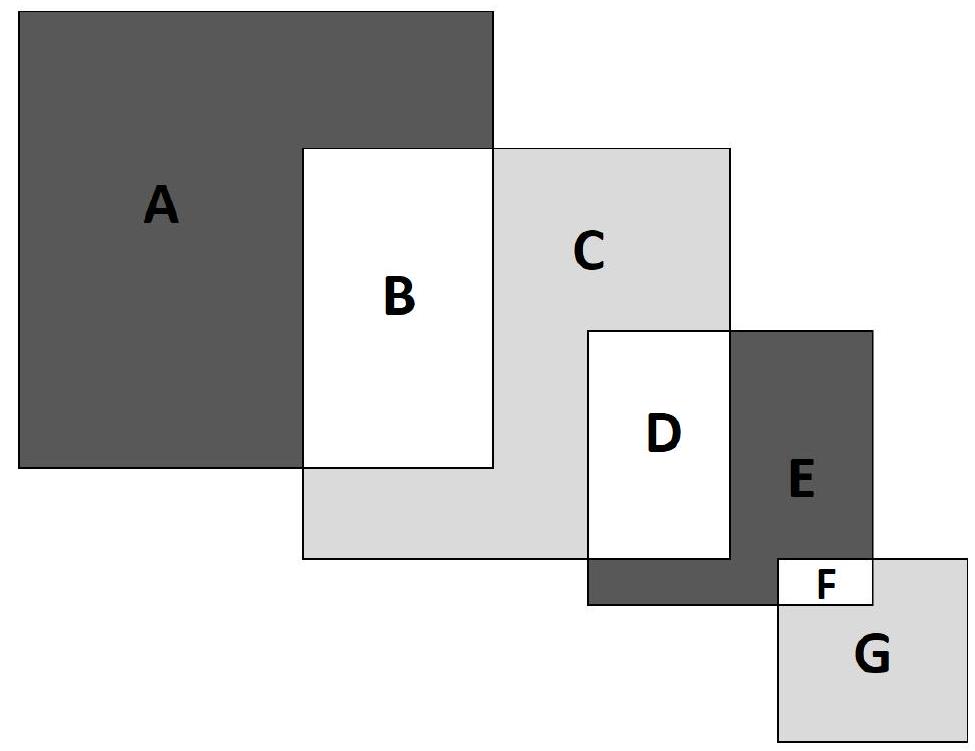
We will compute the desired difference in areas:
$$
\begin{aligned}
A+E-(C+G) & =A-C+E-G=A+B-B-C-D+D+E+F-F-G= \\
& =(A+B)-(B+C+D)+(D+E+F)-(F+G)= \\
& =12^{2}-9^{2}+7^{2}-3^{2}=103
\end{aligned}
$$
|
103
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.7. In triangle $ABC$, the bisector $AL$ is drawn. Points $E$ and $D$ are marked on segments $AB$ and $BL$ respectively such that $DL = LC$, $ED \parallel AC$. Find the length of segment $ED$, given that $AE = 15$, $AC = 12$.
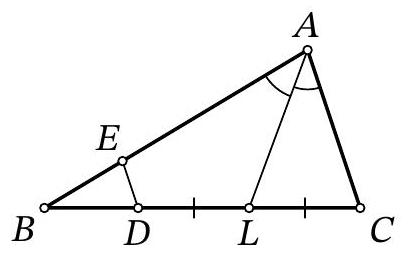
|
Answer: 3.
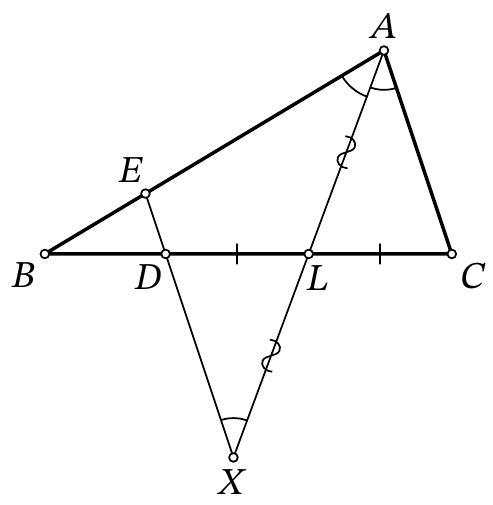
Fig. 5: to the solution of problem 9.7
Solution. On the ray $AL$ beyond point $L$, mark a point $X$ such that $XL = LA$ (Fig. 5). Since in the quadrilateral $ACXD$ the diagonals are bisected by their intersection point $L$, it is a parallelogram (in particular, $AC = DX$). Therefore, $DX \parallel AC$. Since $AC \parallel ED$ by the problem's condition, the points $X, D, E$ lie on the same line.
Since $AC \parallel EX$, then $\angle EAX = \angle CAX = \angle AXE$, i.e., triangle $AEX$ is isosceles, $EA = EX$. Then
$$
ED = EX - XD = EA - AC = 15 - 12 = 3
$$
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.1. In each cell of a $5 \times 5$ table, a natural number is written in invisible ink. It is known that the sum of all the numbers is 200, and the sum of three numbers located inside any $1 \times 3$ rectangle is 23. What is the central number in the table?
|
Answer: 16.
Solution. Divide the $5 \times 5$ square without the central cell into four $2 \times 3$ rectangles, and each of these into two $1 \times 3$ rectangles.
This results in 8 rectangles of $1 \times 3$, the sum of the numbers in each of which is 23. Since the sum of all the numbers is 200, we find the number in the central cell as $200 - 23 \cdot 8 = 16$.
|
16
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.8. Rectangle $ABCD$ is such that $AD = 2AB$. Point $M$ is the midpoint of side $AD$. Inside the rectangle, there is a point $K$ such that $\angle AMK = 80^{\circ}$ and ray $KD$ is the bisector of angle $MKC$. How many degrees does angle $KDA$ measure?
|
Answer: 35.
Solution. Let's start with the assumption that the quadrilateral KMDС is inscribed (several proofs of this fact will be proposed below).
Using the fact that in the inscribed quadrilateral $K M D C$ the sum of opposite angles is $180^{\circ}$, we get $\angle M K D=\frac{\angle M K C}{2}=\frac{180^{\circ}-\angle M D C}{2}=45^{\circ}$. The angle $A M K$ as an external angle for triangle $K D M$ is equal to the sum of angles $M K D$ and $K D A$, so the required angle КDA is $80^{\circ}-45^{\circ}=35^{\circ}$.
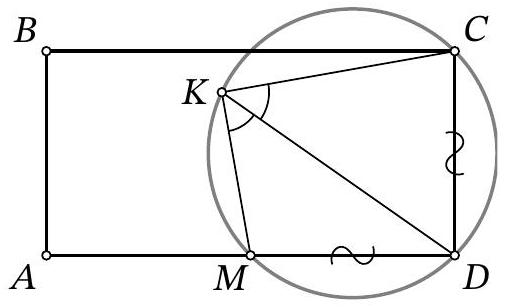
Fig. 8: to the solution of problem 10.8
Let's provide the first possible proof of the inscribed nature of quadrilateral KMDC. Consider triangle $M K C$ and its circumscribed circle. Note that point $D$ lies on the bisector of angle $M K C$, and is equidistant from vertices $M$ and $C$ (Fig. 8). However, the bisector of an angle in a non-isosceles triangle and the perpendicular bisector of its opposite side, as is known, intersect at the midpoint of the "smaller" arc of the circumscribed circle of the triangle. In other words, $D$ is the midpoint of the arc $M C$ of the circumscribed circle of triangle $M K C$, not containing point $K$. It should also be noted that $M K \neq K C$ (otherwise, triangles $K M D$ and $K C D$ would be equal, but $\angle K M D>90^{\circ}>\angle K C D$ ).
Let's provide the second possible proof of the inscribed nature of quadrilateral KMDC. It will use the fourth criterion for the equality of triangles: if two sides and an angle not between them are equal in two triangles, then these triangles are either equal or the sum of the other two angles not between them is $180^{\circ}$. The fourth criterion is satisfied for triangles $M D K$ and $C D K (M D=D C, D K$ - common, $\angle M K D=\angle C K D)$. However, angles $K M D$ and $K C D$ are not equal (again, the first is obtuse, and the second is acute), so their sum is $180^{\circ}$, which are the opposite angles of quadrilateral KMDC. Therefore, it is inscribed.
## 11th grade
|
35
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.6. Inside the cube $A B C D A_{1} B_{1} C_{1} D_{1}$, there is the center $O$ of a sphere with radius 10. The sphere intersects the face $A A_{1} D_{1} D$ along a circle with radius 1, the face $A_{1} B_{1} C_{1} D_{1}$ along a circle with radius 1, and the face $C D D_{1} C_{1}$ along a circle with radius 3. Find the length of the segment $O D_{1}$.
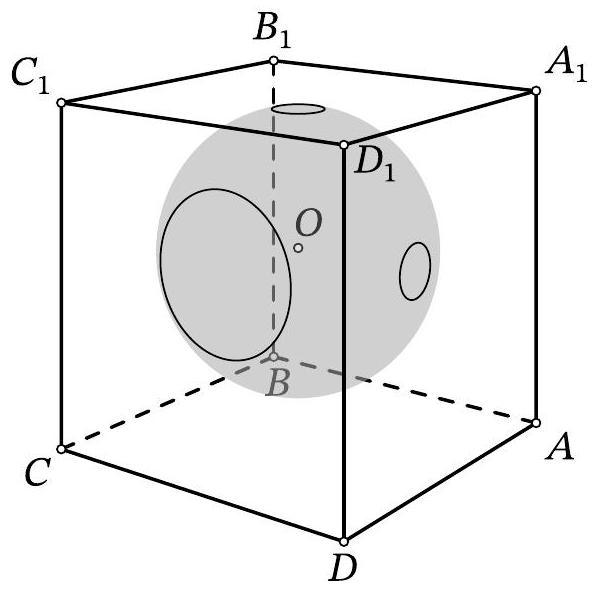
|
Answer: 17.
Solution. Let $\omega$ be the circle that the sphere cuts out on the face $C D D_{1} C_{1}$. From point $O$
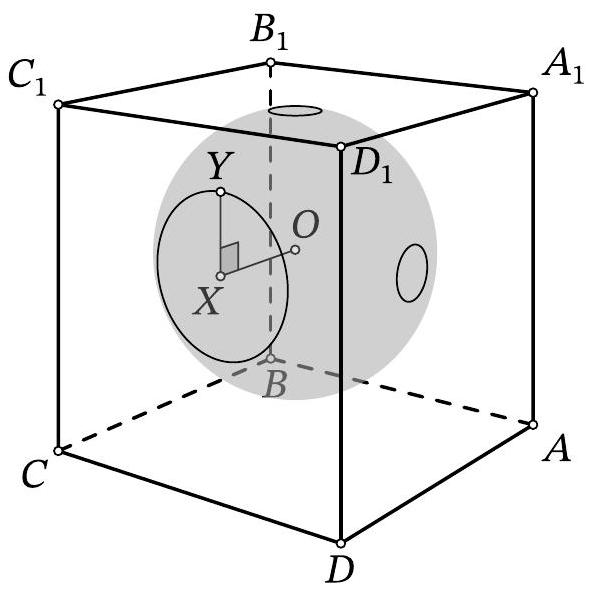
Fig. 10: to the solution of problem 11.6
drop a perpendicular $O X$ to this face, then point $X$ is the center of $\omega$ (point $O$ is equidistant from all points of $\omega$, so the projection of $O$ onto the plane of $\omega$ is also equidistant from them). Let $Y$ be an arbitrary point on $\omega$ (Fig. 10). Triangle $OXY$ is a right triangle; by the problem's condition, $X Y=3$ and $O Y=10$. By the Pythagorean theorem, we get $O X^{2}=10^{2}-3^{2}=91$.
Similarly, we find the squares of the distances from point $O$ to the planes $A_{1} B_{1} C_{1} D_{1}$ and $A D D_{1} A_{1}$, which are both equal to $10^{2}-1^{2}=99$.
By the spatial Pythagorean theorem, the square of the length of segment $O D_{1}$ is equal to the sum of the squares of the distances from point $O$ to the three faces containing point $D_{1}$. Therefore, $O D_{1}^{2}=$ $91+99+99=289$, from which $O D_{1}=17$.
|
17
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. In the parliament of the island state of Promenade-and-Tornado, only the indigenous inhabitants of the island can be elected, who are divided into knights and liars: knights always tell the truth, liars always lie. A secret ballot on 8.09.19 re-elected 2019 deputies. At the first meeting, all deputies were present: 2016 of them sat in the deputies' chairs, arranged in the hall in a rectangle $42 \times 48$, three - in the chairs of the chairman and his deputies in the presidium. During the meeting, each one stated that among his neighbors in the chair were only liars (neighbors - those who sit to the left, right, in front, behind, and diagonally: there can be from 3 to 8 in the hall and 1 or 2 in the presidium). Determine the minimum number of knights in the parliament.
|
Solution. A rectangle $42 \times 48$ can be tiled with $3 \times 3$ squares (224 are required). In each such square, there must be at least one knight (otherwise - if the square contains only liars, the liar in the central cell would have told the truth, which is impossible). Thus, the minimum number of knights in the hall is 224 (in the centers of the squares with which we tiled the rectangle - in this case, all knights in the hall told the truth, and all liars lied as they should). The minimum number of knights in the presidium is 1 (in the center).
Answer: 225.
|
225
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.2. It is known that $\frac{1}{\cos (2022 x)}+\operatorname{tg}(2022 x)=\frac{1}{2022}$.
Find $\frac{1}{\cos (2022 x)}-\operatorname{tg}(2022 x)$.
|
Answer. 2022.
## Solution.
Consider the product $\left(\frac{1}{\cos \alpha}+\operatorname{tg} \alpha\right)\left(\frac{1}{\cos \alpha}-\operatorname{tg} \alpha\right)=\frac{1}{\cos ^{2} \alpha}-\operatorname{tg}^{2} \alpha=\frac{1-\sin ^{2} \alpha}{\cos ^{2} \alpha}=1$. Therefore, the desired expression is 2022.
Comment. A correct answer without justification - 0 points.
|
2022
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.4. One hundred and one non-zero integers are written in a circle such that each number is greater than the product of the two numbers following it in a clockwise direction. What is the maximum number of negative numbers that can be among these 101 written numbers?
|
Answer: 67.
Solution: Consider any 3 consecutive numbers. All of them cannot be negative. Among them, there is a positive one. Fix this positive number and its neighbor (this number can be negative), and divide the remaining 99 numbers into 33 groups of 3 consecutive numbers. In each such group, there will be no more than two negative numbers. Thus, the total number of negative numbers is no more than $1 + 2 \times 33 = 67$. Such a situation is possible. Number the numbers in a circle. Let the positive numbers be those with indices $1, 4, 7, 10$, ..., 100, and the rest be negative. It is easy to verify that if all positive numbers are equal to 5, and all negative numbers are equal to -2, then each number is greater than the product of the two numbers following it in the clockwise direction.
Comment: Correct answer without justification - 0 points.
Proved that the number of negative numbers is no more than 67 - 4 points.
Provided an example with 67 negative numbers - 3 points.
|
67
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.5. The lateral faces of the pentagonal pyramid $S A B C D E$ are acute-angled triangles. We will call a lateral edge of the pyramid good if it is equal to the height of the opposite lateral face, drawn from the vertex of the pyramid (for example, the edge $S A$ is good if it is equal to the height of the triangle $S C D$, drawn from the vertex $S$). What is the maximum number of good edges that the pyramid can have?
|
# Answer. 2.
Solution. We will show that two non-adjacent lateral edges of the pyramid cannot both be good. Suppose this is not the case, and, for example, edges $S A$ and $S C$ are good, meaning $S A = S P$ is the height of face $S C D$, and $S C = S Q$ is the height of face $S A E$. However, by the property of the height in an acute triangle, $S P < S C$, and $S Q < S A$. Therefore, $S A = S P < S C = S Q < S A$ - a contradiction.
Now, note that among the three lateral edges of a pentagonal pyramid, there will always be two non-adjacent edges. Thus, the pyramid can have no more than two good edges. We will show that there exists a pentagonal pyramid with two good lateral edges. Consider a square $A M N E$ with center $O$. Let the line passing through vertex $M$ and perpendicular to $E M$, and the line passing through vertex $N$ and perpendicular to $A N$, intersect at point $C$. Choose points $B$ and $D$ such that points $M$ and $N$ are the midpoints of segments $B C$ and $D C$, respectively. Choose an arbitrary point $S$ on the perpendicular to the plane $A B C$ passing through point $O$. Then, by the theorem of three perpendiculars, $S M$ and $S N$ are the heights of triangles $S B C$ and $S D C$. And, as follows from the isosceles nature of triangles $E S M$ and $A S N$, edges $S E$ and $S A$ are good.
Comment. Correct answer without justification - 0 points.
Proved that the pyramid cannot have more than 2 good edges - 4 points.
Provided an example of a pyramid with 2 good edges - 3 points.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Martians love to dance dances where they have to hold hands. In the dance "Pyramid," no more than 7 Martians can participate, each of whom has no more than three hands. What is the maximum number of hands that the dancers can have if any hand of one Martian holds exactly one hand of another Martian?
|
Solution. In each handshake, two hands are involved, so the total number of hands shaken will be even. The maximum variant (7 Martians with three hands) gives 21 hands. Therefore, the greatest number of hands will be achieved if 6 Martians have three hands each and one has two hands. The dancers have 20 hands.
Comment. Justification of the even number of hands in the correct answer - 2 points. For the maximum score, a diagram illustrating the described situation should be constructed.
|
20
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The number 98 is written on the board. Every minute, the number is erased and replaced with the product of its digits, increased by 15. What number will be on the board after an hour?
|
Solution. Starting from the fourth minute, a periodic sequence with a period length of 6 is formed: 98, 87, 71, 22, 19, 24, 23, 21, 17, 22, ..
On the 60th minute, just like on the 6th minute, the number 24 will appear on the board, and therefore, after an hour, that is, on the 61st minute, the number 23 will be on the board.
Comment. The periodic sequence is correctly identified - 4 points.
|
23
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. Oleg drew an empty $50 \times 50$ table and wrote a number above each column and to the left of each row. It turned out that all 100 written numbers are distinct, with 50 of them being rational and the other 50 being irrational. Then, in each cell of the table, he wrote the sum of the numbers written next to its row and its column (a "sum table"). What is the maximum number of sums in this table that could be rational numbers?
(O. Podlipsky)
|
Answer: 1250 sums.
Solution. First, we show that there are at least 1250 irrational numbers in the table. Let there be $x$ irrational and $50-x$ rational numbers along the left side of the table. Then, along the top side, there are $50-x$ irrational and $x$ rational numbers. Since the sum of a rational and an irrational number is always irrational, there are at least $x^2 + (50-x)^2$ irrational numbers in the table. Furthermore, $x^2 + (50-x)^2 = 2x^2 - 100x + 50^2 = 2(x-25)^2 + 2 \cdot 25^2 \geq 2 \cdot 25^2 = 1250$, which is what we needed to show. Therefore, there are no more than $2500 - 1250 = 1250$ rational numbers in the table.
Exactly 1250 rational numbers in the table can occur, for example, in the following case. Along the left side, the numbers are $1, 2, \ldots, 24, 25, 1+\sqrt{2}, 2+\sqrt{2}, \ldots, 25+\sqrt{2}$, and along the top side, the numbers are $26, 27, \ldots, 49, 50, 26-\sqrt{2}, 27-\sqrt{2}, \ldots, 50-\sqrt{2}$. Then, the only irrational sums will be $2 \cdot 25^2 = 1250$ sums of a rational and an irrational number.
Comment. Only the correct answer - 0 points.
Proof that there are no more than 1250 rational numbers in the table - 4 points.
If this proof is only conducted in a special case where there are an equal number of rational and irrational numbers along the left (or top) side - 1 point instead of four.
The inequality $x^2 + (50-x)^2 \geq 1250$ (or an equivalent one) is used without proof - 1 point is deducted.
A correct example showing that there could be exactly 1250 rational numbers - 3 points.
The statement that the sum of a rational and an irrational number is irrational can be used without proof. 9.6. In an acute triangle $ABC$, the median $AM$ and the altitude $BH$ are drawn. The perpendicular from point $M$ to line $AM$ intersects ray $HB$ at point $K$. Prove that if $\angle MAC = 30^\circ$, then $AK = BC$.
(B. Obukhov)
First Solution. Since $\angle AHK = \angle AMK = 90^\circ$, points $A, H, M$, and $K$ lie on a circle $\omega$ with diameter $AK$ (see Fig. 1). By the problem's condition, the chord $HM$ of this circle subtends an angle $\angle MAH = 30^\circ$, so $HM = 2R \sin 30^\circ = AK / 2$. On the other hand, $HM$ is the median of the right triangle $BHC$, so $BC = 2HM = AK$, which is what we needed to prove.
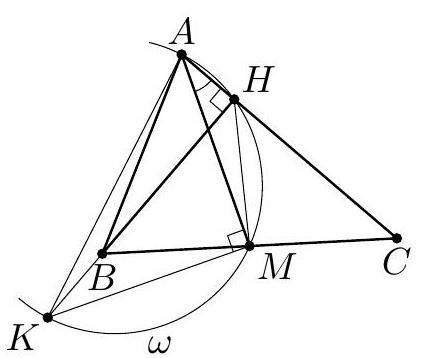
Fig. 1
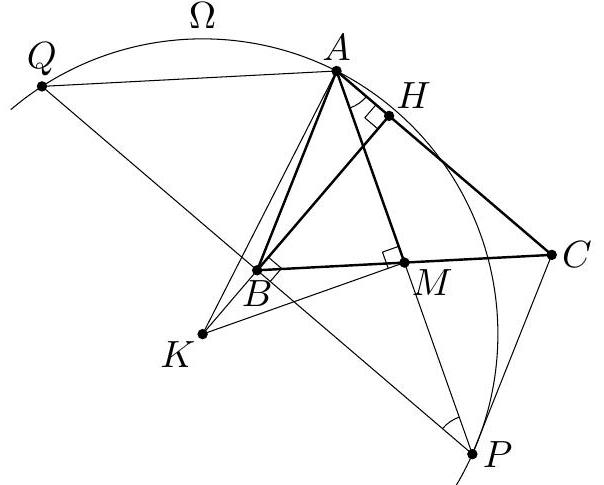
Fig. 2
Second Solution. Extend triangle $ABC$ to parallelograms $ABPC$ and $AQB C$ (see Fig. 2); then $BP = AC = BQ$ and $KH \perp PQ$. Moreover, point $M$ is the midpoint of $AP$ (as the intersection of the diagonals of parallelogram $ABPC$). Therefore, lines $MK$ and $HK$ are the perpendicular bisectors of segments $AP$ and $PQ$. Consequently, point $K$ is the center of the circle $\Omega$ circumscribed around triangle $APQ$. Further, $\angle APQ = \angle PAC = 30^\circ$, so the chord $AQ$ of circle $\Omega$ equals the radius $AK$. Finally, from parallelogram $AQB C$, we get $BC = AQ = AK$.
Comment. Noted that points $A, H, M$, and $K$ lie on the same circle - 2 points.
|
1250
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.1 Two couples want to sit on a bench. In how many ways can they sit so that each boy sits next to his girlfriend, if the left and right sides of the bench are distinguishable?
|
# Answer: 8
Solution. Let's number the seats from 1 to 4. If one of the couple sits in seat number 1, then the second must sit in seat 2. Thus, each couple either sits on the left (seats 1 and 2) or on the right (seats 3 and 4). Each couple can sit in two ways (boy on the left or right), and the couples themselves can switch places. In total, $2 \cdot 2 \cdot 2=8$ ways.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 4.1.2. A sports team consists of two boys and two girls. In the relay, the stages run by girls must alternate with the stages run by boys. In how many ways can the stages be distributed
#
|
# Answer: 8
Solution. Boys can run stages 1 and 3, or stages 2 and 4. If they run stages 1 and 3, they can be distributed in two ways, and girls can be distributed in two ways, making a total of 4 ways. In the second case, there are another 4 ways, making a total of 8 ways.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 4.1.3 Two mothers with their children want to sit on a bench with 4 seats. In how many ways can they sit so that each mother sits next to her child? Each mother is walking with one child.
#
|
# Answer: 8
Solution. Let's number the seats from 1 to 4. If someone from a family sits in seat number 1, then the second person must sit in seat 2. Thus, each family either sits on the left (seats 1 and 2) or on the right (seats 3 and 4). Each family can sit in two ways (child on the left or right), and the families can switch places. In total, $2 \cdot 2 \cdot 2=8$ ways.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.1 In a closed bag lie apples. Three friends tried to lift the bag and guess how many fruits were inside. The first one said that, in his opinion, there were 20 apples, the second thought there were 22, and the third said 25. When the friends opened the bag, it turned out that one of them was off by 1, another by 3, and the third by 6. How many apples were in the bag? Find all possible answers.
#
|
# Answer: 19
Solution. Note that the first and second friends give even predictions, which means they make an error of the same parity, while the third makes an error of a different parity. Therefore, the third friend was off by 6 apples, so there were either 19 or 31 apples in the bag. Checking both options, we get the answer.
|
19
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.2 In a closed bag lie apples. Three friends tried to lift the bag and guess how many fruits were inside. The first said that, in his opinion, there were 19 apples, the second thought there were 22, and the third said 23. When the friends opened the bag, it turned out that one of them was off by 1, another by 2, and the third by 3. How many apples were in the bag? Find all possible answers.
|
Answer: 20
Solution. Note that the first and third friends give odd predictions, which means they make errors of one parity, while the second makes errors of the other parity. Therefore, the second friend was off by 2 apples, so there are either 20 or 24 apples in the bag. Checking both options, we get the answer.
|
20
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.3 In a closed bag lie apples. Three friends tried to lift the bag and guess how many fruits were inside. The first one said that, in his opinion, there were 16 apples, the second thought there were 19, and the third said 25. When the friends opened the bag, it turned out that one of them was off by 2, another by 4, and the third by 5. How many apples were in the bag? Find all possible answers.
#
|
# Answer: 21
Solution. Notice that the second and third friends give odd predictions, which means they make an error of one parity, while the first makes an error of the other parity. Therefore, the first one was off by 5 apples, and the number of apples in the bag is either 11 or 21. Checking both options, we get the answer.
|
21
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.4 In a closed bag lie apples. Three friends tried to lift the bag and guess how many fruits were inside. The first one said that, in his opinion, there were 18 apples, the second thought there were 21, and the third said 22. When the friends opened the bag, it turned out that one of them was off by 2, another by 3, and the third by 6. How many apples were in the bag? Find all possible answers.
|
Answer: 24 apples
Solution. Note that the first and third give even predictions, which means they make an error of one parity, while the third makes an error of the other parity. Therefore, the second one was off by 3 apples, so there are either 18 or 24 apples in the bag. Checking both options, we get the answer.
|
24
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1 For Eeyore's Birthday, Winnie-the-Pooh, Owl, and Piglet decided to give balloons. Winnie-the-Pooh prepared twice as many balloons as Piglet, and Owl prepared three times as many balloons as Piglet. When Piglet was carrying his balloons, he was in a hurry, stumbled, and some of the balloons burst. Eeyore received a total of 31 balloons for his party. How many balloons did Piglet end up giving?
|
# Answer: 1
Solution. If Piglet hadn't burst his balloons, then Eeyore would have received exactly 6 times more balloons than Piglet prepared. The next number after 31 that is a multiple of 6 is $36, 36: 6=6$, which means Piglet prepared no less than 6 balloons.
If all of Piglet's balloons had burst, then Eeyore would have received exactly 5 times more than Piglet prepared. If Piglet initially had 7 or more balloons, then even now Eeyore would have received at least 35 balloons, which is not the case. Therefore, Piglet prepared exactly 6 balloons. If everything had been fine, Eeyore would have received 36 balloons, but since 5 burst, Piglet gave 1 balloon.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.2 For Eeyore's Birthday, Winnie-the-Pooh, Owl, and Piglet decided to give balloons. Winnie-the-Pooh prepared three times as many balloons as Piglet, and Owl prepared four times as many balloons as Piglet. When Piglet was carrying his balloons, he was in a great hurry, stumbled, and some of the balloons burst. Eeyore received a total of 60 balloons for his party. How many balloons did Piglet end up giving?
|
# Answer: 4
Solution. If Piglet hadn't burst his balloons, then Eeyore would have received exactly 8 times more balloons than Piglet prepared. The next number after 60 that is a multiple of 8 is $64, 64: 8=8$, which means Piglet prepared no less than 8 balloons.
If all of Piglet's balloons had burst, then Eeyore would have received exactly 7 times more than Piglet prepared. If Piglet initially had 9 or more balloons, then even now Eeyore would have received at least 63 balloons, which is not the case. Therefore, Piglet prepared exactly 8 balloons. If everything had been fine, Eeyore would have received 64 balloons, but since 4 burst, it means Piglet gave 4 balloons.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.3 For Eeyore's Birthday, Winnie-the-Pooh, Owl, and Piglet decided to give balloons. Winnie-the-Pooh prepared twice as many balloons as Piglet, and Owl prepared four times as many balloons as Piglet. When Piglet was carrying his balloons, he was in a great hurry, stumbled, and some of the balloons burst. Eeyore received a total of 44 balloons for his party. How many balloons did Piglet end up giving?
|
# Answer: 2
Solution. If Piglet hadn't burst his balloons, then Eeyore would have received exactly 7 times more balloons than Piglet prepared. The next number after 44 that is a multiple of 7 is 49, $49: 7=7$, which means Piglet prepared no less than 6 balloons.
If all of Piglet's balloons had burst, then Eeyore would have received exactly 6 times more than Piglet prepared. If Piglet initially had 8 or more balloons, then even now Eeyore would have received at least 48 balloons, which is not the case. Therefore, Piglet prepared exactly 7 balloons. If everything had been fine, Eeyore would have received 36 balloons, but it turned out that 5 burst, so Piglet gave 2 balloons.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1 Six children stood in a circle and whispered their favorite number to the neighbors on their right and left. Each child added the two numbers they heard and said them out loud. The picture shows what three of the children said. What number did the girl think of, next to whom there is a question mark?

#
|
# Answer: 6.
Solution. Let's add the numbers we know: $16+12+8=36$. We get that 36 is the sum of the numbers marked on the diagram as A, B, and the question mark, but taken twice. Therefore, $36: 2=18$, and the sum of numbers A and B is 12. This means the girl guessed the number 6, which can be found by subtracting 12 from 18.

|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.2 Six children stood in a circle and whispered their favorite number to the neighbors on their right and left. Each child added the two numbers they heard and said them out loud. The picture shows what three of the children said. What number did the girl think of, next to whom there is a question mark?

|
Answer: 5.
Solution. Let's add the numbers we know: $8+14+12=34$. We get that 34 is the numbers marked on the diagram as A, B, and under the question mark, but taken twice. Therefore, 34:2 = 17, and the sum of the numbers A and B is 12. Thus, the girl guessed the number 5, which can be found by subtracting 12 from 17.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. A rectangle with a perimeter of 100 cm was divided into 88 smaller identical rectangles by seven vertical and ten horizontal cuts. What is the perimeter of each of them, if the total length of all the cuts is 434 cm?
## Answer: 11
|
Solution. Note that the sum of seven vertical and seven horizontal cuts is 7.50 $=350$ cm, so the three extra horizontal cuts have a total length of 84 cm, each of which is 28 cm. This is the length of the horizontal side of the original rectangle. The vertical side of it is $50-28=22$ cm. After the cuts, the resulting rectangle has a horizontal side of $28 / 8=3.5$ cm and a vertical side of $22 / 11=2$ cm, so its perimeter is 11 cm.
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.6.2 A rectangle with a perimeter of 100 cm is divided into 70 identical smaller rectangles by six vertical and nine horizontal cuts. What is the perimeter of each of them, if the total length of all the cuts is 405 cm $?$
|
# Answer: 13
Solution. Note that the sum of six vertical and six horizontal cuts is $6 \square 50=300$ cm, so the three extra horizontal cuts have a total length of 105 cm, each being 35 cm. This is the length of the horizontal side of the original rectangle. The vertical side of the rectangle is $50-35=15$ cm. After the cuts, the resulting rectangle has a horizontal side of $35 / 7=5$ cm and a vertical side of $15 / 10=1.5$ cm, so its perimeter is 13 cm.
|
13
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.6.3 A rectangle with a perimeter of 96 cm was divided into 108 smaller identical rectangles by eight vertical and eleven horizontal cuts. What is the perimeter of each of them, if the total length of all the cuts is 438 cm?
|
# Answer: 9
Solution. Note that the sum of eight vertical and eight horizontal cuts is $8 \square 48=384$ cm, so the three extra horizontal cuts have a total length of 54 cm, each of which is 18. This is the length of the horizontal side of the original rectangle. The vertical side of it is $48-18=30 \text{~cm}$. After the cuts, the resulting rectangle has a horizontal side of $18 / 9=2$ cm, and a vertical side of $30 / 12=2.5$ cm, so its perimeter is 9 cm.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1 On the Island of Truth and Lies, there are knights who always tell the truth, and liars who always lie. One day, 20 residents of the island lined up by height (from tallest to shortest, the tallest being the first) for a game. Each had to say one of the following phrases: "There is a liar below me" or "There is a knight above me." In the end, those standing from the third to the seventh position said the first phrase, while the rest said the second. How many knights were among these 20 people, given that all residents have different heights?
|
Answer: 17
Solution. The formation cannot consist of only liars (in such a case, the 3-7th person would be telling the truth). Consider the tallest knight, let's call him P. He could only say the first phrase, so the 1st and 2nd places must be occupied by liars, and P stands from the 3rd to the 7th place. Moreover, there is a liar who is shorter than P, let's call him L. This liar cannot say the second phrase, so he must say the first phrase and stand no later than the 7th place, but not earlier than the 4th place. Therefore, from the 8th to the 20th place, only knights stand. The 3rd place cannot be occupied by a liar, as there is a liar L who is shorter than him. Therefore, the 3rd place is occupied by P. If there are other liars between P and L, they must also say the first phrase, but L is shorter than them, which is a contradiction.
Thus, liars stand at the 1st, 2nd, and 7th places, while the remaining places are occupied by knights.
|
17
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2 On the Island of Truth and Lies, there are knights who always tell the truth, and liars who always lie. One day, 15 residents of the island lined up by height (from tallest to shortest, the tallest being the first) for a game. Each had to say one of the following phrases: "There is a liar below me" or "There is a knight above me." In the end, those standing from the fourth to the eighth position said the first phrase, while the rest said the second. How many knights were among these 15 people, given that all residents have different heights?
|
# Answer: 11
Solution. The formation cannot consist of only liars (in such a case, 4-8 would be telling the truth). Consider the tallest knight, let's call him R. He could only say the first phrase, so the positions 1, 2, and 3 must be occupied by liars, and R stands from 4 to 8. In addition, there is a liar who is shorter than R, let's call him L. This liar cannot say the second phrase, so he must say the first phrase and stand no later than the 8th position but no earlier than the 5th position. Therefore, from the 9th to the 15th position, only knights stand. A liar cannot stand at the 4th position, as L is shorter than him. Therefore, R stands at the 4th position. If there are other liars between R and L, they must also say the first phrase, but L is shorter than them, which is a contradiction.
We conclude that liars stand at positions $1, 2, 3,$ and 8, while the remaining positions are occupied by knights.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3 On the Island of Truth and Lies, there are knights who always tell the truth, and liars who always lie. One day, 17 residents of the island lined up by height (from tallest to shortest, the tallest being the first) for a game. Each had to say one of the phrases: "There is a liar below me" or "There is a knight above me." In the end, those standing from the third to the sixth position said the first phrase, while the rest said the second. How many knights were among these 17 people, if all residents have different heights?
|
Answer: 14
Solution. The formation cannot consist of only liars (in such a case, 3-6 would be telling the truth). Consider the tallest knight, let's call him P. He could only say the first phrase, so the 1st and 2nd positions must be occupied by liars, and P stands from the 3rd to the 6th position. Moreover, there is a liar who is shorter than P, let's call him L. This liar cannot say the second phrase, so he must say the first phrase and stand no later than the 6th position but not earlier than the 4th position. Therefore, from the 7th to the 17th position, only knights stand. The 3rd position cannot be occupied by a liar, as there is a liar L who is shorter than him. Therefore, the 3rd position is occupied by P. If there are other liars between P and L, they must also say the first phrase, but L is shorter than them, which is a contradiction.
We conclude that liars stand at the 1st, 2nd, and 6th positions, while the remaining positions are occupied by knights.
|
14
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. Each student in the 7th grade attends a math club or an informatics club, and two students attend both the math club and the informatics club. Two-thirds of all students attend the math club, and $40 \%$ attend the informatics club. How many students are there in this class?
|
Answer: 30.
Solution: Note that $40\%$ is $\frac{2}{5}$ of all students. Adding $\frac{2}{3}$ and $\frac{2}{5}$ gives $\frac{16}{15}$. The two students who are involved in both the math and informatics clubs were counted twice. Therefore, these two students represent $\frac{1}{15}$ of the entire class, meaning there are $2 \cdot 15 = 30$ students in the class.
Comment: Correct solution - 7 points. Correct idea but incorrect answer - 3 points. Problem solved by trial and error, no proof that there are no other solutions - 2 points. Solution started, some progress made - 1 point. Correct answer given without explanation - 1 point.
|
30
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. How many seven-digit natural numbers exist, for which the product of the first three digits is 30, the product of the three digits in the center is 7, and the product of the last three digits is 15?
|
Answer: 4.
Solution: Let the number be $\overline{\operatorname{abcdefg}}$. According to the condition, $c d e=7$, which means one of these digits is 7, and the other two are 1. Since 30 and 15 are not divisible by $7, d=7, c=e=1$. The number $30=5 \cdot 6 \cdot 1$, so we get two three-digit numbers $\overline{a b c}$: 561 and 651. The number $15=1 \cdot 3 \cdot 5$, from which we get two three-digit numbers $\overline{e f g}$: 135 and 153. Finally, we get $2 \cdot 2=4$ numbers.
Comment: Full solution of the problem - 7 points. Only the values of the three middle digits found - 2 points. Correct answer given without explanation - 0 points.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. At a round table, 10 people are sitting, each of whom is either a knight, who always tells the truth, or a liar, who always lies. Each of them was given a token. Then each of them passed their token to one of their two neighbors. After that, 5 people said: "I have one token," while the other 5 said: "I have no tokens." What is the maximum number of knights that could have been among these 10 people?
|
# Answer. 7.
Solution. Evaluation. After passing the chips, each person sitting at the table can have 0, 1, or 2 chips. The total number of chips will be 10. Note that if a person lies, they will state a number of chips that differs from the actual number by 1 or 2. Since the total number of chips according to the answers differs from the actual number by \(10-5=5\), at least 3 people must have lied. Therefore, there are no more than 7 knights at the table.
Example. Suppose the knights sitting at the table pass the chips as follows (arrows indicate the direction of the chip transfer; the number of chips after the transfer is in parentheses):
$$
\leftarrow \mathrm{P}(0)-\mathrm{P}(0) \rightarrow \mathrm{P}(1) \rightarrow \mathrm{P}(1) \rightarrow \mathrm{P}(1) \rightarrow \mathrm{P}(1) \rightarrow \mathrm{P}(1) \rightarrow \mathrm{L}(1) \rightarrow \mathrm{L}(2) \leftrightarrow \mathrm{L}(2) \leftarrow
$$
In this case, all knights tell the truth, while the liars lie, saying they have 0 chips.
Comment. A fully justified solution - 7 points. Correct evaluation - 5 points, a correct example constructed - 2 points, points are cumulative. The problem is not solved or solved incorrectly - 0 points.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Having walked $4 / 9$ of the length of the bridge, the traveler noticed that a car was catching up to him, but it had not yet entered the bridge. Then he turned back and met the car at the beginning of the bridge. If he had continued his movement, the car would have caught up with him at the end of the bridge. Find the ratio of the car's speed to the traveler's speed.
#
|
# Solution
From the condition, it follows that the time it takes for the car to approach the bridge is equal to the time it takes for the traveler to walk $4 / 9$ of the bridge. Therefore, if the traveler continues moving, by the time the car reaches the bridge, he will have walked ${ }^{8} / 9$ of the bridge. This means that during the time it takes for the car to cross the bridge, the traveler manages to walk one-ninth of the bridge, so the speed of the car is 9 times greater than the speed of the traveler.
## Answer 9.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Vovochka is playing a computer game. If he scores less than 1000 points, the computer will add $20 \%$ of his score. If he scores from 1000 to 2000 points, the computer will add $20 \%$ of the first thousand points and $30 \%$ of the remaining points. If Petya scores more than 2000 points, the computer will add $20 \%$ of the first thousand points, $30 \%$ of the second thousand, and $50 \%$ of the remaining points. How many bonus points did Petya receive if he had 2370 points at the end of the game?
|
# Solution
It is clear that Petya scored more than 1000 points (otherwise his result would not exceed 1200) and less than 2000 (otherwise the result would not be less than 2500). Let's discard the 1200 points (the first thousand plus the prize for it). The remaining 1170 points constitute $130 \%$ of the points Petya scored in the second thousand. $3 / 13$ of this amount, that is, 270 points - is the prize. And the total number of prize points is $200+270=470$.
Answer: 470 points.
|
470
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Given various real numbers $p$ and $q$. It is known that there exists a number $x$ such that the equations $x^{2} + p x + q = 0$ and $x^{2} + q x + p = 0$ are satisfied. What values can the sum $p + q$ take?
|
Solution. Let $x$ be such that both equalities from the problem statement are satisfied. Then $x^{2}+p x+q=x^{2}+q x+p$, from which $(p-q) x=p-q$. Since $p \neq q$, it follows that $x=1$. Substituting this value into any of the equations, we find that $p+q+1=0$, that is, $p+q=-1$. Answer: -1.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In a football tournament, seven teams played: each team played once with each other. Teams that scored thirteen or more points advance to the next round. Three points are awarded for a win, one point for a draw, and zero points for a loss. What is the maximum number of teams that can advance to the next round?
|
Solution. Evaluation. Note that the total number of games will be $\frac{7 \cdot 6}{2}=21$. Then the total number of points does not exceed $21 \cdot 3=63$. This means that no more than $\left[\frac{63}{13}\right]=4$ teams can advance to the next round.
Example. We will show that 4 teams can advance to the next round. For this, we will provide an example of a suitable tournament table (the symbol "x" denotes insignificant results):
| $№$ | $\mathbf{1}$ | $\mathbf{2}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{5}$ | $\mathbf{6}$ | $\mathbf{7}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $\mathbf{1}$ | - | 1 | 3 | 3 | 3 | 3 | 0 |
| $\mathbf{2}$ | 1 | - | 0 | 3 | 3 | 3 | 3 |
| $\mathbf{3}$ | 0 | 3 | - | 3 | 3 | 3 | 1 |
| $\mathbf{4}$ | 0 | 0 | 0 | - | $\mathrm{x}$ | $\mathrm{x}$ | 0 |
| $\mathbf{5}$ | 0 | 0 | 0 | $\mathrm{x}$ | - | $\mathrm{x}$ | 0 |
| $\mathbf{6}$ | 0 | 0 | 0 | $\mathrm{x}$ | $\mathrm{x}$ | - | 0 |
| $\mathbf{7}$ | 3 | 0 | 1 | 3 | 3 | 3 | - |
Answer: 4.
Comment. The correct evaluation is obtained - no more than 3 points.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.1. Students from 9A, 9B, and 9C gathered for a line-up. Maria Ivanovna decided to count the number of attendees from each class. She found that there were 27 students from 9A, 29 students from 9B, and 30 students from 9C. Ilya Grigoryevich decided to count the total number of attendees from all three classes, and he got 96 students.
It turned out that when counting the number of students in each class, Maria Ivanovna was off by no more than 2. And when counting the total number of students, Ilya Grigoryevich was off by no more than 4.
How many students from 9A were present at the line-up?
|
Answer: 29.
Solution. Let $a, b, c$ be the actual number of students from 9 "A", 9 "B", 9 "C" respectively. From Maria Ivanovna's counts, it follows that $a \leqslant 29, b \leqslant 31, c \leqslant 32$, and from Ilya Grigoryevich's counts, it follows that $a+b+c \geqslant 92$. We get that
$$
92 \leqslant a+b+c \leqslant 29+31+32=92
$$
From this, it follows that all the considered inequalities must turn into equalities, in particular $a=29$.
|
29
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.4. An empty $3 \times 51$ table is drawn on the board. Masha wants to fill its cells with numbers, following these rules:
- each of the numbers $1, 2, 3, \ldots, 153$ must be present in the table;
- the number 1 must be in the bottom-left cell of the table;
- for any natural number $a \leqslant 152$, the numbers $a$ and $a+1$ must be in adjacent cells.
(a) (1 point) What is the largest number that can be in the cell adjacent to the number 1?
(b) (3 points) We will call a cell of the table good if the number 153 can be in it. How many good cells are there?
|
Answer: (a) 152. (b) 76.
Solution. Let's color the table in black and white so that the cell where the number 1 should be is black. The third rule in the condition means that consecutive numbers in the table are placed in a "snake" pattern, and the colors of their cells alternate, that is, all odd numbers, including 153, will also be in black cells.
| | | | | | | |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| | | | | | | |
| 1 | | | | | | |
| | | | | | | |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| | | | | | | |
(a) We already understand that the number 153 cannot be in a cell adjacent to 1. Let's prove that 152 can. For this, it is enough to provide a suitable arrangement of numbers:
| 153 | 150 | 149 | 146 | 145 | 142 | 141 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 152 | 151 | 148 | 147 | 144 | 143 | 140 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 65 | 62 | 61 | 58 | 57 | 54 | 53 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 64 | 63 | 60 | 59 | 56 | 55 | 52 |
| 45 | 46 | 47 | 48 | 49 | 50 | 51 |
(b) The number 153 can be in any black cell (in the above coloring), except for the one where the number 1 should be. Let's provide a series of corresponding examples. For the top row:
| 149 | 150 | 151 | 152 | 153 | 142 | 141 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 148 | 147 | 146 | 145 | 144 | 143 | 140 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 65 | 62 | 61 | 58 | 57 | 54 | 53 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 64 | 63 | 60 | 59 | 56 | 55 | 52 |
| 45 | 46 | 47 | 48 | 49 | 50 | 51 |
For the middle row:
| 147 | 146 | 145 | 144 | 143 | 142 | 141 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 148 | 149 | 150 | 151 | 152 | 153 | 140 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 65 | 62 | 61 | 58 | 57 | 54 | 53 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 64 | 63 | 60 | 59 | 56 | 55 | 52 |
| 45 | 46 | 47 | 48 | 49 | 50 | 51 |
For the bottom row:
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 2 | 149 | 148 | 147 | 146 | 145 | 142 |
| 1 | 150 | 151 | 152 | 153 | 144 | 143 |
| 47 | 48 | 49 | 50 | 51 | 52 | 53 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 66 | 65 | 62 | 61 | 58 | 57 | 54 |
| 67 | 64 | 63 | 60 | 59 | 56 | 55 |
If we exclude the cell with the number 1, then there are an equal number of black and white cells (for example, because any "snake" breaks down into pairs of adjacent cells of different colors). Therefore, there are 76 good cells.
|
152
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.5. Sides $A D$ and $D C$ of the inscribed quadrilateral $A B C D$ are equal. A point $X$ is marked on side $B C$ such that $A B = B X$. It is known that $\angle B = 34^{\circ}$ and $\angle X D C = 52^{\circ}$.
(a) (1 point) How many degrees does the angle $A X C$ measure?
(b) (3 points) How many degrees does the angle $A C B$ measure?
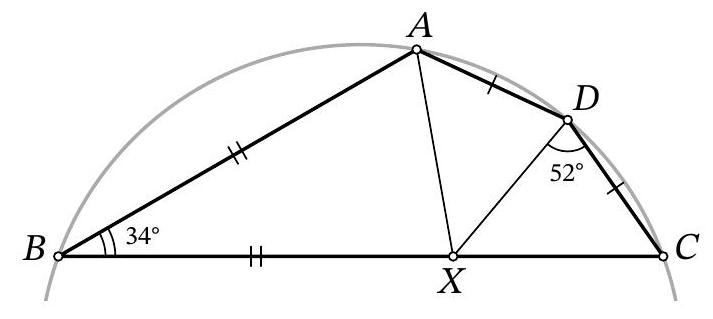
|
Answer: (a) $107^{\circ}$. (b) $47^{\circ}$.
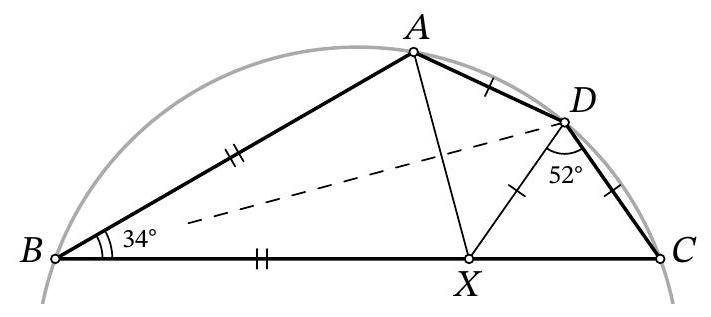
Fig. 5: to the solution of problem 9.5
Solution. Given $A B=B X$ and $\angle B=34^{\circ}$, therefore $\angle A X B=\angle X A B=\frac{1}{2}\left(180^{\circ}-34^{\circ}\right)=73^{\circ}$. Then $\angle A X C=180^{\circ}-73^{\circ}=107^{\circ}$.
Since $A D=D C$, we get that arcs $A D$ and $D C$ are equal. This means that $B D$ is the bisector of angle $A B C$. From the equality of triangles $A B D$ and $X B D$, it follows that $X D=A D=C D$ (Fig. 5).
Since quadrilateral $A B C D$ is cyclic, $\angle A C D=\angle A B D=\frac{1}{2} \cdot 34^{\circ}=17^{\circ}$. Since $X D=C D$ and $\angle X D C=52^{\circ}$, we get that $\angle X C D=\angle C X D=\frac{1}{2}\left(180^{\circ}-52^{\circ}\right)=64^{\circ}$. We have
$$
\angle A C B=\angle X C D-\angle A C D=64^{\circ}-17^{\circ}=47^{\circ}
$$
Remark. The angle $A C X$ could also have been found by considering that point $D$ is the center of the circumcircle of triangle $A C X$.
|
107
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.6. The graph of the line $y=k x+l$ intersects the $O x$ axis at point $B$, the $O y$ axis at point $C$, and the graph of the function $y=1 / x$ at points $A$ and $D$, as shown in the figure. It turns out that $A B=B C=C D$. Find $k$, given that $O C=3$.
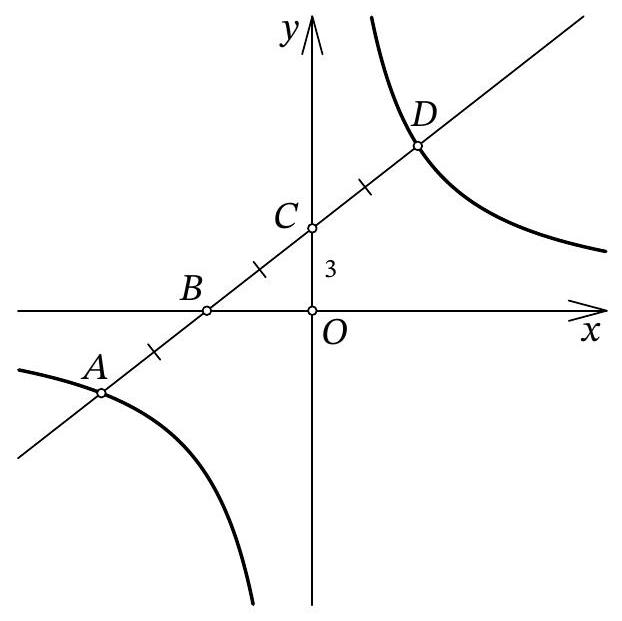
|
Answer: 18.
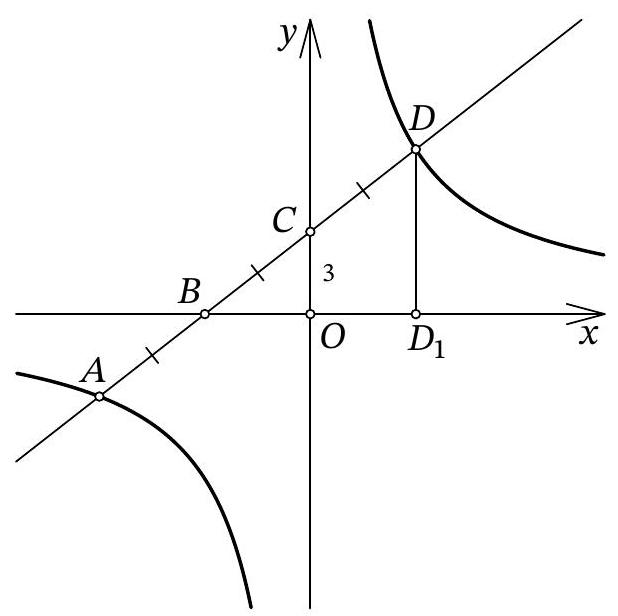
Fig. 6: to the solution of problem 9.6
Solution. Draw a line through point $D$ parallel to the $O y$ axis; let it intersect the $O x$ axis at point $D_{1}$ (Fig. 6). It is easy to see that segment $OC$ is the midline of triangle $B D D_{1}$, so $D D_{1}=2 \cdot O C=2 \cdot 3=6$.
Point $D$ lies on the graph of $y=1 / x$ and has an ordinate of 6, so its coordinates are $\left(\frac{1}{6} ; 6\right)$. The line $y=k x+l$ passes through points $C(0 ; 3)$ and $D\left(\frac{1}{6} ; 6\right)$, therefore,
$$
k=\frac{6-3}{\frac{1}{6}-0}=18
$$
Another solution. Notice that $l=O C=3$, i.e., the equation of the line is $y=k x+3$. Then the coordinates of points $A$ and $D$ are the solutions to the system of equations
$$
\left\{\begin{array}{l}
y=k x+3 \\
y=\frac{1}{x}
\end{array}\right.
$$
By equating the right-hand sides of the equations, this system reduces to solving the quadratic equation
$$
k x^{2}+3 x-1=0
$$
Let $x_{0}$ be the abscissa of point $D$. Then $-2 x_{0}$ is the abscissa of point $A$. Both of these numbers are roots of the given quadratic equation. From Vieta's theorem, it follows that
$$
\left\{\begin{array}{l}
x_{0}-2 x_{0}=-\frac{3}{k} \\
x_{0} \cdot\left(-2 x_{0}\right)=-\frac{1}{k}
\end{array}\right.
$$
This is equivalent to
$$
\left\{\begin{aligned}
x_{0} & =\frac{3}{k} \\
x_{0}^{2} & =\frac{1}{2 k}
\end{aligned}\right.
$$
From this, we derive that $9 / k^{2}=1 / 2 k$, i.e., $18 / k=1$ and $k=18$.
|
18
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.7. In front of a sweet-tooth lie five boxes of candies: the first box contains 11 candies, the second - 22 candies, the third - 33 candies, the fourth - 44 candies, the fifth - 55 candies. In one move, the sweet-tooth can take four candies from one box and distribute them, one candy to each of the remaining four boxes.
At any point, the sweet-tooth can take the candies from any box and leave. What is the maximum number of candies he can take?
|
Answer: 159.
Solution. Consider the number of candies in the boxes. Initially, these are 5 natural numbers that give different remainders when divided by 5. We will prove that as long as the sweet-tooth does not take candies from any box, these 5 numbers will always give different remainders when divided by 5. For this, it is sufficient to understand that the difference between any two of these 5 numbers is never divisible by 5.
Suppose at some point, there were $x$ and $y$ candies in two of the boxes, and the difference $x - y$ is not divisible by 5. After the sweet-tooth rearranges the candies, this difference will take one of the following values:
$$
(x+1)-(y+1)=x-y, \quad(x-4)-(y+1)=x-y-5, \quad(x+1)-(y-4)=x-y+5
$$
Clearly, none of these values are divisible by 5.
Suppose the sweet-tooth at some point takes all the candies from one of the boxes. Let's look at the remaining four boxes: the total number of candies in them is no less than the sum of the remainders when the corresponding numbers are divided by 5. Thus, there are at least $0+1+2+3=6$ candies left in them. Accordingly, the sweet-tooth has taken no more than $11+22+33+44+55-6=159$ candies.
Now let's provide an example of how the sweet-tooth can take exactly 159 candies. Suppose he moves 4 candies from the first four boxes to the fifth box, as long as possible (i.e., as long as there are at least 4 candies in one of these boxes). This process will eventually end, since with each such move, the total number of candies in the first four boxes decreases by exactly 1 (the number of candies in one box decreases by 4, and in the other three, it increases by 1).
At the moment when this process ends, there will be from 0 to 3 candies in each of the first four boxes. But we have proven earlier that the number of candies in these four boxes must give different remainders when divided by 5. Therefore, in one box there are 0 candies, in another 1, in the third 2, and in the fourth 3 candies. This means that the remaining 159 candies are in the fifth box, which the sweet-tooth will take.
|
159
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.8. For real numbers $x$ and $y$, define the operation $\star$ as follows: $x \star y=x y+4 y-3 x$.
Calculate the value of the expression
$$
((\ldots)(((2022 \star 2021) \star 2020) \star 2019) \star \ldots) \star 2) \star 1
$$
|
Answer: 12.
Solution. Let $t=(\ldots(((2022 \star 2021) \star 2020) \star 2019) \star \ldots) \star 4$. Then the value of the expression from the problem condition is
$$
\begin{aligned}
((t \star 3) \star 2) \star 1 & =((3 t+12-3 t) \star 2) \star 1=12 \star 2 \star 1= \\
& =(24+8-36) \star 1=(-4) \star 1=-4+4+12=12
\end{aligned}
$$
## 9th grade
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 9.2.2. On the sides $AB$ and $AD$ of rectangle $ABCD$, points $M$ and $N$ are marked, respectively. It is known that $AN=11$, $NC=39$, $AM=12$, $MB=3$.
(a) (1 point) Find the area of rectangle $ABCD$.
(b) (3 points) Find the area of triangle $MNC$.
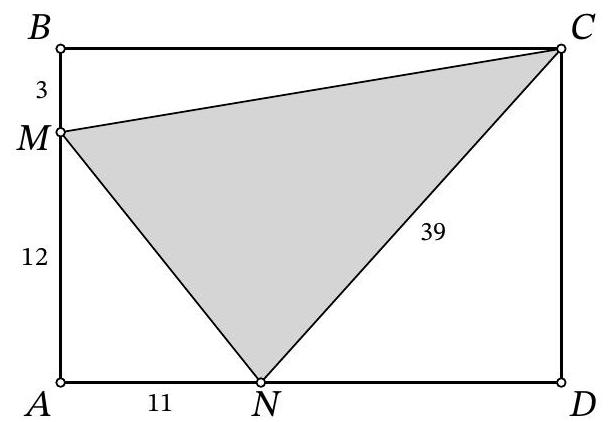
|
Answer: (a) 705. (b) 298.5.
|
705
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 9.2.3. On the sides $AB$ and $AD$ of rectangle $ABCD$, points $M$ and $N$ are marked, respectively. It is known that $AN=3$, $NC=39$, $AM=10$, $MB=5$.
(a) (1 point) Find the area of rectangle $ABCD$.
(b) (3 points) Find the area of triangle $MNC$.
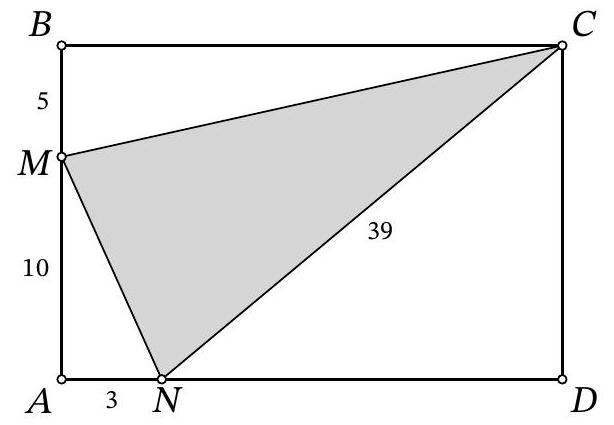
|
Answer: (a) 585. (b) 202.5.
|
585
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 9.2.4. On the sides $AB$ and $AD$ of rectangle $ABCD$, points $M$ and $N$ are marked, respectively. It is known that $AN=9$, $NC=39$, $AM=10$, $MB=5$.
(a) (1 point) Find the area of rectangle $ABCD$.
(b) (3 points) Find the area of triangle $MNC$.
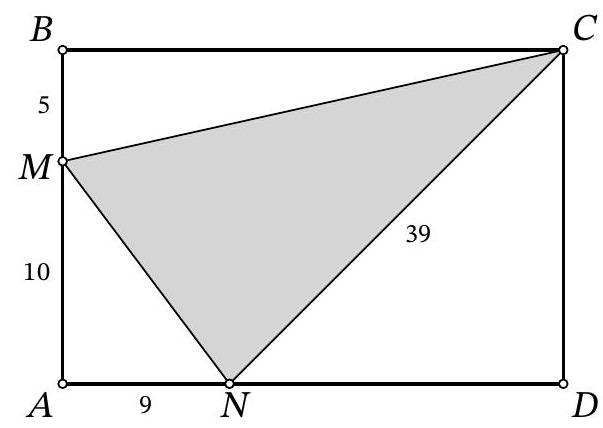
|
Answer: (a) 675. (b) 247.5.
|
675
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 9.4.1. An empty $3 \times 51$ table is drawn on the board. Masha wants to fill its cells with numbers, following these rules:
- each of the numbers $1, 2, 3, \ldots, 153$ must be present in the table;
- the number 1 must be in the bottom-left cell of the table;
- for any natural number $a \leqslant 152$, the numbers $a$ and $a+1$ must be in adjacent cells.
(a) (1 point) What is the largest number that can be in the cell adjacent to the number 1?
(b) (3 points) We will call a cell of the table good if the number 153 can be in it. How many good cells are there?
|
Answer: (a) 152. (b) 76.
|
152
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 9.4.2. An empty $3 \times 53$ table is drawn on the board. Masha wants to fill its cells with numbers, following these rules:
- each of the numbers $1,2,3, \ldots, 159$ must be present in the table;
- the number 1 must be in the bottom-left cell of the table;
- for any natural number $a \leqslant 158$, the numbers $a$ and $a+1$ must be in adjacent cells.
(a) (1 point) What is the largest number that can be in the cell adjacent to the number 1?
(b) (3 points) We will call a cell of the table good if the number 159 can be in it. How many good cells are there?
|
Answer: (a) 158. (b) 79.
|
158
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 9.4.3. An empty $3 \times 55$ table is drawn on the board. Masha wants to fill its cells with numbers, following these rules:
- each of the numbers $1,2,3, \ldots, 165$ must be present in the table;
- the number 1 must be in the bottom-left cell of the table;
- for any natural number $a \leqslant 164$, the numbers $a$ and $a+1$ must be in adjacent cells.
(a) (1 point) What is the largest number that can be in the cell adjacent to the number 1?
(b) (3 points) We will call a cell of the table good if the number 165 can be in it. How many good cells are there?
|
Answer: (a) 164 . (b) 82.
|
82
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 9.4.4. An empty $3 \times 57$ table is drawn on the board. Masha wants to fill its cells with numbers, following these rules:
- each of the numbers $1, 2, 3, \ldots, 171$ must be present in the table;
- the number 1 must be in the bottom-left cell of the table;
- for any natural number $a \leqslant 170$, the numbers $a$ and $a+1$ must be in adjacent cells.
(a) (1 point) What is the largest number that can be in the cell adjacent to the number 1?
(b) (3 points) We will call a cell of the table good if the number 171 can be in it. How many good cells are there?
|
Answer: (a) 170 . (b) 85.
|
170
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 9.5.1. Sides $A D$ and $D C$ of the inscribed quadrilateral $A B C D$ are equal. A point $X$ is marked on side $B C$ such that $A B = B X$. It is known that $\angle B = 34^{\circ}$ and $\angle X D C = 52^{\circ}$.
(a) (1 point) How many degrees does the angle $A X C$ measure?
(b) (3 points) How many degrees does the angle $A C B$ measure?
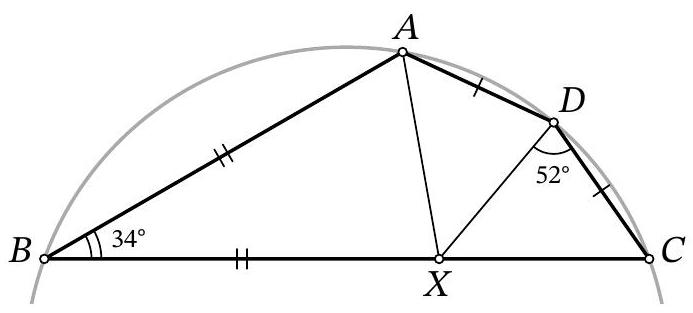
|
Answer: (a) $107^{\circ}$. (b) $47^{\circ}$.
|
107
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 9.5.2. Sides $A D$ and $D C$ of the inscribed quadrilateral $A B C D$ are equal. A point $X$ is marked on side $B C$ such that $A B = B X$. It is known that $\angle B = 32^{\circ}$ and $\angle X D C = 52^{\circ}$.
(a) (1 point) How many degrees does the angle $A X C$ measure?
(b) (3 points) How many degrees does the angle $A C B$ measure?
|
Answer: (a) $106^{\circ}$. (b) $48^{\circ}$.
|
106
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 9.5.3. Sides $A D$ and $D C$ of the inscribed quadrilateral $A B C D$ are equal. A point $X$ is marked on side $B C$ such that $A B = B X$. It is known that $\angle B = 36^{\circ}$ and $\angle X D C = 52^{\circ}$.
(a) (1 point) How many degrees does the angle $A X C$ measure?
(b) (3 points) How many degrees does the angle $A C B$ measure?
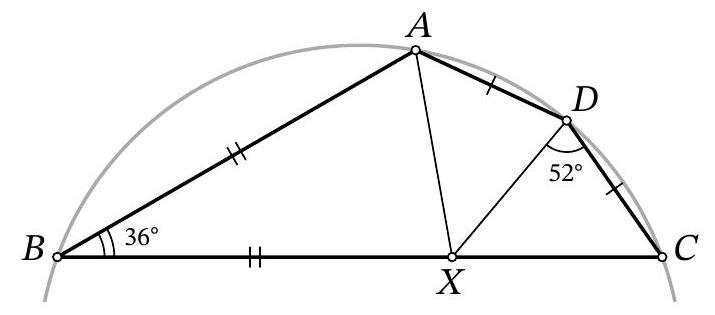
|
Answer: (a) $108^{\circ}$. (b) $46^{\circ}$.
|
108
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 9.5.4. Sides $A D$ and $D C$ of the inscribed quadrilateral $A B C D$ are equal. A point $X$ is marked on side $B C$ such that $A B = B X$. It is known that $\angle B = 38^{\circ}$ and $\angle X D C = 54^{\circ}$.
(a) (1 point) How many degrees does the angle $A X C$ measure?
(b) (3 points) How many degrees does the angle $A C B$ measure?
|
Answer: (a) $109^{\circ}$. (b) $44^{\circ}$.
|
109
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. The numbers $a$ and $b$ are such that each of the two quadratic trinomials $x^{2} + a x + b$ and $x^{2} + b x + a$ has two distinct roots, and the product of these trinomials has exactly three distinct roots. Find all possible values of the sum of these three roots.
(S. Berlov)
|
Answer: 0.
Solution: From the condition, it follows that the quadratic polynomials $x^{2}+a x+b$ and $x^{2}+b x+a$ have a common root $x_{0}$, as well as roots $x_{1}$ and $x_{2}$ different from it; in particular, $a \neq b$. Then $0=\left(x_{0}^{2}+a x_{0}+b\right)-\left(x_{0}^{2}+b x_{0}+a\right)=(a-b)\left(x_{0}-1\right)$, that is, $x_{0}=1$. Substituting this root into any quadratic polynomial, we get $0=1+a+b$, that is, $b=-a-1$. Thus, our quadratic polynomials have the form $x^{2}+a x-(a+1)=(x-1)(x+a+1)$ and $x^{2}-(a+1) x+a=(x-1)(x-a)$. Their roots are the numbers $1, a$, and $-(a+1)$ (for $a \neq 1,-2,-1 / 2$ they are distinct), the sum of which is zero.
Remark. After obtaining the equality $0=1+a+b$, the solution can be completed differently. By Vieta's theorem, we have $x_{0}+x_{1}=-a, x_{0}+x_{2}=-b$, from which $x_{0}+x_{1}+x_{2}=-a-b-x_{0}=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. Parallelogram $A B C D$ is such that $\angle B<90^{\circ}$ and $A B<B C$. Points $E$ and $F$ are chosen on the circle $\omega$ circumscribed around triangle $A B C$ such that the tangents to $\omega$ at these points pass through $D$. It turns out that $\angle E D A=\angle F D C$. Find the angle $A B C$.
(A. Yakubov)
|
Answer: $60^{\circ}$.
Solution. Let $\ell$ be the bisector of angle $E D F$. Since $D E$ and $D F$ are tangents to $\omega$, the line $\ell$ passes through the center $O$ of the circle $\omega$.
Perform a reflection about $\ell$. Since $\angle E D A = \angle F D C$, the ray $D C$ will be transformed into the ray $D A$. Since $\ell$ passes through $O$, the circle $\omega$ will map to itself; hence, point $C$ will map to a point $C^{\prime}$ lying on $D A$ and on $\omega$. At the same time, since $A D \neq D C$, points $C^{\prime}$ and $A$ are distinct (see Fig. 1).
Fig. 1
From the same reflection, we have $\angle D C C^{\prime} = \angle D C^{\prime} C$. Since points $A, B, C$, and $C^{\prime}$ lie on $\omega$, we have $\angle D C^{\prime} C = \angle A B C = \angle A D C$. Therefore, all three angles of triangle $D C C^{\prime}$ are equal, from which it follows that $\angle A B C = \angle C D C^{\prime} = 60^{\circ}$.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.