problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
9.3. Natural numbers $a, x$ and $y$, greater than 100, are such that $y^{2}-1=$ $=a^{2}\left(x^{2}-1\right)$. What is the smallest value that the fraction $a / x$ can take?
|
# Answer. 2.
First solution. Rewrite the condition of the problem as $y^{2}=a^{2} x^{2}-a^{2}+1$. Notice that $y100$, if we set $a=2 x, y=a x-1=2 x^{2}-1$.
Second solution. We provide another proof of the estimate $a / x \geqslant 2$. Rewrite the equality from the condition as
$$
(a x-y)(a x+y)=a^{2} x^{2}-y^{2}=a^{2}-1
$$
The numbers $a^{2}-1$ and $a x+y$ are positive, so the number $k=a x-y$ is also positive (and natural). Then $a x+y=\frac{a^{2}-1}{k}$. Adding the two equations, we get
$$
2 a x=\frac{a^{2}-1}{k}+k=a^{2}+\frac{(k-1)\left(k-a^{2}+1\right)}{k} \leqslant a^{2}
$$
since $1 \leqslant k \leqslant a^{2}-1$. Thus, $2 a x \leqslant a^{2}$, which means $a / x \geqslant 2$.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3. The number 2019 is represented as the sum of different odd natural numbers. What is the maximum possible number of addends?
|
Answer: 43.
Solution. Evaluation. Let's calculate the sum of the 45 smallest odd natural numbers: 1 + 3 + ... + 87 + 89 = (1 + 89) / 2 * 45 = 2025 > 2019. Therefore, there are fewer than 45 addends, but the sum of 44 odd addends is an even number, so there are no more than 43 addends. Example. 2019 = 1 + 3 + ... + 81 + 83 + 255.
Evaluation Criteria.
“+” A complete and well-reasoned solution is provided
“土” A generally correct reasoning is provided, containing minor gaps or inaccuracies
“干” The correct answer and correct evaluation are provided, but the example is missing
“干” The correct answer and correct example are provided, but the evaluation is missing or incorrect
“-” Only the answer is provided
“-” The problem is not solved or is solved incorrectly
|
43
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.6. Find the largest $n$ such that the sum of the fourth powers of any $n$ prime numbers greater than 10 is divisible by $n$.
|
Answer: $n=240$.
Solution. In fact, it is required that the fourth powers of all prime numbers greater than 10 give the same remainder when divided by $n$. Indeed, if the fourth powers of some two numbers give different remainders, then one can take $n-1$ of the first number and one of the second, then the sum of the fourth powers of these numbers will not be divisible by $n$.
We will prove that the fourth power of any prime number $p$, greater than 10, when divided by 3, 5, and 16, gives a remainder of 1, then it will also give a remainder of 1 when divided by $3 \cdot 5 \cdot 16=240$. We will use the fact that $p^{4}-1=\left(p^{2}-1\right)\left(p^{2}+1\right)=(p-1)(p+1)\left(p^{2}+1\right)$.
Since $p$ is not divisible by three, either $p-1$ or $p+1$ is divisible by 3.
Consider the remainders of $p$ when divided by 5. If the remainder is 1, then $p-1$ is divisible by 5; if the remainder is 4, then $p+1$ is divisible by 5; and if the remainder is 2 or 3, then $p^{2}+1$ is divisible by 5.
Since $p$ is odd, each of the factors $p-1, p+1$, and $p^{2}+1$ is even. Moreover, one of the numbers $p-1$ or $p+1$ is divisible by 4, so the product of these three factors is divisible by 16.
It remains to show that if a number is greater than 240, it does not satisfy the condition. Note that the difference of the fourth powers of any prime numbers greater than 10 must be divisible by $n$. First, take the prime numbers 13 and 11 and compute the difference of their fourth powers: $13^{4}-11^{4}=(13-11)(13+11)\left(13^{2}+11^{2}\right)=2 \cdot 24 \cdot 290=240 \cdot 2 \cdot 29$. Now, take the numbers 17 and 11: $17^{4}-11^{4}=(17-11)(17+11)\left(17^{2}+11^{2}\right)=6 \cdot 28 \cdot 410=240 \cdot 7 \cdot 41$. Since the GCD $(240 \cdot 2 \cdot 29,240 \cdot 7 \cdot 41)=240$, $n$ cannot be greater than 240.
Grading criteria.
“+” A complete and well-reasoned solution is provided
“土” A generally correct reasoning is provided, containing minor gaps or inaccuracies
“-” The problem is not solved or solved incorrectly
|
240
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. A six-digit number $A$ is divisible by 19. The number obtained by removing its last digit is divisible by 17, and the number obtained by removing the last two digits of $A$ is divisible by 13. Find the largest $A$ that satisfies these conditions.
|
2. Answer: 998412.
Solution. The largest four-digit number divisible by 13 is 9997. Among the numbers from 99970 to 99979, there is a number 99977 divisible by 17, but among the numbers from 999770 to 999779, there is no number divisible by 19. However, for the next number 9984, which is divisible by 13, the number 99841 is divisible by 17, and the number 998412 is divisible by 19.
Criteria. Correct and justified answer - 7 points; correct answer, but not proven to be the largest - 4 points; incorrect answer - 0 points.
|
998412
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A row of 50 people, all of different heights, stands. Exactly 15 of them are taller than their left neighbor. How many people can be taller than their right neighbor? (Provide all possible answers and prove that there are no others)
|
Answer: 34.
Solution. Let's call 15 people who are taller than their left neighbor - tall people.
If someone has a tall person to their right, then they are shorter than them, otherwise, they are taller.
There are a total of 49 pairs of adjacent people.
Tall people are on the right in exactly 15 pairs. In the remaining $49-15=34$ pairs, the person on the right is not a tall person. It is in these pairs that the person is taller than their neighbor on the right.
|
34
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.1. On 40 cells of an $8 \times 8$ chessboard, stones were placed. The product of the number of stones lying on white cells and the number of stones lying on black cells was calculated. Find the minimum possible value of this product.
|
Answer: 256
Solution. Let $b$ and $w=40-b$ be the number of stones on black and white cells, respectively. Without loss of generality, assume that $b \geqslant w$, so $b$ can take any integer value from 20 to 32. We are interested in the minimum value of the product $b(40-b)$. The quadratic function $x(40-x)=-x^{2}+40 x$ reaches its maximum value at $x_{b}=20$ and decreases for $x \geqslant 20$. Therefore, the answer to the problem is $f(32)=32 \cdot 8=256$.
|
256
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.1. Kolya had 10 sheets of paper. On the first step, he chooses one sheet and divides it into two parts. On the second step, he chooses one sheet from the available ones and divides it into 3 parts, on the third step, he chooses one sheet from the available ones and divides it into 4, and so on. After which step will the number of sheets first exceed 500?
|
# Answer: 31
Solution. On the $k$-th step, the number of leaves increases by $k$, so after $k$ steps, the number of leaves will be $10+(1+2+\ldots+k)=10+\frac{k(k+1)}{2}$. When $k=30$, this number is less than 500 (it equals 475), and when $k=31$, it is already more than 500 (it equals 506), so the answer to the problem is 31.
|
31
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1. A two-digit natural number $\overline{a b}$ is randomly selected from 21 to 45 (the probability of selecting each number is the same). The probability that the number $\overline{a 8573 b}$ is divisible by 6 is $n$ percent. Find $n$.
|
Answer: 16
Solution. There are a total of 25 options. The number $\overline{a 8573 b}$ is divisible by 6 if and only if both conditions are met simultaneously: $b$ is even and the sum of the digits $a+8+5+7+3+b$ is divisible by 3. Among the numbers from 21 to 45, the numbers $22,28,34,40$ (every sixth number) fit - this is 4 options. Therefore, the desired probability is $\frac{4}{25}$ or 16 percent.
|
16
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
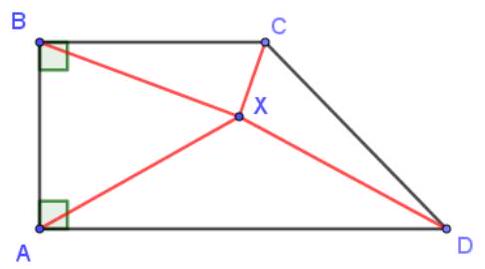
5.1. $B$ of trapezoid $A B C D: \angle A=\angle B=90^{\circ}, A D=2 \sqrt{7}, A B=\sqrt{21}, B C=2$. What is the minimum value that the sum of the lengths $X A+X B+X C+X D$ can take, where $X-$ is an arbitrary point in the plane?
|
# Answer: 12
Solution. By the triangle inequality $X A+X C \geqslant A C$, and equality is achieved when $X$ lies on the segment $A C$. Similarly, $X B+X D \geqslant B D$, and equality is achieved when $X$ lies on the segment
$B D$. Thus, $X A+X B+X C+X D \geqslant A C+B D$, and equality is achieved when $X$ is the intersection point of the diagonals. By the Pythagorean theorem $A C=\sqrt{A B^{2}+B C^{2}}=5, B D=\sqrt{A B^{2}+A D^{2}}=7$, hence $A C+B D=12$.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
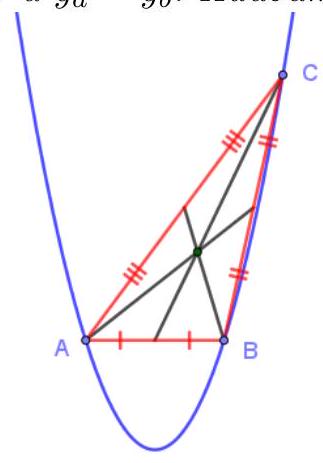
6.1. On the parabola $y=x^{2}-4 x-1$, three different points $A\left(x_{a}, y_{a}\right), B\left(x_{b}, y_{b}\right), C\left(x_{c}, y_{c}\right)$ are taken. It is known that $x_{c}=5$ and $y_{a}=y_{b}$. Find the abscissa of the point of intersection of the medians of triangle $A B C$.
|
# Answer: 3
Solution. Since $y_{a}=y_{b}$, points $A$ and $B$ are symmetric with respect to the axis of the parabola, which means the midpoint $K$ of segment $A B$ has an abscissa equal to the abscissa of the vertex of the parabola $x_{k}=2$. Next, by the property of the median, the point of intersection of the medians $M$ divides the median $C K$ in the ratio $2: 1$, counting from the vertex, so the abscissa $x_{m}$ of point $M$ is found from the equality $x_{c}-x_{k}=3\left(x_{m}-x_{k}\right)$. Finally: $x_{m}=\frac{x_{c}+2 x_{k}}{3}=3$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. In a row, the numbers $\sqrt{7.301}, \sqrt{7.302}, \sqrt{7.303}, \ldots, \sqrt{16.002}, \sqrt{16.003}$ are written (under the square root - consecutive terms of an arithmetic progression with a common difference of 0.001). Find the number of rational numbers among the listed ones.
|
# Answer: 13
Solution. Multiply the numbers by 100, we get $\sqrt{73010}, \sqrt{73020}, \sqrt{73030}, \ldots, \sqrt{160030}$ (in this case, rational numbers will remain rational, and irrational numbers will remain irrational). The square root of a natural number $n$ is a rational number if and only if $n$ is a perfect square. Furthermore, a natural number ending in 0 (i.e., divisible by 2 and 5) can only be a perfect square if it ends in 00 (i.e., divisible by $2^{2}$ and $5^{2}$).
Thus, the required number is the number of perfect squares in the sequence of numbers $731, 732, 733, \ldots$, 1600. Since $27^{2}<731<28^{2}$ and $40^{2}=1600$, the answer is $40-27=13$.
|
13
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. 72 vertices of a regular 3600-gon are painted red such that the painted vertices are the vertices of a regular 72-gon. In how many ways can 40 vertices of this 3600-gon be chosen so that they are the vertices of a regular 40-gon and none of them are red?
|
Answer: 81
Solution. Number the vertices in order $1,2, \ldots, 3600$, so that the painted vertices are those with numbers divisible by $3600 / 72=50$. 40 vertices form the vertices of a regular 40-gon if their numbers give the same remainder when divided by $3600 / 40=90$. There are 90 ways to choose a regular 40-gon. Consider one of these variants, in which the vertex numbers have the form $a+90 k$, where $a \in$ $\{1,2, \ldots, 90\}$. In $90-9=81$ cases, $a$ is not divisible by 10; in such cases, $a+90 k$ is not divisible by 10, and thus not divisible by 50, making these variants suitable. If, however, $a=10 m$, then for some $k \in\{1,2,3,4,5\}$, the number $m+9 k$ will be divisible by 5, and thus, $a+90 k=10(m+9 k)$ will be divisible by 50. Therefore, variants where $a$ is divisible by 10 are not suitable.
|
81
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4. Little One gave Karlson 111 candies. They immediately ate some of them together, $45\%$ of the remaining candies went to Karlson for lunch, and a third of the candies left after lunch were found by Fräulein Bok during cleaning. How many candies did she find?
|
Answer: 11.
First method. Let Carlson have had $n$ candies before lunch. Then, after lunch, there were $\frac{55}{100} n$ left, and Fräulein Bock found $\frac{1}{3} \cdot \frac{55}{100} n=\frac{11 n}{60}$ candies. Since the number of candies must be an integer, $11 n$ is divisible by 60. Since the numbers 11 and 60 are coprime, $n$ must be a multiple of 60. There is only one number that is divisible by 60 and less than 111, which is 60. Therefore, $n=60$, meaning Fräulein Bock found 11 candies.
Similar reasoning: if Carlson had $n$ candies before lunch, then he ate $0.45 n=\frac{9 n}{20}$ candies, and since the numbers 9 and 20 are coprime, $n$ is divisible by 20. After lunch, there were $0.55 n=\frac{11 n}{20}$ candies left, and this number must be divisible by 3. But 11 is not divisible by 3, so $n$ must be divisible by 3. Thus, $n$ is divisible by 3 and on
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (7 points) A seller bought a batch of pens and sold them. Some customers bought one pen for 10 rubles, while others bought 3 pens for 20 rubles. It turned out that the seller made the same profit from each sale. Find the price at which the seller bought the pens.
|
Answer: 5 rubles.
Solution. Let the purchase price of a pen be $x$. Then the profit from one pen is $10-x$, and from 3 pens is $20-3x$. Solving the equation $10-x=20-3x$, we get $x=5$.
Criteria. Correct solution by any method: 7 points.
If it is not justified that the purchase price of the pen should be 5 rubles, but it is verified that the condition is met in this case: 4 points.
Only the correct answer without any explanation: 2 points.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11-5. Santa Claus is preparing gifts. He has distributed 115 candies into bags, with each bag containing a different number of candies. In the three smallest gifts, there are 20 candies, and in the three largest - 50. How many bags are the candies distributed into? How many candies are in the smallest gift?
|
Answer: 10 packages, 5 candies.
Solution. Let's number the gifts from the smallest to the largest, from 1 to n. If the third gift has 7 or fewer candies, then the three smallest gifts have no more than $7+6+5=18$ candies. This contradicts the condition. Therefore, the third gift has at least 8 candies. Similarly, the third from the last gift has no more than 15 candies $(16+17+18=51>50)$.
Remove the three largest and the three smallest gifts. In the remaining gifts, there will be 115 - 20 $50=45$ candies, and each will have between 9 and 14 candies. Three packages are clearly not enough ( $14+13+12=39$ ), and five would be too many ( $9+10+11+12+13=55$ ). Therefore, 45 candies are distributed in 4 packages. This is possible: $47=9+11+12+13$. Note that the fourth package cannot have more than 9 candies: $10+11+12+13=46>45$.
If the fourth package has 9 candies, then the third has no more than 8, the second no more than 7, so the first package has at least $20-8-7=5$ candies. But no more, since $6+7+8=21$.
Criteria. Only the answer - 0 points. Only correct estimates for $a_{3}$ and $a_{n-3}-3$ points. Only a justified answer for the number of packages - 5 points. Full solution - 7 points.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 1. CONDITION
On a line, several points were marked. Then, between each pair of adjacent points, one more point was marked, and this operation was repeated once more. As a result, 101 points were obtained. How many points were marked initially?
|
Solution. Let there be $k$ points marked initially. Then $k-1$ more points were added to them (one between the first and second, second and third, $\ldots, (k-1)$-th and $k$-th marked points), and then another $(k+(k-1))-1=2k-2$ points. In total, the number of points became $4k-3$. Solving the equation $4k-3=101$, we find the answer.
Answer: 26.
|
26
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. If a class of 30 people is seated in a cinema hall, then in any case, at least two classmates will end up in the same row. If the same is done with a class of 26 people, then at least three rows will be empty. How many rows are there in the hall?
|
Answer: 29.
There are no more than 29 rows in the hall. Otherwise, a class of 30 students can be seated with one student per row. On the other hand, if a class of 26 students is seated with one student per row, at least three rows will be empty, which means there are no fewer than 29 rows.
Comment. An answer without justification - 2 points.
|
29
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.4. In triangle $A B C$, points $E$ and $D$ are on sides $A B$ and $B C$ respectively, such that segments $A D$ and $C E$ are equal, $\angle B A D=\angle E C A$ and $\angle A D C=\angle B E C$. Find the angles of the triangle.
|
Answer: All angles are $60^{\circ}$.
Triangles $C E A$ and $A D B$ are equal (by side and adjacent angles). Therefore, sides $A C$ and $A B$ are equal, and angles $C A E$ and $A B D$ are equal, which means angles $C A B$ and $A B C$ are equal. This implies the equality of sides $A C$ and $B C$. Thus, triangle $A B C$ is equilateral.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. The numbers from 1 to 10 were written in some order and resulted in the numbers \(a_{1}, a_{2}, a_{3}, \ldots, a_{10}\), and then the sums \(S_{1}=a_{1}\), \(S_{2}=a_{1}+a_{2}\), \(S_{3}=a_{1}+a_{2}+a_{3}\), \ldots, \(S_{10}=a_{1}+a_{2}+a_{3}+\ldots+a_{10}\) were calculated. What is the maximum number of prime numbers that could be among the numbers \(S_{1}, S_{2}\), \(S_{3}, \ldots, S_{10}\)?
|
Answer: 7.
Among the numbers from 1 to 10, there are five odd numbers. Adding an odd number changes the parity of the sum. Let $y_{1}^{\prime}, y_{2}, y_{3}, y_{4}, y_{5}$ be the odd numbers, in the order they appear on the board. After adding $y_{2}$, the sum will become even and greater than 2, as it will after adding $y_{4}$. These sums are composite numbers, as is $S_{10}=55$. Therefore, among the sums, there are no more than 7 prime numbers.
Example of writing the numbers: $2,1,4,3,7,6,8,10,5,9$. The resulting sums: $2,3,7,10,17,23,31,41,46,55$.
Comment. An answer without justification - 0 points. A correct answer with an example - 3 points (the example provided in the solution is not unique). An estimate of the number of prime sums (without an example) - 3 points.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. 50 businessmen - Japanese, Koreans, and Chinese - are sitting at a round table. It is known that between any two nearest Japanese, there are as many Chinese as there are Koreans at the table. How many Chinese can there be at the table?
## Answer: 32.
|
Solution. Let there be $-x$ Koreans and $y$ Japanese at the table, then there are $-x y$ Chinese. According to the condition: $x+y+x y=50$. By adding 1 to both sides of the equation and factoring both sides, we get: $(x+1)(y+1)=17 \times 3$. Since $x \neq 0$ and $y \neq 0$, one of the factors is 3, and the other is 17.
Thus, $x=2, y=16$ or $x=16, y=2$. In both cases, $x y=32$.
Criteria. If the solution is incorrect - 0 points.
Only the correct answer - 1 point.
If only one case is considered, $x=2, y=16$ or $x=16, y=2-5$ points. If the solution is correct - 7 points.
|
32
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. In a row, there are 20 free chairs. From time to time, a person approaches and sits on one of the free chairs, at which point one of their neighbors, if any, immediately stands up and leaves (the two of them do not sit together). What is the maximum number of chairs that can be occupied?
|
Answer: 19.
Note that all chairs cannot be occupied, otherwise, when the 20th person sat down, no one would leave, and the neighboring chair would be occupied. We will show how 19 chairs can be occupied. The first person takes the first chair, the next person takes the third chair, the third person takes the second chair, and the third person leaves. Then the next person takes the fourth chair, the next takes the third chair, and the fourth person leaves, and so on. By such operations, the first 19 chairs can be filled.
Remarks. The algorithm is provided for occupying 19 chairs without proving maximality - 5 points.
|
19
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
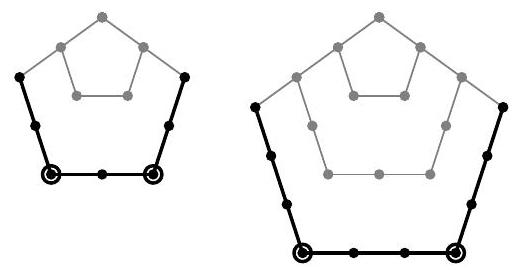
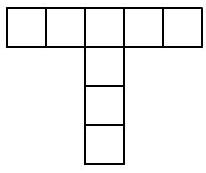
Problem 4.3. Zhenya drew a square with a side of 3 cm, and then erased one of these sides. A figure in the shape of the letter "P" was obtained. The teacher asked Zhenya to place dots along this letter "P", starting from the edge, so that the next dot was 1 cm away from the previous one, as shown in the picture, and then count how many dots he got. He got 10 dots.
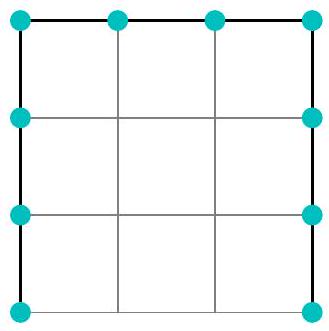
Then the teacher decided to complicate the task and asked to count the number of dots, but for the letter "P" obtained in the same way from a square with a side of 10 cm. How many dots will Zhenya have this time?
|
Answer: 31.
Solution. Along each of the three sides of the letter "П", there will be 11 points. At the same time, the "corner" points are located on two sides, so if 11 is multiplied by 3, the "corner" points will be counted twice. Therefore, the total number of points is $11 \cdot 3-2=31$.
|
31
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
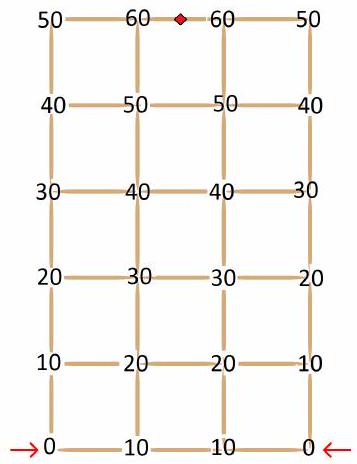
Problem 4.5. Hooligan Dima made a construction in the shape of a $3 \times 5$ rectangle using 38 wooden toothpicks. Then he simultaneously set fire to two adjacent corners of this rectangle, marked in the figure.
It is known that one toothpick burns for 10 seconds. How many seconds will it take for the entire construction to burn?
(Fire spreads along the toothpicks at a constant speed. The fire continues to spread from each burned toothpick to all adjacent unburned toothpicks.)

|
Answer: 65.
Solution. In the picture below, for each "node", the point where the toothpicks connect, the time in seconds it takes for the fire to reach it is indicated. It will take the fire another 5 seconds to reach the middle of the middle toothpick in the top horizontal row (marked in the picture).
|
65
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.4. The school principal, the caretaker, and the parent committee, failing to agree with each other, each bought a carpet for the school auditorium, which is $10 \times 10$. After thinking about what to do, they decided to place all three carpets as shown in the picture: the first carpet $6 \times 8$ - in one corner, the second carpet $6 \times 6$ - in the opposite corner, and the third carpet $5 \times 7$ - in one of the remaining corners (all dimensions are in meters).
Find the area of the part of the hall covered by carpets in three layers (give the answer in square meters).
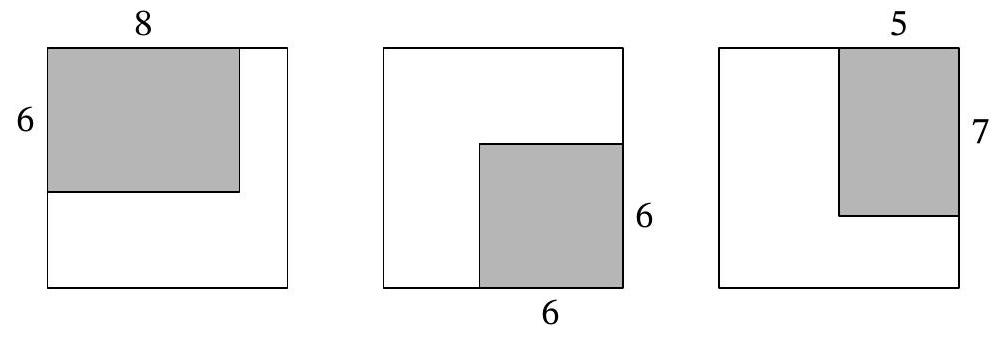
|
Answer: 6.
Solution. We will measure all dimensions in meters and the area in square meters.
Let's look at the overlap of the second and third carpets. This will be a rectangle $5 \times 3$ (5 along the horizontal, 3 along the vertical), adjacent to the right side of the square room, 4 units from the top side, and 3 units from the bottom side.
The first carpet intersects this rectangle horizontally between the 5th and 8th meters from the left side of the square room, and vertically between the 4th and 6th meters from the top side. In the end, we get a rectangle $2 \times 3$, the area of which is 6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
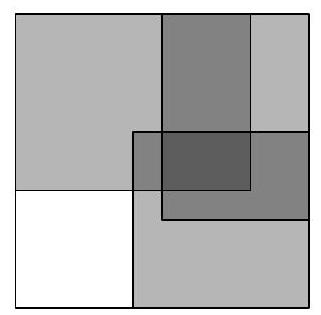
Problem 5.8. Inside a large triangle with a perimeter of 120, several segments were drawn, dividing it into nine smaller triangles, as shown in the figure. It turned out that the perimeters of all nine small triangles are equal to each other. What can they be equal to? List all possible options.
The perimeter of a figure is the sum of the lengths of all its sides.
|
Answer: 40.
Solution. Let's add the perimeters of the six small triangles marked in gray in the following figure:
From the obtained value, subtract the perimeters of the other three small white triangles. Since the perimeters of the small triangles are equal, on one side, we get three times the perimeter of a small triangle. On the other side, in this sum, there will only be segments that make up the perimeter of the large triangle, which is 120. Therefore, the perimeter of a small triangle is $120: 3=40$.
## 6th grade
|
40
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.4. Misha made himself a homemade dartboard during the summer at the cottage. The round board is divided by circles into several sectors - darts can be thrown into it. Points are awarded for hitting a sector as indicated on the board.
Misha threw 8 darts 3 times. The second time he scored twice as many points as the first time, and the third time he scored 1.5 times as many points as the second time. How many points did he score the second time?
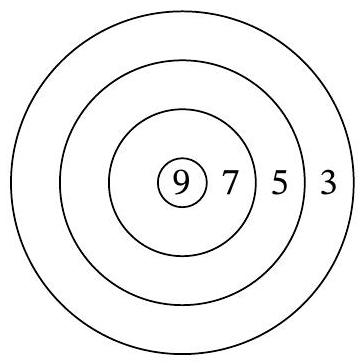
|
Answer: 48.
Solution. The smallest possible score that can be achieved with eight darts is $3 \cdot 8=24$. Then, the second time, Misha scored no less than $24 \cdot 2=48$ points, and the third time, no less than $48 \cdot 1.5=72$.
On the other hand, $72=9 \cdot 8$ is the highest possible score that can be achieved with eight darts. Therefore, the third time, Misha scored exactly 72 points, and the second time, exactly 48.
|
48
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.7. Anya places pebbles on the sand. First, she placed one stone, then added pebbles to form a pentagon, then made a larger outer pentagon with pebbles, then another outer pentagon, and so on, as shown in the picture. The number of stones she had arranged on the first four pictures: 1, 5, 12, and 22. If she continues to create such pictures, how many stones will be on the 10th picture?
-
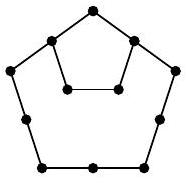
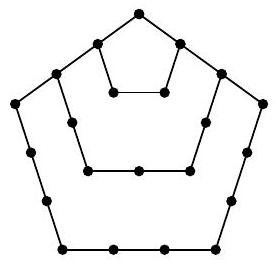
|
Answer: 145.
Solution. On the second picture, there are 5 stones. To get the third picture from it, you need to add three segments with three stones on each. The corner stones will be counted twice, so the total number of stones in the third picture will be $5+3 \cdot 3-2=12$.
To get the fourth picture from the third, you need to add three segments with four stones on each. The corner stones will be counted twice, so the total number of stones will be $12+3 \cdot 4-2=22$.
Similarly, we will calculate the number of stones on each of the remaining pictures:
on the 5th: $22+3 \cdot 5-2=35$;
on the 6th: $\quad 35+3 \cdot 6-2=51$;
on the 7th: $51+3 \cdot 7-2=70$;
on the 8th: $\quad 70+3 \cdot 8-2=92$;
on the 9th: $92+3 \cdot 9-2=117$
on the 10th: ~ 117+3 \cdot 10-2=145$.
|
145
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.2. In the chat of students from one of the schools, a poll was being held: "On which day to hold the disco: October 22 or October 29?"
The graph shows how the votes were distributed an hour after the start of the poll.
Then, 80 more people participated in the poll, voting only for October 22. After that, the poll ended. The final distribution of votes is also shown on the graph.
How many people participated in the poll?
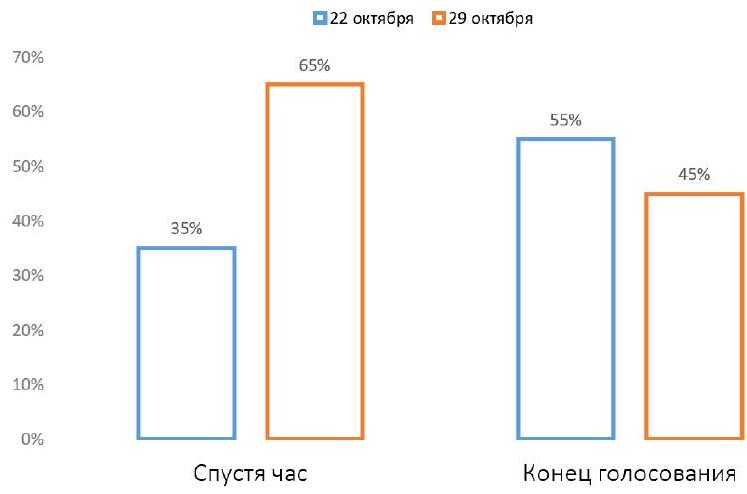
|
Answer: 260.
Solution. Let $x$ be the number of people who voted an hour after the start. From the left chart, it is clear that $0.35 x$ people voted for October 22, and $-0.65 x$ people voted for October 29.
In total, $x+80$ people voted, of which $45\%$ voted for October 29. Since there are still $0.65 x$ of them, we get the equation
$0.65 x=0.45(x+80)$, from which we find $x=180$. Therefore, a total of $180+80=260$ people participated in the voting.
|
260
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.7. In the figure, two equal triangles are depicted: $A B C$ and $E B D$. It turns out that $\angle D A E = \angle D E A = 37^{\circ}$. Find the angle $B A C$.
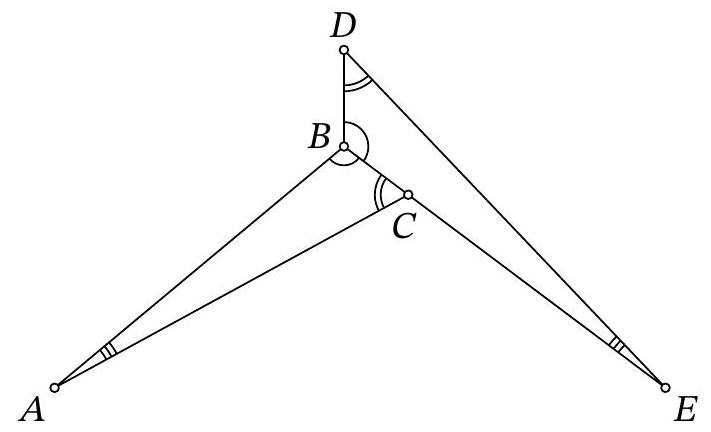
|
Answer: 7.
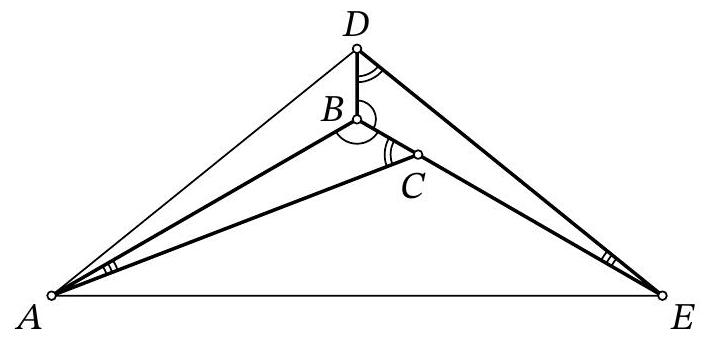
Fig. 4: to the solution of problem 8.7
Solution. Draw segments $A D$ and $A E$ (Fig. 4). Since $\angle D A E=\angle D E A=37^{\circ}$, triangle $A D E$ is isosceles, $A D=D E$.
Notice that triangle $A B D$ is equal to triangle $E B D$ by three sides: $B D$ is a common side, $A D=D E, A B=B E$ from the equality of triangles $A B C$ and $E B D$. Then $\angle D A B=$ $\angle B E D=\angle B A C$ and $\angle A B D=\angle D B E=\angle A B E=\frac{1}{3} \cdot 360^{\circ}=120^{\circ}$.
Since $A B=B E$, triangle $A B E$ is isosceles with an angle of $120^{\circ}$, so $\angle B A E=\frac{1}{2}\left(180^{\circ}-120^{\circ}\right)=30^{\circ}$. Therefore,
$$
\angle B A C=\angle D A B=\angle D A E-\angle B A E=37^{\circ}-30^{\circ}=7^{\circ}
$$
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.4. A line $\ell$ is drawn through vertex $A$ of rectangle $ABCD$, as shown in the figure. Perpendiculars $BX$ and $DY$ are dropped from points $B$ and $D$ to line $\ell$. Find the length of segment $XY$, given that $BX=4$, $DY=10$, and $BC=2AB$.
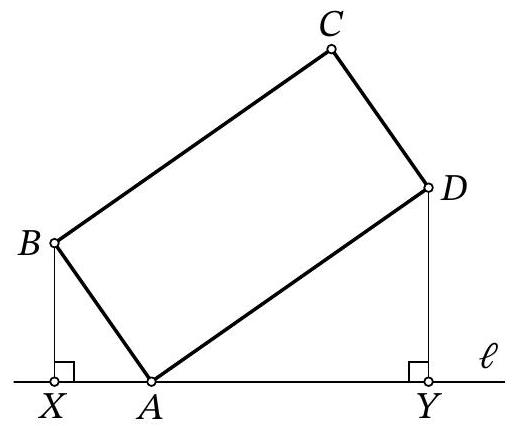
|
Answer: 13.
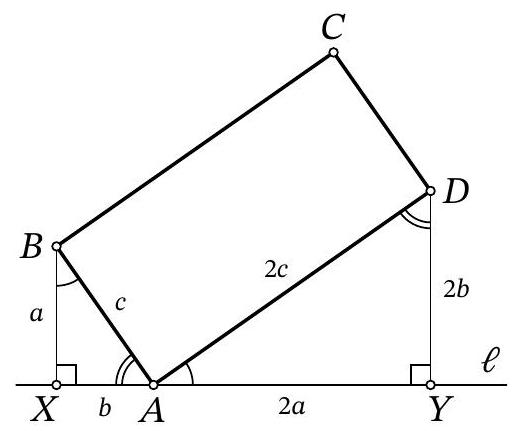
Fig. 5: to the solution of problem 9.4
Solution. Note that since $\angle Y A D=90^{\circ}-\angle X A B$ (Fig. 5), the right triangles $X A B$ and $Y D A$ are similar by the acute angle $\angle Y A D=\angle X B A$. The similarity coefficient is the ratio $A B: A D$, which is $\frac{1}{2}$. From this, we get $X A=\frac{1}{2} D Y=5$ and $A Y=2 B X=8$, which in total gives $X Y=13$.
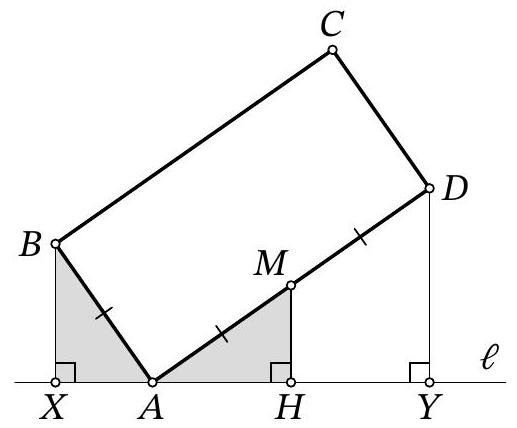
Fig. 6: to the solution of problem 9.4
Another solution. Let $M$ be the midpoint of segment $A D$, then $A M=M D=\frac{A D}{2}=\frac{B C}{2}=A B$ (Fig. 6). Drop a perpendicular from $M$ to $M H$ on line $\ell$. Since in triangle $A D Y$ the segment $M H$ passes through the midpoint of side $A D$ and is parallel to side $D Y$, it is the midline, $A H=H Y$ and $M H=\frac{D Y}{2}=\frac{10}{2}=5$.
Note that $\angle A B X=90^{\circ}-\angle B A X=90^{\circ}-\left(180-90^{\circ}-\angle M A H\right)=\angle M A H$. Then the right triangles $A B X$ and $M A H$ are equal by hypotenuse $A B=A M$ and acute angle $\angle A B X=\angle M A H$. From this, it follows that $A X=M H=5$ and $A H=B X=4$.
Thus, $X Y=A X+A H+H Y=5+4+4=13$.
|
13
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.6. In triangle $A B C$, the angles $\angle B=30^{\circ}$ and $\angle A=90^{\circ}$ are known. On side $A C$, point $K$ is marked, and on side $B C$, points $L$ and $M$ are marked such that $K L=K M$ (point $L$ lies on segment $B M$).
Find the length of segment $L M$, if it is known that $A K=4, B L=31, M C=3$.
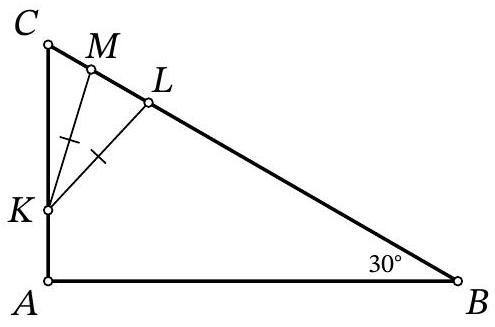
|
Answer: 14.
Solution. In the solution, we will use several times the fact that in a right-angled triangle with an angle of $30^{\circ}$, the leg opposite this angle is half the hypotenuse. Drop the height $K H$ from the isosceles triangle $K M L$ to the base (Fig. 7). Since this height is also a median, then $M H=H L=x$. In the right-angled triangle $C K H$ we have $\angle C K H=90^{\circ}-\angle C=\angle A=30^{\circ}$, so $K C=2 \cdot C H=2 \cdot(C M+M H)=$ $2 \cdot(3+x)=6+2 x$. In the right-angled triangle $A B C$ we have $\angle A=30^{\circ}$, so $B C=2 \cdot A C$. Setting up and solving the corresponding equation $31+2 x+3=2 \cdot(4+6+2 x)$, we find $x=7$. Then $L M=2 x=2 \cdot 7=14$.
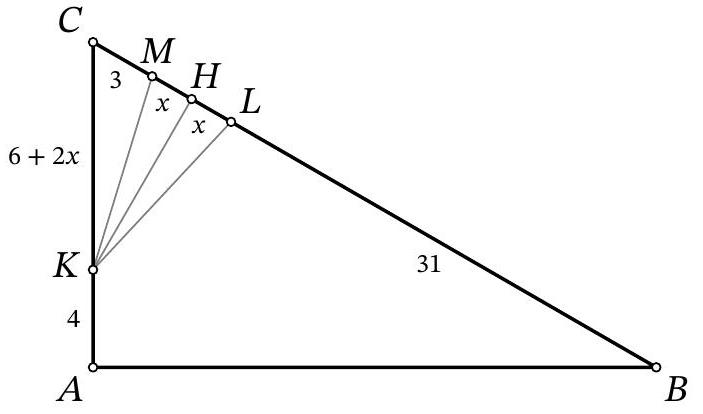
Figure 7: to the solution of problem 9.6
|
14
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.2. Points $A, B, C, D, E, F, G$ are located clockwise on a circle, as shown in the figure. It is known that $A E$ is the diameter of the circle. Also, it is known that $\angle A B F=81^{\circ}, \angle E D G=76^{\circ}$. How many degrees does the angle $F C G$ measure?
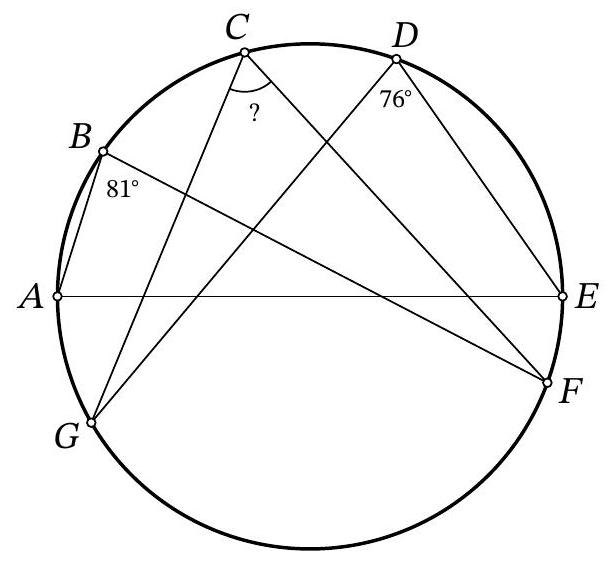
|
Answer: 67.
Solution. Since inscribed angles subtended by the same arc are equal, then $\angle A C F=$ $\angle A B F=81^{\circ}$ and $\angle E C G=\angle E D G=76^{\circ}$. Since a right angle is subtended by the diameter,
$$
\angle F C G=\angle A C F+\angle E C G-\angle A C E=81^{\circ}+76^{\circ}-90^{\circ}=67^{\circ}
$$
|
67
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.7. The graph of the function $f(x)=\frac{1}{12} x^{2}+a x+b$ intersects the $O x$ axis at points $A$ and $C$, and the $O y$ axis at point $B$, as shown in the figure. It turned out that for the point $T$ with coordinates $(3 ; 3)$, the condition $T A=T B=T C$ is satisfied. Find $b$.
|
Answer: -6.
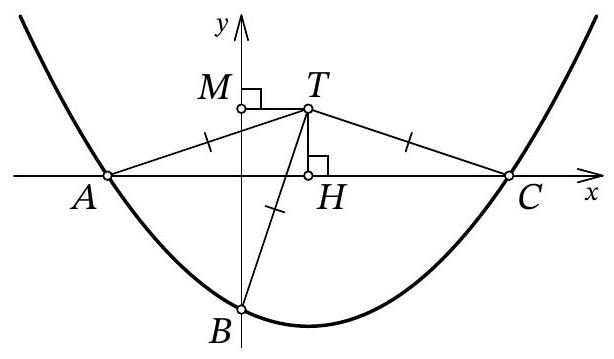
Fig. 11: to the solution of problem 10.7
Solution. Let point $A$ have coordinates $\left(x_{1} ; 0\right)$, and point $C$ have coordinates $\left(x_{2} ; 0\right)$. From the condition, it is clear that $x_{1} < 0$ and $x_{2} > 0$. Since $x_{1}$ and $x_{2}$ are the roots of the quadratic trinomial $f(x)$, by Vieta's theorem, we have $x_{1} \cdot x_{2} = 12b$, from which we get $b = \frac{x_{1} \cdot x_{2}}{12} < 0$.
Let $H$ be the point with coordinates $(3 ; 0)$ (Fig. 11). Clearly, in the isosceles triangle $A T C$, the segment $T H$ is the height, and therefore it is also the median. Thus, $3 - x_{1} = A H = H C = x_{2} - 3$, from which we get $x_{1} = 6 - x_{2}$.
Let $M$ be the point with coordinates $(0, 3)$. Since $T H = T M = 3$ and $T A = T B$, the right triangles $A T H$ and $B T M$ are equal by the leg and hypotenuse. Therefore, $3 - x_{1} = H A = M B = 3 - b$, that is, $x_{1} = b = \frac{x_{1} \cdot x_{2}}{12}$ (by Vieta's theorem), from which we find $x_{2} = 12$. Finally, $x_{1} = 6 - x_{2} = 6 - 12 = -6$ and $b = x_{1} = -6$.
Another solution. As in the previous solution, let the abscissas of points $A$ and $C$ be $x_{1}$ and $x_{2}$, respectively; we will also use the fact that point $B$ has coordinates $(0 ; b)$. Immediately, we understand that $O A = |x_{1}| = -x_{1}$, $O C = |x_{2}| = x_{2}$, and $O B = |b| = -b$.
Let's find the second intersection of the circle with the y-axis, let this be point $D$ with coordinates $(0 ; d)$ (Fig. 12). The chords $A C$ and $B D$ of the circle intersect at the origin $O$; from the properties of the circle, we know that $O A \cdot O C = O B \cdot O D$. We get $-x_{1} \cdot x_{2} = -b \cdot d$, from which, replacing $x_{1} \cdot x_{2}$ with $12b$ by Vieta's theorem, we get $d = 12$.
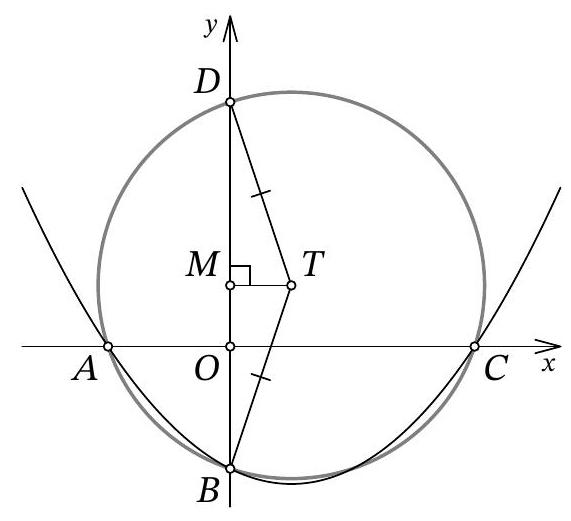
Fig. 12: to the solution of problem 10.7
It remains to note that triangle $BTD$ is isosceles, and the midpoint of its base, point $M$, has coordinates $(0 ; 3)$. Reflecting point $D(0 ; 12)$ relative to it, we get $B(0 ; -6)$.
|
-6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.1. The product of nine consecutive natural numbers is divisible by 1111. What is the smallest possible value that the arithmetic mean of these nine numbers can take?
|
Answer: 97.
Solution. Let these nine numbers be $-n, n+1, \ldots, n+8$ for some natural number $n$. It is clear that their arithmetic mean is $n+4$.
For the product to be divisible by $1111=11 \cdot 101$, it is necessary and sufficient that at least one of the factors is divisible by 11, and at least one of the factors is divisible by 101. Therefore, one of the nine numbers must be at least 101, so $n+8 \geqslant 101$ and $n+4 \geqslant 97$. It is also clear that for the nine numbers $93,94, \ldots, 101$, the value $n+4=97$ is achieved, since 99 is divisible by 11, and 101 is divisible by 101.
|
97
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.2. A square was cut into five rectangles of equal area, as shown in the figure. The width of one of the rectangles is 5. Find the area of the square.
|
Answer: 400.
Solution. The central rectangle and the rectangle below it have a common horizontal side, and their areas are equal. Therefore, the vertical sides of these rectangles are equal, let's denote them by $x$ (Fig. 13). The vertical side of the lower left rectangle is $2x$, and we will denote its horizontal side by $y$. Since its area $2xy$ is the same as the area of the central rectangle, the horizontal side of the central rectangle is $2y$. Then the horizontal side of the upper left rectangle is $3y$, and its area $3y \cdot 5 = 15y$ should be equal to $2xy$, from which we find $x=7.5$. Then the side of the entire square is $5+2x=5+2 \cdot 7.5=20$, and its area is $20^2=400$.
|
400
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.3. In a football tournament, 15 teams participated, each playing against each other exactly once. For a win, 3 points were awarded, for a draw - 1 point, and for a loss - 0 points.
After the tournament ended, it turned out that some 6 teams scored at least $N$ points each. What is the greatest integer value that $N$ can take?
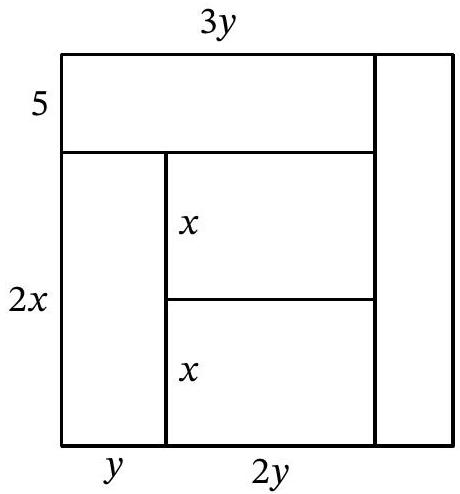
Fig. 13: to the solution of problem 11.2
#
|
# Answer: 34.
Solution. Let's call these 6 teams successful, and the remaining 9 teams unsuccessful. We will call a game between two successful teams an internal game, and a game between a successful and an unsuccessful team an external game.
First, note that for each game, the participating teams collectively earn no more than 3 points. Clearly, there were exactly $\frac{6 \cdot 5}{2}=15$ internal games, and only from these games did all successful teams collectively earn no more than $15 \cdot 3=45$ points. There were exactly $6 \cdot 9=54$ external games, and in each such game, a successful team earned no more than 3 points. Therefore, collectively, all successful teams earned no more than $54 \cdot 3=162$ points from external games. According to the problem, the successful teams collectively earned at least $6 \mathrm{~N}$ points, so we get the inequality $6 N \leqslant 45+162$. From this, it follows that $N \leqslant \frac{207}{6}<35$ and $N \leqslant 34$. Now let's provide an example for $N=34$. Number the teams from 1 to 15. We will show how teams from 1 to 6 can earn at least 34 points.
- Suppose each team from 1 to 6 won against each team from 7 to 15, then each team from 1 to 6 earned $9 \cdot 3=27$ points just from these games.
- Suppose the teams from 1 to 6 played among themselves as indicated in the following table (in each cell, the number of points is shown that the team from the corresponding row received in the game with the team from the corresponding column):
| | $\mathbf{1}$ | $\mathbf{2}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{5}$ | $\mathbf{6}$ |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| $\mathbf{1}$ | | 3 | 3 | 1 | 0 | 0 |
| $\mathbf{2}$ | 0 | | 3 | 3 | 1 | 0 |
| $\mathbf{3}$ | 0 | 0 | | 3 | 3 | 1 |
| $\mathbf{4}$ | 1 | 0 | 0 | | 3 | 3 |
| $\mathbf{5}$ | 3 | 1 | 0 | 0 | | 3 |
| $\mathbf{6}$ | 3 | 3 | 1 | 0 | 0 | |
- Suppose in each game between teams from 7 to 15, the team with the higher number won (the outcome of these games does not matter).
In total, teams from 1 to 6 earned at least $27+7=34$ points.
|
34
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.8. Given a parallelepiped $A B C D A_{1} B_{1} C_{1} D_{1}$. A point $X$ is chosen on the edge $A_{1} D_{1}$, and a point $Y$ is chosen on the edge $B C$. It is known that $A_{1} X=5, B Y=3, B_{1} C_{1}=14$. The plane $C_{1} X Y$ intersects the ray $D A$ at point $Z$. Find $D Z$.
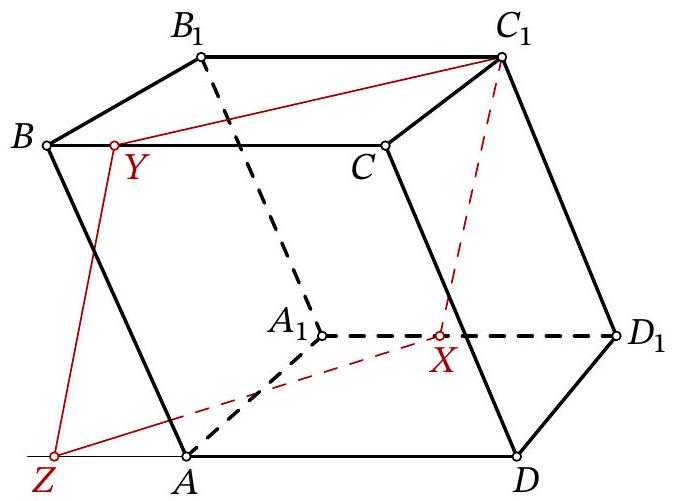
|
Answer: 20.
Solution. Lines $C_{1} Y$ and $Z X$ lie in parallel planes $B B_{1} C_{1} C$ and $A A_{1} D_{1} D$, so they do not intersect. Since these two lines also lie in the same plane $C_{1} X Z Y$, they are parallel. Similarly, lines $Y Z$ and $C_{1} X$ are parallel. Therefore, quadrilateral $C_{1} X Z Y$ is a parallelogram.
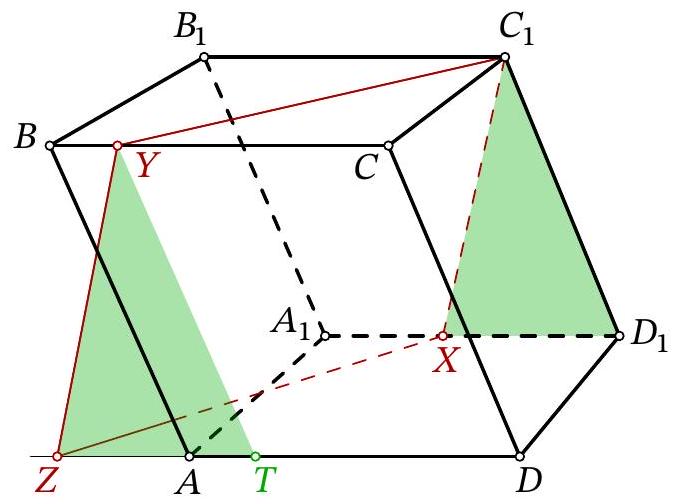
Fig. 15: to the solution of problem 11.8
Let us lay off segment $A T$ on $A D$, equal to $B Y$ (Fig. 15). Quadrilateral $B Y T A$ is a parallelogram, meaning segments $Y T, B A$, and $C_{1} D_{1}$ are parallel and equal. Additionally, segments $Y Z$ and $C_{1} X$ are parallel and equal; from the parallelism follows the equality of angles $Z Y T$ and $X C_{1} D_{1}$, which gives the equality of triangles $Z Y T$ and $X C_{1} D_{1}$.
Then
$$
\begin{aligned}
D Z & =Z T+A D-A T=X D_{1}+B_{1} C_{1}-B Y= \\
& =\left(A_{1} D_{1}-A_{1} X\right)+B_{1} C_{1}-B Y=(14-5)+14-3=20
\end{aligned}
$$
Another solution. As in the previous solution, we will use the fact that $C_{1} X Z Y$ is a parallelogram.
Consider the chain of vector equalities:
$$
\overrightarrow{D Z}=\overrightarrow{D C}+\overrightarrow{C Y}+\overrightarrow{Y Z}=\overrightarrow{D_{1} C_{1}}+\overrightarrow{C Y}+\overrightarrow{C_{1} X}=\overrightarrow{C Y}+\overrightarrow{D_{1} X}
$$
In the last part, all vectors are oriented the same as $\overrightarrow{D Z}$, so we can transition to the equality of segments and continue:
$$
D Z=C Y+D_{1} X=(C B-B Y)+\left(D_{1} A_{1}-A_{1} X\right)=2 B_{1} C_{1}-B Y-A_{1} X
$$
Substituting the lengths given in the problem, we get $D Z=2 \cdot 14-3-5=20$.
|
20
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. For some natural numbers $n>m$, the number $n$ turned out to be representable as the sum of 2021 addends, each of which is some integer non-negative power of the number $m$, and also as the sum of 2021 addends, each of which is some integer non-negative power of the number $m+1$. For what largest $m$ could this have happened (for some $n>m$)?
(A. Kuznetsov)
|
Answer. $m=2021$.
Solution. Let $m>2021$. Since any power of the number $m+1$ gives a remainder of 1 when divided by $m$, the sum of 2021 such powers gives a remainder of 2021 when divided by $m$. On the other hand, powers of the number $m$ give only remainders of 0 or 1 when divided by $m$, so the sum of 2021 powers of the number $m$ can give a remainder of 2021 when divided by $m$ only if all the terms are equal to 1. But then $n=2021m$, which in bases $m$ and $m+1$ when $m=2021$ has a digit sum of 2021 (thus, it also satisfies the condition of the problem): $n=m^{2}+m(m-1)=(m+1)^{2}+(m+$ $+1)(m-4)+3$
|
2021
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 4. CONDITION
The sequence of numbers $\mathrm{a}_{1}, \mathrm{a}_{2}, \mathrm{a}_{3}, \ldots, \mathrm{a}_{\mathrm{n}}, \ldots$ satisfies the relations $\mathrm{a}_{\mathrm{n}}=\mathrm{a}_{\mathrm{n}-1} \cdot \mathrm{a}_{\mathrm{n}-3}$ for $\mathrm{n}=4,5,6, \ldots$ Find $\mathrm{a}_{2019}$, given that $\mathrm{a}_{1}=1, \mathrm{a}_{2}=1, \mathrm{a}_{3}=-1$.
|
Solution. It is clear that all members of this sequence are equal to $\pm 1$. We find:
$$
\begin{aligned}
& a_{n}=\left(a_{n-1}\right) \cdot a_{n-3}=\left(a_{n-2} \cdot a_{n-4}\right) \cdot a_{n-3}=\left(a_{n-2}\right) \cdot a_{n-4} \cdot a_{n-3}= \\
& =\left(a_{n-3} \cdot a_{n-4}\right) \cdot a_{n-4} \cdot a_{n-3}=a_{n-3}^{2} \cdot a_{n-4} \cdot a_{n-5}=a_{n-4} \cdot a_{n-5}= \\
& =\left(a_{n-4}\right) \cdot a_{n-5}=\left(a_{n-5} \cdot a_{n-7}\right) \cdot a_{n-5}=a_{n-5}^{2} \cdot a_{n-7}=a_{n-7}
\end{aligned}
$$
That is, the sequence is periodic with a period of 7. Therefore,
$$
\mathrm{a}_{2019}=\mathrm{a}_{288 \cdot 7+3}=\mathrm{a}_{3}=-1
$$
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Around a circle, 100 integers are written, the sum of which is 1. A chain is defined as several numbers (possibly one) standing consecutively. Find the number of chains, the sum of the numbers in which is positive.
|
Answer: 4951.
Solution. We will divide all chains (except the chain consisting of all numbers) into pairs that complement each other. If the sum of the numbers in one chain of the pair is $s$, and in the second is $t$, then $s+t=1$. Since $s$ and $t$ are integers, exactly one of them is positive. Therefore, exactly half of all chains have a positive sum. The total number of chains is $100 \cdot 99$ (two complementary chains are determined by the choice of two positions between them). This gives us 4950 chains with a positive sum. Adding to them the chain of all numbers.
|
4951
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A 2019-digit number written on the board is such that any number formed by any two adjacent digits (in the order they follow) is divisible by 13. Find the last digit of this number, given that the first digit is 6.
|
1. Answer: 2.
Two-digit numbers divisible by 13: $13,26,39,52,65,78,91$. If the first digit of the number is 6, then the second digit must be 5 (forming the number 65, which is divisible by 13), the third digit is 2 (forming 52), and the fourth digit is again 6 (forming 26). Thus, the digits will be arranged in triplets: $652652 \ldots$ Since 2019 is divisible by 3, the last digit is 2.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. If a number is added to the sum of its digits, the result is 328. Find this number.
|
# 3. Answer: 317
Let's denote the digits of the desired number as a, b, c, and their sum as s. Then abc $+\mathrm{s}=328$. Since $s$ is the sum of three single-digit numbers, s does not exceed 27, so a $=3$. At the same time, b cannot be zero, because otherwise the maximum value of s would be $3+0+9=12$. If $\mathrm{b}=1$, then $31 \mathrm{c}+(4+\mathrm{c})=328$, c $=7$. If $\mathrm{b}=2$, then $32 \mathrm{c}+(5+\mathrm{c})$ $=328$, there are no integer solutions here.
Comment on checking.
The digits of the number are correctly and justifiedly found: 3 points.
|
317
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Petya wants to color several cells of a $6 \times 6$ square so that there are as many vertices as possible that belong to exactly three colored squares. What is the maximum number of such vertices he can achieve?
|
Answer: 25.
Solution. Each vertex of the grid belongs to one, two, or four squares, and the latter are 25. Therefore, the number of vertices in question is no more than 25. An example is shown in the figure.
Criteria. Example: 4 points. Evaluation: 3
points.

|
25
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.3. How many rectangles exist on this picture with sides running along the grid lines? (A square is also a rectangle.)
|
Answer: 24.
Solution. In a horizontal strip $1 \times 5$, there are 1 five-cell, 2 four-cell, 3 three-cell, 4 two-cell, and 5 one-cell rectangles. In total, $1+2+3+4+5=15$ rectangles.
In a vertical strip $1 \times 4$, there are 1 four-cell, 2 three-cell, 3 two-cell, and 4 one-cell rectangles. In total, $1+2+3+4=10$ rectangles. At the same time, one one-cell rectangle at the intersection of the strips is counted twice (and only it is). Therefore, the answer to the problem is the number $15+10-1=24$.
|
24
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.3. A cuckoo clock is hanging on the wall. When a new hour begins, the cuckoo says "cuckoo" a number of times equal to the number the hour hand points to (for example, at 19:00, "cuckoo" sounds 7 times). One morning, Maxim approached the clock when it was 9:05. He started turning the minute hand until he advanced the clock by 7 hours. How many times did "cuckoo" sound during this time?

|
Answer: 43.
Solution. The cuckoo will say "cuckoo" from 9:05 to 16:05. At 10:00 it will say "cuckoo" 10 times, at 11:00 - 11 times, at 12:00 - 12 times. At 13:00 (when the hand points to the number 1) "cuckoo" will sound 1 time. Similarly, at 14:00 - 2 times, at 15:00 - 3 times, at 16:00 - 4 times. In total
$$
10+11+12+1+2+3+4=43
$$
|
43
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.5. In the park, paths are laid out as shown in the figure. Two workers started to asphalt them, starting simultaneously from point $A$. They lay asphalt at constant speeds: the first on the section $A-B-C$, the second on the section $A-D-E-F-C$. In the end, they finished the work simultaneously, spending 9 hours on it. It is known that the second works 1.2 times faster than the first. How many minutes did the second spend laying asphalt on the section $D E$?
|
Answer: 45.
Solution. Let the line $A D$ intersect the line $C F$ at point $G$, as shown in the figure below. Since $A B C G$ and $D E F G$ are rectangles, we have $A B=C G, B C=A G, E F=D G$ and $D E=F G$.
The second worker works 1.2 times faster than the first, and the working time was the same, so the second worker laid 1.2 times more asphalt than the first. Let the first worker lay $x=A B+B C$ asphalt on the section $A-B-C$, then the second worker on the section $A-D-E-F-C$ laid
$$
\begin{aligned}
1.2 x & =A D+D E+E F+F G+G C=(A D+E F+C G)+(D E+F G)= \\
& =(B C+A B)+(D E+D E)=x+2 D E
\end{aligned}
$$
From this, we find that $D E=0.1 x$, which is 12 times less than the total amount of asphalt on the second section. Therefore, the second worker spent 12 times less time on the section $D E$ than on his entire path. He worked a total of $9 \cdot 60=540$ minutes, so he spent $\frac{540}{12}=45$ minutes on $D E$.
|
45
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.8. There are exactly 120 ways to color five cells in a $5 \times 5$ table so that each column and each row contains exactly one colored cell.
There are exactly 96 ways to color five cells in a $5 \times 5$ table without a corner cell so that each column and each row contains exactly one colored cell.
How many ways are there to color five cells in a $5 \times 5$ table without two corner cells so that each column and each row contains exactly one colored cell?

|
Answer: 78.
Solution. Consider the colorings of a $5 \times 5$ table described in the problem (i.e., such that in each column and each row exactly one cell is colored).
For convenience, let's introduce some notations. Let the top-left corner cell of the $5 \times 5$ table be called $A$, and the bottom-right corner cell be called $B$. Suppose that among the colorings of the first table, exactly $a$ have the cell $A$ colored, and exactly $b$ have the cell $B$ colored. Clearly, $a=b$ due to symmetry.
Notice that the number of colorings of the second table is equal to the number of colorings of the first table where the cell $A$ is not colored. The number of colorings of the third table is equal to the number of colorings of the first table where neither $A$ nor $B$ is colored. To find this, we subtract from 120 the number of colorings of the first table where $A$ or $B$ is colored. To count the number of such colorings, we add $a$ and $b$, and then subtract what has been counted twice - the ways where both $A$ and $B$ are colored.
All colorings of the first table can be divided into two types: those in which the cell $A$ is colored, and those in which it is not. This leads to the equation $120=a+96$, i.e., $a=24$. Then $b=24$ as well.
The number of colorings where both $A$ and $B$ are colored is the same as the number of ways to color the central $3 \times 3$ square. It is easy to see that there are exactly $3!=6$ such ways (to choose the colored cell in its top row, there are 3 ways, in the middle row - 2 ways, and in the bottom row - 1 way).
Thus, the answer to the problem is the number $120-(24+24-6)=78$.
## 7th grade
|
78
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.7. In three of the six circles of the diagram, the numbers 4, 14, and 6 are recorded. In how many ways can natural numbers be placed in the remaining three circles so that the products of the triples of numbers along each of the three sides of the triangular diagram are the same?
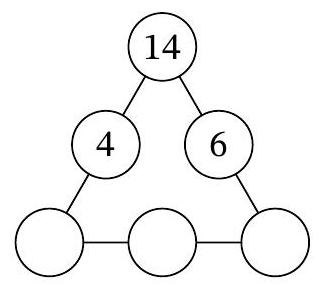
|
Answer: 6.
Solution. Let $a, b, c$ be the natural numbers in the three lower circles, from left to right. According to the condition, $14 \cdot 4 \cdot a = 14 \cdot 6 \cdot c$, i.e., $2a = 3c$. From this, it follows that $3c$ is even, and therefore $c$ is even. Thus, $c = 2k$ for some natural number $k$, and from the equation $2a = 3c$ it follows that $a = 3k$.
It must also hold that $14 \cdot 4 \cdot 3k = 3k \cdot b \cdot 2k$, which means $b \cdot k = 28$. Note that by choosing the number $k$, which is a natural divisor of 28, the natural numbers $a, b, c$ are uniquely determined. The number 28 has exactly 6 natural divisors: $1, 2, 4, 7, 14, 28$. Therefore, there are also 6 ways to place the numbers in the circles.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.8. Given an isosceles triangle $ABC (AB = BC)$. On the ray $BA$ beyond point $A$, point $E$ is marked, and on side $BC$, point $D$ is marked. It is known that
$$
\angle ADC = \angle AEC = 60^{\circ}, AD = CE = 13.
$$
Find the length of segment $AE$, if $DC = 9$.
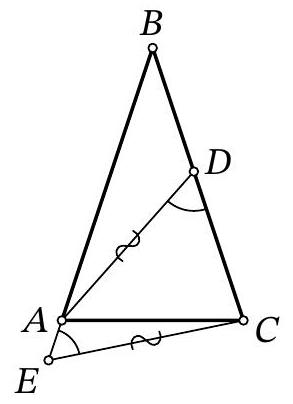
|
Answer: 4.
Solution. Mark point $K$ on ray $B C$ such that $B E=B K$. Then $A E=C K$ as well.
Notice that triangles $A C E$ and $C A K$ are congruent by two sides ($A E=C K, A C$ - common side) and the angle between them ($\angle C A E=\angle A C K$ - adjacent to the equal base angles of the isosceles triangle). Therefore, $A K=C E=13$ and $\angle A K C=\angle A E C=60^{\circ}$.
In triangle $A D K$, the angles at vertices $D$ and $K$ are both $60^{\circ}$, so it is an equilateral triangle, and $D K=A K=A D=13$. Therefore, $A E=C K=D K-D C=13-9=4$.
## 8th grade
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.1. In a $5 \times 5$ square, some cells have been painted black as shown in the figure. Consider all possible squares whose sides lie along the grid lines. In how many of them is the number of black and white cells the same?

|
Answer: 16.
Solution. An equal number of black and white cells can only be in squares $2 \times 2$ or $4 \times 4$ (in all other squares, there is an odd number of cells in total, so there cannot be an equal number of black and white cells). There are only two non-fitting $2 \times 2$ squares (both of which contain the center of the table, but do not contain any cells above the center), so there are exactly $16-2=14$ fitting $2 \times 2$ squares. And among the $4 \times 4$ squares, only the two lower ones fit.
Thus, the total number of squares with an equal number of black and white cells is exactly $14+2=16$.
|
16
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.3. In triangle $ABC$, the sides $AC=14$ and $AB=6$ are known. A circle with center $O$, constructed on side $AC$ as the diameter, intersects side $BC$ at point $K$. It turns out that $\angle BAK = \angle ACB$. Find the area of triangle $BOC$.
|
Answer: 21.
Solution. Since $AC$ is the diameter of the circle, point $O$ is the midpoint of $AC$, and $\angle AKC=90^{\circ}$.
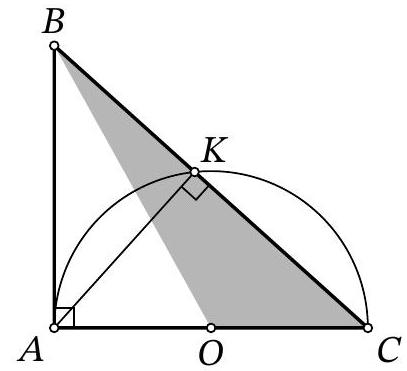
Then
$$
\angle BAC = \angle BAK + \angle CAK = \angle BCA + \angle CAK = \angle BKA = 90^{\circ}.
$$
The area of the right triangle $ABC$ can be found as $\frac{1}{2} \cdot AB \cdot AC = \frac{1}{2} \cdot 6 \cdot 14 = 42$. Since the median $BO$ divides its area in half, the area of triangle $BOC$ is $\frac{42}{2} = 21$.
|
21
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.7. Given an isosceles triangle $A B C$, where $A B=A C$ and $\angle A B C=53^{\circ}$. Point $K$ is such that $C$ is the midpoint of segment $A K$. Point $M$ is chosen such that:
- $B$ and $M$ are on the same side of line $A C$;
- $K M=A B$
- angle $M A K$ is the maximum possible.
How many degrees does angle $B A M$ measure?
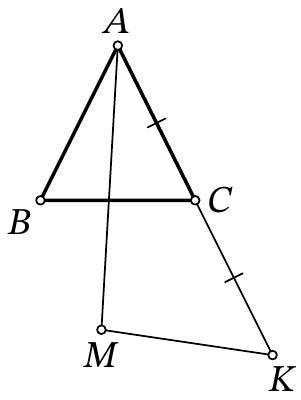
|
Answer: 44.
Solution. Let the length of segment $AB$ be $R$. Draw a circle with center $K$ and radius $R$ (on which point $M$ lies), as well as the tangent $AP$ to it such that the point of tangency $P$ lies on the same side of $AC$ as $B$. Since $M$ lies inside the angle $PAK$ or on its boundary, the angle $MAK$ does not exceed the angle $PAK$, and these angles are equal only if points $M$ and $P$ coincide. Therefore, $M$ is this point of tangency.
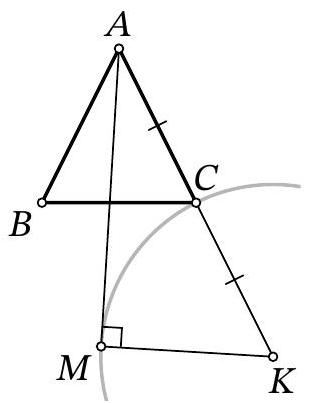
The radius $KM$ of the circle is perpendicular to the tangent $AM$. Also, in the right triangle $AMK$, the leg $MK$ is half the hypotenuse $AK$, so $\angle MAK=30^{\circ}$. Additionally, from the condition, we get that $\angle BAC=180^{\circ}-2 \cdot 53^{\circ}=74^{\circ}$. Therefore,
$$
\angle BAM=\angle BAC-\angle MAK=74^{\circ}-30^{\circ}=44^{\circ}
$$
|
44
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.1. An equilateral triangle with a side of 10 is divided into 100 small equilateral triangles with a side of 1. Find the number of rhombi consisting of 8 small triangles (such rhombi can be rotated).
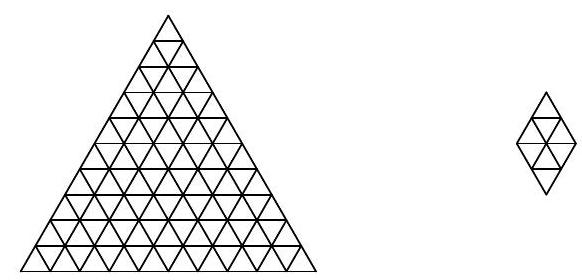
|
Answer: 84.
Solution. Rhombuses consisting of eight triangles can be of one of three types:

It is clear that the number of rhombuses of each orientation will be the same, so let's consider only the vertical ones. Each of them is uniquely determined by its top triangle. Now it is easy to count the number of such triangles.
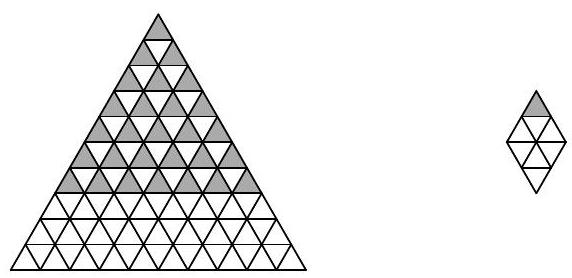
In the first row, there is 1 such triangle, in the second - 2, in the third - 3, ..., in the seventh - 7. In total, \(1+2+3+\ldots+7=28\) vertical rhombuses, and therefore, the answer to the problem is \(28 \cdot 3 = 84\).
|
84
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.5. A circle $\omega$ is inscribed in trapezoid $A B C D$, and $L$ is the point of tangency of $\omega$ and side $C D$. It is known that $C L: L D=1: 4$. Find the area of trapezoid $A B C D$, if $B C=9$, $C D=30$.
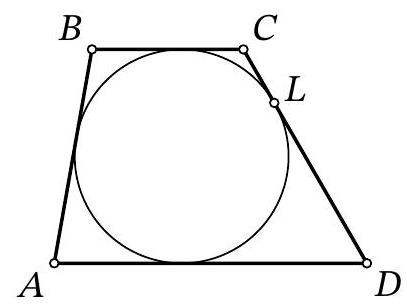
|
Answer: 972.
Solution. Let's mark the center of the circle as $I$, and the points of tangency as $P, Q, K$ with sides $B C$, $A D, A B$ respectively. Note that $I P \perp B C, I Q \perp A D$, i.e., points $P, I, Q$ lie on the same line, and $P Q$ is the height of the given trapezoid, equal to the diameter of its inscribed circle. Also, the segments of tangents $A K=A Q, B K=B P, C P=C L, D L=D Q$ are equal.
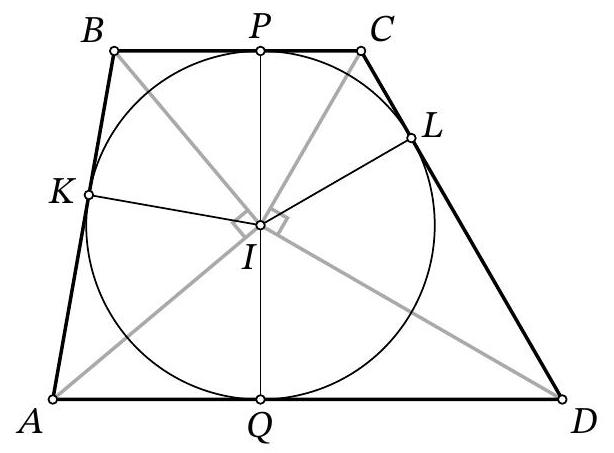
From the condition, it follows that $C P=C L=\frac{1}{5} \cdot 30=6, D Q=D L=\frac{4}{5} \cdot 30=24$. Then $B K=B P=$ $B C-C P=9-6=3$.
Since lines $C I$ and $D I$ are the angle bisectors of angles $C$ and $D$ of the trapezoid, we have $\angle I C D+$ $\angle I D C=\frac{1}{2}(\angle C+\angle D)=\frac{180^{\circ}}{2}=90^{\circ}$, i.e., triangle $C I D$ is a right triangle with a right angle at vertex $I$. Since $I L$ is its height dropped to the hypotenuse, $I L=$ $\sqrt{C L \cdot D L}=12$. This is the radius of the circle.
Similarly, considering the height $I K$ in the right triangle $A I B$, we get $12=$ $I K=\sqrt{A K \cdot B K}$. Using $B K=3$, we extract $A K=A Q=48$.
Thus, the area of the trapezoid is
$$
S_{A B C D}=\frac{B C+A D}{2} \cdot C H=\frac{9+(48+24)}{2} \cdot 24=972
$$
|
972
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. If $x=5 m+4$, then $(5 m+4)^{2}+1=25 m^{2}+40 m+17$ is not divisible by 5.
|
Answer: $\left\{\begin{array}{c}x=5 m+2, \\ y=5 m^{2}+4 m+1 .\end{array}\right.$ or $\left\{\begin{array}{c}x=5 m+3, \\ y=5 m^{2}+6 m+2 .\end{array}\right.$ where $m \in \mathbb{Z}$.
5 points - the solution is correct, complete, and contains no errors.
4 points - if the answer is incorrect, the solution method is correct, but a computational error or typo has been made, and the solution is completed with this error.
3 points - the problem is solved to the correct answer by trial and error, but not all possible cases are considered or the sequence of trials is not completed.
1 point - the solution is incorrect, but contains reasonable considerations, has some progress in solving the problem.
0 points - the solution is incorrect or missing.
## №3. (6 points)
In an isosceles triangle $ABC$, a circle is inscribed. A tangent to the circle, parallel to the base $AC$, intersects the lateral sides at points $D$ and $E$. Find the radius of the circle if $DE=8$ and $AC=18$.
Solution: Drop perpendiculars from points $D$ and $E$ to side $AC$ - we get a rectangle $DEMK$, in which $KM=DE=8$.
The diameter of the circle is equal to the perpendicular $DK$, to calculate the length of which we first need to find the length of segment $AD$.
Consider the right triangles $ADK$ and $CEM$. They are equal by the leg ($DK=EM$) and the acute angle ($\angle A = \angle C$ since $\triangle ABC$ is isosceles). From the equality of the triangles, it follows that the segments $AK=MC=5$.
Since in a quadrilateral circumscribed around a circle, the sums of the lengths of opposite sides are equal,
$AD + EC = DE + AC = 8 + 18 = 26 \Rightarrow AD = EC = \frac{26}{2} = 13$. The diameter of the circle is $DK = \sqrt{AD^2 - AK^2} = \sqrt{13^2 - 5^2} = 12$. Therefore, the radius is $\frac{12}{2} = 6$.
Answer: 6.
6 points - the solution is correct, complete, and contains no errors.
5 points - the solution is correct, but insufficiently justified or contains inaccuracies.
2 points - the solution is incorrect, but contains reasonable considerations, has some progress in solving the problem.
1 point - only the answer is recorded.
0 points - the solution is incorrect or missing.
## №4. (7 points)
Solve the equation: $x \sqrt{1-y^{2}} + y \sqrt{2-z^{2}} + z \sqrt{3-x^{2}} = 3$.
Solution: Applying the inequality between the arithmetic mean and the geometric mean to the numbers $x^2$ and $1-y^2$, we get: $|x| \sqrt{1-y^2} \leq \frac{x^2 + 1 - y^2}{2}$.
Similarly, $|y| \sqrt{2-z^2} \leq \frac{y^2 + 2 - z^2}{2}$ and $|z| \sqrt{3-x^2} \leq \frac{z^2 + 3 - x^2}{2}$. Adding these inequalities and considering that $U \leq |l|$, we have
$$
x \sqrt{1-y^2} + y \sqrt{2-z^2} + z \sqrt{3-x^2} \leq 3
$$
Therefore, equality is achieved in all the above inequalities. This is possible only if $x^2 = 1 - y^2$, $y^2 = 2 - z^2$, and $z^2 = 3 - x^2$. Solving the system, we get:
$x = \pm 1, y = 0, z = \pm \sqrt{2}$. Note that for negative values of $x$ and $z$, the inequality $(*)$ is strict. Therefore, the equation has a unique solution when: $x = 1, y = 0, z = \sqrt{2}$.
Answer: $x = 1, y = 0, z = \sqrt{2}$
7 points - the solution is correct, complete, and contains no errors.
6 points - the solution is correct, but insufficiently justified or contains inaccuracies.
4 points - the solution is found, but the uniqueness of the solution is not proven.
3 points - the solution is constructed without justification, assuming each term equals one.
2 points - the solution is incorrect, but contains reasonable considerations, has some progress in solving the problem.
1 point - only the answer is recorded.
0 points - the solution is incorrect or missing.
## №5. (7 points)
How many different pairs can be formed from 28 domino tiles so that the tiles in the pair can be placed next to each other? (Tiles can be placed next to each other if some number of dots appears on both tiles).
## Solution
Choosing a pair of tiles is simpler to consider as choosing two cards, but it is clear that there are half as many unordered pairs as ordered ones. It is easier to find the number of ordered pairs, as in this case, the rule of product can be applied.
Choose the first tile - this can be done in 28 ways, of which in 7 cases the tile will be a double, i.e., a tile of the form

In 21 cases, it will be a tile of the form $a < b$. In the first case, the second tile can be chosen in 6 ways, and the number of ways to choose a pair of tiles by the rule of product is $7 \cdot 6 = 42$.
In the second case, the second tile can be chosen in 12 ways - 6
pairs, so the number of ways is $21 \cdot 12 = 252$.
Therefore, by the rule of sum, the total number of ways to choose an ordered pair is $42 + 252 = 294$.
Answer: 147 pairs.
7 points - the task is completed correctly.
5 points - the solution contains minor errors, gaps in justification, but is generally correct and can become fully correct after minor corrections or additions.
2 points - important cases are considered in the absence of a solution (or an incorrect solution).
1 point - only the answer is recorded.
0 points - the solution is incorrect or missing.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Given positive numbers $x>y$. Let $z=\frac{x+y}{2}$ and $t=\sqrt{x y}$. It turns out that $(x-y)=3(z-t)$. Find
$x / y$.
|
Answer: 25 (in the second variant 9). Note that $z-t=(\sqrt{} x-\sqrt{} y)^{2} / 2$. Denoting $a=\sqrt{} x, b=\sqrt{} y$, we get that $a^{2}-b^{2}=3(a-b)^{2} / 2$, which transforms into $\kappa(a-b)(2 a+2 b-3 a+3 b)=(a-b)(5 b-a)=0$. By the condition $a \neq b$, therefore $a=5 b$, i.e. $x / y=25$.
|
25
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In a regular 20-gon, four consecutive vertices $A, B, C$ and $D$ are marked. Inside it, a point $E$ is chosen such that $A E=D E$ and $\angle B E C=2 \angle C E D$. Find the angle $A E B$.
|
Answer: $39^{\circ}$ (in the 2nd variant: $36^{\circ}$).
Note that $ABCD$ is an isosceles trapezoid with angles $\angle ABC = \angle DBC = 180^{\circ} \cdot 18 / 20 = 162^{\circ}$. Point $E$ lies on the perpendicular bisector of the base $AC$, and therefore, triangle $BEC$ is isosceles. Draw the height $EH$ in it, and drop a perpendicular $CK$ from point $C$ to line $ED$. We have: $\angle CEH = \angle BEC / 2 = \angle CED$. Therefore, right triangles $CEN$ and $CEK$ are equal by the acute angle and hypotenuse. In particular, $CK = CH = DC / 2 = CD / 2$, so in the right triangle $CKD$, the angle $KDC$ is $30^{\circ}$. In quadrilateral $CDEH$, three angles are $30^{\circ}$, $162^{\circ}$, and $90^{\circ}$, so the last angle $HED$ is $78^{\circ}$. Finally, $\angle CEK = \angle HED / 2 = 39^{\circ}$, and $\angle AEB$ is the same.
|
39
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The company specializes in manufacturing "boards with a hole": this is a $300 \times 300$ grid board, in which a hole in the form of a rectangle, not extending to the board's edge, is cut out by cells. Each such board comes with a tag indicating the maximum number of non-attacking rooks that can be placed on this board. (It is assumed that rooks do not attack through the hole.) For the company's anniversary, it was decided to manufacture a board with the highest number on the tag. What is this number?
|
Answer: 400 rooks (in the $2-nd$ variant 440 rooks).
Let the hole have dimensions $a \times b$. Note that all cells of the board with the hole are covered by $300-b$ columns and 300 - a rows. If $a, b \geqslant 100$, then all cells are covered by no more than 400 lines, and it is impossible to place more than 400 rooks on them. If one of the sides (for example, a) is less than 100, then the board is covered by 300 - a rows and $2 a$ pieces of rows, and no more than $300+a \leqslant 400$ rooks can be placed on them.
If, however, a hole of size $100 \times 100$ is cut out in the center of the board, then rooks can be placed in cells with coordinates $(1,200),(2,199), \ldots,(100,101),(101,100), \ldots,(200,1) u(101,300),(102,299), \ldots,(200,201)$, $(201,200), \ldots,(300,101)$.
|
400
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Along the school corridor, there is a New Year's garland consisting of red and blue bulbs. Next to each red bulb, there is definitely a blue one. What is the maximum number of red bulbs that can be in this garland if there are 50 bulbs in total?
#
|
# Solution
Let's calculate the minimum number of blue bulbs that can be in the garland. We can assume that the first bulb is red. Since there must be a blue bulb next to each red bulb, three red bulbs cannot go in a row. Therefore, among any three consecutive bulbs, at least one bulb must be blue. Then, among the first 48 bulbs, there will be no fewer than $48: 3=16$ blue bulbs. Both bulbs numbered 49 and 50 cannot be red at the same time. Thus, there must be at least 17 blue bulbs in the garland. Such a case is possible: if the bulbs numbered $2,5,8,11, \ldots, 50$ are blue, and the rest are red, then there will be 33 red bulbs in the garland.
Answer: 33 bulbs.
|
33
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.6. Let $a, b, c$ be natural numbers, and the product $ab$ is divisible by $5c$, the product $c$ is divisible by $13a$, and the product $ca$ is divisible by $31b$. Find the smallest possible value of the product $abc$. Justify your answer.
|
Solution: From the condition that $ab$ is divisible by $5c$, it follows that at least one of the numbers $a$ and $b$ is divisible by 5. If this number is $a$, then from the condition that $bc$ is divisible by $13a$, it follows that one of the numbers $b$ or $c$ is also divisible by 5; if this number is $b$, then one of the numbers $a$ or $c$ is also divisible by 5 (due to the divisibility of $ca$ by $31b$). Thus, at least two of the numbers $a, b, c$ are divisible by 5. Similarly, at least two of these numbers are divisible by 13 and two by 31. Therefore, the product $abc$ is divisible by $5^2 \cdot 13^2 \cdot 31^2 = 2015^2 = 4060225$. Hence, $abc \geq 4060225$. The example $a = 5 \cdot 31 = 155, b = 5 \cdot 13 = 65, c = 13 \cdot 31 = 403$ shows that the obtained estimate is achievable.
Answer: $5^2 \cdot 13^2 \cdot 31^2 = 2015^2 = 4060225$.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and fully justified answer | 7 points |
| Noted that the answer should be divisible by 9 and proved that the number in the answer is no more than 45, while the correct answer may be missing | 3 points |
| Provided the correct answer, supported by examples (in any quantity), but the uniqueness of the answer is not proven | 1 point |
| Answer without justification and/or incorrect answer | 0 points |
|
4060225
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. What is the maximum number of cells that can be painted on a $6 \times 6$ board so that it is impossible to select four painted cells such that the centers of these cells form a rectangle with sides parallel to the sides of the board.
#
|
# Solution
Let $n$ be the number of cells that can be painted. Denote by $x_{1}, x_{2}, \ldots, x_{6}$ the number of painted cells in the 1st, 2nd, ..., 6th columns, respectively. Then $x_{1}+x_{2}+\ldots+x_{6}=n$. Let's count the number of pairs of cells in the columns that can form the sides of the desired rectangle. In the first column, there are $\frac{x_{1}(x_{1}-1)}{2}$ such pairs, and similarly in the others $\frac{x_{2}(x_{2}-1)}{2}, \ldots, \frac{x_{6}(x_{6}-1)}{2}$. Then the total number of such pairs is $\frac{x_{1}(x_{1}-1)}{2}+\ldots+\frac{x_{6}(x_{6}-1)}{2}=\frac{x_{1}^{2}+\ldots+x_{6}^{2}}{2}-\frac{x_{1}+\ldots+x_{6}}{2} \geq \frac{1}{2} \frac{(x_{1}+\ldots+x_{6})^{2}}{6}-\frac{n}{2}=$ $=\frac{n^{2}}{12}-\frac{n}{2}=\frac{n^{2}-6 n}{12} \cdot$ Each such pair corresponds to a pair of rows in which they lie, and there are a total of such pairs $C_{6}^{2}=\frac{6!}{2!4!}=15$. Then if $\frac{n^{2}-6 n}{12}>15$, two different pairs of painted cells in different columns will correspond to the same pair of rows, and the four found cells will form the desired rectangle. Therefore, $\frac{n^{2}-6 n}{12}<15$, solving the inequality we get that $n \leq 16$. For $n=16$, the cells can be painted as follows:

## Recommendations for Checking
1) Proven only that $n \leq 16$ - 4 points.
2) Only an example for $n=16$ is provided - 3 points.
|
16
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In a school chess tournament, boys and girls competed, with the number of boys being five times the number of girls. According to the tournament rules, each chess player played against every other player twice. How many players in total participated if it is known that the boys scored exactly twice as many points in total as the girls? (1 point is awarded for a win, -0.5 points for a draw, and 0 points for a loss.)
|
Answer: 6 players.
Solution. Let $d$ girls and $5d$ boys participate in the tournament. Then the total number of players was $d + 5d = 6d$; playing two matches each with every other, they played a total of $2 \cdot \frac{1}{2} \cdot 6d(6d-1) = 6d(6d-1)$ matches. Since each match awards one point, the total number of points scored by all participants is also $6d(6d-1)$. Of these, two-thirds of the points belong to the boys, and one-third to the girls, meaning the girls scored $\frac{1}{3} \cdot 6d(6d-1) = 2d(6d-1)$ points.
Note that if each girl won against all the boys, the girls together could have scored a maximum of $2 \cdot d \cdot 5d = 10d^2$ points, and playing against each other, the girls distributed $2 \cdot \frac{1}{2} \cdot d(d-1)$ points. Therefore, the maximum number of points the girls could have scored is $10d^2 + d(d-1) = 11d^2 - d$. Thus,
$$
2d(6d-1) \leq 11d^2 - d \quad \Longleftrightarrow \quad d^2 \leq d
$$
Therefore, there could not have been more than one girl. If there was one girl, then there were five boys, making a total of 6 players. Six players played a total of $6 \cdot 5 = 30$ matches and awarded 30 points. The girl scored 10 points, winning two matches against each of the five boys. Playing against each other, the boys distributed the remaining 20 points.
Criteria. Only the answer - 0 points. Correct example - 2 points. Calculation of the total number of points scored by all girls - 2 points. Estimation of the number of points scored by the girls - 4 points. Criteria are not cumulative. Full solution - 7 points.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Angle $A$ of the rhombus $A B C D$ is $60^{\circ}$. A line passing through point $C$ intersects segment $A B$ at point $M$ and line $A D$ - at point $N$. Prove that the angle between lines $M D$ and $N B$ is $60^{\circ}$. -
|
Solution. Let $K$ be the intersection point of the lines $M D$ and $N B$ (Fig. 4). Note that triangle $A B D$ is equilateral, $\angle B A D=\angle A B D=\angle B D A=60^{\circ}$. From the similarity of triangles $B M C$ and $A M N$, as well as $M A N$ and $C D N$, it follows that
$$
\frac{M B}{A B}=\frac{M C}{C N}, \quad \frac{M C}{C N}=\frac{A D}{D N} .
$$
Since $A B=B D=A D$, we have
$$
\frac{M B}{B D}=\frac{M B}{A B}=\frac{M C}{C N}=\frac{A D}{D N}=\frac{B D}{D N}
$$
Triangles $M B D$ and $B D N$ have equal angles: $\angle A B D=\angle B D A$ and proportional adjacent sides. Therefore, triangles $M B D$ and $B D N$ are similar. Since the angles between corresponding sides of similar triangles are equal, angles $B D M$ and $D N B$ are equal. The desired angle $B K D$ is the exterior angle of triangle $N K D$ and is equal to $\angle D N K+\angle K D N=\angle B D M+\angle K D N=60^{\circ}$.
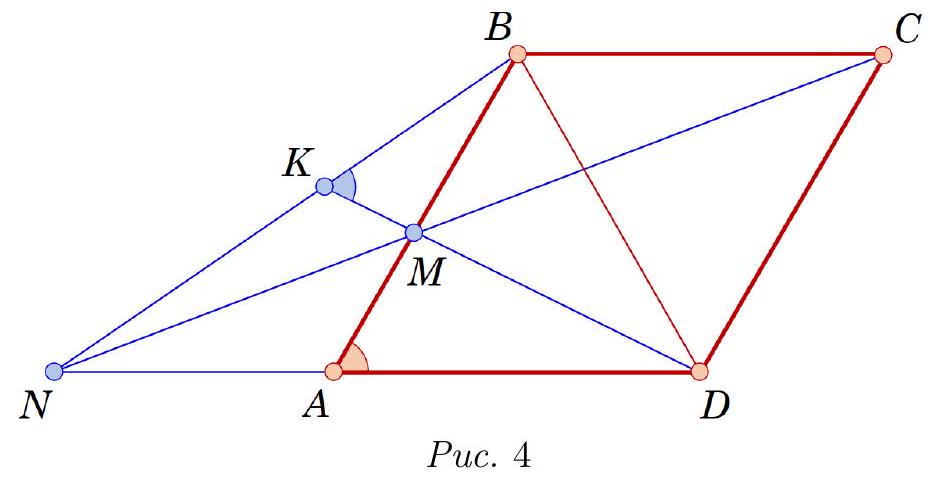
Criteria. The similarity of triangles $B M C$ and $A M N$ (or $M A N$ and $C D N$) is noted - 1 point. The similarity of triangles $M B D$ and $B D N$ is proven - 4 points. The equality $\angle B D M=\angle D N B$ is obtained - 5 points. The criteria are not cumulative. Full solution - 7 points.
|
60
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
10.7. For natural numbers $a>b>1$, define the sequence $x_{1}, x_{2}, \ldots$ by the formula $x_{n}=\frac{a^{n}-1}{b^{n}-1}$. Find the smallest $d$ such that this sequence does not contain $d$ consecutive terms that are prime numbers, for any $a$ and $b$.
(V. Senderov)
|
10.7. Answer. 2.
For $a=4, b=2$ we have $\frac{a^{1}-1}{b^{1}-1}=3, \frac{a^{2}-1}{b^{2}-1}=5$. It remains to show that more than two consecutive prime numbers will not occur.
We will prove a stronger statement than required: for $n \geqslant 2$ at least one of the numbers $\frac{a^{n}-1}{b^{n}-1}, \frac{a^{n+1}-1}{b^{n+1}-1}$ is not prime. Suppose the opposite; then
\[
\begin{aligned}
& (a-1)\left(a^{n-1}+\ldots+a+1\right)=p(b-1)\left(b^{n-1}+\ldots+b+1\right) \\
& (a-1)\left(a^{n}+\ldots+a+1\right)=q(b-1)\left(b^{n}+\ldots+b+1\right)
\end{aligned}
\]
where $p$ and $q$ are prime numbers.
Suppose that $a-1$ does not divide $b-1$. Then some prime number $r$ appears in the factorization of the number $b-1$ with a power greater than in $a-1$. From (1) and (2) we get that $r$ is a common divisor of the numbers $a^{n-1}+\ldots+a+1$ and $a^{n}+\ldots+a+1$, but
\[
\begin{aligned}
& \text{GCD}\left(a^{n-1}+\ldots+a+1, a^{n}+\ldots+a+1\right)= \\
&= \text{GCD}\left(a^{n-1}+\ldots+a+1, a^{n}\right)=1
\end{aligned}
\]
Contradiction.
Thus, the number $k=\frac{a-1}{b-1}$ is an integer. From (1) we have
\[
k\left(a^{n-1}+\ldots+a+1\right)=p\left(b^{n-1}+\ldots+b+1\right)
\]
where $1<k<p$, since $b^{n-1}+\ldots+b+1<a^{n-1}+\ldots+a+1$. Therefore, $\text{GCD}(k, p)=1$, so $b^{n-1}+\ldots+b+1 \vdots k$. Similarly, from (2) it follows that $k<q$ and $b^{n}+\ldots+b+1 \vdots k$. But this contradicts the fact that $\text{GCD}\left(b^{n-1}+\ldots+b+1, b^{n}+\ldots+b+1\right)=1$.
Remark. Two consecutive prime numbers in such a sequence can be any two prime numbers of the form $p=b+1, q=b^{2}+1$. Indeed, setting $a=b^{2}$, we have $p=\frac{a-1}{b-1}, q=\frac{a^{2}-1}{b^{2}-1}$. Such pairs include, for example, $(7,37),(11,101)$ and $\left(2^{2^{3}}+1,2^{2^{4}}+1\right)$.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. On the board, three quadratic equations are written:
$$
\begin{gathered}
2020 x^{2}+b x+2021=0 \\
2019 x^{2}+b x+2020=0 \\
x^{2}+b x+2019=0
\end{gathered}
$$
Find the product of the roots of all the equations written on the board, given that each of them has two real roots.
|
Solution. According to the theorem converse to Vieta's theorem, the product of the roots of the first equation is $-\frac{2021}{2020}$, the product of the roots of the second equation is $\frac{2020}{2019}$, and the third is 2019. Therefore, the product of the roots of all equations is $\frac{2021}{2020} \cdot \frac{2020}{2019} \cdot 2019=2021$. Answer: 2021.
Comment. The statement of the theorem converse to Vieta's theorem is mistakenly called Vieta's theorem by the olympiad participant - no points should be deducted.
|
2021
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The equation $x^{2}-a x+2022=0$ has 2 positive integer roots. What is the smallest value of $a$ for which this is possible?
|
Solution. According to the theorem converse to Vieta's theorem, we have: $x_{1}+x_{2}=a$, $x_{1} \cdot x_{2}=2022$. Note that the product of the roots can be factored into two factors in 4 ways: $1 \cdot 2022, 2 \cdot 1011, 3 \cdot 674, 6 \cdot 337$. The smallest sum of the factors is $6+337=343$. Answer: 343.
|
343
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. There are 25 coins, 12 of which are counterfeit and differ in weight by exactly 1 g from the genuine ones. All coins weigh an integer number of grams. Some may be lighter than the genuine ones, while others may be heavier. There are balance scales without weights, with a needle that shows the difference in weight. What is the minimum number of weighings needed to determine whether a given coin is counterfeit or not?
|
Solution. We will prove that one weighing is sufficient. Set aside the coin under investigation, and place the rest on the scales, 12 coins on each side. If the scales show a difference in an even number of grams, then the coin is genuine; if in an odd number, then it is counterfeit. Indeed, if an odd number of counterfeit coins lie on the pan, then its mass differs from the mass of 12 genuine coins by an odd number of grams (the sum of an odd number of odd numbers), otherwise - by an even number. Depending on the coin under investigation, there are 11 or 12 counterfeit coins on the pans, which can be divided into two groups with different or the same parity of the number of coins, respectively. Answer: one weighing.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Find the hypotenuse of a right triangle if the height drawn to it is 1 cm, and one of the angles of the triangle is $15^{\circ}$. If the answer is not an integer, round it to the tenths.
|
Solution. Let's call the original triangle $ABC$. Let $CH$ be the height drawn to the hypotenuse; $\angle C=90^{\circ}$, and $\angle A=15^{\circ}$. Draw the median $CM$. It is clear that $CM=MA=MB$, so triangle $CMA$ is isosceles $\left(CM=MA \text{ and } \angle MCA=\angle MAC=15^{\circ}\right)$. Note that $\angle BMC=30^{\circ}$ (the exterior angle of the triangle), but then $CM=2 \cdot CH=2$. Since $CM=MA=MB=2$, the hypotenuse $AB=4$.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. How many even six-digit numbers exist, in the notation of which identical digits do not stand next to each other
|
Solution. Let $N_{k}(k>1)$ denote the number of even $k$-digit numbers in which identical digits do not stand next to each other. Similarly, define $N_{1}$, but exclude the number 0, so $N_{1}=4$. We can directly calculate $N_{2}=41$. Let $k>2$. Notice that from $k$-digit numbers satisfying the condition, we can form suitable $(k+1)$-digit numbers by adding one of the 8 permissible digits (not zero and not the one in the highest place) to the left. In addition, $(k+1)$-digit numbers can be formed from $(k-1)$-digit numbers by adding one of the 9 non-zero digits and zero to the left. There are no other options. From this, we obtain the recurrence relation: $N_{k+1}=8 \cdot N_{k}+9 \cdot N_{k-1}$. Sequentially calculating the values using this formula, we find the answer: $N_{6}=265721$.
Remark. One can also construct a proof based on the idea that among numbers in which identical digits do not stand next to each other, there are roughly equal numbers of even and odd numbers (for example, the correspondence is built by replacing digits according to the rule $d \rightarrow 9-d$). Specifically, it can be proven that when the number of digits is odd, there is one more even number than odd, and vice versa when the number of digits is even. However, this fact also requires a careful proof.
|
265721
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. From the set $\{10 ; 11 ; 12 ; \ldots ; 19\}$, 5 different numbers were chosen, and from the set $\{90 ; 91 ; 92 ; \ldots ; 99\}$, 5 different numbers were also chosen. It turned out that the difference between any two of the ten chosen numbers is not divisible by 10. Find the sum of all 10 chosen numbers.
|
Solution. Obviously, all the selected numbers have different last digits. Therefore, the sum can be found by separately adding the tens and units of these numbers. Among the tens, there are five 10s and five 90s, so the sum of the tens is $5 \cdot 10 + 5 \cdot 90 = 500$. And among the units, each digit appears exactly once, so their sum is: $0 + 1 + 2 + \ldots + 9 = 45$. Therefore, the sum of all ten numbers is 545.
Answer: 545.
|
545
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2 In the fishing, 11 experienced fishermen and $n$ children participated. Together they caught $n^{2}+$ $5 n+22$ fish, with all experienced fishermen catching the same amount, and all children catching the same amount, but each 10 less than an experienced fisherman. Who was there more of at the fishing - experienced fishermen or children?
|
Solution: Let each child catch $m$ fish. Then $n m+11(m+10)=n^{2}+5 n+22$. From this, $(n+11) m=n^{2}+3 n-88$. Therefore, the right side is divisible by $n+11$. We have $n^{2}+5 n-88=$ $(n+11)(n-6)-22$, so 22 is divisible by $n+11$. The only divisor of 22 greater than 11 is 22 itself, so $n+11=22, n=11$. Therefore, the experienced fishermen and children were equal in number.
## Criteria:
- No points are deducted for the absence of an example for $n=11$.
- It is shown that $n=11$ works, but it is not proven that there are no other options - 1 point.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4 Is there a rectangular box, all three dimensions of which (height, width, and depth) are expressed as irrational numbers, while the surface area and volume are integers?
|
Solution 1: Consider a box with sides $\sqrt{2}-1, \sqrt{2}-1,3+2 \sqrt{2}$. Its volume is $(\sqrt{2}-1)^{2}(3+2 \sqrt{2})=(3-2 \sqrt{2})(3+2 \sqrt{2})=1$, and the surface area is $2(\sqrt{2}-1)^{2}+4(\sqrt{2}-1)(3+2 \sqrt{2})=2(3-2 \sqrt{2})+4(\sqrt{2}+1)=10$.
Solution 2: Consider the polynomial $f(x)=x^{3}-30 x^{2}+31 x-1$. Since $f(0) < 0, f(2) > 0$, the equation $f(x)=0$ has three positive roots. The numbers $\pm 1$ are not roots, so all roots of the equation are irrational. Take them as the dimensions of the box. By Vieta's theorem, their sum of pairwise products is 31 (from which the surface area is 62), and their product is 1.
## Criteria:
- If the irrationality of the box's sides, their positivity, and/or the integrity of the volume and surface area are not obvious - up to 3 points are deducted;
- If the measurements are given as roots of a polynomial, but it is not verified that this polynomial has three irrational positive roots - no more than 3 points are awarded;
- The statement "the root of an integer to an integer power is either an integer or an irrational number" and its consequences are accepted without proof.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5 What is the largest number of non-overlapping groups into which all integers from 1 to 20 can be divided so that the sum of the numbers in each group is a perfect square?
|
Solution: A group consisting of a single number can only be formed by 4 squares. The remaining 16 numbers must be divided into groups of at least two. Therefore, there will be no more than 12 groups in total. Let's check that exactly 12 groups are not possible. Indeed, in such a case, the numbers 1, 4, 9, 16 would form separate groups, and the remaining numbers would be divided into pairs. Then, the number 8 can only be paired with 17, and the number 19 can only be paired with 6, so the number 10 can only be paired with 15. The number 12 can only be paired with 13, the number 18 only with 7, the number 20 only with 5, and then the number 11 can only be paired with 14. Thus, for all non-squares except 2 and 3, we have uniquely restored the pairs, but 2 and 3 cannot form a group because their sum is not a square. Contradiction.
An example of a partition into 11 groups is the specified partition of non-squares into pairs, and the numbers 2 and 3 are combined into a group with 4.
## Criteria:
- Only proved that there are no more than 11 groups, no example provided - 4 points;
- Provided an example, but did not prove that 12 groups are not possible - 2 points.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the numerical value of the expression
$$
\frac{1}{a^{2}+1}+\frac{1}{b^{2}+1}+\frac{2}{a b+1}
$$
if it is known that $a$ is not equal to $b$ and the sum of the first two terms is equal to the third.
|
Answer: 2.
Solution. Let's bring the condition to a common denominator
$$
\frac{1}{a^{2}+1}+\frac{1}{b^{2}+1}=\frac{2}{a b+1}
$$
we get
$$
\frac{\left(a^{2}+b^{2}+2\right)(a b+1)-2\left(a^{2}+1\right)\left(b^{2}+1\right)}{\left(a^{2}+1\right)\left(b^{2}+1\right)(a b+1)}=0
$$
expand all brackets in the numerator, combine like terms, we get the equality $(a-b)^{2}(a b-1)=0$. Since $a \neq b$, then $a b=1$. From this, the third term equals 1, and then the entire sum equals 2.
Criteria. Full solution - 7 points. Correctly brought to a common denominator, like terms correctly combined, but without further progress - 1 point. Reasoning of the type "if $a$ is taken this way, and $b$ another way, then something will result" is rated 0 points.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10-6-1. In the figure, there are two circles with centers $A$ and $B$. Additionally, points $A, B$, and $C$ lie on the same line, and points $D, B$, and $E$ also lie on the same line. Find the degree measure of the angle marked with a “?”.
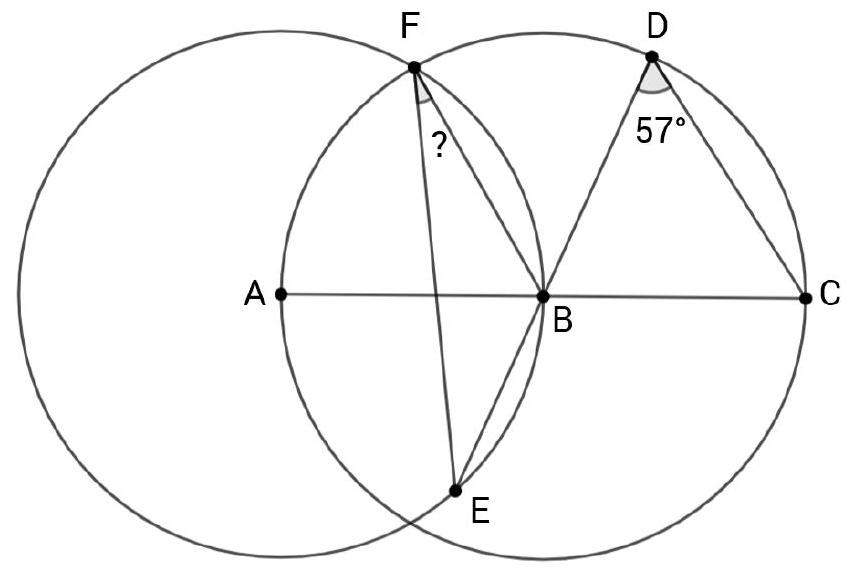
|
Answer: $24^{\circ}$.
Solution Variant 1. The inscribed angle $BFE$ is half the central angle $BAE$, so we will find the angle $BAE$. This angle can be found from the isosceles triangle $BAE$ ($AB=AE$ as radii of the circle). Angles $ABE$ and $DBC$ are equal as vertical angles. Note that triangle $DBC$ is isosceles with $BD$ and $BC$ equal as radii. Thus:
$$
\begin{gathered}
\angle ABE = \angle DBC = 180^{\circ} - 57^{\circ} - 57^{\circ} = 66^{\circ} \\
\angle BAE = 180^{\circ} - 66^{\circ} - 66^{\circ} = 48^{\circ} \\
\angle BFE = \frac{1}{2} \angle BAE = \frac{1}{2} \cdot 48^{\circ} = 24^{\circ}
\end{gathered}
$$
|
24
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10-8-1. There is a magical grid sheet of size $2000 \times 70$, initially all cells are gray. The painter stands on a certain cell and paints it red. Every second, the painter takes two steps: one cell to the left and one cell down, and paints the cell red where he ends up after the two steps. If the painter is in the leftmost column and needs to take a step to the left, he teleports to the rightmost cell of the same row with that step; if the painter is in the bottom row and needs to take a step down, he teleports to the top cell of the same column with that step. After several moves, the painter returns to the cell where he started. How many red cells are on the sheet at this moment?
The image below shows an example of the painter's moves: first the painter is in cell 1, then in cell 2, and so on.
Comment. Let's provide another, equivalent, formulation of this problem. A grid sheet of size $2000 \times 70$ is glued into a torus, as shown in the picture.
The painter walks on the torus "diagonally". After several moves, the painter returns to the cell where he started. How many red cells are on the sheet at this moment?
|
Answer: 14000.
Solution variant 1. We need to understand how many cells will be painted by the time the painter returns to the initial cell. Note that after every 2000 moves, the painter returns to the starting column, and after every 140 moves, he returns to the starting row. Therefore, he will return to the initial cell for the first time after $\operatorname{LCM}(2000,140)=14000$ moves. Thus, a total of 14000 cells will be painted red.
Comment. Note that the number of painted cells does not depend on which cell the painter starts from! This may not be obvious in the formulation with a sheet of paper, but it is clearer in the formulation with a torus: see the two paths starting from the red and blue cells in the figure. Intuitively, it is clear that these two paths are obtained from each other by a "shift" on the surface of the torus.
|
14000
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The distance between cities $A$ and $B$ is 435 km. A train departed from $A$ at a speed of 45 km/h. After 40 minutes, another train departed from city $B$ towards it at a speed of 55 km/h. How far apart will they be one hour before they meet?
|
Answer: The trains are approaching each other at a speed of 100 km/h. Therefore, in the last hour, they will together cover 100 km. This is the distance that will be between them one hour before the meeting.
Evaluation. 7 points for the correct solution.
|
100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. How many ways are there to rearrange the letters of the word ГЕОМЕТРИЯ so that no two consonants stand next to each other?
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。
|
Answer: 21600.
Solution. First, arrange the vowels, among which there are two letters E. They can be permuted in $5!/2=60$ ways. Now, 6 positions are formed where consonants can be placed (no more than one consonant per position) - these are the four gaps between the vowels, as well as the positions at the beginning and the end. The letter $\Gamma$ can be placed in any of the 6 positions. Then, there are 5 positions available for M. After that, we choose a position for $\mathrm{T}$ in 4 ways, and finally for $\mathrm{P}$ in 3 ways. By the rule of product, the total is $60 \cdot 6 \cdot 5 \cdot 4 \cdot 3=21600$.
Grading. 7 points for a correct solution. Minus one point for an arithmetic error (with correct reasoning). If the number of permutations of the vowels is calculated incorrectly, but the second part of the solution is correct, 2 points.
|
21600
|
Combinatorics
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the number of integer points $(x, y)$ satisfying the equation $\frac{1}{|x|}+\frac{1}{|y|}=\frac{1}{2017}$.
|
Solution. Transform the original equation $\frac{1}{|x|}+\frac{1}{|y|}=\frac{1}{2017} \Rightarrow$
$2017(|x|+|y|)-|x||y|=0 \Rightarrow 2017 \cdot|x|+2017 \cdot|y|-|x||y|-2017^{2}=-2017^{2}$, from which it follows that $(|x|-2017)(|y|-2017)=2017^{2}$. Since 2017 is a prime number and $|x|$ and $|y|$ are natural numbers, the last equation is equivalent to the union of systems of equations $\left\{\begin{array}{c}|x|-2017=1 \\ |y|-2017=2017^{2}\end{array},\left\{\begin{array}{c}|x|-2017=2017 \\ |y|-2017=2017\end{array},\left\{\begin{array}{c}|x|-2017=2017^{2} \\ |y|-2017=1\end{array}\right.\right.\right.$. Each system of equations has four distinct solutions that do not coincide with the solutions of the other systems. Therefore, the number of points sought is 12.
Answer. 12.
Recommendations for checking. The factorization of the form $(|x|-2017)(|y|-2017)=2017^{2}$ or an equivalent form within another solution method - 3 points.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The brother left the house 6 minutes after his sister, following her, and caught up with her after 12 minutes. How many minutes would it have taken him to catch up if he had walked twice as fast? Both the brother and the sister walk at a constant speed.
|
# Answer: 3 minutes.
Solution. Since the brother walked for 12 minutes before meeting his sister, and the sister walked for 18 minutes, the brother's speed was $3 / 2$ times the sister's speed. If the brother's speed is 3 times the sister's speed, which is 2 times faster than before, then the difference of 6 minutes will be covered 4 times faster than before, that is, in 3 minutes.
## Grading Criteria:
- The correct answer with a complete justification is given - 7 points;
- The correct answer and a generally correct justification, with gaps or inaccuracies, is given - 5 points;
- The correct answer with verification is given, but the uniqueness is not proven - no more than 3 points;
- The correct answer is given without justification - 1 point;
- The incorrect answer is given - 0 points.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the neighboring houses on Happy Street in Sunny Village, two families of 10 people each lived, with the average weight of the members of one family being 1 kg more than the average weight of the members of the other family. After the eldest sons from both families left to study in the city, it turned out that the average weight of the remaining members of one of these families was 1 kg more than the average weight of the remaining members of the other family. By how many kilograms is the weight of one of the departed sons greater than the weight of the other? List all possible options and prove that there are no others.
|
Answer: by 1 kg or by 19 kg.
Solution. The total weight of the members of one of the families before the departure of the elder sons was 10 kg more than the total weight of the members of the other family. If the heavier family remained heavier, then its total weight became 9 kg more than the total weight of the other family, meaning the weight of its departed son was 1 kg more than the other departed son. In the opposite case, its total weight became 9 kg less, meaning the weight of its departed son was 19 kg less than the other departed son.
## Grading Criteria:
- Both answers are provided with full justification - 7 points;
- The correct answer and a generally correct justification are provided, but with gaps or inaccuracies - 5 points;
- One answer is provided with justification - 4 points;
- The correct answer is provided without justification - 2 points;
- An incorrect answer is provided - 0 points.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. From one point on a straight highway, three cyclists start simultaneously (but possibly in different directions). Each of them rides at a constant speed without changing direction. An hour after the start, the distance between the first and second cyclist was 20 km, and the distance between the first and third - 5 km. At what speed is the third cyclist riding, if it is known that he is riding slower than the first, and the speed of the second is 10 km/h? List all possible options.
|
Answer: 25 km/h or 5 km/h.
Solution. Let's draw a numerical axis along the highway, taking the starting point of the cyclists as the origin and directing it in the direction of the second cyclist's movement. His speed is 10 km/h, so after an hour, he was at point B with a coordinate of 10. The distance from him to the first cyclist is 20 km, which means the first cyclist was at point $\mathrm{A}_{1}$ with a coordinate of 30 (if he was moving in the same direction as the second) or at point $A_{2}$ with a coordinate of -10 (if he was moving in the opposite direction). Let's determine the coordinate of the third cyclist. The distance between him and the first cyclist was 5 km. However, since his speed is lower, he could not have moved further from the starting point. Therefore, in the first case, he was at point $\mathrm{C}_{1}$ with a coordinate of $30-5=25$, and in the second case, at point $C_{2}$ with a coordinate of $-10+5=-5$. Accordingly, in the first case, his speed is 25 km/h (and all cyclists are moving in the same direction), and in the second case, his speed is 5 km/h (and the direction of movement of the 1st and 3rd cyclists is opposite to the direction of the 2nd cyclist).
Criteria. Only the answer (if both options are specified) - 1 point. If only one case is considered in the solution - no more than 3 points.
|
25
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. Petya wrote ten natural numbers on the board, none of which are equal. It is known that among these ten numbers, three can be chosen that are divisible by 5. It is also known that among the ten numbers written, four can be chosen that are divisible by 4. Can the sum of all the numbers written on the board be less than $75?$
(P. Kozhevnikov)
|
Answer. It can.
Solution. Example: $1,2,3,4,5,6,8,10,12,20$. In this set, three numbers $(5,10,20)$ are divisible by 5, four numbers $(4,8,12,20)$ are divisible by 4, and the total sum is 71.
Remark. It can be proven (but, of course, this is not required in the problem), that in any example satisfying the problem's conditions, the numbers $1,2,3,4,5,8,10,12$ and 20 must necessarily be present, and instead of the number 6, one can take 7 or 9.
Comment. To receive full marks (7 points for the problem), it is sufficient to have a correct example without specifying which numbers are divisible by 4 and 5, and an explicit calculation of the sum is also not required. Any non-working example is scored 0 points.
|
71
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5 The numbers $x$, $y$, and $z$ satisfy the equations
$$
x y + y z + z x = x y z, \quad x + y + z = 1
$$
What values can the sum $x^{3} + y^{3} + z^{3}$ take?
|
Solution 1: Let $x y z=p$. Then, from the condition $x y+y z+z x$ is also equal to $p$. Therefore, by Vieta's theorem, the numbers $x, y$, and $z$ are the roots of the polynomial $t^{3}-t^{2}+p t-p$. However, the number 1 is a root of such a polynomial, so one of the numbers is equal to 1. Then the other two numbers are opposite, and the sum of the cubes of all three is 1.
Solution 2: From the condition $x y z=x y+y z+z x$. Then $x^{3}+y^{3}+z^{3}=3 x y z+(x+y+z)\left(x^{2}+y^{2}+\right.$ $\left.z^{2}-x y-y z-z x\right)=3(x y+y z+z x)+\left(x^{2}+y^{2}+z^{2}-x y-y z-z x\right)=(x+y+z)^{2}=1$.
Solution 3: From the condition
$$
0=(x y z-x y-y z-z x)+(x+y+z-1)=(x-1)(y-1)(z-1) .
$$
Therefore, one of the numbers is equal to 1. Then the other two numbers are opposite, and the sum of the cubes of all three is 1.
## Criteria:
- If it is stated without proof that one of the numbers is equal to 1, and the answer to the problem is derived from this -1 point;
- If it is proven that one of the numbers is equal to 1, but the problem is not solved to the answer -6 points.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (7 points) Two vertices, the incenter of the inscribed circle, and the intersection point of the altitudes of an acute triangle lie on the same circle. Find the angle at the third vertex.
|
Answer: $60^{\circ}$.
Solution. Consider triangle $ABC$, in which altitudes $AA_1$ and $BB_1$ are drawn. Let point $H$ be the orthocenter, and point $I$ be the incenter.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.3 The number $\sqrt{1+2019^{2}+\frac{2019^{2}}{2020^{2}}}+\frac{2019}{2020}$ is an integer. Find it.
|
Solution. Let $a=2020$. Then the desired number is $\sqrt{1+(a-1)^{2}+\frac{(a-1)^{2}}{a^{2}}}+$ $\frac{a-1}{a}$. We will perform equivalent transformations:
$$
\begin{gathered}
\sqrt{1+(a-1)^{2}+\frac{(a-1)^{2}}{a^{2}}}+\frac{a-1}{a}=\frac{\sqrt{a^{2}(a-1)^{2}+(a-1)^{2}+a^{2}}}{a}+\frac{a-1}{a}= \\
=\frac{\sqrt{a^{4}-2 a^{3}+3 a^{2}-2 a+1}}{a}+\frac{a-1}{a}=\frac{\sqrt{\left(a^{2}-a+1\right)^{2}}}{a}+\frac{a-1}{a}=\frac{a^{2}-a+1+a-1}{a}=a
\end{gathered}
$$
Thus, the given number is 2020.
Answer: 2020.
| THERE IS IN THE SOLUTION | SCORE |
| :--- | :---: |
| Correct and justified answer | 7 points |
| Calculations are done "head-on", with arithmetic errors | deduct 1 point for each error |
| In the correct solution, formulas not included in the school curriculum are used but not proven (e.g., $\left.\sqrt{a^{2}+(a+1)^{2}+a^{2} \cdot(a+1)^{2}}=a^{2}+a+1\right)$ | 5 points |
| The problem is reduced to an algebraic one by a successful substitution, but there are errors in further transformations | 3 points |
| Correct answer without justification or with incorrect justification | 0 points |
|
2020
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5 On an island, there live 25 people: knights, liars, and tricksters. Knights always tell the truth, liars always lie, and tricksters answer the questions posed to them in turn, alternating between truth and lies. All the islanders were asked three questions: "Are you a knight?", "Are you a trickster?", "Are you a liar?" (the questions were asked in the exact order specified). To the first question, 21 people answered affirmatively, to the second - 17 people, to the third - 6 people. How many knights live on this island?
|
Solution. Each knight will answer "yes" to the first question and "no" to the other two. Each liar will answer "yes" to the first two questions and "no" to the last one. The tricksters can be divided into those who answered the first question truthfully (tricksters of the first type) and those who answered the first question falsely (tricksters of the second type). Tricksters of the first type will answer "no" to all questions, while tricksters of the second type will answer "yes" to all questions. The results can be recorded in a table:
| Type of inhabitant | Are you a knight? | Are you a trickster? | Are you a liar? |
| :---: | :---: | :---: | :---: |
| Knight | yes | no | no |
| Liar | yes | yes | no |
| Trickster 1 type | no | no | no |
| Trickster 2 type | yes | yes | yes |
| Number of "yes" answers | 21 | 17 | 6 |
Note that only tricksters of the second type will answer affirmatively to the last question. Therefore, there are 6 tricksters of the second type. Only tricksters of the first type will not answer affirmatively to the first question, and there are $25-21=4$ of them. The second question will be answered affirmatively by liars and tricksters of the second type (and only them), so there are $17-6=11$ liars. Therefore, the number of knights on the island is $25-6-4-11=4$.
Answer: 4 knights.
| IS IN THE SOLUTION | SCORE |
| :--- | :---: |
| Correct and justified answer | 7 points |
| Correct approach with arithmetic errors, possibly leading to an incorrect answer | deduct 1 point for each error |
| Correctly and justifiedly found only the number of liars or only the number of tricksters | 3 points |
| Considering two types of tricksters (not leading to a solution) | 2 points |
| Correct answer without justification | 1 point |
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.6 Each student in the eighth grade is friends with exactly two students in the seventh grade, and each student in the seventh grade is friends with exactly three students in the eighth grade. There are no more than 29 students in the eighth grade, and no fewer than 17 in the seventh grade. How many students are there in the eighth grade? And in the seventh grade? Provide all possible answers and prove that there are no others.
|
Solution. Let there be $s$ students in the 8th grade and $-t$ in the 7th grade. Then the number of pairs of friends from different grades is $2s$ and it is also equal to $3t$. From the equality $2s = 3t$, we see that $s$ is a multiple of 3, and $t$ is a multiple of 2. Therefore, $2s = 3t$ is a multiple of 6. Additionally, $2s \leq 58$, $3t \geq 51$. Hence, $2s = 3t = 54$, $s = 27$, $t = 18$.
Answer: There are 27 students in the 8th grade and 18 in the 7th grade.
Note. The problem does not require constructing an example of a friendship system that satisfies the condition of the problem. It is assumed a priori that the situation described in the condition is possible.
| INCLUDED IN THE SOLUTION | SCORE |
| :---: | :---: |
| Correct and justified answer | 7 points |
| Three statements are proven: - there are one and a half times more 8th graders than 7th graders - the number of 8th graders is a multiple of $3$; - the number of 7th graders is even | 6 points |
| Two out of three statements (see 6 points item) are proven | 4 points; |
| One out of three statements (see 6 points item) is proven | 2 points |
| Correct answer without justification or a correct example of such classes and a system of friendships among students | 1 point |
|
27
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.4. Ivan Ivanovich's age is 48 years 48 months 48 weeks 48 days 48 hours. How many full years old is Ivan Ivanovich? Don't forget to explain your answer.
|
Answer: 53 years.
48 months is 4 years, 48 weeks is 336 days, 48 days and 48 hours is 50 days, in total 53 years and 21 or 20 days, hence the answer.
Comment. Correct answer only - 3 points; answer with explanations or calculations leading to the answer - 7 points.
|
53
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem №1
Misha suggested that Yulia move a chip from cell $A$ to cell $B$ along the shaded cells. In one step, you can move the chip to an adjacent cell by side or corner. To make it more interesting, Misha put 30 candies in the prize fund, but said he would take 2 candies for each horizontal or vertical move and 3 candies for each diagonal move. Yulia gets the remaining candies as a reward. What is the maximum number of candies Yulia can win?
|
Answer: 14.
Solution. From $A$ to $B$, one can travel via the top or the bottom. If traveling via the top, the first 2 moves are diagonal (a diagonal move is more advantageous than 2 horizontal moves), and the next 5 moves are horizontal. Misha will collect $2 \cdot 3 + 5 \cdot 2 = 16$ candies, and Yulia will win 14. If traveling via the bottom, the first 5 moves are diagonal, and the last move is vertical. In this case, Misha will collect $5 \cdot 3 + 1 \cdot 2 = 17$ candies, and Yulia will win 13 candies. We conclude that the first option is more advantageous, and the win will be 14 candies.
|
14
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem №3
A New Year's garland hanging along the school corridor consists of red and blue bulbs. Next to each red bulb, there is definitely a blue one. What is the maximum number of red bulbs that can be in this garland if there are 50 bulbs in total?
|
Answer: 33 bulbs
## Solution
Let's calculate the minimum number of blue bulbs that can be in the garland. We can assume that the first bulb is red. Since there must be a blue bulb next to each red bulb, three red bulbs cannot go in a row. Therefore, among any three consecutive bulbs, at least one bulb must be blue. Then, among the first 48 bulbs, there will be no fewer than $48: 3=16$ blue ones. Both bulbs numbered 49 and 50 cannot be red. Thus, there should be no fewer than 17 blue bulbs in the garland. Such a case is possible: if the bulbs numbered $2,5,8,11, \ldots, 50$ are blue, and the rest are red, then there will be 33 red bulbs in the garland.
|
33
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem №4
On a grid paper, a square with a side of 5 cells is drawn. It needs to be divided into 5 parts of equal area by drawing segments inside the square only along the grid lines. Can it be such that the total length of the drawn segments does not exceed 16 cells?
|
Answer: yes, it can
(the total length of the segments drawn is 16). (
#
|
16
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem №5
In a train, there are 18 identical cars. In some of the cars, exactly half of the seats are free, in some others, exactly one third of the seats are free, and in the rest, all seats are occupied. At the same time, in the entire train, exactly one ninth of all seats are free. In how many cars are all seats occupied?
|
Answer: in 13 carriages.
Solution. Let's take the number of passengers in each carriage as a unit. We can reason in different ways.
First method. Since exactly one ninth of all seats in the train are free, this is equivalent to two carriages being completely free. The number 2 can be uniquely decomposed into the sum of thirds and halves: $2=3 \cdot 1 / 3+2 \cdot 1 / 2$. This means that there are free seats in five carriages, so in 13 carriages all seats are occupied.
Second method. Let in $x$ carriages half of the seats are free, and in $y$ carriages a third of the seats are free. Then $\mathrm{x} \cdot 1 / 2+\mathrm{y} \cdot 1 / 3=18 \cdot 1 / 9$. Eliminating the denominators of the fractions, we get: $3 \mathrm{x}+2 \mathrm{y}=12$. Since $x$ and $y$ are natural numbers, by enumeration we can confirm that $x=2, y=3$. Then the required number of carriages is: $18-2-3=13$.
Note: The natural solutions to the equation $3 x+2 y=12$ can also be found from considerations of divisibility if one variable is expressed in terms of the other.
## Evaluation Criteria.
«+» A complete and justified solution is provided
«士» A correct reasoning is provided, but a computational error is made
«士» A generally correct reasoning and the correct answer are provided, but the uniqueness of the solution to the equation or the uniqueness of the decomposition of 2 into a linear combination of fractions $1 / 2$ and $1 / 3$ is not explained.
«-|+» The equation is correctly set up, but further reasoning is incorrect or absent «-/+» Only the correct answer is provided
«-» The problem is not solved or is solved incorrectly
|
13
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Variant 1.
Write the smallest number with a digit sum of 62, in the notation of which at least three different digits are used.
|
Answer: 17999999.
Solution: $62=9 \cdot 6+8$. That is, the number is at least a seven-digit number. But if it is a seven-digit number, then in its decimal representation there are exactly 6 nines and 1 eight. According to the problem, the number must contain at least three different digits, so it is at least an eight-digit number. The first digit is no less than 1, and the sum of the first and second digits is no less than 8. By splitting 8 into $1+7$, we get the answer 17999999.
|
17999999
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Variant 1.
Café "Buratino" operates 6 days a week with a day off on Mondays. Kolya made two statements: "from April 1 to April 20, the café was open for 18 days" and "from April 10 to April 30, the café was also open for 18 days." It is known that he was wrong once. How many days was the café open from April 1 to April 27?
|
Answer: 23
Solution: In the period from April 10 to April 30, there are exactly 21 days. Dividing this period into three weeks: from April 10 to April 16, from April 17 to April 23, and from April 24 to April 30, we get exactly one weekend (Monday) in each of the three weeks. Therefore, in the second statement, Kolya told the truth, and in the first statement, he was wrong.
The period from April 1 to April 20 can be divided into two weeks: from April 1 to April 7, and from April 8 to April 14, and a six-day period (from April 15 to April 20). In the two weeks, there are 12 working days, so in the period from April 15 to April 20, there could be either six working days or five. Since Kolya was wrong here, there were five. That is, in the period from April 15 to April 20, there was definitely a weekend, as well as in the period from April 22 to April 27 (since it is obtained by shifting the previous period exactly by 7 days).
In total, from April 1 to April 21, the cafe was open $3 \cdot 6=18$ days, and in the period from April 22 to April 27, another $6-1=5$ days, that is, a total of $18+5=23$ days.
|
23
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 3. Option 1.
The Ivanov family consists of three people: dad, mom, and daughter. Today, on the daughter's birthday, the mother calculated the sum of the ages of all family members and got 74 years. It is known that 10 years ago, the total age of the Ivanov family members was 47 years. How old is the mother now, if she gave birth to her daughter at the age of 26?
|
Answer: 33.
Solution: If the daughter had been born no less than 10 years ago, then 10 years ago the total age would have been $74-30=44$ years. But the total age is 3 years less, which means the daughter was born 7 years ago. The mother is now $26+7=33$ years old.
|
33
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Variant 1.
The figure shows a rectangle composed of twelve squares. The perimeter of this rectangle is 102 cm. What is its area? Express your answer in square centimeters.
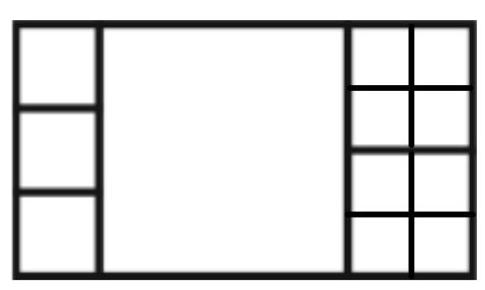
|
Answer: 594.
Solution. We will call the squares large (one such), medium (three such), and small (eight such). Let's denote the side of the medium square as $4a$. Then the side of the large square is $12a$, and the side of the small squares is $12a: 4=3a$. Therefore, the sides of the rectangle are $12a$ and $4a+12a+3a+3a=22a$, and the perimeter is $2(12a+22a)=68a \cdot a=102: 68=\frac{3}{2}$. The area is $12a \cdot 22a=264a^{2}=66 \cdot 9=594$.
|
594
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 5. Variant 1.
The organizers of a ping-pong tournament have only one table. They call up two participants who have not yet played against each other. If, after the game, the losing participant has suffered their second defeat, they are eliminated from the tournament (there are no draws in tennis). After 29 games have been played, it turned out that all participants except two were eliminated. How many players participated in the tournament
|
Answer: 16.
Solution: Each player is eliminated after exactly two losses. In the situation where two "finalists" remain, the total number of losses is 29. If $n$ people have been eliminated from the tournament, they have collectively suffered $2n$ losses, while the "finalists" could have $0 (0+0)$, $1 (0+1)$, or $2 (1+1)$ losses. Considering that $2n$ and $2n+2$ are even numbers, we arrive at the equation $2n+1=29$, from which $n=14$, and the total number of participants is 16.
|
16
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 6. Variant 1.
A diagonal of a 20-gon divides it into a 14-gon and an 8-gon (see figure). How many of the remaining diagonals of the 20-gon intersect the highlighted diagonal? The vertex of the 14-gon is not considered an intersection.
|
Answer: 72.
Solution. On one side of the drawn diagonal, there are 12 vertices, and on the other side - 6. Therefore, $12 \cdot 6=72$ diagonals intersect the highlighted one.
|
72
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Variant 1.
Petya has seven cards with digits $2,2,3,4,5,6,8$. He wants to use all the cards to form the largest natural number divisible by 12. What number should he get?
|
Answer: 8654232.
Solution. Since the number is divisible by 12, it is also divisible by 4, which means the number formed by its last two digits is divisible by 4. Such a number cannot consist of the two smallest digits (22), but it can consist of 2 and 3, and it equals 32. Arranging the remaining digits in descending order, we get the number 8654232.
|
8654232
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.