problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
# 8. Variant 1.
On the Island of Misfortune, there live knights who always tell the truth, and liars who always lie. One day, 2023 natives, among whom $N$ are liars, stood in a circle and each said: "Both of my neighbors are liars." How many different values can $N$ take?
|
Answer: 337.
Solution: Both neighbors of a knight must be liars, and the neighbors of a liar are either two knights or a knight and a liar. Therefore, three liars cannot stand in a row (since in this case, the middle liar would tell the truth). We can divide the entire circle into groups of consecutive liars/knights. These groups alternate. Each "group of knights" consists of one person, and each "group of liars" consists of one or two people. Let \( x \) be the number of "single" liars, and \( y \) be the number of "pairs of liars." Then the number of knights will be \( x + y \). We get that \((x + y) + (2y + x) = 2023\), \(3y + 2x = 2023\), \(N = x + 2y\). It is easy to see that \( y \) must be odd. \( x \geq 2 \) (since \( 2x \) must give the same remainder as 2023 when divided by 3), therefore, \( 3y \leq 2019 \), \( 1 \leq y \leq 673 \). In this range, there are \( 674 / 2 = 337 \) odd numbers, i.e., \( y \) can take 337 different values. For each of these values, the number of knights \( x + y \) is uniquely determined, and consequently, the number of liars \( x + 2y \) (since \( 2y + x = 2023 - (x + y) \)).
|
337
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. The students of a school went on a trip in six buses. The number of students in the buses was not necessarily equal, but on average, there were 28 students per bus. When the first bus arrived at the destination, the average number of students in the buses that continued moving became 26. How many students were in the first bus
|
Answer: 38.
Solution: The initial total number of schoolchildren was $28 \cdot 6=168$. After the first bus finished its trip, there were $26 \cdot 5=130$ schoolchildren left. Therefore, there were $168-130=38$ schoolchildren in the first bus.
Comment: A correct answer without justification - 0 points.
|
38
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. On weekdays (from Monday to Friday), Petya worked out in the gym five times. It is known that in total he spent 135 minutes in the gym, and the time spent in the gym on any two different days differed by at least 7 minutes. What is the maximum duration that the shortest workout could have been?
|
Answer: 13 minutes.
Solution. Let the minimum training time be $x$ minutes, then the second (in terms of duration) is no less than $x+7$, the third is no less than $x+14$, the fourth is no less than $x+21$, and the fifth is no less than $x+28$. Therefore, the total duration of the trainings is no less than $5 x+70$ minutes.
Solving the inequality $135 \geq 5 x+70$, we get $x \leq 13$. A suitable duration for the trainings is 13, 20, 27, 34, and 41 minutes.
Comment. Correct answer without justification - 0 points.
Proved that the shortest session cannot last more than 13 minutes - 5 points. Provided an example - 2 points.
|
13
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. One hundred and one numbers are written in a circle. It is known that among any five consecutive numbers, there are at least two positive numbers. What is the minimum number of positive numbers that can be among these 101 written numbers?
|
Answer: 41.
Solution. Consider any 5 consecutive numbers. Among them, there is a positive one. Fix it, and divide the remaining 100 into 20 sets of 5 consecutive numbers. In each such set, there will be at least two positive numbers. Thus, the total number of positive numbers is at least $1+2 \cdot 20=41$. Such a situation is possible. Number the numbers in a circle. The positive ones can be those with numbers $1,3,6,8,11, \ldots, 98,101$.
Comment. Correct answer without justification - 0 points.
Proved that the number of positive numbers is not less than 41 - 5 points. Provided an example with 41 positive numbers - 2 points.
|
41
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. What is the maximum number of L-shaped pieces
| |
| :--- |
consisting of three $1 x 1$ squares, that can be placed in a 5x7 rectangle? (The L-shaped pieces can be rotated and flipped, but they cannot overlap).
|
Solution: The area of the corner is 3, and the area of the rectangle is 35, so 12 corners cannot fit into the rectangle. The image below shows one way to place 11 corners in the rectangle.

Answer: 11
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On the board, three two-digit numbers are written, one of which starts with 5, the second with 6, and the third with 7. The teacher asked three students to each choose any two of these numbers and add them. The first student got 147, and the answers of the second and third students are different three-digit numbers starting with 12. What can the number starting with 7 be? If there are multiple answers, list them all.
|
Answer: Only 78.
Solution: Let the number starting with 7 be denoted as $a$, the number starting with 6 as $b$, and the number starting with 5 as $c$. The sum $a+b \geqslant 70+60=130$, so it must be equal to 147. The maximum sum of numbers starting with 7 and 6 is $69+79=148$. The number 147 is only 1 less than 148, so the numbers $a$ and $b$ are 79 and 68 or 78 and 69.
We will show that $a$ is not equal to 79. Suppose $a=79$. The sum $a+c \leqslant 129$, so $c \leqslant 129-79=50$. But then the sum $b+c \leqslant 69+50=119$ cannot start with 12. Therefore, $a$ is not equal to 79.
Thus, $a=78$ and $b=69$. If we take $c=51$, we get a set that fits the condition.
Comment: The problem did not require this, but let's prove that nothing other than $c=51$ works. Note that $c$ is not equal to 50, because otherwise the sum $b+c \leqslant 69+50=119$ cannot start with 12. Also, $c<52$ because otherwise the sum $a+c \geqslant 78+52=130$ cannot start with 12. Therefore, $c=51$.
|
78
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In a deck of 52 cards, each person makes one cut. A cut consists of taking the top $N$ cards and placing them at the bottom of the deck, without changing their order.
- First, Andrey cut 28 cards,
- then Boris cut 31 cards,
- then Vanya cut 2 cards,
- then Gena cut several cards,
- then Dima cut 21 cards.
The last cut restored the original order. How many cards did Gena cut?
|
Answer: 22.
Solution: Removing $N$ cards will result in the same outcome as moving $N$ cards one by one from the top to the bottom. We will consider that each of the boys moved one card several times.
After the last move, the order of the cards returned to the initial state, meaning the total number of card moves was a multiple of 52. The number of cards moved by all the boys except Gena is $28+31+2+21=82$. To reach the next multiple of 52, we are short of $2 \cdot 52-82=104-82=22$ cards.
|
22
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
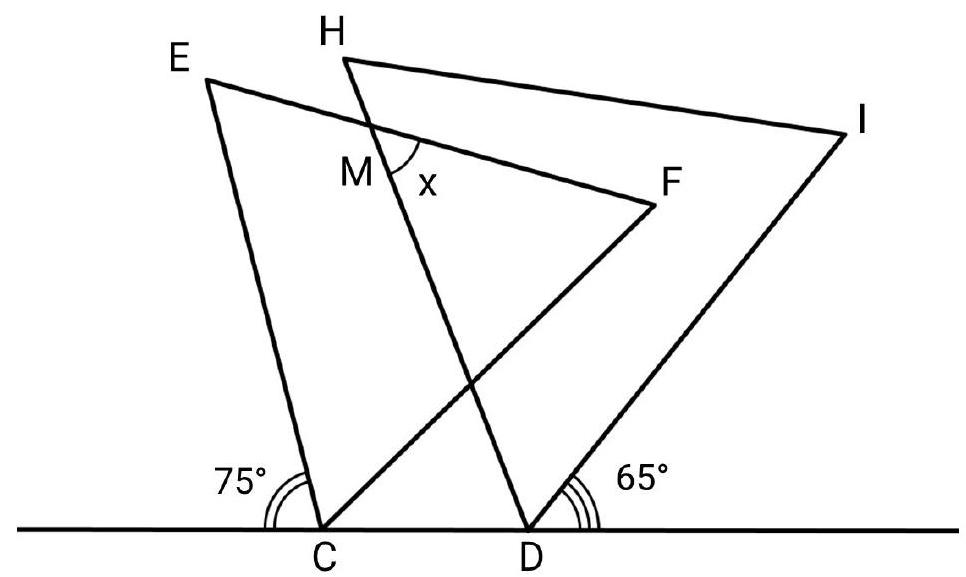
5. Two equilateral triangles $C E F$ and $D I H$ are positioned as shown in the diagram. The diagram indicates the measures of some angles. Find the measure of angle $x$. Provide your answer in degrees.
|
Answer: 40.
Solution. Let's find the degree measures of the angles of quadrilateral $C D M E$:
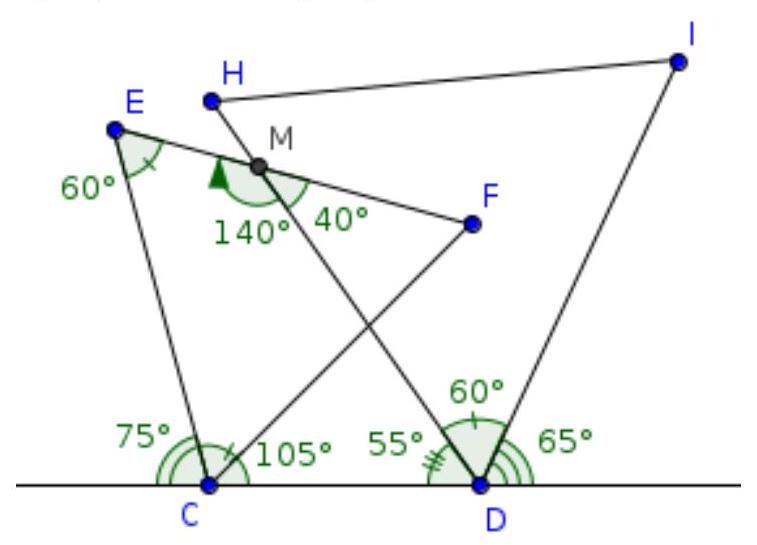
- $\angle C E M=60^{\circ}$: this is the angle of the equilateral triangle $C E F$;
- $\angle E C D=180^{\circ}-75^{\circ}=105^{\circ}$: angle $\angle E C D$ is adjacent to the angle of $75^{\circ}$;
- $\angle C D M=180^{\circ}-60^{\circ}-65^{\circ}=55^{\circ}$: angle $\angle C D M$ is adjacent to the angle formed by angle $\angle H D I$, which is $60^{\circ}$, as it is an angle of the equilateral triangle, and an angle of $65^{\circ}$;
- $\angle E M D=360^{\circ}-60^{\circ}-105^{\circ}-55^{\circ}=140^{\circ}$: the sum of the angles of quadrilateral $C E M D$ is $360^{\circ}$.
The required angle is adjacent to angle $\angle E M D$, so it is equal to $180^{\circ}-140^{\circ}=40^{\circ}$.
|
40
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
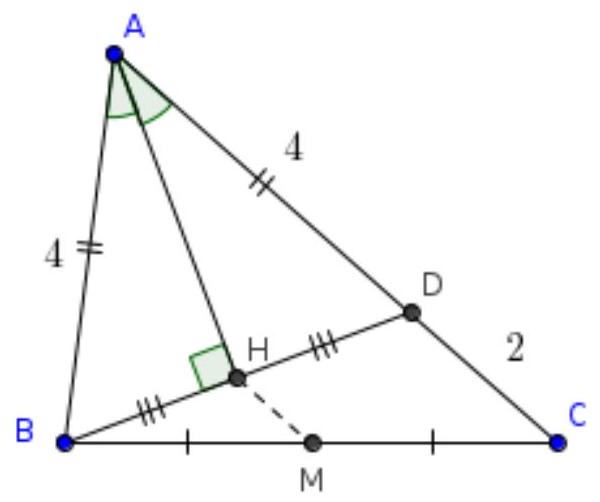
6. In triangle $A B C$, the lengths of the sides are known: $A B=4, B C=5, C A=6$. Point $M$ is the midpoint of segment $B C$, and point $H$ is the foot of the perpendicular dropped from $B$ to the angle bisector of angle $A$. Find the length of segment $H M$. If necessary, round your answer to the hundredths.
#
|
# Answer. 1.
Solution. Let $D$ be the intersection point of line $B H$ with line $A C$. Triangle $A B D$ is isosceles because in it the bisector and the altitude from vertex $A$ coincide. Therefore, $H$ is the midpoint of segment $B D$. Then $H M$ is the midline of triangle $B C D$. Note that $C D = A C - A D = A C - A B = 6 - 4 = 2$, from which $H M = C D / 2 = 1$.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. The school stage of the Magic and Wizardry Olympiad consists of 5 spells. Out of 100 young wizards who participated in the competition,
- 95 correctly performed the 1st spell
- 75 correctly performed the 2nd spell
- 97 correctly performed the 3rd spell
- 95 correctly performed the 4th spell
- 96 correctly performed the 5th spell.
What is the minimum number of students who could have correctly performed exactly 4 out of 5 spells under the described conditions?
|
# Answer: 8.
Solution. The number of students who correctly performed all spells is no more than 75, since only 75 students correctly performed the second spell. The number of students who made mistakes in the 1st, 3rd, 4th, or 5th spells is no more than $(100-95)+(100-97)+(100-95)+(100-96)=$ $5+3+5+4=17$. If a student made a mistake in at least two spells, then they definitely made a mistake in a spell other than the second. Therefore, the number of students who made a mistake in at least two spells does not exceed 17. Then the desired number of students is no less than $100-75-17=8$.
It remains to show that such a number of students is possible. Indeed, let the first 25 students make a mistake in the second spell. Among them, five made a mistake in the first, three in the third, five in the fourth, and four in the fifth. Since $5+3+5+4=17$ is less than 25, these 17 students can be different.
## Information about other clones
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Rational numbers a, b, and c are such that $(a+b+c)(a+b-c)=4 c^{2}$. Prove that $\mathrm{a}+\mathrm{b}=0$.
---
The translation maintains the original text's line breaks and formatting.
|
Solution. The initial equality is equivalent to the following $(a+b)^{2}-c^{2}=4 c^{2}$, or $(a+b)^{2}=5 c^{2}$. If $c \neq 0$, we get $((a+b) / c)^{2}=5 .|(a+b) / c|={ }^{-}$. On the left, we have a rational number, since the sum, quotient, and absolute value of rational numbers are rational, while on the right, we have an irrational number, and the equality is impossible. Therefore, $c=0$ and, consequently, $(a+b)^{2}=0$, and $a+b=0$.
Criteria. The equality $(a+b)^{2}=5 c^{2}$ is obtained, but there is no further progress: 1 point.
|
0
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
5. The bisectors $\mathrm{AD}$ and $\mathrm{BE}$ of triangle $\mathrm{ABC}$ intersect at point I. It turns out that the area of triangle ABI is equal to the area of quadrilateral CDIE. Find $AB$, if $CA=9, CB=4$.
|
Answer: 6.
Solution. Let $\mathrm{S}(\mathrm{CDIE})=\mathrm{S}_{1}, \mathrm{~S}(\mathrm{ABI})=\mathrm{S}_{2}$, $S(B D I)=S_{3}, S(A I E)=S_{4}$ (see figure). Since the ratio of the areas of triangles with a common height is equal to the ratio of the bases, and the angle bisector divides the opposite side in the ratio of the adjacent sides, we have $\left(\mathrm{S}_{1}+\mathrm{S}_{4}\right) /\left(\mathrm{S}_{2}+\mathrm{S}_{3}\right)=\mathrm{CD} / \mathrm{BD}$ $=\mathrm{AC} / \mathrm{AB} . \quad$ Similarly, $\left(\mathrm{S}_{2}+\mathrm{S}_{4}\right) /\left(\mathrm{S}_{1}+\mathrm{S}_{3}\right)$ $=A E / E C=A B / B C$. Since $S_{1}=S_{2}$, then $\left(\mathrm{S}_{1}+\mathrm{S}_{4}\right) /\left(\mathrm{S}_{2}+\mathrm{S}_{3}\right)=\quad\left(\mathrm{S}_{2}+\mathrm{S}_{4}\right) /\left(\mathrm{S}_{1}+\mathrm{S}_{3}\right) \quad$ from which $A B / B C=A C / A B . \quad A B / 4=9 / A B . \quad A B^{2}=36$,

$\mathrm{AB}=6$ (since the length of a segment is a positive number). It is not difficult to verify that such a triangle exists $(4+6>9)$.
Criteria. The length of the side is found correctly, but there is no check for the existence of the triangle: 6 points.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A road 28 kilometers long was divided into three unequal parts. The distance between the midpoints of the extreme parts is 16 km. Find the length of the middle part.
|
Answer: 4 km.
Solution. The distance between the midpoints of the outermost sections consists of half of the outer sections and the entire middle section, i.e., twice this number equals the length of the road plus the length of the middle section. Thus, the length of the middle section $=16 * 2-28=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. Solve the system of equations
$$
\left\{\begin{aligned}
10 x^{2}+5 y^{2}-2 x y-38 x-6 y+41 & =0 \\
3 x^{2}-2 y^{2}+5 x y-17 x-6 y+20 & =0
\end{aligned}\right.
$$
|
Solution: We will eliminate the product $xy$. For example, multiply the first equation by 5, the second by 2, and add the left and right parts of the obtained equations. We get $56x^2 + 21y^2 - 224x - 42y + 245 = 0$. Divide the equation by 7, and then complete the squares for $x$ and $y$. We have $8(x-2)^2 + 3(y-1)^2 = 0$, from which $x=2, y=1$. By verification, we can ensure that the found pair of numbers is indeed a solution.
Answer: $x=2, y=1$.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and fully justified answer | 7 points |
| The pair $x=2$ is justified (other pairs $(x, y)$ are not solutions), but there is no check that it solves the system | 4 points |
| The equation not containing the product $xy$ is correctly obtained by valid transformations; no further progress | 2 points |
| Answer without justification or with a check that the pair $x=2$, $y=1$ is a solution | 1 point |
| Transformations not leading to a solution | 0 points |
|
21
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
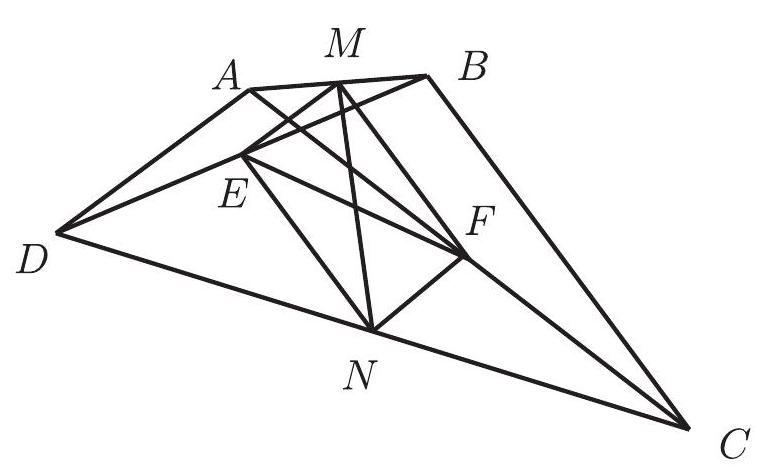
9.4. The distance between the midpoints of sides $AB$ and $CD$ of a convex quadrilateral $ABCD$ is equal to the distance between the midpoints of its diagonals. Find the angle formed by the lines $AD$ and $BC$ at their intersection. Justify your answer.
$\mathrm{K}$ to the solution of problem 9.4
|
Solution: We will apply the theorem of the midline of a triangle four times and obtain that 1) $E M=A D / 2=F N ; 2) F M=B C / 2=E N$ (points $M, N, E, F-$ are the midpoints of segments $A B, C D, D B, A C$, respectively). Therefore, quadrilateral $E M F N$ is a parallelogram. According to the condition, its diagonals are equal, which means this parallelogram is actually a rectangle. Since the angle between lines $A D$ and $B C$ is equal to the angle $E M F$ of the rectangle, it is equal to $90^{\circ}$.
Answer: $90^{\circ}$.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and fully justified answer | 7 points |
| Proven that quadrilateral $E M F N$ is a parallelogram | 4 points |
| Theorem of the midline of a triangle applied (at least once) | 2 points |
| Answer without justification and/or incorrect answer | 0 points |
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. The older brother took identical uncolored cubes from Misha and used them to build a large cube. After that, he completely painted some (not all) faces of the large cube red. When the paint dried, Misha disassembled the large cube and found that exactly 343 small cubes had no red faces. How many faces of the large cube did Misha's brother paint? Justify your answer.
|
Solution: We will call a small cube that has a red face painted. The size of the large cube is greater than 7 (since only the unpainted cubes amount to $343=7^{3}$, and there are also painted ones), but less than 9 (since all "internal" cubes are unpainted - no more than $7^{3}$). Therefore, it is equal to 8. Out of $8^{3}=512$ cubes that make it up, $6^{3}=216$ are "internal." There remain $343-216=127$ unpainted cubes, which lie on the boundary of the large cube. Each unpainted face will give 36 such cubes (the inner square $6 \times 6$), so there are fewer than four unpainted faces. We will prove that there are at least three. Indeed, if there are fewer, then all corner cubes are painted, and the number of unpainted boundary cubes is even. Therefore, three faces, which have a common vertex, are not painted. Let's check that an $8 \times 8 \times 8$ cube with three unpainted adjacent faces fits. In it, there are $3 \cdot 6^{2}=108$ unpainted cubes (inner cubes of the faces) plus $3 \cdot 6=18$ - cubes on the common edge of two unpainted faces plus one corner - exactly 127 cubes.
Answer: 3 faces.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and fully justified answer | 7 points |
| Proven that there can only be 3 faces, but not shown that the described situation is possible | 6 points |
| Justified that the cube has a size of $8 \times 8 \times 8$, but not proven that the number of painted faces cannot differ from 3 | 4 points |
| Correct answer and an example of a cube and coloring, but the uniqueness is not justified | 2 points |
| Answer without justification and/or incorrect answer | 0 points |
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In the class, there are 30 students: excellent students, average students, and poor students. Excellent students always answer questions correctly, poor students always make mistakes, and average students answer the questions given to them strictly in turn, alternating between correct and incorrect answers. All students were asked three questions: "Are you an excellent student?", "Are you an average student?", "Are you a poor student?". 19 students answered "Yes" to the first question, 12 to the second, and 9 to the third. How many average students are there in this class?
|
Answer: 20 C-students
Solution. Let $a$ be the number of excellent students, $b$ be the number of poor students, $c$ be the number of C-students who answered the first question incorrectly, answered the second question correctly, and answered the third question incorrectly (we will call these C-students of the first type), and $d$ be the number of C-students who answered the first question correctly, answered the second question incorrectly, and answered the third question correctly (we will call these C-students of the second type).
To the first question, "Yes" was answered by excellent students, poor students, and C-students of the first type, so $a+b+c=19$. To the second question, "Yes" was answered by poor students and C-students of the first type, that is, $b+c=12$. To the third question, "Yes" was answered only by C-students of the first type, so $c=9$. Then from the second equation, we get that $b=3$, and from the first equation: $a=7$. There are 30 students in the class, so $d=30-19=11$, therefore, the total number of C-students:
$9+11=20$.
Grading criteria.
“+" - a complete and well-reasoned solution is provided
“ $\pm$ " - a generally correct reasoning is provided, containing minor gaps or inaccuracies
“耳” - it is indicated in the provided reasoning that C-students can be of two types, but there is no further progress or a computational error is made.
"-" - the problem is not solved or solved incorrectly
|
20
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. What is the maximum number of natural numbers not exceeding 2016 that can be marked so that the product of any two marked numbers is a perfect square?
|
Answer: 44.
Solution. Let's find the number of natural numbers whose squares are no greater than 2016. There are 44 such numbers, since $44^{2}=1936 < 2016$. Since the product of two perfect squares is a perfect square, the numbers $1=1^{2}, 4=2^{2}, \ldots, 1936=44^{2}$ can be marked.
We will prove that it is impossible to mark a larger number of numbers. Indeed, consider the desired set of numbers and divide each number in this set by the largest perfect square that divides it. We will get a new set of numbers, and in the factorization of each of the resulting numbers into prime factors, these factors can only enter to the first power. Note that each prime factor (if it exists) must be present in all factorizations, since when multiplying any two numbers in the resulting set, it must end up in an even power. This means that after dividing each number in the desired set by the largest squares, we should get the same number $q$. If $q=1$, we get a set of 44 numbers that are perfect squares themselves (see above), and if $q>1$, we get a set of fewer numbers, since $1936 q > 2016$.
Grading Criteria
“+" - a complete and well-reasoned solution is provided
“士” - a generally correct reasoning is provided, containing minor gaps or inaccuracies
"Ғ" - only the correct answer and a correct example are provided
“-” - only the answer is provided
“-” - the problem is not solved or solved incorrectly
|
44
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.1. If you add the last digit of a number to the number itself, you get 5574, and if you add the second-to-last digit, you get 557. What is this number?
|
Answer: 5567
Solution. Note that the guessed number differs from 5574 by one digit, so the guessed number is not less than $5574-9=5565$ and not more than 5574. Then the second to last digit of the number is 6 or 7, so our number is 5566 or 5567. The first one does not fit, but the second one does.
|
5567
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.1. In the table, there are numbers. It turned out that six sums: three sums by rows and three sums by columns are the same. The minimum of the numbers $a, b$, and $c$ is 101. Find the sum $a+b+c$.
| $\mathrm{a}$ | 1 | 4 |
| :---: | :---: | :---: |
| 2 | $\mathrm{~b}$ | 5 |
| 3 | 6 | $\mathrm{c}$ |
|
Answer: 309
Solution. Note that $a+5=b+7=c+9$, therefore, the number $c$ is the smallest, and the others are 2 and 4 more, that is, 103 and 105. The sum of all three numbers $101+103+105=309$
|
309
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.1. Alina and Masha wanted to create an interesting version of the school tour olympiad. Masha proposed several problems and rejected every second problem of Alina's (exactly half), Alina also proposed several problems and did not reject only every third problem of Masha's (exactly a third). In the end, there were 10 problems, and initially, 27 were proposed. How many more problems did Masha propose than Alina?
|
Answer: 15
Solution. In total, 17 tasks were rejected. Note that among the tasks proposed by Alina, an equal number were included and rejected, and among the tasks proposed by Masha, the number of rejected tasks is twice the number of tasks that remained in the variant. Since the number of rejected tasks is 7 more than those included, exactly 7 of Masha's tasks were included in the variant, meaning she proposed 21. Since 3 of Alina's tasks were included, she proposed 6. The difference in the number of proposed tasks is $21-6=15$.
|
15
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1. On a grid sheet, a $1 \times 5$ rectangle was painted. Each minute, all those uncolored cells that have at least one side-adjacent cell already colored are colored. For example, after one minute, 17 cells will be colored. How many cells will be colored after 5 minutes?
|
Answer: 105
Solution 1. Note that after 5 minutes, we will get a stepped figure, in which the rows will have $5,7,9,11,13,15,13,11,9,7$ and 5 cells. In total, this is 105.
Solution 2. Note that if we shorten the strip to $1 \times 1$, 44 cells will disappear, which is $4 \cdot 11=44$. If there is only one cell at the beginning, then in the first move, 4 cells will appear, in the second 8, then $12,16,20$. Adding them up, we get $44+4+8+12+16+20=104$, and one more initial cell.
|
105
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. A cube lies on a plane. Each face is marked with 1 to 6 points such that the sum of points on opposite faces is always 7. The cube is rolled over the plane as shown in the picture. How many points will be on the top face of the cube when it lands on the last cell?
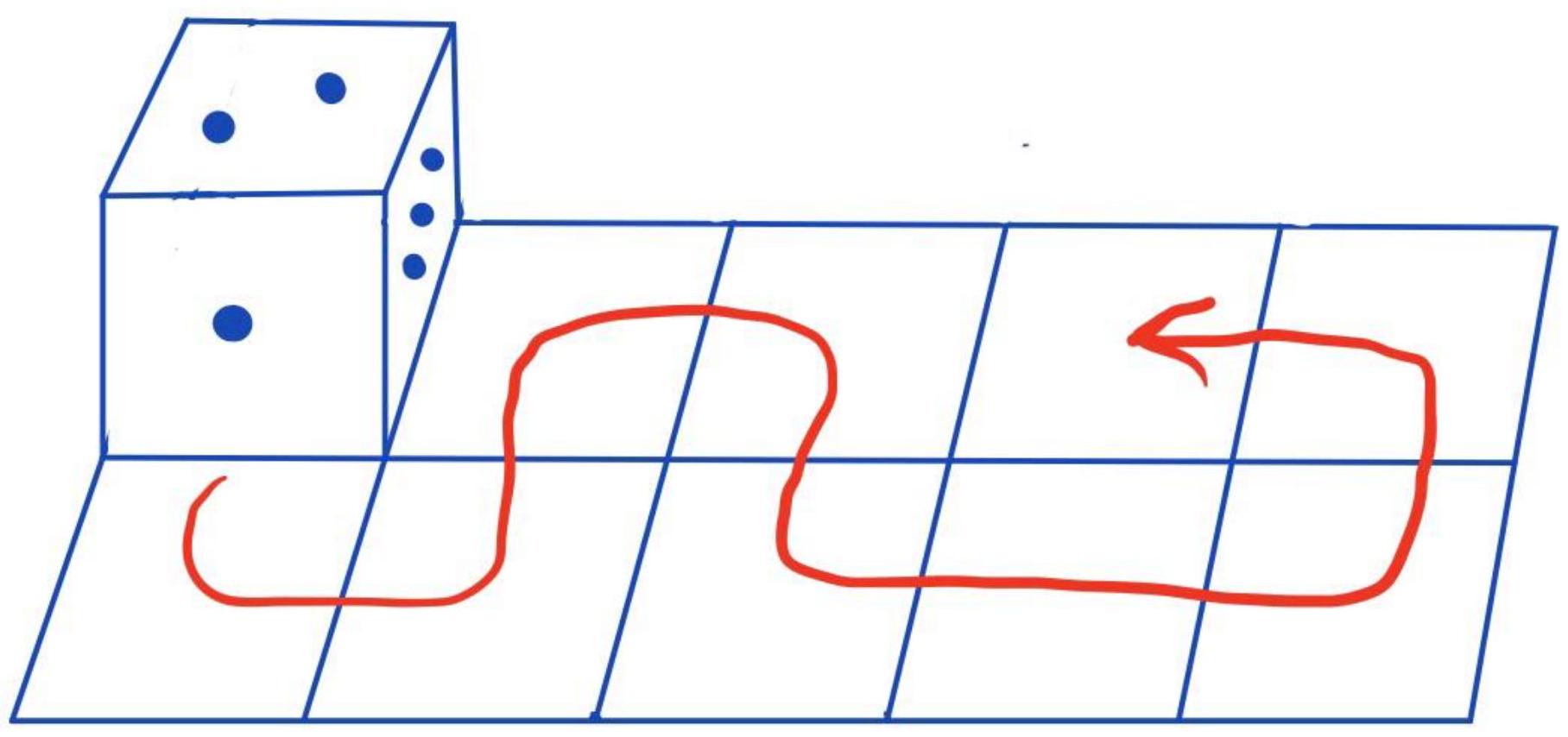
|
Answer: 5
Solution. To find out the answer, you need to imagine rolling the die in the opposite direction and each time keep track of where the face that will end up on top will be. It turns out that this face will be at the bottom in the initial position of the die. Since the top face has 2 dots, the bottom face now has 5 dots.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. A four-digit number is called "beautiful" if it is impossible to append a digit to the right so that the resulting five-digit number is divisible by 11. How many beautiful numbers are there that are greater than 3100 and less than 3600?
|
Answer: 46
Solution. Note that the number 3101 is beautiful because 31009 and 31020 are divisible by 11, so 3101* cannot be divisible by 11. Suppose the number is beautiful, then we have found 10 consecutive numbers, none of which are divisible by 11, but among 11 consecutive numbers, at least one is divisible by 11, which means the next number is divisible by 11. This number is one more than our four-digit number to which we appended 0. Therefore, the number $\overline{3 a b c}$ is beautiful if $\overline{3 a b c}+1$ is divisible by 11.
Note that the smallest number in the given set that is divisible by 11 is 3102, and the largest is 3597. There are as many such numbers as there are quotients from dividing them by $11: 282, \ldots, 327$, and this is $327-281=46$ numbers.
|
46
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the minimum value of the expression $\frac{25 x^{2} \sin ^{2} x+16}{x \sin x}$ for $0<x<\pi$.
|
Answer: 40.
Solution. Let $y = x \sin x$. Then the expression can be written as
$$
\frac{25 y^{2} + 16}{y} = 25 y + \frac{16}{y}.
$$
Note that $y > 0$ (since $x > 0$ and $\sin x > 0$), so we can apply the inequality between the means:
$$
25 y + \frac{16}{y} \geq 2 \sqrt{25 y \cdot \frac{16}{y}} = 40.
$$
Equality holds when $25 y = \frac{16}{y}$, i.e., $y = \frac{4}{5}$, which is a valid value.
Comment. A complete and justified solution is given - 7 points. A generally correct reasoning with minor gaps or inaccuracies - 6 points. The correct answer is obtained, but its minimality is not proven - 2 points. A new variable is introduced without further progress - 1 point. Only special cases or specific examples are considered - 1 point. The problem is not solved or solved incorrectly - 0 points.
|
40
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In a right-angled triangle, the lengths of the leg $a$ and the hypotenuse $c$ are expressed as two-digit integers, and both numbers use the same set of digits. The length of the leg $b$ is a positive rational number. What can the length of the hypotenuse be? (Provide all answers and prove that there are no others.)
|
Answer: 65.
Solution. Since $a \neq c$, in two-digit numbers, two different digits must be used, and they will stand in different places. Let $a=10 e+d, c=10 d+e$. Then $b=\sqrt{(10 d+e)^{2}-(10 e+d)^{2}}=3 \sqrt{11(d-e)(d+e)}$.
By the condition, $b$ is rational, so it cannot contain square roots. The number 11 is prime, so one of the factors must be divisible by 11. The factor $d-e<11$ (since $d$ and $e$ are digits), therefore, $d+e$ is divisible by 11. But the maximum value of the sum of two different digits is $9+8=17$, so $d+e=11$. At the same time, $d-e$ must be a perfect square. Checking the possible options $9+2,8+3,7+4,6+5$, we see that this condition is only met for $d=6, e=5$. The triangle has sides $33,56,65$.
Comment. A complete and justified solution is provided - 7 points. A generally correct reasoning containing minor gaps or inaccuracies is provided - 6 points. The notation for two-digit numbers is obtained - 1 point. The expression for $b$ through the radical is obtained - another 2 points. The correct answer is found by trial and error, and it is not proven that there are no other solutions - 1 point. The problem is not solved or solved incorrectly - 0 points.
|
65
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the smallest natural number $N$, which is divisible by $r$, ends in $r$, and has the sum of its digits equal to $p$, given that $p$ is a prime number and $2p+1$ is the cube of a natural number.
|
Answer: 11713.
Solution. Let $2 p+1=n^{3}$. Then $(n-1)\left(n^{2}+n+1\right)=2 p$. The number $2 p$ can only have the following positive divisors: $1,2, p, 2 p$. The number $n$ is obviously odd, so $n-1$ is divisible by 2. The number $n^{2}+n+1$ is greater than 1, so $n-1=2, n^{2}+n+1=p$. From this, $n=3, p=13$.
The desired number $N$ can be represented as $N=X \cdot 100+13$, where the number $X$ is the number $N$ without the last two digits. Since $N$ is divisible by 13, then $X$ is also divisible by 13. The sum of the digits of the number $X$ is $13-(1+3)=$ 9, so $X$ is divisible by 9, and since 9 and 13 are coprime, $X$ is divisible by $9 \cdot 13=117$.
The smallest of such numbers is the number $X=117$, then $N=117 \cdot 100+13=11713$.
Comment. A correct and justified solution - 7 points. The value found by trial and not shown to be unique - 1 point; the value found and its uniqueness proven - 3 points. If the value of $N$ is found by trial but not shown to be the smallest, 1 point is added. If the solution is not completed, 1-2 points are awarded for proving useful auxiliary statements.
|
11713
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A paper triangle with sides $34, 30, 8 \sqrt{13}$ was folded along the midlines and formed into a triangular pyramid. Through the opposite edges of the pyramid, parallel planes were drawn (a total of 6 planes). Prove that the parallelepiped formed by the intersection of these planes is a rectangular parallelepiped, and find its volume.
|
Answer: 1224.
Solution: All four faces of the pyramid are equal, so the opposite edges of the pyramid are pairwise equal. On opposite faces of the parallelepiped, different diagonals are equal, as they are the opposite edges of the pyramid (see figure). Thus, in the parallelogram, which is a face of the parallelepiped, the diagonals are equal, and therefore it is a rectangle, and the parallelepiped is a rectangular one.
Let's denote its edges as $a, b, c$. The edges of the pyramid are equal to the lengths of the medians of the triangle: $17, 15, 4 \sqrt{13}$. We can set up the following system of equations:
$$
\left\{\begin{array}{l}
a^{2}+b^{2}=289 \\
a^{2}+c^{2}=225 \\
b^{2}+c^{2}=208
\end{array}\right.
$$
Solving the system, we find $a^{2}=153=17 \cdot 3^{2}, b^{2}=136=17 \cdot 2^{3}, c^{2}=72=2^{3} \cdot 3^{2}$.
The volume of the parallelepiped is $V=a b c=\sqrt{a^{2} b^{2} c^{2}}=17 \cdot 2^{3} \cdot 3^{2}=1224$.
Comment: A correct and justified solution - 7 points. Proving that the parallelepiped is rectangular - 4 points, finding the lengths of the edges - 3 points. In a correct solution with some non-obvious and unexplained transitions - 5 points. If the solution is not completed, points are given for proving useful auxiliary statements - 1-2 points.
|
1224
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. On the board, there are five "equations" of the form $x^{2}+\ldots x+\ldots=0$. Two players take turns filling in the dots with natural numbers from 1 to 10, with each number being used only once. The game ends when all numbers are filled in. The player who makes the first move wants to have as many equations as possible with two distinct roots at the end of the game, while his opponent wants to have as few as possible. What is the best result the first player can achieve regardless of the second player's moves?
|
Answer. 3. Solution. To obtain three equations, each having two distinct roots, the first player needs to use the three initial moves to write the largest of the numbers not yet written in the place of the coefficient of $x$ in the "equation" where no number has yet been written. This is possible because if no more than two pairs of moves have been made, the coefficients could have appeared in a maximum of four "equations."
Let $x^{2}+p x+q=0$ be one of the equations obtained at the end of the game, where the coefficient $p$ was written by the first player on one of the first three moves. Then, obviously, $q \leq p-1$, from which $p^{2}-4 q \geq p^{2}-4(p-1)=(p-2)^{2}>0$, because even on the third move of the first player, $p \geq 6$, as only four numbers were used in the first two pairs of moves. Thus, the first player can ensure three equations with two roots each.
To prevent the first player from obtaining more than three equations with two roots, the second player needs to use the first two moves to write the smallest of the numbers not yet written in the place of the coefficient of $x$ in the "equation" where no number has yet been written. Let $x^{2}+p x+q=0$ be one of the equations obtained at the end of the game, where the coefficient $p$ was written by the second player on one of the first two moves. Then, obviously, $p \leq 4$ and $q \geq p+1$, from which $p^{2}-4 q \geq p^{2}-4(p+1)=p(p-4)-4<0$, meaning the equation has no roots.
- Answer without justification - 0 points. If there is a strategy for only one of the players, the solution is evaluated out of 4 points: 2 points for describing the strategy and 2 points for its justification.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the store, apples were sold. On the second day, they sold a quarter of the amount of apples sold on the first day, and an additional eight kilograms. On the third day, they sold a quarter of the amount of apples sold on the second day, and an additional eight kilograms. How many kilograms of apples were sold on the first day if 18 kilograms were sold on the third day?
|
Solution. Let's reason from the end. On the third day, 18 kg of apples were sold. If we subtract 8 kilograms, the remaining 10 kg will be a quarter of the amount sold on the second day. Therefore, 40 kilograms of apples were sold on the second day. Of these, 32 kilograms are a quarter of the amount sold on the first day. Therefore, 128 kilograms of apples were sold on the first day.
Answer. 128 kilograms.
|
128
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
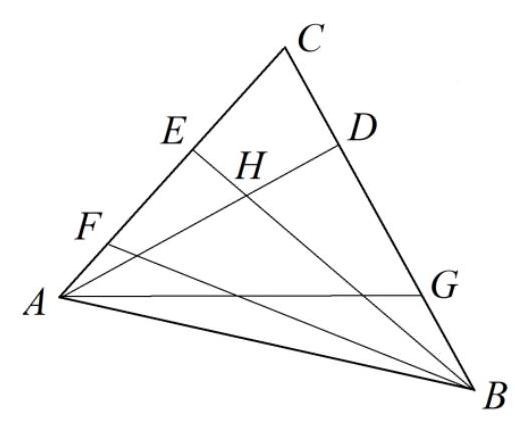
# Task 10.5
The altitudes AD and $\mathrm{BE}$ of an acute-angled triangle $\mathrm{ABC}$ intersect at point $\mathrm{H}$.
The circumcircle of triangle $\mathrm{ABH}$ intersects sides $\mathrm{AC}$ and $\mathrm{BC}$ at points $\mathrm{F}$ and $\mathrm{G}$, respectively. Find FG, if $\mathrm{DE}=5$ cm.
## Number of points 7
#
|
# Answer:
$\mathrm{FG}=10 \mathrm{~cm}$
## Solution
We have only one numerical given.
So, the length of FG will either be equal to ED or a multiple of it. It doesn't seem to be equal. It should be larger (judging by the diagram), by some factor. What do we know about such relationships? There is the midline of a triangle, which is half the length of the base. Let's try to show that ED is the midline in triangle FCG. We need E to be the midpoint of FC. Let's look at triangle FCB. It has a height BE. Let's try to show that it is also a bisector (since we also have a circumscribed circle, and a circle involves angles). On FH, there are two angles: FAH and HBF. They are equal. Let's denote them as $\alpha$. Then from the right triangles, we get $\angle \mathrm{C}=90^{0}-\alpha$ and $\angle \mathrm{CBE}=90^{0}-\left(90^{0}-\alpha\right)=\alpha$. We have confirmed that BE is both a height and a bisector, and therefore a median. Similarly, $\mathrm{AD}$ is a median for triangle CAG. Thus, ED is the midline in triangle FCG, and therefore $\mathrm{FG}=10 \mathrm{~cm}$.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. On the swamp, there are 64 bumps, they are arranged in an $8 \times 8$ square. On each bump sits a frog or a toad. Frogs never lie, while toads only tell lies. Each of them, both frogs and toads, croaked: “At least one of the neighboring bumps has a toad.” What is the maximum number of toads that could sit on these bumps?
Neighboring bumps are those located horizontally and vertically in the rows of the square, diagonal bumps are not considered neighbors.
|
Solution. Note that frogs cannot sit on adjacent lily pads, otherwise they would be telling the truth. If we divide the lily pads into pairs, there will be no more than one frog in each pair, otherwise they would be telling the truth. Therefore, there can be no more than 32 frogs, as the lily pads can be divided into 32 pairs. Let's provide an example of how 32 frogs can be seated. We will color the 64 lily pads in a chessboard pattern with two colors. If we place the frogs on the black lily pads and the toads on the white ones, the condition of the problem will be satisfied.
Answer: 32
|
32
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Vanya thought of a seven-digit number, and then subtracted from it the sum of all the digits except one. He got 9875352. What number would Vanya have gotten if he had subtracted the sum of all the digits except the second from the left?
|
Solution. Since the number is a seven-digit number, the sum of its digits is no more than 63. Adding 63 to 9875352, we get an upper estimate for the original number: 9875415. We see that in the intended number, after subtracting the sum of all digits, the first four digits do not change (the hundreds place initially has a 4 or 3, so there is no need to borrow from the fourth place). Let the original number be $\overline{9875 a b c}$. If Vanya did not subtract the digit $x$, then the result of obtaining the number 9875352 can be written as:
$$
\overline{9875 a b c}-(9+8+7+5+a+b+c-x)=9875352
$$
Then
$1000000 \cdot 9+100000 \cdot 8+10000 \cdot 7+1000 \cdot 5+100 \cdot a+10 \cdot b+c-(9+8+7+5+a+b+c-x)=$
$$
\begin{gathered}
=1000000 \cdot 9+100000 \cdot 8+10000 \cdot 7+1000 \cdot 5+100 \cdot 3+10 \cdot 5+2 \\
100 \cdot a+10 \cdot b+c-(29+a+b+c-x)=100 \cdot 3+10 \cdot 5+2 \\
100 a+10 b+x-29-a-b=352 \\
99 a+9 b+x=381
\end{gathered}
$$
Since $a, b$, and $x$ are digits, only $a=3$ (2 is not enough, 4 is too much). Then $9 b+x=84$, and from this $b=9, x=3$. Therefore, Vanya did not subtract 3 the first time. Then, if instead of 3, 8 is not subtracted, the result will be 5 more. That is, 9875357.
Answer. 9875357
|
9875357
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the largest natural number without repeating digits, in which the product of any two consecutive digits is divisible by 6.
|
3. Answer: 894326705.
Among two adjacent digits, there is certainly one divisible by 3, and there are only four such digits. Therefore, a 10-digit number is impossible. Let's try to construct a 9-digit number. The digits $0,3,6,9$, which are multiples of three, must be in even positions. Moreover, next to 3 and 9, there are even digits on both sides. Since 9 is not in the first position, the maximum first digit is 8, and then, to get the maximum, we place 9. After 9, the maximum digit is 4, as 6 is in another place. Since both digits next to 3 are even, and they are not 0 or 6, the digit 3 is adjacent to 2 and 4. We have $89432 \ldots$, and the continuation is unique: 894326705.
|
894326705
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. How many four-digit numbers are there for which the sum of the digits is a multiple of ten?
|
4. Answer: 900.
To any three-digit number, you can append exactly one decimal digit on the right so that the sum of the digits becomes a multiple of 10. For example, to 780, we append 5; to 202, we append 6; to 334, we append 0, and so on. Since three-digit numbers range from 100 to 999 inclusive, there are exactly $999-(100-1)=900$ of them. There will be the same number of four-digit numbers that meet the condition of the problem.
|
900
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Cut a $3 \times 9$ rectangle into 8 squares.
7 points are awarded for a complete solution to each problem
The maximum total score is 35
|
5. First, cut the rectangle into three squares of size $3 \times 3$. Leave two of them, and from the third, cut out a square of size $2 \times 2$. Cut the remaining part into 5 squares of size $1 \times 1$. In total, you will have 8 squares.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.1. The cells of the pyramid are filled according to the following rule: above every two adjacent numbers, their arithmetic mean is written. Some numbers were erased, and the structure shown in the figure was obtained. What number was in the bottom right cell? (The arithmetic mean of two numbers is their sum divided by 2.)
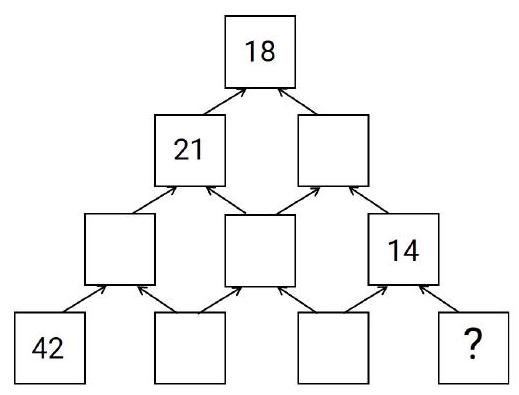
|
Answer: 6.
Solution. Let's restore the numbers in the table by going through it from top to bottom. For example, if the numbers 21 and $x$ are in the second row, then from $18=\frac{1}{2}(21+x)$ we get $x=15$. Similarly, in the third row, we get that next to the number 14 is 16, and next to it is -26; in the last row, the numbers are $42,10,22$ and 6.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.3. On the side $B C$ of rectangle $A B C D$, a point $K$ is marked. Point $H$ on segment $A K$ is such that $\angle A H D=90^{\circ}$. It turns out that $A K=B C$. How many degrees does angle $A D H$ measure if $\angle C K D=71^{\circ}$?
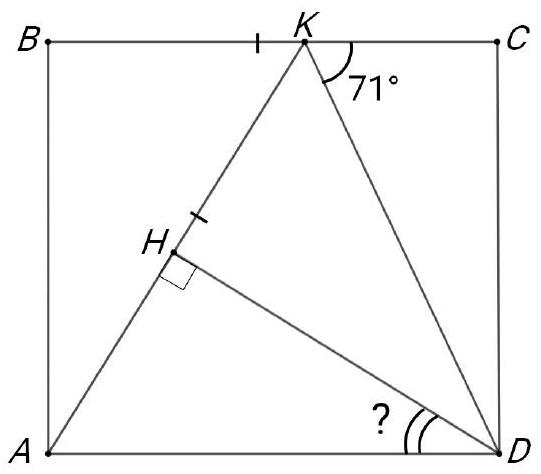
|
Answer: 52.
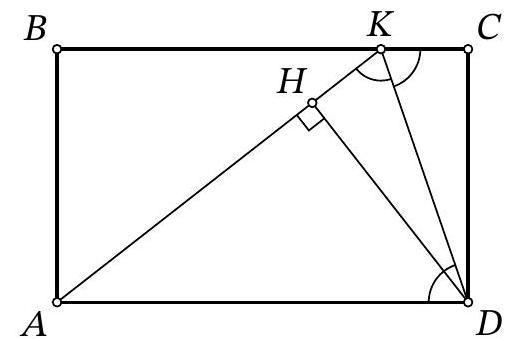
Fig. 5: to the solution of problem 8.3
Solution. Since $B C \| A D$, we get $\angle A D K=\angle C K D=71^{\circ}$ (Fig. 5).
Since $A K=B C=A D$, triangle $A K D$ is isosceles and $\angle A K D=$ $\angle A D K=71^{\circ}$. Then $\angle K A D=180^{\circ}-2 \cdot 71^{\circ}=38^{\circ}$ and $\angle A D H=90^{\circ}-\angle K A D=52^{\circ}$.
|
52
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.4. Thirty-six children are standing in a circle, each dressed in a red or blue sweater. It is known that next to each boy stands a girl, and next to each girl stands a person in a blue sweater. Find the maximum possible number of girls in red sweaters.
#
|
# Answer: 24.
Solution. Note that there will not be 3 girls in red sweaters standing in a row (otherwise, the condition would not be satisfied for the middle one). By dividing 36 children into 12 triplets, we get that in each of them there are no more than 2 girls in red sweaters, and the total number of girls in red sweaters is no more than \(2 \cdot 12 = 24\).
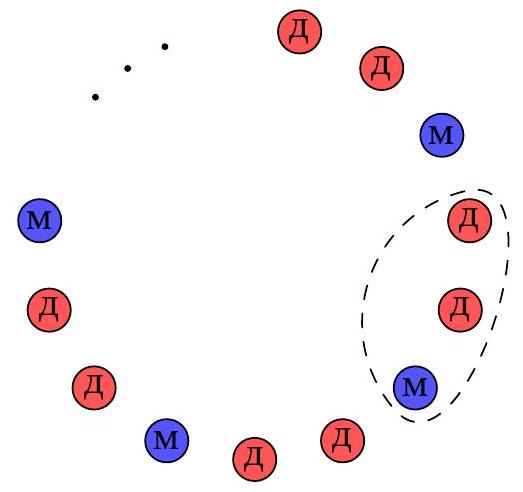
Fig. 6: to the solution of problem 8.4
It is easy to construct an example: in each of the 12 triplets, two girls in red sweaters are arranged clockwise, followed by a boy in a blue sweater (Fig. 6). It is clear that all the conditions of the problem are satisfied.
|
24
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.5. A car left the city for the village at the same time a cyclist left the village for the city. When the car and the cyclist met, the car immediately turned around and headed back to the city. As a result, the cyclist arrived in the city 35 minutes after the car. How many minutes did the cyclist spend on the entire journey, given that his speed is 4.5 times slower than the speed of the car?
|
Answer: 55.
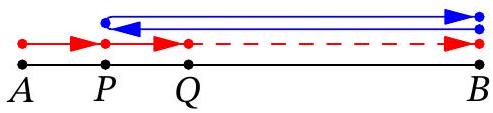
Fig. 7: to the solution of problem 8.5
Solution. In Fig. 7, let's mark village $A$, city $B$, point $P$ where the car and the cyclist meet, and point $Q$, where the cyclist was when the car returned to the city. Since the speeds of the car and the cyclist differ by 4.5 times, then $A P: P B=1: 4.5=2: 9$. Since the car spent the same amount of time on the movements $B \rightarrow P$ and $P \rightarrow B$, the cyclist also spent the same amount of time on the corresponding movements $A \rightarrow P$ and $P \rightarrow Q$. Therefore, $A P: P Q: Q B=2: 2: 7$.
Since the cyclist spent exactly 35 minutes on the movement $Q \rightarrow B$, the total time spent on the movement $A \rightarrow B$ is proportional: $35 \cdot \frac{11}{7}=55$ minutes.
Pasha listed all natural divisors of a natural number $k$ in ascending order and numbered them: the first, the second,
Pasha noticed that if the sixth divisor is multiplied by the thirteenth divisor, the result is the original number $k$.
How many natural divisors does the number $k$ have?
Answer: 18.
Solution. Let the natural divisors of the number $k$ be ordered as follows:
$$
1=d_{1}<d_{2}<\ldots<d_{6}<\ldots<d_{13}<\ldots<d_{m-1}<d_{m}=k
$$
The numbers
$$
1=\frac{k}{d_{m}}<\frac{k}{d_{m-1}}<\ldots<\frac{k}{d_{6}}<\ldots<\frac{k}{d_{13}}<\ldots<\frac{k}{d_{2}}<\frac{k}{d_{1}}=k
$$
are also divisors of the number $k$, they are distinct, and there are as many of them. Thus, these are the same numbers, only in reverse order. We get that
$$
d_{1}=\frac{k}{d_{m}}, d_{2}=\frac{k}{d_{m-1}}, \ldots, \quad d_{m}=\frac{k}{d_{1}}
$$
Thus, the divisors are divided into pairs of "opposite" divisors, which give the original number $k$ when multiplied:
$$
k=d_{1} \cdot d_{m}=d_{2} \cdot d_{m-1}=\ldots
$$
In each such pair, the sum of the indices of the divisors is $m+1$. Since by the condition $d_{6} \cdot d_{13}=k$, we get that $m=6+13-1=18$.
|
55
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.7. In an acute-angled triangle $A B C$, the altitude $B H$ is drawn. It turns out that $C H=A B+A H$. How many degrees does the angle $B A C$ measure if $\angle A B C=84^{\circ}$ ?
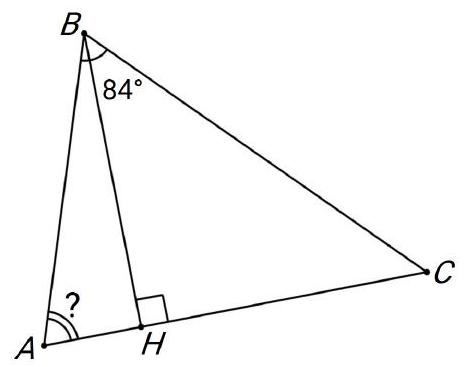
|
Answer: 64.
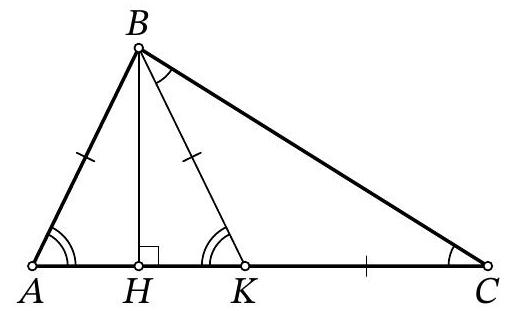
Fig. 8: to the solution of problem 8.7
Solution. Mark a point \( K \) on the segment \( CH \) such that \( AH = HK \). Then, from the condition, it follows that \( AB = CK \) (Fig. 8).
In triangle \( ABK \), the height \( BH \) coincides with the median, so it is isosceles, \( AB = BK \), and \( \angle BAH = \angle BKA \).
Let \( \angle ACB = x \). Since \( CK = AB = BK \), triangle \( BCK \) is isosceles, and \( \angle KBC = \angle KCB = x \). Then \( \angle AKB = 2x \), \( \angle KAB = 2x \), and \( \angle ABC = 180^\circ - 3x \).
Since \( 84^\circ = \angle ABC = 180^\circ - 3x \), we find \( x = 32^\circ \). Therefore, \( \angle BAC = 2 \cdot 32^\circ = 64^\circ \).
|
64
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (7 points) The king decided to test his hundred sages and announced that the next day he would line them up with their eyes blindfolded and put a black or white hat on each of them. After their eyes are uncovered, each, starting from the last in line, will name the supposed color of their hat. If he fails to guess correctly, he will be executed. The sages still have time to agree on how they will act tomorrow. How many sages can definitely be saved?
|
Solution. Let's describe the strategy that the sages should adhere to. The last in line looks ahead, counts the number of black hats, and says "black" if this number is even. In doing so, he cannot save himself for sure. However, the 99th, 98th, ..., 1st in line receive very important information. Thus, the 99th counts the number of black hats on the sages standing ahead, and if the parity of this number has changed, then he has a black hat, and he says "black." Then the 98th counts the number of black hats on those standing ahead and, knowing the parity of the number of black hats on those standing ahead without him and together with him, can uniquely determine the color of his hat, and so on. The sages from the 99th to the 1st will survive.
Answer. 99 sages will definitely manage to save themselves.
|
99
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The parabola $y=x^{2}-20 x+c$, where $c \neq 0$, intersects the $O x$ axis at points $A$ and $B$, and the $O y$ axis at point $C$. It is known that points $A$ and $C$ are symmetric with respect to the line $y=-x$. Find the area of triangle $A B C$.
|
Answer: 231.
Solution. Since $y(0)=c$, we have $C(0, c)$ and $A(-c, 0)$. Therefore, one of the roots of the equation $x^{2}-20 x+c=0$ is $-c$, i.e., $c^{2}+20 c+c=0$, from which $c=-21, x_{1}=21$. By Vieta's theorem, $x_{1}+x_{2}=20$. Thus, $x_{2}=-1$. The length of the base of the triangle is $x_{1}-x_{2}=22$, and the height is 21.
Evaluation. 7 points for a correct solution.
|
231
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. Find $x^{2}+y^{2}+z^{2}$, if $x+y+z=2, \frac{1}{x}+\frac{1}{y}+\frac{1}{z}=0$.
|
# 9.1. Answer: 4.
## 9th grade
By getting rid of the denominators in the second equation, we get $x y + y z + z x = 0$. Squaring the first equation, we get $x^{2} + y^{2} + z^{2} + 2(x y + y z + z x) = 4$. From this, we obtain the answer.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. Petya had a large wooden cube with dimensions $30 \times 30 \times 30$ cm $^{3}$. Petya decided to paint the entire cube, which took 100 grams of paint. Later, Petya needed smaller cubes, so he cut the large cube with 6 cuts, parallel to the faces of the cube (2 cuts parallel to each pair of faces), into 27 cubes with dimensions $10 \times 10 \times 10 \mathrm{~cm}^{3}$. How much paint is needed to finish painting all the resulting cubes? Petya does not repaint the already painted surfaces.
|
Answer: 200 grams.
First solution. Each cut increases the unpainted surface area by an amount equal to twice the area of the cut. It is clear that the area of the cut is the same as the area of a face. Therefore, it is necessary to paint an additional surface area equal to \(6 \cdot 2 = 12\) faces, which is twice the surface area of the cube. Thus, \(100 \cdot 2 = 200\) grams of paint are required.
Second solution. The 27 smaller cubes have a total of \(27 \cdot 6 = 162\) faces. Of these, \(6 \cdot 9 = 54\) faces are already painted. Therefore, \(162 - 54 = 108\) faces remain to be painted, which is twice as many as 54. Thus, painting 108 faces will require \(100 \cdot 2 = 200\) grams of paint.
Third solution. After the cuts, we have 8 corner cubes, each with 3 unpainted faces, 12 non-corner cubes along the edges of the large cube, each with 4 unpainted faces, 6 cubes adjacent to the centers of the faces of the large cube, each with 5 unpainted faces, and one central cube with all faces unpainted. Therefore, we need to paint \(8 \cdot 3 + 12 \cdot 4 + 6 \cdot 5 + 6 = 24 + 48 + 30 + 6 = 108\) faces of the smaller cubes. Initially, we painted \(6 \cdot 9 = 54\) such faces, which required 100 grams of paint. Therefore, painting \(108 = 54 \cdot 2\) faces will require 200 grams of paint.
Comment. Only the answer - 2 points.
The solution follows the first author's solution, but it forgets about the doubling of the unpainted surface area - 2 points.
|
200
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. For four consecutive natural numbers, it is known that the largest of them is a divisor of the product of the other three. Find all values that the largest of these numbers can take.
|
Answer: 6.
First solution. Let our numbers be $n-3, n-2, n-1, n$, where $n-3 \geqslant 1, n \geqslant 4$. Since the numbers $n-1$ and $n$ are coprime, $(n-3)(n-2)$ is divisible by $n$. Note that $(n-3)(n-2) = n^2 - 5n + 6 = n(n-5) + 6$, and since both numbers $(n-3)(n-2)$ and $n(n-5)$ are divisible by $n$, 6 is also divisible by $n$. Therefore, $n \leqslant 6$, and since the largest number is not greater than 6, we need to check the cases $n=4, n=5$, and $n=6$. Clearly, only $n=6$ works.
Second solution. Let our numbers be $n, n+1, n+2, n+3$. Note that if the largest of these numbers is divisible by a prime $p$, then one of the remaining numbers must also be divisible by $p$, but then their difference, which is no more than 3, must also be divisible by $p$, so $p \leqslant 3$. Therefore, $n+3 = 2^m 3^k$.
If $n+3$ is divisible by 9, then the numbers $n+1$ and $n+2$ are not divisible by 3, so $n$ must be divisible by 9. But then $3 = n+3 - n$ would be divisible by 9. This contradiction shows that $k \leqslant 1$. If $n+3$ is divisible by 4, then the numbers $n$ and $n+2$ are not divisible by 2, so $n+1$ must be divisible by 4. But then $2 = n+3 - (n+1)$ would be divisible by 4. This contradiction shows that $m \leqslant 1$. Therefore, the possible values for the largest number are $1, 2, 3, 6$. Clearly, only the last option works.
Comment. Only the answer - 1 point.
Proved that the largest number has the form $2^m 3^k - 2$ points.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.4. Every day, from Monday to Friday, the old man went to the blue sea and cast his net into the water. Each day, the net caught no more fish than the previous day. In total, over the five days, the old man caught exactly 100 fish. What is the smallest total number of fish he could have caught on the three days - Monday, Wednesday, and Friday?
|
Answer: 50.
Solution. If the old man caught 25 fish each of the first four days and caught nothing on Friday, the conditions of the problem are met, and exactly 50 fish were caught over the specified three days.
Let's prove that in the specified days, fewer than 50 fish could not have been caught. Indeed, suppose fewer than 50 fish were caught in these days. Since on Tuesday and Thursday the old man caught no more fish than on Monday and Wednesday, on Tuesday and Thursday fewer than 50 fish were also caught. Thus, in total over the five days, fewer than 100 fish were caught, which contradicts the condition.
The estimate (the second part of the solution) can be written algebraically in various ways. Let the old man catch $a_{1} \geqslant a_{2} \geqslant a_{3} \geqslant a_{4} \geqslant a_{5}$ fish from Monday to Friday. Then:
1) If $a_{1}+a_{2}+a_{3}+a_{4}+a_{5}=100$, then $a_{1}+a_{3}+a_{5}=100-\left(a_{2}+a_{4}\right) \geqslant 100-\left(a_{1}+a_{3}\right)$. Therefore, $2 a_{1}+2 a_{3}+a_{5} \geqslant 100$. Since $2 a_{5} \geqslant a_{5}$, then $a_{1}+a_{3}+a_{5} \geqslant 50$.
2) Since $a_{1} \geqslant \frac{a_{1}+a_{2}}{2}, a_{3} \geqslant \frac{a_{3}+a_{4}}{2}, a_{5} \geqslant \frac{a_{5}}{2}$, then $a_{1}+a_{3}+a_{5} \geqslant \frac{a_{1}+a_{2}}{2}+\frac{a_{3}+a_{4}}{2}+\frac{a_{5}}{2}=$ $=\frac{a_{1}+a_{2}+a_{3}+a_{4}+a_{5}}{2}=50$.
## Grading Criteria
+ Correct answer and a fully justified solution are provided
干 Only the correct answer and an example are provided
$\mp$ Only the estimate is proven
- Only the answer is provided
- The problem is not solved or is solved incorrectly
The jury believes that the plot of the problem should not lead the solver to think that the old man necessarily catches at least one fish each day (and in Pushkin's fairy tale, the old man only pulled out mud). However, if the solver clearly demonstrates this understanding and justifiably finds the answer 51, they should be given a grade of +. Intermediate criteria do not apply to this situation.
|
50
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.5. In triangle $A B C$, points $M$ and $N$ are the midpoints of sides $A C$ and $B C$ respectively. It is known that the point of intersection of the medians of triangle $A M N$ is the point of intersection of the altitudes of triangle $A B C$. Find the angle $A B C$.
|
Answer: $45^{\circ}$.
Solution. Let $H$ be the orthocenter (the point of intersection of the altitudes) of triangle $ABC$. Then the altitude $AT$ of triangle $ABC$ contains the median of triangle $AMN$, that is, it intersects segment $MN$ at its midpoint - point $E$ (see Fig. 10.5a, b). We can reason in different ways.
First method. Since $MN \| AB$, triangles $ETN$ and $ATB$ are similar (see Fig. 10.5a), hence $\frac{TN}{TB}=\frac{TE}{TA}=\frac{EN}{AB}=\frac{1}{4}$. Let $TN=x, TE=y$, then $BN=3x, AE=3y$.
Therefore, $CT=CN-TN=2x$, and $EH=\frac{1}{3}AE=y$ (by the property of the centroid of a triangle).
Notice that in right triangles $CTH$ and $BTA$, $\frac{CT}{BT}=\frac{2x}{4x}=\frac{1}{2}$ and $\frac{HT}{AT}=\frac{2y}{4y}=\frac{1}{2}$. Thus, these triangles are similar. Therefore, $\angle TCH=\angle TBA$. But $CH$ is part of the altitude $CQ$ of triangle $ABC$, so these equal angles are the acute angles of the right triangle $CQB$, that is, each of them is $45^{\circ}$.
Fig. $10.5a$

Fig. 10.5b
Second method. Mark point $K$ - the midpoint of side $AB$ (see Fig. 10.5b). Then $AMNK$ is a parallelogram, its diagonal $MK$ passes through the midpoint of $AN$, so it also passes through point $H$.
Since $MH \| BC$, triangles $EMH$ and $ENT$ are equal (by side and two adjacent angles), hence $EH=ET$. The median $CK$ of triangle $ABC$ passes through point $E$ and is bisected at it, so $CHKT$ is a parallelogram, thus $TK \| CH$.
But $CH$ is part of the altitude $CQ$ of triangle $ABC$, so $TK \perp AB$. Thus, $TK$ is both an altitude and a median of the right triangle $ATB$, meaning this triangle is isosceles, so $\angle ABC=45^{\circ}$.
There are other ways to solve this problem. In particular, it is not difficult to prove that in this triangle, the Euler line $OH$ (where $O$ is the center of the circumscribed circle of triangle $ABC$) is parallel to $AB$. Then the equality $\operatorname{tg} \angle A \cdot \operatorname{tg} \angle B = 3$ holds (see, for example, V. V. Prasolov. Problems in Plane Geometry, No. 5.110). Using this fact and some additional considerations that follow from the problem's condition, one can not only compute the angle $ABC$ but also the other angles of this triangle.
## Evaluation Criteria
+ A complete and well-reasoned solution is provided
$\pm$ A generally correct reasoning is provided, with minor gaps or inaccuracies
- Only the answer is provided
- The problem is not solved or is solved incorrectly
|
45
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In the drawer, there are 23 socks: 8 white and 15 black. Every minute, Marina approaches the drawer and pulls out a sock. If at any moment Marina pulls out more black socks than white ones, she exclaims: "Finally!" - and ends the process.
What is the maximum number of socks Marina can pull out before she exclaims: "Finally!"? The answer should include the last sock that Marina pulled out.
|
Answer: 17.
Solution: If Marina takes out 17 socks, then among them there will be no more than 8 white ones, which means there will be at least 9 black ones. Therefore, at this moment, she will definitely exclaim, "Finally!"
On the other hand, if she takes out only 16 socks, she might be unlucky: if she sequentially takes out a white sock, a black sock, a white sock, a black sock, .... In this situation, after each even-numbered sock, there will be an equal number of black and white socks, and after each odd-numbered sock, there will be more white ones.
Comment: Another example of when Marina might be unlucky: if she first takes out 8 white socks, and then 8 black ones.
|
17
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
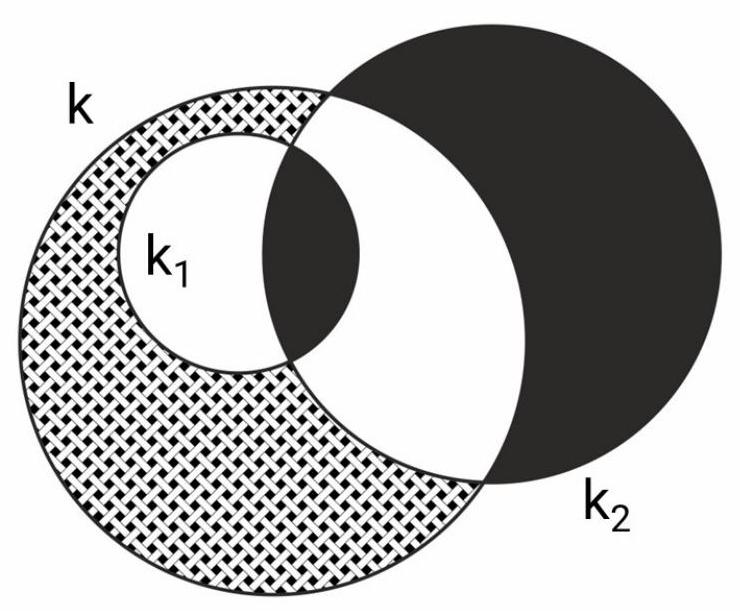
6. Circle $k_{1}$ with a radius of 8 cm lies inside circle $k$. Both circles intersect circle $k_{2}$ with a radius of 15 cm, as shown in the figure. What is the radius of $k$ if the shaded area inside $k$ but outside $k_{1}$ is equal to the total shaded area inside $k_{2}$?
|
Answer: 17.
Solution. Let the area inside circle $k_{1}$ but outside circle $k_{2}$ be denoted by $T_{1}$; inside circle $k_{2}$ but outside circle $k$ by $T_{2}$; inside circle $k$ but outside circles $k_{1}$ and $k_{2}$ by $T_{3}$; and inside circles $k$ and $k_{2}$ but outside circle $k_{1}$ by $T$ (see the figure below). Additionally, let the radius of circle $k$ be denoted by $R$.
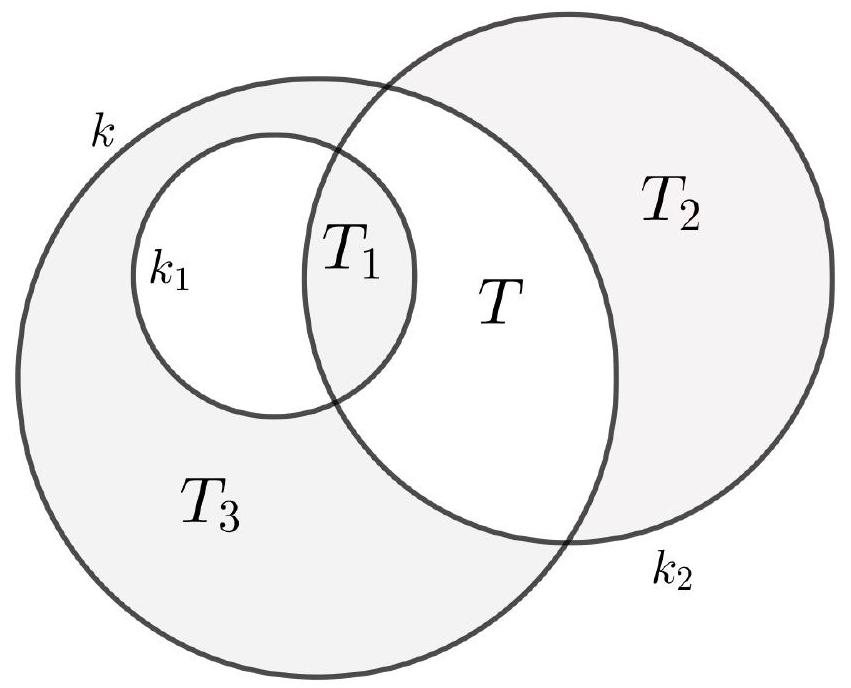
By the problem's condition, $T_{3}=T_{1}+T_{2}$. Let's write down the areas of circles $k_{2}$ and $k$: $T+T_{1}+T_{2}=15^{2} \pi, 8^{2} \pi+T+T_{3}=R^{2} \pi$. It remains to notice that $T+T_{3}=T+T_{1}+T_{2}=15^{2} \pi$, from which we get $R^{2} \pi=8^{2} \pi+15^{2} \pi, R^{2}=289, R=17$.
Remark. One could immediately notice that the difference between the sum of the areas of circles $k_{1}$ and $k_{2}$ and the area of circle $k$ equals the difference between the black and shaded areas.
|
17
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Builders need to tile the floor in a small house with small square tiles. The client says that the variant with more red tiles is preferable. For variants with the same number of red tiles, the one with more orange tiles is preferable; and generally, the client's preferences for colors are: red, orange, yellow, green, blue, indigo. His wife, however, wants the opposite:
- the number of indigo tiles should be at least as many as the total number of red, orange, yellow, green, and blue tiles;
- the number of blue tiles should be at least as many as the total number of red, orange, yellow, and green tiles;
- the number of green tiles should be at least as many as the total number of red, orange, and yellow tiles;
- the number of yellow tiles should be at least as many as the total number of red and orange tiles;
- the number of orange tiles should be at least as many as the number of red tiles.
The floor requires 100 tiles.
How many green tiles will be needed if the most preferable variant for the client is chosen, which also meets the conditions set by his wife?
|
Answer: 13.
Solution: According to the conditions set by the customer's wife, there must be at least as many indigo tiles as all the others combined. This means there must be at least 50 tiles, which is half of all the tiles. The customer clearly wants the number of indigo tiles to be as few as possible. Therefore, in the desired variant, there will be exactly 50 indigo tiles.
Now we have moved to a similar problem: without the indigo color, and we need $100-50=50$ tiles. Reasoning similarly, we get that there should be 25 blue tiles.
And once again, we have moved to a similar problem: now without the blue color, and we need $50-25=25$ tiles. Then, in the desired variant, there will be 13 green tiles.
Comment: Continuing the reasoning, we will get the quantities of tiles of the other colors.
|
13
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. The number $a$ is a root of the equation $x^{11}+x^{7}+x^{3}=1$. Indicate all natural values of $n$ for which the equality $a^{4}+a^{3}=a^{n}+1$ holds.
|
Answer: Only 15.
Solution: Since $a$ is a root of the equation $x^{11} + x^{7} + x^{3} = 1$, then $a^{11} + a^{7} + a^{3} = 1$.
If we factor out $a^{3}$ from the left side, we get $a^{8} + a^{4} + 1$ - this is the expression $s^{2} + s + 1$ for $s = a^{4}$, which we have seen in the formula for the difference of cubes $s^{3} - 1 = (s - 1)(s^{2} + s + 1)$. Multiplying the equation by $a^{4} - 1$, we get $a^{3}(a^{12} - 1) = a^{4} - 1$, from which, after transformations, we obtain $a^{15} + 1 = a^{3} + a^{4}$.
It remains to note that $a \neq \pm 1$ and $a \neq 0$, since these numbers are not roots of the original equation. Therefore, all powers of $a$ are distinct, so nothing other than 15 is the answer.
Remark: The number $a$ exists: the value of $x^{11} + x^{7} + x^{3}$ at $x = 0$ is 0, i.e., less than 1, and at $x = 1$ it is 3, i.e., greater than 1. By the Intermediate Value Theorem, somewhere on the interval $[0,1]$ it must equal 1.
## Information about other clones
|
15
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The value of the parameter $a$ is chosen so that the number of roots of the first equation $4^{x}-4^{-x}=2 \cos a x, 4^{x}+4^{-x}=2 \cos a x+4$ is 2021. How many roots does the second equation have for the same $a$?
|
Solution. Transform the second equation:
$\left.4^{x}+4^{-x}=2 \cos a x+4 \Leftrightarrow 4^{x}-2+4^{-x}=2(1+\cos a x) \Leftrightarrow\left(2^{x}-2^{-x}\right)^{2}=4 \cos ^{2 a x} / 2\right) \Leftrightarrow$
$$
\left[\begin{array} { l }
{ 4 ^ { x / 2 } - 4 ^ { - x / 2 } = 2 \operatorname { cos } \frac { a x } { 2 } , } \\
{ 4 ^ { x / 2 } - 4 ^ { - x / 2 } = - 2 \operatorname { cos } \frac { a x } { 2 } }
\end{array} \Leftrightarrow \left[\begin{array}{l}
4^{x / 2}-4^{-x / 2}=2 \cos \frac{a x}{2} \\
4^{-x / 2}-4^{x / 2}=2 \cos \frac{a x}{2}
\end{array}\right.\right.
$$
Both equations in this system reduce to the first equation from the problem's condition by the substitutions $x=2 y$ and $x=-2 z$ respectively. Therefore, each of these two equations has 2021 roots. If these equations have a common root $x=x_{0}$, then $4^{x_{0}{ }^{\prime 2}}-4^{-x_{0} / 2}=0$ and $\cos ^{a x_{0} / 2}=0$, which is impossible. Consequently, these equations do not have common roots, and the second equation from the condition has $2 \cdot 2021=4042$ roots.
Answer: 4042.
## General grading criteria:
| Points | Correctness (incorrectness) of the solution |
| :---: | :---: |
| 7 | Complete correct solution. |
| $6-7$ | Correct solution. There are minor flaws, which do not significantly affect the solution. |
| $5-6$ | The solution is generally correct. However, it contains several errors, or the omission of individual cases, but can become correct after minor corrections or additions. |
| 4 | One of the two (more complex) significant cases is correctly considered, or in a problem of the type "estimate + example" the estimate is correctly obtained. |
| $2-3$ | Auxiliary statements that help in solving the problem are proved. |
| $0-1$ | Individual important cases are considered in the absence of a solution (or in the case of an incorrect solution). |
| 0 | The solution is incorrect, no progress is made. |
| 0 | The solution is absent. |
|
4042
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.2. For the angles of triangle $ABC$, it is known that $\sin \angle A + \cos \angle B = \sqrt{2}$ and $\cos \angle A + \sin \angle B = \sqrt{2}$. Find the measure of angle $C$.
|
Answer: $90^{\circ}$.
Solution. Square both equalities and add them. Then use the fundamental trigonometric identity, and after transformations, we get $2 \sin \angle A \cos \angle \mathrm{B}+2 \sin \angle B \cos \angle \mathrm{A}=2 \sin (\angle A+\angle \mathrm{B})=2 \quad, \quad$ that is, $\quad \sin (\angle A+\angle \mathrm{B})=1$. Therefore, $\angle A+\angle \mathrm{B}=90^{\circ}, \angle \mathrm{C}=180^{\circ}-(\angle A+\angle \mathrm{B})=90^{\circ}$.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.4 The Oddball marked the centers of 17 cells in an $N \times N$ grid such that the distance between any two marked points is greater than 2. What is the smallest value that $N$ can take?
|
Solution: We will show that in an $8 \times 8$ square (and then in any smaller size), it is impossible to mark the cells in this way. Indeed, let's divide the square into $2 \times 2$ squares. In each of them, the pairwise distances between the centers of the cells do not exceed $\sqrt{2}$, so no more than one cell is marked in each of the four cells. Therefore, the total number of marked cells does not exceed 16.
Example for a $9 \times 9$ square:
| | | $\mathrm{X}$ | | | | | $\mathrm{X}$ | |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $\mathrm{X}$ | | | | | $\mathrm{X}$ | | | |
| | | | X | | | | | $\mathrm{X}$ |
| | $\mathrm{X}$ | | | | | $\mathrm{X}$ | | |
| | | | | $\mathrm{X}$ | | | | |
| | | $\bar{X}$ | | | | | $\mathrm{X}$ | |
| $\mathrm{X}$ | | | | | X | | | |
| | | | X | | | | | $\mathrm{X}$ |
| | $\mathrm{X}$ | | | | | X | | |
## Criteria:
- Only proved that $N>8-3$ points;
- Only provided an example for $N=9-3$ points;
- No points are deducted for the lack of justification in the example.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.6. Points $M$ and $N$ are the midpoints of sides $B C$ and $A D$ of quadrilateral $A B C D$. It is known that $\angle B=$ $150^{\circ}, \angle C=90^{\circ}$ and $A B=C D$. Find the angle between the lines $M N$ and $B C$.
|
Answer: $60^{\circ}$.
Solution. First method. Construct parallelogram $A B M K$ and rectangle $C D L M$ (see Fig. 8.6a). Since $A K\|B C\| L D$ and $A K=B M=$ $M C=L D$, then $A K D L$ is also a parallelogram. Therefore, the midpoint $N$ of its diagonal $A D$ is also the midpoint of diagonal $K L$.
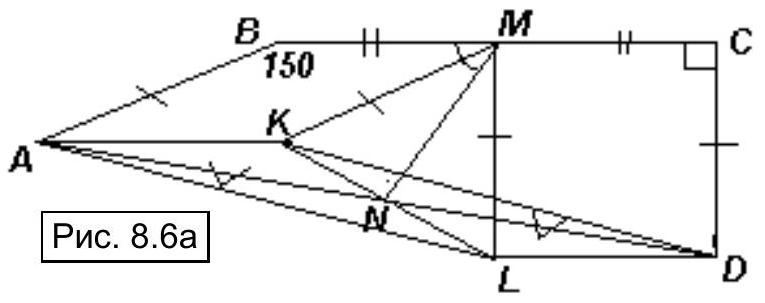
In triangle $K M L: K M=A B=C D=M L$ and $\angle K M L=\angle K M C-\angle L M C=150^{\circ}-90^{\circ}=60^{\circ}$. Therefore, this triangle is equilateral. Hence, its median $M N$ is also its bisector, so $\angle L M N=30^{\circ}$, which means $\angle B M N=60^{\circ}$.
Second method. Draw perpendiculars $A Q$ and $N P$ to line $B C$ (see Fig. 8.6b). Let $A Q=a, C M=B M=b$. Since $\angle A B Q$ $=30^{\circ}$, then $A B=C D=2 a, B Q=\frac{a \sqrt{3}}{2}$.
By Thales' theorem, $Q P=P C$, so $N P$ is the midline of trapezoid $A D C Q$. Then $N P=\frac{3}{2} a$.
$P M=C P-C M=\frac{1}{2} C Q-b=\frac{(a \sqrt{3}+2 b)}{2}-b=\frac{a \sqrt{3}}{2}$. From triangle $NPM$ by the Pythagorean theorem, we get that $M N=a \sqrt{3}$, then $\angle P N M=30^{\circ}$, and $\angle P M N=60^{\circ}$.
Grading criteria.
“+" A complete and well-justified solution is provided
" $\pm$ " A generally correct solution is provided, containing minor gaps or inaccuracies, for example, in the first method, correct additional constructions are made and the correct answer is obtained using the fact that $AKDL$ is a parallelogram, but this is not separately proven
“Ғ” The idea of additional construction is present, but there is no further progress
“-" Only the answer is provided
“-" An incorrect solution is provided or it is absent
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Dima wrote a sequence of zeros and ones in his notebook. Then he noticed that a one follows a zero 16 times, a one follows 01 seven times, and a zero follows 01 eight times. What could be the last two digits on the board? (In your answer, indicate all options and prove that there are no others).
|
Answer. 01.
Solution. The combination 01 occurs 16 times in the tetrad. After it, $7+8=15$ times there is a 0 or 1, and one time there is not. Therefore, one of the combinations 01 stands at the end of the line.
Criteria. Full solution - 7 points. Partial examples of sequences with the correct answer - 1. Only answer - 0 -
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. There are 21 different applications installed on the phone. In how many ways can six applications be selected for deletion so that among them are three applications from the following six $T V F T' V' F'$, but none of the pairs $T T', V V', F F'$ are included?
|
Answer. $8 \cdot C_{15}^{3}=3640$.
Solution. Choose one application from each pair $T T^{\prime}, V V^{\prime}, F F^{\prime}-8$ ways. Thus, out of 21 applications, 6 have already been excluded, leaving 15. Choose 3 applications from the remaining 15, which can be done in $\frac{15 \cdot 14 \cdot 13}{3!}$ (or $C_{15}^{3}$) ways. In total, $8 \cdot C_{15}^{3}=3640$.
Criteria. Full solution - 7 points. The idea to choose one application from each pair without further progress - 16.
|
3640
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Petya ran down the escalator, counting the steps. Exactly halfway down, he stumbled and the rest of the way he tumbled down (Petya flies three times faster than he runs). How many steps are there on the escalator if Petya counted 20 steps with his feet (i.e., before falling) and 30 steps with his sides (after falling)?
|
Answer: 80
Solution. Let the escalator have a length of $2 \mathrm{~L}$ (steps), the speed of the escalator be $u$, and Petya runs with a speed of $\mathrm{x}$, and flies with a speed of $3 \mathrm{x}$. Then the time until the fall is $\frac{L}{u+x}$ and during this time Petya will count $\frac{L x}{u+x}$ steps. From this: $\frac{1}{20}=\frac{1}{L}\left(1+\frac{u}{x}\right)$. A similar equation is obtained "after the fall": $\frac{1}{30}=\frac{1}{L}\left(1+\frac{u}{3 x}\right)$. Multiplying by 3, and subtracting the first, we get: $\frac{3}{30}-\frac{1}{20}=\frac{2}{L}$, so $\mathrm{L}=40$, and $2 \mathrm{~L}=80$.
Grading. Full solution - 7 points.
|
80
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. We will call a right-angled triangle elegant if one of its legs is 10 times longer than the other. Is it possible to cut a square into 2020 identical elegant triangles?
|
Answer: Yes
Solution. An elegant triangle with legs of 10 and 100 can be cut into 100 triangles with legs of 1 and 10 (the cuts are straight lines parallel to its sides). From four such large triangles, we can form a square (its sides will be the hypotenuses of these triangles) with a hole (in the shape of a square with side $100-10=90$). This square can be divided into rectangles with sides 1 and 10 (there will be 810 such rectangles), and each such rectangle can be divided into two triangles with legs of 1 and 10. In total, we get $4 \cdot 100 + 2 \cdot 810 = 2020$ elegant triangles.
Grading. Full solution - 7 points.
|
2020
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 5. CONDITION
A tourist goes on a hike from $A$ to $B$ and back, and completes the entire journey in 3 hours and 41 minutes. The route from $A$ to $B$ first goes uphill, then on flat ground, and finally downhill. Over what distance does the road pass on flat ground, if the tourist's speed is 4 km/h when climbing uphill, 5 km/h on flat ground, and 6 km/h when descending, and the distance $AB$ is 9 km?
|
Solution. Let $x$ km of the path be on flat ground, then $9-x$ km of the path (uphill and downhill) the tourist travels twice, once (each of the ascent or descent) at a speed of 4 km/h, the other at a speed of 6 km/h, and spends $(9-x) / 4+(9-x) / 6$ hours on this part. Since the tourist walks $2 x / 5$ hours on flat ground, and the round trip takes 3 hours and 41 minutes, then $2 x / 5+(9-x) / 4+(9-x) / 6=221 / 60$, from which $x=4$ km.
Answer: 4 km.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A three-digit number, all digits of which are different and non-zero, will be called balanced if it is equal to the sum of all possible two-digit numbers formed from the different digits of this number. Find the smallest balanced number.
|
Answer: 132.
Solution: Let the desired number be of the form $\overline{a b c}$. Then it can be represented as the sum of six different two-digit numbers: $\overline{a b c}=\overline{a b}+\overline{b a}+\overline{a c}+\overline{c a}+\overline{b c}+\overline{c b}$.
From the last equality, we get $100 a+10 b+c=22 a+22 b+22 c$, then, combining like terms and dividing both sides of the equation by 2, we reduce it to the form $26 a=4 b+7 c$.
Next, let $a=1$. Clearly, if we get a balanced number starting with 1, it will be less than any number with $a \geq 2$. Then we have $4 b+7 c=26$. Since $c$ is not less than 1, $b$ does not exceed 4. For $b=4$, we immediately get a contradiction, and for $b=3$, we find $c=2$. The smallest balanced number is 132.
Grading criteria: Correct and justified solution - 7 points, only the correct answer with verification - 2 points, the equation in integers using the digits of the number is obtained - $\mathbf{1}$ point, the solution is incorrect or only the answer without verification - 0 points.
|
132
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Three circles with radii 1, 2, 3 touch each other externally at three points. Find the radius of the circle passing through these three points.
|
Answer: 1.
Solution: Let $\mathrm{O}_{1}, \mathrm{O}_{2}$ and $\mathrm{O}_{3}$ be the centers of the given circles, K, M, N the points of tangency, such that $\mathrm{O}_{1} \mathrm{~K}=\mathrm{O}_{1} \mathrm{~N}=1, \mathrm{O}_{2} \mathrm{~K}=\mathrm{O}_{2} \mathrm{M}=2$ and $\mathrm{O}_{3} \mathrm{~N}=$ $\mathrm{O}_{3} \mathrm{M}=3$. It is known that when two circles touch, the point of tangency lies on the segment connecting their centers. Therefore, K, M, N are points on the sides of the triangle $\mathrm{O}_{1} \mathrm{O}_{2} \mathrm{O}_{3}$. Note that the desired circle coincides with the circle inscribed in the triangle $\mathrm{O}_{1} \mathrm{O}_{2} \mathrm{O}_{3}$. Indeed, since the equalities $\mathrm{O}_{1} \mathrm{~K}=\mathrm{O}_{1} \mathrm{~N}, \mathrm{O}_{2} \mathrm{~K}=\mathrm{O}_{2} \mathrm{M}$ and $\mathrm{O}_{3} \mathrm{~N}=\mathrm{O}_{3} \mathrm{M}$ hold, the points $\mathrm{K}, \mathrm{M}, \mathrm{N}$ are the points of tangency of the inscribed circle with the sides of the triangle $\mathrm{O}_{1} \mathrm{O}_{2} \mathrm{O}_{3}$.
Let $r$ be the desired radius, write the area of the triangle $\mathrm{O}_{1} \mathrm{O}_{2} \mathrm{O}_{3}$ in terms of the perimeter and $r$, and using Heron's formula. We get the equation:
$$
\frac{1}{2}(3+4+5) r=\sqrt{6(6-3)(6-4)(6-5)} \Rightarrow 6 r=6 \Rightarrow r=1
$$
## ALL-RUSSIAN SCHOOL OLYMPIAD 2022/23
## MATHEMATICS 11th GRADE
Grading criteria: Correct and justified solution - 7 points, incorrect solution or only answer - $\mathbf{0}$ points.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1 In a competition of meaningless activity, a participant recorded 2022 numbers in a circle such that each number is equal to the product of its two neighbors. What is the maximum number of different numbers that could have been used?
|
Solution: If there is a zero among the numbers, then its neighbors are also zeros, so all the recorded numbers will be equal to zero. We will assume that there are no zeros among the numbers. Let $a$ and $b$ be two adjacent numbers. Then on the other side of $a$ stands $a / b$, and on the other side of $b$ stands $b / a$. In other words, two numbers at a distance of 3 are reciprocals of each other, and then numbers at a distance of 6 are equal, so there are no more than $2022 / 6 = 337$ different numbers. An example can be constructed from repeating cycles of six numbers: $2, 6, 3, 1/2, 1/6, 1/3$.
## Criteria:
- Only the answer with an example without proving the maximum - 1 point.
|
337
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. Each student in class 7B ate the same number of chocolate bars during math lessons over the week. Nine of them together ate fewer than 288 chocolate bars in a week, while ten of them together ate more than 300 chocolate bars. How many chocolate bars did each student in class 7B eat? Explain your answer.
|
Answer: 31 chocolates each
Solution 1: Since ten students ate more than 300 chocolates, nine students ate more than (310:10)$\cdot$9 = 270 chocolates. It is also known that nine students together ate less than 288 chocolates. The only number divisible by 9 in the range from 271 to 287 is 279. Therefore, nine students ate 279 chocolates, and one student ate 31 chocolates.
Solution 2: Since nine students together ate less than 288 chocolates in a week, one student ate less than $288: 9=32$ chocolates in a week. Since ten students together ate more than 300 chocolates in a week, one student ate more than 300:10 = 30 chocolates in a week. Ultimately, each student ate more than 30 but less than 32, i.e., 31 chocolates.
Criteria: Only the answer - 0 points. 7 points for the correct answer with correct reasoning. 3-5 points for partial progress in the solution.
|
31
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. Find the largest natural number in which each digit, starting from the third, is equal to the sum of all the previous digits of the number.
|
Answer: 101248.
Solution: Let the first digit of the number be $a$, the second digit be $b$. Then the third digit is $(a+b)$, the fourth digit is $(2a+2b)$, the fifth digit is $(4a+4b)$, and the sixth digit is $(8a+8b)$. There cannot be a seventh digit, because if it exists, it would be equal to $(16a+16b)$, but this expression can only be a digit if $a=b=0$. Therefore, the desired number is a six-digit number. Now we need to find the maximum possible value of $a$ such that the sixth digit remains a "digit," i.e., the inequality $8a+8b<10$ is satisfied. This is possible when $a=1, b=0$, so the desired number is 101248.
Criteria: Correct answer - 4 points (may be without explanation). Correct reasoning that the desired number is a six-digit number, but the example is not constructed - 3 points. 7 points are given if there is a proof that numbers greater than 101248 cannot exist (a correct method of constructing the example can be considered as a proof).
|
101248
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. Given an equilateral triangle $\mathrm{ABC}$. On the sides $\mathrm{AB}$ and $\mathrm{BC}$, isosceles right triangles ABP and BCQ are constructed externally with right angles $\angle \mathrm{ABP}$ and $\angle \mathrm{BCQ}$. Find the angle $\angle \mathrm{PAQ}$.
|
Answer: 90.
Solution: Consider triangle ACQ. It is isosceles because $\mathrm{AC}=\mathrm{BC}$ (by the condition of the equilateral triangle $\mathrm{ABC}$), and $\mathrm{BC}=\mathrm{CQ}$ (by the condition of the isosceles triangle BCQ). The angle at the vertex $\angle A C Q=60 \circ+90 \circ=150$ . Then $\angle \mathrm{CAQ}=(180 \circ-150 \circ): 2=15$ degrees. The required angle $\angle \mathrm{PAQ}$ $=\angle \mathrm{PAB}+\angle \mathrm{BAQ}=\angle \mathrm{PAB}+\angle \mathrm{BAC}-\angle \mathrm{CAQ}=45 \circ+60 \circ-$ $15 \circ=90 \circ$.
Criteria: Only the answer - 0 points. Partially correct progress in the solution - 3-5 points. 7 points - correct answer with a correct solution.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. What is the minimum number of cells that need to be marked on a 5 by 5 board so that among the marked cells there are no adjacent ones (having a common side or a common vertex), and adding any one cell to these would violate the first condition?
|
Answer: 4 cells.
Solution: Estimation. Divide the board into four parts (see fig.). In each of them, a cell must be marked, otherwise the black cell contained in it can be added.
Example. The four black cells in the figure satisfy both conditions.
Criteria: Answer only - 0 points. Estimation only - 5 points. Example only - 2 points. 7 points are given if both estimation and example are present.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. How many five-digit numbers exist that are not divisible by 1000, and have the first, third, and last digits even?
Otvet: 9960.
|
Solution. The first digit of the number can be any of the four (2, 4, 6, or 8), the second and fourth can be any of ten each, and the third and fifth, if we abandon the condition "not divisible by a thousand," can be any of five (0, 2, 4, 6, or 8). Therefore, there are $4 \times 10 \times 5 \times 10 \times 5=10000$ five-digit numbers in which the first, third, and last digits are even; since among them $4 \times 10 \times 1 \times 1 \times 1=40$ numbers are divisible by 1000, the numbers that satisfy the condition of the problem will be $10000-40=9960$.
Criteria. If the solution is incorrect - 0 points.
Only the correct answer - 0 points.
If the reasoning is correct and there is a computational error - 3 points. If the solution is correct - 7 points.
|
9960
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In a white $10 \times 10$ square, on the first move, a $1 \times 1$ cell rectangle is painted, on the second move - a $1 \times 2$ cell rectangle, on the third - $1 \times 3$ and so on, as long as it is possible to do so. After what minimum number of moves could this process end? (Cells cannot be painted over again.)
#
|
# Answer: after 6 moves.
Solution. Evaluation. On the board, 16 rectangles of size $1 \times 6$ can be highlighted, of which a maximum of $1+2+3+4+5=15$ will contain colored cells, meaning that a sixth move is always possible. Example. The process is illustrated in the diagram, showing a scenario where a seventh move is no longer possible.
Criteria. If the solution is incorrect - 0 points.
If only a correct example is provided - 3 points.
If only the correct evaluation is provided - 3 points.
If the solution is correct (any correct example and justification of the evaluation) - 7 points.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task No. 6.1
## Condition:
A sheet of paper was folded like an accordion as shown in the figure, and then folded in half along the dotted line. After that, the entire resulting square stack was cut along the diagonal.
How many pieces of paper were obtained after this?
|
Answer: 9
Exact match of the answer - 1 point
## Solution.
Unfold the paper and mark the lines of the cuts.
Now it is easy to count the resulting pieces. For convenience, they are highlighted in color.
## Problem:
A sheet of paper was folded like an accordion as shown in the picture, and then folded in half along the dotted line. After that, the entire resulting square stack was cut along the diagonal.
How many pieces of paper were obtained after this?
Answer: 8
Exact match of the answer - 1 point
Solution by analogy with problem № 6.1.
#
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task No. 6.3
## Condition:
A sheet of paper was folded like an accordion as shown in the figure, and then folded in half along the dotted line. After that, the entire resulting square stack was cut along the diagonal.
How many pieces of paper were obtained after this?
|
Answer: 9
Exact match of the answer -1 point
Solution by analogy with task No. 6.1.
## Condition:
A sheet of paper was folded like an accordion as shown in the figure, and then folded in half along the dotted line. After that, the entire resulting square stack was cut along the diagonal.
How many pieces of paper were obtained after this
## Answer: 7
Exact match of the answer -1 point
Solution by analogy with task No. 6.1.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. In a box, there are several (more than three) balls. Each is painted in some color. If you take out any three balls from the box, there will definitely be at least one red and at least one blue among them. How many balls can be in the box
|
Answer: 4. Solution. In the box, there are no more than two red and blue balls (otherwise, it would be possible to draw three red or three blue balls) and no more than one ball of other colors (otherwise, it would be possible to draw one blue or red ball and two balls of other colors). Therefore, there are no more than five balls in the box, and if there are five, then among them are two blue and two red balls and one of some third color. But then we could draw a ball of the third color and two blue balls. This means that there cannot be five balls in the box. Therefore, there are four: two blue and two red.
Comment. Answer - 0 points, example - 2 points.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.4. On each of 2013 cards, a number is written, and all these 2013 numbers are distinct. The cards are face down. In one move, it is allowed to point to ten cards, and in response, one of the numbers written on them will be reported (it is unknown which one). For what largest $t$ can it be guaranteed to find $t$ cards, for which it is known what number is written on each of them?
(I. Bogdanov)
|
Answer. $t=1986=2013-27$.
Solution. 1. First, we will show that it is impossible to guess 1987 cards. Number the cards $A_{1}, \ldots, A_{2013}$; we will demonstrate how to arrange the answers so that none of the numbers on the cards $A_{1}, \ldots, A_{27}$ can be determined.
For each $i=1, \ldots, 9$, combine the cards $A_{3 i-2}, A_{3 i-1}, A_{3 i}$ into a triplet $T_{i}$. If among the specified 10 cards there is a card $A_{n}$ with $n>27$, we will answer the number $n$. If all 10 cards lie within the triplets, then in some triplet $T_{i}$ there are at least two cards; in this case, we will answer the number on the edge between these cards as shown in Fig. 8. These answers are satisfied by two scenarios: the numbers on the cards with numbers greater than 27 are their own numbers, and either on each card in the triplets, the number on the edge coming out of it counterclockwise is written, or on each such card, the number on the edge clockwise is written. Therefore, none of the numbers on the cards in the triplets can be determined.
|
1986
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 1. Option 1.
A confectionery factory received 5 rolls of ribbon, each 50 m long, for packaging cakes. How many cuts need to be made to get pieces of ribbon 2 m long?
|
Answer: 120.
Solution. From one roll, 25 pieces of ribbon, each 2 m long, can be obtained. For this, 24 cuts are needed. Therefore, a total of $5 \cdot 24=120$ cuts are required.
|
120
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 3. Option 1.
In a box, there are chips. Tolya and Kolya were asked how many chips are in the box. Tolya answered: “Less than 7”, and Kolya answered: “Less than 5”. How many chips can be in the box if it is known that one of the answers is correct? Find all the options. In the answer, write their sum.
|
Answer: 11.
Solution: If there are 7 or more chips in the box, then both boys are lying. If there are 4 or fewer chips in the box, then both boys are telling the truth. If there are 5 or 6 chips in the box, then Tolya is telling the truth, and Kolya is lying.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 4. Option 1.
In a box, there are red, blue, and green pencils. It is known that if you remove two red pencils, the number of pencils of all colors will be equal. And if after that you add 10 red pencils to the box, the number of red pencils will be exactly half of all the pencils. How many pencils were in the box initially?
|
Answer: 32.
Solution. Before adding pencils, it could be considered that there were as many red ones as green ones. Then, the 10 added pencils are the number of blue ones. So, at the moment of adding, there were 10 red, blue, and green pencils each.
#
|
32
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 5. Option 1.
The chocolate bar has the shape of a square with a side of 100 cm, divided into pieces with a side of 1 cm. The sweet tooth ate all the pieces along each of the four sides, as shown in the figure. How many pieces did the sweet tooth eat in total?
|
Answer: 784.
Solution (1st method). The chocolate bar consists of $100 \times 100=10000$ pieces in total. If 2 rows of pieces are removed from each side, a square with a side length of 96 cm remains. Thus, the sweet tooth will eat $10000-96 \cdot 96=784$ pieces.
Solution (2nd method). First, let's count the pieces eaten along two opposite sides: $2 \cdot 100 \cdot 2=400$ pieces. Remove them. Notice that on the other two sides, there are 2 rows left to eat, each containing $100-4=96$ pieces. Thus, a total of $400+2 \cdot 96 \cdot 2=784$ pieces were eaten.
Solution (3rd method). Divide all the eaten pieces into 4 equal groups as shown in the figure:
Each of these groups forms a rectangle of $2 \times 98$. Therefore, a total of $2 \cdot 98 \cdot 4=784$ pieces were eaten.
|
784
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Variant 1. In the kindergarten, 5 children eat porridge every day, 7 children eat porridge every other day, and the rest never eat porridge. Yesterday, 9 children ate porridge. How many children will eat porridge today?
|
Answer: 8.
Solution. Of the 9 boys who ate porridge yesterday, 5 boys eat it every day, so the remaining $9-5=4$ eat it every other day. Therefore, these four will not eat porridge today, while the other $7-4=3$ of those who eat every other day will. So today, these three, as well as the five who always eat porridge, will eat it. We get the answer $3+5=8$.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Variant 1. On a rectangular plot measuring $5 \times 6$ meters, there is a triangular flower bed (see figure). Find the area of this flower bed (in square meters).
|
Answer: 10.
Solution. The area of the flower bed can be calculated as the difference between the area of the plot and the sum of the areas of the two triangular parts not occupied by the flower bed:
1) $(6 \cdot 5): 2=15\left(\mathrm{m}^{2}\right)-$ area of the red part
2) $(5 \cdot 2): 2=5\left(\mathrm{m}^{2}\right)-$ area of the blue part
3) $5 \cdot 6=30\left(\mathrm{~m}^{2}\right)-$ area of the plot
4) $30-15-5=10\left(\mathrm{~m}^{2}\right)-$ area of the flower bed
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Variant 1. A dishonest seller attached a nut to the correct scales, and now the scales overestimate the weight. First, a large apple was placed on the scales, and they showed 300 g. Then a small apple was placed on the scales, and they showed 200 g. When both apples were placed on the scales, they showed 480 g. How many grams does the nut weigh?
|
Answer: 20.
Solution: The nut's weight affects the total of $300+200=500$ g twice, but only once in the weight of 480 g. Therefore, the weight of the nut is $500-480=20$ g.
|
20
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The sequence is defined recursively: $a_{1}=1, a_{2}=2, a_{n+2}=\frac{a_{n+1}}{a_{n}}$. Find the sum of the first 1730 terms of this sequence.
|
Solution. Let's find the first few terms of the sequence: $a_{3}=a_{2} / a_{1}=$ $2 / 1=2 ; a_{4}=a_{3} / a_{2}=2 / 2=1 ; a_{5}=a_{4} / a_{3}=0.5 ; a_{6}=a_{5} / a_{4}=0.5 / 1=0.5 ;$ $a_{7}=a_{6} / a_{5}=0.5 / 0.5=1$ and $a_{8}=a_{7} / a_{6}=1 / 0.5=2$. Notice that the sequence turned out to be periodic, its first six terms $1 ; 2 ; 2 ; 1 ; 0.5 ; 0.5$ will repeat infinitely. Since the sequence is periodic, with a period of six, and $1728: 6=288$ and $a_{1}+a_{2}+\ldots+a_{6}=7$, then $\sum_{i=1}^{1730} a_{i}=\sum_{i=1}^{1728} a_{i}+a_{1729}+a_{1730}=288 \cdot 7+1+2=2019$. Answer: 2019.
|
2019
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The book is sewn from 12 identical booklets. Each booklet consists of several double sheets nested within each other. The booklets of the book are sewn sequentially one after another. All pages of the book are numbered, starting from 1. The sum of the numbers of four pages of one of the double sheets in the fourth booklet is 338. How many pages are in this book?
|
Solution. Let the book have $x$ pages, then each notebook has $\frac{x}{12}$ pages, the first three notebooks have $\frac{3 x}{12}=\frac{x}{4}$ pages, and the first four notebooks have $\frac{4 x}{12}=\frac{x}{3}$ pages. The numbers of the first and second pages of the fourth notebook will be $\frac{x}{4}+1$ and $\frac{x}{4}+2$, and the numbers of the second-to-last and last pages will be $\frac{x}{3}-1$ and $\frac{x}{3}$. Since the sums of the numbers of all double pages for each of the notebooks are the same, we get the equation $\left(\frac{x}{4}+1\right)+\left(\frac{x}{4}+2\right)+\left(\frac{x}{3}-1\right)+\frac{x}{3}=338$, so $x=288$. Answer: 288.
|
288
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 7.1. Condition:
A carpenter took a wooden square and cut out 4 smaller equal squares from it, the area of each of which was $9 \%$ of the area of the larger one. The remaining area of the original square was $256 \mathrm{~cm}^{2}$.
Find the side of the original square. Express your answer in centimeters.
|
Answer: 20
Solution.
Let the side of the larger square be 10x. The area of the smaller square is $9 \%$ of the area of the larger square, which is $9 / 100 \cdot 100 x^{2}=9 x^{2}$. After removing four smaller squares, the remaining area is $100 x^{2}-4 \cdot 9 x^{2}=64 x^{2}=256 \text{ cm}^{2}$. Therefore, $x^{2}=4$. Hence, $x=2$ cm, and the entire side is $10 x=20$ cm.
|
20
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. There is a paper square $7 \times 7$, all cells of which are white. What is the minimum number of cells that need to be painted black so that it is impossible to cut out a rectangle from it with at least 10 cells, all of which are white?
|
# Answer: 4.
Solution. Divide the $7 \times 7$ square into 5 rectangles (see figure): four $3 \times 4$ and a $1 \times 1$ square. If only three cells are shaded, there will be a white rectangle of 12 cells. How to shade 4 cells is shown in the following figure:
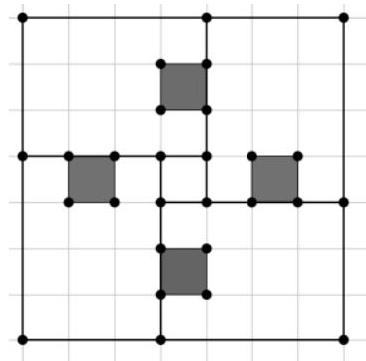
Grading criteria.
Example of four black cells: 3 points.
Estimation that three are not enough: 4 points.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 1. A group of schoolchildren decided to buy pizza. Each pizza is cut into 12 pieces. They calculated that if each boy eats 7 pieces and each girl eats 2 pieces, then three pizzas would not be enough. If they buy four pizzas, then each boy can have 8 pieces and each girl can have 4 pieces, and there will still be some left over. How many boys and how many girls are in this group?
|
Answer: 1 girl and 5 boys.
Solution: Let the number of boys be $m$, and the number of girls be $d$. Notice that $7 m+2 d > 36, 8 m+4 d \geq 14$, from which we get $m \geq 5$. But then from the inequality $4 m+2 d \leq 22$ we get that $d \leq 1$, so either $d=0$ or $d=1$. If $d=0$, then $7 m > 36, m > 5$, and $8 m \leq 44, m \leq 5$, a contradiction. If $d=1$, then $7 m > 34, m \geq 5$, and $8 m \leq 40, m \leq 5$, from which $m=5$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The number $N$ has the smallest positive divisor 1, the second largest positive divisor $k$, and the third largest positive divisor $m$. Given that $k^{k}+m^{m}=N$. What is $N$?
|
Solution. Answer: $N=260$. If $N$ were odd, then both $k$ and $m$ would be odd, which means $k^{k}+m^{m}$ would be an even number. Therefore, the equation $N=k^{k}+m^{m}$ would be impossible in this case.
Now let $N$ be even. Then $k=2$ and $m$ is also even. Since $4=N-m^{m}$ is divisible by $m$, we have $m=4$ (since $m>k$). Therefore, $N=2^{2}+4^{4}=260$.
|
260
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. What is the minimum number of 3-cell corners that need to be painted in a $5 \times 5$ square so that no more corners can be painted? (Painted corners should not overlap.)
|
# 3. Answer. 4.
Let the cells of a $5 \times 5$ square be painted in such a way that no more corners can be painted. Consider the 4 corners marked on the diagram. Since none of these corners can be painted, at least one cell in each of them must be painted. Note that one corner cannot paint cells of two marked corners. Therefore, at least 4 corners must be painted.

The following diagram shows how to paint 4 corners so that no more corners can be painted.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. We will call a number greater than 25 semi-prime if it is the sum of some two distinct prime numbers. What is the maximum number of consecutive natural numbers that can be semi-prime?
|
4. Answer. 5.
Note that an odd semiprime number can only be the sum of two and an odd prime number.
Let's show that three consecutive odd numbers \(2n+1, 2n+3\), and \(2n+5\), greater than 25, cannot all be semiprimes simultaneously. Assuming the contrary, we get that the numbers \(2n-1, 2n+1\), and \(2n+3\) are prime, and all of them are greater than 3. But one of these three numbers is divisible by 3, which is a contradiction. Note that among any six consecutive numbers, there are three consecutive odd numbers; therefore, there cannot be more than five consecutive semiprime numbers. Five consecutive numbers can be semiprimes; for example, \(30 = 17 + 13\),
The segment \(C_1M\) is the median of the right triangle \(CC_1A\), so \(CM = \underline{AC} = MA\) (see the figure). Then \(\angle CMA = \pi - 2\angle BAC\). Similarly, \(\angle AMC = \pi - 2\angle BCA\).
From this, \(\angle C_1MA + \angle A_1MC = 2(\pi - \angle BAC - \angle BCA) = 2\angle ABC\),
\(\angle A_1MC_1 = \pi - (\angle AMC_1 + \angle CMA_1) = \pi - 2\angle ABC\).
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. One degree on the Celsius scale is equal to 1.8 degrees on the Fahrenheit scale, while $0^{\circ}$ Celsius corresponds to $32^{\circ}$ Fahrenheit. Can a temperature be expressed by the same number of degrees on both the Celsius and Fahrenheit scales?
|
Answer: Yes, it can.
From the condition, it follows that the temperature in Fahrenheit is expressed through the temperature in Celsius as follows: $T_{F}=1.8 T_{C}+32^{\circ}$. If $T_{F}=T_{C}$, then $0.8 T_{C}+32=0$, that is, $T_{C}=-40$.
Remarks. An answer without explanations - 0 points; an answer with explanations (it is not necessary to find the root of the equation - it is enough to note that the graphs of linear functions with unequal slopes intersect) - 7 points.
|
-40
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. The monthly pension of football fan Ivan Ivanovich is
$$
\frac{149^{6}-199^{3}}{149^{4}+199^{2}+199 \cdot 149^{2}}
$$
rubles, and the cost of a ticket to a World Cup match is 22000 rubles. Will Ivan Ivanovich's pension for one month be enough to buy one ticket? Justify your answer.
|
Solution: Let $149^{2}=a, 199=b$. Then Ivan Ivanovich's monthly pension (in rubles) is
$$
\frac{a^{3}-b^{3}}{a^{2}+b^{2}+a \cdot b}=\frac{(a-b)\left(a^{2}+a b+b^{2}\right)}{a^{2}+a b+b^{2}}=a-b=149^{2}-199=22002
$$
Thus, his pension will be enough for one ticket.
Answer: It will be enough.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and fully justified answer | 7 points |
| Arithmetic errors were made in the calculations, possibly leading to an incorrect answer | deduct 2 points for each |
| The formula for the difference of cubes was applied and the fraction was simplified | 5 points |
| The problem was reduced to algebra by introducing variables (one or two), but not solved | 3 points |
| Answer without justification and/or incorrect answer | 0 points |
|
22002
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. The first two digits of a natural four-digit number are either each less than 5, or each greater than 5. The same can be said about the last two digits. How many such numbers are there? Justify your answer.
|
Solution: There are $4^{2}=16$ two-digit numbers where both digits are greater than 5, and there are $4 \cdot 5=20$ (the first digit is not zero) where both digits are less than 5. In total, there are $16+20=36$ such numbers. This is the conclusion about the first two digits of the number. The last two digits will provide the same number of options plus another 5: 00, 01, 02, 03, and 04, totaling 41 options. The total number of numbers is $36 \cdot 41=1476$.
Note: 1476 numbers.
Recommendations for checking:
| included in the work | points |
| :--- | :--- |
| Correct and fully justified answer | 7 points |
| Answer is incorrect due to arithmetic errors | 6 points |
| Answer is fully justified but not written as a natural number | no points deducted |
| In a correct reasoning, it is not taken into account that the first digit of the number is never zero | 5 points |
| In a correct solution approach, the number of pairs of the first (and/or last) two digits of the number is incorrectly calculated; the error is not in arithmetic | 4 points |
| Attempt to separately count the number of pairs of the first two digits of the number and the last two digits of the number without further progress in the solution | 2 points |
| Correct answer without justification or by enumeration, if the completeness of the latter is not proven and not obvious | 1 point |
| Attempts to solve by enumeration, not leading to the correct answer | 0 points |
|
1476
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. There is an unlimited number of chips in six colors. What is the smallest number of chips that need to be arranged in a row so that for any two different colors, there are two adjacent chips of these colors in the row.
|
5. It follows from the condition that for each fixed color A, a chip of this color must be paired with a chip of each of the other 5 colors. In a row, a chip has no more than two neighbors, so a chip of color A must appear at least 3 times. Similarly for each other color. Thus, there should be no fewer than 3*6=18 chips in total. Here is one example of the desired arrangement of chips: 123456246325164135 (the colors are denoted by digits).
|
18
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.7. Denis threw darts at four identical dartboards: he threw exactly three darts at each board, where they landed is shown in the figure. On the first board, he scored 30 points, on the second - 38 points, on the third - 41 points. How many points did he score on the fourth board? (For hitting each specific zone - ring or central field - a certain number of points is awarded.)
|
Answer: 34.
Solution. "Add" the first two dart fields: we get 2 hits in the central field, 2 hits in the inner ring, 2 hits in the outer ring. Thus, the sum of points on the first and second fields is twice the number of points obtained for the fourth field.
From this, it is not difficult to get the answer
$$
(30+38): 2=34
$$
|
34
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.1. After a football match, the coach lined up the team as shown in the figure, and commanded: "Run to the locker room, those whose number is less than that of any of their neighbors." After several people ran away, he repeated his command. The coach continued until only one player was left. What is Igor's number, if it is known that after he ran away, 3 people remained in the line? (After each command, one or several players ran away, after which the line closed, and there were no empty spaces between the remaining players.)

|
Answer: 5.
Solution. It is clear that after the first command, the players left are $9,11,10,6,8,5,4,1$. After the second command, the players left are $11,10,8,5,4$. After the third - $11,10,8,5$. After the fourth - $11,10,8$. Therefore, Igor had the number 5.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.5. The figure shows 4 squares. It is known that the length of segment $A B$ is 11, the length of segment $F E$ is 13, and the length of segment $C D$ is 5. What is the length of segment $G H$?
|
Answer: 29.
Solution. The side of the largest square (with vertex $A$) is greater than the side of the second largest square (with vertex $C$) by the length of segment $A B$, which is 11. Similarly, the side of the second largest square is greater than the side of the third largest square (with vertex $E$) by the length of segment $C D$, which is 5. And its side is greater than the side of the smallest square by the length of segment $E F$, which is 13. In total, the side of the largest square is greater than the side of the smallest square by the length of segment $G H$, which is $11+5+13=29$.
|
29
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.5. A rectangle was cut into nine squares, as shown in the figure. The lengths of the sides of the rectangle and all the squares are integers. What is the smallest value that the perimeter of the rectangle can take?
|
Answer: 52.
Solution. Inside the square, we will write the length of its side. Let the sides of the two squares be $a$ and $b$, and we will sequentially calculate the lengths of the sides of the squares.

The sum of the lengths of the sides of the two squares adjacent to the left side of the rectangle is equal to the sum of the lengths of the sides of the two squares adjacent to the right side of the rectangle. We get the equation
$$
\begin{aligned}
(2 a+b)+(3 a+b) & =(12 a-2 b)+(8 a-b) \\
5 a+2 b & =20 a-3 b \\
b & =3 a
\end{aligned}
$$
Thus, to minimize the perimeter of the rectangle, we need to choose $a=1$, $b=3$. It is easy to check that with these values, the rectangle will have dimensions $11 \times 15$, and its perimeter will be 52.
|
52
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.1. A square was cut into four equal rectangles, and from them, a large letter P was formed, as shown in the figure, with a perimeter of 56.
What is the perimeter of the original square
|
Answer: 32.
Solution. Let the width of the rectangle be $x$. From the first drawing, we understand that the length of the rectangle is four times its width, that is, it is equal to $4 x$. Now we can calculate the dimensions of the letter P.

From this, we get the equation
$$
\begin{gathered}
28 x=56 \\
x=2
\end{gathered}
$$
The perimeter of the square is $16 x=32$.
|
32
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.2. The numbers from 1 to 9 were placed in the cells of a $3 \times 3$ table such that the sum of the numbers on one diagonal is 7, and on the other diagonal is 21. What is the sum of the numbers in the five shaded cells?
|
Answer: 25.
Solution. Note that 7 can be represented uniquely as the sum of numbers from 1 to 9 - this is $1+2+4=7$.
Let's look at the other diagonal with a sum of 21. The largest possible value of the sum in it is $9+8+4=21$ (since the number in the central cell is no more than 4). Therefore, it must contain the numbers $9,8,4$.
Thus, the number 4 is in the central cell, and the numbers 1, 2, 8, and 9 are at the corners. Now it is not difficult to find the sum of the numbers in the shaded cells: $3+4+5+6+7=25$.
|
25
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.6. For quadrilateral $ABCD$, it is known that $AB=BD, \angle ABD=\angle DBC, \angle BCD=$ $90^{\circ}$. A point $E$ is marked on segment $BC$ such that $AD=DE$. What is the length of segment $BD$, if it is known that $BE=7, EC=5$?
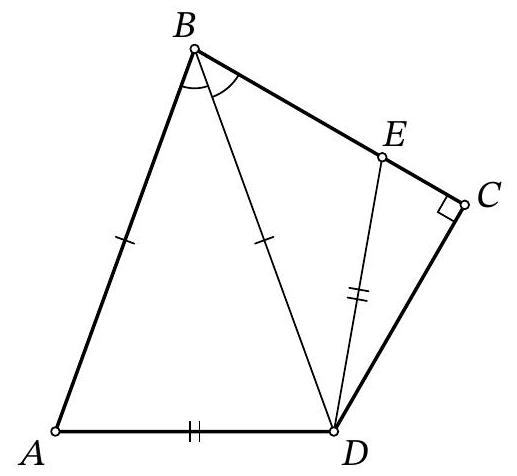
|
Answer: 17.
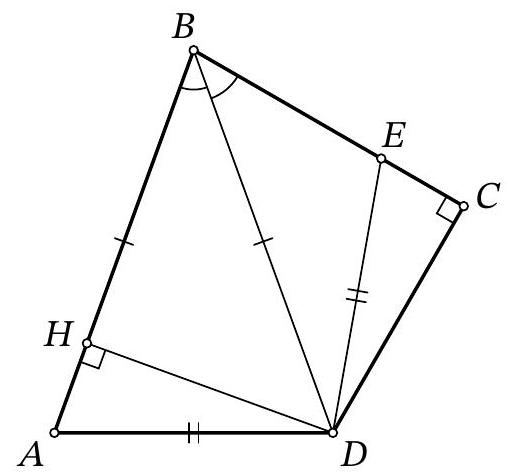
Fig. 3: to the solution of problem 8.6
Solution. In the isosceles triangle $ABD$, drop a perpendicular from point $D$, let $H$ be its foot (Fig. 3). Since this triangle is acute-angled ($\angle ABD = \angle CBD < 90^\circ$, $\left.\angle BAD = \angle ADB = \frac{180^\circ - \angle ABD}{2} < 90^\circ\right)$, point $H$ lies on the segment $AB$.
Notice that the right triangles $BDH$ and $BDC$ are equal by the common hypotenuse $BD$ and the acute angle at vertex $B$. Therefore, $BH = BC$ and $DH = CD$.
Now, notice that the right triangles $ADH$ and $EDC$ are also equal by the hypotenuse $AD = ED$ and the leg $DH = CD$. Therefore, $EC = AH$.
Thus, $BD = BA = BH + AH = BC + EC = (7 + 5) + 5 = 17$.
|
17
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.