problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
Problem 6.7. Anya places pebbles on the sand. First, she placed one stone, then added pebbles to form a pentagon, then made a larger outer pentagon with pebbles, then another outer pentagon, and so on, as shown in the picture. The number of stones she had arranged on the first four pictures: 1, 5, 12, and 22. If she continues to create such pictures, how many stones will be on the 10th picture?
-
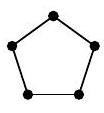
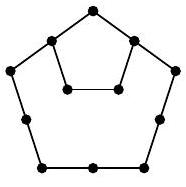
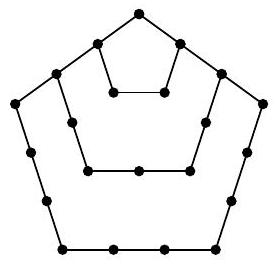
|
Answer: 145.
Solution. On the second picture, there are 5 stones. To get the third picture from it, you need to add three segments with three stones on each. The corner stones will be counted twice, so the total number of stones in the third picture will be $5+3 \cdot 3-2=12$.
To get the fourth picture from the third, you need to add three segments with four stones on each. The corner stones will be counted twice, so the total number of stones will be $12+3 \cdot 4-2=22$.
Similarly, we will calculate the number of stones on each of the remaining pictures:
on the 5th: $22+3 \cdot 5-2=35$;
on the 6th: $\quad 35+3 \cdot 6-2=51$;
on the 7th: $51+3 \cdot 7-2=70$;
on the 8th: $\quad 70+3 \cdot 8-2=92$;
on the 9th: $92+3 \cdot 9-2=117$
on the 10th: ~ 117+3 \cdot 10-2=145$.
|
145
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.2. In the chat of students from one of the schools, a vote was held: "On which day to hold the disco: October 22 or October 29?"
The graph shows how the votes were distributed an hour after the start of the voting.
Then, 80 more people participated in the voting, voting only for October 22. After that, the voting ended. The final distribution of votes is also shown on the graph.
How many people participated in the voting?
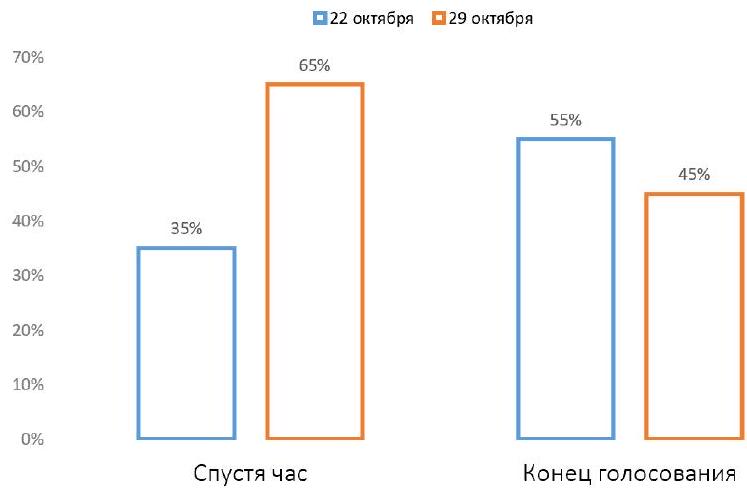
|
Answer: 260.
Solution. Let $x$ be the number of people who voted an hour after the start. From the left chart, it is clear that $0.35 x$ people voted for October 22, and $-0.65 x$ people voted for October 29.
In total, $x+80$ people voted, of which $45\%$ voted for October 29. Since there are still $0.65 x$ of them, we get the equation
$0.65 x=0.45(x+80)$, from which we find $x=180$. Therefore, a total of $180+80=260$ people participated in the voting.
|
260
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.7. The figure shows two equal triangles: $A B C$ and $E B D$. It turns out that $\angle D A E = \angle D E A = 37^{\circ}$. Find the angle $B A C$.
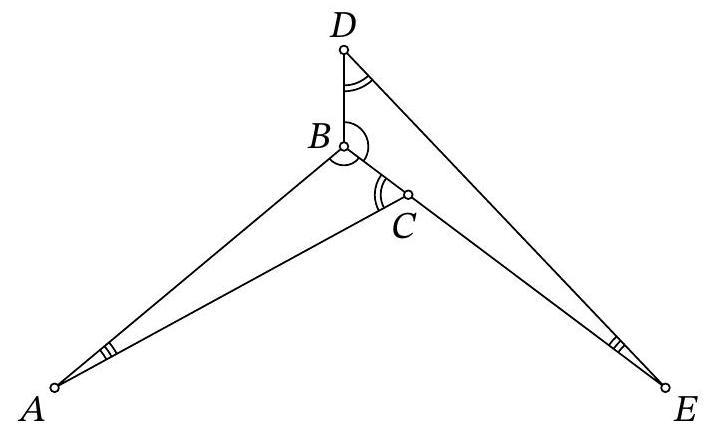
|
Answer: 7.
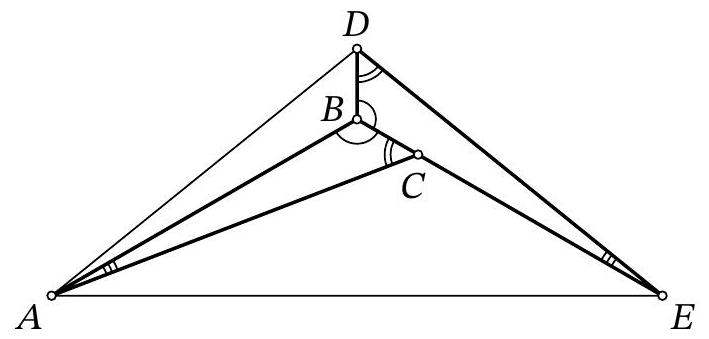
Fig. 4: to the solution of problem 8.7
Solution. Draw segments $A D$ and $A E$ (Fig. 4). Since $\angle D A E=\angle D E A=37^{\circ}$, triangle $A D E$ is isosceles, $A D=D E$.
Notice that triangle $A B D$ is equal to triangle $E B D$ by three sides: $B D$ is a common side, $A D=D E, A B=B E$ from the equality of triangles $A B C$ and $E B D$. Then $\angle D A B=$ $\angle B E D=\angle B A C$ and $\angle A B D=\angle D B E=\angle A B E=\frac{1}{3} \cdot 360^{\circ}=120^{\circ}$.
Since $A B=B E$, triangle $A B E$ is isosceles with an angle of $120^{\circ}$, so $\angle B A E=\frac{1}{2}\left(180^{\circ}-120^{\circ}\right)=30^{\circ}$. Therefore,
$$
\angle B A C=\angle D A B=\angle D A E-\angle B A E=37^{\circ}-30^{\circ}=7^{\circ}
$$
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.4. A line $\ell$ is drawn through vertex $A$ of rectangle $ABCD$, as shown in the figure. Perpendiculars $BX$ and $DY$ are dropped from points $B$ and $D$ to line $\ell$. Find the length of segment $XY$, given that $BX=4$, $DY=10$, and $BC=2AB$.
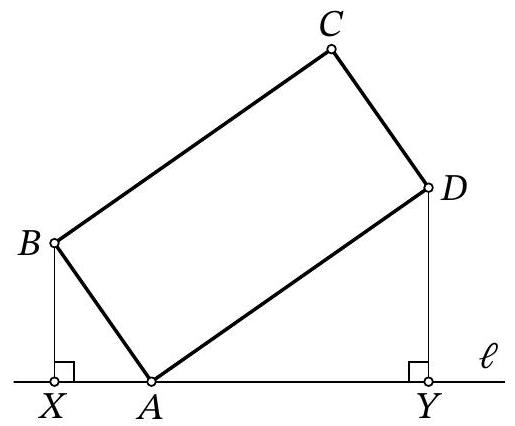
|
Answer: 13.
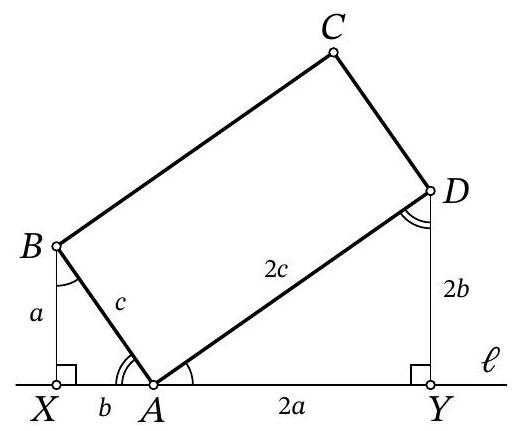
Fig. 5: to the solution of problem 9.4
Solution. Note that since $\angle Y A D=90^{\circ}-\angle X A B$ (Fig. 5), right triangles $X A B$ and $Y D A$ are similar by the acute angle $\angle Y A D=\angle X B A$. The similarity coefficient is the ratio $A B: A D$, which is $\frac{1}{2}$. From this, we get $X A=\frac{1}{2} D Y=5$ and $A Y=2 B X=8$, which in total gives $X Y=13$.
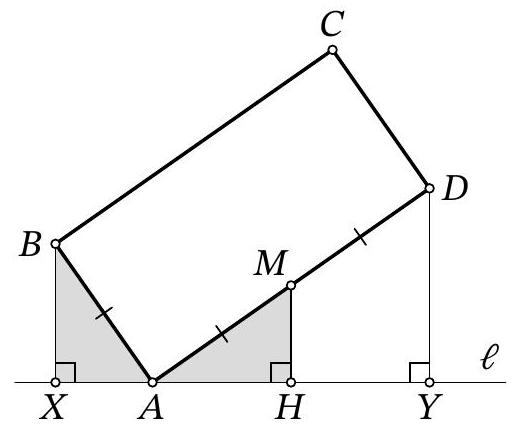
Fig. 6: to the solution of problem 9.4
Another solution. Let $M$ be the midpoint of segment $A D$, then $A M=M D=\frac{A D}{2}=\frac{B C}{2}=A B$ (Fig. 6). Drop a perpendicular from $M$ to $M H$ on line $\ell$. Since in triangle $A D Y$ the segment $M H$ passes through the midpoint of side $A D$ and is parallel to side $D Y$, it is the midline, $A H=H Y$ and $M H=\frac{D Y}{2}=\frac{10}{2}=5$.
Note that $\angle A B X=90^{\circ}-\angle B A X=90^{\circ}-\left(180-90^{\circ}-\angle M A H\right)=\angle M A H$. Then right triangles $A B X$ and $M A H$ are equal by hypotenuse $A B=A M$ and acute angle $\angle A B X=\angle M A H$. From this, it follows that $A X=M H=5$ and $A H=B X=4$.
Thus, $X Y=A X+A H+H Y=5+4+4=13$.
|
13
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.6. In triangle $A B C$, the angles $\angle B=30^{\circ}$ and $\angle A=90^{\circ}$ are known. On side $A C$, point $K$ is marked, and on side $B C$, points $L$ and $M$ are marked such that $K L=K M$ (point $L$ lies on segment $B M$).
Find the length of segment $L M$, if it is known that $A K=4, B L=31, M C=3$.
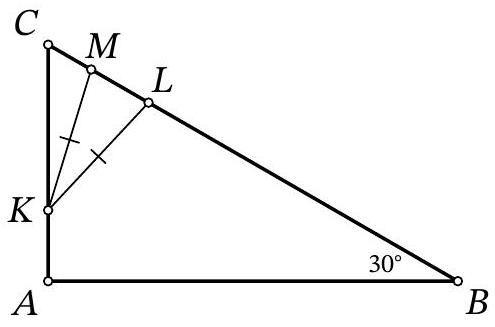
|
Answer: 14.
Solution. In the solution, we will use several times the fact that in a right-angled triangle with an angle of $30^{\circ}$, the leg opposite this angle is half the hypotenuse. Drop the height $K H$ from the isosceles triangle $K M L$ to the base (Fig. 7). Since this height is also a median, then $M H=H L=x$. In the right-angled triangle $C K H$ we have $\angle C K H=90^{\circ}-\angle C=\angle A=30^{\circ}$, so $K C=2 \cdot C H=2 \cdot(C M+M H)=$ $2 \cdot(3+x)=6+2 x$. In the right-angled triangle $A B C$ we have $\angle A=30^{\circ}$, so $B C=2 \cdot A C$. Setting up and solving the corresponding equation $31+2 x+3=2 \cdot(4+6+2 x)$, we find $x=7$. Then $L M=2 x=2 \cdot 7=14$.
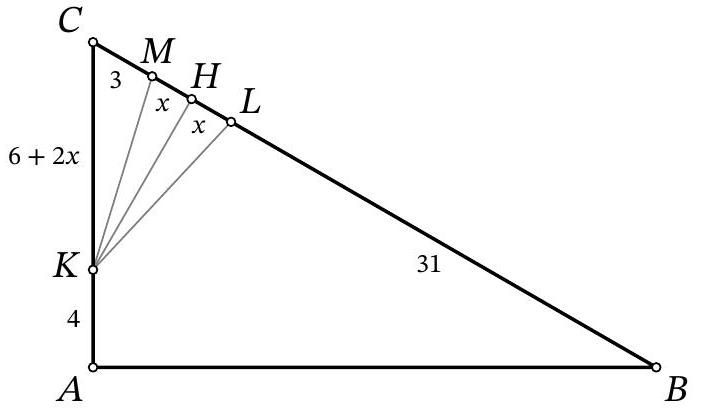
Figure 7: to the solution of problem 9.6
|
14
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.2. Points $A, B, C, D, E, F, G$ are located clockwise on a circle, as shown in the figure. It is known that $A E$ is the diameter of the circle. Also, it is known that $\angle A B F=81^{\circ}, \angle E D G=76^{\circ}$. How many degrees does the angle $F C G$ measure?
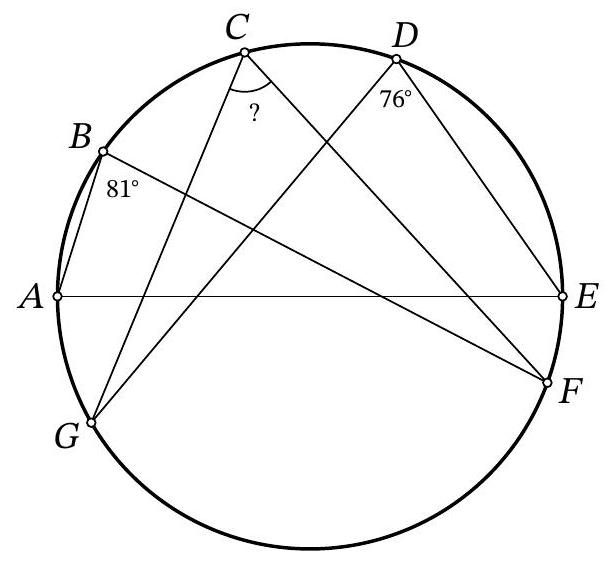
|
Answer: 67.
Solution. Since inscribed angles subtended by the same arc are equal, then $\angle A C F=$ $\angle A B F=81^{\circ}$ and $\angle E C G=\angle E D G=76^{\circ}$. Since a right angle is subtended by the diameter,
$$
\angle F C G=\angle A C F+\angle E C G-\angle A C E=81^{\circ}+76^{\circ}-90^{\circ}=67^{\circ}
$$
|
67
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.7. The graph of the function $f(x)=\frac{1}{12} x^{2}+a x+b$ intersects the $O x$ axis at points $A$ and $C$, and the $O y$ axis at point $B$, as shown in the figure. It turned out that for the point $T$ with coordinates $(3 ; 3)$, the condition $T A=T B=T C$ is satisfied. Find $b$.
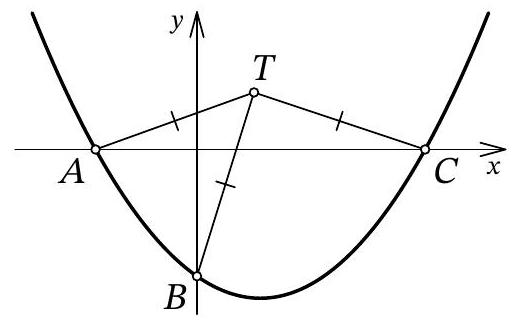
|
Answer: -6.
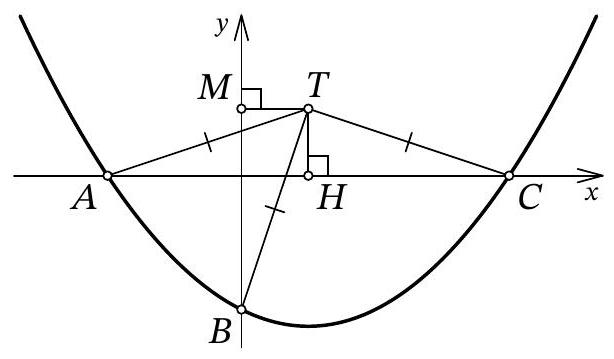
Fig. 11: to the solution of problem 10.7
Solution. Let point $A$ have coordinates $\left(x_{1} ; 0\right)$, and point $C$ have coordinates $\left(x_{2} ; 0\right)$. From the condition, it is clear that $x_{1} < 0$ and $x_{2} > 0$. Since $x_{1}$ and $x_{2}$ are the roots of the quadratic trinomial $f(x)$, by Vieta's theorem, we have $x_{1} \cdot x_{2} = 12b$, from which we get $b = \frac{x_{1} \cdot x_{2}}{12} < 0$.
Let $H$ be the point with coordinates $(3 ; 0)$ (Fig. 11). Clearly, in the isosceles triangle $A T C$, the segment $T H$ is the height, and therefore it is also the median. Thus, $3 - x_{1} = A H = H C = x_{2} - 3$, from which we get $x_{1} = 6 - x_{2}$.
Let $M$ be the point with coordinates $(0, 3)$. Since $T H = T M = 3$ and $T A = T B$, the right triangles $A T H$ and $B T M$ are equal by the leg and hypotenuse. Therefore, $3 - x_{1} = H A = M B = 3 - b$, that is, $x_{1} = b = \frac{x_{1} \cdot x_{2}}{12}$ (by Vieta's theorem), from which we find $x_{2} = 12$. Finally, $x_{1} = 6 - x_{2} = 6 - 12 = -6$ and $b = x_{1} = -6$.
Another solution. As in the previous solution, let the abscissas of points $A$ and $C$ be $x_{1}$ and $x_{2}$, respectively; we will also use the fact that point $B$ has coordinates $(0 ; b)$. Immediately, we understand that $O A = |x_{1}| = -x_{1}$, $O C = |x_{2}| = x_{2}$, and $O B = |b| = -b$.
Let's find the second intersection of the circle with the y-axis, let this be point $D$ with coordinates $(0 ; d)$ (Fig. 12). The chords $A C$ and $B D$ of the circle intersect at the origin $O$; from the properties of the circle, we know that $O A \cdot O C = O B \cdot O D$. We get $-x_{1} \cdot x_{2} = -b \cdot d$, from which, replacing $x_{1} \cdot x_{2}$ with $12b$ by Vieta's theorem, we get $d = 12$.

Fig. 12: to the solution of problem 10.7
It remains to note that triangle $BTD$ is isosceles, and the midpoint of its base, point $M$, has coordinates $(0 ; 3)$. Reflecting point $D(0 ; 12)$ relative to it, we get $B(0 ; -6)$.
|
-6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.2. A square was cut into five rectangles of equal area, as shown in the figure. The width of one of the rectangles is 5. Find the area of the square.
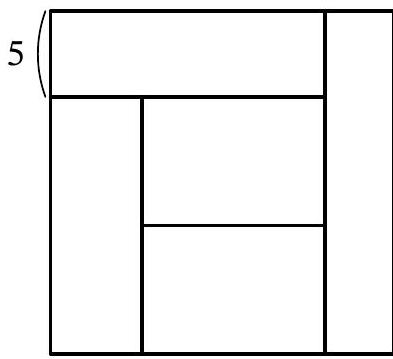
|
Answer: 400.
Solution. The central rectangle and the rectangle below it have a common horizontal side, and their areas are equal. Therefore, the vertical sides of these rectangles are equal, let's denote them by $x$ (Fig. 13). The vertical side of the lower left rectangle is $2x$, and we will denote its horizontal side by $y$. Since its area $2xy$ is the same as the area of the central rectangle, the horizontal side of the central rectangle is $2y$. Then the horizontal side of the upper left rectangle is $3y$, and its area $3y \cdot 5 = 15y$ should be equal to $2xy$, from which we find $x=7.5$. Then the side of the entire square is $5+2x=5+2 \cdot 7.5=20$, and its area is $20^2=400$.
|
400
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.3. In a football tournament, 15 teams participated, each playing against each other exactly once. For a win, 3 points were awarded, for a draw - 1 point, and for a loss - 0 points.
After the tournament ended, it turned out that some 6 teams scored at least $N$ points each. What is the greatest integer value that $N$ can take?

Fig. 13: to the solution of problem 11.2
#
|
# Answer: 34.
Solution. Let's call these 6 teams successful, and the remaining 9 teams unsuccessful. We will call a game between two successful teams an internal game, and a game between a successful and an unsuccessful team an external game.
First, note that for each game, the participating teams collectively earn no more than 3 points. Clearly, there were exactly $\frac{6 \cdot 5}{2}=15$ internal games, and only from these games did all successful teams collectively earn no more than $15 \cdot 3=45$ points. There were exactly $6 \cdot 9=54$ external games, and in each such game, a successful team earned no more than 3 points. Therefore, collectively, all successful teams earned no more than $54 \cdot 3=162$ points from external games. According to the problem, the successful teams collectively earned at least $6 \mathrm{~N}$ points, so we get the inequality $6 N \leqslant 45+162$. From this, it follows that $N \leqslant \frac{207}{6}<35$ and $N \leqslant 34$. Now let's provide an example for $N=34$. Number the teams from 1 to 15. We will show how teams from 1 to 6 can earn at least 34 points.
- Suppose each team from 1 to 6 won against each team from 7 to 15, then each team from 1 to 6 earned $9 \cdot 3=27$ points just from these games.
- Suppose the teams from 1 to 6 played among themselves as indicated in the following table (in each cell, the number of points is shown that the team from the corresponding row received in the game with the team from the corresponding column):
| | $\mathbf{1}$ | $\mathbf{2}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{5}$ | $\mathbf{6}$ |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| $\mathbf{1}$ | | 3 | 3 | 1 | 0 | 0 |
| $\mathbf{2}$ | 0 | | 3 | 3 | 1 | 0 |
| $\mathbf{3}$ | 0 | 0 | | 3 | 3 | 1 |
| $\mathbf{4}$ | 1 | 0 | 0 | | 3 | 3 |
| $\mathbf{5}$ | 3 | 1 | 0 | 0 | | 3 |
| $\mathbf{6}$ | 3 | 3 | 1 | 0 | 0 | |
- Suppose in each game between teams from 7 to 15, the team with the higher number won (the outcome of these games does not matter).
In total, teams from 1 to 6 earned at least $27+7=34$ points.
|
34
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.8. Given a parallelepiped $A B C D A_{1} B_{1} C_{1} D_{1}$. A point $X$ is chosen on the edge $A_{1} D_{1}$, and a point $Y$ is chosen on the edge $B C$. It is known that $A_{1} X=5, B Y=3, B_{1} C_{1}=14$. The plane $C_{1} X Y$ intersects the ray $D A$ at point $Z$. Find $D Z$.
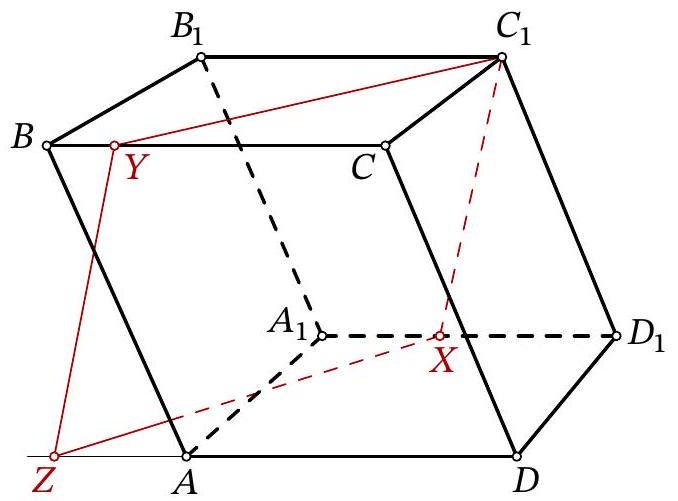
|
Answer: 20.
Solution. Lines $C_{1} Y$ and $Z X$ lie in parallel planes $B B_{1} C_{1} C$ and $A A_{1} D_{1} D$, so they do not intersect. Since these two lines also lie in the same plane $C_{1} X Z Y$, they are parallel. Similarly, lines $Y Z$ and $C_{1} X$ are parallel. Therefore, quadrilateral $C_{1} X Z Y$ is a parallelogram.
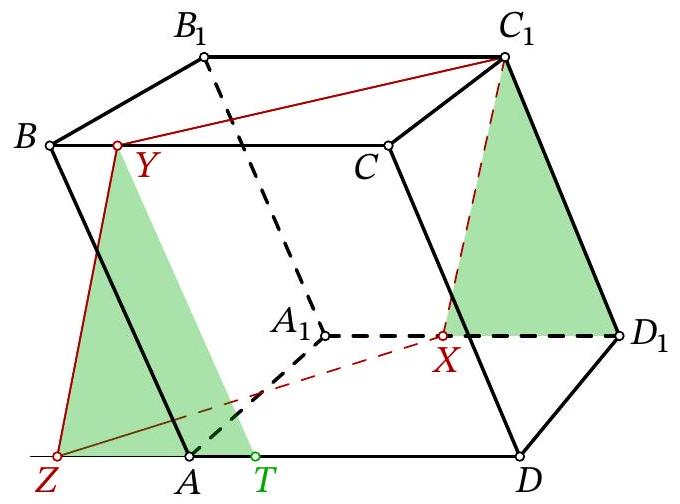
Fig. 15: to the solution of problem 11.8
Let us lay off segment $A T$ on $A D$, equal to $B Y$ (Fig. 15). Quadrilateral $B Y T A$ is a parallelogram, meaning segments $Y T, B A$, and $C_{1} D_{1}$ are parallel and equal. Additionally, segments $Y Z$ and $C_{1} X$ are parallel and equal; from the parallelism follows the equality of angles $Z Y T$ and $X C_{1} D_{1}$, which gives the equality of triangles $Z Y T$ and $X C_{1} D_{1}$.
Then
$$
\begin{aligned}
D Z & =Z T+A D-A T=X D_{1}+B_{1} C_{1}-B Y= \\
& =\left(A_{1} D_{1}-A_{1} X\right)+B_{1} C_{1}-B Y=(14-5)+14-3=20
\end{aligned}
$$
Another solution. As in the previous solution, we will use the fact that $C_{1} X Z Y$ is a parallelogram.
Consider the chain of vector equalities:
$$
\overrightarrow{D Z}=\overrightarrow{D C}+\overrightarrow{C Y}+\overrightarrow{Y Z}=\overrightarrow{D_{1} C_{1}}+\overrightarrow{C Y}+\overrightarrow{C_{1} X}=\overrightarrow{C Y}+\overrightarrow{D_{1} X}
$$
In the last part, all vectors are oriented the same as $\overrightarrow{D Z}$, so we can transition to the equality of segments and continue:
$$
D Z=C Y+D_{1} X=(C B-B Y)+\left(D_{1} A_{1}-A_{1} X\right)=2 B_{1} C_{1}-B Y-A_{1} X
$$
Substituting the lengths given in the condition, we get $D Z=2 \cdot 14-3-5=20$.
|
20
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.3. How many points (different from the origin) are there on the parabola $y=x^{2}$, such that the tangent at these points intersects both coordinate axes at points with integer coordinates not exceeding 2020 in absolute value?
|
Answer: 44. Solution. The equation of the tangent to the parabola $y=x^{2}$ at the point $\left(x_{0}, y_{0}\right)$, where $y_{0}=x_{0}^{2}$, is $y-y_{0}=2 x_{0}\left(x-x_{0}\right)$. From this, we find the coordinates of the points of intersection of the tangent with the axes, namely $x_{1}=\frac{x_{0}}{2}, y_{1}=-x_{0}^{2}$. Thus, $x_{0}$ must be an even number not exceeding $\sqrt{2020}$ in absolute value. Since $44<\sqrt{2020}<45$, there are 22 positive values of $x_{0}$, and considering the symmetric negative values, there will be twice as many.
|
44
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In a certain company, there are 100 shareholders, and any 66 of them own no less than $50 \%$ of the company's shares. What is the largest percentage of all shares that one shareholder can own?
|
4. Let $M$ be the shareholder owning the largest percentage of shares - $\mathrm{x} \%$ of shares. Divide the other 99 shareholders into three groups A, B, C, each with 33 shareholders. Let them own a, b, c percentages of shares, respectively. Then $2(100-x)=2(a+b+c)=(a+b)+(b+c)+(c+a) \geq 50+50+50$, i.e., $x \leq 25$. If each of the 99 shareholders, except M, owns 75/99=25/33\% of shares, then any 66 of them own exactly $50 \%$, and M owns exactly $25 \%$ of the shares.
|
25
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. The age of a certain person in 1988 was equal to the sum of the digits of their birth year. How old was he
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。
However, it seems there is a repetition. Here is the requested translation:
9.2. The age of a certain person in 1988 was equal to the sum of the digits of their birth year. How old was he
|
Answer: 22.
Solution. The number of years a person has lived is equal to the sum of the digits of a four-digit number, each of which is no more than 9. Therefore, he is no more than 36 years old, and he was born in the 20th century. Let $x$ be the number of tens, $y$ be the number of units in his birth year.
Then, according to his age, we get the equation
$$
1+9+x+y=88-(10 x+y), \text{ or } 11 x+2 y=78
$$
From this, $x=6, y=6$, which means he was born in 1966, and in 1988 he was 22 years old.
|
22
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.2 A group of friends went for a morning run around a lake. During the run, one by one they realized they had miscalculated their strength, and switched from running to walking. One of the friends calculated that he had run one-eighth of the total distance that the entire group had run, and walked one-tenth of the total distance that they had walked. How many people were on the outing?
|
Solution 1: Let the person who ran cover $x$ part of the road, then $0<x<1$, and he walked $(1-x)$ part of the way. If there were $n$ people in total, then according to the condition, the total distance covered by the group (expressed in terms of parts) is on one side $n$, and on the other side $8 x + 10(1-x) = 10 - 2 x$. Therefore, $2 x$ is an integer, so the only option is $x=0.5$, and $n=9$.
Solution 2: If this friend ran $a$ km and walked $b$ km, then the total distance covered by the group on one side is $8 a + 10 b$, and on the other side $n(a + b)$. Thus, $n = \frac{8 a + 10 b}{a + b} = 9 + \frac{b - a}{a + b}$. Since $a$ and $b$ are non-zero numbers, the last fraction can only be an integer if $a = b$, otherwise the absolute value of the non-zero numerator will be less than the absolute value of the denominator, and the fraction will not be an integer.
Criteria: The correct equation for the total distance was set up, but no conclusions were drawn, -2 points.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.4 For each integer from 10 to 2021, we found the product of the digits, and then added all the obtained results. What is the sum that was obtained?
|
Solution: Consider the product $(1+2+3+\cdots+9) \cdot(0+1+2+\cdots+9)$. If we expand the brackets, we get the products of pairs of digits that form all two-digit numbers. Similarly, in the product
$$
(1+2+3+\cdots+9) \cdot(0+1+2+\cdots+9) \cdot(0+1+2+\cdots+9)
$$
after expanding the brackets, we get all combinations of digits from three-digit numbers, and
$$
1 \cdot(0+1+2+\cdots+9) \cdot(0+1+2+\cdots+9) \cdot(0+1+2+\cdots+9)
$$
gives all combinations for numbers from 1000 to 1999. Numbers from 2000 to 2021 give a zero product of digits. Therefore, the answer is $45^{2}+45^{3}+45^{3}=184275$.
Criteria:
- The answer is given by the formula $45^{2}+45^{3}+45^{3}$ and the final answer in decimal form is not calculated - no points deducted
- Only the sum of the products for two-digit numbers is correctly calculated - 1 point
|
184275
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.3 There are 12 natural numbers. It is known that the sum of any three of them is not less than 100. Prove that the sum of all the numbers is not less than 406.
|
Solution. Arrange these numbers in non-decreasing order: $\mathrm{a}_{1} \leq \mathrm{a}_{2} \leq \mathrm{a}_{3} \leq \mathrm{a}_{4} \leq \ldots \leq \mathrm{a}_{12}$. By the condition $\mathrm{a}_{1}+\mathrm{a}_{2}+\mathrm{a}_{3} \geq 100$, therefore $3 \mathrm{a}_{3} \geq 100, \mathrm{a}_{3} \geq \frac{100}{3}>33$. Since $\mathrm{a}_{3}$ is an integer, the inequality $\mathrm{a}_{3} \geq 34$ holds. Therefore, $\mathrm{a}_{4} \geq 34, \mathrm{a}_{5} \geq 34, \ldots, \mathrm{a}_{12} \geq 34$.
But then $\left(a_{1}+a_{2}+a_{3}\right)+\left(a_{4}+a_{5}+\ldots+a_{12}\right) \geq 100+9 \cdot 34=406$.
|
406
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
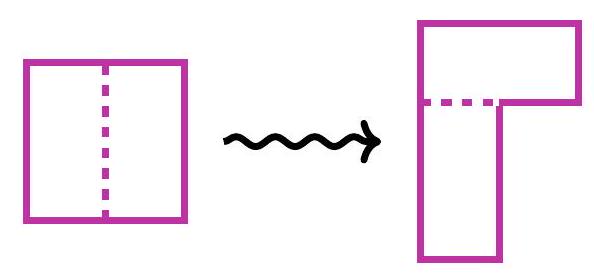
1. The midpoints of adjacent sides of a rectangle with a perimeter of 32 were connected by segments. The same operation was performed on the resulting quadrilateral: the midpoints of adjacent sides were connected by segments (see figure). How many times in total does one need to perform such an operation so that the perimeter of the resulting quadrilateral first becomes less than 1?
|
Answer: 11.
Solution: After two operations, a quadrilateral is obtained, the sides of which are the midlines of triangles with bases parallel to the sides of the original rectangle. Therefore, this quadrilateral is a rectangle, and each of its sides is half the length of the corresponding side of the original rectangle. Thus, after 2 operations, the perimeter is halved. After 5 pairs of operations, the perimeter will decrease by a factor of $2^{5}=32$ and will become equal to 1. From the triangle inequality, it is clear that the perimeter decreases with each operation. Therefore, after 11 operations, the perimeter will be less than 1.
Comment: A specific case is considered (for example, calculations are performed for a rectangle with sides given by specific numbers), but the method of calculations can be applied to any rectangle - 4 points; the method is applicable only to rectangles of a certain type - 1-2 points. If the first two operations were not taken into account when counting the number of operations, deduct 1 point. If it is not proven that the perimeter decreases with each operation, deduct 1 point.
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. A semicircle with diameter $A B$ and center at point $O$ is divided into three parts by points $C$ and $D$ such that point $C$ lies on the arc $A D$. Perpendiculars $D E$ and $D F$ are dropped from point $D$ to segments $O C$ and $A B$ respectively. It turns out that $D E$ is the angle bisector of triangle $A D C$, and $D O$ is the angle bisector of triangle $A D F$. Find the angle $C A D$.
|
Answer: $20^{\circ}$.
Solution. Triangle $A O D$ is isosceles ($O D=O A$, as radii), hence, $\angle O A D=\angle O D A$. Since $D O$ is the bisector of angle $A D F$, then $\angle O A D=$ $\angle O D F$. Calculation of angles in the right triangle $A F D$ shows that $\angle O A D=30^{\circ}$. Let $G$ be the point of intersection of segments $A D$ and $O C$. Segment $D E$ is the height and bisector in triangle $D G C$; therefore, this triangle is isosceles with angle $E C D$ at the base. Triangle $O C D$ is also isosceles with angle $E C D$ at the base, hence, the angles at the vertices of these two triangles are also equal, i.e., $\angle C D G=\angle C O D$. Let $\angle C D G=\angle C O D=a$, then $\angle G C D=$ $\angle O D C=30^{\circ}+a$. By calculating the sum of the angles in triangle $C O D$, we get that $a=40^{\circ}$. The desired angle $C A D$ is inscribed and subtends the same arc as the central angle $D O C$, therefore, $\angle C A D=20^{\circ}$.
Comment. A complete and justified solution - 7 points. A generally correct reasoning containing minor gaps or inaccuracies - up to 5 points. Only the value of $\angle O A D$ found - 2 points.
|
20
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.2. Vlad and Dima decided to earn some money. Each of them decided to deposit 3000 rubles in the bank and withdraw all the money after a year.
Vlad chose the deposit "Confidence": the amount increases by $20\%$ over the year, but the bank charges a $10\%$ fee upon withdrawal.
Dima chose the deposit "Reliability": the amount increases by $40\%$ over the year, but the bank charges a $20\%$ fee upon withdrawal.
("The bank charges a fee of $n\%$" means that the bank keeps $n\%$ of the current deposit amount and returns the remaining part to the owner.)
Who will receive a higher annual profit from the deposit?
What will the difference be? Express the answer in rubles. If the profit is the same, write 0.
|
Answer: Dima will earn 120 rubles more.
Solution. Vlad's deposit amount will increase to $3000 \cdot 1.2$ rubles in a year, and after withdrawal, it will decrease to $3000 \cdot 1.2 \cdot 0.9=3240$ rubles.
Dima's deposit amount will increase to $3000 \cdot 1.4$ rubles in a year, and after withdrawal, it will decrease to $3000 \cdot 1.4 \cdot 0.8=3360$ rubles.
Therefore, Dima will earn 120 rubles more.
|
120
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.3. The Smeshariki Kros, Yozhik, Nyusha, and Barash ate a total of 86 candies, and each of them ate no fewer than 5 candies. It is known that:
- Nyusha ate more candies than each of the other Smeshariki;
- Kros and Yozhik together ate 53 candies.
How many candies did Nyusha eat
|
Answer: 28.
Solution. Krosh or Yozhik ate at least 27 candies (otherwise, they would have eaten no more than $26+26=52$ candies in total), so Nusha ate at least 28 candies. Considering that Barash ate at least 5 candies, we get that all of them together ate at least $53+28+5=86$ candies. Therefore, this is only possible if Nusha ate exactly 28 candies, and Barash exactly 5 candies.
|
28
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.5. A store sells four types of nuts: hazelnuts, almonds, cashews, and pistachios. Stepan wants to buy 1 kilogram of nuts of one type and another 1 kilogram of nuts of a different type. He calculated how much such a purchase would cost him depending on which two types of nuts he chooses. Five out of six possible purchases by Stepan would cost 1900, 2070, 2110, 2330, and 2500 rubles. How many rubles does the cost of the sixth possible purchase amount to?
|
Answer: 2290.
Solution. Let $a, b, c, d$ be the cost of 1 kilogram of hazelnuts, almonds, cashews, and pistachios, respectively. From the condition, it follows that the set $A=\{1900,2070,2110,2330,2500\}$ is contained in the set $B=\{a+b, b+c, c+d, d+a, a+c, b+d\}$.
Note that the 6 elements of set $B$ can be divided into 3 pairs $(a+b, c+d),(b+c, d+a)$, $(a+c, b+d)$ with the same sum $a+b+c+d$. This means that in set $A$, 2 pairs of numbers with the same sum can be identified.
It is not difficult to understand that these can only be the pairs $(1900,2500)$ and $(2070,2330)$ with a sum of 4400 (for example, one can notice that all other pairs either intersect or their sums differ in the last two digits). Then the unknown sixth cost is easily calculated: $4400-2110=2290$ rubles.
Remark. The condition of the problem is satisfied for $a=930, b=970, c=1140, d=1360$.
|
2290
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.6. A magic square is a $3 \times 3$ table in which numbers are arranged so that the sums of all rows, columns, and the two main diagonals are the same. The figure shows a magic square in which all numbers except three have been erased. Find what the number in the upper left corner of the square is.
| $?$ | 31 | 9 |
| :---: | :---: | :---: |
| 13 | | |
| | | |
|
Answer: 14.
Solution. Let the unknown number be $x$, then the sums in all rows, columns, and on the main diagonals are $9+31+x=40+x$.
1) Considering the left column, we get that the number in the lower left corner of the square is 27.
2) Considering the main diagonal going up to the right, we get that the number in the center of the square is $4+x$.
3) Considering the main diagonal going down to the right, we get that the number in the lower right corner of the square is $36-2x$.
4) Considering the right column, we get that the number in the middle cell of this column is $2x-5$.
5) Considering the middle row, we get the necessary equation for $x$:
$$
40+x=13+(4+x)+(2x-5)
$$
Solving it, we find $x=14$.
|
14
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.7. All 25 students in class 7A participated in a quiz consisting of three rounds. In each round, each participant scored a certain number of points. It is known that in each round, as well as in the total of all three rounds, all participants scored a different number of points.
Student Kolya from 7A was third in the first round of the quiz, fourth in the second, and fifth in the third. What is the lowest place Kolya could have taken among all classmates in the total points for all three rounds of the quiz?
|
Answer: 10.
Solution. In the first round, 2 classmates overtook Kolya, in the second - 3, in the third - 4. Then, in the sum of all three rounds, he could be overtaken by no more than $2+3+4=9$ classmates, i.e., in the sum of the three rounds, he could not end up lower than 10th place.
Now let's provide an example of how Kolya could end up exactly in 10th place. Suppose
- in each of the rounds, Kolya scored 100 points;
- in the first round, Andrey and Boris scored 1000 and 2000 points respectively and took the first two places
- in the second round, Vlad, Gennady, and Denis scored 10000, 20000, 30000 points respectively and took the first three places
- in the third round, Masha, Svetlana, Tanya, and Katya scored 100000, 200000, 300000, 400000 points respectively and took the first four places;
- in each of the rounds, all other participants after Kolya were ordered alphabetically and scored a number of points equal to their position in the ranking from the end.
It is easy to see that all the conditions of the problem are satisfied.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
84. a) Prove that there exists a pair of two-digit numbers such that if 20 is added to the first number and 15 is subtracted from the second, the resulting numbers will remain two-digit, and their product will be equal to the product of the original numbers? b) How many such pairs are there?
|
Answer: b) 16 pairs. Hint For part a), it is sufficient to provide a specific example (see problem 7.4). b) Let $a, b$ be the desired pair of numbers. Then $(a+20)(b-15)=a b$. From this, $20 b-15 a=20 \cdot 15 \Leftrightarrow 4 b-3 a=60$.
Since 60 and $3a$ are divisible by 3, $b$ must also be divisible by 3, i.e., $b=3 b_{1}$ for some natural number $b_{1}$. Similarly, $a=4 a_{1}$. Then, by dividing the last equation by 12, we get $b_{1}=a_{1}+5$. From the condition that the numbers $a+20$ and $b-15$ are two-digit, we will have the restrictions $4 a_{1}+20<100$ and $3 a_{1}+15<100$. Taking any natural number $a_{1}$ from 4 to 19, we get 16 different values, and for them, the numbers $a=4 a_{1}$ and $b=3\left(a_{1}+5\right)$ will be the desired pairs.
|
16
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.3. Given a convex quadrilateral $ABCD$, $X$ is the midpoint of diagonal $AC$. It turns out that $CD \parallel BX$. Find $AD$, if it is known that $BX=3, BC=7, CD=6$.
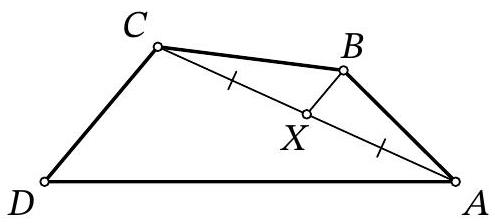
|
Answer: 14.
Solution. Double the median $B X$ of triangle $A B C$, to get point $M$. Quadrilateral $A B C M$ is a parallelogram (Fig. 1).
Notice that $B C D M$ is also a parallelogram, since segments $B M$ and $C D$ are equal in length (both 6) and parallel. This means that point $M$ lies on segment $A D$, since $A M \| B C$ and $M D \| B C$.
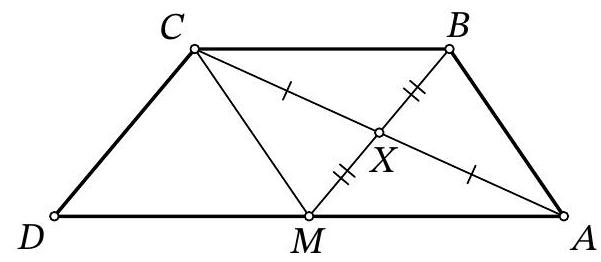
Fig. 1: to the solution of problem 9.3
Now it is easy to find the desired segment:
$$
A D=A M+M D=B C+B C=14
$$
|
14
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.7. The sides of the square $A B C D$ are parallel to the coordinate axes, with $A B$ lying on the y-axis, and the square is positioned as shown in the figure. The parabola defined by the equation
$$
y=\frac{1}{5} x^{2}+a x+b
$$
passes through points $B$ and $C$. Additionally, the vertex of this parabola (point $E$) lies on the segment $A D$. Find the sum of the roots of the quadratic trinomial whose graph is the parabola.
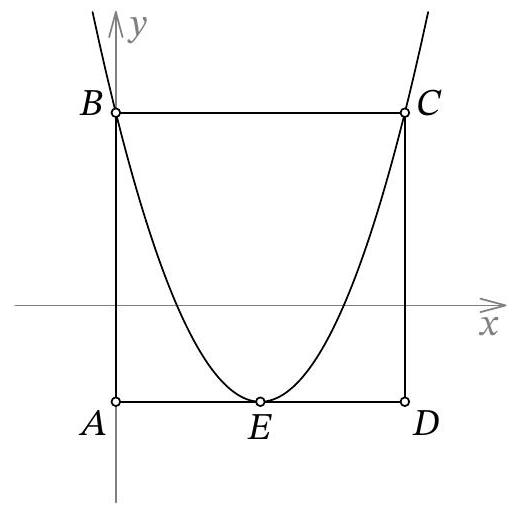
|
Answer: 20.
Solution. Note that the parabola is symmetric with respect to the vertical axis passing through its vertex, point $E$. Since points $B$ and $C$ are on the same horizontal line, they are symmetric with respect to this axis. This means that this axis passes through the midpoint of $B C$, and therefore, through the midpoint of $A D$.
Now that we have established that $E$ is the midpoint of $A D$, let's find the length of the side of the square $A B C D$. By completing the square in the quadratic polynomial, we get
$$
y=\frac{1}{5}\left(x-x_{E}\right)^{2}+y_{E}
$$
where $\left(x_{E}, y_{E}\right)$ are the coordinates of the vertex of the parabola (we will similarly denote the coordinates of other marked points). Substituting $x=x_{B}, y=y_{B}$ (the equality will hold since $B$ lies on the parabola) and moving $y_{E}$ to the left side, we get:
$$
y_{B}-y_{E}=\frac{1}{5}\left(x_{B}-x_{E}\right)^{2}
$$
If we denote the unknown side length of the square by $L$, then $y_{B}-y_{E}=L$ and $x_{B}-x_{E}=L / 2$. We obtain the relation $L=\frac{1}{5}(L / 2)^{2}$, from which it is not difficult to extract $L=20$.
It remains to recall that the points on the graph corresponding to the roots of the polynomial are also symmetric with respect to the axis of the parabola, which means that the semi-sum of the roots is equal to the abscissa of the vertex $x_{E}=L / 2$. Therefore, the sum of the roots is $L=20$.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.4. An isosceles trapezoid $ABCD$ with bases $BC$ and $AD$ is such that $\angle ADC = 2 \angle CAD = 82^{\circ}$. Inside the trapezoid, a point $T$ is chosen such that $CT = CD, AT = TD$. Find $\angle TCD$. Give your answer in degrees.
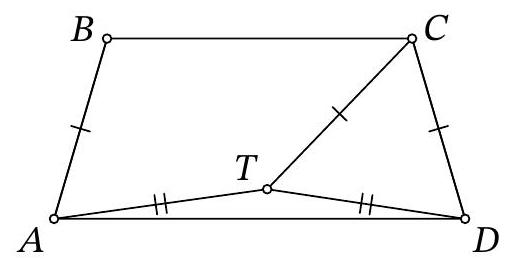
|
Answer: $38^{\circ}$.
Solution. Let $a$ be the length of the lateral side of the trapezoid. Note that point $T$ lies on the perpendicular bisector of the bases of the trapezoid, that is, on its axis of symmetry. From symmetry, we get that $B T=T C=a$ (Fig. 5).
Fig. 5: to the solution of problem 10.4
Next, note that $\angle B A D=\angle C D A=2 \angle C A D$, so $A C$ is the bisector of angle $B A D$. Since $\angle C A D=\angle A C B$ due to parallelism, triangle $A B C$ is isosceles. Therefore, $B C$ is also equal to $a$.
We have obtained that triangle $B T C$ is equilateral, and its angles are each $60^{\circ}$. Now it is not difficult to calculate the required angle:
$$
\angle T C D=\angle B C D-\angle B C T=\left(180^{\circ}-\angle A D C\right)-60^{\circ}=120^{\circ}-\angle A D C=38^{\circ} .
$$
|
38
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
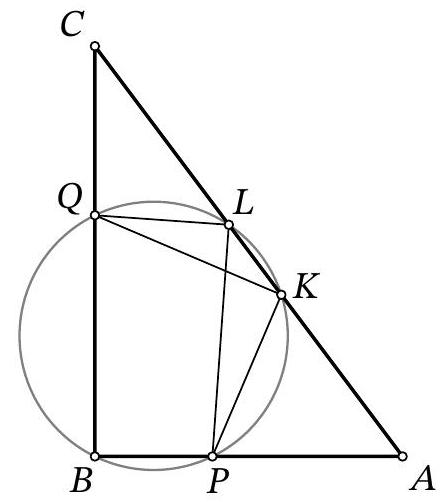
Problem 10.7. Given a right triangle $ABC$ with legs $AB=42$ and $BC=56$. A circle passing through point $B$ intersects side $AB$ at point $P$, side $BC$ at point $Q$, and side $AC$ at points $K$ and $L$. It is known that $PK=KQ$ and $QL: PL=3: 4$. Find $PQ^2$.
|
Answer: 1250.
Solution. Since in a cyclic quadrilateral the sum of opposite angles is $180^{\circ}$, then $\angle P K L=\angle P L Q=90^{\circ}$. From the condition, it also follows that right triangles $A B C$ and $Q L P$ are similar (Fig. 6). From this similarity and the cyclic nature of the pentagon
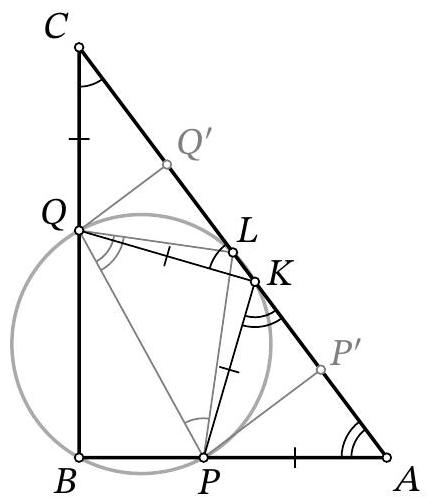
Fig. 6: to the solution of problem 10.7
$B Q L K P$, we get that $\angle C=\angle Q P L=\angle Q K L$, so triangle $C Q K$ is isosceles and $C Q=Q K$. Similarly, $\angle A=\angle P Q L=180^{\circ}-\angle P K L=\angle A K P$, so $A P=P K$. Also, by the condition, $P K=K Q$.
Thus, $C Q=Q K=P K=A P=x$. From the condition, we have
$$
A C=\sqrt{A B^{2}+B C^{2}}=\sqrt{14^{2}\left(3^{2}+4^{2}\right)}=14 \cdot 5=70
$$
and also $\cos A=\frac{3}{5}$ and $\cos C=\frac{4}{5}$. Drop perpendiculars $P P^{\prime}$ and $Q Q^{\prime}$ to the hypotenuse $A C$. Then
$$
70=A C=A K+K C=2 A P^{\prime}+2 C Q^{\prime}=2 x \cos A+2 x \cos C=2 x\left(\frac{3}{5}+\frac{4}{5}\right)=\frac{14}{5} x
$$
from which $x=25$. By the Pythagorean theorem in triangle $P K Q$, we get
$$
P Q^{2}=P K^{2}+Q K^{2}=25^{2}+25^{2}=1250
$$
Another solution. As in the previous solution, by the Pythagorean theorem, we find $A C=70$. Also, from the similarity and the cyclic nature, we get $\angle C=\angle Q P L=\angle Q B L$, so triangle $C L B$ is isosceles and $C L=L B$. Similarly, $\angle A=\angle P Q L=\angle P B L$, so $A L=B L=C L$, i.e., $L$ is the midpoint of the hypotenuse.
Point $K$ is equidistant from points $P$ and $Q$, i.e., it is the midpoint of the arc $P L Q$ of the given circle and lies on the angle bisector of $\angle B$. Then, by the property of the angle bisector, we get $A K: K C=$ $A B: B C=3: 4$, which gives us $A K=\frac{3}{7} A C=30$ and $C K=\frac{4}{7} A C=40$. From the properties of secants to a circle drawn from the same point, we get $A K \cdot A L=A B \cdot A P$ and $C K \cdot C L=C Q \cdot C B$, from which respectively
$$
A P=\frac{A K \cdot A L}{A B}=\frac{30 \cdot 35}{42}=25 \quad \text { and } \quad C Q=\frac{C K \cdot C L}{C B}=\frac{40 \cdot 35}{56}=25
$$
Then $B P=A B-A P=17$ and $B Q=B C-C Q=31$, from which by the Pythagorean theorem in triangle $P B Q$ we get $P Q^{2}=P B^{2}+B Q^{2}=17^{2}+31^{2}=1250$.
|
1250
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.4. On the side $AC$ of triangle $ABC$, points $M$ and $N$ are marked ($M$ lies on the segment $AN$). It is known that $AB = AN$, $BC = MC$. The circumcircles of triangles $ABM$ and $CBN$ intersect at points $B$ and $K$. How many degrees does the angle $AKC$ measure if $\angle ABC = 68^\circ$?
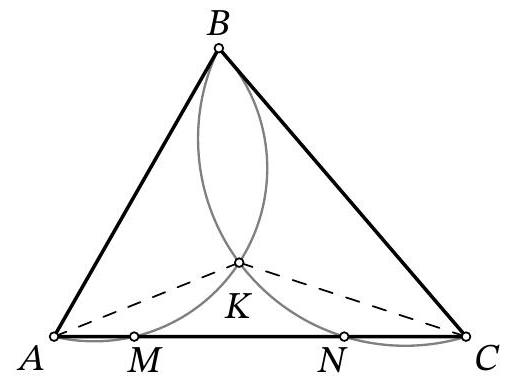
|
Answer: 124.
Solution. From the given in the problem, it follows that $68^{\circ}+\alpha+\gamma=180^{\circ}$, where $\alpha$ and $\gamma$ denote the measures of angles $A$ and $C$ of the triangle, respectively. Since triangle $BAN$ is isosceles, $\angle BNA=90^{\circ}-\frac{1}{2} \alpha$, so $\angle BNC=90^{\circ}+\frac{1}{2} \alpha$. Similarly, $\angle BMA=90^{\circ}+\frac{1}{2} \gamma$.
From the fact that these angles are inscribed in the corresponding circles, we get $\angle BKA=90^{\circ}+\frac{1}{2} \alpha$ and $\angle BKC=90^{\circ}+\frac{1}{2} \gamma$ (Fig. 7). It remains
$$
\angle AKC=360^{\circ}-\angle BKA-\angle BKC=180^{\circ}-\frac{1}{2}(\alpha+\gamma)=90^{\circ}+\frac{1}{2} \cdot 68^{\circ}=124^{\circ}
$$
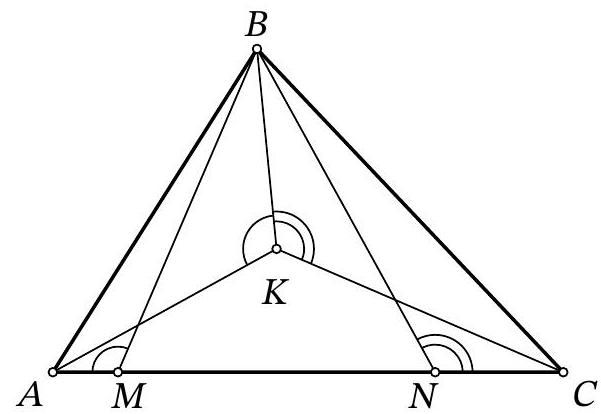
Fig. 7: to the solution of problem 11.4
Remark. Point $K$ is the incenter of triangle $ABC$.
|
124
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. Sixty students went on a trip to the zoo. Upon returning to school, it turned out that 55 of them had forgotten their gloves, 52 - their scarves, and 50 had managed to forget their hats. Find the smallest number of the most absent-minded students - those who lost all three items.
|
Answer: 37 students.
Solution: From the condition, it follows that five students have gloves, eight have a scarf, and ten have a hat. Thus, at least one item is owned by no more than $5+8+10=23$ people. Therefore, no fewer than $60-23=$ 37 people have lost all three items. All three items will be lost by exactly 37 people if each of the remaining 23 loses exactly two items.
|
37
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.2. There are 7 safes and 7 codes for them, but it is unknown which code belongs to which safe. What is the minimum number of attempts required to guarantee matching the codes to the safes?
|
Answer: 21 attempts.
Solution. We enter the first code in sequence on each of the safes. If one of the safes opens - we leave this safe and the code. If none of the first 6 safes open, then this code corresponds to the seventh safe. No more than six attempts have been used, and there are 6 safes and 6 codes left. We take another code and enter it on all the safes in sequence. To determine which safe this code corresponds to, no more than 5 attempts are needed. And so on. In total, no more than $6+5+4+3+2+1$ = 21 attempts are required.
|
21
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.3. The teacher is going to give the children a problem of the following type. He will inform them that he has thought of a polynomial $P(x)$ of degree 2017 with integer coefficients, the leading coefficient of which is 1. Then he will tell them $k$ integers $n_{1}, n_{2}, \ldots, n_{k}$, and separately inform them of the value of the expression $P\left(n_{1}\right) \cdot P\left(n_{2}\right) \cdot \ldots \cdot P\left(n_{k}\right)$. Based on this data, the children are supposed to find the polynomial that the teacher could have thought of. For what smallest $k$ can the teacher formulate such a problem so that the polynomial found by the children necessarily coincides with the one thought of?
(G. Zhukov)
|
Answer. For $k=2017$.
Solution. First, we prove that $k>2016$. Suppose the teacher used some $k \leqslant 2016$, thinking of the polynomial $P(x)$. Consider the polynomial $Q(x)=P(x)+(x-n_{1})(x-n_{2}) \ldots(x-n_{k})$. Note that the degree of the polynomial $Q(x)$ is also 2017, and its leading coefficient is also 1. Moreover, $P\left(n_{1}\right) P\left(n_{2}\right) \ldots P\left(n_{k}\right)=Q\left(n_{1}\right) Q\left(n_{2}\right) \ldots Q\left(n_{k}\right)$, but $P(x) \neq Q(x)$. Therefore, the children could have found the polynomial $Q(x)$ instead of $P(x)$, meaning the teacher did not achieve the required result.
It remains to prove that for $k=2017$ the teacher can come up with the required problem.
Lemma. Let $P(x)$ be a polynomial with integer coefficients, and let $a$ and $b$ be different integers. Then $P(a)-P(b)$ is divisible by $a-b$.
Proof. In the difference $P(a)-P(b)$, we group the terms by powers: if $P(x)=p_{n} x^{n}+p_{n-1} x^{n-1}+\ldots+p_{1} x+p_{0}$, then $P(a)-P(b)=p_{n}\left(a^{n}-b^{n}\right)+p_{n-1}\left(a^{n-1}-b^{n-1}\right)+\ldots+p_{1}(a-b)$, where each term is divisible by $a-b$.
Let $k=2017$. Set $n_{i}=4 i$ for $i=1,2, \ldots, k$; suppose the teacher tells the children that $P\left(n_{1}\right) P\left(n_{2}\right) \ldots P\left(n_{k}\right)=1$. Then the polynomial $P(x)=\left(x-n_{1}\right)\left(x-n_{2}\right) \ldots\left(x-n_{k}\right)+1$ fits the condition. Suppose there is another polynomial $Q(x)$ that also fits the condition. Then, since $Q\left(n_{1}\right) Q\left(n_{2}\right) \ldots Q\left(n_{k}\right)=1$ and the coefficients of the polynomial $Q(x)$ are integers, $Q\left(n_{i}\right)= \pm 1$ for any $i=1,2, \ldots, k$.
If there exist $i$ and $j$ such that $Q\left(n_{i}\right)=1$ and $Q\left(n_{j}\right)=-1$, then the difference $Q\left(n_{i}\right)-Q\left(n_{j}\right)=2$ is not divisible by $n_{i}-n_{j}$, which contradicts the lemma. Therefore, all values $Q\left(n_{i}\right)$ are equal to each other and are all either 1 or -1. However, all values cannot be -1, because in the product $Q\left(n_{1}\right) Q\left(n_{2}\right) \ldots Q\left(n_{k}\right)$ there are an odd number of factors and the product would be -1. Thus, $Q\left(n_{i}\right)=1$ for any $i=1,2, \ldots, k$. Then the difference $P(x)-Q(x)$ is a polynomial of degree less than $k$, having at least $k$ roots, meaning this polynomial is identically zero, and $P(x)=Q(x)$. Contradiction.
Remark. Using the lemma, it can be shown that the polynomial $P(x)=\left(x-n_{1}\right)\left(x-n_{2}\right) \ldots\left(x-n_{2017}\right) \pm 1$ fits for any different integers $n_{1}, n_{2}, \ldots, n_{2017}$.
Comment. Only the correct answer - 0 points.
A complete solution to the problem consists of two parts:
(a) proving that the required cannot be achieved for $k \leqslant 2016$ - evaluated out of 2 points;
(b) proving that for $k=2017$ the required can be achieved - evaluated out of 5 points.
If in part (b) the polynomial $P(x)=\left(x-n_{1}\right)(x-\left.n_{2}\right) \ldots\left(x-n_{k}\right) \pm 1$ (for some different integers $n_{1}, n_{2}, \ldots, n_{k}$) is presented, but it is not proven that no other polynomial $Q(x)$ satisfies the condition - 2 points (out of five).
Using the lemma about the divisibility of $P(a)-P(b)$ by $a-b$ without proof does not result in point deductions.
|
2017
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. What is the minimum number of unit-radius circles required to completely cover a triangle with sides $2 ; 3 ; 4$?
|
Answer: three circles. Solution. Let $A C=4, A B=2, B C=3$ and let $C_{1}, A_{1}$ and $B_{1}$ be the midpoints of sides $A B, B C$ and $A C$ respectively. Note that angle $B$ is obtuse, since $A C^{2}>A B^{2}+B C^{2}$. Therefore, points $B$ and $B_{1}$ lie inside the circle of radius 1 with center at point $O$ - the midpoint of segment $C_{1} A_{1}$ (here we take into account that $\angle C_{1} B_{1} A_{1}=\angle B$ and that the length of the midline is half of $A C$). Thus, the parallelogram $B A_{1} B_{1} C_{1}$ is covered by a unit circle with center $O$. Two other unit circles with centers $M$ and $N$ at the midpoints of $A B_{1}$ and $B_{1} C$ will cover triangles $A C_{1} B_{1}$ and $B_{1} A_{1} C$ (here again we use the fact that angles $A C_{1} B_{1}$ and $B_{1} A_{1} C$ are equal to angle $B$, and thus are obtuse). We will now show that two unit circles are insufficient. Otherwise, their centers must coincide with points $M$ and $N$ (otherwise, segment $A C$ of length 4 could not be covered by two circles of diameter 2). But then point $B$ lies outside both of these circles, since otherwise
the triangle inequality would be violated for triangle $A B M \quad(A B<A M+M B)$ or for triangle $N B C(B C<N B+N C)^{\circ}$.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4-1. Katya attached a square with a perimeter of 40 cm to a square with a perimeter of 100 cm as shown in the figure. What is the perimeter of the resulting figure in centimeters?
|
Answer: 120.
Solution: If we add the perimeters of the two squares, we get $100+40=140$ cm. This is more than the perimeter of the resulting figure by twice the side of the smaller square. The side of the smaller square is $40: 4=10$ cm. Therefore, the answer is $140-20=120$ cm.
|
120
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5-1. A square with a side of 100 was cut into two equal rectangles. They were placed next to each other as shown in the figure. Find the perimeter of the resulting figure.
|
Answer: 500.
Solution. The perimeter of the figure consists of 3 segments of length 100 and 4 segments of length 50. Therefore, the length of the perimeter is
$$
3 \cdot 100 + 4 \cdot 50 = 500
$$
|
500
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5-5. Along a straight alley, 400 lamps are placed at equal intervals, numbered in order from 1 to 400. At the same time, from different ends of the alley, Alla and Boris started walking towards each other at different constant speeds (Alla from the first lamp, Boris from the four hundredth). When Alla was at the 55th lamp, Boris was at the 321st lamp. At which lamp will their meeting occur? If the meeting occurs between two lamps, indicate the smaller number of these two.

|
Answer. At the 163rd lamppost.
Solution. There are a total of 399 intervals between the lampposts. According to the condition, while Allа walks 54 intervals, Boris walks 79 intervals. Note that $54+79=133$, which is exactly three times less than the length of the alley. Therefore, Allа should walk three times more to the meeting point than to the 55th lamppost, i.e., $54 \cdot 3=162$ intervals. And she will be at the 163rd lamppost.
|
163
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
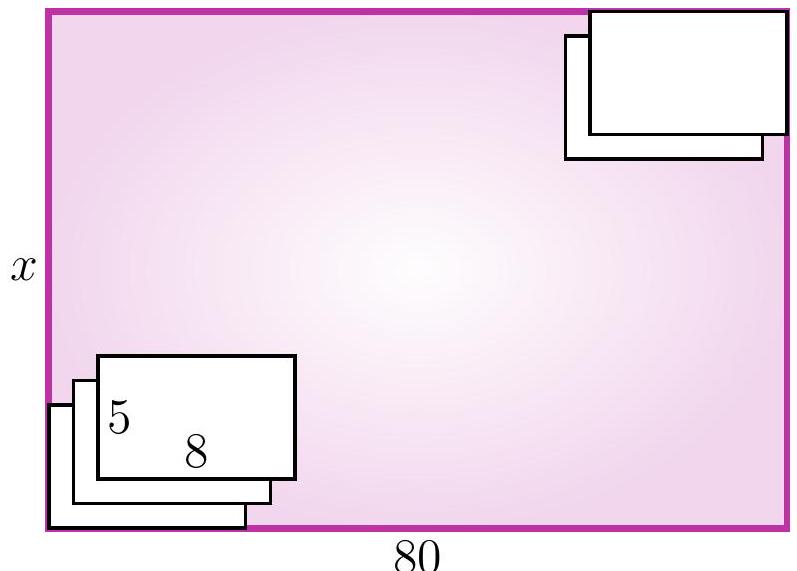
5-6. A rectangular table of size $x$ cm $\times 80$ cm is covered with identical sheets of paper of size 5 cm $\times 8$ cm. The first sheet touches the bottom left corner, and each subsequent sheet is placed one centimeter higher and one centimeter to the right of the previous one. The last sheet touches the top right corner. What is the length $x$ in centimeters?
|
Answer: 77.
Solution I. Let's say we have placed another sheet of paper. Let's look at the height and width of the rectangle for which it will be in the upper right corner.
Let's call such a rectangle the current one. Notice that for each new current rectangle, both the width and the height are 1 cm larger than the previous one. Initially, when there was only one sheet of paper, the width of the large rectangle was 8 cm, and at the end, it was 80 cm. Thus, a total of $(80-8): 1=72$ sheets of paper were added. The height of the current rectangle also increased by $72 \cdot 1$ cm, initially it was 5 cm, so $x=5+72=77$.
Solution II. As in the first solution, let's look at the length and width of the current rectangles. Again, notice that for each new current rectangle, both the length and the width are 1 cm larger than the previous one. However, we will draw a different conclusion: specifically, the difference between the width and the height of the current rectangle is always the same! (Such a value that does not change during a certain process is called an invariant.) Since initially the width was 3 cm greater than the height, i.e., $8-5=3$ cm, at the end it should also be 3 cm greater, so the answer is $x=80-3=77$ cm.
|
77
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
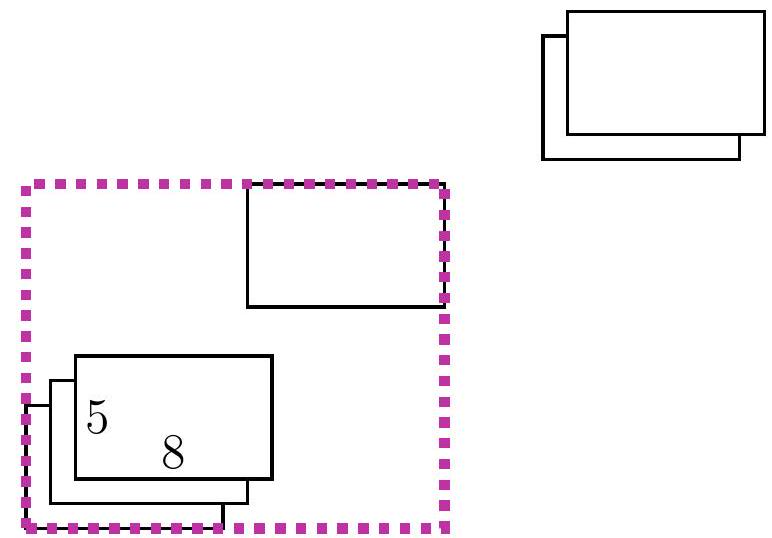
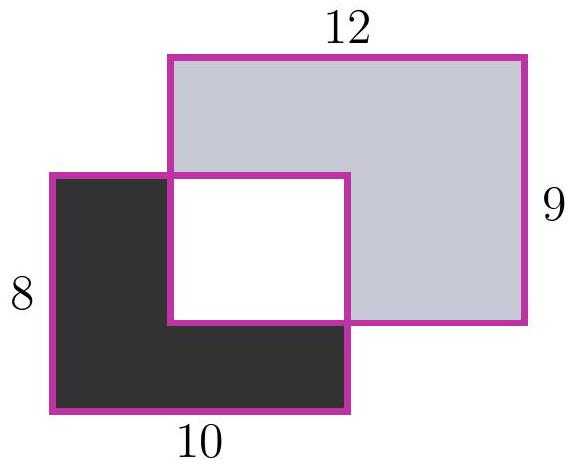
8-1. Two rectangles $8 \times 10$ and $12 \times 9$ are overlaid as shown in the figure. The area of the black part is 37. What is the area of the gray part? If necessary, round the answer to 0.01 or write the answer as a common fraction.
|
Answer: 65.
Solution. The area of the white part is $8 \cdot 10-37=43$, so the area of the gray part is $12 \cdot 9-43=65$
|
65
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
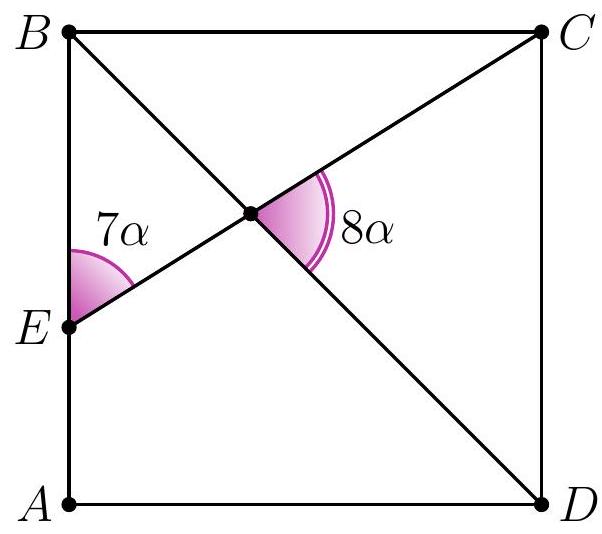
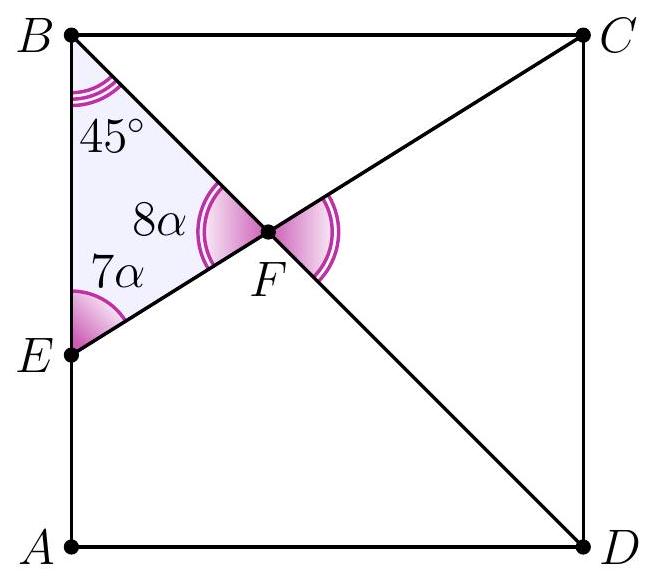
8-2. In square $A B C D$, a segment $C E$ is drawn such that the angles shown in the diagram are $7 \alpha$ and $8 \alpha$. Find the value of angle $\alpha$ in degrees. If necessary, round the answer to 0.01 or write the answer as a common fraction.
|
Answer: $9^{\circ}$.
Solution. In triangle $D F E$, the angles are $7 \alpha, 8 \alpha$ and $45^{\circ}$.
Since the sum of the angles in triangle $D F E$ is $180^{\circ}$, we have $7 \alpha + 8 \alpha + 45^{\circ} = 180^{\circ}$, from which $\alpha = \frac{1}{15} \cdot 135^{\circ} = 9^{\circ}$.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10-3. Point $O$ is the center of the circle. What is the value of angle $x$ in degrees?
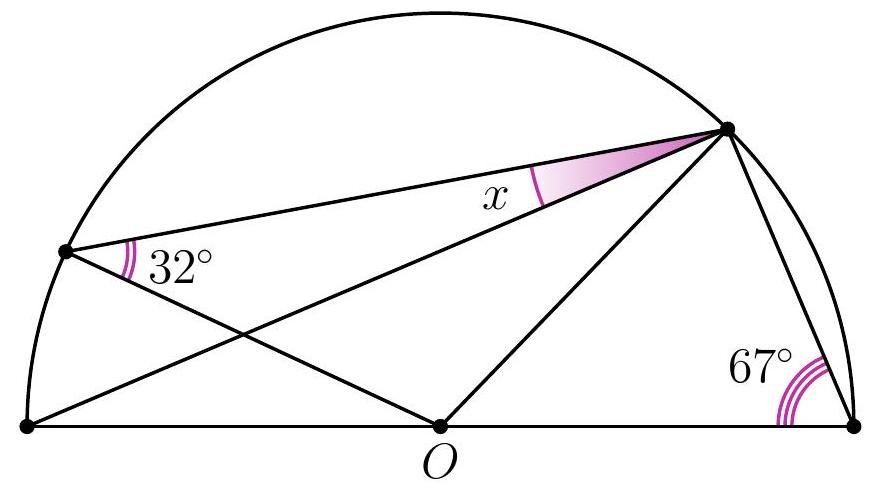
|
Answer: 9.
Solution. Since $O B=O C$, then $\angle B C O=32^{\circ}$. Therefore, to find angle $x$, it is sufficient to find angle $A C O: x=32^{\circ}-\angle A C O$.
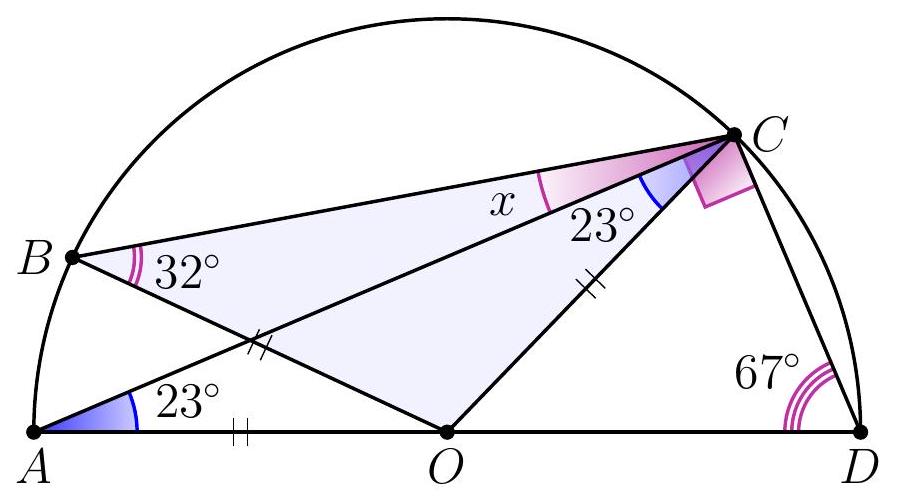
Since $O A=O C$, then $\angle A C O=\angle O A C=90^{\circ}-67^{\circ}=23^{\circ}$ (here we used the fact that triangle $A C D$ is a right triangle: angle $A C D$, which subtends the diameter, is a right angle).
Thus, $x=32^{\circ}-23^{\circ}=9^{\circ}$.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11-3. Point $O$ is the center of the circle. What is the value of angle $x$ in degrees?
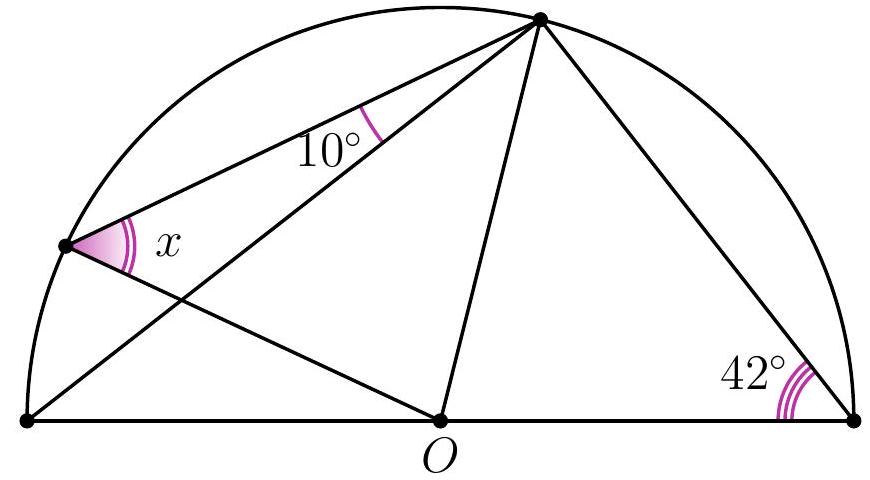
|
Answer: 58.
Solution. Angle $ACD$ is a right angle since it subtends the diameter of the circle.
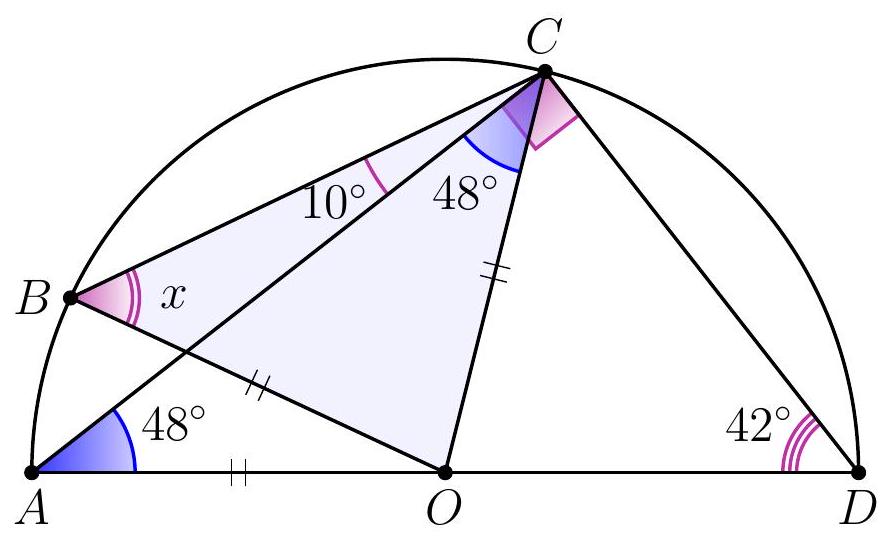
Therefore, $\angle CAD = 90^{\circ} - \angle CDA = 48^{\circ}$. Also, $AO = BO = CO$ as they are radii of the circle, so $\angle OCA = \angle ACO = 48^{\circ}$ and $x = \angle OBC = \angle OCB = 48^{\circ} + 10^{\circ} = 58^{\circ}$.
|
58
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. After teacher Mary Ivanovna moved Vovochka from the first row to the second, Vanechka from the second row to the third, and Mashenka from the third row to the first, the average age of students sitting in the first row increased by one week, those sitting in the second row increased by two weeks, and those sitting in the third row decreased by four weeks. It is known that there are 12 people sitting in the first and second rows. How many people are sitting in the third row?
|
3. Let there be x people in the third row. Since the average age is the sum of the ages divided by the number of people, after the rearrangement, the total age of the children in the first row increased by 12 weeks, in the second row by 24 weeks, and in the third row by -4x weeks. Since the total sum of the ages of all students could not have changed, $4x = 12 + 24$, i.e., $x = 9$.
Answer: 9 people.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. From Zlatoust to Miass, "GAZ", "MAZ", and "KamAZ" set off simultaneously. "KamAZ", having reached Miass, immediately turned back and met "MAZ" 18 km from Miass, and "GAZ" - 25 km from Miass. "MAZ", having reached Miass, also immediately turned back and met "GAZ" 8 km from Miass. What is the distance from Zlatoust to Miass
|
Answer: 60 km.
Solution. Let the distance between the cities be $x$ km, and the speeds of the trucks: "GAZ" $-g$ km/h, "MAZ" - $m$ km/h, "KAMAZ" - $k$ km/h. For each pair of vehicles, we equate their travel time until they meet.
We get $\frac{x+18}{k}=\frac{x-18}{m}, \frac{x+25}{k}=\frac{x-25}{g}$ and $\frac{x+8}{m}=\frac{x-8}{g}$. From this,
$\frac{x+18}{x-18} \cdot \frac{x-25}{x+25} \cdot \frac{x+8}{x-8}=\frac{k}{m} \cdot \frac{g}{k} \cdot \frac{m}{g}=1$.
Transform the obtained equation $x^{3}+x^{2}+(18 \cdot 8-18 \cdot 25-8 \cdot 25) x-18 \cdot 8 \cdot 25=x^{3}-x^{2}+(18 \cdot 8$ $-18 \cdot 25-8 \cdot 25) x+18 \cdot 8 \cdot 25 \square 2 x^{2}=2 \cdot 18 \cdot 8 \cdot 25$. Since $x>0$, then $x=60$.
|
60
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. While waiting for customers, the watermelon seller sequentially weighed 20 watermelons (weighing 1 kg, 2 kg, 3 kg, ..., 20 kg), balancing the watermelon on one scale pan with one or two weights on the other pan (possibly identical). The seller recorded on a piece of paper the weights of the weights he used. What is the smallest number of different numbers that could have appeared in his records, if the weight of each weight is an integer number of kilograms?
|
Answer: 6.
Solution. With one or two weights of 1 kg, 3 kg, 5 kg, 7 kg, 9 kg, and 10 kg, any of the given watermelons can be weighed. Indeed, $2=1+1, 4=3+1$, $6=5+1, 8=7+1, 11=10+1, 12=9+3, 13=10+3, 14=9+5, 15=10+5, 16=9+7, 17$ $=10+7, 18=9+9, 19=10+9, 20=10+10$. Thus, six different numbers could have been recorded.
We will show that five types of weights are insufficient for the required weighings. If there are five weights, then, generally speaking, twenty watermelons can be weighed. Specifically: five watermelons can be balanced with single weights, five with double weights, and the remaining $5 \cdot 4: 2=10$ watermelons with pairs of different weights. However, each combination of weights must be used exactly once.
Notice that half of the watermelons have an odd mass. Let $k$ of the five weights have an odd mass, and $5-k$ have an even mass. Then the number of ways to weigh a watermelon with an odd mass is exactly $k+k(5-k)=6k-k^2$. However, for no $k=0,1,2,3,4,5$ does this expression equal 10 (this can be verified either by substitution or by solving the quadratic equation $6k-k^2=10$).
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Two types of tiles were laid on the wall in a checkerboard pattern. Several tiles fell off the wall. The remaining tiles are shown in the picture. How many striped tiles fell off? Be sure to explain your answer.
|
Answer: 15.
## Solution.
Method 1. Draw additional cells and count them.
Method 2. Look at the number of fallen cells by rows: in the second row from the top, 2 tiles fell out, of which 1 is striped, in the third row - 5 tiles, of which 2 are striped, in the fourth row - 7 tiles (3 striped) and so on. There are five rows in total, so the number of tiles that fell out is
$$
1+2+3+4+5=15 \text{ tiles. }
$$
Method 3. If the tiles had not fallen out, there would be 6 striped tiles in the odd rows and 7 striped tiles in the even rows on the original picture. Subtract the existing striped tiles from each row and add up the missing ones in each row.
$$
\begin{gathered}
(6-6)+(7-6)+(6-4)+(7-4)+(6-2)+(7-2)+(6-6)= \\
=0+1+2+3+4+5+0=15
\end{gathered}
$$
## Grading Criteria.
- Any correct solution - 7 points.
- A solution consisting of the line $1+2+3+4+5=15$ without explanations - 5 points.
- A correct approach in methods 2 or 3, but an incorrect answer due to an arithmetic error - 4 points.
- Only the correct answer (without the redrawn picture) - 2 points.
|
15
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Mowgli asked five monkeys to bring him some nuts. The monkeys collected an equal number of nuts and carried them to Mowgli. On the way, they quarreled, and each monkey threw one nut at each of the others. As a result, they brought Mowgli half as many nuts as they had collected. How many nuts did Mowgli receive? Be sure to explain your answer.
|
Answer: 20 nuts.
## Solution.
Each monkey threw 4 nuts, so the monkeys threw a total of $5 \cdot 4=20$ nuts together.
If half of the nuts remained, it means that Mowgli brought as many nuts as were thrown, which is 20 nuts.
## Grading Criteria.
- Correct solution - 7 points.
- Very brief solution (such as "5 - $4=20$ nuts, and since half remained, 20 nuts") - 5-6 points.
- Generally correct approach, but the student thinks each monkey threw 5 nuts and gets the wrong answer - 2 points.
- Only the correct answer - 2 points.
|
20
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The distance from the home of Vintik and Shpuntik to school is 6 kilometers. Vintik and Shpuntik left for school at the same time, with Vintik spending half of the time riding a scooter at a speed of 10 km/h and then walking, while Shpuntik traveled half the distance by bicycle and then walked. They arrived at school at the same time. Both walk at a speed of 5 km/h. At what speed does Shpuntik ride his bicycle?
|
Answer: 15 km/h.
## Solution:
First method.
Since Shtyubik rides twice as fast as he walks, he also covers twice the distance he walks (since he spends the same amount of time on both), which is 4 km. Since Shtyubik and Shpuntyk walk at the same speed, the last 2 km they walked together. Therefore, while Shtyubik was riding 4 km on the scooter, Shpuntyk rode 3 km on the bicycle and then walked another 1 km. Since Shtyubik rides the scooter twice as fast as he walks, while Shpuntyk walked 1 km, Shtyubik rode 2 km. Consequently, while Shtyubik was riding the first 2 km on the scooter, Shpuntyk covered 3 km on his bicycle, so he rides the bicycle one and a half times faster than Shtyubik on the scooter, which is 15 km/h.
Second method.
As in the first method, we get that Shtyubik rode 4 km on the scooter and walked 2 km - for which he spent $4 / 10 + 2 / 5 = 4 / 5$ (hours). Let the speed of Shpuntyk on the bicycle be $x$ km/h. He rode 3 km on the bicycle, spending $3 / x$ (hours) on it, and then walked 3 km, spending $3 / 5$ (hours) on it. Shtyubik and Shpuntyk spent the same amount of time on the road, so $3 / x + 3 / 5 = 4 / 5$, from which $3 / x = 1 / 5$, and then $x = 15$.
## Criteria:
Correct answer without correct justification - 2 points.
Correctly formulated equation (for the time spent by Shtyubik and Shpuntyk) - another 2 points.
|
15
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In the notebook, all irreducible fractions with the numerator 15 are written down, but which are greater than $\frac{1}{16}$ and less than $\frac{1}{15}$. How many such fractions are written in the notebook?
|
Answer: 9 fractions.
## Solution:
We are looking for all suitable irreducible fractions of the form $\frac{15}{n}$. Since $\frac{1}{16}<\frac{15}{n}<\frac{1}{15}$, then $15 \cdot 15<n<15 \cdot 16$ or $225<n<240$ (with the fraction $\frac{15}{n}$ being irreducible, meaning $n$ is not divisible by 3 or 5). It is not difficult to verify that from this range (of 14 numbers), we need to exclude the numbers 228, 230, 231, 234, 235, 237 - 6 numbers. This leaves 9 possible values for $n$.
## Criteria:
Correct answer without a correct justification - 1 point.
Participants might try to list all such fractions and then justify why the denominator cannot be larger or smaller - carefully monitor the accuracy of such justifications.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In each cell of a $2 \times 2$ table, a number was written, and all the numbers are different. It turned out that the sum of the numbers in the first row is equal to the sum of the numbers in the second row, and the product of the numbers in the first column is equal to the product of the numbers in the second column. What can the sum of all four numbers in the table be? Find all possible options and explain why there are no others.
|
# Answer: 0.
## Solution:
| $a$ | $b$ |
| :--- | :--- |
| $c$ | $d$ |
Let's denote the numbers in the table as shown on the left. According to the condition, $a+b=c+d$, $ac=bd$. Then $a=c+d-b$, substitute this into the product equality: $(c+d-b)c=bd$. Expand the brackets and move everything to the left: $c^2 + cd - bc - bd = 0$. Factorize: $(c+d)(c-b)=0$. Since $c-b \neq 0$ (all numbers are different), then $c+d=0$. Therefore, the sum in the first row is also 0, and accordingly, the sum in the entire table is also 0.
## Criteria:
Correct answer without correct justification - 1 point.
If it is not justified why $c$ can be canceled out - deduct 2 points.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In triangle $A B C$, the median $B M$ was drawn. It turned out that $A B=2 B M$ and $\angle M B A=40^{\circ}$. Find $\angle C B A$.
#
|
# Answer: $110^{\circ}$.
## Solution:
Extend the median $B M$ beyond point $M$ by its length and obtain point $D$. Since $A B=2 B M$, then $A B=B D$, which means triangle $A B D$ is isosceles. Therefore, angles $B A D$ and $B D A$ are each equal to $\left(180^{\circ}-40^{\circ}\right): 2=70^{\circ}$. $A B C D$ is a parallelogram because its diagonals are bisected by their point of intersection. Thus, angle $C B D$, like $A D B$, is $70^{\circ}$, and angle $A B C$, which is the sum of $C B D$ and $A B D$, is $110^{\circ}$.
## Criteria:
Correct answer without correct justification - 1 point.
The idea of extending the triangle to form a parallelogram without further substantial progress - 2 points (not combined with the point for the correct answer).
|
110
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The organizers of a mathematics olympiad decided to photograph 60 participants. It is known that no more than 30 participants can fit in a single photograph, however, any two students must appear together in at least one photograph. What is the minimum number of photographs needed to achieve this?
|
# Answer: 6.
## Solution:
Example with 6 photos: divide 60 participants into 4 groups of 15 people (groups $A, B, B$, Г). Take 6 photos of all possible pairs of groups: $A+D, A+B, A+\Gamma, B+B, B+\Gamma, B+\Gamma$ - in each photo, there will be 30 people, and it is easy to see that in this way any two people will be photographed together.
We will prove that fewer photos are not sufficient. Suppose no more than 5 photos were taken. After each photo, give each photographed person a candy. Then, in total, the participants received no more than $30 \cdot 5 = 150$ candies (since no more than 30 people are in each photo, and there are no more than 5 photos). Since there are 60 participants, there will be a participant who received no more than 2 candies (otherwise, a total of at least $60 \cdot 3 = 180$ candies would have been given). Then he was photographed with no more than 29 other participants in one photo and with no more than 29 other participants in another photo (if there is such a photo) - that is, with no more than $29 \cdot 2 = 58$ other participants of the olympiad, while he should have been photographed with all 59 participants (i.e., with everyone except himself). This is a contradiction, so five or fewer photos are insufficient to meet the condition of the problem.
## Criteria:
A correct answer without a correct example is not scored.
Example for 6 photos - 2 points.
Correct estimation (justification why 5 or fewer photos are insufficient) - another 5 points.
Examples or estimates for 7 or more photos are not scored.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.5. Five athletes came to training with their balls, and when leaving, each took someone else's. In how many ways is this possible.
|
Answer: 44.
Solution. First, let's assume that no two athletes have exchanged balls. Imagine them sitting around a round table. Then, depending on their different relative positions, they would choose the ball of the next (for example, clockwise) athlete. However, this is only possible if 5 are seated at one table, which can be done in $4!=24$ ways.
Now consider the case where two athletes have exchanged balls. These two out of five can be chosen in 10 ways, and the remaining three can be seated around the round table as in the first case, which can be done in $2!=2$ ways. Thus, in this case, we get 20 ways.
Since only one pair of athletes can exchange balls, the total number of ways will be $24+20=44$.
Comment. Consider only one of the cases -3 points.
|
44
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.2 The sequence of numbers $\mathrm{x}_{1}, \mathrm{x}_{2}, \mathrm{x}_{3}, \ldots$ is formed according to the rule: $\mathrm{x}_{1}=1, \mathrm{x}_{\mathrm{n}+1}=1+\frac{\mathrm{x}_{\mathrm{n}}^{2}}{\mathrm{n}}$ for $\mathrm{n}=1,2,3, \ldots$ Find $\mathrm{x}_{2019}$.
|
Answer: 2019
Reasoning. $x_{2}=1+\frac{1^{2}}{1}=2, x_{3}=1+\frac{2^{2}}{2}=3$. Hypothesis: $x_{n}=n$. We proceed by induction. If $x_{n}=n$, then $x_{n+1}=1+\frac{n^{2}}{n}=1+n$. The hypothesis is confirmed.
|
2019
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 8.2. (7 points)
Twelve people are carrying 12 loaves of bread. Each man carries 2 loaves, each woman carries half a loaf, and each child carries a quarter of a loaf. How many men, women, and children were there?
|
Answer: 5 men, one woman, and 6 children.
Solution: Let $x$ be the number of men, $y$ be the number of women, and $z$ be the number of children; $x, y, z$ are natural numbers.
Then $x+y+z=12$ and $2 x+\frac{y}{2}+\frac{z}{4}=12$. From the last equation, it follows that $8 x+2 y+z=48$.
Transform the last equation: $7 x+y+(x+y+z)=48$. Considering the first equality, we get: $7 x+y=36, x=\frac{36-y}{7}$.
Since $x, y$ are natural numbers, $y$ can take the values 1, 8, 15, 22, 29. The values of $y$, equal to 15, 22, and 29, do not meet the condition of the problem $(y<12)$.
When $y=8: x=4, z=0$ - this contradicts the condition of the problem.
Let $y=1$, then $x=5, z=6$.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. Solve the equation $1+\frac{3}{x+3}\left(1+\frac{2}{x+2}\left(1+\frac{1}{x+1}\right)\right)=x$.
Answer: 2
|
Solution.
$1+\frac{1}{x+1}=\frac{x+2}{x+1}$, therefore the given equation is equivalent to the equation $1+\frac{3}{x+3}\left(1+\frac{2}{x+1}\right)=x$ under the condition that $\mathrm{x} \neq-2$. Acting similarly, we get that $1+\frac{3}{x+3}=x$, where $\mathrm{x} \neq-2$ and $\mathrm{x} \neq-3$. The roots of this equation are the numbers 2 and -2, so the only root of the original equation is the number 2.
## Grading Criteria
- Only the correct answer is provided - 1 point.
- The correct solution process, but the extraneous root is not discarded - 3 points.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. The median $\mathrm{AA}_{0}$ of triangle $\mathrm{ABC}$ is laid off from point $\mathrm{A}_{0}$ perpendicular to side $\mathrm{BC}$ to the outside of the triangle. Denote the second endpoint of the constructed segment as $\mathrm{A}_{1}$. Similarly, points $\mathrm{B}_{1}$ and $\mathrm{C}_{1}$ are constructed. Find the angles of triangle $\mathrm{A}_{1} \mathrm{~B}_{1} \mathrm{C}_{1}$, if the angles of triangle $\mathrm{ABC}$ are $30^{\circ}, 30^{\circ}$, and $120^{\circ}$.
|
Answer._ $\triangle \mathrm{A}_{1} \mathrm{~B}_{1} \mathrm{C}_{1}$ is equilateral, all angles are $60^{\circ}$.
## Solution.
Since $\triangle \mathrm{ABC}$ is isosceles, $\mathrm{BB}_{0}$ is the perpendicular bisector of the base AC. Therefore, $\mathrm{B}_{1}$ lies on this perpendicular and $\mathrm{CB}_{0} \perp \mathrm{BB}_{1}$. In $\Delta \mathrm{BCB}_{1}$, point $\mathrm{B}_{0}$ is the foot of the altitude and median on side $\mathrm{BB}_{1}$, hence $\mathrm{BC}=\mathrm{B}_{1} \mathrm{C}$, and since
$\angle \mathrm{B}_{1} \mathrm{BC}=1 / 2 \angle \mathrm{ABC}=60^{\circ}$. Therefore, $\Delta \mathrm{B}_{1} \mathrm{BC}$ is equilateral, and $\mathrm{A}_{0}$, being the midpoint of side $\mathrm{BC}$, is the foot of the altitude in triangle $\mathrm{B}_{1} \mathrm{BC}$. This means that points $\mathrm{A}_{1}$ and $\mathrm{B}_{1}$ lie on the perpendicular bisector of segment $\mathrm{BC}$. Similarly, $\mathrm{C}_{1}$ and $\mathrm{B}_{1}$ lie on the perpendicular bisector of segment AB. Therefore, $\angle \mathrm{C}_{1} \mathrm{~B}_{1} \mathrm{~A}_{1}=180^{\circ}-\angle \mathrm{ABC}=60^{\circ}, \mathrm{B}_{1} \mathrm{~A}_{1}=\mathrm{B}_{1} \mathrm{~A}_{0}$ $+\mathrm{A}_{0} \mathrm{~A}_{1}=\mathrm{B}_{1} \mathrm{~A}_{0}+\mathrm{A}_{0} \mathrm{~A}=\mathrm{B}_{1} \mathrm{C}_{0}+\mathrm{C}_{0} \mathrm{C}=\mathrm{B}_{1} \mathrm{C}_{0}+\mathrm{C}_{0} \mathrm{C}_{1}=\mathrm{B}_{1} \mathrm{C}_{1}$, i.e., $\Delta \mathrm{A}_{1} \mathrm{~B}_{1} \mathrm{C}_{1}$ is isosceles with the vertex angle $60^{\circ}$.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. The math teacher agreed with the eleven students who came to the elective that he would leave the classroom, and the students would agree among themselves who would be a liar (always lie) and who would be a knight (always tell the truth). When the teacher returned to the class, he asked each student to say about each of the others whether they were a knight or a liar. Out of 110 answers, 56 were "He is a liar." What is the maximum number of knights that could have been among the students?
|
Answer: 7.
Solution: The phrase "He is a knight" would be said by a knight about a knight and by a liar about a liar, while the phrase "He is a liar" would be said by a knight about a liar and by a liar about a knight. Therefore, in each pair of "knight-liar," the phrase "He is a liar" will be said twice. Since this phrase was said 56 times in total, there are 28 pairs of "knight-liar," from which we find that there are 7 knights and 4 liars, or vice versa.
Comment: A correct answer without justification - 0 points.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.5. A circle is inscribed with 103 numbers. It is known that among any five consecutive numbers, there are at least two positive numbers. What is the minimum number of positive numbers that can be among these 103 written numbers?
|
Answer: 42.
Solution. We will show that there will be 3 consecutive numbers, among which there are at least 2 positive ones. This can be done, for example, as follows. Consider 15 consecutive numbers. They can be divided into 3 sets of 5 consecutive numbers, so among them, there are at least 6 positive numbers. But these 15 numbers can also be divided into 5 sets of 3 consecutive numbers. Therefore, by the Pigeonhole Principle, in one of these triplets, there are at least 2 positive numbers.
Fix these 3 consecutive numbers. Among them, there are at least 2 positive ones. The remaining 100 numbers can be divided into 20 sets of 5 consecutive numbers. In each such set, there will be at least 2 positive numbers. Thus, the total number of positive numbers is at least $2 + 2 \cdot 20 = 42$. Such a situation is possible. Number the numbers in a circle. The positive numbers can be those with indices $1, 2, 6, 7, \ldots, 96, 97, 101, 102$.
Comment. A correct answer without justification - 0 points. Proving that the number of positive numbers is not less than 42 - 5 points. Providing an example with 42 positive numbers - 2 points.
|
42
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.2. In the bottom left corner of a $7 \times 7$ chessboard, there is a king. In one move, he can move one square to the right, or one square up, or one square diagonally to the right and up. In how many different ways can the king travel to the top right corner of the board, if he is forbidden to visit the central cell?
|
Answer: 5020.
Solution. We will construct a $7 \times 7$ table, in each cell of which we will write the number equal to the number of allowed paths by which the king can reach this cell from the bottom left corner. First, we fill the left column and the bottom row with ones and write 0 in the central cell (as per the condition). Then we fill the second column from the left and the second row from the bottom, and so on, according to the rule: in the current cell, we place the sum of the numbers in the three adjacent cells below, to the left, and diagonally (below and to the left). As a result, we get the table
| 1 | 13 | 85 | 314 | 848 | 2078 | 5020 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 1 | 11 | 61 | 168 | 366 | 864 | 2078 |
| 1 | 9 | 41 | 66 | 132 | 366 | 848 |
| 1 | 7 | 25 | 0 | 66 | 168 | 314 |
| 1 | 5 | 13 | 25 | 41 | 61 | 85 |
| 1 | 3 | 5 | 7 | 9 | 11 | 13 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
The answer is the number in the top right corner, 5020.
|
5020
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.4. At competitions, an athlete's performance is evaluated by 7 judges, each of whom gives a score (an integer from 0 to 10). To obtain the final score, the best and worst scores from the judges are discarded, and the arithmetic mean is calculated. If the average score were calculated based on all seven scores, the athletes would be ranked in the exact reverse order. What is the maximum number of athletes that could have participated in the competition?
|
# Answer. 5.
Solution. Suppose there are no fewer than six dancers. Let $A, a, S_{A}$ be the best score, the worst score, and the sum of all non-discarded scores of the winner, respectively, and $B, b, S_{B}$ be the same for the last athlete. Instead of averages, we can arrange the dancers by the sum of all scores or the sum of all except the extreme ones. From the condition, it follows that such sums are different for all and go in the opposite order. Since the sums are integers and there are at least six dancers, the inequalities must hold:
$$
S_{A}-S_{B} \geq 5 \text { and }\left(B+b+S_{B}\right)-\left(A+a+S_{A}\right) \geq 5 \text {. }
$$
Adding these inequalities, we get $B+b-A-a \geq 10$.
From this, $b \geq A+a+(10-B) \geq A$, i.e., the worst score of the last athlete is not less than the best score of the winner. But then each score of the last athlete is not less than that of the winner, i.e., $S_{B} \geq S_{A}$. We have reached a contradiction.
Example of score distribution among athletes: $0-0-0-0-0-0-10,0-0-0-0-0-1-8$, $0-0-0-0-1-1-6,0-0-0-1-1-1-4,0-0-1-1-1-1-2$.
Comment. Example - 3 points, evaluation - 4 points.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.5. In a regular pentagon $A B C D E$, a point $F$ is marked on side $A B$, and a point $G$ is marked on side $B C$ such that $F G=G D$. Find the angle $C D G$, if the angle $F D E$ is $60^{\circ}$.
|
Answer: $6^{\circ}$.
Solution. The angles of a regular pentagon are each $108^{\circ}, \angle E D A = 36^{\circ}, \angle F D E = 60^{\circ}$. Therefore, $\angle A D F = 24^{\circ}$.
Additional construction: Take point $O$ such that $B O = C O = B C$. Then $\triangle B O C$ is equilateral, $\angle A B O = O C D = 108^{\circ} - 60^{\circ} = 48^{\circ}$. We get that $\triangle A B O = \triangle O C D$, where $\angle B A O = \angle B O A = \angle C O D = \angle C D O = 66^{\circ}, A O = O D$.
Thus, there exists a circle with center at point $O$ and radius $r = O A = O D$. Let this circle intersect side $A B$ at point $K$. Then
$\angle A K O = \angle K A O = 66^{\circ}, \angle K O A = 48^{\circ}$. We obtain that $\angle A D K = A D F = 24^{\circ}$. Therefore, $K = F$. Then $\angle K A D = \angle B A D = \angle B A E - \angle D A E = 72^{\circ}$, and $\angle A F D = 84^{\circ}$, $\angle O F D = 18^{\circ}$.
Let $H$ be the midpoint of $F D$, then $O H$ and $G H$ are medians, altitudes, and angle bisectors of $\triangle F O D$ and $\triangle F G D$ respectively (thus, $G O \perp F D$). We get $\angle F O H = \angle D O H = \angle D O G = 90^{\circ} - 18^{\circ} = 72^{\circ}$.
$\angle G O D + G C D = 180^{\circ} \Rightarrow O G C D$ is inscribed in a circle $\Rightarrow O C D = \angle O G D = 48^{\circ} = \angle H G D$. Then $\angle G D H = 90^{\circ} - 48^{\circ} = 42^{\circ}$. We obtain that $\angle C D G = 108^{\circ} - 60^{\circ} - 42^{\circ} = 6^{\circ}$.
Comment. It is proven that point $O$, the vertex of the equilateral triangle constructed on segment $B C$, is equidistant from vertices $A, F, D$ - 3 points.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the maximum value of the expression $x^{2}+y^{2}+z^{2}$, if $x, y, z$ are integers satisfying the system
$$
\left\{\begin{array}{l}
x y+x+y=20 \\
y z+z+y=6 \\
x z+x+z=2
\end{array}\right.
$$
|
Solution. Adding 1 to both sides of each equation in the system, we get:
$$
\left\{\begin{array}{l}
x y + x + y + 1 = 21 \\
y z + z + y + 1 = 7 \\
x z + x + z + 1 = 3
\end{array}\right.
$$
Factoring the left-hand sides, we obtain:
$$
\left\{\begin{array}{l}
(x+1)(y+1) = 21 \\
(y+1)(z+1) = 7 \\
(z+1)(x+1) = 3
\end{array}\right.
$$
Multiplying the left and right sides of the obtained equations, we arrive at the equality $((x+1)(y+1)(z+1))^2 = 21^2$. There are two cases:
1) $(x+1)(y+1)(z+1) = 21$. Considering that the factors are of the same sign (which follows from the form of the last system), we get $x+1=3, y+1=7, z+1=1$ (the order may be different, but it does not affect the final answer), so $x=2, y=6, z=0$, hence $x^2 + y^2 + z^2 = 2^2 + 6^2 + 0^2 = 40$.
2) $(x+1)(y+1)(z+1) = -21$. Since the factors are of the same sign, we get $x+1=-3, y+1=-7, z+1=-1$ (the order may be different, but it does not affect the final answer), so $x=-4, y=-8, z=-2$, hence $x^2 + y^2 + z^2 = (-4)^2 + (-8)^2 + (-2)^2 = 84$.
Answer: 84.
|
84
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. During a physical education class, all students in the class lined up in a row. It turned out that boys and girls alternated in the row. It is known that exactly $52 \%$ of the students are girls. Find the number of boys in the class. Justify your answer.
|
Solution: Since there are more than half girls, the first and last student in the row are girls. Let's remove the last girl from the row - there will be an equal number of boys and girls left. In this row, all the boys in the class make up $48 \%$. There are as many girls, another $48 \%$. The remaining $100-2 \cdot 48=4 \%$ corresponds to the removed girl. Thus, one person constitutes $4 \%$, and the number of students in the class is $100: 4=25, 48$ percent of this number is 12 people.
Answer: 12 boys.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and justified answer | 7 points |
| In the correct solution, there is an arithmetic error, possibly leading to an incorrect answer | 6 points |
| Noted that there is one more girl than boys | 1 point |
| Correct answer without any justification | 0 points |
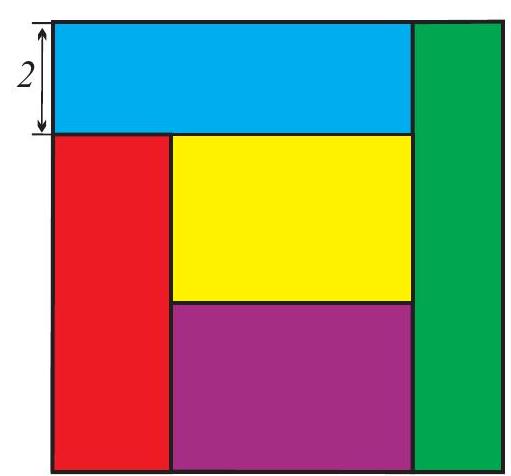
To the condition of problem 7.2
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. While Cheburashka eats two portions of ice cream, Winnie-the-Pooh manages to eat five such portions, and while Winnie-the-Pooh eats three portions, Karlson eats seven. Working together, Cheburashka and Karlson ate 82 portions. How many portions did Winnie-the-Pooh eat during this time? Justify your answer.
|
Solution: Suppose Winnie-the-Pooh ate exactly 15 portions of ice cream. Since $15=3 \cdot 5$, Cheburashka ate $3 \cdot 2=6$ portions, and Karlson ate $-5 \cdot 7=35$ portions. Together, Karlson and Cheburashka ate $6+35=41$ portions, which is half of the 82 portions given in the problem. Therefore, the feast actually lasted twice as long as assumed, and each participant ate twice as much ice cream. In particular, Winnie-the-Pooh ate $15 \cdot 2=30$ portions.
Answer: 30 portions.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and justified answer | 7 points |
| The answer is incorrect due to an arithmetic error, but the approach is correct | 6 points |
| Correctly found the ratio of the number of portions that Winnie-the-Pooh, Karlson, and Cheburashka eat in the same amount of time | 3 points |
| Correct answer without justification or with incorrect justification | 1 point |
|
30
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. It is known that the equations $x^{2}+a x+b=0$ and $x^{3}+b x+a=0$ have a common root and $a>b>0$. Find it.
|
Answer: -1.
Solution. Multiply the first equation by $x$ and subtract the second from it. The common root of the original equations will also be a root of the resulting equation
$$
\left(x^{3}+a x^{2}+b x\right)-\left(x^{3}+b x+a\right)=0 \quad \Longleftrightarrow \quad a\left(x^{2}-1\right)=0
$$
The last equation has two roots, which are 1 and -1. If the common root is $x=1$, then substituting it into each equation yields the equality $1+a+b=0$, which cannot hold given the condition $a>b>0$, leading to a contradiction.
If the common root is $x=-1$, then substituting it into the equations yields $1-a+b=0$, which does not contradict the condition.
Remark. Other methods of solution are possible.
Criteria. Only the answer - 0 points. Excess roots not eliminated - 2 points deducted. No verification of the root $x=-1$ for compliance with the condition - another 2 points deducted. One of the possible roots is missed - no more than 3 points. Complete solution - 7 points.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Points $O$ and $I$ are the centers of the circumcircle and incircle of triangle $ABC$, and $M$ is the midpoint of the arc $AC$ of the circumcircle (not containing $B$). It is known that $AB=15, BC=7$, and $MI=MO$. Find $AC$.
|
Answer: $A C=13$.
Solution. (Fig. 3). First, we prove that $M I=M A$ (trident lemma).
Indeed, the external angle $A I M$ of triangle $A I B$ is equal to the sum of angles $B A I$ and $A B I$, and since $A I$ and $B I$ are angle bisectors, $\angle A I M=\frac{1}{2} \angle A+\frac{1}{2} \angle B$. Angle $I A M$ is equal to the sum of angles $I A C$ and $C A M$. But $\angle I A C=\frac{1}{2} \angle A$, and $\angle C A M=\angle C B M=\frac{1}{2} \angle B$ as inscribed angles.
From this, it follows that $\angle I A M=\frac{1}{2} \angle A+\frac{1}{2} \angle B=\angle A I M$, and therefore, triangle $A M I$ is isosceles, $M I=M A$. By the condition $M O=$ $M I$, so by the trident lemma $A O=M O=M I=M A$. This means that triangle $A O M$ is equilateral and $\angle A O M=60^{\circ}$. Since the central angle $A O M$ is twice the inscribed angle $A B M$, we have $\frac{1}{2} \angle B=30^{\circ}$, that is, $\angle B=60^{\circ}$.
By the cosine theorem, $A C^{2}=A B^{2}+B C^{2}-2 \cdot A B \cdot B C \cos 60^{\circ}=$ $13^{2}$.
Criteria. Answer without explanation - 0 points. Proved that angle $B$ is $60^{\circ}-5$ points. Points are not deducted for the absence of proof of the trident lemma. Full solution - 7 points.
Fig. 3
|
13
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. There are 55 boxes standing in a row, numbered in order from 1 to 55. Each box contains no more than 10 balls, and the number of balls in any two adjacent boxes differs by exactly 1. It is known that the boxes numbered $1,4,7,10, \ldots, 55$ contain a total of 181 balls. What is the minimum total number of balls that can be in all 55 boxes?
|
Solution. Since the number of balls in two adjacent boxes differs by 1, the parity of this number always differs. Therefore, throughout the entire row of boxes, the parity alternates - the number of balls in boxes with different parity numbers also has different parity. We will divide the boxes into pairs: 1 with 4, 7 with 10, 13 with 16, ..., 49 with 52 - a total of 9 pairs. In each pair, one of the quantities is even, the other is odd. Therefore, in two boxes of one pair, there are no more than $10+9=19$ balls. Then in the 55th box, there are no fewer than $181-19 \cdot 9=10$ balls. Therefore, the condition of the problem can only be met in one situation: in the 55th box, there are exactly 10 balls, and in the specified pairs - exactly 19 each. Moreover, the boxes with 10 and 9 balls in the pairs alternate. Then we notice that each interval between the specified boxes can only be of two types: 9 and 10 balls or 8 and 9 balls. In the second case, there are fewer balls. We calculate the minimum number of balls: $181+18 \cdot(8+9)=487$.
Answer. 487 balls.
|
487
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. Pasha is playing a computer game. The game takes place on an infinite grid. Each cell contains either a treasure or a natural number. The number indicates the distance to the nearest treasure in cells (if it takes $A$ steps vertically and $B$ steps horizontally to reach the treasure, the cell contains the number $A+B$). In one move, Pasha can reveal the contents of one cell. The goal of the game is to find at least one treasure.
a) Pasha revealed three cells in a row horizontally. Each of them contained the number 5. What is the minimum number of additional moves Pasha needs to make to definitely find a treasure?
(2 points)
b) Pasha revealed some three cells, and they contained numbers. Could it be that from this information, Pasha can definitely find a treasure with the next move?
(3 points)
c) Pasha knows that each number on the field does not exceed some fixed $K \geqslant 3$. Can Pasha definitely find a treasure by making no more than $K+3$ moves?
2) Pasha knows that each number on the field does not exceed 2023. Will 20 moves be enough for Pasha to definitely find a treasure?
|
Solution. a) Note that if Pasha finds a certain number $K$ in a cell, then at least one treasure must be located in the cells along the perimeter of a square rotated by $45^{\circ}$ relative to the grid lines, where the side of the square is exactly $K+1$ cells. At the same time, there cannot be any treasures inside such a square. Let's construct such squares around the fives found by Pasha. The treasure related to the central five can only be located above or below it at a distance of 5 cells, as the other cells on the perimeter will be covered by other squares. But one of these cells may not contain a treasure, so Pasha will need more than one move to guarantee finding it. For other fives or cells outside the squares, it is also impossible to determine the exact location of the treasure. Therefore, Pasha needs at least two moves (these moves are marked with a star in the figure).
To the solution of problem $7.5 \mathrm{a}$
To the solution of problem $7.5 \mathrm{b}$
b) The figure shows one of the possible situations where the position of the treasure can be determined unambiguously. The treasure is located in the cell marked with a star, as the other cells of the square around the one are covered by the inner cells of the squares around the twos.
c) Suppose Pasha checks two adjacent cells horizontally with his first two moves. The numbers in these cells are either equal or differ by 1 (if, of course, a treasure is found, then Pasha has completed the task). In both cases, the squares around these two numbers will overlap such that the treasure related to the smaller number (or any of the equal numbers) will be located in cells forming only two sides of the square. Let the smaller number be $N \leqslant K$, and, without loss of generality, the specified sides will be to the left of it. The situation is shown in the figure (the sizes of the square are shown schematically).
With the next moves, Pasha will check the cells from left to right, from 1 to a maximum of $N-1$—until the number in the cell matches the number of this cell. If 1 matches, then the treasure should be searched in the three cells around it, and if it does not match, then there is definitely no treasure in these three cells. If 2 matches, the treasure should be searched two cells above or below, and if it does not match, then there is definitely no treasure in these two cells, and so on. If, as a result of such actions, no number matches in any cell, including the number $N-1$, then the treasure should be searched in the last two cells—above or below the number $N$.
Thus, to find the treasure, Pasha will spend: 2 initial moves, no more than $K-1$ moves horizontally, 2 moves to find the treasure above or below the number (3 moves if he gets lucky on the first cell). In total, $2+(K-1)+2=K+3$ moves. Or $2+1+3=6$ moves, but $6 \leqslant K+3$ by the condition.
d) The first two moves will be made in the same way as in part c). For the remaining corner of two sides of the square around the number $N$, we will make three more moves—to its ends and the central cell. If the treasure is still not found, then the suspicious cells will remain in two diagonal segments, containing $N-1 \leqslant 2022$ cells.
Now let's describe the next operation. If in such a segment we select $M+1$ consecutive cells, then there exists a square for which the selected cells form a side. At the same time, all other cells of the square lie strictly inside the square with side $N$ obtained by the first two moves, and therefore definitely do not contain the treasure. Then Pasha can check the central cell of the square—if it turns out to be the number $M$, then among the selected $M+1$ cells there is a treasure, and if not $M$—then there is no treasure. For convenience, this operation will be performed for any $M \geqslant 0$, and for $M=0$ the square together with the boundary is just one cell.
Using the described operation, Pasha will first leave one of the two segments. Then we will divide the segment in half—selecting half of the cells from one of the edges (if the number of cells is odd—half of all, not counting the central one). Then even in the worst case, he will need no more than 12 moves, since $2^{11}>2022$. Indeed, the number of unverified options in 11 moves will not exceed 1011, 506, 253, 127, 64, 32, 16, 8, 4, 2, 1 cells, respectively. In total, Pasha will spend no more than $2+3+1+12=18$ moves, which is even less than the proposed twenty.
Answer. a) 2 moves b) It could.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. Find the smallest six-digit number that is a multiple of 11, where the sum of the first and fourth digits is equal to the sum of the second and fifth digits and is equal to the sum of the third and sixth digits.
|
Solution. Let the desired number have the form $\overline{1000 x y}$, where $x, y$ are some digits. Then, by the condition, the sum of the first and fourth digits is 1, from which $x=y=1$. But the number 100011 is not divisible by 11. Therefore, we will look for a number of the form $\overline{1001 x y}$. Then $x=y=2$, and the number 100122 is divisible by 11.
Answer. 100122.
|
100122
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. Evgeny is tiling the floor of his living room, which measures 12 by 16 meters. He plans to place 1 m $\times$ 1 m square tiles along the perimeter of the room, and the rest of the floor will be covered with 2 m $\times$ 2 m square tiles. How many tiles will he need in total?
|
Solution. Let's step back 1 meter from the living room's boundaries. We will be left with a rectangle of size $10 \times 14$, which needs to be covered with $2 \times 2$ tiles. The area of the rectangle is 140, and the area of one tile is 4, so we will need $140: 4=35$ large tiles. The area of the boundary strip is $12 \cdot 16-140=52$ and it needs to be covered with tiles of area 1. Therefore, 52 small tiles will be required. The total number of tiles is $35+52=87$.
Answer. 87 tiles.
|
87
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.4. Daniil and Pasha were driving in a car along a straight road at a constant speed. While Daniil was driving, Pasha had nothing to do and was looking at the kilometer markers. Pasha noticed that exactly at noon they passed a marker with the number $X Y$ (where $X, Y$ are some digits), at $12:42$ - a marker with the number $Y X$, and at 1 PM - a marker with the number $X0Y$. At what speed were they traveling?
|
Solution. Method 1. In 42 minutes from 12:00 to 12:42, the car traveled no more than 100 km, and in the remaining 18 minutes, it traveled even less (in $42 / 18=7 / 3$) times. Therefore, by 13:00, the car had not reached the sign with the number 200. Then $X=1$. In this case, regardless of the number $Y$, the car traveled 90 km from 12 to 1 o'clock, and its speed is 90 km/h. It remains to show that at such a speed, the described situation is possible, that is, that the problem's condition is not contradictory. Indeed: in 42 minutes (which is $7 / 10$ of an hour), the car traveled 63 km. And with $Y=8$ (incidentally, such a $Y$ is unique), it will be exactly opposite the sign with the number $63+18=81$. In the remaining 18 minutes until 1 o'clock (which is $3 / 10$ of an hour), the car will travel another 27 km and will be opposite the sign with the number $81+2=108$.
Method 2. From the sign with the number $Y X=10 Y+X$ to the sign with the number $X Y=10 X+Y$, there are exactly $\overline{(10 Y+X)}-(10 X+Y)=9(Y-X)$ km. Similarly, between the signs with the numbers $X O Y$ and $Y X$, there are exactly $9(11 X-Y)$ km. The constant speed of the car means that the segments of the path it has traveled are proportional to the time spent overcoming them. In other words, we have the equation $\frac{9(Y-X)}{9(11 X-Y)}=\frac{42}{60-42}$. After solving the obtained proportion, we get the equality $Y=8 X$. This equality has two solutions in digits: $X=Y=0$, which is impossible because the first digit on the kilometer sign is different from zero, and $X=1$, $Y=8$, which is what happened. Then in one hour, the car traveled $108-18=90$ km. This is its speed.
Answer. 90 km/h.
|
90
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.4. Ivan on a tractor and Petr in a "Mercedes" left point A for point B. Petr arrived at point B, waited for 10 minutes, and called Ivan to find out that Ivan had only covered a third of the distance and was currently passing by a cafe. Petr drove to meet him. Not noticing Ivan, he reached the cafe and spent half an hour on a snack, then drove to point B. In the end, Petr arrived at point B at the same time as Ivan. How much time did Ivan spend on the entire journey, if both he and Petr traveled at constant speeds?
|
Solution. From the fact that Ivan had traveled a third of the distance by the time Peter had traveled the whole distance and waited for 10 minutes, we can conclude that by the time Ivan reaches point B, Peter could have traveled the route three times and waited for half an hour. Instead, he traveled the route $1+2 / 3+2 / 3=7 / 3$ times and waited for 40 minutes. This means that for Peter, $2 / 3$ of the journey in the first ratio is equivalent to 10 minutes of waiting in the second. From this, we can conclude that Peter takes 15 minutes to travel the entire route, and a third of Ivan's journey is 25 minutes. Therefore, Ivan's entire journey is 75 minutes.
Answer. 1 hour and 15 minutes.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 11.1. Solve the equation
$$
x^{4}+2 x \sqrt{x-1}+3 x^{2}-8 x+4=0
$$
|
Solution. Let's check that $x=1$ is a root. Indeed,
$$
1^{4}+2 \sqrt{1-1}+3 \cdot 1^{2}-8+4=1+3-8+4=0
$$
We will show that there are no other roots. Since the left side of the equation is defined only for $x \geqslant 1$, it is sufficient to consider the case $x>1$. Using the valid inequalities in this case $x^{4}>x^{2}, x \sqrt{x-1}>0$ and $(x-1)^{2}>0$, we obtain for the left side the inequality
$$
x^{4}+2 x \sqrt{x-1}+3 x^{2}-8 x+4>4 x^{2}-8 x+4=4(x-1)^{2}>0
$$
which holds for all $x>1$. Thus, there are no roots for $x>1$.
Answer. $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.4. In how many ways can all natural numbers from 1 to $2 n$ be arranged in a circle so that each number is a divisor of the sum of its two neighboring numbers? (Ways that differ only by rotation or symmetry are considered the same)
|
Solution. Note that if the numbers in the circle do not alternate in parity, then some two even numbers are adjacent. An even number is a divisor of the sum of the even number adjacent to it and the second adjacent number, which means the latter is also even. Continuing this reasoning around the circle, we get that all numbers in the circle are even, which is incorrect. Consider the number $2n-1$. By the proven fact, both of its neighbors are even, and their sum is divisible by $2n-1$, so the sum is at least $4n-2$. The maximum sum of the two remaining numbers is $2n + (2n-2) = 4n-2$. Therefore, the numbers adjacent to $2n-1$ are $2n$ and $2n-2$. Without loss of generality, let them be in descending order clockwise. Now and further, the situation will be as follows: around the circle, the numbers from $2n$ to $k$ are already placed in descending order clockwise, where $k>1$. One of the neighbors of the number $k$ is $k+1$, and the other neighbor is no more than $k-1$, so the sum of the adjacent numbers is greater than $k$ and no more than $2k$, which means it is equal to $2k$. It turns out that the next number after $k$ is $k-1$. We again get the situation described above. Therefore, the numbers are arranged in a circle from $2n$ to 1 in descending order clockwise or counterclockwise (these are the same options) and no other way.
Answer. 1 option.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
36. A pair of natural numbers $a>b$ is called good if the least common multiple (LCM) of these numbers is divisible by their difference. Among all natural divisors of the number $n$, exactly one good pair was found. What can $n$ be?
|
36. Answer: $n=2$. Two odd numbers cannot form a good pair. Therefore, the number $n$ has an even divisor, and thus it is even. But then it has two good pairs of divisors: $(2,1)$ and $(n, n / 2)$.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
40. At the vertices of a convex 2020-gon, numbers are placed such that among any three consecutive vertices, there is both a vertex with the number 7 and a vertex with the number 6. On each segment connecting two vertices, the product of the numbers at these two vertices is written. Andrey calculated the sum of the numbers written on the sides of the polygon and obtained a total of $A$, while Sasha calculated the sum of the numbers written on the diagonals connecting vertices two apart and obtained a total of $C$. Find the maximum possible value of the difference $C-A$.
|
40. Answer: 1010. This answer is achieved if the numbers 7 and 6 alternate.
We can assume that all numbers are equal to 6 or 7. Indeed, if a number is different from 6 and 7, then among its neighbors, one is 6 and one is 7, and the same is true for the neighbors two steps away. Then, replacing this number with 7 does not change the difference $C-A$.
Now, let's reduce all numbers by 6.5 and prove that the value $C-A$ does not change. Let Sash's sum become $C_{1}$, and Andrey's sum become $A_{1}$. If before the reduction, the number $ab$ stood on some segment, then after we reduced the numbers, the number $(a-6.5)(b-6.5)=ab-6.5(a+b)+6.5^{2}$ stands on this segment. Then $C-C_{1}=2S \cdot 2020 \cdot 6.5-2020 \cdot 6.5^{2}=A-A_{1}$, where $S$ is the sum of all original numbers. From this, it follows that $C-A=C_{1}-A_{1}$.
Now $C_{1}-A_{1} \leqslant 2020 \cdot \frac{1}{4}-2020 \cdot \frac{-1}{4}=1010$, since after the reduction, all numbers are equal to $\pm \frac{1}{2}$, and the product on each segment is $\pm \frac{1}{4}$. In particular, equality is achieved if the original numbers 6 and 7 alternated.
|
1010
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. On a circle, 2021 points are marked. Kostya marks a point, then marks the next point to the right, then he marks the point to the right of the last marked point, skipping one, then the point to the right of the last marked point, skipping two, and so on. On which move will a point be marked for the second time?
|
Answer: on the 67th move. The question is about the smallest natural $b$ for which $(a+1)+(a+2)+\cdots+(b-1)+b$ is divisible by $2021=43 \cdot 47$. This sum is equal to $b(b+1) / 2-a(a+1) / 2=$ $(b-a)(b+a+1) / 2$ and it is not hard to see that the smallest $b=(b-a) / 2+(b+a) / 2$ is achieved with the factorization $(66-19)(66+19+1) / 2=47 \cdot 86 / 2=47 \cdot 43$. In this case, $b=66$, i.e., this happened on the 67th move.
|
67
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find all integers $x, y$ for which $x+y, 2x+3y$ and $3x+y$ are perfect squares.
|
Answer: $x=y=0$. Let $x+y=a^{2}, 2 x+3 y=b^{2}$ and $3 x+y=c^{2}$. Note that $2 b^{2}+c^{2}=7 a^{2}$. We will prove that this equation has a unique solution: $a=b=c=0$. Indeed, let $(a, b, c)$ be a solution with the minimal sum $a^{2}+b^{2}+c^{2}$, in which not all numbers $a, b, c$ are equal to 0. Then $2 b^{2}+c^{2}: 7$. It is easy to see that this is possible only if $b \vdots 7$ and $c \vdots 7$. But then $7 a^{2} \vdots 49$, from which $a \vdots 7$. Reducing $a, b, c$ by 7, we get a new non-zero solution with a smaller sum $a^{2}+b^{2}+c^{2}$. Contradiction. Thus, $a=b=c=0$. Then $x=\frac{c^{2}-a^{2}}{2}=0$ and $y=a^{2}-x=0$.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On the table, there are 100 weights of different masses. A weight is called successful if its mass is equal to the sum of the masses of some two other weights on the table. What is the smallest number of successful weights that would allow us to assert with certainty that the masses of some two weights differ by at least a factor of three?
|
Answer: 87. Let there be 87 lucky numbers. If one of the two addends of a lucky number $a=b+c$ is itself lucky, for example, $b=d+e$, then $a=c+d+e \geqslant 3 \min (c, d, e)$, which means there will be two numbers differing by at least a factor of three. If, however, all the addends of the eighty-seven lucky numbers are among the 13 unlucky ones, then each lucky number is one of the $13 \cdot 12 / 2=78$ pairwise sums of these - a contradiction.
Example with 86 lucky numbers: take 14 almost identical numbers and 86 of their $14 \cdot 13 / 2=91$ pairwise sums and declare them to be lucky numbers. For instance, consider the numbers $1+\varepsilon, 1+2 \varepsilon, 1+2^{2} \varepsilon, \ldots, 1+2^{12} \varepsilon$. All their pairwise sums are distinct, greater than the original numbers, and the largest of them $2+2^{12} \varepsilon+2^{13} \varepsilon=2+3 \cdot 2^{12} \varepsilon < 3(1+\varepsilon)=3+3 \varepsilon$ for a very small $\varepsilon$.
|
87
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
25. The sequence $\left(x_{n}\right)$ is defined by the conditions: $x_{1}=1$, and for each natural number $n$, the number $x_{n+1}$ is the largest number that can be obtained by rearranging the digits of the number $x_{n}+1$. Find the smallest $n$ for which the decimal representation of the number $x_{n}$ has exactly 2017 digits.
|
25. Answer: the smallest such number $n$ is $18298225=9(1+2+3+\ldots+2016)+1$.
To understand how this sequence is constructed, let's write out the first few terms. Initially, the sequence contains single-digit numbers:
$$
1, \quad 2, \quad 3, \quad \ldots, \quad 9 .
$$
Next come the two-digit numbers:

Then the three-digit numbers:
$$
100,110,111, \quad 211,221,222, \quad 322,332,333, \ldots, 988,998,999 .
$$
What is the pattern here? Let's think about how many terms in the sequence can have exactly $k$ digits.
The first $k$-digit number can appear in this sequence only as a result of the operation $99 \ldots 9 + 1 = 100 \ldots 0$ (no digit rearrangement is required). Next, we claim that the sum of the digits of each subsequent $k$-digit number is 1 greater than the sum of the digits of the previous number. Indeed, digit rearrangement does not change the sum of the digits, and adding 1 always increases the sum of the digits by 1, except in the case where the last digit is 9. However, in the representation of all numbers in our sequence, the digits are arranged in descending order, and if the last digit is 9, then the number consists entirely of 9s, and the next term in the sequence is a $(k+1)$-digit number.
Thus, the sums of the digits of consecutive $k$-digit terms in the sequence are $1, 2, 3, \ldots, 9k$, i.e., the sequence contains exactly $9k$ $k$-digit numbers.
It remains to calculate the answer. We have found 9 single-digit terms in the sequence, $9 \cdot 2$ two-digit terms, $9 \cdot 3$ three-digit terms, and so on, $9 \cdot 2016$ terms with 2016 digits. Therefore, the number of the first 2017-digit term in the sequence is
$$
9(1+2+3+\cdot+2016)+1=\frac{9 \cdot 2016 \cdot 2017}{2}+1=18298225 .
$$
|
18298225
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
28. When preparing a district olympiad, each jury member participated in no more than 10 discussions. Discussions can be large or small. In a small discussion, 7 jury members participate, each sending exactly one email to each of the other 6. In a large discussion, 15 jury members participate, each sending exactly one email to each of the other 14. A total of 1994 emails were sent, not counting the emails sent by the jury secretary. In how many discussions did the secretary participate?
|
28. Answer: The secretary participated in 6 small discussions and 2 large ones.
In a small discussion, 7 jury members participate, each sending exactly one email to each of the 6 others, so in the end, 42 emails are sent in a small discussion. Similarly, participants in a large discussion send 210 emails.
Let a total of $M$ small and $B$ large discussions take place, and the secretary participated in $m \leqslant M$ small and $b \leqslant B$ large discussions, with $m+b \leqslant 10$ by condition. A participant in a small discussion sends 6 emails, and a participant in a large discussion sends 14 emails. Thus, the secretary sent $6 m+14 b$ emails. Adding to this the 1994 emails sent by the other jury members, we get all the emails written as a result of all discussions, i.e., $42 M+210 B$ emails. Therefore,
$$
1994+6 m+14 b=42 M+210 B
$$
The right-hand side of this equation is divisible by 42. Thus,
$$
6 m+14 b \equiv-1994 \equiv 22 \quad(\bmod 42)
$$
Thus, theoretically, the sum $6 m+14 b$ can take values $22, 22+42=64, 22+42 \cdot 2=106$, $22+42 \cdot 3=148$, etc. But since $m+b \leqslant 10$, the sum $6 m+14 b$ cannot be too large:
$$
6 m+14 b \leqslant 14 m+14 b=14(m+b) \leqslant 14 \cdot 10=140 .
$$
Thus, we only need to check whether the equations
$$
6 m+14 b=22, \quad 6 m+14 b=64, \quad 6 m+14 b=106
$$
have solutions in non-negative integers $m$ and $b$, where $m+b \leqslant 10$. This check is performed by a simple enumeration. As a result, we find that the first and third equations do not have such solutions. The second equation has a solution $m=6, b=2$, which seems to suit us.
Now we need to ensure that for the found values of $m$ and $b$, we can choose numbers $M \geqslant m$, $B \geqslant b$ such that the equation $(*)$ is satisfied, i.e.,
$$
42 M+210 B=2058
$$
For example, we can take $B=b=2$, then we find that $M=39$.
Thus, we have found that the situation described in the condition is possible only in the case where the secretary participated in 8 discussions.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. There are $2 n$ cards, each with a number from 1 to $n$ (each number appears on exactly two cards). The cards are lying on the table face down. A set of $n$ cards is called good if each number appears exactly once. Baron Munchausen claims that he can point out 80 sets of $n$ cards, at least one of which is guaranteed to be good. For what largest $n$ can Baron's words be true?
|
Answer: $n=7$. We will present an algorithm for how to indicate $2^{n-1}$ sets on $2n$ cards, one of which is suitable. (In our case, this is $2^{6}=64<80$ sets.) Imagine that identical cards are connected by (invisible to us for now) red edges. We will arbitrarily pair the cards with blue edges. The red-blue graph is a collection of cycles, and any set of the form "cards every other in each cycle" will suit us. Any such set has the obvious property: on each blue edge, exactly one vertex is selected. Therefore, by checking all $2^{n}$ sets with this property, we will certainly find the suitable one. Moreover, all such sets are divided into pairs of opposites (and in each pair, either both sets are suitable or both are not), so it is enough to check $2^{n-1}$ sets.
Now suppose that for 16 cards, 80 sets of 8 cards each are indicated. We will prove that it is possible to write numbers on the cards so that none of these sets are suitable.
For each set, mark all $8^{2}$ pairs of cards where one card is in the set and the other is not; in total, $80 \cdot 8^{2}$ pairs will be marked. There are $16 \cdot 15 / 2$ pairs in total, so some pair will be marked no more than $80 \cdot 8^{2} /(16 \cdot 15 / 2)=(8 / 15) \cdot 80$ times. Therefore, this pair is "split" by no more than 42 sets. We will write the number 1 on this pair of cards. All sets that contain both of these cards or neither of them are already rejected. We will now consider only the remaining $a \leqslant 42$ sets that potentially could be suitable.
Each of them contains exactly 7 of the remaining 14 cards. Similarly to the previous step, some pair of them will be "split" by no more than $[(7 / 13) \cdot a] \leqslant[7 / 13] \cdot 42]=22$ sets. We will write the number 2 on this pair and thereby reject all sets except no more than 22.
We continue in the same manner, eventually leaving 4 free cards and one set of two cards. We will write the number 7 on the cards of this set, and the number 8 on the two remaining cards; this set will also be rejected.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
31. Let's call a number complex if it has at least two different prime divisors. Find the largest natural number that cannot be represented as the sum of two complex numbers.
|
31. The numbers $6, 12, 15$, and 21 are composite and give all possible remainders when divided by 4. Therefore, from any number $n>23$, one of these numbers can be subtracted so that the result is a number of the form $4k+2=2(2k+1)$. Clearly, this difference will be a composite number.
|
23
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
34. In the gym, 200 schoolchildren gathered. Every pair of acquaintances shook hands. It turned out that any two strangers made at least 200 handshakes in total. Prove that there were at least 10000 handshakes in total.
|
34. Let's write the solution in the language of graphs. If the degree of a vertex is not less than 100, we call it rich; if it is less than 100, we call it poor. From the condition, it follows that all poor vertices are pairwise adjacent to each other.
We will prove that each poor vertex can be paired with a non-adjacent rich vertex such that different poor vertices correspond to different rich vertices. Suppose we have constructed pairs for $k$ poor vertices. If there are still poor vertices left, then $k < 100$. Take the next poor vertex; it is non-adjacent to at least 100 (rich) vertices. Out of these, no more than $k$ have already been paired with some poor vertex, so there will be at least one that has not yet been included in any pair.
As a result, we have several non-adjacent pairs of vertices, and in each such pair, the sum of the degrees is at least 200, and there are still several rich vertices with a degree of at least 100. In total, the sum of all degrees is at least $200 \cdot 100$, and the number of edges is at least 10000.
|
10000
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
6. Find the minimum value of the expression $\left[\frac{7(a+b)}{c}\right]+\left[\frac{7(a+c)}{b}\right]+\left[\frac{7(b+c)}{a}\right]$, where $a, b$ and $c$ are arbitrary natural numbers.
|
Answer: 40. Evaluation: the sum of the fractions under the integer parts is no less than $14 \cdot 3=42$ (we add three inequalities of the form $7(a / b+b / a) \geqslant 14$, and each integer part is greater than the fraction reduced by 1. Therefore, the desired value is greater than $42-3=39$, i.e., not less than 40. Example: 99, 100, 100.
|
40
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
24. A polynomial of degree 10 has three distinct roots. What is the maximum number of zero coefficients it can have?
(A. Khryabrov)
|
24. Answer: Answer: 9 zero coefficients. For example, the polynomial $x^{10}-x^{8}$ has roots $0,1,-1$. If a polynomial has only one non-zero coefficient, it is of the form $a x^{10}$, and therefore has exactly one root.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On the bank of the river stand 10 sheikhs, each with a harem of 100 wives. Also at the bank stands an $n$-person yacht. By law, a woman should not be on the same bank, on the yacht, or even at a transfer point with a man if her husband is not present. What is the smallest $n$ for which all the sheikhs and their wives can cross to the other bank without breaking the law?
|
Answer: 10. Example: first, all 1000 wives move quietly, then one returns and 10 sheikhs leave. Finally, another returns and picks up the first. Evaluation: let the number of places not exceed 9. Consider the moment when the first sheikh appears on the other shore - or several at once, but not all, for they could not have crossed all at once. Then, together with them, their harems are also there, and with the remaining sheikhs, their harems are there. But then for the return trip, there is only one option: all the sheikhs present on the second shore return immediately, and they accumulate again on the first shore. Thus, all the sheikhs will never leave from there.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Given a prime number $p$. All natural numbers from 1 to $p$ are written in a row in ascending order. Find all $p$ for which this row can be divided into several blocks of consecutive numbers so that the sums of the numbers in all blocks are equal.
|
Answer: $p=3$. Let $k-$ be the number of blocks, $S-$ be the sum in each block. Since $p(p+1) / 2=k S$, either $k$ or $S$ is divisible by $p$. Clearly, $k<p$, so $S$ is a multiple of $p$. Let the leftmost group consist of numbers from 1 to $m$. Then $m(m+1) / 2$ is a multiple of $p$, from which $m \geqslant p-1$, i.e., $m=p-1$. But this means that the sum of the numbers from 1 to $p-1$ is equal to $p$, which is only possible when $p=3$.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The cells of a $100 \times 100$ table are painted white. In one move, it is allowed to select any 99 cells from one row or one column and repaint each of them to the opposite color - from white to black, and from black to white. What is the minimum number of moves required to obtain a table with a checkerboard pattern of cells?
|
Answer: in 100 moves. Evaluation: to repaint each of the cells on the black diagonal, a move is required. Example: repaint all rows and columns with odd numbers. In this case, in the $k$-th row and $u$-th column, we will not repaint their common cell. It is easy to see that as a result, we will get a chessboard coloring (with a white diagonal of cells of the form $(k, k)$).
|
100
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A $10 \times 10$ table is filled with numbers from 1 to 100: in the first row, the numbers from 1 to 10 are written in ascending order from left to right; in the second row, the numbers from 11 to 20 are written in the same way, and so on; in the last row, the numbers from 91 to 100 are written from left to right. Can a fragment of 7 cells in the shape $\quad$ be found in this table, the sum of the numbers in which is $455?$ (The fragment can be rotated.)
|
1. Answer: Yes. If $x$ is in the center of the fragment, then the sum of the numbers in it is $7x$ and then with 646566 $x=65$ the sum will be exactly 455 (see figure).
|
65
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Given $n$ distinct natural numbers, any two of which can be obtained from each other by permuting the digits (zero cannot be placed in the first position). For what largest $n$ can all these numbers be divisible by the smallest of them?
|
Answer: 9. It is clear that there cannot be more than nine numbers.
We will use a known property of the period of a purely periodic rational fraction $\alpha=$ $a / b<1$ with coprime $(a, b)$: the length of the period is the smallest natural $t$ for which $\left(10^{t}-1\right) \vdots b$, and the period $T$ itself is the number $\left(10^{t}-1\right) \alpha$.
From this, it follows that if $a_{1} / b$ and $a_{2} / b$ are two proper irreducible fractions, and $a_{1}=k a_{2}$, then the period of the first fraction is exactly $k$ times the period of the second.
Consider the fractions 2/19, 4/19, 6/19, 8/19, 10/19, 12/19, 14/19, 16/19, 18/19. They have periods of the same length, and all of them are divisible by the period of 2/19, which is 105263157894736842. On the other hand, it can be verified that 10 is a primitive root modulo 19. Therefore, the numbers $2 \cdot 10^{s} / 19$ for $0 \leqslant s \leqslant 17$
It can be verified that 10 is a primitive root modulo 19. Therefore, the numbers $10^{s} / 19$ for $0 \leqslant s \leqslant 17$ after removing the integer part are all 18 proper irreducible fractions with the denominator 19. Their periods have the same length and are obtained from the period of the fraction $2 / 19$ by cyclic shifts of $s$ digits to the right. In particular, they all consist of the same set of digits. (And all, except $1 / 19$, do not start with zero, i.e., they represent natural numbers of the same length). From the previous paragraph, it follows that the periods of the fractions $4 / 19,6 / 19,8 / 19,10 / 19,12 / 19,14 / 19,16 / 19,18 / 19$ are divisible by the period of the fraction $2 / 19$ and together they form an example of 9 numbers.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
34. A company gathered for a meeting. Let's call a person sociable if in this company they have at least 20 acquaintances, and at least two of them are acquainted with each other. Let's call a person shy if in this company they have at least 20 strangers, and at least two of them are strangers to each other. It turned out that in the gathered company there are neither sociable nor shy people. What is the maximum number of people that can be in it
$\left(\right.$ Folklore $^{(2)}$
|
34. Answer: 40.
Evaluation: Suppose that a certain person (let's call him Kostya) is acquainted with at least 20 people. If some of Kostya's acquaintances know each other, then Kostya is sociable. Let's consider the case where all of Kostya's acquaintances do not know each other. In this case, if Kostya is acquainted with at least 21 people, then any of his acquaintances are shy.
Similarly, if Kostya is not acquainted with 20 people, among whom there are some who do not know each other, then Kostya is shy. And in the case where Kostya is not acquainted with 21 people, and all those who are not acquainted with Kostya know each other, then all of them are sociable.
This means that if there are at least 41 people in the company, then Kostya is acquainted with exactly 20 people and is not acquainted with exactly 20 people. In this case, all of Kostya's acquaintances do not know each other, and all those who are not acquainted with Kostya know each other. Consider any person acquainted with Kostya, Vasya, and any person not acquainted with Kostya, Petya. If Vasya and Petya know each other, then Petya is sociable, as he knows Vasya and 19 other people who are not acquainted with Kostya, while those not acquainted with Kostya know each other. Similarly, if Vasya and Petya do not know each other, then Vasya is shy.
Example: Let's divide a company of 40 people into two groups of 20 people each. Suppose that people in one group know each other, while people from different groups do not know each other. Then, if there were a sociable person, all his acquaintances would be in the same group with him, and then there would be at least 21 people in this group. If a shy person were found, then all people not acquainted with him would be in the same group, and thus would know each other.
|
40
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
50. In the city, 2019 metro stations have been built. Some pairs of stations are connected by tunnels, and from any station, you can reach any other station via the tunnels. The mayor ordered the organization of several metro lines: each line must include several different stations, sequentially connected by tunnels (the same tunnel can be part of several lines). Each station must lie on at least one line. To save funds, no more than $k$ lines should be created.
It turned out that the mayor's order was impossible to implement. For what largest $k$ could this have happened? (S. Berlov)
|
50. Answer: $k=1008$. Let's provide an example of a connected graph with 2019 vertices that cannot be covered by 1008 simple paths: one vertex is connected to 2018 vertices of degree 1. Any simple path contains no more than two pendant vertices, so at least 1009 paths are required for coverage.
We will prove that 1009 paths are always sufficient. Choose any vertex $A$ of degree at least 2 (such a vertex obviously exists), and two of its neighbors $B$ and $C$. The remaining 2016 vertices can be arbitrarily divided into 1008 pairs, and we will draw simple paths between the vertices in each pair, as well as the path $B A C$ - a total of 1009 paths.
|
1008
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
52. Olya wrote fractions of the form $1 / n$ on cards, where $n-$ are all possible divisors of the number $6^{100}$ (including one and the number itself). She arranged these cards in some order. After that, she wrote the number on the first card on the board, then the sum of the numbers on the first and second cards, then the sum of the numbers on the first three cards, and so on, finally, the sum of the numbers on all the cards. Each sum Olya wrote on the board as an irreducible fraction. What is the smallest number of different denominators that could appear on the board?
(O. Ivanova)
|
52. Answer: two denominators. Let's represent all fractions in the form $a_{n} / 6^{100}$, then $a_{1}, a_{2}, \ldots$ are again all divisors of the number $6^{100}$, each appearing once. Let the partial sums be denoted by $S_{n} / 6^{100}$. Then the denominator of the irreducible representation of the partial sum depends on the powers of the prime factors 2 and 3 in the numerator $S_{n}$.
It is not difficult to understand that among $S_{n}$ there are both even and odd numbers, so in some $S_{n}$, the factor 2 enters with a zero power, and in others, with a non-zero power. Therefore, the answer in the problem is at least 2.
Let's provide an example of an arrangement with two different denominators. First, write down the divisor $a_{1}=1$. Then write down in any order all divisors that are multiples of 2 and 3. Up to this point, all partial sums $S_{n}$ are neither divisible by 2 nor by 3, i.e., they contain 2 and 3 in the same (zero) power, and the last of them gives a remainder of 1 when divided by both 2 and 3. It remains to write down all divisors of the form $2^{k}$ and $3^{k}$ ( $k$ from 1 to 100). First, write down the powers of two, alternating $2^{k} \equiv 1(\bmod 3)$ and $2^{k} \equiv 2(\bmod 3)$ (i.e., powers with even and odd exponents). All the resulting partial sums will still be odd and not divisible by three. Finally, write down the powers of three, alternating their remainders modulo 4 so that all remaining partial sums are not divisible by 4. In this case, they will remain not divisible by three, and the factor 2 will enter them no more than in the first power! Thus, in this example, the factor 3 enters all $S_{n}$ in the zero power, and the factor 2 in the zero or first power.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13. A grasshopper starts moving in the top-left cell of a $10 \times 10$ square. It can jump one cell down or to the right. Additionally, the grasshopper can fly from the bottom cell of any column to the top cell of the same column, and from the rightmost cell of any row to the leftmost cell of the same row. Prove that the grasshopper will need at least 9 flights to visit each cell of the square at least once.
(N. Vlasova)
|
13. Consider the diagonal running from the bottom-left corner to the top-right corner. We will paint all 10 cells on this diagonal red. Note that from any red cell, without making any jumps, you can only move to cells that are to the right of it, below it, or to the right and below it. Therefore, it is impossible to move from one red cell to another red cell without jumping. The grasshopper must visit all 10 red cells in some order, so it must make at least 9 jumps between these visits.
|
9
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
66. An isosceles triangle \(ABC\) with a perimeter of 12 is inscribed in a circle \(\omega\). Points \(P\) and \(Q\) are the midpoints of the arcs \(ABC\) and \(ACB\) respectively. The tangent to the circle \(\omega\) at point \(A\) intersects the ray \(PQ\) at point \(R\). It turns out that the midpoint of segment \(AR\) lies on the line \(BC\). Find the length of segment \(BC\).
\[
\text{(A. Kuznetsov)}
\]
|
66. Answer: 4. Let $I_{A}, I_{B}, I_{C}$ be the centers of the excircles of triangle $ABC$, touching sides $BC, CA$, and $AB$ respectively. Then the lines $A I_{A}, B I_{B}, C I_{C}$ will be the angle bisectors of triangle $ABC$, and the lines $I_{B} I_{C}, I_{C} I_{A}, I_{A} I_{B}$ will be its external angle bisectors. Therefore, points $A, B, C$ will be the feet of the altitudes of triangle $I_{A} I_{B} I_{C}$, and circle $\omega$ will be its nine-point circle. Then point $P$ is the point of intersection of $I_{A} I_{C}$ with $\omega$ other than $B$. Therefore, $P$ is the midpoint of $I_{A} I_{C}$. Similarly, $Q$ is the midpoint of $I_{A} I_{B}$. Thus, $PQ$ is the midline of triangle $I_{A} I_{B} I_{C}$.
Let $K$ and $L$ be the feet of the external and internal angle bisectors of angle $A$ of triangle $ABC$, and let $M$ be the point of intersection of lines $AR$ and $BC$. By the problem's condition, we know that $AM = MR$. We will prove that $AM = ML = MK$. Indeed, $\angle MAL = \angle MAC + \angle CAL = \angle ABC + \angle LAB = \angle ALM$ (point $M$ lies on ray $BC$ since $R$ lies on $PQ$). Therefore, $AM = ML$, and since triangle $AKL$ is right-angled, $AM = MK$.
Thus, $AM = ML = MK = MR$. Therefore, $ALRK$ is a rectangle and $LR \parallel I_{B} I_{C}$. We obtain that lines $PQ$ and $LR$ are parallel to $I_{B} I_{C}$ and have a common point $R$. Then these lines coincide. This means that point $L$ lies on the midline of triangle $I_{A} I_{B} I_{C}$ and, therefore, divides segment $A I_{A}$ in half. Further, applying the property of the external angle bisector to triangles $ABL$ and $ACL$, we get $AB / BL = AC / CL = AI_{A} / I_{A} L = 2$. Then $AB + AC = 2BC$ and, therefore, $BC = 4$.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
49. What is the maximum number of solutions that the equation $\max \left\{a_{1} x+b_{1}, \ldots, a_{10} x+b_{10}\right\}=0$ can have, if $a_{1}, \ldots, a_{10}, b_{1}, \ldots, b_{10}$ are real numbers, and all $a_{i}$ are not equal to 0?
|
49. Answer: 2 solutions. For example, 5 functions $-x-1$ and 5 functions $x-1$.
Suppose this equation has three roots: $u<v<w$. At point $v$, one of the linear functions $a_{i} x+b_{i}$ is zero. On the other hand, its values at points $u$ and $w$ do not exceed zero. However, such a linear function can only be a constant, which is prohibited by the condition.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
52. In the table, there are 25 columns and 300 rows, and Kostya painted all its cells in three colors. Then Lesha, looking at the table, names one of the three colors for each row and marks all the cells of this color in that row. (If there are no cells of the specified color in the row, he marks nothing in it.) After that, all columns that contain at least one marked cell are erased from the table. Kostya wants as few columns as possible to remain in the table, while Lesha wants as many as possible. What is the maximum number of columns that Lesha can guarantee to leave?
|
52. Answer: Two columns. To leave at least two columns, Lesha must for each row name a color that does not appear in the first two cells of that row. With this strategy, the first two columns will not be crossed out.
Note now that $300=C_{25^{2}}$. Using this observation, we can associate each row with its own pair of columns. Let Kostya paint in each row the cells in the corresponding two columns in the 1st and 2nd colors, and the rest of the cells in the third color. If Lesha chooses the 3rd color in some row, this will immediately cross out everything except two columns. If, however, Lesha always chooses the 1st or 2nd color, then at most one column will remain! Indeed, suppose some two columns remain. Since there is a row in which the cells of these columns are painted in the 1st and 2nd colors, one of these columns must be destroyed by Lesha's choice for that row!
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
55. In a $10 \times 10$ grid (the sides of the cells have a unit length), $n$ cells were chosen, and in each of them, one of the diagonals was drawn and an arrow was placed on this diagonal in one of two directions. It turned out that for any two arrows, either the end of one coincides with the beginning of the other, or the distance between their ends is at least 2. What is the largest $n$ for which this is possible?
|
55. Answer: when $n=48$.
For each arrow, consider the three-cell corner obtained by removing from a $2 \times 2$ square, centered at the end of the arrow, a $1 \times 1$ square, the diagonal of which is this arrow. Note that such corners do not intersect and are contained within a $12 \times 12$ square. Therefore, there are no more than $12^{2} / 3=48$ such corners.
An example of placing 48 arrows is shown in the figure.
|
48
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
46. In a convex quadrilateral $A B C D$, point $M$ is the midpoint of side $A D$, $C M \| A B$, $A D=B D$ and $3 \angle B A C=\angle A C D$. Find the angle $A C B$.
(S. Berlov)
|
46. Answer: $\angle A C B=90^{\circ}$.
Notice that $\angle B A C=\angle A C M$, hence $\angle D C M=\angle A C D-\angle A C M=2 \angle A C M$. Let $N$ be the midpoint of segment $A B$. Then $D N$ is the median, bisector, and altitude of the isosceles triangle $A B D$. Next, point $C$ lies on the midline of this triangle, which is clearly the perpendicular bisector of $D N$, so $C D=C N$. Thus, triangle $N C D$ is isosceles and $C M$ is its bisector. Therefore, $\angle N C M=\angle D C M=2 \angle A C M$, hence $\angle N C A=\angle A C M=\angle N A C$. This means that triangle $A N C$ is isosceles and $N C=A N=N B$, but then
$\angle A C B=90^{\circ}$.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.