problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
Problem 8.4. Given a square $A B C D$. Point $L$ is on side $C D$ and point $K$ is on the extension of side $D A$ beyond point $A$ such that $\angle K B L=90^{\circ}$. Find the length of segment $L D$, if $K D=19$ and $C L=6$.
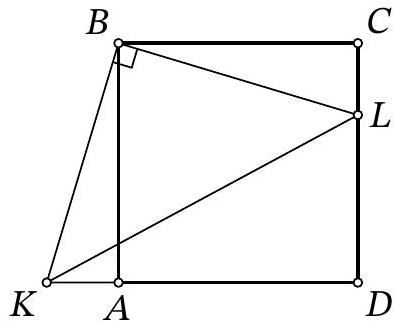
|
Answer: 7.
Solution. Since $ABCD$ is a square, then $AB=BC=CD=AD$.
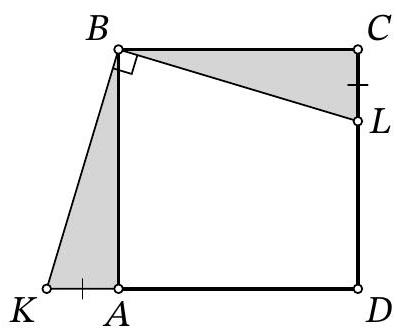
Fig. 1: to the solution of problem 8.4
Notice that $\angle ABK = \angle CBL$, since they both complement $\angle ABL$ to $90^{\circ}$. Therefore, right triangles $ABK$ and $CBL$ are congruent by the acute angle and the leg $AB = BC$ (Fig. 1). Consequently, $AK = CL = 6$. Then
$$
LD = CD - CL = AD - CL = (KD - AK) - CL = KD - 2 \cdot CL = 19 - 2 \cdot 6 = 7
$$
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.5. There are 7 completely identical cubes, each of which has 1 dot marked on one face, 2 dots on another, ..., and 6 dots on the sixth face. Moreover, on any two opposite faces, the total number of dots is 7.
These 7 cubes were used to form the figure shown in the diagram, such that on each pair of glued faces, the same number of dots is marked. All dots were erased from all faces except nine, as shown in the diagram. What is the total number of dots that were initially marked on the surface of the figure?
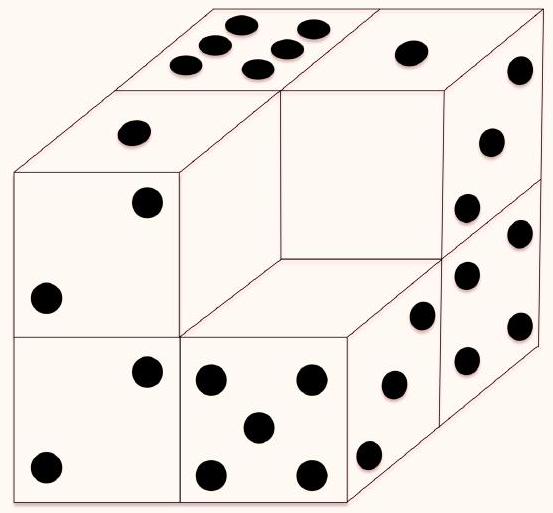
|
Answer: 75.
Solution. There are 9 ways to cut off a "brick" consisting of two $1 \times 1 \times 1$ cubes from our figure. In each such "brick," there are two opposite faces $1 \times 1$, the distance between which is 2. Let's correspond these two faces to each other.
Consider one such pair of faces: on one of them, the dots were not erased, while on the other, they were erased. It is not difficult to understand that originally there were the same number of dots on these faces.
Let's calculate the total number of dots that were originally on all 9 pairs of faces. We get
$$
2 \cdot(1+1+6+2+2+5+3+3+4)=54
$$
There are 6 faces $1 \times 1$ left, about which we still know nothing. However, it can be noticed that they are divided into pairs according to the following principle: in one pair, there will be faces from one $1 \times 1 \times 1$ cube. In each such pair, the sum of the numbers was 7. Then we get that the number of dots on the surface of the figure originally was
$$
54+3 \cdot 7=75
$$
|
75
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.7. For quadrilateral $A B C D$, it is known that $\angle B A C=\angle C A D=60^{\circ}, A B+A D=$ $A C$. It is also known that $\angle A C D=23^{\circ}$. How many degrees does the angle $A B C$ measure?
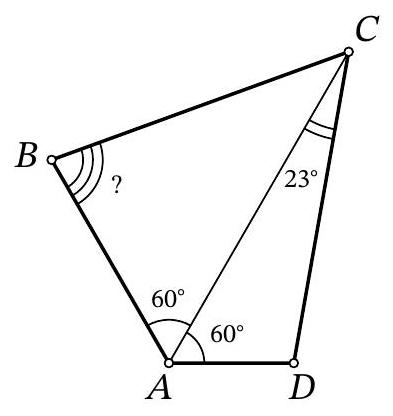
|
Answer: 83.
Solution. Mark a point $K$ on the ray $AB$ such that $AK = AC$. Then the triangle $KAC$ is equilateral; in particular, $\angle AKC = 60^{\circ}$ and $KC = AC$. At the same time, $BK = AK - AB = AC - AB = AD$. This means that triangles $BKC$ and $DAC$ are equal by two sides and the angle $60^{\circ}$ between them (Fig. 2).
It remains to note that the angle $\angle ABC$ - the exterior angle of triangle $BKC$ - is equal to the exterior angle at vertex $D$ of triangle $DAC$, which is calculated as the sum of two interior angles: $60^{\circ} + 23^{\circ} = 83^{\circ}$.
|
83
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
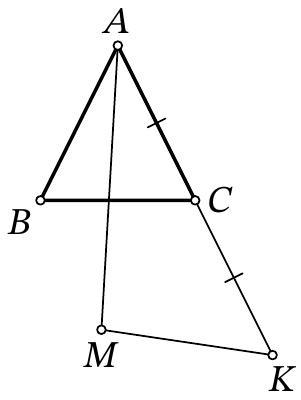
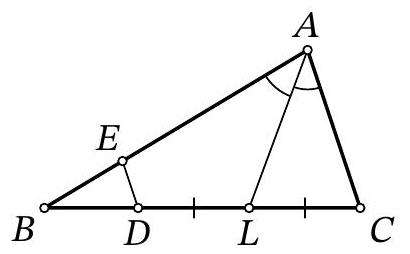
Problem 9.5. On the base $AC$ of isosceles triangle $ABC (AB = BC)$, a point $M$ is marked. It is known that $AM = 7, MB = 3, \angle BMC = 60^\circ$. Find the length of segment $AC$.
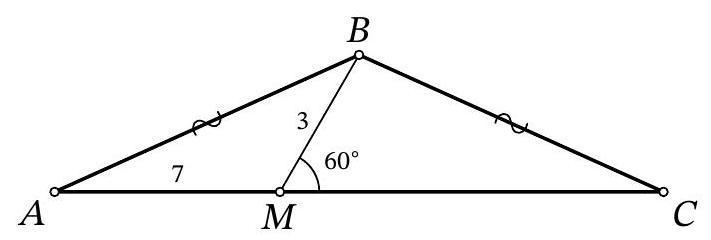
|
Answer: 17.
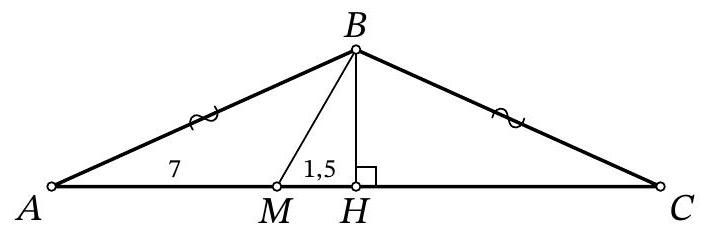
Fig. 3: to the solution of problem 9.5
Solution. In the isosceles triangle \(ABC\), draw the height and median \(BH\) (Fig. 3). Note that in the right triangle \(BHM\), the angle at vertex \(B\) is \(30^\circ\), so \(HM = \frac{1}{2} BM = 1.5\). Then \(AC = 2AH = 2(AM + MH) = 2 \cdot (7 + 1.5) = 17\).
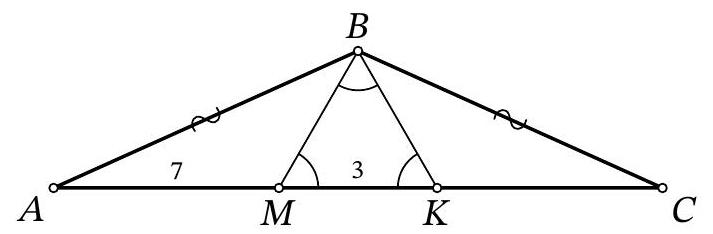
Fig. 4: to the solution of problem 9.5
Another solution. Mark a point \(K\) on \(MC\) such that \(\angle BKM = 60^\circ\) (Fig. 4; such a point lies exactly on the segment \(MC\) because \(\angle BCM = \angle BAM = \angle BMC - \angle ABM < 60^\circ\)). Note that in triangle \(BMK\), two angles are \(60^\circ\), so it is equilateral and \(BK = MK = BM = 3\). Also note that triangles \(ABM\) and \(CBK\) are equal because \(BC = AB\), \(\angle A = \angle C\), \(\angle AMB = \angle CKB = 120^\circ\) (therefore, \(\angle ABM = \angle CBK\)). Then \(CK = AM = 7\) and \(AC = AM + MK + KC = 7 + 3 + 7 = 17\).
|
17
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
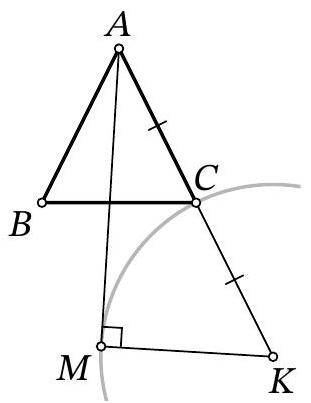
Problem 9.8. On the side $CD$ of trapezoid $ABCD (AD \| BC)$, a point $M$ is marked. A perpendicular $AH$ is dropped from vertex $A$ to segment $BM$. It turns out that $AD = HD$. Find the length of segment $AD$, given that $BC = 16$, $CM = 8$, and $MD = 9$.
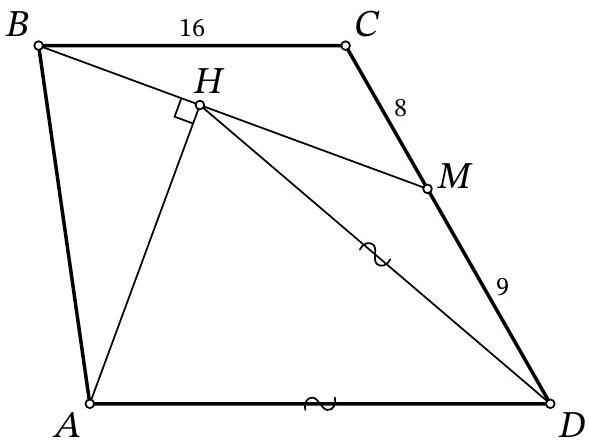
|
Answer: 18.
Solution. Let the lines $B M$ and $A D$ intersect at point $K$ (Fig. 5). Since $B C \| A D$, triangles $B C M$ and $K D M$ are similar by angles, from which we obtain $D K = B C \cdot \frac{D M}{C M} = 16 \cdot \frac{9}{8} = 18$.
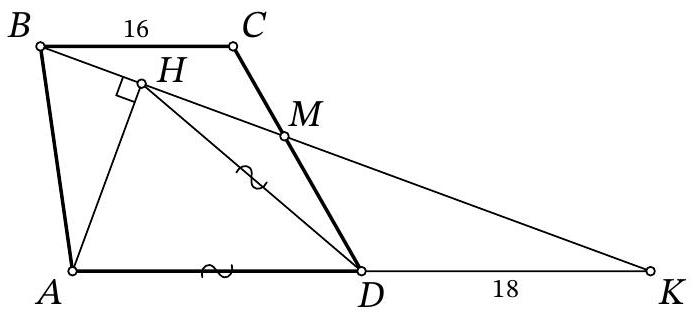
Fig. 5: to the solution of problem 9.8
In the isosceles triangle $A D H$, draw the height and median $D S$. Then, in triangle $A H K$, the segment $D S$ passes through the midpoint of side $A H$ and is parallel to $H K$. Therefore, $D S$ is the midline of this triangle, and $A D = D K = 18$.
Remark. If in a right triangle a point on the hypotenuse is equidistant from two vertices of the triangle, then it is equidistant from all three vertices of the triangle.
## 10th Grade
|
18
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
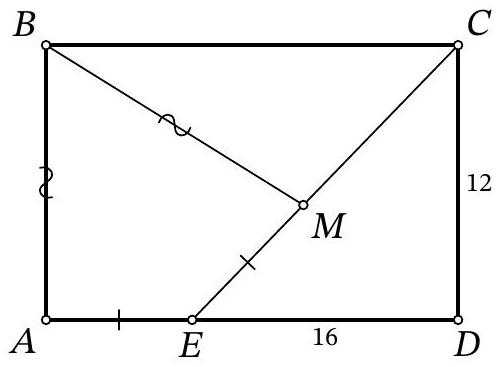
Problem 10.3. On the side $AD$ of rectangle $ABCD$, a point $E$ is marked. On the segment $EC$, there is a point $M$ such that $AB = BM, AE = EM$. Find the length of side $BC$, given that $ED = 16, CD = 12$.
|
Answer: 20.
Solution. Note that triangles $A B E$ and $M B E$ are equal to each other by three sides. Then $\angle B M E=\angle B A E=90^{\circ}$.
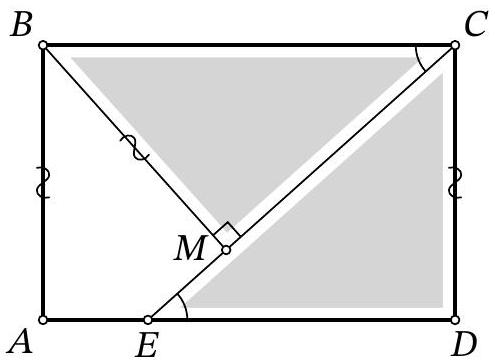
Fig. 6: to the solution of problem 10.3
From the parallelism of $A D$ and $B C$, it follows that $\angle B C M=\angle C E D$ (Fig. 6). Therefore, right triangles $B C M$ and $C E D$ are equal by an acute angle and the leg $B M=A B=C D$. Using the Pythagorean theorem for triangle $C D E$, we conclude
$$
B C=C E=\sqrt{C D^{2}+E D^{2}}=\sqrt{12^{2}+16^{2}}=20
$$
|
20
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
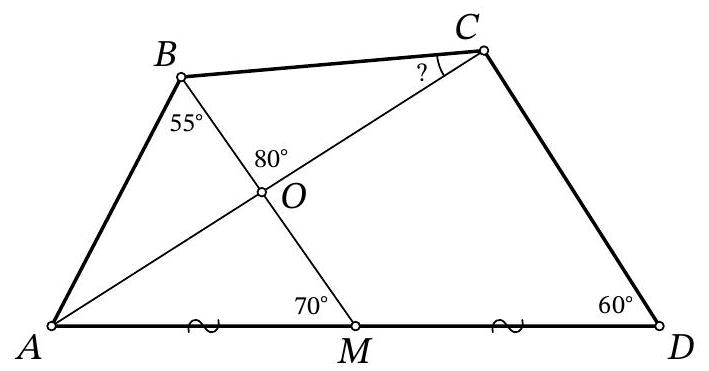
Problem 10.6. In a convex quadrilateral $A B C D$, the midpoint of side $A D$ is marked as point $M$. Segments $B M$ and $A C$ intersect at point $O$. It is known that $\angle A B M=55^{\circ}, \angle A M B=$ $70^{\circ}, \angle B O C=80^{\circ}, \angle A D C=60^{\circ}$. How many degrees does the angle $B C A$ measure?
|
Answer: 35.
Solution. Since
$$
\angle B A M=180^{\circ}-\angle A B M-\angle A M B=180^{\circ}-55^{\circ}-70^{\circ}=55^{\circ}=\angle A B M
$$
triangle $A B M$ is isosceles, and $A M=B M$.
Notice that $\angle O A M=180^{\circ}-\angle A O M-\angle A M O=180^{\circ}-80^{\circ}-70^{\circ}=30^{\circ}$, so $\angle A C D=$ $180^{\circ}-\angle C A D-\angle A D C=180^{\circ}-30^{\circ}-60^{\circ}=90^{\circ}$.
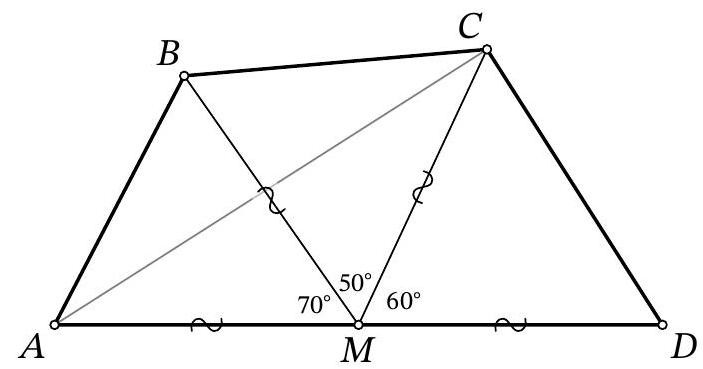
Fig. 7: to the solution of problem 10.6
Draw segment $C M$ (Fig. 7). Since in a right triangle, the median to the hypotenuse is equal to half of it, we have $C M=D M=A M=B M$. Triangle $M C D$ is isosceles with an angle of $60^{\circ}$ at the base, so it is equilateral, and $\angle C M D=60^{\circ}$. Then $\angle B M C=180^{\circ}-\angle A M B-\angle C M D=180^{\circ}-70^{\circ}-60^{\circ}=50^{\circ}$. Since triangle $B M C$ is isosceles with vertex $M$, we have $\angle C B M=$ $\frac{1}{2}\left(180^{\circ}-\angle B M C\right)=\frac{1}{2}\left(180^{\circ}-50^{\circ}\right)=65^{\circ}$. Finally,
$$
\angle B C A=180^{\circ}-\angle C B M-\angle B O C=180^{\circ}-65^{\circ}-80^{\circ}=35^{\circ} \text {. }
$$
Remark. There are other solutions that use the fact that $A B C D$ is a cyclic quadrilateral with the center of the circumscribed circle $M$.
|
35
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.5. Quadrilateral $ABCD$ is inscribed in a circle. It is known that $BC=CD, \angle BCA=$ $64^{\circ}, \angle ACD=70^{\circ}$. A point $O$ is marked on segment $AC$ such that $\angle ADO=32^{\circ}$. How many degrees does the angle $BOC$ measure?
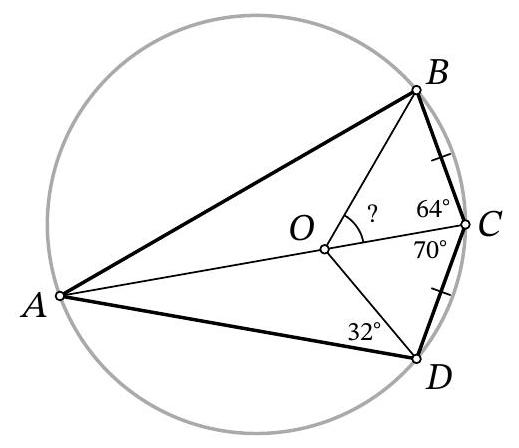
|
Answer: 58.
Solution. As is known, in a circle, inscribed angles subtended by equal chords are either equal or supplementary to $180^{\circ}$. Since $B C=C D$ and $\angle B A D<180^{\circ}$, we get that $\angle B A C=\angle D A C$.
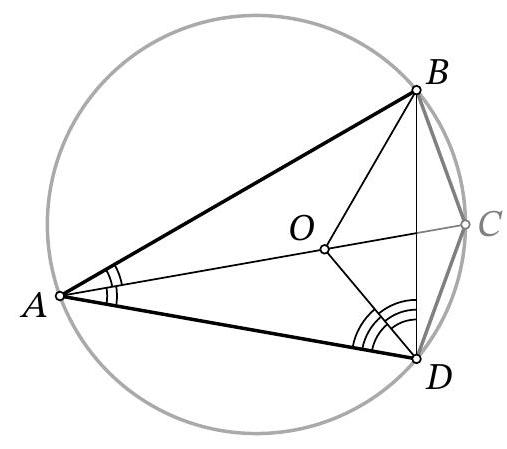
Fig. 9: to the solution of problem 11.5
Since $\angle B D A=\angle B C A=64^{\circ}$, we get that $\angle B D O=\angle A D O=32^{\circ}$. Therefore, point $O$ lies on the two angle bisectors of triangle $A B D$, i.e., it is the intersection point of the angle bisectors (Fig. 9). Then
$$
\angle B O C=\angle B A O+\angle A B O=\frac{\angle B A D+\angle A B D}{2}=\frac{180^{\circ}-\angle B D A}{2}=\frac{180^{\circ}-64^{\circ}}{2}=58^{\circ}
$$
Remark. The solution could also have been completed differently: since $O$ is the intersection point of the angle bisectors of triangle $A B D$, by the trident lemma $C D=C B=C O$, from which $\angle C O B$ is easily found.
|
58
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 4. CONDITION
The square of a natural number $a$ when divided by a natural number $n$ gives a remainder of 8. The cube of the number $a$ when divided by $n$ gives a remainder of 25. Find $n$.
|
Solution. Note that the number $\mathrm{x}=\mathrm{a}^{6}-8^{3}=\left(\mathrm{a}^{2}\right)^{3}-8^{3}=\left(\mathrm{a}^{2}-8\right)\left(\mathrm{a}^{4}+8 \mathrm{a}^{2}+64\right)$ is divisible by $n$. Also note that the number $\mathrm{y}=\mathrm{a}^{6}-25^{2}=\left(\mathrm{a}^{3}\right)^{2}-25^{2}=\left(\mathrm{a}^{3}-25\right)\left(\mathrm{a}^{3}+25\right)$ is divisible by $n$. Then the difference $\mathrm{x}-\mathrm{y}=\left(\mathrm{a}^{6}-8^{3}\right)-\left(\mathrm{a}^{6}-25^{2}\right)=625-512=113$ is divisible by $n$. The number 113 is a prime number, it has only two divisors: 1 and 113. Since by the condition $\mathrm{n}>25$, then $\mathrm{n}=113$.
Answer: $\mathrm{n}=113$.
|
113
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.4. A magician and an assistant have a deck of cards; one side (the "back") of all cards is the same, while the other is painted in one of 2017 colors (the deck contains 1,000,000 cards of each color). The magician and the assistant are going to perform the following trick. The magician leaves the room, and the audience lays out a row of $n>1$ cards face down on the table. The assistant looks at these cards and then turns all but one of them face up, without changing their order. Then the magician enters, looks at the table, points to one of the face-down cards, and names its color. For what smallest $n$ can the magician and the assistant agree in advance so that the trick is guaranteed to succeed?
(I. Bogdanov, K. Knop)
|
Answer. $n=2018$.
Solution. Let $k=2017$.
For $n=k+1$, the trick is easy to arrange. The magician and the assistant number the colors from 1 to $k$. The assistant, seeing the color of the last, $(k+1)$-th card (let its number be $a$), leaves the $a$-th card open. The magician, seeing which numbered card is open, can restore the color of the last card.
It remains to show that the trick cannot be performed for $n \leqslant k$. Suppose the contrary and consider the possible actions of the magician. Let, seeing a card of color $a$ in the $i$-th position, he announces that the card in the $j$-th position is of color $b$ (then $i \neq j$); we will call this an instruction $(a, i) \rightarrow(b, j)$. We can assume that for each pair $(a, i)$ there is only one instruction of the form $(a, i) \rightarrow(b, j)$ (and the magician always applies it when possible - since he has no information on which of such instructions to apply). Then there are no more than $k n$ instructions.
We will say that the initial layout of cards satisfies the instruction $(a, i) \rightarrow(b, j)$ if in it the $i$-th and $j$-th positions have cards of colors $a$ and $b$ respectively. Then each instruction is satisfied by exactly $k^{n-2}$ layouts. On the other hand, if the trick is guaranteed to succeed, then each possible layout satisfies at least one instruction - the one that the assistant and the magician will apply. Therefore, the total number of layouts cannot exceed $k n \cdot k^{n-2}$, that is, $k^{n} \leqslant k^{n-1} n$, from which $k \leqslant n$. Thus, $k=n$, and the inequality above turns into an equality. This means that each layout satisfies exactly one instruction, and from each pair $(a, i)$ exactly one instruction starts.
Consider an arbitrary instruction $(a, i) \rightarrow(b, j)$; then there is also an instruction of the form $(b, j) \rightarrow(c, k)$. Since there is no layout that satisfies both instructions, the conditions $i=k$ and $a \neq c$ must be met.
On the other hand, for any two instructions $(a, i) \rightarrow(b, j)$ and $(c, k) \rightarrow(d, \ell)$, among the numbers $i, j, k, \ell$ there must be coinciding ones - otherwise there is again a layout that satisfies both instructions. Consider a graph with vertices $1,2, \ldots, k$, in which $i$ and $j$ are connected by an edge $[i, j]$, if there is an instruction of the form $(a, i) \rightarrow(b, j)$ (by the above, there is also an instruction of the form $\left.(b, j) \rightarrow\left(a^{\prime}, i\right)\right)$. Then any two edges in this graph have a common vertex, and from each vertex at least one edge goes out. Let, for definiteness, $[1,2]$ be an edge of this graph. From vertex 3 an edge goes out, having a common vertex with the first - let, for definiteness, this be $[1,3]$. Then any edge from vertex $k>3$ must have the form $[1, k]$, to have a common vertex with each of the edges $[1,2]$ and $[1,3]$. Finally, any edge must have a common vertex with each of the edges $[1,2],[1,3]$ and $[1,4]$, that is, it must contain vertex 1. Thus, in each instruction one of the position numbers is 1.
Finally, we associate with each position $i>1$ all such colors $a$ for which there is an instruction of the form $(c, i) \rightarrow(a, 1)$. From the above, it follows that different positions cannot be associated with the same color. Since there are $k-1$ such positions and $k<2(k-1)$ colors, some position $i$ is associated with only one color $a$, that is, there are all $k$ instructions of the form $(c, i) \rightarrow(a, 1)$ for all possible $c$. However, there is also an instruction of the form $(a, 1) \rightarrow(c, i)$ for some $c$. But it cannot exist together with the instruction $(c, i) \rightarrow(a, 1)$; contradiction.
|
2018
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Petya runs down from the fourth floor to the first floor 2 seconds faster than his mother rides the elevator. Mother rides the elevator from the fourth floor to the first floor 2 seconds faster than Petya runs down from the fifth floor to the first floor. How many seconds does it take for Petya to run down from the fourth floor to the first floor? (The lengths of the stair flights between all floors are the same).
|
Answer: 12 seconds.
Solution. Between the first and fourth floors, there are 3 flights, and between the fifth and first floors, there are 4. According to the problem, Petya runs 4 flights 2 seconds longer than it takes his mother to ride the elevator, and 3 flights 2 seconds faster than his mother. Therefore, it takes Petya 4 seconds to run one flight. Then from the fourth floor to the first (i.e., 3 flights), Petya runs down in $4 \cdot 3=12$ seconds.
Grading criteria.
- Correct answer with a complete solution - 7 points.
- Explained that it takes 4 seconds for one flight, and the answer is 4 seconds - 5 points.
- Correct reasoning assuming the distance from the fifth floor to the first is 1.25 times the distance from the fourth floor to the first, and the answer is 16 seconds - 3 points.
- Only the answer - 0 points.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. On the number line, points with integer coordinates are painted red and blue according to the following rules: a) points whose coordinate difference is 7 must be painted the same color; b) points with coordinates 20 and 14 should be painted red, and points with coordinates 71 and 143 - blue. In how many ways can all points with integer coordinates be painted, while adhering to these rules?
|
Answer. In eight ways.
Solution. From part a), it follows that the coloring of all points with integer coordinates is uniquely determined by the coloring of the points corresponding to the numbers $0,1,2,3,4,5$, and 6. The point $0=14-2 \cdot 7$ must be colored the same as 14, i.e., red. Similarly, the point $1=71-10 \cdot 7$ must be colored blue, the point $3=143-20 \cdot 7$ - blue, and $6=20-2 \cdot 7$ - red. Therefore, it remains to count the number of different ways to color the points corresponding to the numbers 2, 4, and 5. Since each point can be colored in two ways - red or blue - the total number of ways is $2 \cdot 2 \cdot 2=8$.
Note. When counting the number of ways to color the points 2, 4, and 5, one can simply list all the ways, for example, in a table:
| 2 | 4 | 5 |
| :--- | :--- | :--- |
| $\kappa p$ | $\kappa p$ | $\kappa p$ |
| $\kappa p$ | $\kappa p$ | $c i n$ |
| $\kappa p$ | $c u n$ | $\kappa p$ |
| $\kappa p$ | $c u n$ | $c i n$ |
| $c u n$ | $\kappa p$ | $\kappa p$ |
| $c i n$ | $\kappa p$ | $c i n$ |
| $c i n$ | $c i n$ | $\kappa p$ |
| $c i n$ | $c i n$ | $c i n$ |
Grading criteria.
- Correct answer with proper justification - 7 points.
- The problem is reduced to counting the number of ways to color 3 points, but the answer is 6 or 7 - 4 points.
- The problem is reduced to counting the number of ways to color 3 points, but the calculation of the number of ways is missing or the answer is different from the ones mentioned earlier - 3 points.
- Answer (including the correct one) without justification - 0 points.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Given a rectangle $A B C D$. Point $M$ is the midpoint of side $A B$, point $K$ is the midpoint of side $B C$. Segments $A K$ and $C M$ intersect at point $E$. How many times smaller is the area of quadrilateral $M B K E$ compared to the area of quadrilateral $A E C D$?
|
Answer: 4 times.
Solution. Draw segments $MK$ and $AC$. Quadrilateral $MBKE$ consists of triangles $MBK$ and $MKE$, while quadrilateral $AEC D$ consists of triangles $AEC$ and $ACD$. We can reason in different ways.
1st method. Triangles $MBK$ and $ACD$ are right-angled, and the legs of the first are half the length of the legs of the second, so they are similar, and the area of triangle $ACD$ is 4 times the area of triangle $MBK$.
Since $M$ and $K$ are the midpoints of $AB$ and $BC$ respectively, $MK$ is the midline of triangle $ABC$, so $MK \parallel AC$ and $MK = 0.5 AC$. From the parallelism of lines $MK$ and $AC$, it follows that triangles $MKE$ and $AEC$ are similar, and since the similarity coefficient is 0.5, the area of triangle $AEC$ is 4 times the area of triangle $MKE$.
Now: $S_{AEC D} = S_{AEC} + S_{ACD} = 4 S_{MKE} + 4 S_{MBK} = 4 (S_{MKE} + S_{MBK}) = 4 S_{MBKE}$.
2nd method. Let the area of rectangle $ABCD$ be $S$. Then the area of triangle $ACD$ is $\frac{1}{2} S$ (the diagonal of the rectangle divides it into two equal triangles), and the area of triangle $MBK$ is $\frac{1}{2} MB \cdot BK = \frac{1}{2} \cdot \frac{1}{2} AB \cdot \frac{1}{2} BC = \frac{1}{8} AB \cdot BC = \frac{1}{8} S$.
Since $M$ and $K$ are the midpoints of segments $AB$ and $BC$, $AK$ and $CM$ are medians of triangle $ABC$, so $E$ is the centroid of triangle $ABC$, i.e., the distance from $E$ to $AC$ is $\frac{1}{3} h$, where $h$ is the height of triangle $ABC$ from vertex $B$. Then the area of triangle $AEC$ is $\frac{1}{2} AC \left(\frac{1}{3} h\right) = \frac{1}{3} \left(\frac{1}{2} AC h\right) = \frac{1}{3} S_{ABC} = \frac{1}{3} \left(\frac{1}{2} S\right) = \frac{1}{6} S$. Therefore, for the area of quadrilateral $AEC D$, which is the sum of the areas of triangles $AEC$ and $ACD$, we get: $\frac{1}{2} S + \frac{1}{6} S = \frac{2}{3} S$.
Furthermore, since $MK$ is the midline of triangle $ABC$, the area of triangle $MKE$ is $\frac{1}{2} MK \cdot \left(\frac{1}{2} h - \frac{1}{3} h\right) = \frac{1}{2} \left(\frac{1}{2} AC\right) \left(\frac{1}{6} h\right) = \frac{1}{12} \left(\frac{1}{2} AC h\right) = \frac{1}{12} S_{ACD} = \frac{1}{24} S$. Therefore, for the area of quadrilateral $MBKE$, which is the sum of the areas of triangles $MBK$ and $MKE$, we get: $\frac{1}{8} S + \frac{1}{24} S = \frac{1}{6} S$.
Thus, the ratio of the areas of quadrilaterals $AEC D$ and $MBKE$ is $\frac{2}{3} S : \left(\frac{1}{6} S\right) = 4$.
Grading criteria.
- Correct solution and correct answer - 7 points.
- Correct solution, but incorrect answer due to an arithmetic error - 5 points.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. There are 40 pencils of four colors - 10 pencils of each color. They were distributed among 10 children so that each received 4 pencils. What is the smallest number of children that can always be selected to ensure that pencils of all colors are found among them, regardless of the distribution of pencils?
(I. Bogdanov, O. Podlipsky)
|
10.1. Answer. 3 boys.
We will show that it is always possible to choose three boys such that they have pencils of all colors. Since there are 10 pencils of each color and each boy received 4 pencils, at least one boy must have received pencils of at least two different colors. It remains to add to him two boys who have pencils of the remaining two colors.
Now, let's show how to distribute the pencils to the boys so that any two of them together have pencils of no more than three colors. Distribute 4 pencils of the second color to two boys, 4 pencils of the third color to two boys, 4 pencils of the fourth color to two boys, 4 pencils of the first color to one boy, 2 pencils of the first and second colors to one boy, 2 pencils of the first and third colors to one boy, and 2 pencils of the first and fourth colors to one boy.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. Plot the graph of the function $\mathrm{y}=\sqrt{4 \sin ^{4} x-2 \cos 2 x+3}+\sqrt{4 \cos ^{4} x+2 \cos 2 x+3}$.
|
Answer. The graph of the function will be the line $y = 4$.
## Solution.
$\mathrm{y}=\sqrt{4 \sin ^{4} x-2 \cos 2 x+3}+\sqrt{4 \cos ^{4} x+2 \cos 2 x+3}$
$\mathrm{y}=\sqrt{4 \sin ^{4} x-2+4 \sin ^{2} x+3}+\sqrt{4 \cos ^{4} x+4 \cos ^{2} x-2+3}$
$\mathrm{y}=\sqrt{4 \sin ^{4} x+4 \sin ^{2} x+1}+\sqrt{4 \cos ^{4} x+4 \cos ^{2} x+1}$
$\mathrm{y}=2 \sin ^{2} x+1+2 \cos ^{2} x+1, \mathrm{y}=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.3. How many rectangles exist on this picture with sides running along the grid lines? (A square is also a rectangle.)
|
Answer: 24.
Solution. In a horizontal strip $1 \times 5$, there are 1 five-cell, 2 four-cell, 3 three-cell, 4 two-cell, and 5 one-cell rectangles. In total, $1+2+3+4+5=15$ rectangles.
In a vertical strip $1 \times 4$, there are 1 four-cell, 2 three-cell, 3 two-cell, and 4 one-cell rectangles. In total, $1+2+3+4=10$ rectangles. At the same time, one one-cell rectangle at the intersection of the strips is counted twice (and only it is). Therefore, the answer to the problem is the number $15+10-1=24$.
|
24
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.3. A cuckoo clock is hanging on the wall. When a new hour begins, the cuckoo says "cuckoo" a number of times equal to the number the hour hand points to (for example, at 19:00, "cuckoo" sounds 7 times). One morning, Maxim approached the clock when it was 9:05. He started turning the minute hand until he advanced the clock by 7 hours. How many times did "cuckoo" sound during this time?

|
Answer: 43.
Solution. The cuckoo will say "cuckoo" from 9:05 to 16:05. At 10:00 it will say "cuckoo" 10 times, at 11:00 - 11 times, at 12:00 - 12 times. At 13:00 (when the hand points to the number 1) "cuckoo" will sound 1 time. Similarly, at 14:00 - 2 times, at 15:00 - 3 times, at 16:00 - 4 times. In total
$$
10+11+12+1+2+3+4=43
$$
|
43
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.5. From a $6 \times 6$ grid square, gray triangles have been cut out. What is the area of the remaining figure? The side length of each cell is 1 cm. Give your answer in square centimeters.
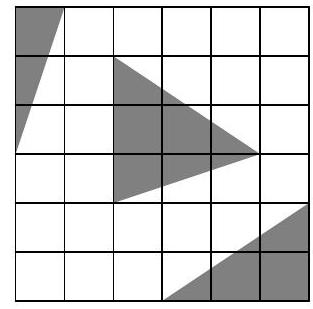
|
Answer: 27.
Solution. The area of the entire square is $6 \cdot 6=36$ sq. cm.
Divide the triangle located in the middle of the square into two smaller triangles, as shown in the picture on the left. Then the dark gray triangles can be combined into a rectangle $1 \times 3$, and the light gray triangles into a rectangle $2 \times 3$. Therefore, the area of the figure that remains after cutting out all the triangles is 36-3-6 $=27$ sq. cm.
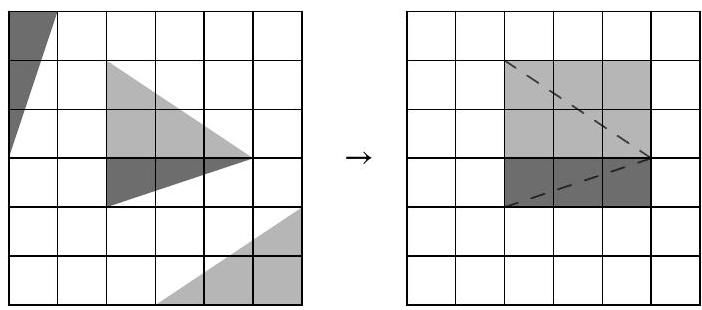
|
27
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.5. In the park, paths are laid out as shown in the figure. Two workers started to asphalt them, starting simultaneously from point $A$. They lay asphalt at constant speeds: the first on the section $A-B-C$, the second on the section $A-D-E-F-C$. In the end, they finished the work simultaneously, spending 9 hours on it. It is known that the second works 1.2 times faster than the first. How many minutes did the second spend laying asphalt on the section $D E$?
|
Answer: 45.
Solution. Let the line $A D$ intersect the line $C F$ at point $G$, as shown in the figure below. Since $A B C G$ and $D E F G$ are rectangles, we have $A B=C G, B C=A G, E F=D G$ and $D E=F G$.
The second worker works 1.2 times faster than the first, and the working time was the same, so the second worker laid 1.2 times more asphalt than the first. Let the first worker lay $x=A B+B C$ asphalt on the section $A-B-C$, then the second worker on the section $A-D-E-F-C$ laid
$$
\begin{aligned}
1.2 x & =A D+D E+E F+F G+G C=(A D+E F+C G)+(D E+F G)= \\
& =(B C+A B)+(D E+D E)=x+2 D E
\end{aligned}
$$
From this, we find that $D E=0.1 x$, which is 12 times less than the total amount of asphalt on the second section. Therefore, the second worker spent 12 times less time on the section $D E$ than on his entire path. He worked a total of $9 \cdot 60=540$ minutes, so he spent $\frac{540}{12}=45$ minutes on $D E$.
|
45
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.8. There are exactly 120 ways to color five cells in a $5 \times 5$ table so that each column and each row contains exactly one colored cell.
There are exactly 96 ways to color five cells in a $5 \times 5$ table without a corner cell so that each column and each row contains exactly one colored cell.
How many ways are there to color five cells in a $5 \times 5$ table without two corner cells so that each column and each row contains exactly one colored cell?

|
Answer: 78.
Solution. Consider the colorings of a $5 \times 5$ table described in the problem (i.e., such that in each column and each row exactly one cell is colored).
For convenience, let's introduce some notations. Let the top-left corner cell of the $5 \times 5$ table be called $A$, and the bottom-right corner cell be called $B$. Suppose that among the colorings of the first table, exactly $a$ have the cell $A$ colored, and exactly $b$ have the cell $B$ colored. Clearly, $a=b$ due to symmetry.
Notice that the number of colorings of the second table is equal to the number of colorings of the first table where the cell $A$ is not colored. The number of colorings of the third table is equal to the number of colorings of the first table where neither $A$ nor $B$ is colored. To find this, we subtract from 120 the number of colorings of the first table where $A$ or $B$ is colored. To count the number of such colorings, we add $a$ and $b$, and then subtract what has been counted twice - the ways where both $A$ and $B$ are colored.
All colorings of the first table can be divided into two types: those in which the cell $A$ is colored, and those in which it is not. This leads to the equation $120=a+96$, i.e., $a=24$. Then $b=24$ as well.
The number of colorings where both $A$ and $B$ are colored is the same as the number of ways to color the central $3 \times 3$ square. It is easy to see that there are exactly $3!=6$ such ways (to choose the colored cell in its top row, there are 3 ways, in the middle row - 2 ways, and in the bottom row - 1 way).
Thus, the answer to the problem is the number $120-(24+24-6)=78$.
## 7th grade
|
78
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
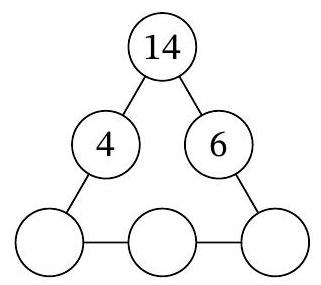
Problem 7.7. In three of the six circles of the diagram, the numbers 4, 14, and 6 are recorded. In how many ways can natural numbers be placed in the remaining three circles so that the products of the triples of numbers along each of the three sides of the triangular diagram are the same?
|
Answer: 6.
Solution. Let $a, b, c$ be the natural numbers in the three lower circles, from left to right. According to the condition, $14 \cdot 4 \cdot a = 14 \cdot 6 \cdot c$, i.e., $2a = 3c$. From this, it follows that $3c$ is even, and therefore $c$ is even. Thus, $c = 2k$ for some natural number $k$, and from the equation $2a = 3c$ it follows that $a = 3k$.
It must also hold that $14 \cdot 4 \cdot 3k = 3k \cdot b \cdot 2k$, which means $b \cdot k = 28$. Note that by choosing the number $k$, which is a natural divisor of 28, the natural numbers $a, b, c$ are uniquely determined. The number 28 has exactly 6 natural divisors: $1, 2, 4, 7, 14, 28$. Therefore, there are also 6 ways to place the numbers in the circles.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.8. Given an isosceles triangle $ABC (AB = BC)$. On the ray $BA$ beyond point $A$, point $E$ is marked, and on side $BC$, point $D$ is marked. It is known that
$$
\angle ADC = \angle AEC = 60^{\circ}, AD = CE = 13.
$$
Find the length of segment $AE$, if $DC = 9$.

|
Answer: 4.
Solution. Mark point $K$ on ray $B C$ such that $B E=B K$. Then $A E=C K$ as well.
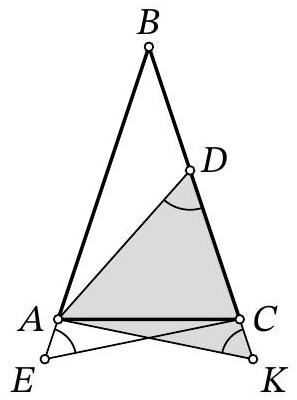
Notice that triangles $A C E$ and $C A K$ are congruent by two sides ($A E=C K, A C$ - common side) and the angle between them ($\angle C A E=\angle A C K$ - adjacent to the equal base angles of the isosceles triangle). Therefore, $A K=C E=13$ and $\angle A K C=\angle A E C=60^{\circ}$.
In triangle $A D K$, the angles at vertices $D$ and $K$ are $60^{\circ}$, so it is equilateral, and $D K=A K=A D=13$. Therefore, $A E=C K=D K-D C=13-9=4$.
## 8th grade
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.1. In a $5 \times 5$ square, some cells have been painted black as shown in the figure. Consider all possible squares whose sides lie along the grid lines. In how many of them is the number of black and white cells the same?

|
Answer: 16.
Solution. An equal number of black and white cells can only be in squares $2 \times 2$ or $4 \times 4$ (in all other squares, there is an odd number of cells in total, so there cannot be an equal number of black and white cells). There are only two non-fitting $2 \times 2$ squares (both of which contain the center of the table, but do not contain any cells above the center), so there are exactly $16-2=14$ fitting $2 \times 2$ squares. And among the $4 \times 4$ squares, only the two lower ones fit.
Thus, the total number of squares with an equal number of black and white cells is exactly $14+2=16$.
|
16
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
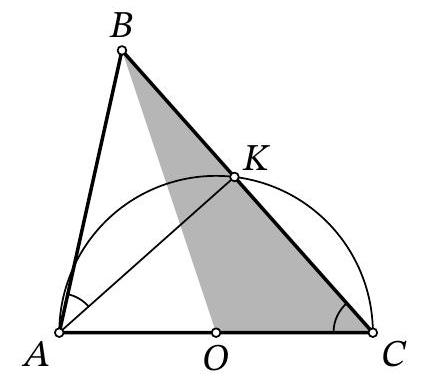
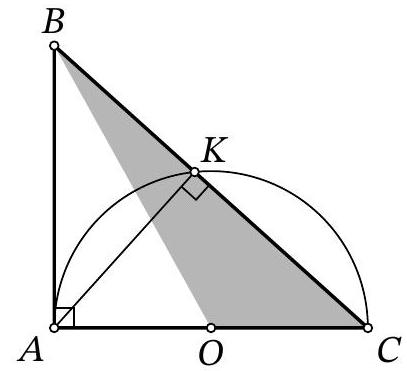
Problem 8.3. In triangle $ABC$, the sides $AC=14$ and $AB=6$ are known. A circle with center $O$, constructed on side $AC$ as the diameter, intersects side $BC$ at point $K$. It turns out that $\angle BAK = \angle ACB$. Find the area of triangle $BOC$.
|
Answer: 21.
Solution. Since $AC$ is the diameter of the circle, point $O$ is the midpoint of $AC$, and $\angle AKC = 90^{\circ}$.
Then
$$
\angle BAC = \angle BAK + \angle CAK = \angle BCA + \angle CAK = \angle BKA = 90^{\circ}.
$$
The area of the right triangle $ABC$ can be found as $\frac{1}{2} \cdot AB \cdot AC = \frac{1}{2} \cdot 6 \cdot 14 = 42$. Since the median $BO$ divides its area in half, the area of triangle $BOC$ is $\frac{42}{2} = 21$.
|
21
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.7. Given an isosceles triangle $A B C$, where $A B=A C$ and $\angle A B C=53^{\circ}$. Point $K$ is such that $C$ is the midpoint of segment $A K$. Point $M$ is chosen such that:
- $B$ and $M$ are on the same side of line $A C$;
- $K M=A B$
- angle $M A K$ is the maximum possible.
How many degrees does angle $B A M$ measure?
|
Answer: 44.
Solution. Let the length of segment $AB$ be $R$. Draw a circle with center $K$ and radius $R$ (on which point $M$ lies), as well as the tangent $AP$ to it such that the point of tangency $P$ lies on the same side of $AC$ as $B$. Since $M$ lies inside the angle $PAK$ or on its boundary, the angle $MAK$ does not exceed the angle $PAK$, and these angles are equal only if points $M$ and $P$ coincide. Therefore, $M$ is this point of tangency.
The radius $KM$ of the circle is perpendicular to the tangent $AM$. Also, in the right triangle $AMK$, the leg $MK$ is half the hypotenuse $AK$, so $\angle MAK=30^{\circ}$. Additionally, from the condition, we get that $\angle BAC=180^{\circ}-2 \cdot 53^{\circ}=74^{\circ}$. Therefore,
$$
\angle BAM=\angle BAC-\angle MAK=74^{\circ}-30^{\circ}=44^{\circ}
$$
|
44
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
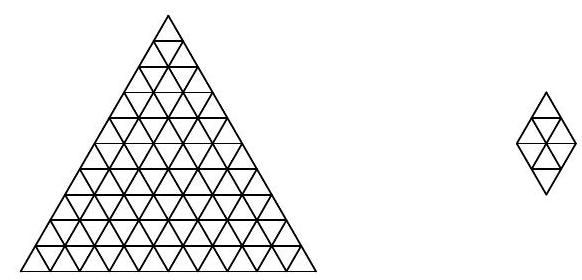
Problem 10.1. An equilateral triangle with a side of 10 is divided into 100 small equilateral triangles with a side of 1. Find the number of rhombi consisting of 8 small triangles (such rhombi can be rotated).
|
Answer: 84.
Solution. Rhombuses consisting of eight triangles can be of one of three types:

It is clear that the number of rhombuses of each orientation will be the same, so let's consider only the vertical ones. Each of them is uniquely determined by its top triangle. Now it is easy to count the number of such triangles.
In the first row, there is 1 such triangle, in the second row - 2, in the third row - 3, ..., in the seventh row - 7. In total, \(1+2+3+\ldots+7=28\) vertical rhombuses, and therefore, the answer to the problem is \(28 \cdot 3 = 84\).
|
84
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.5. A circle $\omega$ is inscribed in trapezoid $A B C D$, and $L$ is the point of tangency of $\omega$ and side $C D$. It is known that $C L: L D=1: 4$. Find the area of trapezoid $A B C D$, if $B C=9$, $C D=30$.
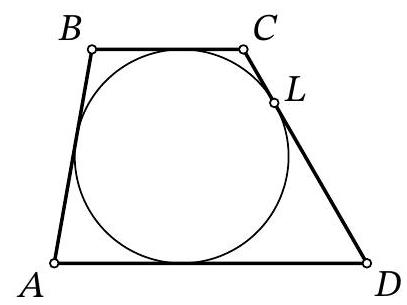
|
Answer: 972.
Solution. Let's mark the center of the circle $I$, and the points of tangency $P, Q, K$ with the sides $B C$, $A D, A B$ respectively. Note that $I P \perp B C, I Q \perp A D$, i.e., points $P, I, Q$ lie on the same line, and $P Q$ is the height of the given trapezoid, equal to the diameter of its inscribed circle. Also, the segments of tangents $A K=A Q, B K=B P, C P=C L, D L=D Q$ are equal.
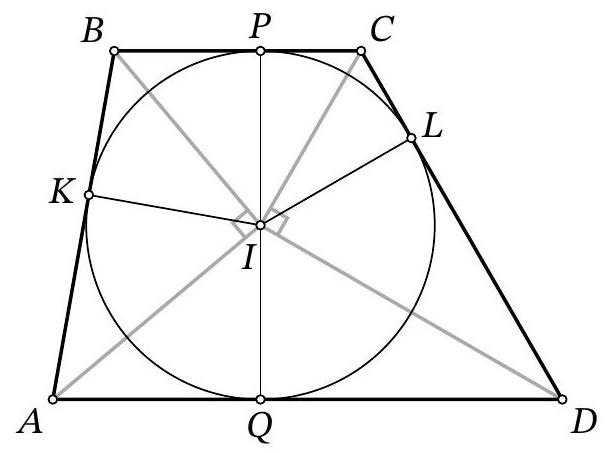
From the condition, it follows that $C P=C L=\frac{1}{5} \cdot 30=6, D Q=D L=\frac{4}{5} \cdot 30=24$. Then $B K=B P=$ $B C-C P=9-6=3$.
Since the lines $C I$ and $D I$ are the angle bisectors of angles $C$ and $D$ of the trapezoid, we have $\angle I C D+$ $\angle I D C=\frac{1}{2}(\angle C+\angle D)=\frac{180^{\circ}}{2}=90^{\circ}$, i.e., triangle $C I D$ is a right triangle with a right angle at vertex $I$. Since $I L$ is its height dropped to the hypotenuse, $I L=$ $\sqrt{C L \cdot D L}=12$. This is the radius of the circle.
Similarly, considering the height $I K$ in the right triangle $A I B$, we get $12=$ $I K=\sqrt{A K \cdot B K}$. Using $B K=3$, we extract $A K=A Q=48$.
Thus, the area of the trapezoid is
$$
S_{A B C D}=\frac{B C+A D}{2} \cdot C H=\frac{9+(48+24)}{2} \cdot 24=972
$$
|
972
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.3. What is the maximum number of digits that a natural number can have, where all digits are different, and it is divisible by each of its digits?
|
Answer: 7 digits.
Evaluation. There are 10 digits in total. The number cannot contain the digit 0, so there are no more than 9. If all 9, then the digit 5 must be at the end of the number (divisibility rule for 5), but in this case, the number must also be divisible by 2. Therefore, the digit 5 is not in this number. If the number lacks only 0 and 5, then it contains 9, and the sum of the digits of this number will be 40, which contradicts divisibility by 9. Thus, there are no more than seven digits.
An example of such a number is 9176328. Verification. The three-digit number formed by the last three digits is 328, which is divisible by 8, meaning the given number is divisible by its digits 2 and 8. The sum of the digits of this number is 36, so it is divisible by 3 and 9, and also by 6. It is easy to see that it is divisible by 7: $9176328: 7=1310904$.
Remarks. An example of a seven-digit number with verification is provided - 3 points. It is proven that there are no more than seven digits, but an example of such a number is not provided - 3 points. If both are present, 7 points.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In triangle $A B C$, the median $B M$ is twice as short as side $A B$ and forms an angle of $40^{\circ}$ with it. Find the angle $A B C$.
|
Solution. Extend median $B M$ beyond point $M$ by the same length to get point $D$ (see figure). Since $A B = B D$, triangle $A B D$ is isosceles. Therefore, $\angle B A D = \angle B D A = (180^{\circ} - 40^{\circ}) : 2 = 70^{\circ}$.
Quadrilateral $A B C D$ is a parallelogram because its diagonals bisect each other. Thus, $\angle C B D = 2 B M = 70^{\circ}$. Then $\angle A B C = \angle A B D + \angle C B D = 110^{\circ}$.
Answer $110^{\circ}$.
|
110
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. In the parliament of the island state of Promenade-and-Tornado, 2019 indigenous inhabitants were elected, who are divided into knights and liars: knights always tell the truth, liars always lie. At the first meeting, 2016 of them sat in the parliamentary seats arranged in the hall in a rectangle of $42 \times 48$, three - in the seats of the chairman and his deputies in the presidium. During the meeting, each one stated that among their neighbors in the seat there are both knights and liars (neighbors are those who sit to the left, right, in front, behind, and diagonally: there can be from 3 to 8 in the hall and 1 or 2 in the presidium). Determine the minimum number of liars at the meeting.
|
Solution. If two liars are adjacent in the hall, then the entire hall is filled with only liars, which corresponds to the maximum number of liars in the hall. For the minimum number of liars, each liar is adjacent only to knights. The rectangle $42 \times 48$ can be tiled with 224 squares of $3 \times 3$. The minimum number of liars in each such square is 1 (otherwise, if the square contains only knights, the central knight would have lied). Therefore, the minimum number of liars in the hall is 224 (in the centers of the $3 \times 3$ squares). In the presidium - all are liars (three).
Answer: 227.
|
227
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Dima was supposed to arrive at the station at 18:00. By this time, his father was supposed to pick him up in a car. However, Dima managed to catch an earlier train and arrived at the station at 17:05. He didn't wait for his father and started walking towards him. On the way, they met, Dima got into the car, and they arrived home 10 minutes earlier than the planned time. At what speed was Dima walking before the meeting with his father, if the car's speed was $60 \mathrm{km} / \mathrm{h}$?
|
Answer: 6 km/h
Solution. Dima arrived home 10 minutes earlier, during which time the car would have traveled the distance Dima walked twice. Therefore, on the way to the station, the father saved 5 minutes and met Dima at 17:55. This means Dima walked the distance from the station to the meeting point in 50 minutes, so he walked 10 times slower than the car, and his speed was 6 km/h.
## Grading Criteria.
- Complete correct solution - 7 points.
- Generally correct solution with insufficient justifications (in particular, a diagram of the movement is drawn with incomplete justifications) - 5 points.
- Correct approach but incorrect answer due to arithmetic error - 4 points.
- It is found that the meeting time is 17:55, but there is no further progress - 2 points.
- It is found that the father saved 5 minutes on the way to the station, but it is incorrectly assumed that Dima walked for 55 minutes before the meeting - 2 points.
- Only the correct answer is provided - 1 point.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. "Did you answer the previous questions honestly?"
40 gnomes answered "yes" to the first question, 50 to the second, 70 to the third, and 100 to the fourth. How many honest gnomes are there in the underground kingdom?
|
Answer: 40 honest gnomes.
## Solution.
On the 4th question, both an honest and a liar will answer "yes," so there are 100 gnomes in the underground kingdom.
An honest gnome will answer "yes" to one of the first three questions and "no" to two. A liar, on the other hand, will answer "yes" to two of the first three questions and "no" to one.
The answer can be obtained either by an equation or by reasoning.
Method 1. Let $x$ be the number of honest gnomes. Then, the total number of "yes" answers to the first three questions will be $x + 2 \cdot (100 - x) = 200 - x$, i.e., $200 - x = 40 + 50 + 70 = 160$, from which $x = 40$.
Method 2. In total, there were $40 + 50 + 70 = 160$ "yes" answers to the first three questions. If all the gnomes were telling the truth, there would be 100 "yes" answers to the first three questions. Since each liar gives one more "yes" answer, there were $160 - 100 = 60$ liars. Therefore, there are 40 honest gnomes.
## Grading Criteria.
- Correct solution - 7 points.
- Reasoning to find the number of liars but not the number of honest gnomes - 5 points.
- Correct answer without justification - 2 points.
|
40
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In triangle $ABC$, the median from vertex $A$ is perpendicular to the bisector of angle $B$, and the median from vertex $B$ is perpendicular to the bisector of angle $A$. It is known that side $AB=1$. Find the perimeter of triangle $ABC$.
|
Answer: 5.
Solution. Let $A M$ be the median drawn from vertex $A$. Then, in triangle $A B M$, the bisector of angle $B$ is perpendicular to side $A M$, i.e., the bisector is also an altitude. Therefore, this triangle is isosceles, $A B = B M = 1$. Hence, $B C = 2 B M = 2$. Similarly, from the second condition, we get that side $A C$ is twice the length of $A B$, so the perimeter of triangle $A B C$ is $1 + 2 + 2 = 5$.

## Grading Criteria.
- Correct solution - 7 points.
- It is determined that the triangle cut off by one of the medians is isosceles, but there is no further progress - 3 points.
- Only the correct answer is provided - 1 point.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. There are three vessels with volumes of 3 liters, 4 liters, and 5 liters, without any markings, a water tap, a sink, and 3 liters of syrup in the smallest vessel. Can you, using pourings, obtain 6 liters of a water-syrup mixture such that the amount of water is equal to the amount of syrup in each vessel?
|
Solution.
For example, as follows (see the table below, c - syrup, w - water, f - final mixture).
| |  | 4-liter container | 5-liter container |
| :---: | :---: | :---: | :---: |
| Pour the syrup into the 5-liter container, and using the 3- and 4-liter containers, get 2 liters of water in the 4-liter container. | $3 \mathrm{c}$ | 0 | 0 |
| | 0 | 0 | $3 \mathrm{c}$ |
| | Zw | 0 | $3 \mathrm{c}$ |
| | 0 | Zw | $3 \mathrm{c}$ |
| | Zw | Zw | $3 \mathrm{c}$ |
| | 2B | 4B | $3 \mathrm{c}$ |
| | 2B | 0 | $3 \mathrm{c}$ |
| | 0 | 2B | $3 \mathrm{c}$ |
| Then fill the 4-liter container with syrup to get 4 liters of the required mixture. | 0 | $2 \mathrm{~B}+2 \mathrm{c}=4$ f | $1 \mathrm{c}$ |
|  | Zi | 1f | $1 \mathrm{c}$ |
| | Zi | $1 f+1 c$ | 0 |
| | 0 | $1 f+1 c$ | Zi |
| | $1 f+1 c$ | 0 | Zi |
| | 1 f $+1 c+1$ w $=3$ f | 0 | Zi |
## Grading Criteria.
- Correct algorithm - 7 points.
- Less than 6 liters of the required mixture obtained (i.e., the required mixture is obtained in one container, but the ratio is not maintained in the other) — no more than 1 point.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. What is the maximum number of sides a polygon can have if each of its angles is either $172^{\circ}$ or $173^{\circ}$?
Let the number of angles with a degree measure of $172^{\circ}$ be $a$, and those with $173^{\circ}-b$. Then the sum of all angles of the polygon will be $172a + 173b$. On the other hand, the sum of the angles of a convex $n$-sided polygon is $180(n-2)$. Therefore, the following equation must hold:
$172a + 173b = 180(a + b - 2)$, or $8a + 7b = 360$. \quad 7(a + b) + a = 360
The sum $a + b$ reaches its maximum value when $a$ is minimal. The smallest possible value of $a = 3$. Then $a + b = 51$.
|
Answer: 51.
Criteria: correct answer without explanation - 2 points.
|
51
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.7. Denis threw darts at four identical dartboards: he threw exactly three darts at each board, where they landed is shown in the figure. On the first board, he scored 30 points, on the second - 38 points, on the third - 41 points. How many points did he score on the fourth board? (For hitting each specific zone - ring or central field - a certain number of points is awarded.)
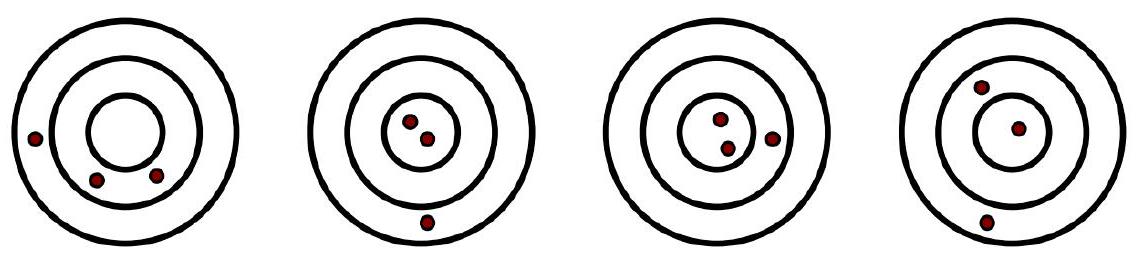
|
Answer: 34.
Solution. "Add" the first two dart fields: we get 2 hits in the central field, 2 hits in the inner ring, 2 hits in the outer ring. Thus, the sum of points on the first and second fields is twice the number of points obtained for the fourth field.
From this, it is not difficult to get the answer
$$
(30+38): 2=34
$$
|
34
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.1. After a football match, the coach lined up the team as shown in the figure, and commanded: "Run to the locker room, those whose number is less than that of any of their neighbors." After several people ran away, he repeated his command. The coach continued until only one player was left. What is Igor's number, if it is known that after he ran away, 3 people remained in the line? (After each command, one or several players ran away, after which the line closed, and there were no empty spaces between the remaining players.)

|
Answer: 5.
Solution. It is clear that after the first command, the players left are $9,11,10,6,8,5,4,1$. After the second command, the players left are $11,10,8,5,4$. After the third - $11,10,8,5$. After the fourth - $11,10,8$. Therefore, Igor had the number 5.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
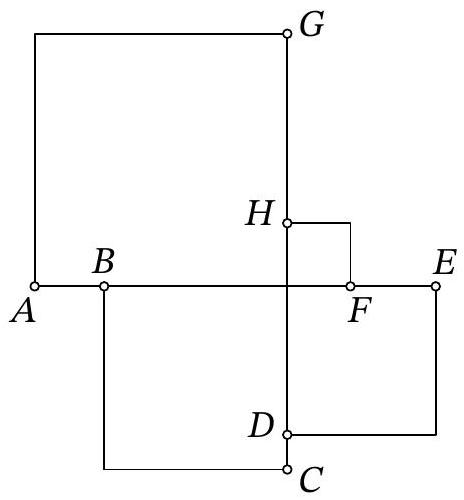
Problem 6.5. The figure shows 4 squares. It is known that the length of segment $A B$ is 11, the length of segment $F E$ is 13, and the length of segment $C D$ is 5. What is the length of segment $G H$?
|
Answer: 29.
Solution. The side of the largest square (with vertex $A$) is greater than the side of the second largest square (with vertex $C$) by the length of segment $A B$, which is 11. Similarly, the side of the second largest square is greater than the side of the third largest square (with vertex $E$) by the length of segment $C D$, which is 5. And its side is greater than the side of the smallest square by the length of segment $E F$, which is 13. In total, the side of the largest square is greater than the side of the smallest square by the length of segment $G H$, which is $11+5+13=29$.
|
29
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
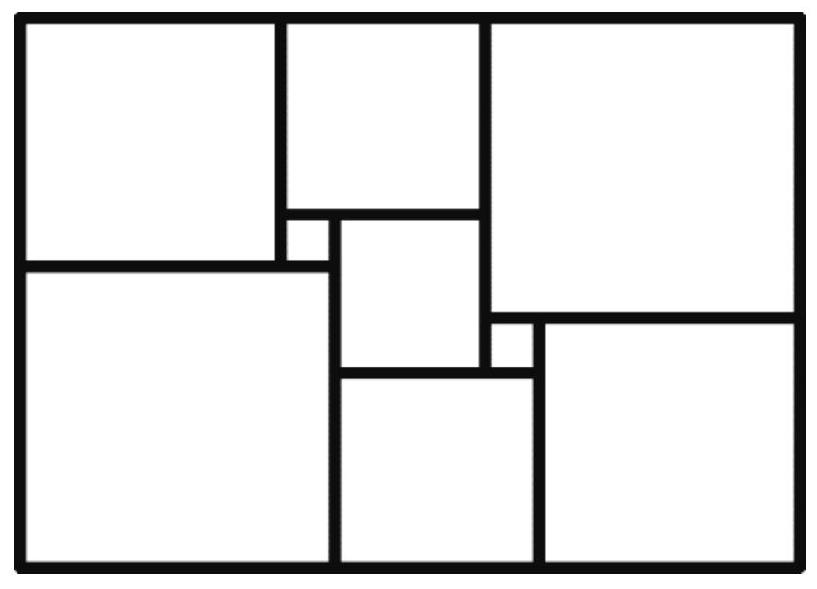
Problem 7.5. A rectangle was cut into nine squares, as shown in the figure. The lengths of the sides of the rectangle and all the squares are integers. What is the smallest value that the perimeter of the rectangle can take?
|
Answer: 52.
Solution. Inside the square, we will write the length of its side. Let the sides of the two squares be $a$ and $b$, and we will sequentially calculate the lengths of the sides of the squares.
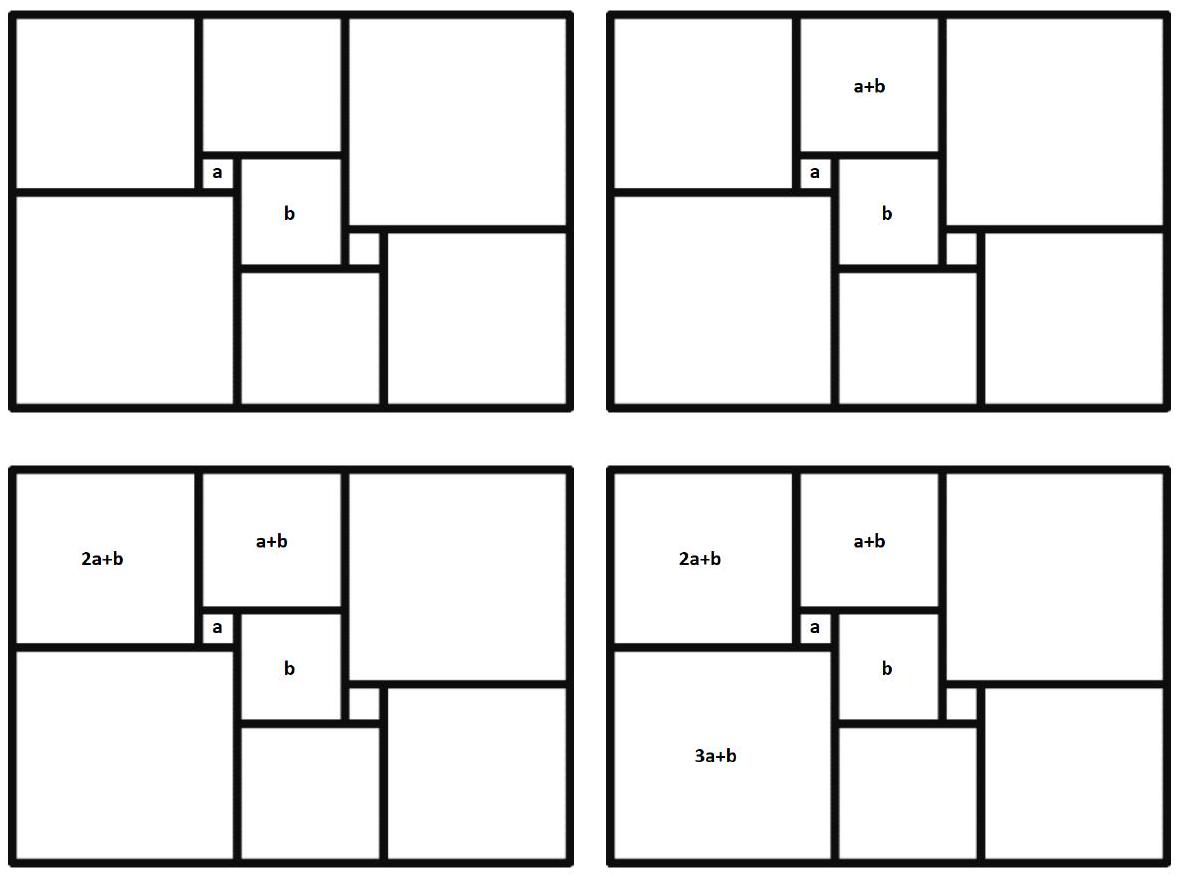
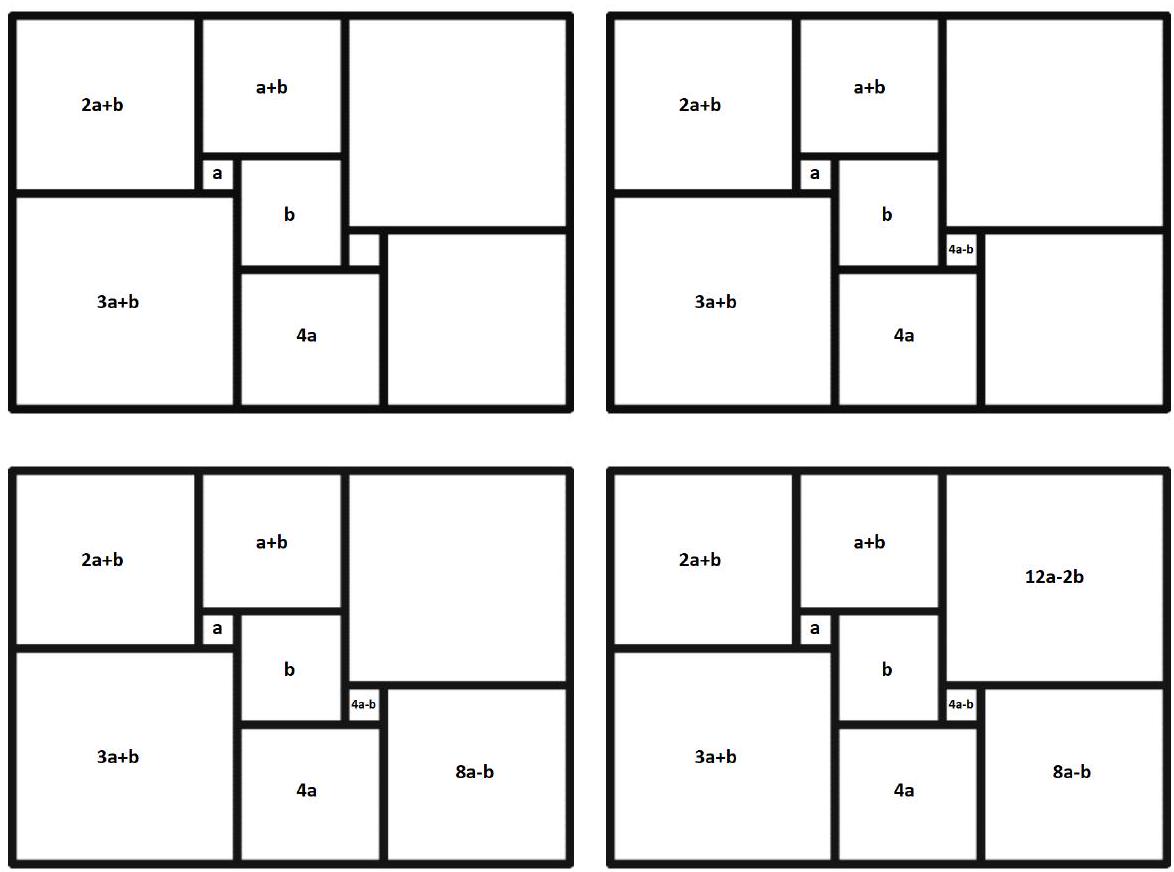
The sum of the lengths of the sides of the two squares adjacent to the left side of the rectangle is equal to the sum of the lengths of the sides of the two squares adjacent to the right side of the rectangle. We get the equation
$$
\begin{aligned}
(2 a+b)+(3 a+b) & =(12 a-2 b)+(8 a-b) \\
5 a+2 b & =20 a-3 b \\
b & =3 a
\end{aligned}
$$
Thus, to minimize the perimeter of the rectangle, we need to choose $a=1$, $b=3$. It is easy to check that with these values, the rectangle will have dimensions $11 \times 15$, and its perimeter will be 52.
|
52
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.1. A square was cut into four equal rectangles, and from them, a large letter P was formed, as shown in the figure, with a perimeter of 56.
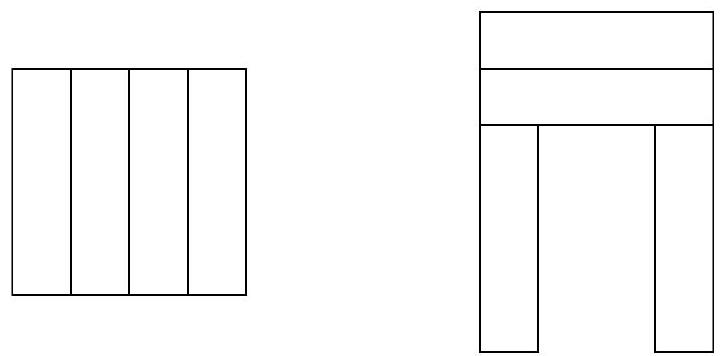
What is the perimeter of the original square
|
Answer: 32.
Solution. Let the width of the rectangle be $x$. From the first drawing, we understand that the length of the rectangle is four times its width, that is, it is equal to $4x$. Now we can calculate the dimensions of the letter P.

From this, we get the equation
$$
\begin{gathered}
28 x=56 \\
x=2
\end{gathered}
$$
The perimeter of the square is $16 x=32$.
|
32
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.2. The numbers from 1 to 9 were placed in the cells of a $3 \times 3$ table such that the sum of the numbers on one diagonal is 7, and on the other diagonal is 21. What is the sum of the numbers in the five shaded cells?
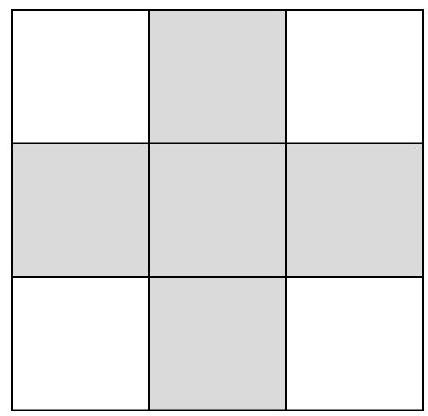
|
Answer: 25.
Solution. Note that 7 can be represented uniquely as the sum of numbers from 1 to 9 - this is $1+2+4=7$.
Let's look at the other diagonal with a sum of 21. The largest possible value of the sum in it is $9+8+4=21$ (since the number in the central cell is no more than 4). Therefore, it must contain the numbers $9,8,4$.
Thus, the number 4 is in the central cell, and the numbers 1, 2, 8, and 9 are at the corners. Now it is not difficult to find the sum of the numbers in the shaded cells: $3+4+5+6+7=25$.
|
25
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.6. For quadrilateral $ABCD$, it is known that $AB=BD, \angle ABD=\angle DBC, \angle BCD=$ $90^{\circ}$. A point $E$ is marked on segment $BC$ such that $AD=DE$. What is the length of segment $BD$, if it is known that $BE=7, EC=5$?
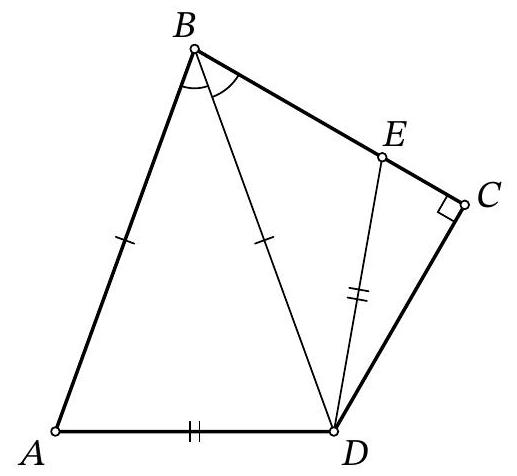
|
Answer: 17.
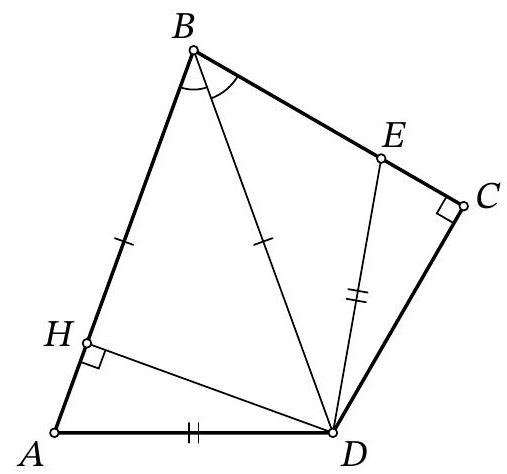
Fig. 3: to the solution of problem 8.6
Solution. Drop a perpendicular from point $D$ in the isosceles triangle $ABD$, let $H$ be its foot (Fig. 3). Since this triangle is acute-angled ($\angle ABD = \angle CBD < 90^\circ$, $\left.\angle BAD = \angle ADB = \frac{180^\circ - \angle ABD}{2} < 90^\circ\right)$, point $H$ lies on the segment $AB$.
Notice that right triangles $BDH$ and $BDC$ are equal by the common hypotenuse $BD$ and the acute angle at vertex $B$. Therefore, $BH = BC$ and $DH = CD$.
Now, notice that right triangles $ADH$ and $EDC$ are also equal by the hypotenuse $AD = ED$ and the leg $DH = CD$. Therefore, $EC = AH$.
Thus, $BD = BA = BH + AH = BC + EC = (7 + 5) + 5 = 17$.
|
17
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.4. From left to right, intersecting squares with sides $12, 9, 7, 3$ are depicted respectively. By how much is the sum of the black areas greater than the sum of the gray areas?
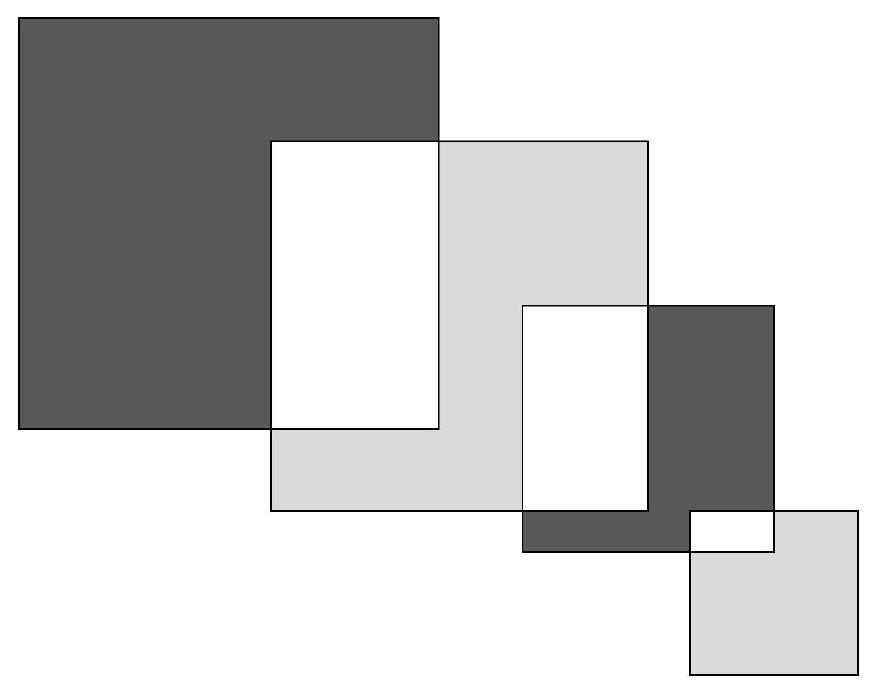
|
Answer: 103.
Solution. Let's denote the areas by $A, B, C, D, E, F, G$.
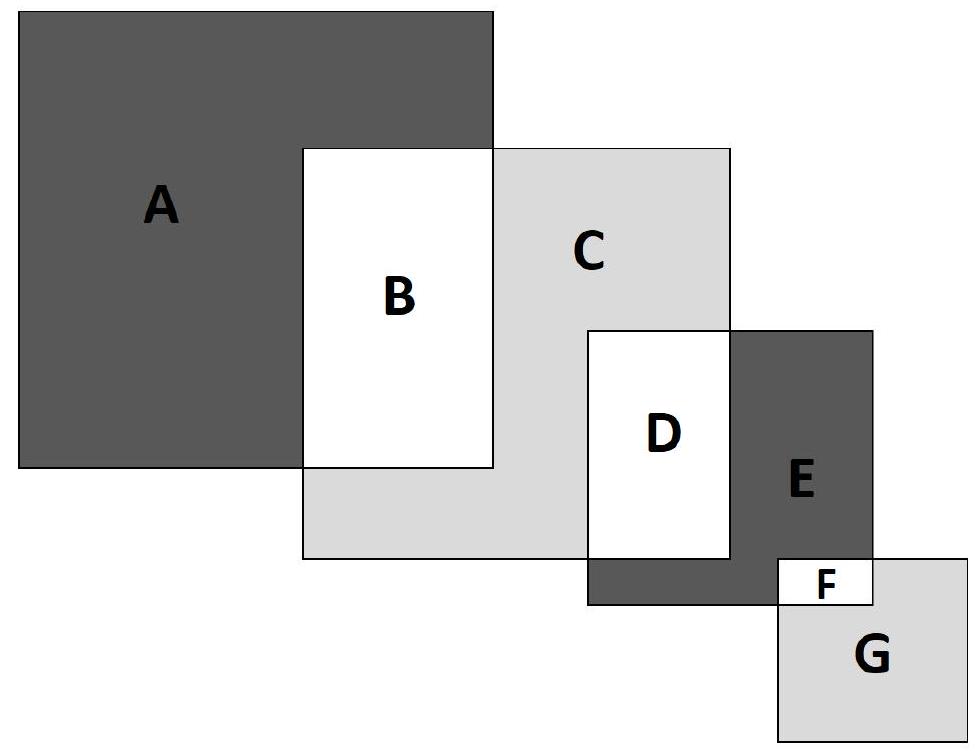
We will compute the desired difference in areas:
$$
\begin{aligned}
A+E-(C+G) & =A-C+E-G=A+B-B-C-D+D+E+F-F-G= \\
& =(A+B)-(B+C+D)+(D+E+F)-(F+G)= \\
& =12^{2}-9^{2}+7^{2}-3^{2}=103
\end{aligned}
$$
|
103
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.7. In triangle $ABC$, the bisector $AL$ is drawn. Points $E$ and $D$ are marked on segments $AB$ and $BL$ respectively such that $DL = LC$, $ED \parallel AC$. Find the length of segment $ED$, given that $AE = 15$, $AC = 12$.
|
Answer: 3.
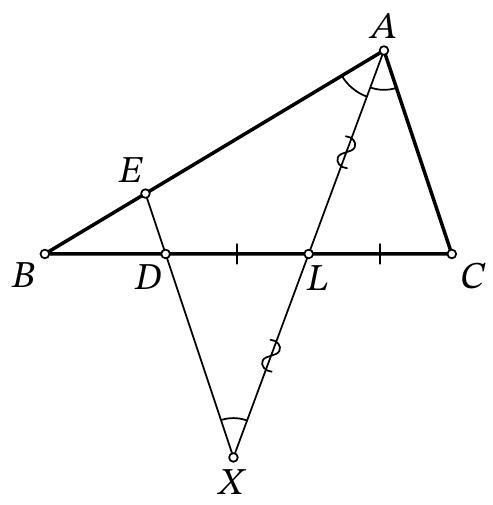
Fig. 5: to the solution of problem 9.7
Solution. On the ray $AL$ beyond point $L$, mark a point $X$ such that $XL = LA$ (Fig. 5). Since in the quadrilateral $ACXD$ the diagonals are bisected by their intersection point $L$, it is a parallelogram (in particular, $AC = DX$). Therefore, $DX \parallel AC$. Since $AC \parallel ED$ by the condition, the points $X, D, E$ lie on the same line.
Since $AC \parallel EX$, then $\angle EAX = \angle CAX = \angle AXE$, i.e., triangle $AEX$ is isosceles, $EA = EX$. Then
$$
ED = EX - XD = EA - AC = 15 - 12 = 3
$$
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.1. In each cell of a $5 \times 5$ table, a natural number is written in invisible ink. It is known that the sum of all the numbers is 200, and the sum of three numbers inside any $1 \times 3$ rectangle is 23. What is the central number in the table?
|
Answer: 16.
Solution. Divide the $5 \times 5$ square without the central cell into four $2 \times 3$ rectangles, and each of these into two $1 \times 3$ rectangles.
We get 8 rectangles of $1 \times 3$, the sum of the numbers in each of which is 23. Since the sum of all the numbers is 200, we find the number in the central cell as $200 - 23 \cdot 8 = 16$.
|
16
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.8. Rectangle $ABCD$ is such that $AD = 2AB$. Point $M$ is the midpoint of side $AD$. Inside the rectangle, there is a point $K$ such that $\angle AMK = 80^{\circ}$ and ray $KD$ is the bisector of angle $MKC$. How many degrees does angle $KDA$ measure?
|
Answer: 35.
Solution. Let's start with the assumption that the quadrilateral KMDС is inscribed (several proofs of this fact will be proposed below).
Using the fact that in the inscribed quadrilateral $K M D C$ the sum of opposite angles is $180^{\circ}$, we get $\angle M K D=\frac{\angle M K C}{2}=\frac{180^{\circ}-\angle M D C}{2}=45^{\circ}$. The angle $A M K$ as an exterior angle for triangle $K D M$ is equal to the sum of angles $M K D$ and $K D A$, so the required angle КDA is $80^{\circ}-45^{\circ}=35^{\circ}$.
Fig. 8: to the solution of problem 10.8
Let's provide the first possible proof of the inscribed nature of quadrilateral KMDC. Consider triangle $M K C$ and its circumcircle. Note that point $D$ lies on the bisector of angle $M K C$, and is equidistant from vertices $M$ and $C$ (Fig. 8). However, the bisector of an angle in a non-isosceles triangle and the perpendicular bisector of its opposite side, as is known, intersect at the midpoint of the "smaller" arc of the circumcircle of the triangle. In other words, $D$ is the midpoint of the arc $M C$ of the circumcircle of triangle $M K C$, not containing point $K$. It should also be noted that $M K \neq K C$ (otherwise, triangles $K M D$ and $K C D$ would be equal, but $\angle K M D>90^{\circ}>\angle K C D$ ).
Let's provide the second possible proof of the inscribed nature of quadrilateral KMDC. It will use the fourth criterion for the congruence of triangles: if two sides and an angle not between them are equal in two triangles, then these triangles are either congruent or the sum of the other two angles not between them is $180^{\circ}$. The fourth criterion is satisfied for triangles $M D K$ and $C D K (M D=D C, D K$ - common, $\angle M K D=\angle C K D)$. However, angles $K M D$ and $K C D$ are not equal (again, the first is obtuse, and the second is acute), so their sum is $180^{\circ}$, which are the opposite angles of quadrilateral KMDC. Therefore, it is inscribed.
## 11th grade
|
35
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.6. Inside the cube $A B C D A_{1} B_{1} C_{1} D_{1}$, there is the center $O$ of a sphere with radius 10. The sphere intersects the face $A A_{1} D_{1} D$ along a circle with radius 1, the face $A_{1} B_{1} C_{1} D_{1}$ along a circle with radius 1, and the face $C D D_{1} C_{1}$ along a circle with radius 3. Find the length of the segment $O D_{1}$.
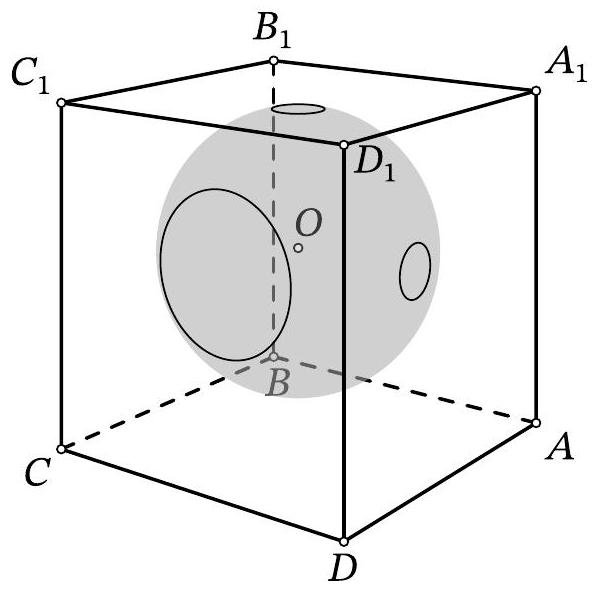
|
Answer: 17.
Solution. Let $\omega$ be the circle that the sphere cuts out on the face $C D D_{1} C_{1}$. From point $O$
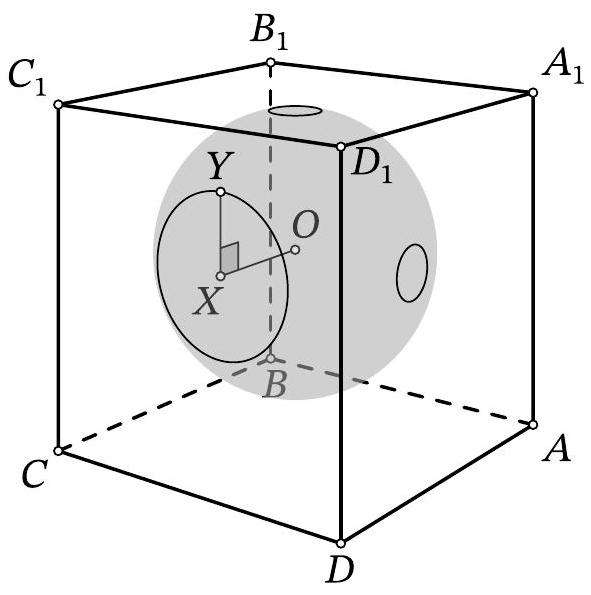
Fig. 10: to the solution of problem 11.6
drop a perpendicular $O X$ to this face, then point $X$ is the center of $\omega$ (point $O$ is equidistant from all points of $\omega$, so the projection of $O$ onto the plane of $\omega$ is also equidistant from them). Let $Y$ be an arbitrary point on $\omega$ (Fig. 10). Triangle $OXY$ is a right triangle; by the problem statement, $X Y=3$ and $O Y=10$. By the Pythagorean theorem, we get $O X^{2}=10^{2}-3^{2}=91$.
Similarly, we find the squares of the distances from point $O$ to the planes $A_{1} B_{1} C_{1} D_{1}$ and $A D D_{1} A_{1}$, which are both equal to $10^{2}-1^{2}=99$.
By the spatial Pythagorean theorem, the square of the length of segment $O D_{1}$ is equal to the sum of the squares of the distances from point $O$ to the three faces containing point $D_{1}$. Therefore, $O D_{1}^{2}=$ $91+99+99=289$, from which $O D_{1}=17$.
|
17
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task No. 1.1
## Condition:
Kirill Konstantinovich's age is 48 years 48 months 48 weeks 48 days 48 hours. How many full years old is Kirill Konstantinovich?
|
Answer: 53
Exact match of the answer -1 point
## Solution.
48 months is exactly 4 years. 48 weeks is $48 \times 7=336$ days. Together with another 48 days, this totals 384 days, which is 1 year and another 18 or 19 days, depending on whether the year is a leap year. In any case, the remaining days plus another 48 hours add up to less than one year. In total: $48+4+1=53$.
|
53
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 1.3
Condition:
Anna Alexandrovna's age is 60 years 60 months 60 weeks 60 days 60 hours. How many full years old is Anna Alexandrovna
|
Answer: 66
Exact match of the answer -1 point
Solution by analogy with task №1.1.
#
|
66
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 1.4
Condition:
Tatyana Timofeevna's age is 72 years 72 months 72 weeks 72 days 72 hours. How many full years old is Tatyana Timofeevna
|
Answer: 79
Exact match of the answer -1 point
Solution by analogy with task №1.1.
#
|
79
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 2.1
Condition:
Dmitry has socks in his wardrobe: 6 pairs of blue socks, 18 pairs of black socks, and 12 pairs of white socks. Dmitry bought some more pairs of black socks and found that now the black socks make up 3/5 of the total number of socks. How many pairs of black socks did Dmitry buy?
|
Answer: 9
Exact match of the answer -1 point
## Solution.
Dmitry had an equal number of pairs of black and all other pairs of socks, and after the purchase, it turned out that the black pairs make up three parts of all socks, while the other pairs make up two parts. This means that Dmitry bought half of the number of pairs of black socks he already had, that is, 9 pairs.
## Condition:
Dmitry has socks in his wardrobe: 16 pairs of blue, 20 pairs of black, and 4 pairs of white. Dmitry bought several more pairs of black socks and found that now the black socks make up $2 / 3$ of the total number of socks. How many pairs of black socks did Dmitry buy?
Answer: 20
Exact match of the answer -1 point
Solution by analogy with task №2.1.
#
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 2.3
## Condition:
Dmitry has socks in his wardrobe: 14 pairs of blue socks, 24 pairs of black socks, and 10 pairs of white socks. Dmitry bought some more pairs of black socks and found that now the black socks make up 3/5 of the total number of socks. How many pairs of black socks did Dmitry buy?
|
Answer: 12
Exact match of the answer -1 point
Solution by analogy with task №2.1.
#
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 3.1
## Condition:
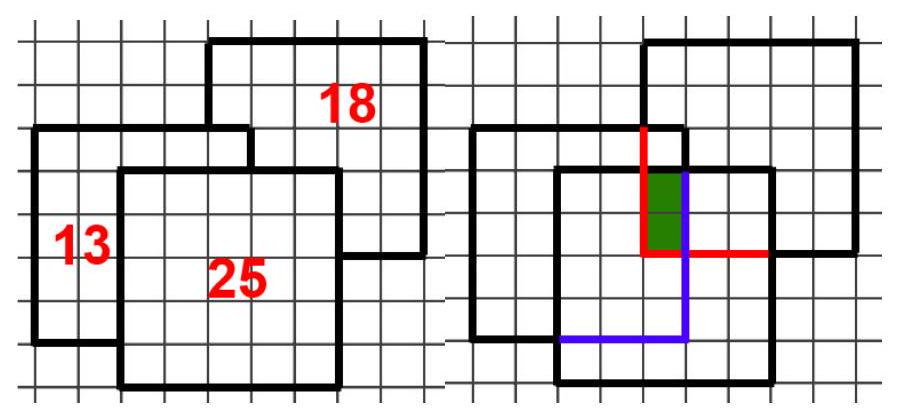
On a sheet of graph paper, there are three $5 \times 5$ squares, as shown in the figure. How many cells are covered by exactly two squares?
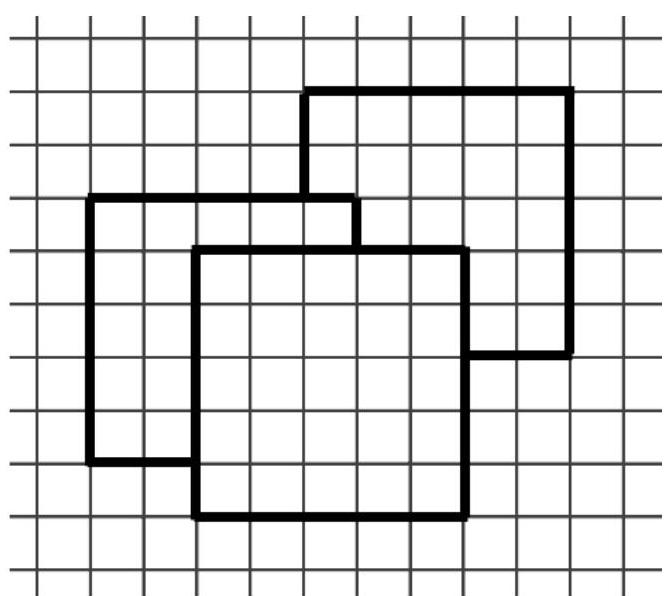
|
Answer: 15
Exact match of the answer -1 point
## Solution 1
Direct calculation. We will draw the squares and shade the cells that are covered exactly twice.
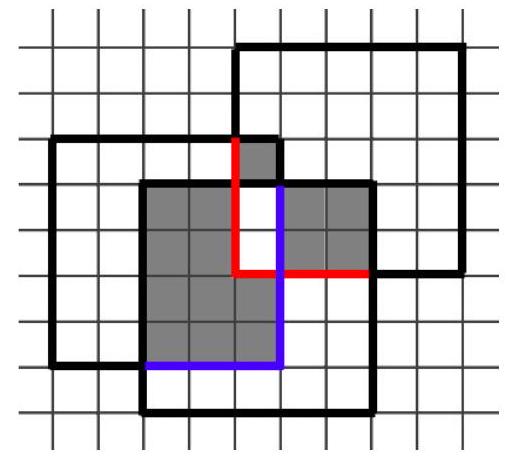
Solution 2.
The total area covered by the squares is $13+25+18=56$. It is easy to understand that all three squares cover exactly two cells. The total area of all squares is 75. The cells covered once (56 cells) are counted once, the cells covered twice (x cells) are counted twice, and the cells covered three times (2 cells) are counted three times. Thus, when adding the areas of all squares, the number $x$ is counted twice, and the number 2 is counted three times. Therefore, we need to subtract one extra $x$ and two times the number 2. We get the equation $56=75-x-2 \cdot 2$, from which $x=15$.
|
15
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
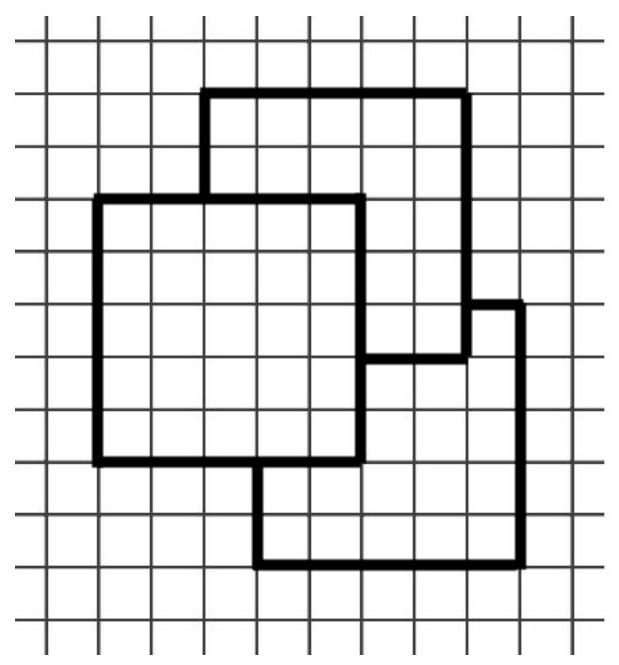
# Task № 3.3
## Condition:
On a sheet of graph paper, there are three $5 \times 5$ squares, as shown in the figure. How many cells are covered by exactly two squares?
|
Answer: 13
Exact match of the answer -1 point
Solution by analogy with task №3.1.
#
|
13
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 5.2
## Condition:
A car number contains three letters and three digits, for example A123BE. The letters allowed for use are А, В, Е, К, М, Н, О, Р, С, Т, У, Х (a total of 12 letters) and all digits except the combination 000. Katya considers a number lucky if the second letter is a consonant, the first digit is odd, and the third digit is even (there are no restrictions on the other characters). How many numbers does Katya consider lucky?
|
Answer: 288000
Exact match of the answer -1 point
Solution by analogy with task №5.1.
#
|
288000
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 5.3
## Condition:
A car number contains three letters and three digits, for example A123BE. The letters allowed for use are А, В, Е, К, М, Н, О, Р, С, Т, У, Х (a total of 12 letters) and all digits except the combination 000. Tanya considers a number lucky if the first letter is a consonant, the second letter is also a consonant, and the third digit is odd (there are no restrictions on the other characters). How many lucky numbers does Tanya consider to exist?
|
Answer: 384000
Exact match of the answer -1 point
Solution by analogy with task №5.1.
#
|
384000
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task № 5.4
## Condition:
A car number contains three letters and three digits, for example A123BE. The letters allowed for use are А, В, Е, К, М, Н, О, Р, С, Т, У, Х (a total of 12 letters) and all digits except the combination 000. Kira considers a number lucky if the second letter is a vowel, the second digit is odd, and the third digit is even (there are no restrictions on the other characters). How many numbers does Kira consider lucky?
|
Answer: 144000
Exact match of the answer -1 point
Solution by analogy with task №5.1.
#
|
144000
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task No. 6.4
## Condition:
On the faces of a cube, 6 letters are drawn: A, B, V, G, D, E. The picture shows three images of the cube from different angles. Which letter is drawn on the face opposite the face with the letter $\mathrm{A}$?

## Answer Options:
○ A
$\circ$ B
$\circ$ V
$\circ$ G
$\circ$ D
○ E
## Correct Answer:
○ B
Exact match of the answer - 1 point
|
Solution by analogy with problem №6.1.
## Condition:
Anya, Borya, and Vasya took the same test consisting of 6 questions, each of which can be answered with "yes" or "no." The answers are presented in the table:
| Question No. | 1 | 2 | 3 | 4 | 5 | 6 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| Anya | no | no | yes | yes | yes | yes |
| Borya | yes | no | no | yes | yes | yes |
| Vasya | no | yes | no | no | no | no |
It turned out that Anya has two incorrect answers, and Borya has only two correct answers. How many correct answers does Vasya have?
Answer: 3
Exact match of the answer - 1 point
## Solution.
Anya has 4 correct answers, and Borya has 2. Therefore, there are at least two questions on which Anya answered correctly, and Borya answered incorrectly. However, Anya and Borya gave different answers to exactly two questions: the first and third. Therefore, it is precisely on these questions that Anya answered correctly, and Borya answered incorrectly. Vasya's answer to the first question matches Anya's, and on the third question, it does not. Therefore, among these two of Vasya's answers, exactly one is correct. Anya's and Borya's answers to the four remaining questions coincide. Therefore, among them, two are correct and two are incorrect. Vasya's answers to all these questions are opposite to Anya's and Borya's. Therefore, among them, two are correct (where Anya and Borya's answers are incorrect) and two are incorrect (where Anya and Borya's answers are correct). Adding 1 and 2, we get the answer.
## Condition:
Anya, Borya, and Vasya took the same test consisting of 6 questions, each of which can be answered with "yes" or "no." The answers are presented in the table:
| Question No. | 1 | 2 | 3 | 4 | 5 | 6 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| Anya | yes | no | no | yes | no | yes |
| Borya | no | no | yes | yes | no | yes |
| Vasya | no | yes | no | no | yes | no |
It turned out that Anya has two incorrect answers, and Borya has only two correct answers. How many incorrect answers does Vasya have?
Answer: 3
Exact match of the answer - 1 point
Solution by analogy with problem №7.1.
## Condition:
Anya, Borya, and Vasya took the same test consisting of 6 questions, each of which can be answered with "yes" or "no." The answers are presented in the table:
| Question No. | 1 | 2 | 3 | 4 | 5 | 6 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| Anya | no | no | yes | yes | yes | yes |
| Borya | yes | no | yes | yes | yes | no |
| Vasya | no | yes | no | no | no | no |
It turned out that Anya has two incorrect answers, and Borya has only two correct answers. How many correct answers does Vasya have?
Answer: 3
Exact match of the answer - 1 point
Solution by analogy with problem №7.1.
|
3
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
# Task No. 8.1
## Condition:
For the "Handy Hands" club, Anton needs to cut several identical pieces of wire (the length of each piece is a whole number of centimeters). Initially, Anton took a piece of wire 10 meters long and was able to cut only 9 needed pieces from it. Then Anton took a piece 11 meters long, but it also only provided 9 pieces. What length of pieces did Anton need to cut? Express the answer in centimeters.
|
Answer: 111
Exact match of the answer -1 point
## Solution.
First, note that 9 pieces of 111 cm each make up 999 cm. Therefore, both the first and the second piece are enough for 9 parts, but the second piece is not enough for 10 parts: $10 \times 111=1110>1100$.
We will prove that if the length of the piece is not 111 cm, then one of the conditions of the problem will not be met. If the length of the piece is no more than 110 cm, then from a piece of 11 m in length, it would be possible to cut at least 10 parts, which contradicts the condition.
If the length of the piece is at least 112 cm, then 9 parts would require at least 1008 cm, that is, they could not be cut from a ten-meter piece.
|
111
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Variant 1.
Currently, the mother is 24 years and 3 months old, and her daughter is 5 months old. After how many months will the number of years in the mother's age be equal to the number of months in the daughter's age?
|
Answer: 21.
Solution. Let $x$ be the required number of months. Then we get the equation: $24+(x+3) / 12=x+5$. From this, $x=21$.
|
21
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Variant 2.
Currently, mom is 23 years and 8 months old, and her daughter is 9 months old. In how many months will the number of years in mom's age be equal to the number of months in her daughter's age?
|
Answer: 16.
Option 3.
Currently, the mother is 19 years and 4 months old, and her daughter is 1 month old. After how many months will the number of years in the mother's age be equal to the number of months in the daughter's age?
Answer: 20.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Variant 1.
In the game "Mathematical Running," nine teams participated (not necessarily equal in the number of participants). On average, there were 7 people in each team. After one team was disqualified, the average number of participants in the remaining teams decreased to 6. How many participants were in the disqualified team?
|
Answer: 15.
Solution. The total number of participants before disqualification was $7 \cdot 9=63$. After the disqualification of participants, $6 \cdot 8=48$ remained. Therefore, the number of participants in the disqualified team was $63-48=15$.
|
15
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Variant 1.
The height $A H$ and the bisector $C L$ of triangle $A B C$ intersect at point $O$. Find the angle $B A C$, if it is known that the difference between the angle $C O H$ and half the angle $A B C$ is $46^{\circ}$.
|
Answer: 92.
Solution. Let the halves of the angles $A, B, C$ of triangle $ABC$ be denoted by $x, y$, and $z$ respectively. Then, $\angle COH = 90^{\circ} - z$ and $46^{\circ} = 90^{\circ} - z - y$. Since $x + y + z = 90^{\circ}$, we have $x = 44$ and $\angle BAC = 92^{\circ}$.
|
92
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 4. Option 1.
Find the number of four-digit numbers where the digit in the units place is exactly 1 more than the digit in the tens place. The number cannot start with zero.
|
Answer: 810.
Solution. The leading digit of the number can be chosen in 9 ways (any digit except zero). The digit in the hundreds place can be chosen in 10 ways (any digit will do). The digit in the tens place can be any digit from 0 to 8, and the digit in the units place is uniquely determined by the chosen digit in the tens place. In total, there are $9 \cdot 10 \cdot 9=810$ options.
|
810
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Variant 1.
An artistic film with a duration of 192 minutes consists of four parts. It is known that the duration of any two parts differs by at least 6 minutes. What is the maximum duration that the shortest part can have? Express your answer in minutes.
|
Answer: 39.
Solution. Let the shortest part be $x$ minutes, then the second (in terms of duration) is no less than $x+6$, the third is no less than $x+12$, and the fourth is no less than $x+18$. Therefore, the entire film lasts no less than $4 x+36$ minutes. Solving the inequality $192 \geq 4 x+36$, we get $x \leq 39$. The durations of the parts being 39, 45, 51, and 57 minutes fit.
|
39
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Variant 1.
In a convex $n$-gon, a diagonal is highlighted. The highlighted diagonal is intersected by exactly 14 other diagonals of this $n$-gon. Find the sum of all possible values of $n$. A vertex of the $n$-gon is not considered an intersection.
|
Answer: 28.
Solution. Let there be $x$ sides on one side of the diagonal, and $-n-x$ on the other. Then there are $-x-1$ vertices on one side, and $-n-x-1$ on the other. They can be the endpoints of the required diagonals. We get $14=(x-1)(n-x-1)$.
The following cases are possible:
$x-1=14, n-x-1=1$, then $n=17$
$x-1=1, n-x-1=14$, then $n=17$
$x-1=2, n-x-1=7$, then $n=11$;
$x-1=7, n-x-1=2$, then $n=11$.
|
28
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 8. Variant 1.
On the Island of Misfortune, there live truth-tellers, who always tell the truth, and liars, who always lie. One day, 2023 natives, among whom $N$ are liars, stood in a circle, and each said: "Both of my neighbors are liars." How many different values can $N$ take?
|
Answer: 337.
Solution: Both neighbors of a knight must be liars, and the neighbors of a liar are either two knights or a knight and a liar. Therefore, three liars cannot stand in a row (since in this case, the middle liar would tell the truth). We can divide the entire circle into groups of liars/knights standing in a row. These groups alternate. Each "group of knights" consists of one person, and each "group of liars" consists of one or two people. Let \( x \) be the number of "single" liars, and \( y \) be the number of "pairs of liars." Then the number of knights will be \( x + y \), and \( x + y + 2y + x = 2023, 3y + 2x = 2023, N = x + y \). It is easy to notice that \( y \) must be odd, \( x \geq 2 \) (since \( 2x \) must give the same remainder when divided by 3 as 2023), accordingly, \( 3y \leq 2019, 1 \leq y \leq 673 \). In this range, there are \( 674 / 2 = 337 \) odd numbers, i.e., \( y \) can take 337 different values. For each of these values, the number of knights \( x + y \) is uniquely determined, and thus the number of liars \( x + 2y \) \( (2y + x = 2023 - (x + y)) \).
|
337
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.6. On the board, the expression $\cos x$ is written. It is allowed to add or multiply several expressions written on the board (an expression can be used multiple times) and write the new obtained expression on the board. Is it possible to get an expression that takes the value 0 when $x=\pi$ after several actions?
(N. Agakhanov)
|
Answer. Yes, it is possible.
Solution. The first action is to append $\cos ^{2} x$, the second is to append $\cos ^{2} x+\cos x$. Since $\cos \pi=-1$, the value of the last expression at $x=\pi$ is 0.
Comment. An answer without presenting the required expression - 0 points.
Only presenting any correct required expression without indicating the sequence of steps leading to it - 6 points.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. Three lines intersect to form 12 angles, and $n$ of them turn out to be equal. What is the maximum possible value of $n$?
|
Answer: 6.
Solution: Three lines limit a certain triangle. If this triangle is equilateral, then out of twelve angles, six are $60^{\circ}$, and the other six are $120^{\circ}$.
Can any external angle of the triangle be equal to its internal angle? It is equal to the sum of the non-adjacent internal angles, so it is greater than each of the non-adjacent ones. Therefore, it can only be equal to the adjacent one. Then each of them is $90^{\circ}$, and there are 4 such angles (they share a common vertex). There are no other right angles in this construction. But then the other external angles are not equal to the internal ones. Equal can only be the internal ones (and the vertical ones to them) or only the external ones (and the vertical ones to them). Then there will be no more than 4 equal angles of each type.
Criteria: 3 points for an example with six equal angles, 3 points for comparing external and internal angles. 1 point for an answer without justification.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the sum of the coefficients of the polynomial obtained after expanding the brackets and combining like terms in the expression
$\left(2 x^{2021}-x^{2020}+x^{2019}\right)^{11}-29$.
|
Solution. First, note that the sum of the coefficients of any polynomial in canonical form $P(x)=a_{0} x^{n}+a_{1} x^{n-1}+\ldots+a_{n-1} x+a_{n}$ is $P(1)$. Next, note that after raising the bracket to the 11th power, the polynomial $Q(x)=\left(2 x^{2021}-x^{2020}+x^{2019}\right)^{11}-29$ will take a canonical form (some of the coefficients may turn out to be zero). Thus, the sum of the coefficients of the polynomial $Q(x)$ is $Q(1)=2^{11}-29=$ 2019. Answer: 2019.
Comment. Solutions in which the value of the polynomial at the point 1 appears in some form are scored full marks. For example, “It is obvious that the sum of the coefficients of the polynomial is equal to its value at the point 1. Answer: 2019.” or $\ll Q(1)=2019 »$. Only the correct answer is given - 3 points.
|
2019
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 2. Option 1
Masha wrote the number 547654765476 on a piece of paper. She erased several digits so that the resulting number is the largest possible multiple of 9. What is this number?
|
Answer: 5476547646.
Solution: The sum of the digits of the original number is $3 \cdot(7+6+5+4)=66$. From the divisibility rule by 9, it follows that the sum of the erased digits must give a remainder of 3 when divided by 9. It is impossible to select digits with a sum of 3. Digits with a sum of $3+9=12$ can be chosen, and with a sum of $12+9=21$ or more, at least 3 digits can be taken. Of the two numbers, the larger one is the one with more digits, so you need to remove two digits with a sum of $12-7$ and 5 or 6 and 6. Of the two ten-digit numbers, the larger one is the one with larger digits in the higher places. Therefore, you need to erase the last "5" and the last "7".
## Variant 2
Masha wrote the number 564756475647 on a piece of paper. She erased several digits so that the resulting number is the largest possible multiple of 9. What is this number?
Answer: 6475647564.
## Variant 3
Masha wrote the number 576457645764 on a piece of paper. She erased several digits so that the resulting number is the largest possible multiple of 9. What is this number?
Answer: 7645764564.
## Variant 4
Masha wrote the number 675467546754 on a piece of paper. She erased several digits so that the resulting number is the largest possible multiple of 9. What is this number?
Answer: 7547546754.
## Variant 5
Masha wrote the number 457645764576 on a piece of paper. She erased several digits so that the resulting number is the largest possible multiple of 9. What is this number?
Answer: 4764576456.
|
5476547646
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 4. Variant 1
A number with the sum of its digits equal to 2021 was divided by 7, resulting in a number that is written only with the digit 7. How many digits 7 can be in it? If there are multiple answers, indicate their sum.
|
Answer: 503.
Solution. By multiplying $777 \ldots 77$ and 7 in a column, we get 54...439. Let $x$ be the number of sevens in the original number, then the number of fours in the resulting product is $x-2$. Its sum of digits is $4(x-2)+5+3+9=4x+9$, but on the other hand, it is equal to 2021, so $x=\frac{2021-9}{4}=$ $\frac{2012}{4}=503$.
## Variant 2
A number with a digit sum of 3333 was divided by 7, resulting in a number that is written only with the digit 7. What can be the number of sevens in it? If there are several answers, indicate their sum.
Answer: 831.
## Variant 3
A number with a digit sum of 7777 was divided by 7, resulting in a number that is written only with the digit 7. What can be the number of sevens in it? If there are several answers, indicate their sum.
Answer: 1942
## Variant 4
A number with a digit sum of 4321 was divided by 7, resulting in a number that is written only with the digit 7. What can be the number of sevens in it? If there are several answers, indicate their sum.
Answer: 1078.
## Variant 5
A number with a digit sum of 2345 was divided by 7, resulting in a number that is written only with the digit 7. What can be the number of sevens in it? If there are several answers, indicate their sum.
Answer: 584.
|
503
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 5. Option 1
Unit cubes were used to build a large cube. Two cubes will be called adjacent if they touch by faces. Thus, one cube can have up to 6 neighbors. It is known that the number of cubes that have exactly 4 neighbors is 132. Find the number of cubes that have exactly 5 neighbors.
|
Answer: 726.
Solution: Cubes that have exactly 4 neighbors touch exactly one edge of the large cube. There are 12 edges in total, so 11 such cubes touch each edge. Therefore, the number of cubes that are strictly inside each face is $11 \cdot 11 = 121$. Since there are 6 faces, the answer is: $121 \cdot 6 = 726$.
## Variant 2
Unit cubes were used to build a large cube. Two cubes are called neighbors if they touch by a face. Thus, one cube can have up to 6 neighbors. It is known that the number of cubes with exactly 4 neighbors is 84. Find the number of cubes with exactly 5 neighbors.
Answer: 294.
## Variant 3
Unit cubes were used to build a large cube. Two cubes are called neighbors if they touch by a face. Thus, one cube can have up to 6 neighbors. It is known that the number of cubes with exactly 4 neighbors is 156. Find the number of cubes with exactly 5 neighbors.
Answer: 1014.
## Variant 4
Unit cubes were used to build a large cube. Two cubes are called neighbors if they touch by a face. Thus, one cube can have up to 6 neighbors. It is known that the number of cubes with exactly 4 neighbors is 108. Find the number of cubes with exactly 5 neighbors.
Answer: 486.
## Variant 5
Unit cubes were used to build a large cube. Two cubes are called neighbors if they touch by a face. Thus, one cube can have up to 6 neighbors. It is known that the number of cubes with exactly 4 neighbors is 180. Find the number of cubes with exactly 5 neighbors.
Answer: 1350.
|
726
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 7. Variant 1
In the garden, there are 46 trees - apple trees and pears. It turned out that among any 28 trees, there is at least one apple tree, and among any 20 trees, there is at least one pear. How many pears are there in the garden?
|
Answer: 27.
Solution: Since among 28 trees there is at least one apple tree, the number of pears is no more than 27. Since among any 20 trees there is at least one pear, the number of apple trees is no more than 19. There are 46 trees in total, so there are 19 apple trees and 27 pears.
## Variant 2
In the garden, there are 46 trees - apple and pear trees. It turned out that among any 28 trees, there is at least one apple tree, and among any 20 trees, there is at least one pear tree. How many apple trees are there in the garden?
Answer: 19.
## Variant 3
In the garden, there are 47 trees - apple and pear trees. It turned out that among any 29 trees, there is at least one apple tree, and among any 20 trees, there is at least one pear tree. How many pear trees are there in the garden?
Answer: 28.
## Variant 4
In the garden, there are 47 trees - apple and pear trees. It turned out that among any 28 trees, there is at least one apple tree, and among any 21 trees, there is at least one pear tree. How many apple trees are there in the garden?
Answer: 20.
## Variant 5
In the garden, there are 49 trees - apple and pear trees. It turned out that among any 29 trees, there is at least one apple tree, and among any 22 trees, there is at least one pear tree. How many apple trees are there in the garden?
Answer: 21.
|
27
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 8. Variant 1
In trapezoid $A B C D(A D \| B C)$, the bisectors of angles $D A B$ and $A B C$ intersect on side $C D$. Find $A B$, if $A D=5, B C=2$.
|
Answer: 7.
Solution.
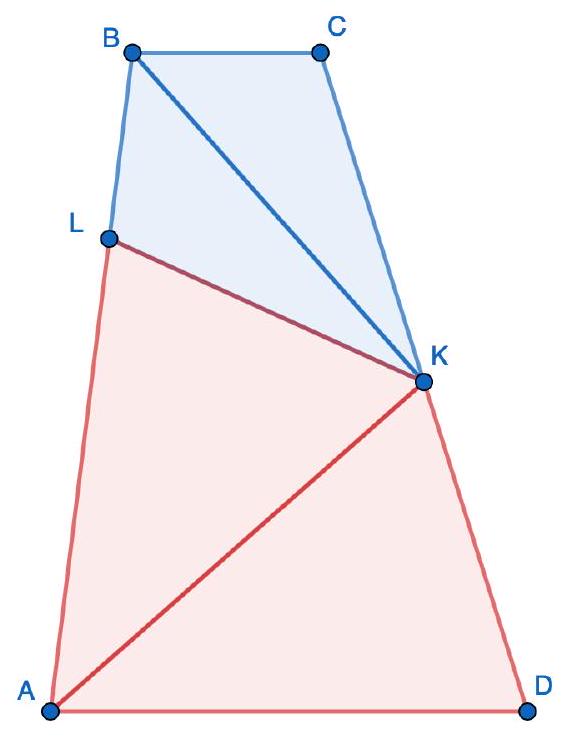
Mark point $L$ on side $AB$ such that $LB = BC$. Let $K$ be the intersection point of the angle bisectors of $\angle DAB$ and $\angle ABC$. Then triangles $LBK$ and $BCK$ are congruent by angle and two adjacent sides $\Rightarrow \angle BLK = \angle BCK$. Therefore, $\angle ALK = 180^\circ - \angle BLK = 180^\circ - \angle BCK = \angle ADC$ (the last equality holds because $AD \parallel BC$). Finally, $\triangle ALK = \triangle ADC$ by angles and a common side. Thus, $AB = AD + BC$.
## Variant 2
In trapezoid $ABCD (AD \parallel BC)$, the angle bisectors of $\angle DAB$ and $\angle ABC$ intersect on side $CD$. Find $AB$ if $AD = 5$, $BC = 3$.
Answer: 8.
## Variant 3
In trapezoid $ABCD (AD \parallel BC)$, the angle bisectors of $\angle DAB$ and $\angle ABC$ intersect on side $CD$. Find $AB$ if $AD = 7$, $BC = 2$.
Answer: 9.
## Variant 4
In trapezoid $ABCD (AD \parallel BC)$, the angle bisectors of $\angle DAB$ and $\angle ABC$ intersect on side $CD$. Find $AB$ if $AD = 11$, $BC = 5$.
Answer: 16.
## Variant 5
In trapezoid $ABCD (AD \parallel BC)$, the angle bisectors of $\angle DAB$ and $\angle ABC$ intersect on side $CD$. Find $AB$ if $AD = 10$, $BC = 3$.
Answer: 13.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.2. Masha eats a bowl of porridge in 12 minutes, and Bear eats it twice as fast. How long will it take them to eat six bowls of porridge?
|
Answer: 24 min.
Solution: In 12 minutes, Masha eats one bowl of porridge, and Bear eats 2 bowls. In total, 3 bowls of porridge are eaten in 12 minutes. Six bowls of porridge will be eaten in twice the time, i.e., $12 * 2=24$ min.
Comment: A correct answer without justification - 3 points.
|
24
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.5. The hedgehogs collected 65 mushrooms and divided them so that each hedgehog got at least one mushroom, but no two hedgehogs had the same number of mushrooms. What is the maximum number of hedgehogs that could be
|
Answer: 10
Solution: If there were 11 hedgehogs, then together they would have collected no less than $1+2+3+\ldots+10+11=66$ mushrooms, which exceeds the total number of mushrooms collected. Therefore, there were fewer than 11 hedgehogs. We will show that there could have been 10 hedgehogs. Suppose the first found 1 mushroom, the second found 2 mushrooms, the third found 3, and so on, the ninth found 9 mushrooms. Then the nine hedgehogs collected $1+2+\ldots+8+9=45$ mushrooms. If the tenth found 20, then all together they collected 65 mushrooms.
Comment. Only the correct answer - 0 points. If an example for 10 hedgehogs is shown without proving the impossibility for 11, then - 4 points.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.5. Given an odd number $n>10$. Find the number of ways to arrange the natural numbers $1,2,3, \ldots, n$ in a circle in some order so that each number is a divisor of the sum of the two adjacent numbers. (Ways that differ by rotation or reflection are considered the same.) (D. Khramov)
|
Answer. Two ways
Solution. Consider an arbitrary arrangement of numbers from 1 to $n$ that satisfies the conditions. Suppose that two even numbers $x$ and $y$ are adjacent, and the next number is $z$. Since $x+z$ is divisible by $y$, the number $z$ is also even. Continuing this movement around the circle, we get that all numbers in the arrangement are even, which is impossible. Therefore, no two even numbers are adjacent; hence, some two odd numbers are adjacent, and the even and odd numbers alternate.
Note that both neighbors of the number $n$ cannot be even; indeed, otherwise their sum would be divisible by $2n$, i.e., it would be at least $2n$. Therefore, for any odd number less than $n$, either both neighbors are even, or one of the neighbors is the number $n$.
Suppose that the numbers $n$ and $n-2$ are neighbors, and the other neighbor of the number $n-2$ is the number $t$. The number $t+n=(n-2)+(t+2)$ must be divisible by $n-2$, which is only possible if $t=n-4$. But then three odd numbers $n, n-2, n-4$ are adjacent, which, as we have shown, is impossible.
Thus, both neighbors of the odd number $n-2$ are even, and therefore their sum is divisible by $2(n-2)$, i.e., this sum is at least $2(n-2)$; this is only possible if these neighbors are $n-1$ and $n-3$. In particular, the numbers $n-1$ and $n-2$ are neighbors. If the pair $n-1, n-2$ continues with numbers in descending order up to the number 1, we arrive at the circular arrangement $n-1, n-2, n-3, n-4, \ldots, 3, 2, 1, n$, which obviously satisfies the condition.
Now suppose that the pair $n-1, n-2$ continues with numbers in descending order up to the number $d>1$, and after it follows the number $x \neq d-1$. Thus, we have the numbers $n-1, n-2, \ldots, d+1, d, x, y, \ldots$ in a row around the circle. Since $x+(d+1)=(x+1)+d$ is divisible by $d$, then $x+1$ is divisible by $d$, in particular, $x \geq d-1$. But $x$ is different from the numbers $d-1, d, \ldots, n-2, n-1$; hence, the only remaining option is $x=n$.
Let $n=2k+1$. We have obtained that the number $n+1=2k+2$ is divisible by $d$; since $d<10$, the only possible values for $d$ are 1, 2, or 4. If $d=1$, the arrangement is $n, n-1, n-2, n-3, \ldots, 3, 2, 1$, which satisfies the condition. If $d=2$, the arrangement is $2k, 2k-1, 2k-2, \ldots, k+1, 2k+1, k, k-1, k-2, \ldots, 1$, which also satisfies the condition. If $d=4$, the arrangement is $2k, 2k-1, 2k-2, \ldots, k+1, 2k+1, k, k-1, k-2, \ldots, 1$, which also satisfies the condition.
For $n>10$, the arrangement $n, n-1, n-2, n-3, \ldots, 3, 2, 1$ is the only one that satisfies the condition.
Comment. Only the correct answer or the correct answer with the presentation of one of the two required arrangements - 0 points.
Points for the following advancements from different parts a), b), c) are summed.
a) Two examples of arrangements that satisfy the condition are found - 1 point.
b) It is proven that the numbers $n-1$ and $n-2$ are adjacent - 2 points.
If it is only proven that two even numbers do not stand next to each other - 1 point out of these 2.
c) Assuming that $n-1$ and $n-2$ are adjacent, it is proven that the chain uniquely continues to one of the examples $(n-1, n-2, n-3, \ldots, 2, 1, n)$ or $(2k, 2k-1, 2k-2, \ldots, k+1, 2k+1, k, k-1, k-2, \ldots) - 4$ points.
If it is only proven that the continuation has the form $(n-1, n-2, \ldots, d+1, d, n, \ldots)$ for some $d$ - 1 point out of these 4.
If it is proven that the continuation has the form $(n-1, n-2, n-3, \ldots, 2, 1, n)$ or $(2k, 2k-1, 2k-2, \ldots, k+1, 2k+1, k, \ldots) - 3$ points out of these 4.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. Given quadratic trinomials $f_{1}(x), f_{2}(x), \ldots, f_{100}(x)$ with the same coefficients for $x^{2}$, the same coefficients for $x$, but different constant terms; each of them has two roots. For each trinomial $f_{i}(x)$, one root was chosen and denoted by $x_{i}$. What values can the sum $f_{2}\left(x_{1}\right)+f_{3}\left(x_{2}\right)+\ldots+f_{100}\left(x_{99}\right)+f_{1}\left(x_{100}\right)$ take?
(N. Agakhanov)
|
Answer: Only 0.
Solution: Let the $i$-th quadratic polynomial have the form $f_{i}(x)=a x^{2}+b x+c_{i}$. Then
$f_{2}\left(x_{1}\right)=a x_{1}^{2}+b x_{1}+c_{2}=\left(a x_{1}^{2}+b x_{1}+c_{1}\right)+\left(c_{2}-c_{1}\right)=c_{2}-c_{1}$, since $f_{1}\left(x_{1}\right)=0$. Similarly, we obtain the equalities $f_{3}\left(x_{2}\right)=$ $=c_{3}-c_{2}, \ldots, f_{100}\left(x_{99}\right)=c_{100}-c_{99}$ and $f_{1}\left(x_{100}\right)=c_{1}-c_{100}$.
By adding the obtained equalities, we get $f_{2}\left(x_{1}\right)+f_{3}\left(x_{2}\right)+\ldots+f_{1}\left(x_{100}\right)=\left(c_{2}-c_{1}\right)+\ldots+\left(c_{1}-c_{100}\right)=0$. Therefore, the only possible value of the sum is zero.
Comment: A correct answer without justification - 0 points.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. King Hiero has 11 metal ingots that are indistinguishable in appearance; the king knows that their weights (in some order) are 1, $2, \ldots, 11$ kg. He also has a bag that will tear if more than 11 kg is placed in it. Archimedes has learned the weights of all the ingots and wants to prove to Hiero that the first ingot weighs 1 kg. In one step, he can load several ingots into the bag and demonstrate to Hiero that the bag does not tear (the bag cannot be torn!). What is the minimum number of bag loadings Archimedes needs to achieve the required result?
(I. Bogdanov, K. Knop)
|
Answer. In 2 loads.
Solution. We will show that Archimedes can use the bag only twice. Let him first put in the bag ingots weighing 1, 2, 3, and 5 kg, and then ingots weighing 1, 4, and 6 kg. In both cases, the bag will not tear.
We will prove that this could only happen if the 1 kg ingot was used twice. Indeed, if Archimedes used ingots weighing $w_{1}, \ldots, w_{6}$ kg instead of ingots weighing 1, ..., 6 kg, these weights would satisfy the system of inequalities $w_{1}+w_{2}+w_{3}+w_{5} \leqslant 11, w_{1}+w_{4}+w_{6} \leqslant 11$. Adding these inequalities, we get $w_{1}+(w_{1}+w_{2}+\ldots+w_{6}) \leqslant 22$. The sum in parentheses is the sum of six different natural numbers, so it is at least $1+2+\ldots+6=21$. Therefore, $w_{1} \leqslant 22-21=1$. Hence, $w_{1}=1$, which means the 1 kg ingot is uniquely determined.
It remains to show that one load is insufficient. If Archimedes loads only one ingot, the bag will not tear in any case, so no ingot can be identified. Suppose Archimedes loads more than one ingot, and the bag does not tear. If the 1 kg ingot is not loaded into the bag, then replacing it with any ingot in the bag will not change the result; in this case, Hiero will not be able to determine whether this ingot is in the bag. If the required ingot is in the bag, then Hiero will not be able to determine which of the (at least two) loaded ingots is the required one.
Remark. After the specified two loads, the group of weights 2, 3, and 5 kg, as well as the group of weights 4 and 6 kg, are also uniquely determined.
Comment. Only proved that one load is insufficient - 1 point.
Only provided a correct example of two loads, but did not prove that it works - 3 points (these points can be combined with the previous one).
Provided a correct example of two loads, proved that it works, but did not prove that one load is insufficient - 6 points.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. Given quadratic trinomials $f_{1}(x), f_{2}(x), \ldots, f_{100}(x)$ with the same coefficients for $x^{2}$, the same coefficients for $x$, but different constant terms; each of them has two roots. For each trinomial $f_{i}(x)$, one root was chosen and denoted by $x_{i}$. What values can the sum $f_{2}\left(x_{1}\right)+f_{3}\left(x_{2}\right)+\ldots+f_{100}\left(x_{99}\right)+f_{1}\left(x_{100}\right)$ take?
|
Answer: Only 0.
Solution. Let the $i$-th quadratic polynomial have the form $f_{i}(x)=a x^{2}+b x+c_{i}$. Then
$$
f_{2}\left(x_{1}\right)=a x_{1}^{2}+b x_{1}+c_{2}=\left(a x_{1}^{2}+b x_{1}+c_{1}\right)+\left(c_{2}-c_{1}\right)=c_{2}-c_{1},
$$
since $f_{1}\left(x_{1}\right)=0$. Similarly, we obtain the equalities $f_{3}\left(x_{2}\right)=$ $=c_{3}-c_{2}, \ldots, f_{100}\left(x_{99}\right)=c_{100}-c_{99}$ and $f_{1}\left(x_{100}\right)=c_{1}-c_{100}$.
Adding the obtained equalities, we get $f_{2}\left(x_{1}\right)+f_{3}\left(x_{2}\right)+\ldots+f_{1}\left(x_{100}\right)=\left(c_{2}-c_{1}\right)+\ldots+\left(c_{1}-c_{100}\right)=0$. Therefore, the only possible value of the sum is zero.
Comment. A correct answer without justification - 0 points.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.4. A $100 \times 100$ grid is given, with cells colored black and white. In each column, there are an equal number of black cells, while in each row, the number of black cells is different. What is the maximum possible number of pairs of adjacent cells of different colors? (I. Bogdanov)
|
Answer. $6 \cdot 50^{2}-5 \cdot 50+1=14751$ pairs.
Solution. Let the side length of the table be $2 n = 100$ (so $n=50$) and number the rows from top to bottom and the columns from left to right with numbers from 1 to $2 n$.
In each row, there can be from 0 to $2 n$ black cells. Since the number of black cells in all rows is different, these numbers are all numbers from 0 to $2 n$, except one (say, except $k$). Then the total number of black cells is $(0+1+\ldots+2 n)-k=2 n^{2}+n-k$. On the other hand, since the number of cells in all columns is the same, the total number of black cells must be divisible by $2 n$. Therefore, $k=n$, and in all columns there are $2 n^{2} / (2 n) = n$ black cells.
Now let's estimate the number of pairs of adjacent cells of different colors, considering separately pairs of cells adjacent horizontally and vertically.
If there are $i \leqslant n-1$ black cells in a row, then they can participate in no more than $2 i$ horizontal pairs. If there are $i \geqslant n+1$ black cells in a row, the same reasoning can be applied to the white cells, of which there are $2 n-i \leqslant n-1$. Therefore, the number of horizontal pairs of different colors is no more than $2 \cdot(2 \cdot 0+2 \cdot 1+\ldots+2 \cdot(n-1))=2 n(n-1)$.
Now let's estimate the number of vertical pairs. Consider any row with an even number from 2 to $2(n-1)$; let there be $i$ black cells in it. Then either in the row above or in the row below it, the number of black cells is not equal to $100-i$; therefore, one of the vertical pairs in which the cells of our row participate will be of the same color. Therefore, there are at least $n-1$ same-color vertical pairs. Since the total number of vertical pairs is $2 n(2 n-1)$, the number of different-color vertical pairs is no more than $2 n(2 n-1)-(n-1)$. Therefore, the total number of different-color pairs is no more than $2 n(n-1)+\left(4 n^{2}-3 n+1\right)=6 n^{2}-5 n+1=14751$.
It remains to provide an example in which the specified number of pairs is achieved. Draw a diagonal from the upper left corner to the lower right corner in our $2 n \times 2 n$ table. All cells lying on or below the diagonal will be painted black if they are in even rows, and white otherwise (coloring "by rows"). All cells lying above the diagonal will be painted black if the sum of their row and column numbers is even, and white otherwise (checkerboard coloring). An example of such a coloring for $n=4$ is shown in Fig. 3. It is easy to verify that in each column there are exactly $n$ black cells, in the $2 i$-th row there are $n+i$ black cells, and in the $(2 i-1)$-th row there are $-n-i$ black cells. Moreover, all the estimates above are achieved.
Comment. Only the answer - 0 points.
Only the answer and a correct example - 2 points.
Only the proof of the exact estimate - 4 points.
Proof of the exact estimate only for the number of vertical or only for the number of horizontal different-color pairs - 2 points (can be combined with points for a correct example).
Proved that there is no row containing exactly 50 black cells - 1 point, if there are no other significant advances in the work (otherwise this point is not added).
|
14751
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. What different values can the digit U take in the puzzle U$\cdot$LAN + U$\cdot$DE = 2020? Justify your answer. (Identical digits are replaced by the same letters, different digits by different letters.)
|
Answer: two. $\mathrm{V}=2, \mathrm{y}=5$.
Solution: Factor out the common factor: У$\cdot$(ЛАН + ДЭ) $=2020$. Note that У, Л, and Э are not equal to 0.
Factorize the right-hand side: $2020=1 \cdot 2 \cdot 2 \cdot 5 \cdot 101$. Since У is a digit, consider all possible values: $\mathrm{V}=1,2,4,5$.
1) $У=1$. Then ЛАН + ДЭ $=2020$, but ЛАН + ДЭ $<999+99=1098<2020$. No solutions.
2) $\mathbf{y}=2$, ЛАН + ДЭ $=1010$.
There are 8 different solutions, for example, $2 \cdot 974+2 \cdot 36=2020$
3) $У=4$, ЛАН + ДЭ $=505$. Clearly, Л $\leq 5$.
Л $\neq 5$, because otherwise ЛАН $\geq 501$, but then ДЭ cannot be a two-digit number.
$Л \neq 4$, because $У=4$.
For Л $=3$, АН + ДЭ $=205$. But АН + ДЭ $\leq 99+99=198$ < 205. No solutions.
4) $\mathbf{y}=\mathbf{5}$, ЛАН + ДЭ $=404$.
There are 14 different solutions, for example, $5 \cdot 306+5 \cdot 98=2020$
# Criteria:
7 points - correct answer and complete correct solution;
only one answer found and justified - 4 points;
only answer - 0 points.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. A student-entrepreneur bought several packs of masks from a pharmacy and sold them to classmates at a higher price, making a profit of 1000 rubles. With all the money earned, he again bought masks from the pharmacy (at the same price as the first time) and sold them to classmates (at the same price as the first time). This time, the profit was 1500 rubles. How much money did he spend on the first purchase?
|
Answer: 2000 rubles.
Solution 1: Let the package of masks in the pharmacy cost x rubles, and the student sold the masks for y rubles, and bought a packages of masks the first time. Then, according to the condition, $a(y-x)=1000$.
The revenue amounted to ay rubles, so the second time the student was able to buy $\frac{a y}{x}$ packages of masks. In this case, the profit amounted to $\frac{a y}{x} \cdot y-a y=\frac{a y(y-x)}{x}$ rubles. According to the condition, $\frac{a y(y-x)}{x}=1500$. From the two obtained equations, it follows that $\frac{1000 y}{x}=1500$, that is, $y=\frac{3}{2} x$. Substituting this result into the first equation, we get $a y-a x=a \frac{3}{2} x-a x=\frac{a x}{2}=1000$, from which $a x=2000$.
Solution 2: Let the student paid x rubles for the masks at the first purchase in the pharmacy. Then he sold them for $1000+x$ rubles. The second time he spent $x+1000+1500=x+2500$ rubles. Since the price ratio did not change, we form the proportion: $\frac{x}{x+1000}=\frac{x+1000}{x+2500}$. Solving the equation, we get $x=2000$.
## Criteria:
7 points - correct answer and complete correct solution;
6 points - correct solution with minor gaps or individual unclear places;
3 points - correct answer obtained based on reasoning with specific numerical data;
1 point - correct answer provided and only checked that it satisfies the condition;
only answer or answer with unclear calculations without explanations - 0 points.
|
2000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3. In triangle $M P Q$, a line parallel to side $M Q$ intersects side $M P$, median $M M_{1}$, and side $P Q$ at points $D, E$, and $F$ respectively. It is known that $D E=5$, and $E F=7$. What is the length of $M Q$?
|
Answer: 17.
Solution: Draw a line through point $E$ parallel to $P Q$ ( $K$ and $L$ - the points of intersection of this line with sides $M P$ and $M Q$ respectively). Since $M M_{1}$ is a median, then $L E = E K$, and since $D F \parallel M Q$, it follows that $D E$ is the midline of triangle $M K L$. Therefore, $M L = 2 D E = 10$. Moreover, $E L \parallel F Q$ and $E F \parallel L Q$, so $L E F Q$ is a parallelogram, from which $L Q = E F = 7$. Thus, $M Q = M L + L Q = 10 + 7 = 17$.
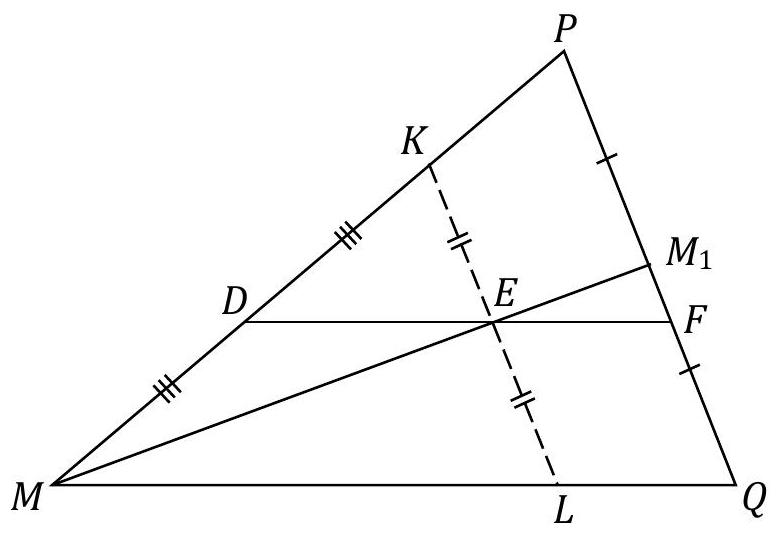
## Criteria:
7 points - correct answer and complete correct solution;
$3-5$ points - partially correct solution;
answer only - 0 points.
|
17
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the smallest 10-digit number, the sum of whose digits is greater than that of any smaller number.
|
Answer: 1999999999.
Solution. Among 9-digit numbers, the largest sum of digits is for the number 999999 999, which is 81. Since the sought 10-digit number is greater than 999999 999, we need to find the smallest number with a sum of digits no less than 82. If the first digit of this number is 1, then the sum of the remaining digits must be no less than 81, which means the other nine digits are nines.
Criteria. Correct answer without explanation - 1 point. Proven that the sum of digits of the sought number is greater than 81 - 3 points. Complete solution - 7 points.
|
1999999999
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In a chess tournament, everyone played against each other once. The winner won half of the games and drew the other half. It turned out that he scored 9 times fewer points than all the others combined. (1 point for a win, 0.5 for a draw, 0 for a loss.) How many chess players were there in the tournament?
|
# Answer: 15 chess players.
Solution. If the number of participants is $n$, then each played $n-1$ games. The winner won half of the games and scored $\frac{1}{2}(n-1)$ points. They drew the other half of the games and scored another $\frac{1}{4}(n-1)$ points. In total, the winner scored $\frac{1}{2}(n-1)+\frac{1}{4}(n-1)=\frac{3}{4}(n-1)$ points.
In the tournament, $\frac{1}{2} n(n-1)$ games were played. In each game, the players played for one point, so they scored a total of $\frac{1}{2} n(n-1)$ points. Therefore,
$$
9 \cdot \frac{3(n-1)}{4}=\frac{n(n-1)}{2}-\frac{3(n-1)}{4}
$$
from which $n=15$. Thus, in a tournament of 15 chess players, the winner played 14 games and scored $7+3.5=10.5$ points, while the others scored $\frac{1}{2} \cdot 15(15-1)-10.5=94.5$ points, which is 9 times more than the winner.
Criteria. Only the answer -0 points. Proven that for $n=15$ the tournament meets the condition, but not justified that there are no other solutions -2 points. The equation for the number of participants is correctly set up -5 points. Complete solution -7 points.
|
15
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Side $A B$ of triangle $A B C$ is greater than side $B C$, and angle $B$ is $40^{\circ}$. A point $P$ is taken on side $A B$ such that $B P = B C$. The bisector $B M$ intersects the circumcircle of triangle $A B C$ at point $T$. Find the angle $M P T$.
|
Answer: $20^{\circ}$.
Solution. (Fig. 3.) In the quadrilateral $A P M T$, the angle at vertex $A$ is measured by half the arc $T C B$. Triangles $P M B$ and $C M B$ are equal by two sides and the angle between them, so $\angle P M B = \angle C M B = \angle A M T$. The angle $\angle A M T$ is measured by half the sum of the arcs $A T$ and $C B$, and:
$$
\frac{1}{2}(\overparen{A T} + \overparen{C B}) = \frac{1}{2}(\overparen{T C} + \overparen{C B}) = \frac{1}{2} \overparen{T C B}
$$
Thus, $\angle C M B = \angle B A T$. Therefore, $\angle P M B = \angle B A T$ and $\angle B A T + \angle P M T = \angle B A T + (180^{\circ} - \angle P M B) = 180^{\circ}$. Consequently, the sum of the opposite angles of the quadrilateral $A P M T$ is $180^{\circ}$, meaning $A P M T$ is cyclic. By the property of inscribed angles,
Fig. 3 $\angle M P T = \angle M A T = \angle C A T = \angle T B C = \frac{1}{2} \angle A B C = 20^{\circ}$.
Criteria. The equality of angles $P M B$ and $C M B$ (or $A M T$) is noted - 1 point. It is proven that the angle $A M T$ or $C M B$ is equal to the angle $B A T$ - 2 points. It is proven that the quadrilateral $A P M T$ is cyclic - 5 points. The criteria are not cumulative. Full solution - 7 points.
|
20
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. Does there exist a natural number $n$, greater than 1, such that the value of the expression $\sqrt{n \sqrt{n \sqrt{n}}}$ is a natural number?
|
Answer: Yes, it exists.
Solution. For example, $n=2^{8}=256$.
Indeed, $\sqrt{n \sqrt{n \sqrt{n}}}=\sqrt{n \sqrt{n \cdot n^{\frac{1}{2}}}}=\sqrt{n \sqrt{n^{\frac{3}{2}}}}=\sqrt{n \cdot n^{\frac{3}{4}}}=\sqrt{n^{\frac{7}{4}}}=n^{\frac{7}{8}}$. Then, for $n=2^{8}$, the value of this expression is $\left(2^{8}\right)^{\frac{7}{8}}=2^{7}=128$.
Other examples are possible: any numbers that are the eighth power of any natural number other than 1.
## Grading Criteria
+ A complete and justified solution is provided
$\pm$ A correct example is provided, but the calculation showing that it fits is not shown
- Only the answer ("yes" or "no") is provided
- The problem is not solved or is solved incorrectly
|
128
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.6. Each cell of a $7 \times 8$ table (7 rows and 8 columns) is painted in one of three colors: red, yellow, or green. In each row, the number of red cells is not less than the number of yellow cells and not less than the number of green cells, and in each column, the number of yellow cells is not less than the number of red cells and not less than the number of green cells. How many green cells can there be in such a table?
|
Answer: 8.
Solution. 1) In each row of the table, there are no fewer red cells than yellow ones, so in the entire table, there are no fewer red cells than yellow ones.
In each column of the table, there are no fewer yellow cells than red ones, so in the entire table, there are no fewer yellow cells than red ones.
Thus, in the table, there is an equal number of red
| 3 | 3 | ॠ | $\mathbf{K}$ | Ж世 | К | WK | $\mathbf{K}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| К | Ж | 3 | 3 | К | Ж | $\mathbf{K}$ | Ж |
| З | $\boldsymbol{\kappa}$ | $\mathbf{K}$ | Ж | 3 | 6 | ऊ | |
| К | Ж | ЖК | $\mathbf{K}$ | ЗК | К | 3 | 3 |
| ЗК | $\mathbf{K}$ | $\mathbf{K}$ | Ж | K | Ж | $\mathbf{K}$ | |
| K | ऊ币 | $\overline{\mathbf{K}}$ | Ж | $\mathbf{K}$ | ऊ | $\mathbf{K}$ | ज्ञ |
| Ж | $\mathbf{K}$ | З | $\mathbf{K}$ | ЗK | K | Ж | |
and yellow cells.
2) Suppose that in some column, there are more yellow cells than red ones. Since in each of the other columns, there are no fewer yellow cells than red ones, then in the entire table, there would be more yellow cells than red ones, but this is not the case (see 1). Therefore, in each of the eight columns, there are an equal number of red and yellow cells.
3) Since in each column, there are no fewer yellow cells than green ones, the cases where in each column: a) 1 yellow, 1 red, 5 green cells and b) 2 yellow, 2 red, 3 green cells are excluded.
The only remaining case is when in each column there are 3 red, 3 yellow, and 1 green cell. Then, in total, there are 8 green cells in the table.
This case is possible. For example, see the table.
## Evaluation Criteria
+ A complete and well-reasoned solution is provided
$\pm$ A generally correct solution is provided, containing minor gaps or inaccuracies
干 It is proven that there can only be 8 green cells, but an example is not provided
Ғ Only the correct answer and an example are provided
- Only the answer is provided
- The problem is not solved or is solved incorrectly
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.3. On the $O x$ axis, points $0,1,2, \ldots, 100$ were marked and graphs of 200 different quadratic functions were drawn, each of which passes through two of the marked points and touches the line $y=-1$. For each pair of graphs, Oleg wrote on the board a number equal to the number of common points of these graphs. After that, he added all 19900 numbers written on the board. Could he have obtained the number 39699?
|
Answer: Could not.
Solution. Each of our 200 polynomials corresponds to two integer points $a$ and $b$ on the $O x$ axis. Without loss of generality, we will assume that $a < b$. The width of the polynomial is $w=b-a$, and the axis is $c=\frac{a+b}{2}$. If the width is $w>0$ and the axis is $c$, then it is written as $f(x)=\frac{4}{w^{2}}(x-c)^{2}-1$.
We will show that the graphs of two different polynomials of this form have exactly two common points when they have different widths and axes. If they have the same width or axis, then they have exactly one common point.
Indeed, $\frac{4}{w_{1}^{2}}\left(x-c_{1}\right)^{2}-1=\frac{4}{w_{2}^{2}}\left(x-c_{2}\right)^{2}-1$ is equivalent to $\left(x-c_{1}\right) w_{2}= \pm\left(x-c_{2}\right) w_{1}$. If $w_{1} \neq w_{2}$, then each of the two linear equations has roots, and they coincide only if $c_{1}=c_{2}$. If $w_{1}=w_{2}$, then $c_{1} \neq c_{2}$ (the polynomials are different) and one of the two linear equations has no roots, while the other has.
Note that the width of a polynomial can take a value from 1 to 100, and there will be no more than one polynomial with a width of 100. Let $x_{i}$ be the number of polynomials with width $i$. We estimate the number of pairs of polynomials with the same width:
$$
\begin{aligned}
\sum_{i=1}^{100} \frac{x_{i}\left(x_{i}-1\right)}{2} & =\sum_{i=1}^{100} \frac{\left(x_{i}^{2}-4 x_{i}+4\right)+3 x_{i}-4}{2}= \\
& =\sum_{i=1}^{100} \frac{\left(x_{i}-2\right)^{2}}{2}+\frac{3 \cdot 200-4 \cdot 100}{2} \geqslant 1+100
\end{aligned}
$$
In the last inequality, we used the following reasoning: since the sum of one hundred numbers $x_{i}$ is 200 and $x_{100} \neq 2$, there will be at least one more $x_{i} \neq 2$, therefore, $\sum_{i=1}^{100}\left(x_{i}-\right.$ $-2)^{2} \geqslant 2$.
The axis of a polynomial can be any integer or half-integer from $\frac{1}{2}$ to $99 \frac{1}{2}$, such numbers are 199, therefore, there will be at least one pair of polynomials with a common axis. This will be a previously unaccounted pair, since polynomials with the same width and axis coincide.
To find the number of intersection points of the graphs, we need to subtract the number of pairs with the same width or axis from twice the number of pairs of polynomials. Thus, the number of intersection points is no more than $2 \cdot \frac{200 \cdot 199}{2}-101-1=39698$, which is less than 39699.
Comment. The correct answer without explanation - 0 points.
The conditions under which a pair of graphs has exactly one common point are formulated - 1 point.
Proved the conditions under which a pair of graphs has exactly one common point - another 1 point.
Proved that the number on the board is no more than 39699 - 5 points (these points are not cumulative with the previous ones).
|
39698
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.5. In Flower City, there live $99^{2}$ dwarfs. Some of the dwarfs are knights (always tell the truth), while the rest are liars (always lie). The houses in the city are located in the cells of a $99 \times 99$ square (a total of $99^{2}$ houses, arranged in 99 vertical and 99 horizontal streets). Each house is inhabited by exactly one dwarf. The house number is denoted by a pair of numbers $(x ; y)$, where $1 \leqslant x \leqslant 99$ is the number of the vertical street (numbers increase from left to right), and $1 \leqslant y \leqslant 99$ is the number of the horizontal street (numbers increase from bottom to top). The Flower City distance between two houses with numbers $\left(x_{1} ; y_{1}\right)$ and $\left(x_{2} ; y_{2}\right)$ is the number $\rho=\left|x_{1}-x_{2}\right|+\left|y_{1}-y_{2}\right|$. It is known that on each street, whether vertical or horizontal, there live at least $k$ knights. In addition, all dwarfs know which house Knight Knowitall lives in. You want to find his house, but you do not know what Knowitall looks like. You can approach any house and ask the dwarf living there: “What is the Flower City distance from your house to the house of Knowitall?”. For what smallest $k$ can you guarantee to find the house of Knowitall? (V. Novikov)
|
Answer: 75.
Solution: Example. Let's show that if $k=74$, we cannot guarantee finding the house of Znayka. Place Znayka and the liar Neznayka in houses with numbers $(50 ; 49)$ and $(49 ; 50)$, respectively. We will show that it might be such that from the answers of the residents, we cannot uniquely determine which of these two houses Znayka lives in.
In the lower left square $49 \times 49$, we will settle the knights. Their distances to Znayka and Neznayka are the same. In the upper right square $50 \times 50$, we will also settle the knights, and their distances are also the same. In the lower right rectangle (49 rows and 50 columns), we will settle the knights so that in each row there are exactly 25 knights and 25 liars, and in each column at least 24 knights and 24 liars. In the upper left rectangle, we will settle the dwarfs diagonally symmetric to the upper right, but swap the knights and liars. In it, each column will have 25 knights and 25 liars, and each row will have at least 24 knights and 24 liars. For each dwarf in these rectangles, the distances to Znayka and Neznayka are different. Let all the liars in them say the distance not to Znayka, but to Neznayka. Then, when the places of the knights and liars in these rectangles are swapped (in particular, when Znayka and Neznayka are swapped), everyone will say the same thing, but Znayka will live in a different house.
Estimate. Let's show that if $k \geqslant 75$, we can guarantee finding the house of Znayka. Suppose that, after asking all the dwarfs, we cannot determine where Znayka is, i.e., there are at least two houses where he could be. Let one have the number $(x ; y)$, and the other $(u ; v)$. We can assume that $x \leqslant u, y \leqslant v$, since we can rotate the square as required. Since both inequalities cannot be equalities at the same time, without loss of generality, we will assume that $yv-y$ or $(u-x)+(v-y)$ is odd, then in these columns there is no dwarf whose distance to both marked houses is the same.
If $x=u$ and $v-y$ is even, then in the column $(x, \ldots)$ there is one dwarf whose distance to both houses is the same.
If $u-x<v-y$ and $(u-x)+(v-y)$ is even, then in the columns $(x, \ldots)$ and $(u, \ldots)$ there is one dwarf in each whose distance to both houses is the same.
If $u-x=v-y$, then in the column $(x, \ldots)$, the places from which the distances to $(x ; y)$ and $(u ; v)$ are the same have the form $(x ; V)$, where $V \geqslant v$, and there are exactly $100-v$ such places. Similarly, in the column $(u, \ldots)$, the places from which the distances to $(x ; y)$ and $(u ; v)$ are the same have the form $(u ; Y)$, where $Y \leqslant y$, and there are exactly $y$ such places.
Notice that $y+(100-v) \leqslant 99$. Therefore, one of the numbers $y, 100-v$ is not greater than 49.
Thus, in all cases, there will be a column where no more than 49 knights indicate both places, while on the incorrect place, no more than these knights and all the liars (no more than $99-75=24$) point, i.e., no more than $49+24=73$ dwarfs. At the same time, on the correct place, in any column, at least all the knights point, i.e., no fewer than 75 dwarfs. Thus, from the two suspicious places, one can always be excluded (since the row or column we rely on depends only on the position of the places, not on the arrangement of the knights/liars). This means that the correct place can always be found.
Comment: The correct answer without explanation - 0 points. Only the example - 3 points.
Only the estimate - 4 points.
|
75
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Alyosha and Vitya set off from point $N$ to point $M$, the distance between which is 20 km. Unfortunately, they have only one bicycle between them. From $N$, Alyosha sets off on the bicycle, while Vitya starts walking. Alyosha can leave the bicycle at any point along the road and continue on foot. When Vitya reaches this point, he switches to the bicycle. Alyosha's walking speed is 4 km/h, and his cycling speed is 15 km/h. Vitya's walking speed is 5 km/h, and his cycling speed is 20 km/h. At what point should Alyosha leave the bicycle so that they both arrive in $M$ at the same time?
|
Answer. 12 km from point $N$.
Solution. Let $x$ (km) be the distance from $N$ to the point where Alyosha leaves the bicycle. Then Alyosha will spend $\frac{x}{15}+\frac{20-x}{4}$ hours on the entire journey, and Vitya will spend $\frac{x}{5}+\frac{20-x}{20}$ hours. By setting up and solving the equation, we find $x=12$ (km).
Comment. Only the answer - 1 point. The equation for finding the distance is correctly set up, but not solved - 3 points. An arithmetic error is made in solving the equation, but the rest is correct - 5 points.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In an equilateral triangle $\mathrm{ABC}$, the height $\mathrm{BH}$ is drawn. On the line $\mathrm{BH}$, a point $\mathrm{D}$ is marked such that $\mathrm{BD}=\mathrm{AB}$. Find $\angle \mathrm{CAD}$.
|
Answer: $15^{\circ}$ or $75^{\circ}$.
Solution. Obviously, $\triangle \mathrm{ADH}=\Delta \mathrm{CDH}$ (right-angled, by two legs), hence $\mathrm{AD}=\mathrm{CD}$. Therefore, $\triangle \mathrm{BDA}=\triangle \mathrm{BDC}$ (by three sides) $\Rightarrow \angle \mathrm{DAB}=\angle \mathrm{DCB}, \angle \mathrm{BDA}=\angle \mathrm{BDC}$.
Moreover, $\triangle \mathrm{ABD}$ is isosceles $(\mathrm{BD}=\mathrm{AB}) \Rightarrow \angle \mathrm{BDA}=\angle \mathrm{BAD}$, that is, $\angle \mathrm{BDC}=\angle \mathrm{BDA}=\angle \mathrm{BAD}=\angle \mathrm{DCB}=\alpha$.
Consider $\triangle \mathrm{ADC}$ and the sum of its angles.
Next, we need to consider two cases for the position of point $\mathrm{D}$: on the same side as point B relative to AC and on opposite sides. In the first case,
$\angle \mathrm{CDA}+\angle \mathrm{DAC}+\angle \mathrm{DCA}=\angle \mathrm{CDB}+\angle \mathrm{BDA}+\angle \mathrm{DAB}+\angle \mathrm{BAC}+\angle \mathrm{DCB}+\angle \mathrm{CBA}=$ $=\alpha+\alpha+\alpha+60^{\circ}+\alpha+60^{\circ}=4 \cdot \alpha+120^{\circ}=180^{\circ}$ (sum of angles in a triangle), from which $\alpha=60^{\circ} / 4=15^{\circ} . \angle \mathrm{CAD}=\angle \mathrm{CAB}+\angle \mathrm{BAD}=60^{\circ}+\alpha=75^{\circ}$.
In the second case,
$\angle \mathrm{CDA}+\angle \mathrm{DAC}+\angle \mathrm{DCA}=\angle \mathrm{CDB}+\angle \mathrm{BDA}+\angle \mathrm{DAB}-\angle \mathrm{BAC}+\angle \mathrm{DCB}-\angle \mathrm{CBA}=$ $=\alpha+\alpha+\alpha-60^{\circ}+\alpha-60^{\circ}=4 \cdot \alpha-120^{\circ}=180^{\circ}$ (sum of angles in a triangle), from which $\alpha=300^{\circ} / 4=75^{\circ} . \angle \mathrm{CAD}=\angle \mathrm{BAD}-\angle \mathrm{BAC}=\alpha-60^{\circ}=15^{\circ}$.
Comment. Only the answer - 0 points. Only one case of the position of point $\mathrm{D}$ is considered (correspondingly, only one value is obtained) - 4 points.
|
15
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Indicate the largest possible number, in decimal notation, in which all digits are different, and the sum of its digits is 37.
#
|
# Answer: 976543210.
Sketch of the solution. The sum of all ten digits is 45, so to achieve the maximum, we exclude only one digit. It will be 8. Among the nine-digit numbers, the larger one has the higher significant digits. Hence the answer.
|
976543210
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. There is a contour of a square with a side of 20 cm, it was cut into two groups of equal segments consisting of three and four segments. What is the length of these segments? Find all possible answers.
|
Answer: 20 cm and 5 cm.
Sketch of the solution.
If each side of the square is cut into at least two segments, there will be 8 segments, and their $4+3=7$. This means one of the segments is equal to the side of the square, and there are three such segments, each 20 cm long. Four segments are obtained by cutting one side of the square into four equal segments, the length of which is 20:4=5(cm).
Criteria. Correct answer, without justification: 1 point.
|
20
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. A rectangle $3 \times 100$ consists of 300 squares $1 \times 1$. What is the maximum number of diagonals that can be drawn in the squares so that no two diagonals share a common endpoint? (In one square, two diagonals can be drawn without sharing endpoints. Common internal points are allowed.)
|
Answer: 200.
Example. Let's number the rows and columns containing the squares. In each square with both odd numbers, we will draw two diagonals.
Another example. In all cells of the first and third rows, we will draw parallel diagonals.
Estimate. We will color the vertices in two colors: vertices from odd-numbered columns in white, and even-numbered columns in black (see figure). There will be 200 white vertices and 204 black vertices. Each diagonal has ends of different colors, and

therefore, it is impossible to draw more than 200 diagonals.
Criteria. Estimate without an example: 4 points. Example without an estimate: 2 points.
|
200
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4-1. Katya attached a square with a perimeter of 40 cm to a square with a perimeter of 100 cm as shown in the figure. What is the perimeter of the resulting figure in centimeters?
|
Answer: 120.
Solution: If we add the perimeters of the two squares, we get $100+40=140$ cm. This is more than the perimeter of the resulting figure by twice the side of the smaller square. The side of the smaller square is $40: 4=10$ cm. Therefore, the answer is $140-20=120$ cm.
|
120
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4-8. In a chess club, 90 children attend. During the session, they divided into 30 groups of 3 people, and in each group, everyone played one game with each other. No other games were played. In total, there were 30 games of "boy+boy" and 14 games of "girl+girl". How many "mixed" groups were there, that is, groups in which there were both a boy and a girl?
|
Answer: 23.
Solution: There were a total of 90 games, so the number of games "boy+girl" was $90-30-14=46$. In each mixed group, two "boy+girl" games are played, while in non-mixed groups, there are no such games. In total, there were exactly $46 / 2=23$ mixed groups.
## Grade 5
|
23
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5-1. A square with a side of 100 was cut into two equal rectangles. They were placed next to each other as shown in the figure. Find the perimeter of the resulting figure.
|
Answer: 500.
Solution. The perimeter of the figure consists of 3 segments of length 100 and 4 segments of length 50. Therefore, the length of the perimeter is
$$
3 \cdot 100 + 4 \cdot 50 = 500
$$
|
500
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.