problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
30. What is the minimum number of colors needed to color the cells of a $5 \times 5$ square so that among any three consecutive cells in a row, column, or diagonal, there are no cells of the same color?
(M. Antipov)
|
30. Answer: in five colors.
Consider a cross of five cells, the central cell of which coincides with the central cell of the square. By the condition, three cells in its column have different colors. Similarly, the colors of the three cells in its row are also different. Finally, any two cells at the "ends" of the cross are also of different colors. For example, cells $A$ and $B$ in the figure have different colors, since by the condition
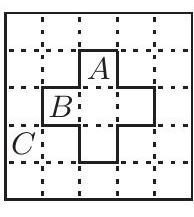
among the cells $A, B, C$ there are no cells of the same color. Thus, the colors of all five cells in the cross are different, so there are at least five colors.
An example of coloring in five colors is shown on the right. In this example, each subsequent row is obtained from the previous one by a cyclic shift of two cells to the left.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
31. Around a round table, 300 people are sitting: some of them are knights, and the rest are liars. Anton asked each of them: "How many liars are among your neighbors?" and added up the numbers he received. Then Anya did the same. When answering the question, knights always tell the truth, while liars always lie, but they only say the numbers 0, 1, or 2. It turned out that the sum of the numbers Anton received is 400 more than the sum Anya received. How many liars are there at the table? Find all possible answers and prove that there are no others.
(A. Chukhnov)
|
31. Answer: there are 200 liars at the table.
It is clear that the knights gave two identical answers, so the difference between the sums of Anton and Anya could have arisen because some liars gave Anton and Anya different answers. At the same time, the answers of any liar differ by only 1 or 2. The total difference of 400 could have accumulated only if there were no fewer than 200 liars.
Let's divide all the people sitting at the table into groups of consecutive knights and groups of consecutive liars. We will give a banana to each liar who gave Anya an answer one less than Anton, and two bananas to liars who gave Anya an answer two less than Anton. Liars who did not change or even increased their answers will be left without bananas. The total reduction in all answers is at least 400 (it can be strictly greater if some liars increased their answers), so all the participants received no less than 400 bananas.
Note that two bananas could only be received by liars at the edges of their groups. Indeed, such a liar must have answered "two" to Anton and "zero" to Anya, and both answers must be false; therefore, this liar is actually adjacent to exactly one liar and one knight. We will ask each liar who has two bananas to give one of their bananas to the adjacent knight. After this, all 300 liars sitting at the table will have no more than one banana, and the knights will have no more than two. Since there are no fewer than 400 bananas, the number of knights must be no less than 100. Then the number of liars is no more than 200. But we have already established at the beginning that there must be no fewer than 200 liars. Therefore, there are exactly 200 liars at the table.
|
200
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Inside an isosceles triangle $A B C (A B=A C)$, a point $K$ is marked. Point $L$ is the midpoint of segment $B K$. It turns out that $\angle A K B=\angle A L C=90^{\circ}, A K=C L$. Find the angles of triangle $A B C$.
|
Answer: the triangle is equilateral. Note that $\triangle A L C=\triangle B K A$ by the leg and hypotenuse. Therefore, $A L=B K=2 K L$, so $\angle K A L=30$. In addition, the sum of angles $B A K$ and $C A L$ in these triangles is 90, so $\angle B A C=90-30-60$.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
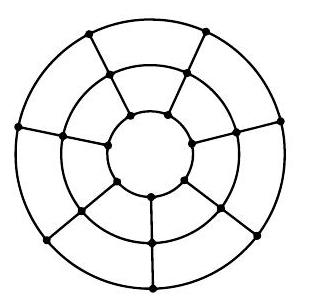
7. The figure shows a city plan. Nodes are intersections, and the 35 lines connecting them are streets. There are $N$ buses operating on these streets. All buses start simultaneously at intersections and move to adjacent intersections along the streets every minute. Each bus follows a closed, non-self-intersecting route. Multiple buses can be at the same intersection, but no more than one bus can be on any street at the same time. Find the maximum possible value of $N$.
|
Answer: 35 (by the number of streets), i.e., it is possible to launch the minibuses so that at any moment in time, exactly one minibus is moving along each street. Obviously, $N$ cannot be greater than 35, because otherwise, in the first minute, some two minibuses will inevitably end up on the same street. Let's provide an example for 35 minibuses. Seven minibuses will be launched clockwise around the middle ring. The remaining 28 minibuses will move clockwise around the perimeters of seven $2 \times 2$ squares, with four on each, initially positioned at the vertices of these squares. It is not difficult to verify (taking into account the circular symmetry of the construction) that at any moment in time, exactly one minibus is driving along each street.
|
35
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
35. In the cells of a $9 \times 9$ square, non-negative numbers are placed. The sum of the numbers in any two adjacent rows is at least 20, and the sum of the numbers in any two adjacent columns does not exceed 16. What can the sum of the numbers in the entire table be?
(A. Chukhnov)
|
35. The total sum is no less than $4 \cdot 20=80$ (since the entire table is divided into 4 pairs of columns) and does not exceed $5 \cdot 16=80$ (since the table is covered by five pairs of rows with an overlap at the 8th row), therefore it is equal to 80.
|
80
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
36. Many city residents engage in dancing, many in mathematics, and at least one in both. Those who engage only in dancing are exactly $p+1$ times more than those who engage only in mathematics, where $p-$ is some prime number. If you square the number of all mathematicians, you get the number of all dancers. How many residents are interested in both mathematics and dancing at the same time?
|
36. Answer: 1 person is engaged in both dancing and mathematics.
Let $a$ people be engaged only in mathematics, and $b \geqslant 1$ people be engaged in both dancing and mathematics. Then, according to the condition, $(a+b)^{2}=(p+1) a+b$. Subtract $a+b$ from both sides: $(a+b)^{2}-(a+b)=p a$. Factor out the common term on the left side: $(a+b)(a+b-1)=p a$. Since $p$ is prime, one of the brackets on the left side must be divisible by $p$. Then $a$ must be divisible by the other bracket! But it is clear that the first bracket is greater than $a$, and the second is not less than $a$. Therefore, $a$ can only be divisible by the second bracket, and only in the case where the second bracket equals $a$. This is possible only when $b=1$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
64. A nearsighted rook attacks all the cells in its row and column that can be reached in no more than 60 steps, moving from cell to adjacent cell by side. What is the maximum number of non-attacking nearsighted rooks that can be placed on a $100 \times 100$ square?
|
64. Answer: 178 myopic rooks.
Evaluation. Divide the $100 \times 100$ square into a central $22 \times 22$ square and $4 \cdot 39=156$ rectangles of $1 \times 61$. In each rectangle of the partition and in each row of the $22 \times 22$ square, no more than one rook can be placed, so there are no more than 178 rooks.
Example: Place the rooks on the cells of the main diagonal and two diagonals parallel to it, consisting of 39 cells each. In this arrangement, there are exactly 60 empty cells between any two rooks located in the same column or row, so no two rooks attack each other.
|
178
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
66. The sum
$$
\begin{gathered}
2 \\
3 \cdot 6
\end{gathered}+\begin{gathered}
2 \cdot 5 \\
3 \cdot 6 \cdot 9
\end{gathered}+\ldots+\begin{gathered}
2 \cdot 5 \cdot \ldots \cdot 2015 \\
3 \cdot 6 \cdot \ldots \cdot 2019
\end{gathered}
$$
was written as a decimal fraction. Find the first digit after the decimal point.
|
66. Answer: the first digit after the decimal point is 5.
To start, let's simplify the given sum. Each term can be written as a difference
$$
\begin{aligned}
\frac{2 \cdot 5 \cdot \ldots \cdot(3 k-1)}{3 \cdot 6 \cdot 9 \cdot \ldots \cdot(3 k+3)}=\frac{2 \cdot 5 \cdot \ldots \cdot(3 k-1) \cdot(3 k+3)}{3 \cdot 6 \cdot 9 \cdot \ldots \cdot(3 k+3)}- & \frac{2 \cdot 5 \cdot \ldots \cdot(3 k-1) \cdot(3 k+2)}{3 \cdot 6 \cdot 9 \cdot \ldots \cdot(3 k+3)}= \\
& =\frac{2 \cdot 5 \cdot \ldots \cdot(3 k-1)}{3 \cdot 6 \cdot 9 \cdot \ldots \cdot 3 k}-\frac{2 \cdot 5 \cdot \ldots \cdot(3 k-1) \cdot(3 k+2)}{3 \cdot 6 \cdot 9 \cdot \ldots \cdot(3 k+3)}
\end{aligned}
$$
Then the entire sum will telescope to the difference of the extreme terms $\frac{2}{3}-\frac{2 \cdot 5 \cdot \ldots \cdot 2018}{3 \cdot 6 \cdot \ldots \cdot 2019}$.
Now let's estimate the subtrahend. Introduce the variables
$$
\begin{gathered}
A=\frac{1 \cdot 3 \cdot 6 \cdot \ldots \cdot 2016}{1 \cdot 4 \cdot 7 \cdot \ldots \cdot 2017}, \quad B=\frac{1 \cdot 4 \cdot 7 \cdot \ldots \cdot 2017}{2 \cdot 5 \cdot 8 \cdot \ldots \cdot 2018}, \quad C=\frac{2 \cdot 5 \cdot 8 \cdot \ldots \cdot 2018}{3 \cdot 6 \cdot 9 \cdot \ldots \cdot 2019}, \quad D=\frac{3 \cdot 6 \cdot 9 \cdot \ldots \cdot 2019}{4 \cdot 7 \cdot 10 \cdot \ldots \cdot 2020} \\
E=\frac{4 \cdot 7 \cdot 10 \cdot \ldots \cdot 2020}{5 \cdot 8 \cdot 11 \cdot \ldots \cdot 2022}
\end{gathered}
$$
We want to estimate the value of the number $C$.
Since $\frac{a-1}{a}<\frac{a}{a+1}$ for natural $a$, the inequalities $A<B<C<D<E$ hold, from which $A B C<C^{3}<C D E$. Substituting these inequalities into the formulas for our numbers and simplifying the fractions, we get
$$
\frac{1}{2019}<C^{3}<\frac{2}{2022}, \quad \frac{1}{15}<\sqrt[3]{\frac{1}{2019}}<C<\sqrt[3]{\frac{2}{2022}}<\frac{1}{6}, \text { and thus, } \quad \frac{1}{2}<\frac{2}{3}-\frac{2 \cdot 5 \cdot \ldots \cdot 2018}{3 \cdot 6 \cdot \ldots \cdot 2019}<\frac{3}{5}
$$
Thus, the first digit after the decimal point of the original number is 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13. Leshа wrote on the board in ascending order all natural divisors of a natural number $n$, and Dima erased several first and several last numbers of the resulting sequence, leaving 151 numbers. What is the maximum number of these 151 divisors that could be fifth powers of natural numbers?
(M. Achtipov)
|
13. Answer: 31.
Lemma. If $n$ is divisible by $a^{5}$ and $b^{5}$, then $n$ is also divisible by $a^{4} b, a^{3} b^{2}, a^{2} b^{3}, a b^{4}$.
Proof of the lemma. Note that $n^{5}=n^{4} \cdot n$ is divisible by $a^{20} \cdot b^{5}$; taking the fifth root, we get that $n$ is divisible by $a^{4} b$. Similarly, $n^{5}=n^{3} \cdot n^{2}$ is divisible by $a^{15} \cdot b^{10}$, from which it follows that $n$ is divisible by $a^{3} b^{2}$. The proof for the other two divisors is completely analogous.
Let's proceed to solving the problem. We will prove the estimate, i.e., that the number of fifth powers is always no more than 31. Arrange the listed divisors in a row in ascending order. We will prove that there are at least four numbers between any two fifth powers in this row. Indeed, if $a^{5}, b^{5}$ are divisors of the number $n$, then the four divisors mentioned in the lemma are located in the row between $a^{5}$ and $b^{5}$: if, for example, $a > b$, then $a^{5} > a^{4} b > a^{3} b^{2} > a^{2} b^{3} > a b^{4} > b^{5}$.
If there were at least 32 fifth powers in the row, then there would be at least $4 \cdot 31 = 124$ numbers in the intervals between them, i.e., there would be at least 156 numbers in total in the row—contradicting the condition! Therefore, there cannot be more than 31 fifth powers.
Let's provide an example. Suppose $n=2^{150}$. This number has exactly 151 divisors (including 1 and $n$), and the fifth powers among them are the numbers $2^{5 k}, 0 \leqslant k \leqslant 30$—exactly 31 numbers.
|
31
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
60. In a class, there are 25 students. The teacher wants to stock $N$ candies, conduct an olympiad, and distribute all $N$ candies for success in it (students who solve the same number of problems should receive the same number of candies, those who solve fewer should receive fewer, including possibly zero candies). What is the smallest $N$ for which this will be possible regardless of the number of problems in the olympiad and the success of the students?
|
60. Answer: $600=25 \cdot 24$ candies.
Let's show that a smaller number of candies might not be enough. If all participants solved the same number of problems, the number of candies must be a multiple of 25. Let $N=25 k$. Imagine that 24 people solved the same number of problems, while the 25th solved fewer. If each of the first 24 participants receives $k$ candies or even fewer, there will be extra candies left. Therefore, each of them must receive at least $k+1$ candies, which means $25 k \geqslant 24(k+1)$, or $k \geqslant 24$.
Now we will prove by induction that it is possible to distribute $m$ participants $m(m-1)$ candies such that each receives fewer than $2 s$ candies. The base case for $m=1$ is obvious: give the only participant 0 candies.
The transition from $m-1$ to $m$. Suppose there are $s \geqslant 1$ participants with the highest score, and besides them, there are $t$ participants, $s+t=m$. To the less successful participants, we will distribute $t(t-1)$ candies (each receiving fewer than $2 t$) by the induction hypothesis. After this, $(s+t)(s+t-1)-t(t-1)=s(s+2 t-1)$ candies will remain, and we will distribute them equally among the $s$ "top" participants. Each of them will receive $s+2 t-1$ candies. This number is not less than $2 t$, so it is more than what we distributed to each of the others. Additionally, $s+2 t-1 < 2 s+2 t=2 m$, which completes the transition.
|
600
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. From the edge of a large square sheet, a small square was cut off, as shown in the figure, and as a result, the perimeter of the sheet increased by $10 \%$. By what percent did the area of the sheet decrease?
|
5. Answer: by $4 \%$.
Let the side of the larger square be denoted by $a$, and the side of the smaller square by $b$. As a result of cutting out the smaller square from the perimeter of the sheet, one segment of length $b$ disappears, and three such segments appear instead, meaning the perimeter increases by $2 b$. Therefore, $2 b$ constitutes $10 \%$ of the old perimeter: $2 b=0.1 \cdot 4 a$. From this, $b=0.2 a$. Thus, the area of the sheet has decreased by $b^{2}=0.04 a^{2}$, i.e., by $4 \%$.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Sasha went to bed at 10 PM and set the alarm clock (with hands and a 12-hour dial) for 7 AM. During the night, at some point, the alarm clock, which had been working properly, broke, and its hands started moving in the opposite direction (at the same speed). Nevertheless, the alarm rang exactly at the scheduled time in the morning. At what time did the alarm clock break? Justify your answer.
(A. Kuznetsov, D. Shiryayev)
|
1. Answer: the alarm clock broke at 1 o'clock at night.
Let's imagine that the minute hand on the alarm clock is missing, and the hour hand, at the moment when the alarm clock broke, split into two halves, one of which (as stated in the condition) started moving in the opposite direction, while the other continued its normal movement. Then at 7 o'clock in the morning, both hands will meet! This means that both hands have traveled half the clock face and the split occurred directly "opposite" the 7 mark, i.e., at 1 o'clock at night.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
47. Inside an equilateral triangle $A B C$, points $P$ and $Q$ are chosen such that $P$ is inside triangle $A Q B$, $P Q = Q C$, and $\angle P A Q = \angle P B Q = 30$. Find $\angle A Q B$.
|
47. We construct regular triangles $A P X$ and $B P Y$ on the sides $A P$ and $P B$ of triangle $A P B$. Triangle $A X C$ is obtained by rotating triangle $A P B$ by $60^{\circ}$ around point $A$, so these triangles are equal. Therefore, $X C = P B = P Y$. Similarly, $C Y = A P = X P$. Consequently, quadrilateral $P X C Y$ is a parallelogram. Further, since $\angle P B Q = 30^{\circ}$, $B Q$ is the angle bisector of the regular triangle $B P Y$. Therefore, $B Q$ is the perpendicular bisector of $P Y$, and thus $Q P = Q Y$. Similarly, $Q P = Q X$. Since by the condition $Q P = Q C$, we get that point $Q$ is equidistant from all vertices of parallelogram $P X C Y$. Such a point can only be the intersection of its diagonals. But then the diagonals of parallelogram $P X C Y$ are equal, so $P X C Y$ is a rectangle. We have already proven that segments $B Q$ and $A Q$ are perpendicular to the sides of this rectangle. Thus, $\angle A Q B = 90^{\circ}$.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the number of all natural numbers in which each subsequent digit is less than the previous one. (8 points)
|
Solution. The largest possible number that satisfies the condition of the problem is 9876543210. In addition, the number must be at least two digits. All other such numbers can be obtained from 9876543210 by deleting one, two, three, four, five, six, seven, or eight digits out of ten. Then the total number
$$
\begin{gathered}
1+C_{10}^{1}+C_{10}^{2}+C_{10}^{3}+C_{10}^{4}+C_{10}^{5}+C_{10}^{6}+C_{10}^{7}+C_{10}^{8}= \\
=1+C_{10}^{1}+\left(C_{10}^{2}+C_{10}^{3}+C_{10}^{4}\right) \cdot 2+C_{10}^{8}=1+10+(45+120+210) \cdot 2+252=1013
\end{gathered}
$$
Answer. 1013.
|
1013
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the sum of the first 10 elements that are found both in the arithmetic progression $\{5,8,11,14, \ldots\}$ and in the geometric progression $\{10,20,40,80, \ldots\} \cdot(10$ points $)$
|
Solution. The members of the arithmetic progression $\{5,8,11,14,17,20,23, \ldots\}$ are given by the formula
$$
a_{n}=5+3 n, n=0,1,2, \ldots
$$
The members of the geometric progression $\{10,20,40,80, \ldots\}$ are given by the formula
$$
b_{n}=10 \cdot 2^{k}, k=0,1,2, \ldots
$$
For the common elements, the equality $5+3 n=10 \cdot 2^{k}$ must hold, from which
$$
n=\frac{10 \cdot 2^{k}-5}{3}=\frac{5 \cdot\left(2^{k+1}-1\right)}{3}, \text { i.e., }\left(2^{k+1}-1\right): 3
$$
It is clear that $2^{k+1}-1$ is divisible by 3 for odd $k$ (the remainder of the division of $2^{k+1}$ by 3 is 2 or 1).
For $k=1, n=5$ the common element is $a_{5}=b_{1}=20$;
for $k=3, n=25$ the common element is $a_{25}=b_{3}=80$;
for $k=5, n=105$ the common element is $a_{105}=b_{5}=320$ and so on.
Thus, the required elements are: $20,80,320, \ldots$ - the members of the original geometric progression with odd indices. They form a geometric progression with a common ratio of 4 and the first term 20. The sum of the first 10 terms can be found using the formula $S=c_{1} \frac{q^{n}-1}{q-1}=20 \cdot \frac{4^{10}-1}{4-1}=20 \cdot \frac{\left(2^{10}\right)^{2}-1}{3}=20 \cdot \frac{1024^{2}-1}{3}=6990500$.
Answer. 6990500.
|
6990500
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the sum of all four-digit numbers in which only the digits $1,2,3,4,5$ appear, and each digit appears no more than once. (8 points)
|
Solution. Any of these digits appears in any place as many times as the remaining four digits can be distributed among the remaining three places. This number is $4 \cdot 3 \cdot 2=24$. Therefore, the sum of the digits in each of the four places, taken over all four-digit numbers satisfying the conditions of the problem, is $24 \cdot(1+2+3+4+5)=24 \cdot 15=360$, and the sum of the four-digit numbers themselves is $360 \cdot\left(10^{3}+10^{2}+10+1\right)=360 \cdot 1111=399960$.
Answer. 399960.
|
399960
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the sum of the first 10 elements that are found both in the arithmetic progression $\{4,7,10,13, \ldots\}$ and in the geometric progression $\{10,20,40,80, \ldots\} \cdot(10$ points $)$
|
Solution. The members of the arithmetic progression $\{4,7,10,13,16,19, \ldots\}$ are given by the formula
$$
a_{n}=4+3 n, n=0,1,2, \ldots
$$
The members of the geometric progression $\{10,20,40,80, \ldots\}$ are given by the formula
$$
b_{n}=10 \cdot 2^{k}, k=0,1,2, \ldots
$$
For the common elements, the equality $4+3 n=10 \cdot 2^{k}$ must hold, from which
$$
n=\frac{10 \cdot 2^{k}-4}{3}=\frac{2 \cdot\left(5 \cdot 2^{k}-2\right)}{3}, \text { i.e., }\left(5 \cdot 2^{k}-2\right) \vdots 3 .
$$
It is clear that ( $\left.5 \cdot 2^{k}-2\right)$ is divisible by 3 for even $k$ (the remainder of the division of $2^{k}$ by 3 is 2 or 1).
For $k=0, n=2$ the common element is $a_{2}=b_{0}=10$;
for $k=2, n=12$ the common element is $a_{12}=b_{2}=40$;
for $k=4, n=52$ the common element is $a_{52}=b_{4}=160$ and so on.
Thus, the sought elements are: $10,40,160, \ldots$ - the members of the original geometric progression with even indices. They form a geometric progression with a common ratio of 4 and the first term 10. The sum of the first 10 terms can be found using the formula $S=c_{1} \frac{q^{n}-1}{q-1}=10 \cdot \frac{4^{10}-1}{4-1}=10 \cdot \frac{\left(2^{10}\right)^{2}-1}{3}=10 \cdot \frac{1024^{2}-1}{3}=3495250$.
Answer. 3495250.
|
3495250
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the number of all natural numbers in which each subsequent digit is greater than the previous one. (8 points)
|
Solution. The largest possible number satisfying the condition of the problem is 123456789. Moreover, the number must be at least two digits. All other such numbers can be obtained from 123456789 by erasing one, two, three, four, five, six, or seven digits out of nine. Then the total number
$1+C_{9}^{1}+C_{9}^{2}+C_{9}^{3}+C_{9}^{4}+C_{9}^{5}+C_{9}^{6}+C_{9}^{7}=1+9+(36+84+126) \cdot 2=502$.
Answer. 502 .
|
502
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the sum of the first 10 elements that are found both among the members of the arithmetic progression $\{5,8,11,13, \ldots\}$, and among the members of the geometric progression $\{20,40,80,160, \ldots\} \cdot(10$ points)
|
Solution. The members of the arithmetic progression $\{5,8,11,14,17,20,23, \ldots\}$ are given by the formula
$$
a_{n}=5+3 n, n=0,1,2, \ldots
$$
The members of the geometric progression $\{20,40,80,160, \ldots\}$ are given by the formula
$$
b_{n}=20 \cdot 2^{k}, k=0,1,2, \ldots
$$
For common elements, the equality $5+3 n=20 \cdot 2^{k}$ must hold, from which $n=\frac{20 \cdot 2^{k}-5}{3}=\frac{5 \cdot\left(2^{k+2}-1\right)}{3}$, that is, $\left(2^{k+2}-1\right) \vdots 3$.
It is clear that $2^{k+2}-1$ is divisible by 3 for even $k$ (the remainder of the division of $2^{k+2}$ by 3 is 1 or 2).
For $k=0, n=5$ the common element is $a_{5}=b_{0}=20$;
for $k=2, n=25$ the common element is $a_{25}=b_{2}=80$;
for $k=4, n=105$ the common element is $a_{105}=b_{4}=320$ and so on.
Thus, the required elements are: $20,80,320, \ldots$ - the members of the original geometric progression with even indices. They form a geometric progression with a common ratio of 4 and the first term 20. The sum of the first 10 terms can be found using the formula
$S=c_{1} \frac{q^{n}-1}{q-1}=20 \cdot \frac{4^{10}-1}{4-1}=20 \cdot \frac{\left(2^{10}\right)^{2}-1}{3}=20 \cdot \frac{1024^{2}-1}{3}=6990500$.
Answer. 6990500.
|
6990500
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the sum of the first 10 elements that are found both in the arithmetic progression $\{4,7,10,13, \ldots\}$ and in the geometric progression $\{20,40,80,160, \ldots\} \cdot(10$ points $)$
|
Solution. The members of the arithmetic progression $\{4,7,10,13,16,19, \ldots\}$ are given by the formula
$$
a_{n}=4+3 n, n=0,1,2, \ldots
$$
The members of the geometric progression $\{20,40,80, \ldots\}$ are given by the formula
$$
b_{n}=20 \cdot 2^{k}, k=0,1,2, \ldots
$$
For common elements, the equation $4+3 n=20 \cdot 2^{k}$ must hold, from which $n=\frac{20 \cdot 2^{k}-4}{3}=\frac{4 \cdot\left(5 \cdot 2^{k}-1\right)}{3}$, that is, $\left(5 \cdot 2^{k}-1\right): 3$.
It is clear that $5 \cdot 2^{k}-1$ is divisible by 3 for odd $k$ (the remainder of the division of $2^{k}$ by 3 is 2 or 1).
For $k=1, n=12$ the common element is $a_{12}=b_{1}=40$;
for $k=3, n=52$ the common element is $a_{52}=b_{3}=160$;
for $k=5, n=212$ the common element is $a_{212}=b_{5}=640$ and so on.
Thus, the required elements are: $40,160,640, \ldots$ - the members of the original geometric progression with odd indices. They form a geometric progression with a common ratio of 4 and the first term 40. The sum of the first 10 terms can be found using the formula $S=c_{1} \frac{q^{n}-1}{q-1}=40 \cdot \frac{4^{10}-1}{4-1}=40 \cdot \frac{\left(2^{10}\right)^{2}-1}{3}=40 \cdot \frac{1024^{2}-1}{3}=13981000$.
Answer. 13981000.
|
13981000
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Solve the inequality $2021 \cdot \sqrt[202]{x^{2020}}-1 \geq 2020 x$ for $x \geq 0$. (10 points)
|
Solution. Transform the inequality into the form:
$$
\begin{aligned}
& \frac{2020 x+1}{2021} \leq \sqrt[202]{x^{2020}}, \text { from which } \\
& x+x+\ldots+x+1
\end{aligned}
$$
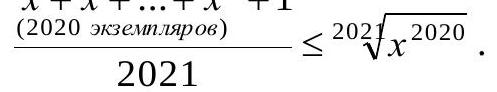
But by the relation for the arithmetic mean and the geometric mean, $x+x+\ldots+x+1$
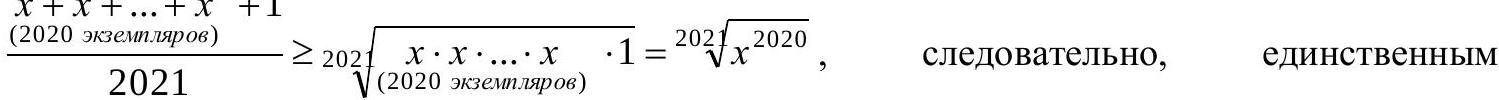
the solution to the inequality is $x=1$.
Answer. $x=1$.
|
1
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Solve the equation $2021 x=2022 \cdot \sqrt[2022]{x^{2021}}-1 .(10$ points $)$
|
Solution. $x \geq 0$. Transform the equation to the form:
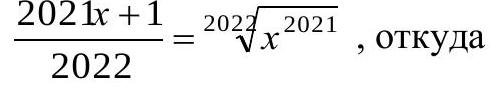
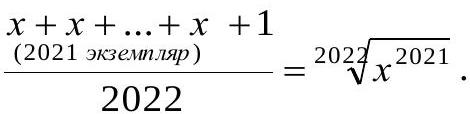
But by the relation for the arithmetic mean and the geometric mean
$x+x+\ldots+x+1$
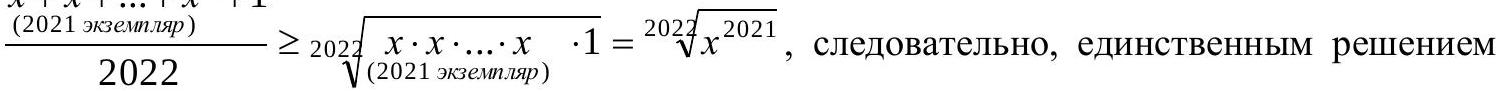
the inequality holds for $x=1$.
Answer. $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Solve the equation $2021 \cdot \sqrt[202]{x^{2020}}-1=2020 x$ for $x \geq 0 \cdot$ (10 points)
|
Solution. Transform the equation to the form:
$$
\begin{aligned}
& \frac{2020 x+1}{2021}=\sqrt[202]{x^{2020}}, \text { from which } \\
& x+x+\ldots+x+1 \\
& \frac{(2020 \text { instances) }}{2021}=\sqrt[202]{x^{2020}}
\end{aligned}
$$
But by the relation for the arithmetic mean and the geometric mean
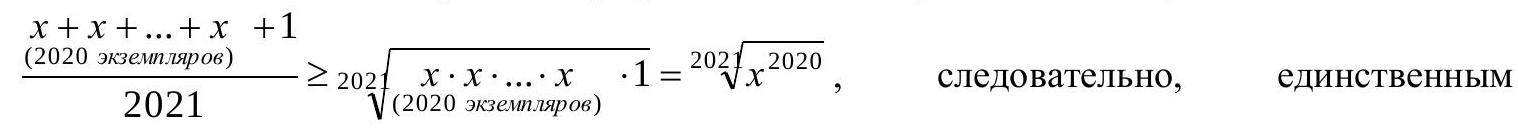
the solution to the equation is $x=1$.
Answer. $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the sum of the first 10 elements that are found both in the arithmetic progression $\{5,8,11,14, \ldots\}$ and in the geometric progression $\{10,20,40,80, \ldots\} \cdot(10$ points)
|
Solution. The members of the arithmetic progression $\{5,8,11,14,17,20,23, \ldots\}$ are given by the formula
$$
a_{n}=5+3 n, n=0,1,2, \ldots
$$
The members of the geometric progression $\{10,20,40,80, \ldots\}$ are given by the formula
$$
b_{n}=10 \cdot 2^{k}, k=0,1,2, \ldots
$$
For the common elements, the equation $5+3 n=10 \cdot 2^{k}$ must hold, from which
$$
n=\frac{10 \cdot 2^{k}-5}{3}=\frac{5 \cdot\left(2^{k+1}-1\right)}{3}, \text { i.e., }\left(2^{k+1}-1\right): 3
$$
It is clear that $2^{k+1}-1$ is divisible by 3 for odd $k$ (the remainder of the division of $2^{k+1}$ by 3 is 2 or 1).
For $k=1, n=5$ the common element is $a_{5}=b_{1}=20$;
for $k=3, n=25$ the common element is $a_{25}=b_{3}=80$;
for $k=5, n=105$ the common element is $a_{105}=b_{5}=320$ and so on.
Thus, the sought elements are: $20,80,320, \ldots$ - the members of the original geometric progression with odd indices. They form a geometric progression with a common ratio of 4 and the first term 20. The sum of the first 10 terms can be found using the formula $S=c_{1} \frac{q^{n}-1}{q-1}=20 \cdot \frac{\cdot^{10}-1}{4-1}=20 \cdot \frac{\left(2^{10}\right)^{2}-1}{3}=20 \cdot \frac{1024^{2}-1}{3}=6990500$.
Answer. 6990500.
|
6990500
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the sum of the first 10 elements that are found both in the arithmetic progression $\{4,7,10,13, \ldots\}$ and in the geometric progression $\{10,20,40,80, \ldots\} \cdot(10$ points)
|
Solution. The members of the arithmetic progression $\{4,7,10,13,16,19, \ldots\}$ are given by the formula
$$
a_{n}=4+3 n, n=0,1,2, \ldots
$$
The members of the geometric progression $\{10,20,40,80, \ldots\}$ are given by the formula
$$
b_{n}=10 \cdot 2^{k}, k=0,1,2, \ldots
$$
For the common elements, the equality $4+3 n=10 \cdot 2^{k}$ must hold, from which
$$
n=\frac{10 \cdot 2^{k}-4}{3}=\frac{2 \cdot\left(5 \cdot 2^{k}-2\right)}{3} \text {, that is }\left(5 \cdot 2^{k}-2\right): 3
$$
It is clear that ( $5 \cdot 2^{k}-2$ ) is divisible by 3 for even $k$ (the remainder of $2^{k}$ divided by 3 is 2 or 1).
For $k=0, n=2$ the common element $a_{2}=b_{0}=10$;
for $k=2, n=12$ the common element $a_{12}=b_{2}=40$;
for $k=4, n=52$ the common element $a_{52}=b_{4}=160$ and so on.
Thus, the sought elements: $10,40,160, \ldots$ - are the members of the original geometric progression with even indices. They form a geometric progression with a common ratio of 4 and the first term 10. The sum of the first 10 terms can be found using the formula $S=c_{1} \frac{q^{n}-1}{q-1}=10 \cdot \frac{\cdot 4^{10}-1}{4-1}=10 \cdot \frac{\left(2^{10}\right)^{2}-1}{3}=10 \cdot \frac{1024^{2}-1}{3}=3495250$.
Answer. 3495250.
|
3495250
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Two adjacent faces of a tetrahedron, which are isosceles right triangles with a hypotenuse of 2, form a dihedral angle of 60 degrees. The tetrahedron is rotated around the common edge of these faces. Find the maximum area of the projection of the rotating tetrahedron onto the plane containing
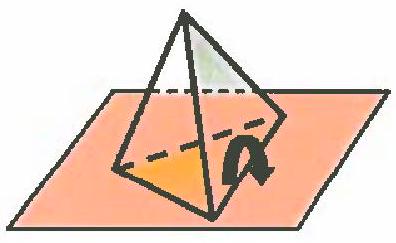
the given edge. (12 points)
Solution. Let the area of each of the given faces be \( S \). If the face lies in the plane of projection, then the projection of the tetrahedron is equal to the area of this face \( \Pi = S \).
When rotated by an angle \( 0 < \varphi < 30^\circ \), the area of the projection is \( \Pi = S \cos \varphi < S \).
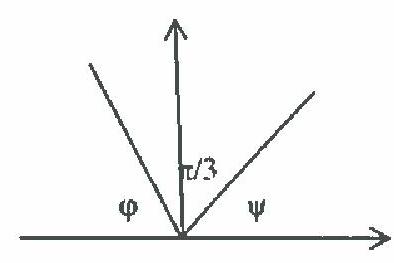
When rotated by an angle \( 30^\circ < \varphi < 90^\circ \), the area of the projection is
\[
\Pi = S \cos \varphi + S \cos \psi = S \cos \varphi + S \cos \left(\pi - \frac{\pi}{3} - \varphi\right) = S \cos \varphi + S \cos \left(\frac{2\pi}{3} - \varphi\right).
\]
\[
\Pi' = S \left(-\sin \varphi + \sin \left(\frac{2\pi}{3} - \varphi\right)\right), \quad \Pi' = 0 \text{ when } \varphi = \frac{\pi}{3}.
\]
The maximum of the function in the considered interval is achieved at
\[
\varphi = \frac{\pi}{3}, \quad \Pi = 2 S \cos \left(\frac{\pi}{3}\right) = 2 S \cdot \frac{1}{2} = S.
\]
When rotated by an angle \( 90^\circ < \varphi < 120^\circ \), the area of the projection is \( \Pi = S \cos \left(\frac{\pi}{2} - \varphi\right) = S \sin \varphi < S \).
When \( \varphi = \frac{2\pi}{3} \), the area \( \Pi = S \).
|
Answer. $\Pi=S=\frac{1}{2} \cdot \sqrt{2}^{2}=1$.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the sum of the first 10 elements that are common to both the arithmetic progression $\{5,8,11,13, \ldots\}$ and the geometric progression $\{20,40,80,160, \ldots\}$. (10 points)
|
Solution. The members of the arithmetic progression $\{5,8,11,14,17,20,23, \ldots\}$ are given by the formula
$$
a_{n}=5+3 n, n=0,1,2, \ldots
$$
The members of the geometric progression $\{20,40,80,160, \ldots\}$ are given by the formula
$$
b_{n}=20 \cdot 2^{k}, k=0,1,2, \ldots
$$
For the common elements, the equation $5+3 n=20 \cdot 2^{k}$ must hold, from which $n=\frac{20 \cdot 2^{k}-5}{3}=\frac{5 \cdot\left(2^{k+2}-1\right)}{3}$, meaning $\left(2^{k+2}-1\right): 3$.
It is clear that $2^{k+2}-1$ is divisible by 3 for even $k$ (the remainder of the division of $2^{k+2}$ by 3 is 1 or 2).
For $k=0, n=5$ the common element is $a_{5}=b_{0}=20$;
for $k=2, n=25$ the common element is $a_{25}=b_{2}=80$;
for $k=4, n=105$ the common element is $a_{105}=b_{4}=320$ and so on.
Thus, the sought elements are: $20,80,320, \ldots$ - the members of the original geometric progression with even indices. They form a geometric progression with a common ratio of 4 and the first term 20. The sum of the first 10 terms can be found using the formula $S=c_{1} \frac{q^{n}-1}{q-1}=20 \cdot \frac{4^{10}-1}{4-1}=20 \cdot \frac{\left(2^{10}\right)^{2}-1}{3}=20 \cdot \frac{1024^{2}-1}{3}=6990500$.
Answer. 6990500.
|
6990500
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the sum of the first 10 elements that are found both in the arithmetic progression $\{4,7,10,13, \ldots\}$ and in the geometric progression $\{20,40,80,160, \ldots\} .(10$ points $)$
|
Solution. The members of the arithmetic progression $\{4,7,10,13,16,19, \ldots\}$ are given by the formula
$$
a_{n}=4+3 n, n=0,1,2, \ldots
$$
The members of the geometric progression $(20,40,80, \ldots\}$ are given by the formula
$$
b_{n}=20 \cdot 2^{k}, k=0,1,2, \ldots
$$
For common elements, the equality $4+3 n=20 \cdot 2^{k}$ must hold, from which $n=\frac{20 \cdot 2^{k}-4}{3}=\frac{4 \cdot\left(5 \cdot 2^{k}-1\right)}{3}$, that is, $\left(5 \cdot 2^{k}-1\right): 3$.
It is clear that $5 \cdot 2^{k}-1$ is divisible by 3 for odd $k$ (the remainder of the division of $2^{k}$ by 3 is 2 or 1).
For $k=1, n=12$ the common element is $a_{12}=b_{1}=40$;
for $k=3, n=52$ the common element is $a_{52}=b_{3}=160$;
for $k=5, n=212$ the common element is $a_{212}=b_{5}=640$ and so on.
Thus, the required elements are: $40,160,640, \ldots$ - the members of the original geometric progression with odd indices. They form a geometric progression with a common ratio of 4 and the first term 40. The sum of the first 10 terms can be found using the formula $S=c_{1} \frac{q^{n}-1}{q-1}=40 \cdot \frac{4^{10}-1}{4-1}=40 \cdot \frac{\left(2^{10}\right)^{2}-1}{3}=40 \cdot \frac{1024^{2}-1}{3}=13981000$.
Answer. 13981000.
|
13981000
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Solve the equation $2021 \cdot \sqrt[202]{x^{2020}}-1=2020 x$ for $x \geq 0$. (10 points)
|
Solution. Transform the equation to the form:
$$
\begin{aligned}
& \frac{2020 x+1}{2021}=\sqrt[202]{x^{2020}}, \text { from which } \\
& \frac{\begin{array}{l}
x+x+\ldots+x+1 \\
(2020 \text { terms) }
\end{array}}{2021}=\sqrt[202]{x^{2020}} .
\end{aligned}
$$
But by the inequality between the arithmetic mean and the geometric mean
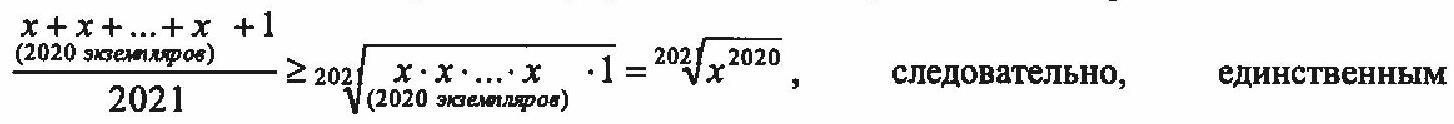
the solution to the equation is $x=1$.
Answer: $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. An athlete with a mass of 78.75 kg is testing a net used by firefighters to save people. The net sags by 100 cm when the athlete jumps from a height of 15 m. Assuming the net behaves elastically like a spring, calculate how much it will sag when a person with a mass of 45 kg jumps from a height of 29 m.
Given:
$m_{1}=78.75$ kg;
$x_{1}=1 \mathrm{~m} ;$
$h_{1}=15 \mathrm{~m} ;$
$m_{2}=45 \mathbf{~ kg ; ~}$
$h_{2}=29 \mathrm{~m}:$
|
Solution. The mechanical system "Earth-athlete-net" $x_{2}-?$ can be considered closed. According to the law of conservation of energy, when the athlete jumps, his potential energy should completely transform into the energy of the elastic deformation of the net: $m_{2} g\left(h_{2}+x_{2}\right)=\frac{k x_{2}^{2}}{2} ;$
$m_{1} g\left(h_{1}+x_{1}\right)=\frac{k x_{1}^{2}}{2} ;$
$\frac{m_{2}}{m_{1}} \cdot \frac{\left(h_{2}+x_{2}\right)}{\left(h_{1}+x_{1}\right)}=\frac{x_{2}^{2}}{x_{1}^{2}} ;$
$\frac{45}{78.75} \cdot \frac{\left(29+x_{2}\right)}{(15+1)}=x_{2}^{2}$;
$\frac{\left(29+x_{2}\right)}{16}=\frac{x_{2}^{2} \cdot 78.75}{45} ;$
$29+x_{2}=x_{2}^{2} \cdot 1.75 \cdot 16$
$28 x_{2}^{2}-x_{2}-29=0$
$D=1+4 \cdot 28 \cdot 29=3249=57^{2}$
$x_{2}=\frac{1+57}{56} \approx 1.04 \mathrm{M}$.
3. Mass spectrometry is one of the most precise methods of substance identification, used in almost all areas of human activity: pharmaceuticals, medicine, ecology,
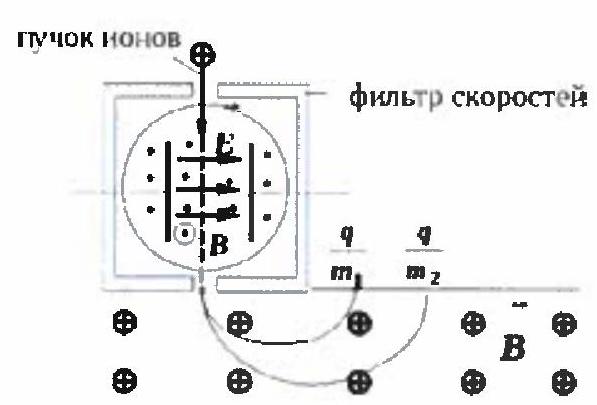
oil and gas industry, nuclear energy. It is a kind of "weighing" of molecules: components are ionized, and then the mass-to-charge ratio of the ions is determined. It turned out that when separating ions with comparable mass, for example, two isotopes of argon ( ${ }^{36} \mathrm{Ar}$ and ${ }^{38} \mathrm{Ar}$ ), difficulties arise. Calculate the radius of curvature required for these particles to be 1.2 mm apart.
Ions, after passing through crossed electric and magnetic fields, and after the velocity selector, enter only the magnetic field and move along the arc of a circle.
$\left\{\begin{array}{c}v=\frac{E}{B} \\ q v B^{\prime}=\frac{m v^{2}}{R}\end{array} \rightarrow m=\frac{q B B^{\prime} R}{E}\right.$.
$x=D_{2}-D_{1}=2\left(R_{2}-R_{1}\right)$
All quantities except $R$ in formula (1) are determined by the parameters of the setup, therefore, for particles with the same charge, it is valid
$\frac{R_{2}}{R_{1}}=\frac{m_{2}}{m_{1}}=38 / 36=1.056$
$R_{2}-R_{1}=\frac{x}{2}=0.6(\mathrm{MM})$
$0.6+R_{1}=1.056 R_{1}$
$R_{1}=10.7$ mm
$R_{2}=11.3 \mathrm{Mm}$
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Solve the equation $9^{x}+4 \cdot 3^{x+1}=13$.
|
Solution: $3^{2 x}+4 \cdot 3^{x+1}=13, 3^{2 x}+12 \cdot 3^{x}-13=0$,
$\left(3^{x}\right)_{1,2}=\frac{-12 \pm \sqrt{144+52}}{2}=\frac{-12 \pm 14}{2}=\left[\begin{array}{l}1, \\ -13 .- \text { n.s. }\end{array} 3^{x}=1 \Rightarrow x=0\right.$. Answer: $x=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. Find the maximum value of the function $f(x)=3 \sin x+4 \cos x$.
|
Solution: $f(x)=3 \sin x+4 \cos x=\sqrt{3^{2}+4^{2}} \sin \left(x+\operatorname{arctg} \frac{4}{3}\right)=5 \sin \left(x+\operatorname{arctg} \frac{4}{3}\right)$.
Answer: The maximum value is 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Solve the equation $9^{x-1}+3^{x+2}=90$.
|
Solution: $9^{x-1}+3^{x+2}=90,\left(3^{x-1}\right)^{2}+27 \cdot 3^{x-1}=90$, $3^{x-1}=\frac{-27 \pm \sqrt{3^{6}+4 \cdot 3^{2} \cdot 10}}{2}=\frac{-27 \pm 3 \sqrt{121}}{2}=\frac{-27 \pm 33}{2}=\left[\begin{array}{l}3, \\ -30 .\end{array} \quad x-1=1, x=2\right.$ Answer: $x=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Solve the equation $\sqrt{\frac{x-3}{2 x+1}}+2=3 \sqrt{\frac{2 x+1}{x-3}}$.
|
Solution: $t=\frac{x-3}{2 x+1}>0 ; \sqrt{t}+2=\frac{3}{\sqrt{t}}, \sqrt{t}+2 \sqrt{t}-3=0, \sqrt{t}=\left[\begin{array}{l}1 \\ -3 \text {, but this is not valid }\end{array}\right.$
$\frac{x-3}{2 x+1}=1 ; x-3=2 x+1, x=-4, \sqrt{\frac{-7}{-7}}+2=3 \sqrt{\frac{-7}{-7}}$. Answer: $x=-4$.
|
-4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Solve the equation $\sqrt{\frac{2 x+2}{x+2}}-\sqrt{\frac{x+2}{2 x+2}}=\frac{7}{12}$.
|
Solution: $\sqrt{\frac{2 x+2}{x+2}}-\sqrt{\frac{x+2}{2 x+2}}=\frac{7}{12} ; t=\frac{2 x+2}{x+2}>0, \sqrt{t}-\sqrt{\frac{1}{t}}=\frac{7}{12}$,
$\sqrt{t}=\frac{7 \pm \sqrt{49+4 \cdot 144}}{24}=\frac{7 \pm 25}{24}=\left[\begin{array}{l}\frac{32}{24}=\frac{4}{3} \\ -\frac{18}{24}=-\frac{3}{4}\end{array}, \frac{2 x+2}{x+2}=\frac{16}{9}, 16 x+18=16 x+32\right.$,
$2 x=14, x=7$. Verification: $\sqrt{\frac{16}{9}}-\sqrt{\frac{9}{16}}=\frac{7}{12}$. Answer: $x=7$.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. Find the maximum value of the function $f(x)=6 \sin x+8 \cos x$.
|
Solution: $f(x)=6 \sin x+8 \cos x=\sqrt{6^{2}+8^{2}} \sin \left(x+\operatorname{arctg} \frac{8}{6}\right)$.
Answer: The maximum value is 10.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. For a sports parade, the coach decided to line up the children in rows of 8, but 5 children were left over. Then he lined them up in rows of 10, but 3 places were left empty. It is known that there were no fewer than 100 and no more than 150 children. How many children were there?
|
Solution: $a=8 x+5=8(x+1)-3, a+3 \vdots 8$,
$$
\begin{array}{lc}
a=8 x+5=8(x+1)-3, & a+3 \vdots 8 \\
a=10 y-3, & a+3 \vdots 10,
\end{array} \Rightarrow a+3 \vdots 40, a+3=\underline{120,160}
$$
Answer: 117.
TICKET № 4
|
117
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the greatest and least values of the function $y=x^{3}-3 x^{2}+5$ on the interval $[1 ; 3]$.
|
Solution: $y=x^{3}-3 x^{2}+5,[1 ; 3] ; y^{\prime}=3 x^{2}-6 x=3 x(x-2) \Rightarrow x=0 ; 2$
$y(1)=3 ; y(3)=5 ; y(2)=1$.
|
5
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Calculate $\sqrt{4+\sqrt{12}}-\sqrt{4-\sqrt{12}}$.
|
Solution: $\sqrt{4+\sqrt{12}}-\sqrt{4-\sqrt{12}}=A ; A^{2}=8-2 \sqrt{16-12}=4 ; \quad A= \pm 2$ Answer: $A=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. In the packaging workshop, there are 2 types of boxes: one for 20 parts and one for 27 parts. A batch of parts between 500 and 600 pieces has arrived for packaging. When the parts are packed in the first type of box, 13 parts are left unpacked, and when packed in the second type of box, 7 spaces are left unfilled. How many parts were in the batch?
|
Solution: ${ }^{a=20 x+13=20(x+1)-7,} a+7 \vdots 20 ; a+7 \vdots 27, \Rightarrow a+7 \vdots 540$.
$$
a=27 x-7
$$
Answer: $a=533$.
## TICKET № 5
|
533
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Calculate $\sqrt{3+\sqrt{8}}-\sqrt{3-\sqrt{8}}$.
|
Solution: $\sqrt{3+\sqrt{8}}-\sqrt{3-\sqrt{8}}=A ; A^{2}=6-2 \sqrt{9-8}=4, \quad A= \pm 2, \quad A=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. Find the maximum value of the function $f(x)=5 \sin x+12 \cos x$.
|
Solution: $f(x)=5 \sin x+12 \cos x=\sqrt{5^{2}+12^{2}}\left(\sin \left(x+\operatorname{arctg} \frac{12}{5}\right)\right)=\sqrt{13^{2} \sin x}$.
Answer: 13 .
|
13
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. A florist received between 300 and 400 roses for a celebration. When he arranged them in vases with 21 roses in each, 13 roses were left. But when arranging them in vases with 15 roses in each, 8 roses were missing. How many roses were there in total?
|
Solution: $\left\{\begin{array}{ll}a=21 x+13=21(x+1)-8, & a+8 \vdots 21, \\ a=15 y-8, & a+8 \vdots 15,\end{array}\right\} \Rightarrow a+8 \vdots 105$. Answer: $a=307$.
$$
a+8=105,210, \underline{315,} 420
$$
## TICKET № 6
|
307
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Solve the equation $3 \cdot 9^{x}+2 \cdot 3^{x}=1$.
|
Solution: $3 \cdot 9^{x}+2 \cdot 3^{x}=1,3 \cdot\left(3^{x}\right)^{2}+2 \cdot 3^{x}-1=0,3^{x}=\frac{-2 \pm \sqrt{4+12}}{6}=\left[\begin{array}{l}\frac{1}{3}, \\ -1-\text { not valid }\end{array} \quad x=-1\right.$.
Answer: $x=-1$
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Two vertices of a square with an area of $256 \mathrm{~cm}^{2}$ lie on a circle, while the other two vertices lie on a tangent to this circle. Find the radius of the circle.
|
Solution: $S_{A B C D}=256 \, \text{cm}^{2} \Rightarrow a=16 \, \text{cm}=x$,
$E F=2 R-x, F O=R-E F=R-(2 R-x)=x-R$,
$\triangle F C O: F O^{2}=R^{2}-F C^{2} \Rightarrow(x-R)^{2}=R^{2}-8^{2}$,
$x^{2}-2 R x+R^{2}=R^{2}-8^{2}, 2 R x=16^{2}+8^{2} \Rightarrow R=\frac{16^{2}+8^{2}}{2 \cdot 16}=10$. Answer:
$R=10$.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. Koschei is counting his gold coins. When he counts them by tens, there are 7 coins left, and he is 3 coins short of a whole number of dozens. Koschei's wealth is estimated at $300-400$ coins. How many coins does Koschei have?
|
Solution: $\left\{\begin{array}{ll}a=10 x+7=10(x+1)-3, & a+3 \mid 10, \\ a=12 y-3, & a+3 \mid 12,\end{array}\right\} \Rightarrow a+3 \mid 60$. Answer: $a=357$.
$$
a+3=300,360,420
$$
## TICKET № 7
|
357
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the eleventh term of the arithmetic progression if the sum of the first seven terms $S_{7}=77$, and the first term $a_{1}=5$.
|
Solution: $S_{7}=77 ; a_{1}=5, a_{11}=$ ?
$S_{7}=\frac{2 a_{1}+d(7-1)}{2} \cdot 7=\frac{10+6 d}{2} \cdot 7=(5+3 d) 7=77 \Rightarrow d=2, a_{11}=a_{1}+10 d=25$.
|
25
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Solve the equation $\sqrt{\frac{x+3}{3 x-5}}+1=2 \sqrt{\frac{3 x-5}{x+3}}$.
|
Solution:
$$
\sqrt{\frac{x+3}{3 x-5}}+1=2 \sqrt{\frac{3 x-5}{x+3}}
$$
$\frac{x+3}{3 x-5}>0$
$t=\frac{x+3}{3 x-5}, \sqrt{t}+1=\frac{2}{\sqrt{t}}, \frac{t+\sqrt{t}-2}{\sqrt{t}}=0, \sqrt{t}=\frac{-1 \pm \sqrt{1+8}}{2}=\frac{-1 \pm 3}{2}=\left[\begin{array}{l}-2 \\ 1\end{array}\right.$
$t=1, \frac{x+3}{3 x-5}=1,3 x-5=x+3,2 x=8, x=4$. Verification: $\sqrt{\frac{7}{7}}+1=2 \sqrt{\frac{7}{7}}$. Answer: $x=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. The distance from the point of intersection of the diameter of a circle with a chord of length 18 cm to the center of the circle is $7 \mathrm{~cm}$. This point divides the chord in the ratio $2: 1$. Find the radius.
$$
A B=18, E O=7, A E=2 B E, R=?
$$
|
Solution: $2 B E \cdot B E=(R-7)(7+R)$
$$
A E \cdot B E=D E \cdot E C, \quad A E+B E=18, \quad B E=6
$$
$$
2 \cdot 6 \cdot 6=\left(R^{2}-7^{2}\right), R^{2}=72+49=121=11^{2}
$$
Answer: $R=11$.
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. Find the maximum value of the function $f(x)=9 \sin x+12 \cos x$.
|
Solution: $f(x)=9 \sin x+12 \cos x=\sqrt{9^{2}+12^{2}} \sin \left(x-\operatorname{arctg} \frac{12}{9}\right)$. Answer: 15 .
|
15
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Solve the equation $7^{-x}-3 \cdot 7^{1+x}=4$.
|
Solution: $7^{-x}-3 \cdot 7^{1+x}=4, \frac{1}{7^{x}}-21 \cdot 7^{x}=4,-21\left(7^{x}\right)^{2}-4 \cdot 7^{x}+1=0$,
$\left(7^{x}\right)=\frac{4 \pm \sqrt{16+84}}{-42}=\frac{4 \pm 10}{-42}=\left[\begin{array}{l}-\frac{14}{42}=-\frac{1}{3} \text {, not valid } \\ \frac{1}{7}\end{array}, x=-1\right.$. Answer: $x=-1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Calculate $\sqrt{6+\sqrt{20}}-\sqrt{6-\sqrt{20}}$.
|
Solution: $\sqrt{6+\sqrt{20}}-\sqrt{6-\sqrt{20}}=A, A^{2}=12-2 \sqrt{36-20}=4, A= \pm \sqrt{4}=2$. Answer: 2 .
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. Find the maximum value of the function $f(x)=8 \sin x+15 \cos x$.
|
Solution: $f(x)=8 \sin x+15 \cos x=\sqrt{8^{2}+15^{2}} \sin \left(x+\operatorname{arctg} \frac{15}{8}\right)=17 \sin \left(x+\operatorname{arctg} \frac{15}{8}\right)$
Answer: The maximum value of $f(x)=17$.
|
17
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. Between 200 and 300 children enrolled in the first grade of school. It was decided to form classes of 25 students, but it turned out that ten would not have a place. Then they formed classes of 30 students, but in one of the classes, there were 15 fewer students. How many children enrolled in the first grade?
|
Solution: $\left\{\begin{array}{ll}a=25 R+10=25(R+1)-15, & a+15: 25, \\ a=30 l-15, & a+15: 30,\end{array}\right\} \Rightarrow a+15 \vdots 150$. Answer: $a=285$.
$$
a+15=150, \underline{300,} 450
$$
|
285
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Solve the equation $9 \cdot 3^{2 x-1}+3^{x}-30=0$.
|
Solution: $9 \cdot 3^{2 x-1}+3^{x}-30=0,3 \cdot 3^{2 x}+3^{x}-30=0$, $3^{x}=\frac{-1 \pm \sqrt{1+360}}{6}=\frac{-1 \pm 19}{6}=\left[\begin{array}{l}3 \\ -\frac{10}{3} \text {, not valid }\end{array}, x=1\right.$.
Answer: $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Solve the equation $\sqrt{\frac{x^{2}-16}{x-3}}+\sqrt{x+3}=\frac{7}{\sqrt{x-3}}$.
|
Solution: $\sqrt{\frac{x^{2}-16}{x-3}}+\sqrt{x+3}=\frac{7}{\sqrt{x-3}}$, Domain of Definition $\frac{x^{2}-16}{x-3} \geq 0, x>3 \Rightarrow x \geq 4$,
$\sqrt{x^{2}-16}+\sqrt{x^{2}-9}=7, x^{2}-16=t, \sqrt{t}+\sqrt{t+7}=7, t+2 \sqrt{t(t+7)}+t+7=49$,
$2 \sqrt{t(t+7)}=42-2 t, \sqrt{t^{2}+7 t}=21-t, t \leq 21, t^{2}+7 t=21^{2}-42 t+t^{2}, 49 t=21^{2}$,
$t=\frac{3^{2} \cdot 7^{2}}{49}=9, x^{2}-16=9, x^{2}=25, x= \pm 5, x=5$.
Verification: $\sqrt{\frac{9}{2}}+\sqrt{8}=\frac{7}{\sqrt{2}}, \frac{3}{\sqrt{2}}+\frac{4}{\sqrt{2}}=\frac{7}{\sqrt{2}}$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Two vertices of a square lie on a circle with a radius of $5 \mathrm{~cm}$, while the other two lie on a tangent to this circle. Find the area of the square.
|
Solution: $R=5, A B C D$-square, $S_{A B C D}=$ ?
$A B=x, E F=2 R-x, E O=R-E F=x-R$
$\Delta E O C: E C^{2}=O C^{2}-E O^{2}=R^{2}-(x-R)^{2} \Rightarrow\left(\frac{x}{2}\right)^{2}=R^{2}-x^{2}+2 R x-R^{2}$,
$\frac{x^{2}}{4}=2 R x-x^{2}, \frac{5}{4} x=2 R, x=\frac{2 R \cdot 4}{5}=8$. Answer: $S_{\triangle A B C D}=64$.
|
64
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. To pack books when moving a school library, you can buy small boxes that hold 12 books or large ones that hold 25 books. If all the books are packed in small boxes, 7 books will be left, and if all the books are packed in large boxes, there will be room for 5 more books. The library's collection contains between 500 and 650 books. How many books are in the library?
|
Solution: $\left\{\begin{array}{ll}a=12 R+7=12(R+1)-5, & a+5 \vdots: 12, \\ a=25 l-5, & a+5 \vdots 25,\end{array}\right\} a+5: 300$. Answer: $a=595$.
$$
a+5=300, \underline{600,} 900
$$
|
595
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Two adjacent faces of a tetrahedron, which are isosceles right triangles with a hypotenuse of 2, form a dihedral angle of 60 degrees. The tetrahedron is rotated around the common edge of these faces. Find the maximum area of the projection of the rotating tetrahedron onto the plane containing
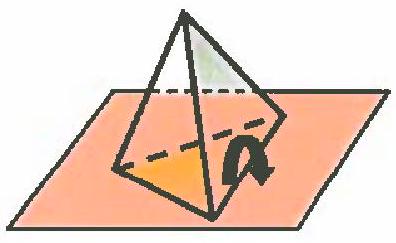
the given edge. (12 points)
Solution. Let the area of each of the given faces be \( S \). If the face lies in the plane of projection, then the projection of the tetrahedron is equal to the area of this face \( \Pi = S \).
When rotated by an angle \( 0 < \varphi < 30^\circ \), the area of the projection is \( \Pi = S \cos \varphi < S \).
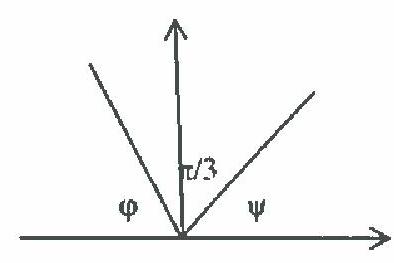
When rotated by an angle \( 30^\circ < \varphi < 90^\circ \), the area of the projection is
\[
\Pi = S \cos \varphi + S \cos \psi = S \cos \varphi + S \cos \left(\pi - \frac{\pi}{3} - \varphi\right) = S \cos \varphi + S \cos \left(\frac{2\pi}{3} - \varphi\right).
\]
\[
\Pi' = S \left(-\sin \varphi + \sin \left(\frac{2\pi}{3} - \varphi\right)\right), \quad \Pi' = 0 \text{ when } \varphi = \frac{\pi}{3}.
\]
The maximum of the function in the considered interval is achieved at
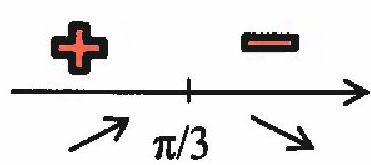
\[
\varphi = \frac{\pi}{3}, \quad \Pi = 2 S \cos \left(\frac{\pi}{3}\right) = 2 S \cdot \frac{1}{2} = S.
\]
When rotated by an angle \( 90^\circ < \varphi < 120^\circ \), the area of the projection is \( \Pi = S \cos \left(\frac{\pi}{2} - \varphi\right) = S \sin \varphi < S \).
When \( \varphi = \frac{2\pi}{3} \), the area \( \Pi = S \).
|
Answer. $\Pi=S=\frac{1}{2} \cdot \sqrt{2}^{2}=1$.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. To pack books when moving a school library, you can buy small boxes that hold 12 books or large ones that hold 25 books. If all the books are packed in small boxes, 7 books will remain, and if all the books are packed in large boxes, there will be room for 5 more books. The library's collection contains between 500 and 650 books. How many books are in the library?
|
Solution: $\left\{\begin{array}{ll}a=12 R+7=12(R+1)-5, & a+5 \vdots: 12, \\ a=25 l-5, & a+5 \vdots 25,\end{array}\right\} a+5: 300$. Answer: $a=595$.
$$
a+5=300, \underline{600,} 900
$$
|
595
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the sum of the first 10 elements that are found both in the arithmetic progression $\{5,8,11,13, \ldots\}$ and in the geometric progression $\{20,40,80,160, \ldots\}$. (10 points)
|
Solution. The members of the arithmetic progression $\{5,8,11,14,17,20,23, \ldots\}$ are given by the formula
$$
a_{n}=5+3 n, n=0,1,2, \ldots
$$
The members of the geometric progression $\{20,40,80,160, \ldots\}$ are given by the formula
$$
b_{n}=20 \cdot 2^{k}, k=0,1,2, \ldots
$$
For the common elements, the equation $5+3 n=20 \cdot 2^{k}$ must hold, from which $n=\frac{20 \cdot 2^{k}-5}{3}=\frac{5 \cdot\left(2^{k+2}-1\right)}{3}$, meaning $\left(2^{k+2}-1\right): 3$.
It is clear that $2^{k+2}-1$ is divisible by 3 for even $k$ (the remainder of the division of $2^{k+2}$ by 3 is 1 or 2).
For $k=0, n=5$ the common element is $a_{5}=b_{0}=20$;
for $k=2, n=25$ the common element is $a_{25}=b_{2}=80$;
for $k=4, n=105$ the common element is $a_{105}=b_{4}=320$ and so on.
Thus, the sought elements are: $20,80,320, \ldots$ - the members of the original geometric progression with even indices. They form a geometric progression with a common ratio of 4 and the first term 20. The sum of the first 10 terms can be found using the formula $S=c_{1} \frac{q^{n}-1}{q-1}=20 \cdot \frac{4^{10}-1}{4-1}=20 \cdot \frac{\left(2^{10}\right)^{2}-1}{3}=20 \cdot \frac{1024^{2}-1}{3}=6990500$.
Answer. 6990500.
|
6990500
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the smallest possible value of the function
$$
f(x)=|x+1|+|x+2|+\ldots+|x+100|
$$
$(25$ points. $)$
|
Answer: 2500.
Using the known inequality $|a|+|b| \geqslant|a-b|$, then $|x+k|+|x+m| \geqslant|k-m|$. Grouping in the original sum the terms equally distant from the ends, we get
$$
\begin{aligned}
f(x) & =(|x+1|+|x+100|)+(|x+2|+|x+99|)+\ldots+(|x+50|+|x+51|) \geqslant \\
& \geqslant(100-1)+(99-2)+\ldots+(51-50)
\end{aligned}
$$
The last sum of 50 terms is an arithmetic progression, it equals $\frac{1}{2} 100 \cdot 50=2500$. This value is the minimum for $f(x)$, it is achieved, for example, at $x=-50$.
Criteria. Only the answer - 0 points. The minimum value found - 18 points. The value of $x$ at which it is achieved is indicated - another 7 points.
|
2500
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.
The answer to the task should be an integer. Enter all characters without spaces. Do not indicate units of measurement.
Doughnut eats a cake in 5 minutes, and Nosy eats it in 7 minutes. How many seconds will it take for the boys to eat the cake together if they do not conflict?
|
# 1. /2 points/
The answer to the task should be an integer. Enter all characters without spaces. Do not indicate units of measurement.
Doughnut eats a cake in 5 minutes, and Nosy eats it in 7 minutes. How many seconds will it take for the boys to eat the cake together if they do not conflict
Answer: 175
#
|
175
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 3.
The answer to the task should be an integer. Enter all characters without spaces.
Find $n$, if $9^{n}+9^{n}+9^{n}+9^{n}+9^{n}+9^{n}+9^{n}+9^{n}+9^{n}=3^{2012}$.
|
# 3. /2 points/
The answer to the task should be an integer. Enter all characters without spaces.
Find $n$, if $9^{n}+9^{n}+9^{n}+9^{n}+9^{n}+9^{n}+9^{n}+9^{n}+9^{n}=3^{2012}$.
Answer: 1005
#
|
1005
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 7.
Among the statements given below, select the correct ones. In your answer, write down the numbers of these statements (in ascending order, without using spaces, commas, or other separators).
Example of answer format: 12345
1) Among the numbers $123,365,293,18$, exactly three numbers are divisible by 3.
2) If the radius of a circle is increased by $20 \%$, then the area of this circle will increase by $44 \%$.
3) The number 45 has more divisors than the number 36.
4) In a geometric progression with a common ratio of -2, the arithmetic mean of the first three terms is equal to the first term.
5) If the tenth term of an arithmetic progression is less than 5, and the twelfth term is greater than 7, then the common difference of this progression is greater than 1.
6) The number $6.4 \cdot 10^{11}$ is a square of a natural number.
|
# 7. /3 points/
Among the statements given below, select the correct ones. In your answer, write down the numbers of these statements (in ascending order, without using spaces, commas, or other separators). Example of answer format: $\quad 12345$
1) Among the numbers $123,365,293,18$, exactly three numbers are divisible by 3.
2) If the radius of a circle is increased by $20 \%$, then the area of this circle will increase by $44 \%$.
3) The number 45 has more divisors than the number 36.
4) In a geometric progression with a common ratio of -2, the arithmetic mean of the first three terms is equal to the first term.
5) If the tenth term of an arithmetic progression is less than 5, and the twelfth term is greater than 7, then the common difference of this progression is greater than 1.
6) The number $6.4 \cdot 10^{11}$ is a square of a natural number.
Answer: 2456
|
2456
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 8.
The answer to the task should be some integer or a number written as a finite decimal. If the answer contains a fractional number, use a comma when writing it. Enter all characters (comma, digits) without spaces. There is no need to indicate units of measurement.
The base and the side of the triangle are 30 and 14, respectively. Find the area of this triangle if the median drawn to the base is 13.
|
# 8. /3 points/
The answer to the problem should be a certain integer or a number written as a finite decimal. If the answer contains a fractional number, use a comma when writing it. Enter all characters (comma, digits) without spaces. Do not specify units of measurement.
The base and the side of the triangle are 30 and 14, respectively. Find the area of this triangle if the median drawn to the base is 13.
Answer: 168
#
|
168
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 9.
The answer to the task should be some integer or a number written as a finite decimal fraction. If the answer contains a fractional number, use a comma when writing it. Enter all characters (minus sign, comma, digits) without spaces.
Find all distinct values of the parameter $p$, for each of which the equation given below has a unique root. In the answer, specify the sum of the found values of the parameter $p$. $\frac{x^{2}-2 p x+p^{2}+p-20}{x}=0$
|
# 9. /3 points/
The answer to the task should be some integer or a number written as a finite decimal. If the answer contains a fractional number, use a comma when writing it. Enter all characters (minus sign, comma, digits) without spaces.
Find all distinct values of the parameter $p$ for which the equation given below has a unique root. In your answer, specify the sum of the found values of the parameter $p$. $\frac{x^{2}-2 p x+p^{2}+p-20}{x}=0$
Answer: 19
#
|
19
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. What is the smallest natural number that is divisible by 2022 and whose notation starts with 2023?
|
Answer: 20230110.
Solution. Let the number we are looking for have $n+4$ digits, then it has the form $2023 \cdot 10^{n}+a, a<10^{n}$. Subtract from it $2022 \cdot 10^{n}$, we get that $b=10^{n}+a$ is also divisible by 2022. That is, we need to find a number that starts with 1 and is divisible by 2022. Numbers divisible by 2022 are 0, 2022, $4044,6066,8088,10110, \ldots$. Thus, the number $b$ is at least five digits, so $n \geq 4$. Under this condition, the smallest value of $b$ is 10110, so the number we are looking for is $10110+20220000=20230110$.
Grading criteria: 20 points for a complete solution. 5 points deducted for estimating $b$ without estimating $n-$ 5 points. 0 points for an answer without justification.
|
20230110
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. (3 points)
Find the smallest natural number that starts with the digit 3 and which, after erasing this digit, decreases by 25 times.
|
Answer: 3125
## Interregional Subject Olympiad KFU 2013-2014, MATHEMATICS 9th grade, 2nd variant, Internet round
The answer in each task should be an integer or a number written as a finite decimal. If the answer contains a fractional number, then when writing it, use a comma. All symbols (minus sign, comma, digits) should be entered without spaces. There is no need to indicate units of measurement.
|
3125
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. In the club, 36 schoolchildren are attending. If any 33 of them come to the lesson, then girls will always be more than half. But if 31 students come to the lesson, it may turn out that more than half of them are boys. How many girls are attending the club? (20 points)
|
Answer: 20.
Solution: Since among any 33 children, there are more girls than half, then boys among them are less than half, that is, no more than 16. Therefore, there are no more than 16 boys in total, because if there were at least 17, it could happen that 17 boys and another 16 students came, and the boys would already be more than half.
Since there is a group of 31 students in which there are more boys than half, there are at least 16 boys in this group. Therefore, there are exactly 16 boys in total. Then the number of girls is $36-16=20$.
Criteria: Only shown that there are no fewer than 16 boys - 4 points.
Only shown that there are no more than 16 boys - 8 points.
|
20
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 3. Sasha chose five numbers from the numbers 1, 2, 3, 4, 5, 6, and 7 and told Anna their product. Based on this information, Anna realized that she could not uniquely determine the parity of the sum of the numbers chosen by Sasha. What number did Sasha tell Anna? (20 points)
|
Answer: 420.
Solution: Let's look at the two remaining numbers. Since Anya knows the sum of all numbers from 1 to 7 (which is 28), these two remaining numbers are such that their product cannot determine the parity of their sum. Therefore, their product can be represented in two ways: \( ab = xy \), where numbers \( a \) and \( b \) are of different parity, and numbers \( x \) and \( y \) are of the same parity. Then \( ab \) is even, so \( xy \) is even, which means one of them is divisible by 2, but then \( x \) and \( y \) are both even. Therefore, \( xy = ab \) is divisible by 4, and thus the even number among \( a \) and \( b \) is 4 (Anya simply has no other multiples of four). Then the pair of numbers \( x \) and \( y \) must be 2 and 6. Their product is 12, so the number paired with 4 is 3.
Thus, the product of the two remaining numbers is necessarily 12. Therefore, the product of Sasha's numbers is \( 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7 / 12 = 420 \).
Criteria: Only the answer - 5 points.
|
420
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 10. $/ 3$ points/
The answer to the task should be some integer or a number written as a finite decimal. If the answer contains a fractional number, use a comma when writing it. Enter all characters (comma, digits) without spaces. There is no need to specify units of measurement.
The bisector of angle $N$ of triangle $M N P$ divides side $M P$ into segments whose lengths are 28 and 12, and $M N - N P = 12$. Find the perimeter of triangle $M N P$.
|
Answer: 70
The answer to the task should be some integer or a number written as a finite decimal. If the answer contains a fractional number, use a comma when writing it. Enter all symbols (minus sign, comma, digits) without spaces.
Find all different values of the parameter $p$ for which the equation given below has a single root. In your answer, specify the sum of the found values of the parameter $p$.
$$
\frac{x^{2}-2 p x+p^{2}+p-20}{x}=0
$$
Answer: 19
|
70
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Given 50 numbers. It is known that among their pairwise products, exactly 500 are negative. Determine the number of zeros among these numbers.
|
Solution. Let $m, n$ and $p-$ be the number of negative, zero, and positive numbers among the given 50 numbers. Then from the condition of the problem we have: $m+n+p=50$ and $m \cdot p=500$. It follows that $m$ and $p$ are divisors of 500, the sum of which does not exceed 50. Among all divisors of the number 500, only the pair 20 and 25 has this property, i.e. $m+p=45$, hence $n=5$.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In triangle $ABC$, two altitudes $AK$ and $CL$ are drawn. Find the measure of angle $B$, given that $AC = 2 \cdot LK$.
|
Solution. Construct a circle on side $AC$ as its diameter, which will pass through points $L$ and $K$, since $\angle ALC = \angle AKC = 90^{\circ}$. According to the condition, $AC = 2 \cdot LK$, and thus, the segment $LK$ is equal to the radius of the constructed circle, so the arc subtended by the chord $LK$ is $60^{\circ}$. Therefore, the angle $\angle LCK$, which subtends this arc, is $30^{\circ}$. Next, if angle $B$ is acute, then $\angle B = 90^{\circ} - \angle LCB = 60^{\circ}$ (Fig. $2, a$); if angle $B$ is obtuse, then $\angle CBL = 90^{\circ} - \angle BCL = 60^{\circ}$ (Fig. 2, b), and thus, $\angle B = 180^{\circ} - \angle CBL = 120^{\circ}$.
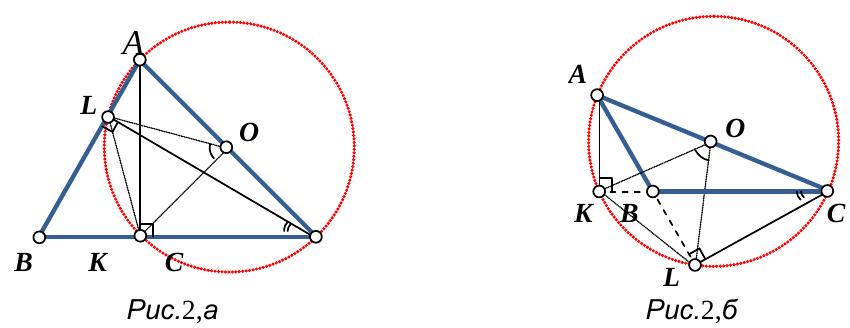
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In how many ways can 8 identical rooks be placed on an $8 \times 8$ board symmetrically with respect to the diagonal passing through the bottom-left corner?
|
Solution. On an $8 \times 8$ board, there are 8 diagonal and 56 non-diagonal cells, the latter of which can be divided into 28 pairs of cells symmetric relative to the diagonal. All placements of rooks will be divided into 5 non-overlapping classes - in the $m$-th class, we will include placements where $m$ pairs of rooks fall on the diagonal.
When $m=0$, no rook stands on the diagonal, and thus all rooks occupy 4 out of 28 pairs of symmetric non-diagonal cells. There will be $C_{28}^{4}=\frac{28 \cdot 27 \cdot 26 \cdot 25}{4 \cdot 3 \cdot 2 \cdot 2 \cdot 1}=20475$ such placements. When $m=1$, exactly two rooks are on the diagonal, which can be arranged in $C_{8}^{2}=$ 28 ways. The remaining 6 rooks occupy 3 out of 28 pairs of symmetric non-diagonal cells. Therefore, there will be $C_{8}^{2} \cdot C_{28}^{3}=91728$ such placements.
By similar reasoning, we find the number of required placements for $m=1$ and $m=3$, which are $C_{8}^{4} \cdot C_{28}^{2}=26460$ and $C_{8}^{6} \cdot C_{28}^{1}=784$ respectively. Finally, when $m=4$, there is only one placement where all rooks fall on the diagonal. The total number of symmetric placements is
$$
C_{28}^{4}+C_{8}^{2} \cdot C_{28}^{3}+C_{8}^{4} \cdot C_{28}^{2}+C_{8}^{6} \cdot C_{28}^{1}+1=139448
$$
|
139448
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Solve the equation
$$
2(x-6)=\frac{x^{2}}{(1+\sqrt{x+1})^{2}}
$$
|
Solution 1. Rewrite the equation as $2(x-6)(1+\sqrt{x+1})^{2}=x^{2}$ and make the substitution $\sqrt{x+1}=y$. Then $x=y^{2}-1$ and $y \geq 0$. After the substitution, we get $2\left(y^{2}-7\right)(y+1)^{2}=$ $\left(y^{2}-1\right)^{2}$. Factor the right side as $(y+1)^{2}(y-1)^{2}$, move it to the left, and factor out $(y+1)^{2}$. We get $(y+1)^{2}\left(2 y^{2}-14-(y-1)^{2}\right)=(y+1)^{2}\left(y^{2}+\right.$ $2 y-15)=(y+1)^{2}(y-3)(y+5)=0$. This equation has three solutions $y_{1}=3, y_{2}=$ $-1, y_{3}=-5$. The last two do not satisfy the condition $y \geq 0$, so they are extraneous. If $y=3$, then $x=8$. Clearly, this solution is valid.
Solution 2. Transform the equation to the form
$$
2(x-6)(x+2+2 \sqrt{x+1})-x^{2}=0
$$
and denote the expression on the left side by $f(x)$. We have
$$
f(x)=2 x^{2}-8 x-24+4(x-6) \sqrt{x+1}-x^{2}=x^{2}-8 x-24+4(x-6) \sqrt{x+1}
$$
We need to solve the equation $f(x)=0$. It is clear that all roots of this equation satisfy the condition $x>6$ (otherwise, the left side of the original equation is non-positive, while the right side is positive). Find the derivative $f^{\prime}(x)$ :
$$
f^{\prime}(x)=(2 x-8)+4 \sqrt{x+1}+\frac{2(x-6)}{\sqrt{x+1}}
$$
It is clear that for $x>6$ each term in the last sum is non-negative. Therefore, the function $f(x)$ is increasing on the interval $(6,+\infty)$. Hence, the equation $f(x)=$ 0 can have no more than one solution. One solution $x=8$ can be easily found by trial.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. How many positive numbers are there among the 2014 terms of the sequence: $\sin 1^{\circ}, \sin 10^{\circ}$, $\sin 100^{\circ}, \sin 1000^{\circ}, \ldots ?$
|
Solution. For $n>3$ we have
$10^{n}-1000=10^{3}\left(10^{n-3}-1\right)=25 \cdot 40 \cdot\left(10^{n-3}-1\right)$.
Since $10^{n-3}-1$ is divisible by 9, it follows that $10^{n}-1000$ is divisible by 360. Therefore, all terms of the sequence, starting from the fourth, coincide with $\sin 1000^{\circ}=\sin \left(3 \cdot 360^{\circ}-80^{\circ}\right)=\sin \left(-80^{\circ}\right)<0$. Thus, the positive terms in the sequence are $\sin 1^{\circ}, \sin 10^{\circ}, \sin 100^{\circ}$.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. Let's call a year interesting if a person turns as many years old as the sum of the digits of their birth year in that year. A certain year turned out to be interesting for Ivan, who was born in the 20th century, and for Vovochka, who was born in the 21st century. What is the difference in their ages?
Note. For convenience, we assume they were born on the same day, and all calculations are done in whole years.
|
Answer: 18 years.
Solution. Let Ivan's year of birth be $\overline{19 x y}$, and Vovochka's $-\overline{20 z t}$. An interesting year for Ivan will be $1900+10 x+y+10+x+y$, and for Vovochka $-2000+10 z+t+2+z+t$, according to the condition these values are equal, that is, $2002+11 z+2 t=1910+11 x+2 y$, from which $11(x-z)+2(y-t)=92$ or $11 a+2 b=92$, where the numbers $a=x-z$ and $b=y-t-$ are integers, ranging from -9 to 9.
We have $a=\frac{92-2 b}{11}$. The numerator here is an even number from 74 to 110, and it must be divisible by 11. Therefore, it is equal to 88 or 110. The second option does not fit, as $a \leq 9$. In the first case, we have $a=8 ; b=$ 2.
According to the condition of the problem, we need to find the number
$$
20 z t-19 x y=100-10(x-z)-(y-t)=100-10 a-b=18
$$
Let's check if this case is realized. For example, $8=9-1 ; 2=7-5$. Let Ivan be born in 1997, Vovochka - in 2015. For Ivan, the interesting year is $1997+1+9+9+7=2023$, for Vovochka $2015+2+0+1+5=2023$. At the same time, Ivan is older by $2015-1997=18$ years.
Note that we did not consider a special case when Ivan was born in 2000 (this year also belongs to the 20th century). In this case, the interesting year is 2002. But it will not be interesting for those born in 2001 (the interesting year is 2004), and even more so for subsequent years of birth (the interesting year comes after the year of birth).
Grading criteria: The correct answer (18) is given and one or several examples are provided when it is achieved - 5 points. An equation of the form $11 \mathrm{a}+2 \mathrm{~b}=92$ is obtained - 10 points. The complete solution of the previous equation ($a=8, b=2)$ - 5 points. A complete solution without considering the special case
(Ivan's year of birth is 2000) - 15 points. The special case is considered and it is shown that it does not fit - 5 points.
|
18
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. Given a triangle $ABC$ with sides $AB=5$; $BC=8$. The bisector of angle $B$ intersects the circumcircle of the triangle at point $D$. a) It is known that the area of triangle $ABD$ is 10. Find the area of triangle $BCD$. b) Can it be that $S_{ABD}$ equals 100?
|
Solution. a) The fact that point $D$ lies on the circle is irrelevant. The areas of triangles $A B O$ and $O B C$ are in the ratio $A O: O C$. The same applies to triangles $A O D$ and $D O C$. Therefore,
$$
S_{A B D}: S_{B C D}=A O: O C=A B: B C=5: 8
$$
by the property of the angle bisector.
b) 1st method. Let the angle $A B D$ be $\alpha, A B=a=5, B C=b=8, A C=c$. Clearly, $D$ is the midpoint of the arc $A C$, so $A D=C D=\frac{A C}{2} / \cos \alpha=\frac{c}{2 \cos \alpha}$. By Ptolemy's theorem, $B D \cdot c=a \cdot C D+b \cdot A D=(a+b) \frac{c}{2 \cos \alpha}$, from which $B D=\frac{a+b}{2 \cos \alpha}$
We have
$$
S_{A B D}=\frac{1}{2} a \cdot B D \sin \alpha=\frac{a(a+b)}{4} \operatorname{tg} \alpha
$$
This value can take any positive value for a suitable $\alpha$.
2nd method. From the previously proven condition, $S_{A B D}=S_{0}$ is equivalent to $S=S_{A B C D}=\frac{a+b}{a} S_{0}$.
Let's calculate the area of the quadrilateral $A B C D$.
$$
\begin{gathered}
S=\frac{1}{2} a b \sin 2 \alpha+\frac{1}{2} A D \cdot C D \sin 2 \alpha=\frac{1}{2}\left(a b+\frac{1}{4} \frac{c^{2}}{\cos ^{2} \alpha}\right) \sin 2 \alpha= \\
=\frac{4 a b \cos ^{2} \alpha+c^{2}}{8 \cos ^{2} \alpha} \sin 2 \alpha=\left(4 a b \cos ^{2} \alpha+a^{2}+b^{2}-2 a b \cos 2 \alpha\right) \frac{\sin 2 \alpha}{8 \cos ^{2} \alpha}= \\
\left(a^{2}+b^{2}+2 a b\left(2 \cos ^{2} \alpha-\cos 2 \alpha\right)\right)=\frac{(a+b)^{2}}{4} \operatorname{tg} \alpha
\end{gathered}
$$
This value can take all possible positive values for suitable $\alpha$.
Grading criteria: A complete solution to part a) with the correct answer 16 - 10 points. The correct answer in part b) without rigorous or incomplete proofs - 0 points. A complete solution to part b) with the condition(s) specified when it is possible. For example, stating that $\operatorname{tg} \alpha=80 / 13$ or $B D=\sqrt{6569} / 2-10$ points.
|
16
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. A rectangular grid, both sides of which are even numbers, was cut into figures of the form $\square$ and $\square \square$ such that both types of figures are present. What is the smallest area that such a rectangle could have? Provide an example of the corresponding cutting and explain why a smaller area is impossible. The figures can be rotated and flipped. The length of a side of the rectangle is the number of cells adjacent to it. The area of a grid rectangle is the number of cells it contains. (20 points)
|
Answer: 40.
Solution: Since the area of both figures is 5, and the sum of numbers divisible by 5 is also divisible by 5, the area of the rectangle must be divisible by 5. Since 5 is a prime number, the length of one of the sides must be divisible by 5. Since the lengths of the sides are even numbers, it must be divisible by 10. The smallest even number is 2, but a rectangle of $2 \times 10$ does not work because the second type of figure can only fit horizontally, leaving one uncovered cell inside it, which cannot be covered by other figures. Therefore, the minimum possible value for the length of the other side is 4. A rectangle of $4 \times 10$ can be cut, for example, as shown in the figure. Therefore, the smallest area is 40.

Criteria: Only the example of cutting - 10 points.
Only the estimate with incorrect or missing cutting - 10 points.
|
40
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. Mom baked a cake for Anya's birthday, which weighs an integer number of grams. Before decorating it, Mom weighed the cake on digital scales that round the weight to the nearest ten grams (if the weight ends in 5, the scales round it down). The result was 1440 g. When Mom decorated the cake with identical candles, the number of which was equal to Anya's age, the scales showed 1610 g. It is known that the weight of each candle is an integer number of grams, and if you put one candle on the scales, they will show 40 g. How old can Anya be? List all possible answers and explain why there are no others. (20 points)
|
Answer: 4 years.
Solution: From the condition, it follows that the cake weighed from 1436 to 1445 grams before decoration, and from 1606 to 1615 grams after decoration. Therefore, the total weight of the candles is between 161 and 179 grams. Since the weight of each candle is given as 40 grams, the weight of one candle is between 36 and 45 grams. If Anya is less than 4 years old, the total weight of the candles is no more than $45 \cdot 3 = 135$ grams, and if she is more than 4 years old, the total weight of the candles is no less than $5 \cdot 36 = 180$ grams. Neither of these values is possible. Therefore, Anya is exactly 4 years old.
Criteria: Correctly determined the weight limits of the cake - 3 points.
Correctly determined the weight limits of all candles - 2 points.
Correctly determined the weight limits of one candle - 3 points.
Correctly verified only one of the inequalities $n \leqslant 4$ or $n \geqslant 4-4$ points. All these criteria are cumulative.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 5. In class 5A, a survey was conducted on what fruits the students like. It turned out that 13 students like apples, 11 like plums, 15 like peaches, and 6 like melons. A student can like more than one fruit. Every student who likes plums also likes either apples or peaches (but not both at the same time). And every student who likes peaches also likes either plums or melons (but not both at the same time). What is the minimum number of people that can be in $5 A$? (20 points)
|
Answer: 22 people.
Solution. Estimate. Since 15 people like peaches and 6 people like melons, there are at least 9 people who like peaches but do not like melons. Then all these people like plums but do not like apples. Therefore, in addition to these people, there are at least 13 people who like apples. Thus, the total number of people is no less than 22.
Example. Suppose 6 people like melons, peaches, and apples, 9 people like plums and peaches, 2 people like plums and apples, and 5 people like only apples. It is easy to see that in this case, the total number of people is 22, and all other conditions of the problem are satisfied.
Criteria. Estimate - 10 points.
Example - 10 points.
|
22
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. Masha has a piggy bank where she puts a 50 or 100 ruble bill every week. At the end of every 4 weeks, she picks the bill of the smallest denomination from the piggy bank and gives it to her little sister. After a year, it turned out that she had given her sister 1250 rubles. What is the minimum amount of money that could have accumulated with her over this time?
|
Answer: 3750 rubles.
Solution. Let's call a 4-week period a "month", there are 13 such "months" in a year. If all the bills given by Masha were hundred-ruble bills, her sister would have received 1300 rubles. This means Masha gave 100 rubles twelve times and 50 rubles once. If in any "month" Masha gave 100 rubles, it means that in her piggy bank there were only hundreds. So, over these 12 "months" she kept 12 * 300 = 3600 rubles for herself.
Thus, 50-ruble bills could appear in Masha's possession only in one month out of 13. If in a "month" only one 50-ruble bill was put into the piggy bank, she gave it to her sister at the end of the month, so her "income" remained 300 rubles.
If in any "month" Masha saves not less than two 50-ruble bills, she gives them to her sister over consecutive "months", which contradicts the condition. The exception is the case when they all come in the 13th "month", then she won't have time to give them away. So, in this case, for the first 12 "months" Masha received 300 rubles each, and in the last one, she could put in the piggy bank from zero to three 50-ruble bills, that is, she could fall short of 300 rubles by a maximum of 150 rubles.
Grading criteria: It is stated that Masha gave money 13 times, 12 times 100 rubles and once 50 rubles - 5 points. The correct answer without mentioning that the 50 rubles are given only in the last month - 10 points. The correct solution to the problem, but the answer indicates the sum including the money given to her sister (3750 + 1250 = 5000) - 17 points.
|
3750
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. Amir is 8 kg heavier than Ilnur, and Daniyar is 4 kg heavier than Bulat. The sum of the weights of the heaviest and lightest boys is 2 kg less than the sum of the weights of the other two. The total weight of all four is 250 kg. How many kilograms does Amir weigh? (20 points)
|
Answer: 66 kg.
Solution. Let the weight of Bulat in kilograms be denoted by $x$, and the weight of Ilnur by $y$. Then Amir weighs $y+8$, and Daniyar weighs $-x+4$. Note that the heaviest is either Amir or Daniyar, and the lightest is either Ilnur or Bulat.
If the heaviest is Daniyar, then $x+4>y+8$, so $x>y$ and the lightest is Ilnur. In this case, the combined weight of the heaviest and the lightest is $x+4+y$, which is 4 kg less than the combined weight of the other two. This is a contradiction. Therefore, the heaviest is Amir.
Suppose Bulat is the lightest. Then together with Amir, they weigh $x+y+8$, which is 4 kg more than the other two boys. This is a contradiction.
The only remaining case is when the lightest is Ilnur. In this case, Ilnur and Amir together weigh $2y+8$. From the problem statement, it follows that Bulat and Daniyar together weigh $2y+10$. Therefore, the total weight of all four boys is $4y+18=250$, from which $y=58$. Therefore, Amir weighs 66 kg.
Criteria. Only the correct answer with an incorrect or missing solution -3 points. Missing cases during enumeration - no more than 10 points depending on the number and severity of the missed cases.
In the case of a solution like the jury's, missing any of the first two cases (with the rest of the solution correct) - 10 points; missing both of the first two cases with the third case correctly analyzed - 6 points.
|
66
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. Timofey placed 10 grid rectangles on a grid field, with areas of $1, 2, 3, \ldots, 10$ respectively. Some of the rectangles overlapped each other (possibly completely, or only partially). After this, he noticed that there is exactly one cell covered exactly once; there are exactly two cells covered exactly twice; there are exactly three cells covered exactly three times, and exactly four cells covered exactly four times. What is the maximum number of cells that could be covered at least five times? The area of a grid rectangle is the number of cells it contains. Each rectangle lies on the field exactly along the grid cells. (20 points)
|
Answer: 5 cells.
Solution. Estimation. There are a total of $1+2+\ldots+10=55$ cell coverings. The ten cells described in the condition are covered in total exactly $1 \cdot 1+2 \cdot 2+3 \cdot 3+4 \cdot 4=30$ times. There remain $55-30=25$ cell coverings. Therefore, the number of cells covered at least five times is no more than $25 / 5=5$.
Example. Let's assume that all rectangles have the form $1 \times n$. We will combine them into rectangles of area $15=3+4+8$, $14=1+6+7$, and $12=2+10$. There are still two rectangles of area 5 and 9 left. We will overlay all five rectangles so that their leftmost cells coincide. It is easy to verify that the example works.
Criteria. Example only -10 points.
Estimation only -10 points.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. (20 points) How many zeros does the number $4^{5^{6}}+6^{5^{4}}$ end with in its decimal representation?
#
|
# Answer: 5
Solution. Consider the number $4^{25}+6$. Let's check that it is divisible by 5 and not divisible by 25. We have
$$
\begin{gathered}
4^{25}+6 \equiv(-1)^{25}+6 \equiv 0 \quad(\bmod 5) \\
4^{25} \equiv 1024^{5}+6 \equiv(-1)^{5}+6 \equiv 5 \quad(\bmod 25)
\end{gathered}
$$
We will write $5^{t} \| c$, if $5^{t} \mid c, 5^{t+1} \nmid c$. For arbitrary integers $a, b$, not divisible by 5, such that $5^{k} \| a-b, k>0$, we will prove that $5^{k+1} \| a^{5}-b^{5}$.
Let $a-b=s, 5^{k} \| s$. We have
$$
a^{5}-b^{5}=s\left(a^{4}+a^{3} b+a^{2} b^{2}+a b^{3}+b^{4}\right)=\quad=s\left((b+s)^{4}+(b+s)^{3} b+(b+s)^{2} b^{2}+(b+s) b^{3}+b^{4}\right)
$$
Expand the brackets using the binomial theorem and consider the expression $\left((b+s)^{4}+(b+s)^{3} b+(b+s)^{2} b^{2}+(b+s) b^{3}+b^{4}\right)$ modulo 25. Clearly, from each bracket only the terms where $s$ is raised to a power no greater than 1 remain. Thus, we have
$$
\begin{aligned}
&(b+s)^{4}+(b+s)^{3} b+(b+s)^{2} b^{2}+(b+s) b^{3}+b^{4} \equiv \\
& \equiv 5 b^{4}+(4+3+2+1) b^{3} s \equiv
\end{aligned}
$$
$$
\equiv 5 b^{4}+10 b^{3} s \equiv 5 b^{4} \quad(\bmod 25)
$$
Thus,
$$
5^{1} \|\left(a^{4}+a^{3} b+a^{2} b^{2}+a b^{3}+b^{4}\right)
$$
Therefore, $5^{k+1} \| a^{2}-b^{2}$.
Now, let's proceed to solving the problem. We have
$$
4^{5^{6}}+6^{5^{4}}=\left(1025^{5}\right)^{5^{4}}-(-6)^{5^{4}}
$$
Let $a=1025^{5}, b=-6$. Apply the proven statement. We get that
$$
5^{2} \|\left(1025^{5}\right)^{5}-(-6)^{5}
$$
Applying the statement three more times, we get that
$$
5^{5} \|\left(1025^{5}\right)^{5^{4}}-(-6)^{5^{4}}
$$
It remains to note that the number from the condition is divisible by $2^{5}$. Thus, the number ends with exactly 5 zeros.
Remark. If we use Hensel's Lemma, the solution becomes obvious.
However, proving the lemma is more complicated than solving this problem.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (5 points) Find the value of $n$ for which the following equality holds:
$$
\frac{1}{1+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+\frac{1}{\sqrt{3}+\sqrt{4}}+\ldots+\frac{1}{\sqrt{n}+\sqrt{n+1}}=2018
$$
|
Answer: 4076360
Solution: Notice that $\frac{1}{\sqrt{k}+\sqrt{k+1}}=\sqrt{k+1}-\sqrt{k}$. Then $\frac{1}{1+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+\frac{1}{\sqrt{3}+\sqrt{4}}+$ $\ldots+\frac{1}{\sqrt{n}+\sqrt{n+1}}=\sqrt{2}-1+\sqrt{3}-\sqrt{2}+\ldots+\sqrt{n+1}-\sqrt{n}=\sqrt{n+1}-1=2018$. From which $n=(2018+1)^{2}-1=4076360$.
|
4076360
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (5 points) On Valentine's Day, every student in the school gave a valentine to every female student. It turned out that the number of valentines was 16 more than the total number of students. How many valentines were given?
|
Answer: 36
Solution: Let $x, y$ be the number of boys and girls in the school, respectively. According to the condition, $x y=x+y+16$. Then $(x-1)(y-1)=17$. Therefore, the numbers $x-1$ and $y-1$ are 1 and 17. The number of valentines is $2 \cdot 18=36$.
|
36
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (7 points) There are 5 blue, 6 red, and 7 white bulbs. In how many ways can they be arranged into a garland (using all the bulbs) so that no two white bulbs are adjacent?
|
Answer: 365904
Solution: First, arrange all the blue and red bulbs in $C_{11}^{5}$ ways. In the gaps between them and at the ends, choose 7 positions and insert the white bulbs. There are $C_{12}^{7}$ ways to do this. In total, there are $C_{11}^{5} \cdot C_{12}^{7}$ ways to compose the garland from the available bulbs.
|
365904
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (7 points) The numbers $a, b, c, d$ belong to the interval $[-4.5 ; 4.5]$. Find the maximum value of the expression $a+2 b+c+2 d-a b-b c-c d-d a$.
|
Answer: 90
Solution: Note that $a+2 b+c+2 d-a b-b c-c d-d a=(a+c)+2(b+d)-(a+c)(b+d)$. Let $x=a+c, y=b+d$, then we will find the maximum value of the expression $x+2 y-x y=(y-1)(2-x)+2$, where $-10 \leqslant y-1 \leqslant 8$ and $-7 \leqslant 2-x \leqslant 11$. Therefore, $(y-1)(2-x)+2 \leqslant 8 \cdot 11+2=90$. The maximum value of the expression is achieved when $a=c=-4.5, b=d=4.5$.
|
90
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (8 points) On the radius $A O$ of a circle with center $O$, a point $M$ is chosen. On one side of $A O$ on the circle, points $B$ and $C$ are chosen such that $\angle A M B = \angle O M C = \alpha$. Find the length of $B C$ if the radius of the circle is $10$, and $\cos \alpha = \frac{2}{5}$?
|
Answer: 8.
## Solution:
Consider point $B_{1}$, which is symmetric to point $B$ with respect to the line $O A$. It also lies on the circle and $\angle A M B=\alpha$. Notice that points $B_{1}, M, C$ lie on the same straight line, and $\Delta B B_{1} M$ is isosceles. Therefore, the inscribed angle $\angle B B_{1} M=90^{\circ}-\alpha$, and the central angle $\angle B O C=180^{\circ}-2 \alpha$. $\triangle B O C$ is isosceles and $\angle O B C=\alpha$. We find the base of the isosceles triangle using the formula $B C=2 \cdot \cos \alpha \cdot B O=2 \cdot \frac{2}{5} \cdot 10=8$
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (8 points) By expanding the expression $(1+\sqrt{7})^{205}$ using the binomial theorem, we obtain terms of the form $C_{205}^{k}(\sqrt{7})^{k}$. Find the value of $k$ for which such a term attains its maximum value.
|
Answer: 149
Solution: The ratio of two consecutive terms $\frac{C_{205}^{k+1}(\sqrt{7})^{k+1}}{C_{205}^{k}(\sqrt{7})^{k}}$ is greater than 1 when $k<$ $\frac{205 \sqrt{7}-1}{\sqrt{7}+1}$. Then the terms increase up to $\left[\frac{205 \sqrt{7}-1}{\sqrt{7}+1}\right]+1$, and then decrease.
|
149
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. (10 points) On the board, 25 ones are written. Every minute, Karlson erases two arbitrary numbers and writes their sum on the board, and then eats a number of candies equal to the product of the two erased numbers. What is the maximum number of candies he could have eaten in 25 minutes?
|
Answer: 300.
Solution: Let's represent 25 units as points on a plane. Each time we combine two numbers, we will connect the points corresponding to one group with all the points of the second group with line segments. Note that if we replace numbers $x$ and $y$ with $x+y$, the groups " $x$ " and " $y$ " will be connected by $x y$ line segments. Carlson eats as many candies as the number of line segments. After 25 minutes, all points will be connected. In total, $\frac{25 \cdot(25-1)}{2}=300$ line segments will be drawn. Therefore, Carlson will eat 300 candies.
|
300
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (10 points) In the inscribed quadrilateral $A B C D$, the degree measures of the angles are in the ratio $\angle A: \angle B: \angle C=2: 3: 4$. Find the length of $A C$, if $C D=18, B C=12 \sqrt{3}-9$.
|
Answer: 30
## Solution:
The quadrilateral is inscribed, hence $\angle A+\angle C=180^{\circ}$. From the given ratio, $\angle A=2 x, \angle C=4 x$. Therefore, $x=30^{\circ}$ and $\angle A=60^{\circ}, \angle B=3 x=90^{\circ}$. Extend $A B$ and $C D$ until they intersect at point $K$. Then $\angle K=30^{\circ}, K C=2 B C=24 \sqrt{3}-18, K D=K C+C D=24 \sqrt{3}$ and $A D=24$. Using the Pythagorean theorem, we get $A C=30$.
## Solve the following problems with justification for your answer
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (5 points) Find the value of $n$ for which the following equality holds:
$$
\frac{1}{1+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+\frac{1}{\sqrt{3}+\sqrt{4}}+\ldots+\frac{1}{\sqrt{n}+\sqrt{n+1}}=2017
$$
|
Answer: 4072323
Solution: Notice that $\frac{1}{\sqrt{k}+\sqrt{k+1}}=\sqrt{k+1}-\sqrt{k}$. Then $\frac{1}{1+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+\frac{1}{\sqrt{3}+\sqrt{4}}+$ $\ldots+\frac{1}{\sqrt{n}+\sqrt{n+1}}=\sqrt{2}-1+\sqrt{3}-\sqrt{2}+\ldots+\sqrt{n+1}-\sqrt{n}=\sqrt{n+1}-1=2017$. From which $n=(2017+1)^{2}-1=4072323$.
|
4072323
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (5 points) On Valentine's Day, every student in the school gave each female student a valentine. It turned out that the number of valentines was 18 more than the total number of students. How many valentines were given?
|
Answer: 40
Solution: Let $x, y$ be the number of boys and girls in the school, respectively. According to the condition, $x y=x+y+18$. Then $(x-1)(y-1)=19$. Therefore, the numbers $x-1$ and $y-1$ are 1 and 19. The number of valentines is $2 \cdot 20=40$.
|
40
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (7 points) There are 7 blue, 6 red, and 10 white light bulbs. In how many ways can they be arranged into a garland (using all the bulbs) so that no two white bulbs are adjacent?
|
Answer: 1717716
Solution: First, arrange all the blue and red bulbs in $C_{13}^{7}$ ways. In the gaps between them and at the ends, choose 10 positions and insert the white bulbs. There are $C_{14}^{10}$ ways to do this. In total, there are $C_{13}^{7} \cdot C_{14}^{10}$ ways to compose the garland from the available bulbs.
|
1717716
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (7 points) The numbers $a, b, c, d$ belong to the interval $[-5.5 ; 5.5]$. Find the maximum value of the expression $a+2 b+c+2 d-a b-b c-c d-d a$.
|
Answer: 132
Solution: Note that $a+2 b+c+2 d-a b-b c-c d-d a=(a+c)+2(b+d)-(a+$ $c)(b+d)$. Let $x=a+c, y=b+d$, then we will find the maximum value of the expression $x+2 y-x y=(y-1)(2-x)+2$, where $-12 \leqslant y-1 \leqslant 10$ and $-9 \leqslant 2-x \leqslant 13$. Therefore, $(y-1)(2-x)+2 \leqslant 10 \cdot 13+2=132$. The maximum value of the expression is achieved when $a=c=-5.5, b=d=5.5$.
|
132
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (8 points) On the radius $A O$ of a circle with center $O$, a point $M$ is chosen. On one side of $A O$ on the circle, points $B$ and $C$ are chosen such that $\angle A M B = \angle O M C = \alpha$. Find the length of $B C$ if the radius of the circle is $8$ and $\cos \alpha = \frac{3}{4}$?
|
Answer: 12.
## Solution:
Consider point $B_{1}$, which is symmetric to point $B$ with respect to the line $O A$. It also lies on the circle and $\angle A M B=\alpha$. Note that points $B_{1}, M, C$ lie on the same straight line, and $\Delta B B_{1} M$ is isosceles. Therefore, the inscribed angle $\angle B B_{1} M=90^{\circ}-\alpha$, and the central angle $\angle B O C=180^{\circ}-2 \alpha$. $\triangle B O C$ is isosceles and $\angle O B C=\alpha$. We find the base of the isosceles triangle using the formula $B C=2 \cdot \cos \alpha \cdot B O=2 \cdot \frac{3}{4} \cdot 8=12$
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (8 points) By expanding the expression $(1+\sqrt{5})^{206}$ using the binomial theorem, we obtain terms of the form $C_{206}^{k}(\sqrt{5})^{k}$. Find the value of $k$ for which such a term attains its maximum value.
|
Answer: 143
Solution: The ratio of two consecutive terms $\frac{C_{206}^{k+1}(\sqrt{5})^{k+1}}{C_{206}^{k}(\sqrt{5})^{k}}$ is greater than 1 when $k<$ $\frac{206 \sqrt{5}-1}{\sqrt{5}+1}$. Then the terms increase up to $\left[\frac{206 \sqrt{5}-1}{\sqrt{5}+1}\right]+1$, and then decrease.
|
143
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.