problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
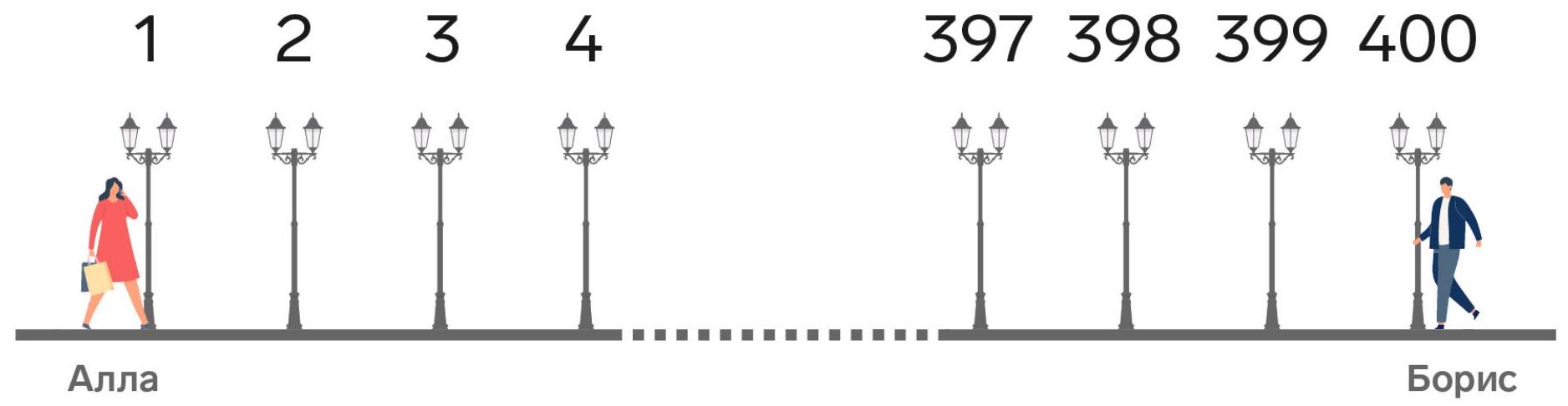
5-5. Along a straight alley, 400 lamps are placed at equal intervals, numbered in order from 1 to 400. At the same time, from different ends of the alley, Alla and Boris started walking towards each other at different constant speeds (Alla from the first lamp, Boris from the four hundredth). When Alla was at the 55th lamp, Boris was at the 321st lamp. At which lamp will their meeting occur? If the meeting occurs between two lamps, indicate the smaller number of these two.
|
Answer. At the 163rd lamppost.
Solution. There are a total of 399 intervals between the lampposts. According to the condition, while Allа walks 54 intervals, Boris walks 79 intervals. Note that $54+79=133$, which is exactly three times less than the length of the alley. Therefore, Allа should walk three times more to the meeting point than to the 55th lamppost, i.e., $54 \cdot 3=162$ intervals. And she will be at the 163rd lamppost.
|
163
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
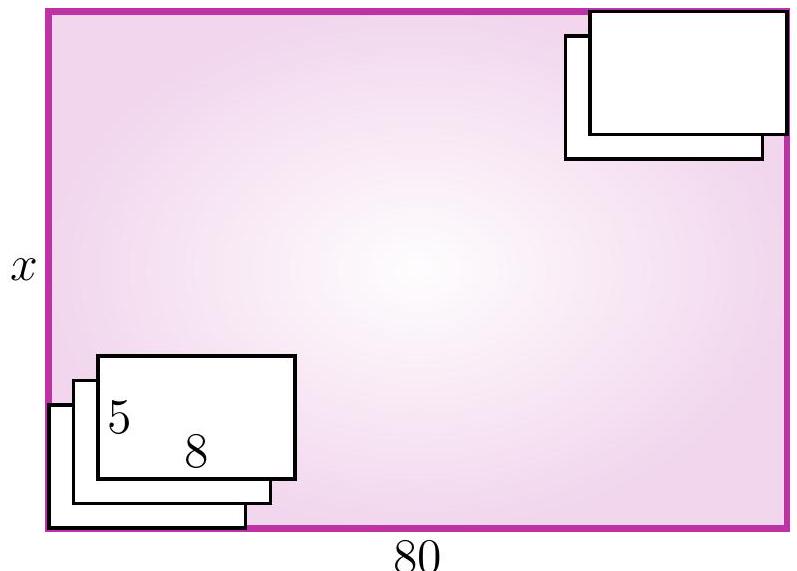
5-6. A rectangular table of size $x$ cm $\times 80$ cm is covered with identical sheets of paper of size 5 cm $\times 8$ cm. The first sheet touches the bottom left corner, and each subsequent sheet is placed one centimeter higher and one centimeter to the right of the previous one. The last sheet touches the top right corner. What is the length $x$ in centimeters?
|
Answer: 77.
Solution I. Let's say we have placed another sheet of paper. Let's look at the height and width of the rectangle for which it will be in the upper right corner.

We will call such a rectangle the current one. Notice that for each new current rectangle, both the width and the height are 1 cm larger than the previous one. Initially, when there was only one sheet of paper, the width of the large rectangle was 8 cm, and at the end, it was 80 cm. Thus, a total of $(80-8): 1=72$ sheets of paper were added. The height of the current rectangle also increased by $72 \cdot 1$ cm, initially it was 5, so $x=5+72=77$.
Solution II. As in the first solution, let's look at the length and width of the current rectangles. Again, notice that for each new current rectangle, both the length and the width are 1 cm larger than the previous one. However, we will draw a different conclusion: specifically, the difference between the width and the height of the current rectangle is always the same! (Such a value that does not change during a certain process is called an invariant.) Since initially the width was 3 cm greater than the height, i.e., $8-5=3$ cm, at the end it should also be 3 cm greater, so the answer is $x=80-3=77$ cm.
|
77
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
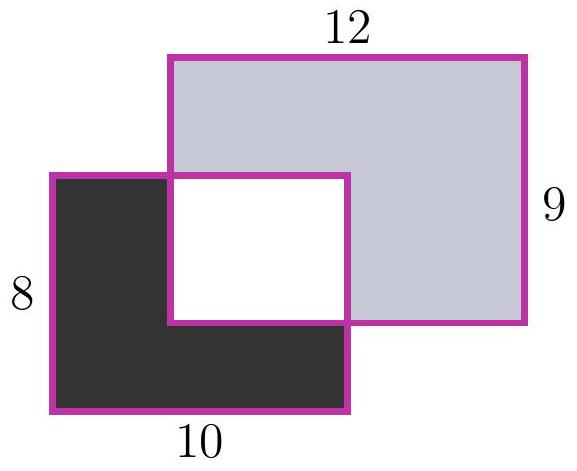
8-1. Two rectangles $8 \times 10$ and $12 \times 9$ are overlaid as shown in the figure. The area of the black part is 37. What is the area of the gray part? If necessary, round the answer to 0.01 or write the answer as a common fraction.
|
Answer: 65.
Solution. The area of the white part is $8 \cdot 10-37=43$, so the area of the gray part is $12 \cdot 9-43=65$
|
65
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
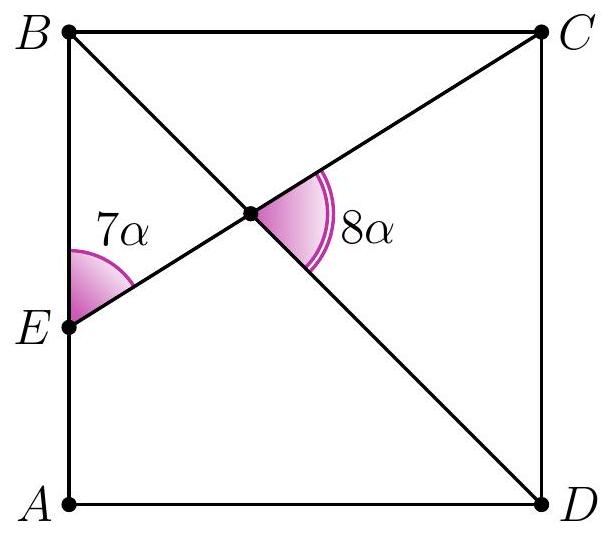
8-2. In square $A B C D$, a segment $C E$ is drawn such that the angles shown in the diagram are $7 \alpha$ and $8 \alpha$. Find the value of angle $\alpha$ in degrees. If necessary, round the answer to 0.01 or write the answer as a common fraction.
|
Answer: $9^{\circ}$.
Solution. In triangle $D F E$, the angles are $7 \alpha, 8 \alpha$ and $45^{\circ}$.
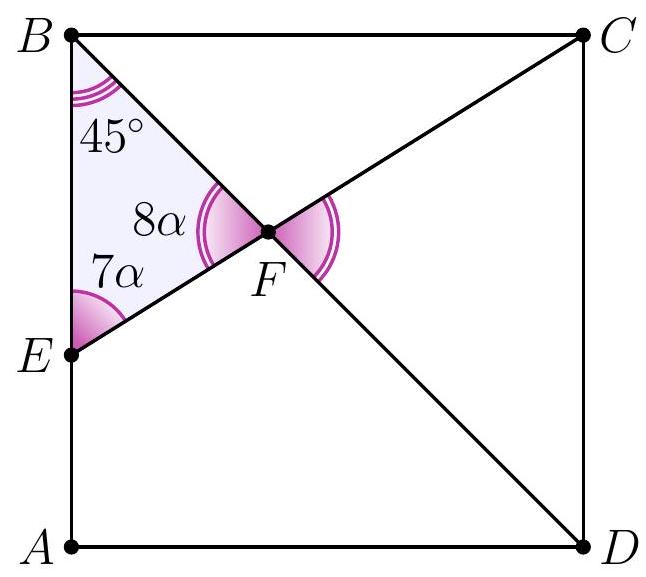
Since the sum of the angles in triangle $D F E$ is $180^{\circ}$, we have $7 \alpha + 8 \alpha + 45^{\circ} = 180^{\circ}$, from which $\alpha = \frac{1}{15} \cdot 135^{\circ} = 9^{\circ}$.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9-1. Segment $P Q$ is divided into several smaller segments. On each of them, a square is constructed (see figure).
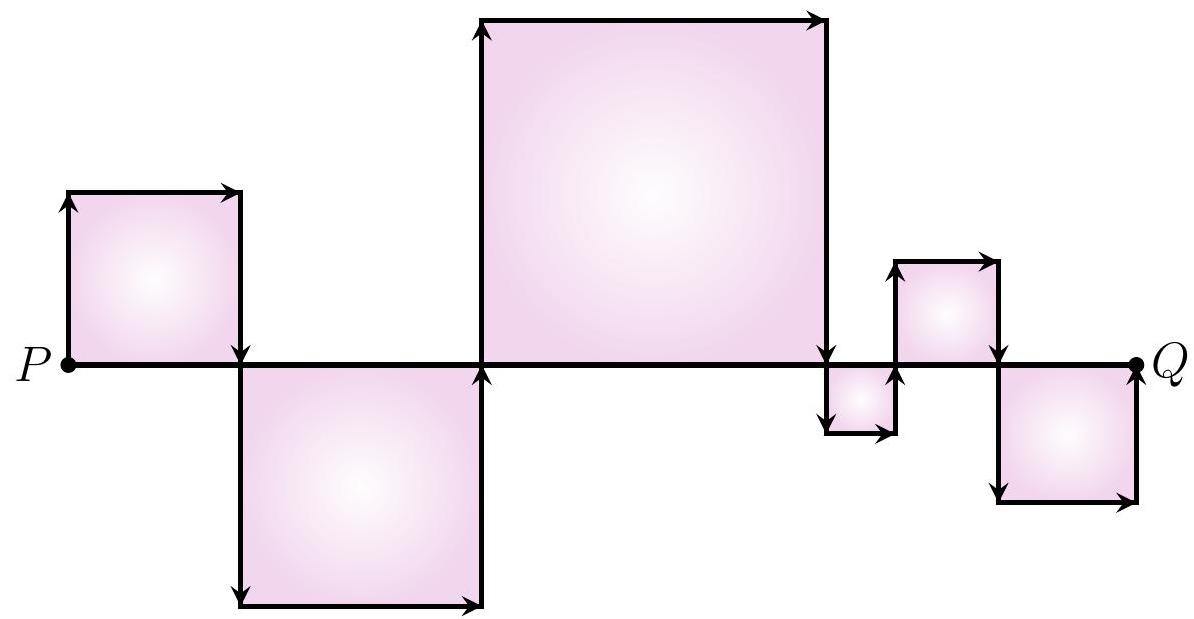
What is the length of the path along the arrows if the length of segment $P Q$ is 73? If necessary, round the answer to 0.01 or write the answer as a common fraction.
|
Answer: 219.
Solution. Note that in each square, instead of going along one side, we go along three sides. Therefore, the length of the path along the arrows is 3 times the length of the path along the segment, hence the answer $73 \cdot 3=219$.
|
219
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10-3. Point $O$ is the center of the circle. What is the value of angle $x$ in degrees?
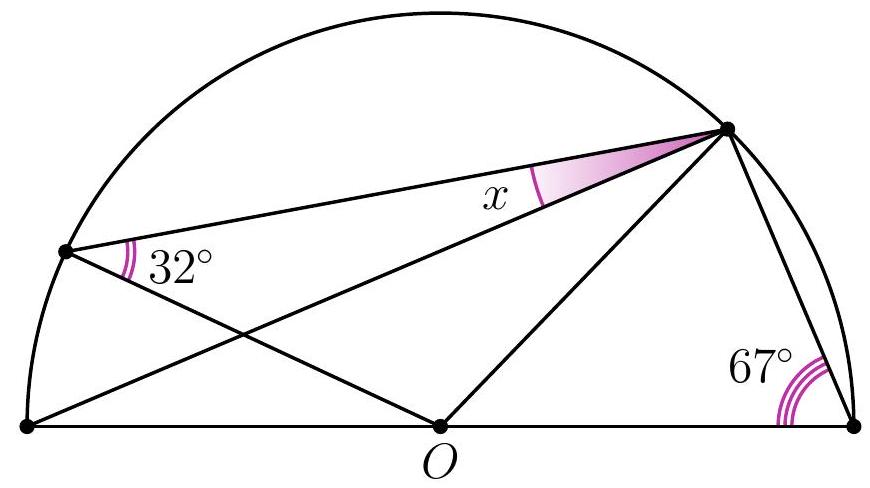
|
Answer: 9.
Solution. Since $O B=O C$, then $\angle B C O=32^{\circ}$. Therefore, to find angle $x$, it is sufficient to find angle $A C O: x=32^{\circ}-\angle A C O$.
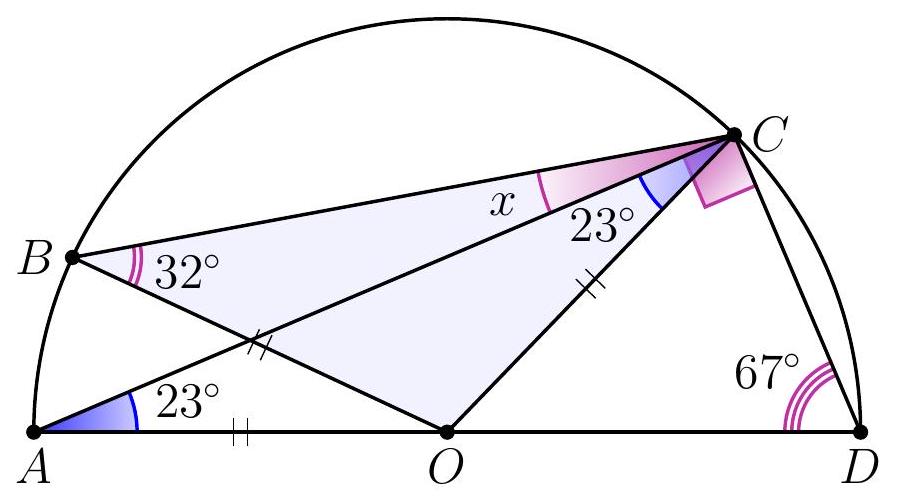
Since $O A=O C$, then $\angle A C O=\angle O A C=90^{\circ}-67^{\circ}=23^{\circ}$ (here we used the fact that triangle $A C D$ is a right triangle: angle $A C D$, which subtends the diameter, is a right angle).
Thus, $x=32^{\circ}-23^{\circ}=9^{\circ}$.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11-3. Point $O$ is the center of the circle. What is the value of angle $x$ in degrees?
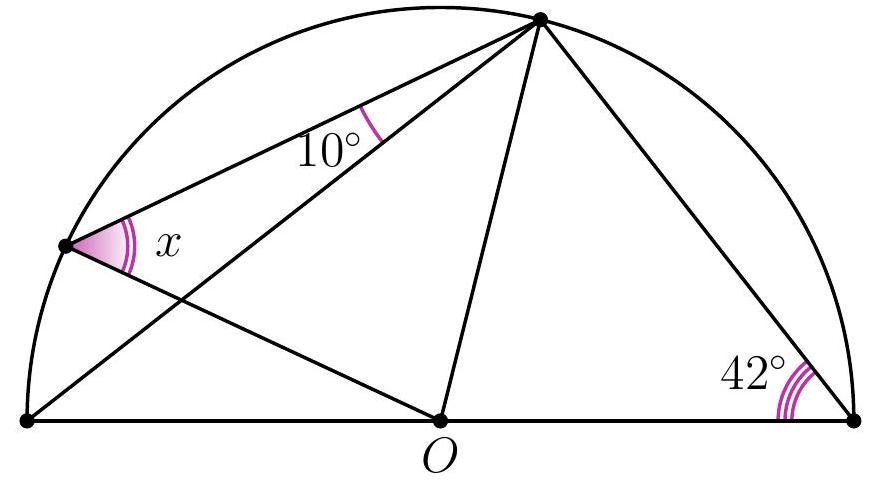
|
Answer: 58.
Solution. Angle $ACD$ is a right angle since it subtends the diameter of the circle.
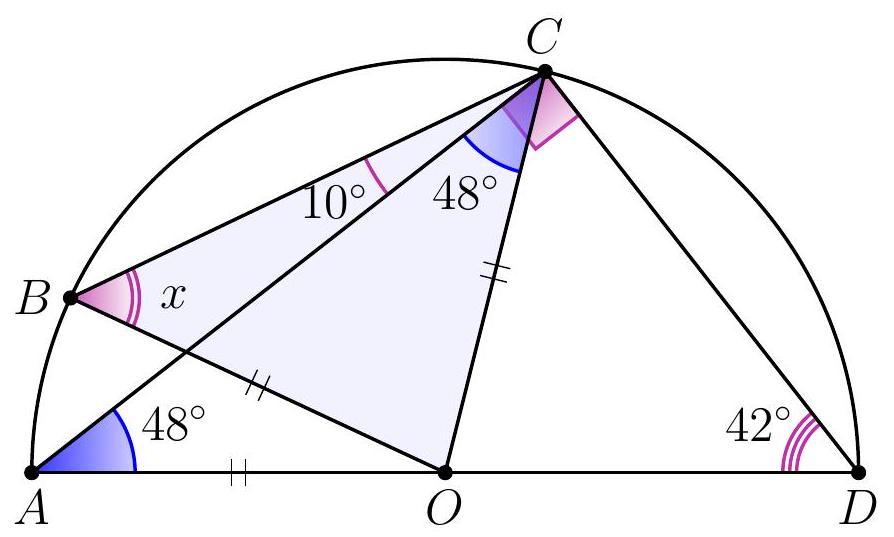
Therefore, $\angle CAD = 90^{\circ} - \angle CDA = 48^{\circ}$. Also, $AO = BO = CO$ as they are radii of the circle, so $\angle OCA = \angle ACO = 48^{\circ}$ and $x = \angle OBC = \angle OCB = 48^{\circ} + 10^{\circ} = 58^{\circ}$.
|
58
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Winnie-the-Pooh stocked up on chocolate bars for the winter: $60\%$ of the total number were "Snickers", $30\%$ were "Mars", and $10\%$ were "Bounty". In the spring, it turned out that the number of "Bounty" bars eaten by Winnie-the-Pooh was $120\%$ of the number of "Mars" bars eaten and $30\%$ of the number of "Snickers" bars eaten. How many chocolate bars did Winnie-the-Pooh stock up for the winter if $2/3$ of all "Bounty" bars were left uneaten and no more than 150 "Snickers" bars were left uneaten.
|
# Solution.
Let there be $3 k$ "Bounty" chocolate bars in total. Then there were $9 k$ "Mars" bars and $18 k$ "Snickers" bars. Since $k$ "Bounty" bars were eaten, $\frac{k}{1.2}=\frac{5 k}{6}$ "Mars" bars were eaten. Therefore, $k$ is divisible by 6. "Snickers" bars eaten were $\frac{k}{0.3}=\frac{10 k}{3}$, and the remaining "Snickers" bars are $18 k-\frac{10 k}{3}=\frac{44 k}{3} \leq 150$. Thus, $k \leq \frac{450}{44}=10 \frac{5}{22}$. Since $k$ is divisible by $6, k=6$. The total number of chocolate bars was $18 k+9 k+3 k=30 k=180$.
Answer: 180.
Remarks for checking. Guessed answer without justification - 0 points.
|
180
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. In a bag, there were cards with numbers from 1 to 20. Vlad drew 6 cards and said that all these cards can be divided into pairs so that the sums of the numbers in each pair are the same. Lena managed to peek at 5 of Vlad's cards: the numbers on them were $2, 4, 9, 17, 19$. What number was on the card that Lena didn't manage to peek at? (It is sufficient to provide one suitable answer.)
|
Answer: 12.
Solution. To calculate the answer, one needs to select four numbers out of the given five such that the sum of two of them equals the sum of the other two. By enumeration, it is not difficult to verify that these numbers are $2,4,17,19(2+19=4+17)$.
Thus, the number on the remaining card is $12(2+19=4+17=9+12)$.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
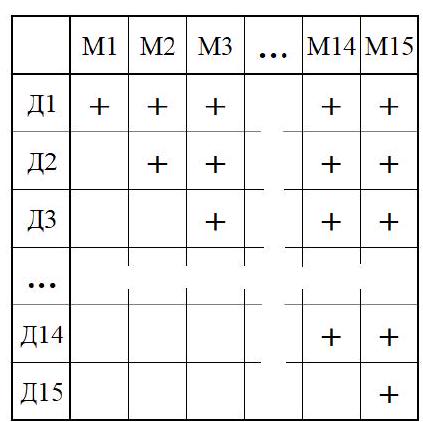
Problem 2. Anya, Borya, Vika, and Gena are on duty at school for 20 days. It is known that exactly three of them are on duty each day. Anya was on duty 15 times, Borya - 14 times, Vika - 18 times. How many times was Gena on duty
|
Answer: 13.
Solution. Since 3 people are on duty in school every day, a total of $3 \cdot 20=60$ people are needed for the duty. Therefore, Gena was on duty $60-15$ (Anya's duties) -14 (Borya's duties) -18 (Vika's duties) $=13$ times.
| Anya | $\checkmark$ | $\checkmark$ | $\checkmark$ | | $\checkmark$ | $\checkmark$ | | $\checkmark$ | $\checkmark$ | | $\checkmark$ | $\checkmark$ | | $\checkmark$ | $\checkmark$ | $\checkmark$ | | $\checkmark$ | $\checkmark$ | $\checkmark$ |
| :--- | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| Borya | $\checkmark$ | | $\checkmark$ | $\checkmark$ | | $\checkmark$ | $\checkmark$ | | $\checkmark$ | $\checkmark$ | | $\checkmark$ | $\checkmark$ | | $\checkmark$ | $\checkmark$ | $\checkmark$ | | $\checkmark$ | $\checkmark$ |
| Vika | $\checkmark$ | $\checkmark$ | $\checkmark$ | $\checkmark$ | $\checkmark$ | $\checkmark$ | $\checkmark$ | $\checkmark$ | $\checkmark$ | $\checkmark$ | $\checkmark$ | $\checkmark$ | $\checkmark$ | $\checkmark$ | | $\checkmark$ | $\checkmark$ | $\checkmark$ | | $\checkmark$ |
| Gena | | $\checkmark$ | | $\checkmark$ | $\checkmark$ | | $\checkmark$ | $\checkmark$ | | $\checkmark$ | $\checkmark$ | | $\checkmark$ | $\checkmark$ | $\checkmark$ | | $\checkmark$ | $\checkmark$ | $\checkmark$ | |
The above table shows an example of a suitable duty schedule.
|
13
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. During the physical education class, the entire class lined up by height (all children have different heights). Dima noticed that the number of people taller than him is four times the number of people shorter than him. And Lёnya noticed that the number of people taller than him is three times less than the number of people shorter than him. How many people are there in the class, if it is known that there are no more than 30 people?
|
Answer: 21.
Solution. Let $x$ be the number of people who are shorter than Dima. Then, the total number of students in the class is $x$ (people who are shorter than Dima) $+4 x$ (people who are taller than Dima) +1 (Dima) $=5 x+1$ (total number of people in the class).
Let $y$ be the number of people who are taller than Lёnya. Then, the total number of students in the class is $y$ (people who are taller than Lёnya) $+3 y$ (people who are shorter than Lёnya) +1 (Lёnya) $=4 y+1$ (total number of people in the class).
Then, if we subtract 1 from the total number of children in the class, the resulting number will be divisible by both 4 and 5. That is, it will be divisible by 20. In the required range, there is only one such number - 20, so there are 21 people in the class.
|
21
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. A row of 11 numbers is written such that the sum of any three consecutive numbers is 18. Additionally, the sum of all the numbers is 64. Find the central number.
|
Answer: 8.
Solution. Number the numbers from left to right from 1 to 11.
Notice that the sum of the five central numbers (from the fourth to the eighth) is 64 (the sum of all numbers) $-2 \cdot 18$ (the sum of the numbers in the first and last triplets) $=28$.
Then the sixth (central) number is 18 (the sum of the fourth, fifth, and sixth numbers) +18 (the sum of the sixth, seventh, and eighth numbers) -28 (the sum of the central five numbers) $=8$.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. Koschei the Deathless has 11 large chests. In some of them lie 8 medium chests. And in some of the medium chests lie 8 small chests. The chests contain nothing else. In total, Koschei has 102 empty chests. How many chests does Koschei have in total?
|
Answer: 115.
Solution. Let $x$ be the number of non-empty chests.
Consider the process when Koschei just started placing chests inside each other. Initially, he had 11 empty large chests. Each time he placed 8 smaller chests into a single empty chest, the total number of empty chests increased by 7 ( -1 old empty chest and +8 new empty chests).
This results in the equation $11+7x=102$. Then $x=13$. The total number of chests Koschei has is 115.
|
115
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7. The dragon has 40 piles of gold coins, and the number of coins in any two of them differs. After the dragon plundered a neighboring city and brought back more gold, the number of coins in each pile increased by either 2, 3, or 4 times. What is the smallest number of different piles of coins that could result?
|
Answer: 14.
Solution. Evaluation. Suppose that no more than 13 piles increased by the same factor. Then no more than 13 piles increased by a factor of 2, no more than 13 by a factor of 3, and no more than 13 by a factor of 4. Thus, the dragon has no more than 39 piles in total. Contradiction.
Therefore, there will be 14 piles where the number of coins increased by the same factor. Since the initial number of coins in these piles was different, the final number of coins will also be different.
Example. Suppose the dragon initially had piles with the following number of coins:
$$
\begin{aligned}
& \frac{12}{2}, \frac{12}{3}, \frac{12}{4}, \frac{120}{2}, \frac{120}{3}, \frac{120}{4}, \frac{1200}{2}, \frac{1200}{3}, \frac{1200}{4}, \ldots \\
& \ldots \frac{12 \overbrace{0 \ldots 0}^{12}}{2}, \frac{12 \overbrace{0 \ldots 0}^{12}}{3}, \frac{12 \overbrace{0 \ldots 0}^{12}}{4}, \frac{12 \overbrace{0 \ldots 0}^{13}}{2} .
\end{aligned}
$$
In each pile with a denominator of 2, he increased the number of coins by a factor of 2, in each pile with a denominator of 3 by a factor of 3, and in each pile with a denominator of 4 by a factor of 4. After this, he will have 14 different
$$
12 \text { zeros } 13 \text { zeros }
$$
values: $12,120,1200$
$\overbrace{0 \ldots 0}, 12 \overbrace{0 \ldots 0}$.
|
14
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8. On one face of a die, one dot is drawn, on another face - two, on the third - three, and so on. Four identical dice are stacked as shown in the figure. How many dots in total are on the 6 faces where the dice touch?
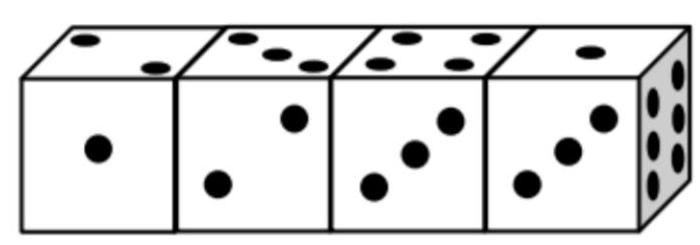
Answer: 20 dots.
|
Solution. Note that on the faces adjacent to the three, there are one, two, four, and six. Therefore, five and three are on opposite faces. Then, adjacent to the one are two, three, five, and six. Therefore, one and four are on opposite faces. From this, two and six are also on opposite faces.
If we look down at the last cube, we will see one, and on the side faces in clockwise order, there will be six, three, two, and five. Then on the left face of the first cube, there should be three dots, and on the right - five.
On the second cube, the side faces have four dots and one dot. On the third cube - six dots and two dots. On the left face of the fourth cube, there are two dots. Then the desired sum is $5+(4+1)+(6+2)+2=20$.
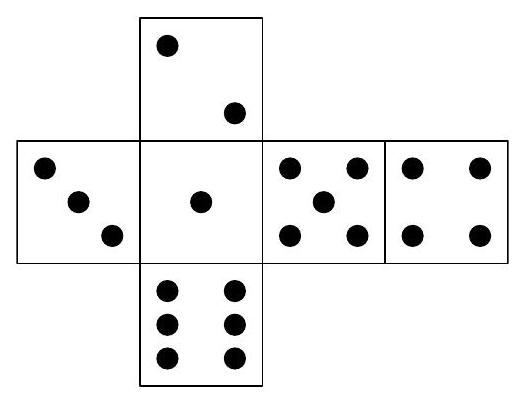
|
20
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. On his birthday, Nikita decided to treat his classmates and took 4 bags of candies to school, each containing the same number of candies. He gave out 20 candies to his classmates, which was more than $60 \%$ but less than $70 \%$ of all the candies he had. How many candies did Nikita have in total?
|
Answer: 32.
Solution. Suppose there were $x$ candies in each bag.
Then $\frac{6}{10}<\frac{20}{4 x}<\frac{7}{10}$. Therefore, $\frac{50}{7}<x<\frac{50}{6}$, i.e., $7<x \leq 8, x=8$. Total candies - 32.
|
32
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. Masha and Sasha take turns (starting with Masha) writing 10 digits on the board from left to right to form a ten-digit number. Moreover, it is not allowed to write two consecutive identical digits. If the resulting number is divisible by 9, then Sasha wins; otherwise, Masha wins. Who will win with correct play from both sides?
|
Answer: Sasha.
Solution. A number is divisible by 9 if the sum of its digits is divisible by 9. Therefore, one of Sasha's possible strategies is to complement each of Masha's digits to 9. That is, if Masha writes 0, then Sasha writes 9; if Masha writes 1, then Sasha writes 8, and so on. Thus, after each pair of moves, the sum of the digits will increase by 9. By the time the entire number is written, it will be equal to $9 \cdot 5=45$.
|
45
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the numerical value of the expression
$$
\frac{1}{x^{2}+1}+\frac{1}{y^{2}+1}+\frac{2}{x y+1}
$$
if it is known that $x$ is not equal to $y$ and the sum of the first two terms is equal to the third.
|
Answer: 2.
Solution. Let's bring the condition to a common denominator
$$
\frac{1}{x^{2}+1}+\frac{1}{y^{2}+1}=\frac{2}{x y+1}
$$
we get
$$
\frac{\left(x^{2}+y^{2}+2\right)(x y+1)-2\left(x^{2}+1\right)\left(y^{2}+1\right)}{\left(x^{2}+1\right)\left(y^{2}+1\right)(x y+1)}=0
$$
expand all brackets in the numerator, combine like terms, we get the equality $(x-y)^{2}(x y-1)=0$. Since $x \neq y$, then $x y=1$. From this, the third term equals 1, and then the entire sum equals 2.
Criteria. Full solution - 7 points. Correctly brought to a common denominator, like terms correctly combined, but without further progress - 1 point. Reasoning of the type "if $x$ is taken this way, and $y$ another way, then something will result" is rated 0 points.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1 Karlson eats three jars of jam and one jar of honey in 25 minutes, while Little Man takes 55 minutes. One jar of jam and three jars of honey Karlson eats in 35 minutes, while Little Man takes 1 hour 25 minutes. How long will it take them to eat six jars of jam together?
|
9.1 20 minutes.
From the condition, it follows that if Karlson eats three jars of jam and one jar of honey, and then immediately eats one jar of jam and three jars of honey, he will spend $25+35=60$ minutes. For Little Man, this time will be 140 minutes. Therefore, Karlson will spend 15 minutes on one jar of jam and one jar of honey, and 10 minutes on two jars of jam, which is $25-15=10$ minutes. For Little Man, this time is 35 minutes and 20 minutes, respectively. In the end, they will eat 6 jars in 20 minutes.
9.2 $a=b=c=1$.
Let's move all the terms to the left side. After transformations, we get $a(a-1)^{2}+b(b-1)^{2}+c(c-1)^{2}=0$. Since $a, b, c$ are positive numbers, on the left we have a sum of non-negative terms. Their sum is zero only if each term is zero. This is possible only when $a=b=c=1$.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. A football team coach loves to experiment with the lineup. During training sessions, he divides 20 available field players into two teams of 10 players each, adds goalkeepers, and arranges a game between the teams. He wants any two field players to end up on different teams at some training session. What is the minimum number of training sessions that must take place for this to happen?
|
# 9.5. 5 Training Sessions.
Note that four training sessions are insufficient. Let's take 10 football players who played on the same team during the first training session. During the second training session, at least five of them will be on the same team again. During the third training session, at least three of these five will be on the same team again. Finally, two of these three will be on the same team during the fourth training session.
However, five training sessions are sufficient. Here is an example of team distribution.
| | Team 1 | Team 2 |
| :--- | :---: | :---: |
| Training 1 | $1-10$ | $11-20$ |
| Training 2 | $1-5,11-15$ | $6-10,16-20$ |
| Training 3 | $1-3,6-7,11-13,16-17$ | $4-5,8-10,14-15,18-20$ |
| Training 4 | $1-2,4,6,8,11-12,14,16,18$ | $3,5,7,9-10,13,15,17,19-20$ |
| Training 5 | $2,4,6,8,10,12,14,16,18,20$ | $1,3,5,7,9,11,13,15,17,19$, |
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. At the first stop, 18 passengers entered an empty bus. Then at each stop, 4 people got off and 6 people got on. How many passengers were in the bus between the fourth and fifth stops?
|
Answer: 24 people.
## Solution.
## Method 1.
After each stop, except the first one, the number of passengers in the bus increases by 2 people. Therefore, from the second to the fourth stop, the number of people increased by 6 people. That is, it became $18+6=24$ people.
Method 2.
From the second to the fourth stop, $3 \cdot 4=12$ people got off, and $3 \cdot 6=18$ people got on. That is, the number of people in the bus became $18-12+18=24$ people.
## Grading Criteria.
- Correct solution - 7 points.
- Incorrect answer, but a correct part of the solution. For example, it is found that the number of passengers increases by 2 after each stop - 2-3 points.
- Only the correct answer - $\mathbf{1}$ point.
|
24
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. A sign engraver makes signs with letters. He engraves identical letters in the same amount of time, and different letters possibly in different times. For two signs “ДОМ МОДЫ” and “ВХОД” together, he spent 50 minutes, and one sign “В ДЫМОХОД” he made in 35 minutes. How long will it take him to make the sign “ВЫХОД”?
|
Answer: 20 minutes.
## Solution.
In the signs FASHION HOUSE ENTRANCE and IN CHIMNEY, we separate the letters that form the word EXIT, then from the first sign, D, O, M, M, O, D will remain, and from the second - D, M, O. Note that FASHION HOUSE ENTRANCE differs from IN CHIMNEY by the letters D, O, M, and in time - by 15 minutes (50-35=15). Therefore, it takes 15 minutes to manufacture the letters D, O, M.
Now we know that when manufacturing IN CHIMNEY, 15 minutes were spent on manufacturing the letters D, M, O, i.e., the remaining 35-15=20 minutes were needed to manufacture the letters V, Y, X, O, D.
## Grading Criteria.
- Correct solution - 7 points.
- Time required for engraving the letters D, O, M found - 2 points.
- Arithmetic error in performing calculations - minus 1 point.
|
20
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. The younger brother takes 25 minutes to reach school, while the older brother takes 15 minutes to walk the same route. How many minutes after the younger brother leaves home will the older brother catch up to him if he leaves 8 minutes later?
|
Answer: in 17 minutes. Solution: Let $S$ be the distance from home to school. Since the younger brother covers this distance in 25 minutes, in 8 minutes he will cover the distance $\frac{8 S}{25}$. After the older brother leaves the house, the rate at which they are closing the distance between them will be $\frac{S}{15}-\frac{S}{25}=\frac{2 S}{75}$. To find the time from this moment until they meet, we divide the distance between them by the rate of closing. We get $\frac{8 S}{25}: \frac{2 S}{75}=12$ (minutes). Taking into account the 5-minute delay, we get the answer of 17 minutes (and since this is less than 25 minutes, the older brother does catch up with the younger one).
|
17
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. Petya tells his neighbor Vova: «In our class, there are 30 people, and there is an interesting situation: any two boys have a different number of girlfriends in the class, and any two girls have a different number of friends among the boys in the class. Can you determine how many boys and how many girls we have in the class?» Vova replies: «You must be mistaken, such a situation is impossible!». a) Is Vova right? b) And how would you answer Petya's question?
|
Answer. a) Vova is wrong; b) 15 boys and 15 girls. Solution. a) To show that Vova is wrong, we will provide an example of a class that meets the conditions of the problem. For a class with 15 girls and 15 boys, we will number them and present a "friendship" table. In the cells of the table, there is a "+", if the corresponding boy and girl are friends. It is easy to see that the table, presented in the figure, meets the conditions of the problem. b) We will show that in the situation described by Petya, the number of boys and girls must be the same. Suppose the opposite and assume, for example, that there are more boys than girls. Then there are at least 16 boys in the class. However, the number of girlfriends each boy can have can take no more than 15 values (from 0 to 14). Therefore, not all boys have a different number of girlfriends. The contradiction proves our
statement.
|
15
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In the USA, the date is typically written as the month number, followed by the day number, and then the year. In Europe, however, the day comes first, followed by the month and the year. How many days in a year cannot be read unambiguously without knowing which format it is written in?
|
2. It is clear that these are the days whose date can be the number of the month, i.e., takes values from 1 to 12. There are such days $12 \cdot 12=144$. However, the days where the number matches the month are unambiguous. There are 12 such days. Therefore, the number of days sought is $144-12=132$.
|
132
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. A traveler arrived on an island inhabited by liars (L) and truth-tellers (P). Each L, when asked a question "How many..?", gives a number that is 2 more or 2 less than the correct answer, while each P answers correctly. The traveler met two residents of the island and asked each how many L and P live on the island. The first answered: "If you don't count me, there are 1001 L and 1002 P," and the second: "If you don't count me, there are 1000 L and 999 P." How many L and P are on the island? Who are the first and second residents of the island?
|
5. I - L, II - P. On the island, there are 1000 L and 1000 P. The answers of the first and second are different, so the option P and P is impossible. The option L and L is also impossible, because the numbers 1001 and 1000 differ by 1, while the answers of the liars regarding the number of L should differ by 4, or coincide. The option I - P, II - L is also impossible, because in this case, 1003 P live on the island, and thus L could not have given the answer 999 P. The only remaining option is I - L, II - P. From the answer of II, we get 1000 L and 1000 P, which corresponds to the answer of I.
|
1000
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.2. Fishermen caught several carp and pike. Each caught as many carp as all the others caught pike. How many fishermen were there if the total number of carp caught was 10 times the number of pike? Justify your answer.
|
# Solution:
Method 1. Each fisherman caught as many carp and pike together as the total number of pike caught. Summing the catches of all fishermen, we get that the total catch of all fishermen (in terms of the number of fish) is equal to the total number of pike caught, multiplied by the number of fishermen. On the other hand, there are 10 times more carp than pike, so the total catch in terms of the number of fish is 11 times the number of pike. Therefore, there are 11 fishermen in total.
Method 2. Let the total number of fishermen be $n$, and the $i$-th fisherman caught $a_{i}$ pike and $b_{i}$ carp $(i=\overline{1, n})$. Then $b_{k}=\left(\sum_{i=1}^{n} a_{i}\right)-a_{k}$ for all $k$. Summing these equalities over $k$, we get
$\sum_{i=1}^{n} b_{i}=n \cdot \sum_{i=1}^{n} a_{i}-\sum_{i=1}^{n} a_{i}=(n-1) \cdot \sum_{i=1}^{n} a_{i}$. But $\sum_{i=1}^{n} b_{i}=10 \cdot \sum_{i=1}^{n} a_{i}$, from which $n-1=10$ and $n=11$.
Answer: 11 fishermen.
Recommendations for checking:
| present in the work | points |
| :--- | :--- |
| Correct and fully justified answer | 7 points |
| A correct approach but an incorrect answer due to arithmetic or algebraic errors | 5 points |
| Correctly formulated but unsolved system of equations, fully describing the problem's conditions | 3 points |
| Only specific cases are considered, for example, when all fishermen caught the same number of pike | 1 point |
| Correct answer without justification or illustrated by a finite number of examples | 0 points |
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. We consider all possible pairs of quadratic equations $x^{2} + p x + q = 0$ and $x^{2} + q x + p = 0$ such that each equation has two distinct roots. Is it true that the expression $\frac{1}{x_{1} x_{3}} + \frac{1}{x_{1} x_{4}} + \frac{1}{x_{2} x_{3}} + \frac{1}{x_{2} x_{4}}$, where the numbers $x_{1}, x_{2}$ are the roots of the first equation, and the numbers $x_{3}, x_{4}$ are the roots of the second, is the same for all such pairs (i.e., does not depend on the numbers $p$ and $q$)? Justify your answer.
|
Solution: According to Vieta's theorem
$$
x_{1} x_{2}=-\left(x_{3}+x_{4}\right)=q \text { and } x_{3} x_{4}=-\left(x_{1}+x_{2}\right)=p
$$
Then
$$
\frac{1}{x_{1} x_{3}}+\frac{1}{x_{1} x_{4}}=\frac{x_{3}+x_{4}}{x_{1} x_{3} x_{4}}=-\frac{q}{p x_{1}}
$$
Similarly
$$
\frac{1}{x_{2} x_{3}}+\frac{1}{x_{2} x_{4}}=-\frac{q}{p x_{2}}
$$
Then
$$
\frac{1}{x_{1} x_{3}}+\frac{1}{x_{1} x_{4}}+\frac{1}{x_{2} x_{3}}+\frac{1}{x_{2} x_{4}}=-\frac{q}{p}\left(\frac{1}{x_{1}}+\frac{1}{x_{2}}\right)=-\frac{q}{p} \cdot \frac{x_{2}+x_{1}}{x_{1} x_{2}}=-\frac{q}{p} \cdot\left(-\frac{p}{q}\right)=1
$$
that is, the same for all pairs of equations.
Note 1: Such pairs of equations exist. The task does not require providing examples of such pairs.
Note 2: The problem can also be solved "head-on," by writing the roots of the equations using the root formula (via discriminants), substituting them into the expression, and performing the necessary transformations. The solution will be somewhat longer, but that's all.
Answer: Correct.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and fully justified answer | 7 points |
| The solution does not include examples of pairs of such equations | points not reduced |
| Roots of the equations are correctly found and substituted into the expression Or Vieta's theorem is correctly written for both equations, but further transformations are incorrect or incomplete | 2 points |
| :--- | :--- |
| The correct answer is illustrated with several examples | 1 point |
| Answer without justification and/or incorrect answer | 0 points |
|
1
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
10.3. In the distant times of stagnation in the Soviet Union, 15 and 20 kopeck coins were in circulation. Schoolboy Valera had a certain amount of money only in such coins. Moreover, the number of 20 kopeck coins was greater than the number of 15 kopeck coins. Valera spent one-fifth of all his money, paying two coins for a movie ticket. He then spent half of the remaining money on lunch, paying with three coins. How many coins of each denomination did Valera have initially? Justify your answer.
|
Solution: One fifth of Valera's capital could be either 30, 35, or 40 kopecks. Then, after buying the ticket, he should have had 120, 140, or 160 kopecks left, and the cost of the lunch was either 60, 70, or 80 kopecks. The maximum value of three coins is 60 kopecks, so the last two scenarios are impossible. Therefore, Valera had lunch for 60 kopecks, paying with three "twenty-kopeck" coins, paid 30 kopecks for the movie ticket (using 2 "fifteen-kopeck" coins), and had 60 kopecks left. This amount could be made up either with 4 coins of 15 kopecks each, or 3 coins of 20 kopecks each. In the first case, it turns out that Valera had 6 "fifteen-kopeck" coins and 3 "twenty-kopeck" coins, which contradicts the condition. The second case leads to the correct answer: 2 coins of 15 kopecks and 6 coins of 20 kopecks.
Answer: 2 coins of 15 kopecks and 6 coins of 20 kopecks.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and fully justified answer | 7 points |
| In the correct solution, there are computational errors (possibly leading to an incorrect answer) | deduct 1 point for each error |
| In the exhaustive solution, exactly one case was not considered | 4 points |
| :--- | :--- |
| In the exhaustive solution, more than one case was not considered | 2 points |
| Correct answer supported by calculations, but without proof of its uniqueness | 1 point |
| Answer without justification and/or incorrect answer | 0 points |
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A mathematician left point A for point B. After some time, a physicist also left point A for point B. Catching up with the mathematician after 20 km, the physicist, without stopping, continued to point B and turned back. They met again 20 km from B. Then each continued in their respective directions. Upon reaching points A and B respectively, they turned and walked towards each other again. How many kilometers from point A will they meet for the third time, if the distance between points A and B is 100 km?
|
# Answer: 45.
Solution. From the first meeting to the second meeting, the mathematician walked a total of 100 - 20 - 20 = 60 km, while the physicist walked -100 - 20 + 20 = 100 km. It is clear from this that the ratio of their speeds is 6:10 or 3:5. From the second to the third meeting, they will walk together 100 + 100 = 200 km, during which the mathematician will walk \(\frac{3}{8}\), and the physicist \(\frac{5}{8}\) of this distance, meaning the mathematician will walk 75 km. Thus, he will first walk the remaining 20 km to point B, and then, turning back, he will walk another 75 - 20 = 55 km. Therefore, he will be 100 - 55 = 45 km from point A.
## Criteria.
If the solution is incorrect - 0 points.
If the system of equations is correctly set up - 3 points.
If there is a computational error - 5 points.
If the solution is correct - 7 points.
|
45
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The city center is a rectangle measuring $5 \times 8$ km, consisting of 40 blocks, each $1 \times 1$ km, with boundaries formed by streets that create 54 intersections. What is the minimum number of police officers needed to be placed at the intersections so that any intersection can be reached by at least one police officer driving no more than 2 km along the city streets?
Answer: 6 police officers.
|
Solution. Evaluation. Consider the intersections on the boundary. There are 26 in total. Each police officer can control no more than 5 intersections (if he is on the boundary, then exactly 5, if he is inside the city, then no more than 3 on each side and no more than 5 in the corner). Therefore, at least 6 police officers are needed.
Example (see fig).
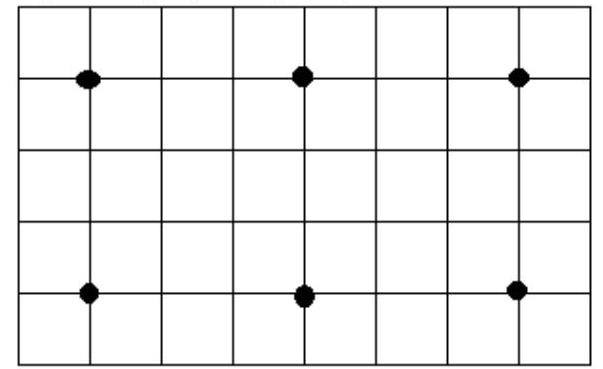
Criteria. If the solution is incorrect - 0 points.
If only an example is constructed - 2 points.
If only the evaluation is proven - 4 points.
If the correct solution (both example and evaluation) - 7 points.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.3. The hunter told a friend that he saw a wolf with a one-meter tail in the forest. That friend told another friend that a wolf with a two-meter tail had been seen in the forest. Passing on the news further, ordinary people doubled the length of the tail, while cowards tripled it. As a result, the 10th channel reported about a wolf with a tail 864 meters long. How many ordinary and how many cowardly people "grew" the wolf's tail? Provide all possible answers and prove that there are no others.
|
Solution: Note that when information is transmitted by ordinary people, the length of the tail is multiplied by 2, and when transmitted by cowardly people, it is multiplied by 3. Therefore, the number of twos in the product equals the number of ordinary people (and the number of threes equals the number of cowardly people) through whom the information has passed. This number does not depend on the order in which the information reached these people. Let's factorize the number 864 into prime factors. We get $864=2^{5} \cdot 3^{3}$. Therefore, the number of ordinary and cowardly people who grew the wolf's tail was 5 and 3, respectively.
Answer: 5 ordinary people and 3 cowardly people.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and justified answer | 7 points |
| Answer is incorrect only due to arithmetic errors | 6 points |
| Correct answer is confirmed by an example showing how the wolf's tail length could have "changed" | 4 points |
| It is justified that the length of the "grown" tail does not depend on the order in which the information was transmitted by ordinary and cowardly people, but there is no solution. | 2 points |
| Correct answer without justification | 1 point |
| Principally incorrect reasoning | 0 points |
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.4. Three pirates were dividing a bag of coins. The first took 3/7 of all the coins; the second took 51 percent of the remainder. After this, the third received 8 fewer coins than the second. How many coins were in the bag? Justify your answer.
|
Solution: The third pirate received $49\%$ of the remainder, which is $2\%$ less than the third. These two percent of the remainder amount to 8 coins, so one percent is
4 coins, and the entire remainder is 400 coins. These 400 coins make up $1-\frac{3}{7}=\frac{4}{7}$ of the total. Therefore, the total number of coins in the bag was $400: \frac{4}{7}=700$.
Answer: 700 coins.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and justified answer | 7 points |
| Answer is incorrect only due to arithmetic errors | 6 points |
| Correctly and justifiedly found the number of coins received by one or two pirates | 4 points |
| Correctly formulated, but not solved (or solved incorrectly) equation (or system of equations) that fully describes the problem | 3 points |
| There is an idea (not brought to a solution) to solve the problem from the "end" | 2 points |
| Correct answer without justification | 1 point |
| Principally incorrect reasoning | 0 points |
|
700
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.5. On cards, all two-digit numbers from 10 to 99 are written (one number per card). All these cards are lying on the table face down. What is the minimum number of cards that need to be flipped to guarantee that at least one of the revealed numbers is divisible by 7? Justify your answer.
|
Solution: There are exactly 13 two-digit numbers divisible by 7 (14 = 7 * 2, 21 = 7 * 3, ..., 98 = 7 * 14). If at least 13 cards are not flipped, it is impossible to exclude the situation where all these numbers remain covered. Therefore, no more than 12 cards can be left in their original position, and the rest must be flipped. Since there are 90 cards in total, at least 90 - 12 = 78 cards should be flipped.
Answer: 78 cards.
Recommendations for checking:
| is in the work | points |
| :--- | :--- |
| Correct and justified answer | 7 points |
| Correctly and justifiedly found the maximum number of cards that can be left unflipped | 5 points |
| Correct reasoning but incorrect answer due to incorrect total number of two-digit numbers found | 4 points |
| Incorrect number of two-digit numbers divisible by 7 found, which may have led to an incorrect answer | 3 points |
| There is an idea (not developed into a solution) to find the number of cards with a number divisible by 7 | 2 points |
| Correct answer without justification | 1 point |
| Fundamentally incorrect reasoning | 0 points |
|
78
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.1. January first of a certain non-leap year fell on a Saturday. And how many Fridays are there in this year?
|
Answer: 52
Solution. In a non-leap year, there are 365 days. The first two days fell on Saturday and Sunday, followed by 51 full weeks ( $51 \cdot 7=357$ days) and 6 more days. In total, there are 52 Fridays.
|
52
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.1. Lisa wrote a quadratic equation. Artem erased its free term, so the equation now looks like $\operatorname{\operatorname {mak}} 2 x^{2}+20 x+\ldots=0$. Lisa doesn't remember what number Artem erased, but she remembers that the equation has exactly one real root. What is this root?
|
# Answer: -5
Solution. A quadratic equation has one root if and only if its discriminant is 0. And if the discriminant is 0, then the root is calculated using the formula $x_{1}=-b /(2 a)=-20 / 4=-5$.
|
-5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.1. Lisa drew graphs of all functions of the form $y=a x+b$, where $a$ and $b$ take all natural values from 1 to 100. How many of these graphs pass through the point $(3,333)$?
|
Answer: 23
Solution. We are looking for such $a$ and $b$ that $333=3a+b$. That is, $b=3(111-a)$. Therefore, $0<111-a \leqslant 33$, $78 \leqslant a$. There are exactly 23 such $a$ and for each of them, $b$ can be uniquely determined.
|
23
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1. The sea includes a bay with more saline water. The salinity of the water in the sea is 120 per mille, in the bay 240 per mille, in the part of the sea not including the bay - 110 per mille. How many times is the volume of water in the sea larger than the volume of water in the bay? The volume of water is considered, including the volume of salt. Per mille - one-thousandth of a number; salinity is determined as the ratio of the volume of salt to the total volume of the mixture.
|
Answer: 13
Solution. Let the volume of salt in the bay be $s_{1}$, and the volume of water $v_{1}$; in the part of the sea not including the bay, the volume of salt is $s_{2}$, and the total volume is $v_{2}$. We have the equations
$$
\frac{s_{1}}{v_{1}}=\frac{240}{1000} ; \quad \frac{s_{2}}{v_{2}}=\frac{110}{1000} ; \quad \frac{s_{1}+s_{2}}{v_{1}+v_{2}}=\frac{120}{1000}
$$
Thus, $120\left(v_{1}+v_{2}\right)=1000\left(s_{1}+s_{2}\right)=240 v_{1}+110 v_{2}$, from which $120 v_{1}=10 v_{2}, 12 v_{1}=v_{2}$. We need to find the ratio $\left(v_{1}+v_{2}\right) / v_{1}$. It equals 13.
|
13
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. A paper rectangle $4 \times 8$ was folded along the diagonal as shown in the figure. What is the area of the triangle that is covered twice?
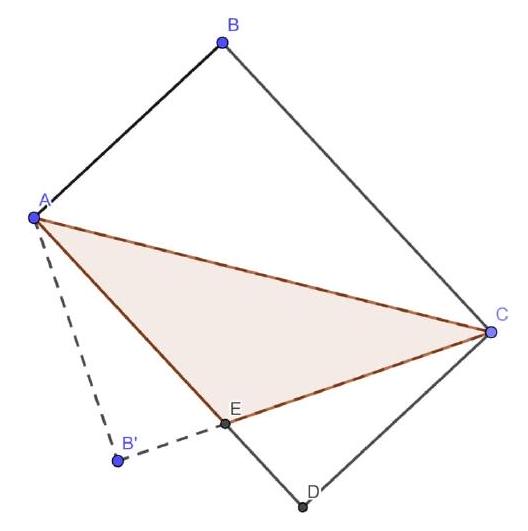
|
Answer: 10.
Solution. By the Pythagorean theorem, $A C=\sqrt{A B^{2}+B C^{2}}=4 \sqrt{5}$. Triangle $A E C$ is isosceles, and if we drop the height $E H$ in it, then triangle $A E H$ will be similar to triangle $A C D$. Therefore, $A H / E H=A D / D C=2 . A H=2 \sqrt{5}$, since the height in an isosceles triangle is also a median. Thus, $E H=\sqrt{5}, S(A E C)=\sqrt{5} \cdot 4 \sqrt{5} / 2=10$.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. In the club, there are 9 people. Every day, some three of them went to the cafe together, while the others did not go to the cafe. After 360 days, it turned out that any two people from the club had been to the cafe together the same number of times. How many times?
|
Answer: 30
Solution. The total number of pairs of people in the circle is $9 \cdot 8 / 2=36$. Over 360 days, the cafe was visited by $360 \cdot 3$ pairs (since three new pairs are added each day). Since all pairs visited the cafe an equal number of times, this number is $360 \cdot 3 / 36=30$.
|
30
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. Real $x, y, z$ are such that $x y + x z + y z + x + y + z = -3, x^{2} + y^{2} + z^{2} = 5$. What is $x + y + z$?
|
Answer: -1
Solution. Add twice the first equation to the second, we get $(x+y+z)^{2}+2(x+y+z)=-1$. Therefore, $(x+y+z+1)^{2}=0, x+y+z=-1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. Of all numbers with the sum of digits equal to 25, find the one whose product of digits is maximal. If there are several such numbers, write the smallest of them in the answer.
|
Answer: 33333334
Solution. Obviously, there is no 0 in the number. If the number contains the digit 1, then it can be removed and one of the remaining digits can be increased by 1, which does not change the sum, but increases the product. If the number contains a digit $x \geqslant 5$, then it can be replaced by the digits 2 and $x-2$, and the product will increase: $2(x-2)>x$ for $x>4$. Finally, if the number contains at least three twos or a two and a four, they can be replaced by two threes. If the number contains at least two fours, they can be replaced by 3, 3, and 2. Thus, in the number with the maximum product, in addition to threes, there can be no more than one four or no more than two twos. This is only possible if the number has 7 threes and either one four or two twos (in both cases, the products are the same). The smallest of the resulting numbers is 33333334.
|
33333334
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1 The number 890 has the property that by changing any of its digits to 1 (increasing or decreasing), you can obtain a number that is a multiple of 11. Find the smallest three-digit number with the same property.
|
Answer: 120.
Solution. Since the last digit of the number must be changed to obtain a number divisible by 11, the required number should differ from it by 1. The smallest three-digit number divisible by 11 is 110. However, the numbers adjacent to it, 109 and 111, do not have the required property. Indeed, if the second digit of the number 109 is changed to 1, the only number that can be obtained is 119, which is not divisible by 11. If the first digit of the number 111 is changed to 1, the only number that can be obtained is 211, which is not divisible by 11.
The next three-digit number divisible by 11 is 121. Consider the number 120. Numbers that are multiples of 11 can be obtained from it according to the condition. The modified numbers 121, 110, 220 are divisible by 11.
Grading criteria.
«+» A complete and justified solution is provided.
«士» A justified solution with the answer 111 is provided, meaning the student considered that the first digit of the number can be zero (resulting in a two-digit number).
«Ғ» Only the correct answer (120 or 111) is provided, meaning it is not justified that this number is the smallest.
«-» The problem is not solved or is solved incorrectly.
|
120
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.5. A $7 \times 7$ checkered board was assembled using three types of figures (see the image), not necessarily all. How many figures, composed of four cells, could have been used?
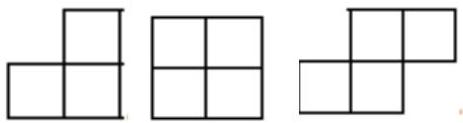
|
Answer: only one.
Solution. We will prove that only one figure consisting of four cells can be used. We will color the cells of the board as shown in Fig. 11.5a: Each of the given figures can cover no more than one shaded cell, therefore, the number of figures must be no less than 16.
Since 16 three-cell figures cover 48 cells, one such figure consisting of four cells must be used. More than one cannot be used.

Indeed, if at least two figures consisting of four cells are used, and the remaining 14 figures are three-cell ones, together they will occupy \(2 \cdot 4 + 14 \cdot 3 = 50\) cells, which exceeds the size of the board.
An example of a board composed of one four-cell figure and fifteen three-cell figures is shown in Fig. 11.56.
There are other examples as well. They can be obtained by highlighting 7 rectangles of size \(3 \times 2\) on the board, each of which can be divided into two three-cell corners, and placing one three-cell and one four-cell figure in the remaining part of the board.
Evaluation criteria.
«+» A complete and justified solution is provided
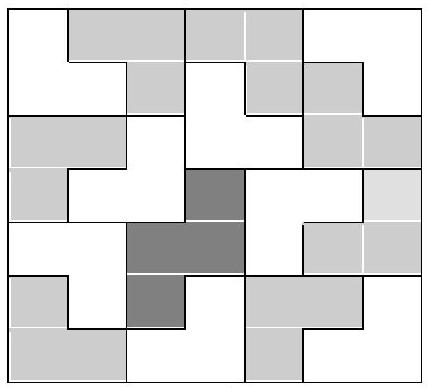
Fig. 11.56 «士» It is proven that there are no fewer than 16 figures and the correct answer is given, but the example is missing
«Ғ» Only the correct answer and the correct example are provided
«-» Only the answer is provided
«-» The problem is not solved or is solved incorrectly
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. All graduates of the mathematics school took the Unified State Exam (USE) in mathematics and physical education. Each student's result in mathematics turned out to be equal to the sum of the results of all other students in physical education. How many graduates are there in the school if the total number of points scored by the students in mathematics was 50 times greater than in physical education?
#
|
# Answer: 51.
## Solution:
Let the total number of graduates be $n$. Denote the total score in mathematics by $M$. This sum is equal to the sum of the physical education scores of all students, counted $(n-1)$ times.
Thus, we have the equation: $M=50 \frac{M}{n-1}$.
From this, the answer is
Instructions for checking:
If the problem is solved with additional assumptions, for example, that everyone scored the same, then give 1 point.
|
51
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. The letters А, Б, К, М, П, У, Ш were encoded with sequences of zeros and ones (each with its own). Then, in the word ПАПАМАМАБАБУШКА, the letters were replaced with their codes. Could the length of the resulting sequence be shorter than 40 characters, if the sequence can be uniquely decoded?
|
Answer: She could.
## Solution:
Here is an example of a code table:
| A | B | K | M | P | U | Sh |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 0 | 110 | 1111 | 100 | 101 | 11100 | 11101 |
The word will look like this: 10101010100010001100110111001110111110 - a total of 38 characters. Decoding is unambiguous. To verify this, start from the left edge. The leftmost can only be the code 101, as no other code starts with the same combination of characters. Next, similarly, as no code starts with a combination of characters that matches any other code.
## Comment:
A uniform code (3 symbols per letter) gives 45 characters. Therefore, it is necessary to use codes of variable length for different letters. The more frequently a letter appears, the shorter its code should be. This consideration can help with verification. Be careful.
Participants can justify the unambiguousness of decoding not by sequentially examining the code sequence (from left to right), but by referring to a correct fact about such codes. The given code is an example of a prefix code - the code of any letter is not the beginning of the code of any other letter (Fano's condition), and for it, the theorem of unambiguous decoding is true. A reference to the corresponding theorem can be counted as justification (naturally, provided that it is correctly formulated).
## Instructions for Checking:
Score - either 0 if the answer is incorrect or the code table does not give the required result, or 4 points if the codes are correct but there is no justification for the unambiguousness of decoding, or 7 points.
|
38
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.2. A travel agency ran a promotion: "Buy a trip to Egypt, bring four friends who also buy a trip, and get the cost of your trip back." During the promotion, 13 customers came on their own, and the rest were brought by friends. Some of them brought exactly four new customers, while the other 100 did not bring anyone. How many tourists went to the Land of Pyramids for free?
|
Answer: 29.
Let each of the $x$ potential "lucky ones" bring 4 friends. Then the number of "brought" customers is $4 x$, and 13 came on their own, so the total number of tourists was $13+4 x$.
On the other hand, $x$ people brought new customers, while 100 people did not, so the total number of tourists was $x+100$.
We get the equation: $13+4 x=x+100$, from which $x=29$.
+ complete justified solution
$\pm$ the equation is correctly formulated and the correct answer is obtained, but there are no explanations
a arithmetic error is made in the solution
- the equation is incorrectly formulated
- only the answer is provided
|
29
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Papa always picked up Misha from kindergarten at the same time and in the same car. But today, after firmly establishing that there would be pea porridge for dinner, Misha resolutely left the kindergarten and set off down the road to meet Papa. Having walked 5 km, Misha met Papa, got into the car, and they arrived home 10 minutes earlier than usual. At what speed does Misha's Papa drive?
|
3. Speed: 60 km/h (or 1 km/min). Today, Misha and his dad saved 10 minutes that were previously spent driving 10 km (from the meeting point to the kindergarten and back). This means that in 1 minute, Misha's dad drives 1 km, i.e., his speed is 60 km/h.
Criteria: Correct reasoning and correct answer - 7 points; only answer - 0 points.
|
60
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. How many natural numbers greater than one exist, the product of which with their smallest prime divisor does not exceed 100?
|
Answer: 33.
Sketch of the solution. The smallest prime divisor can be 2. These are the numbers: $2, 4, \ldots, 50$ (25 numbers). The smallest prime divisor can be 3. These are the numbers: 3, 9, 15, 21, 27, 33 (6 numbers). The smallest prime divisor can be 5. This number: 5 (1 number). The smallest prime divisor can be 7. This number: 7 (1 number). Since $11 \times 11=121>100$, there are no other prime divisors with this property. Total numbers: $25+5+1+1=33$.
Criteria. Correct answer only: 1 point.
|
33
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Every week, listeners choose the ten most popular songs via SMS. It is known that 1) the same set of songs in the same order is never chosen twice in a row; 2) a song that has once dropped in the ranking will not rise again in the future. What is the maximum number of weeks that the same 10 songs can remain in the ranking?
|
Answer: 46 weeks.
Sketch of the solution. Suppose that for two consecutive weeks, the same set of 10 songs was on the list. Since the order of the songs is different, at least one song in the list has moved up in the ranking, and at least one has moved down. Since a song, once it has moved down, does not move up in the ranking, let's count the total number of possible rises. The last song in the initial list could rise no more than 9 times, the second-to-last no more than 8 times, and so on. Thus, there are no more than $9+8+\ldots+2+1=45$ rises. Therefore, the list can stay in the ranking for no more than 46 weeks.
It remains to provide the necessary example. First, the song that was in first place drops 9 weeks to the last place, then the second song drops 8 weeks. The third song in the initial list drops 7 weeks, and so on.
|
46
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A student's income comes from three sources: scholarship, temporary part-time work, and parental support. If the government doubles the scholarship, the income will increase by $5 \%$. If the time spent on part-time work is doubled, the income will increase by $15 \%$. By what percentage will the student's income increase if his father and mother send twice as much money?
|
Solution. Let $\mathrm{S}$ be the student's monthly income, $a, b$ and $c$ be the amounts of the scholarship, part-time job, and parental support, respectively (expressed, for example, in rubles). Clearly, $S=a+b+c$. Then, according to the conditions, $2 a+b+c=1.05 S$ and $a+2 b+c=1.15 S$. From the first equation, $a=0.05 S$, and from the second, $b=0.15 S$, then $c=S-a-b=0.8 S, a+b+2 c=1.8 S$, which means the student's income will increase by $80 \%$. Answer: $80 \%$.
|
80
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In the basket, there are fruits (no less than five). If you randomly pick three fruits, there will definitely be an apple among them. If you randomly pick four fruits, there will definitely be a pear among them. What fruits can be picked and in what quantities if you randomly pick five fruits?
|
Solution. From the condition of the problem, it follows that the "non-apples" in the box are no more than two fruits (otherwise, you could pull out 3 fruits, none of which would be apples). Similarly, "non-pears" are no more than three fruits (otherwise, you could pull out 4 fruits, none of which would be pears). Thus, there are exactly 5 fruits in the box: three apples and two pears. These are the ones that will be pulled out. Answer: three apples and two pears.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Solve the equation: $\cos ^{4}\left(\sqrt{\frac{\pi^{2}}{4}-|x|}\right)+\sin ^{4}\left(\sqrt{\frac{\pi^{2}}{4}-|x|}\right)=\sin ^{-2}\left(\sqrt{\frac{\pi^{2}}{4}-|x|}\right)$.
|
# Solution.
Let's make the substitution $t=\left(\sqrt{\frac{\pi^{2}}{4}-|x|}\right)$. Clearly, $0<t \leq \frac{\pi}{2}$.
$\cos ^{4} t+\sin ^{4} t=\sin ^{-2} t$.
$\cos ^{4} t+\sin ^{4} t=\left(\cos ^{2} t+\sin ^{2} t\right)^{2}-2 \sin ^{2} t \cdot \cos ^{2} t=1-2 \sin ^{2} t \cdot \cos ^{2} t \leq 1 . \frac{1}{\sin ^{2} t} \geq 1$.
Equality is possible only if $\cos ^{4} t+\sin ^{4} t=1$ and $\sin ^{-2} t=1$ simultaneously. This is possible only when $\sin ^{2} t=1$.
Considering that $0<t \leq \frac{\pi}{2}, t=\frac{\pi}{2}$. Then $x=0$.
## Answer: 0
## Recommendations for checking.
The answer $x=0$ is given, but it is not proven that there are no other roots - 0 points.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Find the height of the pyramid if, by cutting it only along the lateral edges and unfolding the lateral faces onto the plane of the base, outside of it, you get a square with a side of 18. If it is impossible to get such a square, explain why.
#
|
# Solution:
The figure shows such a net. If we flip the pyramid and place it on the face $A B C$, it is easy to calculate the volume of the pyramid $V=\frac{1}{3} \cdot \frac{1}{2} \cdot 9 \cdot 9 \cdot 18=3^{5}$. We determine the area of the base $B D C$ as the difference between the area of the square and the areas of three triangles. $18^{2}-\frac{1}{2}(9 \cdot 9+9 \cdot 18+9 \cdot 18)=\frac{3^{5}}{2}$
We determine the volume of the pyramid in two ways. $V=\frac{1}{3} H \cdot \frac{3^{5}}{2}=3^{5}$, where H is the height of the pyramid we are looking for. From the equality, we find that $H=6$.
## Answer: 6
## Recommendations for checking.
The net of the pyramid is correctly drawn - 4 points.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. In each cell of a table consisting of 10 columns and $n$ rows, a digit is written. It is known that for any row $A$ and any two columns, there exists a row that differs from $A$ exactly in these two columns. Prove that $n \geqslant 512$.
(P. Karasev)
|
10.1. Let $R_{0}$ be the first row of the table. Consider any set of an even number of columns and number them from left to right: $C_{1}, \ldots, C_{2 m}$. Then there is a row $R_{1}$ that differs from $R_{0}$ exactly in columns $C_{1}$ and $C_{2}$; further, there is a row $R_{2}$ that differs from $R_{1}$ exactly in columns $C_{3}$ and $C_{4} ; \ldots ;$ finally, there is a row $R_{m}$ that differs from $R_{m-1}$ exactly in columns $C_{2 m-1}$ and $C_{2 m}$ (if $m=0$, then $R_{m}=R_{0}$). Thus, the row $R_{m}$ differs from $R_{0}$ exactly in columns $C_{1}, C_{2}, \ldots, C_{2 m}$. Therefore, the rows $R_{m}$, constructed from different sets of columns, are different. Since the number of sets of an even number of columns is $2^{10} / 2=512$, the number of rows in the table is at least 512.
Remark. The table can have exactly 512 rows - for example, if its rows contain all 512 sequences of 10 zeros and ones, among which there is an even number of zeros.
|
512
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
10.2. On the board, nine quadratic trinomials are written: $x^{2}+a_{1} x+b_{1}, x^{2}+a_{2} x+b_{2}, \ldots, x^{2}+a_{9} x+b_{9}$. It is known that the sequences $a_{1}, a_{2}, \ldots, a_{9}$ and $b_{1}, b_{2}, \ldots, b_{9}$ are arithmetic progressions. It turned out that the sum of all nine trinomials has at least one root. What is the maximum number of the original trinomials that can have no roots?
(I. Bogdanov)
|
10.2. Answer. 4.
Let $P_{i}(x)=x^{2}+a_{i} x+b_{i}, P(x)=P_{1}(x)+\ldots+P_{9}(x)$. Notice that $P_{i}(x)+P_{10-i}(x)=2 x^{2}+\left(a_{i}+a_{10-i}\right) x+\left(b_{i}+b_{10-i}\right)=$ $=2 P_{5}(x)$. Therefore, $P(x)=9 P_{5}(x)$, and the condition is equivalent to $P_{5}(x)$ having at least one root.
Let $x_{0}$ be any of its roots. Then $P_{i}\left(x_{0}\right)+P_{10-i}\left(x_{0}\right)=2 P_{5}\left(x_{0}\right)=0$, which means that either $P_{i}\left(x_{0}\right) \leqslant 0$ or $P_{10-i}\left(x_{0}\right) \leqslant 0$. Since the leading coefficients of the quadratic polynomials are positive, this implies that in each of the pairs $(P_{1}, P_{9})$, $\left(P_{2}, P_{8}\right),\left(P_{3}, P_{7}\right),\left(P_{4}, P_{6}\right)$, at least one of the polynomials has a root. Therefore, there are at least five polynomials that have at least one root. Hence, there are no more than four polynomials without roots.
It remains to provide an example where exactly five polynomials (one of them being $-P_{5}$) have at least one root. For example, the polynomials $x^{2}-4, x^{2}-3, x^{2}-2, \ldots, x^{2}+4$ will do.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Write the number 2021 using each of the digits from 0 to 9 exactly once, along with parentheses and arithmetic operations. (Parentheses and arithmetic operations can be used in any quantity. "Sticking" digits together to form a single number is allowed)
|
For example, $43 \cdot (8 \cdot 5 + 7) + 0 \cdot 1 \cdot 2 \cdot 6 \cdot 9 = 2021$.
|
2021
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Anya has a chocolate bar of size 5 x 6 squares. It contains 6 squares, forming a $2 \times 3$ rectangle, in which there are nuts (the rectangle can be positioned either vertically or horizontally). Anya does not know exactly where the nuts are. She wants to eat the smallest number of squares, but in such a way that at least one of them contains nuts. How many squares does she need to eat? Show which squares she should eat and prove that a smaller number is not sufficient.
|
2. Answer: 5.
Solution. An example of which slices to eat.
Evaluation. Let's number the slices as shown in the figure.
| 1 | 1 | 2 | 2 | 3 | 3 |
| :--- | :--- | :--- | :--- | :--- | :--- |
| 1 | 1 | 2 | 2 | 3 | 3 |
| 1 | 1 | 2 | 2 | 3 | 3 |
| 4 | 4 | 4 | 5 | 5 | 5 |
| 4 | 4 | 4 | 5 | 5 | 5 |
Note that we need to eat at least one slice with each number, otherwise the nuts could be in all the slices marked with the number we did not touch.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A mathematician and a physicist started running on a running track towards the finish line at the same time. After finishing, the mathematician said: "If I had run twice as fast, I would have beaten the physicist by 12 seconds." And after finishing, the physicist said: "If I had run twice as fast, I would have beaten the mathematician by 36 seconds." By how many seconds did the winner beat the second participant?
|
# Answer: 16.
Solution: Let the time it took the mathematician to run the entire distance be $2 x$ seconds, and the time it took the physicist be $2 y$ seconds. Then, under the condition that the mathematician ran twice as fast, we get $2 y-x=12$. And from the condition that the physicist ran twice as fast, we get $2 x-y=36$. From this, we get $x+y=48$. Then $3 x$ $=84, x=28, y=20$. Therefore, $2 x-2 y=16$.
Criteria. If the solution is incorrect - 0 points.
Only the correct answer - 0 points.
If the system of equations is correctly derived - 3 points.
If there is a computational error - 5 points.
If the solution is correct - 7 points.
|
16
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. On the island, there live 7 natives who know mathematics and physics, 6 natives who know physics and chemistry, 3 natives who know chemistry and mathematics, and 4 natives who know physics and biology. In how many ways can a team of three people be formed who together know at least three subjects out of the four? The four subjects are: mathematics, physics, chemistry, and biology.
#
|
# Answer: 1080.
## Solution.
Let's choose three people. If this trio includes representatives of at least two different groups of aborigines, then together they know no fewer than three subjects.
If this trio includes representatives of only one group, then together they know only two subjects.
Therefore, we will find the number of all possible trios and subtract from it the number of trios from representatives of one group. In total, there are $7+6+3+4=20$.
The first person can be chosen in 20 ways, the second in 19 ways, and the third in 18 ways. In total, by the multiplication rule, $20 \times 19 \times 18$. However, the chosen aborigines can be enumerated differently. The first can be appointed in 3 ways, the second in 2 ways, and the third in 1 way. In total, 6 ways of enumeration.
By the multiplication rule, $3 \times 2 \times 1=6$. Therefore, due to the enumeration of aborigines, we get 6 identical teams. Thus, the total number of trios is $(20 \times 19 \times 18): 6=20 \times 19 \times 3=1140$.
The number of trios from representatives of the first group will be ( $7 \times 6 \times 5$ ) : $6=35$.
The number of trios from representatives of the second group will be ( $6 \times 5 \times 4$ ): $6=20$.
The number of trios from representatives of the third group will be ( $3 \times 2 \times 1$ ): $6=1$.
The number of trios from representatives of the fourth group will be ( $4 \times 3 \times 2$ ): $6=4$.
Then the number of teams we need will be $1140-(35+20+1+4)=1080$.
Criteria. If the solution is incorrect - 0 points.
Only the correct answer, without justification - 1 point.
Only the number of all possible trios from representatives of two groups is found - 3 points.
Only the number of all possible trios from representatives of one group is found - 3 points.
The solution is completed with a computational error - 5 points. If the solution is correct - 7 points.
|
1080
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Islandland consists of ten islands, some of which are connected by two-way air routes. If you choose any 9 islands, you can fly around them one by one and return to the starting island at the end. Find the minimum number of air routes that can exist in this country.
|
Answer: 15 airlines.
Solution. Evaluation. Let islands $A$ and $B$ be connected by an airline. If we choose 9 islands for the tour, excluding $A$, then a circular path passes through $B$, meaning $B$ is connected by airlines to at least two other islands. Thus, at least three airlines depart from $B$, and a similar statement holds for each island. Therefore, there are at least $\frac{10 \cdot 3}{2}=15$ airlines.
Example with 15 airlines - placing the islands at the vertices of a pentagonal prism. Denote the vertices of the prism as $A B C D E A_{1} B_{1} C_{1} D_{1} E_{1}$ and provide an example of a cycle that forms when one city is removed (for example, $E_{1}$, since all cities are equal): $A-A_{1}-$ $B_{1}-B-C-C_{1}-D_{1}-D-E-A$. The cycle is constructed, meaning this configuration satisfies the problem's condition.
Criteria. If the solution is incorrect - 0 points.
Only the correct answer - 0 points.
If there is only a correct example without justification - 2 points.
If there is only a correct example with justification - 3 points.
If there is only a correct evaluation - 4 points.
If the solution is correct - 7 points.
|
15
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.5. A large rectangle consists of three identical squares and three identical small rectangles. The perimeter of the square is 24, and the perimeter of the small rectangle is 16. What is the perimeter of the large rectangle?
The perimeter of a figure is the sum of the lengths of all its sides.
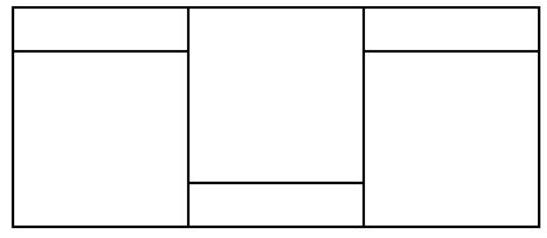
|
Answer: 52.
Solution. All sides of a square are equal, and its perimeter is 24, so each side is $24: 4=6$. The perimeter of the rectangle is 16, and its two largest sides are each 6, so the two smallest sides are each $(16-6 \cdot 2): 2=2$. Then the entire large rectangle has dimensions $8 \times 18$, and its perimeter is $2 \cdot(8+18)=$ 52.
|
52
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.1. The set includes 8 weights: 5 identical round, 2 identical triangular, and one rectangular weight weighing 90 grams.
It is known that 1 round and 1 triangular weight balance 3 round weights. Additionally, 4 round weights and 1 triangular weight balance 1 triangular, 1 round, and 1 rectangular weight.
How much does the triangular weight weigh?
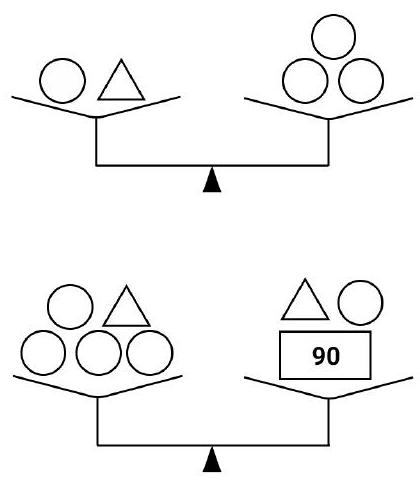
|
Answer: 60.
Solution. From the first weighing, it follows that 1 triangular weight balances 2 round weights.
From the second weighing, it follows that 3 round weights balance 1 rectangular weight, which weighs 90 grams. Therefore, a round weight weighs $90: 3=30$ grams, and a triangular weight weighs $30 \cdot 2=60$ grams.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.2. A jeweler has six boxes: two contain diamonds, two contain emeralds, and two contain rubies. On each box, it is written how many precious stones are inside.
It is known that the total number of rubies is 15 more than the total number of diamonds. How many emeralds are there in total in the boxes?

#
|
# Answer: 12.
Solution. The total number of rubies is no more than $13+8=21$, and the number of diamonds is no less than $2+4=6$. According to the condition, their quantities differ by 15. This is only possible if the rubies are in the boxes with 13 and 8 stones, and the diamonds are in the boxes with 2 and 4 stones. Then the emeralds are in the two remaining boxes, and there are a total of $5+7=12$.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.4. Seven boxes are arranged in a circle, each containing several coins. The diagram shows how many coins are in each box.
In one move, it is allowed to move one coin to a neighboring box. What is the minimum number of moves required to equalize the number of coins in all the boxes?
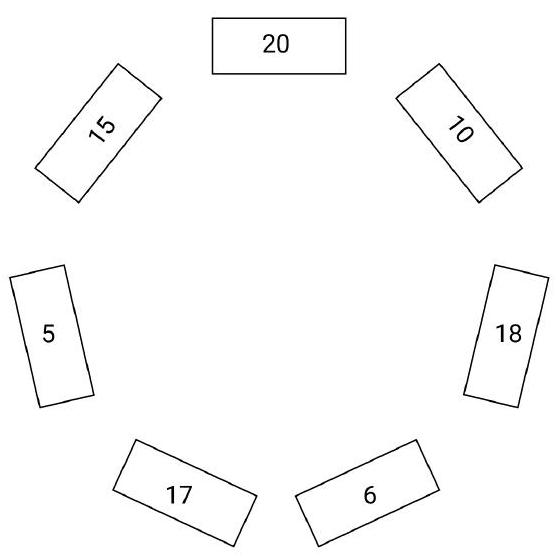
|
Answer: 22.
Solution. Note that there are a total of 91 coins, so after all moves, each box should have exactly 13 coins. At least 7 coins need to be moved from the box with 20 coins. Now consider the boxes adjacent to the box with 20 coins. Initially, they have a total of 25 coins, and at least 7 more coins will be transferred from the box with 20 coins. In the end, these two boxes should have a total of 26 coins, so at least \(25 + 7 - 26 = 6\) coins need to be moved from these boxes. Next, consider the boxes with 17 and 18 coins, from which at least 4 and 5 coins need to be moved, respectively. In total, there should be at least \(7 + 6 + 4 + 5 = 22\) moves.
Let's provide an example of how to equalize all the boxes in exactly 22 moves. From the box with 20 coins, we move 3 coins to the box with 10 (which then becomes 13), and 4 coins to the box with 15 (which then becomes 19). From the box that now has 19 coins, we move 6 coins to the box with 5 coins (which then becomes 11). From the box with 17 coins, we move 2 coins to the box with 11, and 2 coins to the box with 6 (which then becomes 8). Finally, we move 5 coins from the box with 18 coins to the box with 8 coins. In the end, each box has exactly 13 coins. It is easy to verify that exactly 22 moves were made.
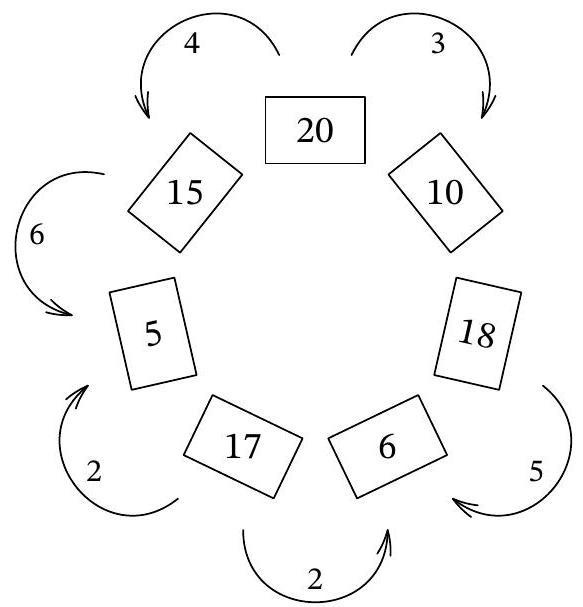
|
22
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.4. Given a square $A B C D$. Point $L$ is on side $C D$ and point $K$ is on the extension of side $D A$ beyond point $A$ such that $\angle K B L=90^{\circ}$. Find the length of segment $L D$, if $K D=19$ and $C L=6$.

|
Answer: 7.
Solution. Since $A B C D$ is a square, then $A B=B C=C D=A D$.

Fig. 1: to the solution of problem 8.4
Notice that $\angle A B K=\angle C B L$, since they both complement $\angle A B L$ to $90^{\circ}$. Then the right triangles $A B K$ and $C B L$ are equal by the acute angle and the leg $A B=B C$ (Fig. 1). Therefore, $A K=C L=6$. Then
$$
L D=C D-C L=A D-C L=(K D-A K)-C L=K D-2 \cdot C L=19-2 \cdot 6=7
$$
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.5. There are 7 completely identical cubes, each of which has 1 dot marked on one face, 2 dots on another, ..., and 6 dots on the sixth face. Moreover, on any two opposite faces, the total number of dots is 7.
These 7 cubes were used to form the figure shown in the diagram, such that on each pair of glued faces, the same number of dots is marked. All dots were erased from all faces except nine, as shown in the diagram. What is the total number of dots that were initially marked on the surface of the figure?
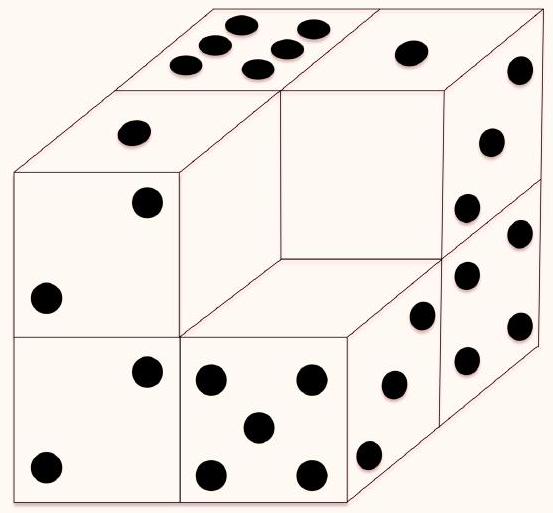
|
Answer: 75.
Solution. There are 9 ways to cut off a "brick" consisting of two $1 \times 1 \times 1$ cubes from our figure. In each such "brick," there are two opposite faces $1 \times 1$, the distance between which is 2. Let's correspond these two faces to each other.
Consider one such pair of faces: on one of them, the dots were not erased, while on the other, they were erased. It is not difficult to understand that originally there were the same number of dots on these faces.
Let's calculate the total number of dots that were originally on all 9 pairs of faces. We get
$$
2 \cdot(1+1+6+2+2+5+3+3+4)=54
$$
There are 6 faces $1 \times 1$ left, about which we still know nothing. However, it can be noticed that they are divided into pairs according to the following principle: in one pair, there will be faces from one $1 \times 1 \times 1$ cube. In each such pair, the sum of the numbers was 7. Then we get that the number of dots on the surface of the figure originally was
$$
54+3 \cdot 7=75
$$
|
75
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.7. For quadrilateral $A B C D$, it is known that $\angle B A C=\angle C A D=60^{\circ}, A B+A D=$ $A C$. It is also known that $\angle A C D=23^{\circ}$. How many degrees does the angle $A B C$ measure?
|
Answer: 83.
Solution. Mark a point $K$ on the ray $AB$ such that $AK = AC$. Then the triangle $KAC$ is equilateral; in particular, $\angle AKC = 60^{\circ}$ and $KC = AC$. At the same time, $BK = AK - AB = AC - AB = AD$. This means that triangles $BKC$ and $DAC$ are equal by two sides and the angle $60^{\circ}$ between them (Fig. 2).
It remains to note that the angle $\angle ABC$ - the exterior angle of triangle $BKC$ - is equal to the exterior angle at vertex $D$ of triangle $DAC$, which is calculated as the sum of two interior angles: $60^{\circ} + 23^{\circ} = 83^{\circ}$.
|
83
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.5. On the base $AC$ of isosceles triangle $ABC (AB = BC)$, a point $M$ is marked. It is known that $AM = 7, MB = 3, \angle BMC = 60^\circ$. Find the length of segment $AC$.
|
Answer: 17.
Fig. 3: to the solution of problem 9.5
Solution. In the isosceles triangle \(ABC\), draw the height and median \(BH\) (Fig. 3). Note that in the right triangle \(BHM\), the angle at vertex \(B\) is \(30^\circ\), so \(HM = \frac{1}{2} BM = 1.5\). Then \(AC = 2AH = 2(AM + MH) = 2 \cdot (7 + 1.5) = 17\).
Fig. 4: to the solution of problem 9.5
Another solution. Mark a point \(K\) on \(MC\) such that \(\angle BKM = 60^\circ\) (Fig. 4; such a point lies exactly on the segment \(MC\) because \(\angle BCM = \angle BAM = \angle BMC - \angle ABM < 60^\circ\)). Note that in triangle \(BMK\), two angles are \(60^\circ\), so it is equilateral and \(BK = MK = BM = 3\). Also note that triangles \(ABM\) and \(CBK\) are equal because \(BC = AB\), \(\angle A = \angle C\), \(\angle AMB = \angle CKB = 120^\circ\) (therefore, \(\angle ABM = \angle CBK\)). Then \(CK = AM = 7\) and \(AC = AM + MK + KC = 7 + 3 + 7 = 17\).
|
17
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.8. On the side $CD$ of trapezoid $ABCD (AD \| BC)$, a point $M$ is marked. A perpendicular $AH$ is dropped from vertex $A$ to segment $BM$. It turns out that $AD = HD$. Find the length of segment $AD$, given that $BC = 16$, $CM = 8$, and $MD = 9$.
|
Answer: 18.
Solution. Let the lines $B M$ and $A D$ intersect at point $K$ (Fig. 5). Since $B C \| A D$, triangles $B C M$ and $K D M$ are similar by angles, from which we get $D K = B C \cdot \frac{D M}{C M} = 16 \cdot \frac{9}{8} = 18$.
Fig. 5: to the solution of problem 9.8
In the isosceles triangle $A D H$, draw the height and median $D S$. Then, in triangle $A H K$, the segment $D S$ passes through the midpoint of side $A H$ and is parallel to $H K$. Therefore, $D S$ is the midline of this triangle, and $A D = D K = 18$.
Remark. If in a right triangle a point on the hypotenuse is equidistant from two vertices of the triangle, then it is equidistant from all three vertices of the triangle.
## 10th Grade
|
18
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.3. On the side $AD$ of rectangle $ABCD$, a point $E$ is marked. On the segment $EC$, there is a point $M$ such that $AB = BM, AE = EM$. Find the length of side $BC$, given that $ED = 16, CD = 12$.
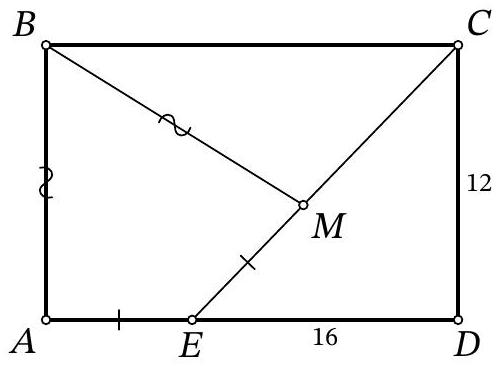
|
Answer: 20.
Solution. Note that triangles $A B E$ and $M B E$ are equal to each other by three sides. Then $\angle B M E=\angle B A E=90^{\circ}$.
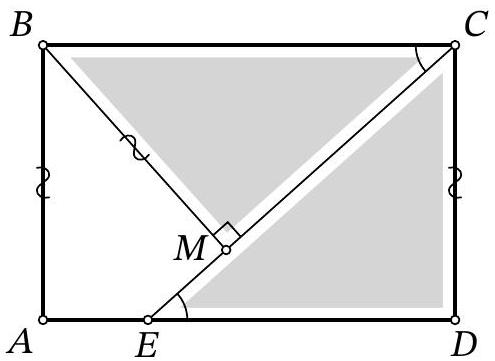
Fig. 6: to the solution of problem 10.3
From the parallelism of $A D$ and $B C$, it follows that $\angle B C M=\angle C E D$ (Fig. 6). Therefore, right triangles $B C M$ and $C E D$ are equal by an acute angle and the leg $B M=A B=C D$. Using the Pythagorean theorem for triangle $C D E$, we conclude
$$
B C=C E=\sqrt{C D^{2}+E D^{2}}=\sqrt{12^{2}+16^{2}}=20
$$
|
20
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.6. In a convex quadrilateral $A B C D$, the midpoint of side $A D$ is marked as point $M$. Segments $B M$ and $A C$ intersect at point $O$. It is known that $\angle A B M=55^{\circ}, \angle A M B=$ $70^{\circ}, \angle B O C=80^{\circ}, \angle A D C=60^{\circ}$. How many degrees does the angle $B C A$ measure?
|
Answer: 35.
Solution. Since
$$
\angle B A M=180^{\circ}-\angle A B M-\angle A M B=180^{\circ}-55^{\circ}-70^{\circ}=55^{\circ}=\angle A B M
$$
triangle $A B M$ is isosceles, and $A M=B M$.
Notice that $\angle O A M=180^{\circ}-\angle A O M-\angle A M O=180^{\circ}-80^{\circ}-70^{\circ}=30^{\circ}$, so $\angle A C D=$ $180^{\circ}-\angle C A D-\angle A D C=180^{\circ}-30^{\circ}-60^{\circ}=90^{\circ}$.
Fig. 7: to the solution of problem 10.6
Draw segment $C M$ (Fig. 7). Since in a right triangle, the median to the hypotenuse is equal to half of it, we have $C M=D M=A M=B M$. Triangle $M C D$ is isosceles with an angle of $60^{\circ}$ at the base, so it is equilateral, and $\angle C M D=60^{\circ}$. Then $\angle B M C=180^{\circ}-\angle A M B-\angle C M D=180^{\circ}-70^{\circ}-60^{\circ}=50^{\circ}$. Since triangle $B M C$ is isosceles with vertex $M$, we have $\angle C B M=$ $\frac{1}{2}\left(180^{\circ}-\angle B M C\right)=\frac{1}{2}\left(180^{\circ}-50^{\circ}\right)=65^{\circ}$. Finally,
$$
\angle B C A=180^{\circ}-\angle C B M-\angle B O C=180^{\circ}-65^{\circ}-80^{\circ}=35^{\circ} \text {. }
$$
Remark. There are other solutions that use the fact that $A B C D$ is a cyclic quadrilateral with the center of the circumscribed circle $M$.
|
35
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.5. Quadrilateral $ABCD$ is inscribed in a circle. It is known that $BC=CD, \angle BCA=$ $64^{\circ}, \angle ACD=70^{\circ}$. A point $O$ is marked on segment $AC$ such that $\angle ADO=32^{\circ}$. How many degrees does the angle $BOC$ measure?
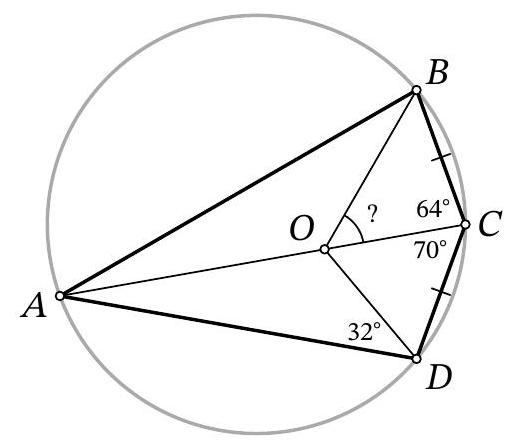
|
Answer: 58.
Solution. As is known, in a circle, inscribed angles subtended by equal chords are either equal or supplementary to $180^{\circ}$. Since $B C=C D$ and $\angle B A D<180^{\circ}$, we get that $\angle B A C=\angle D A C$.
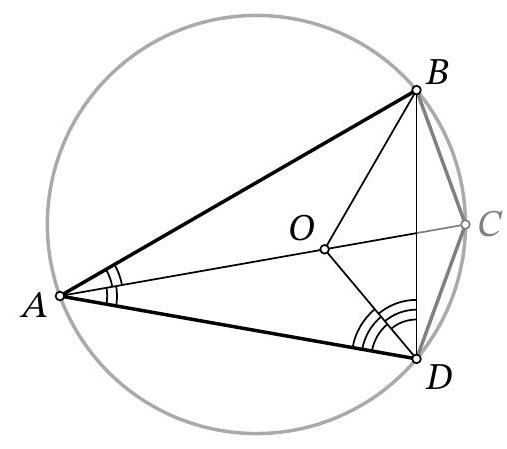
Fig. 9: to the solution of problem 11.5
Since $\angle B D A=\angle B C A=64^{\circ}$, we get that $\angle B D O=\angle A D O=32^{\circ}$. Therefore, point $O$ lies on the two angle bisectors of triangle $A B D$, i.e., it is the point of intersection of the angle bisectors (Fig. 9). Then
$$
\angle B O C=\angle B A O+\angle A B O=\frac{\angle B A D+\angle A B D}{2}=\frac{180^{\circ}-\angle B D A}{2}=\frac{180^{\circ}-64^{\circ}}{2}=58^{\circ}
$$
Remark. The solution could also have been completed differently: since $O$ is the point of intersection of the angle bisectors of triangle $A B D$, by the trident lemma $C D=C B=C O$, from which $\angle C O B$ is easily found.
|
58
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (7 points) Mom is walking around a lake with a stroller and completes a full lap around the lake in 12 minutes. Vanya rides a scooter on the same path in the same direction and meets (overtakes) mom every 12 minutes. At what intervals will Vanya meet mom if he rides at the same speed but in the opposite direction?
|
Answer: Every 4 minutes.
Solution. Since Mom completes a full lap around the lake in 12 minutes and meets Vanya every 12 minutes, in 12 minutes Vanya rides around the lake exactly 2 times, while Mom completes one lap. Therefore, Vanya's speed is twice that of Mom's. From this, it follows that when Vanya was riding in the same direction as Mom, their closing speed was equal to Mom's speed. If Vanya rides in the opposite direction, their closing speed will be three times Mom's speed, i.e., three times faster. Therefore, he will meet Mom three times more frequently, i.e., every 4 minutes.
This reasoning can be conducted by introducing a notation for the length of the path.
Let \( l \) be the length of the path around the lake (in meters), then Mom's speed is \( \frac{l}{12} \) (m/min), and Vanya's speed is \( -\frac{l}{6} \) (m/min). The closing speed when Mom and Vanya are riding towards each other is \( \frac{3l}{12} = \frac{l}{4} \) (m/min). Therefore, with this speed, they will cover \( l \) meters together in 4 minutes, i.e., they will meet every 4 minutes.
## Grading Criteria.
- Any complete and correct solution - 7 points.
- Correctly found that Vanya's speed is twice that of Mom's, correctly found the sum of speeds, but the final conclusion is incorrect - 2 points.
- Correctly and justifiedly found that Vanya's speed is twice that of Mom's, but further reasoning is either unjustified or not completed - 1 point.
- A solution that provides specific distances and speeds and arrives at the correct answer - 1 point.
- Only the correct answer - 0 points.
Maximum score for all completed tasks - 35.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 8.2. Condition:
On an island, there are two tribes: knights, who always tell the truth, and liars, who always lie. Four islanders lined up, each 1 meter apart from each other.
- The leftmost in the row said: "My fellow tribesman in this row stands 2 meters away from me."
- The rightmost in the row said: "My fellow tribesman in this row stands 2 meters away from me."
It is known that there are two knights and two liars in the row. What distances could the second and third islanders from the left have mentioned? List all possible options.
## Options for matching:
Second islander 1 m
Third islander $\quad 2 \mathrm{~m}$
3 m
$4 \mathrm{M}$
#
|
# Answer:
The second islander is 1 m
The third islander is 1 m.
## Solution.
Let's number the islanders from left to right. Suppose the first one is a knight. Then from his statement, it follows that the third one is also a knight; by the principle of exclusion, the second and fourth must be liars. The fourth said that his fellow islander stands two meters away. This is true, but the fourth is a liar, which leads to a contradiction. Therefore, the first one must be a liar.
Notice that a similar situation is created for the fourth and the first: if we look at the row from right to left, the fourth will be the first in it, and the same reasoning will apply to him. That is, the fourth must also be a liar. It follows that the second and third are knights, as the liars are the first and fourth.
From the above, it follows that the second and third are knights, who will say "one meter."
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.2.1. Given trapezoid $A B C D(A D \| B C)$. It turns out that $\angle A B D=\angle B C D$. Find the length of segment $B D$, if $B C=36$ and $A D=64$.
|
Answer: 48.
Solution. Since $A D \| B C$, we have $\angle C B D=\angle B D A$. Then triangles $A B D$ and $D C B$ are similar by the first criterion. Therefore, $\frac{64}{B D}=\frac{A D}{B D}=\frac{B D}{B C}=\frac{B D}{36}$, from which we find $B D=\sqrt{64 \cdot 36}=48$.
|
48
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.4.1. A rectangle was cut into six smaller rectangles, the areas of five of them are marked on the diagram. Find the area of the remaining rectangle.
|
Answer: 101.
Solution. Let's introduce the notation as shown in the figure.
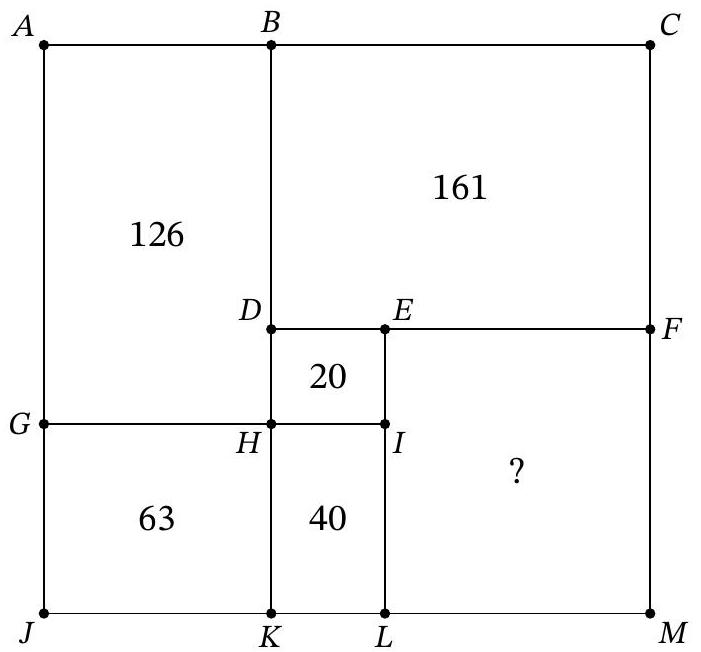
Notice that
$$
2=\frac{40}{20}=\frac{S_{H I L K}}{S_{D E I H}}=\frac{H K \cdot H I}{H D \cdot H I}=\frac{H K}{H D} \quad \text { and } \quad 2=\frac{126}{63}=\frac{S_{A B H G}}{S_{G H K J}}=\frac{B H \cdot G H}{H K \cdot G H}=\frac{B H}{H K}
$$
Therefore, if $H D=x$, then $H K=2 x$, and $B H=4 x$. From this, it follows immediately that $B D=3 x=D K$.
We obtain that the rectangles $B C F D$ and $D F M K$ are equal, as are their areas. Thus,
$$
S_{E F M L}=S_{D F M K}-S_{D E I H}-S_{H I L K}=161-20-40=101
$$
|
101
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. There is a set of 2021 numbers. Moreover, it is known that if each number in the set is replaced by the sum of the others, the same set will be obtained. Prove that the set contains a zero.
|
Solution. Let the sum of the numbers in the set be $M$, then the number $a$ in the set is replaced by the number $b=M-a$. Summing these equations for all $a$:
$$
b_{1}+\ldots+b_{2021}=2021 M-\left(a_{1}+\ldots+a_{2021}\right)
$$
from which $M=0$, since $b_{1}+\ldots+b_{2021}=a_{1}+\ldots+a_{2021}=M$. Therefore, for any $a$ the number $b=-a$ is also in the set, and all numbers can be paired as $(a,-a)$. From the odd number of elements, it follows that the set includes a number $a=-a$, that is, $a=0$.
|
0
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
9.2. Toshа travels from point A to point B via point C. From A to C, Toshа travels at an average speed of 75 km/h, and from C to B, Toshа travels at an average speed of 145 km/h. The entire journey from A to B took Toshа 4 hours and 48 minutes. The next day, Toshа travels back at an average speed of 100 km/h. The journey from B to C took Toshа 2 hours, and the journey from C to A was completed at an average speed of 70 km/h. Find the distance between B and C.
|
Answer: 290 km.
Solution. Let $\mathrm{X}$ km be the distance between B and C, and $y$ km be the distance between A and C. From the system of equations $x / 145 + y / 75 = 24 / 5$ and $(x + y) / 100 = 2 + y / 70$, we find: $x = 290$ and $y = 210$.
Computational error - 5 points.
|
290
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5 On a board of $20 \times 15$ cells, some cells contain chips (no more than one chip per cell). Two chips are called "connected" if they are in the same column or row, and there are no other chips between them. What is the maximum number of chips that can be placed on the board so that each has no more than two "connected" chips?
|
Answer: 35.
Solution. Let $x_{1}, x_{2}, \ldots, x_{20}$ be the number of chips in rows $1,2, \ldots, 20$, and $y_{1}, y_{2}, \ldots, y_{15}$ be the number of chips in columns $1,2, \ldots, 15$. Then the total number of chips $S=x_{1}+x_{2}+\ldots+x_{20}=y_{1}+y_{2}+\ldots+y_{15}$. The number of "connectivities" $k \geq\left(2 x_{1}-2\right)+\left(2 x_{2}-2\right)+\ldots+\left(2 x_{20}-2\right)+\left(2 y_{1}-2\right)+\left(2 y_{2}-2\right)+\ldots+\left(2 y_{15}-2\right)=4 S-70$. Since each chip has no more than two connected chips, $2 S \geqslant k \geqslant 4 S-70$, which means $S \leqslant 35$. It is possible to place 35 chips on the board by filling the bottom row and the left column, and placing one more chip in the top right corner.
Comments. Only the correct answer - $\underline{0 \text { points. Correct justified estimate }-\underline{4} \text { points. }}$.
Correct example - 3 points.
|
35
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Variant 1. Petya thought of two numbers and wrote down their product. After that, he decreased the first of the thought numbers by 3, and increased the other by 3. It turned out that the product increased by 900. By how much would the product have decreased if Petya had done the opposite: increased the first number by 3, and decreased the second by 3?
|
Answer: 918.
Solution: Let these numbers be $a$ and $b$. Then, according to the condition, $(a-3)(b+3)-ab=600$. Expanding the brackets: $ab+3a-3b-9-ab=900$, so $a-b=303$. We need to find the difference $ab-(a+3)(b-3)=$ $ab-ab+3a-3b+9=3(a-b)+9=3 \cdot 303+9=918$.
|
918
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Variant 1. At the intersection of perpendicular roads, a highway from Moscow to Kazan and a road from Vladimir to Ryazan intersect. Dima and Tolya set out with constant speeds from Moscow to Kazan and from Vladimir to Ryazan, respectively. When Dima passed the intersection, Tolya had 3500 meters left to reach it. When Tolya passed the intersection, Dima was 4200 meters away from it. How many meters will be between the boys when Dima has traveled 4200 meters from the moment Tolya crossed the intersection?
|
Answer: 9100.
Solution. When Tolya has traveled 3500 meters, Dima will have traveled 4200 meters, so at the moment when Dima is 8400 meters past the intersection, Tolya will be 3500 meters past the intersection. By the Pythagorean theorem, the distance between the boys is 9100 meters.
|
9100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Variant 1. Find the largest root of the equation
$(x+1)(x+2)-(x+2)(x+3)+(x+3)(x+4)-(x+4)(x+5)+\cdots-(x+1000)(x+1001)=0$.
|
Answer: -501.
Solution. Let's break the terms into pairs of adjacent terms and factor out the common factor, we get $(x+2)(x+1-x-3)+\cdots+(x+1000)(x+999-x-1001)=-2 \cdot(x+2+x+4+\cdots+x+1000)=$ $-2 \cdot\left(500 x+\frac{2+1000}{2} \cdot 500\right)=-1000 \cdot(x+501)=0$. From this, $x=-501-$ the only root.
|
-501
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 5. Variant 1
It is known that $\cos \alpha+\cos \beta+\cos \gamma=\sqrt{\frac{1}{5}}, \sin \alpha+\sin \beta+\sin \gamma=\sqrt{\frac{4}{5}}$. Find $\cos (\alpha-\beta)+\cos (\beta-$ $\gamma)+\cos (\gamma-\alpha)$
|
Answer: -1.
Solution. Consider the expression $(\cos \alpha+\cos \beta+\cos \gamma)^{2}+(\sin \alpha+\sin \beta+\sin \gamma)^{2}$ and expand the brackets: $\cos ^{2} \alpha+\cos ^{2} \beta+\cos ^{2} \gamma+2(\cos \alpha \cdot \cos \beta+\cos \alpha \cdot \cos \gamma+\cos \beta \cdot \cos \gamma)+\sin ^{2} \alpha+\sin ^{2} \beta+\sin ^{2} \gamma+2(\sin \alpha \cdot \sin \beta+\sin \alpha \cdot \sin \gamma+\sin \beta \cdot \sin \gamma)$. We transform, then apply the fundamental trigonometric identity and the cosine difference formula: $\left(\cos ^{2} \alpha+\sin ^{2} \alpha\right)+\left(\cos ^{2} \beta+\sin ^{2} \beta\right)+\left(\cos ^{2} \gamma+\sin ^{2} \gamma\right)+2(\cos \alpha \cdot \cos \beta+\sin \alpha \cdot \sin \beta)+2(\cos \alpha \cdot \cos \gamma+\sin \alpha \cdot \sin \gamma)+2(\cos \beta \cdot \cos \gamma+\sin \beta \cdot \sin \gamma)=3+2(\cos (\alpha-\beta)+\cos (\beta-\gamma)+\cos (\gamma-\alpha))$. Substituting the initial expression $\cos \alpha+\cos \beta+\cos \gamma=\sqrt{\frac{1}{5}}, \sin \alpha+\sin \beta+\sin \gamma=\sqrt{\frac{4}{5}}$ we get the equation: $\left(\sqrt{\frac{1}{5}}\right)^{2}+\left(\sqrt{\frac{4}{5}}\right)^{2}=3+2(\cos (\alpha-\beta)+\cos (\beta-\gamma)+\cos (\gamma-\alpha))$, from which we find the answer.
## Variant 2
It is known that $\cos \alpha+\cos \beta+\cos \gamma=\sqrt{\frac{10}{7}}, \sin \alpha+\sin \beta+\sin \gamma=\sqrt{\frac{11}{7}}$. Find $\cos (\alpha-\beta)+\cos (\beta-\gamma)+\cos (\gamma-\alpha)$
## Answer: 0.
## Variant 3
It is known that $\cos \alpha+\cos \beta+\cos \gamma=\sqrt{\frac{10}{3}}, \sin \alpha+\sin \beta+\sin \gamma=\sqrt{\frac{17}{3}}$. Find $\cos (\alpha-\beta)+\cos (\beta-\gamma)+\cos (\gamma-\alpha)$
Answer: 3.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 6. Option 1
Initially, there were 20 balls of three colors in the box: white, blue, and red. If we double the number of blue balls, the probability of drawing a white ball will be $\frac{1}{25}$ less than it was initially. If we remove all the white balls, the probability of drawing a blue ball will be $\frac{1}{16}$ greater than the probability of drawing a blue ball at the beginning. How many white balls were in the box?
|
Answer: 4.
Solution: Let there be $a$ white balls, $b$ blue balls, and $c$ red balls in the box. We can set up the following equations:
$$
\begin{gathered}
a+b+c=20 \\
\frac{a}{20}=\frac{a}{20+b}+\frac{1}{25} \\
\frac{b}{20}+\frac{1}{16}=\frac{b}{20-a}
\end{gathered}
$$
Transform the second equation: $\frac{a b}{20(20+b)}=\frac{1}{25}$ and the third equation: $\frac{1}{16}=\frac{a b}{20(20-a)}$. Finally, $\frac{20+b}{25}=\frac{20-a}{16}$ and, substituting into the second equation, after simplification, we get a quadratic equation for $a$ (for $a \neq 20$): $\frac{a}{20}=\frac{16 a}{25(20-a)}+\frac{1}{25} \Leftrightarrow$ $100 a-5 a^{2}=64 a+80-4 a \Leftrightarrow a^{2}-8 a+16=0 \Leftrightarrow a=4$. Then, from the first and second equations, we have: $b=5, c=11$.
## Variant 2
Initially, there were 30 balls of three colors in the box: white, blue, and red. If we double the number of blue balls, the probability of drawing a white ball will be $\frac{1}{36}$ less than it was initially. If we remove all the white balls, the probability of drawing a blue ball will be $\frac{1}{25}$ greater than the probability of drawing a blue ball at the beginning. How many white balls were in the box?
Answer: 5.
## Variant 3
Initially, there were 42 balls of three colors in the box: white, blue, and red. If we double the number of blue balls, the probability of drawing a white ball will be $\frac{1}{49}$ less than it was initially. If we remove all the white balls, the probability of drawing a blue ball will be $\frac{1}{36}$ greater than the probability of drawing a blue ball at the beginning. How many white balls were in the box?
Answer: 6.
## Variant 4
Initially, there were 56 balls of three colors in the box: white, blue, and red. If we double the number of blue balls, the probability of drawing a white ball will be $\frac{1}{64}$ less than it was initially. If we remove all the white balls, the probability of drawing a blue ball will be $\frac{1}{49}$ greater than the probability of drawing a blue ball at the beginning. How many white balls were in the box?
Answer: 7.
## Variant 5
Initially, there were 72 balls of three colors in the box: white, blue, and red. If we double the number of blue balls, the probability of drawing a white ball will be $\frac{1}{81}$ less than it was initially. If we remove all the white balls, the probability of drawing a blue ball will be $\frac{1}{64}$ greater than the probability of drawing a blue ball at the beginning. How many white balls were in the box?
Answer: 8.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 7. Variant 1
Unit cubes were used to assemble a large parallelepiped with sides greater than 4. Two cubes will be called adjacent if they touch by faces. Thus, one cube can have up to 6 neighbors. It is known that the number of cubes that have exactly 6 neighbors is 836. Find the number of cubes that have no more than four neighbors.
|
Answer: 144.
Solution. Let $a, b$ and $c$ be the lengths of the sides of the large parallelepiped. Then, the number of cubes with exactly 6 neighbors is: $(a-2)(b-2)(c-2)$. Since each of the factors $a-2, b-2$ and $c-2$ is greater than 2 and their product equals the product of four prime numbers $2,2,11$ and 19, we have that the numbers $a-2$, $b-2$ and $c-2$ are 4, 11, and 19 in some order. The number of cubes with exactly 4 neighbors is $4 \cdot(a-2+b-2+c-2)$ (since each such cube is adjacent to exactly one edge). Thus, we get the answer: $4 \cdot(4+11+19)+8=144$.
## Variant 2
A large parallelepiped was assembled from unit cubes with sides greater than 4. Two cubes are called neighboring if they touch by faces. Thus, a cube can have up to 6 neighbors. It is known that the number of cubes with exactly 6 neighbors is 1564. Find the number of cubes with no more than four neighbors.
Answer: 184.
## Variant 3
A large parallelepiped was assembled from unit cubes with sides greater than 4. Two cubes are called neighboring if they touch by faces. Thus, a cube can have up to 6 neighbors. It is known that the number of cubes with exactly 6 neighbors is 812. Find the number of cubes with no more than four neighbors.
Answer: 168.
## Variant 4
A large parallelepiped was assembled from unit cubes with sides greater than 4. Two cubes are called neighboring if they touch by faces. Thus, a cube can have up to 6 neighbors. It is known that the number of cubes with exactly 6 neighbors is 1012. Find the number of cubes with no more than four neighbors.
Answer: 160.
## Variant 5
A large parallelepiped was assembled from unit cubes with sides greater than 4. Two cubes are called neighboring if they touch by faces. Thus, a cube can have up to 6 neighbors. It is known that the number of cubes with exactly 6 neighbors is 868. Find the number of cubes with no more than four neighbors.
Answer: 176.
|
144
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 8. Variant 1
At the base of the quadrilateral pyramid $S A B C D$ lies a square $A B C D, S A$ - the height of the pyramid. Let $M$ and $N$ be the midpoints of the edges $S C$ and $A D$. What is the maximum value that the area of triangle $B S A$ can have if $M N=3 ?$
|
Answer: 9.
Solution: Let $O$ be the center of the square $ABCD$. Then $MO$ is the midline of the triangle $SAC$, so $SA = 2MO$. Similarly, $ON$ is the midline of the triangle $BDA$, so $AB = 2ON$. Therefore, $SA^2 + AB^2 = 4(MO^2 + ON^2) = MN^2 = 36$. Let $SA = x, AB = y$. From the formula $S = 0.5 \cdot SA \cdot AB = 0.5xy$, the equality $x^2 + y^2 = SB^2 = 36$, and the inequality $x^2 + y^2 \geq 2xy$, it follows that the area of the triangle is maximized when $2xy = x^2 + y^2$, and it is equal to 9.
## Variant 2
In the base of the quadrilateral pyramid $SABCD$ lies a square $ABCD$, and $SA$ is the height of the pyramid. Let $M$ and $N$ be the midpoints of the edges $SC$ and $AD$. What is the maximum value that the area of the triangle $BSA$ can have if $MN = 4$?
Answer: 16.
## Variant 3
In the base of the quadrilateral pyramid $SABCD$ lies a square $ABCD$, and $SA$ is the height of the pyramid. Let $M$ and $N$ be the midpoints of the edges $SC$ and $AD$. What is the maximum value that the area of the triangle $BSA$ can have if $MN = 5$?
Answer: 25.
## Variant 4
In the base of the quadrilateral pyramid $SABCD$ lies a square $ABCD$, and $SA$ is the height of the pyramid. Let $M$ and $N$ be the midpoints of the edges $SC$ and $AD$. What is the maximum value that the area of the triangle $BSA$ can have if $MN = 6$?
Answer: 36.
## Variant 5
In the base of the quadrilateral pyramid $SABCD$ lies a square $ABCD$, and $SA$ is the height of the pyramid. Let $M$ and $N$ be the midpoints of the edges $SC$ and $AD$. What is the maximum value that the area of the triangle $BSA$ can have if $MN = 2$?
Answer: 4.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. In the village, seven people live. Some of them are liars (always lie), and the rest are knights (always tell the truth). Each of them said about each of the others whether they are a knight or a liar. Out of the 42 answers received, 24 were “He is a liar.” What is the smallest number of knights that can live in the village?
|
Answer: 3.
Solution: The phrase "He is a knight" would be said by a knight about a knight and by a liar about a liar, while the phrase "He is a liar" would be said by a knight about a liar and by a liar about a knight. Therefore, in each pair of knight-liar, the phrase "He is a liar" will be said twice. Since this phrase was said 24 times in total, there are 12 pairs of knight-liar, from which we find that there are 3 knights and 4 liars, or vice versa.
Comment: A correct answer without justification - 0 points.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.5. Three hundred non-zero integers are written in a circle such that each number is greater than the product of the next three numbers in the clockwise direction. What is the maximum number of positive numbers that can be among these 300 written numbers?
|
Answer: 200.
Solution: Note that three consecutive numbers cannot all be positive (i.e., natural numbers). Suppose the opposite. Then their product is positive, and the number preceding them (counterclockwise) is also a natural number. Since it is greater than the product of these three natural numbers, it is greater than each of them. Continuing this reasoning, we will conclude that all numbers are natural, and if we move counterclockwise, the numbers will increase. However, when the "circle closes," we will arrive at a contradiction.
Thus, in any triplet of adjacent numbers, there is at least one negative number. Dividing our 300 numbers into 100 triplets, we get that there are no fewer than 100 negative numbers, and therefore, no more than 200 positive numbers. If we alternate two positive numbers 2 and one negative number -2, we will get an example of the arrangement of 200 positive and 100 negative numbers that satisfy the problem's condition.
Comment: A correct answer without justification - 0 points.
Proving the impossibility of placing three positive numbers consecutively - 3 points. Proving that there are no more than 200 positive numbers - another 1 point.
Providing an example with 200 positive numbers - 3 points.
|
200
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.1. Misha and Grisha are writing numbers on the board. Misha writes threes, and Grisha writes fives. In total, they wrote 20 numbers. How many fives were written if the sum of all the numbers is 94?
|
Answer: 17
Solution. If all 20 numbers were "5", their sum would be 100. We will replace "5" with "3". With each replacement, the sum decreases by 2. Since $100-94=6, 6: 2=3$, we need 3 replacements. Therefore, the number of fives is $20-3=17$.
|
17
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.1. Five identical squares, standing in a row, were cut by two horizontal lines. The sum of the perimeters of the resulting 15 rectangles is 800 cm. Indicate in centimeters the length of the original squares.
| | | | | |
| :--- | :--- | :--- | :--- | :--- |
| | | | | |
|
# Answer: 20
Solution. Let's calculate how many times the side of the original square is repeated in the sum of all perimeters. The sides of the rectangle are counted once (a total of 12), and the crossbars are counted twice ($4 \cdot 2 + 10 \cdot 2 = 28$). In total, $40.800: 40=20$ cm - the side of the square.
|
20
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1. In a row, 64 people are standing - each one is either a knight, who always tells the truth, or a liar, who always lies. One of the standing knights said that he stands next to a knight and a liar, and all the other 63 people repeated his phrase. Indicate how many of them were knights.
|
Answer: 42
Solution. The people at the ends must be liars, as they do not have a second neighbor, and by saying this phrase, those standing there lied. All others can be liars, in which case there are no knights at all, but this option contradicts the condition that at least one knight is present. If there is a knight, then next to him stand a knight and a liar: KKL or LKK. A liar cannot tell the truth, so if there is a knight on one side, there must be a knight on the other side (if the liar is not at the end). We get ...KKLKK... or ...KLKK... A knight cannot stand between two liars, so knights always stand in pairs. We have ...KKLKK... in both cases. Thus, the following arrangement is obtained: LKKLKKLKK...LKKL - if we do not count the last liar, the remaining 63 people can be divided into 21 triplets LKK, each containing 42 knights.
|
42
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. In a row, there are 27 matchboxes, each containing a certain number of matches. It is known that in any four consecutive boxes, the total is 25 matches, and in all of them, the total is 165. How many matches are in the eighth box?
|
Answer: 10
Solution. In the first 24 boxes, there are a total of $6 \cdot 25=150$ matches. In the last three boxes, there are 15 matches. Therefore, the 4th from the end (or 24th from the start) has 10 matches. Then, in boxes $24, 23, 22, 21$, there are 25 matches in total, meaning in boxes $21, 22, 23$, there are 15 matches. But in boxes $23, 22, 21$, and 20, there are also 25 matches, so box 20 has 10 matches, the same as box 24. Thus, in every 4th box with a number divisible by 4, there will be 10 matches, including the box with number 8.
On the same road, Emilia and Eduard set out at the same speed. It is known that Arkady met Emilia at 13:00, and Eduard at 16:00. Arina met Emilia at 15:00. At what time will Arina meet Eduard?
Answer: 18
Solution. Arkady and Arina met Emilia with a 2-hour interval. The speeds of Arina and Arkady are equal, as are the speeds of Emilia and Eduard. Therefore, the distance between Arkady and Arina is constant, as is the distance between Emilia and Eduard. This means the speed of approach between Arkady and Emilia is equal to the speed of approach between Arkady and Eduard, and the same speed of approach will be between Arina and Emilia, and Arina and Eduard. Since the speeds of approach of Emilia and Eduard to the pair Arkady-Arina are equal, they will each pass the pair Arkady-Arina in the same amount of time, i.e., 2 hours. If Arkady met Eduard at 16:00, then Arina will meet him 2 hours later, i.e., at 18:00.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. A $7 \times 7$ board has a chessboard coloring. In one move, you can choose any $m \times n$ rectangle of cells and repaint all its cells to the opposite color (black cells become white, white cells become black). What is the minimum number of moves required to make the board monochromatic?
Answer: in 6 moves.
|
Solution. Consider segments of length equal to the side of a cell, separating pairs of cells adjacent to the side of the board. Along each side of the board, there are 6 such segments, totaling $6 \cdot 4=24$. Each of these segments separates cells that initially have different colors, so each segment must end up on the side of at least one of the chosen rectangles. It is easy to see that no more than four of the considered segments can lie on the sides of one rectangle. Thus, to make the board monochromatic, at least $24: 4=6$ moves are required. It remains to show that six moves are sufficient. We choose 6 rectangles of size $1 \times 6$, covering the cells of the second, fourth, and sixth rows and the second, fourth, and sixth diagonals.
Criteria for evaluation.
Only the answer - 0 points.
An example of repainting in 6 moves without proving minimality - 2 points.
Proof of minimality without an example - 5 points.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. There is a ruler 10 cm long without divisions. What is the smallest number of intermediate divisions that need to be made on the ruler so that segments of length 1 cm, 2 cm, 3 cm, ..., 10 cm can be laid off, applying the ruler in each case only once.
|
Answer: 4
Solution: First, let's prove that three divisions are not enough. There are a total of 10 segments with endpoints at five points. Therefore, if three divisions are made, each length from 1 to 10 should be obtained exactly once. If any division is made at a non-integer distance from the left end, there will be segments of non-integer length, meaning not all lengths from 1 to 10 can be obtained. Therefore, for each division, only nine options are possible. Thus, a segment of length 9 can only be obtained in one way: by making a division at a distance of 1 from one of the ends of the ruler. Without loss of generality, we can assume that this division is made at a distance of 1 from the left end, and denote this division as T. How can a segment of length 8 be obtained? Again, consider the fact that segments of non-integer length should not be formed. This means that a segment of length 8 can be obtained either by making a division at a distance of 2 from one of the ends, or from two divisions, each made at a distance of 1 from the left and right ends of the ruler. The second case is impossible, as it results in two identical segments (length 1). If the division is made at a distance of 2 from the left end, two segments of length 1 are again formed. Therefore, the only option left is to make the division at a distance of 2 from the right end. Denote this division as S. A segment of length 3 cannot be obtained using the ends of the ruler: it results in extra segments of length 1 or 2. Therefore, the third point N is such that either NT=3 or NS=4 (in each case, uniqueness follows from the fact that N lies on the ruler). Denote the left end of the ruler as A, and the right end as B. If NT=3, then AN=NS=4, leading to a contradiction. If SN=3, then AN=NB=5, again contradicting the fact that all segment lengths are different. Thus, we have proven that three divisions are not enough to complete the task.
Four points are sufficient, as they can be arranged as follows: AC=1, AD=4, AE=5, AF=8, where A is the left end of the segment.
Criteria:
Only the answer without construction --- 0 points.
Proving that all segments from 1 to 10 must be obtained exactly once --- 2 points.
Proving that three points are not enough --- 6 points.
Proving that four points are sufficient --- 1 point.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.10. In the company, there are 100 children, some of whom are friends (friendship is always mutual). It is known that by selecting any child, the remaining 99 children can be divided into 33 groups of three such that in each group, all three are pairwise friends. Find the minimum possible number of pairs of friends.
(S. Berlov, N. Vlasova)
|
Answer: 198.
Solution: Let's translate the problem into the language of graphs, associating each child with a vertex and each friendship with an edge. Then we know that in this graph with 100 vertices, after removing any vertex, the remaining vertices can be divided into 33 triples such that the vertices in each triple are pairwise connected. We need to find the minimum possible number of edges in such a graph.
First, let's construct an example with exactly 198 edges. Divide 99 vertices, except for vertex $A$, into 33 groups of 3 vertices each. Connect the vertices pairwise within each triple; finally, connect $A$ to all other vertices. Then the conditions of the problem are satisfied: if $A$ is removed, the division into triples is already given, and if any other vertex $B$ is removed, in this division, it is sufficient to replace $B$ with $A$. In this described graph, there are a total of $33 \cdot 3 + 99 = 198$ edges.
It remains to prove that this number is the smallest. We will call a graph on $3k+1$ vertices good if, after removing any vertex, the remaining $3k$ vertices can be divided into $k$ triples that are pairwise connected. We will prove by induction on $k$ that in a good graph on $3k+1$ vertices, there are at least $6k$ edges; for $k=33$, we will get the required estimate. The base case for $k=1$ is simple: since after removing any vertex, the remaining three are pairwise connected, any two vertices must be connected, so the number of edges is $C_{4}^{2}=6$.
Let's prove the inductive step. If from each vertex at least 4 edges come out, the total number of edges is not less than $(3k+1) \cdot 4 / 2 = 2(3k+1)$, which is even more than the required $6k$. Otherwise, there is a vertex $A$ connected to no more than three other vertices. If any vertex other than $A$ is removed, $A$ will end up in some triple, which means it is connected to at least two vertices. If one of these vertices is removed, $A$ will still have at least two adjacent vertices, so there were at least three. Thus, $A$ is connected to exactly three vertices $B, C$, and $D$. Then, when, for example, $B$ is removed, the vertices $A, C$, and $D$ form a triple, so $C$ and $D$ are connected; similarly, we get that $B, C$, and $D$ are pairwise connected.
Now, let's remove from our graph the vertices $A, B, C$, and $D$, and add one vertex $X$ connected to all those with whom at least one of the vertices $B, C$, and $D$ was connected. Note that in this case, the number of edges decreases by at least 6 (i.e., by the number of edges between $A, B, C$, and $D$). We will show that the new graph is good; from this, the inductive step will follow, and in the new graph, there will be at least $6(k-1)$ edges, which means in the original graph, there are at least $6(k-1) + 6 = 6k$ edges.
Suppose some vertex $Y \neq X$ is removed from the new graph. If it is removed from the original graph, the remaining vertices will be divided into triples; let's say vertex $A$ ends up in a triple with $B$ and $C$, and vertex $D$ in another triple. Then the new graph can be divided in the same way, placing vertex $X$ in the triple where vertex $D$ was. Finally, if vertex $X$ is removed from the new graph, the same operation can be performed, considering that vertex $D$ is removed from the original graph (then $A, B$, and $C$ will automatically end up in one triple). Thus, the inductive step is proven.
Remark. The provided example is not the only one. The reasoning from the second part of the solution essentially shows that many different optimal examples can be constructed in the following inductive manner. For $k=1$, take 4 vertices and connect all pairs with edges. When transitioning from $k$ to $k+1$, add three vertices $B, C, D$, connect them pairwise with each other, and also connect them all to some already existing vertex $A$.
In such an example, there will always be $6k$ edges, and it will satisfy the conditions of the problem.
Comment. Only the correct answer - 0 points.
Only provided an example with 198 pairs of friends - 1 point.
Examples with more pairs of friends are not scored.
Only proved that the number of pairs of friends is not less than $198-6$ points.
|
198
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.3. Zhenya drew a square with a side of 3 cm, and then erased one of these sides. A figure in the shape of the letter "P" was obtained. The teacher asked Zhenya to place dots along this letter "P", starting from the edge, so that the next dot was 1 cm away from the previous one, as shown in the picture, and then count how many dots he got. He got 10 dots.
Then the teacher decided to complicate the task and asked to count the number of dots, but for the letter "P" obtained in the same way from a square with a side of 10 cm. How many dots will Zhenya have this time?
|
Answer: 31.
Solution. Along each of the three sides of the letter "П", there will be 11 points. At the same time, the "corner" points are located on two sides, so if 11 is multiplied by 3, the "corner" points will be counted twice. Therefore, the total number of points is $11 \cdot 3-2=31$.
|
31
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4.5. Hooligan Dima made a construction in the shape of a $3 \times 5$ rectangle using 38 wooden toothpicks. Then he simultaneously set fire to two adjacent corners of this rectangle, marked in the figure.
It is known that one toothpick burns for 10 seconds. How many seconds will it take for the entire construction to burn?
(Fire spreads along the toothpicks at a constant speed. The fire continues to spread from each burned toothpick to all adjacent unburned toothpicks.)

|
Answer: 65.
Solution. In the picture below, for each "node", the point where the toothpicks connect, the time in seconds it takes for the fire to reach it is indicated. It will take the fire another 5 seconds to reach the middle of the middle toothpick in the top horizontal row (marked in the picture).
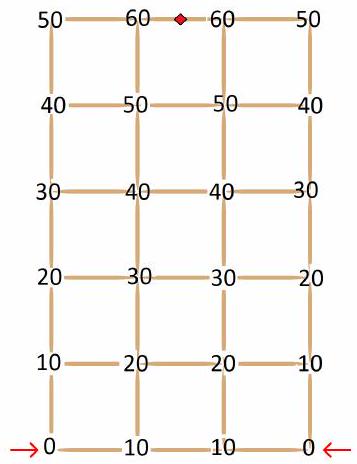
|
65
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.4. The school principal, the caretaker, and the parent committee, failing to agree with each other, each bought a carpet for the school auditorium, which is $10 \times 10$. After thinking about what to do, they decided to place all three carpets as shown in the picture: the first carpet $6 \times 8$ - in one corner, the second carpet $6 \times 6$ - in the opposite corner, and the third carpet $5 \times 7$ - in one of the remaining corners (all dimensions are in meters).
Find the area of the part of the hall covered by carpets in three layers (give the answer in square meters).
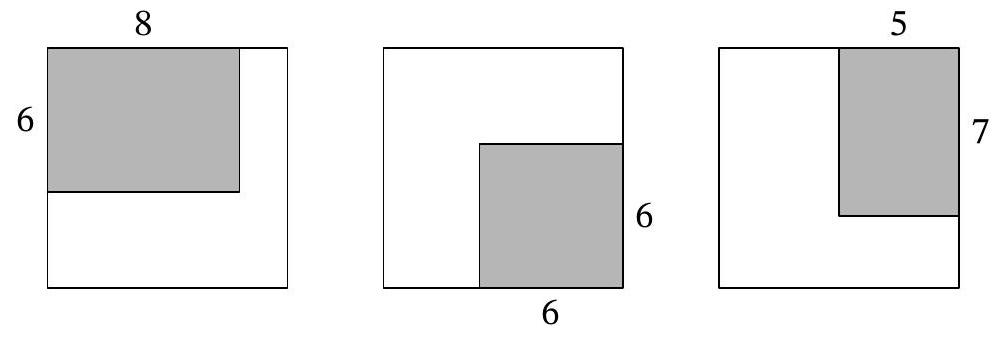
|
Answer: 6.
Solution. We will measure all dimensions in meters and the area in square meters.
Let's look at the overlap of the second and third carpets. This will be a rectangle $5 \times 3$ (5 along the horizontal, 3 along the vertical), adjacent to the right side of the square room, 4 units from the top side, and 3 units from the bottom side.
The first carpet intersects this rectangle horizontally between the 5th and 8th meters from the left side of the square room, and vertically between the 4th and 6th meters from the top side. In the end, we get a rectangle $2 \times 3$, the area of which is 6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5.8. Inside a large triangle with a perimeter of 120, several segments were drawn, dividing it into nine smaller triangles, as shown in the figure. It turned out that the perimeters of all nine small triangles are equal to each other. What can they be equal to? List all possible options.
The perimeter of a figure is the sum of the lengths of all its sides.
|
Answer: 40.
Solution. Let's add the perimeters of the six small triangles marked in gray in the following figure:
From the obtained value, subtract the perimeters of the other three small white triangles. Since the perimeters of the small triangles are equal, on one side, we get three times the perimeter of a small triangle. On the other side, in this sum, there will only be segments that make up the perimeter of the large triangle, which is 120. Therefore, the perimeter of a small triangle is $120: 3=40$.
## 6th grade
|
40
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.