problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
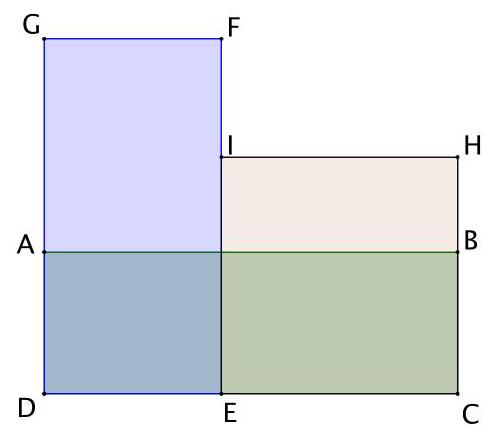
5. (8 points) Rectangles $A B C D, D E F G, C E I H$ have equal areas and integer sides. Find $D G$, if $B C=31$.
|
Answer: 992
Solution: Let $D E=a$ and $E C=b$. Then the area of the rectangles $S=31(a+b)$. According to the condition, $S$ is divisible by $a$ and $b$, that is, $S=a k$ and $S=b l$, where $k=D G$ and $l=C H-$ are natural numbers. Then $a=\frac{S}{k}$ and $b=\frac{S}{l}$. We get that $S=\frac{31 S}{k}+\frac{31 S}{l}$. Therefore, $k l=31(k+l)=>$ $k l-31 k-31 l+961=961=>(k-31)(l-31)=961$. Since $l<k$, that is, $l-31<k-31$. Therefore, $l-31=1$ and $k-31=961$. Thus, $k=D G=992$.
|
992
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (8 points) Let for positive numbers $x, y, z$ the following system of equations holds:
$$
\left\{\begin{array}{l}
x^{2}+x y+y^{2}=75 \\
y^{2}+y z+z^{2}=49 \\
z^{2}+x z+x^{2}=124
\end{array}\right.
$$
Find the value of the expression $x y+y z+x z$.
|
Answer: 70
Solution: Let there be three rays with vertex $O$, forming angles of $120^{\circ}$ with each other. On these rays, we lay off segments $O A=x, O B=y, O C=z$. Then, by the cosine theorem, $A B^{2}=75$, $B C^{2}=49, A C^{2}=124$. Note that triangle $A B C$ is a right triangle with hypotenuse $A C$. The sum of the areas of triangles $A O B, B O C, A O C$ is equal to the area of triangle $A B C$. This gives us the relation $\frac{1}{2}(x y+y z+x z) \sin 120^{\circ}=\frac{1}{2} \cdot 5 \sqrt{3} \cdot 7$. From this, we obtain the answer.
|
70
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (10 points) In the expression $(x+y+z)^{2026}+(x-y-z)^{2026}$, the brackets were expanded and like terms were combined. How many monomials $x^{a} y^{b} z^{c}$ with a non-zero coefficient were obtained?
|
Answer: 1028196
Solution: Let $t=y+z$, then the polynomial can be rewritten as $(x+t)^{2026}+(x-t)^{2026}$. We expand both brackets using the binomial theorem and get
$$
\begin{aligned}
& (x+t)^{2026}=x^{2026}+a_{1} x^{2025} t+\ldots+a_{2025} x t^{2025}+t^{2026} \\
& (x-t)^{2026}=x^{2026}-a_{1} x^{2025} t+\ldots-a_{2025} x t^{2025}+t^{2026}
\end{aligned}
$$
Adding them up, we get
$$
(x+t)^{2026}+(x-t)^{2026}=2\left(x^{2026}+a_{2} x^{2024} t^{2}+\ldots+a_{2024} x^{2} t^{2024}+t^{2026}\right)
$$
Notice that when expanding different $t_{1}^{n}$ and $t_{2}^{n}$, we will get different monomials (since the degrees of $x$ will be different). Also, when expanding $t^{n}$, we will get $n+1$ different monomials, so the final answer will be
$$
1+3+\ldots+2025+2027=1014^{2}=1028196
$$
## Solve the following problems with justification of the answer
|
1028196
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (5 points) Find the degree measure of the angle
$$
\delta=\arccos \left(\left(\sin 2907^{\circ}+\sin 2908^{\circ}+\cdots+\sin 6507^{\circ}\right)^{\cos } 2880^{\circ}+\cos 2881^{\circ}+\cdots+\cos 6480^{\circ}\right)
$$
|
Answer: $63^{\circ}$
Solution: From the statement $\cos \alpha+\cos \left(\alpha+180^{\circ}\right)=0$ it follows that $\cos \alpha+\cos \left(\alpha+1^{\circ}\right)+$ $\cdots+\cos \left(\alpha+179^{\circ}\right)=0$. Then $\cos 2880^{\circ}+\cos 2881^{\circ}+\cdots+\cos 6479^{\circ}=0$ and in the exponent only $\cos 6480^{\circ}=1$ remains. Similarly, $\sin \alpha+\sin \left(\alpha+1^{\circ}\right)+\cdots+\sin \left(\alpha+179^{\circ}\right)=0$ and $\sin 2907^{\circ}+\sin 2908^{\circ}+\cdots+\sin 6506^{\circ}=0 \cdot \sin 6507^{\circ}=\sin 27^{\circ}$. Then $\delta=\arccos \left(\sin 27^{\circ}\right)=63^{\circ}$.
|
63
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (7 points) On the radius $A O$ of a circle with center $O$, a point $M$ is chosen. On one side of $A O$ on the circle, points $B$ and $C$ are chosen such that $\angle A M B = \angle O M C = \alpha$. Find the length of $B C$ if the radius of the circle is $28$, and $\sin \alpha = \frac{\sqrt{45}}{7}$?
|
Answer: 16.
## Solution:
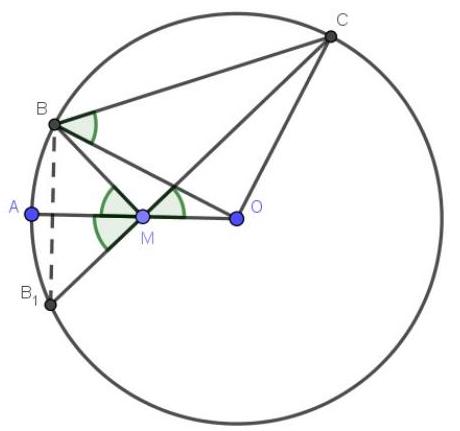
Consider point $B_{1}$, which is symmetric to point $B$ with respect to the line $O A$. It also lies on the circle and $\angle A M B=\alpha$. Note that points $B_{1}, M, C$ lie on the same straight line, and $\Delta B B_{1} M$ is isosceles. Therefore, the inscribed angle $\angle B B_{1} M=90^{\circ}-\alpha$, and the central angle $\angle B O C=180^{\circ}-2 \alpha$. $\triangle B O C$ is isosceles and $\angle O B C=\alpha \cdot \cos \alpha=\sqrt{1-\sin ^{2} \alpha}=\frac{2}{7}$. We find the base of the isosceles triangle using the formula $B C=2 * \cos \alpha * B O=2 * \frac{2}{7} * 28=16$
|
16
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (7 points) On the board, 46 ones are written. Every minute, Karlson erases two arbitrary numbers and writes their sum on the board, and then eats a number of candies equal to the product of the two erased numbers. What is the maximum number of candies he could have eaten in 46 minutes?
|
Answer: 1035.
Solution: Let's represent 46 units as points on a plane. Each time we combine numbers, we will connect the points of one group with all the points of the second group with line segments. Note that if we replace numbers $x$ and $y$ with $x+y$, the groups " $x$ " and " $y$ " will be connected by $x y$ line segments. This is the same number of candies that Karlson eats. After 46 minutes, all points will be connected. In total, $\frac{46 \cdot(46-1)}{2}=1035$ line segments will be drawn. Therefore, Karlson will eat 1035 candies.
|
1035
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
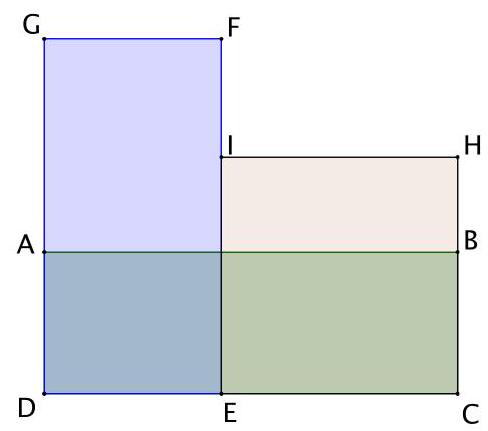
5. (8 points) Rectangles $A B C D, D E F G, C E I H$ have equal areas and integer sides. Find $D G$, if $B C=29$.
|
Answer: 870
Solution: Let $D E=a$ and $E C=b$. Then the area of the rectangles $S=29(a+b)$. According to the condition, $S$ is divisible by $a$ and $b$, that is, $S=a k$ and $S=b l$, where $k=D G$ and $l=C H-$ are natural numbers. Then $a=\frac{S}{k}$ and $b=\frac{S}{l}$. We get that $S=\frac{29 S}{k}+\frac{29 S}{l}$. Therefore, $k l=29(k+l)=>$ $k l-29 k-29 l+841=841=>(k-29)(l-29)=841$. Since $l<k$, that is, $l-29<k-29$. Therefore, $l-29=1$ and $k-29=841$. Thus, $k=D G=870$.
|
870
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (8 points) Let for positive numbers $x, y, z$ the following system of equations holds:
$$
\left\{\begin{array}{l}
x^{2}+x y+y^{2}=75 \\
y^{2}+y z+z^{2}=64 \\
z^{2}+x z+x^{2}=139
\end{array}\right.
$$
Find the value of the expression $x y+y z+x z$.
|
Answer: 80
Solution: Let there be three rays with vertex $O$, forming angles of $120^{\circ}$ with each other. On these rays, we lay off segments $O A=x, O B=y, O C=z$. Then, by the cosine theorem, $A B^{2}=75$, $B C^{2}=64, A C^{2}=139$. Note that triangle $A B C$ is a right triangle with hypotenuse $A C$. The sum of the areas of triangles $A O B, B O C, A O C$ is equal to the area of triangle $A B C$. This gives us the relation $\frac{1}{2}(x y+y z+x z) \sin 120^{\circ}=\frac{1}{2} \cdot 5 \sqrt{3} \cdot 8$. From this, we obtain the answer.
|
80
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (10 points) In the expression $(x+y+z)^{2028}+(x-y-z)^{2028}$, the brackets were expanded and like terms were combined. How many monomials $x^{a} y^{b} z^{c}$ with a non-zero coefficient were obtained?
|
Answer: 1030225
Solution: Let $t=y+z$, then the polynomial can be rewritten as $(x+t)^{2028}+(x-t)^{2028}$. We expand both brackets using the binomial theorem and get
$$
\begin{aligned}
& (x+t)^{2028}=x^{2028}+a_{1} x^{2027} t+\ldots+a_{2027} x t^{2027}+t^{2028} \\
& (x-t)^{2028}=x^{2028}-a_{1} x^{2027} t+\ldots-a_{2027} x t^{2027}+t^{2028}
\end{aligned}
$$
Adding them up, we get
$$
(x+t)^{2028}+(x-t)^{2028}=2\left(x^{2028}+a_{2} x^{2026} t^{2}+\ldots+a_{2026} x^{2} t^{2026}+t^{2028}\right)
$$
Notice that when expanding different $t_{1}^{n}$ and $t_{2}^{n}$, we will get different monomials (since the degrees of $x$ will be different). Also, when expanding $t^{n}$, we will get $n+1$ different monomials, so the final answer will be
$$
1+3+\ldots+2027+2029=1015^{2}=1030225
$$
## Solve the following problems with justification of the answer
|
1030225
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (5 points) Find the degree measure of the angle
$$
\delta=\arccos \left(\left(\sin 3269^{\circ}+\sin 3270^{\circ}+\cdots+\sin 6869^{\circ}\right)^{\cos } 3240^{\circ}+\cos 3241^{\circ}+\cdots+\cos 6840^{\circ}\right)
$$
|
Answer: $61^{\circ}$
Solution: From the statement $\cos \alpha+\cos \left(\alpha+180^{\circ}\right)=0$ it follows that $\cos \alpha+\cos \left(\alpha+1^{\circ}\right)+$ $\cdots+\cos \left(\alpha+179^{\circ}\right)=0$. Then $\cos 3240^{\circ}+\cos 3241^{\circ}+\cdots+\cos 6839^{\circ}=0$ and in the exponent only $\cos 6840^{\circ}=1$ remains. Similarly, $\sin \alpha+\sin \left(\alpha+1^{\circ}\right)+\cdots+\sin \left(\alpha+179^{\circ}\right)=0$ and $\sin 3269^{\circ}+\sin 3270^{\circ}+\cdots+\sin 6868^{\circ}=0 \cdot \sin 6869^{\circ}=\sin 29^{\circ}$. Then $\delta=\arccos \left(\sin 29^{\circ}\right)=61^{\circ}$.
|
61
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (5 points) Two different natural numbers end with 7 zeros and have exactly 72 divisors. Find their sum.
#
|
# Answer: 70000000
Solution: Since the number ends with 7 zeros, it has the form $N=10^{7} k$. The smallest number of this form $10^{7}$ has 64 divisors: all divisors are of the form $2^{a} 5^{b}$, where $a$ and $b$ range from 0 to 7. We will show that $k$ does not have any prime divisors other than 2 and 5. If $k$ has other prime divisors, the number of divisors of $N$ increases by at least a factor of two: in addition to the original $1,2,5,10,20 \ldots$, there will also be $k, 2 k, 5 k, 10 k, 20 k$ and so on.
Therefore, $10^{7} k=2^{a} 5^{b}$, and the number of its divisors is $(a+1)(b+1)$. The number 72 can be represented as a product of two factors greater than 7 in only one way: $72=8 \cdot 9$. Then, $N=2^{7} 5^{8}$ or $N=2^{8} 5^{7}$. Their sum is 70000000.
|
70000000
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (7 points) On the radius $A O$ of a circle with center $O$, a point $M$ is chosen. On one side of $A O$ on the circle, points $B$ and $C$ are chosen such that $\angle A M B = \angle O M C = \alpha$. Find the length of $B C$ if the radius of the circle is $21$, and $\sin \alpha = \frac{\sqrt{40}}{7}$?
|
Answer: 18.
## Solution:
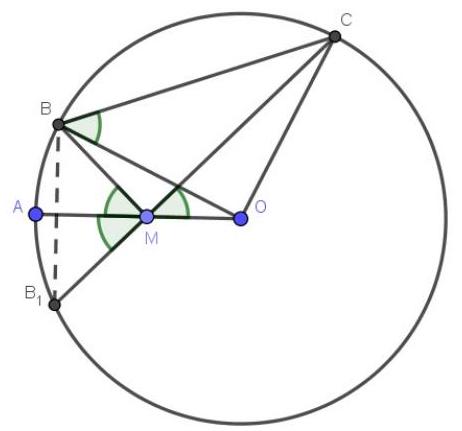
Consider point $B_{1}$, which is symmetric to point $B$ with respect to the line $O A$. It also lies on the circle and $\angle A M B=\alpha$. Note that points $B_{1}, M, C$ lie on the same straight line, and $\Delta B B_{1} M$ is isosceles. Therefore, the inscribed angle $\angle B B_{1} M=90^{\circ}-\alpha$, and the central angle $\angle B O C=180^{\circ}-2 \alpha$. $\triangle B O C$ is isosceles and $\angle O B C=\alpha \cdot \cos \alpha=\sqrt{1-\sin ^{2} \alpha}=\frac{3}{7}$. We find the base of the isosceles triangle using the formula $B C=2 * \cos \alpha * B O=2 * \frac{3}{7} * 21=18$
|
18
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (7 points) On the board, 47 ones are written. Every minute, Karlson erases two arbitrary numbers and writes their sum on the board, and then eats a number of candies equal to the product of the two erased numbers. What is the maximum number of candies he could have eaten in 47 minutes?
|
Answer: 1081.
Solution: Let's represent 47 units as points on a plane. Each time we combine numbers, we will connect the points of one group with all the points of the second group with line segments. Note that if we replace numbers $x$ and $y$ with $x+y$, the groups " $x$ " and " $y$ " will be connected by $x y$ line segments. This is the same number of candies that Karlson eats. After 47 minutes, all points will be connected. In total, $\frac{47 \cdot(47-1)}{2}=1081$ line segments will be drawn. Therefore, Karlson will eat 1081 candies.
|
1081
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
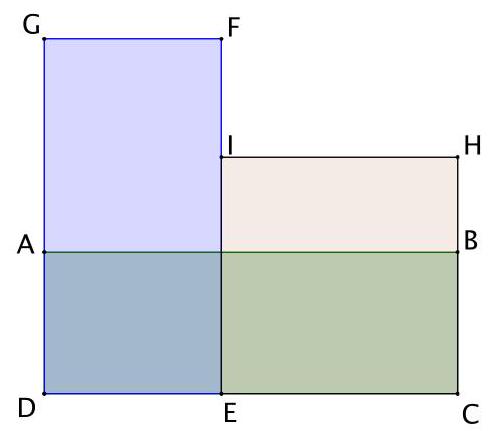
5. (8 points) Rectangles $A B C D, D E F G, C E I H$ have equal areas and integer sides. Find $D G$, if $B C=23$.
|
Answer: 552
Solution: Let $D E=a$ and $E C=b$. Then the area of the rectangles $S=23(a+b)$. According to the condition, $S$ is divisible by $a$ and $b$, that is, $S=a k$ and $S=b l$, where $k=D G$ and $l=C H-$ are natural numbers. Then $a=\frac{S}{k}$ and $b=\frac{S}{l}$. We get that $S=\frac{23 S}{k}+\frac{23 S}{l}$. Therefore, $k l=23(k+l)=>$ $k l-23 k-23 l+529=529=>(k-23)(l-23)=529$. Since $l<k$, that is, $l-23<k-23$. Therefore, $l-23=1$ and $k-23=529$. Thus, $k=D G=552$.
|
552
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (8 points) Let for positive numbers $x, y, z$ the following system of equations holds:
$$
\left\{\begin{array}{l}
x^{2}+x y+y^{2}=108 \\
y^{2}+y z+z^{2}=64 \\
z^{2}+x z+x^{2}=172
\end{array}\right.
$$
Find the value of the expression $x y+y z+x z$.
|
Answer: 96
Solution: Let there be three rays with vertex $O$, forming angles of $120^{\circ}$ with each other. On these rays, we lay off segments $O A=x, O B=y, O C=z$. Then, by the cosine theorem, $A B^{2}=108$, $B C^{2}=64, A C^{2}=172$. Note that triangle $A B C$ is a right triangle with hypotenuse $A C$. The sum of the areas of triangles $A O B, B O C, A O C$ is equal to the area of triangle $A B C$. This gives us the relation $\frac{1}{2}(x y+y z+x z) \sin 120^{\circ}=\frac{1}{2} \cdot 6 \sqrt{3} \cdot 8$. From this, we obtain the answer.
|
96
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (10 points) In the expression $(x+y+z)^{2030}+(x-y-z)^{2030}$, the brackets were expanded and like terms were combined. How many monomials $x^{a} y^{b} z^{c}$ with a non-zero coefficient were obtained?
|
Answer: 1032256
Solution: Let $t=y+z$, then the polynomial can be rewritten as $(x+t)^{2030}+(x-t)^{2030}$. We expand both brackets using the binomial theorem and get
$$
\begin{aligned}
& (x+t)^{2030}=x^{2030}+a_{1} x^{2029} t+\ldots+a_{2029} x t^{2029}+t^{2030} \\
& (x-t)^{2030}=x^{2030}-a_{1} x^{2029} t+\ldots-a_{2029} x t^{2029}+t^{2030}
\end{aligned}
$$
Adding these, we get
$$
(x+t)^{2030}+(x-t)^{2030}=2\left(x^{2030}+a_{2} x^{2028} t^{2}+\ldots+a_{2028} x^{2} t^{2028}+t^{2030}\right)
$$
Notice that when expanding different $t_{1}^{n}$ and $t_{2}^{n}$, we will get different monomials (since the powers of $x$ will be different). Also, when expanding $t^{n}$, we will get $n+1$ different monomials, so the final answer will be
$$
1+3+\ldots+2029+2031=1016^{2}=1032256
$$
## Solve the following problems with justification for the answer
|
1032256
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (5 points) Find the degree measure of the angle
$$
\delta=\arccos \left(\left(\sin 3271^{\circ}+\sin 3272^{\circ}+\cdots+\sin 6871^{\circ}\right)^{\cos } 3240^{\circ}+\cos 3241^{\circ}+\cdots+\cos 6840^{\circ}\right)
$$
|
Answer: $59^{\circ}$
Solution: From the statement $\cos \alpha+\cos \left(\alpha+180^{\circ}\right)=0$ it follows that $\cos \alpha+\cos \left(\alpha+1^{\circ}\right)+$ $\cdots+\cos \left(\alpha+179^{\circ}\right)=0$. Then $\cos 3240^{\circ}+\cos 3241^{\circ}+\cdots+\cos 6839^{\circ}=0$ and in the exponent only $\cos 6840^{\circ}=1$ remains. Similarly, $\sin \alpha+\sin \left(\alpha+1^{\circ}\right)+\cdots+\sin \left(\alpha+179^{\circ}\right)=0$ and $\sin 3271^{\circ}+\sin 3272^{\circ}+\cdots+\sin 6870^{\circ}=0 \cdot \sin 6871^{\circ}=\sin 31^{\circ}$. Then $\delta=\arccos \left(\sin 31^{\circ}\right)=59^{\circ}$.
|
59
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (7 points) On the radius $A O$ of a circle with center $O$, a point $M$ is chosen. On one side of $A O$ on the circle, points $B$ and $C$ are chosen such that $\angle A M B = \angle O M C = \alpha$. Find the length of $B C$ if the radius of the circle is $14$, and $\sin \alpha = \frac{\sqrt{33}}{7}$?
|
Answer: 16
## Solution:
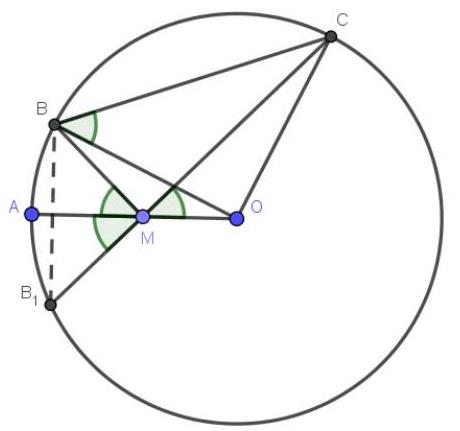
Consider point $B_{1}$, which is symmetric to point $B$ with respect to the line $O A$. It also lies on the circle and $\angle A M B=\alpha$. Notice that points $B_{1}, M, C$ lie on the same straight line, and $\Delta B B_{1} M$ is isosceles. Therefore, the inscribed angle $\angle B B_{1} M=90^{\circ}-\alpha$, and the central angle $\angle B O C=180^{\circ}-2 \alpha$. $\triangle B O C$ is isosceles and $\angle O B C=\alpha \cdot \cos \alpha=\sqrt{1-\sin ^{2} \alpha}=\frac{4}{7}$. We find the base of the isosceles triangle using the formula $B C=2 * \cos \alpha * B O=2 * \frac{4}{7} *$ $14=16$
|
16
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (7 points) On the board, 48 ones are written. Every minute, Karlson erases two arbitrary numbers and writes their sum on the board, and then eats a number of candies equal to the product of the two erased numbers. What is the maximum number of candies he could have eaten in 48 minutes?
|
Answer: 1128.
Solution: Let's represent 48 units as points on a plane. Each time we combine numbers, we will connect the points of one group to all the points of the second group with line segments. Note that if we replace numbers $x$ and $y$ with $x+y$, the groups " $x$ " and " $y$ " will be connected by $x y$ line segments. This is the same number of candies that Karlson eats. After 48 minutes, all points will be connected. In total, $\frac{48 \cdot(48-1)}{2}=1128$ line segments will be drawn. Therefore, Karlson will eat 1128 candies.
|
1128
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
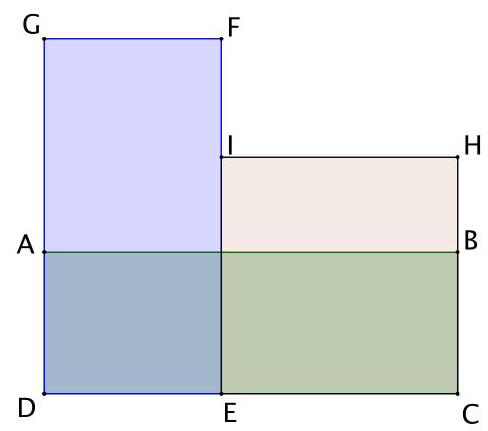
5. (8 points) Rectangles $A B C D, D E F G, C E I H$ have equal areas and integer sides. Find $D G$, if $B C=19$.
|
Answer: 380
Solution: Let $D E=a$ and $E C=b$. Then the area of the rectangles $S=19(a+b)$. According to the condition, $S$ is divisible by $a$ and $b$, that is, $S=a k$ and $S=b l$, where $k=D G$ and $l=C H-$ are natural numbers. Then $a=\frac{S}{k}$ and $b=\frac{S}{l}$. We get that $S=\frac{19 S}{k}+\frac{19 S}{l}$. Therefore, $k l=19(k+l)=>$ $k l-19 k-19 l+361=361=>(k-19)(l-19)=361$. Since $l<k$, that is, $l-19<k-19$. Therefore, $l-19=1$ and $k-19=361$. Thus, $k=D G=380$.
|
380
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (8 points) Let for positive numbers $x, y, z$ the system of equations holds:
$$
\left\{\begin{array}{l}
x^{2}+x y+y^{2}=108 \\
y^{2}+y z+z^{2}=49 \\
z^{2}+x z+x^{2}=157
\end{array}\right.
$$
Find the value of the expression $x y+y z+x z$.
|
Answer: 84
Solution: Let there be three rays with vertex $O$, forming angles of $120^{\circ}$ with each other. On these rays, we lay off segments $O A=x, O B=y, O C=z$. Then, by the cosine theorem, $A B^{2}=108$, $B C^{2}=49, A C^{2}=157$. Note that triangle $A B C$ is a right triangle with hypotenuse $A C$. The sum of the areas of triangles $A O B, B O C, A O C$ is equal to the area of triangle $A B C$. This gives us the relation $\frac{1}{2}(x y+y z+x z) \sin 120^{\circ}=\frac{1}{2} \cdot 6 \sqrt{3} \cdot 7$. From this, we obtain the answer.
|
84
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (10 points) In the expression $(x+y+z)^{2032}+(x-y-z)^{2032}$, the parentheses were expanded and like terms were combined. How many monomials $x^{a} y^{b} z^{c}$ with a non-zero coefficient were obtained?
|
Answer: 1034289
Solution: Let $t=y+z$, then the polynomial can be rewritten as $(x+t)^{2032}+(x-t)^{2032}$. We expand both brackets using the binomial theorem and get
$$
\begin{aligned}
& (x+t)^{2032}=x^{2032}+a_{1} x^{2031} t+\ldots+a_{2031} x t^{2031}+t^{2032} \\
& (x-t)^{2032}=x^{2032}-a_{1} x^{2031} t+\ldots-a_{2031} x t^{2031}+t^{2032}
\end{aligned}
$$
Adding these, we get
$$
(x+t)^{2032}+(x-t)^{2032}=2\left(x^{2032}+a_{2} x^{2030} t^{2}+\ldots+a_{2030} x^{2} t^{2030}+t^{2032}\right)
$$
Notice that when expanding different $t_{1}^{n}$ and $t_{2}^{n}$, we will get different monomials (since the degrees of $x$ will be different). Also, when expanding $t^{n}$, we will get $n+1$ different monomials, so the final answer will be
$$
1+3+\ldots+2031+2033=1017^{2}=1034289
$$
## Solve the following problems with justification of the answer
|
1034289
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (5 points) Find the degree measure of the angle
$$
\delta=\arccos \left(\left(\sin 2193^{\circ}+\sin 2194^{\circ}+\cdots+\sin 5793^{\circ}\right)^{\cos 2160^{\circ}+\cos 2161^{\circ}+\cdots+\cos 5760^{\circ}}\right)
$$
|
# Answer: $57^{\circ}$
Solution: From the statement $\cos \alpha+\cos \left(\alpha+180^{\circ}\right)=0$, it follows that $\cos \alpha+\cos \left(\alpha+1^{\circ}\right)+$ $\cdots+\cos \left(\alpha+179^{\circ}\right)=0$. Then $\cos 2160^{\circ}+\cos 2161^{\circ}+\cdots+\cos 5759^{\circ}=0$ and in the exponent only $\cos 5760^{\circ}=1$ remains. Similarly, $\sin \alpha+\sin \left(\alpha+1^{\circ}\right)+\cdots+\sin \left(\alpha+179^{\circ}\right)=0$ and $\sin 2193^{\circ}+\sin 2194^{\circ}+\cdots+\sin 5792^{\circ}=0 \cdot \sin 5793^{\circ}=\sin 33^{\circ}$. Then $\delta=\arccos \left(\sin 33^{\circ}\right)=57^{\circ}$.
|
57
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (7 points) On the radius $A O$ of a circle with center $O$, a point $M$ is chosen. On one side of $A O$ on the circle, points $B$ and $C$ are chosen such that $\angle A M B = \angle O M C = \alpha$. Find the length of $B C$ if the radius of the circle is $16$, and $\sin \alpha = \frac{\sqrt{55}}{8}$?
|
Answer: 12.
## Solution:
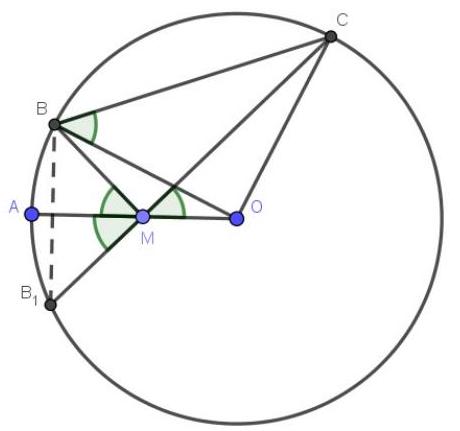
Consider point $B_{1}$, which is symmetric to point $B$ with respect to the line $O A$. It also lies on the circle and $\angle A M B=\alpha$. Note that points $B_{1}, M, C$ lie on the same straight line, and $\Delta B B_{1} M$ is isosceles. Therefore, the inscribed angle $\angle B B_{1} M=90^{\circ}-\alpha$, and the central angle $\angle B O C=180^{\circ}-2 \alpha$. $\triangle B O C$ is isosceles and $\angle O B C=\alpha \cdot \cos \alpha=\sqrt{1-\sin ^{2} \alpha}=\frac{3}{8}$. We find the base of the isosceles triangle using the formula $B C=2 * \cos \alpha * B O=2 * \frac{3}{8} * 16=12$
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (7 points) On the board, 49 ones are written. Every minute, Karlson erases two arbitrary numbers and writes their sum on the board, and then eats a number of candies equal to the product of the two erased numbers. What is the maximum number of candies he could have eaten in 49 minutes?
|
Answer: 1176.
Solution: Let's represent 49 units as points on a plane. Each time we combine numbers, we will connect the points of one group with all the points of the second group with line segments. Note that if we replace numbers $x$ and $y$ with $x+y$, the groups " $x$ " and " $y$ " will be connected by $x y$ line segments. This is the same number of candies that Karlson eats. After 49 minutes, all points will be connected. In total, $\frac{49 \cdot(49-1)}{2}=1176$ line segments will be drawn. Therefore, Karlson will eat 1176 candies.
|
1176
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (8 points) Rectangles $A B C D, D E F G, C E I H$ have equal areas and integer sides. Find $D G$, if $B C=17$.
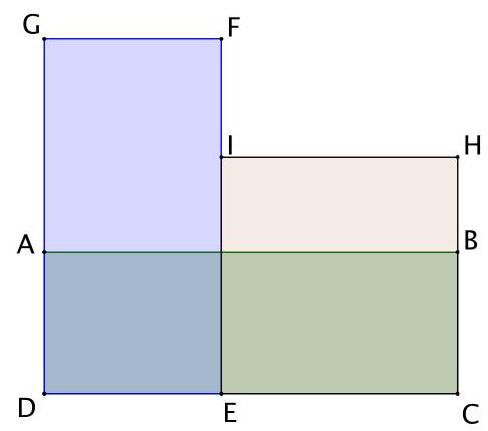
|
Answer: 306
Solution: Let $D E=a$ and $E C=b$. Then the area of the rectangles $S=17(a+b)$. According to the condition, $S$ is divisible by $a$ and $b$, that is, $S=a k$ and $S=b l$, where $k=D G$ and $l=C H-$ are natural numbers. Then $a=\frac{S}{k}$ and $b=\frac{S}{l}$. We get that $S=\frac{17 S}{k}+\frac{17 S}{l}$. Therefore, $k l=17(k+l)=>$ $k l-17 k-17 l+289=289=>(k-17)(l-17)=289$. Since $l<k$, that is, $l-17<k-17$. Therefore, $l-17=1$ and $k-17=289$. Thus, $k=D G=306$.
|
306
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (8 points) Let for positive numbers $x, y, z$ the following system of equations holds:
$$
\left\{\begin{array}{l}
x^{2}+x y+y^{2}=108 \\
y^{2}+y z+z^{2}=9 \\
z^{2}+x z+x^{2}=117
\end{array}\right.
$$
Find the value of the expression $x y+y z+x z$.
|
Answer: 36
Solution: Let there be three rays with vertex $O$, forming angles of $120^{\circ}$ with each other. On these rays, we lay off segments $O A=x, O B=y, O C=z$. Then, by the cosine theorem, $A B^{2}=108$, $B C^{2}=9, A C^{2}=117$. Note that triangle $A B C$ is a right triangle with hypotenuse $A C$. The sum of the areas of triangles $A O B, B O C, A O C$ is equal to the area of triangle $A B C$. This gives us the relation $\frac{1}{2}(x y+y z+x z) \sin 120^{\circ}=\frac{1}{2} \cdot 6 \sqrt{3} \cdot 3$. From this, we obtain the answer.
|
36
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (10 points) In the expression $(x+y+z)^{2034}+(x-y-z)^{2034}$, the brackets were expanded and like terms were combined. How many monomials $x^{a} y^{b} z^{c}$ with a non-zero coefficient were obtained?
|
Answer: 1036324
Solution: Let $t=y+z$, then the polynomial can be rewritten as $(x+t)^{2034}+(x-t)^{2034}$. We expand both brackets using the binomial theorem and get
$$
\begin{aligned}
& (x+t)^{2034}=x^{2034}+a_{1} x^{2033} t+\ldots+a_{2033} x t^{2033}+t^{2034} \\
& (x-t)^{2034}=x^{2034}-a_{1} x^{2033} t+\ldots-a_{2033} x t^{2033}+t^{2034}
\end{aligned}
$$
Adding these, we get
$$
(x+t)^{2034}+(x-t)^{2034}=2\left(x^{2034}+a_{2} x^{2032} t^{2}+\ldots+a_{2032} x^{2} t^{2032}+t^{2034}\right)
$$
Notice that when expanding different $t_{1}^{n}$ and $t_{2}^{n}$, we will get different monomials (since the degrees of $x$ will be different). Also, when expanding $t^{n}$, we will get $n+1$ different monomials, so the final answer will be
$$
1+3+\ldots+2033+2035=1018^{2}=1036324
$$
## Solve the following problems with justification of the answer
|
1036324
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (5 points) Find the degree measure of the angle
$$
\delta=\arccos \left(\left(\sin 2195^{\circ}+\sin 2196^{\circ}+\cdots+\sin 5795^{\circ}\right)^{\cos } 2160^{\circ}+\cos 2161^{\circ}+\cdots+\cos 5760^{\circ}\right)
$$
|
Answer: $55^{\circ}$
Solution: From the statement $\cos \alpha+\cos \left(\alpha+180^{\circ}\right)=0$ it follows that $\cos \alpha+\cos \left(\alpha+1^{\circ}\right)+$ $\cdots+\cos \left(\alpha+179^{\circ}\right)=0$. Then $\cos 2160^{\circ}+\cos 2161^{\circ}+\cdots+\cos 5759^{\circ}=0$ and in the exponent only $\cos 5760^{\circ}=1$ remains. Similarly, $\sin \alpha+\sin \left(\alpha+1^{\circ}\right)+\cdots+\sin \left(\alpha+179^{\circ}\right)=0$ and $\sin 2195^{\circ}+\sin 2196^{\circ}+\cdots+\sin 5794^{\circ}=0 \cdot \sin 5795^{\circ}=\sin 35^{\circ}$. Then $\delta=\arccos \left(\sin 35^{\circ}\right)=55^{\circ}$.
|
55
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (7 points) On the radius $A O$ of a circle with center $O$, a point $M$ is chosen. On one side of $A O$ on the circle, points $B$ and $C$ are chosen such that $\angle A M B = \angle O M C = \alpha$. Find the length of $B C$ if the radius of the circle is $16$, and $\sin \alpha = \frac{\sqrt{39}}{8}$?
|
Answer: 20.
## Solution:
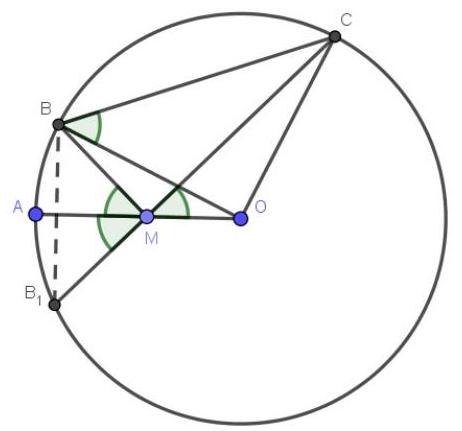
Consider point $B_{1}$, which is symmetric to point $B$ with respect to the line $O A$. It also lies on the circle and $\angle A M B=\alpha$. Note that points $B_{1}, M, C$ lie on the same straight line, and $\Delta B B_{1} M$ is isosceles. Therefore, the inscribed angle $\angle B B_{1} M=90^{\circ}-\alpha$, and the central angle $\angle B O C=180^{\circ}-2 \alpha$. $\triangle B O C$ is isosceles and $\angle O B C=\alpha \cdot \cos \alpha=\sqrt{1-\sin ^{2} \alpha}=\frac{5}{8}$. We find the base of the isosceles triangle using the formula $B C=2 * \cos \alpha * B O=2 * \frac{5}{8} * 16=20$
|
20
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (7 points) On the board, 50 ones are written. Every minute, Karlson erases two arbitrary numbers and writes their sum on the board, and then eats a number of candies equal to the product of the two erased numbers. What is the maximum number of candies he could have eaten in 50 minutes?
|
Answer: 1225.
Solution: Let's represent 50 units as points on a plane. Each time we combine two numbers, we will connect the points corresponding to one group with all the points of the second group with line segments. Note that if we replace numbers $x$ and $y$ with $x+y$, the groups " $x$ " and " $y$ " will be connected by $x y$ line segments. This is the same number of candies that Karlson eats. After 50 minutes, all points will be connected. In total, $\frac{50 \cdot(50-1)}{2}=1225$ line segments will be drawn. Therefore, Karlson will eat 1225 candies.
|
1225
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (8 points) Rectangles $A B C D, D E F G, C E I H$ have equal areas and integer sides. Find $D G$, if $B C=13$.
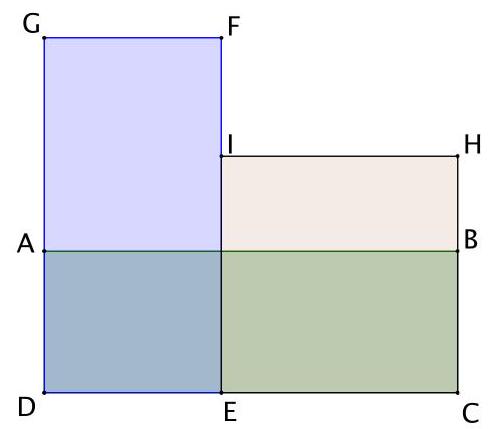
|
Answer: 182
Solution: Let $D E=a$ and $E C=b$. Then the area of the rectangles $S=13(a+b)$. According to the condition, $S$ is divisible by $a$ and $b$, that is, $S=a k$ and $S=b l$, where $k=D G$ and $l=C H-$ are natural numbers. Then $a=\frac{S}{k}$ and $b=\frac{S}{l}$. We get that $S=\frac{13 S}{k}+\frac{13 S}{l}$. Therefore, $k l=13(k+l)=>$ $k l-13 k-13 l+169=169=>(k-13)(l-13)=169$. Since $l<k$, that is, $l-13<k-13$. Therefore, $l-13=1$ and $k-13=169$. Thus, $k=D G=182$.
|
182
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (8 points) Let for positive numbers $x, y, z$ the following system of equations holds:
$$
\left\{\begin{array}{l}
x^{2}+x y+y^{2}=147 \\
y^{2}+y z+z^{2}=9 \\
z^{2}+x z+x^{2}=156
\end{array}\right.
$$
Find the value of the expression $x y+y z+x z$.
|
Answer: 42
Solution: Let there be three rays with vertex $O$, forming angles of $120^{\circ}$ with each other. On these rays, we lay off segments $O A=x, O B=y, O C=z$. Then, by the cosine theorem, $A B^{2}=147$, $B C^{2}=9, A C^{2}=156$. Note that triangle $A B C$ is a right triangle with hypotenuse $A C$. The sum of the areas of triangles $A O B, B O C, A O C$ is equal to the area of triangle $A B C$. This gives us the relation $\frac{1}{2}(x y+y z+x z) \sin 120^{\circ}=\frac{1}{2} \cdot 7 \sqrt{3} \cdot 3$. From this, we obtain the answer.
|
42
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (10 points) In the expression $(x+y+z)^{2036}+(x-y-z)^{2036}$, the brackets were expanded and like terms were combined. How many monomials $x^{a} y^{b} z^{c}$ with a non-zero coefficient were obtained?
|
Answer: 1038361
Solution: Let $t=y+z$, then the polynomial can be rewritten as $(x+t)^{2036}+(x-t)^{2036}$. We expand both brackets using the binomial theorem and get
$$
\begin{aligned}
& (x+t)^{2036}=x^{2036}+a_{1} x^{2035} t+\ldots+a_{2035} x t^{2035}+t^{2036} \\
& (x-t)^{2036}=x^{2036}-a_{1} x^{2035} t+\ldots-a_{2035} x t^{2035}+t^{2036}
\end{aligned}
$$
Adding these, we get
$$
(x+t)^{2036}+(x-t)^{2036}=2\left(x^{2036}+a_{2} x^{2034} t^{2}+\ldots+a_{2034} x^{2} t^{2034}+t^{2036}\right)
$$
Notice that when expanding different $t_{1}^{n}$ and $t_{2}^{n}$, we will get different monomials (since the degrees of $x$ will be different). Also, when expanding $t^{n}$, we will get $n+1$ different monomials, so the final answer will be
$$
1+3+\ldots+2035+2037=1019^{2}=1038361
$$
## Solve the following problems with justification of the answer
|
1038361
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In a $4 \times 4$ table, 16 different natural numbers are arranged. For each row and each column of the table, the greatest common divisor (GCD) of the numbers located in it was found. It turned out that all eight found numbers are different. For what largest $n$ can we assert that there is a number in such a table that is not less than $n ?$
(A. Khryabrov)
|
# Answer: 32.
Solution. If the greatest common divisor (GCD) in some row is $n$, then there are four numbers in that row that are divisible by $n$, meaning there is a number no less than $4n$. Since the greatest common divisors in all rows are distinct, one of them is certainly no less than 8. Then, in the corresponding row, there must be a number no less than 32. Now, let's provide an example of a table where all numbers are no greater than 32. The greatest common divisors of the rows are $5, 6, 7$, and 8, while those of the columns are 1, 2, 3, and 4.
| 5 | 10 | 15 | 20 |
| :---: | :---: | :---: | :---: |
| 30 | 6 | 18 | 12 |
| 7 | 14 | 21 | 28 |
| 8 | 16 | 24 | 32 |
Remark. The greatest common divisors must certainly be numbers from 1 to 8, and the rows with GCDs of 6, 7, and 8 should be composed of the numbers that appear in the corresponding rows in the example table (possibly in a different order).
|
32
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (8 points) Given an isosceles right triangle with a leg of 10. An infinite number of equilateral triangles are inscribed in it as shown in the figure: the vertices lie on the hypotenuse, and the bases are sequentially laid out on one of the legs starting from the right angle vertex. Find the sum of the areas of the equilateral triangles.
|
Answer: 25 .
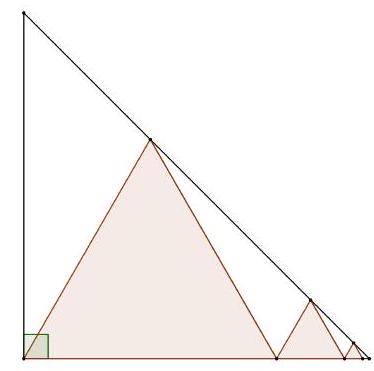
|
25
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. (20 points) Inside an acute triangle $A B C$, a point $M$ is marked. The lines $A M, B M$, $C M$ intersect the sides of the triangle at points $A_{1}, B_{1}$ and $C_{1}$ respectively. It is known that $M A_{1}=M B_{1}=M C_{1}=3$ and $A M+B M+C M=43$. Find $A M \cdot B M \cdot C M$.
|
Answer: 441.
Solution. Let $A M=x, B M=y, C M=z$. Note that $\frac{M C_{1}}{C C_{1}}=\frac{S_{A M B}}{S_{A B C}}$ and similarly for the other two segments. From the equality $\frac{S_{A M B}}{S_{A B C}}+\frac{S_{B M C}}{S_{A B C}}+\frac{S_{A M C}}{S_{A B C}}=1$ it follows that $\frac{3}{x+3}+\frac{3}{y+3}+\frac{3}{z+3}=1$, which transforms into $x y z=2 \cdot 3^{3}+3^{2}(x+y+z)=2 \cdot 3^{3}+3^{2} \cdot 43$
|
441
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. (20 points) Find all values of the parameter $c$ such that the system of equations has a unique solution
$$
\left\{\begin{array}{l}
2|x+7|+|y-4|=c \\
|x+4|+2|y-7|=c
\end{array}\right.
$$
|
Answer: $c=3$.
Solution. Let $\left(x_{0} ; y_{0}\right)$ be the unique solution of the system. Then $\left(-y_{0} ;-x_{0}\right)$ also satisfies the conditions of the system. This solution coincides with the first, so $y_{0}=-x_{0}$. The equation $2|x+7|+|x+4|=$ $c$ has a unique solution $x_{0}=-7$ when $c=|7-4|$, since the function $f(x)=2|x+7|+|x+4|$ decreases on the interval $\left(-\infty ; x_{0}\right]$ and increases on $\left[x_{0} ;+\infty\right)$. Similarly, $2|y-7|+|y-4| \geqslant|7-4|$. Therefore, when $c=|7-4|$, the equality $f(x)+f(-y)=2 c$ holds only when $x=-y=-7$, i.e., the system has a unique solution.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. What is the minimum number of cells on a $3 \times 2016$ board that can be painted so that each cell has a side-adjacent painted cell?
(A. Khryabrov)
|
Answer: 2016.
Solution: Let's divide our board as follows:
We have obtained two three-cell corners and 1007 D-hexomino figures. In our three-cell corners, at least one cell must be shaded (either the corner cell or a cell adjacent to the corner). We will prove that in each D-hexomino of the partition, at least two cells will be shaded. Let's number the cells of an arbitrary D-hexomino as follows:
If one of the cells 2 or 3 is shaded, then the adjacent cell belonging to the D-hexomino will also be shaded. If neither 2 nor 3 are shaded, then 1 or 5 (as a neighbor of cell 2) and 6 or 4 (as a neighbor of cell 3) must be shaded. In any case, our D-hexomino will have at least two shaded cells.
In the end, we get an estimate for the number of shaded cells, which is at least \(1007 \cdot 2 + 2 = 2016\).
Now let's provide an example where this estimate is achieved:
We shade 2016 cells, located on the second horizontal row.
|
2016
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (5 points) Find the remainder when $20^{16}+201^{6}$ is divided by 9.
|
Answer: 7
Solution. $201^{16}$ is divisible by 9. 20 gives a remainder of $2.2^{6}$ gives a remainder of $1,2^{16}=2^{6} \cdot 2^{6} \cdot 2^{4}$ gives the same remainder as 16.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (10 points) A hare jumps in one direction along a strip divided into cells. In one jump, it can move either one or two cells. In how many ways can the hare reach the 12th cell from the 1st cell?
#
|
# Answer: 144
Solution. In each cell, we write the number of ways the rabbit can get there. In the first cell, it's 1, in the second cell, it's 1, and so on. In each subsequent cell, the number of paths the rabbit can take splits into two groups: the last jump is 2 cells or the last jump is 1 cell. Therefore, the number in the cell is the sum of the numbers from the two previous cells (this is the Fibonacci sequence).
|
144
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (12 points) On the coordinate plane, all points whose coordinates satisfy the condition
$$
|2 x-2|+|3 y-3| \leq 30
$$
are shaded. Find the area of the resulting figure.
|
Answer: 300
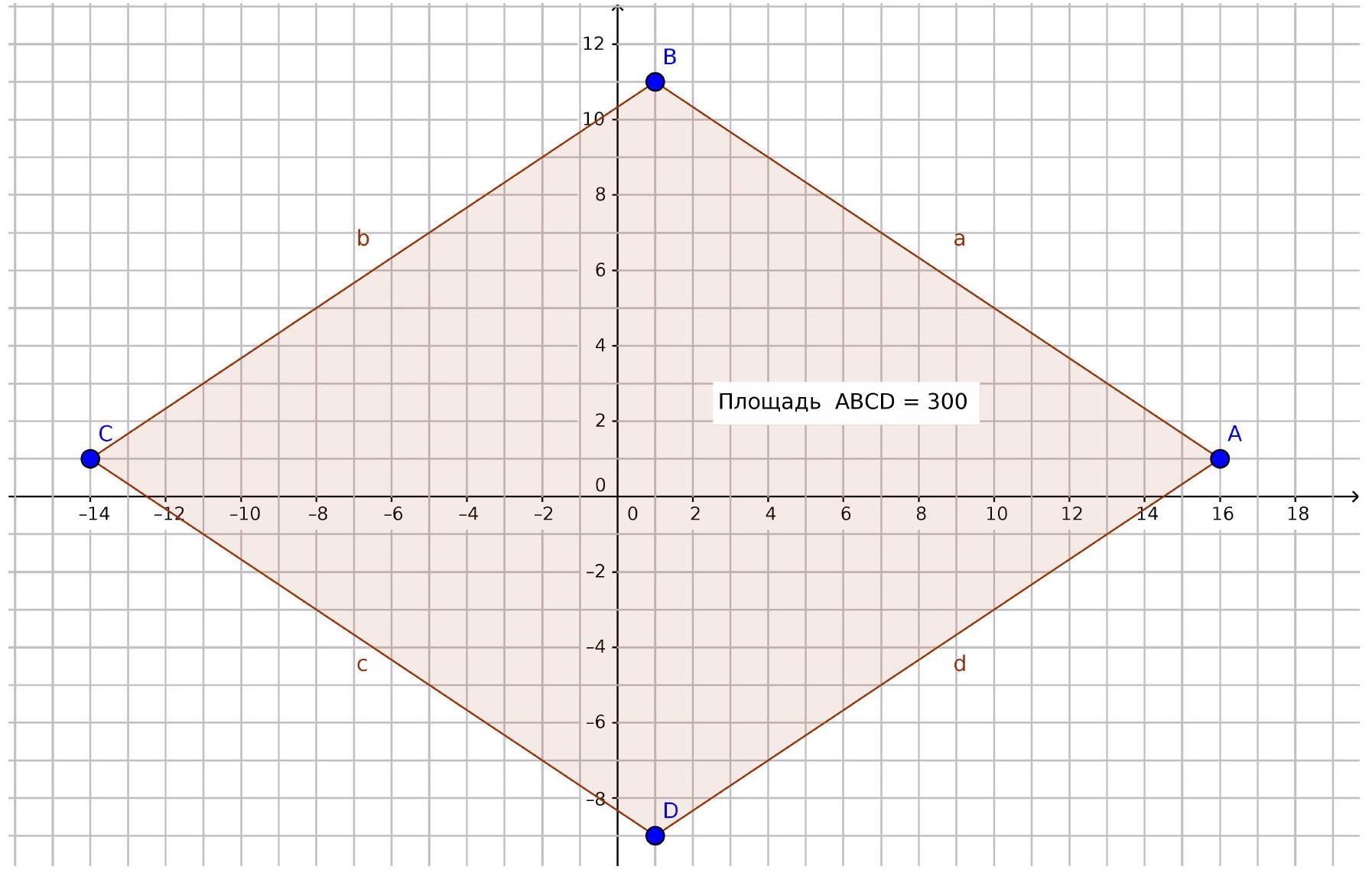
|
300
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. For a natural number $n$, the smallest divisor $a$, different from 1, and the next largest divisor $b$ were taken. It turned out that $n=a^{a}+b^{b}$. Find $n$.
|
Answer: $n=2^{2}+4^{4}=260$.
Solution. If $n$ is odd, then all its divisors are also odd. Then $a$ and $b$ are odd and $a^{a}+b^{b}$ is even. Therefore, $n$ is even. Then its smallest divisor, different from 1, is 2, and thus $a=2$. Therefore, $n=2^{2}+b^{b}$. Consequently, $4=n-b^{b}$ is divisible by $b$. Then $b=4$, since $b>2$. Thus, $n=2^{2}+4^{4}=260$.
|
260
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. (20 points) A four-digit number $\overline{a b c d}$ is called perfect if $a+b=c+d$. How many perfect numbers can be represented as the sum of two four-digit palindromes?
|
Solution: Let the number $\overline{a b c d}=\overline{n m m n}+\overline{x y y x}$, then
$$
\overline{a b c d}=1001(n+x)+110(m+y) \vdots 11
$$
From the divisibility rule by 11, it follows that $b+d=a+c$. Since the number $\overline{a b c d}$ is perfect, we get $a=d$ and $b=c$, hence the original number is a palindrome, and the first digit is not equal to 1 (otherwise it cannot be represented as the sum of two four-digit numbers). All four-digit palindromes are determined by the first two digits, where the first digit can be chosen in 8 ways, and the second in 10 ways. In total, we get that there are $8 \cdot 10=80$ such numbers. It remains to note that each obtained number can be represented in the form $\overline{\overline{b b b a}}=1001+\overline{(a-1) b b(a-1)}$.
Answers: 80.
|
80
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (5 points) Find the value of the function $f(x)$ at the point $x_{0}=1000$, if $f(0)=1$ and for any $x$ the equality $f(x+2)=f(x)+4 x+2$ holds.
|
Answer: 999001
Solution: In the equation $f(x+2)-f(x)=4 x+2$, we will substitute for $x$ the numbers $0,2,4, \ldots, 998$. We get:
$$
\begin{aligned}
& f(2)-f(0)=4 \cdot 0+2 \\
& f(4)-f(2)=4 \cdot 2+2
\end{aligned}
$$
$$
f(1000)-f(998)=4 \cdot 998+2
$$
Adding the equations, we get: $f(1000)-f(0)=4 \cdot(0+2+4+\cdots+998)+2 \cdot 500=4$. $\frac{998 \cdot 500}{2}+1000=999000$. Then $f(1000)=999001$.
|
999001
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (5 points) At the World Meteorologists Conference, each participant in turn announced the average monthly temperature in their hometown. At this moment, all the others recorded the product of the temperatures in their and the speaker's cities. In total, 62 positive and 70 negative numbers were recorded. What is the smallest number of times a positive temperature could have been announced?
|
Answer: 5
Solution: When solving, we will not consider cities with a zero temperature, as no positive or negative numbers arise from their interactions.
1) Let there be $x$ participants at the conference, each giving $x-1$ answers, so $x(x-1)=70+62$, which means $x=12$.
2) Let there be $y$ people with "positive temperature" at the conference, then there were $(12-y)$ people with "negative temperature". Each "positive" person recorded a positive number $(y-1)$ times, and each "negative" person recorded a negative number $-(11-y)$ times. Then $y(y-1)+(12-y)(11-y)=62 \Rightarrow$ $y^{2}-12 y+35=0 \Rightarrow y=5$ or $y=7$. Both answers satisfy the condition (in both cases, 70 negative numbers are recorded).
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (7 points) Four mole burrows $A, B, C, D$ are connected sequentially by three tunnels. Each minute, the mole runs through a tunnel to one of the adjacent burrows. In how many ways can the mole get from burrow $A$ to $C$ in 30 minutes?

|
Answer: 832040
Solution: After an even number of minutes, the mole can be only at vertices $A$ and $C$. Let $a_{k}$ and $c_{k}$ denote the number of paths of length $2 k$ leading from $A$ to $A$ and from $A$ to $C$, respectively. Note that the equalities $c_{k+1}=a_{k}+2 c_{k}, a_{k+1}=a_{k}+c_{k}$ hold. Therefore, $c_{k+2}=a_{k+1}+$ $2 c_{k+1}=a_{k}+c_{k}+2 c_{k+1}=c_{k+1}-2 c_{k}+c_{k}+2 c_{k+1}=3 c_{k+1}-c_{k}$.
| $C_{0}$ | $C_{1}$ | $C_{2}$ | $C_{3}$ | $C_{4}$ | $C_{5}$ | $C_{6}$ | $C_{7}$ | $C_{8}$ | $C_{9}$ | $C_{10}$ | $C_{11}$ | $C_{12}$ | $C_{13}$ | $C_{14}$ | $C_{15}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 0 | 1 | 3 | 8 | 21 | 55 | 144 | 377 | 987 | 2584 | 6765 | 17711 | 46368 | 121393 | 317811 | 832040 |
|
832040
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (7 points) The numbers $a, b, c, d$ belong to the interval $[-4.5,4.5]$. Find the maximum value of the expression $a+2 b+c+2 d-a b-b c-c d-d a$.
|
Answer: 90
Solution: Note that $a+2 b+c+2 d-a b-b c-c d-d a=(a+c)+2(b+d)-(a+c)(b+d)$. Let $x=a+c, y=b+d$, then we will find the maximum value of the expression $x+2 y-x y=(y-1)(2-x)+2$, where $-10 \leqslant y-1 \leqslant 8$ and $-7 \leqslant 2-x \leqslant 11$. Therefore, $(y-1)(2-x)+2 \leqslant 8 \cdot 11+2=90$. The maximum value of the expression is achieved when $a=c=-4.5, b=d=4.5$.
|
90
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (8 points) In $\triangle A B C, A B=86$, and $A C=97$. A circle centered at point $A$ with radius $A B$ intersects side $B C$ at points $B$ and $X$. Moreover, $B X$ and $C X$ have integer lengths. What is the length of $B C ?$
|
Answer: 61
Solution: Let $x=B X$ and $y=C X$. We will calculate the power of point $C$ in two ways
$$
y(y+x)=97^{2}-86^{2}=2013
$$
Considering all divisors of the number 2013 and taking into account the triangle inequality $\triangle A C X$, we obtain the unique solution 61.
|
61
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (8 points) On the board, 34 ones are written. Every minute, Karlson erases two arbitrary numbers and writes their sum on the board, and then eats a number of candies equal to the product of the two erased numbers. What is the maximum number of candies he could have eaten in 34 minutes?
|
Answer: 561.
Solution: Let's represent 34 units as points on a plane. Each time we combine numbers, we will connect the points of one group with all the points of the second group with line segments. Note that if we replace numbers $x$ and $y$ with $x+y$, the groups " $x$ " and " $y$ " will be connected by $x y$ line segments. This is the same number of candies that Karlson eats. After 34 minutes, all points will be connected. In total, $\frac{34 \cdot(34-1)}{2}=561$ line segments will be drawn. Therefore, Karlson will eat 561 candies.
|
561
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (10 points) Let for positive numbers $x, y, z$ the following system of equations holds:
$$
\left\{\begin{array}{l}
x^{2}+x y+y^{2}=12 \\
y^{2}+y z+z^{2}=25 \\
z^{2}+x z+x^{2}=37
\end{array}\right.
$$
Find the value of the expression $x y+y z+x z$.
|
Answer: 20
Solution: Let there be three rays with vertex $O$, forming angles of $120^{\circ}$ with each other. On these rays, we lay off segments $O A=x, O B=y, O C=z$. Then, by the cosine theorem, $A B^{2}=12$, $B C^{2}=25$, and $A C^{2}=37$. Note that triangle $A B C$ is a right triangle with hypotenuse $A C$. The sum of the areas of triangles $A O B, B O C, A O C$ is equal to the area of triangle $A B C$. This gives us the relation $\frac{1}{2}(x y+y z+x z) \sin 120^{\circ}=\frac{1}{2} \cdot 2 \sqrt{3} \cdot 5$. From this, we obtain the answer.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (5 points) Find the value of the function $f(x)$ at the point $x_{0}=2000$, if $f(0)=1$ and for any $x$ the equality $f(x+2)=f(x)+4 x+2$ holds.
|
Answer: 3998001
Solution: In the equation $f(x+2)-f(x)=4 x+2$, we will substitute for $x$ the numbers $0, 2, 4, \ldots, 1998$. We get:
$$
\begin{aligned}
& f(2)-f(0)=4 \cdot 0+2 \\
& f(4)-f(2)=4 \cdot 2+2
\end{aligned}
$$
$$
f(2000)-f(1998)=4 \cdot 1998+2
$$
Adding the equations, we get: $f(2000)-f(0)=4 \cdot(0+2+4+\cdots+1998)+2 \cdot 1000=$ $4 \cdot \frac{1998 \cdot 1000}{2}+2000=3998000$. Then $f(2000)=3998001$.
|
3998001
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (5 points) At the World Meteorologists Conference, each participant in turn announced the average monthly temperature in their hometown. At this moment, all the others recorded the product of the temperatures in their and the speaker's cities. In total, 68 positive and 64 negative numbers were recorded. What is the smallest number of times a positive temperature could have been announced?
|
Answer: 4
Solution: When solving, we will not consider cities with a zero temperature, as no positive or negative numbers appear when interacting with them.
1) Let there be $x$ participants at the conference, each giving $x-1$ answers, so $x(x-1)=64+68$, which means $x=12$.
2) Let there be $y$ people with "positive temperature" at the conference, then there were $(12-y)$ people with "negative temperature". Each "positive" person recorded a positive number $(y-1)$ times, and each "negative" person recorded a negative number $-(11-y)$ times. Then $y(y-1)+(12-y)(11-y)=68 \Rightarrow$ $y^{2}-12 y+32=0 \Rightarrow y=4$ or $y=8$. Both answers satisfy the condition (in both cases, 64 negative numbers are recorded).
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (7 points) Four mole burrows $A, B, C, D$ are connected sequentially by three tunnels. Each minute, the mole runs through a tunnel to one of the adjacent burrows. In how many ways can the mole get from burrow $A$ to $C$ in 28 minutes?
|
# Answer: 317811
Solution: After an even number of minutes, the mole can be only at vertices $A$ and $C$. Let $a_{k}$ and $c_{k}$ denote the number of paths of length $2 k$ leading from $A$ to $A$ and from $A$ to $C$, respectively. Note that the equalities $c_{k+1}=a_{k}+2 c_{k}, a_{k+1}=a_{k}+c_{k}$ hold. From this, $c_{k+2}=a_{k+1}+2 c_{k+1}=a_{k}+c_{k}+2 c_{k+1}=c_{k+1}-2 c_{k}+c_{k}+2 c_{k+1}=3 c_{k+1}-c_{k}$.
| $C_{0}$ | $C_{1}$ | $C_{2}$ | $C_{3}$ | $C_{4}$ | $C_{5}$ | $C_{6}$ | $C_{7}$ | $C_{8}$ | $C_{9}$ | $C_{10}$ | $C_{11}$ | $C_{12}$ | $C_{13}$ | $C_{14}$ | $C_{15}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 0 | 1 | 3 | 8 | 21 | 55 | 144 | 377 | 987 | 2584 | 6765 | 17711 | 46368 | 121393 | 317811 | 832040 |
|
317811
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (7 points) The numbers $a, b, c, d$ belong to the interval $[-5.5,5.5]$. Find the maximum value of the expression $a+2 b+c+2 d-a b-b c-c d-d a$.
|
Answer: 132
Solution: Note that $a+2 b+c+2 d-a b-b c-c d-d a=(a+c)+2(b+d)-(a+$ $c)(b+d)$. Let $x=a+c, y=b+d$, then we will find the maximum value of the expression $x+2 y-x y=(y-1)(2-x)+2$, where $-12 \leqslant y-1 \leqslant 10$ and $-9 \leqslant 2-x \leqslant 13$. Therefore, $(y-1)(2-x)+2 \leqslant 10 \cdot 13+2=132$. The maximum value of the expression is achieved when $a=c=-5.5, b=d=5.5$.
|
132
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (8 points) In $\triangle A B C, A B=86$, and $A C=97$. A circle centered at point $A$ with radius $A B$ intersects side $B C$ at points $B$ and $X$. Additionally, $B X$ and $C X$ have integer lengths. What is the length of $B C ?$
|
Answer: 61
Solution: Let $x=B X$ and $y=C X$. We will calculate the power of point $C$ in two ways
$$
y(y+x)=97^{2}-86^{2}=2013
$$
Considering all divisors of the number 2013 and taking into account the triangle inequality $\triangle A C X$, we obtain the unique solution 61.
|
61
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (8 points) On the board, 33 ones are written. Every minute, Karlson erases two arbitrary numbers and writes their sum on the board, and then eats a number of candies equal to the product of the two erased numbers. What is the maximum number of candies he could have eaten in 33 minutes?
|
Answer: 528.
Solution: Let's represent 33 units as points on a plane. Each time we combine numbers, we will connect the points of one group to all the points of the second group with line segments. Note that if we replace numbers $x$ and $y$ with $x+y$, the groups " $x$ " and " $y$ " will be connected by $xy$ line segments. This is the same number of candies that Karlson eats. After 33 minutes, all points will be connected. In total, $\frac{33 \cdot (33-1)}{2}=528$ line segments will be drawn. Therefore, Karlson will eat 528 candies.
|
528
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (10 points) Let for positive numbers $x, y, z$ the following system of equations holds:
$$
\left\{\begin{array}{l}
x^{2}+x y+y^{2}=12 \\
y^{2}+y z+z^{2}=16 \\
z^{2}+x z+x^{2}=28
\end{array}\right.
$$
Find the value of the expression $x y+y z+x z$.
|
Answer: 16
Solution: Let there be three rays with vertex $O$, forming angles of $120^{\circ}$ with each other. On these rays, we lay off segments $O A=x, O B=y, O C=z$. Then, by the cosine theorem, $A B^{2}=12$, $B C^{2}=16, A C^{2}=28$. Note that triangle $A B C$ is a right triangle with hypotenuse $A C$. The sum of the areas of triangles $A O B, B O C, A O C$ is equal to the area of triangle $A B C$. This gives us the relation $\frac{1}{2}(x y+y z+x z) \sin 120^{\circ}=\frac{1}{2} \cdot 2 \sqrt{3} \cdot 4$. From this, we obtain the answer.
|
16
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (5 points) Find the value of the function $f(x)$ at the point $x_{0}=3000$, if $f(0)=1$ and for any $x$ the equality $f(x+2)=f(x)+3 x+2$ holds.
|
Answer: 6748501
Solution: In the equation $f(x+2)-f(x)=3 x+2$, we will substitute for $x$ the numbers $0, 2, 4, \ldots, 2998$. We get:
$$
\begin{aligned}
& f(2)-f(0)=3 \cdot 0+2 \\
& f(4)-f(2)=3 \cdot 2+2
\end{aligned}
$$
$$
f(3000)-f(2998)=3 \cdot 2998+2
$$
Adding the equations, we get: $f(3000)-f(0)=3 \cdot(0+2+4+\cdots+2998)+2 \cdot 1500=$ $3 \cdot \frac{2998 \cdot 1500}{2}+3000=6748500$. Then $f(3000)=6748501$.
|
6748501
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (5 points) At the World Meteorologists Conference, each participant in turn announced the average monthly temperature in their hometown. At this moment, all the others recorded the product of the temperatures in their and the speaker's cities. In total, 78 positive and 54 negative numbers were recorded. What is the smallest number of times a positive temperature could have been announced?
|
Answer: 3
Solution: When solving, we will not consider cities with a zero temperature, as no positive or negative numbers appear when interacting with them.
1) Let there be $x$ participants at the conference, each giving $x-1$ answers, so $x(x-1)=54+78$, which means $x=12$.
2) Let there be $y$ people with "positive temperature" at the conference, then there were $(12-y)$ people with "negative temperature". Each "positive" person recorded a positive number $(y-1)$ times, and each "negative" person recorded a negative number $-(11-y)$ times. Then $y(y-1)+(12-y)(11-y)=78 \Rightarrow$ $y^{2}-12 y+27=0 \Rightarrow y=3$ or $y=9$. Both obtained answers satisfy the condition (in both cases, 54 negative numbers are recorded).
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (7 points) Four mole burrows $A, B, C, D$ are connected sequentially by three tunnels. Each minute, the mole runs through a tunnel to one of the adjacent burrows. In how many ways can the mole get from burrow $A$ to $C$ in 26 minutes?

|
Answer: 121393
Solution: After an even number of minutes, the mole can be only at vertices $A$ and $C$. Let $a_{k}$ and $c_{k}$ denote the number of paths of length $2 k$ leading from $A$ to $A$ and from $A$ to $C$, respectively. Note that the equalities $c_{k+1}=a_{k}+2 c_{k}, a_{k+1}=a_{k}+c_{k}$ hold. Therefore, $c_{k+2}=a_{k+1}+$ $2 c_{k+1}=a_{k}+c_{k}+2 c_{k+1}=c_{k+1}-2 c_{k}+c_{k}+2 c_{k+1}=3 c_{k+1}-c_{k}$.
| $C_{0}$ | $C_{1}$ | $C_{2}$ | $C_{3}$ | $C_{4}$ | $C_{5}$ | $C_{6}$ | $C_{7}$ | $C_{8}$ | $C_{9}$ | $C_{10}$ | $C_{11}$ | $C_{12}$ | $C_{13}$ | $C_{14}$ | $C_{15}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 0 | 1 | 3 | 8 | 21 | 55 | 144 | 377 | 987 | 2584 | 6765 | 17711 | 46368 | 121393 | 317811 | 832040 |
|
121393
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (7 points) The numbers $a, b, c, d$ belong to the interval $[-6.5,6.5]$. Find the maximum value of the expression $a+2 b+c+2 d-a b-b c-c d-d a$.
|
Answer: 182
Solution: Note that $a+2 b+c+2 d-a b-b c-c d-d a=(a+c)+2(b+d)-(a+$ $c)(b+d)$. Let $x=a+c, y=b+d$, then we will find the maximum value of the expression $x+2 y-x y=(y-1)(2-x)+2$, where $-14 \leqslant y-1 \leqslant 12$ and $-11 \leqslant 2-x \leqslant 15$. Therefore, $(y-1)(2-x)+2 \leqslant 12 \cdot 15+2=182$. The maximum value of the expression is achieved when $a=c=-6.5, b=d=6.5$.
|
182
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (8 points) On the board, 32 ones are written. Every minute, Karlson erases two arbitrary numbers and writes their sum on the board, and then eats a number of candies equal to the product of the two erased numbers. What is the maximum number of candies he could have eaten in 32 minutes?
|
Answer: 496.
Solution: Let's represent 32 units as points on a plane. Each time we combine numbers, we will connect the points of one group with all the points of the second group with line segments. Note that if we replace numbers $x$ and $y$ with $x+y$, the groups " $x$ " and " $y$ " will be connected by $x y$ line segments. This is the same number of candies that Karlson eats. After 32 minutes, all points will be connected. In total, $\frac{32 \cdot(32-1)}{2}=496$ line segments will be drawn. Therefore, Karlson will eat 496 candies.
|
496
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (10 points) Let for positive numbers $x, y, z$ the following system of equations holds:
$$
\left\{\begin{array}{l}
x^{2}+x y+y^{2}=12 \\
y^{2}+y z+z^{2}=9 \\
z^{2}+x z+x^{2}=21
\end{array}\right.
$$
Find the value of the expression $x y+y z+x z$.
|
Answer: 12
Solution: Let there be three rays with vertex $O$, forming angles of $120^{\circ}$ with each other. On these rays, we lay off segments $O A=x, O B=y, O C=z$. Then, by the cosine theorem, $A B^{2}=12$, $B C^{2}=9, A C^{2}=21$. Note that triangle $A B C$ is a right triangle with hypotenuse $A C$. The sum of the areas of triangles $A O B, B O C, A O C$ is equal to the area of triangle $A B C$. This gives us the relation $\frac{1}{2}(x y+y z+x z) \sin 120^{\circ}=\frac{1}{2} \cdot 2 \sqrt{3} \cdot 3$. From this, we obtain the answer.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (5 points) Find the value of the function $f(x)$ at the point $x_{0}=4000$, if $f(0)=1$ and for any $x$ the equality $f(x+2)=f(x)+3 x+2$ holds.
|
Answer: 11998001
Solution: In the equation $f(x+2)-f(x)=3 x+2$, we will substitute for $x$ the numbers $0,2,4, \ldots, 3998$. We get:
$$
\begin{aligned}
& f(2)-f(0)=3 \cdot 0+2 \\
& f(4)-f(2)=3 \cdot 2+2
\end{aligned}
$$
$$
f(4000)-f(3998)=3 \cdot 3998+2
$$
Adding the equations, we get: $f(4000)-f(0)=3 \cdot(0+2+4+\cdots+3998)+2 \cdot 2000=$ $3 \cdot \frac{3998 \cdot 2000}{2}+4000=11998000$. Then $f(4000)=11998001$.
|
11998001
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (5 points) At the World Meteorologists Conference, each participant in turn announced the average monthly temperature in their hometown. At this moment, all the others recorded the product of the temperatures in their and the speaker's cities. In total, 92 positive and 40 negative numbers were recorded. What is the smallest number of times a positive temperature could have been announced?
|
Answer: 2
Solution: When solving, we will not consider cities with a zero temperature, as no positive or negative numbers appear when interacting with them.
1) Let there be $x$ participants at the conference, each giving $x-1$ answers, so $x(x-1)=40+92$, which means $x=12$.
2) Let there be $y$ people with "positive temperature" at the conference, then there were $(12-y)$ people with "negative temperature". Each "positive" person recorded a positive number $(y-1)$ times, and each "negative" person recorded a negative number $-(11-y)$ times. Then $y(y-1)+(12-y)(11-y)=92 \Rightarrow$ $y^{2}-12 y+20=0 \Rightarrow y=2$ or $y=10$. Both obtained answers satisfy the condition (in both cases, 40 negative numbers are recorded).
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (7 points) Four mole burrows $A, B, C, D$ are connected sequentially by three tunnels. Each minute, the mole runs through a tunnel to one of the adjacent burrows. In how many ways can the mole get from burrow $A$ to $C$ in 24 minutes?

|
Answer: 46368
Solution: After an even number of minutes, the mole can only be at vertices $A$ and $C$. Let $a_{k}$ and $c_{k}$ denote the number of paths of length $2 k$ leading from $A$ to $A$ and from $A$ to $C$, respectively. Note that the equalities $c_{k+1}=a_{k}+2 c_{k}, a_{k+1}=a_{k}+c_{k}$ hold. Therefore, $c_{k+2}=a_{k+1}+2 c_{k+1}=a_{k}+c_{k}+2 c_{k+1}=c_{k+1}-2 c_{k}+c_{k}+2 c_{k+1}=3 c_{k+1}-c_{k}$.
| $C_{0}$ | $C_{1}$ | $C_{2}$ | $C_{3}$ | $C_{4}$ | $C_{5}$ | $C_{6}$ | $C_{7}$ | $C_{8}$ | $C_{9}$ | $C_{10}$ | $C_{11}$ | $C_{12}$ | $C_{13}$ | $C_{14}$ | $C_{15}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 0 | 1 | 3 | 8 | 21 | 55 | 144 | 377 | 987 | 2584 | 6765 | 17711 | 46368 | 121393 | 317811 | 832040 |
|
46368
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (7 points) The numbers $a, b, c, d$ belong to the interval $[-7.5,7.5]$. Find the maximum value of the expression $a+2 b+c+2 d-a b-b c-c d-d a$.
|
Answer: 240
Solution: Note that $a+2 b+c+2 d-a b-b c-c d-d a=(a+c)+2(b+d)-(a+$ $c)(b+d)$. Let $x=a+c, y=b+d$, then we will find the maximum value of the expression $x+2 y-x y=(y-1)(2-x)+2$, where $-16 \leqslant y-1 \leqslant 14$ and $-13 \leqslant 2-x \leqslant 17$. Therefore, $(y-1)(2-x)+2 \leqslant 14 \cdot 17+2=240$. The maximum value of the expression is achieved when $a=c=-7.5, b=d=7.5$.
|
240
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (8 points) On the board, 31 ones are written. Every minute, Karlson erases two arbitrary numbers and writes their sum on the board, and then eats a number of candies equal to the product of the two erased numbers. What is the maximum number of candies he could eat in 31 minutes?
|
Answer: 465.
Solution: Let's represent 31 units as points on a plane. Each time we combine numbers, we will connect the points of one group with all the points of the second group with line segments. Note that if we replace numbers $x$ and $y$ with $x+y$, the groups " $x$ " and " $y$ " will be connected by $xy$ line segments. This is the same number of candies that Karlson eats. After 31 minutes, all points will be connected. In total, $\frac{31 \cdot(31-1)}{2}=465$ line segments will be drawn. Therefore, Karlson will eat 465 candies.
|
465
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (10 points) Let for positive numbers $x, y, z$ the following system of equations holds:
$$
\left\{\begin{array}{l}
x^{2}+x y+y^{2}=27 \\
y^{2}+y z+z^{2}=25 \\
z^{2}+x z+x^{2}=52
\end{array}\right.
$$
Find the value of the expression $x y+y z+x z$.
|
Answer: 30
Solution: Let there be three rays with vertex $O$, forming angles of $120^{\circ}$ with each other. On these rays, we lay off segments $O A=x, O B=y, O C=z$. Then, by the cosine theorem, $A B^{2}=27$, $B C^{2}=25, A C^{2}=52$. Note that triangle $A B C$ is a right triangle with hypotenuse $A C$. The sum of the areas of triangles $A O B, B O C, A O C$ is equal to the area of triangle $A B C$. This gives us the relation $\frac{1}{2}(x y+y z+x z) \sin 120^{\circ}=\frac{1}{2} \cdot 3 \sqrt{3} \cdot 5$. From this, we obtain the answer.
|
30
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (5 points) Find the value of the function $f(x)$ at the point $x_{0}=1500$, if $f(0)=1$ and for any $x$ the equality $f(x+3)=f(x)+2 x+3$ holds.
|
Answer: 750001
Solution: In the equation $f(x+3)-f(x)=2 x+3$, we will substitute the numbers $0,3,6, \ldots, 1497$ for $x$. We get:
$$
\begin{aligned}
& f(3)-f(0)=2 \cdot 0+3 \\
& f(6)-f(3)=2 \cdot 3+3
\end{aligned}
$$
$$
f(1500)-f(1497)=2 \cdot 1497+3
$$
Adding the equations, we get: $f(1500)-f(0)=2 \cdot(0+3+6+\cdots+1497)+3 \cdot 500=$ $2 \cdot \frac{1497 \cdot 500}{2}+1500=750000$. Then $f(1500)=750001$.
|
750001
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (5 points) At the World Meteorologists Conference, each participant in turn announced the average monthly temperature in their hometown. At this moment, all the others recorded the product of the temperatures in their and the speaker's cities. In total, 50 positive and 60 negative numbers were recorded. What is the smallest number of times a positive temperature could have been announced?
|
Answer: 5
Solution: When solving, we will not consider cities with a zero temperature, as no positive or negative numbers arise from their interactions.
1) Let there be $x$ participants at the conference, each giving $x-1$ answers, so $x(x-1)=60+50$, which means $x=11$.
2) Let there be $y$ people with "positive temperature" at the conference, then there were $(11-y)$ people with "negative temperature". Each "positive" person recorded a positive number $(y-1)$ times, and each "negative" person recorded a negative number $-(10-y)$ times. Then $y(y-1)+(11-y)(10-y)=50 \Rightarrow$ $y^{2}-11 y+30=0 \Rightarrow y=5$ or $y=6$. Both answers satisfy the condition (in both cases, 60 negative numbers are recorded).
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (7 points) Four mole burrows $A, B, C, D$ are connected sequentially by three tunnels. Each minute, the mole runs through a tunnel to one of the adjacent burrows. In how many ways can the mole get from burrow $A$ to $C$ in 22 minutes?

|
Answer: 17711
Solution: After an even number of minutes, the mole can be only at vertices $A$ and $C$. Let $a_{k}$ and $c_{k}$ denote the number of paths of length $2 k$ leading from $A$ to $A$ and from $A$ to $C$, respectively. Note that the equalities $c_{k+1}=a_{k}+2 c_{k}, a_{k+1}=a_{k}+c_{k}$ hold. Therefore, $c_{k+2}=a_{k+1}+$ $2 c_{k+1}=a_{k}+c_{k}+2 c_{k+1}=c_{k+1}-2 c_{k}+c_{k}+2 c_{k+1}=3 c_{k+1}-c_{k}$.
| $C_{0}$ | $C_{1}$ | $C_{2}$ | $C_{3}$ | $C_{4}$ | $C_{5}$ | $C_{6}$ | $C_{7}$ | $C_{8}$ | $C_{9}$ | $C_{10}$ | $C_{11}$ | $C_{12}$ | $C_{13}$ | $C_{14}$ | $C_{15}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 0 | 1 | 3 | 8 | 21 | 55 | 144 | 377 | 987 | 2584 | 6765 | 17711 | 46368 | 121393 | 317811 | 832040 |
|
17711
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (7 points) The numbers $a, b, c, d$ belong to the interval $[-8.5,8.5]$. Find the maximum value of the expression $a+2 b+c+2 d-a b-b c-c d-d a$.
|
Answer: 306
Solution: Notice that $a+2 b+c+2 d-a b-b c-c d-d a=(a+c)+2(b+d)-(a+$ $c)(b+d)$. Let $x=a+c, y=b+d$, then we will find the maximum value of the expression $x+2 y-x y=(y-1)(2-x)+2$, where $-18 \leqslant y-1 \leqslant 16$ and $-15 \leqslant 2-x \leqslant 19$. Therefore, $(y-1)(2-x)+2 \leqslant 16 \cdot 19+2=306$. The maximum value of the expression is achieved when $a=c=-8.5, b=d=8.5$.
|
306
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (8 points) On the board, 30 ones are written. Every minute, Karlson erases two arbitrary numbers and writes their sum on the board, and then eats a number of candies equal to the product of the two erased numbers. What is the maximum number of candies he could have eaten in 30 minutes?
|
Answer: 435.
Solution: Let's represent 30 units as points on a plane. Each time we combine numbers, we will connect the points of one group to all the points of the second group with line segments. Note that if we replace numbers $x$ and $y$ with $x+y$, the groups " $x$ " and " $y$ " will be connected by $x y$ line segments. This is the same number of candies that Karlson eats. After 30 minutes, all points will be connected. In total, $\frac{30 \cdot(30-1)}{2}=435$ line segments will be drawn. Therefore, Karlson will eat 435 candies.
|
435
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (10 points) Let for positive numbers $x, y, z$ the following system of equations holds:
$$
\left\{\begin{array}{l}
x^{2}+x y+y^{2}=27 \\
y^{2}+y z+z^{2}=16 \\
z^{2}+x z+x^{2}=43
\end{array}\right.
$$
Find the value of the expression $x y+y z+x z$.
|
Answer: 24
Solution: Let there be three rays with vertex $O$, forming angles of $120^{\circ}$ with each other. On these rays, we lay off segments $O A=x, O B=y, O C=z$. Then, by the cosine theorem, $A B^{2}=27$, $B C^{2}=16, A C^{2}=43$. Note that triangle $A B C$ is a right triangle with hypotenuse $A C$. The sum of the areas of triangles $A O B, B O C, A O C$ is equal to the area of triangle $A B C$. This gives us the relation $\frac{1}{2}(x y+y z+x z) \sin 120^{\circ}=\frac{1}{2} \cdot 3 \sqrt{3} \cdot 4$. From this, we obtain the answer.
|
24
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (5 points) Find the value of the function $f(x)$ at the point $x_{0}=3000$, if $f(0)=1$ and for any $x$ the equality $f(x+3)=f(x)+2 x+3$ holds.
|
Answer: 3000001
Solution: In the equation $f(x+3)-f(x)=2 x+3$, we will substitute for $x$ the numbers $0,3,6, \ldots, 2997$. We get:
$$
\begin{aligned}
& f(3)-f(0)=2 \cdot 0+3 \\
& f(6)-f(3)=2 \cdot 3+3
\end{aligned}
$$
$$
f(3000)-f(2997)=2 \cdot 2997+3
$$
Adding the equations, we get: $f(3000)-f(0)=2 \cdot(0+3+6+\cdots+2997)+3 \cdot 1000=$ $2 \cdot \frac{2997 \cdot 1000}{2}+3000=3000000$. Then $f(3000)=3000001$.
|
3000001
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (5 points) At the World Meteorologists Conference, each participant in turn announced the average monthly temperature in their hometown. At this moment, all the others recorded the product of the temperatures in their and the speaker's cities. In total, 54 positive and 56 negative numbers were recorded. What is the smallest number of times a positive temperature could have been announced?
|
Answer: 4
Solution: When solving, we will not consider cities with a zero temperature, as no positive or negative numbers appear when interacting with them.
1) Let there be $x$ participants at the conference, each giving $x-1$ answers, so $x(x-1)=56+54$, which means $x=11$.
2) Let there be $y$ people with "positive temperature" at the conference, then there were $(11-y)$ people with "negative temperature". Each "positive" person recorded a positive number $(y-1)$ times, and each "negative" person recorded a negative number $-(10-y)$ times. Then $y(y-1)+(11-y)(10-y)=54 \Rightarrow$ $y^{2}-11 y+28=0 \Rightarrow y=4$ or $y=7$. Both obtained answers satisfy the condition (in both cases, 56 negative numbers are recorded).
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (7 points) Four mole burrows $A, B, C, D$ are connected sequentially by three tunnels. Each minute, the mole runs through a tunnel to one of the adjacent burrows. In how many ways can the mole get from burrow $A$ to $C$ in 20 minutes?

|
Answer: 6765
Solution: After an even number of minutes, the mole can be only at vertices $A$ and $C$. Let $a_{k}$ and $c_{k}$ denote the number of paths of length $2 k$ leading from $A$ to $A$ and from $A$ to $C$, respectively. Note that the equalities $c_{k+1}=a_{k}+2 c_{k}, a_{k+1}=a_{k}+c_{k}$ hold. Therefore, $c_{k+2}=a_{k+1}+$ $2 c_{k+1}=a_{k}+c_{k}+2 c_{k+1}=c_{k+1}-2 c_{k}+c_{k}+2 c_{k+1}=3 c_{k+1}-c_{k}$.
| $C_{0}$ | $C_{1}$ | $C_{2}$ | $C_{3}$ | $C_{4}$ | $C_{5}$ | $C_{6}$ | $C_{7}$ | $C_{8}$ | $C_{9}$ | $C_{10}$ | $C_{11}$ | $C_{12}$ | $C_{13}$ | $C_{14}$ | $C_{15}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 0 | 1 | 3 | 8 | 21 | 55 | 144 | 377 | 987 | 2584 | 6765 | 17711 | 46368 | 121393 | 317811 | 832040 |
|
6765
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (7 points) The numbers $a, b, c, d$ belong to the interval $[-9.5,9.5]$. Find the maximum value of the expression $a+2 b+c+2 d-a b-b c-c d-d a$.
|
Answer: 380
Solution: Note that $a+2 b+c+2 d-a b-b c-c d-d a=(a+c)+2(b+d)-(a+$ $c)(b+d)$. Let $x=a+c, y=b+d$, then we will find the maximum value of the expression $x+2 y-x y=(y-1)(2-x)+2$, where $-20 \leqslant y-1 \leqslant 18$ and $-17 \leqslant 2-x \leqslant 21$. Therefore, $(y-1)(2-x)+2 \leqslant 18 \cdot 21+2=380$. The maximum value of the expression is achieved when $a=c=-9.5, b=d=9.5$.
|
380
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (8 points) On the board, 29 ones are written. Every minute, Karlson erases two arbitrary numbers and writes their sum on the board, and then eats a number of candies equal to the product of the two erased numbers. What is the maximum number of candies he could have eaten in 29 minutes?
|
Answer: 406.
Solution: Let's represent 29 units as points on a plane. Each time we combine two numbers, we will connect the points corresponding to one group with all the points of the second group with line segments. Note that if we replace numbers $x$ and $y$ with $x+y$, the groups " $x$ " and " $y$ " will be connected by $x y$ line segments. This is the same number of candies that Karlson eats. After 29 minutes, all points will be connected. In total, $\frac{29 \cdot(29-1)}{2}=406$ line segments will be drawn. Therefore, Karlson will eat 406 candies.
|
406
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (10 points) Let for positive numbers $x, y, z$ the following system of equations holds:
$$
\left\{\begin{array}{l}
x^{2}+x y+y^{2}=27 \\
y^{2}+y z+z^{2}=9 \\
z^{2}+x z+x^{2}=36
\end{array}\right.
$$
Find the value of the expression $x y+y z+x z$.
|
Answer: 18
Solution: Let there be three rays with vertex $O$, forming angles of $120^{\circ}$ with each other. On these rays, we lay off segments $O A=x, O B=y, O C=z$. Then, by the cosine theorem, $A B^{2}=27$, $B C^{2}=9, A C^{2}=36$. Note that triangle $A B C$ is a right triangle with hypotenuse $A C$. The sum of the areas of triangles $A O B, B O C, A O C$ is equal to the area of triangle $A B C$. This gives us the relation $\frac{1}{2}(x y+y z+x z) \sin 120^{\circ}=\frac{1}{2} \cdot 3 \sqrt{3} \cdot 3$. From this, we obtain the answer.
|
18
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (5 points) Find the value of the function $f(x)$ at the point $x_{0}=4500$, if $f(0)=1$ and for any $x$ the equality $f(x+3)=f(x)+2 x+3$ holds.
|
Answer: 6750001
Solution: In the equation $f(x+3)-f(x)=2 x+3$, we will substitute for $x$ the numbers $0,3,6, \ldots, 4497$. We get:
$$
\begin{aligned}
& f(3)-f(0)=2 \cdot 0+3 \\
& f(6)-f(3)=2 \cdot 3+3
\end{aligned}
$$
$$
f(4500)-f(4497)=2 \cdot 4497+3
$$
Adding the equations, we get: $f(4500)-f(0)=2 \cdot(0+3+6+\cdots+4497)+3 \cdot 1500=$ $2 \cdot \frac{4497 \cdot 1500}{2}+4500=6750000$. Then $f(4500)=6750001$.
|
6750001
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (5 points) At the World Meteorologists Conference, each participant in turn announced the average monthly temperature in their hometown. At this moment, all the others recorded the product of the temperatures in their and the speaker's cities. In total, 62 positive and 48 negative numbers were recorded. What is the smallest number of times a positive temperature could have been announced?
|
Answer: 3
Solution: When solving, we will not consider cities with a zero temperature, as no positive or negative numbers appear when interacting with them.
1) Let there be $x$ participants at the conference, each giving $x-1$ answers, so $x(x-1)=48+62$, which means $x=11$.
2) Let there be $y$ people with "positive temperature" at the conference, then there were $(11-y)$ people with "negative temperature". Each "positive" person recorded a positive number $(y-1)$ times, and each "negative" person recorded a negative number $-(10-y)$ times. Then $y(y-1)+(11-y)(10-y)=62 \Rightarrow$ $y^{2}-11 y+24=0 \Rightarrow y=3$ or $y=8$. Both obtained answers satisfy the condition (in both cases, 48 negative numbers are recorded).
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (7 points) Four mole burrows $A, B, C, D$ are connected sequentially by three tunnels. Each minute, the mole runs through a tunnel to one of the adjacent burrows. In how many ways can the mole get from burrow $A$ to $C$ in 18 minutes?

|
Answer: 2584
Solution: After an even number of minutes, the mole can be only at vertices $A$ and $C$. Let $a_{k}$ and $c_{k}$ denote the number of paths of length $2 k$ leading from $A$ to $A$ and from $A$ to $C$, respectively. Note that the equalities $c_{k+1}=a_{k}+2 c_{k}, a_{k+1}=a_{k}+c_{k}$ hold. Therefore, $c_{k+2}=a_{k+1}+$ $2 c_{k+1}=a_{k}+c_{k}+2 c_{k+1}=c_{k+1}-2 c_{k}+c_{k}+2 c_{k+1}=3 c_{k+1}-c_{k}$.
| $C_{0}$ | $C_{1}$ | $C_{2}$ | $C_{3}$ | $C_{4}$ | $C_{5}$ | $C_{6}$ | $C_{7}$ | $C_{8}$ | $C_{9}$ | $C_{10}$ | $C_{11}$ | $C_{12}$ | $C_{13}$ | $C_{14}$ | $C_{15}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 0 | 1 | 3 | 8 | 21 | 55 | 144 | 377 | 987 | 2584 | 6765 | 17711 | 46368 | 121393 | 317811 | 832040 |
|
2584
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (7 points) The numbers $a, b, c, d$ belong to the interval $[-10.5,10.5]$. Find the maximum value of the expression $a+2 b+c+2 d-a b-b c-c d-d a$.
|
Answer: 462
Solution: Note that $a+2 b+c+2 d-a b-b c-c d-d a=(a+c)+2(b+d)-(a+$ $c)(b+d)$. Let $x=a+c, y=b+d$, then we will find the maximum value of the expression $x+2 y-x y=(y-1)(2-x)+2$, where $-22 \leqslant y-1 \leqslant 20$ and $-19 \leqslant 2-x \leqslant 23$. Therefore, $(y-1)(2-x)+2 \leqslant 20 \cdot 23+2=462$. The maximum value of the expression is achieved when $a=c=-10.5, b=d=10.5$.
|
462
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (8 points) On the board, 28 ones are written. Every minute, Karlson erases two arbitrary numbers and writes their sum on the board, and then eats a number of candies equal to the product of the two erased numbers. What is the maximum number of candies he could have eaten in 28 minutes?
|
Answer: 378.
Solution: Let's represent 28 units as points on a plane. Each time we combine numbers, we will connect the points of one group to all the points of the second group with line segments. Note that if we replace numbers $x$ and $y$ with $x+y$, the groups " $x$ " and " $y$ " will be connected by $x y$ line segments. This is the same number of candies that Karlson eats. After 28 minutes, all points will be connected. In total, $\frac{28 \cdot(28-1)}{2}=378$ line segments will be drawn. Therefore, Karlson will eat 378 candies.
|
378
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (10 points) Let for positive numbers $x, y, z$ the following system of equations holds:
$$
\left\{\begin{array}{l}
x^{2}+x y+y^{2}=48 \\
y^{2}+y z+z^{2}=25 \\
z^{2}+x z+x^{2}=73
\end{array}\right.
$$
Find the value of the expression $x y+y z+x z$.
|
Answer: 40
Solution: Let there be three rays with vertex $O$, forming angles of $120^{\circ}$ with each other. On these rays, we lay off segments $O A=x, O B=y, O C=z$. Then, by the cosine theorem, $A B^{2}=48$, $B C^{2}=25, A C^{2}=73$. Note that triangle $A B C$ is a right triangle with hypotenuse $A C$. The sum of the areas of triangles $A O B, B O C, A O C$ is equal to the area of triangle $A B C$. This gives us the relation $\frac{1}{2}(x y+y z+x z) \sin 120^{\circ}=\frac{1}{2} \cdot 4 \sqrt{3} \cdot 5$. From this, we obtain the answer.
|
40
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (5 points) Find the value of the function $f(x)$ at the point $x_{0}=6000$, if $f(0)=1$ and for any $x$ the equality $f(x+3)=f(x)+2 x+3$ holds.
|
Answer: 12000001
Solution: In the equation $f(x+3)-f(x)=2 x+3$, we will substitute for $x$ the numbers $0,3,6, \ldots, 5997$. We get:
$$
\begin{aligned}
& f(3)-f(0)=2 \cdot 0+3 \\
& f(6)-f(3)=2 \cdot 3+3
\end{aligned}
$$
$$
f(6000)-f(5997)=2 \cdot 5997+3
$$
Adding the equations, we get: $f(6000)-f(0)=2 \cdot(0+3+6+\cdots+5997)+3 \cdot 2000=$ $2 \cdot \frac{5997 \cdot 2000}{2}+6000=12000000$. Then $f(6000)=12000001$.
|
12000001
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (5 points) At the World Meteorologists Conference, each participant in turn announced the average monthly temperature in their hometown. At this moment, all the others recorded the product of the temperatures in their and the speaker's cities. In total, 42 positive and 48 negative numbers were recorded. What is the smallest number of times a positive temperature could have been announced?
|
Answer: 4
Solution: When solving, we will not consider cities with a zero temperature, as no positive or negative numbers appear when interacting with them.
1) Let there be $x$ participants at the conference, each giving $x-1$ answers, so $x(x-1)=48+42$, which means $x=10$.
2) Let there be $y$ people with "positive temperature" at the conference, then there were $(10-y)$ people with "negative temperature". Each "positive" person recorded a positive number $(y-1)$ times, and each "negative" person recorded a negative number $-(9-y)$ times. Then $y(y-1)+(10-y)(9-y)=42 \Rightarrow$ $y^{2}-10 y+24=0 \Rightarrow y=4$ or $y=6$. Both answers satisfy the condition (in both cases, 48 negative numbers are recorded).
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (7 points) Four mole burrows $A, B, C, D$ are connected sequentially by three tunnels. Each minute, the mole runs through a tunnel to one of the adjacent burrows. In how many ways can the mole get from burrow $A$ to $C$ in 16 minutes?

|
Answer: 987
Solution: After an even number of minutes, the mole can be only at vertices $A$ and $C$. Let $a_{k}$ and $c_{k}$ denote the number of paths of length $2 k$ leading from $A$ to $A$ and from $A$ to $C$, respectively. Note that the equalities $c_{k+1}=a_{k}+2 c_{k}, a_{k+1}=a_{k}+c_{k}$ hold. Therefore, $c_{k+2}=a_{k+1}+$ $2 c_{k+1}=a_{k}+c_{k}+2 c_{k+1}=c_{k+1}-2 c_{k}+c_{k}+2 c_{k+1}=3 c_{k+1}-c_{k}$.
| $C_{0}$ | $C_{1}$ | $C_{2}$ | $C_{3}$ | $C_{4}$ | $C_{5}$ | $C_{6}$ | $C_{7}$ | $C_{8}$ | $C_{9}$ | $C_{10}$ | $C_{11}$ | $C_{12}$ | $C_{13}$ | $C_{14}$ | $C_{15}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 0 | 1 | 3 | 8 | 21 | 55 | 144 | 377 | 987 | 2584 | 6765 | 17711 | 46368 | 121393 | 317811 | 832040 |
|
987
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (7 points) The numbers $a, b, c, d$ belong to the interval $[-11.5,11.5]$. Find the maximum value of the expression $a+2 b+c+2 d-a b-b c-c d-d a$.
|
Answer: 552
Solution: Notice that $a+2 b+c+2 d-a b-b c-c d-d a=(a+c)+2(b+d)-(a+c)(b+d)$. Let $x=a+c, y=b+d$, then we will find the maximum value of the expression $x+2 y-x y=(y-1)(2-x)+2$, where $-24 \leqslant y-1 \leqslant 22$ and $-21 \leqslant 2-x \leqslant 25$. Therefore, $(y-1)(2-x)+2 \leqslant 22 \cdot 25+2=552$. The maximum value of the expression is achieved when $a=c=-11.5, b=d=11.5$.
|
552
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (8 points) On the board, 27 ones are written. Every minute, Karlson erases two arbitrary numbers and writes their sum on the board, and then eats a number of candies equal to the product of the two erased numbers. What is the maximum number of candies he could have eaten in 27 minutes?
|
Answer: 351.
Solution: Let's represent 27 units as points on a plane. Each time we combine numbers, we will connect the points of one group to all the points of the second group with line segments. Note that if we replace numbers $x$ and $y$ with $x+y$, the groups " $x$ " and " $y$ " will be connected by $x y$ line segments. Carlson eats as many candies as the number of line segments. After 27 minutes, all points will be connected. In total, $\frac{27 \cdot(27-1)}{2}=351$ line segments will be drawn. Therefore, Carlson will eat 351 candies.
|
351
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (10 points) Let for positive numbers $x, y, z$ the following system of equations holds:
$$
\left\{\begin{array}{l}
x^{2}+x y+y^{2}=48 \\
y^{2}+y z+z^{2}=16 \\
z^{2}+x z+x^{2}=64
\end{array}\right.
$$
Find the value of the expression $x y+y z+x z$.
|
Answer: 32
Solution: Let there be three rays with vertex $O$, forming angles of $120^{\circ}$ with each other. On these rays, we lay off segments $O A=x, O B=y, O C=z$. Then, by the cosine theorem, $A B^{2}=48$, $B C^{2}=16, A C^{2}=64$. Note that triangle $A B C$ is a right triangle with hypotenuse $A C$. The sum of the areas of triangles $A O B, B O C, A O C$ is equal to the area of triangle $A B C$. This gives us the relation $\frac{1}{2}(x y+y z+x z) \sin 120^{\circ}=\frac{1}{2} \cdot 4 \sqrt{3} \cdot 4$. From this, we obtain the answer.
|
32
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (5 points) Find the value of the function $f(x)$ at the point $x_{0}=2000$, if $f(0)=1$ and for any $x$ the equality $f(x+4)=f(x)+3 x+4$ holds.
|
Answer: 1499001
Solution: In the equation $f(x+4)-f(x)=3 x+4$, we will substitute for $x$ the numbers $0, 4, 8, \ldots, 1996$. We get:
$$
\begin{aligned}
& f(4)-f(0)=3 \cdot 0+4 \\
& f(8)-f(4)=3 \cdot 4+4
\end{aligned}
$$
$$
f(2000)-f(1996)=3 \cdot 1996+4
$$
Adding the equations, we get: $f(2000)-f(0)=3 \cdot(0+4+8+\cdots+1996)+4 \cdot 500=$ $3 \cdot \frac{1996 \cdot 500}{2}+2000=1499000$. Then $f(2000)=1499001$.
|
1499001
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (5 points) At the World Meteorologists Conference, each participant in turn announced the average monthly temperature in their hometown. At this moment, all the others recorded the product of the temperatures in their and the speaker's cities. In total, 48 positive and 42 negative numbers were recorded. What is the smallest number of times a positive temperature could have been announced?
|
Answer: 3
Solution: When solving, we will not consider cities with a zero temperature, as no positive or negative numbers appear when interacting with them.
1) Let there be $x$ participants at the conference, each of them gave $x-1$ answers, so $x(x-1)=42+48$, which means $x=10$.
2) Let there be $y$ people with "positive temperature" at the conference, then there were $(10-y)$ people with "negative temperature". Each "positive" person recorded a positive number $(y-1)$ times, and each "negative" person recorded a negative number $-(9-y)$ times. Then $y(y-1)+(10-y)(9-y)=48 \Rightarrow$ $y^{2}-10 y+21=0 \Rightarrow y=3$ or $y=7$. Both obtained answers satisfy the condition (in both cases, 42 negative numbers are recorded).
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (7 points) Four mole burrows $A, B, C, D$ are connected sequentially by three tunnels. Each minute, the mole runs through a tunnel to one of the adjacent burrows. In how many ways can the mole get from burrow $A$ to $C$ in 14 minutes?

|
Answer: 377
Solution: After an even number of minutes, the mole can be only at vertices $A$ and $C$. Let $a_{k}$ and $c_{k}$ denote the number of paths of length $2 k$ leading from $A$ to $A$ and from $A$ to $C$, respectively. Note that the equalities $c_{k+1}=a_{k}+2 c_{k}, a_{k+1}=a_{k}+c_{k}$ hold. From this, $c_{k+2}=a_{k+1}+$ $2 c_{k+1}=a_{k}+c_{k}+2 c_{k+1}=c_{k+1}-2 c_{k}+c_{k}+2 c_{k+1}=3 c_{k+1}-c_{k}$.
| $C_{0}$ | $C_{1}$ | $C_{2}$ | $C_{3}$ | $C_{4}$ | $C_{5}$ | $C_{6}$ | $C_{7}$ | $C_{8}$ | $C_{9}$ | $C_{10}$ | $C_{11}$ | $C_{12}$ | $C_{13}$ | $C_{14}$ | $C_{15}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 0 | 1 | 3 | 8 | 21 | 55 | 144 | 377 | 987 | 2584 | 6765 | 17711 | 46368 | 121393 | 317811 | 832040 |
|
377
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (7 points) The numbers $a, b, c, d$ belong to the interval $[-12.5,12.5]$. Find the maximum value of the expression $a+2 b+c+2 d-a b-b c-c d-d a$.
|
Answer: 650
Solution: Note that $a+2 b+c+2 d-a b-b c-c d-d a=(a+c)+2(b+d)-(a+c)(b+d)$. Let $x=a+c, y=b+d$, then we will find the maximum value of the expression $x+2 y-x y=(y-1)(2-x)+2$, where $-26 \leqslant y-1 \leqslant 24$ and $-23 \leqslant 2-x \leqslant 27$. Therefore, $(y-1)(2-x)+2 \leqslant 24 \cdot 27+2=650$. The maximum value of the expression is achieved when $a=c=-12.5, b=d=12.5$.
|
650
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (8 points) On the board, 26 ones are written. Every minute, Karlson erases two arbitrary numbers and writes their sum on the board, and then eats a number of candies equal to the product of the two erased numbers. What is the maximum number of candies he could have eaten in 26 minutes?
|
Answer: 325.
Solution: Let's represent 26 units as points on a plane. Each time we combine two numbers, we will connect the points corresponding to one group with all the points of the second group with line segments. Note that if we replace numbers $x$ and $y$ with $x+y$, the groups " $x$ " and " $y$ " will be connected by $x y$ line segments. This is the same number of candies that Karlson eats. After 26 minutes, all points will be connected. In total, $\frac{26 \cdot(26-1)}{2}=325$ line segments will be drawn. Therefore, Karlson will eat 325 candies.
|
325
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (10 points) Let for positive numbers $x, y, z$ the following system of equations holds:
$$
\left\{\begin{array}{l}
x^{2}+x y+y^{2}=48 \\
y^{2}+y z+z^{2}=9 \\
z^{2}+x z+x^{2}=57
\end{array}\right.
$$
Find the value of the expression $x y+y z+x z$.
|
Answer: 24
Solution: Let there be three rays with vertex $O$, forming angles of $120^{\circ}$ with each other. On these rays, we lay off segments $O A=x, O B=y, O C=z$. Then, by the cosine theorem, $A B^{2}=48$, $B C^{2}=9, A C^{2}=57$. Note that triangle $A B C$ is a right triangle with hypotenuse $A C$. The sum of the areas of triangles $A O B, B O C, A O C$ is equal to the area of triangle $A B C$. This gives us the relation $\frac{1}{2}(x y+y z+x z) \sin 120^{\circ}=\frac{1}{2} \cdot 4 \sqrt{3} \cdot 3$. From this, we obtain the answer.
|
24
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.