problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
1. (5 points) Find the value of the function $f(x)$ at the point $x_{0}=4000$, if $f(0)=1$ and for any $x$ the equality $f(x+4)=f(x)+3 x+4$ holds.
|
Answer: 5998001
Solution: In the equation $f(x+4)-f(x)=3 x+4$, we will substitute for $x$ the numbers $0,4,8, \ldots, 3996$. We get:
$$
\begin{aligned}
& f(4)-f(0)=3 \cdot 0+4 \\
& f(8)-f(4)=3 \cdot 4+4
\end{aligned}
$$
$$
f(4000)-f(3996)=3 \cdot 3996+4
$$
Adding the equations, we get: $f(4000)-f(0)=3 \cdot(0+4+8+\cdots+3996)+4 \cdot 1000=$ $3 \cdot \frac{3996 \cdot 1000}{2}+4000=5998000$. Then $f(4000)=5998001$.
|
5998001
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (5 points) At the World Meteorologists Conference, each participant in turn announced the average monthly temperature in their hometown. At this moment, all the others recorded the product of the temperatures in their and the speaker's cities. In total, 36 positive and 36 negative numbers were recorded. What is the smallest number of times a positive temperature could have been announced?
|
Answer: 3
Solution: When solving, we will not consider cities with a zero temperature, as no positive or negative numbers appear when interacting with them.
1) Let there be $x$ participants at the conference, each giving $x-1$ answers, so $x(x-1)=36+36$, which means $x=9$.
2) Let there be $y$ people with "positive temperature" at the conference, then there were $(9-y)$ people with "negative temperature". Each "positive" person recorded a positive number $(y-1)$ times, and each "negative" person recorded a negative number $-(8-y)$ times. Then $y(y-1)+(9-y)(8-y)=36 \Rightarrow$ $y^{2}-9 y+18=0 \Rightarrow y=3$ or $y=6$. Both obtained answers satisfy the condition (in both cases, 36 negative numbers are recorded).
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (7 points) Four mole burrows $A, B, C, D$ are connected sequentially by three tunnels. Each minute, the mole runs through a tunnel to one of the adjacent burrows. In how many ways can the mole get from burrow $A$ to $C$ in 12 minutes?

|
Answer: 144
Solution: After an even number of minutes, the mole can be only at vertices $A$ and $C$. Let $a_{k}$ and $c_{k}$ denote the number of paths of length $2 k$ leading from $A$ to $A$ and from $A$ to $C$, respectively. Note that the equalities $c_{k+1}=a_{k}+2 c_{k}, a_{k+1}=a_{k}+c_{k}$ hold. From this, $c_{k+2}=a_{k+1}+$ $2 c_{k+1}=a_{k}+c_{k}+2 c_{k+1}=c_{k+1}-2 c_{k}+c_{k}+2 c_{k+1}=3 c_{k+1}-c_{k}$.
| $C_{0}$ | $C_{1}$ | $C_{2}$ | $C_{3}$ | $C_{4}$ | $C_{5}$ | $C_{6}$ | $C_{7}$ | $C_{8}$ | $C_{9}$ | $C_{10}$ | $C_{11}$ | $C_{12}$ | $C_{13}$ | $C_{14}$ | $C_{15}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 0 | 1 | 3 | 8 | 21 | 55 | 144 | 377 | 987 | 2584 | 6765 | 17711 | 46368 | 121393 | 317811 | 832040 |
|
144
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (7 points) The numbers $a, b, c, d$ belong to the interval $[-13.5,13.5]$. Find the maximum value of the expression $a+2 b+c+2 d-a b-b c-c d-d a$.
|
Answer: 756
Solution: Note that $a+2 b+c+2 d-a b-b c-c d-d a=(a+c)+2(b+d)-(a+c)(b+d)$. Let $x=a+c, y=b+d$, then we will find the maximum value of the expression $x+2 y-x y=(y-1)(2-x)+2$, where $-28 \leqslant y-1 \leqslant 26$ and $-25 \leqslant 2-x \leqslant 29$. Therefore, $(y-1)(2-x)+2 \leqslant 26 \cdot 29+2=756$. The maximum value of the expression is achieved when $a=c=-13.5, b=d=13.5$.
|
756
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (8 points) On the board, 25 ones are written. Every minute, Karlson erases two arbitrary numbers and writes their sum on the board, and then eats a number of candies equal to the product of the two erased numbers. What is the maximum number of candies he could have eaten in 25 minutes?
|
Answer: 300.
Solution: Let's represent 25 units as points on a plane. Each time we combine two numbers, we will connect the points corresponding to one group with all the points of the second group with line segments. Note that if we replace numbers $x$ and $y$ with $x+y$, the groups " $x$ " and " $y$ " will be connected by $x y$ line segments. Carlson eats as many candies as the number of line segments. After 25 minutes, all points will be connected. In total, $\frac{25 \cdot(25-1)}{2}=300$ line segments will be drawn. Therefore, Carlson will eat 300 candies.
|
300
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (10 points) Let for positive numbers $x, y, z$ the following system of equations holds:
$$
\left\{\begin{array}{l}
x^{2}+x y+y^{2}=75 \\
y^{2}+y z+z^{2}=4 \\
z^{2}+x z+x^{2}=79
\end{array}\right.
$$
Find the value of the expression $x y+y z+x z$.
|
Answer: 20
Solution: Let there be three rays with vertex $O$, forming angles of $120^{\circ}$ with each other. On these rays, we lay off segments $O A=x, O B=y, O C=z$. Then, by the cosine theorem, $A B^{2}=75$, $B C^{2}=4, A C^{2}=79$. Note that triangle $A B C$ is a right triangle with hypotenuse $A C$. The sum of the areas of triangles $A O B, B O C, A O C$ is equal to the area of triangle $A B C$. This gives us the relation $\frac{1}{2}(x y+y z+x z) \sin 120^{\circ}=\frac{1}{2} \cdot 5 \sqrt{3} \cdot 2$. From this, we obtain the answer.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. (20 points) Given various natural numbers $a, b, c, d$, for which the following conditions are satisfied: $a>d, a b=c d$ and $a+b+c+d=a c$. Find the sum of all four numbers.
|
Answer: 12
Solution. From the relations $a>d$ and $ab=cd$, we have the inequality $ba+d$ and $\frac{ac}{2} \geqslant 2c > b+c$. Adding them, we get a contradiction with the condition.
Therefore, without loss of generality, assume that $a \geqslant 3$. Since $a$ is a natural number, then $a \in\{1,2,3\}$. Moreover, $d$ is a natural number less than $a$, so $a \neq 1$. Let's consider two cases.
Case 1. $a=3$. The relations can be rewritten as
$$
3b=cd, 3+b+c+d=3c, 3>d
$$
From the last inequality, in particular, it follows that $(3, d)=1$. Therefore, $3 \mid c$. Since all numbers are distinct, $c \geqslant 6$. Then we have a chain of inequalities
$$
3+b+c+d < 3c \Rightarrow b+c+d < 2c \Rightarrow b+d < c
$$
Since $3>d$ implies $d=1$. The relations can be rewritten as $2b=c, 3+b=c$. The only solution to this system of equations is the pair $(b, c)=(3,6)$. We find the solution $(2,3,6,1)$, the sum of which is 12.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (5 points) When dividing the numbers 312837 and 310650 by a certain three-digit natural number, the remainders were the same. Find this remainder.
|
Answer: 96
Solution. $312837-310650=2187=3^{7}$. The three-digit divisors of this number are also powers of three, i.e., $3^{6}=729,3^{5}=243$. By dividing these numbers by 729 and 243 with a remainder, we find that the remainder is always 96.
|
96
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (10 points) The area of a sector of a circle is 100. For what value of the radius of the circle will the perimeter of this sector be minimal? If the answer is not an integer, round to the tenths.
Answer: 10
|
Solution. The area of the sector corresponding to $\alpha$ radians $S_{\alpha}=\frac{1}{2} R^{2} \alpha=100$. The length of the perimeter is $L(R)=2 R+R \alpha=2 R+\frac{200}{R}$, which reaches a minimum at the point $R=10$.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
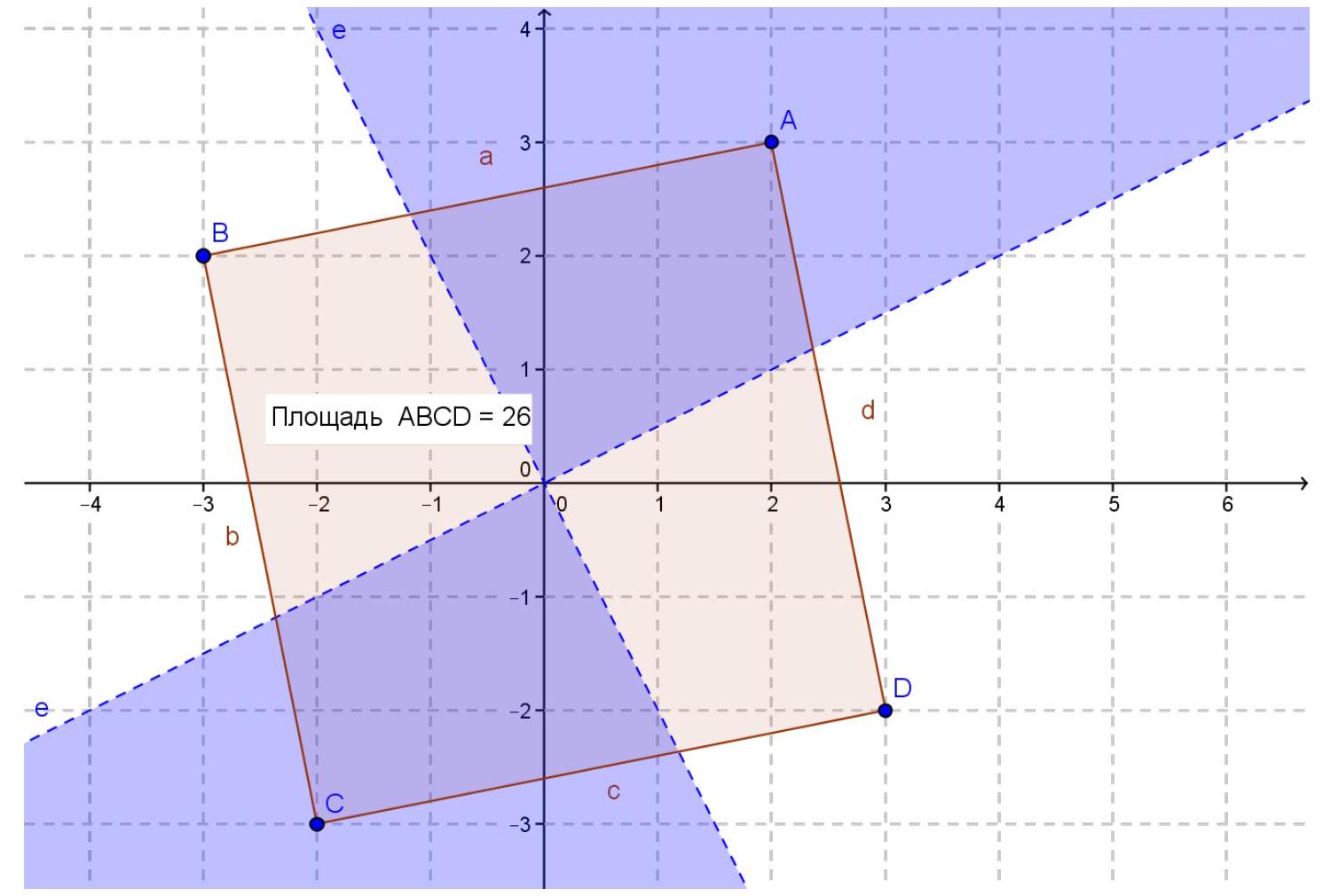
8. (13 points) On the coordinate plane, all points whose coordinates satisfy the conditions
$$
\left\{\begin{array}{l}
|2 x+3 y|+|3 x-2 y| \leq 13 \\
2 x^{2}-3 x y-2 y^{2} \leq 0
\end{array}\right.
$$
are shaded. Find the area of the resulting figure.
#
|
# Answer: 13
Solution. The solution to the first inequality defines the square $ABCD$, the solution to the second inequality is the shaded part of the plane between the perpendicular lines $2x + y = 0$ and $x - 2y = 0$.
|
13
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. (20 points) Find the smallest value of the parameter $c$ such that the system of equations has a unique solution
$$
\left\{\begin{array}{l}
2(x+7)^{2}+(y-4)^{2}=c \\
(x+4)^{2}+2(y-7)^{2}=c
\end{array}\right.
$$
|
Answer: $c=6.0$.
Solution. By the Cauchy-Bunyakovsky-Schwarz inequality, we have
$$
\begin{aligned}
& \left(\frac{1}{2}+1\right)\left(2(x+\alpha)^{2}+(y-\beta)^{2}\right) \geqslant(|x+\alpha|+|y-\beta|)^{2} \\
& \left(1+\frac{1}{2}\right)\left((x+\beta)^{2}+2(y-\alpha)^{2}\right) \geqslant(|x+\beta|+|y-\alpha|)^{2}
\end{aligned}
$$
Therefore, for any solution $(x, y)$ of the system, we have
(3) $3 c \geqslant(|x+\alpha|+|y-\beta|)^{2}+(|x+\beta|+|y-\alpha|)^{2} \geqslant$
$$
\begin{aligned}
\geqslant(\alpha-\beta+x+y)^{2}+(\alpha-\beta-(x+y))^{2} & = \\
& =2(\alpha-\beta)^{2}+2(x+y)^{2} \geqslant 2(\alpha-\beta)^{2}
\end{aligned}
$$
Thus, if $c<\frac{2}{3}(\alpha-\beta)^{2}$, the system has no solutions.
If $c=\frac{2}{3}(\alpha-\beta)^{2}$, then equality must be achieved in all inequalities (1)-(3). Therefore, $x+y=0$, the numbers $x+\alpha$ and $x+\beta$ must have different signs, and
$$
\frac{2(x+\alpha)^{2}}{(x+\beta)^{2}}=\frac{1}{2}
$$
From these conditions, it follows that when $c=\frac{2}{3}(\alpha-\beta)^{2}$, there is only one solution $\left(-\frac{2 \alpha+\beta}{3}, \frac{2 \alpha+\beta}{3}\right)$. Remark. One can immediately notice that the solution of the system is symmetric with respect to the line $y=-x$ (two ellipses with centers at points $(-\alpha ; \beta)$ and $(-\beta ; \alpha)$). The solution will be unique if one of the ellipses touches this line. This is satisfied if the equation $2(x+\alpha)^{2}+(x+\beta)^{2}=c$ has a unique solution. Setting the discriminant to zero, we find the solution. https://ggbm.at/FVmUGS4Y
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (6 points) It is known that no digit of a three-digit number is zero and the sum of all possible two-digit numbers formed from the digits of this number is equal to this number. Find the largest such three-digit number.
|
# Answer: 396
Solution. If there are identical digits, then the sum of three two-digit numbers is less than 300. If the digits are different, then $\overline{a b c}=\overline{a b}+\overline{a c}+\overline{b a}+\overline{b c}+\overline{c a}+\overline{c b}=22(a+b+c)$. The sum of the digits gives the same remainder when divided by 9 as the number itself. Therefore, $a+b+c$ is divisible by 9, and thus does not exceed 18. Then $\overline{a b c} \leq 22 \cdot 18=396$ fits.
|
396
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (10 points) A square is divided into 2016 triangles, with the vertices of no triangle lying on the sides or inside another triangle. The sides of the square are sides of some triangles in the partition. How many points, which are vertices of the triangles, are located inside the square?
|
Answer: 1007
Solution. Let us have $k$ points inside the square. Then the sum of the angles of all triangles is $360 k+4 \cdot 90=180 \cdot 2016$ degrees.
|
1007
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (10 points) Anton, Boris, Vadim, Gena, Dima, and Egor gathered at the cinema. They bought 6 seats in a row. Anton and Boris want to sit next to each other, while Vadim and Gena do not want to. In how many ways can the boys sit in their seats considering these preferences?
#
|
# Answer: 144
Solution. The total number of seating arrangements where Anton and Boris sit next to each other is $2 \cdot 5!=240$. The number of seating arrangements where the pairs Anton-Boris and Vadim-Gena end up next to each other is $2 \cdot 2 \cdot 4!=96$. Subtracting the second set from the first gives the answer.
|
144
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (12 points) On the coordinate plane, all points whose coordinates satisfy the condition
$$
|| x|-2|+|y-3| \leq 3
$$
are shaded. Find the area of the resulting figure.
|
Answer: 34
Solution. The polygon that results from solving the equation ||$x|-2|+$ $|y-3|=3$ consists of segments of straight lines, glued together at special points: $x=0, x=2, x=$ $-2, y=3$.
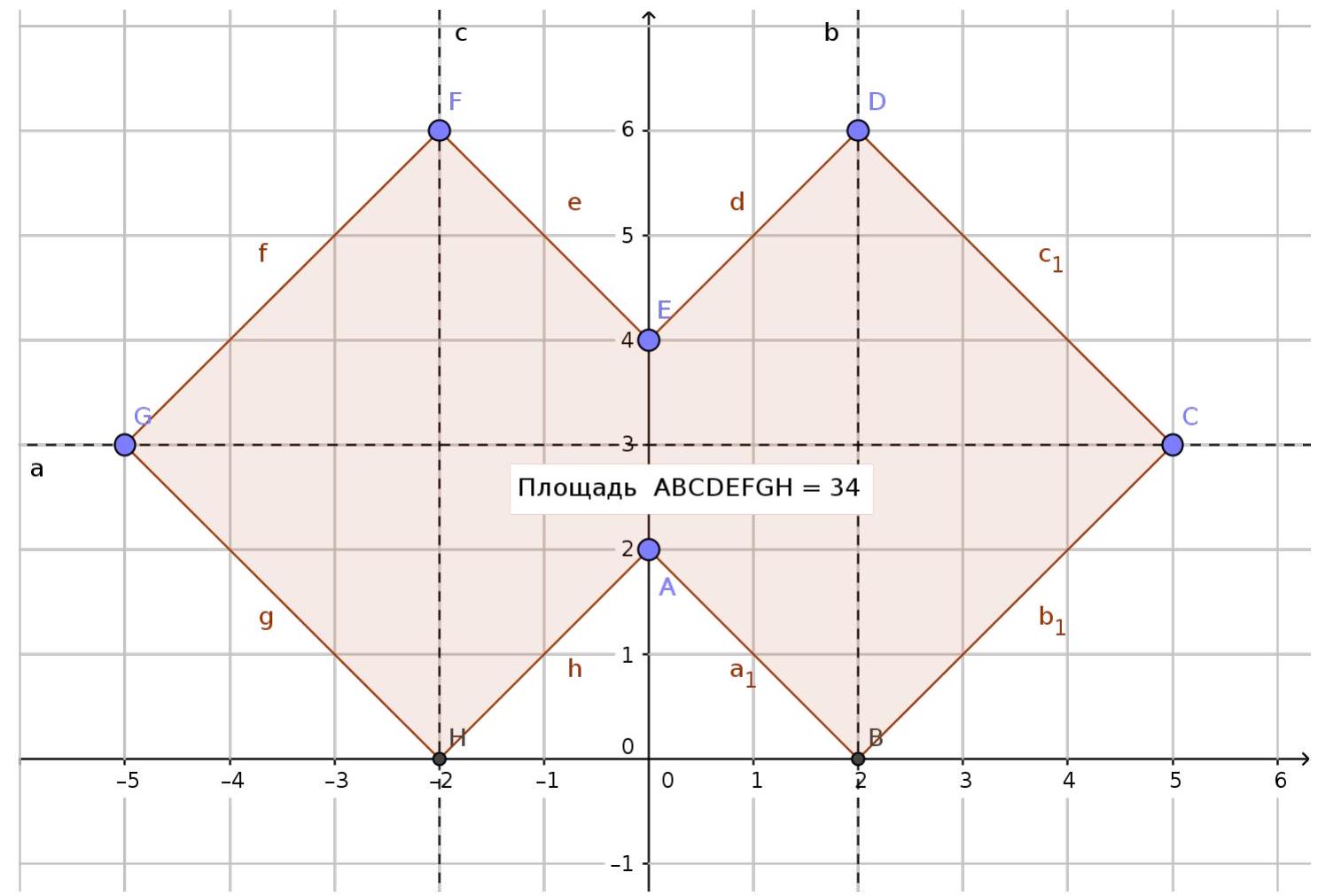
|
34
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Triples of natural numbers $\left(a_{i}, b_{i}, c_{i}\right)$, where $i=1,2, \ldots, n$ satisfy the following conditions:
1) $a_{i}+b_{i}+c_{i}=2017$ for all $i=1,2, \ldots, n$;
2) if $i \neq j$, then $a_{i} \neq a_{j}, b_{i} \neq b_{j}$ and $c_{i} \neq c_{j}$. What is the maximum possible value of $n$? (M. Popov)
|
Answer: 1343.
Solution: Note that
$$
\sum_{i=1}^{n} a_{i} \geqslant \sum_{i=1}^{n} i=\frac{n(n+1)}{2} .
$$
A similar inequality is written for the sums $b_{i}$ and $c_{i}$. Adding the three obtained inequalities, we get
$$
\begin{gathered}
3 \cdot \frac{n(n+1)}{2} \leqslant \sum_{i=1}^{n} a_{i}+\sum_{i=1}^{n} b_{i}+\sum_{i=1}^{n} c_{i}= \\
=\sum_{i=1}^{n}\left(a_{i}+b_{i}+c_{i}\right)=2017 n .
\end{gathered}
$$
Thus, we obtain the upper bound
$$
\frac{3(n+1)}{2} \leqslant 2017 \Longrightarrow n \leqslant 1343
$$
Now let's provide an example where this bound is achieved ( $n=1343$ )
| $a_{i}$ | $b_{i}$ | $c_{i}$ |
| :---: | :---: | :---: |
| 1 | 672 | 1344 |
| 2 | 673 | 1342 |
| $\vdots$ | $\vdots$ | $\vdots$ |
| 672 | 1343 | 2 |
| 673 | 1 | 1343 |
| 674 | 2 | 1341 |
| $\vdots$ | $\vdots$ | $\vdots$ |
| 1343 | 671 | 3 |
|
1343
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Several people played a round-robin table tennis tournament. At the end of the tournament, it turned out that for any four participants, there would be two who scored the same number of points in the games between these four participants. What is the maximum number of tennis players that could have participated in this tournament? In table tennis, there are no ties; one point is awarded for a win, and zero points for a loss.
(from materials of international olympiads)
|
Answer: 7 tennis players.
Solution. Let $n \geqslant 8$ be the number of tennis players in the tournament. Then the total number of matches played is $\frac{1}{2} n(n-1)$, and thus the total number of victories is also $\frac{1}{2} n(n-1)$. Therefore, there must be a participant who has won at least $\frac{n-1}{2}$ matches. Hence, some participant must have won at least 4 matches.
Let's call this participant Andrei. Consider those he has defeated. Let these be Borya, Vasya, Grisha, and Dima. In the matches among them, 6 matches were played, so at least one of them must have won at least two matches.
Let's assume, for definiteness, that this is Borya, and he won against Vasya and Grisha. Then consider the quartet of players Andrei, Borya, Vasya, and Grisha. Andrei won all his matches among these four players, so he scored three points, Borya won exactly two matches, so he scored two points, the winner of the match between Vasya and Grisha scored one point, and the loser scored no points.
Therefore, they scored different numbers of points in their matches against each other, which means that such a quartet does not satisfy the condition of the problem. Hence, there are no more than seven players.
Let's provide an example of a tournament with seven participants. A victory is denoted by a plus, and a loss by a minus.
| | + | + | + | - | - | - |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| - | | + | - | + | + | - |
| - | - | | + | + | - | + |
| - | + | - | | - | + | + |
| + | - | - | + | | + | - |
| + | - | + | - | - | | + |
| + | + | - | - | + | - | |
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Cinderella, together with her fairy godmother, released a collection of crystal slippers featuring 7 new models. The fairy tale heroines organized a presentation of the collection for some guests: the audience was supposed to say which slippers they liked. The guests wrote in a questionnaire which models they thought were the best. It is known that no two guests chose the same set of favorite slippers. What is the maximum number of people (excluding Cinderella and the fairy) who could have attended the presentation?
|
Solution. Suppose that the guests were given a questionnaire where they could put a "1" next to each pair of shoes they liked and a "0" next to the pair they did not select as the best. Thus, the opinion of each guest can be recorded as a string of "1"s and "0"s. Then, the number of different sets of favorite shoes is the same as the number of evaluation strings, which means the maximum number of guests at the presentation is $2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2=2^{7}=128$ people.
## Answer: 128 guests.
|
128
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. On the side $AB$ of triangle $ABC$, a point $M$ is taken. It starts moving parallel to $BC$ until it intersects with $AC$, then it moves parallel to $AB$ until it intersects with $BC$, and so on. Is it true that after a certain number of such steps, point $M$ will return to its original position? If this is true, what is the minimum number of steps sufficient for the return?
|
Solution. Let the length of side $AB$ be 1, and let point $M$ be at a distance $a$ from point $B$. From the properties of the parallelogram, the small triangles are equal, so after 3 steps, point $M$ will be at a distance $a$ from point $A$, which is at a distance $1-a$ from point $B$. After another 3 steps, the point will be at a distance $1-(1-a)=a$ from point $B$, meaning it will return to its initial position.
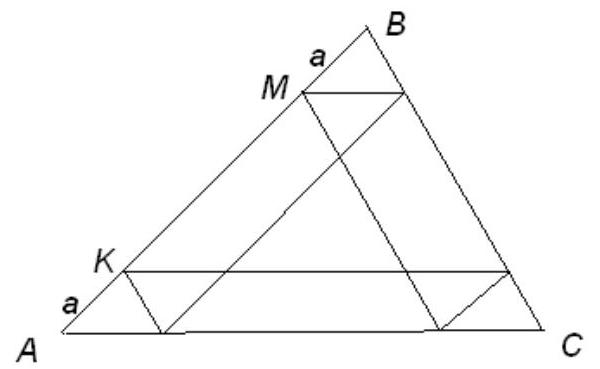
A special case is when $a=1/2$. Then $1-a=a$, and the return will occur after 3 steps.
Answer: Correct.
It takes 3 steps if point $M$ divides side $AB$ in half, and 6 steps in other cases.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. The set $M$ consists of $n$ numbers, $n$ is odd, $n>1$. It is such that when any of its elements is replaced by the sum of the other $n-1$ elements from $M$, the sum of all $n$ elements does not change. Find the product of all $n$ elements of the set $M$.
|
Solution. Let
$$
M=\left\{x_{1}, \ldots, x_{n}\right\}, \quad x_{1}+\cdots+x_{n}=S
$$
Replace the element $x_{1}$ with the sum of the others. Then
$$
S=\left(S-x_{1}\right)+x_{2}+x_{3}+\cdots+x_{n}=\left(S-x_{1}\right)+\left(S-x_{1}\right)
$$
Reasoning similarly for the other elements, we get that
$$
2 x_{k}=S, \quad k=1 \ldots n \text {. }
$$
Thus, all elements of the set are equal to each other. Since the sum does not change when one addend is replaced, this addend must be equal to what it is replaced with, i.e.,
$$
x_{1}=x_{2}+x_{3}+\cdots+x_{n}
$$
Considering the equality of the elements, we get $x_{1}=(n-1) x_{1}$, hence, $x_{1}=0$. Therefore, the product of all numbers in the set $M$ is 0.
## Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The integer part $[x]$ of a number $x$ is defined as the greatest integer $n$ such that $n \leqslant x$, for example, $[10]=10,[9.93]=9,\left[\frac{1}{9}\right]=0,[-1.7]=-2$. Find all solutions to the equation $\left[\frac{x+3}{2}\right]^{2}-x=1$.
|
# Solution.
From the equation, it follows that $x=\left[\frac{x+3}{2}\right]^{2}-1$ is an integer. Therefore, $x=n \in \mathbb{Z}$, but we need to consider the cases of even and odd $n$ separately.
First, let's move all terms to the left side of the equation.
1) If $x=2 k$.
$$
\left[\frac{2 k+3}{2}\right]^{2}-2 k-1=\left[k+1+\frac{1}{2}\right]^{2}-2 k-1=\quad=(k+1)^{2}-2 k-1=k^{2}=0
$$
The obtained equation has a solution $k=0$, which gives $x=0$.
2) If $x=2 k+1$.
$$
\begin{aligned}
& {\left[\frac{2 k+4}{2}\right]^{2}-(2 k+1)-1=(k+2)^{2}-2 k-2=k^{2}+2 k+2=} \\
& \quad=\left(k^{2}+k\right)+(k+1)+1=k(k+1)+(k+1)+1=(k+1)(k+1)+1 \geqslant 1
\end{aligned}
$$
Since the obtained expression is strictly positive, solutions of the form $x=2 k+1$ are not possible.
Answer. $x=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 2.
What is the last digit of the value of the sum $2019^{2020}+2020^{2019} ?$
|
# Solution.
The number $2019^{n}$ for $n \in \mathbb{N}$ ends in 9 if $n$ is odd, and in 1 if $n$ is even. Therefore, $2019^{2020}$ ends in 1. The number $2020^{n}$ ends in 0 for any $n \in \mathbb{N}$, so $2020^{2019}$ ends in 0. Thus, the sum $2019^{2020} +$ $2020^{2019}$ ends in the digit 1.
Answer. The digit 1.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 3.
On the coordinate plane, a square $K$ is marked with vertices at points $(0,0)$ and $(10,10)$. Inside this square, draw the set $M$ of points $(x, y)$ whose coordinates satisfy the equation
$$
[x]=[y],
$$
where $[a]$ denotes the integer part of the number $a$ (i.e., the greatest integer not exceeding $a$; for example, $[10]=10,[9.93]=9,[1/9]=0,[-1.7]=-2$). What fraction of the area of square $K$ is the area of set $M$?
|
Solution. Let $n \leq x < n+1$, where $n$ is an integer from 0 to 9. Then $[x]=n$ and $[y]=n$. The solution to the latter equation is all $y \in [n, n+1)$. Thus, the solution will be the union of unit squares
$$
\{x \in [n, n+1), y \in [n, n+1), n \in \mathbb{Z}\}
$$
Inside the square $K$ specified in the problem, ten such squares will fit. Since $K$ consists of 100 unit squares, the ratio of the areas is $\frac{S_{M}}{S_{K}}=\frac{10}{100}=0.1=10\%$.
The answer is represented by dotted hatching in the figure below (the left and lower boundaries are included in $M$, the right and upper boundaries are not). The area of the set $M$ is $10\%$ of the area of the square $K$.
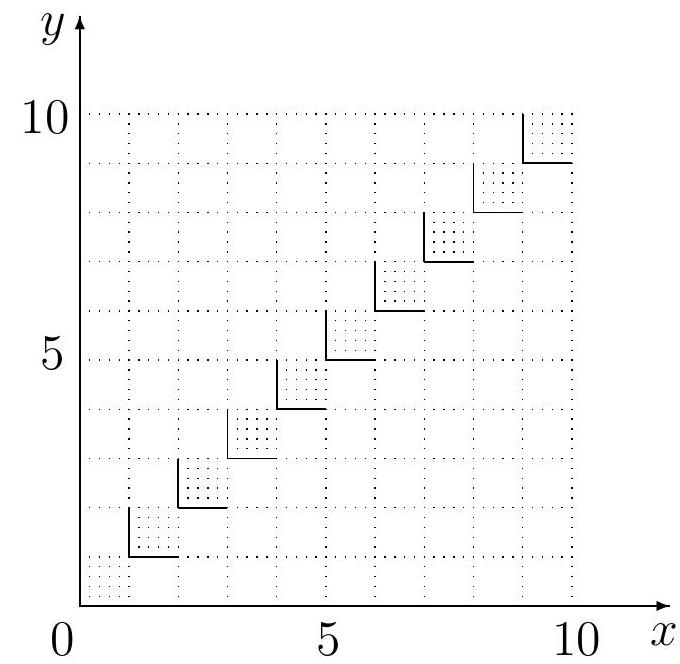
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 4.
In modern conditions, digitalization - the conversion of all information into digital code - is considered relevant. Each letter of the alphabet can be assigned a non-negative integer, called the code of the letter. Then, the weight of a word can be defined as the sum of the codes of all the letters in that word. Is it possible to encode the letters Е, О, С, Т, Ш, Ь with elementary codes, each consisting of a single digit from 0 to 9, so that the weight of the word "СТО" is not less than the weight of the word "ШЕСТЬСОТ"? If such encoding is possible, in how many ways can it be implemented? If such encoding is possible, does it allow for the unambiguous restoration of a word from its code?
|
# Solution.
Let $k(x)$ denote the elementary code of the letter $x$. We have
$k(C)+k(T)+k(O) \geq k(\amalg)+k(\mathrm{E})+k(C)+k(T)+k(\mathrm{~b})+k(C)+k(O)+k(T)$, which is equivalent to
$$
k(\amalg)+k(\mathrm{E})+k(C)+k(T)+k(\mathrm{~b})=0 .
$$
Thus,
$$
k(\amalg)=k(\mathrm{E})=k(C)=k(T)=k(\mathrm{~b})=0 .
$$
The elementary code $k(O)$ can be any digit from 0 to 9. Therefore, there are exactly 10 ways to encode.
However, for any choice of $k(O)$, the words "TOCT" and "TOT" (for example) will have the same code $k(O)$, which cannot be decoded uniquely.
Answer. The inequality for the weights holds if and only if $k(\amalg)=k(\mathrm{E})=k(C)=k(T)=k(\mathrm{~b})=0$.
There are exactly 10 ways to encode.
In any of them, unique decoding is impossible.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 4.
Over two days, 50 financiers raised funds to combat a new virus. Each of them made a one-time contribution of a whole number of thousands of rubles, not exceeding 100. Each contribution on the first day did not exceed 50 thousand, while on the second day, it was more than this amount; and no pair of the 50 contributions differed by exactly 50 thousand. What amount was raised?
|
The solution significantly depends on whether all contributions were distinct or could repeat.
Let's first consider the case where all contributions are distinct. Any natural number greater than 50 but not exceeding 100 can be represented as $50+n$, where $n \in [1, 2, 3, \ldots, 50]$. According to the condition, there are no two numbers that differ exactly by 50, so $n$ takes all the remaining values from the first 25 numbers. Therefore, the sum of all 50 numbers is $1+2+3+\ldots+50+50 \cdot 25=2525$.
If contributions could repeat, a definitive answer cannot be given, but estimates can be made. Note that according to the condition, there was at least one contribution each day. The smallest sum would occur if there were 49 contributions of 1 on the first day, and one contribution of 52 on the second day (51 is not possible). The total sum would be $49 \cdot 1 + 52 = 101$. The largest sum would occur if there was 1 contribution of 49 on the first day, and 49 contributions of 100 on the second day. The total sum would be $49 \cdot 100 + 49 = 4949$.
Answer. If all contributions are distinct, then the total collected is 2525 thousand. If not, the minimum possible sum is 101 thousand, and the maximum possible sum is 4949 thousand.
|
2525
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. A triangle was cut into two triangles. Find the greatest value of $N$ such that among the 6 angles of these two triangles, exactly $N$ are the same.
|
Solution. For $N=4$, an example is an isosceles right triangle divided into two isosceles right triangles: four angles of $45^{\circ}$. Suppose there are five equal angles. Then in one of the triangles, all three angles are equal, meaning all of them, and two angles of the other triangle are $60^{\circ}$. But then both these triangles are equilateral, and it is impossible to form a triangle from two equilateral triangles.
Answer: $\mathrm{N}=4$.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. The set $M$ consists of $n$ numbers, $n$ is odd, $n>1$. It is such that when any of its elements is replaced by the sum of the other $n-1$ elements
from $M$, the sum of all $n$ elements does not change. Find the product of all $n$ elements of the set $M$.
|
# Solution. Let
$$
M=\left\{x_{1}, \ldots, x_{n}\right\}, \quad x_{1}+\cdots+x_{n}=S
$$
Replace the element $x_{1}$ with the sum of the others. Then
$$
S=\left(S-x_{1}\right)+x_{2}+x_{3}+\cdots+x_{n}=\left(S-x_{1}\right)+\left(S-x_{1}\right)
$$
Reasoning similarly for the other elements, we get that
$$
2 x_{k}=S, \quad k=1 \ldots n
$$
Thus, all elements of the set are equal to each other. Since the sum does not change when one addend is replaced, this addend must be equal to what it is replaced with, i.e.,
$$
x_{1}=x_{2}+x_{3}+\cdots+x_{n}
$$
Considering the equality of the elements, we get $x_{1}=(n-1) x_{1}$, hence, $x_{1}=0$. Therefore, the product of all numbers in the set $M$ is 0.
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. After another labor season, the electrified part of the Mediterranean Tundra doubled. At the same time, its non-electrified part decreased by $25 \%$. What fraction of the entire Tundra was not supplied with electricity at the beginning of the labor season?
|
# Solution
Let $x$ and $y$ be the fractions of the electrified and non-electrified parts, respectively. Clearly, $x+y=1$. According to the condition, $2x + 0.75y = 1$. We obtain the equation
$$
x+y=2x+0.75y
$$
from which we can find the ratio
$$
\frac{x}{y}=\frac{1}{4}
$$
Now we can find the required ratio
$$
\frac{y}{x+y}=\frac{1}{x / y+1}=\frac{1}{1 / 4+1}=\frac{4}{5}=0.8=80\%
$$
## Answer: $80\%$
|
80
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. A table of numbers with 20 rows and 15 columns, $A_{1}, \ldots, A_{20}$ are the sums of the numbers in the rows, $B_{1}, \ldots, B_{15}$ are the sums of the numbers in the columns.
a) Is it possible that $A_{1}=\cdots=A_{20}=B_{1}=\cdots=B_{15}$?
b) If the equalities in part a) are satisfied, what is the sum $A_{1}+\cdots+A_{20}+$ $B_{1}+\cdots+B_{15}?$
|
Let $A_{i}=B_{j}=X$ for $i=1, \ldots 20$ and $j=1, \ldots, 15$. Consider the sum $S$ of all elements in the table. We have $S=20 X=15 X, X=0$ and $A_{1}+\cdots+A_{20}+B_{1}+\cdots+B_{15}=0$. An example of such a table is, for instance, a table consisting entirely of zeros. There is no need to consider other cases.
Answer: a) - yes, b) - 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Early in the morning, the pump was turned on and they started filling the pool. At 10 am, another pump was connected and by 12 pm the pool was half full. By 5 pm, the pool was full. What could be the latest time the first pump was turned on?
|
Solution. Let the volume of the pool be $V$. Denote by $x$ and $y$ the capacities of the pumps, and by $t$ the time the first pump operates before the second pump is turned on.
Then $t x + 2 x + 2 y = V / 2.5 x + 5 y = V / 2$.
From this, $t x + 2 x + 2 y = 5 x + 5 y$ or $t x = 3 x + 3 y$.
In the end, $t = 3 + 3 y / x$. Since $x > 0$ and $y > 0$, then $t \geqslant 3$.
Answer. The first pump was turned on no later than 7 a.m.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The integer part $[x]$ of a number $x$ is defined as the greatest integer $n$ such that $n \leqslant x$, for example, $[10]=10,[9.93]=9,\left[\frac{1}{9}\right]=0,[-1.7]=-2$. Find all solutions to the equation $\left[\frac{x-1}{2}\right]^{2}+2 x+2=0$.
|
Solution. From the equation, it follows that $2 x=2-\left[\frac{x-1}{2}\right]^{2}-$ is an integer. Therefore, either $2 x=n \in \mathbb{Z}$, or $x=n+\frac{1}{2} \quad(n \in \mathbb{Z})$. In this case, we need to separately consider the cases of even and odd $n$.
1) If $x=2 k$, then
$$
\begin{aligned}
& {\left[\frac{2 k-1}{2}\right]^{2}+2(2 k)+2=\left[k-\frac{1}{2}\right]^{2}+4 k+2=(k-1)^{2}+4 k+2=} \\
& =k^{2}-2 k+1+4 k+2=\left(k^{2}+2 k+1\right)+2=(k+1)^{2}+2 \geqslant 2
\end{aligned}
$$
Since the obtained expression is strictly positive, solutions of the form $x=2 k$ are impossible.
2) If $x=2 k+1$, then
$$
\left[\frac{2 k}{2}\right]^{2}+2(2 k+1)+2=k^{2}+4 k+4=(k+2)^{2}=0
$$
The obtained equation has a solution $k=-2$, which gives $x=-3$.
3) If $x=2 k+\frac{1}{2}$, then
$$
\begin{aligned}
& {\left[\frac{2 k-\frac{1}{2}}{2}\right]^{2}+2\left(2 k+\frac{1}{2}\right)+2=\left[k-\frac{1}{4}\right]^{2}+4 k+3=(k-1)^{2}+4 k+3=} \\
& =k^{2}-2 k+1+4 k+3=\left(k^{2}+2 k+1\right)+3=(k+1)^{2}+3 \geqslant 3
\end{aligned}
$$
Since the obtained expression is strictly positive, solutions of the form $x=2 k+\frac{1}{2}$ are impossible.
4) If $x=2 k+1+\frac{1}{2}$, then
$$
\begin{aligned}
{\left[\frac{2 k+\frac{1}{2}}{2}\right]^{2}+2\left(2 k+\frac{3}{2}\right)+2=\left[k+\frac{1}{4}\right]^{2} } & +4 k+3+2=k^{2}+4 k+5= \\
& =k^{2}+4 k+4+1=(k+2)^{2}+1 \geqslant 1
\end{aligned}
$$
Since the obtained expression is strictly positive, solutions of the form $x=2 k+1+\frac{1}{2}$ are impossible.
Answer. $x=-3$.
|
-3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The Atelier "Heavy Burden" purchased a large batch of cast iron buttons. If they sew two buttons on each coat or if they sew three buttons on each coat, in each case 1 piece will remain from the entire batch. If, however, they sew four buttons on each coat or if they sew five buttons on each coat, in each case 3 pieces will remain from the entire batch. How many buttons will remain if they sew twelve buttons on each coat?
|
# Solution
Let $a$ be the desired number. From the condition, it follows that the number $a-1$ is divisible by 2 and 3. Therefore, $a=6k+1$. Also, the number $a-3$ is divisible by 4 and 5. Therefore, $a=20n+3$. We solve the equation
$$
6k+1=20n+3
$$
Or, equivalently,
$$
3k=10n+1
$$
Its general solution is
$$
k=7+10s, \quad n=2+3s, \quad \Rightarrow \quad a=60s+43
$$
We find the remainder of the division of $a$ by 12. Since 60 is divisible by 12, the desired remainder is the remainder of the division of 43 by 12, which is 7.
Answer: 7.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Given a rectangular parallelepiped. The perimeters of each of its three mutually perpendicular faces are equal to the sides of a new rectangular parallelepiped. What can be the minimum ratio of the volume of the new parallelepiped to the volume of the original?
#
|
# Solution
Let $x, y, z$ be the sides of the original parallelepiped. Then the volume of the new one is
$$
V_{2}=2 \cdot(x+y) \cdot 2 \cdot(y+z) \cdot 2 \cdot(z+x)
$$
The desired ratio of volumes is
$$
\begin{gathered}
\frac{V_{2}}{V_{1}}=\frac{8(x+y)(y+z)(z+x)}{x y z}=\frac{8\left(x y+y^{2}+x z+y z\right)(z+x)}{x y z}= \\
=\frac{8\left(2 x y z+y^{2} z+x z^{2}+y z^{2}+x^{2} y+x y^{2}+x^{2} z\right)}{x y z}= \\
=8\left(2+\frac{y}{x}+\frac{x}{y}+\frac{z}{y}+\frac{y}{z}+\frac{z}{x}+\frac{x}{z}\right)
\end{gathered}
$$
We use the fact that $\frac{a}{b}+\frac{b}{a} \geq 2$, thus we get
$$
\frac{V_{2}}{V_{1}} \geq 8(2+2+2+2)=64
$$
Answer: 64.
|
64
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Find the maximum value of the quantity $x^{2}+y^{2}$, given that
$$
x^{2}+y^{2}=3 x+8 y
$$
|
# Solution
## Method 1
Introduce a Cartesian coordinate system and consider an arbitrary vector $\mathbf{a}$ with coordinates $(x, y)$ and a fixed vector $\mathbf{c}$ with coordinates $(3, 8)$.
Then the left side of the condition represents the square of the length of vector $\mathbf{a}$, and the right side represents the dot product of vectors $\mathbf{a}$ and $\mathbf{c}$:
$$
|\mathbf{a}|^{2} = (\mathbf{a}, \mathbf{c})
$$
Estimating the dot product through the lengths of the factors, we get
$$
|\mathbf{a}|^{2} \leq |\mathbf{a}| \cdot |\mathbf{c}| \Leftrightarrow |\mathbf{a}| \leq |\mathbf{c}|
$$
As is known, equality is possible and is achieved when the vectors lie on the same line. Therefore, the maximum value will be achieved, for example, when $\mathbf{a} = \mathbf{c}$.
Substituting the values, we get $3^{2} + 8^{2} = 73$.
## Method 2
Transform the condition by completing the square.
$$
x^{2} + y^{2} = 3x + 8y \quad \Leftrightarrow \quad \left(x - \frac{3}{2}\right)^{2} + (y - 4)^{2} = \frac{73}{4}
$$
Thus, the points of the given set lie on a circle with center at $\left(\frac{3}{2}, 4\right)$. Points with a fixed value of $x^{2} + y^{2}$ also lie on a circle (with center at the origin), so the desired point will be the point of tangency of the obtained circle internally with the circle $x^{2} + y^{2} = \text{Const}$. This point of tangency, in turn, lies on the diameter connecting the centers of the circles, so it remains to substitute $y = \frac{8}{3} x$ into the condition.
$$
\left(x - \frac{3}{2}\right)^{2} + \left(\frac{8}{3} x - 4\right)^{2} = \frac{73}{4} \Leftrightarrow \frac{73}{9} \left(x - \frac{3}{2}\right)^{2} = \frac{73}{4},
$$
from which $x = 0$ or $x = 3$. For the second value, we get $y = \frac{8}{3} \cdot 3 = 8$, from which $x^{2} + y^{2} = 9 + 64 = 73$.
Answer: 73.
|
73
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 4.
In modern conditions, digitalization - the conversion of all information into digital code - is considered relevant. Each letter of the alphabet can be assigned a non-negative integer, called the code of the letter. Then, the weight of a word can be defined as the sum of the codes of all the letters in that word. Is it possible to encode the letters О, П, С, Т, Ь, Я with elementary codes, each consisting of a single digit from 0 to 9, so that the weight of the word "СТО" is not less than the weight of the word "ПЯТЬСОТ"? If such encoding is possible, in how many ways can it be implemented? If such encoding is possible, does it allow for the unambiguous restoration of a word from its code?
|
# Solution.
Let $k(x)$ denote the elementary code of the letter $x$. We have:
$$
k(C)+k(T)+k(O) \geq k(\Pi)+k(\text { Ya) }+k(T)+k(\text{ b })+k(C)+k(O)+k(T)
$$
which is equivalent to
$$
k(\Pi)+k(T)+k(\text{ b })+k(\text { Ya) }=0
$$
from which it follows that
$$
k(\Pi)=k(T)=k(\text{ b })=k(\text { Ya) }=0
$$
The elementary codes of the two remaining letters $k(C)$ and $k(O)$ can be any digits from 0 to 9. Therefore, there are exactly $10^{2}$ ways to encode them. However, for any choice of $k(O)$ and $k(C)$, the words "POP" and "TOT" will have the same codes $k(O)$, which cannot be decoded uniquely.
Answer. The inequality for the weights holds if and only if $k(\Pi)=k(T)=k(\text{ b })=k(\text { Ya) }=0$.
There are exactly 100 ways to encode them.
In any of these ways, unique decoding is impossible.
|
100
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 4.
Over two days, 100 bankers collected funds to fight a new virus. Each of them made a one-time contribution of a whole number of thousands of rubles, not exceeding 200. Each contribution on the first day did not exceed 100 thousand, while on the second day it was more than this amount; and no pair of all 100 contributions differed by exactly 100 thousand. What amount was collected?
|
The solution significantly depends on whether all contributions were distinct or could repeat.
Let's first consider the case where all contributions are distinct. Any natural number greater than 100 but not exceeding 200 can be represented as $100+n$, where $n \in [1,2,3, \ldots, 100]$. According to the condition, there are no two numbers that differ exactly by 100, so $n$ takes all the remaining values from the first 50 numbers. Therefore, the sum of all 100 numbers is $1+2+3+\ldots+100+100 \cdot 50=10050$.
If contributions could repeat, a definitive answer cannot be given, but estimates can be made. Note that according to the condition, there was at least one contribution each day. The smallest sum would occur if there were 99 contributions of 1 on the first day, and one contribution of 102 on the second day (101 is not possible). The total sum would be $99 \cdot 1 + 102 = 201$. The largest sum would occur if there was 1 contribution of 99 on the first day, and 99 contributions of 200 on the second day. The total sum would be $99 \cdot 200 + 99 = 19899$.
Answer. If all contributions are distinct, then the total collected is 10050 thousand. If not, the minimum possible sum is 201 thousand, and the maximum possible sum is 19899 thousand.
|
10050
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Each of the six houses on one side of the street is connected by cable lines to each of the eight houses on the opposite side. How many pairwise intersections do the shadows of these cables form on the surface of the street, if no three of them intersect at the same point? Assume that the light causing these shadows falls vertically downward.
|
# Solution
Let's take an arbitrary pair of houses on one side of the street and an arbitrary pair on the other. They are the vertices of a convex quadrilateral (since two sides of the quadrilateral, coming from each chosen pair, lie on one side of the line, i.e., the angles do not exceed $180^{\circ}$), so its diagonals intersect.
Each pairwise intersection of shadows (cables) is a point of intersection of the diagonals of such a quadrilateral. Thus, it remains to find their number, which is equal to the product of the ways to choose an ordered pair of houses on each side of the street.
Answer: $C_{6}^{2} \cdot C_{8}^{2}=420$.
|
420
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the maximum value of the quantity $x^{2}+y^{2}+z^{2}$, given that
$$
x^{2}+y^{2}+z^{2}=3 x+8 y+z
$$
|
# Solution
## 1st Method
Introduce a Cartesian coordinate system and consider an arbitrary vector $\mathbf{a}$ with coordinates $(x, y, z)$ and a fixed vector $\mathbf{c}$ with coordinates $(3, 8, 1)$. Then, the left side of the condition represents the square of the length of vector $\mathbf{a}$, and the right side represents the dot product of vectors $\mathbf{a}$ and $\mathbf{c}$:
$$
|\mathbf{a}|^{2}=(\mathbf{a}, \mathbf{c})
$$
By estimating the dot product through the lengths of the multipliers, we get
$$
|\mathbf{a}|^{2} \leq|\mathbf{a}| \cdot|\mathbf{c}| \Leftrightarrow|\mathbf{a}| \leq|\mathbf{c}|
$$
As is known, equality is possible and is achieved when the vectors lie on the same line. Therefore, the maximum value will be achieved, for example, when $\mathbf{a}=\mathbf{c}$.
Substituting the values, we get $3^{2}+8^{2}+1^{2}=74$.
## 2nd Method
Transform the condition by isolating complete squares.
$$
x^{2}+y^{2}+z^{2}=3 x+8 y+z \quad \Leftrightarrow \quad\left(x-\frac{3}{2}\right)^{2}+(y-4)^{2}+\left(z-\frac{1}{2}\right)^{2}=\frac{74}{4}
$$
Thus, the points of the given set lie on a sphere with center at the point $\left(\frac{3}{2}, 4, \frac{1}{2}\right)$. Points with a fixed value of the quantity $x^{2}+y^{2}+z^{2}$ also lie on a sphere (with center at the origin), so the desired point will be the point of tangency of the obtained sphere internally with the sphere $x^{2}+y^{2}=$ Const. This point of tangency, in turn, lies on the diameter connecting the centers of the spheres, so it remains to substitute $y=\frac{8}{3} x, z=\frac{1}{3} x$ into the condition.
$$
\left(x-\frac{3}{2}\right)^{2}+\left(\frac{8}{3} x-4\right)^{2}+\left(\frac{1}{3} x-\frac{1}{2}\right)^{2}=\frac{74}{4} \quad \Leftrightarrow \quad \frac{74}{9}\left(x-\frac{3}{2}\right)^{2}=\frac{74}{4},
$$
from which $x=0$ or $x=3$.
The first value gives a zero sum of squares. For the second value, we get $y=\frac{8}{3} \cdot 3=8, z=\frac{1}{3} \cdot 3=1$, from which $x^{2}+y^{2}+z^{2}=9+64+1=74$.
Answer: 74.
|
74
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 4.
Four brigades were developing an open coal deposit for three years, working with a constant productivity for each brigade. In the second year, due to weather conditions, work was not carried out for four months, and for the rest of the time, the brigades worked in rotation (one at a time). The ratio of the working times of the first, second, third, and fourth brigades and the amount of coal mined respectively are: in the first year 4:1:2:5 and 10 million tons; in the second year $2: 3: 2: 1$ and 7 million tons; in the third year 5:2:1:4 and 14 million tons. How much coal would these four brigades have mined in 4 months if they worked together?
|
Solution. Let the $i$-th brigade mine $x_{i}$ coal per month. Then we have the system
$$
\left\{\begin{array}{l}
4 x_{1}+x_{2}+2 x_{3}+5 x_{4}=10 \\
2 x_{1}+3 x_{2}+2 x_{3}+x_{4}=7 \\
5 x_{1}+2 x_{2}+x_{3}+4 x_{4}=14
\end{array}\right.
$$
By adding twice the first equation to thrice the second and subtracting the third equation, we get
$$
9\left(x_{1}+x_{2}+x_{3}+x_{4}\right)=27 \text {. }
$$
Then
$$
4\left(x_{1}+x_{2}+x_{3}+x_{4}\right)=12 \text {. }
$$
Answer: 12 million tons.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 2.
What is the last digit of the value of the sum $5^{2020}+6^{2019} ?$
|
# Solution.
The number 5 to any power ends in 5.
The number 6 to any power ends in 6.
Therefore, the sum $5^{2020}+6^{2019}$ ends in the digit 1.
Answer. The digit 1.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 4.
In modern conditions, digitalization - the conversion of all information into digital code - is considered relevant. Each letter of the alphabet can be assigned a non-negative integer, called the letter code. Then, the weight of a word can be defined as the sum of the codes of all the letters in that word. Is it possible to encode the letters O, P, S, T, Ь, Я with elementary codes, each consisting of a single digit from 0 to 9, so that the weight of the word "СТО" is not less than the weight of the word "ПЯТЬСОТ"? If such encoding is possible, does it allow for the unambiguous restoration of a word from its code?
|
# Solution.
Let $k(x)$ denote the elementary code of the letter $x$. We have:
$$
k(C)+k(T)+k(O) \geq k(\Pi)+k(\text { ( })+k(T)+k(\mathrm{~b})+k(C)+k(O)+k(T)
$$
which is equivalent to
$$
k(\Pi)+k(T)+k(\mathrm{~b})+k(\text { Я) }=0
$$
from which it follows that
$$
k(\Pi)=k(T)=k(\mathrm{~b})=k(\text { Я })=0
$$
The elementary codes of the two remaining letters $k(C)$ and $k(O)$ can be any digits from 0 to 9. Therefore, there are exactly $10^{2}$ ways to encode them. However, for any choice of $k(O)$ and $k(C)$, the words "ПОП" and "ТОТ" will have the same codes $k(O)$, which cannot be decoded uniquely.
Answer. The inequality for the weights holds if and only if $k(\Pi)=k(T)=k(\mathrm{~b})=k($ Я $)=0$
There are exactly 100 ways to encode them.
In any of these ways, unique decoding is impossible.
|
100
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 5.
The carriages of the express train "Moscow - Yalta" must be numbered consecutively, starting from one. But in a hurry, two adjacent carriages received the same number. As a result, it turned out that the sum of the numbers of all carriages is 111. How many carriages are in the train and which number was used twice?
#
|
# Solution.
Let's start calculating the sums sequentially
$$
\begin{aligned}
& 1+2=3 \\
& 1+2+3=6 \\
& \cdots \\
& 1+2+\ldots+14=105 \\
& 1+2+\ldots+14+15=120
\end{aligned}
$$
From this, it is clear that the first 14 wagons had the first 14 sequential numbers, which sum up to 105, and one more wagon had a number equal to \(111-105=6\).
Answer. There were 15 wagons in the train, two of which had the number 6.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 1.
Three electric generators have powers $x_{1}, x_{2}, x_{3}$, the total power of all three does not exceed 2 MW. In the power system with such generators, a certain process is described by the function
$$
f\left(x_{1}, x_{2}, x_{3}\right)=\sqrt{x_{1}^{2}+x_{2} x_{3}}+\sqrt{x_{2}^{2}+x_{1} x_{3}}+\sqrt{x_{3}^{2}+x_{1} x_{2}} .
$$
Find the maximum and minimum values of this function.
|
# Solution.
It is clear that the minimum value of the function is zero (achieved when $\left.x_{1}=x_{2}=x_{3}=0\right)$.
Let's find the maximum. We can assume that $x_{1} \geq x_{2} \geq x_{3} \geq 0$. We will prove two inequalities:
$$
\begin{gathered}
\sqrt{x_{1}^{2}+x_{2} x_{3}} \leq x_{1}+\frac{x_{3}}{2} \\
\sqrt{x_{2}^{2}+x_{3} x_{1}}+\sqrt{x_{3}^{2}+x_{1} x_{2}} \leq \frac{2 x_{1}+3 x_{2}+x_{3}}{2}
\end{gathered}
$$
The first inequality is equivalent to the inequality $4 x_{3}\left(x_{1}-x_{2}\right)+x_{3}^{2} \geq 0$.
To prove the second inequality, we use the fact that for $u \geq 0$ and $v \geq 0$, $\sqrt{u}+\sqrt{v} \leq \sqrt{2(u+v)}$ holds.
Thus,
$$
\sqrt{x_{2}^{2}+x_{3} x_{1}}+\sqrt{x_{3}^{2}+x_{1} x_{2}} \leq \sqrt{2\left(x_{2}^{2}+x_{3} x_{1}+x_{3}^{2}+x_{1} x_{2}\right)}
$$
It is not difficult to verify that
$2\left(x_{2}^{2}+x_{3} x_{1}+x_{3}^{2}+x_{1} x_{2}\right) \leq\left(\frac{x_{1}+3 x_{2}+2 x_{3}}{2}\right)^{2} \Leftrightarrow\left(x_{1}-x_{2}-2 x_{3}\right)^{2}+8 x_{3}\left(x_{2}-x_{3}\right) \geq 0$.
We have:
$$
\begin{aligned}
\sqrt{x_{1}^{2}+x_{2} x_{3}}+\sqrt{x_{2}^{2}+x_{1} x_{3}}+\sqrt{x_{3}^{2}+x_{1} x_{2}} \leq & x_{1}+\frac{x_{3}}{2}+\frac{x_{1}+3 x_{2}+2 x_{3}}{2}= \\
& =\frac{3}{2}\left(x_{1}+x_{2}+x_{3}\right) \leq \frac{3}{2} \cdot 2=3 .
\end{aligned}
$$
Answer: $\quad \max f\left(x_{1}, x_{2}, x_{3}\right)=3, \min f\left(x_{1}, x_{2}, x_{3}\right)=0$
for $x_{1} \geq 0, x_{2} \geq 0, x_{3} \geq 0$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 3.
A polynomial $P(x)$ with integer coefficients has the properties
$$
P(1)=2019, \quad P(2019)=1, \quad P(k)=k,
$$
where the number $k$ is an integer. Find this number $k$.
#
|
# Solution.
Since the polynomial $P(x)$ has integer coefficients, $P(a)-P(b)$ is divisible by $a-b$ for any integers $a$ and $b$.
We get that
$$
\begin{gathered}
P(k)-P(1)=(k-2019) \text { is divisible by }(k-1), \\
P(k)-P(2019)=(k-1) \text { is divisible by }(k-2019) .
\end{gathered}
$$
This can only be true if $|k-1|=|k-2019|$.
The solution to the obtained equation is $k=1010$.
Answer: $\quad k=1010$.
|
1010
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. It is known that there are four ways to prepare magical pollen to create elixirs of kindness, joy, wisdom, luck, health, friendliness, and creativity. But elixirs of kindness, joy, and wisdom are made from fairy pollen, while elixirs of luck, health, friendliness, and creativity are made from elf pollen. Among the instructions for preparing the pollen, there are two methods for fairy pollen and two methods for elf pollen. How many ways are there to prepare all the elixirs?
|
Solution. Four methods of preparing pollen are represented by four branches of a tree. From two branches with methods of preparing fairy pollen, three branches of elixirs (of goodness, joy, and wisdom) branch off, and from two branches with methods of preparing elf pollen, four branches (of luck, health, friendliness, and creativity) branch off. This results in the following scheme:
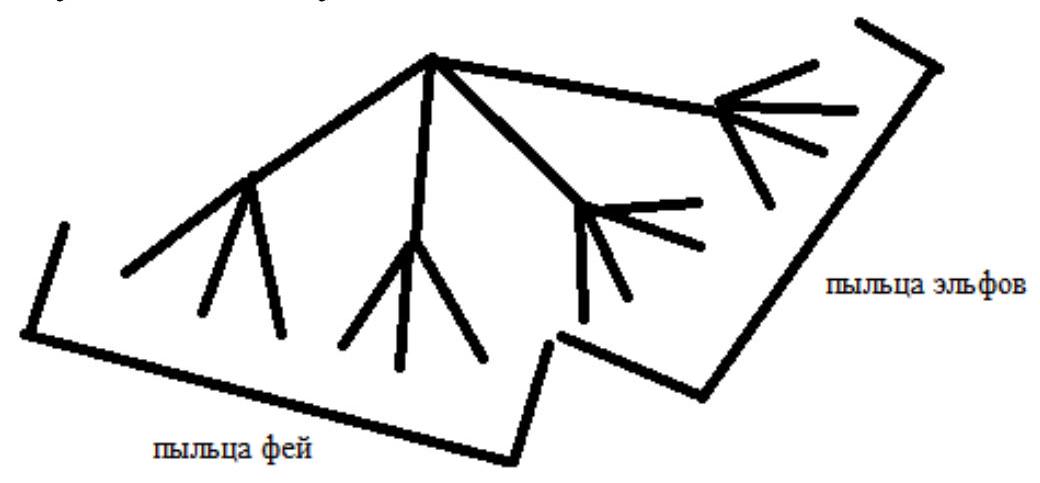
Thus, we have the answer: $2 \cdot 3 + 2 \cdot 4 = 14$ (types)
## Answer: 14 types of elixirs.
|
14
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. It is known that the free term $a_{0}$ of the polynomial $P(x)$ with integer coefficients is less than 100 in modulus, and $P(20)=P(16)=2016$. Find $a_{0}$.
|
Solution. We can write $P(x)-2016=(x-16)(x-20) Q(x)$, where $Q(x)$ is a polynomial with integer coefficients. The constant term of the right side is $320 k$, where $k$ is an integer. Thus, $a_{0}=2016-320 k$. The condition is satisfied only by the value $k=6, a_{0}=96$.
Answer. $a_{0}=96$.
|
96
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The council of the secret pipeline village is gathering around a round table, where each arriving member can sit in any free seat. How many different seating arrangements are possible if 7 participants will attend the council? (Two seating arrangements are considered the same if the same people sit to the left and right of each participant, empty seats are not considered.)
|
# Solution
Since empty seats are not taken into account, we can consider only the ways of arranging on seven seats. The first person can sit in any of the 7 seats, the next in any of the 6 remaining seats, and so on until the last. In total, there are $7 \cdot 6 \cdot \ldots \cdot 1=7!$ ways.
However, each arrangement that can be obtained from another by a cyclic shift (rotation clockwise or counterclockwise) is considered the same. For each fixed arrangement, there will be 7 such variants. Therefore, the final number is
$$
7 \cdot 6 \cdot \ldots \cdot 1 / 7=6!=720
$$
It is also worth noting that a mirror reflection transforms one seating arrangement into another, as the right and left neighbors switch places.
Answer: $6!=720$ ways.
|
720
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In the summer, Ponchik eats honey cakes four times a day: instead of morning exercise, instead of a daytime walk, instead of an evening run, and instead of a nighttime swim. The quantities of cakes eaten instead of exercise and instead of a walk are in the ratio of $3: 2$; instead of a walk and instead of a run - as $5: 3$; and instead of a run and instead of a swim - as $6: 5$. By how many more or fewer cakes did Ponchik eat instead of exercise compared to instead of swimming on the day when a total of 216 cakes were eaten?
|
# Solution
According to the problem, we can establish the following ratios for the number of doughnuts eaten instead of engaging in a particular useful activity:
$$
\frac{\text { Morning Exercise }}{\text { Walk }}=\frac{3}{2} \quad \frac{\text { Walk }}{\text { Jog }}=\frac{5}{3} \quad \frac{\text { Jog }}{\text { Swim }}=\frac{6}{5}
$$
or equivalently,
$$
\frac{\text { Morning Exercise }}{\text { Walk }}=\frac{15}{10} \quad \frac{\text { Walk }}{\text { Jog }}=\frac{10}{6} \quad \frac{\text { Jog }}{\text { Swim }}=\frac{6}{5}
$$
From this, we can denote: Morning Exercise $=15 x$, Walk $=10 x$, Jog $=$ $6 x$, Swim $=5 x$. It is known that a total of 216 doughnuts were eaten, so
$$
15 x+10 x+6 x+5 x=216 \Rightarrow x=6
$$
Therefore, instead of morning exercise, Donut ate 90 doughnuts, and instead of swimming, he ate 30. Answering the question of the problem, Donut ate 60 more doughnuts instead of morning exercise than instead of swimming.
Answer: 60 more doughnuts.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 3.
Two swimmers are training in a rectangular quarry. The first swimmer finds it more convenient to exit at a corner of the quarry, so he swims along the diagonal to the opposite corner and back. The second swimmer finds it more convenient to start from a point that divides one of the quarry's shores in the ratio $2018: 2019$. He swims along a quadrilateral, visiting one point on each shore, and returns to the starting point. Can the second swimmer choose points on the other three shores such that his path is shorter than the first swimmer's? What is the minimum value that the ratio of the length of the longer path to the shorter can have?
|
# Solution.
Let's draw a rectangular quarry $A D C D$ and the inscribed quadrilateral route of the second swimmer $N L M K$.
Reflect the drawing symmetrically first with respect to side $C D$, then with respect to side $C B^{\prime}$, and finally with respect to side $A^{\prime} B^{\prime}$.
By construction, segments $N D$ and $N^{\prime} D^{\prime}$ are equal and parallel to each other. Therefore, $A A^{\prime} N^{\prime} N$ is a parallelogram, and its side $N N^{\prime}$ is equal to twice the diagonal of the original rectangle $A C$ (i.e., the length of the first swimmer's path).
Olympiad for schoolchildren "Nadezhda Energetiki". Final stage. Solutions
It is clear that the sum of the lengths of segments $N K, K M^{\prime}, M^{\prime} L^{\prime}$, and $L^{\prime} N^{\prime}$ is equal to the perimeter of the quadrilateral $N L M K$ (i.e., the length of the second swimmer's path).
But the length of the broken line $N K M^{\prime} L^{\prime} N^{\prime}$ cannot be less than the length of the segment $N N^{\prime}$, which is the shortest distance between points $N$ and $N^{\prime}$. From this, it follows that the second swimmer's path cannot be shorter than the first swimmer's path.
The paths can be made equal if we transfer (using the symmetry of the construction) the points of intersection of the segment $N N^{\prime}$ with the sides $D C, C B^{\prime}$, and $B^{\prime} A^{\prime}$ to the original rectangle. (It can be shown that the resulting figure will be a parallelogram, but this is not part of the problem statement.)
With such a construction, the swimmers' paths will be equal, and their ratio will be 1.
Note that nowhere in the reasoning is it used that the initial point $N$ divides the corresponding side of the rectangle $A D$ in a certain proportion.
## Answer:
the second swimmer's path cannot be shorter than the first swimmer's path; the minimum ratio of the length of the longer path to the shorter one is 1.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 1. In the country of "Energetika," there are 150 factories, and some of them are connected by bus routes that do not stop anywhere except at these factories. It turned out that any four factories can be divided into two pairs such that there is a bus route between the factories of each pair. Find the smallest number of pairs of factories that can be connected by bus routes.
|
Solution. Suppose that some factory $X$ is connected by bus routes to no more than 146 factories. Then a quartet of factories, consisting of $X$ and any three with which it is not connected, does not satisfy the problem's condition, since $X$ cannot be paired with any of the three remaining factories. Therefore, each factory is connected to at least 147 factories. Consequently, the total number of pairs of factories connected by bus routes is no less than $\frac{147 \cdot 150}{2}=11025$.
Now, we will show that there can be exactly 11025 pairs of factories. Number the factories from 1 to 150 and connect by bus routes all factories except the first and the 150th, as well as factories whose numbers differ by one. We will check that this construction satisfies the problem's condition. Since each factory is connected by bus routes to 147 factories, the total number of connected factory pairs is exactly $\frac{147 \cdot 150}{2}=11025$.
Now, take any quartet of factories. There are two cases.
1) There is a factory not connected to two of the other three factories. Let factory A not be connected to factories B and C, but connected to factory D. Then factories B and C must be connected to each other, since the remainders of their numbers when divided by 150 differ by 2. Therefore, the pairs (A,D) and (B,C) are suitable.
2) All factories are connected to at least two of the other three factories. Let factory A be connected to factories B and C. By assumption, factory D must be connected to B or C. If it is connected to B, then the pairs (A,C) and (B,D) are suitable, and if it is connected to C, then the pairs (A,B) and (C,D) are suitable.
Answer: 11025.
|
11025
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. There are 4 numbers, not all of which are the same. If you take any two of them, the ratio of the sum of these two numbers to the sum of the other two numbers will be equal to the same value k. Find the value of k. Provide at least one set of four numbers that satisfy the condition. Describe all possible sets of such numbers and determine how many there are.
|
Solution. Let $x_{1}, x_{2}, x_{3}, x_{4}$ be such numbers. Write the relations for the sums of pairs of numbers:
$$
\begin{aligned}
& \frac{x_{1}+x_{2}}{x_{3}+x_{4}}=\frac{x_{3}+x_{4}}{x_{1}+x_{2}}=k \\
& \frac{x_{1}+x_{3}}{x_{2}+x_{4}}=\frac{x_{2}+x_{4}}{x_{1}+x_{3}}=k \\
& \frac{x_{1}+x_{4}}{x_{2}+x_{3}}=\frac{x_{2}+x_{3}}{x_{1}+x_{4}}=k
\end{aligned}
$$
Let $A=x_{1}+x_{2}, B=x_{3}+x_{4}$. Then from (2) we get $A=k B, B= k A, A B \neq 0$, from which $(k^{2}-1) A=0, k= \pm 1$. The same values will be obtained by analyzing relations (3) and (4).
If $k=1$, then equations (2)-(4) take the form $x_{1}+x_{2}=x_{3}+x_{4}, x_{1}+x_{3}= x_{2}+x_{4}, x_{1}+x_{4}=x_{2}+x_{3}$, from which we find the general solution $x_{1}=x_{2}=x_{3}= x_{4}=C \neq 0$. This case does not meet the condition (all numbers turned out to be equal).
If $k=-1$, then each of equations (2)-(4) takes the form $x_{1}+x_{2}+x_{3}+ x_{4}=0$, and the general solution is
$x_{1}=A, x_{2}=B, \quad x_{3}=C, \quad x_{4}=-A-B-C, \quad(A+B)(A+C)(B+C) \neq 0$.
Answer: $k=-1$.
$x_{1}=A, \quad x_{2}=B, \quad x_{3}=C, \quad x_{4}=-A-B-C, \quad(A+B)(A+C)(B+C) \neq 0$.
The set of tuples $\left(x_{1}, x_{2}, x_{3}, x_{4}\right)$ is infinite.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 4.
Find the number of numbers $N$ in the set $\{1,2, \ldots, 2018\}$ for which there exist positive solutions $x$ to the equation
$$
x^{[x]}=N
$$
( $[x]$ is the integer part of the real number $x$, i.e., the greatest integer not exceeding $x$)
|
# Solution.
Notice that suitable numbers $N$ for $x$ such that $[x]=n$ are the numbers from $n^{n}$ to $(n+1)^{n-1}$, that is, exactly the numbers for which $[\sqrt[n]{N}]=n$. Such numbers (among the numbers from 1 to 2018) are the number 1, the numbers from $2^{2}$ to $3^{2-1}$ (there are exactly 5 of them), the numbers from $3^{3}$ to $4^{3-1}$ (there are exactly 37 of them), and the numbers from $4^{4}$ to $5^{4-1}$ (there are exactly 369 of them).
In total, we get $1+5+37+369=412$ numbers.
Answer: 412 numbers.
|
412
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 5.
An electric cable 21 meters long is cut into 21 pieces. For any two pieces, their lengths differ by no more than a factor of three. What is the smallest $m$ such that there will definitely be two pieces whose lengths differ by no more than a factor of $m$?
|
# Solution.
If among the pieces of cable there are at least two that differ in length, then by taking the ratio of the smaller to the larger, we get that $m \leq 1$.
However, the cable can be cut in such a way that all pieces are equal. This implies that if $m<1$, then a way of cutting has been found where no two pieces differ by more than a factor of $m$.
The constructed example proves that the smallest value of $m$ is 1.
Answer: $m=1$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. Boys and girls formed a circle in such a way that the number of children whose right neighbor is of the same gender is equal to the number of children whose right neighbor is of a different gender. What could be the total number of children in the circle?
|
Solution. Let $n$ be the number of children next to whom stands a child of the opposite gender, and $m$ be the number of children next to whom stands a child of the same gender. Initially, $n=m$, i.e., the total number of children ($n+m$) is even. We will swap the positions of two adjacent children so that all boys gather in a row on one side of the circle, and all girls on the other. Then $n$ will become 2. With each such swap of children, the numbers $n$ and $m$ either do not change, or one increases by 2, and the other decreases by 2. This means that the remainder of the division of the difference ($m \sim n$) by 4 does not change.
Initially, this remainder was 0.
If the total number of children is $2k$, $n=2$, then $m=2k \curlyvee 2$. Then $m^{\llcorner} n=2k^{\llcorner} 4$.
For the remainder of the division of $m^{\llcorner} n$ by 4 to be zero, $k$ must be divisible by 2. That is, the total number of children must be a multiple of 4.
Answer. Any natural number that is a multiple of four.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. There are 4 numbers, not all of which are the same. If you take any two of them, the ratio of the sum of these two numbers to the sum of the other two numbers will be the same value $\mathrm{k}$. Find the value of $\mathrm{k}$. Provide at least one set of four numbers that satisfy the condition. Describe all possible sets of such numbers and determine how many there are.
|
Solution. Let $x_{1}, x_{2}, x_{3}, x_{4}$ be such numbers. Write the relations for the sums of pairs of numbers:
$$
\begin{aligned}
& \frac{x_{1}+x_{2}}{x_{3}+x_{4}}=\frac{x_{3}+x_{4}}{x_{1}+x_{2}}=k \\
& \frac{x_{1}+x_{3}}{x_{2}+x_{4}}=\frac{x_{2}+x_{4}}{x_{1}+x_{3}}=k \\
& \frac{x_{1}+x_{4}}{x_{2}+x_{3}}=\frac{x_{2}+x_{3}}{x_{1}+x_{4}}=k
\end{aligned}
$$
Let $A=x_{1}+x_{2}, B=x_{3}+x_{4}$. Then from (2) we get $A=k B, B= k A, A B \neq 0$, from which $\left(k^{2}-1\right) A=0, k= \pm 1$. The same values will be obtained by analyzing relations (3) and (4).
If $k=1$, then equations (2)-(4) take the form $x_{1}+x_{2}=x_{3}+x_{4}, x_{1}+x_{3}=$ $x_{2}+x_{4}, x_{1}+x_{4}=x_{2}+x_{3}$, from which we find the general solution $x_{1}=x_{2}=x_{3}=$ $x_{4}=C \neq 0$. This case does not meet the condition (all numbers turned out to be equal).
If $k=-1$, then each of equations (2)-(4) takes the form $x_{1}+x_{2}+x_{3}+$ $x_{4}=0$, and the general solution is
$x_{1}=A, \quad x_{2}=B, \quad x_{3}=C, \quad x_{4}=-A-B-C, \quad(A+B)(A+C)(B+C) \neq 0$.
Answer: $k=-1$.
$x_{1}=A, \quad x_{2}=B, \quad x_{3}=C, \quad x_{4}=-A-B-C, \quad(A+B)(A+C)(B+C) \neq 0$. The set of tuples $\left(x_{1}, x_{2}, x_{3}, x_{4}\right)$ is infinite.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 1.
The Triassic Discoglossus tadpoles have five legs, while the saber-toothed frog tadpoles grow several tails (all have the same number of tails). An employee of the Jurassic Park scooped up several tadpoles with water. It turned out that the captured tadpoles had a total of 100 legs and 64 tails. How many tails does each saber-toothed frog tadpole have, if all five-legged tadpoles have one tail, and all multi-tailed tadpoles have four legs?
|
# Solution.
Let $x$ be the number of tails of the saber-toothed frog's pollywog. Suppose $n$ five-legged and $k$ many-tailed pollywogs were caught. Counting the total number of legs and tails gives the equations
$$
\left\{\begin{aligned}
5 n+4 k & =100 \\
n+x k & =64
\end{aligned}\right.
$$
From the first equation, we have $n \leq 100 / 5=20, \quad k \leq 100 / 4=25$.
Moreover, $4 k=5(20-n)$, so $k$ must be a multiple of 5.
Now, multiply the second equation of the system by 5 and subtract the first from the result. We get
$$
(5 x-4) k=64 \cdot 5-100=220=2 \cdot 2 \cdot 5 \cdot 11 .
$$
Since the left side is the product of two natural numbers and considering the obtained limits, we find that $k$ can only take the values
$$
k=5 \quad \text { or } \quad k=10 \quad \text { or } \quad k=20 .
$$
Substitute them one by one into the system of equations. For $k=5$, we have
$$
\left\{\begin{aligned}
5 n+20 & =100 \\
n+5 x & =64
\end{aligned}\right.
$$
from which $n=16$. But $64-16=48$ is not a multiple of 5. There are no solutions.
For $k=10$, we get
$$
\left\{\begin{array}{r}
5 n+40=100 \\
n+10 x=64
\end{array}\right.
$$
from which $n=12$. But $64-12=52$ is not a multiple of 10. There are no solutions again.
Olympiad for Schoolchildren "Hope of Energy". Final Stage. Solutions
Finally, for $k=20$, we find
$$
\left\{\begin{array}{l}
5 n+80=100 \\
n+20 x=64
\end{array}\right.
$$
from which $n=4$ and $n=3$.
Answer: 3 tails.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 1.
A rule is given by which each pair of integers $X$ and $Y$ is assigned a number $X \nabla Y$. (The symbol «»» means applying the rule to the numbers $X$ and $Y$.) It is known that for any integers $X, Y$ the following properties hold:
1) $X \nabla 0=X$
2) $X \nabla(Y-1)=(X \nabla Y)-2$
3) $X \nabla(Y+1)=(X \nabla Y)+2$.
Find the formula that describes the given rule, and solve the equation
$$
X \nabla X=-2019
$$
#
|
# Solution.
Let's start writing down in order the result of applying the operation $X \nabla Y$ for $Y=0,1,2, \ldots$, using property 3.
$$
\begin{aligned}
& X \nabla 0=0, \\
& X \nabla 1=X \nabla(0+1)=(X \nabla 0)+2=X+2, \\
& X \nabla 2=X \nabla(1+1)=(X \nabla 1)+2=X+4, \\
& X \nabla 3=X \nabla(2+1)=(X \nabla 2)+2=X+6
\end{aligned}
$$
and so on. It is clear that the result can be calculated using the formula $x+2 y$.
Similarly, writing down the results of applying the operation $X \nabla Y$ for $Y=-1,-2,-3, \ldots$ (using property 2) also leads to the formula $x+2 y$.
It remains to solve the equation
$$
X \nabla X=X+2 X=3 X=-2019
$$
Answer. $X \nabla Y=X+2 Y$, the solution to the equation is $X=-673$
|
-673
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 5.
Once upon a time, Baba Yaga and Koschei the Deathless tried to divide a magical powder that turns everything into gold equally. Baba Yaga took out a scale and weighed all the powder. The scales showed 6 zolotniks. Then she started removing the powder until the scales showed 3 zolotniks. However, Koschei suspected that the scales were lying and weighed the portion that had been removed separately on the same scales (there were no others). The scales showed 2 zolotniks. Determine the exact weight of the two parts into which Baba Yaga divided the powder. Assume that if the scales are lying, they always lie by the same amount.
|
# Solution.
Let $A$ be the weight of the first part (the one that remained on the scales), $B$ be the weight of the second part (the one that was poured off), and $d$ be the error of the scales.
Then the result of the first weighing (of the entire powder) gives
$$
A+B+d=6,
$$
the result of the second weighing (after pouring off) gives
$$
A+d=3
$$
and the result of the last weighing (of the poured-off part) gives
$$
B+d=2
$$
Adding the last two equations, we get
$$
A+B+2 d=5
$$
Subtracting the first equation from the obtained one, we get
$$
d=-1
$$
Thus, the scales reduce all readings by 1 zolotnik. From this, the answer immediately follows.
Answer: 4 and 3 zolotniks.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Does there exist a convex polygon with 2015 diagonals?
#
|
# Solution.
The number of diagonals in a convex $n$-gon is
$$
\frac{n(n-1)}{2}-n=\frac{n^{2}-3 n}{2}
$$
Solve the equation
$$
\frac{n^{2}-3 n}{2}=2015 \quad \Longleftrightarrow \quad n^{2}-3 n-4030=0
$$
Its discriminant $D=9+4 \cdot 4030=16129$. Note that $120^{2}<16129<130^{2}$ and $D$ ends with the digit 9. If $D$ is the square of an integer $m$, then $m$ ends with the digit 3 or 7, i.e., only two cases are possible: $m=123$ or $m=127$. It is easy to check that $123^{2}=(120+3)^{2} \neq 16129$, while $127^{2}=(130-3)^{2}=$ $16900+9-2 \cdot 3 \cdot 130=16129$. Hence, $n=\frac{3 \pm 127}{2}$. Choosing the positive value, we get $n=65$. Therefore, the specified polygon exists, it is a 65-gon.
Answer. Yes. It is a 65-gon.
|
65
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 2.
In a football tournament, each team is supposed to play one match against each of the others. But during the tournament, half of all the teams were disqualified and withdrew from further participation. As a result, 77 matches were played, and the teams that withdrew had managed to play all their matches among themselves, with each of the withdrawn teams playing the same number of matches. How many teams were there at the beginning of the tournament?
|
# Solution.
According to the condition, an even number of teams $2n$ started, of which $n$ were disqualified. The eliminated teams played $\frac{n(n-1)}{2}$ matches among themselves. The same number of matches were played by the teams that remained in the tournament.
Let each of the eliminated teams have played with $k$ teams from among the remaining ones $(k>1$. Clearly, $k=1$ is not a solution, so $n+k-1>n$. Factoring $77=7 \cdot 11$, we get
$$
n=7, \quad n+k-1=11
$$
from which $k=5$.
## Answer: 14 teams.
|
14
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 4.
At 9:00 AM, ships "Anin" and "Vinin" departed from port O to port E. At the same moment, ship "Sanin" departed from port E to port O. All three vessels are traveling on the same course ("Sanin" heading towards "Anin" and "Vinin") at constant but different speeds. At 10:00 AM, "Vinin" was at the same distance from "Anin" and "Sanin". At 10:30 AM, "Sanin" was at the same distance from "Anin" and "Vinin". At what moment will "Anin" be exactly in the middle between "Vinin" and "Sanin"?
|
# Solution.
For simplicity, let's assume the distance between the ports is 1. Let $x$ be the speed of "Anina", $y$ be the speed of "Vanina", and $z$ be the speed of "Sanina". Then at 10 o'clock (i.e., one hour after departure),
$$
2 y = x + 1 - z,
$$
and one and a half hours after departure,
$$
2(1 - 1.5 z) = 1.5 x + 1.5 y.
$$
After time $t$ from departure, the condition should be met:
$$
2 x t = 1 - t z + t y,
$$
which simplifies to
$$
t(2 x + z - y) = 1.
$$
From (1) and (2),
$$
3 z + 1.5 x + 1.5 y = 4 y + 2 z - 2 x
$$
or $z = 2.5 y - 3.5 x$. Substituting this expression into (1), we get $y - x = 2 / 9$. Considering this, from (1) we have $y + z + y - x = y + z + 2 / 9$. Therefore, $t + z = 7 / 9$. Thus, from (3) we get
$$
\begin{gathered}
t(2 x + z - y) = t(z + y - 2 x + 2 y) = 1 \\
t(7 / 9 - 4 / 9) = 1
\end{gathered}
$$
which gives $t = 3$.
Answer: at 12 o'clock noon.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In a square table with 2015 rows and columns, positive numbers are arranged. The product of the numbers in each row and each column is 1, and the product of the numbers in any 1008 x 1008 square is 2. What number is in the center of the table?
#
|
# Solution
Consider the first 1008 rows of the table. From the additional condition, it follows that if these rows are covered by two squares of size $1008 \times 1008$, then these squares will overlap by one column. Denote the product of the numbers in this column (1008 numbers) by $M$.
Then the product of all the numbers in the first 1008 rows of the table is, on the one hand, 1, and on the other hand, $2^{2} / M$.
Thus, $\quad M=4$.
Now consider the middle column of the table. It is similarly divided into two blocks of 1008 elements, which overlap at the central element of the table (if moving from the top and bottom towards each other). Denote this element $C$.
The product of all the numbers in this column is 1. Therefore, $1=M^{2} / C$.
From which $C=M^{2}=16$.
Answer. The number in the center of the table is 16.
|
16
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Clever Dusya arranges six cheat sheets in four secret pockets so that the 1st and 2nd cheat sheets end up in the same pocket, the 4th and 5th cheat sheets also end up in the same pocket, but not in the same pocket as the 1st. The others can be placed anywhere, but only one pocket can remain empty (or all can be filled). In how many different ways can this be done?
#
|
# Solution
Let's reason constructively and straightforwardly. Place the 1st and 2nd cheat sheets in any pocket. This can be done in 4 ways. Now place the 4th and 5th cheat sheets in any free pocket. This can be done in 3 ways. In total, there are 12 ways. There remain two cheat sheets (3rd and 6th) and two free pockets. There are two possible scenarios. If there are no empty pockets, there are two ways to arrange the remaining cheat sheets. If one of the two pockets is empty, the remaining cheat sheets can be placed in the three non-empty pockets in three different ways.
In total, this results in \(12 \cdot (2 + 2 \cdot (2 + 3)) = 144\) ways.
Answer: 144 ways.
|
144
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Four managers of responsibility shifting reported: "If they are arranged in pairs, there will be 1 left. If they are arranged in threes, there will also be 1 left. If they are arranged in fours, there will be 2 left, and if they are arranged in fives, there will also be 2 left." Should the head of the report reception department believe such a report? Determine the maximum number of true statements among these four statements (possibly all) and for each maximum set of non-contradictory statements, find the smallest number of objects being arranged, considering that there are at least a thousand.
|
# Solution
Let $a$ be the desired quantity. If when dividing by 4, 2 remains, then $a$ is even. But then when dividing by two, 1 cannot remain. Therefore, these two statements are contradictory and the message as a whole is false.
Remove one of the contradictory statements.
1st var.: leave the division by 3, by 4, and by 5. From the condition, it follows that the number $a-2$ is divisible by 4 and by 5. Therefore, $a=20n+2$. Also, by the condition, $a=3k+1$. Form the equation $3k+1=20n+2$. Or, equivalently,
$$
3k=20n+1 \quad \Rightarrow \quad k=\frac{20n+1}{3}
$$
The smallest $n$ for which $a \geq 1000$ is $n=50$. By simple enumeration, we find that at $n=52$ the fraction gives an integer $k$. Thus, in this case, $a=1042$.
2nd var.: leave the division by 2, by 3, and by 5. From the condition, it follows that the number $a-1$ is divisible by 2 and by 3. Therefore, $a=6n+1$. Also, by the condition, $a=5k+2$. Form the equation $5k+2=6n+1$. Or, equivalently,
$$
6n=5k+1 \Rightarrow n=\frac{5k+1}{6}
$$
The smallest $k$ for which $a \geq 1000$ is $k=200$. By simple enumeration (over odd $k$), we find that at $k=205$ the fraction gives an integer $n$. Thus, in this case, $a=1027$.
Answer: Should not believe.
If leaving the division by 3, by 4, and by 5, then $a=1042$.
If leaving the division by 2, by 3, and by 5, then $a=1027$.
|
1042
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.2. (15 points) Real numbers $x_{1}, x_{2}, x_{3}, x_{4}$ are such that
$$
\left\{\begin{array}{l}
x_{1}+x_{2} \geqslant 12 \\
x_{1}+x_{3} \geqslant 13 \\
x_{1}+x_{4} \geqslant 14 \\
x_{3}+x_{4} \geqslant 22 \\
x_{2}+x_{3} \geqslant 23 \\
x_{2}+x_{4} \geq 24
\end{array}\right.
$$
What is the smallest value that the sum $x_{1}+x_{2}+x_{3}+x_{4}$ can take?
|
Answer: 37.
Solution. By adding the second equality to the last one, we get $x_{1}+x_{2}+x_{3}+x_{4} \geqslant 37$.
It is also worth noting that the value of the expression $x_{1}+x_{2}+x_{3}+x_{4}$ can be equal to 37, for example, when $x_{1}=1, x_{2}=11, x_{3}=12, x_{4}=13$. It is easy to verify that such numbers satisfy all the conditions of the problem.
## Criteria
The points for the estimate and the example are summed up:
+7 p. Estimate - it is proven that the considered sum is not less than 37.
+8 p. Example - numbers are provided for which the sum is 37 (or it is otherwise proven that such numbers exist).
|
37
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.3. (15 points) In one move, you can choose a natural number $x$ and cross out all natural numbers $y$ such that $|x-y|$ is a natural composite number. At the same time, $x$ can be chosen from already crossed out numbers.
What is the minimum number of moves needed to cross out all numbers from the natural number sequence?
|
Answer: 2.
Solution. First, note that one move is not enough, because if we choose some natural number $x$, then the number $y=x$ will remain unchecked. Let's prove that two moves are enough.
We will look for two suitable numbers $x_{1}$ and $x_{2}$ of different parity. Then one of the differences $\left|y-x_{1}\right|$ or $\left|y-x_{2}\right|$ will be even. This means it will be composite - except for the cases when it equals 2 or 0. These cases need to be considered separately. For $y=x_{1}-2, y=x_{1}$, and $y=x_{1}+2$, the difference $\left|y-x_{2}\right|$ must be a composite number; and for $y=x_{2}-2, y=x_{2}$, and $y=x_{2}+2$, the difference $\left|y-x_{1}\right|$ must be a composite number.
In any case, it is sufficient for the differences $\left|x_{1}-x_{2}-2\right|, \left|x_{1}-x_{2}\right|$, and $\left|x_{1}-x_{2}+2\right|$ to be odd composite numbers. Since the expressions under the modulus cannot have different signs (otherwise one of them would be equal to 1), they must be three consecutive odd composite numbers.
Now it is enough to find three consecutive odd composite numbers $a-2, a, a+2$ (or even just prove that such numbers exist). Then we can choose, for example, $x_{1}=a+1$ and $x_{2}=1$ and get the required result.
There are different ways to prove that three consecutive odd composite numbers exist. Here are some of them.
Method 1. Consider the consecutive odd numbers $7!+3, 7!+5$, and $7!+7$. They are divisible by the prime numbers 3, 5, and 7, respectively, but are not equal to them, so they are composite.
Method 2. If we assume that $a-2$ is divisible by 3, $a$ is divisible by 5, and $a+2$ is divisible by 7, then the number $a$ must give remainders 2, 0, and 5 when divided by 3, 5, and 7, respectively, and a remainder of 1 when divided by 2. By the Chinese Remainder Theorem, there are infinitely many such $a$, and they form an arithmetic progression with a common difference of $2 \cdot 3 \cdot 5 \cdot 7 = 210$. The first such number is obviously $a=5$, but it does not work; the next one is $a=215$, which gives the triplet of composites $213, 215, 217$.
Method 3. We can also try odd numbers and find a suitable triplet. The smallest such triplet is $91, 93, 95$, which corresponds to $x_{1}=1$ and $x_{2}=94$.
## Criteria
The highest applicable criterion is used:
15 p. Any complete solution to the problem.
0 p. Proved that one move is not enough.
0 p. Only the answer is provided.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 7. Problem 7.1*
Misha thought of a five-digit number, all digits of which are different, and Igor is trying to guess it. In one move, Igor can choose several digits of the number, and Misha, in any order, tells the digits that stand in these places. The order in which to tell the digits is chosen by Misha. For example, if the number thought of is 67890, and Igor asked about the digits in the 1st and 5th places, then Misha can answer either "6 and 0" or "0 and 6". In what minimum number of moves can Igor guarantee to find out the number? Points for the problem: 13.
#
|
# 7. Problem $7.1^{*}$
Misha thought of a five-digit number, all digits of which are different, and Igor is trying to guess it. In one move, Igor can choose several digits of the number, and Misha reports the digits in these positions in any order. The order in which to report the digits is chosen by Misha. For example, if the number thought of is 67890, and Igor asks about the digits in the 1st and 5th positions, Misha can answer either "6 and 0" or "0 and 6". What is the minimum number of moves Igor needs to guarantee he can determine the number? Points for the problem: 13.
## Answer: 3
#
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 9. Problem 9.1*
Petya came up with four different natural numbers, wrote down all their pairwise sums on the board, and in the row below, all their sums of three. It turned out that the sum of the two largest numbers in the top row and the two smallest numbers in the bottom row (a total of four numbers) is 2017. Find the largest possible value of the sum of the four numbers that Petya came up with. Points for the problem: 13.
#
|
# 9. Problem 9.1*
Petya came up with four different natural numbers, wrote down all their pairwise sums on the board, and in the row below, all their sums of three. It turned out that the sum of the two largest numbers in the top row and the two smallest numbers in the bottom row (a total of four numbers) is 2017. Find the largest possible value of the sum of the four numbers that Petya came up with. Points for the problem: 13.
Answer: 806
|
806
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.1. (15 points) Do there exist polynomials $P(x), Q(x)$, and $R(x)$ with real coefficients such that the polynomials $P(x) \cdot Q(x), Q(x) \cdot R(x)$, and $P(x) \cdot R(x)$ have the same degree, while the polynomials $P(x)+Q(x), P(x)+R(x)$, and $Q(x)+R(x)$ have pairwise distinct degrees? (We consider that the zero polynomial has no degree, so the specified polynomials cannot be equal to it.)
|
Answer: $: 2$.
Solution. It is sufficient to take, for example, $P(x)=x^{2}, Q(x)=-x^{2}+1, R(x)=x^{2}+x$. Then the polynomials $P(x) \cdot Q(x), Q(x) \cdot R(x)$, and $P(x) \cdot R(x)$ have degree 4 (these are products of two polynomials of degree 2); the polynomial $P(x)+Q(x)$ equals 1 and has degree 0; the polynomial $P(x)+R(x)$ equals $2 x^{2}+x$ and has degree 2; the polynomial $Q(x)+R(x)$ equals $x+1$ and has degree 1.
## Criteria
The highest applicable criterion is used:
15 p. A correct example of polynomials $P(x), Q(x), R(x)$ is provided (or it is otherwise proven that such polynomials exist).
0 p. Only the answer is provided.
|
2
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10.4. (15 points) Once, 45 friends living in different parts of the world decided to exchange news with each other. To do this, they plan to arrange $k$ video meetings, at each of which every person will share their news, as well as all the news from other people they have learned previously.
For the video meetings, 10 days were proposed, but it turned out that each friend can only be present on 8 of them. What is the smallest natural number $k$ that guarantees we can select $k$ days for the video meetings from the proposed 10 so that everyone learns the news from everyone else?
(Between the proposed days, no new news arises among the people, and they do not communicate with each other in any other way. On each of the proposed days, one video meeting is held, which is attended by everyone who can be present on that day.)
|
Answer: 5 days.
Solution. Let's provide an example of a situation where 4 days would not be enough. Suppose each of the 45 people has their own unique pair of days when they cannot participate in the meeting. Since the number of ways to choose a pair of days from the 10 offered is $\mathrm{C}_{10}^{2}=45$, for any pair of days, there will be a person who cannot be present on exactly those two days. Suppose we managed to choose some 4 days such that everyone learns all the news. Then there exists a person $A$ who cannot be present on the first two of these four days, and a person $B$ who cannot be present on the last two of these four days. Notice that then $B$ will not be able to learn the news from $A$. Contradiction.
Now let's understand that 5 days will always be enough. Choose 5 days arbitrarily. We will prove that any two people will be present together at some meeting. Indeed, among these 5 days, there are no more than 2 days when the first person cannot be present, and no more than 2 days when the second person cannot be present. Therefore, there will be a day when both can be present. Thus, each pair of people will be able to exchange news, i.e., everyone will learn the news from everyone else.
## Criteria
## Points for evaluation and example are summed up:
+9 p. Evaluation - it is proven that 4 days may not be enough.
In the absence of this proof, the following progress is evaluated:
+1 p. Mentioned that different pairs of missed days can correspond to all people.
+6 p. Example - it is proven that 5 days are guaranteed to be enough.
The following progress is not evaluated:
0 p. Only the correct answer is provided.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 10.5. (20 points) Find all composite natural numbers $n$ that have the following property: each natural divisor of the number $n$ (including $n$ itself), decreased by 1, is a square of an integer.
|
Answer: 10.
Solution. Suppose that $n$ is divisible by the square of some prime number $p$. Then it has a divisor $p^{2}=b^{2}+1$; but two squares of integers can only differ by 1 if they are 0 and 1.
Let $n$ be divisible by some two prime numbers $p$ and $q$. Without loss of generality, we can assume that $p>q$. From the condition that any divisor, decreased by 1, is a square, we can write
\[
\begin{gathered}
p=a^{2}+1 \\
q=b^{2}+1 \\
p q=c^{2}+1
\end{gathered}
\]
Subtract the first equation from the third, we get $p q-p=c^{2}-a^{2}$. This can be rewritten as
\[
p(q-1)=(c-a)(c+a)
\]
Since $p$ is a prime number, one of the factors on the right side must be divisible by $p$. Note that from the condition $p>q$ it follows that $p>q-1$, so $p$ cannot divide $q-1$. Therefore, $p$ must divide $c-a$ or $c+a$. Since $p>q$, we get that $q=2$.
Substituting $q=2$, we get $2=c-a+1=p-2a+1$, from which, first, $c=a+1$, and second, $p=2a+1$. Then $p q=2 p=4a+2$ and $p q=c^{2}+1=(a+1)^{2}+1$. Equating, we get the quadratic equation $a^{2}+2a+2=4a+2$, the roots of which are 2 and 0, from which $p$ equals 5 or 1. But since $p$ must be prime, the only option left is $p=5$.
Thus, the only possible case is $p=5, q=2$. It is clear that there cannot be any other prime numbers in the factorization of $n$.
## Criteria
The highest applicable criterion is used:
20 points. Any complete solution to the problem is provided.
16 points. It is proven that $n$ is even.
4 points. The case of even $n$ is correctly analyzed.
In the absence of the above advancements, the following criteria are summed up:
+1 point. The correct answer is provided.
+1 point. It is proven that $n$ is square-free.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 8. Problem $8^{*}$
A natural number $\mathrm{N}$ ends in 5. Ninth-grader Dima found all its divisors and discovered that the sum of the two largest proper divisors does not divide evenly by the sum of the two smallest proper divisors. Find the smallest possible value of the number N. A divisor of a natural number is called proper if it is different from 1 and the number itself. Points for the problem: 13.
#
|
# 8. Problem $\mathbf{8}^{2}$
A natural number $\mathrm{N}$ ends with 5. Ninth-grader Dima found all its divisors and noticed that the sum of the two largest proper divisors does not divide evenly by the sum of the two smallest proper divisors. Find the smallest possible value of the number N. A divisor of a natural number is called proper if it is different from 1 and the number itself. Points for the problem: 13.
## Answer: 725
|
725
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In an acute-angled triangle $A B C$, the altitude $A A_{1}$ is drawn. $H$ is the orthocenter of triangle $A B C$. It is known that $A H=3, A_{1} H=2$, and the radius of the circumcircle of triangle $A B C$ is 4. Find the distance from the center of this circle to $H$.
|
Solution. Draw the altitudes $B B_{1}$ and $C C_{1}$ in the triangle. Then the quadrilateral $A C_{1} H B_{1}$ is cyclic, since its opposite angles $C_{1}$ and $B_{1}$ are right angles. Therefore: $\angle B H C=$ $\angle C_{1} H B_{1}=180^{\circ}-\angle C_{1} A B_{1}$. Reflect point $H$ symmetrically with respect to the line $B C$ and denote the resulting point by $H_{1}$. Then $\angle B H_{1} C=\angle B H C=180^{\circ}-\angle C_{1} A B_{1}$,
so the quadrilateral $B A C H_{1}$ is cyclic and point $H_{1}$ lies on the circumcircle of triangle $A B C$. Denote the center of this circle by $O$.
By construction, we have $H_{1} A_{1}=H A_{1}=2$, therefore, in the isosceles triangle $O A H_{1}$, the base $A H_{1}$ is $3+2+2=7$, and the lateral side is equal to the radius of the circle: that is, 4. The height dropped to the base is
$$
\sqrt{4^{2}-(7 / 2)^{2}}=\sqrt{15} / 2
$$
and the distance from the base $O_{1}$ of this height to $H$ is $A H_{1} / 2-A H=7 / 2-3=1 / 2$. Therefore,
$$
O H=\sqrt{O O_{1}^{2}+O_{1} H^{2}}=\sqrt{(\sqrt{15} / 2)^{2}+(1 / 2)^{2}}=2
$$
Answer: 2.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Let $x$ be a number from the interval $(\pi / 2, \pi)$ such that
$$
\frac{4}{3}\left(\frac{1}{\sin x}+\frac{1}{\cos x}\right)=1
$$
Prove that the number
$$
\left(\frac{4}{3}\right)^{4}\left(\frac{1}{\sin ^{4} x}+\frac{1}{\cos ^{4} x}\right)
$$
is an integer and find it.
|
Solution. For brevity, let $s=\sin x, c=\cos x$. We need to find the number $t=$ $1 / c s$. For this, we square the relation $\left(s^{-1}+c^{-1}\right)=3 / 4$. We get $s^{2}+c^{2}+2 c s=$ $9(c s)^{2} / 16$. Considering that $s^{2}+c^{2}=1$, we obtain the following quadratic equation for $t$:
$$
t^{2}+2 t-9 / 16=0
$$
This equation has two solutions $1 / 4$ and $-9 / 4$. Since $cs$ must be negative, we get $t=-9 / 4$.
Consider the sequence $A_{n}=(4 / 3)^{n}\left(s^{-n}+c^{-n}\right)$. We will derive a recurrence relation for the numbers $A_{n}$.
$$
\begin{aligned}
& A_{n}=\frac{4^{n+1}}{3^{n+1}}\left(s^{-1}+c^{-1}\right)\left(s^{-n}+c^{-n}\right)= \\
& =A_{n+1}+\frac{4^{2}}{3^{2} c s} A_{n-1}=A_{n+1}-4 A_{n-1}
\end{aligned}
$$
Thus, $A_{n+1}=A_{n}+4 A_{n-1}$. Using the fact that $A_{0}=2, A_{1}=1$, we find the subsequent $A_{n}$ from the recurrence relation:
$$
A_{2}=9, A_{3}=13, A_{4}=49
$$
Answer: 49.
|
49
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
4. On the board, the numbers $1 / 1, 1 / 2, 1 / 3, 1 / 4, \ldots 1 / 100$ are written.
It is allowed to erase any two numbers a, b and write $a b + a + b$ in their place,
then do the same with any two of the remaining numbers, and so on. What number can be left last?
|
Solution. If initially on the board there were not one hundred, but three numbers: a, b, c, then at the end on the board there would be the number abc + ab + bc + ac + a + b + c. That is, the sum of all possible monomials composed of the numbers a, b, c, taken no more than once each.
In the case when one hundred numbers are written on the board. It is easy to see that the last number on the board will be a number represented as the sum of (2^100)-1 different monomials of the form (1/a_1)*(1/a_2)*....(1/a_k) for all possible natural numbers $\mathrm{k}$ in $[1,100]$ and a_i in [1,100], with a_i < a_i+1 for all i. The schoolchildren will need to prove this.
Now notice that this sum can be represented as $(1+1 / 1) *(1+1 / 2) *(1+1 / 3) * \ldots *(1+1 / 100)-1$.
Transform it: $(1+1 / 1) *(1+1 / 2) *(1+1 / 3) * . . .(1+1 / 100)-1=$ $(2 / 1) *(3 / 2) *(3 / 4) * \ldots *(101 / 100)-1=101-1=100$.
## Criteria
+/2 or -+ - it is proven that the last remaining number is representable as the correct sum of monomials. +- - it is noted that this sum is equal to $(1+1 / 1) *(1+1 / 2) *(1+1 / 3)^{*} . . *(1+1 / 100)$ -
|
100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 3. Problem 3
In an isosceles triangle $A B C$, the perpendicular bisector of the lateral side $B C$ intersects the base $A B$ at point $D$ such that $A C=A D$. Find the angle $A B C$.
Write the answer in degrees without the degree symbol.
|
# 3. Problem 3
In an isosceles triangle $ABC$, the perpendicular bisector of the lateral side $BC$ intersects the base $AB$ at point $D$ such that $AC = AD$. Find the angle $ABC$.
Write the answer in degrees without the degree symbol.
Answer: 36
|
36
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9-1. Calculate the sum $1^{2}+2^{2}-3^{2}-4^{2}+5^{2}+6^{2}-7^{2}-8^{2}+9^{2}+10^{2}-\ldots+2017^{2}+2018^{2}$.
|
Answer: 4074341.
Solution. Note that for any $k$ the equality $k^{2}-(k+1)^{2}-(k+2)^{2}+(k+3)^{2}=4$ holds. Therefore, the entire sum is equal to $1+504 \cdot 4+2018^{2}=4074341$.
| Rating | Score | Content of the criterion |
| :---: | :---: | :--- |
| + | 20 | Complete solution |
| $+/-$ | 16 | Correct solution with an arithmetic error |
| $-/+$ | 8 | Correct idea of the solution with completely incorrect calculation and answer |
| - | 0 | Solution is completely incorrect/only answer |
|
4074341
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9-3. In a right triangle $A B C$, angle $B$ is a right angle. On the leg $A B$, a point $M$ is chosen such that $A M=B C$, and on the leg $B C$, a point $N$ is chosen such that $C N=M B$. Find the acute angle between the lines $A N$ and $C M$.
Answer: $45^{\circ}$.
|
Solution. Complete the triangle $A B C$ to a rectangle $A B C D$ and choose a point $P$ on its side $C D$ such that $A P$ is parallel to $C M$. Then $P C = A D$, $D P = C N$, and the right triangles $A D P$ and $C P N$ are equal, with $\angle D A P = \angle C P N$. Therefore, $\angle A P D + \angle C P N = 90^{\circ}$ and $\angle A P N = 90^{\circ}$, meaning that $A P N$ is an isosceles right triangle. Thus, $\angle P A N = 45^{\circ}$ and, due to the parallelism of lines $A P$ and $C M$, the acute angle between the lines $A N$ and $C M$ also measures 45 degrees.
| Rating | Score | Content criterion |
| :---: | :---: | :--- |
| + | 20 | Complete solution |
| - | 0 | Solution is completely incorrect/only answer |
|
45
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9-4. From $n$ regular hexagons with side 1, a polygon on the plane was made by gluing hexagons along their sides. Any two hexagons either have exactly one common side or have no common points at all. There are no holes inside the polygon. Moreover, each hexagon has at least one side lying on the boundary of the polygon. What is the smallest perimeter that the polygon can have under these conditions?
|
Answer: $2 n+6$ for $n \geq 2$, $6$ for $n=1$.
Solution. It is easy to understand that if a point is an endpoint for at least one side of a hexagon, it is an endpoint for two or three sides: more than three is impossible because all angles are $120^{\circ}$.
Let's draw a bit. Imagine that in each point that is an endpoint for three sides of a hexagon, we place a red dot. And each path along the sides of the hexagons from a red dot to a red dot we outline with a blue marker. Thus, the blue lines go along the sides of the hexagons and through vertices from which only two sides emerge (in other words, which are vertices of exactly one hexagon). Note that the blue lines do not intersect except at their endpoints, which are red dots. It is easy to understand that if a point is an endpoint for at least one side of a hexagon, it is an endpoint for two or three sides: more than three is impossible because all angles are $120^{\circ}$.
Let's draw a bit. Imagine that in each point that is an endpoint for three sides of a hexagon, we place a red dot. And each path along the sides of the hexagons from a red dot to a red dot we outline with a blue marker. Thus, the blue lines go along the sides of the hexagons and through vertices from which only two sides emerge (in other words, which are vertices of exactly one hexagon). Note that the blue lines do not intersect except at their endpoints, which are red dots.
Thus, we have obtained a drawing of a multigraph on the plane. For it, Euler's formula $F-E+V=2$ holds, where $F, E, V$ are the number of faces, edges, and vertices, respectively. Since all vertices have degree $3, 3V = 2E$. Additionally, $F = n + 1$, since these are all the hexagons and the external face. From these three equations, we derive $E = 3n - 3$. Traversing the external cycle, we walked along all $n$ hexagons, so for $n > 1$, we changed the hexagon we were walking along at least $n$ times (note: this statement is not true if $n = 1$: we walked along one hexagon and never changed it). Thus, in the external cycle, there are at least $n$ edges, so in the rest of the graph, there are no more than $2n - 3$ edges. Each of these consists of exactly one segment that was a side for two hexagons, since inside the polygon, there cannot be points that are endpoints for exactly two side segments. Thus, inside there are no more than $4n - 6$ sides of hexagons, glued in pairs, so on the boundary, there are at least $2n + 6$ sides.
| Evaluation | Score | Content Criterion |
| :---: | :---: | :--- |
| + | 20 | Complete solution |
| .+ | 18 | Minor errors in the proof |
| $+/-$ | 14 | Significant gaps in the proof (e.g., existence of a hexagon touching others by no more than 2 sides is not proven) |
| $+/2$ | 10 | There is a statement that the minimum perimeter for $n$ and $n+1$ differs by 2, but the proof is missing. Example is provided |
| $-/+$ | 6 | There is an example for $2n + 6$. There is a statement that the minimum perimeter for $n$ and $n+1$ differs by 2, but the proof is missing |
| - | 0 | Solution is completely incorrect/only the answer |
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9-5. A divisor of a natural number is called proper if it is different from 1 and the number itself. Find all natural numbers for which the difference between the sum of the two largest proper divisors and the sum of the two smallest proper divisors is a prime number.
|
Answer: $12(2,3,4,6)$.
Solution. One of two cases applies.
A) Suppose the two smallest divisors $p$ and $q$ are prime numbers. Then the number $r=(n / p+n / q)-(p+q)$ is also prime, and $p q r=(p+q)(n-p q)$. Since the numbers $p+q$ and $p q$ are coprime, we get $r=p+q$, from which $p=2$ and $n=4 q$. But then, due to the choice of $q$, we get $q=3$ and $n=12$.
B) Suppose the smallest divisors are of the form $p$ and $p^{2}$, where $p$ is a prime number. This case is analyzed similarly.
Remark. It is possible that a number has only three proper divisors. Then the difference mentioned in the condition is the difference between the largest and the smallest of the proper divisors. But any number with three proper divisors is a power of a prime $p^{4}$, and the difference $p^{3}-p$ cannot be a prime number.
| Evaluation | Score | Content of the criterion |
| :---: | :---: | :--- |
| + | 20 | Complete solution |
| .+ | 16 | Minor errors |
| $+/ 2$ | 10 | Significant gaps in the solution |
| .- | 6 | The idea that $p n q=(p+q)(n-p q)$ is present |
| - | 0 | The solution is completely incorrect/only the answer |
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.5. On a plane, there are eight different points. A numbering of these points with numbers from 1 to 8 is called good if the following condition is met:
there exists a line such that all points lie on one side of it and at different distances from it, and the distances from the points to this line increase with the increase in the number. That is, the closest point is number 1, the next in distance is number 2, and so on.
What is the maximum number of different good numberings that a given set of eight points can have?
|
Answer. $2 C_{8}^{2}=56$.
Solution. Note that when numbering points relative to a line, we are only interested in its direction and which side of it the points are on. All this information can be uniquely restored from a unit normal to it, directed towards the points. Therefore, the numbering of the octet is derived from a vector of unit length. Let's parameterize such vectors by points on a circle.
For a moment, consider only two points $A$ and $B$ from the octet. These two points can be associated with two opposite points on the circle: the two normals to the line $A B$. The circle is divided into two arcs. It is clear that the numbering of $A$ and $B$ on one arc is the same, and on the other arc, it is the remaining one.
Next, note that the numbering can be uniquely restored based on the order of each separate pair. Therefore, if we mark all the resulting $C_{8}^{2}$ pairs of opposite points on the circle, the numbering on each of the resulting arcs will be fixed. Consequently, for any octet of points, the number of numberings will not exceed the number of arcs, i.e., not more than $2 C_{8}^{2}$. On the other hand, we can imagine a sufficiently general octet of points for which no pairs of opposite points coincide. Then the circle will be divided into exactly $2 C_{8}^{2}$ arcs. Finally, any two arcs can be separated by some pair of opposite points, meaning that the numbering on any two different arcs is different. Therefore, $2 C_{8}^{2}$ is achievable.
Criteria.
(-.) Correctly found and justified the number of numberings for some non-maximal configuration.
(-/+) Correct reasoning, not leading to the correct answer due to a minor error.
(+/2) Correct answer + significant progress in justification.
(+/-) Fully proven that 56 is achievable, $\underline{and}$ and that more than 56 is not possible.
(+) Fully proven that 56 is achievable, and more than 56 is not possible.
|
56
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. Along the shore of a circular lake with a perimeter of 1 km, two salmons are swimming - one at a constant speed of $500 \mathrm{m} /$ min clockwise, the other at a constant speed of 750 m/min counterclockwise. Along the edge of the shore, a bear is running, always moving along the shore at a speed of 200 m/min in the direction of the nearest salmon to it. How many full laps around the lake will the bear make in one hour?
ANSWER: 7.
CRITERIA
-/. For a specific initial position of the bear and the fish, direct calculations of their movements over the course of two or more laps of the bear around the lake are provided, followed by an explicit but unproven (though intuitively correct) statement that the average speed of the bear's rotation around the lake is approximately equal to that obtained in this numerical experiment. Based on this, the answer is obtained with an accuracy of $10 \%$.
|
Solution. Note that the bear runs to the nearest salmon if and only if it runs from a point on the shore that is equidistant from the salmons and not separated from the bear by the salmons. Since both points equidistant from the salmons move counterclockwise at a speed of $|750-500| / 2=125<200$ m/min, they will never catch up to the bear, and the bear will never be at such a point (except possibly at the initial moment). Since each of these points will run $125 \cdot 60$ meters in an hour, they will make exactly $125 \cdot 60 / 1000=15 / 2=7.5$ laps around the lake. Therefore, the bear, which never crosses either of these points, will make strictly more than 7 but strictly less than 8 laps, that is, 7 full laps.
|
7
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 6. Problem 6
In triangle $A B C$, points $M$ and $N$ are chosen on sides $A B$ and $B C$ respectively, such that $A M=2 M B$ and $B N=N C$. Segments $A N$ and $C M$ intersect at point $P$. Find the area of quadrilateral $M B N P$, given that the area of triangle $A B C$ is 30.
|
# 6. Problem 6
In triangle $A B C$, points $M$ and $N$ are chosen on sides $A B$ and $B C$ respectively such that $A M=2 M B$ and $B N=N C$. Segments $A N$ and $C M$ intersect at point $P$. Find the area of quadrilateral $M B N P$, given that the area of triangle $A B C$ is 30.
## Answer: 7
#
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10-1. For real numbers $a, b$, and $c$, it is known that $a b c + a + b + c = 10$, and $a b + b c + a c = 9$. For which numbers $x$ can it be asserted that at least one of the numbers $a, b, c$ is equal to $x$? (Find all such numbers $x$ and prove that there are no others.)
Answer: 1.
|
Solution. We will provide two solutions to the problem.
First Solution. Let $a+b+c=\lambda$. Vieta's theorem allows us to write a cubic equation depending on the parameter $\lambda$, whose roots are the set $a, b, c$ corresponding to the given $\lambda$:
$$
t^{3}-\lambda t^{2}+9 t-(10-\lambda)=0 \quad \Leftrightarrow \quad(t-1)\left(t^{2}-(\lambda-1) t+(10-\lambda)\right)=0
$$
From this, it is clear that for any $\lambda$ there is a root $t=1$, so the value $x=1$ works. It remains to prove that there are no other values that are roots for any $\lambda$ (although this is obvious). Indeed, $t^{2}-(\lambda-1) t+(10-\lambda)=0$ implies $t=\frac{\lambda-1 \pm \sqrt{\lambda^{2}+2 \lambda-39}}{2}$. Take any pair of values of $\lambda$ for which the discriminant takes the same positive value, for example, for $\lambda=10$ and $\lambda=-12$ we have $t \in\{0,9\}$ and $t \in\{-11,-2\}$ - there are no intersections. Therefore, the answer is $x=1$.
Second Solution. Subtract the second equation from the first, transforming it, we get $(a-1)(b-1)(c-1)=0$. From this, it follows that one of $a, b, c$ is equal to one. Other $x$ do not work, as the triples $(a, b, c)=(4,1,1)$ and $(a, b, c)=(0,9,1)$ satisfy the condition.
| Grade | Score | Content Criterion |
| :---: | :---: | :--- |
| + | 20 | Complete solution |
| .+ | 18 | Not proven why there are no others besides 1, or there is a minor error in the proof. |
| $+/-$ | 16 | Significant errors in the proof (several transitions with division by possibly zero, misunderstanding of the condition (with necessary calculations for the proof)). |
| $-/+$ | 10 | Two specific cases are considered, which show that it can only be equal to 1. But there is no proof that $= 1$. |
| .- | 6 | Only one case is found (it is claimed that $\in\{1,4\}$ or $\in\{0,1,9\}$. |
| - | 0 | The solution is completely incorrect/only the answer. |
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 10-5. Consider all reduced quadratic trinomials $x^{2}+p x+$ $q$ with integer coefficients $p$ and $q$. Let's call the range of such a trinomial the set of its values at all integer points $x=0, \pm 1, \pm 2, \ldots$ What is the maximum number of such trinomials that can be chosen so that their ranges do not intersect pairwise?
Answer: 2.
|
Solution. Note that the substitution of the variable $x \rightarrow x+k$ for any integer $k$ does not change the range of the polynomial. Then, by making the substitution $x \rightarrow x-\left[\frac{p}{2}\right]$ (square brackets denote the integer part), we can assume that any polynomial has one of two forms: $x^{2}+q$ or $x^{2}+x+q$.
The ranges of any two polynomials of different forms intersect: indeed, the values of the polynomials $x^{2}+q$ and $x^{2}+x+q^{\prime}$ coincide at $x=q-q^{\prime}$. Therefore, polynomials of different forms cannot be chosen.
Polynomials of the first form can be chosen no more than two, since if the ranges of $f_{1}(x)=x^{2}+q$ and $f_{2}(x)=x^{2}+q^{\prime}$ do not intersect, then $q-q^{\prime}=4 k+2$ for some $k \in \mathbb{Z}$. Indeed, for an odd difference of the constant terms $q-q^{\prime}=2 k+1$, we have $f_{1}(k)=f_{2}(k+1)$. For a difference of the constant terms divisible by 4, $q-q^{\prime}=4 k$, we have $f_{1}(k-1)=f_{2}(k+1)$. But if at least three polynomials are chosen, then among the pairwise differences of the constant terms, at least one does not have the form $4 k+2$.
Polynomials of the second form can also be chosen no more than two, since if the ranges of $f_{1}(x)=x^{2}+x+q$ and $f_{2}(x)=x^{2}+x+q^{\prime}$ do not intersect, then $q-q^{\prime}=2 k+1$ for some $k \in \mathbb{Z}$. Indeed, for an even difference of the constant terms $q-q^{\prime}=2 k$, we have $f_{1}(k-1)=f_{2}(k)$. Again, if at least three polynomials are chosen, then among the pairwise differences of the constant terms, at least one is even.
Thus, more than two polynomials cannot be chosen. Example for two: $f_{1}(x)=x^{2}$ and $f_{2}(x)=x^{2}+2$.
| Grade | Score | Content criterion |
| :---: | :---: | :--- |
| + | 20 | Complete solution |
| .+ | 18 | Solution is correct modulo minor inaccuracies |
| $+/-$ | 14 | There is a proof that for each type of values $\left(x^{2}+q\right.$ and $\left.x^{2}+x+q\right)$ no more than two trinomials can be taken |
| $-/+$ | 8 | Complete solution, but only for the case $x^{2}+q$ |
| .- | 4 | Example of two trinomials whose ranges do not intersect |
| - | 0 | Solution is completely incorrect/only answer |
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7-5. In the garden of the oracle, there live four turtles. A visitor can choose any subset of turtles in a move and ask the oracle how many of these turtles are males (the oracle's answers are always truthful). What is the minimum number of moves required to find out the gender of all the turtles?
Answer: 3.
|
Solution. In three questions, the answer can be obtained as follows. The first two questions are about turtles 1 and 2, and 2 and 3. If at least one of the answers is 0 or 2, we know who they are for the corresponding pair, and for the remaining one of the three, we know from the other question, leaving one question for the 4th turtle. If both answers are 1, then turtles 1 and 3 are of the same gender. Then we ask about $1, 3, 4$. We will hear an answer of at least 2 if turtles 1 and 3 were males, and an answer of no more than 1 otherwise. In this case, the gender of turtle 4 is also uniquely determined, and one question remains to determine the gender of turtle 2.
We will prove that two questions are insufficient. First, note that: a) in one question, without knowing the total number of males, we cannot figure out even two turtles; b) knowing the total number of males, we can figure out two, but not three turtles. Therefore, in the situation with four turtles and two questions, asking the first question about all turtles at once or about one turtle is meaningless. Since when asking about a group of three or two turtles, we can hear an answer of 1, such a question will also not lead to success.
| Rating | Score | Content of the criterion |
| :---: | :---: | :--- |
| + | 20 | Complete solution |
| $+/-$ | 14 | Correct answer, but not proven that it cannot be less |
| $+/ 2$ | 10 | Correct answer with minor flaws in the solution and not proven that it cannot be less |
| .- | 4 | Attempt to analyze cases with 2 and 3 questions, but made an incorrect conclusion that the minimum number is 4 |
| - | 0 | Solution is completely incorrect/only answer |
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.3. (15 points) Natural numbers $a, b, c$ are such that $1 \leqslant a<b<c \leqslant 3000$. Find the greatest possible value of the quantity
$$
\text { GCD }(a, b)+\text { GCD }(b, c)+\text { GCD }(c, a)
$$
|
Answer: 3000.
Solution. Note that GCD $(a, b)=$ GCD $(a, b-a) \leqslant b-a$, since the GCD of two natural numbers does not exceed either of them. Similarly, we obtain that GCD $(b, c) \leqslant c-b$, and also GCD $(c, a) \leqslant a$.
Adding these three inequalities, we get
$$
\text { GCD }(a, b)+\text { GCD }(b, c)+\text { GCD }(c, a) \leqslant(b-a)+(c-b)+a=c \leqslant 3000
$$
As an example for 3000, we can provide, for instance, $a=1000, b=2000, c=3000$. In this case, GCD $(a, b)+$ GCD $(b, c)+$ GCD $(c, a)=1000+1000+1000=3000$.
## Criteria
The points for the estimate and the example are summed.
+14 p. Estimate - it is proven that the considered sum does not exceed 3000.
In the absence of such a proof, the following progress is evaluated:
+4 p. It is noted that the GCD of different natural numbers does not exceed their difference, but there is no further progress.
+1 p. Example - numbers $a, b, c$ are provided for which the considered sum equals 3000 (or it is otherwise proven that such numbers exist).
The following progress is not evaluated:
0 p. Only the answer is provided.
0 p. An incomplete enumeration, in which one of the cases is not considered, and this case is not analogous to the considered ones.
|
3000
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.6. (20 points) Quadratic trinomials $P(x)$ and $Q(x)$ with real coefficients are such that together they have 4 distinct real roots, and each of the polynomials $P(Q(x))$ and $Q(P(x))$ has 4 distinct real roots. What is the smallest number of distinct real numbers that can be among the roots of the polynomials $P(x), Q(x), P(Q(x))$, and $Q(P(x))$?
|
# Answer: 6.
Solution. Note that if among the roots of the polynomial $P(Q(x))$ there is a root of $Q(x)$, say, the number $x_{0}$, then $P\left(Q\left(x_{0}\right)\right)=P(0)=0$, from which 0 is a root of $P(x)$. Similarly, if among the roots of $Q(P(x))$ there is a root of $P(x)$, then 0 is a root of $Q(x)$. However, $P(x)$ and $Q(x)$ cannot both have the root 0, otherwise, in total, they would have fewer than 4 roots.
From this, we can obtain an estimate of the total number of distinct roots. If there are no more than 5, then $P(Q(x))$ and $Q(x)$ have a common root, and $Q(P(x))$ and $P(x)$ have a common root, which cannot be according to the above.
Now let's construct an example where there are exactly 6 distinct roots. Let $P(x)=\frac{1}{2} x(x-3), Q(x)=$ $-\frac{3}{2}(x+1)(x-2)$. Then the roots of $P(x)$ will be the numbers 0 and 3; the roots of $Q(x)$ will be the numbers -1 and 2; the roots of $P(Q(x))$ will be the numbers -1, 0, 1, 2; the roots of $Q(P(x))$ will be the numbers -1, 1, 2, 4. In total, the roots of all polynomials together are the integers from -1 to 4.
Remark. There are other examples where there are exactly 6 distinct roots; in all examples, one of the quadratic polynomials $P(x)$ and $Q(x)$ has the root 0. For example, the pair of quadratic polynomials $P(x)=$ $x(x-3)$ and $Q(x)=-\frac{3}{4}(x+1)(x-4)$ also works.
## Criteria
The points for the estimate and the example are summed.
+6 points. Estimate - it is proven that there cannot be fewer than 6 distinct numbers among the roots of the considered polynomials.
In the absence of this proof, the following progress is evaluated:
+3 points. It is noted that if the polynomials $P(Q(x))$ and $Q(x)$ have a common root, then the polynomial $P(x)$ has the root 0.
+14 points. Example - suitable quadratic polynomials $P(x)$ and $Q(x)$ are provided, and it is shown that among the roots of all four considered polynomials, there are exactly 6 distinct numbers (or it is otherwise proven that such polynomials exist).
In the absence of such an example with justification, the highest of the following criteria is used:
+10 points. Correct example of quadratic polynomials $P(x)$ and $Q(x)$.
+12 points. Correct example of quadratic polynomials $P(x)$ and $Q(x)$, and the work also includes a correct estimate. (Thus, for a solution with a correct estimate and a correct pair of $P(x)$ and $Q(x)$ without proof that they fit, a total of 18 points is given.)
The following progress is not evaluated:
0 points. Only the answer is provided.
0 points. A correct example with 7 or more roots is provided.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8-2. Calculate the sum $1^{2}+2^{2}-3^{2}-4^{2}+5^{2}+6^{2}-7^{2}-8^{2}+9^{2}+10^{2}-\ldots+2017^{2}+2018^{2}$.
|
Solution. Note that for any $k$ the equality $k^{2}-(k+1)^{2}-(k+$ $2)^{2}+(k+3)^{2}=4$ holds. Therefore, the entire sum is equal to $1+504 \cdot 4+2018^{2}=4074341$.
| Grade | Score | Content criterion |
| :---: | :---: | :--- |
| + | 20 | Complete solution |
| .+ | 18 | Solution is correct, but there are minor flaws that do not affect the solution or the final number is not calculated |
| $+/-$ | 17 | Arithmetic error with correct reasoning |
| $+/ 2$ | 12 | Correct idea with errors |
| $-/+$ | 8 | Description of the counting method without the actual counting or multiple errors |
| - | 0 | Solution is completely incorrect/only the answer |
|
4074341
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8-3. $\quad$ In a right triangle $A B C$, angle $B$ is a right angle. On the leg $A B$, a point $M$ is chosen such that $A M=B C$, and on the leg $B C$, a point $N$ is chosen such that $C N=M B$. Find the acute angle between the lines $A N$ and $C M$.
Answer: $45^{\circ}$.
|
Solution. Complete the triangle $A B C$ to a rectangle $A B C D$ and choose a point $P$ on its side $C D$ such that $A P$ is parallel to $C M$. Then $P C = A D$, $D P = C N$, and the right triangles $A D P$ and $C P N$ are equal, with $\angle D A P = \angle C P N$. Therefore, $\angle A P D + \angle C P N = 90^{\circ}$ and $\angle A P N = 90^{\circ}$, meaning that $A P N$ is an isosceles right triangle. Thus, $\angle P A N = 45^{\circ}$ and, due to the parallelism of lines $A P$ and $C M$, the acute angle between the lines $A N$ and $C M$ also measures 45 degrees.
| Rating | Score | Content Criterion |
| :---: | :---: | :--- |
| + | 20 | Full solution |
| - | 0 | Solution is completely incorrect/only answer |
|
45
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8-4. In the garden of the oracle, there live four turtles. A visitor can choose any subset of turtles in a move and ask the oracle how many of these turtles are males (the oracle's answers are always truthful). What is the minimum number of moves required to find out the gender of all the turtles?
Answer: 3.
|
Solution. In three questions, the answer can be obtained as follows. The first two questions are about turtles 1 and 2, and 2 and 3. If at least one of the answers is 0 or 2, we know who they are for the corresponding pair, and for the remaining one of the three, we know from the other question, leaving one question for the 4th turtle. If both answers are 1, then turtles 1 and 3 are of the same gender. Then we ask about $1, 3, 4$. We will hear an answer of at least 2 if turtles 1 and 3 were males, and an answer of no more than 1 otherwise. In this case, the gender of turtle 4 is also uniquely determined, and one question remains to determine the gender of turtle 2.
We will prove that two questions are insufficient. First, note that: a) in one question, without knowing the total number of males, we cannot figure out even two turtles; b) knowing the total number of males, we can figure out two, but not three turtles. Therefore, in the situation with four turtles and two questions, asking the first question about all turtles at once or about one turtle is meaningless. Since when asking about a group of three or two turtles, we can hear an answer of 1, such a question will also not lead to success.
| Rating | Score | Content of the criterion |
| :---: | :---: | :--- |
| + | 20 | Complete solution |
| $+/-$ | 14 | Correct answer, but not proven that it cannot be less |
| $+/ 2$ | 10 | Correct answer with minor flaws in the solution and not proven that it cannot be less |
| .- | 4 | Attempt to analyze cases with 2 and 3 questions, but made an incorrect conclusion that the minimum number is 4 |
| - | 0 | Solution is completely incorrect/only answer |
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8-5. 8 8-5. A divisor of a natural number is called proper if it is different from 1 and the number itself. Find all natural numbers for which the difference between the sum of the two largest proper divisors and the sum of the two smallest proper divisors is a prime number.
|
Answer: $12(2,3,4,6)$.
Solution. One of two cases applies.
A) Suppose the two smallest divisors $p$ and $q$ are prime numbers. Then the number $r=(n / p+n / q)-(p+q)$ is also prime, and $p q r=(p+q)(n-p q)$. Since the numbers $p+q$ and $p q$ are coprime, we get $r=p+q$, from which $p=2$ and $n=4 q$. But then, due to the choice of $q$, we get $q=3$ and $n=12$.
B) Suppose the smallest divisors are of the form $p$ and $p^{2}$, where $p$ is a prime number. This case is analyzed similarly.
Remark. It is possible that a number has only three proper divisors. Then the difference mentioned in the condition is the difference between the largest and the smallest of the proper divisors. But any number with three proper divisors is a power of a prime $p^{4}$, and the difference $p^{3}-p$ cannot be a prime number.
| Evaluation | Score | Content of the criterion |
| :---: | :---: | :--- |
| + | 20 | Complete solution |
| .+ | 16 | Minor errors |
| $+/ 2$ | 10 | Significant gaps in the solution |
| .- | 6 | The idea that $p n q=(p+q)(n-p q)$ is present |
| - | 0 | The solution is completely incorrect/only the answer |
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.3. The sequence $a_{n}$ is constructed as follows: $a_{1}, a_{2}$ are arbitrary real numbers, and for $n \geq 3$, the number $a_{n}$ is the smallest of the numbers $\left|a_{i}-a_{j}\right|, 1 \leq$ $i<j \leq n-1$. For example, if $a_{1}=6, a_{2}=\frac{19}{2}$, then we get the sequence $6, \frac{19}{2}, \frac{7}{2}, \frac{5}{2}, 1,1,0,0,0 \ldots$ For some choice of $a_{1}, a_{2}$, the sequence resulted in $a_{10}=1$. Find the smallest possible value of $a_{3}$ in such a sequence.
|
Solution. Let $S_{n}$ be the set of all numbers $\left|a_{i}-a_{j}\right|, 1 \leq i<j \leq n-1, \quad n \geq 3$. Then $a_{n}$ is the smallest number in the set $S_{n}$. Since $S_{n} \subset S_{n+1}$, then $a_{n} \geq a_{n+1}$, i.e., starting from $a_{3}$, the sequence is non-increasing. Therefore, $a_{9} \geq a_{10}=1$. Further, from the definition of the sequence, it follows that $a_{10} \leq\left|a_{8}-a_{9}\right|=a_{8}-a_{9} \Rightarrow a_{8} \geq a_{9}+a_{10} \geq 2$. Similarly, $a_{7} \geq a_{8}+a_{9} \geq 2+1=3, a_{6} \geq a_{7}+a_{8} \geq 3+2=5, \ldots, a_{3} \geq a_{4}+a_{5} \geq 13+8=21$. This value is achieved if we take $a_{1}=55, a_{2}=34$.
Criteria.
(-.) It is strictly proven that $a_{n} \geq a_{n+1}$ for $n \geq 3$.
$(-/+)$ Answer + incomplete example: it is stated that $\min \left(a_{3}\right)=21$, and for this case, all terms of the sequence except $a_{1}, a_{2}$ are written out.
$(+/ 2)$ Answer + example (including $\left.a_{1}, a_{2}\right)$, or it is proven that $a_{3} \geq 21$, but without proof, it is used that $a_{n} \geq a_{n+1}$, an example of the sequence for $a_{3}=21$ is missing, or answer + incomplete example (without $a_{1}, a_{2}$) + significant progress in justifying the minimality.
$(+/-)$ It is strictly and without gaps proven that $a_{3} \geq 21$, the example is missing, or answer + example (including $\left.a_{1}, a_{2}\right)+$ justification of minimality with minor gaps.
(+.) Logically correct and complete solution with no significant gaps except the following:
- incomplete example (not explicitly written $a_{1}, a_{2}$),
- the fact that $a_{n} \geq a_{n+1}$ for $n \geq 3$ is used without proof,
- an arithmetic error is made in calculating $a_{3}$.
(+) It is strictly and without gaps proven that $a_{3} \geq 21$, and $a_{1}, a_{2}$ are explicitly written out, for which $a_{3}=21$.
|
21
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 2. Task 2
In a dumpling shop, you can order dumplings in portions of 6, 9, and 20 pieces. Thus, not every number of dumplings can be ordered with these sets, for example, 1, 2, 3, 4, 5, 7, and 8 cannot be bought. What is the largest number of dumplings that cannot be ordered in the dumpling shop?
|
# 2. Task 2
In a dumpling shop, you can order dumplings in portions of 6, 9, and 20 pieces. Thus, not every number of dumplings can be ordered with these sets, for example, 1, 2, 3, 4, 5, 7, and 8 cannot be bought. What is the largest number of dumplings that cannot be ordered in the dumpling shop?
## Answer: 43
|
43
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Natural numbers $x$ and $y$ are such that the following equality holds:
$$
x^{2}-3 x=25 y^{2}-15 y
$$
How many times greater is the number $x$ than the number $y$?
|
Answer. 5
Solution. The equality $x^{2}-3 x=25 y^{2}-15 y$ is equivalent to the equality $(5 y-x)(5 y+x-3)=$ 0. Since $x$ and $y$ are natural numbers, $x, y \geq 1$. Therefore, the second bracket $5 y+x-3 \geq 3$, in particular, is non-zero. Therefore, the first bracket $5 y-x$ is zero, meaning $x$ is 5 times $y$.
Criteria.
## $(-)$
$(-$.$) An example of specific numbers is considered.$
$(-/+)$ From the equality $x(x-3)=5 y(5 y-3)$, the conclusion $x=5 y$ is drawn without satisfactory explanations.
(+/2) A complete square is factored out on both sides, but an incorrect conclusion is made $(x-1.5)^{2}=$ $(5 y-1.5)^{2} \Rightarrow x-1.5=5 y-1.5$. The second case $(x-1.5)=-(5 y-1.5)$ is not considered.
(+/-) The equality $(x-5 y)(x+5 y-3) \neq 0$ is obtained, from which it is concluded that $x-5 y=0$, but it is not explained why $(x+5 y-3) \neq 0$.
(+.) Minor logical steps are omitted
$(+)$
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Pete, Sasha, and Misha are playing tennis in a knockout format. A knockout format means that in each match, two players compete while the third waits. The loser of the match gives up their place to the third player and becomes the waiting player in the next match. Pete played a total of 12 matches, Sasha played 7 matches, and Misha played 11 matches. How many times did Pete win against Sasha?
|
Answer: 4
Solution. First, let's find the total number of games played. Petya, Pasha, and Misha participated in a total of $12+7+11=30$ games. Since each game involves two participants, the number of games is half of this: $30 / 2=15$.
Thus, Petya did not participate in $15-12=3$ games, Pasha in $15-7=8$ games, and Misha in $15-11=4$ games.
Notice now that in a round-robin tournament, one player cannot skip two consecutive games. Since Pasha did not participate in 8 out of 15 games, it means he did not participate in the very first game and then skipped every second game. This means Pasha lost all his games.
Therefore, the number of Petya's wins over Pasha is equal to the number of games in which Petya and Pasha met. This number is equal to the number of games in which Misha did not participate, which is 4, as found earlier.
Criteria.
$(-$.$) Correct answer for a specific case, or it is proven that 15 games were played.
(-/+) Correct answer for a specific case + it is proven that 15 games were played
(+/2) It is proven that Sasha lost all his games, and the correct answer for a specific example, without sufficient justification.
$(+/-)$
(+.) The problem is solved correctly with one flaw: there is no strict proof that 15 games were played.
$(+)$ The answer is correct and strictly justified.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 1. Task 1.1
Timur and Alexander are counting the trees growing around their house. Both are moving in the same direction but start counting from different trees. What is the total number of trees growing around the house if the tree that Timur called the 12th, Alexander counted as $33-\mathrm{m}$, and the tree that Timur called $105-\mathrm{m}$, Alexander counted as the 8th?
|
# 1. Task 1.1
Timur and Alexander are counting the trees growing around their house. Both are moving in the same direction but start counting from different trees. What is the total number of trees growing around the house if the tree that Timur called the 12th, Alexander counted as $33-\mathrm{m}$, and the tree that Timur called $105-\mathrm{m}$, Alexander counted as the 8th?
## Answer: 118
|
118
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 8. Problem 8.1
Pentagon $A B C D E$ is circumscribed around a circle.
Angles $\angle A B C, \angle B A E, \angle C D E$ are each $104^{\circ}$. Find $\angle A D B$. Write the answer in degrees (the number only, without specifying the unit of measurement).
#
|
# 8. Problem 8.1
Pentagon $A B C D E$ is circumscribed around a circle.
Angles $\angle A B C, \angle B A E, \angle C D E$ are each $104^{\circ}$. Find $\angle A D B$. Write the answer in degrees (the number only, without specifying the unit of measurement).
## Answer: 38
|
38
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. How many different (i.e., not equal to each other) acute triangles with integer side lengths and a perimeter of 24 exist? List the lengths of the three sides of all these triangles and prove that there are no others.
ANSWER: 6.
CRITERIA
b - correct criterion for acuteness and either a correct list of acute triangles but without full justification (it is stated without justification that only these sets of lengths satisfy the criterion, or the enumeration is incomplete), or a complete enumeration with an arithmetic error leading to the erroneous inclusion or exclusion of a triangle.
$d$ - correct criterion for acuteness and either an incorrect list without detailed proof or with significant errors in the proof, or no list.
* - a complete list of all triangles, not just acute ones.
|
Solution. Note that a triangle with sides $a \geqslant b \geqslant c$ is obtuse if and only if $a^{2}>b^{2}+c^{2}$. Indeed, if $A B C$ is a triangle with sides $a \geqslant b \geqslant c$ opposite vertices $A, B$, and $C$ respectively, and $A B^{\prime} C$ is a triangle with a right angle $\angle A$ and $A B^{\prime}=A B$, then $B$ and $C$ lie on opposite sides of the line $A B^{\prime}$, otherwise in the triangle $C B B^{\prime}$ it would be $\angle C B B^{\prime}>\angle A B B^{\prime}=\angle A B^{\prime} B>\angle B B^{\prime} C$, and $B C=ab^{2}+c^{2}$ follows that $\angle C A B>\angle C A B^{\prime}=90^{\circ}$, the converse is proved similarly.
Let's count the triples of natural numbers satisfying the conditions $a>b \geqslant c, a^{2}a^{2}$.
For $a=8$ there is one pair of numbers $(b, c)$ such that $8 \geqslant b \geqslant c$ and $b+c=16$: this is $(8,8)$, and the corresponding triangle is equilateral.
For $a=9$ there are two pairs of numbers $(b, c)$ such that $9 \geqslant b \geqslant c$ and $b+c=15$: these are $(8,7)$ and $(9,6)$, both satisfy the inequality $b^{2}+c^{2}>a^{2}$.
For $a=10$ there are four pairs of numbers $(b, c)$ such that $10 \geqslant b \geqslant c$ and $b+c=14$: these are $(7,7),(8,6),(9,5)$ and $(10,4)$. The last two satisfy the inequality $b^{2}+c^{2}>a^{2}$, while the first two do not.
For $a=11$ there are five pairs of numbers $(b, c)$ such that $11 \geqslant b \geqslant c$ and $b+c=13$: these are $(7,6),(8,5),(9,4),(10,3)$ and $(11,2)$. Only the last one satisfies the inequality $b^{2}+c^{2}>a^{2}$.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.5. (20 points) Real numbers $a, b, c, d$ are such that $a+b=\frac{9}{c-d}$ and $c+d=$ $=\frac{25}{a-b}$. What is the smallest value that the quantity $a^{2}+b^{2}+c^{2}+d^{2}$ can take?
|
# Answer: 34.
Solution. If the given equalities are multiplied by the denominators of the corresponding fractions and added, we get $2(a c-b d)=34$. We will prove that $a^{2}+b^{2}+c^{2}+d^{2} \geqslant 2(a c-b d)$. This follows from $a^{2}+c^{2} \geqslant 2 a c$ (equivalent to $(a-c)^{2} \geqslant 0$) and $b^{2}+d^{2} \geqslant-2 b d$ (equivalent to $\left.(b+d)^{2} \geqslant 0\right)$. Therefore, $a^{2}+b^{2}+c^{2}+d^{2} \geqslant 34$.
Equality is achieved if all the above inequalities turn into equalities, i.e., when $a=c$ and $b=-d$. Substituting these relations into the equalities given in the problem, it is not difficult to find suitable values, for example, $a=4, b=-1, c=4, d=1$.
Another solution. Let $a+b$ be denoted by $x$, and $a-b$ by $y$. We get $a=\frac{1}{2}(x+y)$ and $b=\frac{1}{2}(x-y)$, which gives
$$
a^{2}+b^{2}=\frac{(x+y)^{2}}{4}+\frac{(x-y)^{2}}{4}=\frac{x^{2}+y^{2}}{2}
$$
On the other hand, from the condition we have $c-d=\frac{9}{x}$ and $c+d=\frac{25}{y}$, from which $c=\frac{1}{2}\left(\frac{9}{x}+\frac{25}{y}\right)$ and $d=\frac{1}{2}\left(\frac{9}{x}-\frac{25}{y}\right)$. Similarly, we get
$$
c^{2}+d^{2}=\frac{1}{4}\left(\frac{9}{x}+\frac{25}{y}\right)^{2}+\frac{1}{4}\left(\frac{9}{x}-\frac{25}{y}\right)^{2}=\frac{1}{2}\left(\frac{9^{2}}{x^{2}}+\frac{25^{2}}{y^{2}}\right)
$$
Adding, we have
$$
a^{2}+b^{2}+c^{2}+d^{2}=\frac{1}{2}\left(x^{2}+\frac{9^{2}}{x^{2}}+y^{2}+\frac{25^{2}}{y^{2}}\right)
$$
Noting that $x^{2}+9^{2} / x^{2} \geqslant 2 \cdot 9$ (which follows from $(x-9 / x)^{2} \geqslant 0$) and similarly $y^{2}+25^{2} / y^{2} \geqslant 2 \cdot 25$, we get
$$
a^{2}+b^{2}+c^{2}+d^{2} \geqslant \frac{1}{2}(2 \cdot 9+2 \cdot 25)=9+25=34
$$
Equality can only be achieved if all inequalities turn into equalities. From $x-9 / x=0$ we get $x= \pm 3$, and from $y-25 / y=0$ we get $y= \pm 5$, from which it is not difficult to obtain suitable examples of the values of the original variables.
Remark. From the given solutions, it can be understood that the expression takes the value 34 only for four sets of $(a, b, c, d)$:
$$
(4,-1,4,1) ; \quad(-1,4,-1,-4) ; \quad(1,-4,1,4) ; \quad(-4,1,-4,-1)
$$
## Criteria
Points for the estimate and example are summed:
+17 p. Estimate - it is proven that $a^{2}+b^{2}+c^{2}+d^{2} \geqslant 34$.
In the absence of a complete proof of the estimate, the highest suitable criterion is used:
+3 p. The work contains the equality $2\left(a^{2}+b^{2}+c^{2}+d^{2}\right)=(a+b)^{2}+(a-b)^{2}+(c+d)^{2}+(c-d)^{2}$.
+3 p. The work contains the equality $a c-b d=17$ or $2 a c-2 b d=34$.
+0 p. The work contains the equality $a d-b c=8$ or $2 a d-2 b c=16$.
+0 p. The problem is solved under the assumption that the numbers $a, b, c, d$ are integers.
+3 p. Example - suitable numbers $a, b, c, d$ are provided for which $a^{2}+b^{2}+c^{2}+d^{2}=34$ (or it is proven that such exist).
The following advancement is not evaluated:
0 p. Only the answer is provided.
|
34
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.