problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
Problem 9.6. (20 points) There were $n$ identical-looking coins weighing $x_{1}, x_{2}, \ldots, x_{n}$ grams (the weights of the coins are pairwise distinct positive real numbers), and also weightless stickers with numbers $x_{1}, x_{2}, \ldots, x_{n}$. At night, a lab assistant weighed the coins and labeled them with stickers. It is required to check using a balance scale that he did not mix anything up. For example, if $n=6, x_{1}=1, \ldots, x_{6}=6$, then this can be done in 2 weighings, verifying that
$$
\begin{aligned}
& 1+2+3=6 \\
& 1+6<3+5
\end{aligned}
$$
Does there exist for $n=8$ a set of weights $x_{1}, x_{2}, \ldots, x_{8}$, the correct labeling of which can be verified in 2 weighings?
|
Answer: 2 yes
Solution. Consider the weights 10, 20, 25, 30, 35, 201, 203, 207 (weights will be measured in grams hereafter). We will perform two checks:
$$
\begin{aligned}
10+20+30 & =25+35 \\
10+25+201 & <30+207
\end{aligned}
$$
First, consider the first weighing. We will prove that if some three coins balance some two coins, then these must be 10, 20, 30 on one side and 25, 35 on the other.
We will call the coins 10, 20, 25, 30, 35 small, and the coins 201, 203, 207 - large.
If among the five coins participating in the first weighing there are large ones, then on each side there must be exactly one such coin (otherwise, the side with more such coins would outweigh). At the same time, the weights of all small coins are divisible by 5, while the weights of large coins give different remainders when divided by 5. Then the total weights on the sides give different remainders when divided by 5, which is impossible in the case of equality.
Therefore, all five coins are small. Then each side weighs $\frac{1}{2}(10+20+25+30+35)=$ $=60$. It is easy to understand that the sum of the weights of two coins can be 60 only if these two coins weigh 25 and 35. Then the other three coins weigh 10, $20,30$.
Thus, if the first weighing shows equality, then 10, 20, 30 are on the side with 3 coins (this group will be called $A$), and 25, 35 - on the side with two coins (this group will be called $B$). At the same time, the coins 201, 203, 207 (this group will be called $C$) do not participate in the first weighing.
Now consider the second weighing. On one side, one coin from each of the three groups $A, B, C$ is taken, the minimum sum of the weights of such coins is $10+25+201=236$. On the other side, one coin from groups $A$ and $C$ is taken, the maximum sum of the weights of such coins is $30+$ $207=237$. Given that 237 is only 1 more than 236, the inequality in the second weighing will not hold for any other coins. Therefore, on one side lie the coins $10,25,201$, and on the other - $30,207$.
Thus, in each weighing, we uniquely determined the set of coins on each side. At the same time, for all 8 coins, the pairs of groups they belong to in the first and second weighings (either on the side with 3 coins, or on the side with 2 coins, or not weighed) are different. Therefore, the weight of each coin is uniquely determined.
Remark. In any correct algorithm, one weighing must establish the equality of the weights of two coins on one side with three coins on the other, and the other weighing must establish that two coins on one side are heavier than three coins on the other. This can be understood from the following considerations.
- Coins that are in one of the three groups (on the first side, on the second, or not weighed) in one weighing must end up in different groups in the second weighing. (Indeed, if two coins ended up in the same groups in both weighings, the lab assistant could mix them up and we would not notice.)
- From the previous point, it follows that no weighing can create a group of 4 or more coins. This means that in each weighing, there are either 3 coins on each side, or 3 and 2.
- Also from the first point, it follows that the coins can be arranged in a $3 \times 3$ table, with the groups of the first weighing along the rows and the groups of the second weighing along the columns; exactly one cell will remain without a coin.
| $a_{1}$ | $a_{2}$ | $a_{3}$ |
| :--- | :--- | :--- |
| $b_{1}$ | $b_{2}$ | $b_{3}$ |
| $c_{1}$ | | $c_{3}$ |
- Both weighings cannot have the same format and outcome. (For example, it cannot be that in both weighings 2 coins on one side outweigh 3 coins on the other.) Indeed, in this case, if the rows and columns in the table above are ordered in the same way (for example, in the order light/heavy/unweighed), the empty cell would be on the main diagonal; then the lab assistant could mix up the labels in such a way that the coins would be reflected relative to this diagonal, and we would not notice this.
- There cannot be a weighing in which there are 3 coins on each side, and they balance each other. For example, let the first weighing be set up this way; its sides correspond to the first and second rows of our table. Then the lab assistant could mix up the labels in such a way that the first and second rows would swap places. This would not affect the results of our weighings, that is, we would not notice such an error.
- There cannot be a weighing in which there are 3 coins on each side, and one side is heavier than the other. To prove this, assume the contrary - let this be the first weighing. The lighter side of this weighing corresponds to the first row, and the heavier side to the third row; the columns are ordered so that the group of 2 coins from the second weighing is in the last column (regardless of the structure of the second weighing).
| $a_{1}$ | $a_{2}$ | $a_{3}$ |
| :--- | :--- | :--- |
| $b_{1}$ | $b_{2}$ | |
| $c_{1}$ | $c_{2}$ | $c_{3}$ |
If we now reorder the numbers in the columns from top to bottom in ascending order (leaving the empty cell empty), the weight readings will not change: the composition of the columns will not change, and the bottom row will be heavier than the top row. But if we then swap, for example, the two lower coins in the central column, the bottom row will still be heavier than the top row! It turns out that we cannot uniquely determine the placement of the coins, that is, the lab assistant has a chance to deceive us again.
- Similarly, it can be shown that there cannot be a weighing in which the side with three coins outweighs the side with two.
It is also not difficult to understand from similar considerations that for 9 coins, it is impossible to get by with two weighings in any situation.
## Criteria
The highest suitable criterion is used:
20 points. A correct example of a set of masses and a description of two weighings that allow checking the correctness of the labeling is provided.
3 points. The work contains an indication that coins that end up in the same group during the first weighing must end up in different groups during the second weighing.
3 points. The work provides an example of a set of masses and a description of two weighings that do not allow checking the correctness of the labeling, but coins that end up in the same group during each weighing end up in different groups during the other weighing.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Kolya came up with an entertainment for himself: he rearranges the digits in the number 2015, then places a multiplication sign between any two digits. In this process, none of the resulting two factors should start with zero. Then he calculates the value of this expression. For example: $150 \cdot 2=300$, or $10 \cdot 25=250$. What is the largest number he can get as a result of such a calculation?
|
Answer: 1050
Solution. Note three facts (their justification is obvious). First, in the case of the maximum product, the digits in each of the factors are in descending order. That is, 0 should be at the end of one of the factors. Second, it does not matter at the end of which of the two factors to place 0, the product will not change. Therefore, it can be rearranged so that both factors become two-digit numbers. After that, only 3 options remain to be considered:
$$
21 \cdot 50=1050, \quad 52 \cdot 10=520, \quad 51 \cdot 20=1020
$$
Criteria.
## $(-)$
(-.) Correct answer with an example. It is not explained why it is correct.
$(-/+)$ A significant number of cases are missing
(+/2) It is stated that only half of the cases need to be considered (for example, the case of a three-digit and a one-digit number), but the explanation is unsatisfactory
$(+/-)$ 1-2 cases are missing
$(+$.
(+) Correct answer with a review of all cases.
|
1050
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Pete, Sasha, and Misha are playing tennis in a knockout format. A knockout format means that in each match, two players compete while the third waits. The loser of the match gives up their place to the third player and becomes the waiting player in the next match. Pete played a total of 12 matches, Sasha - 7 matches, Misha - 11 matches. How many times did Pete win against Sasha?
|
Answer: 4
Solution. First, let's find the total number of games played. Petya, Pasha, and Misha participated in a total of $12+7+11=30$ games. Since each game involves two participants, the number of games is half of this: $30 / 2=15$.
Thus, Petya did not participate in $15-12=3$ games, Pasha in $15-7=8$ games, and Misha in $15-11=4$ games.
Notice now that in a round-robin tournament, one player cannot skip two consecutive games. Since Pasha did not participate in 8 out of 15 games, it means he did not participate in the very first game and then skipped every second game. This means Pasha lost all his games.
Therefore, the number of Petya's wins over Pasha is equal to the number of games in which Petya and Pasha met. This number is equal to the number of games in which Misha did not participate, which is 4, as found earlier.
Criteria.
$(-$.$) Correct answer for a specific case, or it is proven that 15 games were played.
$(-/+)$ Correct answer for a specific case + it is proven that 15 games were played
(+/2) It is proven that Pasha lost all his games, and the correct answer for a specific example, without sufficient justification.
$(+/-)$
(+.) The problem is solved correctly with one flaw: there is no strict proof that 15 games were played.
$(+)$ The answer is correct and strictly justified.
## Mathematics - solutions
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. The numbers $x$ and $y$ are such that $x+y=xy=17$. Find the value of the expression:
$$
\left(x^{2}-17 x\right)\left(y+\frac{17}{y}\right)
$$
|
Answer: -289
Solution. $x-17=-y, \frac{17}{y}=x$. The desired expression is:
$$
x(x-17)(y+x)=-x y \cdot 17=-289 .
$$
Criteria.
$(-)$
$(-$.
(-/+) Serious arithmetic error affecting the solution process, or several arithmetic errors.
$(+/ 2)$
(+/-) One arithmetic error in an otherwise correct solution (for example, incorrectly multiplying 17 and 17 in the last step).
(+.) Omission of minor calculations.
(+)
|
-289
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 4. Problem $4.1 *$
In the class, 6 students received a grade of 5, 7 received a grade of 4, and 1 received a grade of 3. The teacher told them to form pairs with different grades, where the student with the better grade would explain to the student with the worse grade where they made a mistake.
In how many ways could the students form pairs under this condition? Points for the problem: 9.
#
|
# 4. Problem $4.1 *$
In the class, 6 students received a grade of 5, 7 received a grade of 4, and 1 received a grade of 3. The teacher told them to form pairs with different grades, where the student with the better grade would explain to the student with the worse grade where they made a mistake.
In how many ways could the students form pairs under these conditions? Points for the problem: 9.
## Answer: 5040
|
5040
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Kolya came up with an entertainment for himself: he rearranges the digits in the number 2015, then places a multiplication sign between any two digits and calculates the value of the resulting expression. For example: $150 \cdot 2=300$, or $10 \cdot 25=250$. What is the largest number he can get as a result of such a calculation?
|
Answer: 1050
Solution. Note three facts (their justification is obvious). First, in the case of the maximum product, the digits in each of the factors are in descending order. That is, 0 should be at the end of one of the factors. Second, it does not matter at the end of which of the two factors to place 0, the product will not change. Therefore, it can be rearranged so that both factors become two-digit numbers. After that, only 3 options remain to be considered:
$$
21 \cdot 50=1050, \quad 52 \cdot 10=520, \quad 51 \cdot 20=1020
$$
Criteria.
## $(-)$
(-.) Correct answer with an example. It is not explained why it is correct.
$(-/+)$ A significant number of cases are missing
(+/2) It is stated that only half of the cases need to be considered (for example, the case of a three-digit and a one-digit number), but the explanation is unsatisfactory
$(+/-)$ 1-2 cases are missing
$(+$.
$(+)$ Correct answer with a review of all cases.
|
1050
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The numbers $x$ and $y$ are such that $x+y=xy=17$. Find the value of the expression:
$$
\left(x^{2}-17 x\right)\left(y+\frac{17}{y}\right)
$$
|
Answer: -289
Solution. $x-17=-y, \frac{17}{y}=x$. The desired expression is:
$$
x(x-17)(y+x)=-x y \cdot 17=-289
$$
Criteria.
$(-)$
$(-$.
(-/+) Serious arithmetic error affecting the solution process, or several arithmetic errors.
$(+/ 2)$
(+/-) One arithmetic error in an otherwise correct solution.
(+.) Omission of minor calculations.
(+)
|
-289
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 2. Problem 2
Angles $A, B, C$ of triangle $A B C$ are $44^{\circ}, 66^{\circ}$, and $70^{\circ}$ respectively. The bisector of angle $A B C$ and the perpendicular bisector of side $A C$ intersect at point $D$. How many degrees is angle $A D C$? (Write the answer without the degree symbol.)
#
|
# 2. Task 2
Angles $A, B, C$ of triangle $A B C$ are $44^{\circ}, 66^{\circ}$, and $70^{\circ}$ respectively.
The bisector of angle $A B C$ and the perpendicular bisector of side $A C$ intersect at point $D$. How many degrees does angle $A D C$ measure? (Write the answer without the degree symbol.)
## Answer: 114
|
114
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. In the expression
$$
(* *+*)(* *+*)=* * * *
$$
insert digits instead of asterisks so that a correct equality is obtained and no more than 4 different digits are used. (A number cannot start with zero).
|
Solution. For example, $(90+9)(10+1)=1089$. Or: $(99+1)(10+9)=1900$. Criteria.
(+.) Correct left side.
$(+)$ Correct answer.
|
1089
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11-1. For real numbers $a, b$, and $c$, it is known that $a b c + a + b + c = 10$, and $a b + b c + a c = 9$. For which numbers $x$ can it be asserted that at least one of the numbers $a, b, c$ is equal to $x$? (Find all such numbers $x$ and prove that there are no others.)
Answer: 1.
|
Solution. We will provide two solutions to the problem.
First Solution. Let $a+b+c=\lambda$. Vieta's theorem allows us to write a cubic equation depending on the parameter $\lambda$, whose roots are the set $a, b, c$ corresponding to the given $\lambda$:
$$
t^{3}-\lambda t^{2}+9 t-(10-\lambda)=0 \quad \Leftrightarrow \quad(t-1)\left(t^{2}-(\lambda-1) t+(10-\lambda)\right)=0
$$
From this, it is clear that for any $\lambda$ there is a root $t=1$, so the value $x=1$ works. It remains to prove that there are no other values that are roots for any $\lambda$ (although this is obvious). Indeed, $t^{2}-(\lambda-1) t+(10-\lambda)=0$ implies $t=\frac{\lambda-1 \pm \sqrt{\lambda^{2}+2 \lambda-39}}{2}$. Take any pair of values of $\lambda$ for which the discriminant takes the same positive value, for example, for $\lambda=10$ and $\lambda=-12$ we have $t \in\{0,9\}$ and $t \in\{-11,-2\}$ - there are no intersections. Therefore, the answer is $x=1$.
Second Solution. Subtract the second equation from the first, transforming it, we get $(a-1)(b-1)(c-1)=0$. From this, it follows that one of $a, b, c$ is equal to one. Other $x$ do not work, as the triples $(a, b, c)=(4,1,1)$ and $(a, b, c)=(0,9,1)$ satisfy the condition.
| Grade | Score | Content Criterion |
| :---: | :---: | :--- |
| + | 20 | Complete solution |
| .+ | 18 | Not proven why there are no others besides 1, or there is a minor error in the proof. |
| $+/-$ | 16 | Significant errors in the proof (several transitions with division by possibly zero, misunderstanding of the condition (with necessary calculations for the proof)). |
| $-/+$ | 10 | Two specific cases are considered, which show that it can only be equal to 1. But there is no proof that $= 1$. |
| .- | 6 | Only one case is found (it is claimed that $\in\{1,4\}$ or $\in\{0,1,9\}$. |
| - | 0 | The solution is completely incorrect/only the answer. |
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11-2. Mr. $A$ stood at the point with coordinates $(0,0)$ for an hour. During the same hour, moving uniformly and in a straight line, Mr. $B$ traveled from the point $(22,0)$ to the point $(2,20)$. During this same hour, Miss $C$, also moving uniformly and in a straight line, traveled from the point $(30,4)$ to the point $(0,24)$. How many times during the observation period did the area of triangle $A B C$ take on integer values? The initial and final moments are included.
|
Answer: 53.
Solution. Informally speaking, the problem in this task is not to find a path of calculations leading to the answer; but to find a path to the answer that passes through not too many intermediate calculations. Let's show how to do this.
As is known, the area of a triangle formed by vectors $\overrightarrow{\left(x_{1}, y_{1}\right)}$ and $\overrightarrow{\left(x_{2}, y_{2}\right)}$ is $\left|\frac{1}{2}\left(x_{1} y_{2}-x_{2} y_{1}\right)\right|$. If the point $\overrightarrow{(x, y)}$ moves uniformly and in a straight line, then its coordinates depend on time $t$ as $x=x_{0}+x^{\prime} t$, $y=y_{0}+y^{\prime} t$. Then the value $f(t)=\frac{1}{2}\left(x_{1} y_{2}-x_{2} y_{1}\right)$ as a function of $t$ is a polynomial of the second degree. Let's choose the time axis so that zero is in the middle of the observation interval, and the initial and final moments have coordinates -1 and 1, respectively. Let $f(t)=a x^{2}+b x+c$. The coordinates of points $B$ and $C$ in the middle of the observation interval are easily calculated, these are $(12,10)$ and $(15,14)$, respectively. Thus, $f(-1)=\frac{1}{2}(22 \cdot 4-30 \cdot 0)=$ 44, $f(0)=\frac{1}{2}(12 \cdot 14-15 \cdot 10)=9, f(1)=\frac{1}{2}(2 \cdot 24-0 \cdot 20)=24$. From which
$c=f(0)=9, b=\frac{f(1)-f(-1)}{2}=-10, a=\frac{f(1)+f(-1)-2 f(0)}{2}=25$. The minimum of the quadratic trinomial is reached at the point $\frac{-b}{2 a}=\frac{1}{5} ; f\left(\frac{1}{5}\right)=8$. Thus, we see that the minimum of the expression $\frac{1}{2}\left(x_{1} y_{2}-x_{2} y_{1}\right)$ fell within the observation interval, moreover, it is positive, that is, the modulus is equal to the expression under the modulus. In total, the area first decreased from 44 to 8, then increased from 8 to 24, thus taking integer values $1+(44-8)+(24-8)=53$ times.
| Rating | Score | Content of the criterion |
| :---: | :---: | :--- |
| + | 20 | Full solution |
| .+ | 17 | Only an arithmetic error. Ignoring the second passage of the same integer area. |
| $+/ 2$ | 16 | The formula for $S(\mathrm{t})\left(100 t^{2}-120 t+44\right.$ or $44-2 t+t^{2} / 36$ or $\left.t^{2} / 4-6 t+44\right)$, or $2 S$ is correctly found, further reasoning is absent |
| $-/+$ | 10 | The idea of continuity, giving only a lower bound (the values at the initial and final moments are found, the difference between them is calculated) or an arithmetic error in calculating the formula for $S(t)$ |
| - | 0 | The solution is completely incorrect/only the answer |
|
53
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11-5. Consider all reduced quadratic trinomials $x^{2}+p x+$ $q$ with integer coefficients $p$ and $q$. Let's call the range of such a trinomial the set of its values at all integer points $x=0, \pm 1, \pm 2, \ldots$ What is the maximum number of such trinomials that can be chosen so that their ranges do not intersect pairwise?
Answer: 2.
|
Solution. Note that the substitution of the variable $x \rightarrow x+k$ for any integer $k$ does not change the range of the polynomial. Then, by making the substitution $x \rightarrow x-\left[\frac{p}{2}\right]$ (square brackets denote the integer part), we can assume that any polynomial has one of two forms: $x^{2}+q$ or $x^{2}+x+q$.
The ranges of any two polynomials of different forms intersect: indeed, the values of the polynomials $x^{2}+q$ and $x^{2}+x+q^{\prime}$ coincide at $x=q-q^{\prime}$. Therefore, polynomials of different forms cannot be chosen.
Polynomials of the first form can be chosen no more than two, since if the ranges of $f_{1}(x)=x^{2}+q$ and $f_{2}(x)=x^{2}+q^{\prime}$ do not intersect, then $q-q^{\prime}=4 k+2$ for some $k \in \mathbb{Z}$. Indeed, for an odd difference of the constant terms $q-q^{\prime}=2 k+1$, we have $f_{1}(k)=f_{2}(k+1)$. For a difference of the constant terms divisible by 4, $q-q^{\prime}=4 k$, we have $f_{1}(k-1)=f_{2}(k+1)$. But if at least three polynomials are chosen, then among the pairwise differences of the constant terms, at least one does not have the form $4 k+2$.
Polynomials of the second form can also be chosen no more than two, since if the ranges of $f_{1}(x)=x^{2}+x+q$ and $f_{2}(x)=x^{2}+x+q^{\prime}$ do not intersect, then $q-q^{\prime}=2 k+1$ for some $k \in \mathbb{Z}$. Indeed, for an even difference of the constant terms $q-q^{\prime}=2 k$, we have $f_{1}(k-1)=f_{2}(k)$. Again, if at least three polynomials are chosen, then among the pairwise differences of the constant terms, at least one is even.
Thus, more than two polynomials cannot be chosen. Example for two: $f_{1}(x)=x^{2}$ and $f_{2}(x)=x^{2}+2$.
| Grade | Score | Content criterion |
| :---: | :---: | :--- |
| + | 20 | Complete solution |
| .+ | 18 | Solution is correct modulo minor inaccuracies |
| $+/-$ | 14 | There is a proof that for each type of values $\left(x^{2}+q\right.$ and $\left.x^{2}+x+q\right)$ no more than two trinomials can be taken |
| $-/+$ | 8 | Complete solution, but only for the case $x^{2}+q$ |
| .- | 4 | Example of two trinomials whose ranges do not intersect |
| - | 0 | Solution is completely incorrect/only answer |
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. In the expression
$$
(* *+*)(* *+*)=* * * *
$$
insert digits instead of asterisks so that a correct equality is obtained and no more than 4 different digits are used. (A number cannot start with zero).
|
Solution. For example, $(90+9)(10+1)=1089$. Or: $(99+1)(10+9)=1900$.
Criteria.
(+.) Correct left side.
$(+)$ Correct answer.
|
1089
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.6. The altitudes of an acute-angled scalene triangle $ABC$ intersect at point $H$. $I$ is the incenter of triangle $ABC$, $O$ is the circumcenter of triangle $BHC$. It is known that point $I$ lies on the segment $OA$. Find the angle $BAC$.
|
Answer: $60^{\circ}$
Solution. Note that point $O$ lies on the perpendicular bisector of segment $B C$. On the other hand, point $O$ lies on the bisector of angle $A$. However, these two lines intersect at a point lying on the circumcircle of triangle $A B C$, and dividing the arc $B C$ in half. Therefore, point $O$ lies on the circumcircle of triangle $A B C$.
The angles at the vertices of triangle $A B C$ will be denoted by the same letter. Consider the isosceles triangle $O H C, O H=O C$. Then, from the observation about the location of point $O$ and the properties of inscribed angles, we immediately get that the angles at the base of this isosceles triangle are equal to $90^{\circ}-B+A / 2$. Similarly, the angle at the base of the isosceles triangle $O H B(O H=$ $O B)$ is equal to $90^{\circ}-C+A / 2$. But the sum of these two angles is equal to the angle $B H C$, which, in turn, is equal to the angle $180^{\circ}-A$ (by the theorem of vertical angles). Therefore, $180^{\circ}-B-C+A=180^{\circ}-A$, or $3 A=180$.
## Criteria.
(-.) The answer is incorrect and there is no complete solution, but there are significant advances in the solution.
(-/+) The correct answer is obtained, but the solution uses without proof that point $O$ belongs to the circumcircle of $\triangle A B C$.
(+/-) It is proven that point $O$ lies on the circumcircle of $\triangle A B C$.
(+.) The answer is incorrect due to an arithmetic error.
$(+)$ Correct answer + full justification.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. Point $B$ is the midpoint of segment $A C$. Square $A B D E$ and equilateral triangle $B C F$ are located in the same half-plane relative to line $A C$. Find (in degrees) the measure of the acute angle between lines $C D$ and $A F$.
|
Answer: $75^{\circ}$.
Solution. Note that points $A D F C$ lie on the same circle with center at point $B$. The arc $F C$ is $60^{\circ}$. Therefore, the angle $F A C$ is $30^{\circ}$ (by the inscribed angle theorem). Triangle $B D C$ is isosceles with a right angle at vertex $B$. Therefore, the angle $D C A$ is $\pi / 4$. Thus, the acute angle between the lines $A F$ and $D C$ is $30^{\circ}+45^{\circ}=75^{\circ}$.
Criteria.
(-.) Progress in the problem (finding many equal segments and angles) without obtaining the answer.
(+/2) Correct answer, significant gaps in justification (but without logical errors),
or errors that did not affect the answer.
(+.) Insufficient justification of some (not difficult) facts or omission of some more or less obvious steps, or the obtuse angle was calculated instead of the acute one, or a minor arithmetic error that did not affect the answer.
(+) Correct answer with full justification and no errors in the solution.
|
75
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. The lines containing the altitudes of the non-isosceles triangle \(ABC\) intersect at point \(H\). \(I\) is the incenter of triangle \(ABC\), \(O\) is the circumcenter of triangle \(BHC\). It is known that point \(I\) lies on the segment \(OA\). Find the angle \(BAC\).
|
Answer: $60^{\circ}$
Solution. Note that point $O$ lies on the bisector (perpendicular through the midpoint) of segment $B C$. On the other hand, point $O$ lies on the bisector of angle $A$. However, these two lines intersect at a point lying on the circumcircle of triangle $B A C$, and dividing the arc $B C$ in half. Thus, point $O$ lies on the circumcircle of triangle $B A C$.
The angles at the vertices of triangle $B A C$ will be denoted by the same letter. Consider the isosceles triangle $O H C, O H=O C$. Then, from the observation about the location of point $O$ and the properties of inscribed angles, we immediately get that the angles at the base of this isosceles triangle are $90^{\circ}-B+A / 2$. Similarly, the angle at the base of the isosceles triangle $O H B(O H=$ $O B)$ is $90^{\circ}-C+A / 2$. But the sum of these two angles is equal to the angle $B H C$, which, in turn, is equal to the angle $180-A$ (by the theorem of vertical angles). Therefore, $180-B-C+A=180-A$, from which $3 A=180$.
Criteria.
(-.) The answer is incorrect and there is no complete solution, but there are significant advances in the solution.
(-/+) The correct answer is obtained, but the solution uses without proof that point $O$ belongs to the circumcircle of $\triangle A B C$.
(+/-) It is proven that point $O$ lies on the circumcircle of $\triangle A B C$.
(+.) The answer is incorrect due to an arithmetic error.
$(+)$ Correct answer + full justification.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.6. The sequence $a_{n}$ is constructed as follows: $a_{1}, a_{2}$ are arbitrary real numbers, and for $n \geq 3$, the number $a_{n}$ is the smallest of the numbers $\left|a_{i}-a_{j}\right|, 1 \leq i<j \leq n-1$. For example, if $a_{1}=6, a_{2}=\frac{19}{2}$, then we get the sequence $6, \frac{19}{2}, \frac{7}{2}, \frac{5}{2}, 1,1,0,0,0 \ldots$ For some choice of $a_{1}$ and $a_{2}$, the sequence resulted in $a_{10}=1$. Find the smallest possible value of $a_{3}$ in such a sequence.
|
Solution. Let $S_{n}$ be the set of all numbers $\left|a_{i}-a_{j}\right|, 1 \leq i<j \leq n-1, n \geq 3$. Then $a_{n}$ is the smallest number in the set $S_{n}$. Since $S_{n-1} \subset S_{n}$, then $a_{n-1} \geq a_{n}$, i.e., starting from $a_{3}$, the sequence is non-increasing. Therefore, $a_{9} \geq a_{10}=1$. Further, from the definition of the sequence, it follows that $a_{10} \leq\left|a_{8}-a_{9}\right|=a_{8}-a_{9} \Rightarrow a_{8} \geq a_{9}+a_{10} \geq 2$. Similarly, $a_{7} \geq a_{8}+a_{9} \geq 2+1=3$, $\quad a_{6} \geq a_{7}+a_{8} \geq 3+2=5, \ldots, a_{3} \geq a_{4}+a_{5} \geq 8+13=21$. This value is achieved if we take $a_{1}=55, a_{2}=34$.
Criteria.
(-.) It is strictly proven that $a_{n} \geq a_{n+1}$ for $n \geq 3$.
$(-/+)$ Answer + incomplete example: it is stated that $\min \left(a_{3}\right)=21$, and for this case, all terms of the sequence except $a_{1}, a_{2}$ are written out,
$(+/ 2)$ answer + example (including $a_{1}, a_{2}$), justification of minimality is absent or contains gross errors (for example, it is stated that in any such sequence, each number starting from the 3rd is equal to the difference of the two preceding ones,
or
it is proven that $a_{3} \geq 21$, but without proof, it is used that $a_{n} \geq a_{n+1}$, an example of a sequence for $a_{3}=21$ is absent, or
answer + incomplete example (without $\left.a_{1}, a_{2}\right)+$ significant progress in justifying minimality.
(+/-) It is strictly and without gaps proven that $a_{3} \geq 21$, an example is absent, or
answer + example (including $a_{1}, a_{2}$) + justification of minimality with minor gaps.
(+.) Logically correct and complete solution with no significant gaps except the following
- incomplete example (not explicitly written $a_{1}, a_{2}$),
- the fact that $a_{n} \geq a_{n+1}$ for $n \geq 3$ is used without proof,
- an arithmetic error is made in calculating $a_{3}$.
(+) It is strictly and without gaps proven that $a_{3} \geq 21$, and $a_{1}, a_{2}$ are explicitly written out, for which $a_{3}=21$.
|
21
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.1. (15 points) Find the smallest ten-digit natural number, all digits of which are different, such that when all even digits are erased, 97531 remains, and when all odd digits are erased, 02468 remains.
|
Answer: 9024675318.
Solution. Let $A=9024675318$. Consider an arbitrary number $N=\overline{a_{1} a_{2} \ldots a_{10}}$ that satisfies the conditions of the problem. Clearly, $a_{1}=9$, since $a_{1} \neq 0$. Let $7=a_{k}$ for some $k$. We will consider several cases.
- If $k>6$, then $N=9024687531>A$.
- If $kA$.
- If $k=6$, then $N=\overline{902467 a_{7} a_{8} a_{9} a_{10}}$. If $a_{10} \neq 8$, then $N=\overline{902467 \ldots 8 \ldots a_{10}}>A$. If $a_{10}=8$, then $N=9024675318=A$.
Thus, we have considered all possible cases and confirmed that $A$ is the smallest number.
## Criteria
The largest suitable criterion is used:
15 points. The correct answer is provided with justification of minimality.
8 points. The correct answer is provided without justification of minimality.
|
9024675318
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.2. (15 points) Given an isosceles triangle $A B C(A B=B C)$. On the sides $A B, B C, A C$ points $K, L, M$ are marked respectively such that $\angle A K M=90^{\circ}, \angle B L K=90^{\circ}$ and $K M=K L$. What is the measure of angle $C M L ?$
|
Answer: $90^{\circ}$.
Solution. From the condition, it follows that $\angle M K L + \angle L K B = 90^{\circ} = \angle L K B + \angle L B K$, from which $\angle M K L = \angle L B K$ (Fig. 1). Triangles $A B C$ and $M K L$ are isosceles with equal angles at the vertex, so the base angles are also equal: $\angle K L M = \angle M C L$. It remains to note that $90^{\circ} = \angle K L M + \angle C L M = \angle M C L + \angle C L M$, so $\angle C M L = 180^{\circ} - \angle M C L - \angle C L M = 90^{\circ}$.
Criteria
The largest suitable criterion is used:
15 p. Any complete solution to the problem.
5 p. The similarity (i.e., equality of corresponding angles) of triangles $A B C$ and $M K L$ is proven.
8 p. The problem is solved using the similarity of triangles $A B C$ and $M K L$, but their similarity is not proven.
0 p. Only the answer is provided.
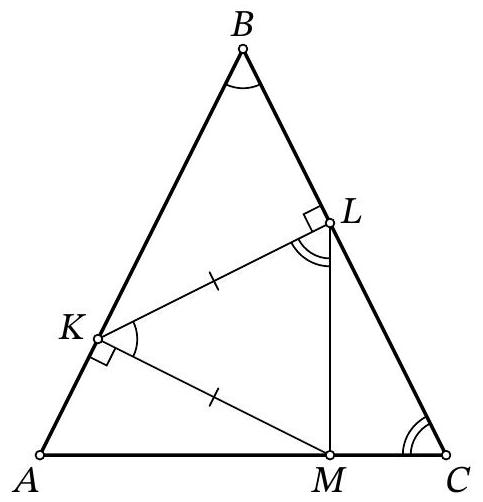
Fig. 1: to the solution of problem 7.2.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.3. (15 points) Several boxes are stored in a warehouse. It is known that there are no more than 60 boxes, and each of them contains either 59 apples or 60 oranges. After a box with a certain number of oranges was brought to the warehouse, the number of fruits in the warehouse became equal. What is the smallest number of oranges that could have been in the brought box?
|
Answer: 30.
Solution. Let the number of boxes with oranges be denoted by $n$, the number of boxes with apples by $m$, and the number of oranges in the brought box by $x$. According to the problem, $59 m = 60 n + x$. By moving $59 n$ to the left side, we get $59(m - n) = n + x$. From this, it follows that $n + x$ is a natural number divisible by 59, so it is at least 59. Also, since both sides of the equation are positive, we have $m > n$.
If $x \leq 29$, then $n \geq 30$ and $m \geq 31$, which contradicts the condition $n + m \leq 60$. Therefore, $x \geq 30$.
It remains to note that for $m = 30$, $n = 29$, and $x = 30$, the condition of the problem is satisfied, meaning there could be exactly 30 oranges in the brought box.
Alternative solution. Consider the situation with the smallest possible number of oranges in the box. Note that there must be more boxes with apples than boxes with oranges (otherwise, there would already be fewer apples than oranges in the boxes, and the brought box with oranges would not be able to equalize the number of fruits). Let the number of boxes with oranges be denoted by $n$; then $n \leq 29$, otherwise the total number of boxes would exceed 60.
We will prove that the number of boxes with apples is exactly one more than the number of boxes with oranges. Indeed, in any other case, there are at least $n + 2$ boxes with apples. This means that the number of apples in the boxes is at least
$$
59(n + 2) - 60 n = 118 - n
$$
Since $n \leq 29$, this difference is at least 89. But then one box with apples can be removed, and the number of oranges in the brought box can be reduced by 59. This means that the considered case does not give the minimum number of oranges in the box, a contradiction.
Then the difference between the number of apples and the number of oranges in the boxes is
$$
59(n + 1) - 60 n = 59 - n
$$
This difference decreases as $n$ increases, so the smallest value of the difference is achieved at the largest value of $n$. Therefore, this difference (equal to the number of oranges in the box) reaches its smallest value, 30, at the largest value of $n = 29$ (the total number of boxes is then exactly 59).
## Criteria
The highest applicable criterion is used:
15 points. Any complete solution to the problem.
12 points. The estimate is proven that there are at least 30 oranges in the box.
Alternatively (if the above criteria are not applicable or give fewer points), the following advancements are summed:
+8 points. It is proven that to achieve the minimum difference between the number of apples and the number of oranges, the number of boxes with apples must be exactly one more.
In the absence of a proof of this fact, the following criterion is used:
+6 points. This fact is stated without proof.
+7 points. All cases for $n < 30$ are considered, where there are $n + 1$ boxes with apples and $n$ boxes with oranges. (For example, it may be noted that when $n$ increases by 1, the difference $59(n + 1) - 60 n = 59 - n$ decreases by 1.)
In the absence of a complete consideration of these cases, the following criterion is used:
+3 points. An example is given where there are exactly 30 oranges in the box (or it is otherwise proven that such a situation is possible).
The following advancement is not scored:
0 points. The correct answer is given.
|
30
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.4. (15 points) On an island, there live knights who always tell the truth, and liars who always lie. One day, 100 residents of this island lined up, and each of them said one of the following phrases:
- "To the left of me, there are as many liars as there are knights."
- "To the left of me, there are 1 more liar than there are knights."
- "To the left of me, there are 2 more liars than there are knights."
- "To the left of me, there are 99 more liars than there are knights."
It is known that each phrase was said by exactly one person. What is the smallest number of liars that can be among these 100 residents?
|
Answer: 50.
Solution. Suppose there are no fewer than 51 knights in the row. Consider the rightmost of them. To his left, there are at least 50 knights and no more than 49 liars, so he could not have said any of the listed phrases, leading to a contradiction. Therefore, the total number of knights cannot exceed 50.
Now let's provide an example where there are exactly 50 knights. Suppose the leftmost 50 people are liars, who respectively say the phrases "To my left, there are 99 more liars than knights," "To my left, there are 98 more liars than knights," ..., "To my left, there are 51 more liars than knights," and "To my left, there are as many liars as knights." The next 50 people are knights, who respectively say "To my left, there are 50 more liars than knights," "To my left, there are 49 more liars than knights," ..., "To my left, there is 1 more liar than knights." It is clear that the liars' statements are false, as there are no more than 49 liars to the left of each of them. The statement of the leftmost knight is true, as there are 50 liars and 0 knights to his left. The statements of the subsequent knights are also true, as for each subsequent knight, the number of liars remains unchanged, while the number of knights increases by 1, i.e., the difference between liars and knights decreases by 1.
## Criteria
The points for the estimate and example are summed:
+8 p. Estimate - it is proven that there are no fewer than 50 liars.
In the absence of a correct estimate, the following progress is evaluated:
+6 p. It is proven that if there are \( k \) liars, then the phrases starting from "To my left, there are \( k+1 \) more liars than knights" to "To my left, there are 99 more liars than knights" are false.
+7 p. Example - a correct arrangement of knights and liars with the phrases they say is provided (or it is otherwise proven that such an arrangement exists).
In the absence of a correct example, the highest applicable criterion is used:
+3 p. A suitable arrangement of knights and liars is provided without specifying the phrases they say.
+5 p. An arrangement of LL...LRR...R is provided, and it is incorrectly stated that the first liar says "To my left, there are as many liars as knights."
+6 p. An arrangement of LL...LRR...R is provided, and it is not specified what the first liar says.
The following progress is not evaluated:
0 p. Only the answer is provided.
|
50
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. On side $AB$ of triangle $ABC$, a point $D$ is taken. In triangle $ADC$, the angle bisectors $AP$ and $CQ$ are drawn. On side $AC$ of triangle $ADC$, a point $R$ is taken such that $PR \perp CQ$. It is known that the angle bisector of angle $D$ of triangle $BCD$ is perpendicular to segment $PB$, $AB=18$, $AP=12$. Find $AR$. 8.
|
Solution. Let $A B=n, A P=m, A D=c, A C=b, D P=p, C P=q, B D=D P=p, C P=C R=q$.
Using the property of the angle bisector and the formula for the length of the angle bisector, we get $\left\{\begin{array}{l}\frac{c}{b}=\frac{p}{q}, \\ c+p=A B=n, \\ m^{2}=b c-p q,\end{array}\right.$
$\left\{\begin{array}{l}c=\frac{b p}{q}, \\ \frac{b p}{q}+p=n, \\ m^{2}=b \frac{b p}{q}-p q:\end{array}\left\{\begin{array}{l}c=\frac{b p}{q}, \\ b p+p q=q n, \\ m^{2}=b \frac{b p}{q}-p q,\end{array}\left\{\begin{array}{l}c=\frac{b p}{q}, \\ p=\frac{q n}{b q}, \\ m^{2}=b \frac{b}{q} \frac{q n}{b+q}-q \frac{q n}{b+q}:\end{array} m^{2}=\frac{b^{2} n}{b+q}-\frac{q^{2} n}{b+q}, m^{2}=\frac{\left(b^{2}-q^{2}\right) n}{b+q}:\right.\right.\right.$ $m^{2}=\frac{(b-q)(b+q) n}{b+q}, m^{2}=(b-q) n, b-q=\frac{m^{2}}{n}, b-q=\frac{12^{2}}{18}=8$.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Given three points $A, B, C$, forming a triangle with angles $30^{\circ}, 45^{\circ}, 105^{\circ}$. Two of these points are chosen, and the perpendicular bisector of the segment connecting them is drawn, after which the third point is reflected across this perpendicular bisector. This results in a fourth point $D$. With the resulting set of 4 points, the same procedure is carried out - two points are chosen, the perpendicular bisector is drawn, and all points are reflected across it. What is the maximum number of distinct points that can be obtained by repeatedly performing this procedure?
|
Answer: 12 points.
## Solution. FIRST WAY.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 2. Task 2*
The number 2017 has 7 ones and 4 zeros in its binary representation. When will the next year come, in which the number of the year in binary representation will have no more ones than zeros? (Enter the year.) Points for the task: 8.
#
|
# 2. Task 2*
The number 2017 has 7 ones and 4 zeros in its binary representation. When will the next year come, in which the number of the year in binary representation will have no more ones than zeros? (Enter the year.) Points for the task: 8.
## Answer: 2048
|
2048
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 7. Problem 7*
Petya came up with four different natural numbers, wrote down all their pairwise sums on the board, and in the row below, all their sums of three. It turned out that the sum of the two largest numbers in the top row and the two smallest numbers in the bottom row (a total of four numbers) is 2017. Find the largest possible value of the sum of the four numbers that Petya came up with. Points for the problem: 8.
#
|
# 7. Problem $7 *$
Petya came up with four different natural numbers, wrote down all their pairwise sums on the board, and in the row below, all their sums of three. It turned out that the sum of the two largest numbers in the top row and the two smallest numbers in the bottom row (a total of four numbers) is 2017. Find the largest possible value of the sum of the four numbers that Petya came up with. Points for the problem: 8.
## Answer: 806
#
|
806
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 8. Problem 8.10
Pentagon $A B C D E$ is circumscribed around a circle.
Angles $\angle A B C, \angle B A E, \angle C D E$ are each $104^{\circ}$. Find $\angle A D B$. Write the answer in degrees (the number only, without specifying the unit of measurement).
#
|
# 8. Problem 8.10
Pentagon $A B C D E$ is circumscribed around a circle.
Angles $\angle A B C, \angle B A E, \angle C D E$ are each $104^{\circ}$. Find $\angle A D B$. Write the answer in degrees (the number only, without the unit of measurement).
## Answer: 38
|
38
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 9. Problem 9.10
In a convex 10-gon \(A_{1} A_{2} \ldots A_{10}\), all sides and all diagonals connecting vertices every other one (i.e., \(A_{1} A_{3}, A_{2} A_{4}\), etc.) are drawn, except for the side \(A_{1} A_{10}\) and the diagonals \(A_{1} A_{9}, A_{2} A_{10}\).
We call a path leading from \(A_{1}\) to \(A_{10}\) a non-self-intersecting broken line (i.e., one in which non-adjacent segments do not have common points) with endpoints \(A_{1}\) and \(A_{10}\), each segment of which coincides with one of the drawn sides or diagonals. Find the number of such paths.
|
# 9. Problem 9.10
In a convex 10-gon $A_{1} A_{2} \ldots A_{10}$, all sides and all diagonals connecting vertices every other one (i.e., $A_{1} A_{3}, A_{2} A_{4}$, etc.) are drawn, except for the side $A_{1} A_{10}$ and the diagonals $A_{1} A_{9}, A_{2} A_{10}$.
A path from $A_{1}$ to $A_{10}$ is defined as a non-self-intersecting broken line (i.e., one where non-adjacent segments do not have common points) with endpoints $A_{1}$ and $A_{10}$, each segment of which coincides with one of the drawn sides or diagonals. Find the number of such paths.
## Answer: 55
|
55
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 1. Problem 1*
Let $S$ be the sum of the digits of the number $11^{2017}$. Find the remainder when $S$ is divided by 9. Points for the problem: 8.
## Answer: 2
#
|
# 1. Problem 1*
Let $S$ be the sum of the digits of the number $11^{2017}$. Find the remainder when $S$ is divided by 9. Points for the problem: 8.
## Answer: 2
#
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 2. Task 2*
The number 2017 has 7 ones and 4 zeros in its binary representation. When will the next year come, in which the number of the year in binary representation will have no more ones than zeros? Enter the year. Points for the task: 8.
## Answer: 2048
|
# 2. Task 2*
The number 2017 has 7 ones and 4 zeros in its binary representation. When will the next year come, in which the number of the year in binary representation will have no more ones than zeros? Enter the year. Points for the task: 8.
## Answer: 2048
|
2048
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 7. Problem $7 *$
Petya came up with four different natural numbers, wrote down all their pairwise sums on the board, and in the row below, all their sums of three. It turned out that the sum of the two largest numbers in the top row and the two smallest numbers in the bottom row (a total of four numbers) is 2017. Find the largest possible value of the sum of the four numbers that Petya came up with. Points for the problem: 8.
## Answer: 806
#
|
# 7. Problem $7 *$
Petya came up with four different natural numbers, wrote down all their pairwise sums on the board, and in the row below, all their sums of three. It turned out that the sum of the two largest numbers in the top row and the two smallest numbers in the bottom row (a total of four numbers) is 2017. Find the largest possible value of the sum of the four numbers that Petya came up with. Points for the problem: 8.
## Answer: 806
#
|
806
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Each move of a chess knight is a move of one square horizontally and two squares vertically, or vice versa - one square vertically and two squares horizontally. (In the diagram on the right, the knight marked with the letter $\mathrm{K}$ can move to any of the shaded squares in one move.)
A chess knight is placed in an arbitrary square of a rectangular board measuring $2 \times$ 2016 squares. Moving according to the described rules (and not going beyond the edges of the board), it can move from this square to some other squares on the board, but not to all. What is the minimum number of squares that need to be added to the board so that the knight can move from any square of the board to all other squares? (Adding a square is done so that it shares a common side with one of the existing squares. Any number of squares can be added, and the resulting board does not necessarily have to be rectangular).
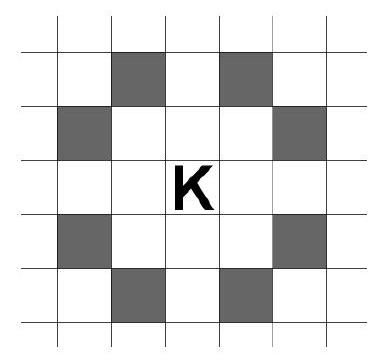
|
Answer: 2
Solution. Let's number the cells as shown in Figure 1. The knight can move from any cell to any cell with the same number, and cannot move to other cells.
| $\mathbf{2}$ | $\mathbf{3}$ | $\mathbf{1}$ | $\mathbf{4}$ | $\mathbf{2}$ | $\mathbf{3}$ | $\mathbf{1}$ | $\mathbf{4}$ | $\mathbf{2}$ | $\mathbf{3}$ | $\ldots$ |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| $\mathbf{1}$ | $\mathbf{4}$ | $\mathbf{2}$ | $\mathbf{3}$ | $\mathbf{1}$ | $\mathbf{4}$ | $\mathbf{2}$ | $\mathbf{3}$ | $\mathbf{1}$ | $\mathbf{4}$ | $\ldots$ |
Fig. 1
Thus, all cells are divided into 4 sets, such that the knight cannot jump from one set to another, but can freely move within one set.
Let's add two cells as shown in Figure 2. We will prove that now the knight can move from any cell to any other cell. Cell A "connects" the cells marked in pink, i.e., through it, one can jump from set 1 to set 4. (Being in any cell with number 1, one can reach the pink cell with number 1, then through A reach the pink cell with number 4, and from there - to any cell with number 4. In the end, from any cell with number 1, one can reach any cell with number 4 using A.)
Cell B connects the cells marked in green, i.e., through it, one can jump from any of the sets 2, 3, 4 to any of these sets.
In the end, by combining cells A and B, one can move from any set to any other set. For example, to move from set 1 to set 2, first use A to move from 1 to 4, then use B to move from 4 to 2.
| | $\mathrm{B}$ | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 2 | 3 | 1 | 4 | 2 | 3 | 1 | 4 | 2 | 3 | $\ldots$ | | | | | | | | | | | | | | | | | | | |
| 1 | 4 | 2 | 3 | 1 | 4 | 2 | 3 | 1 | 4 | $\ldots$ | | | | | | | | | | | | | | | | | | | |
Fig. 2
It remains to be convinced that one cell is not enough. From Figure 3, it is clear that all added cells are divided into two types: cells A can be reached from no more than 3 cells on the board, cells B can be reached from 4 cells, but among them, there are always two from the same set (marked with the same number). That is, a cell that can be reached from all 4 sets does not exist.
| | $A$ | $A$ | $B$ | $B$ | $\cdots$ | | | | | $\cdots$ | B | B | A | A | |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| A | $\mathbf{2}$ | $\mathbf{3}$ | $\mathbf{1}$ | $\mathbf{4}$ | $\mathbf{2}$ | $\mathbf{3}$ | $\mathbf{1}$ | $\mathbf{4}$ | $\mathbf{2}$ | $\mathbf{3}$ | $\cdots$ | $\mathbf{O}$ | $\mathbf{1}$ | $\mathbf{4}$ | A |
| A | $\mathbf{1}$ | $\mathbf{4}$ | $\mathbf{2}$ | $\mathbf{3}$ | $\mathbf{1}$ | $\mathbf{4}$ | $\mathbf{2}$ | $\mathbf{3}$ | $\mathbf{1}$ | $\mathbf{4}$ | $\cdots$ | | $\mathbf{2}$ | $\mathbf{3}$ | A |
| | A | A | B | B | $\cdots$ | | | | | $\cdots$ | B | B | A | A | |
Fig. 3
Criteria for evaluating solutions. The solution is evaluated based on the presence of three components:
a) The correct method of adding two cells is shown,
b) It is proven that with this method of adding two cells, the knight can indeed traverse the entire board,
c) It is proven that one cell is not enough.
(-) The solution does not meet any of the criteria listed below.
$(-/+)$ The solution only contains a).
(+/2) a) and b) are present, c) is missing or incorrect.
(+/-) a) and c) are present, b) is missing or incorrect.
$(+)$ a), b), and c) are present.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 5. (based on materials from the Ural Tournaments)
In triangle $ABC$, angle $B$ is $80^{\circ}$. On side $BC$, point $D$ is marked such that $AB = AD = CD$. On side $AB$, point $F$ is marked such that $AF = BD$. On segment $AC$, point $E$ is marked such that $AB = AE$. Find angle $AEF$.
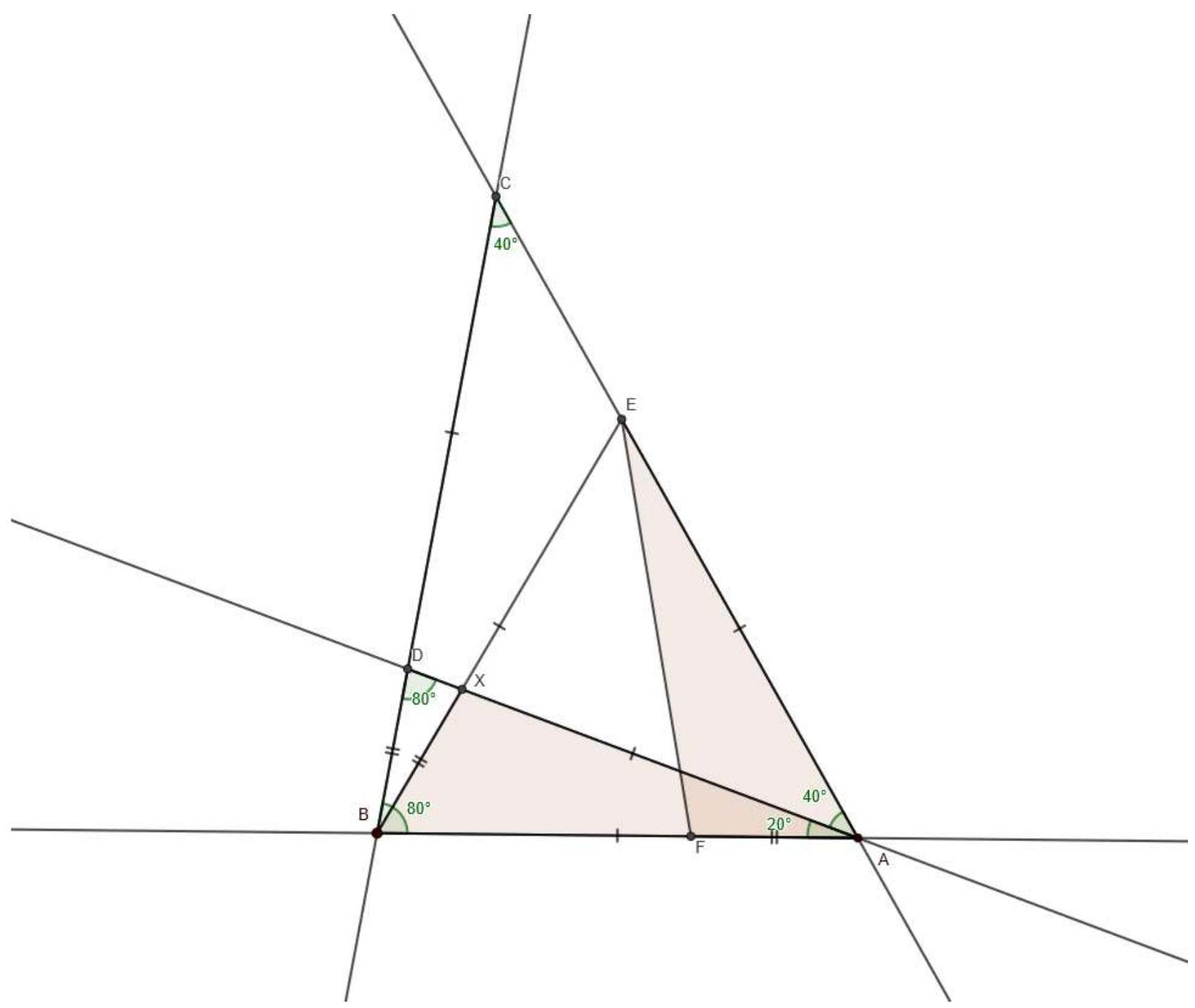
|
Answer: $20^{\circ}$. Solution:
Since $A B=A D$ we have $\angle A D B=\angle A B D=80^{\circ}$, and since $A D=D C$, we have $\angle D A C=\angle D C A=40^{\circ}$. Therefore, $\angle B A E=60^{\circ}$, hence triangle $A B E-$ is equilateral.
Then denoting by $X$ the intersection point of $A D$ and $B E$ we have $\angle B X D=\angle B A X+\angle A B X=80^{\circ}=\angle B D X$, that is, $B X=B D$.
From this it follows that triangles $A B X$ and $E A F$ are equal by two sides and the angle between them.
Thus, $\angle A E F=\angle B A X=20^{\circ}$.
Criteria: Correct solution: 15 points (+)
Found and proved the equilateral triangle: no less than 6 points (〒)
#
|
20
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 6.
There are $n$ houses in a row, painted in $k$ different colors, and for any color, there are 100 consecutive houses, among which the number of houses of this color is strictly greater than the number of houses of any other color. What is the largest $k$ for which this is possible if: a) $n=404$? b) $n=406$?
|
Answer: 202 colors in both parts. Solution:
Example for part a) with 202 colors:
Let's call a 198-block a sequence of 198 consecutive houses, where any pair of houses 99 apart is painted in a unique color (i.e., among all 404 houses, there are no other houses of that color).
Let's call a 2-block a pair of houses painted in a unique color.
Now, paint the 404 houses as follows: 2-block, 198-block, 2-block, 2-block, 198-block, 2-block
406 houses can also be painted in 202 colors by adding two houses at the end, whose color matches the last 2-block.
Estimate for part a):
For each color, there must be at least 2 houses → a maximum of 404 houses
Estimate for part b):
Suppose we could paint 406 houses in 203 colors, meaning each color was used twice.
Number the colors in the order they appear when traversing the houses, so for the $i$-th color, the houses with numbers $a_{i}$ and $b_{i}$ are painted, and $a_{i} < b_{i}$. If $a_{i} < a_{j} < b_{j} < b_{i}$, then any segment containing both houses of the $i$-th color also contains both houses of the $j$-th color.
Now, instead of painting the houses, consider a sequence of letters $a$ and $b$, where $a$ represents the houses with numbers of the form $a_{i}$ (where $b$ represents $b_{i}$).
Among the first 100 letters, there is exactly one $b$, since for the 1st color, the segment can only be from the 1st to the 100th house
(That is, the first color appears twice in this segment, while any other color appears at most once)
This means that among the first 100 letters, there are 99 $a$s. Therefore, among the letters from 100 to 199, there are at least 98 $b$s
(Since there are 98 numbers $a_{i \geq 2}$ for which $b_{i} \geq 100$, but $b_{i} \leq 199$, since $b_{i} - a_{i} \leq 99$)
Then, among the first 199 houses, there are at most 100 $a$s, so $a_{101} \geq 200$
Similarly, among the last 199 houses, there are at most 100 $b$s, so $b_{103} \leq 206$, which means
$$
200 \leq a_{101} < a_{102} < a_{103} < b_{103} \leq 206, \quad 200 \leq a_{101} < b_{101} < b_{102} < b_{103} \leq 206
$$
Now consider the hundred for $a_{102}$ and $b_{102}$.
Either it contains 206, in which case it contains $a_{103}$ and $b_{103}$, or it contains 200, in which case it also contains $a_{101}$ and $b_{101}$
Then this hundred contains two houses of another color, a contradiction
Criteria: Correct solution: 25 points (+)
Checking the correct example is not required, the example in part b) is not evaluated separately
Part a) (example plus simple estimate): 13 points $(+/ 2)$
Only example: 8 points ( (
|
202
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 1. (Folklore)
There are balls in three boxes. In the first - red ones, in the second - white ones, in the third - both red and white balls. Each box has a label: "red," "white," "mixed," but it is known that none of the labels correspond to the actual contents. Seventh-grader Sergey wants to find out which balls are in which box. To do this, he can open exactly one box and take out exactly one ball. Can he achieve his goal?
|
Answer: Yes. Solution:
Take from the box "mixed":
Red $\Rightarrow$ in the box with mixed balls red $\Rightarrow$ in the box with white balls not white and not red (then mixed) $\Rightarrow$ in the box with red balls white
Criteria: Correct solution: 15 points (+)
Non-obvious and unclear consequence of the form “in mixed red $\Rightarrow$ in red white”: 11 points ( $\pm$ )
## Problem 2
(Stern A.) On the board, a positive number is written, with which the following operations are allowed:
1) multiply by two
2) add one.
Each of the three students applied the first operation once and the second operation twice in some order. As a result, all three numbers turned out to be different, and the number obtained by the first student exceeds the number obtained by the second student by more than $60 \%$. Prove that the number obtained by the third student exceeds the number obtained by the second student by more than $30 \%$.
Solution: From $x$ you can get $2 x+2,2 x+3,2 x+4$
For $x>0: 2 x+4$ cannot be more than $60 \%$ greater than $2 x+3$ (since 1 is more than $60 \%$ of $2 x+3$)
$(2 x+2) * 160 \%<2 x+4 \Rightarrow 1.2 x<0.8 \Rightarrow x<\frac{2}{3}$
Then $(2 x+3) * 130 \%<2 x+4$
Criteria: Correct solution: 15 points (+)
Not considered the case with a different correspondence of numbers and students: 11 points ( $\pm$ )
Obtained the estimate $x<\frac{2}{3}$ : no less than 8 points $(+/ 2)$
Only matched numbers and students: 6 points (†)
## Problem 3
(Stern A.) In a right triangle $K L M$, the bisectors $K E$ and $L F$ are drawn, intersecting at point $O$. The line that bisects angle $E O L$ cuts off an isosceles triangle from the original triangle. Find the acute angles of triangle $K L M$.
Answer: $\left(45^{\circ}, 45^{\circ}\right),\left(18^{\circ}, 72^{\circ}\right),\left(\frac{270^{\circ}}{7}, \frac{360^{\circ}}{7}\right)$
Solution:
Case 1: the bisectors of two acute angles are drawn.
Let the bisector of angle $E O L$ intersect the leg $K M$ at point $T$, the leg $L M$ at point $S$, and $\angle E K M=\alpha$.
Then $\angle K O F=45^{\circ} \Rightarrow \angle S T M=\alpha+22.5^{\circ}, \angle T S M=67.5^{\circ}-\alpha$.
The triangle $S T M$ is cut off, in which there is a right angle $\Rightarrow$ if it is isosceles,
$$
\angle S T M=\angle T S M \Rightarrow \alpha+22.5^{\circ}=67.5^{\circ}-\alpha \Rightarrow \alpha=22.5^{\circ} \Rightarrow \text { the sought angles }\left(45^{\circ}, 45^{\circ}\right)
$$
Case 2: the bisector of the acute angle $L$ and the right angle $K$ is drawn.
Let the bisector of angle $E O L$ intersect the leg $K M$ at point $S$, the leg $L M$ at point $T$, and $\angle K L O=\alpha$.
Then $\angle E O L=45^{\circ}+\alpha, \angle E T O=22.5^{\circ}+\frac{3 \alpha}{2} \Rightarrow \angle T S M=67.5^{\circ}+\frac{\alpha}{2}$
Thus, the angles of the cut-off triangle $STM$ are $22.5^{\circ}+\frac{3 \alpha}{2}, 67.5^{\circ}+\frac{\alpha}{2}$, and $90^{\circ}-2 \alpha$.
Among them, there are two equal ones.
The angles $22.5^{\circ}+\frac{3 \alpha}{2}$ and $67.5^{\circ}+\frac{\alpha}{2}$ cannot be equal.
The other two equalities lead to $\alpha=9^{\circ}$ and $\alpha=\frac{135^{\circ}}{7}$, that is, to the answers $\left(18^{\circ}, 72^{\circ}\right),\left(\frac{270^{\circ}}{7}, \frac{360^{\circ}}{7}\right)$.
## Criteria:
To solve the problem, you need to consider 4 sub-cases (one in the first case and 3 in the second).
If correctly considered
one: 6 points ( $($ )
two: 8 points $(+1 / 2)$
three: 11 points $( \pm)$
all four: : 15 points (+)
## Problem 4
(Based on materials from American mathematical competitions) A proper divisor of a number is any divisor other than 1 and the number itself. Find the number of ways to color the numbers $2,3,4,5,6,7,8,9$ in three colors such that the color of each number is different from the color of any of its proper divisors. Don't forget to explain your proposed method of counting.
Answer: 432 Solution:
Color 5 and 7 (9 options)
Color $2,4,8(3 * 2 * 1=6$ options $)$
Left to color 3,6 and 9
Color 3. If 3 and 2 are the same color - 2 ways for 6 and 9 each
If different - uniquely 6 and 2 ways for 9
In total $2 * 2+2=8$ ways for $3,6,9$ and $9 * 6 * 8$ ways in total
Criteria: Correct solution: 15 points (+)
Correctly calculated the number of ways to color $2,3,6: 8$ points ( + ( $/ 2$ )
Incorrectly calculated only the number of ways to color 2,3,6 (for example, always color 2 and 3 different colors) : no more than 6 points ( $(+)$
|
432
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
26. The demand and supply functions for a good in the market are linear. Initially, equilibrium in the market was established at a price of $14 per unit of the good and a quantity of 42 units. The government decided to support producers: for this purpose, it buys any quantity of the good that producers are willing to sell at a price of $20 per unit. The good purchased by the government never reappears on the market. It is known that as a result of these purchases, the quantity of the good sold on the market increased by 12 units compared to the initial equilibrium, at
Social Studies (Economic Sphere), 10th Grade
this price, no unit of the good will be sold for more than $29. How much of the good did the government purchase?
|
Solution: demand has increased, it is necessary to find a new demand function from two points: $p 1=20$, $q 1=42+12=54 ; \quad p 2=29, \quad q 2=0 . \quad p=a-b q, \quad b=(29-20) / 54=1 / 6 ; \quad a=29$. The new demand function is $p=29-1 / 6 q: p=14, q=90$. The state will purchase 90-42=48 units
|
48
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
27. On a perfectly competitive market for a good, the market demand and market supply functions are given respectively as: $Q^{d}=60-14 P$ and $Q^{s}=20+6 P$. It is known that if the amount of labor used by a typical firm is $\mathbf{L}$ units, then the marginal product of labor is $\frac{160}{L^{2}}$. Determine how many units of labor a typical firm will hire in a competitive labor market if the equilibrium price of a unit of labor is 5 rubles.
|
Solution: find the equilibrium price of the good $60-14 P=20+6 P, P=2$. Optimal choice of the firm: MPL $x P=w ; \frac{160}{L^{2}} \times 2=5 ; \boldsymbol{L}=\boldsymbol{8}$.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Given three points $A, B, C$, forming a triangle with angles $30^{\circ}, 45^{\circ}, 105^{\circ}$. Two of these points are chosen, and the perpendicular bisector of the segment connecting them is drawn, after which the third point is reflected across this perpendicular bisector. This results in a fourth point $D$. With the resulting set of 4 points, the same procedure is repeated - two points are chosen, the perpendicular bisector is drawn, and all points are reflected across it. What is the maximum number of distinct points that can be obtained by repeatedly performing this procedure?
|
Answer: 12 points.
## Solution. FIRST WAY.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. a) Find at least two different natural numbers $n$, for each of which the number $n^{2}+2015 n$ is a perfect square of a natural number.
b) Find the number of all natural numbers $n$, for each of which the number $n^{2}+$ $2015 n$ is a perfect square of a natural number.
|
Answer. a) For example $n=496$ and $n=1007^{2}=1014049$. b) 13.
## Solution. FIRST METHOD.
Let $n^{2}+2015 n=m^{2}$. Denote $d=$ GCD $(n, 2015), n=d \nu, 2015=d r$. Then $\nu$ and $r$ are coprime, and
$$
d^{2} \nu(\nu+r)=m^{2}
$$
Since $\nu$ and $\nu+r$ are coprime, each of them must be a square of a natural number, i.e., $\nu=a^{2}, \nu+r=b^{2}$. Then $r=(b-a)(b+a)$.
a) To obtain some values of $n$, we can choose $d, a, b$ according to the above scheme. The number $d$ is a divisor of the number $2015=5 \cdot 13 \cdot 31$. For example, let's choose $d=1$. Then $r=2015=(b-a)(b+a)$. Let $b-a=1, b+a=2015$. Then $b=1008, a=1007$, and we get the first value $n=a^{2} d=1007^{2}$.
Now let's take $d=31$. Then $r=65=(b-a)(b+a)$. Let $b-a=5, b+a=13$. Then $b=9, a=4, n=a^{2} d=496$.
b) From the above reasoning, it follows that this scheme gives all solutions. Moreover, since $d$ is not divisible by the square of a prime number, different $d, a$ will correspond to different $n$. Let's count how many different $n$ can be obtained. The number $d$ is a divisor of the number $2015=5 \cdot 13 \cdot 31$. Consider 4 cases:
- $d=1$. Then $r=2015=(b-a)(b+a)$. The number 2015 has 8 different divisors, and thus can be represented in 4 ways as $2015=(b-a)(b+a)$. (Considering that $b-a<b+a$). For each such representation, both numbers $b-a, b+a$ are odd, and thus $a, b$ are uniquely determined. Knowing $a, b, d$, we can uniquely find $n=d \cdot a^{2}$. Thus, in this case, we have 4 different numbers $n$.
- $d=5,13$ or 31. Then $r$ is the product of two prime numbers and can be represented in the form $r=(b-a)(b+a)$ in two ways. Thus, we have $3 \cdot 2=6$ answers.
- $d=65,155$ or 403. Then $r$ is a prime number, and can be represented in the form $r=(b-a)(b+a)$ in a unique way. Thus, we have 3 more answers.
- $d=2015$. Then $r=1$, and the equation $r=(b-a)(b+a)$ is impossible, since $a, b$ are natural numbers.
In total, $4+6+3=13$ different numbers $n$.
## SECOND METHOD.
Let $n^{2}+2015 n=m^{2}$. Multiplying by 4 and completing the square on the left side, we transform the equation to
$$
(2 n+2015)^{2}=4 m^{2}+2015^{2} \Rightarrow(2 n-4 m+2015)(2 n+4 m+2015)=2015^{2}
$$
Denoting $2 n-4 m+2015=a, 2 n+4 m+2015=b$, we get that all sought values of $n$ are determined by the conditions
$$
a<b, a b=2015^{2}, \quad n=\frac{a+b-2 \cdot 2015}{4}
$$
a) To obtain some specific values of $n$, we can take specific factorizations $a b=2015^{2}=5^{2} \cdot 13^{2} \cdot 31^{2}$. For example, if $a=1, b=2015^{2}$, then $n=4060226$. If $a=25 \cdot 31, b=169 \cdot 31$, then $n=496$.
b) Note that for any factorization $2015^{2}=a b$, the number $n$, determined by the equation $n=\frac{a+b-2 \cdot 2015}{4}$, is an integer. This follows from the fact that $a b=2015^{2} \equiv 1(\bmod 4)$, so either $a \equiv b \equiv 1(\bmod 4)$ or $a \equiv b \equiv 3(\bmod 4)$. In both cases, $a+b \equiv 2 \equiv 2 \cdot 2015(\bmod 4)$. Thus, the number of sought numbers $n$ is equal to the number of factorizations $a b=2015^{2}, a<b$. The number $2015^{2}$ has exactly 27 different divisors. One of them is 2015, and the rest form pairs $(a, b), a<b, a b=2015^{2}$. Therefore, the number of such pairs is $\frac{27-1}{2}=13$.
Criteria.
## $(-)$
(-.) One value in part a)
$(-/+)$ Correctly solved part a)
$(+/ 2)$ or (+/-) Part a) and progress in part b) (depending on progress)
$$
(+/-)
$$
$$
\text { (+.) }
$$
$(+)$ clean solution
|
13
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (3 points) In triangle $A B C$, a square $K L M N$ with side length 1 is inscribed: points $K$ and $L$ lie on side $A C$, points $M$ and $N$ lie on sides $A B$ and $B C$ respectively. The area of the square is half the area of the triangle. Find the length of the height $B H$ of triangle $A B C$.
|
Answer: 2.
Solution 1:
$A C \cdot B H=2 S_{A B C}=4 S_{K L M N}=4$.
Points $A, L, K, C$ lie on a straight line in that exact order. Moreover, triangle $A B C$ is clearly acute. From the condition, it follows that
$$
\begin{gathered}
S_{A M L}+S_{C K N}+S_{B M N}=S_{K L M N} \\
\frac{A L \cdot 1}{2}+\frac{C K \cdot 1}{2}+\frac{(B H-1) \cdot 1}{2}=1 \\
A L+C K+B H-1=2 \\
A C-1+B H-1=2 \\
A C+B H=4=A C \cdot B H=2+\frac{A C \cdot B H}{2} . \\
2 A C+2 B H=A C+B H+4 \\
(A C-2)(B H-2)=0 \\
{\left[\begin{array}{l}
A C=2 \\
B H=2
\end{array}\right.}
\end{gathered}
$$
If only one of the equalities in this system is satisfied, then $A C \cdot B H$ will be either greater or less than 4, which is impossible. Therefore, $A C=B H=2$.
## Solution 2:
Points $A, L, K, C$ lie on a straight line in that exact order. Moreover, triangle $A B C$ is clearly acute.
On ray $L K$, take a point $X$ such that $A L=L X$. Then triangles $A M L$ and $X M L$ are equal. Similarly, on ray $K L$, take a point $Y$ such that $C K=K X$. Then triangles $C K N$ and $Y N L$ are equal. Let $Z$ be the intersection of $M X$ and $N Y$. Triangle $M N Z$ is equal to triangle $M N B$ by side $M N$ and the angles adjacent to it.
We obtain the equality:
$$
S_{K L M N}=S_{A M L}+S_{C K N}+S_{B M N}=S_{X M L}+S_{Y K N}+S_{M N Z}=S_{K L M N} \pm S_{X Y Z}
$$
where the sign $\pm$ depends on whether point $Z$ lies inside or outside triangle $A B C$. This area must be equal to 0, i.e., point $Z$ lies on $A C$. From this, the height of triangle $Z M N$, dropped from $Z$ to $M N$, is equal to the side of the square. But this height is equal to the height of triangle $B M N$, dropped from $B$ to $M N$. If we add the side of the square to this height, we get the height $B H$, from which $B H=2$.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (3 points) The rivers Stuka and Turka merge into the river Stukatura at some point. Cities $A$ and $B$ are located on the rivers Stuka and Turka, respectively, with city $A$ being twice as far from the confluence as city $B$. A steamboat takes the same amount of time to travel from $A$ to $B$ via these rivers as it does to travel from $B$ to $A$. Prove that the speeds of the currents of Stuka and Turka differ by no more than a factor of two.
|
# Solution:
Let the distance from the confluence of the rivers to city $B$ be $S$, the own speed of the steamboat be $x$, and the speeds of Shchuk and Turk be $u$ and $v$ respectively. We form the equation:
$$
\frac{2 S}{x+u}+\frac{S}{x-v}=\frac{S}{x+v}+\frac{2 S}{x-u}
$$
By canceling $S$ and moving the terms related to one city to one side, we get:
$$
\frac{1}{x-v}-\frac{1}{x+v}=\frac{2}{x-u}-\frac{2}{x+u}
$$
$$
\begin{aligned}
\frac{2 v}{x^{2}-v^{2}} & =\frac{4 u}{x^{2}-u^{2}} \\
v\left(x^{2}-u^{2}\right) & =2 u\left(x^{2}-v^{2}\right)
\end{aligned}
$$
Solving for $x^{2}$:
$x^{2}=\frac{u v(u-2 v)}{v-2 u}$.
Since $x^{2}$ and $u v$ are positive, $u-2 v$ and $v-2 u$ must have the same sign. However, they cannot both be positive, as this would imply $u>2 v>4 u$. Therefore, they must both be negative, which clearly leads to the statement of the problem.
7. (5 points) In the cells of a $5 \times 13$ table, the numbers 0, 1, and 2 are arranged such that in any $2 \times 2$ square, there are all three different numbers. What is the maximum value that the sum of the numbers in the entire table can take?
Answer: 92
## Solution:
Example:
| 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
Estimation:
Consider the top-left $2 \times 2$ square of the $5 \times 13$ rectangle. In it, there are at least two non-twos, and at least one of them is on the side or in the corner of the rectangle. Call this cell marked. By considering the other corners of the rectangle, we get at least four marked cells, i.e., cells on the boundary of the rectangle that are not twos.
The top-left and bottom-right $4 \times 12$ rectangles do not share any marked cells, so one of them contains no more than two marked cells. This rectangle can be divided into $2 \times 2$ squares, the sum of the numbers in each of which is no more than 5. Therefore, the total sum of the numbers in this rectangle is no more than 60.
Outside this $4 \times 12$ rectangle, there are 17 cells, at least two of which are marked. The sum of the numbers in these cells is no more than $15 \cdot 2 + 2 \cdot 1 = 32$. In total, we get a sum of no more than 92.
|
92
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3. Natural numbers $x_{1}, x_{2}, \ldots, x_{13}$ are such that $\frac{1}{x_{1}}+\frac{1}{x_{2}}+\ldots+\frac{1}{x_{13}}=2$. What is the minimum value that the sum of these numbers can take?
|
Answer: 85
# Examples of answer recording: 14
#
|
85
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Between cities A and B, there are three buses: a regular one, which stops in cities V, G, and D (in that order); a fast one, which stops only in city $\Gamma$; and an express, which does not stop anywhere along the way.
All buses travel on different roads at a constant speed and take an integer number of hours to travel between any two stops. The road segments between stops are straight.
The regular bus travels from A to B in 20 hours (excluding the time spent at stops). What is the maximum time (in hours) that the express bus can take to travel from A to B?
|
Answer: 17
## Examples of answer notation:
14
#
|
17
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the number of solutions of the equation $x y + 5 x + 7 y = 29$ in integers (i.e., the number of pairs of integers (x, y) that satisfy the given equality).
|
Answer: 14
## Examples of answer notation:
14
#
|
14
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Given a rectangle $\mathrm{ABCD}$. The length of side $\mathrm{BC}$ is one and a half times less than the length of side $\mathrm{AB}$. Point $\mathrm{K}$ is the midpoint of side $\mathrm{AD}$. Point $\mathrm{L}$ on side $\mathrm{CD}$ is such that $\mathrm{CL}=\mathrm{AK}$. Point $\mathrm{M}$ is the intersection of line $\mathrm{BL}$ and the perpendicular bisector of segment $\mathrm{DL}$. It is known that $\mathrm{KL}=4$. Find the length of segment $\mathrm{BM}$.
|
Answer: 8
## Examples of answer recording: 14 0.5
#
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In a watch repair shop, there is a certain number of electronic watches (more than one), displaying time in a 12-hour format (the number of hours on the watch face changes from 1 to 12). All of them run at the same speed, but show completely different times: the number of hours on the face of any two different watches is different, and the number of minutes is also different.
One day, the master added up the number of hours on the faces of all the watches, then added up the number of minutes on the faces of all the watches, and remembered the two resulting numbers. After some time, he did the same again and found that both the total number of hours and the total number of minutes had decreased by 1. What is the maximum number of electronic watches that could have been in the shop?
|
Answer: 11
## Examples of answer notation:
14
#
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. A $10 \times 10$ grid is filled with non-negative numbers. It is known that in each (vertical or horizontal) strip of 1x3, the sum of the numbers is 9. What is the maximum value that the sum of all numbers in the grid can take?
|
Answer: 306
## Examples of answer recording: 14
#
|
306
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Six children are sledding in a train formation down a hill. In how many different ways can they slide down if one of the children, who has peculiarities, believes that it is contraindicated for him to sit in even-numbered positions.
|
Answer: 360
## Examples of answer recording:
14
#
|
360
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. $\mathrm{ABCD}$ is a parallelogram with an area of $120 . \mathrm{K}$ is the midpoint of side $\mathrm{AD}, \mathrm{L}$ is the midpoint of $\mathrm{CD}$. Find the area of triangle BKL.
|
Answer: 45
## Examples of answer notation:
14
|
45
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Natural numbers a and b are such that 5 LCM $(a, b)+2$ GCD $(a, b)=120$. Find the greatest possible value of the number a.
|
Answer: 20
## Examples of answer notation:
14
|
20
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 3. (3 points)
In the country of Taxia, everyone pays as many percent in taxes as thousands of tugriks their salary amounts to. What salary is the most advantageous to have?
(Salary is measured in a positive, not necessarily integer number of tugriks)
|
Answer: 50000 tugriks
Solution:
Let's denote the salary as $x$. Then what remains after the tax deduction is $x-\frac{x^{2}}{100000}$. This is a quadratic trinomial with a negative leading coefficient, it reaches its maximum at the vertex when $x=50000$.
|
50000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 8. (5 points)
For each pair of numbers $\overline{a b b}$ and $\overline{a b b}$, where $a$ and $b$ are different digits, the GCD of these numbers was calculated. Find the greatest of these GCDs.
$\overline{a b b}$ is the standard notation for a number consisting of the digits $a, b$, and $b$ in that exact order.
Answer: 45
|
Solution:
45 is the greatest common divisor (GCD) of the numbers 585 and 855.
Note that \(a\) and \(b\) are not equal to 0, as numbers cannot start with 0.
Suppose there are two numbers for which this GCD is greater than 45. Note that \(\overline{b a b} - \overline{a b b} = 90(b - a)\) is divisible by this GCD. Divisibility by 2 and 5 is determined by the last digit, which is \(b\), and it cannot be zero, so the GCD cannot be both even and divisible by 5.
\(|a - b| \leqslant 8\), so if the GCD is not divisible by 3, it cannot be greater than \(2|a - b| \leqslant 16\) or \(5|a - b| \leqslant 40\) depending on the case we are considering.
Therefore, for the GCD to be greater than 45, it must be divisible by 3, and thus the original numbers must be divisible by 3.
For the number \(\overline{b a b}\) to be divisible by 3, the numbers \(a\) and \(b\) must give the same remainder when divided by 3. Thus, \(|a - b|\) can take the values 3 or 6, and consequently, the GCD must be a divisor of the number \(540 = 3^3 \cdot 2^2 \cdot 5\), and it still cannot contain both 2 and 5 simultaneously. If we are interested in a GCD greater than 45, it must be divisible by 9, and more specifically, by 27. This means the number \(\overline{b a b}\) must be divisible by 9. When this condition is met, the digit \(a\) almost uniquely determines the digit \(b\) according to the divisibility rule for 9.
Thus, for \(\overline{b a b}\), it makes sense to consider only the numbers 171, 252, 333, 414, 585, 666, 747, 828, 909, and 999 (some of which do not fit because \(a \neq b\), for example, 999). The remaining numbers form two arithmetic progressions with a common difference of 81 each. Since 81 is divisible by 27, it is sufficient to check that 171 and 585 are not divisible by 27, and the other numbers will also not be divisible.
Therefore, the GCD is not divisible by 27, and 45 is the greatest possible value.
## 2nd Variant
#
|
45
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 3. (3 points)
In the country of Taxia, everyone pays as many thousandths of their salary in taxes as tugriks the salary amounts to. What salary is the most advantageous to have?
(Salary is measured in a positive, not necessarily integer number of tugriks)
|
Answer: 500 tugriks
Solution:
Let the salary be $x$. Then what remains after the tax deduction is $x-\frac{x^{2}}{1000}$. This is a quadratic trinomial with a negative leading coefficient, it reaches its maximum at the vertex when $x=500$.
|
500
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 4. (3 points)
In triangle $A B C$, the median $B M$ is drawn, in triangle $M C B$ - the median $B N$, in triangle $B N A$ - the median $N K$. It turned out that $N K \perp B M$. Find $A C: B C$.
Answer: 2
#
|
# Solution:
Let $\vec{b}=\overrightarrow{C B}$ and $\vec{a}=\overrightarrow{C A}$.
$\overrightarrow{N K}=\overrightarrow{C K}-\overrightarrow{C N}=\frac{\vec{a}+\vec{b}}{2}-\frac{\vec{a}}{4}=\frac{\vec{a}+2 \vec{b}}{4}$.
$\overrightarrow{B M}=\overrightarrow{C M}-\overrightarrow{C B}=\frac{\vec{a}}{2}-\vec{b}$
$0=\overrightarrow{B M} \cdot \overrightarrow{N K}=\frac{\vec{a}^{2}-4 \vec{b}^{2}}{8}$, from which $|\vec{a}|=2|\vec{b}|$, that is, $A C: B C=2$.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 8. (5 points)
For each pair of numbers $\overline{a b b}$ and $\overline{a b a}$, where $a$ and $b$ are different digits, the GCD of these numbers was calculated. Find the greatest of these GCDs.
$\overline{a a b}$ - standard notation for a number consisting of digits $a, a$ and $b$ in exactly that order.
Answer: 18
|
Solution:
18 is the greatest common divisor (GCD) of the numbers 828 and 882.
Suppose there are two numbers for which this GCD is greater than 18. Note that $\overline{a a b}-\overline{a b a}=9(a-b)$ is divisible by this GCD. $|a-b| \leqslant 9$ so for the GCD to be greater than 9, it must contain factors from both the number 9 and $a-b$. In particular, for the GCD to be greater than 9, it must be divisible by 3, which means the original numbers are divisible by 3.
For the number $\overline{a a b}$ to be divisible by 3, the numbers $a$ and $b$ must give the same remainder when divided by 3. Therefore, $|a-b|$ can take the values 3, 6, or 9, and consequently, the GCD is a divisor of 27, 54, or 81. If we are interested in a GCD greater than 18, it must be divisible by 9, and more specifically, by 27. This means the number $\overline{a a b}$ is divisible by 9. Under this condition, by the divisibility rule for 9, the digit $a$ almost uniquely determines the digit $b$.
Thus, as $\overline{a a b}$, it makes sense to consider only the numbers 117, 225, 333, 441, 558, 666, 774, 882, 990, and 999 (some of these do not fit because $a \neq b$, in particular, 999. The remaining numbers form two arithmetic progressions with a common difference of 108 each). Since 108 is divisible by 27, it is enough to check that 117 and 558 are not divisible by 27, and the other numbers will also not be divisible.
Thus, the GCD is not divisible by 27. Therefore, 18 is the greatest option.
## 9th grade
#
|
18
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On side $AB$ of triangle $ABC$, point $D$ is marked, and on side $BC$, point $E$ is marked. Segments $CD$ and $AE$ intersect at point $L$. It turns out that $CL = CE$, $AL = DL$. The angle $ACE$ is 24 degrees. Find the degree measure of angle $ABC$.
|
Answer: 27
## Examples of answer notation:
45
#
|
27
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the store, they sell bags of apples weighing 3 kg (one bag costs 20 rubles), bags of pears weighing 4 kg (one bag costs 35 rubles), and bags of plums weighing 5 kg (one bag costs 50 rubles). Anya has 155 rubles, what is the maximum number of kg of fruit she can buy?
|
Answer: 22
## Examples of answer notation:
11
#
|
22
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 2. (3 points)
In a certain company, the $20 \%$ most useful employees perform $80 \%$ of the work. What is the smallest percentage of work that the $40 \%$ most useful employees can perform?
We will consider an employee more useful if they perform more work.
|
Answer: $85 \%$
## Solution:
$40 \%$ of the most useful employees are divided into $20 \%$ who perform $80 \%$ of the work, and the next $20 \%$ who are part of the $80 \%$ performing the remaining $20 \%$. These second $20 \%$ make up a quarter of the $80 \%$. Since they are the most useful among these $80 \%$, they perform no less than a quarter of the work of these $80 \%$, which is no less than $20 \%: 4=5 \%$ of the total work.
Therefore, $40 \%$ of the most useful employees perform no less than $85 \%$ of the total work. Equality is achieved when the $80 \%$ least useful employees work equally.
|
85
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 3. (3 points)
30 people are standing in a row, each of them is either a knight, who always tells the truth, or a liar, who always lies. They were numbered from left to right, after which each person with an odd number said: "All people with higher numbers than mine are liars," and each person with an even number said: "All people with lower numbers than mine are liars."
How many liars could there be? If there are multiple correct answers, list them in ascending order separated by semicolons.
|
# Answer: 28
## Solution:
We will prove that under the given conditions, there must be exactly two knights, and all others are liars.
Consider the people with odd numbers. If a person with an odd number $n$ is telling the truth, then the person with the odd number $n+2$ must also be telling the truth, since all people with numbers greater than his are liars. On the other hand, if the person with number $n$ is telling the truth, the person with number $n+2$, according to his statement, is also a liar. This leads to a contradiction. This means that the only person with an odd number who can be telling the truth is the one with the largest odd number, which is the second-to-last person.
Similarly, it can be proven that the only person with an even number who can be a knight is the person numbered 2.
At the same time, since the first and the last are definitely liars, the second and the second-to-last are telling the truth.
#
|
28
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 6. (3 points)
Three runners are moving along a circular track at constant equal speeds. When two runners meet, they instantly turn around and start running in opposite directions.
At some point, the first runner meets the second. After 15 minutes, the second runner meets the third for the first time. Another 25 minutes later, the third runner meets the first for the first time.
How many minutes does it take for one runner to complete the entire track?
|
# Answer: 80
## Solution:
Let the first runner meet the second, then after $a$ minutes the second runner meets the third for the first time, and after another $b$ minutes the third runner meets the first for the first time.
Let the first and second runners meet at point $A$, the second and third at point $B$, and the first and third at point $C$. Additionally, let the first runner be at point $D$ at the moment the second and third runners meet.
Then the points are arranged on the circle in the following order: $D, A, B, C$, where the first runner ran from $D$ to $A$ in $a$ minutes, the second runner ran from $A$ to $B$ in $a$ minutes, the third runner ran from $B$ to $C$ in $b$ minutes, and the first runner ran from $D$ to $C$ in $b$ minutes. These four segments together form the entire track, so it is covered in $2a + 2b$ minutes.
|
80
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 7. (4 points)
Natural numbers $a, b, c$ are such that $\operatorname{GCD}(\operatorname{LCM}(a, b), c) \cdot \operatorname{LCM}(\operatorname{GCD}(a, b), c)=200$.
What is the greatest value that $\operatorname{GCD}(\operatorname{LCM}(a, b), c)$ can take?
|
Answer: 10
## Solution:
Note that $\operatorname{LCM}(\operatorname{GCD}(x, y), z)$ is divisible by $z$, and $z$ is divisible by $\operatorname{GCD}(\operatorname{LCM}(x, y), z)$, so $\operatorname{LCM}(\operatorname{GCD}(x, y)$ is divisible by $\operatorname{GCD}(\operatorname{LCM}(x, y), z)$.
$200=2^{3} \cdot 5^{2}$ and in the second factor, each prime number enters with an exponent no less than in the first. Therefore, the maximum possible value of $\operatorname{GCD}(\operatorname{LCM}(x, y), z)$ is $2 \cdot 5=10$. This value is achieved when $x=y=10, z=20$.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The three heights of a tetrahedron are three, four, and four times greater than the radius of its inscribed sphere, respectively. How many times greater is the fourth height than the radius of the inscribed sphere?
|
Answer: 6
## Examples of answer notations:
14
$1 / 4$
#
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The AC-2016 calculator can perform two operations: taking the cube root and calculating the tangent. Initially, the number $2^{-243}$ was entered into the calculator. What is the minimum number of operations required to obtain a number greater than 1?
|
Answer: 7
## Examples of answer notation:
## 10
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the country, there are 9 cities, some of which are connected by postal flights. To send a letter from one city to another, you need to stick as many stamps on it as the number of flights required (the route with the fewest flights is used). It is known that even if two cities are not connected by a flight, it is always possible to send a letter from one to the other.
Under the New Year, the mayors of all cities sent congratulatory letters to each other. What is the maximum number of stamps they could have needed?
|
Answer: 240
## Examples of answer recording:
1000
#
|
240
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Dima took the fractional-linear function $\frac{a x+2 b}{c x+2 d}$, where $a, b, c, d-$ are positive numbers, and added it to all the remaining 23 functions that result from it by permuting the numbers $a, b, c, d$. Find the root of the sum of all these functions, independent of the numbers $a, b, c, d$.
|
Answer: -1
## Examples of answer notation:
14
$1 / 4$
$-1.4$
#
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the last digit of the integer part of the number $(\sqrt{37}+\sqrt{35})^{2016}$.
|
Answer: 1
## Examples of answer recording:
## 0
#
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. A cube is circumscribed around a sphere of radius 1. From one of the centers of the cube's faces, vectors are drawn to all other centers of the faces and vertices. The scalar products of each pair of different vectors were calculated, a total of 78. What is the sum of these scalar products?
|
Answer: 76
## 10th grade
#
|
76
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. For the function $\mathrm{f}(\mathrm{x})$, the condition $\mathrm{f}(\mathrm{f}(\mathrm{f}(\mathrm{x})))+3 \mathrm{f}(\mathrm{f}(\mathrm{x}))+9 \mathrm{f}(\mathrm{x})+27 \mathrm{x}=0$ is satisfied. Find $\mathrm{f}(\mathrm{f}(\mathrm{f}(\mathrm{f}(2))))$.
|
Answer: 162
## Examples of how to write answers:
14
$1 / 4$
$-0.25$
#
|
162
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 4. (3 points)
Petya wrote the number 11234567 on the board, and then all the numbers obtained from it by rearranging the digits, in ascending order. What was the position of the number $46753211$?
|
Answer: 12240
## Solution:
The number of a number is the quantity of numbers that are listed no later than it. The numbers listed no later than 46753211 are:
(1) Numbers starting with 1. In this case, the remaining digits can be arranged in 7! = 5040 ways.
(2) Numbers starting with 2 or 3. For each variant of the first digit, the remaining digits can be arranged in $\frac{7!}{2}$ ways. In total, this results in another 5040 numbers.
(3) Numbers starting with 41. The remaining six digits can be arranged in 6! = 720 ways.
(4) Numbers starting with 42, 43, 45, and 46 (including our number, which is the last in the list of numbers starting with 46). The remaining six digits for each variant can be arranged in $\frac{6!}{2}$ ways.
In total, we get $5040 \cdot 2 + 720 + 360 \cdot 4 = 12240$.
|
12240
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 5. (3 points)
Circles $O_{1}, O_{2}$, and $O_{3}$ are located inside circle $O_{4}$ with radius 6, touching it internally, and touching each other externally. Moreover, circles $O_{1}$ and $O_{2}$ pass through the center of circle $O_{4}$. Find the radius of circle $O_{3}$.
#
|
# Answer: 2
## Solution:
We will solve the problem in general for all cases, specifically proving that if the radius of circle $O_{4}$ is $R$, then the radius of circle $O_{3}$ is $\frac{R}{3}$.
Since circles $O_{1}$ and $O_{2}$ pass through the center of circle $O_{4}$ and are internally tangent to it, for each of them, the center of circle $O_{4}$ is diametrically opposite to the point of tangency. This means that the radius of each of them is $\frac{R}{2}$. Additionally, they touch each other at the center of circle $O_{4}$, which means that the centers of all three circles lie on the same straight line.
Now consider the triangle formed by the centers of circles $O_{1}$ and $O_{2}$ (let's call them $A$ and $B$) and the point of tangency of circles $O_{2}$ and $O_{3}$ (let's call it $C$). By symmetry, it is clear that $A C = B C$. Moreover, point $O$ (the center of circle $O_{4}$) is the midpoint of side $A B$. Therefore, triangle $O A C$ is a right triangle, with $O A = \frac{R}{2}$ and $O C = R$.
Now consider point $X$ (the center of circle $O_{3}$). It lies on segment $O C$, so triangle $O A X$ is also a right triangle. Its legs are $O A = \frac{R}{2}$ and $O X = R - r$, and the hypotenuse is $A X = \frac{R}{2} + r$, where $r$ is the desired radius of circle $O_{3}$. By the Pythagorean theorem, $\frac{R^{2}}{4} + R^{2} - 2 R r + r^{2} = \frac{R^{2}}{4} + R r + r^{2} = R^{2}$, from which $3 R r = R^{2}$ and $r = \frac{R}{3}$.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 7. (4 points)
In a $7 \times 7$ table, some cells are black, and the rest are white. In each white cell, the total number of black cells on the same row or column is written; nothing is written in the black cells. What is the maximum value that the sum of the numbers in the entire table can take?
#
|
# Answer: 168
## Solution:
The number in the white cell consists of two addends: a "horizontal" and a "vertical" one. Consider the sum of all "horizontal" addends and the sum of all "vertical" addends separately across the entire table. If we maximize each of these two sums separately, the total sum will also be the largest.
Consider the sum of the "horizontal" addends. If a row contains $x$ black cells and 7 - $x$ white cells, then the sum of the horizontal addends in this row is $x(7-x)$. This value is maximized when $x=3$ and $x=4$, and equals 12. Therefore, the maximum sum of "horizontal" addends is $7 \cdot 12=84$, and the total of all numbers is 168.
This value is achieved, for example, with a checkerboard pattern—easily verified, as each row and each column indeed contains 3 or 4 black cells.
|
168
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Given a regular hexagon $A B C D E F$, with side $10 \sqrt[4]{27}$. Find the area of the union of triangles ACE and BDF.
|
Answer: 900
## Examples of how to write answers:
14
$1 / 4$
1.4
#
|
900
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Given triangle $\mathrm{ABC}: \mathrm{BK}, \mathrm{CL}$ - angle bisectors, M - the point of their intersection. It turns out that triangle $\mathrm{AMC}$ is isosceles, one of whose angles is 150 degrees. Find what the perimeter of triangle $\mathrm{ABC}$ can be, if it is known that $\mathrm{BK}=4-2 \sqrt{3}$.
|
Answer: 4
## Examples of how to write answers:
14
$1 / 4$
0.25
#
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the number of solutions in natural numbers for the equation $(x-4)^{2}-35=(y-3)^{2}$.
|
Answer: 3
## Examples of answer notation:
14
#
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. At the hitmen convention, 1000 participants gathered, each receiving a registration number from 1 to 1000. By the end of the convention, it turned out that all hitmen, except number 1, were killed. It is known that each hitman could only kill hitmen with higher numbers, and the number of his victims could not exceed his number. What is the minimum number of hitmen who could have participated in the killings at the convention?
|
Answer: 10
## Examples of answer notation:
5
#
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the country of Aviania, there are 40 cities, some of which are connected by two-way flights. Moreover, between any two cities, there is only one reasonable air route (i.e., a route where the same flight is not used in different directions).
For each city, the air distance to the capital was calculated. It is calculated as the minimum number of flights required to fly from this city to the capital. For any two cities A and B connected by a flight, the cost of a ticket from city A to city B (and vice versa) in marks is equal to the maximum of the air distances from A and B to the capital. In particular, a ticket to the capital from any city connected to it by a direct flight costs 1 mark; all other flights departing from these cities cost 2 marks, and so on.
Petya traveled a lot in Aviania (not only by plane) and at the end of the year, it turned out that he used each air route exactly once (i.e., for any two cities A and B connected by a direct flight, he flew either from A to B or from B to A, but only in one of these directions). What is the maximum number of marks he could have spent on air travel?
|
Answer: 780.
## Examples of answer recording:
45
|
780
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Given a regular 11-gon. In how many ways can 3 diagonals be drawn in it so that every two of them intersect (inside the 11-gon)?
|
Answer: 462
## Examples of answer recording:
45
## Problem 6 (3 points).
|
462
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (2 points) Anya and Kolya were collecting apples. It turned out that Anya collected as many apples as the percentage of the total apples collected by Kolya, and vice versa, Kolya collected as many apples as the percentage of the total apples collected by Anya. How many apples did Anya collect and how many did Kolya collect?
|
Answer: 50 apples each.
Solution: If we add the two given conditions, it turns out that the total number of apples equals the total percentage. Therefore, Anya and Kolya collected a total of 100 apples. If one of them had collected more apples, they would have also collected more percentages. On the other hand, the condition states that the other would have collected more percentages. Therefore, both collected 50 apples each.
|
50
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (3 points) Point $C$ is located on the segment $A E$. On one side of the line $A E$, points $B$ and $D$ are marked such that $A B C$ is an equilateral triangle, and $C D E$ is an isosceles right triangle with a right angle at $D$. It turns out that triangle $B C D$ is isosceles with base $B C$. Find the angle $A D E$.
|
# Answer: $105^{\circ}$
Solution: The acute angles of triangle $C D E$ are each $45^{\circ}$, and the angles of triangle $A B C$ are each $60^{\circ}$. Therefore, angle $B C D$ is $75^{\circ}$. Consequently, $\angle C B D=75^{\circ}, \angle C D B=30^{\circ}$.
The altitudes of triangles $A B C$ and $B C D$, dropped to side $B C$, fall at its midpoint, meaning they are extensions of each other. Since they are also angle bisectors, $\angle A D C=\frac{\angle B D C}{2}=15^{\circ}$.
Thus, $\angle A D E=\angle A D C+\angle C D E=15^{\circ}+90^{\circ}=105^{\circ}$.
|
105
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (3 points) Given the puzzle: AB + BC + DE = FGH. Different letters represent different digits, no digit is equal to 9, and a number cannot start with 0. Find the smallest possible value of FGH.
|
Answer: 108.
## Solution:
The sum of all the digits at our disposal is 36. Therefore, AB $+\mathrm{B} \Gamma+\mathrm{DE}+$ ZHI is divisible by 9. But AB + BG + DE + ZHI $=2$ ZHI, so ZHI is divisible by 9.
The smallest three-digit number divisible by 9 is 108. Since, for example, $108=25+36+$ 47, this number fits our criteria.
|
108
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (5 points) In the cells of a $5 \times 7$ table, the numbers 1, 2, and 3 are arranged such that in any $2 \times 2$ square, there are all three different numbers. What is the smallest value that the sum of the numbers in the entire table can take?
|
Answer: 55
Solution:
Example:
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 2 | 3 | 2 | 3 | 2 | 3 | 2 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 3 | 2 | 3 | 2 | 3 | 2 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Evaluation
Consider the left upper $2 \times 2$ square of the $5 \times 7$ rectangle. In it, there are at least two non-ones, and at least one of them is on the side or in the corner of the rectangle. Let's call this cell marked. By considering the other corners of the rectangle, we get a total of at least four marked cells, i.e., cells on the boundary of the rectangle that are not ones.
The left upper and right lower $4 \times 6$ rectangles do not share any marked cells, so in one of them, there are no more than two marked cells. This rectangle can be divided into $2 \times 2$ squares, the sum of the numbers in each of which is at least 7. Therefore, the total sum of the numbers in this rectangle is at least 42.
Outside this $4 \times 6$ rectangle, there are 11 cells, at least two of which are marked. The sum of the numbers in these cells is at least $9 \cdot 1 + 2 \cdot 2 = 13$. In total, we get a sum of at least 55.
## 7th grade
## 2nd variant
|
55
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 5. (3 points)
$A B C D$ is a cyclic quadrilateral. The extension of side $A B$ beyond point $B$ and the extension of side $C D$ beyond point $C$ intersect at point $P$. The extension of side $A D$ beyond point $D$ and the extension of side $B C$ beyond point $C$ intersect at point $Q$. It turns out that angles $B P C$ and $C Q D$ are equal. It is also known that $C Q=20, D Q=12, B P=3$. Find the square of the length of diagonal $A C$. If there are multiple possible answers, list them in ascending order separated by commas or semicolons.
|
# Problem 5. (3 points)
$A B C D$ is a cyclic quadrilateral. The extension of side $A B$ beyond point $B$ and the extension of side $C D$ beyond point $C$ intersect at point $P$. The extension of side $A D$ beyond point $D$ and the extension of side $B C$ beyond point $C$ intersect at point $Q$. It turns out that angles $B P C$ and $C Q D$ are equal. It is also known that $C Q=20, D Q=12, B P=3$. Find the square of the length of diagonal $A C$. If there are multiple possible answers, list them in ascending order separated by commas or semicolons.
Answer: 1040
|
1040
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 2. (3 points)
Natural numbers $a$ and $b$ are such that $2a + 3b = \operatorname{LCM}(a, b)$. What values can the number $\frac{\operatorname{LCM}(a, b)}{a}$ take? List all possible options in ascending or descending order, separated by commas. If there are no solutions, write the number 0.
|
Answer: 0 (no solutions)
## Solution:
Let $d=\operatorname{GCD}(a, b)$. Then $a=x d, b=y d, \operatorname{LCM}(a, b)=x y d$, where $x$ and $y$ are coprime. We get $2 x d+3 y d=x y d$. Dividing by $d$ yields $2 x+3 y=x y$.
The right side of this equation is divisible by $x$, so $2 x+3 y$ is divisible by $x$, which means $3 y$ is divisible by $x$. Since $x$ and $y$ are coprime, 3 must be divisible by $x$. Therefore, $x=3$ or $x=1$. Similarly, 2 must be divisible by $y$.
If $x=3$, the equation becomes $6+3 y=3 y$, which is false. If $x=1$, we get $2+3 y=y$, from which $y$ is negative, which is also impossible.
Therefore, there are no solutions.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 4. (3 points)
Inside a pentagon, 1000 points were marked and the pentagon was divided into triangles such that each of the marked points became a vertex of at least one of them. What is the smallest number of triangles that could have resulted?
#
|
# Answer: 1003
## Solution:
The sum of the angles of a pentagon is $540^{\circ}$. The sum of the angles at each internal point is either $180^{\circ}$, if it lies on the side of one of the triangles and is the vertex of several others, or $360^{\circ}$, if angles of triangles are located on all sides. That is, the sum of the angles at each internal point is at least $180^{\circ}$.
Therefore, for a thousand points, the sum of the angles of all triangles is at least $540^{\circ} + 1000 \cdot 180^{\circ} = 1003 \cdot 180^{\circ}$. For this, we need at least 1003 triangles, since the sum of the angles in each is $180^{\circ}$.
An example where the value 1003 is achieved is constructed as follows: first, divide the pentagon into three triangles using diagonals emanating from one of the vertices. Then, mark 1000 points on one of the diagonals and connect them to the opposite vertex of the triangle for which this diagonal is a side. The triangle will be divided into 1001 parts, giving us another 1000 new triangles.
|
1003
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 5. (3 points)
In trapezoid $ABCD$ with base $AD$, the diagonals are the angle bisectors of $\angle B$ and $\angle C=110^{\circ}$. Find the degree measure of $\angle BAC$.
#
|
# Solution:
$\angle B D A=\angle C B D$ as alternate interior angles, and $\angle C B D=\angle A B D$, since $B D$ is the bisector. Therefore, triangle $B D A$ is isosceles, that is, $A B=A D$. Similarly, $C D=A D$, so our trapezoid is isosceles (equilateral) and $\angle B=\angle C=110^{\circ}$.
$$
\angle B A C=180^{\circ}-\angle B-\angle B C A=180^{\circ}-110^{\circ}-55^{\circ}=15^{\circ} .
$$
Answer: 15
|
15
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 6. (3 points)
In an $8 \times 10$ table (8 rows, 10 columns), some cells are black, and the rest are white. In each white cell, the total number of black cells in the same row is written; nothing is written in the black cells. What is the maximum value that the sum of the numbers in the entire table can take?
|
Answer: 200
## Solution:
If a row contains $x$ black cells and $10-x$ white cells, then the sum of the horizontal terms in this row is $x(10-x)$. This value is maximized when $x=5$ and equals 25. This can be understood as $x(10-x)-25=-x^{2}+10 x-25=-(x-5)^{2}$. Therefore, the maximum sum of all numbers is $8 \cdot 25=200$. An example is easily constructed.
|
200
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (3 points) On the side $AC$ of triangle $ABC$, a circle with a radius of 10 cm is constructed with $AC$ as its diameter. This circle intersects sides $AB$ and $BC$ at points $X$ and $Y$ respectively. Find $AX \cdot AB + CY \cdot BC$.
|
Answer: 400
Solution: Let point $M$ be the midpoint of side $AC$, which is also the center of the circle. Then $AB \cdot BX = BC \cdot BY = (BM + 10)(BM - 10)$. Therefore, $BX = \frac{BM^2 - 100}{AB} = \frac{2AB^2 + 2BC^2 - 400 - 400}{4AB}$. Accordingly, $AX = AB - \frac{2AB^2 + 2BC^2 - 800}{4AB} = \frac{2AB^2 - 2BC^2 + 800}{4AB}$.
Similarly, $CY = \frac{2BC^2 - 2AB^2 + 800}{4BC}$. Then $AX \cdot AB + CY \cdot BC = \frac{1600}{4} = 400$.
|
400
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (5 points) A $10 \times 10$ table is filled with zeros. In one operation, the smallest number in the table (if there are several, any one is chosen) is found, and one is added to it, as well as to all numbers in the cells adjacent to it by side or corner. What is the largest number that can appear in one of the cells of the table after 80 operations?
|
Answer: 20.
Solution: Let's call the $n$-th phase a sequence of consecutive operations applied to numbers equal to $n$. If such operations did not occur, we will say that this phase consists of zero operations. Everything starts with the zero phase.
During one phase, no number can increase by more than 4. Indeed, if we increased the number itself, then neither to it nor to its neighbors can our operation be applied during this phase, neither before nor after, since a number increased by one in some phase cannot be the minimum during the same phase. Among the neighbors of a number, no more than 4 non-adjacent ones can be chosen, so indeed, we can increase a number by no more than 4 in one phase.
Consider the first, fourth, seventh, and tenth cells in the first, fourth, seventh, and tenth rows of the table, a total of 16 cells. Note that no operation affects two of them. Therefore, to change $n$ phases, at least $16n$ operations are needed. (Important! We cannot claim that one phase lasts at least 16 operations, as some of our numbers could have been increased in previous phases)
Thus, no more than 5 phases have passed, and in each, no number could increase by more than 4. Therefore, in 80 operations, no number could become greater than 20.
The example is constructed as follows: consider the second, fourth, seventh, and tenth cells in the second, fourth, seventh, and tenth rows of the table, a total of 16 cells. We will apply operations only to them. Operations applied to one of these cells do not affect the other 15, and after applying operations to all 16 cells, all numbers in the table increase by at least 1. Meanwhile, the number in the third cell of the third row will increase by 4 each phase.
Of course, the example is not unique.
|
20
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (3 points) On the side $B C$ of triangle $A B C$ as a diameter, a circle with a radius of 20 cm is constructed. This circle intersects sides $A B$ and $A C$ at points $X$ and $Y$ respectively. Find $B X \cdot A B + C Y \cdot A C$.
|
Answer: 1600
Solution: Let point $M$ be the midpoint of side $B C$, which is also the center of the circle. Then $A B \cdot A X = A C \cdot A Y = (A M + 20)(A M - 20)$. Therefore, $A X = \frac{A M^{2} - 400}{A B} = \frac{2 A B^{2} + 2 A C^{2} - 1600 - 1600}{4 A B}$. Accordingly, $B X = A B - \frac{2 A B^{2} + 2 A C^{2} - 3200}{4 A B} = \frac{2 A B^{2} - 2 A C^{2} + 3200}{4 A B}$.
Similarly, $C Y = \frac{2 A C^{2} - 2 A B^{2} + 3200}{4 A C}$. Then $B X \cdot A B + C Y \cdot A C = \frac{6400}{4} = 1600$.
|
1600
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (5 points) A $7 \times 7$ table is filled with zeros. In one operation, the smallest number in the table (if there are several, any one is chosen) is found, and one is added to it, as well as to all numbers in the cells adjacent to it by side or corner. What is the largest number that can appear in one of the cells of the table after 90 operations?
Answer: 40.
|
Solution: Let's call the $n$-th phase a sequence of consecutive operations applied to numbers equal to $n$. If such operations did not occur, we will say that this phase consists of zero operations. Everything starts with the zero phase.
During one phase, no number can increase by more than 4. Indeed, if we increased the number itself, then neither to it nor to its neighbors can our operation be applied during this phase, neither before nor after, since a number increased by one in some phase cannot be the minimum during the same phase. Among the neighbors of a number, no more than 4 non-adjacent ones can be chosen, so indeed, we can increase a number by no more than 4 in one phase.
Consider the first, fourth, and seventh cells in the first, fourth, and seventh rows of the table, a total of 9 cells. Note that no operation affects two of them. Therefore, to change $n$ phases, at least $9n$ operations are needed. (Important! We cannot claim that one phase lasts at least 9 operations, as some of our numbers could have been increased in previous phases.)
Thus, no more than 10 phases have passed, and in each, no number could have increased by more than 4. Therefore, in 90 operations, no number could have become greater than 40.
The example is constructed as follows: consider the second, fourth, and sixth cells in the second, fourth, and sixth rows of the table, a total of 9 cells. We will apply operations only to them. Operations applied to one of these cells do not affect the other 8, and after applying operations to all 9 cells, all numbers in the table increase by at least 1. At the same time, the number in the third cell of the third row will increase by 4 in each phase.
Of course, the example is not unique.
|
40
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (2 points) Find the minimum value of the expression $x^{2}+4 x \sin y-4 \cos ^{2} y$.
|
Answer: -4.
Solution: Add and subtract $4 \sin ^{2} y$. We get the expression $x^{2}+4 x \sin y+4 \sin ^{2} y-4=(x+2 \sin y)^{2}-4$. It is clear that this expression has a minimum value of -4.
Idea of Solution 2: To find the minimum value, we can take the derivatives of this expression with respect to $x$ and $y$ and find the point where both these derivatives are zero. The derivative with respect to $x$ is zero when $x=-2 \sin y$.
The derivative with respect to $y$ is $4 x \cos y+8 \sin y \cos y$. It is zero in two cases: when $x=-2 \sin y$ and when $\cos y=0$. After this, it is necessary to determine which of these points are indeed local minima and why a global minimum exists.
A rigorous proof of this in terms of derivatives unfortunately goes beyond the school curriculum, so for school students, this solution can serve more as a hint to the answer and to the solution presented above.
|
-4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (3 points) Let $x_{1}, x_{2}, \ldots, x_{100}$ be natural numbers greater than 1 (not necessarily distinct). In a $100 \times 100$ table, the numbers are arranged as follows: at the intersection of the $i$-th row and the $k$-th column, the number $\log _{x_{k}} \frac{x_{i}}{4}$ is written. Find the smallest possible value of the sum of all numbers in the table.
|
Answer: -10000
Solution: $\log _{x_{k}} \frac{x_{i}}{4}=\log _{x_{k}} x_{i}-\log _{x_{k}}$ 4. Add the minuend to the similar minuend in the symmetric cell: $\log _{x_{k}} x_{i}+\log _{x_{i}} x_{k}=\log _{x_{k}} x_{i}+\frac{1}{\log _{x_{k}} x_{i}} \geqslant 2$, since this logarithm is positive. If $i=k$, then this logarithm
equals one.
Thus, the sum of the minuends in all expressions $\log _{x_{k}} x_{i}-\log _{x_{k}} 4$ is no less than the number of cells, i.e., $100^{2}$. The subtrahends are maximized when $x_{k}=2$ is minimal and equal to 2. Therefore, the sum of the numbers in the entire table is no less than $100^{2}(1-2)=-100^{2}$, and equality is achieved when all $x_{k}=2$.
|
-10000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (2 points) Find the minimum value of the expression $x^{2}-6 x \sin y-9 \cos ^{2} y$.
|
Answer: -9.
Solution: Add and subtract $9 \sin ^{2} y$. We get the expression $x^{2}-6 x \sin y+9 \sin ^{2} y-9=(x-3 \sin y)^{2}-9$. It is clear that this expression has a minimum value of -9.
Idea of Solution 2: To find the minimum value, we can take the derivatives of this expression with respect to $x$ and $y$ and find the point where both these derivatives are zero. The derivative with respect to $x$ is zero when $x=3 \sin y$.
The derivative with respect to $y$ is $-6 x \cos y+18 \sin y \cos y$. It is zero in two cases: when $x=3 \sin y$ and when $\cos y=0$. After this, it is necessary to determine which of these points are indeed local minima and why a global minimum exists.
A rigorous proof of this in terms of derivatives unfortunately goes beyond the school curriculum, so for school students, this solution can serve more as a hint to the answer and to the solution presented above.
|
-9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (2 points) Find the minimum value of the expression $4 x^{2}+4 x \sin y-\cos ^{2} y$.
|
Answer: -1.
Solution: Add and subtract $\sin ^{2} y$. We get the expression $4 x^{2}+4 x \sin y+\sin ^{2} y-1=(x+2 \sin y)^{2}-1$. It is clear that this expression has a minimum value of -1.
Idea of Solution 2: To find the minimum value, we can take the derivatives of this expression with respect to $x$ and $y$ and find the point where both these derivatives are zero. The derivative with respect to $x$ is zero when $2 x=-\sin y$.
The derivative with respect to $y$ is $4 x \cos y-2 \sin y \cos y$. It is zero in two cases: when $x=-2 \sin y$ and when $\cos y=0$. After this, it is necessary to determine which of these points are indeed local minima and why a global minimum exists.
A rigorous proof of this in terms of derivatives unfortunately goes beyond the school curriculum, so for school students, this solution can serve more as a hint to the answer and to the solution presented above.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (3 points) Let $x_{1}, x_{2}, \ldots, x_{200}$ be natural numbers greater than 2 (not necessarily distinct). In a $200 \times 200$ table, the numbers are arranged as follows: at the intersection of the $i$-th row and the $k$-th column, the number $\log _{x_{k}} \frac{x_{i}}{9}$ is written. Find the smallest possible value of the sum of all numbers in the table.
|
Answer: -40000
Solution: $\log _{x_{k}} \frac{x_{i}}{4}=\log _{x_{k}} x_{i}-\log _{x_{k}}$ 9. Add the minuend with the similar minuend in the symmetric cell: $\log _{x_{k}} x_{i}+\log _{x_{i}} x_{k}=\log _{x_{k}} x_{i}+\frac{1}{\log _{x_{k}} x_{i}} \geqslant 2$, since this logarithm is positive. If $i=k$, then this logarithm equals one.
Thus, the sum of the minuends in all expressions $\log _{x_{k}} x_{i}-\log _{x_{k}} 9$ is no less than the number of cells, i.e., $200^{2}$. The subtrahends are maximized when $x_{k}=3$ is minimal and equal to 2. Therefore, the sum of the numbers in the entire table is no less than $200^{2}(1-2)=-200^{2}$, and equality is achieved when all $x_{k}=3$.
|
-40000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (3 points) Let $x_{1}, x_{2}, \ldots, x_{100}$ be natural numbers greater than 1 (not necessarily distinct). In an $80 \times 80$ table, the numbers are arranged as follows: at the intersection of the $i$-th row and the $k$-th column, the number $\log _{x_{k}} \frac{x_{i}}{16}$ is written. Find the smallest possible value of the sum of all numbers in the table.
|
Answer: -19200
Solution: $\log _{x_{k}} \frac{x_{i}}{16}=\log _{x_{k}} x_{i}-\log _{x_{k}}$ 16. Add the minuend with the similar minuend in the symmetric cell: $\log _{x_{k}} x_{i}+\log _{x_{i}} x_{k}=\log _{x_{k}} x_{i}+\frac{1}{\log _{x_{k}} x_{i}} \geqslant 2$, since this logarithm is positive. If $i=k$, then this logarithm
equals one.
Thus, the sum of the minuends in all expressions $\log _{x_{k}} x_{i}-\log _{x_{k}} 16$ is no less than the number of cells, i.e., $80^{2}$. The subtrahends are maximal when $x_{k}=2$ and equal 4. Therefore, the sum of the numbers in the entire table is no less than $80^{2}(1-4)=-80^{2} \cdot 3=-19200$ and equality is achieved when all $x_{k}=2$.
|
-19200
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (2 points) Among six different quadratic trinomials that differ by the permutation of coefficients, what is the maximum number that can have no roots?
|
Answer: 6
Solution:
Consider, for example, the coefficients 1000, 1001, 1002. The square of any of them is obviously less than the quadruple product of the other two, so all discriminants will be negative.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (3 points) Equilateral triangles $A B C$ and $A_{1} B_{1} C_{1}$ with side length 10 are inscribed in the same circle such that point $A_{1}$ lies on the arc $B C$, and point $B_{1}$ lies on the arc $A C$. Find $A A_{1}^{2}+B C_{1}^{2}+C B_{1}^{2}$.
|
Answer: 200
Solution:
Notice that the arcs $A B_{1}, B A_{1}$, and $C C_{1}$ are equal. Let their degree measure be $2 \alpha$. Then the lengths of the arcs $A C_{1}=B B_{1}=C A_{1}=120^{\circ}-2 \alpha$.
By the Law of Sines in triangle $A C A_{1}$, we get $\frac{A A_{1}}{\sin A C A_{1}}=$ $\frac{A C}{A A_{1} C}$, from which $A A_{1}=\frac{12 \sin \left(60^{\circ}+\alpha\right)}{\sin 60^{\circ}}$.
Similarly, $B B_{1}=\frac{10 \sin \left(60^{\circ}-\alpha\right)}{\sin 60^{\circ}}$ and $C C_{1}=\frac{12 \sin \alpha}{\sin 60^{\circ}}$.
$$
\begin{aligned}
& \left.A A_{1}^{2}+B B_{1}^{2}+C C_{1}^{2}=\frac{10^{2}}{\sin ^{2} 60^{\circ}}\left(\sin ^{2}\left(60^{\circ}+\alpha\right)+\sin ^{2}\left(60^{\circ}-\alpha\right)+\sin ^{2} \alpha\right)\right)= \\
& =\frac{200}{3} \cdot\left(\left(\frac{\sqrt{3}}{2} \cos \alpha+\frac{1}{2} \sin \alpha\right)^{2}+\left(\frac{\sqrt{3}}{2} \cos \alpha-\frac{1}{2} \sin \alpha\right)^{2}+\sin ^{2} \alpha\right)= \\
& =\frac{200}{3}\left(3 \cos ^{2} \alpha+3 \sin ^{2} \alpha\right)=200
\end{aligned}
$$
|
200
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (4 points) For February 23, the boy Zhenya was given a chocolate bar of size $3 \times 3$, on each piece of which a unique picture is drawn, with each picture appearing only once. In each move, Zhenya can bite off one piece that has no more than three common sides with other pieces that have not yet been eaten. In how many ways can Zhenya eat his chocolate bar?
Answer: $\frac{4}{5} \cdot 9!=290304$.
|
Solution:
If Zhenya had no restrictions, he could eat the pieces in any order, and he would have $9!=362880$ ways.
Not suitable are the ways in which the central cell is eaten before any of the four adjacent to it. Since for each of these five cells, there is an equal number of options where it is earlier than the others, every fifth option is not suitable. This leaves $\frac{4}{5} \cdot 9!=290304$.
## Open Mathematics Olympiad for School Students
March 11, 2018
## 9th grade 2nd variant Solutions
|
290304
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (2 points) Among six different quadratic trinomials that differ by the permutation of coefficients, what is the maximum number that can have two distinct roots
|
Answer: 6
Solution: Let's take, for example, the coefficients, $-5,1,2$.
If the number -5 is the leading coefficient or the constant term, the equation obviously has two roots of different signs.
For the case when -5 is the second coefficient, let's calculate the discriminant: $5^{2}-1 \cdot 2=23>0$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (3 points) Equilateral triangles $A B C$ and $A_{1} B_{1} C_{1}$ with side length 12 are inscribed in circle $S$ such that point $A$ lies on arc $B_{1} C_{1}$, and point $B$ lies on arc $A_{1} B_{1}$. Find $A A_{1}^{2}+B B_{1}^{2}+C C_{1}^{2}$.
|
Answer: 288
Solution:
Notice that the arcs $A B_{1}, B A_{1}$, and $C C_{1}$ are equal. Let their degree measure be $2 \alpha$. Then the lengths of the arcs $A C_{1}=B B_{1}=C A_{1}=120^{\circ}-2 \alpha$.
By the Law of Sines in triangle $A C A_{1}$, we get $\frac{A A_{1}}{\sin A C A_{1}}=$ $\frac{A C}{A A_{1} C}$, from which $A A_{1}=\frac{12 \sin \left(60^{\circ}+\alpha\right)}{\sin 60^{\circ}}$.
Similarly, $B B_{1}=\frac{12 \sin \left(60^{\circ}-\alpha\right)}{\sin 60^{\circ}}$ and $C C_{1}=\frac{12 \sin \alpha}{\sin 60^{\circ}}$.
$$
\left.A A_{1}^{2}+B B_{1}^{2}+C C_{1}^{2}=\frac{12^{2}}{\sin ^{2} 60^{\circ}}\left(\sin ^{2}\left(60^{\circ}+\alpha\right)+\sin ^{2}\left(60^{\circ}-\alpha\right)+\sin ^{2} \alpha\right)\right)=
$$
$$
=96 \cdot\left(\left(\frac{\sqrt{3}}{2} \cos \alpha+\frac{1}{2} \sin \alpha\right)^{2}+\left(\frac{\sqrt{3}}{2} \cos \alpha-\frac{1}{2} \sin \alpha\right)^{2}+\sin ^{2} \alpha\right)=
$$
$=96\left(3 \cos ^{2} \alpha+3 \sin ^{2} \alpha\right)=288$.
|
288
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.