problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
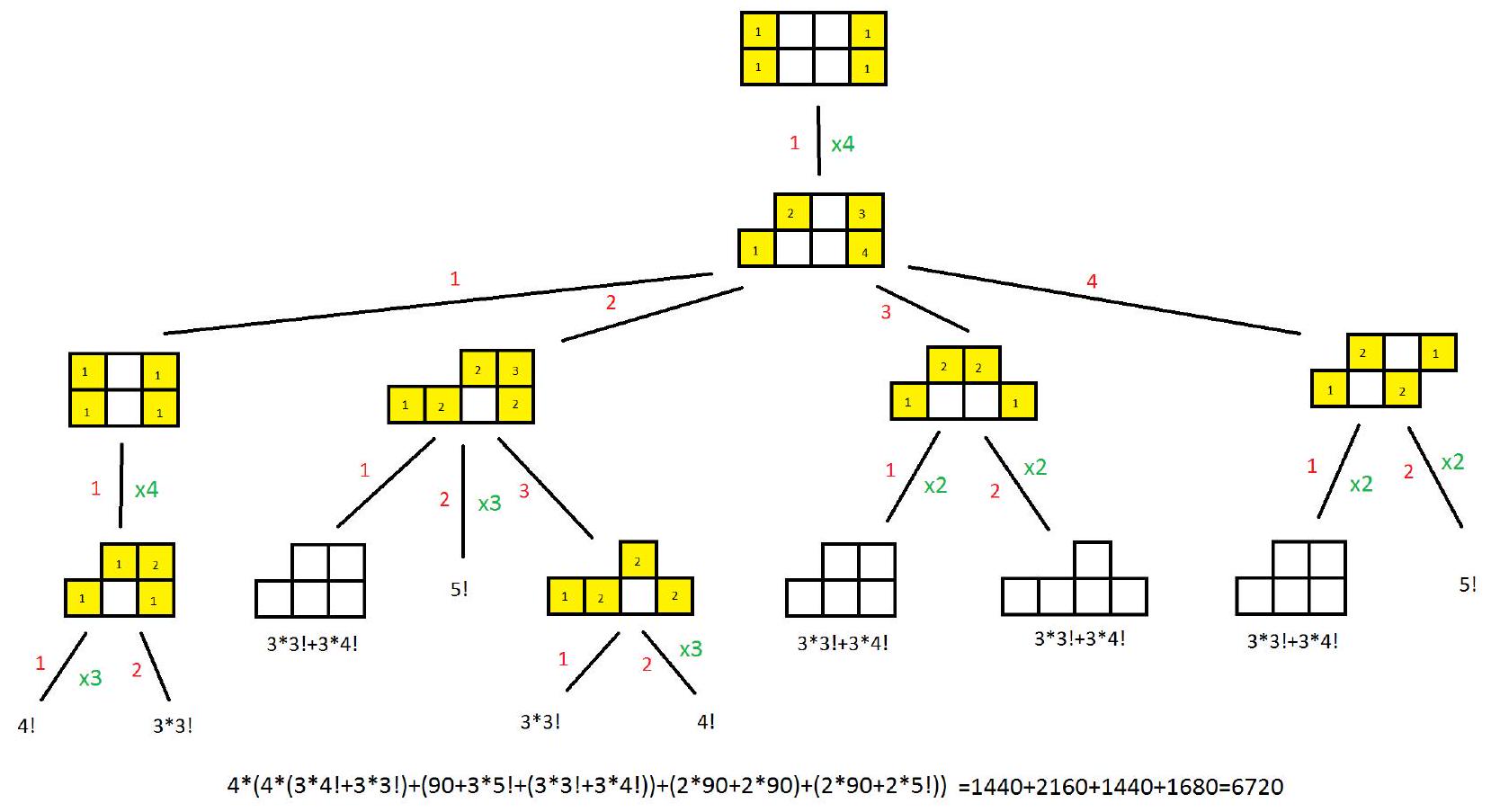
8. (4 points) For Valentine's Day, the boy Zhenya was given a chocolate bar of size $2 \times 4$, on each piece of which a unique picture is drawn. In each move, Zhenya can bite off one piece that has no more than two common sides with other pieces that have not yet been eaten. In how many ways can Zhenya eat his chocolate bar?
|
Answer: 6720.
## Solution:
The first cell to be eaten is necessarily a corner cell (4 ways). After this, there are 4 options:
1) The second cell to be eaten is the adjacent corner cell (1 way). A $2 \times 3$ rectangle remains. From this, the first cell to be eaten is again a corner cell (4 ways). After this, one cell remains inaccessible.
1.1) The fourth cell to be eaten is the only cell not adjacent to the inaccessible cell (1 way). Then, the cell adjacent to the inaccessible cell is eaten (3 ways). The remaining 3 cells can be eaten in any order (3! ways). In total, $4 \cdot 1 \cdot 4 \cdot 1 \cdot 3 \cdot 3! = 288$ ways.
1.2) The fourth cell to be eaten is adjacent to the inaccessible cell (3 ways). The remaining 4 cells can be eaten in any order (4! ways). In total, $4 \cdot 1 \cdot 4 \cdot 3 \cdot 4! = 1152$ ways.
In total, 1440 ways for case 1).
2) The second cell to be eaten is an adjacent non-corner cell (1 way). After this, one cell remains inaccessible, with three adjacent cells.
2.1) The third cell to be eaten is one of the three cells adjacent to the inaccessible cell (3 ways). Then, all cells can be eaten in $5!$ ways. In total, $4 \cdot 1 \cdot 3 \cdot 5! = 1440$ ways.
2.2) The third cell to be eaten is not adjacent to the inaccessible cell (2 ways).
2.2.1) The fourth cell to be eaten is one of the three cells adjacent to the inaccessible cell (3 ways). Then, all cells can be eaten in 4! ways. In total, $4 \cdot 1 \cdot 2 \cdot 3 \cdot 4! = 576$ ways.
2.2.2) The fourth cell to be eaten is not adjacent to the inaccessible cell (1 way). Then, one of the cells adjacent to the inaccessible cell is eaten (3 ways). Then, all cells can be eaten in $3!$ ways. In total, $4 \cdot 1 \cdot 2 \cdot 1 \cdot 3 \cdot 3! = 144$ ways.
In total, 2160 ways for case 2).
3) The second cell to be eaten is a corner cell on the same long side as the already eaten one. After this, two cells remain inaccessible, each with three adjacent cells. Further reasoning is similar to case 1). In the end, the same 1440 ways.
4) The second cell to be eaten is the cell opposite the eaten one (1 way).
4.1) If after this we eat a corner cell, we are left with a figure identical to case 1), which can be eaten in $3 \cdot 4! + 3 \cdot 3!$ ways. This number must be multiplied by 8, resulting in 720 ways.
4.2) If a non-corner cell is eaten, all cells become accessible and can be eaten in 5! ways. In total, $4 \cdot 1 \cdot 2 \cdot 5! = 960$ ways.
In total, 1680 ways for case 4).
In total, 6720 ways.
|
6720
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. What is the greatest value that the sum $\sin ^{2} a+\sin ^{2}\left(a+60^{\circ}\right)+\sin ^{2}\left(a+120^{\circ}\right)+\ldots+\sin ^{2}\left(a+300^{\circ}\right)$ can take?
|
Answer: 3
## Examples of how to write the answer:
1,7
$1 / 7$
17
#
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. All seven-digit numbers consisting of different digits from 1 to 7 were listed in ascending order. What is the position of the number 3241765?
|
Answer: 1590
## Examples of how to write the answer:
1,7
#
|
1590
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. What integer can be written in the form $\sqrt{12-\sqrt{12-\sqrt{12-\ldots}}}$ (the number of roots is infinite).
|
Answer: 3
## Examples of how to write the answer:
1,7
#
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On a unit cube, a vector was drawn along each edge in one of the two possible directions. On each face, one diagonal was chosen and a vector was drawn along it in one of the two possible directions, and the 6 drawn diagonals turned out to be non-parallel. In total, 18 vectors were obtained. What is the maximum value that the square of the sum of these vectors can take?
|
Answer: 116
## Examples of how to write the answer:
## 1,7
$1 / 7$
17
#
|
116
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In a $13 \times 13$ grid, numbers are arranged such that the numbers in each row and each column form an arithmetic progression in the order they are written. The grid is colored in two colors in a checkerboard pattern. The numbers on the corner white cells of the grid are $1, 2, 3,$ and $6$. Find the sum of the numbers on the black cells of the grid.
|
Answer: 252
## Examples of how to write the answer:
1,7
#
|
252
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. At a rock festival, vocalists, guitarists, and drummers met, a total of 121 people. Each vocalist gave a slap on the back of each guitarist, each guitarist gave a slap on the back of each drummer, and each drummer gave a slap on the back of each vocalist. What is the maximum number of slaps on the back that the participants of the festival could have received?
|
Answer: 4880.
## Examples of how to write the answer:
17
#
|
4880
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. A 101-gon is inscribed in a circle with diameter $\mathrm{XY}=6$ and has an axis of symmetry perpendicular to this diameter. Find the sum of the squares of the distances from the vertices of the 101-gon to the point $\mathrm{X}$.
|
Answer: 1818
## Examples of how to write the answer:
#
|
1818
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Around a circle, 300 (not necessarily integer) numbers from 20 to 400 inclusive were written. From each number, the logarithm to the base of the next number in the clockwise direction was taken, and then all the obtained logarithms were summed. What is the greatest value that the sum of these logarithms can take?
|
Answer: 375
## Examples of how to write the answer:
## Grade 9
#
|
375
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Four different numbers $a, b, c, d$, greater than one and not divisible by 5, are such that $\operatorname{GCD}(a, b)=\operatorname{GCD}(c, d)$ and $\operatorname{LCM}(a, b)=\operatorname{LCM}(c, d)$. What is the smallest possible value of $a+b+c+d$?
|
Answer: 24
## Examples of how to write the answer:
17
|
24
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The fox builds "pyramids" from 5 cubes in the following way: each "pyramid" consists of one or several levels; on each level, the number of cubes is strictly less than on the previous one; each new level consists of one or several consecutive cubes. You can see an example of a "pyramid" made of ten cubes in the picture:
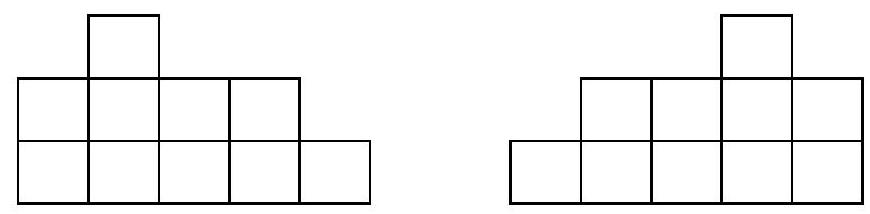
How many different "pyramids" can the fox build?
(It is important where the right edge and the left edge of the "pyramid" are — the "pyramids" in the picture are different).
|
Answer: 7
## Examples of answer notation:
12
#
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. $A B C D E$ - a pentagon inscribed in circle $S$. Lines $D E$ and $A B$ are parallel, $B C=C D$, $A D=D E=20, B C: B D=4: 5$. Find the radius of circle $S$.
|
Answer: 16
## Examples of how to write answers: $1 / 4$ 0.25
#
|
16
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. $A B D E, B C E F, C D F A$ - cyclic quadrilaterals with the intersection points of the diagonals $K, L$ and $M$ respectively. It is known that point $K$ lies on segments $B L$ and $A M$, point $M$ - on segment $C L$. Moreover, $E L=F L=K L=5, D M=4, A K=M K=6$. Find the length of segment $M C$. If there are multiple possible answers, list them in any order separated by a semicolon.
|
Answer: 4
## Examples of how to write answers:
$1 / 4$
0.25
$4 ; 10$
#
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Given two quadratic trinomials with the leading coefficient $\frac{\sqrt{3}}{8}$. The vertices and the intersection point of their graphs form an equilateral triangle. Find the length of its side. If there are multiple possible answers, list them in any order separated by a semicolon.
|
Answer: 16
## Examples of answer notations:
$1 / 4$
$-0.25 ; 10$
8th grade.
|
16
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 9. (4 points)
$A B C D$ is a cyclic quadrilateral. The extension of side $A B$ beyond point $B$ and the extension of side $C D$ beyond point $C$ intersect at point $P$. The extension of side $A D$ beyond point $D$ and the extension of side $B C$ beyond point $C$ intersect at point $Q$. It turns out that angles $B P C$ and $C Q D$ are equal. It is also known that $C Q=20, D Q=12, B P=3$. Find the square of the length of diagonal $A C$. If there are multiple possible answers, list them in ascending order separated by commas or semicolons.
|
# Problem 9. (4 points)
$A B C D$ is a cyclic quadrilateral. The extension of side $A B$ beyond point $B$ and the extension of side $C D$ beyond point $C$ intersect at point $P$. The extension of side $A D$ beyond point $D$ and the extension of side $B C$ beyond point $C$ intersect at point $Q$. It turns out that angles $B P C$ and $C Q D$ are equal. It is also known that $C Q=20, D Q=12, B P=3$. Find the square of the length of diagonal $A C$. If there are multiple possible answers, list them in ascending order separated by commas or semicolons.
Answer: 1040
|
1040
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. (1 point)
Find the largest three-digit number ABC that is divisible by the two-digit numbers AB and BC. (Different letters do not necessarily represent different digits)
|
Answer: 990
Solution:
The number 990 clearly fits. A larger answer is not possible, as all three-digit numbers greater than 990 do not divide by 99: the next number divisible by 99 is 1089.
#
|
990
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 3. (2 points)
What is the maximum number of different reduced quadratic equations that can be written on the board, given that any two of them have a common root, but no four have a root common to all.
|
Answer: 3
Solution:
Consider three such equations. There are two cases:
1) These equations have a common root $a$. Then they can be represented in the form $(x-a)(x-b)=0, (x-a)(x-c)=0$ and $(x-a)(x-d)=0$, where $b, c$ and $d$ are their remaining roots (they are not equal to each other, otherwise the equations coincide; one of these numbers can coincide with $a$, which is not important).
The fourth equation cannot have the root $a$; then it must have the roots $b, c$ and $d$ simultaneously, which means it is not quadratic.
We get a contradiction.
2) The equations do not have a common root. Then they can be represented as $(x-a)(x-b)=0$, $(x-a)(x-c)=0$ and $(x-b)(x-c)=0$. In this case, the fourth equation can only have one of the roots $a, b$ and $c$, otherwise it coincides with one of the previously described.
If it has a root, for example, $a$, then it cannot have a common root with $(x-$ $b)(x-c)=0$. Again, we get a contradiction.
Therefore, there cannot be more than three different equations.
An example can easily be constructed for the first case by taking arbitrary numbers $a, b, c, d$.
#
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 5. (3 points)
In trapezoid $ABCD$, a point $X$ is taken on the base $AD$ such that segments $XB$ and $XC$ divide the trapezoid into three triangles that are similar to each other but pairwise unequal and non-isosceles. The side $AB$ has a length of 6. Find $AX \cdot DX$.
|
Answer: 36
## Solution:
The triangles are scalene, meaning all their angles are different.
$\alpha=\angle B X A=\angle X B C \neq \angle B X C=\beta$. The angle $\angle C X D$ together with these angles sums to $180^{\circ}$, so it is the third angle of the triangle and cannot be equal to either $\alpha$ or $\beta$.
If $\angle A B X=\beta$, we get equal angles around the common side in triangles $A B X$ and $C B X$, meaning these triangles are congruent. This contradicts the condition, so $\angle A B X=\gamma$, and accordingly, $\angle B A D=\beta$.
Similarly, we get $\angle X C D=\alpha$ and $\angle X D C=\beta$, from which the trapezoid is isosceles.
Now, let's write the ratio of the sides in similar triangles $A B X$ and $C D X$:
$$
\frac{D X}{C D}=\frac{A B}{A X}
$$
from which $D X \cdot A X=A B \cdot C D=36$.
|
36
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 1. (2 points)
Find the smallest three-digit number ABC that is divisible by the numbers AB and BC (the digit A cannot be 0, and the digit B can be; different letters do not necessarily represent different digits)
|
Answer: 110
Solution:
The number 110 clearly fits. A smaller answer cannot be, as all three-digit numbers less than 110 start with 10. At the same time, none of them are divisible by 10, except for 100, and 100 is not divisible by 0.
|
110
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 3. (2 points)
What is the maximum number of different reduced quadratic equations that can be written on the board, given that any two of them have a common root, but no five have a root common to all.
|
Answer: 4
## Solution:
Consider 4 such equations. There are two cases:
1) These equations have a common root $a$. Then they can be represented in the form $(x-a)(x-b)=0,(x-a)(x-c)=0,(x-a)(x-d)=0$ and $(x-a)(x-e)=0$, where $b, c, d$ and $e$ are their remaining roots (they are not equal to each other, otherwise the equations coincide; one of these numbers can coincide with $a$, which is not important).
The fifth equation cannot have the root $a$; then it must have the roots $b, c, d$ and $e$ simultaneously, which means it is not quadratic. This leads to a contradiction.
2) The equations do not have a common root. Then three of them can be represented as $(x-$ $a)(x-b)=0,(x-a)(x-c)=0$ and $(x-b)(x-c)=0$. In this case, the fourth equation can only have one of the roots $a, b$ and $c$, otherwise it coincides with one of the previously described equations.
If it has a root, for example, $a$, then it cannot have a common root with $(x-$ b) $(x-c)=0$. Again, we get a contradiction. Therefore, in this case, there cannot be more than three different equations.
An example can easily be constructed for the first case by taking arbitrary numbers $a, b, c, d$ and $e$.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 5. (3 points)
In trapezoid $ABCD$, a point $X$ is taken on the base $BC$ such that segments $XA$ and $XD$ divide the trapezoid into three triangles that are similar to each other but pairwise unequal and non-isosceles. The side $AB$ has a length of 5. Find $XC \cdot BX$.
Answer: 25
|
Solution:
The triangles are scalene, meaning all their angles are different.
$\alpha=\angle B X A=\angle X A D \neq \angle A X D=\beta$. The angle $\angle C X D$ together with these angles sums up to $180^{\circ}$, so it is the third angle of the triangle and cannot be equal to either $\alpha$ or $\beta$.
If $\angle B A X=\beta$, we get in triangles $B A X$ and $D A X$ equal angles around the common side, meaning these triangles are congruent. This contradicts the condition, so $\angle B A X=\gamma$, and accordingly, $\angle A B C=\beta$.
Similarly, we get $\angle X D C=\alpha$ and $\angle X C D=\beta$, from which the trapezoid is isosceles.
Now, let's write the ratio of the sides in similar triangles $A B X$ and $C D X$:
$$
\frac{X C}{C D}=\frac{A B}{B X}
$$
from which $X C \cdot B X=A B \cdot C D=25$.
|
25
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. How many pairs of natural numbers exist for which the number 189 is the LCM? (The numbers in the pair can be the same, the order of the numbers in the pair does not matter)
|
Answer: 11
Only digits are allowed as input
#
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the largest three-digit number that gives a remainder of 2 when divided by 13, and a remainder of 6 when divided by 15.
|
Answer: 951
2nd option. Find the largest three-digit number that gives a remainder of 3 when divided by 13, and a remainder of 2 when divided by 14.
Answer: 926
3rd option. Find the largest three-digit number that gives a remainder of 5 when divided by 14, and a remainder of 3 when divided by 15.
Answer: 873
Only digits are allowed in the input
#
|
951
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 1. (2 points)
$A B C$ is an equilateral triangle with a side length of 10. On side $A B$, a point $D$ is taken; on side $A C$, a point $E$ is taken; on side $B C$, points $F$ and $G$ are taken such that triangles $A D E$, $B D G$, and $C E F$ are also equilateral. $A D=3$. Find $F G$.
|
# Answer: 4
## Solution:
$B D=A B-A D=10-3=7$, so all sides of triangle $B D G$ are equal to 7.
$C E=A C-A E=A C-A D=10-3=7$, so all sides of triangle $C E F$ are also equal to 7.
Thus, $B G+C F=14$. This is greater than the length of segment $B C=10$, so $G F=14-10=4$.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. (3 points)
Alice the Fox thought of a two-digit number and told Pinocchio that this number is divisible by $2, 3, 4, 5$, and $6$. However, Pinocchio found out that exactly two of these five statements are actually false. What numbers could Alice the Fox have thought of? In your answer, indicate the number of possible variants.
|
# Answer: 8
## Solution:
If a number is not divisible by 2, then it is not divisible by 4 or 6 either, and we already have three false statements. Therefore, the number must be divisible by 2. If an even number is divisible by 3, it is also divisible by 6, which means the statements about divisibility by 4 and 5 are false. If the number is not divisible by 3, it is not divisible by 6, and the statements about divisibility by 4 and 5 should be true instead.
In the first case, we get numbers that are divisible by 6 but not by 4 or 5. There are exactly five such two-digit numbers: 18, 42, 54, 66, and 78. In the second case, we get numbers that are divisible by 20 but not by 3. There are three such numbers: 20, 40, and 80. In total, we have 8 numbers.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 3. (3 points)
All residents of the island are either blondes or brunettes with green or blue eyes. The proportion of brunettes among blue-eyed residents is $65 \%$. The proportion of blue-eyed residents among blondes is $70 \%$. Finally, the proportion of blondes among green-eyed residents is 10\%. What percentage of the island's population are green-eyed brunettes?
|
Answer: 54
## Solution:
Let the number of blue-eyed brunettes be $a$, blue-eyed blondes be $b$, green-eyed blondes be $c$, and green-eyed brunettes be $d$.
Then $\frac{a}{a+b}=0.65$, from which $\frac{a+b}{a}=\frac{20}{13}$ and $\frac{b}{a}=\frac{20}{13}-1=\frac{7}{13}$.
Similarly, $\frac{b}{b+c}=0.7$, from which $\frac{b+c}{b}=\frac{10}{7}$ and $\frac{c}{b}=\frac{10}{7}-1=\frac{3}{7}$, and $\frac{c}{a}=\frac{c}{b} \cdot \frac{b}{a}=\frac{7}{13} \cdot \frac{3}{7}=\frac{3}{13}$.
Finally, $\frac{c}{c+d}=0.1$, from which $\frac{c+d}{c}=10$ and $\frac{d}{c}=10-1=9$, and $\frac{d}{a}=\frac{d}{c} \cdot \frac{c}{a}=9 \cdot \frac{3}{13}=\frac{27}{13}$.
Then $\frac{a+b+c+d}{a}=1+\frac{b}{a}+\frac{c}{a}+\frac{d}{a}=1+\frac{7}{13}+\frac{3}{13}+\frac{27}{13}=\frac{50}{13}$.
Accordingly, $\frac{d}{a+b+c+d}=\frac{d}{a} \cdot \frac{a}{a+b+c+d}=\frac{27}{13} \cdot \frac{13}{50}=\frac{27}{50}=54\%$.
|
54
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 5. (3 points)
In the cells of a $7 \times 7$ table, pairwise distinct non-negative integers are written. It turns out that for any two numbers in the same row or column, the integer parts of their quotients when divided by 8 are different. What is the smallest value that the largest number in the table can take?
|
# Answer: 54
Solution: Each row must contain seven numbers that give different incomplete quotients when divided by 8. This means that in each row, there is at least one number with an incomplete quotient of 6 or more when divided by 8 (6, not 7, since the minimum value of the incomplete quotient is 0). Therefore, the table contains at least 7 numbers that are not less than $6 \cdot 8=48$. The largest of these is not less than $48+6=54$.
This is indeed possible if numbers with the same incomplete quotients are arranged along the diagonals:
| $0 \cdot 8+1$ | $1 \cdot 8+1$ | $2 \cdot 8+1$ | $3 \cdot 8+1$ | $4 \cdot 8+1$ | $5 \cdot 8+1$ | $6 \cdot 8+1$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $6 \cdot 8+2$ | $0 \cdot 8+2$ | $1 \cdot 8+2$ | $2 \cdot 8+2$ | $3 \cdot 8+2$ | $4 \cdot 8+2$ | $5 \cdot 8+2$ |
| $5 \cdot 8+3$ | $6 \cdot 8+3$ | $0 \cdot 8+3$ | $1 \cdot 8+3$ | $2 \cdot 8+3$ | $3 \cdot 8+3$ | $4 \cdot 8+3$ |
| $4 \cdot 8+4$ | $5 \cdot 8+4$ | $6 \cdot 8+4$ | $0 \cdot 8+4$ | $1 \cdot 8+4$ | $2 \cdot 8+4$ | $3 \cdot 8+4$ |
| $3 \cdot 8+5$ | $4 \cdot 8+5$ | $5 \cdot 8+5$ | $6 \cdot 8+5$ | $0 \cdot 8+5$ | $1 \cdot 8+5$ | $2 \cdot 8+5$ |
| $2 \cdot 8+6$ | $3 \cdot 8+6$ | $4 \cdot 8+6$ | $5 \cdot 8+6$ | $6 \cdot 8+6=54$ | $0 \cdot 8+6$ | $1 \cdot 8+6$ |
| $1 \cdot 8+0$ | $2 \cdot 8+0$ | $3 \cdot 8+0$ | $4 \cdot 8+0$ | $5 \cdot 8+0$ | $6 \cdot 8+0$ | $0 \cdot 8+7$ |
#
|
54
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 8. (4 points)
In the Magic Country, there are 100 cities, some of which are connected by two-way air routes. Any two cities can be reached from each other with no more than 11 transfers, and there is a unique way to do so. If it is impossible to travel from city $A$ to city $B$ with 10 or fewer transfers, both cities are called peripheral. What is the maximum number of peripheral cities that can exist in the country?
|
Answer: 89
## Solution:
Consider two peripheral cities and the route between them. All 11 cities where transfers are made on this route cannot be peripheral. All other cities can be peripheral if there are direct flights from them to the first or last of these 11 intermediate cities.
Thus, the maximum number of peripheral cities is $100-11=89$.
|
89
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Given a cube and 12 colors. Find the number of ways to paint the faces of this cube using these colors (each face in one color) such that adjacent faces are of different colors. Colorings that differ by a rotation are considered different.
|
Answer: 987360
## Examples of writing the answer:
## 7th grade
#
|
987360
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In a four-digit number, the first digit was crossed out. The resulting number is 9 times smaller than the original. What is the largest value the original number could have had?
|
Answer: 7875
## Examples of how to write the answer:
1234
|
7875
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On a plane, a certain number of triangles are drawn, the lengths of whose sides are ten-digit natural numbers, containing only threes and eights in their decimal representation. No segment belongs to two triangles, and the sides of all triangles are distinct. What is the maximum number of triangles that can be drawn?
|
Answer: 341
## Examples of how to write the answer:
## 17
#
|
341
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. At a round table sat raccoons, hedgehogs, and hamsters, a total of 134 animals. When asked: "Are any of your neighbors the same type of animal as you?", everyone answered "No." What is the maximum number of hedgehogs that could have been sitting at the table, given that hamsters and hedgehogs always tell the truth, raccoons almost always lie (except when a raccoon is sitting between two raccoons - then he tells the truth), and hamsters heard the question differently: "Are your neighbors of the same type of animal?"
|
Answer: 44
## Examples of how to write the answer:
17
#
|
44
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The polynomial $P(x)=(x-4)^{4}\left(x^{2}+\frac{3}{2} x-1\right)^{5}$ is represented in the form $\sum_{k=0}^{14} a_{k}(x+1)^{k}$. Find $a_{0}+a_{2}+\ldots+a_{14}$.
|
Answer: -256
Allowed for input are digits, minus sign, and division sign, a dot or comma as a decimal separator
#
|
-256
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. How many pairs of natural numbers exist for which the number 392 is the LCM? (The numbers in the pair can be the same, the order of the numbers in the pair does not matter)
|
Answer: 18
Only digits are allowed as input
#
|
18
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The gnomes dug a system of tunnels that formed a rectangular grid 7 by 2. The main entrance is located at the bottom-left vertex $(0,0)$, and the main exit is at the top-right vertex $(7,2)$. The tunnels are numbered as follows: the tunnel connecting vertices $(x, k)$ and $(x+1, k)$ has a number equal to $7 k + x + 1$, and the tunnel connecting vertices $(m, y)$ and $(m, y+1)$ has a number equal to $21 + 8 y + m + 1$. A collapse occurred, as a result of which all tunnels with numbers that are prime numbers became non-functional. In how many ways can one now travel from the main entrance to the main exit, passing through each tunnel no more than once?
|
Answer: 8
Only digits are allowed as input
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 1. (2 points)
Let $p_{1}, p_{2}, \ldots, p_{97}$ be prime numbers (not necessarily distinct). What is the largest integer value that the expression
$$
\sum_{i=1}^{97} \frac{p_{i}}{p_{i}^{2}+1}=\frac{p_{1}}{p_{1}^{2}+1}+\frac{p_{2}}{p_{2}^{2}+1}+\ldots+\frac{p_{97}}{p_{97}^{2}+1}
$$
can take?
|
# Answer: 38
Solution: Note that the function $\frac{x}{x^{2}+1}$ decreases when $x \geqslant 2$, which means $\sum_{i=1}^{97} \frac{p_{i}}{p_{i}^{2}+1} \leqslant 97 \cdot \frac{2}{2^{2}+1}=$ $97 \cdot 0.4=38.8$. Therefore, the answer cannot be greater than 38.
At the same time, $\frac{3}{3^{2}+1}=0.3$, which is 0.1 less than the value for $p=2$. Therefore, if in the above maximum sum, eight twos are replaced by threes, the result will be exactly 38.
|
38
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 4. (3 points)
On the side $B C$ of triangle $A B C$, points $A_{1}$ and $A_{2}$ are marked such that $B A_{1}=6, A_{1} A_{2}=8$, $C A_{2}=4$. On the side $A C$, points $B_{1}$ and $B_{2}$ are marked such that $A B_{1}=9, C B_{2}=6$. Segments $A A_{1}$ and $B B_{1}$ intersect at point $K$, and $A A_{2}$ and $B B_{2}$ intersect at point $L$. Points $K, L$ and $C$ lie on the same line. Find $B_{1} B_{2}$.
|
# Answer: 12
## Solution:
Let $M$ be the point of intersection of line $KL$ and side $AB$. We write two Ceva's theorems, for point $K$ and for point $L$:
$$
\frac{AM}{MB} \cdot \frac{BA_1}{A_1C} \cdot \frac{CB_1}{B_1A}=1 ; \quad \frac{AM}{MB} \cdot \frac{BA_2}{A_2C} \cdot \frac{CB_2}{B_2A}=1
$$
From this, we get $\frac{BA_1}{A_1C} \cdot \frac{CB_1}{B_1A}=\frac{BA_2}{A_2C} \cdot \frac{CB_2}{B_2A}$. Four segments in this equality are known to us. $A_1C = A_2C \pm A_1A_2 = A_2C + A_1A_2$, since $A_1A_2 > A_2C$. Similarly, $BA_2 = BA_1 + A_1A_2$. For the other two segments, $AB_2 = AB_1 \pm B_1B_2$ and $CB_1 = CB_2 \pm B_1B_2$ (the signs $\pm$ are the same). Substituting, we get
$$
\begin{gathered}
\frac{BA_1}{A_2C + A_1A_2} \cdot \frac{CB_2 \pm B_1B_2}{B_1A} = \frac{BA_1 + A_1A_2}{A_2C} \cdot \frac{CB_2}{AB_1 \pm B_1B_2} \\
(CB_2 \pm B_1B_2)(AB_1 \pm B_1B_2) = \frac{(BA_1 + A_1A_2)CB_2(A_2C + A_1A_2)B_1A}{A_2C \cdot BA_1} \\
(6 \pm B_1B_2)(9 \pm B_1B_2) = \frac{14 \cdot 6 \cdot 12 \cdot 9}{4 \cdot 6} = 378
\end{gathered}
$$
Since $378 > 6 \cdot 9$, the signs $\pm$ are resolved as +, and we get the quadratic equation $B_1B_2^2 + 15B_1B_2 - 324 = 0$. This equation has roots 12 and -27, of which we are interested in the positive one.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 3. (3 points)
$4^{27000}-82$ is divisible by $3^n$. What is the greatest natural value that $n$ can take?
|
Answer: 5
Solution:
$4^{27000}=(1+3)^{27000}=1+27000 \cdot 3+\frac{27000 \cdot 26999 \cdot 3^{2}}{2}+\frac{27000 \cdot \ldots \cdot 26998 \cdot 3^{3}}{6}+$
$+\frac{27000 \cdot \ldots \cdot 26997 \cdot 3^{4}}{24}+\frac{27000 \cdot \ldots \cdot 26996 \cdot 3^{5}}{120} \ldots$
The last two terms listed are divisible by $3^{6}$, as are all other terms included in the ellipsis.
$$
1+27000 \cdot 3+\frac{27000 \cdot 26999 \cdot 3^{2}}{2}+\frac{27000 \cdot 26999 \cdot 26998 \cdot 3^{3}}{6}=1+81000+
$$
$$
+\frac{27000 \cdot 26999 \cdot 3^{2}+27000 \cdot 26999 \cdot 26998 \cdot 3^{2}}{2}
$$
$1+81000=1+81(1+999)=1+81+81 \cdot 999=1+82+81 \cdot 999$, which gives a remainder of 82 when divided by $3^{6}$, since the last term is divisible by $3^{6}$.
$\frac{27000 \cdot 26999 \cdot 3^{2}+27000 \cdot 26999 \cdot 26998 \cdot 3^{2}}{2}=\frac{27000 \cdot 26999 \cdot 3^{2} \cdot(1+26998)}{2}$, and this number is clearly divisible by $3^{5}$, but not by $3^{6}$. Therefore, $4^{27000}-82$ is also divisible by $3^{5}$, but not by $3^{6}$.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 5. (3 points)
Positive numbers $x, y$, and $z$ are such that $x+y+z=5$. What is the smallest value that the quantity $x^{2}+y^{2}+2 z^{2}-x^{2} y^{2} z$ can take?
|
# Answer: -6
## Solution:
Rewrite the condition as $\frac{x}{2}+\frac{x}{2}+\frac{y}{2}+\frac{y}{2}+z=5$ and write the inequality for the arithmetic mean and the quadratic mean of these five numbers:
$$
1=\frac{\frac{x}{2}+\frac{x}{2}+\frac{y}{2}+\frac{y}{2}+z}{5} \leqslant \sqrt{\frac{\frac{x^{2}}{4}+\frac{x^{2}}{4}+\frac{y^{2}}{4}+\frac{y^{2}}{4}+z^{2}}{5}}=\sqrt{\frac{x^{2}+y^{2}+2 z^{2}}{10}}
$$
from which $x^{2}+y^{2}+2 z^{2} \geqslant 10$. Now write the inequality for the arithmetic mean and the geometric mean of these same numbers:
$$
1=\frac{\frac{x}{2}+\frac{x}{2}+\frac{y}{2}+\frac{y}{2}+z}{5} \geqslant \sqrt[5]{\frac{x}{2} \cdot \frac{x}{2} \cdot \frac{y}{2} \cdot \frac{y}{2} \cdot z}
$$
from which $x^{2} y^{2} z \leqslant 16$. Therefore, $x^{2}+y^{2}+2 z^{2}-x^{2} y^{2} z \geqslant 10-16=-6$. The minimum is achieved when all numbers for which the inequalities of means are applied are equal, that is, $x=y=2$, $z=1$.
#
|
-6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 8. (5 points)
In an $8 \times 8$ table, some 23 cells are black, and the rest are white. In each white cell, the sum of the number of black cells on the same row and the number of black cells on the same column is written; nothing is written in the black cells. What is the maximum value that the sum of the numbers in the entire table can take?
|
Answer: 234
## Solution:
The number in the white cell consists of two addends: "horizontal" and "vertical". Consider the sum of all "horizontal" addends and the sum of all "vertical" addends separately across the entire table. If we maximize each of these two sums separately, the total sum will also be the largest.
Consider the sum of the "horizontal" addends. If a row contains $x_{i}$ black cells and $8-x_{i}$ white cells, then the sum of the horizontal addends in this row is $x_{i}(8-x_{i})$. Summing this sum over all rows, we get $8(x_{1}+\ldots+x_{8})-x_{1}^{2}-\ldots-x_{8}^{2}=8 \cdot 23-(x_{1}^{2}+\ldots+x_{8}^{2})$. We need to maximize this expression, i.e., minimize the sum of the squares of eight numbers whose sum is 23. As is known, the sum of the squares of numbers decreases as these numbers approach their arithmetic mean, so for integers, the minimum is achieved when seven of the eight numbers are 3, and the remaining one is 2.
Thus, we get that the smallest possible sum of "horizontal" addends is $8 \cdot 23-7 \cdot 3^{2}-2^{2}=117$. A similar estimate can be obtained for the sum of "vertical" addends, which gives us a final value of 234.
It remains to ensure that there is a coloring of the table in which both sums are maximal simultaneously, i.e., in which each column or row contains 2 or 3 shaded cells.
|
234
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Six natural numbers are written on the board, such that for any two $a$ and $b$ among them, $\log _{a} b$ or $\log _{b} a$ is an integer (the second logarithm does not necessarily exist). What is the smallest value that the maximum of these numbers can take?
|
The answer can be written in the form of a power of a number: $m^{n}$ is denoted as $\mathrm{m}^{\wedge} \mathrm{n}$.
Answer: 65536 || $2 \wedge 16\left\|4^{\wedge} 8\right\| 16^{\wedge} 4 \| 256^{\wedge} 2$
|
65536
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. $A B C A_{1} B_{1} C_{1}$ - a right triangular prism with a circumscribed sphere. The perimeter of the base $A B C$ is 32 units, and the product of the sides is 896 cubic units. The surface area of the prism is 192 square units. Find the square of the radius of its circumscribed sphere.
|
Answer: 53
## Examples of answer notations:
7.4
$7 / 14$
714
#
|
53
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (3 points) From the set of three-digit numbers that do not contain the digits $0,1,2$, $3,4,5$ in their notation, several numbers were written on paper in such a way that no two numbers can be obtained from each other by swapping two adjacent digits. What is the maximum number of such numbers that could have been written?
|
Answer: 40
Solution:
Whether a number can be written or not depends only on numbers consisting of the same set of digits.
Suppose a number ABC, consisting of three different digits, is written. This means that the numbers BAC and ACB cannot be written. Among the numbers consisting of these same digits, BVA, VAB, and VBA remain. The first two can be written together, but the third cannot be written with any of the others. Therefore, among the six numbers consisting of the digits A, B, and V, a maximum of 3 can be written. There are 4 ways to choose the digits A, B, and V from 6, 7, 8, and 9. In total, this gives a maximum of 12 numbers.
Among the numbers AAB, ABA, and BAA, a maximum of 2 can be written: AAB and BAA. The digit A can be chosen in 4 ways, and the digit B in 3 ways, so this results in 24 numbers.
Finally, all 4 numbers consisting of three identical digits each can be written.
In total, this gives 40 numbers.
|
40
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (3 points) On a $3 \times 3$ chessboard, there are knights, who always tell the truth, and liars, who always lie. Each of them said: "Among my neighbors, there are exactly three liars." How many liars are on the board?
Neighbors are considered to be people on cells that share a common side.
|
Answer: 5.
Solution: The people in the corner cells are obviously liars: they simply do not have three neighbors.
If the person in the center is a knight, then all the people in the side cells are also liars. But in this case, the knight has 4 liar neighbors, not three. This leads to a contradiction.
If the person in the center is a liar, then the people in the side cells each have three liar neighbors, so they are knights. Now we check that the person in the center is indeed a liar: they do not have three liar neighbors.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (2 points) Does there exist a rectangular parallelepiped with integer sides, for which the surface area is numerically equal to the sum of the lengths of all twelve edges?
|
Answer: Yes, it exists.
Solution: For example, a $2 \times 2 \times 2$ cube fits. Both the surface area and the sum of the lengths of the edges are 24.
|
24
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (3 points) From the set of three-digit numbers that do not contain the digits 0, 6, 7, 8, 9 in their notation, several numbers were written on paper in such a way that no two numbers can be obtained from each other by swapping two adjacent digits. What is the maximum number of such numbers that could have been written?
|
Answer: 75
Solution:
Whether a number can be written or not depends only on numbers consisting of the same set of digits.
Suppose a number ABC, consisting of three different digits, is written. This means that the numbers BAC and ACB cannot be written. Among the numbers consisting of these same digits, BVA, VAB, and VBA remain. The first two can be written together, but the third cannot be written with any of the others. Therefore, among the six numbers consisting of the digits A, B, and V, a maximum of 3 can be written. There are 10 ways to choose the digits A, B, V from $1,2,3,4$ and 5. In total, this gives a maximum of 30 numbers.
Among the numbers AAB, ABA, BAA, a maximum of 2 can be written: AAB and BAA. The digit A can be chosen in five ways, and the digit B in four ways, so this results in 40 numbers.
Finally, all 5 numbers, each consisting of three identical digits, can be written.
In total, this gives 75 numbers.
|
75
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (3 points) On a $2 \times 4$ chessboard, there are knights, who always tell the truth, and liars, who always lie. Each of them said: "Among my neighbors, there are exactly three liars." How many liars are on the board?
Neighbors are considered to be people on cells that share a common side.
|
Answer: 6.
Solution: On the corner cells, liars are obviously standing: they simply do not have three neighbors.
A situation where all people on the board are liars is impossible, as it would mean that four of these liars are telling the truth.
Therefore, there is at least one knight. Then all his neighbors are liars, and we get the following situation (accurate up to symmetry):
| $L$ | $\mathrm{P}$ | $L$ | $L$ |
| :---: | :---: | :---: | :---: |
| $L$ | $L$ | $?$ | $L$ |
The cell marked with a question mark can only be a knight, since all his neighbors are liars. Don't forget to check that the left and upper neighbors of this knight have only two liar neighbors, meaning they are indeed lying.
Thus, we end up with 6 liars.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Given the function $f(x)=\frac{\sqrt{3} x-1}{x+\sqrt{3}}$. Find $\underbrace{f(f(\ldots(1) \ldots))}_{2013 \text { times }}$.
|
Answer: -1
## Examples of how to write answers:
$1 / 4$
0.25
10
#
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The polynomial $P(x)$ of the third degree, as well as its first, second, and third derivatives, take the value 1 at $x=-3$. Find $\mathrm{P}(0)$.
|
Answer: 13
## Examples of how to write answers:
$1 / 4$
0.25
$-10$
#
|
13
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In space, there are 37 different vectors with integer non-negative coordinates, starting from the point $(0 ; 0 ; 0)$. What is the smallest value that the sum of all their coordinates can take?
|
Answer: 115
## Examples of answer notation:
239
Answer: $[-1 ; 7]$
|
115
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Four spheres of radius $r$ touch each other externally. A sphere of radius $\sqrt{6}+2$ touches all of them internally. Find $r$.
|
Answer: 2
## Examples of how to write answers:
$1 / 4$
0.25
10
#
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the city of Gentle-city, there live 19 gentlemen, any two of whom are either friends or enemies. At some point, each gentleman asked each of his friends to send a hate card to each of his enemies (gentleman A asks gentleman B to send a card to all enemies of gentleman B). Each gentleman fulfilled all the requests, and he sent each of his enemies as many cards as he was asked to. What is the maximum number of cards that could have been sent?
|
Answer: 1538.
## Examples of answer recording:
100
#
|
1538
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. $\mathrm{ABCD}$ is a trapezoid with bases $A D=15$ and $\mathrm{BC}=10$. $O$ is one of the intersection points of the circles constructed on the lateral sides of the trapezoid as diameters, and this point lies inside the trapezoid. Triangle $B C M$ is constructed on side $B C$ on the external side relative to the trapezoid and is similar to triangle $A D O$ (the vertices of the triangles are listed in the order in which they correspond to each other). Line $O M$ intersects the bases $B C$ and $A D$ at points $K$ and $L$ respectively. It is known that $O K=4, O L=9$. Find the smallest possible value of the length of segment $B K$.
|
Answer: 4
## Examples of answer notations:
$1 / 4$
0.25
10
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (2 points) In a row without spaces, all natural numbers are written in ascending order: $1234567891011 . .$. What digit stands at the 2017th place in the resulting long number?
|
Answer: 7.
Solution: The first 9 digits are contained in single-digit numbers, the next 180 - in two-digit numbers. $2017-180-9=1828$. Next, $1828: 3=609 \frac{1}{3}$. This means that the 2017-th digit is the first
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (3 points) Does there exist a four-digit natural number with the sum of its digits being 23, which is divisible by 23?
|
Answer: Yes, for example $7682=23 \cdot 334$.
Solution: Generally speaking, the solution is contained in the answer, but let's explain how to find such a number. The sum of the digits of the product gives the same remainder when divided by 9 as the sum of the original numbers. Represent 23 as the difference between a multiple of 5 and a multiple of 9: $23=5 \cdot 10-3 \cdot 9$. Therefore, we need to find a three-digit multiplier with a digit sum of 10.
Here are all possible options: $1679,1886,3749,3956,4577,4784,4991,5198,5819,6647,6854$, $7268,7475,7682,8096,8717,8924,9338,9545,9752$.
|
7682
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (3 points) Given the cryptarithm: ЖАЛО + ЛОЖА = ОСЕНЬ. Identical letters represent identical digits, different letters represent different digits. Find the value of the letter А.
|
Answer: 8
Solution: The rebus can be rewritten as ОСЕНЬ $=($ ЖА + ЛО $) \cdot 101$. First, this means that the last digit of ЖА + ЛО is Ь. Second, if ЖА + ЛО $<100$, the result will be a four-digit number. Let $Ж А+Л О=1 Х Ь$, where $X$ is some digit.
Then ОСЕНЬ $=1 Х Ь 00+1 Х Ь$. If $\mathrm{b}<9$, then the second and fourth digits of this number should match, but they do not. Therefore, $\mathrm{b}=9$. Consequently, $\mathrm{A}+\mathrm{O}=9$. But О is 1, so А is 8.
There are many examples, for instance, $7861+6178=14039$.
7. (4 points) Alice and Bob each have three equal segments. First, Alice breaks one of the segments into two unequal parts. Then, Bob breaks another of the original segments into any two parts. As a result, there are five segments, from which ten sets of three segments can be chosen. Alice wins if at least 4 of these ten sets form a triangle. Otherwise, Bob wins. Who will win if both players play optimally?
Answer: Bob wins.
Solution: Let the original segments have a length of 1, and Alice breaks one of the segments into parts $x$ and $1-x$, with $x<1-x$ for definiteness. Then Bob needs to break another segment into parts $1-y$ and $y$ such that $y$ is very small, specifically, the inequalities $y<x$, $y<(1-x)-x$, and $y<(1-y)-(1-x)$, or $2 y<x$, are satisfied. Clearly, he can choose such a $y$.
Using the triangle inequality: to form a triangle, it is necessary and sufficient that the largest side of the triangle is less than the sum of the other two. With such a choice of $y$, it is not greater than the difference between any two other segments, and therefore cannot form a triangle with any of them. There are exactly 6 sets of three segments that include the segment $y$. Additionally, the remaining segment of length 1 and the segments Alice obtained also do not form a triangle. This is the seventh set of segments that does not form a triangle. Thus, Alice is left with only 3 sets of segments that can form a triangle, and she loses.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (4 points) A triangle is divided into 1000 triangles. What is the maximum number of different points at which the vertices of these triangles can be located?
|
Answer: 1002
Solution: The sum of the angles of a triangle is $180^{\circ}$, thousands of triangles $-180000^{\circ}$. Where did the extra $179820^{\circ}$ come from? Each internal vertex, where only the angles of triangles meet, adds $360^{\circ}$. Each vertex on the side of the original triangle or on the side of one of the triangles in the partition adds $180^{\circ}$. To achieve the maximum, it is necessary that there are only points of the second type and there are $179820: 180=999$ of them. An example is constructed by sequentially adding new vertices to the sides of the existing triangles.
Adding the three vertices of the original triangle, we get the answer 1002.
## 7th grade
2nd variant
|
1002
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (2 points) In a row without spaces, all natural numbers from 999 to 1 are written in descending order: 999998 ...321. What digit is in the 2710th position of the resulting long number?
|
Answer: 9.
Solution: The first $3 \cdot 900=2700$ digits are contained in three-digit numbers. Therefore, we need to count another 10 digits in two-digit numbers. That is, we need the first digit of the fourth largest two-digit number. This number is 96, so we need the digit 9.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (3 points) Given the cryptarithm: RIVER + SQUARE = ABVAD. Identical letters represent identical digits, different letters represent different digits. Find the value of the letter B.
|
Answer: 2
Solution: The rebus can be rewritten as ABVAD $=(\mathrm{KA}+\mathrm{PE}) \cdot 101$. First, this means that the last digit of $\mathrm{KA}+\mathrm{PE}$ is D. Second, if $\mathrm{KA}+\mathrm{PE}<100$, the result will be a four-digit number. Let $\mathrm{KA}+\mathrm{PE}=1X$D, where $X$ is some digit.
Then ABVAD $=1X$D$00+1X$D. If D $<9$, then the second and fourth digits of this number should match, but they do not. Therefore, D $=9$ and the second digit of the number ABVAD is one more than the fourth. But A is 1, so B is 2.
There are many examples, for instance, $5861+6158=12019$.
7. (4 points) Alice and Bob have three equal segments. First, Alice breaks one of the segments into two parts. Then, Bob breaks another of the original segments into two arbitrary parts. As a result, five segments are obtained, from which ten ways to choose three segments are possible. Alice wins if at least 4 of these ten ways give triples of segments that form a triangle. Otherwise, Bob wins. Who will win with correct play by both opponents?
Answer: Alice wins.
Solution: We use the triangle inequality: to form a triangle, it is necessary and sufficient that the largest side of the triangle is less than the sum of the other two.
Let the original segments have a length of 1. Alice breaks one of the segments into two equal parts. Let Bob break his segment into parts of length $x$ and $1-x$, and for definiteness, let $x<1-x$. $1-x<\frac{1}{2}+\frac{1}{2}$, so this triple forms a triangle. Also, the triple formed by Alice's segments and Bob's smaller segment forms a triangle. Two more suitable triples are obtained when we take the segments $1,1-x$ and $\frac{1}{2}$.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. (4 points) A triangle is divided into 1000 triangles. What is the minimum number of distinct points at which the vertices of these triangles can be located?
|
Answer: 503
Solution: The sum of the angles of a triangle is $180^{\circ}$, so for a thousand triangles, it is $180000^{\circ}$. Where did the extra $179820^{\circ}$ come from? Each internal vertex where only the angles of triangles meet adds $360^{\circ}$. Each vertex on the side of the original triangle or on the side of one of the triangles in the partition adds $180^{\circ}$. To achieve the minimum, we need as many points of the first type as possible. $179820: 360=499.5$. Therefore, we need 499 points of the first type and one point of the second type. The example is constructed by sequentially adding new points inside (not on the boundary) of the existing triangles and one point on the boundary.
Adding the three vertices of the original triangle, we get the answer 503.
|
503
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 4. (3 points)
Three runners are moving along a circular track at constant equal speeds. When two runners meet, they instantly turn around and start running in opposite directions.
At some point, the first runner meets the second. Twenty minutes later, the second runner meets the third for the first time. Another thirty minutes after that, the third runner meets the first for the first time.
How many minutes does it take for one runner to complete the entire track?
|
# Answer: 100
Solution: (in general form)
Let the first runner meet the second, then after $a$ minutes the second runner meets the third for the first time, and after another $b$ minutes the third runner meets the first for the first time.
Let the first and second runners meet at point $A$, the second and third at point $B$, and the first and third at point $C$. Additionally, let the first runner be at point $D$ at the moment the second and third runners meet.
Then the points are arranged on the circle in the following order: $D, A, B, C$, where the first runner ran from $D$ to $A$ in $a$ minutes, the second runner ran from $A$ to $B$ in $a$ minutes, the third runner ran from $B$ to $C$ in $b$ minutes, and the first runner ran from $D$ to $C$ in $b$ minutes. These four segments together form the entire track, so it is covered in $2a + 2b$ minutes.
|
100
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 5. (3 points)
In an isosceles trapezoid $A B C D$, the bisectors of angles $B$ and $C$ intersect on the base $A D$. $A B=50, B C=128$. Find the area of the trapezoid.
|
Answer: 5472
## Solution:
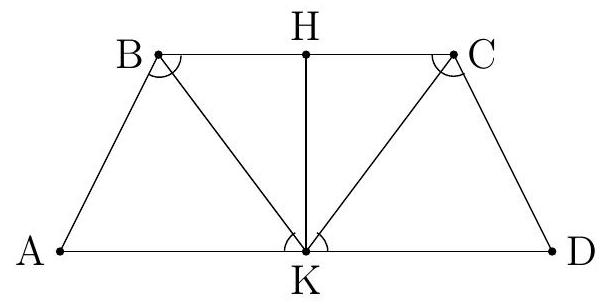
Let $K$ be the point of intersection of the angle bisectors. Angles $\angle B=\angle C$ are equal as the base angles of an isosceles trapezoid, so their halves are also equal, that is, $\angle K B A=\angle K B C=\angle K C B=\angle K C D$. Additionally, $\angle K B C=\angle A K B$ and $\angle K C B=\angle D K C$ as alternate interior angles.
Thus, triangles $A K B$ and $K C D$ are isosceles, and $A D=A K+K D=A B+C D=2 A B$.
Moreover, triangles $A K B$ and $K B C$ are similar, so $B K^{2}=A B \cdot B C$. We can calculate the height of the isosceles triangle $K B C$ using the Pythagorean theorem:
$$
K H^{2}=B K^{2}-B H^{2}=A B \cdot B C-\frac{B C^{2}}{4}
$$
from which the area of the trapezoid is $\frac{1}{2}(2 A B+B C) \sqrt{A B \cdot B C-\frac{B C^{2}}{4}}$.
#
|
5472
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 6. (3 points)
Natural numbers $x, y, z$ are such that $\operatorname{GCD}(\operatorname{LCM}(x, y), z) \cdot \operatorname{LCM}(\operatorname{GCD}(x, y), z)=1400$.
What is the greatest value that $\operatorname{GCD}(\operatorname{LCM}(x, y), z)$ can take?
#
|
# Answer: 10
## Solution:
Notice that $\operatorname{LCM}(\operatorname{GCD}(x, y), z)$ is divisible by $z$, and $z$ is divisible by $\operatorname{GCD}(\operatorname{LCM}(x, y), z)$, so $\operatorname{LCM}(\operatorname{GCD}(x, y), z)$ is divisible by $\operatorname{GCD}(\operatorname{LCM}(x, y), z)$.
$1400=2^{3} \cdot 5^{2} \cdot 7$ and in the second factor, each prime number appears with an exponent no less than in the first. Therefore, the maximum possible value of $\operatorname{GCD}(\operatorname{LCM}(x, y), z)$ is $2 \cdot 5=10$. This value is achieved when $x=y=10, z=140$.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 7. (3 points)
On an island, there live vegetarians who always tell the truth, and cannibals who always lie. 50 residents of the island, including both women and men, gathered around a campfire. Each of them said either "All men at this campfire are cannibals" or "All women at this campfire are vegetarians," and both phrases were spoken. What is the maximum number of vegetarian women that could have been at the campfire?
|
Answer: 48
## Solution:
We will prove that if we have $n$ people, the maximum number of vegetarian women is $n-2$.
First, note that if someone has called someone a cannibal, then we definitely have at least one cannibal.
Second, according to the condition, there is at least one man. Therefore, the only case where we can have $n-1$ vegetarians is the case where the remaining person is a male cannibal. However, in this case, he cannot say either of the two phrases from the condition. Therefore, this case is impossible, and besides the vegetarians, there must be at least two more people.
If we have $n-2$ vegetarian women, the remaining two can either be two men (a cannibal and a vegetarian) or two cannibals (a man and a woman).
|
48
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On a piece of paper, a square with a side length of 1 was drawn, next to it a square with a side length of 2, then a square with a side length of 3, and so on. It turned out that the area of the entire resulting figure is 42925. How many squares were drawn?
|
Answer: 50
## Examples of answer notation: 45
#
|
50
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. $\mathrm{ABCD}$ is an isosceles trapezoid, $\mathrm{AB}=\mathrm{CD}=25, \mathrm{BC}=40, \mathrm{AD}=60$. $\mathrm{BCDE}$ is also an isosceles trapezoid. Find AE. (Points A and E do not coincide)
If there are multiple possible values, list them in any order separated by a semicolon.
|
Answer: 44.
## Examples of answer recording:
45
$45 ; 56$
## Problem 7 (3 points).
|
44
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Let $f(x)=\frac{34^{x}}{4^{x}+2}$. Find the sum $f(0)+f\left(\frac{1}{2017}\right) \ldots f\left(\frac{2}{2017}\right) f(1)$.
|
Answer: 3027
## Examples of answer recording:
45
## Problem 9 (4 points).
|
3027
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Two tangents are drawn from point A to a circle. The distance from point A to the point of tangency is 10, and the distance between the points of tangency is 16. Find the greatest possible distance from point A to a point on the circle.
|
Answer: 30
## Examples of answer recording:
## Problem 10 (2 points).
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (3 points) From cards with letters, you can form the word KARAKATITSA. How many words (not necessarily meaningful) can be formed from these cards, in which the letters R and T are adjacent?
|
Answer: $\frac{9!}{4!}=9 \cdot 8 \cdot 7 \cdot 6 \cdot 5=15120$
## Solution:
Let's replace the adjacent letters R and T with one letter, for example, the letter Sh, since they stand together. Then we are left with 9 letters, and among them, 4 letters A and 2 letters K.
Thus, the number of ways to rearrange the letters in this word is $\frac{9!}{4! \cdot 2!}$. Additionally, the letter Sh can be decoded in two ways: as RT and as TR, which doubles the number of ways. Therefore, we get $\frac{9!}{4!}$.
|
15120
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Given a convex hexagon ABCDEF such that AB $\|\mathrm{CF}\| \mathrm{DE}, \mathrm{BC}\|\mathrm{AD}\| \mathrm{EF}$ and $\mathrm{CD} \| \mathrm{BE}$ $\| \mathrm{FA}$ and $\mathrm{AB}=\mathrm{DE}=\mathrm{CD}=\mathrm{AF}=13, \mathrm{BD}=24$. Find the area of the union of triangles $\mathrm{ACE}$ and BDF.
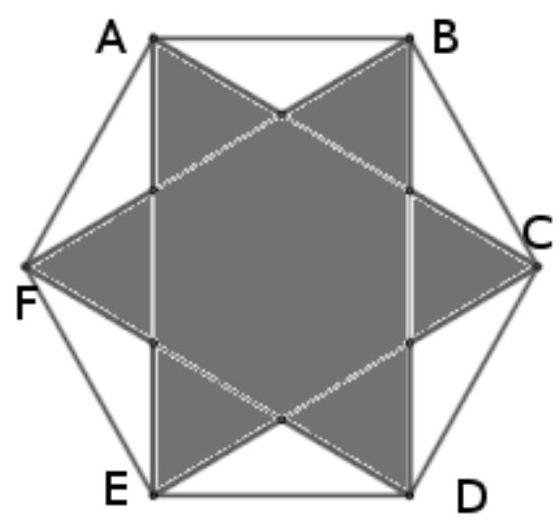
|
Answer: 240
## Examples of how to write answers:
14
$1 / 4$
0.25
#
|
240
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On a $6 \times 6$ checkerboard, there are chips. It turns out that for each number $n$ from 2 to 10, there is a chip such that in the same column and the same row with it, there are exactly $n$ chips in total (not counting the chip itself). What is the maximum number of chips that can be on the board?
|
Answer: 21
## Examples of answer recording:
14
## 9th grade.
#
|
21
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 1. (2 points)
Let $x, y, z$ be pairwise coprime three-digit natural numbers. What is the greatest value that the GCD $(x+y+z, x y z)$ can take?
|
Answer: 2994
Solution:
The GCD of two numbers cannot be greater than either of them. The maximum possible value of $x+$ $y+z=997+998+999=2994$ and for these numbers, $x y z$ is indeed divisible by $x+y+z=2994=3 \cdot 998$.
|
2994
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. (2 points)
On a circle, 10 points are marked. Any three of them form three inscribed angles. Petya calculated the number of different values that these angles can take. What is the maximum number he could have obtained?
|
Answer: 80
Solution:
Any two points form two arcs. All inscribed angles subtending the same arc are equal. For two adjacent points, on one of the two arcs between them, no other point lies, meaning a pair of adjacent points gives us one possible angle value, while a pair of non-adjacent points gives two values.
In total, we have 45 pairs of points, of which 35 pairs are non-adjacent. We get the answer $35 \cdot 2 + 10 = 80$.
An example clearly exists. It is sufficient to take the lengths of the arcs between adjacent points in the ratio $1: 2: 4: 8 \ldots$
|
80
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. (3 points)
Let $f(x)$ be a quadratic trinomial with integer coefficients. Given that $f(\sqrt{3}) - f(\sqrt{2}) = 4$. Find $f(\sqrt{10}) - f(\sqrt{7})$.
|
# Answer: 12
## Solution:
Let $f(x)=c x^{2}+d x+e$. Then $f(\sqrt{3})-f(\sqrt{2})=3 c+\sqrt{3} d+e-(2 c+\sqrt{2} d+e)=c+d(\sqrt{3}-\sqrt{2})$. This number can only be an integer if $d=0$. Therefore, $f(x)=c x^{2}+e$ and $f(\sqrt{3})-f(\sqrt{2})=c$.
Then $f(\sqrt{10})-f(\sqrt{7})=10 c+e-(7 c+e)=3 c=12$.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 5. (3 points)
In triangle $A B C$, the midpoints of sides $A B=40$ and $B C=26$ are marked as points $K$ and $L$ respectively. It turns out that the quadrilateral $A K L C$ is a tangential quadrilateral. Find the area of triangle $A B C$.
|
# Answer: 264
## Solution:
According to the Midline Theorem, $K L=\frac{1}{2} A C$. In a cyclic quadrilateral, the sums of the opposite sides are equal, that is, $K L+A C=A K+C L=\frac{A B+B C}{2}$, so $\frac{3 A C}{2}=\frac{66}{2}$ and $A C=22$. Knowing the sides of the triangle, the area can be calculated using Heron's formula.
#
|
264
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 6. (3 points)
Positive numbers $x, y, z$ are such that $x y + y z + x z = 12$.
Find the smallest possible value of $x + y + z$.
#
|
# Answer: 6
## Solution:
By adding the inequalities $x^{2}+y^{2} \geqslant 2 x y, x^{2}+z^{2} \geqslant 2 x z$ and $y^{2}+z^{2} \geqslant 2 y z$ and dividing by 2, we get $x^{2}+y^{2}+z^{2} \geqslant x y+y z+x z$.
$(x+y+z)^{2}=x^{2}+y^{2}+z^{2}+2(x y+y z+x z) \geqslant 3(x y+y z+x z)=36$, from which $x+y+z \geqslant 6$. Equality is achieved when $x=y=z=2$.
#
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 7. (3 points)
From point $K$ on side $A C$ of triangle $A B C$, perpendiculars $K L_{1}$ and $K M_{1}$ were dropped to sides $A B$ and $B C$ respectively. From point $L_{1}$, a perpendicular $L_{1} L_{2}$ was dropped to $B C$, and from point $M_{1}$, a perpendicular $M_{1} M_{2}$ was dropped to $A B$.
It turned out that triangles $B L_{1} M_{1}$ and $B L_{2} M_{2}$ are similar (point $L_{1}$ in the first triangle corresponds to point $M_{2}$ in the second). In addition, $B L_{2}=6$ and $L_{2} M_{1}=4$. Find $L_{1} L_{2}$.
|
# Answer: 8
## Solution:
Notice that the quadrilateral $L_{1} M_{2} L_{2} M_{1}$ is cyclic, since $\angle L_{1} M_{2} M_{1}=\angle L_{1} L_{2} M_{1}=$ $90^{\circ}$. Therefore, $\angle B M_{2} L_{2}=180^{\circ}-\angle L_{1} M_{2} L_{2}=\angle L_{2} M_{1} L_{1}=\angle B M_{1} L_{1}$. Similarly, $\angle B L_{2} M_{2}=\angle B L_{1} M_{1}$, so triangles $B L_{1} M_{1}$ and $B L_{2} M_{2}$ are similar, with point $L_{1}$ in the first triangle corresponding to point $L_{2}$ in the second. However, the problem states that they are similar in another way, which means these two triangles are isosceles. From this, we get $B L_{1}=B M_{1}=B L_{2}+L_{2} M_{1}$ and, by the Pythagorean theorem, we find $L_{1} L_{2}=\sqrt{B L_{1}^{2}-B L_{2}^{2}}=\sqrt{\left(B L_{2}+L_{2} M_{1}\right)^{2}-B L_{2}^{2}}$.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 1. (2 points)
A cubic polynomial has three roots. The greatest value of the polynomial on the interval $[4 ; 9]$ is achieved at $x=5$, and the smallest value is achieved at $x=7$. Find the sum of the roots of the polynomial.
#
|
# Answer: 18
## Solution:
Since in all options the minimum and maximum on the interval are not reached at its ends, they are reached at the roots of the polynomial's derivative. Let the polynomial be of the form $a x^{3}+b x^{2}+c x+d$, and its derivative, respectively, $3 a x^{2}+2 b x+c$. In this case, the sum of the roots of the polynomial is $\frac{-b}{a}$, and the sum of the roots of the derivative is $\frac{-2 b}{3 a}$, which is $\frac{2}{3}$ of the sum of the roots of the polynomial.
Therefore, the sum of the roots of the polynomial is $\frac{3}{2}\left(x_{1}+x_{2}\right)$.
| $x_{0}$ | 4 |
| :---: | :---: |
| $x_{1}$ | 5 |
| $x_{2}$ | 7 |
| $x_{3}$ | 9 |
| Answer | 18 |
|
18
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 2. (3 points)
Find the sum of natural numbers from 1 to 3000 inclusive that have common divisors with the number 3000, greater than 1.
|
# Answer: 3301500
## Solution:
$3000=2^{3} \cdot 3 \cdot 5^{3}$, so we are interested in numbers divisible by 2, 3, or 5. First, let's find the number of such numbers. For this, we will use the principle of inclusion and exclusion. There are exactly $\frac{3000}{2}=1500$ even numbers from 1 to 3000, $\frac{3000}{3}=1000$ numbers divisible by 3, and $\frac{3000}{5}=600$ numbers divisible by 5. However, if we simply add the numbers 1500, 1000, and 600, we will count some numbers twice, specifically, numbers divisible by $2 \cdot 3=6$, $2 \cdot 5=10$, and $3 \cdot 5=15$. Therefore, we need to subtract $\frac{3000}{6}=500$, $\frac{3000}{10}=300$, and $\frac{3000}{15}=200$ from the sum. However, $1500+1000+600-500-300-200=2100$ is still incorrect. Since in this expression, numbers that have all three prime factors are counted three times and then subtracted three times, we need to add these numbers again. The number of such numbers is $\frac{3000}{2 \cdot 3 \cdot 5}=100$, so the number of numbers that have common divisors with 3000 and do not exceed it is 2200.
Notice now that if a number $x$ has common divisors with a number $N$, then the number $N-x$ also has the same common divisors with $N$. Therefore, all the numbers of interest, except for the numbers 1500 and 3000, can be paired with a sum of 3000 (the number 3000 would have to be paired with 0, and the number 1500 with itself). There are 1099 such pairs, so the final answer is $1099 \cdot 3000 + 3000 + 1500 = 1100 \cdot 3000 + 1500 = 3301500$.
Note: Numbers less than 3000 and coprime with it can also be paired in the same way, so participants familiar with Euler's function could derive the formula for the answer as $\frac{N(N+1)-N \cdot \varphi(N)}{2}$.
|
3301500
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 6. (4 points)
Quadrilateral $A B C D$ is circumscribed around a circle with center at point $O, K, L, M, N$ - the points of tangency of sides $A B, B C, C D$ and $A D$ respectively, $K P, L Q, M R$ and $N S$ - the altitudes in triangles $O K B, O L C, O M D, O N A . O P=15, O A=32, O B=64$.
Find the length of the segment $Q R$.
|
# Answer: 30
## Solution:
Triangles $O K A$ and $O N A$ are right triangles with a common hypotenuse and a leg equal to the radius of the circle, so they are congruent. Therefore, their altitudes fall on the same point of the common hypotenuse, meaning $K S$ is the altitude in triangle $O K A$. Thus, points $S$ and $P$ lie on a circle with diameter $O K$. Similarly, points $R$ and $S$ lie on a circle with diameter $O N$. Since the diameters of these circles are equal, the degree measures of arc $O S$ in these circles coincide. In the first circle, this arc is subtended by $\angle O P S$, and in the second by $\angle O R S$, so these angles are equal. (They are exactly equal, not supplementary to $180^{\circ}$, because points $P$ and $R$ lie on opposite sides of line $O S$, and the circles are symmetric with respect to it).
Similarly, $\angle O P Q = \angle O R Q$. Adding this to the previous equality, we get $\angle S P Q = \angle S R Q$. Similarly, $\angle P S R = \angle P Q R$, so quadrilateral $P R Q S$ is a parallelogram. Therefore, instead of the length of segment $Q R$, we can find the length of segment $P S$.
(For participants familiar with the concept of inversion: we can understand that the vertices of quadrilateral $P Q R S$ are the inverses of the vertices of quadrilateral $A B C D$ relative to our circle, meaning we have just repeated the proof of the theorem that a quadrilateral inverse to a circumscribed one is a parallelogram).
By the property of the altitude in a right triangle, $O K^{2} = O S \cdot O A$. Similarly, $O K^{2} = O P \cdot O B$, so $\frac{O S}{O B} = \frac{O P}{O A} = k$. Additionally, angle $\angle O$ is common in triangles $O B A$ and $O S P$, so they are similar with a ratio of $k$. Therefore, $P S = k \cdot A B = k(A K + K B) = k\left(\sqrt{O A^{2} - O K^{2}} + \sqrt{O B^{2} - O K^{2}}\right) = \frac{O P}{O A}\left(\sqrt{O A^{2} - O B \cdot O P} + \sqrt{O B^{2} - O B \cdot O P}\right) = 30$.
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 7. (4 points)
Two cubes with an edge of $12 \sqrt[4]{\frac{8}{11}}$ share a common face. A section of one of these cubes by a certain plane is a triangle with an area of 16. The section of the other by the same plane is a quadrilateral. What is the maximum value that its area can take?
|
# Answer: 128
## Solution:
Let our cubes be $A B C D A_{1} B_{1} C_{1} D_{1}$ and $A B C D A_{2} B_{2} C_{2} D_{2}$ with a common face $A B C D$. Let the triangular section of the first cube be $K L M$, where point $K$ lies on $A A_{1}$, point $L$ on $A B$, and point $M$ on $A D$. One side of the quadrilateral section of the second cube is the segment $L M$. The other two sides are the extensions of segments $K L$ and $K M$ to the faces of the second cube, which we will call segments $L P$ and $M Q$. For the section to be a quadrilateral, points $P$ and $Q$ must lie on the same face of the second cube, which can only be the face $A_{2} B_{2} C_{5} D_{2}$.
Thus, the quadrilateral section of the second cube is a trapezoid $L M Q P$. Finding its maximum area is equivalent to finding the maximum area of triangle $K P Q$, which is similar to triangle $K L M$. Let the similarity coefficient be $k=\frac{K P}{K L}$. Then $k^{2}=\frac{S_{K P Q}}{S_{K L M}}=\frac{S_{K P Q}}{S}$. Therefore, our problem is equivalent to finding the maximum similarity coefficient.
On the other hand, by Thales' theorem, $k=\frac{K P}{K L}=\frac{K A_{2}}{K A}=\frac{K A+A A_{2}}{K A}=1+\frac{A A_{2}}{K A}$. Thus, the similarity coefficient is greater the smaller $K A$ is, which means our task is to minimize $K A$, or equivalently, to minimize $K A_{2}$.
Suppose we have a triangle with vertices located on three edges of the cube, at distances $x, y$, and $z$. Let's find the formula for the area of this triangle. This can be done in different ways, for example, using the vector product, or by calculating the area of the tetrahedron formed by the vertices of the triangle and the vertex of the cube in two ways, but we will compute this area using Heron's formula, knowing the sides of the triangle: $a=\sqrt{x^{2}+y^{2}}, b=\sqrt{x^{2}+z^{2}}$, and $c=\sqrt{y^{2}+z^{2}}$.
$$
\begin{aligned}
& S=\frac{\sqrt{(a+b+c)(a+b-c)(c+(b-a))(c-(b-a))}}{4}=\frac{\sqrt{\left((a+b)^{2}-c^{2}\right)\left(c^{2}-(b-a)^{2}\right)}}{4}= \\
= & \frac{\sqrt{\left(a^{2}+b^{2}+c^{2}-2 a b\right)\left(c^{2}-a^{2}-b^{2}+c^{2}+2 a b\right)}}{4}=\underbrace{\frac{\sqrt{4 a^{2} b^{2}-\left(a^{2}+b^{2}-c^{2}\right)^{2}}}{4}}_{\text {This formula is also sometimes called Heron's formula }}=
\end{aligned}
$$
$$
\begin{gathered}
=\frac{\sqrt{4\left(x^{2}+y^{2}\right)\left(x^{2}+z^{2}\right)-\left(\left(x^{2}+y^{2}\right)+\left(x^{2}+z^{2}\right)-\left(y^{2}+z^{2}\right)\right)^{2}}}{4}=\frac{\sqrt{4 x^{4}+4 x^{2} y^{2}+4 x^{2} z^{2}+4 y^{2} z^{2}-\left(2 x^{2}\right)^{2}}}{4}= \\
=\frac{\sqrt{x^{2} y^{2}+x^{2} z^{2}+y^{2} z^{2}}}{2}
\end{gathered}
$$
Let's look at this formula for triangle $K P Q$ and segments $x=A_{2} P, y=A_{2} Q, z=A_{2} K$. On the one hand, we need to minimize $z$, and on the other hand, maximize the area. Clearly, for this, $x$ and $y$ should be as large as possible, that is, equal to the edge $\ell$.
As we know, $k=\frac{K A+A A_{2}}{K A}=\frac{K A+\ell}{K A}$, so $K A \cdot k=K A+\ell$, from which $K A=\frac{\ell}{k-1}$, $K A_{2}=K A+\ell=\frac{k \ell}{k-1}$.
Substituting these values into the formula, we get:
$S_{K P Q}=\frac{1}{2} \sqrt{\ell^{4}+\ell^{2} \cdot\left(\frac{k \ell}{k-1}\right)^{2}+\ell^{2} \cdot\left(\frac{k \ell}{k-1}\right)^{2}}=\frac{\ell^{2}}{2(k-1)} \sqrt{(k-1)^{2}+2 k^{2}}$.
Accordingly, $S=\frac{S_{K P Q}}{k^{2}}=\frac{\ell^{2} \sqrt{(k-1)^{2}+2 k^{2}}}{2 k^{2}(k-1)}$, from which $\frac{4 S^{2}}{\ell^{4}}=\frac{(k-1)^{2}+2 k^{2}}{k^{4}(k-1)^{2}}=\frac{1}{k^{4}}+\frac{2}{k^{2}(k-1)^{2}}$. The right-hand side of this equation decreases for $k>1$, so the equation has no more than one solution. The specific solution is often easily found from this equation, as it is usually an integer.
For example, in the first variant, we get the equation $\frac{1}{k^{4}}+\frac{2}{k^{2}(k-1)^{2}}=\frac{4 \cdot 16^{2}}{12^{4} \cdot \frac{8}{11}}=\frac{11}{2 \cdot 3^{4}}$, from which it is immediately desirable to check $k=3$, which turns out to be correct.
The answer is the difference in the areas of the two triangles and is equal to $\left(k^{2}-1\right) S$.
| $S$ | 16 |
| :---: | :---: |
| $\ell$ | $12 \sqrt[4]{\frac{8}{11}}$ |
| $k$ | 3 |
| Answer | 128 |
|
128
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 8. (4 points)
Hansel and Gretel are playing a game, with Hansel going first. They take turns placing tokens on a $7 \times 8$ grid (7 rows and 8 columns). Each time Gretel places a token, she earns 4 points for each token already in the same row and 3 points for each token already in the same column.
Only one token can be placed on each cell. The game ends when all cells on the board are filled.
What is the maximum number of points Gretel can score regardless of Hansel's actions?
|
# Answer: 700
## Solution:
Let's say that Hansel also earns points according to the same principle as Gretel. In this case, each pair of cells in the same row will ultimately give one of the players 4 points, and each pair of cells in the same column will give 3 points. In one row, there are $\frac{8 \cdot 7}{2}=28$ pairs of cells, and in one column, there are $-\frac{7 \cdot 6}{2}=21$ pairs. The total score accumulated by both players at the end of the game will be $7 \cdot 28 \cdot 4 + 8 \cdot 21 \cdot 3 = 1288$.
We can present a strategy for Gretel that allows her to gain 4 more points with each move than Hansel did before. For this, we can divide each row into 8 rectangles of $1 \times 2$. As soon as Hansel places a token in one of the cells of a rectangle, Gretel immediately occupies the second one. The columns in which these cells are located are identical due to Gretel's strategy, and in the row, by the time of her move, there is one more token—exactly the one placed by Hansel.
On the other hand, if Hansel always chooses the cell that yields the maximum number of points, Gretel can, with her next move, score at most 4 more points, since adding one token by Hansel increases the "value" of each of the remaining cells by no more than 4.
Each player will make 28 moves, and with the correct play, Gretel will score 112 more points. Knowing the sum and difference of two numbers, it is easy to find the numbers themselves, which are 700 and 588.
In all other scenarios, the second player always scores more points per token in a row of even length, so the described strategy for the second player always works.
|
700
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 1. (2 points)
The graphs of the quadratic trinomials $f(x)$ and $g(x)$ intersect at the point $(3 ; 8)$. The trinomial $f(x)+g(x)$ has a single root at 5. Find the leading coefficient of the trinomial $f(x)+g(x)$.
#
|
# Answer: 4
## Solution:
Since the quadratic polynomial $f(x)+g(x)$ has a unique root 5, it can be represented as $a(x-5)^{2}$, where $a$ is precisely the leading coefficient we are looking for. Additionally, the value of this quadratic polynomial at the point 3 is equal to the sum of the values of the polynomials $f(x)$ and $g(x)$, which is 16.
Thus, $a \cdot(-2)^{2}=16$, from which we get $a=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 2. (2 points)
A natural number $n$ when divided by 12 gives a remainder $a$ and an incomplete quotient $b$, and when divided by 10, it gives a remainder $b$ and an incomplete quotient $a$. Find $n$.
|
Answer: 119
## Solution:
From the condition, it follows that $n=12 b+a=10 a+b$, from which $11 b=9 a$. Therefore, $b$ is divisible by 9, and $a$ is divisible by 11. On the other hand, $a$ and $b$ are remainders from division by 12 and 10, respectively, so $0 \leqslant a \leqslant 11$ and $0 \leqslant b \leqslant 9$. We get two options: $a=b=0$ and $n=0$ (which does not fit, since $n$ is a natural number) or $a=11, b=9, n=119$.
|
119
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 3. (3 points)
It is known that $a^{2} b+a^{2} c+b^{2} a+b^{2} c+c^{2} a+c^{2} b+3 a b c=30$ and $a^{2}+b^{2}+c^{2}=13$.
Find $a+b+c$.
|
Answer: 5
## Solution:
$(a+b+c)^{3}-(a+b+c)\left(a^{2}+b^{2}+c^{2}\right)=2\left(a^{2} b+a^{2} c+b^{2} a+b^{2} c+c^{2} a+c^{2} b+3 a b c\right)$. Let $a+b+c$ be $x$, substitute the known values of the expressions from the condition, and we get the equation $x^{3}-13 x-60=0$.
It is not hard to notice that the number 5 is a root of this equation. Dividing $x^{3}-13 x-60$ by $x-5$, we get $x^{2}+5 x+12$. This quadratic has no roots, so 5 is the only possible answer.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 4. (3 points)
Circles $O_{1}$ and $O_{2}$ touch circle $O_{3}$ with radius 13 at points $A$ and $B$ respectively and pass through its center $O$. These circles intersect again at point $C$. It is known that $O C=12$. Find $A B$.
|
# Answer: 10
## Solution:
Since circles $O_{1}$ and $O_{2}$ touch circle $O_{3}$ at points $A$ and $B$ respectively and pass through its center $O$, $AO$ and $BO$ are their diameters. Therefore, angles $\angle OCA$ and $\angle OCB$ are right angles. These cannot be the same angle, as this would mean that circles $O_{1}$ and $O_{2}$ coincide, so they are adjacent angles. Right triangles $OCA$ and $OCB$ are equal by the leg $OC$ and hypotenuses. Therefore, $AB = 2AC = 2\sqrt{OA^2 - OC^2} = 2\sqrt{13^2 - 12^2} = 10$.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 6. (4 points)
Six positive numbers, not exceeding 3, satisfy the equations $a+b+c+d=6$ and $e+f=2$. What is the smallest value that the expression
$$
\left(\sqrt{a^{2}+4}+\sqrt{b^{2}+e^{2}}+\sqrt{c^{2}+f^{2}}+\sqrt{d^{2}+4}\right)^{2}
$$
can take?
|
Answer: 72
In the image, there are three rectangles $2 \times (a+b)$ and three rectangles $2 \times (c+d)$, forming a $6 \times 6$ square, since $a+b+c+d=6$. The segment of length 2 in the center of the image is divided into segments $e$ and $f$, which sum to 2, as required by the condition.
The broken line depicted in the image, going from one corner of the square to the other, by the Pythagorean theorem, has a square of its length equal to the expression whose minimum value we need to find. Such a broken line can be constructed for each set of six numbers, so we only need to find the length of the shortest broken line, which is the diagonal of the square. The square of its length is $2 \cdot 6^{2}=$ 72.
|
72
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 7. (4 points)
In an $8 \times 8$ table, some cells are black, and the rest are white. In each white cell, the total number of black cells on the same row or column is written; nothing is written in the black cells. What is the maximum value that the sum of the numbers in the entire table can take?
|
Answer: 256
## Solution:
The number in the white cell consists of two addends: a "horizontal" and a "vertical" one. Consider the sum of all "horizontal" addends and the sum of all "vertical" addends separately across the entire table. If we maximize each of these two sums separately, the total sum will also be the greatest.
Consider the sum of the "horizontal" addends. If a row contains $x$ black cells and $8-x$ white cells, then the sum of the horizontal addends in this row is $x(8-x)$. This value is maximized when $x=4$ and equals 16. Therefore, the maximum sum of "horizontal" addends is $8 \cdot 16 = 128$, and the total of all numbers is 256.
This value is achieved, for example, with a checkerboard pattern—where it is easy to verify that each row and each column indeed has 4 black cells.
|
256
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 8. (5 points)
32 volleyball teams participate in a tournament according to the following scheme. In each round, all remaining teams are randomly paired; if the number of teams is odd, one team skips this round. In each pair, one team wins and the other loses, as there are no draws in volleyball. After three losses, a team is eliminated from the tournament. When all teams except one are eliminated, this team is declared the winner and the tournament ends.
What is the minimum number of rounds the tournament can last?
|
# Solution:
For all teams to be eliminated except one, they must suffer at least 93 losses, meaning at least 93 matches must be played.
We also note that after each round, the number of teams decreases by at most half, because no more than half of the teams lose. In particular, in the final round, only 2 teams could have participated, and they played one match. In the penultimate round, a maximum of 4 teams participated and played a maximum of 2 matches. One round before that, a maximum of 4 matches were played, and another round before that, a maximum of 8. In total, in the last 4 rounds, no more than 15 matches were played.
This means that at least 78 matches were played before that. In each of the remaining rounds, no more than 16 matches were played, so there were at least 5 such rounds. In total, we get at least $4+5=9$ rounds.
The teams could manage in 9 rounds. Indeed, in the first 4 rounds, the teams could pair up, and in each pair, they could inflict 2 losses on each other. After this, each team has one loss left, and we get a standard Olympic system of 5 rounds, in each of which half of the teams are eliminated.
Answer: 9
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 1. (2 points)
In a class, each student has either 5 or 6 friends (friendship is mutual), and any two friends have a different number of friends in the class. What is the smallest number of students, greater than 0, that can be in the class?
|
Answer: 11
## Solution:
Let's look at some person. Suppose he has five friends. Then each of these five people has six friends. Similarly, there are at least another 6 people with five friends each. In total, there are 11 people.
It is quite easy to construct an example: two groups of 5 and 6 people, people from different groups are friends with each other, but not within the same group.
#
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 2. (2 points)
In a positive non-constant geometric progression, the arithmetic mean of the second, seventh, and ninth terms is equal to some term of this progression. What is the minimum possible number of this term?
|
Answer: 3
Solution:
The second element is either the larger or the smaller of the three specified, so it cannot be equal to the arithmetic mean of all three. The first element is even less suitable.
To prove that the answer "3" is possible, let's introduce the notation: let $b_{n}=$ $b q^{n-1}$. Then we need to solve the equation $3 b q^{2}=b q+b q^{6}+b q^{8}$. Simplifying it, we get $q^{7}+q^{5}-$ $3 q+1=0$.
This equation has a root $q=1$, but it does not suit us because the progression is not constant. $q^{7}+q^{5}-3 q+1=(q-1)\left(q^{6}+q^{5}+2 q^{4}+2 q^{3}+q^{2}+2 q-1\right)$. The second factor is negative at $q=0$ and positive at $q=1$, so this expression has a root between zero and one. Thus, we can choose the common ratio of the progression and take any positive number as the first term for the answer 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 4. (2 points)
How many negative numbers are there among the numbers of the form $\operatorname{tg}\left(\left(15^{n}\right)^{\circ}\right)$, where $\mathrm{n}$ is a natural number from 1 to 2019?
|
Answer: 1009
Solution:
$\operatorname{tg} 15^{\circ}>0$.
$15^{2}=225 ; \operatorname{tg} 225^{\circ}>0$.
Further, $225 \cdot 15=3375$, this number gives a remainder of 135 when divided by $360 . \operatorname{tg} 135^{\circ}<0$.
$135 \cdot 15=2025$, this number gives a remainder of 225 when divided by 360. The sequence of remainders when divided by 360 then repeats, meaning that positive and negative tangents will alternate.
The first number does not enter this cycle and it is positive. Among the remaining numbers, exactly half are negative, that is 1009.
|
1009
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 7. (4 points)
Can the numbers from 0 to 9999 (each used exactly once) be arranged in a $100 \times 100$ square table so that the sum of the numbers in each $2 \times 2$ square is the same?
|
Answer: Yes, it can.
Solution:
The desired table is obtained as the sum of two tables.
The first table looks like this:
| 0 | 99 | 0 | 99 | 0 | 99 | $\ldots$ |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 0 | 99 | 0 | 99 | 0 | 99 | $\ldots$ |
| 1 | 98 | 1 | 98 | 1 | 98 | $\ldots$ |
| 1 | 98 | 1 | 98 | 1 | 98 | $\ldots$ |
| 2 | 97 | 2 | 97 | 2 | 97 | $\ldots$ |
| 2 | 97 | 2 | 97 | 2 | 97 | $\ldots$ |
| $\ldots$ | | | | | | |
| 49 | 50 | 49 | 50 | 49 | 50 | $\ldots$ |
In this table, any number, together with its horizontal neighbor, sums to 99, so the sum in any $2 \times 2$ square is 198.
| 9900 | 0 | 9800 | 100 | 9700 | 200 | $\ldots$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 0 | 9900 | 100 | 9800 | 200 | 9700 | $\ldots$ |
| 9900 | 0 | 9800 | 100 | 9700 | 200 | $\ldots$ |
| 0 | 9900 | 100 | 9800 | 200 | 9700 | $\ldots$ |
| 9900 | 0 | 9800 | 100 | 9700 | 200 | $\ldots$ |
| 0 | 9900 | 100 | 9800 | 200 | 9700 | $\ldots$ |
| $\ldots$ | | | | | | |
In this table, any number, together with its vertical neighbor, sums to 9900, so the sum in any $2 \times 2$ square is 19800.
When these tables are summed, the sum in each $2 \times 2$ square will obviously be 19998.
It remains to understand that all numbers will appear in the table.
Consider the placement of a number of the form $100k$ in the second table. This number is located in two adjacent columns on cells that, when colored in a checkerboard pattern, are of the same color. In the first table, in these two columns, all numbers from 0 to 99 appear, with each number appearing once on a black cell and once on a white cell. Therefore, the number $100k$ will be summed with each number from 0 to 99 exactly once. Thus, we will get all numbers from $100k$ to $100k+99$ each exactly once, and therefore, in the entire table, we will get all numbers from 0 to 9999.
|
19998
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 1. (2 points)
In a class, each student has either 5 or 7 friends (friendship is mutual), and any two friends have a different number of friends in the class. What is the smallest number of students, greater than 0, that can be in the class?
Answer: 12
|
Solution:
Let's look at some person. Suppose he has five friends. Then each of these five people has seven friends. Similarly, there are at least seven more people with five friends each. In total, there are 12 people.
It is quite easy to construct an example: two groups of 5 and 7 people, people from different groups are friends with each other, but not within the same group.
#
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 2. (2 points)
In a positive non-constant geometric progression, the arithmetic mean of the third, fourth, and eighth terms is equal to some term of this progression. What is the minimum possible number of this term?
|
Answer: 4
Solution:
The third element is either the larger or the smaller of the three specified, so it cannot be equal to the arithmetic mean of all three. The first and second elements are even less suitable.
To prove that the answer "4" is possible, let's introduce the notation: let $b_{n}=$ $b q^{n-1}$. Then we need to solve the equation $3 b q^{3}=b q^{2}+b q^{3}+b q^{7}$. Simplifying it, we get $q^{5}-$ $2 q+1=0$.
This equation has a root $q=1$, but it does not suit us because the progression is not constant. $q^{5}-2 q+1=(q-1)\left(q^{4}+q^{3}+q^{2}+q-1\right)$. The second factor is negative at $q=0$ and positive at $q=1$, so this expression has a root between zero and one. Thus, we can choose the common ratio of the progression and take any positive number as the first term for the answer 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 4. (2 points)
How many positive numbers are there among the numbers of the form $\operatorname{ctg}\left(\left(15^{n}\right)^{\circ}\right)$, where $\mathrm{n}$ is a natural number from 1 to 2019?
|
Answer: 1010
Solution:
$\operatorname{ctg} 15^{\circ}>0$.
$15^{2}=225 ; \operatorname{ctg} 225^{\circ}>0$.
Next, $225 \cdot 15=3375$, this number gives a remainder of 135 when divided by $360 . \operatorname{ctg} 135^{\circ}<0$.
$135 \cdot 15=2025$, this number gives a remainder of 225 when divided by 360. The sequence of remainders when divided by 360 then repeats, meaning that positive and negative cotangents will alternate.
The first number does not enter this cycle and it is positive. Among the remaining numbers, exactly half are positive, that is, 1009. Therefore, the answer is 1010.
|
1010
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 7. (4 points)
Can the numbers from 0 to 999 (each used exactly once) be arranged in a $100 \times 10$ rectangular table so that the sum of the numbers in each $2 \times 2$ square is the same?
|
Answer: Yes, it can.
Solution:
The desired table is obtained as the sum of two tables.
The first table looks like this:
| 0 | 99 | 0 | 99 | 0 | 99 | $\ldots$ |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 0 | 99 | 0 | 99 | 0 | 99 | $\ldots$ |
| 1 | 98 | 1 | 98 | 1 | 98 | $\ldots$ |
| 1 | 98 | 1 | 98 | 1 | 98 | $\ldots$ |
| 2 | 97 | 2 | 97 | 2 | 97 | $\ldots$ |
| 2 | 97 | 2 | 97 | 2 | 97 | $\ldots$ |
| $\ldots$ | | | | | | |
| 49 | 50 | 49 | 50 | 49 | 50 | $\ldots$ |
In this table, any number, together with its horizontal neighbor, sums to 99, so the sum in any $2 \times 2$ square is 198.
| 900 | 0 | 800 | 100 | 700 | 200 | $\ldots$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 0 | 900 | 100 | 800 | 200 | 700 | $\ldots$ |
| 900 | 0 | 800 | 100 | 700 | 200 | $\ldots$ |
| 0 | 900 | 100 | 800 | 200 | 700 | $\ldots$ |
| 900 | 0 | 800 | 100 | 700 | 200 | $\ldots$ |
| 0 | 900 | 100 | 800 | 200 | 700 | $\ldots$ |
| $\ldots$ | | | | | | |
In this table, any number, together with its vertical neighbor, sums to 900, so the sum in any $2 \times 2$ square is 1800.
When these tables are summed, the sum in each $2 \times 2$ square will obviously be 1998.
It remains to understand that all numbers will appear in the table.
Consider the placement of a number of the form $100k$ in the second table. This number is located in two adjacent columns on cells that, when colored in a checkerboard pattern, are of the same color. In the first table, in these two columns, all numbers from 0 to 99 appear, with each number appearing once on a black cell and once on a white cell. Therefore, the number $100k$ will be summed with each number from 0 to 99 exactly once. Thus, we will get all numbers from $100k$ to $100k+99$ each exactly once, and therefore, in the entire table, we will get all numbers from 0 to 999.
|
1998
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. $\mathrm{ABCD}$ is a trapezoid with bases $\mathrm{AD}=6$ and $\mathrm{BC}=10$. It turns out that the midpoints of all four sides of the trapezoid lie on the same circle. Find its radius.
If there are multiple correct answers, list them in any order separated by a semicolon.
|
Answer: 4.
## Examples of answer notation:
45
$4 ; 5$
#
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Given a regular tetrahedron with edge lengths that are integers. Two of these edges have lengths 9 and 11. What is the greatest possible value of the perimeter of the tetrahedron?
|
Answer: 68.
## Examples of answer recording: 45
#
|
68
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Given a cubic polynomial $p(x)$. It is known that $p(-6)=30, p(-3)=45, p(-1)=15, p(2)=30$.
Find the area of the figure bounded by the lines $x=-6, y=0, x=2$ and the graph of the given polynomial, if it is also known that on the interval from -6 to 2 the given polynomial takes only positive values.
|
Answer: 240.
## Examples of answer recording:
45
|
240
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.