problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
6. Find a two-digit number if it is known that the sum of its digits is 13, and the difference between the sought number and the number written with the same digits but in reverse order is a two-digit number with 7 units.
|
6. The desired number $N=10 x+y$, where $x=1,2,3,4,5,6,7,8,9 ; y=0,1,2$, $3,4,5,6,7,8,9$. Let's write down the two-digit numbers whose sum of digits is 13. Such numbers will be $49,58,67,76,85,94$. Let's write down the reversed numbers: $94,85,76,67,58,49$. The condition of the problem is satisfied only by the pair of numbers 85 and 58. $85-58=27$. The desired number $N=85$.
|
85
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. The dividing circle of the dividing head is uniformly marked with 24 holes. What regular polygons can be marked using this instrument?
|
10. By connecting all 24 holes sequentially, we get a twenty-four-sided polygon, connecting every other hole - a twelve-sided polygon,
connecting every two holes - an eight-sided polygon, connecting every three holes - a six-sided polygon, and connecting every seven holes - a three-sided polygon. If $n$ is the number of vertices of the inscribed polygon, $3 \leqslant n \leqslant 24$, then $\frac{24-n}{n}=k-$ $5^{*}$
is an integer. Then $n=\frac{24}{k+1}$. Therefore, $0 \leqslant k \leqslant 7$.
Answer. Using a dividing circle with 24 holes, 6 different regular polygons can be marked.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13. In what ways can you give 78 rubles, having only five-ruble and three-ruble banknotes?
|
13. Let $x$ be the number of 5-ruble stamps, and $y$ be the number of 3-ruble stamps, then $78 = 5x + 3y$, from which $x = 15 - \frac{3(y-1)}{5}$. Since $x$ is a positive integer, $15 - \frac{3(y-1)}{5} > 0$, and thus $y < 26$. Additionally, $\frac{3(y-1)}{5}$ is an integer, meaning $y-1$ is a multiple of 5. Let $y-1 = 5k$, $0 \leq k < 5$.
Answer. 78 rubles can be paid in five ways.
| $k$ | 0 | 1 | 2 | 3 | 4 |
| :--- | :--- | :--- | :--- | :--- | :--- |
| $y$ | 1 | 6 | 11 | 16 | 21 |
| $x$ | 15 | 12 | 9 | 6 | 3 |
|
78
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
14. The purchase costs 19 rubles. The buyer has only three-ruble bills, and the cashier has only five-ruble bills. Can the purchase be paid for with the available money, and if so, how exactly? (Limit the case to when the buyer and the cashier each have 15 bills of the specified denomination).
|
14. 19 rubles can be paid in two ways:
1) the buyer gives 24 rubles and receives 5 rubles in change. 2) gives 39 rubles and receives 20 rubles in change.
|
19
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
14. $\log _{\frac{\sqrt{3}}{3}}\left(\log _{8} \frac{\sqrt{2}}{2}-\log _{3} \frac{\sqrt{3}}{3}\right)$.
In № $15-27$ solve the equations:
|
14. We should switch to the logarithm with base $\frac{\sqrt{3}}{3}$.
Then replace $\frac{1}{3}$ with $\left(\frac{\sqrt{3}}{3}\right)^{2}$. Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
16. $\log _{4}\left\{2 \log _{3}\left[1+\log _{2}\left(1+3 \log _{2} x\right)\right]\right\}=\frac{1}{2}$.
|
16. Gradually potentiating, we arrive at the equation $1+3 \log _{2} x=4$. From which $x=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
19. $\log _{5} 120+(x-3)-2 \log _{5}\left(1-5^{x-3}\right)=-\log _{5}\left(0.2-5^{x-4}\right)$.
|
19. $1-5^{x-3} \neq 0, x \neq 3,0,2-5^{x-4}=\frac{1}{5}\left(1-5^{x-3}\right)$.
Raising the entire expression, we get
$$
\frac{120 \cdot 5^{x-3}}{\left(1-5^{x-3}\right)^{2}}=\frac{5}{1-5^{x-3}} ; \quad 5^{x-3}=5^{-2} . \quad \text { Hence } x=1
$$
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
26. $5^{\lg x}-3^{\lg x-1}=3^{\lg x+1}-5^{\lg x-1}$.
|
26. Grouping the powers with bases 5 and 3, we get
$$
5^{\lg x}\left(1+\frac{1}{5}\right)=3^{\lg x}\left(3+\frac{1}{3}\right) . \quad \text { Hence }\left(\frac{5}{3}\right)^{\lg \cdot x}=\left(\frac{5}{3}\right)^{2} ; \quad x=100
$$
|
100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
14. Calculate the product $p=1 \cdot 2^{\frac{1}{2}} \cdot 4^{\frac{1}{4}} \cdot 8^{\frac{1}{8}} \cdot 16^{\frac{1}{16}} \cdot \ldots$
In № $15-20$ find the sums:
|
14. Let's write all powers as powers with base 2
$$
p=1 \cdot 2^{\frac{1}{2}} \cdot 2^{\frac{2}{4}} \cdot 2^{\frac{3}{8}} \cdot 2^{\frac{4}{16}} \ldots=2^{\frac{1}{2}+\frac{2}{4}+\frac{3}{8}+\frac{4}{16}+\cdots}
$$
The problem has been reduced to finding the sum $S=\frac{1}{2}+\frac{2}{4}+\frac{3}{8}+\frac{4}{16}+\ldots$
Divide each term of this equality by 2 and subtract the obtained result from the first equality
$$
\frac{1}{2} S=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\ldots ; \quad \frac{1}{2} S=1, \quad S=2, \quad p=4
$$
86
15, 16, 17. $S=\frac{n}{n+1}, \quad S=\frac{n}{3 n+1}, S=\frac{n}{2 n+1}$ respectively. The specified sums can be found by constructing sequences of partial sums or by decomposing the terms of these sums into simpler fractions.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
21. Find the sum $\frac{1}{2!}+\frac{2}{3!}+\frac{3}{4!}+\ldots+\frac{n}{(n+1)!}$ and compute its limit as $n \rightarrow \infty$.
|
21. By forming the sequence of partial sums, we get
$$
S_{1}=\frac{2!-1}{2!}, \quad S_{2}=\frac{3!-1}{3!}, \ldots \quad \text { Hence } S_{n}=\frac{(n+1)!-1}{(n+1)!}, \quad S=\lim _{n \rightarrow \infty} S_{n}=1
$$
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
15. $y=\frac{|x|-2}{|x|}$.
Translate the text above into English, keeping the original text's line breaks and format, and output the translation result directly.
15. $y=\frac{|x|-2}{|x|}$.
|
15. (Fig. 15) The root of the submodular expression is 0.
For $x>0, \quad y=1-\frac{2}{x}$.
For $x<0, \quad y=1+\frac{2}{x}$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
31. How many planes of symmetry do the following have: a) a cube; b) a regular tetrahedron?
|
31. a) A cube has 9 planes of symmetry; b) a regular tetrahedron has 6 planes of symmetry.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
32. How many axes of symmetry do the following have: a) a cube; b) a regular tetrahedron
|
32. a) A cube has 13 axes of symmetry; b) a regular tetrahedron has 7 axes of symmetry.
|
13
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
21. What is the maximum area that a triangle with sides \(a, b, c\) can have, given that the sides are within the following limits: \(0 \leqslant a \leqslant 1 \leqslant b \leqslant 2 \leqslant c \leqslant 3\) ?
|
21. $S=\frac{1}{2} a b \sin \alpha$. Takes the maximum value when $a=1, b=2, \sin \alpha=1$,
$S=\frac{1}{2} \cdot 1 \cdot 2 \cdot 1=1$. Under these conditions, $c=\sqrt{1+4}=\sqrt{5}$, which satisfies the problem's condition ( $2 \leqslant c \leqslant 3$).
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
33. Determine $a$ so that the sum of the squares of the roots of the equation $x^{2}+(2-a) x-a-3=0$ is the smallest.
|
33. $a=1$
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
35. Find the maximum value of the expression $\log _{2}^{4} x+12 \log _{2}^{2} x \log _{2} \frac{8}{x}$, assuming that $x$ varies from 1 to 64.
|
35. Let's denote the given expression by $y$. Then it is easy to see that $y=\log _{2}^{2} x\left(6-\log _{2} x\right)^{2}$. But $1<x<64$, so $0<\log _{2} x<6$. The maximum value of $y$ coincides with the maximum value of the product. Since $\log _{2} x+(6-$ $\left.-\log _{2} x\right)=6$, the product will be the largest under the condition that
$\frac{\log _{2} x}{2}=\frac{6-\log _{2} x}{2}$; from which $\log _{2} x=3, x=8$. The maximum value of $y$ is 81.
|
81
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
43. Points $A$ and $B$ are located on a straight highway running from west to east. Point $B$ is 9 km east of $A$. A car departs from point $A$ heading east at a speed of 40 km per hour. At the same time, a motorcycle departs from $B$ in the same direction with a constant acceleration of 32 km/hour ${ }^{2}$. Determine the greatest distance between the car and the motorcycle during the first two hours of travel.
Hint. It is useful to draw a graph of the distance as a function of time.
|
43. At time $t$, the car is at a distance of $40 t$ km from point $A$, and the motorcycle is at a distance of $\left(\frac{32 t^{2}}{2}+9\right)$ km from the same point. The distance between them is $\left|16 t^{2}+9-40 t\right|$ (Fig. 29). The greatest distance of 16 km will be reached in 1 hour 15 minutes.
|
16
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
30. Several families lived in one house. In total, there are more children in these families than adults: there are more adults than boys; more boys than girls; and more girls than families. There are no childless families, and no families have the same number of children. Each girl has at least one brother and at most one sister. In one of the families, there are more children than in all the others combined. How many families lived in the house? How many boys and how many girls are there in each of these families?
|
30. Three families lived in the house. In one of these families, there is a single child, a boy. In another family - two girls and a boy. In the third - two girls and three boys.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
32. During the lunch break, the members of the communist labor brigade started talking about how many newspapers each of them reads. It turned out that each member subscribes to and reads exactly two newspapers, each newspaper is read by five people, and any combination of two newspapers is read by one person. How many newspaper titles do the members of the brigade subscribe to? How many members are in the brigade?
|
32. 6 newspaper names, 15 members.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
51. There are three villages: $A, B$, and $C$. The inhabitants of $A$ always tell the truth, the inhabitants of $B$ always lie, and the inhabitants of $C$, depending on their mood, tell the truth or lie. Since the villages are located close to each other, the inhabitants visit each other. A tourist ended up in one of these villages. What is the minimum number of questions and what specific questions will he have to ask the first person he meets (who can only answer “yes” or “no”) to find out which village he is in and which village this person he met lives in?
|
51. Four questions: 1) Am I in one of the settlements $A$ and $B$? 2) Am I in settlement C? 3) Do you live in settlement C? 4) Am I in settlement $A^{*}$?
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
52. My friend has thought of an integer between 10 and 19. To guess which number he has in mind, I can ask him questions that he will answer with "yes" or "no": What is the smallest number of questions and which specific questions can I ask to determine which number he thought of?
|
52. The least number of questions is three. The first question: "Is the number you are thinking of among the first four numbers (11-14)?" If the answer is "Yes," then the second question can be: "Is the number you are thinking of among the numbers 11 and 12?" If the answer is "No," then the third question can be: "Is the number you are thinking of 13?" If the answer is "No," then the number you are thinking of is 14.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (7th grade) Several girls (all of different ages) were collecting white mushrooms in the forest. The collected mushrooms they distributed as follows: the youngest received 20 mushrooms and 0.04 of the remainder. The next oldest received 21 mushrooms and 0.04 of the remainder, and so on. It turned out that everyone received an equal amount. How many mushrooms were collected and how many girls were there?
|
1. Let the number of collected mushrooms be denoted by $x$. Then the youngest girl received $20+(x-20) \cdot 0.04$ mushrooms. The second girl received $19.392+0.0384 x$. Both received the same amount. By setting up the equation and solving it, we find $x=120$. There were 5 girls, each received 24 mushrooms.
|
120
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11. (9th grade) Find a natural number $n$, knowing that the sum $1+2+3+\ldots+n$ is a three-digit number consisting of identical digits.
|
11. $1+2+3+\ldots+n=\frac{n+1}{2} n$. This sum equals a three-digit number $\overline{a a a}$, where $\overline{a a a}=100 a+10 a+a=111 a$. We get the equation $\frac{n+1}{2} n=111 a$. From this, $a=\frac{n(n+1)}{2 \cdot 3 \cdot 37}$. Since $a$ is an integer, $n(n+1)$ must be divisible by 2, 3, and 37. This is only possible when $n=36$.
|
36
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
21. (7th grade) (Newton's problem) Grass grows at the same rate and density everywhere in the corner. It is known that 70 cows would eat it in 24 days, and 30 cows in 60 days. How many cows would eat all the grass in 96 days? (It is assumed that the cows eat the grass uniformly).
|
21. In one day, $x$ amount of grass grows. If the initial amount of grass is taken as 1, then over 24 days, the cows eat $1+24 x$ amount of grass, and one cow eats $\frac{1+24 x}{24 \cdot 70}$ amount of grass per day. But according to the second condition, a cow eats $\frac{1+60 x}{30 \cdot 60}$ amount of grass per day. By equating the first and second results, we get $x=\frac{1}{480}$. A cow eats $\frac{1}{1600}$ of the initial amount of grass per day. In 96 days, 20 cows will eat all the grass.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
29. (8th grade) When asked what his ticket number was, someone answered like this: "If all six two-digit numbers that can be formed from the digits of the number are added together, then half of the resulting sum will be exactly my ticket number." Determine the ticket number.
|
29. Let's denote the ticket number as: $N=100 x+10 y+\boldsymbol{z}$. According to the problem,
$$
\begin{gathered}
2 N=10 x+y+10 x+z+10 y+x+10 y+z+10 z+x+10 z+y= \\
=22 x+22 y+22 z, \text { i.e. } N=11(x+y+z)
\end{gathered}
$$
By equating the first and second results, we get the following equation: $100 x+10 y+z=11(x+y+z)$. The right side is divisible by 11, and the left side must also be divisible by 11. This is possible if $x+\boldsymbol{z}-\boldsymbol{y}=11 k$. Since $x+\boldsymbol{z}$ can take a value from 0 to 18, and $y$ from 0 to 9, the equation is possible only for $k=0, k=1$. Answer: $N=198$.
|
198
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
37. (10-11 grades) How many planes are equidistant from four points that do not lie in the same plane?
|
37. Taking these points as the vertices of a tetrahedron, it is easy to establish that only seven planes can be drawn equidistant from its vertices.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
41. (8th grade) Find the smallest natural number that has the following properties: a) its representation in the decimal system ends with the digit 6; b) if the last digit 6 is erased and this digit 6 is written in front of the remaining digits, the resulting number is four times the original number.
|
41. The desired number can be written as: $N=\overline{a_{1} a_{2} a_{3} \ldots a_{n-1}}-1$. After rearranging the digit 6, we get the number $K=4 N=6 \bar{a}_{1} a_{2} a_{3} \ldots a_{n-1}$. Since the last digit of the number $N$ is 6, the last digit of the number $K$ is 4, i.e., $a_{n-1}=4$.
Substituting the value $a_{n-1}=4$ into $N$ and multiplying $N$ by 4, we find that $a_{n-2}=8$. Substituting the value $a_{n-2}=8$ into $N$ and multiplying $N$ by 4, we find that $a_{n-3}=3$, and so on, until we get the digit 6 in the number $4 N$. The number 153846 satisfies all the conditions of the problem and is the smallest. The problem has other solutions as well.
|
153846
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
45. (9th grade) Find a four-digit number that is a perfect square, knowing that the first two digits, as well as the last two, are equal to each other.
|
45. The desired number can be written as: $N=\overline{a a b} b$ or $N=1100 a+11 b=$ $=11(99 a+a+b)$. For the desired number to be a perfect square, it is necessary that the factor 11 appears in the number $N$ twice, i.e., the sum $a+b$ must be divisible by $11.1<a+b<18$, hence, $a+b=11$. Then $N=11^{2}(9 a+1)$. The binomial $9 a+1$ must be a square of some number. This is possible only when $a=7$. Then $b=4, N=7744=88^{2}$.
|
7744
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
58. (8th grade) Given a thousand-sided polygon. Inside it, 500 points are taken, which are connected to each other and to the vertices of the thousand-sided polygon. How many triangles will be formed? (The sides of the triangles do not intersect).
|
58. Let $x$ be the number of triangles, $2 d(n-2)$ be the sum of the interior angles of a polygon, $2 d x$ be the sum of the interior angles of the triangles, and $4 d \cdot 500$ be the sum of the full angles at the given 500 points. We can set up the equation $2 d x = 500 \cdot 4 d + 2 d(n-2)$, where $n=1000$. Answer: $x=1998$.
|
1998
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
61. (9th grade) In a square table consisting of $8 \times 8$ cells, natural numbers from 1 to 64 are arranged in order. A number is selected, and the row and column in which it is located are crossed out. From the remaining numbers, another number is selected, and the row and column in which it is located are crossed out again. This continues until all rows and columns are crossed out. Find the sum of the eight selected numbers.
|
61. The chosen number $N=M_{i}+8\left(n_{k}-1\right)$, where $M_{i}$ is the column number, and $n_{k}$ is the row number in which it stands. Then the total sum of the eight chosen numbers can be written as:
$$
S=\sum_{i=1, k=1}^{i=8, k=8} M_{i}+8\left(n_{k}-1\right)=\frac{8+1}{3} 8+8 \frac{7+1}{2} 7=260
$$
|
260
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
64. (9th grade) The number 7 is raised to the seventh power, the resulting number is again raised to the seventh power, and so on. This process is repeated 1000 times. What is the last digit of this number?
|
64. Considering the powers of the number 7 in sequence, we notice that the last digits of these powers repeat every four, so the number given in the problem ends with the digit 7.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
65. (10-11 grades) Into how many parts do the planes of the faces of a tetrahedron divide space?
|
65. The calculation is easiest to perform as follows: inside the tetrahedron - 1 part, at the vertices of the trihedral angles - 4 parts, along the edges - 10 parts. In total, 15 parts.
|
15
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
81. The difference $\sqrt{|40 \sqrt{2}-57|}-\sqrt{40 \sqrt{2}+57}$ is an integer. Find this number.
|
Solution. Since $40 \sqrt{2}-57<0$, then $|40 \sqrt{2}-57|=$ $=57-40 \sqrt{2}$. Then
$$
\begin{aligned}
A & =\sqrt{|40 \sqrt{2}-57|}-\sqrt{40 \sqrt{2}+57}= \\
& =\sqrt{57-40 \sqrt{2}}-\sqrt{57+40 \sqrt{2}}
\end{aligned}
$$
Let $57-40 \sqrt{2}=(a+b \sqrt{2})^{2}$, where $a$ and $b$ are unknown coefficients. Then
$$
57-40 \sqrt{2}=a^{2}+2 b^{2}+2 \sqrt{2} a b
$$
from which
$$
\left\{\begin{array}{l}
a^{2}+2 b^{2}=57 \\
2 a b=-40
\end{array}\right.
$$
Solving this system of equations, we get $a=5, b=-4$. Therefore, $\sqrt{57-40 \sqrt{2}}=\sqrt{(5-4 \sqrt{2})^{2}}=|5-4 \sqrt{2}|=4 \sqrt{2}-5, \quad$ since $5-4 \sqrt{2}<0$.
Similarly, it is established that $\sqrt{57+40 \sqrt{2}}=4 \sqrt{2}+5$. Consequently, $A=4 \sqrt{2}-5-(4 \sqrt{2}+5)=-10$.
## Elimination of Irrationality in the Denominator
|
-10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
89. Simplify the expression:
a) $\sqrt{|40 \sqrt{2}-57|}-\sqrt{40 \sqrt{2}+57}$
b) $\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}$
|
Solution. a) Let $\sqrt{57-40 \sqrt{2}}-\sqrt{57+40 \sqrt{\overline{2}}}=x ; x<0$, since $\sqrt{57-40 \sqrt{2}}<\sqrt{57+40 \sqrt{2}}$.
Square both sides of the equation:
$$
x^{2}=57-40 \sqrt{2}-2 \sqrt{57^{2}-(40 \sqrt{2})^{2}}+57+40 \sqrt{2}
$$
from which
$$
x^{2}=114-2 \sqrt{49}, x^{2}=100, x=-10
$$
(Solution by the method of undetermined coefficients see p. 51.)
b) Let the value of the expression be $x$, i.e.
$$
\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}=x
$$
Cube both sides of the equation:
$$
\begin{aligned}
& 4+3 \cdot(\sqrt[3]{2+\sqrt{5}})^{2} \cdot \sqrt[3]{2-\sqrt{5}}+ \\
& +3 \cdot \sqrt[3]{2+\sqrt{5}} \cdot(\sqrt[3]{2-\sqrt{5}})^{2}=x^{3}
\end{aligned}
$$
or
$$
3 \sqrt[3]{2+\sqrt{5}} \cdot \sqrt[3]{2-\sqrt{5}} \cdot(\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}})=x^{3}-4
$$
or (see (1))
$$
\begin{aligned}
3 \cdot \sqrt[3]{2^{2}-(\sqrt{5})^{2}} \cdot x & =x^{3}-4, \text { i.e. } \\
x^{3}+3 x-4 & =0
\end{aligned}
$$
Thus, the value $x$ of the expression is a root of equation (2).
It is obvious that the number $x=1$ is a root of equation (2).
|
-10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
90. Prove that $\sqrt[3]{9+\sqrt{80}}+\sqrt[3]{9-\sqrt{80}}=3$.
|
Solution. Let the value of the expression on the left side of the equality be denoted by $x$. Reasoning as in the solution of Example 89, b, we obtain the equation $x^{3}-3 x-18=0$, from which $x=3$.
## Solving Equations
|
3
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
91. Let's solve the equation
$$
(3 x-1) \sqrt{x-4}=17 \sqrt{2}
$$
|
Solution. Method 1. The domain of expression (3) is the interval $[4 ;+\infty)$. Squaring both sides of the equation, we obtain the equivalent equation
$$
9 x^{3}-42 x^{2}+25 x-582=0
$$
We find the critical points of the function $f(x)=9 x^{3}-42 x^{2}+25 x-582$:
$$
f^{\prime}(x)=27 x^{2}-84 x+25=0
$$
from which $x=\frac{1}{3}$ and $x=\frac{25}{9}$. Both critical points do not belong to the domain of equation (3). Therefore, we look for the zero of the function in the interval $[4 ;+\infty)$, where $f^{\prime}(x)>0$. In this interval, the function is increasing, and it has a unique zero. Since
$$
\begin{aligned}
& f(4)=9 \cdot 4^{3}-42 \cdot 4^{2}+25 \cdot 4-5820
\end{aligned}
$$
by the Bolzano-Cauchy theorem, the zero of the function belongs to the interval $[4 ; 10]$. By trial, we find the root of the equation—it is equal to 6.
Method 2. Suppose that the factors containing radicals are equal. Then the system holds
$$
\left\{\begin{array}{l}
3 x-1=17 \\
\sqrt{x-4}=\sqrt{2}
\end{array}\right.
$$
Solving it, we get $x=6$. It is easy to verify that the number 6 is a root of the given equation. We will prove that the equation has no other roots.
Indeed, for $x>6$, the system of inequalities holds
$$
\left\{\begin{array}{l}
3 x-1>17 \\
\sqrt{x-4}>\sqrt{2}
\end{array}\right.
$$
Then
$$
(3 x-1) \cdot \sqrt{x-4}>17 \sqrt{2}
$$
If $4 \leqslant x<6$, then the system of inequalities holds
$$
\left\{\begin{array}{l}
3 x-1<17 \\
\sqrt{x-4}<\sqrt{2}
\end{array}\right.
$$
i.e.
$$
(3 x-1) \cdot \sqrt{x-4}<17 \sqrt{2}
$$
Therefore, the original equation has a unique root $x=6$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
29. Space Division. Through a fixed point in space, we draw planes to divide the space into as many parts as possible. One plane will divide the space into two parts, two intersecting planes will divide it into four parts, and three planes intersecting at a point and having no other common point will divide the space into eight parts. What is the maximum number of parts that can be obtained with four planes? And what about with $n$ planes?
|
29. Instead of the entire space, we will divide the tar, through the center of which we draw planes. On the surface of the sphere (bounded by its sphere), intersecting great circles will arise. We will take one of them as the әquator and project all other circles from the center of the sphere onto a plane tangent to the sphere at the pole. The projections of our circles (except for one, which is the әquator and does not project at all) will be straight lines. Therefore, we need to calculate the maximum number of regions on the plane divided by \( n-1 \) lines. By induction, it is easy to obtain that this number is \( 1+1+2+3+\ldots+(n-1) = 1 + \frac{1}{2} n(n-1) \), because with \( k-1 \) existing lines, the \( k \)-th line can increase the number of regions by at most \( k \). Since there are twice as many regions on the sphere as on its planar projection, the desired number will be twice the one we calculated above, i.e., it is \( n(n-1) + 2 \). In particular, for \( n=4 \), the desired number is 14.
Fig. 38.
|
14
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
31. Cube. Holding a model of a cube in your hand so that it can rotate around its longest axis (i.e., around the line connecting opposite vertices), you can wind black yarn around it without any gaps. The yarn will shade only half of the cube (why?). The same can be done with another axis; there are four in total, and each time we use a different color of yarn (black, red, blue, and
yellow). The entire model will be covered with different colors, and from their mixing, mixed colors will emerge (the model of the cube is white and we do not consider this color). How many color shades will there be on the cube and which ones?
|
31. The yarn wound around a cube rotating about one of its axes (Fig. 41) will remain only on those edges that do not have common points with the axis of rotation; the yarn will cover half of each face of the cube, i.e., half of the cube's surface.
Now, let's rotate the cube sequentially around each of the four axes, each time winding yarn of a different color.
Thus, when rotating around the axis $A C^{\prime}$, we will use yarn of color $a$ (black); when rotating around the axis $D B^{\prime}$, we will use yarn of color $b$ (red); when rotating around the axis $B D^{\prime}$, we will use yarn of color $c$ (yellow); and finally, when rotating around the axis $C A^{\prime}$, we will use yarn of color $d$ (blue).
The cube will be colored as shown in Fig. 42, where each face is divided into four triangles; the letters placed in the corresponding triangles denote the colors of the yarn covering that triangle.
It is easy to notice that:
$1^{\circ}$ six shades will appear on the surface of the cube, i.e., as many as there are combinations of four elements taken two at a time, namely: $a b, a c, a d, b c, b d$, and $c d$;
$2^{\circ}$ each face will have four different shades;
$3^{\circ}$ the surface of the cube will be covered by two layers of yarn;
$4^{\circ}$ opposite faces of the cube will be colored in the same shades, arranged in reverse cyclic order.
*) See, for example, I. M. Yaglom, Geometric Transformations II, Moscow, Gostekhizdat, 1956, §§ 1 and 4 of Chapter II; H. S. M. Coxeter, Introduction to Geometry, Chapter 6; G. Rademacher, O. Toeplitz, Numbers and Figures, Topic 18; D. Hilbert, S. Cohn-Vossen, Anschauliche Geometrie, Moscow, Gostekhizdat, 1951, § 36.

Fig. 41.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
32. Geodesics. This problem does not require knowledge of mathematics. Let's place a rubber band (so-called "prescription", used in pharmacies for packaging medicines) on a stationary cube in such a way that it holds on the cube and does not cross itself.
The line along which this rubber band will lie is called a geodesic line.
1) How many times will all geodesic lines cover the surface of the cube (i.e., how many geodesic lines will pass through each point on the surface of the cube)?
2) How many different families of geodesic lines cover the surface of the cube?
|
32. We will prove that through each point on the surface of a cube, there pass four different geodesics, and in total, we have seven families of geodesic lines.
If we assume that the cube is smooth, then a rubber band wrapped around it will be arranged in such a way that the perimeter of the polygon it forms will reach a minimum.
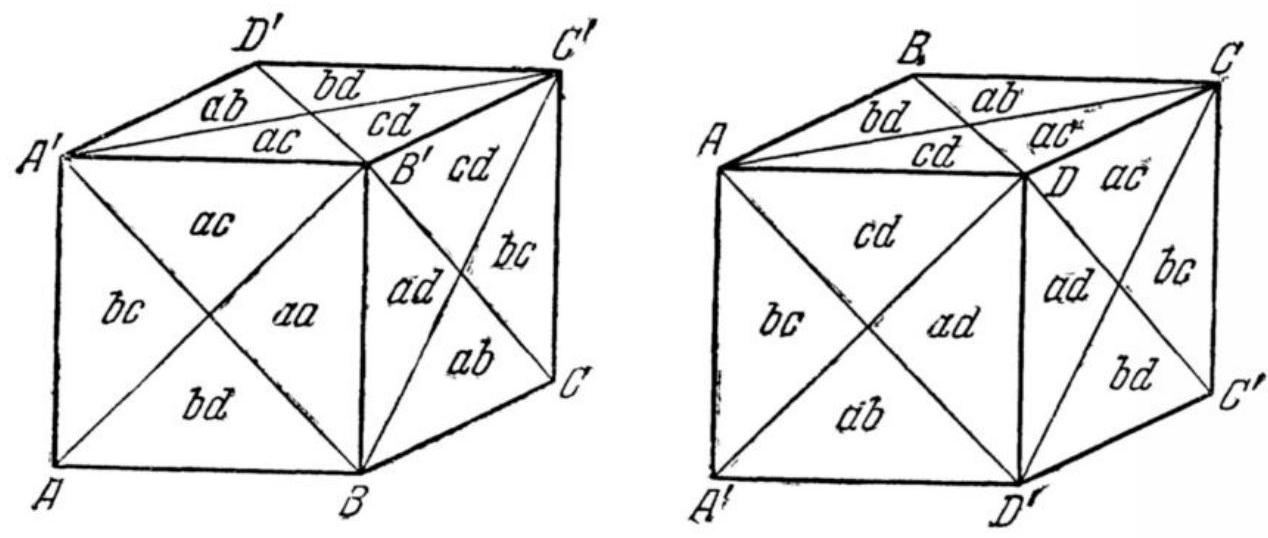
Fig. 42.
Three types of such positions, and therefore, three families of such geodesics, are shown in Fig. 43; they lie in planes parallel to the faces of the cube. To convince ourselves that there are other families of geodesics, let's cut the cube with a plane parallel to the diagonal of the base (Fig. 44),
Then, using the notations indicated in Fig. 44, we will have:
$$
\begin{gathered}
x+y=a \\
P K=a \sqrt{2}-2 x \operatorname{tg} \alpha, \quad K L=x \sqrt{1+2 \operatorname{tg}^{2} \alpha} \\
M N=a \sqrt{2}-2 y \operatorname{tg} \alpha, \quad L M=y \sqrt{1+2 \operatorname{tg}^{2} \alpha}
\end{gathered}
$$
and for the perimeter \( p \) of the hexagon \( K L M N O P \), we get:
$$
p=2 a \sqrt{2}-2 a \operatorname{tg} \alpha+2 a \sqrt{1+2 \operatorname{tg}^{2} \alpha}
$$
Thus, the perimeter \( p \) depends only on the angle \( \alpha \) and remains the same in all parallel planes; this perimeter
Fig. 43.
Fig. 44.
reaches a minimum if \( \operatorname{tg} \alpha=1 / \sqrt{2} \). The sides of the hexagon \( K L M N O P \) will be parallel to the diagonals of the faces of the cube, and this hexagon represents a geodesic. There are four families of such geodesics, as indicated in Fig. 45, and therefore, together with the previous three, there are a total of seven families.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
34. Unfolding a Cube. Models of polyhedra are made from flat nets. In a net, faces are adjacent to each other along edges, and the model is constructed by folding the cardboard net along the edges. A regular tetrahedron has two such different nets. How many does a cube have?
|
34. All existing nets (a total of 11) are shown in Fig. 49. The first six solutions give nets in which four faces of the cube are arranged in one strip of the net. No other solutions of this type exist. The next four nets are those in which there are three faces in one
Fig. 48.

Fig. 49.
strip, but not four faces. Finally, in the last net, there are no three faces in any strip.
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
37. Tetrahedron. There are 6 rods of different lengths, and it is known that in any order, a tetrahedron (triangular pyramid) can be formed from them. How many different tetrahedrons can result from this?
|
37. The answer depends on whether we consider two tetrahedra different if one can be obtained from the other by a mirror reflection. We will show that in the first case, there are 60 different tetrahedra; in the second case, the number will obviously be reduced to 30.
Consider Fig. 55, which shows a tetrahedron with edges labeled $a, b, c, d, e, f$. Let's number the rods from which we assembled the tetrahedron from 1 to 6; a rod can be used as any of the edges $a, b, c, d, e, f$. Therefore, we can form $6!=720$ tetrahedra, although some of them will differ only by their position in space.
Temporarily assume that the tetrahedron shown in Fig. 55 is regular. Let's determine how many ways this tetrahedron can be superimposed on itself by moving it in space. Clearly, the position of the tetrahedron is completely determined by $1^{\circ}$ which of the four faces of the tetrahedron is placed at the base and $2^{\circ}$ which of the three edges of this face is aligned with a fixed edge of the base, for example, with edge $a$. Therefore, there are a total of $3 \cdot 4 = 12$ different positions of the tetrahedron.
Thus, the 720 possible permutations of our rods, taken as edges $a-f$, form each tetrahedron 12 times, and therefore, there are $720: 12=60$ different tetrahedra that can be assembled from six different rods. If we identify tetrahedra that can be obtained from each other by a mirror reflection, then the number of different tetrahedra will be half as many, i.e., $60: 2=30$.
|
30
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
53. How old is Sofia Sergeyevna? Our acquaintance Sofia Sergeyevna is not old, as she was born after World War I, but she does not like to answer directly when asked how old she is.
When asked on July 27, 1950, how old she was, she replied: I am only one year old, because I only celebrate my birthday when it falls on the same day of the week as the day I was born, and I have only celebrated such a birthday once.
How old is Sofia Sergeyevna?
|
53. Let's denote the days of the week as I, II, ..., VII and construct a table, agreeing that the day of the week that fell on a certain specific date in 1911 is denoted by the number I.
| $\boldsymbol{A}$ | B | c | $D$ | $A$ | $B$ | $c$ | D |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 1911 | I | I | | 1931 | v | $\mathbf{V}$ | |
| 1912 | II | III | I | 1932 | VI | VII | V |
| 1913 | IV | IV | | 1933 | I | I | |
| 1914 | $\mathrm{~V}$ | $\mathrm{~V}$ | | 1934 | II | II | |
| 1915 | VI | VI | | 1935 | III | III | |
| 1916 | VII | I | VI | 1936 | IV | $\mathrm{V}$ | III |
| 1917 | II | II | | 1937 | VI | VI | |
| 1918 | III | III | | 1938 | VII | VII | |
| 1919 | IV | IV | | 1939 | I | I | |
| 1920 | V | VI | IV | 1940 | II | III | I |
| 1921 | VII | VII | | 1941 | IV | IV | |
| 1922 | I | I | | 1942 | $\mathrm{~V}$ | $\mathrm{v}$ | |
| 1923 | II | II | | 1943 | VI | VI | |
| 1924 | III | IV | II | 1944 | VII | I | VI |
| 1925 | $\mathrm{~V}$ | $\mathrm{~V}$ | | 1945 | II | II | |
| 1926 | VI | VI | | 1946 | III | III | |
| 1927 | VII | VII | | 1947 | IV | IV | |
| 1928 | I | II | VII | 1948 | $\mathrm{~V}$ | VI | IV |
| 1929 | III | III | | 1949 | VII | VII | |
| 1930 | IV | IV | | 1950 | I | I | |
In column $A$, the years are listed (leap years are printed in bold). In column $B$, the days of the week are listed that fall on the same date as in 1911, if this date is between January 1 and February 28. In column $C$, the days of the week are listed that fall on the same date as in 1911, if this date is between March 1 and December 31. In column $D$, the days of the week are listed that fall on February 29 in certain leap years.
From this table, it is clear that the day of the week that falls on a certain date before March 1 moves forward by 1 after a common year, and by 2 after a leap year; the day of the week that falls on a certain date after March 1 moves forward by 1 before a common year, and by 2 before a leap year.
From this table, it is also clear that if a certain date (other than February 29) falls on, for example, a Monday in a certain year, then it will fall on the same day of the week again either after 5 years, or after 6 years, or after 11 years (if the period under consideration does not include a year whose number is divisible by 100 but not by 400).
If Sofia Sergeyevna were born on any day other than February 29, and by July 27, 1950, she had celebrated her birthday only once, then she would still be a minor, and there would be no reason to call her Sofia Sergeyevna or to say that she is not old.
Therefore, let's assume that Sofia Sergeyevna was born on February 29. The day of the week that falls on this date moves forward by 5 every four years, as a result, February 29 falls on the same day of the week every $7 \cdot 4=28$ years (if the period does not include a year whose number is divisible by 100 but not by 400). Since Sofia Sergeyevna is "only one year old," she celebrated her first birthday as early as 1924 and as late as 1948.
But since it is known that Sofia Sergeyevna was born after World War I, she celebrated her first birthday in 1948 and was born on February 29, 1920.
|
28
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
54. How many fish are in the pond? A certain ichthyologist wanted to determine how many fish in the pond were suitable for catching. For this purpose, he cast a net with a pre-selected mesh size and, pulling it out, found 30 fish, marked each of them, and threw them back into the pond. The next day, he cast the same net and caught 40 fish, two of which had his marks. How did he approximately calculate the number of fish in the pond based on these data?
|
54. Let $n$ denote the number of fish in the pond suitable for catching. Then the ratio of the number of marked fish to the total number of fish is $30 / n$.
The second time, the ichthyologist caught 40 fish, two of which were marked. The ratio of the number of marked fish to the total number of fish caught is $1 / 20$.
If we assume that the marked fish are evenly distributed among all the fish in the pond, then both ratios should be the same, i.e.,
$$
\frac{30}{n}=\frac{1}{20}
$$
from which $n=600$.
Therefore, the number of fish in the pond suitable for catching with the given net is approximately 600.
|
600
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
72. Railway Network (I). There are five cities; no three of them lie on the same straight line. These cities need to be connected by a railway network consisting of four straight roads; at that, railway lines can be built one over another on viaducts.
How many such different railway networks exist?
|
72. There can exist three types of railway networks, as shown in Fig. 149.
1) In the first case, each city can be a node where four lines converge, so there will be five different networks of this kind.
2) In the second case, a city that will be a node where three lines converge can be connected to three other cities in four ways (the number of combinations of four elements taken three at a time), and the fifth city in each of these cases can be connected to each of these three cities, so there are a total of $4 \cdot 3=12$ possible connections. Since any of the five cities can be the node, the total number of different networks of this kind will be $5 \cdot 12=60$.
3) In the third case, in the network connecting the cities, the order of the cities can be changed arbitrarily, so we will have as many networks as there are permutations of five elements, i.e., $5!=120$. But each permutation and its reverse permutation define the same network, so the number of different networks will be $120: 2=60$.
In total, there are $5+60+60=125$ networks.
Fig. 149.
|
125
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
87. Four dogs. Four dogs $A, B, C$, and $D$ stand at the corners of a square meadow and suddenly start chasing each other as indicated by the arrows in Fig. 2.
Each dog runs straight towards the next: $A$ towards $B$, $B$ towards $C$, $C$ towards $D$, and $D$ towards $A$. The side of the meadow is 100 m, and the speed of the dogs is $10 \mathrm{m} / \mathrm{s}$.
After what time interval will the dogs meet? Will their paths intersect and where? What is the length of each path?

Fig. 2.
|
87. Since each dog runs at a right angle to the direction of the dog chasing it, and the one chasing runs straight toward the fleeing one, the chasing dog approaches the next dog at a speed of $10 \mathrm{m} /$ s and will catch it after 10 seconds. As a result, the path of each dog is $100 \mathrm{~m}$. At every moment, the four dogs form a square. This square rotates and shrinks: its sides decrease uniformly at a speed of $10 \mathrm{m} /$. . The paths will intersect at the center $S$ of the initial square. These will be curved lines (logarithmic spirals). They will not intersect earlier, because if any dog had crossed another's path, it would mean that it had been in that place earlier, which is impossible due to the equal distance of all dogs from $S$ at every moment.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
88. The Chase (I). Ship $P$ has spotted ship $Q$, which is sailing in a direction perpendicular to $P Q$, maintaining its course. Ship $P$ is chasing $Q$, always heading directly towards $Q$; the speed of both ships is the same at any moment (but can vary over time). Without calculations, it is clear that $P$ is sailing along a curved path; if the chase lasts long enough, the trajectory of the pursuing ship and the trajectory of the fleeing ship will eventually become almost identical. What will then be the distance $P Q$, if initially it was 10 nautical miles?
|
88. Let $\alpha$ denote the instantaneous angle between the direction $P Q$ and the path of ship $Q$ (Fig. 163), and $v$ - the speed of ships $P$ and $Q$ at that moment. The mutual approach of the ships is influenced by the speed $v$ of ship $P$, directed towards $Q$, and the component $v \cos \alpha$ of the speed of ship $Q$, both in the same direction. Therefore, the speed of approach of the ships is $v(1-\cos \alpha)$.
The projection $S$ of point $P$ on the path of ship $Q$ moves along this path with a speed of $v \cos \alpha$, while ship $Q$ moves away with a speed of $v$, so the distance $S Q$ increases at a speed of $v(1-\cos \alpha)$. Since the distance $P Q$ decreases, as we noted earlier, at the same speed, the sum $P Q + S Q$ is constant, and therefore equals 10 miles, as it did at the initial moment.
After an infinitely long
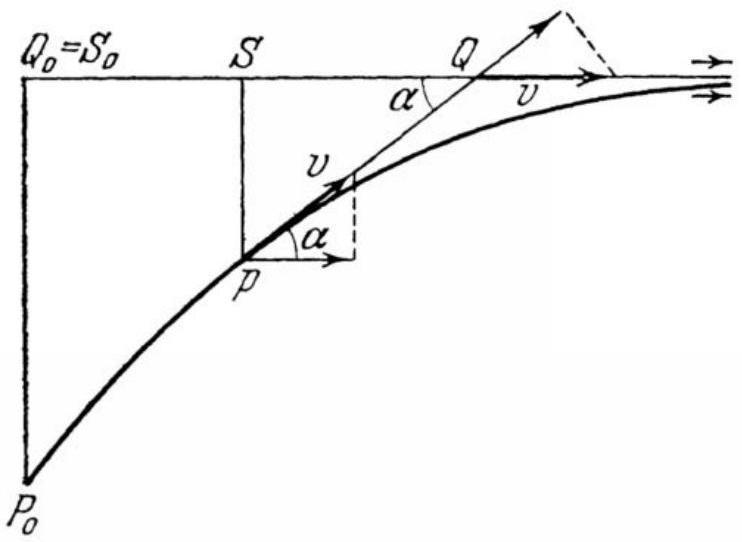
Fig. 163. time, $P$ will coincide with $S$ and will be equal to $P Q + S Q = 2 P Q = 10$ miles, and $P Q = 5$ miles.
|
5
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
95. Word game. Dr. Sylvester Sharadek announced that he can always guess the word you think of if he is allowed to ask 20 questions, to which the answers should be only "yes" or "no," and if the word is in the dictionary. Do you think he is boasting?
|
95. There are no dictionaries containing more than a million words. For example, if a dictionary has 500 pages, we will open it in the middle and find the last word on page 250, let's say, "narcissus." The first question should be: is the word we are guessing located after the word "narcissus" in the dictionary? If the answer is "yes," we will open the dictionary to page 375, and if "no," we will open it to page 125 and again ask about the position of the guessed word relative to the last word on the opened page, and so on. If at any point we get a fractional page number (for example, 62.5), we will round it up to the nearest whole number. After nine such questions, the search for the word will be narrowed down to one page. If there are 2 columns on this page, the 10th question will determine the column. In a column, there are no more than 64 words, and thus, the 16th question will lead us to one word, which, if we haven't already guessed the correct word, we will indicate to the person who thought of it.
The dictionary we used as an example contains no more than $128 \cdot 500 = 64000$ words. Since the number of words in a dictionary is limited to a million, it can contain no more than 16 times as many words as the dictionary considered above ($64000 \cdot 16 = 1024000$). For a dictionary with the maximum number of words, 4 additional questions will be required $\left(2^4 = 16\right)$, i.e., a total of 20 questions.
Thus, we see that Dr. Sharadek is telling the truth.
|
20
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
100. French cities. Dr. Sharadek, who knew strategy well, was interested in the latest war and in 1940 became acquainted with the map of the French theater of military operations. From this, the following problem probably arose. The distance (as the crow flies, as are all distances in this problem) from Chalon to Vitry is 30 km, from Vitry to Chaumont 80 km, from Chaumont to Saint-Quentin 236 km, from Saint-Quentin to Reims 86 km, from Reims to Chalon 40 km. Calculate in this closed polygon the distance from Reims to Chaumont. Only Silvester Sharadek can do this without a map!
|
100. The five cities of Chalon, Vitry, Chaumont, Sän-Cantän, and Reims form a closed pentagon; one of its sides (the side Chaumont - Sän-Cantän) is the sum of the other four, since $236=86+40+30+80$. This is only possible when the vertices of the pentagon lie on a straight line. The cities are arranged on the line in the following order: Sän-Cantän, Reims, Chalon, Vitry, and Chaumont. The distance between Reims and Chaumont, therefore, is $40+30+80=150$ km.
|
150
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2. Let's determine in which numeral system the following multiplication was performed: $352 \cdot 31=20152$.
|
Solution. Let $x$ be the base of the numeral system, then the given equality can be written in the form of an equation
$$
\left(3 x^{2}+5 x+2\right)(3 x+1)=2 x^{4}+x^{2}+5 x+2
$$
By performing the multiplication and combining like terms, we get:
$$
2 x^{4}-9 x^{3}-17 x^{2}-6 x=0
$$
It is clear that $x \neq 0$ and therefore the equation will take the form:
$$
2 x^{3}-9 x^{2}-17 x-6=0
$$
Since $x$ as the base of the numeral system can only take natural values, among the divisors of the constant term, only the numbers $1,2,3,6$ need to be tested. If we also consider that the digit 5 is the largest in the given equality, then only $x=6$ needs to be checked.
Let's divide the polynomial $2 x^{3}-9 x^{2}-17 x-6$ by $(x-6)$ using Horner's scheme:
6 | 2 | -9 | -17 | -6 |
| ---: | ---: | ---: | ---: |
| 2 | 3 | 1 | 0 |
We obtained zero as the remainder. This means that $x=6$ is a root of the obtained equation and is the base of the desired numeral system.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2. Let's find the sum of the cubes of the roots of the equation
$$
x^{3}+2 x^{2}+x-3=0
$$
|
S o l u t i o n. This can be done in various ways, for example, by sequentially calculating the sum of the squares of the roots and then the sum of the cubes of the roots. However, we will use a frequently applied identity in mathematics:
$$
\begin{aligned}
a^{3}+b^{3}+c^{3}-3 a b c= & (a+b+c)\left(a^{2}+b^{2}+c^{2}-a b-\right. \\
& -a c-b c) .
\end{aligned}
$$
In our case, this identity will take the form:
$$
\begin{gathered}
x_{1}^{3}+x_{2}^{3}+x_{3}^{3}=3 x_{1} x_{2} x_{3}+\left(x_{1}+x_{2}+x_{3}\right)\left(x_{1}^{2}+x_{2}^{2}+\right. \\
\left.+x_{3}^{2}-x_{1} x_{2}-x_{2} x_{3}-x_{3} x_{1}\right)
\end{gathered}
$$
We will express \( S_{3}=x_{1}^{3}+x_{2}^{3}+x_{3}^{3} \) in terms of \( \sigma_{1}, \sigma_{2} \) and \( \sigma_{3} \), where \( \sigma_{1}=x_{1}+x_{2}+x_{3}, \sigma_{2}=x_{1} x_{2}+x_{2} x_{3}+x_{3} x_{1}, \sigma_{3}=x_{1} x_{2} x_{3} \).
The sum \( x_{1}^{2}+x_{2}^{2}+x_{3}^{2} \) can be easily expressed in terms of \( \sigma_{1} \) and \( \sigma_{2} \):
$$
x_{1}^{2}+x_{2}^{2}+x_{3}^{2}=\sigma_{1}^{2}-2 \sigma_{2}
$$
Finally, we get:
$$
x_{1}^{3}+x_{2}^{3}+x_{3}^{3}=\sigma_{1}^{3}-3 \sigma_{1} \sigma_{2}+3 \sigma_{3} .
$$
Since by the condition (by Vieta's formulas) \( \sigma_{1}=-2 \),
$$
\sigma_{2}=1, \sigma_{3}=3, \text { then } x_{1}^{3}+x_{2}^{3}+x_{3}^{3}=7
$$
E x a m p l e. Solve the system of equations:
$$
\left\{\begin{array}{l}
x+y+z=2 \\
x^{2}+y^{2}+z^{2}=6 \\
x^{3}+y^{3}+z^{3}=8
\end{array}\right.
$$
S o l u t i o n. Consider the triplet of variables \( x, y, z \) as the roots of some cubic equation \( t^{3}+a t^{2}+b t+c=0 \) and find the coefficients \( a, b, c \).
By Vieta's formulas
$$
\sigma_{1}=-a, \quad \sigma_{2}=b, \quad \sigma_{3}=-c
$$
But from the previous example,
$$
\begin{aligned}
x^{2}+y^{2}+z^{2}=\sigma_{1}^{2}-2 \sigma_{2} & =a^{2}-2 b \\
x^{3}+y^{3}+z^{3}=\sigma_{1}^{3}-3 \sigma_{1} \sigma_{2}+3 \sigma_{3} & =-a^{3}+3 a b-3 c
\end{aligned}
$$
Substituting these expressions into the original system of equations, we get:
$$
\left\{\begin{array}{l}
-a=2 \\
a^{2}-2 b=6 \\
-a^{3}+3 a b-3 c=8
\end{array}\right.
$$
from which we easily find: \( a=-2, b=-1, c=2 \).
Therefore, the desired equation will be:
$$
t^{3}-2 t^{2}-t+2=0
$$
or
$$
\left(t^{2}-1\right)(t-2)=0
$$
Its roots are: \( -1, 1, 2 \). Since the original system is symmetric, any combination of this triplet of numbers is its solution.
## EXERCISES
11. Formulate an equation whose roots are the lengths of the radii \( r_{a}, r_{b}, r_{c} \) of the excircles.
12*. Formulate a cubic equation whose roots are
$$
\cos \frac{\pi}{7}, \cos \frac{3 \pi}{7}, \cos \frac{5 \pi}{7}
$$
13*. Find the sum of the 16th powers of the roots of the equation
$$
x^{3}-x+1=0 \text {. }
$$
14. Calculate the area of a quadrilateral whose side lengths are the roots of the equation \( x^{4}+k x^{3}+m x^{2}+n x+5=0 \), and the sum of the measures of the opposite angles is \( \pi \).
15. If the equation \( a x^{3}-3 b x^{2}+3 c x-d=0 \) has roots \( \frac{b}{a} \), \( \frac{c}{b} \), \( \frac{d}{c} \), then these roots are either equal or form an arithmetic progression. Prove it.
16. Calculate the values of the expressions: \( x_{1}^{2} x_{2}^{2}+x_{2}^{2} x_{3}^{2}+x_{3}^{2} x_{1}^{2} \); \( x_{1}^{2} x_{2}+x_{1} x_{2}^{2}+x_{2}^{2} x_{3}+x_{2} x_{3}^{2}+x_{1}^{2} x_{3}+x_{1} x_{3}^{2} \), if \( x_{1}, x_{2}, x_{3} \) are the roots of the equation \( x^{3}-x+3=0 \).
17. Find the real roots of the systems of equations:
a) \( \left\{\begin{aligned} x+y+z & =4 \\ x y+y z+z x & =5 \\ \frac{1}{x}+\frac{1}{y}+\frac{1}{z} & =\frac{5}{2}\end{aligned}\right. \)
b) \( \left\{\begin{aligned} x^{3}+y^{3}+z^{3} & =\frac{73}{8}, \\ x y+x z+y z & =x+y+z \\ x y z & =1 .\end{aligned}\right. \)
18. Given the equation
$$
x^{3}+p x^{2}+q x+z=0
$$
Find the relationship between the coefficients under which one root is equal to the sum of the other two.
19. Given the equation \( x^{4}+a x^{3}+b x^{2}+c x+d=0 \), in which: a) \( x_{1}+x_{2}=x_{3}+x_{4} \); b) \( x_{1} x_{2}=x_{3} x_{4} \). Find the relationship between the coefficients. Find ways to solve the equation under these conditions.
20. Determine the condition that the coefficients of the equation \( x^{3}+p x^{2}+q x+r=0 \) must satisfy for its three roots to form an arithmetic progression.
21. What necessary and sufficient condition must the coefficients of the equation \( x^{8}+p x^{2}+q x+r=0 \), where \( r \neq 0 \), \( q \neq 0 \), satisfy if its roots are related by the equation \( \frac{1}{x_{1}}+\frac{1}{x_{2}}=\frac{1}{x_{3}} \) ?
22. Determine \( \lambda \) so that one of the roots of the equation \( x^{3}+7 x+\lambda=0 \) is twice the second.
12
Problems on forming equations of the 3rd and 4th degrees. The solutions to the geometric problems presented in this section mainly reduce to solving reciprocal or other equations, which in turn can be appropriately reduced to quadratic equations.
Let's consider this on a specific example.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 1. Let's find pairs of real numbers $x$ and $y$ that satisfy the equation
$$
x^{2}+4 x \cos x y+4=0
$$
|
S o l u t i o n. Several methods can be proposed to solve the given equation.
1st method. Since the equation is quadratic (if we do not consider $x$ under the cosine sign), we can express $x$ in terms of trigonometric functions of the angle $x y$:
$$
x=-2 \cos x y \pm \sqrt{4 \cos ^{2} x y-4}=-2 \cos x y \pm 2 \sqrt{-\sin ^{2} x y}
$$
Since by condition $x$ and $y$ are real numbers, then $-\sin ^{2} x y \geqslant 0$. This inequality is only satisfied when $\sin x y=0$, i.e., when $x y=k \pi, k \in \mathbf{Z}$.
Now we have:
$$
x=-2 \cos x y=-2 \cos k \pi .
$$
If $k$ is even, then $\cos k \pi=1$ and $x=-2$, so $y=n \pi, n \in \mathbf{Z}$; if $k$ is odd, then $\cos k \pi=-1$ and $x=2$, so $y=\frac{\pi}{2}(2 m+$ $+1)$, where $m \in \mathbf{Z}$.
2nd method. Transform the equation so that the left side becomes a sum of non-negative numbers, for example by adding and correspondingly subtracting $4 \cos ^{2} x y$. We get:
$$
(x+2 \cos x y)^{2}+4\left(1-\cos ^{2} x y\right)=0
$$
or
$$
(x+2 \cos x y)^{2}+4 \sin ^{2} x y=0
$$
Since the sum of squares of real numbers equals zero only when each term is zero, we arrive at the system:
$$
\left\{\begin{array}{c}
x+2 \cos x y=0 \\
\sin x y=0
\end{array}\right.
$$
Solving this system, we find the same values of $x$ and $y$.
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 5. Let's find all values of $a$ for which the system
$$
\left\{\begin{array}{l}
2^{b x}+(a+1) b y^{2}=a^{2} \\
(a-1) x^{3}+y^{3}=1
\end{array}\right.
$$
has at least one solution for any value of $b,(a, b, x, y \in \mathbf{R})$.
|
S o l u t i o n. Suppose there exists some value $a$ for which the system has at least one solution, for example, for $b=0$.
In this case, the system will take the form:
$$
\left\{\begin{array}{l}
1=a^{2} \\
(a-1) x^{3}+y^{3}=1
\end{array}\right.
$$
It is clear that this system is consistent only if $a=1$ or $a=-1$. Therefore, if $b=0$, then for these values of $a$ the original system is consistent. We will now prove that the original system will be consistent for any value of $b$.
32
Let $a=1$. Then the original system will take the form:
$$
\left\{\begin{array}{l}
2^{b x}+2 b y^{2}=1 \\
y^{3}=1
\end{array}\right.
$$
From the second equation, we find: $y=1$ (by the condition $y \in \mathbf{R}$). Substituting $y=1$ into the first equation, we get:
$$
2^{b x}=1-2 b
$$
It is easy to see that this equation has no solutions for $b \geqslant \frac{1}{2}$. Therefore, when $a=1$, the system has solutions, but not for any value of $b$, i.e., the value $a=1$ does not satisfy the condition of the problem.
Now let's check $a=-1$. Then the original system will take the form:
$$
\left\{\begin{array}{l}
2^{b x}=1 \\
-2 x^{3}+y^{3}=1
\end{array}\right.
$$
It is completely obvious that the first equation has a solution $x=0$ for any $b$. Then $y=1$. Therefore, the condition of the problem is satisfied only by $a=-1$.
## EXERCISES
57. Prove that the equation
$$
x^{2}-x \sin x y+1=0
$$
has no solutions.
58. Find all pairs of real values of $x$ and $y$ that satisfy the equations:
a) $\sin 2 x+\cos (x+y)=2$
b) $4^{\sin x}-2^{1+\sin x} \cos x y+2^{|y|}=0$;
c) $\operatorname{tg}^{2} x+2 \operatorname{tg} x(\sin x+\cos y)+2=0$;
d) $\left(\sin ^{2} x+\frac{1}{\sin ^{2} x}\right)^{2}+\left(\cos ^{2} x+\frac{1}{\cos ^{2} y}\right)^{2}=12+\frac{1}{2} \sin x y$;
e) $\operatorname{tg}^{4} x+\operatorname{tg}^{4} y+2 \operatorname{ctg}^{2} x \operatorname{ctg}^{2} y=3+\sin ^{2}(x+y)$.
59. Solve the inequalities:
a) $\cos x \geqslant y^{2}+\sqrt{y-x^{2}-1}$
b) $y \geqslant\left|\sec ^{2} x\right|+\sqrt{1-y-x^{2}}$
c) $x-|y| \geqslant 1+\sqrt{x^{2}+y^{2}-1}$.
60. Find the general form of the solution of the system:
$$
\left\{\begin{array}{l}
\operatorname{tg} x=\operatorname{tg}(y-z), \\
\operatorname{tg} y=\operatorname{tg}(z-x) .
\end{array}\right.
$$
61. Find the real solutions of the systems:
a) $\left\{\begin{array}{l}x^{2}+4 y^{2}+5=4 z \\ x-y \geqslant z\end{array}\right.$
2 Order 454
b) $\left\{\begin{array}{l}x^{2}+y^{2}+20=z \\ 8 x+4 y \geqslant z .\end{array}\right.$
62. Find the real solutions of the system:
$$
\left\{\begin{array}{l}
x+y+z=2 \\
2 x y-z^{2}=4
\end{array}\right.
$$
63. Prove that if three numbers $x, y, z$ satisfy the system of equations:
$$
\left\{\begin{array}{l}
x+y+z=a \\
\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=\frac{1}{a}
\end{array}\right.
$$
then at least one of these numbers is equal to $a$.
64. Find all values of $a$ for which the system
$$
\left\{\begin{array}{l}
2^{|x|}+|x|=y+x^{2}+a \\
x^{2}+y^{2}=1
\end{array}\right.
$$
has only one solution.
65. Find all values of $a$ and $b$ for which the system
$$
\left\{\begin{array}{l}
\left|\frac{x^{y}-1}{x^{y}+1}\right|=a \\
x^{2}+y^{2}=b
\end{array}\right.
$$
has only one solution ( $a, b, x, y \in \mathbf{R}, x>0, x \neq 1$ ).
66. Find all values of $a$ for which the system
$$
\left\{\begin{array}{l}
\left(x^{2}+1\right)^{a}+\left(b^{2}+1\right)^{y}=2 \\
a+b x y+x^{2} y=1
\end{array}\right.
$$
has at least one solution for any $b(a, b, x, y \in \mathbf{R})$.
67. Determine for which values of the parameter $a$ the system
$$
\left\{\begin{array}{l}
a x^{2}+a-1=y-|\sin x| \\
\operatorname{tg}^{2} x+y^{2}=1
\end{array}\right.
$$
has a unique real solution.
68. Given the system:
$$
\left\{\begin{array}{l}
x^{y}=a, x>0 \\
\operatorname{arctg} x=\frac{\pi}{4}+y
\end{array}\right.
$$
For which values of $a$ does the system have a unique solution?
69. Find all values of $a$ for which the system
$$
\left\{\begin{array}{l}
x^{3}-a y^{3}=\frac{1}{2}(a+1)^{2} \\
x^{3}+a x^{2} y+x y^{2}=1
\end{array}\right.
$$
has at least one solution and any solution satisfies the equation $x+y=0 \quad(a, x, y \in \mathbf{R})$.
34
70. Given the system of equations:
$$
\left\{\begin{array}{l}
\frac{x}{y}+\sin x=a \\
\frac{y}{x}+\sin y=a
\end{array}\right.
$$
For which values of $a$ does the system have a unique solution satisfying the conditions: $0 \leqslant x \leqslant 2 \pi, 0 \leqslant y \leqslant 2 \pi$ ?
## Chapter II
## POWER MEAN AND ITS APPLICATIONS
The expression of the form
$$
C_{\alpha}(a)=\left(\frac{a_{1}^{\alpha}+a_{2}^{\alpha}+\ldots+a_{n}^{\alpha}}{n}\right)^{\frac{1}{\alpha}}
$$
is called the power mean of order $\alpha$ of positive numbers $a_{1}, a_{2}, \ldots, a_{n}$.
In particular, for $\alpha=-1$ we get the harmonic mean
$$
C_{-1}(a)=\frac{n}{\frac{1}{a_{1}}+\frac{1}{a_{2}}+\ldots+\frac{1}{a_{n}}}
$$
for $\alpha=1$ we get the arithmetic mean
$$
C_{1}(a)=\frac{a_{1}+a_{2}+\ldots+a_{n}}{n}
$$
for $\alpha=2$ we get the quadratic mean
$$
C_{2}(a)=\sqrt{\frac{a_{1}^{2}+a_{2}^{2}+\ldots+a_{n}^{2}}{n}}
$$
Let us note some properties of the power mean:
$1^{0}$. The following equality holds:
$$
\lim _{\alpha \rightarrow 0} C_{\alpha}(a)=G
$$
where $G=\sqrt[n]{a_{1} a_{2} \ldots a_{n}}$ is the geometric mean. Therefore, we adopt
$$
C_{0}(a)=\sqrt[n]{a_{1} a_{2} \ldots a_{n}}
$$
$2^{0}$. For any real $\alpha$ and $\beta$, such that $\alpha \leqslant \beta$, the following inequality holds (monotonicity property):
$$
C_{\alpha}(a) \leqslant C_{\beta}(a)
$$
$3^{0}$. Let $\min a$ be the smallest among the numbers $a_{1}, a_{2}, \ldots a_{n}$, and $\max a$ be the largest among these same numbers. Then
$$
\lim _{\alpha \rightarrow-\infty} C_{\alpha}(a)=\min a, \lim _{\alpha \rightarrow+\infty} C_{\alpha}(a)=\max a
$$
2*
From this, the following chain of inequalities follows:
$\min a \leqslant \ldots \leqslant C_{-2} \leqslant C_{-1} \leqslant C_{0} \leqslant C_{1} \leqslant C_{2} \leqslant \ldots \leqslant \max a$.
Equality occurs only when $a_{1}=a_{2}=\ldots=a_{n}$.
## § 1. Proof of Inequalities
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 3. Compare the number $a$ with one, if
$$
a=0.99999^{1.00001} \cdot 1.00001^{0.99999} .
$$
|
S o l u t i o n. Let's represent the numbers in the given expression as follows:
$$
0.99999=1-\alpha, \quad 1.00001=1+\alpha
$$
where $\alpha=0.00001$. Then
$$
a=(1-\alpha)^{1+\alpha}(1+\alpha)^{1-\alpha}=\left(1-\alpha^{2}\right)\left(\frac{1-\alpha}{1+\alpha}\right)^{\alpha}
$$
Since $1-\alpha^{2}<1$, then $a<1$
b) $\frac{1}{2}<5$
$$
156. Prove that
$$
\begin{gathered}
\log _{\sqrt{2}+\sqrt{3}}(4 \sqrt{2}+3 \sqrt{\overline{3}}) \cdot \log _{\sqrt{6}+1}(\sqrt{3}-\sqrt{2})+ \\
+\log ^{2} \sqrt{6}+7 \\
(2 \sqrt{6}+5)+1=0
\end{gathered}
$$
## § 2. Systematic Fractions and Irrationalities
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
E x a m p l e 1. Let's find the limit of the sum
$$
S_{n}=\frac{3}{4}+\frac{5}{36}+\ldots+\frac{2 n+1}{n^{2}(n+1)^{2}}
$$
as $n \rightarrow \infty$.
|
S o l u t i o n. First, let's try to simplify $S_{n}$. Since the fraction 56
$\frac{2 k+1}{k^{2}(k+1)^{2}}$ can be represented as the difference $\frac{1}{k^{2}}-\frac{1}{(k+1)^{2}}$, then
$$
\begin{gathered}
\frac{3}{4}=1-\frac{1}{2^{2}} \\
\frac{5}{36}=\frac{1}{2^{2}}-\frac{1}{3^{2}} \\
\frac{2 n+1}{n^{2}(n+1)^{2}}=\frac{1}{n^{2}}-\frac{1}{(n+1)^{2}}
\end{gathered}
$$
By adding these equalities, we get:
$$
S_{n}=1-\frac{1}{(n+1)^{2}}
$$
Then
$$
\lim _{n \rightarrow \infty} S_{n}=\lim _{n \rightarrow \infty}\left(1-\frac{1}{(n+1)^{2}}\right)=1
$$
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2. Let $y \neq-1$. We set,
$$
x_{1}=\frac{y-1}{y+1}, \quad x_{2}=\frac{x_{1}-1}{x_{1}+1}, \quad x_{3}=\frac{x_{2}-1}{x_{2}+1}, \ldots
$$
What is $y$ if $x_{1978}=-\frac{1}{3}$?
|
Solution. Substituting the value of $x_{1}$ into the second equality, after simplifications we get:
$$
x_{2}=-\frac{1}{y}
$$
Further,
$$
x_{3}=\frac{y+1}{1-y}, \quad x_{4}=y, \quad x_{5}=\frac{y-1}{y+1}=x_{1}
$$
Therefore,
$$
x_{5}=x_{1}, \quad x_{6}=x_{2}, \quad x_{7}=x_{3}, \quad x_{8}=x_{4}, \ldots, \quad x_{1978}=x_{2}=-\frac{1}{y}
$$
from which $y=3$.
## EXERCISES
174. Let a number $N$ be given and a sequence of positive numbers $x_{1}, x_{2}, \ldots, x_{n}$, where each subsequent term is formed by the rule
$$
x_{n}=\frac{1}{2}\left(x_{n-1}+\frac{N}{x_{n-1}}\right)
$$
Prove that
$$
\lim _{n \rightarrow \infty} x_{n}=\sqrt{N}
$$
175. A sequence is defined by the recurrence formula
$$
u_{n}=(\alpha+\beta) u_{n-1}-\alpha \beta u_{n-2}
$$
and initial values $u_{1}=\alpha+\beta, u_{2}=\frac{\alpha^{3}-\beta^{3}}{\alpha-\beta}$. Find the general term of the sequence.
176. Two sequences are given: $x_{0}, x_{1}, \ldots, x_{n}, \ldots\left(x_{0}>0\right)$ and $y_{0}, y_{1}, \ldots, y_{n}, \ldots\left(y_{0}>0\right)$, where
$$
x_{n}=\frac{x_{n-1}+y_{n-1}}{2}, \quad y_{n}=\sqrt{x_{n-1} y_{n-1}}
$$
Prove that the limits $\lim _{n \rightarrow \infty} x_{n}$ and $\lim _{n \rightarrow \infty} y_{n}$ exist and are equal to each other.
177. Two positive numbers $a$ and $b(a>b)$ and two sequences are given:
$$
\begin{array}{ll}
a_{1}=\frac{a+b}{2}, & b_{1}=\frac{2 a b}{a+b} \\
a_{2}=\frac{a_{1}+b_{1}}{2}, & b_{2}=\frac{2 a_{1} b_{1}}{a_{1}+b_{1}} \\
\cdots \cdot \cdot \cdot \cdot, & . \cdot \cdot \cdot \cdot \\
a_{n+1}=\frac{a_{n}+b_{n}}{2}, & b_{n+1}=\frac{2 a_{n} b_{n}}{a_{n}+b_{n}}
\end{array}
$$
Find the limits of these sequences.
178. Given 1979 numbers: $x_{1}=0, x_{2}, \ldots, x_{1978}, x_{1979}=0$. Moreover, $x_{i}=\frac{x_{i-1}+x_{i+1}}{4}+1$ for any $i=2,3, \ldots, 1978$. Prove that:
a) $0 \leqslant x_{i} \leqslant 2$ for $i=1,2, \ldots, 1979$
b) $x_{1}x_{992}>\ldots>x_{1979}$
c) $x_{1}=x_{1979}, x_{2}=x_{1978}, \ldots$.
179. Find the sum $\frac{1}{2!}+\frac{2}{3!}+\ldots+\frac{n}{(n+1)!}$ and its limit as $n \rightarrow \infty$.
180. Compute the limits:
a) $\lim \sqrt[n]{n}$;
b) $\lim _{n \rightarrow \infty} \sqrt[n]{\frac{1}{n!}}$
c) $\lim _{n \rightarrow \infty}\left(\frac{5}{9} \cdot \frac{14}{20} \cdot \frac{27}{35} \ldots \frac{2 n^{2}-n-1}{2 n^{2}+n-1}\right)$.
181. Prove that for $x \neq 0$ we have:
$$
\lim _{n \rightarrow \infty}\left(\cos \frac{x}{2} \cdot \cos \frac{x}{4} \ldots \cos \frac{x}{2^{n}}\right)=\frac{\sin x}{x}
$$
182. Find $\lim _{n \rightarrow \infty} x_{n}$, if:
58
a) $x_{n}=\sqrt{\underbrace{2+\sqrt{2+\sqrt{2+\ldots+\sqrt{2}}}}_{n \text { times }}} ;$
b) $x_{n}=\sqrt{\underbrace{2 \sqrt{2 \sqrt{2 \ldots \sqrt{2}}}}_{n \text { times }}}$;
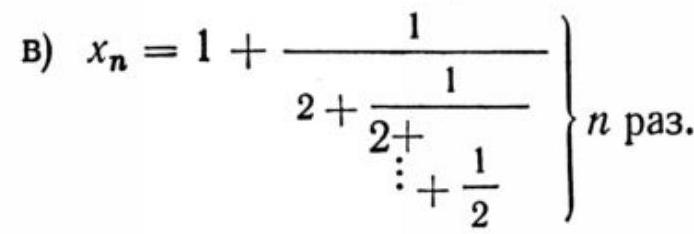
## § 4. Various Algebraic Problems
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2. Let's calculate the sum
$$
a^{2000}+\frac{1}{a^{2000}}
$$
if $a^{2}-a+1=0$.
|
S o l u t i o n. From the equality $a^{2}-a+1=0$, it follows that:
$$
a-1+\frac{1}{a}=0 \text { or } a+\frac{1}{a}=1
$$
Moreover,
$$
a^{3}+1=(a+1)\left(a^{2}-a+1\right)=0
$$
from which $a^{3}=-1$. Now we have:
$$
\begin{aligned}
& a^{2000}+\frac{1}{a^{2000}}=\left(a^{3}\right)^{666} a^{2}+\frac{1}{\left(a^{3}\right)^{666} a^{2}}=a^{2}+\frac{1}{a^{2}}=\left(a+\frac{1}{a}\right)^{2}-2= \\
& =1-2=-1
\end{aligned}
$$
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Points on a Line. If 10 points are placed at equal intervals on a line, they will occupy a segment of length s, and if 100 points are placed, the segment will have a length S. How many times greater is S than s?
|
6. Between ten points there are nine intervals, and between a hundred points - ninety-nine. Therefore, $S$ is greater than $s$ by 11 times.
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Stereometric problem. How many faces does a hexagonal pencil have?
|
7. It is important to ask: which pencil? If the pencil has not been sharpened yet, then 8, otherwise there may be variations...
Translating the text as requested, while preserving the original line breaks and formatting.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12. The Musketeers' Journey. The distance between Athos and Aramis, riding on the road, is 20 leagues. In one hour, Athos travels 4 leagues, and Aramis - 5 leagues. What distance will be between them after an hour?
|
12. Well, in which direction was each of the musketeers traveling? The problem statement does not mention this. If they were traveling towards each other, the distance between them would be 11 leagues. In other cases (make a diagram!), the possible answers are: 29 leagues; 19 leagues; 21 leagues.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
16.On a circular route, two buses are operating, with an interval of 21 minutes. What would be the interval if three buses were operating on the route?
|
16. Since the interval between buses is 21 minutes, the entire route is covered by a bus in 42 minutes. If there are 3 buses, the intervals between them will be 14 minutes.
|
14
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
17. Economic forecast. Three chickens laid three eggs in three days. How many eggs will twelve chickens lay in twelve days?
|
17. Of course not 12, as sometimes answered (inertial thinking!), but 48.
|
48
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12. Buying an album. To buy the album, Masha was short of 2 kopecks, Kolya was short of 34 kopecks, and Fedia was short of 35 kopecks. When they combined their money, it still wasn't enough to buy the album. How much does the album cost?
|
12.Since Kolya has one kopek more than Fyodor, he has at least 1 kopek, and 1 kopek is added to Masha's money. But Masha was short of money for the album, so she was given less than 2 kopeks, which means Fyodor has no money at all and is short of the full cost of the album. Answer: the album costs 35 kopeks.
|
35
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13. An Arabic Tale. A Flock of Pigeons
$>\Delta \theta \Pi \mathrm{V} \oplus \theta\mathbf{v} \Pi \square \nabla \square \Lambda$
$\oplus \Lambda \nabla \theta \Pi \oplus \mathbf{V V} \varnothing \odot$
ロจ৫ఠ<>VIVOO flew up to a tall tree.
Some of the pigeons perched on the branches, while others settled under the tree. "Those perched on the branches said to those below: If one of you flew up to us, then you would be three times fewer than all of us together, and if one of us flew down to you, then we would be equal in number." How many pigeons were perched on the branches and how many were under the tree? (Tales from One Thousand and One Nights. Night 458)
|
13. From the condition of the problem, it is clear that the number of pigeons sitting on the branches is two more than those sitting below. Further, it follows from the condition that after one of the pigeons flew up to the branch, the number of pigeons sitting on the branch became twice as many as those sitting on the ground. In addition, at this point, there were four more of them. Therefore, 7 pigeons are sitting on the tree, and 5 under the tree.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
14.Strike out a hundred digits from the number $12345678910111213 \ldots 5960 \quad$ so that the resulting number is the largest possible.
|
14. The largest possible number should start with the maximum number of nines. We will "move" along the number from left to right, crossing out all digits except 9. We will cross out 27 digits: $12345678910111213141516171819 . . .5960$, 8 digits 19 digits
then 19 digits: $99 \underbrace{20212223242526272829 \ldots .5960}_{19 \text { digits }}$ and so on. Note that we "reach" the next nine by crossing out 19 digits. After two more steps, we will have crossed out 38 digits: 999995051525354555657585960. In the previous 15 steps, we crossed out 84 digits (we need to cross out 16 more digits), so we will not "reach" the next nine. The largest digit we can "reach" by crossing out 15 digits is 7. Then, by crossing out 5 more, we get the largest possible number: 99999785960.
|
99999785960
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In the government of the country of knights and liars, there are 12 ministers. Some of them are liars, and the rest are knights. Once, at a government meeting, the following opinions were expressed: the first minister said, “There is not a single honest person here,” the second said, “There is no more than one honest person here,” the third said, “There are no more than two honest people here,” and so on until the twelfth, who said, “There are no more than eleven honest people here.” How many liars are in the government of the country?
23 In the country of knights and liars
|
4. Note that the number of true statements must match the number of honest people in the government. Further, if a statement from any minister is true, then the statements of each minister who spoke after him are also true. In this case, the only statement that would not lead to a contradiction is: "there are no more than 6 honest people," since in this case, exactly 6 statements would be true. Therefore, there are exactly 6 liars in the government.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Around a round table, eight people are sitting, each of whom is either a knight or a liar. When asked who their neighbors are, each of them answered: “My neighbors are a liar and a knight.” How many of them were liars? How would the answer change if nine people were sitting at the table?
|
5. 6. At the table, there is at least one liar. Indeed, if only knights were sitting at the table, each knight's statement "next to me sits a knight and a liar" would be false, which is impossible. 2. The neighbors
Fig. 1
Who can sit here? Both possible assumptions lead to a contradiction
Fig. 2
of a liar can be either two liars or two knights. 3. If both neighbors of a liar are liars, then further around the table sit only liars, otherwise, one of the liars' statements "next to me sits a knight and a liar" would be true, which is impossible. Thus, one of the possible answers is all liars. 4. If the neighbors of a liar are knights, then after each knight must sit another knight, then a liar, then again two knights, then a liar, and so on. If there are 9 people at the table, then there are 3 liars (Fig. 1), if 8 people, then we get a contradiction (Fig. 2$)^{1}$.
Answer: 1. If there are 8 people at the table, then all are liars. 2. If there are 9 people at the table, then the number of liars is either 9 or 3.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11. In the bookbinding workshop. A piece fell out of the book, the first page of which is numbered 328, and the number of the last page is written with the same digits but in a different order. How many pages are in the missing piece?
|
11. Since the last page must have a higher number of a different parity than the initial one, its number is 823. Answer: 496 pages fell out.
${ }^{1}$ Notation: $p-p$ king, $l-l$ liar.
27 In a country of knights and liars
|
496
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.From Wittenberg to Göttingen, two students are walking. The first one walked 7 miles daily. The second one walked 1 mile on the first day, 2 miles on the second day, 3 miles on the third day, and so on, walking 1 mile more each day than the previous day. When will the second catch up with the first?
|
12. On the first day, the second student walked 6 miles less than the first, on the second day 5 miles less, and so on. By the seventh day, the students will walk the same distance. After that, on the eighth day, the second student will walk 1 mile more, on the ninth day 2 miles more, and so on. They will meet at the end of the 13th day.
|
13
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
14. Insert parentheses in the equation: $1: 2: 3: 4: 5: 6: 7: 8: 9: 10=7$, to make it true.
|
14. Answer: $1: 2: 3: 4: 5:(6: 7: 8: 9: 10)=7$.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. What can you buy for a ruble? Nine boxes of matches cost 9 rubles and some kopecks, while ten such boxes cost 11 rubles and some kopecks. How much does one box cost?
|
6. Note that a box of matches costs more than $\frac{11}{10}$ rubles, but less than $\frac{10}{9}$ rubles. That is, more than 1.10 rubles, but less than 1.111 rubles. Answer: 1 ruble 11 kopecks.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12. The Big Laundry. After seven hours of washing, the length, width, and height of the soap piece were halved. For how many washes will the remaining soap last?
|
12. Since the length, width, and height of the soap piece have been halved, its volume has decreased by 8 times, meaning that in 7 hours, the soap piece has decreased by $\frac{7}{8}$ of its volume (by $\frac{1}{8}$ of its volume per hour). Therefore, the soap will last for one more hour of heavy washing.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. How has the purchasing power of the population changed? The product has become cheaper by $20 \%$. By what percentage can more of the product be bought for the same amount of money?
|
5. The product became cheaper by $20 \%$. Therefore, all the previously purchased goods could be bought by spending $80 \%$ of the money, and the remaining $20 \%$ could buy an additional $\frac{1}{4}$ of the goods, which constitutes $25 \%$.
|
25
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. At the conference. $85 \%$ of the delegates at the conference know English, and $75 \%$ know Spanish. What fraction of the delegates know both languages?
|
7. Note that $85 \%+75 \%=160 \%$, which exceeds the total number of conference delegates by $60 \%$. The excess is due to those people who know both languages - we counted them twice. Thus, not less than $60 \%$ of the conference delegates know both languages.
|
60
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. Seawater contains $5 \%$ salt. How many kilograms of fresh water need to be added to 40 kg of seawater to make the salt content $2 \%$?
|
9. In 40 kg of seawater, there is $40 \cdot 0.05=2$ (kg) of salt, which in the new solution constitutes $2\%$, therefore, the solution should be $2: 0.02=100$ (kg). Answer: 60 kg of fresh water should be added.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. Vера and Аnya attend a math club, in which there are more than $91 \%$ boys. Find the smallest possible number of club participants.
|
10. Let $x$ be the number of participants in the club, and $y$ be the number of girls. Then, according to the conditions of the problem, $0.09 x > y$ or $9 x > 100 y$, where $x$ and $y$ are natural numbers. Solving the problem by enumeration, we will verify that the smallest possible solution for $y=2$ is achieved at $x=23$. Therefore, there are no fewer than 23 people in the club.
## Percentages
|
23
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
14. A painted cube with an edge of 10 cm was sawn into cubes with an edge of $1 \mathrm{~cm}$. How many of them will have one painted face? How many will have two painted faces?
|
14. $K$ each face of the cube adjoins $8 \times 8=64$ cubes, painted only on one side (make a drawing!). There are 6 faces, so 384 cubes are painted on one side. Reasoning similarly, we get that 96 cubes are painted on two sides.
|
384
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12. To number the pages of an encyclopedia, 6869 digits were required. How many pages are there in it?
|
12.Note that there are 9 single-digit numbers, 99-9=90 two-digit numbers, digits - 90 × 2=180; 999-99=900 three-digit numbers; digits - 900 × 3=2700. Let's calculate the number of four-digit numbers in the page numbering of the book: 6869-2700-180-9=3980, 3980: 4=995. Adding up the obtained results, we get: 9+90+900+995=1094 pages in the encyclopedia.
|
1094
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13. About the cat. A ribbon was stretched around the Earth along the equator. Then the length of the ribbon was increased by 1 meter and again evenly positioned around the equator. Will a cat be able to crawl through the resulting gap?
|
13. Let the radius of the Earth be $R$, and the formed gap be $h$, then $2 \pi(R+h)-2 \pi R=1$ and $2 \pi h=1$. Therefore, the size of the gap $h=\frac{1}{2 \pi} \approx 15$ cm - a gap quite sufficient for a cat to squeeze through.
|
15
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. $о$ about the fisherman and the fish. When asked how big the fish he caught was, the fisherman said: “I think that its tail is 1 kg, the head is as much as the tail and half of the body, and the body is as much as the head and the tail together.” How big is the fish?
|
3. Let $2 x$ kg be the weight of the torso, then the head will weigh $x+1$ kg. From the condition that the torso weighs as much as the head and tail together, we get the equation: $2 x=x+1+1$. From this, $x=2$, and the whole fish weighs - 8 kg.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. A Herd of Elephants. Springs are bubbling at the bottom of the lake. A herd of 183 elephants could drink it dry in one day, while a herd of 37 elephants would take 5 days. How many days would it take for 1 elephant to drink the lake?
|
6. Let's translate the problem into the language of algebra. Let the volume of the lake be $V$ liters, the elephant drinks $C$ liters of water per day, and $K$ liters of water flow into the lake from the springs per day. Then the following two equations hold: $183 C = V + K$ and $37 \cdot 5 C = V + 5 K$; from which we get: $C = 2 K$ and $V = 365 K$. Let one elephant drink the lake dry in $t$ days. Then: $t C = V + t K$, or $2 K t = 365 K + K t$, from which we get $t = 365$. Answer: in 365 days.
|
365
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11. The Clock Hands Problem. At what time after 12:00 will the minute hand first catch up with the hour hand?
|
11. At 13:00, the minute hand will lag behind the hour hand by 5 minute divisions. Before the "meeting," the hour hand will travel $x$ divisions, and the minute hand will travel $12x$ divisions. From the equation $x + 5 = 12x$, we get that $x = \frac{5}{11}$ minute divisions on the clock face. Answer: 1 hour $5 \frac{5}{11}$ minutes.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.Cunning manipulations. With the number written on the board, it is allowed to perform the following operations: replace it with its double, or erase its last digit. How can you use these operations to get from the number 458 to the number 14?
|
12.Let A be the doubling of a number, and B be the erasing of the last digit. Then: $458-\mathrm{B} \Rightarrow 45-\mathrm{A} \Rightarrow 90-\mathrm{B} \Rightarrow 9-\mathrm{A} \Rightarrow 18-\mathrm{A} \Rightarrow 36-\mathrm{A} \Rightarrow 72-\mathrm{B} \Rightarrow 7-\mathrm{A} \Rightarrow 14$.
|
14
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Divide equally. There is milk in an eight-liter bucket. How can you measure out 4 liters of milk using a five-liter bucket and a three-liter jar?
|
4. It is convenient to write the solution in the form of a table:
| 8-liter can | 8 | 3 | 3 | 6 | 6 | 1 | 1 | 4 |
| :--- | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 5-liter can | 0 | 5 | 2 | 2 | 0 | 5 | 4 | 4 |
| 3-liter jar | 0 | 0 | 3 | 0 | 2 | 2 | 3 | 0 |
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The Zmey Gorynych has 2000 heads. A legendary hero can cut off $1, 17, 21$ or 33 heads with one blow, but in return, $10, 14, 0$ or 48 heads grow back, respectively. If all heads are cut off, no new ones grow. Can the hero defeat the Zmey?
|
5. We can propose the following tactic for cutting off the heads of the Snake: 1. Initially, we will cut off 21 heads (94 times); no new heads will grow, and the Snake will be left with 26 heads. 2. Next, we will cut off 17 heads three times (remember, 14 new heads will grow back each time) - after which 17 heads will remain to be cut off. 3. With the final blow, we will cut off the remaining 17 heads.
|
17
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In a family, there are six children. Five of them are respectively 2, 6, 8, 12, and 14 years older than the youngest, and the age of each child is a prime number. How old is the youngest?
|
4. Suppose the child's age does not exceed 35 years. Let's list all the prime numbers: $2,3,5,7,11,13,17,19,23$, 29,31. It is clear that the age of the younger child is an odd number. The numbers 29 and 31 also do not fit. Let's find the age of the younger child. He cannot be 1 year old, because $1+8=9$. His age cannot end in 3, because $3+2=5$. This leaves $5,7,11,17$ and 19. Not 7 years old, because $7+2=9$. Not 17 years old, because $17+8=25$. Not 19 years old: $19+2=21$. And not 11: $11+14=25$. Therefore, the younger one is 5 years old. Answer: $5,7,11,13,17$ and 19 years.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. The Eight Queens Problem. Can eight queens be placed on a chessboard so that they do not threaten each other?
|
7. There are 92 solutions to this problem. The figure shows one of them.
|
92
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13. In the senate of the country of knights and liars - there are 100 senators. Each of them is either a knight or a liar. It is known that: 1. At least one of the senators is a knight. 2. Out of any two arbitrarily chosen senators, at least one is a liar. Determine how many knights and how many liars are in the senate.
|
13. Only one of the senators is a knight. The fact that there is at least one knight among the senators follows from the first statement, the existence of a second knight contradicts the second statement.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Scientific organization of labor. There are logs of two types: 6 meters and 7 meters long. They need to be sawn into 1-meter logs. Which logs are more profitable to saw?
|
1. To saw 42 one-meter logs from six-meter logs requires 35 cuts, while from seven-meter logs - 36. It can be considered that sawing six-meter logs is more profitable.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. To the Mechanics and Mathematics Faculty! Several identical books and identical albums were bought. The books cost 10 rubles 56 kopecks. How many books were bought if the price of one book is more than one ruble higher than the price of an album, and 6 more books were bought than albums?
|
5. Since each book is more expensive than a ruble, no more than 10 books were bought. Moreover, it is clear that no fewer than 7 books were bought (since at least one album was bought). The number 1056 is divisible by 8 and not divisible by $7,9,10$. Therefore, 8 books were bought. (MSU, Mechanics and Mathematics, 1968)
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. 175 shaltev cost more than 125 boltayev, but less than 126 boltayev. Prove that 80 kopecks will not be enough to buy 3 shaltev and 1 boltayev.
|
6. Let's prove that 80 kopecks are not enough to buy 3 shaltays and 1 boltay. Let one shaltay cost $x$ kopecks, and one boltay $y$ kopecks, then $126 y > 175 x > 125 y$. From this, it follows that $y > 25(7 x - 5 y) > 0$ and $y \geq 26$. Further, $7 x \geq 5 \cdot 26 = 130$. Hence:
63 Natural numbers
$x \geq 19$. Therefore, $3 x + y \geq 83$, which is what we needed to prove.
|
83
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
8. One or two? Let's take all natural numbers from 1 to 1000000 and for each of them, calculate the sum of its digits. For all the resulting numbers, we will again find the sum of their digits. We will continue this process until all the resulting numbers are single-digit. Among the million resulting numbers, 1 and 2 will appear. Which number will be more frequent: 1 or 2?
|
8. Let's use the statement: if a number when divided by 9 has a remainder of \( d \), then the sum of its digits will have the same remainder. Which numbers from 1 to 1000000 are more: those that have a remainder of 1 when divided by 9, or those that have a remainder of 2? In the range from 1 to 999999, there are an equal number of each. 1000000 when divided by 9 gives a remainder of 1. Therefore, 1 is more.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. Centipedes and three-headed dragons. In a certain herd of centipedes and three-headed dragons, there are a total of 26 heads and 298 legs. Each centipede has one head. How many legs does a three-headed dragon have?
|
10.Note: 1. the number of heads of dragons is divisible by 3, and the number of centipedes cannot exceed 7 (otherwise, there would be more than 298 legs), so the number of centipedes is either 2 or 5. 2. If there are 2 centipedes, then there are 8 dragons, and each dragon would have $\frac{218}{8}$ legs, which is impossible. 3. If there are 5 centipedes, then there are 7 dragons, and thus each dragon has 14 legs.
|
14
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Two detectives met. Here is their dialogue:
- Do you have two sons?
- Yes, they are young, they don't go to school.
- By the way, the product of their ages equals the number of pigeons near us.
- That's not enough information.
- And I named the older one after you.
- Now I know how old they are.
How old are the sons?
|
7. The ages of the sons could have been equal, hence the product of their ages - a perfect square. Upon receiving information about the product of the ages, the second detective could not answer the question, therefore, the product can be factored in two ways. Answer: 1 and 4 years.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Boxing Championship. In the Olympic boxing tournament, 247 people participated. How many matches were needed to determine the winner?
|
1. In the Olympic tournament, when after each match one boxer is eliminated, and only the winner continues to compete, 246 matches will be required.
|
246
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In a round-robin chess tournament, 7 players participated. How many games did they play?
|
2. Let's calculate the total number of games played in the tournament. Each player played 6 games - in total: $6 \times 7=42$. Notice that in this way, we counted each game twice (since two players participate in each game!), so the total number of games played in the tournament is $42: 2=21$. We can also solve this using a table:
| № | Participants | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| :--- | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 1 | Ivanov | 口口 | | 1 | | | | |
| 2 | Svirin | | 口口 | | | | | |
| 3 | Sherstnev | 0 | | 口■ | \| | | | |
| 4 | Sudo | | | $\mid$ | $\square \square$ | | | |
| 5 | Makarov | | | | | $\square \square$ | | |
| 6 | Romanov | | | | | | $\square \square$ | |
| 7 | Novikov | | | | | | | $\square \square$ |
Tournaments $\quad 72$
From the table, it becomes clear that the total number of games played is $7+6+5+\ldots+1$ - the number of cells located above the diagonal.
|
21
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. How many chess players participated in the round-robin tournament if a total of 190 games were played in this competition?
|
3. Since $19 \times 20: 2=190$, there were 20 chess players in the tournament.
|
20
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In a chess tournament (played in a round-robin system) with 30 participants, to achieve the 4th category rating, a player needs to score $60 \%$ of the points. What is the maximum number of chess players who can achieve the category rating by the end of the tournament?
|
5. In total, $30 \cdot 29: 2=435$ games are played in the tournament, and thus 435 points are contested. The number of participants who become rated players cannot exceed $435: 17.5=24$ people. If 24 participants draw all their games against each other and win the rest of their games, they will accumulate the required 17.5 points. Answer: 24 people.
|
24
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. In a chess tournament, 8 players participated. They scored $7, 6, 4, 4, 3, 2, 1, 5$ and 0.5 points respectively. How many points did the players who took the first four places lose in matches against the others?
|
7. From the condition of the problem, it follows that the tournament winner and the participant who took second place did not lose a single point in their matches against the others. Further, the participants who shared third and fourth places could have scored 8 points against the rest, but scored 7 (they played one point in their match against each other). Thus, the players who took the first four places lost 1 point in their matches against the others.
73 Tournaments
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11. Homework. Fedya was supposed to divide a certain number by 4 and add 15 to it, but Fedya multiplied this number by 4 and subtracted 15, yet he still got the correct answer. What was this number?
|
11. Solving the equation: $0.25 x + 15 = 4 x - 15$, we get the answer: 8.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Linear function. The distance between villages $\mathcal{A}$ and $B$ is 3 km. In village $\mathcal{A}-300$ students, and in village $B-$ 200 students. Where should a school be built to minimize the total distance traveled by students on their way to school?
|
4. It is clear that the school should be built on the segment $A B$, but where exactly? Let the distance from village $A$ to the school be $x$, then the total distance traveled by all schoolchildren on the way
77 What is the best?
to school is $f(x)=300 x+200(a-x)=200 a+100 x$, where $a-$ is the length of segment $A B$. The minimum value of $f(x)$ is achieved at $x=0$. Therefore, the school should be built in village $A$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.