problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
329. Find the value of the arbitrary function $f(x)=\sin ^{4} x-$ $-\cos ^{4} x$ at $x=\pi / 12$.
|
Solution. First, we transform the given function:
$$
f(x)=\left(\sin ^{2} x+\cos ^{2} x\right)\left(\sin ^{2} x-\cos ^{2} x\right)=-\cos 2 x
$$
(since $\sin ^{2} \alpha+\cos ^{2} \alpha=1, \cos ^{2} \alpha-\sin ^{2} \alpha=\cos 2 \alpha$). Using the rule for differentiating a composite function, we get
$$
f^{\prime}(x)=(-\cos 2 x)^{\prime}=-(\cos 2 x)^{\prime}=-(-\sin 2 x) \cdot(2 x)^{\prime}=2 \sin 2 x
$$
At $x=\frac{\pi}{12}$, we have $f^{\prime}\left(\frac{\pi}{12}\right)=2 \sin \frac{\pi}{6}=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
374. Find the slope of the tangent line drawn to the curve $y=x^{3}$ at the point $C(-2;-8)$.
|
Solution. Let's find the derivative of the function $y=x^{3}$ at the point $x=-2$:
$$
y^{\prime}=\left(x^{3}\right)^{\prime}=3 x^{2} ; \quad y_{x=-2}^{\prime}=3(-2)^{2}=12
$$
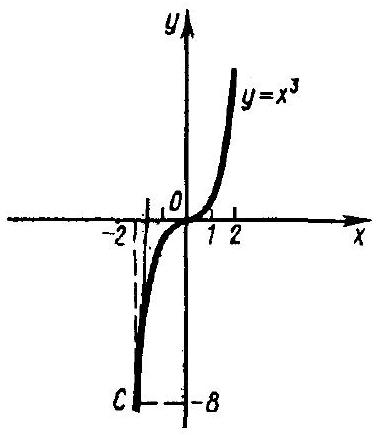
Thus, the slope of the tangent line to the curve $y=x^{3}$ at the point $C(-2 ;-8)$ is 12 (Fig. 104).
Fig. 104
|
12
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
410. The height of a body thrown vertically upwards changes with time according to the law $H=200 t-4.9 t^{2}$. Find the velocity of the body at the end of the 10th second. How many seconds will the body fly upwards and what is the greatest height it will reach?
|
Solution. The velocity of the body is determined by the expression $v=\frac{d H}{d t}=$ $=200-9.8 t$; at $t=10$ we have $v=102($ m $/ \mathrm{s})$.
At the moment when the body reaches its maximum height, its velocity is zero. Therefore, for this moment $\frac{d H}{d t}=200-$ $-9.8 t=0$, from which $t=\frac{200}{9.8} \approx 20.4$ (s)
Substituting this value into the equation of motion, we get the maximum height to which the body rises:
$$
s=200 \cdot 20.4-4.9 \cdot 20.4^{2} \approx 2040 ; 8(\mathrm{m})
$$
|
102
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
413. A body with a mass of 8 kg moves in a straight line according to the law $s=$ $=2 t^{2}+3 t-1$. Find the kinetic energy of the body $\left(m v^{2} / 2\right)$ 3 seconds after the start of the motion.
|
Solution. Let's find the velocity of the body at any moment of time $t$:
$$
v=\frac{d s}{d t}=4 t+3
$$
Calculate the velocity of the body at the moment $t=3$:
$$
v_{t=3}=4 \cdot 3+3=15(\mathrm{M} / \mathrm{c})
$$
Determine the kinetic energy of the body at the moment $t=3$:
$$
\frac{m v^{2}}{2}=\frac{8 \cdot 15^{2}}{2}=900(\text { J })
$$
|
900
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
434. A material point moves according to the law $s=2 t^{3}-6 t^{2}+$ $+4 t$. Find its acceleration at the end of the 3rd second.
|
Solution. We find $v=s^{\prime}=6 t^{2}-12 t+4, a=s^{\prime \prime}=12 t-12$, from which at $t=3$ we get $a=12 \cdot 3-12=24\left(\mathrm{m} / \mathrm{c}^{2}\right)$.
|
24
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
435. At time $t$, the body is at a distance of $s=\frac{1}{4} t^{4}+4 t^{3}+16 t^{2}$ km from the starting point. Find its acceleration after 2 hours.
|
Solution. We find $v=s^{\prime}=t^{3}+12 t^{2}+32 t, a=v^{\prime}=s^{\prime \prime}=3 t^{2}+$ $+24 t+32$. For $t=2$ we have $a=3 \cdot 4+24 \cdot 2+32=92$ (km $\left./ \mathrm{u}^{2}\right)$.
|
92
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
448. The sides $a$ and $b$ of a rectangle change according to the laws $a=(2 t+1)$ cm, $b=(3 t+2)$ cm. At what rate is its area $S$ changing at the moment $t=4$ s?
|
Solution. We find $S=a b=(2 t+1)(3 t+2)=6 t^{2}+7 t+2, \quad v=$ $=S_{t}^{\prime}=\left(6 t^{2}+7 t+2\right)^{\prime}=12 t+7$. For $t=4$ we get $v_{t=4}=12 \cdot 4+7=$ $=55(\mathrm{~cm} / \mathrm{s})$.
|
55
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
455. The amount of electricity flowing through a conductor, starting from the moment of time $t=0$, is given by the formula $Q=$ $=3 t^{2}-3 t+4$. Find the current strength at the end of the 6th second.
|
Solution. The current is the derivative of the quantity of electricity with respect to time: therefore, we need to find the derivative of the function $Q=3 t^{2}-3 t+4$ and calculate its value at $t=6 \mathrm{c}$. We have $I=Q^{\prime}=$ $=6 t-3$, from which at $t=6$ we get $I=33$ (A).
|
33
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
461. The law of temperature change $T$ of a body depending on time $t$ is given by the equation $T=0.2 t^{2}$. At what rate is this body heating at the moment of time $10 \mathrm{c}$?
|
Solution. The heating rate of a body is the derivative of temperature $T$ with respect to time $t$:
$$
\frac{d T}{d t}=\left(0.2 t^{2}\right)^{\prime}=0.4 t
$$
Determine the heating rate of the body at $t=10$:
$$
\left(\frac{d T}{d t}\right)_{t=10}=0.4 \cdot 10=4(\text{ deg } / \mathrm{s})
$$
|
4
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
564. $y=x^{2}+2$.
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
564. $y=x^{2}+2$.
|
Solution. $1^{0}$. Find the derivative: $y^{\prime}=\left(x^{2}+2\right)^{\prime}=2 x$.
$2^{0}$. Set it to zero; $2 x=0$, from which $x=0$ - the critical point.
$3^{\circ}$. Determine the sign of the derivative at the value $x0$, for example at $x=1$: $y_{x=1}^{\prime}=2 \cdot 1=2$. Since the derivative changes sign from negative to positive as we pass through $x=0$, the function has a minimum at $x=0$.
$4^{0}$. Find the minimum value of the function, i.e., $f(0)=0^{2}+2=2$.
Now we can sketch the curve near the point $A(0 ; 2)$ (Fig. 121).
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
582. $y=4x-x^{2}$.
|
Solution. $1^{0}$. Find the first derivative: $y^{\prime}=4-2 x$. $2^{0}$. Solving the equation $4-2 x=0$, we get the critical point $x=2$. $3^{0}$. Calculate the second derivative: $y^{\prime \prime}=-2$.
$4^{0}$. Since $y^{\prime \prime}$ is negative at any point, then $y^{\prime \prime}(2)=-2<0$. This means that the function has a maximum at the point $x=2$. Let's find its value: $y(2)=4 \cdot 2-2^{2}=4$, i.e., $y_{\max }=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
585. $y=x^{6}$.
|
Solution. $1^{0} . y^{\prime}=6 x^{5}$.
$2^{0} .6 x^{5}=0$, i.e. $x=0$.
$3^{0} \cdot y^{\prime \prime}=30 x^{4}$.
$4^{0}$. Since $y^{\prime \prime}(0)=0$, the method of investigation using the second derivative is not applicable.
We will investigate the function for an extremum using the first derivative. If $x<0$, then $y^{\prime}<0$; if $x>0$, then $y^{\prime}>0$. Therefore, at the point $x=0$ the function has a minimum $y=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
614. There is a square sheet of tin, the side of which $a=$ $=60 \mathrm{~cm}$. By cutting out equal squares from all its corners and folding up the remaining part, a box (without a lid) needs to be made. What should be the dimensions of the squares to be cut out so that the box has the maximum volume?
|
Solution. According to the condition, the side of the square $a=60$. Let the side of the squares cut out from the corners be denoted by $x$. The bottom of the box is a square with side $a-2 x$, and the height of the box is equal to the side $x$ of the cut-out square. Therefore, the volume of the box can be expressed by the function
$$
V=(a-2 x)^{2} x
$$
To find the value of $x$ at which the function will take the maximum value, we first transform the function and then investigate it for an extremum:
$$
\begin{gathered}
V=\left(a^{2}-4 a x+4 x^{2}\right) x ; \quad V=4 x^{3}-4 a x^{2}+a^{2} x \\
V^{\prime}=12 x^{2}-8 a x+a^{2} ; \quad 12 x^{2}-8 a x+a^{2}=0 \\
x=\frac{4 a \pm \sqrt{16 a^{2}-12 a^{2}}}{12}=\frac{4 a \pm \sqrt{4 a^{2}}}{12}=\frac{4 a \pm 2 a}{12} ; \quad x_{1}=\frac{a}{2}, \quad x_{2}=\frac{a}{6}
\end{gathered}
$$
Obviously, the value $x=a / 2$ does not meet the condition, as in this case the square would be cut into four equal parts and no box would be formed. Therefore, we investigate the function for an extremum at the critical point $x_{2}=a / 6$ :
$$
V^{\prime \prime}=24 x-8 a ; V^{\prime \prime}\left(\frac{a}{6}\right)=24 \frac{a}{6}-8 a=4 a-8 a=-4 a<0
$$
i.e., the maximum is achieved at $x=a / 6$. Thus, the side of the cut-out square should be equal to $x=a / 6$. In this specific case, when $a=60$ cm, we get $x=10$ cm.
|
10
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
616. An irrigation channel has the shape of an isosceles trapezoid, the lateral sides of which are equal to the smaller base. At what angle of inclination of the lateral sides is the cross-sectional area of the channel the largest?
|
Solution. Let the smaller base of the trapezoid be denoted by $a$, the angle of inclination of the lateral sides by $\alpha$, and the area of the section by $S$ (Fig. 124). According to the condition, $|A B|=|A D|=|B C|=a$.
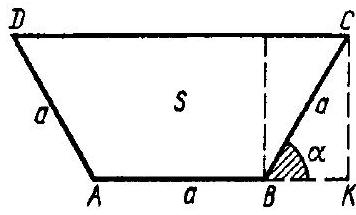
Fig. 124 From triangle $B C K$, we find $|B K| = a \cos \alpha$. Then $|C D| = a + 2a \cos \alpha$. The height of the trapezoid is $|C K| = a \sin \alpha$. Let's determine the area of the trapezoid:
$$
\begin{gathered}
S = \frac{|A B| + |D C|}{2} |C K| = \frac{a + a + 2a \cos \alpha}{2} a \sin \alpha = \\
= a^2 (1 + \cos \alpha) \sin \alpha.
\end{gathered}
$$
To find the maximum value of the area $S = S(\alpha)$, we need to find the critical points within the interval $(0, \pi / 2)$, compute the values of the function $S(\alpha)$ at these points and at the endpoints of the interval $(0, \pi / 2)$, and then select the largest value from the obtained results.
Let's find the derivative:
$$
\begin{aligned}
& S'(\alpha) = a^2 \left( (1 + \cos \alpha)' \sin \alpha + (1 + \cos \alpha) (\sin \alpha)' \right) = \\
= & a^2 \left( -\sin^2 \alpha + \cos \alpha + \cos^2 \alpha \right) = a^2 \left( 2 \cos^2 \alpha + \cos \alpha - 1 \right)
\end{aligned}
$$
Set the derivative to zero and solve the resulting equation:
$$
2 \cos^2 \alpha + \cos \alpha - 1 = 0 ; \quad \cos \alpha_1 = 1 / 2 ; \quad \cos \alpha_2 = -1
$$
from which $\alpha_1 = \pm \pi / 3 + 2 \pi n, \alpha_2 = \pi + 2 \pi n$. Only the critical point $\alpha_1 = \pi / 3$ belongs to the interval $(0, \pi / 2)$.
Let's find $S(\alpha_1) = S\left(\frac{\pi}{3}\right) = a^2 \left(1 + \cos \frac{\pi}{3}\right) \sin \frac{\pi}{3} = \frac{3 \sqrt{3}}{4} a^2, S(0) = 0$, $S\left(\frac{\pi}{2}\right) = a^2$. Comparing the obtained results, we conclude that the function $S(\alpha)$ attains its maximum value at $\alpha = \pi / 3$.
Thus, the area of the channel section is the largest when the angle of inclination of the lateral sides is $60^{\circ}$.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
228. Given the function $f(x)=2 x+4$. Find the increment of any of its antiderivatives when $x$ changes from -2 to 0.
|
Solution. Let's find the antiderivative of the given function:
$$
F=\int(2 x+4) d x=x^{2}+4 x+C
$$
Consider, for example, the antiderivatives $F_{1}=x^{2}+4 x, F_{2}=x^{2}+4 x+2$, $F_{3}=x^{2}+4 x-1$, and compute the increment of each of them on the interval $[-2,0]: \quad F_{1}(0)-F_{1}(-2)=0-(-4)=4 ; \quad F_{2}(0)-F_{2}(-2)=2-(-2)=4 ;$ $F_{3}(0)-F_{3}(-2)=1-(-5)=4$. Thus, the increments of these antiderivatives are equal to each other.
Now consider the increment of any antiderivative $F=x^{2}+4 x+$ $+C$ on the interval $[-2,0]$. We have
$$
\left(x^{2}+4 x+C\right)_{x=0}-\left(x^{2}+4 x+C\right)_{x=-2}=4
$$
Therefore, the increment of any antiderivative of the function $f(x)=$ $=2 x+4$ when $x$ changes from -2 to 0 is 4, i.e., the increments of all antiderivatives of this function are equal to each other and do not depend on $C$.
Let's find the increment of any antiderivative of the function $f(x)$ when the argument $x$ changes from $x=a$ to $x=b$:
$$
(F(x)+C)_{x=b}-(F(x)+C)_{x=0}=F(b)-F(a)
$$
The obtained result means that when the argument $x$ changes from $x=a$ to $x=b$, all antiderivatives of the given function have the same increment, equal to $F(b)-F(a)$.
This increment is called the definite integral.
Definition 2. If $F(x)+C$ is an antiderivative of $f(x)$, then the increment $F(b)-F(a)$ of the antiderivatives when the argument $x$ changes from $x=a$ to $x=b$ is called the definite integral and is denoted by the symbol
$$
\begin{aligned}
& \text { } \int_{a}^{b} f(x) d x, \text { i.e., } \\
& \qquad \int_{a}^{b} f(x) d x=F(b)-F(a)
\end{aligned}
$$
where $a$ is the lower limit, and $b$ is the upper limit of the definite integral.
The symbol $\int_{a}^{b} f(x) d x$ is read as: "the definite integral from $a$ to $b$ of $f$ of $x$ $d x$."
The function $f(x)$ is assumed to be continuous in the interval of the argument $x$ from $a$ to $b$.
To compute the definite integral $\int_{a}^{b} f(x) d x$, one finds:
1) the indefinite integral $\int f(x) d x=F(x)+C$;
2) the value of the integral $F(x)+C$ at $x=b, C=0$, i.e., compute $F(b)$
3) the value of the integral $F(x)+C$ at $x=a, C=0$, i.e., compute $F(a)$;
4) the difference $F(b)-F(a)$.
The process of computation is evident from the formula
$$
\int_{a}^{b} f(x) d x=\left.F(x)\right|_{a} ^{b}=F(b)-F(a)
$$
Equality (2) is called the Newton-Leibniz formula.
Remarks. 1. Under $F(x)$ in formula (2), the simplest of the antiderivatives is meant, for which $C=0$.
|
4
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
244. Find $\int_{1}^{2}\left(5 x^{4}+2 \dot{x}-8\right) d x$.
|
Solution. $\int_{1}^{2}\left(5 x^{4}+2 x-8\right) d x=\int_{1}^{2} 5 x^{4} d x+\int_{1}^{2} 2 x d x-\int_{1}^{2} 8 d x=\left.x^{5}\right|_{1} ^{2}+$ $+x^{2}-\left.8 x\right|_{1} ^{2}=\left(2^{5}-1^{5}\right)+\left(2^{2}-1^{2}\right)-8(2-1)=26$.
|
26
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
245. Find $\int_{\pi / 2}^{\pi} \frac{2 \sin x d x}{(1-\cos x)^{2}}$.
|
Solution. Let's use the substitution $u=1-\cos x$, from which $d u=$ $=\sin x d x$. Then we will find the new limits of integration; substituting into the equation $u=1-\cos x$ the values $x_{1}=\pi / 2$ and $x_{2}=\pi$, we will respectively obtain $u_{1}=1-\cos (\pi / 2)=1$ and $u_{2}=1-\cos \pi=2$. The solution is written as follows:
$$
\begin{aligned}
& \int_{\pi / 2}^{\pi} \frac{2 \sin x d x}{(1-\cos x)^{2}}=\left|\begin{array}{l}
u=1-\cos x, u_{1}=1-\cos (\pi / 2)=1, \\
d u=\sin x d x ; u_{2}=1-\cos \pi=2
\end{array}\right|=2 \int_{u}^{u_{2}} \frac{d u}{u^{2}}=2 \int_{1}^{2} u^{-2} d u= \\
& =-\left.2 u^{-1}\right|_{1} ^{2}=-1+2=1
\end{aligned}
$$
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
246. $\int 8 x^{3} d x$
|
Solution. $\int_{1}^{3} 8 x^{3} d x=\left.8 \cdot \frac{x^{4}}{4}\right|_{1} ^{3}=\left.2 x^{4}\right|_{1} ^{3}=2\left(3^{4}-1^{4}\right)=160$.
|
160
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
294. $\int_{1}^{e} \frac{3 \ln ^{2} x d x}{x}$.
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
294. $\int_{1}^{e} \frac{3 \ln ^{2} x \, dx}{x}$.
|
Solution. $\int_{1}^{e} \frac{3 \ln ^{2} x d x}{x}=\left|\begin{array}{l}\ln x=t, t_{1}=\ln 1=0, \\ \frac{d x}{x}=d t ; t_{2}=\ln e=1\end{array}\right|=3 \int_{0}^{1} t^{2} d t=\left.t^{3}\right|_{0} ^{1}=1$.
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
307. $y^{2}=9 x, x=16, x=25$ and $y=0$ (Fig. 150).
|
Solution. For any $x \in [16,25]$, the function $y=\sqrt{9 x}$ takes positive values; therefore, to calculate the area of the given curvilinear trapezoid, we should use formula (1):
$$
S=\int_{16}^{25} \sqrt{9} x d x=\int_{16}^{25} 3 x^{1 / 2} d x=\left.3 \frac{x^{3 / 2}}{3 / 2}\right|_{16} ^{25}=\left.2 x \sqrt{x}\right|_{16} ^{25}=2(125-64)=2 \cdot 61=
$$
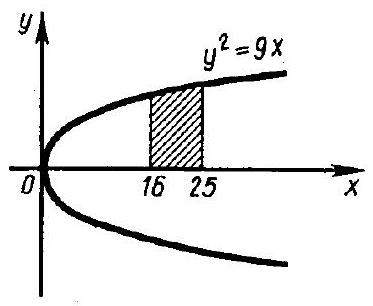
Fig. 150 $=122$ (sq. units).
|
122
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
320. $y=4x-x^2$, $y=0$ and $x=5$.
|
The parabola $y=4 x-x^{2}$ intersects the x-axis at points $x=0$ and $x=4$. The figure whose area we need to find is marked in color in Fig. 167. Let $S_{1}$ and $S_{2}$ be the areas of the parts of this figure corresponding to the segments $[0,4]$ and $[4, 5]$, and let $S$ be the required area; then $S=S_{1}+S_{2}$. Using formula (1), we get
Fig. 166
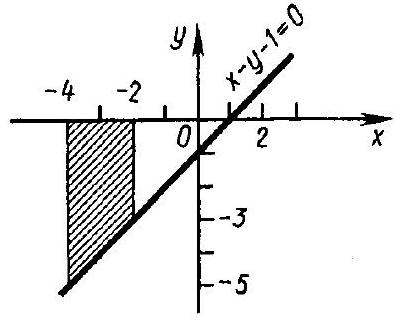
Fig. 168
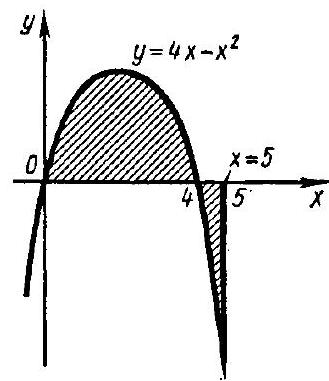
Fig. 167
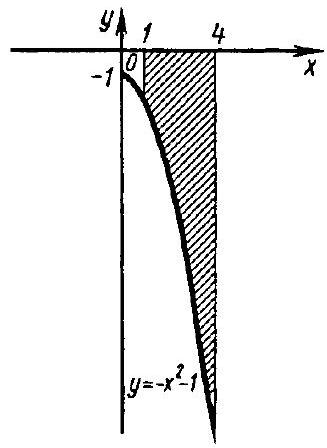
Fig. 169
$$
S_{1}=\int_{0}^{4}\left(4 x-x^{2}\right) d x=\left.\left(2 x^{2}-\frac{x^{3}}{3}\right)\right|_{0}^{4}=32-\frac{64}{3}=\frac{32}{3} \text { (sq. units) }
$$
and using formula (2) we find
$$
\begin{gathered}
S_{2}=\left|\int_{4}^{5}\left(4 x-x^{2}\right) d x\right|=\left|\left(\frac{x^{3}}{3}-2 x^{2}\right)\right|_{4}^{5}=\left(\frac{125}{3}-50\right)-\left(\frac{64}{3}-32\right)= \\
=\frac{7}{3} \text { (sq. units) }
\end{gathered}
$$
Therefore, $S=S_{1}+S_{2}=32 / 3+7 / 3=13$ (sq. units).
|
13
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
324. $y=\frac{1}{2} x^{3}, x=-2, x=4$ and $y=0$.
|
Solution. The graph of the function $y=\frac{1}{2} x^{3}$ lies below the $O x$ axis on the interval $[-2,0]$, and above the $O x$ axis on the interval $[0,4]$ (Fig. 171). Therefore,
$S=\left|\int_{-2}^{0} \frac{1}{2} x^{3} d x\right|+\int_{0}^{4} \frac{1}{2} x^{3} d x=\left|\frac{1}{8} x^{4}\right|_{-2}^{0}+\left.\frac{1}{8} x^{4}\right|_{0} ^{4}=2+32=34$ (sq. units).
|
34
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
358. Calculate the integral $\int_{1}^{9} \sqrt{6 x-5} d x$ using the Newton-Leibniz formula and approximate formulas for rectangles and trapezoids, dividing the interval of integration into 8 equal parts. Estimate the error of the results.
|
Solution. According to the Newton-Leibniz formula, we find
$$
I=\int_{1}^{9} \sqrt{6 x-5} d x=\frac{1}{6} \int_{1}^{9}(6 x-5)^{1 / 2} d(6 x-5)=\left.\frac{1}{9}(6 x-5)^{3 / 2}\right|_{1} ^{9}=\frac{7^{3}-1}{9}=38
$$
Since the interval $[1,9]$ is divided into 8 equal parts, then $\Delta x=1$. We find the values $y_{i}(i=1,2, \ldots, 8)$ of the integrand function $y=\sqrt{6 x-5}$ at the division points $x_{i}: x_{0}=1, y_{0}=\sqrt{1}=1,0000 ; x_{1}=2, y_{1}=\sqrt{7}=$ $=2,6458 ; \quad x_{2}=3, \quad y_{2}=\sqrt{13}=3,6056 ; \quad x_{3}=4, \quad y_{3}=\sqrt{19}=4,3589 ; \quad x_{4}=5$, $y_{4}=\sqrt{25}=5,0000 ; \quad x_{5}=6, \quad y_{5}=\sqrt{31}=5,5678 ; \quad x_{6}=7, \quad y_{6}=\sqrt{37}=6,0828 ;$ $x_{7}=8, y_{7}=\sqrt{43}=6,5574 ; x_{8}=9, y=\sqrt{49}=7,0000$.
We will compute this integral using approximate formulas. Using the rectangle formula (10), we find
$$
I=\sum_{i=0}^{7} y_{i}=34,8183
$$
The absolute error of this approximate value (by deficiency) is 3.1817, and the relative error is $\frac{3.1817 \cdot 100 \%}{38} \approx 8.37 \%$.
According to the rectangle formula (11), we get
$$
I=\sum_{i=1}^{8} y_{i}=40,8183
$$
Here the absolute error (by excess) is 2.8183, and the relative error is $\frac{2.8183 \cdot 100 \%}{38} \approx 7.42 \%$.
Using the trapezoidal formula (12), we find
$$
I \approx 4+\sum_{i=1}^{7} y_{i}=37,8183
$$
The absolute error of this result is 0.1817, and the relative error is $\frac{0.1817 \cdot 100 \%}{38} \approx 0.48 \%$.
|
38
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
362. Calculate the integral $\int_{1}^{4} x^{2} d x$ using Simpson's formula.
|
Solution. Divide the interval of integration into 10 equal parts. Then $(b-a) / 3 n=3 / 30=1 / 10=0.1$. Substituting into the integrand function $y=x^{2}$ the values of the argument $x_{0}=1, x_{1}=1.3 ; x_{2}=1.6, \ldots$, $x_{10}=4$, we find the corresponding values of the ordinates: $y_{0}=1 ; y_{1}=1.69$; $y_{2}=2.56 ; \quad y_{3}=3.61 ; \quad y_{4}=4.84 ; \quad y_{5}=6.25 ; \quad y_{6}=7.84 ; \quad y_{7}=9.61 ; \quad y_{8}=11.56 ;$ $y_{9}=13.69 ; y_{10}=16$.
Applying formula (14), we get
$$
\begin{gathered}
\int_{1}^{4} x^{2} d x=0.1((1+16)+2(2.56+4.84+7.84+11.56)+4(1.69+3.61+6.25+ \\
+9.61+13.69))=21
\end{gathered}
$$
Evaluating the integral using the Newton-Leibniz formula gives
$$
\int_{1}^{4} x^{2} d x=\left.\frac{x^{3}}{3}\right|_{1} ^{4}=\frac{64}{3}-\frac{1}{3}=21
$$
Thus, by applying Simpson's formula, in this case, we obtained the exact value of the integral.
Note that although the method of rectangles is the simplest method for approximate calculation of definite integrals, it provides the least accurate results. The choice of the method of approximate integration depends on the integrand function and the required accuracy of the calculation.
## $\S$ 10. Application of the Definite Integral to Solving Physical Problems
Scheme for solving problems on the application of the definite integral Finding the path traveled by a body in rectilinear motion Calculating the work done by a force in rectilinear motion of a body Calculating the work expended on stretching or compressing a spring Determining the force of liquid pressure on a vertically positioned plate
|
21
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
363. The velocity of a material point is given by the formula $v=\left(4 t^{3}-2 t+1\right)$ m/s. Find the distance traveled by the point in the first 4 s from the start of the motion.
|
Solution. According to formula (1), we have
$$
s=\int_{0}^{4}\left(4 t^{3}-2 t+1\right) d t=\left.\left(t^{4}-t^{2}+t\right)\right|_{0} ^{4}=256-16+4=244(\text { m })
$$
Thus, in 4 s, the point has traveled 244 m.
|
244
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
370. The velocity of a body is given by the equation $v=$ $=\left(12 t-3 t^{2}\right) \mathrm{m} / \mathrm{s}$. Determine the distance traveled by the body from the start of the motion until it stops.
|
Solution. The speed of the body is zero at the beginning of its motion and at the moment of stopping. To find the moment of stopping, we set the speed to zero and solve the equation with respect to $t$; we get $12 t-3 t^{2}=0 ; 3 t(4-t)=0 ; t_{1}=0, t_{2}=4$. Therefore,
$$
s=\int_{0}^{4}\left(12 t-3 t^{2}\right) d t=\left.\left(6 t^{2}-t^{3}\right)\right|_{0} ^{4}=6 \cdot 4^{2}-4^{3}=32(\mathrm{M})
$$
|
32
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
380. Two bodies simultaneously started linear motion from a certain point in the same direction with speeds $v_{1}=$ $=\left(6 t^{2}+4 t\right) \mathrm{m} /$ s and $v_{2}=4 t \mathrm{m} / \mathrm{s}$. After how many seconds will the distance between them be 250 m?
|
Solution. Let $t_{1}$ be the moment of the meeting. Then
$$
s_{1}=\int_{0}^{t_{1}}\left(6 t^{2}+4 t\right) d t=\left.\left(2 t^{3}+2 t^{2}\right)\right|_{0} ^{t_{1}}=2 t_{1}^{3}+2 t_{1}^{2} ; \quad s_{2}=\int_{0}^{t_{1}} 4 t d t=2 t_{1}^{2}
$$
Since $s_{1}-s_{2}=250$, we get the equation $2 t_{1}^{3}+2 t_{1}^{2}-2 t_{1}^{2}=250$ or $2 t_{1}^{3}=250$, from which $t_{1}^{3}=125$, i.e., $t=5$ (s).
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
392. A rectangular plate is immersed in water, positioned vertically. Its horizontal side is 1 m, the vertical side is $2 \mathrm{m}$. The top side is at a depth of 0.5 m. Determine the force of water pressure on the plate.
|
Solution. Here $y=1, \quad a=0.5, \quad b=2+0.5=2.5$ (m), $\gamma=$ $=1000 \mathrm{kr} / \mathrm{m}^{3}$. Therefore,
$$
\begin{gathered}
P=9810 \int_{a}^{b} x y d x=9810 \int_{a}^{b} x d x=\left.9810 \frac{x^{2}}{2}\right|_{0.5} ^{2.5}=9810 \frac{2.5^{2}-0.5^{2}}{2}= \\
=29430 \text { (N) }
\end{gathered}
$$
|
29430
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
400. Calculate the force of water pressure on a dam that has the shape of a trapezoid, where the upper base, coinciding with the water surface, is $10 \mathrm{~m}$ long, the lower base is $20 \mathrm{~m}$, and the height is $3 \mathrm{m}$.
|
Solution. Using formula (6), we find
$$
P=9810 \frac{(10+2 \cdot 20) 3^{2}}{6}=9810 \cdot \frac{450}{6}=735750(\mathrm{H})
$$
|
735750
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
403. Determine the force of water pressure on a vertical parabolic segment, the base of which is $4 \mathrm{m}$ and is located on the water surface, while the vertex is at a depth of $4 \mathrm{m}$ (Fig. 204).
|
Solution. We have $|B A|=2 x=4$ (m). Point $A$ in the chosen coordinate system has coordinates $(2 ; 4)$. The equation of the parabola relative to this system is $y = a x^{2}$ or $4=a \cdot 2^{2}$, from which $a=1$, i.e., $y=x^{2}$.
Consider an elementary area $d S$ at a distance $y$ from the origin. The length of this area is $2 x$, and its area is $d S=2 x d y$, where $d y$ is the width of the area. This area will experience a pressure force
$$
d P=9.81 \gamma(4-y) d S=9.81 \gamma(4-y) 2 x d y
$$
Summing all the elementary forces of pressure as $y$ changes from 0 to 4 and taking the limit as $\Delta y \rightarrow 0$, the force of pressure on the entire segment will be expressed by the following integral:
$$
P=9.81 \gamma \int_{0}^{4}(4-y) 2 x d y
$$
To find this integral, express $x$ in terms of $y$; since $y=x^{2}$, then $x=\sqrt{y}$. Then we get
$$
\begin{aligned}
& P=19.62 \cdot 1000 \int_{0}^{4}(4-y) \sqrt{y} d y=19620\left(\int_{0}^{4} 4 \sqrt{y} d y-\int_{0}^{4} y \sqrt{y} d y\right)= \\
&=19620\left(4 \int_{0}^{4} y^{1 / 2} d y-\int_{0}^{4} y^{3 / 2} d y\right)=\left.19620\left(\frac{4 y^{3 / 2}}{3 / 2}-\frac{y^{5 / 2}}{5 / 2}\right)\right|_{0} ^{4}= \\
&=\left.19620\left(\frac{8}{3} y^{3 / 2}-\frac{2}{5} y^{5 / 2}\right)\right|_{0} ^{4}=19620\left(\frac{8 \cdot 2}{3}-\frac{2 \cdot 32}{5}\right)= \\
&=\frac{19620 \cdot 128}{15}=167424 \text { (N). }
\end{aligned}
$$
|
167424
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
65. The speed of a body coming out of a state of rest is equal to $5 t^{2} \mathrm{m} / \mathrm{s}$ after $t$ seconds. Determine the distance the body will travel in 3 s (see problem 20).
|
Solution. Using the condition, we form the differential equation: $\frac{d s}{d t}=5 t^{2}$, since velocity $v=\frac{d s}{d t}$.
Let's find the general solution of this equation:
$$
d s=5 t^{2} d t ; \int d s=5 \int t^{2} d t ; s=\frac{5}{3} t^{3}+C
$$
Now, let's find the particular solution of this equation. The initial conditions are determined by the fact that the body starts from rest, i.e., $s=0$ when $t=0$. Substituting these values into the general solution, we get $C=0$. Therefore, the particular solution is $s=\frac{5}{3} t^{3}$.
Let's determine the distance traveled by the body in $3 \mathrm{~s}$:
$$
s=\frac{5}{3} \cdot 3^{3}=\frac{5}{3} \cdot 27=45(\mathrm{~m})
$$
|
45
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
192. A metal ball, the temperature of which at the beginning of the experiment was $12^{\circ} \mathrm{C}$, is cooled by a stream of water having a temperature of $0^{\circ}$. After 8 minutes, the ball cooled down to $9^{\circ}$. Assuming the cooling rate is proportional to the difference between the temperature of the body and the temperature of the cooling medium, determine how long it took for the ball to cool down to $7^{\circ}$.
|
Solution. $1^{\circ}$. Let $T$ denote the temperature of the sphere, and $t-$ the time elapsed since the start of the experiment. Then the cooling rate of the sphere is the derivative $\frac{d T}{d t}\left(T^{\prime}\right)$. According to the condition, $T^{\prime}=k(T-0)=k T$, where $k$ is the proportionality coefficient.
$2^{0}$. This is a separable differential equation. Separating the variables, we have $\frac{d T}{d t}=k T, \frac{d T}{T}=k d t$, from which $\ln T=k t+\ln C$, or $\ln T=\ln e^{k t}+\ln C$. Finally, after exponentiating, we get
$$
T=C e^{k t}
$$
$3^{0}$. To find the constants $C$ and $k$, we use the data from the problem: at $t=0$ the temperature of the sphere $T=12^{\circ}$, and at $t=8$ it is $T=9^{\circ}$. Substituting the values of $t$ and $T$ into equation (1), we get $12=C e^{0}$ and $9=C e^{8 k}$. From the first equation, we have $C=12$, and from the second, $e^{8 k}=0.75$. To find $e^{k}$, we take the eighth root of both sides of the equation:
$$
e^{k}=\sqrt[8]{0.75}=0.75^{1 / 8}
$$
Raising both sides of this equation to the power of $t$, we have
$$
e^{k t}=0.75^{t / 8}
$$
Substituting the found values of $C$ and $e^{k t}$ into equation (1), we get
$$
T=12 \cdot(0.75)^{1 / 8}
$$
To answer the question of the problem, we take the logarithm base 10 of equation (2):
$$
\lg T=\lg 12+\frac{t}{8} \lg 0.75
$$
and set $T=7$ in the obtained equation:
$$
\lg 7=\lg 12+\frac{t}{8} \lg 0.75
$$
From this, we finally find
$$
t=\frac{8(\lg 7-\lg 12)}{\lg 0.75}=\frac{8(0.8451-1.0792)}{\overline{1}, 8751}=\frac{-8 \cdot 0.2341}{-0.1249}=\frac{1.8728}{0.1249} \approx 15 \text{ min }
$$
|
15
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
195. In a motorboat with an initial speed of $v_{0}=$ $=5 \mathrm{m} / \mathrm{s}$, the engine was turned off. During movement, the boat experiences water resistance, the force of which is proportional to the square of the boat's speed, with a proportionality coefficient of $m / 50$, where $m$ is the mass of the boat. After what time interval will the boat's speed decrease by half, and what distance will the boat travel during this time?
|
Solution. $1^{0}$. According to the condition, we can take the function as the path $s$, and the argument as time $t$. Using Newton's second law $F=m a$, we obtain the equation
$$
m s_{(t)}^{\prime \prime}=-\frac{m}{50}\left(s_{(t)}^{\prime}\right)^{2}, \text { or } s_{(t)}^{\prime \prime} \doteq-\frac{1}{50}\left(s_{(t)}^{\prime}\right)^{2}
$$
where the minus sign indicates that the resistance force is directed opposite to the motion.
$2^{0}$. This is a second-order differential equation. We reduce its order. Since $s_{(t)}^{\prime}=v_{(t)}$ and $s^{\prime \prime}(t)=v^{\prime}(t)$, we arrive at the first-order equation
$$
\frac{d v}{d t}=-\frac{1}{50} v^{2}
$$
We separate the variables and integrate:
$$
\frac{d v}{v^{2}}=-\frac{1}{50} d t ; \frac{1}{v}=\frac{t}{50}+C_{1}
$$
$3^{0}$. Using the condition $v_{0}=5$ m $/ \mathrm{c}$, we find $C_{1}=\frac{1}{5}$, from which $v=$ $=\frac{50}{t+10} \cdot$ Then we get
$$
\frac{d s}{d t}=\frac{50}{t+10} ; d s=\frac{50 d t}{t+10} ; s=50 \ln (t+10)+C_{2}
$$
From the condition $s=0$ at $t=0$ we find $C_{2}=-50 \ln 10$, from which
$$
s=50 \ln \frac{t+10}{10}
$$
We need to determine the time interval during which the speed will decrease by half. Substituting into the formula for $v$ the value $\frac{1}{2} v_{0}=2.5$, we find $2.5=\frac{50}{t+10} ; t=10$ s. During this time, the boat will travel the distance $s=50 \ln 2 \approx 34.5$ (m).
|
10
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
18. How many two-digit numbers can be formed from the five digits $1,2,3,4,5$ if no digit is repeated?
|
Solution. Since two-digit numbers differ from each other either by the digits themselves or by their order, the desired number is equal to the number of arrangements of two out of five elements: \(A_{5}^{2}=5 \cdot 4=20\). Therefore, 20 different two-digit numbers can be formed.
When finding the number of arrangements, we multiply \(n\) consecutive decreasing integers, i.e., we are short of ( \(m-n\) ) consecutive decreasing integer factors to form a complete factorial.
Therefore, the formula for the number of arrangements can be written as
\[
A_{m}^{n}=\frac{\overbrace{m(m-1)(m-2) \ldots(m-n)(m-n-1) \ldots 2 \cdot 1}^{(m \text { factors }}}{(m-n)(m-n-1) \ldots 2 \cdot 1}
\]
From this, considering that the numerator is equal to \(m\) !, and the denominator is equal to \((m-n)\) !, we can write this formula in factorial form:
\[
A_{m}^{n}=\frac{m!}{(m-n)!}
\]
|
20
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
19. Calculate in factorial form $A_{6}^{3}$.
|
Solution. $A_{6}^{3}=\frac{6!}{(6-3)!}=6 \cdot 5 \cdot 4=120$.
20-25. Calculate in any way:
|
120
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
30. Calculate: a) $C_{8}^{3}$; b) $C_{10}^{8}$.
|
Solution. a) Applying formula (6) for $m=8, n=3$, we find
$$
C_{8}^{3}=-\frac{8!}{(8-3)!3!}=-\frac{8!}{5!3!}=\frac{5!6 \cdot 7 \cdot 8}{5!3 \cdot 2 \cdot 1}=56
$$
b) $C_{10}^{\beta}=\frac{10!}{(10-8)!\cdot 8!}=\frac{10!}{2!\cdot 8!}=\frac{8!9 \cdot 10}{1 \cdot 2 \cdot 8!}=45$.
Let's note the main property of the number of combinations:
$$
C_{m}^{n}=C_{m}^{m-n}
$$
Indeed,
$$
C_{m}^{n}=\frac{m!}{(m-n)!n!}, C_{m}^{m-n}=\frac{m!}{(m-m+n)!(m-n)!}=\frac{m!}{n!(m-n)!}
$$
We see that the right-hand sides of these equalities are equal; therefore, the left-hand sides are also equal.
This property of the number of combinations allows simplifying the calculation of the number of combinations of $m$ elements taken $n$ at a time, when $n$ exceeds $\frac{1}{2} m$.
|
56
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
129. The probability of an event occurring in each of the independent trials is 0.8. How many trials need to be conducted to expect with a probability of 0.9 that the event will occur at least 75 times?
|
Solution. According to the condition, $p=0.8 ; q=0.2 ; k_{i}=75 ; k_{2}=n$; $P_{n}=(75, n)=0.9$.
Let's use the integral theorem of Laplace:
$$
P_{n}\left(k_{1} ; n\right)=\Phi\left(x^{\prime \prime}\right)-\Phi\left(x^{\prime}\right)=\Phi\left[\frac{k_{2}-n p}{\sqrt{n p q}}\right]-\Phi\left[\frac{k_{1}-n p}{\sqrt{n p q}}\right]
$$
Substituting the data from the problem, we get
$$
0.9=\Phi\left[\frac{n-0.8 n}{\sqrt{n \cdot 0.8 \cdot 0.2}}\right]-\Phi\left[\frac{75-0.8 n}{\sqrt{n \cdot 0.8 \cdot 0.2}}\right]
$$
or
$$
0.9=\Phi\left[\frac{\sqrt{n}}{2}\right]-\Phi\left[\frac{75-0.8 n}{0.4 \sqrt{n}}\right]
$$
Obviously, the number of trials $n>75$, so $\sqrt{n / 2}>\sqrt{75} / 2 \simeq$ $\simeq 4.33$. Since the Laplace function is increasing and $\Phi(4) \simeq 0.5$, we can set $\Phi(\sqrt{n} / 2)=0.5$. Therefore,
$$
0.9=0.5-\Phi\left[\frac{75-0.8 n}{0.4 \sqrt{n}}\right]
$$
Thus,
$$
\Phi\left[\frac{75-0.8 n}{0.4 \sqrt{n}}\right]=-0.4
$$
From the table in Appendix 2, we find $\Phi(1.28)=0.4$. Hence, from the relation (*), considering that the Laplace function is odd, we get
$$
(75-0.8 n) /(0.4 \sqrt{n})=-1.28
$$
Solving this equation as a quadratic equation in terms of $\sqrt{n}$, we get $\sqrt{n}=10$. Therefore, the required number of trials $n=100$.
|
100
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
136. How many times should a die be thrown so that the probability of the inequality
$$
|m / n-1 / 6| \leqslant 0.01
$$
is not less than the probability of the opposite inequality, where $m$ is the number of times one dot appears in $n$ throws of a die?
|
Solution. We will use the formula
$$
P\left(\left|\frac{m}{n}-p\right|<\varepsilon\right)=1-2 \Phi\left(\varepsilon \sqrt{\frac{n}{p q}}\right)
$$
According to the condition, the inequality should hold
$$
2 \Phi\left(\varepsilon \sqrt{\frac{n}{p q}}\right) \geqslant 1-2 \Phi\left(\varepsilon \sqrt{\frac{n}{p q}}\right)
$$
or
$$
4 \Phi\left(\varepsilon \sqrt{\frac{n}{p q}}\right) \geqslant 1
$$
From this,
$$
\Phi\left(\varepsilon \sqrt{\frac{n}{p q}}\right) \geqslant 0.25
$$
Using the table in Appendix 2, we find $\Phi(0.67)=0.2486 ; \Phi(0.68)=0.2517$. Performing linear interpolation, we get $\Phi(0.6745)=0.25$.
Considering the relation (*) and taking into account that the function $\Phi(x)$ is increasing, we have
$$
\varepsilon \sqrt{\frac{n}{p q}} \geqslant 0.6745, \text { or } 0.01 \sqrt{\frac{n}{1 / 6 \cdot 5 / 6}}=0.6745
$$
From this, the required number of coin tosses $n \geqslant 632$.
|
632
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
145. Each of the 15 elements of a certain device is tested. The probability that an element will withstand the test is 0.9. Find the most probable number of elements that will withstand the test.
|
Solution. According to the condition, $n=15, p=0.9, q=0.1$. Let's find the most probable number $k_{0}$ from the double inequality
$$
n p-q<k_{0}<n p+p
$$
Substituting the data from the problem, we get
$$
15 \cdot 0.9-0.1 \leqslant k_{0}<15 \cdot 0.9+0.9, \text{ or } 13.5 \leqslant k_{0}<14.4 \text{. }
$$
Since $k_{0}$ is an integer and since there is only one integer between 13.4 and 14.4, namely 14, the most probable number $k_{0}=14$.
|
14
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
150. Two shooters shoot at a target. The probability of a miss with one shot for the first shooter is 0.2, and for the second shooter it is 0.4. Find the most probable number of volleys in which there will be no hits on the target, if the shooters will make 25 volleys.
|
Solution. Misses by the shooters are independent events, so the multiplication theorem of probabilities of independent events applies. The probability that both shooters will miss in one volley, $p=0.2 \cdot 0.4=0.08$.
Since the product $n p=25 \cdot 0.08=2$ is an integer, the most probable number of volleys in which there will be no hits, $k_{0}=n p=2$.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
172. After the student answers the questions in the examination ticket, the examiner asks the student additional questions. The teacher stops asking additional questions as soon as the student shows ignorance of the given question. The probability that the student will answer any additional question is 0.9. Required: a) construct the distribution law of the random discrete variable $X$ - the number of additional questions the teacher will ask the student; b) find the most probable number $k_{0}$ of additional questions asked to the student.
|
Solution. a) The discrete random variable $X$ - the number of additional questions asked - has the following possible values: $x_{1}=1, x_{2}=2, x_{3}=3, \ldots, x_{k}=k, \ldots$ Let's find the probabilities of these possible values.
The variable $X$ will take the possible value $x_{i}=1$ (the examiner will ask only one question) if the student does not answer the first question. The probability of this possible value is $1-0.9=0.1$. Thus, $P(X=1)=0.1$.
The variable $X$ will take the possible value $x_{2}=2$ (the examiner will ask only two questions) if the student answers the first question (the probability of this event is 0.9) and does not answer the second (the probability of this event is 0.1). Thus, $P(X=2)=0.9 \cdot 0.1=0.09$.
Similarly, we find
$$
P(X=3) \leftrightharpoons 0.9^{2} \cdot 0.1=0.081, \ldots, P(X=k)=0.9^{k-1} \cdot 0.1, \ldots
$$
Let's write the required distribution law:
| $X$ | 1 | 2 | 3 | $\ldots$ | $k$ | $\ldots$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $p$ | 0.1 | 0.09 | 0.081 | $\ldots$ | $0.9^{k-1} \cdot 0.1$ | $\ldots$ |
b) The most probable number $k_{0}$ of questions asked (the most probable possible value of $X$), i.e., the number of questions asked by the teacher, which has the highest probability, as follows from the distribution law, is one.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
183. The probability of winning with one lottery ticket is $p=0.01$. How many tickets need to be bought to win at least one of them with a probability $P$, not less than 0.95?
|
Solution. The probability of winning is small, and the number of tickets that need to be purchased is obviously large, so the number of winning tickets is approximately Poisson distributed.
It is clear that the events "none of the purchased tickets are winning" and "at least one ticket is winning" are opposite. Therefore, the sum of the probabilities of these events is one:
$$
P_{n}(0)+P=1 \text {, or } P=1-P_{n}(0) \text {. }
$$
By setting $k=0$ in the Poisson formula $P_{n}(k)=\lambda^{k} \mathrm{e}^{-\lambda} / k!$, we get
$$
P_{n}(0)=\mathrm{e}^{-\lambda}
$$
Therefore, the relation (*) will take the form
$$
P=1-\mathrm{e}^{-\lambda}
$$
By the condition, $P \geqslant 0.95$, or $1-\mathrm{e}^{-\lambda} \geqslant 0.95$. From this,
$$
\mathrm{e}^{-\lambda} \leq 0.05
$$
Using the table of the function $e^{-x}$, we find $e^{-3}=0.05$. Considering that the function $\mathrm{e}^{-x}$ is decreasing, we conclude that the inequality (**) is satisfied for $\lambda \geqslant 3$, or for $n p \geqslant 3$. Therefore, $n \geqslant 3 / p=$ $=3 / 0.01=300$. Thus, one needs to buy at least 300 tickets to win at least one of them.
## § 2. Simplest Event Flow
An event flow is a sequence of events that occur at random moments in time.
A simplest (Poisson) event flow is one that has the following three properties: stationarity, "lack of aftereffect," and ordinarity.
The property of stationarity means that the probability of $k$ events occurring in any time interval depends only on the number $k$ and the duration $t$ of the time interval and does not depend on the start of its measurement. In other words, the probability of $k$ events occurring over a time interval of duration $t$ is a function that depends only on $k$ and $t$.
The property of "lack of aftereffect" means that the probability of $k$ events occurring in any time interval does not depend on whether events occurred or did not occur at moments of time preceding the start of the considered interval. In other words, the history of the flow does not affect the probabilities of events occurring in the near future.
The property of ordinarity means that the occurrence of two or more events over a small time interval is practically impossible. In other words, the probability of more than one event occurring over a small time interval is negligible compared to the probability of only one event occurring.
The intensity of the flow $\lambda$ is the average number of events that occur per unit of time.
If the constant intensity of the flow $\lambda$ is known, then the probability of $k$ events occurring in the simplest flow over time $t$ is determined by the Poisson formula
$$
P_{t}(k)=\frac{(\lambda t)^{k} \cdot \mathrm{e}^{-\lambda t}}{k!}
$$
Remark. A flow that has the property of stationarity is called stationary; otherwise, it is called non-stationary.
|
300
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
189. Find the mathematical expectation of the random variable $Z$, if the mathematical expectations of $X$ and $Y$ are known:
a) $Z=X+2 Y, M(X)=5, M(Y)=3 ;$ b) $Z=3 X+4 Y$, $M(X)=2, M(Y)=6$
|
Solution. a) Using the properties of mathematical expectation (the expectation of a sum is equal to the sum of the expectations of the terms; a constant factor can be factored out of the expectation), we get
$$
\begin{aligned}
M(Z)=M(X+2 Y)= & M(X)+M(2 Y)=M(X)+2 M(Y)= \\
& =5+2 \cdot 3=11 .
\end{aligned}
$$
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
208. Random variables $X$ and $Y$ are independent. Find the variance of the random variable $Z=3X+2Y$, given that $D(X)=5, D(Y)=6$.
|
Solution. Since the variables $X$ and $Y$ are independent, the variables $3X$ and $2Y$ are also independent. Using the properties of variance (the variance of the sum of independent random variables is equal to the sum of the variances of the addends; a constant factor can be factored out of the variance sign, squaring it), we get
$D(Z)=D(3X+2Y)=D(3X)+D(2Y)=9D(X)+4D(Y)=9 \cdot 5+4 \cdot 6=69$.
|
69
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
277. The random variable $X$ in the interval (-c, c) is given by the probability density function $f(x)=1 /\left(\pi \sqrt{c^{2}-x^{2}}\right)$; outside this interval, $f(x)=0$. Find the mathematical expectation of the variable $X$.
|
Solution. We use the formula $M(X)=\int_{a} x f(x) \mathrm{d} x$. Substituting $a=-c, b=c, f(x)=1 /\left(\pi \sqrt{c^{2}-x^{2}}\right)$, we get
$$
M(X)=\frac{1}{\pi} \int_{-c}^{c} \frac{x d x}{\sqrt{c^{2}-x^{2}}}
$$
Considering that the integrand is an odd function and the limits of integration are symmetric with respect to the origin, we conclude that the integral is zero. Therefore, $M(X)=0$.
This result can be obtained immediately if we take into account that the distribution curve is symmetric about the line $\boldsymbol{x}=\mathbf{0}$.
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
280. Find the mathematical expectation of the random variable $X$, given by the distribution function
$$
F(x)=\left\{\begin{array}{ccr}
0 & \text { for } & x \leqslant 0 \\
x / 4 & \text { for } & 0 < x \leqslant 4 \\
1 & \text { for } & x > 4
\end{array}\right.
$$
|
Solution. Find the density function of the random variable $\boldsymbol{X}$:
$$
f(x)=F^{\prime}(x)=\left\{\begin{array}{ccc}
0 & \text { for } & x4 .
\end{array}\right.
$$
Find the required expected value:
$$
M(X)=\int_{0}^{4} x f \cdot(x) \mathrm{d} x=\int_{0}^{4} x \cdot(1 / 4) \mathrm{d} x=2
$$
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
334. A machine manufactures balls. A ball is considered suitable if the deviation $X$ of the ball's diameter from the design size in absolute value is less than 0.7 mm. Assuming that the random variable $X$ is normally distributed with a standard deviation $\sigma=0.4$ mm, find how many suitable balls on average will be among a hundred manufactured.
|
Solution. Since $X$ is the deviation (of the diameter of the ball from the design size), then $M(X)=a=0$.
Let's use the formula $P(|X|<\delta)=2 \Phi(\delta / \sigma)$. Substituting $\delta=0.7, \sigma=0.4$, we get
$$
P(|X|<0.7)=2 \Phi\left(\frac{0.7}{0.4}\right)=2 \Phi(1.75)=2 \cdot 0.4599=0.92
$$
Thus, the probability of a deviation less than 0.7 mm is 0.92. From this, it follows that approximately 92 out of 100 balls will be suitable.
|
92
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
453. Find the sample mean for the given distribution of sample size $n=10$ :
| $x_{i}$ | 1250 | 1270 | 1280 |
| :--- | :---: | :---: | :---: |
| $n_{i}$ | 2 | 5 | 3 |
|
Solution. The initial variants are large numbers, so we will switch to conditional variants $u_{i}=x_{i}-1270$. As a result, we will get the distribution of conditional variants:
$$
\begin{array}{rrrr}
u_{i} & -20 & 0 & 10 \\
n_{i} & 2 & 5 & 3
\end{array}
$$
We will find the required sample mean:
$$
\bar{x}_{\mathrm{B}}=C+\frac{\sum n_{i} u_{i}}{n}=1270+\frac{2 \cdot(-20)+5 \cdot 0+3 \cdot 10}{10}=1270-1=1269
$$
|
1269
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
506. Find the minimum sample size for which with a reliability of 0.975, the accuracy of estimating the mean $a$ of the population using the sample mean is $\delta=0.3$, given that the standard deviation $\sigma=1.2$ of the normally distributed population is known.
|
Solution. We will use the formula that defines the accuracy of estimating the mathematical expectation of the general population by the sample mean: $\delta=t \sigma / \sqrt{n}$. From this,
$$
n=t^{2} \sigma^{2} / \delta^{2}
$$
According to the condition, $\gamma=0.975$; therefore, $\Phi(t)=0.975 / 2=0.4875$. From the table in Appendix 2, we find $t=2.24$. Substituting $t=2.24, \sigma=1.2$, and $\delta=0.3$ into (*), we obtain the required sample size $n=81$.
|
81
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
576. a) From a sample of size $n$, extracted from a normal general population with a known standard deviation $\sigma$, the sample mean $\bar{x}$ is found. At a significance level $\alpha$, it is required: 1) to find the critical region if the null hypothesis $H_{0}$: $a=a_{0}$ about the equality of the general mean $a$ to the hypothetical value $a_{0}$ is tested against the alternative hypothesis $H_{1}: a>a_{0}$; 2) to find the power function of the considered criterion, taking the hypothetical value of the general mean $a=a_{1}\left(a_{1}>a_{0}\right)$ as the argument; 3) to verify that increasing the sample size leads to an increase in the power of the criterion; 4) to verify that increasing the significance level leads to an increase in the power of the criterion.
$\mathrm{Solution.} \mathrm{1)} \mathrm{The} \mathrm{alternative} \mathrm{hypothesis} \mathrm{is} \mathrm{of} \mathrm{the} \mathrm{form} a>a_{0}$, so the critical region is right-sided. Using rule 2, we find the critical point $u_{\text {cr }}$ from the equality $\Phi\left(u_{\text {cr }}\right)=(1-2 \alpha) / 2$. Therefore, the right-sided critical region is defined by the inequality $U>u_{\text {cr }}$, or in more detail $\frac{\bar{x}-a_{0}}{\sigma \sqrt{n}}>u_{\text {cr }}$. Hence,
$$
\bar{x}>u_{\text {cr }}(\sigma / \sqrt{n})+a_{0} .
$$
At these values of the sample mean, the null hypothesis is rejected; in this sense, $\bar{x}=u_{\text {cr }}(\sigma / \sqrt{n})+a_{0}$ can be considered the critical value of the sample mean.
2) To calculate the power of the considered criterion, we first find its value under the condition that the alternative hypothesis is true (i.e., when $a=a_{1}$), setting $\bar{x}=u_{\text {cr }}(\sigma / \sqrt{n})+a_{0}:$
$$
U=\frac{\bar{x}-a_{1}}{\sigma / \sqrt{n}}=\frac{u_{\text {cr }}(\sigma / \sqrt{n})+a_{0}-a_{1}}{\sigma / \sqrt{n}}=u_{\text {cr }}-\frac{a_{1}-a_{0}}{\sigma / \sqrt{n}} .
$$
Thus,
$$
U=u_{\text {cr }}-\lambda, \text { where } \lambda=\left(a_{1}-a_{0}\right) \sqrt{n} / \sigma
$$
When $U>u_{\text {cr }}-\lambda$, the null hypothesis is rejected, so the power of the considered criterion at $a=a_{1}$ is
$$
\begin{aligned}
1-\beta & =P\left(U>u_{\text {cr }}-\lambda\right)=1-P\left(U<u_{\text {cr }}-\lambda\right)=1-\Phi\left(u_{\text {cr }}-\lambda\right) .
\end{aligned}
$$
3) To verify that increasing the sample size leads to an increase in the power of the criterion, we note that as $n$ increases, $\lambda$ increases, and thus $u_{\text {cr }}-\lambda$ decreases. Since $\Phi$ is an increasing function, $1-\Phi\left(u_{\text {cr }}-\lambda\right)$ increases, indicating an increase in the power of the criterion.
4) To verify that increasing the significance level leads to an increase in the power of the criterion, we note that as $\alpha$ increases, $u_{\text {cr }}$ decreases. Thus, $u_{\text {cr }}-\lambda$ decreases, and since $\Phi$ is an increasing function, $1-\Phi\left(u_{\text {cr }}-\lambda\right)$ increases, indicating an increase in the power of the criterion.
$\mathrm{2)} \mathrm{Given} \mathrm{the} \mathrm{values} \mathrm{of} \mathrm{the} \mathrm{parameters} \sigma=1, \alpha=0.05, a_{0}=3, n=16, \mathrm{and} \mathrm{the} \mathrm{alternative} \mathrm{hypothesis} \mathrm{is} \mathrm{of} \mathrm{the} \mathrm{form} a>a_{0}$. It is required: 1) to find the power of the right-sided criterion for testing the considered hypothesis for the hypothetical value of the general mean $a=a_{1}=3.2$; 2) to find the sample size $n_{1}$ for which the power of the criterion is 0.6.
|
Solution. 1) We use the formula
$$
1-\beta=0.5-\Phi\left(u_{\mathrm{kp}}-\lambda\right) .
$$
By rule 2, we find the critical point of the right-sided critical region $u_{\text {kp}}=1.65$.
We calculate $\lambda$, considering that, according to the condition, $a_{1}=3, a_{0}=2, n=16$, $\sigma=4:$
$$
\lambda=\left(a_{1}-a_{0}\right) \sqrt{ } \bar{n} / \sigma=(3-2) \sqrt{16} / 4=1 .
$$
Substituting $u_{\mathrm{kp}}=1.65$ and $\lambda=1$ into formula (*), we get
$$
1-\beta=0.5-\Phi(1.65-1)=0.5-\Phi(0.65)
$$
From the Laplace function table (see Appendix 2), we find $\Phi(0.65)=$ $=0.2422$. The required power $1-\beta=0.5-0.2422=0.2578$.
2) To find the "new" sample size $n_{1}$, for which the power of the criterion is 0.6, we find the "new" value of the parameter $\lambda$ (denote it as $\lambda_{1}$) from the relation $0.6=0.5-\Phi\left(1.65-\lambda_{1}\right)$. Hence,
$$
\Phi\left(\lambda_{1}-1.65\right)=0.1 \text {. }
$$
From the Laplace function table (see Appendix 2), we find $\lambda_{1}$ $-1.65=0.253$. Therefore, $\lambda_{1}=1.903$.
Considering that $\lambda_{1}=\left(a_{1}-a_{0}\right) \sqrt{n_{1}} / \sigma$, and, according to the condition, $a_{1}=3$, $a_{0}=2, \sigma=4$, we get $1.903=(3-2) \sqrt{n_{1}} / 4$. Hence, the required sample size $n_{1}=58$.
c) From a sample of size $n=9$, drawn from a normal general population with a known standard deviation $\sigma=4$, at a significance level of 0.05, the null hypothesis $H_{0}: a=a_{0}=15$ is tested for the equality of the general mean $a$ to the hypothetical value $a_{0}=15$ under the alternative hypothesis $a>15$. Required: 1) find the power of the right-sided criterion for the hypothetical value of the general mean $a=$ $=a_{1}=17 ; 2$ ) find the sample size $n_{1}$, for which the power of the criterion is 0.8 .
|
58
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
647. Why, when checking the hypothesis of exponential distribution of the population by the Pearson criterion, is the number of degrees of freedom determined by the equation $k=s-2$, where $s$ is the number of sample intervals?
|
Solution. When using the Pearson criterion, the number of degrees of freedom is $k=s-1-r$, where $r$ is the number of parameters estimated from the sample. The exponential distribution is defined by one parameter $\lambda$. Since this parameter is estimated from the sample, $r=1$, and therefore, the number of degrees of freedom is $k=s-1-1=s-2$.
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
657. Why, when testing the hypothesis of a uniform distribution of the population $X$ using the Pearson's criterion, is the number of degrees of freedom determined by the equation $k=s-3$, where $s$ is the number of intervals in the sample?
|
Solution. When using the Pearson criterion, the number of degrees of freedom $k=s-1-r$, where $r$ is the number of parameters estimated from the sample. The uniform distribution is defined by two parameters $a$ and $b$. Since these two parameters are estimated from the sample, $r=2$, and therefore, the number of degrees of freedom $k=s-1-2=s-3$.
|
-3
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
732. In a single-channel queuing system with rejections, a Poisson flow of requests arrives.
The time between the arrival of two consecutive requests is distributed according to the law \( f(\tau)=0.8 \mathrm{e}^{-0.8 \tau} \); the service time for requests is random and distributed according to the law \( f_{1}(t)=1.5 \mathrm{e}^{-1.5 t} \). Using the Monte Carlo method over a period of \( T=30 \) minutes, find: a) the average number of served requests; b) the average service time per request; c) the probability of service; d) the probability of rejection. Conduct six trials.
|
The solution is as follows. The time between the arrival of two consecutive requests is distributed according to the law $f(\tau)=0.8 \mathrm{e}^{-0.8 \tau}$, so the values $\tau_{i}$ will be generated using the formula
$$
\tau_{i}=-(1 / 0.8) \ln r_{i}=1.25\left(-\ln r_{i}\right)
$$
Random numbers $r_{i}$ are taken from the table in Appendix 9, starting from the first row from the bottom.
The service time for requests is distributed according to the law $f_{1}(t)=1.5 \mathrm{e}^{-1.5 t}$, so the values $t_{i}$ will be generated using the formula
$$
t_{i}=-(1 / 1.5) \ln R_{i}=0.67\left(-\ln R_{i}\right)
$$
Random numbers $R_{i}$ are taken from the same table, starting from the first row from the top.
Let $T_{1}=0$ be the moment of arrival of the first request. Using the random number $R_{1}=0.10$, we will generate the duration of the service time for the first request (in minutes):
$$
t_{1}=0.67(-\ln 0.10)=0.67 \cdot 2.30=1.54
$$
The moment of completion of service for the first request is $T_{1}=1.54=0+1.54=1.54$. We record one in the counter of served requests.
Using the random number $r_{2}=0.69$, we will generate the time (in minutes) between the arrival of the first and second requests:
$$
\tau_{2}=1.25(-\ln 0.69)=1.25 \cdot 0.37=0.46.
$$
The first request arrived at the moment $T_{1}=0$. Therefore, the second request will arrive at the moment $T_{2}=T_{1}+0.46=0+0.46=0.46$.
At this moment, the channel is busy serving the first request $(0.46 < 1.54)$, so it will serve the third request. We add one to the counter of served requests.
The further calculation is clear from tables 60 and 61. The test ends when the arrival moment of the request $T_{i} \geqslant 30$. For example, in the first test, as seen from table 60, the 23rd request arrived at the moment
*) The first random number is intentionally indexed 2 to avoid discrepancies with the notation in table 60.
$T_{23}=31.35>30$, so we exclude this request («Stop») and end the first test.
The other tests are conducted similarly.
Table 60
| Number of request $i$ | Random number $\boldsymbol{r}_{\boldsymbol{i}}$ | $-\ln \boldsymbol{r}_{i}$ | Time between two consecutive requests $\tau_{i}^{\Sigma}=1.25\left(-\ln r_{i}\right)$ | Moment of arrival of the request $T_{i}=T_{i-1}+\tau_{i}$ |
| :---: | :---: | :---: | :---: | :---: |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | 0.69 0.07 0.49 0.41 0.38 0.87 0.63 0.79 0.19 0.76 0.35 0.58 0.40 0.44 0.01 0.10 0.51 0.82 0.16 0.15 0.48 0.32 | 0.37 2.66 0.71 0.89 0.97 0.14 0.46 0.24 1.66 0.27 1.05 0.54 0.92 0.82 4.60 2.30 0.67 0.20 1.83 1.90 0.73 1.14 | 0.46 3.32 0.89 1.11 1.21 0.18 0.58 0.30 2.08 0.34 1.31 0.68 1.15 1.02 5.75 2.88 0.84 0.25 2.29 2.38 0.91 1.42 | 0 0.46 3.78 4.67 5.78 6.99 7.17 7.75 8.05 10.13 10.47 11.78 12.46 13.61 14.63 20.38 23.26 24.10 24.35 26.64 29.02 29.93 31.35 (Stop) |
The other tests are conducted similarly. Table 62 provides the results of six tests, including the first one.
Using table 62, we will find the required values: a) the average number of requests served in 30 minutes $\bar{N}_{\text {served}}=93 / 6=15.5$,
b) the average service time for one request $\bar{t}_{\text {served}}=4.49 / 6=0.748$,
c) the probability of service $P_{\text {served}}=3.974 / 6=0.662$,
d) the probability of rejection $P_{\text {rejection}}=1-P_{\text {served}}=1-0.662=0.338$.
Thus, approximately $66\%$ of the requests will be served, and $34\%$ will be rejected.
|
66
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
910. A stationary random function $X(t)$ with mean $m_{x}=5$ is input to a linear stationary dynamic system described by the equation $Y^{\prime}(t)+2 Y(t)=5 X^{\prime}(t)+$ $+6 X(t)$. Find the mean of the random function $Y(t)$ at the output of the system in the steady state (after the transient process has decayed).
|
Solution. Let's equate the mathematical expectations of the left and right parts of the given differential equation:
$$
\begin{aligned}
M\left[Y^{\prime}(t)+2 Y(t)\right]= & M\left[5 X^{\prime}(t)+6 X(t)\right], \text{ or } M\left[Y^{\prime}(t)\right]+2 m_{y}= \\
& =5 M\left[X^{\prime}(t)\right]+6 m_{x} .
\end{aligned}
$$
By the condition, $X(t)$ and $Y(t)$ are stationary functions, and the mathematical expectation of the derivative of a stationary function is zero, so
$2 m_{y}=6 m_{x}$. Therefore, the required mathematical expectation $m_{y}=3 m_{x}=$ $=3 \cdot 5=15$.
|
15
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 1. Find $\lim _{x \rightarrow 2}\left(4 x^{2}-6 x+3\right)$.
|
Solution. Since the limit of the algebraic sum of variables is equal to the same algebraic sum of the limits of these variables (formula (1.42)), a constant multiplier can be factored out of the limit sign (formula (1.44)), the limit of an integer positive power is equal to the same power of the limit (formula (1.45)), and the limit of a constant is the constant itself (formula (1.48)), we sequentially obtain
$$
\begin{gathered}
\lim _{x \rightarrow 2}\left(4 x^{2}-6 x+3\right)=\lim _{x \rightarrow 2} 4 x^{2}-\lim _{x \rightarrow 2} 6 x+\lim _{x \rightarrow 2} 3= \\
=4 \lim _{x \rightarrow 2} x^{2}-6 \lim _{x \rightarrow 2} x+\lim _{x \rightarrow 2} 3=4\left(\lim _{x \rightarrow 2} x\right)^{2}-6 \lim _{x \rightarrow 2} x+3= \\
=4 \cdot 2^{2}-6 \cdot 2+3=16-12+3=7 .
\end{gathered}
$$
Remark 1. The calculation of the limit of a second-degree polynomial has been reduced to calculating its value at the limit of the argument.
Remark 2. To calculate the limit of an n-th degree polynomial
$$
P_{n}(x)=b_{0}+b_{1} x+b_{2} x^{2}+\ldots+b_{n} x^{n} \text { as } x \rightarrow b
$$
it is sufficient to find \( P_{n}(b) \), i.e., its value at \( x=b \). For example,
$$
\lim _{x \rightarrow 1}\left(2 x^{5}-4 x^{4}+3 x^{3}-6 x^{2}+8 x+2\right)=2 \cdot 1^{5}-4 \cdot 1^{4}+3 \cdot 1^{3}-6 \cdot 1^{2}+8 \cdot 1+2=5
$$
Example 2. Find \(\lim _{x \rightarrow 1} \frac{3 x^{2}-4 x+7}{2 x^{2}-5 x+6}\).
Solution. Since the limit of a quotient is equal to the quotient of the limits, based on formula (1.46), and using formulas (1.42), (1.44), (1.45), and (1.48), we sequentially obtain
$$
\lim _{x \rightarrow 1} \frac{3 x^{2}-4 x+7}{2 x^{2}-5 x+6}=\frac{\lim _{x \rightarrow 1}\left(3 x^{2}-4 x+7\right)}{\lim _{x \rightarrow 1}\left(2 x^{2}-5 x+6\right)}=\frac{\lim _{x \rightarrow 1} 3 x^{2}-\lim _{x \rightarrow 1} 4 x+\lim _{x \rightarrow 1} 7}{\lim _{x \rightarrow 1} 2 x^{2}-\lim _{x \rightarrow 1} 5 x+\lim _{x \rightarrow 1} 6}=
$$
$$
=\frac{3 \lim _{x \rightarrow 1} x^{2}-4 \lim _{x \rightarrow 1} x+\lim _{x \rightarrow 1} 7}{2 \lim _{x \rightarrow 1} x^{2}-5 \lim _{x \rightarrow 1} x+\lim _{x \rightarrow 1} 6}=\frac{3 \cdot 1^{2}-4 \cdot 1+7}{2 \cdot 1^{2}-5 \cdot 1+6}=\frac{6}{3}=2
$$
Remark 1. The calculation of the limit of a rational function (the ratio of two polynomials) has been reduced to calculating the value of this function at the limit of the argument.
Remark 2. To calculate the limit of a rational function
$$
R(x)=\frac{b_{0}+b_{1} x+b_{2} x^{2}+\ldots+b_{n} x^{n}}{c_{0}+c_{1} x+c_{2} x^{2}+\ldots+c_{m} x^{m}}
$$
as \( x \rightarrow a \), it is sufficient to find its value at \( x=a \).
For example,
$$
\lim _{x \rightarrow 2} \frac{x^{5}-2 x^{4}+3 x^{2}-6 x+9}{3 x^{4}-12 x^{2}+7 x-11}=\frac{2^{5}-2 \cdot 2^{4}+3 \cdot 2^{2}-6 \cdot 2+9}{3 \cdot 2^{4}-12 \cdot 2^{2}+7 \cdot 2-11}=\frac{9}{3}=3
$$
Remark 3. The limit of an elementary function \( f(x) \) as \( x \rightarrow a \), where \( a \) belongs to its domain, is equal to the value of the function at \( x=a \), i.e.,
$$
\lim _{x \rightarrow a} f(x)=f(a)
$$
For example,
$$
\text { 1) } \begin{gathered}
\lim _{x \rightarrow 4} \frac{\sqrt{x^{2}-7}+\sqrt[3]{x+60}}{2 x^{2}-5 x-8}=\frac{\sqrt{4^{2}-7}+\sqrt[3]{4+60}}{2 \cdot 4^{2}-5 \cdot 4-8}= \\
=\frac{\sqrt{9}+\sqrt[3]{64}}{32-20-8}=\frac{3+4}{4}=\frac{7}{4}
\end{gathered}
$$
2). \(\lim \left[\lg \left(t+\sqrt{t^{2}+80}\right)\right]+t \sqrt{t^{2}+8}=\lg (1+\sqrt{81})+1 \sqrt{1+8}=1+3=4\). \(t \rightarrow 1\)
|
7
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 3. Find $\lim _{x \rightarrow 4} \frac{x^{2}-6 x+8}{x-4}$.
|
Solution. When $x=4$, both the numerator and the denominator of the given function become zero. This results in an indeterminate form $\frac{0}{0}$, which needs to be resolved. We will transform the given function by factoring the numerator using the formula
$$
x^{2}+p x+q=\left(x-x_{1}\right)\left(x-x_{2}\right)
$$
where $x_{1}$ and $x_{2}$ are the roots of the equation $x^{2}+p x+q=0$.
Since the equation $x^{2}-6 x+8=0$ has roots $x_{1}=2, x_{2}=4$, we have $x^{2}-6 x+8=(x-2)(x-4)$. Substituting this expression into the given function and canceling the common factor $(x-4) \neq 0$, we get
$$
\lim _{x \rightarrow 4} \frac{x^{2}-6 x+8}{x-4}=\lim _{x \rightarrow 4} \frac{(x-2)(x-4)}{x-4}=\lim _{x \rightarrow 4}(x-2)=4-2=2
$$
Remark 1. When canceling the common factor, we assumed that $x-4 \neq 0$. This is indeed the case. According to the definition of the limit of a function, the argument $x$ approaches its limiting value $a$ without ever coinciding with it, i.e., $x \neq a$ and $x-a \neq 0$. (See formula (1.26).)
Remark 2. The limit of a function does not depend on whether the function is defined at the limiting point or not.
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 6. Find $\lim _{x \rightarrow+\infty} \frac{6 x^{2}+5 x+4}{3 x^{2}+7 x-2}$.
|
Solution. As $x \rightarrow+\infty$, the numerator and denominator increase without bound (we get an indeterminate form of $\frac{\infty}{\infty}$). To find the limit, we transform the given fraction by dividing its numerator and denominator by $x^{2}$, i.e., by the highest power of $x$. Using the properties of limits, we get
$$
\begin{gathered}
\lim _{x \rightarrow+\infty} \frac{6 x^{2}+5 x+4}{3 x^{2}+7 x-2}=\lim _{x \rightarrow+\infty} \frac{6+\frac{5}{x}+\frac{4}{x^{2}}}{3+\frac{7}{x}-\frac{2}{x^{2}}}=\frac{\lim _{x \rightarrow+\infty}\left(6+\frac{5}{x}+\frac{4}{x^{2}}\right)}{\lim _{x \rightarrow+\infty}\left(3+\frac{7}{x}-\frac{2}{x^{2}}\right)}= \\
=\frac{6+0+0}{3+0-0}=2
\end{gathered}
$$
Here it is taken into account that
$$
\lim _{x \rightarrow+\infty} \frac{c}{x}=0, \lim _{x \rightarrow+\infty} \frac{c}{x^{2}}=0(c=\text { const })
$$
(See formula (1.54)).
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 7. Find $\lim _{x \rightarrow+\infty} \frac{7 x^{2}+6 x-3}{9 x^{3}+8 x^{2}-2}$.
|
Solution. By dividing the numerator and the denominator of the fraction by $x^{3}$, i.e., by the highest degree, we get
$$
\begin{aligned}
\lim _{x \rightarrow+\infty} \frac{7 x^{2}+6 x-3}{9 x^{3}+8 x^{2}-2}= & \lim _{x \rightarrow+\infty} \frac{\frac{7}{x}+\frac{6}{x^{2}}-\frac{3}{x^{3}}}{9+\frac{8}{x}-\frac{2}{x^{3}}}=\frac{\lim _{x \rightarrow+\infty}\left(\frac{7}{x}+\frac{6}{x^{2}}-\frac{3}{x^{3}}\right)}{\lim _{x \rightarrow+\infty}\left(9+\frac{8}{x}-\frac{2}{x^{3}}\right)}= \\
& =\frac{0+0-0}{9+0-0}=\frac{0}{9}=0
\end{aligned}
$$
Remark. To resolve the indeterminacy of the form $\frac{\infty}{\infty}$, given by the ratio of two polynomials, one must divide the numerator and the denominator by the highest power of $x$ present in them, and then take the limit.
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 9. Find $\lim _{x \rightarrow 3} \frac{x^{2}-9}{\sqrt{x+1}-2}$.
|
Solution. When $x=3$, both the numerator and the denominator of the fraction become zero. The denominator contains an irrational expression $\sqrt{x+1}$. To eliminate the irrationality in the denominator, we multiply the numerator and the denominator by $(\sqrt{x+1}+2)$. We get
$$
\begin{gathered}
\lim _{x \rightarrow 3} \frac{x^{2}-9}{\sqrt{x+1}-2}=\lim _{x \rightarrow 3} \frac{(x-3)(x+3)(\sqrt{x+1}+2)}{(\sqrt{x+1}-2)(\sqrt{x+1}+2)}= \\
=\lim _{x \rightarrow 3} \frac{(x-3)(x+3)(\sqrt{x+1}+2)}{(\sqrt{x+1})^{2}-2^{2}}=\lim _{x \rightarrow 3} \frac{(x-3)(x+3)(\sqrt{x+1}+2)}{(x+1)-4}= \\
=\lim _{x \rightarrow 3}(x+3)(\sqrt{x+1}+2)=(3+3)(\sqrt{3+1}+2)=24 .
\end{gathered}
$$
Remark. To resolve an indeterminate form of the type $\frac{0}{0}$, where the numerator or the denominator contains an irrationality, one should appropriately eliminate the irrationality.
|
24
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 11. Find $\lim _{n \rightarrow \infty} \frac{1+3+5+\ldots+(2 n-1)}{1+2+3+\ldots+n}$.
|
Solution. The numerator and denominator of the fraction are the sums of $n$ terms of the corresponding arithmetic progressions. Finding these sums using the known formula, we get
\[
\begin{gathered}
\lim _{n \rightarrow \infty} \frac{1+3+5+\ldots+(2 n-1)}{1+2+3+\ldots+n}=\lim _{n \rightarrow \infty} \frac{\frac{1+(2 n-1)}{2} \cdot n}{\frac{1+n}{2} \cdot n}= \\
=\lim _{n \rightarrow \infty} \frac{1+(2 n-1)}{1+n}=\lim _{n \rightarrow \infty} \frac{2 n}{n+1}=2 \lim _{n \rightarrow \infty} \frac{n}{n+1}=2 \lim _{n \rightarrow \infty} \frac{1}{1+\frac{1}{n}}=2 .
\end{gathered}
\]
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 14. Find $\lim _{n \rightarrow \infty} \frac{12 n+5}{\sqrt[3]{27 n^{3}+6 n^{2}+8}}$.
|
Solution. As $n \rightarrow \infty$, the numerator and denominator also tend to infinity, resulting in an indeterminate form $\frac{\infty}{\infty}$. To find the limit, we divide the numerator and denominator by $\boldsymbol{n}$ and bring $\boldsymbol{n}$ under the root sign:
$$
\lim _{n \rightarrow \infty} \frac{12 n+5}{\sqrt[3]{27 n^{3}+6 n^{2}+8}}=\lim _{n \rightarrow \infty} \frac{12+\frac{5}{n}}{\sqrt[3]{27+\frac{6}{n}+\frac{8}{n^{3}}}}=\frac{12}{\sqrt[3]{27}}=\frac{12}{3}=4
$$
(Here it is taken into account that $\lim _{n \rightarrow \infty} \frac{5}{n}=0, \lim _{n \rightarrow \infty} \frac{6}{n}=0, \lim _{n \rightarrow \infty} \frac{8}{n^{3}}=0$.)
## Problems
Find the limits:
1. $\lim _{x \rightarrow 3}\left(2 x^{2}-7 x+6\right)$.
2. $\lim _{x \rightarrow 1}\left(3 x^{4}-5 x^{3}+6 x^{2}-4 x+7\right)$.
3. $\lim _{x \rightarrow 2} \frac{4 x^{2}-5 x+2}{3 x^{2}-6 x+4}$.
4. $\lim _{x \rightarrow 4} \frac{x^{2}-5 x+4}{x^{2}-7 x+6}$.
5. $\lim _{x \rightarrow 5} \frac{x^{2}-7 x+12}{x^{2}-6 x+5}$.
6. $\lim _{t \rightarrow 3}\left[2 t \sqrt{t^{2}-8}+\lg \left(3 t+\sqrt{t^{2}-8}\right)-\frac{\sqrt[3]{t^{2}-1}+\sqrt[4]{t^{3}-2 t^{2}+7}}{t^{3}-2 t^{2}+t-11}\right]$.
7. $\lim _{x \rightarrow 6} \frac{x^{2}-8 x+12}{x^{2}-7 x+6}$.
8. $\lim _{x \rightarrow 2} \frac{3 x^{2}-7 x+2}{4 x^{2}-5 x-6}$.
9. $\lim _{x \rightarrow 1} \frac{x^{3}-3 x+2}{x^{4}-4 x+3}$.
10. $\lim _{x \rightarrow \infty} \frac{10 x^{3}-6 x^{2}+7 x+5}{8-4 x+3 x^{2}-2 x^{3}}$.
11. $\lim _{x \rightarrow \infty} \frac{2 x^{4}-5 x^{3}+7 x^{2}+8 x-9}{3 x^{5}-6 x^{3}+4 x^{2}-2 x+11}$.
12. $\lim _{x \rightarrow \infty} \frac{x^{7}+8 x^{6}+5 x^{4}-3 x^{2}-12}{10 x^{6}+7 x^{5}-6 x^{3}-4 x+17}$.
13. $\lim _{x \rightarrow 5} \frac{x^{2}-25}{2-\sqrt{x-1}}$.
14. $\lim _{n \rightarrow \infty} \frac{\sqrt{4 n^{2}-3}}{2 n+1}$.
15. $\lim _{x \rightarrow \infty} \frac{6 x-5}{1+\sqrt{x^{2}+3}}$.
16. $\lim _{n \rightarrow \infty} \frac{1+2+3+\ldots+n}{n^{2}-1}$.
17. $\lim _{x \rightarrow \frac{\pi}{4}} \frac{\sin 2 x-\cos 2 x-1}{\cos x-\sin x}$.
18. $\lim _{x \rightarrow \pi} \frac{\sqrt{1-\operatorname{tg} x}-\sqrt{1+\operatorname{tg} x}}{\sin 2 x}$.
19. $\lim _{x \rightarrow \infty}\left(\frac{2 x^{2}}{1-x^{2}}+3^{\frac{1}{x}}\right)$.
## Answers
1.3. 2. 7. 3. 2. 4.0. 5. $\infty$. 6.4. 7. $\frac{4}{5}$. 8. $\frac{15}{44}$. 9. $\frac{1}{2}$ 10. -5 . 11. 0 . 12. $\infty$.
13. -40 . 14. $\frac{3}{4}$. Hint. Let $x=t^{12}$. 15. 1. 16.6. 17. $\frac{1}{2}$.
14. $-\sqrt{2} \cdot 19 \cdot-\frac{1}{2} \cdot 20 \cdot-1$.
§ 1.5. The number e, $\lim _{\alpha \rightarrow 0} \frac{\sin \alpha}{\alpha}=1$
1. The number e is the limit
$$
\lim _{x \rightarrow \infty}\left(1+\frac{1}{x}\right)^{x}=e
$$
or
$$
\lim _{\alpha \rightarrow 0}(1+\alpha)^{\frac{1}{\alpha}}=e
$$
The number $e$ is useful for resolving indeterminate forms of the type $1^{\infty}$.
If the base of logarithms is the number $e$, then the logarithms are called natural:
$$
\ln x=\log _{e} x
$$
2. If the angle $\alpha$ is expressed in radians, then
$$
\lim _{\alpha \rightarrow 0} \frac{\sin \alpha}{\alpha}=1
$$
3. When finding limits of the form
$$
\lim _{x \rightarrow a}[\varphi(x)]^{\psi(x)}=C
$$
the following should be kept in mind:
1) if there exist finite limits
$$
\lim _{x \rightarrow a} \varphi(x)=A \text { and } \lim _{x \rightarrow a} \psi(x)=B
$$
then
$$
C=A^{B}
$$
2) if
$$
\lim _{x \rightarrow a} \varphi(x)=A \neq 1 \text { and } \lim _{x \rightarrow a} \psi(x)=\infty \text {, }
$$
then the limit is found using formulas (1.55) and (1.56);
3) if
$$
\lim _{x \rightarrow a} \varphi(x)=1, \lim _{x \rightarrow a} \psi(x)=\infty
$$
then we set $\varphi(x)=1+\alpha(x)$, where $\alpha(x) \rightarrow 0$ as $x \rightarrow a$ and, consequently,
$$
\begin{gathered}
C=\lim _{x \rightarrow a}\left\{[1+\alpha(x)]^{\frac{1}{\alpha(x)}}\right\}^{\alpha(x) \psi(x)}=e^{\lim _{x \rightarrow \alpha} \alpha(x) \psi(x)}= \\
=e^{\lim _{x \rightarrow a}[\varphi(x)-1] \psi(x)}
\end{gathered}
$$
|
4
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2. Find $\lim _{x \rightarrow 0} \frac{\ln (1+x)}{x}$.
|
Solution. Since
$$
\frac{\ln (1+x)}{x}=\frac{1}{x} \ln (1+x)=\ln (1+x)^{\frac{1}{x}}
$$
then based on formula (1.58) we find
$$
\lim _{x \rightarrow 0} \frac{\ln (1+x)}{x}=\lim _{x \rightarrow 0}\left[\ln (1+x)^{\frac{1}{x}}\right]=\ln \left[\lim _{x \rightarrow 0}(1+x)^{\frac{1}{x}}\right]=\ln e=1
$$
Therefore,
$$
\lim _{x \rightarrow 0} \frac{\ln (1+x)}{x}=1
$$
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 6. Find $\lim _{x \rightarrow 0} \frac{\tan x}{x}$.
|
Solution. Taking into account that $\operatorname{tg} x=\frac{\sin x}{\cos x}$ and $\lim _{x \rightarrow 0} \cos x=\cos 0=1$, based on the properties of limits (1.43) and (1.46) and formula (1.59), we obtain
$$
\begin{aligned}
\lim _{x \rightarrow 0} \frac{\operatorname{tg} x}{x} & =\lim _{x \rightarrow 0}\left(\frac{\sin x}{\cos x} \cdot \frac{1}{x}\right)=\lim _{x \rightarrow 0}\left(\frac{1}{\cos x} \cdot \frac{\sin x}{x}\right)= \\
& =\lim _{x \rightarrow 0} \frac{1}{\cos x} \cdot \lim _{x \rightarrow 0} \frac{\sin x}{x}=1 \cdot 1=1
\end{aligned}
$$
Thus,
$$
\lim _{x \rightarrow 0} \frac{\operatorname{tg} x}{x}=1
$$
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 9. Find $\lim _{x \rightarrow 0} \frac{\sin x}{\sqrt{x+9}-3}$.
|
Solution. When $x=0$, both the numerator and the denominator become zero. The denominator contains an irrationality. We will eliminate the irrationality and use formula (1.59)
$$
\begin{gathered}
\lim _{x \rightarrow 0} \frac{\sin x}{\sqrt{x+9}-3}=\lim _{x \rightarrow 0} \frac{\sin x(\sqrt{x+9}+3)}{(\sqrt{x+9}-3)(\sqrt{x+9}+3)}= \\
=\lim _{x \rightarrow 0} \frac{\sin x(\sqrt{x+9}+3)}{(x+9)-9}=\lim _{x \rightarrow 0} \frac{\sin x}{x} \cdot \lim _{x \rightarrow 0}(\sqrt{x+9}+3)=1(3+3)=6
\end{gathered}
$$
|
6
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 10. Find $\lim _{x \rightarrow 0}\left(\frac{\sin 3 x}{x}\right)^{x+2}$.
|
Solution. This is a limit of the form (1.60), where $\varphi(x)=\frac{\sin 3 x}{x}, \psi(x)=x+2$.
From (1.67)
$$
\lim _{x \rightarrow 0} \frac{\sin 3 x}{x}=3, \lim _{x \rightarrow 0}(x+2)=2
$$
According to formula (1.62), we get
$$
\lim _{x \rightarrow 0}\left(\frac{\sin 3 x}{x}\right)^{x+2}=3^{2}=9
$$
|
9
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 11. Find $\lim _{x \rightarrow \infty}\left(\frac{2 x-1}{3 x+4}\right)^{x^{2}}$.
|
Solution. This is also a limit of the form $(1.60)$, where $\varphi(x)=\frac{2 x-1}{3 x+4}, \psi(x)=x^{2}$
Since
$$
\lim _{x \rightarrow \infty} \frac{2 x-1}{3 x+4}=\lim _{x \rightarrow \infty} \frac{2-\frac{1}{x}}{3+\frac{4}{x}}=\frac{2}{3}, \lim _{x \rightarrow \infty} x^{2}=\infty
$$
then according to formula (1.55)
$$
\lim _{x \rightarrow \infty}\left(\frac{2 x-1}{3 x+4}\right)^{x^{2}}=0
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 13. Find $\lim _{x \rightarrow 0}(\cos x)^{\frac{1}{x}}$.
|
Solution. By adding and subtracting 1 from $\cos x$ and applying the corresponding formula, we get
$$
\begin{aligned}
& \lim _{x \rightarrow 0}(\cos x)^{\frac{1}{x}}=\lim _{x \rightarrow 0}[1-(1-\cos x)]^{\frac{1}{x}}=\lim _{x \rightarrow 0}\left(1-2 \sin ^{2} \frac{x}{2}\right)^{\frac{1}{x}}= \\
& =\lim _{x \rightarrow 0}\left[\left(1-2 \sin ^{2} \frac{x}{2}\right)^{-\frac{1}{2 \sin ^{2} \frac{x}{2}}}\right]^{-\frac{2 \sin ^{2} \frac{x}{2}}{x}}=e^{\lim _{x \rightarrow 0}\left(-\frac{2 \sin ^{2} \frac{x}{2}}{x}\right)}
\end{aligned}
$$
Since
$$
\begin{aligned}
& \lim _{x \rightarrow 0}\left(-\frac{2 \sin ^{2} \frac{x}{2}}{x}\right)=-\lim _{x \rightarrow 0} \frac{\sin ^{2} \frac{x}{2}}{\frac{x}{2}}= \\
= & -\lim _{x \rightarrow 0} \frac{\sin \frac{x}{2}}{\frac{x}{2}} \cdot \lim _{x \rightarrow 0} \sin \frac{x}{2}=-1 \cdot 0=0
\end{aligned}
$$
$$
\lim _{x \rightarrow 0}(\cos x)^{\frac{1}{x}}=e^{0}=1
$$
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 1. Find $\lim _{x \rightarrow+\infty}\left(\sqrt{x^{2}+6 x+5}-x\right)$.
|
Solution. When $x \rightarrow+\infty$, the given function represents the difference of two infinitely large quantities taking positive values (case $\infty-\infty$). By multiplying and dividing the given function by $\left(\sqrt{x^{2}+6 x+5}+x\right)$, we get
$$
\begin{gathered}
\lim _{x \rightarrow+\infty}\left(\sqrt{x^{2}+6 x+5}-x\right)=\lim _{x \rightarrow+\infty} \frac{\left(\sqrt{x^{2}+6 x+5}-x\right)\left(\sqrt{x^{2}+6 x+5}+x\right)}{\sqrt{x^{2}+6 x+5}+x}= \\
=\lim _{x \rightarrow+\infty} \frac{\left(x^{2}+6 x+5\right)-x^{2}}{\sqrt{x^{2}+6 x+5+x}}=\lim _{x \rightarrow+\infty} \frac{6 x+5}{\sqrt{x^{2}+6 x+5+x}}=
\end{gathered}
$$
$$
=\lim _{x \rightarrow+\infty} \frac{6+\frac{5}{x}}{\sqrt{1+\frac{6}{x}+\frac{5}{x^{2}}}+1}=\frac{6}{1+1}=3
$$
|
3
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 4. Find $\lim _{x \rightarrow 0} x \operatorname{ctg} \frac{x}{3}$.
|
Solution. When $x \rightarrow 0$, we get an indeterminate form of $0 \cdot \infty$. Rewriting the given function in another form and applying formula (1.59), we find
$$
\lim _{x \rightarrow 0} x \operatorname{ctg} \frac{x}{3}=\lim _{x \rightarrow 0} x \frac{\cos \frac{x}{3}}{\sin \frac{x}{3}}=\lim _{x \rightarrow 0} \frac{x}{\sin \frac{x}{3}} \cos \frac{x}{3}=
$$
$$
=\lim _{x \rightarrow 0} \frac{\frac{1}{3} x}{\frac{1}{3} \sin \frac{x}{3}} \cdot \cos \lim _{x \rightarrow 0} \frac{x}{3}=\frac{1}{\frac{1}{3}} \cdot 1=3
$$
|
3
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 6. Find $\lim _{x \rightarrow+\infty} x\left(\operatorname{arctg} x-\frac{\pi}{2}\right)$.
|
Solution. Let $\operatorname{arctg} x=\alpha$, then $x=\operatorname{tg} \alpha$, if $x \rightarrow+\infty$, then $\alpha \rightarrow \frac{\pi}{2}$.
Consequently,
$$
\begin{gathered}
\lim _{x \rightarrow+\infty} x\left(\operatorname{arctg} x-\frac{\pi}{2}\right)=\lim _{\alpha \rightarrow \frac{\pi}{2}} \operatorname{tg} \alpha\left(\alpha-\frac{\pi}{2}\right)= \\
=-\lim _{\alpha \rightarrow \frac{\pi}{2}} \frac{\sin \alpha}{\cos \alpha}\left(\frac{\pi}{2}-\alpha\right)=-\lim _{\alpha \rightarrow \frac{\pi}{2}} \sin \alpha \frac{\frac{\pi}{2}-\alpha}{\sin \left(\frac{\pi}{2}-\alpha\right)}= \\
=-\lim _{\alpha \rightarrow \frac{\pi}{2}} \sin \alpha \cdot \lim _{\alpha \rightarrow \frac{\pi}{2}} \frac{\frac{\pi}{2}-\alpha}{\sin \left(\frac{\pi}{2}-\alpha\right)}=-1 \cdot 1=-1
\end{gathered}
$$
## Problems
Find the limits:
1. $\lim _{x \rightarrow+\infty}\left(\sqrt{x^{2}+5 x+4}-\sqrt{x^{2}+x}\right)$.
2. $\lim _{x \rightarrow-4}\left(\frac{1}{x+4}-\frac{8}{16-x^{2}}\right)$.
3. $\lim _{x \rightarrow 0}\left(\frac{\cos x}{\sin ^{2} x}-\operatorname{ctg}^{2} x\right)$.
4. $\lim _{x \rightarrow 0}(\operatorname{ctg} x-\operatorname{cosec} x)$.
5. $\lim _{x \rightarrow 0} x \operatorname{ctg} \frac{\pi}{2} x$.
6. $\lim _{x \rightarrow \frac{\pi}{2}}\left(x-\frac{\pi}{2}\right) \operatorname{tg} x$.
7. $\lim _{x \rightarrow 0} \frac{e^{-x}-1}{3 x}$.
8. $\lim _{m \rightarrow \infty} m[\ln (m+4)-\ln m]$.
9. $\lim _{x \rightarrow 0} \frac{\sqrt{x+9}-3}{\sin 6 x}$.
10. $\lim _{n \rightarrow \infty} \frac{5-2^{n}}{5+2^{n+1}}$.
11. $\lim _{x \rightarrow 0}(\cos 2 x)^{\operatorname{ctg}^{2} 2 x}$.
12. $\lim _{x \rightarrow 0} \frac{1+x^{2}-\cos x}{\sin ^{2} x}$.
## Answers
1.2.2. $-\frac{1}{8}$. 3. $\frac{1}{2}$. 4. 0. 5. $\frac{2}{\pi}$. 6. -1 . Hint. Let $x=\frac{\pi}{2}+\alpha$. 7. $-\frac{1}{3}$. 8.4.9. $\frac{1}{36} \cdot 10 .-\frac{1}{2} \cdot 11 \cdot \frac{1}{\sqrt{e}} \cdot$ 12. $\frac{3}{2}$.
## § 1.7. Comparison of Infinitesimals
1. Two infinitesimals $\alpha$ and $\beta$ are called infinitesimals of the same order if the limit of their ratio is not zero, i.e.
$$
\lim \frac{\alpha}{\beta}=a(a \neq 0)
$$
2. The quantity $\alpha$ is called an infinitesimal of higher order compared to $\beta$ if the limit of the ratio of $\alpha$ to $\beta$ is zero, i.e.
$$
\lim \frac{\alpha}{\beta}=0
$$
3. The quantity $\alpha$ is called an infinitesimal of lower order compared to $\beta$ if the ratio of $\alpha$ to $\beta$ is an infinitely large quantity, i.e.
$$
\lim \frac{\alpha}{\beta}=\infty
$$
4. Infinitesimals $\alpha$ and $\beta$ are called equivalent if the limit of their ratio is one, i.e.
$$
\lim \frac{\alpha}{\beta}=1
$$
Notation for equivalent infinitesimals $\alpha$ and $\beta$:
$$
\alpha \sim \beta
$$
Equivalent infinitesimals have the following properties:
1) the difference of two equivalent infinitesimals is an infinitesimal of higher order compared to each of them;
2) when finding the limit of the ratio of two infinitesimals, each of them (or only one) can be replaced by another infinitesimal equivalent to it, i.e., if $\alpha \sim \alpha_{1}$ and $\beta \sim \beta_{1}$, then
$$
\lim \frac{\alpha}{\beta}=\lim \frac{\alpha_{1}}{\beta}=\lim \frac{\alpha}{\beta_{1}}=\lim \frac{\alpha_{1}}{\beta_{1}}
$$
Remark 1. The product of two infinitesimals is an infinitesimal of higher order compared to each of them.
Remark 2. To compare infinitesimals, find the limit of their ratio. If this ratio does not have a limit, then the quantities are incomparable.
|
-1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 6. Find $\lim _{x \rightarrow 3} \frac{\ln \left(x^{2}-5 x+7\right)}{x-3}$.
|
Solution. When $x \rightarrow 3$, we get an indeterminate form of $\frac{0}{0}$, since $x^{2}-5 x+7 \rightarrow 1$ and $\ln \left(x^{2}-5 x+7\right) \rightarrow 0$. The expression $x^{2}-5 x+7$ can be represented as:
$$
x^{2}-5 x+7=1+\left(x^{2}-5 x+6\right)=1+z
$$
where $\left(x^{2}-5 x+6\right)=z \rightarrow 0$ as $x \rightarrow 3$.
Since $\ln (1+z) \sim z$ as $z \rightarrow 0$ (see example 2), then
$$
\ln \left(x^{2}-5 x+7\right) \sim x^{2}-5 x+6
$$
Applying formula (1.74), we get
$$
\lim _{x \rightarrow 3} \frac{\ln \left(x^{2}-5 x+7\right)}{x-3}=\lim _{x \rightarrow 3} \frac{x^{2}-5 x+6}{x-3}=\lim _{x \rightarrow 3} \frac{(x-2)(x-3)}{x-3}=
$$
$$
=\lim _{x \rightarrow 3}(x-2)=1
$$
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 3. Calculate the value of the derivative of the implicit function $x y^{2}=4$ at the point $M(1,2)$.
|
Solution. First, let's find the derivative:
$$
x^{\prime} y^{2}+x 2 y y^{\prime}=0, y^{\prime}=-\frac{y}{2 x}
$$
Substituting the values \(x=1\), \(y=2\) into the right-hand side of the last equation, we get
$$
y^{\prime}=-\frac{2}{2 \cdot 1}=-1
$$
|
-1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2. Find the third-order derivative of the function $y=x^{2}+3 x+2$.
|
Solution. Differentiating successively, we obtain:
$$
\begin{gathered}
y^{\prime}=\left(x^{2}+3 x+2\right)^{\prime}=2 x+3 ; y^{\prime \prime}=(2 x+3)^{\prime}=2 \\
y^{\prime \prime \prime}=(2)^{\prime}=0
\end{gathered}
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 4. Find the derivative $y_{x}^{\prime}$ of the function $x=e^{t} \cos t$; $y=e^{t} \sin t$ at $t=0$.
|
Solution. The functions $x$ and $y$ have the following derivatives with respect to $t$:
$$
\begin{aligned}
& x_{i}^{\prime}=e^{t} \cos t-e^{t} \sin t=e^{t}(\cos t-\sin t) \\
& y_{t}^{\prime}=e^{t} \sin t+e^{t} \cos t=e^{t}(\sin t+\cos t)
\end{aligned}
$$
therefore
$$
y_{x}^{\prime}=\frac{\sin t+\cos t}{\cos t-\sin t}
$$
At $t=0$, we get $y_{x}^{\prime}=1$.
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 3. Find $\lim _{x \rightarrow \frac{\pi}{2}} \frac{\tan x}{\tan 3 x}$.
|
Solution. Using the L'Hôpital-Bernoulli rule, we get
$$
\lim _{x \rightarrow \frac{\pi}{2}} \frac{\tan x}{\tan 3 x}=\lim _{x \rightarrow \frac{\pi}{2}} \frac{\frac{1}{\cos ^{2} x}}{\frac{3}{\cos ^{2} 3 x}}=\lim _{x \rightarrow \frac{\pi}{2}} \frac{\cos ^{2} 3 x}{3 \cos ^{2} x}
$$
The limit of the ratio of the first derivatives is an indeterminate form of $\frac{0}{0}$. We resolve this indeterminate form:
$$
\lim _{x \rightarrow \frac{\pi}{2}} \frac{\cos ^{2} 3 x}{3 \cos ^{2} x}=\lim _{x \rightarrow \frac{\pi}{2}} \frac{-6 \cos 3 x \sin 3 x}{-6 \cos x \sin x}=\lim _{x \rightarrow \frac{\pi}{2}} \frac{\sin 6 x}{\sin 2 x}
$$
Again, we have an indeterminate form of $\frac{0}{0}$. Applying the L'Hôpital-Bernoulli rule once more, we find
$$
\lim _{x \rightarrow \frac{\pi}{2}} \frac{\sin 6 x}{\sin 2 x}=\lim _{x \rightarrow \frac{\pi}{2}} \frac{6 \cos 6 x}{2 \cos 2 x}=\frac{6}{2}=3
$$
Thus,
$$
\lim _{x \rightarrow \frac{\pi}{2}} \frac{\tan x}{\tan 3 x}=3
$$
|
3
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 6. Find $\lim _{x \rightarrow 0}\left(\frac{1}{x}-\frac{1}{\sin x}\right)$.
|
Solution. When $x \rightarrow \mathbf{0}$, we get an indeterminate form of $\infty-\infty$. We will resolve this indeterminacy by converting it to an indeterminate form of $\frac{0}{0}$ and applying L'Hôpital-Bernoulli's rule,
$$
\begin{gathered}
\lim _{x \rightarrow 0}\left(\frac{1}{x}-\frac{1}{\sin x}\right)=\lim _{x \rightarrow 0} \frac{\sin x-x}{x \sin x}=\lim _{x \rightarrow 0} \frac{\cos x-1}{\sin x+x \cos x}= \\
=\lim _{x \rightarrow 0} \frac{-\sin x}{\cos x+\cos x-x \sin x}=0
\end{gathered}
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 7. Find $\lim _{x \rightarrow 0}[(x-\sin x) \ln x]$.
|
Solution. Here we have an indeterminate form $0 \cdot \infty$. The given function can be represented as
$$
(x-\sin x) \ln x=\frac{\ln x}{\frac{1}{x-\sin x}}
$$
The resulting indeterminate form $\frac{\infty}{\infty}$ is resolved using L'Hôpital's rule:
$$
\lim _{x \rightarrow 0} \frac{\ln x}{\frac{1}{x-\sin x}}=\lim _{x \rightarrow 0} \frac{\frac{1}{x}}{\frac{-(1-\cos x)}{(x-\sin x)^{2}}}=\lim _{x \rightarrow 0} \frac{(x-\sin x)^{2}}{x(\cos x-1)}
$$
This is an indeterminate form of $\frac{0}{0}$, so
$$
\begin{aligned}
& \lim _{x \rightarrow 0} \frac{(x-\sin x)^{2}}{x(\cos x-1)}=\lim _{x \rightarrow 0} \frac{2(x-\sin x)(1-\cos x)}{\cos x-1-x \sin x}= \\
& =2 \lim _{x \rightarrow 0} \frac{(1-\cos x)^{2}+(x-\sin x) \sin x}{-\sin x-\sin x-x \cos x}= \\
& =2 \lim _{x \rightarrow 0} \frac{1-2 \cos x+\cos ^{2} x+x \sin x-\sin ^{2} x}{-2 \sin x-x \cos x}= \\
& \quad=2 \lim _{x \rightarrow 0} \frac{1-2 \cos x+x \sin x+\cos 2 x}{-2 \sin x-x \cos x}= \\
& =2 \lim _{x \rightarrow 0} \frac{2 \sin x+\sin x+x \cos x-2 \sin 2 x}{-3 \cos x+x \sin x}=0
\end{aligned}
$$
Thus,
$$
\lim _{x \rightarrow 0}(x-\sin x) \ln x=0
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 8. Find $\lim _{x \rightarrow 1}(x-1)^{\ln x}$.
|
Solution. When $x \rightarrow 1$, we have the indeterminate form $0^{0}$. We will use the identity
$$
[f(x)]^{\varphi(x)}=e^{\varphi(x) \ln f(x)}
$$
which in this case will be
$$
(x-1)^{\ln x}=e^{\ln x \cdot \ln (x-1)}
$$
We have
$$
\lim _{x \rightarrow 1}(x-1)^{\ln x}=\lim _{x \rightarrow 1} e^{\ln x \cdot \ln (x-1)}=e^{\lim _{x \rightarrow 1}^{\ln x \cdot \lim _{x \rightarrow 1} \ln (x-1)}}
$$
Now we will find $\lim _{x \rightarrow 1}[\ln x \cdot \ln (x-1)]$. This is an indeterminate form of type $0 \cdot \infty$. Resolving this indeterminate form, we get
$$
\begin{gathered}
\lim _{x \rightarrow 1}[\ln x \cdot \ln (x-1)]=\lim _{x \rightarrow 1} \frac{\ln (x-1)}{\frac{1}{\ln x}}=\lim _{x \rightarrow 1} \frac{\frac{1}{1-x}}{-\frac{1}{x(\ln x)^{2}}}= \\
=-\lim _{x \rightarrow 1} \frac{x(\ln x)^{2}}{x-1}=-\lim _{x \rightarrow 1} \frac{(\ln x)^{2}+x 2 \ln x \cdot \frac{1}{x}}{1}= \\
=\lim _{x \rightarrow 1}\left[(\ln x)^{2}+2 \ln x\right]=0
\end{gathered}
$$
Therefore,
$$
\lim _{x \rightarrow 1}(x-1)^{\ln x}=e^{0}=1
$$
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 9. Find $\lim _{x \rightarrow 0}\left[\frac{\sin x}{x}\right]^{\frac{1}{x}}$.
|
Solution. Since $\lim _{x \rightarrow 0} \frac{\sin x}{x}=1, \lim _{x \rightarrow 0} \frac{1}{x}=\infty$, we have an indeterminate form of $1^{\infty}$ here.
Taking into account identity (A) (see example 8), using L'Hôpital-Bernoulli's rule, we find
$$
\lim _{x \rightarrow 0}\left[\frac{\sin x}{x}\right]^{\frac{1}{x}}=\lim _{x \rightarrow 0} e^{\frac{1}{x} \ln \frac{\sin x}{x}}=e^{\lim _{x \rightarrow 0} \frac{\ln \frac{\sin x}{x}}{x}}
$$
We need to find $\lim _{x \rightarrow 0} \frac{\ln \frac{\sin x}{x}}{x}$, which is an indeterminate form of $\frac{0}{0}$:
$$
\begin{gathered}
\lim _{x \rightarrow 0} \frac{\ln \frac{\sin x}{x}}{x}=\lim _{x \rightarrow 0} \frac{\frac{x}{\sin x} \cdot \frac{x \cos x-\sin x}{x^{2}}}{1}=\lim _{x \rightarrow 0} \frac{x \cos x-\sin x}{x \sin x}= \\
=\lim _{x \rightarrow 0} \frac{\cos x-x \sin x-\cos x}{\sin x+x \cos x}=-\lim _{x \rightarrow 0} \frac{x \sin x}{\sin x+x \cos x}= \\
=-\lim _{x \rightarrow 0} \frac{\sin x+x \cos x}{\cos x+\cos x-x \sin x}=0
\end{gathered}
$$
Thus, 104
$$
\lim _{x \rightarrow 0}\left[\frac{\sin x}{x}\right]^{\frac{1}{x}}=e^{0}=1
$$
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 11. Find $\lim _{x \rightarrow \infty} \frac{x-\sin x}{x+\sin x}$.
|
Solution. Apply L'Hôpital's rule:
$$
\lim _{x \rightarrow \infty} \frac{x-\sin x}{x+\sin x}=\lim _{x \rightarrow \infty} \frac{1-\cos x}{1+\cos x}
$$
In the right-hand side of the last equality, the limit does not exist, so L'Hôpital's rule is not applicable here.
The specified limit can be found directly:
$$
\lim _{x \rightarrow \infty} \frac{x-\sin x}{x+\sin x}=\lim _{x \rightarrow \infty} \frac{1-\frac{\sin x}{x}}{1+\frac{\sin x}{x}}=1
$$
## Problems
Find the limits:
1. $\lim _{x \rightarrow 0} \frac{\tan x-\sin x}{x-\sin x}$.
2. $\lim _{x \rightarrow 0} \frac{\frac{\pi}{x}}{\cot \frac{\pi x}{2}}$.
3. $\lim _{x \rightarrow \frac{\pi}{2}} \frac{\tan x}{\tan 5 x}$.
4. $\lim _{x \rightarrow 0}(1-\cos x) \cot x$.
5. $\lim _{x \rightarrow 1}(1-x) \tan \frac{\pi x}{2}$.
6. $\lim _{x \rightarrow 1}\left(\frac{x}{x-1}-\frac{1}{\ln x}\right)$.
6. $\lim _{x \rightarrow 3}\left(\frac{1}{x-3}-\frac{5}{x^{2}-x-6}\right)$.
7. $\lim _{x \rightarrow 0} x^{x}$.
8. $\lim _{x \rightarrow 0}\left(\frac{1}{x}\right)^{\tan x}$.
9. $\lim _{x \rightarrow 0}(\cot x)^{\sin x}$.
10. $\lim _{x \rightarrow 0}\left(\frac{\sin x}{x}\right)^{\frac{1}{1-\cos x}}$.
11. $\lim _{x \rightarrow+\infty}\left(\frac{\pi}{2}-\arctan x\right)^{\frac{1}{\ln x}}$.
## Answers
1.3. 2. $\frac{\pi^{2}}{2}$. 3.5. 4.0.5. $\frac{2}{\pi}$. 6. $\frac{1}{2}$. 7. $\frac{1}{5}$. 8.1. Hint. Let $x^{x}=y$, take the logarithm of this equation, and take the limit. 9.1. 10. 1. 11. $\frac{1}{\sqrt[3]{e}}$. 12. $\frac{1}{e}$.
## §3.2. Tangent and Normal to a Plane Curve. Angle Between Curves. Curvature of a Plane Curve. Velocity and Acceleration
The tangent to a curve $y=f(x)$ at its point $M_{0}\left(x_{0}, y_{0}\right)$ is the limiting position $M_{0} T$ of the secant $M M_{0}$, as the point $M$ approaches $M_{0}$ along the given curve (Fig. 3.1).
The equation of the tangent to the curve $y=f(x)$ at the point $M_{0}\left(x_{0}, y_{0}\right)$ is:
$$
y-y_{0}=f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)
$$
The normal to the curve at the point $M_{0}\left(x_{0}, y_{0}\right)$ is the line passing through $M_{0}$ and perpendicular to the tangent at that point.
The equation of the normal to the curve $y=f(x)$ at the point $M_{0}\left(x_{0}, y_{0}\right)$ is:
$$
y-y_{0}=-\frac{1}{f^{\prime}\left(x_{0}\right)}\left(x-x_{0}\right)
$$
The curvature of a curve at its point $M$ is the limit of the absolute value of the ratio of the angle $\Delta \alpha$ between the tangents at points $M$ and $N$ of the curve to the length of the arc $\breve{M N}=\Delta s$, as $N \rightarrow M$ (Fig. 3.2), i.e.,
$$
k=\lim _{\Delta s \rightarrow 0}\left|\frac{\Delta \alpha}{\Delta s}\right|
$$
where the angle $\alpha$ is expressed in radians.

Fig. 3.1
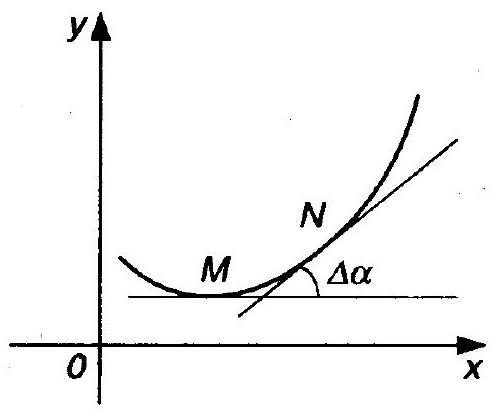
Fig. 3.2
The curvature of the curve $y=f(x)$ is calculated by the formula
$$
k=\frac{\left|y^{\prime \prime}\right|}{\left(1+y^{\prime 2}\right)^{\frac{3}{2}}}
$$
If the curve is given parametrically by $x=\varphi(t)$, $y=\varphi(t)$, then its curvature is determined by the formula
$$
k=\frac{\left|x^{\prime} y^{\prime \prime}-x^{\prime \prime} y^{\prime}\right|}{\left(x^{\prime 2}+y^{\prime 2}\right)^{\frac{3}{2}}}
$$
The radius of curvature of a curve at a point is the reciprocal of its curvature at that point. If the radius of curvature is denoted by $R$, then
$$
R=\frac{1}{k}
$$
The circle of curvature (osculating circle) of a curve at its point $M$ is the limiting position of the circle passing through the point $M$ and two other points $L$ and $N$ of the curve, as $L \rightarrow M$ and $N \rightarrow M$.
The radius of the circle of curvature is equal to the radius of curvature of the curve at the corresponding point.
The center of the circle of curvature is called the center of curvature of the curve at the given point $M$. The coordinates $X$ and $Y$ of the center of curvature of the curve $y=f(x)$ are calculated by the formulas:
$$
X=x-\frac{y^{\prime}\left(1+y^{\prime 2}\right)}{y^{\prime \prime}} ; Y=y+\frac{1+y^{\prime 2}}{y^{\prime \prime}}
$$
The evolute of a curve is the geometric locus of its centers of curvature.
Formulas (3.6) give the parametric equations of the evolute with parameter $x$ or $y$.
If the curve is given parametrically, then the equations of its evolute are:
$$
X=x-y^{\prime} \frac{x^{\prime 2}+y^{\prime 2}}{x^{\prime} y^{\prime \prime}-y^{\prime} x^{\prime \prime}} ; Y=y+x^{\prime} \frac{x^{\prime 2}+y^{\prime 2}}{x^{\prime} y^{\prime \prime}-y^{\prime} x^{\prime \prime}}
$$
The involute of a curve is a curve for which the given curve is the evolute.
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 1. Calculate the definite integral $\int_{1}^{4} x^{2} d x$.
|
Solution. By formula (5.3) we have
$$
\int_{1}^{4} x^{2} d x=\left.\frac{x^{3}}{3}\right|_{1} ^{4}=\frac{4^{3}}{3}-\frac{1^{3}}{3}=\frac{64}{3}-\frac{1}{3}=21
$$
Remark According to the Newton-Leibniz theorem, we can take any antiderivative of the integrand. In this case, instead of $\frac{x^{3}}{3}$, we could have taken $\frac{x^{3}}{3}+5$, which is also an antiderivative of the function $y=x^{2}$:
$$
\int_{1}^{4} x^{2} d x=\left(\frac{x^{3}}{3}+5\right)_{1}^{4}=\left(\frac{4^{3}}{3}+5\right)-\left(\frac{1^{3}}{3}+5\right)=\frac{64}{3}+5-\frac{1}{3}-5=\frac{63}{3}=21
$$
The same result is obtained in the general case:
$$
\int_{1}^{4} x^{2} d x=\left(\frac{x^{3}}{3}+C\right)_{1}^{4}=\left(\frac{4^{3}}{3}+C\right)-\left(\frac{1^{3}}{3}+C\right)=\frac{64}{3}+C-\frac{1}{3}-C=21
$$
In the future, we will consider only the antiderivative for which the constant term is zero.
|
21
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2. Calculate the integral $\int_{0}^{\frac{\pi}{2}} \cos x d x$.
|
Solution.
$$
\int_{0}^{\frac{\pi}{2}} \cos x d x=\left.\sin x\right|_{0} ^{\frac{\pi}{2}}=\sin \frac{\pi}{2}-\sin 0=1-0=1
$$
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 3. Calculate $\int_{4}^{9}\left(\frac{2 x}{5}+\frac{1}{2 \sqrt{x}}\right) d x$.
|
Solution. Based on properties 5 and 6 of the definite integral and formula (5.3), we obtain
$$
\begin{aligned}
& \int_{4}^{9}\left(\frac{2 x}{5}+\frac{1}{2 \sqrt{x}}\right) d x=\frac{2}{5} \int_{4}^{9} x d x+\int_{4}^{9} \frac{1}{2 \sqrt{x}} d x=\left.\frac{2}{5} \cdot \frac{x^{2}}{2}\right|_{4} ^{9}+ \\
& +\left.\sqrt{x}\right|_{4} ^{9}=\frac{1}{5}\left(9^{2}-4^{2}\right)+(\sqrt{9}-\sqrt{4})=\frac{1}{5} \cdot 65+1=14
\end{aligned}
$$
|
14
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 6. Calculate $\int_{1}^{e} \ln x d x$.
|
Solution. We apply the integration by parts formula (5.5).
Letting $u=\ln x, d v=d x$, we determine $d u=\frac{1}{x} d x, v=x$.
Therefore,
$$
\begin{gathered}
\int_{1}^{e} \ln x d x=\left.x \ln x\right|_{1} ^{e}-\int_{1}^{e} \frac{1}{x} x d x=\left.x \ln x\right|_{1} ^{e}-\int_{1}^{e} d x=\left.x \ln x\right|_{1} ^{e}-\left.x\right|_{1} ^{e}= \\
=e \ln e-1 \cdot \ln 1-(e-1)=e-0-e+1=1
\end{gathered}
$$
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 8. Determine the area bounded by the arc of the cosine curve from $x=-\frac{\pi}{2}$ to $x=\frac{\pi}{2}$ and the $O x$ axis.
|
Solution. Based on the geometric meaning of the definite integral, we conclude that the desired area is expressed by the integral
$$
S=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \cos x d x
$$
Evaluating this integral, we get
$$
S=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \cos x d x=\left.\sin x\right|_{-\frac{\pi}{2}} ^{\frac{\pi}{2}}=\sin \frac{\pi}{2}-\sin \left(-\frac{\pi}{2}\right)=1-(-1)=2 \text { (sq. units) }
$$
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 1. Determine the area bounded by the lines $x y=6$, $x=1, x=e, y=0$ (Fig. 5.5).

Fig. 5.5
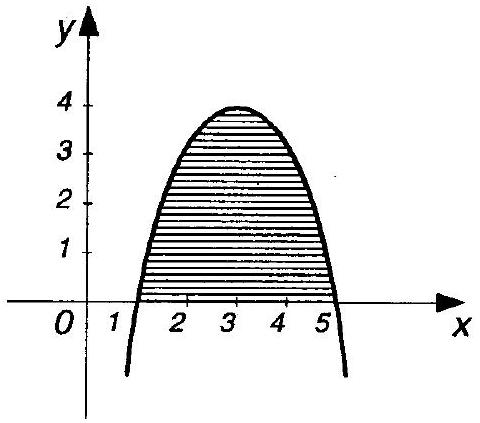
Fig. 5.6
|
Solution. Defining $y$ from the hyperbola equation $x y=6$, we get $y=\frac{6}{x}$. From the condition, it follows that $a=1, b=e$. Substituting the values of $a, b$ and $\frac{6}{x}$ (the expression for $y$) into formula (5.13), we find:
$$
S=\int_{1}^{e} \frac{6}{x} d x=6 \int_{1}^{e} \frac{d x}{x}=\left.6 \ln x\right|_{1} ^{e}=6(\ln e-\ln 1)=6(1-0)=6
$$
|
6
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 6. Calculate the area bounded by the parabola $x=8 y-y^{2}-7$ and the $O y$ axis.
|
Solution. To determine the limits of integration, we find the points of intersection of the curve with the $O y$ axis.
Solving the system of equations $x=8 y-y^{2}-7, x=0$, we get $\quad y_{1}=1, \quad y_{2}=7$
(Fig. 5.10). By formula (5.16) we find
$$
\begin{aligned}
& S=\int_{1}^{7}\left(8 y-y^{2}-7\right) d y=8 \int_{1}^{7} y d y-\int_{1}^{7} y^{2} d y-7 \int_{1}^{7} d y= \\
& =\left.8 \cdot \frac{y^{2}}{2}\right|_{1} ^{7}-\left.\frac{y^{3}}{3}\right|_{1} ^{7}-\left.7 y\right|_{1} ^{7}=4(49-1)-\frac{1}{3}(343-1)- \\
& -7(7-1)=192-114-42=36
\end{aligned}
$$
|
36
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 1. Find the length of the arc of the astroid $x^{\frac{2}{3}}+y^{\frac{2}{3}}=a^{\frac{2}{3}}$. What is the length of the astroid when $a=1, a=\frac{2}{3}?$
|
Solution. Since the astroid
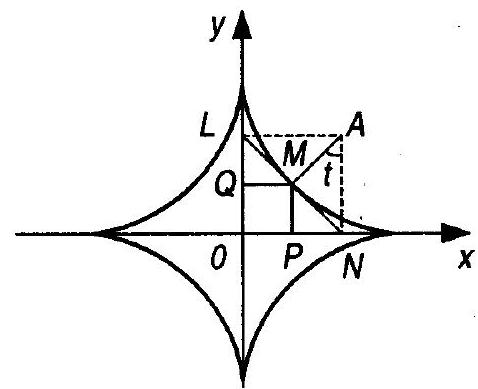
Fig. 5.13 is symmetric with respect to the coordinate axes (Fig. 5.13), it is sufficient to compute the length of the arc $AB$ and multiply the result by 4.
Differentiating the function $x^{\frac{2}{3}} + y^{\frac{2}{3}} = a^{\frac{2}{3}}$ implicitly, we get
$$
\frac{2}{3} x^{-\frac{1}{3}} + \frac{2}{3} y^{-\frac{1}{3}} y' = 0, \quad y' = -\frac{y^{\frac{1}{3}}}{x^{\frac{1}{3}}}
$$
We find the expression for the integrand in formula (2.18). We have
$$
\sqrt{1 + y'^2} = \sqrt{1 + \frac{y^{\frac{2}{3}}}{x^{\frac{2}{3}}}} = \sqrt{\frac{x^{\frac{2}{3}} + y^{\frac{2}{3}}}{x^{\frac{2}{3}}}} = \sqrt{\frac{a^{\frac{2}{3}}}{x^{\frac{2}{3}}}} = \frac{a^{\frac{1}{3}}}{x^{\frac{1}{3}}}
$$
Using formula (5.18), we find
$$
\begin{aligned}
\frac{1}{4} l & = \int_{0}^{a} \sqrt{1 + y'^2} \, dx = \int_{0}^{a} \frac{a^{\frac{1}{3}}}{x^{\frac{1}{3}}} \, dx = a^{\frac{1}{3}} \int_{0}^{a} x^{-\frac{1}{3}} \, dx = \\
& = \left. a^{\frac{1}{3}} \frac{x^{\frac{2}{3}}}{\frac{2}{3}} \right|_{0}^{a} = \left. \frac{3}{2} a^{\frac{1}{3}} x^{\frac{2}{3}} \right|_{0}^{a} = \frac{3}{2} a, \quad l = 6a
\end{aligned}
$$
For $a = 1$, we get $l = 6$, and for $a = \frac{2}{3}$, we get $l = 4$.
|
4
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 1. Find $\lim _{\substack{x \rightarrow 2 \\ y \rightarrow 0}} \frac{\sin x y}{y}$.
|
Solution. At the point $M(2,0)$, the function $z=\frac{\sin x y}{y}$ is undefined.
By multiplying and dividing the given function by $x \neq 0$, we get
$$
\frac{\sin x y}{y}=\frac{x \sin x y}{x y}=x \frac{\sin x y}{x y}
$$
Taking the limit in the last equality, we obtain
$$
\lim _{\substack{x \rightarrow 2 \\ y \rightarrow 0}} \frac{\sin x y}{y}=\lim _{\substack{x \rightarrow 2 \\ y \rightarrow 0}} x \cdot \frac{\sin x y}{x y}=\lim _{\substack{x \rightarrow 2 \\ y \rightarrow 0}} x \cdot \lim _{\substack{x \rightarrow 2 \\ y \rightarrow 0}} \frac{\sin x y}{x y}=2 \cdot 1=2
$$
since $\lim _{\alpha \rightarrow 0} \frac{\sin \alpha}{\alpha}=1$.
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2. Given the function
$$
f(x, y)=x \sin \frac{1}{y}+y \sin \frac{1}{x} \quad\left(x^{2}+y^{2} \neq 0\right), \quad f(0, y)=0, \quad f(x, 0)=0
$$
find $\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}} f(x, y)$.
|
Solution. Let $\varepsilon>0$, then for $|x|<\frac{\varepsilon}{2},|y|<\frac{\varepsilon}{2}$ we get $\rho=$
$$
=\sqrt{\left(\frac{\varepsilon}{2}\right)^{2}+\left(\frac{\varepsilon}{2}\right)^{2}}=\frac{\sqrt{2}}{2} \varepsilon . \text { We form the difference } f(x, y)-0 \text { and estimate it: }
$$
$$
|f(x, y)-0| \leq|x| \cdot\left|\sin \frac{1}{y}\right|+|y| \cdot\left|\sin \frac{1}{x}\right| \leq|x|+|y|<\frac{\varepsilon}{2}+\frac{\varepsilon}{2}=\varepsilon
$$
Thus,
$$
|f(x, y)-0|<\varepsilon
$$
Based on formula (6.10), we conclude that
$$
\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}} f(x, y)=0
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 3. Find $\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}} \frac{x^{2} y}{x^{2}+y^{2}}$.
|
Solution. The given function can be represented as:
$$
f(x, y)=\frac{x^{2} y}{x^{2}+y^{2}}=\frac{x y}{x^{2}+y^{2}} x .
$$
Since
$$
\left|\frac{x y}{x^{2}+y^{2}}\right| \leq \frac{1}{2}
$$
(this can be derived from the inequality $(x-y)^{2} \geq 0$ : $x^{2}-2 x y+y^{2} \geq 0$, $\left.x^{2}+y^{2} \geq 2 x y, \frac{1}{2} \geq \frac{x y}{x^{2}+y^{2}}\right)$, then
$$
|f(x, y)|=\left|\frac{x y}{x^{2}+y^{2}}\right| \cdot|x| \leq \frac{1}{2}|x|
$$
If given $\varepsilon>0$, then for $|x|<\delta$ and $\delta=2 \varepsilon$ we get
$$
|f(x, y)-0| \leq \frac{1}{2}|x|<\frac{1}{2} \cdot 2 \varepsilon=\varepsilon
$$
That is,
$$
|f(x, y)-0|<\varepsilon
$$
Therefore,
$$
\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}} \frac{x^{2} y}{x^{2}+y^{2}}=0
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 1. Investigate the function for extremum
$$
f(x, y)=x^{3}+y^{3}+9 x y
$$
|
Solution. We find the first and second partial derivatives:
$$
\begin{gathered}
f_{x}^{\prime}(x, y)=3 x^{2}+9 y ; f_{y}^{\prime}(x, y)=3 y^{2}+9 x \\
f_{x x}^{\prime \prime}(x, y)=6 x ; f_{x y}^{\prime \prime}(x, y)=9 ; f_{y y}^{\prime \prime}(x, y)=6 y
\end{gathered}
$$
Setting the first derivatives to zero, we obtain a system of equations to determine the critical points:
$$
\left.\left.\begin{array}{c}
3 x^{2}+9 y=0 \\
3 y^{2}+9 x=0
\end{array}\right\} \text { or } \begin{array}{r}
x^{2}+3 y=0 \\
y^{2}+3 x=0
\end{array}\right\}
$$
Solving for $y$ from the first equation and substituting its expression
$$
y=-\frac{1}{3} x^{2}
$$
into the second equation, we get
$$
\left(-\frac{1}{3} x^{2}\right)^{2}+3 x=0, x^{4}+27 x=0
$$
or
$$
x\left(x^{3}+27\right)=0
$$
from which
$$
x_{1}=0, x_{2}=-3
$$
(We do not consider the complex roots of the equation $x^{3}+27=0$ or $(x+3)\left(x^{2}-3 x+\right.$ $+9)=0$.)
We find the values of $y$ corresponding to the values $x_{1}=0, x_{2}=-3$. From equation (A), we have $y_{1}=0, y_{2}=-3$. We have obtained two critical points $M_{1}(0,0), M_{2}(-3,-3)$.
We compute the values of the second partial derivatives at these points:
$$
\begin{gathered}
A_{1}=f_{x x}^{\prime \prime}(0,0)=0, B_{1}=f_{x y}^{\prime \prime}(0,0)=9, C_{1}=f_{y y}^{\prime \prime}(0,0)=0 \\
A_{2}=f_{x x}^{\prime \prime}(-3,-3)=-18, B_{2}=f_{x y}^{\prime \prime}(-3,-3)=9 \\
C_{2}=f_{y y}^{\prime \prime}(-3,-3)=-18
\end{gathered}
$$
We find the determinant (8.9):
$$
\begin{gathered}
\Delta_{1}=A_{1} C_{1}-B_{1}^{2}=0 \cdot 0-9^{2}=-81 \\
\Delta_{2}=A_{2} C_{2}-B_{2}^{2}=(-18)(-18)-9^{2}=243
\end{gathered}
$$
By the sufficient conditions, we conclude that there is no extremum at point $M_{1}$, since $\Delta_{1}<0$, and there is a maximum at point $M_{2}$, since $\Delta_{2}>0$ and $A_{2}<0$, and
$$
\max f(x, y)=f(-3,-3)=27
$$
|
27
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2. Find the maximum and minimum values of the function $z=f(x, y)=x^{3}+y^{3}+6 x y \quad$ in the rectangle with vertices $A(-3,-3), B(-3,2), C(1,2), D(1,-3)$.
|
Solution. We take the partial derivatives of the given function:
$$
f_{x}^{\prime}(x, y)=3 x^{2}+6 y ; f_{y}^{\prime}(x, y)=3 y^{2}+6 x
$$
From the system of equations
$$
\left.\left.\begin{array}{c}
3 x^{2}+6 y=0 \\
3 y^{2}+6 x=0
\end{array}\right\} \text { or } \begin{array}{r}
x^{2}+2 y=0 \\
y^{2}+2 x=0
\end{array}\right\}
$$
we find two critical points $M_{1}(0,0), M_{2}(-2,-2)$, both of which belong to the rectangle $A B C D$ (Fig. 8.1).
We calculate the values of the function at these points:
$$
z_{1}=f(0,0)=0, z_{2}=f(-2,-2)=8
$$

Fig. 8.1
We find the maximum and minimum values of the function on the boundary of the rectangle $A B C D$. It is convenient to divide this boundary into four segments $A B, B C, C D, D A$, on each of which there may be critical points. In addition, we must take into account the endpoints of the segments, i.e., the points $A, B, C$ and $D$.
We look for critical points on the segment $A B$, the equation of which is $x=-3$, and $-3 \leq y \leq 2$. On this segment, the given function becomes a function of one variable $y$:
$$
z=f(-3, y)=-27+y^{3}-18 y ; z(y)=y^{3}-18 y-27
$$
The derivative of this function
$$
z^{\prime}=3 y^{2}-18
$$
is zero at $y=-\sqrt{6} \approx-2.45, y=\sqrt{6} \approx 2.45$. We will not consider the second value, as it does not belong to the segment $A B$, for which $-3 \leq y \leq 2$. We calculate the value of the function $z(y)$ at $y=-\sqrt{6}$:
$$
\begin{gathered}
z_{3}=z(-\sqrt{6})=(-\sqrt{6})^{3}-18(-\sqrt{6})-27=12 \sqrt{6}- \\
-27 \approx 2.4
\end{gathered}
$$
On the segment $B C \quad y=2(-3 \leq x \leq 1)$, therefore,
$$
z=f(x, 2)=x^{3}+8+12 x
$$
The function $z(x)=x^{3}+12 x+8$ has no critical points, as its derivative $z^{\prime}(x)=3 x^{2}+12$ does not equal zero.
On the segment $C D$, where $x=1(-3 \leq y \leq 2)$,
$$
z=f(1, y)=1+y^{3}+6 y
$$
there are also no critical points.
On the segment $D A \quad y=-3(-3 \leq x \leq 1)$, therefore
$$
z=f(x,-3)=x^{3}-27-18 x
$$
The function $z(x)=x^{3}-18 x-27$ has a critical point at $x=-\sqrt{6}$ (the point $x=\sqrt{6}$, where the derivative $z^{\prime}(x)=3 x^{2}-18$ also equals zero, does not belong to the segment $D A$).
We calculate the value of the function $z(x)$ at the point $x=-\sqrt{6}$:
$$
\begin{gathered}
z_{4}=z(-\sqrt{6})=(-\sqrt{6})^{3}-18(-\sqrt{6})-27= \\
=12 \sqrt{6}-27 \approx 2.4
\end{gathered}
$$
It remains to find the values of the function $z=f(x, y)=x^{3}+y^{3}+6 x y$ at the vertices $A, B, C, D$:
$$
\begin{gathered}
z_{5}=f(A)=f(-3,-3)=(-3)^{3}+(-3)^{3}+6(-3)(-3)=0 \\
z_{6}=f(B)=f(-3,2)=(-3)^{3}+2^{3}+6(-3) 2=-55 \\
z_{7}=f(C)=f(1,2)=1^{3}+2^{3}+6 \cdot 1 \cdot 2=21 \\
z_{8}=f(D)=f(1,-3)=1^{3}+(-3)^{3}+6(-3) 1=-44
\end{gathered}
$$
By comparing $z_{1}, z_{2}, z_{3}, z_{4}, z_{5}, z_{6}, z_{7}, z_{8}$, we conclude that the function $z=x^{3}+y^{3}+6 x y$ in the rectangle $A B C D$ reaches its minimum value, equal to -55, at point $B$, and its maximum value, equal to 21, at point $C$.
|
-55
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2. Into how many parts should the interval of integration be divided to calculate $\int_{2}^{7} \frac{d x}{\sqrt{x+2}}$ with an accuracy of 0.1?
|
Solution. The absolute error in calculating a definite integral using the rectangle method is determined by inequality (13.4). In the problem, the condition $\left|R_{n}(f)\right| \leq \varepsilon$ is set, where $\varepsilon=0.1$. The inequality $\left|R_{n}(f)\right| \leq \varepsilon$ will be satisfied if $\frac{(b-a)^{2} M}{2 n} \leq \varepsilon$, from which
$$
n \geq \frac{(b-a)^{2} M}{2 \varepsilon}
$$
In this case, $a=2, b=7, \varepsilon=0.1$. Since $f(x)=\frac{1}{\sqrt{x+2}}$,
$$
\begin{aligned}
f^{\prime}(x)=-\frac{1}{2 \sqrt{(x+2)^{3}}}, M & =\max _{2 \leq x \leq 7}\left|f^{\prime}(x)\right|=\frac{1}{16}, \text { then } \\
n & \geq \frac{(7-2)^{2} \cdot \frac{1}{16}}{2 \cdot 0.1} \approx 7.8
\end{aligned}
$$
Since $n$ is an integer, we need to take $n=8$. (For convenience in calculations, $n=10$ can be taken).
## Problems
Using the rectangle formulas, with $n=10$, calculate the definite integrals:
1. $\int_{1}^{11} \frac{d x}{x+2}$.
2. $\int_{0}^{\frac{\pi}{6}} \sin 3 x d x$.
3. $\int_{0}^{10} \sqrt{x^{2}+2} d x$.
4. $\int_{0}^{1} \frac{\cos x}{1+x} d x$.
5. $\int_{0}^{0.9} \sin x^{2} d x$.
6. $\int_{0}^{1} \frac{d x}{\sqrt{x^{3}+1}}$.
How many parts should the integration interval be divided into to calculate the integrals with an accuracy of 0.1 using the rectangle formulas:
7. $\int_{1}^{2} \ln x d x$.
8. $\quad \int_{0}^{1} \frac{d x}{x+1}$.
9. $\int_{0}^{\frac{\pi}{8}} \cos 4 x d x$. \quad 10. $\int_{0}^{\frac{\pi}{8}} \sin \frac{x}{2} d x$.
## Answers
1. $J_{n}=1.603 ; J_{n}=1.348$. 2. $J_{n}=0.303 ; J_{n}=0.314$. 3. $J_{n}=48.891$. 4. $J_{n}=0.565 ; J_{n}=0.640$. 5. $J_{n}=0.266$. 6. $J_{n}=0.444$. 7.5. 8.5. 9.3.
## § 13.2. Trapezoidal Rule
The trapezoidal rule is given by
$$
\int_{a}^{b} f(x) d x \approx h\left(\frac{y_{0}}{2}+y_{1}+y_{2}+\ldots+y_{n-1}+\frac{y_{n}}{2}\right)
$$
where
$$
h=\frac{b-a}{n}, x_{k}=a+k h, y_{k}=f\left(x_{k}\right)(k=0,1,2, \ldots, n)
$$
The right-hand side of formula (13.5) represents the area of a figure consisting of trapezoids, each with height $h$ (Fig. 13.2). If $R_{n}$ is the remainder term of the approximate formula (13.5), then
$$
\left|R_{n}\right| \leq \frac{(b-a)^{3} M}{12 n^{2}}
$$
where $M=\max _{a \leq x \leq b}\left|f^{\prime \prime}(x)\right|$.
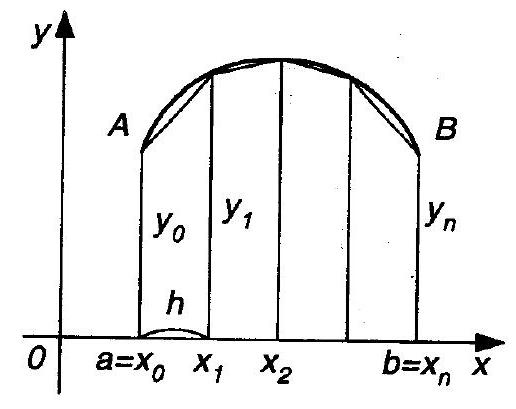
Fig. 13.2
|
8
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 1. Construct a table of differences of various orders for the following values of $x$ and $f(x)$:
\[
\begin{gathered}
x_{0}=-1, x_{1}=-2, x_{2}=1, x_{3}=2, x_{4}=3 \\
y_{0}=0, y_{1}=7, y_{2}=30, y_{3}=-16, y_{4}=-45
\end{gathered}
\]
|
Solution. Using formulas (15.4), we find the first differences:
$$
\begin{gathered}
\Delta y_{0}=y_{1}-y_{0}=7-0=7 ; \Delta y_{1}=y_{2}-y_{1}=30-7=23 \\
\Delta y_{2}=y_{3}-y_{2}=-16-30=-46 ; \Delta y_{3}=y_{4}-y_{3}=-45-(-16)=-29
\end{gathered}
$$
In accordance with formulas (15.5), we calculate the second-order differences:
$$
\begin{gathered}
\Delta^{2} y_{0}=\Delta y_{1}-\Delta y_{0}=23-7=16 ; \Delta^{2} y_{1}=\Delta y_{2}-\Delta y_{1}=-46-23=-69 \\
\Delta^{2} y_{2}=\Delta y_{3}-\Delta y_{2}=-29-(-46)=17
\end{gathered}
$$
Using the definitions and corresponding formulas, we obtain the third-order differences:
$$
\begin{aligned}
& \Delta^{3} y_{0}=\Delta^{2} y_{1}-\Delta^{2} y_{0}=-69-16=-85 \\
& \Delta^{3} y_{1}=\Delta^{2} y_{2}-\Delta^{2} y_{1}=17-(-69)=86
\end{aligned}
$$
and the fourth-order difference $\Delta^{4} y_{0}=\Delta^{3} y_{1}-\Delta^{3} y_{0}=86-(-85)=171$.
The obtained differences can be represented in the form of Table 15.2.
Table 15.2
| $x$ | $y$ | $\Delta y$ | $\Delta^{2} y$ | $\Delta^{3} y$ | $\Delta^{4} y$ |
| :---: | :---: | :---: | :---: | :---: | :---: |
| -1 | 0 | 7 | | | |
| -2 | 7 | 23 | 16 | -85 | 171 |
| 1 | 30 | -46 | -69 | 86 | |
| 2 | -16 | -29 | 17 | | |
| 3 | -45 | | | | |
| $\Sigma$ | | -45 | -36 | 1 | |
| $S$ | -45 | -36 | 1 | | |
Remark. The last two rows serve for checking the calculations: in the $\sum$ row, the numbers are equal to the sums of the numbers in the corresponding columns, in the $S$ row - the differences between the last and first numbers in the corresponding columns. The coincidence of these numbers (along the diagonal) means that the calculations are correct.
|
171
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2. Construct a table of divided differences of various orders for the following values of $x$ and $y=f(x)$:
\[
\begin{gathered}
x_{0}=-3, x_{1}=-2, x_{2}=-1, x_{3}=1, x_{4}=2 \\
y_{0}=-9, y_{1}=-16, y_{2}=-3, y_{3}=11, y_{4}=36
\end{gathered}
\]
|
Solution. According to the definitions, we find the divided differences of the first order:
$$
\begin{gathered}
f\left(x_{1}, x_{0}\right)=\frac{y_{1}-y_{0}}{x_{1}-x_{0}}=\frac{-16-(-9)}{-2-(-3)}=-7 ; f\left(x_{2}, x_{1}\right)=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-3-(-16)}{-1-(-2)}=13 \\
f\left(x_{3}, x_{2}\right)=\frac{y_{3}-y_{2}}{x_{3}-x_{2}}=\frac{11-(-3)}{1-(-1)}=7 ; f\left(x_{4}, x_{3}\right)=\frac{y_{4}-y_{3}}{x_{4}-x_{3}}=\frac{36-11}{2-1}=25
\end{gathered}
$$
differences of the second order:
$$
\begin{aligned}
& f\left(x_{2}, x_{1}, x_{0}\right)=\frac{f\left(x_{2}, x_{1}\right)-f\left(x_{1}, x_{0}\right)}{x_{2}-x_{0}}=\frac{13-(-7)}{-1-(-3)}=10 \\
& f\left(x_{3}, x_{2}, x_{1}\right)=\frac{f\left(x_{3}, x_{2}\right)-f\left(x_{2}, x_{1}\right)}{x_{3}-x_{1}}=\frac{7-13}{1-(-2)}=-2 \\
& f\left(x_{4}, x_{3}, x_{2}\right)=\frac{f\left(x_{4}, x_{3}\right)-f\left(x_{3}, x_{2}\right)}{x_{4}-x_{2}}=\frac{25-7}{2-(-1)}=6
\end{aligned}
$$
differences of the third order:
$$
\begin{aligned}
& f\left(x_{3}, x_{2}, x_{1}, x_{0}\right)=\frac{f\left(x_{3}, x_{2}, x_{1}\right)-f\left(x_{2}, x_{1}, x_{0}\right)}{x_{3}-x_{0}}=\frac{-2-10}{1-(-3)}=-3 \\
& f\left(x_{4}, x_{3}, x_{2}, x_{1}\right)=\frac{f\left(x_{4}, x_{3}, x_{2}\right)-f\left(x_{3}, x_{2}, x_{1}\right)}{x_{4}-x_{1}}=\frac{6-(-2)}{2-(-2)}=2
\end{aligned}
$$
difference of the fourth order:
$$
f\left(x_{4}, x_{3}, x_{2}, x_{1}, x_{0}\right)=\frac{f\left(x_{4}, x_{3}, x_{2}, x_{1}\right)-f\left(x_{3}, x_{2}, x_{1}, x_{0}\right)}{x_{4}-x_{0}}=\frac{2-(-3)}{2-(-3)}=1
$$
The obtained divided differences can be represented in the form of Table 15.3.
Table 15.3
| $x$ | $y$ | Divided differences | | | |
| :---: | ---: | ---: | ---: | ---: | ---: |
| -3 | -9 | -7 | 10 | | |
| -2 | -16 | 13 | 10 | -3 | 1 |
| -1 | -3 | 7 | -2 | 2 | |
| 1 | 11 | 25 | 6 | | |
| 2 | 36 | | | | |
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2. How many elementary outcomes favor the event "the same number of points fell on both dice" when two gaming dice are rolled?
|
Solution. This event is favored by 6 elementary outcomes (see Table 1.1$):(1 ; 1),(2 ; 2),(3 ; 3),(4 ; 4),(5 ; 5),(6 ; 6)$.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 1. In how many different ways can three people be selected for three different positions from ten candidates?
|
Solution. We will use formula (1.3.3). For $n=10, m=3$ we get
$$
A_{10}^{3}=10 \cdot 9 \cdot 8=720
$$
|
720
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 3. In how many ways can three people be selected for three identical positions from ten candidates?
|
Solution. According to formula (1.3.4), we find
$$
C_{10}^{3}=\frac{10!}{3!\cdot(10-3)!}=\frac{10!}{3!\cdot 7!}=\frac{10 \cdot 9 \cdot 8}{1 \cdot 2 \cdot 3}=120
$$
|
120
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 4. How many different six-digit numbers can be written using the digits $1 ; 1 ; 1 ; 2 ; 2 ; 2$?
|
Solution. Here we need to find the number of permutations with repetitions, which is determined by formula (1.3.7). For $k=2, n_{1}=3, n_{2}=3, n=6$ this formula gives us
$$
P_{6}(3 ; 3)=\frac{6!}{3!\cdot 3!}=\frac{1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6}{1 \cdot 2 \cdot 3 \cdot 1 \cdot 2 \cdot 3}=20
$$
|
20
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.