problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
Example 5. How many different permutations of letters can be made from the words: zamok, rotor, topor, kolokol?
|
Solution. In the word "замок" (lock), all letters are different, and there are five of them. According to formula (1.3.1), we get
$$
P_{5}=5!=1 \cdot 2 \cdot 3 \cdot 4 \cdot 5=120
$$
In the word "ротор" (rotor), consisting of five letters, the letters $p$ and о are repeated twice. To count the different permutations, we use formula (1.3.7). For $n=5, n_{1}=2, n_{2}=2$, by this formula we find
$$
P_{5}(2 ; 2)=\frac{5!}{2!\cdot 2!}=\frac{1 \cdot 2 \cdot 3 \cdot 4 \cdot 5}{1 \cdot 2 \cdot 1 \cdot 2}=30
$$
In the word "топор" (hatchet), the letter о is repeated twice, so
$$
P_{5}(2)=\frac{5!}{2!}=\frac{1 \cdot 2 \cdot 3 \cdot 4 \cdot 5}{1 \cdot 2}=60
$$
In the word "колокол" (bell), consisting of seven letters, the letter $к$ appears twice, the letter $o$ - three times, and the letter $л$ - twice. According to formula (1.3.7) for $n=7, n_{1}=2, n_{2}=3, n_{3}=2$, we get
$$
P_{7}(2 ; 3 ; 2)=\frac{7!}{2!\cdot 3!\cdot 2!}=\frac{1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7}{1 \cdot 2 \cdot 1 \cdot 2 \cdot 3 \cdot 1 \cdot 2}=210
$$
17р and mer 6. On five identical cards, the letters $U, K, M$, $H, C$ are written. The cards are shuffled and randomly laid out in a row. What is the probability that the word "МИНСК" (MINSK) will be formed?
Solution. From five different elements, $P_{5}$ permutations can be formed: $P_{5}=1 \cdot 2 \cdot 3 \cdot 4 \cdot 5=120$. Therefore, there will be 120 equally possible outcomes, and only one of them is favorable to the given event. Thus,
$$
P=\frac{1}{120}
$$
|
210
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 5. When shooting at a target, the frequency of hits $W=0.75$. Find the number of hits in 40 shots.
|
Solution. From formula (1.4.1), it follows that $m=W n$. Since $W=0.75, n=40$, then $m=0.75 \cdot 40=30$. Therefore, 30 hits were obtained.
|
30
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 6. The frequency of normal seed germination $W=0.97$. Out of the sown seeds, 970 germinated. How many seeds were sown?
|
Solution. From formula (1.4.1), it follows that $n=\frac{m}{W}$. Since $m=970, \quad W=0.97$, then $n=970 / 0.97=1000$. Therefore, 1000 seeds were sown.
|
1000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 22. How many times do you need to roll two dice so that the probability of rolling at least one double six is greater than $1 / 2$? (This problem was first posed by the French mathematician and writer de Mere ( $1610-1684$ ), hence the problem is named after him).
|
Solution. Let the event $A_{i}$ be "rolling two sixes on the $i$-th throw". Since any of the six faces of the first die can match any of the six faces of the second die, there are $6 \cdot 6=36$ equally likely and mutually exclusive events. Only one of these - rolling a six on both the first and the second die - is favorable to the event $A_{i}$. Therefore,
$$
P\left(A_{i}\right)=\frac{1}{36}
$$
from which
$$
q=1-p=1-\frac{1}{36}=\frac{35}{36}
$$
The throws of the dice are independent trials, so we can use formula (1.8.17), which in this case takes the form
$$
1-\left(\frac{35}{36}\right)^{n}>\frac{1}{2}
$$
or
$$
\left(\frac{35}{36}\right)^{n}\frac{\ln 2}{\ln 36-\ln 35}=\frac{0.6931}{0.0284}=24.4
$$
Thus, to have the probability of rolling two sixes greater than $1 / 2$, the dice need to be thrown at least 25 times.
|
25
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 5. The distribution law of a discrete random variable is given by the following table:
| $X$ | 0 | 1 | 2 | 3 |
| :---: | :---: | :---: | :---: | :---: |
| $P$ | 0.2 | 0.4 | 0.3 | 0.1 |
Find the distribution function of this random variable.
|
Solution. To construct the distribution function $F(x)$ of a discrete random variable $X$, we use formula (2.2.11).
1. For $x \leq 0 \quad F(x)=\sum_{x_{k}3 \quad F(x)=P(X=0)+P(X=1)+P(X=2)+P(X=3)=$
$$
=0.2+0.4+0.3+0.1=1
$$
The graph of the function $F(x)$ is shown in Fig. 2.7.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 4. The mathematical expectations of two independent random variables $X$ and $Y$ are known: $M(X)=4, M(Y)=5$.
Find the mathematical expectation of their product.
|
Solution. Applying formula (2.4.15), we find
$$
M(X \cdot Y)=M(X) \cdot M(Y)=4 \cdot 5=20
$$
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 5. Find the mathematical expectation of the random variable $Y=2X+7$, given that $M(X)=4$.
|
Solution. Using formulas (2.4.10), (2.4.11), (2.4.12), we find
$$
\begin{aligned}
& M(Y)=M(2 X+7)=M(2 X)+M(7)= \\
& =2 M(X)+7=2 \cdot 4+7=15
\end{aligned}
$$
|
15
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 7. Two dice are rolled. The discrete random variable $X$ is the sum of the points that appear on both dice. Find the mathematical expectation of this random variable.
|
Solution. This random variable takes all integer values from 2 to 12. The distribution law can be given by the following table:
| $X$ | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $P$ | $\frac{1}{36}$ | $\frac{2}{36}$ | $\frac{3}{36}$ | $\frac{4}{36}$ | $\frac{5}{36}$ | $\frac{6}{36}$ | $\frac{5}{36}$ | $\frac{4}{36}$ | $\frac{3}{36}$ | $\frac{2}{36}$ | $\frac{1}{36}$ |
By formula (2.4.3) we find
$$
\begin{aligned}
& M(X)=2 \cdot \frac{1}{36}+3 \cdot \frac{2}{36}+4 \cdot \frac{3}{36}+5 \cdot \frac{4}{36}+6 \cdot \frac{5}{36}+ \\
& +7 \cdot \frac{6}{36}+8 \cdot \frac{5}{36}+9 \cdot \frac{4}{36}+10 \cdot \frac{3}{36}+11 \cdot \frac{2}{36}+12 \cdot \frac{1}{36}= \\
& =\frac{2+6+12+20+30+42+40+36+30+22+12}{36}=\frac{252}{36}=7
\end{aligned}
$$
Remark 1. This result can be obtained more easily. Let the random variable for the number of points that fall on one die be denoted by $X$, and on the other die by $Y$. These random variables have the same distribution laws (see Example 6). By formula (2.4.12) we get
$$
M(X+Y)=M(X)+M(Y)=3.5+3.5=7
$$
Remark 2. Since the variables $X$ and $Y$ are independent, we can also find the mathematical expectation of the random variable $Z=XY$ - the product of the number of points that fall when two dice are rolled simultaneously. By formula (2.4.15) we have:
$$
M(Z)=M(X \cdot Y)=M(X) \cdot M(Y)=3.5 \cdot 3.5=12.25
$$
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 13. Find the mathematical expectation of a random variable $X$, the distribution function of which is given by
$$
F(x)= \begin{cases}0 & \text { if } x \leq -a \\ \frac{(a+x)^{2}}{2 a^{2}} & \text { if } -a < x \leq a \\ 1 & \text { if } x > a\end{cases}
$$
|
Solution. First, let's find the probability density function of this random variable. Since \( p(x) = F'(x) \), we have:
\[
p(x)= \begin{cases}0 & \text{if } x \leq -a \\ \frac{1}{a}\left(1+\frac{x}{a}\right) & \text{if } -a < x \leq 0 \\ \frac{1}{a}\left(1-\frac{x}{a}\right) & \text{if } 0 < x \leq a \\ 0 & \text{if } x > a\end{cases}
\]
Using formula (2.4.7), we find the required expected value:
\[
\begin{aligned}
& M(X)=\int_{-a}^{a} x p(x) d x=\int_{-a}^{0} \frac{1}{a}\left(1+\frac{x}{a}\right) x d x+\int_{0}^{a} \frac{1}{a}\left(1-\frac{x}{a}\right) x d x= \\
& =\frac{1}{a} \int_{-a}^{0}\left(x+\frac{x^{2}}{a}\right) d x+\frac{1}{a} \int_{0}^{a}\left(x-\frac{x^{2}}{a}\right) d x=\left.\frac{1}{a}\left(\frac{x^{2}}{2}+\frac{x^{3}}{3 a}\right)\right|_{-a} ^{0}+ \\
& +\left.\frac{1}{a}\left(\frac{x^{2}}{2}-\frac{x^{3}}{3 a}\right)\right|_{0} ^{a}=\frac{1}{a}\left(-\frac{(-a)^{2}}{2}-\frac{(-a)^{3}}{3 a}\right)+\frac{1}{a}\left(\frac{(a)^{2}}{2}-\frac{(a)^{3}}{3 a}\right)=0
\end{aligned}
\]
## Problems
1. Find the expected value of a discrete random variable whose distribution is given by the table:
| $X$ | 1 | 2 | 3 | 4 | 5 |
| :---: | :---: | :---: | :---: | :---: | :---: |
| $P$ | 0.15 | 0.25 | 0.3 | 0.2 | 0.1 |
2. The distribution of a discrete random variable is given by the table:
| $X$ | 3 | 6 | 9 | 12 |
| :---: | :---: | :---: | :---: | :---: |
| $P$ | 0.1 | 0.2 | 0.3 | 0.4 |
Write the distribution laws for the random variables $2X$, $X/3$. Find the expected values of the random variables $X$, $2X$, $X/3$.
3. The expected values of two random variables $X$ and $Y$ are known: $M(X)=7$, $M(Y)=4$. Find the expected values of the sum and difference of these variables.
4. The expected values of two independent random variables $X$ and $Y$ are known: $M(X)=6$, $M(Y)=8$. Find the expected value of their product.
5. Find the expected value of the random variable $Y=8X+5$, if it is known that $M(X)=1.5$.
6. A discrete random variable $X$, which can take an infinite sequence of values, is given by the following distribution:
| $X$ | $1/4$ | $1/4^2$ | $1/4^3$ | $\ldots$ | $1/4^k$ | $\ldots$ |
| :--- | :---: | :---: | :---: | :---: | :---: | :---: |
| $P$ | $1/2$ | $1/2^2$ | $1/2^3$ | $\ldots$ | $1/2^k$ | $\ldots$ |
\[
\sum_{k=1}^{\infty} \frac{1}{2^k}=1
\]
Find the expected value of this random variable.
7. The probability density function of a random variable $X$ is given by
\[
p(x)= \begin{cases}0 & \text{if } x \leq 0 \\ 3x^2 & \text{if } 0 < x \leq 1 \\ 0 & \text{if } x > 1\end{cases}
\]
Find the expected value of the random variable $X$.
8. Find the expected value of the random variable $X$, if the distribution function of this variable is given by
\[
F(x)= \begin{cases}0 & \text{if } x \leq 0 \\ x/3 & \text{if } 0 < x \leq 3 \\ 1 & \text{if } x > 3\end{cases}
\]
9. Find the expected value of the random variable $X$, if the distribution function is given by
\[
F(x)=\begin{cases}
0 & \text{if } x \leq 0 \\
1-e^{-\alpha x} & \text{if } x > 0
\end{cases} \quad (\alpha > 0)
\]
## Answers
1. 2.85. 2. 9, 18, 3. 11, 3. 4. 48. 5. 17. 6. 1/7. 7. 0.75. 8. 4.5. 9. 1/α.
## Questions
1. How is the expected value of a discrete random variable $X$ defined, which takes a finite set of values?
2. What other names are used for the expected value? What explains these names?
3. What is the expected value of a discrete random variable $X$ that takes a countable set of values?
4. How is the expected value of a continuous random variable defined, all values of which belong to the interval $[\alpha, \beta]$?
5. How is the expected value of a continuous random variable defined, all values of which belong to the infinite interval $(-\infty, +\infty)$?
6. What are the properties of the expected value of a random variable?
7. What conditions must random variables $X$ and $Y$ satisfy for equation (2.4.15) to hold?
8. Prove that the expected value of a non-negative discrete variable is non-negative.
## § 2.5. Variance of a Random Variable. Mean Square Deviation
The difference $X - M(X)$ is called the deviation of the random variable $X$ from its expected value $M(X)$. The expected value of the deviation is zero:
\[
M(X - M(X)) = 0
\]
The variance, or dispersion, of a random variable $X$ is the expected value of the square of its deviation:
\[
D(X) = M\left((X - M(X))^2\right)
\]
From the definition and properties of the expected value, it follows that the variance of any random variable is non-negative, i.e.,
\[
D(X) \geq 0
\]
For calculating the variance, the formula
\[
D(X) = M(X^2) - (M(X))^2
\]
is used.
The variance of a random variable has the following properties:
1. The variance of a constant is zero:
\[
D(C) = 0 \quad (C = \text{const})
\]
2. A constant factor can be factored out of the variance, squaring it:
\[
D(CX) = C^2 D(X) \quad (C = \text{const})
\]
4. The variance of the sum of two independent random variables is equal to the sum of their variances:
\[
D(X + Y) = D(X) + D(Y)
\]
5. The variance of the difference of two independent random variables is equal to the sum of their variances:
\[
D(X - Y) = D(X) + D(Y)
\]
Remark. Property 3 extends to $n$ independent random variables:
\[
D(X_1 + X_2 + \ldots + X_n) = D(X_1) + D(X_2) + \ldots + D(X_n)
\]
The variance of a discrete random variable with the distribution
\[
\begin{aligned}
& P(X = x_k) = p_k \quad (k = 1, 2, \ldots, n) \\
& \sum_{k=1}^{n} p_k = 1
\end{aligned}
\]
is defined by the formula
\[
D(X) = \sum_{k=1}^{n} (x_k - M(X))^2 p_k
\]
or the formula
\[
D(X) = \sum_{k=1}^{n} (x_k - a)^2 p_k
\]
where
\[
a = M(X)
\]
is another notation for the expected value. We will use this notation in the future, depending on the circumstances.
If a discrete random variable takes an infinite sequence of values with the distribution
\[
\begin{aligned}
& P(X = x_k) = p_k \quad (k = 1, 2, 3, \ldots) \\
& \sum
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 8. The average germination rate of seeds is $80 \%$. Find the most probable number of germinated seeds among nine seeds.
|
Solution. The number $k_{0}$ will be determined using inequalities (3.1.5). Since $n=9, p=0.8$, and $q=0.2$, then $9 \cdot 0.8 - 0.2 \leq k_{0} \leq 9 \cdot 0.8 + 0.8 = 8$. An integer is obtained; hence, there are two most probable numbers of germinated seeds: 8 and 7. Their probabilities are the highest and equal to each other.
Indeed,
$$
\begin{aligned}
& P_{9}(7)=C_{9}^{7} p^{7} q^{9-7}=C_{9}^{7} \cdot(0.8)^{7} \cdot(0.2)^{2}=36 \cdot 0.2097 \cdot 0.04 \approx 0.302 \\
& P_{9}(8)=C_{9}^{8} p^{8} q^{9-8}=C_{9}^{8} \cdot(0.8)^{8} \cdot 0.2=9 \cdot 0.1678 \cdot 0.2 \approx 0.302
\end{aligned}
$$
|
78
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2. Prove that
$$
\sum_{k=0}^{\infty} p_{k}=\sum_{k=0}^{\infty} \frac{a^{k} e^{-a}}{k!}=1
$$
|
Solution. Taking into account the power series expansion of the function $f(x)=e^{x}$
$$
e^{x}=1+\frac{x}{1!}+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\ldots+\frac{x^{k}}{k!}+\ldots
$$
and the resulting equality
$$
e^{a}=1+\frac{a}{1!}+\frac{a^{2}}{2!}+\frac{a^{3}}{3!}+\ldots+\frac{a^{k}}{k!}+\ldots
$$
we obtain
$$
\sum_{k=0}^{\infty} \frac{a^{k} e^{-a}}{k!}=e^{-a} \sum_{k=0}^{\infty} \frac{a^{k}}{k!}=e^{-a}\left(1+\frac{a}{1!}+\frac{a^{2}}{2!}+\frac{a^{3}}{3!}+\ldots+\frac{a^{k}}{k!}+\ldots\right)=e^{-a} e^{a}=1
$$
Thus, the series of probabilities of the Poisson distribution converges and its sum is equal to one, i.e., condition (2.1.4) in the definition of the distribution law of a discrete random variable is satisfied.
|
1
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Example 12. A factory sent 5000 good-quality items to a base. The probability that an item will be damaged during transportation is 0.0002. What is the probability that 3 defective items will arrive at the base?
$\mathrm{Pe} \mathrm{sh} \mathbf{e n i e . ~ F r o m ~ t h e ~ c o n d i t i o n ~ i t ~ f o l l o w s ~ t h a t ~} n=5000, p=0.0002, \text{ and } np=5000 \cdot 0.0002=1$. According to formula (3.3.1) we have
$$
P_{5000}(3)=\frac{1^{3}}{3!} e^{-1}=\frac{1}{6 e} \approx 0.0613
$$
Example 13. A radio apparatus consists of 1000 electrical elements. The probability of failure of one element in one year of operation is 0.001 and is independent of the state of other elements. What is the probability of the failure of two elements? What is the probability of the failure of at least two elements in a year?
|
Solution. Here it is required to find the probabilities: 1) $P_{1000}(2)$;
2) $P_{1000}(k \geq 2)$. According to the condition, $n=1000, p=0.001, a=n p=1000 \cdot 0.001=1$.
The probability of exactly two elements failing:
$$
P_{1000}(2)=\frac{a^{2}}{2!} e^{-a}=\frac{1}{2 e} \approx 0.1831
$$
The probability of at least two elements failing:
$$
P_{1000}(k \geq 2)=\sum_{k=2}^{\infty} p_{k}=1-p_{0}-p_{1}=1-e^{-a}(1+a)=1-\frac{2}{e} \approx 0.2642
$$
|
0
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 9. Find the mathematical expectation of a random variable $X$,
uniformly distributed on the interval $[2,8]$.
|
Solution. The mathematical expectation of a random variable $X$, uniformly distributed on the interval $[\alpha, \beta]$, is defined by formula (3.4.7). Since in this case $\alpha=2, \beta=8$, then
$$
M(X)=\frac{8+2}{2}=5
$$
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 1. Prove that the function (3.5.1), defining the density of the normal distribution, satisfies condition (2.3.6), i.e.
$$
\int_{-\infty}^{+\infty} p(x) d x=1
$$
|
Solution. In the integral
$$
\int_{-\infty}^{+\infty} p(x) d x=\frac{1}{\sigma \sqrt{2 \pi}} \int_{-\infty}^{+\infty} e^{-(x-a)^{2} / 2 \sigma^{2}} d x
$$
we will transition to a new variable \( t \) using the formula
$$
t=\frac{x-a}{\sigma}
$$
Then \( x=a+\sigma t, d x=\sigma d t \). Since the new limits of integration are the same as the old ones, we have
$$
\frac{1}{\sigma \sqrt{2 \pi}} \int_{-\infty}^{+\infty} e^{-(x-a)^{2} / 2 \sigma^{2}} d x=\frac{1}{\sigma \sqrt{2 \pi}} \int_{-\infty}^{+\infty} e^{-t^{2} / 2} \sigma d t=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{+\infty} e^{-t^{2} / 2} d t=\frac{1}{\sqrt{2 \pi}} \cdot \sqrt{2 \pi}=1 .
$$
Here it is taken into account that
$$
\int_{-\infty}^{+\infty} e^{-t^{2} / 2} d t=\sqrt{2 \pi}
$$
Thus,
$$
\frac{1}{\sigma \sqrt{2 \pi}} \int_{-\infty}^{+\infty} e^{-(x-a)^{2} / 2 \sigma^{2}} d x=1
$$
|
1
|
Calculus
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Example 14. A machine manufactures bearings, which are considered suitable if the deviation $X$ from the design size in absolute value does not exceed 0.77 mm. What is the most probable number of suitable bearings out of 100, if the random variable $X$ is normally distributed with the parameter $\sigma=0.4$ mm?
|
Solution. First, we find the probability of deviation using formula (3.5.4) with $\delta=0.77$ and $\sigma=0.4$:
$$
P(|X-a|<0.77)=2 \Phi\left(\frac{0.77}{0.4}\right) \approx 2 \Phi(1.93)=2 \cdot 0.473197=0.946394
$$
Approximating $p=0.95$ and $q=0.05$, according to formula (3.1.5), i.e., $n p-q \leq k_{0} \leq n p+p$, we find for $n=100$:
$$
100 \cdot 0.95-0.05 \leq k_{0} \leq 100 \cdot 0.95+0.95
$$
from which $k_{0}=95$.
|
95
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 4. Prove that the function (3.6.2) satisfies condition (2.3.6), i.e. $\int_{-\infty}^{+\infty} p(x) d x=1$.
|
Solution. Indeed,
$$
\int_{-\infty}^{+\infty} p(x) d x=\int_{-\infty}^{0} p(x) d x+\int_{0}^{+\infty} p(x) d x=\int_{-\infty}^{0} 0 \cdot d x+\int_{0}^{+\infty} \alpha e^{-\alpha x} d x=
$$
$$
=-\int_{0}^{+\infty} d\left(e^{-\alpha x}\right)=-\left.e^{-\alpha x}\right|_{0} ^{+\infty}=-\left(e^{-\infty}-e^{0}\right)=1
$$
|
1
|
Calculus
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Example 11. Find the mathematical expectation of the random variable
$X$, the density of which is determined by the function $p(x)=0.2 e^{-0.2 x}$ for $x \geq 0$.
|
Solution. Since in this case $\alpha=0.2$ and $M(X)=\frac{1}{\alpha}$, then
$$
M(X)=\frac{1}{2 / 10}=\frac{10}{2}=5, \quad M(X)=5
$$
|
5
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 3. For what number of independent trials will the probability of the inequality $\left|\frac{m}{n}-p\right|<0.2$ being satisfied exceed 0.96, if the probability of the event occurring in a single trial $p=0.7$?
|
Solution. According to the problem, we have: $\varepsilon=0.2, p=0.7$, so $q=0.3$; it is required to determine $n$ using inequality (4.2.5). The condition $P>0.96$ is equivalent to the inequality
$$
\frac{p q}{n \varepsilon^{2}} < 0.04
$$
or
$$
n > \frac{p q}{\varepsilon^{2} \cdot 0.04}
$$
Substituting the values $p=0.7, q=0.3$, and $\varepsilon=0.2$ into the last inequality, we find that
$$
n > \frac{0.7 \cdot 0.3}{(0.2)^{2} \cdot 0.04} = \frac{0.21}{0.0016} = 131.25
$$
Therefore, the required inequality is satisfied for the number of independent trials starting from 132.
Example 4. To determine the average yield of a field with an area of 1800 hectares, a sample of $1 \mathrm{~m}^{2}$ was taken from each hectare. It is known that the variance on each hectare of the field does not exceed 6. Estimate the probability that the deviation of the average sample yield from the average yield of the entire field does not exceed 0.25 centners.
Solution. In the right-hand side of inequality (4.2.1.), which defines the required probability, the values are given: $\varepsilon=0.25, C=6$, and $n=1800$. Therefore,
$$
P > 1 - \frac{C}{n \varepsilon^{2}} = 1 - \frac{6}{1800 \cdot 0.0625} = 1 - 0.053 = 0.947
$$
Example 5. The variance of each of the 1000 independent random variables $X_{\kappa} (\kappa=1,2, \ldots, 1000)$ is 4. Estimate the probability that the deviation of the arithmetic mean of these variables from the arithmetic mean of their mathematical expectations in absolute value does not exceed 0.1.
Solution. According to inequality (4.2.1.) with $C=4, \varepsilon=0.1$, we get
$$
P\left(\left|\frac{1}{1000} \sum_{k=1}^{1000} X_{k} - \frac{1}{1000} \sum_{k=1}^{1000} M\left(X_{\kappa}\right)\right| \leq 0.1\right) \geq 1 - \frac{4}{1000 \cdot 0.1^{2}} = 0.6
$$
Thus, $P \geq 0.6$.
|
132
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 6. Determine how many measurements of the cross-sectional diameter of trees need to be made on a large plot so that the average diameter of the trees differs from the true value $a$ by no more than 2 cm with a probability of at least 0.95. The standard deviation of the cross-sectional diameter of the trees does not exceed $10 \mathrm{~cm}$ and measurements are taken without error.
|
Solution. We will consider the selection of trees for measurements such that the measurement results can be regarded as independent random variables. Let $X_{i}$ denote the measurement result of the cross-section of the $i$-th tree. According to the problem, $\sigma\left(X_{i}\right)=\sqrt{D\left(X_{i}\right)} \leq 10$, hence, $D\left(X_{i}\right) \leq 100$.
Assuming in inequality (4.2.3.) $\varepsilon=2, C=100$, we get
$$
P\left(\left|\frac{1}{n} \sum_{i=1}^{n} X_{i}-a\right|<2\right) \geq 1-\frac{100}{n \cdot 2^{2}} \geq 0.95
$$
Since
$$
1-\frac{100}{n \cdot 2^{2}} \geq 0.95, \text { then } 0.05 \geq \frac{100}{n \cdot 4}, n \geq \frac{100}{4 \cdot 0.05}=500
$$
Therefore, it is sufficient to perform 500 measurements of the cross-section of the trees.
|
500
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 11. On average, $85 \%$ of the items coming off the conveyor are of the first grade. How many items need to be taken so that with a probability of 0.997, the deviation of the frequency of first-grade items from the probability $p=0.85$ in absolute value does not exceed $0.01?$
|
Solution. We will use the formula
$$
P\left(\left|\frac{m}{n}-p\right| \leq \varepsilon\right)=2 \Phi\left(\varepsilon \sqrt{\frac{n}{p q}}\right)
$$
From the condition, it follows that $p=0.85, q=1-0.85=0.15, \varepsilon=0.01$, $P=0.997$. We need to determine the value of $n$. Since
$$
2 \Phi\left(\varepsilon \sqrt{\frac{n}{p q}}\right)=0.997, \quad \Phi\left(\varepsilon \sqrt{\frac{n}{p q}}\right)=0.4985
$$
we first solve the equation $\Phi(t)=0.4985 ; t=2.96$. Therefore,
$$
\varepsilon \sqrt{\frac{n}{p q}}=2.96, \quad \text { from which } \quad n=(2.96)^{2} \cdot \frac{p q}{\varepsilon^{2}}
$$
Substituting the values of $p, q$ and $\varepsilon$ into the last equation, we find $n$ :
$$
n=(2.96)^{2} \cdot \frac{0.85 \cdot 0.15}{(0.01)^{2}}, \quad n=11171
$$
|
11171
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 1. Find the zeros of the function $f(z)=e^{z}-1-z$ and determine their order.
|
Solution.
1. Find the zeros of the function $f(z)$ by solving the equation $e^{z}-1-z=0$. We get $z=0$.
2. Determine the order of the obtained zero $z=0$. For this, we use the Taylor series expansion of the function $f(z)$ in powers of $z$:
$$
e^{z}-1-z=\left(1+z+\frac{z^{2}}{2!}+\frac{z^{3}}{3!}+\ldots\right)-1-z=\frac{z^{2}}{2!}+\frac{z^{3}}{3!}+\ldots
$$
Since in the obtained expansion the coefficients $c_{0}=c_{1}=0$, and $c_{2}=1 / 2 \neq 0$, the point $z=0$ is a zero of the 2nd order of the function $f(z)$.
Answer. $z=0$ is a zero of the 2nd order of the function $f(z)$.
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2. How to find out how many fish are in the pond?
We catch $n_{a}=20$ fish, mark them, and release them back into the pond. After some time, sufficient for the marked fish to disperse throughout the pond, we catch $m=50$ fish. Suppose that among them, $k_{1}=7$ are marked. Determine the number of fish in the pond $N$ using the method of maximum likelihood.
|
## Solution.
1. The random variable $\xi$ - the number of marked fish among $m$ caught - is determined by the probabilities
$$
\mathrm{P}(\xi=k)=p(k ; N)=\frac{C_{n_{a}}^{k} C_{N-n_{a}}^{m-k}}{C_{N}^{m}}=\frac{C_{20}^{k} C_{N-20}^{50-k}}{C_{N}^{50}}(k=0,1, \ldots, 50)
$$
2. We define the likelihood function
$$
L(N)=\frac{C_{20}^{7} C_{N-20}^{43}}{C_{N}^{50}}
$$
In this case, the sample consists of a single number $k_{1}=7$.
3. We find the unknown parameter $N$ (the number of fish in the pond) from the condition
$$
L(N) \longrightarrow \max
$$
i.e., the value of $N$ for which the likelihood function $L(N)$ has the maximum value.
The function $L(N)$ is not differentiable, as its argument $N$ takes only discrete values $63,64, \ldots$ Therefore, the value of $N$ for which $L(N)$ reaches its maximum value is found by enumeration.
We have
$$
L(N)=C_{20}^{7} \frac{(N-20)!50!(N-50)!}{43!(N-63)!N!}=A \frac{(N-50) \cdot \ldots \cdot(N-62)}{N(N-1) \cdot \ldots \cdot(N-19)}
$$
where $A=\frac{50!}{43!} C_{20}^{7}$ is an insignificant multiplier. A simple program provides a table of values of $L(N)$ for $N=63 \div 1000$. In the table, we find that $L(N)$ reaches its maximum value at $N=142$.
Answer. $\quad N=142$.
Conditions of the problems. Using the method of maximum likelihood, find the parameters of the distribution based on the sample.
1. Binomial distribution $p(k ; n, p)=C_{n}^{k} p^{k} q^{n-k}, \quad n=10$, sample: $6,5,9,5,8,7,9,6,6,7$.
2. Poisson distribution $p(k ; a)=e^{-a} a^{k} / k!$, sample: $5,3,3,3,5,5,1,2,3,0$.
3. Geometric distribution $p(k ; q)=(1-q) q^{k}$, sample: $1,2,0,4,1,4,4,1,2,2$.
4. Hypergeometric distribution $p\left(k ; n_{A}, n_{B}, m\right)=\frac{C_{n_{a}}^{k} C_{n_{b}}^{m-k}}{C_{n_{a}+n_{b}}^{m}}$, $m=10$, sample: $6,3,7,6,4,4,5,5,6,8$.
5. Distribution of stellar multiplicity $p(k ; q)=(1-q)^{2} k q^{k-1}$, sample: $1,2,1,3,2,1,1,2,1,2$.
6. Uniform distribution $p(x ; a, b)=\frac{1}{b-a}$ for $a \leq x \leq b$, $p(x ; a, b)=0$ for $x < a$ or $x > b$, sample:
$0.35,1.83,0.14,0.64,2.08,-0.46,2.0,-0.31,-0.30,1.87$.
7. Exponential distribution $p(x ; \lambda)=\lambda e^{-\lambda x}$ for $x>0$, $p(x ; \lambda)=0$ for $x \leq 0$, sample:
$1.63,1.35,1.80,1.51,1.56,2.10,1.36,1.48,1.24,1.39$.
8. Rayleigh distribution $p(x ; t)=\frac{x}{t^{2}} e^{-x^{2} / (2 t^{2})}$ for $x>0$, $p(x ; t)=0$ for $x \leq 0$, sample:
$1.63,1.35,1.80,1.51,1.56,2.10,1.36,1.48,1.24,1.39$.
9. Gamma distribution $p(x ; \lambda, \alpha)=\frac{\lambda^{\alpha}}{\Gamma(\alpha)} x^{\alpha-1} e^{-\lambda x}$ for $x>0$, $p(x ; \lambda, \alpha)=0$ for $x \leq 0$, sample:
$1.63,1.35,1.80,1.51,1.56,2.10,1.36,1.48,1.24,1.39$.
10. Weibull distribution $p(x ; a, \alpha)=\frac{\alpha}{a} \left(\frac{x}{a}\right)^{\alpha-1} e^{-(x/a)^{\alpha}}$ for $x \geq a$, $p(x ; a, \alpha)=0$ for $x < a$, sample:
$1.63,1.35,1.80,1.51,1.56,2.10,1.36,1.48,1.24,1.39$.
Answers. 1. $p=0.68$. 2. $a=3.235$. 3. $q=0.677$. 4. $n_{a}=17$, $n_{b}=25$. 5. $q=0.23$. 6. $a=-0.46, b=2.08$. 7. $\lambda=1.17$. 8. $t=1.8$. 9. $\lambda=3.60$. 10. $a=1.24, \alpha=2.88$.
### 7.13. Method of Least Squares
PROBLEM STATEMENT. To determine the parameters $a_{1}, \ldots, a_{j}$ in the formula $y=f\left(x ; a_{1}, \ldots, a_{j}\right)$, values of $y$ were measured at different values of $x$. The sample obtained is $\left(x_{1}, y_{1}\right), \ldots,\left(x_{n}, y_{n}\right)$. Using these data, determine the parameters $a_{1}, \ldots, a_{j}$ by the method of least squares. Errors in the measurements of $x_{1}, \ldots, x_{n}$ and computational errors can be neglected.
PLAN OF SOLUTION. The quantities $\xi_{k}=y_{k}-f\left(x_{k} ; a_{1}, \ldots, a_{j}\right)$ are non-zero due to measurement errors in $y_{k}$, since errors in the measurements of $x_{k}$ and the computation of $f\left(x_{k} ; a_{1}, \ldots, a_{j}\right)$ can be neglected. It is assumed that measurement errors are normally distributed with a mean of 0 (no systematic errors) and some variance $\sigma^{2}$, determined by the accuracy of the instrument. Therefore, the likelihood function has the form
$$
\begin{aligned}
L\left(a_{1}, \ldots, a_{j}\right)= & \frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{-\xi_{1}^{2} /\left(2 \sigma^{2}\right)} \cdot \ldots \cdot \frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{-\xi_{n}^{2} /\left(2 \sigma^{2}\right)}= \\
& =\frac{1}{\left(2 \pi \sigma^{2}\right)^{n / 2}} \exp \left[-\frac{1}{2 \sigma^{2}} \sum_{k=1}^{n}\left(y_{k}-f\left(x_{k} ; a_{1}, \ldots, a_{j}\right)\right)^{2}\right]
\end{aligned}
$$
This function reaches its maximum value for those $a_{1}, \ldots, a_{j}$ for which
$$
S\left(a_{1}, \ldots, a_{j}\right)=-\ln L\left(a_{1}, \ldots, a_{j}\right)=\sum_{k=1}^{n}\left(y_{k}-f\left(x_{k} ; a_{1}, \ldots, a_{j}\right)\right)^{2}
$$
reaches its minimum value.
1. We find the partial derivatives
$$
\frac{\partial S}{\partial a_{k}} \quad(k=1, \ldots, j)
$$
2. We determine the parameters $a_{1}, \ldots, a_{j}$ as the solution to the system of equations
$$
\frac{\partial S}{\partial a_{1}}=0, \quad \frac{\partial S}{\partial a_{2}}=0, \ldots, \frac{\partial S}{\partial a_{j}}=0
$$
Remarks.
1. After the parameters $a_{1}, \ldots, a_{j}$ are determined,
|
142
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.7. Calculate the determinant
$$
\Delta=\left|\begin{array}{cccc}
3 & 1 & -1 & 2 \\
-3 & 1 & 4 & -5 \\
2 & 0 & 1 & -1 \\
3 & -5 & 4 & -4
\end{array}\right|
$$
|
S o l u t i o n. Notice that the second column of the determinant already contains one zero element. Add to the elements of the second row the elements of the first row multiplied by -1, and to the elements of the fourth row - the elements of the first row multiplied by 5. We get:
$$
\Delta=\left|\begin{array}{cccc}
3 & 1 & -1 & 2 \\
(-3-3) & (1-1) & (1+4) & (-2-5) \\
2 & 0 & 1 & -1 \\
(15+3) & (5-5) & (-5+4) & (10-4)
\end{array}\right|=\left|\begin{array}{cccc}
3 & 1 & -1 & 2 \\
-6 & 0 & 5 & -7 \\
2 & 0 & 1 & -1 \\
18 & 0 & -1 & 6
\end{array}\right| .
$$
Expanding the obtained determinant along the second row, we have:
$$
\Delta=(-1)^{1+2} \cdot 1 \cdot\left|\begin{array}{ccc}
-6 & 5 & -7 \\
2 & 1 & -1 \\
18 & -1 & 6
\end{array}\right|=-2 \cdot\left|\begin{array}{ccc}
-3 & 5 & -7 \\
1 & 1 & -1 \\
9 & -1 & 6
\end{array}\right|
$$
(Then we factored out the multiplier 2 from the first column based on property 4.) Next, add to the elements of the first and second columns the elements of the third column of the determinant. We get:
$$
\Delta=-2 \cdot\left|\begin{array}{ccc}
-10 & -2 & -7 \\
0 & 0 & -1 \\
15 & 5 & 6
\end{array}\right|=-2 \cdot 5 \cdot\left|\begin{array}{ccc}
-2 & -2 & -7 \\
0 & 0 & -1 \\
3 & 5 & 6
\end{array}\right|=10 \cdot\left|\begin{array}{ccc}
2 & 2 & 7 \\
0 & 0 & -1 \\
3 & 5 & 6
\end{array}\right|
$$
Here we factored out the multiplier in the first column, and then the common multiplier $(-1)$ in the first row. Expanding the resulting third-order determinant along the elements of the second row, we get:
$$
\Delta=10 \cdot(-1) \cdot(-1)^{2+3}\left|\begin{array}{cc}
2 & 2 \\
3 & 5
\end{array}\right|=10 \cdot(10-6)=40
$$
Here the second-order determinant is calculated according to its definition, by the formula
$$
\left|\begin{array}{ll}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{array}\right|=a_{11} \cdot a_{12}-a_{21} \cdot a_{22}
$$
|
40
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.9. Using the property that the determinant of the matrix $C=A \cdot B$, which represents the product of square matrices $A$ and $B$ of the same order, is equal to the product of the determinants of matrices $A$ and $B$, i.e., $\operatorname{det} C=\operatorname{det} A \cdot \operatorname{det} B$, calculate the determinant of the matrix $\operatorname{det} C$.
$$
A=\left(\begin{array}{lll}
3 & 2 & 5 \\
0 & 2 & 8 \\
4 & 1 & 7
\end{array}\right), B=\left(\begin{array}{ccc}
-2 & 3 & 4 \\
-1 & -3 & 5 \\
0 & 4 & 3
\end{array}\right)
$$
|
Solution. We will find the determinants of matrices $A$ and $B$ and then multiply them. We have
$$
\operatorname{det} A=\left|\begin{array}{lll}
3 & 2 & 5 \\
0 & 2 & 8 \\
4 & 1 & 7
\end{array}\right|=\left|\begin{array}{ccc}
3 & 2 & -3 \\
0 & 2 & 0 \\
4 & 1 & 3
\end{array}\right|=2 \cdot(-1)^{2+2}\left|\begin{array}{cc}
3 & -3 \\
4 & 3
\end{array}\right|=2 \cdot(9+12)=42
$$
Here we multiplied the second column of the determinant by $(-4)$, added it to the third column, and then expanded the resulting determinant along the second row.
Similarly,
$$
\operatorname{det} B=\left|\begin{array}{ccc}
-2 & 3 & 4 \\
-1 & -3 & 5 \\
0 & 4 & 3
\end{array}\right|=\left|\begin{array}{ccc}
0 & 9 & -6 \\
-1 & -3 & 5 \\
0 & 4 & 3
\end{array}\right|=(-1) \cdot(-1)^{1+2}\left|\begin{array}{cc}
9 & -6 \\
4 & 3
\end{array}\right|=51
$$
Here we multiplied the second row by $(-2)$ and added it to the first row, and then expanded the resulting determinant along the first column. Multiplying the obtained values of the determinants, we find that $\operatorname{det} C=51 \cdot 42=2142$. It is easy to verify that we get the same result if we first find the matrix $C$ by multiplying matrices $A$ and $B$, in which case the matrix $C$ has the form:
$$
C=\left(\begin{array}{lll}
-8 & 23 & 37 \\
-2 & 26 & 34 \\
-9 & 37 & 42
\end{array}\right)
$$
and then compute $\operatorname{det} C$.
In addition to the method of reducing the order of the determinant (Example 1.7) and the method of reducing to a triangular form (Example 1.8), the method of recurrence relations is used when calculating determinants. The essence of the method is that the initial determinant $D_{n}$ of order $n$ is expressed in terms of determinants of the same type but of a lower order, i.e., by a recurrence formula of the form: $D_{n}=f\left(D_{n-1}, D_{n-2}, \ldots, D_{n-k}\right)$, valid for all natural numbers $n$ greater than $k$. From this relation, using the method of mathematical induction, a formula is obtained that expresses the determinant $D_{n}$ in terms of the determinants $D_{n-1}, D_{n-2}, \ldots, D_{n-k}$.
As an example of applying the specified method, we will compute the Vandermonde determinant:
$$
D_{n}=\left|\begin{array}{ccccc}
1 & 1 & 1 & \ldots & 1 \\
a_{1} & a_{2} & a_{3} & \ldots & a_{n} \\
a_{1}^{2} & a_{2}^{2} & a_{3}^{2} & \ldots & a_{n}^{2} \\
\ldots & \ldots & \ldots & \ldots & \ldots \\
a_{1}^{n-1} & a_{2}^{n-1} & a_{3}^{n-1} & \ldots & a_{n}^{n-1}
\end{array}\right|
$$
We will show that for any $n \geqslant 2$ the Vandermonde determinant is equal to the product of all possible differences $a_{i}-a_{j}$, where $1 \leqslant j<i \leqslant n$. Indeed, for $n=2$ we have
$$
D_{2}=\left|\begin{array}{cc}
1 & 1 \\
a_{1} & a_{2}
\end{array}\right|=a_{2}-a_{1}
$$
Suppose the statement is proved for Vandermonde determinants of order $n-1$:
$$
D_{n-1}=\prod_{1 \leqslant j<i \leqslant n-1}\left(a_{i}-a_{j}\right)
$$
where the symbol
$$
\prod_{i=1}^{n} a_{i}
$$
denotes the product of the elements $a_{i}$, i.e.,
$$
\prod_{i=1}^{n} a_{i}=a_{1} \cdot a_{2} \cdot \ldots \cdot a_{n}
$$
We will prove that this formula is also valid for $D_{n}$. For this, we subtract the $(n-1)$-th row from the last $n$-th row, multiplied by $a_{1}$, and then sequentially subtract the $(k-1)$-th row from the $k$-th row, multiplied by $a_{1}$. As a result, we get
$$
D_{n}=\left|\begin{array}{ccccc}
1 & 1 & 1 & \ldots & 1 \\
0 & a_{2}-a_{1} & a_{3}-a_{1} & \ldots & a_{n}-a_{1} \\
0 & a_{2}^{2}-a_{2} a_{1} & a_{3}^{2}-a_{3} a_{1} & \ldots & a_{n}^{2}-a_{n} a_{1} \\
\ldots & \ldots & \ldots & \ldots & \ldots \\
0 & a_{2}^{n-1}-a_{2}^{n-2} a_{1} & a_{3}^{n-1}-a_{3}^{n-2} a_{1} & \ldots & a_{n}^{n-1}-a_{n}^{n-2} a_{1}
\end{array}\right|
$$
Next, we expand this determinant along the first column and factor out the common factors from all columns. As a result, we obtain the recurrence relation:
$$
\begin{aligned}
D_{n}=\left(a_{2}-a_{1}\right) & \cdot\left(a_{3}-a_{1}\right) \ldots\left(a_{n}-a_{1}\right) \cdot\left|\begin{array}{cccc}
1 & 1 & & 1 \\
a_{2} & a_{3} & & a_{n} \\
a_{2}^{2} & a_{3}^{2} & & a_{n}^{2} \\
\ldots & \ldots & & \ldots \\
a_{2}^{n-2} & a_{3}^{n-2} & \ldots & a_{n}^{n-2}
\end{array}\right|= \\
& =\left(a_{2}-a_{1}\right) \cdot\left(a_{3}-a_{1}\right) \ldots\left(a_{n}-a_{1}\right) \times \\
& \times \prod_{2 \leqslant j<i \leqslant n}\left(a_{i}-a_{j}\right)=\prod_{1 \leqslant j<i \leqslant n}\left(a_{i}-a_{j}\right) .
\end{aligned}
$$
|
2142
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.13. Using the method of bordering minors, find the rank of the matrix
$$
A=\left(\begin{array}{ccccc}
2 & 1 & 2 & 1 & 2 \\
1 & 1 & 5 & -2 & 3 \\
-1 & 0 & -4 & 4 & 1 \\
3 & 3 & 8 & 1 & 9
\end{array}\right)
$$
|
Solution. The second-order minor
$$
M_{2}=\left|\begin{array}{ll}
2 & 1 \\
1 & 1
\end{array}\right|=2 \cdot 1-1 \cdot 1=1 \neq 0
$$
is non-zero and located in the upper left corner of matrix $A$. The third-order minor
$$
M_{3}=\left|\begin{array}{ccc}
2 & 1 & 2 \\
1 & 1 & 5 \\
-1 & 0 & 4
\end{array}\right|=\left|\begin{array}{ccc}
1 & 0 & -3 \\
1 & 1 & 5 \\
-1 & 0 & 4
\end{array}\right|=\left|\begin{array}{cc}
1 & -3 \\
-1 & 4
\end{array}\right|=4-3=1 \neq 0
$$
enclosing the minor $M_{2}$, is also non-zero. However, both fourth-order minors enclosing $M_{3}$,
$$
M_{4}=\left|\begin{array}{cccc}
2 & 1 & 2 & 1 \\
1 & 1 & 5 & -2 \\
-1 & 0 & -4 & 4 \\
3 & 3 & 8 & 1
\end{array}\right|, M_{4}=\left|\begin{array}{cccc}
2 & 1 & 2 & 2 \\
1 & 1 & 5 & 3 \\
-1 & 0 & -4 & 1 \\
3 & 3 & 8 & 9
\end{array}\right|
$$
are equal to zero. Therefore, the rank of matrix $A$ is 3, and a basis minor is, for example, the minor $M$ presented above.
The method of elementary transformations is based on the fact that elementary transformations of a matrix do not change its rank. Using these transformations, the matrix can be brought to a form where all its elements, except for $a_{11}, a_{22}, \ldots$, $a_{r r}(r \leqslant \min (m, n))$, are zero. This obviously means that rang $A=r$. Note that if an $n$-order matrix has the form of an upper triangular matrix, i.e., a matrix where all elements below the main diagonal are zero, then its determinant is equal to the product of the elements on the main diagonal. This property can be used when calculating the rank of a matrix using the method of elementary transformations: it is necessary to use them to bring the matrix to a triangular form, and then, by isolating the corresponding determinant, we find that the rank of the matrix is equal to the number of elements on the main diagonal that are non-zero.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.14. Using elementary transformations, find the rank of the matrix
$$
A=\left(\begin{array}{ccccc}
5 & 7 & 12 & 48 & -14 \\
9 & 16 & 24 & 98 & -31 \\
14 & 24 & 25 & 146 & -45 \\
11 & 12 & 24 & 94 & -25
\end{array}\right)
$$
|
Solution. Let's denote the $i$-th row of matrix $A$ by the symbol $\alpha_{i}$. In the first stage, we perform elementary transformations $\alpha_{2}^{\prime}=\alpha_{2}-\alpha_{3}+\alpha_{1}, \alpha_{3}^{\prime}=\alpha_{3}-\alpha_{2}-\alpha_{1} ; \alpha_{4}^{\prime}=\alpha_{4}-\alpha_{3}+\alpha_{1}$.
In the second stage, we perform the transformations
$$
\alpha_{3}^{n}=\alpha_{3}^{\prime}+\alpha_{2}^{\prime}, \alpha_{4}^{\prime \prime}=\alpha_{4}^{\prime}-\alpha_{2}^{\prime}
$$
As a result, we get
$$
\begin{aligned}
& \left(\begin{array}{ccccc}
5 & 7 & 12 & 48 & -14 \\
9 & 16 & 24 & 98 & -31 \\
14 & 24 & 25 & 146 & -45 \\
11 & 12 & 24 & 94 & -25
\end{array}\right) \xrightarrow{1}\left(\begin{array}{ccccc}
5 & 7 & 12 & 48 & -14 \\
0 & -1 & 11 & 0 & 0 \\
0 & 1 & -11 & 0 & 0 \\
0 & 0 & 0 & 0 & 0
\end{array}\right) \xrightarrow{2} \\
& \xrightarrow{2}\left(\begin{array}{ccccc}
5 & 7 & 12 & 48 & -14 \\
0 & -1 & 11 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & -4 & 6
\end{array}\right) \xrightarrow{3}\left(\begin{array}{ccccc}
5 & 7 & 12 & 48 & -14 \\
0 & -1 & 11 & 0 & 0 \\
0 & 0 & 0 & -4 & 6 \\
0 & 0 & 0 & 0 & 0
\end{array}\right) \xrightarrow{4} \\
& \xrightarrow{4}\left(\begin{array}{ccccc}
5 & 7 & 12 & 12 & -7 \\
0 & -1 & 0 & 2 & 0 \\
0 & 0 & -1 & 0 & 3 \\
0 & 0 & 0 & 0 & 0
\end{array}\right)
\end{aligned}
$$
In the third stage, we swapped the fourth row with the third row, and the third row with the fourth row. In the fourth stage, we divided the elements of the fourth and fifth columns by 4 and 2, respectively, and swapped the third and fourth columns. From the form of the matrix obtained after the fourth stage of transformation, it follows that
rank $A=3$. We could continue transforming matrix $A$, aiming to zero out the remaining elements of the matrix with different indices, but this is probably not advisable when finding the rank of the matrix. It is also worth noting that the resulting zero row from the elementary transformations could have been omitted in further transformations of the matrix, simply by deleting it, which, obviously, would not affect the rank of the original matrix.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.27. Given a linear transformation using a system of equations
$$
\left\{\begin{array}{l}
g_{1}=-x_{1}+0 \cdot x_{2}+0 \cdot x_{3} \\
g_{2}=0 \cdot x_{1}+1 \cdot x_{2}+0 \cdot x_{3} \\
g_{3}=0 \cdot x_{1}+0 \cdot x_{2}+1 \cdot x_{3}
\end{array}\right.
$$
Find the transformation matrix, will it be singular?
|
Solution. With the matrix representation of the transformation, we get:
$$
\left(\begin{array}{l}
g_{1} \\
g_{2} \\
g_{3}
\end{array}\right)=\left(\begin{array}{ccc}
-1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right) \cdot\left(\begin{array}{l}
x_{1} \\
x_{2} \\
x_{3}
\end{array}\right)
$$
Here, the transformation matrix
$$
A=\left(\begin{array}{ccc}
-1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right)
$$
has a non-zero determinant, equal to the product of all elements on the main diagonal \(\operatorname{det} A=(-1) \cdot 1 \cdot 1=-1 \neq 0\) (the mapping is also non-degenerate).
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.13. Are the vectors coplanar
$$
\vec{a}, \vec{b}, \vec{c}: \vec{a}=\{1,-2,1\}, \vec{b}=\{3,1,-2\}, \vec{c}=\{7,14,-13\} ?
$$
|
Solution. To answer the given question, it is necessary to calculate the mixed product of these vectors, and if it turns out to be zero, this will indicate that the vectors $\ddot{a}, \vec{b}, \vec{c}$ are coplanar. We find the mixed product $\vec{a} \cdot \vec{b} \cdot \vec{c}$ using formula (2.40).
$$
\begin{aligned}
\vec{a} \times \vec{b} \cdot \vec{c} & =\left|\begin{array}{ccc}
1 & -2 & 1 \\
3 & 1 & -2 \\
7 & 14 & -13
\end{array}\right|=1\left|\begin{array}{cc}
1 & -2 \\
14 & -13
\end{array}\right|-(-2)\left|\begin{array}{cc}
3 & -2 \\
7 & -13
\end{array}\right|+1\left|\begin{array}{cc}
3 & 1 \\
7 & 14
\end{array}\right|= \\
& =-13+28+2(-39+14)+42-7=15-50+35=0
\end{aligned}
$$
Since the mixed product $\vec{a} \cdot \vec{b} \cdot \vec{c}$ turned out to be zero, the vectors $\vec{a}, \ddot{b}, \vec{c}$ are coplanar.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.3. Obtain the equation of the line passing through two given points $P_{0}(1 ; 2)$ and $P_{1}(3 ; 2)$.
|
Solution.
1st step. Make a schematic drawing (Fig. 3.3).
2nd step. Write down the coordinates of the vectors defining the given geometric object - the line. This is the current vector lying on the line $\overrightarrow{P_{0} M}=\{x-1 ; y-2\}$ and the vector formed by two points on the line
$$
\overrightarrow{P_{0} P_{1}}=\{3-1 ; 2-2\}=\{1 ; 0\} .
$$
3rd step. Write down one of the conditions - orthogonality or collinearity, according to the problem. According to the problem, $\vec{P}_{0} M \| \bar{P}_{0} \vec{P}_{1}$, so we will use the condition of collinearity of two vectors in coordinate form $(x-1) / 2=(y-2) / 0$. We obtain the canonical equation of the line. Sometimes in the answer to the considered problem, it is mistakenly not written that part of the equation where zero appears in the denominator, referring to the fact that division by zero is not allowed. However, the equation $(x-1) / 2=(y-2) / 0$ does not describe division by zero; here only a symbolic notation is made that the current vector $\overrightarrow{P_{0} M}$ is collinear with the vector $\widetilde{P}_{0} \vec{P}_{1}$, one of whose components is zero.

Fig. 3.2
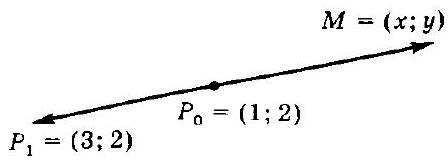
Fig. 3.3
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.23. Derive the polar equation of the ellipse $x^{2} / a^{2}+$ $+y^{2} / b^{2}=1$ under the condition that the direction of the polar axis coincides with the positive direction of the x-axis, and the pole is at the center of the ellipse.
|
Solution. Substitute into the ellipse equation the expressions for $x$ and $y$ in terms of the polar radius $\rho$ and the angle $\varphi$.
We have
$$
\frac{\rho^{2} \cos ^{2} \varphi}{a^{2}}+\frac{\rho^{2} \sin ^{2} \varphi}{b^{2}}=1, \rho^{2} \frac{b^{2} \cos ^{2} \varphi+a^{2} \sin ^{2} \varphi}{a^{2} b^{2}}=1
$$
Replace $b^{2}$ in the numerator with $a^{2}-c^{2}$ and use the fundamental trigonometric identity
$$
\begin{aligned}
& \cos ^{2} \varphi+\sin ^{2} \varphi=1, \quad \rho^{2} \frac{\left(a^{2}-c^{2}\right) \cos ^{2} \varphi+a^{2} \sin ^{2} \varphi}{a^{2} b^{2}}=1 \\
& \rho^{2} \frac{a^{2}-c^{2} \cos ^{2} \varphi}{a^{2} b^{2}}=1, \frac{\rho^{2}}{b^{2}}\left(1-\frac{c^{2}}{a^{2}} \cos ^{2} \varphi\right)=1
\end{aligned}
$$
Substitute $\varepsilon^{2}=c^{2} / a^{2}$, then we get $\rho^{2}=b^{2} /\left(1-\varepsilon^{2} \cos ^{2} \varphi\right)$. 3.24. At what point does the linear function $L(x, y)=\sqrt{2} x-y$ reach its maximum in the region described by the inequality $x^{2} / 9+y^{2} / 7 \leqslant 1 ?$
Solution. Applying Theorems 3.3 and 3.4, we get that the maximum of $L(x, y)$ is achieved at the point of tangency of the right tangent to the given ellipse, parallel to the line $\sqrt{2} x-y=0$. Using condition 3.39:
$$
k=\sqrt{2}=\sqrt{2} x-2 y, a=3, b=\sqrt{7} ; 2 \cdot 9+7=m^{2}
$$
From the two values $m= \pm 5$ we choose $m=-5$, since the function $L(x, y)=\sqrt{2} x-y$ will reach its maximum in the given region in the direction of the vector $\vec{n}=\{\sqrt{2} ;-1\}$ on the right tangent $y=\sqrt{2} x-5$. Determine the coordinates of the point of tangency by substituting $y$ with $\sqrt{2} x-5$ in the ellipse equation. Hence
$$
\begin{aligned}
& \frac{x^{2}}{9}+\frac{(\sqrt{2} x-5)^{2}}{7}=1 \\
& 25 x^{2}-90 \sqrt{2} x+162=0, \Rightarrow x_{1}=x_{2}=1.8 \sqrt{2}
\end{aligned}
$$
Substitute $x_{1}$ into the tangent equation and find $y_{1}=$ $=-1.4$. For these $x_{1}$ and $y_{1}$, the linear function reaches the following maximum value:
$$
L_{\max }(1.8 \sqrt{2},-1.4)=\sqrt{2} \cdot 1.8 \cdot \sqrt{2}-(-1.4)=5
$$
## 3.5 . PROBLEMS
## STRAIGHT LINE
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.2. Two planes are given by their general equations:
$$
\begin{aligned}
& 5 x-4 y+z-1=0 \\
& 10 x+2 y+4 z-7=0
\end{aligned}
$$
Determine the magnitude of the dihedral angle between these planes.
|
Solution. The dihedral angle between planes is measured, as is known, by a linear angle, and the latter is equal to the angle between vectors perpendicular to the planes. The vector perpendicular to the first plane has coordinates $\vec{n}_{1}=(5,-4,1)$, to the second plane $\ddot{n}_{2}=(10,2,4)$. Let's use the formula for the cosine of the angle between two vectors
$$
\begin{aligned}
& \cos \varphi=\frac{\dot{n_{1}} \cdot \ddot{n}_{2}}{\left|\ddot{n}_{1}\right| \cdot\left|\vec{n}_{2}\right|}=\frac{5 \cdot 10+(-4) \cdot 2+1 \cdot 4}{\sqrt{5^{2}+(-4)^{2}+1^{2}} \cdot \sqrt{10^{2}+2^{2}+1^{2}}} \cong 0.69, \\
& \varphi=\arccos (0.69) \cong 52^{\circ} .
\end{aligned}
$$
|
52
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.2. Find the limit of the sequence
$$
\lim _{n \rightarrow \infty} \frac{\sqrt{2 n-1}-\sqrt[3]{n^{3}+10}}{\sqrt{n^{2}+1}-\sqrt[4]{n+1}}
$$
|
Solution. Divide the numerator and the denominator of the fraction by $n$. After transformations and discarding infinitely small quantities, we obtain the required result:
$$
\begin{gathered}
\lim _{n \rightarrow \infty} \frac{\sqrt{2 n-1}-\sqrt[3]{n^{3}+10}}{\sqrt{n^{2}+1}-\sqrt[4]{n+1}}=\lim _{n \rightarrow \infty} \frac{\sqrt{2 n-1} / n-\sqrt[3]{n^{3}+10} / n}{\sqrt{n^{2}+1} / n-\sqrt[4]{n+1} / n}= \\
=\lim _{n \rightarrow \infty} \frac{\sqrt{2 / n-1 / n^{2}}-\sqrt[3]{1+10 / n^{3}}}{\sqrt{1+1 / n^{2}}-\sqrt[4]{1 / n^{3}+1 / n^{4}}}=-1
\end{gathered}
$$
|
-1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.9. Calculate the limit
$$
\lim _{x \rightarrow \pm \infty}\left(\sqrt{x^{2}+1}-\sqrt{x^{2}-1}\right)
$$
|
Solution. In this case, we have an indeterminate form of type «$\infty - \infty$». To resolve it, we multiply and divide the given expression by its conjugate. We get
$$
\begin{gathered}
\lim _{x \rightarrow \pm \infty}\left(\sqrt{x^{2}+1}-\sqrt{x^{2}-1}\right)=\lim _{x \rightarrow \pm \infty} \frac{x^{2}+1-x^{2}+1}{\sqrt{x^{2}+1}+\sqrt{x^{2}-1}}= \\
=\lim _{x \rightarrow \pm \infty} \frac{2}{\sqrt{x^{2}+1}+\sqrt{x^{2}-1}}=0
\end{gathered}
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.10. Calculate the limit
$$
\lim _{x \rightarrow 0} \frac{\tan 6 x}{\sin 3 x}
$$
|
Solution. To calculate this limit, which represents an indeterminate form of the type "0/0", it is best to use the theorem on the replacement of infinitesimal functions with equivalent quantities.
According to this theorem, as $x \rightarrow 0, \operatorname{tg} 6 x \sim 6 x$, $\sin 3 x \sim 3 x$. Taking this into account, we have
$$
\lim _{x \rightarrow 0} \frac{\operatorname{tg} 6 x}{\sin 3 x}=\lim _{x \rightarrow 0} \frac{6 x}{3 x}=2
$$
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
### 5.11. Compute the limit
$$
\lim _{x \rightarrow 0} \frac{1+\sin 2 x-\cos 2 x}{1-\sin 2 x-\cos 2 x}
$$
|
Solution. Under the limit sign, we have an indeterminate form of type "0/0". To resolve this, we will use the known trigonometric formulas:
$$
\sin 2 x=2 \sin x \cos x, \quad 1-\cos 2 x=2 \sin ^{2} x
$$
Taking this into account, we get
$$
\begin{aligned}
& \lim _{x \rightarrow 0} \frac{1+\sin 2 x-\cos 2 x}{1-\sin 2 x-\cos 2 x}=\lim _{x \rightarrow 0} \frac{2 \sin ^{2} x+2 \sin x \cos x}{2 \sin ^{2} x-2 \sin x \cos x}= \\
& =\lim _{x \rightarrow 0} \frac{2 \sin x(\sin x+\cos x)}{2 \sin x(\sin x-\cos x)}=\lim _{x \rightarrow 0} \frac{\sin x+\cos x}{\sin x-\cos x}=\frac{0+1}{0-1}=-1 .
\end{aligned}
$$
|
-1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
### 5.13. Calculate
$$
\lim _{x \rightarrow \pi}(\pi-x) \cot x
$$
|
Solution. The given limit represents an indeterminate form of type «0 $\cdot \infty »$. To resolve this, we introduce a new variable $\pi-x=t$. Then
$\lim _{x \rightarrow \pi}(\pi-x) \operatorname{ctg} x=\lim _{t \rightarrow 0} t \operatorname{ctg}(\pi-t)=-\lim _{t \rightarrow 0} t \operatorname{ctg} t=-\lim _{t \rightarrow 0} \frac{t}{\operatorname{tg} t}=-1$.
|
-1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.18. Calculate the limit
$$
\lim _{x \rightarrow \infty}\left(\frac{4 x^{2}-x+1}{2 x^{2}+x+1}\right)^{\frac{x^{3}}{2-x}}
$$
|
Solution. This limit is not an indeterminate form, since when
$$
x \rightarrow \infty \frac{4 x^{2}-x+1}{2 x^{2}+x+1} \rightarrow 2, \text { and } \frac{x^{3}}{2-x} \sim -x^{2} \rightarrow -\infty
$$
Therefore:
$$
\begin{gathered}
\lim _{x \rightarrow \infty}\left(\frac{4 x^{2}-x+1}{2 x^{2}+x+1}\right)^{\frac{x^{3}}{2-x}}=\lim _{x \rightarrow \infty}\left(2-\frac{3 x-1}{2 x^{2}+x+1}\right)^{\frac{x^{3}}{2-x}}= \\
=\left(\lim _{x \rightarrow \infty}\left(2-\frac{3 x-1}{2 x^{2}+x+1}\right)\right)^{\lim _{x \rightarrow x} \frac{x^{3}}{2-x}}=2^{-\infty}=0
\end{gathered}
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.22. Let
$$
f(x)=\left\{\begin{array}{l}
e^{3 x}, \text { if } x<0, \\
a+5 x, \text { if } x \geqslant 0
\end{array}\right.
$$
For which choice of the number $a$ will the function $f(x)$ be continuous?
|
The problem is solved. Let's write down the condition for the continuity of the function at the point \( x=0 \), where it is currently not continuous due to the arbitrariness of the number \( a \). We have
\[
\lim _{x \rightarrow 0-0} f(x)=\lim _{x \rightarrow 0+0} f(x)=f(0)
\]
In this case,
\[
\begin{aligned}
& \lim _{x \rightarrow 0-0} f(x)=\lim _{x \rightarrow 0-0} e^{3 x}=e^{0}=1 ; \\
& \lim _{x \rightarrow 0+0} f(x)=\lim _{x \rightarrow 0-0}(a+5 x)=a ; \\
& f(0)=\left.(a+5 x)\right|_{x=0}=a
\end{aligned}
\]
For the function to be continuous at the point \( x=0 \), the condition \( a=1 \) must be satisfied.
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
### 5.24. Investigate the function
$$
f(x)=\frac{5^{1 / x}}{1+5^{1 / x}}
$$
for continuity and determine the nature of the points of discontinuity.
|
Solution. The function is defined everywhere except at the point $x=0$. Let's investigate the behavior of the function in the neighborhood of the point $x=0$. We will find the one-sided limits
$$
\lim _{x \rightarrow 0-0} f(x)=\lim _{x \rightarrow 0-0} \frac{5^{1 / x}}{1+5^{1 / x}}=0
$$
since as $x \rightarrow 0-0$, i.e., from the left of zero, $1 / x \rightarrow-\infty \Rightarrow$ $5^{1 / x} \rightarrow 0$.
$$
\lim _{x \rightarrow 0+0} f(x)=\lim _{x \rightarrow 0+0} \frac{5^{1 / x}}{1+5^{1 / x}}=\lim _{x \rightarrow 0+0} \frac{1}{5^{-1 / x}+1}=1
$$
since as $x \rightarrow 0+0$, $1 / x \rightarrow+\infty \Rightarrow 5^{-1 / x} \rightarrow 0$.
Thus, the one-sided limits of the function at the point $x=0$ exist but are not equal to each other. Therefore, the function $f(x)$ has a discontinuity of the first kind at the point $x=0$.
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.14. Find the derivative of the function
$$
f(x)=\left\{\begin{array}{l}
\operatorname{arctg}\left(x^{2} \cdot \sin (1 /(5 x))\right), \quad x \neq 0, \\
0, x=0
\end{array}\right.
$$
and compute its value at the point $x_{0}=0$.
|
Solution. Let's find the derivatives for $x \neq 0$. We have
$$
\begin{gathered}
f^{\prime}(x)=\frac{1}{1+\left(x^{2} \cdot \sin (1 / 5 x)\right)^{2}} \cdot\left(x^{2} \cdot \sin (1 /(5 x))\right)^{\prime}= \\
=\frac{1}{1+\left(x^{2} \cdot \sin (1 /(5 x))\right)^{2}} \cdot\left(\left(x^{2}\right)^{\prime} \cdot \sin (1 /(5 x))+x^{2} \cdot(\sin (1 /(5 x)))^{\prime}\right)= \\
=\frac{1}{1+\left(x^{2} \cdot \sin (1 /(5 x))\right)^{2}} \cdot\left(2 x \cdot \sin (1 /(5 x))+x^{2} \cdot \cos (1 /(5 x)) \cdot\left(-1 /\left(5 x^{2}\right)\right)\right)= \\
=\frac{1}{1+\left(x^{2} \cdot \sin (1 /(5 x))\right)^{2}} \cdot\left(2 x \cdot \sin (1 /(5 x))-\frac{\cos (1 /(5 x))}{5}\right), x \neq 0 .
\end{gathered}
$$
Since the one-sided limits
$$
\lim _{x \rightarrow 0 \pm 0} \sin (1 / 5 x)
$$
do not exist, the one-sided limits of $f^{\prime}(x)$ at $x_{0}=0$ do not exist either.
To find the derivative at the given point, we will use the definition of the derivative.
$$
f^{\prime}(0)=\lim _{\Delta x \rightarrow 0} \frac{\operatorname{arctg}\left((0+\Delta x)^{2} \cdot \sin \left(\frac{1}{5(0+\Delta x)}\right)\right)-0}{\Delta x}
$$
Since the limit of the product of the bounded function $\sin (1 /(5 \Delta x))$ and the infinitesimal $\Delta x$ is zero, we get that $y^{\prime}(0)=0$.
Note that the original function $f(x)$ is continuous at the point $x_{0}=0$. Indeed, the function is defined both at the point $x_{0}=0$ and in some neighborhood of it, and
$$
\lim _{x \rightarrow 0} \operatorname{arctg}(x \cdot \sin (1 /(5 x)))=0=f(0)
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.28. Determine the angle at which the graph of the curve $f(x)=e^{x}-x$ intersects the y-axis.
|
Solution. $f_{x}^{\prime}(x)=e^{x}-1, f_{x}^{\prime}(0)=e^{0}-1=0$, hence the angle of intersection is $\alpha=0^{\circ}$.
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.31. Find the first differential of the function $y(x)=$ $=e^{3 x} \ln \left(1+x^{2}\right)$ and calculate its value at $x=0, d x=$ $=\Delta x=0.1$.
|
Solution. The first method is based on the direct application of the formula $d y(x)=y^{\prime}(x) d x$.
We have
$$
y^{\prime}(x)=3 e^{3 x} \cdot \ln \left(1+x^{2}\right)+\frac{e^{3 x} \cdot 2 x}{1+x^{2}}
$$
hence
$$
d y(x)=\left(3 e^{3 x} \cdot \ln \left(1+x^{2}\right)+\frac{e^{3 x} \cdot 2 x}{1+x^{2}}\right) \cdot d x
$$
The second method is based on the application of the rules for finding the differential of a product:
$$
\begin{aligned}
& d y(x)=d\left(e^{3 x}\right) \ln \left(1+x^{2}\right)+e^{3 x} d\left(\ln \left(1+x^{2}\right)\right)= \\
& \quad=3 e^{3 x} \ln \left(1+x^{2}\right) d x+\frac{e^{3 x} 2 x}{1+x^{2}} d x \\
& d y(0)=\left(3 e^{3 \cdot 0} \ln \left(1+0^{2}\right)+\frac{e^{3 \cdot 0} 2 \cdot 0}{1+0^{2}}\right) \cdot 0.1=0
\end{aligned}
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.50. $\lim _{x \rightarrow 1} \frac{x^{4}-1}{\ln x}$.
|
Solution. Let's check the conditions for applying L'Hôpital's rule: 1) there is an indeterminate form
$$
\left.\frac{x^{4}-1}{\ln x}\right|_{x=1}=\frac{0}{0}
$$
2) the functions $x^{4}-1$ and $\ln x$ are differentiable in a neighborhood of the point $\left.x=1 ; 3)(\ln x)_{x=1}^{\prime} \neq 0 ; 4\right)$ the limit exists
$$
\lim _{x \rightarrow 1} \frac{\left(x^{4}-1\right)^{\prime}}{(\ln x)^{\prime}}=\lim _{x \rightarrow 1} \frac{4 x^{3}}{1 / x}=\lim _{x \rightarrow 1} 4 x^{4}=4
$$
Therefore, $\lim _{x \rightarrow 1} \frac{x^{4}-1}{\ln x}=\lim _{x \rightarrow 1} \frac{\left(x^{4}-1\right)^{\prime}}{(\ln x)^{\prime}}=4$.
|
4
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.52. $\lim _{x \rightarrow+\infty} \frac{\ln x}{x}$.
|
Solution.
$$
\lim _{x \rightarrow+\infty} \frac{\ln x}{x}=(\infty / \infty)=\lim _{x \rightarrow+\infty} \frac{(\ln x)^{\prime}}{(x)^{\prime}}=\lim _{x \rightarrow+\infty} \frac{1 / x}{1}=\lim _{x \rightarrow+\infty} \frac{1}{x}=0
$$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.53. $\lim _{x \rightarrow \infty} \frac{x}{e^{x}}$.
|
Solution.
$$
\lim _{x \rightarrow \infty} \frac{x}{e^{x}}=(\infty / \infty)=\lim _{x \rightarrow \infty} \frac{(x)^{\prime}}{\left(e^{x}\right)^{\prime}}=\lim _{x \rightarrow \infty} \frac{1}{e^{x}}=0
$$
## INDETERMINACY OF THE FORM «0 $\cdot$
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.54. $\lim _{x \rightarrow \pi / 2}(x-\pi / 2) \cdot \tan x$.
|
Solution.
$$
\begin{aligned}
& \lim _{x \rightarrow \pi / 2}(x-\pi / 2) \cdot \tan x=(0 \cdot \infty)=\lim _{x \rightarrow \pi / 2} \frac{x-\pi / 2}{\cot x}= \\
& =(0 / 0)=\lim _{x \rightarrow \pi / 2} \frac{(x-\pi / 2)'}{(\cot x)'}=\lim _{x \rightarrow \pi / 2} \frac{1}{-\frac{1}{\sin ^{2} x}}=-1
\end{aligned}
$$
|
-1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.55. $\lim _{x \rightarrow 1+0}(\ln x \cdot \ln (x-1))$.
6.55. $\lim _{x \rightarrow 1+0}(\ln x \cdot \ln (x-1))$.
(No change needed as the text is already in English and contains mathematical notation which is universal.)
|
Solution.
$$
\begin{aligned}
& \lim _{x \rightarrow 1+0}(\ln x \cdot \ln (x-1))=(0 \cdot(-\infty))=\lim _{x \rightarrow 1+0} \frac{\ln (x-1)}{\frac{1}{\ln x}}=(-\infty /-\infty)= \\
& \quad=\lim _{x \rightarrow 1+0} \frac{(\ln (x-1))^{\prime}}{\left(\frac{1}{\ln x}\right)^{\prime}}=\lim _{x \rightarrow 1+0} \frac{\frac{1}{x-1}}{\frac{1}{x \ln ^2 x}}=\lim _{x \rightarrow 1+0} \frac{x \ln ^{2} x}{x-1}= \\
& \quad=\lim _{x \rightarrow 1+0} \frac{\ln ^{2} x}{1-\frac{1}{x}}=(0 / 0)=\lim _{x \rightarrow 1+0} \frac{\frac{\ln x}{x}}{\frac{1}{x^{2}}}=\lim _{x \rightarrow 1+0} 2 x \ln x=0 .
\end{aligned}
$$

|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.58. $\lim _{x \rightarrow+0} x^{x}$.
|
Solution.
$\lim _{x \rightarrow+0} x^{x}=e^{\lim _{x \rightarrow 0} x \ln x}=e^{\lim _{x \rightarrow 0 \rightarrow 0(1)}\left(\frac{(\ln x)'}{(1 / x)'}\right)}=e^{\lim _{x \rightarrow-0} \frac{1 / x}{-1 / x^{2}}}=e^{\lim _{x \rightarrow+0}(-x)}=e^{0}=1$.
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.59. $\lim _{x \rightarrow 0}(1-\cos x)^{x}$.
|
Solution.
$$
\lim _{x \rightarrow 0}(1-\cos x)^{x}=\left(0^{0}\right)=e^{\lim _{x \rightarrow 0} x \ln (1-\cos x)}
$$
## Find separately
$$
\begin{aligned}
& \lim _{x \rightarrow 0} x \cdot \ln (1-\cos x)=(0 \cdot(-\infty))=\lim _{x \rightarrow 0} \frac{(\ln (1-\cos x))^{\prime}}{(1 / x)^{\prime}}=\lim _{x \rightarrow 0} \frac{\frac{\sin x}{1-\cos x}}{-\frac{1}{x^{2}}}= \\
& =-\lim _{x \rightarrow 0} \frac{x^{2} \cdot 2 \sin \frac{x}{2} \cos \frac{x}{2}}{2 \sin ^{2} \frac{x}{2}}=-\lim _{x \rightarrow 0} 2 x \cdot \lim _{x / 2 \rightarrow 0} \frac{x / 2}{\sin \frac{x}{2}} \cdot \lim _{x \rightarrow 0} \cos \frac{x}{2}=0
\end{aligned}
$$
Here, the first remarkable limit was used
$$
\lim _{\alpha \rightarrow 0} \frac{\alpha}{\sin \alpha}=1
$$
From here $e^{\lim _{x \rightarrow 0} x \ln (1-\cos x)}=e^{0}=1$.
## INDETERMINACY OF THE FORM « 1 *
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13. Let $X, Y$ be random variables, $\mathbf{E}|X|, \mathrm{E}|Y|<\infty$ and $\mathrm{E}(Y \mid X)=0$ a.s. Show that from the condition $\mathrm{E}(Y \mid X+Y)=0$ a.s. it follows that $Y=0$ with probability one.
|
Solution. Let $f(x)=|x|-\operatorname{arctg}|x|, x \in \mathbb{R}$. The function $f=f(x)$ is increasing on $\mathbb{R}_{+}$ and is an even, strictly convex function on $\mathbb{R}$, and $0 \leqslant f(x) \leqslant|x|$ for all $x \in \mathbb{R}$. By Jensen's inequality for conditional expectations, we have
$$
\begin{gathered}
\mathrm{E} f(X+Y)=\mathrm{E} f(\mathrm{E}[X+Y \mid X+Y])=\mathrm{E} f(\mathrm{E}[X \mid X+Y]) \leqslant \mathrm{E} f(X), \\
\mathrm{E} f(X)=\mathrm{E} f(\mathrm{E}[X+Y \mid X]) \leqslant \mathrm{E} f(X+Y),
\end{gathered}
$$
i.e., $\mathrm{E} f(X+Y)=\mathrm{E} f(\mathrm{E}[X+Y \mid X])$. The latter (in view of the remark to problem II.7.10) is possible only if $\mathrm{E}(X+Y \mid X)=X+Y$ a.s., which is equivalent to the equality $Y=\mathrm{E}(Y \mid X)=0$ a.s.
|
0
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
47. Find the limit of the function:
1) $f(x)=x^{3}-5 x^{2}+2 x+4$ as $x \rightarrow-3$;
2) $\varphi(t)=t \sqrt{t^{2}-20}-\lg \left(t+\sqrt{t^{2}-20}\right)$ as $t \rightarrow 6$.
|
Solution. The given function is elementary, it is defined at the limit point, so we find the limit of the function as its particular value at the limit point:
1) $\lim _{x \rightarrow-3} f(x)=f(-3)=(-3)^{3}-5 \cdot(-3)^{2}+2 \cdot(-3)+4=-74$;
2) $\lim \varphi(t)=\varphi(6)=6 \sqrt{6^{2}-20}-\lg \left(6+\sqrt{6^{2}-20}\right)=23$.
Find the following limits:
|
23
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
232.
$$
\text { 1) }\left\{\begin{array}{l}
x=k \sin t+\sin k t \\
y=k \cos t+\cos k t ;\left(\frac{d y}{d x}\right)_{t=0} ?
\end{array}\right.
$$
What is the geometric meaning of the result?
2) $\left\{\begin{array}{l}x=\alpha^{2}+2 \alpha \\ y=\ln (\alpha+1) ; \frac{d^{2} y}{d x^{2}} ?\end{array}\right.$
3) $\left\{\begin{array}{l}x=1+e^{a \varphi} \\ y=a \varphi+e^{-a_{\varphi} \varphi} ; \frac{d^{3} y}{d x^{3}} ?\end{array}\right.$
|
Solution. 1) We find the derivatives of $x$ and $y$ with respect to the parameter $t$:
$$
\frac{d x}{d t}=k \cos t+k \cos k t ; \quad \frac{d y}{d t}=-k \sin t-k \sin k t
$$
The desired derivative of $y$ with respect to $x$ is found as the ratio of the derivatives of $y$ and $x$ with respect to $t$:
$\frac{d y}{d x}=\frac{\frac{d y}{d t}}{\frac{d x}{d t}}=-\frac{k(\sin t+\sin k t)}{k(\cos t+\cos k t)}=-\frac{2 \sin \frac{t+k t}{2} \cos \frac{t-k t}{2}}{2 \cos \frac{t+k t}{2} \cos \frac{t-k t}{2}}=-\operatorname{tg} \frac{k+1}{2} t$.
At $t=0$, we get $\frac{d y}{d x}=0$. According to the geometric meaning of the derivative (§ 1), at the point $(0 ; k+1)$, where $t=0$, the tangent to the graph of the given function is parallel to the $O x$ axis.
2) We find the derivatives of $x$ and $y$ with respect to the parameter $\alpha$:
$$
\frac{d x}{d a}=2 \alpha+2 ; \frac{d y}{d \alpha}=\frac{1}{\alpha+1}
$$
and the desired derivative of $y$ with respect to $x$:
$$
y^{\prime}=\frac{d y}{d x}=\frac{d y}{d \alpha}: \frac{d x}{d \alpha}=\frac{1}{2(\alpha+1)^{2}}=\frac{1}{2}(\alpha+1)^{-2}
$$
Next, we find the derivative of $y^{\prime}$ with respect to $\alpha$, and then the desired second derivative of $y$ with respect to $x$ as the ratio of the derivatives of $y^{\prime}$ and $x$ with respect to $\alpha$:
$$
\frac{d y^{\prime}}{d \alpha}=-(\alpha+1)^{-3} ; \quad y^{\prime \prime}=\frac{d y^{\prime}}{d x}=\frac{d y^{\prime}}{d \alpha}: \frac{d x}{d \alpha}=\frac{-(\alpha+1)^{-3}}{2(\alpha+1)}=-\frac{1}{2(\alpha+1)^{4}}
$$
3) Using the general formulas (A) for the derivatives of a function given parametrically, we obtain
$$
\begin{aligned}
& y^{\prime}=\frac{d y}{d x}=\frac{d y}{d \varphi}: \frac{d x}{d \varphi}=\frac{a-a e^{-a \varphi}}{a e^{a \varphi}}=e^{-a \varphi}-e^{-2 \alpha \varphi} ; \\
& y^{\prime \prime}=\frac{d y^{\prime}}{d x}=\frac{d y^{\prime}}{d \varphi}: \frac{d x}{d \varphi}=\frac{2 a e^{-2 a \varphi}-a e^{-\alpha \varphi}}{a e^{a \varphi}}=2 e^{-3 a \varphi}-e^{-2 a \varphi} \\
& y^{\prime \prime \prime}=\frac{d y^{\prime \prime}}{d x}=\frac{d y^{\prime \prime}}{d \varphi}: \frac{d x}{d \varphi}=\frac{2 a e^{-2 a \varphi}-6 a e^{-3 a^{\prime} \varphi}}{a e^{a \varphi}}=2 e^{-3 a \varphi}-6 e^{-4 a \varphi} \\
& \text { 233. }\left\{\begin{array}{l}
x=t^{2} \\
y=t^{3} ; \frac{d y}{d x}
\end{array}\right. \\
& \text { 234. }\left\{\begin{array}{l}
x=\frac{3 a t}{1+t^{3}} \\
y=\frac{3 a t^{2}}{1+t^{3}} ; \frac{d y}{d x} ?
\end{array}\right. \\
& \text { 235. }\left\{\begin{array}{l}
x=a \cos t \\
y=a \sin t ; \frac{d^{2} y}{d x^{2}} ?
\end{array}\right. \\
& \text { 236. }\left\{\begin{array}{l}
p=\cos \alpha+\alpha \sin \alpha \\
q=\sin \alpha-\alpha \cos \alpha ; \frac{d^{2} q}{d p^{2}} ?
\end{array}\right. \\
& \text { 237. }\left\{\begin{array}{l}
x=z^{2} \\
y=z^{3}+z ;\left(\frac{d^{2} y}{d x^{2}}\right)_{z=1}
\end{array}\right\} \\
& \text { 238. }\left\{\begin{array}{l}
x=a \cos ^{3} t \\
y=a \sin ^{3} t
\end{array}\left(\frac{d^{2} y}{d x^{2}}\right)_{t=\frac{\pi}{6}} ?\right.
\end{aligned}
$$
## § 11. Tangent and Normal to a Plane Curve. Angle Between Two Curves
If a plane curve is referred to a rectangular coordinate system (Fig. 33), then the equations of the tangent and normal to it at the point $M\left(x_{0}, y_{0}\right)$ are:
$$
y-y_{0}=y_{0}^{\prime}\left(x-x_{0}\right) ; \quad y-y_{0}=-\frac{1}{y_{0}^{\prime}}\left(x-x_{0}\right)
$$
where $y_{0}^{\prime}$ is the value at the point $x_{0}$ of the derivative $\frac{d y}{d x}$ from the equation of the curve.
The direction of the curve at each of its points is determined by the direction of the tangent to it at that point. The angle between two intersecting curves is defined as the angle between two lines tangent to the curves at their point of intersection (Fig. 34) by the formula
$$
\operatorname{tg} \varphi=\frac{k_{1}-k_{2}}{1+k_{1} k_{2}}
$$
where $k_{1}$ and $k_{2}$ are the slopes of the tangents to the curves at their point of intersection $P\left(x_{0}, y_{0}\right)$, i.e., the particular values at the point $x_{0}$ of the derivatives of $y$ with respect to $x$ from the equations of these curves:
$$
k_{1}=\operatorname{tg} \alpha_{1}=\left(\frac{d y_{1}}{d x}\right)_{x=x_{0}} ; k_{2}=\operatorname{tg} \alpha_{2}=\left(\frac{d y_{2}}{d x}\right)_{x=x_{0}}
$$
Fig. : 3

Fig. 34
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
315. Find the limits:
1) $\lim x \operatorname{ctg} 2 x$
2) $\lim _{x \rightarrow+0} \sqrt[3]{x} \ln x$
3) $\lim (\operatorname{tg} \varphi-\sec \varphi)$; $\varphi \rightarrow \frac{\pi}{2}$
4) $\lim _{x \rightarrow 1}\left(\frac{1}{\ln x}-\frac{x}{x-1}\right)$;
5) $\lim _{t \rightarrow 0}\left(\frac{1}{\sin t}-\frac{1}{t}\right)$
|
Solution. By establishing that the case is $0 \cdot \infty$ or $\infty - \infty$, we transform the function into a fraction where both the numerator and the denominator simultaneously tend to zero or infinity, then apply L'Hôpital's rule:
1) $\lim _{x \rightarrow 0} x \operatorname{ctg} 2 x=\lim \frac{x}{\operatorname{tg} 2 x}=\lim \frac{1}{2 \sec ^{2} 2 x}=\frac{1}{2}$;
3) $\lim _{\varphi \rightarrow-\frac{\pi}{2}}(\operatorname{tg} \varphi-\sec \varphi)=\lim \frac{\sin \varphi-1}{\cos \varphi}=\lim \frac{\cos \varphi}{-\sin \varphi}=0$;
4) $\lim _{x \rightarrow 1}\left(\frac{1}{\ln x}-\frac{x}{x-1}\right)=\lim \frac{x-1-x \ln x}{(x-1) \ln x}=\lim \frac{-\ln x}{\ln x+\frac{x-1}{x}}=$
$$
:=-\lim \frac{x \ln x}{x \ln x+x-1}=-\lim \frac{1+\ln x}{2+\ln x}=\cdots \frac{1}{2}
$$
here L'Hôpital's rule is applied twice;
5) $\lim _{t \rightarrow 0}\left(-\frac{1}{\sin t}-\frac{1}{t}\right)=\lim \frac{t-\sin t}{t \sin t}=\lim \frac{1-\cos t}{\sin t+t \cos t}=$
$$
=\lim \frac{\sin t}{2 \cos t-t \sin t}=0
$$
here L'Hôpital's rule is applied twice.
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
411. Find the curvature of the curve: 1) $x=t^{2}, y=2 t^{3}$ at the point where $t=1$; 2) $y=\cos 2 x$ at the point where $x=\frac{\pi}{2}$.
|
Solution. 1) We find the derivatives $\dot{x}=2 t, \ddot{x}=2, \dot{y}=6 t^{2}$, $\ddot{y}=12 t$, and compute their values at the point where $t=1$:
$$
\dot{x}=2, \ddot{x}=2, \dot{y}=6, \ddot{y}=12
$$
and, substituting into formula (1), we get
$$
K=\frac{|\ddot{x} \ddot{y}-\ddot{y} x|}{\left(\dot{x}^{2}+\dot{y}^{2}\right)^{\frac{3}{2}}}=\frac{2 \cdot 12-0.2}{\left(2^{2}+6^{2}\right)^{\frac{3}{2}}}=\frac{3}{20 \sqrt{10}}
$$
2) From the given equation, we find the first and second derivatives of $y$ with respect to $x$:
$$
y^{\prime}=-2 \sin 2 x, y^{\prime \prime}=-4 \cos 2 x
$$
we compute their values at the given point: $y^{\prime}\left(\frac{\pi}{2}\right)=0, y^{\prime \prime}\left(\frac{\pi}{2}\right)=4$ and, substituting into formula (1), we get $K=\frac{\left|y^{\prime \prime}\right|}{\left[1+\left(y^{\prime}\right)^{2}\right]^{\frac{3}{2}}}=4$.
|
4
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
665. A rectangular reservoir with a horizontal cross-sectional area of $S=6 \mathrm{~m}^{2}$ is filled with water to a height of $H=5$ m. Determine the time it takes for all the water to flow out of the reservoir through a small hole in its bottom with an area of $s=0.01 \mu^{2}$, assuming that the velocity of the water flow is $0.6 \sqrt{2 \text { g } h}$, where $h$ is the height of the water level above the hole, and $g$ is the acceleration due to gravity.
|
Solution. According to the general scheme (1), divide the desired time $T$ into a large number $n$ of small intervals $\Delta t_{1}, \Delta t_{2}, \ldots, \Delta t_{n}$, and let the water level in the reservoir decrease by an amount $\Delta x=\frac{H}{n}$ during each such interval (Fig. 124).[^20]
If we assume that during each small time interval $\Delta t_{i}$ the speed of water flowing out through the hole at the bottom remains constant, equal to its value at the beginning of the interval $0.6 \sqrt{2 \mathrm{~g}\left(H-x_{i}\right)}$, then, equating the volume of water that flows out at this speed through the hole at the bottom over the interval $\Delta t_{i}$ to the volume of the part of the reservoir that has emptied over the same interval, we obtain the approximate equality
$$
0.6 s \sqrt{2 g\left(H-x_{i}\right)} \Delta t_{i} \approx S \Delta x
$$
from which
$$
\Delta t_{i} \approx \frac{S \Delta x}{0.6 s \sqrt{2 g\left(H-x_{i}\right)}}
$$
The approximate value of the total desired time $T$ will be equal to the sum
$$
T=\sum_{i=1}^{n} \Delta t_{i} \approx \sum_{i=1}^{n} \frac{S \Delta x}{0.6 s \sqrt{2 g\left(H-x_{i}\right)}}
$$
where, according to the problem statement, the points $x_{i}$ are contained in the interval $[0, H]$.
Having verified that the error in the obtained approximate value of $T$ tends to zero as $n$ increases, we find the exact value of $T$ as the limit of the integral sum (*) as $n \rightarrow+\infty$, i.e., as the corresponding definite integral
$$
T=\frac{S}{0.6 s \sqrt{2 g}} \int_{0}^{H}(H-x)^{-\frac{1}{2}} d x=\left.\frac{2 S}{0.6 s \sqrt{2 g}}(H-x)^{\frac{1}{2}}\right|_{H} ^{0}=\frac{S}{0.6 s} \sqrt{\frac{2 \overline{I}}{G}}
$$
Substituting the numerical values of the parameters, we get $T \approx$ $\approx 1010$ sec $\approx 16.83$ min.
If the decrease in water in the reservoir were constantly replenished, i.e., if the water level in it remained constant, then the speed of water flowing out would also be constant, equal to $0.6 \sqrt{2 \mathrm{~g} H}$. In this case, in each second, the volume of water flowing out through the hole at the bottom of the reservoir would be $0.6 s \sqrt{2 g H}$, equal to the volume of a right cylinder with base area $s$ and height $0.6 \sqrt{2 g H}$. Therefore, under the given assumption, the volume of water contained in the reservoir would flow out of it in time
$$
T_{1}=\frac{S H}{0.6 s \sqrt{2 g H}}=\frac{1}{2} \frac{S}{0.6 s} \sqrt{\frac{2 H}{g}} .
$$
Comparing this result with the previous one shows that the time of outflow $T$, without replenishing the decrease in water in the reservoir, is twice the time of outflow $T_{1}$, when the decrease in water is constantly replenished; $T=2 T_{1}$.
|
1010
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
701. Calculate the integral $\int_{1}^{9} \sqrt{6 x-5} d x$ using the Newton-Leibniz formula and approximate formulas for rectangles, trapezoids, and Simpson's method, dividing the integration interval into 8 equal parts. Then estimate the percentage error of the results obtained using the approximate formulas.
|
Solution. By the Newton-Leibniz formula
$$
I=\int_{1}^{9} \sqrt{6 x-5} d x=\frac{1}{6} \int_{1}^{9}(6 x-5)^{\frac{1}{2}} d(6 x-5)=\left.\frac{1}{9}(6 x-5)^{\frac{3}{2}}\right|_{1} ^{9}=38
$$
Next, we divide the integration interval $[1 ; 9]$ into 8 equal parts, find the length of one part $h=1$, the division points $x_{i}$, and the values $y_{i}$ of the integrand function $y=\sqrt{6 x-5}$ at these points:
$$
\begin{aligned}
x_{0}=1 & y_{0}=\sqrt{\bar{I}}=1,0000 \\
x_{1}=2 & y_{1}=\sqrt{7}=2,6458 \\
x_{2}=3 & y_{2}=\sqrt{13}=3,6056 \\
x_{3}=4 & y_{3}=\sqrt{19}=4,3589 \\
x_{4}=5 & y_{4}=\sqrt{25}=5,0000 \\
x_{5}=6 & y_{6}=\sqrt{3 \overline{1}}=5,5678 \\
x_{6}=7 & y_{6}=\sqrt{37}=6,0828 \\
x_{7}=8 & y_{7}=\sqrt{43}=6,5574 \\
x_{8}=9 & y_{8}=\sqrt{49}=7,0000
\end{aligned}
$$
and we calculate the integral using approximate formulas.
By the rectangle formula (1) $/ \approx \sum_{i=n}^{7} y_{l}=34,8183$.
The absolute error of this approximate value (by deficiency) is $38-34,8183=3,1817$, and the relative (percentage) error is $\frac{3,1817 \cdot 100}{38} \approx 8,37 \%$.
By the rectangle formula ( $1 a$ ) $I \approx \sum_{i=1}^{8} y_{i}=40,8183$.
Here, the absolute error (by excess) is 2,8183, and the relative error is $\frac{2,8183 \cdot 100}{38} \approx 7,42 \%$.
By the trapezoidal formula $I \approx 4+\sum_{i=1}^{?} y_{i}=37,8183$.
The absolute error of this result is 0,1817, and the relative error is $\frac{0,1817 \cdot 100}{38} \approx 0,48 \%$.
By the Simpson's formula
$$
I \approx \frac{1}{3}(8+4 \cdot 19,1299+2 \cdot 14,6884) \approx 37,9655
$$
The absolute error is only 0,0345, and the relative error is $\frac{0,0345 \cdot 100}{38} \approx 0,09 \%$.
|
38
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
702. Using Simpson's formula, calculate the approximate value of the integral $\int_{0} \cos x d x$ with an accuracy of 0.00001.
|
Solution. First, we determine the number $n$ of parts into which the integration interval $\left[0, \frac{\pi}{2}\right]$ should be divided to achieve the required accuracy of the computation.
Assuming the error $\delta(n)$ of Simpson's formula is less than $10^{-5}$, we have
$$
\frac{(b-a)^{5}}{180 n^{4}} y_{H L}^{(4)}5 \pi \sqrt[4]{\frac{\pi}{36}}=8.5
$$
Next, assuming $n=10$ (the nearest even number greater than 8.5), we determine the division points $x_{i}$ and the corresponding values $y_{i}$ of the integrand function $y:=\cos x$ (with one extra decimal place, $\pi \approx 3.141592$):
$$
\begin{array}{ll}
x_{0}=0.000000 & y_{0}=1.000000 \\
x_{1}=0.157080 & y_{1}=0.987688 \\
x_{2}=0.314159 & y_{2}=0.951057 \\
x_{3}=0.471239 & y_{3}=0.891007 \\
x_{4}=0.628318 & y_{4}=0.809017 \\
x_{5}=0.785398 & y_{5}=0.707107 \\
x_{8}=0.942478 & y_{6}=0.587785 \\
x_{7}=1.099557 & y_{7}=0.453991 \\
x_{8}=1.256637 & y_{8}=0.309017 \\
x_{9}=1.413716 & y_{9}=0.156435 \\
x_{10}=1.570796 & y_{10}=0.000000
\end{array}
$$
Substituting into Simpson's formula, we obtain the desired value of the integral with an accuracy of $10^{-6}$:
$$
\int_{0}^{\frac{\pi}{2}} \cos x d x \approx 0.0523599(1+4 \cdot 3.196228+2 \cdot 2.656876) \approx 1.00000
$$
This solution demonstrates that for computing an integral with a given accuracy, when the analytical expression of the integrand function is known, one can determine in advance the necessary number of divisions of the integration interval, which would ensure the required accuracy, based on the specified inequalities for estimating the error of approximate formulas.
However, in many cases, the analytical expression of the integrand function is such that it is difficult to find the maximum value over the entire integration interval for the first, second, or fourth-order derivatives, which are contained in the inequalities determining the errors of the rectangle, trapezoidal, or Simpson's formulas. Therefore, in computational practice, other criteria are often used for estimating the error of approximate integration, which can be found in specialized manuals on approximate computations.
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
714. Find the limits:
1) $\lim _{\substack{x \rightarrow 3 \\ y \rightarrow 0}} \frac{\tan(x y)}{y}$
2) $\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}} \frac{x}{x+y}$.
|
Solution. Having made sure that the function is not defined at the limit point, we perform transformations, guided by the instructions in § 7, Chapter I:
1) $\lim _{\substack{x \rightarrow 3 \\ y \rightarrow 0}} \frac{\tan(x y)}{y}=\lim x \cdot \lim \frac{\tan(x y)}{x y}=3 \cdot 1=3$, since $\lim _{a \rightarrow 0} \frac{\tan \alpha}{a}=1$.
2) $\lim _{\substack{x \rightarrow 0 \\ y \rightarrow 0}} \frac{x}{x+y}=\lim \frac{1}{1+\frac{y}{x}}$ - does not exist, because the ratio $\frac{y}{x}$
does not have a limit as the point $M(x, y)$ approaches the point $M_{0}(0 ; 0)$ arbitrarily. Thus, if $M \rightarrow M_{0}$ along different lines $y=k x$, then $\frac{y}{x}=k$, i.e., it depends on the slope of the line along which the point $M$ moves.
|
3
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
874. Given points $A(3, -6, 0)$ and $B(-2, 4, 5)$. Compute the line integral $I=\int_{C} x y^{2} d x + y z^{2} d y - z x^{2} d z$:
1) along the straight line segment $O B$ and
2) along the arc $A B$ of the circle defined by the equations $x^{2} + y^{2} + z^{2} = 45, 2 x + y = 0$.
|
Solution. 1) First, we write the equation of the line passing through two points $\frac{x-x_{1}}{x_{2}-x_{1}}=\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{z-z_{1}}{z_{2}-z_{1}}$, obtaining $\frac{x}{-2}=\frac{y}{4}=\frac{z}{5}$. By equating these equal ratios to the parameter $t$, we transform the canonical equations of the line $O B$ into parametric form: $x=-2 t, y=4 t, z=5 t$.
Next, using these equations, we transform the given line integral into an ordinary integral with the variable $t$, and then compute it
$$
\begin{gathered}
I_{1}=\int_{t_{0}=0}^{t_{B}=1}-2 t(4 t)^{2}(-2 d t)-4 t(5 t)^{2} 4 d t-5 t(-2 t)^{2} 5 d t= \\
=364 \int_{0}^{1} t^{3} d t=91
\end{gathered}
$$
2) Transform the given equations of the circle into parametric form. Setting $x=t$, we get $y=-2 t$ (from the second given equation), $z=\sqrt{45-5 t^{2}}$ (from the first equation). Hence, $d x=d t, d y=-2 d t, d z=-\frac{5 t d t}{\sqrt{4.5-5 t^{2}}}$
$$
\begin{gathered}
I_{2}=\int_{t_{A^{\prime}}=3}^{t_{B}=-2} t(-2 t)^{2} d t+(-2 t)\left(45-5 t^{2}\right)(-2 d t)- \\
-\sqrt{45-5 t^{2}} t^{2}\left(-\frac{5 t d t}{\sqrt{45-5 t^{2}}}\right)=\int_{3}^{-2}\left(180 t-17 t^{3}\right) d t=-173 \frac{3}{4}
\end{gathered}
$$
|
91
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
875. Compute the line integrals:
1) $\oint_{-i} 2 x d x-(x+2 y) d y \quad$ and
2) $\oint_{+l} y \cos x d x+\sin x d y$
along the perimeter of the triangle with vertices $A(-1 ; 0), B(0 ; 2)$ and $C(2 ; 0)$.
|
Solution. 1) Here (Fig. 186) the integration line (closed) consists of three segments lying on different lines (with different equations). Accordingly, the line integral along the broken line $A B C A$ is calculated as the sum of integrals taken over the segments $A B, B C$, and $C A$.
By formulating the equation of the line $A B$,
Fig. 186 $y-2 x=2$, and based on this equation, we transform the line integral over the segment $A B$ into an ordinary integral with the variable $x$:
$$
\begin{gathered}
x=2 x+2, \quad d y=2 d x, \quad \int_{A B}=-8 \int_{x_{A}=-1}^{x_{B}=0}(x+1) d x= \\
=-\left.4(x+1)^{2}\right|_{-1} ^{0}=-4
\end{gathered}
$$
Similarly, calculating the line integral over the segments $B C$ and $C A$, we get
$$
\begin{aligned}
& x=2-y, d x=-d y, \quad \int_{B C}==\int_{u_{R}=2}^{4 / c^{=0}}(y-6) d y=\left.\frac{(y-6)^{2}}{2}\right|_{2} ^{0}=10 ; \\
& y=0, \quad d y=0, \int_{C A}=2 \int_{x_{C}=2}^{x_{A}=-1} x d x=\left.x^{2}\right|_{2} ^{-1}=-3
\end{aligned}
$$
Therefore,
$$
\oint_{A B C A}=\int_{A B}+\int_{B C}+\int_{C A}=-4+10-3=3
$$
2) Here the integrand is a complete differential of a function of two variables, since $(y \cos x)_{y}^{\prime}=(\sin x)_{x}^{\prime}=\cos x$. Therefore, this line integral, taken over the perimeter of the given triangle, is equal to zero. It will also be equal to zero over any other closed contour.
Calculate the line integrals:
|
3
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1167. A locomotive is moving along a horizontal section of the track c) at a speed of 72 km/hour. In what time and at what distance will it be stopped by the brake, if the resistance to motion after the start of braking is equal to 0.2 of its weight.
|
Solution. According to Newton's second law in mechanics, the differential equation of motion for the locomotive will be
$$
m \frac{d^{2} s}{d t^{2}}=-0.2 m g
$$
where $s$ is the distance traveled in time $t$, $m$ is the mass of the locomotive, and $g$ is the acceleration due to gravity.
Multiplying both sides of this equation by $d l$ and then integrating twice, we get
$$
\frac{d s}{d t}=-0.2 g t + c_{1}, \quad s=-0.1 g t^{2} + c_{1} t + c_{2}
$$
The values of the constants $c_{1}$ and $c_{2}$ are determined by the initial conditions: at $t=0$, $s=0$, and $\frac{d s}{d t}=72 \kappa \text{ m/h} = 20 \text{ m/s}$.
From the first condition, we have $c_{2}=0$. From the second condition, it follows that $c_{1}=20$.
Therefore, the equations of motion for the locomotive will be:
$$
\begin{gathered}
\frac{d s}{d t}=v=20-0.2 g t (\mu ; \text{sec}) \\
s=20 t-0.1 g t^{2} (\mu)
\end{gathered}
$$
Setting $v=0$ in equation (5), we find the braking time during which the locomotive will be stopped by the brake:
$$
t=\frac{20}{0.2 g} \approx \frac{100}{9.8} \approx 10.2 \text{ sec}
$$
Setting $t \approx 10.2$ in equation (6), we find the braking distance:
$$
s \approx 20 \cdot 10.2 - 0.1 \cdot 9.8 \cdot 10.2^{2} \approx 102 \text{ m}
$$
|
102
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 4. Find the singular solutions of the differential equation
$$
\left(y^{\prime}\right)^{2}=4 x^{2}
$$
|
Solution. Differentiating (23) with respect to $y_{1}$:
$$
2 y^{\prime}=0
$$
Excluding $y^{\prime}$ from (23) and (24), we get $x^{2}=0$. The discriminant curve is the y-axis. It is not an integral curve of equation (23), but according to scheme (16) it can be the geometric locus of points of tangency of integral curves.
The solutions of equation (23) are parabolas
$$
y=x^{2}+C, \quad y=-x^{2}+C
$$
and any smooth curves that can be composed from their parts (Fig. 21).
From the drawing, it is clear that the line $x=0$ is indeed the geometric locus of points of tangency of the integral curves of equation (23).
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 5. Find the singular solutions of the differential equation
$$
\left(y^{\prime}\right)^{2}(2-3 y)^{2}=4(1-y)
$$
|
Solution. Let's find the PDK. Excluding $y^{\prime}$ from the system of equations
$$
\left\{\begin{aligned}
\left(y^{\prime}\right)^{2}(2-3 y)^{2}-4(1-y) & =0 \\
y^{\prime}(2-3 y)^{2} & =0
\end{aligned}\right.
$$
we obtain
$$
(2-3 y)^{2}(1-y)=0 .
$$
Transforming equation (25) to the form
$$
\frac{d x}{d y}= \pm \frac{2-3 y}{2 \sqrt{1-y}}
$$
we find its general integral
$$
y^{2}(1-y)=(x-C)^{2}
$$
Let's find the CDK. Excluding $C$ from the system of equations
$$
\left\{\begin{array}{r}
y^{2}(1-y)-(x-C)^{2}=0 \\
2(x-C)=0
\end{array}\right.
$$
we will have
$$
y^{2}(1-y)=0
$$
Thus, from (26) and (27) we have
$$
\begin{aligned}
& \text { PDK } \equiv(1-y)(2-3 y)^{2}=0 \\
& \text { CDK } \equiv(1-y) y^{2}=0
\end{aligned}
$$
The factor $1-y$ appears in the $p$-discriminant and in the $C$-discriminant to the first degree and gives the envelope, i.e., the function $y=1$ is a special solution of the differential equation (25). By direct substitution, we verify that $y=1$ indeed satisfies the equation.
The equation $2-3 y=0$, appearing in the $p$-discriminant to the second degree and not appearing in the $C$-discriminant at all, gives the place of tangency points ( $\Pi^{2}$ ).
Finally, the equation $y=0$, appearing in the $C$-discriminant to the second degree and not appearing in the $p$-discriminant at all, gives the place of nodal points $\left(P^{2}\right)$ (Fig. 22).
Fig. 22
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 8. Find the Wronskian determinant for the functions: $y_{1}(x)=\sin x$,
$$
y_{2}(x)=\sin \left(x+\frac{\pi}{8}\right), y_{3}(x)=\sin \left(x-\frac{\pi}{8}\right)
$$
|
Solution. We have
$$
W\left[y_{1}, y_{2}, y_{3}\right]=\left|\begin{array}{rrr}
\sin x & \sin \left(x+\frac{\pi}{8}\right) & \sin \left(x-\frac{\pi}{8}\right) \\
\cos x & \cos \left(x+\frac{\pi}{8}\right) & \cos \left(x-\frac{\pi}{8}\right) \\
-\sin x & -\sin \left(x+\frac{\pi}{8}\right) & -\sin \left(x-\frac{\pi}{8}\right)
\end{array}\right|=0
$$
since the first and last rows of the determinant are proportional.
Theorem. If the system of functions $y_{1}(x), y_{2}(x), \ldots, y_{n}(x)$ is linearly dependent on the interval $[a, b]$, then its Wronskian determinant is identically zero on this interval.
For example, the system of functions $\sin x, \sin \left(x+\frac{\pi}{8}\right), \sin \left(x-\frac{\pi}{8}\right)$ is linearly dependent in the interval $(-\infty,+\infty)$, and the Wronskian determinant of these functions is zero everywhere in this interval (see examples 4 and 8).
This theorem provides a necessary condition for the linear dependence of a system of functions. The converse statement is false, i.e., the Wronskian determinant can be identically zero even when the given functions form a linearly independent system on some interval.
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 2. Investigate the stability of the solution of the degenerate equation for the equation
$$
\varepsilon \frac{d x}{d t}=x\left(e^{x}-2\right)
$$
|
Solution. The degenerate equation $x\left(e^{x}-2\right)=0$ has two solutions
$$
\text { 1) } x=0, \quad 2) x=\ln 2 \text {. }
$$
We have
$$
\left.\frac{\partial f(t, x)}{\partial x}\right|_{x=0}=\left.\left(e^{x}-2+x e^{x}\right)\right|_{x=0}=-1
$$
so the solution $x=0$ is stable;
$$
\left.\frac{\partial f(t, x)}{\partial x}\right|_{x=\ln 2}=\left.\left(e^{x}-2+x e^{x}\right)\right|_{x=\ln 2}=2 \ln 2>0,
$$
so the solution $x=\ln 2$ of the degenerate equation is unstable (Fig. 51).
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
88. Calculate the sum:
$$
S=\frac{1}{(a-b)(a-c)}+\frac{1}{(b-a)(b-c)}+\frac{1}{(c-a)(c-b)}
$$
|
$$
\begin{aligned}
& S=\frac{1}{(a-b)(b-c)(c-a)}(-(b-c)-(c-a)-(a-b))= \\
& =\frac{-1}{(a-b)(b-c)(c-a)}(b-c+c-a+a-b)=0
\end{aligned}
$$
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
114. Calculate the sum:
$$
x=\sqrt[3]{9+4 \sqrt{5}}+\sqrt[3]{9-4 \sqrt{5}}
$$
|
$$
\triangle$ Let's raise the equality to the third power, using the formula
$$
(a+b)^{3}=a^{3}+b^{3}+3 a b(a+b)
$$
We get:
$$
\begin{aligned}
& x^{3}=(9+4 \sqrt{5})+(9-4 \sqrt{5})+3 \sqrt[3]{81-80} \cdot(\sqrt[3]{9+4 \sqrt{5}}+\sqrt[3]{9-4 \sqrt{5}}) \\
& x^{3}=18+3 x, \quad x^{3}-3 x-18=0
\end{aligned}
$$
The last equation has an integer root $x=3$. It can be rewritten as
$$
(x-3)\left(x^{2}+3 x+6\right)=0
$$
The equation has no other real roots.
Answer: 3.
$$
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
128. Knowing that $x+\frac{1}{x}=4$, calculate $x^{2}+\frac{1}{x^{2}}$.
|
$\triangle$ It seems that the equation $x+\frac{1}{x}=4$ should be transformed into a quadratic equation, find $x$ from the quadratic equation, and substitute the obtained value of $x$ into the sum $x^{2}+\frac{1}{x^{2}}$. However, this path is long, especially since the quadratic equation has two roots.
It is simpler to square the original equation:
$$
x^{2}+2+\frac{1}{x^{2}}=16, \quad x^{2}+\frac{1}{x^{2}}=14
$$
Answer: 14.
|
14
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
172. Prove that the numbers formed by the last two digits of the sequence $a_{n}=6^{n}$ form a periodic sequence. Find the period of such a sequence.
|
$\triangle$ That such a sequence is periodic is almost obvious: after all, the numbers formed by the last two digits of the power $6^{n}$ do not exceed 10: from 06 to 96. To find the period of the sequence, we will compute its first few terms:
$$
06,36,16,96,76,56,36,16
$$
It turned out that $a_{7}=a_{2}$, which means that for any natural $n \geq 2, a_{n+5}=a_{n}$. Therefore, the period of the sequence is 5.
Answer: 5.
|
5
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
253. The digits of a three-digit number form a geometric progression with different terms. If this number is decreased by 200, the result is a three-digit number whose digits form an arithmetic progression. Find the original three-digit number.
|
$\triangle$ The number of three-digit numbers with distinct digits forming a geometric progression is small, and all of them can be easily found by enumeration:
$124,421,139,931,248,842,469,964$.
We will discard the numbers 124 and 139, as they are less than 200. Subtract 200 from the remaining numbers and find the number (or numbers) whose digits form an arithmetic progression.
There is only one such number - 642. The original number is 842.
Answer: 842.
|
842
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
390. Solve the equation:
$$
\sqrt[3]{x-1}+\sqrt[3]{2 x-1}=1
$$
|
$\triangle$ Let's raise both sides of the equation to the third power, using the formula
$$
(a+b)^{3}=a^{3}+b^{3}+3 a b(a+b)
$$
We will have:
$x-1+2 x-1+3 \sqrt[3]{(x-1)(2 x-1)} \cdot(\sqrt[3]{x-1}+\sqrt[3]{2 x-1})=1$,
$\sqrt[3]{(x-1)(2 x-1)} \cdot(\sqrt[3]{x-1}+\sqrt[3]{2 x-1})=1-x$.
But what now? Now let's use the original equation, according to which the sum in parentheses equals 1:
$$
\sqrt[3]{(x-1)(2 x-1)}=1-x
$$
We will also raise the last equation to the third power:
$(x-1)(2 x-1)=(1-x)^{3}, \quad(x-1)\left(2 x-1+(x-1)^{2}\right)=0$, $(x-1) x^{2}=0$.
From this
$$
x_{1}=1, \quad x_{2}=x_{3}=0
$$
It is interesting to check the original equation. It shows that the value $x=1$ satisfies it, while the value $x=0$ does not satisfy it.
Answer: 1.
A problem for reflection: Do you think at which step in the transition from the given original equation to the last one and for what reason did the extraneous root $x=0$ of the original equation appear? After all, it seems that we only used raising the equation to the third power, and as a result, we get an equation equivalent to the original one...
Note. The solution to problem 390 shows that when solving equations of the type
$$
\sqrt[3]{f_{1}(x)}+\sqrt[3]{f_{2}(x)}=\varphi(x)
$$
using this method, extraneous roots can appear. (When solving such equations by other methods, they may not appear.) Therefore, it is necessary to check the obtained roots by the original equation.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
394. Solve the equation:
$$
\sqrt[3]{x}+\sqrt[3]{x+19}=5
$$
|
$\triangle$ Equations of this type have already been encountered in section 11.1, with a different method of solution (see the solution to problem 390). Let's introduce two new variables:
$$
\sqrt[3]{x}=y, \quad \sqrt[3]{x+19}=z
$$
We obtain a system of rational equations:
$$
\left\{\begin{array}{l}
y+z=5 \\
y^{3}=x \\
z^{3}=x+19
\end{array}\right.
$$
Subtract the second equation from the third to eliminate $x$: $z^{3}-y^{3}=19$.
To solve the system of two equations
$$
y+z=5, \quad z^{3}-y^{3}=19
$$
express $z$ from the first equation and substitute this expression into the second equation:
$z=5-y, \quad(5-y)^{3}-y^{3}=19, \quad 125-75 y+15 y^{2}-2 y^{3}=19$, $2 y^{3}-15 y^{2}+75 y-106=0$.
Among the divisors of the free term, the last equation is satisfied by $y=2$. Then the equation reduces to:
$$
(y-2)\left(2 y^{2}-11 y+51\right)=0 .
$$
From this, it is clear that the equation has no other roots.
Therefore,
$$
x=y^{3}=2^{3}=8
$$
Answer: 8.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
403*. Solve the equation:
$$
\sqrt[4]{1-x^{2}}+\sqrt[4]{1-x}+\sqrt[4]{1+x}=3
$$
|
$\triangle$ The domain of the equation is the interval $[-1 ; 1]$. In this domain, we can apply the inequality between the geometric mean and the arithmetic mean of two non-negative numbers to each of the radicals in the left-hand side:
$\sqrt[4]{1-x^{2}}=\sqrt{\sqrt{1+x} \cdot \sqrt{1-x}} \leq \frac{\sqrt{1+x}+\sqrt{1-x}}{2}$,
$\sqrt[4]{1+x}=\sqrt{1 \cdot \sqrt{1+x}} \leq \frac{1+\sqrt{1+x}}{2}$,
$\sqrt[4]{1-x}=\sqrt{1 \cdot \sqrt{1-x}} \leq \frac{1+\sqrt{1-x}}{2}$.
We will add these three inequalities term by term, and apply the same inequality twice more to the expression in the right-hand side of the new inequality:
$$
\sqrt[4]{1-x^{2}}+\sqrt[4]{1+x}+4 \sqrt[4]{1-x} \leq 1+\sqrt{1+x}+\sqrt{1-x} \leq 1+\frac{1+(1+x)}{2}+\frac{1+(1-x)}{2}=3
$$
The obtained inequality must turn into an equality according to the condition. However, this is only possible if each of the inequalities used here turns into an equality. It is known that the geometric mean of two non-negative numbers equals their arithmetic mean only when these numbers are equal. In this case, we will have:
$$
1=1+x=1-x
$$
from which $x=0$.
Answer: 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
447. A motorcyclist left point A at a speed of 45 km/h. After 40 minutes, a car left A in the same direction at a speed of 60 km/h. How much time after the car's departure will the distance between it and the motorcyclist be 36 km?
|
$\triangle$ Important question: at the moment when the car is 36 km away from the motorcycle, will it be ahead or behind the motorcycle?
In 40 minutes, the motorcycle will travel a distance of $45 \cdot \frac{2}{3}$ km $=30$ km, which is less than 36 km. Therefore, at the moment the car departs, it is 30 km behind the motorcycle, and the distance between them will continue to decrease until the car overtakes the motorcycle. This means that the car will be 36 km ahead of the motorcycle after the overtaking.
Fig. 1
In Fig. 1, points A and B denote the locations of the car and the motorcycle, respectively, at the moment the car departs, and points $\mathrm{A}_{1}$ and $\mathrm{B}_{1}$ denote their locations at the moment the car is 36 km ahead of the motorcycle. Then $\mathrm{AB}=30$ km, $\mathrm{B}_{1} \mathrm{~A}_{1}=36$ km.
Let the unknown be the distance $\mathrm{BB}_{1}: \mathrm{BB}_{1}=x$ km. If we find this distance, we will also find the time the car takes to travel the path $\mathrm{AA}_{1}$.
The verbal "equation" here is: the time the car takes to travel the path $\mathrm{AA}_{1}$ equals the time the motorcycle takes to travel the path $\mathrm{BB}_{1}$. Express both times in terms of $x$ and set the expressions equal:
$$
\frac{30+x+36}{60}=\frac{x}{45}
$$
Solve this equation:
$$
3(66+x)=4 x, \quad 198+3 x=4 x, \quad x=198
$$
From this, the time the car takes to travel the path $\mathrm{AA}_{1}$ is $\frac{198}{45}=\frac{22}{5}=4 \frac{2}{5}$ (hours), i.e., 4 hours 24 minutes. Answer: 4 hours 24 minutes.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
448. A cyclist set off from point A to point B, and 15 minutes later, a car set off after him. Halfway from A to B, the car caught up with the cyclist. When the car arrived at B, the cyclist still had to cover another third of the entire distance. How long will it take the cyclist to travel the distance from A to B?
|
$\triangle$ Let's take the path AB as a unit. (This can be done in cases where there is no distance given in linear units in the problem data.) Let's denote the speed of the cyclist by $x$ (in fractions of the path per hour).
During the time it took the car to travel the second half of the path, the cyclist traveled $\frac{1}{2}-\frac{1}{3}=\frac{1}{6}$ of the path AB. Therefore, the car's speed is $\frac{1}{2}: \frac{1}{6}=3$ times greater than the cyclist's speed, i.e., it is $3x$.
The verbal "equation" here is: the time it took the cyclist to travel the first half of the path AB is 15 minutes $=\frac{1}{4}$ hour more than the time it took the car to travel the same half. We get:
$$
\frac{1}{2 x}-\frac{1}{2 \cdot 3 x}=\frac{1}{4}
$$
Solving this equation, we find $x: x=\frac{4}{3}$. Then the time it took the cyclist to travel the path AB is $1: \frac{4}{3}=\frac{3}{4}$ hours, i.e., 45 minutes.
Answer: 45 minutes.
|
45
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
455*. From point A to point B, which is 40 km away from A, two tourists set off simultaneously: the first on foot at a speed of 6 km/h, and the second on a bicycle. When the second tourist overtook the first by 5 km, the first tourist got into a passing car traveling at a speed of 24 km/h. Two hours after leaving A, the first tourist caught up with the second and arrived in B before him. Find the speed of the tourist who was riding the bicycle.
|
$\triangle$ Let's make a drawing (Fig. 2). $\qquad$
Fig. 2
Let $\mathrm{A}_{1}$ and $\mathrm{B}_{1}$ be the points where the first and second tourists are, respectively, at the moment when the second tourist overtakes the first by $5 \mathrm{km}$, and let $\mathrm{K}$ be the point where the first tourist catches up with the second.
Denote the time the first tourist takes to travel $\mathrm{AA}_{1}$ (and simultaneously the second tourist to travel $\mathrm{AB}_{1}$) by $t_{1}$ hours, and the time the first tourist takes to travel $\mathrm{A}_{1} \mathrm{~K}$ (and the second to travel $\mathrm{B}_{1} \mathrm{~K}$) by $t_{2}$ hours. Let the speed of the cyclist be $v$ km/h.
Since each tourist traveled the distance $\mathrm{AK}$ in 2 hours, we have $t_{1}+t_{2}=2$.
Since in time $t_{1}$ the cyclist traveled 5 km more than the first tourist, we have $v t_{1}-6 t_{1}=5$.
Finally, express the distance $\mathrm{AK}$ in two ways - using quantities related to the first tourist and quantities related to the second, and equate the resulting expressions:
$$
6 t_{1}+24 t_{2}=v\left(t_{1}+t_{2}\right)
$$
We have the system of equations:
$$
\left\{\begin{array}{l}
t_{1}+t_{2}=2 \\
v t_{1}-6 t_{1}=5 \\
6 t_{1}+24 t_{2}=v\left(t_{1}+t_{2}\right)
\end{array}\right.
$$
From the first equation, $t_{2}=2-t_{1}$, and from the second, $-v=\frac{6 t_{1}+5}{t_{1}}$. Substitute these expressions for $t_{2}$ and $v$ into the third equation and solve the new equation with the unknown $t_{1}$:
$6 t_{1}+24\left(2-t_{1}\right)=\frac{2\left(6 t_{1}+5\right)}{t_{1}}, \quad 6 t_{1}^{2}+48 t_{1}-24 t_{1}^{2}=12 t_{1}+10$,
$18 t_{1}^{2}-36 t_{1}+10=0, \quad 9 t_{1}^{2}-18 t_{1}+5=0 ; \quad t_{1}=\frac{9 \pm 6}{9}$.
Thus, $t_{1}=\frac{5}{3}$ or $t_{1}=\frac{1}{3}$. Accordingly, $v=9$ or $v=21$.
Do both these values of $v$ fit? It turns out, no: if $v=21$ km/h, then the cyclist will travel a distance of 42 km in 2 hours, and this distance is greater than $A B=40$ km.
Answer: 9 km/h.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
457. A motorcyclist and a cyclist set off towards each other from points A and B simultaneously and met 4 km from B. At the moment when the motorcyclist arrived at B, the cyclist was 15 km from A. Find the distance AB.
|
$\triangle$ Let the distance AB be denoted as $x$ km.
By the time they meet, the motorcyclist and the cyclist have traveled $(x-4)$ km and $x$ km, respectively, and by the time the motorcyclist arrives at $\mathrm{B}$, the distances are $x$ km and $(x-4)$ km, respectively.
Thus, the ratio of the speeds of the motorcyclist and the cyclist is, on one hand, $\frac{x-4}{x}$ (since the ratio of distances traveled by two bodies moving at a constant speed over the same time is equal to the ratio of their speeds), and on the other hand, $-\frac{x}{x-15}$. Therefore,
$$
\frac{x-4}{x}=\frac{x}{x-15}
$$
Solving this equation, we get: $x_{1}=20, x_{2}=3$. Only $x=20$ is valid.
Answer: 20 km.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
463. From two ports A and B, two steamships set off simultaneously towards each other across the sea. The speed of each is constant. The first steamship arrived at B 16 hours after the meeting, while the second arrived at A 25 hours after the meeting. How long does it take for each steamship to travel the entire distance?
|
$\triangle$ Let the path AB be a unit. Denote the speeds of the steamships as $v_{1}$ and $v_{2}$ (in fractions of a unit per hour).
Suppose the steamships met at point C. Then $\frac{A C}{C B}=\frac{v_{1}}{v_{2}}$. From this,
$$
\frac{A C}{C B}+1=\frac{v_{1}}{v_{2}}+1, \quad \frac{1}{C B}=\frac{v_{1}+v_{2}}{v_{2}}, \quad C B=\frac{v_{2}}{v_{1}+v_{2}}, \quad A C=\frac{v_{1}}{v_{1}+v_{2}}
$$
Since the first steamship traveled the path CB in 16 hours, and the second steamship traveled the path CA in 25 hours, then
$$
\left\{\begin{array}{l}
\frac{v_{2}}{\left(v_{1}+v_{2}\right) v_{1}}=16 \\
\frac{v_{1}}{\left(v_{1}+v_{2}\right) v_{2}}=25
\end{array}\right.
$$
Solving this system of equations, we determine $v_{1}$ and $v_{2}: v_{1}=\frac{1}{36}, v_{2}=\frac{1}{45}$.
Therefore, the time for the steamships to complete the entire path is
$$
1: \frac{1}{36}=36(h), \quad 1: \frac{1}{45}=45(h)
$$
Answer: 36 h, 45 h.
|
36
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
489*. Three cyclists set off simultaneously: the first and second from point A, and the third towards them from point B. After 1.5 hours, the first cyclist was at an equal distance from the other two, and after 2 hours from the start, the third cyclist was at an equal distance from the first and second. How many hours after departure was the second cyclist at an equal distance from the first and third?
|
$\triangle$ Let's take the path AB as a unit. Denote the speeds of the first, second, and third cyclists as $v_{1}, v_{2}$, and $v_{3}$ (in fractions of this path per hour).
We will denote the positions of the first, second, and third cyclists in each of the three specified situations by the letters $\mathbf{M}_{1}, \mathbf{M}_{2}$, and $\mathbf{M}_{3}$, respectively.
After 1.5 hours from the start of the movement, the first cyclist was halfway between the second and the third (Fig. 4), and after 2 hours, the third cyclist was halfway between the first and the second (Fig. 5).
Fig. 4

Fig. 5
Since on Fig. $4 \mathrm{M}_{2} \mathrm{M}_{1}=\mathrm{M}_{1} \mathrm{M}_{3}$, where
$$
\mathbf{M}_{2} \mathbf{M}_{1}=1.5\left(v_{1}-v_{2}\right), \quad \mathbf{M}_{1} \mathbf{M}_{3}=1-1.5 v_{1}-1.5 v_{3},
$$
then
$$
1.5\left(v_{1}-v_{2}\right)=1-1.5\left(v_{1}+v_{3}\right)
$$
Since on Fig. $5 M_{2} M_{3}=M_{3} M_{1}$, where
$$
\mathbf{M}_{2} \mathbf{M}_{3}=1-2\left(v_{2}+v_{3}\right), \quad \mathbf{M}_{3} \mathbf{M}_{1}=2\left(v_{1}+v_{3}\right)-1
$$
then
$$
1-2\left(v_{2}+v_{3}\right)=2\left(v_{1}+v_{3}\right)-1
$$
We obtain the system of equations:
$$
\left\{\begin{array}{l}
1.5\left(v_{1}-v_{2}\right)=1-1.5\left(v_{1}+v_{3}\right) \\
1-2\left(v_{2}+v_{3}\right)=2\left(v_{1}+v_{3}\right)-1
\end{array}\right.
$$
From this, we find that
$$
v_{3}=\frac{1}{2}\left(1-v_{1}-v_{2}\right), \quad v_{1}-v_{2}=\frac{1}{9}
$$
(consider how to derive these equalities).
We are interested in the third position, when the second cyclist is halfway between the first and the third (Fig. 6).

Fig. 6
Let $t$ hours be the time from the start of the movement to this position. Since $\mathrm{M}_{3} \mathrm{M}_{2}=\mathrm{M}_{2} \mathrm{M}_{1}$, where
$$
\mathrm{M}_{3} \mathrm{M}_{2}=\left(v_{2}+v_{3}\right) t-1, \quad \mathbf{M}_{2} \mathbf{M}_{1}=\left(v_{1}-v_{2}\right) t
$$
then
$$
\left(v_{1}+v_{3}\right) t-1=\left(v_{1}-v_{2}\right) t .
$$
Solve for $t$, and then, using the obtained expressions for $v_{3}$ and $v_{1}-v_{2}$, calculate $t$:
$t=\frac{1}{2 v_{2}+v_{3}-v_{1}}=\frac{1}{2 v_{2}+\frac{1}{2}\left(1-v_{1}-v_{2}\right)-v_{1}}=\frac{2}{1-3 v_{1}+3 v_{2}}=2:\left(1-\frac{3}{9}\right)=3$.
Answer: after 3 hours.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
493. Four pumps of the same capacity, working together, filled the first tanker and a third of the second tanker (of a different volume) in 11 hours. If three pumps had filled the first tanker and then one of them filled a quarter of the second tanker, the work would have taken 18 hours. How many hours would it take for three pumps to fill the second tanker?
|
$\triangle$ Let one pump fill the first tanker in $x$ hours, and the second tanker in $y$ hours. Then four pumps, working together, will fill the first tanker in $\frac{x}{4}$ hours, and the second in $\frac{y}{4}$ hours.
We have the system of equations:
$$
\left\{\begin{array}{l}
\frac{x}{4}+\frac{y}{4 \cdot 3}=11 \\
\frac{x}{3}+\frac{y}{4}=18
\end{array}\right.
$$
From this, we find that $y=24$ hours. Therefore, three pumps can fill the second tanker in $\frac{24}{3}=8$ hours.
Answer: in 8 hours.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
498. Three automatic lines produce the same product, but have different productivity. The combined productivity of all three lines working simultaneously is 1.5 times the productivity of the first and second lines working simultaneously. A shift assignment for the first line can be completed by the second and third lines working simultaneously 4 hours and 48 minutes faster than the first line. The same assignment is completed by the second line 2 hours faster than the first line. How many hours does the first line take to complete its shift assignment?
|
$\triangle$ Let's accept the shift task for the first line as a unit.
Let the first line complete its shift task in $x$ hours, and the third line the same task in $y$ hours. Then the second line completes the task of the first in $(x-2)$ hours.
Therefore, the productivity of the first, second, and third lines are respectively $\frac{1}{x}, \frac{1}{x-2}$, and $\frac{1}{y}$ (in fractions of the first line's task per hour).
Since the combined productivity of all three lines is 1.5 times greater than the combined productivity of the first and second lines, then
$$
\frac{1}{x}+\frac{1}{x-2}+\frac{1}{y}=1.5\left(\frac{1}{x}+\frac{1}{x-2}\right)
$$
Since the second and third lines, working simultaneously, can complete the shift task of the first line 4 hours and 48 minutes $=\frac{24}{5}$ hours faster than the first line, then
$$
x-\frac{24}{5}=1:\left(\frac{1}{x-2}+\frac{1}{y}\right)
$$
After simplifications, this equation reduces to the following form:
$$
1+\frac{x-2}{y}=\frac{5 x-10}{5 x-24}
$$
We obtain the system of equations:
$$
\left\{\begin{array}{l}
\frac{1}{x}+\frac{1}{x-2}+\frac{1}{y}=1.5\left(\frac{1}{x}+\frac{1}{x-2}\right) \\
1+\frac{x-2}{y}=\frac{5 x-10}{5 x-24}
\end{array}\right.
$$
From the first equation of the system, express $y$ in terms of $x$:
$$
\frac{1}{y}=0.5\left(\frac{1}{x}+\frac{1}{x-2}\right), \quad \frac{1}{y}=\frac{1}{2} \cdot \frac{2 x-2}{x(x-2)}, \quad y=\frac{x(x-2)}{x-1}
$$
Substitute this expression into the second equation of the system:
$$
1+(x-2) \cdot \frac{x-1}{x(x-2)}=\frac{5 x-10}{5 x-24}, \quad 1+\frac{x-1}{x}=\frac{5 x-10}{5 x-24}
$$
The last equation reduces to the quadratic equation $5 x^{2}-43 x+24=0$. Its roots are $-x_{1}=8$ and $x_{2}=\frac{3}{5}$. Only the first root fits.
Answer: 8 hours.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
503. Three workers need to make 80 identical parts. Together, they make 20 parts per hour. The first worker started the job alone. He made 20 parts, spending more than 3 hours on their production. The remaining work was done by the second and third workers together. The entire job took 8 hours. How many hours would it take the first worker to make all 80 parts?
|
Let's denote the productivity of the first, second, and third workers as \( x, y, \) and \( z \) parts per hour, respectively. Based on the conditions of the problem, we obtain a system of two equations with three unknowns:
\[
\left\{\begin{array}{l}
x+y+z=20 \\
\frac{20}{x}+\frac{60}{y+z}=8
\end{array}\right.
\]
To find \( x \), we express \( y+z \) in terms of \( x \) from the first equation: \( y+z=20-x \), and then substitute this expression into the second equation:
\[
\frac{20}{x}+\frac{60}{20-x}=8
\]
This equation can be reduced to a quadratic equation \( x^{2}-15 x+50=0 \). The roots of this equation are \( x_{1}=10 \) and \( x_{2}=5 \). Do both fit? According to the condition, the first worker spent more than 3 hours on 20 parts. But \( \frac{20}{10}=2 \), so only \( x=5 \) is valid. Then he will manufacture all 80 parts in \( \frac{80}{5}=16 \) hours.
Answer: 16 hours.
|
16
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
507. Fresh mushrooms contain $90\%$ water, while dried ones contain $12\%$ water. How many kilograms of dried mushrooms can be obtained from 44 kg of fresh mushrooms?
|
$\triangle$ According to the condition, 44 kg of fresh mushrooms contain $44 \cdot 0.9 = 39.6$ kg of water, which means there is $44 - 39.6 = 4.4$ kg of dry matter.
Let's denote the mass of dried mushrooms that can be obtained from 44 kg of fresh mushrooms by $x$ kg. These $x$ kg consist of $0.12 x$ kg of water and $0.88 x$ kg of dry matter.
Since the mass of the dry matter is the same in both fresh and dried mushrooms,
$$
0.88 x = 4.4
$$
Therefore, $x = \frac{4.4}{0.88} = 5$.
This problem could also be solved without algebra - arithmetically.
Answer: 5 kg.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. A mowing team had to mow two meadows, one twice as large as the other. For half a day, the team mowed the larger meadow. After that, they split in half: one half stayed on the large meadow and finished it by evening, while the other half mowed the smaller meadow but did not finish it. How many mowers were in the team, if it is known that the remaining work was completed by one mower on the following day?
|
7. If the whole brigade mowed a large meadow for half a day and half of the brigade mowed for another half a day, it is clear that the brigade mowed $\frac{2}{3}$ of the meadow in half a day, and half of the brigade mowed $\frac{1}{3}$ of the meadow in half a day. Since the second meadow is half the size of the first, after working on it with half of the brigade for half a day, the uncut area is $\frac{1}{2}-\frac{1}{3}=\frac{1}{6}$. This area was mowed by one mower in one day. Therefore, one mower mows $\frac{1}{6}$ of the meadow in one day, and the whole brigade mows $\frac{4}{3}$. Answer: there were 8 mowers in the brigade.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
14. A box with a square base is required to be made for laying boxes that are 9 cm wide and 21 cm long. What should be the minimum length of the side of the square base so that the boxes fit snugly in the box?
|
14. The side of the base of the box is 63 cm (you need to find the LCM of the numbers 9 and 21).
|
63
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
15. When adding several numbers, the following errors were made: in one of the numbers, the digit 3 in the tens place was taken for 8, and the digit 7 in the hundreds place was taken for 4; in another, the digit 2 in the thousands place was taken for 9. The sum obtained was 52000. Find the correct sum.
|
15. The obtained sum is greater than the true one by 7 thousand and 5 tens, but less than it by three hundred. To get the true sum, you need to subtract 7050 from 52000 and add 300 to the result. Answer: 42250.
|
42250
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
16. Columbus discovered America in the 15th century. In which year did this discovery take place, if the following is known:
a) the sum of the digits representing this year is 16,
b) if the tens digit is divided by the units digit, the quotient is 4 and the remainder is 1.
|
16. Let $x$ be the number of tens, $y$ be the number of units of the year of discovery. Then: $\left\{\begin{array}{l}x+y=11 \\ x=4 y+1 .\end{array}\right.$ Answer: 1492.
|
1492
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
23. A pond is overgrown with duckweed in 64 days. In how many days will a quarter of the pond be overgrown if the amount of duckweed doubles every day?
|
23. 62 days (the problem should be solved from the end).
|
62
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
25. In the wallet, there are 71 kopecks in coins of 5, 2, and 1 kopeck. The number of 1 and 2 kopeck coins is the same. How many coins of each denomination are in the wallet if there are 31 of them in total?
|
25. 1 kopeck - 12 coins, 2 kopecks - 12 coins, and 5 kopecks - 7 coins.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12. Find the remainder of the division of $67^{283}$ by 13.
|
12. $65=13 \cdot 5$, then $67^{283}=(65+2)^{283}=65^{283}+283 \cdot 65^{282} \cdot 2+\ldots+2^{283}$. Each term, except the last one, contains a factor of 65, and therefore, is divisible by 13.
$$
2^{283}=16^{70} \cdot 2^{3}=(13+3)^{70} \cdot 2^{3}=\left(13^{70}+70 \cdot 13^{69} \cdot 3+\ldots+3^{70}\right) \cdot 2^{3}
$$
Each term, except the last one, is divisible by 13.
Consider the last term:
$$
3^{70} \cdot 2^{3}=27^{23} \cdot 3 \cdot 2^{3}=(26+1)^{23} \cdot 3 \cdot 2^{3}=\left(26^{23}+23 \cdot 26^{22}+\ldots+1\right) \cdot 3 \cdot 2^{3}
$$
Each term, except the last one, is divisible by 13, as it contains a factor of 26. Consider the last term.
$$
1 \cdot 3 \cdot 2^{3}=24=13+11 \text{. Answer: the remainder is } 11.
$$
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
14. What digit does the number $777^{777}$ end with?
|
14. Let's determine the last digits of the powers of 777. \(777^1\) ends in 7. \(777^2\) ends in 9; \(777^3\) ends in 3; \(777^4\) ends in 1; \(777^5\) ends in 7; \(777^6\) ends in 9; \(777^7\) ends in 3; \(777^8\) ends in 1, and so on. We establish that 777776 ends in 1, therefore, \(777^{777}\) ends in 7.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
18. How many digits does the number $2^{100}$ have?
|
18. The number of digits in the representation of a number is always one more than the characteristic of the decimal logarithm of the number. In our case
$$
\lg 2^{100}=100 \lg 2 \approx 100 \cdot 0.3010=30.10
$$
Therefore, the number $2^{100}$ contains 31 digits.
|
31
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
19. Find the last two digits of the number $99^{99}-51^{51}$.
|
19. Let's determine the last digits of the powers $99^{99}$ and $5151.99^{1}-99$, $99^{2}-01,99^{3}-99,99^{4}-01$ and so on. $99^{99} - 99$, i.e., $99^{99}=100 M+99$.
Similarly, we establish that $51^{51}=100 N+51$, then $99^{99}-5151=$ $=100(M-N)+99-51=100(M-N)+48$.
Answer: the last two digits are 4 and 8.
|
48
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
39. Find a two-digit number that has the following properties:
a) if the desired number is multiplied by 2 and 1 is added to the product, the result is a perfect square;
b) if the desired number is multiplied by 3 and 1 is added to the product, the result is a perfect square.
|
39. The condition of the problem can be written as: $2 a+1=N^{2}, 3 a+1=M^{2}$. The squares of numbers can end with the digits $0,1,4,5,6,9$. Then $2 a$ can end with $0,4,8$ (since $2 a$ is an even number) and $a$ can end with 5,2, 4, and 0. $10 \leqslant a \leqslant 99$, i.e., $21<2 a+1<199,31<3 a+1<298$ or $21<N^{2}<199$, $31<M^{2}<298$. $N^{2}$ is an odd number, so $N^{2}$ can have the values 24, 49, 81, 121, 169, i.e., $a$ can be equal to $12,24,40,60,34$.
$M^{2}-1$ is divisible by 3, so $M^{2}$ can have the values $49,64,100,121,169$, $196,256,289$ and $a$ can be equal to $40,65,85$. Thus, $a=40$.
|
40
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
40. Find a five-digit number that has the following property: when multiplied by 9, the result is a number composed of the same digits but in reverse order, i.e., the number is reversed.
|
40. Multiply the desired number by 10 and subtract the desired number from the product, which is equivalent to multiplying by 9, then $\overline{a b c d e o}-\overline{a b c d e}=\overline{e d c b a}$. It is easy to establish that $a=1$, then $e=9, b=0, d=8, c=9$. The desired number is 10989.
|
10989
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
43. Find a four-digit number that is a perfect square, where the digit in the thousands place is the same as the digit in the tens place, and the digit in the hundreds place is 1 more than the digit in the units place.
|
43. The desired number is $1000a + 100(b+1) + 10a + b = 1010a + 101b + 100$. $1010a + 101b + 100 = x^2$ or $101(10a + b) = (x-10)(x+10)$.
The left side has a factor of 101, so the right side must also have such a factor. Since $x$ is a two-digit number, $x-10 < 101$. Therefore, $x+10 = 101$, from which $x = 91$.
The desired number is 8281.
|
8281
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
56. If the thought number is multiplied by 3, 2 is appended to the right, the resulting number is divided by 19, and 7 is added to the quotient, the result is three times the thought number. What is this number?
|
56. Let $x$ be the thought-of number. Then the condition of the problem can be written as: $(3 x \cdot 10 + 2) : 9 + 7 = 3 x$.
From which $x = 5$.
## $\S 3$
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The square root of a two-digit number is expressed as an infinite decimal fraction, the first four digits of which (including the integer part) are the same. Find this number without using tables.
|
2. Let the desired number be $N_{\bullet}$ Then $10 \leqslant N \leqslant 100$. Therefore, $3, \ldots \leqslant$ $10,89$, i.e., $N=11 ; 12 ; \ldots$
But $\sqrt{11}=3.31662$. Therefore, there does not exist a two-digit number, the first four digits of the square root of which are written only with threes. By performing similar trials, we find that the desired number is 79, the square root of which is $8.888 \ldots$
|
79
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find a six-digit number that, when multiplied by 2, 3, 4, 5, and 6, gives other six-digit numbers composed of the same digits but in a different order.
|
3. Let the desired number be denoted as: \( N = \overline{a_{6} a_{5} a_{4} a_{3} a_{2} a_{1}} \), with \( a_{6} \neq 0 \), because otherwise \( N \) would not be a six-digit number. \( a_{6} \neq 2 \), because \( 5N \) would then be a seven-digit number. Therefore, \( a_{6} = 1 \).
It is clear that the first digits of the six numbers \( N, 2N, 3N, 4N, 5N \), and \( 6N \) increase, starting from 1. Among them, there is no zero. All these digits are different. \( a_{1} \neq 0 \), \( a_{1} \neq 1 \), because the first digits of all six numbers are different and all digits \( a_{6}, a_{5}, a_{4}, a_{3}, a_{2}, a_{1} \) are distinct. \( a_{1} \neq 5 \). If \( a_{1} = 5 \), then \( 2N \) ends in zero, and zero is not among the desired digits. \( a_{1} \) cannot be even, otherwise \( 5N \) would end in zero. If \( a_{1} = 3 \), then \( N \) ends in 3, \( 2N \) in 6, \( 3N \) in 9, \( 4N \) in 2, \( 5N \) in 5, and \( 6N \) in 8. Considering that \( a_{6} = 1 \), we get 7, not 6 digits. Therefore, \( a_{1} \neq 3 \). If \( a_{1} = 7 \), then the numbers \( N, 2N, 3N, 4N, 5N, 6N \) end in 7, 4, 1, 8, 5, and 2. We get six different digits, and among them is 1. If \( a_{1} = 9 \), then these same numbers would end in 9, 8, 7, 6, 5, and 4. Among them, there is no digit 1, although \( a_{6} = 1 \). Therefore, \( a_{1} \neq 9 \). Thus, \( a_{1} = 7 \).
Fig. 10
Summing up, we get \( 21N = 2999997 \), from which \( N = 142857 \). The numbers \( N, 2N, 3N, 4N, 5N \), and \( 6N \) can be easily read using the circle (Fig. 10).
74
|
142857
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Find the smallest four-digit number that is equal to the square of the sum of the numbers formed by its first two digits and its last two digits.
|
4. Let the desired number be $N=100 a+b$, where $a$ is the number written by the first two digits of the desired number, and $b$ is the last two digits. According to the problem, $100 a+b=(a+b)^{2}$. From this equation, we express $a+b$ in terms of $a$. By trial and error, we establish that $a+b$ will be an integer when $a=20, b=25, N=2025$.
|
2025
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.