problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
272. Calculation of the sum. Let $n$ be a fixed positive number. Set $x_{0}=\frac{1}{n}$ and $x_{j}=\frac{1}{n-1} \sum_{i=0}^{j-1} x_{i}$ for $j=$ $1,2, \ldots, n-1$. Compute the sum $\sum_{j=0}^{n-1} x_{j}$.
|
272. We will prove by induction that $\sum_{j=0}^{k} x_{j}=\frac{1}{(n-k)}, k=$ $0,1, \ldots, n-1$. For $k=0$, the given equality is trivially satisfied by definition. Suppose now that $\sum_{j=0}^{k} x_{j}=\frac{1}{(n-k)}$ for some $k, 0 \leqslant k \leqslant n-2$. Then
$$
\sum_{j=0}^{k+1} x_{j}=x_{k+1}+\sum_{j=0}^{k} x_{j}=\sum_{j=0}^{k} \frac{x_{j}}{n-k-1}+\sum_{j=0}^{k} x_{j}
$$
by the definition of $x_{k+1}$. Using the induction hypothesis, we get
$$
\sum_{j=0}^{k+1} x_{j}=\frac{1}{(n-k-1)(n-k)}+\frac{1}{n-k}=\frac{1}{n-k-1}
$$
From this, taking $k=n-1$, we find the desired sum
$$
\sum_{j=0}^{n-1} x_{j}=1
$$
[E. Lengyel, A. M. M., 76, 86 (January 1969).]
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
275. Maximum Number. Let a set of distinct complex numbers $z_{i}, i=1,2, \ldots, n$, be given, satisfying the inequality
$$
\min _{i \neq j}\left|z_{i}-z_{j}\right| \geqslant \max _{i}\left|z_{i}\right|
$$[^16]
Find the maximum possible $n$ and for this $n$ all sets satisfying the condition of the problem.
|
275. Let $\left|z_{m}\right|=\max _{i}\left|z_{i}\right|$. Then on the complex plane, all points $z_{i}$ will be located inside the circle $R$ of radius $\left|z_{m}\right|$ centered at the point $z=0$. Clearly, 6 points $z_{i}$, located on the circumference of $R$ and forming a regular hexagon, together with the point $z_{1}=0$ give $n=7$. If, however, $n \geqslant 7$ and some point $z \neq 0$ is not on the circumference of $R$, then by applying the cosine theorem, we will get that $\left|z_{i}-z_{j}\right|0$ and $0 \leqslant \delta<\frac{\pi}{3}$.
[P. Kornya, A. M. M., 76, 91 (January 1969).]
|
7
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
308. A simple "game". In the following cryptarithm
| $M A T H$ |
| :--- |
| $M A G S$ |
| $M A T H$ |
| GAME |
the word $G A M E^{*}$ is used instead of some prime number. Find this number.
|
308. The letter $M$ must represent one of the elements of the set $\{1,2,3\}$, the letter $A$ one of the elements of the set $\{4,5,9\}$, from which it follows that the letter $G$ coincides with some element of the set $\{4,7,8\} . .^{*}$ Looking at the table of prime numbers, we will find that the only suitable prime number can be only 8923.
After this, it is already easy to decipher the entire cryptarithm:

$[C$. Diano, M. M., 43, 227 (May 1970).]
|
8923
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
322. Limit of a Sum. Calculate the value of the expression
$$
\lim _{n \rightarrow \infty} \sum_{k=0}^{n} \frac{k^{2}+3 k+1}{(k+2)!}
$$
|
322.
$$
\begin{gathered}
\sum_{k=0}^{n} \frac{k^{2}+3 k+1}{(k+2)!}=\sum_{k=0}^{n}\left(\frac{1}{k!}-\frac{1}{(k+2)!}\right)= \\
=\left(\frac{1}{0!}+\frac{1}{2!}\right)+\left(\frac{1}{1!}-\frac{1}{3!}\right)+\cdots+\left(\frac{1}{n!}-\frac{1}{(n+2)!}\right)= \\
=\frac{1}{0!}+\frac{1}{1!}-\frac{1}{(n+1)!}-\frac{1}{(n+2)!}=2-\frac{n+3}{(n+2)!}
\end{gathered}
$$
From this, it follows that the desired limit is 2.
[E. Just and H. Geck, M. M., 44, 56 (January 1971).]
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
342. Simple calculation. Let $\left(x+\frac{1}{x}\right)^{2}=3$; determine what $x^{3}+\frac{1}{x^{3}}$ is equal to.
|
342.
$$
\begin{aligned}
x^{3} & +\frac{1}{x^{3}}=\left(x+\frac{1}{x}\right)^{3}-3\left(x+\frac{1}{x}\right)= \\
& =\left(x+\frac{1}{x}\right)\left[\left(x+\frac{1}{x}\right)^{2}-3\right]=0
\end{aligned}
$$
[M. Demos, M. M., 45, 102 (February 1972).]
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
373. Cutting a Cube. In a mathematical journal, the following question and answer appeared.
Question: "A carpenter wants to cut a wooden cube with a side of 3 inches into 27 cubes with a side of 1 inch. He can easily do this by making 6 cuts while keeping the pieces together so they don't fall apart. What is the minimum number of cuts if the carpenter is allowed to rearrange the pieces in any way during the cutting process $?$"
Answer: "The minimum number of cuts is 6, since it takes 6 cuts, one for each face, to separate the inner cube."
Now, suppose the inner cube is missing. What is the minimum number of cuts in this case if the pieces can be rearranged in any way during the cutting process $?$
|
373. After the first cut, the cube splits into 2 parts. The larger of these (consisting of 17 one-inch cubes) contains one central cube, for four faces of which another cut is required. After the last of these is made, there will remain at least two one-inch cubes undivided - regardless of any rearrangement of the pieces - for which another cut will be required. Thus, the minimum number of cuts is 6.
[C. Newman, M. M., 41, 102 (February 1968).]
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
388. Three Napkins. One lady made 3 round napkins with radii of 2, 3, and 10 inches, respectively. She placed them on a round table so that each napkin touched the other two and the edge of the table. What is the radius of the table top?
|
388. If the centers of napkins with radii of 2, 3, and 10 inches are located at points \( C, A \), and \( B \) respectively, then these points form the vertices of a right triangle with sides 5, 12, and 13 inches. Completing the figure \( ABC \) to a rectangle, we denote its fourth vertex as \( O \). From point \( O \), draw lines through points \( B, C \), and \( A \), intersecting the given circles at points \( P, Q \), and \( R \) respectively. Then \( OP = OQ = OR = 15 \) inches. This is the desired radius. [For a more general solution, see Scripta Mathematica 21, 46-47 (1955)].
[U. Howard, M. M., 41, 295 (May 1968).]
|
15
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Ex. 1. Find the area of a right triangle if the length of the shortest median is 13, and one of the legs is 10.
|
Ex. 1. 120.
Translate the text above into English, please retain the original text's line breaks and format, and output the translation result directly.
|
120
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
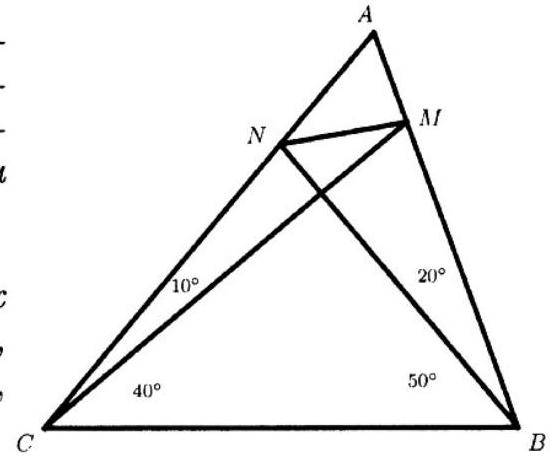
Ex. 19. In triangle $ABC$, points $M$ and $N$ are chosen on sides $AB$ and $AC$. It is known that $\angle ABC=70^{\circ}, \angle ACB=50^{\circ}, \angle ABN=20^{\circ}$, $\angle ACM=10^{\circ}$. Find $\angle NMC$.
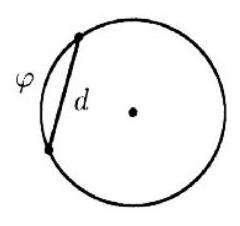
## Generalized Sine Theorem
The length of a chord is equal to the product of the diameter of the circle and the sine of half the angular length of the arc whose ends the chord connects
$$
d=2 R \sin \frac{\varphi}{2}
$$
|
Ex. 19. Answer: $\angle N M C=30^{\circ}$. Solution. Construct $\angle B C D$, equal to $\angle M C A$, equal to $10^{\circ}$. Lay off $D P$, equal to $A N$. Draw $P N$ and $P M . \quad \triangle C P N-$ is equilateral, therefore, $P N=C N$.
$\triangle C B N-$ is isosceles $\Rightarrow P M=B N=C N$. Hence, $P N=P M$.
Thus, $\angle P M N=80^{\circ}$. But $\angle M P=50^{\circ}$.
Therefore, $\angle N M C=80^{\circ}-50^{\circ}=30^{\circ}$.
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Ex. 104. A regular triangle $ABC$ is inscribed in a circle. Another, smaller circle, is inscribed in the sector bounded by the chord $BC$, touching the larger circle at point $M$, and the chord $BC$ at point $K$. The ray $MK$ intersects the larger circle a second time at point $N$. Find the length of $MN$, if the sum of the distances from point $M$ to the ends of the chord $BC$ is 6.
|
Ex. 104. 6. Hint. Show that point $N$ coincides with $A$ and use the result of Ex. 28.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Ex. 118. A circle with center on side $AB$ of triangle $ABC$ touches sides $AC$ and $BC$. Find the radius of the circle, given that it is expressed as an integer, and sides $AC$ and $BC$ are equal to 5 and 3.
|
Ex. 118. Answer: $r=1$. Solution. By equating the expressions for the area of triangle $ABC$, we get that $\frac{a+b}{2} r=\frac{a b}{2} \sin C$. From this, it follows that $r=\frac{a b}{a+b} \sin C$. In our case, $r=\frac{15}{8} \sin C$. If $r \geq 2$, then $\sin C>1$. This solves the problem.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Ex. 119. The lengths of the sides of a triangle are integers. It is known that the height, drawn to one of the sides, divides it into integer segments, the difference of which is 7. For what smallest value of the length of this side is the height, drawn to it, also an integer?
|
Ex. 119. 25. Solution. Let $A B C$ be the considered triangle, $B D$ be the height. Denote $A D=x, D C=y, A D=h$. Let $y>x \Rightarrow y-x=7 \Rightarrow x=\frac{b-7}{2}$. Expressing the height in two ways, we get the equality $a^{2}-y^{2}=c^{2}-x^{2} \Rightarrow$ $(y-x)(y+x)=(a-c)(a+c) \Rightarrow 7 b=(a-c)(a+c)$. Since $a+c>b$, then $a-c=k, a+c=7 n$, where $1 \leq k<7, b=k n, x=\frac{k n-7}{2}$. From this, $a=\frac{7 n+k}{2}, c=$ $\frac{7 n-k}{2} \Rightarrow \frac{(7 n+k)^{2}}{4}-\frac{(k n-7)^{2}}{4}=h^{2} \Rightarrow\left(n^{2}-1\right)\left(49-k^{2}\right)=h^{2}$. Note that $k$ and $n$ must be odd numbers. Thus, for $k$ there are only the following cases: $k=1,3,5$. By trying the possibilities, we find that $k=5, n=5$ give the smallest value of $b$. From this, $a=20, b=25, c=15$ (the triangle is right-angled). In this case, $x=9, y=16$. Note. If we allow that the length of one of the segments into which the height divides the side $A C$ can be zero, then another option is possible: $a=25, c=24, b=7(x=0)$.
|
25
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Ex. 129. In an integer-sided triangle, two sides are equal to 10. Find the third side, given that the radius of the inscribed circle is an integer.
|
Ex. 129. Answer: 12. Solution. Let the third side be denoted by $a$, and the angle subtending it by $\alpha$. Then $\sin \alpha=\frac{10+10+a}{10 \cdot 10} \cdot r$. At the same time, $1 \leq a \leq 19 \Rightarrow r \leq 4$. If $\sin \alpha=1$, then $x=5, r=4$, but a triangle with such data does not exist. According to the result of Ex. 124, $\sin \alpha=\frac{m}{n}$, where $n$ is either 5 or 25. In the first case, either $\sin \alpha=\frac{3}{5}$ or $\sin \alpha=\frac{4}{5}$. In both cases, a triangle with such data does not exist. If $n=25$, then $\sin \alpha=\frac{7}{25}$ or $\frac{24}{25}$. After verification, we get $a=12, r=3$.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 7. At the Dentist's Office
In the waiting room, two women and ten men are waiting for their turn. At their disposal are eight copies of the latest magazine and four copies of the morning newspaper. In how many ways can they distribute the newspapers and magazines among themselves, if both women insist on reading the same thing?
|
7. If both women will be reading a newspaper, then the corresponding number of distribution options for newspapers and magazines will be equal to the number of ways in which the remaining two copies of the newspaper can be distributed among ten men, i.e.
$$
C_{10}^{2}=\frac{10!}{2!8!}=45
$$
If the two women will be reading a magazine, then the corresponding number of options is equal to the number of ways in which four copies of the newspaper can be distributed among ten men, i.e.
$$
C_{10}^{4}=\frac{10!}{4!6!}=210
$$
Thus, the total number of possible distributions is $210+45=255$.
|
255
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 10. Auto Rally
This was an extremely dangerous auto rally. It started with a small and very narrow bridge, where one out of five cars fell into the water. Then came a terrible sharp turn, where three out of ten cars ended up in the ditch. Further along the way, there was such a dark and winding tunnel that one out of ten cars crashed in it. And the final stretch of the route was a sandy road, where two out of five cars got hopelessly stuck in the sand.
The task is to find the overall percentage of cars that were involved in accidents during the rally.
|
10. For a car to successfully complete an auto rally, it must not get into an accident on the bridge (which happens in 4 out of 5 cases), nor on a curve (7 out of 10), nor in a tunnel (9 out of 10), nor, finally, on a sandy road (3 out of 5). Thus, we get
$$
\frac{4 \cdot 7 \cdot 9 \cdot 3}{5 \cdot 10 \cdot 10 \cdot 5}=0.302
$$
Therefore, the percentage of cars that got into an accident during the auto rally is
$$
100-(100 \cdot 0.302) \approx 70 \%
$$
|
70
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 11. How Many Are We?
To help you answer this question, let's say that the probability that at least two of us have the same birthday is less than $1 / 2$, but this would be false if one more person joined us.
|
11. The probability that two people do not share the same birthday is $364 / 365$. For three people, the probability that no two of them share the same birthday is (364/365)$\cdot$(363/365), and so on. In the case of $n$ people, the same probability is
$$
(364 / 365) \cdot(363 / 365) \cdot \ldots \cdot(365-n+1) / 365
$$
This product crosses the threshold of $1 / 2$ when $n$ changes from 22 to 23. Therefore, we are - 22 people.
|
22
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 12. Convoy of Ships
In 1943, in one American port, there were four escort ships, seven cargo ships, and three aircraft carriers. From these ships, a transport convoy was formed to deliver food and ammunition to Europe. At the head was an escort ship, followed by three cargo ships, then an aircraft carrier, and lastly, another escort ship.
In how many different ways can such a convoy be organized?
|
12. The number of ways to choose the first escort ship is 4. The selection of three cargo ships can be carried out
$$
C_{3}^{3}=\frac{7!}{3!4!}=35
$$
ways.
The number of ways to choose an aircraft carrier is 3. The last escort ship can be chosen in 3 ways (since only three unused ships remain).
Thus, there are $4 \cdot 35 \cdot 3 \cdot 3=1260$ ways to form the transport heading to Europe.
|
1260
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 18. Expected Lifespan
An ethnographer found that in a certain primitive tribe he studied, the distribution of the lifespan of the tribe members could be described as follows: $25 \%$ of them only lived up to 40 years, $50 \%$ died at 50 years, and $25 \%$ - at 60 years. He then randomly selected two individuals to study in more detail. What is the expected lifespan of the one of the two randomly selected individuals who will live longer?
|
18. If the one of the two members of the tribe who lives longer reaches 40 years, then obviously both "subjects" will live only to 40 years; the corresponding probability is
$$
25 \cdot 25 \% = 1 / 4 \cdot 1 / 4 = 1 / 16
$$
If the "long-liver" reaches 50 years, this means that either the first of the two will live only 40 years, and the second will live 50, or they will both live 50 years, or finally, the first will live 50 years, and the second will live 40 years. The corresponding probability, as is easy to see, is
$$
\begin{aligned}
& (25 \cdot 50) \% + (50 \cdot 50) \% + (50 \cdot 25) \% = \\
& = 1 / 4 \cdot 1 / 2 + 1 / 2 \cdot 1 / 2 + 1 / 2 \cdot 1 / 4 = 1 / 2
\end{aligned}
$$
Finally, if the one of the two chosen members of the tribe who will live longer dies at 60 years, then neither of the events whose probabilities we have just calculated has occurred. The corresponding probability is
$$
1 - 1 / 16 - 1 / 2 = 7 / 16 \text{. }
$$
The expected average life expectancy is
$$
(1 / 16) \cdot 40 + (1 / 2) \cdot 50 + (7 / 16) \cdot 60 = 53 \text{ years } 9 \text{ months. }
$$
|
53
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 33. In Search of a Job
To find a job after demobilization, soldier Maurice began sending letters to various companies where people of his specialty can be employed. He believes that each of his applications has a one in five chance of being accepted, and he stops sending letters as soon as he finds that he has at least a three in four chance of finding a job.
How many letters will Maurice have to write? (The decimal logarithms of 3, 4, and 5 are approximately 0.477, 0.602, and 0.699.
|
33. The probability that Maurice will remain unemployed after sending $n$ letters is $(1-1 / 5)^{n}=(4 / 5)^{n}$. Therefore, the probability of finding a job is $1-(4 / 5)^{n}$.
Maurice will stop writing when $n$ becomes such that this probability is not less than $3 / 4$, i.e., when the inequality
$$
(4 / 5)^{n} \leqslant 1 / 4
$$
holds, from which
$$
n \geqslant \frac{\lg 4}{\lg 5-\lg 4}=\frac{0.602}{0.097} \approx 6.2 .
$$
Thus, Maurice will have to write 7 letters.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 36. Daily Newspapers
In a small town where many vacationers spend their holidays, $28 \%$ of the adult vacationers read "Mond", $25 \%$ read "Figaro", and $20 \%$ read "Orore". Additionally, $11 \%$ of the vacationers read both "Mond" and "Figaro", $3 \%$ read both "Mond" and "Orore", and $2 \%$ read both "Figaro" and "Orore", while $42 \%$ of the vacationers do not read any of these three newspapers. What is the percentage of adult vacationers who read all three newspapers, "Mond", "Figaro", and "Orore"?
|
36. Let $x$ be the desired percentage. Denote by $V$ the set of all vacationers, by $M$ the set of "Mond" readers, by $F$ the set of "Figaro" readers, and finally by $A$ the set of "Aurore" readers. To determine the desired percentage, we will use the Venn diagram provided below.
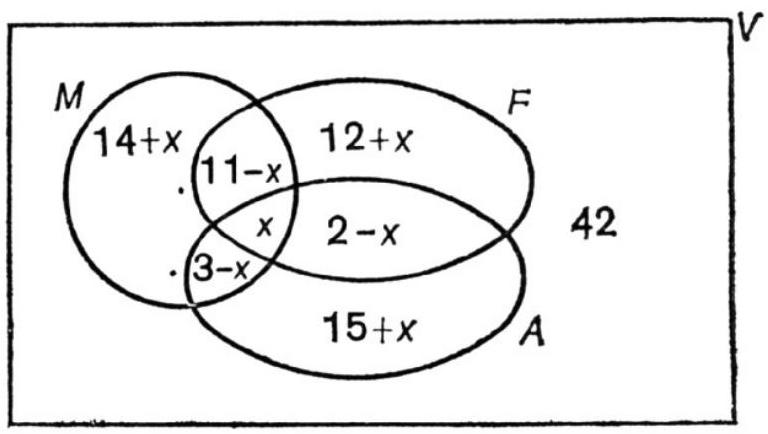
The entire set $V$ corresponds, of course, to $100 \%$. From this, we obtain the equation
$$
\begin{gathered}
42+(14+x)+(12+x)+(15+x)+(11-x)+ \\
+(2-x)+(3-x)+x=100
\end{gathered}
$$
i.e., $x=1 \%$.
Thus, $1 \%$ of adult vacationers read all three newspapers simultaneously.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 37. International Conference
Four French, two representatives from the Republic of Ivory Coast, three English and four Swedes gathered at a conference to discuss forestry issues. The conference participants from the same country initially sat next to each other on a bench with 13 seats during the opening ceremony, and later, during the working sessions, at a round table with 13 seats.
In how many different ways can the conference participants sit next to each other in each of these two cases?
|
37. The number of ways in which 4 French people can sit next to each other on a bench is 4!; representatives from Ivory Coast can be arranged in 2! ways; the English - in 3! ways, and the Swedes - in 4! ways.
From this, we get that the number of ways in which all 13 people can sit on a bench, given that the order of the national delegations is fixed, is
$$
4! \cdot 2! \cdot 3! \cdot 4! = 6912
$$[^23]
The number of ways in which the 4 national delegations can be arranged among themselves on a bench is 4!
Therefore, the total number of possible arrangements of 13 people on a bench is
$$
4! \cdot 6912 = 165888
$$
The number of ways in which the national delegations can be arranged around a round table is, obviously, not 4!, but 3!. Therefore, the total number of possible arrangements of 13 people around a round table is
$$
3! \cdot 6912 = 41472
$$
Explanation. Let's denote the delegations participating in the conference with letters: F - French, C - Ivory Coast, E - English, S - Swedes. The possible arrangements of the delegations around a round table are: FCES, FCSE, FCEC, FSEC, FSCC, FSEC.
The total number of such arrangements is 6, or 3!. On a bench, we have 4 times more arrangements, since, for example, ECF and FSEC are two different orders of arrangement of the delegations, while around a round table, such two arrangements are no longer distinguishable from each other.
|
165888
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 30. New City
The New City is built in the form of 12 rectangular blocks of houses, separated by streets; there is a mailbox at each corner of a block and at each street intersection. The blocks touch each other with entire sides or have only one common corner.
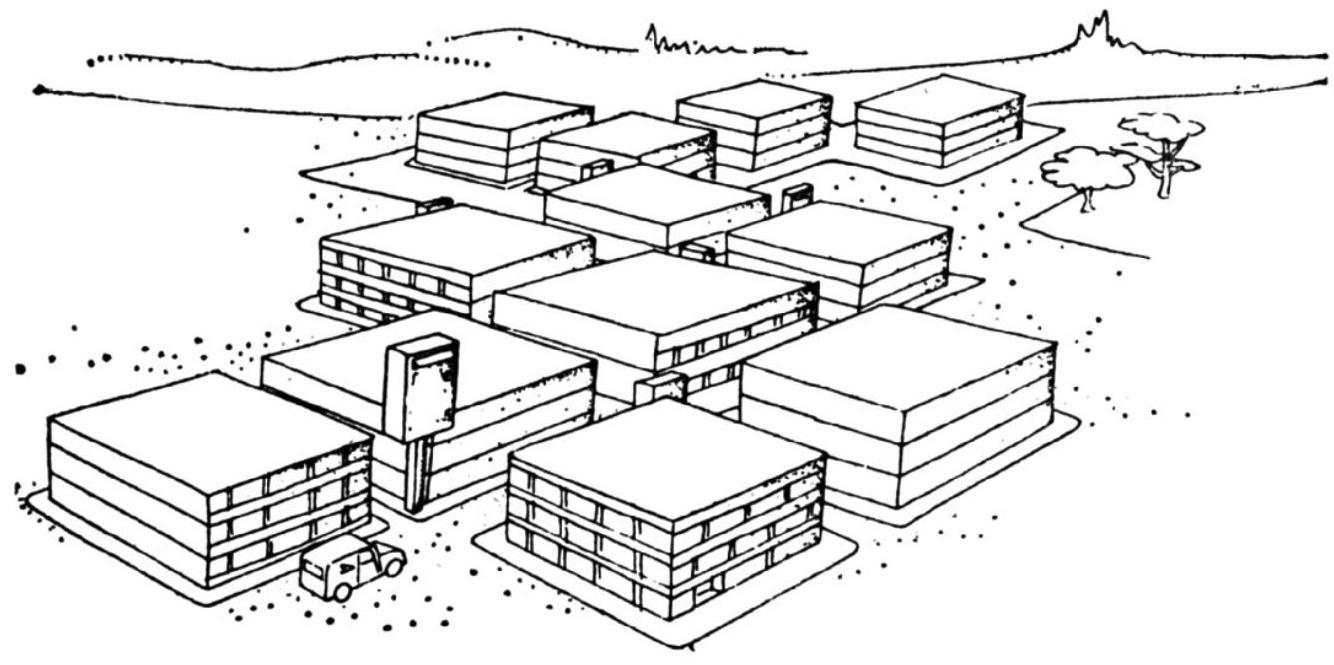
Suppose there are a total of 37 street segments that define the city blocks, i.e., 37 intervals between mailboxes. How many mailboxes are there in this city?
|
30. Let's examine two arbitrarily chosen possible configurations of 12 blocks.
We can observe that for each of these configurations, the number of mailboxes is 26. In fact, this number does not depend on the details of the city plan. Euler ${ }^{1}$ proved the following theorem g $^{2}$.[^25]
If the number of vertices, edges, and faces (i.e., regions bounded by edges) of any planar graph are $b, p$, and $r$ respectively, then
$$
b-p+r=2
$$
In our case, $b$ is the number of vertices, i.e., mailboxes, $p=27$ is the number of edges, i.e., street segments, and $r=12+1=13$ is the number of faces, i.e., the number of blocks plus 1, which is due to the presence of the external (infinite) face. Thus, we have
$$
b-37+13=2 \text {, i.e., } b=26 .
$$
|
26
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 4. From Bordeaux to Saint-Jean-de-Luz
Two cyclists set out simultaneously from Bordeaux to Saint-Jean-de-Luz (the distance between these cities is approximately 195 km). One of the cyclists, whose average speed is 4 km/h faster than the second cyclist, arrives at the destination 1 hour earlier. What is the speed of this cyclist?
|
4. Let $v$ (km/h) be the desired speed, and $t$ (h) be the time it takes for the cyclist moving at the higher speed $v$ to cover the entire distance.
The speed of the second cyclist, who is moving slower, is $v-4$. The time spent by him on the entire journey is $t+1$. Thus, we have
$$
195=v t=(v-4)(t+1),
$$
from which 1) $t=195 / v ;$ 2) $v-4 t-4=0$.
Expressing time in terms of speed, we get the equation
$$
v-4(195 / v)-4=0 \text {, or } v^{2}-4 v-4(195)=0 \text {. }
$$
Since the discriminant of the last quadratic equation is
$$
\Delta=4+195 \cdot 4=4 \cdot 196=(28)^{2} \text {, then } v=2+28=30 \text {. }
$$
(Clearly, the root of the equation $v=2-28=-26$ does not provide a meaningful solution.) Therefore, the desired speed is $30 \mathrm{km} /$ h.
The time it takes for the first cyclist to cover the entire distance is $195 / 30=6.5$ h. The time required by the second cyclist is $195 / 26=7.5$ h (i.e., exactly 1 h more than the first cyclist), which corresponds to the condition of the problem.
## 138
|
30
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 5. The Story of the Vagabonds
At the very moment when Pierrot left the "Commercial" bar, heading for the "Theatrical" bar, Jeanno was leaving the "Theatrical" bar, making his way to the "Commercial" bar. They were walking at a constant (but different) speed. When the vagabonds met, Pierrot proudly noted that he had walked 200 meters more than Jeanno. Already quite drunk, Jeanno got offended and hit Pierrot. Of course, Pierrot didn't hesitate to respond... When the fight was over, they hugged and cried, and each continued on their way, but at half the speed they had before, as the beatings were taking their toll. Therefore, Pierrot reached the "Theatrical" bar in 8 minutes, and Jeanno reached the "Commercial" bar in 18 minutes. What is the distance between the bars?
|
5. Let $x$ (m) - be the distance between the bars we are looking for; $d$ - the distance traveled by Pierrot by the time of the meeting; $V$ (m/s) - Pierrot's speed, and $v$ - Jeanno's speed before the fight.
The sum of the distances traveled by the vagrants is
$$
d+(d-200)=x, \quad \text { from which } \quad x=2 d-200 .
$$
Before the meeting, each traveled their path in the same amount of time; therefore,
$$
d / V=(d-200) / v
$$
After the meeting, Pierrot walked for 8 minutes:
$$
\frac{d-200}{V / 2}=8, \quad \text { or } \quad V=\frac{d-200}{4}
$$
and Jeanno - for 18 minutes:
$$
d /(v / 2)=18, \quad \text { or } \quad v=d / 9 .
$$
Substituting the values of $V$ and $v$, expressed in terms of $d$ from (3) and (4), into equation (2), we get
$\frac{4 d}{d-200}=\frac{9(d-200)}{d}$, or $5 d^{2}-3600 d+360000=0$.
The discriminant of this quadratic equation in $d \Delta^{\prime}=(1800)^{2}-5 \cdot 360000=(1200)^{2}$. Therefore,
$$
d=\frac{1800 \pm 1200}{5} \text {, i.e., } d=600 \text { or } 120 \text { (m). }
$$
Since $x=2 d-200$ [see (1)], we get two values for $x: 1000$ or 40.
However, since, according to the condition, the distance $d$ is only a part of the sought distance $x$, the second solution should be discarded. The first solution remains. Thus, the bars are 1 km apart.
|
1000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 6. Invited Evening
To celebrate her husband being awarded the Legion of Honor, his wife, a well-known lady from the Paris region, decided to order cookies from the best pastry shop in Paris.
- Our evening, - she clarifies on the phone, - will start exactly at 6 PM. I want the fresh cookies to be delivered precisely at this time.
- Madam, - they respond, - the delivery vehicles leave at specific times, as soon as the cookies are baked. If there is not too much traffic, the vehicles can travel at an average speed of 60 km/h; then we will arrive at your place at 5:45 PM. But if there are traffic jams along the way, the average speed will drop to 20 km/h, and we will only arrive at 6:15 PM.
Try to determine at what average speed the delivery vehicle should travel to arrive at your place exactly at the start of the evening?
|
6. Let $v$ be the speed of interest (but currently unknown), $t$ the corresponding delivery time, and $d$ (km) the distance the car must travel. We obtain the following system of equations:
$$
\text { 1) } t=d / v, \text { 2) } t+1 / 4=d / 20, \text { 3) } t-1 / 4=d / 60 \text {. }
$$
From equations (2) and (3), it follows that
$$
20 t+5=d, \quad 60 t-15=d
$$
Therefore,
$$
40 t-20=0
$$
and, thus,
$$
t=1 / 2, \quad d=15 \text { and } v=30
$$
Thus, the car should move at a speed of 30 km/h.
|
30
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 8. The Emir and His Chauffeur
Emir Ben Sidi Mohammed always drives from his palace to the airport at the same speed along a magnificent highway that runs through the desert. If his chauffeur increased the average speed of the car by $20 \mathrm{km} /$ h, the Emir would save 2 minutes, and if the chauffeur drove at a speed 20 km/h slower, the Emir would lose 3 minutes.
How far is the Emir's palace from the airport?
|
8. Let $I$ (km) be the unknown distance; $v$ (km/h) the speed of the emir's car, and finally, $t$ (h) the time it takes for the emir to travel from the palace to the airport. We obtain the following system of equations:
$$
v=I / t ; \quad v+20=I /(t-2 / 60) ; \quad v-20=I /(t+3 / 60) .
$$
Excluding the first equation, we find
$$
(v-20)(t-3 / 60)=v t, \quad(v+20)(t+3 / 60)=v t,
$$
or
$$
\begin{gathered}
-v / 30+20 t-2 / 3=0 \\
v / 20-20 t-1=0 .
\end{gathered}
$$
From the last two equations (add them!), we find: $v=100$, and $t=1 / 5=12$ min. Therefore, $I=v t=20$.
The airport and the emir's palace are separated by a distance of 20 km.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 10. Escalator in the Metro
Usually, I go up the escalator in the metro. I calculated that when I walk up the stairs of the moving upward escalator, I climb 20 steps myself, and the entire ascent takes me exactly $60 \mathrm{c}$. My wife walks up the stairs more slowly and only climbs 16 steps; therefore, the total time she spends on the ascent is longer - it takes her 72 seconds.
How many steps would I have to climb if the escalator suddenly breaks down?
|
10. Let $x$ be the unknown number of steps on the stationary escalator. When the escalator is working, it rises at a speed of $x-20$ steps in 60 seconds (this follows from calculations related to my ascent) or at a speed of $x-16$ steps in 72 seconds (which follows from how my wife ascends). Thus, the speed of the escalator's movement is $[(x-16)-(x-20)]$ in 12 seconds (72-60). Therefore, in 60 seconds, the escalator moves up 20 steps. From this, it follows that the full span of the escalator contains 20 plus 20 steps, i.e., a total of 40 steps.
|
40
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 11. Polar Expedition
A polar explorer set out from one point to another on a sled pulled by a team of five dogs. But after 24 hours, two of the dogs died, causing the explorer's speed to decrease to $3 / 5$ of the original speed, and he was delayed by two days.
- Oh! - exclaimed the polar explorer. - If the two dogs that died had run another 120 km, I would have been delayed by only one day.
What distance did the polar explorer travel?
|
11. If two dogs had run 120 km more, the polar explorer's delay would have been reduced by 24 hours (48-24). Therefore, if these dogs had run 240 km further, the polar explorer's delay would have been 48-24-24=0 hours, i.e., he would have arrived on time; hence, the distance from the place where the dogs fell to the destination is 240 km. Let $v$ be the initial speed of the polar explorer. From the moment the dogs fell until arrival at the destination, the time taken is
$$
48+240 / v, \text { or } 5 / 3 \cdot 240 / v .
$$
Therefore,
$$
48+240 / v=400 / v, \quad \text { i.e., } \quad v=10 / 3 \text{ km} / \text { h. }
$$
Before the dogs fell, the polar explorer had traveled (in 24 hours)
$$
24 \cdot 10 / 3=80 \text{ km}
$$
Thus, the total distance is
$$
80+240=320 \text{ km. }
$$
|
320
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 12. Punctual Wife
Every Saturday between 15 and 16, I play tennis with my friend Philippe. My wife arrives to pick me up in the car precisely at 16:10. One day, Philippe fell ill. Unaware of this, I set out for tennis as usual. However, at 15:05, realizing that Philippe wasn't coming, I gathered my things and started walking home. On the way, I met my wife, who was driving to pick me up. I got into the car, and we arrived home 10 minutes earlier than usual.
This might not seem very interesting, but could you determine from this story the ratio between my walking speed and the speed at which my wife drives?
|
12. On the day when Philip fell ill, my wife drove the car for 10 minutes less than usual; that means she drove 5 minutes less in each direction. Therefore,
I met her at 4:05 PM, instead of 4:10 PM as usual. But then I walked for 60 minutes to cover the distance my wife drives in 5 minutes. Thus, I walk 12 times slower than my wife drives.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 13. The Scout and the Drummer
On the occasion of the village festival, a procession was organized that stretched for 250 m; the scouts led the procession, and the musicians brought up the rear. Soon after the march began, the youngest scout remembered that he had not tied his neckerchief, which was left with his friend, the drummer, who was in the last row of the musicians. So the scout ran to get the neckerchief and returned to his place in 3 minutes and 18 seconds.
What was the speed of the procession, assuming the scout ran at a speed of 10 km/h?
|
13. Let $x$ be the unknown speed of the procession. When the scout ran to the end of the procession, he moved relative to the procession (considered stationary!) at a speed of $10+x$; when he returned, he moved relative to the procession at a speed of $10-x$. Since the length of the procession is 250 m, the total time spent by the scout is
$$
\frac{250}{1000} \cdot \frac{1}{10+x}+\frac{250}{1000} \cdot \frac{1}{10-x}=\frac{3}{60}+\frac{18}{3600}
$$
(here we measure distance in kilometers, time in hours, and speeds in km/h).
Transform our equation:
$$
(10-x)+(10+x)=4(10+x)(10-x)(3 / 60+18 / 3600)
$$
or
$$
20=4\left(100-x^{2}\right) \cdot(198 / 3600)
$$
From this, we find
$$
x^{2}=100 / 11, \quad x=\sqrt{100 / 11} \approx 3
$$
The speed of the procession is approximately 3 km/h.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 15. Metro in Mexico City
A worker is walking along the tracks in one of the tunnels of the capital's subway, on a section between two stations that are far apart. Every 5 minutes a train passes him coming from the opposite direction, and every 6 minutes another train overtakes him. The worker walks at a constant speed, the speeds of the subway trains (which are the same for trains going in both directions) do not change, nor do the intervals between trains (which are also the same for trains going in both directions).
When the worker stopped to fix a malfunction that had forced him to set out on his journey, a train passed by. How long will it take for the next train going in the same direction to pass by?
|
15. Let $x$ be the time between the passage of two consecutive trains moving in the same direction; $I$ be the distance between two consecutive trains; $V$ be the speed of each train, and finally, $v$ be the speed of the worker. Then, relative to the worker, each following train moves at a speed of $V-v$, and each oncoming train moves at a speed of $V+v$.
From this, we obtain the following system of equations:
1) $5=I / (V+v)$
2) $6=I / (V-v)$,
3) $x=I / V$.
It is easy to see that [due to (1)-(3)] $x=60 / 11=5$ min $27 \mathrm{s}$.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 21. Rue Sainte-Catherine
I was walking with my mother-in-law. We were slowly, at a speed of 3 km/h, walking down Rue Sainte-Catherine in Bordeaux, which, as everyone knows (or maybe doesn't know), is straight. Suddenly, I remembered that I needed to drop a letter in a mailbox located a bit further down the street. Leaving my mother-in-law, who continued her walk calmly, I hurried ahead, and after dropping the letter, I walked back to meet her at the same speed (5 km/h). I clearly remember that I left her alone for only 3 minutes.
How far from the mailbox were we when we parted?
|
21. Let's choose meters and minutes as units of measurement. Then my speed after I left my mother-in-law is $5000 / 60 = 250 / 3 \, \text{m} /$ min, and my mother-in-law's speed (and our common speed during the walk) is 3000/60 = $50$ m $/$ min. Let $S$ be the point where we parted, $R$ the point where we met again, and $B$ the point where the mailbox is located. The distance my mother-in-law walked in 3 minutes is
$$
S R = 50 \cdot 3 = 150
$$
In this time, I walked the distance
$$
S B + B R = S R + 2 B R = (250 / 3) \cdot 3 = 250
$$
Therefore, $2 B R = 100$ and $B R = 50$. Thus,
$$
S B = S R + R B = 200
$$
So, at the moment we parted, we were 200 meters away from the mailbox.
|
200
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 12. Figure
On a plane, there are five points such that no three of them lie on the same line. The points are connected by straight lines. What is the number of intersection points of the lines (excluding the original five points), if none of the drawn lines are parallel to each other?
|
12. Let $A, B, C, D$ and $E$ be five given points. The line $A B$ is intersected by the lines forming three sides of the triangle $C D E$. This gives three points of intersection. The same applies to each other line. The total number of lines is equal to the number of ways to choose two points from five, i.e., 10. Thus, we get $3 \cdot 10=30$ points, but each point is counted twice (why?). In fact, the actual number of intersection points of the lines is only 15, not 30.
## 154
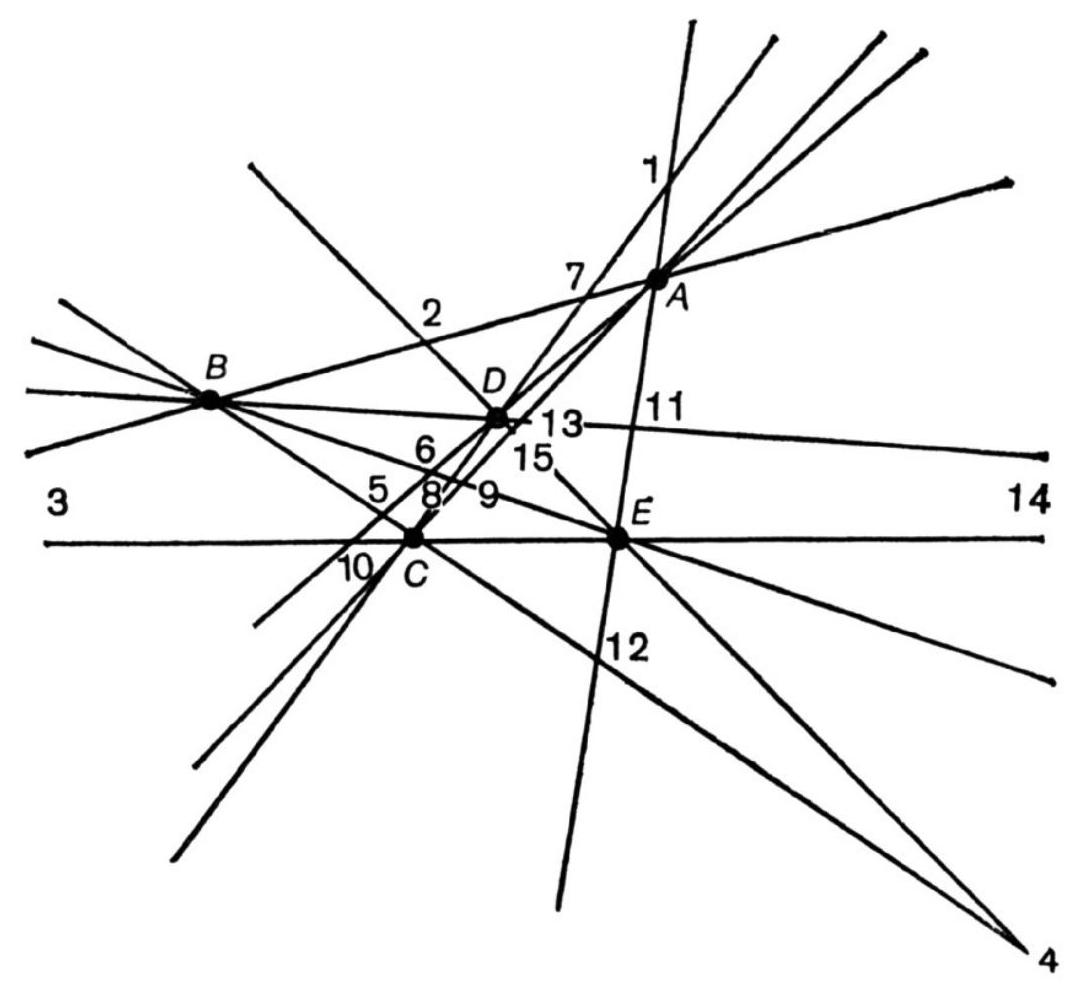
|
15
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 14. "Revolutionary" ${ }^{1}$ Geometry
Let in triangle $A B C$ angle $B$ be a right angle, and $M$ be a point on the hypotenuse, equidistant from the two sides of the triangle. Could you find the value of the following expression:
$$
\begin{aligned}
E & =\sqrt{1830}\left(A C-\sqrt{A B^{2}+B C^{2}}\right) \\
& +1789-\frac{\frac{1}{A B}+\frac{1}{B C}-\frac{\sqrt{2}}{B M}}{(1848)^{3}} ?
\end{aligned}
$$
|
14. 15) By the Pythagorean theorem $A C^{2}=A B^{2}+B C^{2}$; therefore,
$$
A C-\sqrt{\overline{A B^{2}+B C^{2}}}=0
$$
2) The area of $A B C=$ area of $A B M+$ area of $B M C$. Therefore, if point $M$ is at a distance $d$ from the legs of the triangle, then
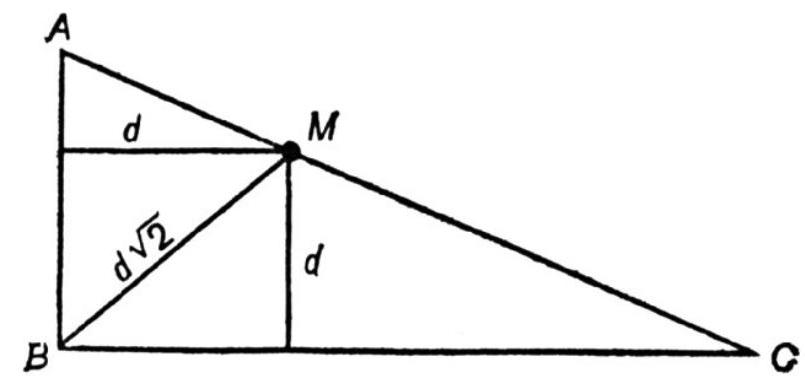
$A B \cdot B C / 2=A B \cdot d / 2+B C \cdot d / 2$,
or
$$
1 / d=1 / B C+1 / A B
$$
But $B M=d \sqrt{2}$; therefore,
$$
1 / A B+1 / B C-\sqrt{2} / B M=0
$$
3) From the two previous observations, it follows that
$$
E=1789 \text {. }
$$
|
1789
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 22. Lighthouse
From the tower of the lighthouse, located 125.7 m above sea level, the horizon line is visible. At what approximate distance from the tower is this line, if we assume that the Earth's surface is spherical and its great circle is 40,000 km?
|
22. Let $S$ be the top of the lighthouse, $A$ be the point on the horizon, and $O$ be the center of the Earth. Triangle $O A S$ is a right triangle because line $S A$ is tangent to the spherical surface of the Earth. Therefore,
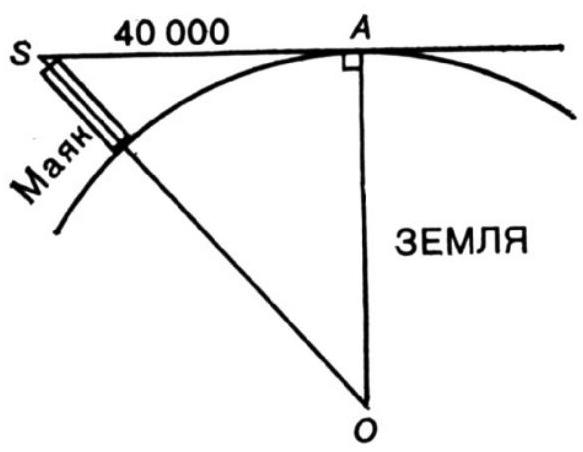
$$
O S^{2}=A O^{2}+A S^{2}
$$
But (in meters)
$$
O A=\frac{40000000}{2 \pi}
$$[^27]a
$$
O S=O A+125.7 \approx \frac{40000000}{2 \pi}+40 \pi
$$
Therefore,
$$
A S=\sqrt{O S^{2}-O A^{2}} \approx \sqrt{2 \frac{40 \pi \cdot 40000000}{2 \pi}} \approx 40000
$$
Thus, the horizon is approximately 40 km from the lighthouse.
|
40
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 32. Siesta
Albert lay lazily on the sun-drenched terrace, drifting into a sweet doze. This did not prevent him, however, from observing his right hand. "My index and middle fingers," he thought, "form an angle of about $20^{\circ}$. Can I, while keeping their relative position, turn my hand so that the shadows of my fingers are perpendicular to each other?" A minute later, having found the answer to his question, he sighed contentedly—and fell asleep immediately.
Could you, in his place, fall asleep just as quickly?
|
32. Albert placed the tips of his index and middle fingers on the terrace (a horizontal plane), maintaining a constant angle between them ($20^{\circ}$). When his hand rotates around these two points of support, the angle formed by the shadows of his fingers changes: it is $20^{\circ}$ when the hand lies on the terrace, and $180^{\circ}$ when the hand lies in a plane parallel to the sun's rays. Since this change in angle occurs continuously, at some point the two shadows will form exactly a right angle ($90^{\circ}$ is between $20^{\circ}$ and $180^{\circ}$). This conclusion is simple enough that, were we in Albert's place, we too would quickly fall asleep.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 1. Bark
One smart dog knew how to count in the quaternary number system. She conveyed zero in her dog language with the sound "o", one with the sound "u", two with the sound "v", and finally, three with the sound "a". What number, in this case, did her bark "ouavoouav" represent?
|
1. Ouoouo $=\left(2 \cdot 4^{0}\right)+\left(3 \cdot 4^{1}\right)+\left(1 \cdot 4^{2}\right)+\left(0 \cdot 4^{3}\right)+\left(2 \cdot 4^{4}\right)+$ $+\left(3 \cdot 4^{5}\right)+\left(1 \cdot 4^{6}\right)+\left(0 \cdot 4^{7}\right)=2+12+16+0+512+3072+0+$ $+4096+0=7710$.
|
7710
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 8. At the Restaurant
Monsieur Dupont remembered that today was their wedding anniversary and invited his wife to have lunch at a good restaurant. Leaving the restaurant, he found that he had only one-fifth of the money he had brought with him left, and the number of centimes left was the same as the number of francs he initially had (1 franc $=100$ centimes), while the number of francs left was five times less than the number of centimes he initially had.
How much did Monsieur Dupont's visit to the restaurant cost?
|
8. Let $F$ be the initial number of francs, $C$ be the initial number of centimes, $F^{\prime}$ be the remaining number of francs, and $C^{\prime}$ be the remaining number of centimes.
Since after dining at the restaurant, Monsieur Dupont had only one-fifth of his money left, we have
$$
100 F + C = 5 \left(100 F^{\prime} + C^{\prime}\right)
$$
On the other hand, we know that
$$
C^{\prime} = F \quad \text{and} \quad F^{\prime} = C / 5.
$$
From this system of three equations with four unknowns, we can easily obtain that
$$
C = (95 / 99) F
$$
However, the number of centimes is an integer and less than 100. Therefore, the initial number of francs $F$ can only be 99, which means,
$$
C = 95, \quad F^{\prime} = C / 5 = 19, \quad C^{\prime} = F = 99
$$
Thus, initially, Monsieur Dupont had 99 francs and 95 centimes, and he was left with 19 francs and 99 centimes. Therefore, the dinner at the restaurant cost him 79 francs and 96 centimes.
|
79
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 10. Anniversary
"Do you remember Leonitina's fortieth birthday? It was December 28, $19 \ldots$ Since then, Leonitina has aged. I noticed that half of her age equals twice the sum of its digits."
Please fill in the missing digits in the date of Leonitina's fortieth birthday.
|
10. So, Leontina's age is equal to four times the sum of its digits. Therefore, she is less than 100 years old (and not less than 10 years old). Let $d$ be the number of tens, and $u$ be the number of units in the notation of her age. Then
$$
10 d+u=4(d+u)
$$
from which
$$
2 d=u \text {. } \quad \text {. }
$$
Thus, the number of units is twice the number of tens, which corresponds to ages of 12, 24, 36, and 48 years. Since Leontina is over forty years old, on December 28, 1978, she was exactly 48 years old. Therefore, she celebrated her fortieth birthday on December 28, 1970.
|
1970
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 16. How many of you were there, children?
If you had asked me such a question, I would have answered you only that my mother dreamed of having no fewer than 19 children, but she did not manage to fulfill her dream; however, I had three times as many sisters as cousins, and brothers - half as many as sisters. How many children did my mother have?
|
16. From the conditions of the problem, it follows that the number of my sisters is divisible by both 3 and 2. Therefore, it is divisible by 6. Hence, the total number of children is
$$
[(\text { number divisible by } 6) \cdot(1+1 / 2)]+1
$$
(the last 1 corresponds to myself). This number must be strictly less than 19, so it inevitably equals 6.
Therefore, I had 6 sisters and 3 brothers, and my mother had a total of 10 children.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 17. Airline
One American airline serves several major cities, establishing direct flights between each pair of these cities. Next year, it plans to increase the number of flights by 76, which will allow it to serve some additional cities under the same conditions.
How many cities does this airline currently serve, and how many cities does it plan to serve next year?
|
17. Let $n$ be the number of cities currently served. The corresponding number of flights is $n(n-1)$, since each city is connected to $n-1$ cities served by the airline. For the next year, the airline plans
$$
(n+k)(n+k-1)
$$
flights, where $k$ is the additional number of cities. Therefore,
$$
(n+k)(n+k-1)-n(n-1)=76
$$
From this,
$$
k(k+2 n-1)=76(=4 \cdot 19=2 \cdot 39=1 \cdot 76)
$$
Thus, $k=4$, or $k=2$, or, finally, $k=1$.
But if $k=2$, then $k+2 n-1=38$, i.e., $2 n-1=36$, which is impossible since $(2 n-1)$ is an odd number. Therefore, the only possible cases are: $k=4$ - and then $k+2 n-1=19$, i.e., $n=8$, and $k=1$ - and then $k+2 n-1=76$, i.e., $n=38$.
Thus, either the airline currently serves 8 cities, and next year it will serve 12 cities, or it currently serves 38 cities, and next year the number will increase to 39.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 22. Age Difference
The sums of the digits that make up the birth years of Jean and Jacques are equal to each other, and the age of each of them starts with the same digit. Could you determine the difference in their ages?
|
22. Let $(m, c, d, u)$ be the number of thousands, hundreds, tens, and units in Jean's birth year, and let $\left(m^{\prime}, c^{\prime}, d^{\prime}, u^{\prime}\right)$ be the corresponding digits of Jacques' birth year. Then Jean's age is
$$
1979-(1000 m+100 c+10 d+u)
$$
Jacques' age is
$$
1979-\left(1000 m^{\prime}+100 c^{\prime}+10 d^{\prime}+u^{\prime}\right)
$$
The difference in their ages is
$$
1000\left(m-m^{\prime}\right)+100\left(c-c^{\prime}\right)+10\left(d-d^{\prime}\right)+\left(u-u^{\prime}\right)
$$
But according to the problem statement,
$$
m+c+d+u=m^{\prime}+c^{\prime}+d^{\prime}+u^{\prime}
$$
i.e.,
$$
\left(m-m^{\prime}\right)+\left(c-c^{\prime}\right)+\left(d-d^{\prime}\right)+\left(u-u^{\prime}\right)=0
$$
Subtracting the last expression from the difference in Jean's and Jacques' ages term by term, we get the number
$$
999\left(m-m^{\prime}\right)+99\left(c-c^{\prime}\right)+9\left(d-d^{\prime}\right)
$$
which is clearly divisible by 9.
But this number is less than 10 (since Jean's and Jacques' ages are written as numbers starting with the same digit), and therefore it equals 9.
Thus, the difference in Jean's and Jacques' ages is 9 years.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 23. Division
Division of integers is performed. If the dividend is increased by 65 and the divisor is increased by 5, both the quotient and the remainder remain unchanged. What is this quotient?
|
23. Let $D$ - the dividend, $d$ - the divisor, $q$ - the quotient, and $r$ - the remainder. The conditions of the problem can be written as two equations:
$$
D=q d+r, \quad D+65=q(d+5)+r
$$
Subtracting the first equation from the second, we get
$$
65=5 q
$$
from which
$$
q=13
$$
|
13
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 24. Permutations
A certain three-digit number will increase by 45 if the two rightmost digits are swapped, and it will decrease by 270 if the two leftmost digits are swapped. What will happen to this number if the two outermost digits are swapped?
|
24. Let $c, d$ and $u$ be the number of hundreds, tens, and units of a given number, respectively. According to the problem, we have the following equations:
$$
\begin{aligned}
& (100 c+10 d+u)=(100 c+10 u+d)-45 \\
& (100 c+10 d+u)=(100 d+10 c+u)+270
\end{aligned}
$$
From this, we get
$$
\begin{gathered}
9 d-9 u+45=0 \\
90 c-90 d-270=0
\end{gathered}
$$
That is,
$$
u=d+5, \quad c=d+3
$$
If we swap the two extreme digits, the difference between the resulting values will be
$$
\begin{gathered}
(100 u+10 d+c)-(100 c+10 d+u)= \\
=99(u-c)=99[(d+5)-(d+3)]=198
\end{gathered}
$$
Thus, with this permutation of digits, the number will increase by 198.
|
198
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 25. School
In all the classes of one school, the same number of students studied. After a fire, six classes of the school became unsuitable for lessons, and therefore, five more students had to be added to each class where lessons were held. But then, due to water damage from the fire hoses, another ten classes were recognized as being in a threatened condition. Then, fifteen more students had to be added to each class that remained in good condition.
How many students are there in this school?
|
25. Let $c$ be the number of students in each class before the fire, and $n$ be the number of classes at that time. Then the following relationships hold:
$$
\begin{gathered}
n c=(n-6)(c+5) \\
n c=(n-16)(c+20)
\end{gathered}
$$
From these two equations, it follows that
$$
\begin{gathered}
-6 c+5 n-30=0 \\
-16 c+20 n-320=0
\end{gathered}
$$
Therefore, $c=25, n=36$.
Thus, the number of students in the school is
$$
n c=36 \cdot 25=900
$$
|
900
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 27. Large Families
The Martens have more children than the Duponts. Suppose the difference of the squares of these two numbers is 24 and that both families have more than one child. How many children do the Martens have?
70
|
27. Let $m$ and $d$ be the number of children in the Marten and Dupont families, respectively. According to the problem,
$$
m^{2}-d^{2}=24 \text {, i.e., }(m+d)(m-d)=24\left(=2^{3} \cdot 3\right) \text {. }
$$
Therefore, the following values for $m+d, m-d$, and thus $2 m[=(m+d)+(m-d)]$, $m$, and $d$ are possible:
| $m+d$ | $m-d$ | $2 m$ | $m$ | $d$ |
| :---: | :---: | :---: | :---: | :---: |
| 24 | 1 | 25 | $12 \frac{1}{2} ?$ | $11 \frac{1}{2} ?$ |
| 12 | 2 | 14 | 7 | 5 |
| 8 | 3 | 11 | $5 \frac{1}{2} ?$ | $2 \frac{1}{2} ?$ |
| 6 | 4 | 10 | 5 | $1 ?$ |
The only valid value, therefore, is $m=7$. The Martens have 7 children.
Remark. The first and third possibilities are not valid because the number of children must be an integer, and the last one is not valid because, according to the problem, each family has more than one child.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 28. At the Ball
When I saw Eleanor, I found her very pretty. After a brief banal conversation, I told her how old I was and asked about her age. She replied:
- When you were as old as I am now, you were three times as old as I was. When I am three times as old as I am now, together we will be exactly a century old.
I didn't understand a word of this gibberish and told her so. Then she decided that I didn't deserve her attention and left without giving me an answer.
How old is this stubborn creature?
|
28. So, let's turn to the conversation of two individuals. Let $e-$ be Eleonora's age, and $m$ - my age. When I was as old as she is now, Eleonora's age was
$$
e-(m-e)=2 e-m .
$$
Therefore, from her first statement, the following equality follows:
$$
e=3(2 e-m) \text{, or } 3 m=5 e \text{. }
$$
When Eleonora becomes three times as old as she is now, I will be
$$
m+(3 e-e)=m+2 e
$$
years old. From Eleonora's second statement, it follows that
$$
3 e+(m+2 e)=100 \text{, or } 5 e+m=100 \text{. }
$$
Considering the first equation, we get
$$
3 m+m=100 \text{, or } m=25 \text{. }
$$
Therefore,
$$
e=3 m / 5=15
$$
So, Eleonora is 15 years old.
|
15
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 29. Leonie and Cats
When old lady Leonie is asked how many cats she has, she melancholically replies: “Four fifths of my cats plus four fifths of a cat.” How many cats does she have?

|
29. Let $n$ be the number of cats Leonie has. From her last words, we can write the relationship
$$
n=(4 / 5) n+4 / 5, \text { i.e. } \quad n=4 .
$$
Thus, Leonie has 4 cats.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 30. New Mathematics
My son has learned to count in a numeral system different from the decimal system, and instead of 136, he writes 253 in this system. In what numeral system is my son counting?
|
30. Let $a$ be the base of an unknown numeral system. When my son writes "253" in this system, it represents $2 a^{2}+5 a+3$; according to the problem, this corresponds to the number 136 in the decimal system. Therefore, we can write
$$
2 a^{2}+5 a+3=136
$$
i.e.
$$
2 a^{2}+5 a-133=0
$$
or
$$
(a-7)(2 a+19)=0
$$
Since $a$ is a positive integer, the only solution to this equation is 7. My son was using the septenary (base-7) system. 31.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 33. Least Number
What is the least number that, when divided by $2, 3, 4, 5$, and 6, gives remainders of $1, 2, 3, 4$, and 5 respectively?
|
33. Let $n$ be an unknown number. Since $n$ when divided by 2 leaves a remainder of 1, the number $n+1$ is divisible by 2. Since $n$ when divided by 3 leaves a remainder of 2, the number $n+1$ is divisible by 3, and so on. Similarly, $n+1$ is divisible by 4, 5, and 6. But the least common multiple of 2, 3, 4, 5, and 6 is 60. Therefore, $n=59$.
|
59
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 36. San Salvador Embankment
Would you come to have dinner with me tonight? I live in one of the eleven houses on San Salvador Embankment; however, to find out which one, you will have to think.
When, from my home, I look at the sea and multiply the number of houses to my left by the number of houses to my right, I get a number that is 5 more than the similar number obtained by my left neighbor when he does the same.
|
36. Let $d$ be the number of houses to the right of my house when I look at the sea, and $g$ be the number of houses to the left of it. Then
$$
d+g=10,
$$
and
$$
d g-(d+1)(g-1)=5
$$
or
$$
d+g=10, \quad d-g=4 .
$$
From this, $2 d=14, d=7$ and, therefore, $g=3$.
Thus, my house is the fourth from the left when looking at the sea, or the fourth from the right if you turn your back to the sea.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 38. How old is the eldest brother?
Determine this yourself, if it is known that the age of the middle brother is equal to the product of the ages of his two brothers, that the sum of the ages of all three brothers is 35, while the sum of the decimal logarithms of their ages is 3.
|
38. Let $a$ be the age of the oldest, $c$ the age of the middle, and $b$ the age of the youngest brother. Then, based on the conditions of the problem, the following relationships hold:
$$
\begin{gathered}
c^{2}=a b \\
a+b+c=35 \\
\lg a+\lg b+\lg c=3
\end{gathered}
$$
From the first equation, it follows that
$$
2 \lg c=\lg a+\lg b
$$
However, in this case, the third equation implies that
$$
\lg c=1 . \quad
$$
Thus, $c=10$, i.e., the middle brother is 10 years old. Therefore,
$$
a b=100 \text { and } a+b=25 .
$$
Hence, $a$ and $b$ are the roots of the equation
$$
x^{2}-25 x+100=0
$$
Since $a$ is greater than $b$, then $a=20, b=5$. Therefore, the age of the oldest brother is 20 years. (Since the age of the youngest brother $b=5$ years, indeed, $\lg a+\lg b+$ $+\lg c=\lg (a b c)=\lg (20 \cdot 5 \cdot 10)=\lg 1000=3$).
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 39. How old am I?
Try to answer this question if it is known that Alfred's age is obtained by rearranging the digits of my age, that the quotient of the number equal to my age divided by the sum of these two digits differs from the analogous quotient for Alfred by a number equal to the difference between these two digits, and that, finally, the product of these two quotients is exactly equal to my age.
|
39. Let $x$ be my age, $d$ be the number of tens in it, and $u$ be the number of units. Then $x=10 d+u$, and Alfred's age is $10 u+d$. The first condition of the problem can be written as:
$$
\left|\frac{10 d+u}{d+u}-\frac{10 u+d}{d+u}\right|=|d-u| \cdot
$$
Simplifying this equality, we get
$$
9|d-u|=(d+u) \cdot|d-u|
$$
from which
$$
d+u=9 \text {, i.e., } d=9-u \text {. }
$$
192
Now let's write the second condition of the problem
$$
\frac{10 d+u}{d+u} \cdot \frac{10 u+d}{d+u}=10 d+u
$$
or
$$
10 u+d=(d+u)^{2}
$$
Replacing $d$ with $9-u$, we get
$$
9 u+9=81
$$
Therefore,
$$
u=8 \text { and } d=1 \text {. }
$$
So, I am 18 years old, and Alfred is 81 years old.
|
18
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 40. Question about age
One fine spring Sunday morning, the head of the family went for a walk with his sons.
- Have you noticed,- he said to them,- that the age of the oldest of you is equal to the sum of the ages of the other two brothers?
- Yes. And we also noticed,一 they replied in unison,一 that the product of our ages and your age is equal to the sum of the cube of the number of your sons, multiplied by a thousand, and ten times the square of this number.
Could you determine from this conversation the age of the head of the family at the time of the birth of the second son?
|
40. The head of the family has three sons. The product of the ages of the father and all his sons is
$$
3^{3} \cdot 1000 + 3^{2} \cdot 10 = 27090 = 43 \cdot 7 \cdot 5 \cdot 3^{2} \cdot 2
$$
Since the age of the oldest son is equal to the sum of the ages of his brothers, the only possible factorization of the obtained number is
$$
43 \cdot 14 \cdot 9 \cdot 5
$$
Thus, the father is 43 years old, the second son is 9 years old. Therefore, when the middle son was born, the father was 34 years old.
|
34
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 43. Rue Saint-Nicaise
On December 24, 1800, First Consul Bonaparte was heading to the Opera along Rue Saint-Nicaise. A bomb exploded on his route with a delay of a few seconds. Many were killed and wounded. Bonaparte accused the Republicans of the plot; 98 of them were exiled to the Seychelles and Guiana. Several people were executed. Suppose the number of wounded is equal to twice the number of killed (in the explosion) plus four-thirds of the number of those executed, that the sum of the number of killed or wounded and the number of those executed is slightly less than the number of those exiled, and that if you subtract 4 from the number of killed, you get exactly twice the number of those executed.
Could you, without referring to history books, determine how many people Bonaparte executed after the attack on Rue Saint-Nicaise?
|
43. Let $x$ be the number of those executed; then, according to the last condition of the problem, the number of those killed in the explosion is $2 x+4$, and the number of wounded is
$$
2(2 x+4)+(4 / 3) x=5 x+x / 3+8
$$
(hence, $x$ is a multiple of 3).
It is also known that
$$
(2 x+4)+(5 x+x / 3+8)+x<98
$$
or
$$
x<10
$$
Since $x$, on the one hand, is slightly less than 10, and on the other - a multiple of 3, then, apparently, $x=9$.
Thus, after the assassination attempt on the rue Saint-Nicaise, Bonaparte executed nine republicans.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 47. Suez and Panama
A meeting took place between Egyptians and Panamanians, where issues regarding the operation of the Suez and Panama Canals were discussed. In total, there were twelve participants from both sides, with more Egyptians than Panamanians. Upon arriving at the meeting place, the Egyptians greeted each other in pairs in Arabic. The Panamanians did the same, but in Spanish. However, the Panamanians did not exchange greetings with the Egyptians, either due to language barriers or for some political reasons.
Assuming there were a total of 31 greetings exchanged, how many Egyptians and how many Panamanians were present at the meeting?
|
47. If $n$ people greet each other in pairs, then a total of $n(n-1) / 2$ greetings take place. Therefore, we can create the following table:
In order for there to be exactly 31 greetings, there must have been seven Egyptians and five Panamanians at the meeting.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 48. Sequence of Numbers
To write the sequence of numbers from 1 to $n$, it took 2893 digits. What is the number $n$?
|
48. To write the first nine single-digit numbers, it is necessary
$$
9 \cdot 1=9 \text{ digits. }
$$
To write the next 90 two-digit numbers, 180 digits are required, and to write the next 900 three-digit numbers, 2700 digits are required.
In total, we get 2889 digits. This is four digits less than the number of digits needed to write all numbers from one to $n$. Therefore, $n$ coincides with the first four-digit number, i.e., with the number 1000.
|
1000
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 51. Congratulations from Methuselah
Every New Year, starting from the first year of our era, Methuselah, who is still alive to this day, sends a greeting to his best friend, who, naturally, has changed many times over the centuries and decades. However, the formula for the greeting, on the contrary, has remained unchanged for almost two millennia. It is very simple: "Happy New Year 1", "Happy New Year 2", "Happy New Year 3", and so on, "Happy New Year 1978" and finally, "Happy New Year 1979".
Which digit has Methuselah used the least so far?
|
51. From the 1st to the 999th year, all digits were used an equal number of times, except for 0 (all digits were used exactly the same number of times if the first years were recorded by Methuselah as: year 0001, year 0002, ..., year 0999; however, since he did not do this, the digit 0 was used 111 times less frequently than the others). For similar reasons, in the records from 1000 to 1999, all digits appear the same number of times, except for 1 (the digit 1 is used here 1000 times more frequently than the others). But we are only considering the series of years ending in 1979. The years 1980, 1981, 1982, ..., 1999 remain. In this new series, the digit 9 appears most frequently (31 times). But this shortage of nines due to the "discarded" series is much less significant than the shortage of 0 in the first 1000 numbers.
Thus, Methuselah used the digit 0 the least frequently (and, obviously, the digit 1 the most frequently).
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 55. 100 years among the three
Patrick was walking with his father and grandfather. He wanted to imagine the time when all of them together would be 100 years old.
His father said on this matter: “I will be 28 years older than you, and you will be six-fifths of your current age.” And his grandfather added: “I will be twice as old as your father would have been at the time of your birth, if you had been born one and a half years later.”
Patrick thought deeply, trying to figure out how much time would pass until they could celebrate their combined century.
Please help him.
|
55. Let $e$ be Patrick's age, $p$ be the father's age, and $g$ be the grandfather's age; let $x$ be the time interval after which all three will be 100 years old. Then the following equations hold:
1) $(g+x)+(p+x)+(e+x)=100$
2) $e+x=(6 / 5) e$,
3) $(p+x)-(e+x)=28$,
4) $g+x=2(p-e+1.5)$.
From the last two equations, we get
$$
g+x=59 \text {. }
$$
Then from equation (1), we find
$$
59+(p+x)+(e+x)=100
$$
Since
$$
p+x=28+(e+x) \text { and } e+x=(6 / 5) e \text {, }
$$
it follows that
$$
59+28+(12 / 5) e=100
$$
Therefore, $e=5$ years 5 months, and $x=e / 5=1$ year 1 month.
Thus, all three will be 100 years old together in 1 year and 1 month (or 13 months).
|
13
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 1. British Hospital
In a British hospital, the following announcement can be read: "Surgeon $X$ and Nurse $Y$ have the pleasure of announcing their forthcoming marriage." Suppose that at the time the hospital was opened, the groom was as old as the bride is now, and that the product of the ages of the groom and the bride and the number of years the hospital has been in existence minus the age of the surgeon equals 1539. When was the hospital opened?
|
1. Let $x$ be the age (number of full years) of the surgeon (groom or bride), $y$ be the number of years of the paramedic (groom or bride), and $h$ be the number of years the hospital has been in existence.
The conditions of the problem can be written as the following two equations:
$$
\begin{gathered}
|x-y|=h \\
x(y h-1)=1539=3^{4} \cdot 19
\end{gathered}
$$
Since, by the context of the problem, $x$ is obviously greater than 9 and less than 171, there are four possible values for $x$: $19, 27, 57, 81$.
These correspond to four values of the expression ($y h - 1$): $81, 57, 27, 19$ and, therefore, four values for $y h$: 82, 58, 28, and 20.
But if $y h=82=2 \cdot 41$, then $y=41, \quad h=2$,
$$
\begin{array}{lll}
y h=58=2 \cdot 29 & y=29, & h=2 \\
y h=28=2^{2} \cdot 7, & y=28 & h=1 \\
y h=20=2^{2} \cdot 5, & y=20, & h=1 .
\end{array}
$$
We obtained these four solutions using only the second equation. If we also use the first equation ($|x-y|=h$), then only the second solution remains, i.e., $x=27, y=29$, and $h=2$.
Thus, the problem is about the marriage of a 29-year-old paramedic to a 27-year-old female surgeon, who work in a hospital that opened 2 years ago.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 2. Clock
At the moment, according to my watch, it is more than 3:20 but less than 3:25. I observe the exact position of the hands on my watch, and then I move the hands so that the minute hand is in the position previously occupied by the hour hand, and the hour hand is in the position previously occupied by the minute hand.
Can you accurately indicate what time the watch shows at the moment.
|
2. If $p$ and $g$ are the angles (in radians) that the hour and minute hands form with the direction from the center of the clock face to the 12 o'clock mark, then
$$
g=12(p-h \cdot 2 \pi / 12)
$$
where $h=0,1,2, \ldots$ or 12 is the number of hours ${ }^{1}$. If the angles $p_{0}$
${ }^{1}$ The angles $p$ and $g$ are measured here in the direction of the clockwise rotation; with $0 \leqslant p, g \leqslant 2 \pi, -\text{Note, } \text{pre}$,
and $g_{0}$ characterize the initial positions of the hands, and the angles $p_{1}$ and $g_{1}$ their positions after we have set the clock, then
1) $g_{0}=12\left(p_{0}-\pi / 2\right)$
2) $g_{1}=12\left(p_{1}-2 \pi / 3\right)$
3) $p_{1}=g_{0}, g_{1}=p_{0}$.
## From this
$$
p_{0}=12\left(g_{0}-2 \pi / 3\right)
$$
Substituting this expression into (1), we get
$$
g_{0}=12\left[12\left(g_{0}-2 \pi / 3\right)-\pi / 2\right]
$$
or
$$
143 g_{0}=6 \cdot 17 \pi
$$
But $g_{0}$ is the angle formed with the chosen direction by the minute hand, for which $2 \pi$ corresponds to 60 minutes. Therefore,
$$
g_{0}=\frac{3 \cdot 17 \cdot 60}{143} \text { min. }
$$
Thus, at this moment, the clock shows 3 hours 21 minutes $23(131 / 143)$ seconds $\approx 3$ hours 21 minutes 23 seconds 55 thirds, where 60 thirds $=1$ second.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 3. In the Cafeteria
Every day while having breakfast in the cafeteria, I noticed that snacks are always served between 7 and 8 o'clock, when both the hour and minute hands are equally distant from the number 6, and coffee is placed on the table at the moment when the minute hand catches up with the hour hand.
How much time does it take me to have breakfast in this cafeteria (or more precisely, to eat the appetizer and the main course - before the coffee)?
|
3. Let 7 hours $x$ minutes be the time when the appetizer is served. The angle formed by the hour hand and the segment connecting the center of the clock face with the number 6 is (in degrees
$$
\frac{360}{12}+\left(\frac{x}{60} \cdot \frac{360}{12}\right)=30\left(1+\frac{x}{60}\right)=30+\frac{x}{2}
$$
The angle formed by the minute hand with the same segment is
$$
180-x \frac{360}{60}=180-6 x
$$
Since these two angles are equal,
$$
x=300 / 13 \approx 23 \text { min } 5 \text{ s. }
$$
So, the appetizers are served at approximately 7:23:05. Let 7 hours $y$ minutes be the time when the coffee is served. The angle formed by the hour hand with the same ray directed at the number 6 is
$$
30+y / 2
$$
The angle formed by the minute hand with the same direction is
$$
6 y-180
$$
Since these two angles are equal, then
$$
y=420 / 11 \approx 38 \text { min } 11 \text { s, }
$$
i.e., the coffee is served at approximately 7:38:11.
Thus, in this cafeteria, it takes about 15 min 6 s to eat the appetizers and the main course.
|
15
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 6. Coffee is served
Coffee is always served to me between 1 and 2 o'clock, at a moment when the bisector of the angle formed by the two hands of my clock points exactly at the "12" (hour) mark. At what exact time is my coffee served?
|
6. Let's denote this unknown moment of time as 1 hour $x$ minutes (since it is between 1 hour and 2 hours!). The angle formed by the hour hand with the bisector of the angle between the two hands is (in degrees)
$$
\frac{360}{12}+\frac{x}{60} \cdot \frac{360}{12}=30+\frac{x}{2}
$$
(here we use the fact that the bisector of the angle points to the 12 o'clock mark).
The angle formed by the minute hand with this same bisector is
$$
360-x \cdot(360 / 60)=360-6 x
$$
${ }^{1}$ In Venn diagrams (cf. footnote on p. 119), each subset $Z$ is symbolically represented by a circle, making it easy to trace all possible unions and intersections of these sets, - Note by the translator.
Thus, we have
$$
30+x / 2=360-6 x
$$
from which
$$
x=(2 / 13) \cdot 300 \approx 50 \text { min } 46 \text{s}.
$$
Therefore, my coffee is served at approximately 1 hour 50 minutes $46 \text{s}$.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 10. Confession
The confessor has a habit of assigning penances "by the tariff" - in exact proportion to the gravity of the sins committed. Thus, before absolving the sin of pride, he requires the penitent to recite the "Te Deum" once and the "Pater Noster" twice. Slander is "priced" at two "Pater Noster" and seven "Credo." Laziness "costs" two "Te Deum." Adultery is only absolved after ten "Te Deum," ten "Pater Noster," and ten "Credo," while gluttony is punished with only one penitential prayer, the "Te Deum." Self-love costs the penitent three "Pater Noster" and one "Credo," while jealousy costs three "Pater Noster." Finally, backbiting is "priced" at seven "Pater Noster" and two "Credo." Suppose since my last confession, I must repent for a dozen sins, for which I will have to recite the "Te Deum" nine times, the "Pater Noster" twelve times, and the "Credo" ten times.
What, then, are my sins?
|
10. Since I will have to repeat the "Te Deum" only nine times, it is clear that I am not guilty of adultery.
I confess to one instance of slander, for ten "Credo" would be too few for two instances of slander, and if I had not slandered at all, the "Credo" would correspond to such a number of sins of pride and slander, for which more than a dozen "Pater Noster" would be required to atone.
Having fulfilled the penance imposed for slander, I will still have to repeat the prayer "Credo" three more times. This corresponds to three sins of pride or one sin of pride and one sin of slander. But three sins of pride require nine "Pater Noster" for atonement, and since I am also guilty of slander, there will be a total of eleven "Pater Noster," not twelve as required by the condition of the problem; this remains unexplained and, moreover, inexplicable. Therefore, the three "Credo" I must read are for the atonement of one instance of slander and one instance of pride.
There remain nine sins for which there are nine "Te Deum." Thus, these sins can be nothing other than nine instances of gluttony.
Thus, I confess to one instance of slander, one instance of slander, one sin of pride, and nine instances of gluttony.
(We recommend that the reader first prepare a table in which the number of repetitions of each of the twenty prayers is indicated, corresponding to each of the eight named sins.)
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 13. Friendly Lunch
Ten married couples, who were friends with each other, met to have lunch together. First, they had an aperitif in the living room, and then all twenty people followed each other into the dining room. What is the minimum number of people that must go into the dining room so that among them there are:
1) at least one married couple;
2) at least two people of the same gender?
|
13. It is clear that as soon as thirteen people enter the dining room, there will inevitably be at least one married couple among them.
As soon as three people enter the dining room, there will certainly be at least two people of the same gender among them.
|
13
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 14. Dromedaries ${ }^{1}$
Some of the dromedaries are sleeping, while others are awake; the number of sleeping dromedaries is seven eighths of the number of awake dromedaries plus another seven eighths of a dromedary. If half of the sleeping dromedaries woke up, the number of awake dromedaries would be between 25 and 65. And if all the sleeping dromedaries woke up, the number of awake dromedaries would be equal to...
Complete, please, the last sentence.
|
14. Let $d$ be the number of sleeping, and $r$ be the number of awake dromedaries. According to the problem, we have
$$
d=(7 / 8) r+7 / 8
$$
or
$$
8 d=7 r+7
$$
Thus, $d$ must be a multiple of 7.
On the other hand, this number must be such that it can be divided into two equal parts, i.e., it must be even; therefore, $d$ is divisible by 14. Further, we have the following possibilities:
| $d$ | 14 | 28 | 42 | 56 | and so on |
| :---: | :---: | :---: | :---: | :---: | :---: |
| $r$ | 15 | 31 | 47 | 63 | and so on |
| $r+d / 2$ | 22 | 45 | 68 | 91 | and so on |
In the third row of this table, the number of awake dromedaries is shown as it would be if half of the sleeping dromedaries woke up. Since, according to the problem, this number is between 25 and 65, it equals 45. Thus, $d=28$ and $r=31$. The total number of dromedaries is 59, which is what we needed to find.
|
59
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 16. Grandmother, the Mark, and the Kittens
If you write down my mark, which I received in school for Latin ${ }^{1}$, twice in a row, you will get my grandmother's age. And what would you get if you divide this age by the number of my kittens? Imagine this - you would get my morning mark, increased by fourteen thirds?
How old is my grandmother?
|
16. Let $a$ be the age of my grandmother, $c$ be the number of my kittens, and $l$ be my grade in Latin. From the first condition of the problem, it follows that $l$ is an integer less than 10 (since it is clear that the age of my grandmother is less than 1010 years), and that $a=11 l$.
The second condition of the problem can be written as the equation
$$
a / c=3 l+14 / 3,
$$
or
$$
a=3 c l+14 c / 3 \text { . }
$$
Thus, $c$ is a multiple of 3; and since $3 c$ must be less than 11, $c$ equals 3. Therefore, we have
$$
a=11 l \text { and } a=9 l+14 \text {, }
$$
from which it is easy to find
$$
l=7, \quad a=77
$$
Thus, my grandmother is 77 years old.
|
77
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 17. Mathematical Puzzle
This week's mathematical puzzle in the "Modern Values" magazine was particularly difficult. When I started thinking about it (it was between 9 and 10 o'clock), I noticed that the two hands of my clock were in a straight line, one continuing the other. And I found the solution only at the moment when the hands merged with each other.
How long did my reflections last?
|
17. Let 9 hours $x$ minutes be the time when I started solving the problem. The angle formed by the hour hand with the common direction of the clock hands at noon is (in degrees)
$$
2 \cdot 360 / 12 + [(60 - x) / 60] \cdot 30
$$
The angle formed by the minute hand with the same direction is
$$
(360 / 60) \cdot x
$$
Since the hands were extensions of each other, these two angles must be supplementary to $180^{\circ}$:
$$
60 + (60 - x) / 2 + 6x = 180 \text{ or } 30 + (11 / 2) \cdot x = 120
$$
from which
$$
x = (2 / 11) \cdot 90 \approx 16 \text{ min } 22 \text{s}
$$
Let 10 hours minus $y$ minutes be the time when I finished my thoughts. The angle formed by the hour hand with the common direction of the clock hands at noon is (in degrees)
$$
2 \cdot (360 / 12) + (y / 60) \cdot 30
$$
The angle formed by the minute hand with the same direction is
$$
(360 / 60) \cdot y
$$
Since the two hands merged, these angles must be equal to each other
$$
6y = 60 + y / 2
$$
from which
$$
y = 120 / 11 \approx 10 \text{ min } 54 \text{s}.
$$
Thus, I started working at approximately 9:16:22, and finished at approximately 9:49:06. My thoughts on the puzzle took me about 32 minutes and 45 seconds.
|
32
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 18. Seals
Once I entered a maritime museum and saw some seals there. There were not many of them - just seven eighths of all the seals plus another seven eighths of a seal that I counted in the pool. How many seals were there in the pool in total?
dili in two rounds). According to the French constitution, a second round of elections is not held if one candidate has already received an absolute majority of the votes in the first round; if no such candidate exists, only the two candidates who received the most votes in the first round participate in the second round.-Note by nepes.
${ }^{1}$ In French high schools, a 20-point grading system is used - from 1 (complete lack of knowledge of the subject) to 20 (the highest grade in French secondary education, which gives the right to continue education at a university). - Note by the editor.
|
18. Let $n$ be the total number of seals. In this case,
$$
n=(7 / 8) n+7 / 8
$$
from which it follows that $n=7$.
There were seven seals in the marine museum.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 19. Tram
On one tram line, trams depart regularly every 10 minutes throughout the day. A tram takes one hour to travel from one end of the line to the other. A passenger boards a tram at one terminal stop and rides to the last stop of the tram; out of boredom, he looks out the window and counts the oncoming trams of the same route. How many tram sets will he count in total.
|
19. The passenger will encounter all the tram cars that departed from the other end of the tram line less than an hour before his departure; generally speaking, there are six such trains. He will also encounter all the trains that will depart from the opposite end of the line within the next hour; generally speaking, there are also six such trains. Therefore, the passenger will count a total of twelve tram cars on the way.
Special case. If the departure of the tram cars from both terminal stations occurs simultaneously, then our passenger will encounter only eleven cars on the way, but he will see one additional oncoming car at each of the terminal stations.
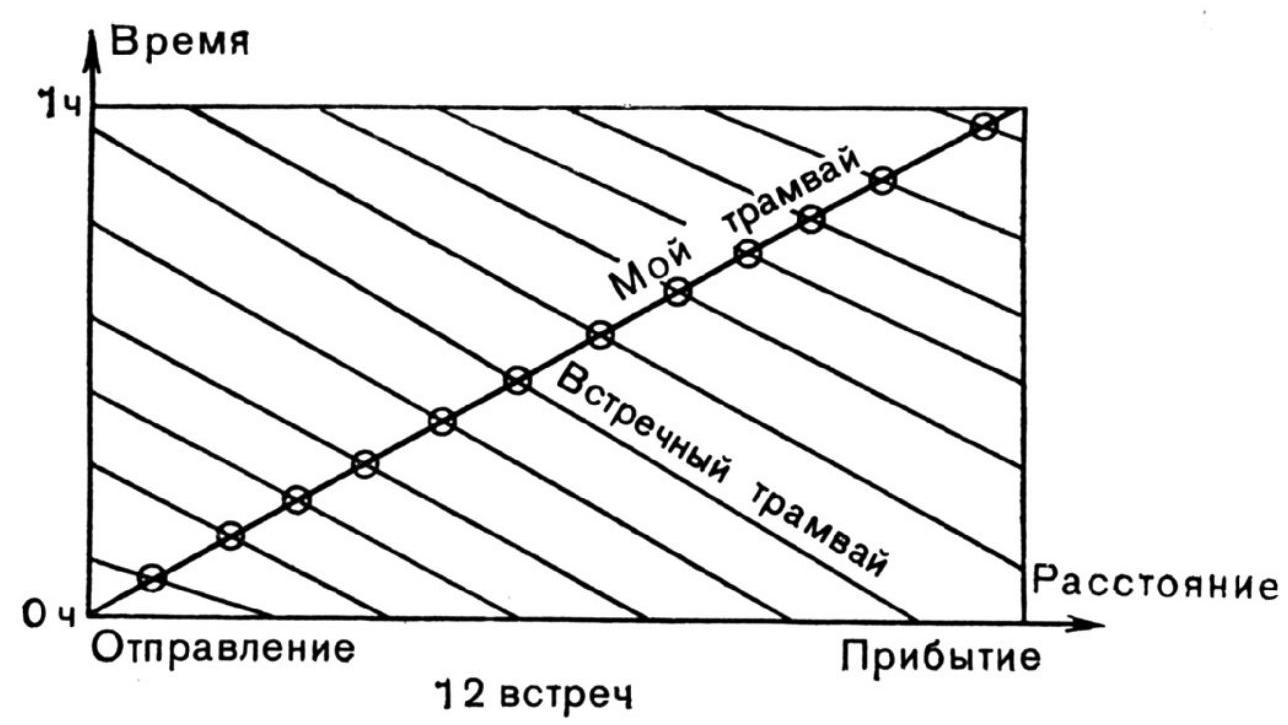
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 20. Nicolas plays
## with tin soldiers
Nicolas has the same number of tin Indians, Arabs, cowboys, and Eskimos. After his cousin Sebastian's visit, he indignantly discovered the disappearance of a third of his soldiers. Suppose the number of Eskimos remaining is the same as the number of cowboys that disappeared, and that only two Indians out of every three remain. How many Arabs did cousin Sebastian take?
|
20. Let $x$ be the number of soldiers of each type that Nicolas had initially, and $y$ be the number of cowboys taken by Sebastian (or the number of remaining Eskimos); in this case, the number of Eskimos taken is $x-y$.
On the other hand, it is known that the number of Indians taken is $x / 3$. Let $z$ be the number of Arabs taken. The total number of soldiers taken is $4 x / 3$, since it constitutes one third of the total number of soldiers. But it is easy to see that it also equals
$$
y+(x-y)+x / 3+z
$$
From this, we get the equation
$$
4 x / 3=4 x / 3+z
$$
from which it follows that $z=0$.
Thus, cousin Sebastian did not take any Arabs.
|
0
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 22. General Cleaning
A solid joint-stock company occupies three floors in a tower, which has the shape of a parallelepiped and is located in Paris in the La Défense district: the 13th and 14th floors, where the company's offices are located, and the 25th floor, where its board of directors is situated.
To clean these premises, a cleaning crew is called in, who work for four hours in the offices. Then the crew splits into two parts: half goes to clean the 25th floor, while the other half continues to clean the 13th and 14th floors. After another four hours, the crew stops working: the two lower floors are already completely cleaned, while the 25th floor is scheduled to receive another cleaner the next day, who will complete the work in 8 hours.
Assuming that the time required for cleaning is proportional only to the area of the cleaned premises, how many cleaners were in the crew called by the company?
|
22. Let $n$ be the unknown number of cleaners. The number of man-hours required to clean two floors of the bureau is
$$
4 \cdot(n+n / 2)
$$
The number of man-hours required to clean the 25th floor is
$$
4 \cdot(n / 2)+8
$$
But this last number is half of the previous one, since the area of one floor is half the area of the other two. Therefore,
$$
4(n+n / 2)=2(4 n / 2+8)
$$
From this, $n=8$, i.e., there were eight cleaners in the team.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 29. Apples
Amelie picked apples, ate a quarter of them herself, and gave the rest to her little sisters Bertha, Charlotte, and Dorothy. Bertha ate a quarter of her apples and gave the rest to her three sisters. Charlotte ate one apple and gave the rest to her three sisters. As for little Dorothy, she also ate a quarter of her share before giving the rest to her three sisters.
"Look," said Bertha to Charlotte, "I have twice as many apples left as you do."
How many apples did Amelie pick?
|
29. Let $a$ be the number of apples Amelie ends up with, $c$ be the number of apples Charlotte has at this stage, and $2c - y$ be the number of apples Berta has (0 being the number of apples Dorothy has). In the following table, we will represent all events in reverse order of their actual occurrence:
| | Amelie | Berta | Charlotte | Dorothy |
| :--- | :---: | :---: | :---: | :---: |
| In the end | $a$ | $2c$ | $c$ | 0 |
| Before Dorothy distributed the apples | $a-c$ | $c$ | 0 | $4+3c$ |
| Before Charlotte distributed the apples | $a-2c$ | 0 | $1+3c$ | $4+2c$ |
| Before Berta distributed the apples, but after Amelie did | 0 | $4a-8c$ | $1+5c-a$ | $4+4c-a$ |
The last three parts should be equal. Therefore,
$$
4a-8c=1+5c-a
$$
and
$$
4a-8c=4+4c-a,
$$
from which $c=3, a=8$.
Thus, Amelie gave her sisters 8 apples each, and she herself picked 32 apples.
|
32
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 35. Parent Meeting
At the end of the school year, the third-grade teachers met with some of their students' parents; exactly 31 people were present at this meeting. The Latin teacher was asked questions by 16 parents, the French teacher by 17, the English teacher by 18, and so on up to the math teacher, who was asked questions by all the parents present at the meeting. How many parents were present at the meeting?
|
35. Let $n$ be the number of parents present at the meeting, and $m$ be the number of teachers. The first teacher talked to $15+1$ parents, the second to $15+2$, and so on, ..., the $m$-th teacher talked to $15+m$ parents. But the last teacher was the math teacher, with whom all the parents talked. Therefore,
$$
15+m=n
$$
Since there were a total of 31 people at the meeting, then
$$
n+m=31
$$
Subtracting the first equation from the second, we get
$$
n-15=31-n
$$
i.e., $n=23$.
At the mentioned meeting, there were 23 parents of students (and 8 teachers).
|
23
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 36. Sacks of Flour
Two trucks are transporting identical sacks of flour from France to Spain. The first one carries 118 sacks, while the second one carries only 40. Since the drivers of these trucks do not have enough pesetas to pay the customs duty, the first one leaves 10 sacks for the customs officials, as a result of which he only has to pay 800 pesetas. The second one does the same, but he had to unload only 4 sacks, and the customs official even paid him 800 pesetas.
How much does each sack of flour cost, given that in these calculations the customs officials took exactly as much flour as was required to fully pay the customs duty?
|
36. Let $x$ be the cost of one sack of flour, and $y$ be the duty charged per sack.
If the first driver left 10 sacks at the customs, he should pay duty only for 108 sacks. Similarly, the second driver should pay duty only for 36 sacks. As a result, we get the following system of equations:
$$
\begin{aligned}
10 x+800 & =108 y, \\
4 x-800 & =36 y .
\end{aligned}
$$
Multiplying the second equation by 3 and subtracting the first equation from it, we get
$$
2 x-3200=0
$$
Therefore, $x=1600$.
Each sack of flour costs 1600 pesetas.
|
1600
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 38. Simone and Her Complexes
Simone suffered from numerous complexes. Therefore, she decided to go to one psychoanalyst and after a course of treatment, she got rid of half of her complexes and half of one of the remaining complexes. Then she went to another psychoanalyst, thanks to which she got rid of half of the remaining complexes and half of one of the still remaining complexes. The result of her visit to the third psychoanalyst was exactly the same. After this, Simone was left with only one complex, from which she will not part until the end of her days.
How much did Simone's treatment cost, assuming that each psychoanalyst charged 197 francs for each cured complex?
|
38. Consider the following table:
| Stage of Treatment | Number of Complexes |
| :--- | :---: |
| | 1 |
| At the end | $(1+1 / 2) \cdot 2=3$ |
| Before the 3rd psychoanalyst | $(3+1 / 2) \cdot 2=7$ |
| Before the 2nd psychoanalyst | $(7+1 / 2) \cdot 2=15$ |
| Before the 1st psychoanalyst | $(7+1)$ |
Thus, at the beginning, Simone suffered from 15 complexes. For the entire treatment, she had to pay
$$
14 \cdot 197=2758 \text { francs. }
$$
|
2758
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 39. Square Plot
Mathieu has a square plot of land. Surrounding this plot is an alley of constant width with an area of $464 \mathrm{~m}^{2}$. Walking around his plot, Mathieu noticed that the difference in length between the outer and inner edges of the alley is 32 m.
What is the total area of Mathieu's plot, including the alley?
|
39. Let $x$ be the length of the outer edge of the alley, and $y$ be the length of the inner edge of the alley. We have the following system of equations:
$$
\begin{gathered}
x^{2}-y^{2}=464 \\
4 x-4 y=32
\end{gathered}
$$
From the second equation, it follows that $x=y+8$. Then the first equation gives $x=33$ and $y=25$. (Note that, by dividing the first equation by the second, we get $x+y=$ $=464: 8=58$.)
Thus, the total area of Mathieu's plot is 1089 m.
|
1089
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 40. Tennis Tournament
199 people have registered to participate in a tennis tournament. In the first round, pairs of opponents are selected by lottery. The same process is used to select pairs in the second, third, and all subsequent rounds. After each match, one of the two opponents is eliminated, and whenever the number of participants in the tournament is odd, one of them skips the current round.
Assume that in each match between two tennis players, a new can of balls is used. How many cans of balls will be needed for the entire tournament?
|
40. After each match, one of the opponents is eliminated, and since 199 people are participating in the tournament, by the end, 198 athletes must be eliminated. Therefore, for the entire tournament, 198 boxes of balls will be needed.
|
198
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 42. Barrels
In how many ways can a 10-liter barrel be emptied using two containers with capacities of 1 liter and 2 liters?
|
42. Let $u_{n}$ be the number of ways to empty a barrel of capacity $n$ liters using two vessels of capacity 1 and 2 liters.
A barrel of $n$ liters will be emptied if we first use either the 1-liter vessel [and then we need to choose $(n-1)$ liters more from the barrel], or the 2-liter vessel [and then we need to choose $(n-2)$ liters more]. This gives us the recurrence relation
$$
u_{n}=u_{n-1}+u_{n-2}
$$
Obviously, $u_{0}=1, u_{1}=1$.
We obtain sequentially
$$
\begin{array}{ll}
u_{2}=2, & u_{5}=13, \\
u_{3}=3, & u_{7}=21, \\
u_{4}=5, & u_{8}=34, \\
u_{5}=8, & u_{9}=55, \\
& u_{10}=89 .
\end{array}
$$
Thus, there are 89 ways to empty a barrel of capacity 10 liters using the two specified vessels ${ }^{1}$.
|
89
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 43. Calves, Cows, Pigs, Chickens
The dowry of a young peasant girl consists of a cow, a calf, a pig, and a chicken. Her fiancé knew that five cows, seven calves, nine pigs, and one chicken together cost 108210 francs, and also that a cow is 4000 francs more expensive than a calf, that three calves cost as much as ten pigs, and that 3000 chickens cost as much as five calves. Based on all this information, he tried to calculate the value of his bride's dowry - but he failed. Could you help him?
|
43. Let $c$ be the price of a pig. Then the price of a calf is $(10 / 3) c$, and therefore, the price of a cow is $(10/3)c+4000$ and the price of a chicken is $(5 / 3000) \cdot(10 / 3) \cdot c$.
Considering the first piece of information the suitor had, we get
$$
(50 / 3) c+20000+(70 / 3) c+9 c+c / 180=108210
$$
from which it follows that
$$
c=1800 \text {. }
$$
The dowry of the bride, therefore, amounts to
$$
6000+10000+1800+10=17810 \text { francs. }
$$
|
17810
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 2. Marel
Take a piece of cardboard and draw the following diagram on it:
Also, take three silver and three gold coins (if you are on the beach, draw the diagram directly in the sand and play with three white and three black pebbles).
Now choose a suitable partner; each player starts the game with three coins (one player with gold, the other with silver). The player who starts places one of their coins on any of the nine circles. Then the second player places their coin on any of the remaining eight circles; after that, the first player places their second coin, and so on. When all the coins are placed, the players take turns moving one of their three coins along one of the sixteen segments, provided that the other end of the segment is free. The player who first aligns their three coins in a straight line wins.
I. After playing several rounds, you will undoubtedly notice that the player who starts the game can always win if they follow the appropriate strategy. What does it consist of?
II. Let's introduce an additional rule: the player who starts is not allowed to place their first coin in the center. In this case, the second player usually places their coin in the center. Then the first player has six different possible strategies:
1) place the first two coins at the midpoints of two opposite sides of the diagram;
2) place them at the midpoints of two adjacent sides of the diagram;
3) place one coin in a corner and the second in the midpoint of one of the opposite sides to that corner;
4) place one coin in a corner and the second in the midpoint of one of the sides converging at that corner;
${ }^{1}$ If you don't have gold coins, you can use copper ones,
5) place two coins in two opposite corners of the diagram;
6) place two coins in two adjacent corners.
Which of these strategies do you think is the best?
Historical information: Marel (or Merel) is a very ancient game, widely spread in the East under the name "game of three roads." The first definite mention of it appears in the works of Ovid ("Tristia" and "Ars Amatoria"). There it is said: "This game is played on a special small board with three coins that each player has; to win, one must align their three coins in a straight line."
|
2. Let's renumber our nine circles (nine positions of the scheme):
Let $C$ be the player who starts, and $F$ be the player who finishes placing their coins.

I. The player who starts the game places a coin in the center. First case. $F$ places their first coin in a corner. Then the game will develop as follows:
| $C$ | 5 | 8 | 3 | $8 \rightarrow 9$ | $5 \rightarrow 6$ | Victory! |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $F$ | 1 | 2 | 7 | - | - | |
Initial placement of 3 coins
Regular moves from 8 to 9, from 5 to 6, etc. ...
Second case. $F$ places their first coin in the middle of a side. The game develops as follows:
| $C$ | 5 | 1 | 7 | $1 \rightarrow 2$ | $2 \rightarrow 3$ | Victory! |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $F$ | 8 | 9 | 4 | - | - | |
In both cases, $C$ wins.
II. The starting player is prohibited from placing their first coin in the center.
Let's analyze the six game tactics listed in the problem statement.
1) The game develops as follows:
| $C$ | 2 | 8 | 1 | - | |
| :---: | :---: | :---: | :---: | :---: | :---: |
| $F$ | 5 | 9 | 4 | $9 \rightarrow 6$ | Victory! |
2) The game develops as follows:
| $C$ | 2 | 6 | 3 | - | |
| :---: | :---: | :---: | :---: | :---: | :---: |
| $F$ | 5 | 7 | 9 | $5 \rightarrow 8$ | Victory! |
3) The game develops as follows:
| $C$ | 1 | 6 | 3 | - | |
| :---: | :---: | :---: | :---: | :---: | :---: |
| $F$ | 5 | 7 | 2 | $7 \rightarrow 8$ | Victory! |
4) The game develops as follows:
| $C$ | 1 | 2 | 7 | - | |
| :---: | :---: | :---: | :---: | :---: | :---: |
| $F$ | 5 | 3 | 9 | $5 \rightarrow 6$ | Victory! |
5) The game develops as follows:
| $C$ | 1 | 9 | 2 | - | |
| :---: | :---: | :---: | :---: | :---: | :---: |
| $F$ | 5 | 8 | 3 | $8 \rightarrow 7$ | Victory! |
6) The game develops as follows:
| $C$ | 1 | 3 | 8 | Draw |
| :---: | :---: | :---: | :---: | :---: |
| $F$ | 5 | 2 | | Draw |
Thus, for the player $C$, who starts the game, the sixth tactic (placing the first two coins in two adjacent corners) is the best, as it is the only one that does not lead to a loss for $C$ (if the second player $F$ plays optimally), but to a draw.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
150*. Prove that if $a+b+c=0$, then
$$
\left(\frac{a-b}{c}+\frac{b-c}{a}+\frac{c-a}{b}\right)\left(\frac{c}{a-b}+\frac{a}{b-c}+\frac{b}{c-a}\right)=9
$$
where $a \neq 0, \quad b \neq 0, c \neq 0, a \neq b, \quad a \neq c, b \neq c$.
|
Proof.
$$
\begin{gathered}
\left(\frac{a-b}{c}+\frac{b-c}{a}+\frac{c-a}{b}\right) \cdot\left(\frac{c}{a-b}+\frac{a}{b-c}+\frac{b}{c-a}\right)= \\
=1+\frac{(b-c) c}{a(a-b)}+\frac{(c-a) c}{b(a-b)}+\frac{a(a-b)}{c(b-c)}+ \\
+1+\frac{(c-a) a}{b(b-c)}+\frac{b(a-b)}{c(c-a)}+\frac{(b-c) b}{a(c-a)}+1= \\
=3+\frac{c}{a-b}\left(\frac{b^{2}-b c+a c-a^{2}}{a b}\right)+\frac{a}{b-c}\left(\frac{a b-b^{2}+c^{2}-a c}{b c}\right)+ \\
+\frac{b}{c-a}\left(\frac{a^{2}-a b+b c-c^{2}}{a c}\right)=3+2\left(\frac{c^{2}}{a b}+\frac{a^{2}}{b c}+\frac{b^{2}}{a c}\right)
\end{gathered}
$$
since
$$
\frac{c}{a-b}\left(\frac{b^{2}-b c+a c-a^{2}}{a b}\right)=\frac{c(c-b-a)}{a b}=\frac{2 c^{2}}{a b}
$$
since
$$
a+b+c=0, \quad c-b-a=2 c
$$
## Similarly:
$$
\frac{a}{b-c}\left(\frac{a b-b^{2}+c^{2}-a c}{b c}\right)=\frac{2 a^{2}}{b c} ; \frac{b}{c-a}\left(\frac{a^{2}-a b+b c-c^{2}}{a c}\right)=\frac{2 b^{2}}{a c}
$$
## Transform the expression
$$
\frac{c^{2}}{a b}+\frac{a^{2}}{b c}+\frac{b^{2}}{a c}=\frac{c^{3}+a^{3}+b^{3}}{a b c}=\frac{3 a b c}{a b c}=3
$$
(see problem 113). Therefore,
$$
\left(\frac{a-b}{c}+\frac{b-c}{a}+\frac{c-a}{b}\right)\left(\frac{c}{a-b}+\frac{a}{b-c}+\frac{b}{c-a}\right)=3+2 \cdot 3=9
$$
|
9
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
233. If $x_{1}$ and $x_{2}$ are the roots of the equation
$$
\frac{3 a-b}{c} x^{2}+\frac{c(3 a+b)}{3 a-b}=0
$$
then, without solving it, find $x_{1}^{117}+x_{2}^{117}$.
|
Solution.
$x_{1}^{117}+x_{2}^{117}=\left(x_{1}+x_{2}\right)\left(x_{1}^{116}-x_{1}^{115} x_{2}+\ldots+x_{2}^{116}\right), \quad$ but $\quad x_{1}+x_{2}=0$, so, $x_{1}^{117}+x_{2}^{117}=0$.
Note. It is useful to solve problem 233 when reviewing, after discussing the equality:
$$
a^{n}+b^{n}=(a+b)\left(a^{n-1}-a^{n-2} b+\ldots+b^{n-1}\right)
$$[^5]
62
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
352. Find a natural number that is equal to the sum of all its preceding natural numbers. Does more than one such number exist, or is there only one?
|
Let $n$ be the desired natural number; the sum of the numbers preceding this natural number is expressed by the formula
$$
S_{n-1}=\frac{n(n-1)}{2}
$$
According to the problem, $\frac{n(n-1)}{2}=n$, from which $n^{2}-3 n=0$ or $n_{1}=3, n_{2}=0$. The desired number is 3. It is the only one, as the second root of the obtained equation (zero) cannot be considered, since no natural number precedes it.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. What will be the result if we add:
a) the smallest three-digit and the largest two-digit number;
b) the smallest odd one-digit and the largest even two-digit number.
|
a) The smallest three-digit number is 100, and the largest two-digit number is 99.
$$
100+99=199
$$
b) The smallest odd one-digit number is 1, and the largest even two-digit number is 98.
$$
1+98=99
$$
Answer: a) 199 ; b) 99 .
|
99
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. The perimeter of a cardboard sheet in the shape of a square is 28 dm. How many square centimeters does its area contain?
|
4. 5) $28: 4=7$ (dm) - the length of the side of the square;
2) $7 \times 7=49$ (sq. dm) - the area of the square;
3) $100 \times 49=4900$ (sq. cm).
Answer: the area of the square is 4900 sq. cm.
|
4900
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. A part is machined from a metal blank. The chips obtained from machining 8 parts can be remelted into one blank. How many parts can be made from 64 blanks?
|
5. 6) $64: 8=8$ (blanks) - can be manufactured from the waste when machining 64 parts;
2) $8: 8=1$ (blank) - can be manufactured from the waste when machining 8 parts;
3) $64+8+1=73$ (parts).
Answer: from 64 blanks, 73 parts can be manufactured.
|
73
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. How many strikes do the clocks make in a day if they strike once every half hour, and at each hour $1,2,3 \ldots 12$ times?
|
1. $(1+2+3+4+5+6+7+8+9+10+11+12) \times 2+24=180$.
Answer: 180 hits.
|
180
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. What is the least number greater than 1992 that gives a remainder of $7$ when divided by $9$?
|
5. Divide 1992 by 9 with a remainder
| $-1992\llcorner 9$ |
| :--- |
| $\frac{18}{-19}$ |
| $\frac{-18}{221}$ |
| $\frac{-12}{9}$ |
| 3 |
We obtained a remainder of 3. To make the remainder equal to 7, the divisor needs to be increased by four:
$$
1992+4=1996 \text {. }
$$
Answer: 1996.
|
1996
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Find the sum of all even numbers from 10 to 31. Calculate in different ways.
|
6. Let's list all even numbers from 10 to 31:
$$
10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30
$$
a) Let's add the obtained numbers:
$$
10 + 12 + 14 + 16 + 18 + 20 + 22 + 24 + 26 + 28 + 30 = 220.
$$
b) We can notice that the sum of numbers equally distant from the ends is 40:
$$
10 + 30 = 12 + 28 = 14 + 26 = \ldots = 40
$$
There will be five such pairs, and the number 20 will remain. Let's calculate the sum:
$$
40 \times 5 + 20 = 220
$$
c) We can group the addends in such a way that their sum is a round number:
$$
\begin{gathered}
10 + 12 + 14 + 16 + 18 + 20 + 22 + 24 + 26 + 28 + 30 = \\
= 10 + (12 + 18) + (14 + 16) + 20 + (22 + 28) + (24 + 26) + 30 = \\
= 10 + 30 + 30 + 20 + 50 + 50 + 30 = 220
\end{gathered}
$$
Answer: The sum of all even numbers from 10 to 31 is 220.
## THIRD
|
220
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. What will be the result if we add the largest odd two-digit number and the smallest even three-digit number?
|
1. The largest odd two-digit number is 99, and the smallest even three-digit number is 100.
$$
99+100=199
$$
Answer: The sum of the largest odd two-digit number and the smallest even three-digit number is 199.
|
199
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Write in digits the number equal to the sum of 22 million, 22 thousand, 22 hundred, and 22 units.
|
2. Many believe that this number will be 22022222.
In fact, this number is 22024222, because if you add 22 thousand, which is 22000, and 22 hundred, which is 2200, and 22 units to 22 million, which is 22000000, you get 22024222.
Answer: 22024222.
|
22024222
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In a two-digit number, the number of tens is two times less than the number of units. If you subtract the sum of its digits from this two-digit number, you get 18. Find this number.
|
5. According to the condition, in a two-digit number, the number of tens is twice less than the number of units, i.e., the number of units is twice the number of tens.
Two-digit numbers that satisfy this condition:
$$
12 ; \quad 24 ; \quad 36 ; \quad 48 .
$$
The sum of the digits of each of the obtained numbers:
$$
1+2=3 ; \quad 2+4=6 ; \quad 3+6=9 ; \quad 4+8=12
$$
Subtract the sum of the digits from the given numbers.
$$
12-3=9 ; \quad 24-6=18 ; \quad 36-9=27 ; \quad 48-12=36
$$
Thus, the number that satisfies the condition of the problem is 24.
Answer: 24.
|
24
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. What is the greatest number of Saturdays that can be in a year?
|
2. Since a year can have 365 or 366 days, we will choose the larger of these numbers - 366. Saturday occurs once every seven days. Therefore, to find the number of Saturdays in a year, we need to divide 366 by 7 with a remainder. We get
Thus, there will be 52 Saturdays and 2 additional days, one of which can also be a Saturday. Therefore, the maximum number of Saturdays will be $52+1=53$.
Answer: 53 Saturdays.
|
53
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The sum of the digits of a two-digit number is equal to some two-digit number, and the digit in the tens place is four times smaller than the digit in the units place. Find this number.
|
3. First method of solving. Let's list the single-digit numbers for which the second condition is met - one of them is four times smaller than the other. These numbers are: 1 and 4, 2 and 8.
From the obtained pairs, we will choose the one that satisfies the first condition - the sum of the digits should equal a certain two-digit number:
$1+4=5$ - does not satisfy;
$2+8=10-$ satisfies.
Second method of solving. Let's represent the problem condition in the form of a diagram.
Let $x$ be the number of tens. Then $4x$ is the number of units. The smallest two-digit number is 10. We will form an equation:
$$
\begin{aligned}
& x+4x=10 \\
& 5x=10 \\
& x=2
\end{aligned}
$$
Then $2 \times 4=8$.
Therefore, the number 28 satisfies the condition. Similarly, we can form equations for other numbers from 11 to 18 and draw a conclusion.
Third method of solving. Based on the problem condition, the sum of the digits must be divisible by 5. There are two such numbers:
$$
\begin{aligned}
& 10: 5=2 \\
& 2 \times 4=8
\end{aligned}
$$
We get the number 28.
$$
\begin{aligned}
& 15: 5=3 \\
& 3 \times 4=12
\end{aligned}
$$
In this case, we do not get a two-digit number.
Answer: 28.
|
28
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. How many zeros does the product of numbers from 1 to 100 inclusive end with?
|
4. First method of solution. To find out how many zeros the product of numbers from 1 to 100 ends with, we need to determine how many times the factor 5 will appear. Among the factors of the number \(1 \times 2 \times 3 \times \ldots \times 99 \times 100\), 20 numbers are divisible by 5 \((100: 5=20)\).
Of these, 4 numbers are divisible by 25 \((20: 5=4)\). Therefore, all fives appear as a factor 24 times. Among the factors of the number
\(1 \times 2 \times 3 \times \ldots \times 99 \times 100\) there are 50 even numbers, so the factor 2 will appear 24 times for sure. Hence, the product ends with 24 zeros.
Second method of solution (Anna Sonkina, 3a grade student of School No. 24).
Let's factorize all composite numbers into prime factors. We need to find out how many fives are in the factorization. They are in the numbers 5, \(10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100\). There are 10 multiples of 10; two numbers give two fives when factorized. These are 50 and 100. This results in 12 fives. There are also 10 numbers ending in 5, but two numbers give two fives when factorized. These are 25 and 75. This results in 12 fives. In total, there are 24 fives. There are more than 24 twos in the factorization. Therefore, the product ends with 24 zeros. The other numbers in the product do not contribute any zeros.
Answer: 24 zeros.
|
24
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Find the sum of all possible different two-digit numbers, all digits of which are odd.
|
7. To find out how many such numbers there are, let's try to determine which digits can stand in the tens place. There are five such digits: $1,3,5,7,9$.
The second digit must also be odd, so it can also be chosen in five ways.
$\begin{array}{llll}13 & 5 & 7 & 9\end{array}$
$\begin{array}{llllllllll}1 & 3 & 5 & 7 & 9 & 13 & 5 & 9\end{array}$
$\begin{array}{lllll}135 & 5 & 9\end{array}$
$\begin{array}{llllll}1 & 3 & 5 & 7 & 9\end{array}$
In total, there will be $5 \times 5=25$ such numbers. Let's list these numbers and find their sum.
$11+13+15+17+\ldots+93+95+97+99=(11+99) \times 12+55=1375$.
Answer: 1375.
# FIFTH
|
1375
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. How many four-digit numbers can be formed, the sum of whose digits is 3? List these numbers.
|
2. For writing numbers, we use digits
$0,1,2,3,4,5,6,7,8,9$
Since the sum of the digits is three, we can exclude all digits starting from four.
$0,1,2,3,4,5,6,7,8,9$
A number cannot start with zero, so the first digit can be one of the three digits $1,2,3$. The further solution will be represented in the form of a diagram:
Now we need to choose the second digit for each of the three cases.
Similarly, we will determine the third and fourth digits.
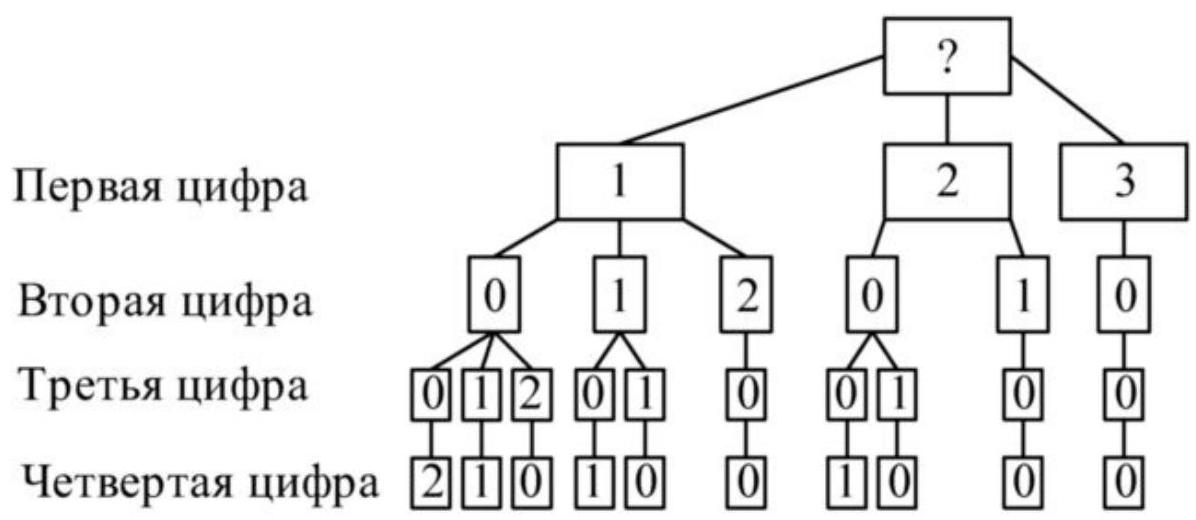
The obtained numbers are:
| $1002 ;$ | $1101 ;$ | $2001 ;$ | $3000 ;$ |
| :--- | :--- | :--- | :--- |
| $1011 ;$ | $1110 ;$ | $2010 ;$ | |
| $1020 ;$ | $1200 ;$ | 2100. | |
Answer: 10 numbers.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Ducks were flying. One in front, two behind, one behind and two in front, one between two and three in a row. How many ducks were flying in total?
|
3. Let's schematically depict how the ducks flew.
As can be seen from the diagram, the problem is about three ducks.
Answer: 3 ducks.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. There were plates on the shelf. First, from all the plates except two, $1 / 3$ part was taken, and then $1 / 2$ of the remaining plates. After this, 9 plates were left on the shelf. How many plates were on the shelf?
|
4. Let's represent the condition of the problem in a drawing
1) $9 \times 2=18$ (plates) — remain after the first time plates were taken
2) $18-2=16$ (plates) - corresponds to $2 / 3$;
3) $16: 2=8$ (plates) - corresponds to $1 / 3$;
4) $8 \times 3=24$ (plates) - corresponds to all plates minus two;
5) $24+2=26$ (plates) - was.
Answer: 26 plates.
|
26
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.