problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
3.46 The path from $A$ to $B$ is traveled by a passenger train 3 hours and 12 minutes faster than by a freight train. In the time it takes the freight train to travel from $A$ to $B$, the passenger train travels 288 km more. If the speed of each train is increased by $10 \mathrm{km} / \mathrm{h}$, the passenger train will travel from $A$ to $B$ 2 hours and 24 minutes faster than the freight train. Determine the distance from $A$ to $B$.
|
3.46 In Fig. 3.9, the graphs of train movements before the speed changes are shown.
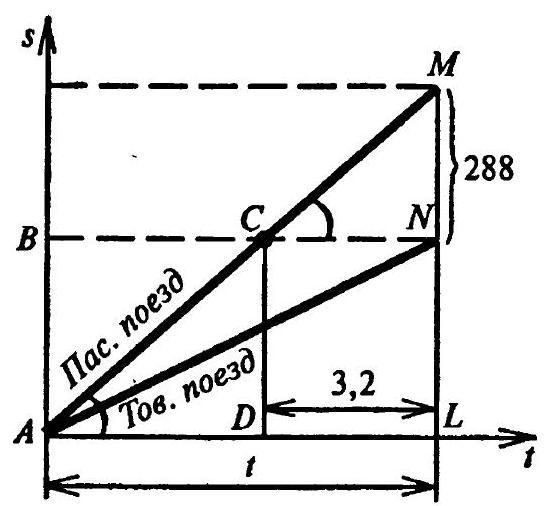
Fig. 3.9
We find $\operatorname{tg} \angle M C N=v^{(0)}{ }_{\text {пас }}=288: 3.2=90$ (km/h). Let $v^{(0)}{ }_{\text {тов }}=x$ km/h; then $A B=N L=x t$ km; $C D=90(t-3.2)=x t$, from which
$$
t=\frac{288}{90-x}
$$
After the speed changes, we have $v^{(1)}{ }_{\text {пас }}=100 \text{ km/h}$, $v_{\text {тов }}^{(1)}=x+10$ km/h. According to the condition,
$\frac{x t}{x+10}-\frac{x t}{100}=2.4$.
Solving the system of equations (1) and (2), we get $x=50 \text{ km/h}$, $t=7.2$ h. Thus, $A B=x t=50 \cdot 7.2=360$ (km).
Answer: $360 \text{ km}$.
|
360
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.48 A young man was returning home from vacation on a bicycle. At first, after traveling several kilometers, he spent one day more than half the number of days remaining after this until the end of his vacation. Now the young man has two options to travel the remaining distance to arrive home on time: to travel $h$ km more daily than originally planned, or to maintain the original daily travel distance, exceeding it only once - on the last day of the journey by $2 h$ km. How many days before the end of his vacation did the young man set out for home?
|
3.48 Let the segment $A B$ (Fig. 3.11) represent the entire journey of the young man and the number of days ($x$) it should take him to travel it at a rate of $v$ km per day. According to the problem, the time segment $A C$ is one unit more than half of the time segment $C B$; therefore,
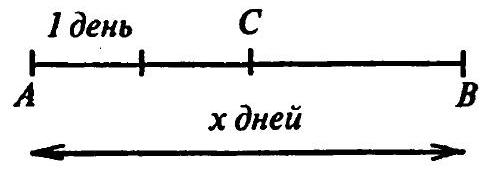
Fig. 3.11
$A C-1=\frac{C B}{2}$, or $x-C B-1=\frac{C B}{2}$,
from which $C B=\frac{2 x-2}{3}$ days. Let the distance represented by the segment $C B$ be taken as the unit. Then, according to the first option, $\frac{2 x-2}{3}(v+h)=1$, and according to the second, $\left(\frac{2 x-2}{3}-1\right) v+(v+2 h) \cdot 1=1$. By eliminating $v$ from these two equations, we find $x=4$.
Answer: $\quad$ in 4 days.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.49 A mail truck left $A$ for $B$. After 20 minutes, a second car left on the same route with a speed of 45 km/h. Catching up with the first car, the driver handed over a package and immediately returned at the same speed (the time spent on the stop and turn is negligible). At the moment when the first car arrived in $B$, the second car had only reached the midpoint of the way from the meeting point with the first car to point $A$. Find the speed of the first car, if the distance between $\boldsymbol{A}$ and $B$ is $40 \mathrm{kM}$.
|
3.49 Consider a coordinate system "path" ($s$ - in kilometers), "time" ($t$ - in hours). Let $AC$ (Fig. 3.12) be the graph of the motion of the first car with the desired speed $v = \tan \alpha$; $DE$ and $EF$ be the graph of the "there and back" motion of the second car with speed $\tan \beta = 45$; $AD = \frac{1}{3}$. It is known that $AB = 40$ and $G$ is the midpoint of the path $AH$. Let $AG = NK = y$. Then the time interval $DK = \frac{y}{\tan \beta} = \frac{y}{45}$. Geometrically, it is clear that $DK = KL = LM$, so the time interval of the first car's motion $AM = \frac{1}{3} + \frac{3y}{45}$, from which $\left(\frac{1}{3} + \frac{y}{15}\right) v = 40$.
The time interval $AL = \frac{1}{3} + \frac{2y}{45}$, $LE = AH = 2y$, so
$\left(\frac{1}{3} + \frac{2y}{45}\right) v = 2y$.
Solving the equations (1) and (2) simultaneously, we find $y = 15 \text{km}$ and $v = 30 \text{km/h}$.
|
30
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.53 Usually, two mechanisms are involved in performing a certain task simultaneously. The productivity of these mechanisms is not the same, and when working together, they complete the task in 30 hours. Once, the joint operation of the two mechanisms lasted only 6 hours, after which the first mechanism was stopped, and the second mechanism completed the remaining part of the task in 40 hours. How long would it take for each mechanism to complete the same task individually, working at its inherent productivity?
|
3.53 Let's accept the entire volume of work as a unit. Let the first mechanism complete the task in $x$ hours, and the second in $y$ hours. Since when working together, the capacities (productivities) add up, we have the system of equations
$$
\left\{\begin{array}{l}
\frac{1}{x}+\frac{1}{y}=\frac{1}{30} \\
1-6\left(\frac{1}{x}+\frac{1}{y}\right)=\frac{40}{y}
\end{array}\right.
$$
Solving it, we find $x=75$ hours, $y=50$ hours.
Answer: $\quad z a ~ 75$ and 50 hours.
|
75
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.56 Two pipes of different cross-sections are connected to a swimming pool, one uniformly supplying water, the other uniformly draining it, with the first pipe filling the pool 2 hours longer than the second pipe takes to empty it. When the pool was filled to $\frac{1}{3}$ of its capacity, both pipes were opened, and the pool was found to be empty after 8 hours. How many hours does it take for the first pipe to fill the pool and for the second pipe to empty it when acting separately?
## Mixtures, Alloys
A certain alloy consists of two metals in the ratio $1: 2$, while another contains the same metals in the ratio 2:3. How many parts of each alloy are needed to obtain a third alloy containing the same metals in the ratio 17:27?
A container with a capacity of 8 liters is filled with a mixture of oxygen and nitrogen, with oxygen accounting for $16 \%$ of the container's capacity. A certain amount of the mixture is released from this container and an equal amount of nitrogen is added, after which the same amount of the mixture is released again and the same amount of nitrogen is added. In the new mixture, the oxygen content is $9 \%$. What amount of the mixture was released from the container each time?
|
3.56 Let's write down the values of the required and given quantities in the form of a table:
| Pipe | Time, h | Capacity | Productivity |
| :---: | :---: | :---: | :---: |
| Supply | $x$ | 1 | $\frac{1}{x}$ |
| Discharge | $x+2$ | 1 | $\frac{1}{x+2}$ |
| Both together | 8 | 1 | $\frac{1}{24}$ |
According to the condition, $\frac{1}{x}-\frac{1}{x+2}=\frac{1}{24}$, from which $x=6$.
Answer: $\quad$ in 6 and 8 h.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.59 Impurities constitute $20 \%$ of the total volume of the solution. What is the smallest number of filters through which the solution must be passed so that the final impurity content does not exceed $0.01 \%$, if each filter absorbs $80 \%$ of the impurities? (It is known that $\lg 2 \approx 0.30$.)
|
3.59 Impurities constitute $\frac{1}{5}$ of the solution. After the first filtration, $\left(\frac{1}{5}\right)^{2}$ impurities remain, and after the $k$-th filtration, $-\left(\frac{1}{5}\right)^{k+1}$ impurities remain. According to the condition, $\left(\frac{1}{5}\right)^{k+1} \leqslant 10^{-4}$; $-(k+1) \lg 5 \leqslant-4$, from which $k \geqslant 4.7$.
Answer: 5 filters.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$4.35 \operatorname{tg} 435^{\circ}+\operatorname{tg} 375^{\circ}$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
$4.35 \tan 435^{\circ}+\tan 375^{\circ}$.
|
### 4.35 We have
$$
\begin{aligned}
& \tan 435^{\circ} + \tan 375^{\circ} = \tan 75^{\circ} + \tan 15^{\circ} = \frac{\sin 90^{\circ}}{\cos 75^{\circ} \cos 15^{\circ}} = \\
& = \frac{2}{\cos 90^{\circ} + \cos 60^{\circ}} = 4
\end{aligned}
$$
Here, reduction formulas, as well as (4.23) and (4.26), were used.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$4.47 \frac{\sin ^{2}\left(\frac{3 \pi}{2}-\alpha\right)\left(\tan^{2} \alpha-1\right) \cot\left(\alpha-\frac{5 \pi}{4}\right)}{\sin ^{2}\left(\frac{5 \pi}{4}+\alpha\right)}=2$.
|
4.47 Note that
$$
\begin{aligned}
& \sin ^{2}\left(\frac{3 \pi}{2}-\alpha\right)=\cos ^{2} \alpha \\
& \operatorname{tg}^{2} \alpha-1=\frac{\sin ^{2} \alpha-\cos ^{2} \alpha}{\cos ^{2} \alpha}=\frac{(\sin \alpha-\cos \alpha)(\sin \alpha+\cos \alpha)}{\cos ^{2} \alpha} \\
& \sin \alpha-\cos \alpha=\sqrt{2} \sin \left(\alpha-\frac{\pi}{4}\right) \\
& \sin \alpha+\cos \alpha=\sqrt{2} \sin \left(\frac{\pi}{4}+\alpha\right) \\
& \operatorname{ctg}\left(\alpha-\frac{5 \pi}{4}\right)=\operatorname{ctg}\left(\alpha-\frac{\pi}{4}\right)
\end{aligned}
$$
Then the left side of the identity can be written as:
$$
\frac{\cos ^{2} \alpha \cdot \sqrt{2} \sin \left(\alpha-\frac{\pi}{4}\right) \cdot \sqrt{2} \sin \left(\frac{\pi}{4}+\alpha\right) \cos \left(\alpha-\frac{\pi}{4}\right)}{\cos ^{2} \alpha \sin ^{2}\left(\frac{\pi}{4}+\alpha\right) \sin \left(\alpha-\frac{\pi}{4}\right)}=2
$$
$$
\text { since } \cos \left(\alpha-\frac{\pi}{4}\right)=\sin \left(\frac{\pi}{4}+\alpha\right) \text {. }
$$
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$4.77 \operatorname{tg} 9^{\circ}+\operatorname{tg} 15^{\circ}-\operatorname{tg} 27^{\circ}-\operatorname{ctg} 27^{\circ}+\operatorname{ctg} 9^{\circ}+\operatorname{ctg} 15^{\circ}=8$.
|
### 4.77 We have
$$
\begin{aligned}
& \tan 9^{\circ} + \tan 81^{\circ} - (\tan 27^{\circ} + \tan 63^{\circ}) + \tan 15^{\circ} + \tan 75^{\circ} = \\
& = \frac{2}{\cos 90^{\circ} + \cos 72^{\circ}} - \frac{2}{\cos 90^{\circ} + \cos 36^{\circ}} + \frac{2}{\cos 90^{\circ} + \cos 60^{\circ}} = \\
& = \frac{2}{\cos 72^{\circ}} - \frac{2}{\cos 36^{\circ}} + 4 = \frac{2(\cos 36^{\circ} - \cos 72^{\circ}) \cdot 2}{\cos 36^{\circ} + \cos 108^{\circ}} + 4 = 8
\end{aligned}
$$
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.88 Prove that the expression
$$
\frac{1-2 \sin ^{2}\left(\alpha-\frac{3 \pi}{2}\right)+\sqrt{3} \cos \left(2 \alpha+\frac{3 \pi}{2}\right)}{\sin \left(\frac{\pi}{6}-2 \alpha\right)}
$$
does not depend on $\alpha$, where $\alpha \neq \frac{\pi n}{2}+\frac{\pi}{12}$.
|
4.88 After applying the reduction formulas, we get
\[
\begin{aligned}
& \frac{1-2 \cos ^{2} \alpha+\sqrt{3} \sin 2 \alpha}{\sin \left(\frac{\pi}{6}-2 \alpha\right)}=\frac{-2 \cos 2 \alpha+\sqrt{3} \sin 2 \alpha}{\sin \left(\frac{\pi}{6}-2 \alpha\right)}= \\
& =\frac{2\left(\frac{\sqrt{3}}{2} \sin 2 \alpha-\frac{1}{2} \cos 2 \alpha\right)}{\sin \left(\frac{\pi}{6}-2 \alpha\right)}=2 \frac{\sin \left(2 \alpha-\frac{\pi}{6}\right)}{\sin \left(\frac{\pi}{6}-2 \alpha\right)}=-2
\end{aligned}
\]
|
-2
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
6.1 In a shooting competition, for each miss in a series of 25 shots, the shooter received penalty points: for the first miss - one penalty point, and for each subsequent miss - 0.5 points more than for the previous one. How many times did the shooter hit the target, receiving 7 penalty points?
|
6.1 Let $x$ be the number of misses in a series of 25 shots. Then, using formula (6.3), we get the equation
$$
\frac{2 \cdot 1+0.5(x-1)}{2} x=7, \text{ or } x^{2}+3 x-28=0
$$
from which $x_{1}=4, x_{2}=-7$ (does not fit). Therefore, the shooter hit the target 21 times.
Answer: 21 times.
|
21
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.6 Calculate
$$
\begin{aligned}
& \left(1+3^{2}+5^{2}+\ldots+(2 n-1)^{2}+\ldots+199^{2}\right)- \\
& -\left(2^{2}+4^{2}+6^{2}+\ldots+(2 n)^{2}+\ldots+200^{2}\right)
\end{aligned}
$$
|
6.6 Note that $(2 n)^{2}-(2 n-1)^{2}=4 n-1$. The number $n$ can be found from the equation $4 n-1=200^{2}-199^{2}$, or $4 n-1=399$, from which $n=100$. We will show that the sequence $a_{n}=(2 n)^{2}-(2 n-1)^{2}$ is an arithmetic progression. Indeed,
$a_{n}-a_{n-1}=\left((2 n)^{2}-(2 n-1)^{2}\right)-\left((2 n-2)^{2}-(2 n-3)^{2}\right)=$
$=4 n-1-4 n+5=4$,
i.e., $d=4$. Now we find
$-S_{100}=\frac{3+399}{3} \cdot 100=20100$, from which $S=-20100$.
Answer: -20100.
|
-20100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.7 The denominator of the geometric progression is $\frac{1}{3}$, the fourth term of this progression is $\frac{1}{54}$, and the sum of all its terms is $\frac{121}{162}$. Find the number of terms in the progression.
|
6.7 Since $b_{4}=b_{1} q^{3}$, then $\frac{1}{54}=b_{1} \cdot \frac{1}{27}$, from which $b_{1}=\frac{1}{2}$. Now, using formula (6.7a), we get the equation
$$
\frac{\frac{1}{2}\left(1-\frac{1}{3^{n}}\right)}{\frac{2}{3}}=\frac{121}{162}, \text { or } 1-\frac{1}{3^{n}}=\frac{121 \cdot 4}{162 \cdot 3}, \text { or } 1-\frac{1}{3^{n}}=\frac{242}{243}
$$
from which we find $n=5$.
Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.15 The sum of the first three terms of an increasing arithmetic progression is 15. If 1 is subtracted from the first two terms of this progression, and 1 is added to the third term, the resulting three numbers will form a geometric progression. Find the sum of the first ten terms of the arithmetic progression.
|
6.15 Let $a_{1}$ be the first term of an arithmetic progression, and $d$ its difference. According to the condition, $\frac{\left(2 a_{1}+2 d\right) 3}{2}=15$, from which $a_{1}+d=5$.
Further, since the numbers $a_{1}-1, a_{1}+d-1, a_{1}+2 d+1$ form a geometric progression, by formula (6.8) we have
$$
\left(a_{1}+d-1\right)^{2}=\left(a_{1}-1\right)\left(a_{1}+2 d+1\right)
$$
Solving the system of equations (1), (2), we get two solutions: 1) $\left.a_{1}=3, d=2 ; 2\right) a_{1}=9, d=-4$. However, the second solution does not fit $(d=-4<0)$. Therefore,
$$
S_{10}=\frac{2 \cdot 3+2 \cdot 9}{2} \cdot 10=120
$$
Answer: 120.
|
120
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.23 The sum of the first three terms of an increasing arithmetic progression is 21. If 1 is subtracted from the first two terms of this progression, and 2 is added to the third term, the resulting three numbers will form a geometric progression. Find the sum of the first eight terms of the geometric progression.
|
6.23 Let $a_{1}$ be the first term of an arithmetic progression, and $d$ its difference. Then, according to formula (6.2), we have $S_{3}=\frac{2 a_{1}+2 d}{2} \cdot 3=21$, or $a_{1}+d=7$. By the condition, $a_{1}-1$, $a_{1}+d-1, a_{1}+2 d+2$ are three consecutive terms of a geometric progression. Using formula (6.8), we get
$$
\left(a_{1}+d-1\right)^{2}=\left(a_{1}+2 d+2\right)\left(a_{1}-1\right)
$$
from which, after substituting $a_{1}=7-d$ and expanding the brackets, we arrive at the quadratic equation $d^{2}+3 d-18=0$, and thus $d_{1}=3, d_{2}=-6$. Only $d_{1}=3$ satisfies the condition; then $a_{1}=4$. Next, we find $b_{1}=a_{1}-1=3$, $b_{2}=a_{1}+d-1=6$, and therefore, $q=2$. Finally, using formula (6.7a), we get
$$
S_{8}=\frac{a_{1}\left(q^{8}-1\right)}{q-1}=\frac{3\left(2^{8}-1\right)}{2-1}=765
$$
Answer: 765.
|
765
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.7 $\quad 2^{\log _{3} x^{2}} \cdot 5^{\log _{3} x}=400$.
|
7.7 The logarithmic function $y=\log _{3} x$ is defined for $x>0$. Therefore, according to formula (7.6), we have $\log _{3} x^{2}=2 \log _{3} x$. Consequently, $2^{2 \log _{3} x} \cdot 5^{\log _{3} x}=20^{2} ; 4^{\log _{3} x} \cdot 5^{\log _{3} x}=20^{2} ; 20^{\log _{3} x}=20^{2}$. From this, $\log _{3} x=2$, i.e., $x=3^{2}=9$.
Answer: $x=9$.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$7.8 \quad 4^{\sqrt{x}}-9 \cdot 2^{\sqrt{x}-1}+2=0$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
$7.8 \quad 4^{\sqrt{x}}-9 \cdot 2^{\sqrt{x}-1}+2=0$.
|
7.8 Since $4^{\sqrt{x}}=2^{2 \sqrt{x}}$ and $2^{\sqrt{x}-1}=2^{\sqrt{x}} \cdot 2^{-1}=\frac{1}{2} \cdot 2^{\sqrt{x}}$, the given equation will take the form
$$
2^{2 \sqrt{x}}-\frac{9}{2} \cdot 2^{\sqrt{x}}+2=0
$$
Let's make the substitution $2^{\sqrt{x}}=y$, where $y>0$ due to the property of the exponential function $2^{0}$. Then we get the equation $y^{2}-\frac{9}{2} y+2=0$, the roots of which are $y_{1}=4$, $y_{2}=\frac{1}{2}$, both positive. From the equation $2^{\sqrt{x}}=4$ we have $2^{\sqrt{x}}=2^{2}, \sqrt{x}=2$, hence $x=4$. From the equation $2^{\sqrt{x}}=\frac{1}{2}$ we find $2^{\sqrt{x}}=2^{-1}$, hence $\sqrt{x}=-1$, which is impossible.
Thus, $x=4$.
Answer: $x=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$7.9 \quad 3 \cdot 5^{2x-1}-2 \cdot 5^{x-1}=0.2$.
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
$7.9 \quad 3 \cdot 5^{2x-1}-2 \cdot 5^{x-1}=0.2$.
|
7.9 We have $5^{2 x-1}=5^{2 x} \cdot 5^{-1} ; 5^{x-1}=5^{x} \cdot 5^{-1} ; 0.2=5^{-1}$. After dividing all terms of the given equation by $5^{-1}$, it will take the form
$3 \cdot 5^{2 x}-2 \cdot 5^{x}=1$.
Let $5^{x}=y$, where $y>0$. Then we get the equation $3 y^{2}-2 y-1=0$, from which $y_{1}=1, y_{2}=-\frac{1}{3}$ (does not fit because the condition $y>0$ is not met). Therefore, $y=1$, from which $\boldsymbol{x}=\mathbf{0}$.
Answer: $x=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$7.23 \quad 7^{\lg x}-5^{\lg x+1}=3 \cdot 5^{\lg x-1}-13 \cdot 7^{\lg x-1}$
|
7.23 Group the powers with base 7 on the left side of the equation, and the powers with base 5 on the right side: $7^{\lg x}+13 \cdot 7^{\lg x-1}=3 \cdot 5^{\lg x-1}+5^{\lg x+1}$.
By factoring out the power with the smaller exponent and performing further transformations, we get
$$
\begin{aligned}
& 7^{\lg x-1}(7+13)=5^{\lg x-1}\left(3+5^{2}\right) ; \frac{7^{\lg x-1} \cdot 20}{5^{\lg x-1} \cdot 28}=1 ; \\
& \left(\frac{7}{5}\right)^{\lg x-2}=\left(\frac{7}{5}\right)^{0}
\end{aligned}
$$
From this, $\lg x-2=0$, i.e., $x=100$.
Answer: $x=100$.
|
100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$7.25 \lg (\sqrt{6+x}+6)=\frac{2}{\log _{\sqrt{x}} 10}$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
$7.25 \lg (\sqrt{6+x}+6)=\frac{2}{\log _{\sqrt{x}} 10}$.
|
7.25 From the definition of the logarithm, it follows that $\sqrt{x}>0, \sqrt{x} \neq 1$, i.e., $x>0, x \neq 1$. Applying formulas (7.8) and (7.6), we get $\lg (\sqrt{6+x}+6)=\lg x$. According to the hint $4^{0}$, we transition to an equivalent system of equations:
$\left\{\begin{array}{l}x>0, x \neq 1, \\ \sqrt{6+x}+6=x,\end{array}\right.$ or $\left\{\begin{array}{l}x>0, x \neq 1, \\ \sqrt{6+x}=x-6 .\end{array}\right.$
In the left part of the equation $\sqrt{6+x} \geq 0$, therefore $x-6 \geq 0$, i.e., $x \geq 6$, and both sides of the equation can be squared. We have
$$
\left\{\begin{array} { l }
{ x \geq 6 } \\
{ 6 + x = x ^ { 2 } - 1 2 x + 3 6 , }
\end{array} \text { or } \left\{\begin{array}{l}
x \geq 6 \\
x^{2}-13 x+30=0
\end{array}\right.\right.
$$
We find the roots of the equation: $x_{1}=3, x_{2}=10$; of these, only $x=10$ satisfies the inequality $x \geq 6$.
Answer: $x=10$.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$7.27 \lg (3-x)-\frac{1}{3} \lg \left(27-x^{3}\right)=0$.
|
7.27 We have $\lg (3-x)^{3}=\lg \left(27-x^{3}\right)$, which is equivalent to the system
$$
\left\{\begin{array} { l }
{ 3 - x > 0 , } \\
{ ( 3 - x ) ^ { 3 } = 2 7 - x ^ { 3 } , }
\end{array} \text { or } \left\{\begin{array}{l}
x<3, \\
(3-x)^{3}=(3-x)\left(9+3 x+x^{2}\right)
\end{array}\right.\right.
$$
Further, we get
$$
(3-x)\left(9-6 x+x^{2}-9-3 x-x^{2}\right)=0, \text { or }(3-x)(-9 x)=0 \text {, }
$$
from which $x_{1}=0, x_{2}=3$ (does not satisfy the inequality $x<3$). Therefore, $x=0$.
Answer: $x=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$7.28 \frac{2-\lg 4+\lg 0.12}{\lg (\sqrt{3 x+1}+4)-\lg 2 x}=1$.
$7.29 0.5\left(\lg \left(x^{2}-55 x+90\right)-\lg (x-36)\right)=\lg \sqrt{2}$.
|
7.28 Given the domains of the logarithmic function and the square root, we have the system of inequalities $3 x+1 \geq 0$ (under this condition $\sqrt{3 x+1}+4>0$), $x>0$, the solution of which is $\boldsymbol{x}>0$. This equation is equivalent to the system
$$
\left\{\begin{array}{l}
x>0 \\
\lg (\sqrt{3 x+1}+4)-\lg 2 x \neq 0 \\
2-\lg 4+\lg 0.12=\lg (\sqrt{3 x+1}+4)-\lg 2 x
\end{array}\right.
$$
Using the hint $5^{0}$, we transition to the equation
$$
\lg \frac{100 \cdot 0.12}{4}=\lg \frac{\sqrt{3 x+1}+4}{2 x}, \text{ or } 3=\frac{\sqrt{3 x+1}+4}{2 x}
$$
After multiplying both sides of the equation by $2 x$ (no extraneous roots will be introduced since $x>0$), we obtain the irrational equation
$$
\sqrt{3 x+1}=6 x-4
$$
Since $\sqrt{3 x+1} \geq 0$, then $6 x-4 \geq 0$, from which $x \geq \frac{2}{3}$.
Square both sides of equation (2):
$3 x+1=36 x^{2}-48 x+16$, or $36 x^{2}-51 x+15=0$.
From here, we find $x_{1}=1, x_{2}=\frac{5}{12}$ (does not satisfy the condition $x \geq \frac{2}{3}$). It remains to verify that for $x=1$, the second condition of system (1) is satisfied: $\lg (\sqrt{3 x+1}+4)-\lg 2 x=\lg 6-\lg 2=\lg 3 \neq 0$. Thus, $x=1$.
Answer: $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$7.30 \lg (\lg x)+\lg \left(\lg x^{3}-2\right)=0$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
$7.30 \lg (\lg x)+\lg \left(\lg x^{3}-2\right)=0$.
|
7.30 For the existence of logarithms, it is necessary that the inequalities $x>0$, $\lg x>0$, $3 \lg x-2>0$ are satisfied simultaneously, i.e., $x>0, x>1, \lg x>\frac{2}{3}$. Hence, $\lg x>\frac{2}{3}$. Now we transition to the equivalent system of equations given by
$$
\left\{\begin{array}{l}
\lg x>\frac{2}{3} \\
\lg x(3 \lg x-2)=1
\end{array}\right.
$$
After substituting the variable $y=\lg x$, we obtain the equation $3 y^{2}-2 y-1=0$, whose roots are $y_{1}=1, y_{2}=-\frac{1}{3}$. Of these values, only the first satisfies the inequality $\lg x>\frac{2}{3}$. Therefore, $\lg x=1$, from which $x=10$.
Answer: $x=10$.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$7.33 \log _{2} x+\log _{4} x+\log _{8} x=11$.
|
7.33 Using formula (7.7), we get the equation
$$
\log _{2} x+\frac{\log _{2} x}{\log _{2} 4}+\frac{\log _{2} x}{\log _{2} 8}=11, \text { or } \log _{2} x\left(1+\frac{1}{2}+\frac{1}{3}\right)=11
$$
from which $\log _{2} x=6$, i.e., $x=64$.
Answer: $x=64$.
|
64
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$7.36 \quad 3 \log _{5} 2+2-x=\log _{5}\left(3^{x}-5^{2-x}\right)$.
$7.37 \quad 25^{\log _{2} \sqrt{x+3}-0.5 \log _{2}\left(x^{2}-9\right)}=\sqrt{2(7-x)}$.
|
7.36 Here
$3^{x}-5^{2-x}>0$.
Let's use the fact that $2-x=\log _{5} 5^{2-x}$, and write the equation in the form
$\log _{5}\left(2^{3} \cdot 5^{2-x}\right)=\log _{5}\left(3^{x}-5^{2-x}\right)$
Then we have
$2^{3} \cdot 5^{2-x}=3^{x}-5^{2-x} ; 5^{2-x}\left(2^{3}+1\right)=3^{x} ; 5^{2-x}=3^{x-2}$.
Finally, multiplying both sides of the equation by $3^{2-x} \neq 0$, we get
$(5 \cdot 3)^{2-x}=1 \Rightarrow 15^{2-x}=15^{0} \Rightarrow 2-x=0 \Rightarrow x=2$.
This root satisfies the inequality (1).
Answer: $x=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$7.43 \quad 5^{x} \sqrt[x]{8^{x-1}}=500$.
$7.44 \quad 5^{\frac{x}{\sqrt{x}+2}} \cdot 0.2^{\frac{4}{\sqrt{x}+2}}=125^{x-4} \cdot 0.04^{x-2}$.
|
7.43 According to the definition of the root, $x \neq 0$. Let's write the equation as
$$
5^{x} \cdot 2^{\frac{3 x-3}{x}}=5^{3} \cdot 2^{2}
$$
Dividing both sides by $5^{3} \cdot 2^{2} \neq 0$, we get
$$
5^{x-3} \cdot 2^{\frac{3 x-3}{x}-2}=1, \text { or } 5^{x-3} \cdot 2^{\frac{x-3}{x}}=1, \text { or }\left(5 \cdot 2^{\frac{1}{x}}\right)^{x-3}=1
$$
Since $5 \cdot 2^{\frac{1}{x}}>0$ and $5 \cdot 2^{\frac{1}{x}} \neq 1$, then $x-3=0$, i.e., $x=3$.
Answer: $x=3$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.58 $2 \lg x^{2}-\lg ^{2}(-x)=4$.
Translate the above text into English, please keep the original text's line breaks and format, and output the translation result directly.
7.58 $2 \log x^{2}-\log ^{2}(-x)=4$.
|
7.58 Here it should be $-x>0$, hence $x<0$. Then $\lg x^{2}=2 \lg (-x)$ and the given equation will take the form $4 \lg (-x)-\lg ^{2}(-x)=4$.
Letting $\lg (-x)=y$, we find $y=2$, hence $\lg (-x)=2$, i.e. $-x=100, x=-100$.
Answer: $x=-100$.
|
-100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$7.73 \sqrt{\log _{0.04} x+1}+\sqrt{\log _{0.2} x+3}=1$.
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
$7.73 \sqrt{\log _{0.04} x+1}+\sqrt{\log _{0.2} x+3}=1$.
|
7.73 Given the domains of the logarithmic function and the square root, we obtain the system of inequalities
$$
\left\{\begin{array}{l}
x>0 \\
\log _{0.04} x+1 \geq 0 \\
\log _{0.2} x+3 \geq 0
\end{array}\right.
$$
We use the fact that $\log _{0.2} x=\log _{0.04} x^{2}=2 \log _{0.04} x$ (since $x>0$). Then, setting $\log _{0.04} x=y$, we get the equation
$$
\sqrt{y+1}+\sqrt{2 y+3}=1, \text { or } \sqrt{2 y+3}=1-\sqrt{y+1} \text {. }
$$
Squaring both sides of the equation, we get:
$2 y+3=1+y+1-2 \sqrt{y+1}$, or $2 \sqrt{y+1}=-1-y$.
Since $2 \sqrt{y+1} \geq 0$, then $-1-y \geq 0$, from which $y \leq-1$. Squaring both sides of the equation again, we have $4(y+1)=1+y^{2}+2 y$, or $y^{2}-2 y-3=0$, from which $y_{1}=-1, \quad y_{2}=3$ (does not satisfy the condition $y \leq-1$). Therefore, $\log _{0.04} x=-1$, i.e., $x=0.04^{-1}=25$. In this case, the conditions (1) are satisfied.
Answer: $x=25$.
|
25
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1 $\quad A_{x}^{2} C_{x}^{x-1}=48$.
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
9.1 $\quad A_{x}^{2} C_{x}^{x-1}=48$.
|
9.1 According to formula (9.1), we find
$$
A_{x}^{2}=\frac{x!}{(x-2)!}=\frac{x(x-1)(x-2)!}{(x-2)!}=x(x-1)
$$
Further, using formulas (9.6) and (9.4), we have
$$
C_{x}^{x-1}=C_{x}^{x-(x-1)}=C_{x}^{1}=\frac{x!}{1!(x-1)!}=x
$$
Therefore, the given equation will take the form
$x^{2}(x-1)=48$, or $x^{2}(x-1)=4^{2} \cdot 3$.
Consequently, $x=4$.
Answer: $x=4$.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$9.2 \quad C_{x+1}^{x-2}+2 C_{x-1}^{3}=7(x-1)$.
|
9.2 Let's use formula (9.4):
$$
\frac{(x+1)!}{(x-2)!3!}+\frac{2(x-1)!}{(x-4)!3!}=7(x-1)
$$
from which, after simplifying the first fraction by $(x-2)!$ and the second fraction by $(x-4)!$, we get
$$
(x+1) x(x-1)+2(x-1)(x-2)(x-3)=42(x-1)
$$
Further, considering that $x \neq 1$, we arrive at the quadratic equation
$$
x^{2}+x+2\left(x^{2}-5 x+6\right)=42, \text{ or } x^{2}-3 x-10=0
$$
which has roots $x_{1}=5, x_{2}=-2$ (not suitable by the context of the problem).
Answer: $x=5$.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.7 For what value of $x$ is the fourth term of the expansion $\left(\sqrt{2^{x-1}}+\sqrt[3]{2^{-x}}\right)^{m}$ 20 times greater than $m$, if the binomial coefficient of the fourth term is to the binomial coefficient of the second term as $5: 1 ?$
|
9.7 The binomial coefficients of the fourth and second terms are $C_{m}^{3}$ and $m$, respectively. Therefore, $\frac{m(m-1)(m-2)}{3!m}=5$, or $(m-1)(m-2)=30$, from which $m=7$. Then the fourth term of the expansion has the form $T_{4}=C_{7}^{3} 2^{2(x-1)} \cdot 2^{-x}$, and we arrive at the equation $C_{7}^{3} 2^{x-2}=140$, from which we find $\frac{7 \cdot 6 \cdot 5}{6} \cdot 2^{x-2}=140$; $2^{x-2}=4 ; x=4$.
Answer: $x=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.8 The commission consists of a chairman, his deputy, and five other people. In how many ways can the commission members distribute among themselves the duties of chairman and deputy?
|
9.8 When choosing a chairman and his deputy from the given seven people, it matters not only how these two people are chosen from the seven candidates, but also how their positions are distributed between them (i.e., both the composition and the order of the selected elements matter).
This means we are dealing with permutations (without repetition) of seven elements taken two at a time. Using formula (9.1), we find $A_{7}^{2}=7 \cdot 6=42$.
Answer: 42 ways.
|
42
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.9 How many three-digit numbers can be formed from the digits 1, 2, $3,4,5,6?$
|
9.9 Each three-digit number composed of the specified digits can be considered as an arrangement with repetitions, made up of three digits taken from the given six digits. The desired number of numbers can be found using the formula (9.2):
$\widetilde{A}_{6}^{3}=6^{3}=216$.
Answer: 216 numbers.
|
216
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.10 In how many ways can three duty officers be selected from a group of 20 people?
|
9.10 The desired number of ways is equal to the number of combinations (without repetition) that can be formed from 20 elements taken three at a time. According to formula (9.4), we get
$C_{20}^{3}=\frac{20!}{17!3!}=\frac{20 \cdot 19 \cdot 18}{6}=1140$.
Answer: 1140 ways.
|
1140
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.11 In a confectionery shop, three types of pastries are sold: Napoleons, eclairs, and sponge cakes. In how many ways can you buy 9 pastries?
|
9.11 Here, we need to find the number of all possible combinations of 9 elements that can be formed from the given three elements, where these elements can repeat in each combination, and the combinations differ from each other by at least one element. This means we are looking for the number of combinations with repetitions of 3 elements taken 9 at a time. Using formula (9.5), we find
$$
\widetilde{C}_{3}^{9}=C_{11}^{9}=C_{11}^{2}=\frac{11 \cdot 10}{2}=55
$$
Answer: 55 ways.
|
55
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.12 How many different four-digit numbers can be formed from the digits $0,1,2,3$, if each digit appears only once in the representation of the number?
|
9.12 The considered four-digit number can be represented as some permutation of the digits $0,1,2, 3$, where the first digit is not zero. Since four digits can form $P_{4}=4$! permutations and of these, $P_{3}=3$! start with zero, the desired number is $4!-3!=3 \cdot 3!=1 \cdot 2 \cdot 3 \cdot 3=18$.
Answer: 18 numbers.
|
18
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.13 How many different sound combinations can be taken from ten selected piano keys, if each sound combination can contain from three to ten sounds?
|
9.13 For each sound combination, the Slavic keys are pressed simultaneously, so for $k$ sounds we have $C_{10}^{k}$ combinations. Thus, the desired number is $C_{10}^{3}+C_{10}^{4}+\ldots+C_{10}^{10}=C_{10}^{0}+C_{10}^{1}+C_{10}^{2}+\ldots+C_{10}^{10}-$ $-C_{10}^{0}-C_{10}^{1}-C_{10}^{2}=2^{10}-1-10-45=968$.
Answer: 968 sound combinations.
|
968
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.14 The lock opens only if a specific three-digit number is entered. An attempt consists of randomly selecting three digits from the five given. The number was guessed only on the last of all attempts. How many attempts preceded the successful one?
|
9.14 I method. The first digit could be chosen in five ways, the second also in five ways, i.e., for a two-digit number there were $5^{2}$ options. Thus, the total number of three-digit numbers under these conditions was $5^{3}=125$, and 124 unsuccessful attempts preceded the successful one.
II method. The total number of attempts is equal to the number of arrangements with repetitions of five elements taken three at a time, i.e., $\widetilde{A}_{5}^{3}=5^{3}=125$. Therefore, the number of unsuccessful attempts is 124.
Answer: 124 attempts.
|
124
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.15 In how many ways can two rooks be placed on a chessboard so that one cannot capture the other? (One rook can capture another if it is on the same row or the same column of the chessboard).
## Group 5
Solve the equations (9.16-9.17):
|
9.15 The first rook can be placed on any of the 64 squares. In this case, 14 squares are under threat, so for the second rook, there are any of $64-15=49$ squares left. Thus, the total number of options is $64 \cdot 49=3136$.
Answer: 3136 ways.
|
3136
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$9.17 C_{x}^{x-1}+C_{x}^{x-2}+C_{x}^{x-3}+\ldots+C_{x}^{x-9}+C_{x}^{x-10}=1023$.
|
9.17 Obviously, when $x=10$ the left side of the equation is 1 less than the sum of the binomial coefficients in the expansion of the binomial $(a+b)^{10}$. This sum is 1024. Therefore, $x=10$ is a solution to the equation. There are no other solutions, as for $x>10$ the left side of the equation is greater than 1023.
Answer: $x=10$.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.20 Find the largest binomial coefficient in the expansion of $\left(n+\frac{1}{n}\right)^{n}$, if the product of the fourth term from the beginning and the fourth term from the end is 14400.
|
9.20 The fourth term from the beginning has the form $T_{4}=C_{n}^{3} n^{n-3} \frac{1}{n^{3}}$, and the fourth term from the end has the form $T_{n-2}=C_{n}^{n-3} n^{3} \frac{1}{n^{n-3}}$.
Therefore, $T_{4} T_{n-2}=\left(C_{n}^{3}\right)^{2}=14400$, from which $C_{n}^{3}=120$. Further, we have
$$
n(n-1)(n-2)=720 ; n(n-1)(n-2)=10 \cdot 9 \cdot 8 ; n=10
$$
Thus, the largest binomial coefficient, which is equally distant from the ends of the expansion, is $C_{10}^{5}=252$.
Answer: 252.
|
252
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.21 The sum of the third from the beginning and the third from the end binomial coefficients in the expansion of $(\sqrt[4]{3}+\sqrt[3]{4})^{n}$ is 9900. How many rational terms are contained in this expansion?
|
9.21 The coefficients specified in the condition are equal to $C_{n}^{2}$. We have $2 \cdot \frac{n(n-1)}{2}=9900$, or $n(n-1)=100 \cdot 99$,
from which $n=100$. Then $T_{k+1}=C_{100}^{k} 3^{\frac{100-k}{4}} 4^{\frac{k}{3}} ;$ according to the condition, $\frac{k}{3}$ and $\frac{100-k}{4}$ are integers, i.e., $k$ is divisible by 12. For $n=100$, there are $\left[\frac{100}{12}\right]+1=9$ such numbers.
Answer: 9 terms.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.23 How many four-digit numbers, composed of the digits $0,1,2,3,4,5$, contain the digit 3 (the digits in the numbers do not repeat)?
|
9.23 From the six digits $0,1,2,3,4,5$, one can form $A_{6}^{4}$ different four-digit combinations (including those that start with the digit 0). Among these combinations, there are $A_{5}^{3}$ combinations with zero as the first digit, so we get $A_{6}^{4}-A_{5}^{3}$ four-digit numbers composed of the given six digits. Now, from this set, we need to exclude all four-digit numbers that do not contain the digit 3, i.e., those consisting of the five digits 0,1, $2,4,5$. Reasoning as before, we conclude that there are $A_{5}^{4}-A_{4}^{3}$ four-digit numbers in which the digit 3 is absent. Therefore, the desired quantity is
$$
\begin{aligned}
& \left(A_{6}^{4}-A_{5}^{3}\right)-\left(A_{5}^{4}-A_{4}^{3}\right)= \\
& =(6 \cdot 5 \cdot 4 \cdot 3-5 \cdot 4 \cdot 3)-(5 \cdot 4 \cdot 3 \cdot 2-4 \cdot 3 \cdot 2)= \\
& =5 \cdot 60-4 \cdot 24=204
\end{aligned}
$$
Answer: 204 numbers.
|
204
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.24 How many four-digit numbers divisible by 5 can be formed from the digits $0,1,3,5,7$, if each number must not contain identical digits?
|
9.24 The desired numbers end with five or zero. If the last digit is 0, then there are $A_{4}^{3}=4 \cdot 3 \cdot 2=24$ such numbers. If the last digit is 5, then the first digit cannot be 0 (the desired numbers are four-digit); in this case, there are $A_{4}^{3}-A_{3}^{2}=18$ such numbers. Therefore, 42 numbers satisfy the condition of the problem.
Answer: 42 numbers.
|
42
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.26 In a tournament, 16 chess players are participating. Determine the number of different first-round schedules (schedules are considered different if they differ in the participants of at least one game; the color of the pieces and the board number are not taken into account).
|
9.26 The participants of the first party can be chosen in $C_{16}^{2}$ ways, and the participants of the second party in $C_{14}^{2}$ ways. Since the order of selecting pairs does not matter, the participants of two parties can be chosen in $\frac{C_{16}^{2} C_{14}^{2}}{2!}$ ways, the participants of three parties in $\frac{C_{16}^{2} C_{14}^{2} C_{12}^{2}}{3!}$ ways, ..., and finally, the participants of eight parties
$$
\begin{aligned}
& \frac{C_{16}^{2} C_{14}^{2} C_{12}^{2} \ldots C_{2}^{2}}{8!}=\frac{16 \cdot 15 \cdot 14 \cdot 13 \cdot 12 \cdot 11 \ldots 2 \cdot 1}{2^{8} \cdot 8 \cdot 7 \cdot 6 \ldots 2 \cdot 1}= \\
& =15 \cdot 13 \cdot 11 \cdot 9 \cdot 7 \cdot 5 \cdot 3 \cdot 1=2027025 \text { ways }
\end{aligned}
$$
Answer: 2027025 options.
|
2027025
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.29 The letters of the Morse alphabet consist of symbols (dots and dashes). How many letters can be represented if we require that each letter contain no more than five symbols?
|
9.29 Letters containing exactly $k$ characters are $2^{k}$; therefore, in total, we can represent
$2^{1}+2^{2}+2^{3}+\ldots+2^{5}=\frac{2\left(2^{5}-1\right)}{2-1}=62$ letters.
Answer: 62 letters.
|
62
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.30 A gardener has to plant 10 trees over the course of three days. In how many ways can he distribute the work over the days, if he will plant no less than one tree per day
|
9.30 Let's separate the trees designated for planting on each day with boundaries. There are two such boundaries, and there are 9 possible places for them (the number of intervals between ten trees). We have $C_{9}^{2}=36$.
Answer: 36 ways.
|
36
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.3 Find the sum $A=i+i^{2}+i^{3}+\ldots+i^{15}$.
Translate the text above into English, keeping the original text's line breaks and format, and output the translation result directly.
|
10.3 Let's group the terms as follows:
$$
\begin{aligned}
& A=\left(i+i^{2}+i^{3}+i^{4}\right)+\left(i^{5}+i^{6}+i^{7}+i^{8}\right)+ \\
& +\left(i^{9}+i^{10}+i^{11}+i^{12}\right)+\left(i^{13}+i^{14}+i^{15}\right)
\end{aligned}
$$
from which
$$
A=\left(i+i^{2}+i^{3}+i^{4}\right)\left(1+i^{4}+i^{8}\right)+i^{13}+i^{14}+i^{15}
$$
Since
$$
\begin{aligned}
& i+i^{2}+i^{3}+i^{4}=i-1-i+1=0 \\
& A=i^{13}+i^{14}+i^{15}=i-1-i=-1
\end{aligned}
$$
Answer: -1.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.36 Find the real number $b$ from the condition that the points representing the complex numbers $3-5 i, 1-i$ and $-2+b i$ lie on the same straight line.
|
10.36 The numbers $3-5i, 1-i$ and $-2+bi$ correspond to the points $A(3, -5), B(1, -1)$ and $C(-2, b)$ on the plane (Fig. 10.10). We find the coordinates of the vectors $\overline{A B}$ and $\overline{A C}$; we have $\overline{A B}(-2, 4), \overline{A C}(-5, b+5)$.
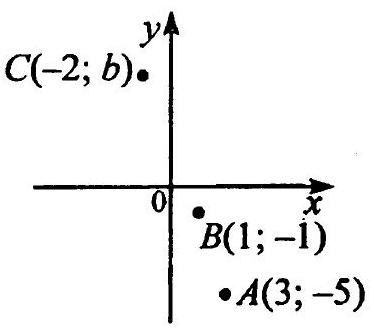
Fig. 10.10
Since these points lie on the same line, the equality $\overline{A C}=k \overline{A B}$ must hold,
i.e.
$$
\left\{\begin{array}{l}
-2k = -5 \\
4k = b + 5
\end{array}\right.
$$
From this system, we find $b=5$.
Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.47 Given complex numbers $z_{1}=1+a i$ and $z_{2}=2^{\frac{3}{4}}\left(\cos \frac{3 \pi}{8}+i \sin \frac{3 \pi}{8}\right)$. Find all real values of $a$ for which $z_{1}^{3}=z_{2}^{2}$.
|
10.47 We find
\[
\begin{aligned}
& z_{1}^{3}=(1+a i)^{3}=\left(1-3 a^{2}\right)+\left(3 a-a^{3}\right) i \\
& z_{2}^{2}=\left(2^{\frac{3}{4}}\left(\cos \frac{3 \pi}{8}+i \sin \frac{3 \pi}{8}\right)\right)^{2}= \\
& =2^{\frac{3}{2}}\left(\cos \frac{3 \pi}{4}+i \sin \frac{3 \pi}{4}\right)=2^{\frac{3}{2}}\left(-\frac{\sqrt{2}}{2}+i \frac{\sqrt{2}}{2}\right)=-2+2 i
\end{aligned}
\]
Since the numbers $z_{1}^{3}$ and $z_{2}^{2}$ are equal, we arrive at the system
\[
\left\{\begin{array}{l}
1-3 a^{2}=-2 \\
3 a-a^{3}=2
\end{array}\right.
\]
from which, considering that $a \in \boldsymbol{R}$, we obtain $a=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.2 Solve the equation $|x+1|+|x-1|=2 x^{3}$.
|
11.2 We have $|x+1|=0$ when $x=-1$, and $|x-1|=0$ when $x=1$. We will solve the given equation in the intervals $(-\infty,-1)$, $[-1,1)$, $[1, \infty)$.
1) If $x<0$ for any $x$, then $x=0$; this value does not belong to the interval $(-\infty,-1)$.
2) If $-1 \leq x<1$, then $x+1-x+1=2 x^{3} ; 2 x^{3}=2 ; x^{3}=1$; $x=1 \notin[-1,1)$.
3) If $\quad x \geq 1, \quad$ then $\quad x+1+x-1=2 x^{3} ; \quad x^{3}-x=0$; $x\left(x^{2}-1\right)=0 ; x(x-1)(x+1)=0 ; \quad x_{1}=-1, x_{2}=0, x_{3}=1$. Only the value $x=1$ belongs to the interval $[1, \infty)$. Therefore: $x=1$.
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.16 For what value of $m$ does the system of equations
$$
\left\{\begin{array}{l}
2 x+(m-1) y=3 \\
(m+1) x+4 y=-3
\end{array}\right.
$$
have an infinite number of solutions? No solutions?
|
11.16 The system has an infinite number of solutions or no solutions if the coefficients of $x$ and $y$ are proportional. Therefore, $\frac{2}{m+1}=\frac{m-1}{4}$ (here $m+1 \neq 0$; it is easy to verify that when $m=-1$, the system has a unique solution). Further, we have $(m+1)(m-1)=8 ; m^{2}-1=8$, from which $m= \pm 3$. When $m=3$, we get $\frac{2}{4}=\frac{2}{4} \neq \frac{3}{-3}$, i.e., the system has no solutions. When $m=-3$, we get $\frac{2}{-2}=\frac{-4}{4}=\frac{3}{-3}$, i.e., the system has an infinite number of solutions.
Answer: an infinite number of solutions when $m=-3$; no solutions when $m=3$.
|
-3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.27 The price of a certain item was reduced twice - first by $15 \%$, and then by another $20 \%$. What is the overall percentage reduction in price?
## Group B
|
11.27 Let's take the original price as $100 \%$. Then after the first reduction, the new price will be $100 \%$ $-15 \%=85 \%$ of the original. The second price reduction of $20 \%$ relative to the first will be $85 \% \cdot 0.2=17 \%$ of the original price. Thus, after the second reduction, the new price will be $85 \%-17 \%=68 \%$ of the original. Therefore, the total price reduction is $100 \%-68 \%=32 \%$.
Answer: $32 \%$.
|
32
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.36 Solve graphically the equation
$$
|x-1|+2x-5=0
$$
|
11.36 Let's write the equation as $|x-1|=5-2 x$. Since $|x-1| \geq 0$ for any $x$,
Fig. 11.11
and $\quad 5-2 x \geq 0$, i.e., $x \leq 2.5$.
Consider the functions $y_{1}=|x-1|, y_{2}=5-2 x$ and plot their graphs on the same diagram for $\quad x \leq 2.5 \quad$ (Fig.
11.12). The solution to the given equation is the points of intersection of these graphs. Using Fig. 11.12, we establish that $x=2$.
Answer: $x=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.40 How many real solutions does the system of equations have
$\left\{\begin{array}{l}x^{2}+y=5 \\ x+y^{2}=3 ?\end{array}\right.$
|
11.40 The solutions of the system are the coordinates of the points of intersection of the graphs of the functions given by these equations. Let's write the original system in the form
$\left\{\begin{array}{l}y=5-x^{2}, \\ x=3-y^{2} .\end{array}\right.$
The graph of the first equation is a parabola with the axis of symmetry $O y$, and the graph of the second equation is a parabola with the axis of symmetry $O x$. By plotting these graphs (Fig. 11.14), we obtain four points of their intersection, i.e., the system has four real solutions.
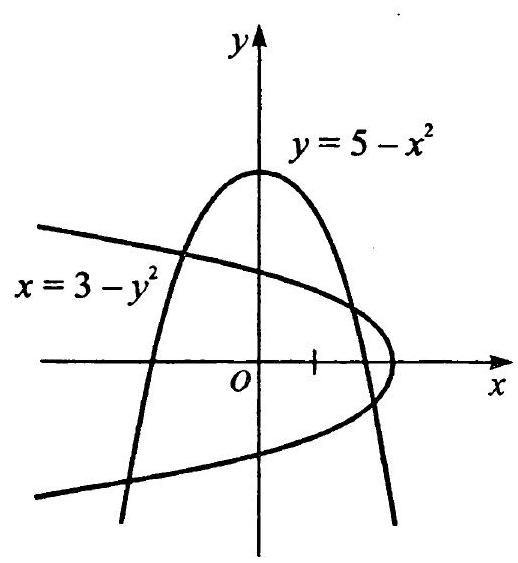
Fig. 11.14
Fig. 11.15
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.41 For what value of a is the sum of the squares of the roots of the equation $x^{2}+a x+a-2=0$ the smallest?
|
11.41 Let $x_{1}$ and $x_{2}$ be the roots of the equation. Then $x_{1} x_{2}=a-2$, $x_{1}+x_{2}=-a$. From this, we can express the sum of the squares of the roots:
$$
x_{1}^{2}+x_{2}^{2}=\left(x_{1}+x_{2}\right)^{2}-2 x_{1} x_{2}=a^{2}-2 a+4=f(a)
$$
Since $f(a)$ is a quadratic function with a positive leading coefficient, $f(a)$ attains its minimum value. This minimum value is achieved at $a=1$.
Answer: at $a=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.43 Solve the equation $x+\lg \left(1+4^{x}\right)=\lg 50$.
|
11.43 Let's write the equation as $x+\lg \left(1+4^{x}\right)=1+\lg 5$. It is not difficult to establish that the value $x=1$ satisfies the equation. The left side of the equation is $f(x)=x+\lg \left(1+4^{x}\right)$ - an increasing function; therefore, if $x<1$, then $f(x)<1+\lg 5$, and if $x>1$, then $f(x)>1+\lg 5$. This means the equation has a unique root $x=1$.
Answer: $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.1 $\lim _{x \rightarrow 2} \frac{x^{3}-8}{2 x-4}$.
|
12.1 The function $f(x)=\frac{x^{3}-8}{2 x-4}$ is undefined at the point $x=2$. By factoring the numerator using formula (1.14), we can represent this function as
$f(x)=\frac{(x-2)\left(x^{2}+2 x+4\right)}{2(x-2)}$.
In the domain of the function $f(x)$, the expression $x-2 \neq 0$, so the fraction can be simplified by canceling out $x-2$. Then we get
$$
\lim _{x \rightarrow 2} f(x)=\lim _{x \rightarrow 2} \frac{x^{2}+2 x+4}{2}=f(2)=6
$$
Answer: 6.
|
6
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$12.3 \lim _{x \rightarrow-1} \frac{\sqrt{2 x+3}-1}{\sqrt{5+x}-2}$.
$12.3 \lim _{x \rightarrow-1} \frac{\sqrt{2 x+3}-1}{\sqrt{5+x}-2}$.
The above text is already in a mathematical expression format, so the translation is the same as the original text. If you need an explanation or solution for the limit, please let me know!
|
12.3 Multiplying the numerator and the denominator of the fraction by $(\sqrt{2 x+3}+1)(\sqrt{5+x}+2)$, we get $\lim _{x \rightarrow-1} \frac{(2 x+3-1)(\sqrt{5+x}+2)}{(5+x-4)(\sqrt{2 x+3}+1)}=\lim _{x \rightarrow-1} \frac{2(x+1)(\sqrt{5+x}+2)}{(x+1)(\sqrt{2 x+3}+1)}=$ $\lim _{x \rightarrow-1} \frac{2(\sqrt{5+x}+2)}{\sqrt{2 x+3}+1}=\frac{2 \cdot 4}{2}=4$.
Answer: 4.
|
4
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.8 $f(x)=\sqrt{x^{2}+3}+\frac{2 x}{x+1} ; f^{\prime}(1)=?$
|
12.8 First, we find
$$
f^{\prime}(x)=\frac{x}{\sqrt{x^{2}+3}}+2 \frac{x+1-x}{(x+1)^{2}}=\frac{x}{\sqrt{x^{2}+3}}+\frac{2}{(x+1)^{2}}
$$
Now, setting $x=1$, we get $f^{\prime}(1)=\frac{1}{2}+\frac{2}{4}=1$.
Answer: 1.
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.9 $f(x)=\sin 4 x \cos 4 x ; f^{\prime}\left(\frac{\pi}{3}\right)=$ ?
|
12.9 We have
$f^{\prime}(x)=4 \cos 4 x \cdot \cos 4 x+\sin 4 x(-4 \sin 4 x)=$ $=4\left(\cos ^{2} 4 x-\sin ^{2} 4 x\right)=4 \cos 8 x$.
At $x=\frac{\pi}{3}$ we find $f^{\prime}\left(\frac{\pi}{3}\right)=4 \cos \frac{8 \pi}{3}=4 \cos \frac{2 \pi}{3}=-2$.
Answer: -2.
|
-2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.11 $f(x)=\frac{(x-2)^{2}}{x^{2}}$.
|
12.11 The domain of the function is the entire number line, except for the point $x=0$. Using formula (12.4) and the table of derivatives, we find
$$
f^{\prime}(x)=\frac{2(x-2) x^{2}-(x-2)^{2} 2 x}{x^{4}}=\frac{4(x-2)}{x^{3}}
$$
$f^{\prime}(x)=0$ only at $x=2$. We will construct a table:
| Interval | $(-\infty, 0)$ | $(0,2)$ | 2 | $(2, \infty)$ |
| :---: | :---: | :---: | :---: | :---: |
| $f^{\prime}(x)$ | + | - | 0 | + |
| $f(x)$ | $\nearrow$ | $\searrow$ | $\min$ | $\nearrow$ |
Therefore, $x=2$ is a point of minimum; the function is increasing on $(-\infty, 0)$ and on $(2, \infty)$, and decreasing on $(0,2)$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.17 A rectangular plot of land with an area of $294 \mathrm{~m}^{2}$ needs to be fenced and then divided into two equal parts by another fence. What should the linear dimensions of the plot be for the total length of the fence to be the smallest?
|
12.17 Let $x$ and $y$ (Fig. 12.2) (linear dimensions of the plot in meters), then the area of the plot is $x y=294$, from which $y=\frac{294}{x}$. The length of the entire fence

Fig. 12.2 can be expressed by the function
$$
f(x)=3 x+2 y=3 x+\frac{588}{x}=\frac{3 x^{2}+588}{x}
$$
where, by the context of the problem, $x>0$. Further, we have $f^{\prime}(x)=\frac{3 x^{2}-588}{x^{2}}$, from which $\quad f^{\prime}(x)=0 \quad$ when $\quad x=14$ (since $x>0$). If $014$, then $f^{\prime}(x)>0$; therefore, $x=14$ is a point of minimum of the function $f(x)$. As a result, we get $x=14$, $y=21$.
Answer: 14 and 21 m.
|
14
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.18 A pedestrian set out for a walk from point $A$ at a speed of $v$ km/h. After he had walked 6 km from $A$, a cyclist set out after him from $A$ at a speed 9 km/h greater than the pedestrian's speed. When the cyclist caught up with the pedestrian, they turned back and returned to $A$ together at a speed of 4 km/h. For what value of $v$ will the pedestrian's walking time be the shortest?
|
12.18 The time it takes for the cyclist to catch up with the pedestrian is $\frac{6}{9}=\frac{2}{3}$ (hours). Before the meeting, the pedestrian had been walking for $\frac{6}{v}+\frac{2}{3}$ (hours) and covered $v\left(\frac{6}{v}+\frac{2}{3}\right)$ (km). They covered this same distance on the way back at a constant speed of 4 km/h and spent $\frac{v\left(\frac{6}{v}+\frac{2}{3}\right)}{4}$ (hours). Therefore, the total time spent by the pedestrian on the walk can be expressed by the function
$$
t(v)=\frac{6}{v}+\frac{2}{3}+\frac{v\left(\frac{6}{v}+\frac{2}{3}\right)}{4}=\frac{6}{v}+\frac{2}{3}+\frac{3}{2}+\frac{v}{6}=\frac{v^{2}+13 v+36}{6 v}
$$
where $v>0$. We find
$$
t^{\prime}(v)=\frac{(2 v+13) v-\left(v^{2}+13 v+36\right)}{6 v^{2}}=\frac{v^{2}-36}{6 v^{2}}
$$
from which $t^{\prime}(v)=0$ when $v=6$. It is easy to verify that $v=6$ is a minimum point of the function $t(v)$. Therefore, the pedestrian will spend the least amount of time on the walk if they initially walk at a speed of 6 km/h.
Answer: 6 km/h
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
$12.28 \int_{8}^{27} \frac{d x}{\sqrt[3]{x^{2}}}$
|
12.28 We have
$$
\int_{8}^{27} \frac{d x}{\sqrt[3]{x^{2}}}=\int_{8}^{27} x^{-2 / 3} d x=\left.\frac{x^{1 / 3}}{1 / 3}\right|_{8} ^{27}=3\left(27^{1 / 3}-8^{1 / 3}\right)=3
$$
Answer: 3.
|
3
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.35 $\lim _{x \rightarrow 4} \frac{x+\sqrt{x}-6}{x-5 \sqrt{x}+6}$.
|
12.35 The numerator and denominator of the given fraction are quadratic functions of $\sqrt{x}$. We have
$$
\lim _{x \rightarrow 4} \frac{(\sqrt{x}+3)(\sqrt{x}-2)}{(\sqrt{x}-3)(\sqrt{x}-2)}=\lim _{x \rightarrow 4} \frac{\sqrt{x}+3}{\sqrt{x}-3}=\frac{5}{-1}=-5
$$
Answer: -5.
|
-5
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
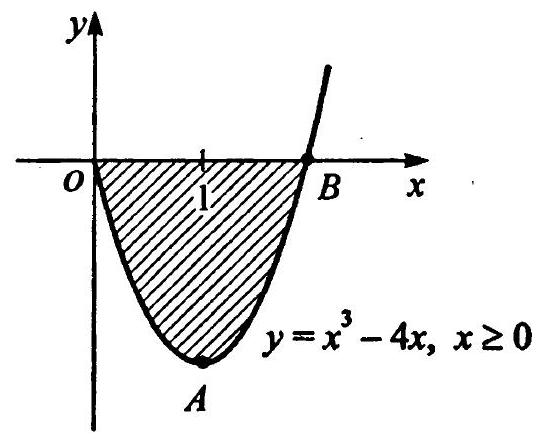
12.59 Find the area of the figure bounded by the lines $y=x^{3}-4 x$ and $y=0$ for $x \geq 0$.
Translate the text above into English, please keep the original text's line breaks and format, and output the translation result directly.
|
12.59 First, let's construct the graph of the function $y=x^{3}-4 x$ for $x \geq 0$. We find the extrema:
$y^{\prime}=3 x^{2}-4$;
$3 x^{2}-4=0 ;$
$x= \pm \frac{2}{\sqrt{3}} \approx \pm 1.1$.
For
$x \geq 0$ the function is decreasing
on $\left(0, \frac{2}{\sqrt{3}}\right)$, increasing
Fig. 12.11
on $\left(\frac{2}{\sqrt{3}}, \infty\right)$, and $x=\frac{2}{\sqrt{3}}$ is a point of minimum, with $y_{\min }=-\frac{16}{3 \sqrt{3}} \approx-3$. Therefore, we need to find the area of the figure $O A B$ (Fig. 12.11). Since the function $y=x^{3}-4 x$ takes negative values on $(0,2)$, we have $S=\left|\int_{0}^{2}\left(x^{3}-4 x\right) d x\right|$. We get
$\int_{0}^{2}\left(x^{3}-4 x\right) d x=\left.\left(\frac{x^{4}}{4}-4 \frac{x^{2}}{2}\right)\right|_{0} ^{2}=-4$,
from which we obtain $S=4$ (sq. units).
Answer: 4 sq. units.
|
4
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.1. The lengths of the sides of a right-angled triangle form an arithmetic progression with a common difference of 1 cm. Find the length of the hypotenuse.
|
1.1. Let $c$ be the length of the hypotenuse. Then the lengths of the legs are $c-1$ and $c-2$. We have
$$
(c-1)^{2}+(c-2)^{2}=c^{2}, \text { or } c^{2}-6 c+5=0
$$
from which $c=5$ (cm) (the second root of the equation does not satisfy the condition).
Answer: 5 cm.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.2. A point on the hypotenuse, equidistant from both legs, divides the hypotenuse into segments of 30 and 40 cm. Find the legs of the triangle.
|
1.2. By the condition, $\angle C=90^{\circ}, A D=30 \text{ cm}$, $D B=40$ cm (Fig. 1.1). Let $A C=x, B C=y$. Since the point equidistant from the sides of the angle lies on its bisector, then $\frac{x}{y}=\frac{30}{40}$, i.e., $y=\frac{4 x}{3}$. But $x^{2}+y^{2}=A B^{2}$ and, therefore,

Fig. 1.1
$x^{2}+\frac{16 x^{2}}{9}=70^{2}$, from which $x^{2}=1764$. Thus, $x=42$ (cm), then $y=\frac{4}{3} \cdot 42=56(\text{ cm})$
Answer: 42 and 56 cm.

Fig. 1.2
|
42
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.6. The legs of a right triangle are 9 and 12 cm. Find the distance between the point of intersection of its angle bisectors and the point of intersection of the medians.
|
1.6. In $\triangle A B C$ (Fig. 1.5), we have $A B=\sqrt{9^{2}+12^{2}}=15$ (cm); the median $C D$ is half the hypotenuse, i.e., $\frac{15}{2}$ cm. Let $E$ be the point of intersection of the medians; then $C E=\frac{2}{3} C D=\frac{2}{3} \cdot \frac{15}{2}=5$ (cm) (according to the additional relations, point $1^{\circ}$). Draw $D F \perp A C$; since $D F$ is the midline in $\triangle A B C$, we have $C F=6$ cm, $D F=\frac{9}{2}$ cm. Next, draw $E K \perp A C$; then $E K \| D F$ and $\triangle C E K \sim \triangle C D F$, from which
$$
E K=\frac{2}{3} D F=\frac{2}{3} \cdot \frac{9}{2}=3(\mathrm{~cm}), C K=\frac{2}{3} C F=\frac{2}{3} \cdot 6=4(\mathrm{~cm})
$$
Let $M$ be the point of intersection of the angle bisectors of $\angle C B A$ and $\angle B C A$,
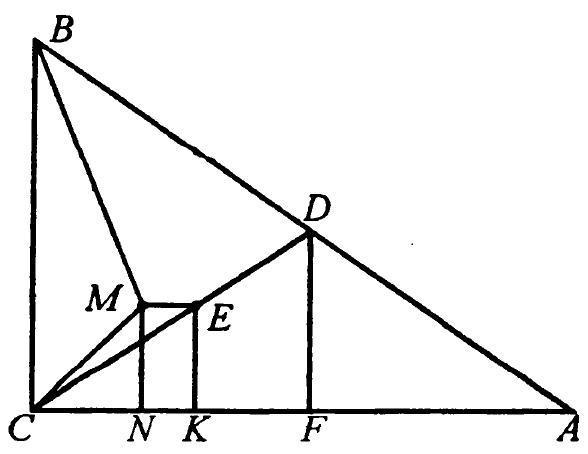
Fig. 1.5
i.e., the center of the inscribed circle in $\triangle A B C$; then $M N \perp A C$, where $r=M N$ is the radius of this circle. By formula (1.4), we have $r=\frac{S}{p}$, where $S=\frac{1}{2} \cdot 9 \cdot 12=54\left(\mathrm{~cm}^{2}\right), p=\frac{1}{2}(9+12+15)=18$ (cm); thus, $r=\frac{54}{18}=3$ (cm). Finally, considering that $\angle M C N=45^{\circ}$, i.e., $C N=M N$, we get $N K=M E=C K-C N=4-3=1$ (cm).
Answer: 1 cm.

Fig. 1.6
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.8. In an isosceles triangle, the heights drawn to the base and to the lateral side are equal to 10 and 12 cm, respectively. Find the length of the base.
|
1.8. In $\triangle A B C$ we have $A B=B C$, $A E \perp B C, B D=10$ cm and $A E=12$ cm (Fig. 1.7). Let $A C=x, A B=B C=y$. Right triangles $A E C$ and $B D C$ are similar (angle $C$ is common); therefore, $B C: A C=B D: A E$, or $y: x=10: 12=5: 6$. Applying the Pythagorean theorem (1.13) to $\triangle B D C$, we have $B C^{2}=B D^{2}+D C^{2}$, i.e.,
$y^{2}=100+\frac{x^{2}}{4}$. Thus, we arrive at the system of equations
$$
\left\{\begin{array}{l}
\frac{y}{x}=\frac{5}{6} \\
y^{2}=100+\frac{x^{2}}{4}
\end{array}\right.
$$
solving which we get $x=15$.
Answer: 15 cm.
|
15
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.9. Two circles touch each other externally. A tangent is drawn to the first circle, passing through the center of the second circle. The distance from the point of tangency to the center of the second circle is three times the radius of this circle. How many times greater is the length of the first circle compared to the length of the second circle?
|
1.9. Let $O_{1}$ and $O_{2}$ be the centers of the circles, and $A$ be the point of tangency (Fig. 1.8). Then $O_{1} A = R_{1}, O_{1} O_{2} = R_{1} + R_{2}, O_{2} A = 3 R_{2}$ (by the condition). We need to find the ratio $2 \pi R_{1} : 2 \pi R_{2} = R_{1} : R_{2}$. In the right triangle $O_{1} A O_{2} \left(\angle A = 90^{\circ}\right)$, we have
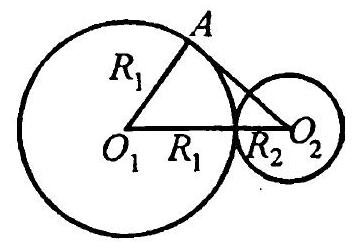
Fig. 1.8
$$
O_{1} O_{2}^{2} = O_{1} A^{2} + O_{2} A^{2}, \text{ or } \left(R_{1} + R_{2}\right)^{2} = R_{1}^{2} + \left(3 R_{2}\right)^{2}
$$
Simplifying this equation, we get $R_{1} = 4 R_{2}$, hence $R_{1} : R_{2} = 4$.
Answer: 4 times.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.13. Inside a circle with a radius of 15 cm, a point $M$ is taken at a distance of 13 cm from the center. A chord of length 18 cm is drawn through this point. Find the lengths of the segments into which point $M$ divides the chord.
|
1.13. Draw $O C \perp A B$ (Fig.
1.11). Then $C B=\frac{1}{2} A B=9 \quad \text{cm}$.
From $\triangle O B C$ it follows that
$O C=\sqrt{O B^{2}-B C^{2}}=12(\text{cm})$, and from
$\triangle O M C$ - that $M C=\sqrt{O M^{2}-O C^{2}}=5$ (cm). Therefore, $A M=9+5=14$ (cm), $M B=9-5=4$ (cm).
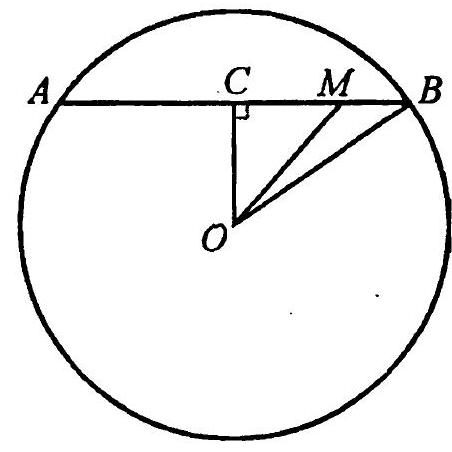
Fig. 1.11
Answer: 14 and 4 cm.
|
14
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.20. A tangent, parallel to the base, is drawn to the circle inscribed in an isosceles triangle with a base of 12 cm and a height of 8 cm. Find the length of the segment of this tangent, enclosed between the sides of the triangle.
|
1.20. Let's find the length of the side $B C$ (Fig. 1.18); $B C=\sqrt{B M^{2}+M C^{2}}=\sqrt{6^{2}+8^{2}}=10$ (cm). Considering that $A O$ is the bisector of $\triangle A B M$, we have $\frac{M O}{O B}=\frac{A M}{A B}$, or $\frac{r}{8-r}=\frac{6}{10}$, from which $r=3$ (cm). Since $D E \| A C$, then $\triangle D B E \sim \triangle A B C$. That is, $\frac{D E}{A C}=\frac{B N}{B M}$, or $\frac{D E}{12}=\frac{8-2 r}{8}$, from which $D E=3 \text{ cm}$.
Answer: 3 cm.
Fig. 1.18
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.26. The area of an isosceles triangle is equal to $\frac{1}{3}$ of the area of the square constructed on the base of the given triangle. The lengths of the lateral sides of the triangle are shorter than the length of its base by 1 cm. Find the lengths of the sides and the height of the triangle, drawn to the base.
|
1.26. By the condition, $B C^{2}=$ $=3 \cdot \frac{1}{2} B C \cdot A H$ (Fig. 1.22), or $A H=$ $=\frac{2}{3} B C$. But $A H^{2}=A B^{2}-\left(\frac{1}{2} B C\right)^{2}$ and, therefore, $\frac{4}{9} B C^{2}=A B^{2}-\frac{1}{4} B C^{2}$, or $A B^{2}=\frac{25}{36} B C^{2}$, i.e., $A B=\frac{5}{6} B C$. Then we get $A B=\frac{5}{6}(A B+1)$, from which $A B=5$ (cm). Therefore, $B C=6 \mathrm{~cm}, A H=4 \mathrm{~cm}$.
Answer: 5 and 6 cm; 4 cm.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.28. One of the angles of the parallelogram is $60^{\circ}$, and the shorter diagonal is $2 \sqrt{31}$ cm. The length of the perpendicular dropped from the point of intersection of the diagonals to the longer side is $\frac{\sqrt{75}}{2}$ cm. Find the lengths of the sides and the longer diagonal of the parallelogram.
|
### 1.28. Let's conduct
Fig. 1.23 $B N \perp A D$ (Fig. 1.24); since $B N=2 O M$, then $B N=\sqrt{75}$ cm. Considering that in $\triangle A N B \angle A B N=30^{\circ}$, we have $A B=2 A N$ and, therefore, $4 A N^{2}=75+A N^{2}$, from which $A N=5$ cm and $A B=10$ cm. Further, from $\triangle B D N$ we get
Fig. 1.24 $N D^{2}=B D^{2}-B N^{2}=124-75=49$; hence, $N D=7$ cm and $A D=12$ cm. Finally, from the equality $A C^{2}+B D^{2}=2 A B^{2}+2 A D^{2}$ we find $A C^{2}=200+288-124=364$, i.e., $A C=2 \sqrt{91}$ cm.
Answer: 10 and 12 cm; $2 \sqrt{91}$ cm.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.30. The lengths of the parallel sides of the trapezoid are 25 and 4 cm, and the lengths of the non-parallel sides are 20 and 13 cm. Find the height of the trapezoid.
|
1.30. Given that $B C=$ $=4 \text{ cm}, A D=25 \text{ cm}, A B=20$ cm, $C D=13$ cm (Fig. 1.26). Draw $B E \perp A D$ and $C F \perp A D$. Let $B E=C F=$ $=h, A E=x, F D=y$. Then from $\triangle A B E$ and $\triangle C F D$ we find $h=\sqrt{20^{2}-x^{2}}=\sqrt{13^{2}-y^{2}}$. Considering that $y=25-4-$ $-x=21-x$, we have
$$
20^{2}-x^{2}=13^{2}-(21-x)^{2} \text {, or } 42 x=672 \text {, }
$$
from which $x=16$ (cm). Thus, $h=\sqrt{20^{2}-16^{2}}=12$ (cm).
Answer: $12 \text{ cm}$.
Fig. 1.27
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.31. The diagonal of an isosceles trapezoid bisects its obtuse angle. The smaller base of the trapezoid is $3 \mathrm{~cm}$, and the perimeter is $42 \mathrm{~cm}$. Find the area of the trapezoid.
|
1.31. By the condition, $\angle B C A=$ $=\angle A C D$ (Fig. 1.27). But $\angle B C A=$ $=\angle C A D$, so $\triangle A C D$ is isosceles and $A D=C D$. We have $3 A D+B C=42$; since $B C=3$ cm, then $A D=13$ cm. Draw $B K \perp A D$; then $A K=\frac{1}{2}(13-3)=5$ (cm) and from $\triangle A K B$ we find $B K=\sqrt{13^{2}-5^{2}}=$ $=12$ (cm). Therefore,
$$
S=\frac{1}{2}(3+13) \cdot 12=96\left(\mathrm{~cm}^{2}\right)
$$
|
96
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.36. Inside a right angle, there is a point $M$, the distances from which to the sides of the angle are 4 and $8 \mathrm{~cm}$. A line passing through point $M$ cuts off a triangle from the right angle with an area of $100 \mathrm{~cm}^{2}$. Find the legs of the triangle.
|
1.36. According to the condition, $\angle C=90^{\circ}, M P=$ $=4 \text{ cm}, M Q=8 \text{ cm}, S_{\triangle A B C}=100 \text{ cm}^{2}$ (Fig. $1.30$); it is required to find $B C$ and $A C$. Let $B C=x, A C=y$; then $0.5 x y=100$, i.e., $x y=200$. Since $\triangle B P M \sim \triangle M Q A$, we have
$$
\frac{M P}{A Q}=\frac{B P}{M Q}, \text { or } \frac{4}{y-4}=\frac{x-8}{8} . \text { Therefore, }
$$
we have the system of equations
$$
\left\{\begin{array}{l}
\frac{4}{y-4}=\frac{x-8}{8}, \\
x y=200
\end{array} \text { or } \left\{\begin{array}{l}
x+2 y=50 \\
x y=200
\end{array}\right.\right.
$$
which reduces to the quadratic equation $y^{2}-25 y+100=0$, from which we find $y_{1}=5 \text{ cm} ; y_{2}=20 \text{ cm}$. As a result, we get two solutions: $x_{1}=40 \text{ cm}, y_{1}=5 \text{ cm} ; x_{2}=10 \text{ cm}, y_{2}=20 \text{ cm}$.
Answer: 40 and 5 cm or 10 and 20 cm.
|
40
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.37. The perimeter of a right triangle \(ABC (\angle C = 90^\circ)\) is 72 cm, and the difference between the lengths of the median \(CM\) and the altitude \(CK\) is 7 cm. Find the length of the hypotenuse.
|
1.37. According to the condition, $\angle C=90^{\circ}, A B+B C+A C=72 \text{ cm}, C M$ is the median, $C K$ is the altitude, $C M-C K=7$ cm (Fig. 1.31); we need to find $A B$. Since $M$ is the center of the circumscribed circle,
Fig. 1.31
$A M=M B=M C=\frac{1}{2} A B$. We use the equality $A B^{2}=B C^{2}+$ $+A C^{2}$. Note that $B C^{2}+A C^{2}=(B C+A C)^{2}-2 B C \cdot A C$, hence $A B^{2}=(72-A B)^{2}-2 A B \cdot C K$, since $B C \cdot A C=A B \cdot C K=2 S$, where $S$ is the area of the triangle. Thus, we arrive at the equation $A B^{2}=(72-A B)^{2}-2 A B\left(\frac{1}{2} A B-7\right)$, or $A B^{2}+130 A B-5184=0$, from which $A B=-65+\sqrt{9409}=32$ cm (the second root of the equation does not satisfy the condition).
Answer: $32 \text{ cm}$
|
32
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.44. In a circle with center $O$, a chord $A B$ is drawn, intersecting the diameter at point $M$ and forming an angle of $60^{\circ}$ with the diameter. Find $O M$, if $A M=10$ cm, and $B M=4$ cm.
|
1.44. Draw $O P \perp A B$ (Fig. 1.36). Then $A P=B P=7$ cm and, therefore, $M P=3$ cm. Since $\angle P M O=60^{\circ}$, then $\angle M O P=30^{\circ}$ and $O M=2 M P=6 \text{ cm}$.
Answer: 6 cm.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.49. The area of a right triangle is $24 \mathrm{~cm}^{2}$, and the hypotenuse is 10 cm. Find the radius of the inscribed circle.
|
1.49. I n d i c a t i o n. Denoting the legs of the triangle by $a$ and $b$, solve the system of equations
$$
\left\{\begin{array}{l}
a b=48 \\
a^{2}+b^{2}=100
\end{array}\right.
$$
and then use the formula $S=p r$.
Answer: 2 cm.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.57. The vertices of a rectangle inscribed in a circle divide it into four arcs. Find the distance from the midpoint of one of the larger arcs to the vertices of the rectangle, if its sides are 24 and 7 cm.
|
1.57. Since $A C$ is the diameter of the circle (Fig. 1.44), then $R=0.5 \sqrt{24^{2}+7^{2}}=12.5 \quad$ (cm). In $\triangle B O F$ we have $O F=$ $=\sqrt{O B^{2}-B F^{2}}=\sqrt{12.5^{2}-12^{2}}=3.5$ (cm); hence, $M F=12.5-3.5=9$ (cm), $M K=12.5+3.5=16$ (cm). From $\triangle M B F$ and $\triangle M A K$ we find the required distances: $\quad M B=\sqrt{M F^{2}+B F^{2}}=\sqrt{9^{2}+12^{2}}=15(\mathrm{~cm})$, $M A=\sqrt{M K^{2}+K A^{2}}=\sqrt{16^{2}+12^{2}}=20(\mathrm{~cm})$.
Answer: 15 and 20 cm.
|
15
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.43. Find the distance between the midpoints of two skew edges of a cube, the total surface area of which is $36 \mathrm{~cm}^{2}$.
|
2.43. Since the total surface area of the cube $S_{\text {full }}=36 \mathrm{~cm}^{2}$, the area of one face $S=6 \mathrm{~cm}^{2}$ and the edge of the cube
Fig. 2.37
$A D=a=\sqrt{6}$ cm (Fig. 2.37). The required distance
$$
\begin{gathered}
K M=\sqrt{A K^{2}+A M^{2}} \text {, where } A K=\frac{a}{2}=\frac{\sqrt{6}}{2}(\text { cm }), \\
A M=\sqrt{A D^{2}+D M^{2}}=\sqrt{a^{2}+\frac{a^{2}}{4}}=\frac{a \sqrt{5}}{2}=\frac{\sqrt{30}}{2} \text { (cm). }
\end{gathered}
$$
Finally, we get $K M=\sqrt{\frac{6}{4}+\frac{30}{4}}=3$ (cm).
Answer: 3 cm.
Fig. 2.38
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.46. In a slanted parallelepiped, the projection of a lateral edge onto the base plane is 5 dm, and the height is 12 dm. A section perpendicular to the lateral edge is a rhombus with an area of 24 dm ${}^{2}$ and a diagonal of 8 dm. Find the lateral surface area and the volume of the parallelepiped.
|
2.46. According to the condition, $A_{1} K=12$ dm, $A K=5$ dm, $A_{1} K \perp A K$ (Fig. 2.40); therefore, $A A_{1}=\sqrt{A_{1} K^{2}+A K^{2}}=13$ (dm). Since $S_{A_{1} L M N}=$ $=24$ dm $^{2}$ and $A A_{1}$ is perpendicular to the section, the required volume is
$$
V=S_{A_{1} L M N} \cdot A A_{1}=24 \cdot 13=312\left(\text { dm }^{3}\right)
$$

Fig. 2.40
Next, considering that $A_{1} L M N$ is a rhombus, we have $S_{\text {side }}=4 A A_{1} \cdot A_{1} N$: To find the side of the rhombus, we use the equality
$$
S_{A_{1} L M N}=\frac{1}{2} A_{1} M \cdot L N, \text { or } 24=\frac{1}{2} \cdot 8 \cdot L N,
$$
from which $L N=6$ (dm); then $A_{1} N=\sqrt{3^{2}+4^{2}}=5$ (dm). Thus,
$$
S_{\text {side}}=4 \cdot 13 \cdot 5=260 \text { dm }^{2}
$$
Answer: 260 dm $^{2} ; 312$ dm $^{3}$.
|
260
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.16. The height of an isosceles trapezoid is equal to \( h \). The upper base of the trapezoid is seen from the midpoint of the lower base at an angle of \( 2 \alpha \), and the lower base from the midpoint of the upper base at an angle of \( 2 \beta \). Find the area of the trapezoid in this general case and calculate it without tables if \( h=2, \alpha=15^{\circ}, \beta=75^{\circ} \).
|
3.16. Given that in trapezoid $ABCD$ we have: $AB = CD, BC \parallel AD$, $M \in AD, AM = MD, N \in BC, BN = NC, BE \perp AD, BE = h, \angle BMC = 2\alpha$,
Fig. 3.18
$\angle AND = 2\beta$ (Fig. 3.18). Since $\triangle ABM = \triangle CMD$ and $\triangle ABN = \triangle CDN$ (by two sides and the included angle), we have $BM = MC, AN = ND$. From $\triangle AMN$ and $\triangle BMN$ we find $AM = h \operatorname{tg} \beta, BN = h \operatorname{tg} \alpha$. Therefore,
$$
S_{ABCD} = (AM + BN) h = h^2 (\operatorname{tg} \alpha + \operatorname{tg} \beta) = \frac{h^2 \sin (\alpha + \beta)}{\cos \alpha \cos \beta}
$$
For $h = 2, \alpha = 15^\circ$ and $\beta = 75^\circ$ we get
$$
S_{ABCD} = \frac{4 \sin 90^\circ}{\cos 15^\circ \cos 75^\circ} = \frac{4}{\cos 15^\circ \sin 15^\circ} = \frac{8}{\sin 30^\circ} = 16
$$
|
16
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.67. In a trapezoid, the smaller base is equal to 2, the adjacent angles are $135^{\circ}$ each. The angle between the diagonals, facing the base, is $150^{\circ}$. Find the area of the trapezoid.
|
3.67. By the condition, $A D \| B C, B C=2, \angle A B C=\angle B C D=135^{\circ}$, $\angle A O D=150^{\circ}$ (Fig. 3.69). Since the angles at the base of the trapezoid are equal, the trapezoid is isosceles, i.e., $A B=C D$. We find
Fig. 3.69 $\angle A D C=180^{\circ}-135^{\circ}=45^{\circ} ;$
$\angle O D A=\frac{180^{\circ}-150^{\circ}}{2}=15^{\circ}$;
$\angle B D C=45^{\circ}-15^{\circ}=30^{\circ}$. From $\triangle B D C$ by the Law of Sines we have $\frac{B C}{\sin 30^{\circ}}=\frac{B D}{\sin 135^{\circ}}$, hence
$B D=\frac{2 \sin 45^{\circ}}{\sin 30^{\circ}}=2 \sqrt{2}$. Therefore,
$$
S_{A B C D}=\frac{1}{2} B D^{2} \sin 150^{\circ}=\frac{1}{2} \cdot 8 \cdot \frac{1}{2}=2
$$
(since the area of a convex quadrilateral is equal to $\frac{1}{2} d_{1} d_{2} \sin \alpha$, where $\alpha$ is the angle between the diagonals).
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.6. The lengths of the sides of an acute-angled triangle form an arithmetic progression with a common difference of 5 cm. Find the greatest number with the following property: the length of the largest side of any triangle of the specified type is greater than this number.
|
4.6. Let in $\triangle A B C$ (Fig. 4.5) $A B=x, B C=$ $=x+5$ and $A C=x+10$, where $x>5$. According to the Law of Cosines, we have
$$
(x+10)^{2}=x^{2}+(x+5)^{2}-2 x(x+5) \cos B
$$
from which
$$
\cos B=\frac{x^{2}-10 x+75}{2 x(x+5)}=\frac{(x+5)(x-15)}{2 x(x+5)}=\frac{x-15}{2 x}
$$
Fig. 4.5
$$
\text { Since } 0<\cos B<1, \text { then } 0<\frac{x-15}{2 x}<1 \text {. The }
$$
smallest value of $x$ for which this inequality holds is $x=15$. Therefore, the largest number with the property specified in the condition is $x+10=25$.
Answer: 25 cm.
|
25
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.15. Find the angle between the intersecting diagonals of adjacent faces of a cube.
|
4.15. Let the edge of the cube be $a$; we need to find the angle between the diagonals $A_{1} B$ and $B_{1} C$ (Fig. 4.13). This angle is equal to the angle between the lines $D_{1} C$ and $B_{1} C$, since $D_{1} C \| A_{1} B$. In $\Delta B_{1} D_{1} C$, we have $B_{1} D_{1}=D_{1} C=B_{1} C=a \sqrt{2}$, and therefore, $\angle B_{1} C D_{1}=60^{\circ}$.
Answer: $60^{\circ}$.
Fig. 4.14
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.29. A regular $n$-sided polygon is inscribed in a circle of radius $R$, the area of which is equal to $3 R^{2}$. Find $n$.
|
4.29. We have $\angle A O B=\frac{360^{\circ}}{n}$ and, therefore, $S_{\triangle A O B}=\frac{R^{2}}{2} \sin \frac{360^{\circ}}{n}$ (Fig. 4.26). Thus, we obtain the equation $\frac{R^{2}}{2} \sin \frac{360^{\circ}}{n}=\frac{3 R^{2}}{n}$, which holds
Fig. 4.26 for $n=12$.
Answer: $\boldsymbol{n}=12$.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.5. The vector $\overline{O A}$ forms angles with the axes $O x, O y, O z$ that are respectively equal to $\alpha=\frac{\pi}{3}, \beta=\frac{\pi}{3}, \gamma=\frac{\pi}{4}$; the point $B$ has coordinates $(-2; -2; -2 \sqrt{2})$. Find the angle between the vectors $\overline{O A}$ and $\overline{O B}$.
|
5.5. Let $\bar{n}$ be a unit vector in the direction of $\overline{O A};$ then $\quad \bar{n}\left(\cos \frac{\pi}{3} ; \cos \frac{\pi}{3} ; \cos \frac{\pi}{4}\right)$, or $\quad \bar{n}\left(\frac{1}{2} ; \frac{1}{2} ; \frac{\sqrt{2}}{2}\right)$, and $\overline{O B}(-2 ;-2 ;-2 \sqrt{2})$. Denoting the angle between $\overline{O A}$ and $\overline{O B}$ by $\varphi$, we find
$$
\cos \varphi=\frac{\bar{n} \cdot \overline{O B}}{|\bar{n}||\overline{O B}|}=\frac{\frac{1}{2}(-2)+\frac{1}{2}(-2)+\frac{\sqrt{2}}{2}(-2 \sqrt{2})}{1 \cdot 4}=-1
$$
from which we obtain the answer: $\varphi=180^{\circ}$.
Answer: $180^{\circ}$.
|
180
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.8. Find the modulus of the projection of vector $\bar{a}(7; -4)$ onto the axis parallel to vector $\bar{b}(-8; 6)$.
untranslated text:
5.8. Найти модуль проекции вектора $\bar{a}(7 ;-4)$ на ось, параллельную вектору $\bar{b}(-8 ; 6)$.
|
5.8. We have $O K=$ proj $_{\bar{b}} \bar{a}=|\bar{a}| \cos \varphi$ (Fig. 5.5). From here, using
Fig. 5.5 the equality $\quad \bar{a} \bar{b}=|\bar{a}||\vec{b}| \cos \varphi, \quad$ we find proj $_{\bar{b}} \bar{a}=\frac{\bar{a} \bar{b}}{|\bar{b}|}$. Since $\bar{b}$ is the direction vector of the axis onto which the vector is projected,
$$
\operatorname{proj}_{\bar{b}} \bar{a}=\frac{7(-8)+(-4) 6}{\sqrt{64+36}}=\frac{-56-24}{10}=-8 \text {, i.e. }\left|\operatorname{proj}_{\bar{b}} \bar{a}\right|=8
$$
Answer: 8.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.10. Given vectors $\bar{a}(6 ;-8 ; 5 \sqrt{2})$ and $\bar{b}(2 ;-4 ; \sqrt{2})$. Find the angle formed by the vector $\bar{a}-\bar{b}$ with the $O z$ axis.
|
5.10. The vector $\bar{a}-\bar{b}$ has coordinates $(4; -4; 4 \sqrt{2})$. Let $\bar{k}(0; 0; 1)$ be the unit vector directed along the $O z$ axis. Assuming $(\widehat{a}-\bar{b}; \bar{k})=\gamma$, we find
$$
\cos \gamma=\frac{(\bar{a}-\bar{b}) \bar{k}}{|\bar{a}-\bar{b}||\bar{k}|}=\frac{4 \sqrt{2}}{\sqrt{16+16+32 \cdot 1}}=\frac{\sqrt{2}}{2}, \text{ i.e. } \gamma=45^{\circ}
$$
Answer: $45^{\circ}$.
|
45
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.11. Given a triangle $A B C ; B D$ is a median, $\angle D B C=90^{\circ}$, $B D=\frac{\sqrt{3}}{4} A B$. Find $\angle A B D$.
|
5.11. According to the condition, $\angle D B C=90^{\circ}, B D=\frac{\sqrt{3}}{4} A B, A D=D C$ (Fig. 5.6); we need to find $\angle A B D=$ $=\alpha$. To find the angle $\alpha$, we will use the formula $\cos \alpha=\frac{\overline{B A} \cdot \overline{B D}}{|\overrightarrow{B A}||\overline{B D}|}$. Since $B D$ is the median of $\triangle A B C$,
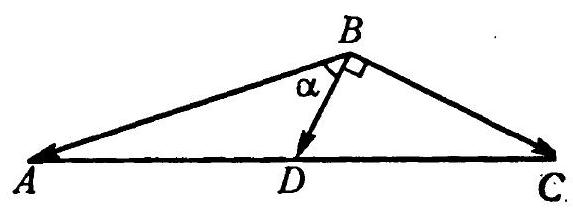
Fig. 5.6 then $B D=\frac{1}{2}(\overline{B A}+\overline{B C})$, from which $\overline{B A}=2 \overline{B D}-\overline{B C}$. Therefore,
$$
\cos \alpha=\frac{(2 \overline{B D}-\overline{B C}) \overline{B D}}{|\overline{B A}||| \overline{B D} \mid}=\frac{2 B D^{2}-\overline{B C} \cdot \overline{B D}}{|\overline{B A}||| B D}
$$
But $\overline{B C} \perp \overline{B D}$, i.e., $\overline{B C} \cdot \overline{B D}=0$, and from the equality $B D=\frac{\sqrt{3}}{4} A B$ it follows that $A B=\frac{4}{\sqrt{3}} B D$. Then the equality (1) will take the form
$$
\cos \alpha=\frac{2 B D^{2}}{\frac{4}{\sqrt{3}} B D^{2}}=\frac{\sqrt{3}}{2} \text {, from which } \alpha=30^{\circ}
$$
Answer: $30^{\circ}$.
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.18. In parallelogram $A B C D$, point $K$ is the midpoint of side $B C$, and point $M$ is the midpoint of side $C D$. Find $A D$, if $A K=6$ cm, $A M=3$ cm, and $\angle K A M=60^{\circ}$.
|
5.18. I n d i c a t i o n. Decompose the vector $\overline{A D}$ into vectors $\overline{A K}$ and $\overline{A M}$.
Answer: 4 cm.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.001. $\frac{(7-6.35): 6.5+9.9}{\left(1.2: 36+1.2: 0.25-1 \frac{5}{16}\right): \frac{169}{24}}$.
|
## Solution.
$$
\begin{aligned}
& \frac{(7-6.35): 6.5+9.9}{\left(1.2: 36+1.2: 0.25-1 \frac{5}{16}\right): \frac{169}{24}}=\frac{0.65: 6.5+9.9}{\left(\frac{1}{30}+\frac{24}{5}-\frac{21}{16}\right) \cdot \frac{24}{169}}=\frac{0.1+9.9}{\frac{169}{48} \cdot \frac{24}{169}}= \\
& =\frac{10}{\frac{1}{2}}=20 .
\end{aligned}
$$
Answer: 20.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.002. $\left(\left(\frac{7}{9}-\frac{47}{72}\right): 1.25+\left(\frac{6}{7}-\frac{17}{28}\right):(0.358-0.108)\right) \cdot 1.6-\frac{19}{25}$.
|
## Solution.
$$
\begin{aligned}
& \left(\left(\frac{7}{9}-\frac{47}{72}\right): 1.25+\left(\frac{6}{7}-\frac{17}{28}\right):(0.358-0.108)\right) \cdot 1.6-\frac{19}{25}= \\
& =\left(\frac{56-47}{72} \cdot \frac{4}{5}+\frac{24-17}{28}: 0.25\right) \cdot 1.6-\frac{19}{25}=(0.1+1) \cdot 1.6-\frac{19}{25}=1.76-0.76=1 .
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.005. $\frac{2 \frac{3}{4}: 1.1+3 \frac{1}{3}}{2.5-0.4 \cdot 3 \frac{1}{3}}: \frac{5}{7}-\frac{\left(2 \frac{1}{6}+4.5\right) \cdot 0.375}{2.75-1 \frac{1}{2}}$.
|
Solution.
$$
\frac{2 \frac{3}{4}: 1.1+3 \frac{1}{3}}{2.5-0.4 \cdot 3 \frac{1}{3}}: \frac{5}{7}-\frac{\left(2 \frac{1}{6}+4.5\right) \cdot 0.375}{2.75-1 \frac{1}{2}}=\frac{\frac{5}{2}+\frac{10}{3}}{\frac{5}{2}-\frac{4}{3}} \cdot \frac{7}{5}-\frac{\frac{20}{3} \cdot \frac{3}{8}}{1.25}=7-2=5
$$
Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.006. $\frac{\left(13.75+9 \frac{1}{6}\right) \cdot 1.2}{\left(10.3-8 \frac{1}{2}\right) \cdot \frac{5}{9}}+\frac{\left(6.8-3 \frac{3}{5}\right) \cdot 5 \frac{5}{6}}{\left(3 \frac{2}{3}-3 \frac{1}{6}\right) \cdot 56}-27 \frac{1}{6}$.
|
## Solution.
$$
\begin{aligned}
& \frac{\left(13.75+9 \frac{1}{6}\right) \cdot 1.2}{\left(10.3-8 \frac{1}{2}\right) \cdot \frac{5}{9}}+\frac{\left(6.8-3 \frac{3}{5}\right) \cdot 5 \frac{5}{6}}{\left(3 \frac{2}{3}-3 \frac{1}{6}\right) \cdot 56}-27 \frac{1}{6}=\frac{\left(\frac{55}{4}+\frac{55}{6}\right) \cdot \frac{6}{5}}{(2.3-0.5) \cdot \frac{5}{9}}+\frac{\left(\frac{34}{5}-\frac{18}{5}\right) \cdot \frac{35}{6}}{\left(\frac{4}{6}-\frac{1}{6}\right) \cdot 56}- \\
& -\frac{163}{6}=\frac{11\left(1+\frac{3}{2}\right)}{\frac{18}{10} \cdot \frac{5}{9}}+\frac{\frac{16}{5} \cdot \frac{35}{6}}{28}-\frac{163}{6}=\frac{55}{2}+\frac{2}{3}-\frac{163}{6}=\frac{169}{6}-\frac{163}{6}=1
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.008. $\left(\frac{3 \frac{1}{3}+2.5}{2.5-1 \frac{1}{3}} \cdot \frac{4.6-2 \frac{1}{3}}{4.6+2 \frac{1}{3}} \cdot 5.2\right):\left(\frac{0.05}{\frac{1}{7}-0.125}+5.7\right)$.
|
Solution.
$$
\begin{aligned}
& \left(\frac{3 \frac{1}{3}+2.5}{2.5-1 \frac{1}{3}} \cdot \frac{4.6-2 \frac{1}{3}}{4.6+2 \frac{1}{3}} \cdot 5.2\right):\left(\frac{0.05}{\frac{1}{7}-0.125}+5.7\right)= \\
& =\left(\frac{\frac{10}{3}+\frac{5}{2}}{\frac{5}{2}-\frac{4}{3}} \cdot \frac{\frac{23}{5}-\frac{7}{3}}{\frac{23}{5}+\frac{7}{3}} \cdot \frac{26}{5}\right):\left(\frac{\frac{1}{20}}{\frac{1}{7}-\frac{1}{8}}+\frac{57}{10}\right)= \\
& =\left(\frac{35}{7} \cdot \frac{34}{104} \cdot \frac{26}{5}\right):\left(\frac{28}{10}+\frac{57}{10}\right)=\frac{17}{2} \cdot \frac{2}{17}=1
\end{aligned}
$$
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.