problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
9.5. Let $M$ - be a finite set of numbers (distinct). It is known that among any three of its elements, there will be two whose sum belongs to $M$. What is the maximum number of elements that can be in $M$?
|
Answer: 7.
Solution: An example of a set with 7 elements: $\{-3,-2,-1,0,1,2,3\}$.
We will prove that a set $M=\left\{a_{1}, a_{2}, \ldots, a_{n}\right\}$ with $n>7$ numbers does not have the required property.
We can assume that $a_{1}>a_{2}>a_{3}>\ldots>a_{n}$ and $a_{4}>0$ (changing the signs of all elements does not change our property). Then $a_{1}+a_{2}>a_{1}+a_{3}>a_{1}+a_{4}>a_{1}$, i.e., none of the sums $a_{1}+a_{2}, a_{1}+a_{3}$, and $a_{1}+a_{4}$ belong to the set $M$. Moreover, the sums $a_{2}+a_{3}$ and $a_{2}+a_{4}$ cannot both belong to $M$, since $a_{2}+a_{3}>a_{2}+a_{4}>a_{2}$. This means that for at least one of the triples ( $a_{1}, a_{2}, a_{3}$ ) and ( $a_{1}, a_{2}, a_{4}$ ), the sum of any two of its elements does not belong to the set $M$.
Grading criteria: Proved that there are no more than 7 elements in M: 5 points. Example for 7 elements: 2 points.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. In the wagon, several kilograms of apple jam were loaded, of which $20 \%$ was good and $80 \%$ was bad. Every day, half of the existing bad jam rotted, and it was thrown away. After several days, it turned out that $20 \%$ of the jam in the wagon was bad and $80 \%$ was good. How many days have passed since the loading?
|
Answer: 4 days.
Solution 1: Let the initial total amount be $x$, and the final amount be $y$ kilograms of jam. Then, since the amount of good jam did not change, $0.2 x = 0.8 y$, which means $x = 4 y$. Therefore, initially, the amount of bad jam was $0.8 x = 3.2 y$, and it became $0.2 y$, meaning the mass of bad jam decreased by a factor of 16. Given that the amount of bad jam halved each day, it is clear that 4 days have passed.
Solution 2: Initially, there were 100 arbitrary units of jam: 20 good and 80 bad. In the end, the amount of bad jam became $20 \%$, and the amount of good jam became $80 \%$ of the new quantity, meaning the amount of good jam increased by a factor of 4. Therefore, the new amount of bad jam is 5 arbitrary units. Since it decreased by a factor of 2 each time and ultimately decreased by a factor of 16, 4 days have passed.
Criteria: Only the answer, answer with verification - 1 point. In a solution similar to the second one, if abstract units of measurement are not used but specific ones are used without any explanation that the units of measurement are not important - 1 point.
|
4
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. Once Alexei and Daniil were playing such a game. If a number \( x \) is written on the board, it can be erased and replaced with \( 2x \) or \( x - 1000 \). The player who gets a number not greater than 1000 or not less than 4000 loses. Both players aim to win. At some point, the boys stopped playing. Who lost if the first number was \( 2017 \)?
|
Answer: no one lost.
Solution: note that if a number is less than 2000 but greater than 1000, then by multiplying by 2, you can get a number that is less than 4000. If a number is less than 4000 but greater than 2000, then by subtracting 1000 (possibly twice), you can get a number between 1000 and 2000. Thus, the only number from which no move can be made is 2000.
We will prove that no one could have obtained 2000. Note that the initial number is not divisible by 5. If we multiply it by 2 or subtract 1000 from it, the new number will again not be divisible by 5.
Thus, Alexei and Danila could have continued their game indefinitely, and no one would have lost.
Criteria:
Noted only that from numbers less than 2000 and greater than 2000, a move can always be made - 3 points. Proved only that 2000 cannot be obtained - 3 points.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. Around a round table, 15 boys and 20 girls sat down. It turned out that the number of pairs of boys sitting next to each other is one and a half times less than the number of pairs of girls sitting next to each other. Find the number of boy - girl pairs sitting next to each other.
|
Answer: 10.
Solution. Let's call a group several children of the same gender sitting in a row, with children of the opposite gender sitting to the left and right of the outermost ones. Let $X$ be the number of groups of boys, which is equal to the number of groups of girls sitting in a row. It is easy to see that the number of pairs of adjacent children in each group is one less than the number of children in that group, so the number of pairs of boys sitting next to each other is $15-X$, and the number of pairs of girls sitting next to each other is $20-X$. According to the condition, $3(15-X)=2(20-X)$, from which $X=5$. Therefore, the number of pairs of adjacent boys is 10, the number of pairs of adjacent girls is 15, and the number of mixed adjacent pairs is $15+20-(10+15)=10$.
Grading criteria. Noted that the number of pairs of adjacent children in each group is one less than the number of children in that group: 1 point. Noted that the number of pairs of boys sitting next to each other is $15-X$, and the number of pairs of girls sitting next to each other is $20-X$: 2 points. Noted that the number of groups of boys is equal to the number of groups of girls: 1 point.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. What is the maximum number of triangles with vertices at the vertices of a regular 18-gon that can be marked so that no two different sides of these triangles are parallel? The triangles can intersect and have common vertices, coinciding segments are considered parallel.
|
Answer: 5.
Solution. Estimating the number of triangles. Let's number the vertices of the 18-gon from 1 to 18 clockwise. The sides of the triangles are the sides and diagonals of the regular 18-gon. We will call a diagonal even if an even number of sides lies between its ends, and odd otherwise. The parity of a diagonal coincides with the parity of the difference in the numbers of its ends. Due to the evenness of the total number of sides of the polygon, it does not matter from which side of the diagonal to count the number of sides. We also consider the sides as odd diagonals. Two diagonals $\mathrm{AB}$ and $\mathrm{CD}$, where $\mathrm{AC}$ and $\mathrm{BD}$ do not intersect, are parallel if and only if the number of sides between A and C, and B and D, is the same, that is, the positive difference in the numbers of A and C is equal to the positive difference in the numbers of B and D. It is not difficult to notice that any odd diagonal is parallel to one of the nine sides of the 18-gon, and any even diagonal is parallel to one of the nine diagonals that cut off a triangle from the 18-gon (two sides of which are sides of the polygon). In total, there are 18 families of diagonals, any two diagonals of the same family are parallel, and any two diagonals of different families are not parallel. Nine of these families contain even diagonals and nine contain odd diagonals. As representatives of the odd families, we can take the sides with ends $1223, \ldots, 89,910$ and the diagonals $13,24, \ldots, 810,911$. Therefore, triangles with pairwise non-parallel sides, constructed on the vertices of a regular 18-gon, cannot use more than one from each of these families of diagonals, and the total number of such triangles does not exceed $18: 3=6$. Moreover, any triangle constructed on three vertices of the 18-gon can contain either three even diagonals or one even and two odd, since the sum of the parities of its three sides equals the parity of the number 18. Consequently, the total number of odd sides in any set of triangles with pairwise non-parallel sides must be even, and we will not be able to use all 18 families of diagonals for their sides. Thus, the number of triangles with pairwise non-parallel sides, constructed on the vertices of a regular 18-gon, does not exceed five.
Example. Five triangles with vertices $\{1,2,3\},\{3,4,5\},\{5,6,7\},\{7,8,9\},\{1,5,9\}$.
Grading criteria. It is shown that there are 18 pairwise non-parallel families of diagonals: 2 points. It is shown that all 9 non-parallel odd diagonals cannot be used as sides of triangles: 2 points. Example: 2 points. Justification of the example: 1 point.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.3. Find the maximum length of a horizontal segment with endpoints on the graph of the function $y=x^{3}-x$
|
Answer: 2.
Solution 1. A horizontal segment of length $a>0$ with endpoints on the graph of the function $y=x^{3}-x$ exists if and only if the equation $(x+a)^{3}-(x+a)=x^{3}-x$ has at least one solution for the given value of the parameter $a$. Expanding the brackets, combining like terms, and dividing by $a>0$, we obtain the quadratic equation $3 x^{2}+3 a x+a^{2}-1=0$, which is solvable when $D=12-3 a^{2} \geq 0$, from which $0<a \leq 2$. Therefore, the length of the desired segment does not exceed 2. When $a=2$, the solution to the equation is $x=-1$, from which it follows that the length 2 is achieved for the segment with endpoints $(-1,0)$ and $(1,0)$ on the graph of the function $y=x^{3}-x$.
## Solution 2.
As in Solution 1, we obtain the equation $3 x^{2}+3 a x+a^{2}-1=0$, which we consider as a quadratic equation in $a$ with parameter $x: a^{2}+3 x a+3 x^{2}-1=0$. We find its roots $a_{1,2}=\frac{-3 x \pm \sqrt{4-3 x^{2}}}{2}$, and since $a$ is positive, we consider only the one with the plus sign: $a=\frac{\sqrt{4-3 x^{2}}-3 x}{2}$. This function of $x$ is defined for $|x| \leq \frac{2}{\sqrt{3}}$ and is positive for $-\frac{2}{\sqrt{3}} \leq x \leq \frac{1}{\sqrt{3}}$. Its derivative, equal to
$a^{\prime}(x)=-\frac{3 x+3 \sqrt{4-3 x^{2}}}{2 \sqrt{4-3 x^{2}}}$, is zero at $x=-1$, is greater than zero to the left, and less than zero to the right. Therefore, its value is maximal at $x=-1$ and equals $a_{\max }=2$. Indeed, in this case, the segment of length 2 connects on the x-axis the two roots $x_{1}=-1$ and $x_{2}=1$ of the equation $x^{3}-x=0$.
Grading criteria. The answer 2 and an example of a segment of such length are provided: 1 point. Lack of an explicit example in the solution: minus 2 points.
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.4. From identical isosceles triangles, where the angle opposite the base is $45^{\circ}$ and the lateral side is 1, a figure was formed as shown in the diagram. Find the distance between points $A$ and $B$.
|
Answer: 2.
Solution: Let's denote the points $K, L, M$, as shown in the figure. We will construct an isosceles triangle $A K C$ equal to the original one. Connect vertex $C$ to other points as shown in the figure.
In the original triangles, the angle at the vertex is $45^{\circ}$. Therefore, the other two angles are each $62.5^{\circ}$. Then the angle $\angle C K L = 360^{\circ} - 62.5^{\circ} - 62.5^{\circ} - 45^{\circ} - 45^{\circ} - 62.5^{\circ} = 62.5^{\circ}$. Therefore, triangles $A K C$ and $K L C$ are equal by two sides and the angle between them. Similarly, it can be proven that triangles $L M C$ and $M B C$ are equal to the original ones. Then the angle $\angle A C B$ is $4 \times 45^{\circ} = 180^{\circ}$, which means points $A, C, B$ lie on the same line. Therefore,
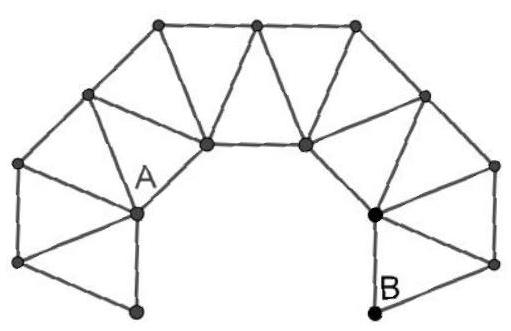
$A B = A C + C B = 2$.
## Criteria:
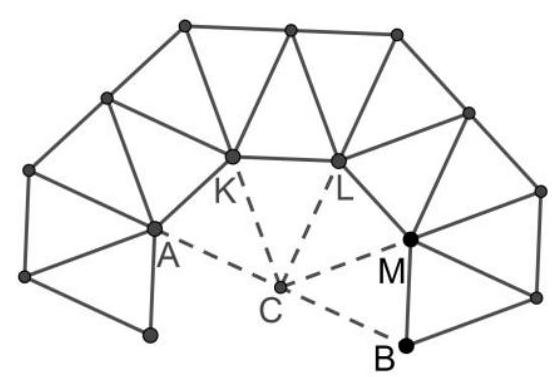
A suitable construction is made, but it is not justified that points $A, C, B$ lie on the same line (or point $C$ is the midpoint of segment $A B$, but it is not justified that the resulting triangles are equal to the original ones) - 1 point.
The solution refers to the fact that a regular octagon has a center and other obvious properties of the octagon - no more than 1 point should be deducted.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. On a plane, there are points $A, B, C, D, X$. Some segment lengths are known: $A C=2$, $A X=5$, $A D=11$, $C D=9$, $C B=10$, $D B=1$, $X B=7$. Find the length of the segment $C X$.
|
Answer: 3.
Solution: Note that $A D=11=2+9=A C+C D$. Therefore, points $A, C, D$ lie on the same line $C D$ (since the triangle inequality becomes an equality). Note that $C B=10=9+1=C D+D B$. Therefore, points $C, D, B$ lie on the same line $C D$ (since the triangle inequality becomes an equality). Therefore, all four points lie on the same line $C D$, with $C$ between $A D$ and $D$ between $C$ and $B$, i.e., in the order $A, C, D, B$. Note that $A B=A D+D B=11+1=5+7=A X+X B$. Therefore, points $A, X, B$ lie on the same line $A B$ (since the triangle inequality becomes an equality).
Thus, all points lie on the segment $A B$. Therefore, $C X=A X-A C=5-2=3$.
## Criteria:
Answer only - 0 points.
Answer with verification - 1 point.
Solution based on the assumption that all points lie on one line - no more than 3 points.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.5. In each cell of a 5 by 5 table, a letter is written such that in any row and in any column there are no more than three different letters. What is the maximum number of different letters that can be in such a table
|
Answer: 11.
Solution: If each row contains no more than two different letters, then the total number of letters does not exceed $10=5 * 2$. Further, we can assume that the first row contains exactly three different letters. If each of the remaining rows has at least one letter in common with the first, then the total number of letters does not exceed $3+4 * 2=11$. Suppose there is a row, which we can consider the second, with three different letters, distinct from the letters in the first row. Then, in each column, apart from the letters in the first and second rows, there can be no more than one new letter, totaling no more than $3+3+5 * 1=11$. An example of arranging 11 different letters: along the main diagonal of the table from the bottom left corner to the top right, the first five different letters are written, along the next lower diagonal - the next four, in the top left corner - the tenth, and in the remaining cells - the eleventh letter.
Grading criteria. The maximum of 11 is proven: 5 points. Example for 11: 2 points. Any incorrect answer and an attempt to prove it: 0 points.
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. Let $a^{2}+b^{2}=c^{2}+d^{2}=1$ and $a c+b d=0$ for some real numbers $a, b, c, d$. Find all possible values of the expression $a b+c d$.
|
Answer: 0.
Solution: Let's first assume $b \neq 0$. From the second equation, express $d=\frac{-a c}{b}$ and substitute it into the equation $c^{2}+d^{2}=1$. Eliminating the denominator, we get $c^{2}\left(a^{2}+b^{2}\right)=b^{2}$, from which, given $a^{2}+b^{2}=1$, we obtain $b= \pm c$. Substituting this into the equation $a^{2}+b^{2}=c^{2}+d^{2}$, we get $a= \pm d$. Given the equation ${ }^{a c}+b d=0$, we have either $b=c, a=-d$, or $b=-c, a=d$. In both cases, $a b+c d=0$.
If $b=0$, then from $a c+b d=0$ it follows that ${ }^{a=0}$ or ${ }^{c=0}$. The first is impossible due to $a^{2}+b^{2}=1$, so $c=0$, from which we again get $a b+c d=0$.
Grading criteria. Only the answer even with the corresponding $a, b, c, d$: 0 points. Failure to consider the case ${ }^{b=0}$ (if necessary in the solution): minus 1 point.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. Large sandglasses measure an hour, and small ones measure 11 minutes. How can you use these sandglasses to measure a minute?
|
Solution: We will run the large hourglass twice in a row and the small one eleven times in a row. A minute will be measured between the second time the large hourglass finishes (120 minutes) and the 11th time the small one finishes (121 minutes).
Criteria: Any correct example - 7 points.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. Vikentiy walked from the city to the village, and at the same time Afanasiy walked from the village to the city. Find the distance between the village and the city, given that the distance between the pedestrians was 2 km twice: first, when Vikentiy had walked half the way to the village, and then, when Afanasiy had walked a third of the way to the city.
|
Answer: 6 km.
Solution. Let the distance between the village and the city be denoted as $S$ km, the speeds of Vikentiy and Afanasy as $x$ and $y$, and calculate the time spent by the travelers in the first and second cases. In the first case, we get: $\frac{S / 2}{x}=\frac{S / 2-2}{y}$, in the second case $\frac{2 S / 3+2}{x}=\frac{S / 3}{y}$. From here, eliminating $x$ and $y$, we have $S^{2}-2 S-24=0$, from which $S=6$ km.
Instructions. Answer with verification: 1 point. Formulation of equations: 3 points.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. From two cities, the distance between which is 105 km, two pedestrians set out simultaneously towards each other at constant speeds and met after 7.5 hours. Determine the speed of each of them, knowing that if the first walked 1.5 times faster, and the second 2 times slower, they would have met after $8 \frac{1}{13}$ hours.
|
Answer: 6 and 8 km per hour.
Solution: Let their speeds be $x$ and $y$ km per hour, respectively. From the condition, we get: $\frac{15}{2}(x+y)=105, \frac{105}{13}\left(\frac{3}{2} x+\frac{1}{2} y\right)=105$, from which $x=6, y=8$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.3. Two circles intersect at points A and B. A tangent to the first circle is drawn through point A, intersecting the second circle at point C. A tangent to the second circle is drawn through point B, intersecting the first circle at point D. Find the angle between the lines $\mathrm{AD}$ and $\mathrm{BC}$.
|
Answer. The lines are parallel, the angle is $0^{\circ}$.
Solution. Mark point $\mathrm{P}$ on the extension of $\mathrm{CA}$ beyond point A and point M on the extension of DB beyond point B. The inscribed angle ABD in the first circle, which subtends the chord AD, is equal to the angle PAD between the chord AD and the tangent AC to the first circle. The inscribed angle CAB in the second circle, which subtends the chord BC, is equal to the angle CBM between the chord BC and the tangent BD to the second circle. Then, the angle BAD between the secant line AB and the line AD is equal to the difference of $180^{\circ}$ and the sum of angles PAD and CAB, which is equal to the difference of $180^{\circ}$ and the sum of angles ABD and CBM, that is, the angle ABC between the secant line AB and the line BC. Therefore, the lines AD and BC are parallel.
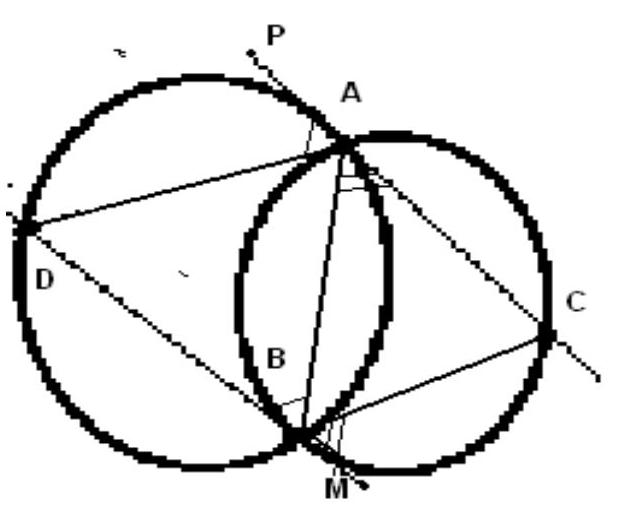
Grading criteria. Only answer: 0 points.
|
0
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. There are two ingots of different copper and tin alloys weighing 6 and 12 kg respectively. From each of them, a piece of the same weight was cut off and the first piece was alloyed with the remainder of the second ingot, and the second piece - with the remainder of the first ingot, after which the ratio of copper to tin in the two resulting new ingots turned out to be the same. Find the weight of each of the cut-off pieces.
|
Answer: 4 kilograms.
Solution: Let the weight of each of the cut pieces be $x$ kg, and the proportions of tin in the first and second ingots be $a \neq b$ respectively. Then, the proportion of tin after remelting in the first ingot will be $\frac{b x + a(6 - x)}{6}$, and in the second ingot $\frac{a x + b(12 - x)}{12}$, and they are equal according to the condition. Solving the obtained equation, we find $x = 4$ for all $a \neq b$.
Grading criteria. Correct answer with verification for arbitrary $a \neq b: 1$ point. Analysis of a specific case: 0 points.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. In the tournament, each of the six teams played against each other exactly once. In the end, the teams scored 12, 10, 9, 8, 7, and 6 points respectively. a) How many points were awarded for a win in a match, if 1 point was awarded for a draw, and 0 points for a loss? The answer, of course, should be a natural number. b) Find the number of wins, draws, and losses for each team and prove the uniqueness of these numbers. c) Provide an example of a corresponding tournament.
|
Answer. a) 4 points.
b) The first team had three wins, the second team had two wins and two draws, the third team had two wins and one draw, the fourth team had two wins, the fifth team had one win and three draws, the sixth team had one win and two draws. The rest of the matches were lost by the teams.
c) One example that meets the condition is as follows: the first team won against the fourth, fifth, and sixth teams, the second team won against the first and third teams, the third team won against the first and sixth teams, the fourth team won against the second and third teams, the fifth team won against the fourth team, and the sixth team won against the fourth team. In addition, the fifth team drew with the sixth, third, and second teams, and the sixth and second teams also drew with each other.
Solution. a) Let $n$ be the number of points awarded for a win in a match. There were a total of 15 matches played in the tournament, of which $x$ ended in a win for one of the teams, and the remaining $15-x$ ended in draws. In drawn matches, the participants collectively score 2 points, while in the others, they score $n$ points, so the total number of points scored by all teams in the tournament is $n x + 2(15-x) = (n-2)x + 30 = 12 + 10 + 9 + 8 + 7 + 6 = 52$ points, from which $(n-2)x = 22$. There were a total of 15 games, so $x$ can be 1, 2, or 11. In the first two cases, $n$ equals 24 or 13, which exceeds the maximum number of points scored by the teams, which is impossible because a win in a match would then be impossible in principle, meaning all matches would end in draws, which contradicts the assumption about $x$. In the remaining case, $x$ equals 11, then $n$ equals 4, which is the number of points awarded for a win.
b) We will find the number of wins, draws, and losses for each team. There were a total of four draws and 11 matches that ended in a win for one of the teams. Each team played five games, so it was impossible to score 6 or more points solely from draws, meaning the sixth and fifth teams each won once and drew two and three times, respectively.
If the fourth team had won no more than once, it would have had at least four draws, together with the fifth and sixth teams, there would already be at least $(2+3+4)/2 = 4.5$ draws, which exceeds the total of 4. Therefore, the fourth team won twice and lost three times.
For the same reasons, the third team had two wins and one draw, and the second team had two wins and two draws. For all teams except the first, there are at least $(2+3+1+2)/2 = 4$ draws, which equals their total number. Therefore, the first team had three wins and two losses.
c) Let's provide an example of a corresponding tournament. The fifth team drew three times, while the first and fourth teams had no draws. Therefore, the fifth team drew with the sixth, third, and second teams. In addition to these draws, the sixth and second teams each had one draw, so they drew with each other. All draws are thus uniquely determined. However, the decisive matches cannot be uniquely determined. One example that meets the condition is as follows: the first team won against the fourth, fifth, and sixth teams, the second team won against the first and third teams, the third team won against the first and sixth teams, the fourth team won against the second and third teams, the fifth team won against the fourth team, and the sixth team won against the fourth team.
Grading criteria. Correct and justified answer in part a): 3 points. Found the number of wins and draws for each team with justification: 2 points. Provided any valid example of a tournament in part c): 2 points.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.2. Three people are playing table tennis, with the player who loses a game giving way to the player who did not participate in it. In the end, it turned out that the first player played 21 games, and the second - 10. How many games did the third player play?
|
Answer: 11.
Solution: According to the problem, the first player played 21 games, so there were at least 21 games in total. Out of any two consecutive games, the second player must participate in at least one, which means there were no more than \(2 \cdot 10 + 1 = 21\) games. Therefore, a total of 21 games were played, and the first player participated in all of them. In 10 games, he played against the second player, and in the remaining 11 games, he played against the third player. An example of such a tournament: the first player plays against the second player in games with even numbers, and against the third player in games with odd numbers.
Grading Criteria: If the answer is guessed and an example of the tournament is provided: 1 point. If it is noted that out of any two consecutive games, the second player must participate in at least one: 2 points. If an example of the tournament is not provided: minus 1 point.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.5. On the board, 10 natural numbers are written, some of which may be equal, and the square of each of them divides the sum of all the others. What is the maximum number of different numbers that can be among the written ones?
|
Answer. Four
Solution. An example for four different numbers: 1,1,1,2,2,3,5,5,5,5.
Let among the listed numbers there are exactly $n \geq 2$ different ones, the maximum of which we denote by $x$, and the sum of all numbers by $\mathrm{S}$. Then the sum of all numbers except the maximum does not exceed $(9-n) x + x - 1 + x - 2 + \ldots + x - (n-1) = 9x - \frac{n(n-1)}{2}$, which is not less than $x^2$, since it is divisible by it. Therefore, the inequality $x^2 - 9x + \frac{n(n-1)}{2} \leq 0$ has solutions in natural numbers, and $\frac{9 - \sqrt{81 - 2n(n-1)}}{2} \leq x \leq \frac{9 + \sqrt{81 - 2n(n-1)}}{2}$. The positivity of the discriminant gives us $n \leq 6$, and $x \leq 8, S - x \leq 72 - 1 = 71$. Consider each case of the maximum number separately.
a) $x=8$, then $S - x \leq 71$ and is divisible by 64, so $S = 72$. Then $72 - k$ is divisible by $k^2, k \leq 7$ only for $k=1$, so in this case $n \leq 2$.
b) $x=7$, then $S - x \leq 62$ and is divisible by 49, so $S = 56$. Then $56 - k$ is divisible by $k^2, k \leq 6$ only for $k=1$, so in this case $n \leq 2$.
c) $x=6$, then $S - x \leq 53$ and is divisible by 36, so $S = 42$. Then $42 - k$ is divisible by $k^2, k \leq 5$ only for $k=1,2$, so in this case $n \leq 3$.
d) $x=5$, then $S - x \leq 44$ and is divisible by 25, so $S = 30$. Then $30 - k$ is divisible by $k^2, k \leq 4$ for $k=1,2,3$, so in this case $n \leq 4$. The desired set must contain 10 natural numbers with a sum of 30, among which there must be $1,2,3,5$. Now it is not difficult to construct an example for $n=4: 1,1,1,2,2,3,5,5,5,5$. This example is not unique.
Grading criteria. It is proven that $n \leq 4: 5$ points. Example for $n=4: 2$ points. Estimate $n \leq 6: 2$ points.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. The bathtub fills up from the hot water tap in 17 minutes, and from the cold water tap in 11 minutes. After how many minutes from opening the hot water tap should the cold water tap be opened so that by the time the bathtub is full, there is one third more hot water than cold water?
|
Answer. In 5 minutes.
Solution. Let the volume of the bathtub be $V$, then by the time it is filled, there should be $\frac{3}{7} V$ of cold water and $\frac{4}{7} V$ of hot water in it. The filling rates of cold and hot water are $\frac{V}{11}$ and $\frac{V}{17}$, respectively. Therefore, the desired time is the difference between the time to fill $\frac{4}{7} V$ of the bathtub with hot water and the time to fill $\frac{3}{7} V$ of the bathtub with cold water, that is, $\frac{4}{7} V / \frac{V}{17} - \frac{3}{7} V / \frac{V}{11} = \frac{68 - 33}{7} = 5$ minutes.
Instructions. Answer with verification: 2 points. Formulation of equations: 3 points.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.3. Find the smallest natural number $n$ such that in any set of $n$ distinct natural numbers, not exceeding 1000, it is always possible to select two numbers, the larger of which does not divide the smaller one.
|
Answer. $n=11$.
Solution. Among the first 10 powers of two $1=2^{0}, 2=2^{1}, 4=2^{2}, \ldots, 512=2^{9}$, in each pair of numbers, the larger number is divisible by the smaller one, hence $n \geq 11$.
On the other hand, let there be some set of $n \geq 11$ numbers where the larger number of each pair is divisible by the smaller one. Arrange all the numbers in ascending order; from the assumption, it follows that each subsequent number is at least twice the previous one. Therefore, the largest number is at least $2^{10}=1024$ times larger than the first, meaning it is greater than 1000 - a contradiction.
Instructions. Proving $n \geq 11$ with an example: 3 points. Proving only $n \leq 11$ (the second part): 4 points.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. Anya wrote down 100 numbers in her notebook. Then Sonya wrote down in her notebook all the pairwise products of the numbers written by Anya. Artem noticed that there were exactly 2000 negative numbers in Sonya's notebook. How many zeros did Anya initially write down in her notebook?
|
Answer: 10 zeros.
Solution: Let Anya write down $n$ positive numbers, $m$ negative numbers, and $100-n-m$ zeros in her notebook. Then, by the condition, $n m=2000$, since a negative number can only be obtained by multiplying numbers of different signs.
Let's list all the divisors of the number $2000=2^{4} * 5^{3}$:
| | $2^{0}$ | $2^{1}$ | $2^{2}$ | $2^{3}$ | $2^{4}$ |
| :--- | :--- | :--- | :--- | :--- | :--- |
| $5^{0}$ | 1 | 2 | 4 | 8 | 16 |
| $5^{1}$ | 5 | 10 | 20 | 40 | 80 |
| $5^{2}$ | 25 | 50 | 100 | 200 | 400 |
| $5^{3}$ | 125 | 250 | 500 | 1000 | 2000 |
They can be paired such that the product of each pair is 2000. Let's write them in pairs and list their sums:
| 1 | 2 | 4 | 5 | 8 | 10 | 16 | 20 | 25 | 40 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 2000 | 1000 | 500 | 400 | 250 | 200 | 125 | 100 | 80 | 50 |
| 2001 | 1002 | 504 | 405 | 258 | 210 | 141 | 120 | 105 | 90 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
Only in one of these cases is the sum less than 100, so this is the case that is realized. Thus, there are 90 non-zero numbers and 10 zeros.
Criteria: Only the answer - 0 points.
Only the answer with verification - 1 point.
Not all cases of divisors are considered - no more than 3 points.
No explanation of why there are no other divisors - deduct 1 point.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4. Arseny sat down at the computer between 4 and 5 PM, when the hour and minute hands were pointing in opposite directions, and got up from it on the same day between 10 and 11 PM, when the hands coincided. How long did Arseny sit at the computer?
|
Solution: Let's see where the hands will be 6 hours after Arseny sat down at the computer. The minute hand will go around the clock 6 times and return to its place. The hour hand will move exactly half a circle. Therefore, the angle between the hands will change by 180 degrees, i.e., the hands will coincide. It is obvious that there is exactly one moment between 22 and 23 hours when the hands coincide, so this will be the time when Arseny gets up from the computer. Thus, Arseny sat at the computer for 6 hours.
## Criteria:
Only the answer - 1 point.
If in a similar solution it is not noted that such a moment between 22 and 23 is exactly one, deduct 1 point.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.5. Several seventh-graders were solving problems. The teacher does not remember how many children there were and how many problems each of them solved. However, he remembers that, on the one hand, each solved more than a fifth of what the others solved, and on the other hand, each solved less than a third of what the others solved. How many seventh-graders could there be? Find all the options and prove that there are no others.
|
Answer: 5 seventh-graders.
Solution: Let one seventh-grader solve $a$ problems, and the rest solve $S - a$. Then
$$
\begin{gathered}
a < (S-a) / 3 \\
3a < S - a \\
4a < S \\
a < S / 4
\end{gathered}
$$
Similarly,
$$
\begin{gathered}
(S-a) / 5 < a \\
S - a < 5a \\
S < 6a \\
S / 6 < a
\end{gathered}
$$
Thus, if there are 4 or fewer students, and each solved less than a quarter of all problems, then together they solved fewer than all the problems, which is impossible. Similarly, if there are 6 or more students, and each solved more than a fifth of all problems, then together they solved more than all the problems, which is also impossible. Therefore, there must be 5 students in total.
## Criteria:
Answer - 0 points.
Solved under the assumption that each solved more than a fifth of all problems and less than a quarter of all problems - 3 points.
|
5
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Point $M$ lies on the leg $A C$ of the right triangle $A B C$ with a right angle at $C$, such that $A M=2, M C=16$. Segment $M H$ is the altitude of triangle $A M B$. Point $D$ is located on the line $M H$ such that the angle $A D B$ is $90^{\circ}$, and points $C$ and $D$ lie on the same side of the line $A B$. Find the length of segment $B L$, if $L$ is the intersection of $B D$ and $A C$, and the tangent of angle $A C H$ is 1/18. (16 points)
|
Solution. 1. A circle can be circumscribed around quadrilateral $A B C D$ with diameter $A B$ (angles $A D B$ and $A C B$ are right angles). Then $\angle A B D=\angle A C D$,
$$
\angle H A D=90^{\circ}-\angle A B D, \angle A D H=\angle A B D=\angle A C D
$$
Triangles $A C D$ and $A D M$ are similar, and $\frac{A D}{A C}=\frac{A M}{A D}=$ $\frac{M D}{D C}, A D^{2}=A C \cdot A M=2 \cdot 18=36, A D=6$.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.
Find the roots of the equation $f(x)=8$, if $4 f(3-x)-f(x)=3 x^{2}-4 x-3$ for any real value of $x$. In your answer, specify the product of the found roots. #
|
# Solution:
Notice that when $x$ is replaced by $3-x$, the expression $3-x$ changes to $x$. That is, the pair $f(x)$ and $f(3-x)$ is invariant under this substitution. Replace $x$ with $3-x$ in the equation given in the problem. We get:
$4 f(x) - f(3-x) = 3(3-x)^2 - 4(3-x) - 3 = 3x^2 - 14x + 12$. Express $f(x)$ from the system: $\left\{\begin{array}{l}4 f(3-x) - f(x) = 3x^2 - 4x - 3 \\ 4 f(x) - f(3-x) = 3x^2 - 14x + 12\end{array}\right.$. Multiply the second equation of the system by 4 and add it to the first, we get: $15 f(x) = 15x^2 - 60x + 45$; $f(x) = x^2 - 4x + 3$. Form the equation: $x^2 - 4x + 3 = 8 ; x^2 - 4x - 5 = 0$; its roots are $x_1 = -1 ; x_2 = 5$. The product of the roots is ( -5 ).
|
-5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Find all values of the parameter $a$, for each of which the solution set of the inequality $\frac{x^{2}+(a+1) x+a}{x^{2}+5 x+4} \geq 0$ is the union of three non-overlapping intervals. In your answer, specify the sum of the three smallest integer values of $a$ from the obtained interval.
|
# Solution
Let's factorize the numerator and the denominator of the left part of the inequality, it will take the form: $\frac{(x+1)(x+a)}{(x+1)(x+4)} \geq 0$. There are five possible cases for the placement of the number ($-a$) relative to the numbers (-4) and (-1). In each case, the inequality is solved using the interval method on the number line (see Fig.2). Let's list the results of the investigation: 1 )
$-a > -1 ; a < 4 \quad x \in (-\infty ; -4) \cup (-4 ; -a] \cup (-1 ; +\infty)$ - does not fit. 2 )
$-a = -1 ; a = 1 \quad x \in (-\infty ; -4) \cup (-1 ; +\infty)$ - does not fit. 3 )
$-4 < -a < -1 ; 1 < a < 4 \quad x \in (-\infty ; -4) \cup (-4 ; -a] \cup (-1 ; +\infty)$ - does not fit. 4 )
$-a = -4 ; a = 4 \quad x \in (-\infty ; -4] \cup (-1 ; +\infty)$ - does not fit. 5 )
$-a < -4 ; a > 4 \quad x \in (-\infty ; -a] \cup (-4 ; -1) \cup (-1 ; +\infty)$ - fits. Thus, the answer to the problem satisfies $a \in (1 ; +\infty)$. The smallest integers that fall within this interval are 2, 3, and 4. $2 + 3 + 4 = 9$.
Answer: 9.
|
9
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.
Calculate the number $8^{2021}$, find the sum of the digits in this number, and write down the result. Then, in the newly written number, find the sum of the digits and write down the result again. These actions were repeated until a single-digit number was obtained. Find this number.
|
# Solution.
Consider the natural powers of 8. Notice that even powers of the number 8 give a remainder of 1 when divided by 9, while odd powers (including the number \(8^{2021}\)) give a remainder of 8. Indeed, let's analyze the powers of 8:
\[
\begin{gathered}
8^{2}=(9-1)^{2}=9 n+1, n \in N \\
8^{3}=(9 n+1) \cdot 8=9 k+8, k \in N \\
8^{4}=(9 k+8) \cdot 8=9 k \cdot 8+8^{2}=9 k \cdot 8+9 n+1=9 \cdot s+1, s \in N
\end{gathered}
\]
Assuming that \(8^{2 m-1}=9 t+8, t \in N, m \in N, m \geq 2\), we get:
\[
\begin{aligned}
& 8^{2 m}=8^{2 m-1} \cdot 8=(9 t+8) \cdot 8=9 t \cdot 8+8^{2}=9 t \cdot 8+9 n+1=9 q+1, q \\
& \quad \in N
\end{aligned}
\]
\[
8^{2 m+1}=8^{2 m} \cdot 8=(9 q+1) \cdot 8=9 q \cdot 8+8
\]
Since an integer when divided by 9 gives the same remainder as the sum of its digits, the sum of the digits of the number \(8^{2021}\) and the sum of the digits of subsequent summation results, when divided by 9, have the same remainder of 8.
Answer. 8.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Solve the equation $8 \sin ^{4}(\pi x)-\sin ^{2} x=\cos ^{2} x-\cos (4 \pi x)$. In your answer, specify the sum of the roots that belong to the interval $[-1 ; 2]$.
(5 points)
|
Solution. Considering the basic trigonometric identity, we get
$8 \sin ^{4}(\pi x)-1+\cos (4 \pi x)=0 \quad \Rightarrow \quad 8 \sin ^{4}(\pi x)-2 \sin ^{2}(2 \pi x)=0 \quad \Rightarrow$
$\left(2 \sin ^{2}(\pi x)-2 \sin (\pi x) \cos (\pi x)\right)\left(2 \sin ^{2}(\pi x)+2 \sin (\pi x) \cos (\pi x)\right)=0 \Rightarrow$
$\sin ^{2}(\pi x)\left(\sin ^{2}(\pi x)-\cos ^{2}(\pi x)\right)=0 \Rightarrow \sin ^{2}(\pi x)(\cos (2 \pi x))=0$.
Therefore, $\left[\begin{array}{l}\sin (\pi x)=0, \\ \cos (2 \pi x)=0,\end{array} \Rightarrow\left[\begin{array}{l}\pi x=\pi k, k \in Z, \\ 2 \pi x=\frac{\pi}{2}+\pi n, n \in Z,\end{array} \Rightarrow\left[\begin{array}{l}x=k, k \in Z, \\ x=\frac{1}{4}+\frac{n}{2}, n \in Z,\end{array}\right.\right.\right.$ then the roots of the equation belonging to the interval $[-1 ; 2]$, will be $-1,1,2,-0.75,-0.25,0.25,0.75,1.25,1.75$. Their sum is 5.
Answer: 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. What is the smallest area that a right triangle can have, if its hypotenuse lies on the tangent to the graph of the function $y=\sqrt{x-3}$, one of its legs lies on the $y$-axis, and one of its vertices coincides with the point of tangency
|
Solution. $\quad f(x)=\sqrt{x-3}, \quad f^{\prime}\left(x_{0}\right)=\frac{1}{2 \sqrt{x-3}}$
$$
\begin{aligned}
& S_{A B C}=\frac{1}{2} A B \cdot B C, x_{0}-\text { abscissa of the point of tangency } A, \\
& A\left(x_{0}, f\left(x_{0}\right)\right), \quad B\left(0, f\left(x_{0}\right)\right), \quad C \quad \text { - intersection point }
\end{aligned}
$$
with the y-axis. Let $C(0, c)$. The equation of the tangent line to the graph of the function $f(x)=\sqrt{x-3}$ is $y=f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)+f\left(x_{0}\right)$. Point $C$ lies on the tangent line, so we substitute its coordinates into the equation of the tangent line: $c=-f^{\prime}\left(x_{0}\right) x_{0}+f\left(x_{0}\right)$.
Then $A B=x_{0}, \quad B C=f\left(x_{0}\right)-c=f^{\prime}\left(x_{0}\right) x_{0}, \quad S_{A B C}=\frac{1}{2} A B \cdot B C=\frac{1}{2} f^{\prime}\left(x_{0}\right)\left(x_{0}\right)^{2}=\frac{x_{0}^{2}}{2 \sqrt{x_{0}-3}}$. To find the extrema of the function $\quad S_{A B C}=S\left(x_{0}\right)=\frac{x_{0}^{2}}{4 \sqrt{x_{0}-3}}$ we find the zeros of the derivative of this function $S^{\prime}\left(x_{0}\right)=\frac{3\left(x_{0}^{2}-4 x_{0}\right)}{8 \sqrt{\left(x_{0}-3\right)^{3}}}$. Since $x_{0} \geq 3$, the only extremum point, and specifically, the point of minimum for this function is the point $\quad x_{0}=4, \quad S_{\min }=S(4)=\frac{4^{2}}{4 \sqrt{4-3}}=4$.
Answer: 4.
|
4
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. In triangle $A B C$, altitudes $A D, B E, C F$ are drawn. The length of side $A C$ is $1+\sqrt{3}$. The distances from the center of the inscribed circle in triangle $D E F$ to points $A$ and $C$ are $\sqrt{2}$ and 2, respectively. Find the length of side $A B$.
|
Solution. $\quad A D, B E, C F$ are the altitudes of triangle $A B C, D A, E B, F C$ are the angle bisectors of angles $D, E, F$ of triangle $D E F, O$ is the point of intersection of the altitudes of triangle $A B C$, which is also the center of the inscribed circle of triangle $D E F$. Thus, $A O=\sqrt{2}, C O=2$. Let $O E=x, A E=y$. Then we arrive at the system $\left\{\begin{array}{c}x^{2}+y^{2}=2, \\ (1+\sqrt{3}-y)^{2}+x^{2}=4\end{array}\right.$. Solving the system, we get $\quad y=1, x=1$. Then $\quad \angle D A C=\angle B C A=45^{\circ}$, $B C=\sqrt{6}, \angle F C A=\operatorname{arctg} \frac{1}{\sqrt{3}}=30^{\circ}$,
$\angle A B E=30^{\circ}, \quad A B=2$.
Answer: 2.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A vessel with a capacity of 10 liters is filled with air containing $24\%$ oxygen. A certain volume of air was pumped out of the vessel and the same volume of argon was added. Then, the same volume of the mixture as the first time was pumped out and again the same volume of argon was added. In the new mixture, $11.76\%$ oxygen was found. How many liters of the mixture were released each time from the vessel? Give your answer as a number without specifying the unit.
(5 points)
|
Solution. Let $x$ liters of the mixture be released each time from the vessel. Then, the first time, the amount of oxygen left in the vessel is $2.4 - 0.24x$. The percentage of oxygen in the mixture after adding argon is $(2.4 - 0.24x) \times 10$. The second time, the amount of oxygen left in the vessel is $2.4 - 0.24x - (2.4 - 0.24x) \times 0.1x$. The percentage of oxygen in the mixture after adding argon in this case is $10(2.4 - 0.24x - (2.4 - 0.24x) \times 0.1x)$. According to the condition, $10(2.4 - 0.24x - (2.4 - 0.24x) \times 0.1x) = 11.76$. Solving the equation, we arrive at the quadratic equation $x^2 - 20x + 51 = 0$, with roots $x_1 = 3$, $x_2 = 17$. The second root does not fit the condition.
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. In triangle $A B C$, the altitudes $A D, B E, C F$ are drawn. The length of side $A C$ is $\sqrt{6}+\sqrt{2}$. The distances from the center of the inscribed circle of triangle $D E F$ to points $A$ and $C$ are 2 and $2 \sqrt{2}$, respectively. Find the radius of the circumscribed circle around triangle $D E F$. (16 points)
|
Solution. $\quad A D, B E, C F$ are the altitudes of triangle $A B C, D A, E B, F C$ are the angle bisectors of angles $D, E, F$ of triangle $D E F, O$ is the point of intersection of the altitudes of triangle $A B C$, which is also the center of the inscribed circle of triangle $D E F$. Thus, $A O=2, C O=2 \sqrt{2}$. Let $O E=x, A E=y$. Then we arrive at the system $\left\{\begin{array}{c}x^{2}+y^{2}=4, \\ (\sqrt{2}+\sqrt{6}-y)^{2}+x^{2}=8 .\end{array}\right.$ Solving the system, we get $y=\sqrt{2}, x=\sqrt{2}$. Then $\quad \angle D A C=\angle B C A=45^{\circ}, \quad B C=2 \sqrt{3}$,
$\angle F C A=\operatorname{arctg} \frac{1}{\sqrt{3}}=30^{\circ}, \quad \angle A B E=30^{\circ}, \quad A B=2 \sqrt{2}$. $\angle D F E=90^{\circ}, D E=A B \cos 45^{\circ}=2 . \quad R_{o n .}=D E / 2=1$.
## Answer: 1.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Given 2019 indistinguishable coins. All coins have the same weight, except for one, which is lighter. What is the minimum number of weighings required to guarantee finding the lighter coin using a balance scale without weights?
|
Solution. $\quad$ We will prove the following statement by induction on $k$: if there are $N$ visually identical coins, with $3^{k-1}<N \leq 3^{k}$, and one of them is lighter, then it can be found in $k$ weighings. Base case: $k=0, N=1$, no weighing is needed for a single coin. Inductive step: suppose the statement is true for $0,1,2, \ldots, k$. Now let $3^{k}<N \leq 3^{k+1}$. Place no less than $N / 3$ coins, but no more than $3^{k}$ coins, on the left pan, and the same number on the right pan. If the left pan is lighter, then the lighter coin is on it; if the right pan is lighter, then the lighter coin is on it; if the scales are balanced, then the lighter coin is among the remaining coins, the number of which is less than or equal to $N / 3 \leq 3^{k}$. As a result, we need to find the lighter coin among no more than $3^{k}$ coins, and it will take no more than $k$ additional weighings. Since $3^{6}<2019 \leq 3^{7}$, the number of weighings $k$ is 7.
Answer: 7.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (15 points) In a convex quadrilateral $A B C D, A B=10, C D=15$. Diagonals $A C$ and $B D$ intersect at point $O, A C=20$, triangles $A O D$ and $B O C$ have equal areas. Find $A O$.
#
|
# Solution:
From the equality of the areas of triangles $A O D$ and $B O C$ and the equality of angles $\angle A O D=\angle B O C$, it follows that $\frac{A O \cdot O D}{B O \cdot O C}=1$ (by the theorem on the ratio of areas of triangles with one equal angle). From this, we get $\frac{A O}{O C}=\frac{B O}{O D}$. Additionally, $\angle A O B=\angle D O C$ as vertical angles. Therefore, triangles $A O B$ and $C O D$ are similar. $\frac{A B}{B C}=\frac{A O}{O C}=\frac{2}{3}$, which means $A O=8$.
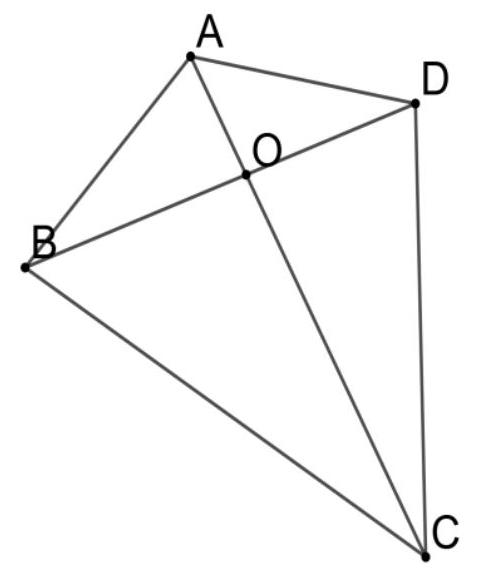
Answer: 8.
Criteria:
| Points | Conditions for awarding |
| :---: | :--- |
| 15 points | Complete, justified solution |
| 12 points | The solution approach is correct, but a computational error has been made. |
| 10 points | Similarity of triangles $A O B$ and $C O D$ is proven, but further actions are not performed or are performed incorrectly. |
| 5 points | The theorem on the ratio of areas of triangles with one equal angle is correctly applied, but further actions are not performed or are performed incorrectly. |
| 0 points | The solution does not meet the criteria listed above |
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the largest integer \( a \) such that the expression
\[
a^{2}-15 a-(\tan x-1)(\tan x+2)(\tan x+5)(\tan x+8)
\]
is less than 35 for any value of \( x \in (-\pi / 2, \pi / 2) \).
(6 points)
|
Solution. Let's make the substitution $t=\operatorname{tg} x$. We need to determine for which values of $a$ the inequality $a^{2}-15 a-(t-1)(t+2)(t+5)(t+8)a^{2}-15 a-35,\left(t^{2}+7 t-8\right)\left(t^{2}+7 t+10\right)>a^{2}-15 a-35$
$z=t^{2}+7 t+1,(z-9)(z+9)>a^{2}-15 a-35, z^{2}>a^{2}-15 a+46$, $0>a^{2}-15 a+46, \sqrt{D}=\sqrt{41},(15-\sqrt{41}) / 2<a<(15-\sqrt{41}) / 2, \Rightarrow a=10$.
Answer: 10.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. On the plane $x O y$, the lines $y=3 x-3$ and $x=-1$ intersect at point $\mathrm{B}$, and the line passing through point $M(1 ; 2)$ intersects the given lines at points A and C respectively. For what positive value of the abscissa of point A will the area of triangle $\mathrm{ABC}$ be the smallest?
(12 points)
|
# Solution.
$A C: \quad y=k x+d, \quad M \in A C \Rightarrow d=2-k$
$A(a ; 3 a-3) \in A C \Rightarrow 3 a-3=k a+2-k \Rightarrow a=\frac{5-k}{3-k}$,
$C(-1 ; c) \in A C \Rightarrow c=-2 k+2$,
$S_{A B C}=\frac{1}{2}(c+6) \cdot(a+1)=\frac{2(k-4)^{2}}{3-k}$
$S^{\prime}=\frac{2(k-4)(2-k)}{(3-k)^{2}}=0, k_{\min }=2, \quad a_{\text {min }}=3$.
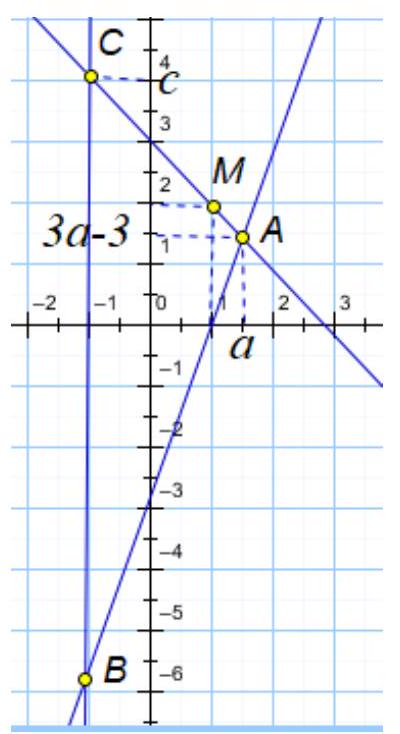
Answer: 3.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Specify the smallest integer value of \(a\) for which the system has a unique solution
\[
\left\{\begin{array}{l}
\frac{y}{a-\sqrt{x}-1}=4 \\
y=\frac{\sqrt{x}+5}{\sqrt{x}+1}
\end{array}\right.
\]
|
# Solution.
Solving the system by substitution, we arrive at an equation with constraints on the unknown quantity ${ }^{x}$.
$$
\left\{\begin{array} { l }
{ \frac { y } { a - \sqrt { x } - 1 } = 4 } \\
{ y = \frac { \sqrt { x } + 5 } { \sqrt { x } + 1 } }
\end{array} \Rightarrow \left\{\begin{array} { l }
{ x \geq 0 } \\
{ \sqrt { x } \neq a - 1 } \\
{ \frac { \sqrt { x } + 5 } { \sqrt { x } + 1 } = 4 ( a - \sqrt { x } - 1 ) }
\end{array} \Rightarrow \left\{\begin{array}{l}
x \geq 0 \\
\sqrt{x} \neq a-1 \\
\sqrt{x}+5=4(a-\sqrt{x}-1)(\sqrt{x}+1)
\end{array}\right.\right.\right.
$$
First, let's check for which values of the parameter the case $\sqrt{x}=a-1$ is possible. $4(a-1)^{2}+(9-4 a)(a-1)+(9-4 a)=0 \Rightarrow 4(a-1)^{2}+9 a-4 a^{2}=0 \Rightarrow a=-4$.
For this value of the parameter, we get a root equal to a negative number, which is impossible.
We solve the quadratic equation $4 x+(9-4 a) \sqrt{x}+(9-4 a)=0$.
$D=(4 a-9)(4 a+7) \Rightarrow \sqrt{x}_{1,2}=\frac{4 a-9 \pm \sqrt{(4 a-9)(4 a+7)}}{8}$.
The only non-negative solution will be under the conditions
$$
\left[\begin{array}{l}
\left\{\begin{array}{l}
(4 a-9)(4 a+7)=0 \\
\frac{4 a-9}{8} \geq 0
\end{array}\right. \\
\left\{\begin{array} { l }
{ a \in ( - \infty , - 7 / 4 ) \cup ( 9 / 4 , + \infty ) } \\
{ [ \begin{array} { l }
{ \frac { 9 - 4 a } { 4 } < 0 }
\end{array} } \\
{ \{ \begin{array} { l }
{ x _ { 1 } x _ { 2 } = \frac { 9 - 4 a } { 4 } = 0 } \\
{ x _ { 1 } + x _ { 2 } = \frac { 4 a - 9 } { 4 } < 0 }
\end{array} }
\end{array} \Rightarrow \left[\begin{array}{l}
a=9 / 4 \\
a \in(9 / 4,+\infty)
\end{array}\right.\right.
\end{array}\right.
$$
Choosing the smallest integer value of the parameter, we get $a=3$.
## Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find all pairs of integers $(x, y)$ that satisfy the equation $x^{2}-x y-6 y^{2}-11=0$. For each pair $(x, y)$ found, calculate the product $x y$. In the answer, write the sum of these products.
|
Solution. $x^{2}-x y-6 y^{2}-11=0,(x-3 y)(x+2 y)=11$. Since $x$ and $y$ are integers, we have four cases:
$\left\{\begin{array}{c}x-3 y=11 \\ x+2 y=1\end{array} \Leftrightarrow\left\{\begin{array}{c}y=-2 \\ x=5\end{array}\right.\right.$
2)
$\left\{\begin{array}{c}x-3 y=-11 \\ x+2 y=-1,\end{array} \Leftrightarrow\left\{\begin{array}{c}y=2 \\ x=-5\end{array}\right.\right.$
$\left\{\begin{array}{c}x-3 y=1, \\ x+2 y=11,\end{array} \Leftrightarrow\left\{\begin{array}{l}y=2 \\ x=7\end{array}\right.\right.$
$\left\{\begin{array}{c}x-3 y=-1 \\ x+2 y=-11\end{array} \Leftrightarrow\left\{\begin{array}{l}y=-2 \\ x=-7\end{array}\right.\right.$
Answer: 8.
$$
\begin{aligned}
& \text { 3. Let } \\
& g(x)=\frac{2}{x^{2}-8 x+17} . \text { Find all possible } \\
& a^{2}+6 a+\frac{727}{145} \leq g\left(g^{4}(x)\right) \leq 10 a^{2}+29 a+2
\end{aligned}
$$
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Find all integer values of the parameter \(a\) for which the system has at least one solution
\[
\left\{\begin{array}{l}
y-2=x(x+2) \\
x^{2}+a^{2}+2 x=y(2 a-y)
\end{array}\right.
\]
In the answer, specify the sum of the found values of the parameter \(a\).
|
Solution. Transform the system
$$
\left\{\begin{array} { l }
{ y - 1 = ( x + 1 ) ^ { 2 } , } \\
{ ( x + 1 ) ^ { 2 } + ( y - a ) ^ { 2 } = 1 }
\end{array} \Rightarrow \left\{\begin{array}{l}
y-1=(x+1)^{2} \\
y-2+(y-a)^{2}=0
\end{array}\right.\right.
$$
Consider the second equation of the system
$$
y^{2}-y(2 a-1)+a^{2}-2=0, \quad D=(2 a-1)^{2}-4\left(a^{2}-2\right)=9-4 a
$$
For the existence of a solution, the following conditions must be satisfied
$$
\left\{\begin{array} { l }
{ D = 9 - 4 a \geq 0 } \\
{ [ \begin{array} { l }
{ f ( 1 ) = a ^ { 2 } - 2 a > 0 } \\
{ \frac { 2 a - 1 } { 2 } > 1 } \\
{ f ( 1 ) = a ^ { 2 } - 2 a \leq 0 }
\end{array} }
\end{array} \Rightarrow \left\{\begin{array}{l}
a \leq 9 / 4 \\
{\left[\begin{array}{l}
\left\{\begin{array}{l}
a-2)>0 \\
2 a-1>2
\end{array}\right. \\
a(a-2) \leq 0
\end{array}\right.}
\end{array} \Rightarrow a \in[0,9 / 4]\right.\right.
$$
Summing the integer values of the parameter, we get $0+1+2=3$.
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. During the shooting practice, each soldier fired 10 times. One of them completed the task successfully and scored 90 points. How many times did he score 9 points, if there were 4 tens, and the results of the hits were sevens, eights, and nines. There were no misses at all.
|
Solution: Since the soldier scored 90 points and 40 of them were scored in 4 attempts, he scored 50 points with the remaining 6 shots. Since the soldier only hit the seven, eight, and nine, let's assume that in three shots (once each in seven, eight, and nine), he scored 24 points. Then, for the remaining three shots, he scored 26 points, which is only possible with the unique combination of numbers $7,8,9: 8+9+9=26$. Therefore, the shooter hit the seven once, the eight twice, and the nine three times.
Answer: 3.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Ivan Ivanovich approached a source with two empty cans, one with a capacity of 10 liters, and the other - 8 liters. Water from the source flowed in two streams - one stronger, the other weaker. Ivan Ivanovich simultaneously placed the cans under the streams and, when half of the smaller can was filled, he switched the cans. To Ivan Ivanovich's surprise, the cans filled up simultaneously. How many times more water does the stronger stream provide compared to the weaker one?
|
Solution. Let $x$ liters of water fill the larger can while 4 liters fill the smaller can. After the switch, $(10-x)$ liters fill the larger can, and 4 liters fill the smaller can again. Since the flow rates are constant, the ratio of the volumes of water filled in the same time is also constant. We can set up the equation: $\frac{4}{x}=\frac{10-x}{4} ; x^{2}-10 x+16=0$, which has two roots $x_{1}=2, x_{2}=8$. The two roots of the equation correspond to two possibilities: placing the smaller can under the stronger or the weaker stream first. However, in both cases, the answer is the same: one stream provides twice as much water as the other.
Answer. 2.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find all values of $n, n \in N$, for which the sum of the first terms of the sequence $a_{k}=3 k^{2}-3 k+1, \quad k \in N, \quad$ is equal to the sum of the first $n$ terms of the sequence $b_{k}=2 k+89, k \in N$ (12 points)
|
Solution. Note that $a_{k}=3 k^{2}-3 k+1=k^{3}-(k-1)^{3}$, and the sum is $S_{n}=n^{3}$.
For the second sequence $\quad b_{k}=2 k+89=(k+45)^{2}-(k+44)^{2}, \quad$ the sum is $S_{n}=(n+45)^{2}-45^{2}=n(n+90)$.
We get the equation $n^{3}=n(n+90) \Rightarrow n^{2}-n-90=0 \Rightarrow n=10$.
Answer: 10.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 6. (Option 2).
Translate the text above into English, preserving the original text's line breaks and formatting, and output the translation result directly.
|
Solution: A total of $68+59+46=173$ "yes" answers were given to the three questions. Note that since each resident of Kashino lives in exactly one district, if every resident were a knight (i.e., told the truth only), the number of "yes" answers would be equal to the number of residents in the city (a knight says "yes" only once when the question is about the district where they live). However, if every resident were a liar, the number of "yes" answers would be exactly twice the number of residents in the city (since each liar resident says "yes" exactly twice, when the question is about the districts where they do not live). Therefore, the number of liars in Kashino is the difference between the number of "yes" answers and the number of residents in the state, i.e., 173-120=53. After Doctor Aibolit visited the Mankino district, all residents of the district started telling the truth, so if they previously answered "yes" to the question "Do you live in Ovsyanikino?", they would now answer "no". Therefore, the number of liars in the Mankino district is the difference between the number of "yes" answers in the first and second surveys (i.e., 59-34=25). Similarly, the number of liars in Grechkin is $59-43=16$. Therefore, the total number of liars in the Mankino and Grechkin districts is $25+16=41$. Since there are 53 liars in total in the city, 53-41=12 liars live in the Ovsyanikino district. Answer: 12 liars
## Criteria for checking tasks
|
12
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
1. $x_{1}^{2}+x_{2}^{2}=\left(x_{1}+x_{2}\right)^{2}-2 x_{1} x_{2}$, but according to Vieta's theorem $\left\{\begin{array}{l}D \geq 0 \\ x_{1}+x_{2}=-(m+1) . \text { Then, } \mathrm{c} \\ x_{1} x_{2}=2 m-2\end{array}\right.$
considering that $D=(m+3)^{2} \geq 0$, we have $x_{1}^{2}+x_{2}^{2}=$
$(-(m+1))^{2}-2(2 m-2)=m^{2}+2 m+1-4(m-1)=m^{2}-2 m+5=(m-1)^{2}+4$
From which $y=(m-1)^{2}+4$ and $y_{\text {min }}=4$ when $m=1$.
|
Answer: For the equation $x^{2}+(m+1) x+2 m-2=0$, the smallest sum of the squares of its roots is 4 when $m=1$.
Grading criteria.
| 15 points | Correct and justified solution. |
| :--- | :--- |
| 10 points | Using Vieta's theorem, the expression for the sum of the squares of the roots is correctly written, but there is an error in the transformation of the expression. |
| 5 points | Vieta's theorem (considering D) is correctly written. |
| 0 points | Other solutions that do not meet the above criteria. |
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (10 points) Solve the equation
$$
\sqrt{7-x^{2}+6 x}+\sqrt{6 x-x^{2}}=7+\sqrt{x(3-x)}
$$
|
# Solution:
The domain of the variable x in our problem is the interval [0;3]. By completing the square in the expressions under the square roots on the left side of the equation or by plotting the graphs, we notice that the values of the first root do not exceed 4, and the second does not exceed 3, with the minimum values being reached at $\mathrm{x}=3$. The value of the left side of the equation does not exceed 7, while the right side is no less than 7. Therefore, equality is possible only when both sides of the equation are simultaneously equal to 7, which is achieved at $x=3$.
Answer: 3
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the value of the expression $2 a-\left(\frac{2 a-3}{a+1}-\frac{a+1}{2-2 a}-\frac{a^{2}+3}{2 a^{2-2}}\right) \cdot \frac{a^{3}+1}{a^{2}-a}+\frac{2}{a}$ when $a=1580$.
|
Solution:
1) $2 a-\frac{2(a-1)(2 a-3)+(a+1)(a+1)-\left(a^{2}+3\right)}{2(a-1)(a+1)} \cdot \frac{(a+1)\left(a^{2}-a+1\right)}{a^{2}-a}+\frac{2}{a}$
2) $2 a-\frac{2(a-1)(2 a-3)+(a+1)(a+1)-\left(a^{2}+3\right)}{2(a-1)} \cdot \frac{\left(a^{2}-a+1\right)}{a^{2}-a}+\frac{2}{a}$
3) $2 a-\frac{\left(-4 a+2+2 a^{2}\right)}{(a-1)} \cdot \frac{\left(a^{2}-a+1\right)}{a \cdot(a-1)}+\frac{2}{a}$
4) $2 a-\frac{2(a-1)^{2}}{(a-1)} \cdot \frac{\left(a^{2}-a+1\right)}{a \cdot(a-1)}+\frac{2}{a}$
5) $2 a-\frac{2 a^{2}-2 a+2}{a}+\frac{2}{a}$
6) $\frac{2 a^{2}-2 a^{2}+2 a-2+2}{a}=\frac{2 a}{a}$
We get the answer to the problem: $\frac{2 a}{a}=2$
Answer: 2
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In a convex quadrilateral $A B C D$, the angles at vertices $B, C$, and $D$ are $30^{\circ}, 90^{\circ}$, and $120^{\circ}$ respectively. Find the length of segment $A B$, if $A D=C D=2$.
|
Solution:
Extend lines $A B$ and $C D$ to intersect at point $E$, the resulting triangle $A D E$ is equilateral, so $E D=E A=2$, the leg $E C=E D+D C=2+2=4$, since it lies in the right triangle $B C E$ opposite the angle $30^{\circ}$, then the hypotenuse $B E=8$, and the segment $A B=B E-E A=8-2=6$.
Answer: 6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. In an acute-angled triangle $ABC$ with sides $AB=4, AC=3$, a point $N$ is marked on the median $AM$ such that $\angle BNM = \angle MAC$. Find the length of the segment $BN$.
|
Solution:
Let's make an additional construction, doubling the median $A M$ beyond point $M$, thereby obtaining point $K$ such that $K \in A M, K M=A M$. Triangles $K M B$
Preliminary (correspondence) online stage of the "Step into the Future" School Students' Olympiad in the subject of Mathematics
and $A M C$ are equal by two sides and the angle between them, hence the corresponding sides and angles are equal: $B K=A C=3, \quad \angle M K B=\angle M A C$. Then we get that triangle $K B N$ is isosceles $\angle B N M=\angle B K N$ and $B N=B K=3$.
Answer: 3.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. Solve the equation $a^{2}+2=b$ !, given that a, b belong to N. In the answer, indicate the sum of the product of all possible a and the product of all possible b (if the equation has no solutions, indicate 0; if there are infinitely many solutions, indicate 1000).
|
Solution:
$b!-2=a^{2} ; x, y \in N$
$a \geq 1$, i.e. $a^{2} \geq 1 \Rightarrow b!\geq 3$, i.e. $b \geq 3$
If $x \geq 5$, then $x!$ ends in 0, then $y^{2}$ ends in 8, but there is no number whose square ends in 8, i.e. $x<5$.
This gives us:
$\left[\begin{array}{l}b=3 \\ b=4\end{array} \Rightarrow\left[\begin{array}{c}a^{2}=4 \\ a^{2}=22\end{array} \Rightarrow\left[\begin{array}{c}a=2 \\ a=-2, \notin N \\ a= \pm \sqrt{22, \notin N}\end{array}\right.\right.\right.$, i.e. $b=3, a=2$.
We get the answer to the problem: $a+b=2+3=5$
Answer: 5
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (20 points) For what values of the parameter $a$ does the equation
$$
(a+1)(|x-2.3|-1)^{2}-2(a-3)(|x-2.3|-1)+a-1=0
$$
have exactly two distinct solutions?
|
Solution. Let $|x-2.3|-1=t$ (1), then the original equation will take the form: $(a+1) t^{2}-2(a-3) t+a-1=0$ (2). Let's analyze equation (1): when $t>-1$, it corresponds to two different values of x. Thus, the original equation can have from zero to four solutions. It has two distinct roots in the following three cases for equation (2):
1) the linear case, if the only root is greater than $(-1)$;
2) $D=0 ; t_{b}>-1$;
3) equation (2) has two distinct roots, one of which is greater than (-1), and the other is less than (-1).
The case where one root is greater than (-1) and the other is equal to (-1) does not suit us, as in this case there will be three solutions. Let's investigate the above cases. 1) $a=-1 ; 8 t-2=0 ; t=\frac{1}{4}>-1$ therefore, this value of the parameter is included in the answer.
2) $\frac{D}{4}=(a-3)^{2}-(a+1)(a-1)=10-6 a=0 ; \quad a=\frac{5}{3}$. The only root $-t_{b}=\frac{a-3}{a+1}$; $t_{6}\left(\frac{5}{3}\right)=\frac{\frac{5}{3}-3}{\frac{5}{3}+1}=-\frac{1}{2}>-1, a=\frac{5}{3}$ is included in the answer.
3) The general case - the roots are on different sides of (-1) - is described by the inequality $(a+1) f(-1) the correct answer is insufficiently justified. | 15 |
| The substitution of the variable is made and the correct restrictions for the new variable are defined. Attempts are made to write down some restrictions for the coefficients in connection with the conditions for the new variable, but they are only partially correct. | 10 |
| The substitution of the variable is made, the problem is reduced to the study of a quadratic trinomial with a parameter, but the reasoning is limited to considering the discriminant. | 5 |
| The solution does not correspond to any of the criteria listed above. | 0 |
| Maximum score | 20 |
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (20 points) Given a cyclic quadrilateral $A B C D$. The rays $A B$ and $D C$ intersect at point $E$, and the rays $D A$ and $C B$ intersect at point $F$. The ray $B A$ intersects the circumcircle of triangle $D E F$ at point $L$, and the ray $B C$ intersects the same circle at point $K$. The length of segment $L K$ is $5$, and $\angle E B C=15^{0}$. Find the radius of the circumcircle of triangle $E F K$.
#
|
# Solution.

$\angle F L E = \angle F D E = \angle F K E = \alpha$, since these angles subtend the arc $F E$.
$\angle E B K = \angle F D E = \alpha$, since quadrilateral $A B C D$ is cyclic.
$\triangle B L F$ is isosceles, as $\angle F L B = \angle F B L = \angle E B K = \alpha$.
Then $\angle B F L = 180 - 2 \alpha \Rightarrow \sin \angle B F L = \sin 2 \alpha = \sin 30^{\circ} = \frac{1}{2} . \quad 2 R = \frac{L K}{\sin \angle L F K} = 10 \Rightarrow R = 5$.
Answer: 5.
| Criterion | Points |
| :--- | :---: |
| The correct answer is obtained with justification. | 20 |
| It is proven that $\triangle B L F$ is isosceles. | 15 |
| It is proven that $\angle E B K = \angle F D E = \alpha$. | 10 |
| It is proven that $\angle F L E = \angle F D E = \angle F K E = \alpha$. | 5 |
| The solution does not meet any of the criteria listed above. | 0 |
| Maximum score | 20 |
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (20 points) A circle passes through the vertices $A$ and $C$ of an isosceles triangle $ABC (AB = BC)$ and intersects the sides $AB$ and $BC$ at points $M$ and $N$, respectively. $MK$, a chord of this circle, equal in length to $2 \sqrt{5}$, contains point $H$, which lies on $AC$ and is the foot of the altitude of triangle $ABC$. The line passing through point $C$ and perpendicular to $BC$ intersects the line $MN$ at point $L$. Find the radius of the circumcircle of triangle $MKL$, if $\cos \angle ABK = \frac{2}{3}$.
|
# Solution.
Quadrilateral $A M N C$ is an isosceles trapezoid. $\triangle A M H = \Delta H N C$ - by two sides and the angle between them.
$$
\begin{gathered}
\angle A H M = \angle H M N = \angle M N H = \angle N H C = \angle C H K = 180^{\circ} - \angle N C K \\
\angle M A C = \angle A C N = \angle N C A
\end{gathered}
$$
$$
\angle K H B = \angle K H C + 90^{\circ} = 180^{\circ} - \angle N C K + 90^{\circ} = \angle K C L,
$$
$\angle A M K = \angle A C K = \angle H N C$ - as angles of equal triangles and as angles subtending the same arc. Therefore, $\triangle H N C$ is similar to $\triangle H C K$ and $\triangle B H C$ is similar to $\triangle N L C$ by two angles. $\frac{K C}{K H} = \frac{N C}{C H} = \frac{L C}{H B}$ and considering that $\angle K H B = \angle K C L$, we get the similarity of $\triangle K C L$ and $\triangle B H K$ $\Rightarrow \angle C L K = \angle H B K \Rightarrow \angle M B K = \angle M L K$, which means points $K, M, B, L$ lie on the same circle and $R = \frac{M K}{2 \sin \angle A B K} = \frac{2 \sqrt{5}}{2 \sqrt{5} / 3} = 3$.
Answer: 3.
| Criterion | Points |
| :--- | :---: |
| The problem is solved correctly. | 20 |
| It is proven that points $K, M, B, L$ lie on the same circle. | 17 |
| It is proven that $\triangle K C L$ is similar to $\triangle B H K$. | 15 |
| It is proven that $\triangle B H C$ is similar to $\triangle N L C$. | 12 |
| It is proven that $\triangle A M H = \Delta H N C$ or $\triangle H N C$ is similar to $\triangle H C K$. | 5 |
| The solution does not meet any of the criteria listed above. | 0 |
| Maximum score | 20 |
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the minimum value of the expression $\frac{3 f(1)+6 f(0)-f(-1)}{f(0)-f(-2)}$, if $f(x)=a x^{2}+b x+c$ is an arbitrary quadratic function satisfying the condition $b>2 a$ and taking non-negative values for all real $x$.
(12 points)
|
Solution. We have $f(1)=a+b+c, \quad f(0)=c, \quad f(-1)=a-b+c, f(-2)=4 a-2 b+c$, $\frac{3 f(1)+6 f(0)-f(-1)}{f(0)-f(-2)}=\frac{3(a+b+c)+6 c-a+b-c}{c-4 a+2 b-c}=\frac{2 a+4 b+8 c}{2 b-4 a}=\frac{a+2 b+4 c}{b-2 a}$.
Since $f(x)=a x^{2}+b x+c \quad-$ is an arbitrary quadratic function that takes non-negative values for all real $x$, then $a>0, \quad D=b^{2}-4 a c \leq 0 \Rightarrow c \geq b^{2} / 4 a$.
Then $\quad \frac{a+2 b+4 c}{b-2 a} \geq \frac{a+2 b+b^{2} / a}{b-2 a}=\frac{a\left(1+2 b / a+b^{2} / a^{2}\right)}{a(b / a-2)}=\frac{t^{2}+2 t+1}{t-2}=\frac{(t+1)^{2}}{t-2}, \quad$ where $\quad t=b / a, \quad t>2$. Consider the function $g(t)=\frac{(t+1)^{2}}{t-2}$ and find its minimum value for $t>2$. $g^{\prime}(t)=\frac{2(t+1)(t-2)-(t+1)^{2}}{(t-2)^{2}}=\frac{(t+1)(2(t-2)-(t+1))}{(t-2)^{2}}=\frac{(t+1)(t-5)}{(t-2)^{2}}$, at $t=5$ the derivative $g^{\prime}(t)$ is 0 and, passing through this point, changes sign from "minus" to "plus", therefore, $t_{\min }=5, \quad g_{\min }=g(5)=12$.
Answer: 12.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In triangle $A B C$, the bisector $A D$ is drawn. It is known that the centers of the inscribed circle of triangle $A B D$ and the circumscribed circle of triangle $A B C$ coincide. Find $C D$, if $A C=\sqrt{5}+1$. The answer should not include trigonometric function notations or their inverses.
(20 points)
|
Solution: Let $\angle A=\alpha, \quad B=\beta$. Point $O$ is the center of the inscribed circle of triangle $ABD$. $\angle BAO=\alpha / 4, \angle ABO=\beta / 2$. Since $O$ is the center of the circumscribed circle around triangle $ABC$, triangle $AOB$ is isosceles, and $\angle BAO=\angle ABO, \beta=\alpha / 2$. Triangles $AOC$ and $BOC$ are isosceles, and $\angle ACO=3 \alpha / 4, \angle BCO=\alpha / 4$. Since $\angle A+\angle B+\angle C=180^{\circ}$, then $\alpha+\alpha / 2+3 \alpha / 4+\alpha / 4=180^{\circ}$, and $\alpha=72^{\circ}$. Triangle $ABC$ is isosceles, $\angle A=\angle C=72^{\circ}, \angle B=36^{\circ}$.

$\frac{x}{y}=\frac{x+y}{x}, \quad x^{2}-x y-y^{2}=0$.
By the condition $x=\sqrt{5}+1, y=x(\sqrt{5}-1) / 2, \quad y=2$.
Answer: 2.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A workshop produces transformers of types $A$ and $B$. For one transformer of type $A$, 5 kg of transformer iron and 3 kg of wire are used, and for a transformer of type $B$, 3 kg of iron and 2 kg of wire are used. The profit from selling a transformer of type $A$ is 12 thousand rubles, and for type $B$ it is 10 thousand rubles. The shift fund of iron is 481 kg, and wire is 301 kg. How many transformers of types $A$ and $B$ should be produced per shift to maximize the profit from selling the products, if the resource consumption should not exceed the allocated shift funds? What will be the maximum profit in this case?
$(12$ points)
|
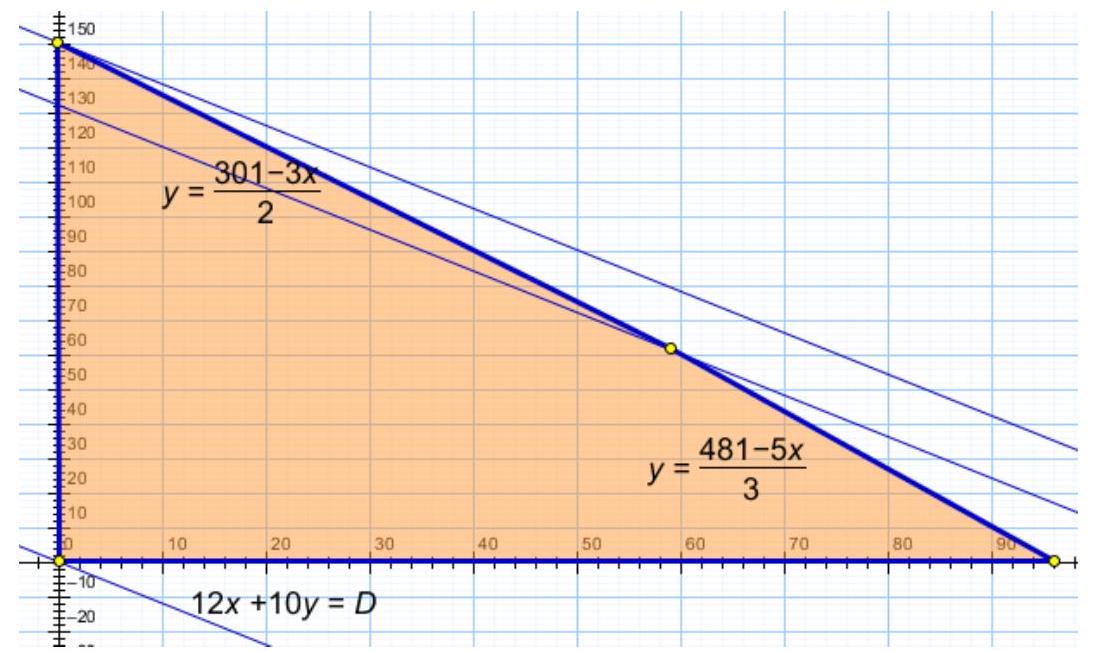
Solution. Let $x$ be the number of transformers of type $A$, and $y$ be the number of transformers of type $B$. Then the profit per shift is calculated by the formula $D=12 x+10 y$, with the conditions
$5 x+3 y \leq 481, \quad 3 x+2 y \leq 301, x$ and $y$ - non-negative integers.
$5 x+3 y \leq 481 \Leftrightarrow y \leq 160 \frac{1}{3}-\frac{5 x}{3}, \quad 3 x+2 y \leq 301 \Leftrightarrow y \leq 150.5-\frac{3 x}{2}$. The intersection point of the lines $5 x+3 y=481$ and $3 x+2 y=301$ is the point with coordinates $x=59, y=62$. In this case, $D=12 \cdot 59+10 \cdot 62=1328$, but for $x=0, y=150.5$ we have the maximum value of the function $D=12 x+10 y$ for non-negative $x$ and $y$ satisfying the inequalities $5 x+3 y \leq 481, 3 x+2 y \leq 301$. This value is 1505. Since $x$ and $y$ are integers, for $x=0, y=150$ the revenue $D=1500$, for $x=1, y \leq 150.5-1.5, y=149, D=1502$, for $x=2, y \leq 150.5-3, y=147, D<1502$.
Thus, the maximum revenue is 1502 thousand rubles, provided that one transformer of type $A$ and 149 transformers of type $B$ are produced.
Answer: 1 transformer of type $A$ and 149 transformers of type $B$, 1502 thousand rubles.
Solution. $\left(2+\sin ^{2}(x+y)+2 \sin (x+y)\right) \log _{2}\left(3^{x}+3^{-x}\right) \leq 1$,
$\left(1+(\sin (x+y)+1)^{2}\right) \log _{2}\left(3^{x}+3^{-x}\right) \leq 1$. Since $1+(\sin (x+y)+1)^{2} \geq 1$, and $3^{x}+3^{-x} \geq 2$, $\log _{2}\left(3^{x}+3^{-x}\right) \geq 1$ for any values of $x$ and $y$, then $\left(2+\sin ^{2}(x+y)+2 \sin (x+y)\right) \log _{2}\left(3^{x}+3^{-x}\right) \geq 1$, and the inequality $\left(2+\sin ^{2}(x+y)+2 \sin (x+y)\right) \log _{2}\left(3^{x}+3^{-x}\right) \leq 1$ is valid only for those $x$ and $y$ for which $\left\{\begin{array}{c}\sin (x+y)=-1, \\ 3^{x}+3^{-x}=2,\end{array}\left\{\begin{array}{c}y=-\pi / 2+2 \pi n, n \in N, \\ x=0 .\end{array}\right.\right.$
Answer: $x=0, y=-\pi / 2+2 \pi n, n \in N$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The numbers from 100 to 999 are written without spaces. What is the remainder when the resulting 2700-digit number is divided by 7?
|
Solution.
Since 1001 is divisible by 7, we get $1000 \equiv-1(\bmod 7) \Longrightarrow 1000^{n} \equiv(-1)^{n}(\bmod 7)$. Therefore, the given number is congruent modulo 7 to the number
$$
999-998+997-996+\ldots+101-100=450 \equiv 2(\bmod 7)
$$
Answer: 2
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Two balls, the sizes of which can be neglected in this problem, move along a circle. When moving in the same direction, they meet every 20 seconds, and when moving in opposite directions - every 4 seconds. It is known that when moving towards each other along the circle, the distance between the approaching balls decreases by 75 cm every 3 seconds (until they meet). Find the speed of the slower ball (in cm/sec).
|
# Solution:
Let the speed of the faster ball be $v$, and the slower one be $u$. When moving in the same direction, the faster ball catches up with the slower one when the difference in the distances they have traveled equals the length of the circle. According to the problem, we set up a system of two linear equations.
$$
\left\{\begin{array}{l}
(u+v) \cdot 4=(v-u) \cdot 20 \\
(u+v) \cdot 3=75
\end{array} . \text { From which } u=\frac{2}{3} v, v=15 \text{ cm/s }; u=10 \text{ cm/s}\right.
$$
Answer: 10.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. For what values of the parameter $\boldsymbol{a}$ does the equation $|f(x)-4|=p(x)$, where $f(x)=\left|\frac{x^{2}+3 x}{x+3}-\frac{x^{2}-4 x+4}{2-x}\right|$, $p(x)=a$ have three solutions? If there is more than one value of the parameter, indicate their product in the answer.
|
# Solution:
Simplify $f(x)=\left|\frac{x^{2}+3 x}{x+3}-\frac{x^{2}-4 x+4}{2-x}\right|$, we get $f(x)=|2 x-2|$, where $x \neq-3, x \neq 2$.
Solve the equation || $2 x-2|-4|=a$, where $x \neq-3, x \neq 2$ graphically in the system $x O a$.
The equation has three solutions when $a=2$.
The product is 2.
## Answer: 2.
## Solution for Variant #2
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Masha, Dasha, and Sasha are tasked with harvesting all the currants from the bushes on the garden plot. Masha and Dasha together can collect all the berries in 7 hours 30 minutes, Masha and Sasha - in 6 hours, and Dasha and Sasha - in 5 hours. How many hours will it take the children to collect all the berries if they work together?
|
Solution: Let the entire work be 1. Let $x$ (parts of the entire work per hour) be Masha's labor productivity, $y$ be Dasha's, and $z$ be Sasha's. Since the labor productivity adds up when working together, we can set up a system of equations based on the problem's conditions: $\left\{\begin{array}{l}(x+y) \cdot 7.5=1 \\ (x+z) \cdot 6=1 \\ (y+z) \cdot 5=1\end{array} ;\left\{\begin{array}{l}(x+y)=\frac{2}{15} \\ (x+z)=\frac{1}{6} . \\ (y+z)=\frac{1}{5}\end{array}\right.\right.$. By adding all the equations in the system, we get: $2(x+y+z)=\frac{2}{15}+\frac{1}{6}+\frac{1}{5}=\frac{15}{30}=\frac{1}{2} ; x+y+z=\frac{1}{4}$. Therefore, the three children will gather all the currants together in 4 hours.
Answer: 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On the sides $AB$ and $BC$ of triangle $ABC$, points $M$ and $N$ are marked respectively such that $\angle CMA = \angle ANC$. Segments $MC$ and $AN$ intersect at point $O$, and $ON = OM$. Find $BC$, if $AM = 5 \, \text{cm}, BM = 3 \, \text{cm}$.
|
# Solution:
Triangles $A M O$ and $C N O$ are congruent ($\angle A M O=\angle C N O, O N=O M, \angle M O A=\angle N O C$, as vertical angles). From the congruence of the triangles, it follows that $A M=N C, \angle M A O=\angle N C O$ and $O A=O C$. Therefore, triangle $A O C$ is isosceles, which means angles $C A O$ and $A C O$ are equal. Hence, triangle $A B C$ is isosceles and $A B=B C=8 \text{ cm}$.
Answer: 8 cm.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. During the shooting practice, each soldier fired 10 times. One of them completed the task successfully and scored 90 points. How many times did he score 7 points, if he hit the bullseye 4 times, and the results of the other hits were sevens, eights, and nines? There were no misses at all.
|
# Solution:
Since the soldier scored 90 points and 40 of them were scored in 4 shots, he scored 50 points with the remaining 6 shots. As the soldier only hit the 7, 8, and 9, let's assume that in three shots (once each in 7, 8, and 9), he scored 24 points. Then, for the remaining three shots, he scored 26 points, which is only possible with the unique combination of numbers $7, 8, 9$: $8+9+9=26$. Therefore, the shooter hit the 7 once.
## Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Boys are dividing the catch. The first one took $r$ fish and a seventh part of the remainder; the second - $2 r$ fish and a seventh part of the new remainder; the third - $3 r$ fish and a seventh part of the new remainder, and so on. It turned out that in this way all the caught fish were divided equally. How many boys were there?
|
# Solution:
Let $x$ be the number of boys; $y$ be the number of fish each received. Then the last boy took $x r$ fish (there could be no remainder, otherwise there would not have been an even distribution), so $y=x r$. The second-to-last boy took $(x-1) r+\frac{x r}{6}=y$; i.e., $x r$ is $\frac{6}{7}$ of the second-to-last remainder, so the last remainder is $\frac{7}{6} x r$, and its seventh part is $\frac{x r}{6}$.
Then $(x-1) r+\frac{x r}{6}=x r ; 6 r=x r ; x=6$.
Answer: 6.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. In rectangle $A B C D$, point $E$ is located on diagonal $A C$ such that $B C=E C$, point $M$ is on side $B C$ such that $E M=M C$. Find the length of segment $M C$, if $B M=5, A E=2$.
|
# Solution:

Draw $A F$ parallel to $B E$ (point $F$ lies on line $B C$), then $\angle C B E=\angle C F A$, $\angle C E B=\angle C A F$. Considering that $B C=C E$, we get that triangle $FCA$ is isosceles, hence $F C=A C$ and $F B=A E$. Triangles $F B A$ and $A E F$ are congruent, as $F B=A E, \angle A F B=$ $\angle F A E, A F$ is common. We obtain that $\angle F B A=\angle A E F=90^{\circ}$, from which $\angle F E C=90^{\circ}$. Triangle $F C E$ is right-angled and $M C=M E$, so $\mathrm{FM}=\mathrm{MC}$ and $F M=F B+B M=A E+B M=M C=7$.
Answer: 7.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Task: On an $8 \times 8$ chessboard, 64 checkers numbered from 1 to 64 are placed. 64 students take turns approaching the board and flipping only those checkers whose numbers are divisible by the ordinal number of the current student. A "Queen" is a checker that has been flipped an odd number of times. How many "Queens" will be on the board after the last student has stepped away from it?
|
Solution: It is clear that each checker is flipped as many times as the number of divisors of its number. Therefore, the number of "queens" will be the number of numbers from 1 to 64 that have an odd number of divisors, and this property is only possessed by perfect squares. That is, the numbers of the "queens" remaining on the board will be \(1, 4, 9, 16, 25, 36, 49\), and 64, which totals 8.
## Answer: 8.
#
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. One worker in two hours makes 5 more parts than the other, and accordingly spends 2 hours less to manufacture 100 parts. How much time does each worker spend on manufacturing 100 parts?
#
|
# Solution:
Let the second worker make 100 parts in $x$ hours, and the first worker in $x-2$ hours.
$\frac{100}{x-2}-\frac{100}{x}=\frac{5}{2} ; \frac{40}{x-2}-\frac{40}{x}=1 ; x^{2}-2 x-80=0, x=1+9=10$. Answer: 8 and 10 hours.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. In triangle $A B C$, angles $A$ and $B$ are $45^{\circ}$ and $30^{\circ}$ respectively, and $C M$ is the median. The incircles of triangles $A C M$ and $B C M$ touch segment $C M$ at points $D$ and $E$. Find the radius of the circumcircle of triangle $A B C$ if the length of segment $D E$ is $4(\sqrt{2}-1)$.
|
# Solution:
By the property of tangents to a circle, we have:
$$
A G=A K=x, C G=C D=y, C E=C F=z, B F=B H=u, D M=\frac{A B}{2}-A K=\frac{A B}{2}-x
$$
$M E=\frac{A B}{2}-B H=\frac{A B}{2}-u$,
Then $D E=z-y, D E=D M-M E=u-x$. Therefore, $2 D E=z-y+u-x=C B-$ AC. Let $C B=a, A C=b$. Then $a-b=8(\sqrt{2}-1)$. By the Law of Sines, we have
$\frac{a}{\sin 45^{\circ}}=\frac{b}{\sin 30^{\circ}}$, or $\sqrt{2} a=2 b$,
i.e., $a=\sqrt{2} b$. Thus,
$b=8, a=8 \sqrt{2}$.
The radius of the circumcircle of triangle
$A B C$ is found using the formula
$R=\frac{b}{2 \sin 30^{\circ}}=b=8$.
## Answer: 8.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. One tourist covers a distance of 20 km 2.5 hours faster than the other. If the first tourist reduced their speed by 2 km/h, and the second increased their speed by 50%, they would spend the same amount of time on the same distance. Find the speeds of the tourists.
|
Solution: Let $\mathrm{x}$ be the speed of the first tourist, and $y$ be the speed of the second tourist.
\[
\frac{20}{x}+\frac{5}{2}=\frac{20}{y}, \quad x-2=1.5 y, \quad \frac{4}{x}+\frac{1}{2}=\frac{6}{x-2}, \quad x^{2}-6 x-16=0, \quad x=8, \quad y=4
\]
Answer: $8 \mathrm{km} / \mathrm{u}, 4 \mathrm{km} / \mathrm{q}$.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Since $\mathrm{x} \leq \mathrm{P}$ and Р:х, let $2 \mathrm{x} \leq \mathrm{P} => \mathrm{x} \leq \mathrm{P} / 2$, and also $\mathrm{y} \leq \mathrm{P} ; \kappa \leq \mathrm{P} ; \mathrm{e} \leq \mathrm{P} ; =>$
$$
\mathrm{x}+\mathrm{y}+\mathrm{K}+\mathrm{e} \leq 3.5 \mathrm{P} ; => \mathrm{P} \geq \frac{2}{7}(\mathrm{x}+\mathrm{y}+\mathrm{K}+\mathrm{e})=\frac{2}{7} \cdot 2023=578
$$
$\mathrm{x}=289 ; 2 \mathrm{x}=\mathrm{y}=\mathrm{K}=\mathrm{e}=578 . \mathrm{x}+\mathrm{y}+\mathrm{\kappa}+\mathrm{e}=2023$. $\mathrm{P}=578$. Answer: 578.
## №5: Percentages.
From a bottle filled with a $12 \%$ salt solution, 1 liter was poured out and the bottle was topped up with water, then another 1 liter was poured out and topped up with water again. The bottle ended up with a $3 \%$ salt solution. What is the capacity of the bottle?
|
Answer: 2 l
## №6: Planimetry.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. (10 points) In a row, 2018 digits are written consecutively. It is known that in this row, every two-digit number formed by two adjacent digits (in the order they are written) is divisible by 17 or 23. The last digit in this row is 5. What is the first digit in the row? Provide a justified answer.
#
|
# Solution:
All two-digit numbers divisible by 17 or 23:
$$
\begin{aligned}
& 17,34,51,68,85 \\
& 23,46,69,92
\end{aligned}
$$
The following diagram shows with arrows which digit can follow which in the row:
$$
\begin{aligned}
& 1 \rightarrow 7 \quad 9 \rightarrow 2 \rightarrow 3 \\
& \uparrow \quad \uparrow \\
& 5 \leftarrow 8 \longleftarrow 6 \leftarrow 4
\end{aligned}
$$
Traversing the digits in the row from right to left corresponds to moving against the direction of the arrows. If in this diagram we take steps against the direction of the arrows, starting from the digit 5, we end up at 6 in two steps, and then we will be moving in a cycle, landing back at 6 every 5 steps.
Since \(2017 = 2 + 5 \cdot 403\), the first digit will be 6.
Answer. 6.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. Rectangle $ABCD$ with sides $AB=1$ and $AD=10$ serves as the base of pyramid $SABCD$, and the edge $SA=4$ is perpendicular to the base. Find a point $M$ on edge $AD$ such that triangle $SMC$ has the smallest perimeter. Find the area of this triangle.
#
|
# Solution:
Let's lay off $A T=A S$ on the extension of edge $A B$. For any position of point $M$ on side $A D$, $T M=S M$, so the minimum value of the sum $S M+M C$ will be when $M=T C \cap A D$.
Let's introduce the notation
$A B=a, A D=b, A S=c, A M=x$. From
$\triangle T A M \sim \triangle C D M$ it follows that
$\frac{T A}{C D}=\frac{A M}{D M}, \frac{c}{a}=\frac{x}{b-x}$,
$x=\frac{b c}{a+c}=A M, \frac{a b}{a+c}=D M$.
Draw $A K \perp T C$ and connect $K$ and $S$.
$A K=\frac{T A \cdot A M}{\sqrt{T A^{2}+A M^{2}}}=\frac{c x}{\sqrt{c^{2}+x^{2}}}=$
$=\frac{b c}{\sqrt{(a+c)^{2}+b^{2}}} \cdot S K=\sqrt{A S^{2}+A K^{2}}=\sqrt{c^{2}+\frac{b^{2} c^{2}}{(a+c)^{2}+b^{2}}}=c \frac{\sqrt{(a+c)^{2}+2 b^{2}}}{\sqrt{(a+c)^{2}+b^{2}}}$.
$M C=\sqrt{D C^{2}+M D^{2}}=\sqrt{a^{2}+\frac{a^{2} b^{2}}{(a+c)^{2}}}=\frac{a \sqrt{(a+c)^{2}+b^{2}}}{a+c}$.
$S_{\triangle M C S}=\frac{1}{2} \cdot M C \cdot S K=\frac{1}{2} \cdot \frac{a c}{a+c} \cdot \sqrt{(a+c)^{2}+2 b^{2}}=\frac{1}{2} \cdot a c \sqrt{1+2\left(\frac{b}{a+c}\right)^{2}}$.
Answer: when $a=1, b=10, c=4 \quad x=8, S_{\triangle M C S}=6$.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 1. (Option 1)
Calculate $x^{3}+3 x$, where $x=\sqrt[3]{2+\sqrt{5}}-\frac{1}{\sqrt[3]{2+\sqrt{5}}}$.
|
Solution: Let $\sqrt[3]{2+\sqrt{5}}=a$, then $x=a-\frac{1}{a}$,
$$
\begin{aligned}
& x^{3}+3 x=\left(a-\frac{1}{a}\right)^{3}+3\left(a-\frac{1}{a}\right)=a^{3}-\frac{1}{a^{3}}=2+\sqrt{5}-\frac{1}{2+\sqrt{5}}=\frac{(2+\sqrt{5})^{2}-1}{2+\sqrt{5}}= \\
& =\frac{8+4 \sqrt{5}}{2+\sqrt{5}}=4
\end{aligned}
$$
Answer: 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. There are two lead-tin alloys. In the first alloy, the mass of lead is to the mass of tin as $1: 2$; in the second - as $2: 3$. How many grams of the first alloy are needed to obtain 22 g of a new alloy with the mass ratio of lead to tin being 4:7?
|
Solution. Let the first alloy contain x g of lead and 2x g of tin. In the second alloy, there are 2y g of lead and 3y g of tin. Then $k \cdot 3x + n \cdot 5y = 22 ; \frac{kx + n \cdot 2y}{k \cdot 2x + n \cdot 3y} = \frac{4}{7} ; \quad$ we need to find $k \cdot 3x$ and $5ny$. Let $ny = b ; kx = a \cdot \frac{a + 2b}{2a + 3b} = \frac{4}{7} ; 7a + 14b = 8a + 12b ; 2b = a$. Using the first equation $3a + 5b = 22 ; 11b = 22 ; b = 2 ; a = 4$. Therefore, $k \cdot 3x = 12 ; 5ny = 10$.
Answer: 12.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The number $\overline{6 x 62 y 4}$ is divisible by 11, and when divided by 9, it gives a remainder of 6. Find the remainder when this number is divided by $13 .(15$ points)
|
# Solution
By the divisibility rule for 11, we get
$((x+2+4)-(6+6+y)) \vdots 11$ or $(x-6-y) \vdots 11$
Let's find suitable options: $(0 ; 5)(1 ; 6)(2 ; 7)(3 ; 8)(4 ; 9)(6 ; 0)(7 ; 1)(8 ; 2)$ $(9 ; 3)$.
If the number $\overline{6 x 62 y 4}$ gives a remainder of 6 when divided by 9, then by the divisibility rule for 9 we get
$$
\begin{aligned}
& (6+x+6+2+y+4)-6: 9 \\
& \text { or }(12+x+y) \vdots 9
\end{aligned}
$$
The combination $(6 ; 0)$ fits, so the original number is 666204.
The remainder when this number is divided by 13 is 6.
Answer: 6.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Find the sum of the integers that belong to the set of values of the function $f(x)=\log _{3}(40 \cos 2 x+41)$ for $x \in[(5 / 3)(\operatorname{arctg}(1 / 5)) \cos (\pi-\arcsin (-0.8)) ; \operatorname{arctg} 3]$ (10 points)
|
Solution: Since $\cos (\pi-\arcsin (-0.8))=\cos (\pi+\arcsin 0.8)=-\cos (\arcsin 0.8)=-0.6$, then $x \in[(5 / 3)(\operatorname{arctg}(1 / 5)) \cos (\pi-\arcsin (-0.8)) ; \operatorname{arctg} 3]=[-\operatorname{arctg}(1 / 5) ; \operatorname{arctg} 3]$. $2 x \in[-2 \operatorname{arctg}(1 / 5) ; 2 \operatorname{arctg} 3]$. Since $\quad 0<\operatorname{arctg}(1 / 5)<\operatorname{arctg} 1=\pi / 4, \quad 0<2 \operatorname{arctg}(1 / 5)<\pi / 2$, $-\pi / 2<-2 \operatorname{arctg}(1 / 5)<0$, and also $\pi / 4<\operatorname{arctg} 3<\pi / 2, \pi / 2<2 \operatorname{arctg} 3<\pi$, then $\cos 2 x \in[\cos (2 \operatorname{arctg} 3) ; 1]$. Using the formula $\cos 2 \alpha=\frac{1-\operatorname{tg}^{2} \alpha}{1+\operatorname{tg}^{2} \alpha}$, we get $\cos (2 \operatorname{arctg} 3)=-0.8$, and $\cos 2 x \in[-0.8 ; 1]$. From this, we have $40 \cos 2 x+41 \in[9 ; 81]$, and $f(x)=\log _{3}(40 \cos 2 x+41) \in\left[\log _{3} 9 ; \log _{3} 81\right]=[2 ; 4]$.
The interval $[2 ; 4]$ is the range of the function $f(x)=\log _{3}(40 \cos 2 x+41)$ for $x \in[(5 / 3)(\operatorname{arctg}(1 / 5)) \cos (\pi-\arcsin (-0.8)) ; \operatorname{arctg} 3]$. The sum of the integers in the interval $[2 ; 4]$ is 9.
Answer: $E_{f}=[2 ; 4]$, the sum of the integers is 9.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. On the side $AC$ of triangle $ABC$, a circle is constructed with $AC$ as its diameter, which intersects sides $AB$ and $BC$ at points $D$ and $E$ respectively. The angle $EDC$ is $30^{\circ}$, $AE = \sqrt{3}$, and the area of triangle $DBE$ is to the area of triangle $ABC$ as $1:2$. Find the length of segment $BO$, where $O$ is the intersection point of segments $AE$ and $CD$.
|
# Solution:
1) $\angle E D C=\angle E A C=30^{\circ}$ (inscribed angles subtending the same arc);
2) $A C$ - diameter of the circle $\Rightarrow \triangle A E C$ - right triangle, $\angle A E C=90^{\circ}, \angle E C A=60^{\circ}$, $A C=\frac{A E}{\cos 30^{\circ}}=2, E C=A C \sin 30^{\circ}=1$
3) $\angle A D C=90^{\circ}, \angle E D C=30^{\circ} \Rightarrow \angle B D E=60^{\circ} \Rightarrow \triangle D B E \approx \triangle C B A \Rightarrow \frac{D E}{A C}=\frac{B D}{B C}=\frac{B E}{A B}=k$, $k^{2}=\frac{S_{D B E}}{S_{A B C}}=\frac{1}{2} \Rightarrow k=\frac{1}{\sqrt{2}} \Rightarrow D E=\sqrt{2} ;$
4) $\triangle D E C$ - Law of Sines: $\frac{D E}{\sin (\angle D C E)}=\frac{E C}{\sin 30^{\circ}} \Rightarrow \frac{\sqrt{2}}{\sin (\angle D C E)}=2 \Rightarrow \sin (\angle D C E)=\frac{\sqrt{2}}{2}$ $\Rightarrow \angle D C E=45^{\circ} \Rightarrow \triangle E O C$ - isosceles right triangle, $E O=E C=1$;
5) $\angle D A E=45^{\circ} \Rightarrow \triangle A B E$ - isosceles right triangle, $B E=A E=\sqrt{3}$;
6) $\triangle B E O$ - right triangle $\Rightarrow B O^{2}=B E^{2}+E O^{2}$ (Pythagorean theorem) $\Rightarrow$ $B O^{2}=3+1=4 \Rightarrow B O=2$.
Answer: 2 .
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Find the sum of the integers that belong to the set of values of the function $f(x)=\log _{3}(10 \cos 2 x+17)$ for $x \in[1,25(\operatorname{arctg} 0.25) \cos (\pi-\arcsin (-0.6)) ; \operatorname{arctg} 3] . \quad(10$ points $)$
|
# Solution:
Since $\quad$ $\cos (\pi-\arcsin (-0.6))=\cos (\pi+\arcsin 0.6)=-\cos (\arcsin 0.6)=-0.8, \quad$ then $x \in[1.25(\operatorname{arctg} 0.25) \cos (\pi-\arcsin (-0.6)) ; \operatorname{arctg} 3]=[-\operatorname{arctg} 0.25 ; \operatorname{arctg} 3] \quad$ Therefore, $2 x \in[-2 \operatorname{arctg} 0.25 ; 2 \operatorname{arctg} 3]$ Since $\quad 0<\operatorname{arctg} 0.25<\operatorname{arctg} 1=\pi / 4, \quad 0<2 \operatorname{arctg} 0.25<\pi / 2$, $-\pi / 2<-2 \operatorname{arctg} 0.25<0, \quad$ and $\quad \pi / 4<\operatorname{arctg} 3<\pi / 2, \quad \pi / 2<2 \operatorname{arctg} 3<\pi, \quad$ then $\cos 2 x \in[\cos (2 \operatorname{arctg} 3) ; 1] . \quad$ Using $\quad$ the formula $\cos 2 \alpha=\frac{1-\operatorname{tg}^{2} \alpha}{1+\operatorname{tg}^{2} \alpha}, \quad$ we get $\cos (2 \operatorname{arctg} 3)=-0.8, \quad$ and $\cos 2 x \in[-0.8 ; 1]$. From this, we have $10 \cos 2 x+17 \in[9 ; 27]$, and $f(x)=\log _{3}(10 \cos 2 x+17) \in\left[\log _{3} 9 ; \log _{3} 27\right]=[2 ; 3]$.
The interval $[2 ; 3]$ is the range of the function $f(x)=\log _{3}(10 \cos 2 x+17)$ for $x \in[1.25(\operatorname{arctg} 0.25) \cos (\pi-\arcsin (-0.6)) ; \operatorname{arctg} 3]$.
The sum of the integers in the interval $[2 ; 3]$ is 5.
Answer: $E_{f}=[2 ; 3]$, the sum of the integers is 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. On the side $AC$ of triangle $ABC$, a circle is constructed with $AC$ as its diameter, which intersects sides $AB$ and $BC$ at points $D$ and $E$ respectively. The angle $EDC$ is $30^{\circ}$, $EC=1$, and the area of triangle $DBE$ is to the area of triangle $ABC$ as $1:2$. Find the length of segment $BO$, where $O$ is the intersection point of segments $AE$ and $CD$.
|
# Solution:
1) $\angle E D C=\angle E A C=30^{\circ}$ (inscribed angles subtending the same arc);
2) $A C$ - diameter of the circle $\Rightarrow \triangle A E C$ - right triangle, $\angle A E C=90^{\circ}, \angle E C A=60^{\circ}$,
$$
A C=\frac{E C}{\sin 30^{\circ}}=2, \quad A E=E C \operatorname{tg} 60^{\circ}=\sqrt{3}
$$
3) $\angle A D C=90^{\circ}, \angle E D C=30^{\circ} \Rightarrow \angle B D E=60^{\circ} \Rightarrow \triangle D B E \approx \triangle C B A \Rightarrow \frac{D E}{A C}=\frac{B D}{B C}=\frac{B E}{A B}=k$, $k^{2}=\frac{S_{D B E}}{S_{A B C}}=\frac{1}{2} \Rightarrow k=\frac{1}{\sqrt{2}} \Rightarrow D E=\sqrt{2} ;$
4) $\triangle D E C$ - law of sines: $\frac{D E}{\sin (\angle D C E)}=\frac{E C}{\sin 30^{\circ}}$ $\Rightarrow \frac{\sqrt{2}}{\sin (\angle D C E)}=2 \Rightarrow \sin (\angle D C E)=\frac{\sqrt{2}}{2} \Rightarrow$ $\angle D C E=45^{\circ} \Rightarrow \triangle E O C$ - isosceles right triangle, $E O=E C=1$;
5) $\angle D A E=45^{\circ} \Rightarrow \triangle A B E$ - isosceles right triangle, $B E=A E=\sqrt{3}$;
6) $\triangle B E O$ - right triangle $\Rightarrow$ $B O^{2}=B E^{2}+E O^{2}($ Pythagorean theorem $) \Rightarrow$ $B O^{2}=3+1=4 \Rightarrow B O=2$.
Answer: 2 .
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Find the sum of the integers that belong to the set of values of the function $f(x)=\log _{2}(5 \cos 2 x+11)$ for $x \in[1,25(\operatorname{arctg}(1 / 3)) \cos (\pi+\arcsin (-0.6)) ; \operatorname{arctg} 2] \quad$ (10 points)
|
# Solution:
Since $\quad$ $\cos (\pi+\arcsin (-0.6))=\cos (\pi-\arcsin 0.6)=-\cos (\arcsin 0.6)=-0.8, \quad$ then $x \in[1.25(\operatorname{arctg}(1 / 3)) \cos (\pi+\arcsin (-0.6)) ; \operatorname{arctg} 2]=[-\operatorname{arctg}(1 / 3) ; \operatorname{arctg} 2]$ Therefore, $2 x \in[-2 \operatorname{arctg}(1 / 3) ; 2 \operatorname{arctg} 2]$ Since $\quad 0<\operatorname{arctg}(1 / 3)<\operatorname{arctg} 1=\pi / 4, \quad 0<2 \operatorname{arctg}(1 / 3)<\pi / 2$, $-\pi / 2<-2 \operatorname{arctg}(1 / 3)<0, \quad$ and $\quad \pi / 4<\operatorname{arctg} 2<\pi / 2, \quad \pi / 2<2 \operatorname{arctg} 2<\pi, \quad$ then $\cos 2 x \in[\cos (2 \operatorname{arctg} 2) ; 1] . \quad$ Using the formula $\cos 2 \alpha=\frac{1-\operatorname{tg}^{2} \alpha}{1+\operatorname{tg}^{2} \alpha}, \quad$ we get $\cos (2 \operatorname{arctg} 2)=-0.6, \quad$ and $\quad \cos 2 x \in[-0.6 ; 1]$. From this, we have $5 \cos 2 x+11 \in[8 ; 16]$, and $f(x)=\log _{2}(5 \cos 2 x+11) \in\left[\log _{2} 8 ; \log _{2} 16\right]=[3 ; 4]$.
The interval $[3 ; 4]$ is the range of the function $f(x)=\log _{2}(5 \cos 2 x+11)$ for $x \in[1.25(\operatorname{arctg}(1 / 3)) \cos (\pi+\arcsin (-0.6)) ; \operatorname{arctg} 2]$.
The sum of the integers in the interval $[3 ; 4]$ is 7.
Answer: $E_{f}=[3 ; 4]$, the sum of the integers is 7.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. On the side $AC$ of triangle $ABC$, a circle is constructed with $AC$ as its diameter, which intersects sides $AB$ and $BC$ at points $D$ and $E$ respectively. The angle $EDC$ is $30^{\circ}$, the area of triangle $AEC$ is $\sqrt{3} / 2$, and the area of triangle $DBE$ is to the area of triangle $ABC$ as $1: 2$. Find the length of segment $BO$, where $O$ is the intersection point of segments $AE$ and $CD$.
|
Solution:
1) $\angle E D C=\angle E A C=30^{\circ}$ (inscribed angles subtending the same arc);
2) $A C$ - diameter of the circle $\Rightarrow \triangle A E C$ - right-angled, $\angle A E C=90^{\circ}, \angle E C A=60^{\circ}$, $A C=\frac{E C}{\sin 30^{\circ}}=2 E C, A E=E C \operatorname{tg} 60^{\circ}=\sqrt{3} E C ;$ $S_{A E C}=\frac{A E \cdot E C}{2}=\frac{\sqrt{3} E C^{2}}{2}=\frac{\sqrt{3}}{2} \Rightarrow E C=1$, $A C=2, A E=\sqrt{3} ;$
3) $\angle A D C=90^{\circ}, \angle E D C=30^{\circ} \Rightarrow \angle B D E=60^{\circ} \Rightarrow$ $\triangle D B E \approx \triangle C B A \Rightarrow \frac{D E}{A C}=\frac{B D}{B C}=\frac{B E}{A B}=k$, $k^{2}=\frac{S_{D B E}}{S_{A B C}}=\frac{1}{2} \Rightarrow k=\frac{1}{\sqrt{2}} \Rightarrow D E=\sqrt{2} ;$
4) $\triangle D E C$ - law of sines: $\frac{D E}{\sin (\angle D C E)}=\frac{E C}{\sin 30^{\circ}}$
$\Rightarrow \frac{\sqrt{2}}{\sin (\angle D C E)}=2 \Rightarrow \sin (\angle D C E)=\frac{\sqrt{2}}{2} \Rightarrow \angle D C E=45^{\circ} \Rightarrow \triangle E O C$ - isosceles right-angled triangle, $E O=E C=1$;
5) $\angle D A E=45^{\circ} \Rightarrow \triangle A B E$ - isosceles right-angled triangle, $B E=A E=\sqrt{3}$
6) $\triangle B E O$ - right-angled triangle $\Rightarrow B O^{2}=B E^{2}+E O^{2}$ (Pythagorean theorem) $\Rightarrow$ $B O^{2}=3+1=4 \Rightarrow B O=2$.
Answer: 2
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Solve the equation $\quad \sqrt{x+\sqrt{x}-\frac{71}{16}}-\sqrt{x+\sqrt{x}-\frac{87}{16}}=\frac{1}{2}$.
|
Solution. Taking into account that $x$ is non-negative, we make the substitution $u=\sqrt{x+\sqrt{x}-\frac{71}{16}}, v=\sqrt{x+\sqrt{x}-\frac{87}{16}}, u \geq 0, v \geq 0$.
Then we obtain the system $\left\{\begin{array}{l}u-v=1 / 2, \\ u^{2}-v^{2}=1,\end{array} \Rightarrow\left\{\begin{array}{l}u-v=1 / 2, \\ u+v=2,\end{array} \Rightarrow\left\{\begin{array}{l}u=5 / 4, \\ v=3 / 4,\end{array} \Rightarrow\right.\right.\right.$ reverse substitution: $\left\{\begin{array}{l}x+\sqrt{x}-\frac{71}{16}=\frac{25}{16}, \\ x+\sqrt{x}-\frac{87}{16}=\frac{9}{16} .\end{array} \Rightarrow x+\sqrt{x}-6=0 \Rightarrow x=4\right.$.
## Answer: 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. What is the maximum possible number of consecutive terms of an increasing geometric progression that can be three-digit natural numbers? Provide an example of such a sequence. (16 points)
|
Solution. Let the required members of the progression be $a_{0}, a_{1}, \ldots, a_{n}, a_{k}=a_{0} q^{k}$, the common ratio - an irreducible fraction $q=r / s, r>s$. Then $a_{0}=b s^{n}, a_{n}=b r^{n}, b \in \mathbb{N}$, since $r^{n}$ and $s^{n}$ are coprime. We obtain the restriction
$$
r^{n}<1000 / b, \quad s^{n} \geq 100 / b
$$
1) Let $r=2$, then $q=2 / 1, (2) \Longrightarrow n \leq 9$. For $n=9$ we have
$$
r=2, \quad s=1, \quad\left\{\begin{array}{c}
a_{0}=b \geq 100 \\
a_{n}=512 b<1000
\end{array} \Longrightarrow b=1\right.
$$
However, $a_{9}=512$ is not a valid solution since $a_{9} \geq 1000$ is required. Thus, $r=2$ is not useful.
2) Let $r=3$, then $q=3 / 2, (2) \Longrightarrow n \leq 5$. For $n=5$ we have
$$
r=3, \quad s=2, \quad\left\{\begin{array}{c}
a_{0}=32 b \geq 100 \\
a_{n}=243 b<1000
\end{array} \Longrightarrow b=4\right.
$$
3) Let $r \geq 4$, then ( 1$) \Longrightarrow n \leq 4$. The record $n=5$ cannot be broken.
Answer: 6. The only example: $128,192,288,432,648,972$.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. $f(-x)=3(-x)^{3}-(-x)=-3 x^{3}+x=-\left(3 x^{3}-x\right)=-f(x)$ $g(-x)=f^{3}(-x)+f\left(\frac{1}{-x}\right)-8(-x)^{3}-\frac{2}{-x}=-f^{3}(x)-f\left(\frac{1}{x}\right)+8 x^{3}+\frac{2}{x}=-g(x)$
Therefore, $g$ is an odd function $\Rightarrow$ if $x_{0}$ is a root of the original equation, then $-x_{0}$ is also a root of the equation $\Rightarrow$ the sum of the roots is zero, if the roots exist
Check $\quad x=1: \quad f(1)=3 \cdot 1^{3}-1=2, \quad f\left(\frac{1}{1}\right)=f(1)=2, \quad$ substitute $\quad$ into the original equation:10=10 - correct $\Rightarrow x=1$ is a root $\Rightarrow$ the roots exist
|
Answer: 0.
Problem 8 (2nd version).
Find the sum of the roots of the equation $g^{3}(x)-g\left(\frac{1}{x}\right)=5 x^{3}+\frac{1}{x}$, where $g(x)=x^{3}+x$.
## Solution.
Consider the function $f(x)=g^{3}(x)-g\left(\frac{1}{x}\right)-5 x^{3}-\frac{1}{x}$, then the roots of the original equation are the roots of the equation $f(x)=0$.
Investigate the function $f$ for evenness:
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. $g(-x)=(-x)^{3}+(-x)=-x^{3}-x=-\left(x^{3}+x\right)=-g(x)$
$$
f(-x)=g^{3}(-x)-g\left(\frac{1}{-x}\right)-5(-x)^{3}-\frac{1}{-x}=-g^{3}(x)+g\left(\frac{1}{x}\right)+5 x^{3}+\frac{1}{x}=-f(x)
$$
Therefore, $f$ is an odd function $\Rightarrow$ if $x_{0}$ is a root of the original equation, then $-x_{0}$ is also a root of the equation $\Rightarrow$ the sum of the roots is zero, if the roots exist
Check $x=1: g(1)=1^{3}+1=2, g\left(\frac{1}{1}\right)=g(1)=2$, substitute into the original equation: $6=6$ - true $\Rightarrow x=1$ is a root $\Rightarrow$ the roots exist
|
# Answer: 0.
Task 9 (1st variant). In each vertex of an equilateral triangle with side $\sqrt{10}$, circles of radius $\sqrt{5}$ were constructed, the inner areas of which were painted gray, brown, and raspberry. Find the area of the gray-brown-raspberry region.
Solution. By symmetry, the areas of the figures formed by the intersection of the circles and the triangle are equal. The area of the entire triangle is $3 s+3 p+x=\frac{\sqrt{3}}{4} a^{2}=\frac{5 \sqrt{3}}{2}\left(a\right.$-side of the triangle), the area of a sector with an angle of $60^{\circ}$ is $s+2 p+x=\frac{\pi R^{2}}{6}=\frac{5 \pi}{6}$ ( $R$-radius of the circle). From the right triangle DEC we have
$D E=\sqrt{D C^{2}-E C^{2}}=\sqrt{R^{2}-\frac{a^{2}}{4}}=\frac{\sqrt{10}}{2}=E C$.
Therefore, triangle $\quad D E C$
is isosceles and $\angle D C E=45^{\circ}, \quad$ hence,
$\angle D C F=90^{\circ}$ and the area of the sector $D C F$ is
$S_{\text {secm }}=\frac{\pi R^{2}}{4}=\frac{5 \pi}{4}$.
Since the area of triangle $D C F$ is $S_{D C F}=\frac{1}{2} D F \cdot E C=\frac{5}{2}$, the area of the segment with arc
DF is $S_{\text {segm }}=\frac{5 \pi}{4}-\frac{5}{2}$.
Thus, we have the system of equations $\left\{\begin{array}{l}3 s+3 p+x=\frac{5 \sqrt{3}}{2} \\ s+2 p+x=\frac{5 \pi}{6} \\ p+x=\frac{5 \pi}{4}-\frac{5}{2}\end{array}\right.$, solving which, we find that $x=\frac{5 \pi}{4}-\frac{15}{2}+\frac{5 \sqrt{3}}{2}$.
Answer: $\frac{5 \pi}{4}-\frac{15}{2}+\frac{5 \sqrt{3}}{2}$.
Task 9 (2nd variant). In each vertex of a square with side $\sqrt{6}$, circles of radius $\sqrt{6}$ were constructed, the inner areas of which were painted in different colors: gray, brown, raspberry, and polka dot. Find the area of the region painted with all four colors.
Solution. The area of the square is $4 s+4 p+x=R^{2}=6(R$-radius of the circle), the area of a sector with an angle of $90^{\circ}$ is $2 s+3 p+x=\frac{\pi R^{2}}{4}=\frac{3 \pi}{2}$.
The area of the segment with arc $B D$ is the area of the sector with arc $B D$ minus the area of triangle $B C D$, so, $x+2 p+s=\frac{\pi R^{2}}{3}-\frac{1}{2} B D \cdot A C$, from which (considering that for triangle $A B C$ we have $A C=\frac{1}{2} B C$ )
$x+2 p+s=\frac{\pi R^{2}}{3}-\frac{\sqrt{3} R^{2}}{4}$.
We get the system of equations $\left\{\begin{array}{l}4 s+4 p+x=6 \\ 2 s+3 p+x=\frac{3 \pi}{2} \\ x+2 p+s=2 \pi-\frac{3 \sqrt{3}}{2}\end{array}\right.$, solving which, we find that $x=2 \pi-6 \sqrt{3}+6$.
Answer: $2 \pi-6 \sqrt{3}+6$.
Task 10 (1st variant). Given a triangle with sides $2 \sqrt{13}, 2 \sqrt{5}, 8$. On its sides, squares are constructed outward. Find the area of the triangle with vertices at the centers of these squares.
Solution. Let $A B C$ be the given triangle and $A B=2 \sqrt{13}, B C=2 \sqrt{5}, A C=8$. Let $K$, $M, N$ be the centers of the squares constructed on sides $A B, B C, A C$, respectively.
Then, by the cosine theorem for triangles $A K N$ (considering that the diagonals of the square form an angle of $45^{\circ}$ with the sides and $A K=\frac{A B}{\sqrt{2}}, A N=\frac{A C}{\sqrt{2}}$ ) we get
$$
\begin{aligned}
& K N^{2}=A K^{2}+A N^{2}-2 A K \cdot A N \cdot \cos \left(\angle A+\frac{\pi}{2}\right)= \\
& =A K^{2}+A N^{2}+2 A K \cdot A N \cdot \sin \angle A=
\end{aligned}
$$
$$
=\frac{A B^{2}}{2}+\frac{A C^{2}}{2}+A B \cdot A C \cdot \sin \angle A=\frac{A B^{2}}{2}+\frac{A C^{2}}{2}+2 S_{A B C}
$$
Similarly, for triangles $B K M, C M N$ we get $K M^{2}=\frac{A B^{2}}{2}+\frac{B C^{2}}{2}+2 S_{A B C}$ and $N M^{2}=\frac{A C^{2}}{2}+\frac{B C^{2}}{2}+2 S_{A B C}$
We find the area of triangle $A B C$. We can calculate this area by first finding the height of the triangle (the height is 4), or by using Heron's formula, we get $S_{A B C}=16$.
Substituting the numerical values, we find, $K N^{2}=90, K M^{2}=68, N M^{2}=74$.
By Heron's formula for the area of a triangle through the squares of its sides, we have $S_{K M N}=\frac{1}{4} \sqrt{4 K M^{2} \cdot M N^{2}-\left(K M^{2}+M N^{2}-K N^{2}\right)^{2}}=33$.
Answer: 33.
Task 10 (2nd variant). Given a triangle with sides $2 \sqrt{13}, 2 \sqrt{5}, 8$. On its sides, squares are constructed inward. Find the area of the triangle with vertices at the centers of these squares.
Solution. Let $A B C$ be the given triangle and $A B=2 \sqrt{13}, B C=2 \sqrt{5}, A C=8$. Let $K$, $M, N$ be the centers of the squares constructed on sides $A B, B C, A C$, respectively.
Then, by the cosine theorem for triangles $A K N$ (considering that the diagonals of the square form an angle of $45^{\circ}$ with the sides and $\left.A K=\frac{A B}{\sqrt{2}}, A N=\frac{A C}{\sqrt{2}}\right)$ we get
$$
\begin{aligned}
& K N^{2}=A K^{2}+A N^{2}-2 A K \cdot A N \cdot \cos \left(\frac{\pi}{4}-\left(\angle A-\frac{\pi}{4}\right)\right)= \\
& =A K^{2}+A N^{2}-2 A K \cdot A N \cdot \sin \angle A= \\
& =\frac{A B^{2}}{2}+\frac{A C^{2}}{2}-A B \cdot A C \cdot \sin \angle A=\frac{A B^{2}}{2}+\frac{A C^{2}}{2}-2 S_{A B C}
\end{aligned}
$$
Similarly, for triangles $B K M, C M N$ we get $K M^{2}=\frac{A B^{2}}{2}+\frac{B C
|
0
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
1. Two trucks were transporting fertilizers, making the same number of trips. It turned out that 4 tons less could be loaded onto the first truck and 3 tons less onto the second truck than planned, so each truck had to make 10 extra trips. As a result, the first truck transported 60 tons more than the second, as planned. How much fertilizer was loaded onto each truck and how many trips were made?
|
# Solution:
Let $x, y$ - capacity, $t-$ number of trips as planned.
$$
\left\{\begin{array}{l}
x t=(x-4)(t+10), \\
y t=(y-3)(t+10), \Leftrightarrow\left\{\begin{array} { l }
{ 1 0 x - 4 t = 4 0 } \\
{ \quad x t - y t = 6 0 }
\end{array} \quad \left\{\begin{array}{l}
10 y-3 t=30, \\
(x-y) t=60
\end{array} \Rightarrow 10(x-y)-t=10 \Rightarrow t^{2}+10 t-600=0\right.\right.
\end{array}\right.
$$
From here $t_{1}=20, t_{2}=-30-$ extraneous root; $x=12, y=9$. The first truck was loaded with 8 tons, the second with 6 tons, and 30 trips were completed.
Answer: 8 tons, 6 tons, 30 trips.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The numerical sequence $\left\{a_{n}\right\}_{n=1}^{\infty}$ is defined such that $a_{1}=\log _{2}\left(\log _{2} f(2)\right), \quad a_{2}=$ $\log _{2}\left(\log _{2} f(f(2))\right), \ldots, a_{n}=\log _{2}(\log _{2} \underbrace{f(f(\ldots f}_{n}(2)))), \ldots$, where $f(x)=x^{x}$. Determine the index $n$ for which $a_{n}=2059+2^{2059}$.
(12 points)
|
# Solution.
If $\log _{2}\left(\log _{2} u\right)=t$, then $u=2^{2^{t}}, f(u)=\left(2^{2^{t}}\right)^{2^{2^{t}}}=2^{2^{t+2^{t}}}, \log _{2}\left(\log _{2} f(u)\right)=t+2^{t} . \quad$ If $u=2,2=2^{2^{t}}, t=0, a_{1}=\log _{2}\left(\log _{2} f(2)\right)=0+2^{0}=1$. If $u=f(2)$, then $t=\log _{2}\left(\log _{2} u\right)=$ 1 , and $a_{2}=\log _{2}\left(\log _{2} f(f(2))\right)=\log _{2}\left(\log _{2} f(u)\right)=t+2^{t}=1+2^{1}=3$. If $u=f(f(2))$, then $t=\log _{2}\left(\log _{2} u\right)=3$, and $a_{3}=\log _{2}\left(\log _{2} f(f(f(2)))\right)=\log _{2}\left(\log _{2} f(u)\right)=t+2^{t}=3+2^{3}=11$. If $u=f(f(f(2)))$, then $t=\log _{2}\left(\log _{2} u\right)=11$, and $a_{4}=\log _{2}\left(\log _{2} f(f(f(f(2))))\right)=\log _{2}\left(\log _{2} f(u)\right)=t+2^{t}=11+2^{11}=2059$. If $u=f(f(f(f(2))))$, then $t=\log _{2}\left(\log _{2} u\right)=2059$, and $a_{5}=\log _{2}\left(\log _{2} f(f(f(f(f(2)))))\right)=\log _{2}\left(\log _{2} f(u)\right)=2059+2^{2059}$.
## Answer: 5
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. More and more countries are exploring space. The number of states that launch their satellites using their own launch vehicles is already 12. There are also countries that use the services of the main space powers to launch their satellites for economic purposes. Due to the increasing number of participants in space activities and the intensification of these activities, issues of ensuring the safety of space operations are arising. For example, NASA has approached the corporation "Energia" with a request to reduce the altitude of the ISS orbit.
a) Considering the Earth as a sphere with radius $R$, determine the maximum number of satellites that can simultaneously be in orbits around the Earth at the same height $H$ from its surface, such that the distance between the satellites is greater than $\sqrt{2}(R+H)$.
b) For the maximum number of satellites found, specify the coordinates of their possible locations in a coordinate system with the origin at the center of the Earth and the x-axis directed along the vector connecting the center of the Earth with one of the satellites. (20 points)
|
Solution. According to the condition, at the current moment, all satellites should be located on a sphere with radius $R+H$. Let $O$ be the center of the sphere, and its radius $R_{H}=R+H$. Denote the satellites by points $C_{i}, i=1, \ldots, n$. We need to determine the maximum value of $n$.
Let's find the distance $C_{i} C_{j}$, using the cosine theorem for triangle $O C_{i} C_{j}$.
$C_{i} C_{j}^{2}=O C_{i}^{2}+O C_{j}^{2}-2 O C_{i} \cdot O C_{j} \cdot \cos \left(\angle O C_{i}, O C_{j}\right)=2 R_{H}^{2}-2 R_{H}^{2} \cdot \cos \alpha=2 R_{H}^{2}(1-\cos \alpha)>2 R_{H}^{2}$,
Thus, $1-\cos \alpha>1 \Rightarrow \cos \alpha<0$, and the third axis is directed towards the nearest to $C_{3}\left(x_{3}, y_{3}, z_{3}\right)$, so that the z-coordinate is positive, i.e., $z_{3}>0$. Consider the scalar products of the vectors, noting that all of them are negative.
$\overrightarrow{O C_{1}} \cdot \overrightarrow{O C_{i}}=x_{i}, \quad i=\overline{2, n}, \quad \overrightarrow{O C_{2}} \cdot \overrightarrow{O C_{i}}=x_{2} x_{i}+y_{2} y_{i}, i=\overline{3, n}, \quad \overrightarrow{O C_{3}} \cdot \overrightarrow{O C_{i}}=x_{3} x_{i}+y_{3} y_{i}+z_{3} z_{i}, i=\overline{4, n}$.
Since $\cos \left(\angle O C_{i}, O C_{j}\right)<0$, the scalar products of the vectors are negative, and thus, $\quad x_{i}<0, i=\overline{2, n}, \quad$ meaning all $y_{i}<0, i=\overline{3, n}, \quad x_{3} x_{i}+y_{3} y_{i}+z_{3} z_{i}<0, i=\overline{4, n}$. Therefore, all $z_{i}<0, i=\overline{4, n}$. Thus, the coordinates of all vectors starting from $\overrightarrow{O C_{4}}$ will be negative. Consequently, the scalar product of vectors $\overrightarrow{O C_{4}}, \overrightarrow{O C_{5}}$ will be positive. We have reached a contradiction. The assumption of the existence of more than 4 satellites satisfying the required conditions is incorrect. Answer: 4 satellites.
b) 4 satellites are possible, for example, with coordinates that can be written as follows:
if the $o x$ axis is directed from the center of the sphere in the direction of one of the satellites, then the coordinates of this satellite will be $\left(R_{H}, 0,0\right)$, the other three satellites will be located on the plane $x=-R_{H} / 3$ and their coordinates will be respectively
$$
\left(-R_{H} / 3,0, r\right), \quad\left(-R_{H} / 3, \sqrt{3} r / 2,-r / 2\right), \quad\left(-R_{H} / 3,-\sqrt{3} r / 2,-r / 2\right)
$$
where $r=\sqrt{R_{H}^{2}-R_{H}^{2} / 9}=R_{H} \sqrt{8} / 3$.
These relationships are derived from considering the relationships between the elements of a regular
tetrahedron with side $a$. The height $H=\sqrt{a^{2}-\left(a \frac{\sqrt{3}}{2} \cdot \frac{2}{3}\right)^{2}}=a \sqrt{\frac{2}{3}} . \quad$ The radius $\quad$ of the sphere circumscribed around a regular tetrahedron is found from the similarity of triangles
$\frac{H}{a}=\frac{a}{2 R} \Rightarrow R=\frac{a^{2}}{2 \sqrt{\frac{2}{3}} a}=\frac{a \sqrt{3}}{2 \sqrt{2}} \Rightarrow \frac{H}{R}=\frac{\sqrt{\frac{2}{3}} a}{\frac{a \sqrt{3}}{2 \sqrt{2}}}=\frac{4}{3}$.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 1. Option I.
The decimal representation of a natural number $N$ contains 1580 digits. Among these digits are threes, fives, and sevens, and no other digits. It is known that the number of sevens is 20 less than the number of threes. Find the remainder when the number $N$ is divided by 3.
|
Solution. Let $x$ be the number of threes in the number $N$. The sum of the digits of the number $N$ is $S=3 x+7(x-20)+5(1580-(2 x-20))=7860$.
The remainder of $S$ divided by 3 is equal to the remainder of $N$ divided by 3 and is 0.
Answer: 0.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. II variant.
The decimal representation of a 2015-digit natural number $N$ contains the digits 5, 6, 7 and no other digits. Find the remainder of the division of the number $N$ by 9, given that the number of fives in the representation of the number is 15 more than the number of sevens.
|
Solution. Let the number $N$ contain $x$ sevens. Then the sum of the digits of the number $N$ is $S=7x+5(x+15)+6(2015-(2x+15))=12075$.
$N \equiv S \equiv 6(\bmod 9)$.
Answer: 6.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 4. Option I.
Find the set of values of the parameter $a$, for which the sum of the cubes of the roots of the equation $x^{2}-a x+a+2=0$ is equal to -8.
#
|
# Solution.
1) $x_{1}^{3}+x_{2}^{3}=\left(x_{1}+x_{2}\right)\left(\left(x_{1}+x_{2}\right)^{2}-3 x_{1} x_{2}\right)=a\left(a^{2}-3(a+2)\right)=a^{3}-3 a(a+2)$.
2) $a^{3}-3 a(a+2)=-8 \Leftrightarrow\left[\begin{array}{l}a=-2, \\ a=1, \\ a=4 .\end{array}\right.$
3) $D=a^{2}-4 a-8$.
For $a=-2 \quad D=4+8-8=4>0$, therefore, $a=-2$ is a solution.
For $a=1 \quad D=1-4-8<0$ - no roots; hence, $a=1$ is not a solution.
For $a=4 \quad D=16-16-8<0$, $a=4$ is also not a solution.
Answer: $\{-2\}$.
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. II variant.
Find the set of values of the parameter $a$, for which the sum of the cubes of the roots of the equation $x^{2}+a x+a+1=0$ is equal to 1.
|
# Solution.
1) $x_{1}^{3}+x_{2}^{3}=\left(x_{1}+x_{2}\right)\left(\left(x_{1}+x_{2}\right)^{2}-3 x_{1} x_{2}\right)=-a\left(a^{2}-3(a+1)\right)=-a^{3}+3 a(a+1)$.
2) $-a^{3}+3 a(a+1)=1 \Leftrightarrow\left[\begin{array}{l}a=-1, \\ a=2 \pm \sqrt{3} \text {. }\end{array}\right.$
3) $D=a^{2}-4 a-4$.
For $a=-1 \quad D=1+4-4>0$, therefore, $a=-1$ is a solution.
For $a=2 \pm \sqrt{3} \quad D=7 \pm 4 \sqrt{3}-8 \mp 4 \sqrt{3}-4=-5<0$; hence, the values $a=2 \pm \sqrt{3}$ are not solutions.
Answer: $\{-1\}$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 7. Option 1.
Given a triangle with sides 6, 8, and 10. Find the length of the shortest segment connecting points on the sides of the triangle and dividing it into two equal areas.
|
Solution. 1) Note that the given triangle is a right triangle: $6^{2}+8^{2}=10^{2}$.
2) Suppose first (and we will justify this later) that the ends of the desired segment $D E=t$ lie on the larger leg $A C=8$ and the hypotenuse $A B=10$ (see figure). Let $A D=x$, $A E=y, \angle B A C=\alpha$. Then
$S_{A D E}=\frac{1}{2} x y \sin \alpha=\frac{3}{10} x y$.
3) By the problem's condition $S_{A D E}=\frac{1}{2} S_{A B C}$,
$\frac{3}{10} x y=\frac{1}{2} \cdot \frac{1}{2} \cdot 6 \cdot 8$,
$x y=40$.
4) $\triangle A D E: t^{2}=x^{2}+y^{2}-2 x y \cos \alpha=$
$$
\begin{aligned}
& =x^{2}+y^{2}-2 \cdot 40 \cdot \frac{8}{10}= \\
& =x^{2}+y^{2}-64= \\
& =x^{2}+\frac{1600}{x^{2}}-64
\end{aligned}
$$
By the Cauchy-Schwarz inequality $t^{2} \geq 2 \sqrt{x^{2} \cdot \frac{1600}{x^{2}}}-64=16$.
The minimum value $t_{\min }=4$ is achieved when $x=y=\sqrt{40}=2 \sqrt{10}$.
5) In an isosceles triangle with base $t$ and vertex angle $\alpha$, the area is
$$
S=\frac{1}{2} t \cdot \frac{1}{2} t \operatorname{ctg} \frac{\alpha}{2}=\frac{1}{4} t^{2} \operatorname{ctg} \frac{\alpha}{2} .
$$
From this, $t=2 \sqrt{S \operatorname{tg} \frac{\alpha}{2}}$.
It is clear that for a fixed area $S$, as $\alpha$ increases, the base $t$ will also increase. Therefore, the found value $t_{\min }$, corresponding to the segment opposite the smallest of the three angles of the triangle, is indeed the desired one.
Answer: 4.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 3.
One side of the parallelogram is $\sqrt{3}$ times larger than the other side. One diagonal of the parallelogram is $\sqrt{7}$ times larger than the other diagonal. How many times larger is one angle of the parallelogram than the other angle?
|
Solution. Let $x$ be the smaller side, then $\sqrt{3} x$ is the larger side. Let $y$ be the smaller diagonal, then $\sqrt{7} y$ is the larger diagonal. We have:
$2 x^{2}+2(\sqrt{3} x)^{2}=y^{2}+(\sqrt{7} y)^{2}$,
from which $x=y$.
We get: the acute angle of the parallelogram is $30^{\circ}$, the obtuse angle is $150^{\circ}$.
Answer: 5 times.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. From point $A$ to point $B$, which are 8 km apart, a tourist and a cyclist set out simultaneously. The cyclist, who took no less than half an hour to travel from $A$ to $B$, without stopping, turned back and started moving towards point $A$, increasing his speed by $25 \%$. After 10 minutes from his departure from point $B$, the cyclist met the tourist. Determine the greatest possible integer value of the tourist's speed (in km/h), and for this value of the tourist's speed, find the initial speed of the cyclist.
|
Solution: Let $x$ (km/h) be the speed of the tourist, $y$ (km/h) be the initial speed of the cyclist, and $t$ (h) be the time spent by the cyclist traveling from $A$ to $B$. Then
$$
\left\{\begin{array}{c}
x(t+1 / 6)+5 y / 24=8, \\
y t=8, \\
t \geq 0.5,
\end{array} \Rightarrow x(8 / y+1 / 6)+5 y / 24=8, \Rightarrow 5 y^{2}+(4 x-192) y+192 x=0\right.
$$
For the quadratic equation to have a solution, it is necessary that $D / 4=(2 x-96)^{2}-960 x \geq 0$. Therefore, $x^{2}-336 x+2304 \geq 0, D / 4=(72 \sqrt{5})^{2}$, $x \in(-\infty ; 168-72 \sqrt{5}] \cup[168+72 \sqrt{5} ;+\infty)$. Since by the condition $x \in \mathbb{N}$, and $x / 6<8$, i.e., $x<48$, then $x \in[1 ; 168-72 \sqrt{5}] \cap \mathbb{N}$. Using the estimate $2.23<\sqrt{5}<2.24$, we get the estimate $160<72 \sqrt{5}<161$, and $7<168-72 \sqrt{5}<8$. The largest possible integer value of the speed $x=7$. We find the initial speed of the cyclist when $x=7$ from the equation $5 y^{2}-164 y+192 \cdot 7=0, y_{1}=84 / 5$, $y_{2}=16$. Since $t \geq 0.5, \quad t=\frac{8}{y} \geq \frac{1}{2}$, and $y \leq 16$, then $y=16$.
Answer: 7 km/h, 16 km/h.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Two numbers x and y satisfy the equation $280 x^{2}-61 x y+3 y^{2}-13=0$ and are the fourth and ninth terms, respectively, of a decreasing arithmetic progression consisting of integers. Find the common difference of this progression.
|
Solution: We factorize the expression $280 x^{2}-61 x y+3 y^{2}$. For $y \neq 0$, we have $y^{2}\left(280\left(\frac{x}{y}\right)^{2}-61\left(\frac{x}{y}\right)+3\right)=280 y^{2}\left(\frac{x}{y}-\frac{3}{40}\right)\left(\frac{x}{y}-\frac{1}{7}\right)=(40 x-3 y)(7 x-y)$. This formula is also valid for all real numbers $y$. According to the problem, the integers $x$ and $y$ satisfy the equation $(40 x-3 y)(7 x-y)=13$. The integers $40 x-3 y$ and $7 x-y$ are divisors of the number 13, and the following cases are possible:
$$
\left\{\begin{array} { c }
{ 4 0 x - 3 y = 1 3 , } \\
{ 7 x - y = 1 ; }
\end{array} \text { 2) } \left\{\begin{array} { c }
{ 4 0 x - 3 y = - 1 3 , } \\
{ 7 x - y = - 1 ; }
\end{array} \text { 3) } \left\{\begin{array} { c }
{ 4 0 x - 3 y = - 1 , } \\
{ 7 x - y = - 1 3 ; }
\end{array} \text { 4) } \left\{\begin{array}{c}
40 x-3 y=1, \\
7 x-y=13
\end{array}\right.\right.\right.\right.
$$
We solve each system using the method of addition. We multiply both sides of the second equation of the system by -3 and add it to the first:
$$
\left\{\begin{array} { l }
{ 1 9 x = 1 0 , } \\
{ 7 x - y = 1 ; }
\end{array} \text { 2) } \left\{\begin{array} { l }
{ 1 9 x = - 1 0 , } \\
{ 7 x - y = - 1 ; }
\end{array} \text { 3) } \left\{\begin{array} { c }
{ 1 9 x = 3 8 , } \\
{ 7 x - y = - 1 3 ; }
\end{array} \text { 4) } \left\{\begin{array}{l}
19 x=-38 \\
7 x-y=13
\end{array}\right.\right.\right.\right.
$$
Systems 1) and 2) do not have integer solutions. Since the progression is decreasing, we have $x < y$, which is satisfied by the solutions of system 4): $x=-2$, $y=-27$. Thus, $a_{4}=-2, a_{9}=-27$, or $a_{1}+3 d=-2, \quad a_{1}+8 d=-27$. From this, we get $d=-5$.
Answer: $d=-5$.
|
-5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. From point $A$ to point $B$, which are 24 km apart, a pedestrian and a cyclist set out simultaneously. The cyclist, who spent no less than two hours on the journey from $A$ to $B$, without stopping, turned back and started moving towards point $A$ at a speed twice the initial speed. After 24 minutes from his departure from point $B$, the cyclist met the pedestrian. Determine the greatest possible integer value of the pedestrian's speed (in km/h), and for this value of the pedestrian's speed, find the initial speed of the cyclist.
|
Solution: Let $x$ (km/h) be the speed of the cyclist, $y$ (km/h) be the initial speed of the truck, and $t$ (h) be the time spent by the truck traveling from $A$ to $B$. Then
$$
\left\{\begin{array}{rl}
x(t+0.4)+0.8 y=24, \\
y t & =24, \\
t & \geq 2,
\end{array} \Rightarrow x(24 / y+0.4)+0.8 y=24, \Rightarrow 2 y^{2}+(x-60) y+60 x=0\right.
$$
For the quadratic equation to have a solution, it is necessary that $D=(x-60)^{2}-480 x \geq 0$. Therefore, $x^{2}-600 x+3600 \geq 0, D / 4=(120 \sqrt{6})^{2}$, and
$x \in(-\infty ; 300-120 \sqrt{6}] \cup[300+120 \sqrt{6} ;+\infty)$. Since by the condition $x \in \mathbb{N}$, and $0.2 x<12$, i.e., $x<60$, then $\quad x \in[1 ; 300-120 \sqrt{6}] \cap \mathbb{N}$. Using the estimate $2.44<\sqrt{6}<2.45$, we get the estimate $293<120 \sqrt{6}<294$, and $6<300-120 \sqrt{6}<7$. The largest possible integer value of the speed $x=6$. We find the initial speed of the truck when $x=6$ from the equation $2 y^{2}-54 y+360=0$, or $y^{2}-27 y+180=0, \quad y_{1}=12, \quad y_{2}=15$. Since $t \geq 2, \quad t=\frac{24}{y} \geq 2$, and $y \leq 12$, then $y=12$.
Answer: 6 km/h, 12 km/h.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Two numbers \(x\) and \(y\) satisfy the equation \(26 x^{2} + 23 x y - 3 y^{2} - 19 = 0\) and are the sixth and eleventh terms, respectively, of a decreasing arithmetic progression consisting of integers. Find the common difference of this progression.
|
Solution: Factorize the expression $26 x^{2}+23 x y-3 y^{2}$. For $y \neq 0$, we have $y^{2}\left(26\left(\frac{x}{y}\right)^{2}+23\left(\frac{x}{y}\right)-3\right)=26 y^{2}\left(\frac{x}{y}+1\right)\left(\frac{x}{y}-\frac{3}{26}\right)=(x+y)(26 x-3 y)$. This formula is valid for all real numbers $y$. According to the problem, the integers $x$ and $y$ satisfy the equation $(x+y)(26 x-3 y)=19$. The integers $x+y$ and $26 x-3 y$ are divisors of the number 19, and the following cases are possible:
1) $\left\{\begin{array}{c}x+y=19 \\ 26 x-3 y=1\end{array}\right.$
2) $\left\{\begin{array}{c}x+y=-19 \\ 26 x-3 y=-1\end{array}\right.$
3) $\left\{\begin{array}{c}x+y=-1 \\ 26 x-3 y=-19\end{array}\right.$
4) $\left\{\begin{array}{c}x+y=1 \\ 26 x-3 y=19\end{array}\right.$
We solve each system by the method of addition. Multiply both sides of the first equation of the system by 3 and add to the second:
1) $\left\{\begin{array}{l}29 x=58 \\ x+y=19\end{array}\right.$
2) $\left\{\begin{array}{c}29 x=-58 \\ x+y=-19\end{array}\right.$
3) $\left\{\begin{array}{l}29 x=-22 \\ x+y=-1\end{array}\right.$
4) $\left\{\begin{array}{l}29 x=22, \\ x+y=1 .\end{array}\right.$
Systems 3) and 4) do not have integer solutions. Since the progression is decreasing, it follows that $x<y$, which is satisfied by the solutions of system 2): $x=-2$, $y=-17$. Thus, $a_{6}=-2, a_{11}=-17$, or $a_{1}+5 d=-2, a_{1}+10 d=-17$. From this, we get $d=-3$.
Answer: $d=-3$.
|
-3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Indicate the smallest value of the parameter $a$ for which the equation has at least one solution
$2 \sin \left(\pi-\frac{\pi x^{2}}{12}\right) \cos \left(\frac{\pi}{6} \sqrt{9-x^{2}}\right)+1=a+2 \sin \left(\frac{\pi}{6} \sqrt{9-x^{2}}\right) \cos \left(\frac{\pi x^{2}}{12}\right)$.
|
Solution.
Rewrite the equation as
$2 \sin \left(\pi-\frac{\pi x^{2}}{12}\right) \cos \left(\frac{\pi}{6} \sqrt{9-x^{2}}\right)-2 \sin \left(\frac{\pi}{6} \sqrt{9-x^{2}}\right) \cos \left(\pi-\frac{\pi x^{2}}{12}\right)=a-1$, or
$\sin \left(\pi-\frac{\pi x^{2}}{12}-\frac{\pi}{6} \sqrt{9-x^{2}}\right)=\frac{a-1}{2}$.
Consider the expression $t=\pi-\frac{\pi x^{2}}{12}-\frac{\pi}{6} \sqrt{9-x^{2}}$ separately, which can be rewritten as:
$$
\begin{gathered}
\pi-\frac{\pi x^{2}}{12}-\frac{\pi}{6} \sqrt{9-x^{2}}=\frac{\pi}{12}\left(12-x^{2}-2 \sqrt{9-x^{2}}\right)=\frac{\pi}{12}\left(9-x^{2}-2 \sqrt{9-x^{2}}+3\right) \\
=\frac{\pi}{12}\left(\left(\sqrt{9-x^{2}}-1\right)^{2}+2\right)
\end{gathered}
$$
Considering that the root takes values from 0 to 3, then $t \in\left[\frac{\pi}{6} ; \frac{\pi}{2}\right]$, so $\sin t \in$ $\left[\frac{1}{2} ; 1\right]$. Let's find the range in which the parameter varies: $\frac{1}{2} \leq \frac{a-1}{2} \leq 1 \Rightarrow 2 \leq a \leq 3$.
Answer: 2
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. Rhombus $ABCD$ is the base of a pyramid with vertex $S$. All its lateral faces are inclined to the base plane at the same angle of $60^{\circ}$. Points $M, N, K$, and $L$ are the midpoints of the sides of rhombus $ABCD$. A rectangular parallelepiped is constructed on rectangle $MNKL$ as its base. The edges of the upper face of the parallelepiped (opposite to face $MNKL$) intersect the lateral edges of the pyramid $SABCD$ at points $F, P, R$, and $Q$, respectively. The volume of the polyhedron with vertices at points $M, N, K, L, F, P, R, Q$ is $12 \sqrt{3}$, and the radius of the circle inscribed in rhombus $ABCD$ is 2.4. Find the side of rhombus $ABCD$. (16 points)
|
Solution.
The height of the pyramid $SO = h$. The diagonals of the rhombus $AC = d_1, BD = d_2$.
The height of the parallelepiped is $h / 2$, and the sides of the base of the parallelepiped are $d_1 / 2$ and $d_2 / 2$.
The volume of the parallelepiped is
$$
V_{\Pi} = \frac{d_1}{2} \cdot \frac{d_2}{2} \cdot \frac{h}{2}
$$
The volume of the polyhedron is
$$
V_{\mathrm{M}} = V_{\Pi} - 4 \cdot \frac{1}{3} \cdot \frac{1}{2} \cdot \frac{d_1}{4} \cdot \frac{d_2}{4} \cdot \frac{h}{2} = \frac{d_1 d_2 h}{8} - \frac{d_1 d_2 h}{48} = \frac{5 d_1 d_2 h}{48}
$$
According to the condition $\frac{5 d_1 d_2 h}{48} = 12 \sqrt{3}$.
Since the radius of the circle inscribed in this rhombus is 2.4, and all lateral faces of the pyramid are inclined to the base plane at an angle of $60^{\circ}$, then $h = 2.4 \sqrt{3}$. Therefore,
$$
\frac{5 d_1 d_2 \cdot 2.4 \sqrt{3}}{48} = 12 \sqrt{3}, \text{ and } d_1 d_2 = 48
$$
Since $\quad S_{ABCD} = \frac{d_1 d_2}{2}, \quad$ and $S_{ABCD} = \frac{4 AB \cdot r_{\mathrm{B}}}{2} = 4.8 \cdot AB, \quad$ then $4.8 \cdot AB = 24 \Rightarrow AB = 5$.
## Answer: 5
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Specify the greatest value of the parameter $p$ for which the equation has at least one solution
$2 \cos \left(2 \pi-\frac{\pi x^{2}}{6}\right) \cos \left(\frac{\pi}{3} \sqrt{9-x^{2}}\right)-3=p-2 \sin \left(-\frac{\pi x^{2}}{6}\right) \cos \left(\frac{\pi}{3} \sqrt{9-x^{2}}\right)$. (16 points)
|
# Solution.
Let's rewrite the equation as
$$
\cos \left(2 \pi-\frac{\pi x^{2}}{6}\right) \cos \left(\frac{\pi}{3} \sqrt{9-x^{2}}\right)+\sin \left(2 \pi-\frac{\pi x^{2}}{6}\right) \sin \left(\frac{\pi}{3} \sqrt{9-x^{2}}\right)=\frac{p+3}{2} \text {, or }
$$
$\cos \left(2 \pi-\frac{\pi x^{2}}{6}-\frac{\pi}{3} \sqrt{9-x^{2}}\right)=\frac{p+3}{2}$.
Consider the expression $t=2 \pi-\frac{\pi x^{2}}{6}-\frac{\pi}{3} \sqrt{9-x^{2}}$ separately, which can be rewritten as:
$$
\begin{aligned}
2 \pi-\frac{\pi x^{2}}{6}- & \frac{\pi}{3} \sqrt{9-x^{2}}=\frac{\pi}{6}\left(12-x^{2}-2 \sqrt{9-x^{2}}\right)=\frac{\pi}{6}\left(9-x^{2}-2 \sqrt{9-x^{2}}+3\right) \\
= & \frac{\pi}{6}\left(\left(\sqrt{9-x^{2}}-1\right)^{2}+2\right)
\end{aligned}
$$
Considering that the root takes values from 0 to 3, then $t \in\left[\frac{\pi}{3} ; \pi\right]$, so $\cos t \in$ $\left[-1 ; \frac{1}{2}\right]$. Let's find the range in which the parameter varies: $-1 \leq \frac{p+3}{2} \leq \frac{1}{2} \Rightarrow-5 \leq p \leq-2$
## Answer: -2
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (1b, 8-11) The probability that a purchased light bulb will work is 0.95. How many light bulbs need to be bought to ensure that with a probability of 0.99, there are at least 5 working ones among them?
|
# Solution.
Let's take 6 light bulbs. The probability that at least 5 of them will work is the sum of the probabilities that 5 will work and 1 will not, and that all 6 will work, i.e.,
$$
C_{6}^{5} \cdot 0.95^{5} \cdot 0.05 + C_{6}^{6} \cdot 0.95^{6} = 6 \cdot 0.95^{5} \cdot 0.05 + 0.95^{6} = 0.9672
$$
Let's take 7 light bulbs. The desired probability is
$$
\begin{aligned}
& C_{7}^{5} \cdot 0.95^{5} \cdot 0.05^{2} + C_{7}^{6} \cdot 0.95^{6} \cdot 0.05 + C_{7}^{7} \cdot 0.95^{7} = \\
= & 21 \cdot 0.95^{5} \cdot 0.05^{2} + 7 \cdot 0.95^{6} \cdot 0.05 + 0.95^{7} = 0.9962
\end{aligned}
$$
The minimum number of light bulbs required is 7.
Answer: 7.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.