problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
25.15. Calculate $\lim _{n \rightarrow \infty}(\sqrt{n+1}-\sqrt{n})$.
|
25.15. Answer: 0. It is clear that
$$
0<\sqrt{n+1}-\sqrt{n}=\frac{(\sqrt{n+1}-\sqrt{n})(\sqrt{n+1}+\sqrt{n})}{\sqrt{n+1}+\sqrt{n}}=\frac{1}{\sqrt{n+1}+\sqrt{n}}<\frac{1}{\sqrt{n}}
$$
Therefore, $\lim _{n \rightarrow \infty}(\sqrt{n+1}-\sqrt{n})=0$.
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
25.35. Find the first digit of the number $2^{400}$.
|
25.35. Answer: 2. The first digit of the number $2^{400}=\left(2^{10}\right)^{40}=1024^{40}$ coincides with the first digit of the number $1,024^{40}$. On the one hand, according to problem 25.34, we get $1,024^{40}1+40 \cdot 0,024+\frac{40 \cdot 39}{2} 0,024^{2}=2,40928>2$.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
25.40. Does the sequence $a_{n}=\sin (2 \pi n!e)$ converge?
|
25.40. A n s w e r: yes, converges to 0. According to problem 25.39, the fractional part of the number $n!e$ is between 0 and $1 / n$. Therefore, $0<\sin (2 \pi n!e)<$ $<\sin (2 \pi / n)$ for $n \geqslant 4$.
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
27.13. Solve the equation $5^{2 x-1}+5^{x+1}=250$.
Translate the text above into English, please keep the original text's line breaks and format, and output the translation result directly.
|
27.13. Answer: $x=2$. The function $f(x)=5^{2 x-1}+5^{x+1}$ is monotonically increasing, so it takes the value 250 at only one value of $x$. It is also clear that $f(2)=5^{3}+5^{3}=250$.
|
2
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
27.26. Provide an example of positive irrational numbers $a$ and $b$ such that the number $a^{b}$ is an integer.
## 27.6. Some Notable Limits
|
27.26. Let $a=\sqrt{2}$ and $b=\log _{\sqrt{2}} 3$. The numbers $a$ and $b$ are irrational (problems 6.16 and 27.25). In this case, $a^{b}=(\sqrt{2})^{\log _{\sqrt{2}} 3}=3$.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
28.62. Calculate the limit $\lim _{x \rightarrow 0} \frac{\tan x - x}{x - \sin x}$.
### 28.10. The number of roots of the equation
|
28.62. Answer: 2. Transform the ratio of derivatives:
$$
\frac{\frac{1}{\cos ^{2} x}-1}{1-\cos x}=\frac{1}{\cos ^{2} x} \cdot \frac{1-\cos x^{2}}{1-\cos x}=\frac{1+\cos x}{\cos ^{2} x}
$$
The last expression tends to 2 as $x \rightarrow 0$.
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
29.27. Calculate the area under the graph of the function $y=$ $=\sin x$ on the interval from 0 to $\pi$.
## 29.5. Calculation of Volumes
Let a body be located in space with rectangular coordinates $O x y z$, such that the projection of this body onto the $O x$ axis is the segment $[a, b]$. Suppose that a plane passing through
a point $x$ of the segment $[a, b]$ perpendicular to the $O x$ axis cuts out a figure of area $S(x)$ on this body. Then the volume of this body is given by $\int_{a}^{b} S(x) d x$.
|
29.27. The desired area is equal to $\int_{0}^{\pi} \sin x d x=-\left.\cos x\right|_{0} ^{\pi}=2$.
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
32.15. Prove that if $a+b+c+d=2$ and $1 / a+1 / b+1 / c+$ $+1 / d=2$, then
$$
\frac{1}{1-a}+\frac{1}{1-b}+\frac{1}{1-c}+\frac{1}{1-d}=2
$$
$$
\% * *
$$
|
32.15. Let $\sigma_{k}$ be the $k$-th elementary symmetric function of $a, b, c, d$. Given that $\sigma_{1}=2$ and $\sigma_{3}=2 \sigma_{4}$. Therefore,
$$
\begin{aligned}
\frac{1}{1-a}+\frac{1}{1-b}+\frac{1}{1-c}+\frac{1}{1-d}=\frac{4-3 \sigma_{1}+2 \sigma_{2}-\sigma_{3}}{1-\sigma_{1}+\sigma_{2}-\sigma_{3}+\sigma_{4}} & = \\
& =\frac{4-6+2 \sigma_{2}-2 \sigma_{4}}{1-2+\sigma_{2}-2 \sigma_{4}+\sigma_{4}}=2
\end{aligned}
$$
|
2
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
2. Write down and read all seven-digit numbers, the sum of the digits in each of which is equal to 2. How many such numbers are there?
|
2. $2000000,1100000,1010000,1001000,1000100,1000010,1000001$. Bcero 7 numbers.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
27. Find the digit that has the property that if it is appended to the end of any natural number, the resulting number is equal to the sum of three terms, the first of which is the original number, the second is the number represented by the sought digit, and the third is the product of the first two terms.
|
27. Let the natural number be $a$, and the appended digit be $x$. Then according to the condition $a \cdot 10 + x = a + x + a x$, from which $9 a = a x$, and therefore, $x = 9$.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
37. In the hundred-digit number $12345678901234567890 \ldots 1234567890$, all digits in odd positions were erased. In the resulting fifty-digit number, digits in odd positions were erased again. The erasing continued until nothing was left. What was the last digit to be erased?
|
37. The first time, 50 odd digits were crossed out, leaving 50 even ones. The second time, 25 digits were crossed out, including 5 twos, 5 fours, 5 sixes, 5 eights, and 5 zeros. 25 remained in the following sequence: $4,8,2,6,0,4$, $8,2,6,0, \ldots, 2,6,0$. (The group of digits 4, 8, 2, 6,0 is written in sequence 5 times.) During the third crossing out, 13 digits will be crossed out, leaving 12 such digits: $8,6,4,2,0,8,6,4,2,0,8,6$. After the fourth crossing out, $6,2,8,4$, 0,6 will remain, after the fifth $-2,4,6$ and after the sixth - 4. Therefore, the last (seventh) time, the digit 4 will be crossed out.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. How many different products divisible by ten can be formed from the numbers $2,3,5,7,9 ?$
|
8. For the product of numbers to be divisible by 10, the factors must include the numbers 2 and 5. Taking this into account, the following products satisfy the condition of the problem:
1) $2 \cdot 5$
2) $2 \cdot 5 \cdot 3$
3) $2 \cdot 5 \cdot 7$
4) $2 \cdot 5 \cdot 9$;
5) $2 \cdot 5 \cdot 3 \cdot 7$
6) $2 \cdot 5 \cdot 3 \cdot 9$
7) $2 \cdot 5 \cdot 7 \cdot 9$
8) $2 \cdot 5 \cdot 3 \cdot 7 \cdot 9$.
In total, there are 8 products.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. A store needed to receive 185 kg of candies in closed boxes from the warehouse. The warehouse has boxes of candies weighing 16 kg, 17 kg, and 21 kg. What boxes and how many could the store receive?
|
9. We notice that $185=37 \cdot 5$ and $16+21=37$. Therefore, the store could have received 5 boxes weighing 21 kg each and 5 boxes weighing 16 kg each. Since the number 185 has been factored into prime factors, the problem has a unique solution.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. A kilogram of one type of candy is 80 k more expensive than another. Andrey and Yura bought 150 g of candies, which included both types of candies, with Andrey having twice as much of the first type as the second, and Yura having an equal amount of each. Who paid more for their purchase and by how much?
14
|
10. Andrei has 100 g of one type of candy and 50 g of another, while Yura has 75 g of each type. Andrei's candies are more expensive than Yura's by the same amount that 25 g of one type is more expensive than 25 g of the other. Since 1 kg is more expensive by 80 k., then 25 g is more expensive by 2 k. $(80: 40=2)$. Therefore, Andrei paid 2 k. more for his candies than Yura.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
30. Think of a single-digit number: double it, add 3, multiply by 5, add 7, using the last digit of the resulting number, write down a single-digit number, add 18 to it, and divide the result by 5. What number did you get? No matter what number you thought of, you will always get the same number in the final result. Explain why.
|
30. Let the number thought of be $x$. Then we sequentially obtain:
1) $2 x ; 2) 2 x+3 ; 3) 10 x+15=10(x+1)+5$
2) $10(x+1)+12 ; 5) 2 ; 6) 2+18=20$; 7) $20: 5=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
31. The quotient of dividing one number by another is an integer that is two times smaller than one of them and six times larger than the other. Find this quotient.
|
31. Let the dividend be $a$, and the divisor be $b$, then according to the condition, the quotient is $a: 2$ or $6 b$, i.e., $a: 2 = 6 b$, from which $a = 12 b$ and $a: b = 12$. Therefore, the quotient $a: b$ is 12.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
40. In a football tournament, each of the participating teams played against each other once. The teams scored $16,14,10,10,8,6,5,3$ points. How many teams participated in the tournament and how many points did the teams that played and finished in the top 4 positions lose? (A team gets 2 points for a win and 1 point for a draw.)
|
40. If the number of teams is $n$, then the total number of games is $\frac{n(n-1)}{2}$, and the total number of points scored by them is $(n-1) n$. In our example, we have $16+14+10+10+8+$ $+6+5+3=72$. Therefore, $(n-1) \cdot n=72$, or $(n-1) \cdot n=8 \cdot 9$, so $n=9$, i.e., there were 9 teams. The maximum number of points a team can score is: $2 \cdot 8=16$. This means the first team did not lose any points, the second team lost 2 points, the third and fourth teams lost 6 points each, and in total they lost 14 points $(2+6 \cdot 2=14)$. (One team did not score any points.)
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
47. Over the past five years, 27 collective farmers have been awarded. Moreover, in each subsequent year, more were awarded than in the previous year. In the last year, three times as many were awarded as in the first year. How many collective farmers were awarded in the third year?
|
47. If in the first year $x$ collective farm workers are awarded, then in the last year it is $3x$, and for these two years it is $4x$. The values $x=1$ and $x=2$ do not satisfy the condition, as in the second, third, and fourth years, 23 (27-4=23) and 19 (27-8=19) would be awarded, which does not meet the condition that "in each subsequent year, more were awarded than in the previous year." Let's try $x=3$. In this case, in the first year, 3 collective farm workers were awarded, and in the fifth year, 9. In the remaining three years, 15 collective farm workers were awarded. Since $15=4+5+6$, in the third year, 5 collective farm workers were awarded ( $3<4<5<6<9$ ).
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
64. First, two numbers 2 and 3 are written, then they are multiplied and their product, the number 6, is recorded, then the product of the two last single-digit numbers $3 \cdot 6=18$, then $1 \cdot 8=8$, then $8 \cdot 8=64$ and so on. As a result, we get the following sequence of digits:
## $2361886424 \ldots$
Which digits cannot appear in such a sequence? Which digit stands at the thousandth place?
|
64. As a result of analyzing the sequence of digits $236188642483261224832612248 \ldots$, we notice that starting from the tenth digit, the group of digits 48326122 repeats (as in the previous problem, let's call it the period). Before the first period, there are 9 digits, and the period itself consists of 8 digits. Among these digits, there are no $5, 7, 9$, and 0. Therefore, these digits will be absent in the sequence, no matter how long it is extended. To find the digit in the thousandth place, since there are 9 digits before the period, there will be 991 digits in the first and subsequent periods up to the desired digit $(1000-9=991)$. Since the period consists of 8 digits, there will be 123 complete periods plus 7 more digits of the 124th period $(991=8 \cdot 123+7)$. The seventh digit of the period is 2. Therefore, the digit in the thousandth place in the sequence is 2.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Tourists from one of the groups bought various souvenirs, with each of them taking a set of souvenirs of the same cost and as many as the cost of one souvenir in rubles. All tourists paid with ten-ruble bills (one or several), and each received change that did not match the change received by any of the other tourists. What change could each tourist have received, and what is the maximum number of tourists that could have been in the group?
|
5. The amount in rubles that each tourist paid for a set of souvenirs is expressed by a number of the form $a^{2}$, where $a$ is the number of souvenirs or the price of one souvenir in rubles. Since the squares of natural numbers can only end in the digits $1,4,5,6,9$, there can only be 5 different changes, namely 9 p., 6 p., 5 p., 4 p., and 1 p. The maximum possible number of tourists is 5.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. To the question: "How many two-digit numbers are there such that the sum of their digits is 9?" - Stepa Verkhoglyadkin started listing all two-digit numbers in a row, selecting the ones he needed. Show him a shorter way to solve the problem.
|
6. For two-digit numbers, except for 99, the statement is true: “If a number is divisible by 9, then the sum of its digits is 9, and vice versa.” Up to 99 inclusive, there are 11 numbers divisible by 9 (99: 9=11). However, among them, two numbers (9 and 99) are not considered in this problem, so the number of numbers satisfying the condition of the problem is 9 (11-2=9).
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
24. Mowgli asked his monkey friends to bring him some nuts. The monkeys gathered an equal number of nuts and carried them to Mowgli. But on the way, they quarreled, and each monkey threw a nut at every other monkey. As a result, Mowgli received only 35 nuts. How many nuts did the monkeys gather, if it is known that each of them brought more than one nut?
|
24. Since the monkeys collected nuts equally and threw them away equally, they brought them equally. The number 35 is divisible by 5, so we have $35=5 \cdot 7$. There can be 2 cases:
1) There were 5 monkeys, each brought 7 nuts, and each threw away 4 nuts, so each collected $7+4=11$.
2) There were 7 monkeys, each brought 5 nuts, and each threw away 6 nuts, so each collected $5+6=11$.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. On New Year's Eve, Father Frost gave the children the following task: using all nine digits from 1 to 9 once each, insert "+" or "-" between every two adjacent digits so that after performing the operations, all possible two-digit prime numbers can be obtained. Help the children complete this task. How many such numbers can be obtained
|
8. If we place only the "+" sign between the digits, we will get 45 after performing the operations. There are only 10 prime two-digit numbers less than 45. These numbers are $11,13,17,19,23,29,31,37,41,43$. They can be obtained as follows:
1) $1+2+3+4+5+6-8-9=11$
2) $1+2+3+4+5+6-7+8-9=13$
3) $1+2+3+4-5+6+7+8-9=17$
4) $1+2+3-4+5+6+7+8-9=19$
5) $1-2+3+4+5+6+7+8-9=23$
6) $1+2+3+4+5+6+7-8+9=29$;
7) $1+2+3+4+5+6-7+8+9=31$
8) $1+2+3-4+5+6+7+8+9=37$
9) $1-2+3+4+5+6+7+8+9=41$
10) $2-1+3+4+5+6+7+8+9=43$.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
20. Find $p$, if each of the numbers $p, p+10$, and $p+14$ is prime.
|
20. All natural numbers can be divided into 3 groups:
1) divisible by 3, i.e., of the form $3 k$;
2) giving a remainder of 1 when divided by 3, i.e., of the form $3 k+1$;
3) giving a remainder of 2 when divided by 3, i.e., of the form $3 k+2$.
If $p=3 k$, then it is prime only when $k=1$; then $p+10=13$ and $p+14=17$. If $p=3 k+1$, then $p+14=3 k+15=3(k+5)$-composite. If $p=3 k+2$, then $p+10=3 k+12=3(k+4)$-composite. We have the solution: $p=3$.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
21. Find $p$, if each of the numbers $p, 2p+1$, and $4p+1$ is prime.
|
21. The number $p$ can be represented in one of three forms: $3 k, 3 k+1$ or $3 k+2$. For $p=3 k+1$, we have:
$2 p+1=2(3 k+1)+1=6 k+3=3(2 k+1)$ - a composite number. For $p=3 k+2$, we have:
$4 p+1=12 k+9=3(4 k+3)$ - a composite number.
Fig. 12
If $p=3 k$, then only when $k=1$ is the number $p$ prime. This number is $p=3$. Then $2 p+1=7$ and $4 p+1=13$ are also prime numbers. Therefore, when $p=3$, all three numbers are prime.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
23. Find all such prime numbers, so that each of them can be represented as the sum and difference of two prime numbers.
|
23. Since the desired number $p$ must be the sum of two prime numbers, $p>2$. All such prime numbers are odd. To get odd numbers when adding and subtracting two numbers, one of the components must be odd and the other even. Since the only even prime number is 2, then $p=p_{1}+2$ and $p=p_{2}-2$. Therefore, the prime numbers $p, p_{1}$, and $p_{2}$ are consecutive odd numbers, and the only such numbers are $3, 5, 7; p=5; 5=3+2$ and $5=7-2$.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
28. In all the carriages of a passenger train, 737 tourists were evenly distributed. How many carriages were there and how many tourists were in each carriage?
|
28. Since $737=67 \cdot 11$ and the numbers 67 and 11 are prime, it is clear that there were 11 cars, and in each car there were 67 tourists.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
33. To answer the question: "Is the difference $9^{1986}-8^{1980}$ divisible by 5 and by 10?" - one could call upon a computer. But perhaps you would like to compete with it? Give it a try.
|
33. Since $9^{1}=9, 9^{2}=81, 9^{3}=729$, it is clear that the odd powers of nine end in the digit 9, and the even powers end in the digit 1. Let's consider the powers of the number 8: $8^{1}=8 ; 8^{2}=64$-ends in the digit $4 ; 8^{3}$ ends in the digit $2 ; 8^{4}$ ends in the digit $6 ; 8^{5}$ ends in the digit 8, and so on. Thus, we have a repeating group of digits $8,4,2$ and 6, which are the last digits of the powers of 8. Since 1980 is divisible by 4, $8^{1980}$ ends in the digit 6, and therefore, the given difference ends in the digit 5. Hence, it is divisible by 5, but not by 10.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
34. To calculate the product of all natural numbers from 1 to 50 inclusive, of course, it's better to use a computer. However, you can easily state the number of zeros at the end of this product without resorting to a computer. How many are there?
|
34. Among the factors of the number $1 \cdot 2 \cdot 3 \cdot \ldots \cdot 50$, 10 numbers are divisible by 5 $(50: 5=10)$, and out of these, 2 numbers are divisible by $5^{2}=25$. Therefore, the product of the numbers from 1 to 50, when factored into prime factors, will contain 12 fives, and there will undoubtedly be more twos. Since $5 \cdot 2=10$, then $(5 \cdot 2)^{12}=10^{12}$, which means that the given product ends with twelve zeros.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
40. The steamship has $a$ funnels, $b$ screws, and $c$ people on board. It set off on the $n$-th day, $k$-th month, of the year $(1900+p)$. The product of the six numbers $a$, $b$, $c$, $n$, $k$, $p$, increased by the number whose cube is the captain's age in years, equals 4752862. Determine the unknowns.
|
40. Since $2^{3}=8,3^{3}=27,4^{3}=64,5^{3}=125$, it is clear that the captain is either 27 years old or 64 years old. If the captain is 64 years old, then from the number 4752862, 4 should be subtracted and the resulting number should be factored into 6 factors ( $4752862-4=$ $=4752858 ; 4752858=2 \cdot 3 \cdot 11 \cdot 23 \cdot 31 \cdot 101$ ). From this, it follows that the most plausible answer could be: the ship has 2 propellers, 3 funnels, 101 people on board, and it set sail on November 23, 1931. Checking shows that the captain being 27 years old does not satisfy the condition.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. Find the greatest common divisor of all five-digit numbers written using the digits
$$
1,2,3,4,5
$$
without repetition.
|
10. Each of such five-digit numbers is divisible by 3, since $1+2+$ $+3+4+5=15$, and $15: 3$. These numbers do not have any common divisors greater than 3, as, for example, $12345=3 \cdot 5 \cdot 823$, but the number 12354 does not divide evenly by either 5 or 823. Therefore, the greatest common divisor of these numbers is 3.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11. In one class, there are fewer than 50 students. On Gorky Street, $\frac{1}{7}$ of the students from this class live, on Pushkin Street - $\frac{1}{3}$, on Gaidar Street - $\frac{1}{2}$, and on Shipbuilding Street - the remaining students. How many students live on Shipbuilding Street?
|
11. The number of students in the class must be a multiple of the numbers 7, 3, and 2. The least common multiple of these numbers is $42(7 \cdot 3 \cdot 2=42)$. It is less than 50, so it satisfies the condition. Then $42 \cdot \frac{1}{7}=6 ; 42 \cdot \frac{1}{3}=14 ; 42 \cdot \frac{1}{2}=21$; $42-(6+21+14)=1$. Therefore, 1 student of this class lives on Shipbuilding Street.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13. At the lumber yard, there were logs 6 m and 8 m long of the same thickness. Which logs are more advantageous to take in order to get more pieces with fewer cuts when cutting them into 1-meter pieces?
|
13. It is more profitable to take logs from which more pieces can be obtained with fewer or the same number of cuts. From a six-meter log, 6 pieces can be obtained with 5 cuts, while from an eight-meter log, 8 pieces can be obtained with 7 cuts. Let's compare the number of pieces obtained from these logs with the same number of cuts. For the numbers 5 and 7, the least common multiple is 35. Therefore, taking 7 six-meter logs and making 35 cuts, we will get $6 \cdot 7=42$ pieces, while from five eight-meter logs with the same number of cuts, we will get $8 \cdot 5=40$ pieces. Therefore, it is more profitable to take six-meter logs.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. Half of the way the tourists walked, and the other half they traveled by bus, spending a total of 5.5 hours on the entire journey. If they had traveled the entire distance by bus, it would have taken them 1 hour. How much time in total will the tourists spend if they walk the entire distance? How many times faster is it to travel by bus than to walk?
|
9. Half of the way the tourists traveled by bus in 0.5 hours (1:2=0.5), then on foot they walked the other half in 5 hours (5.5-0.5). Therefore, the entire journey will take the tourists 10 hours (5 * 2=10). Traveling by bus is 10 times faster than walking.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11. The bear was carrying pastries from the bazaar,
But on the forest edge
He ate half the pastries
And plus half a pastry.
He walked, walked, sat down to rest
And to the "coo-coo" of the cuckoo
He ate half the pastries again
And plus half a pastry.
It got dark, he quickened his pace,
But on the porch of the cottage
He ate half of what was left
And plus half a pastry.
With an empty wallet—alas!
He entered the house sadly...
Tell me, how many pastries were there?
|
11. On the porch of the little house, the bear ate all the remaining cookies, which were half a cookie and half a cookie. This means that half a cookie is half of the remainder, i.e., the third time he ate one cookie. Therefore, when he ate half the cookies and another half cookie the second time, one cookie was left. So, $1+0.5=1.5$ is half of the cookies he had at that point, and there were a total of $1.5 \cdot 2=3$ cookies. The first time he ate half the cookies and another half cookie, so 3.5 is half of the cookies he had. This means there were initially $3.5 \cdot 2=7$ cookies.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
18. A group of tourists was supposed to arrive at the station at 5 o'clock. By this time, a bus was supposed to arrive from the tourist base to pick them up. However, arriving at the station at 3:15 PM, the tourists, not waiting for the bus, started walking to the tourist base. Meeting the bus on the way, they got in and arrived at the tourist base 15 minutes earlier than the scheduled time. At what speed were the tourists walking before they met the bus, if the bus's speed was 60 km/h?
|
18. Since the bus arrived at the tourist base 15 minutes earlier, it should have traveled from the meeting point with the tourists to the station for $\frac{1}{8}$ hours (15 minutes / 2 = $=7.5$ minutes $=\frac{1}{8}$ hours). In this time, it would travel 7.5 km $(60: 8=7.5)$, which means the tourists walked 7.5 km on foot. They covered this distance in 1.5 hours $(5-3.25=$ $=1.75 ; 1.75-0.25=1.5)$. Therefore, their speed was 5 km/h $(7.5: 1.5=5)$.
150
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
45. Calculate in the most rational way:
$$
x=\frac{225+375 \cdot 138}{375 \cdot 139-150}
$$
|
45. Since $375 \cdot 139-150=375 \cdot 138+375-150=375 \cdot 138+225$, then $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
48. On the sheet, several non-zero numbers are written, each of which is equal to half the sum of the others. How many numbers are written?
|
48. Let there be $n$ numbers, then
$$
\begin{aligned}
a_{1} & =\frac{a_{2}+a_{3}+\ldots a_{n}}{2} ; \\
a_{2} & =\frac{a_{1}+a_{3}+\ldots+a_{n}}{2} ; \\
\ldots & \ldots \ldots \ldots+a_{n-1} \\
a_{n} & =\frac{a_{1}+a_{2}+\ldots+a_{n}}{2} ; \\
2\left(a_{1}\right. & \left.+a_{2}+\ldots+a_{n}\right)=(n-1) \cdot\left(a_{1}+a_{2}+\ldots+a_{n}\right), \text { hence } 2=n-1 ; n=3 .
\end{aligned}
$$
Thus, there were 3 numbers written.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
59. Find the non-negative integer values of $n$ for which $\frac{30 n+2}{12 n+1}$ is an integer.
|
59. $\frac{30 n+2}{12 n+1}=\frac{(24 n+2)+6 n}{12 n+1}=2+\frac{6 n}{12 n+1}; \quad \frac{6 n}{12 n+1}$
will be an integer only when $n=0$, for other values of $n$ it is a proper fraction. Therefore, only when $n=0$ is $\frac{30 n+2}{12 n+1}$ an integer (2).
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
60. A barrel contains exactly 30 liters of linseed oil. For three construction brigades, 3 barrels were filled from it, each of which holds a whole number of liters, and the capacity of the first is $\frac{2}{3}$ of the capacity of the second or $\frac{3}{5}$ of the capacity of the third. How many liters of linseed oil are left in the barrel?
|
60. Let's express the capacities of the second and third buckets in terms of the capacity of the first one and schematically write it as: $\mathrm{II}=\frac{3}{2} \mathrm{I} ; \mathrm{III}=\frac{5}{3} \mathrm{I}$. Since each bucket contains a whole number of liters and the smallest number divisible by 2 and 3 is 6, the capacity of the first bucket is 6 liters, the second is 9 liters, and the third is 10 liters. Therefore, 5 liters remain in the barrel $(30-(6+9+10)=5)$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
66. After the tourists have walked 1 km and half of the remaining distance, they still have to walk a third of the entire distance and 1 km. What is the total distance?
|
66. After the tourists have walked 1 km, half of the remaining distance is one third of the entire distance plus 1 km, which means the entire remaining distance is $\frac{2}{3}$ of the entire distance plus 2 km. Thus, the entire distance is $\frac{2}{3}$ of the entire distance plus $2+1=3$ (km), which means 3 km is $\frac{1}{3}$ of the entire distance $\left(1-\frac{2}{3}=\frac{1}{3}\right)$. Therefore, the entire distance is 9 km $(3 \cdot 3=9)$.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
70. A certain amount was spent on strawberries at 2 r. 40 k. per 1 kg of one variety and the same amount on another variety at 1 r. 60 k. Find the average price of 1 kg of the strawberries purchased.
|
70. Let the amount spent on each type of strawberry be $a$ r. Then the first type purchased is $a: 2.4=\frac{a}{2.4}$ (kg), and the second type is $-\frac{a}{1.6}$ kg. In total, $\left(\frac{a}{2.4}+\frac{a}{1.6}\right)$ kg were purchased for a total of $2a$ r. The average price per 1 kg is
$$
2 a:\left(\frac{a}{2.4}+\frac{a}{1.6}\right)=\frac{2 \cdot 2.4 \cdot 1.6}{2.4+1.6}=1.92, \text{ i.e., } 1 \text{ r. } 92 \text{ k. }
$$
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
81. At exactly 24:00, the battery received an order to begin artillery preparation at the earliest time that will pass until the hour and minute hands overlap again. At what time should the artillery preparation begin?
|
81. In 1 hour, the minute hand makes a full revolution and will point to 12, while the hour hand will have traveled $\frac{1}{12}$ of the circumference and will point to 1. This means that after 1 hour, the minute hand, following the hour hand, will be at a distance equal to $\frac{1}{12}$ of the circumference from it. Since in 1 hour the minute hand will travel $\frac{11}{12}$ of the circumference more than the hour hand ($1-\frac{1}{12}=\frac{11}{12}$), it will "catch up" with the hour hand after 1 hour plus an additional $\frac{1}{11}$ hour $\left(\frac{1}{12} : \frac{11}{12} = \frac{1}{11}\right)$. Therefore, the hour and minute hands will coincide again, starting from 12, after $1 \frac{1}{11}$ hours, i.e., at 1 hour 5 minutes 27 seconds. This is the time (to the nearest second) when the artillery preparation should begin.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
82. Andrey and Grandpa Grisha went mushroom picking sometime between six and seven in the morning, at the moment when the clock hands were aligned. They returned home between twelve and one in the afternoon, at the moment when the clock hands were pointing in exactly opposite directions. How long did their mushroom "hunt" last?
|
82. In 1 hour, the minute hand makes a full revolution (its end describes a circle), while the hour hand travels $\frac{1}{12}$ of the circumference. Therefore, in one hour, the minute hand will travel more than the hour hand by $\frac{11}{12}$ of the circumference. By the time the minute hand travels from 12 to 6, i.e., $\frac{1}{2}$ of the circumference, the hour hand will travel $\frac{1}{24}$ of the circumference, i.e., at 6:30, the minute hand will lag behind the hour hand by $\frac{1}{24}$ of the circumference. It will catch up with the hour hand in $\frac{1}{22}$ of an hour $\left(\frac{1}{24} : \frac{11}{12} = \frac{1}{22}\right)$. The clock will show $6 \frac{6}{11}$ hours $\left(6 \frac{1}{2} + \frac{1}{22} = 6 \frac{6}{11}\right)$. Similar reasoning leads to the conclusion that when the hour hand is between 12 and 1, and the minute hand is directly opposite to it, the clock will show $12 \frac{6}{11}$ hours. Therefore, the mushroom "hunt" lasted 6 hours $\left(12 \frac{6}{11} - 6 \frac{6}{11} = 6\right)$.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
85. To which number can the expression
$$
\frac{(a+b)(b+c)(a+c)}{a b c}
$$
be equal if the numbers $a, b$ and $c$ satisfy the condition of problem 84?
|
85. From the solution of the previous problem, we have $a+b=c n ; b+c=a n ; a+c=b n$. After subtracting, we get $a-c=n(c-a)$. The equality is possible when $a-c=0$, i.e., $a=c$. Similarly, $a=b$, so $a=b=c$, and from this, $\frac{a+b}{c}=\frac{b+c}{a}=\frac{a+c}{b}=2$. Therefore, $\frac{(a+b)(b+c)(a+c)}{a b c}=8$.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. On a horizontal coordinate line, several integers are marked as points, the sum of which is equal to 25. If each point is moved 5 unit segments to the left, then the sum of the numbers corresponding to these points will become equal to -35. How many numbers were marked on the line?
|
1. The sum of the numbers decreased by $25-(-35)=60$. Therefore, $60: 5=12$ numbers were marked.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. In one line, 19 numbers were written. The sum of any three consecutive numbers is positive. Can the sum of all 19 numbers be negative?
|
9. Consider, for example, the sequence of numbers $\underbrace{-7,4,4, \ldots,-7,4,4,-7}_{19 \text { numbers }}$. The sum of any 3 consecutive numbers in this sequence is 1, i.e., positive, while the sum of all 19 numbers is -1, i.e., negative. Answer: It can. Find another similar example.
|
-1
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12. Based on the first three lines, establish the rule by which the number $c$ is obtained from the numbers $a$ and $b$, and fill in the missing numbers in the empty cells:
| $a$ | $b$ | $c$ |
| :---: | :---: | :---: |
| 5 | -11 | 6 |
| $-2.7$ | $-2.3$ | 5 |
| 32 | -18 | -14 |
| -17 | 5 | |
| 14 | -14 | |
|
12. Obviously, $c=-(a+b)$, so the missing numbers are $-(-17+5)=12$; $-(14-14)=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
19. On the number line, points $A, B, C, D$ were marked. It is known that the first three points correspond to the numbers 5, 8, and -10. What number corresponds to point $D$, if when the direction of the number line is reversed, the sum of the four numbers corresponding to these points does not change?
|
19. Let the point $D$ correspond to the number $x$. The sum of the numbers before changing the direction of the line is $5+8-10+x$, and after changing the direction it is $-5-8+10-x$. According to the condition, $5+8-10+x=5-8+10-x$, from which $2x = -6$ and $x = -3$. The problem can be solved more simply without resorting to an equation. Since the sum did not change when the signs were reversed, it is equal to zero. And if we have the terms 8, 5, and -10, then the fourth term is -3, because in this case $8+5-10-3=0$. Therefore, the point $D$ corresponds to the number -3.
|
-3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
21. Simplify the expression
$-1-(-1-(-1-(-1-(\ldots$, if the expression contains:
a) 1989 ones; b) 1990 ones.
|
21. Observing
$$
\begin{aligned}
& -1-(-1)=-1+1=0 \\
& -1-(-1-(-1))=-1 ; \\
& -1-(-1-(-1-(-1)))=0 ; \\
& -1-(-1-(-1-(-1-(-1))))=-1
\end{aligned}
$$
we notice that with an even number of ones, the result is 0, and with an odd number of ones, the result is -1. Therefore, in case a) we have -1, and in case b) we have 0. [^0]
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
22. Given 5 numbers: $a_{1}=-1, a_{2}=0, a_{3}=1, a_{4}=2, a_{5}=3$. The sixth is the product of the first and the second, the seventh is the product of the second and the third, the eighth is the product of the third and the fourth, and so on. What is the last non-zero number in this sequence?
|
22. Let's construct a table:
| $a_{1}$ | $a_{2}$ | $a_{3}$ | $a_{4}$ | $a_{5}$ | $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ | $a_{13}$ | $a_{14}$ | $a_{15}$ | $a_{16}$ | $a_{17}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| -1 | 0 | 1 | 2 | 3 | 0 | 0 | 2 | 6 | 0 | 0 | 0 | 12 | 0 | 0 | 0 | 0 |
Starting from $a_{14}$, all numbers will be zeros, so the last non-zero number will be $a_{13}=12$.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
23. Given 5 numbers: $a_{1}=1, a_{2}=-1, a_{3}=-1, a_{4}=1, a_{5}=-1$. The following numbers are determined as follows: $a_{6}=a_{1} \cdot a_{2}, a_{7}=a_{2} \cdot a_{3}, a_{8}=a_{3} \cdot a_{4}$ and so on. What is $a_{1988}$?
|
23. Let's construct a table:
| $a_{1}$ | $a_{2}$ | $a_{3}$ | $a_{4}$ | $a_{5}$ | $a_{6}$ | $a_{7}$ | $a_{8}$ | $a_{9}$ | $a_{10}$ | $a_{11}$ | $a_{12}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 1 | -1 | -1 | 1 | -1 | -1 | 1 | -1 | -1 | 1 | -1 | -1 |
We notice that in the obtained sequence, the group of numbers $1, -1, -1$ repeats periodically. If there are 1988 numbers, then the number of complete periods will be $662 (1988: 3=$
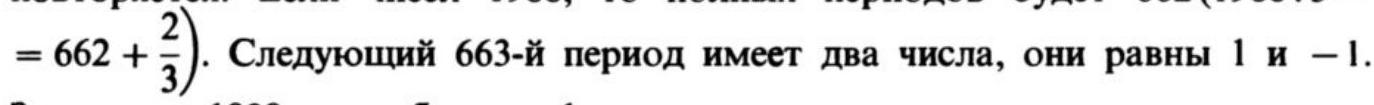
This means that the number at the 1988th position will be -1.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. Petya has as many sisters as brothers, while his sister Ira has twice as few sisters as brothers. How many boys and how many girls are there in this family?
|
9. If there are $x$ girls, then there are $x+1$ boys. Without Irina, there will be $x-1$ girls, then from the condition we have
$$
2(x-1)=x+1
$$
from which $x=3$. Therefore, there are 3 girls and 4 boys in the family.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. Aunt Masha is three years younger than Sasha and his same-aged friend Pasha combined. How old is Sasha when Aunt Masha was as old as Pasha is now?
|
10. Let Sasha and Pasha be $a$ years old, then Aunt Masha is $(2 a-3)$ years old. Aunt Masha was $a$ years old $(a-3)$ years ago $(2 a-3-a=a-3)$. But so many years ago, Sasha was 3 years old $(a-(a-3)=3)$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
14. In the workshop, five clocks were checked. It turned out that clock No. 3 is 3 minutes behind clock No. 2 per day. Clock No. 1 is 1 minute behind clock No. 2 per day, clock No. 4 is behind clock No. 3, and clock No. 5 is behind clock No. 1. If the readings of all five clocks are added together and the sum is divided by 5, the exact time is obtained. It is also known that one of these clocks is accurate. Which one exactly?
|
14. Let clock No. 1 show $x$ min, then clock No. $2-(x+1)$, clock No. $3-(x-2)$, clock No. $4-(x-3)$ and clock No. $5-(x-1)$. The sum of the readings of all clocks $x+(x+1)+(x-2)+(x-3)+(x-1)=5 x-5$. Since $(5 x-5): 5=$ $=x-1$, and this is the reading of clock No. 5, then these clocks show the exact time.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
15. How many people are in the team if the average age of all team members is 25 years, the team leader is 45 years old, and the average age of the team members without the team leader is 23 years?
|
15. Let there be $x$ people in the brigade, then we have $25 x=23(x-1)+45$, from which $2 x=22$ and $x=11$.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
22. Yura left the house for school 5 minutes later than Lena, but walked twice as fast as she did. How many minutes after leaving will Yura catch up to Lena?
|
22. If Lena walks $a$ m in 1 min, then Yura walks $2a$ m. Let him catch up with her after $x$ min from his start. Then we have $a \cdot 5 + a \cdot x = 2a \cdot x$, from which $x=5$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
24. Preparing his son for school, the father bought him a new uniform for 24 r. How did he pay for the purchase, if he only had 5 r bills, and the cashier only had 3 r bills?
|
24. If the buyer gave the cashier $x$ bills and received $y$ bills as change, we have the equation $5 x-3 y=24$, from which $x=\frac{24+3 y}{5}$. Since $x$ must be an integer, $24+3 y$ must be divisible by 5. This is possible with the smallest value of $y=2$. Therefore, the buyer gave 6 bills (30 p.) and received 6 p. as change (2 bills of 3 p.).
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
26. In a competition of fun and ingenuity, 9 points were awarded for each correctly completed task, and 5 points were deducted for each uncompleted or incorrectly completed task. It is known that the team was offered no more than 15 tasks and scored 57 points. How many tasks did the team complete correctly?
|
26. Let $x$ be the number of tasks completed correctly, and $y$ be the number of tasks completed incorrectly or not at all. Then we have $9 x-5 y=57$, from which $x=\frac{57+5 y}{9}$. Since $x$ is a natural number, $(57+5 y)$ must be divisible by 9. The smallest value of $y$ for which this condition is met is 3. In this case, $x=8$. Since $8+3=11$ and $11<15$, the found value of $x$ satisfies the condition.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
27. If the team had scored 97 points in the last sport, the average number of points scored by it in one sport would have been 90; if it had scored 73 points in this last sport, the average number of points per sport would have been 87. In how many sports did the team compete?
|
27. Let the team compete in $x$ sports and score $n$ points in all sports except the last one. Then we have
$$
(97+n): x=90 ;(73+n): x=87
$$
which means $97+n=90 x$ and $73+n=87 x$, so $x=8$.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
30. Several girls were picking mushrooms. They divided the collected mushrooms among themselves as follows: one of them was given 20 mushrooms and 0.04 of the remainder, another - 21 mushrooms and 0.04 of the new remainder, the third - 22 mushrooms and 0.04 of the remainder, and so on. It turned out that everyone received an equal share. How many girls were there and how many mushrooms did they collect?
|
30. Let the girls collected $x$ mushrooms. The first one received $20+0.04(x-20)$, the second one received $21+0.04(x-21-20-0.04(x-20))$ mushrooms. According to the condition $20+0.04 x-$ $-0.8=21+0.04(x-21-20-0.04(x-20))$, from which
$$
0.0016 x=0.192 \text { and } x=120 .
$$
Thus, 120 mushrooms were collected, each girl received 24 mushrooms, and there were 5 girls.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
37. Two people, who have one bicycle, need to get from point $A$ to point $B$, which is 40 km away from $A$. The first person walks at a speed of 4 km/h and rides the bicycle at 30 km/h, while the second person walks at a speed of 6 km/h and rides the bicycle at 20 km/h. What is the minimum time they can take to reach point $B$? (The bicycle can be left unattended.)
|
37. Let the first person travel $x$ hours by vehicle and $y$ hours on foot, then the second person travels $y$ hours by vehicle and $x$ hours on foot. We have the equation $30 x + 4 y = 20 y + 6 x$, from which $x = \frac{2}{3} y$. Therefore, the first person walked $y$ hours and traveled $\frac{2}{3} y$ hours by vehicle, while the second person walked $\frac{2}{3} y$ hours and traveled $y$ hours by vehicle. Knowing the total distance, we can form the equation $4 y + \frac{2}{3} y \cdot 30 = 40$, from which $y = \frac{5}{3}$ hours. The first person was on the road for $\frac{5}{3} + \frac{2}{3} \cdot \frac{5}{3} = 2 \frac{7}{9}$ (hours), and the second person was on the road for the same amount of time, as he walked $1 \frac{1}{9}$ hours and traveled $1 \frac{2}{3}$ hours. Therefore, the minimum time it takes for them to reach point $B$ is 2 hours 46 minutes 40 seconds.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
42. Ten identical books cost no more than 11 p., while 11 such books cost more than $12 \mathrm{p}$. How much does one book cost?
|
42. Let one book cost $x$ k. Then we have $x \cdot 10 \leqslant 1100$ and $x \cdot 11 > 1200$ or $x \leqslant 110$ and $x > 109 \frac{1}{11}$. Therefore, $x=110$ k., i.e., the book costs 1 p. 10 k.
|
1
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the length of the side of a square whose area is numerically equal to its perimeter.
|
2. Let the side length of the square be $a$, then the area $S=a \cdot a$, and the perimeter $P=4 a$. According to the condition $a \cdot a=4 a$, from which $a=4$.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
25. A scout is in a house with four windows arranged in a rectangular shape. He needs to signal to the sea at night by lighting a window or several windows. How many different signals can he send?
|
25. Let's schematically represent the windows and measure them:
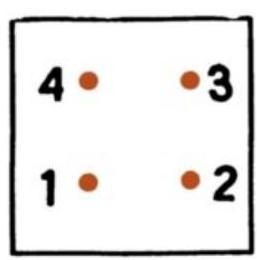
a) Lighting all four windows gives one signal;
b) Lighting one of the windows is perceived as one signal, as in the dark, the position of the windows relative to the house cannot be distinguished;
c) Lighting two windows can give 4 different signals: one signal by lighting windows 1,4 or 2,3; one signal by lighting windows 1,2 or 4,3; two signals by lighting windows 1,3 and 2,4, i.e., we have the following configurations:
1)
2) $\bullet \cdot 3)$
- 4)
d) Lighting three windows can give four signals: $1,2,3$; $2,3,4$; $3,4,1$ and $4,1,2$, i.e., we have the following configurations:
1)
2)
3)
4)
In total, we have different signals: $1+1+4+4=10$.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. Working in a collective farm orchard harvesting fruits, schoolchildren collected 22 crates, some of which contained apples, others pears, and still others plums. Can it be asserted that there are at least 8 crates, the contents of which are one of the specified types of fruit?
|
10. Let's consider the most "unfavorable" case. Suppose there are 7 boxes of apples, pears, and plums each. This makes a total of 21 boxes. If the 22nd box is with apples, then there will be 8 boxes of apples; if this box is with pears, then there will be 8 boxes of pears; if this box is with plums, then there will be 8 boxes of plums. In other cases, there will be more than 8 boxes containing one of the three types of fruits.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
18. The traffic inspector noticed that out of 20 cars that passed on the road to the airport, 14 were "Ladas," 15 were dark-colored, 17 were driven by men, and in 18 cars, there were passengers besides the driver. For what minimum number of cars could all 4 of these characteristics be true?
|
18. Out of the total number of cars, 6 did not have the first feature (not "Zhiguli"), 5 did not have the second, 3 did not have the third, and 2 did not have the fourth. Therefore, the maximum number of cars that do not have at least one feature is 16 $(6+5+3+2=16)$. The remaining $4(20-16=4)$ have all four features.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
22. The chain has broken into five parts,
But I hope you will
Join them as quickly as you can,
Doing the minimum work.
To cut and solder a link-
It takes two minutes...
Remember, the task is given
For a very thoughtful look.
Note. Each link has three rings.
|
22. Cut 3 rings of one link and join the remaining 4 links with the three resulting rings (by welding). This will take 6 minutes.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
28. A problem solved by Poisson (1781-1840) in his youth. Someone has 12 pints (a unit of volume) of honey and wants to pour out half of this amount, but he does not have a container with a capacity of 6 pints. He has 2 containers: one with a capacity of 8 pints, and the other with a capacity of 5 pints. How can he pour 6 pints of honey into the 8-pint container? What is the minimum number of transfers required to do this? (This problem determined Poisson's life path: he dedicated his entire life to mathematics.)
|
28. Let's represent it with such a diagram:
| Vessel | | |
| :---: | :---: | :---: |
| 12 pints | 8 pints | 5 pints |
| 12 | - | - |
| 4 | 8 | - |
| 4 | 3 | 5 |
| 9 | - | - |
| 1 | 8 | 3 |
| 1 | 6 | 3 |
| 6 | 6 | - |
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
29. How can you use a balance scale and a 200g weight to divide 9 kg of sugar into two bags - 2 kg and 7 kg, if you are allowed to weigh no more than three times?
|
29. Place a weight on one pan and distribute the available sugar across the pans so that the scales are in balance. Then, on one pan there will be 4 kg 600 g of sugar, and on the other (where the weight is) - 4 kg 400 g of sugar. The second time, distribute 4 kg 600 g of sugar across the pans. On one of them (without the weight) there will be 2 kg 400 g of sugar, and on the other - 2 kg 200 g. The last (third) time, from 2 kg 200 g of sugar, weigh out 200 g using the available weight, and 2 kg will remain. (During the second weighing, the weight can be not used, and 2 kg 400 g can be evenly distributed on the pans.)
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
32. In which cases does a month have the maximum number of Saturdays? What is this number?
|
32. The maximum number of Saturdays in one month is 5, since $7 \cdot 4=28 ; 28<30$ and $28<31$. In February, there can be 5 Saturdays if it is a leap year and the month starts on a Saturday. April, June, September, and November will have 5 Saturdays if they start on a Saturday or a Friday. The remaining months can have 5 Saturdays if they start on a Saturday, Friday, or Thursday.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
37. Football teams were holding a round-robin tournament. One of the fans of this game, returning from vacation, found the following situation: the total number of points scored by all teams was 44; one team, which scored the fewest points, received one point; the two teams occupying the first and second places scored the same number of points. How many teams are participating in the tournament and how many games do they still have to play?
|
37. Since $1+2+3+4+5+6+7+8+8=44$, there are 9 teams participating in the tournament. In total, they should score 72 points ( $8 \cdot 9=72$ ). Therefore, they still need to score 28 points $(72-44=28)$, which can be achieved in 14 games $(28: 2=14)$.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
38. In a tournament where each pair of teams played each other twice, 4 teams participated. For each win, two points were awarded, for a draw - one, and for a loss - 0. The team that finished in last place scored 5 points. How many points did the team that finished in first place score?
|
38. There were 12 games in total $(3 \cdot 4=12)$. In each match, -2 points were awarded, and the total points were -24. Since $5+6+7+8=26>24$, this case is impossible.
Therefore, $5+6+6+7=24$. This means the winning team scored 7 points.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
39. In a chess tournament, each of the 8 participants plays one game with each other. All participants scored a different number of points (an integer), and the second-place finisher scored as many points as all the chess players who finished from fifth to eighth place combined. How did the players who finished in third and fifth place play against each other?
|
39. The participant who took second place, out of a total of 28 points scored by all participants together, scored no more than six points, as otherwise, they would have taken either first place or shared the first and second places, which contradicts the condition. The only possible scenario is: $28=7+6+5+4+3+2+1+0$. On the other hand, if the participants who took fifth through eighth place inclusive scored 6 points, then these points were earned by playing against each other, losing all games to the chess players who took the top four places. Therefore, the participant who took third place won against the one who took fifth.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 22. Find the minimum value of the expression $(x+y) \cdot(x+z),$ if $x, y, z-$ are positive numbers and $x \cdot y \cdot z \cdot(x+y+z)=1$.
|
Solution. Let $a=y+z ; b=x+z ; c=x+y$. Consider a triangle with sides $a, b, c$ (it is not difficult to verify that such a triangle exists for any $x, y, z$). Then:
$$
\begin{gathered}
(x+y) \cdot(x+z)=b \cdot c \\
x y z(x+y+z)=(p-a)(p-b)(p-c) p=S^{2}=1
\end{gathered}
$$
But $b \cdot c=\frac{2 S}{\sin A}=\frac{2}{\sin A}$, and $|\sin A| \leq 1$. In this case, it is clear that the minimum value of the product $b \cdot c$ is 2. Therefore, the minimum value of the expression $(x+y) \cdot(x+z)$ under the given conditions is 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
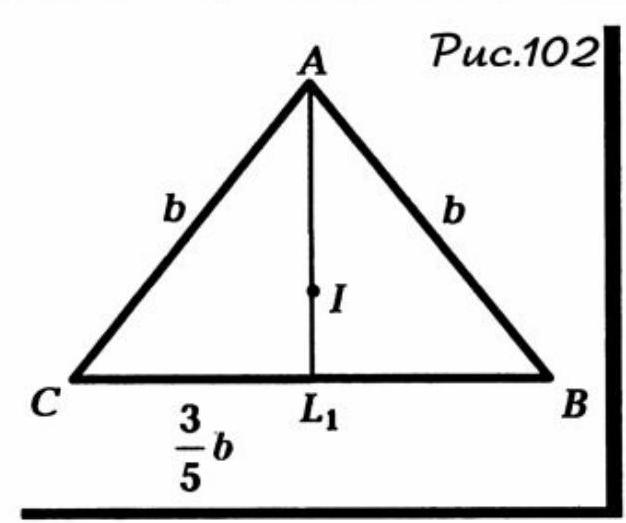
Problem 101. The center of the inscribed circle divides the height of an isosceles triangle, drawn to the base, into segments of 5 cm and 3 cm, measured from the vertex. Find the sides of the triangle.
|
Solution. Let in triangle $A B C \quad b=c$ and $\frac{A I}{I L_{1}}=\frac{5}{3}$ (Fig. 102). Then $\frac{b+c}{a}=\frac{2 b}{a}=\frac{5}{3}$, or $a=\frac{6}{5} b$. Then $\quad C L_{1}=B L_{1}=\frac{a}{2}=\frac{3}{5} b . \quad$ By the Pythagorean theorem for triangle $A L_{1} C \quad A L_{1}=\frac{4}{5} b$. Thus:
76
$$
\frac{4}{5} b=8 \text { cm, from which } b=10 \text { cm. Therefore } a=\frac{6}{5} b=12 \text { cm. }
$$
We will demonstrate how the property $\frac{A I}{I L_{1}}=\frac{b+c}{a}$ can be applied in trigonometry.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
19. Two natural numbers both give a remainder of 2 when divided by 3. What remainder does their product give when divided by 3?
|
19. $(3 m+2)(3 n+2)=3(m n+m+n+1)+1$.
Translating the above text into English, while preserving the original text's line breaks and format, results in:
19. $(3 m+2)(3 n+2)=3(m n+m+n+1)+1$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
65. What whole number is equal to the sum of all the whole numbers preceding it? Is there only one such number?
|
65. $1+2=3$. No other number $>3$ has the required property: indeed, if we move forward in the sequence of natural numbers, then with each step taken, the sum of natural numbers increases by $3, 4, 5$, etc., while each subsequent natural number increases only by 1, and therefore the difference between the sum of natural numbers preceding a given number and this number will continue to grow. -Otherwise: the sum of integers preceding the number $n$ is $\frac{(n-1) n}{2}$. If it is to equal $n$, then $\frac{n-1}{2}=1$, from which $n-1=2, \quad n=3$
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
102. A certain number is written in the duodecimal system; for which divisor $m$ is the following divisibility rule valid: if the sum of the digits of the number is divisible by $m$, then the number is also divisible by $m$?
|
102. $m=11$, because $12=11\cdot1+1, \quad 12^{2}=11\cdot13+1$ and so on.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
140. How to express with one equality sign that among three numbers $a, b, c$ at least one is equal to zero
|
140. $a b c=0$.
The above text has been translated into English, maintaining the original text's line breaks and format.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
287. How many solutions does the system of equations generally have
$$
\begin{gathered}
a x^{2}+b x y+c y^{2}=d \\
a_{1} x^{2}+b_{1} x y+c_{1} y^{2}=d_{1} ?
\end{gathered}
$$
In particular, how many solutions does the system of question 280 have?
|
287. Generally four. Excluding $d$ and $d_{1}$, we obtain a homogeneous equation of the second degree, which, generally, will determine two values of the ratio $\frac{x}{y}$ (see question 284) $\frac{x}{y}=k_{1}$ and $\frac{x}{y}=k_{2}$, from which $x=k_{1} y, x=k_{2} y$. Substituting each of these expressions sequentially into one of the given equations, we will obtain a quadratic equation each time, which will determine two values for $y$, and consequently for $x$. In total, generally, four solutions will be obtained.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
423. Can the sum of a finite number of terms of a geometric progression be zero?
|
423. If all members of the progression are real numbers, then in the trivial case only, when the progression coefficient \( q = -1 \) and the number of terms is even.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
454. Prove that the third difference of the function $n^{3}$ is constantly equal to 6. Give the general form of a function that possesses this property.
|
454. The first differences of the function $n^{3}$ are expressed by the function $3 n^{2}+3 n+1$, the second differences by $6 n+6$; consequently, the third differences are constant and equal to 6. If we add to $n^{3}$ an arbitrary function $\varphi(n)$, the third differences of which are zero, then the third differences of the resulting function $n^{3}+\varphi(n)$ will also be 6.
As is known (question 453), the most general form of $\varphi(n)$ is a quadratic trinomial.
|
6
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
456. Prove that the third difference of the function
$$
f(n)=1^{2}+2^{2}+\ldots+n^{2}
$$
is constantly equal to 2.
|
456. $f(n+1)-f(n)=(n+1)^{2}$; therefore, the first differences of $f(n)$ are $(n+1)^{2}$; the second differences are $(n+1)^{2}-n^{2}=2 n+1$, from which it is clear that the third differences are constantly equal to 2.
|
2
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
521. Through a point lying outside a plane, how many: a) lines perpendicular to the plane can be drawn? b) lines parallel to it? c) planes perpendicular to this plane? d) planes parallel to it?
|
521. a) One, b) an infinite set - generating a plane parallel to the given one, c) an infinite set - passing through the perpendicular dropped from this point, d) one (see b).
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
551. On one of the sides of triangle $A B C$ there is a point $P$; draw a line through $\boldsymbol{P}$ that cuts off from triangle $\boldsymbol{A} \boldsymbol{B} \boldsymbol{C}$ a triangle similar to it. How many solutions?
|
551. In general, there are 4 solutions. If the triangle is isosceles or equilateral, the number of solutions decreases accordingly.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
641. Study the symmetric properties of an equilateral triangle.
|
641. 3 axes of symmetry; no center of symmetry, for if such existed, it could only be (see question 634) the point of intersection of the altitudes. But it divides the altitudes in the ratio $1: 2$.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
740. Show that a rectangle is the only convex polygon in which all angles are right angles.
|
740. From the equation $\frac{180^{\circ}(n-2)}{n}=90^{\circ}$ it follows that $n=4$.
|
4
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
833. How many different values does the expression $\sin \frac{k \pi}{3}$ take when $k$ takes all integer values from 0 to $+\infty$?
|
833. Let $q$ be the integer quotient of the division of $k$ by $3$, and $r$ the remainder, which lies between -2 and 2, then $k=3 q+r$.
We have $\sin \frac{k \pi}{3}=\sin \left(q \pi+\frac{r \pi}{3}\right)=\sin \left( \pm \frac{r \pi}{3}\right)$. Everything reduces to the number of different values of the seven members of the series
$$
\sin \left(-\frac{2 \pi}{3}\right), \sin \left(-\frac{\pi}{3}\right), \sin 0^{\circ}, \sin \frac{\pi}{3}, \sin \frac{2 \pi}{3}
$$
In this series, the first two and the last two members are equal; as a result, we have 3 different values, two of which differ only in sign.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 11. Are the equations
$$
\frac{2(x-10)}{x^{2}-13 x+30}=1 \quad \text { and } \quad x^{2}-15 x+50=0
$$
equivalent?
|
Solution. We will solve the first equation. By getting rid of the denominator, i.e., multiplying both sides of the original equation by the expression $x^{2}-13 x+30$, we obtain the equation
$$
2 x-20=x^{2}-13 x+30
$$
The set of all roots of this equation consists of two numbers: $x_{1}=10$ and $x_{2}=5$. As a result of the transformation, extraneous roots could have appeared; therefore, it is necessary to check. The check shows that the number $x_{1}=10$ is not a root of the original equation, while the number $x_{2}=5$ is its root, i.e., the first equation has a single root $x=5$.
The equation $x^{2}-15 x+50=0$ has two solutions: $x_{1}=5$ and $\boldsymbol{x}_{2}=10$. Comparing the sets of roots of the given equations, we get: the second equation is a consequence of the first.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 19. Solve the equation
$$
\sqrt{x+11}=x-1
$$
|
Solution.
The first method. The domain of definition (DOD) of equation (7) is given by the condition $x \geqslant-11$. Considering that
$$
f(x)=g(x) \Rightarrow f^{2}(x)=g^{2}(x)
$$
we have
$$
\text { (7) } \begin{aligned}
\Rightarrow x+11=x^{2}-2 x+1 \Leftrightarrow x^{2}-3 x-10=0 \Leftrightarrow \\
\Leftrightarrow(x-5)(x+2)=0 \Leftrightarrow\left[\begin{array}{l}
x=5 \\
x=-2
\end{array}\right.
\end{aligned}
$$
## 14 CH. 1. EQUIVALENT EQUATIONS AND INEQUALITIES
Thus, the solutions of the original equation are among the numbers $x_{1}=5$ and $x_{2}=-2$.
Before making the check, let us draw the reader's attention to a common mistake. Transitioning from the given equation to its consequence, roots are found. Then, it is checked whether the found roots belong to the DOD of the original equation. The roots that do not belong to the DOD are discarded, and the remaining ones (belonging to the DOD of the original equation) are listed in the answer. This is where the mistake lies. It is not enough to check whether the found roots belong to the DOD of the equation. It is necessary to check whether the roots of the consequence, which belong to the DOD of the original equation, satisfy the original equation itself. This is confirmed by the given example.
Indeed, both roots of the system satisfy the DOD, but the number 5 satisfies equation (7), while the number -2 does not satisfy it. Therefore, equation (7) has a single root $x=5$.
The second method. The equation $\sqrt{\alpha(x)}=\beta(x)$ is equivalent to the system
$$
\left\{\begin{array}{l}
\beta(x) \geqslant 0 \\
\alpha(x)=\beta^{2}(x)
\end{array}\right.
$$
since $\beta^{2}(x) \geqslant 0$, and the equality $\alpha(x)=\beta^{2}(x)$ imposes a non-negativity condition on $\alpha(x)$.
When solving equations of type (7) by equivalent transitions, it is not necessary to find the DOD of this equation, but it is mandatory to impose the non-negativity condition on the function $\beta(x)$.
Considering this, for the given example, we have
(7) $\Leftrightarrow\left\{\begin{array}{l}x-1 \geqslant 0, \\ x+11=x^{2}-2 x+1\end{array} \Leftrightarrow\left\{\begin{array}{l}x \geqslant 1, \\ x^{2}-3 x-10=0\end{array} \Leftrightarrow\right.\right.$
$$
\Leftrightarrow\left\{\begin{array}{l}
x \geqslant 1 \\
{\left[\begin{array}{l}
x=-2, \\
x=5
\end{array}\right.}
\end{array} \Leftrightarrow x=5\right.
$$
Thus, $x=5$ is the only solution to equation (7).
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 4. Solve the equation
$$
\left|\frac{x^{2}-6 \sqrt{x}+7}{x^{2}+6 \sqrt{x}+7}\right|=1
$$
|
Solution. The given equation is equivalent to the system of equations
$\left[\begin{array}{l}\frac{x^{2}-6 \sqrt{x}+7}{x^{2}+6 \sqrt{x}+7}=1, \\ \frac{x^{2}-6 \sqrt{x}+7}{x^{2}+6 \sqrt{x}+7}=-1\end{array} \Leftrightarrow\right.$
$$
\Leftrightarrow\left[\begin{array}{l}
\frac{-12 \sqrt{x}}{x^{2}+6 \sqrt{x}+7}=0 \\
\frac{2 x^{2}+14}{x^{2}+6 \sqrt{x}+7}=0
\end{array} \Leftrightarrow \sqrt{x}=0 \Leftrightarrow x=0\right.
$$
Thus, the only solution to the original equation is the number 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 7. Solve the equation
$$
|x-| 4-x||-2 x=4
$$
|
Solution. The given equation is equivalent to the combination of two systems:
$$
\left\{\begin{array} { l }
{ 4 - x \geqslant 0 } \\
{ | x - ( 4 - x ) | - 2 x = 4 , }
\end{array} \quad \left\{\begin{array}{l}
4-x4 \\
-2 x=0
\end{array}\right.\right.
$$
The second system of the combination (4) has no solutions.
The first system of the combination (4) is equivalent to the combination of the following two systems:
$$
\left\{\begin{array} { l }
{ x \leqslant 4 , } \\
{ 2 x - 4 \geqslant 0 , } \\
{ ( 2 x - 4 ) - 2 x = 4 , }
\end{array} \quad \left\{\begin{array}{l}
x \leqslant 4 \\
2 x-4<0 \\
-(2 x-4)-2 x=4
\end{array}\right.\right.
$$
i.e., the combination
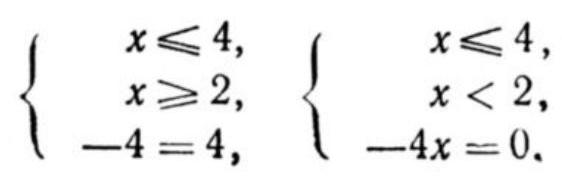
The only solution to the combination (5), and therefore to the original equation, is the number 0.
Consider an equation of the form
$$
\left|f_{1}(x)\right|+\left|f_{2}(x)\right|+\left|f_{3}(x)\right|+\ldots+\left|f_{n}(x)\right|=g(x)
$$
where \( f_{1}(x), \ldots, f_{n}(x), g(x) \) are some functions. If this equation is solved by sequentially opening the absolute value signs, then after opening one absolute value sign, a combination of two systems is obtained, after opening the second absolute value sign, a combination of four systems, and so on. This method is very cumbersome. Such equations are easier to solve using the interval method. For this, first find all points where at least one of the functions \( f_{1}(x), f_{2}(x), \ldots, f_{n}(x) \) changes sign. These points divide the domain of admissible values of equation (6) into intervals, on each of which all functions \( f_{1}(x), f_{2}(x), \ldots, f_{n}(x) \) retain their sign. Then, using the definition of absolute value, transition
Fig. 2.2
from equation (6) to a combination of systems without absolute value signs.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 4. Solve the equation
$$
3 \sqrt{x+3}-\sqrt{x-2}=7
$$
|
Solution. Isolate one of the roots on the left side:
$$
3 \sqrt{x+3}=\sqrt{x-2}+7
$$
By squaring both sides of the obtained equation, we have
$$
9(x+3)=x-2+14 \sqrt{x-2}+49
$$
Combining like terms and isolating the radical on the right side, we get the equation
$$
4 x-10=7 \sqrt{x-2}
$$
By squaring both sides of the obtained equation, we have
$$
16 x^{2}-80 x+100=49(x-2)
$$
i.e., the equation
$$
16 x^{2}-129 x+198=0
$$
which is a consequence of the original equation. We find the roots of this equation: $x_{1}=6, x_{2}=2 \frac{1}{16}$.
Substitute each of these roots into the original equation.
For $x=6$, we get a true numerical equality. Therefore, $x_{1}=6$ is a root of the original equation.
For $x=2 \frac{1}{16}$, the left side of the original equation equals $6 \frac{1}{2}$, and its right side equals 7. Since $6 \frac{1}{2} \neq 7$, the number $x_{2}=2 \frac{1}{16}$ does not satisfy the original equation, i.e., it is an extraneous root for it.
Thus, $x_{1}=6$ is the only root of the original equation.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 5. Solve the equation
$$
\sqrt{11 x+3}-\sqrt{2-x}-\sqrt{9 x+7}+\sqrt{x-2}=0
$$
|
Solution. Isolate two radicals on each side so that after squaring we get the simplest equation:
$$
\sqrt{11 x+3}-\sqrt{2-x}=\sqrt{9 x+7}-\sqrt{x-2}
$$
Perform a chain of transformations:
$$
\begin{gathered}
11 x+3-2 \sqrt{(11 x+3)(2-x)}+2-x= \\
=9 x+7-2 \sqrt{(9 x+7)(x-2)}+x-2 \\
\sqrt{6+19 x-11 x^{2}}=\sqrt{9 x^{2}-11 x-14} \\
6+19 x-11 x^{2}=9 x^{2}-11 x-14 \\
20 x^{2}-30 x-20=0 \\
2 x^{2}-3 x-2=0
\end{gathered}
$$
The last equation is a consequence of the original equation and has roots $x_{1}=2$ and $x_{2}=-0.5$.
When $x=2$, the original equation turns into a true numerical equality. Therefore, $x_{1}=2$ is its root.
When $x=-0.5$, in the left part of the original equation, we have the expression $\sqrt{-0.5-2}$, which is meaningless; therefore, the number $x_{2}=-0.5$ does not satisfy the original equation.
Thus, $x_{2}=2$ is the only root of the original equation.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 6. Solve the equation
$$
\sqrt[3]{2 x-1}+\sqrt[3]{x-1}=1
$$
|
Solution. Raising both sides of the equation to the third power, we get
$$
3 x-2+3 \sqrt[3]{(2 x-1)(x-1)}(\sqrt[3]{2 x-1}+\sqrt[3]{x-1})=1
$$
By the condition, the expression $\sqrt[3]{2 x-1}+\sqrt[3]{x-1}$ equals one. Substituting this expression with one in the obtained equation, we get the equation
$$
3 x-2+3 \sqrt[3]{(2 x-1)(x-1)}=1
$$
which is a consequence of the original equation, since equation (1) may have a root that does not necessarily satisfy the relation:
$$
1=\sqrt[3]{2 x-1}+\sqrt[3]{x-1}
$$
Raising equation (1) to the third power:
$$
(2 x-1)(x-1)=(1-x)^{3}
$$
The last equation has roots $x_{1}=0$ and $x_{2}=1$.
Verification shows that $x_{1}=0$ is an extraneous root of the original equation, while $x_{2}=1$ satisfies it.
Thus, $x_{2}=1$ is the only root of the original equation.
For an equation of the form
$$
\sqrt[3]{f(x)}+\sqrt[3]{g(x)}=\varphi(x)
$$
where $f(x), g(x), \varphi(x)$ are some functions, they are usually solved as follows. Both sides of the equation are raised to the third power to obtain the equation
$$
f(x)+g(x)+3 \sqrt[3]{f(x) g(x)}(\sqrt[3]{f(x)}+\sqrt[3]{g(x)})=\varphi^{3}(x)
$$
In this equation, the expression $\sqrt[3]{f(x)}+\sqrt[3]{g(x)}$, which is the left-hand side of the original equation, is replaced by $\varphi(x)$, which is its right-hand side. As a result, we get the equation
$$
f(x)+g(x)+3 \sqrt[3]{f(x) g(x)} \varphi(x)=\varphi^{3}(x)
$$
which (since it is solved under the condition $\sqrt[3]{f(x)}+\sqrt[3]{g(x)}=$ $=\varphi(x)$) is a consequence of the original equation. After isolating the radical and raising the obtained equation to the third power, we find its roots, and then by direct substitution of each of the found numbers into the original equation, we select those that are roots of the original equation.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 10. Solve the equation
$$
\sqrt{x+16}-x+4=0
$$
|
Solution. The domain of the equation: $x \geqslant-16$. Isolating the radical, we get the equation $\sqrt{x+16}=x-4$. Squaring both sides of this equation and combining like terms, we obtain the equation $x^{2}-9 x=0$, the roots of which are: $x_{1}=0$ and $x_{2}=9$. Each of these roots belongs to the domain of the original equation.
For the root $x_{1}=0$, the parts of the equation $\sqrt{x+16}=x-4$ being squared have different signs; therefore, $x_{1}=0$ is an extraneous root of the original equation.
By substitution, we verify that $x=9$ is the only root of the original equation.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 11. Solve the equation
$$
\sqrt{x^{2}+3 x-4}=\sqrt{2 x+2}
$$
|
Solution. Solving the system of inequalities
$$
\left\{\begin{array}{l}
x^{2}+3 x-4 \geqslant 0 \\
2 x+2 \geqslant 0
\end{array}\right.
$$
we find the domain of the equation: $x \geqslant 1$.
By squaring both sides of the original equation, we obtain the equation
$$
x^{2}+3 x-4=2 x+2
$$
which is a consequence of it. The roots of this equation are: $x_{1}=2$ and $x_{2}=-3$.
The root $x_{2}=-3$ does not belong to the domain of the original equation and is therefore extraneous.
Substituting the number 2 into the original equation, we get a true equality; hence, $x=2$ is its only root.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 12. Solve the equation
$$
\sqrt{2 x+5}+\sqrt{x-1}=8
$$
|
Solution. Domain of the equation: $x \geqslant 1$. Squaring both sides of the equation and performing transformations, we obtain the equation
$$
2 \sqrt{2 x^{2}+3 x-5}=60-3 x
$$
After squaring both sides of this equation, we get the equation
$$
4\left(2 x^{2}+3 x-5\right)=(60-3 x)^{2}
$$
which is a consequence of the original equation. The roots of this equation are: $x_{1}=10$ and $x_{2}=362$.
The number $x_{2}=362$ is an extraneous root of the original equation, as for it, the equation being squared $2 \sqrt{2 x^{2}+3 x-5}=60-3 x$ has parts of different signs.
The number $x_{1}=10$ belongs to the domain of the original equation and satisfies it; therefore, it is its only root.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 15. Solve the equation
$$
\sqrt{x+7} \sqrt{3 x-2}=3 \sqrt{x-1} \sqrt{x+2}
$$
|
Solution. Solving the system of inequalities
$$
\left\{\begin{array}{r}
x+7 \geqslant 0 \\
3 x-2 \geqslant 0 \\
x-1 \geqslant 0 \\
x+2 \geqslant 0
\end{array}\right.
$$
we find the domain of the equation: $x \geqslant 1$. Squaring both sides of the equation and combining like terms, we obtain the equation
$$
3 x^{2}-5 x-2=0
$$
which is a consequence of the original equation. The roots of this equation are $x_{1}=-1 / 3$ and $x_{2}=2$.
The root $x_{1}=-1 / 3$ does not belong to the domain of the original equation.
The root $x_{2}=2$ belongs to the domain of the original equation and, when substituted, turns it into a true numerical equality.
Thus, $x_{1}=2$ is the only root of the original equation.
The equation $f(x)=g(x) \alpha(x)$ is a consequence of the equation
$$
\frac{f(x)}{\alpha(x)}=g(x)
$$
If the domain of the function $\varphi(x)$ is not narrower than the domain of the equation $f(x)=g(x)$, then the equation
$$
f(x) \varphi(x)=g(x) \varphi(x)
$$
is a consequence of the equation
$$
f(x)=g(x)
$$
Therefore, if in the process of solving an equation, transformations are performed that consist of eliminating the denominator from the equation or multiplying the equation by an expression whose domain is not narrower than the domain of the given equation, the domain of the original equation may be expanded, and, consequently, extraneous roots may appear. In this case, verification is also a necessary part of solving the equation.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.