problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
Example 18. Solve the equation
$$
x=(\sqrt{1+x}+1)(\sqrt{10+x}-4)
$$
|
Solution. The domain of definition (DOD) of equation (6): $x \geqslant-1$. Multiplying both sides of equation (6) by the expression $\sqrt{1+x}-1$, we obtain the equation
$$
x(\sqrt{1+x}-\sqrt{10+x}+3)=0
$$
which is a consequence of equation (6). This equation has two roots: $x_{1}=0$ and $x_{2}=-1$ (note that the DOD has not been extended). Both found roots belong to the DOD of equation (6); nevertheless, checking shows that $x_{1}=0$ is an extraneous root of equation (6), while $x_{2}=-1$ satisfies it.
Thus, equation (6) has a unique root $x=-1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 25. Solve the equation
$$
\sqrt{4-6 x-x^{2}}=x+4
$$
|
Solution. The given equation is equivalent to the system
$$
\left\{\begin{array}{l}
x+4 \geqslant 0 \\
4-6 x-x^{2}=(x+4)^{2}
\end{array}\right.
$$
i.e., the system
$$
\left\{\begin{array}{l}
x \geqslant-4 \\
x^{2}+7 x+6=0
\end{array}\right.
$$
## 68
Solving the equation \(x^{2}+7 x+6=0\), we find its two roots: \(x_{1}=-1\) and \(x_{2}=-6\). The condition \(x \geqslant-4\) is satisfied only by \(x_{1}=-1\). Therefore, the only root of the original equation is the number \((-1)\).
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 26. Solve the equation
$$
\sqrt{x+5}+\sqrt{2 x+8}=7
$$
|
Solution. Solving the system of inequalities
$$
\left\{\begin{array}{r}
x+5 \geqslant 0 \\
2 x+8 \geqslant 0
\end{array}\right.
$$
we find the domain of the equation (12): $x \geqslant-4$. We have:
$$
\text { (12) } \begin{aligned}
\Leftrightarrow & \left\{\begin{array}{l}
x \geqslant-4 \\
x+5+2 \sqrt{x+5} \sqrt{2 x+8}+2 x+8=49
\end{array} \Leftrightarrow\right. \\
& \Leftrightarrow\left\{\begin{array}{l}
x \geqslant-4, \\
2 \sqrt{(x+5)(2 x+8)}=3(12-x)
\end{array} \Leftrightarrow\right. \\
& \Leftrightarrow\left\{\begin{array} { l }
{ x \geqslant - 4 , } \\
{ x \leqslant 1 2 , } \\
{ 4 ( x + 5 ) ( 2 x + 8 ) = 9 ( 1 2 - x ) ^ { 2 } }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
-4 \leqslant x \leqslant 12, \\
x^{2}-288 x+1136=0
\end{array}\right.\right.
\end{aligned}
$$
Solving the equation $x^{2}-288 x+1136=0$, we find its roots: $x_{1}=284$ and $x_{2}=4$. The condition $-4 \leqslant x \leqslant 12$ is satisfied only by $x_{2}=4$. Therefore, $x=4$ is the only root of equation (12).
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 9. Solve the equation
$$
5^{2 x}-2 \cdot 5^{x}-15=0
$$
|
Solution. Let $t=5^{x}$. Then $t^{2}-2 t-15=0$. From this, we find $t_{1}=5, t_{2}=-3$. Thus, the given equation is equivalent to the system of equations
$$
5^{x}=5, \quad 5^{x}=-3
$$
## § 3. EXPONENTIAL EQUATIONS
The second equation of this system has no roots, since $-3<0$ for any $x$, while from the first equation we find that $x=1$ is the only root of the original equation.
An equation of the form
$$
a^{f(x)}=b
$$
where $a>0, a \neq 1, b>0$, can be solved by taking the logarithm of both sides (this is possible since both sides of the equation are positive). Taking the logarithm, we obtain the equation
$$
f(x)=\log _{a} b,
$$
which is equivalent to equation (3).
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 15. Solve the equation
$$
27^{x}+12^{x}=2 \cdot 8^{x}
$$
|
Solution. This equation is similar in appearance to equation (6): the exponent of the bases is the same, but the bases 27, 12, and 8 of the three consecutive terms of a geometric progression do not form one.
Consecutive (but four) terms of a geometric progression are the numbers $27, 18, 12$, and 8. Therefore, we can assume that the term containing $18^{x}$ enters the given equation with a zero coefficient.
We divide all terms of equation (11) by $8^{x}$ and obtain
$$
(3 / 2)^{3 x}+(3 / 2)^{x}=2
$$
Let $t=(3 / 2)^{x}$; then we have the equation $t^{3}+t-2=0$. Since $t^{3}+t-2=(t-1)\left(t^{2}+t+2\right)$, this equation has a unique root $t_{1}=1$. Thus, the original equation is equivalent to the equation
$$
(3 / 2)^{x}=1
$$
the only root of which is $x=0$.
An equation of the form
$$
\alpha \cdot a^{f(x)}+\beta \cdot b^{f(x)}+c=0
$$
where $\alpha, \beta, c$ are real numbers, and the bases $a$ and $b$ are positive numbers that are reciprocals of each other (i.e., $a b=1$), can be solved as follows.
Introduce the variable $t=a^{f(x)}$ and, using the equality $a b=1$, transition from equation (12) to the equation
$$
\alpha t^{2}+c t+\beta=0
$$
Then equation (12) will be equivalent to the combination of two exponential equations:
$$
a^{f(x)}=t_{1}, \quad a^{f(x)}=t_{2},
$$
where $t_{1}, t_{2}$ are the roots of equation (12'). If equation (12') has no solutions, then equation (12) also has no solutions.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 16. Solve the equation
$$
5 \cdot 2^{3 x-3}-3 \cdot 2^{5-3 x}+7=0
$$
|
Solution. Using the properties of exponents, rewrite the given equation as
$$
\frac{5}{8} \cdot 2^{3 x}-\frac{96}{2^{3 x}}+7=0
$$
This equation is of the form (12).
Let $t=2^{3 x}$; then we have $\frac{5}{8} t-\frac{96}{t}+7=0$, i.e., $5 t^{2}+56 t-768=0$. From this, we find $t_{1}=-96 / 5, t_{2}=8$.
Thus, equation (13) is equivalent to the equation
$$
2^{3 x}=8
$$
from which $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 6. Solve the equation:
a) $\log _{x+1}\left(x^{2}-3 x+1\right)=1$
b) $\log _{x}\left(2 x^{2}-3 x-4\right)=2$.
|
Solution. a) The given equation is equivalent to the system
$$
\left\{\begin{array} { l }
{ x + 1 > 0 } \\
{ x + 1 \neq 1 , } \\
{ x ^ { 2 } - 3 x + 1 = x + 1 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x>-1 \\
x \neq 0 \\
x^{2}-4 x=0
\end{array} \Leftrightarrow x=4\right.\right.
$$
Therefore, the only root of the equation is the number 4.
b) The original equation is equivalent to the system
$$
\left\{\begin{array} { l }
{ x > 0 , } \\
{ x \neq 1 , } \\
{ 2 x ^ { 2 } - 3 x - 4 = x ^ { 2 } }
\end{array} \Leftrightarrow \left\{\begin{array} { l }
{ x > 0 , } \\
{ x \neq 1 , } \\
{ x ^ { 2 } - 3 x - 4 = 0 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x>0, \\
x \neq 1, \\
(x+1)(x-4)=0
\end{array} \Leftrightarrow\right.\right.\right.
$$
Thus, the only root of the equation is the number 4.
An equation of the form
$$
\log _{f(x)} g(x)=\log _{f(x)} h(x)
$$
can be replaced by an equivalent system in two ways.
First method:
$$
\log _{f(x)} g(x)=\log _{f(x)} h(x) \Leftrightarrow\left\{\begin{array}{l}
g(x)>0 \\
f(x)>0 \\
f(x) \neq 1 \\
g(x)=h(x)
\end{array}\right.
$$
102
CH. 2. EQUATIONS WITH ONE UNKNOWN
Second method:
$$
\log _{f(x)} g(x)=\log _{f(x)} h(x) \Leftrightarrow\left\{\begin{array}{l}
h(x)>0 \\
f(x)>0 \\
f(x) \neq 1 \\
g(x)=h(x)
\end{array}\right.
$$
An equation of the form
$$
\log _{g(x)} f(x)=\log _{p(x)} f(x)
$$
can be replaced by an equivalent system in two ways.
First method:
$$
\log _{g(x)} f(x)=\log _{p(x)} f(x) \Leftrightarrow\left\{\begin{array}{l}
f(x)>0 \\
g(x)>0 \\
g(x) \neq 1 \\
g(x)=p(x)
\end{array}\right.
$$
Second method:
$$
\log _{g(x)} f(x)=\log _{p(x)} f(x) \Leftrightarrow\left\{\begin{array}{l}
f(x)>0 \\
p(x)>0 \\
p(x) \neq 1 \\
g(x)=p(x)
\end{array}\right.
$$
Note that the choice of a system equivalent to the given equation is determined by which of the inequalities $g(x)>0$ or $h(x)>0(p(x)>0)$ is easier to solve.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 15. Solve the equation
$$
\log _{1 / 3}\left(x^{2}+3 x-4\right)=\log _{1 / 3}(2 x+2)
$$
|
Solution. Solving the system of inequalities
$$
\left\{\begin{array}{l}
x^{2}+3 x-4>0 \\
2 x+2>0
\end{array}\right.
$$
we find the domain of definition (ODZ) of equation (10): $x>1$.
Potentiating equation (10), we obtain the equation
$$
x^{2}+3 x-4=2 x+2
$$
which is a consequence of it.
Equation (11) has two roots: $x_{1}=2$ and $x_{2}=-3$. The number $x_{1}=2$ falls within the ODZ of equation (10) and is therefore its root. The number $x_{2}=-3$ does not fall within the ODZ of equation (10) and is thus an extraneous root.
Thus, the number 2 is the only root of equation (10).
Formulas of logarithms. Let $f$ and $g$ be some functions and $a>0, a \neq 1$. Then, if $f>0$ and $g>0$, we have
$1^{\circ} . \log _{a}(f g)=\log _{a} f+\log _{a} g$.
2.. $\log _{a} \frac{f}{g}=\log _{a} f-\log _{a} g$.
$3^{\circ} . \log _{a} f^{\alpha}=\alpha \log _{a} f$.
$4^{\circ} . \log _{a^{\beta}} f^{\alpha}=\frac{\alpha}{\beta} \log _{a} f$.
Applying any of these formulas formally (without considering the inequalities $f>0$ and $g>0$), one should keep in mind that the domains of definition (ODZ) of the left and right parts of each of them may be different. For example, the expression $\log _{a} f+\log _{a} g$ is defined for $f>0$ and $g>0$, while the expression $\log _{a}(f g)$ is defined both for $f>0, g>0$ and for $f<0, g<0$. Similarly, the ODZ of the left part of formulas $2^{\circ}-4^{\circ}$ may be wider than the ODZ of the right part.
Thus, transforming an equation by formally using formulas $1^{\circ}-4^{\circ}$ "from right to left" leads to an equation that is a consequence of the original equation (its ODZ may be wider). In this case, extraneous roots of the original equation may appear; therefore, at the end of the solution, one must check the membership of each root of the last equation to the ODZ of the original equation.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 6. Solve the inequality
$$
\sqrt{6-x}\left(5^{x^{2}-7.2 x+3.9}-25 \sqrt{5}\right) \geqslant 0
$$
|
Solution. The domain of definition of inequality (1) is determined by the condition $6-x \geqslant 0$, i.e., $x \leqslant 6$. Inequality (1) is equivalent to a combination consisting of an equation and a system of two inequalities:
$$
\sqrt{6-x}=0, \quad\left\{\begin{array}{l}
5^{x^{2}-7.2 x+3.9}-25 \sqrt{5} \geqslant 0 \\
x<6
\end{array}\right.
$$
From the equation $\sqrt{6-x}=0$ we find $x=6$.
Since $25 \sqrt{5}=5^{2} \cdot 5^{1 / 2}=5^{2.5}$, the first inequality of the system is equivalent to the inequality
$$
5^{x^{2}-7.2 x+3.9} \geqslant 5^{2.5}
$$
which is equivalent to the inequality
$x^{2}-7.2 x+3.9 \geqslant 2.5 \Leftrightarrow x^{2}-7.2 x+1.4 \geqslant 0 \Leftrightarrow(x-1 / 5)(x-7) \geqslant 0$.
Therefore, the first inequality of the system is equivalent to the combination of simple inequalities
$$
x \leqslant 1 / 5, \quad x \geqslant 7
$$
Considering the condition $x<6$, we obtain the solution of the system, which is the interval $-\infty<x \leqslant 1 / 5$.
Therefore, the solutions of inequality (1) are the number $x=6$ and all numbers in the interval $-\infty<x \leqslant 1 / 5$.
|
6
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Example 22. Solve the inequality
$$
\left(\sqrt{x^{2}-4 x+3}+1\right) \log _{2} \frac{x}{5}+\frac{1}{x}\left(\sqrt{8 x-2 x^{2}-6}+1\right) \leqslant 0
$$
|
Solution. The domain of admissible values of the original inequality consists of all $x$ satisfying the system
$$
\left\{\begin{array}{l}
x>0 \\
x^{2}-4 x+3 \geqslant 0 \\
8 x-2 x^{2}-6 \geqslant 0
\end{array}\right.
$$
i.e., the system
$$
\left\{\begin{array}{l}
x>0 \\
x^{2}-4 x+3 \geqslant 0 \\
x^{2}-4 x+3 \leqslant 0
\end{array}\right.
$$
It follows that the domain of admissible values consists of all $x$ satisfying the system
$$
\left\{\begin{array}{l}
x>0 \\
x^{2}-4 x+3=0
\end{array}\right.
$$
Since the quadratic equation $x^{2}-4 x+3=0$ has positive roots $x_{1}=1$ and $x_{2}=3$, the domain of admissible values of the original inequality is $x=1$ and $x=3$. The solutions of the original inequality lie within its domain of admissible values; therefore, the solutions are among the numbers 1 and 3.
Let $x=1$. Substituting this value into the left-hand side of inequality (18), we get $\log _{5} \frac{1}{5}+1=-1+1=0$, i.e., the value $x=1$ is a solution of the inequality.
Let $x=3$. Then the left-hand side of the original inequality is
$$
\log _{5} \frac{3}{5}+\frac{1}{3}=\log _{5} 3-1+\frac{1}{3}=\log _{5} 3-\frac{2}{3}=\log _{5} \frac{3}{5^{2 / 3}}
$$
Since $27>25$, then $3>5^{2 / 3}$, i.e., $\frac{3}{5^{2 / 3}}>1$; therefore, $\log _{5} \frac{3}{5^{2 / 3}}>0$. Hence, the value $x=3$ is not a solution of the original inequality.
Thus, the set of solutions of the original inequality consists of the single number $x=1$.
|
1
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12. Find an integer whose cube is equal to the sum of the cubes of the three preceding consecutive numbers.
|
12. Answer. 6. We obtain an interesting identity:
$$
3^{3}+4^{3}+5^{3}=6^{3}
$$
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
52. Find the remainder when the number $50^{13}$ is divided by 7.
|
52. $50^{13}=(49+1)^{13}=49 n+1$ (by the binomial theorem); therefore, the remainder of the division of $50^{13}$ by 7 (and also by 49) is 1.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
98. For what integer values of $x$ is the number $a\left(x^{3}+a^{2} x^{2}+\right.$ $\left.+a^{2}-1\right)$ divisible by 6 for any integer $a$?
As is known, the difference $a^{n}-b^{n}$ is divisible by $a-b$ for any natural number $n$; $a^{n}-b^{n}$ is divisible by $a+b$ for even $n$; $a^{n}+b^{n}$ is divisible by $a+b$ for odd $n$.
Prove the following statements (Nos. 99 - 127):
|
98. $x=3 t$ and $x=3 t-a^{2}$.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
162. Find a perfect number of the form $p q$, where $p$ and $q$ are prime numbers.
|
162. $\frac{\left(p^{2}-1\right)\left(q^{2}-1\right)}{(p-1)(q-1)}-p q=p q, \quad q=1+\frac{2}{p-1}, \quad$ from here $p_{1}=2, p_{2}=3, q_{1}=3, q_{2}=2$.
Answer. 6 .
42
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
262. Find a triangular number whose square is also a triangular number.
|
262. From the equation $\left[\frac{x(x+1)}{2}\right]^{2}=\frac{y(y+1)}{2}$, we find:
$$
y=\frac{-1+\sqrt{2 x^{2}(x+1)^{2}+1}}{2}
$$
Let $x(x+1)=z$, then $2 z^{2}+1=t^{2}, t^{2}-2 z^{2}=1$.
Solving this Pell's equation, we get an infinite set of values $z=2,12,70,408 \ldots$. From the equation $x(x+1)=2$, we have $x=1$, the corresponding triangular number is 1. From the equation $x(x+1)=12$, we find $x=3$, the triangular number will be 6. The values $z=70$ and $z=408$ do not lead to triangular numbers.
60
It has been proven that, apart from 1 and 6, there are no triangular numbers that satisfy the requirement of the problem.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
296. The difference between a number and the product of its digits is equal to the sum of the digits of this number. Find this number.
## Chapter $I X$.
## VARIOUS PROBLEMS
|
296. Let the desired number contain $n$ digits $a, b, c$, $\ldots, k, l$. According to the condition $a \cdot 10^{n-1}+b \cdot 10^{n-2}+\ldots+$ $+k \cdot 10+l-a b c d \ldots k l=a+b+c+\ldots+k+l, \quad$ from which $9 k=a\left(b c \ldots k l+1-10^{n-1}\right)+b\left(1-10^{n-2}\right)+c\left(1-10^{n-3}\right)+$ $+\ldots(1)$.
In the general case, this equality is impossible. Indeed,
$$
b c \ldots k l-\left(10^{n-1}-1\right)<10^{n-1}-\left(10^{n-1}-1\right)
$$
$b c \ldots k l-\left(10^{n-1}-1\right)<1$; since $b c \ldots k l-\left(10^{n-1}-1\right)-$ is an integer, not equal to zero, it is negative; thus, the right side of equality (1) is negative, while the left side is non-negative.
The only possible case is $n=2$ (by the problem's meaning $n \neq 1$), then $10 a+b-a b=a+b$, from which $b=9 ; a-$ is any digit (not zero). The problem is satisfied by two-digit numbers ending in 9.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Charity. A generous person distributed the same amount of money equally among those who asked him for assistance every week. One day he noticed:
- If the number of petitioners is five less next week, each will receive two dollars more.
But, alas, after a week, the number of petitioners did not decrease but increased by four.
- This means,--the benefactor noted,--that each will receive one dollar less.
How much did each petitioner receive this last time?
|
4. At first, there were 20 people and each received 6 dollars. Fifteen people (five fewer) would have received 8 dollars each. But their number increased to 24 (by four people), and each received only 5 dollars. Thus, the weekly donation amount is 120 dollars.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. The "Reverse" Game. Seven friends decided to play cards by somewhat unusual rules. The one who won had to pay each of the other players as much money as they had in their pocket. The players played seven rounds and, strangely enough, they won in alphabetical order of their names, starting with $A, B, C, D, E, F$ and $G$.
After finishing the game, the friends discovered that each of them had exactly 1 dollar and 28 cents left. How much money did each player have before the game started?
|
8. Players \(A, B, C, D, E, F\) and \(G\) had, before the game began, 4 dollars 49 cents, 2 dollars 25 cents, 1 dollar 13 cents, 57 cents, 29 cents, 15 cents, and 8 cents, respectively. The answer can be obtained by working from the end of the problem to the beginning, but a simpler method is as follows: \(7+1=8 ; 2 \times 7+1=15 ; 4 \times 7+1=29\) and so on (the first multipliers represent successive powers of two, that is, the numbers \(2,4,8,16,32\) and 64\()\).
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
46. The Clocks from the Land of Dreams. In a dream, I traveled to a country where wondrous things happened. One incident was so memorable that I didn't forget it even after I woke up. In my dream, I saw a clock and spoke aloud the time it showed, but my guide corrected me. He said:
- Clearly, you don't know that our minute hands always move in the direction opposite to the hour hands. In every other way, our clocks are exactly the same as the ones you are used to.
If at the moment I was looking at the clock, both hands coincided and were between the four and five o'clock marks, and at noon they both pointed to XII, then what time was it on a regular clock?
|
46. If these were ordinary clocks, they would show 4 hours \(23 \frac{1}{13}\) minutes. But since the minute hand moved in the direction opposite to the hour hand, the true time was 4 hours \(36 \frac{12}{13}\) minutes. To get the true time, you need to subtract from 60 the number of minutes that the clock shows.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
48. Indistinguishable Clock Hands. A person had a clock on which it was impossible to distinguish the hour hand from the minute hand. If this clock was started at noon, when would it first be impossible to tell the exact time?
The reader should remember that in such clock puzzles, there is a convention that we are able to determine fractions of a second. With this assumption, an exact answer can be given.
|
48. This will first occur at 12 hours \(5 \frac{5}{143}\) minutes, which could be incorrectly interpreted (due to the identical positions of the hands) as 1 hour \(\frac{60}{143}\) minutes.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 51. Mixed-Up Hands.
- Yesterday, between two and three o'clock, - said Colonel Crackham, - I looked at my watch and, mistaking the hour hand for the minute hand, I was wrong in my estimate of the time. The erroneous time was 55 minutes less than the actual time. What was the actual time?
|
51. The true time was 2 hours \(5 \frac{5}{11}\) minutes.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
52. Equal Distances. A few days ago, Professor Rackbrain stunned his students with the following puzzle:
- When between three and four o'clock is the minute hand at the same distance from VIII as the hour hand is from XII?
|
52. At 3 hours \(23 \frac{1}{13}\) minutes.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
53. To the right and to the left. At what time between three and four o'clock is the minute hand the same distance to the left of XII as the hour hand is to the right of XII?
|
53. At 3 hours \(41 \frac{7}{13}\) minutes.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
54. At a Right Angle. Once during breakfast, Professor Rackbrain asked his young friends a simple question:
- When between five and six o'clock will the hour and minute hands be exactly at a right angle?
|
54. For the angle between the hands to be a right angle, the minute hand must be exactly 15 minutes ahead of or behind the hour hand. Each of these positions will occur 11 times in 12 hours, that is, every 1 hour \(5 \frac{5}{11}\) minutes. If eight such intervals pass after 9 o'clock, the clock will show 5 hours \(43 \frac{7}{11}\) minutes. On the other hand, if two such intervals pass after 3 o'clock, we get 5 hours \(10 \frac{10}{11}\) minutes. These are the two moments in time,
\footnotetext{
* Here M. Gardner is not entirely correct, as Dudeney considers IX as a combination of two digits: I and X.
}
that were required to find in the problem, with the second moment, of course, occurring earlier than the first.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
59. A Walk. One man set out for a walk from Appleminster to Boniham at noon, and his friend left Boniham for Appleminster at two o'clock of the same day. On the way, they met. The meeting took place at five minutes to five, after which the friends arrived simultaneously at their final destinations. When did they finish their journey
|
59. It should be noted (and this is the key to the solution) that the person from B. covers 7 km in the same time that the person from E. covers 5 km. Let's assume, for example, that the distance between the cities is 24 km, then they met 14 km from E. The person from E. was moving at a speed of \(3 \frac{3}{7}\) km/h, and the person from B. - at a speed of \(4 \frac{4}{5}\) km/h. Both completed their journey at 7 p.m.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
65. Motorcycle with a sidecar. Atkins, Baldwin, and Clark decided to go on a trip. Their journey will be 52 km. Atkins has a motorcycle with a one-person sidecar. He needs to take one of his companions for some distance, drop him off to walk the rest of the way, return, pick up the other companion who started walking at the same time, and continue so that all three arrive at the destination at the same time. How can this be done?
The motorcycle's speed is 20 km/h, Baldwin can walk at a speed of 5 km/h, and Clark at 4 km/h. Of course, each one tries to move as quickly as possible and does not stop anywhere along the way.
The problem could be made more complex by introducing more passengers, but in our case, it is so simplified that even all distances are expressed in whole kilometers.
|
65. Atkins drives Clark 40 km and drops him off to walk the remaining 12 km. Then he returns and picks up Baldwin 16 km from the start and drives him to the end. The three of them spend 5 hours on the road. Another solution is for Atkins to first drive Baldwin 36 km and return for Clark, who by this time has walked 12 km. In both cases, the motorcycle has traveled 100 km, including 24 km without passengers.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
74. Baxter's Dog. Here is an interesting puzzle, complementing the previous one. Anderson left the hotel in San Remo at 9 o'clock and was on the road for a whole hour when Baxter set out after him along the same route. Baxter's dog ran out at the same time as its owner and kept running back and forth between him and Anderson until Baxter caught up with Anderson. Anderson's speed is 2 km/h, Baxter's is 4 km/h, and the dog's is 10 km/h. How many kilometers did the dog run by the time Baxter caught up with Anderson?
The reader who sent me this problem, being a meticulous person, deemed it necessary to specify that "the length of the dog and the time spent turning can be neglected." I would add, on my part, that the dog's name and the day of the week can equally be neglected.
|
74. It is quite obvious that Baxter will catch up with Anderson in one hour, by which time they will have each traveled 4 km in the same direction. Furthermore, the dog’s speed is 10 km/h; therefore, in this hour, it will have run 10 km! When this puzzle was presented to a French mathematics professor, he exclaimed, “Mon Dieu, quelle série!”*, completely failing to notice how simple it was to solve.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
79. Oncoming Trains. At Wurzltown station, an old lady, looking out the window, shouted:
- Conductor! How long is it from here to Madville?
- All trains take 5 hours in either direction, ma'am, - he replied.
- And how many trains will I meet on the way?
This absurd question puzzled the conductor, but he readily answered:
- Trains from Wurzltown to Madville and from Madville to Wurzltown depart at five minutes past one, five minutes past two, and so on, with an interval of exactly one hour.
The old lady made one of her fellow passengers in the compartment find the answer to her question.
So how many trains will she meet on the way?
|
79. Since the train travels for 5 hours, we will divide the journey into 5 equal intervals. When the lady departs from Wurzeltown, 4 oncoming trains are already en route, and the fifth one is just leaving the station. She will meet each of these 5 trains. When the lady has traveled \(\frac{1}{5}\) of the distance, a new oncoming train will depart from Madville, when she has traveled \(\frac{2}{5}\) of the distance - another one, \(\frac{3}{5}\) - another one, \(\frac{4}{5}\) - another one, and finally, when she arrives in Madville, another, the fifth, train will be just departing from there. If we assume, as we should, that
\footnotetext{
* The answer follows directly from the theorem of velocity addition in mechanics, and the author's solution is merely an explanation of this theorem for the specific case under consideration.
}
she does not meet the last train "on the way" or the one that arrived in Wurzeltown when her train departed from there, then on the way from Wurzeltown to Madville, the lady will meet 9 trains.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
85. The Fly and the Cars. The length of the road is 300 km. Car $A$ starts at one end of the road at noon and moves at a constant speed of 50 km/h. At the same time, at the other end of the road, car $B$ starts at a constant speed of 100 km/h and a fly, flying at 150 km/h. Upon meeting car $A$, the fly turns and flies towards $B$.
1) When will the fly meet $B$?
2) If, upon meeting $B$, the fly turned, flew towards $A$, met him, turned again, and continued flying back and forth between $A$ and $B$ until they collided, when would the cars crush the fly?
|
85. 1) The fly will meet \(B\) in 1 hour 48 minutes.
2) There is no need to determine the distance the fly will fly. This is too difficult a task. Instead, we can simply find the time when the cars could have collided, which is 2 hours. In reality, the fly flies (in kilometers):
\[
\frac{270}{1}+\frac{270}{10}+\frac{270}{100}+\frac{270}{1000}+\cdots \text { to infinity; }
\]
the sum of this infinite decreasing geometric progression is 300 km.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
88. Transportation Puzzle. Twelve soldiers need to get to a point 20 km away from their location as quickly as possible. To do this, they stopped a small car.
- I drive at a speed of 20 km/h, - the driver said, - but I can only take four of you at a time. How fast do you walk?
- Each of us walks 4 km/h, - one of the soldiers replied.
- Excellent, - the driver exclaimed, - then I will drive forward with four of you, take them part of the way, then return and pick up another four, take them as well, and return for the rest. All you need to do is walk whenever you are not in the car, I will take care of the rest.
The soldiers set off at exactly noon. When will they arrive at their destination[^5]
|
88. The driver must transport four soldiers 12 km and drop them off 8 km from the destination. Then he must return 8 km and pick up another four soldiers (out of eight) who will be there by then, transport them 12 km and drop them off 4 km from the destination. Returning 8 km to pick up the remaining soldiers, who by then will have walked 8 km from the starting point, he must transport them 12 km to the end. All soldiers will arrive at the destination simultaneously, and the car will have traveled 52 km in \(2 \frac{3}{5}\) hours. Therefore, the soldiers will arrive at the destination in 2 hours and 36 minutes.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
99. Fruits for Jam. For making jam, it was necessary to weigh fresh fruits. It turned out that apples, pears, and plums balance each other as shown in the figure.

Could you tell how many plums would balance one pear? The relative sizes of the fruits in the figure are depicted incorrectly (this is done intentionally), but we should assume that fruits of the same type weigh the same.
Obviously, 3 apples and a pear weigh as much as 10 plums, and that an apple and 6 plums balance one pear. But how many plums would be needed to balance a pear?
|
99. On the first scales, we see that an apple and 6 plums weigh the same as a pear, so on the second scales, we can replace the pear with an apple and 6 plums without disrupting the balance. Then we can remove 6 plums from each side and find that 4 apples weigh the same as 4 plums. Therefore, one apple weighs the same as one plum. By replacing the apple with a plum on the first scales, we get that one pear weighs the same as 7 plums. As they write in old textbooks: Q.E.D.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
122. Digits and Cubes. Professor Rackbrain recently asked his young friends to find all five-digit squares for which the sum of the numbers formed by the first two and the last two digits is a perfect cube. For example, if we take the square of 141, which is 19881, and add 81 to 19, we get 100 - a number that, unfortunately, is not a perfect cube.
How many solutions exist?
|
122. There are three solutions: \(56169\left(237^{2}\right)\), where \(56+69=125\) \(\left(5^{3}\right) ; 63001\left(251^{2}\right)\), where \(63+01=64\left(4^{3}\right)\) and \(23104\left(152^{2}\right)\), where \(23+04=\) \(27\left(3^{3}\right)\).
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
140. An example of multiplication. One morning at breakfast, the Crackhams were discussing high matters, when suddenly George asked his sister Dora to quickly multiply
$$
1 \times 2 \times 3 \times 4 \times 5 \times 6 \times 7 \times 8 \times 9 \times 0
$$
How long will it take the reader to find this product?
|
140. George's question did not catch Dora off guard. She immediately gave the correct answer: 0.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 163. The Cat and the Mouse.
- One of these barrels has a mouse in it,- said the dog.
- Which one? - asked the cat.
- Well, the five hundredth.
- What do you mean by that? There are only five barrels here.
- The barrel I mean will be the five hundredth if you start counting forward and backward like this.
And the dog explained how exactly one should count:
| 1 | 2 | 3 | 4 | 5 |
| ---: | ---: | ---: | ---: | ---: |
| 9 | 8 | 7 | 6 | |
| | 10 | 11 | 12 | 13 |
For example, the seventh barrel will coincide with the one that has the number 3, and the twelfth barrel with the one that has the number 4.
- This will take a lot of time,- said the cat and began to count patiently. Several times she got confused and started all over again.
- Damn it!-exclaimed the dog.-Hurry up, or it will be too late!
- Be damned yourself! You made me lose my count again, now I have to start all over.
Meanwhile, the mouse, having heard the entire conversation, gnawed a hole and slipped away just as the cat jumped into the right barrel.
- I knew it would happen, - said the dog. - Your education I would not dare to call too brilliant. A little familiarity with arithmetic would not hurt any cat, just as it does not hurt any dog. What am I saying! Even some snakes are so diligent in this science that they have to wear glasses!
Which of the barrels was the five hundredth? Could you find the answer without counting to 500?

|
163. You just need to divide the given number by 8. If it divides evenly, with no remainder, the mouse is in the second barrel. If the remainder is 1, 2, 3, 4, or 5, the barrel number will match this remainder. If the remainder is greater than 5, subtract it from 10. The resulting difference is the barrel number. The number 500, when divided by 8, gives a remainder of 4, so the number on the sought-after barrel is 4.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
182. Quarrelsome Children. A man married a widow, and each of them had children from their previous marriages. After 10 years, a battle broke out in which all the children (by then there were 12) participated. The mother ran to the father, shouting:
- Come quickly. Your children and my children are beating our children!
Each now had 9 children of their own.
How many children were born in these 10 years?
|
182. Each of the parents had 3 children from their first marriage, and 6 children were born from their second marriage.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
216. Blindness in Bats. One naturalist, trying to mystify Colonel Crackham, told him that he had studied the question of blindness in bats.
- I found,- he said, - that the ingrained habit of bats to sleep during the day in dark corners and fly only at night has led to the spread of blindness among them, although some individuals saw well with both or one eye. Two of the bats I examined saw with the right eye, three with the left, four did not see with the left eye, and five did not see with the right eye.
Could you calculate the smallest number of bats the naturalist had to examine to obtain such results?
|
216. The smallest number of mice is 7, with three possible cases:
1) 2 see well, 1 is blind only in the right eye, and 4 are completely blind
2) 1 sees well, 1 is blind only in the left eye, 2 are blind only in the right eye, and 3 are completely blind;
3) 2 are blind only in the left eye, 3 only in the right eye, and 2 are completely blind.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
239. Fence Order. One person ordered a fence with a total length of 297 m. The fence was to consist of 16 sections, each containing a whole number of meters. Moreover, 8 sections were to have the maximum length, while the others were to be 1, 2, or 3 meters shorter.
How should this order be carried out? Suppose that the 8 sections of maximum length contain 15 m each, then the remaining sections have lengths of 14, 13, or 12 m; naturally, it is not necessary to take sections of each of these sizes.
|
239. 8 sections of 20 m each, 1 section 18 m long, and 7 sections of 17 m each were manufactured. Thus, a total of 16 sections with a total length of \(297 \mathrm{m}\) were obtained, as required by the customer.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
243. Обезьяна и груз. Вот одна забавная задачка, которая представляет собой симбиоз нескольких головоломок, в том числе головоломок Льюиса Кэрролла «Обезьяна и груз» и Сэма Лойда «Сколько лет Мэри?» Хорошенько подумав, вы ее безусловно решите.
Через блок перекинута веревка, на одном конце которой висит обезьяна, а на другом груз. Длина обоих концов веревки одинакова, и система находится в равновесии. Каждый фут веревки весит
4 унции. Возраст обезьяны вместе с возрастом ее матери составляет 4 года. Обезьяна весит столько фунтов ${ }^{*}$, сколько лет ее матери. Мать обезьяны вдвое старше, чем была обезьяна, когда ее мать была вдвое моложе, и чем будет обезьяна, когда она станет в три раза старше, чем была ее мать, когда та была втрое старше обезьяны. Вес веревки с грузом в полтора раза больше разницы между весом груза и еще таким весом и весом обезьяны.
Чему равна длина веревки
|
243. Сначала мы находим возраст обезьяны ( \(1 \frac{1}{2}\) года) и возраст ее матери ( \(2 \frac{1}{2}\) года). Следовательно, обезьяна весит \(2 \frac{1}{2}\) фунта и столько же весит груз. Затем мы находим, что вес веревки составляет \(1 \frac{1}{4}\) фунта, или 20 унций, а поскольку каждый фут весит 4 унции, то длина веревки равна 5 футам.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
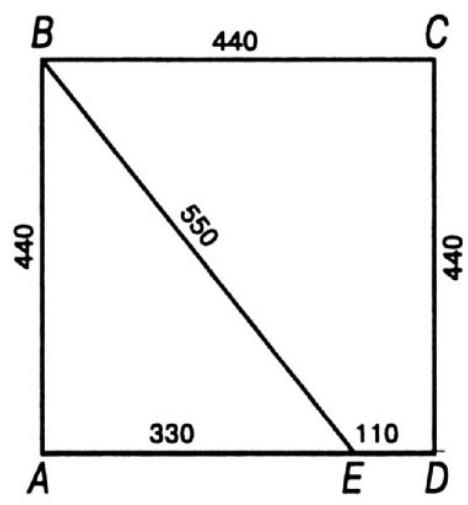
270. The Runner's Puzzle. $A B C D$ is a square field with an area of 19.36 hectares. $B E$ is a straight path, and $E$ is 110 meters from $D$. During the competition, Adams ran straight from $A$ to $D$, while Brown started running from $B$, reached $E$, and then continued towards $D$.
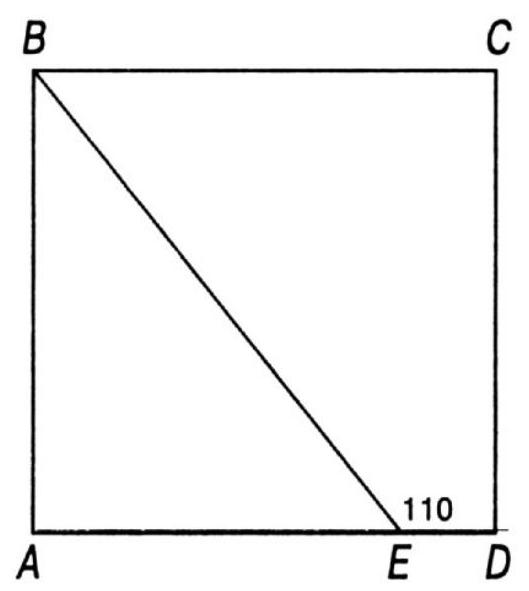
Each ran at a constant speed, and when Brown reached $E$, he saw Adams 30 meters ahead of him.
Who won the competition and by what margin?
|
270. Each side of the field is 440 m, \(B A E\) is a right-angled triangle. Therefore, \(A E=330\) m, \(B E=550\) m. If Brown runs 550 m in the same time it takes Adams to run 360 m \((330+30)\), then Brown can run the remaining 100 m in the time it takes Adams to run only \(72 \mathrm{m}\). But \(30+72=102 \mathrm{m}\), so Brown wins, beating his opponent by 8 m.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
282. Cross of chips. Arrange 20 chips in the shape of a cross, as shown in the figure. How many different cases can you count where four chips form a perfect square?
For example, squares are formed by the chips at the ends of the cross, the chips located in the center, as well as the chips marked with the letters $A$ and $B$.
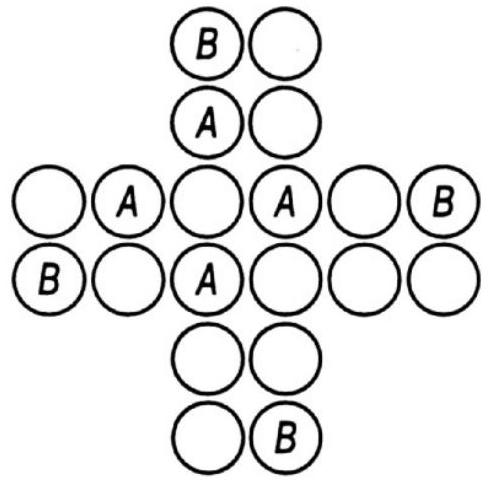
Which 6 chips should be removed so that no four of the remaining chips are located at the vertices of any square?
|
282. There are 19 such squares in total. Of these, 9 are the same size as the square marked with the letters \(a\), 4 are the same size as the square marked with the letters \(b\), 4 are the size of \(c\), and 2 are the size of \(d\). If 6 chips marked with the letter \(e\) are removed, it will be impossible to form any square from the remaining chips.
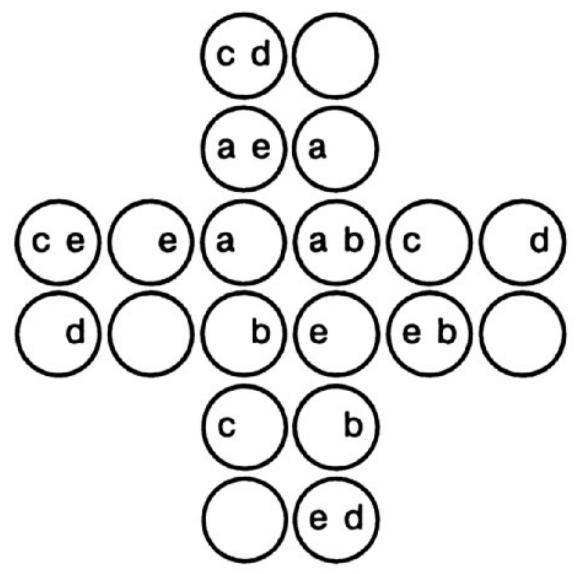
[In fact, there are 21 squares. Will the reader be able to find the two squares that Dudeney missed? The answer to the second part of the problem remains correct, nevertheless. - M. G.]
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
368. Black and White. One day over a cup of tea, Professor Rackbrain showed his friends the following old puzzle.

Arrange 4 white and 4 black chips in a row, alternating as shown in the picture. The puzzle is to move two adjacent chips to one of the ends, then move two other adjacent chips to the vacated space, and so on, until after 4 moves all the chips form a straight line without gaps, with the 4 black chips followed by the 4 white chips. Remember, you can only move adjacent chips.
- Now,- said Rackbrain,-since you have learned how to play this game, try another version. The conditions remain the same, but when moving two adjacent chips, you must swap their positions. For example, if you move chips 5,6 to the end, you must place them in the order 6,5. How many moves will it take now?
|
368. In the first case, move the pairs in the following order: place 6 and 7 before 1, then 3 and 4, 7 and 1, and 4 and 8 in the free spaces. This will result in the following arrangement of chips: 6,4, 8,2,7,1,5,3.
In the second case, move the chips 3,4 and place them in reverse order (4,3) before chip 1. Then move, simultaneously reversing the order of the chips, the pairs 6,7 (after rearrangement 7,6), 6,5 (after rearrangement 5,6), 3,1 (after rearrangement 1,3), and 6,8 (after rearrangement 8,6). The chips will be arranged in the sequence \(4,8,6,2,7,1,3,5\) in just 5 moves.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
377. Difference Squares. Can you arrange 9 digits in a square so that in any row, any column, and on each of the main diagonals, the differences between the sum of two digits and the third digit are the same? In the square provided in our diagram, all rows and columns meet the required condition - the difference in them is 3 (for example, $4+2-3,1+9-7,6+5-8$, etc.), but the diagonals "fall short," since the differences $8-(4+1)$ and $6-(1+2)$ are obtained in a prohibited manner: one digit should not be subtracted from the sum of two others, but rather the sum of two minus one.
How many solutions exist in total?
| 4 | 3 | 2 |
| :--- | :--- | :--- |
| 7 | 1 | 9 |
| 6 | 5 | 8 |
|
377. Apparently, there are only three solutions provided here. In each case, the difference is 5.
OTBETM
277

|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
436. The Crossing. Six relatives need to cross a river in a small boat that can only hold two people at a time. Mr. Webster, who was in charge of the crossing, had a falling out with his father-in-law and son. Unfortunately, I must also note that Mrs. Webster is not speaking to her mother and her daughter-in-law. The tension between them is so high that it would be unsafe to allow feuding parties to cross together or to remain on the same bank of the river. Additionally, to prevent further disputes, no man can be left with two women or two men with three women.
How can this respectable family cross to the opposite bank in the fewest number of trips? No tricks such as using a rope or swimming to another bank are allowed.
|
436. The puzzle can be solved in 9 crossings as follows:
1) Mr. and Mrs. Webster cross together;
2) Mrs. Webster returns;
3) the mother and daughter-in-law cross
4) Mr. Webster returns;
5) the father-in-law and son cross
6) the daughter-in-law returns;
7) Mr. Webster and the daughter-in-law cross;
8) Mr. Webster returns;
9) Mr. and Mrs. Webster cross together.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
484. Zero from fifty-seven. After the previous puzzle, this one will seem quite simple.
In our drawing, you see 6 cigarettes (matches would work just as well) arranged to form the number 57. The puzzle is to move two of the cigarettes without touching the others to get 0.
Remember, you can only move two cigarettes. There are two completely different solutions. Can you find one or even both?
|
484. Move the two cigarettes forming the letter \(L\), and place them as shown in the figure. We have the square root of 1 minus 1 (i.e., \(1-1\)), which is obviously equal to 0. In the second case, we can move the same two cigarettes, placing one next to V and the other next to the second I, so that the word NIL (nothing) is formed.
|
0
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The Absent-Minded Secretary. The typist typed ten letters and addresses on ten envelopes, but the absent-minded secretary placed these letters into the envelopes without any regard for the correspondence between the letter and the addressee. However, she did place only one letter in each envelope. What is the probability that exactly nine letters ended up in their intended envelopes?
|
1. If nine letters have gone into their intended envelopes, then the tenth letter will certainly do the same. Therefore, the probability that exactly nine letters have gone into their envelopes is zero.
$$
[M . M ., \mathbf{3 3}, 210(\text { March 1950).] }
$$
|
0
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Zero-sum test. A certain test consists of 26 questions. For each incorrect answer, five points are deducted from the test-taker, and for each correct answer, eight points are awarded.
The test-taker answered all the questions. How many questions did he answer correctly if the total number of points he received was zero?
|
4. The ratio of the number of answers of each type is equal to the inverse ratio of the corresponding points. Therefore, the number of correct answers is $\frac{5}{5+8} \cdot 26=10$.
[M. M., 31, 237 (March 1958).]
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Fourth-order equation. How many negative roots does the equation
$$
x^{4}-5 x^{3}-4 x^{2}-7 x+4=0 ?
$$
have?
|
8. The equation $x^{4}-5 x^{3}-4 x^{2}-7 x+4=0$ can be rewritten as $\left(x^{2}-2\right)^{2}=5 x^{3}+7 x$. Since for any negative $x$ the left side of the equation is positive, while the right side is negative, the original equation cannot have negative roots.
[P. E. Horton, M. M., 24, 114 (November 1950).]
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
20. Flower Seller. A girl bought $x$ roses in the store, paying $y$ dollars for all ( $x$ and $y$ are integers). When she was about to leave, the seller told her: "If you bought 10 more roses, I would give you all the roses for 2 dollars, and you would save 80 cents on each dozen." Find $x$ and $y$.
|
20. Since $y$ is an integer $<2, y=1^{\star}$. Then, expressing the cost of one rose in cents, we get
$$
\frac{100}{x}-\frac{200}{x+10}=\frac{80}{12}, \text{ or } x^{2}+25 x-150=0.
$$
The only positive root of this equation is $x=5$. This is the number of roses the girl initially bought.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
30. Unknown remainder. Find the remainder of the division of $f\left(x^{5}\right)$ by $f(x)$, if
$$
f(x)=x^{4}+x^{3}+x^{2}+x+1
$$
|
30. Since $f(x)=x^{4}+x^{3}+x^{2}+x+1,(x-1) f(x)=x^{5}-1$. Further, $f\left(x^{5}\right)=\left(x^{20}-1\right)+\left(x^{15}-1\right)+\left(x^{10}-1\right)+\left(x^{5}-1\right)+4+1$. But $x^{5}-1$, and therefore $f(x)$, are divisors of each of the brackets. Hence,
$$
f\left(x^{5}\right)=[\text { multiple of } f(x)]+5
$$
[N. Anning, S. S. M., 54, 576 (October 1954).]
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
35. Simplifying Radicals. Simplify the expression
$$
\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}
$$
|
35. Let $\sqrt[3]{2+\sqrt{5}}=a, \quad \sqrt[3]{2-\sqrt{5}}=b, \quad a+b=x$. Then
$$
x^{3}=a^{3}+3 a^{2} b+3 a b^{2}+b^{3}=a^{3}+b^{3}+3 a b(a+b)=4+3(\sqrt[3]{-1}) x
$$
Thus, $x^{3}+3 x-4=0$, and the only real root of this equation is 1.
$[$ [K. Adler, A. M. M., 59, 328 (May 1952).]
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
41. The Dozing Schoolboy. A schoolboy, waking up at the end of an algebra lesson, heard only a fragment of the teacher's phrase: "… I will only say that all the roots are real and positive." Glancing at the board, he saw there a 20th-degree equation assigned as homework, and tried to quickly write it down. He managed to write down only the first two terms $x^{20}-20 x^{19}$, before the teacher erased the board; however, he remembered that the constant term was +1. Could you help our unfortunate hero solve this equation?
|
41. The roots are positive; their arithmetic mean is $-\frac{(-20)}{20}$, and their geometric mean is $(+1)^{\frac{1}{20}}$. Since both these values coincide, it follows that all roots are equal to 1.
[D. S. Greenstein, A. M. M., 63, 493 (September 1956).]
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
51. An equation containing sums. Find $n$, if
$$
\frac{1^{3}+3^{3}+5^{3}+\cdots+(2 n-1)^{3}}{2^{3}+4^{3}+6^{3}+\cdots+(2 n)^{3}}=\frac{199}{242}
$$
|
51. First, note that if \(a: b = c: d\), then obviously \((a+b): b = (c+d): d\). Applying such a transformation to the fractions in our equation, we get
\[
\frac{1^{3}+2^{3}+3^{3}+\cdots+(2 n)^{3}}{2^{3}\left(1^{3}+2^{3}+3^{3}+\cdots+n^{3}\right)}=\frac{441}{242}
\]
Then, applying the known formula for the sum of cubes of natural numbers \({ }^{*}\), we get
\[
\begin{aligned}
\frac{(2 n)^{2}(2 n+1)^{2}}{4}: \frac{8 n^{2}(n+1)^{2}}{4} & =\frac{441}{242}=\frac{(21)^{2}}{2 \cdot(11)^{2}} \\
\frac{(2 n+1)^{2}}{(n+1)^{2}} & =\frac{(21)^{2}}{(11)^{2}}
\end{aligned}
\]
From this, it is clear that \(n=10\). (The negative square root leads to a negative \(n\).)
52*. If we place a stack of \((k-1)\) rectangular parallelepipeds, each of length \(2x\), on the \(k\)-th horizontal parallelepiped of the same kind and shift our stack until its center of gravity is vertically aligned with the edge of this \(k\)-th parallelepiped, then the center of gravity of the entire configuration will be horizontally distant from the edge of the \(k\)-th parallelepiped by a distance of \(\frac{x}{k}\).
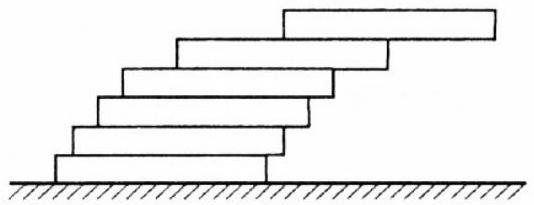
From this, it follows that \(n\) domino tiles in our stack (with \(x = 1\) inch) can be shifted between two vertical parallel planes, which are 1 inch apart, such that the total length of the "protruding" edges, moving from top to bottom, is expressed as \(1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{n-1}\). In this case, the domino tiles form a semi-arch that will be in equilibrium. This sum represents a partial sum of the harmonic series; since this series diverges, we can, by choosing a sufficiently large \(n\), achieve any horizontal distance between the edge of the top tile and the edge of the bottom tile.
To have the entire top tile extend beyond the edge of the bottom tile, \(n\) must be at least 5. In this case, the total length of the "protruding" edges will be \(1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4}\), or approximately 2.083 inches.
If we now shift our tiles so that all the \(2 \times 0.25\) faces are parallel to the same plane, and the center of gravity of each upper part of our stack is located above the corner of the nearest lower tile, then the horizontal distance between the corners of the topmost and bottommost tiles will increase compared to the previous case by \(\left[1^{2} + \left(\frac{1}{2}\right)^{2}\right]^{\frac{1}{2}} = \frac{\sqrt{5}}{2}\) times.
\[
\text { [P. M. E. J., 1, } 411 \text { (April 1954).] }
\]
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
56. Probability of divisibility. Find the probability that if the digits $0,1,2, \ldots, 9$ are placed in random order in the empty spaces in the sequence of digits
$$
5-383-8-2-936-5-8-203-9-3-76
$$
then the resulting number will be divisible by 396.
|
56. The number 76, formed by the last two digits, is divisible by 4. The difference between 73 (the sum of all digits in even positions) and $17+45$ (the sum of all digits in odd positions) is divisible by 11 regardless of the order in which the empty places are filled*. The sum of all digits, $90+45$, is divisible by 9. Therefore, our number is divisible by $4 \cdot 11 \cdot 9=396$. Hence, the desired probability is 1.
[P. Nagara, A. M. M., 58, 700 (December 1951).]
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
58. The son of a mathematics professor. The mathematics professor wrote a polynomial $f(x)$ with integer coefficients on the board and said:
- Today is my son's birthday. If his age $A$ is substituted into this polynomial instead of $x$, then the equation $f(A)=A$ holds. Note also that $f(0)=P$, where $P$ is a prime number greater than $A$.
How old is the professor's son?
|
58. Since $f(0)=P$,
$$
f(x)=x \cdot q(x)+P \quad \text { and } \quad f(A)=A \cdot q(A)+P=A .
$$
Therefore, $P$ is divisible by $A$. Since $P>A$ and $P$ is prime, $A=1$. Thus, the professor's son is 1 year old. The professor could have written down any polynomial from an infinite class of such polynomials, for example $x^{3}-3 x^{2}+3$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
60. Meteorological observations. At a weather station, it was noticed that during a certain period of time, if it rained in the morning, it was clear in the evening, and if it rained in the evening, it was clear in the morning. In total, there were 9 rainy days, with clear evenings 6 times and clear mornings 7 times. How many days did this entire period cover?
|
60. There were $\frac{1}{2}(6+7-9)=2$ completely clear days, so the period under consideration covered $9+2=11$ days.
$[$ [M. M., 34, 244 (March 1961).]
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
81. Sheep Buyers. A farmer died, leaving a herd of cows to his two sons. The sons sold the herd, receiving as many dollars for each head as there were heads in the herd. With the money, the brothers bought sheep at 10 dollars each and one lamb, which cost less than 10 dollars. Then they divided the sheep and the lamb between themselves so that each brother received the same number of animals. How much should the brother who received only sheep pay to his brother to ensure that each heir receives an equal share?
|
81. Let $x$ be the number of cows in the herd, $y$ the number of sheep, and $z$ the cost of a lamb. Then $x^{2}=10 y+z$, where $y$ is an odd number, and $z<10$. But the second-to-last digit of a square is odd if and only if the last digit is $6^{*}$. Thus, $z=6$, and the luckier son should pay his brother 2 dollars.
[И. Kaplansky, A. M. M., 51, 166 (March 1944).]
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
88. Choosing a pair. Among the pairs of numbers listed below, one and only one does not satisfy the equation $187 x-104 y=41$. Which one exactly
1) $x=3, \quad y=5$
2) $x=107, \quad y=192$
3) $x=211, \quad y=379$
4) $x=314, \quad y=565$
5) $x=419, \quad y=753$.
|
88. Since the difference between the two terms on the left side of the equation is the odd number 41, one of these terms must be odd and the other even. Since $104 y$ is even, $187 x$ is odd, and therefore $x$ is odd. Thus, the pair $x=314$, $y=565$ does not satisfy our equation.
[D. Woods, S. S. M., 64, 242 (March 1964).]
|
4
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
104. Divisibility condition. For which integer $a$ does the polynomial $x^{13}+x+90$ divide by $x^{2}-x+a ?$
|
Let $f(x)=x^{2}-x+a, g(x)=x^{13}+x+90$. Then $f(0)=$ $a, f(1)=a, g(0)=90, g(1)=92$. Therefore, the greatest common divisor of 90 and 92, which is 2, must divide $a$. Further, $f(-1)=$ $a+2, g(-1)=88$; hence $a$ is neither 1 nor $-2 ; f(-2)=a+6$, $g(-2)=-8104$, so $a \neq-1$. Therefore,
$$
\begin{gathered}
a=2^{\star} \quad \text { and } \frac{x^{13}+x+90}{x^{2}-x+2}= \\
=x^{11}+x^{10}-x^{9}-3 x^{8}-x^{7}+5 x^{6}+7 x^{5}- \\
-3 x^{4}-17 x^{3}-11 x^{2}+23 x+45
\end{gathered}
$$
[L. E. Bash, A. M. M., 71, 640 (June 1964).]
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
105. The Farmer's Task. A certain farmer must buy 100 heads of cattle for 100 dollars. If each calf costs 10 dollars, each lamb 3, and each piglet 0.5 dollars, then how many calves, lambs, and piglets will the farmer buy?
|
105. The average cost of one head of cattle is 1 dollar. The cost of each calf differs from the average by +9 dollars, each lamb by +2 dollars, and each piglet by $-\frac{1}{2}$ dollar. Therefore, for each calf, the farmer must buy 18 piglets, and for each lamb, 4 piglets. Consequently, since $5(1+18)+(1+4)=100$, he must buy 5 calves, 1 lamb, and 94 piglets.
[B. E. Mitchell, M. M., 26, 153 (January 1953).]
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
108. Unique Square. What square is equal to the product of four consecutive odd numbers?
|
108. If $n(n+2)(n+4)(n+6)=m^{2}$, then $\left(n^{2}+6 n+4\right)^{2}=m^{2}+16$. However, among the squares, only 0 and 9 have the form $a^{2}-16$; and since $m^{2}$ is odd, the sought square is $9=(-3)(-1)(1)(3)$.
[D. L. Silverman, M. M., 38, 60 (January 1965).]
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
110. Sum of Cosines. Calculate the sum
$$
\cos 5^{\circ}+\cos 77^{\circ}+\cos 149^{\circ}+\cos 221^{\circ}+\cos 293^{\circ}
$$
|
110. Project the sides of an arbitrary polygon onto a line lying in the plane of this polygon. Then the sum of such projections, taken with the appropriate sign, is zero. Now let's take a regular pentagon with a unit side and note that its exterior angle is $72^{\circ}$. The terms
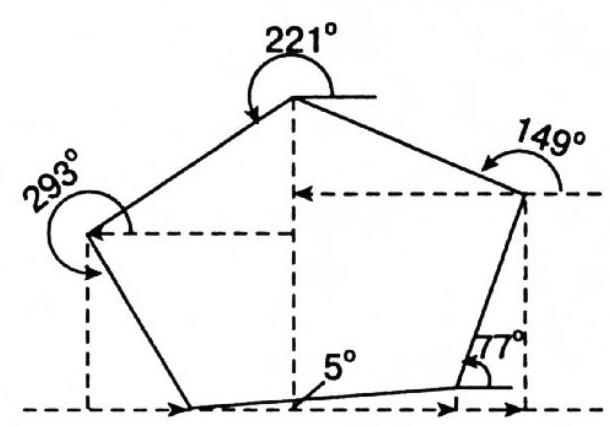
of our sum represent the projections of the sides of this pentagon onto a line that forms an angle of $5^{\circ}$ with one of these sides. Therefore,
$$
\cos 5^{\circ}+\cos 77^{\circ}+\cos 149^{\circ}+\cos 221^{\circ}+\cos 293^{\circ}=0
$$
[M. S. Klamkin, M. M., 28, 293 (May 1955).]
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
136. Joint system. For which values of $k$ is the system given below consistent?
$$
\left\{\begin{aligned}
x+y & =1 \\
k x+y & =2 \\
x+k u & =3
\end{aligned}\right.
$$
|
136. Adding the second and third equations of the given system, we get
$$
x+y+k(x+y)=5
$$
Considering the first equation, we find from here the desired value $k=4$. For this $k$ we have $x=\frac{1}{3}, y=\frac{2}{3}$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
157. Ballot Papers. A physical society needed to hold elections for three leadership positions. For each of the three positions, there were 3, 4, and 5 candidates, respectively. To ensure that the number under which each candidate is listed on the ballot does not influence the voting results, it was decided to apply a rule that in the list of candidates for each position, each candidate must appear under each number an equal number of times. What is the minimum number of different ballots required to comply with this rule?
|
157. Perhaps someone will immediately say that it is necessary to take $3 \cdot 4 \cdot 5=60$ different ballots. However, if we add two fictitious names to the group of three candidates and one fictitious name to the group of four candidates, then only 5 different ballots will be required. This technique not only reduces printing costs but also allows for the collection of statistical[^31] material, which can help determine what has a greater influence on the voting results: the number under which a candidate is listed, or their surname.
[М. S. Klamkin, M. M., 30, 110 (November 1956).]
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
163. Reduced Share. A father gave his children 6 dollars for entertainment, which was to be divided equally. But two young cousins joined the company. The money was divided equally among all the children, so that each child received 25 cents less than originally intended. How many children were there in total?
|
163. The share of each child decreased by $\frac{2}{24}$ of the entire sum. Further, $24=2 \cdot 12=3 \cdot 8=4 \cdot 6$. From these representations of the number 24, we choose the pair $q_{1} c_{1}=q_{2} c_{2}$ such that $q_{1}+1=q_{2}$, and $c_{1}=c_{2}+2$. Thus, there were initially 6 children, and then there were 8.
$[$ [
$164^{\star}$. Let
$$
\begin{gathered}
S=1+2 x+3 x^{2}+4 x^{3}+\ldots \\
x S=\quad x+2 x^{2}+3 x^{3}+\ldots \\
(1-x) \cdot S=1+x+x^{2}+x^{3}+\cdots=\frac{1}{(1-x)}
\end{gathered}
$$
From this, $S=\frac{1}{(1-x)^{2}}$.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
167. Inscribed Circles. Which of the two triangles has a larger inscribed circle: the triangle with sides 17, 25, and 26, or the triangle with sides 17, 25, and 28?
|
167. Answer: none. The radius of the inscribed circle of a triangle with sides $a, b, c$ is calculated by the formula
$$
r=\frac{S}{p}=\left[\frac{(p-a)(p-b)(p-c)}{p}\right]^{\frac{1}{2}}, \quad \text { where } \quad 2 p=a+b+c
$$
From this, for each of our triangles, the radius value will be 6.
A rare example of "obtuse twins" are triangles with sides equal to $97,169,122$ and 97,169, 228. Each of them has an inscribed circle radius of 30.
[B. H. Brown, M. M., 29, 275-276 (May 1956).]
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
170. Antifreeze. The radiator of a car with a capacity of 21 quarts* is filled with an 18% alcohol solution. How many quarts of this solution need to be drained from the radiator so that, by replacing them with the same amount of 90% solution, a 42% alcohol solution is obtained in the end.
|
170. The percentage of alcohol in the old solution differs from the percentage of alcohol in the new (or mixed) solution by $-24 \%$, and the percentage of alcohol in the solution added to the radiator differs from the percentage of alcohol in the new solution by $+48 \%$. Therefore, for each quart of $90 \%$ solution added to the radiator, there should be 2 quarts of the old $18 \%$ solution. Hence, $\frac{1}{3}$ of the total volume, or 7 quarts of the old solution, should be drained from the radiator.
[B. E. Mitchell, M. M., 26, 153 (January 1953).]
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
179. Determinant of Pascal's Triangle. Pascal arranged the binomial coefficients in the following table (Pascal's Triangle) $)^{*}$
| 1 | 1 | 1 | 1 | 1 | 1 | $\ldots$ |
| ---: | ---: | ---: | ---: | ---: | ---: | :--- |
| 1 | 2 | 3 | 4 | 5 | 6 | $\cdots$ |
| 1 | 3 | 6 | 10 | 15 | 21 | $\cdots$ |
| 1 | 4 | 10 | 20 | 35 | 56 | $\cdots$ |
| 1 | 5 | 15 | 35 | 70 | 126 | $\cdots$ |
| 1 | 6 | 21 | 56 | 126 | 252 | $\cdots$ |
| . | . | . | . | . | . | $\cdots$ |
Prove that if we cut out any square of any size from this infinite table, the first row (or column) of which is not located on the first row (column) of this table, then the determinant of any such square will be equal to 1.
|
179. The law according to which our table is composed is that each element is equal to the sum of two other elements, one of which is directly above the given element, and the other is to the left of the given element. Applying to our determinant of the $n$-th order the operation of subtracting columns (column) $_{i} - $ (column) $_{i-1}$, where $i=n, (n-1), \ldots, 2$, and then expanding it along the first row, we will obtain a determinant of the $(n-1)$-th order, equal to the minor defined by the element in the lower left corner of the original determinant. Continuing this process, we will eventually arrive at the value 1.
For example:
$$
\begin{aligned}
& \left|\begin{array}{rrrr}
1 & 1 & 1 & 1 \\
3 & 4 & 5 & 6 \\
6 & 10 & 15 & 21 \\
10 & 20 & 35 & 56
\end{array}\right|=\left|\begin{array}{rrrr}
1 & 0 & 0 & 0 \\
3 & 1 & 1 & 1 \\
6 & 4 & 5 & 6 \\
10 & 10 & 15 & 21
\end{array}\right|=\left|\begin{array}{rrr}
1 & 1 & 1 \\
4 & 5 & 6 \\
10 & 15 & 21
\end{array}\right|= \\
& =\left|\begin{array}{rrr}
1 & 0 & 0 \\
4 & 1 & 1 \\
10 & 5 & 6
\end{array}\right|=\left|\begin{array}{ll}
1 & 0 \\
5 & 1
\end{array}\right|=1
\end{aligned}
$$
Since the original table is symmetric with respect to the main diagonal, the proof provided remains valid for determinants whose first column is located in the first column of the table. In this case, rows should be subtracted instead of columns.
|
1
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
197. Test Series. Professor Tester conducts a series of tests, based on which he assigns the test subject an average score. After answering the last test, John realized that if he had scored 97 points on this last test, his average score would have been 90. On the other hand, if he had scored only 73 points on the last test, his average score would still have been 87. How many tests are in Professor Tester's series?
|
197. If the difference in points obtained in one test, equal to $97-73=24$ points, causes a change in the average score by $90-87=3$ points, then the series contains a total of $\frac{24}{3}=8$ tests.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
209. "Fibonacci Tetrahedron". Find the volume of the tetrahedron whose vertices are located at the points with coordinates $\left(F_{n}, F_{n+1}, F_{n+2}\right), \quad\left(F_{n+3}, F_{n+4}, F_{n+5}\right), \quad\left(F_{n+6}, F_{n+7}, F_{n+8}\right)$ and $\left(F_{n+9}, F_{n+10}, F_{n+11}\right)$, where $F_{i}$ is the $i$-th term of the Fibonacci sequence: $1,1,2,3,5,8 \ldots$.
|
209. The Fibonacci sequence satisfies the recurrence relation $F_{n}+F_{n+1}=F_{n+2}$, so any three consecutive Fibonacci numbers satisfy the equation $x+y=z$. Consequently, all four vertices of our tetrahedron lie in the same plane, and its volume is 0.
We can observe that all the reasoning remains valid even if the coordinates of the vertices do not coincide with 12 consecutive Fibonacci numbers. It is sufficient for the coordinates of each vertex to coincide with any three consecutive Fibonacci numbers.
|
0
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
231. Henry's Walk. Henry went for a walk in the countryside sometime between 8 and 9 in the morning, when the hands of his clock were aligned. He arrived at his destination between 2 and 3 in the afternoon; at this time, the hands of his clock were pointing in exactly opposite directions. How long did Henry's walk last?
|
231. The walk lasted 6 hours. Suppose we extended the hour hand in the opposite direction. If at the beginning of the walk the hour and minute hands were coincident, then after six hours the hour hand and its extension will simply have swapped places, while the minute hand, having completed exactly six full circles, will return to its initial position and, consequently, will coincide with the extension of the hour hand.
[Ch. Salkind, M. M., 28, 241 (March 1955).]
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
251. Packing Cylinders. Forty cylinders with a diameter of 1 cm and the same height were tightly packed in a box in 5 rows of 8 cylinders each so that they would not "rattle" during transportation. How many cylinders need to be removed from the box so that, by moving the remaining cylinders and adding the removed cylinders and one more cylinder at the end, 41 cylinders of the same size can be packed in this box? Will the cylinders "rattle" in this case?
|
251. Only two cylinders need to be removed from the box. Let's renumber the cylinders as shown in the figure. Remove cylinders 6 and 16.
Move cylinders $7-10$ to the right and up (see the figure). Move cylinders 11-15 to the left, cylinders 17-20 up and to the left, and cylinders 21-25 to the left. The remaining cylinders can be moved in different ways. For example, move cylinders 26, 28, 29, 30, 31 to the left; press cylinder 32 against cylinders 31 and 37; move cylinder 27 against cylinders 28 and 32; move cylinder 26 against cylinders 21 and 22. Move cylinder 31 to the left; press cylinder 32 against cylinders 36 and 37; move cylinder 27 up to cylinder 31; move cylinders $28, 29, 30$ up and to the left; move cylinders $33, 34, 35$ up and to the right. Insert cylinders 6, 16, and 41 into the positions indicated in the figure. If the cylinders in the new arrangement are tightly pressed against each other, the distance between the lines of centers of adjacent "columns" will be $\sqrt{\frac{3}{2}}$ cm. Therefore, the entire packaging will take up a length of $8\left(\frac{\sqrt{3}}{2}\right)+1=4 \sqrt{3}+1 \approx 7.928 < 8$ cm.
Thus, the cylinders will now "rattle" slightly during transportation.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
266. When division is exact. For which positive integer $n$ will the quantity $n^{4}+n^{2}$ be divisible by $2 n+1$?
|
266.
$$
\begin{aligned}
f(n) & =\frac{n^{4}+n^{2}}{2 n+1}=\frac{n^{2}\left(n^{2}+1\right)}{2 n+1}=\frac{n^{2}}{4}\left[\frac{4 n^{2}+4}{2 n+1}\right]= \\
& =\left(\frac{n}{2}\right)^{2} \cdot\left[2 n-1+\frac{5}{2 n+1}\right]
\end{aligned}
$$
It is obvious that the greatest common divisor of the numbers $n$ and $2n+1$ is 1. Therefore, $f(n)$ can be an integer only when $\frac{5}{2n+1}$ is an integer, which occurs when $n=2, 0, -1$, or $-3$. Consequently, the only positive integer for which $f(n)$ will be an integer is $n=2$. [In this case, $f(n)=4$.]
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
272. Calculation of the sum. Let $n$ be a fixed positive number. Set $x_{0}=\frac{1}{n}$ and $x_{j}=\frac{1}{n-1} \sum_{i=0}^{j-1} x_{i}$ for $j=$ $1,2, \ldots, n-1$. Compute the sum $\sum_{j=0}^{n-1} x_{j}$.
|
272. We will prove by induction that $\sum_{j=0}^{k} x_{j}=\frac{1}{(n-k)}, k=$ $0,1, \ldots, n-1$. For $k=0$, the given equality is trivially satisfied by definition. Suppose now that $\sum_{j=0}^{k} x_{j}=\frac{1}{(n-k)}$ for some $k, 0 \leqslant k \leqslant n-2$. Then
$$
\sum_{j=0}^{k+1} x_{j}=x_{k+1}+\sum_{j=0}^{k} x_{j}=\sum_{j=0}^{k} \frac{x_{j}}{n-k-1}+\sum_{j=0}^{k} x_{j}
$$
by the definition of $x_{k+1}$. Using the induction hypothesis, we get
$$
\sum_{j=0}^{k+1} x_{j}=\frac{1}{(n-k-1)(n-k)}+\frac{1}{n-k}=\frac{1}{n-k-1}
$$
From this, taking $k=n-1$, we find the desired sum
$$
\sum_{j=0}^{n-1} x_{j}=1
$$
[E. Lengyel, A. M. M., 76, 86 (January 1969).]
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
275. Maximum Number. Let a set of distinct complex numbers $z_{i}, i=1,2, \ldots, n$, be given, satisfying the inequality
$$
\min _{i \neq j}\left|z_{i}-z_{j}\right| \geqslant \max _{i}\left|z_{i}\right|
$$[^16]
Find the maximum possible $n$ and for this $n$ all sets satisfying the condition of the problem.
|
275. Let $\left|z_{m}\right|=\max _{i}\left|z_{i}\right|$. Then on the complex plane, all points $z_{i}$ will be located inside the circle $R$ of radius $\left|z_{m}\right|$ centered at the point $z=0$. Clearly, 6 points $z_{i}$, located on the circumference of $R$ and forming a regular hexagon, together with the point $z_{1}=0$ give $n=7$. If, however, $n \geqslant 7$ and some point $z \neq 0$ is not on the circumference of $R$, then by applying the cosine theorem, we will get that $\left|z_{i}-z_{j}\right|0$ and $0 \leqslant \delta<\frac{\pi}{3}$.
[P. Kornya, A. M. M., 76, 91 (January 1969).]
|
7
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
322. Limit of a Sum. Calculate the value of the expression
$$
\lim _{n \rightarrow \infty} \sum_{k=0}^{n} \frac{k^{2}+3 k+1}{(k+2)!}
$$
|
322.
$$
\begin{gathered}
\sum_{k=0}^{n} \frac{k^{2}+3 k+1}{(k+2)!}=\sum_{k=0}^{n}\left(\frac{1}{k!}-\frac{1}{(k+2)!}\right)= \\
=\left(\frac{1}{0!}+\frac{1}{2!}\right)+\left(\frac{1}{1!}-\frac{1}{3!}\right)+\cdots+\left(\frac{1}{n!}-\frac{1}{(n+2)!}\right)= \\
=\frac{1}{0!}+\frac{1}{1!}-\frac{1}{(n+1)!}-\frac{1}{(n+2)!}=2-\frac{n+3}{(n+2)!}
\end{gathered}
$$
From this, it follows that the desired limit is 2.
[E. Just and H. Geck, M. M., 44, 56 (January 1971).]
|
2
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
342. Simple calculation. Let $\left(x+\frac{1}{x}\right)^{2}=3$; determine what $x^{3}+\frac{1}{x^{3}}$ is equal to.
|
342.
$$
\begin{aligned}
x^{3} & +\frac{1}{x^{3}}=\left(x+\frac{1}{x}\right)^{3}-3\left(x+\frac{1}{x}\right)= \\
& =\left(x+\frac{1}{x}\right)\left[\left(x+\frac{1}{x}\right)^{2}-3\right]=0
\end{aligned}
$$
[M. Demos, M. M., 45, 102 (February 1972).]
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
373. Cutting a Cube. In a mathematical journal, the following question and answer appeared.
Question: "A carpenter wants to cut a wooden cube with a side of 3 inches into 27 cubes with a side of 1 inch. He can easily do this by making 6 cuts while keeping the pieces together so they don't fall apart. What is the minimum number of cuts if the carpenter is allowed to rearrange the pieces in any way during the cutting process $?$"
Answer: "The minimum number of cuts is 6, since it takes 6 cuts, one for each face, to separate the inner cube."
Now, suppose the inner cube is missing. What is the minimum number of cuts in this case if the pieces can be rearranged in any way during the cutting process $?$
|
373. After the first cut, the cube splits into 2 parts. The larger of these (consisting of 17 one-inch cubes) contains one central cube, for four faces of which another cut is required. After the last of these is made, there will remain at least two one-inch cubes undivided - regardless of any rearrangement of the pieces - for which another cut will be required. Thus, the minimum number of cuts is 6.
[C. Newman, M. M., 41, 102 (February 1968).]
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Ex. 104. A regular triangle $ABC$ is inscribed in a circle. Another, smaller circle, is inscribed in the sector bounded by the chord $BC$, touching the larger circle at point $M$, and the chord $BC$ at point $K$. The ray $MK$ intersects the larger circle a second time at point $N$. Find the length of $MN$, if the sum of the distances from point $M$ to the ends of the chord $BC$ is 6.
|
Ex. 104. 6. Hint. Show that point $N$ coincides with $A$ and use the result of Ex. 28.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Ex. 118. A circle with center on side $AB$ of triangle $ABC$ touches sides $AC$ and $BC$. Find the radius of the circle, given that it is expressed as an integer, and sides $AC$ and $BC$ are equal to 5 and 3.
|
Ex. 118. Answer: $r=1$. Solution. By equating the expressions for the area of triangle $ABC$, we get that $\frac{a+b}{2} r=\frac{a b}{2} \sin C$. From this, it follows that $r=\frac{a b}{a+b} \sin C$. In our case, $r=\frac{15}{8} \sin C$. If $r \geq 2$, then $\sin C>1$. This solves the problem.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Ex. 129. In an integer-sided triangle, two sides are equal to 10. Find the third side, given that the radius of the inscribed circle is an integer.
|
Ex. 129. Answer: 12. Solution. Let the third side be denoted by $a$, and the angle subtending it by $\alpha$. Then $\sin \alpha=\frac{10+10+a}{10 \cdot 10} \cdot r$. At the same time, $1 \leq a \leq 19 \Rightarrow r \leq 4$. If $\sin \alpha=1$, then $x=5, r=4$, but a triangle with such data does not exist. According to the result of Ex. 124, $\sin \alpha=\frac{m}{n}$, where $n$ is either 5 or 25. In the first case, either $\sin \alpha=\frac{3}{5}$ or $\sin \alpha=\frac{4}{5}$. In both cases, a triangle with such data does not exist. If $n=25$, then $\sin \alpha=\frac{7}{25}$ or $\frac{24}{25}$. After verification, we get $a=12, r=3$.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 33. In Search of a Job
To find a job after demobilization, soldier Maurice began sending letters to various companies where people of his specialty can be employed. He believes that each of his applications has a one in five chance of being accepted, and he stops sending letters as soon as he finds that he has at least a three in four chance of finding a job.
How many letters will Maurice have to write? (The decimal logarithms of 3, 4, and 5 are approximately 0.477, 0.602, and 0.699.
|
33. The probability that Maurice will remain unemployed after sending $n$ letters is $(1-1 / 5)^{n}=(4 / 5)^{n}$. Therefore, the probability of finding a job is $1-(4 / 5)^{n}$.
Maurice will stop writing when $n$ becomes such that this probability is not less than $3 / 4$, i.e., when the inequality
$$
(4 / 5)^{n} \leqslant 1 / 4
$$
holds, from which
$$
n \geqslant \frac{\lg 4}{\lg 5-\lg 4}=\frac{0.602}{0.097} \approx 6.2 .
$$
Thus, Maurice will have to write 7 letters.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 36. Daily Newspapers
In a small town where many vacationers spend their holidays, $28 \%$ of the adult vacationers read "Mond", $25 \%$ read "Figaro", and $20 \%$ read "Orore". Additionally, $11 \%$ of the vacationers read both "Mond" and "Figaro", $3 \%$ read both "Mond" and "Orore", and $2 \%$ read both "Figaro" and "Orore", while $42 \%$ of the vacationers do not read any of these three newspapers. What is the percentage of adult vacationers who read all three newspapers, "Mond", "Figaro", and "Orore"?
|
36. Let $x$ be the desired percentage. Denote by $V$ the set of all vacationers, by $M$ the set of "Mond" readers, by $F$ the set of "Figaro" readers, and finally by $A$ the set of "Aurore" readers. To determine the desired percentage, we will use the Venn diagram provided below.
The entire set $V$ corresponds, of course, to $100 \%$. From this, we obtain the equation
$$
\begin{gathered}
42+(14+x)+(12+x)+(15+x)+(11-x)+ \\
+(2-x)+(3-x)+x=100
\end{gathered}
$$
i.e., $x=1 \%$.
Thus, $1 \%$ of adult vacationers read all three newspapers simultaneously.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 12. Punctual Wife
Every Saturday between 15 and 16, I play tennis with my friend Philippe. My wife arrives to pick me up in the car precisely at 16:10. One day, Philippe fell ill. Unaware of this, I set out for tennis as usual. However, at 15:05, realizing that Philippe wasn't coming, I gathered my things and started walking home. On the way, I met my wife, who was driving to pick me up. I got into the car, and we arrived home 10 minutes earlier than usual.
This might not seem very interesting, but could you determine from this story the ratio between my walking speed and the speed at which my wife drives?
|
12. On the day when Philip fell ill, my wife drove the car for 10 minutes less than usual; that means she drove 5 minutes less in each direction. Therefore,
I met her at 4:05 PM, instead of 4:10 PM as usual. But then I walked for 60 minutes to cover the distance my wife drives in 5 minutes. Thus, I walk 12 times slower than my wife drives.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 13. The Scout and the Drummer
On the occasion of the village festival, a procession was organized that stretched for 250 m; the scouts led the procession, and the musicians brought up the rear. Soon after the march began, the youngest scout remembered that he had not tied his neckerchief, which was left with his friend, the drummer, who was in the last row of the musicians. So the scout ran to get the neckerchief and returned to his place in 3 minutes and 18 seconds.
What was the speed of the procession, assuming the scout ran at a speed of 10 km/h?
|
13. Let $x$ be the unknown speed of the procession. When the scout ran to the end of the procession, he moved relative to the procession (considered stationary!) at a speed of $10+x$; when he returned, he moved relative to the procession at a speed of $10-x$. Since the length of the procession is 250 m, the total time spent by the scout is
$$
\frac{250}{1000} \cdot \frac{1}{10+x}+\frac{250}{1000} \cdot \frac{1}{10-x}=\frac{3}{60}+\frac{18}{3600}
$$
(here we measure distance in kilometers, time in hours, and speeds in km/h).
Transform our equation:
$$
(10-x)+(10+x)=4(10+x)(10-x)(3 / 60+18 / 3600)
$$
or
$$
20=4\left(100-x^{2}\right) \cdot(198 / 3600)
$$
From this, we find
$$
x^{2}=100 / 11, \quad x=\sqrt{100 / 11} \approx 3
$$
The speed of the procession is approximately 3 km/h.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 15. Metro in Mexico City
A worker is walking along the tracks in one of the tunnels of the capital's subway, on a section between two stations that are far apart. Every 5 minutes a train passes him coming from the opposite direction, and every 6 minutes another train overtakes him. The worker walks at a constant speed, the speeds of the subway trains (which are the same for trains going in both directions) do not change, nor do the intervals between trains (which are also the same for trains going in both directions).
When the worker stopped to fix a malfunction that had forced him to set out on his journey, a train passed by. How long will it take for the next train going in the same direction to pass by?
|
15. Let $x$ be the time between the passage of two consecutive trains moving in the same direction; $I$ be the distance between two consecutive trains; $V$ be the speed of each train, and finally, $v$ be the speed of the worker. Then, relative to the worker, each following train moves at a speed of $V-v$, and each oncoming train moves at a speed of $V+v$.
From this, we obtain the following system of equations:
1) $5=I / (V+v)$
2) $6=I / (V-v)$,
3) $x=I / V$.
It is easy to see that [due to (1)-(3)] $x=60 / 11=5$ min $27 \mathrm{s}$.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 16. How many of you were there, children?
If you had asked me such a question, I would have answered you only that my mother dreamed of having no fewer than 19 children, but she did not manage to fulfill her dream; however, I had three times as many sisters as cousins, and brothers - half as many as sisters. How many children did my mother have?
|
16. From the conditions of the problem, it follows that the number of my sisters is divisible by both 3 and 2. Therefore, it is divisible by 6. Hence, the total number of children is
$$
[(\text { number divisible by } 6) \cdot(1+1 / 2)]+1
$$
(the last 1 corresponds to myself). This number must be strictly less than 19, so it inevitably equals 6.
Therefore, I had 6 sisters and 3 brothers, and my mother had a total of 10 children.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 17. Airline
One American airline serves several major cities, establishing direct flights between each pair of these cities. Next year, it plans to increase the number of flights by 76, which will allow it to serve some additional cities under the same conditions.
How many cities does this airline currently serve, and how many cities does it plan to serve next year?
|
17. Let $n$ be the number of cities currently served. The corresponding number of flights is $n(n-1)$, since each city is connected to $n-1$ cities served by the airline. For the next year, the airline plans
$$
(n+k)(n+k-1)
$$
flights, where $k$ is the additional number of cities. Therefore,
$$
(n+k)(n+k-1)-n(n-1)=76
$$
From this,
$$
k(k+2 n-1)=76(=4 \cdot 19=2 \cdot 39=1 \cdot 76)
$$
Thus, $k=4$, or $k=2$, or, finally, $k=1$.
But if $k=2$, then $k+2 n-1=38$, i.e., $2 n-1=36$, which is impossible since $(2 n-1)$ is an odd number. Therefore, the only possible cases are: $k=4$ - and then $k+2 n-1=19$, i.e., $n=8$, and $k=1$ - and then $k+2 n-1=76$, i.e., $n=38$.
Thus, either the airline currently serves 8 cities, and next year it will serve 12 cities, or it currently serves 38 cities, and next year the number will increase to 39.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 22. Age Difference
The sums of the digits that make up the birth years of Jean and Jacques are equal to each other, and the age of each of them starts with the same digit. Could you determine the difference in their ages?
|
22. Let $(m, c, d, u)$ be the number of thousands, hundreds, tens, and units in Jean's birth year, and let $\left(m^{\prime}, c^{\prime}, d^{\prime}, u^{\prime}\right)$ be the corresponding digits of Jacques' birth year. Then Jean's age is
$$
1979-(1000 m+100 c+10 d+u)
$$
Jacques' age is
$$
1979-\left(1000 m^{\prime}+100 c^{\prime}+10 d^{\prime}+u^{\prime}\right)
$$
The difference in their ages is
$$
1000\left(m-m^{\prime}\right)+100\left(c-c^{\prime}\right)+10\left(d-d^{\prime}\right)+\left(u-u^{\prime}\right)
$$
But according to the problem statement,
$$
m+c+d+u=m^{\prime}+c^{\prime}+d^{\prime}+u^{\prime}
$$
i.e.,
$$
\left(m-m^{\prime}\right)+\left(c-c^{\prime}\right)+\left(d-d^{\prime}\right)+\left(u-u^{\prime}\right)=0
$$
Subtracting the last expression from the difference in Jean's and Jacques' ages term by term, we get the number
$$
999\left(m-m^{\prime}\right)+99\left(c-c^{\prime}\right)+9\left(d-d^{\prime}\right)
$$
which is clearly divisible by 9.
But this number is less than 10 (since Jean's and Jacques' ages are written as numbers starting with the same digit), and therefore it equals 9.
Thus, the difference in Jean's and Jacques' ages is 9 years.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 27. Large Families
The Martens have more children than the Duponts. Suppose the difference of the squares of these two numbers is 24 and that both families have more than one child. How many children do the Martens have?
70
|
27. Let $m$ and $d$ be the number of children in the Marten and Dupont families, respectively. According to the problem,
$$
m^{2}-d^{2}=24 \text {, i.e., }(m+d)(m-d)=24\left(=2^{3} \cdot 3\right) \text {. }
$$
Therefore, the following values for $m+d, m-d$, and thus $2 m[=(m+d)+(m-d)]$, $m$, and $d$ are possible:
| $m+d$ | $m-d$ | $2 m$ | $m$ | $d$ |
| :---: | :---: | :---: | :---: | :---: |
| 24 | 1 | 25 | $12 \frac{1}{2} ?$ | $11 \frac{1}{2} ?$ |
| 12 | 2 | 14 | 7 | 5 |
| 8 | 3 | 11 | $5 \frac{1}{2} ?$ | $2 \frac{1}{2} ?$ |
| 6 | 4 | 10 | 5 | $1 ?$ |
The only valid value, therefore, is $m=7$. The Martens have 7 children.
Remark. The first and third possibilities are not valid because the number of children must be an integer, and the last one is not valid because, according to the problem, each family has more than one child.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 29. Leonie and Cats
When old lady Leonie is asked how many cats she has, she melancholically replies: “Four fifths of my cats plus four fifths of a cat.” How many cats does she have?

|
29. Let $n$ be the number of cats Leonie has. From her last words, we can write the relationship
$$
n=(4 / 5) n+4 / 5, \text { i.e. } \quad n=4 .
$$
Thus, Leonie has 4 cats.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 30. New Mathematics
My son has learned to count in a numeral system different from the decimal system, and instead of 136, he writes 253 in this system. In what numeral system is my son counting?
|
30. Let $a$ be the base of an unknown numeral system. When my son writes "253" in this system, it represents $2 a^{2}+5 a+3$; according to the problem, this corresponds to the number 136 in the decimal system. Therefore, we can write
$$
2 a^{2}+5 a+3=136
$$
i.e.
$$
2 a^{2}+5 a-133=0
$$
or
$$
(a-7)(2 a+19)=0
$$
Since $a$ is a positive integer, the only solution to this equation is 7. My son was using the septenary (base-7) system. 31.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 36. San Salvador Embankment
Would you come to have dinner with me tonight? I live in one of the eleven houses on San Salvador Embankment; however, to find out which one, you will have to think.
When, from my home, I look at the sea and multiply the number of houses to my left by the number of houses to my right, I get a number that is 5 more than the similar number obtained by my left neighbor when he does the same.
|
36. Let $d$ be the number of houses to the right of my house when I look at the sea, and $g$ be the number of houses to the left of it. Then
$$
d+g=10,
$$
and
$$
d g-(d+1)(g-1)=5
$$
or
$$
d+g=10, \quad d-g=4 .
$$
From this, $2 d=14, d=7$ and, therefore, $g=3$.
Thus, my house is the fourth from the left when looking at the sea, or the fourth from the right if you turn your back to the sea.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 43. Rue Saint-Nicaise
On December 24, 1800, First Consul Bonaparte was heading to the Opera along Rue Saint-Nicaise. A bomb exploded on his route with a delay of a few seconds. Many were killed and wounded. Bonaparte accused the Republicans of the plot; 98 of them were exiled to the Seychelles and Guiana. Several people were executed. Suppose the number of wounded is equal to twice the number of killed (in the explosion) plus four-thirds of the number of those executed, that the sum of the number of killed or wounded and the number of those executed is slightly less than the number of those exiled, and that if you subtract 4 from the number of killed, you get exactly twice the number of those executed.
Could you, without referring to history books, determine how many people Bonaparte executed after the attack on Rue Saint-Nicaise?
|
43. Let $x$ be the number of those executed; then, according to the last condition of the problem, the number of those killed in the explosion is $2 x+4$, and the number of wounded is
$$
2(2 x+4)+(4 / 3) x=5 x+x / 3+8
$$
(hence, $x$ is a multiple of 3).
It is also known that
$$
(2 x+4)+(5 x+x / 3+8)+x<98
$$
or
$$
x<10
$$
Since $x$, on the one hand, is slightly less than 10, and on the other - a multiple of 3, then, apparently, $x=9$.
Thus, after the assassination attempt on the rue Saint-Nicaise, Bonaparte executed nine republicans.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 47. Suez and Panama
A meeting took place between Egyptians and Panamanians, where issues regarding the operation of the Suez and Panama Canals were discussed. In total, there were twelve participants from both sides, with more Egyptians than Panamanians. Upon arriving at the meeting place, the Egyptians greeted each other in pairs in Arabic. The Panamanians did the same, but in Spanish. However, the Panamanians did not exchange greetings with the Egyptians, either due to language barriers or for some political reasons.
Assuming there were a total of 31 greetings exchanged, how many Egyptians and how many Panamanians were present at the meeting?
|
47. If $n$ people greet each other in pairs, then a total of $n(n-1) / 2$ greetings take place. Therefore, we can create the following table:
In order for there to be exactly 31 greetings, there must have been seven Egyptians and five Panamanians at the meeting.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 51. Congratulations from Methuselah
Every New Year, starting from the first year of our era, Methuselah, who is still alive to this day, sends a greeting to his best friend, who, naturally, has changed many times over the centuries and decades. However, the formula for the greeting, on the contrary, has remained unchanged for almost two millennia. It is very simple: "Happy New Year 1", "Happy New Year 2", "Happy New Year 3", and so on, "Happy New Year 1978" and finally, "Happy New Year 1979".
Which digit has Methuselah used the least so far?
|
51. From the 1st to the 999th year, all digits were used an equal number of times, except for 0 (all digits were used exactly the same number of times if the first years were recorded by Methuselah as: year 0001, year 0002, ..., year 0999; however, since he did not do this, the digit 0 was used 111 times less frequently than the others). For similar reasons, in the records from 1000 to 1999, all digits appear the same number of times, except for 1 (the digit 1 is used here 1000 times more frequently than the others). But we are only considering the series of years ending in 1979. The years 1980, 1981, 1982, ..., 1999 remain. In this new series, the digit 9 appears most frequently (31 times). But this shortage of nines due to the "discarded" series is much less significant than the shortage of 0 in the first 1000 numbers.
Thus, Methuselah used the digit 0 the least frequently (and, obviously, the digit 1 the most frequently).
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 1. British Hospital
In a British hospital, the following announcement can be read: "Surgeon $X$ and Nurse $Y$ have the pleasure of announcing their forthcoming marriage." Suppose that at the time the hospital was opened, the groom was as old as the bride is now, and that the product of the ages of the groom and the bride and the number of years the hospital has been in existence minus the age of the surgeon equals 1539. When was the hospital opened?
|
1. Let $x$ be the age (number of full years) of the surgeon (groom or bride), $y$ be the number of years of the paramedic (groom or bride), and $h$ be the number of years the hospital has been in existence.
The conditions of the problem can be written as the following two equations:
$$
\begin{gathered}
|x-y|=h \\
x(y h-1)=1539=3^{4} \cdot 19
\end{gathered}
$$
Since, by the context of the problem, $x$ is obviously greater than 9 and less than 171, there are four possible values for $x$: $19, 27, 57, 81$.
These correspond to four values of the expression ($y h - 1$): $81, 57, 27, 19$ and, therefore, four values for $y h$: 82, 58, 28, and 20.
But if $y h=82=2 \cdot 41$, then $y=41, \quad h=2$,
$$
\begin{array}{lll}
y h=58=2 \cdot 29 & y=29, & h=2 \\
y h=28=2^{2} \cdot 7, & y=28 & h=1 \\
y h=20=2^{2} \cdot 5, & y=20, & h=1 .
\end{array}
$$
We obtained these four solutions using only the second equation. If we also use the first equation ($|x-y|=h$), then only the second solution remains, i.e., $x=27, y=29$, and $h=2$.
Thus, the problem is about the marriage of a 29-year-old paramedic to a 27-year-old female surgeon, who work in a hospital that opened 2 years ago.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 2. Clock
At the moment, according to my watch, it is more than 3:20 but less than 3:25. I observe the exact position of the hands on my watch, and then I move the hands so that the minute hand is in the position previously occupied by the hour hand, and the hour hand is in the position previously occupied by the minute hand.
Can you accurately indicate what time the watch shows at the moment.
|
2. If $p$ and $g$ are the angles (in radians) that the hour and minute hands form with the direction from the center of the clock face to the 12 o'clock mark, then
$$
g=12(p-h \cdot 2 \pi / 12)
$$
where $h=0,1,2, \ldots$ or 12 is the number of hours ${ }^{1}$. If the angles $p_{0}$
${ }^{1}$ The angles $p$ and $g$ are measured here in the direction of the clockwise rotation; with $0 \leqslant p, g \leqslant 2 \pi, -\text{Note, } \text{pre}$,
and $g_{0}$ characterize the initial positions of the hands, and the angles $p_{1}$ and $g_{1}$ their positions after we have set the clock, then
1) $g_{0}=12\left(p_{0}-\pi / 2\right)$
2) $g_{1}=12\left(p_{1}-2 \pi / 3\right)$
3) $p_{1}=g_{0}, g_{1}=p_{0}$.
## From this
$$
p_{0}=12\left(g_{0}-2 \pi / 3\right)
$$
Substituting this expression into (1), we get
$$
g_{0}=12\left[12\left(g_{0}-2 \pi / 3\right)-\pi / 2\right]
$$
or
$$
143 g_{0}=6 \cdot 17 \pi
$$
But $g_{0}$ is the angle formed with the chosen direction by the minute hand, for which $2 \pi$ corresponds to 60 minutes. Therefore,
$$
g_{0}=\frac{3 \cdot 17 \cdot 60}{143} \text { min. }
$$
Thus, at this moment, the clock shows 3 hours 21 minutes $23(131 / 143)$ seconds $\approx 3$ hours 21 minutes 23 seconds 55 thirds, where 60 thirds $=1$ second.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 6. Coffee is served
Coffee is always served to me between 1 and 2 o'clock, at a moment when the bisector of the angle formed by the two hands of my clock points exactly at the "12" (hour) mark. At what exact time is my coffee served?
|
6. Let's denote this unknown moment of time as 1 hour $x$ minutes (since it is between 1 hour and 2 hours!). The angle formed by the hour hand with the bisector of the angle between the two hands is (in degrees)
$$
\frac{360}{12}+\frac{x}{60} \cdot \frac{360}{12}=30+\frac{x}{2}
$$
(here we use the fact that the bisector of the angle points to the 12 o'clock mark).
The angle formed by the minute hand with this same bisector is
$$
360-x \cdot(360 / 60)=360-6 x
$$
${ }^{1}$ In Venn diagrams (cf. footnote on p. 119), each subset $Z$ is symbolically represented by a circle, making it easy to trace all possible unions and intersections of these sets, - Note by the translator.
Thus, we have
$$
30+x / 2=360-6 x
$$
from which
$$
x=(2 / 13) \cdot 300 \approx 50 \text { min } 46 \text{s}.
$$
Therefore, my coffee is served at approximately 1 hour 50 minutes $46 \text{s}$.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 10. Confession
The confessor has a habit of assigning penances "by the tariff" - in exact proportion to the gravity of the sins committed. Thus, before absolving the sin of pride, he requires the penitent to recite the "Te Deum" once and the "Pater Noster" twice. Slander is "priced" at two "Pater Noster" and seven "Credo." Laziness "costs" two "Te Deum." Adultery is only absolved after ten "Te Deum," ten "Pater Noster," and ten "Credo," while gluttony is punished with only one penitential prayer, the "Te Deum." Self-love costs the penitent three "Pater Noster" and one "Credo," while jealousy costs three "Pater Noster." Finally, backbiting is "priced" at seven "Pater Noster" and two "Credo." Suppose since my last confession, I must repent for a dozen sins, for which I will have to recite the "Te Deum" nine times, the "Pater Noster" twelve times, and the "Credo" ten times.
What, then, are my sins?
|
10. Since I will have to repeat the "Te Deum" only nine times, it is clear that I am not guilty of adultery.
I confess to one instance of slander, for ten "Credo" would be too few for two instances of slander, and if I had not slandered at all, the "Credo" would correspond to such a number of sins of pride and slander, for which more than a dozen "Pater Noster" would be required to atone.
Having fulfilled the penance imposed for slander, I will still have to repeat the prayer "Credo" three more times. This corresponds to three sins of pride or one sin of pride and one sin of slander. But three sins of pride require nine "Pater Noster" for atonement, and since I am also guilty of slander, there will be a total of eleven "Pater Noster," not twelve as required by the condition of the problem; this remains unexplained and, moreover, inexplicable. Therefore, the three "Credo" I must read are for the atonement of one instance of slander and one instance of pride.
There remain nine sins for which there are nine "Te Deum." Thus, these sins can be nothing other than nine instances of gluttony.
Thus, I confess to one instance of slander, one instance of slander, one sin of pride, and nine instances of gluttony.
(We recommend that the reader first prepare a table in which the number of repetitions of each of the twenty prayers is indicated, corresponding to each of the eight named sins.)
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 18. Seals
Once I entered a maritime museum and saw some seals there. There were not many of them - just seven eighths of all the seals plus another seven eighths of a seal that I counted in the pool. How many seals were there in the pool in total?
dili in two rounds). According to the French constitution, a second round of elections is not held if one candidate has already received an absolute majority of the votes in the first round; if no such candidate exists, only the two candidates who received the most votes in the first round participate in the second round.-Note by nepes.
${ }^{1}$ In French high schools, a 20-point grading system is used - from 1 (complete lack of knowledge of the subject) to 20 (the highest grade in French secondary education, which gives the right to continue education at a university). - Note by the editor.
|
18. Let $n$ be the total number of seals. In this case,
$$
n=(7 / 8) n+7 / 8
$$
from which it follows that $n=7$.
There were seven seals in the marine museum.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.