problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
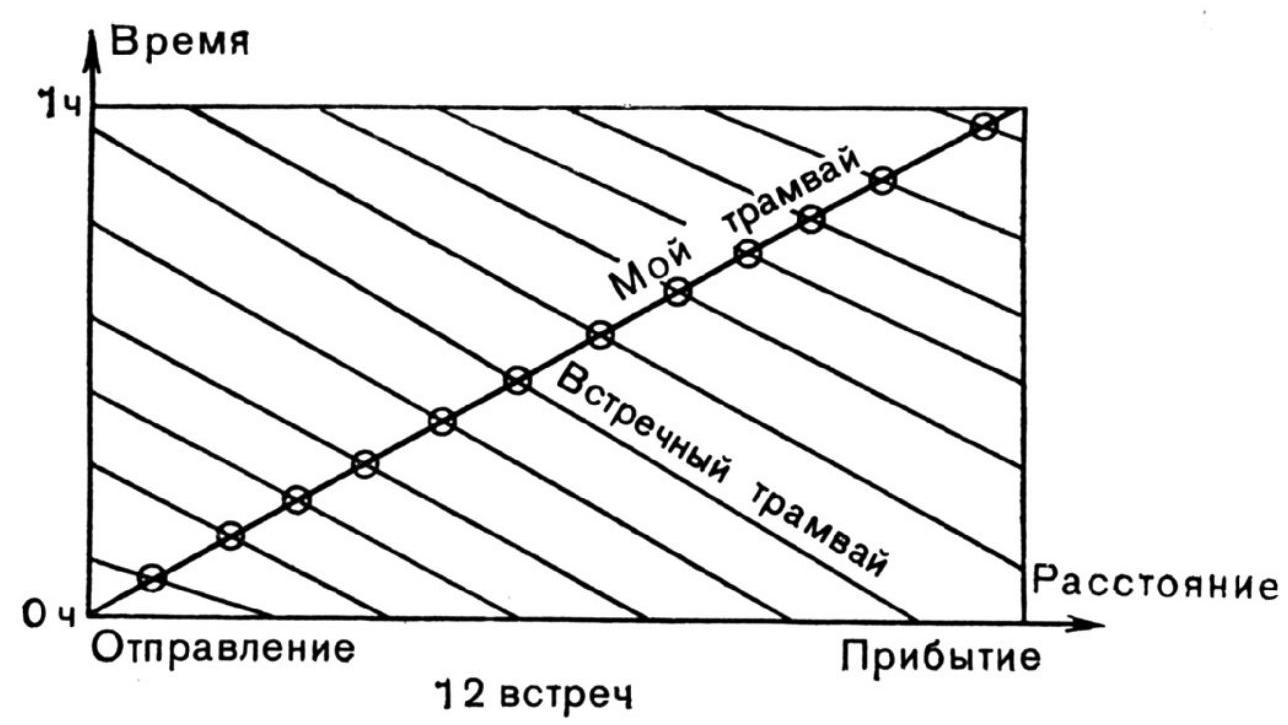
## 19. Tram
On one tram line, trams depart regularly every 10 minutes throughout the day. A tram takes one hour to travel from one end of the line to the other. A passenger boards a tram at one terminal stop and rides to the last stop of the tram; out of boredom, he looks out the window and counts the oncoming trams of the same route. How many tram sets will he count in total.
|
19. The passenger will encounter all the tram cars that departed from the other end of the tram line less than an hour before his departure; generally speaking, there are six such trains. He will also encounter all the trains that will depart from the opposite end of the line within the next hour; generally speaking, there are also six such trains. Therefore, the passenger will count a total of twelve tram cars on the way.
Special case. If the departure of the tram cars from both terminal stations occurs simultaneously, then our passenger will encounter only eleven cars on the way, but he will see one additional oncoming car at each of the terminal stations.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 20. Nicolas plays
## with tin soldiers
Nicolas has the same number of tin Indians, Arabs, cowboys, and Eskimos. After his cousin Sebastian's visit, he indignantly discovered the disappearance of a third of his soldiers. Suppose the number of Eskimos remaining is the same as the number of cowboys that disappeared, and that only two Indians out of every three remain. How many Arabs did cousin Sebastian take?
|
20. Let $x$ be the number of soldiers of each type that Nicolas had initially, and $y$ be the number of cowboys taken by Sebastian (or the number of remaining Eskimos); in this case, the number of Eskimos taken is $x-y$.
On the other hand, it is known that the number of Indians taken is $x / 3$. Let $z$ be the number of Arabs taken. The total number of soldiers taken is $4 x / 3$, since it constitutes one third of the total number of soldiers. But it is easy to see that it also equals
$$
y+(x-y)+x / 3+z
$$
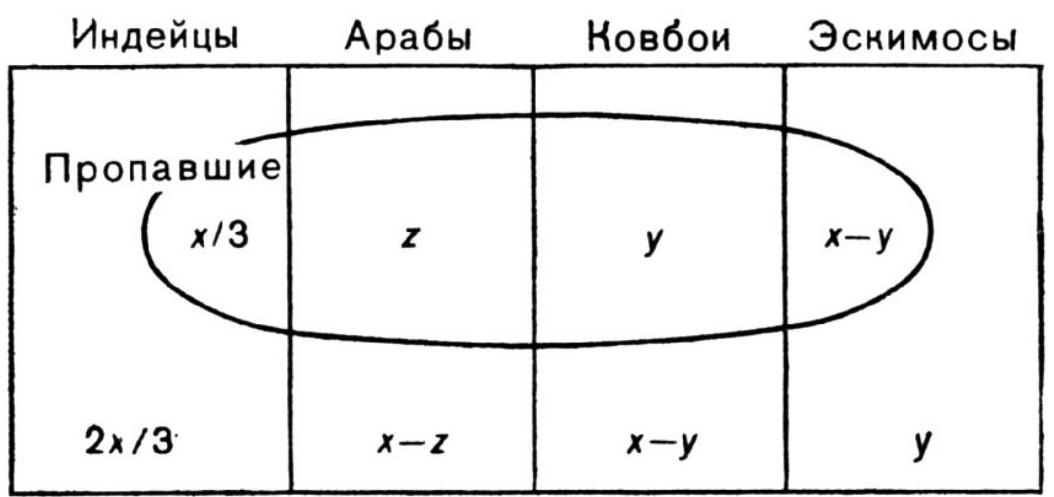
From this, we get the equation
$$
4 x / 3=4 x / 3+z
$$
from which it follows that $z=0$.
Thus, cousin Sebastian did not take any Arabs.
|
0
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 22. General Cleaning
A solid joint-stock company occupies three floors in a tower, which has the shape of a parallelepiped and is located in Paris in the La Défense district: the 13th and 14th floors, where the company's offices are located, and the 25th floor, where its board of directors is situated.
To clean these premises, a cleaning crew is called in, who work for four hours in the offices. Then the crew splits into two parts: half goes to clean the 25th floor, while the other half continues to clean the 13th and 14th floors. After another four hours, the crew stops working: the two lower floors are already completely cleaned, while the 25th floor is scheduled to receive another cleaner the next day, who will complete the work in 8 hours.
Assuming that the time required for cleaning is proportional only to the area of the cleaned premises, how many cleaners were in the crew called by the company?
|
22. Let $n$ be the unknown number of cleaners. The number of man-hours required to clean two floors of the bureau is
$$
4 \cdot(n+n / 2)
$$
The number of man-hours required to clean the 25th floor is
$$
4 \cdot(n / 2)+8
$$
But this last number is half of the previous one, since the area of one floor is half the area of the other two. Therefore,
$$
4(n+n / 2)=2(4 n / 2+8)
$$
From this, $n=8$, i.e., there were eight cleaners in the team.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## 2. Marel
Take a piece of cardboard and draw the following diagram on it:
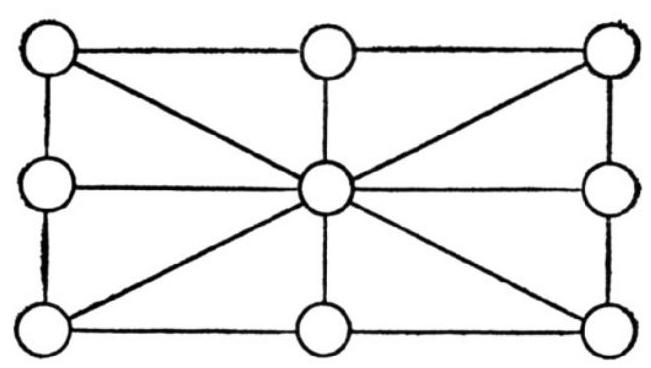
Also, take three silver and three gold coins (if you are on the beach, draw the diagram directly in the sand and play with three white and three black pebbles).
Now choose a suitable partner; each player starts the game with three coins (one player with gold, the other with silver). The player who starts places one of their coins on any of the nine circles. Then the second player places their coin on any of the remaining eight circles; after that, the first player places their second coin, and so on. When all the coins are placed, the players take turns moving one of their three coins along one of the sixteen segments, provided that the other end of the segment is free. The player who first aligns their three coins in a straight line wins.
I. After playing several rounds, you will undoubtedly notice that the player who starts the game can always win if they follow the appropriate strategy. What does it consist of?
II. Let's introduce an additional rule: the player who starts is not allowed to place their first coin in the center. In this case, the second player usually places their coin in the center. Then the first player has six different possible strategies:
1) place the first two coins at the midpoints of two opposite sides of the diagram;
2) place them at the midpoints of two adjacent sides of the diagram;
3) place one coin in a corner and the second in the midpoint of one of the opposite sides to that corner;
4) place one coin in a corner and the second in the midpoint of one of the sides converging at that corner;
${ }^{1}$ If you don't have gold coins, you can use copper ones,
5) place two coins in two opposite corners of the diagram;
6) place two coins in two adjacent corners.
Which of these strategies do you think is the best?
Historical information: Marel (or Merel) is a very ancient game, widely spread in the East under the name "game of three roads." The first definite mention of it appears in the works of Ovid ("Tristia" and "Ars Amatoria"). There it is said: "This game is played on a special small board with three coins that each player has; to win, one must align their three coins in a straight line."
|
2. Let's renumber our nine circles (nine positions of the scheme):
Let $C$ be the player who starts, and $F$ be the player who finishes placing their coins.

I. The player who starts the game places a coin in the center. First case. $F$ places their first coin in a corner. Then the game will develop as follows:
| $C$ | 5 | 8 | 3 | $8 \rightarrow 9$ | $5 \rightarrow 6$ | Victory! |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $F$ | 1 | 2 | 7 | - | - | |
Initial placement of 3 coins
Regular moves from 8 to 9, from 5 to 6, etc. ...
Second case. $F$ places their first coin in the middle of a side. The game develops as follows:
| $C$ | 5 | 1 | 7 | $1 \rightarrow 2$ | $2 \rightarrow 3$ | Victory! |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $F$ | 8 | 9 | 4 | - | - | |
In both cases, $C$ wins.
II. The starting player is prohibited from placing their first coin in the center.
Let's analyze the six game tactics listed in the problem statement.
1) The game develops as follows:
| $C$ | 2 | 8 | 1 | - | |
| :---: | :---: | :---: | :---: | :---: | :---: |
| $F$ | 5 | 9 | 4 | $9 \rightarrow 6$ | Victory! |
2) The game develops as follows:
| $C$ | 2 | 6 | 3 | - | |
| :---: | :---: | :---: | :---: | :---: | :---: |
| $F$ | 5 | 7 | 9 | $5 \rightarrow 8$ | Victory! |
3) The game develops as follows:
| $C$ | 1 | 6 | 3 | - | |
| :---: | :---: | :---: | :---: | :---: | :---: |
| $F$ | 5 | 7 | 2 | $7 \rightarrow 8$ | Victory! |
4) The game develops as follows:
| $C$ | 1 | 2 | 7 | - | |
| :---: | :---: | :---: | :---: | :---: | :---: |
| $F$ | 5 | 3 | 9 | $5 \rightarrow 6$ | Victory! |
5) The game develops as follows:
| $C$ | 1 | 9 | 2 | - | |
| :---: | :---: | :---: | :---: | :---: | :---: |
| $F$ | 5 | 8 | 3 | $8 \rightarrow 7$ | Victory! |
6) The game develops as follows:
| $C$ | 1 | 3 | 8 | Draw |
| :---: | :---: | :---: | :---: | :---: |
| $F$ | 5 | 2 | | Draw |
Thus, for the player $C$, who starts the game, the sixth tactic (placing the first two coins in two adjacent corners) is the best, as it is the only one that does not lead to a loss for $C$ (if the second player $F$ plays optimally), but to a draw.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
150*. Prove that if $a+b+c=0$, then
$$
\left(\frac{a-b}{c}+\frac{b-c}{a}+\frac{c-a}{b}\right)\left(\frac{c}{a-b}+\frac{a}{b-c}+\frac{b}{c-a}\right)=9
$$
where $a \neq 0, \quad b \neq 0, c \neq 0, a \neq b, \quad a \neq c, b \neq c$.
|
Proof.
$$
\begin{gathered}
\left(\frac{a-b}{c}+\frac{b-c}{a}+\frac{c-a}{b}\right) \cdot\left(\frac{c}{a-b}+\frac{a}{b-c}+\frac{b}{c-a}\right)= \\
=1+\frac{(b-c) c}{a(a-b)}+\frac{(c-a) c}{b(a-b)}+\frac{a(a-b)}{c(b-c)}+ \\
+1+\frac{(c-a) a}{b(b-c)}+\frac{b(a-b)}{c(c-a)}+\frac{(b-c) b}{a(c-a)}+1= \\
=3+\frac{c}{a-b}\left(\frac{b^{2}-b c+a c-a^{2}}{a b}\right)+\frac{a}{b-c}\left(\frac{a b-b^{2}+c^{2}-a c}{b c}\right)+ \\
+\frac{b}{c-a}\left(\frac{a^{2}-a b+b c-c^{2}}{a c}\right)=3+2\left(\frac{c^{2}}{a b}+\frac{a^{2}}{b c}+\frac{b^{2}}{a c}\right)
\end{gathered}
$$
since
$$
\frac{c}{a-b}\left(\frac{b^{2}-b c+a c-a^{2}}{a b}\right)=\frac{c(c-b-a)}{a b}=\frac{2 c^{2}}{a b}
$$
since
$$
a+b+c=0, \quad c-b-a=2 c
$$
## Similarly:
$$
\frac{a}{b-c}\left(\frac{a b-b^{2}+c^{2}-a c}{b c}\right)=\frac{2 a^{2}}{b c} ; \frac{b}{c-a}\left(\frac{a^{2}-a b+b c-c^{2}}{a c}\right)=\frac{2 b^{2}}{a c}
$$
## Transform the expression
$$
\frac{c^{2}}{a b}+\frac{a^{2}}{b c}+\frac{b^{2}}{a c}=\frac{c^{3}+a^{3}+b^{3}}{a b c}=\frac{3 a b c}{a b c}=3
$$
(see problem 113). Therefore,
$$
\left(\frac{a-b}{c}+\frac{b-c}{a}+\frac{c-a}{b}\right)\left(\frac{c}{a-b}+\frac{a}{b-c}+\frac{b}{c-a}\right)=3+2 \cdot 3=9
$$
|
9
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
233. If $x_{1}$ and $x_{2}$ are the roots of the equation
$$
\frac{3 a-b}{c} x^{2}+\frac{c(3 a+b)}{3 a-b}=0
$$
then, without solving it, find $x_{1}^{117}+x_{2}^{117}$.
|
Solution.
$x_{1}^{117}+x_{2}^{117}=\left(x_{1}+x_{2}\right)\left(x_{1}^{116}-x_{1}^{115} x_{2}+\ldots+x_{2}^{116}\right), \quad$ but $\quad x_{1}+x_{2}=0$, so, $x_{1}^{117}+x_{2}^{117}=0$.
Note. It is useful to solve problem 233 when reviewing, after discussing the equality:
$$
a^{n}+b^{n}=(a+b)\left(a^{n-1}-a^{n-2} b+\ldots+b^{n-1}\right)
$$[^5]
62
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
352. Find a natural number that is equal to the sum of all its preceding natural numbers. Does more than one such number exist, or is there only one?
|
Let $n$ be the desired natural number; the sum of the numbers preceding this natural number is expressed by the formula
$$
S_{n-1}=\frac{n(n-1)}{2}
$$
According to the problem, $\frac{n(n-1)}{2}=n$, from which $n^{2}-3 n=0$ or $n_{1}=3, n_{2}=0$. The desired number is 3. It is the only one, as the second root of the obtained equation (zero) cannot be considered, since no natural number precedes it.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. How many four-digit numbers can be formed, the sum of whose digits is 3? List these numbers.
|
2. For writing numbers, we use digits
$0,1,2,3,4,5,6,7,8,9$
Since the sum of the digits is three, we can exclude all digits starting from four.
$0,1,2,3,4,5,6,7,8,9$
A number cannot start with zero, so the first digit can be one of the three digits $1,2,3$. The further solution will be represented in the form of a diagram:
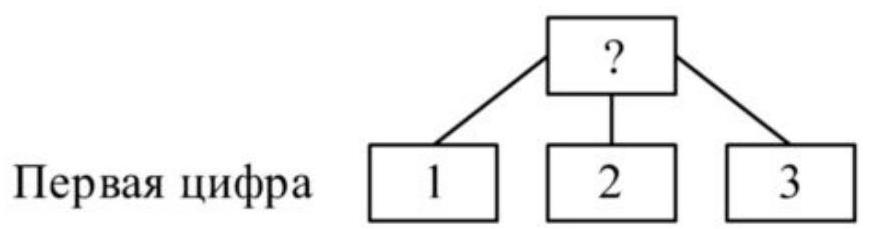
Now we need to choose the second digit for each of the three cases.
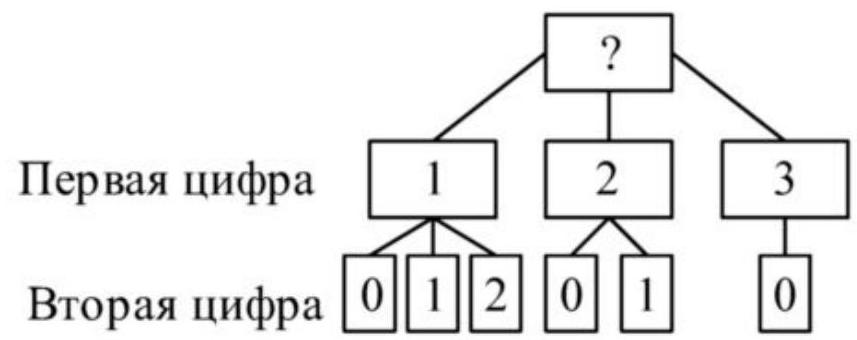
Similarly, we will determine the third and fourth digits.
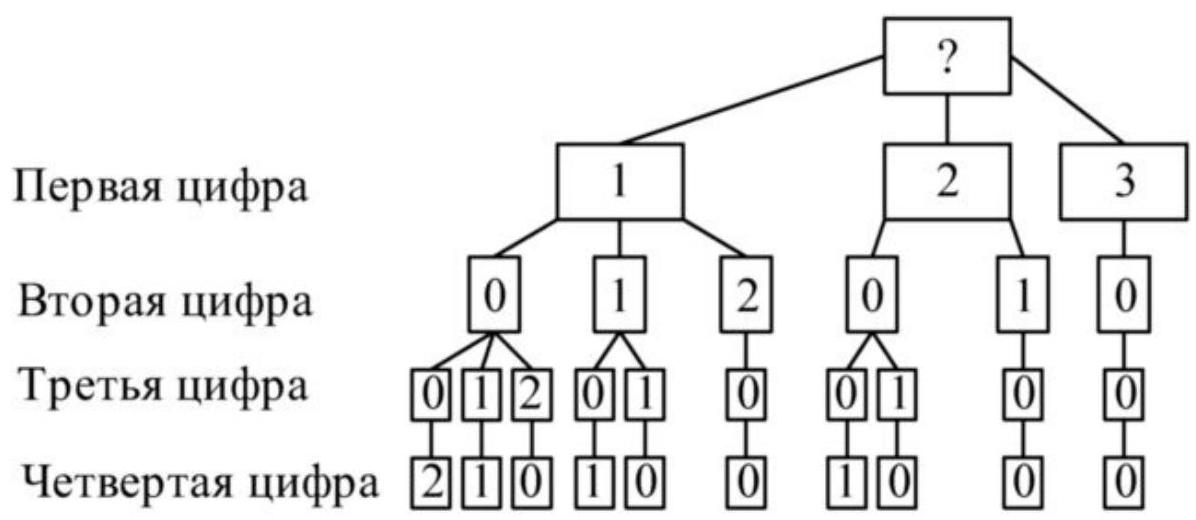
The obtained numbers are:
| $1002 ;$ | $1101 ;$ | $2001 ;$ | $3000 ;$ |
| :--- | :--- | :--- | :--- |
| $1011 ;$ | $1110 ;$ | $2010 ;$ | |
| $1020 ;$ | $1200 ;$ | 2100. | |
Answer: 10 numbers.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Ducks were flying. One in front, two behind, one behind and two in front, one between two and three in a row. How many ducks were flying in total?
|
3. Let's schematically depict how the ducks flew.
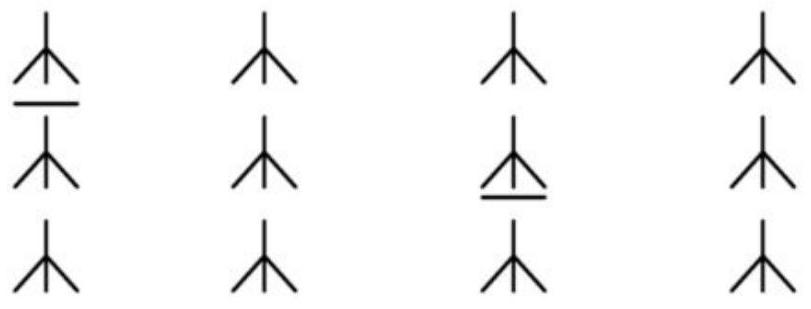
As can be seen from the diagram, the problem is about three ducks.
Answer: 3 ducks.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. There were 5 times more strawberry bushes on the first bed than on the second. When 22 bushes were transplanted from the first bed to the second, the number of strawberry bushes on each bed became the same. How many bushes were there on each bed?
|
## 5. First method of solving.
Let's build a graphical model of the problem's condition
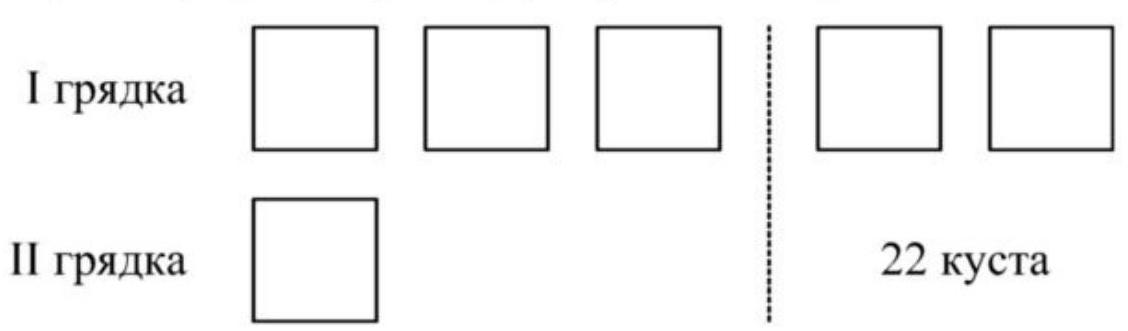
1) $22: 2=11$ (bushes) - this is $1/5$ of all the bushes (that were on the second bed);
2) $11 \times 5=55$ (bushes) - this was on the first bed.
Second method of solving (Nikolai Zherebtsov - student of School No. 46).
1) $5+1=6$ (parts) - in total;
2) $6: 2=3$ (parts) - this is how many parts each bed has;
3) $5-3=2$ (parts) - this is how many parts were transplanted from the first bed to the second;
4) $22: 2=11$ (bushes) - this is how many bushes are in one part (there were on the second bed)
5) $11 \times 5=55$ (bushes) - this was on the first bed.
Third method of solving (Vitaliy Semikin - student of School No. 48).
1) $22+22=44$ (bushes) - this is how many fewer bushes there are on the second bed compared to the first;
2) $44: 4=11$ (bushes) - this is how many bushes are in one part (there were on the second bed)
3) $11 \times 5=55$ (bushes) - this was on the first bed.
Answer: 11 bushes were on the second bed, 55 bushes were on the first.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Let 2 cups and 2 pitchers weigh as much as 14 plates, 1 pitcher weighs as much as 1 cup and 1 plate. How many plates will balance a pitcher
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。
|
4. First method of solution (graphical).
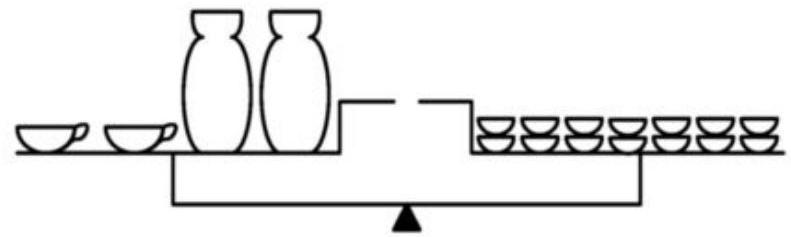
Reduce the number of items on each scale by half.

Now replace the jug on the left scale with a plate and a cup.
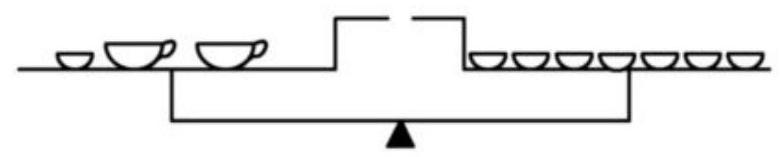
Remove a plate from each scale.
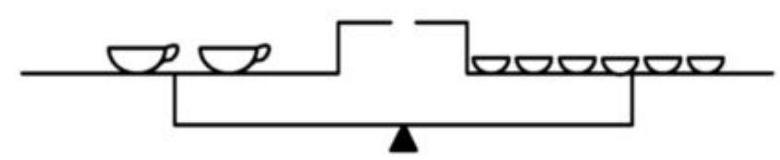
Reduce the number of items on each scale by half.

Since one jug weighs as much as one cup and one plate, we get:
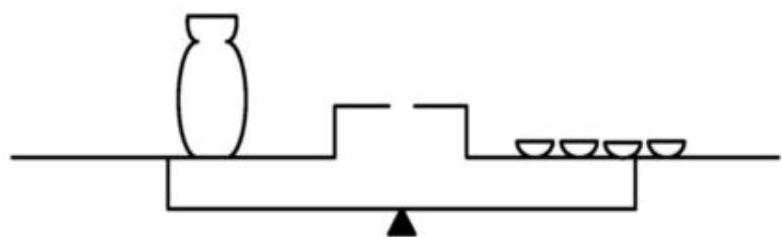
Second method of solution (analytical).
According to the problem, 2 cups + 2 jugs = 14 plates. Dividing both sides of the equation by 2, we get 1 cup + 1 jug = 7 plates. According to the second condition, 1 jug = 1 cup + 1 plate. From the subsequent two equations, we have:
$$
\begin{aligned}
& 1 \text{ cup } + 1 \text{ jug } = 7 \text{ plates; } \\
& 1 \text{ jug } = 1 \text{ cup } + 1 \text{ plate; } \\
& 1 \text{ cup } + 1 \text{ cup } + 1 \text{ plate } = 7 \text{ plates; } \\
& 2 \text{ cups } = 6 \text{ plates; } \\
& 1 \text{ cup } = 3 \text{ plates; } \\
& 1 \text{ jug } = 1 \text{ cup } + 1 \text{ plate } = 3 \text{ plates } + 1 \text{ plate } = 4 \text{ plates. }
\end{aligned}
$$
Third method of solution (arithmetic).
1) $14 \div 2 = 7$ (plates) - will balance 1 cup and 1 plate;
2) $7 - 1 = 6$ (plates) - will balance 2 cups;
3) $6 \div 2 = 3$ (plates) - will balance 1 cup;
4) $3 + 1 = 4$ (plates) - will balance 1 jug.
Answer: one jug balances 4 plates.
|
4
|
Logic and Puzzles
|
other
|
Yes
|
Yes
|
olympiads
| false
|
5. A group of third-graders decided to go on a trip to Moscow on March 19 after a math olympiad. Each student contributed the same amount of money monthly, and over 9 months, they collected 22725 rubles. How many students were in the class and how much did each student contribute monthly?
|
5. 6) $22725: 9=2525$ (rubles) — the amount the students paid for one month.
To determine how much each student paid monthly, we need to know the number of students in the class. This is unknown in the problem. However, from the problem's condition, it follows that this is a natural number that is a divisor of 2525.
$$
\begin{gathered}
2525: 5=505 \\
505: 5=101
\end{gathered}
$$
Thus, there could have been 5, 25, or 101 students in the class. Since it is impossible to have 101 students in a class, the number of students was either 5 or 25.
2) $2525: 5=505$ (rubles)
3) $2525: 25=101$ (rubles)
Answer: 5 students paid 505 rubles each or 25 students paid 101 rubles each.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the smallest number that gives a remainder of 1 when divided by 2, and a remainder of 2 when divided by 3.
|
3. First, let's write down the numbers that give a remainder of 1 when divided by 2:
$$
3,5,7,9,11 \ldots
$$
Next, let's write down the numbers that give a remainder of 2 when divided by 3:
$$
5,8,11,14,17 \ldots
$$
We will choose from the obtained numbers the one that satisfies both conditions and is the smallest. This number is 5.
We could have reasoned differently. After writing down the numbers that give a remainder of 1 when divided by 2, we find which of them will give a remainder of 2 when divided by 3, and then choose the smallest one among them (5, 11, 17 ...), or we could first write down the numbers that give a remainder of 2 when divided by 3, and then choose the smallest one among them that gives a remainder of 1 when divided by 2.
Answer: 5.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. It is known that the perimeter of one rectangle is greater than the perimeter of another rectangle. Compare the areas of these rectangles.
Translate the above text into English, please keep the original text's line breaks and format, and output the translation result directly.
|
6. The solution to this problem can be obtained by students as a result of conducting a computational experiment with various rectangles, for example:
a) $a=3 \text{~cm}, b=4 \text{~cm}$;
$$
\begin{aligned}
& a=4 \text{~cm}, b=2 \text{~cm} ; \\
& p_{2}=12 \text{~cm} ; \\
& S_{2}=8 \text{~cm}^{2}
\end{aligned}
$$
$$
\begin{aligned}
& p_{1}=14 \text{~cm} ; \\
& S_{1}=12 \text{~cm}^{2} ;
\end{aligned}
$$
$$
S_{1}>S_{2}
$$
b) $a=6 \text{~cm}, b=1 \text{~cm}$;
$$
\begin{aligned}
& a=4 \text{~cm}, b=2 \text{~cm} ; \\
& p_{2}=12 \text{~cm} \\
& S_{2}=8 \text{~cm}^{2}
\end{aligned}
$$
$$
\begin{aligned}
& p_{1}=14 \text{~cm} \\
& S_{1}=6 \text{~cm}^{2}
\end{aligned}
$$
$$
S_{1}<S_{2} .
$$
c) $a=10 \text{~cm}, b=2 \text{~cm}$;
$$
\begin{aligned}
& a=5 \text{~cm}, b=4 \text{~cm} \\
& p_{1}=18 \text{~cm} \\
& S_{1}=20 \text{~cm}^{2}
\end{aligned}
$$
$$
\begin{aligned}
& p_{1}=24 \text{~cm} ; \\
& S_{1}=20 \text{~cm}^{2}
\end{aligned}
$$
$$
S_{1}=S_{2} .
$$
Thus, we have three variants of the relationships between the areas of the rectangles.
Answer: the area of one rectangle can be greater than, less than, or equal to the area of another rectangle.
|
1
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the box, there are geometric shapes: triangles, squares, and circles. In total, there are 24 shapes. There are 7 times as many triangles as squares. How many of each shape could be in the box?
|
3. The first method of solving. Let's represent the condition of the problem in the form of a drawing.
squares

triangles

circles

From this, it is clear that the sum of the triangles and squares should be divisible by eight. There are only two numbers less than 24 and divisible by eight - these are 16 and 8. Let's check each of them.
1) \(16 \div 8 = 2\) (squares); \(\quad\) 1) \(8 \div 8 = 1\) (squares);
2) \(2 \times 7 = 14\) (triangles)
3) \(1 \times 7 = 7\) (triangles);
4) \(24 - 16 = 8\) (circles).
5) \(24 - 8 = 16\) (circles).
The second method of solving. Since, according to the condition, there are 7 times more triangles than squares, there could not be more than three squares, otherwise, the total number of figures would exceed 24.
Let's assume there was 1 square, then there were 7 times more triangles, that is, 7. The number of circles can be determined by calculating the difference between 24 and 8. There were 16 circles.
Let's assume there were 2 squares, then there were \(14 = 2 \times 7\) triangles, and \(8 (24 - (14 + 2)) = 8\) circles.
Let's assume there were 3 squares, then there would be 21 triangles, and their sum would be 24. In this case, there would be no circles, which contradicts the condition of the problem.
The third method of solving (by Yelena Viazmina, a student of School No. 46).
There are 7 times more triangles than squares. In total, there are 8 such parts. 24 is divisible by 8, but we still have circles. We take the nearest number that is divisible by 8. This number is 16.
1) \(16 \div 8 = 2\) (squares)
2) \(2 \times 7 = 14\) (triangles)
3) \(24 - 16 = 8\) (circles).
Answer: 2 squares, 14 triangles, 8 circles or 1 square, 7 triangles, 16 circles.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Anton was given a scale, and he started weighing his toys. A car was balanced by a ball and two cubes, and a car with a cube - two balls. How many cubes balance a car? (All of Anton's balls are the same, and the cubes are the same too.)
|
4. First method of solving. Since the machine is balanced by the ball and two cubes, the machine with a cube will be balanced by the ball and three cubes. From the second condition, we have that 2 balls balance a ball and 3 cubes, meaning one ball by mass is equal to 3 cubes. Thus, the machine can be balanced by 5 cubes.
Second method of solving. This problem can be solved analytically, for which each condition of the problem can be written as an equality:
$$
\begin{aligned}
& \mathrm{M}=\mathrm{Mball}+2 \mathrm{~K} \\
& \mathrm{M}+\mathrm{K}=2 \mathrm{Mball}
\end{aligned}
$$
Substituting into the second equality the sum of Mball $+2 K$ for M, we get
$$
\text { Mball + } 2 \mathrm{~K}+\mathrm{K}=2 \text { Mball. }
$$
From which it is easy to find that
$$
\text { 3K = Mball. }
$$
From the obtained ratio and the first equality, we get:
$$
\begin{gathered}
\mathrm{M}=2 \mathrm{~K}+3 \mathrm{~K} \\
\mathrm{M}=5 \mathrm{~K}
\end{gathered}
$$
Answer: the machine can be balanced by 5 cubes.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Two numbers were first multiplied, and then the larger number was divided by the smaller one, resulting in equal outcomes. What are these numbers? How many such pairs of numbers exist?
|
2. Let $a$ and $b$ be the two numbers mentioned in the problem, with $a > b$. According to the problem,
$$
a \times b = a : b
$$
or
$$
a b^{2} - a = 0
$$
Factoring out the common factor, we get
$$
a \left(b^{2} - 1\right) = 0
$$
From this, we can conclude that $b = 1$, and $a$ can be any number.
Students might reason as follows: find a number such that when multiplied and divided by it, the result is the same. This number is one. Then the first number can be any number, because multiplying it by one and dividing it by one will yield the same number.
Answer: $b = 1$, $a$ can be any number. There are infinitely many such pairs.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Given a triangle with side lengths of 7 cm, 12 cm, and 9 cm respectively. Explain how to construct a segment connecting a vertex and the opposite side with a length of 9 cm so that the perimeters of the two resulting triangles are equal.
|
6. First method of solution. Since in the obtained triangles one side will be common ( $A D$ ), in order for the perimeters to be equal, it is necessary that the side of 9 cm be divided into parts, the difference in lengths of which would equal the difference of the other two sides ( $12-7=5 \text{ cm}$ ). Based on this, the number 9 should be represented as the sum of two addends, one of which is 5 more than the other. The numbers that satisfy this condition are 2 and 7. Thus, we get the following solution:
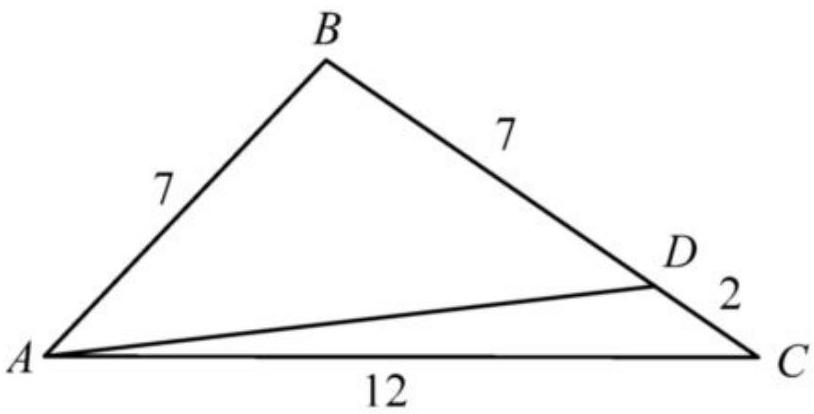
Second method of solution. The solution to this problem will be easily found if the perimeter is represented as the sum of segments:
$$
\begin{aligned}
& P_{\triangle A D C}=A C+C D+D A \\
& P_{\triangle A B D}=A B+B D+D A
\end{aligned}
$$
1) $12-7=5$ (cm) - by this much $B D$ should be longer than $D C$;
2) $9-5=4$ (cm) - two segments $C D$;
3) $4: 2=2$ (cm) - the length of segment $C D$;
4) $2+5=7$ (cm) - the length of segment $B D$.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Carlson has a runny nose. He uses square handkerchiefs measuring 25 cm $\times 25 \mathrm{~cm}$. Over eight days, Carlson used $3 \mathrm{~m}^{2}$ of fabric. How many handkerchiefs did Carlson use per day?
|
2. First method of solving.
1) $25 \times 25=625\left(\mathrm{~cm}^{2}\right)-$ area of one handkerchief;
2) $3 \times 10000=30000\left(\mathrm{~cm}^{2}\right)$ - contained in $3 \mathrm{~m}^{2}$;
3) $30000: 625=48$ (handkerchiefs) - Carlson used over 8 days
4) $48: 8=6$ (handkerchiefs) - Carlson used per day.
Second method of solving (Setov Mikhail, student of School No. 15).
From 1 m², 16 handkerchiefs can be obtained (see diagram). Carlson used $3 \mathrm{~m}^{2}$, which means $3 \times 16=48$ handkerchiefs over 8 days. Therefore, he used 6 handkerchiefs per day $(48: 8=6)$.
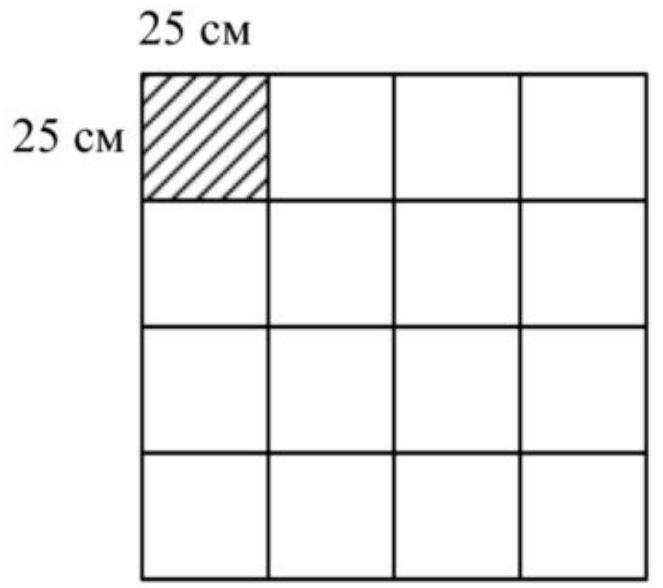
Third method of solving (Babenko Dima, student of School No. 28).
1) $300 \cdot 100=30000\left(\mathrm{~cm}^{2}\right)-$ was in $3 \mathrm{~m}^{2}$;
2) $300: 25=12$ (h.) - on one side
3) $100: 25=4$ (h.) - on the other side.
4) $12 \times 4=48$ (h.) — in total.
5) $48: 8=6$ (h.) — Carlson used per day.
Fourth method of solving (Selemin Alexei, student of School No. 9)
1) $25 \times 25=625\left(\mathrm{~cm}^{2}\right)$ - area of one handkerchief;
2) $3 \times 10000=30000\left(\mathrm{~cm}^{2}\right)$ - contained in 3 square meters;
3) $30000: 8=3750\left(\mathrm{~cm}^{2}\right)$ — fabric Carlson used per day;
4) $3750: 625=6$ (h.) — Carlson used per day.
Answer: 6 handkerchiefs.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In a box, there are 7 blue and 5 red balls. What is the minimum number of balls that need to be taken out to ensure that among them there are at least 2 blue and 1 red?
|
5. The worst-case scenario is if we draw 7 balls and they all turn out to be blue. To get another red ball, we need to draw one more ball. In this case, there will definitely be one red ball and 2 blue balls among the balls.
Answer: 8 balls.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The boy caught a fish. When asked how much the caught fish weighed, he said: “I think the tail weighs 1 kg, and the head weighs as much as the tail and half the body, and the body weighs as much as the head and the tail together.” How much does the fish weigh?
|
2. From the problem statement, it is known that the tail ( $X$ ) weighs 1 kg. The weight of the head is equal to the weight of the tail plus an additional $1 / 2$ of the body weight (T):
$$
\Gamma=\mathrm{X}+\mathrm{T} / 2 \text { or } 2 \Gamma=2 \mathrm{X}+\mathrm{T} .
$$
Since the tail weighs 1 kg, then $2 \Gamma=2+$ T .
From another condition, it is known that $\mathrm{T}=\Gamma+\mathrm{X}$ or $\mathrm{T}=\Gamma+1$.
From the obtained equations, we have:
$$
2 \Gamma=2+\Gamma+1, \Gamma=3, \mathrm{a} T=4 .
$$
Thus, the fish weighs $1+3+4=8$ (kg).
Answer: 8 kg.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. If from each of two numbers you subtract half of the smaller one, the remainder of the larger one is three times the remainder of the smaller one. How many times larger is the larger number than the smaller one?
|
1. The first way to solve the problem is to represent the condition of the problem in the form of a drawing.
From the drawing, it is clear that the first number is twice as large as the second.
The second way to solve the problem is to solve it without relying on a drawing. Since the remainder of the smaller number is half of the number itself, the larger number contains 4 halves of the smaller number and is therefore twice as large as the smaller one.
The third way to solve (Shabanov Konstantin, student of Gymnasium No. 24).
Let there be two numbers \(a\) and \(b\), where \(a > b\). Then
\[
\begin{aligned}
& a - b / 2 = x \\
& b - b / 2 = y, \quad y = b / 2
\end{aligned}
\]
By the condition
\[
x : y = 3, \quad x = 3 y
\]
that is
\[
x = 3 b / 2 \text{.}
\]
Since \(a - b / 2 = x\) and \(x = 3 b / 2\), we can find
\[
a = b / 2 + x = x = b / 2 + 3 b / 2 = 2 b \text{.}
\]
The larger number \(a\) is twice as large as the smaller \(b\).
The fourth way to solve (Lakhov Evgeny, student of School No. 12).
It became: the larger one \(-3x\), the smaller one \(-x\).
It was: the larger one \(3x + x = 4x\)
The smaller one \(x + x = 2x, \quad 4x : 2x = 2\) (times).
Answer: the larger number is 2 times larger.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. One side of the square was increased by 5 times, and the other side was reduced by 2 times, resulting in a rectangle with an area of $160 \mathrm{~cm}^{2}$. What is the side length of the square
|
6. First method of solution.
1) $160: 5=32\left(\mathrm{~cm}^{2}\right)$ - area of half the square;
2) $32 \times 2=64\left(\mathrm{~cm}^{2}\right)$ - area of the original square;
3) $64: 8=8$ (cm) - side of the square.
Second method of solution. The algebraic solution of this problem is as follows: let $x$ be the side of the square, then $x / 2$ and $5 x$ are the sides of the rectangle. Its area is 160 sq.cm.
$$
5 x \times x / 2=160 \text { or } 5 x \times x=320, x \times x=64, x=8(\text { cm). }
$$
Answer: the side of the square is 8 cm.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. In 1996, a farmer bought two sheep. This year he did not get any offspring. The first sheep gave birth to 1 sheep every three years, and the second sheep gave birth to 1 sheep every two years. All the born sheep gave birth to 1 sheep annually. How many sheep will the farmer have in the year 2000?
|
6. Let's draw a diagram according to the problem statement.

Answer: 9 sheep.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. From 16 m of fabric, 4 men's and 2 children's coats were sewn. How many meters of fabric are needed to sew one men's and one children's coat, if from 18 m of the same fabric, 2 men's and 6 children's coats can be sewn
|
7. Let's make a brief record of the problem's condition:
$$
\begin{aligned}
& 4 \text { m, } 2 \text { d }-16 \text { m; } \\
& 2 \text { m, } 6 \text { d }-18 \text { m. }
\end{aligned}
$$
To ensure that the brief record contains the same quantities, we will double the second order:
$$
\begin{aligned}
& 4 \text { m, } 2 \text { d }-16 \text { m} ; \\
& 4 \text { m, } 12 \text { d }-36 \text { m} .
\end{aligned}
$$
1) $12-2=10$ (d) - by this much more children's coats were ordered the second time;
2) $36-16=20$ (m) - by this much more fabric was used for children's coats the second time;
3) $20: 10=2$ (m) - the amount of fabric needed to sew one children's coat;
4) $16-2 \times 2=12$ (m) - the amount of fabric remaining for the first order of 4 men's coats;
5) $12: 4=3$ (m) - the amount of fabric needed to sew one men's coat.
Answer: 3 meters of fabric are needed to sew one men's coat, and 2 meters for one children's coat.
## SEVENTEENTH
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. At the mathematics olympiad in two rounds, it is necessary to solve 14 problems. For each correctly solved problem, 7 points are given, and for each incorrectly solved problem, 12 points are deducted. How many problems did the student solve correctly if he scored 60 points?
|
3. Let's determine the number of problems solved by the student, given that he received 7 points for each problem: $60: 7=8$ (remainder 4). Since 12 points were deducted for each incorrectly solved problem, the number of correctly solved problems was more than 8. Further, by trial and error, we can establish that there were 12.
Answer: The student solved 12 problems correctly.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. One side of a rectangle is $5 \mathrm{~cm}$, and the other is the smallest two-digit number that is divisible by 3. For the second rectangle, one side is equal to the shorter side of the first. The area of one rectangle is $25 \mathrm{~cm}^{2}$ greater than the area of the other. Determine the unknown side of the second rectangle.
|
6. First, let's determine the unknown side of the rectangle. For this, we will find the smallest two-digit number that is divisible by 3, which is 12. According to the problem, one side of the second rectangle is $5 \mathrm{~cm}$. Let's determine the area of the first rectangle $(12 \times 5=60)$. Since the problem does not specify which rectangle's area is larger by $25 \mathrm{~cm}^{2}$, we need to consider two cases.
First case. Suppose the area of the first rectangle is $25 \mathrm{~cm}^{2}$ larger than the area of the second rectangle. In this case, the area of the second rectangle is $35 \mathrm{~cm}^{2}(60-25=35)$. Knowing that one side of the second rectangle is 5 cm and its area is 35 $\mathrm{cm}^{2}$, we can determine the second side $-7 \mathrm{~cm}(35: 5=7)$.
Second case. Suppose the area of the second rectangle is $25 \mathrm{~cm}^{2}$ larger than the area of the first rectangle. In this case, the area of the second rectangle is $85 \mathrm{~cm}^{2}(60+25=85)$. Knowing that one side of the second rectangle is 5 cm and its area is 85 $\mathrm{cm}^{2}$, we can determine the second side $-17 \mathrm{~cm}(85: 5=17)$.
Answer: 7 cm or 17 cm.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A sheet of cardboard measuring 48 cm in length and 36 cm in width needs to be cut into cards measuring 16 cm in length and 12 cm in width. How can this be done to obtain the maximum number of cards?
|
1. In the first step, it is necessary to determine how many cards will fit if the length of each is $16 (48: 16=3)$. Then determine how many cards will fit in the width (36:12 = 3).
Finally, find the number of cards $(3 \times 3=9)$. Then conduct similar reasoning for the case where the cards are laid out by width ( $48: 12=4,36: 16=2$ (remainder 4), $4 \times 2=8$ ). Now we can conclude that the maximum number of cards is 9.
Answer: cut the length into three equal parts of 16 cm, and then cut each of the resulting parts into 3 more parts - 12 cm each.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (Ancient Indian problem 3-4th century AD). Of the four sacrificial donors, the second gave twice as many coins as the first, the third three times as many as the second, the fourth four times as many as the third, and all together gave 132 coins. How many did the first give?
|
4. The first method of solving. By analyzing the condition of the problem, one can conclude that the number of coins given by the first person will not be more than 10. We will then refine this number through trial and error. Let's try the number 5.
$$
5+5 \times 2+5 \times 2 \times 3+5 \times 2 \times 3 \times 4=5+10+30+120=165
$$
Since the obtained number is greater than the given number, we made a mistake in our choice. Let's take the number 4. Checking shows that it satisfies the conditions of the problem.
The second method of solving. When solving this problem, it is useful to make a drawing, representing each number as a segment. This way, it will be immediately clear that 33 identical segments equal 132. From this, it is easy to determine the amount of money given by the first donor.
The third method of solving. This problem can also be solved using an equation. For this, let $x$ be the amount of money given by the first donor. Based on the condition, the following equation can be formed:
$$
\begin{gathered}
x+2 x+(2 x) \times 3+(2 x \times 3) \times 4=132 \\
x+2 x+6 x+24 x=132,33 x=132, x=4
\end{gathered}
$$
Answer: the first person gave four coins.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Two boats departed from piers $A$ and $C$. The speed of the boat traveling from $A$ is 7 km per hour, and from $C$ is 3 km per hour. Determine after how much time the boats will meet, if the distance between the piers is 20 km, and the speed of the river current from $A$ to $C$ is 2 km per hour.
|
4. Since the problem does not specify the direction in which the boats are moving, we need to consider various scenarios: they are moving towards each other; they are moving in the same direction downstream; they are moving in the same direction upstream; they are moving in opposite directions. Given that the boats must meet, we can exclude the last two cases.
Case one - the boats are moving towards each other.
1) $7+2=9$ km/h - the speed of the first boat;
2) $3-2=1 \text{ km/h} -$ the speed of the second boat;
3) $9+1=10$ km/h - the closing speed;
4) $20: 10=2$ hours.
Case two - the boats are moving downstream.
1) $7+2=9$ km/h - the speed of the first boat;
2) $3+2=5$ km/h - the speed of the second boat;
3) $9-5=4$ km/h - the closing speed;
4) $20: 4=5$ hours.
Answer: They will meet in 2 or 5 hours.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (An old entertaining problem). Divide 46 rubles into 8 parts so that each part is 50 kopecks (50 cents) more than the previous one.
|
5. First method of solution. Let the first part be $x$, then the second is $x+50$, the third is $-x+50 \times 2$, the fourth is $-x+50 \times 3$, the fifth is $x+50 \times 4$, the sixth is $-x+50 \times 5$, the seventh is $-x+50 \times 6$, and the eighth is $x+50 \times 7$. We will calculate the sum of all parts.
$$
\begin{gathered}
x+x+50+x+50 \times 2+x+50 \times 3+x+50 \times 4+ \\
x+50 \times 5+x+50 \times 6+x+50 \times 7= \\
=8 x+50 \times 28=8 x+1400 .
\end{gathered}
$$
Since 1400 kopecks is equal to 14 rubles, we get $8 x+14$. According to the problem, this sum is equal to 46 rubles.
We get the equation
$$
8 x+14=46,8 x=32, x=4
$$
The first part is 4 rubles, the second is 4 rubles 50 kopecks (4 rubles + 50 kopecks = 4 rubles 50 kopecks), the third is 5 rubles, the fourth is 5 rubles 50 kopecks, the fifth is 6 rubles, the sixth is 6 rubles 50 kopecks, the seventh is 7 rubles, and the eighth is 7 rubles 50 kopecks.
Second method of solution. The problem can be solved using a brief record of the problem's condition in the form of a diagram.
1) $50 \times 28=1400$ kopecks - was more than if all parts were like the first;
2) $4600-1400=3200$ kopecks - is the amount for eight equal parts;
3) $3200: 8=400$ kopecks $=4$ rubles - the first part.
Answer: 4 rubles, 4 rubles 50 kopecks, 5 rubles, 5 rubles 50 kopecks, 6 rubles, 6 rubles 50 kopecks, 7 rubles, 7 rubles 50 kopecks.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. How many numbers less than 2011 are divisible by 117 and 2?
|
7. When solving this problem, one can reason as follows. First, list the numbers less than 2011 and divisible by 117 (2), then among them, select those that are divisible by 2 (117), and determine how many there are.
Since the number is divisible by both 2 and 117, it will also be divisible by their product $2 \times 117=234$. By dividing 2011 by 234, we can determine the number of such numbers (2011:234 $=8$ (remainder 128).
Answer: eight numbers.
## TWENTY-SECOND
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. What digits stand in the natural number sequence at the thirteenth and one hundred twentieth positions?
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。
|
2. Let's write down the first fifteen numbers:
$$
1,2,3,4,5,6,7,8,9,10,11,12,13,14,15
$$
To fill the first nine positions, 9 digits are required, and then two digits are needed to write each two-digit number. Starting from the tenth position, two-digit numbers are written. For each of them, two places are allocated. To determine which digit is in the thirteenth position, we need to find out which digit of the units or tens of which two-digit number will be written. For this, we find the difference between thirteen and nine (four) and divide it by two $(4: 2=2)$. This means that the thirteenth position is occupied by the units digit of the second two-digit number, which is 1. Similarly, the 120th position is occupied by the tens digit of $55(120-9): 2=55$ (remainder 1).
Answer: 6.
|
6
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
7. How many different products that are divisible by 10 (order does not matter) can be formed from the numbers $2,3,5,7,9$? Numbers in the product do not repeat!
|
7. For a number to be divisible by 10, it must be divisible by 2 and 5.
Thus, the product must necessarily include 2 and 5. We get the first product $-2 \times 5$.
Now, let's add one more factor to this product:
$$
2 \times 5 \times 3, 2 \times 5 \times 7, 2 \times 5 \times 9
$$
Add one more factor to the obtained products:
$$
2 \times 5 \times 3 \times 7, 2 \times 5 \times 3 \times 9, 2 \times 5 \times 7 \times 9
$$
Add one more factor:
$$
2 \times 5 \times 3 \times 7 \times 9
$$
In total, we have eight products $1+3+3+1=8$.
Answer: eight products.
## TWENTY-THIRD
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. In village $A$, there are 100 schoolchildren, and in village $B$, there are 50 schoolchildren. The distance between the villages is 3 kilometers. At what point on the road from $A$ to $B$ should a school be built to minimize the total distance traveled by all schoolchildren?
|
$\triangle$ It seems fair to build the school closer to $A$, as there are more students there. But how much closer? Sometimes it is suggested to build the school one kilometer from $A$ and two kilometers from $B$ (twice as many students, so the school is twice as close). However, from the perspective of the given problem (minimizing the total distance traveled), this option is not the best; it is better to build the school directly at $A$.
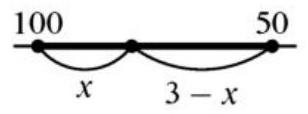
This can be verified as follows: if the distances from the school to $A$ and $B$ are $x$ and $3-x$ respectively, then the total distance traveled by all students is $100x + 50(3-x) = 100x + 150 - 50x = 50x + 150$, so it is minimized (and equals 150 km) when $x=0$. $\triangleleft$
The same can be explained without formulas: each meter the school is moved towards $A$ reduces the distance for 100 students by one meter and increases the distance for 50 students by one meter, thus reducing the total distance by 50 meters.
It can also be said this way: divide all students at $A$ arbitrarily into two groups of 50 people each. If the second group did not exist, it would not matter where to build the school (the problem of the well) - but from the perspective of the second group, it is best to build it at $A$.
## A Few More Problems
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
18. How many degrees does the minute hand turn in a minute? The hour hand?
|
$\Delta$ In one hour, the minute hand makes a full revolution, and in half an hour, it turns by $180^{\circ}$ (a straight angle). Half an hour is 30 minutes, so in one minute, it turns by $1 / 30$ of the angle in $180^{\circ}$, which is $180 / 30=6^{\circ}$.
The hour hand moves $1 / 12$ of a circle in one hour, meaning it moves 12 times slower than the minute hand. In one minute, it turns by $0.5^{\circ} . \triangleleft$
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
449. Two points $A$ and $B$ are 8 units apart. How many lines exist that are 5 units away from point $A$ and 3 units away from point $B$?
|
$\triangleright$ The line $l$ is at a distance $d$ from the point $A$ when it is tangent to the circle of radius $d$ centered at $A$. Therefore, the problem can be restated as follows: given two circles with radii 3 and 5, and the distance between their centers is 8. How many common tangents exist?
We have already solved this problem; since $3+5=8$, the circles touch each other externally, and there will be three common tangents. $\triangleleft$
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
521. By what factor should the side of a square be increased to make its area four times larger?
|
$\triangleright$ The area of a rectangle with sides $a$ and $b$ is $a b$, so the area of a square with side $a$ is $a \cdot a=a^{2}$. By doubling the side of the square, we increase its area by four times: $(2 a)^{2}=2^{2} a^{2}=4 a^{2} . \triangleleft$
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
577. Draw an isosceles right triangle on graph paper with the legs equal to the side of a cell, and check the Pythagorean theorem for it: the area of the square built on the hypotenuse is equal to the sum of the areas of the squares built on the legs.
|
$\triangleright$ The squares built on the legs have a unit area. The square built on the hypotenuse is divided into four triangles, each of which makes up half of a grid square, and thus has an area of 2 - as required. $\triangleleft$
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
578. Check the Pythagorean theorem for a right triangle with legs 1 and 2.
|
$\triangleright$ The squares constructed on the legs have areas of 1 and 4. It remains to find the area of the square constructed on the hypotenuse. This can be done in two ways. First, it can be cut into 4 triangles and a central square. The triangles are equal to the original (legs 1 and 2) and have an area of 1. The area of four such triangles is 4, plus the unit square in the center, totaling 5, as required.
Another way to calculate the area of the square constructed on the hypotenuse is to surround it with triangles on all four sides, completing it to a larger square. By adding four triangles equal to the original, we get a square $3 \times 3=9$, thus the desired area is $9-4=5 . \triangleleft$
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
662. Point $A$ was moved 13 units to the right and resulted in a point with a coordinate of 8. What was the coordinate of point $A$?
|
$\triangleright$ Let $A$ have the coordinate $a$. Then $a+13=8$, and $a=8-13=(-5) . \triangleleft$
|
-5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
664. Given two points $A(-3)$ and $B(7)$ (the coordinates are given in parentheses). Find the coordinate of the midpoint of segment $A B$.
|
$\triangle$ The distance $A B$ is $7-(-3)=10$, half of the distance is 5. Shifting $A$ 5 units to the right (or $B$ 5 units to the left), we get the point with coordinate 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
694. Find the slope of a line that forms an angle of $45^{\circ}$ with the horizontal.
|
$\triangleright$ We already know that such a line is given by the equation $y=x$, so the slope is $1 . \triangleleft$
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
735. Find the greatest divisor of the pair of numbers 123456789 and 987654321 (in other words, the greatest common measure of segments of such lengths).
|
$\triangleright$ In principle, this problem can be solved by brute force (and even in a reasonable time if you have a computer at hand), trying all numbers from 1 to 123456789 (larger numbers clearly do not fit).
However, it can also be done without a computer, using the Euclidean algorithm. The number 987654321 can be replaced by $987654321-123456789=864197532$. Subtracting 123456789 again, we get 740740743, then 617283954, 493827165, 370370376, 246913587, 123456798, and finally, $123456798-123456789=9$. (In the end, we divided 987654321 by 123456789 with a remainder and got a remainder of 9.) As we have seen, the common divisors of the original pair and the pair 123456789, 9 are the same, and according to the Euclidean algorithm, we need to subtract 9 from 123456789. The number 123456789 is divisible by 9 (it equals $9 \cdot 13717421$), so when subtracting, we get 9 (and then 0). Answer: the greatest common divisor is $9. \triangleleft$
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the minimum value of the expression $2 x+y$, defined on the set of all pairs $(x, y)$ satisfying the condition
$$
3|x-y|+|2 x-5|=x+1
$$
|
1.I.1. The following figure shows a set defined by the equation $3|x-y|+|2 x-5|=x+1$.
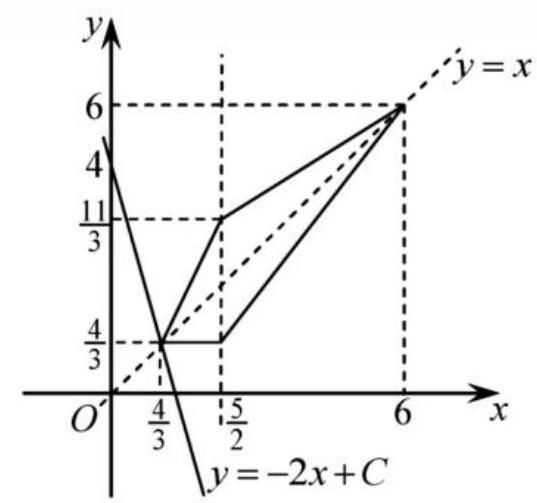
Let $C=2 x+y$. The problem requires finding the minimum value of $C$ for all points in the depicted set. Rewriting this relation as $y=C-2 x$, from a geometric perspective, we need to find the smallest $C$ such that the line $y=C-2 x$ intersects the given set. Clearly, the desired value of $C$ is the one for which this line passes through the point $\left(\frac{4}{3} ; \frac{4}{3}\right)$. Thus, $C=\frac{8}{3}+\frac{4}{3}=4$.
Answer: 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Find the minimum value of the function
$$
f(x)=4^{x}+4^{-x}-2^{x+1}-2^{1-x}+5
$$
Solution: Since
$$
\begin{aligned}
4^{x}+4^{-x}-2^{x+1}-2^{1-x}+5=2^{2 x}+ & 2^{-2 x}-2\left(2^{x}+2^{-x}\right)+5= \\
=2^{2 x}+2 \cdot 2^{x} \cdot 2^{-x}+2^{-2 x} & -2-2\left(2^{x}+2^{-x}\right)+5= \\
& =\left(2^{x}+2^{-x}\right)^{2}-2\left(2^{x}+2^{-x}\right)+3
\end{aligned}
$$
then the substitution $t=2^{x}+2^{-x}$ reduces the problem to finding the minimum value of the quadratic polynomial $g(t)=t^{2}-2 t+3$, which is $g(1)=2$.
Answer: 2.
|
1.I.8. Comment. The following error was made in the given solution. Since $2^{x}>0$, the range of the function $y=2^{x}+2^{-x}$ is the interval $[2 ;+\infty)$. Therefore, it is necessary to find the minimum value of the function $g(t)=t^{2}-2 t+3$ on the interval $[2 ;+\infty)$. On this interval, the function $g(t)$ is increasing, so its minimum value is achieved at $t=2$.
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. The radii of the excircles of a certain triangle are 2, 3, and 6 cm. Find the radius of the circle inscribed in this triangle.
|
3.II.4. First, let's derive the formula for the radius of the excircle. Let $P$ be the center of the circle with radius $r_{3}$, which touches the side $AB$ and the extensions of the sides $CA$ and $CB$ of triangle $ABC$. From the equality $S_{PAB} + S_{ABC} = S_{PAC} + S_{PBC}$, it follows that
$$
S_{ABC} = S = \frac{a r_{3}}{2} + \frac{b r_{3}}{2} - \frac{c r_{3}}{2}
$$
from which $r_{3} = \frac{2 S}{a + b - c}$. The radii of the other two excircles are found by analogous formulas: $r_{1} = \frac{2 S}{b + c - a}$ and $r_{2} = \frac{2 S}{a + c - b}$. Since the radius of the circle inscribed in the given triangle is found by the formula $r = \frac{2 S}{a + b + c}$, the following relationship holds:
$$
\frac{1}{r_{1}} + \frac{1}{r_{2}} + \frac{1}{r_{3}} = \frac{b + c - a}{2 S} + \frac{a + c - b}{2 S} + \frac{a + b - c}{2 S} = \frac{a + b + c}{2 S} = \frac{1}{r}
$$
According to the problem, $r_{1} = 2$, $r_{2} = 3$, and $r_{3} = 6$, from which $r = 1$. A triangle with the given radii of the excircles exists; it is a right triangle with legs 3 and 4, known as the "Egyptian" triangle.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Compute $\operatorname{tg} \alpha$, if $3 \operatorname{tg} \alpha-\sin \alpha+4 \cos \alpha=12$.
|
4.II.1. We have,
$$
\begin{aligned}
& 3 \operatorname{tg} \alpha - \sin \alpha + 4 \cos \alpha = 12 \\
& \Longleftrightarrow \operatorname{tg} \alpha (3 - \cos \alpha) - 4 (3 - \cos \alpha) = 0 \Longleftrightarrow \\
& (\operatorname{tg} \alpha - 4)(3 - \cos \alpha) = 0 \Longleftrightarrow \operatorname{tg} \alpha = 4
\end{aligned}
$$
Answer: 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Let $x$ and $y$ be positive numbers whose sum is 2. Find the maximum value of the expression $x^{2} y^{2}\left(x^{2}+y^{2}\right)$.
|
Solution 1. The idea is suggested by the formula for $(x+y)^{4}$. Since
$(x+y)^{4}-8 x y\left(x^{2}+y^{2}\right)=x^{4}-4 x^{3} y+6 x^{2} y^{2}-4 x y^{3}+y^{4}=(x-y)^{4} \geqslant 0$, then $8 x y\left(x^{2}+y^{2}\right) \leqslant(x+y)^{4}$. It is clear that $4 x y \leqslant(x+y)^{2}$. Therefore,
$$
32 x^{2} y^{2}\left(x^{2}+y^{2}\right) \leqslant(x+y)^{6}
$$
Since $x+y=2$, then $x^{2} y^{2}\left(x^{2}+y^{2}\right) \leqslant 2$. It is clear that when $x=y=1$ we get equality.
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Solve the equation $\frac{3}{\log _{2} x}=4 x-5$.
Answer: 2.
Solution: The function $y=\log _{2} x$ is increasing, therefore $y=\frac{3}{\log _{2} x}$ is a decreasing function. On the other hand, the function $y=4 x-5$ is increasing, therefore, the given equation has no more than one root. By trial, we find that $x=2$ is a solution to the equation.
|
5.I.8. Comment. The error in the given solution is that the function $y=\frac{3}{\log _{2} x}$ is decreasing not on its entire domain, but only on each of the intervals $(0 ; 1)$ and $(1 ;+\infty)$. Therefore, this equation has no more than one root in each of them. In addition to $x=2$, the solution to the equation is the number $x=\frac{1}{2}$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11. Solve the equation $27^{x}-7 \sqrt[3]{7 \cdot 3^{x}+6}=6$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
|
Solution 1. Let $z=\sqrt[3]{7 y+6}$ and transition to the system
$$
\left\{\begin{array}{l}
y^{3}=7 z+6 \\
z^{3}=7 y+6
\end{array}\right.
$$
Then $y^{3}-z^{3}=7(z-y)$, from which it follows that $y=z$, since $y^{2}+y z+z^{2}$ cannot be equal to -7. As a result, we get the equation $y^{3}-7 y-6=0$, the roots of which are the numbers $-1, -2, 3$. Since $3^{x}>0$, then $3^{x}=3$, hence $x=1$.
Answer: 1.
Topic: "Methods for solving irrational equations"
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In a row, all natural numbers less than a billion that have exactly 13 natural divisors (including one and the number itself) were written down. How many of them have an even sum of digits?
|
6.I.3. If $n=p_{1}^{s_{1}} p_{2}^{s_{2}} \ldots p_{k}^{s_{k}}$, then the number of divisors of the number $n$ is $\left(s_{1}+1\right)\left(s_{2}+1\right) \ldots\left(s_{k}+1\right)$. Since the number of divisors of the given number is a prime number, the number itself is a power of a prime number; in this case $n=p^{12}$. From the following table, it is clear that the required numbers are $3^{12}$ and $5^{12}$.
| $p$ | 2 | 3 | 5 | 7 |
| :---: | :---: | :---: | :---: | :---: |
| $p^{12}$ | 4096 | 531441 | 244140625 | 13841287201 |
Answer: two numbers.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Solve the equation $3^{x^{2}+x-2}-3^{x^{2}-4}=80$.
|
6.II.1. Let's rewrite the equation as $3^{x^{2}-4}\left(3^{x+2}-1\right)=80$ and set $f(x)=3^{x^{2}-4}\left(3^{x+2}-1\right)$. If $x \leqslant -2$, then $f(x) \leqslant 0$, hence the equation has no solutions on the interval $(-\infty; -2]$. If $-2 < x \leqslant 0$, then $0 < 3^{x+2} - 1 \leqslant 8$ and $3^{x^{2}-4} \leqslant 1$, so $f(x) \leqslant 1$, hence the equation has no solutions on the interval $(-2; 0]$. Now notice that the function $f(x)$ is increasing on the interval $[0; +\infty)$, so the equation has at most one solution. It remains to note that $f(2)=80$, so $x=2$ is a solution to the equation. Answer: $\{2\}$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Find the smallest prime number $p$ such that $n^{2}+n+11$ is divisible by $p$ for some integer $n$.
untranslated text is preserved in terms of line breaks and format, as requested.
|
6.II.5. Since $n(n+1)$ is an even number, the number $n^{2}+n+11$ is odd, and therefore this number is not divisible by 2. Since $n^{2}+n+11=$ $(n-1)^{2}+1+3n+9$, the number $n^{2}+n+11$ is not divisible by 3, because no perfect square can have a remainder of 2 when divided by 3. Since $n^{2}+n+11=(n-2)^{2}+2+5n+5$, by similar reasoning, this number is not divisible by 5. Further, since $n^{2}+n+11=$ $(n-3)^{2}+2+7n$, this number is not divisible by 7 because no perfect square can have a remainder of 5 when divided by 7. Finally, note that when $n=0$, the number $n^{2}+n+11$ is divisible by 11. Therefore, 11 is the smallest prime divisor among all divisors of numbers of the form $n^{2}+n+11$.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. There are 9 sticks of different lengths from 1 cm to 9 cm. What are the side lengths of the squares that can be formed from these sticks, and in how many ways can they be formed? Ways of forming a square are considered different if different sticks are used and not necessarily all of them.
Can squares with side lengths of 1 cm, 2 cm, ... 6 cm be formed? Why? Can a square with a side length of 7 cm be formed? How can it be done? In how many different ways can it be formed? Consider all possible cases. Can a square with a side length of 12 cm or more be formed? Why?
|
1. Solution. One way to form squares is to have side lengths of $7 \mathrm{~cm}, 8 \mathrm{~cm}, 10 \mathrm{~cm}, 11 \mathrm{~cm}$. In five ways, squares can be formed, each with a side length of $9 \mathrm{~cm}$. Thus, there are 9 ways to form the squares.
Hint. The side length of the square must be greater than 6 cm (Why?). Since the total length of all the sticks is 45 cm, the perimeter of the square cannot be more than 44 cm, and the side length of the square cannot be more than $11 \mathrm{~cm}$. (MvSh)
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. The incident took place in 1968. A high school graduate returned from a written university entrance exam and told his family that he couldn't solve the following problem:
Several identical books and identical albums were bought. The books cost 10 rubles 56 kopecks, and the albums cost 56 kopecks. The number of books bought was 6 more than the number of albums. How many books were bought if the price of a book, which is more than one ruble, exceeds the price of an album?
The adults delved into calculations. But the little brother, a fifth-grader, suddenly blurted out:
- There's nothing to solve here. 8 books!
How did he solve the problem?
If solving this problem caused you difficulty, then think it over again and again, delve into the conditions so that they are clearly imprinted in your memory. Look for and seek new approaches to solving the problem. Try to "guess" the answer, find it by making a rough estimate. How many solutions does the problem have? Write down the solution and check your answer.
|
4. S o l u t i o n. Since the book is more expensive than a ruble, no more than 10 books were bought. Moreover, it is clear that no fewer than 7 books were bought. By checking, we find that the number 1056 is divisible by 8 and not divisible by $7,9,10$. A n s w e r: 8 books.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Twelve people are carrying 12 loaves of bread. Each man carries 2 loaves, each woman carries half a loaf, and each child carries a quarter of a loaf, and all 12 people are involved in the carrying. How many men, how many women, and how many children were there?
|
7. 5 men, 1 woman, and 6 children. Show that the number of men cannot be, first, less than five, and second, more than five.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. On the number line, four points are marked. Point $A$ corresponds to the number -3, point $B$ corresponds to the number -5, and point $C$ corresponds to the number 6. Find the fourth number corresponding to point $K$ under the following condition: if the direction of the number line is reversed, the sum of the new numbers corresponding to the "old" points $A, B, C$, and $K$ will not change.
|
10. Solution. When the direction of the number line is changed, the sign of each number (except, of course, zero) changes to the opposite. Since the sum did not change in this case, it can only be equal to zero. Therefore, the fourth number sought is $0-(-5-3+6)=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13. Several points are marked on a number line. The sum of the numbers corresponding to these points is $-1.5$. Each of the marked points was moved two units to the left on the number line, and therefore the sum of the numbers became $-15.5$. How many points were there?
|
13. Solution. When a point is moved two units to the left on the number line, the number corresponding to this point decreases by 2 units. The sum of all numbers decreased by $-1.5-(-15.5)=$ $=14$, so there were a total of $14: 2=7$ points.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12. What digits do the decimal representations of the following numbers end with:
1) $135^{x}+31^{y}+56^{x+y}$, if $x \in N, y \in N$
2) $142+142^{2}+142^{3}+\ldots+142^{20}$
3) $34^{x}+34^{x+1}+34^{2 x}$, if $x \in N$.
|
12. 3) $\mathrm{Solution.} \mathrm{If} \mathrm{a} \mathrm{number} \mathrm{ends} \mathrm{in} \mathrm{four,} \mathrm{then}$ even powers of it end in 6, and odd powers end in 4. Therefore, one of the first two terms ends in four, and the other ends in six. The third term ends in six, so the decimal representation of the sum ends in six.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2(!). Let the formula for the \(n\)-th term of the sequence be \(x=n^{2}\). Write down the first 10 terms of this sequence. Write down the sequence of differences between the second and first terms, the third and second terms, and so on. Write down another sequence of differences between the second and first, the third and second, and so on, of the second sequence. Write down a few terms of the corresponding fourth sequence. What are the terms of the fifth, sixth, ... sequences?
|
2. The results of the calculations can be recorded in the form of the following table:

|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. For what least natural \(m\) are the numbers of the form:
1) \(m^{3}+3^{m}\)
2) \(m^{2}+3^{m}\)
divisible by 7?
|
10. Solution. Let \(r_{1}\) be the remainder of the division of \(m^{3}\) by 7, and \(r_{2}\) be the remainder of the division of \(3^{m}\) by 7. Clearly, the number \(m^{3}+3^{m}\) will be divisible by 7 when the sum of the remainders \(r_{1}+r_{2}\) equals 7. Let's construct the following table:
\begin{tabular}{|c|c|c|c|c|c|c|c|c|c|c|}
\hline\(m\) & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & \(\ldots\) \\
\hline\(r_{1}\) & 1 & 1 & 6 & 1 & 6 & 6 & \(\ldots\). & \(\ldots\) & \(\ldots\) & \(\ldots\) \\
\hline\(r_{2}\) & 3 & 2 & 6 & 4 & 5 & 1 & \(\ldots\) & \(\ldots\) & \(\ldots\). & \(\ldots\) \\
\hline\(r_{1}+r_{2}\) & 4 & 3 & 12 & 5 & 4 & 7 & \(\ldots\) & \(\ldots\) & \(\ldots\) & \(\ldots\) \\
\hline
\end{tabular}
From the table, it is clear that \(r_{1}+r_{2}=7\) when \(m=6\).
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12. Simplify the expression:
\[
-(-(-(\ldots-(-1) \ldots)))
\]
which contains 200 pairs of parentheses.
If solving the problem is difficult, consider the numbers:
\[
\begin{aligned}
& -(-1)=\ldots, \\
& -(-(-1))=\ldots
\end{aligned}
\]
notice the pattern and draw a conclusion.
It is appropriate to inform students that this approach to solving problems was often used by many mathematicians, and in particular one of the greatest mathematicians in the world - Leonhard Euler (1707-1783). He writes: “... properties of numbers known today were for the most part discovered by observation and were discovered long before their truth was confirmed by rigorous proofs. There are even many properties of numbers with which we are well acquainted, but which we are still unable to prove; only observation has led us to their knowledge.”
|
12. -1. 13. 1) \(x=4n-1\); 2) \(y=(-1)^{n+1}\); 3) \(z=n^2+1\); 4) \(t=2^n-1\).
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
16*. Among the first ten thousand numbers, how many of them end in 1 and can be represented in the following form: \(8^{m}+5^{n} ?(m \in N, n \in N)\)
|
16. Five numbers. Hint. Show that \(m=4\). (KvN, 1972, No. 5, p. 81 .)
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Calculate at \(x=7\):
\((x-4)^{(x-5)^{(x-6)}}{ }^{(x+6)^{(x+5)}}\)
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
6. Calculate at \(x=7\):
\((x-4)^{(x-5)^{(x-6)}}{ }^{(x+6)^{(x+5)}}\)
|
6. When \(x=7\), the given expression equals \(3^{2^{1}}=9\).
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
14. Given the monomial \((-1)^{n} a^{n-2} b^{9-n}\). Write in a row the set of all possible forms of this monomial for different permissible natural values of the exponents.
|
14. Instruction. It is clear that \(n>2\) and \(n<9\), i.e., \(n=\{3 ; 4\); \(5 ; 6 ; 7 ; 8\}\). For these values of \(n\), six different monomials will be obtained.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Find \(k\), if it is known that for any \(x\):
\[
\begin{array}{r}
a x^{2}+b x+c \\
+b x^{2}+a x-7 \\
k x^{2}+c x+3 \\
\hline x^{2}-2 x-5
\end{array}
\]
|
7. Solution.
\[
c=-5-(-7+3)=-1
\]
\[
\begin{aligned}
a+b & =-2-(-1) \\
k & =1-(a+b)=1-(-1)=2
\end{aligned}
\]
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11. Find the sum of the values of the polynomial \(x^{5}-1.7 \cdot x^{3}+2.5\) at \(x=19.1\) and \(x=-19.1\).
|
11. Solution. If the sign of \(x\) is changed to the opposite, the given polynomial will take the form: \(-x^{5}+1.7 x^{3}+2.5\). The sum of the given polynomial and the obtained one is 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
13*. Calculate:
1) \(x^{4}-2 x^{3}+3 x^{2}-2 x+2\) given \(x^{2}-x=3\)
2) \(2 x^{4}+3 x^{2} y^{2}+y^{4}+y^{2} \quad\) given \(x^{2}+y^{2}=1\).
|
13. 1) \( \mathrm{P} \) is a solution. \( x^{2}\left(x^{2}-x\right)-x\left(x^{2}-x\right)+2\left(x^{2}-x\right)+2= \) \( =3 x^{2}-3 x+2 \cdot 3+2=3\left(x^{2}-x\right)+8=3 \cdot 3+8=17 \);
2) Solution. \( 2 x^{4}+2 x^{2} y^{2}+x^{2} y^{2}+y^{4}+y^{2}=2 x^{2}\left(x^{2}+\right. \) \( \left.+y^{2}\right)+y^{2}\left(x^{2}+y^{2}\right)+y^{2}=2 x^{2} \cdot 1+y^{2} \cdot 1+y^{2}=2\left(x^{2}+y^{2}\right)=2 \).
If students are already familiar with the formulas for abbreviated multiplication, the exercise can be solved by substitution \( x^{2}=1-y^{2} \).
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. Solve the equation: \(x^{3}+x^{2}+x+1=0\).
|
9. Solution. Factoring the left side of the equation, we get:
\[
(x+1)\left(x^{2}+1\right)=0
\]
Since \(x^{2}+1>0\), then \(x+1=0, x=-1\).
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Find: 1) \(x^{6}+3 x^{2} y^{2}+y^{6}\), if \(x^{2}+y^{2}=1\); 2) \(x^{4}+\) \(+x^{2} y^{2}+y^{4}\), if \(x^{2}+y^{2}=a\) and \(x y=b\).
|
5. 1) \(\mathrm{P}\) is the solution. First method. The given polynomial is equal to
\[
\left(x^{2}+y^{2}\right)\left(x^{4}-x^{2} y^{2}+y^{4}\right)+3 x^{2} y^{2}=\ldots=\left(x^{2}+y^{2}\right)^{2}=1
\]
Second method. Since \(y^{2}=1-x^{2}\), then, performing the substitution, we get that the given polynomial is identically equal to 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
14. Find the distance between the points of intersection of the three lines: \(y = 3x\), \(y = 3x - 6\), and \(y = 1975\).
|
14. 2. Instruction. Show that the desired distance is equal to the distance between points \(A(0 ; 0)\) and \(B(2 ; 0)\).
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Calculate in the most rational way:
\[
\frac{7^{16}-1}{2402000\left(49^{4}+1\right)}
\]
76
|
1. 2,4. Hint. Factor the numerator and reduce the fraction
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。
Note: The last sentence is a note I added for context, and it should not be part of the translation. Here is the requested translation:
1. 2,4. Hint. Factor the numerator and reduce the fraction
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12. The price of a diamond is proportional to the square of its mass. If a diamond is broken into two parts, in which case will the total price of the two parts be the lowest?
|
12. Solution. Let the price of a diamond be calculated by the formula \(y=a m^{2}\), where \(m\) is its mass. Let the mass of the first piece be \(\frac{m}{2}+x\). Then the mass of the second piece will be \(m-\frac{m}{2}-x=\frac{m}{2}-x\). The total cost of the two pieces will be:
\[
a\left(\frac{m}{2}+x\right)^{2}+a\left(\frac{m}{2}-x\right)^{2}=a\left(\frac{m^{2}}{4}+x^{2}\right)
\]
Obviously, this sum will be the smallest if \(x=0\), i.e., if both pieces have the same mass.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
297. The continuations of the medians of a triangle intersect the circumscribed circle at points $A_{1}, B_{1}, C_{1}$. Prove that
$$
\frac{A G}{G A_{1}}+\frac{B G}{G B_{1}}+\frac{C G}{G C_{1}}=3
$$
where $G$ is the centroid of triangle $A B C$.
|
297. Using the concept of the power of a point, establish that
$$
\frac{A G}{G A_{1}}+\frac{B G}{G B_{1}}+\frac{C G}{G C_{1}}=\frac{A G^{2}+B G^{2}+C G^{2}}{R^{2}-d^{2}}
$$
But based on Leibniz's theorem, $A G^{2}+B G^{2}+C G^{2}=3 R^{2}-3 d^{2}$. 116
|
3
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
45. Write the system of equations of a line passing through the origin and forming equal angles with the three coordinate axes. Determine the magnitude of these angles. How many solutions does the problem have?
|
45. According to the problem, $\cos \alpha=\cos \beta=\cos \gamma$ and the equations take the form: $x=y=z$. Further, we have:
$$
\begin{gathered}
\cos ^{2} \alpha+\cos ^{2} \alpha+\cos ^{2} \alpha=1 ; \cos ^{2} \alpha=\frac{1}{3} \\
\cos \alpha= \pm \frac{1}{\sqrt{3}} ; \alpha \approx 54^{\circ} 44^{\prime} 8^{\prime \prime} \text { or } \alpha=125^{\circ} 15^{\prime} 52^{\prime \prime}
\end{gathered}
$$
The coordinate planes divide the space into 8 octants. Each of the desired lines passes through two octants, and therefore there are 4 such lines.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Given three pairwise intersecting lines, not parallel to one plane, and a point $P$ not belonging to any of them, construct a plane through this point so that it forms equal angles with the given lines.
保留源文本的换行和格式,这里直接输出翻译结果。
|
5. Draw through point $P$ the lines $A A^{\prime}, B B^{\prime}$, and $C C^{\prime}$, respectively parallel to the given lines $a, b$, and $c$. Point $P$ divides each of the lines $A A^{\prime}, B B^{\prime}, C C^{\prime}$ into two opposite rays $P A$ and $P A^{\prime}, P B$ and $P B^{\prime}, P C$ and $P C^{\prime}$. The planes of symmetry of the rays $P A$ and $P B, P B$ and $P C$ intersect along the line $l$, through which the plane of symmetry of the rays $P C$ and $P A$ also passes (why?). The line $l$ forms congruent angles with the rays $P A, P B$, and $P C$. This same line $l$ forms congruent angles with the opposite rays $P A^{\prime}, P B^{\prime}$, and $P C^{\prime}$. The plane passing through $P$ perpendicular to $l$ forms congruent angles with the lines $A A^{\prime}, B B^{\prime}, C C^{\prime}$, and thus also with the lines $a, b$, and $c$.
Another solution is obtained by considering the rays $P A, P B$, and $P C^{\prime}$ and their opposite rays $P A^{\prime}, P B^{\prime}$, and $P C$. Two more solutions correspond to the triples of rays $P B, P C$, and $P A^{\prime}$ (with their opposites $P B^{\prime}, P C^{\prime}, P A$) and $P A, P C, P B^{\prime}$ (with their opposites $P A^{\prime}, P C^{\prime}$, $P B$). Thus, there are 4 planes that satisfy the condition of the problem.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11*. From a point $M$ on the edge of a dihedral angle in one of its faces, a ray is drawn. Draw from the same point $M$ in the other face a ray that forms an angle of a given magnitude with the first ray.
|
11. Let's take an arbitrary point $A$ on this ray; let $A^{\prime}$ be the projection of this point onto the other face. Suppose the desired ray is drawn, and we construct a segment $M B$ on it such that $|M B|=|M A|$. Then, in the isosceles triangle $A M B$, the two sides and the angle between them are known, and it can be constructed on a separate drawing. We will then know the length of the slant $|A B|$, and consequently, the length of its projection $\left|A^{\prime} B\right|$ onto the second face. The desired point $B$ must lie on the circle with center at point $A^{\prime}$ and radius $\left|A^{\prime} B\right|$, and at the same time on the circle with center at point $M$ and radius $|M A|$. By constructing point $B$, we will determine the desired ray. Determine how many solutions the problem can have.
142
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
58. Three spheres with different radii and centers not lying on the same straight line lie outside each other. What figure is formed by the lines of intersection of pairs of planes that are symmetric with respect to the plane of the centers of the spheres and simultaneously tangent to all three given spheres?
|
58. The common tangent plane of two spheres passes through the center of their homothety, since the radii drawn to the points of tangency are parallel, and the line passing through the points of tangency also passes through the center of homothety (see the previous problem). The centers of homothety of three spheres belong to the plane of their centers and coincide with the centers of homothety of the circles of section of the spheres by this plane. Therefore, the plane tangent to all three spheres passes through the axes of homothety of these circles (see problem 15 from §2).
Since the spheres are symmetric relative to the plane of their centers, through each axis of homothety there pass pairs of mutually symmetric planes tangent to the three spheres.
Thus, pairs of symmetric planes tangent to three spheres intersect along lines lying in the plane of the centers and form a configuration of 4 lines and 6 points, with 3 points on each line.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
36*. A polyhedron is called regular if all its faces are regular and congruent polygons to each other and all its polyhedral angles are also regular and congruent to each other ${ }^{2}$. Investigate the possibility of constructing simple regular polyhedra with $n$-sided faces and $m$-sided angles and determine the possible number of their types, using the following considerations.
Divide the entire space into $f$ congruent regular $n$-sided angles with a common vertex $S$, with $m$ angles at each edge, and express the magnitudes of their dihedral angles in terms of $n$ and $f$. If a regular $n$-sided pyramid is constructed from the found magnitude of the dihedral angle, with the base being a regular $n$-sided polygon - a face of the desired polyhedron, then from such congruent pyramids, a regular polyhedron can be assembled (for example, a cube is assembled from six regular quadrilateral pyramids with a common vertex at the center of the cube). It can be proven that any regular polyhedron can be obtained by such a construction. (The last remark can be used without proof in solving this and the following problems.)
## 44
|
36. Let the faces of a regular polyhedron be regular $n$-gons, and the polyhedral angles at the vertices be regular $m$-gonal angles; obviously, $m \geqslant 3, n \geqslant 3$. Divide the space into $f$ congruent regular $n$-gonal angles with a common vertex $S$ such that around each edge $[S A)$ there are $m$ angles. Then the magnitude of each of these $f$ polyhedral angles is $\frac{4 \pi}{f}$. Since this magnitude is the difference between the sum of the magnitudes of its dihedral angles and the number $\pi(n-2)$, the sum of all dihedral angles of the $n$-gonal angle is $\frac{4 \pi}{f} + \pi(n-2) = \frac{4 + nf - 2f}{f} \pi$. One dihedral angle has a magnitude that is $n$ times smaller, i.e., $\frac{4 + nf - 2f}{nf} \pi$.
On the other hand, since at each of the $p$ edges of our $n$-gonal angles there are $m$ congruent dihedral angles, the magnitude of each of them is $\frac{2 \pi}{m}$. Thus,
$$
\begin{gathered}
\frac{2 \pi}{m} = \frac{4 + nf - 2f}{nf} \pi \\
2nf + 2mf - mnf = 4m \\
f = \frac{4m}{2m + 2n - mn}
\end{gathered}
$$
## 168
Since $f > 0, m > 0$, from (1) we have $2m + 2n - mn > 0$,
$$
\frac{2}{m} + \frac{2}{n} > 1
$$
Thus, the division of space into congruent polyhedral angles is possible only if the numbers $m \geqslant 3$ and $n \geqslant 3$ satisfy the inequality (2). Clearly, only five cases are possible: 1) $m=3$ and $n=3: \frac{2}{3} + \frac{2}{3} > 1$. From (1) we get $f=4$, the polyhedron is bounded by 4 triangles - this is a tetrahedron. The corresponding values of the numbers $a$ and $p$ are obtained from the formulas in problems 27 and 28: for the tetrahedron $a=6, p=4$.
2) For $m=3, n=4$ we get: $\frac{2}{3} + \frac{2}{4} > 1, f=6$. The polyhedron is bounded by six squares - this is a hexahedron or cube. Here $a=12, p=8$.
3) For $m=4, n=3$ we also get $\frac{2}{4} + \frac{2}{3} > 1 ; f=8$. The polyhedron is bounded by eight triangles - this is an octahedron. In it, $a=12, p=6$.
4) For $m=3, n=5$ we have: $\frac{2}{3} + \frac{2}{5} > 1 ; f=12$. The polyhedron is bounded by twelve pentagons - this is a dodecahedron. In it, $a=30, p=20$.
5) For $m=5, n=3 ; \frac{2}{5} + \frac{2}{3} > 1, f=20$. The polyhedron is bounded by 20 triangles - this is an icosahedron. In it, $a=30, p=12$.
For $m=4$ and $n=4$ we have: $\frac{2}{4} + \frac{2}{4} = 1$, and the inequality (2) is not satisfied. For further increases in the values of $m$ and $n$, the expression on the left side of the inequality (2) becomes even smaller, and it cannot be valid. It can be shown that any regular polyhedron can be obtained by the described construction, and our considerations show that there are only five types of regular polyhedra in space.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
46*. Inscribed a cube in a dodecahedron so that all eight vertices of the cube are vertices of the dodecahedron. How many solutions does the problem have?
|
46. Consider a dodecahedron with center $S$ (Fig. 101). Due to the congruence of the faces, their diagonals are also congruent: $[A B] \cong|B C| \cong \cong[C D] \cong[D A]$. In the regular triangular pyramid $P A B Q$, the edge $[P Q]$ is perpendicular to the base edge $[A B]$ (see problem 8 from § 5). But $(P Q)\|(A D)\|(B C)$, and thus, $A B C D$ is a square. Similarly,
Fig. 101
we will prove that $A B B^{\prime} A^{\prime}, B C C^{\prime} B^{\prime}$, $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$, and $A D D^{\prime} A^{\prime}$ are also squares. Thus, the polyhedron $A B C D C^{\prime} D^{\prime} A^{\prime} B^{\prime}$ is a cube, whose edges are the diagonals of the dodecahedron.
If in the pentagon $A M N B P$ we take another diagonal $[A N]$, we get the square $A N E Q$, which is a face of the cube $A N E Q C^{\prime} N^{\prime} E^{\prime} Q^{\prime}$. From the other three diagonals $[B M \mid, [M P]$, and $\mid N P]$, we obtain three more cubes: $B M F^{\prime} Q D^{\prime} M^{\prime} F Q^{\prime}$, $M P D E^{\prime} M^{\prime} F^{\prime} B^{\prime} E$, and $N P C F N^{\prime} P^{\prime} A^{\prime} F^{\prime}$.
It is not difficult to verify that each diagonal of each face of the dodecahedron is a side of one and only one of these cubes. Therefore, there are exactly five such cubes (60 face diagonals are distributed 12 to each of the 5 cubes).
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In a box, there are 7 red and 4 blue pencils. Without looking into the box, a boy randomly draws pencils. What is the minimum number of pencils he needs to draw to ensure that there are both red and blue pencils among them?
|
1. Answer: 8 pencils.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
39. All odd numbers from 27 to 89 inclusive are multiplied together. What is the last digit of the resulting product?
|
39. The product ends with the digit 5. Indeed, if in the multiplication of several odd numbers at least one factor ends with the digit 5, then the entire product ends with the digit 5.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
43. An adult needs 16 kg of salt for consumption over 2 years and 8 months. How much salt does an adult need for one year?
|
43. 2 years 8 months make up 32 months. If 32 months require 16 kg of salt, then 12 months require 6 kg of salt.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
61. Insert arithmetic operation signs between the digits 12345 so that the result equals 1.
|
61. There are several solutions. For example: $1+2-3-$ $-4+5=1 ; 1-2+3+4-5=1$.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
75. Can the sum of four consecutive integers be a prime number?
## Problems for the ninth grade
|
75. The sum of four consecutive integers is an even number. There is only one even prime number. This number is 2. Since $-1+0+1+2=2$, the answer to the question of the problem is affirmative.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
82. There is a water tap and two containers: a three-liter and a five-liter. How can you get 4 liters of water in the larger one?
|
82. Let's fill a five-liter container and pour 3 liters from it into a three-liter container. Then we will empty the three-liter container and transfer the 2 liters of water remaining in the five-liter container into it. Finally, we will fill the five-liter container from the tap and pour 1 liter from it into the three-liter container. Now we will have 4 liters of water in the five-liter container.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
86. Three numbers end with different digits. Can their pairwise products end with the same digit?
|
86. They can. For example, the three numbers 2, 5, and 10 end in different digits, but their pairwise products all end in the same digit 0.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
101. Write the number 100 using six identical non-zero digits in such a way that the method of writing does not depend on the digits used.
102 Calculate:
$\lg \operatorname{tg} 37^{\circ} \cdot \lg \operatorname{tg} 38^{\circ} \cdot \lg \operatorname{tg} 39^{\circ} \ldots \lg \operatorname{tg} 47^{\circ}$
|
101. Let $x$ be any non-zero digit. Then the expression $(\overline{x x x}-\overline{x x}): x=100$ is true for any digit $x$. 102. Since $\operatorname{tg} 45^{\circ}=1$, then $\lg \operatorname{tg} 45^{\circ}=0$. Therefore, the given product is also zero.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
108. The purchase of a book cost 1 ruble and one third of the book's cost. What is the cost of the book?
|
108. Answer. 1 ruble 50 kopecks.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
109. What is the last digit of the difference
$$
1 \cdot 2 \cdot 3 \cdot 4 \ldots 13-1 \cdot 3 \cdot 5 \cdot 7 \ldots 13 ?
$$
|
109. The minuend ends in 0, and the subtrahend ends in 5. Therefore, the difference ends in 5.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
116. How many lines can divide a plane into 5 parts?
|
116. Two lines can divide the plane only into 3 or 4 parts (see Fig. 15). Three lines can divide the plane only into 4, 6, and 7 parts (see Fig. 16). Four lines can divide the plane into 5 parts only if these lines are parallel (see Fig. 17). It is obvious that with any arrangement of five or more lines, the number of parts of the plane will be more than five.
Fig. $\quad 16$
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
118. A circle is inscribed in a square, and then a new square is inscribed in the circle. Find the ratio of the areas of these squares.
|
118. It is clear that the second square can be placed so that its vertices fall on the points of tangency of the circle with the sides of the first square (see Fig. 18). After this, it is not difficult to verify that the desired ratio of the areas of the squares is 2.
Fig. $\quad 18$
24
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. a) Prove that the square of an integer cannot end in any of the digits $2, 3, 7, 8$.
b) Prove that for no natural number $n$ can the numbers $5n+2$ and $5n+3$ be perfect squares.
c) Prove that for no integer $n$ is the number $n^2 + 3$ divisible by 5.
d) Find all natural values of $n$ for which the number $123 \ldots n + 97$ is a perfect square.
|
7. a) Any integer can be represented in the form: \( n = 10k + r \), where \( k \) is an integer and \( r = 0, 1, 2, \ldots, 9 \). Based on the equality \( n^2 = 10(10k^2 + 2kr) + r^2 \), we conclude that the numbers \( n^2 \) and \( r^2 \) end with the same digit. It remains to verify directly that \( r^2 \) does not end in any of the digits 2, 3, 7, 8.
b) Numbers of this form, when \( n \) is even, end in the digits 2 and 3, and when \( n \) is odd, they end in the digits 7 and 8. As follows from problem 7a, numbers of this form cannot be perfect squares.
c) Since \( n^2 \) cannot end in 2 or 7, \( n^2 + 3 \) cannot end in 5 or 0.
d) Let \( P(n) = 1 \cdot 2 \cdot 3 \ldots n + 97 \). Then \( P(1) = 98 \), \( P(2) = 99 \), \( P(3) = 103 \), \( P(4) = 121 \). Thus, \( P(4) \) is a perfect square. If \( n \geq 5 \), then \( P(n) \) ends in 7 and cannot be a perfect square. Answer: \( n = 4 \).
|
4
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
19. Find all prime numbers $p$ such that the numbers $p+4$ and $p+8$ are also prime.
|
19. It is not hard to notice that the number 3 satisfies the requirements of the problem. Let's show that the problem has no other solutions. Indeed, every prime number not equal to 3 has one of two forms: $3k+1$ or $3k+2$, where $k$ is a non-negative integer. But in the case $p=3k+1$, the number $p+8$ is divisible by 3, and in the case $p=3k+2$, the number $p+4$ is divisible by 3.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
22. Find all natural $n$ for which the number $n^{2}+3 n$ is a perfect square.
|
22. For $n=1$ the number $n^{2}+3 n$ equals 4, i.e., is a perfect square. Let now $n>1$. Obviously, in this case
$$
(n+1)^{2}<n^{2}+3 n<(n+2)^{2}
$$
Since a perfect square cannot exist between the squares of two consecutive natural numbers, the problem has a unique solution $n=1$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
31. Find all prime numbers $p$ such that $p^{2}+14$ is also a prime number.
|
31. It is easy to notice that the prime number $p=3$ satisfies the condition of the problem. If $p \neq 3$, then $p^{2}$ has the form $3 \mathrm{k}+1$ (see problem 5 a). Then $p^{2}+14=3 k+15=3(k+5)$. The obtained number is composite. Therefore, the problem has a unique solution $p=3$.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
18. This square should be cut by a broken line into two parts of equal area so that each segment of the broken line is parallel to the side or diagonal of the square, and the sum of the lengths of the segments parallel to the sides equals the length of the side, while the sum of the lengths of the segments parallel to the diagonals equals the length of the diagonal. What is the minimum number of segments such a broken line can have?
$$
7-8 \text { grades }
$$
|
18. It is obvious that each segment of the broken line must be shorter than the side or diagonal of the square parallel to it, since otherwise, this segment alone would already divide the square into two parts. From this, it follows that the number of segments of the broken line cannot be less than four. We will now show,
Fig. 45
that there exists a broken line with four segments that meets all the requirements of the problem. Divide the given square into 36 equal squares. Construct the broken line shown in Figure 45. It is easy to verify that this broken line is the one we are looking for.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. List all two-element subsets of a five-element set.
|
7. Let's take the five-element set $\{A ; B ; C ; D ; E\}$. We will list its two-element subsets:
$\{A ; B\},\{A ; C\},\{A ; D\},\{A ; E\},\{B ; C\},\{B ; D\},\{B ; E\},\{C ; D\}$, $\{C ; E\},\{D ; E\}$. In total, we have 10 subsets.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Given 5 points, no three of which lie on the same line. How many segments need to be drawn to connect each pair of points?
|
8. The solution to the problem is shown in Figure 93. We will obtain 10 segments. It is useful to compare this problem with problem 7.
Fig. 93
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.