problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
7. A survey was conducted involving 420 families. It was found that $95\%$ of the families own a TV, and $80\%$ of the families own a computer. A family is randomly selected. If it is known that each surveyed family has at least one of the mentioned devices, what is the probability that the selected family owns a computer but not a TV? Express the probability as a percentage.
No calculators or reference materials are allowed.
|
First method:
| $\frac{95}{100}$ | 420 = 399, which means 399 families own a TV. | $1 \text{ POINT}$ |
| :---: | :---: | :---: |
| $\frac{80}{100}$ | $420=336$, which means 336 families own a computer. | 1 POINT |
| $399-$ | $-336=735$ | 1 POINT |
| 735 | $420=315$ | 1 POINT |
| $315$ | families own both a TV and a computer. | |
| 336 | $315=21$, which means 21 families own only a computer. | 1 POINT |
| The number | of all possible outcomes is 420. | $1 \text{ POINT}$ |
| The number | of favorable outcomes is 21, | $1 \text{ POINT}$ |
| so the | probability of a favorable outcome is $p=\frac{21}{420}=\frac{1}{20}=0.05=5\%$. | 2 POINTS |
| The probability | that a family owns a computer but does not own a TV is $5\%$. | $\begin{aligned} 1 \text{ POINT} \\ \text{POINTS} \end{aligned}$ |
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Marko bought $3 \mathrm{~kg}$ of apples, $2 \mathrm{~kg}$ of pears, and $1 \mathrm{~kg}$ of strawberries at the market. He paid 59 kn for all the fruit. Apples are cheaper than pears by $1 \mathrm{kn}$ and 50 lp per kilogram, and they are three times cheaper than strawberries per kilogram. How much does one kilogram of pears cost?
|
First method:
Apples are the cheapest, so the following applies:

$8 \square + 3 = 59 \quad 1$ POINT
$8 = 59 - 3 \quad 1$ POINT
$8 \square = 56 \quad 1$ POINT
$\square = 56 : 8 = 7 \quad 1$ POINT
One kilogram of pears costs $7 \text{kn} + 1 \text{kn} 50 \text{lp} = 8 \text{kn} 50 \text{lp}$ 1 POINT
TOTAL 10 POINTS
##
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Using the digits 0 and 5, write all ten-digit numbers that are divisible by 9. How many such numbers are there?
|
2. The sum of the digits of any ten-digit number composed of the digits 0 and 5 is
a multiple of the number 5.
2 POINTS
Furthermore, since we are looking for numbers that are divisible by 9, the sum of the digits must be divisible by 9.
Since the numbers 5 and 9 are relatively prime, it follows that the desired numbers must have exactly nine fives and one zero. Then the sum of the digits is $9 \cdot 5 = 45$.
2 POINTS
Zero cannot be in the first position, so we have the numbers: $5055555555, 5505555555, 5550555555$,
$5555055555, 5555505555, 5555550555, 5555555055, 5555555505, 55555555550$.
5 POINTS
Thus, there are a total of 9 numbers that satisfy the conditions of the problem.
1 POINT
TOTAL 10 POINTS
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. What is the remainder when the number
$1+1 \cdot 2+1 \cdot 2 \cdot 3+1 \cdot 2 \cdot 3 \cdot 4+1 \cdot 2 \cdot 3 \cdot 4 \cdot 5+\ldots+1 \cdot 2 \cdot 3 \cdot 4 \cdot \ldots \cdot 14+1 \cdot 2 \cdot 3 \cdot 4 \cdot \ldots \cdot 14 \cdot 15$
is divided by 72?
|
First method:
$1+1 \cdot 2+1 \cdot 2 \cdot 3+1 \cdot 2 \cdot 3 \cdot 4+1 \cdot 2 \cdot 3 \cdot 4 \cdot 5+1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6+\ldots+1 \cdot 2 \cdot 3 \cdot 4 \cdot \ldots \cdot 14+1 \cdot 2 \cdot 3 \cdot 4 \cdot \ldots \cdot 14 \cdot 15=$
$=1+2+6+24+120+1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot(1+7+7 \cdot 8+7 \cdot 8 \cdot 9+\ldots+7 \cdot 8 \cdot 9 \cdot 10 \cdot 11 \cdot 12 \cdot 13 \cdot 14 \cdot 15)=$
$=153+720 \cdot(1+7+7 \cdot 8+7 \cdot 8 \cdot 9+\ldots+7 \cdot 8 \cdot 9 \cdot 10 \cdot 11 \cdot 12 \cdot 13 \cdot 14 \cdot 15)=$
$=9+144+72 \cdot 10 \cdot(1+7+7 \cdot 8+7 \cdot 8 \cdot 9+\ldots+7 \cdot 8 \cdot 9 \cdot 10 \cdot 11 \cdot 12 \cdot 13 \cdot 14 \cdot 15)=$
$=9+72 \cdot 2+72 \cdot 10 \cdot(1+7+7 \cdot 8+7 \cdot 8 \cdot 9+\ldots+7 \cdot 8 \cdot 9 \cdot 10 \cdot 11 \cdot 12 \cdot 13 \cdot 14 \cdot 15)=$
$=9+72 \cdot[2+10 \cdot(1+7+7 \cdot 8+7 \cdot 8 \cdot 9+\ldots+7 \cdot 8 \cdot 9 \cdot 10 \cdot 11 \cdot 12 \cdot 13 \cdot 14 \cdot 15)]$
Therefore, the desired remainder is 9.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Twenty students participating in a math camp have decided to send messages to each other, with each of them sending messages to exactly ten of the remaining students. Determine the minimum possible number of mutual messages, i.e., find an example of a message-sending schedule in which the number of mutual messages is the smallest possible and prove that a smaller number of mutual messages cannot be achieved.
(A message between students $\mathrm{A}$ and $\mathrm{B}$ is considered mutual if student $\mathrm{A}$ has sent a message to student B and student B has sent a message to student A.)
|
5. A total of $20 \cdot 10=200$ messages were sent, and the number of pairs of students is $\frac{20 \cdot 19}{2}=190$.
Therefore, at least $200-190=10$ messages must be sent between the same pairs of students, so the minimum possible number of mutual messages is at least 10.
Now, let's construct a schedule of sent messages such that the number of mutual messages is exactly 10.
Let the students be arranged in a circle, and let each student send a message to the ten students who are located after them in the clockwise direction. Note that in this arrangement, only students who are directly opposite each other (diametrically opposite) will send mutual messages.

(Each point represents one student, and the directed line segment represents a one-way message.)
This constructs the desired message schedule, where the number of mutual messages is exactly 10. From the above, we can conclude that the minimum possible number of mutual messages is 10.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Throughout the year, Marko took several exams and scored a certain number of points on them. If Marko were to score 89 points on his next exam, his average score on the exams would be 91. However, if he were to score 64 points on the next exam, his average score on the exams would then be 86. How many exams has Marko taken so far?
|
First method:
Let $n$ be the number of exams Marko has written so far, and $x$ the sum of the scores achieved on them.
From the conditions of the problem, it is clear that:
$\frac{x+89}{n+1}=91, \frac{x+64}{n+1}=86$
$1 \text{ POINT}$
From both equations, express $x$:
$x=91 \cdot(n+1)-89 \quad$ and $\quad x=86 \cdot(n+1)-64$
$1 \text{ POINT}$
Equate the right-hand sides:
$91 \cdot(n+1)-89=86 \cdot(n+1)-64$
$1 \text{ POINT}$
$91 n+91-89=86 n+86-64$
$91 n+2=86 n+22$
$91 n-86 n=22-2$
| $5 n=20$ | 1 POINT |
| :--- | ---: |
| $n=4$ | 1 POINT |
| Marko has written 4 exams so far. | 1 POINT |
| ......................................................................................................... 6 POINTS. | |
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Determine the remainder when the natural number $n$ is divided by 45, given that the number $(n+2$ 020) gives a remainder of 43 when divided by 45.
|
3. The remainder of the division of the number $n$ by 45 is denoted by $\mathrm{s} x$.
The remainder of the division of the number 2020 by 45 is 40.
Since $40<43$, it can be concluded that the remainder of the division of the number ( $n+2020$ ) by 45 is the number $(x+40)$
Now, $x+40=43$, from which it follows that $x=3$.
Therefore, the remainder of the division of the natural number $n$ by 45 is 3.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. On one of two parallel lines, there are 8 points. How many points are on the other line if all the points together determine 640 triangles?
Each task is scored out of 10 points.
The use of a pocket calculator or any reference materials is not allowed.
|
first method):
$x^{2}+16 x-10 x-160=0$
$x \cdot(x+16)-10 \cdot(x+16)=0$
$(x+16) \cdot(x-10)=0$
2 POINTS
From $x+16=0$ we get $x_{1}=-16$, and from $x-10=0$ we get $x_{2}=10$.
1 POINT
Since the number of points must be a natural number, there are 10 points on the second line.
1 POINT
TOTAL 10 POINTS
Note 1: The equation $x^{2}+6 x-160=0$ can also be solved in the following two ways:
##
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Two towers are of heights $20 \mathrm{~m}$ and $30 \mathrm{~m}$. The top of each tower is connected to the base of the other with a taut wire. At what height above the ground do the two wires cross if the distance between the towers is $40 \mathrm{~m}$?
|
8.

According to the K-K theorem on similarity, it follows that $\triangle A C B \sim \triangle F C E$. 2 POINTS
From the similarity, it follows that $20: x = 40 : y$ or $y = 2x$. 2 POINTS
According to the K-K theorem on similarity, it follows that $\triangle A C D \sim \triangle A F E$. 2 POINTS
From the similarity, it follows that $30 : x = 40 : (40 - y)$ or $30 : x = 40 : (40 - 2x)$ 1 POINT, so $x = 12$.
The two wires intersect at a height of 12 meters above the ground.
2 POINTS
TOTAL 10 POINTS
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. To reduce heating costs in a residential building, the tenants decided to change the facade, and they were granted non-repayable funds from the Environmental Protection and Energy Efficiency Fund, which cover 60% of all total costs. The total cost for the new facade is 1,200,000 kn. The new facade guarantees that the average annual heating costs will be reduced by 35%. If the average annual heating cost for the building was 168,000 kn, how many years will it take for this investment to pay off?
|
6. The cost for the facade is 1200000 kn. The non-refundable portion of funds is $60\%$, which means that the residents have to cover $40\%$ of the costs, amounting to $480000 \mathrm{kn}$.
1 POINT
The average annual heating cost was 168000 kn, and with a savings of 35%, it will amount to 109200 kn.
1 POINT
Let $n$ be the number of years needed for the investment to pay off. Then the total cost for $n$ years of heating before the new facade is $168000 n$,
and the total cost for $n$ years of heating after the new facade is $109200 n$.
1 POINT
We need to determine the smallest number of years for which the heating cost before the new facade will be greater than the sum of the total heating costs after the new facade and the costs for the facade paid by the residents.
Determine the smallest natural number $n$ for which the following holds:
$168000 n > 109200 n + 480000$.
1 POINT
$168000 n - 109200 n > 480000$
$58800 n > 480000$
1 POINT
$n > \frac{480000}{58800}$
1 POINT
Since $\frac{480000}{58800} \approx 8.2$,
1 POINT
the smallest natural number that satisfies this condition is 9, meaning the investment will pay off in 9 years.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-1.2. Solve the equation in the set of real numbers:
$$
f(x)+f(2-x)=2
$$
where
$$
f(x)= \begin{cases}|x|, & x \leq 1 \\ 2-x, & x>1\end{cases}
$$
|
Solution.
$$
f(2-x)= \begin{cases}|2-x|, & \text { for } 2-x \leq 1, \text { i.e. } x \geq 1 \\ x, & \text { for } 2-x>1, \text { i.e. } x<1\end{cases}
$$
1. For $x>1$ the equation becomes
$$
\begin{array}{r}
2-x+|2-x|=2 \\
|2-x|=x
\end{array}
$$
Then we have
$$
2-x=x \quad \text { or } \quad 2-x=-x
$$
The solution $x=1$ does not satisfy (because $x>1$).
2. For $x<1$ the equation becomes
$$
|x|=2-x
$$
The solution $x=1$ does not satisfy (because $x<1$).
3. For $x=1$ the equation is
$$
|x|+|2-x|=2
$$
We conclude that $x=1$ is the only solution.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Zadatak B-4.1. Ako je
$$
f\left(\log _{3} x\right)=\frac{\log _{3} \frac{9}{x^{4}}}{\log _{0 . \dot{3}} x-\log _{\sqrt{3}} x} \quad \text { i } \quad(f \circ g)(x)=e^{x}
$$
koliko je $g(\ln 2)$ ?
|
Rješenje. Zapišimo izraz
$$
f\left(\log _{3} x\right)=\frac{\log _{3} \frac{9}{x^{4}}}{\log _{0 . \dot{3}} x-\log _{\sqrt{3}} x}
$$
u jednostavnijem obliku.
$$
f\left(\log _{3} x\right)=\frac{\log _{3} 9-\log _{3} x^{4}}{\log _{3^{-1}} x-\log _{3^{\frac{1}{2}}} x}=\frac{2-4 \log _{3} x}{-\log _{3} x-2 \log _{3} x}
$$
Stavimo li $\log _{3} x=t$, slijedi
$$
f(t)=\frac{2-4 t}{-3 t} \quad \text { ili } \quad f(x)=\frac{4 x-2}{3 x}
$$
Ako je
$$
(f \circ g)(x)=\frac{4 \cdot g(x)-2}{3 g(x)}
$$
rješenje jednadžbe
$$
\frac{4 \cdot g(x)-2}{3 g(x)}=e^{x}
$$
je funkcija $g(x)$,
$$
g(x)=\frac{2}{4-3 e^{x}}
$$
Tada je
$$
g(\ln 2)=\frac{2}{4-6}=-1
$$
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-4.4. Determine all values of the real parameter $p$ for which the equation $x^{4}-(3 p+2) x^{2}+p^{2}=0$ has four solutions that form four consecutive terms of an arithmetic sequence.
|
Solution. Since the equation is biquadratic, its solutions are $x_{1}, -x_{1}, x_{2} \text{ and } -x_{2}$ (symmetric with respect to the origin). Let $x_{1}$ and $x_{2}$ be positive real numbers and let $x_{1} < x_{2}$. Then the order of the terms of the sequence (from the smallest) is $-x_{2}, -x_{1}, x_{1}, x_{2}$.
It follows that $x_{1} = -x_{1} + d$ or $x_{1} = \frac{1}{2} d$.
Then $x_{2} = x_{1} + d = \frac{3}{2} d$, and $-x_{2} = -\frac{3}{2} d$.
The given sequence is of the form $-\frac{3}{2} d, -\frac{1}{2} d, \frac{1}{2} d, \frac{3}{2} d$.
If we let $t = x^{2}$ in the given equation, we get $t^{2} - (3p + 2)t + p^{2} = 0$.
From the previous considerations, we conclude that its solutions are $t_{1} = \frac{1}{4} d^{2}, t_{2} = \frac{9}{4} d^{2}$.
Using Vieta's formulas, the following equalities follow
$$
\begin{array}{rr}
\frac{1}{4} d^{2} + \frac{9}{4} d^{2} = 3p + 2, \quad \text{or} \quad \frac{5}{2} d^{2} = 3p + 2 \\
\frac{1}{4} d^{2} \cdot \frac{9}{4} d^{2} = p^{2}, \quad \text{or} \quad \frac{9}{16} d^{4} = p^{2}
\end{array}
$$
From the second equality,
$$
d^{2} = \frac{4}{3}|p|
$$
which, with the first equality, gives the equation
$$
\frac{10}{3}|p| = 3p + 2
$$
Then
$$
\begin{gathered}
\text{for } p \geq 0 \text{, } 10p = 9p + 6 \text{, and } p = 6 \\
\text{for } p < 0 \text{, } -10p = 9p + 6 \text{ and } p = -\frac{6}{19}
\end{gathered}
$$
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-4.5. In the race, 100 people participated, and no two people finished the race with the same time. At the end of the race, each participant was asked what place they finished in, and everyone answered with a number between 1 and 100.
The sum of all the answers is 4000. What is the smallest number of incorrect answers that the runners could have given? Justify your answer.
|
Solution. If all the runners had accurately answered their finishing positions, the sum of their answers would be
$$
1+2+3+\ldots+100=5050
$$
Thus, some people must have exaggerated their results, and the smallest number of incorrect answers is achieved when the runners at the last positions claim they were first.
If $n$ people at the end of the line lied that they were first, the sum of the answers is
$$
1+2+\ldots+(100-n)+1+1+\ldots+1=\frac{(100-n)(100-n+1)}{2}+n
$$
By direct verification, we can determine that for $n=11$ the sum is 4016, which is greater than 4000, and for $n=12$ the sum is 3928.
Therefore, to have the sum exactly 4000 with the smallest number of incorrect answers, 11 people at the end of the line need to say they were first, and since the difference to 4016 is 16, it is sufficient for the runner with the number 17 to say he was first.
Thus, a minimum of 12 runners gave incorrect answers.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-1.5.
Karlo and Lovro are playing the following game. Karlo will cut a paper of size $9 \times 9$ into rectangles of integer dimensions, where at least one dimension is 1. After that, Lovro will choose a natural number $k \in \{1, \ldots, 9\}$, and Karlo will give him as many coins as the total area of all rectangles of dimensions $1 \times k$ and $k \times 1$. Lovro will choose $k$ to maximize the number of coins he receives, while Karlo wants to save and give Lovro as few coins as possible.
Determine the smallest possible number of coins that Karlo will give to Lovro.
|
## Solution.
We claim that Karlo will give Lovro at least 12 coins.
1 point
Assume there is a way for Karlo to cut the paper such that Lovro has to give (strictly) fewer than 12 coins. By cutting the paper in this way, Karlo would create at most 11 rectangles of dimensions $1 \times 1$, five rectangles of dimensions $1 \times 2$, three rectangles of dimensions $1 \times 3$, two rectangles of dimensions $1 \times 4$, two rectangles of dimensions $1 \times 5$, and one rectangle each of dimensions $1 \times 6$, $1 \times 7$, $1 \times 8$, and $1 \times 9$.
The total area of all these rectangles would be
$$
11 \cdot 1 + 5 \cdot 2 + 3 \cdot 3 + 2 \cdot 4 + 2 \cdot 5 + 6 + 7 + 8 + 9 = 78
$$
Since $78 < 81$, Karlo would have to create at least one more rectangle to use the entire $9 \times 9$ paper. Therefore, it is impossible for Karlo to give Lovro fewer than 12 coins.
The following example shows that Karlo can cut the paper in such a way that he is sure Lovro will have to give at most 12 coins.
| 9 | | | | |
| :---: | :---: | :---: | :---: | :---: |
| 8 | | | | 1 |
| 7 | | |  | |
| 6 | | 3 | | |
| 6 | | 3 | | |
| 5 | | 4 | | |
| 5 | | 4 | | |
| 3 | 2 | 4 | | |
| 3 | 2 | 2 | | |
## COUNTY COMPETITION IN MATHEMATICS
2nd grade - high school - A variant
March 3, 2017.
## IF A STUDENT HAS A DIFFERENT APPROACH TO SOLVING THE TASK, THE COMMITTEE IS OBLIGED TO GRADE AND EVALUATE THAT APPROACH IN AN APPROPRIATE MANNER.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-3.5.
How many integers can a finite set $S$ contain at most such that among any three elements of the set $S$ there are two different numbers whose sum is also in $S$?
|
## Solution.
Let $S$ be a finite set of integers such that among any three elements of the set $S$, there exist two distinct numbers whose sum is also in $S$. We will show that $S$ cannot have more than 7 elements.
Assume that $S$ has at least three positive elements. Let $a, b, c$ be the three smallest positive elements of $S$ with $a < b < c$. Since $a + b > b$ and $a + b < c$, it must be that $a + b \in S$. Since $a + b > b$ and $a + b \in S$, it must be that $a + b = c$.
Let $x$ be the largest element of $S$ that is less than $a$. Consider the elements $x, b, c$. If $x > 0$, then $x + c > c$ and $b + c > c$, so it must be that $x + b \in S$. Since $x + b > b$, it must be that $x + b = c = a + b$, i.e., $a = x$, which is not possible. Therefore, $x$ cannot be positive, i.e., $S$ contains exactly 3 positive numbers.
Similarly, we show the implication: if $S$ contains at least 3 negative numbers, then $S$ contains exactly 3 negative numbers. In other words, the set $S$ can contain at most 3 numbers of the same sign. Therefore, $S$ can contain at most 7 elements (three positive, three negative, and the number 0).
An example of a set $S$ with 7 elements that has the desired property is
$$
S = \{-3, -2, -1, 0, 1, 2, 3\}
$$
## COUNTY COMPETITION IN MATHEMATICS
## 4th grade - high school - A variant
28th February 2017.
## IF A STUDENT HAS A DIFFERENT APPROACH TO SOLVING THE TASK, THE COMMITTEE IS OBLIGED TO GRADE AND EVALUATE THAT APPROACH IN AN APPROPRIATE MANNER.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Zadatak B-2.4.
Na nekom natjecanju iz matematike rješava se $n$ zadataka, $10<n<20$. Za svaki točno riješeni zadatak natjecatelj dobiva 5 bodova, a za svaki neriješeni ili netočno riješen zadatak gubi 3 boda. Ako je Sebastijan imao ukupno 0 bodova, koliko je zadataka riješio točno? Koliko je bilo ukupno zadataka?
|
## Drugo rješenje.
Neka je $x$ broj točno riješenih zadataka, a $y$ broj netočno ili neriješenih zadataka.
Vrijedi da je $10<x+y<20, x, y \in \mathbb{N}$, a tada je $x<20$ i $y<20$.
Ukupni broj bodova iznosi $5 x-3 y$.
Budući da Sebastijan ima 0 bodova, vrijedi
$$
5 x-3 y=0, \text { odnosno } x=\frac{3 y}{5}
$$
Kako $x$ mora biti prirodan broj, slijedi da $y$ mora biti djeljiv s 5 . 1 bod
Tada, budući da je $y<20$, imamo sljedeće mogućnosti:
$$
\begin{aligned}
& y=5 \text { i } x=\frac{3 y}{5}=3, \text { ali je tada } x+y=8 \text { pa to nije rješenje; } \\
& y=10 \text { i } x=6 \\
& y=15 \text { i } x=\frac{3 y}{5}=9, \text { ali je tada } x+y=24 \text { što također ne može biti rješenje. }
\end{aligned}
$$
Sebastijan je točno riješio 6 zadataka, a ukupno je bilo 16 zadataka.
Napomena: Ako učenik ne raspiše sve mogućnosti, odnosno ne pokaže da je $x=10$, $y=6$ jedino rješenje, može dobiti maksimalno 3 boda.
Analogno vrijedi i ukoliko učenik izrazi $y=\frac{5}{3} x$ te raspisuje sve slučajeve za $x<20$.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-3.1.
Solve the equation $5 \cdot 0.16^{x}+8 \cdot 0.4^{x}=4$.
|
## Solution.
Let $t=(0.4)^{x}$. 1 point
After introducing the substitution, the equation takes the form $5 t^{2}+8 t-4=0$.
The solutions of the obtained quadratic equation are:
$t_{1,2}=\frac{-8 \pm \sqrt{64+80}}{10}=\frac{-8 \pm \sqrt{144}}{10}=\frac{-8 \pm 12}{10}$,
which means $t_{1}=\frac{2}{5}$ and $t_{2}=-2$.
It remains to determine the values of the unknown $x$.
From the equation $0.4^{x}=\frac{2}{5}$, we get $\left(\frac{2}{5}\right)^{x}=\frac{2}{5}$ and the solution is $x=1$.
There is no real number $x$ for which $0.4^{x}=-2$.
The solution $x=1$ is the only solution to the original equation.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-3.3.
The function is given by $f(x)=A \sin \left(B x+\frac{7 \pi}{10}\right)+D$, where $A, B$, and $D$ are positive real numbers. The point $M\left(\frac{2 \pi}{3},-8\right)$ is the only minimum point, and the point $N\left(\frac{3 \pi}{2}, 12\right)$ is the only maximum point of the function $f$ in the interval $\left[\frac{2 \pi}{3}, \frac{3 \pi}{2}\right]$. Determine $f\left(\frac{203 \pi}{12}\right)$.
|
## Solution.
Let's plot points $M$ and $N$ in the coordinate system and sketch the graph of the function $f$.
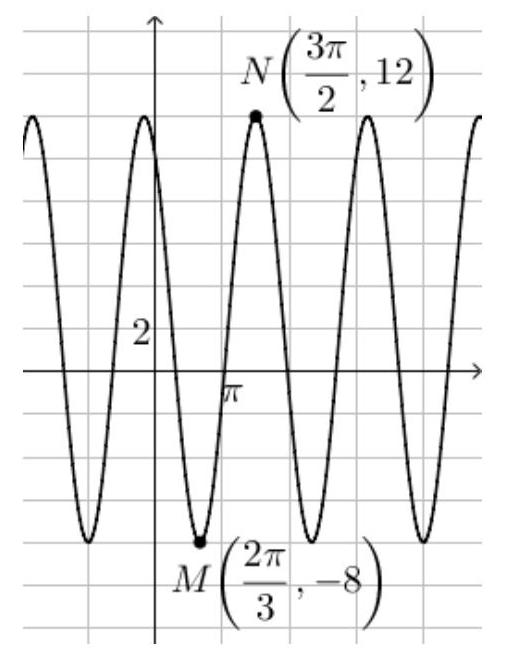
First, let's determine the coefficients $A$ and $D$.
The coefficient $D$ is the vertical shift of the sine function or calculated as:
$$
D=\frac{\text { "maximum value" }+ \text { "minimum value" }}{2}=\frac{12+(-8)}{2}=2
$$
The coefficient $A$ is the amplitude of the given function or calculated as:
$$
A=\frac{\text { "maximum value" }- \text { "minimum value" }}{2}=\frac{12-(-8)}{2}=10
$$
For the fundamental period $T$ of the function $f$, we have $\frac{T}{2}=\frac{3 \pi}{2}-\frac{2 \pi}{3}=\frac{5 \pi}{6}$, hence $T=\frac{5 \pi}{3}$.
Now we can determine the coefficient $B: B=\frac{2 \pi}{T}=\frac{2 \pi}{\frac{5 \pi}{3}}=\frac{6}{5}$.
Therefore, the given function is $f(x)=10 \sin \left(\frac{6}{5} x+\frac{7 \pi}{10}\right)+2$.
Finally, we need to determine $f\left(\frac{203 \pi}{12}\right)$.
$f\left(\frac{203 \pi}{12}\right)=10 \sin \left(\frac{6}{5} \cdot \frac{203 \pi}{12}+\frac{7 \pi}{10}\right)=10 \sin (21 \pi)+2=10 \cdot 0+2=2$.
Note: A student can achieve full points in the problem even if they have not sketched the graph of the function. A student can earn points for accurately determining the coefficients $A$ and $D$ if they read them from the sketch.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-4.5.
A math teacher gave the students ten problems for homework and said that he would select two of them for the next test. How many of the given ten problems does Luka need to solve at minimum to be sure with a probability greater than $\frac{7}{9}$ that at least one of the selected problems will be among those he has solved?
|
## First Solution.
Let $S$ be a set of ten homework problems. Let $L$ be a subset of $S$, i.e., a set of $x$ problems that Luka has solved. Then $10-x$ is the number of problems that Luka has not solved.
Consider the event $A$ - "the professor has chosen at least one problem from the set $L$."
Then the complementary event $\bar{A}$ is - "the professor has not chosen any problem from the set $L$" or $\bar{A}$ - "the professor has chosen both problems from the set $S \backslash L$."
The probability of event $A$ is
$$
p(A)=1-p(\bar{A})=1-\frac{\binom{10-x}{2}}{\binom{10}{2}}=1-\frac{(10-x)(10-x-1)}{10 \cdot 9}
$$
Since $p(A)>\frac{7}{9}$, it follows that
$$
\begin{gathered}
1-\frac{(10-x)(10-x-1)}{10 \cdot 9}>\frac{7}{9} \\
90-\left(100-10 x-10-10 x+x^{2}+x\right)>70 \\
-x^{2}+19 x-70>0
\end{gathered}
$$
The solution to this inequality is the interval $\langle 5,14\rangle$,
Note: For a student who does not describe the analyzed events in text but correctly solves the problem, do not deduct 1 point.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-3.2.
A quadruple of natural numbers $(a, b, c, d)$ is called green if
$$
b=a^{2}+1, \quad c=b^{2}+1, \quad d=c^{2}+1
$$
and $D(a)+D(b)+D(c)+D(d)$ is odd, where $D(k)$ is the number of positive divisors of the natural number $k$.
How many green quadruples are there whose all members are less than 1000000?
|
## Solution.
A natural number has an odd number of divisors if and only if it is the square of some natural number. For a natural number $m$, we have
$$
m^{2}d=c^{2}+1>c^{2}=\left(b^{2}+1\right)^{2}>b^{4}=\left(a^{2}+1\right)^{4}>a^{8}
$$
Therefore, it must be that $a^{8}<10^{6}$. Since $10^{6}=1000^{3}<1024^{3}=2^{20}<2^{24}=8^{8}$, we conclude that $a<8$. The only squares less than 8 are 1 and 4.
By direct verification, we conclude that both quadruples $(1,2,5,26)$ and $(4,17,290,84101)$ are green. Thus, there are two such green quadruples.
Note: The claim that a number is a square of a natural number if and only if it has an odd number of divisors does not need to be proven by the student. A simple proof of this claim follows. All divisors of a number $n$ can be grouped into pairs where the divisor $d$ is paired with $\frac{n}{d}$, except when $n=k^{2}$ for some natural number $k$ (in which case $k$ is paired with itself).
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-1.5.
On a board, there are 2023 different real numbers. If each number on the board (simultaneously) is replaced by the sum of all the other numbers, the 2023 numbers on the board will be the same as at the beginning.
What values can the product of all the numbers on the board take at some point?
|
## First Solution.
Let the numbers initially written on the board be denoted by $x_{1}, x_{2}, \ldots, x_{2023}$, and let $s=x_{1}+x_{2}+\ldots+x_{2023}$.
Since after the first swap the numbers on the board are the same as the initial numbers, it follows that after any other swap, the numbers on the board will also be the initial numbers.
Therefore, the product of all numbers on the board will always be the same as the product of the initial numbers on the board. The same statement holds for the sum of the numbers on the board.
After the first swap, the numbers on the board will be $s-x_{1}, s-x_{2}, \ldots, s-x_{2023}$.
Since these are the same numbers that were initially written on the board, their sum is also equal to $s$, i.e.,
$$
s=\left(s-x_{1}\right)+\left(s-x_{2}\right)+\ldots+\left(s-x_{2023}\right)=2023 s-\left(x_{1}+x_{2}+\ldots+x_{2023}\right)=2022 s . \quad 1 \text { point }
$$
From the above equation, it follows that $s=0$.
Therefore, the numbers on the board after the first swap are $-x_{1},-x_{2}, \ldots,-x_{2023}$.
Since these are the same numbers that were initially on the board, the product of all numbers before and after the swap will be the same, i.e.,
$$
x_{1} \cdot x_{2} \cdot \ldots \cdot x_{2023}=\left(-x_{1}\right) \cdot\left(-x_{2}\right) \cdot \ldots \cdot\left(-x_{2023}\right)=-x_{1} \cdot x_{2} \cdot \ldots \cdot x_{2023}
$$
From the above equality, we have $x_{1} \cdot x_{2} \cdot \ldots \cdot x_{2023}=0$.
Thus, the product of all numbers on the board at any time will always be 0.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-1.5.
On the board, there are 2023 different real numbers. If each number on the board (simultaneously) is replaced by the sum of all the other numbers, the 2023 numbers on the board will be the same as at the beginning.
What values can the product of all the numbers on the board take at some point?
|
## Second Solution.
As in the previous solution, we conclude that if the numbers on the board after the first move are equal to the opposite values of the numbers written on the board at the beginning, and that the product does not change after each move.
Without loss of generality, let $x_{1}>x_{2}>\ldots>x_{2023}$. Then it holds that $-x_{2023}>$ $-x_{2022}>\ldots>-x_{1}$. Since the numbers written on the board at the beginning are equal to those after one move, it must be
$$
x_{1}=-x_{2023}, x_{2}=-x_{2022}, \ldots, x_{2023}=-x_{1}
$$
In particular, $x_{1012}=-x_{1012}$, or $x_{1012}=0$.
Since one of the numbers on the board is zero, we conclude that the product of these numbers is zero, and it will remain so after each move.
Note: The solution earns the first point from the first scoring scheme if it mentions in any form the equality that the sum of all numbers on the board before the swap is equal to the sum of all numbers on the board after the swap, or an analogous statement for the product.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-2.3.
Let $p$ and $q$ be prime numbers such that $p+q+4$ and $p q-12$ are also prime numbers. Determine $p+q$.
|
## Solution.
Numbers $p$ and $q$ cannot have the same parity because then $p+q+4$ would be an even number strictly greater than 2. Therefore, one of the numbers $p$ or $q$ must be equal to 2.
Without loss of generality, we can assume that $p=2$.
According to the conditions of the problem, $q+6$ and $2q-12$ are prime numbers. The number $2q-12$ is clearly even, and since it is also prime, it must be $2q-12=2$, i.e., $q=7$.
The numbers $q=7$ and $p+q+4=13$ are also prime, so all conditions of the problem are satisfied. 1 point Therefore, the final value of $p+q=9$.
Note: The fifth point in the above scoring scheme can only be achieved if the solution verifies (or mentions) that all four numbers $p=2, q=7, p+q+4=13$, and $pq-12=2$ are indeed prime.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-3.4.
How many ordered pairs of natural numbers $(a, b)$ satisfy
$$
\log _{2023-2(a+b)} b=\frac{1}{3 \log _{b} a} ?
$$
|
## Solution.
For the equality to be well-defined, it is necessary that
$$
\begin{aligned}
2023-2(a+b) & \in (0,1) \cup (1,+\infty) \\
b & \in (0,1) \cup (1,+\infty) \\
\log _{b} a & \neq 0
\end{aligned}
$$
Since $a$ and $b$ are natural numbers, the first two conditions become $2023-2(a+b) \geqslant 2$ and $b \geqslant 2$. The last condition is equivalent to $a \geqslant 2$.
We can rearrange the initial equation as follows:
$$
\begin{aligned}
\frac{1}{\log _{b}(2023-2(a+b))} & =\frac{1}{\log _{b} a^{3}} \\
\log _{b}(2023-2(a+b)) & =\log _{b} a^{3} \\
2023-2(a+b)) & =a^{3} \\
a^{3}+2(a+b) & =2023 \\
a^{3}+2 a+2 b & =2023 .
\end{aligned}
$$
Notice that the condition $a^{3}=2023-2(a+b) \geqslant 2$ is automatically satisfied as long as $a \geqslant 2$. Therefore, we are looking for the number of natural solutions $(a, b)$ of the obtained equation that satisfy $a, b \geqslant 2$.
The number of solutions to this equation is equal to the number of odd natural numbers $a$ for which
$$
a^{3}+2 a \leqslant 2019
$$
Indeed, for the left and right sides of the equation to have the same parity, $a^{3}$ must be odd, i.e., $a$ must be odd. On the other hand, for any odd $a$ that satisfies the above inequality, the number $b=\frac{2023-a^{3}-2 a}{2}$ is a unique natural number that satisfies the desired equation.
For $a \leqslant 11$, we have $a^{3}+2 a \leqslant 11^{3}+2 \cdot 11=1353<2019$, while for $a \geqslant 13$, we have $a^{3}+2 a \geqslant 13^{3}+2 \cdot 13=2223$. Since there are 5 odd natural numbers less than or equal to 11 and greater than 2, we conclude that there are 5 ordered pairs that are solutions to the equation in the problem.
Note: The second point in the scoring scheme is achieved if an expression is obtained in which the number $(2023-2(a+b))$ does not appear in the base of the logarithm. The third point is achieved if an equation is obtained that does not include logarithms.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-1.3. If $a+b=2$ and $a^{2}+b^{2}=6$, what is $a^{-1}+b^{-1}$?
|
Solution.
$$
a^{-1}+b^{-1}=\frac{1}{a}+\frac{1}{b}=\frac{b+a}{a b}=\frac{2}{a b}
$$
Let's square the expression $a+b=2$. From
$$
a^{2}+2 a b+b^{2}=4
$$
it follows that $2 a b=4-6$, so $a b=-1$.
Then we have
$$
a^{-1}+b^{-1}=-2
$$
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-1.7. If in a regular hexagon $A B C D E F$ we draw all six of its shorter diagonals, they determine a hexagon GHIJKL. Prove that the hexagon GHIJKL is also a regular hexagon and calculate how many times smaller its area is compared to the area of the original hexagon.
|
Solution. Sketch
(2 points)

Let the side length of the hexagon $A B C D E F$ be $a$. Consider, in the regular hexagon $A B C D E F$, the characteristic triangle $S B C$.
Since this is an equilateral triangle, the length $|I N|=\frac{1}{3}|B N|=\frac{a \sqrt{3}}{6}$,
$$
|S I|=\frac{2}{3} \cdot \frac{a \sqrt{3}}{2}=\frac{a \sqrt{3}}{3}
$$
and the measure of the angle $\angle I S N$ is $30^{\circ}$.
(1 point)
Similarly, from the characteristic triangle $S C D$, $|N J|=\frac{a \sqrt{3}}{6}, |S J|=\frac{a \sqrt{3}}{3}$, and the measure of the angle $\angle J S N=30^{\circ}$. We conclude that $S I J$ is an equilateral triangle with side length $\frac{a \sqrt{3}}{3}$.
(1 point)
The same applies to the triangles $S J K, S K L, S L G, S G H, S H I$. Thus, all internal angles and sides of the hexagon are congruent, making the hexagon $G H I J K L$ regular with side length $b=\frac{a \sqrt{3}}{3}$.
(1 point)
Determine the ratio of the areas.
$$
P_{1}=6 \frac{a^{2} \sqrt{3}}{4}, \quad P_{2}=6 \frac{b^{2} \sqrt{3}}{4}
$$
The ratio of the areas is
$$
\frac{P_{1}}{P_{2}}=\frac{6 \frac{a^{2} \sqrt{3}}{4}}{6 \frac{b^{2} \sqrt{3}}{4}}=\frac{a^{2}}{b^{2}}=\frac{a^{2}}{\frac{a^{2}}{3}}=3
$$
The area of the hexagon $G H I J K L$ is three times smaller than the area of the hexagon $A B C D E F$.
|
3
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Task B-2.5. What is the last digit of the number $2012^{3}+3^{2012}$?
|
Solution. The number $2012^{3}$ ends with the digit 8.
The powers of the number $3, 3^{1}, 3^{2}, 3^{3}, 3^{4}, 3^{5}, 3^{6}, \ldots$ end with the digits $3,9,7,1,3,9, \ldots$,
that is, every fourth digit repeats.
Therefore, the number $3^{2012}=\left(3^{4}\right)^{503}$ has the same units digit as the number $3^{4}$, which is the number 1.
Since $8+1=9$, the number $2012^{3}+3^{2012}$ ends with the digit 9.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-3.1. Solve the equation
$$
\log _{5 x-2} 2+2 \cdot \log _{5 x-2} x=\log _{5 x-2}(x+1)
$$
|
Solution. Let's determine the conditions for which the given equation makes sense.
$$
\begin{aligned}
& 5 x-2>0, \quad 5 x-2 \neq 1, \quad x>0, \quad x+1>0 . \\
& \log _{5 x-2} 2+2 \cdot \log _{5 x-2} x=\log _{5 x-2}(x+1) \\
& \log _{5 x-2}\left(2 x^{2}\right)=\log _{5 x-2}(x+1) \\
& 2 x^{2}=x+1
\end{aligned}
$$
The solutions to this quadratic equation are $x_{1}=1, x_{2}=-\frac{1}{2}$.
However, only $x_{1}=1$ satisfies the condition, so it is the only solution.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-4.1. Calculate the area of a square whose two vertices are at the foci, and the other two at the vertices of the ellipse $\frac{x^{2}}{8}+\frac{y^{2}}{b^{2}}=1$. The foci of the ellipse are on the x-axis.
|
Solution. Sketch
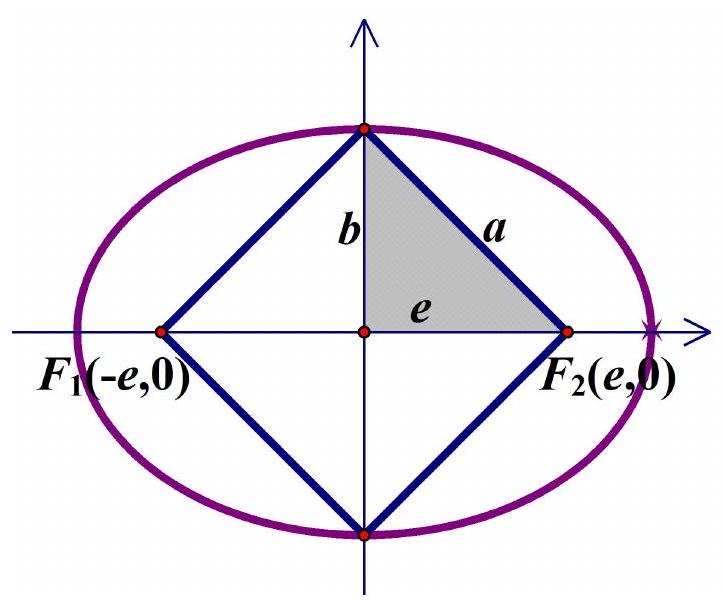
Since it is a square, it must hold that $e=b$,
or $a^{2}=2 b^{2}, b^{2}=4, b=2$.
The area is $P=2 b^{2}=8$ square units.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-4.4.
Let $n$ be a natural number. Determine all positive real numbers $x$ for which
$$
\frac{2^{2}}{x+1}+\frac{3^{2}}{x+2}+\cdots+\frac{(n+1)^{2}}{x+n}+n x^{2}=n x+\frac{n(n+3)}{2}
$$
|
## First Solution.
Since $n x=x+x+\cdots+x$, and $\frac{n(n+3)}{2}=(1+2+3+\cdots+n)+n$, the original equality is equivalent to
$$
\sum_{k=1}^{n} \frac{(k+1)^{2}}{x+k}+n x^{2}-\sum_{k=1}^{n} x-\sum_{k=1}^{n} k-n=0
$$
or equivalently,
$$
\sum_{k=1}^{n}\left(\frac{(k+1)^{2}}{x+k}-(x+k)\right)+n x^{2}-n=0
$$
By simplifying, we get
$$
\frac{(k+1)^{2}}{x+k}-(x+k)=\frac{(k+1)^{2}-(x+k)^{2}}{x+k}=\frac{(x+2 k+1)(1-x)}{x+k}=(1-x)\left(1+\frac{k+1}{x+k}\right)
$$
Thus, the above equality is equivalent to
$$
(1-x)\left(n+\sum_{k=1}^{n} \frac{k+1}{x+k}\right)+n\left(x^{2}-1\right)=0
$$
or equivalently,
$$
(1-x)\left(n+\left(\frac{2}{x+1}+\frac{3}{x+2}+\cdots+\frac{n+1}{x+n}\right)-n(1+x)\right)=0
$$
For $x=1$, the equality clearly holds. For $x \neq 1$, it must hold that
$$
n+\left(\frac{2}{x+1}+\frac{3}{x+2}+\cdots+\frac{n+1}{x+n}\right)=n(1+x)
$$
or equivalently,
$$
\frac{2}{x+1}+\frac{3}{x+2}+\cdots+\frac{n+1}{x+n}=n x
$$
If $0 < x < 1$, the left side is strictly less than $n$, while the right side is strictly greater than $n$. If $x > 1$, the opposite is true: the left side is strictly less than $n$, and the right side is strictly greater than $n$. Therefore, the only solution is $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-4.5.
On a board of dimensions $8 \times 8$, triomino tiles of shape $\exists$ are placed such that each triomino tile covers exactly three squares of the board, and they do not overlap with each other.
How many triomino tiles are needed at a minimum to place on the board so that no additional triomino tile can be placed afterward?
|
## Solution.
Divide the board into 16 squares of $2 \times 2$ as shown in the figure.

In each of these squares, at least two fields must be covered, otherwise a tromino-tile can be placed on the uncovered fields. Therefore, at least 32 fields must be covered, and for that, we need at least 11 tromino-tiles.
To show that 11 tromino-tiles are sufficient, we demonstrate this by construction, as shown in the figure.

|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-1.1.
Determine the minimum value of the expression
$$
|x+1|+|x-2|+|x-3|,
$$
where $x$ is a real number.
|
## Solution.
Let's calculate the value of the given expression depending on where the number $x$ is located on the real number line.
- For $x \leqslant -1$, the given expression is equal to
$$
-x-1-x+2-x+3=4-3x
$$
We conclude that for real numbers $x \leqslant -1$, the given expression achieves its minimum value when $x$ is the largest, i.e., at the point $x=-1$ and this value is equal to 7.
- For $-1 \leqslant x \leqslant 2$, the given expression is equal to
$$
x+1-x+2-x+3=6-x
$$
the minimum value is achieved at $x=2$ and is equal to 4.
- For $2 \leqslant x \leqslant 3$, the given expression is equal to
$$
x+1+x-2-x+3=x+2
$$
the minimum value is achieved at $x=2$ and is equal to 4.
- For $3 \leqslant x$, the given expression is equal to
$$
x+1+x-2+x-3=3x-4
$$
the minimum value is achieved at $x=3$ and is equal to 5.
Finally, we conclude that the minimum value of the expression is achieved at $x=2$ and is equal to 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-1.5.
Ana covered a board of dimensions $2020 \times 2020$ with domino tiles that do not overlap, and each tile covers exactly two squares of the board. Branka wants to color these tiles such that for each tile, among its neighboring tiles, at most two are of the same color. Two tiles are neighbors if they cover squares that share a side.
How many colors are needed at a minimum for Branka to be able to color the tiles in this way, regardless of how Ana arranged them?
|
## Solution.
We will prove that Branka has enough with two colors.
It is obvious that Branka cannot color all the tiles with one color: every tile that is not on the edge has at least four neighboring tiles (which touch it from below, above, left, and right) and which are the same color as the observed one, which is not allowed.
Now let's prove that, regardless of how Ana places the tiles, Branka can color the tiles with two colors in a correct way. Consider all the black fields of a $2020 \times 2020$ board when we would color it black and white like a chessboard. Each tile, regardless of Ana's placement, will cover exactly one black field. Therefore, instead of tiles, it is enough to assign one of two colors to each black field of the $2020 \times 2020$ board. We will color the tile with the color assigned to the black field it covers.
We do this as shown in the figure: we assign the colors 1 and 2 alternately to the fields of the black diagonal. Consider any black field. Without loss of generality, we can assume that the color 1 is assigned to this field. The tile that covers this field will be adjacent to some of the eight black fields that are two fields away from this field. Among these fields, only two have the color 1 assigned to them. Since this is true for any field, we conclude that all tiles will be adjacent to at most two other tiles of the same color.

## NATIONAL MATHEMATICS COMPETITION
## 2nd grade - high school - A variant
## October 26, 2020.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-2.5.
Ana covered a board of dimensions $2020 \times 2020$ with domino tiles that do not overlap, and each tile covers exactly two squares of the board. Branka wants to color these tiles such that for each tile, among its adjacent tiles, at most one is of the same color. Two tiles are adjacent if they cover squares that share a common side.
How many colors are needed at a minimum for Branka to be able to color the tiles in this way, regardless of how Ana arranged them?
|
## Solution.
We will prove that Branka has enough with three colors.
First, we will prove that Branka does not have enough with two colors (and thus not with fewer). We will find an example of Ana's tiling in which Branka cannot color the tiles with two colors.

Suppose Ana tiles the upper left $3 \times 4$ part of the board as shown in the figure, and the remaining part by placing the tiles horizontally. Let's name the tiles as in the figure. Tiles $A, B$, and $C$ are all pairwise adjacent. Since we have two colors (1 and 2), by the Pigeonhole Principle, at least two of these tiles must be the same color (without loss of generality, color 1). If these are tiles $A$ and $B$, then all tiles adjacent to them must be color 2. That is, tiles $C, E$, and $F$ are colored 2, which means that $C$ has two adjacent tiles of the same color.
On the other hand, if $C$ is the same color as one of the tiles $A$ or $B$, then all other adjacent tiles to $C$ must be color 2. Then $D, E$, and $F$ are colored 2, which means that $D$ has two adjacent tiles of the same color.
In both cases, we arrive at a contradiction, so at least three colors are needed.
Now let's prove that, regardless of how Ana places the tiles, Branka can color the tiles with three colors in a valid way. Consider all the black squares of the $2020 \times 2020$ board if we were to color it black and white like a chessboard. Each tile, regardless of how Ana places it, will cover exactly one black square. Therefore, instead of coloring the tiles, it is enough to assign one of the three colors to each black square of the $2020 \times 2020$ board. We will color a tile with the color assigned to the black square it covers.
Additionally, for the construction of the coloring, divide the $2020 \times 2020$ board into $2 \times 2$ blocks. Coloring a block means assigning the same color to its black squares (i.e., the squares in the upper left and lower right corners). We color the blocks by alternating all three colors in sequence, as shown in the figure.

Two tiles can be adjacent only if the distance between the black squares they cover is at most 2. Therefore, consider two squares in the same $2 \times 2$ block to which the same color is assigned (without loss of generality, color 1). From the figure, we see that the squares to which color 1 is assigned have at most one square of the same color in their vicinity. Since this holds for any square with an arbitrarily assigned color, we conclude that all tiles will be adjacent to at most one tile of the same color.
## NATIONAL MATHEMATICS COMPETITION
## 3rd grade - high school - A variant
## October 26, 2020.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-2.6.
Determine the lengths of the sides of a right-angled triangle with a perimeter of $24 \mathrm{~cm}$ and an inradius of $2 \mathrm{~cm}$.
|
## First Solution.
Let $a$ and $b$ be the legs of the right triangle, and $c$ the hypotenuse.
Then the radius of the inscribed circle is $r=\frac{a+b-c}{2}=2$.
From the system $\left\{\begin{array}{l}a+b+c=28 \\ a+b-c=4\end{array}\right.$ we get that $c=10 \text{ cm}$.
Applying the Pythagorean theorem, we have
$$
a^{2}+b^{2}=c^{2} \text { and } a+b-c=4, \text { i.e., } a+b=14
$$
so we need to solve the system
$$
\left\{\begin{array}{c}
a^{2}+b^{2}=100 \\
a+b=14
\end{array}\right.
$$
By substituting $b=14-a$ into the equation $a^{2}+b^{2}=100$, we reduce the system to the equation
$$
a^{2}+(14-a)^{2}=100
$$
This leads to $a^{2}-14 a+48=0$. The solutions to this equation are $a_{1}=6, a_{2}=8$.
Then $b_{1}=8, b_{2}=6$.
Thus, the lengths of the sides of the given triangle are $6 \text{ cm}, 8 \text{ cm}, 10 \text{ cm}$.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-2.3.
Determine all natural numbers $n$ for which the quadratic equation
$$
x^{2}-3 n x+n+3=0
$$
has integer solutions.
|
## First Solution.
Let $x_{1}$ and $x_{2}$ be the solutions of the given quadratic equation. According to Viète's formulas, we have
$$
x_{1} x_{2}=n+3 \quad \text{and} \quad x_{1}+x_{2}=3 n.
$$
First, observe that from the first equation, $x_{1}$ and $x_{2}$ have the same sign, and from the second equation, they are positive.
From $x_{1} x_{2}=n+3$, we see that both roots are less than or equal to $n+3$.
Furthermore, the smaller root must be less than or equal to $\sqrt{n+3}$, i.e., (without loss of generality) $x_{1} \leqslant \sqrt{n+3}$.
Since $n+3 \geqslant 4$, we can also use $\sqrt{n+3} \leqslant \frac{1}{2}(n+3)$.
Now, from $x_{1} \leqslant \frac{1}{2}(n+3)$ and $x_{2} \leqslant n+3$, it follows that $x_{1}+x_{2} \leqslant \frac{3}{2}(n+3)$, i.e., $3 n \leqslant \frac{3}{2}(n+3)$. Simplifying this inequality, we get the condition $n \leqslant 3$.
It remains to check if the equation has integer solutions for $n=1,2,3$. By substitution and direct verification, we find that the initial equation has integer solutions only for $n=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-3.5.
Let $n$ be a natural number. A sequence of $2 n$ real numbers is good if for every natural number $1 \leqslant m \leqslant 2 n$, the sum of the first $m$ or the sum of the last $m$ terms of the sequence is an integer. Determine the smallest possible number of integers in a good sequence.
|
## Solution.
We claim that for every $n$, the smallest possible number of integers is 2.
Let $x_{1}, x_{2}, \ldots, x_{2 n}$ be a good sequence of real numbers. If $n=1$, then $x_{1}$ and $x_{2}$ must be integers. Now let $n>1$.
Due to the condition for $m=1$, either $x_{1}$ or $x_{2 n}$ must be an integer.
Since $x_{1}+\cdots+x_{n}$ or $x_{n+1}+\cdots+x_{2 n}$ is an integer, and their sum is also an integer, we see that both of these numbers must be integers.
Furthermore, $x_{1}+\cdots+x_{n-1}$ or $x_{n+2}+\cdots+x_{2 n}$ must be an integer. If $x_{1}+\cdots+x_{n-1}$ is an integer, since $x_{1}+\cdots+x_{n}$ is an integer, we conclude that $x_{n}$ is an integer. Similarly, if $x_{n+2}+\cdots+x_{2 n}$ is an integer, we see that $x_{n+1}$ must be an integer. Therefore, either $x_{n}$ or $x_{n+1}$ must be an integer.
This shows that at least two terms of a good sequence must be integers.
Now we prove that for every natural number $n$, there exists a good sequence of real numbers with exactly two integers.
1. If $n$ is odd, we define $x_{1}=x_{n+1}=1$ and $x_{k}=\frac{1}{2}$ for all other $k \in\{1, \ldots, 2 n\}$. 1 point
Let $1 \leqslant m \leqslant n$. For odd $m$, the sum of the first $m$ terms is $1+(m-1) \cdot \frac{1}{2}$, which is an integer. For even $m$, the sum of the last $m$ terms is $m \cdot \frac{1}{2}$, which is an integer in this case.
If $m>n$, then by the proven fact, the sum of the first or last $m-n$ terms is an integer, and since $x_{1}+\cdots+x_{2 n}$ is an integer, we see that the sum of the first or last $m$ terms must also be an integer.
2. If $n$ is even, we define the sequence $x_{1}=x_{n}=1$ and $x_{k}=\frac{1}{2}$ for all other $k \in\{1, \ldots, 2 n\}$. For $m<n$. In this case, for odd $m$, the sum of the first $m$ terms is $1+(m-1) \cdot \frac{1}{2}$, and for even $m$, the sum of the last $m$ terms is $m \cdot \frac{1}{2}$, so we see that the given sequence is good.
## COUNTY COMPETITION IN MATHEMATICS
## 4th grade - high school - A variant
## February 28, 2018.
## IF A STUDENT HAS A DIFFERENT APPROACH TO SOLVING THE PROBLEM, THE COMMITTEE IS OBLIGED TO GRADE AND EVALUATE THAT APPROACH APPROPRIATELY.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-1.2. (4 points)
Let $a$ be a real number. Determine the sum of all three solutions of the equation
$$
x^{3}-a^{2} x+a x-x+a^{2}-a=0
$$
|
## Solution.
The expression on the left side of the given equation can be factored as follows:
$$
\begin{aligned}
x^{3}-a^{2} x+a x-x+a^{2}-a & =\left(x^{3}-x\right)+a^{2}(-x+1)+a(x-1) & & 1 \text { point } \\
& =(x-1)\left(x^{2}+x-a^{2}+a\right) & & 1 \text { point } \\
& =(x-1)\left(\left(x^{2}-a^{2}\right)+(x+a)\right) & & \\
& =(x-1)(x+a)(x-a+1) & & 1 \text { point }
\end{aligned}
$$
It is now clear that the solutions to the equation $(x-1)(x+a)(x-a+1)=0$ are the numbers $x=1$, $x=-a$, and $x=a-1$, and their sum is 0.
Note: Since the coefficient of $x^{2}$ is 0, it follows from Vieta's formulas that the sum of the solutions of the given equation is zero.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-1.5. (4 points)
Eleonora has many cubes, all of whose sides are white. First, she separates one cube and puts it in an empty box. Then she takes one cube at a time and paints some of its sides green, but in such a way that this cube differs from all those already in the box, and then she puts this cube in the box as well. How many cubes can there be in the box at most?
|
## Solution.
In the box, there is only one cube without any green sides, and one cube with one green side. Also, there is only one cube with all sides painted and one cube with five painted sides.
Cubes with two green sides are not all the same, as the painted sides can be adjacent or opposite. Therefore, there are two such cubes in the box.
Cubes with four painted sides (and two painted sides) are also two.
Finally, there are two cubes with three green sides: on one, all three sides are painted around one vertex, and on the other, two opposite sides and one side between them are painted.
Thus, Eleonora could have put a maximum of $1+1+2+2+2+1+1=10$ different cubes in the box.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task A-2.6. (10 points)
Determine all natural numbers less than 1000 that are equal to the sum of the squares of their digits.
|
## Solution.
Let the desired number be $n=\overline{a b c}$. (We will allow leading digits to be 0).
We want $a^{2}+b^{2}+c^{2}=100 a+10 b+c$.
Since $a, b$, and $c$ are digits, $a^{2}+b^{2}+c^{2} \leqslant 3 \cdot 9^{2}=243$, so $a \leqslant 2$.
2 points
Furthermore, we conclude that $a^{2}+b^{2}+c^{2} \leqslant 2^{2}+9^{2}+9^{2}=166$, so $a \leqslant 1$.
2 points
1. Case. Let $a=1$. Then $b^{2}+c^{2}=99+10 b+c$.
However, $b^{2} \leqslant 10 b$ and $c^{2} \leqslant 81<99+c$, so the left side is strictly less than the right side, and equality cannot be satisfied.
2. Case. Let $a=0$. Then $b^{2}+c^{2}=10 b+c$,
which we can write in the form $b(10-b)=c(c-1)$.
The expression $b(10-b)$ can be $0 \cdot 10=0,1 \cdot 9=9,2 \cdot 8=16,3 \cdot 7=21,4 \cdot 6=24$, and $5 \cdot 5=25$, while the expression $c(c-1)$ can be $0,2,6,12,20,30,42,56$ or 72.
Therefore, it must be that $b(10-b)=c(c-1)=0$, i.e., $b=0$ and $c \in\{0,1\}$.
The only natural number less than 1000 with the given property is the number 1.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Zadatak A-3.3. (4 boda)
Izračunaj $144^{\log _{5} 1000}: 10^{6 \log _{5} 12}$.
|
## Prvo rješenje.
Vrijedi
$$
\frac{144^{\log _{5} 1000}}{10^{6 \log _{5} 12}}=\frac{\left(12^{2}\right)^{\log _{5} 10^{3}}}{10^{6 \log _{5} 12}}=\frac{12^{6 \log _{5} 10}}{10^{6 \log _{5} 12}}=\left(\frac{12^{\log _{5} 10}}{10^{\log _{5} 12}}\right)^{6}
$$
Općenito je
$$
x^{\log _{a} y}=\left(a^{\log _{a} x}\right)^{\log _{a} y}=a^{\log _{a} x \log _{a} y}=\left(a^{\log _{a} y}\right)^{\log _{a} x}=y^{\log _{a} x}
$$
pa je $12^{\log _{5} 10}=10^{\log _{5} 12}$
i konačno dobivamo $144^{\log _{5} 1000}: 10^{6 \log _{5} 12}=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-3.3. (4 points)
Calculate $144^{\log _{5} 1000}: 10^{6 \log _{5} 12}$.
|
## Second Solution.
Let's determine the logarithm (base 5) of the desired number:
$$
\begin{aligned}
\log _{5} \frac{144^{\log _{5} 1000}}{10^{6 \log _{5} 12}} & =\log _{5}\left(144^{\log _{5} 1000}\right)-\log _{5}\left(10^{6 \log _{5} 12}\right) \\
& =\log _{5} 1000 \cdot \log _{5} 144-6 \log _{5} 12 \cdot \log _{5} 10 \\
& =\log _{5} 10^{3} \cdot \log _{5} 12^{2}-6 \log _{5} 12 \cdot \log _{5} 10 \\
& =3 \log _{5} 10 \cdot 2 \log _{5} 12-6 \log _{5} 12 \cdot \log _{5} 10=0
\end{aligned}
$$
From this, we get $\frac{144^{\log _{5} 1000}}{10^{6 \log _{5} 12}}=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task A-1.4. (4 points)
Let $a, b$ and $c$ be real numbers such that
$$
a+b+c=3 \quad \text { and } \quad \frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0
$$
What is $a^{2}+b^{2}+c^{2}$?
|
## Solution.
Since $(a+b+c)^{2}=a^{2}+b^{2}+c^{2}+2 a b+2 b c+2 c a$
from the first given equality, we get
$$
\begin{aligned}
& a^{2}+b^{2}+c^{2}+2 a b+2 b c+2 c a=9 \\
& a^{2}+b^{2}+c^{2}=9-2(a b+b c+c a)
\end{aligned}
$$
Since from the second given equality it follows that
$$
\frac{b c+c a+a b}{a b c}=0
$$
which means $a b+b c+c a=0$,
we finally get:
$$
\begin{aligned}
a^{2}+b^{2}+c^{2} & =9-2(a b+b c+c a) \\
& =9-2 \cdot 0=9
\end{aligned}
$$
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task A-1.5. (4 points)
How many elements at least need to be removed from the set $\{2,4,6,8,10,12,14,16\}$ so that the product of the remaining elements is a square of a natural number?
|
## Solution.
The product of all elements of the given set is
$$
\begin{aligned}
P & =2 \cdot 4 \cdot 6 \cdot 8 \cdot 10 \cdot 12 \cdot 14 \cdot 16 \\
& =2 \cdot 2^{2} \cdot(2 \cdot 3) \cdot 2^{3} \cdot(2 \cdot 5) \cdot\left(2^{2} \cdot 3\right) \cdot(2 \cdot 7) \cdot 2^{4} \\
& =2^{15} \cdot 3^{2} \cdot 5 \cdot 7
\end{aligned}
$$
The product is divisible by 5, but not by $5^{2}$, so it is clear that the number 10 needs to be removed.
The product is divisible by 7, but not by $7^{2}$, so it is clear that the number 14 also needs to be removed.
The product of the remaining numbers, $2^{13} \cdot 3^{2}$, is not a perfect square, so at least one more number needs to be removed. We see that it is sufficient to remove an odd power of 2, i.e., the number 2 or the number 8.
It is necessary to remove at least three numbers.
## Note.
It is not necessary for the student to list all possible ways to remove three elements, but it is necessary to show that it is not possible to remove only one or two numbers and for the product of the remaining to be a perfect square. The possible ways to remove three numbers are: $\{\mathscr{Z ,} 4,6,8,10,12,14,16\}$ and $\{2,4,6,8,10,12,14,16\}$.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task A-2.6. (10 points)
Let $a, b$, and $c$ be three distinct real numbers, none of which are equal to zero. We consider the quadratic equations:
$$
a x^{2}+b x+c=0, \quad b x^{2}+c x+a=0, \quad c x^{2}+a x+b=0
$$
If $\frac{c}{a}$ is a solution to the first equation, prove that all three equations have a common solution. Determine the product of the other three solutions of these equations (non-common solutions).
|
## First Solution.
Since $\frac{c}{a}$ is a solution to the equation $a x^{2}+b x+c=0$, after substitution we get
$$
a \cdot\left(\frac{c}{a}\right)^{2}+b \cdot \frac{c}{a}+c=0
$$
which simplifies to
$$
c^{2}+b c+a c=0
$$
i.e.,
$$
c(a+b+c)=0
$$
Since $c \neq 0$, it must be that $a+b+c=0$,
so $x_{0}=1$ is a common solution to the given three equations.
Let $x_{1}, x_{2}, x_{3}$ be the other solutions of these equations. According to Vieta's formulas, we have
$$
x_{0} \cdot x_{1}=\frac{c}{a}, \quad x_{0} \cdot x_{2}=\frac{a}{b}, \quad x_{0} \cdot x_{3}=\frac{b}{c}
$$
Since $x_{0}=1$, the desired product is $x_{1} x_{2} x_{3}=\frac{c}{a} \cdot \frac{a}{b} \cdot \frac{b}{c}=1$.
|
1
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
## Zadatak A-3.1. (4 boda)
Ako je $\log _{a} x=3$ i $\log _{a b} x=2$, koliko je $\log _{b} x$ ?
|
## Prvo rješenje.
Iz $\log _{a} x=3$ slijedi $x=a^{3}$, a iz $\log _{a b} x=2$ slijedi $x=(a b)^{2}$.
Sada imamo $a^{3}=a^{2} b^{2}$ pa kako $a \neq 0$, vrijedi $a=b^{2}$.
Stoga je $x=\left(b^{2}\right)^{3}=b^{6}$,
pa je $\log _{b} x=\log _{b} b^{6}=6$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-3.1. (4 points)
If $\log _{a} x=3$ and $\log _{a b} x=2$, what is $\log _{b} x$?
|
## Second solution.
Obviously $x \neq 1$, so from $\log _{a} x=3$ it follows that $\log _{x} a=\frac{1}{3}$,
and from $\log _{a b} x=2$ it follows that $\log _{x} a b=\frac{1}{2}$.
Since $\log _{x} a b=\log _{x} a+\log _{x} b$, it follows that $\frac{1}{3}+\log _{x} b=\frac{1}{2}$,
so $\log _{x} b=\frac{1}{6}$ and finally $\log _{b} x=6$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task A-3.3. (4 points)
Point $D$ is the foot of the altitude from vertex $A$, and point $E$ is the foot of the altitude from vertex $B$ of triangle $A B C$. If $|A E|=5,|C E|=3$ and $|C D|=2$, determine the length of $|B D|$.
|
## First solution.
Notice that triangles $A C D$ and $B C E$ are similar (two angles).
Therefore, $|A C|:|C D|=|B C|:|C E|$.
Let $|B D|=x$.
Now (*) can be written in the form $\frac{5+3}{2}=\frac{x+2}{3}$,
from which it follows that $x+2=3 \cdot \frac{8}{2}=12$ so the desired length $|B D|=x=10$.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Zadatak A-4.2. (4 boda)
Neka je $z$ nultočka polinoma $z^{2}-2 z \cos \frac{\pi}{n}+1$. Odredi sve moguće vrijednosti izraza $z^{n}$.
|
## Rješenje.
Rješenja kvadratne jednadžbe $z^{2}-2 z \cos \frac{\pi}{n}+1=0$ su
$$
z=\frac{2 \cos \frac{\pi}{n} \pm \sqrt{4 \cos ^{2} \frac{\pi}{n}-4}}{2}=\cos \frac{\pi}{n} \pm i \sin \frac{\pi}{n}
$$
pa je
$$
\begin{aligned}
z^{n} & =\left(\cos \frac{\pi}{n} \pm i \sin \frac{\pi}{n}\right)^{n} \\
& =\cos \left(n \cdot \frac{\pi}{n}\right) \pm i \sin \left(n \cdot \frac{\pi}{n}\right) \\
& =\cos \pi \pm i \sin \pi \\
& =-1 \pm i \cdot 0=-1
\end{aligned}
$$
Jedino rješenje je $z^{n}=-1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task A-4.6. (10 points)
Let $a$ and $b$ be natural numbers. Which digits can be in the units place of the decimal representation of the number $(a+b)^{5}-\left(a^{5}+b^{5}\right)$?
|
## Solution.
The given expression can be expanded as follows:
$$
\begin{aligned}
& (a+b)^{5}-\left(a^{5}+b^{5}\right) \\
& =a^{5}+5 a^{4} b+10 a^{3} b^{2}+10 a^{2} b^{3}+5 a b^{4}+b^{5}-a^{5}-b^{5} \\
& =5\left(a^{4} b+2 a^{3} b^{2}+2 a^{2} b^{3}+a b^{4}\right) \\
& =5 a b\left(a^{3}+2 a^{2} b+2 a b^{2}+b^{3}\right) \\
& =5 a b(a+b)\left(a^{2}+a b+b^{2}\right) .
\end{aligned}
$$
From $(*)$ we see that the given expression is always divisible by 5.
(4 points)
Let's prove that it is also divisible by 2.
This is obviously true if at least one of the numbers $a$ and $b$ is even.
Otherwise, $a$ and $b$ are odd, so $a+b$ is an even number.
Thus, in this case, the given expression is also divisible by 2.
We conclude that the given number ends in the digit 0 for all natural numbers $a$ and $b$.
(1 point)
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Using a suitable substitution, determine the number of roots of the equation
$$
8 x\left(1-2 x^{2}\right)\left(8 x^{4}-8 x^{2}+1\right)=1
$$
that lie within the interval $[0,1]$.
|
2. We immediately see that $x=0$ and $x=1$ are not solutions, so we introduce the substitution $x=\cos \varphi$, with $\varphi \in\left(0, \frac{\pi}{2}\right)$. The equation becomes
$$
8 \cos \varphi\left(1-2 \cos ^{2} \varphi\right)\left(8 \cos ^{4} \varphi-8 \cos ^{2} \varphi+1\right)=1
$$
5 points
or, because $\cos 2 \varphi=2 \cos ^{2} \varphi-1$ and $\cos 4 \varphi=8 \cos ^{4} \varphi-8 \cos ^{2} \varphi+1$,
$$
-8 \cos \varphi \cos 2 \varphi \cos 4 \varphi=1
$$
Multiply both sides of the equation by $\sin \varphi$. (The resulting equation is equivalent to the previous one since $\sin \varphi \neq 0$ for $\varphi \in\left(0, \frac{\pi}{2}\right)$.)
$$
\begin{gathered}
-4 \sin 2 \varphi \cos 2 \varphi \cos 4 \varphi=\sin \varphi \\
-2 \sin 4 \varphi \cos 4 \varphi=\sin \varphi \\
\sin 8 \varphi+\sin \varphi=0 \\
2 \sin \frac{9 \varphi}{2} \cos \frac{7 \varphi}{2}=0
\end{gathered}
$$
so the solutions are $\varphi=\frac{2}{9} k \pi$ and $\varphi=\frac{\pi}{7}+\frac{2}{7} k \pi$.
5 points
In the interval $\left(0, \frac{\pi}{2}\right)$, the solutions are $\varphi=\frac{2 \pi}{9}, \varphi=\frac{4 \pi}{9}, \varphi=\frac{\pi}{7}$, and
$\varphi=\frac{3 \pi}{7}$, so the original equation has 4 solutions in the interval $[0,1]$.
5 points
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-2.1.
If $a=\sqrt{\sqrt{3}-\sqrt{2}}(\sqrt{\sqrt{3}-1}+\sqrt{\sqrt{3}+1}), b=\sqrt{\sqrt{3}+\sqrt{2}}(\sqrt{\sqrt{3}-1}-\sqrt{\sqrt{3}+1})$, what is $a+b$?
|
## First Solution.
$$
\begin{aligned}
a^{2} & =(\sqrt{3}-\sqrt{2})(\sqrt{3}-1+2 \sqrt{\sqrt{3}-1} \cdot \sqrt{\sqrt{3}+1}+\sqrt{3}+1) \\
& =2(\sqrt{3}-\sqrt{2})(\sqrt{3}+\sqrt{2})=2 \\
b^{2} & =(\sqrt{3}+\sqrt{2})(\sqrt{3}-1-2 \sqrt{\sqrt{3}-1} \cdot \sqrt{\sqrt{3}+1}+\sqrt{3}+1) \\
& =2(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})=2
\end{aligned}
$$
Therefore, $|a|=\sqrt{2},|b|=\sqrt{2}$.
It is clear that $a>0$, and since $\sqrt{\sqrt{3}+1}>\sqrt{\sqrt{3}-1}$, it follows that $b<0$. Thus, from $a>0, b<0$ we have $a=\sqrt{2}, b=-\sqrt{2}$.
Finally, the sum $a+b=0$.
Note: If a student does not conclude that $b<0$ and obtains the solution $a+b=2 \sqrt{2}$, deduct 2 points.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-3.2.
Determine all even natural numbers $n$ for which
$$
\left|\log _{0.5} 20^{\cos \pi}+\log _{0.5} 30^{\cos 2 \pi}+\log _{0.5} 42^{\cos 3 \pi}+\cdots+\log _{0.5}\left(n^{2}+7 n+12\right)^{\cos n \pi}\right|=1
$$
|
## Solution.
Simplify the given expression.
$$
\begin{array}{cc}
\left|\log _{0.5}\left(20^{\cos \pi} \cdot 30^{\cos 2 \pi} \cdot 42^{\cos 3 \pi} \cdots\left(n^{2}+7 n+12\right)^{\cos n \pi}\right)\right|=1 & \\
\left|\log _{0.5}\left(20^{-1} \cdot 30^{1} \cdot 42^{-1} \cdots\left(n^{2}+7 n+12\right)^{1}\right)\right|=1 & 1 \text { point } \\
\left|\log _{0.5}\left((4 \cdot 5)^{-1} \cdot(5 \cdot 6) \cdot(6 \cdot 7)^{-1} \cdots \cdots(n+3)(n+4)\right)\right|=1 & 1 \text { point } \\
\left|\log _{0.5}\left(\frac{1}{4 \cdot 5} \cdot(5 \cdot 6) \cdot \frac{1}{6 \cdot 7} \cdots(n+3)(n+4)\right)\right|=1 & 1 \text { point } \\
\left|\log _{0.5}\left(\frac{1}{4} \cdot(n+4)\right)\right|=1 \Longrightarrow \log _{0.5}\left(\frac{1}{4} \cdot(n+4)\right)= \pm 1 & 1 \text { point }
\end{array}
$$
From $\frac{n+4}{4}=\frac{1}{2}$, we get $n=-2$, but this is not a natural number.
From $\frac{n+4}{4}=2$, we get the solution $n=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Zadatak B-2.5.
Kružnice $k_{1}$ i $k_{2}$ sijeku se u točkama $A$ i $B$ kao što je prikazano na slici. Točka $C$ nalazi se na kružnici $k_{1}$, a točka $D$ na kružnici $k_{2}$ tako da vrijedi $\varangle A C B=60^{\circ} \mathrm{i} \varangle B D A=30^{\circ}$. Ako su središta kružnica $k_{1}$ i $k_{2}$ udaljena $4 \sqrt{3} \mathrm{~cm}$, kolika je duljina njihove zajedničke tetive $\overline{A B}$ ?
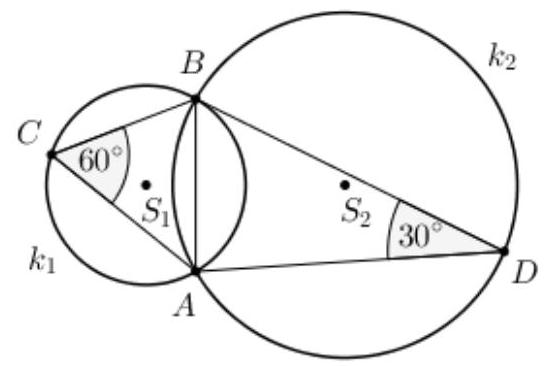
|
## Prvo rješenje.
Označimo s $r_{1} \mathrm{i} r_{2}$ polumjere kružnica $k_{1} \mathrm{i} k_{2}$. Neka je $E$ polovište tetive $\overline{A B}$ i $x=|B E|$.
Kut $\varangle A C B$ je obodni nad lukom $\widehat{A B}$ pa je njegov središnji kut $\varangle A S_{1} B=120^{\circ}$, odnosno $\varangle E S_{1} B=60^{\circ}$.
Kut $\varangle B D A$ je obodni nad lukom $\widehat{B A}$ pa je njegov središnji kut $\varangle B S_{2} A=60^{\circ}$, odnosno $\varangle B S_{2} E=30^{\circ}$.

Trokut $S_{1} S_{2} B$ je pravokutan pa vrijedi $r_{1}^{2}+r_{2}^{2}=(4 \sqrt{3})^{2}=48$.
$\mathrm{U}$ pravokutnome trokutu $E B S_{1}$ vrijedi da je $\sin 60^{\circ}=\frac{x}{r_{1}}=\frac{\sqrt{3}}{2}$, odnosno $r_{1}=\frac{2 x}{\sqrt{3}}$.
Na isti se način iz pravokutnoga trokuta $E B S_{2}$ dobiva da je $\sin 30^{\circ}=\frac{x}{r_{2}}=\frac{1}{2}$, odnosno vrijedi da je $r_{2}=2 x$.
Uvrstimo dobivene izraze u jednakost $r_{1}^{2}+r_{2}^{2}=48$.
Iz jednadžbe $\frac{4 x^{2}}{3}+4 x^{2}=48$ dobivamo da je $x^{2}=9$, odnosno da je $x=3 \mathrm{~cm}$.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-2.5.
Circles $k_{1}$ and $k_{2}$ intersect at points $A$ and $B$ as shown in the figure. Point $C$ is on circle $k_{1}$, and point $D$ is on circle $k_{2}$ such that $\varangle A C B=60^{\circ} \text{ and } \varangle B D A=30^{\circ}$. If the centers of circles $k_{1}$ and $k_{2}$ are $4 \sqrt{3} \text{ cm}$ apart, what is the length of their common chord $\overline{A B}$?

|
## Second Solution.
We use the same sketch and labels as in the first solution.
Angle $\varangle A C B$ is an inscribed angle over the arc $\overparen{A B}$, so its central angle is $\varangle A S_{1} B=120^{\circ}$, or $\varangle E S_{1} B=60^{\circ}$.
Angle $\varangle B D A$ is an inscribed angle over the arc $\widehat{B A}$, so its central angle is $\varangle B S_{2} A=60^{\circ}$, or $\varangle B S_{2} E=30^{\circ}$.
Notice that triangle $S_{1} S_{2} B$ is half of an equilateral triangle with side length $a=\left|S_{1} S_{2}\right|=4 \sqrt{3} \mathrm{~cm}$.
Then, $r_{1}=\left|S_{1} B\right|=\frac{a}{2}=\frac{4 \sqrt{3}}{2}=2 \sqrt{3} \mathrm{~cm}$.
1 point
It also holds that $r_{2}=\left|S_{2} B\right|=\frac{a \sqrt{3}}{2}=\frac{4 \sqrt{3} \cdot \sqrt{3}}{2}=6 \mathrm{~cm}$. 1 point
Since triangle $S_{1} S_{2} B$ is a right triangle, its area can be calculated in two ways, so we have $P=\frac{r_{1} \cdot r_{2}}{2}=\frac{x \cdot\left|S_{1} S_{2}\right|}{2}$.
$2 \sqrt{3} \cdot 6=x \cdot 4 \sqrt{3}$
$x=3 \mathrm{~cm}$
1 point
Finally, we conclude that $|A B|=2 x=6 \mathrm{~cm}$.
Note: After noticing that triangle $S_{1} S_{2} B$ is half of an equilateral triangle with side length $a=4 \sqrt{3} \mathrm{~cm}$, the student does not need to determine $r_{1}$ and $r_{2}$, but can immediately calculate the area of the triangle $P=\frac{1}{2} \cdot \frac{a^{2} \sqrt{3}}{4}=6 \sqrt{3} \mathrm{~cm}^{2}$, for which they receive 2 points.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-4.3.
The sum of all 1002-digit numbers that in their representation have a thousand zeros and two ones is $S$. Determine the remainder obtained when the number $S$ is divided by 3.
|
## First solution.
The number 1 must be in the first position, from which it follows that there are 1001 numbers with the described property.
We can add these numbers by writing one below the other:
$$
\begin{array}{r}
1100000 \ldots 00 \\
1010000 \ldots 00 \\
1001000 \ldots 00 \\
1000100 \ldots 00 \\
\ldots \ldots . \ldots . . \\
1000000 \ldots 10 \\
+1000000 \ldots 01 \\
\hline
\end{array}
$$
Then,
$$
S=1001 \cdot 10^{1001}+\underbrace{111 \ldots 11}_{1001 \text { ones }}=100 \underbrace{1111 \ldots 11}_{1002 \text { ones }}.
$$
The number $S$ has 1003 ones, so the sum of all its digits is 1003.
The number $S$ has the same remainder when divided by 3 as the sum of its digits, the number 1003, which is 1.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-1.2.
Let $n$ be a natural number and let
$$
A=0.1^{n} \cdot 0.01^{n} \cdot 0.001^{n} \cdot 0.0001^{n} \cdot \ldots \cdot 0 . \underbrace{00 \ldots 0}_{199 \text { zeros }} 1^{n} .
$$
The number $A^{-1}$ has 140701 digits. Determine the number $n$.
|
## Solution.
$A=10^{-n} \cdot 10^{-2 n} \cdot 10^{-3 n} \cdot 10^{-4 n} \cdot \ldots \cdot 10^{-200 n}=10^{-n(1+2+3+\ldots+200)} \quad 1 \text{ point}$
Then $A^{-1}=10^{n \cdot \frac{200 \cdot 201}{2}}=10^{20100 n}$. 2 points
This number has a leading digit of one and 20100n zeros in its decimal representation.
It follows that $20100 n+1=140701$.
Then $n=7$.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-1.5.
Determine the last two digits of the number $7^{2016^{2017}}$.
|
## Solution.
The number $7^{2016^{2017}}$ can be written as follows:
$$
7^{2016^{2017}}=7^{2016 \cdot 2016 \cdot 2016 \cdots \cdots \cdot 2016}
$$
The exponent of the given number is divisible by 8 because 2016 is divisible by 8, so we have:
$$
7^{2016^{2017}}=7^{8 x}=\left(7^{4}\right)^{2 x}
$$
where $x$ is some integer. Further, we have
$$
7^{2016^{2017}}=\left(7^{4}\right)^{2 x}=(2400+1)^{2 x}=\left(2400^{2}+4800+1\right)^{x}=(100 y+1)^{x} \quad 1 \text { point }
$$
where $y$ is also some integer.
The last two digits of the given number are 01.
Note: Students can observe the powers of 7 and conclude that they always end in $7,9,3$ and 1, and since the exponent of the given number is divisible by 4, it must have the last digit 1. (3 points)
Since $7^{2016^{2017}}=7^{4 k}=2401 \cdots 2401 \cdot 2401$, the product will certainly end with 0 in the second-to-last position (which is worth the remaining 3 points), and this needs to be justified as in the first solution. Accept also if the student has justified it using part of the written multiplication with the last number 2401.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-2.1.
How many integers $a$ are there for which both solutions of the equation $(x-20)(x+17)=\frac{1}{4} a$ are positive real numbers?
|
## First solution.
$(x-20)(x+17)=\frac{1}{4} a \Leftrightarrow x^{2}-3 x-340-\frac{1}{4} a=0$.
Both solutions of the equation will be positive real numbers if the following conditions are met:
1. $D \geqslant 0 \Leftrightarrow 9+4\left(340+\frac{1}{4} a\right) \geqslant 0 \Rightarrow a \geqslant-1369$.
2 points
2. $x_{1}+x_{2}>0$, and since $x_{1}+x_{2}=3$ this holds for any real number $a$.
1 point
3. $x_{1} x_{2}>0 \Rightarrow-340-\frac{1}{4} a>0 \Rightarrow a<-1360$.
Thus, for $a \in[-1369,-1360\rangle$ both solutions of the given equation are positive real numbers, and there are 9 integers in this interval.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-2.7.
Let $A B C D$ be a parallelogram with side lengths $|A B|=a \mathrm{~cm}$ and $|B C|=b \mathrm{~cm} (a>b)$ and an acute angle $\alpha$. The area of the quadrilateral formed by the intersection of the angle bisectors of the internal angles of the parallelogram is $48 \mathrm{~cm}^{2}$, and $\sin \frac{\alpha}{2}=\frac{3}{5}$. Calculate the difference $a-b$.
|
## Solution.
In triangle $A V D$, $\angle V A D = \frac{\alpha}{2}$ and $\angle A D V = \frac{180^\circ - \alpha}{2} = 90^\circ - \frac{\alpha}{2}$. Therefore, triangle $A V D$ is a right triangle, and $\angle U V X = 90^\circ$. For the same reason, the other angles of quadrilateral $X Y U V$ are right angles, so this quadrilateral is a rectangle.
From triangle $A V D$, we have $|D V| = b \sin \frac{\alpha}{2}$ and $|A V| = b \cos \frac{\alpha}{2}$.
2 points
From triangle $D X C$, we have $|D X| = a \sin \frac{\alpha}{2}$.
1 point
From triangle $A B U$, we have $|A U| = a \cos \frac{\alpha}{2}$.
1 point
Then the lengths of the sides of the rectangle are:
$|V X| = a \sin \frac{\alpha}{2} - b \sin \frac{\alpha}{2} = (a - b) \sin \frac{\alpha}{2}$ and $|V U| = a \cos \frac{\alpha}{2} - b \cos \frac{\alpha}{2} = (a - b) \cos \frac{\alpha}{2}$.
1 point
The area of the rectangle is $P = |V X| \cdot |V U| = (a - b)^2 \sin \frac{\alpha}{2} \cos \frac{\alpha}{2}$.
1 point
Since $\sin \frac{\alpha}{2} = \frac{3}{5}$, it follows that $\cos \frac{\alpha}{2} = \sqrt{1 - \left(\frac{3}{5}\right)^2} = \frac{4}{5}$.
The desired difference is calculated as follows:
$48 = (a - b)^2 \cdot \frac{3}{5} \cdot \frac{4}{5} \Rightarrow (a - b)^2 = 100 \Rightarrow a - b = 10 \text{ cm}$.
## COUNTY COMPETITION IN MATHEMATICS
## 3rd grade - high school - B variant
28th February 2017.
## IF A STUDENT HAS A DIFFERENT APPROACH TO SOLVING THE TASK, THE COMMITTEE IS OBLIGED TO GRADE AND EVALUATE THAT APPROACH APPROPRIATELY.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-2.1. Draw in the complex plane the set of points $(x, y)$, associated with complex numbers $z=x+yi$, for which
$$
\operatorname{Re} z \cdot \operatorname{Im} z<0 \quad \mathrm{and} \quad|z|^{2} \leq \operatorname{Im}\left(z^{2}\right)+1
$$
Calculate the area of this set of points.
|
## Solution.
From the first inequality, it follows that $x \cdot y < 0$, which means that the desired points lie in the second or fourth quadrant.
From the second inequality, it follows that
$$
x^{2} + y^{2} \leq 2 x y + 1
$$
or $(x-y)^{2} \leq 1$ or $|x-y| \leq 1$.
From this, we have $-1 \leq x-y \leq 1$, or $y \leq x+1$ and $y \geq x-1$.
The set of desired points is a part of the plane between the lines $y=x+1$ and $y=x-1$, and within the second and fourth quadrants, as shown in the figure.

From the figure, it is clear that
$$
P=2 \cdot \frac{1 \cdot 1}{2}=1
$$
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-2.2. Rowing evenly, a fisherman traveled upstream as many kilometers as the solution to the equation $\sqrt{5 x}-\frac{4}{\sqrt{3 x+1}}=\sqrt{3 x+1}$, and returned to the harbor without stopping in 1 hour and 20 minutes. At what speed did he row if the river's speed is $2 \mathrm{~km} / \mathrm{h}$?
|
## Solution.
First, let's solve the given equation
$$
\sqrt{5 x}-\frac{4}{\sqrt{3 x+1}}=\sqrt{3 x+1}
$$
Multiply both sides by the denominator.
$$
\begin{aligned}
\sqrt{5 x(3 x+1)}-4 & =3 x+1 \\
\sqrt{5 x(3 x+1)} & =3 x+5
\end{aligned}
$$
If we square both sides, we get
$$
\begin{aligned}
15 x^{2}+5 x & =9 x^{2}+30 x+25 \\
6 x^{2}-25 x-25 & =0
\end{aligned}
$$
The only positive solution to this equation that satisfies the original equation is $x=5$ $\mathrm{km}$.
The fisherman walked a distance of $5 \mathrm{~km}$ upstream and the same distance downstream in a total of $1 \mathrm{~h}$ and $20 \mathrm{~min}$, which is $\frac{4}{3} \mathrm{~h}$.
If the speed at which the fisherman rows is $v$, then
$$
\begin{aligned}
\frac{5}{v-2}+\frac{5}{v+2} & =\frac{4}{3} / \cdot 3(v-2)(v+2) \\
15(v+2)+15(v-2) & =4\left(v^{2}-4\right) \\
2 v^{2}-15 v-8 & =0
\end{aligned}
$$
The positive solution to this equation is $v=8$. The fisherman rowed at a speed of $8 \mathrm{~km} / \mathrm{h}$.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-1.1.
If $x y z=a b c$, what is $\frac{b x}{x y+a b+b x}+\frac{c y}{y z+b c+c y}+\frac{a z}{z x+c a+a z}$?
|
## Solution.
First, extend the first fraction by $z$, and the second by $a$.
$$
\begin{aligned}
& \frac{b x}{x y+a b+b x} \cdot \frac{z}{z}+\frac{c y}{y z+b c+c y} \cdot \frac{a}{a}+\frac{a z}{z x+c a+a z}= \\
& \frac{b x z}{x y z+a b z+b x z}+\frac{c a y}{a y z+a b c+a c y}+\frac{a z}{z x+c a+a z}
\end{aligned}
$$
Replace the expression $xyz$ in the denominator of the first fraction with $abc$, and the expression $abc$ in the denominator of the second fraction with $xyz$.
$$
\begin{gathered}
\frac{b x z}{a b c+a b z+b x z}+\frac{a c y}{a y z+x y z+a c y}+\frac{a z}{z x+c a+a z}= \\
\frac{b x z}{b(a c+a z+x z)}+\frac{a c y}{y(a z+x z+a c)}+\frac{a z}{z x+c a+a z}=\frac{x z+a c+a z}{a c+x z+a z}=1 .
\end{gathered}
$$
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-1.2.
Natural numbers are sequentially written to form a spiral of numbers as shown in the figure:
| 21 | 22 | | 23 | | 24 | | 25 | 26 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| | | | | | | | | $\vdots$ |
| 20 | 7 | $\rightarrow$ | 8 | $\rightarrow$ | 9 | $\rightarrow$ | 10 | |
| | $\uparrow$ | | | | | | | |
| 19 | 6 | | 1 | $\rightarrow$ | 2 | | 11 | |
| | $\uparrow$ | | | | $\downarrow$ | | | |
| 18 | 5 | $\leftarrow$ | 4 | $\leftarrow$ | 3 | 12 | | |
| 17 | 16 | | 15 | | 14 | 13 | | |
The position of a number is determined relative to the number 1. For example, the number 24 is located 1 place to the right and 2 places up from the number 1. Determine the position of the number 2015 relative to the number 1.
|
## Solution.
Notice that the numbers on the diagonal to the right and up are squares of odd natural numbers $1, 9, 25, 49, \ldots$

The number $9=(2 \cdot \mathbf{1}+1)^{2}$ and its position is 1 to the right and 1 up.
The number $25=(2 \cdot \mathbf{2}+1)^{2}$ and its position is 2 to the right and 2 up.
The number $49=(2 \cdot \mathbf{3}+1)^{2}$ and its position is 3 to the right and 3 up...
The square of the odd natural number closest to the number 2015 is $45^{2}=2025$.
Since $45=2 \cdot \mathbf{22}+1$, the position of the number 2025 is 22 places to the right and 22 places up.
Since $2025=2015+10$, the position of the number 2015 relative to the number 1 is $22-10=12$ places to the right and 22 places up.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-1.3.
Each member of Marića's family drank 4 deciliters of a coffee and milk mixture. The amount of coffee and milk is different in each cup, but it is never zero. Marića drank one quarter of the total amount of milk and one sixth of the total amount of coffee. How many members are there in Marića's family?
|
## Solution.
Let $k$ be the amount of coffee, and $m$ be the amount of milk that Marica drank (in dl). Let the family have $n$ members. Since each member of the family drank $4 \mathrm{dl}$ of the coffee and milk mixture, a total of $4 n$ of the mixture was consumed, so the following equations hold:
$$
\begin{aligned}
& k+m=4 \\
& 6 k+4 m=4 n \\
& k>0, m>0, n \in \mathbb{N}
\end{aligned}
$$
Determine $k$ and $m$ in terms of $n$.
$$
\begin{aligned}
& m=4-k \\
& 6 k+4(4-k)=4 n \\
& k=2 n-8 \\
& m=12-2 n
\end{aligned}
$$
Since the amount of coffee and milk cannot be 0, for the numbers $k$ and $m$ it holds that:
$$
2 n-8>0 \text { and } 12-2 n>0
$$
It follows that $n>4$ and $n<6$, so $n=5$.
Marica's family has 5 members.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-2.1.
Determine the real parameter $k$ so that the system of equations
$$
\left[\operatorname{Im}\left(z+\frac{1}{2} i\right)\right]^{2}=|z+2|^{2}+\frac{5}{4} \quad \text { and } \quad \operatorname{Im}(z)-2 \operatorname{Re}(z)=k, z \in \mathbb{C}
$$
has only one solution?
|
## Solution.
Let $z=x+y i ; x, y \in \mathbb{R}$.
Then the first of the given equations becomes
$$
\left[\operatorname{Im}\left(x+y i+\frac{1}{2} i\right)\right]^{2}=|x+y i+2|^{2}+\frac{5}{4}
$$
or
$$
\left(y+\frac{1}{2}\right)^{2}=(x+2)^{2}+y^{2}+\frac{5}{4}
$$
By simplifying, we get the set of points $(x, y)$ that lie on the parabola $y=x^{2}+4 x+5$.
The second equation $\operatorname{Im}(x+y i)-2 \operatorname{Re}(x+y i)=k$ determines the set of points $(x, y)$ that lie on the line $y=2 x+k$.
By solving the system of equations, we get the common points of the parabola and the line:
$$
\begin{aligned}
& y=x^{2}+4 x+5 \\
& y=2 x+k \\
& x^{2}+4 x+5=2 x+k \\
& x^{2}+2 x+5-k=0
\end{aligned}
$$
The obtained quadratic equation will have one real solution if its discriminant ($D=$ $\left.b^{2}-4 a c\right)$ is equal to zero, that is
$4-4(5-k)=0 \Rightarrow k=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-3.1.
Ordered pairs $(a, b)$ and $(c, d)$ are solutions to the system of equations
$$
\begin{aligned}
\log _{225} x+\log _{64} y & =4 \\
\log _{x} 225-\log _{y} 64 & =1
\end{aligned}
$$
Calculate $\log _{30}(a b c d)$.
|
## Solution.
The solutions $x$ and $y$ of the problem must be positive real numbers different from 1. Notice that
$$
\log _{x} 225=\frac{1}{\log _{225} x} \quad \text{and} \quad \log _{y} 64=\frac{1}{\log _{64} y}
$$
If we introduce the substitutions $\log _{225} x=m$ and $\log _{64} y=n$, the system transforms into
$$
\begin{aligned}
m+n & =4 \\
\frac{1}{m}-\frac{1}{n} & =1
\end{aligned}
$$
From the first equation, express $m$ and substitute it into the second equation. We get
$$
\begin{aligned}
\frac{1}{4-n}-\frac{1}{n} & =1 \\
n-(4-n) & =4 n-n^{2} \\
n^{2}-2 n-4 & =0
\end{aligned}
$$
The solutions to the last equation and the corresponding $m_{1}, m_{2}$ are:
$$
n_{1}=1-\sqrt{5}, \quad n_{2}=1+\sqrt{5}, \quad \text { respectively } \quad m_{1}=3+\sqrt{5}, \quad m_{2}=3-\sqrt{5}
$$
Now we calculate $x=225^{m}$ and $y=64^{n}$. We have
$$
a=x_{1}=225^{3+\sqrt{5}}, \quad b=y_{1}=64^{1-\sqrt{5}}, \quad c=x_{2}=225^{3-\sqrt{5}} \quad \text{and} \quad d=y_{2}=64^{1+\sqrt{5}}
$$
Thus, the final solution is
$$
\begin{aligned}
\log _{30}(a b c d) & =\log _{30}\left(225^{3+\sqrt{5}} \cdot 64^{1-\sqrt{5}} \cdot 225^{3-\sqrt{5}} \cdot 64^{1+\sqrt{5}}\right)=\log _{30}\left(225^{6} \cdot 64^{2}\right) \\
& =\log _{30}\left(15^{12} \cdot 2^{12}\right)=\log _{30} 30^{12}=12
\end{aligned}
$$
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Zadatak B-2.1.
Odredite vrijednost brojevnog izraza $\sqrt{2}+\left(\frac{3}{\sqrt[3]{4}-\sqrt[3]{2}+1}-1\right)^{3}-\frac{\sqrt{2}}{2+\sqrt{2}}$.
|
## Rješenje.
Racionalizirajmo najprije nazivnike zadanih razlomaka.
$\frac{3}{\sqrt[3]{4}-\sqrt[3]{2}+1}=\frac{3}{\sqrt[3]{4}-\sqrt[3]{2}+1} \cdot \frac{\sqrt[3]{2}+1}{\sqrt[3]{2}+1}=\frac{3 \cdot(\sqrt[3]{2}+1)}{2+1}=\sqrt[3]{2}+1$
$\frac{\sqrt{2}}{2+\sqrt{2}}=\frac{\sqrt{2}}{2+\sqrt{2}} \cdot \frac{2-\sqrt{2}}{2-\sqrt{2}}=\frac{2 \sqrt{2}-2}{4-2}=\frac{2(\sqrt{2}-1)}{2}=\sqrt{2}-1$
Uvrstimo dobivene vrijednosti u početni brojevni izraz i izračunajmo.
$$
\begin{aligned}
& \sqrt{2}+\left(\frac{3}{\sqrt[3]{4}-\sqrt[3]{2}+1}-1\right)^{3}-\frac{\sqrt{2}}{2+\sqrt{2}}= \\
& \sqrt{2}+(\sqrt[3]{2}+1-1)^{3}-(\sqrt{2}-1)= \\
& \sqrt{2}+(\sqrt[3]{2})^{3}-\sqrt{2}+1= \\
& \sqrt{2}+2-\sqrt{2}+1=
\end{aligned}
$$
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-3.1.
If $\operatorname{ctg} x=\frac{1}{2}$, what is $\frac{(\cos x-1+\sin x)(\cos x+1-\sin x)}{\cos x-\cos x \sin x}$ ?
|
## First Solution.
If in the numerator of the given expression we notice a difference of squares or multiply the parentheses, and in the denominator we factor out $\cos x$, we get successively:
$$
\begin{aligned}
& \frac{(\cos x-1+\sin x)(\cos x+1-\sin x)}{\cos x-\cos x \sin x}=\frac{[\cos x-(1-\sin x)][\cos x+(1-\sin x)]}{\cos x(1-\sin x)}= \\
& \frac{\cos ^{2} x-(1-\sin x)^{2}}{\cos x(1-\sin x)}=\frac{\cos ^{2} x-1+2 \sin x-\sin ^{2} x}{\cos x(1-\sin x)}
\end{aligned}
$$
After applying the fundamental trigonometric identity $\cos ^{2} x+\sin ^{2} x=1$, we get
$$
\begin{gathered}
\frac{\cos ^{2} x-1+2 \sin x-\sin ^{2} x}{\cos x(1-\sin x)}=\frac{-\sin ^{2} x+2 \sin x-\sin ^{2} x}{\cos x(1-\sin x)}= \\
\frac{2 \sin x-2 \sin ^{2} x}{\cos x(1-\sin x)}
\end{gathered}
$$
Then, we factor out $2 \sin x$ in the numerator, simplify the fraction, and apply the given equality.
$$
\begin{gathered}
\frac{2 \sin x-2 \sin ^{2} x}{\cos x(1-\sin x)}=\frac{2 \sin x(1-\sin x)}{\cos x(1-\sin x)}=\frac{2 \sin x}{\cos x}= \\
2 \operatorname{tg} x=\frac{2}{\operatorname{ctg} x}=4
\end{gathered}
$$
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-3.7.
It has been established that the number of student absences in the third grade during the school year can be described by the function $f(t)=2^{t+a}+b$, where $t$ is the number of months that have passed since the start of the school year on September 1st, $f(t)$ is the total number of absences in the first $t$ months, and $a$ and $b$ are constants. This year, students were absent for 128 hours in December.
a) After how many months will the students have 4064 hours of absences?
b) How many unexcused absences did the students have in December if the ratio of excused to unexcused absences in December was 29:3?
|
## Solution.
a) First, let's determine the constants $a$ and $b$ in the function $f(t)=2^{t+a}+b$.
Given that students were absent for 128 hours in December, we write:
$$
f(3)-f(2)=128
$$
According to the given rule, we have:
$$
\begin{gathered}
2^{3+a}+b-\left(2^{2+a}+b\right)=128 \\
8 \cdot 2^{a}-4 \cdot 2^{a}=128 \\
4 \cdot 2^{a}=128 \\
2^{a}=32 \\
a=5
\end{gathered}
$$
Since there were 0 absences at the beginning of the school year, we have $f(0)=2^{a}+b=0$, so $b=-2^{a}$, or $b=-32$.
Thus, $f(t)=2^{t+5}-32$. Now, let's calculate the required number of months. We have:
$$
\begin{gathered}
2^{t+5}-32=4064 \\
2^{t+5}=4096 \\
2^{t+5}=2^{12} \\
t+5=12 \\
t=7
\end{gathered}
$$
After 7 months, they will have 4096 hours of absences.
b) In December, the number of absences is
$$
f(4)-f(3)=2^{4+5}+32-\left(2^{3+5}+32\right)=2^{9}-2^{8}=2^{8}(2-1)=256
$$
The ratio of justified to unjustified absences is $O: N=29: 3$.
$$
\begin{gathered}
O=29 k, \quad N=3 k \\
29 k+3 k=256 \\
32 k=256 \\
k=8
\end{gathered}
$$
The number of unjustified absences is 24.
## SCHOOL/CITY COMPETITION IN MATHEMATICS
4th grade - high school - B variant
January 5, 2023.
## IF A STUDENT HAS A DIFFERENT APPROACH TO SOLVING THE PROBLEM, THE COMMITTEE IS OBLIGED TO GRADE AND EVALUATE THAT APPROACH APPROPRIATELY.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-4.5.
If $z=-\sin \frac{2022 \pi}{5}-i \cos \frac{2023 \pi}{5}$, what is $z^{10}$?
|
## Solution.
By applying the periodicity properties of sine and cosine functions and reduction formulas, we have the following sequence of equalities:
$$
\begin{aligned}
& z=-\sin \frac{2022 \pi}{5}-i \cos \frac{2023 \pi}{5} \\
& z=-\sin \left(404 \pi+\frac{2 \pi}{5}\right)-i \cos \left(404 \pi+\frac{3 \pi}{5}\right) \\
& z=-\sin \frac{2 \pi}{5}-i \cos \frac{3 \pi}{5} \\
& z=-\cos \left(\frac{\pi}{2}-\frac{2 \pi}{5}\right)-i \sin \left(\frac{\pi}{2}-\frac{3 \pi}{5}\right) \\
& z=-\cos \frac{\pi}{10}-i \sin \frac{-\pi}{10}
\end{aligned}
$$
Furthermore, using the odd property of the sine function, we conclude that
$$
z=-\cos \frac{\pi}{10}+i \sin \frac{\pi}{10}
$$
and since $\sin \frac{\pi}{10}=\sin \frac{9 \pi}{10} \text{ and } \cos \frac{\pi}{10}=-\cos \frac{9 \pi}{10}$, we finally get
$$
z=\cos \frac{9 \pi}{10}+i \sin \frac{9 \pi}{10}
$$
Therefore,
$$
\begin{aligned}
z^{10} & =\cos 9 \pi+i \sin 9 \pi & & 1 \text { point } \\
& =\cos \pi+i \sin \pi=-1 & & 1 \text { point }
\end{aligned}
$$
Note: The student can leave the solution in trigonometric or standard form.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-1.3.
In how many ways can the number 455 be written as the sum of an increasing sequence of two or more consecutive natural numbers?
|
## Solution.
Let $n$ be the first number in a sequence of $k+1$ consecutive numbers, $k \geqslant 1$. Then,
$$
\begin{aligned}
455=n+(n+1)+(n+2)+\cdots+(n+k) & =(k+1) n+(1+2+3+\cdots+k) \\
& =(k+1) n+\frac{k(k+1)}{2}=\frac{(k+1)(2 n+k)}{2}
\end{aligned}
$$
which implies $910=(2 n+k)(k+1)$.
The prime factorization of 910 is $910=2 \cdot 5 \cdot 7 \cdot 13$.
Notice that the numbers $(2 n+k)$ and $(k+1)$ have different parities, meaning that one of the parentheses must be equal to an even divisor of 910, which are the numbers 2, 10, 14, 26, 70, 130, 182.
Given that $2 n+k > k+1$, we get 7 linear systems whose solutions yield the numbers $n$ and $k$:
$$
\begin{aligned}
& \begin{array}{lllllll}
k+1=2 & k+1=10 & k+1=14 & k+1=26 & k+1=13 & k+1=7 & k+1=5
\end{array} \\
& 2 n+k=455 \quad 2 n+k=91 \quad 2 n+k=65 \quad 2 n+k=35 \quad 2 n+k=70 \quad 2 n+k=130 \quad 2 n+k=182
\end{aligned}
$$
Each of these systems has a unique solution, so there are a total of 7 ways to represent the number 455 as the desired sum.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Zadatak B-2.1.
Koliko je $1+z^{2}+z^{4}+\cdots+z^{2 \cdot 2019}$, ako je $z=\frac{1+\sqrt{3} i}{2}$ ?
|
## Prvo rješenje.
Izračunajmo redom
$$
\begin{aligned}
& z^{2}=\left(\frac{1+\sqrt{3} i}{2}\right)^{2}=\frac{2 \sqrt{3} i-2}{4}=\frac{\sqrt{3} i-1}{2} \\
& z^{3}=\frac{1+\sqrt{3} i}{2} \cdot \frac{\sqrt{3} i-1}{2}=\frac{-3-1}{4}=-1 \\
& z^{4}=-z \\
& z^{6}=z^{4} \cdot z^{2}=-z^{3}=1 \\
& z^{8}=z^{6} \cdot z^{2}=z^{2}, \quad z^{10}=z^{6} \cdot z^{4}=z^{4}=-z, \quad z^{12}=1, \ldots
\end{aligned}
$$
Svake tri uzastopne parne potencije broja $z$ imaju iste vrijednosti kao
$$
z^{0}=1, \quad z^{2}=\frac{-1+i \sqrt{3}}{2}, \quad z^{4}=-z
$$
pa je
$$
\begin{aligned}
1+z^{2}+z^{4}+\cdots+z^{2 \cdot 2019} & =\left(1+z^{2}-z\right)+\left(1+z^{2}-z\right)+\cdots+\left(1+z^{2}-z\right)+z^{2 \cdot 2019} \\
& =673 \cdot\left(1+z^{2}-z\right)+1=673 \cdot\left(1+\frac{-1+i \sqrt{3}}{2}-\frac{1+i \sqrt{3}}{2}\right)+1=1
\end{aligned}
$$
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-1.2.
All natural numbers from 1 to some number were written on a board. After one of the numbers was erased, the arithmetic mean of the remaining numbers on the board is $\frac{673}{18}$. Which number was erased?
|
## First Solution.
Let the largest written natural number be $n$, and the erased number be $k$. The sum of the first $n$ natural numbers is $\frac{n(n+1)}{2}$.
The condition of the problem can be written as
$$
\frac{\frac{n(n+1)}{2}-k}{n-1}=\frac{673}{18}
$$
If the erased number $k$ were $n$, we would get the smallest possible arithmetic mean. It would be
$$
\frac{\frac{n(n+1)}{2}-n}{n-1}=\frac{n}{2}
$$
and it is less than or equal to the obtained arithmetic mean:
$$
\frac{n}{2} \leqslant \frac{673}{18}
$$
If the erased number $k$ were 1, we would get the largest possible arithmetic mean. It would be
$$
\frac{\frac{n(n+1)}{2}-1}{n-1}=\frac{n+1}{2}
$$
and it is greater than or equal to the obtained arithmetic mean:
$$
\frac{n+1}{2} \geqslant \frac{673}{18}
$$
From the obtained inequalities, it follows that $72<n<75$, so $n=73$ or $n=74$.
If $n=73$, then
$$
\frac{673}{18}=\frac{\frac{73 \cdot(73+1)}{2}-k}{73-1}
$$
From this, we get $k=9$.
If $n=74$, we get
$$
\frac{673}{18}=\frac{\frac{74 \cdot(74+1)}{2}-k}{74-1}
$$
Solving this equation, we get $k=\frac{821}{18}$, which is not a natural number, so we conclude that $n$ cannot be 74.
We conclude that the number erased from the board is 9.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-1.3.
A billiard table has the shape of a rectangle $A B C D$ with dimensions $|A B|=2 \mathrm{~m}$ and $|B C|=1 \mathrm{~m}$. A billiard ball moves straight on the table until it reaches the edge of the rectangle, at which point it bounces off such that the path of the ball before and after the bounce forms equal angles with the edge. If the billiard ball starts moving from point $A$ and after bouncing off the sides $\overline{C D}, \overline{B C}$, and $\overline{A B}$ in sequence, it ends its movement at point $D$, determine the total distance the ball has traveled. The ball is considered as a material point.
|
## First Solution.
Let $E, F,$ and $G$ be the points where the billiard ball bounces off the sides $\overline{C D}, \overline{B C},$ and $\overline{A B}$, respectively. The condition of the billiard ball's bounce means that the following equalities hold:
$$
\varangle A E D = \varangle C E F, \quad \varangle E F C = \varangle G F B, \quad \varangle F G B = \varangle D G A.
$$
Let $l = |A E| + |E F| + |F G| + |G D|$ be the length of the path traveled by the billiard ball.
Consider the triangles $A G D$ and $D E A$. These are right triangles with right angles at vertices $A$ and $D$, respectively, and they share the leg $\overline{A D}$. For the angles opposite this leg, we have:
$$
\varangle D G A = \varangle F G B = 90^{\circ} - \varangle G F B = 90^{\circ} - \varangle E F C = \varangle F E C = \varangle A E D
$$
Therefore, all the angles of these triangles match in pairs, so the triangles are congruent by the $\mathrm{K}-\mathrm{S}-\mathrm{K}$ (Angle-Side-Angle) congruence theorem.
From this congruence, it follows that $|A E| = |D G|$ and $|A G| = |D E|$, and thus $|B G| = |C E|$.
Consider the right triangles $B G F$ and $C E F$. All their angles match in pairs (due to $\varangle E F C = \varangle G F B$), and they have one pair of sides of equal length (due to $|B G| = |C E|$). Therefore, they are also congruent by the $\mathrm{K}-\mathrm{S}-\mathrm{K}$ (Angle-Side-Angle) congruence theorem.
We conclude that
$$
|C F| = |F B| = \frac{1}{2} |B C| = \frac{1}{2} \text{ m}
$$
and $|E F| = |F G|$.
Since $\varangle D G A = \varangle F G B$, the right triangles $D G A$ and $F G B$ are similar. Therefore, we have
$$
\frac{|D G|}{|F G|} = \frac{|A G|}{|G B|} = \frac{|F B|}{|D A|} = \frac{1}{2}
$$
Together with $|A G| + |G B| = 2 \text{ m}$, we get $|B G| = \frac{2}{3} \text{ m}$.
The length of the path traveled by the billiard ball is
$$
\begin{aligned}
l & = |A E| + |E F| + |F G| + |G D| \\
& = |G D| + |F G| + |F G| + |G D| \\
& = 2|F G| + |F G| + |F G| + 2|F G| \\
& = 6|F G|
\end{aligned}
$$
Applying the Pythagorean theorem to triangle $F G B$, we get
$$
|F G| = \sqrt{|F B|^2 + |G B|^2} = \sqrt{\left(\frac{1}{2}\right)^2 + \left(\frac{2}{3}\right)^2} \text{ m} = \frac{5}{6} \text{ m}
$$
Thus, $l = 5 \text{ m}$.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-2.1.
Determine all real solutions of the equation
$$
\sqrt{x^{2}+x+3}-\sqrt{x^{2}-2 x+4}=1
$$
|
## Solution.
By moving one expression from the left side of the equation to the right and squaring, we get
$$
\begin{array}{cc}
-\sqrt{x^{2}-2 x+4}=1-\sqrt{x^{2}+x+3} & \\
x^{2}-2 x+4=1-2 \sqrt{x^{2}+x+3}+x^{2}+x+3 & 1 \text { point } \\
-3 x=-2 \sqrt{x^{2}+x+3} & 3 \text { points } \\
3 x=2 \sqrt{x^{2}+x+3} &
\end{array}
$$
By squaring again and rearranging, we have
$$
\begin{gathered}
9 x^{2}=4\left(x^{2}+x+3\right) \\
9 x^{2}=4 x^{2}+4 x+12 \\
5 x^{2}-4 x-12=0
\end{gathered}
$$
The solutions to this quadratic equation are \( x_{1}=2 \) and \( x_{2}=-\frac{6}{5} \).
By substituting the solution \( x=2 \) into the original equation, we see that it is a solution. 1 point
On the other hand, by substituting \( x=-\frac{6}{5} \) into the original equation, we see that it is not a solution. We conclude that the only solution to the original equation is \( x=2 \).
Note: That \( x=-\frac{6}{5} \) is not a solution to the original equation can also be seen by the fact that it definitely does not satisfy the equality \( 3 x=\sqrt{x^{2}+x+3} \), as one side of the equality is positive and the other is negative.
The solution can be carried out (and scored) analogously even if the term \( \sqrt{x^{2}+x+3} \) is not moved to the right side of the equation, but \( \sqrt{x^{2}-2 x+4} \) is.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-2.4.
A semicircle with diameter $\overline{P Q}$ is inscribed in rectangle $A B C D$ and touches its sides $\overline{A B}$ and $\overline{A D}$. Point $P$ is located on side $\overline{B C}$, and point $Q$ is on side $\overline{C D}$. If $|B P|=2$ and $|D Q|=1$, determine $|P Q|$.
|
## First Solution.

Let $O$ be the center and $r$ the radius of the given semicircle. Let points $K, L, M$, and $N$ be the orthogonal projections of point $O$ onto sides $\overline{C D}, \overline{B C}, \overline{A B}$, and $\overline{A D}$, respectively. Let $\varphi$ be the measure of angle $\varangle C Q P$.
Since the line segment connecting the center and the point of tangency of the semicircle is perpendicular to the side it touches, points $M$ and $N$ are the points of tangency of the semicircle with sides $\overline{A B}$ and $\overline{A D}$. Specifically, $|O M| = |O N| = r$. In the quadrilateral $A M O N$, the angles at vertices $A, M$, and $N$ are right angles, so this quadrilateral is a square with side length $r$.
Similarly, in the right triangle $P L O$, we have $|P L| = r \sin \varphi$.
Consider the quadrilateral $O K D N$. This is a rectangle because the angles at vertices $K, D$, and $N$ are right angles. Therefore, we have
$$
1 + r \sin \varphi = |D Q| + |Q K| = |D K| = |O N| = r
$$
Similarly, from the rectangle $L O M B$, we get $2 + r \cos \varphi = r$. 1 point
If we write these equations as
$$
r \sin \varphi = r - 1, \quad r \cos \varphi = r - 2
$$
and square and add them, we get
$$
\begin{aligned}
r^{2} & = (r - 1)^{2} + (r - 2)^{2} \\
0 & = r^{2} - 6 r + 5
\end{aligned}
$$
The solutions to the resulting quadratic equation are $r = 1$ and $r = 5$.
We discard the solution $r = 1$ because in that case, from the equation $r \cos \varphi = r - 2$, we get $\cos \varphi = -1$, which is impossible if $\varphi$ is the measure of an acute angle in the right triangle $P C Q$. Therefore, $r = 5$, so $|P Q| = 2 r = 10$.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-4.2.
Let $x_{1}, x_{2}$, and $x_{3}$ be distinct roots of the polynomial $P(x)=x^{3}-3 x+1$. Determine
$$
\frac{1}{x_{1}^{2}-3}+\frac{1}{x_{2}^{2}-3}+\frac{1}{x_{3}^{2}-3}
$$
|
## First Solution.
For the root $x_{1}$ of the polynomial $P$, we have
$$
\begin{aligned}
x_{1}^{3}-3 x_{1}+1 & =0 \\
x_{1}^{3}-3 x_{1} & =-1 \\
x_{1}^{2}-3 & =-\frac{1}{x_{1}} \\
\frac{1}{x_{1}^{2}-3} & =-x_{1} .
\end{aligned}
$$
Similarly, this holds for $x_{2}$ and $x_{3}$, so for the desired expression we have
$$
\frac{1}{x_{1}^{2}-3}+\frac{1}{x_{2}^{2}-3}+\frac{1}{x_{3}^{2}-3}=-\left(x_{1}+x_{2}+x_{3}\right)
$$
By Vieta's formulas, $x_{1}+x_{2}+x_{3}=0$, so the expression is equal to zero.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-4.4.
Determine all prime numbers $p$ for which there exist exactly five natural numbers $n$ such that $n+p \mid n^{3}+p^{2}$.
|
## First Solution.
The sum of cubes $n^{3}+p^{3}=(n+p)\left(n^{2}-n p+p^{2}\right)$ is divisible by $n+p$. Since, according to the problem's condition, $n^{3}+p^{2}$ is divisible by $n+p$, it is equivalent to say that
$$
\left(n^{3}+p^{3}\right)-\left(n^{3}+p^{2}\right)=p^{3}-p^{2}=p^{2}(p-1)
$$
is divisible by $n+p$.
Assume there exist $n$ and $p$ such that $n+p \mid p^{2}(p-1)$ and $n$ is not divisible by $p$. Then $n$ and $p$ are relatively prime, and therefore $n+p$ and $p$ are also relatively prime.
Thus, it must be true that $n+p \mid p-1$, which is impossible since $n+p > p-1 > 0$. Therefore, $n$ must be divisible by $p$.
We conclude that there exists $k \in \mathbb{N}$ such that $n=k p$. Finding all prime $p$ for which there exist five natural numbers from the problem's condition is equivalent to finding all prime $p$ for which there exist five natural numbers $k$ such that
$$
k+1 \mid p(p-1)
$$
The number $k$ satisfies this condition if and only if it is of the form $d-1$, where $d$ is a divisor of $p(p-1)$ greater than 1. Since 1 is a divisor of every number, we need to find all $p$ for which the expression $p(p-1)$ has exactly 6 natural divisors.
It is easy to see that $p$ cannot be equal to 2 or 3, and that $p=5$ is a solution because the number $p(p-1)=20$ has six divisors.
1 point
Now assume that $p \geqslant 7$. Then $p-1=2 m$ for some natural $m \geqslant 3$. In this case, the number $p(p-1)=2 m(2 m+1)$ has at least eight different divisors:
$$
1,2, m, 2 m, 2 m+1,2(2 m+1), m(2 m+1), 2 m(m+1)
$$
so for $p \geqslant 7$ we do not get new solutions.
We conclude that $p=5$ is the only prime number that satisfies the problem's condition.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-1.5.
For real numbers $a, b, c$, which are not equal to zero, it holds that $a+b+c=0$. What is
$$
\frac{a^{2}}{b c}+\frac{b^{2}}{a c}+\frac{c^{2}}{a b} ?
$$
|
## Solution.
If $a+b+c=0$, then $c=-(a+b)$.
The given expression is reduced to a common denominator and we substitute $c=-(a+b)$. We get
$$
\begin{array}{rlrl}
\frac{a^{2}}{b c}+\frac{b^{2}}{a c}+\frac{c^{2}}{a b} & =\frac{a^{3}+b^{3}-(a+b)^{3}}{-a b(a+b)} & & 1 \text { point } \\
& =\frac{(a+b)\left(a^{2}-a b+b^{2}\right)-(a+b)^{3}}{-a b(a+b)} & & 1 \text { point } \\
& =\frac{a^{2}-a b+b^{2}-a^{2}-2 a b-b^{2}}{-a b} & & 2 \text { points } \\
& =\frac{-3 a b}{-a b}=3 . & 1 \text { point }
\end{array}
$$
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-1.6.
A student has passed 31 exams over the course of a five-year study. Each year, he took more exams than the previous year, and in the fifth year, he took three times as many exams as in the first year. How many exams did the student take in the fourth year?
|
## Solution.
Let's denote the number of exams the student passed in the $i$-th year by $x_{i}, i \in\{1,2,3,4,5\}$.
Then $x_{5}=3 x_{1}, x_{1}<x_{2}<x_{3}<x_{4}<x_{5}$ and $x_{1}+x_{2}+x_{3}+x_{4}+x_{5}=31$.
1 point
If $x_{1}=1$, then $x_{5}=3$. This is impossible because there are no 3 different natural numbers between 1 and 3.
If $x_{1}=2$, then $x_{5}=6$, and the number of exams in the remaining years must be 3, 4, and 5. However, the sum $2+3+4+5+6$ is not 31.
If $x_{1}=3$, then $x_{5}=9$, so $x_{2}, x_{3}, x_{4}$ are some of the numbers $4,5,6,7,8$. Since $3+9=12$, it must be that $x_{2}+x_{3}+x_{4}=19$, which can be obtained for $4+7+8$ or $5+6+8$.
For the case when $x_{1} \geqslant 4$, there is no solution, because $x_{5}=3 \cdot x_{1} \geqslant 12$, and the sum $x_{2}+x_{3}+x_{4}=$ $31-x_{1}-x_{5} \leqslant 15$. On the other hand, the smallest values that the numbers $x_{2}, x_{3}, x_{4}$ can take are $5,6,7,8,9,10,11, \ldots$, and their sum is at least 18, which is greater than 15.
The student passed 8 exams in the fourth year.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-2.6.
If
$$
f(n)=\left(\frac{1+i}{\sqrt{2}}\right)^{n}+\left(\frac{1-i}{\sqrt{2}}\right)^{n}, \quad \text { where } n \in \mathbb{N}, i^{2}=-1
$$
what is $f(n+2016)-f(n-2016)$?
|
## Solution.
We calculate
$$
\begin{aligned}
f(n+2016) & =\left(\frac{1+i}{\sqrt{2}}\right)^{n+2016}+\left(\frac{1-i}{\sqrt{2}}\right)^{n+2016} \\
& =\left(\frac{1+i}{\sqrt{2}}\right)^{2016}\left(\frac{1+i}{\sqrt{2}}\right)^{n}+\left(\frac{1-i}{\sqrt{2}}\right)^{2016}\left(\frac{1-i}{\sqrt{2}}\right)^{n}
\end{aligned}
$$
Since
$$
\left(\frac{1+i}{\sqrt{2}}\right)^{2016}=\left[\left(\frac{1+i}{\sqrt{2}}\right)^{2}\right]^{1008}=\left(\frac{2 i}{2}\right)^{1008}=i^{1008}=1, \text { and similarly }\left(\frac{1-i}{\sqrt{2}}\right)^{2016}=1
$$
it follows that
$$
f(n+2016)=\left(\frac{1+i}{\sqrt{2}}\right)^{n}+\left(\frac{1-i}{\sqrt{2}}\right)^{n}=f(n)
$$
Similarly, we calculate
$$
\begin{aligned}
f(n+2016) & =\left(\frac{1+i}{\sqrt{2}}\right)^{n-2016}+\left(\frac{1-i}{\sqrt{2}}\right)^{n-2016} \\
& =\left(\frac{1+i}{\sqrt{2}}\right)^{-2016}\left(\frac{1+i}{\sqrt{2}}\right)^{n}+\left(\frac{1-i}{\sqrt{2}}\right)^{-2016}\left(\frac{1-i}{\sqrt{2}}\right)^{n} \\
& =\left(\left(\frac{2 i}{2}\right)^{1008}\right)^{-1}\left(\frac{1+i}{\sqrt{2}}\right)^{n}+\left(\left(\frac{-2 i}{2}\right)^{1008}\right)^{-1}\left(\frac{1-i}{\sqrt{2}}\right)^{n} \\
& =\left(\frac{1+i}{\sqrt{2}}\right)^{n}+\left(\frac{1-i}{\sqrt{2}}\right)^{n}=f(n)
\end{aligned}
$$
We conclude $f(n+2016)-f(n-2016)=f(n)-f(n)=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-4.5.
For real numbers $x_{1}, x_{2}, \ldots, x_{2016}$, the following equalities hold:
$$
\frac{x_{1}}{x_{1}+1}=\frac{x_{2}}{x_{2}+2}=\cdots=\frac{x_{2016}}{x_{2016}+2016}, \quad x_{1}+x_{2}+x_{3}+\cdots+x_{2016}=2017
$$
Calculate $x_{1008}$.
|
## Solution.
Notice
$$
\frac{x_{1}}{x_{1}+1}=\frac{x_{i}}{x_{i}+i}, \text { for all } i \in\{1,2, \ldots, 2016\}
$$
Then $x_{1}(x_{i}+i)=x_{i}(x_{1}+1)$, so $x_{i}=i \cdot x_{1}$ for all $i \in\{1,2, \ldots, 2016\}$. It follows that
$$
\begin{array}{cc}
x_{1}+x_{2}+\cdots+x_{2016}=2017 & \\
x_{1} \cdot(1+2+\cdots+2016)=2017 & \\
x_{1} \cdot \frac{(1+2016) \cdot 2016}{2}=2017 & 1 \text{ point} \\
x_{1}=\frac{1}{1008} & 1 \text{ point} \\
x_{1008}=1008 \cdot x_{1}=1 . & 1 \text{ point}
\end{array}
$$
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-1.8. The perimeter of a right triangle is $14 \mathrm{~cm}$. A square is constructed outward on each side. The sum of the areas of all the squares is $72 \mathrm{~cm}^{2}$. What is the area of the given right triangle?
|
## Solution.
Let $a$ and $b$ be the lengths of the legs, and $c$ be the length of the hypotenuse of a right triangle. It is given that
$$
\begin{aligned}
a+b+c & =14 \\
a^{2}+b^{2}+c^{2} & =72
\end{aligned}
$$
Since, by the Pythagorean theorem, $a^{2}+b^{2}=c^{2}$, the last equation becomes $2 c^{2}=72$ or $c=6 \text{ cm}$.
From the perimeter of the triangle, we get
$$
a+b=14-6=8
$$
We will square this equation and use the fact that the area of a right triangle is $P=\frac{a b}{2}$. Then we have
$$
\begin{aligned}
(a+b)^{2} & =64 \\
a^{2}+2 a b+b^{2} & =64
\end{aligned}
$$
which is equivalent to
$$
\begin{aligned}
& c^{2}+4 P=64 \\
& 36+4 P=64
\end{aligned}
$$
from which we get $P=7 \text{ cm}^{2}$.
(1 point)
## ZUPANIJSKO NATJECANJE IZ MATEMATIKE
## 2nd grade - high school - B variant
February 28, 2011.
IF A STUDENT HAS A DIFFERENT METHOD OF SOLVING THE PROBLEM, THE COMMITTEE IS OBLIGED TO EVALUATE THE METHOD AND SCORE IT APPROPRIATELY.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-2.2. If the graph of the quadratic function $f(x)=x^{2}-(m-n) x+n, m, n \in \mathbb{R}$, has its vertex at point $T(2,3)$, determine the value of $f(m-n)$.
|
## Solution.
The $x$-coordinate of the vertex of the quadratic function $f$ is $\frac{m-n}{2}$. Then $\frac{m-n}{2}=2$, so
$$
m-n=4
$$
(1 point)
Furthermore, the $y$-coordinate of the vertex is $\frac{4 n-(m-n)^{2}}{4}=3$. From this and (1), we get
$$
4 n-(m-n)^{2}=12
$$
or $4 n-16=12$, i.e., $n=7$.
Then $f(m-n)=f(4)=16-16+7=7$.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-4.1. Solve the equation:
$$
2^{\binom{n+1}{2}}-4 \cdot 2^{\binom{n-1}{2}}=7 \cdot 2^{\binom{n}{2}}
$$
|
Solution. We solve the equation under the condition that $n \geq 3$.
$$
2^{\frac{(n+1) n}{2}}-4 \cdot 2^{\frac{(n-1)(n-2)}{2}}=7 \cdot 2^{\frac{n(n-1)}{2}}
$$
After dividing the equation by $2^{\frac{n(n-1)}{2}}$ we get
$$
2^{\frac{(n+1) n}{2}-\frac{n(n-1)}{2}}-4 \cdot 2^{\frac{(n-1)(n-2)}{2}-\frac{n(n-1)}{2}}=7
$$
or
$$
2^{n}-4 \cdot 2^{-n+1}=7
$$
If we let $2^{n}=t$ we get the equation $t^{2}-7 t-8=0$ whose solutions are 8 and -1.
Since $2^{n}>0, 2^{n}=8$ so the solution is $n=3$.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-4.5. If we draw a tangent $t_{1}$ to the ellipse $b^{2} x^{2}+a^{2} y^{2}=a^{2} b^{2}$ at an angle of $45^{\circ}$ to the positive direction of the $x$-axis, its intercept on the $y$-axis is 4. If we draw a tangent $t_{2}$ at an angle of $60^{\circ}$, the intercept on the $y$-axis will increase by 2. Determine the area of the quadrilateral $F_{1} T_{1} F_{2} T_{2}$, where $F_{1}, F_{2}$ are the foci of the ellipse, and $T_{1}, T_{2}$ are the intersections of the tangents $t_{1}, t_{2}$ with the $y$-axis.
|
Solution. Let's write the equations of the given tangents:
$$
\begin{gathered}
t_{1} \ldots k_{1}=\operatorname{tg} 45^{\circ}=1, l_{2}=4, \quad t_{2} \ldots k_{2}=\sqrt{3}, l_{2}=6 \\
t_{1} \ldots y=x+4 \\
t_{2} \ldots y=\sqrt{3} x+6
\end{gathered}
$$
From the condition of tangency $a^{2} k^{2}+b^{2}=l^{2}$, it follows that $a^{2}+b^{2}=16$ and $3 a^{2}+b^{2}=36$, hence $a^{2}=10$, $b^{2}=6$.
(1 point)
Then $e^{2}=10-6=4$, and the coordinates of the foci are $F_{1}=(2,0), F_{2}=(-2,0)$.
Since $T_{1}=(0,4), T_{2}=(0,6)$, the desired area is
$$
P=2 \cdot\left(\frac{2 \cdot 6}{2}-\frac{2 \cdot 4}{2}\right)=4
$$
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-4.7. The base of a triangular pyramid is a triangle with sides $a, b$, and $c$. The length of side $c$ is $7 \, \text{cm}$, $a - b = 5 \, \text{cm}$, and the angle opposite side $c, \gamma = 60^\circ$. The lateral face containing the longest base edge is perpendicular to the base plane and congruent to the base. Calculate the volume of the pyramid and the area of the largest lateral face of the pyramid.
|
## Solution.
Using the Law of Cosines, we will calculate the lengths of sides $a$ and $b$.
$$
\begin{aligned}
& c^{2}=a^{2}+b^{2}-2 a b \cdot \cos \gamma \\
& 49=(b+5)^{2}+b^{2}-2(b+5) b \cdot \frac{1}{2} \\
& b^{2}+5 b-24=0 \\
& b=3 \text{ cm}, \quad a=8 \text{ cm}
\end{aligned}
$$
Since the lateral face $C B D$ is congruent to the base and perpendicular to it, the height of the pyramid is equal to the height of the base, and we have
$$
\sin \gamma=\frac{v}{b} \quad \Rightarrow \quad v=\frac{3 \sqrt{3}}{2} \text{ cm}
$$
The area of the base is $B=\frac{1}{2} a b \sin \gamma=12 \cdot \frac{\sqrt{3}}{2}=6 \sqrt{3}$.
Then the volume of the pyramid is
$$
V=\frac{6 \sqrt{3} \cdot \frac{3 \sqrt{3}}{2}}{3}=9 \text{ cm}^{3}
$$
The area of the lateral face $C B D$ is equal to the area of the base. Since the length of side $b$ is less than the length of side $c$, the lateral face $A B D$ is larger than the lateral face $C A D$, so we will calculate its area.
(1 point)
Let's calculate the length of the unknown edge $x$:
$$
x=v \sqrt{2}=\frac{3 \sqrt{6}}{2} \text{ cm}
$$
The length of the height of the lateral face $A B D$ is
$$
y=\sqrt{c^{2}-\left(\frac{x}{2}\right)^{2}}=\frac{\sqrt{730}}{4}
$$
and its area is
$$
P=\frac{y \cdot x}{2}=\frac{1}{2} \cdot \frac{\sqrt{730}}{4} \cdot \frac{3 \sqrt{6}}{2}=\frac{3}{16} \cdot \sqrt{4380}=\frac{3}{8} \cdot \sqrt{1095} \text{ cm}^{2}
$$
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-4.8. Determine the sum of the reciprocals of all positive divisors of the number $n$, including 1 and $n$, if $n=2^{p-1}\left(2^{p}-1\right)$, and $2^{p}-1$ is a prime number.
|
Solution. The divisors of the number $n$ are the numbers
$$
1,2,2^{2}, 2^{3}, \ldots, 2^{p-1}, 2^{p}-1,2 \cdot\left(2^{p}-1\right), 2^{2} \cdot\left(2^{p}-1\right), \ldots, 2^{p-1} \cdot\left(2^{p}-1\right)
$$
The sum of their reciprocals is
$$
S=1+\frac{1}{2}+\frac{1}{2^{2}}+\ldots+\frac{1}{2^{p-1}}+\frac{1}{2^{p}-1}\left(1+\frac{1}{2}+\frac{1}{2^{2}}+\ldots+\frac{1}{2^{p-1}}\right)
$$
We observe a geometric sequence of $p$ terms with the first term 1 and the common ratio $\frac{1}{2}$. Then,
$$
S=\frac{1-\left(\frac{1}{2}\right)^{p}}{\frac{1}{2}} \cdot\left(1+\frac{1}{2^{p}-1}\right)=2\left(1-2^{-p}\right)\left(\frac{2^{p}}{2^{p}-1}\right)=2\left(\frac{2^{p}-1}{2^{p}-1}\right)=2
$$
(4 points)
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Riješite jednadžbu
$$
\log _{2}^{2}(x+y)+\log _{2}^{2}(x y)+1=2 \log _{2}(x+y)
$$
|
1. Zapišimo jednadžbu u obliku
$$
\log _{2}^{2}(x y)+\left(\log _{2}(x+y)-1\right)^{2}=0
$$
Time dobivamo sustav jednadžbi
$$
\log _{2}(x y)=0, \quad \log _{2}(x+y)=1
$$
Odavde dobivamo jednadžbe
$$
x y=1, \quad x+y=2
$$
čije rješenje je $x=y=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-1.5.
Two friends, Esma and Ljerka, came up with a game: each letter of their names is replaced by a digit from 1 to 5 according to a given table. Thus, the name Esma has the code 4431, and Ljerka has 24351.
The digits of the obtained code $a_{1} a_{2} \ldots a_{k}$ are used for moving in steps of the same length. Starting from the initial point, one moves $a_{1}$ steps north, and for each subsequent digit $a_{i}$, one turns $90^{\circ}$ to the left and walks $a_{i}$ steps in that direction (thus $a_{2}$ steps west, $a_{3}$ steps south, $a_{4}$ steps east, and so on). The process is repeated (after the last digit, it starts again with the first digit of the code)
| 1 | 2 | 3 | 4 | 5 |
| :---: | :---: | :---: | :---: | :---: |
| $\mathrm{A}$ | $\mathrm{B}$ | $\mathrm{C}$ | $\mathrm{C}$ | $\mathrm{C}$ |
| $\mathrm{D}$ | $\mathrm{D} \check{Z}$ | $\mathrm{P}$ | $\mathrm{E}$ | $\mathrm{F}$ |
| $\mathrm{G}$ | $\mathrm{H}$ | $\mathrm{I}$ | $\mathrm{J}$ | $\mathrm{K}$ |
| $\mathrm{L}$ | $\mathrm{LJ}$ | $\mathrm{M}$ | $\mathrm{N}$ | $\mathrm{NJ}$ |
| $\mathrm{O}$ | $\mathrm{P}$ | $\mathrm{R}$ | $\mathrm{S}$ | S S |
| $\mathrm{T}$ | $\mathrm{U}$ | $\mathrm{V}$ | $\mathrm{Z}$ | $\check{Z}$ |
until returning to the initial point.
Esma concluded that she would never return to the starting point with her code. Why?
Ljerka returned to the starting point after exactly $5 n$ steps. Determine $n$ and prove that any person with 5 letters in their name will return to the starting point after at most 4 cycles, or repetitions of the code.
|
## Solution.
Without loss of generality, assume that Esma and Ljerka started from the point $(0,0)$.

Esma's movement looks like this:
First loop: $(0,0),(0,4),(-4,4),(-4,1),(-3,1)$
Second loop: $(-3,1),(-3,5),(-7,5),(-7,2),(-6,2)$
Third loop: $(-6,2),(-6,6),(-10,6),(-10,3),(-9,3)$.
After the $k$-th loop, the coordinates of the final point change to $(-3 k, k)$, so Esma obviously cannot return to the starting point because the final points lie on a single line.
Ljerka's movement looks like this:
First loop: $(0,0),(0,2),(-4,2),(-4,-1),(1,-1),(1,0)$
Second loop: $(1,0),(-1,0),(-1,-4),(2,-4),(2,1),(1,1)$
Third loop: $(1,1),(1,-1),(5,-1),(5,2),(0,2),(0,1)$
Fourth loop: $(0,1),(2,1),(2,5),(-1,5),(-1,0),(0,0)$
Ljerka needed 4 loops to return to the point from which she started.
Since each loop consisted of $2+4+3+5+1=15$ steps, Ljerka needed a total of 60 steps, so the desired $n=12$.
Let the code name be a 5-letter word abcde, where $a, b, c, d, e \in\{1,2,3,4,5\}$. Starting from the point $(x, y)$, we move up by $a$, left by $b$, down by $c$, right by $d$, and up again by $e$, arriving at the point $(x-b+d, y+a-c+e)$.
In the second loop, we start from this point and move left by $a$, down by $b$, right by $c$, up by $d$, and left by $e$, arriving at the point $(x-b+d-a+c-e, y+a-c+e-b+d)$.

In the third loop, we start from this point and move down by $a$, right by $b$, up by $c$, left by $d$, and down again by $e$, arriving at the point $(x-b+d-a+c-e+b-d, y+a-c+e-b+d-a+c-e) = (x-a+c-e, y-b+d)$.
In the fourth loop, we start from this point and move right by $a$, up by $b$, left by $c$, down by $d$, and right by $e$, arriving at the point $(x-a+c-e+a-c+e, y-b+d+b-d) = (x, y)$.
A person with a 5-letter name needs 4 loops to return to the starting point.
## NATIONAL MATHEMATICS COMPETITION
## 2nd grade - high school - B variant
## October 26, 2020.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-2.5.
The math test consisted of three problems. Professor Max informed the students of their test results in a somewhat vague manner, setting a new problem:
The first and second problems were correctly solved by 7 students, the second and third problems by 9 students, and the first and third problems by as many as 13 students. What is the minimum number of students who correctly solved all three problems?
It is known that there are 24 students in the class and that no student failed to solve any of the problems.
|
## Solution.
Let the number of students who solved only the first and second problems be denoted by $a$, only the first and third by $b$, only the second and third by $c$. Let $d$ be the number of students who correctly solved all three problems, $e$ the number who correctly solved only the first problem, $f$ only the second, and $g$ only the third.
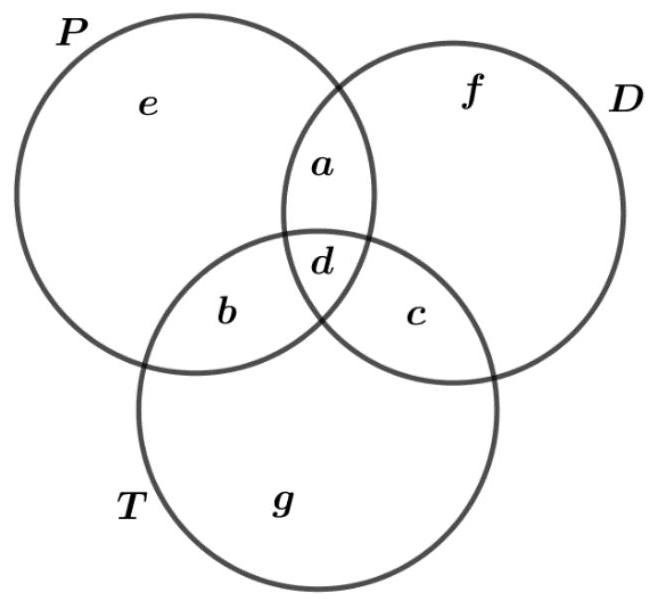
Then we have $a+d=7, b+d=13, c+d=9, a+b+c+d+e+f+g=24$.
Adding the first three equations: $a+b+c+3d=29$. Since $a+b+c+d+e+f+g=24$, it follows that $a+b+c+3d+e+f+g=24+2d, 29+e+f+g=24+2d, e+f+g+5=2d$.
According to the problem's condition, $e+f+g$ is a non-negative number.
If $e+f+g=0$, then $2d=5$, which is impossible.
When $e+f+g=1$, we have $d=3$. This is the smallest possible value for $d$.
The smallest number of students who correctly solved all three problems is three.
## NATIONAL MATHEMATICS COMPETITION
## 3rd grade - high school - B variant
## October 26, 2020.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-3.4.
In a square $A B C D$, a circle $k$ is inscribed. From a point $T$ which lies on the circle $k$, the diagonal $\overline{A C}$ is seen at an angle $\alpha$, and the diagonal $\overline{B D}$ at an angle $\beta$.
Prove that $\operatorname{tg}^{2} \alpha+\operatorname{tg}^{2} \beta=8$.
|
## First Solution.
Let the radius of the circle $k$ be $r$, and its center be the origin of the coordinate system $O$. The coordinates of the vertices of the square are $A(-r,-r), B(r,-r), C(r, r), D(-r, r)$, and the coordinates of point $T$ are $(x, y)$.
Point $T$ is at a distance $r$ from the center, so $\sqrt{x^{2}+y^{2}}=r$, which implies $x^{2}+y^{2}=r^{2}$. The angle $\alpha$ is the angle between the lines $A T$ and $C T$, and the angle $\beta$ is the angle between the lines $B T$ and $D T$. Therefore,
$$
\operatorname{tg} \alpha=\frac{k_{C T}-k_{A T}}{1+k_{C T} k_{A T}}, \quad \operatorname{tg} \beta=\frac{k_{D T}-k_{B T}}{1+k_{D T} k_{B T}}
$$
It follows that
$$
\begin{aligned}
\operatorname{tg} \alpha & =\frac{k_{C T}-k_{A T}}{1+k_{C T} k_{A T}}=\frac{\frac{r-y}{r-x}-\frac{-r-y}{-r-x}}{1+\frac{r-y}{r-x} \cdot \frac{-r-y}{-r-x}} \\
& =\frac{r-y r+x-r+y r-x}{r-x r+x+r-y r+y}=\frac{2 r x-2 r y}{2 r^{2}-x^{2}-y^{2}}
\end{aligned}
$$
Since $x^{2}+y^{2}=r^{2}$, it follows that $\operatorname{tg} \alpha=\frac{2(x-y)}{r}$.
Similarly,
$$
\begin{aligned}
\operatorname{tg} \beta & =\frac{\frac{r-y}{-r-x}-\frac{-r-y}{r-x}}{1+\frac{r-y}{-r-x} \frac{-r-y}{r-x}} \\
& =\frac{r-y r-x-r+y r+x}{-r-x r-x+r-y-r-y}=\frac{-2 r x-2 r y}{-r^{2}}=\frac{2(x+y)}{r} .
\end{aligned}
$$
Then,
$$
\begin{aligned}
\operatorname{tg}^{\alpha}+\operatorname{tg}^{2} \beta & =\frac{4(x-y)^{2}}{r^{2}}+\frac{4(x+y)^{2}}{r^{2}}=\frac{4}{r^{2}}\left(x^{2}-2 x y+y^{2}+x^{2}+2 x y+y^{2}\right) \\
& =\frac{8}{r^{2}}\left(x^{2}+y^{2}\right)=\frac{8}{r^{2}} \cdot r^{2}=8
\end{aligned}
$$
|
8
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
## Task B-1.4.
A lively hedgehog is hopping through a meadow, first moving 4 meters to the east, then 2 meters southwest, and finally 4 meters to the south. How far is the hedgehog from its starting position?
|
## Solution.
For the sketch.
The angle $\measuredangle E B C=45^{\circ}$, so $|E B|=|E C|=\sqrt{2}$.
$$
\begin{aligned}
|A E| & =4-\sqrt{2},|E D|=4+\sqrt{2} \\
|A D| & =\sqrt{|A E|^{2}+|E D|^{2}}=\sqrt{(4-\sqrt{2})^{2}+(4+\sqrt{2})^{2}} \\
& =\sqrt{16-8 \sqrt{2}+2+16+8 \sqrt{2}+2}=\sqrt{36} \\
|A D| & =6 \text{ m}
\end{aligned}
$$
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-3.6. A given isosceles triangle has a base length of $6 \mathrm{~cm}$ and legs of length 5 cm. A circle whose diameter is one of the legs of the triangle intersects the other two sides of the triangle at points $E$ and $F$. Determine the length of the segment $|E F|$.
|
## Solution.
Sketch.
$|A C|=|B C|=5 \text{ cm}, |A B|=6 \text{ cm}$
$\measuredangle C E B=90^{\circ}$ (angle subtended by the diameter of the circle)
(1 point)
We conclude that point E is the foot of the altitude of the given isosceles triangle.
Since triangle $\triangle A B C$ is isosceles, $\measuredangle C A B=\measuredangle C B A=\alpha$.
Quadrilateral $E B C F$ is cyclic, hence
$$
\measuredangle E B C + \measuredangle C F E = 180^{\circ}
$$
Then,
$$
\measuredangle A F E = 180^{\circ} - \measuredangle C F E = \measuredangle E B C = \alpha
$$
We conclude that triangle $\triangle A E F$ is isosceles, so $|E F| = |A E| = 3 \text{ cm}$.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task B-4.3. Find all solutions to the equation
$$
\frac{1}{\binom{4}{x}}-\frac{1}{\binom{5}{x}}=\frac{1}{\binom{6}{x}}
$$
|
Solution. From the definition of the binomial coefficient, we have
$$
\binom{4}{x}=\frac{4!}{x!(4-x)!},\binom{5}{x}=\frac{5!}{x!(5-x)!},\binom{6}{x}=\frac{6!}{x!(6-x)!}
$$
so the given equation becomes
$$
\frac{x!(4-x)!}{4!}-\frac{x!(5-x)!}{5!}=\frac{x!(6-x)!}{6!}, \text { with the condition } x \leq 4
$$
The equation
$$
\frac{(4-x)!}{4!}-\frac{(4-x)!(5-x)}{4!\cdot 5}=\frac{(4-x)!(5-x)(6-x)}{4!\cdot 5 \cdot 6}
$$
after simplification becomes
$$
1-\frac{5-x}{5}=\frac{(5-x)(6-x)}{5 \cdot 6} \text { or } x^{2}-17 x+30=0
$$
The solutions to this equation are 15 and 2, but due to the condition $x \leq 4$, the only solution is $x=2$.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-1.2.
Let $x$ and $y$ be real numbers such that $x+y=1$ and $x^{3}+y^{3}=13$. What is $x^{2}+y^{2}$?
|
## First Solution.
From the formula for the cube of a sum
$$
(x+y)^{3}=x^{3}+3 x^{2} y+3 x y^{2}+y^{3}=x^{3}+y^{3}+3 x y(x+y)
$$
it follows that
$$
3 x y(x+y)=(x+y)^{3}-\left(x^{3}+y^{3}\right)
$$
By substituting $x+y=1$ and $x^{3}+y^{3}=13$, we have
$$
3 x y=1^{3}-13=-12
$$
which means $x y=-4$.
Now, from the formula for the square of a sum $(x+y)^{2}=x^{2}+2 x y+y^{2}$, by substituting $x+y=1$ and $x y=-4$, we have
$$
1^{2}=x^{2}+y^{2}+2 \cdot(-4)=x^{2}+y^{2}-8
$$
which means $x^{2}+y^{2}=1+8=9$.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-1.3.
Dino, Pino, and Tino go to the same kindergarten. For the game, each boy needs two dice of the same color, but it is not necessary that the dice of different boys be of different colors. The caregiver has red, blue, and green dice in one box. If she draws without looking, how many dice does she need to draw from the box to be sure that each boy can take two dice of the same color?
|
## First Solution.
Two dice of the same color form a pair. Therefore, for each color, the caregiver draws some number of pairs and at most one additional die. If the caregiver were to draw dice among which there are no three pairs, the number of pairs could be at most two, and with those two pairs, there could be at most one die of each color. Thus, the maximum number of dice among which there are no three pairs is 7. This means that if the caregiver draws 8 dice, there will certainly be three pairs among them.
Furthermore, if the caregiver draws 7 or fewer dice, it is possible that there will not be three pairs. For example, she could draw 3 red, 3 blue, and 1 green die.
Therefore, the answer is 8.
Note: This way of thinking shows that if the number of children is $n$ and the number of colors is $k$, it would be necessary to draw $2(n-1)+k+1$ dice to ensure that each child can take a pair of dice of the same color.
Note: The answer alone, i.e., the result without justification, is worth 0 points. The proof that for eight dice, we can certainly find three pairs is worth 4 points. An example where for seven dice, we cannot find three pairs is worth 2 points.
It is necessary to provide an example of 7 dice among which there are no three pairs of the same color. Another such example is five dice of one color, and one die of each of the other two colors.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Task A-2.7.
Two teams are playing handball. Neither team has scored 30 or more goals. The recorder at the beginning of the game and after each goal scored records the score and calculates the sum of all digits in the score. For example, with a score of 15 : 6, the sum of the digits is 12. How many times during the game could the recorder have recorded a score where the total sum of the digits is 10?
|
## Solution.
At each change of the result, exactly one of the numbers $\overline{a b}$ and $\overline{c d}$ increases by one, while the other remains unchanged.
Consider some (fixed) $a$ and $c$. Let $b$ and $d$ be such that $a+b+c+d=10$. With each subsequent change of the result, one of them will increase, and the other will not decrease. Therefore, the sum $a+b+c+d$ increases as long as $a$ and $c$ remain unchanged. In other words, for each given pair of numbers $a$ and $c$, there can be at most one result in the same match that satisfies the conditions of the problem.
From the text of the problem, we see that the digits $a$ and $c$ can only be 0, 1, and 2.
The number $a$ initially has the value 0, and later it can only increase from 0 to 1 and then from 1 to 2. The same applies to the number $c$.
Without loss of generality, assume that $a$ is the first of these two numbers to increase from 0 to 1. Then in that match, we can have at most five different pairs $(a, c)$:
$$
(0,0) \rightarrow(1,0) \rightarrow(1,1) \rightarrow(2,1) \rightarrow(2,2)
$$
or
$$
(0,0) \rightarrow(1,0) \rightarrow(1,1) \rightarrow(1,2) \rightarrow(2,2)
$$
or
$$
(0,0) \rightarrow(1,0) \rightarrow(2,0) \rightarrow(2,1) \rightarrow(2,2)
$$
Therefore, the sum can be equal to 10 at most five times.
It remains to show that these results are indeed possible. By solving the equation $a+b+c+d=10$ for each pair $(a, c)$ and considering that the result of a team cannot decrease during the match, we see that one possible sequence of results is, for example:
$$
06: 04, \quad 13: 06, \quad 21: 07, \quad 22: 15, \quad 25: 21
$$
Note: The result alone, i.e., the answer without justification, is worth 0 points. 8 points are awarded for proving that there can be at most five different results, and the remaining 2 points are awarded for an example of such a sequence.
## SCHOOL/CITY COMPETITION IN MATHEMATICS
3rd grade - high school - A variant
January 4, 2020.
## IF A STUDENT HAS A DIFFERENT APPROACH TO SOLVING THE PROBLEM, THE COMMITTEE IS OBLIGED TO GRADE AND EVALUATE THAT APPROACH APPROPRIATELY.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.