problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
4. In each cell of the square field below, a building of height 1, 2, 3, 4, or 5 is placed so that the following rules are met:
- In each (horizontal) row and (vertical) column, each building height appears exactly once.
- The numbers on the sides of the square are the sums of the heights of the visible buildings. These are the buildings (partially) visible in the side view from the number on the side. For example, if the heights 1, 3, 2, 5, and 4 are in a row in that order, then from the left, the buildings with heights 1, 3, and 5 are visible, and from the right, the buildings with heights 4 and 5 are visible.
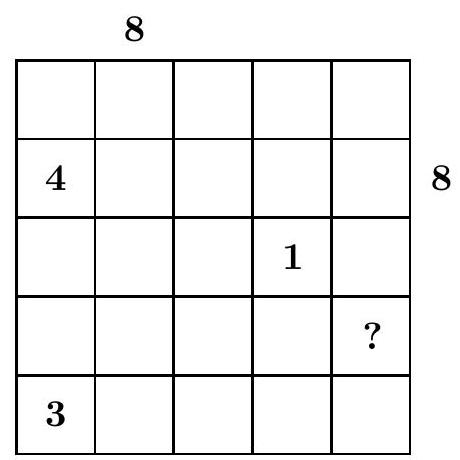
6
How tall is the building that goes in the place of the question mark?
A) 1 tall
B) 2 tall
C) 3 tall
D) 4 tall
E) 5 tall
|
A4. B) 2 First note that the building of 5 stories is always visible. We first look at the middle column, where the 6 is written. It must hold that $6=1+5$: the first building you see is 1 story high, and behind it you see the building of 5 stories. No building can stand between them, because otherwise we would also see it from the side. In this way, we get the numbers in the first picture.
Now we look at the second row, where an 8 stands on the right side. The building of 1 story can only be in the second or fifth column due to the first requirement. If the 1 is in the fifth column, the 8 on the right side only works if the order is $4-3-5-2-1$. But that can't be, because there is already a 5 in the third column. So the 1 is in the second column. We can now only get a sum of 8 from the right side if the buildings of height 3 and 5 are visible. Therefore, the 3 is in the fifth column and due to the first requirement, the 5 is in the fourth column. This gives us the numbers as in the second picture.
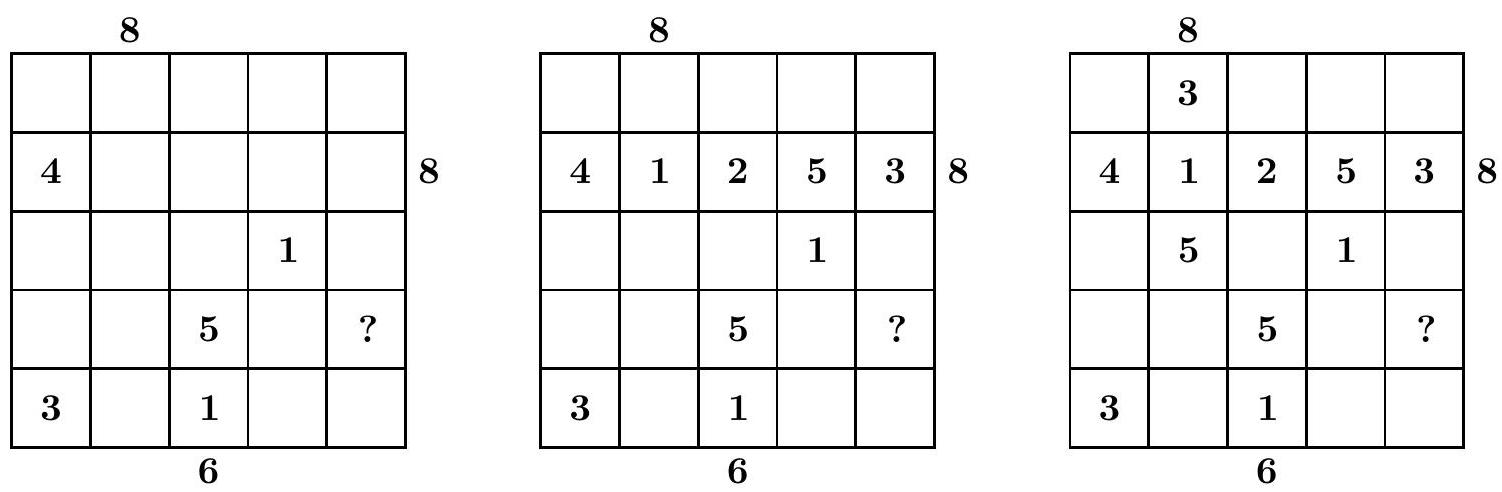
Finally, we look at the 8 above the second column. We already see a 1 in the second row. This building cannot be visible. The visible buildings of this 8 are therefore also buildings of height 3 and 5. The building with height 3 comes in the top row and the 5 in the third row, because there is already a 5 in the fourth row and if the 5 were in the bottom row, the building of height 4 would also be visible.
We now have the numbers filled in as in the third picture. Continue filling in as you would a Sudoku, so that each number appears exactly once in each row and column. You can fill in the first column, the third column, and the middle row completely. Then you see that the number 2 comes at the question mark.
|
2
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
7. On the board are the integers from 1 to $n$. One of the numbers is erased. The average of the remaining numbers is $11 \frac{1}{4}$.
Which number was erased?
A) 6
B) 7
C) 11
D) 12
E) 21
|
A7. A) 6 The average of the numbers from 1 to $n$ is exactly $\frac{n+1}{2}$. We can divide the numbers into pairs, with one number remaining if $n$ is odd: 1 paired with $n$, 2 paired with $n-1$, and so on. The average of each pair is then $\frac{n+1}{2}$.
If we remove a number, the smallest possible average that remains is the average of the numbers from 1 to $n-1$, which is exactly $\frac{n}{2}$. This is because we have removed the largest number. The largest possible average that remains is the average of the numbers from 2 to $n$, which is exactly $\frac{n+2}{2}$.
Thus, we have $\frac{n}{2} \leqslant \frac{45}{4}$ and $\frac{45}{4} \leqslant \frac{n+2}{2}$. Multiplying these inequalities by 2, we get $n \leqslant \frac{45}{2} \cdot 2 = 45/2 \cdot 2 = 22.5$. Therefore, there are two possibilities: $n=21$ or $n=22$. We will now show that $n=22$ is not possible.
If $n$ were 22, then 21 numbers would remain. Taking the average of 21 integers means we first add 21 integers and then divide the result by 21. This gives us a fraction of the form $\frac{S}{21}$. This can never equal $\frac{45}{4}$. The equation $\frac{S}{21}=\frac{45}{4}$ implies $4S = 21 \cdot 45$, but $21 \cdot 45$ is not divisible by 4.
So we start with the numbers from 1 to 21. The sum of these numbers is exactly 21 times the average: $21 \cdot \frac{21+1}{2} = 21 \cdot 11 = 231$. The average of the remaining 20 numbers must be $\frac{45}{4}$, so the sum of the remaining numbers must be $20 \cdot \frac{45}{4} = 225$. This means we must remove the number $231 - 225 = 6$.
|
6
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
A8. Consider all four-digit numbers in which each of the digits $3,4,6$ and 7 appears exactly once. How many of these numbers are divisible by 44?
(A) 2
(B) 4
(C) 6
(D) 8
(E) 12
B-questions
|
A8. Consider all four-digit numbers in which each of the digits 3, 4, 6, and 7 appears exactly once. How many of these numbers are divisible by 44? (A) 2
Solution Let the number $n$ consisting of the digits $a, b, c$, and $d (n=1000a+100b+10c+d)$ satisfy the condition, so it is divisible by 44. It must then certainly be divisible by 11. Since $m=1001a+99b+11c=11(91a+9b+c)$ is also a multiple of 11, $m-n$ must also be a multiple of 11, so $m-n=a-b+c-d$ must be a multiple of 11. But this is at most the two highest minus the two lowest (so $13-7=6$) and at least -6, so it must be 0. Therefore, $a+c=b+d$. And since the digits sum to 20, it follows that $a+c=b+d=10$.
Suppose $d=4$, then $b=6$ and we get 3674 and 7634, but neither of these satisfy the condition (since 74 and 34 are not divisible by 4). Suppose $d=6$, then $b=4$ and we get 3476 and 7436, both of which do satisfy the condition. There are no other options for $d$, as $d$ must be even. This gives a total of 2 solutions.
Alternative solution Check the 24 possibilities, or the 12 even possibilities, or the 6 multiples of 4.
|
2
|
Number Theory
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
B2. How many positive integers $a$ are there, for which it is true that: when you divide 2216 by $a$, the remainder is 29.
|
B2. 4 Dat 2216 bij deling door $a$ rest 29 geeft, betekent precies dat $2216-29=2187$ deelbaar is door $a$ en dat $a$ groter is dan 29 (de rest is altijd kleiner dan de deler $a$). The divisors of $2187=3^{7}$ that are greater than 29 are 81, 243, 729, and 2187. There are thus 4 possibilities in total.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A5. If the number $\left(\left(\left(\left(7^{6}\right)^{5}\right)^{4}\right)^{3}\right)^{2}$ is written out, what is the last digit?
A) 1
B) 3
C) 5
D) 7
E) 9
|
A5. A) 1 The product of two numbers that end in 1 also ends in 1. Since the last digit of $7^{4}=2401$ is 1, this also holds for any power of $7^{4}$. In particular, the last digit of $\left.\left(\left(\left(7^{6}\right)^{5}\right)^{4}\right)^{3}\right)^{2}=7^{6 \cdot 5 \cdot 4 \cdot 3 \cdot 2}=\left(7^{4}\right)^{180}$ is 1.
|
1
|
Number Theory
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
A6. Calculate $\left((\sqrt{2}+1)^{7}+(\sqrt{2}-1)^{7}\right)^{2}-\left((\sqrt{2}+1)^{7}-(\sqrt{2}-1)^{7}\right)^{2}$.
A) 2
B) 4
C) $8 \sqrt{2}$
D) 128
E) 512
|
A6. B) 4 Given $a=(\sqrt{2}+1)^{7}$ and $b=(\sqrt{2}-1)^{7}$. Then the given expression is equal to
$$
(a+b)^{2}-(a-b)^{2}=4 a b=4(\sqrt{2}+1)^{7}(\sqrt{2}-1)^{7}=4((\sqrt{2}+1)(\sqrt{2}-1))^{7}=4 \cdot 1^{7}=4
$$
|
4
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
A1. In the places of the asterisks, there are positive integers arranged in such a way that the multiplication table below is correct.
What is the largest number that appears more than once in the $5 \times 5$ table?
A) 6
B) 8
C) 9
D) 12
E) 18
| $\times$ | $*$ | $*$ | $*$ | 7 |
| :---: | :---: | :---: | :---: | :---: |
| $*$ | 24 | $*$ | $*$ | 56 |
| $*$ | $*$ | 36 | 8 | $*$ |
| $*$ | $*$ | 27 | 6 | $*$ |
| 6 | 18 | $*$ | $*$ | 42 |
|
A1. D) 12 Look at the left picture. At the place of the star, a number must stand that both 27 and 6 are divisible by. This gives two possibilities: 1 or 3. The first possibility is ruled out, because then the number 27 would stand at the place of the double star, while 36 is not divisible by it.
| $\times$ | | $* *$ | | 7 |
| :---: | :---: | :---: | :---: | :---: |
| | 24 | | | 56 |
| | | 36 | 8 | |
| $*$ | | 27 | 6 | |
| 6 | 18 | | | 42 |
| $\times$ | 3 | 9 | 2 | 7 |
| :---: | :---: | :---: | :---: | :---: |
| 8 | 24 | 72 | 16 | 56 |
| 4 | 12 | 36 | 8 | 28 |
| 3 | 9 | 27 | 6 | 21 |
| 6 | 18 | 54 | 12 | 42 |
With the second possibility, we can fill in the entire table step by step (see the right picture). We see that 12 is the largest number that appears twice.
|
12
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
A6. On side $C D$ of a square $A B C D$ lies a point $E$. Line segment $A E$ is divided into four equal parts by the points $P, R$ and $T$. Line segment $B E$ is divided into four equal parts by the points $Q, S$ and $U$. Given that $|P Q|=3$.
What is the area of quadrilateral $P Q U T$?
A) $\frac{15}{4}$
B) 4
C) $\frac{17}{4}$
D) $\frac{9}{2}$
E) 5

|
A6. B) 4 Triangle $E A B$, triangle $E P Q$, and triangle $E T U$ are similar because $|A E|:|P E|:|T E|=4: 3: 1=|B E|:|Q E|:|U E|$ and $\angle A E B=\angle P E Q=\angle T E U$ (SAS). This implies that $|A B|:|P Q|:|T U|=$ $4: 3: 1$. From this, it follows that $|A B|=4$, so the area of triangle $A B E$ is $\frac{1}{2} \times 4 \times 4=8$.
Due to the similarity, triangles $P Q E$ and $T U E$ therefore have areas $\left(\frac{3}{4}\right)^{2} \times 8=\frac{9}{2}$ and $\left(\frac{1}{4}\right)^{2} \times 8=\frac{1}{2}$, respectively. The area of the
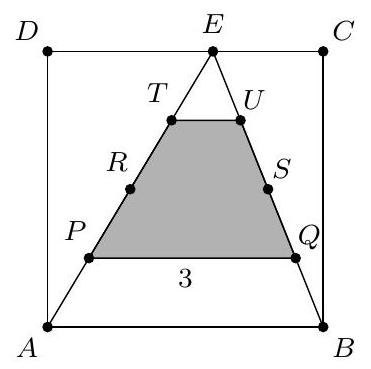
quadrilateral is thus $\frac{9}{2}-\frac{1}{2}=4$.
|
4
|
Geometry
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
A7. Carry has six cards. On each card, a positive integer is written. She chooses three cards and calculates the sum of the numbers on those cards. She does this for all 20 possible combinations of three cards. Ten times Carry gets a result of 16 and ten times a result of 18. What is the smallest number that appears on the cards?
A) 1
B) 2
C) 3
D) 4
E) 5
|
A7. D) 4 Because there are only two different outcomes, only two different numbers can appear on the cards. Indeed, if three cards bear different numbers, then in combination with a pair of the remaining three cards, they would each yield a different result. Let the two numbers that appear be $a$ and $b$. We can assume that $a$ appears on at least three cards. Since $a+a+a$, $a+a+b$, and $a+b+b$ are all different, $b$ can only appear once.
There are now two cases: $a+a+a=16$, $a+a+b=18$ and $a+a+a=18$, $a+a+b=16$. The first possibility is ruled out because 16 is not a multiple of three (since $a$ is an integer). Therefore, we see that $a=\frac{18}{3}=6$ and $b=16-12=4$. The smallest number that appears is thus 4.
|
4
|
Combinatorics
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
1. Frank has two integers that add up to 26. Kees adds two more integers and gets 41. Pieter adds two more integers and gets 58. At least how many of the six added numbers are even?
A) 0
B) 1
C) 2
D) 3
E) 4
|
A1. C) 2 The two numbers Frank has are either both even or both odd; otherwise, their sum would not be even. The two numbers Kees has add up to $41-26=15$, so one of his numbers must be even and the other odd, because otherwise the sum would not be odd. Pieter's numbers add up to $58-41=17$, so one of his numbers must also be even. Therefore, the minimum number of even numbers is 2, and this occurs, for example, if Frank has the numbers 11 and 15, Kees has the numbers 7 and 8, and Pieter has the numbers 4 and 13.
|
2
|
Number Theory
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
3. A positive integer is called fully divisible if it is divisible by each of its digits. These digits must also all be different (and not equal to 0). For example, 162 is fully divisible, because it is divisible by 1, 6, and 2.
How many fully divisible two-digit numbers are there?
A) 4
B) 5
C) 6
D) 7
E) 8
|
A3. B) 5
First, look at the numbers that start with the digit 1. A number is always divisible by 1, so this condition is always met. Now we will check which of the numbers 12, 13, 14, 15, 16, 17, 18, and 19 are also divisible by their last digit, and we see that 12 and 15 are.
Now look at the numbers starting with 2. To be divisible by 2, the last digit of the number must be even. So we only have the possibilities 24, 26, and 28, and we see that only 24 is fully divisible. For the numbers starting with 3, we have the possibilities 36 and 39 (the others are not divisible by 3), and we see that only 36 is fully divisible. For the numbers starting with 4, only 48 is a possibility, and we see that it is also fully divisible. For numbers where the first digit is 5 or greater, there is no second digit such that the number is divisible by the first digit. For example, for the first digit 5, 55 would have been the only possibility, but it is not allowed because the two digits must be different.
In total, there are 5 fully divisible two-digit numbers: $12, 15, 24, 36$, and 48.
|
5
|
Number Theory
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
7. A square board is divided into $4 \times 4$ squares. Initially, all the squares are white. We want to color as many squares blue as possible, in such a way that each blue square has exactly one white neighbor (two squares are neighbors if they share a side). What is the maximum number of squares we can color blue?
A) 6
B) 8
C) 10
D) 12
E) 14
|
A7. D) 12 A filling with 12 blue squares where each blue square has exactly one white neighboring square can be seen in the figure. A coloring with more than 12 blue squares does not exist. With a coloring of 13 or more blue squares, there are at most 3 white squares. These white squares together have no more than $3 \times 4=12$ neighboring squares, so at least one blue square does not have a white neighboring square.

|
12
|
Combinatorics
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
A1. We have a field of $4 \times 4$ square cells. Of these 16 cells, we want to color exactly four black. This must be done in such a way that each row and each column gets exactly one black cell, and no two black cells are diagonally (with a corner) adjacent.
In how many ways can we choose the four cells to color?
A) 1
B) 2
C) 3
D) 4
E) This is not possible.
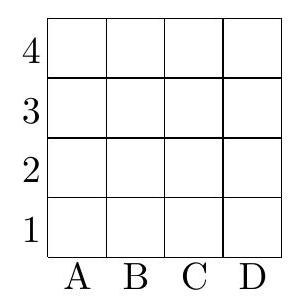
|
A1. B) 2 Suppose we color field B2 black. Then the 8 surrounding fields may not be colored black anymore: the fields above, below, to the left, and to the right of B2 are in the same column or row as B2, and the other four fields touch B2 diagonally. This leaves only row 4 and column D, and in each, we can only color one field black. In total, no more than 3 fields can be colored black. We conclude that B2 may not be colored black.
In the same way, we can deduce that the fields B3, C2, and C3 may not be colored black either. In row 2, we can therefore only color A2 or D2 black. If we color A2 black, then in row 3 we must color D3 black, because A3 is in the same column as A2. For rows 1 and 4, it is then only possible to color C1 and B4 black. This gives one solution. If we color D2 black instead of A2, we find the solution where D2, A3, B1, and C4 are colored black. In total, there are thus 2 ways to choose the black squares.
|
2
|
Combinatorics
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
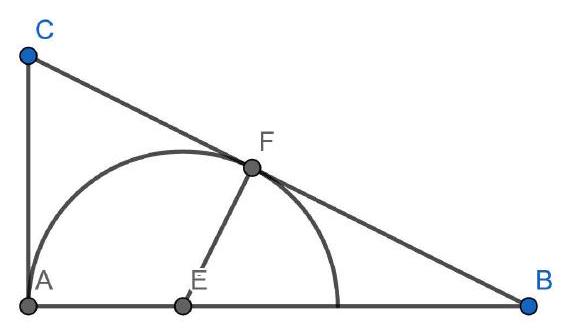
A4. A square paper ring has height 1. The sides have length 4. The ring is depicted in the left figure. By pressing it flat on a table, we get the right figure. In this figure, quadrilateral $A B C D$ is a square.

How long is side $A B$?
A) $\frac{5}{2}$
B) 3
C) $\frac{7}{2}$
D) 4
E) $\frac{9}{2}$
|
A4. B) 3 We look at the top edge of the paper ring. This edge has a length of $4 \times 4=16$. In the folded figure, the top edge follows the rectangle $E F G H$. Since $|A E|=|B F|=|C G|=$ $|D H|=1$, we see that $|A B|+|F G|+|C D|+|E H|=16-4=12$. These four lengths are equal to the lengths of the sides of the square $A B C D$. The sides of the square thus have a length of $\frac{12}{4}=3$.

|
3
|
Geometry
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
B4. We consider $5 \times 5$ tables with 25 numbers written in them. The same number can appear multiple times, but in no row or column does the same number appear five times. We call such a table beautiful if in each row the middle number is the average of the numbers in that row, and in each column the middle number is the average of the numbers in that column. The score of a beautiful table is the number of numbers in the table that are smaller than the number that is exactly in the middle of the table.
What is the smallest possible score of a beautiful table?
|
B4. 3
We first show that every beautiful table has a score of at least 3. Consider such a table and let the number exactly in the middle be $a$. The five numbers in the middle row have $a$ as their average and are not all equal to $a$. At least one of these five numbers must therefore be smaller than $a$. Similarly, (at least) one of the five numbers in the middle column must be smaller than $a$, say the number $b$. Since $b$ is the average of the numbers in its row, one of the five numbers in this row is smaller than $b$ and thus also smaller than $a$. We have now found three numbers in different positions in the table, each smaller than the number exactly in the middle. The score is therefore at least 3.
In the figure on the right, you can see that there exists a beautiful table with a score of 3. A score of 3 is thus the lowest possible score.
| 4 | 4 | 3 | 4 | 0 |
| ---: | ---: | ---: | ---: | ---: |
| 4 | 4 | 3 | 4 | 0 |
| 3 | 3 | 0 | 3 | -9 |
| 4 | 4 | 3 | 4 | 0 |
| 0 | 0 | -9 | 0 | -36 |
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A8. A motorboat moves relative to the water at a constant speed of 25 kilometers per hour. It sails from Arnhem to Zwolle with the constant current. At a certain moment, it has covered $42\%$ of the distance. From that point, it takes the same amount of time to continue sailing to Zwolle as it does to sail back to Arnhem.
What is the speed of the current in kilometers per hour?
A) 3
B) 4
C) $\frac{9}{2}$
D) 5
E) 6
## B-questions
|
A8. B) 4 From the mentioned point, we can travel $42\%$ of the distance upstream and $58\%$ of the distance downstream in the same time. This means that the boat goes $\frac{58}{42}$ times faster with the current than against it. If we denote the current speed as $v$, we then find that $\frac{25+v}{25-v}=\frac{58}{42}$. This gives $58 \cdot(25-v)=42 \cdot(25+v)$, or $1450-58 v=1050+42 v$. We find that $400=100 v$, or $v=4$.
|
4
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
A1. A traffic light alternates between green and red at regular intervals. The green and red periods last the same amount of time, always 1, 2, or 3 minutes. There are four color combinations for the light at the times 12:08 and 12:09: red-red, red-green, green-red, and green-green. How many of the four combinations are possible given that the light was red at exactly 12:05 and also red at exactly 12:12?
A) 1
B) 2
C) 3
D) 4
E) The light cannot be red at both 12:05 and 12:12.
|
A1. B) 2
Given that the traffic light is red at 12:05. For a traffic light of period 1, the colors for the times 12:05 to 12:12 are fixed, alternating between red and green. For period 2, there are two possibilities, and for period 3, there are three possibilities:
| period | 12:05 | 12:06 | 12:07 | 12:08 | 12:09 | $12: 10$ | $12: 11$ | $12: 12$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 1 min | red | green | red | green | red | green | red | green |
| $2 \mathrm{~min}$ | red | red | green | green | red | red | green | green |
| $2 \mathrm{~min}$ | red | green | green | red | red | green | green | red |
| $3 \mathrm{~min}$ | red | red | red | green | green | green | red | red |
| $3 \mathrm{~min}$ | red | red | green | green | green | red | red | red |
| $3 \mathrm{~min}$ | red | green | green | green | red | red | red | green |
Of these six possibilities, three meet the condition that the light is red at 12:12. For the times 12:08 and 12:09, this results in two color combinations: red-red and green-green.
|
2
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
A4. Nine lamps are arranged in a square. Each lamp can be on or off. If you press a lamp, that lamp and the lamps in the same row or column change state: from on to off or vice versa. Initially, all lamps are on.
What is the smallest number of presses needed to turn all the lamps off?

A) 3
B) 4
C) 5
D) 9
E) It is not possible.
|
A4. A) 3 The order in which the lights are pressed does not matter for the final result. By pressing the three lights in the top row, all lights change from on to off. The lights in the top row change state three times, and the other lights change state exactly once.
It is not possible to turn off all the lights by pressing two (or fewer) lights. Indeed, there will then be a light that does not lie in the same row or column as one of the pressed lights. This light will therefore remain on.
|
3
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
A2. In a magic square, the three row sums, the three column sums, and the two diagonal sums are equal to each other. (A row sum is the sum of the numbers in a row, etc.) For the $3 \times 3$ magic square depicted here, three numbers have been filled in.
Which number must be placed in the position of the question mark?
A) 2
B) 4
C) 6
D) 8
E) 9

|
A2. B) $4 \quad$ See figure. From $F+10+3=F+D+7$ it follows that $D=6$. From $7+E+3=C+D+E=C+6+E$ it follows that $C=7+3-6=4$.
|
4
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
B2. From a set of 50 different numbers from the collection $\{1,2,3, \ldots, 100\}$, the sum is equal to 2900. What is the smallest possible number of even numbers among these 50 numbers?
|
B2. 6 If you take all 50 odd numbers from the set $\{1,2,3, \ldots, 100\}$, their sum is $\frac{1}{2} \times 50 \times(1+99)=2500$. That is 400 too little. Therefore, replace the smallest odd numbers with the largest possible even numbers, each time in pairs because 400 is even. If we replace 1 and 3 with 100 and 98, we get 2694. Then $2694-5-7+96+94=2872$. We need to do at least one more such step. And that works: $2872-9-11=2852$, so replace, for example, 20 and 28; then we have found a sum of 2900 with 6 even numbers and we have also shown that it cannot be done with fewer.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A8. How many different (real) solutions does the equation $\left(\left(x^{2}-2\right)^{2}-5\right)^{2}=1 \quad$ have?
A) 4
B) 5
C) 6
D) 7
E) 8
## B-questions
|
A8. B) 5 The equation is equivalent to
$$
\left(x^{2}-2\right)^{2}-5=1 \quad \text { or } \quad\left(x^{2}-2\right)^{2}-5=-1 .
$$
The first part is equivalent to $x^{2}-2=\sqrt{6}$ or $x^{2}-2=-\sqrt{6}$, with 2 and 0 solutions respectively (the latter due to $-\sqrt{6}+2<0$).
The second part is equivalent to $x^{2}-2=2$ or $x^{2}-2=-2$, with 2 and 1 solution(s) respectively. Therefore, in total $2+0+2+1=5$ solutions.
|
5
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
A1. The fields of a $4 \times 4$ board are colored white or black. Next to each row and below each column, it is indicated how many fields in that row or column must be black.
In how many ways can the board be colored?
A) 0
B) 1
C) 4
D) 5
E) 8

|
A1. D) 5 Note first that all boxes in the second row and in the second column must be colored white. We consider two cases, depending on the color of the box in the top left corner.
If this box is white, the last two boxes in the first row and column must be black. This fixes the coloring. See the top figure.
If this box is black, one more box in the first column and one more box in the first row must be black. For each of the $2 \times 2=4$ choices, there is exactly one solution. There is then still one row and one column missing a black box. The box in that row and column must therefore be black, and the rest white, see the bottom four figures.

|
5
|
Combinatorics
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
B1. For the number $x$, it holds that: $x=\frac{1}{1+x}$. Calculate $x-\frac{1}{x}$. Simplify your answer as much as possible.
|
B1. -1 Given that $x=\frac{1}{1+x}$. We see that $x \neq 0$, because $0 \neq \frac{1}{1}$. We can therefore invert the fraction on both sides. This gives $\frac{1}{x}=1+x$. From this, it follows that $x-\frac{1}{x}=x-(1+x)=-1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A6. The number $a=11 \ldots 111$ consists of exactly 2011 ones.
What is the remainder of $a$ when divided by 37?
A) 0
B) 1
C) 3
D) 7
E) 11
|
A6. B) 1 Door with a division of $a=11 \cdots 11$ (2011 ones) to be divided by 37, it quickly becomes apparent that 111 is divisible by 37. We will use this fact. We now see that the number $1110 \cdots 0$ is divisible by 37, regardless of the number of zeros at the end. In particular

$1110 \cdots 0$ (2002 zeros), and so on until 1110 (1 zero). The sum of these numbers is $1 \ldots 10$ (2010 ones) and is therefore also divisible by 37. The remainder of $a$ when divided by 37 is thus equal to 1, because $a-1$ is divisible by 37.
|
1
|
Number Theory
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
A1. A square is divided into two rectangles by a straight line. The combined perimeters of the two rectangles are 30 centimeters. How many centimeters long is the side of the square?
A) 5
B) 6
C) $\frac{15}{2}$
D) 8
E) 12

|
A1. A) 5 If you add the perimeters of the two rectangles, you get the perimeter of the square plus twice the length of the line segment in the middle. That line segment in the middle is exactly as long as the side of the square. The sum of the perimeters of the two rectangles is therefore equal to six times the length of the side of the square. In other words: the side of the square has a length of $\frac{30}{6}=5$.
|
5
|
Geometry
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
A5. Jan has a wooden cube. Each of the faces he divides into a $2 \times 2$ grid of squares, which he then paints in a black-and-white pattern: two diagonally adjacent squares are black, and the other two are white. At each corner of the cube, three squares come together. If two or three of these are black, we call the corner dark.

What is the smallest possible number of dark corners that the cube can have?
A) 0
B) 1
C) 2
D) 3
E) 4
|
A5. C) 2 On the cube, after distribution, there are a total of 24 squares: 12 white and 12 black. The number of dark vertices cannot be zero, because then the number of black squares would not exceed \(8 \times 1=8\) (one per vertex). The number of dark vertices also cannot be one, because then the number of black squares would not exceed \(3+7 \times 1=10\). In the figure, you can see a solution where only two vertices are dark. Therefore, the minimum number is 2.

|
2
|
Combinatorics
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
A6. In how many ways can you make the number 100 by choosing a sequence of consecutive numbers from 1 to 99 and adding them together?
A) 1
B) 2
C) 3
D) 4
E) 5
|
A6. B) 2
Let the number of numbers we add together be $n$. There are two cases.
$n$ is odd In this case, there is a middle number. Let this number be $k$. The sum of the $n$ numbers is then $n \times k=100$. Since $n$ is an odd divisor of 100 (and greater than 1), $n$ must be 5 or 25. In the first case, we find $k=\frac{100}{5}=20$ and the solution $18+19+20+21+22=100$. In the second case, we find $k=4$, but this does not give a solution because the smallest of the 25 numbers would then be equal to $4-12$, which is a negative number.
$n$ is even Let $n=2m$. The sum of the two middle numbers is an odd number, say $k$. The sum now consists of $m$ pairs of numbers, each with a sum of $k$. This means $100=k \times m$. Since $k$ is an odd divisor of 100 (and greater than 1), it follows that $k=5$ or $k=25$. In the first case, $m=20$ and the two middle numbers are 2 and 3. This does not give a solution, because then the smallest number would be equal to $3-20$, which is negative. In the second case, $m=4$ with the solution $100=9+10+11+12+13+14+15+16$.
|
2
|
Number Theory
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
3. In a criminal investigation, five suspects have been arrested. They all make one statement:
Eva: "We are all innocent."
Fatima: "Exactly one of us is innocent."
Kees: "Exactly one of us is guilty."
Manon: "At least two of us are innocent."
Mustafa: "At least two of us are guilty."
It turns out that only the guilty ones lie and the innocent ones tell the truth. How many guilty suspects are there among these five?
A) 1
B) 2
C) 3
D) 4
E) 5
|
A3. C) 3 At most one of the statements made by Eva, Fatima, and Kees can be true. Therefore, at least two of them are lying and are guilty. From this, we can already conclude that Eva and Kees are lying and thus guilty. Therefore, Mustafa is telling the truth and is innocent.
Fatima cannot be telling the truth, because then she and Mustafa would both be innocent, which contradicts her own statement. Therefore, Fatima is guilty.
Manon cannot be lying, because then she would be guilty and Mustafa would be the only innocent person. But then Fatima would indeed be telling the truth.
We conclude that Manon and Mustafa are the only innocent ones. This also matches their own statements and the lies of the other three.
|
3
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
6. A $100 \times 100$ board is filled with numbers. In the bottom-left cell, there is a 0. From any other cell $V$, we consider a path from the bottom-left cell to cell $V$, where you can only move right or up, not diagonally. If you add up all the numbers you encounter along the way and then add 1 for each step you have taken, you get the number that is in cell $V$.

In the partial board shown above, the number 15 is obtained from $(0+1+3+7)+4=15$.
What is the last digit of the number in the top-right cell of the $100 \times 100$ board?
A) 1
B) 3
C) 5
D) 7
E) 9
|
A6. $\quad$ B) 3 We consider a route from the bottom-left square to the top-right square. This route consists of $99+99=198$ steps. The numbers on the squares along this route we call $a_{0}, a_{1}, a_{2}, \ldots, a_{198}$.
We know that $a_{0}=0, a_{1}=1$ and $a_{2}=3$. To calculate the next number, $a_{3}$, we need to add the numbers $a_{0}, a_{1}$ and $a_{2}$, and add 1 for each step we take. We find that $a_{3}=\left(a_{0}+1\right)+\left(a_{1}+1\right)+\left(a_{2}+1\right)=7$. To then calculate the next number, which is $a_{4}$, we need to take the same sum and add $a_{3}+1$. Thus, we see that $a_{4}=a_{3}+\left(a_{3}+1\right)=15$. In general, we see that
$$
a_{k+1}=\left(a_{1}+1\right)+\ldots+\left(a_{k-1}+1\right)+\left(a_{k}+1\right)=a_{k}+\left(a_{k}+1\right)=2 a_{k}+1
$$
If we only look at the last digits, we will notice that they repeat; after the first 0, we get: $1,3,7,5,1,3,7,5$, and so on. It is easy to explain why this regularity occurs. The last digit of $a_{k+1}$ depends only on the last digit of $a_{k}$. For this reason, this regularity continues up to and including $a_{198}$. Therefore, the numbers $a_{2}, a_{6}, a_{10}, a_{14}, \ldots, a_{198}$ all end in 3.
|
3
|
Combinatorics
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
## Problem 3.
Let $a_{n}=1+n^{3}$ be the sequence $\{2,9,28,65, \ldots\}$ and $\delta_{n}=\operatorname{gcd}\left(a_{n+1}, a_{n}\right)$. Find the maximum value that $\delta_{n}$ can take.
|
Solution: $\delta_{n}$ divides $a_{n+1}$ and $a_{n}$, and therefore their difference $b_{n}=a_{n+1}-a_{n}=3 n^{2}+3 n+1$.
It also divides $c_{n}=3 a_{n}-n b_{n}=3-n-3 n^{2}$ and the sum $d_{n}=b_{n}+c_{n}=4+2 n$. But then $\delta_{n}$ also divides $e_{n}=2 b_{n}-3 n d_{n}=2-6 n$. Finally, it divides $3 d_{n}+e_{n}=14$.
But $b_{n}=3 n^{2}+3 n+1=3 n(n+1)+1$ is an odd number, so $\delta_{n}$ can only be 1 or 7. The maximum is 7 since $\operatorname{mcd}\left(5^{3}+1,6^{3}+1\right)=7$.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Let $x, y, z$ be positive real numbers such that $x+y+z=3$. Find the maximum value reached by
$$
\sqrt{x}+\sqrt{2 y+2}+\sqrt{3 z+6}
$$
For what values of $x, y, z$ is this maximum achieved?
|
Solution 1. Consider the vectors $(\sqrt{x}, \sqrt{y+1}, \sqrt{z+2})$ and $(\sqrt{1}, \sqrt{2}, \sqrt{3})$, whose coordinates are all real and positive, whose respective magnitudes are $\sqrt{x+y+z+3}=$ $\sqrt{6}$ and $\sqrt{1+2+3}=\sqrt{6}$, and whose dot product is the expression whose maximum is to be found. By the dot product inequality, the maximum value is equal to the product of the magnitudes of the vectors, which is 6, with equality occurring when both vectors are proportional. In this case, since both vectors have the same magnitude, equality occurs if and only if both vectors are equal, that is,
$$
\sqrt{x}+\sqrt{2 y+2}+\sqrt{3 z+6} \leq 6
$$
with equality if and only if $x=y=z=1$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem 6.
It is known that the polynomial $\mathrm{p}(\mathrm{x})=\mathrm{x}^{3}-\mathrm{x}+\mathrm{k}$ has three roots that are integers.
Determine the number k.
|
For $\mathrm{k}=0$ we have $\mathrm{p}(\mathrm{x})=\mathrm{x}^{3}-\mathrm{x}=\mathrm{x}(\mathrm{x}-1)(\mathrm{x}+1)$, which has roots $0, -1 \text{ and } 1$.
It is shown that this is the only value of $k$ for which $\mathrm{p}(\mathrm{x})$ has three integer roots. Indeed, if $a, b, c$ are integers, and $p(x)=(x-a)(x-b)(x-c)$, we get:
$$
\left.\begin{array}{c}
a+b+c=0 \\
ab+ac+bc=-1 \\
abc=-k
\end{array}\right\}
$$
Then,
$$
(a+b+c)^{2}=0=a^{2}+b^{2}+c^{2}+2(ab+ac+bc)=a^{2}+b^{2}+c^{2}-2
$$
That is, $a^{2}+b^{2}+c^{2}=2$, where $a^{2}, b^{2}, c^{2}$ are non-negative integers. Necessarily, one of the values $a, b$ or $c$ must be zero, so $\mathrm{k}=-\mathrm{abc}=0$.
They can also represent $q(x)=y \quad$ and observe that $q(x)+k$ cannot have three integer roots, as there are no integers in $(-1,0)$ or in $(0,1)$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. We have 50 chips numbered from 1 to 50, and they need to be colored red or blue. We know that chip 5 is blue. For the coloring of the rest of the chips, the following rules are followed:
a) If the chip with the number $x$ and the chip with the number $y$ are of different colors, then the chip with the number $|x-y|$ is painted red.
b) If the chip with the number $x$ and the chip with the number $y$ are of different colors and $x \cdot y$ is a number between 1 and 50 (inclusive), then the chip with the number $x \cdot y$ is painted blue.
Determine how many different colorings can be performed on the set of chips.
|
Solution. Let's observe that two numbers differing by 5 have the same color. Indeed, if they were of different colors, their difference should be red, according to rule a). But their difference is 5, which is blue. Therefore, it is enough to know the color of the first 4 numbers. Here, we distinguish two cases: 1) the tile 1 is blue, and 2) the tile 1 is red.
Case 1) If 1 is blue, the rest of the tiles must be blue, by rule b). This is because if the tile $k \neq 1$ were red, then by b), $k = k \cdot 1$ would have to be blue, which contradicts that $k$ is red.
Case 2) If 1 is red, by rule a) $4 = 5 - 1$ is red. To determine the color of 2 and 3, suppose 3 is blue. Since $2 = 3 - 1$ and 3 and 1 are of different colors, then 2 is red. Now, $3 = 5 - 2$ and 5 is blue and 2 is red, so 3 is red. This cannot be, therefore 3 cannot be blue and is red, which means 2 is also red. Thus, 1, 2, 3, and 4 are red, as are the rest of the tiles that are not multiples of 5.
Therefore, there are only two possible colorings, either all tiles are blue or all are red, except for the multiples of 5 which are blue.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5 Solve the exponential equation
$$
2^{x} \cdot 3^{5^{-x}}+\frac{3^{5^{x}}}{2^{x}}=6
$$
|
Solution. Applying the arithmetic and geometric means inequality and, subsequently, one of its most well-known consequences (the sum of a positive real number and its inverse is always greater than or equal to 2, and equality only holds for the number 1), we have,
$$
6=2^{x} 3^{5^{-x}}+2^{-x} 3^{5^{x}} \geq 2 \sqrt{2^{x} 3^{5^{-x}} 2^{-x} 3^{5 x}}=6 .
$$
And equality will hold when the numbers being averaged are equal.
$$
2^{x} 3^{5^{-x}}=2^{-x} 3^{5^{x}} \Leftrightarrow 2^{2 x}=3^{5^{x}-5^{-x}} \Leftrightarrow 5^{x}=5^{-x}
$$
which is, when $x=0$, which will be, therefore, the only solution to the equation.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In a triangle $ABC$, the angle bisector from $A$, the median from $B$, and the altitude from $C$ are concurrent, and moreover, the angle bisector from $A$ and the median from $B$ are perpendicular. If the side $AB$ measures one unit, find the lengths of the other two sides.
|
Solution. We provide two different solutions.
Solution 1. Let $P, M$, and $Q$ be the feet of the angle bisector from $A$, the median from $B$, and the altitude from $C$, respectively, which intersect at point $X$. In triangle $ABM$, the angle bisector from $A, AX$, is perpendicular to $BM$ (since by hypothesis the median and the angle bisector of $ABC$ are perpendicular), so $\angle ABX = \angle AMX$, which means $ABM$ is isosceles and $AM = AB = 1$, hence $AC = 2$.
Let $BP = x$ and $BQ = y$. By the Angle Bisector Theorem, $BP / AB = PC / AC$, which gives $PC = 2x$. Now, by Ceva's Theorem,
$$
1 = \frac{MC}{CP} \cdot \frac{PB}{BQ} \cdot \frac{QA}{AM} = \frac{1}{2x} \cdot \frac{x}{y} \cdot \frac{1-y}{1}
$$
from which $y = 1 / 3$. We draw the perpendiculars to $AC$ from $B$ and $X$, respectively, with feet $R$ and $S$. Triangles $XQB$ and $XSM$ are congruent (they are right triangles, $XB = XM$ because $AX$ is the altitude of the isosceles triangle $ABM$, and $XQ = XS$ because they are perpendiculars from a point on the angle bisector to the sides $AB$ and $AC$), so $SM = BQ = y = 1 / 3$. On the other hand, by Thales' Theorem, $BX = XM$ implies $RS = SM$, so $RS = 1 / 3$ and $AR = AM - RS - SM = 1 / 3$. Finally, by the Pythagorean Theorem,
$$
BC^2 = BR^2 + RC^2 = AB^2 - AR^2 + RC^2 = 1 - \frac{1}{9} + \left(2 - \frac{1}{3}\right)^2 = \frac{11}{3}
$$
Thus, the other two sides measure 2 and $\frac{\sqrt{33}}{3}$.

Solution 2. As before, $AC = 2$. We fix a coordinate system with origin at $A$ such that $\overrightarrow{AC} = (2, 0)$. Let $\overrightarrow{AB} = (x, y)$. Then
$$
\overrightarrow{CX} = \overrightarrow{CA} + \overrightarrow{AX} = (-2, 0) + \left(\frac{x+1}{2}, \frac{y}{2}\right) = \left(\frac{x-3}{2}, \frac{y}{2}\right)
$$
(note that $X$ is the midpoint of $BM$). But the vectors $\overrightarrow{AB}$ and $\overrightarrow{CX}$ are orthogonal, so $x(x-3) + y^2 = 0$. Since $x^2 + y^2 = 1$, we have $x = 1 / 3$ and $y = \sqrt{8} / 3$. By the Pythagorean Theorem, $BC^2 = y^2 + (2 - x)^2 = 11 / 3$, which means $BC = \sqrt{33} / 3$.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem II - 5
The natural numbers 22, 23, and 24 have the following property: the exponents of the prime factors in their factorization are all odd:
$$
22=2^{1} \cdot 11^{1} ; \quad 23=23^{1} ; \quad 24=2^{3} \cdot 3^{1}
$$
What is the largest number of consecutive natural numbers that can have this property? Justify your answer.
|
## Solution
We will prove that it is impossible to find 8 consecutive numbers with this property. Suppose, for the sake of contradiction, that such 8 consecutive numbers exist. One of them, which we will call $n$, is divisible by 8.
Among the 8 numbers, there must be either $n+4$ or $n-4$. Both are divisible by 4, but not by 8, and this is a contradiction because the exponent of 2 in this number must be even.
The example of the numbers
$$
29,30,31,32,33,34,35
$$
finally demonstrates that the maximum sought is 7, and that it is indeed achieved.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Let $p \geq 3$ be a prime number, and consider the right triangle with the larger leg $p^{2}-1$ and the smaller leg $2p$. We inscribe a semicircle in the triangle whose diameter lies on the larger leg of the triangle and is tangent to the hypotenuse and the smaller leg of the triangle. Find the values of $p$ for which the radius of the semicircle is an integer.
|
Solution. In the right triangle $ABC$, we consider $\overline{AB}=p^{2}-1$, $\overline{AC}=2p$.
By the Pythagorean Theorem, we have $\overline{BC}^{2}=\overline{AC}^{2}+\overline{AB}^{2}$, so
$\overline{BC}^{2}=(2p)^{2}+\left(p^{2}-1\right)^{2}=4p^{2}+p^{4}-2p^{2}+1=p^{4}+2p^{2}+1=\left(p^{2}+1\right)^{2}$, from which we obtain that $\overline{BC}=p^{2}+1$.
Let $r$ be the radius of the semicircle, $E$ the center of the circle on side $AB$, and $F$ the point of tangency of the semicircle with side $BC$. We have $\overline{AE}=\overline{EF}=r$. On one hand, the area of triangle $ABC$ is given by
$$
\text{Area}(ABC)=\frac{1}{2} \overline{AB} \cdot \overline{AC}=\left(p^{2}-1\right) p
$$
On the other hand,
$$
\begin{gathered}
\text{Area}(ABC)=\text{Area}(AEC)+\text{Area}(ECB)=\frac{1}{2} \overline{AE} \cdot \overline{AC}+\frac{1}{2} \overline{BC} \cdot \overline{EF}= \\
\frac{1}{2} r \cdot 2p+\frac{1}{2}\left(p^{2}+1\right) \cdot r=\frac{r}{2}\left(p^{2}+2p+1\right)=\frac{r}{2}(p+1)^{2}
\end{gathered}
$$
Equating the two expressions for the area of triangle $ABC$, we get
$$
\frac{r}{2}(p+1)^{2}=\left(p^{2}-1\right) p
$$
from which
$$
r=\frac{\left(p^{2}-1\right) 2p}{(p+1)^{2}}=\frac{2p(p-1)}{p+1}
$$
It is a simple calculation to verify that
$$
2p-4<\frac{2p(p-1)}{p+1}<2p
$$
so the only possible values for $r$ are $2p-1$, $2p-2$, and $2p-3$.
- If $r=2p-1$, then
$$
2p-1=\frac{2p(p-1)}{p+1} \Longrightarrow 2p^{2}+2p-p-1=2p^{2}-2p \Longrightarrow p=\frac{1}{3}
$$
- If $r=2p-2=2(p-1)$, then
$$
2(p-1)=\frac{2p(p-1)}{p+1} \Longrightarrow 1=\frac{2p}{p+1} \Longrightarrow p=1
$$
- If $r=2p-3$, then
$$
2p-3=\frac{2p(p-1)}{p+1} \Longrightarrow 2p^{2}+2p-3p-3=2p^{2}-2p \Longrightarrow p=3
$$
Therefore, the only valid solution is $p=3$, which gives the value of $r=3$.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. Calculate the maximum number of distinct real roots that a polynomial $P$ can have, which satisfies the following property: the product of two distinct roots of $P$ is still a root of $P$.
|
Solution. The answer is 4. The polynomial $x(x-1 / 2)(x-1)(x-2)$, with roots 0, 1/2, 1, and 2, satisfies the given bound. Suppose there was a polynomial with at least 5 distinct roots. It is important to note that a polynomial has a finite number of roots, which allows us to take maximums and minimums.
If a polynomial has 5 roots, at least 4 would be non-zero, and we distinguish two cases.
1. If -1 is a root, there is at least one root (in fact, at least two) with a non-zero absolute value different from 1. Let $A$ be a root with the largest absolute value among all roots and assume that $|A|>1$. Since -1 and $A$ are roots, $-A$ is a root; but then $-A \cdot A=-A^{2}$ would also be a root and $\left|A^{2}\right|>|A|$, which would contradict the maximality of the absolute value of $A$.
If there are no roots with an absolute value $>1$, take $A$ as one of the roots with the smallest absolute value among all non-zero roots. Then $|A|<1$, and since -1 and $A$ are roots, $-A$ is a root and so is $-A \cdot A=-A^{2}$. But then, $\left|A^{2}\right|<|A|$, which would contradict the minimality of the absolute value of $A$ among the non-zero roots.
2. If -1 is not a root, there are at least three non-zero roots with a modulus different from 1. There are then two roots $A, B$ with the two largest absolute values (greater than 1) or two roots with the two smallest absolute values $A, B$ (less than 1 and non-zero). In either case, multiplying $A \cdot B$ leads to a contradiction with the maximality or minimality.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem 6
Find all positive integers $n$ such that $3^{n}+5^{n}$ is a multiple of $3^{n-1}+5^{n-1}$.
|
## Solution:
For such an $n$, since
$$
3\left(3^{n-1}+5^{n-1}\right)<3^{n}+5^{n}<5\left(3^{n-1}+5^{n-1}\right)
$$
it follows that
$$
3^{n}+5^{n}=4\left(3^{n-1}+5^{n-1}\right)
$$
which reduces to
$$
5^{n-1}=3^{n-1}
$$
implying $n=1$.
Since $n=1$ is a solution (because 8 is a multiple of 2), it is concluded that $n=1$ is the only solution.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Determine all positive integers $x$, such that $2x+1$ is a perfect square, but among the numbers $2x+2, 2x+3, \cdots, 3x+2$, there is no perfect square.
|
Solution. Let $n$ be an integer such that $2 x+1=n^{2}$ and $n^{2} \leq 3 x+2<(n+1)^{2}$. From the first equation, we get $x=\left(n^{2}-1\right) / 2$, and substituting this value into the double inequality, we obtain
$$
n^{2} \leq \frac{3 n^{2}+1}{2}<n^{2}+2 n+1 \Leftrightarrow 2 n^{2} \leq 3 n^{2}+1<2 n^{2}+4 n+2
$$
In the last expression, the first inequality holds for all integer $n$, the second can be written as
$$
n^{2}-4 n-1<0 \Leftrightarrow 2-\sqrt{5}<n<2+\sqrt{5}
$$
and is satisfied for all integers $n \in\{0,1,2,3,4\}$. Among these values, only for $n=3$, we get that $x=\left(3^{2}-1\right) / 2=4$ is a positive integer, and this is the only solution to the problem, since in this case $2 x+1=9$ and among the numbers $10,11,12,13$ and 14 there is no perfect square.
2. $2 n+1$ chips, white and black, are placed in a row $(n \geq 1)$. A chip is said to be balanced if the number of white chips to its left, plus the number of black chips to its right is $n$. Determine, with reasoning, whether the number of chips that are balanced is even or odd.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## - Problem 1
A pucelana sequence is a strictly increasing sequence of sixteen consecutive positive odd numbers, whose sum is a perfect cube. How many pucelana sequences consist only of three-digit numbers?
|
## Solution:
Let the sequence be $n, n+2, \ldots, n+30$. Then the sum is $\frac{1}{2} \cdot 16(2 n+30)=8(2 n+30)$. Therefore, it is necessary that $2 n+30$ be a perfect cube. Now we need to count the number of such $n$ that are odd and satisfy $101 \leq n \leq 969$. The even cubes between 232 and 1968 are 512, 1000, and 1728, which correspond to values of $n$ of 241, 485, and 849. Therefore, there are exactly three such sequences.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Each rational number is painted with one of two colors, white and red. Such a coloring is called sanferminera when for any two rational numbers $x, y$, with $x \neq y$, if one of the following three conditions is met:
a) $x y=1$,
b) $x+y=0$,
c) $x+y=1$,
then $x$ and $y$ are painted in different colors. How many sanferminera colorings are there?
## SOLUTION:
Translate the above text into English, please keep the original text's line breaks and format, and output the translation result directly.
|
If a coloring is sanferminera, we can find another sanferminera coloring by simultaneously swapping the color of each rational, from red to white and from white to red; if in the initial coloring two rationals have different colors, they will also have different colors in the resulting one. Let's then find the number of sanferminera colorings such that, without loss of generality, the rational 1 is painted red, and the total number of sanferminera colorings will be exactly double.
Suppose then that we have a sanferminera coloring with 1 painted red. Given the color of the rational $x>0$, the color of the rational $-xu^{\prime}$, and after at most $u$ steps, we would reach $u^{\prime}=0$, that is, to an integer, which does have an associated color. Note also that the process is unique since, at each step, the values of $m, u, v$ are uniquely determined by the value of the positive rational $q$, so with all positive integers being red, each positive rational will have one and only one associated color. This unique coloring for positive rationals extends uniquely to all rationals, as we have already seen. There is then at most one sanferminera coloring painting the rational 1 red.
Let's check that indeed this unique coloring we have constructed satisfies the conditions of the statement:
1) If $x+y=0$ with $x \neq y$, without loss of generality $x>0>y=-x$, so $y$ has, by the way of extending the coloring to all rationals, a different color from $x$.
2) If $x y=1$ with $x \neq y$, either both are positive, or both are negative, having in the second case $x, y$ colors respectively opposite to those of $-x,-y$, which would be positive, reducing the verification to the first case. If $x, y$ are both positive, without loss of generality $x>1>y$, with $y=0+\frac{u}{v}$ for positive integers $uy$, and either $x=1$ is red, $y=0$ is white, or $x>1>0>y$, or $1>x>y>0$. In the second case, the positive rational $x-1$ has, by construction, the same color as $x$, so by 1), $x$ has the opposite color of $1-x=y$. In the third case, there exist positive integers $u<v$ coprime such that $x=\frac{v}{u+v}, y=\frac{u}{u+v}$. By construction and by 2), $x$ has the opposite color of $\frac{u+v}{v}=1+\frac{u}{v}$, so $x$ has the same color as $\frac{v}{u}$. But also by construction and by 2), $y$ has the opposite color of $y=\frac{u+v}{u}=1+\frac{v}{u}$, so opposite to $\frac{v}{u}$, and opposite to $x$.
Thus, the constructed coloring is sanferminera, and it is the only one that can be sanferminera with the rational 1 painted red. Restoring generality, there are exactly two sanferminera colorings.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Let $n$ be a natural number and a convex polygon with $n$ vertices. Each of the sides and diagonals of this polygon is colored either blue or red. Determine the smallest $n$ such that, for any such coloring, there exist three vertices of the observed polygon that are mutually connected by segments of the same color.
|
5. For $n=4$, we color the sides in one color, for example, blue, and the diagonals in another - red. It is then obvious that there does not exist a triangle whose vertices are the vertices of this quadrilateral, and all sides are colored in the same color.
For $n=5$, we color the sides in one color, for example, blue, and the diagonals in another - red. It is then obvious that there does not exist a triangle whose vertices are the vertices of this pentagon, and all sides are colored in the same color.
This proves that the desired $n>5$.

Now, let's prove that for any hexagon, no matter how we color each of the sides and diagonals of a regular hexagon in blue or red, there must exist at least one triangle whose vertices are also vertices of the hexagon and whose sides are all colored in the same color.
Consider one vertex of the hexagon, let's call it A. From it, there are five connections to other vertices, which are colored either blue or red.
Since $5=2 \cdot 2+1$, by the Dirichlet principle, there exists a color such that at least three of these connections are colored in that color. For example, let's say it is red.
Label the vertices that determine these connections with vertex $A$ as $B, C$, and $D$, so the red connections are $\overline{A B}, \overline{A C}$, and $\overline{A D}$.
If at least one of the connections $\overline{B C}, \overline{B D}$, or $\overline{C D}$ is colored red, we have a monochromatic (red) triangle.
If not, then the triangle $\triangle B C D$ is monochromatic (blue).
Note: If a student does not consider the case $n=4$ but does consider the case $n=5$ and shows that it is possible to color the pentagon such that no triangle has monochromatic sides, they do not lose points.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Calculate: $2022 \cdot 35 - 2022 \cdot 34 + 32 \cdot 2022 - 33 \cdot 2022$.
|
First solution.
```
\(2022 \cdot 35-2022 \cdot 34+32 \cdot 2022-33 \cdot 2022\)
\(=2022 \cdot(35-34+32-33) \quad 4\) POINTS
\(=2022 \cdot 0 \quad 1\) POINT
\(=0 \quad 1\) POINT
TOTAL 6 POINTS
```
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. After conducting a survey among 96 sixth-grade students at his school, Leo drew a bar chart as shown in the image, but he did not highlight the numbers on the vertical axis or the names of the sports on the horizontal axis. He remembered that the number of students who swim is five times the number of students who play tennis, and twice the number of students who play handball. There are fewer basketball players than water polo players. How many students play basketball?

|
First solution.

From the condition of the problem that "five times more students swim than play tennis" and the ratio of the heights of the third and first bars, we conclude that the third bar represents swimmers, and the first bar represents tennis players.
As can be seen from the image, we have 24 unit parts. 1 POINT One unit part is $96: 24=4$. 1 POINT From the condition of the problem that "swimming is twice as popular as handball," we conclude that the fourth bar represents handball players.
1 POINT
From the condition of the problem that "there are fewer basketball players than water polo players," and the remaining are the second and fifth bars, we conclude that the second bar represents basketball players.
1 POINT
12 students play basketball.
1 POINT
TOTAL 6 POINTS
##
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. After conducting a survey among 96 sixth-grade students at his school, Leo drew a bar chart as shown in the image, but he did not highlight the numbers on the vertical axis or the names of the sports on the horizontal axis. He remembered that there are five times more students who swim than those who play tennis, and twice as many as those who play handball. There are fewer basketball players than water polo players. How many students play basketball?

|
Another solution.
From the condition of the problem that "five times more students swim than play tennis" and the ratio of the height of the third and the first column, we conclude that the third column represents swimmers, and the first column represents tennis players.
Let the number of students who play tennis be $x$ (1st column).
Then, $5x$ students swim (3rd column), and $2.5x$ students play handball (4th column). $\quad 1$ POINT
From the diagram, it can be observed, since there are fewer basketball players than water polo players, that $1.5x$ students play basketball (2nd column), and $2x$ students play water polo (5th column). 1 POINT
The equation holds: $\quad x+1.5x+5x+2.5x+2x=96 . \quad 1$ POINT
It follows that $\quad 12x=96$
$x=8$
1 POINT
The number of basketball players is $1.5 \cdot 8$, i.e., 12 students play basketball.
$1$ POINT
TOTAL 6 POINTS
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A polygon has 5 fewer sides than another polygon and 50 fewer diagonals than that other polygon. What is the polygon (the one with fewer sides)?
|
4. Let $n$ be the number of sides (vertices) of the sought polygon.
From one vertex of this polygon, $n-3$ diagonals can be drawn,
and the total number of diagonals of this polygon is $\frac{n(n-3)}{2}$.
In a polygon with $n+5$ sides,
from one vertex, $n+5-3=n+2$ diagonals can be drawn,
and the total number of diagonals of this polygon is $\frac{(n+5)(n+2)}{2}$.
According to the condition of the problem, we have: $\frac{n(n-3)}{2}+50=\frac{(n+5)(n+2)}{2}$
By solving this equation, we get in turn
$n(n-3)+100=(n+5)(n+2)$
$n^{2}-3 n+100=n^{2}+7 n+10$
$10 n=90$
and finally $n=9$.
$1 \text{ POINT}$
TOTAL 6 POINTS
Note: A solution obtained by the method of successive approximation (e.g., filling in a table) can be scored with 10 points. If there are no calculations, but only the correct final result, then it is scored with 2 points.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. The perimeter of a parallelogram is $30 \mathrm{~cm}$. The sum of the areas of the squares constructed on two adjacent sides is $113 \mathrm{~cm}^{2}$. What are the lengths of those sides?
The use of a pocket calculator or any reference materials is not allowed.
|
First method:
Sketch or description (Let $a$ be the length of the longer side, and $b$ be the length of the shorter side.)
Then we have $2a + 2b = 30$ or $a + b = 15$
and $a^2 + b^2 = 113$.
1 POINT
Since $(a + b)^2 = a^2 + 2ab + b^2$, after substitution we get $15^2 = 113 + 2ab$ or
$2ab = 225 - 113 = 112$.
2 POINTS
Since $(a - b)^2 = a^2 - 2ab + b^2$, after substitution we get
$(a - b)^2 = (a^2 + b^2) - 2ab = 113 - 112$, or $(a - b)^2 = 1$.
2 POINTS
If $(a - b)^2 = 1$, then (assuming $a > b$ or $a - b > 0$) it must be $a - b = 1$.
The lengths of the sides satisfy the system of equations $\left\{\begin{array}{l}a + b = 15 \\ a - b = 1\end{array}\right.$
1 POINT
By solving the system, we find the solution $a = 8 \text{ cm}$ and $b = 7 \text{ cm}$.
1 POINT
TOTAL 10 POINTS
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Determine the smallest possible value of the expression $4 x^{2}+4 x y+4 y^{2}+12 x+8$. For which $x$ and $y$ will this expression have the smallest value?
Each task is scored out of 10 points.
The use of a pocket calculator or any reference materials is not allowed.
|
5. Let's rewrite the given expression in another form, using the formula for the square of a sum:
$$
\begin{aligned}
4 x^{2}+4 x y+4 y^{2}+12 x+8 & =x^{2}+4 x y+4 y^{2}+3 x^{2}+12 x+12-4 \\
& =(x+2 y)^{2}+3\left(x^{2}+4 x+4\right)-4 \\
& =(x+2 y)^{2}+3(x+2)^{2}-4
\end{aligned}
$$
Since the square of a number is always non-negative, we conclude that $(x+2 y)^{2} \geq 0$ and $(x+2)^{2} \geq 0$, so the minimum value is achieved when $(x+2 y)^{2}=(x+2)^{2}=0$, and it is equal to -4. The minimum value is achieved when $x+2 y=0$ and $x+2=0$. From the second equation, we get $x=-2$, and from the first, $y=-\frac{x}{2}=-\frac{-2}{2}=1$.
|
-4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In a certain store, 2400 kilograms of flour were ordered. They planned to repackage it into 5 kg bags and sell each bag for 14 kn. When the goods arrived, they noticed that 300 kg of flour had been damaged during transport. By how much should the price of the 5 kg packaging be increased so that the planned profit remains the same despite the reduced amount of flour?
|
4. From the ordered quantity of flour, $2400: 5=480$ packages of $5 \mathrm{~kg}$ can be obtained.
1 POINT
The profit would be $480 \cdot 14=6720 \mathrm{kn}$.
1 POINT
$300 \mathrm{~kg}$ was destroyed, leaving $2100 \mathrm{~kg}$.
1 POINT
From this, $2100: 5=420$ packages of $5 \mathrm{~kg}$ can be made.
1 POINT
To achieve the same profit, the price of one package should be $6720: 420=16 \mathrm{kn}$.
1 POINT
The planned price of a $5 \mathrm{~kg}$ package should be increased by 2 kuna.
1 POINT
TOTAL 6 POINTS
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. A cat can catch 5 mice in 6 days. How many days will it take for 2 cats to catch 3 mice?
|
## 2. 5 cats catch 5 mice in 6 days.
Five times fewer cats catch five times fewer mice in the same time:
1 cat catches 1 mouse in 6 days.
Twice as many cats catch twice as many mice in the same time:
2 cats catch 2 mice in 6 days.
The same number of cats catch half as many mice in half the time:
2 cats catch 1 mouse in 3 days.
The same number of cats catch three times as many mice in three times the time:
2 cats catch 3 mice in 9 days.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The length of the side of the square is 1. Prove that for any line $p$ passing through the intersection of the diagonals, which does not pass through any vertex of the square and is not parallel to any of its sides, the following statement holds: "The sum of the squares of the distances from all four vertices of the square to the line $p$ is equal to 1."
|
5.

Let point $S$ be the intersection of the diagonals of square $ABCD$. Through point $S$, any line $m$ is drawn. Let points $M, N, P,$ and $R$ be the feet of the perpendiculars drawn from vertices $A, B, C, D$ of the square to line $m$.
Consider the right triangles $\triangle DNS$ and $\triangle BPS$. Since $|DS| = |BS|$ and $|\angle DSN| = |\angle BSP|$ (vertical angles) and $|\angle DNS| = |\angle BPS| = 90^\circ$, by the $\mathrm{K}-\mathrm{S}-\mathrm{K}$ theorem, these two triangles are congruent, and thus $|DN| = |BP| = y$.
Consider the right triangles $\triangle ASM$ and $\triangle CSR$. Since $|AS| = |CS|$ and $|\angle ASM| = |\angle CSR|$ (vertical angles) and $|\angle AMS| = |\angle CRS| = 90^\circ$, by the $\mathrm{K}-\mathrm{S}-\mathrm{K}$ theorem, these two triangles are congruent, and thus $|AM| = |CR| = x$.
Consider the right triangles $\triangle ASM$ and $\triangle BPS$. Since $|AS| = |BS|$ and $|\angle ASM| = |\angle S BP|$ (angles with perpendicular sides) and $|\angle AMS| = |\angle BPS| = 90^\circ$, by the $\mathrm{K}-\mathrm{S}-\mathrm{K}$ theorem, these two triangles are congruent, and thus $|AM| = |SP| = x$.
Let the diagonal $|BD| = |AC| = d = \sqrt{2}$. Applying the Pythagorean theorem to triangle $\triangle BPS$, we get
$$
|SP|^2 + |BP|^2 = |SB|^2 \Rightarrow x^2 + y^2 = \left(\frac{d}{2}\right)^2
$$
i.e.,
$$
x^2 + y^2 = \left(\frac{\sqrt{2}}{2}\right)^2 = \frac{1}{2}
$$
Then,
$$
|AM|^2 + |CR|^2 + |DN|^2 + |BP|^2 = x^2 + x^2 + y^2 + y^2 = 2(x^2 + y^2) = 1
$$
|
1
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
1. Andrija read a book over three days. While reading, his reading speed was constant. On the first day, he spent $\frac{1}{32}$ of a day reading, and each subsequent day he read for one-third less time than the previous day. What percentage of the book does Andrija still need to read if it takes him 1 hour and 40 minutes to read the entire book?
|
1. Andrija read a book over three days. While reading, his reading speed was constant. On the first day, he spent $\frac{1}{32}$ of a day reading, and each subsequent day he read for one-third less time than the previous day. What percentage of the book does Andrija still need to read if it takes him 1 hour and 40 minutes to read the entire book?
## Solution.
1 day has 24 hours or $24 \cdot 60=1440$ minutes.
Andrija spent $\frac{1}{32}$ of a day reading on the first day, which is $1440: 32=45$ minutes. $\quad 1$ POINT One-third of 45 is 15, so he spent $45-15=30$ minutes reading on the second day. 2 POINTS One-third of 30 is 10, so he spent $30-10=20$ minutes reading on the third day. $\quad 2$ POINTS Over the three days, Andrija spent a total of $45+30+20=95$ minutes reading. 1 POINT Andrija needs 1 hour and 40 minutes to read the entire book, which is $60+40=100$ minutes.
To finish reading the entire book, he still needs to read for $100-95=5$ minutes. 1 POINT
Expressed as a percentage, this is $\frac{5}{100}=5 \%$.
1 POINT
Andrija still needs to read $5 \%$ of the book.
TOTAL 10 POINTS
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The area of a rectangle is $\overline{3 x x 3}$, and the lengths of its adjacent sides are $\overline{x x}$ and $x^{2}$. Determine the digit $x$.
|
First solution.
The lengths of adjacent sides of the rectangle are $\overline{x x}$ and $x^{2}$, so $x \neq 0$, i.e., $x \in\{1,2, \ldots, 9\}$.
The area of the rectangle is $\overline{x x} \cdot x^{2}=\overline{3 x x 3}$.
1 POINT
The product $\overline{3 x x 3}$ is an odd number, so it is sufficient to consider $x \in\{1,3,5,7,9\}$.
2 POINTS
The last digit of the product $\overline{3 x x 3}$ is 3:
- For $x=1$, the last digit of the product $11 \cdot 1^{2}$ is different from 3, so $x \neq 1$. 1 POINT
- For $x=3$, the last digit of the product $33 \cdot 3^{2}$ is different from 3, so $x \neq 3$. 1 POINT
- For $x=5$, the last digit of the product $55 \cdot 5^{2}$ is different from 3, so $x \neq 5$. 1 POINT
- For $x=9$, the last digit of the product $99 \cdot 9^{2}$ is different from 3, so $x \neq 9$. 1 POINT
By checking $77 \cdot 49=3773 \quad 2$ POINTS
we get the solution $x=7$. 1 POINT
TOTAL 10 POINTS
##
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In September 2014, when they started the first grade, all students in 5.a grade together had 153 years, and in September 2018, at the beginning of the fifth grade, those same students had a total of 245 years. How many of them started school at six, and how many at seven years old?
Each task is scored out of 10 points.
The use of a pocket calculator or any manuals is not allowed.
|
First method:
From September 2014 to September 2018, 4 years have passed.
1 POINT
During this time, the total number of years of all students increased by
$245-153=92$ years.
2 POINTS
Since each student aged 4 years, there are
$92: 4=23$ students in the class.
2 POINTS
If all students started the first grade at 7 years old, they would have a total of $7 \cdot 23=161$ years.
2 POINTS
Since they had 153 years, then 6-year-olds started school
$161-153=8$ students.
2 POINTS
Then, 7-year-olds started school $23-8=15$ students.
1 POINT
TOTAL 10 POINTS
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Determine all natural numbers $n$ for which the number $\left|n^{2}-100\right|$ is prime.
## Problems worth 10 points:
|
5. Let $m=\left|n^{2}-100\right|$.
We have $m=\left|n^{2}-100\right|=|(n-10)(n+10)|$.
The number $m$ is prime if and only if one of the numbers $|n-10|$ and $|n+10|$ is equal to 1, and the other is a prime number.
$1 \text{ POINT}$
Notice that there are no natural numbers $n$ for which $|n+10|=1$.
Let's find all natural numbers $n$ for which $|n-10|=1$.
If $|n-10|=1$, then $n=9$ or $n=11$.
For $n=9$, $m=|(n-10)(n+10)|=19$, which is a prime number.
For $n=11$, $m=|(n-10)(n+10)|=21$, which is not a prime number.
Therefore, there is only one natural number $n$ for which $\left|n^{2}-100\right|$ is a prime number, and that is $n=9$.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Ivana chose two numbers $a$ and $b$ from the set $\{1,2,3,4, \ldots, 25,26\}$. The product $a \cdot b$ is equal to the sum of the remaining 24 numbers in that set of numbers. What is the value of the expression $|a-b|$?
|
First method:
Assume $a \geq b$.
Since $a$ and $b$ are from the set $\{1,2,3,4, \ldots, 25,26\}$ and their product is equal to the sum of the remaining 24 numbers, we have $a+b+a \cdot b=1+2+3+4+\ldots+25+26$ or $a+b+a \cdot b=351$.
Adding 1 to both sides of the equation, we get $a+b+a \cdot b+1=352$.
By factoring the left side, we obtain $(1+b) \cdot(1+a)=352$.
This means that the number 352 is the product of two natural numbers $a+1$ and $b+1$.
By factoring the number 352 into prime factors, we get $352=2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 11$.
Since the numbers $a$ and $b$ are from the set $\{1,2,3,4, \ldots, 25,26\}, a \geq b$, it follows that $a+1=22$ and $b+1=16$.
Thus, $a=21$ and $b=15$.
Therefore, $|a-b|=6$.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. A circle with center $O$ and diameter $|A B|=4 \text{ cm}$ is given. Draw three tangents to this circle, two at points $A$ and $B$, and the third at a point such that the segment $\overline{C D}$ between the first two tangents is $5 \text{ cm}$ long. Explain and describe the procedure.
|
First method: Algebraic approach.
It is necessary to determine the distance of point $C$ from line $A B$.
Sketch:

Draw a parallel line with the diameter $\overline{A B}$ through $C$ and let $x=|A C|=|B E|$.
We obtain a right triangle $C E D$ with the hypotenuse $\overline{C D}$ of length $5 \mathrm{~cm}$ and the leg $\overline{C E}$ of length $4 \mathrm{~cm}$. By applying the Pythagorean theorem, we calculate the length of the other leg $\overline{E D}$, so $|D E|=3 \mathrm{~cm}$. The length of $\overline{C F}$ is $x$ because triangles $A O C$ and $F O C$ are congruent. (Right triangles over the same hypotenuse $\overline{O C}$ - congruent two corresponding sides and congruent angles opposite the larger side.) The length of $\overline{F D}$ is $x+3$ because triangles $B O D$ and $F O D$ are congruent. (Right triangles over the same hypotenuse $\overline{O D}$ - congruent two corresponding sides and congruent angles opposite the larger side.) From the above two statements, it follows that $x+x+3=5$ or $2 x+3=5$ so $x=1 \mathrm{~cm}$.
Since the desired distance can be applied in four different ways, there are four solutions for

the tangent.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The boy thought of a number. He added 5 to that number, then divided the sum by 2, multiplied the quotient by 9, subtracted 6 from the product, divided the difference by 7, and got the number 3. What number did the boy think of?
|
3. We calculate backwards:
$3 \cdot 7=21$
1 POINT
$21+6=27$ 1 POINT
$27: 9=3$ 1 POINT
$3 \cdot 2=6$ 1 POINT
$6-5=1$
1 POINT
The desired number is 1.
1 POINT
(Note: If the student has written that the solution is the number 1 and has only verified the correctness of this solution, they should receive 2 POINTS.)
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Let the expressions $A$ and $B$ be given as:
$$
A=2 x+13+11 x-4-5 x+6 x+12 \text { and } \quad B=9+3 y+14 y-4-5 y+7-y+5
$$
If $x=6$, calculate $y$ so that the values of the expressions $A$ and $B$ are equal.
|
First method:
Simplify each expression:
| $A=2 x+13+11 x-4-5 x+6 x+12=14 x+21$ | 1 POINT |
| :--- | :--- |
| $B=9+3 y+14 y-4-5 y+7-y+5=11 y+17$ | 1 POINT |
| For $x=6, A=14 \cdot 6+21=84+21=105$. | 1 POINT |
| We are looking for $y$ for which the expressions $A$ and $B$ will be equal: | |
| $11 y+17=105$ | 1 POINT |
| $11 y=105-17$ | 1 POINT |
| $11 y=88$ | |
| $y=88: 11$ | 1 POINT |
| $y=8$ | mo............................................................................................ |
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. What is $3 x+2 y$, if $x^{2}+y^{2}+x y=28$ and $8 x-12 y+x y=80$?
The use of a pocket calculator or any manuals is not allowed.
|
7. From the second equation, we have $x y=80-8 x+12 y$.
By substituting into the first equation, we get:
$x^{2}+y^{2}+80-8 x+12 y=28$, or $x^{2}+y^{2}-8 x+12 y+52=0$.
3 POINTS
Then we complete the square:
$x^{2}-8 x+16+y^{2}+12 y+36+52-16-36=0$
$(x-4)^{2}+(y+6)^{2}=0$
3 POINTS
The sum of two squares is zero if and only if both squares are zero.
Thus, $x=4$ and $y=-6$,
2 POINTS
so $3 x+2 y=3 \cdot 4+2 \cdot(-6)=12-12=0$.
2 POINTS
TOTAL 10 POINTS
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Calculate $2015-5 \cdot(25 \cdot 13+13+3 \cdot 25-10)$.
|
First method:
\(2015-5 \cdot(25 \cdot 13+13+3 \cdot 25-10)=2015-5 \cdot(325+13+75-10)=\quad 1\) POINT
\(=2015-5 \cdot(338+75-10)=\quad 1\) POINT
\(=2015-5 \cdot(413-10)=\quad 1\) POINT
\(=2015-5 \cdot 403=\quad 1\) POINT
\(=2015-2015=\quad 1\) POINT
\(=0 \quad 1\) POINT
TOTAL 6 POINTS
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. The annual set of the magazine Blue Swallow consists of 6 issues. Each issue does not have to have the same number of pages, but it is known that each has 40 or 44 pages. Can the annual set have a total of 260 pages?
|
First method:
If each number had 40 pages, the complete set would have $6 \cdot 40=240$ pages. 2 POINTS
To have a total of 260 pages in the set, we would need to add $260-240=20$ pages.
2 POINTS
Since $44-40=4$ and $20 \div 4=5$, the annual set will have 260 pages if 5 numbers have 44 pages each and 1 number has 40 pages.
2 POINTS
TOTAL 6 POINTS
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Calculate: $1325: 5+15: 5-(99-9: 9) \cdot 2-35-30$.
|
1. Calculate: $1325: 5+15: 5-(99-9: 9) \cdot 2-35-30$.
## Solution.
$$
\begin{aligned}
& 1325: 5+15: 5-(99-9: 9) \cdot 2-35-30 \\
& =265+3-(99-9: 9) \cdot 2-35-30 \quad 1 \text { POINT } \\
& =265+3-(99-1) \cdot 2-35-30 \quad 1 \text { POINT } \\
& =268-98 \cdot 2-35-30 \quad 1 \text { POINT } \\
& =268-196-35-30 \quad 1 \text { POINT } \\
& =72-35-30 \quad 1 \text { POINT } \\
& =37-30 \\
& =7 \quad 1 \text{POINT} \\
& \text { TOTAL } 6 \text { POINTS }
\end{aligned}
$$
Note: If a student incorrectly copies part of the problem or makes a calculation error, points are deducted for that part, and further scoring follows the principle of "following the error."
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Four elephants and eight zebras eat a ton of food daily. An elephant eats $214 \mathrm{~kg}$ more food daily than a zebra. If a zebra needs 24 minutes to eat $1 \mathrm{~kg}$ of food, how much time does it need to eat its daily amount of food? Express the obtained time in hours and minutes.
|
4. Four elephants and eight zebras eat a ton of food daily. An elephant eats $214 \mathrm{~kg}$ more food daily than a zebra. If a zebra needs 24 minutes to eat $1 \mathrm{~kg}$ of food, how much time does it need to eat its daily amount of food? Express the obtained time in hours and minutes.
## Solution.
An elephant eats $214 \mathrm{~kg}$ more food daily than a zebra.
Since $214 \cdot 4=856$, four elephants eat as much as four zebras and an additional $856 \mathrm{~kg}$. 1 POINT The amount eaten by twelve zebras plus 856 kg totals one ton.
1 POINT
Since $1000-856=144$, twelve zebras eat 144 kg of food. 1 POINT
A zebra eats 144:12 = 12 kg of food daily. 1 POINT
A zebra eats $12 \cdot 24=288$ minutes daily, 1 POINT
which is 4 hours and 48 minutes. 1 POINT
TOTAL 6 POINTS
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In 6th grade class a, there are 24 students. Half of the students in this class play an instrument. Also, $\frac{5}{8}$ of the students in this class sing in the choir. If it is known that more than a third, but less than $\frac{5}{12}$ of the students in 6th grade class a both play an instrument and sing in the choir, how many students in this class neither play an instrument nor sing in the choir?
|
2. In 6th grade, there are 24 students. Half of the students in this class play an instrument. Also, $\frac{5}{8}$ of the students in this class sing in the choir. If it is known that more than a third, but less than $\frac{5}{12}$ of the students in 6th grade class 6a both play an instrument and sing in the choir, how many students in this class neither play an instrument nor sing in the choir?
## Solution.
The number of students who play an instrument is $24: 2=12$.
$1 \text{ POINT}$
In the choir, $\frac{5}{8} \cdot 24=15$ students sing.
$1 \text{ POINT}$
Since $24: 3=8, \frac{5}{12} \cdot 24=10$,
1 POINT
it follows that 9 students both play an instrument and sing in the choir.
$1 \text{ POINT}$
The number of students who play an instrument, sing in the choir, or do both is
$(12-9)+9+(15-8)=18$.
1 POINT
$24-18=6$ students neither play an instrument nor sing in the choir.
1 POINT
Note: It is not necessary to draw a Venn diagram in the solution. A correct solution that includes all necessary calculations and conclusions is fully recognized even without a Venn diagram.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In a rectangular coordinate system in the plane, a point $S(2,3)$ and a square $A B C D$ are given, with three known vertices $A(3,1), C(-2,6)$, and $D(-2,1)$. The square $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ is the central symmetric image of the square $A B C D$ with respect to the point $S$. Determine the coordinates of the points $B, A^{\prime}, B^{\prime}, C^{\prime}$, and $D^{\prime}$, as well as the area of the figure that is the intersection of the squares $A B C D$ and $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$. The length of the unit segment is $1 \mathrm{~cm}$.
|
3. In a rectangular coordinate system in the plane, a point $S(2,3)$ and a square $A B C D$ are given, with three known vertices $A(3,1), C(-2,6)$, and $D(-2,1)$. The square $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ is the central symmetric image of the square $A B C D$ with respect to the point $S$. Determine the coordinates of the points $B, A^{\prime}, B^{\prime}, C^{\prime}$, and $D^{\prime}$, as well as the area of the figure that is the intersection of the squares $A B C D$ and $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$. The length of the unit segment is $1 \mathrm{~cm}$.
## Solution.
[^0]
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. At the entrance to the cinema hall, among 30 visitors, 58 candies were distributed. Each girl received six candies, each boy received four candies, and each adult received one candy. How many girls, how many boys, and how many adults could there be in the cinema hall?
## Ministry of Science and Education of the Republic of Croatia Agency for Education and Upbringing Croatian Mathematical Society
## SCHOOL COMPETITION IN MATHEMATICS January 26, 2024.
|
First solution.
After each visitor eats 1 candy, there are $58-30=28$ candies left in the hall.
Then the adults do not have any candies.
\[\begin{array}{ll}\text { Each boy has } 3 \text { candies left, so the number of candies with boys is a multiple of 3. } & 1 \text { POINT } \\ \text { Each girl has } 5 \text { candies left, so the number of candies with girls is a multiple of 5. } & 1 \text { POINT } \\ \text { The number of candies with girls is not greater than } 28 \text {, so the possible number of candies with girls is } \\ 5,10,15,20 \text { and } 25 . & \\ \text { 1 POINT }\end{array}\]
Then the boys would have $23,18,13,8$ and 3 candies left, but only 18 and 3 are multiples of 3.
2 POINTS
If the boys have a total of 18 candies, then the girls have 10 candies.
Then there are $18: 3=6$ boys and $10: 5=2$ girls in the hall.
1 POINT
There are $30-(6+2)=22$ adults in the hall.
1 POINT
If the boys have 3 candies, then the girls have 25 candies, so there is $3: 3=1$ boy and $25: 5=5$ girls in the hall.
1 POINT
There are $30-(1+5)=30-6=24$ adults in the hall.
1 POINT
There could be 1 boy, 5 girls, and 24 adults in the hall, or
6 boys, 2 girls, and 22 adults in the hall.
TOTAL 10 POINTS
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In the expression $2: 2: 2: 2: 2$ place parentheses so that the result is equal to 2. Find two different ways!
|
1. $2:(2: 2):(2: 2)=2: 1: 1=2: 1=2$. 2 points
$2:(2: 2:(2: 2))=2:(2: 2: 1)=2:(1: 1)=2: 1=2$. 2 points
ILI
$2:(2:(2: 2): 2)=2:(2: 1: 2)=2:(2: 2)=2: 1=2$
.$U K U P N O 4$ POINTS
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Write all two-digit numbers that can be written using the digits 3, 4, and 9. How many such numbers are there?
|
2. The sought numbers are $33,34,43,39,93,44,49,94,99$.
5 POINTS
There are 9 of these numbers.
Note: For writing 1 or 2 numbers, award 1 point, for 3 or 4 award 2 points, for 5 or 6 award 3 points, for 7 or 8 award 4 points, and for all 9 award 5 points. Grade the answer separately.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Determine the prime number $p$ such that $\frac{4}{23}<\frac{1}{p}<\frac{8}{19}$.
|
First method:
If we expand the fractions so that their numerators are 8, then $\frac{8}{46}<\frac{8}{8 p}<\frac{8}{19}$. 2 POINTS Further, it follows that $19<8 p<46$.
2 POINTS
This means that $8 p \in\{24,32,40\} \quad 2$ POINTS
or $p \in\{3,4,5\}$. 2 POINTS
Since $p$ is a prime number, then $p \in\{3,5\}$. 2 POINTS
TOTAL 10 POINTS
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Determine the unknown number $\mathrm{x}$ from the proportion $\frac{5}{8}:\left(0.4-2-\frac{1}{2} x\right)=1.25:\left(3.8-2 \frac{1}{4} \cdot x+\frac{1}{2}\right)$.
|
First method:
$$
\begin{array}{ll}
\frac{5}{8}:\left(0.4-2-\frac{1}{2} x\right)=1.25:\left(3.8-2 \frac{1}{4} \cdot x+\frac{1}{2}\right) & \\
\frac{5}{8} \cdot\left(3.8-2 \frac{1}{4} \cdot x+\frac{1}{2}\right)=1.25 \cdot\left(0.4-2-\frac{1}{2} x\right) & 1 \text{ POINT} \\
\frac{5}{8} \cdot\left(\frac{19}{5}-\frac{9}{4} \cdot x+\frac{1}{2}\right)=\frac{5}{4} \cdot\left(\frac{2}{5}-2-\frac{1}{2} x\right) & 1 \\
\frac{19}{8}-\frac{45}{32} x+\frac{5}{16}=\frac{1}{2}-\frac{5}{2}-\frac{5}{8} x / \cdot 32 & 1 \text{ POINT} \\
76-45 x+10=16-80-20 x & 1 \text{ POINT} \\
-45 x+20 x=16-80-76-10 & 1 \text{ POINT} \\
-25 x=-150 /:(-25) & 1 \text{ POINT}
\end{array}
$$
$$
\text { POINT }
$$
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Micek is packing candies into bags. He has three types of candies: caramels, chocolate kisses, and gummy candies. If each bag must contain exactly 6 candies and at least 1 candy of each type, how many different bags can he make?
|
First method:
Let $k$ denote a caramel, $p$ denote a chocolate chip, and $g$ denote a gummy candy.
The problem can be solved by writing six-element sets of the form $\{k, p, g, -, -, -\}$.
The missing elements in the positions should be filled with the following subsets:
| $\{k, k, k\},\{p, p, p\},\{g, g, g\}$ | 1 POINT |
| :--- | ---: |
| $\{k, k, p\},\{k, k, g\}$ | 1 POINT |
| $\{p, p, k\},\{p, p, g\}$ | 1 POINT |
| $\{g, g, k\},\{g, g, p\}$ | 1 POINT |
| $\{k, p, g\}$ | 1 POINT |
| 10 different bags of candies can be composed. | 1 POINT |
Note: If the six-element sets (regardless of the order of the elements) are listed, they should be graded as suggested. For three six-element sets, 1 point; for five six-element sets, 2 points; for seven six-element sets, 3 points; for nine six-element sets, 4 points; for ten six-element sets, 5 points. The correct answer is worth 1 point. For repeated solutions, points are deducted, with 1 point deducted for every 2 repetitions, up to a maximum of 0 points.
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Calculate the sum of the expressions $S_{2015}$ and $S_{2016}$ if $S_{2015}=1-2+3-4+5-\ldots-2014+2015$, and $S_{2016}=1-2+3-4+5-\ldots-2014+2015-2016$.
Problems worth 10 points:
|
First method:
```
\(S_{2015}=(1-2)+(3-4)+\ldots+(2013-2014)+2015=(2014: 2) \cdot(-1)+2015=-1007+2015=\)
\(=1008 \quad 3\) POINTS
\(S_{2016}=(1-2)+(3-4)+\ldots+(2015-2016)=(2016: 2) \cdot(-1)=-1008 \quad 2\) POINTS
\(S_{2015}+S_{2016}=1008+(-1008)=0\)
1 POINT
```
TOTAL 6 POINTS
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. A rectangle $A B C D$ with a diagonal of length $20 \text{ cm}$ is circumscribed by a circle. The side $\overline{C D}$ of the rectangle $A B C D$ is the base of an isosceles triangle whose third vertex $E$ is on the shorter arc determined by the chord $\overline{C D}$ of the circle circumscribed around the rectangle. What is the length of the side $\overline{A D}$ of the rectangle if the area of the rectangle $A B C D$ is equal to the area of triangle DCE?
SCHOOL/CITY COMPETITION IN MATHEMATICS21st January 2016.8th grade-elementary school
Problems worth 6 points:
|
First method:

Let $|AB| = |CD| = a$, $|BC| = |AD| = b$, and let $v_a$ be the length of the height to the base of triangle $DCE$.
The radius of the circle circumscribed around the rectangle is $r = 20 / 2 = 10 \text{ cm}$.
1 POINT
Triangle $DCE$ is isosceles with base $\overline{DC}$, so $|SE| = r = v_a + \frac{b}{2}$.
1 POINT
Thus, $\frac{b}{2} + v_a = 10$ or $v_a = 10 - \frac{b}{2}$.
1 POINT
From the equality of the areas of rectangle $ABCD$ and triangle $DCE$, we get
$ab = \frac{1}{2} a v_a \Rightarrow b = \frac{1}{2} v_a \Rightarrow v_a = 2b$
2 POINTS
The equation $2b = 10 - \frac{b}{2} \cdot 2$ holds.
$4b = 20 - b$
$5b = 20$
$b = 4$
Therefore, $|AD| = 4 \text{ cm}$.
Note: A guessed (measured) solution without the procedure is worth 2 points.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. In a mathematics competition, 23 fourth-grade students participated. Some of them were supposed to have four classes that day, while others were supposed to have five. How many had four, and how many had five classes if all together they missed a total of 101 classes?
The use of a pocket calculator or any reference materials is not allowed.
## Ministry of Science and Education of the Republic of Croatia
Agency for Education and Upbringing
Croatian Mathematical Society
## SCHOOL/CITY COMPETITION IN MATHEMATICS
|
First solution.
| $\mathbf{4}$ hours of classes | $\mathbf{5}$ hours of classes | Total hours of classes |
| :---: | :---: | :---: |
| 5 students $\ldots . .20$ hours | $23-5=18$ students $\ldots 90$ hours | 110 hours |
| 6 students $\ldots .24$ hours | $23-6=17$ students $\ldots 85$ hours | 109 hours |
| 7 students $\ldots . .28$ hours | $23-7=16$ students $\ldots 80$ hours | 108 hours |
| 8 students $\ldots .32$ hours | $23-8=15$ students $\ldots 75$ hours | 107 hours |
| 9 students $\ldots .36$ hours | $23-9=14$ students $\ldots 70$ hours | 106 hours |
| 10 students $\ldots . .40$ hours | $23-10=13$ students $\ldots 65$ hours | 105 hours |
| $\ldots$ | $\ldots$ | $\ldots$ |
It is necessary to calculate at least 3 rows in the sequence to observe the rule of increasing and decreasing the total number of hours, which then needs to be explained.
Explanation: Each additional student in the class with 4 hours of classes reduces the total number of hours by one. $\quad 4$ POINTS (Alternatively: Each additional student in the class with 5 hours of classes increases the total number of hours by one.) $105-101=4$ hours less means 4 more students.
Note: If there is no explanation, then all possible options must be listed in the table for the maximum score (8 POINTS) in this part of the task. 2 POINTS are awarded for the written answer about the number of students in both classes.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Calculate:
$$
\frac{1}{\sqrt{2}-1}-\frac{1}{\sqrt{2}+1}+\frac{1}{\sqrt{3}-1}-\frac{1}{\sqrt{3}+1}
$$
|
First solution.
$$
\begin{aligned}
\frac{1}{\sqrt{2}-1} & -\frac{1}{\sqrt{2}+1}+\frac{1}{\sqrt{3}-1}-\frac{1}{\sqrt{3}+1}= \\
& =\frac{\sqrt{2}+1-(\sqrt{2}-1)}{(\sqrt{2}-1)(\sqrt{2}+1)}+\frac{\sqrt{3}+1-(\sqrt{3}-1)}{(\sqrt{3}-1)(\sqrt{3}+1)} \\
& =\frac{\sqrt{2}+1-\sqrt{2}+1}{(\sqrt{2})^{2}-1^{2}}+\frac{\sqrt{3}+1-\sqrt{3}+1}{(\sqrt{3})^{2}-1^{2}} \\
& =\frac{2}{2-1}+\frac{2}{3-1}=2+1=3
\end{aligned}
$$
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Joško added the largest three-digit number divisible by 9 and the smallest three-digit number not divisible by 9, while Fran added the largest three-digit number not divisible by 9 and the smallest three-digit number divisible by 9. Which sum is greater and by how much?
|
2. The largest three-digit number divisible by 9 is 999, and the smallest three-digit number not divisible by 9 is 100.
Joško added $999+100=1099$. 1 point The largest three-digit number not divisible by 9 is 998, and the smallest three-digit number divisible by 9 is 108.
Fran added $998+108=1106$. 1 point
Fran's sum is greater by 1106 - $1099=7$. 2 points
TOTAL 4 POINTS
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. What is the 2012th digit in the sequence 012343210012343210012...?
|
4. In the sequence 012343210012343210012....the "subsequence" 012343210 which has 9 digits repeats.
1 point
$2012: 9=223$
21
32
5
Up to the 2012th digit, the "subsequence" 012343210 repeats 223 times, and there are still five digits remaining.
2 points
This means that the 2012th digit in the given sequence is the 5th digit of the "subsequence" 012343210.
Therefore, the 2012th digit in the given sequence is 4.
1 point
.TOTAL 4 POINTS
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Determine the unknown number $x$ and explain.
| 9 | 22 | 13 | 16 |
| :---: | :---: | :---: | :---: |
| 144 | 176 | 143 | 192 |
| 16 | 8 | 11 | $x$ |
Tasks worth 10 points
|
5. Since $144: 9=16$, $176: 22=8$ and $143: 13=11$, then it must also be so in the last column.
2 points
Therefore, $x=192$ : 16, which means $x=12$.
2 points
TOTAL 4 POINTS
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. The lengths of the sides of a rectangle are expressed as natural numbers (in cm), and the area is $196 \mathrm{~cm}^{2}$. How many such rectangles are there, and which one has the largest perimeter?
|
6. If we factorize the number 196 into prime factors, we have that $196=2 \cdot 2 \cdot 7 \cdot 7$.
3 points
From the prime factorization, it is clear that there are five different pairs of natural numbers whose product is 196, so we have five different rectangles with an area of $196 \mathrm{~cm}^{2}$, and these are: a rectangle whose adjacent side lengths are $1 \mathrm{~cm}$ and $196 \mathrm{~cm}, \quad 1$ point a rectangle whose adjacent side lengths are $2 \mathrm{~cm}$ and $98 \mathrm{~cm}$, 1 point a rectangle whose adjacent side lengths are $4 \mathrm{~cm}$ and $49 \mathrm{~cm}$, 1 point a rectangle whose adjacent side lengths are $7 \mathrm{~cm}$ and $28 \mathrm{~cm}$, 1 point a rectangle whose adjacent side lengths are $14 \mathrm{~cm}$ and $14 \mathrm{~cm}$. 1 point
The rectangle with the largest perimeter has adjacent side lengths of $1 \mathrm{~cm}$ and $196 \mathrm{~cm} .2$ points TOTAL 10 POINTS
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. How many three-digit natural numbers have the product of their digits equal to 28? Write them down!
|
7. Since $28=2 \cdot 2 \cdot 7$, the corresponding triples of digits are:
a) 2, 2, 7;
b) $1,4,7$.
2 points
The required numbers are:
a) $227,272,722$;
2 points
b) $147,174,417,471,714,741$.
4 points
There are 9 numbers with the required properties.
2 points
TOTAL 10 POINTS
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Frane has a total of $108 \mathrm{kn}$ in his piggy bank in $5 \mathrm{kn}$, $2 \mathrm{kn}$, and $1 \mathrm{kn}$ coins. The value of the $5 \mathrm{kn}$ and $2 \mathrm{kn}$ coins is the same. The number of $1 \mathrm{kn}$ coins is equal to the number of $5 \mathrm{kn}$ and $2 \mathrm{kn}$ coins combined. How many coins of each type are in the piggy bank?
|
First solution.
A $1 \mathrm{kn}$ coin has exactly as many as a $5 \mathrm{kn}$ coin and a $2 \mathrm{kn}$ coin together, so we can place a $1 \mathrm{kn}$ coin on each $5 \mathrm{kn}$ coin to form a "packet" of $6 \mathrm{kn}$, and place a $1 \mathrm{kn}$ coin on each $2 \mathrm{kn}$ coin to form a "packet" of $3 \mathrm{kn}$.
2 POINTS

The amounts in the $5 \mathrm{kn}$ and $2 \mathrm{kn}$ coins are equal, so for every two $5 \mathrm{kn}$ coins (i.e., packets of $6 \mathrm{kn}$), there are five $2 \mathrm{kn}$ coins (i.e., packets of $3 \mathrm{kn}$).
2 POINTS

Thus, all the coins can be grouped such that each group has two packets of $6 \mathrm{kn}$ and five packets of $3 \mathrm{kn}$, and it holds that $2 \cdot 6 + 5 \cdot 3 = 27 \mathrm{kn}$.
2 POINTS
The total amount is 108 kn, so we have $108 \div 27 = 4$ such groups.
1 POINT
Each group has 2 coins of 5 kn, so there are 8 such coins in total.
1 POINT
Each group has 5 coins of 2 kn, so there are 20 such coins in total.
1 POINT
Each group has 7 coins of 1 kn, so there are 28 such coins in total.
1 POINT
TOTAL 10 POINTS
##
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Iva and Maja received an order to make 72 greeting cards. Each of them made 36 cards, and each of their cards took the same amount of time to make. Iva made 6 cards in the same time it took Maja to make 5 cards. Iva finished making her 36 cards 1 hour and 48 minutes before Maja finished all of hers. How many cards did Iva and Maja each make in 1 hour?
|
First solution.
Let $x$ be the time it took for Iva to make 6 cards, and for Maja to make 5 cards.
Then, it took Iva $\frac{x}{6}$ hours to make one card, and Maja $\frac{x}{5}$ hours.
This means that Iva made her 36 cards in $\frac{36}{6} x=6 x$ hours, and Maja in $\frac{36}{5} x$ hours.
Convert 1 hour and 48 minutes to hours.
1 minute $=\frac{1}{60}$ hours.
$\Rightarrow$ 1 hour and 48 minutes $=\frac{108}{60}=\frac{9}{5}$ hours.
1 POINT
Since it took Iva 1 hour and 48 minutes less time to make the cards than Maja, the equation holds:
$6 x+\frac{9}{5}=\frac{36}{5} x$
3 POINTS
$30 x+9=36 x$
1 POINT
$6 x=9$
$x=\frac{9}{6}=\frac{3}{2}=1 \frac{1}{2}$
1 POINT
Iva makes 6 cards in 1 hour and 30 minutes, which means she makes 6: $1 \frac{1}{2}=4$ cards in 1 hour.
1 POINT
Maja makes 5 cards in 1 hour and 30 minutes, which means she makes
$5: 1 \frac{1}{2}=3 \frac{1}{3}$ cards in 1 hour.
1 POINT
TOTAL 10 POINTS
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. A sequence of digits consists of the first 222 natural numbers written in a row. In this sequence, we cross out the digits that are in odd positions. After that, we again cross out the digits that are in (new) odd positions. We repeat this procedure until only one digit remains. Which digit will it be?
## Ministry of Science and Education of the Republic of Croatia
Agency for Education and Education
Croatian Mathematical Society
## COUNTY COMPETITION IN MATHEMATICS March 24, 2022.
|
5. The sequence of digits consists of the first 222 natural numbers written in order. In this sequence, we cross out the digits that are in odd positions. After that, we again cross out the digits that are in (new) odd positions. We repeat this process until only one digit remains. Which digit will it be?
## Solution.
The sequence contains $9 \cdot 1 + 90 \cdot 2 + 123 \cdot 3 = 558$ digits. 1 POINT
After the first crossing out, the digits that remain are in the second, fourth, sixth, ... positions, i.e., in even positions. After the second crossing out, the digits that remain are those that were originally in the fourth, eighth, twelfth, ... positions. The remaining digits are those whose original position number is divisible by $4 = 2^2$.
After the third crossing out, the digits that remain are those whose original position number is divisible by $8 = 2^3$.
After the fourth crossing out, the digits that remain are those whose original position number is divisible by $16 = 2^4$.
It can be concluded that after each $k$-th crossing out, the remaining digits are those whose original position number is divisible by $2^k$.
3 POINTS
To determine the position of the digit that will remain last, it is necessary to determine the largest natural number $k$ for which $2^k < 558$ holds.
This occurs for $k = 9$, where $2^k = 512$.
In the end, the digit that remains will be the one in the 512th position in the sequence.
3 POINTS
The first 9 digits are the digits from 1 to 9.
Then come 180 digits that form all two-digit numbers.
Up to the 512th digit, there are $512 - 189 = 323$ digits left that form three-digit numbers, starting from the number 100.
Since $323 = 107 \cdot 3 + 2$, the desired digit is the second digit in the 108th three-digit number. This is the number 207, and the desired digit is the digit 0.
3 POINTS
TOTAL 10 POINTS
## COUNTY COMPETITION IN MATHEMATICS
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. A car left city A heading towards city B, covering $12 \mathrm{~km}$ in 10 minutes. At the same time, a truck left city B heading towards city A, covering 10 $\mathrm{km}$ in 12 minutes. How many kilometers apart will the car and the truck be after 2 hours and 30 minutes of driving if the distance between cities A and B is $300 \mathrm{~km}$?
NATIONAL COMPETITION IN MATHEMATICSŠibenik, April 2-4, 2014.6th grade-elementary school
|
5. A car travels $12 \cdot(60: 10)=72 \text{ km}$ in 1 hour (60 minutes).
A car travels $36 \text{ km}$ in 30 minutes.
A car travels $2 \cdot 72+36=144+36=180 \text{ km}$ in 2 hours and 30 minutes.
A truck travels $10 \cdot(60: 12)=50 \text{ km}$ in 1 hour.
A truck travels $25 \text{ km}$ in 30 minutes.
A truck travels $2 \cdot 50+25=125 \text{ km}$ in 2 hours and 30 minutes.
Since $180+125=305>300$, the car and the truck will meet on the road and continue further to their destination.
Their distance after 2 hours and 30 minutes will be $180+125-300=5 \text{ km}$.
## NATIONAL MATHEMATICS COMPETITION
Šibenik, April 2-4, 2014.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. What is the value of the digit in the units place of the number $1+9^{2014}$?
|
3. The powers of the number 9 are $9^{1}=9,9^{2}=81,9^{3}=729,9^{4}=6561, \ldots$
2 POINTS
It is easy to notice that powers with odd exponents have the units digit 9, while powers with even exponents have the units digit 1.
2 POINTS
The number $9^{2014}$ has an even exponent, so its units digit is 1.
1 POINT
Therefore, the number $1+9^{2014}$ has the units digit 2.
1 POINT
TOTAL 6 POINTS
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Solve the equation $6(x-1)(x+2)-4(x-3)(x+4)=2(x-5)(x-6)$.
|
4. $6\left(x^{2}+2 x-x-2\right)-4\left(x^{2}+4 x-3 x-12\right)=2\left(x^{2}-6 x-5 x+30\right) \quad 1$ BOD
$6\left(x^{2}+x-2\right)-4\left(x^{2}+x-12\right)=2\left(x^{2}-11 x+30\right) \quad 1$ BOD
$6 x^{2}+6 x-12-4 x^{2}-4 x+48=2 x^{2}-22 x+60 \quad$ 1 BOD
$6 x^{2}-4 x^{2}-2 x^{2}+6 x-4 x+22 x=60-48+12 \quad 1$ BOD
$24 x=24 \quad 1$ BOD
$x=1 \quad 1$ BOD
TOTAL 6 POINTS
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Determine the unknown digit $a$ of the number $\overline{401512 a}$ so that the remainders when this number is divided by 3 and 5 are equal.
|
First method:
Possible remainders when dividing by 3 are 0, 1, and 2.
If the remainder when dividing by 3 is 0, then the number $\overline{401512 a}$ is divisible by 3, and the sum of its digits must be divisible by 3.
The sum of the digits of the number $\overline{401512 a}$ is $13+a$, so the digit a can be 2, 5, and 8. The numbers of the given form that are divisible by 3 are 4015122, 4015125, and 4015128. Of these three numbers, only the number 4015125 is divisible by 5.
If the remainder when dividing by 3 is 1, then the digit a can be 0, 3, 6, and 9. The numbers of the given form that have a remainder of 1 when divided by 3 are 4015120, 4015123, 4015126, and 4015129.
Of these four numbers, only the number 4015126 has a remainder of 1 when divided by 5.
If the remainder when dividing by 3 is 2, then the digit a can be 1, 4, and 7. The numbers of the given form that have a remainder of 2 when divided by 3 are 4015121, 4015124, and 4015127.
Of these three numbers, only the number 4015127 has a remainder of 2 when divided by 5.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Let $n>1$ be a natural number. An equilateral triangle with side length $n$ is divided by lines parallel to its sides into congruent equilateral smaller triangles with side length 1. The number of smaller triangles that have at least one side on the side of the original triangle is 1 less than the number of all other smaller triangles. Determine all such $n$.
|
First method:
For $n=2$
the number of small triangles with at least one side lying on the side of the original triangle is 3, and the number of all remaining small triangles is 1, which means the condition is not satisfied.
For $n>2$, let the small triangles at the vertices of the given triangle be black, the small triangles that share exactly one side with the boundary of the triangle (but are not at the vertex of the given triangle) be blue, the small triangles that share only a vertex with the boundary of the original triangle be red, and the small triangles inside the original triangle be white.
The given condition can now be rephrased as: "the total number of black and blue small triangles is 1 less than the total number of white and red small triangles."
We observe that the number of red and blue small triangles is the same (consider one red small triangle, then in the positive direction, a blue one sharing a side, and in the positive direction, a red one sharing a side with the blue one, and so on until we return to the initial red small triangle). This means that the number of black small triangles must be 1 less than the number of white small triangles. However, the number of black small triangles is always 3, so the number of white small triangles must be 4.
This is possible only for $n=5$.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. How many three-digit numbers less than 200 can be expressed in the form $a^{2} \cdot b$, where $a$ and $b$ are prime numbers?
|
4. If $a=2$, then $a^{2}=4$. For the product to be a three-digit number, $b$ must be a prime number greater than or equal to 25. For the product to be less than 200, $b$ must be a prime number less than 50.
Then $b \in\{29,31,37,41,43,47\}$.
1 POINT
If $a=3$, then $a^{2}=9$, so $b$ needs to be a prime number greater than 11 and less than or equal to 22.
Then $b \in\{13,17,19\}$.
1 POINT
For $a=5$, $a^{2}=25$, so $b \in\{5,7\}$.
1 POINT
For $a=7$, $a^{2}=49$, so $b \in\{3\}$.
1 POINT
For $a \geq 11$, $a^{2} \cdot b>200$ for any prime number $b$, so there are no more solutions.
Therefore, the total number of solutions is $6+3+2+1=12$.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Mama, tata, brat i sestra kupili su ukupno 10 kuglica sladoleda. Na koliko različitih načina mogu međusobno raspodijeliti sladoled, pod uvjetom da svatko dobije barem dvije kuglice? Ispiši sve mogućnosti.
4. Mama, tata, brat i sestra bought a total of 10 scoops of ice cream. In how many different ways can they distribute the ice cream among themselves, given that each person gets at least two scoops? List all the possibilities.
|
4. Everyone must receive at least two scoops. That's a total of eight scoops, so there are two more to be distributed.
2 POINTS
Both scoops can belong to one of them (mom, dad, brother, or sister)
3 POINTS
or two people can each get one scoop (mom/dad, mom/brother, mom/sister, dad/brother, dad/sister, or
brother/sister).
4 POINTS
In total, there are 10 distributions as shown in the table:
1 POINT
| Mom | 4 | 2 | 2 | 2 | 3 | 3 | 3 | 2 | 2 | 2 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| Dad | 2 | 4 | 2 | 2 | 3 | 2 | 2 | 3 | 3 | 2 |
| Brother | 2 | 2 | 4 | 2 | 2 | 3 | 2 | 3 | 2 | 3 |
| Sister | 2 | 2 | 2 | 4 | 2 | 2 | 3 | 2 | 3 | 3 |
TOTAL 10 POINTS
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. To the summer math camp, 713 students traveled in 25 buses, some of which have 33 seats, and some have 26 seats. If it is known that the students filled all the seats in the buses, how many buses had 33 seats, and how many buses had 26 seats?
|
First method:
Assume that each of the 25 buses has 26 seats. 1 POINT
Then, they can accommodate $25 \cdot 26=\quad 1 \text{ POINT}$
$=650$ students. 1 POINT
Then, $713-650=\quad 1 \text{ POINT}$
$=63$ students would be left without seats. 1 POINT
Since $33-26=7$, a larger bus can accommodate seven more children than a smaller one. 1 POINT
Since $63: 7=9$,
9 smaller buses need to be replaced with 9 larger buses. 1 POINT
The remaining $25-9=16$ buses are smaller. 1 POINT
There were 9 buses with 33 seats and 16 buses with 26 seats. 2 POINTS
TOTAL 10 POINTS
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Roko and Marko have equally long steps. They are 1600 steps apart from each other. In one minute, Roko takes 80 steps, and Marko takes 60 steps. Who of the two needs to start earlier and how much earlier should they start to meet exactly halfway while walking towards each other? Express the solution in minutes and seconds.
|
First method:
For half the distance, 800 steps are required. 1 POINT
It takes Roku $800: 80=10$ minutes to do this. 1 POINT
In 10 minutes, Marko walks $10 \cdot 60=600$ steps. 1 POINT
$\begin{array}{ll}\text { Marko needs to start earlier. } & 1 \text { POINT }\end{array}$
Marko needs to start earlier by the amount of time it takes him to walk 200 steps. 1 POINT
In 1 minute, Marko walks 60 steps, so in 3 minutes, he walks 180 steps. 1 POINT
Since he walks 60 steps in 60 seconds,
he will walk the remaining 20 steps in 20 seconds.
2 POINTS
Therefore, Marko needs to start $180+20=200$ seconds earlier than Roku.
1 POINT
Marko needs to start 3 minutes and 20 seconds earlier than Roku.
1 POINT
TOTAL 10 POINTS
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. What is the remainder when the number $1+2+2^{2}+2^{3}+\ldots+2^{2021}$ is divided by 9?
|
First method:
The number 1 when divided by 9 gives a remainder of 1.
The number 2 when divided by 9 gives a remainder of 2.
The number $2^{2}$ when divided by 9 gives a remainder of 4.
The number $2^{3}$ when divided by 9 gives a remainder of 8.
The number $2^{4}$ when divided by 9 gives a remainder of 7.
The number $2^{5}$ when divided by 9 gives a remainder of 5.
1 POINT
Since $2^{6}$ gives a remainder of 1 when divided by 9, the remainders of the number $2^{n}$ when divided by 9 repeat periodically with a period of 6.
Therefore, we first calculate the sum of the remainders for the first six addends $1+2+4+8+7+5=27$ and conclude that the sum $1+2+2^{2}+2^{3}+2^{4}+2^{5}$ is divisible by 9.
2 POINTS
Since $2^{6+k}=2^{6} \cdot 2^{k}$, $2^{6+k}$ for any non-negative integer $k$ gives the same remainder when divided by $k$ as $2^{k}$, i.e., since the remainders of the number $2^{n}$ when divided by 9 repeat periodically with a period of 6, we conclude that the sum $2^{6 k}+2^{6 k+1}+2^{6 k+2}+2^{6 k+3}+2^{6 k+4}+2^{6 k+5}$ is divisible by 9 for any non-negative integer $k$. 3 POINTS
The sum $1+2+2^{2}+2^{3}+\ldots+2^{2021}$ has 2022 addends.
1 POINT
Since 2022 is divisible by 6,
1 POINT the addends in the original sum can be grouped into sets of 6 addends (there are 337 such sets because $2022: 6=337$) whose sum is divisible by 9
1 POINT and thus we conclude that the original sum is divisible by 9, i.e., the remainder when the number $1+2+2^{2}+2^{3}+\ldots+2^{2021}$ is divided by 9 is equal to 0.
1 POINT
Note: Instead of writing generally that each sum $2^{6 k}+2^{6 k+1}+2^{6 k+2}+2^{6 k+3}+2^{6 k+4}+2^{6 k+5}$ for any non-negative integer $k$ is divisible by 9, the student can write that, because the remainders of the number $2^{n}$ when divided by 9 repeat periodically with a period of 6, each of the sums $1+2+2^{2}+2^{3}+2^{4}+2^{5}$, $2^{6}+2^{7}+2^{8}+2^{9}+2^{10}+2^{11}$, $2^{12}+2^{13}+2^{14}+2^{15}+2^{16}+2^{17}$, etc., is divisible by 9.
TOTAL 10 POINTS
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Students sit in the classroom in pairs. There are more girls in the class, so four fifths of the total number of students sit in mixed pairs (boy + girl), and there are three pairs that are exclusively female. How many boys, and how many girls are there in this class?
|
First method: In mixed pairs, $\frac{4}{5}$ of the class sits, so in female pairs, $\frac{1}{5}$ of the class sits.
$\mathrm{Here} \frac{1}{5}$ of the class consists of 6 girls sitting together,
1 POINT
which means there are $5 \cdot 6=30$ students in the class.
1 POINT
Of these 30 students, 24 students sit in mixed pairs, so there are 12 boys.
There are then 18 girls.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The average value of twelve numbers is 4.7. By adding two new numbers, the average value changes to 5.6. What is the average value of the two new numbers?
|
2. From the conditions of the problem, it is possible to write the equality $x_{1}+x_{2} \ldots+x_{12}=56.4$. ..... 2 POINTS
After adding two new numbers, the equality becomes $x_{1}+x_{2} \ldots+x_{12}+x_{13}+x_{14}=78.4$. ..... 2 POINTS
By subtracting the first equality from the second, we get $x_{13}+x_{14}=22$. ..... 1 POINT
The average value of the two numbers whose sum is 22 is $x_{\left(x_{13}+x_{14}\right)}=11$. ..... 1 POINT
TOTAL 6 POINTS
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In a drum, there are balls on which all three-digit numbers are written (each one once). One ball is drawn. What is the probability that the sum of the digits of the drawn number is 2 or 5?
|
First method:
There are 900 three-digit numbers, so there are as many balls in the drum. ..... $1 \text{ POINT}$
The sum of 2 can be obtained by drawing three balls (200, 110, 101). ..... $1 \text{ POINT}$
The sum of 5 can be obtained by drawing 15 balls (500, 410, 401, 320, 302, 311, 230, 203, 221, 212,
140, 104, 131, 113, 122). ..... 2 POINTS
The sum of the digits equal to 2 or 5 can be achieved by drawing one of 18 balls. The probability of this happening is 18 : $900=0.02=2 \%$. ..... 2 POINTS
TOTAL 6 POINTS
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Find the smallest natural number $n$ such that for every set of $n$ points with integer coordinates, of which no three lie on the same line, there exists a triangle with vertices from this set for which the midpoints of its sides also have integer coordinates.
No use of a pocket calculator or any manuals is allowed.
## NATIONAL MATHEMATICS COMPETITION
|
5. Find the smallest natural number $n$ such that for any set of $n$ points with integer coordinates, of which no three lie on the same line, there exists a triangle with vertices from this set for which the midpoints of its sides also have integer coordinates.
## Solution.
If the points are $A\left(x_{1}, y_{1}\right)$ and $B\left(x_{2}, y_{2}\right)$, then their midpoint is given by
$$
P\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)
$$
Divide all points with integer coordinates into four sets:
$S_{1}$ - the set of points whose abscissa and ordinate give a remainder of 1 when divided by 2,
$S_{2}$ - the set of points whose abscissa and ordinate are divisible by 2,
$S_{3}$ - the set of points whose abscissa gives a remainder of 1 when divided by 2, and whose ordinate is divisible by 2,
$S_{4}$ - the set of points whose abscissa is divisible by 2, and whose ordinate gives a remainder of 1 when divided by 2.
Among 9 points, by the Dirichlet principle, there must be 3 points that belong to one of the four sets mentioned above. These three points are the vertices of a triangle (since no three points lie on the same line), and for these three points, it is true that the midpoint of each of the three segments they determine (which are the sides of the triangle) has integer coordinates, because the sum of the abscissas, as well as the sum of the ordinates, of any two such points is an even number, as per (1).
If we have a set of 8 points, with two from each of the sets $S_{1}, S_{2}, S_{3}$, and $S_{4}$, for example, the set consisting of the points $(0,0), (0,2), (1,0), (1,2), (2,1), (2,3), (3,1)$, and $(3,3)$, then among any 3 chosen points, there will be at least two points from different sets $S_{1}, S_{2}, S_{3}$, and $S_{4}$. Since the sum of the abscissas or the sum of the ordinates of two points from different sets is not even, according to (1), the abscissa or the ordinate of some midpoint is not an integer.
(The image shows the selected eight points, none of which are on the same line.)
Therefore, the smallest natural number $n$ with the desired property is $n=9$.
## NATIONAL MATHEMATICS COMPETITION
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. One pipe can fill the pool in 5 hours, and the second pipe in 3 hours. How long (in hours, minutes, and seconds) would it take for both pipes to fill the pool if they fill it together?
|
2. The first pipe fills $\frac{1}{5}$ of the pool in 1 hour, and the second pipe fills $\frac{1}{3}$ of the pool in 1 hour. 1 point For 1 hour, these pipes together fill $\frac{1}{5}+\frac{1}{3}=\frac{8}{15}$ of the pool. The pool will be full in $\frac{15}{8}=1 \frac{7}{8}$ hours, which is 1 hour 52 minutes and 30 seconds. $\qquad$
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.