problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
7.5. Determine the integer numbers $x$, for which the numbers $n=x^{2}+5 x+1$ and $m=x^{2}+3 x+$ 7 are simultaneously perfect squares.
|
## Solution:
$\operatorname{Given} x^{2}+3 x+7=k^{2} \Rightarrow 4 x^{2}+12 x+28=4 k^{2} \Leftrightarrow(2 x+3)^{2}+19=4 k^{2} \Leftrightarrow$ $(2 x+3-2 k)(2 x+3+2 k)=-19$.
a) $\left\{\begin{array}{l}2 x+3-2 k=-1 \\ 2 x+3+2 k=19\end{array} \Rightarrow 4 x+6=18 \Leftrightarrow 4 x=12 \Leftrightarrow x=3\right.$.
b) $\left\{\begin{array}{c}2 x+3-2 k=-19 \\ 2 x+3+2 k=1\end{array} \Rightarrow 4 x+6=-18 \Leftrightarrow 4 x=-24 \Leftrightarrow x=-6\right.$.
Thus $x^{2}+3 x+7$ is a perfect square for $x \in\{-6 ; 3\}$. For $x=-6 \Rightarrow x^{2}+5 x+1=$ 7 - which is not a perfect square, and for $x=3 \Rightarrow x^{2}+5 x+1=25=5^{2}$.
Answer: $x=3$.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. On a board, all natural numbers $1,2,3, \ldots, 15$ are written. Determine the minimum number of numbers that can be erased from the board so that with the remaining numbers we can form two non-empty sets of numbers that simultaneously satisfy the following properties:
a) they have no common elements;
b) they have the same number of elements;
c) the product of the elements of the two sets is the same.
|
## Solution:
The product of all the numbers initially written on the board is $n=1 \cdot 2 \cdot 3 \cdot 2^{2} \cdot 5 \cdot 2 \cdot 3 \cdot 7 \cdot 2^{3} \cdot 3^{2} \cdot 2 \cdot 5 \cdot 11 \cdot 2^{2} \cdot 3 \cdot 13 \cdot 2 \cdot 7 \cdot 3 \cdot 5=2^{11} \cdot 3^{6} \cdot 5^{3} \cdot 7^{2} \cdot 11 \cdot 13$. To obtain the same product for the elements of the two sets, it follows that the product of all the remaining numbers must be a perfect square. Thus, we need to delete a factor from $n$ that has an odd exponent, i.e., $2, 5, 11, 13$. Since the cardinality of the two sets formed is the same, it follows that an even number of numbers must remain on the board. As we initially have an odd number of numbers on the board, it follows that an odd number of numbers must be deleted. Thus, we delete the numbers $10, 11, 13$ from the board. The numbers remaining on the board are $1, 2, 3, 4, 5, 6, 7, 8, 9, 12, 14, 15$. From the remaining numbers, we deduce that 5 and 15 do not belong to the same set, just as the numbers 7 and 14 do not belong to the same set. As a result, we can obtain the sets $M=\{2,3,5,8,9,14\}$ and $N=\{1,4,6,7,12,15\}$ or $M=\{1,4,5,9,12,14\}$ and $N=\{2,3,6,7,8,15\}$.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.3. For any natural number $m$, we denote by $S(m)$ the sum of the digits of the number $m$. Calculate $S\left(S\left(S\left(2023^{2023}\right)\right)\right)$.
|
## Solution.
For any natural number $m$, we denote by $S(m)$ the sum of the digits and by $N(m)$ the number of digits of the number $m$. We have $2023^{2023}<\left(10^{4}\right)^{2023}=10^{8092}$, which implies $N\left(2023^{2023}\right) \leq 8092$. The number $2023^{2023}$ has no more than 8092 digits, and the sum of its digits does not exceed $9 \cdot 8092$, that is,
$$
0<S\left(2023^{2023}\right) \leq 9 \cdot 8092=72828
$$
The number $S\left(2023^{2023}\right)$ does not exceed the number 72828, and the sum of its digits does not exceed the sum of the digits of the number 79999 (we keep the value 7 for the first digit (as the maximum value), and replace the other digits with the maximum value 9). As a result, we obtain the inequality
$$
0<S\left(S\left(2023^{2023}\right)\right) \leq S(79999)=43
$$
Similarly, the number $S\left(S\left(2023^{2023}\right)\right)$ does not exceed the number 43, and the sum of its digits does not exceed the sum of the digits of the number 49 (we keep the value 4 for the first digit (as the maximum value), and replace the second digit with the maximum value 9). We obtain
$$
0<S\left(S\left(S\left(2023^{2023}\right)\right)\right) \leq S(49)=13
$$
It is known that at division by 9, any natural number $m$ and the sum of its digits give the same remainder, i.e., $m \equiv S(m)(\bmod 9), \forall m \in \mathbb{N}$. Therefore,
$$
2023^{2023} \equiv(S(2023))^{2023} \equiv 7^{2023} \equiv\left(7^{3}\right)^{674} \cdot 7 \equiv 1^{674} \cdot 7 \equiv 7(\bmod 9)
$$
Correspondingly, applying the congruence property modulo 9 recursively three times, we have
$$
S\left(S\left(S\left(2023^{2023}\right)\right)\right) \equiv S\left(S\left(2023^{2023}\right)\right) \equiv S\left(2023^{2023}\right) \equiv 2023^{2023} \equiv 7(\bmod 9)
$$
Consequently, from relations $(*)$ and $(* *)$, we obtain
$$
S\left(S\left(S\left(2023^{2023}\right)\right)\right)=7
$$
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.4. Let the function $f: \mathbf{R} \rightarrow(0,+\infty)$ be differentiable, strictly decreasing, with $f(0)=1$ and $f^{\prime}(0)=-1$. Let the sequence $\left(a_{n}\right)_{n=1}^{\infty}$ be defined by: $a_{1}=1$ and $a_{n+1}=a_{n} f\left(a_{n}\right), \forall n \geq 1$. Show that the limit $\lim _{n \rightarrow \infty}\left(n a_{n}\right)$ exists and compute this limit.
|
Solution. Since $a_{1}=1>0$ and $a_{n+1}=a_{n} f\left(a_{n}\right), \forall n \geq 1$, by mathematical induction it can be shown that $a_{n}>0, \forall n \geq 1$.
From the fact that the function $f$ is strictly decreasing, the inequalities follow: $0 < a_{n+1} = a_{n} f(a_{n}) < a_{n}, \forall n \geq 1$. Therefore, the sequence $(a_{n})_{n=1}^{\infty}$ is strictly decreasing and bounded below by 0, so it is convergent. Let $L=\lim _{n \rightarrow \infty} a_{n} \geq 0$. If $L>0$, then we would get $f(L)=1=f(0)$, which contradicts the fact that the function $f$ is strictly decreasing. Therefore, $L=\lim _{n \rightarrow \infty} a_{n}=0$, which implies $\lim _{n \rightarrow \infty} \frac{1}{a_{n}}=+\infty$.
Finally, since the sequence $(n)_{n=1}^{\infty}$ is strictly increasing and $\lim _{n \rightarrow \infty} n=+\infty$, we can apply the Stolz-Cesaro lemma. We obtain:
$$
\begin{aligned}
\lim _{n \rightarrow \infty} \frac{1}{n a_{n}} & =\lim _{n \rightarrow \infty} \frac{\frac{1}{a_{n}}}{n}=\lim _{n \rightarrow \infty} \frac{\frac{1}{a_{n+1}}-\frac{1}{a_{n}}}{(n+1)-n}=\lim _{n \rightarrow \infty}\left(\frac{1}{a_{n+1}}-\frac{1}{a_{n}}\right)= \\
& =\lim _{n \rightarrow \infty}\left(\frac{1}{a_{n} f\left(a_{n}\right)}-\frac{1}{a_{n}}\right)=\lim _{n \rightarrow \infty} \frac{1-f\left(a_{n}\right)}{a_{n} f\left(a_{n}\right)}
\end{aligned}
$$
We note that from the differentiability of the function $f$ and its continuity, it follows that the limits exist:
$$
\begin{aligned}
& \lim _{x \rightarrow 0}\left(\frac{1-f(x)}{x \cdot f(x)}\right)=-\lim _{x \rightarrow 0}\left(\frac{f(x)-f(0)}{x-0} \cdot \frac{1}{f(x)}\right)= \\
& -\lim _{x \rightarrow 0} \frac{f(x)-f(0)}{x-0} \cdot \lim _{x \rightarrow 0} \frac{1}{f(x)}=-f^{\prime}(0) \cdot \frac{1}{f(0)}=1
\end{aligned}
$$
Therefore, since $\lim _{n \rightarrow \infty} a_{n}=0$, the limit also exists for the sequence
$$
\lim _{n \rightarrow \infty} \frac{1}{n a_{n}}=\lim _{n \rightarrow \infty}\left(\frac{1-f\left(a_{n}\right)}{a_{n} f\left(a_{n}\right)}\right)=\lim _{x \rightarrow 0}\left(\frac{1-f(x)}{x \cdot f(x)}\right)=1
$$
which implies $\lim _{n \rightarrow \infty}\left(n a_{n}\right)=1$.
|
1
|
Calculus
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
11.8. A student was supposed to multiply a three-digit number by a four-digit number (the numbers do not start with 0). Instead of doing so, he simply appended the four-digit number to the right of the three-digit number, obtaining a seven-digit number, which is $N$ times ($N \in \mathbb{Z}$) larger than the correct result.
a) Can $N$ be equal to 2 or 10?
b) Find the largest possible value of $N$.
|
Solution. Let $\overline{abc}$ be the three-digit number and $\overline{defg}$ be the four-digit number. Then the seven-digit number has the form $\overline{abcdefg}$. From the condition of the problem, we have $\overline{\overline{abcdefg}}=N \cdot \overline{abc} \cdot \overline{defg}$, which is equivalent to $\overline{abc} \cdot 10^{4}=\overline{defg} \cdot(N \cdot \overline{abc}-1)$ (1).
a) Let $N=2$. Then (1) takes the form $\overline{abc} \cdot 10^{4}=\overline{defg} \cdot(2 \cdot \overline{abc}-1)$ (2). Since $(2 \cdot \overline{abc}-1)$ is an odd number, and $\overline{defg}$ does not divide $10^{4}$, then $(2 \cdot \overline{abc}-1)$ must divide a number of the form $5^{m}(m \geq 1)$. For example, let $2 \cdot \overline{abc}-1=5^{4}=625$. Then $\overline{abc}=313$ and, from (2), we obtain $\overline{defg}=5008$, i.e., $\overline{\overline{abcdefg}}=3135008$. Therefore, the value $N=2$ is possible.
For $N=10$ the equality (1) takes the form $\overline{abc} \cdot 10^{4}=\overline{defg} \cdot(10 \cdot \overline{abc}-1)$. The expression $(10 \cdot \overline{abc}-1)$ is an odd number (does not divide by 2) and has the last digit 9 (does not divide by 5). Therefore, $10^{4}$ must divide the number $\overline{defg}\frac{10000}{\overline{defg}}>\frac{10000}{2000}=5$ and, since $N<10$, it follows that $N \in\{6,7,8,9\}$.
Let $N=9$. Then from (4) we get $\frac{10000}{9}<\overline{defg}<\frac{10020}{9}$, which implies $1111<\overline{defg} \leq 1113$, i.e., $\overline{defg} \in\{1112,1113\}$. Considering $\overline{defg}=1112$, from relation (3) we get $1112=\overline{abc} \cdot 8$, i.e., $\overline{abc}=139$. Therefore, $\overline{abcdefg}=1391112$ and $N_{\max }=9$.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. Mihai drew several right-angled triangles on the board, such that any two triangles do not have common points. In each of these triangles, Mihai drew the following important lines (segments): all angle bisectors, all medians, and the altitude to the hypotenuse. Counting, the total number of important lines drawn in all the triangles is 44. Determine how many right-angled isosceles triangles Mihai drew on the board.
|
## Solution:
Right-angled triangles can be scalene or isosceles. In a scalene right-angled triangle, Mihai constructs exactly 7 distinct important segments: 3 angle bisectors, 3 medians, and one altitude. In a right-angled isosceles triangle, Mihai constructs exactly 5 distinct important segments, because the median, altitude, and angle bisector drawn from the right angle vertex coincide. We note that no important segment in one triangle coincides with any important segment in another triangle. Let $x$ be the number of any right-angled triangles, and $y$ be the number of right-angled isosceles triangles drawn by Mihai. Thus, we get $7 x + 5 y = 44$, where $x, y \in \mathbb{N}$. Since $7 x \leq 44$ and $x \in \mathbb{N}$, it follows that $x \in \{0,1,2,3,4,5,6\}$.
For $x=0$, we get $y=\frac{44}{5} \notin \mathbb{N}$. For $x=1$, we get $y=\frac{37}{5} \notin \mathbb{N}$. For $x=2$, we get $y=6$. For $x=3$, we get $y=\frac{23}{5} \notin \mathbb{N}$. For $x=4$, we get $y=\frac{16}{5} \notin \mathbb{N}$. For $x=5$, we get $y=\frac{9}{5} \notin \mathbb{N}$. For $x=6$, we get $y=\frac{2}{5} \notin \mathbb{N}$. Since the only solution to the equation $7 x + 5 y = 44$, where $x, y \in \mathbb{N}$, is $x=2$ and $y=6$, it follows that Mihai drew 6 right-angled isosceles triangles.
Answer: Mihai drew 6 right-angled isosceles triangles.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12.5. Let $I_{n}=\int_{\frac{1}{n}}^{n} \frac{d x}{(x+1)\left(\ln ^{2 n} x+1\right)}, n \geq 2$. Calculate $\lim _{n \rightarrow \infty} I_{n}$.
|
## Solution.
$$
I_{n}=\int_{\frac{1}{n}}^{n} \frac{d x}{(x+1)\left(\ln ^{2 n} x+1\right)}=\int_{\frac{1}{n}}^{1} \frac{d x}{(x+1)\left(\ln ^{2 n} x+1\right)}+\int_{1}^{n} \frac{d x}{(x+1)\left(\ln ^{2 n} x+1\right)}
$$
Consider
$$
\begin{aligned}
& \int_{\frac{1}{n}}^{1} \frac{d x}{(x+1)\left(\ln ^{2 n} x+1\right)}=\left|\begin{array}{l}
t=\frac{1}{x} \Rightarrow x=\frac{1}{t} \\
d x=-\frac{1}{t^{2}} d t \\
x=\frac{1}{n} \Rightarrow t=n \\
x=1 \Rightarrow t=1
\end{array}\right|=\int_{1}^{n} \frac{d t}{\left.t(t+1)\left(\ln ^{2 n} t+1\right)\right)}= \\
& \int_{1}^{n}\left(\frac{1}{t}-\frac{1}{t+1}\right) \frac{d t}{\ln ^{2 n} t+1}=\int_{1}^{n} \frac{d t}{t\left(\ln ^{2 n} t+1\right)}-\int_{1}^{n} \frac{d t}{(t+1)\left(\ln ^{2 n} t+1\right)}
\end{aligned}
$$
Then
$$
I_{n}=\int_{1}^{n} \frac{d t}{t\left(\ln ^{2 n} t+1\right)}-\int_{1}^{n} \frac{d t}{(t+1)\left(\ln ^{2 n} t+1\right)}+\int_{1}^{n} \frac{d x}{(x+1)\left(\ln ^{2 n} x+1\right)}=\int_{1}^{n} \frac{d t}{t\left(\ln ^{2 n} t+1\right)}
$$
Performing the variable substitution in the last integral, we get
$$
\begin{gathered}
I_{n}=\int_{1}^{n} \frac{d t}{t\left(\ln ^{2 n} t+1\right)}=\left|\begin{array}{c}
z=\ln t \\
d z=\frac{1}{t} d t \\
t=1 \Rightarrow z=0 \\
t=n \Rightarrow z=\ln n
\end{array}\right|=\int_{0}^{\ln n} \frac{d z}{z^{2 n}+1}=\int_{0}^{1} \frac{d z}{z^{2 n}+1}+\int_{1}^{\ln n} \frac{d z}{z^{2 n}+1}= \\
=1-\int_{0}^{1} \frac{z^{2 n} d z}{z^{2 n}+1}+\int_{1}^{\ln n} \frac{d z}{z^{2 n}+1}
\end{gathered}
$$
Estimate each integral separately
$$
\begin{gathered}
0 \leq \int_{1}^{\ln n} \frac{d z}{z^{2 n}+1}<\int_{1}^{\ln n} z^{-2 n} d z=\left.\frac{1}{1-2 n} z^{1-2 n}\right|_{1} ^{\ln n}=\frac{1}{(1-2 n)\left(\ln ^{2 n-1} n\right)}+\frac{1}{2 n-1} \rightarrow 0, n \rightarrow \infty \\
0 \leq \int_{0}^{1} \frac{z^{2 n} d z}{z^{2 n}+1} \leq \int_{0}^{1} \frac{z^{2 n-1} d z}{z^{2 n}+1}=\left.\frac{1}{2 n} \ln \left(z^{2 n}+1\right)\right|_{0} ^{1}=\frac{1}{2 n} \ln 2 \rightarrow 0, n \rightarrow \infty
\end{gathered}
$$
and we obtain: $\lim _{n \rightarrow \infty} I_{n}=1$.
|
1
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.3. In triangle $A B C$, point $D$ is the midpoint of side $A C$, and $E$ is an interior point of side $B C$ such that angles $B E A$ and $C E D$ are congruent. Find the numerical value of the ratio $\frac{A E}{D E}$.
|
Solution. On the extension of the ray $(ED$, we take the point $F$ such that $DE = DF$ (see figure).
Since $AD = DC$, it follows that the quadrilateral $AECF$ is a parallelogram. Then the lines $AE$ and $CF$ are parallel, as are the lines $AF$ and $BC$. Then we obtain
$$
m(\angle BEA) = m(\angle EAF) = \alpha = m(\angle CEF) = m(\angle AFE)
$$
It follows that triangle $AEF$ is isosceles with $AE = FE$. Since
$EF = 2 \cdot DE$, we have that $AE = 2 \cdot DE \Leftrightarrow \frac{AE}{DE} = 2$.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.4. A rectangular table has 6 rows and 7 columns and includes 42 squares of size $1 \times 1$. In each square, one of the numbers 0 or 1 is written such that for any two different rows, the sums of the numbers written on them are different, and for any two columns, the sums of the numbers written on them are equal. Find the sum of the numbers written in the first column.
|
Solution. Since the sums of the numbers on the lines are different, it follows that the sum of 7 numbers (0 or 1) written in a line can take only 8 values, namely: $0,1,2,3,4,5,6,7$. Since we have only 6 lines, then two values out of the eight are missing. Let's denote the missing values by $x$ and $y$. Then the sum of all the numbers in the table can be written as:
$$
S=0+1+2+3+4+5+6+7-(x+y)=28-(x+y)=7 k
$$
where $k \in \mathbf{N}$ is the sum of the numbers in any column, including the first.
Since $x+y=28-7 k=7 \cdot(4-k)$, it follows that the sum $x+y$ is a multiple of 7, which shows that $x+y=7$, and $k=3$.
We will show that such a table is possible. The following is an example of filling in the table with 0 and 1, which satisfies the conditions of the statement.
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 |
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.3. Solve in the set of real numbers the equation
$$
\cos \frac{\pi}{x}=-x^{6}-4 x^{5}+2 x^{4}+12 x^{3}-9 x^{2}-1
$$
|
Solution.
We have
$$
\begin{gathered}
1 \geq -\cos \frac{\pi}{x} = x^{6} + 4 x^{5} - 2 x^{4} - 12 x^{3} + 9 x^{2} + 1 = x^{2}\left(x^{4} + 4 x^{3} - 2 x^{2} - 12 x + 9\right) + 1 = \\
= x^{2}\left[\left(x^{2} + 2 x\right)^{2} - 6 x^{2} - 12 x + 9\right] + 1 = x^{2}\left[\left(x^{2} + 2 x\right)^{2} - 6\left(x^{2} + 2 x\right) + 9\right] + 1 = \\
= \left[x\left(x^{2} + 2 x - 3\right)\right]^{2} + 1 = [x(x-1)(x+3)]^{2} + 1 \geq 1
\end{gathered}
$$
which implies $[x(x-1)(x+3)]^{2} + 1 = 1$, i.e., $x=0, x=1$ or $x=-3$.
The value $x=0$ is not a solution because it is not in the domain of the function $f(x) = \cos \frac{\pi}{x}$.
For $x=1$, we have $-\cos \frac{\pi}{x} = -\cos \pi = 1$, so $x=1$ is a solution.
For $x=-3$, we have $-\cos \frac{\pi}{x} = -\cos \left(-\frac{\pi}{3}\right) = -\cos \frac{\pi}{3} = -\frac{1}{2} \neq 1$, so $x=-3$ is not a solution.
In conclusion, the only real solution to the equation in the statement is $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.7. Solve in $\square$ the equation $16 x+(x-1) \cdot 4^{x+1}=x^{2}\left(4^{x}+8+4^{\frac{1}{x}}\right)$.
|
Solution: DVA: $x \neq 0$.
The equation can be written in the form $x^{2} \cdot 4^{\frac{1}{x}}+(2-x)^{2} \cdot 4^{x}=8 x(2-x)$.
We observe that $x=2$ is not a solution.
Since $x \neq 2$, the equation can be brought to the form $\frac{x}{2-x} \cdot 4^{\frac{1}{x}}+\frac{2-x}{x} \cdot 4^{x}=8$.
If $\frac{x}{2-x} > 0$, that is, $x \in(0 ; 2)$. Using the relationship between the arithmetic mean and the geometric mean, we get $\frac{x}{2-x} \cdot 4^{\frac{1}{x}}+\frac{2-x}{x} \cdot 4^{x} \geq 2 \cdot \sqrt{\frac{x}{2-x} \cdot 4^{\frac{1}{x}} \cdot \frac{2-x}{x} \cdot 4^{x}}=2 \cdot \sqrt{4^{\frac{1}{x}+x}}=2^{\frac{1}{x}+x+1}$.
Since $x \in(0 ; 2)$, it follows that $x+\frac{1}{x} \geq 2$. Therefore, $\frac{x}{2-x} \cdot 4^{\frac{1}{x}}+\frac{2-x}{x} \cdot 4^{x} \geq 2^{2+1}=8$.
Equality holds when $\left\{\begin{array}{rl}\frac{x}{2-x} \cdot 4^{\frac{1}{x}} & =\frac{2-x}{x} \cdot 4^{x} \\ x & =1\end{array} \Leftrightarrow x=1 \in(0 ; 2)\right.$.
Answer: $S=\{1\}$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. Let $\left(a_{n}\right)_{n=1}^{\infty}$ be a sequence of integers that satisfies the relation $a_{n+1}=a_{n}^{1009}+3^{2017}, \forall n \geq 1$. How many perfect squares can this sequence contain? Justify your answer.
|
Solution. The possible values of the pairs $\left(a_{n} \bmod 4, a_{n+1} \bmod 4\right)$ are $(0,3),(1,0),(2,3)$ and $(3,2)$. Therefore, regardless of the value of $a_{1}$, all terms $a_{n}, n \geq 3$, are equal to 2 or $3(\bmod 4)$ and, thus, are not perfect squares. In conclusion, we have at most two perfect square terms: $a_{1}$ and $a_{2}$.
Let's prove that $a_{1}$ and $a_{2}$ cannot both be perfect squares. Suppose the contrary, $a_{1}=a^{2}$ and $a_{2}=b^{2}$, where $a$ and $b$ are natural numbers. We have $b^{2}=a^{2018}+3^{2017}$, equivalent to $\left(b-a^{1009}\right)\left(b+a^{1009}\right)=3^{2017}$, which implies $b-a^{1009}=3^{s}$ and $b+a^{1009}=3^{t}$, where the natural numbers $s$ and $t$ satisfy the relations $s+t=2017$ and $s \leq t$. Thus, $2 a^{1009}=3^{s}\left(3^{t-s}-1\right)$, where $s+t=2017$ and $s \leq 1008$.
If $s>0$, then $3^{s}\left(3^{t-s}-1\right) \mathrm{M}$ and, thus, $2 a^{1009} \mathrm{MB}$, which implies $a^{1009}$ M $\mathbb{B}^{1009}$. It follows that the right-hand side $3^{s}\left(3^{t-s}-1\right)$ is divisible by $3^{1009}$, which is impossible due to the inequality $s \leq 1008$.
If $s=0$, then $2 a^{1009}=3^{2017}-1$. We have $a^{1009}<3^{2017}-1<3^{2018}=9^{1009}$ and, thus, $a<9$. Since $3^{2017}-1 \equiv 2(\bmod 4)$, it follows that $a$ is odd, which implies $a \in\{1,3,5,7\}$. The case $a=1$ is impossible since $2 \neq 3^{2017}-1$. The case $a=3$ is impossible since $3^{2017}-1$ is not divisible by 3. The case $a=5$ is impossible since $2 \cdot 5^{1009} \mathrm{M} 0$, but $3^{2017}-1 \equiv 2(\bmod 10)$. The case $a=7$ is impossible since $3^{2017}-1 \equiv 2(\bmod 7)$.
Therefore, the numbers $a_{1}$ and $a_{2}$ cannot both be perfect squares. In conclusion, among the terms of the sequence $\left(a_{n}\right)_{n=1}^{\infty}$, we can find at most one perfect square (for example, if $a_{1}$ is a perfect square).
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. Determine all natural numbers $n$ for which the number $\sqrt{n+\sqrt{n-2}}$ is rational.
|
Solution: Suppose for some value of the number $n, n \geq 2$ we have $m=\sqrt{n+\sqrt{n-2}} \in Q, m \in N^{*}$. The equality $m^{2}=n+\sqrt{n-2}$ holds. Then there exists $k \in N^{*}$, such that $k=\sqrt{n-2}$, i.e., $n=k^{2}+2$. We can write $m^{2}=k^{2}+k+2$.
The inequality $k^{2}<k^{2}+k+2<k^{2}+4 k+4=(k+2)^{2}$ holds, or $k^{2}<m^{2}<(k+2)^{2}$. We obtain that $m=k+1$, then $k=1$ and $n=3$.
Answer: $n=3$
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.6. Let the sequence $\left(a_{n}\right)_{n=0}^{\infty}$ be defined by the relations $a_{0}=1, a_{1}=\frac{1+\sqrt{3}}{2 \sqrt{2}}$ and $a_{n}=2 a_{1} a_{n-1}-a_{n-2}, \forall n \geq 2$. Calculate the value of $a_{2020}$ and determine $\lim _{n \rightarrow \infty} \frac{a_{n}}{n^{2}}$.
|
## Solution.
We have $\quad a_{2}=2 a_{1}^{2}-a_{0}=2\left(\frac{1+\sqrt{3}}{2 \sqrt{2}}\right)^{2}-1=\frac{\sqrt{3}}{2}, \quad a_{3}=2 a_{1} a_{2}-a_{1}=2 \cdot \frac{\sqrt{3}}{2} \cdot\left(\frac{1+\sqrt{3}}{2 \sqrt{2}}\right)-\frac{1+\sqrt{3}}{2 \sqrt{2}}=\frac{\sqrt{2}}{2}$, $a_{4}=2 a_{1} a_{3}-a_{2}=2 \cdot \frac{\sqrt{2}}{2} \cdot\left(\frac{1+\sqrt{3}}{2 \sqrt{2}}\right)-\frac{\sqrt{3}}{2}=\frac{1}{2}$. These values reasonably suggest the hypothesis $a_{n}=\cos \left(\frac{\pi}{12} n\right), \forall n \geq 2$. We will prove its correctness using mathematical induction. Indeed, we have
$$
\cos \left(\frac{\pi}{12} \cdot 2\right)=\cos \left(\frac{\pi}{6}\right)=\frac{\sqrt{3}}{2}=a_{2}
$$
Assume the statement is true for $\forall n<N, N \geq 2$. Let's prove the correctness of the statement for $n=N$. Indeed, we have
$$
\begin{aligned}
& a_{N}=2 a_{1} a_{N-1}-a_{N-2}=2 \cos \frac{\pi}{12} \cdot \cos \left(\frac{\pi}{12}(N-1)\right)-\cos \left(\frac{\pi}{12}(N-2)\right)= \\
& =\cos \left(\frac{\pi}{12}(N-1)+\frac{\pi}{12}\right)+\cos \left(\frac{\pi}{12}(N-1)-\frac{\pi}{12}\right)-\cos \left(\frac{\pi}{12}(N-2)\right)= \\
& =\cos \left(\frac{\pi}{12} N\right)+\cos \left(\frac{\pi}{12}(N-2)\right)-\cos \left(\frac{\pi}{12}(N-2)\right)=\cos \left(\frac{\pi}{12} N\right)
\end{aligned}
$$
By the method of mathematical induction, we have $a_{n}=\cos \left(\frac{\pi}{12} n\right), \forall n \geq 2$.
Since the cosine function is periodic with period $2 \pi$, it follows that the sequence $\left(a_{n}\right)_{n=0}^{\infty}$ is periodic with period 24. Therefore, $a_{2020}=a_{2020 \bmod 24}=a_{4}=\frac{1}{2}$.
We calculate $\lim _{n \rightarrow \infty} \frac{a_{n}}{n^{2}}$. We obtain $0 \leq\left|\frac{a_{n}}{n^{2}}\right|=\left|\frac{1}{n^{2}} \cos \left(\frac{\pi}{12} n\right)\right| \leq \frac{1}{n^{2}}$. Taking the limit as $n \rightarrow \infty$, we get $0 \leq \lim _{n \rightarrow \infty}\left|\frac{a_{n}}{n^{2}}\right| \leq \lim _{n \rightarrow \infty} \frac{1}{n^{2}}=0$, i.e., $\lim _{n \rightarrow \infty}\left|\frac{a_{n}}{n^{2}}\right|=0$, which implies $\lim _{n \rightarrow \infty} \frac{a_{n}}{n^{2}}=0$.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.6. Solve in $R$ the equation
$$
\sqrt{2 x^{5}+x^{4}+4 x^{3}+2 x^{2}+2 x+1}+\sqrt{17-2 x+34 x^{2}-4 x^{3}+17 x^{4}-2 x^{5}}=7 x^{2}-8 x+22
$$
|
Solution: We will apply the inequality $\frac{a+b}{2} \leq \sqrt{\frac{a^{2}+b^{2}}{2}}$, which is true for any real numbers $a$ and $b$.
On $D V A$, the inequality holds:
$$
\frac{\sqrt{2 x^{5}+x^{4}+4 x^{3}+2 x^{2}+2 x+1}+\sqrt{17-2 x+34 x^{2}-4 x^{3}+17 x^{4}-2 x^{5}}}{2} \leq \sqrt{\frac{18 x^{4}+36 x^{2}+18}{2}}=3\left(x^{2}+1\right)
$$
Then
$\sqrt{2 x^{5}+x^{4}+4 x^{3}+2 x^{2}+2 x+1}+\sqrt{17-2 x+34 x^{2}-4 x^{3}+17 x^{4}-2 x^{5}} \leq 6\left(x^{2}+1\right)$.
We will show that on DVA we have $7 x^{2}-8 x+22 \geq 6 x^{2}+6 \Leftrightarrow x^{2}-8 x+16 \geq 0 \Leftrightarrow x \in \mathbb{R}$
Equality holds only for $x=4$.
We verify whether the number 4 is a solution to the equation and convince ourselves that it is a solution.
Answer: $S=\{4\}$
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.8. The natural number $n$ and the prime numbers $p$ and $q$ satisfy the relation $\frac{3}{\sqrt{n}}=\frac{2}{\sqrt{p}}+\frac{1}{\sqrt{q}}$. Determine all possible values of the expression $E=p+q-2 n$.
|
## Solution:
From $\frac{3}{\sqrt{n}}=\frac{2}{\sqrt{p}}+\frac{1}{\sqrt{q}}$, we get $\frac{3}{\sqrt{n}}=\frac{2 \sqrt{q}+\sqrt{p}}{\sqrt{p q}}, 3 \sqrt{p q}=\sqrt{n}(2 \sqrt{q}+\sqrt{p})$. Squaring both sides of the last equality, we obtain $9 p q=n(4 q+p+4 \sqrt{p q})$. Since $9 p q \in \mathbb{N}$, it follows that $\sqrt{p q} \in \mathbb{N}$, which implies $p \cdot q$ - a perfect square. Since $p$ and $q$ are prime numbers, and $p \cdot q$ - a perfect square, it follows that $p=q$. For $p=q$, from $9 p q=n(4 q+p+4 \sqrt{p q})$ we get $9 p^{2}=9 p n$, which implies $p=n$. Thus, $n=p=q$, and the expression $E=p+q-2 n=0$.
## Answer: 0
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. For what real values of the parameter a does the graph of the function $f: \square \rightarrow \square$, $f(x)=x^{4}-8 x^{3}+14 x^{2}+$ ax have an axis of symmetry parallel to the line $x=0$?
|
## Solution.
Since the graph of the function $f(x)$ has an axis of symmetry parallel to the line $x=0$, then the axis of symmetry has the equation $x=c$, where $c$ is a constant real value. Substituting $t=x-c$, we obtain that the graph of the function $f(t)$, as a function of $t$, will be symmetric with respect to the line $t=0$, i.e., the $O y$ axis. We have:
$$
\begin{gathered}
P(t)=x^{4}-8 x^{3}+14 x^{2}+a x=(t+c)^{4}-8(t+c)^{3}+14(t+c)^{2}+a(t+c)= \\
=t^{4}+4 t^{3} c+6 t^{2} c^{2}+4 t c^{3}+c^{4}-8\left(t^{3}+3 t^{2} c+3 t c^{2}+c^{3}\right)+14\left(t^{2}+2 t c+c^{2}\right)+a t+a c= \\
=t^{4}+t^{3}(4 c-8)+t^{2}\left(6 c^{2}-24 c+14\right)+t\left(4 c^{3}-24 c^{2}+28 c+a\right)+\left(c^{4}-8 c^{3}+14 c^{2}+a c\right)
\end{gathered}
$$
The graph of the function $f(t)$ is symmetric with respect to the $O y$ axis if and only if the function $f(t)$ is even, i.e., if and only if the coefficients of the function $f(t)$ corresponding to the odd powers of $t$ are equal to 0. We obtain
$$
\left\{\begin{array} { c }
{ 4 c - 8 = 0 } \\
{ 4 c ^ { 3 } - 2 4 c ^ { 2 } + 2 8 c + a = 0 }
\end{array} \Leftrightarrow \left\{\begin{array} { c }
{ c = 2 } \\
{ a = - 4 c ^ { 3 } + 2 4 c ^ { 2 } - 2 8 c }
\end{array} \Leftrightarrow \left\{\begin{array}{c}
c=2 \\
a=-4 \cdot 8+24 \cdot 4-28 \cdot 2=8
\end{array}\right.\right.\right.
$$
Final answer: $a=8$.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 3. On the ceiling of a room, there are 15 lamps, numbered from 1 to 15. Initially, all the lamps are off. In another room, there are 15 switches: one switch for lamp 1 and 2, one switch for lamp 2 and 3, one switch for lamp 3 and 4, and so on, up to a switch for lamp 15 and 1. When the switch for such a pair of lamps is flipped, the status of each of those two lamps changes (from on to off or vice versa). The switches are arranged in a random order and all look identical. Raymond wants to find out which switch corresponds to which pair of lamps. From the room with the switches, he cannot see the lamps. However, he can flip a number of switches and then go to the other room to see which lamps are on. He can do this multiple times. How many times does he need to go to the other room at a minimum to be certain which switch corresponds to which pair of lamps?
|
Solution. With three rounds of walking, Raymond can never be certain. Indeed, if for each switch you note whether it is in the initial position or the flipped position in the three rounds, then you can get $2^{3}=8$ different patterns. However, there are 15 switches, so there are multiple switches with the same pattern, and Raymond can never distinguish these switches. Therefore, he must walk at least four times. We will prove that this is indeed sufficient.
Assume that Raymond, starting from the situation where all the lights are off, flips a number of switches. If he flips all the switches or none at all, then all the lights will still be off afterward. Otherwise, there will always be a light that has been changed by only one flipped switch, so it will be on. Consider such a light $i$ that is on. Then the switch with $i-1$ and $i$ or the switch with $i$ and $i+1$ has been flipped. (Consider the light numbers modulo 15.) First, assume that the latter is the case. Now consider light $i+1$. If it is off, then the switch with $i+1$ and $i+2$ has also been flipped; if it is on, then that switch has not been used. Next, we can deduce from the status of light $i+2$ whether the switch with $i+2$ and $i+3$ has been flipped or not. By continuing this process, we see that it is determined for all switches whether they have been flipped or not. In the second case, if it is precisely the switch with $i-1$ and $i$ that has been flipped, then it is also determined for all switches whether they have been flipped or not. Therefore, there are exactly two combinations of switches that result in the same status of the lights. If we choose one of these combinations and then flip all 15 switches again, the same lights will be on, so this must result in exactly the second combination of switches. If the first combination of switches contains an even number of switches, then the second combination contains 15 minus that number, so an odd number of switches.
However, Raymond knows himself how many switches he has flipped. He can deduce from the situation of the lights which two combinations of switches are possible, and only one of these can match the number of switches he has flipped. Therefore, he can precisely determine which lights the switches he has flipped correspond to; he only does not know which is which within that group of switches.
Now write the numbers 1 to 15 in binary notation. For this, a maximum of 4 digits are needed; pad with zeros if necessary so that each number is written with exactly 4 digits. Raymond numbers the switches with these binary numbers. In the first round, he flips the switches whose numbers in binary notation start with a 1 and notes the 8 corresponding light pairs. In the second round, he first resets all the switches and then chooses the numbers that have a 1 in the second position in binary notation. Similarly, in the third round, he chooses the third position in the binary notation, and in the fourth round, the fourth position. In each round, he can determine which light pairs the switches he has used correspond to (only not which is which). Since each switch corresponds to a unique combination of rounds, he can then figure out for each switch which light pair it controls. For example, if a certain light pair is turned on in the first round, not in the second round, in the third round, and also in the fourth round, then it corresponds to the switch with binary code 1011, which is switch 11. Therefore, he can succeed in four rounds of walking.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. Let $n$ be an even positive integer. A sequence of $n$ real numbers is called complete if for every integer $m$ with $1 \leq m \leq n$, the sum of the first $m$ terms or the sum of the last $m$ terms of the sequence is an integer. Determine the minimum number of integers in a complete sequence of $n$ numbers.
|
Solution. We prove that the minimum number of integers in a complete sequence is 2. First, consider the case $n=2$. Let $a_{1}$ and $a_{2}$ be the numbers in the sequence. Then $a_{1}$ or $a_{2}$ is an integer, say without loss of generality $a_{1}$. Furthermore, $a_{1}+a_{2}$ is an integer, but then $a_{2}$ is also an integer. Therefore, the sequence contains at least two integers.
Now consider the case $n>2$. Write $n=2k$ (since $n$ is even) with $k \geq 2$. Then $a_{1}+a_{2}+\ldots+a_{k}$ or $a_{k+1}+a_{k+2}+\ldots+a_{2k}$ is an integer. Since the sum of both expressions is also an integer, both are integers. Furthermore, $a_{1}+a_{2}+\ldots+a_{k-1}$ or $a_{k+2}+a_{k+3}+\ldots+a_{2k}$ is an integer. This implies that $a_{k}$ or $a_{k+1}$ is an integer. Additionally, we know that $a_{1}$ or $a_{2k}$ is an integer, and these do not coincide with $a_{k}$ or $a_{k+1}$ because $k \geq 2$. Therefore, at least two different numbers are integers.
Finally, we show that for every even $n$, it is possible to construct a complete sequence with exactly two integers. Write $n=2k$ again. If $k$ is odd, we take
$a_{1}=a_{k+1}=1$ and all other terms equal to $\frac{1}{2}$. The sum of all numbers in the sequence is an integer, so it suffices to show that the sum of the first or last $m$ terms is an integer with $1 \leq m \leq k$; the cases with $m>k$ follow directly. For odd $m \leq k$, the first $m$ terms together are an integer, for even $m \leq k$.
We conclude that the minimum number of integers in a complete sequence of $n$ numbers is 2.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 5. Given a positive integer $n$. Determine all positive real numbers $x$ such that
$$
n x^{2}+\frac{2^{2}}{x+1}+\frac{3^{2}}{x+2}+\ldots+\frac{(n+1)^{2}}{x+n}=n x+\frac{n(n+3)}{2} .
$$
|
Solution. For $1 \leq i \leq n$ we have
$\frac{(i+1)^{2}}{x+i}=i+1+\frac{(i+1)^{2}-(i+1)(x+i)}{x+i}=i+1+\frac{i+1-(i+1) x}{x+i}=i+1+\frac{(i+1)(1-x)}{x+i}$,
so we can rewrite the left side of the given equation to
$$
n x^{2}+2+3+\ldots+(n+1)+\frac{2(1-x)}{x+1}+\frac{3(1-x)}{x+2}+\ldots+\frac{(n+1)(1-x)}{x+n}
$$
It holds that $2+3+\ldots+(n+1)=\frac{1}{2} n(n+3)$, so this sum cancels out with $\frac{n(n+3)}{2}$ on the right side of the given equation. Furthermore, we can move $n x^{2}$ to the other side and factor out $1-x$ in all fractions. The equation can thus be rewritten as
$$
(1-x) \cdot\left(\frac{2}{x+1}+\frac{3}{x+2}+\ldots+\frac{n+1}{x+n}\right)=n x-n x^{2}
$$
The right side can be factored as $n x(1-x)$. We now see that $x=1$ is a solution to this equation. If there were another solution $x \neq 1$, then it would have to satisfy
$$
\frac{2}{x+1}+\frac{3}{x+2}+\ldots+\frac{n+1}{x+n}=n x
$$
For $0 < x < 1$ we have
$$
\frac{2}{x+1}+\frac{3}{x+2}+\ldots+\frac{n+1}{x+n}>\frac{2}{2}+\frac{3}{3}+\ldots+\frac{n+1}{n+1}=n>n x,
$$
while for $x>1$ we have
$$
\frac{2}{x+1}+\frac{3}{x+2}+\ldots+\frac{n+1}{x+n}<\frac{2}{2}+\frac{3}{3}+\ldots+\frac{n+1}{n+1}=n<n x .
$$
Thus, there are no solutions with $x \neq 1$. We conclude that for all $n$, the only solution is $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 4. Let $m \geq 3$ and $n$ be positive integers with $n > m(m-2)$. Find the largest positive integer $d$ such that $d \mid n!$ and $k \nmid d$ for all $k \in \{m, m+1, \ldots, n\}$.
|
Solution. We will prove that $d=m-1$ is the largest that satisfies. First note that $m-1 \mid n$ ! and for $k \geq m$ we have $k \nmid m-1$, so $d=m-1$ indeed satisfies. Now suppose that for some $d$ we have: $d \mid n$ ! and $k \nmid d$ for all $k \in\{m, m+1, \ldots, n\}$. We will prove that $d \leq m-1$. Write $d=p_{1} p_{2} \cdots p_{t}$ with $p_{i}$ prime for all $i$ (not necessarily all distinct). If $t=0$, then $d=1 \leq m-1$, so we may assume $t \geq 1$. From the first condition on $d$ it follows that $p_{i} \leq n$ for all $i$. From the second condition on $d$ it follows that $p_{i} \notin\{m, m+1, \ldots, n\}$ for all $i$. Thus $p_{i} \leq m-1$ for all $i$. Now consider the numbers $p_{1}, p_{1} p_{2}, \ldots, p_{1} p_{2} \cdots p_{t}$. These are all divisors of $d$ and therefore all different from numbers in $\{m, m+1, \ldots, n\}$. Furthermore, we know that $p_{1} \leq m-1$. Now consider the largest $j \leq t$ for which $p_{1} p_{2} \cdots p_{j} \leq m-1$. If $j<t$ then
$$
p_{1} p_{2} \cdots p_{j} p_{j+1} \leq(m-1) p_{j+1} \leq(m-1)(m-1)=m(m-2)+1 \leq n
$$
But that means that $p_{1} p_{2} \cdots p_{j} p_{j+1} \leq m-1$ as well. Contradiction with the maximality of $j$. So it must be that $j=t$, i.e., $d=p_{1} p_{2} \cdots p_{t} \leq m-1$.
We conclude that $d=m-1$ is indeed the largest $d$ that satisfies the conditions.
|
-1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. Determine the largest real number $M$ such that for every infinite sequence $x_{0}, x_{1}, x_{2}, \ldots$ of real numbers that satisfies
a) $x_{0}=1$ and $x_{1}=3$,
b) $x_{0}+x_{1}+\cdots+x_{n-1} \geq 3 x_{n}-x_{n+1}$,
it holds that
$$
\frac{x_{n+1}}{x_{n}}>M
$$
for all $n \geq 0$.
|
Solution. Answer: the largest possible constant for which this holds is $M=2$.
This problem is a typical example where it is beneficial to take a stronger induction hypothesis than strictly necessary: we show by induction that $x_{n+1}>2 x_{n}>x_{n}+x_{n-1}+\ldots+x_{0}$. For $n=0$, this translates to $x_{1}>2 x_{0}>x_{0}$, which, with the given initial values, becomes $3>2>1$. Now assume as the induction hypothesis that $x_{n+1}>2 x_{n}>x_{n}+x_{n-1}+\ldots+x_{0}$. Then for $x_{n+2}$, using the given condition, we have
$$
\begin{aligned}
x_{n+2} & \geq 3 x_{n+1}-\left(x_{n}+\ldots+x_{0}\right) \\
& >2 x_{n+1} \\
& >x_{n+1}+x_{n}+\ldots+x_{0} .
\end{aligned}
$$
This completes the induction step. From this, it follows that for all possible sequences and all possible $n$, $\frac{x_{n+1}}{x_{n}}>2$.
To show that we cannot find a higher value for $M$, consider the sequence for which equality holds in b), i.e., $x_{0}+x_{1}+\cdots+x_{n-1}=3 x_{n}-x_{n+1}$. Then we have
$$
\begin{aligned}
x_{n+1} & =3 x_{n}-\left(x_{n-1}+\ldots+x_{0}\right) \\
& =3 x_{n}-x_{n-1}-\left(x_{n-2}+\ldots+x_{0}\right) \\
& =3 x_{n}-x_{n-1}-\left(3 x_{n-1}-x_{n}\right) \\
& =4 x_{n}-4 x_{n-1} .
\end{aligned}
$$
The characteristic equation of this homogeneous recurrence relation is $\lambda^{2}-4 \lambda+4=(\lambda-2)^{2}=0$. Since this has a double root at $\lambda=2$, the two characteristic solutions are $2^{n}$ and $n 2^{n}$. Solving $x_{n}=B 2^{n}+C n 2^{n}$ for the given initial values, we get $B+0=x_{0}=1$ and $2 B+2 C=x_{1}=3$, so $B=1$ and $C=\frac{1}{2}$. The solution for these initial values is thus $x_{n}=1 \cdot 2^{n}+\frac{1}{2} n 2^{n}=(n+2) 2^{n-1}$.
Now that we have solved the recurrence relation, we simply calculate that
$$
\frac{x_{n+1}}{x_{n}}=\frac{(n+3) 2^{n}}{(n+2) 2^{n-1}}=2 \frac{n+3}{n+2}=2\left(1+\frac{1}{n+2}\right)
$$
For large $n$, this fraction approaches 2 arbitrarily closely. To make this precise: suppose $M=2+\epsilon$ with $\epsilon>0$. Then for this sequence and $n>\frac{2}{\epsilon}-2$, we have $\frac{x_{n+1}}{x_{n}}=2+\frac{2}{n+2}<2+\epsilon=M$. Therefore, such an $M$ does not satisfy the condition. The largest value of $M$ that can satisfy the condition is thus 2, and we have shown above that this value does indeed satisfy the condition.
|
2
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## Problem 3.
(a) Let $a$ and $b$ be positive integers such that $M(a, b)=a-\frac{1}{b}+b\left(b+\frac{3}{a}\right)$ is an integer. Prove that $M(a, b)$ is a perfect square.
(b) Find integers $a$ and $b$, both not equal to zero, such that $M(a, b)$ is a positive integer but not a perfect square.
|
## Solution.
(a) Since $a+b^{2}$ is an integer, $-\frac{1}{b}+\frac{3 b}{a}$ is also an integer. This can be written as $\frac{-a+3 b^{2}}{a b}$. We see that $a b$ is a divisor of $3 b^{2}-a$. In particular, $b$ is a divisor of $3 b^{2}-a$, and thus $b \mid a$. But this means that $b^{2}$ is a divisor of $a b$ and therefore also of $3 b^{2}-a$, which implies $b^{2} \mid a$. We now write $a=m b^{2}$ with $m$ a positive integer. Then $m b^{3}$ is a divisor of $3 b^{2}-m b^{2}$, so $m b$ is a divisor of $3-m$. This implies that $m$ is a divisor of 3 (i.e., $m=1$ or $m=3$) and that $b$ is a divisor of $3-m$.
First, assume that $m=3$. Then $a=3 b^{2}$. Substituting this gives $M\left(3 b^{2}, b\right)=3 b^{2}-\frac{1}{b}+b^{2}+\frac{1}{b}=4 b^{2}$, which is the square of $2 b$.
Now, assume that $m=1$. From $b \mid 3-m$ it follows that $b=1$ or $b=2$. In the first case, $a=1$ and in the second case, $a=4$. Substituting the first possibility gives $M(1,1)=1-1+1+3=4$, which is a square. Substituting the second possibility gives $M(4,2)=4-\frac{1}{2}+4+\frac{3}{2}=9$, which is also a square.
We conclude that $M(a, b)$ is a square in all cases.
(b) Take $a=4$ and $b=-2$. Then $M(4,-2)=7$. This is a positive integer, but not a square. After all the work in part (a), this answer is not hard to find. You know that $a$ must be of the form $m b^{2}$, now with $m \in \mathbb{Z}$, and that $m$ must be a divisor of 3. Moreover, $m=3$ does not work, as it always results in a square. The rest of the possibilities for $m$ can be simply tested.
|
7
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. Determine all positive integers $n$ for which there exist positive integers $a_{1}, a_{2}, \ldots, a_{n}$ such that
$$
a_{1}+2 a_{2}+3 a_{3}+\ldots+n a_{n}=6 n
$$
and
$$
\frac{1}{a_{1}}+\frac{2}{a_{2}}+\frac{3}{a_{3}}+\ldots+\frac{n}{a_{n}}=2+\frac{1}{n}
$$
|
Solution. If we apply the inequality of the arithmetic and harmonic mean to $a_{1}$, twice $a_{2}$, three times $a_{3}, \ldots, n$ times $a_{n}$, then we find
$$
\frac{6 n}{\frac{1}{2} n(n+1)}=\frac{a_{1}+2 a_{2}+3 a_{3}+\ldots+n a_{n}}{\frac{1}{2} n(n+1)} \geq \frac{\frac{1}{2} n(n+1)}{\frac{1}{a_{1}}+\frac{2}{a_{2}}+\frac{3}{a_{3}}+\ldots+\frac{n}{a_{n}}}=\frac{\frac{1}{2} n(n+1)}{2+\frac{1}{n}} .
$$
It holds that
$$
\frac{6 n}{\frac{1}{2} n(n+1)}=\frac{12}{n+1}\frac{\frac{1}{2} n^{2}(n+1)}{2 n+2}=\frac{1}{4} n^{2} .
$$
All together, we find $\frac{12}{n}>\frac{1}{4} n^{2}$, or $48>n^{3}$, from which it follows that $n \leq 3$.
For $n=1$, we get $a_{1}=6$ and $\frac{1}{a_{1}}=3$, which contradicts each other. So $n=1$ is not possible.
For $n=2$, we get $a_{1}+2 a_{2}=12$ and $\frac{1}{a_{1}}+\frac{2}{a_{2}}=2+\frac{1}{2}$. If $a_{2} \geq 2$, then $\frac{1}{a_{1}}+\frac{2}{a_{2}} \leq 1+1$ and that is too small. So $a_{2}$ must be $1$, but then we find $a_{1}=12-2=10$ and thus $\frac{1}{a_{1}}+\frac{2}{a_{2}}=\frac{1}{10}+2$, a contradiction. So $n=2$ is not possible.
For $n=3$, there is a solution, namely $a_{1}=6, a_{2}=3$ and $a_{3}=2$ (substitution shows that this satisfies the conditions). So $n=3$ is possible and we conclude that $n=3$ is the only solution.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 3. Find all positive integers $k$ for which the equation
$$
\operatorname{lcm}(m, n)-\operatorname{gcd}(m, n)=k(m-n)
$$
has no positive integer solutions $(m, n)$ with $m \neq n$.
|
Solution. Let $d=\operatorname{gcd}(m, n)$ and write $m=d a$ and $n=d b$. It holds that $\operatorname{lcm}(m, n) \cdot \operatorname{gcd}(m, n)=m n$, so we can write the given equation as
$$
\frac{d a \cdot d b}{d}-d=k(d a-d b)
$$
or equivalently
$$
a b-1=k(a-b) .
$$
From now on, we will look at the equivalent problem: find all positive integers $k$ for which this new equation has no positive integer solutions $(a, b)$ with $a \neq b$ and $\operatorname{gcd}(a, b)=1$. Note that if a pair $(a, b)$ satisfies this equation, it automatically follows that $\operatorname{gcd}(a, b)=1$. Suppose that $t \mid a$ and $t \mid b$, then $t \mid a b$ and $t \mid a-b$, so $t \mid 1$, so $a$ and $b$ have no common divisor greater than 1.
First, assume that $k \geq 3$. We claim that $(a, b)=\left(k^{2}-k-1, k-1\right)$ is a solution. Indeed, we have
$a b-1=a(k-1)-1=k a-a-1=k a-k^{2}+k+1-1=k a-k^{2}+k=k(a-k+1)=k(a-b)$.
We have already seen that this immediately implies that $\operatorname{gcd}(a, b)=1$. We still need to check that $a$ and $b$ are positive and that they are not equal. Since $k \geq 3$, we have $b=k-1 \geq 2$ and $a=k^{2}-k-1 \geq 2 k-k-1=k-1 \geq 2$, so they are both positive. Suppose that $a=b$, then $k^{2}-k-1=k-1$, or $k^{2}=2 k$, or $k=2$, a contradiction. Thus, our pair $(a, b)$ satisfies all the conditions. For every $k \geq 3$, the equation has at least one solution $(a, b)$ with $a \neq b$ and $\operatorname{gcd}(a, b)=1$.
Now assume that $k=1$. We claim that $(a, b)=(2,1)$ is a solution. Clearly, $a$ and $b$ are positive and not equal. Furthermore, we have
$$
a b-1=2-1=1=1 \cdot(2-1)=k(a-b) .
$$
So for $k=1$, the equation also has at least one solution $(a, b)$ with $a \neq b$ and $\operatorname{gcd}(a, b)=1$.
Finally, assume that $k=2$. The equation becomes
$$
a b-1=2(a-b) .
$$
The right-hand side is at most $2 a-2$ because $b$ is positive and an integer, so $a b-1 \leq 2 a-2$, hence $a b<2 a$, so $b<2$. Therefore, we must have $b=1$. The equation then becomes $a-1=2(a-1)$, which implies $a-1=0$. We then have $a=1$ and $b=1$, so $a=b$. We conclude that there are no solutions $(a, b)$ with $a \neq b$.
Thus, the only $k$ for which the original equation has no positive integer solutions $(m, n)$ with $m \neq n$ is $k=2$.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. The sets $A$ and $B$ are subsets of the positive integers. The sum of any two different elements from $A$ is an element of $B$. The quotient of any two different elements of $B$ (where we divide the larger by the smaller) is an element of $A$. Determine the maximum number of elements in $A \cup B$.
|
Solution. Suppose $A$ contains at least three elements, say $a<b<c$, so $b-a$ is positive, thus it must hold that $a+c \leq b-a$. This gives $c \leq b-2a$. Therefore, $A$ contains at most two elements.
Suppose $B$ contains at least four elements, say $a<b<c<d$. Then $A$ contains the three distinct elements $\frac{d}{a}, \frac{d}{b}$, and $\frac{d}{c}$. But $A$ cannot contain three distinct elements, contradiction. Therefore, $B$ contains at most three elements.
In total, $A \cup B$ contains at most 5 elements. This is possible, for example with $A=\{2,4\}$ and $B=\{3,6,12\}$. Now $2+4=6 \in B$ and $\frac{12}{6}=\frac{6}{3}=2 \in A$ and $\frac{12}{3}=4 \in A$, so this pair of sets satisfies the conditions. We conclude that $A \cup B$ contains at most 5 elements. Finding a pair of sets that satisfies the conditions can be done as follows. Suppose $B$ contains the elements $a<b<c$. Then $A$ contains the elements $\frac{c}{b}$, $\frac{b}{a}$, and $\frac{c}{a}$, with $\frac{c}{a}$ being the largest. Since $A$ contains only two elements, it must hold that $\frac{c}{b}=\frac{b}{a}$. Furthermore, the sum of the two elements in $A$ must be in $B$, so $\frac{b}{a}+\frac{c}{a} \in B$. Write $b=t a$, then $c=t b=t^{2} a$ and $\frac{b}{a}+\frac{c}{a}=t+t^{2}$. Now you see that $b$ can equal $t+t^{2}$ by choosing $a=t+1$. With $t=1$ you get $b=a$, so that does not work; with $t=2$ you get the solution mentioned above.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
B3. One of the four gnomes, Anne, Bert, Chris, and Dirk, has stolen gold from the king. Each of the gnomes, who know each other inside and out, makes two statements. If a gnome is a liar, at least one of those two statements is a lie. If a gnome is not a liar, both statements are true.
Anne says: "Bert is a liar." and "Chris or Dirk did it."
Bert says: "Chris is a liar." and "Dirk or Anne did it."
Chris says: "Dirk is a liar." and "Anne or Bert did it."
Dirk says: "Anne is a liar." and "Bert or Chris did it."
How many of these eight statements are true?
|
B3. 5
First, consider the case where Anne stole from the king. Then the last two statements of Bert and Chris are true, and those of Anne and Dirk are false. Therefore, Anne and Dirk are liars. Since both statements of Chris are true, Chris is not a liar. From this, we conclude that Bert is a liar, because his first statement is a lie. Now that we know whether each person is a liar, we simply count that out of the eight statements, five are true.
You can apply similar reasoning for the cases where Bert, Chris, and Dirk stole from the king. Since the problem is symmetric (cyclically swapping the names 'Anne', 'Bert', 'Chris', and 'Dirk' does not change the problem), we find the same result each time: five of the statements are true.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
B1. We consider numbers of two or more digits where none of the digits is 0. We call such a number thirteenish if every two adjacent digits form a multiple of 13. For example, 139 is thirteenish because $13=1 \times 13$ and $39=3 \times 13$.
How many thirteenish numbers of five digits are there?
|
B1. 6 The multiples of 13 that consist of two non-zero digits are 13, 26, 39, 52, 65, 78, and 91. In a thirteenish number, a 1 can only be followed by a 3, and a 2 can only be followed by a 6. The digit 4 cannot be followed by any digit. In the figure, each digit is marked with the digit that can follow it.
For the first digit of a thirteenish number with more than two digits, we can only choose from $1, 3, 9, 2, 6$, and 5. Subsequently, all following digits are fixed.
We now see that 13913, 26526, 39139, 52652, 65265, and 91391 are the thirteenish numbers of five digits. Thus, there are 6 of them.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
B5. In a $5 \times 5$ table, we place the numbers 1 through 5 such that each number appears exactly once in each row and each column. A number in a specific row and column of the table is correctly placed if the following two conditions are met:
- In that row, all smaller numbers are to the left of the number and all larger numbers are to the right, or vice versa.
- In that column, all smaller numbers are below the number and all larger numbers are above, or vice versa.
What is the maximum number of correctly placed numbers in such a table?
## C-Problems
For the C-Problems, the answer is not the only thing that matters; your reasoning and the method of solving must also be clearly written. Solve each C-Problem on a separate sheet of paper. Each correctly worked-out C-Problem is worth 10 points. Partial solutions can also earn points. Therefore, write everything clearly and submit your scratch paper (for each problem!) as well.
|
B5. 5 See the left figure below. A well-placed one and a well-placed five can only be in a cell with an $A$ because all other numbers must be on the same side of that number in the same row/column. A well-placed two or four can only be in a cell with a $B$, and a well-placed three can only be in a cell with a $C$.
| $A$ | | | | $A$ |
| :--- | :--- | :--- | :--- | :--- |
| | $B$ | | $B$ | |
| | | $C$ | | |
| | $B$ | | $B$ | |
| $A$ | | | | $A$ |
| $A$ | 5 | | | $A$ |
| :---: | :---: | :---: | :---: | :---: |
| 5 | 4 | | $B$ | |
| | | $C$ | | |
| | $B$ | | $B$ | |
| $A$ | | | | $A$ |
Since no two identical numbers can be in the same row or column, there can be no more than two well-placed ones. Similarly, there can be no more than two well-placed twos, fours, or fives. If there is a well-placed four, then the two adjacent cells must contain fives (see the right figure). On three of the four cells with an $A$, a five cannot stand because otherwise, there would be two fives in the same row or column. With two well-placed fours, no fives can stand on any of those four cells. Therefore, the total number of well-placed fours and fives cannot be more than two.
Similarly, it follows that the total number of well-placed twos and ones cannot be more than two. Thus, we can conclude that there cannot be more than $2+2+1=5$ well-placed numbers in total.
Now, we will show that it is indeed possible to have 5 well-placed numbers. Although one example is sufficient for the proof, we provide two different examples of a square with 5 well-placed numbers.
| $\mathbf{1}$ | 3 | 2 | 4 | $\mathbf{5}$ |
| :--- | :--- | :--- | :--- | :--- |
| 2 | 4 | 1 | 5 | 3 |
| 4 | 5 | 3 | 1 | 2 |
| 3 | 1 | 5 | 2 | 4 |
| $\mathbf{5}$ | 2 | 4 | 3 | $\mathbf{1}$ |
| $\mathbf{1}$ | $\mathbf{5}$ | $\mathbf{2}$ | 4 | 3 |
| :--- | :--- | :--- | :--- | :--- |
| 5 | $\mathbf{4}$ | 1 | 3 | 2 |
| 2 | 1 | $\mathbf{3}$ | 5 | 4 |
| 4 | 3 | 5 | $\mathbf{2}$ | 1 |
| 3 | 2 | 4 | 1 | $\mathbf{5}$ |
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
B2. A square with side 2 lies within a square with side 7. The sides of the smaller square are parallel to the sides of the larger square. What is the area of the black region?

|
B2. 10
We split the black area from the problem into four triangles, two of which we have shaded gray. The two gray triangles both have a base of 2 and together have a height of $7-2=5$, which is the height of the large square minus the height of the small square. The combined area of the two gray triangles is thus $\frac{1}{2} \cdot 2 \cdot 5=5$. The same applies to the two black triangles. Therefore, the total area of the region is $5+5=10$.

|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
B3. In a class, there are 23 students, each of whom has chosen exactly one foreign language, either German or French. There are a total of 10 girls in the class, and there are 11 students in total who are taking French. The number of girls who have chosen French plus the number of boys who have chosen German is 16.
How many girls have chosen French?
|
B3. 7 In total, there are 23 students. From the data it follows:
$$
\begin{aligned}
16+11+10= & (\text { girls with French }+ \text { boys with German })+\text { everyone with French }+ \text { all girls } \\
= & (\text { girls with French }+ \text { boys with German }) \\
& +(\text { girls with French }+ \text { boys with French }) \\
& +(\text { girls with French }+ \text { girls with German }) \\
= & 3 \times \text { girls with French }+ \text { boys with German } \\
& + \text { boys with French }+ \text { girls with German } \\
= & 2 \times \text { girls with French }+23 .
\end{aligned}
$$
The number of girls with French is thus equal to $\frac{16+11+10-23}{2}=\frac{14}{2}=7$.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
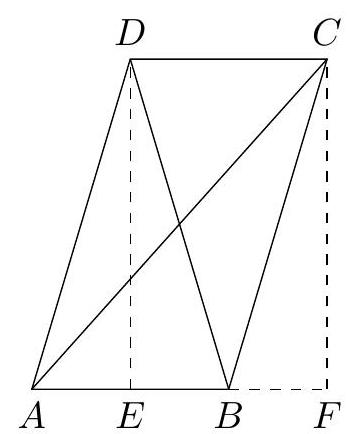
C2. We consider a triangle $A B C$ and a point $D$ on the extension of $A B$ towards $B$. The point $E$ lies on the side $A C$ such that angle $\angle D B C$ and angle $\angle D E C$ are equal. The intersection of $D E$ and $B C$ is $F$. Suppose that $|B F|=2,|B D|=3,|A E|=4$ and $|A B|=5$. (Note: the image below is not to scale.)
(a) Show that the triangles $\triangle A B C$ and $\triangle A E D$ are similar.
(b) Determine $|C F|$.
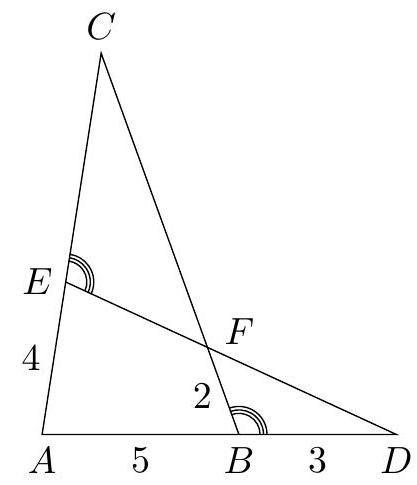
|
C2. (a) The situation is as shown in the figure below. Since angles $\angle A E C$ and $\angle A B D$ are straight, it follows that
$$
\angle A B C=180^{\circ}-\angle D B C=180^{\circ}-\angle D E C=\angle A E D .
$$
Since angle $A$ is present in both triangles, triangles $\triangle A B C$ and $\triangle A E D$ have two equal angles and are therefore similar.
(b) Due to the similarity of triangles $\triangle A B C$ and $\triangle A E D$, the angles at $C$ and $D$ are equal. Together with the equality $\angle D B F=\angle C E F$, it follows that triangles $\triangle D B F$ and $\triangle C E F$ are similar.
In similar triangles, all pairs of
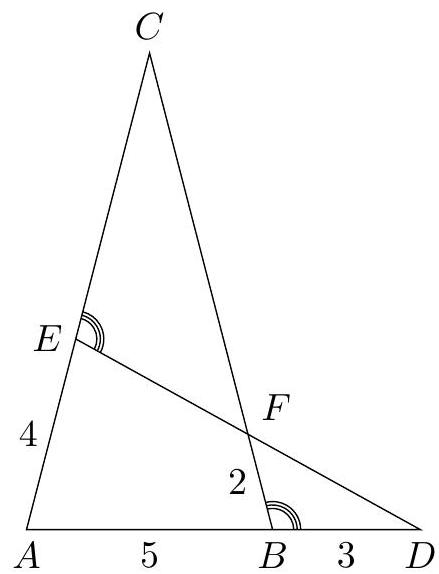
sides have the same ratio. The similarity of triangles $\triangle D B F$ and $\triangle C E F$ thus gives that
$$
\frac{|B F|}{|E F|}=\frac{|F D|}{|F C|}=\frac{|D B|}{|C E|}
$$
Since triangles $\triangle A B C$ and $\triangle A E D$ are similar, we find the ratios
$$
\frac{|A B|}{|A E|}=\frac{|B C|}{|E D|}=\frac{|C A|}{|D A|}
$$
Using equations (1) and (2), we can now find $|C F|$. From the first and last ratios in equation (2), it follows that
$$
\frac{5}{4}=\frac{|A B|}{|A E|}=\frac{|A C|}{|A D|}=\frac{4+|E C|}{5+3}
$$
From this, it follows that $|E C|=6$. We then substitute this into the first and third ratios in equation (1): $\frac{2}{|E F|}=\frac{3}{6}$. From this, it follows that $|E F|=4$. From the first and second ratios in (1), we now find that $\frac{2}{4}=\frac{|F D|}{|F C|}$, so $|F D|=\frac{1}{2}|C F|$. Finally, we substitute this into the first and second ratios in equation (2):
$$
\frac{5}{4}=\frac{|A B|}{|A E|}=\frac{|B C|}{|D E|}=\frac{2+|C F|}{4+\frac{1}{2}|C F|}
$$
Cross-multiplying and solving the equation gives that $|C F|=8$.
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
B4. Een parallellogram heeft twee zijden van lengte 4 en twee zijden van lengte 7. Ook heeft een van de diagonalen lengte 7. (Let op: het plaatje hiernaast is niet op schaal.) Hoe lang is de andere diagonaal?
|
B4. 9 We tekenen enkele hulplijnen, zoals in de figuur. Het parallellogram is $A B C D$ met $|A B|=4$ en $|A D|=|B C|=7$. We zijn op zoek naar $|A C|$.
Aangezien $|A D|=|B D|$, is driehoek $\triangle A B D$ een gelijkbenige driehoek. Laat $E$ het punt zijn midden tussen $A$ en $B$. Dan zijn de driehoeken $\triangle A E D$ en $\triangle B E D$ congruent en hoek $\angle A E D$ is een rechte hoek.
Vanuit het punt $C$ laten we een loodlijn neer op het verlengde van $A B$, noem het snijpunt $F$. Dan is $\angle D A E=\angle C B F$ vanwege $\mathrm{F}$-hoeken, en $\angle A E D=\angle B F C=90^{\circ}$ vanwege de loodlijn. Verder geldt $|A D|=|B C|$,
dus we hebben de congruente driehoeken $\triangle A E D \cong \triangle B F C$. Hieruit volgt dat $|B F|=2$.
We passen nu de stelling van Pythagoras toe in driehoek $\triangle B F C$. Dit geeft dat voor de hoogte $h$ van deze driehoek geldt dat $2^{2}+h^{2}=7^{2}$, dus $h^{2}=45$. Nu passen we de stelling van Pythagoras toe in driehoek $\triangle A F C$ om de diagonaal $d=|A C|$ te vinden: $h^{2}+6^{2}=d^{2}$, oftewel $45+36=d^{2}$, dus $d=9$.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
B2. In a top hat, there are a hundred tickets numbered from 1 to 100. You want to have three tickets with the property that each of the three numbers is smaller than the sum of the other two numbers. For example, the three tickets with numbers 10, 15, and 20 would be suitable (since $10<15+20, 15<10+20$, and $20<10+15$), but the tickets with numbers 3, 4, and 7 would not (since 7 is not less than $3+4$). You may (without looking at the numbers) take a number of tickets from the hat.
How many tickets must you take at a minimum to be sure that there are three tickets among them that meet your requirement?
|
2. 11
Suppose we have drawn 11 lottery tickets with numbers $a_{1}<a_{2}<\cdots<a_{11}$ on them such that no three tickets meet our wish. We know first that $a_{1} \geqslant 1$ and $a_{2} \geqslant 2$. Since the triplet $a_{1}, a_{2}$, and $a_{3}$ does not meet our wish, it must be that $a_{3} \geqslant a_{1}+a_{2} \geqslant 1+2=3$. We then proceed with the triplet $a_{2}, a_{3}$, and $a_{4}$ and find $a_{4} \geqslant a_{2}+a_{3} \geqslant 2+3=5$. If we continue this way, we find
$$
\begin{gathered}
a_{5} \geqslant 3+5=8, \quad a_{6} \geqslant 5+8=13, \quad a_{7} \geqslant 8+13=21, \quad a_{8} \geqslant 13+21=34, \\
a_{9} \geqslant 21+34=55, \quad a_{10} \geqslant 34+55=89 \quad \text { and } \quad a_{11} \geqslant 55+89=144 .
\end{gathered}
$$
The largest number on a ticket, however, is 100. So this is impossible, and we see that there must always be three tickets that meet our wish if we draw 11 tickets.
Moreover, 10 tickets are not enough. If we draw the tickets $1,2,3,5,8,13,21,34,55$ and 89, then we have no triplet of tickets that meets our wish.
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
B3. On each of the twelve edges of a cube, we write the number 1 or -1. We then multiply the four numbers on the edges of each face of the cube and write the result on that face. Finally, we add up the eighteen written numbers.
What is the smallest (most negative) result we can get this way? In the figure, you see an example of such a cube. The numbers on the back of the cube are not visible here.
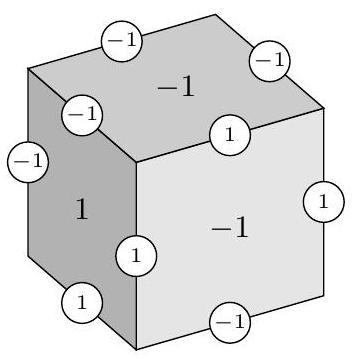
|
3. -12
First, we show that the result is always -12 or more. If we write a -1 on each of the twelve edges, we get a 1 in each face. In that case, the result is $-12+6=-6$. For every -1 on an edge that we change to a 1, at most two faces change from a 1 to a -1. The result thus becomes at most 2 lower $(-1+1+1$ becomes $1-1-1)$. To go below -12, we would need to write a 1 on at least 4 edges. However, in that case, the result is

at least $(4-8)-6=-10$. The result will therefore never be lower than -12.
Finally, we show that you can indeed get -12 as a result. To do this, we write a -1 on each edge, except for the three edges indicated in the figure. On each face, exactly three edges have a -1. Therefore, each face has a -1. The result is thus $(3-9)-6=-12$.
|
-12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
B5. Given is the sequence of numbers $a_{0}, a_{1}, a_{2}, \ldots, a_{2020}$. It is given that $a_{0}=0$. Moreover, for every $k=1,2, \ldots, 2020$ it holds that
$$
a_{k}= \begin{cases}a_{k-1} \cdot k & \text { if } k \text { is divisible by } 8, \\ a_{k-1}+k & \text { if } k \text { is not divisible by } 8 .\end{cases}
$$
What are the last two digits of $a_{2020}$?
## C-Problems
For the C-Problems, not only the answer is important; a reasoning should also be provided that shows your answer is correct. Each correctly worked out C-Problem is worth 10 points. Partial solutions can also earn points. Therefore, write everything clearly and submit your scratch paper for each problem as well.
NOTE: Solve each C-Problem on a separate sheet of paper and also submit the corresponding scratch paper per problem.
|
B5. 02 We see that $a_{2000}=a_{1999} \cdot 2000$ ends in three zeros. We can now determine the last digits of $a_{2001}, a_{2002}$ up to $a_{2020}$ using the formulas. It is only important to keep the last two digits, the rest we will ignore.
| $a_{2001}$ | $a_{2002}$ | $a_{2003}$ | $a_{2004}$ | $a_{2005}$ | $a_{2006}$ | $a_{2007}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $0+1=1$ | $1+2=3$ | $3+3=6$ | $6+4=10$ | $10+5=15$ | $15+6=21$ | $21+7=28$ |
| $a_{2008}$ | $a_{2009}$ | $a_{2010}$ | $a_{2011}$ | $a_{2012}$ | $a_{2013}$ | $a_{2014}$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $28 \cdot 8=224$ | $24+9=33$ | $33+10=43$ | $43+11=54$ | $54+12=66$ | $66+13=79$ | $79+14=93$ |
| $a_{2015}$ | $a_{2016}$ | $a_{2017}$ | $a_{2018}$ | $a_{2019}$ | $a_{2020}$ | |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $93+15=108$ | $8 \cdot 16=128$ | $28+17=45$ | $45+18=63$ | $63+19=82$ | $82+20=102$ | |
We see that $a_{2020}$ ends in the digits 02.
## C-questions
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
B4. For the second round of the Math Olympiad, 999 students are invited. Melanie prepares invitation letters in the order of participant numbers: $1,2,3, \ldots$ For some values of $n \geqslant 100$, she notices the following: the number of participant numbers from $1$ to $n$ that end in a 5 is exactly equal to the number formed by the last two digits of $n$.
For how many values of $n$ (with $100 \leqslant n<1000$) does this hold?
|
B4. 9 Let $a, b$ and $c$ be the digits of $n$; that is, $n=100 a+10 b+c$. Then the number of participant numbers from $1 \mathrm{t} / \mathrm{m} n$ that end in 5 is equal to $10 a+b$ if $c<5$ and equal to $10 a+b+1$ if $c \geqslant 5$. The number formed by the last two digits of $n$ is $10 b+c$.
First, consider the case $c<5$. Then $10 a+b$ must be equal to $10 b+c$. Both are two-digit numbers, one with digits $a$ and $b$, the other with digits $b$ and $c$. We find that $a=b=c \neq 0$ and we get the solutions $n=111,222,333,444$.
The case $c \geqslant 5$ is a bit more complicated. The number $10 a+b+1$ must be equal to $10 b+c$. If $b<9$, then the digits of $10 a+b+1$ are exactly $a$ and $b+1$ and we find $a=b$ and $b+1=c$. This gives the solutions $n=445,556,667,778,889$. If $b=9$, then we get $10 a+10=90+c$. From this, it follows that $c=0$ must hold, which contradicts $c \geqslant 5$.
In total, we have found 9 possible values for $n$.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
B2. Consider a circle with diameter $A B$. Point $C$ lies on the line segment $A B$ such that $2 \cdot|A C|=|B C|$. The points $D$ and $E$ lie on the circle so that $C D$ is perpendicular to $A B$ and $D E$ is also a diameter of the circle. Denote the areas of triangles $A B D$ and $C D E$ as $O(A B D)$ and $O(C D E)$. Determine the value of $\frac{O(A B D)}{O(C D E)}$.
|
B2. Let the center of the circle be $M$. Triangles $C D M$ and $C E M$ have equal areas. Indeed, the two triangles have bases of equal length $|D M|=|E M|$ and the same height. It follows that
$$
O(C D E)=2 \cdot O(C D M)
$$
We have $|A C|=\frac{1}{3}|A B|$ and $|A M|=\frac{1}{2}|A B|$, so $|C M|=|A M|-|A C|=$ $\frac{1}{2}|A B|-\frac{1}{3}|A B|=\frac{1}{6}|A B|$. Triangles $A B D$ and $C D M$ have the same height relative to the bases $A B$ and $C M$, and thus
$$
O(A B D)=6 \cdot O(C D M)
$$
Combining the two equations gives $\frac{O(A B D)}{O(C D E)}=\frac{6}{2}=3$.
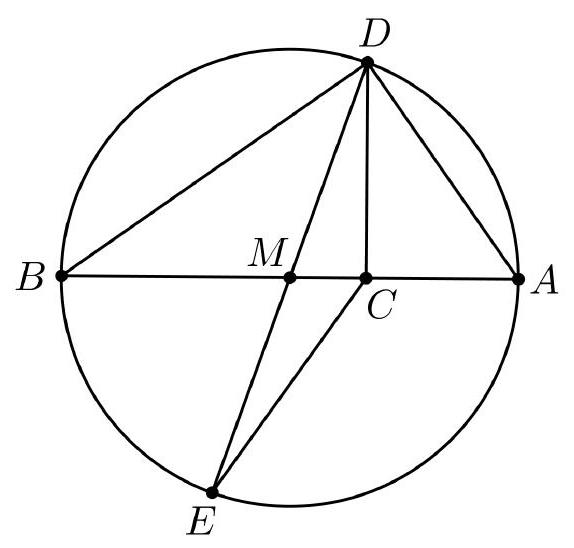
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
B4. Emile stands in a circle with nine other people. Each of the ten people thinks of an integer (which can also be negative) and whispers this number to both of their neighbors. Then, each person loudly states the average of the two numbers they heard from their neighbors. It turns out that Emile says the number 10, his right neighbor says the number 9, the next right neighbor says the number 8, and so on around the circle until Emile's left neighbor, who says the number 1.
What number did Emile have in mind?
|
B4. 5
The number that Emile had in mind we call $c_{10}$, the number of his right neighbor we call $c_{9}$, and so on until the left neighbor of Emile, who had the number $c_{1}$ in mind. We then see that
\[
\begin{aligned}
c_{10}+c_{8} & =2 \cdot 9=18, \\
c_{8}+c_{6} & =2 \cdot 7=14, \\
c_{6}+c_{4} & =2 \cdot 5=10, \\
c_{4}+c_{2} & =2 \cdot 3=6, \\
c_{2}+c_{10} & =2 \cdot 1=2 .
\end{aligned}
\]
Adding gives $2\left(c_{2}+c_{4}+c_{6}+c_{8}+c_{10}\right)=50$, so $c_{2}+c_{4}+c_{6}+c_{8}+c_{10}=25$.
It follows that $c_{10}=\left(c_{2}+c_{4}+c_{6}+c_{8}+c_{10}\right)-\left(c_{2}+c_{4}\right)-\left(c_{6}+c_{8}\right)=25-6-14=5$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
B5. The sum of the number of eyes on opposite sides of a die is always 7. Nine identical dice are glued together in a $3 \times 3$ square. This is done in such a way that two glued sides always have the same number of eyes. In the figure, you see the top view of the result, where the number of eyes is not shown for five dice.
What number of eyes should be on the place of the question mark?

## C-questions
For the C-questions, not only the answer is important; your reasoning and the way of solving it must also be clearly written down. Solve each C-question on a separate sheet of paper. Each correctly worked-out C-question is worth 10 points. Partial solutions can also earn points. Therefore, write everything clearly and submit your scratch paper (per question!) as well.
|
B5. 3 The numbers on opposite sides of a die are called opposite. Together, these numbers always add up to 7. We consider two dice that are touching with the same numbers, but can still rotate relative to each other. Around the two dice, we then see the same numbers, but in reverse cyclic order.
Consider the situation where the numbers on the top of the two dice are opposite, say \(a\) and \(7-a\). This situation is illustrated in the left figure. The left die then has the numbers \(a, b, 7-a\), and \(7-b\) around it for some \(b\). The right die has the numbers in reverse cyclic order: \(7-a, b\), \(a\), and \(7-b\). We see that the dice must have the same numbers on the front and back, namely \(b\) and \(7-b\), respectively.
Conversely, if the two dice have the same numbers on the front (or back), the numbers on the top must be opposite.

We apply this to the six dice in the first two columns of the \(3 \times 3\) table, see the right figure. The two dice in the third row show opposite numbers on the top, namely 2 and 5. The numbers \(c\) and \(d\) with which they touch the two dice in row 2 must therefore be the same. From this, it follows that the numbers \(e\) and \(f\) on the top are again opposite. The numbers \(g\) and \(h\) are therefore the same. Finally, the numbers visible on the top of the two dice in row 1 must again be opposite. We conclude that a 3 must be placed where the question mark is.
## C-problems
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
B2. Given is a square $A B C D$ with side lengths of 4. Inside the square, two semicircles with diameters $A B$ and $B C$ are drawn (see figure).
What is the combined area of the two gray regions?
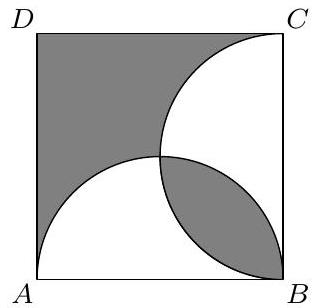
|
B2. 8 Note that both circles pass through the center of the square. The four circular segments marked with $p, q, r$ and $s$ therefore all belong to a quarter of a circle with radius 2 and thus have the same area. The total area of the gray region is therefore equal to the area of triangle $A C D$ and thus equal to $\frac{1}{2} \cdot 4 \cdot 4=8$.

|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
B1. We call a sequence of consecutive positive integers balanced if the number of multiples of three in that sequence is equal to the number of multiples of five. For example, the sequence 30, 31, 32, 33, 34, 35, 36 is not balanced, because out of these 7 numbers, 3 are multiples of three (namely 30, 33, and 36) and only 2 are multiples of five (namely 30 and 35).
How many numbers can a balanced sequence of consecutive positive integers contain at most?
|
B1. 11 Of every three consecutive integers, there is always exactly one that is a multiple of three. Now consider a sequence of $k$ consecutive integers. If $k$ itself is a multiple of three, say $k=3 \ell$, then exactly $\ell$ numbers in the sequence are multiples of three: one in each consecutive group of three numbers. If $k$ is not a multiple of three, say $k=3 \ell+1$ or $k=3 \ell+2$, then at least $\ell$ of the numbers in the sequence are multiples of three, because $k \geqslant 3 \ell$. In all cases, $3 \ell \geqslant k-2$ and the number of multiples of three is thus at least $\ell \geqslant \frac{k-2}{3}$.
Of every five consecutive integers, there is always exactly one that is a multiple of five. Now consider a sequence of $k$ consecutive integers. If $k$ is a multiple of five, say $k=5 m$, then the number of multiples of five in the sequence is exactly $m$. If $k$ is not a multiple of five, say $k=5 m-1$, $k=5 m-2$, $k=5 m-3$, or $k=5 m-4$, then at most $m$ numbers in the sequence are multiples of five. In all cases, $5 m \leqslant k+4$ and the number of multiples of five is thus at most $m \leqslant \frac{k+4}{5}$.
If a balanced sequence has length $k$, then it must hold that $\frac{k-2}{3} \leqslant \frac{k+4}{5}$. Multiplying both sides by 15 gives $5 k-10 \leqslant 3 k+12$. From this, it follows that $2 k \leqslant 22$ and thus that $k \leqslant 11$.
The sequence $10,11, \ldots, 20$ has length 11 and is balanced. Indeed, it contains 3 multiples of three and 3 multiples of five. We therefore conclude that $k=11$ is the maximum length of a balanced sequence.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
B4. A parallelogram $A B C D$ is cut by a line $m$. From the four vertices $A, B, C$ and $D$, we drop perpendiculars to line $m$. The feet of these perpendiculars are $P, Q, R$ and $S$ respectively. Point $S$ is also exactly the intersection of line $m$ and $A B$. The lengths of segments $A P, B Q$ and $D S$ are 6, 7, and 25, respectively.
What is the length of $C R$? Note: the diagram is not to scale.

|
B4. 12 We will prove that:
$$
|A P|+|B Q|+|C R|=|D S| .
$$
From this, the required length follows:
$$
|C R|=|D S|-|A P|-|B Q|=25-6-7=12 .
$$
Let $T$ be the foot of the perpendicular from $A$ to $D S$. It follows that $A P S T$ is a rectangle, so $|S T|=|A P|$.

Now it remains to prove that $|D T|=|B Q|+|C R|$. Let $U$ be the foot of the perpendicular from $B$ to the line through $C$ and $R$. Since $B U R Q$ is a rectangle, it follows that $|R U|=|B Q|$, so $|C U|=|B Q|+|C R|$. Triangles $B U C$ and $A T D$ are similar, because the sides of the two triangles are pairwise parallel. The triangles are also congruent, because $|A D|=|B C|$. It follows that $|D T|=|C U|$ and thus that $|D T|=|B Q|+|C R|$.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In a tournament, each team plays exactly one match against each other team. A won match earns the winner 3 points and 0 for the loser. In case of a draw, both teams receive 1 point each. At the end of the tournament, it turns out that all teams together have scored 15 points. The last team on the final list has scored exactly 1 point. The team that is second to last has not lost any match.
a) How many teams participated in the tournament?
b) How many points did the team that stands in second place on the final ranking score?
|
1. a) In every match of the tournament, 2 or 3 points are scored. In a tournament with four teams, $\left(\begin{array}{l}4 \\ 2\end{array}\right)$, so six matches are played, resulting in a total of 12 to 18 points scored. For three teams, the maximum is $\left(\begin{array}{l}3 \\ 2\end{array}\right) \times 3$, thus 9 points. For five teams, the minimum is $\left(\begin{array}{l}5 \\ 2\end{array}\right) \times 2=20$.
b) Order the teams A, B, C, D from highest to lowest: then team D has lost two matches and drawn one. Team C has not lost any matches. Assume that C only drew matches. Then the competition results would look like those in schema 1.
There are still 3 points to be distributed in the two remaining boxes. Then A must have won against B, and team B has scored a total of 4 points.
If team C has drawn twice and won once, then C would have already scored 5 points, see schema 2. B must have won against A to rank above C, which is contradictory to the ranking (and also to the total points scored).
The answer is thus 4 points for B.

|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. $a_{1}, a_{2}, a_{3}, a_{4}$ and $a_{5}$ are five different real numbers. The number of different values that the sum $a_{i}+a_{j}$ can take for all $i, j$ with $1 \leq i<j \leq 5$ we call $m$.
Determine the smallest possible value of $m$.
|
3. We order the five numbers from smallest to largest and call them $a, b, c, d$, and $e$, so $a<b<c<d<e$. Then it holds that: $a+b<a+c<a+d<a+e<b+e<c+e<d+e$. Therefore, the smallest value of $m$ satisfies: $m \geq 7$. With the example $a=1, b=2, c=3, d=4$ and $e=5$, we find the sums to be $3,4,5,6,7,8$ and 9. Thus, 7 is the smallest possible value of $m$.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A quadruple $(p, a, b, c)$ of positive integers is called a Leiden quadruple if
- $p$ is an odd prime number,
- $a, b$, and $c$ are distinct, and
- $ab+1, bc+1$, and $ca+1$ are divisible by $p$.
a) Prove that for every Leiden quadruple $(p, a, b, c)$, it holds that $p+2 \leqslant \frac{a+b+c}{3}$.
b) Determine all numbers $p$ for which there exists a Leiden quadruple $(p, a, b, c)$ such that $p+2=\frac{a+b+c}{3}$.
|
4. a) Without loss of generality, we assume that $a < b < c$. The numbers $a$ and $c$ are not divisible by $p$, because otherwise $ac + 1$ would be a multiple of $p$ plus 1, and thus not divisible by $p$. Since $bc + 1$ and $ac + 1$ are divisible by $p$, their difference $(bc + 1) - (ac + 1) = (b - a)c$ is also divisible by $p$. Since $c$ is not divisible by $p$, $b - a$ must be divisible by $p$. Similarly, $(ac + 1) - (ab + 1) = a(c - b)$ is divisible by $p$, and since $a$ is not divisible by $p$, $c - b$ must be divisible by $p$.
We see that $b = a + (b - a) \geq a + p$ and that $c = b + (c - b) \geq a + 2p$.
It holds that $a \geq 2$. Suppose that $a = 1$. Then the numbers $b + 1 = ab + 1$ and $b - 1 = b - a$ are divisible by $p$. The difference $(b + 1) - (b - 1) = 2$ is also divisible by $p$. But $p$ is an odd prime and cannot be a divisor of 2.
Using $a \geq 2$, $b \geq a + p$, and $c \geq a + 2p$, we find that
$$
\frac{a + b + c}{3} \geq \frac{a + (a + p) + (a + 2p)}{3} = p + a \geq p + 2
$$
Remark. To conclude from the fact that $p$ is a divisor of $(b - a)c$ that $p$ is a divisor of $b - a$ or of $c$, the proof uses that $p$ is prime. We sketch an alternative proof that shows that the claim in the problem remains valid if we only require that $p$ is an integer greater than 2.
We may again assume that $a < b < c$. Note that $a(bc + 1) = abc + a$, $b(ac + 1) = abc + b$, and $c(ab + 1) = abc + c$ are different multiples of $p$. The differences $(abc + b) - (abc + a) = b - a$ and $(abc + c) - (abc + b) = c - b$ are also multiples of $p$. We can now conclude again that $b \geq a + p$ and $c \geq b + p \geq a + 2p$. The rest of the proof proceeds as in the first proof.
b) We may again assume that $a < b < c$. In part a), we saw that $\frac{a + b + c}{3} \geq \frac{a + (a + p) + (a + 2p)}{3} = p + a \geq p + 2$. The equality $\frac{a + b + c}{3} = p + 2$ can only hold if $b = a + p$, $c = a + 2p$, and $a = 2$. Since $ab + 1 = 2(2 + p) + 1 = 2p + 5$ must be divisible by $p$, 5 must also be divisible by $p$. We conclude that $p = 5$, $b = 7$, and $c = 12$. The quadruple $(p, a, b, c) = (5, 2, 7, 12)$ is indeed a Leids quadruple because $ab + 1 = 15$, $ac + 1 = 25$, and $bc + 1 = 85$ are all divisible by $p$.
Thus, there exists a Leids quadruple $(p, a, b, c)$ with $\frac{a + b + c}{3} = p + 2$ only for $p = 5$.
|
5
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
5. Kira has 3 blocks with the letter A, 3 blocks with the letter B, and 3 blocks with the letter C. She puts these 9 blocks in a sequence. She wants to have as many distinct distances between blocks with the same letter as possible. For example, in the sequence ABCAABCBC the blocks with the letter A have distances 1, 3, and 4 between one another, the blocks with the letter B have distances 2, 4, and 6 between one another, and the blocks with the letter $\mathrm{C}$ have distances 2, 4 , and 6 between one another. Altogether, we got distances of $1,2,3,4$, and 6 ; these are 5 distinct distances.
What is the maximum number of distinct distances that can occur?
|
5. We will show that the maximum number of distinct distances is 7 . First we prove that the number of distinct distances cannot be more than 7 , then we will show that there is a sequence of blocks with 7 distances.
The possible distances between two blocks in the sequence are the numbers 1 to 8 . Therefore, there can certainly be no more than 8 distinct distances. We will show that there is always at least one distance that does not occur.
If in a sequence the distances 8 and 7 do not both occur, we are done. Therefore, suppose we have a sequence in which these two distances do both occur. The distance 8 can only occur between the very first and the very last block, so these should have the same letter on them, say A. The distance 7 can only occur between the first and the eighth (second last) block, or between the second and the last block. Because both outer blocks have an A, the second or eighth block must also have an A. Then the sequence of blocks is AAxxxxxxA (or the other way around: AxxxxxxAA), where on the place of $x$ are blocks with a $B$ or $C$. Now we see that the distance 6 cannot occur anymore: the distances between the blocks with $\mathrm{A}$ are 1, 7, and 8, and the distances between the blocks with B and the blocks with $\mathrm{C}$ are at most 5 . Also in this case, there is at least one distance that does not occur.
We conclude that there is always one of the possible distances $1,2,3,4,5,6,7,8$ that does not occur. Hence, the number of distinct distances cannot be more than 7 .
An example of a sequence of blocks where 7 distinct distances occur, is ABBCACCBA, with distances $4,4,8 ; 1,5,6 ; 1,2,3$ (only the distance 7 is missing). So the maximal number of distinct distances is equal to 7 .
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Daan distributes the numbers 1 through 9 over the nine cells of a $3 \times 3$ table (each cell contains exactly one number). Then Daan circles the middle number in terms of size in each row. For example, if the numbers 8, 1, and 2 are in a row, he circles the number 2. He does this for each column and for each of the two diagonals as well. If a number is already circled, he does not circle it again.
| 8 | 1 | 2 |
| :---: | :---: | :---: |
| 7 | 6 | 3 |
| 9 | 5 | 4 |
The result of this process he calls a median table. Above you see an example of a median table where 5 numbers are circled.
(a) What is the smallest possible number of circled numbers in a median table? Prove that it cannot be less and provide an example where this minimal number is circled.
(b) What is the largest possible number of circled numbers in a median table? Prove that it cannot be more and provide an example where this maximal number is circled.
|
1. (a) The smallest possible number of circled numbers is 3. That it cannot be done with fewer follows from the fact that at least one number is circled in each row (and these are three different numbers).
A median table with only 3 numbers circled is shown alongside. In the rows, the numbers 7, 5, 3 are circled, in the columns the numbers 3, 5, 7, and on the diagonals the numbers 5 and 5. Together, these are three different numbers: 3, 5, and 7.
| 4 | 9 | 7 |
| :---: | :---: | :---: |
| 2 | 5 | 8 |
| 3 | 1 | 6 |
(b) The largest possible number of circled numbers is 7. That it cannot be more follows from the fact that the numbers 9 and 1 are never circled. Thus, no more than \(9 - 2 = 7\) numbers are ever circled.
A median table where actually 7 numbers are circled is shown alongside. In the rows, the numbers 2, 6, 8 are circled, in the columns the numbers 7, 5, 3, and on the diagonals 4 and 5. Together, these are the seven numbers 2, 3, 4, 5, 6, 7, 8.
| 4 | 1 | 2 |
| :--- | :--- | :--- |
| 7 | 5 | 6 |
| 8 | 9 | 3 |
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. We consider sequences of numbers $a_{1}, a_{2}, a_{3}, \ldots$ that satisfy the formula $a_{n+1}=\frac{a_{n}+a_{1}}{a_{n}+1}$ for all $n \geqslant 1$.
(a) Suppose that $a_{1}=-3$. Calculate $a_{2020}$.
(b) Suppose that $a_{1}=2$. Prove that for all $n \geqslant 2$ it holds that $\frac{4}{3} \leqslant a_{n} \leqslant \frac{3}{2}$.
|
## 2. Version for Grade 5 & Grade 4 and lower
(a) If $a_{1}=-3$, then $a_{2}=\frac{a_{1}+a_{1}}{a_{1}+1}=\frac{-6}{-2}=3$. Next, we calculate $a_{3}=\frac{a_{2}+a_{1}}{a_{2}+1}=\frac{0}{4}=0$. Then comes $a_{4}=\frac{a_{3}+a_{1}}{a_{3}+1}=\frac{-3}{1}=-3$. We see that $a_{4}=a_{1}$. Since $a_{n+1}$ depends only on $a_{n}$ and $a_{1}$, we see that $a_{5}=a_{2}=3, a_{6}=a_{3}=0, a_{7}=a_{4}=-3$, and so on. In other words: the sequence is periodic with period 3, and we see that
$$
a_{2020}=a_{2017}=a_{2014}=\cdots=a_{4}=a_{1}=-3 .
$$
(b) We will prove the statement by complete induction. We start with the base case $n=2$. We calculate $a_{2}=\frac{a_{1}+a_{1}}{a_{1}+1}=\frac{4}{3}$ and see that indeed $\frac{4}{3} \leqslant a_{n} \leqslant \frac{3}{2}$.
Now assume that for some $n=k \geqslant 2$ we have proven that $\frac{4}{3} \leqslant a_{n} \leqslant \frac{3}{2}$. We will prove that these inequalities also hold for $n=k+1$.
First, we note that
$$
a_{k+1}=\frac{a_{k}+2}{a_{k}+1}=1+\frac{1}{a_{k}+1} .
$$
From the induction hypothesis $\left(\frac{4}{3} \leqslant a_{k} \leqslant \frac{3}{2}\right)$, it follows that $\frac{7}{3} \leqslant a_{k}+1 \leqslant \frac{5}{2}$ and thus that
$$
\frac{2}{5} \leqslant \frac{1}{a_{k}+1} \leqslant \frac{3}{7} .
$$
By adding 1 to each part of this inequality, we now find
$$
\frac{7}{5} \leqslant 1+\frac{1}{a_{k}+1}=a_{k+1} \leqslant \frac{10}{7} .
$$
Since $\frac{4}{3} \leqslant \frac{7}{5}$ and $\frac{10}{7} \leqslant \frac{3}{2}$, we see that $\frac{4}{3} \leqslant a_{k+1} \leqslant \frac{3}{2}$, as we wanted to prove.
|
-3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. We consider sports tournaments with $n \geqslant 4$ participating teams and where every pair of teams plays against one another at most one time. We call such a tournament balanced if any four participating teams play exactly three matches between themselves. So, not all teams play against one another.
(a) Prove that in a balanced tournament with $n \geqslant 5$ teams, there are no three teams that all play against one another.
(b) Determine the largest value of $n$ for which a balanced tournament with $n$ teams exists.
|
## 2. Version for klas 5 \& klas 4 and below
(a) Suppose towards a contradiction that we can find three teams in a balanced tournament that all play against each other, say teams A, B and C. Because $n \geqslant 5$ there are two other teams, say D and E. Since A, B and C already play three matches between them, there are no other matches between the quadruple A, B, C and D. In other words: D does not play against $\mathrm{A}, \mathrm{B}$ and $\mathrm{C}$. The same holds for team $\mathrm{E}$. If we now consider the quadruple $\mathrm{A}, \mathrm{B}, \mathrm{D}$ and $\mathrm{E}$ we see that there are at most two matches: $\mathrm{A}$ against $\mathrm{B}$, and possibly $\mathrm{D}$ against $\mathrm{E}$. This means that we have found four teams such that there are not exactly three matches between these four teams. This is a contradiction.
(b) We will first show that a balanced tournament is not possible with $n \geqslant 6$ teams. Then we give an example of a balanced tournament for $n=5$. This shows that 5 is the largest value of $n$ for which a balanced tournament with $n$ teams exists.
Suppose that $n \geqslant 6$ and, towards a contradiction, that a balanced tournament with $n$ teams exists. We look at the first six teams, say teams A to F. Suppose that A plays against at most two of these teams, say at most against B and C but not against D, E and F. Since three matches have to be played among the quadruple A, D, E and F, the teams D, E and F all have to play against one another. This is a contradiction with part (a).
We conclude that A has to play against at least three of the teams, for example B, C and D. This gives three matches in the quadruple A, B, C, D, so B, C and D do not play any matches between them. Because the quadruple B, C, D, E also has to play three matches, $\mathrm{E}$ has to play against all of $\mathrm{B}, \mathrm{C}$ and $\mathrm{D}$. But now we find a contradiction in the quadruple A, B, C, E: there are already four matches between these teams (A against B, A against C, $\mathrm{B}$ against $\mathrm{E}$, and $\mathrm{C}$ against $\mathrm{E}$ ). Therefore a balanced tournament with $n \geqslant 6$ does not exist. To make a tournament with five teams, imagine the teams are standing in a circle. Two teams play against each other if they are standing next to each other in the circle. If we look at any quadruple of teams, we see there are exactly three pairs of teams standing next to each other in the circle. So the four teams plays three matches between them. We conclude that 5 is the largest value of $n$ for which a balanced tournament with $n$ teams exists.
|
5
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
1. Niek has 16 square cards that are yellow on one side and red on the other. He lays them out in a $4 \times 4$ square. Some cards may lie with the yellow side up, and some with the red side up. For each color pattern, he calculates the monochromaticity of the pattern as follows. For each pair of cards that share a side, he adds +1 or -1 as follows: +1 if the adjacent cards have the same color facing up, and -1 if the adjacent cards have different colors facing up. Adding everything together gives him the monochromaticity (which can also be negative). For example, if he lays the cards as shown below, there are 15 pairs of adjacent cards with the same color facing up and 9 pairs with different colors.
The monochromaticity of this color pattern is therefore $15 \cdot (+1) + 9 \cdot (-1) = 6$. Niek investigates all possible color patterns and makes a list of all numbers that appear at least once as a value of the monochromaticity. In other words: Niek makes a list of all numbers for which there exists a color pattern with that number as the monochromaticity.
(a) What are the three largest numbers on his list?
(Explain your answer. If your answer, for example, is 12, 9, and 6, you must show that these numbers actually appear on the list by providing a corresponding color pattern for each of these numbers, and also prove that the numbers 7, 8, 10, 11, and all numbers greater than 12 do not appear.)
(b) What are the three smallest (most negative) numbers on his list?
(c) What is the smallest positive number (i.e., greater than 0) on his list?
|
1. (a) First note that there are $3 \cdot 4=12$ horizontal boundaries between two tiles, and also 12 vertical boundaries. Suppose there are $k$ boundaries that count for -1, then there are $24-k$ boundaries that count for +1. This gives a monochromaticity of $(24-k) \cdot (+1) + k \cdot (-1) = 24 - 2k$. Therefore, the monochromaticity is always an even number.
If all tiles are the same color, then all boundaries count for +1, so the monochromaticity can be at most 24. Can a monochromaticity of 22 occur? No, and we prove this by contradiction. Suppose there is a distribution of tiles with a monochromaticity of 22. Then there must be one boundary with -1 and the rest all +1. In other words, all adjacent tiles have the same color, except for one boundary. Consider the two tiles where this boundary lies, and choose two adjacent tiles to form a $2 \times 2$ sub-square. For each pair of tiles, you can find such a $2 \times 2$ sub-square. If you start at the top-left and trace a loop around these four tiles (top-left - top-right - bottom-right - bottom-left - top-left), you will encounter four boundaries. Since you start and end on the same color, you must always encounter an even number of boundaries where the color changes. But this contradicts the assumption that there is only one boundary where the adjacent tiles have different colors. We conclude that a monochromaticity of 22 is not possible.
The next possibilities for a high monochromaticity are 20 and 18. Then there must be 2 or 3 boundaries between tiles of different colors. This can be achieved by giving a tile in the corner or on the side a different color:
The three largest numbers on Niek's list are therefore 24, 20, and 18.
(b) Suppose we have placed the tiles such that the monochromaticity is $x$. Now we flip half of the tiles, in a checkerboard pattern: we flip a tile if and only if we do not flip all adjacent tiles. This changes the sign of all boundaries between two tiles, resulting in a monochromaticity of $-x$. In other words, $x$ is a possible monochromaticity if and only if $-x$ is a possible monochromaticity. The three smallest numbers on Niek's list therefore follow from the three largest possibilities: $-24, -20$, and -18.
(c) We have already seen that the monochromaticity is always an even number. The smallest positive even number is 2. This monochromaticity can be achieved by having 13 boundaries between the same color and 11 with a different color. There are many possibilities for this, for example:
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. We consider sports tournaments with $n \geqslant 4$ teams where each pair of teams plays against each other at most once. We call such a tournament balanced if every quartet of teams plays exactly three matches among themselves. Not all teams play against each other.
(a) Prove that in a balanced tournament with $n \geqslant 5$ teams, there are no three teams that all play against each other.
(b) Determine the largest value of $n$ for which a balanced tournament with $n$ teams exists.
|
## 2. Version for Grade 5 & Grade 4 and Lower
(a) Assume, for the sake of contradiction, that in a balanced tournament, there are three teams that all play against each other, say teams A, B, and C. Since \( n \geqslant 5 \), there are two other teams, say teams D and E. Because A, B, and C already play three matches among themselves, there can be no other matches among the four teams A, B, C, and D. In other words, team D does not play against teams A, B, and C. The same applies to team E. If we now look at the quartet A, B, D, and E, we see that there are at most two matches among them: A against B and possibly D against E. This means that there are not three matches in this quartet. This leads to a contradiction.
(b) First, we will show that it is not possible to have a balanced tournament with \( n \) teams for \( n \geqslant 6 \). Then, we will provide an example of a balanced tournament for \( n=5 \). This will show that 5 is the largest value for \( n \) for which a balanced tournament with \( n \) teams is possible.
Assume that \( n \geqslant 6 \) and that a balanced tournament with \( n \) teams does exist. We now look at the first six teams, teams A through F. Suppose that A plays against at most two of these teams, for example, at most against B and C but not against D, E, and F. The quartet A, D, E, F must, however, play three matches among themselves, so D, E, and F must play against each other. This is in contradiction with part (a).
We conclude that A must play against at least three of the teams, for example, B, C, and D. In the quartet A, B, C, D, three matches are now played, so B, C, and D do not play against each other. Since the quartet B, C, D, E must also play three matches, E must play against each of B, C, and D. But now we find a contradiction in the quartet A, B, C, E: there are now at least four matches (A against B, A against C, B against E, and C against E). Therefore, a balanced tournament with \( n \geqslant 6 \) does not exist.
To create a tournament with five teams, imagine the five teams standing in a circle. Two teams play a match against each other if they are next to each other in the circle. If we then look at any four teams, we see that there are exactly three pairs that are next to each other in the circle. Therefore, exactly three matches are played among them. We conclude that 5 is the largest value for \( n \) for which a balanced tournament exists.
|
5
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
3. In a tournament with six teams, each team plays once against every other team. If a team wins a match, it receives 3 points and the loser gets 0 points. If a match ends in a draw, both teams receive 1 point.
Can the final scores of the teams be exactly six consecutive numbers $a, a+1, \ldots, a+5$? If so, determine all values of $a$ for which this is possible.
|
3. In total, 15 matches are played. In each match, a total of 2 or 3 points are earned. The sum of the six scores therefore lies between $15 \cdot 2=30$ (all matches end in a draw) and $15 \cdot 3=45$ (no match ends in a draw).
The sum of the six scores is also equal to $a+(a+1)+\cdots+(a+5)=15+6a$. We see that $30 \leqslant 15+6a \leqslant 45$, so $3 \leqslant a \leqslant 5$. We will prove that only $a=4$ is possible.
First, consider the case $a=5$. The total number of points is then $15+30=45$, so no match ends in a draw. In each match, a team earns either 0 or 3 points, so all scores are divisible by 3. The scores cannot therefore be six consecutive numbers.
Now consider the case $a=3$. The sum of the scores is $3+4+5+6+7+8=33$. The teams with 6 and 7 points have each won at least one of their five matches.
The team with 8 points has even won at least twice, because $3+1+1+1+1=7<8$. Therefore, there are at least 4 matches that did not end in a draw, so the sum of the scores is at least $4 \cdot 3+11 \cdot 2=34$. But we already saw that this sum is equal to 33. Therefore, the case $a=3$ cannot occur.
Finally, we show that $a=4$ is possible: in the table below, you see one of the possible game outcomes where teams $A$ through $F$ have scores from 4 to 9. The last column shows the scores of the six teams.
| | $A$ | $B$ | $C$ | $D$ | $E$ | $F$ | |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $A$ | - | 3 | 1 | 0 | 0 | 0 | 4 |
| $B$ | 0 | - | 1 | 0 | 3 | 1 | 5 |
| $C$ | 1 | 1 | - | 3 | 0 | 1 | 6 |
| $D$ | 3 | 3 | 0 | - | 1 | 0 | 7 |
| $E$ | 3 | 0 | 3 | 1 | - | 1 | 8 |
| $F$ | 3 | 1 | 1 | 3 | 1 | - | 9 |
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The eight points below are the vertices and the midpoints of the sides of a square. We would like to draw a number of circles through the points, in such a way that each pair of points lie on (at least) one of the circles.
Determine the smallest number of circles needed to do this.
|
5. Four of the eight points are coloured black and the other four points are coloured white in the way indicated in the figure on the left. The circle through the four black points is denoted $C_{1}$ and the circle through the four white points is denoted $C_{2}$. If two points lie on a circle $C$, we say that $C$ covers that pair of points.

Circle $C_{1}$ covers all pairs of black points and circle $C_{2}$ covers all pairs of white points. It is easy to check that each of the $4 \cdot 4=16$ pairs consisting of a white point and a black point is covered by one of the four circles in the figure on the right. It follows that the six circles form a solution.
We will now prove that five or fewer circles do not suffice. First observe that any circle passing through more than two black points must be equal to $C_{1}$ and that any circle passing through more than two white points must be equal to $C_{2}$. Indeed, a circle is already determined by three points.
A circle passing through 2 or fewer black points covers at most one of the $\frac{4 \cdot 3}{2}=6$ pairs of black points. A solution consisting of only five circles must therefore contain circle $C_{1}$ (since otherwise at most 5 pairs of black points are covered). In the same way we see that such a solution must contain circle $C_{2}$.
Each of the remaining three circles in the (hypothetical) solution contains at most 2 black points and at most 2 white points. Such a circle covers at most $2 \cdot 2=4$ pairs consisting of a white and a black point. In total, the five circles can therefore cover at most $0+0+3 \cdot 4=12$ such pairs, while there are 16 to be covered. The five circles can therefore not form a correct solution after all. We conclude that the smallest number of circles in a solution is 6 .
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Kira has 3 blocks with the letter A, 3 blocks with the letter B, and 3 blocks with the letter C. She places these 9 blocks in a row. She wants to have as many different distances between blocks with the same letter as possible. For example, in the sequence ABCAABCBC, the blocks with the letter A have distances of 1, 3, and 4 from each other, the blocks with the letter B have distances of 2, 4, and 6 from each other, and the blocks with the letter C also have distances of 2, 4, and 6 from each other. Altogether, the distances 1, 2, 3, 4, and 6 appear; that makes 5 different distances. What is the maximum number of different distances that can occur?
|
5. We will show that there can be a maximum of 7 different distances. First, we prove that the number of different distances cannot be more than 7, then we show that there is a sequence of blocks with 7 different distances.
The possible distances between two blocks in a row of nine blocks are 1 through 8. Therefore, there can certainly not be more than 8 different distances. We will show that there is always at least one distance that does not occur.
If in a sequence the distances 8 and 7 do not both occur, then we are done. Suppose, however, that we have a sequence in which they do both occur. Distance 8 can only occur between the first and the last block, so these get the same letter, say A. Distance 7 can only occur between either the first and the eighth (second-to-last) block, or between the second and the last block. Since the two outer blocks are already A, the second or the eighth block must also be A. The sequence of blocks is thus AAxxxxxxA (or conversely: AxxxxxxAA), where the x's are filled with blocks B and C. We now see that distance 6 cannot occur anymore: the distances between the A's are 1, 7, and 8, and the distances between the B's and C's among themselves are not higher than 5. Here, too, there is thus at least one possible distance that does not occur.
We conclude that there is always one distance from the possible distances $1,2,3,4,5,6,7,8$ that does not occur. The number of different distances can therefore not be more than 7.
An example of a sequence of blocks in which 7 different distances occur is ABBCACCBA, with mutual distances $4,4,8 ; 1,5,6 ; 1,2,3$ (only distance 7 is missing). Therefore, the maximum number of different distances that can occur is equal to 7.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In a hockey tournament, six teams participate. Each team plays exactly one match against each other team. A team receives 3 points for a win, 1 point for a draw, and 0 points for a loss. At the end of the tournament, a ranking list is compiled. It turns out that there are no shared positions on the ranking list. It also turns out that each team (except the team that finished last) has exactly 2 points more than the team that is one position lower.
Prove that the team that finished fourth has exactly two wins.
|
3. Let the six team scores be equal to $s, s+2, s+4, s+6, s+8$ and $s+10$. Let $T$ be the total number of points scored. Therefore, $T=6s+30$. The total number of points is thus a multiple of six.
In total, $\frac{6 \cdot 5}{2}=15$ matches were played. The number of matches that ended in a draw we call $g$. A draw yields a total of $1+1=2$ points to the participants, while every other match yields $3+0=3$ points. The total number of points scored is thus $T=g \cdot 2 + (15-g) \cdot 3 = 45 - g$.
From $T=45-g$ it follows that $30 \leqslant T \leqslant 45$ because the number of draws satisfies $0 \leqslant g \leqslant 15$. Since we also know that $T$ is a multiple of six, the only possible values are $T=30, T=36$ and $T=42$.
If $T=30$, then $g=45-30=15$. But then all matches ended in a draw and each team has the same score. The case $T=30$ is therefore invalid.
If $T=36$, then $g=45-36=9$ and $s=\frac{T-30}{6}=1$. The scores of the six teams are thus $1, 3, 5, 7, 9, 11$. The team with a score of 1 has lost 4 matches (and drawn one). The team with a score of 3 has lost at least 2 matches (since at most 3 matches were not lost). The team with a score of 11 has won at least 3 matches (with 2 wins, the score is at most $3+3+1+1+1=9$), so in addition to the teams with scores of 1 and 3, at least one more team has lost a match. In total, there are thus at least $4+2+1=7$ matches lost, which contradicts the fact that only $15-9=6$ matches did not end in a draw. The case $T=36$ is therefore invalid.
Finally, we consider the case $T=42$. The scores are then $2, 4, 6, 8, 10, 12$ and $g=3$. Since the points earned from wins are always a multiple of three, the six teams must have earned at least $2, 1, 0, 2, 1, 0$ points from draws. In total, there are $2 \cdot 3=6$ points from draws. Since $2+1+0+2+1+0=6$, the six teams cannot have earned more than the mentioned number of points from draws. In particular, the team that finished fourth (the team with 6 points) has drawn 0 times and thus won twice.
|
2
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
5. The eight points below are the vertices and midpoints of the sides of a square. We want to draw a number of circles through the points in such a way that each pair of points lies on (at least) one of the circles.
Find the smallest possible number of circles with which this can be done.
|
5. Of the eight points, we color four black and the other four white, as indicated in the left figure. The circle through the four black points we call $C_{1}$ and the circle through the four white points we call $C_{2}$. If a pair of points lies on a circle $C$, we say that $C$ covers that pair.

Circle $C_{1}$ covers all pairs of black points and circle $C_{2}$ covers all pairs of white points. It is easy to verify that each of the $4 \cdot 4=16$ pairs consisting of one white and one black point is covered by one of the four circles in the right figure. Together, these six circles thus form a solution.
We will now prove that there is no solution with five (or fewer) circles. First, we note that a circle passing through more than two black points must be identical to $C_{1}$, and a circle passing through more than two white points must be identical to $C_{2}$. A circle is fixed once we choose three points it must pass through.
A circle passing through at most 2 black points covers at most one of the $\frac{4 \cdot 3}{2}=6$ pairs of black points. A solution with five circles must therefore include circle $C_{1}$ (otherwise, at most 5 pairs of black points would be covered). Similarly, the solution must include circle $C_{2}$.
Each of the remaining three circles passes through at most 2 black and at most 2 white points. Thus, such a circle covers at most $2 \cdot 2=4$ pairs consisting of one white and one black point. In total, the five circles cover at most $0+0+3 \cdot 4=12$ such pairs out of the 16 in total. Therefore, the five circles do not form a correct solution.
We conclude that the smallest possible number of circles in a solution is 6.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In a tournament among six teams, every team plays against each other team exactly once. When a team wins, it receives 3 points and the losing team receives 0 points. If the game is a draw, the two teams receive 1 point each.
Can the final scores of the six teams be six consecutive numbers $a, a+1, \ldots, a+5$ ? If so, determine all values of $a$ for which this is possible.
|
3. In all, 15 matches are played. In each match, the two teams together earn 2 or 3 points. The sum of the final scores is therefore an integer between $15 \cdot 2=30$ (all matches end in a draw) and $15 \cdot 3=45$ (no match is a draw).
On the other hand, the sum of the six scores equals $a+(a+1)+\cdots+(a+5)=15+6 a$. Hence $30 \leqslant 15+6 a \leqslant 45$, which shows that $3 \leqslant a \leqslant 5$. We will prove that $a=4$ is the only possibility.
First consider the case $a=5$. The sum of the scores equals $15+30=45$, so no match ends in a draw. Because in every match the teams earn either 0 or 3 points, every team's score is divisible by 3 . Therefore, the scores cannot be six consecutive numbers.
Next, consider the case $a=3$. The scores sum up to $3+4+5+6+7+8=33$. The two teams scoring 6 and 7 points must both have won at least one out of the five matches they played.
The team scoring 8 points must have won at least two matches, because $3+1+1+1+1=7<8$. Hence at least 4 matches did not end in a draw, which implies that the sum of the scores is at least $4 \cdot 3+11 \cdot 2=34$. But we have already see that this sum equals 33 , a contradiction.
Finally, we will show that $a=4$ is possible. The table depicts a possible outcome in which teams $A$ to $F$ have scores 4 to 9 . The rightmost column shows the total scores of the six teams.
| | $A$ | $B$ | $C$ | $D$ | $E$ | $F$ | |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $A$ | - | 3 | 1 | 0 | 0 | 0 | 4 |
| $B$ | 0 | - | 1 | 0 | 3 | 1 | 5 |
| $C$ | 1 | 1 | - | 3 | 0 | 1 | 6 |
| $D$ | 3 | 3 | 0 | - | 1 | 0 | 7 |
| $E$ | 3 | 0 | 3 | 1 | - | 1 | 8 |
| $F$ | 3 | 1 | 1 | 3 | 1 | - | 9 |
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. We call a positive integer a shuffle number if the following hold:
(1) All digits are nonzero.
(2) The number is divisible by 11 .
(3) The number is divisible by 12. If you put the digits in any other order, you again have a number that is divisible by 12 .
How many 10-digit shuffle numbers are there?
|
## 1. Version for klas $4 \&$ below
First observe that a shuffle number can only contain the digits 2, 4, 6, and 8 . Indeed, if we place the digits in any order, we obtain an even number (since it is divisible by 12) because of property (3). Since the last digit of an even number is also even, the digit must be $2,4,6$, or 8 since it cannot be 0 because of property (1). Since we can put any of the digits in the last position, this holds for each digit of a shuffle number.
Next, observe that a shuffle number can only contain the digits 4 and 8 . Indeed, suppose that we had a shuffle number containing the digit 2 . We could reorder the digits so that the last digit is 2 . The last two digits would then be $22,42,62$, or 82 . But then the number would not be divisible by 4 (and hence also not divisible by 12), contradicting property (3). In the same way we see that a shuffle number cannot contain digit 6 because a number ending in digits $26,46,66$, or 86 is not divisible by 4 .
A shuffle number is divisible by 3 (since it is divisible by 12), hence the sum of its digits is divisible by 3 as well. Since each digit is either 4 or 8 , we have the following cases:
- 5 fours and 0 eights. Sum of the digits: 20
- 4 fours and 1 eight. Sum of the digits: 24
- 3 fours and 2 eights. Sum of the digits: 28
- 2 fours and 3 eights. Sum of the digits: 32
- 1 four and 4 eights. Sum of the digits: $\mathbf{3 6}$
- 0 fours and 5 eights. Sum of the digits: 40
The 5-digit numbers for which properties (1) and (3) hold, are precisely the numbers that have 4 fours and 1 eight, or have 1 four and 4 eights. It remains to examine which of these eight numbers are divisible by 11. For this we use the 11-criterion: a number is divisible by 11 if the alternating sum of the digits is divisible by 11. By alternating sum we mean that instead of adding them, we alternately add and subtract. For the eight candidate solutions we find the following alternating sums:
| 84444 | $8-4+4-4+4=8$ | 48888 | $4-8+8-8+8=4$ |
| ---: | :--- | :--- | :--- |
| $\mathbf{4 8 4 4 4}$ | $4-8+4-4+4=0$ | 84888 | $8-4+8-8+8=12$ |
| 44844 | $4-4+8-4+4=8$ | 88488 | $8-8+4-8+8=4$ |
| $\mathbf{4 4 4 8 4}$ | $4-4+4-8+4=0$ | 88848 | $8-8+8-4+8=12$ |
| 44448 | $4-4+4-4+8=8$ | 88884 | $8-8+8-8+4=4$ |
We see that there are precisely two 5-digit shuffle numbers, namely 48444 and 44484.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The numbers 1 to 25 are each coloured blue or red. Determine all possible colourings that satisfy the following rules:
- The number 5 is red.
- If numbers $x$ and $y$ have different colours and $x+y \leqslant 25$, then $x+y$ is blue.
- If numbers $x$ and $y$ have different colours and $x \cdot y \leqslant 25$, then $x \cdot y$ is red.
|
## 2. Version for klas $5 \&$ klas 4 and below
We first consider the case that 1 is red. Then all numbers from 1 to 25 are red. Indeed, suppose that some number $k$ is blue. Then 1 and $k$ have different colours, hence by the third rule the number $1 \cdot k=k$ must be red. But this contradicts the assumption that it was blue. Observe that colouring all numbers red indeed gives a correct colouring.
Now consider the case that 1 is blue. Since 5 is not blue, it follows from the second rule that 1 and 4 have the same colour. Hence, 4 is blue. Similarly, 2 and 3 must have the same colour. In fact, both must be blue since if 2 were red, then $3=1+2$ would have to be blue because of the second rule.
We now know that 1, 2, 3, and 4 are blue. By the second rule, we see that also $6=5+1$, $7=5+2,8=5+3$, and $9=5+4$ are blue. Applying the second rule again, we find in turn that $11,12,13,14$ are blue, that $16,17,18,19$ are blue, and that $21,22,23,24$ are blue.
Because of the third rule, $10=2 \cdot 5,15=3 \cdot 5$, and $20=4 \cdot 5$ are red. Only the colour of 25 is not yet determined by the rules. We find two possible colourings:
(1) Only $5,10,15,20,25$ (the numbers divisible by 5 ) are red.
(2) Only 5, 10,15, 20 are red.
We check that colouring (1) is indeed correct. The second rule is satisfied, because the sum of a number divisible by 5 and a number not divisible by 5 is itself not divisible by 5 . The third rule is satisfied since the product of a number divisible by 5 and a number not divisible by 5 is itself divisible by 5 .
Colouring (2) differs from colouring (1) only in the colour of 25 . To see that colouring (2) is correct, we only need to check the rules in the situation that one of the numbers involved is 25 . We check that 25 is not the product of a blue and a red number (that is correct). We must also check that there is no red number $k$ such that $25+k$ is red or $25 k$ is blue. That is automatically true since the numbers greater than 25 are not coloured.
We conclude that there are 3 correct colourings altogether: the colouring in which all numbers are red, colouring (1), and colouring (2).
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The numbers 1 to 15 are each coloured blue or red. Determine all possible colourings that satisfy the following rules:
- The number 15 is red.
- If numbers $x$ and $y$ have different colours and $x+y \leqslant 15$, then $x+y$ is blue.
- If numbers $x$ and $y$ have different colours and $x \cdot y \leqslant 15$, then $x \cdot y$ is red.
|
## 2. Version for klas 6
We first consider the case that 1 is red. Then all numbers from 1 to 15 are red. Indeed, suppose that some number $k$ is blue. Then 1 and $k$ have different colours, hence by the third rule the number $1 \cdot k=k$ must be red. But this contradicts the assumption that it was blue. Observe that colouring all numbers red indeed gives a correct colouring.
Now we consider the case that 1 is blue. Observe that when two numbers sum to 15, those numbers must have the same colour by the second rule. We get the following pairs of numbers of the same colour: 1 and 14, 2 and 13, 3 and 12,4 and 11,5 and 10,6 and 9, 7 and 8 .
The number 2 is blue. Indeed, suppose that 2 is red. From the second rule, we derive that $3=1+2$ is blue. Repeatedly applying the same rule we find that $5=3+2$ is blue, that $7=5+2$ is blue, and finally that 15 is blue. Since 15 is in fact not blue, 2 cannot be red.
The number 7 is blue. Indeed, suppose that 7 is red. It then follows from the second rule that $8=1+7$ is blue. However, 7 and 8 must have the same colour, so this cannot be the case.
The number 4 is blue. Indeed, suppose that 4 is red. It then follows from the second rule that $11=4+7$ is blue. But 4 and 11 have the same colour, so this cannot be the case.
Recall, that 3 and 12 have the same colour, and so do 6 and 9. In fact, all four numbers must have the same colour. Indeed, otherwise $9=3+6$ would be blue by the second rule and also $12=3+9$ would be blue by the second rule.
So far, we know that 15 is red, that $1,2,4,7,8,11,13,14$ are blue, that $3,6,9,12$ have the same colour, and that 5,10 have the same colour. The numbers 3 and 5 cannot both be red, since if 3 is red, $5=2+3$ is blue by the second rule. The three remaining colour combinations for the numbers 3 and 5 result in the following three colourings:
(1) Only 15 is red.
(2) Only $5,10,15$ (the numbers divisible by 5 ) are red.
(3) Only $3,6,9,12,15$ (the numbers divisible by 3 ) are red.
It is easy to check that all three colourings are indeed correct. We write this out for the third colouring, the other two can be checked in a similar way. That the sum of a red and a blue number is always blue follows from the fact that the sum of a number divisible by 3 and a number not divisible by 3 is itself not divisible by 3 . That the product of a blue and a red number is always red follows from the fact that the product of a number divisible by 3 and a number not divisible by 3 is itself divisible by 3 .
We conclude that there are 4 correct colourings in total: the colouring in which all numbers are red, and colourings (1), (2), and (3).
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. We make groups of numbers. Each group consists of five distinct numbers. A number may occur in multiple groups. For any two groups, there are exactly four numbers that occur in both groups.
(a) Determine whether it is possible to make 2015 groups.
(b) If all groups together must contain exactly six distinct numbers, what is the greatest number of groups that you can make?
(c) If all groups together must contain exactly seven distinct numbers, what is the greatest number of groups that you can make?
|
1. (a) It is possible to make 2015 groups. For example, take the 2015 groups $\{-4,-3,-2,-1, i\}$, where $i$ runs from 1 to 2015. Each group consists of five distinct numbers, as required, and any two groups have exactly four numbers in common: $-4,-3,-2$, and -1 .
(b) Using six available numbers, there are only six possible groups of five numbers (each obtained by leaving out one of the six numbers). Those six groups do satisfy the requirement that any two of them have exactly four numbers in common. We conclude that six is the greatest number of groups we can make in this case.
(c) A way to make three groups is to take $\{1,2,3,4,5\},\{1,2,3,4,6\}$, and $\{1,2,3,4,7\}$.
More than three groups is not possible. Indeed, suppose we have four or more groups. The first two groups are $A=\{a, b, c, d, e\}$ and $B=\{a, b, c, d, f\}$, where $a, b, c, d, e$, and $f$ are distinct numbers. Then there must be a third group $C$ containing a seventh number $g$. The remaining four numbers in $C$ must be in both $A$ and $B$, hence $C=\{a, b, c, d, g\}$.
Now consider a hypothetical fourth group $D$. This group cannot contain the number $g$ since otherwise, using a similar reasoning as for $C$, we would have $D=\{a, b, c, d, g\}$. Because $D$ does not contain the number $g$, it must contain the remaining four numbers $a, b, c$, and $d$ from $C$. Comparison with groups $A$ and $B$ then shows that $D$ can contain neither $e$ nor $f$. It follows that besides $a, b, c$, and $d, D$ cannot contain a fifth number, contradicting the requirements.
We conclude that the greatest number of groups we can make is three.
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Daan distributes the numbers 1 to 9 over the nine squares of a $3 \times 3$-table (each square receives exactly one number). Then, in each row, Daan circles the median number (the number that is neither the smallest nor the largest of the three). For example, if the numbers 8,1 , and 2 are in one row, he circles the number 2. He does the same for each column and each of the two diagonals. If a number is already circled, he does not circle it again.
| 8 | 1 | 2 |
| :---: | :---: | :---: |
| 7 | 6 | 3 |
| 9 | 5 | 4 |
He calls the result of this process a median table. Above, you can see a median table that has 5 circled numbers.
(a) What is the smallest possible number of circled numbers in a median table?
Prove that a smaller number is not possible and give an example in which a minimum number of numbers is circled.
(b) What is the largest possible number of circled numbers in a median table?
Prove that a larger number is not possible and give an example in which a maximum number of numbers is circled.
|
1. (a) The smallest possible number of circled numbers is 3 . Fewer than 3 is not possible since in each row at least one number is circled (and these are three different numbers).
On the right, a median table is shown in which only 3 numbers are circled. In the rows, the numbers $7,5,3$ are circled, in the columns the numbers $3,5,7$, and on the diagonals the numbers 5 and 5 . Together, these are three different numbers: 3,5 , and 7 .
| 4 | 9 | 7 |
| :---: | :---: | :---: |
| 2 | 5 | 8 |
| 3 | 1 | 6 |
(b) The largest possible number of circled numbers is 7 . More than 7 is not possible, since the numbers 9 and 1 are never circled, hence no more than $9-2=7$ numbers are circled.
On the right, a median table is shown in which 7 numbers are circled. In the rows, the numbers $2,6,8$ are circled, in the columns the numbers $7,5,3$, and on the diagonals the numbers 4 and 5 . Together, these are the numbers $2,3,4,5,6,7,8$.
| 4 | 1 | 2 |
| :--- | :--- | :--- |
| 7 | 5 | 6 |
| 8 | 9 | 3 |
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. We consider number sequences $a_{1}, a_{2}, a_{3}, \ldots$ such that $a_{n+1}=\frac{a_{n}+a_{1}}{a_{n}+1}$ holds for all $n \geqslant 1$.
(a) Suppose that $a_{1}=-3$. Compute $a_{2020}$.
(b) Suppose that $a_{1}=2$. Prove that $\frac{4}{3} \leqslant a_{n} \leqslant \frac{3}{2}$ holds for all $n \geqslant 2$.
|
## 2. Version for klas 5 \& klas 4 and below
(a) If $a_{1}=-3$, we have $a_{2}=\frac{a_{1}+a_{1}}{a_{1}+1}=\frac{-6}{-2}=3$. Next, we find $a_{3}=\frac{a_{2}+a_{1}}{a_{2}+1}=\frac{0}{4}=0$. Then, we have $a_{4}=\frac{a_{3}+a_{1}}{a_{3}+1}=\frac{-3}{1}=-3$. We see that $a_{4}=a_{1}$. Since $a_{n+1}$ only depends on $a_{n}$ and $a_{1}$, we see that $a_{5}=a_{2}=3, a_{6}=a_{3}=0, a_{7}=a_{4}=-3$, et cetera. In other words: the sequence is periodic with period 3 , and we see that
$$
a_{2020}=a_{2017}=a_{2014}=\cdots=a_{4}=a_{1}=-3 .
$$
(b) We will prove the statement by induction on $n$. We start with the induction basis $n=2$. We calculate $a_{2}=\frac{a_{1}+a_{1}}{a_{1}+1}=\frac{4}{3}$ and see that indeed $\frac{4}{3} \leqslant a_{n} \leqslant \frac{3}{2}$ holds.
Now suppose that for certain $n=k \geqslant 2$ we have proven that $\frac{4}{3} \leqslant a_{n} \leqslant \frac{3}{2}$. We will show that these inequalities hold for $n=k+1$ as well.
We first observe that
$$
a_{k+1}=\frac{a_{k}+2}{a_{k}+1}=1+\frac{1}{a_{k}+1} .
$$
From the induction hypothesis $\left(\frac{4}{3} \leqslant a_{k} \leqslant \frac{3}{2}\right)$ it follows that $\frac{7}{3} \leqslant a_{k}+1 \leqslant \frac{5}{2}$, and hence that
$$
\frac{2}{5} \leqslant \frac{1}{a_{k}+1} \leqslant \frac{3}{7} .
$$
By adding 1 to all parts of these inequalities, we find
$$
\frac{7}{5} \leqslant 1+\frac{1}{a_{k}+1}=a_{k+1} \leqslant \frac{10}{7} .
$$
Since $\frac{4}{3} \leqslant \frac{7}{5}$ and $\frac{10}{7} \leqslant \frac{3}{2}$, we see that $\frac{4}{3} \leqslant a_{k+1} \leqslant \frac{3}{2}$, completing the induction step.
|
-3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (a) Determine all pairs $(x, y)$ of (real) numbers with $0<x<1$ and $0<y<1$ for which $x+3 y$ and $3 x+y$ are both integers. An example of such a pair is $(x, y)=\left(\frac{3}{8}, \frac{7}{8}\right)$, because $x+3 y=\frac{3}{8}+\frac{21}{8}=\frac{24}{8}=3$ and $3 x+y=\frac{9}{8}+\frac{7}{8}=\frac{16}{8}=2$.
(b) Find the integer $m \geqslant 2$ for which there are exactly 119 pairs $(x, y)$ with $0<x<1$ and $0<y<1$ for which $x+m y$ and $m x+y$ are both integers.
Note: if $u \neq v$, then $(u, v)$ and $(v, u)$ are different pairs.
|
4. (a) Suppose $(x, y)$ is such a pair and consider the integers $a=x+3 y$ and $b=3 x+y$. Since $0<x, y<1$, it follows that $0<a, b<4$, or rather $1 \leqslant a, b \leqslant 3$.
Now, conversely, let $a$ and $b$ be two integers with $1 \leqslant a, b \leqslant 3$. There is exactly one pair of numbers $(x, y)$ for which $a=x+3 y$ and $b=3 x+y$. Indeed, combining the two equations gives $3 b-a=3(3 x+y)-(x+3 y)=8 x$ and $3 a-b=8 y$, or rather $x=(3 b-a) / 8$ and $y=(3 a-b) / 8$ (and these $x$ and $y$ do indeed satisfy the two equations). Substituting $1,2,3$ for $a$ and $b$ gives nine pairs $(x, y)$:
$$
\left(\frac{2}{8}, \frac{2}{8}\right),\left(\frac{5}{8}, \frac{1}{8}\right),\left(\frac{8}{8}, \frac{0}{8}\right), \quad\left(\frac{1}{8}, \frac{5}{8}\right),\left(\frac{4}{8}, \frac{4}{8}\right),\left(\frac{7}{8}, \frac{3}{8}\right), \quad\left(\frac{0}{8}, \frac{8}{8}\right),\left(\frac{3}{8}, \frac{7}{8}\right),\left(\frac{6}{8}, \frac{6}{8}\right).
$$
Due to the requirement that $0<x, y<1$, the two possibilities $(x, y)=\left(\frac{8}{8}, \frac{0}{8}\right),\left(\frac{0}{8}, \frac{8}{8}\right)$ must be excluded. The remaining 7 pairs are thus precisely the pairs asked for in the problem.
(b) Suppose $0<x, y<1$ and that $a=x+m y$ and $b=m x+y$ are integers. Then $1 \leqslant a, b \leqslant m$.
Given integers $a$ and $b$ with $1 \leqslant a, b \leqslant m$, there is exactly one pair $(x, y)$ for which $x+m y=a$ and $m x+y=b$, because combining the two equations gives: $m b-a=\left(m^{2}-1\right) x$ and $m a-b=\left(m^{2}-1\right) y$, or rather $x=(m b-a) /\left(m^{2}-1\right)$ and $y=(m a-b) /\left(m^{2}-1\right)$. These $x$ and $y$ indeed satisfy the two equations.
We now consider for which $a$ and $b$ the corresponding numbers $x$ and $y$ also satisfy $0<x, y<1$. From $1 \leqslant a, b \leqslant m$ it follows that $x \geqslant(m \cdot 1-m) /\left(m^{2}-1\right)=0$ and that $x \leqslant(m \cdot m-1) /\left(m^{2}-1\right)=$ 1. The cases $x=0$ and $x=1$ correspond precisely to $(a, b)=(m, 1)$ and $(a, b)=(1, m)$, respectively. Similarly, $0<y<1$ unless $(a, b)=(1, m)$ or $(a, b)=(m, 1)$. Of the $m^{2}$ possibilities for $(a, b)$, there are thus two without a solution. In total, this gives $m^{2}-2$ solutions $(x, y)$.
From $m^{2}-2=119$ it follows that $m=11$.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In a table consisting of $n$ by $n$ small squares some squares are coloured black and the other squares are coloured white. For each pair of columns and each pair of rows the four squares on the intersections of these rows and columns must not all be of the same colour.
What is the largest possible value of $n$ ?
|
1. We will prove that $n=4$ is the largest possible $n$ for which an $n \times n$-table can be coloured according to the rules. The following figure shows a valid colouring for $n=4$.

Now we prove that there is no colouring of the squares in a $5 \times 5$-table satisfying the requirements. Suppose, for contradiction, that such a colouring exists. Of the squares in each row either the majority is black, or the majority is white. We may suppose that there are at least three rows for which the majority of the squares is black (the case where there are at least three rows for which the majority of the squares is white is treated in an analogous way). We now consider the squares in these three rows. Of these 15 squares at least 9 are black.
If there is a column in which each of the three rows has a black square, then each other column can contain at most one black square in these three rows. The total number of black squares in the three rows will therefore be no more than $3+1+1+1+1=7$, contradicting the fact that the number should be at least 9 .
Hence, in each column at most two of the three rows have a black square. We consider the number of columns with two black squares in the three rows. If there are more then three, then there are two columns in which the same two rows have a black square, which is impossible. It follows that the number of black squares in the three rows is no more than $2+2+2+1+1=8$, again contradicting the fact that this number should be at least 9 .
Hence, it is impossible to colour a $5 \times 5$-table according to the rules. It is clear that it also will be impossible to colour an $n \times n$-table according to the rules if $n>5$.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Call a positive integer a hussel number if:
(1) All digits are not equal to 0.
(2) The number is divisible by 11.
(3) The number is divisible by 12. If you rearrange the digits in any other random order, you always get a number that is divisible by 12.
How many 5-digit hussel numbers are there?
|
## 1. Version for Class 4 and Lower
To begin with, we note that a hussel number can only contain the digits 2, 4, 6, and 8. Indeed, if we arrange the digits in any random order, we get an even number (divisible by 12) due to property (3). Since the last digit of an even number is always even, that digit must be 2, 4, 6, or 8 because 0 is not included due to property (1). Since we can place each digit at the end, this applies to every digit of a hussel number.
Next, we note that a hussel number can only contain the digits 4 and 8. Suppose a hussel number has the digit 2. By suitably swapping the digits, we get a number where the last digit is 2. The last two digits of this number are then 22, 42, 62, or 82. The number is then not divisible by 4 (and thus not divisible by 12), contradicting property (3). Similarly, a hussel number cannot have the digit 6 because a number ending in 26, 46, 66, or 86 is not divisible by 4.
Since a hussel number is divisible by 3 (because it is divisible by 12), the sum of the digits is also divisible by 3. Since each digit is either 4 or 8, we have the following cases:
- 5 fours and 0 eights. Sum of the digits: 20
- 4 fours and 1 eight. Sum of the digits: 24
- 3 fours and 2 eights. Sum of the digits: 28
- 2 fours and 3 eights. Sum of the digits: 32
- 1 four and 4 eights. Sum of the digits: 36
- 0 fours and 5 eights. Sum of the digits: 40
The five-digit numbers that satisfy properties (1) and (3) are therefore exactly the numbers that consist of 4 fours and 1 eight, or 1 four and 4 eights. We now need to check which of these eight numbers are divisible by 11. This is simple using the 11-criterion: a number is divisible by 11 if the alternating sum of the digits is divisible by 11. By alternating sum, we mean that we take the digits alternately with a plus sign and a minus sign. For the eight candidates, we find the following alternating sums:
| 84444 | $8-4+4-4+4=8$ | 48888 | $4-8+8-8+8=4$ |
| ---: | :--- | :--- | :--- |
| $\mathbf{4 8 4 4 4}$ | $4-8+4-4+4=0$ | 84888 | $8-4+8-8+8=12$ |
| 44844 | $4-4+8-4+4=8$ | 88488 | $8-8+4-8+8=4$ |
| $\mathbf{4 4 4 8 4}$ | $4-4+4-8+4=0$ | 88848 | $8-8+8-4+8=12$ |
| 44448 | $4-4+4-4+8=8$ | 88884 | $8-8+8-8+4=4$ |
Thus, there are exactly two hussel numbers of 5 digits, namely 48444 and 44484.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The numbers 1 through 25 are each colored blue or red. Determine all possible colorings that satisfy the following rules:
- The number 5 is red.
- If the numbers $x$ and $y$ have different colors and $x+y \leqslant 25$, then $x+y$ is blue.
- If the numbers $x$ and $y$ have different colors and $x \cdot y \leqslant 25$, then $x \cdot y$ is red.
|
## 2. Version for class $5 \&$ class 4 and lower
First, we consider the case where 1 is red. Then all numbers from 1 to 25 must be red. Suppose a certain number $k$ is blue. Then 1 and $k$ have different colors, so according to the third rule, the number $1 \cdot k = k$ must be red. But this number was blue, which is a contradiction. Note that a coloring where all numbers are red is indeed a valid coloring.
Now we consider the case where 1 is blue. Since 5 is not blue, it follows from the second rule that 1 and 4 have the same color. Therefore, 4 is blue. Also, it follows that 2 and 3 have the same color. If 2 were red, then $3 = 1 + 2$ would have to be blue according to the second rule, so 2 and 3 are both blue.
We now know that 1, 2, 3, and 4 are blue. Applying the second rule again, we find that $6 = 5 + 1, 7 = 5 + 2, 8 = 5 + 3$, and $9 = 5 + 4$ are also blue. Applying the second rule again, we find that 11, 12, 13, 14 are blue, that 16, 17, 18, 19 are blue, and that 21, 22, 23, 24 are blue.
According to the third rule, $10 = 2 \cdot 5, 15 = 3 \cdot 5$, and $20 = 4 \cdot 5$ are red. Only the color of 25 is still undetermined. We find two possible colorings:
(1) Only 5, 10, 15, 20, 25 (the numbers divisible by 5) are red.
(2) Only 5, 10, 15, 20 are red.
We check that coloring (1) is indeed correct. The second rule is satisfied because the sum of a number divisible by 5 and a number not divisible by 5 is itself not divisible by 5. The third rule is satisfied because the product of a number divisible by 5 and a number not divisible by 5 is itself divisible by 5.
Coloring (2) differs from coloring (1) only for the number 25. To check that coloring (2) is correct, we only need to check the rules in the case where one of the involved numbers is 25. We check that 25 is not the product of a blue and a red number (which is true). We also need to check that there is no red number $k$ for which $25 + k$ is red or $25k$ is blue. This is fine because numbers greater than 25 are not colored.
We conclude that there are a total of 3 valid colorings: the coloring where all numbers are red and the colorings (1) and (2).
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The numbers 1 through 15 are each colored blue or red. Determine all possible colorings that satisfy the following rules:
- The number 15 is red.
- If the numbers $x$ and $y$ have different colors and $x+y \leqslant 15$, then $x+y$ is blue.
- If the numbers $x$ and $y$ have different colors and $x \cdot y \leqslant 15$, then $x \cdot y$ is red.
|
## 2. Version for Grade 6
First, let's consider the case where 1 is red. Then all numbers from 1 to 15 must be red. Suppose a certain number $k$ is blue. Then 1 and $k$ have different colors, so according to the third rule, the number $k=1 \cdot k$ must be red. But this number was blue, which is a contradiction. Note that a coloring where all numbers are red is indeed a valid coloring.
$\mathrm{Now}$ let's consider the case where 1 is blue. Note that if two numbers add up to 15, then those numbers must have the same color according to the second rule. The following pairs must therefore always have the same color: 1 and 14, 2 and 13, 3 and 12, 4 and 11, 5 and 10, 6 and 9, 7 and 8.
The number 2 is blue. Suppose 2 is red. Then from the second rule, $3=1+2$ must be blue. Repeated application of the second rule gives that $5=3+2$ is blue, that $7=5+2$ is blue, and eventually that 15 is blue. Since 15 is not blue, 2 cannot be red.
The number 7 is blue. Suppose 7 is red. Then from the second rule, $8=1+7$ must be blue. However, 7 and 8 must have the same color, so that cannot be.
The number 4 is blue. Suppose 4 is red. Then from the second rule, $11=4+7$ must be blue. But 4 and 11 have the same color, so 4 cannot be red.
The pairs 3 and 12 and 6 and 9 must have the same color. Otherwise, $9=3+6$ would be blue according to the second rule, and also $12=3+9$ would be blue according to the second rule.
So far, we know that 15 is red, that 1, 2, 4, 7, 8, 11, 13, 14 are blue, that $3, 6, 9, 12$ have the same color, and that 5, 10 have the same color. The numbers 3 and 5 cannot both be red, because if 3 is red, then $5=2+3$ would be blue according to the second rule. The three remaining possibilities for the colors of 3 and 5 give the following colorings:
(1) Only 15 is red.
(2) Only 5, 10, 15 (the numbers divisible by 5) are red.
(3) Only 3, 6, 9, 12, 15 (the numbers divisible by 3) are red.
It is easy to verify that these three colorings are indeed valid. We will check this for the third coloring, the other two are verified in the same way. That the sum of a red and a blue number is always blue follows from the fact that the sum of a number divisible by 3 and a number not divisible by 3 is also not divisible by 3. That the product of a blue and a red number is always red follows from the fact that the product of a number divisible by 3 and a number not divisible by 3 is again divisible by 3.
We conclude that there are a total of 4 valid colorings: the coloring where all numbers are red and the colorings (1), (2), and (3).
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
B2 The point $S$ lies on the chord $A B$ of a circle such that $S A=3$ and $S B=5$. The radius of the circle from the center $M$ through $S$ intersects the circle at $C$. Given $C S=1$.
Calculate the length of the radius of the circle.
|
B2. Draw the perpendicular from $\mathrm{M}$ to the chord $\mathrm{AB}$.
Let the foot of the perpendicular be $T$.
$T$ is the midpoint of $AB$.
Let the length of the radius be $r$.
$A T^{2}+T M^{2}=r^{2}$, so $16+T M^{2}=r^{2}$
$S T^{2}+T M^{2}=S M^{2}$, so $1+T M^{2}=(r-1)^{2}$
(1) - (2) gives $15=r^{2}-(r-1)^{2}=2 r-1$, so $r=8$.

|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. We call a positive integer squareful if every two adjacent digits in the number form a square. The number 364 is, for example, squareful, because both 36 and 64 are squares.
How many digits does the largest squareful number have?
A) 2
B) 3
C) 4
D) 5
E) 6
|
A1. D) 5 The squares of two digits are $16, 25, 36, 49, 64$, and 81. We start with each of these squares and look for which digit we can append so that the last two digits also form a square. For example: after 16, a 4 can be appended because of 64 (and no other digit can follow the 6), then comes a 9 to form 49, and then it stops because no square starts with a 9. With the six different starting squares, you can form the following numbers at most:
- 1649
- 25
- 3649
- 49
- 649
- 81649
The largest number from this list, 81649, consists of five digits.
|
5
|
Number Theory
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
4. We place the numbers 1 through 9 one by one in a $3 \times 3$ grid. The number 1 can be placed in any cell; each subsequent number must be placed in a cell that is horizontally or vertically adjacent to the cell containing the previous number. See the example picture below. We call such a grid a snake grid. The score of a cell in a snake grid is the sum of the numbers in all cells that share a side with it. The total score of a snake grid is the sum of the scores of all its cells.
| 1 | 2 | 9 |
| :---: | :---: | :---: |
| 4 | 3 | 8 |
| 5 | 6 | 7 |
In the example snake grid (adding row by row, from left to right), the total score is $6+13+10+9+20+19+10+15+14=116$.
How many possible total scores can such a snake grid have?
A) 1
B) 2
C) 3
D) 4
E) 5
|
A4. E) 5
We color the cells of the $3 \times 3$ grid alternately gray and white and assign each cell a letter, as shown in the figure below. A snake always alternates between the white and gray cells, and thus alternates between even and odd numbers. Since there are five odd numbers and five white cells, the odd numbers will be placed on the white cells, at positions $a, c, e, g$, and $i$. We calculate the total score of this grid as follows:
| $a$ | $b$ | $c$ |
| :--- | :--- | :--- |
| $d$ | $e$ | $f$ |
| $g$ | $h$ | $i$ |
$$
\begin{array}{r}
(b+d)+(a+e+c)+(b+f)+(a+e+g)+(b+d+f+h) \\
+(c+e+i)+(d+h)+(e+g+i)+(f+h) \\
=2(a+b+c+d+e+f+g+h+i)+(b+d+f+h)+2 e
\end{array}
$$
This is equal to twice the sum of all numbers, plus the sum of all even numbers, plus twice $e$. The first two terms are the same for every snake. The total score of the grid thus depends only on the number that ends up in position $e$. This is an odd number, as we have already seen, and there are five possibilities for it. The examples below show that each odd number can indeed end up in the middle.
| 5 | 4 | 3 |
| :---: | :---: | :---: |
| 6 | 1 | 2 |
| 7 | 8 | 9 |
| 1 | 2 | 9 |
| :---: | :---: | :---: |
| 4 | 3 | 8 |
| 5 | 6 | 7 |
| 1 | 2 | 3 |
| :---: | :---: | :---: |
| 6 | 5 | 4 |
| 7 | 8 | 9 |
| 1 | 2 | 3 |
| :---: | :---: | :---: |
| 8 | 7 | 4 |
| 9 | 6 | 5 |
| 1 | 2 | 3 |
| :---: | :---: | :---: |
| 8 | 9 | 4 |
| 7 | 6 | 5 |
|
5
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
4. Pjotr has a bathtub with a plug at the bottom that he can fill with two identical taps. The water flows from both taps at the same constant speed, and the bathtub drains (if the plug is not in) at a constant speed.
On Monday, Pjotr lets the bathtub fill to the brim by turning on one tap fully, after which he pulls the plug and waits until the bathtub is empty again. Only when the bathtub is empty does he turn the tap off. On Tuesday, he lets the bathtub fill to the brim by turning on both taps fully, after which he pulls the plug and waits until the bathtub is empty again. Only when the bathtub is empty does he turn the taps off. On both days, Pjotr was busy for exactly 45 minutes from turning on the tap/taps to turning them off again.
How many minutes does it take for a full bathtub to drain completely if both taps are off?
|
B4. 10 Given that water flows from a tap at a rate of $v$ liters per minute and the bathtub drains at a rate of $w$ liters per minute when the taps are off. Assume the bathtub can hold $b$ liters of water. We want to know how long it takes for a full bathtub to drain, which is $\frac{b}{w}$.
On Monday, the bathtub first fills at a rate of $v$ liters per minute, and then drains at a rate of $w-v$ liters per minute. Together, this takes $\frac{b}{v}+\frac{b}{w-v}$ minutes. On Tuesday, the bathtub first fills at a rate of $2v$ liters per minute, and then drains at a rate of $w-2v$ liters per minute. This takes the same amount of time as on Monday. Together, this gives the equation
$$
\frac{b}{v}+\frac{b}{w-v}=\frac{b}{2v}+\frac{b}{w-2v}
$$
Making the fractions have a common denominator, cross-multiplying, and simplifying yields $w=3v$. (You can easily verify this by substituting it into the equation above.) In other words, the bathtub drains three times as fast as it fills with one tap.
Finally, we use the given information that Pjotr spent 45 minutes on both days. Substituting $v=\frac{1}{3}w$ into the formula for Monday, we get
$$
45=\frac{b}{v}+\frac{b}{w-v}=\frac{b}{\frac{1}{3}w}+\frac{b}{\frac{2}{3}w}=\frac{9}{2} \cdot \frac{b}{w}.
$$
From this, it follows that $\frac{b}{w}=10$.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Xander draws five points and a number of infinitely long lines on an infinite sheet of paper, in such a way that at least two of those points lie on each line and that the lines intersect only at points that Xander has drawn.
What is the maximum number of lines that Xander can have drawn?
A) 3
B) 4
C) 5
D) 6
E) 7
|
A5. D) 6 We can get 6 lines as follows. We take the extended sides of a square together with the two diagonals. The 5 points are now the four corners of the square and the center, see also the figure below.
We will show that 7 (or more) lines are not possible. We do this by contradiction: assume that a situation with 7 lines does exist. In
general, 7 lines intersect in $\frac{7 \cdot 6}{2}=21$ points, but there are two reasons why there could be fewer.
First, lines can be parallel, meaning they do not intersect. Since each line must contain at least 2 of the 5 points, it is not possible for 3 lines to be parallel (as that would require $3 \cdot 2=6$ points). Therefore, of the 7 lines, there can be at most 3 pairs that are parallel, and thus at most 3 fewer intersection points due to parallelism. This leaves at least $21-3=18$ intersection points.
Second, intersection points can coincide. This happens when more than two lines pass through the same point. If 3 lines pass through one point, 3 intersection points coincide. If 4 lines pass through one point, 6 intersection points coincide, and so on. The at least 18 remaining intersection points must coincide in the 5 points we started with. This means that there must be a point, say $P$, where at least 4 intersection points coincide (since $5 \cdot 3=15<18$). Therefore, at least 4 different lines, say $\ell_{1}, \ell_{2}, \ell_{3}$, and $\ell_{4}$, pass through this point.
On each of these 4 lines, there must be another one of the 5 points, say points $P_{1}, P_{2}, P_{3}$, and $P_{4}$. These points cannot coincide. Since we have now found all 5 points, there can be no fifth line passing through the point $P$. Each of the remaining 3 lines intersects at least 3 of the lines $\ell_{1}, \ell_{2}, \ell_{3}$, and $\ell_{4}$ (since it can be parallel to at most one of those lines). This means that the remaining lines must contain at least 3 of the points $P_{1}, P_{2}, P_{3}$, and $P_{4}$. However, this implies that the 3 remaining lines are all the same, which is a contradiction.
We conclude that 7 (or more) lines are not possible and that 6 is the maximum number of lines.
|
6
|
Combinatorics
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
1. Arthur writes down five different positive integers less than $10 \mathrm{on}$. If you add any two of these five numbers, the sum is never 10.
Which number has Arthur certainly written down?
A) 1
B) 2
C) 3
D) 4
E) 5
|
A1. E) 5 Of the numbers 1 and 9, Arthur could have written down only one, because no two written numbers add up to 10. The same applies to 2 and 8, for 3 and 7, and also for 4 and 6. Of the eight numbers 1, 2, 3, 4, 6, 7, 8, and 9, Arthur has thus written down at most four. This means that he must have written down the remaining number 5.
|
5
|
Number Theory
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
4. Er zijn 13 verschillende veelvouden van 7 die uit twee cijfers bestaan. Je wilt een zo lang mogelijke keten maken van deze veelvouden, waarbij twee veelvouden alleen naast elkaar mogen staan als het laatste cijfer van het linker veelvoud gelijk is aan het eerste cijfer van het rechter veelvoud. Je mag elk veelvoud hooguit één keer gebruiken. Zo is $21-14-49$ een toegestane keten van lengte 3 .
Wat is de maximale lengte van een toegestane keten?
A) 6
B) 7
C) 8
D) 9
E) 10
|
A4. B) 7 De dertien veelvouden zijn: $14,21,28,35,42,49,56,63,70,77,84,91$ en 98.
In de veelvouden 70 en 77 komen alleen de cijfers 0 en 7 voor. Bovendien zijn het de enige veelvouden met een 0 of 7 . Met 70 of 77 kan de keten dus hooguit lengte 2 hebben.
Op dezelfde manier zijn de veelvouden 35, 56 en 63 de enige veelvouden met een 3,5 of 6 . Met die veelvouden kan een keten dus hooguit lengte 3 hebben.
Een keten van lengte 4 of meer kan dus alleen de veelvouden 14, 21, 28, 42, 49, 84, 91 en 98 bevatten. We kijken eerst of er een keten mogelijk is die alle acht overgebleven veelvouden gebruikt. Omdat twee van de veelvouden eindigen op een 1 en er slechts één met een 1 begint, moet het laatste getal van de keten dus op een 1 eindigen. Er zijn echter ook twee veelvouden die op een 8 eindigen en slechts één veelvoud dat met een 8 begint. Het laatste getal in de keten moet dus ook op een 8 eindigen. Het laatste getal kan niet op zowel een 1 als een 8 eindigen, dus we kunnen geen keten maken van lengte 8 .
Er is wel een keten van lengte 7, namelijk $21-14-42-28-84-49-91$.
|
7
|
Combinatorics
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
4. Alice has a number of cards. On each card, three of the letters A through I are written. For any two letters you choose, there is at least one card where those two letters appear together.
What is the smallest number of cards Alice can have?
|
B4. 12 There are 9 letters, namely $A$ through $I$. The number of possible pairs of letters is $\frac{9 \times 8}{2}=36$. Indeed, each of the 9 letters can form a pair with 8 other letters, but this way we count each pair twice (pair AE is the same as pair EA).
Each card has three different letters that form 3 pairs. Therefore, at least $\frac{36}{3}=12$ cards are needed to get each pair exactly once. That it can actually be done with 12 cards follows by taking the following triplets:
| ABC | DEF | GHI |
| :---: | :---: | :---: |
| ADG | BEH | CFI |
| AEI | CDH | BFG |
| AFH | BDI | CEG |
The triplets are also illustrated in the figure. The twelve triplets are formed by the three horizontal lines, the three vertical lines, the two diagonals, and the four curved lines. It is easy to verify that each pair of letters indeed lies on one of the lines.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. By replacing every $*$ in the expression $1 * 2 * 3 * 4 * 5 * \cdots * 2019 * 2020$ with a plus or minus sign ( + or - ), a long arithmetic expression is formed. Place the plus and minus signs in such a way that the result is the smallest possible positive number (greater than 0).
What is this result?
|
B1. 2 We look at the expression from back to front. By taking $2017-2018-2019+2020$, we get exactly zero. Before that, we choose $2013-2014-2015+2016$ and so on until $5-6-7+8$. At the beginning, we take $1+2+3-4$ and thus we get a result of 2.
Now we only need to show that the result is never equal to 1, making 2 the smallest possible positive result. This is easily seen by noting that the result is always even. The result 2 is even, and if we change a + to a - or vice versa, it does not change whether the result is even or not. All possible results are therefore even.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Annemiek and Bart each wrote three different positive integers on a piece of paper. It turns out that there is exactly one number that appears on both of their papers. Furthermore, if you take two different numbers from Annemiek's paper and add them together, the result is always a number on Bart's paper. One of the three numbers on Annemiek's paper is her favorite number, and if you multiply that by 3, you also get a number on Bart's paper. On Bart's paper, his favorite number is 25.
What is Annemiek's favorite number?
|
B3. Suppose we call the three numbers on Annemieke's note $a, b$, and $c$ and assume that $a<b<c$. Then the three numbers on Bart's note, in order of size, are $a+b, a+c$, and $b+c$. The last two numbers are greater than $c$ and thus greater than any number on Annemieke's note. The number that appears on both notes must therefore be $a+b$ and that must be equal to $c$.
Annemieke thus has the numbers $a, b$, and $a+b$, and Bart has $a+b, 2a+b$, and $a+2b$. If we now look at $3b$ and $3(a+b)=3a+3b$, we see that these numbers are both greater than all the numbers on Bart's note. Annemieke's favorite number, which appears on Bart's note when multiplied by 3, is therefore $a$.
The number $3a$ is thus one of the numbers $a+b, 2a+b, a+2b$ on Bart's note, and since $a$ and $b$ are different, it must be the number $a+b$. In other words: $b=2a$. Bart thus has the numbers $3a$, $4a$, and $5a$. The only one of these three numbers that can be the number 25 is $5a$. We thus see that $a=5$ and that is Annemieke's favorite number.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. We consider rows of 2020 coins. Each coin has a value of 1, 2, or 3. Between two coins with value 1, there is always at least one other coin. Between two coins with value 2, there are always at least two other coins. Between two coins with value 3, there are always at least three other coins.
How many different rows are there that meet these conditions?
|
B4. 10 Consider a continuous segment where no coin of value 3 is present. In this segment, there can be at most one coin of value 2, because otherwise we would have two coins of value 2 with only coins of value 1 in between, which is not allowed. Since there can be at most one coin of value 2, there can also be at most two coins of value 1, because otherwise we would have two coins of value 1 next to each other. The only possibilities for such a segment without coins of value 3 are thus
$$
121,12,21,2,1
$$
A row of 2020 coins must therefore have multiple coins of value 3. Consider in a row two coins of value 3 where no other coin of value 3 lies between them. Between these two coins, there must be at least three other coins. We have just seen that we then have exactly three coins, and 121 is the only possibility.
Our row of 2020 coins thus looks like this:
beginning segment- $\underbrace{312131213 \cdots \cdots 31213}_{\text {number of times the same pattern }}$-end segment,
where the beginning and end segments contain only coins of value 1 and 2. The only possibilities for the beginning and end segments are: $121,12,21,2,1$, or no coins.
The length of the repeating segment is a multiple of four plus one. The length of this segment must be less than $505 \cdot 4+1=2021$ and more than $503 \cdot 4+1=2013$, because otherwise the beginning and end segments together would have more than 6 coins. The length of the middle segment is thus equal to $504 \cdot 4+1=2017$ and the beginning and end segments together have $2020-2017=3$ coins. For the beginning and end segments, there are now 10 possibilities: nothing at the beginning and 121 at the end or vice versa (2 possibilities in total); 1 or 2 at the beginning and 12 or 21 at the end ($2 \cdot 2=4$ possibilities); 12 or 21 at the beginning and 1 or 2 at the end ($2 \cdot 2=4$ possibilities).
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. On a $4 \times 4$ board, there are 16 grasshoppers, each on its own square. At a certain moment, each grasshopper jumps to an adjacent square: a square up, down, to the right, or to the left, but not diagonally and not off the board.
What is the maximum number of squares that can be empty afterward?
A) 8
B) 9
C) 10
D) 11
E) 12
|
A5. C) 10 We color the squares of the $4 \times 4$ board in a checkerboard pattern and name the squares from a1 to d4 as shown in the figure. We see that the grasshoppers on white squares all jump to a black square, and the grasshoppers on black squares jump to a white square.

The squares adjacent to a3, c1, and d4 are all different, so the three grasshoppers from a3, c1, and d4 end up on three different white squares. Similarly, the three grasshoppers from a2, c4, and d1 end up on three different black squares. After jumping, there are thus at least six squares occupied.
We can ensure that only six squares are occupied after jumping. The grasshoppers from the black squares can each jump to one of the squares a2, c4, and d1, and the grasshoppers from the white squares can each jump to one of the squares a3, c1, and d4.
The smallest possible number of occupied squares is thus 6, and the largest possible number of empty squares is $16-6=10$.
|
10
|
Combinatorics
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
6. In the table below, each of the three rows is a correct arithmetic operation (with $\div$ indicating division). Also, each of the three columns (read from top to bottom) is a correct arithmetic operation. However, the digits in the table have been replaced by letters. Different letters stand for different digits, and all digits are not equal to 0.
$$
\begin{array}{cccc}
\mathrm{ABC} & -\mathrm{ADF} & =\mathrm{F} \\
+ & - & - \\
\mathrm{ADD} & \div \mathrm{GC} & =\mathrm{C} \\
= & = & = \\
\mathrm{CEF} & \div \mathrm{GD} & =\mathrm{D}
\end{array}
$$
For which digit does the letter E stand?
A) 1
B) 3
C) 5
D) 7
E) 9
|
A6. E) 9
From the first row, it follows that
$$
\mathrm{ADF}+\mathrm{F}=\mathrm{ABC} .
$$
The digit $\mathrm{C}$ is therefore even and, moreover, not 0. The possibilities are thus: 2, 4, 6, and 8. From the middle row, it follows that
$$
\mathrm{C} \cdot \mathrm{GC}=\mathrm{ADD} .
$$
Since $2 \cdot 2=4, 4 \cdot 4=16, 6 \cdot 6=36$, and $8 \cdot 8=64$, it follows that the digit $\mathrm{D}$ is either 4 or 6. The last row then gives
$$
\mathrm{D} \cdot \mathrm{GD}=\mathrm{CEF} .
$$
Since $4 \cdot 4=16$ and $6 \cdot 6=36$, the digit $\mathrm{F}$ must be 6. Because the digits are different, $\mathrm{D}$ must be 4. The first row now gives
$$
\mathrm{A} 46+6=\mathrm{ABC} .
$$
We see that $\mathrm{B}$ is the digit 5 and $\mathrm{C}$ is the digit 2. The first column is now
$$
\mathrm{A} 52+\mathrm{A} 44=2 \mathrm{E} 6 .
$$
The digit $\mathrm{E}$ is thus 9. Additionally, $\mathrm{A}=1$ and $\mathrm{G}=7$.
|
9
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
8. Lieneke makes beaded bracelets. Each bracelet has six beads: two white, two gray, and two black beads. Some bracelets may seem different at first glance, but they are not: if you rotate or flip one, it turns out to be the same as the other. For example, the three bracelets below are the same.

How many truly different bracelets can Lieneke make?
A) 10
B) 11
C) 12
D) 14
E) 15
## B-questions
|
A8. B) 11 We divide the bracelets into three groups: (I) the black beads are next to each other, (II) there is one bead between the two black beads, and (III) the black beads are opposite each other. In each case, we count how many different ways we can place the remaining beads.

Group (I) We need to choose which two of the positions $a, b, c, d$ will be white beads. There are six possibilities: $a b, a c, a d, b c, b d$, and $c d$. The choice $b d$ gives the same bracelet as $a c$, and the choice $c d$ gives the same bracelet as $a b$. In total, we find 4 different bracelets in group (I).
Group (II) Suppose we choose $a$ to be white. This gives two different bracelets: $a c$ white and $a b$ white. If we choose $a d$ white, we get the same bracelet as when we choose $a b$ white. If we choose $a$ to be gray, we also get two bracelets. Group (II) thus has 4 different bracelets.
Group (III) We find 3 different bracelets: $a b$ white, $a c$ white, or $a d$ white. The other three possibilities $(b c, b d, c d)$ give the same bracelet as (respectively) $a d, a c$, and $a b$.
In total, there are $4+4+3=11$ different bracelets.
|
11
|
Combinatorics
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
A2. In the figure, several angles are given in terms of $x$.
The value of $x$ in degrees is:
(A) 6
(B) 8 (C) 10
(D) 12
(E) 15
|
A2. In the left triangle, the third angle is equal to 180-7 $x$ degrees. In the right triangle, the third angle is equal to 180-13 $x$ degrees. The two base angles of the middle triangle are each equal to one of those angles.
So it must be true that: $5 x+(180-7 x)+(180-13 x)=180$ thus $15 x=180$ and therefore $x=12$.
|
12
|
Geometry
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
A5. In a magic square, the sum of the three numbers in each row, the sum of the three numbers in each column, and the sum of the three numbers in each of the two diagonals is always the same number.
In the magic square below, four of the nine numbers are given.
What is the value of $N$?
| | $\boldsymbol{N}$ | |
| :--- | :--- | :--- |
| 11 | | 15 |
| 12 | | 10 |
(A) 4
(B) 9
(C) 10
(D) 13
(E) 17
|
A5. Compare the left column with the diagonal in which 10 is located. In the middle box (below the $N$), 13 must be placed because it must hold that $13+10=12+11$. In the middle below, 17 must be placed because $(11+13+15)-(12+10)=17$. Therefore, $N=39-13-17=9$.
|
9
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
1. An archipelago consists of a large, a medium, and a small island. The total area of the three islands is $23 \mathrm{~km}^{2}$. The difference between the areas of the large and the medium island turns out to be exactly $1 \mathrm{~km}^{2}$ more than the area of the small island. How many $\mathrm{km}^{2}$ is the area of the large island?
A) 10
B) 11
C) 12
D) 13
E) 14
|
A1. C) 12 The difference between the areas of the large and the medium island is 1 $\mathrm{km}^{2}$ more than the area of the small island. In other words, the area of the medium island plus the area of the small island is $1 \mathrm{~km}^{2}$ less than the area of the large island. Therefore, the sum of the areas of all three islands is $1 \mathrm{~km}^{2}$ less than twice the area of the large island. Twice the area of the large island is thus $23+1=24$, and the large island has an area of $12 \mathrm{~km}^{2}$.
|
12
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
8. Michael prints the result below twice on cardboard and makes two identical dice such that the visible dots are on the outside of the dice. He stacks them to form a tower. The front side of the bottom die shows 3 dots. The total number of dots on the two touching sides of the dice is 9. The total number of dots on the back of the tower is three times the total number of dots on the right side of the tower.
How many dots are on the side that touches the ground?
A) 1
B) 2
C) 4
D) 5
E) 6

## B-questions
|
A8. A) 1 On the bottom die, we see 3 eyes on the front, so there is a 4 on the back. On the right side of the bottom die, there can still be 1, 2, 5, or 6. With 5 or 6, the total number of eyes on the back must be at least 15 or 18, and that is not possible. If there is a 1 on the right side, then there is a 2 on the top (look at the picture), and thus there must be a 7 on the bottom of the top die. That is also not possible. Therefore, there is a 2 on the right side of the bottom die. On the side that touches the ground, there is thus a 1.
To verify, we look at the rest of the tower. On the top of the bottom die, we now find the 6, so there is a 3 on the bottom of the top die. There are then four ways in which we can place the top die. We know that the total number of eyes on the back of the tower is three times the total number of eyes on the right side of the tower. Testing gives that there is a 1 on the right side of the top die and a 5 on the back. Indeed, \(3 \cdot (2+1) = 4+5\).
|
1
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
A4. How many positive integers $N$ of two digits are there with the following property: The sum of $N$ and the reverse of $N$ is a square of an integer (the reverse of $N$ is the number you get by writing $N$ backwards)?
|
A4 If you write the number $N$ as $a b$ then $N=10 a+b$. The reverse of $N$ is then equal to $10 b+a$. Together this gives $11 a+11 b=11(a+b)$. Since the latter must be a square, it must hold that $(a+b)$ is equal to 11 or a square times 11. $(a+b)=11$ gives the solutions $29,38,47,56,65,74,83$ and 92. If $(a+b)$ must be a square times 11, then it is at least 44 and that is not possible because $a$ and $b$ must be less than 10. Therefore, 8 solutions.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In a classroom, there are chairs and stools. A child is sitting on each chair and each stool. Each chair has 4 legs, each stool has 3 legs, and each child has 2 legs. Together, this results in a total of 39 legs and feet.
How many chairs are there in the classroom?
A) 3
B) 4
C) 5
D) 6
E) 9
|
A1. B) 4
A chair with a child on it has a total of 6 legs and feet. A stool with a child on it has a total of 5 legs and feet. With 7 chairs, we already have $7 \times 6 = 42$ legs and feet, which is too many. We create a table with the number of chairs and the number of legs and feet:
| Number of chairs: | 0 | 1 | 2 | 3 | $\mathbf{4}$ | 5 | 6 |
| ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: |
| Number of legs and feet: | 0 | 6 | 12 | 18 | $\mathbf{2 4}$ | 30 | 36 |
| Remaining legs and feet: | 39 | 33 | 27 | 21 | $\mathbf{1 5}$ | 9 | 3 |
The remaining number of legs and feet must come from the children sitting on stools. This number must therefore be divisible by 5. The only number in the third row that is divisible by 5 is 15. Therefore, the number of chairs is 4 (and the number of stools is $\frac{15}{5}=3$).
|
4
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
3. If you continue the chain of squares and regular pentagons in the same way, does it close precisely upon itself after going all the way around? If so, how many pentagons does the chain contain in total?
A) 9
B) 10
C) 11
D) 12
E) It does not close.

|
A3. B) 10 The angles of a regular $n$-gon are equal to $180-\frac{360}{n}$ degrees. Indeed, if you walk around the $n$-gon, you change direction $n$ times, after which you have turned a total of 360 degrees. At each vertex, your direction changes by $\frac{360}{n}$ degrees, and the corresponding angle of the $n$-gon is equal to $180-\frac{360}{n}$ degrees.
The angles of a square are thus $180-90=90$ degrees, and those of a regular pentagon are $180-72=108$ degrees.
If we place a square and a regular pentagon against each other, as shown in the figure, they together enclose an angle of $360-90-108=162$ degrees (angle $A B C$ in the figure). Since $162=180-18$, this is precisely the angle of a regular 20-gon because $18=\frac{360}{20}$. The sides $A B$ and $B C$ are of equal length, so after twenty steps (10 squares and 10 pentagons), we are exactly back where we started, and the inner sides of the squares and pentagons form the sides of a regular 20-gon.

|
10
|
Geometry
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
4. Julian wants to make a list of numbers as long as possible. Each number on the list must consist of one or more of the digits 1 through 9. Additionally, it must be true that
- each of the digits 1 through 9 is used exactly once;
- no number on the list is divisible by any other number on the list.
What is the maximum number of numbers that Julian's list can contain?
A) 4
B) 5
C) 6
D) 7
E) 8
|
A4. D) 7 The only list of 9 numbers that meets the first requirement consists of the nine digits each as a separate number. This list does not meet the second property (since 2, for example, is divisible by 1).
A list of 8 numbers that meets the first requirement must consist of seven single-digit numbers and one two-digit number. According to the second property, however, no more than five digits can appear individually: in addition to the digits 5, 7, 9, at most one of the digits $1, 2, 4, 8$ and at most one of the digits 3, 6 can appear individually.
A list of 7 numbers that meets the requirements does exist, for example: 5, 6, 7, 8, 9, 23, 41. The maximum length of Julian's list is therefore 7.
|
7
|
Number Theory
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
5. At a party, there are nine people. Upon entering, some people greeted each other by shaking hands. Quintijn is present at the party and asks everyone else how many people they have shaken hands with. He receives eight different answers.
How many people did he shake hands with?
A) 0
B) 1
C) 2
D) 3
E) 4
|
A5. E) 4 Of the eight people Quintijn meets at the party, let's call them A, B, C, D, E, F, G, and H in ascending order of the number of hands they shake. Since there are a total of 9 people present, the number of hands someone shakes is always a number from 0 to 8. If someone shakes 8 hands, then he shakes hands with everyone and no one can shake 0 hands. The answers Quintijn hears are therefore either the numbers 0 to 7 or the numbers 1 to 8. We will consider the two cases separately.
- Suppose A, B, .., H shake $0,1, \ldots, 7$ hands.
Person H shakes 7 hands and thus shakes hands with everyone except A. Person B shakes hands with H and no one else.
Person G shakes 6 hands and thus shakes hands with everyone except A and B. Person C has already shaken 2 hands (with H and G) and shakes no one else's hand.
Person F shakes 5 hands and thus shakes hands with everyone except A, B, and C. Person D has then already shaken 3 hands (with H, G, and F) and shakes no one else's hand. Person E shakes 4 hands and thus shakes hands with everyone except A, B, C, and D. We see that Quintijn shakes hands with exactly four people, namely H, G, F, and E.
- Suppose A, B, .., H shake $1,2, \ldots, 8$ hands.
Person H shakes 8 hands and thus shakes hands with everyone. Person A shakes hands with H and no one else.
Person G shakes 7 hands and thus shakes hands with everyone except A. Person B has already shaken 2 hands (with H and G) and shakes no one else's hand.
Person F shakes 6 hands and thus shakes hands with everyone except A and B. Person C has then already shaken 3 hands (with H, G, and F) and shakes no one else's hand.
Person E shakes 5 hands and thus shakes hands with everyone except A, B, and C. Person D has then already shaken 4 hands (with H, G, F, and E) and shakes no one else's hand. We see that Quintijn shakes hands with exactly four people, namely H, G, F, and E.
We conclude that in both cases, Quintijn shakes hands with exactly four people.
|
4
|
Combinatorics
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
A1. The numbers 1, 2, 3, 4, 5, 6, 7, and 8 must be distributed over the circles in the figure such that the sum of the three numbers on each of the four sides of the square is the same.
Provide a solution where this sum is minimized.
|
A1. $1+2+3+4+5+6+7+8=36$. If $S$ is the sum of the three numbers on each side, then $4S=36+$ the four numbers at the corners. To make $S$ as small as possible, the sum of the numbers at the four corners must be as small as possible. This cannot be achieved with $1,2,3,4$ because then $4S=36+10=46$ and 46 is not divisible by 4. The smallest value we can try for $S$ is thus 12, because $48=4 \times 12$.
This gives the possibilities: $48=36+1+2+3+6$ or $48=36+1+2+4+5$.
1 and 2 cannot lie on the same side because you would then need 9 to get 12. Therefore, 1 and 2 must lie on a diagonal, and so must 3 and 6. This gives the
$$
183
$$
solution $5 \quad 7$, apart from rotations and reflections.
$\begin{array}{lll}6 & 4 & 2\end{array}$
The second possibility 1,2,4,5 does not yield a solution.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A4. How many pairs $(a, b)$ of positive integers with $a+b<100$ satisfy the equation: $a+\frac{1}{b}=13 \times\left(b+\frac{1}{a}\right)$?
(A) 5
(B) 7
(C) 9
(D) 13
(E) 28
|
A4. $\frac{a b+1}{b}=13 \times \frac{b a+1}{a}$. Thus $a=13 b$ and hence the seven pairs $(13,1),(26,2), \cdots,(91,7)$. (B)
|
7
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
A6. A sequence of numbers is constructed as follows:
The first number is 2. The second number is 2.
Each subsequent number is the product of its two predecessors.
The sequence thus becomes: $2, 2, 4, 8, 32, \ldots$
What is the last digit of the $2007^{\text{th}}$ number in this sequence?
(A) 0
(B) 2
(C) 4
(D) 6
(E) 8
|
A6. We continue the row with only the last digits of the numbers: we find
$2,2,4,8, \cdot 2, \cdot \cdot 6, \cdot 2, \cdot \cdot 2, \cdot 4, \cdot 8, \cdot 2, \cdot 6, \cdot 2$, etc. We see that a group of six digits repeats itself. Since $2007=334 \times 6+3$, the last digit of the 2007th number is the same as that of the third number, which is 4. (C).
|
4
|
Number Theory
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
2. In a toy store, at the beginning of the day, there are 20 sticker sheets (0.30 euros each), 18 footballs (3 euros each), 5 teddy bears (5 euros each), and 8 water guns (15 euros each) in stock. The new cashier makes a mess of the administration and reports only the total amount of 75.80 euros at the end of the day for the sales of these four items, and that fewer footballs were sold than any other item. How many teddy bears were sold?
A) 1
B) 2
C) 3
D) 4
E) 5
|
A2. D) 4 Because three of the four items have a price in whole euros, the sticker sheets must have either 6 sold (for 1.80 euros) or 16 (for 4.80 euros). More is not possible, as there were only 20 in stock. For the other three items, there is thus 74 or 71 euros left. First, assume that there is 74 euros left. Since the teddy bears and water guns cost a multiple of 5 euros, there must have been 3 soccer balls sold (with 65 euros left) or an additional multiple of 5. But 8 soccer balls is not possible, because then more than 8 teddy bears would have to be sold, and there were not that many in stock. So there are 3. There must be at least 4 water guns sold and at least 4 teddy bears, but that is more than 65 euros together. So this is not possible.
Now assume that there are 71 euros left. According to the same reasoning, 2 soccer balls must have been sold or at least 7, but the latter is not possible again. So there is still 65 euros left for the teddy bears and water guns. Of these, at least 3 must have been sold, for at least $3 \cdot 5 + 3 \cdot 15 = 60$ euros. Therefore, there must have been exactly 3 water guns sold and to complete the amount, exactly 4 teddy bears.
|
4
|
Logic and Puzzles
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
3. A chessboard consists of $8 \times 8$ squares. In a corner square stands a knight. The knight makes jumps of either two squares horizontally and one square vertically, or two squares vertically and one square horizontally. In each square of the chessboard, we write down how many jumps the knight needs to reach it.
Which number have we then written down the most?
A) 2
B) 3
C) 4
D) 5
E) 6
|
A3. C) 4
In each field of the chessboard, we write down how many moves a knight needs to get there. We start with 0 in the corner, then write a 1 in the (empty) squares that can be reached from the 0 in one move, then write a 2 in the (empty) squares that can be reached from a 1 in one move, and so on. Eventually, we count how often each number appears and see that 4 is the most frequent number, appearing 21 times (3 appears 20 times).
| 5 | 4 | 5 | 4 | 5 | 4 | 5 | 6 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 4 | 3 | 4 | 3 | 4 | 5 | 4 | 5 |
| 3 | 4 | 3 | 4 | 3 | 4 | 5 | 4 |
| 2 | 3 | 2 | 3 | 4 | 3 | 4 | 5 |
| 3 | 2 | 3 | 2 | 3 | 4 | 3 | 4 |
| 2 | 1 | 4 | 3 | 2 | 3 | 4 | 5 |
| 3 | 4 | 1 | 2 | 3 | 4 | 3 | 4 |
| 0 | 3 | 2 | 3 | 2 | 3 | 4 | 5 |
|
4
|
Combinatorics
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
4. We have a triangle $\triangle A B C$ and two points $D$ and $E$ on the line segment $B C$, such that $\angle B A D=\angle D A E=\angle E A C$. Furthermore, $|A B|=6,|B D|=4,|D E|=2$ and $|E A|=3$. See the picture below: note that it is not drawn to scale!
What is the length of the line segment $C E$?
A) 2
B) $2 \frac{1}{4}$
C) $2 \frac{1}{2}$
D) $2 \frac{3}{4}$
E) 3
|
A4. E) 3 Name the three equal angles $\alpha$. We see that $|E B|=|E D|+|D B|=2+4=$ $6=|A B|$, and thus triangle $\triangle A B E$ is an isosceles triangle. From this it follows that $\angle A E B=$ $\angle B A E=2 \alpha$ and due to the straight angle at $E$ we find that $\angle A E C=180^{\circ}-2 \alpha$. Since $\angle C A E=\alpha$ and the sum of the angles in $\triangle A C E$ is equal to $180^{\circ}$, it also follows that $\angle A C E=\alpha$. We have thus found another isosceles triangle, namely $\triangle A C E$, and from this it follows that $|C E|=|A E|=3$.
|
3
|
Geometry
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
7. How many pairs of positive integers $a$ and $b$ with $a<b$ are there such that
$$
\frac{1}{a}+\frac{1}{b}=\frac{4}{15} ?
$$
A) 1
B) 2
C) 3
D) 4
E) 5
|
A7. C) 3 Because $a\frac{1}{b}$. In particular, $\frac{1}{a}$ must be more than half of $\frac{4}{15}$: $\frac{1}{a}>\frac{2}{15}$. From this, it follows that $a<\frac{15}{2}<8$. Moreover, $a$ must be at least 4, otherwise $\frac{1}{a}$ would be greater than $\frac{4}{15}$. So we have four possibilities for $a$: 4, 5, 6, and 7. For $a=4$, we find $\frac{1}{b}=\frac{4}{15}-\frac{1}{4}=\frac{1}{60}$ and thus $b=60$. For $a=5$, we find $\frac{1}{b}=\frac{4}{15}-\frac{1}{5}=\frac{1}{15}$ and thus $b=15$. For $a=6$, we find $\frac{1}{b}=\frac{4}{15}-\frac{1}{6}=\frac{1}{10}$ and thus $b=10$. For $a=7$, we find $\frac{1}{b}=\frac{4}{15}-\frac{1}{7}=\frac{13}{105}$ and in this case the solution $b=\frac{105}{13}$ is not an integer. In total, we thus find 3 solutions.
|
3
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
1. For integers $a, b, c$ and $d$, it is given that the difference between $a$ and $b$ is 2, the difference between $b$ and $c$ is 3, and the difference between $c$ and $d$ is 4.
Which of the following values cannot be the difference between $a$ and $d$?
A) 1
B) 3
C) 5
D) 7
E) 9
|
A1. D) 7
From the data in the problem, we deduce that $a-b= \pm 2, b-c= \pm 3$ and $c-d= \pm 4$.
We then get
$$
a-d=(a-b)+(b-c)+(c-d)= \pm 2 \pm 3 \pm 4
$$
We can now go through all eight possibilities for the plus and minus signs:
$$
\begin{array}{rrrr}
2+3+4=9, & 2+3-4=1, & 2-3+4=3, & 2-3-4=-5, \\
-2-3-4=-9, & -2-3+4=-1, & -2+3-4=-3, & -2+3+4=5 .
\end{array}
$$
The only value that does not occur (neither with a plus sign nor with a minus sign) is 7.
|
7
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.