problem
stringlengths 54
2.23k
| solution
stringlengths 134
24.1k
| answer
stringclasses 1
value | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 54
2.21k
| solution_raw
stringlengths 134
24.1k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 23.5k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
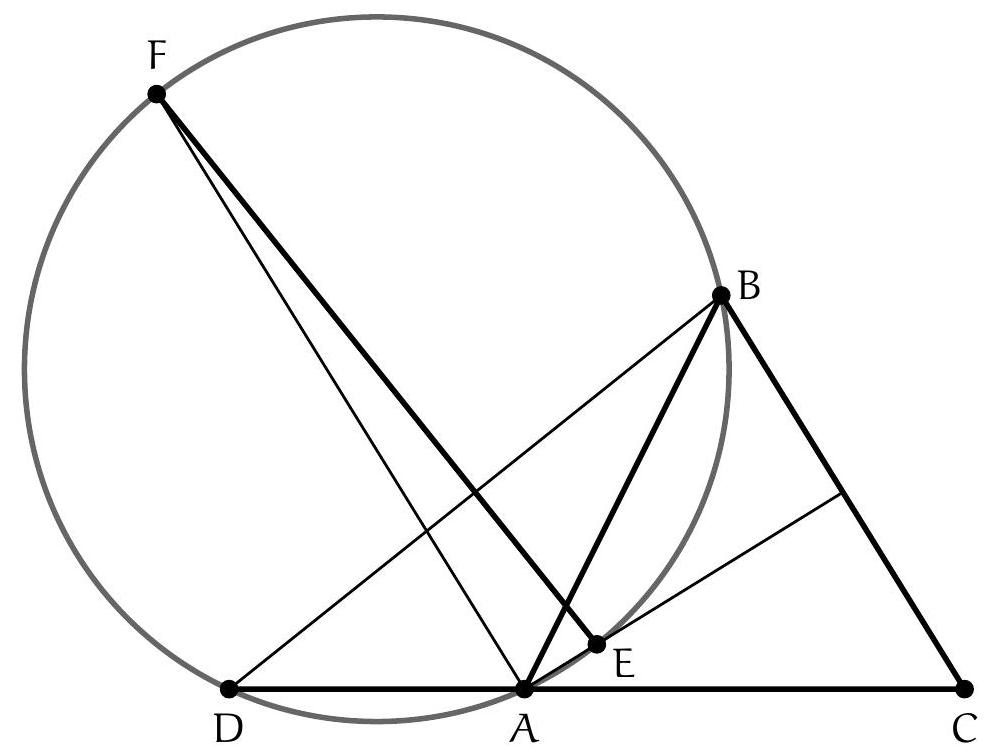
Let $ABC$ be an isosceles triangle at $A$, and let $D$ be a point on ($AC$) such that $A$ is located between $C$ and $D$, but is not the midpoint of [CD].
We denote $d_{1}$ and $d_{2}$ as the internal and external bisectors of the angle $\widehat{BAC}$, and $\Delta$ as the perpendicular bisector of [BD]. Finally, let $E$ and $F$ be the points of intersection of $\Delta$ with the lines $d_{1}$ and $d_{2}$, respectively.
Prove that the points $A, D, E$, and $F$ are concyclic.
|
A pretty figure suggests that points $A, B, D, E$, and $F$ are concyclic: this is what we will show.
Let $\Gamma$ be the circumcircle of $A B D$, and let $G_{1}$ and $G_{2}$ be the points of intersection of lines $d_{1}$ and $d_{2}$ with $\Gamma$, and other than $D$ itself. It suffices to show that $E=G_{1}$ and that $\mathrm{F}=\mathrm{G}_{2}$.
Since $\mathrm{d}_{2}$ is the external bisector of $\widehat{B A C}$, it is the internal bisector of $\widehat{B A D}$, and the South Pole theorem indicates that $\mathrm{G}_{2}$ is equidistant from B and D. Similarly, $\mathrm{d}_{1}$ is the internal bisector of $\widehat{B A C}$, hence the external bisector of $\widehat{B A D}$, and the North Pole theorem indicates that $\mathrm{G}_{1}$ is equidistant from B and D.
But then $\left(G_{1} G_{2}\right)$ is indeed the perpendicular bisector of $[B D]$, so $G_{1}=E$ and $G_{2}=F$, which concludes.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle isocèle en $A$, et soit $D$ un point sur ( $A C$ ) tel que $A$ soit situé entre C et D , mais ne soit pas le milieu de [CD].
On note $d_{1}$ et $d_{2}$ les bissectrices intérieure et extérieure de l'angle $\widehat{B A C}$, et $\Delta$ la médiatrice de [BD]. Enfin, soit $E$ et $F$ les points d'intersection respectifs de $\Delta$ avec les droites $d_{1}$ et $d_{2}$.
Démontrer que les points $A, D, E$ et $F$ sont cocycliques.
|
Une jolie figure suggère même que les points $A, B, D, E$ et $F$ sont cocycliques : c'est ce que nous allons montrer.
Soit $\Gamma$ le cercle circonscrit à $A B D$, et soit $G_{1}$ et $G_{2}$ les points d'intersection respectifs des droites $d_{1}$ et $d_{2}$ avec $\Gamma$, et autres que $D$ lui-même. Il nous suffit de montrer que $E=G_{1}$ et que $\mathrm{F}=\mathrm{G}_{2}$.
Puisque $\mathrm{d}_{2}$ est la bissectrice extérieure de $\widehat{B A C}$, donc la bissectrice intérieure de $\widehat{B A D}$, le théorème du pôle Sud indique que $\mathrm{G}_{2}$ est équidistant de B et D . De même, $\mathrm{d}_{1}$ est la bissectrice intérieure de $\widehat{B A C}$, donc la bissectrice extérieure de $\widehat{B A D}$, et le théorème du pôle Nord indique que $\mathrm{G}_{1}$ est équidistant de B et D .
Mais alors $\left(G_{1} G_{2}\right)$ est bien la médiatrice de $[B D]$, donc $G_{1}=E$ et $G_{2}=F$, ce qui conclut.

|
{
"resource_path": "French/segmented/tests/fr-2018-2019-Test-26-02-Corrige.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
95b7a446-8f33-57be-a3f6-01da78b5a8da
| 605,830
|
In a tournament with $n$ players, numbered from 1 to $n$, each pair of players meets exactly once. This meeting ends with one player winning and the other losing. We denote $v_{\mathrm{k}}$ as the number of victories of player $k$ during the tournament, and $d_{k}$ as their number of defeats.
Prove that $\sum_{k=1}^{n} v_{k}^{2}=\sum_{k=1}^{n} d_{k}^{2}$.
|
Since each player has played $n-1$ games and the total number of wins among all players is $n(n-1) / 2$, we know that
$$
\sum_{k=1}^{n} v_{k}=n(n-1) / 2
$$
and that $v_{k}+d_{k}=n-1$ for all $k \leqslant n$. We deduce that
$$
\sum_{k=1}^{n} d_{k}^{2}=\sum_{k=1}^{n}\left(n-1-v_{k}\right)^{2}=n(n-1)^{2}-2(n-1) \sum_{k=1}^{n} v_{k}+\sum_{k=1}^{n} v_{k}^{2}=\sum_{k=1}^{n} v_{k}^{2}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Dans un tournoi auxquels participent $n$ joueurs, numérotés de 1 à $n$, chaque paire de joueurs se rencontre exactement une fois. Cette rencontre se termine par la victoire d'un des deux joueurs et la défaite de l'autre joueur. On note $v_{\mathrm{k}}$ le nombre de victoires du joueur $k$ au cours du tournoi, et $d_{k}$ son nombre de défaites.
Démontrer que $\sum_{k=1}^{n} v_{k}^{2}=\sum_{k=1}^{n} d_{k}^{2}$.
|
Puisque chaque joueur a disputé $n-1$ parties et que l'ensemble des joueurs a totalisé $n(n-1) / 2$ victoires, on sait que
$$
\sum_{k=1}^{n} v_{k}=n(n-1) / 2
$$
et que $v_{k}+d_{k}=n-1$ pour tout $k \leqslant n$. On en déduit que
$$
\sum_{k=1}^{n} d_{k}^{2}=\sum_{k=1}^{n}\left(n-1-v_{k}\right)^{2}=n(n-1)^{2}-2(n-1) \sum_{k=1}^{n} v_{k}+\sum_{k=1}^{n} v_{k}^{2}=\sum_{k=1}^{n} v_{k}^{2}
$$
|
{
"resource_path": "French/segmented/tests/fr-2018-2019-Test-26-02-Corrige.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "\nSolution de l'exercice 4"
}
|
0fcd75df-2c0f-5135-a4de-f92a47ac6665
| 605,840
|
Let $p$ be a prime number.
Prove that there exists a prime $q$ such that $\mathfrak{n}^{p} \not\equiv p$ for all $n \in \mathbb{Z}$.
|
First, if $p$ does not divide $q-1$, then $x \mapsto x^{p}$ is a bijection of $\mathbb{Z} / q \mathbb{Z}$ onto itself, so $q$ cannot work. We are thus led to seek $q \equiv 1(\bmod p)$ such that for all $n \not \equiv 0(\bmod q), n$ has order $\omega_{q}(n) \neq p \omega_{q}(p)$ modulo $q$, where $\omega_{q}(p)$ is the order of $p$ modulo $q$.
Since the possible orders are exactly the divisors of $q-1$, this means that $q-1$ must be divisible by $p$ and by $\omega_{q}(p)$ but not by $p \omega_{q}(p)$. Consequently, $p$ must necessarily divide $\omega_{q}(p)$, and a first idea would be to check if we can have $\omega_{q}(p)=p$.
In this direction, $q$ must divide $p^{p}-1$ but not $p-1$. Thus, $q$ must divide the integer
$$
\mathbf{N}=\frac{p^{p}-1}{p-1}=1+p+p^{2}+\ldots+p^{p-1}
$$
Under these conditions, if $q$ still divides $p-1$, then $\mathbf{N} \equiv p(\bmod q)$, which is impossible. Thus, we are assured here that $q$ does not divide $p-1$, and therefore that $\omega_{q}(p)=p$.
It remains to ensure that we can choose $q$ so that $q \not \equiv 1\left(\bmod p^{2}\right)$. If such a $q$ did not exist, then $N$ itself would be congruent to $1\left(\bmod p^{2}\right)$. We conclude the problem by noting that $\mathbf{N} \equiv 1+p \not \equiv 1\left(\bmod p^{2}\right)$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit p un nombre premier.
Démontrer qu'il existe un nombre premier $q$ tel que $\mathfrak{n}^{p} \not \equiv p$ pour tout $n \in \mathbb{Z}$.
|
Tout d'abord, si $p$ ne divise pas $q-1$, alors $x \mapsto x^{p}$ est une bijection de $\mathbb{Z} / q \mathbb{Z}$ dans lui-même, donc $q$ ne peut pas convenir. On en vient à chercher $q \equiv 1(\bmod p)$ tel que, pour tout $n \not \equiv 0(\bmod q), n$ soit d'ordre $\omega_{q}(n) \neq p \omega_{q}(p)$ modulo $q$, où $\omega_{q}(p)$ est l'ordre de $p$ modulo $q$.
Puisque les ordres possibles sont exactement les diviseurs de $q-1$, cela signifie que $q-1$ doit être divisible par $p$ et par $\omega_{q}(p)$ mais pas $p \omega_{q}(p)$. Par conséquent, $p$ doit nécessairement diviser $\omega_{q}(p)$, et une première idée serait de vérifier si on ne peut pas justement avoir $\omega_{q}(p)=p$.
Dans cette optique, $q$ doit diviser $p^{p}-1$ mais pas $p-1$. Ainsi, $q$ doit diviser l'entier
$$
\mathbf{N}=\frac{p^{p}-1}{p-1}=1+p+p^{2}+\ldots+p^{p-1}
$$
Dans ces conditions, si $q$ divise quand même $p-1$, alors $\mathbf{N} \equiv p(\bmod q)$, ce qui est impossible. Ainsi, on est ici assuré que $q$ ne divise pas $p-1$, donc que $\omega_{q}(p)=p$.
Il reste donc à s'assurer que l'on peut choisir $q$ de sorte que $q \not \equiv 1\left(\bmod p^{2}\right)$. Si un tel $q$ $n^{\prime}$ existait pas, alors $N$ lui même serait congru à $1\left(\bmod p^{2}\right)$. On conclut donc le problème en remarquant que $\mathbf{N} \equiv 1+p \not \equiv 1\left(\bmod p^{2}\right)$.
|
{
"resource_path": "French/segmented/tests/fr-2018-2019-Test-27-02-Corrige.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
60f65681-543f-5635-8f97-9b594c5b13d0
| 605,874
|
We have, in the plane, 16 distinct points, which we denote by $A_{i, j}$ for $i, j \in\{1,2,3,4\}$. These points satisfy the following alignment and cocyclicity relations:
$\triangleright$ for all $i \in\{1,2,3,4\}$, the points $A_{i, 1}, A_{i, 2}, A_{i, 3}$, and $A_{i, 4}$ are collinear;
$\triangleright$ for all $j \in\{1,2,3,4\}$, the points $A_{1, j}, A_{2, j}, A_{3, j}$, and $A_{4, j}$ are collinear;
$\triangleright$ the quadrilaterals $A_{1,1} A_{1,2} A_{2,2} A_{2,1}, A_{2,1} A_{2,2} A_{3,2} A_{3,1}, A_{3,1} A_{3,2} A_{4,2} A_{4,1}, A_{1,2} A_{1,3} A_{2,3} A_{2,2}$, $A_{1,3} A_{1,4} A_{2,4} A_{2,3}, A_{1,1} A_{2,2} A_{2,3} A_{1,4}$, and $A_{1,1} A_{2,2} A_{3,2} A_{4,1}$ are cyclic.
Show that the quadrilateral $A_{4,1} A_{3,2} A_{3,3} A_{4,4}$ is also cyclic.
Note: a quadrilateral is said to be cyclic if its four vertices lie on the same circle.
|
Below, we will denote $\Delta_{i}$ as the line $\left(A_{i, 1} A_{i, 2}\right)$ and $\Delta^{j}$ as the line $\left(A_{1, j} A_{2, j}\right)$. A figure and angle chasing show that the lines $\Delta_{1}$ and $\Delta_{3}$ are parallel, since ( $\Delta_{1}, \Delta^{1}$ ) $\equiv$ $\left(\Delta^{2}, \Delta_{2}\right) \equiv\left(\Delta_{3}, \Delta^{1}\right)\left(\bmod 180^{\circ}\right)$. Similarly, we know that $\Delta_{2} / / \Delta_{4}$, that $\Delta^{1} / / \Delta^{3}$ and that $\Delta^{2} / / \Delta^{4}$.
Thus, and provided that the quadrilateral $A_{1,1} A_{1,2} A_{2,2} A_{2,1}$ formed by the lines $\Delta_{1}, \Delta^{1}$, $\Delta_{2}$ and $\Delta^{2}$ is cyclic, it suffices to define the point $A_{i, j}$ as the intersection of $\Delta_{i}$ and $\Delta^{j}$ to ensure our alignment relations and to be certain that our first five quadrilaterals are cyclic. In particular, by angle chasing, each quadrilateral $A_{i, j} A_{i+1, j} A_{i+1, j+1} A_{i, j+1}$ is then cyclic.
In the following, we will assume these alignment and cocyclicity relations are established, and we now focus on the quadrilateral $A_{1,1} A_{2,2} A_{2,3} A_{1,4}$. Given the symmetric role it seems to play with the quadrilaterals $A_{1,1} A_{2,2} A_{3,2} A_{4,1}$ on one hand and $A_{1,1} A_{2,2} A_{3,2} A_{4,1}$ on the other, it would be good to find a simple criterion that is equivalent to its cyclic nature.
This criterion only involves the lines $\Delta_{1}$ and $\Delta_{2}$ on one hand, and the four lines $\Delta^{j}$ on the other, with the pairs $\left(\Delta^{1}, \Delta^{2}\right)$ and $\left(\Delta^{3}, \Delta^{4}\right)$ playing symmetric roles. This leads us to consider the intersection points $X=\Delta_{1} \cap \Delta_{2}, Y=\Delta^{1} \cap \Delta^{2}$ and $Z=\Delta^{3} \cap \Delta^{4}$, which the figure seems to show are collinear. This suggests the following lemma.
Lemma: The quadrilateral $A_{1,1} A_{2,2} A_{2,3} A_{1,4}$ is cyclic if and only if $X$, $Y$ and $Z$ are collinear. Proof: Suppose first that $\mathrm{X}, \mathrm{Y}$, and $Z$ are collinear. Thales' theorem then indicates that the quadrilaterals $A_{1,1} A_{1,2} A_{2,2} A_{2,1}$ and $A_{1,3} A_{2,3} A_{2,4} A_{3,4}$ are homothetic to each other, so $\left(A_{2,1} A_{1,2}\right) / /\left(A_{2,3} A_{1,4}\right)$. We deduce that ( $\left.A_{1,1} A_{1,4}, A_{1,1} A_{2,2}\right) \equiv\left(A_{1,1} A_{1,2}, A_{1,1} A_{2,2}\right) \equiv$ $\left(A_{2,1} A_{1,2}, A_{2,1} A_{2,2}\right) \equiv\left(A_{2,3} A_{1,4}, A_{2,3} A_{2,2}\right)\left(\bmod 180^{\circ}\right)$, which means that $A_{1,1} A_{1,4} A_{2,3} A_{2,2}$ is indeed cyclic.
Conversely, once the lines $\Delta_{1}, \Delta_{2}, \Delta^{1}, \Delta^{2}$ and $\Delta^{3}$ are fixed, the point $A_{4,1}$ and then the line $\Delta^{4}$ are uniquely defined, so $Z$ is necessarily collinear with $X$ and $Y$.
We also take $T=\Delta_{3} \cap \Delta_{4}$. Here, since $A_{1,1} A_{2,2} A_{2,3} A_{1,4}$ and $A_{1,1} A_{2,2} A_{3,2} A_{4,1}$ are cyclic, the lemma shows the collinearity of the points $X, Y$ and $Z$, and $X, Y$ and $T$ respectively. Thus, the points $T, Y$ and $Z$ are collinear, and the lemma shows this time that the quadrilateral $A_{4,1} A_{3,2} A_{3,3} A_{4,4}$ is cyclic.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
On dispose, dans le plan, 16 points deux à deux distincts, que l'on note $A_{i, j}$ pour $i, j \in\{1,2,3,4\}$. Ces points vérifient les relations d'alignement et de cocyclicité suivantes :
$\triangleright$ pour tout $i \in\{1,2,3,4\}$, les points $A_{i, 1}, A_{i, 2}, A_{i, 3}$ et $A_{i, 4}$ sont alignés;
$\triangleright$ pour tout $j \in\{1,2,3,4\}$, les points $A_{1, j}, A_{2, j}, A_{3, j}$ et $A_{4, j}$ sont alignés;
$\triangleright$ les quadrilatères $A_{1,1} A_{1,2} A_{2,2} A_{2,1}, A_{2,1} A_{2,2} A_{3,2} A_{3,1}, A_{3,1} A_{3,2} A_{4,2} A_{4,1}, A_{1,2} A_{1,3} A_{2,3} A_{2,2}$, $A_{1,3} A_{1,4} A_{2,4} A_{2,3}, A_{1,1} A_{2,2} A_{2,3} A_{1,4}$ et $A_{1,1} A_{2,2} A_{3,2} A_{4,1}$ sont cycliques.
Montrer que le quadrilatère $A_{4,1} A_{3,2} A_{3,3} A_{4,4}$ est lui aussi cyclique.
Note: on dit qu'un quadrilatère est cyclique si ses quatre sommets sont sur un même cercle.
|
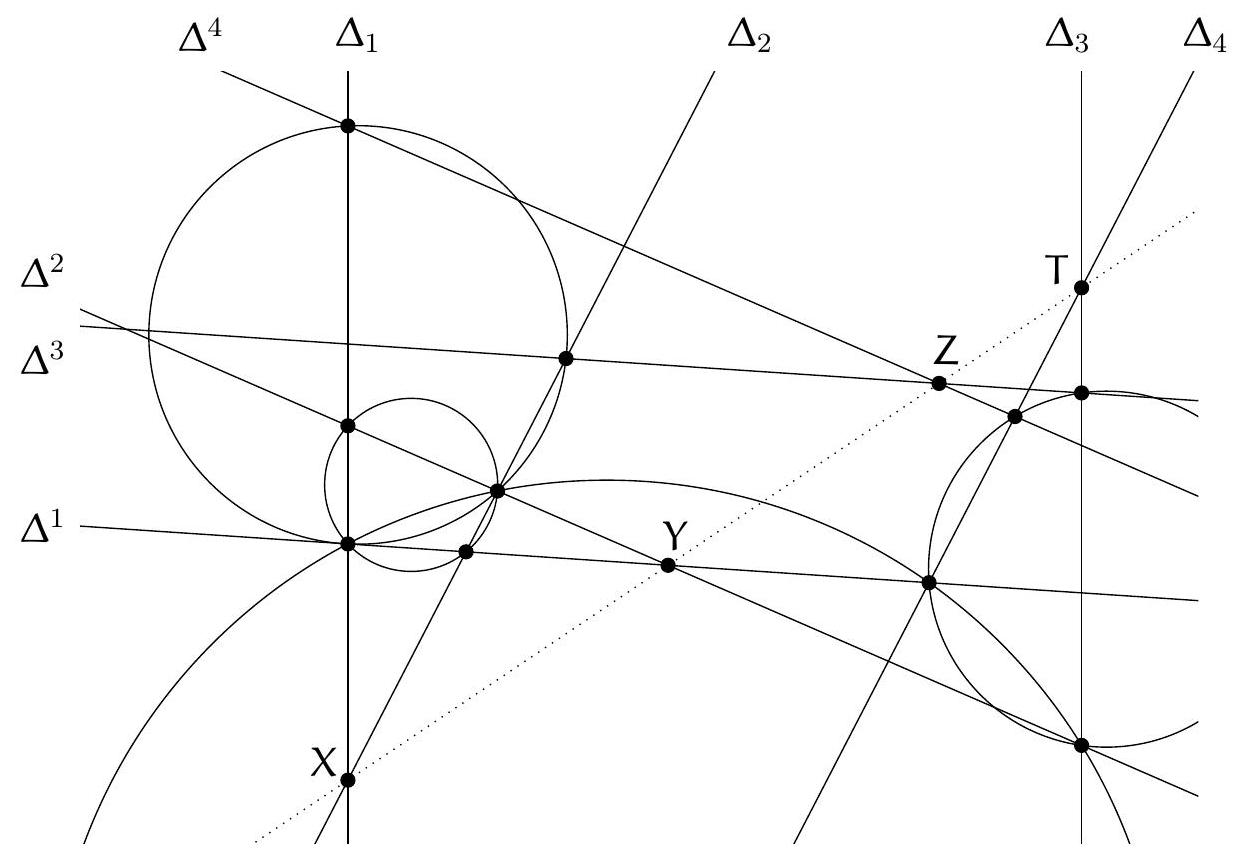
Ci-dessous, on notera $\Delta_{i}$ la droite $\left(A_{i, 1} A_{i, 2}\right)$ et $\Delta^{j}$ la droite $\left(A_{1, j} A_{2, j}\right)$. Une figure et une chasse aux angles nous montrent que les droites $\Delta_{1}$ et $\Delta_{3}$ sont parallèles, puisque ( $\Delta_{1}, \Delta^{1}$ ) $\equiv$ $\left(\Delta^{2}, \Delta_{2}\right) \equiv\left(\Delta_{3}, \Delta^{1}\right)\left(\bmod 180^{\circ}\right)$. De même, on sait que $\Delta_{2} / / \Delta_{4}$, que $\Delta^{1} / / \Delta^{3}$ et que $\Delta^{2} / / \Delta^{4}$.
Ce faisant, et sous réserve que le quadrilatère $A_{1,1} A_{1,2} A_{2,2} A_{2,1}$ formé par les droites $\Delta_{1}, \Delta^{1}$, $\Delta_{2}$ et $\Delta^{2}$ soit cyclique, il suffit de définir le point $A_{i, j}$ comme le point d'intersection de $\Delta_{i}$ et $\Delta^{j}$ pour être assuré de nos relations d'alginement, et pour être certain que nos cinq premiers quadrilatères sont cycliques. En particulier, toujours par chasse aux angles, chaque quadrilatère $A_{i, j} A_{i+1, j} A_{i+1, j+1} A_{i, j+1}$ est alors cyclique.
Dans toute la suite, on supposera ces relations d'alignement et de cocyclicité acquises, et on s'intéresse maintenant au quadrilatère $A_{1,1} A_{2,2} A_{2,3} A_{1,4}$. Vu le rôle symétrique qu'il semble jouer avec les quadrilatères $A_{1,1} A_{2,2} A_{3,2} A_{4,1}$ d'une part et $A_{1,1} A_{2,2} A_{3,2} A_{4,1}$ d'autre part, il serait bon de trouver un critère simple qui soit équivalent avec son caractère cyclique.
Or, il ne met en jeu que les droites $\Delta_{1}$ et $\Delta_{2}$ d'une part, et les quatre droites $\Delta^{j}$ d'autre part, les paires $\left(\Delta^{1}, \Delta^{2}\right)$ et $\left(\Delta^{3}, \Delta^{4}\right)$ jouant des rôles symétriques. On en vient alors à considérer les points d'intersection $X=\Delta_{1} \cap \Delta_{2}, Y=\Delta^{1} \cap \Delta^{2}$ et $Z=\Delta^{3} \cap \Delta^{4}$, dont la figure semble montrer qu'ils sont alignés. Cela suggère le lemme suivant.
Lemme: Le quadrilatère $A_{1,1} A_{2,2} A_{2,3} A_{1,4}$ est cyclique si et seulement si $X$, $Y$ et $Z$ sont alignés. Démonstration : Supposons d'abord $\mathrm{X}, \mathrm{Y}$ et Z alignés. Le théorème de Thalès indique alors que les quadrilatères $A_{1,1} A_{1,2} A_{2,2} A_{2,1}$ et $A_{1,3} A_{2,3} A_{2,4} A_{3,4}$ sont homothétiques l'un de l'autre, doncque $\left(A_{2,1} A_{1,2}\right) / /\left(A_{2,3} A_{1,4}\right)$. On en déduit que ( $\left.A_{1,1} A_{1,4}, A_{1,1} A_{2,2}\right) \equiv\left(A_{1,1} A_{1,2}, A_{1,1} A_{2,2}\right) \equiv$ $\left(A_{2,1} A_{1,2}, A_{2,1} A_{2,2}\right) \equiv\left(A_{2,3} A_{1,4}, A_{2,3} A_{2,2}\right)\left(\bmod 180^{\circ}\right)$, ce qui signifie que $A_{1,1} A_{1,4} A_{2,3} A_{2,2}$ est bien cyclique.
Réciproquement, une fois fixées les droites $\Delta_{1}, \Delta_{2}, \Delta^{1}, \Delta^{2}$ et $\Delta^{3}$, le point $A_{4,1}$ puis la droite $\Delta^{4}$ sont définis de manière unique, donc $Z$ se retrouve nécessairement aligné avec $X$ et $Y$.
On en profite aussi pour poser $T=\Delta_{3} \cap \Delta_{4}$. Ici, puisque $A_{1,1} A_{2,2} A_{2,3} A_{1,4}$ et $A_{1,1} A_{2,2} A_{3,2} A_{4,1}$ sont cycliques, le lemme montre l'alignement des points $X, Y$ et $Z$, et $X, Y$ et $T$ d'autre part. Ainsi, les points $T, Y$ et $Z$ sont alignés, et le lemme montre cette fois-ci que le quadrilatère $A_{4,1} A_{3,2} A_{3,3} A_{4,4}$ est cyclique.
|
{
"resource_path": "French/segmented/tests/fr-2018-2019-Test_RMM_28_novembre_corrige.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
4cd1789d-6736-5be0-847b-0356863e2a65
| 605,893
|
It is said that an integer $k$ is olympic if there exist four integers $a, b, c$ and $d$, all coprime with $k$, such that $k$ divides $a^{4}+b^{4}+c^{4}+d^{4}$. Let $n$ be any integer.
Show that $n^{2}-2$ is olympic.
|
Let $p_{1}^{\alpha_{1}} \cdots p_{\ell}^{\alpha_{\ell}}$ be the prime factorization of $n^{2}-2$. Thanks to the Chinese Remainder Theorem, it suffices to show that each of the integers $p_{i}^{\alpha_{i}}$ is Olympic.
Suppose first that $p_{i}=2$. Since $n^{2}-2 \equiv\{2,3\}(\bmod 4)$, we know that $\alpha_{i} \leqslant 1$. Clearly, 2 is Olympic, since $1+1+1+1 \equiv 0(\bmod 2)$.
Now consider an odd prime divisor $p$ of $n^{2}-2$. Since 2 is not a square modulo 3 or 5, we know that $p \geqslant 7$. Furthermore, if $p^{\alpha}$ is Olympic, then $p$ is clearly so as well. Conversely, if $p$ is Olympic (and odd), Hensel's lemma shows that the fourth powers modulo $p^{k}$ are exactly the integers whose residues (modulo $p$) are fourth powers modulo $p$, and it follows that $p^{\alpha}$ is also Olympic.
We are thus reduced to showing that every prime $p \geqslant 7$ such that 2 is a square modulo $p$ is Olympic. We will proceed by case analysis, depending on the value of $p$ modulo 4 or 8. However, we first recall Fermat's little theorem, which states that the order $\omega_{p}(x)$ of an invertible element modulo $p$ must divide $p-1$. We also recall that $\mathbb{Z} / p \mathbb{Z}$ contains an element of order $p-1$, as indicated by Theorem 17 of the POFM Arithmetic course on the properties of $\mathbb{Z} / \mathrm{n} \mathbb{Z}$. We deduce the following lemma.
Lemma: The $k$-th powers are the elements $x$ whose order $\omega_{p}(x)$ divides $(p-1) / \delta$, where $\delta=\operatorname{GCD}(k, p-1)$.
Proof: Let $z$ be an element of order $p-1$. The $k$-th powers are the elements of the form $z^{a k+b(p-1)}$, with $a$ and $b$ integers, i.e., the elements of the form $z^{\mathrm{c} \delta}$ with $c$ an integer. The order of these elements modulo $p$ clearly divides $(p-1) / \delta$.
Conversely, $\omega_{p}(x)$ divides $(p-1) / \delta$ if and only if $x$ is one of the roots of the polynomial $P(X)=1-X^{(\mathfrak{p}-1) / \delta}$. However, the elements of the form $z^{\mathfrak{c} \delta}$ already constitute $(p-1) / \delta$ roots of $P(X)$. Therefore, the $k$-th powers are exactly the roots of $P(X)$, which concludes the proof of the lemma.
We finally proceed with the case analysis announced above.
1. If $p \equiv 1(\bmod 8)$, and since -1 is of order 2, it is a fourth power. Since $0 \equiv 1+1+(-1)+(-1)(\bmod p)$, the integer $p$ is Olympic.
2. If $p \equiv 5(\bmod 8)$, then -1 is a square. Let $i$ and $-i$ be its square roots. They are of order 4, so they are not squares. However, $(1+i)^{2} \equiv 2 i(\bmod p)$. Since the set of squares is closed under product and inverse (and thus division), 2 is not a square, which actually means that $p$ does not divide $n^{2}-2$. This case is therefore impossible.
3. If $p \equiv 3(\bmod 4)$, then being a fourth power is in fact the same as being a square. It suffices to show that 0 is a sum of four non-zero squares modulo $p$.
We will first show that it is a sum of $\ell$ non-zero squares, with $2 \leqslant \ell \leqslant 4$. Indeed, let $Q$ be the set of squares. Note that $|Q|=(p+1) / 2$, since every non-zero square has exactly two square roots modulo $p$. Thus, for any $k \in \mathbb{Z} / p \mathbb{Z}$, and by the pigeonhole principle, the set $(k-Q) \cap Q$ is non-empty, which means that $k$ is a sum of two squares. If $k \neq 0$, one of these squares is even non-zero. But then, by writing $0 \equiv k+(-k)(\bmod p)$, we can indeed write 0 as a sum of four squares, at least two of which are non-zero.
Furthermore, by the identity $k^{2} \equiv(3 k / 5)^{2}+(4 k / 5)^{2}(\bmod p)$, every non-zero square is in fact a sum of two non-zero squares. Consequently, 0 is indeed a sum of four non-zero squares, which means that $p$ is Olympic.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
On dit qu'un entier $k$ est olympique s'il existe quatre entiers $a, b, c$ et $d$, tous premiers avec $k$, tels que $k$ divise $a^{4}+b^{4}+c^{4}+d^{4}$. Soit $n$ un entier quelconque.
Montrer que $n^{2}-2$ est olympique.
|
Soit $p_{1}^{\alpha_{1}} \cdots p_{\ell}^{\alpha_{\ell}}$ la décomposition de $n^{2}-2$ en produits de facteurs premiers. Grâce au théorème Chinois, il nous suffit en fait de montrer que chacun des entiers $p_{i}^{\alpha_{i}}$ est olympique.
Supposons tout d'abord que $p_{i}=2$. Puisque $n^{2}-2 \equiv\{2,3\}(\bmod 4)$, on sait que $\alpha_{i} \leqslant 1$. Or, il est clair que 2 est olympique, puisque $1+1+1+1 \equiv 0(\bmod 2)$.
On considère maintenant un diviseur premier $p$ impair de $n^{2}-2$. Puisque 2 n'est pas carré modulo 3 ou 5 , on sait en fait que $p \geqslant 7$. Par ailleurs, si $p^{\alpha}$ est olympique, alors $p$ l'est clairement lui aussi. Réciproquement, si $p$ est olympique (et impair), le lemme de Hensel montre que les puissances $4{ }^{\text {èmes }}$ modulo $p^{k}$ sont exactement les entiers dont les résidus (modulo $p$ ) sont des puissances $4^{\text {èmes }}$ modulo $p$, et il s'ensuit que $p^{\alpha}$ est également olympique.
On se ramène donc à montrer que tout nombre premier $p \geqslant 7$ tel que 2 soit un carré modulo $p$ est olympique. On va procéder par disjonction de cas, selon la valeur de $p$ modulo 4 ou 8 . Cependant, on rappelle d'abord le petit théorème de Fermat, qui stipule que l'ordre $\omega_{p}(x)$ d'un élément inversible modulo $p$ doit diviser $p-1$. On rappelle également que $\mathbb{Z} / p \mathbb{Z}$
contient un élément d'ordre $p-1$, comme l'indique le Théorème 17 du cours d'Arithmétique de la POFM sur les propriétés de $\mathbb{Z} / \mathrm{n} \mathbb{Z}$. On en déduit le lemme suivant.
Lemme : Les puissances $k^{\text {èmes }}$ sont les éléments $x$ dont l'ordre $\omega_{p}(x)$ divise $(p-1) / \delta$, où $\delta=\operatorname{PGCD}(k, p-1)$.
Démonstration : Soit $z$ un élément d'ordre $p-1$. Les puissances $k^{\text {èmes }}$ sont les éléments de la forme $z^{a k+b(p-1)}$, avec a et b entiers, c'est-à-dire les éléments de la forme $z^{\mathrm{c} \mathrm{\delta}}$ avec c entier. L'ordre de ces éléments modulo $p$ divise clairement $(p-1) / \delta$.
Réciproquement, $\omega_{p}(x)$ divise $(p-1) / \delta$ si et seulement si $x$ est une des racines du polynôme $P(X)=1-X^{(\mathfrak{p}-1) / \delta}$. Or, les éléments de la forme $z^{\mathfrak{c} \delta}$ constituent déjà $(p-1) / \delta$ racines de $P(X)$. Par conséquent, les puissances ${ }^{k e \text { èmes }}$ sont exactement les racines de $P(X)$, ce qui conclut la preuve du lemme.
On procède enfin à la disjonction de cas annoncée ci-dessus.
1. Si $p \equiv 1(\bmod 8)$, et puisque -1 est d'ordre 2 , c'est une puissance $4^{\text {ème }}$. Comme $0 \equiv$ $1+1+(-1)+(-1)(\bmod p)$, l'entier $p$ est olympique.
2. Si $p \equiv 5(\bmod 8)$, alors -1 est un carré. Soit $i$ et $-i$ ses racines carrées. Elles sont d'ordre 4 , donc ce ne sont pas des carrés. Or, $(1+i)^{2} \equiv 2 i(\bmod p)$. Puisque l'ensemble des carrés est clos par produit et par inverse (donc par division), 2 n'est donc pas un carré, ce qui signifiait en fait que $p$ ne divisait pas $n^{2}-2$. Ce cas s'avère donc impossible.
3. Si $p \equiv 3(\bmod 4)$, alors être une puissance $4{ }^{\text {ème }}$ revient en fait à être un carré. Il suffit donc de montrer que 0 est somme de quatre carrés non nuls modulo $p$.
On va d'abord montrer que c'est une somme de $\ell$ carrés non nuls, avec $2 \leqslant \ell \leqslant 4$. En effet, soit Q l'ensemble des carrés. Notons que $|Q|=(p+1) / 2$, puisque tout carré non nul a exactement deux racines carrés modulo $p$. Ainsi, pour tout $k \in \mathbb{Z} / p \mathbb{Z}$, et par principe des tiroirs, $l^{\prime}$ ensemble $(k-Q) \cap Q$ est non vide, ce qui signifie que $k$ est somme de deux carrés. Si $k \neq 0$, l'un de ces carrés est même non nul. Mais alors, en écrivant $0 \equiv k+(-k)(\bmod p)$, on peut bien écrire 0 comme une somme de quatre carrés dont au moins deux sont non nuls.
Puis, en vertu de l'identité $k^{2} \equiv(3 k / 5)^{2}+(4 k / 5)^{2}(\bmod p)$, tout carré non nul est en fait somme de deux carrés non nuls. Par conséquent, 0 est bien somme de quatre carrés non nuls, ce qui signifie que $p$ est olympique.
|
{
"resource_path": "French/segmented/tests/fr-2018-2019-Test_RMM_28_novembre_corrige.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
238d09b0-0acb-5ddd-bbb4-f3743d3e04c5
| 605,904
|
Let $x$ and $y$ be two real numbers. We define
$$
M=\max \{x y+1, x y-x-y+3,-2 x y+x+y+2\} .
$$
Prove that $M \geqslant 2$, and determine the cases of equality.
|
$n^{\circ} 1$ Here is another way to prove that the equalities of equation (1) are satisfied if and only if $x=y=1$. First, if $x=y=1$, these equalities are clearly satisfied.
Conversely, if they are satisfied, then the equality $x y-x-y+3=2$ can be rewritten as $0=x y-x-y+1=(x-1)(y-1)$. Since $x$ and $y$ play symmetric roles, we can assume, without loss of generality, that $x=1$. For the equality $x y+1=2$ to be satisfied, it is then necessary that $y=1$, which concludes the proof here.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit $x$ et $y$ deux nombres réels. On pose
$$
M=\max \{x y+1, x y-x-y+3,-2 x y+x+y+2\} .
$$
Démontrer que $M \geqslant 2$, et déterminer les cas d'égalité.
|
$n^{\circ} 1$ Voici une autre manière de démontrer que les égalités de l'équation (1) sont vérifiées si et seulement si $x=y=1$. Tout d'abord, si $x=y=1$, ces égalités sont clairement vérifiées.
Réciproquement, si elles sont vérifiées, alors on peut réécrire l'égalité $x y-x-y+3=2$ comme $0=x y-x-y+1=(x-1)(y-1)$. Puisque $x$ et $y$ jouent des rôles symétriques, on peut supposer, sans perte de généralité, que $x=1$. Pour que l'égalité $x y+1=2$ soit vérifiée, il est alors nécessaire que $y=1$, ce qui conclut ici.
|
{
"resource_path": "French/segmented/tests/fr-2019-2020-Corrigé-Web-05-2020.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution alternative"
}
|
5c787f0b-53f0-5268-ab20-677771b96d21
| 605,913
|
Let $x$ and $y$ be two real numbers. We define
$$
M=\max \{x y+1, x y-x-y+3,-2 x y+x+y+2\} .
$$
Prove that $M \geqslant 2$, and determine the cases of equality.
|
$n^{\circ} 2$ The idea of introducing the variables $p$ and $s$, as in the first solution, or directly using the equality $x y - x - y + 3 = 2$ to obtain a factorization, as in the second solution, might seem miraculous. Of course, this is not the case, and these approaches actually stem from what are known as Viète's formulas.
These formulas state that $x$ and $y$ are the two roots, possibly identical, of the polynomial
$$
P(X) = (X - x)(X - y) = X^2 - (x + y)X + xy = X^2 - sX + p.
$$
Since the equalities in equation (1) are symmetric in $x$ and $y$, a general result (which holds even if we had three unknowns $x, y$, and $z$, or even any number of unknowns) allows us to express them directly in terms of the values taken by the polynomial $P$.
For example, the equalities $p + 1 = 2$, $p - s + 3 = 2$, and $-2p + s + 2 = 2$ can be rewritten as $P(0) = 1$, $P(1) = 0$, and $P(1/2) = 1/4$. Here, the equality $P(1) = 0$ means precisely that $(x - 1)(y - 1) = 0$, which is the factorization used in our second solution.
We could also proceed more systematically. Indeed, since $P(1) = 0$, we know that the polynomial $P(X)$ is divisible by $X - 1$. We can therefore write it in the form $P(X) = (X - 1)(X - a)$, and then verify that $P(0) = a$, and thus that $P(X) = (X - 1)^2$.
If we had been less lucky and had not identified a root of our polynomial $P$, it would still have been possible to write $P$ as a Lagrange interpolation polynomial. Here, this method allows us to write
$$
\begin{aligned}
P(X) & = \frac{X - 1}{0 - 1} \frac{X - 1/2}{0 - 1/2} P(0) + \frac{X - 1}{1/2 - 1} \frac{X - 0}{1/2 - 0} P(1/2) + \frac{X - 1/2}{1 - 1/2} \frac{X - 0}{1 - 0} P(1) \\
& = 2(X - 1)(X - 1/2) - X(X - 1) = X^2 - 2X + 1 = (X - 1)^2
\end{aligned}
$$
from which it follows that the two roots of $P$ are $x = y = 1$.
Comment from the graders: The exercise was generally well solved. Few students noticed that the first inequality was a simple consequence of the fact that the maximum is greater than the arithmetic mean.
Be careful with handling inequalities: some students wrote that $xy < 1$ and $x + y \geq xy$ to conclude that $x + y \geq 1$, which is not true. Other students proved the required inequality but forgot to consider the equality cases, which was an important part of the exercise: unlike equality cases in classical inequalities, this one was harder to find, and asserting without proof that $x = y = 1$ was not sufficient.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit $x$ et $y$ deux nombres réels. On pose
$$
M=\max \{x y+1, x y-x-y+3,-2 x y+x+y+2\} .
$$
Démontrer que $M \geqslant 2$, et déterminer les cas d'égalité.
|
$n^{\circ} 2$ Avoir pensé à introduire les variables $p$ et $s$, comme dans la première solution, ou bien à utiliser directement l'égalité $x y-x-y+3=2$ pour obtenir une factorisation, comme dans la deuxième solution, pourrait passer pour miraculeux. Il n'en est bien sûr rien, et ces approchent découlent en fait de ce que l'on appelle les relations de Viète.
Ces relations consistent à dire que $x$ et $y$ sont les deux racines, éventuellement confondues, du polynôme
$$
P(X)=(X-x)(X-y)=X^{2}-(x+y) X+x y=X^{2}-s X+p .
$$
Puisque les égalités de l'équation (1) sont symétriques en $x$ et en $y$, un résultat général (valable même si on avait eu trois inconnues $x, y$ et $z$, ou même un nombre quelconque d'inconnues) permet en fait de démontrer qu'elles peuvent s'exprimer directement à partir des valeurs que prend le polynôme $P$.
Par exemple, les égalités $p+1=2, p-s+3=2$ et $-2 p+s+2=2$ peuvent se réécrire comme $P(0)=1, P(1)=0$ et $P(1 / 2)=1 / 4$. Ici, l'égalité $P(1)=0$ signifie précisément que $(x-1)(y-1)=0$, ce qui est la factorisation utilisée dans notre deuxième solution.
On pourrait également procéder de manière plus systématique. En effet, puisque $P(1)=0$, on sait que le polynôme $P(X)$ est divisible par $X-1$. On peut donc l'écrire sous la forme $P(X)=(X-1)(X-a)$, puis vérifier que $P(0)=a$, et donc que $P(X)=(X-1)^{2}$.
Si l'on avait été moins chanceux, et que l'on n'avait pas identifié de racine de notre polynôme $P$, il aurait toujours été possible d'écrire $P$ comme un polynôme d'interpolation de Lagrange. Ici, cette méthode nous permet d'écrire que
$$
\begin{aligned}
P(X) & =\frac{X-1}{0-1} \frac{X-1 / 2}{0-1 / 2} P(0)+\frac{X-1}{1 / 2-1} \frac{X-0}{1 / 2-0} P(1 / 2)+\frac{X-1 / 2}{1-1 / 2} \frac{X-0}{1-0} P(1) \\
& =2(X-1)(X-1 / 2)-X(X-1)=X^{2}-2 X+1=(X-1)^{2}
\end{aligned}
$$
d'où le fait que les deux racines de $P$ soient $x=y=1$.
Commentaire des correcteurs L'exercice a été plutôt bien résolu. Peu d'élèves ont vu que la première inégalité était une conséquence simple du fait que le maximum est plus grand que la moyenne arithmétique.
Attention au maniement des inégalités : certains élèves ont écrit que $x y<1$ et $x+y \geqslant x y$ pour en conclure que $x+y \geqslant 1$, ce qui n'est pas vrai. D'autres élèves ont démontré l'inégalité demandée mais oublié de regarder les cas d'égalité alors que c'était une partie importante de l'exercice : contrairement à des cas d'égalité dans des inégalités classiques, celui-là était plus dur à trouver, et affirmer sans preuve que $x=y=1$ ne suffisait pas.
|
{
"resource_path": "French/segmented/tests/fr-2019-2020-Corrigé-Web-05-2020.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution alternative"
}
|
5c787f0b-53f0-5268-ab20-677771b96d21
| 605,913
|
Let $ABC$ be a triangle and $\Gamma$ a circle passing through $A$. Suppose that $\Gamma$ intersects the segments $[AB]$ and $[AC]$ at two points, which we call $D$ and $E$ respectively, and that it intersects the segment $[BC]$ at two points, which we call $F$ and $G$, such that $F$ lies between $B$ and $G$. Let $T$ be the point of intersection between the tangent at $F$ to the circumcircle of $BDF$ and the tangent at $G$ to the circumcircle of $CEG$.
Prove that, if the points $A$ and $T$ are distinct, then $(AT)$ and $(BC)$ are parallel.
|
Let's start by drawing a figure.
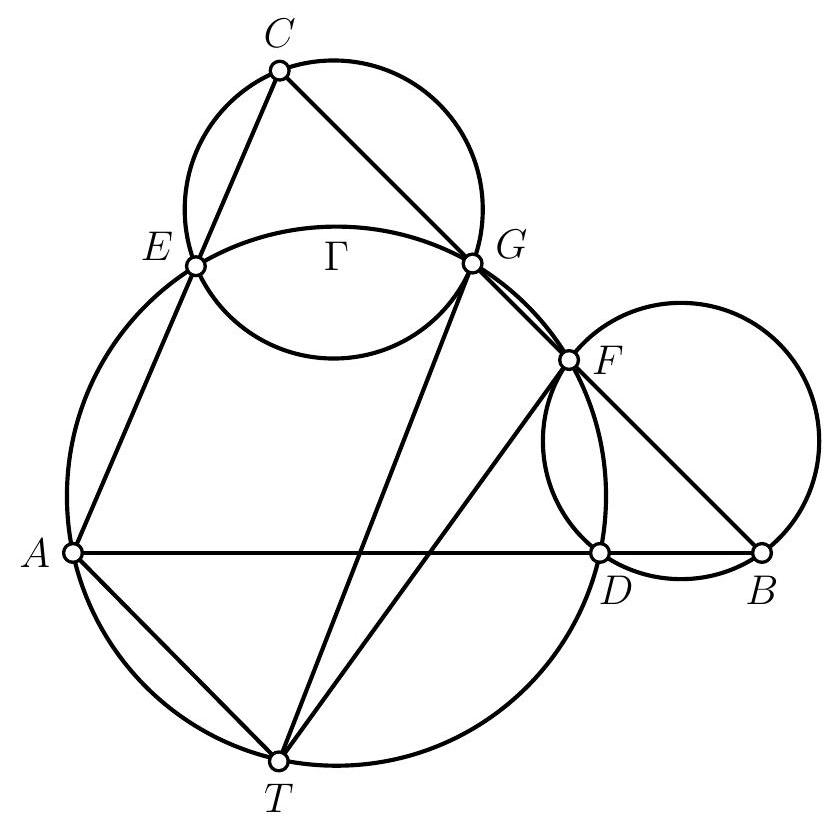
A striking first observation is that $T$ appears to lie on the circle $\Gamma$. After verifying this on a second figure, we promptly set out to prove this first result. To do so, we embark on an angle chase using the properties of cyclic points and the limiting case of the inscribed angle theorem:
$$
\begin{aligned}
(T G, T F) & =(T G, B C)+(B C, T F)=(T G, C G)+(B F, T F)=(E G, E C)+(D B, D F) \\
& =(E G, A E)+(A D, D F)=(D G, A D)+(A D, D F)=(A D, D F)
\end{aligned}
$$
The points $A, F, G$, and $T$ are therefore concyclic, and $T$ lies on $\Gamma$. But then
$$
\begin{aligned}
(A T, B C) & =(A T, A F)+(A F, B C)=(G T, G F)+(A F, G F) \\
& =(G T, G C)+(A E, G E)=(E G, E C)+(C E, G E)=0^{\circ},
\end{aligned}
$$
which means precisely that the lines $(A T)$ and $(B C)$ are parallel.
Comment from the graders: The problem was correctly solved by 7 students. Some students, even if they did not completely solve the problem, used their figure to conjecture that the point $T$ lies on the circle $\Gamma$ and concluded by assuming this result. This approach was highly appreciated as it is the right attitude when facing a geometry problem.
## Senior Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $\Gamma$ un cercle passant par $A$. On suppose que $\Gamma$ recoupe les segments $[A B]$ et $[A C]$ en deux points, que l'on appelle respectivement $D$ et $E$, et qu'il coupe le segment $[B C]$ en deux points, que l'on appelle $F$ et $G$, de sorte que $F$ se trouve entre $B$ et $G$. Soit $T$ le point d'intersection entre la tangente en $F$ au cercle circonscrit à $B D F$ et la tangente en $G$ au cercle circonscrit à $C E G$.
Démontrer que, si les points $A$ et $T$ sont distincts, alors $(A T)$ et $(B C)$ sont parallèles.
|
Commençons par tracer une figure.

Une première remarque frappante est que $T$ semble être situé sur le cercle $\Gamma$. Après avoir vérifié qu'il l'était bien sur une deuxième figure, on s'empresse donc de démontrer ce premier résultat. Pour ce faire, on entame donc une chasse aux angles de droites, en utilisant les relations de cocyclicité et le cas limite du théorème de l'angle au centre :
$$
\begin{aligned}
(T G, T F) & =(T G, B C)+(B C, T F)=(T G, C G)+(B F, T F)=(E G, E C)+(D B, D F) \\
& =(E G, A E)+(A D, D F)=(D G, A D)+(A D, D F)=(A D, D F)
\end{aligned}
$$
Les points $A, F, G$ et $T$ sont donc cocycliques, et $T$ appartient à bien $\Gamma$. Mais alors
$$
\begin{aligned}
(A T, B C) & =(A T, A F)+(A F, B C)=(G T, G F)+(A F, G F) \\
& =(G T, G C)+(A E, G E)=(E G, E C)+(C E, G E)=0^{\circ},
\end{aligned}
$$
ce qui signifie précisément que les droites $(A T)$ et $(B C)$ sont parallèles.
Commentaire des correcteurs L'exercice a été correctement résolu par 7 élèves. Quelques élèves, même s'ils n'ont pas complètement résolu le problème, ont utilisé leur figure pour conjecturer que le point $T$ appartenait au cercle $\Gamma$ et ont conclu en admettant ce résultat. Ce procédé a été grandement apprécié car c'est la bonne attitude face à un problème de géometrie.
## Exercices Senior
|
{
"resource_path": "French/segmented/tests/fr-2019-2020-Corrigé-Web-05-2020.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "\nSolution de l'exercice 4"
}
|
964396e1-1dd0-5302-8450-1ab3e2ea4e11
| 605,983
|
Let $ABC$ be a triangle and $\Gamma$ a circle passing through $A$. Suppose that $\Gamma$ intersects the segments $[AB]$ and $[AC]$ at two points, which we call $D$ and $E$ respectively, and that it intersects the segment $[BC]$ at two points, which we call $F$ and $G$, such that $F$ lies between $B$ and $G$. Let $T$ be the point of intersection between the tangent at $F$ to the circumcircle of $BDF$ and the tangent at $G$ to the circumcircle of $CEG$.
Prove that, if the points $A$ and $T$ are distinct, then $(AT)$ and $(BC)$ are parallel.
|
Let's start by drawing a figure.
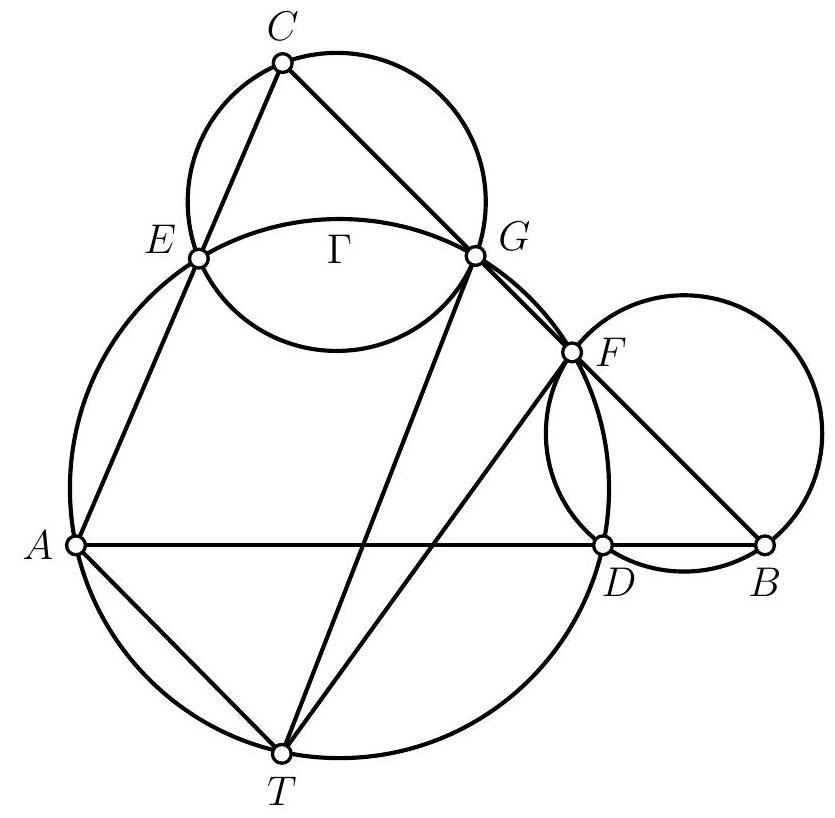
A striking first observation is that $T$ appears to lie on the circle $\Gamma$. After verifying this on a second figure, we promptly set out to prove this first result. To do so, we embark on an angle chase using the properties of cyclic points and the limiting case of the inscribed angle theorem:
$$
\begin{aligned}
(T G, T F) & =(T G, B C)+(B C, T F)=(T G, C G)+(B F, T F)=(E G, E C)+(D B, D F) \\
& =(E G, A E)+(A D, D F)=(D G, A D)+(A D, D F)=(A D, D F) .
\end{aligned}
$$
The points $A, F, G$, and $T$ are therefore concyclic, and $T$ lies on $\Gamma$. But then
$$
\begin{aligned}
(A T, B C) & =(A T, A F)+(A F, B C)=(G T, G F)+(A F, G F) \\
& =(G T, G C)+(A E, G E)=(E G, E C)+(C E, G E)=0^{\circ},
\end{aligned}
$$
which precisely means that the lines $(A T)$ and $(B C)$ are parallel.
Comment from the graders: The exercise was very well done! The most efficient students noted that it was sufficient to show that the point $T'$, the intersection of the line parallel to the line $(B C)$ passing through the point $A$ with the circle $\Gamma$, lies on both tangents. It is a pity to note that several students submitted a very neat figure but did not attempt to make conjectures from this figure, even though the point $T$ clearly lies on the circle $\Gamma$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $\Gamma$ un cercle passant par $A$. On suppose que $\Gamma$ recoupe les segments $[A B]$ et $[A C]$ en deux points, que l'on appelle respectivement $D$ et $E$, et qu'il coupe le segment $[B C]$ en deux points, que l'on appelle $F$ et $G$, de sorte que $F$ se trouve entre $B$ et $G$. Soit $T$ le point d'intersection entre la tangente en $F$ au cercle circonscrit à $B D F$ et la tangente en $G$ au cercle circonscrit à $C E G$.
Démontrer que, si les points $A$ et $T$ sont distincts, alors $(A T)$ et $(B C)$ sont parallèles.
|
Commençons par tracer une figure.

Une première remarque frappante est que $T$ semble être situé sur le cercle $\Gamma$. Après avoir vérifié qu'il l'était bien sur une deuxième figure, on s'empresse donc de démontrer ce premier résultat. Pour ce faire, on entame donc une chasse aux angles de droites, en utilisant les relations de cocyclicité et le cas limite du théorème de l'angle au centre :
$$
\begin{aligned}
(T G, T F) & =(T G, B C)+(B C, T F)=(T G, C G)+(B F, T F)=(E G, E C)+(D B, D F) \\
& =(E G, A E)+(A D, D F)=(D G, A D)+(A D, D F)=(A D, D F) .
\end{aligned}
$$
Les points $A, F, G$ et $T$ sont donc cocycliques, et $T$ appartient à bien $\Gamma$. Mais alors
$$
\begin{aligned}
(A T, B C) & =(A T, A F)+(A F, B C)=(G T, G F)+(A F, G F) \\
& =(G T, G C)+(A E, G E)=(E G, E C)+(C E, G E)=0^{\circ},
\end{aligned}
$$
ce qui signifie précisément que les droites $(A T)$ et $(B C)$ sont parallèles.
Commentaire des correcteurs L'exercice a été très bien réussi! Les élèves les plus efficaces ont noté qu'il suffisait de montrer que le point $T^{\prime} \mathrm{d}^{\prime}$ intersection de la droite parallèle à la droite $(B C)$ passant par le point $A$ avec le cercle $\Gamma$ appartenait aux deux tangentes. Il est dommage de constater que plusieurs élèves ont rendu une figure très propre mais n'ont pas cherché à effectuer de conjectures à partir de cette figure, alors même que le point $T$ appartient visiblement au cercle $\Gamma$.
|
{
"resource_path": "French/segmented/tests/fr-2019-2020-Corrigé-Web-05-2020.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution de l'exercice 5"
}
|
964396e1-1dd0-5302-8450-1ab3e2ea4e11
| 605,983
|
Let $a_{1}, a_{2}, \ldots$ be the sequence of integers such that $a_{1}=1$ and, for all integers $n \geqslant 1$,
$$
a_{n+1}=a_{n}^{2}+a_{n}+1
$$
Prove, for all integers $n \geqslant 1$, that $a_{n}^{2}+1$ divides $a_{n+1}^{2}+1$.
|
For all integers $n \geqslant 1$, let $b_{n}=a_{n}^{2}+1$. We conclude by directly observing that
$$
b_{n+1} \equiv\left(a_{n}^{2}+a_{n}+1\right)^{2}+1 \equiv\left(b_{n}+a_{n}\right)^{2}+1 \equiv a_{n}^{2}+1 \equiv b_{n} \equiv 0 \quad\left(\bmod b_{n}\right)
$$
$\underline{\text { Alternative Solution } n^{\circ} 1}$ It suffices to observe, for all integers $n \geqslant 1$, that
$$
\begin{aligned}
a_{n+1}^{2}+1 & =\left(a_{n}^{2}+a_{n}+1\right)^{2}+1 \\
& =a_{n}^{4}+2 a_{n}^{3}+3 a_{n}^{2}+2 a_{n}+2 \\
& =a_{n}^{2}\left(a_{n}^{2}+1\right)+2 a_{n}^{3}+2 a_{n}^{2}+2 a_{n}+2 \\
& =a_{n}^{2}\left(a_{n}^{2}+1\right)+2 a_{n}\left(a_{n}^{2}+1\right)+2 a_{n}^{2}+2 \\
& =a_{n}^{2}\left(a_{n}^{2}+1\right)+2 a_{n}\left(a_{n}^{2}+1\right)+2\left(a_{n}^{2}+1\right) \\
& =\left(a_{n}^{2}+2 a_{n}+2\right)\left(a_{n}^{2}+1\right)
\end{aligned}
$$
is indeed a multiple of $a_{n}^{2}+1$.
Comment from the graders The exercise was well solved. Some attempted induction, with little success, as it was difficult to obtain the result by induction. Few papers worked modulo $a_{n}^{2}+1$, which greatly simplified the calculations.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $a_{1}, a_{2}, \ldots$ la suite d'entiers telle que $a_{1}=1$ et, pour tout entier $n \geqslant 1$,
$$
a_{n+1}=a_{n}^{2}+a_{n}+1
$$
Démontrer, pour tout entier $n \geqslant 1$, que $a_{n}^{2}+1$ divise $a_{n+1}^{2}+1$.
|
Pour tout entier $n \geqslant 1$, posons $b_{n}=a_{n}^{2}+1$. On conclut en constatant directement que
$$
b_{n+1} \equiv\left(a_{n}^{2}+a_{n}+1\right)^{2}+1 \equiv\left(b_{n}+a_{n}\right)^{2}+1 \equiv a_{n}^{2}+1 \equiv b_{n} \equiv 0 \quad\left(\bmod b_{n}\right)
$$
$\underline{\text { Solution alternative } n^{\circ} 1}$ Il suffit de constater, pour tout entier $n \geqslant 1$, que
$$
\begin{aligned}
a_{n+1}^{2}+1 & =\left(a_{n}^{2}+a_{n}+1\right)^{2}+1 \\
& =a_{n}^{4}+2 a_{n}^{3}+3 a_{n}^{2}+2 a_{n}+2 \\
& =a_{n}^{2}\left(a_{n}^{2}+1\right)+2 a_{n}^{3}+2 a_{n}^{2}+2 a_{n}+2 \\
& =a_{n}^{2}\left(a_{n}^{2}+1\right)+2 a_{n}\left(a_{n}^{2}+1\right)+2 a_{n}^{2}+2 \\
& =a_{n}^{2}\left(a_{n}^{2}+1\right)+2 a_{n}\left(a_{n}^{2}+1\right)+2\left(a_{n}^{2}+1\right) \\
& =\left(a_{n}^{2}+2 a_{n}+2\right)\left(a_{n}^{2}+1\right)
\end{aligned}
$$
est effectivement un multiple de $a_{n}^{2}+1$.
Commentaire des correcteurs L'exercice a été bien résolu. Certains ont tenté une récurrence, sans grand succès, car il était difficile d'obtenir le résultat par récurrence. Peu de copies ont travaillé modulo $a_{n}^{2}+1$, ce qui simplifiait pourtant grandement les calculs.
|
{
"resource_path": "French/segmented/tests/fr-2019-2020-Corrigé-Web.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution de l'exercice 1"
}
|
0a7fe00b-28bf-5b83-ad0d-33b31dbc023e
| 111,051
|
In the land of wonders, there are $n$ cities. Each pair of cities is connected by a one-way road, which starts from one of the two cities and arrives at the other. To find her way, Alice questions the King of Hearts: with each question, Alice chooses a pair of cities, and the King of Hearts tells her which is the starting city of the road connecting these two cities.
Prove that, in $5 n$ questions or fewer, Alice can determine whether there exists a city from which at most one road starts.
|
We will describe a strategy that Alice can implement to achieve her goal in $5 n$ questions or fewer. At any time, we will say that a city $v$ is bad if Alice has already found two roads that leave from $v$, and that $v$ is good otherwise. Similarly, we will say that a pair of cities $\{v, w\}$ is explored if Alice has already asked the Queen of Hearts about this pair, and unexplored otherwise.
In addition, in parallel with these questions, Alice has drawn a map on which the $n$ cities are represented by $n$ vertices, and she adds an edge on this map, between the cities $v$ and $w$ for each question she asks about the pair $\{v, w\}$. In the following, we will identify Wonderland with the graph that Alice is building.
First, Alice clearly has no interest in asking the Queen of Hearts about a pair of cities that would both be bad, or about a pair of cities already explored. Alice's strategy therefore begins as follows. As long as there is an unexplored pair $\{v, w\}$ formed by two good cities, Alice chooses such a pair and asks the Queen of Hearts about this pair. At the end of this first step, no vertex in our graph has strictly more than two outgoing edges. Alice has therefore asked at most $2 n$ questions.
Furthermore, let $X$ be the set of cities that are still good at the end of this step, and let $x$ be the cardinality of $X$, so that there are $x(x-1) / 2$ roads between cities in $X$. Every pair $\{v, w\}$ formed by two cities in $X$ is clearly explored; and every city in $X$, since it is good, is therefore the origin of at most one road going to another city in $X$. There are therefore at most $x$ roads between cities in $X$, which means that $x \leqslant 3$.
Alice therefore only has to ask the Queen of Hearts about all pairs $\{v, x\}$ where $x \in X$: this will make $n x \leqslant 3 n$ additional questions, at the end of which Alice will know exactly how many roads leave from each of the cities in $X$. If, at this stage of the algorithm, there is a good city $v$, it is because there was indeed no more than one road that left from $v$.
Comment from the Examiners Due to its difficulty, this problem was solved by a small number of students. Many noticed that for $n \leqslant 11$, Alice could simply ask the direction of all the roads; unfortunately, this did not advance the problem. The key was to realize that, in general, it was necessary to avoid asking a question about a city from which two roads left.
Some students proposed strategies that did not work in $5 n$ questions, but in $6 n$ questions or more (for example, 10n questions), and this was valued. Some students also scored points by showing that at most 3 cities could have fewer than 2 outgoing roads.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Au pays des merveilles se trouvent $n$ villes. Chaque paire de villes est reliée par une route à sens unique, qui part d'une des deux villes et arrive à l'autre. Afin de s'y retrouver, Alice interroge le roi de cœur : à chaque question, Alice choisit une paire de villes, et le roi de cœur lui dit quelle est la ville de départ de la route qui relie ces deux villes.
Démontrer que, en $5 n$ questions ou moins, Alice peut arriver à savoir s'il existe une ville d'où part au plus une route.
|
Nous allons décrire une stratégie qu'Alice peut mettre en place pour aboutir à ses fins en $5 n$ questions ou moins. À tout moment, on dira qu'une ville $v$ est mauvaise si Alice a déjà trouvé deux routes qui partent de $v$, et que $v$ est bonne sinon. De même, on dira qu'une paire de villes $\{v, w\}$ est explorée si Alice a déjà interrogé le roi de cœur sur cette paire-là, et inexplorée sinon.
Enfin, en parallèle de ces questions, Alice a dessiné une carte sur laquelle les $n$ villes sont représentées par $n$ sommets, et elle ajoute une arête sur cette carte, entre les villes $v$ et $w$ à chaque question qu'elle pose sur la paire $\{v, w\}$. Dans la suite, nous allons identifier le pays des merveilles au graphe qu'Alice est en train de construire.
Tout d'abord, Alice n'a manifestement jamais intérêt à interroger le roi de cœur sur une paire de villes qui seraient toutes deux mauvaises, ou sur une paire de villes déjà explorée. La stratégie d'Alice débute donc comme suit. Tant qu'il existe une paire inexplorée $\{v, w\}$ formée de deux bonnes villes, Alice choisit une telle paire et interroge le roi de cœur sur cette paire. À la fin de cette première étape, nul sommet de notre graphe n'a strictement plus de deux arêtes sortantes. Alice a donc posé au plus $2 n$ questions.
En outre, soit $X$ l'ensemble des villes toujours bonnes à l'issue de cette étape, et soit $x$ le cardinal de $X$, de sorte qu'il y a $x(x-1) / 2$ routes entre villes de $X$. Toute paire $\{v, w\}$ formée de deux villes de $X$ est manifestement explorée; et toute ville de $X$, puisqu'elle est bonne, est donc à l'origine d'au plus une route allant vers une autre ville de $X$. Il y a donc au plus $x$ routes entre villes de $X$, ce qui signifie que $x \leqslant 3$.
Alice n'a donc plus qu'à interroger le roi de cœur sur toutes les paires $\{v, x\}$ où $x \in X$ : cela fera $n x \leqslant 3 n$ questions supplémentaires, à l'issue desquelles Alice saura exactement combien de routes partent de chacune des villes de $X$. Si, à cette étape de l'algorithme, il reste une bonne ville $v$, c'est qu'il n'y avait effectivement pas plus d'une route qui partait de $v$.
Commentaire des correcteurs Du fait de sa difficulté, cet exercice a été résolu par un faible nombre d'élèves. Nombreux sont ceux qui ont remarqué que, pour $n \leqslant 11$, Alice pouvait se contenter de demander le sens de toutes les routes; malheureusement, cela ne faisait pas avancer le problème. La clé consistait à s'apercevoir que, en général, il fallait éviter de poser une question sur une ville dont deux routes sortaient.
Quelques élèves ont proposé des stratégies qui ne marchaient pas en $5 n$ questions, mais en $6 n$ questions ou plus (par exemple 10n questions) et cela a été valorisé. Quelques élèves ont également obtenu des points en montrant qu'au plus 3 villes pouvaient avoir moins de 2 routes sortantes.
## Exercices Senior
|
{
"resource_path": "French/segmented/tests/fr-2019-2020-Corrigé-Web.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "\nSolution de l'exercice 4"
}
|
ce4855dd-a0bf-5c4b-b9fa-29abb14d57be
| 606,060
|
In the land of wonders, there are $n$ cities. Each pair of cities is connected by a one-way road, which starts from one of the two cities and arrives at the other. To find her way, Alice questions the King of Hearts: with each question, Alice chooses a pair of cities, and the King of Hearts tells her which is the starting city of the road connecting these two cities.
Prove that, in $5 n$ questions or fewer, Alice can determine whether there exists a city from which at most one road starts.
|
We will describe a strategy that Alice can implement to achieve her goal in $5 n$ questions or fewer. At any time, we will say that a city $v$ is bad if Alice has already found two roads that leave from $v$, and that $v$ is good otherwise. Similarly, we will say that a pair of cities $\{v, w\}$ is explored if Alice has already asked the Queen of Hearts about this pair, and unexplored otherwise.
In addition, in parallel with these questions, Alice has drawn a map on which the $n$ cities are represented by $n$ vertices, and she adds an edge on this map, between the cities $v$ and $w$ for each question she asks about the pair $\{v, w\}$. In the following, we will identify Wonderland with the graph that Alice is building.
First of all, Alice clearly has no interest in asking the Queen of Hearts about a pair of cities that would both be bad, or about a pair of cities already explored. Alice's strategy therefore begins as follows. As long as there is an unexplored pair $\{v, w\}$ formed of two good cities, Alice chooses such a pair and asks the Queen of Hearts about this pair. At the end of this first step, no vertex in our graph has strictly more than two outgoing edges. Alice has therefore asked at most $2 n$ questions.
Furthermore, let $X$ be the set of cities that are still good at the end of this step, and let $x$ be the cardinality of $X$, so that there are $x(x-1) / 2$ roads between cities in $X$. Every pair $\{v, w\}$ formed of two cities in $X$ is clearly explored; and every city in $X$, since it is good, is therefore the origin of at most one road going to another city in $X$. There are therefore at most $x$ roads between cities in $X$, which means that $x \leqslant 3$.
Alice therefore only has to ask the Queen of Hearts about all pairs $\{v, x\}$ where $x \in X$: this will make $n x \leqslant 3 n$ additional questions, at the end of which Alice will know exactly how many roads leave from each of the cities in $X$. If, at this stage of the algorithm, there is a good city $v$, it is because there was indeed no more than one road that left from $v$.
Comment from the graders: Due to its difficulty, this problem was solved by a small number of students. Many noticed that for $n \leqslant 11$, Alice could simply ask the direction of all the roads; unfortunately, this did not advance the problem. The key was to realize that, in general, it was necessary to avoid asking a question about a city from which two roads left.
Some students proposed strategies that did not work in $5 n$ questions, but in $6 n$ questions or more (for example, 10n questions), and this was valued. Some students also earned points by showing that at most 3 cities could have fewer than 2 outgoing roads.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Au pays des merveilles se trouvent $n$ villes. Chaque paire de villes est reliée par une route à sens unique, qui part d'une des deux villes et arrive à l'autre. Afin de s'y retrouver, Alice interroge le roi de cœur : à chaque question, Alice choisit une paire de villes, et le roi de cœur lui dit quelle est la ville de départ de la route qui relie ces deux villes.
Démontrer que, en $5 n$ questions ou moins, Alice peut arriver à savoir s'il existe une ville d'où part au plus une route.
|
Nous allons décrire une stratégie qu'Alice peut mettre en place pour aboutir à ses fins en $5 n$ questions ou moins. À tout moment, on dira qu'une ville $v$ est mauvaise si Alice a déjà trouvé deux routes qui partent de $v$, et que $v$ est bonne sinon. De même, on dira qu'une paire de villes $\{v, w\}$ est explorée si Alice a déjà interrogé le roi de cœur sur cette paire-là, et inexplorée sinon.
Enfin, en parallèle de ces questions, Alice a dessiné une carte sur laquelle les $n$ villes sont représentées par $n$ sommets, et elle ajoute une arête sur cette carte, entre les villes $v$ et $w$ à chaque question qu'elle pose sur la paire $\{v, w\}$. Dans la suite, nous allons identifier le pays des merveilles au graphe qu'Alice est en train de construire.
Tout d'abord, Alice n'a manifestement jamais intérêt à interroger le roi de cœur sur une paire de villes qui seraient toutes deux mauvaises, ou sur une paire de villes déjà explorée. La stratégie d'Alice débute donc comme suit. Tant qu'il existe une paire inexplorée $\{v, w\}$ formée de deux bonnes villes, Alice choisit une telle paire et interroge le roi de cœur sur cette paire. À la fin de cette première étape, nul sommet de notre graphe n'a strictement plus de deux arêtes sortantes. Alice a donc posé au plus $2 n$ questions.
En outre, soit $X$ l'ensemble des villes toujours bonnes à l'issue de cette étape, et soit $x$ le cardinal de $X$, de sorte qu'il y a $x(x-1) / 2$ routes entre villes de $X$. Toute paire $\{v, w\}$ formée de deux villes de $X$ est manifestement explorée; et toute ville de $X$, puisqu'elle est bonne, est donc à l'origine d'au plus une route allant vers une autre ville de $X$. Il y a donc au plus $x$ routes entre villes de $X$, ce qui signifie que $x \leqslant 3$.
Alice n'a donc plus qu'à interroger le roi de cœur sur toutes les paires $\{v, x\}$ où $x \in X$ : cela fera $n x \leqslant 3 n$ questions supplémentaires, à l'issue desquelles Alice saura exactement combien de routes partent de chacune des villes de $X$. Si, à cette étape de l'algorithme, il reste une bonne ville $v$, c'est qu'il n'y avait effectivement pas plus d'une route qui partait de $v$.
Commentaire des correcteurs Du fait de sa difficulté, cet exercice a été résolu par un faible nombre d'élèves. Nombreux sont ceux qui ont remarqué que, pour $n \leqslant 11$, Alice pouvait se contenter de demander le sens de toutes les routes; malheureusement, cela ne faisait pas avancer le problème. La clé consistait à s'apercevoir que, en général, il fallait éviter de poser une question sur une ville dont deux routes sortaient.
Quelques élèves ont proposé des stratégies qui ne marchaient pas en $5 n$ questions, mais en $6 n$ questions ou plus (par exemple 10n questions) et cela a été valorisé. Quelques élèves ont également obtenu des points en montrant qu'au plus 3 villes pouvaient avoir moins de 2 routes sortantes.
|
{
"resource_path": "French/segmented/tests/fr-2019-2020-Corrigé-Web.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution de l'exercice 5"
}
|
ce4855dd-a0bf-5c4b-b9fa-29abb14d57be
| 606,060
|
Let $ABC$ be an acute triangle such that $\widehat{CAB} > \widehat{BCA}$, and let $P$ be the point on the segment $[BC]$ such that $\widehat{PAB} = \widehat{BCA}$. Let $Q$ be the intersection point, other than $A$, between the circumcircle of $ABP$ and the line $(AC)$. Let $D$ be the point on the segment $[AP]$ such that $\widehat{QDC} = \widehat{CAP}$, and let $E$ be the point on $(BD)$, other than $D$, such that $CE = CD$. Finally, let $F$ be the intersection point, other than $C$, between the circumcircle of $CQE$ and the line $(CD)$, and let $G$ be the intersection point of the lines $(QF)$ and $(BC)$.
Prove that the points $B, D, F$, and $G$ are concyclic.
|
Let's start by drawing a figure. The first difficulty is to construct point $P$: a simple way to proceed is to construct the intersection point, other than $A$, between the circumcircle of $A B C$ and the circle centered at $B$ with radius $A$. Indeed, if we denote this point by $P^{\prime}$, the arcs $\overline{A B}$ and $\overline{B P^{\prime}}$ have the same measure, so $\widehat{B C A}=\widehat{P^{\prime} A B}=\widehat{P A B}$, and it suffices to construct $P$ as the intersection of the lines $(B C)$ and $\left(A P^{\prime}\right)$.
Similarly, since we want $\widehat{Q D C}=\widehat{C A P}=\widehat{Q A P}=\widehat{Q B P}=\widehat{Q B C}$, we can construct point $D$ as the intersection of the line $(A P)$ and the circumcircle of $B C Q$.
We then obtain the following figure, where we have drawn in dashed lines all the circles useful for our construction, in gray the circle we wish to show exists, and of course marked the angles $\widehat{P A B}=\widehat{B C A}$ and $\widehat{Q D C}=\widehat{C A P}$, which are likely to play a role in the following.
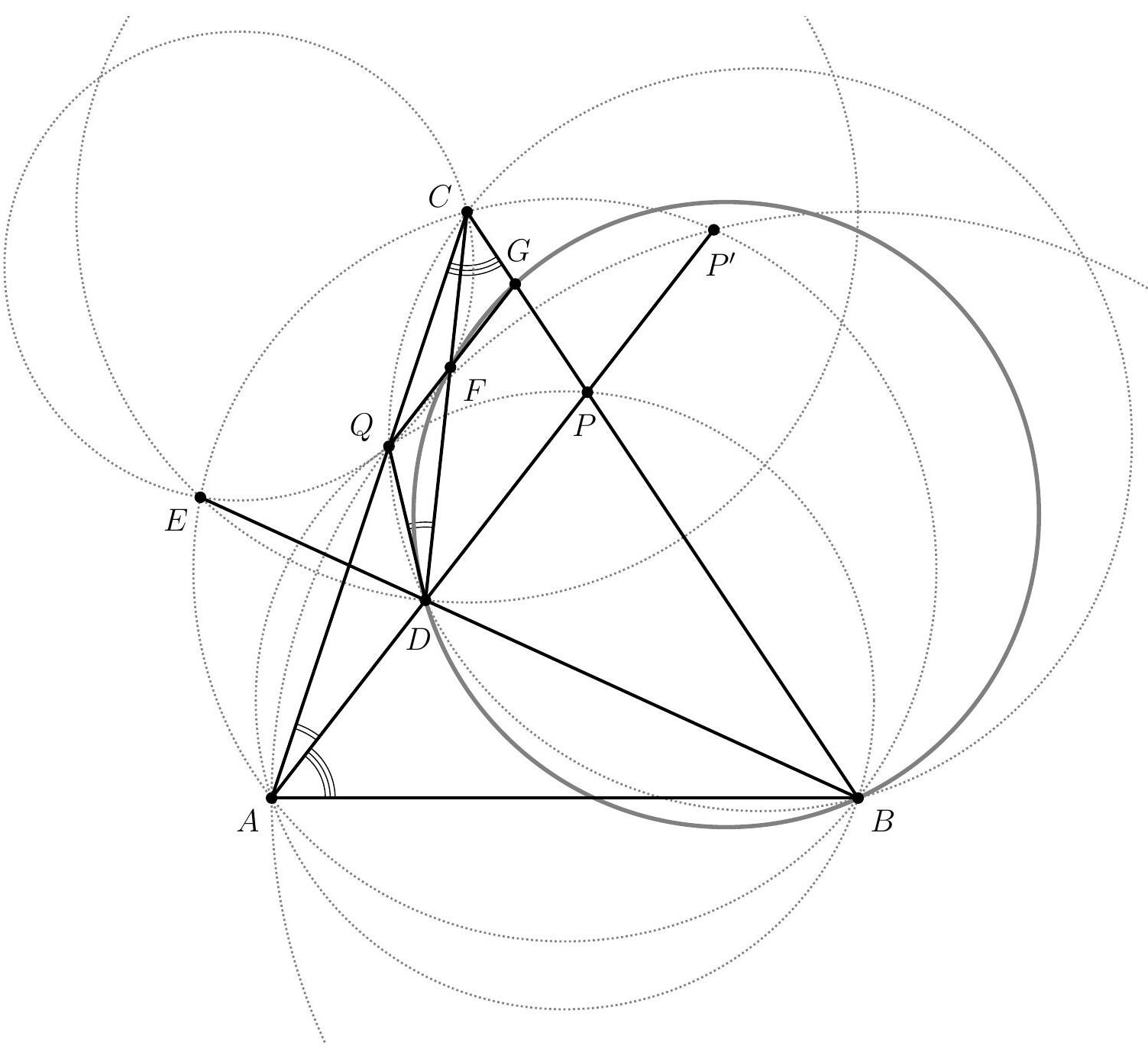
A first clear observation from the figure is that points $A, B, P^{\prime}, C$ and $E$ appear to be concyclic. We therefore start by proving this, using the following angle chasing:
$$
\begin{aligned}
(E C, E B) & =(D B, D C)=(Q B, Q C)=(Q B, Q A)=(P B, P A) \\
& =(C B, P A)=(C B, A B)+(A B, P A) \\
& =(C B, A B)+(A C, C B)=(A C, A B) .
\end{aligned}
$$
Since no other observation is immediately apparent, we focus on the property to be proven, with the aim of transforming it into an equivalent property that is more likely to be easier to observe. Thus, it is necessary to prove that
$$
(D F, D B)=(G F, G B)=(Q F, B C)=(Q F, C F)+(C F, B C)=(Q E, C E)+(D F, B C)
$$
that is, $(Q E, C E)=(B C, D B)=(B C, B E)=(A C, A E)$, or that the triangles $A C E$ and $E C Q$ are (indirectly) similar, since they already have the same angle at $\widehat{C}$.
Given the relation $C D^{2}=C E^{2}$, our goal is therefore to prove that $C A \cdot C Q=$ $C E^{2}=C D^{2}$. But the equality $C A \cdot C Q=C D^{2}$ follows precisely from the fact that the triangles $C A D$ and $C D Q$ are similar, since they have the same angle at $\widehat{C}$ and $\widehat{C A D}=\widehat{Q D C}$. This concludes our solution.
Comment from the graders: The exercise was very successful! Several approaches were possible. Some students were, without knowing it, very close to the conclusion. Others performed an interesting angle chasing without seeing that it implied that certain points were concyclic or that certain lines were parallel, which is always a pity.
Several students attempted to reduce the problem or to bring it back to the proof of another property of the figure. This is a good idea, but most of the time, proving this other property is not particularly simpler than the original problem.
It is worth noting that it was not necessary to deploy technical tools for this exercise, and a simple angle chasing or the use of the power of a point with respect to a circle was more than sufficient.
Once again, we deplore the case of students who did not follow the instructions regarding the figures. We emphasize the importance of neat and accurate figures, which are the basis of geometric reasoning, especially when the exercise becomes really challenging. The habit of drawing accurate figures is therefore essential. Conversely, many students were able to use their figures to conjecture various properties and provide a start to the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle acutangle tel que $\widehat{C A B}>\widehat{B C A}$ et soit $P$ le point du segment $[B C]$ tel que $\widehat{P A B}=\widehat{B C A}$. Soit $Q$ le point d'intersection, autre que $A$, entre le cercle circonscrit à $A B P$ et la droite $(A C)$. Soit ensuite $D$ le point du segment $[A P]$ tel que $\widehat{Q D C}=\widehat{C A P}$, puis $E$ le point de $(B D)$, autre que $D$, tel que $C E=C D$. Enfin, soit $F$ le point d'intersection, autre que $C$, entre le cercle circonscrit à $C Q E$ et la droite ( $C D$ ), et soit $G$ le point d'intersection des droites $(Q F)$ et $(B C)$.
Démontrer que les points $B, D, F$ et $G$ sont cocycliques.
|
Commençons par tracer une figure. Une première difficulté est de construire le point $P$ : une manière simple de procéder est alors de construire le point d'intersection, autre que $A$, entre le cercle circonscrit à $A B C$ et le cercle de centre $B$ et de rayon $A$. En effet, si l'on note $P^{\prime}$ ce point, les arcs $\overline{A B}$ et $\overline{B P^{\prime}}$ ont même mesure, donc $\widehat{B C A}=\widehat{P^{\prime} A B}=\widehat{P A B}$, et il suffit de construire $P$ comme le point d'intersection des droites $(B C)$ et $\left(A P^{\prime}\right)$.
De même, puisque l'on souhaite que $\widehat{Q D C}=\widehat{C A P}=\widehat{Q A P}=\widehat{Q B P}=\widehat{Q B C}$, on peut construire le point $D$ comme le point d'intersection entre la droite $(A P)$ et le cercle circonscrit à $B C Q$.
On obtient alors la figure suivante, où l'on a tracé en pointillés tous les cercle utiles à notre construction, en gris le cercle dont on souhaite montrer qu'il existe, et où l'on a bien sûr marqué les angles $\widehat{P A B}=\widehat{B C A}$ et $\widehat{Q D C}=\widehat{C A P}$, qui ont de fortes chances d'avoir un rôle à jouer dans la suite.

Une première remarque qui apparaît nettement sur la figure est que les points $A, B, P^{\prime}, C$ et $E$ semblent cocycliques. On commence donc par le démontrer, au moyen de la chasse aux angles de droites suivante:
$$
\begin{aligned}
(E C, E B) & =(D B, D C)=(Q B, Q C)=(Q B, Q A)=(P B, P A) \\
& =(C B, P A)=(C B, A B)+(A B, P A) \\
& =(C B, A B)+(A C, C B)=(A C, A B) .
\end{aligned}
$$
Puisque aucune autre remarque ne saute manifestement aux yeux, on se concentre alors sur la propriété à démontrer, dans le but de la transformer en une propriété équivalente qui aura des chances d'être plus facile à observer. Ainsi, il s'agit de démontrer que
$$
(D F, D B)=(G F, G B)=(Q F, B C)=(Q F, C F)+(C F, B C)=(Q E, C E)+(D F, B C)
$$
c'est-à-dire que $(Q E, C E)=(B C, D B)=(B C, B E)=(A C, A E)$, ou encore que les triangles $A C E$ et $E C Q$ sont (indirectement) semblables, puisqu'ils ont déjà même angle en $\widehat{C}$.
Au vu de la relation $C D^{2}=C E^{2}$, notre objectif devient donc de démontrer que $C A \cdot C Q=$ $C E^{2}=C D^{2}$. Mais l'égalité $C A \cdot C Q=C D^{2}$ découle justement du fait que les triangles $C A D$ et $C D Q$ sont semblables, puisqu'ils ont même angle en $\widehat{C}$ et que $\widehat{C A D}=\widehat{Q D C}$. Ceci conclut donc notre solution.
Commentaire des correcteurs L'exercice a été très réussi! Plusieurs approches étaient possibles. Quelques élèves étaient, sans le savoir, très proches de la conclusion. D'autres ont effectué une chasse aux angles intéressante sans pour autant voir que cela impliquait que des points étaient cocycliques ou que des droites étaient parallèles, ce qui est toujours dommage.
Plusieurs élèves ont tenté de réduire le problème ou de le ramener à la démonstration d'une autre propriété de la figure. C'est une bonne idée mais, la plupart du temps, démontrer cette autre propriété n'est pas spécialement plus simple que le problème de départ.
On notera qu'il n'était pas nécessaire de déployer des outils techniques pour cet exercice et qu'une simple chasse aux angles ou l'usage de la puissance d'un point par rapport à un cercle était largement suffisants.
Une fois de plus, on déplore le cas d'élèves n'ayant pas respecté la consigne concernant les figures. On insiste sur l'intérêt de figures propres et exactes qui sont la base de la réflexion en géométrie, surtout lorsque l'exercice devient rééllement corsé. L'habitude de tracer des figures exactes est donc essentiel. À l'inverse, de nombreux élèves ont su utiliser leur figure pour conjecturer diverses propriétés et en fournir un début de démonstration.
|
{
"resource_path": "French/segmented/tests/fr-2019-2020-Corrigé-Web.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "\nSolution de l'exercice 6"
}
|
970b41d9-3bc4-5c45-be9f-7be74364e1d3
| 606,076
|
Let $ABC$ be a triangle and let $\Gamma$ be its circumcircle. Let $P$ be the intersection point of the line $(BC)$ and the tangent to $\Gamma$ at $A$. Let $D$ and $E$ be the symmetrical points of $B$ and $A$ with respect to $P$.
Let $\omega_{1}$ be the circumcircle of triangle $DAC$ and let $\omega_{2}$ be the circumcircle of triangle $APB$. We denote by $F$ the intersection point of the circles $\omega_{1}$ and $\omega_{2}$ other than $A$, and then we denote by $G$ the intersection point, other than $F$, of the circle $\omega_{1}$ with the line $(BF)$.
Prove that the lines $(BC)$ and $(EG)$ are parallel.
|
Let's start by drawing a figure.
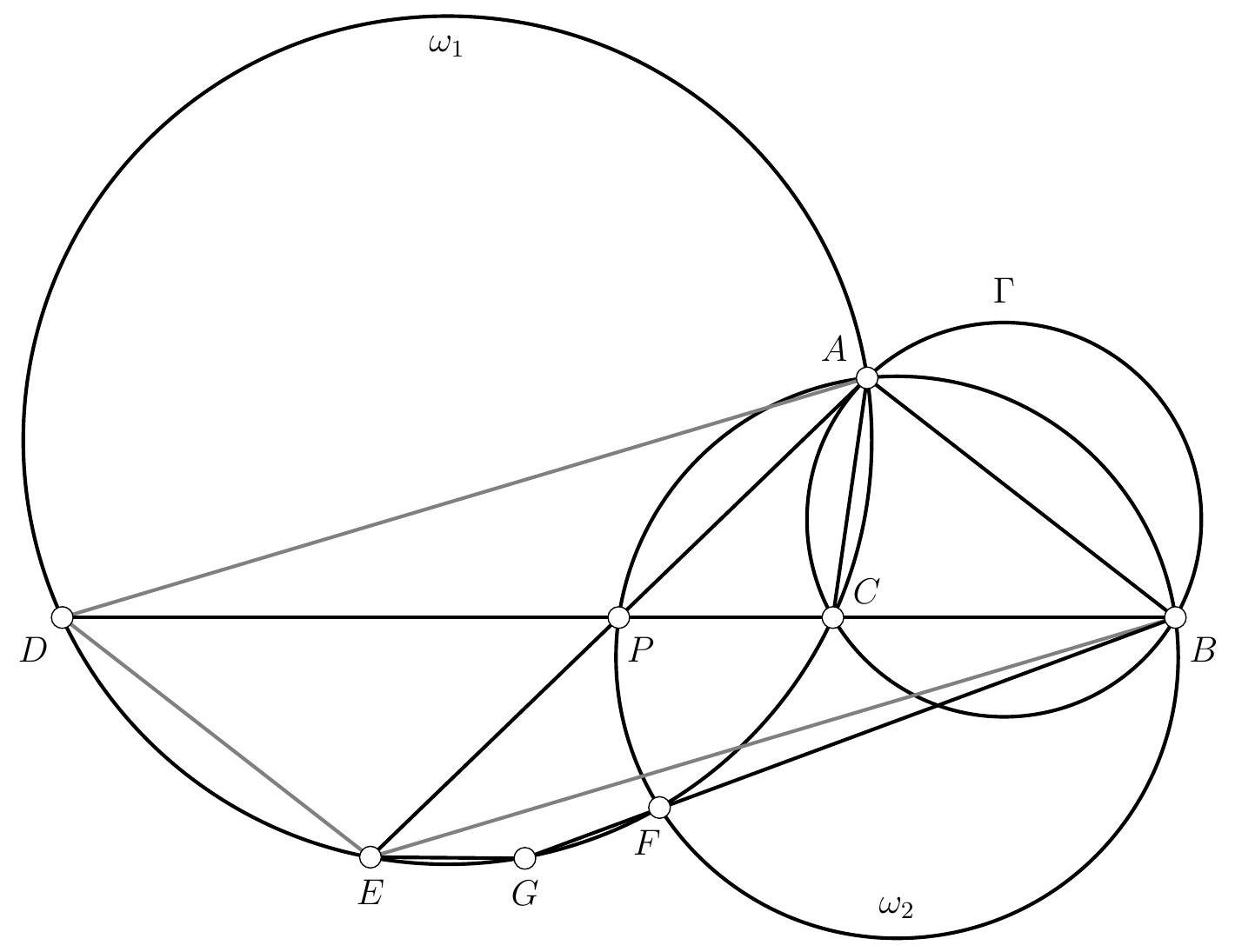
A first observation we can make is that, since $P$ is the midpoint of segments $[A E]$ and $[B D]$, the quadrilateral $A B E D$ is a parallelogram. Therefore, lines $(A B)$ and $(D E)$ are parallel, as are lines $(A D)$ and $(B E)$.
A striking second observation is that $E$ appears to lie on the circle $\omega_{1}$. After verifying on a second figure that this is indeed the case, we promptly set out to prove this first result. To do so, we embark on an angle chase:
$$
(E A, E D)=(E A, A B)=(C A, C B)=(C A, C D)
$$
An angle chase then indicates that
$(B C, E G)=(B C, B G)+(B G, E G)=(P B, B F)+(G F, G E)=(P A, A F)+(A F, A E)=0^{\circ}$, which means that $(B C)$ and $(E G)$ are parallel.
Comment from the graders: One of the reasons we require the presence of a figure is that it serves as a good means of forming intuitions about the problem; it is then necessary to prove that these intuitions are correct. Thus, on many drawings, it was clearly visible that $E$ lies on the circle $\omega_{1}$; however, few students noticed this. Similarly, several students saw on the drawing that $E$ seemed to lie on the circle $\omega_{1}$, and then used this property, but forgot to prove it!
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et soit $\Gamma$ son cercle circonscrit. Soit $P$ le point d'intersection de la droite $(B C)$ et de la tangente à $\Gamma$ en $A$. Soit $D$ et $E$ les symétriques respectifs des points $B$ et $A$ par rapport à $P$.
Soit alors $\omega_{1}$ le cercle circonscrit au triangle $D A C$ et soit $\omega_{2}$ le cercle circonscrit au triangle $A P B$. On note $F$ le point d'intersection des cercles $\omega_{1}$ et $\omega_{2}$ autre que $A$, puis on note $G$ le point d'intersection, autre que $F$, du cercle $\omega_{1}$ avec la droite $(B F)$.
Démontrer que les droites $(B C)$ et $(E G)$ sont parallèles.
|
Commençons par tracer une figure.

Une première remarque que l'on peut formuler est que, puisque $P$ est le milieu des segments $[A E]$ et $[B D]$, le quadrilatère $A B E D$ et un parallélogramme. Les droites $(A B)$ et $(D E)$ sont donc parallèles, de même que les droites $(A D)$ et $(B E)$.
Une seconde remarque frappante est que $E$ semble appartenir au cercle $\omega_{1}$. Après avoir vérifié sur une deuxième figure que c'était bien le cas, on s'empresse donc de démontrer ce premier résultat. Pour ce faire, on entame donc une chasse aux angles de droites :
$$
(E A, E D)=(E A, A B)=(C A, C B)=(C A, C D)
$$
Une chasse aux angles de droites indique alors que
$(B C, E G)=(B C, B G)+(B G, E G)=(P B, B F)+(G F, G E)=(P A, A F)+(A F, A E)=0^{\circ}$, ce qui signifie bien que $(B C)$ et $(E G)$ sont parallèles.
Commentaire des correcteurs Une des raisons pour lesquelles on exige la présence d'une figure est qu'elle constitue un bon moyen de se forger des intuitions sur le problème; c'est alors qu'il faut démontrer que ces intuitions sont correctes. Ainsi, sur beaucoup de dessins on voyait clairement que $E$ est sur le cercle $\omega_{1}$; cependant, peu d'élèves l'ont remarqué. Parallèlement, plusieurs élèves ont vu sur le dessin que $E$ semblait appartenir au cercle $\omega_{1}$, et ont alors utilisé cette propriété, mais ont oublié de la démontrer!
|
{
"resource_path": "French/segmented/tests/fr-2019-2020-corrigé-test-janvier.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
56676006-740c-579d-a8f7-cc9462833fc8
| 606,128
|
Let $n$ be a non-zero natural number. We say that a function $f: \mathbb{R} \rightarrow \mathbb{R}$ is $n$-positive if, for all real numbers $x_{1}, \ldots, x_{n}$ such that $x_{1}+\ldots+x_{n}=0$, we have $f\left(x_{1}\right)+\ldots+f\left(x_{n}\right) \geqslant 0$.
a) Is every 2020-positive function necessarily 1010-positive?
b) Is every 1010-positive function necessarily 2020-positive?
|
In both solutions, we set $n=1010$.
a) Let $f$ be a $2n$-positive function, and let $x_{1}, \ldots, x_{n}$ be real numbers such that $x_{1}+\ldots+x_{n}=0$. Noting that $x_{1}+\ldots+x_{n}+x_{1}+\ldots+x_{n}=0$ and that $f$ is $2n$-positive, we observe that
$$
0 \leqslant f\left(x_{1}\right)+\ldots+f\left(x_{n}\right)+f\left(x_{1}\right)+\ldots+f\left(x_{n}\right)=2\left(f\left(x_{1}\right)+\ldots+f\left(x_{n}\right)\right),
$$
which shows that $f\left(x_{1}\right)+\ldots+f\left(x_{n}\right) \geqslant 0$, and thus that $f$ is $n$-positive. The answer is therefore yes!
b) Let $f$ be the function defined by $f(x)=-1$ if $x$ is an integer such that $x \equiv 1(\bmod 2n)$, and by $f(x)=n$ otherwise. Then $f$ is $n$-positive. Indeed, let $x_{1}, \ldots, x_{n}$ be real numbers such that $x_{1}+\ldots+x_{n}=0:$
$\triangleright$ If there exists an integer $k$ such that $f\left(x_{k}\right)=n$, and since $f\left(x_{i}\right) \geqslant-1$ for all $i \neq k$, we know that $f\left(x_{1}\right)+\ldots+f\left(x_{k}\right) \geqslant f\left(x_{k}\right)-(n-1) \geqslant 1$.
$\triangleright$ Otherwise, then $x_{k} \equiv 1(\bmod 2n)$ for all $k$, so $x_{1}+\ldots+x_{n} \equiv n \not \equiv 0(\bmod 2n)$, which means that this case is actually impossible.
However, $f$ is not $2n$-positive. Indeed, if $x_{1}=1-2n$ and $x_{2}=x_{3}=\ldots=x_{2n}=1$, then $x_{1}+\ldots+x_{2n}=0$ but $f\left(x_{1}\right)+\ldots+f\left(x_{2n}\right)=-2n<0$. The answer is therefore no!
Graders' Comments The graders noted several confusions about the concept of a function. Indeed, the function $f$ considered does not change depending on whether there are 1010 or 2020 real numbers.
Furthermore, if one wants to prove that a statement is false (for example, if one wishes to prove that any function $f$ that is $n$-positive is not necessarily $2n$-positive), the simplest way to proceed is still to present a counterexample.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $n$ un entier naturel non nul. On dit qu'une fonction $f: \mathbb{R} \rightarrow \mathbb{R}$ est $n$-positive si, pour tous les réels $x_{1}, \ldots, x_{n}$ tels que $x_{1}+\ldots+x_{n}=0$, on a $f\left(x_{1}\right)+\ldots+f\left(x_{n}\right) \geqslant 0$.
a) Toute fonction 2020-positive est-elle nécessairement 1010-positive?
b) Toute fonction 1010-positive est-elle nécessairement 2020-positive?
|
Dans les deux solutions, on pose $n=1010$.
a) Soit $f$ une fonction $2 n$-positive, et soit $x_{1}, \ldots, x_{n}$ des réels tels que $x_{1}+\ldots+x_{n}=0$. En notant que $x_{1}+\ldots+x_{n}+x_{1}+\ldots+x_{n}=0$ et que $f$ est $2 n$-positive, on constate que
$$
0 \leqslant f\left(x_{1}\right)+\ldots+f\left(x_{n}\right)+f\left(x_{1}\right)+\ldots+f\left(x_{n}\right)=2\left(f\left(x_{1}\right)+\ldots+f\left(x_{n}\right)\right),
$$
ce qui montre bien que $f\left(x_{1}\right)+\ldots+f\left(x_{n}\right) \geqslant 0$, et donc que $f$ est $n$-positive. La réponse est donc oui!
b) Soit $f$ la fonction définie par $f(x)=-1$ si $x$ est un entier tel que $x \equiv 1(\bmod 2 n)$, et par $f(x)=n$ sinon. Alors $f$ est $n$-positive. En effet, soit $x_{1}, \ldots, x_{n}$ des réels tels que $x_{1}+\ldots+x_{n}=0:$
$\triangleright$ S'il existe un entier $k$ tel que $f\left(x_{k}\right)=n$, et puisque $f\left(x_{i}\right) \geqslant-1$ pour tout $i \neq k$, on sait que $f\left(x_{1}\right)+\ldots+f\left(x_{k}\right) \geqslant f\left(x_{k}\right)-(n-1) \geqslant 1$.
$\triangleright$ Sinon, alors $x_{k} \equiv 1(\bmod 2 n)$ pour tout $k$, donc $x_{1}+\ldots+x_{n} \equiv n \not \equiv 0(\bmod 2 n)$, de sorte que ce cas est en fait impossible.
Cependant, $f$ n'est pas $2 n$-positive. En effet, si $x_{1}=1-2 n$ et $x_{2}=x_{3}=\ldots=x_{2 n}=1$, alors $x_{1}+\ldots+x_{2 n}=0$ mais $f\left(x_{1}\right)+\ldots+f\left(x_{2 n}\right)=-2 n<0$. La réponse est donc non!
Commentaire des correcteurs Les correcteurs ont repéré plusieurs confusions sur la notion de fonction. En effet, lafonction $f$ considérée ne change pas selon qu'il y a 1010 ou 2020 nombres réels.
D'autre part, si l'on veut démontrer qu'une assertion est fausse (par exemple, si l'on souhaite démontrer que toute fonction $f$ qui serait $n$-positive n'est pas nécessairement $2 n$-positive), la manière la plus simple de procéder reste encore de présenter un contre-exemple.
|
{
"resource_path": "French/segmented/tests/fr-2019-2020-corrigé-test-janvier.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
34520bea-1647-551e-ae32-5505c0e6200a
| 606,137
|
Let $a_{0}, a_{1}, a_{2}, \ldots$ be a sequence of non-zero natural numbers, and let $b_{0}, b_{1}, b_{2}, \ldots$ be the sequence such that $b_{n}=\operatorname{GCD}\left(a_{n}, a_{n+1}\right)$ for all integers $n \geqslant 0$. Is it possible that every non-zero natural number is equal to exactly one of the terms $b_{0}, b_{1}, b_{2}, \ldots$?
|
The answer is yes!
In the following, we will say that a sequence $\left(b_{k}\right)_{k \geqslant 0}$ is pleasant if, for all $k \geqslant 0$, the integers $b_{k}$ and $b_{k+2}$ are coprime. Given a pleasant sequence $\left(b_{k}\right)_{k \geqslant 0}$, let $a_{0}=b_{0}$ and then $a_{k}=b_{k-1} b_{k}$ for all $k \geqslant 0$. We then observe that $\operatorname{PGCD}\left(a_{0}, a_{1}\right)=b_{0}$ and that $\operatorname{PGCD}\left(a_{k}, a_{k+1}\right)=b_{k} \operatorname{PGCD}\left(b_{k-1}, b_{k+1}\right)=b_{k}$ for all $k \geqslant 1$. Therefore, it suffices to construct a pleasant sequence $\left(b_{k}\right)_{k \geqslant 0}$ such that every positive integer is equal to exactly one of the integers $b_{0}, b_{1}, b_{2}, \ldots$
To this end, and for all $k \geqslant 1$, let $p_{k}$ be the $k^{\text {th }}$ smallest prime number, and $q_{k}$ the $k^{\text {th }}$ smallest composite number and greater than or equal to 1. It is easily observed that $p_{k} \geqslant 2 k-1$ and that $q_{k} \leqslant 2 k$, hence $p_{k} \geqslant q_{k}-1$. We deduce that $q_{k} \leqslant p_{k}+1<2 p_{k}<2 p_{k+2}$, and thus $\operatorname{PGCD}\left(q_{k}, p_{k}\right)=\operatorname{PGCD}\left(q_{k}, p_{k+2}\right)=1$.
We then set $b_{4 k}=p_{2 k+1}, b_{4 k+1}=p_{2 k+2}, b_{4 k+2}=q_{2 k+1}$ and $b_{4 k+3}=q_{2 k+2}$ for all $k \geqslant 0$. First, every positive integer is indeed equal to exactly one of the integers $b_{0}, b_{1}, b_{2}, \ldots$. Furthermore, for all $k \geqslant 0$, and as shown above:
$\triangleright \operatorname{PGCD}\left(b_{4 k}, b_{4 k+2}\right)=\operatorname{PGCD}\left(p_{2 k+1}, q_{2 k+1}\right)=1$,
$\triangleright \operatorname{PGCD}\left(b_{4 k+1}, b_{4 k+3}\right)=\operatorname{PGCD}\left(p_{2 k+2}, q_{2 k+2}\right)=1$,
$\triangleright \operatorname{PGCD}\left(b_{4 k+2}, b_{4 k+4}\right)=\operatorname{PGCD}\left(p_{2 k+3}, q_{2 k+1}\right)=1$ and
$\triangleright \operatorname{PGCD}\left(b_{4 k+3}, b_{4 k+5}\right)=\operatorname{PGCD}\left(p_{2 k+4}, q_{2 k+2}\right)=1$.
The sequence $\left(b_{k}\right)_{k \geqslant 0}$ is therefore indeed a sequence as sought, which concludes the proof.
Comment from the graders: Many different constructions were found, leading to proofs of varying difficulty. A key idea was to think about choosing the sequence $\left(a_{n}\right)$ to have a simple expression for the sequence $\left(b_{n}\right)$.
Often, a proof by algorithm was used: after reducing the problem to finding a sequence $\left(b_{n}\right)$ such that $b_{n}$ and $b_{n+2}$ would be coprime, some students invoked a greedy algorithm, where at each step the smallest integer $b_{n}$ not yet chosen and suitable was chosen. This algorithm does indeed work, but the proof of its correctness was often incomplete:
$\triangleright$ it is necessary to first specify that such an integer $b_{n}$ can indeed be chosen at each step, for example by invoking the infinitude of the set of prime numbers;
$\triangleright$ it is then necessary to demonstrate that, in this case, all integers will indeed be chosen; for this purpose, it was sufficient, for example, to indicate that an infinite number of integers $b_{n}$ would be prime numbers, and to deduce that every number was indeed chosen.
## Senior Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $a_{0}, a_{1}, a_{2}, \ldots$ une suite d'entiers naturels non nuls, et soit $b_{0}, b_{1}, b_{2}, \ldots$ la suite telle que $b_{n}=\operatorname{PGCD}\left(a_{n}, a_{n+1}\right)$ pour tout entier $n \geqslant 0$. Est-il possible que tout entier naturel non nul soit égal à exactement un des termes $b_{0}, b_{1}, b_{2}, \ldots$ ?
|
La réponse est oui!
Dans la suite, on dira qu'une suite $\left(b_{k}\right)_{k \geqslant 0}$ est agréable si, pour tout $k \geqslant 0$, les entiers $b_{k}$ et $b_{k+2}$ sont premiers entre eux. Étant donnée une suite $\left(b_{k}\right)_{k \geqslant 0}$ agréable, posons $a_{0}=b_{0}$ puis $a_{k}=b_{k-1} b_{k}$ pour tout $k \geqslant 0$. On constate alors que $\operatorname{PGCD}\left(a_{0}, a_{1}\right)=b_{0}$ et que $\operatorname{PGCD}\left(a_{k}, a_{k+1}\right)=b_{k} \operatorname{PGCD}\left(b_{k-1}, b_{k+1}\right)=b_{k}$ pour tout $k \geqslant 1$. Il nous suffit donc de construire une suite $\left(b_{k}\right)_{k \geqslant 0}$ agréable telle que tout entier naturel non nul soit égal à exactement un des entiers $b_{0}, b_{1}, b_{2}, \ldots$
À cette fin, et pour tout $k \geqslant 1$, notons $p_{k}$ le $k^{\text {ème }}$ plus petit nombre premier, et $q_{k}$ le $k^{\text {ème }}$ plus petit entier composé et supérieur ou égal à 1 . On remarque aisément que $p_{k} \geqslant 2 k-1$ et que $q_{k} \leqslant 2 k$, donc que $p_{k} \geqslant q_{k}-1$. On en déduit que $q_{k} \leqslant p_{k}+1<2 p_{k}<2 p_{k+2}$, donc que $\operatorname{PGCD}\left(q_{k}, p_{k}\right)=\operatorname{PGCD}\left(q_{k}, p_{k+2}\right)=1$.
On pose alors $b_{4 k}=p_{2 k+1}, b_{4 k+1}=p_{2 k+2}, b_{4 k+2}=q_{2 k+1}$ et $b_{4 k+3}=q_{2 k+2}$ pour tout $k \geqslant 0$. Tout d'abord, tout entier naturel non nul est bien égal à exactement un des entiers $b_{0}, b_{1}, b_{2}, \ldots$. En outre, pour tout $k \geqslant 0$, et comme démontré ci-dessus :
$\triangleright \operatorname{PGCD}\left(b_{4 k}, b_{4 k+2}\right)=\operatorname{PGCD}\left(p_{2 k+1}, q_{2 k+1}\right)=1$ ,
$\triangleright \operatorname{PGCD}\left(b_{4 k+1}, b_{4 k+3}\right)=\operatorname{PGCD}\left(p_{2 k+2}, q_{2 k+2}\right)=1$ ,
$\triangleright \operatorname{PGCD}\left(b_{4 k+2}, b_{4 k+4}\right)=\operatorname{PGCD}\left(p_{2 k+3}, q_{2 k+1}\right)=1$ et
$\triangleright \operatorname{PGCD}\left(b_{4 k+3}, b_{4 k+5}\right)=\operatorname{PGCD}\left(p_{2 k+4}, q_{2 k+2}\right)=1$.
La suite $\left(b_{k}\right)_{k \geqslant 0}$ est donc bien une suite telle que recherchée, ce qui conclut.
Commentaire des correcteurs Beaucoup de constructions différentes ont été trouvées, menant à des preuves plus ou moins faciles. Une idée clé était de penser à choisir la suite $\left(a_{n}\right)$ pour avoir une expression simple de la suite $\left(b_{n}\right)$.
Souvent, une preuve par algorithme a été utilisée : après s'être ramenés à trouver une suite $\left(b_{n}\right)$ telle que $b_{n}$ et $b_{n+2}$ seraient premiers entre eux, certains élèves ont invoqué un algorithme glouton, où l'on choisissait à chaque fois le plus petit entier $b_{n}$ non pris qui convenait. Cet algorithme fonctionne effectivement, mais la preuve de correction de cet algorithme était très souvent incomplète :
$\triangleright$ il faut tout d'abord préciser que l'on peut bien choisir un tel entier $b_{n}$ à chaque étape, par exemple en invoquant l'infinité de l'ensemble des nombres premiers;
$\triangleright$ il faut ensuite démontrer que, dans ce cas, tous les entiers seront bien pris ; à cette fin, il suffisait par exemple de signaler qu'une infinité d'entiers $b_{n}$ seraient des nombres premiers, et en déduire que tout nombre était effectivement pris.
## Exercices Senior
|
{
"resource_path": "French/segmented/tests/fr-2019-2020-corrigé-test-janvier.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "## Solution de l'exercice 4"
}
|
ad03c9bf-7b89-573d-80de-50c98b32245f
| 606,147
|
Let $a_{0}, a_{1}, a_{2}, \ldots$ be a sequence of non-zero natural numbers, and let $b_{0}, b_{1}, b_{2}, \ldots$ be the sequence such that $b_{n}=\operatorname{GCD}\left(a_{n}, a_{n+1}\right)$ for all integers $n \geqslant 0$. Is it possible that every non-zero natural number is equal to exactly one of the terms $b_{0}, b_{1}, b_{2}, \ldots$?
|
The answer is yes!
In the following, we will say that a sequence $\left(b_{k}\right)_{k \geqslant 0}$ is pleasant if, for all $k \geqslant 0$, the integers $b_{k}$ and $b_{k+2}$ are coprime. Given a pleasant sequence $\left(b_{k}\right)_{k \geqslant 0}$, let $a_{0}=b_{0}$ and then $a_{k}=b_{k-1} b_{k}$ for all $k \geqslant 0$. We then observe that $\operatorname{PGCD}\left(a_{0}, a_{1}\right)=b_{0}$ and that $\operatorname{PGCD}\left(a_{k}, a_{k+1}\right)=b_{k} \operatorname{PGCD}\left(b_{k-1}, b_{k+1}\right)=b_{k}$ for all $k \geqslant 1$. Therefore, it suffices to construct a pleasant sequence $\left(b_{k}\right)_{k \geqslant 0}$ such that every positive integer is equal to exactly one of the integers $b_{0}, b_{1}, b_{2}, \ldots$
To this end, and for all $k \geqslant 1$, let $p_{k}$ be the $k^{\text {th }}$ smallest prime number, and $q_{k}$ the $k^{\text {th }}$ smallest composite number and greater than or equal to 1. It is easily observed that $p_{k} \geqslant 2 k-1$ and that $q_{k} \leqslant 2 k$, hence that $p_{k} \geqslant q_{k}-1$. We deduce that $q_{k} \leqslant p_{k}+1<2 p_{k}<2 p_{k+2}$, thus $\operatorname{PGCD}\left(q_{k}, p_{k}\right)=\operatorname{PGCD}\left(q_{k}, p_{k+2}\right)=1$.
We then set $b_{4 k}=p_{2 k+1}, b_{4 k+1}=p_{2 k+2}, b_{4 k+2}=q_{2 k+1}$ and $b_{4 k+3}=q_{2 k+2}$ for all $k \geqslant 0$. First, every positive integer is indeed equal to exactly one of the integers $b_{0}, b_{1}, b_{2}, \ldots$. Furthermore, for all $k \geqslant 0$, and as shown above:
$$
\begin{aligned}
& \triangleright \operatorname{PGCD}\left(b_{4 k}, b_{4 k+2}\right)=\operatorname{PGCD}\left(p_{2 k+1}, q_{2 k+1}\right)=1, \\
& \triangleright \operatorname{PGCD}\left(b_{4 k+1}, b_{4 k+3}\right)=\operatorname{PGCD}\left(p_{2 k+2}, q_{2 k+2}\right)=1, \\
& \triangleright \operatorname{PGCD}\left(b_{4 k+2}, b_{4 k+4}\right)=\operatorname{PGCD}\left(p_{2 k+3}, q_{2 k+1}\right)=1 \text { and } \\
& \triangleright \operatorname{PGCD}\left(b_{4 k+3}, b_{4 k+5}\right)=\operatorname{PGCD}\left(p_{2 k+4}, q_{2 k+2}\right)=1 .
\end{aligned}
$$
The sequence $\left(b_{k}\right)_{k \geqslant 0}$ is therefore indeed a sequence as sought, which concludes.
Comment from the graders: Many different constructions were found, leading to proofs of varying difficulty. A key idea was to think of choosing the sequence $\left(a_{n}\right)$ to have a simple expression for the sequence $\left(b_{n}\right)$.
Often, a proof by algorithm was used: after reducing to finding a sequence $\left(b_{n}\right)$ such that $b_{n}$ and $b_{n+2}$ would be coprime, some students invoked a greedy algorithm, where at each step the smallest integer $b_{n}$ not yet taken that worked was chosen. This algorithm does indeed work, but the proof of correctness of this algorithm was often incomplete:
$\triangleright$ it is necessary to first specify that one can indeed choose such an integer $b_{n}$ at each step, for example by invoking the infinitude of the set of prime numbers;
$\triangleright$ it is then necessary to show that, in this case, all integers will indeed be taken; for this purpose, it was sufficient, for example, to indicate that an infinite number of integers $b_{n}$ would be prime numbers, and to deduce that every number was indeed taken.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $a_{0}, a_{1}, a_{2}, \ldots$ une suite d'entiers naturels non nuls, et soit $b_{0}, b_{1}, b_{2}, \ldots$ la suite telle que $b_{n}=\operatorname{PGCD}\left(a_{n}, a_{n+1}\right)$ pour tout entier $n \geqslant 0$. Est-il possible que tout entier naturel non nul soit égal à exactement un des termes $b_{0}, b_{1}, b_{2}, \ldots$ ?
|
La réponse est oui!
Dans la suite, on dira qu'une suite $\left(b_{k}\right)_{k \geqslant 0}$ est agréable si, pour tout $k \geqslant 0$, les entiers $b_{k}$ et $b_{k+2}$ sont premiers entre eux. Étant donnée une suite $\left(b_{k}\right)_{k \geqslant 0}$ agréable, posons $a_{0}=b_{0}$ puis $a_{k}=b_{k-1} b_{k}$ pour tout $k \geqslant 0$. On constate alors que $\operatorname{PGCD}\left(a_{0}, a_{1}\right)=b_{0}$ et que $\operatorname{PGCD}\left(a_{k}, a_{k+1}\right)=b_{k} \operatorname{PGCD}\left(b_{k-1}, b_{k+1}\right)=b_{k}$ pour tout $k \geqslant 1$. Il nous suffit donc de construire une suite $\left(b_{k}\right)_{k \geqslant 0}$ agréable telle que tout entier naturel non nul soit égal à exactement un des entiers $b_{0}, b_{1}, b_{2}, \ldots$
À cette fin, et pour tout $k \geqslant 1$, notons $p_{k}$ le $k^{\text {ème }}$ plus petit nombre premier, et $q_{k}$ le $k^{\text {ème }}$ plus petit entier composé et supérieur ou égal à 1 . On remarque aisément que $p_{k} \geqslant 2 k-1$ et que $q_{k} \leqslant 2 k$, donc que $p_{k} \geqslant q_{k}-1$. On en déduit que $q_{k} \leqslant p_{k}+1<2 p_{k}<2 p_{k+2}$, donc que $\operatorname{PGCD}\left(q_{k}, p_{k}\right)=\operatorname{PGCD}\left(q_{k}, p_{k+2}\right)=1$.
On pose alors $b_{4 k}=p_{2 k+1}, b_{4 k+1}=p_{2 k+2}, b_{4 k+2}=q_{2 k+1}$ et $b_{4 k+3}=q_{2 k+2}$ pour tout $k \geqslant 0$. Tout d'abord, tout entier naturel non nul est bien égal à exactement un des entiers $b_{0}, b_{1}, b_{2}, \ldots$. En outre, pour tout $k \geqslant 0$, et comme démontré ci-dessus:
$$
\begin{aligned}
& \triangleright \operatorname{PGCD}\left(b_{4 k}, b_{4 k+2}\right)=\operatorname{PGCD}\left(p_{2 k+1}, q_{2 k+1}\right)=1, \\
& \triangleright \operatorname{PGCD}\left(b_{4 k+1}, b_{4 k+3}\right)=\operatorname{PGCD}\left(p_{2 k+2}, q_{2 k+2}\right)=1, \\
& \triangleright \operatorname{PGCD}\left(b_{4 k+2}, b_{4 k+4}\right)=\operatorname{PGCD}\left(p_{2 k+3}, q_{2 k+1}\right)=1 \text { et } \\
& \triangleright \operatorname{PGCD}\left(b_{4 k+3}, b_{4 k+5}\right)=\operatorname{PGCD}\left(p_{2 k+4}, q_{2 k+2}\right)=1 .
\end{aligned}
$$
La suite $\left(b_{k}\right)_{k \geqslant 0}$ est donc bien une suite telle que recherchée, ce qui conclut.
Commentaire des correcteurs Beaucoup de constructions différentes ont été trouvées, menant à des preuves plus ou moins faciles. Une idée clé était de penser à choisir la suite $\left(a_{n}\right)$ pour avoir une expression simple de la suite $\left(b_{n}\right)$.
Souvent, une preuve par algorithme a été utilisée : après s'être ramenés à trouver une suite $\left(b_{n}\right)$ telle que $b_{n}$ et $b_{n+2}$ seraient premiers entre eux, certains élèves ont invoqué un algorithme glouton, où l'on choisissait à chaque fois le plus petit entier $b_{n}$ non pris qui convenait. Cet algorithme fonctionne effectivement, mais la preuve de correction de cet algorithme était très souvent incomplète :
$\triangleright$ il faut tout d'abord préciser que l'on peut bien choisir un tel entier $b_{n}$ à chaque étape, par exemple en invoquant l'infinité de l'ensemble des nombres premiers;
$\triangleright$ il faut ensuite démontrer que, dans ce cas, tous les entiers seront bien pris; à cette fin, il suffisait par exemple de signaler qu'une infinité d'entiers $b_{n}$ seraient des nombres premiers, et en déduire que tout nombre était effectivement pris.
|
{
"resource_path": "French/segmented/tests/fr-2019-2020-corrigé-test-janvier.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "## Solution de l'exercice 5"
}
|
ad03c9bf-7b89-573d-80de-50c98b32245f
| 606,147
|
Let $P_{1}, P_{2}, \ldots, P_{2019}$ be non-constant polynomials with real coefficients such that
$$
P_{1}\left(P_{2}(x)\right)=P_{2}\left(P_{3}(x)\right)=\ldots=P_{2019}\left(P_{1}(x)\right)
$$
for all real $x$. Prove that $P_{1}=P_{2}=\ldots=P_{2019}$.
|
We will in fact demonstrate the more general result that if $P_{1}, \ldots, P_{2 n+1}$ are non-constant polynomials with real coefficients such that $P_{1} \circ P_{2} = P_{2} \circ P_{3} = \ldots = P_{2 n+1} \circ P_{1}$, then $P_{1} = \ldots = P_{2 n+1}$. For convenience, in the following, we set $P_{2 n+1+k} = P_{k}$ for all $k \geq 1$.
First, we denote $d_{k}$ as the degree of $P_{k}$. Since $P_{k} \circ P_{k+1}$ is a polynomial of degree $d_{k} d_{k+1}$, it follows that $d_{k} d_{k+1} = d_{k+1} d_{k+2}$, and thus $d_{k} = d_{k+2}$ for all $k$. We deduce that all polynomials $P_{k}$ have degree $d_{1}$, and we simply set $d = d_{1}$.
Next, let $p_{k}$ be the leading coefficient of $P_{k}$, i.e., its coefficient of degree $d$, and set $q_{k} = p_{k} / p_{k+1}$. The leading coefficient of $P_{k} \circ P_{k+1}$ is equal to $p_{k} p_{k+1}^{d}$. We deduce that $p_{k} p_{k+1}^{d} = p_{k+1} p_{k+2}^{d}$, which means $q_{k} = q_{k+1}^{-d}$. But then
$$
1 = \prod_{i=k+1}^{k+2 n+1} q_{i} = q_{k}^{s}
$$
where we have set
$$
s = \sum_{i=0}^{2 n} (-d)^{i} \equiv 1 \quad (\bmod 2).
$$
Since $s$ is an odd integer, it follows that $q_{k} = 1$. This means that all polynomials $P_{k}$ have the same leading coefficient $p_{1}$, and we simply set $p = p_{1}$.
Now suppose that $d = 1$. In this case, we can write each polynomial $P_{k}$ in the form $P_{k}(X) = p X + b_{k}$, and then $P_{k}(P_{k+1}(X)) = p^{2} X + p b_{k+1} + b_{k}$. We set $c_{k} = b_{k+1} - b_{k}$, and since the statement indicates that $p b_{k+1} + b_{k} = p b_{k+2} + b_{k+1}$, this means that $c_{k} = -p c_{k+1}$. Again, we deduce that $c_{k} = (-p)^{2 n+1} c_{k}$, so that $c_{k} = 0$ for all $k$, or that $p = -1$; but in the latter case, we still have $c_{k} = c_{k+1}$ for all $k$, so that $0 = \sum_{i=1}^{2 n+1} c_{i} = (2 n+1) c_{k}$ and thus $c_{k} = 0$ in any case. Thus, when $d = 1$, the polynomials $P_{k}$ are indeed equal to each other.
Finally, suppose that $d \geq 2$. We denote $p_{k, \ell}$ as the coefficient of $P_{k}$ of degree $\ell$, and we will prove by induction on $d - \ell$ that $p_{k, \ell} = p_{1, \ell}$. First, for $\ell = d$, we have $p_{k, d} = p = p_{1, d}$. We now assume that $p_{k, m} = p_{1, m}$ for all integers $m \geq \ell + 1$, and we study the coefficient of degree $d^{2} - d + \ell$ of the polynomial $P_{k} \circ P_{k+1}$. Writing $A \approx B$ whenever two polynomials $A$ and $B$ have the same coefficient of degree $d^{2} - d + \ell$, we observe that
$$
\begin{aligned}
P_{k}(P_{k+1}(X)) & = \sum_{i=0}^{d} p_{k, i} \left( \sum_{j=0}^{d} p_{k+1, j} X^{j} \right)^{i} \\
& \approx p \left( \sum_{j=0}^{d} p_{k+1, j} X^{j} \right)^{d} + p_{k, d-1} \left( \sum_{j=0}^{d} p_{k+1, j} X^{j} \right)^{d-1} \\
& \approx p \left( p_{k+1, \ell} X^{\ell} + \sum_{j=\ell+1}^{d} p_{1, j} X^{j} \right)^{d} + p_{k, d-1} (p X^{d})^{d-1} \\
& \approx d p_{k+1, \ell} p^{d} X^{d^{2} - d + \ell} + p \left( \sum_{j=\ell+1}^{d} p_{1, j} X^{j} \right)^{d} + p_{k, d-1} p^{d-1} X^{d^{2} - d}
\end{aligned}
$$
For $\ell \geq 1$, we deduce that $d p_{k+1, \ell} p^{d} = d p_{1, \ell} p^{d}$, which means that $p_{k+1, \ell} = p_{1, \ell}$. Then, for $\ell = 0$, we deduce that $d p_{k+1, 0} p^{d} + p_{k, d-1} = d p_{1, 0} p^{d} + p_{2 n+1, d-1}$. Since $d \geq 2$, when we reach the case $\ell = 0$, we already know that $p_{k, d-1} = p_{2 n+1, d-1}$. We thus deduce as expected that $p_{k+1, 0} = p_{1, 0}$, which concludes the proof.
Comment from the graders: This problem was extremely difficult, and scoring points on it was therefore challenging. Unfortunately, several students lost these hard-earned points by making avoidable errors, which we list below:
$\triangleright$ Many students confused the composition and the product of two polynomials. Thus, the composition $P \circ Q$ of two polynomials $P$ and $Q$ of degrees $d$ and $d'$ is a polynomial of degree $d \times d'$, not $d + d'$. Similarly, if $P$ and $Q$ have leading coefficients $p$ and $q$, then the leading coefficient of $P \circ Q$ is $p \times q^{d}$, not $p \times q$. Finally, the polynomials $P \circ (Q + R)$ and $(P \circ Q) + (P \circ R)$ are, in general, distinct polynomials.
$\triangleright$ Some students did not prove that the polynomials $P_{i}$ have the same degree, claiming it was obvious. However, this assertion depended on the oddness of 2019, making it far less obvious: it is advisable to avoid losing 1 point by saving a line of writing.
$\triangleright$ It is recommended not to call a polynomial $P'$ that one introduces, as $P'$ already denotes the derivative of $P$. Such notation can be confusing, both for the grader and for the student themselves!
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit $P_{1}, P_{2}, \ldots, P_{2019}$ des polynômes non constants à coefficients réels tels que
$$
P_{1}\left(P_{2}(x)\right)=P_{2}\left(P_{3}(x)\right)=\ldots=P_{2019}\left(P_{1}(x)\right)
$$
pour tout réel $x$. Démontrer que $P_{1}=P_{2}=\ldots=P_{2019}$.
|
Nous allons en fait démontrer le résultat plus général suivant : si $P_{1}, \ldots, P_{2 n+1}$ sont des polynômes non constants à coefficients réels et tels que $P_{1} \circ P_{2}=$ $P_{2} \circ P_{3}=\ldots=P_{2 n+1} \circ P_{1}$, alors $P_{1}=\ldots=P_{2 n+1}$. Par commodité, dans la suite, on pose $P_{2 n+1+k}=P_{k}$ pour tout $k \geqslant 1$.
Tout d'abord, on note $d_{k}$ le degré de $P_{k}$. Puisque $P_{k} \circ P_{k+1}$ est un polynôme de degré $d_{k} d_{k+1}$, $c^{\prime}$ est que $d_{k} d_{k+1}=d_{k+1} d_{k+2}$, et donc $d_{k}=d_{k+2}$, pour tout $k$. On en déduit que tous les polynômes $P_{k}$ ont degré $d_{1}$, et on pose simplement $d=d_{1}$.
Ensuite, soit $p_{k}$ le coefficient dominant de $P_{k}$, c'est-à-dire son coefficient de degré $d$, et posons $q_{k}=p_{k} / p_{k+1}$. Le coefficient dominant de $P_{k} \circ P_{k+1}$ est égal à $p_{k} p_{k+1}^{d}$. On en déduit que $p_{k} p_{k+1}^{d}=$ $p_{k+1} p_{k+2}^{d}$ , c'est-à-dire que $q_{k}=q_{k+1}^{-d}$. Mais alors
$$
1=\prod_{i=k+1}^{k+2 n+1} q_{i}=q_{k}^{s}
$$
où l'on a posé
$$
s=\sum_{i=0}^{2 n}(-d)^{i} \equiv 1 \quad(\bmod 2) .
$$
Puisque $s$ est un entier impair, $\mathrm{c}^{\prime}$ est donc que $q_{k}=1$. Cela signifie donc que tous les polynômes $P_{k}$ sont de coefficient dominant $p_{1}$, et on pose simplement $p=p_{1}$.
Supposons maintenant que $d=1$. Dans ce cas, on peut écrire chaque polynôme $P_{k}$ sous la forme $P_{k}(X)=p X+b_{k}$, et alors $P_{k}\left(P_{k+1}(X)\right)=p^{2} X+p b_{k+1}+b_{k}$. On pose alors $c_{k}=b_{k+1}-b_{k}$, et puisque l'énoncé indique entre autres que $p b_{k+1}+b_{k}=p b_{k+2}+b_{k+1}$, cela signifie en fait que $c_{k}=-p c_{k+1}$. Là encore, on en déduit que $c_{k}=(-p)^{2 n+1} c_{k}$, de sorte que $c_{k}=0$ pour tout $k$, ou bien que $p=-1$; mais, dans ce second cas, on a tout de même $c_{k}=c_{k+1}$ pour tout $k$, de sorte que $0=\sum_{i=1}^{2 n+1} c_{i}=(2 n+1) c_{k}$ et que l'on a $c_{k}=0$ de toute façon. Ainsi, quand $d=1$, les polynômes $P_{k}$ sont bien égaux deux à deux.
Supposons enfin que $d \geqslant 2$. On note $p_{k, \ell}$ le coefficient de $P_{k}$ de degré $\ell$, et on va prouver par récurrence sur $d-\ell$ que $p_{k, \ell}=p_{1, \ell}$. Tout d'abord, pour $\ell=d$, on a bien $p_{k, d}=p=p_{1, d}$. On suppose donc maintenant que $p_{k, m}=p_{1, m}$ pour tout entier $m \geqslant \ell+1$, et on étudie le coefficient de degré $d^{2}-d+\ell$ du polynôme $P_{k} \circ P_{k+1}$. En écrivant $A \approx B$ dès lors que deux polynômes $A$ et $B$ ont même coefficient de degré $d^{2}-d+\ell$, on constate que
$$
\begin{aligned}
P_{k}\left(P_{k+1}(X)\right) & =\sum_{i=0}^{d} p_{k, i}\left(\sum_{j=0}^{d} p_{k+1, j} X^{j}\right)^{i} \\
& \approx p\left(\sum_{j=0}^{d} p_{k+1, j} X^{j}\right)^{d}+p_{k, d-1}\left(\sum_{j=0}^{d} p_{k+1, j} X^{j}\right)^{d-1} \\
& \approx p\left(p_{k+1, \ell} X^{\ell}+\sum_{j=\ell+1}^{d} p_{1, j} X^{j}\right)^{d}+p_{k, d-1}\left(p X^{d}\right)^{d-1} \\
& \approx d p_{k+1, \ell} p^{d} X^{d^{2}-d+\ell}+p\left(\sum_{j=\ell+1}^{d} p_{1, j} X^{j}\right)^{d}+p_{k, d-1} p^{d-1} X^{d^{2}-d}
\end{aligned}
$$
Pour $\ell \geqslant 1$, on en déduit que $d p_{k+1, \ell} p^{d}=d p_{1, \ell} p^{d}$, ce qui signifie bien que $p_{k+1, \ell}=p_{1, \ell}$. Puis, pour $\ell=0$, on en déduit aussi que $d p_{k+1,0} p^{d}+p_{k, d-1}=d p_{1,0} p^{d}+p_{2 n+1, d-1}$. Or, puisque $d \geqslant 2$, quand on en arrive à étudier le cas $\ell=0$, on sait déjà que $p_{k, d-1}=p_{2 n+1, d-1}$. On en déduit donc comme prévu que $p_{k+1,0}=p_{1,0}$, ce qui conclut.
Commentaire des correcteurs Ce problème était extrêmement difficile, et y obtenir des points était donc ardu. Malheureusement, plusieurs élèves ont perdu ces points si durement acquis en commettant des erreurs évitables, que nous listons ci-dessous :
$\triangleright$ De nombreux élèves ont confondu la composée et le produit de deux polynômes. Ainsi, la composée $P \circ Q$ de deux polynômes $P$ et $Q$ de degrés $d$ et $d^{\prime}$ est un polynôme de degré $d \times d^{\prime}$, et non pas $d+d^{\prime}$. De même, si $P$ et $Q$ sont de coefficients dominants $p$ et $q$, alors le coefficient dominant de $P \circ Q$ est $p \times q^{d}$, et non pas $p \times q$. Enfin, les polynômes $P \circ(Q+R)$ et $(P \circ Q)+(P \circ R)$ sont, dans le cas général, des polynômes distincts l'un de l'autre.
$\triangleright$ Certains élèves n'ont pas démontré que les polynômes $P_{i}$ avaient même degré, affirmant qu'il s'agissait là d'une évidence. Cependant, cette affirmation dépendait de l'imparité de 2019, ce qui la rendait nettement moins évidente : il faut éviter de perdre bêtement 1 point pour économiser une ligne de rédaction.
$\triangleright$ Il est recommandé de ne pas appeler $P^{\prime}$ un polynôme que l'on introduit, car $P^{\prime}$ désigne déjà le polynôme dérivé de $P$. Une telle notation peut donc prêter à confusion, pour le correcteur mais aussi pour l'élève lui-même !
|
{
"resource_path": "French/segmented/tests/fr-2019-2020-corrigé-test-novembre.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
ab27b1a2-24ae-58af-a875-90af33687052
| 606,242
|
It is said that a sequence $\left(u_{n}\right)_{n \geqslant 0}$ of non-zero natural numbers is Sicilian if $^{-10}$
$$
u_{n+1} \in\left\{u_{n} / 2, u_{n} / 3,2 u_{n}+1,3 u_{n}+1\right\}
$$
for all $n \geqslant 0$. Prove that, for every integer $k \geqslant 1$, there exists a Sicilian sequence $\left(u_{n}\right)_{n \geqslant 0}$ and an integer $\ell \geqslant 0$ such that $u_{0}=k$ and $u_{\ell}=1$.
|
We will demonstrate, for any integer $k \geqslant 2$, the property $\mathcal{P}_{k}$ as follows: there exists a finite Sicilian sequence $\left(u_{0}, \ldots, u_{\ell}\right)$ such that $u_{0}=k$ and $u_{\ell}<k$.
The property $\mathcal{P}_{k}$ is immediate if $k$ is even, since it suffices to choose $u_{1}=k / 2$. Therefore, we assume $k$ is odd. Let $\alpha$ and $\kappa$ be non-zero natural numbers such that $k=2^{\alpha} \kappa-1$, with the integer $\kappa$ being odd. We then construct our Sicilian sequence as follows.
First, for all $i \leqslant \alpha-1$, we set $u_{2 i}=2^{\alpha-i} 3^{i} \kappa-1$ and $u_{2 i+1}=2^{\alpha-i} 3^{i+1} \kappa-2$. We then set $u_{2 \alpha}=3^{\alpha} \kappa-1$ and $u_{2 \alpha+1}=\left(3^{\alpha} \kappa-1\right) / 2$, which is indeed an integer since $\kappa$ is odd. Finally, for all $i \leqslant \alpha$, we set $u_{2 \alpha+2+i}=3^{\alpha-i} \kappa$. We then easily verify that the sequence $\left(u_{0}, \ldots, u_{3 \alpha+2}\right)$ is Sicilian. Indeed, we have $u_{2 i+1}=3 u_{2 i}+1$ and $u_{2 i+2}=u_{2 i+1} / 2$ for all $i \leqslant \alpha$, then $u_{2 \alpha+1}=u_{2 \alpha} / 2$ and $u_{2 \alpha+2}=2 u_{2 \alpha+1}+1$, and we also have $u_{2 \alpha+3+i}=u_{2 \alpha+2+i} / 3$ for all $i \leqslant \alpha-1$. Since $u_{0}=k$ and $u_{3 \alpha+2}=\kappa \leqslant(k+1) / 2<k$, this completes the proof of the property $\mathcal{P}_{k}$.
Armed with this property, we finally prove the statement in the problem by induction on $k$.
Comment from the graders: On this problem, many students had relevant ideas: performing a strong induction or trying to reduce to a term smaller than $u_{0}$ to ensure reaching 1. However, numerous calculation errors were observed when manipulating congruences: to divide a congruence modulo $m$ by $k$, one must also divide $m$ by $\operatorname{PGCD}(k, m)$. For example, we have $6 \equiv 2(\bmod 4)$, so we can deduce that $3 \equiv 1(\bmod 2)$, but certainly not that $3 \equiv 1(\bmod 4)$.
Some students managed to set up rigorous arguments to obtain the result for all values of $k$. Some treated many cases, reducing to increasingly complex cases: $k \equiv 3(\bmod 4)$, then $k \equiv 7(\bmod 8)$, and so on. The key insight was to consider the integer $k+1$ and its 2-adic valuation.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
On dit qu'une suite $\left(u_{n}\right)_{n \geqslant 0}$ d'entiers naturels non nuls est sicilienne si $^{-10}$
$$
u_{n+1} \in\left\{u_{n} / 2, u_{n} / 3,2 u_{n}+1,3 u_{n}+1\right\}
$$
pour tout $n \geqslant 0$. Démontrer que, pour tout entier $k \geqslant 1$, il existe une suite sicilienne $\left(u_{n}\right)_{n \geqslant 0}$ et un entier $\ell \geqslant 0$ tels que $u_{0}=k$ et $u_{\ell}=1$.
|
Nous allons démontrer, pour tout entier $k \geqslant 2$, la propriété $\mathcal{P}_{k}$ suivante : il existe une suite sicilienne finie $\left(u_{0}, \ldots, u_{\ell}\right)$ telle que $u_{0}=k$ et $u_{\ell}<k$.
La propriété $\mathcal{P}_{k}$ est immédiate si $k$ est pair, puisqu'il suffit de choisir $u_{1}=k / 2$. On suppose donc $k$ impair. Soit $\alpha$ et $\kappa$ les entiers naturels non nuls tels que $k=2^{\alpha} \kappa-1$, l'entier $\kappa$ étant impair. On construit alors notre suite sicilienne comme suit.
Tout d'abord, pour tout $i \leqslant \alpha-1$, on pose $u_{2 i}=2^{\alpha-i} 3^{i} \kappa-1$ et $u_{2 i+1}=2^{\alpha-i} 3^{i+1} \kappa-2$. On pose ensuite $u_{2 \alpha}=3^{\alpha} \kappa-1$ et $u_{2 \alpha+1}=\left(3^{\alpha} \kappa-1\right) / 2$, qui est bien un entier puisque $\kappa$ est impair. Enfin, pour tout $i \leqslant \alpha$, on pose $u_{2 \alpha+2+i}=3^{\alpha-i} \kappa$. On vérifie alors aisément que la suite $\left(u_{0}, \ldots, u_{3 \alpha+2}\right)$ est sicilienne. En effet, on a $u_{2 i+1}=3 u_{2 i}+1$ et $u_{2 i+2}=u_{2 i+1} / 2$ pour tout $i \leqslant \alpha$, puis $u_{2 \alpha+1}=u_{2 \alpha} / 2$ et $u_{2 \alpha+2}=2 u_{2 \alpha+1}+1$, et on a également $u_{2 \alpha+3+i}=u_{2 \alpha+2+i} / 3$ pour tout $i \leqslant \alpha-1$. Puisque $u_{0}=k$ et $u_{3 \alpha+2}=\kappa \leqslant(k+1) / 2<k$, cela achève de démontrer la propriété $\mathcal{P}_{k}$.
Forts de cette propriété, on démontre enfin l'assertion de l'énoncé par récurrence sur $k$.
Commentaire des correcteurs Sur ce problème, beaucoup d'élèves ont eu des idées pertinentes : faire une récurrence forte ou essayer de se ramener à un terme plus petit que $u_{0}$ pour s'assurer d'aboutir à 1 . Toutefois, on a constaté de nombreuses erreurs de calcul lors de la manipulation de congruences : pour diviser une égalité modulo $m$ par $k$, il faut également diviser $m$ par $\operatorname{PGCD}(k, m)$. Par exemple, on a $6 \equiv 2(\bmod 4)$, donc on peut en déduire que $3 \equiv 1(\bmod 2)$, mais certainement pas que $3 \equiv 1(\bmod 4)$.
Quelques élèves ont réussi à mettre en place des arguments rigoureux pour obtenir le résultat pour toute valeur de $k$. Certains ont traité de nombreux cas, se ramenant à des cas de plus en plus compliqués : $k \equiv 3(\bmod 4)$, puis $k \equiv 7(\bmod 8)$, et ainsi de suite. Il fallait alors se rendre compte que la bonne idée à avoir était de considérer l'entier $k+1$ et sa valuation 2 -adique.
|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-1.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
245893f1-d994-534a-b8bb-5c7dbad3e5a4
| 604,156
|
Let $ABC$ be a triangle with acute angles, and let $D$ be the foot of the altitude from vertex $A$. Let $X$ and $Y$ be the two points on the circumcircle of $ABC$ such that $AX = AY = AD$, and such that $B$ and $X$ are on the same side of the line $(AD)$. Let $E$ be the intersection point of the lines $(BX)$ and $(CY)$. Finally, let $F$ be the intersection point, other than $E$, between the line $(DE)$ and the circumcircle of $EXY$.
Prove that the circumcircles of triangles $BCF$ and $EXY$ are tangent.
|
In the following, we denote $\mathcal{C}_{U V W}$ as the circumcircle of a triangle $U V W$. Let $i$ be the inversion centered at $E$ that leaves the circle $\mathcal{C}_{A B C}$ globally invariant. This inversion exchanges the points $B$ and $X$, as well as the points $C$ and $Y$. Therefore, it exchanges the circle $\mathcal{C}_{E X Y}$ and the line $(B C)$. Since $i$ leaves the line $(D E)$ globally invariant, it exchanges $F$ with the intersection point of $(D E)$ and $(B C)$, which is the point $D$.
Consequently, the inversion $i$ exchanges the circles $\mathcal{C}_{B C F}$ and $\mathcal{C}_{X Y D}$. The latter circle has a radius $[A D]$, and it is therefore tangent to the line $(B C)$. Thus, the circles $\mathcal{C}_{B C F}$ and $\mathcal{C}_{E X Y}$ are themselves tangent.
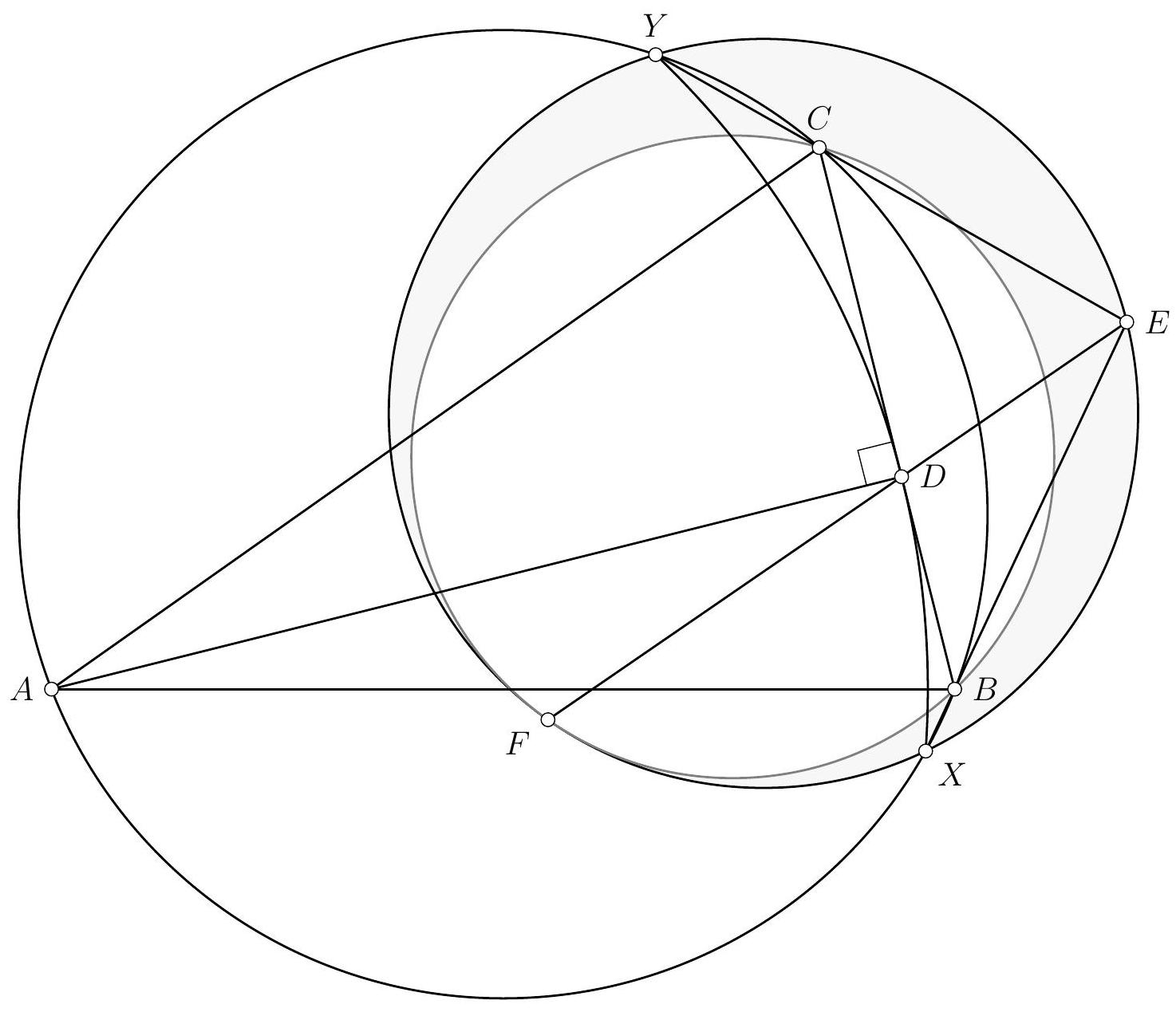
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle dont les angles sont aigus, et soit $D$ le pied de la hauteur issue du sommet $A$. Soit $X$ et $Y$ les deux points du cercle circonscrit à $A B C$ tels que $A X=A Y=A D$, et tels que $B$ et $X$ se trouvent du même côté de la droite $(A D)$. Soit $E$ le point d'intersection des droites $(B X)$ et $(C Y)$. Enfin, soit $F$ le point d'intersection, autre que $E$, entre la droite $(D E)$ et le cercle circonscrit à $E X Y$.
Démontrer que les cercles circonscrits aux triangles $B C F$ et $E X Y$ sont tangents.
|
Dans la suite, on note $\mathcal{C}_{U V W}$ le cercle circonscrit à un triangle $U V W$. Soit $i$ l'inversion de centre $E$ qui laisse le cercle $\mathcal{C}_{A B C}$ globalement invariant. Cette inversion échange les points $B$ et $X$, ainsi que les points $C$ et $Y$. Elle échange donc le cercle $\mathcal{C}_{E X Y}$ et la droite $(B C)$. Puisque $i$ laisse la droite $(D E)$ globalement invariante, elle échange donc $F$ avec le point d'intersection de $(D E)$ et $(B C)$, c'est-à-dire avec le point $D$.
Par conséquent, l'inversion $i$ échange les cercles $\mathcal{C}_{B C F}$ et $\mathcal{C}_{X Y D}$. Or, ce dernier cercle a pour rayon $[A D]$, et il est donc tangent à la droite ( $B C$ ). Ainsi, les cercles $\mathcal{C}_{B C F}$ et $\mathcal{C}_{E X Y}$ sont euxmêmes tangents.

|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-1.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
f1704904-6ba3-51ca-b0ce-172174459678
| 604,169
|
Let $ABC$ be a triangle with acute angles, and let $D$ be the foot of the altitude from vertex $A$. Let $X$ and $Y$ be the two points on the circumcircle of $ABC$ such that $AX = AY = AD$, and such that $B$ and $X$ are on the same side of the line $(AD)$. Let $E$ be the intersection point of the lines $(BX)$ and $(CY)$. Finally, let $F$ be the intersection point, other than $E$, between the line $(DE)$ and the circumcircle of $EXY$.
Prove that the circumcircles of triangles $BCF$ and $EXY$ are tangent.
|
$n^{\circ} 1$ In the following, we denote $\mathcal{C}_{U V W}$ as the circumcircle of triangle $U V W$. If $A B C$ is isosceles at $A$, the line $(A D)$ constitutes an axis of symmetry of the figure, and the result is immediate. Therefore, without loss of generality, we assume that $A B \neq A C$.
When drawing the figure, it is obviously important to highlight the triangle $A B C$ first, the isosceles triangles $A D X, A D Y$, and $A X Y$, and what appears to be the common tangent to the two circles $\mathcal{C}_{B C F}$ and $\mathcal{C}_{E X Y}$. We then notice that these three lines seem to be concurrent, and this is what we set out to prove.
Let $I$ be the intersection point of the lines $(X Y)$ and $(B C)$: this point exists because $A B C$ is not isosceles at $A$. We will prove that the line $(I F)$ is tangent to the circles $\mathcal{C}_{F B C}$ and $\mathcal{C}_{F X Y}$, which will give the desired result. By considering the power of the point $I$ with respect to the circles $\mathcal{C}_{F B C}$ and $\mathcal{C}_{F X Y}$, it is therefore necessary to prove that $I F^{2}$ is equal to $I X \cdot I Y$ and to $I B \cdot I C$. Since the lines $(B C)$ and $(A D)$ are perpendicular, the circle $\mathcal{C}_{X Y D}$ is tangent to the line $(B C)$. By considering the power of the point $I$ with respect to the circles $\mathcal{C}_{X Y D}$ and $\mathcal{C}_{A B C}$, we deduce that $I D^{2}=I X \cdot I Y=I B \cdot I C$. It is therefore necessary to prove that $I F=I D$. From there, we seek additional properties of the point $D$. If $(I F)$ is the common tangent sought and if $I F D$ is isosceles at $I$, then
$$
(F B, F D)=(F B, F I)+(F I, F D)=(C B, C F)+(F D, D I)=(F D, F C),
$$
and $(F D)$ is therefore the bisector of the angle $\widehat{B F C}$.
Conversely, if $(F D)$ is the bisector of $\widehat{B F C}$, and if $J$ is the intersection point between $(B C)$ and the tangent to $\mathcal{C}_{B C F}$ at $F$, the angle chasing above indicates that $J F D$ is isosceles at $J$, so $J D^{2}=J F^{2}=J B \cdot J C$. The point $J$ therefore has the same power with respect to the circles $\mathcal{C}_{B C F}$ and $\mathcal{C}_{D X Y}$, so it lies on their radical axis $(X Y)$, hence $I=J$. Thus, our problem is equivalent to proving that $(F D)$ is the bisector of the angle $\widehat{B F C}$.
To do this, we denote $G$ as the intersection point, other than $D$, between the circles $\mathcal{C}_{D B X}$ and $\mathcal{C}_{C D Y}$. Since
$$
(G Y, G X)=(G Y, G D)+(G D, G X)=(C Y, C D)+(B D, B X)=(E Y, E X)
$$
the point $G$ lies on the circle $\mathcal{C}_{E X Y}$. Furthermore, $E$ is the intersection point of the radical axes of $\mathcal{C}_{A B C}$ with $\mathcal{C}_{D B X}$ and $\mathcal{C}_{C D Y}$. It is therefore the radical center of these three circles, and $E$ lies on the radical axis of $\mathcal{C}_{D B X}$ and $\mathcal{C}_{C D Y}$, which is the line $(G D)$. This means that $F=G$.
We then conclude by simple angle chasing. Indeed,
$$
\begin{aligned}
(F B, F D)+(F C, F D) & =(G B, G D)+(G C, G D) \\
& =(X B, X D)+(Y C, Y D) \\
& =(B X, B C)+(D B, D X)+(C Y, C B)+(D C, D Y) \\
& =(Y X, Y C)+(Y D, Y X)+(X Y, X B)+(X D, X Y) \\
& =(Y D, Y C)+(X D, X B) .
\end{aligned}
$$
Thus, $2(X B, X D)+2(Y C, Y D)=0^{\circ}$, so the angles $\widehat{D F B}$ and $\widehat{C F D}$ are equal modulo $90^{\circ}$. Since $\widehat{D F B}=\widehat{D X B} \leqslant \widehat{C X B}=\widehat{C A B}<90^{\circ}$ and, similarly, $\widehat{C F D}<90^{\circ}$, we deduce that $\widehat{D F B}=\widehat{C F D}$, which concludes the problem.
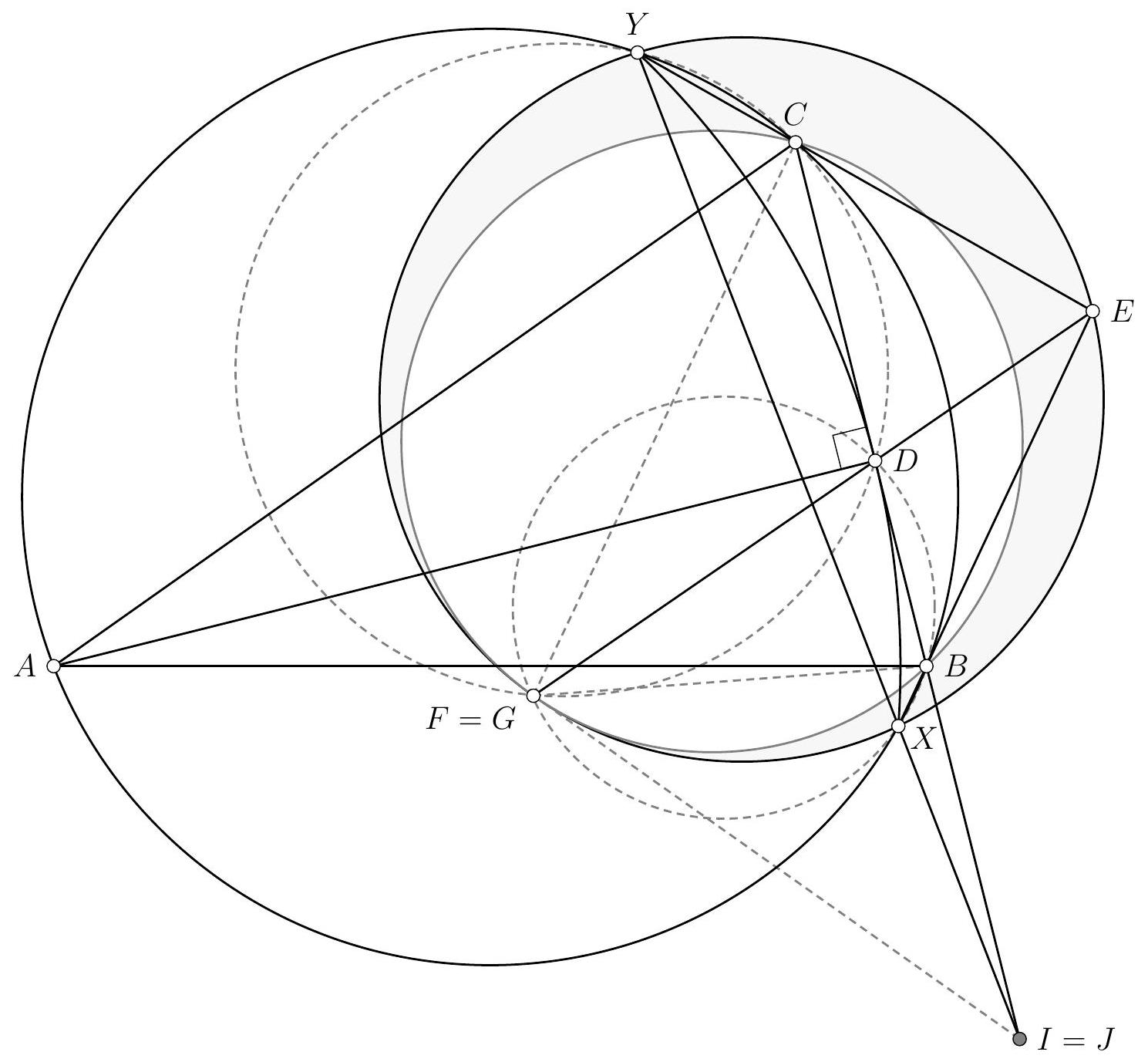
Comment from the graders: For this problem, several students highlighted a solution by inversion that the graders had not thought of: this is the solution $\mathrm{n}^{\circ} 1$ presented above. This method made the exercise significantly less difficult than the difficulty level estimated by the correction team.
Thus, a strong dichotomy was observed between students who recognized this inversion solution and those who did not recognize it or who are not adept at inversion and who, for the most part, were not able to make significant progress in the exercise. However, we commend the efforts and the approaches advanced by the students who attempted the exercise and who sometimes earned their author 1 or 2 partial points.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle dont les angles sont aigus, et soit $D$ le pied de la hauteur issue du sommet $A$. Soit $X$ et $Y$ les deux points du cercle circonscrit à $A B C$ tels que $A X=A Y=A D$, et tels que $B$ et $X$ se trouvent du même côté de la droite $(A D)$. Soit $E$ le point d'intersection des droites $(B X)$ et $(C Y)$. Enfin, soit $F$ le point d'intersection, autre que $E$, entre la droite $(D E)$ et le cercle circonscrit à $E X Y$.
Démontrer que les cercles circonscrits aux triangles $B C F$ et $E X Y$ sont tangents.
|
$n^{\circ} 1$ Dans la suite, on note $\mathcal{C}_{U V W}$ le cercle circonscrit au triangle $U V W . \mathrm{Si}$ $A B C$ est isocèle en $A$, la droite $(A D)$ constitue un axe de symétrie de la figure et le résultat est immédiat. On suppose donc, sans perte de généralité, que $A B \neq A C$.
Lorsque l'on trace la figure, il est évidemment important de mettre en évidence le triangle $A B C$ et départ, les triangles isocèles $A D X, A D Y$ et $A X Y$, et ce qui semble être la tangente commune aux deux cercles $\mathcal{C}_{B C F}$ et $\mathcal{C}_{E X Y}$. On remarque alors que ces trois droites semblent concourantes, et c'est donc ce que l'on entreprend de démontrer.
Soit $I$ le point d'intersection des droites $(X Y)$ et $(B C)$ : ce point existe bien, car $A B C$ n'est pas isocèle en $A$. Nous allons démontrer que la droite $(I F)$ est tangente aux cercles $\mathcal{C}_{F B C}$ et $\mathcal{C}_{F X Y}$, ce qui donnera le résultat désiré. En considérant la puissance du point $I$ par rapport aux cercles $\mathcal{C}_{F B C}$ et $\mathcal{C}_{F X Y}$, il s'agit donc de démontrer que $I F^{2}$ est égal à $I X \cdot I Y$ et à $I B \cdot I C$. Or, puisque les droites $(B C)$ et $(A D)$ sont perpendiculaires, le cercle $\mathcal{C}_{X Y D}$ est tangent à la droite $(B C)$. En considérant la puissance du point $I$ par rapport aux cercles $\mathcal{C}_{X Y D}$ et $\mathcal{C}_{A B C}$, on en déduit donc que $I D^{2}=I X \cdot I Y=I B \cdot I C$. Il s'agit donc de démontrer que $I F=I D$. Dès lors, on cherche des propriétés supplémentaires sur le point $D$. Si $(I F)$ est la tangente commune recherchée et si $I F D$ est isocèle en $I$, alors
$$
(F B, F D)=(F B, F I)+(F I, F D)=(C B, C F)+(F D, D I)=(F D, F C),
$$
et $(F D)$ est donc la bissectrice de l'angle $\widehat{B F C}$.
Réciproquement, si $(F D)$ est la bissectrice de $\widehat{B F C}$, et en notant $J$ le point d'intersection entre $(B C)$ et la tangente à $\mathcal{C}_{B C F}$ en $F$, la chasse aux angles ci-dessus indique que $J F D$ est isocèle en $J$, donc que $J D^{2}=J F^{2}=J B \cdot J C$. Le point $J$ a donc même puissance par rapport aux cercles $\mathcal{C}_{B C F}$ et $\mathcal{C}_{D X Y}$, donc il appartient à leur axe radical $(X Y)$, de sorte que $I=J$. Ainsi, notre problème est équivalent à démontrer que $(F D)$ est donc la bissectrice de l'angle $\widehat{B F C}$.
Pour cela, on note $G$ le point d'intersection, autre que $D$, entre les cercles $\mathcal{C}_{D B X}$ et $\mathcal{C}_{C D Y}$. Puisque
$$
(G Y, G X)=(G Y, G D)+(G D, G X)=(C Y, C D)+(B D, B X)=(E Y, E X)
$$
les point $G$ appartient au cercle $\mathcal{C}_{E X Y}$. En outre, $E$ est le point de concourt des axes radicaux de $\mathcal{C}_{A B C}$ avec $\mathcal{C}_{D B X}$ et $\mathcal{C}_{C D Y}$. Il s'agit donc du centre radical de ces trois cercles, et $E$ appartient donc à l'axe radical de $\mathcal{C}_{D B X}$ et $\mathcal{C}_{C D Y}$, c'est-à-dire à la droite (GD). Cela signifie que $F=G$.
On conclut alors par simple chasse aux angles. En effet,
$$
\begin{aligned}
(F B, F D)+(F C, F D) & =(G B, G D)+(G C, G D) \\
& =(X B, X D)+(Y C, Y D) \\
& =(B X, B C)+(D B, D X)+(C Y, C B)+(D C, D Y) \\
& =(Y X, Y C)+(Y D, Y X)+(X Y, X B)+(X D, X Y) \\
& =(Y D, Y C)+(X D, X B) .
\end{aligned}
$$
Ainsi, $2(X B, X D)+2(Y C, Y D)=0^{\circ}$, de sorte que les angles $\widehat{D F B}$ et $\widehat{C F D}$ sont égaux modulo $90^{\circ}$. Comme $\widehat{D F B}=\widehat{D X B} \leqslant \widehat{C X B}=\widehat{C A B}<90^{\circ}$ et, de même, $\widehat{C F D}<90^{\circ}$, on en déduit que $\widehat{D F B}=\widehat{C F D}$, ce qui conclut le problème.

Commentaire des correcteurs Pour ce problème, plusieurs élèves ont mis en évidence une solution par inversion à laquelle les correcteurs n'avaient pas pensé : il s'agit de la solution $\mathrm{n}^{\circ} 1$ présentée ci-dessus. Cette méthode rendait l'exercice nettement moins difficile que le niveau de difficulté estimé par l'équipe de correction.
Ainsi, on a observé une forte dichotomie entre les élèves ayant repéré cette solution par inversion et les élèves qui ne l'ont pas repérée ou qui ne sont pas adeptes de l'inversion et qui n'ont, pour la plupart, pas pu avancer de façon significative dans l'exercice. Toutefois, nous saluons les efforts et les pistes avancées par les élèves ayant tenté l'exercice et qui ont parfois pu rapporter à leur auteur 1 ou 2 points partiels.
|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-1.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution alternative"
}
|
f1704904-6ba3-51ca-b0ce-172174459678
| 604,169
|
Let $n=2021$. Prove that the number $3^{2 n+1}+2^{n+2}$ is divisible by 35.
|
We will demonstrate that the number $S_{n}=3^{2 n+1}+2^{n+2}$ is simultaneously divisible by 5 and by 7 when $n=2021$.
We immediately verify that
$$
S_{n} \equiv 9^{n} \times 3+2^{n} \times 4 \equiv 2^{n} \times 3+2^{n} \times 4 \equiv 2^{n} \times 7 \equiv 0 \quad(\bmod 7),
$$
which means that $S_{n}$ is indeed divisible by 7.
We then verify that
$$
S_{n} \equiv 9^{n} \times 3+2^{n} \times 4 \equiv(-1)^{n} \times 3+2^{n} \times(-1) \equiv-3-2^{n} \quad(\bmod 5).
$$
The required property clearly depends on the value of $n$, as it would have been invalid if we had chosen $n=3$.
We therefore calculate the first few values of $S_{n}(\bmod 5)$ to get some ideas:
$$
\begin{array}{ll}
\triangleright S_{0} \equiv-3-1 \equiv 1(\bmod 5) ; & \triangleright S_{4} \equiv-3-16 \equiv 1(\bmod 5) ; \\
\triangleright S_{1} \equiv-3-2 \equiv 0(\bmod 5) ; & \triangleright S_{5} \equiv-3-32 \equiv 0(\bmod 5) ; \\
\triangleright S_{2} \equiv-3-4 \equiv 3(\bmod 5) ; & \triangleright S_{6} \equiv-3-64 \equiv 3(\bmod 5) ; \\
\triangleright S_{3} \equiv-3-8 \equiv 4(\bmod 5) ; & \triangleright S_{7} \equiv-3-128 \equiv 4(\bmod 5) .
\end{array}
$$
It is clearly visible that $S_{n} \equiv 0(\bmod 5)$ when $n \equiv 1(\bmod 4)$, and we therefore set out to prove this. If we set $n=4 k+1$, then
$$
S_{n} \equiv-3-2^{4 k+1} \equiv-3-16^{k} \times 2 \equiv-3-1^{k} \times 2 \equiv-3-2 \equiv 0 \quad(\bmod 5)
$$
Thus, when $n=2021$, we indeed have $n \equiv 1(\bmod 4)$, and the integer $S_{n}$ is therefore divisible by 5.
In conclusion, the integer $S_{n}$ is divisible by both 5 and 7, so it is also divisible by their LCM, which is 35.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
On pose $n=2021$. Démontrer que le nombre $3^{2 n+1}+2^{n+2}$ est divisible par 35.
|
Nous allons démontrer que le nombre $S_{n}=3^{2 n+1}+2^{n+2}$ est divisible simultanément par 5 et par 7 lorsque $n=2021$.
On vérifie immédiatement que
$$
S_{n} \equiv 9^{n} \times 3+2^{n} \times 4 \equiv 2^{n} \times 3+2^{n} \times 4 \equiv 2^{n} \times 7 \equiv 0 \quad(\bmod 7),
$$
ce qui signifie bien que $S_{n}$ est divisible par 7 .
On vérifie ensuite que
$$
S_{n} \equiv 9^{n} \times 3+2^{n} \times 4 \equiv(-1)^{n} \times 3+2^{n} \times(-1) \equiv-3-2^{n} \quad(\bmod 5) .
$$
La propriété demandée dépend donc manifestement de la valeur de $n$, puisqu'elle aurait été invalide si on avait choisi $n=3$.
On calcule donc les premières valeurs de $S_{n}(\bmod 5)$ pour se donner des idées :
$$
\begin{array}{ll}
\triangleright S_{0} \equiv-3-1 \equiv 1(\bmod 5) ; & \triangleright S_{4} \equiv-3-16 \equiv 1(\bmod 5) ; \\
\triangleright S_{1} \equiv-3-2 \equiv 0(\bmod 5) ; & \triangleright S_{5} \equiv-3-32 \equiv 0(\bmod 5) ; \\
\triangleright S_{2} \equiv-3-4 \equiv 3(\bmod 5) ; & \triangleright S_{6} \equiv-3-64 \equiv 3(\bmod 5) ; \\
\triangleright S_{3} \equiv-3-8 \equiv 4(\bmod 5) ; & \triangleright S_{7} \equiv-3-128 \equiv 4(\bmod 5) .
\end{array}
$$
Il apparaît visiblement que $S_{n} \equiv 0(\bmod 5)$ lorsque $n \equiv 1(\bmod 4)$, et on entreprend donc de le démontrer. Si l'on pose $n=4 k+1$, alors
$$
S_{n} \equiv-3-2^{4 k+1} \equiv-3-16^{k} \times 2 \equiv-3-1^{k} \times 2 \equiv-3-2 \equiv 0 \quad(\bmod 5)
$$
Ainsi, lorsque $n=2021$, on a bien $n \equiv 1(\bmod 4)$, et l'entier $S_{n}$ est donc divisible par 5 .
En conclusion, l'entier $S_{n}$ est divisible à la fois par 5 et par 7, donc il est également divisible par leur PPCM, c'est-à-dire 35.
|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-2.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution de l'exercice 1"
}
|
0f35cdb3-5eb8-5a33-a362-cc26fe3c199a
| 604,197
|
Let $n=2021$. Prove that the number $3^{2 n+1}+2^{n+2}$ is divisible by 35.
|
$n^{\circ} 1$ Fermat's little theorem assures us that $2^{4} \equiv 3^{4} \equiv 1(\bmod 5)$. Since $2 n+1 \equiv 4043 \equiv 3(\bmod 4)$ and $n+2 \equiv 2023 \equiv 3(\bmod 4)$, we deduce that $S_{n} \equiv$ $3^{3}+2^{3} \equiv 35 \equiv 0(\bmod 5)$.
Similarly, Fermat's little theorem assures us that $2^{6} \equiv 3^{6} \equiv 1(\bmod 7)$. Since $2 n+1 \equiv$ $4043 \equiv-1(\bmod 6)$ and $n+2 \equiv 2023 \equiv 1(\bmod 6)$, we deduce that $S_{n} \equiv 3^{5}+2^{1} \equiv 245 \equiv 0$ $(\bmod 7)$.
In conclusion, the sum $S_{n}$ is divisible by 5 and by 7, hence by 35.
Examiner's Comment This problem was generally well done, to the great satisfaction of the examiners. Most students had good ideas and good reflexes:
$\triangleright$ to reduce the problem to studying the divisibility of $S_{n}$ by 5 and by 7;
$\triangleright$ to study small values of $n$;
$\triangleright$ to consider the powers of 2 and 3 separately and study their last digits, i.e., their congruence modulo 10;
$\triangleright$ to notice that a pattern was repeating.
These are very encouraging signs!
Some students also directly invoked Fermat's little theorem, which states that $a^{p-1} \equiv 1(\bmod p)$ when $p$ is a prime number that does not divide $a$. This result allowed them to reach the solution more quickly, and also made the divisibility by 5 and by 7 symmetric.
However, the examiners also noted several mathematical or strategic errors, which they wish to highlight to prevent students from making them again. Here, first, are the most frequent mathematical errors:
$\triangleright$ Several students made mistakes in manipulating powers and wrote, incorrectly, equalities of the form $a^{k}+b^{\ell}=(a+b)^{k+\ell}$. When one "invents" such an algebraic identity, there is a strong chance that it is false, and a very important step is therefore to look for possible counterexamples: if one does not find any, one will have more confidence in one's identity. Here, taking $a=b=k=\ell=1$ is enough to confirm that $a^{k}+b^{\ell}=1+1=2 \neq 4=2^{2}=(a+b)^{k+\ell}$.
$\triangleright$ Several students incorrectly believed that one could reduce the exponents modulo $m$. Certainly, if $a \equiv b(\bmod m)$, then $a+c \equiv b+c(\bmod m)$ and $a c \equiv b c(\bmod m)$ for any $c$. However, in general, $c^{a} \not \equiv c^{b}(\bmod m)$. This is the case, for example, when $a=1, b=4$, $c=2$ and $m=3$, since then $c^{a} \equiv 2^{1} \equiv 2 \not \equiv 16 \equiv 2^{4} \equiv c^{b}(\bmod m)$.
$\triangleright$ Several students incorrectly claimed that a number is divisible by 7 if and only if the number formed by its last two digits is divisible by 7. This divisibility criterion is clearly incorrect, since 100 and 700 have the same last digits but only 700 is divisible by 7. Moreover, if such a criterion existed, and given its simplicity, it would certainly be taught in school, which is not the case.
$\triangleright$ Many students confused necessary and sufficient conditions. They thus claimed that "if $S_{n}$ is divisible by $35=5 \times 7$", it is also divisible by 5 and by 7. This information is certainly true, but it is also useless to us. What was expected of the students was to formulate the reciprocal implication, which is also the one they used: "if $S_{n}$ is divisible by 5 and by 7, it is also divisible by $35=5 \times 7$".
Here are, next, the most frequent strategic errors:
$\triangleright$ Several students believed, based on a false reasoning or a calculation error, that they had demonstrated that 35 does not divide $S_{n}$. Instead of concluding that the statement was incorrect, it would have been more judicious to first question themselves and recheck the calculations made and the correctness of the arguments invoked.
$\triangleright$ Many students, after studying the last digit of $2^{n}$ and $3^{n}$ to deduce that 5 divides $S_{n}$, did not think to take a step back and realize that it would suffice to do the same but write all our numbers in base 7 rather than base 10. In general, when one breaks down a problem into two sub-problems that appear analogous and solves one of the sub-problems, it is very useful to take the time to think about how one could adapt the reasoning used to solve the other sub-problem.
$\triangleright$ Many students, after noticing that the last digits of $2^{n}$ seemed to repeat in the cycle $2,4,8,6,2,4,8,6, \ldots$, claimed that this was the case without trying to prove it. Instead of a proof, they relied on a mere conjecture. Since this conjecture played a central role in their solution, it was essential to prove it.
The examiners here decided not to penalize the lack of this proof, as it was the first timed POFM test of their lives for most candidates.
However, in other circumstances, omitting this proof could have been quite heavily penalized, to the tune of 2 or 3 points out of 7.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
On pose $n=2021$. Démontrer que le nombre $3^{2 n+1}+2^{n+2}$ est divisible par 35.
|
$n^{\circ} 1$ Le petit théorème de Fermat nous assure que $2^{4} \equiv 3^{4} \equiv 1(\bmod 5)$. Comme $2 n+1 \equiv 4043 \equiv 3(\bmod 4)$ et $n+2 \equiv 2023 \equiv 3(\bmod 4)$, on en déduit que $S_{n} \equiv$ $3^{3}+2^{3} \equiv 35 \equiv 0(\bmod 5)$.
De même, le petit théorème de Fermat nous assure que $2^{6} \equiv 3^{6} \equiv 1(\bmod 7)$. Comme $2 n+1 \equiv$ $4043 \equiv-1(\bmod 6)$ et $n+2 \equiv 2023 \equiv 1(\bmod 6)$, on en déduit que $S_{n} \equiv 3^{5}+2^{1} \equiv 245 \equiv 0$ $(\bmod 7)$.
En conclusion, la somme $S_{n}$ est divisible par 5 et par 7, donc par 35.
Commentaire des correcteurs Cet exercice a été globalement bien réussi, à la grande satisfaction des correcteurs. La plupart des élèves ont eu bonnes idées et de bons réflexes :
$\triangleright$ se ramener à étudier la divisibilité de $S_{n}$ par 5 et par 7;
$\triangleright$ étudier les petites valeurs de $n$;
$\triangleright$ considérer séparément les puissances de 2 et de 3 et étudier leur chiffre des unités, c'est-à-dire leur congruence modulo 10;
$\triangleright$ repérer qu'un motif se répétait.
Il s'agit là de signes très encourageants!
Certains élèves ont aussi invoqué directement le petit théorème de Fermat, qui stipule que $a^{p-1} \equiv 1(\bmod p)$ quand $p$ est un nombre premier qui ne divise pas $a$. Ce résultat permettait d'aboutir plus rapidement à la solution, et avait aussi le bon goût de rendre les divisibilités par 5 et par 7 symétriques.
Néanmoins, les correcteurs ont également repéré plusieurs erreurs, mathématiques ou stratégiques, qu'ils tiennent à souligner pour éviter aux élèves de les commettre à nouveau. Voici, tout d'abord, les erreurs mathématiques les plus fréquentes:
$\triangleright$ Plusieurs élèves se sont trompés en manipulant les puissances, et ont écrit, à tort, des égalités de la forme $a^{k}+b^{\ell}=(a+b)^{k+\ell}$. Quand on « invente» une telle identité algébrique, il y a de fortes chances qu'elle soit fausse, et une étape très importante est donc de rechercher des contre-exemples éventuels : si on n'en trouve pas, on aura davantage confiance en notre identité. Ici, prendre $a=b=k=\ell=1$ suffit à confirmer que $a^{k}+b^{\ell}=1+1=2 \neq 4=2^{2}=(a+b)^{k+\ell}$.
$\triangleright$ Plusieurs élèves ont cru à tort que l'on pouvait réduire les exposants modulo $m$. Certes, si $a \equiv b(\bmod m)$, on a bien $a+c \equiv b+c(\bmod m)$ et $a c \equiv b c(\bmod m)$ pour tout $c$. En revanche, en général, $c^{a} \not \equiv c^{b}(\bmod m)$. C'est le cas, par exemple, quand $a=1, b=4$, $c=2$ et $m=3$, puisque alors $c^{a} \equiv 2^{1} \equiv 2 \not \equiv 16 \equiv 2^{4} \equiv c^{b}(\bmod m)$.
$\triangleright$ Plusieurs élèves ont affirmé, à tort, qu'un nombre est divisible par 7 si et seulement si le nombre formé par ses deux derniers chiffres est divisible par 7. Ce critère de divisibilité est manifestement incorrect, puisque 100 et 700 ont les mêmes derniers chiffres mais que seul 700 est divisible par 7 . En outre, si un tel critère existait, et au vu de sa simplicité, il serait certainement enseigné à l'école, ce qui n'est pas le cas.
$\triangleright$ De nombreux élèves ont confondu conditions nécessaires et suffisantes. Ils ont ainsi affirmé que « si $S_{n}$ est divisible par $35=5 \times 7$ », il est aussi divisible par 5 et par 7 ». Cette information est certes vraie, mais elle nous est aussi inutile. On attendait des élèves qu'ils formulent l'implication réciproque, qui est d'ailleurs celle qu'ils ont utilisée : «si $S_{n}$ est divisible par 5 et par 7, il est aussi divisible par $35=5 \times 7$ ».
Voici, ensuite, les erreurs stratégiques les plus fréquentes :
$\triangleright$ Plusieurs élèves ont cru, en s'appuyant sur un raisonnement faux ou sur une erreur de calcul, démontrer que 35 ne divisait pas $S_{n}$. Dans pareil cas, au lieu de conclure au fait que l'énoncé était incorrect, il aurait été plus judicieux de se remettre d'abord en question, et revérifiant les calculs effectués et la correction des arguments invoqués.
$\triangleright$ De nombreux élèves, après avoir étudié le chiffre des unités de $2^{n}$ et $3^{n}$ pour en déduire que 5 divisait $S_{n}$, n'ont pas pensé à prendre du recul pour se dire qu'il suffisait de faire la même chose mais en écrivant tous nos nombres en base 7 plutôt qu'en base 10. De manière générale, quand on découpe un problème en deux sous-problèmes d'apparences analogues et que l'on résout un des deux sous-problèmes, il est très utile de prendre le temps de réfléchir à la façon dont on pourrait adapter le raisonnement utilisé pour résoudre l'autre sous-problème.
$\triangleright$ De nombreux élèves, après avoir repéré que les chiffres des unités de $2^{n}$ semblaient se répéter en formant le cycle $2,4,8,6,2,4,8,6, \ldots$, ont affirmé que c'était le cas sans essayer de le démontrer. Au lieu d'une démonstration, ils se sont donc appuyés sur une simple conjecture. Puisque cette conjecture tenait un rôle central dans leur solution, il était cependant indispensable de la démontrer.
Les correcteurs ont ici décidé de ne pas pénaliser l'absence de cette démonstration, car il s'agissait du premier test POFM en temps limité de leur vie pour la plupart des candidats.
Cependant, en d'autres circonstances, omettre cette démonstration aurait pu être assez lourdement sanctionné, à hauteur de 2 ou 3 points sur 7.
|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-2.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution alternative"
}
|
0f35cdb3-5eb8-5a33-a362-cc26fe3c199a
| 604,197
|
We define the sequence $a_{1}, a_{2}, a_{3} \ldots$ as follows: $a_{1}=63$ and, for all integers $n \geqslant 2, a_{n}$ is the smallest multiple of $n$ that is greater than or equal to $a_{n-1}$. Prove that the terms of our sequence are pairwise distinct.
|
It is clear that the sequence $\left(a_{n}\right)_{n \geqslant 1}$ is increasing. Therefore, it is necessary to prove that it is strictly increasing.
We calculate the first terms of the sequence: $a_{1}=63, a_{2}=64, a_{3}=66, a_{4}=68, a_{5}=70$, $a_{6}=72, a_{7}=77, a_{8}=80, a_{9}=81, a_{10}=90, a_{11}=99, a_{12}=108, a_{13}=117 . .$.
A property then becomes apparent: it seems that $a_{n}=9 n$ for all $n \geqslant 9$. In practice, it is good to verify this conjecture on a few additional values of $n$ to be convinced that it is true. We therefore set out to prove this property by induction.
First, as mentioned above, we have $a_{9}=9^{2}$. Then, for any integer $n \geqslant 9$ such that $a_{n}=9 n$, we observe that $8(n+1)=a_{n}-(n-8)<a_{n}<9(n+1)$, so that $a_{n+1}=9(n+1)$.
In conclusion, the sequence $\left(a_{n}\right)_{n \geqslant 1}$ is strictly increasing as long as $n \leqslant 9$, and it is clearly so when $n \geqslant 9$. Its terms are therefore indeed distinct from each other.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
On définit la suite $a_{1}, a_{2}, a_{3} \ldots$ de la façon suivante : $a_{1}=63$ et, pour tout entier $n \geqslant 2, a_{n}$ est le plus petit multiple de $n$ qui soit supérieur ou égal à $a_{n-1}$. Démontrer que les termes de notre suite sont deux à deux distincts.
|
Il est clair que la suite $\left(a_{n}\right)_{n \geqslant 1}$ est croissante. Il s'agit donc de démontrer qu'elle est strictement croissante.
On calcule donc les premiers termes de la suite : $a_{1}=63, a_{2}=64, a_{3}=66, a_{4}=68, a_{5}=70$, $a_{6}=72, a_{7}=77, a_{8}=80, a_{9}=81, a_{10}=90, a_{11}=99, a_{12}=108, a_{13}=117 . .$.
Une propriété se dessine alors sous nos yeux : il semble que $a_{n}=9 n$ pour tout $n \geqslant 9$. En pratique, il est bon de vérifier cette conjecture sur quelques valeurs supplémentaires de $n$, pour se convaincre qu'elle est vraie. On entreprend donc de démontrer cette propriété par récurrence.
Tout d'abord, comme mentionné ci-dessus, on a bien $a_{9}=9^{2}$. Puis, pour tout entier $n \geqslant 9$ tel que $a_{n}=9 n$, on constate que $8(n+1)=a_{n}-(n-8)<a_{n}<9(n+1)$, de sorte que $a_{n+1}=9(n+1)$.
En conclusion, la suite $\left(a_{n}\right)_{n \geqslant 1}$ est strictement croissante tant que $n \leqslant 9$, et elle l'est manifestement quand $n \geqslant 9$. Ses termes sont donc en effet distincts deux à deux.
|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-2.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
9fd345aa-b716-59b0-a714-8a815c0914e2
| 604,241
|
We define the sequence $a_{1}, a_{2}, a_{3} \ldots$ as follows: $a_{1}=63$ and, for all integers $n \geqslant 2, a_{n}$ is the smallest multiple of $n$ that is greater than or equal to $a_{n-1}$. Prove that the terms of our sequence are pairwise distinct.
|
$n^{\circ} 1$ As in the previous solution, it is clear that the sequence $\left(a_{n}\right)_{n \geqslant 1}$ is increasing. Therefore, it is necessary to prove, for all integers $n \geqslant 1$, that $a_{n} \neq a_{n+1}$, that is, $n(n+1)$ does not divide $a_{n}$.
We then calculate the first terms of the sequence, up to $a_{9}=81$, and observe that $n(n+1)$ does not divide $a_{n}$ when $n \leqslant 9$. We then prove that $a_{n}<n(n+1)$ for all integers $n \geqslant 9$.
Indeed, this is the case if $n=9$. Then, for all integers $n \geqslant 9$ such that $a_{n}<n(n+1)$, we observe that $a_{n+1} \leqslant a_{n}+n<n(n+2)<(n+1)^{2}$, which concludes the proof.
Comment from the graders: Many students had interesting ideas that allowed them to make progress in solving this difficult problem. When faced with such a statement, it is important to look at how the sequence $\left(a_{n}\right)$ behaves, and therefore to calculate its first terms: one can try to look at the first 10 or 20 terms to get an idea of the sequence. This idea proved particularly fruitful here, as it allowed conjecturing that $a_{n}=9 n$ when $n \geqslant 9$, which seems a priori easier to prove than the initial statement.
However, be careful with the writing! Students who started a recurrence often wrote that $a_{n}=9 n$ since $a_{n+1}=k(n+1)$ for some $k$, and then tried to find $k$, but only managed to show that $k \leqslant 9$ or that $k \geqslant 9$, forgetting the other inequality: it is important to properly justify why $k=9$.
Moreover, in this exercise, it was possible to empirically notice that $a_{n}=9 n$ when $n \geqslant 9$, but without being able to prove it. In such a case, it is obviously necessary to mention such a conjecture, and then see how it could be used to solve the problem. Indeed, the more complete the reasoning is and the fewer elements are missing to justify, the more points it will be worth. Admitting a result obviously costs points (and if the result that is admitted is as difficult to prove as the initial statement, it can even cost all the points), but it is often possible to formulate a conjecture and then deduce the desired result from it.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
On définit la suite $a_{1}, a_{2}, a_{3} \ldots$ de la façon suivante : $a_{1}=63$ et, pour tout entier $n \geqslant 2, a_{n}$ est le plus petit multiple de $n$ qui soit supérieur ou égal à $a_{n-1}$. Démontrer que les termes de notre suite sont deux à deux distincts.
|
$n^{\circ} 1$ Comme dans la solution précédente, il est clair que la suite $\left(a_{n}\right)_{n \geqslant 1}$ est croissante. Il s'agit donc de démontrer, pour tout entier $n \geqslant 1$, que $a_{n} \neq a_{n+1}$, c'est-à-dire que $n(n+1)$ ne divise pas $a_{n}$.
On calcule alors les premiers termes de la suite, jusqu'à $a_{9}=81$, et l'on constate bien que $n(n+1)$ ne divise pas $a_{n}$ lorsque $n \leqslant 9$. On démontre ensuite que $a_{n}<n(n+1)$ pour tout entier $n \geqslant 9$.
En effet, c'est bien le cas si $n=9$. Puis, pour tout entier $n \geqslant 9$ tel que $a_{n}<n(n+1)$, on constate que $a_{n+1} \leqslant a_{n}+n<n(n+2)<(n+1)^{2}$, ce qui conclut.
Commentaire des correcteurs De nombreux élèves ont eu des idées intéressantes et leur permettant d'avancer dans la résolution de ce problème pourtant difficile. Face à un tel énoncé, il est important de regarder comment la suite $\left(a_{n}\right)$ se comporte, et donc en calculer les premiers termes : on peut essayer de regarder les 10 ou 20 premiers termes pour se faire une idée de la suite. Cette idée s'avérait particulièrement fructueuse ici, puisqu'elle permettait de conjecturer que $a_{n}=9 n$ lorsque $n \geqslant 9$, ce qui semble a priori plus facile à prouver que l'énoncé initial.
Néanmoins, attention à la rédaction! Les élèves qui ont entamé une récurrence on souvent écrit que $a_{n}=9 n$ puisque $a_{n+1}=k(n+1)$ pour un certain $k$, et ont ensuite tenté de trouver $k$, mais ont uniquement démontré que $k \leqslant 9$ ou que $k \geqslant 9$, oubliant l'autre inégalité : il est important de bien justifier pourquoi $k=9$.
Par ailleurs, dans cet exercice, il était possible de remarquer empiriquement que $a_{n}=9 n$ lorsque $n \geqslant 9$, mais sans parvenir à le démontrer. Dans ce cas, il faut évidemment mentionner une telle conjecture, puis voir comment on pourrait l'utiliser pour résoudre l'exercice. En effet, plus le raisonnement est complet et moins il manque d'éléments à justifier, et plus il vaudra de points. Admettre un résultat coûte évidemment des points (et si le résultat que l'on admet est aussi difficile à démontrer que l'énoncé initial, cela peut même coûter l'intégralité des points), mais il est souvent possible de formuler une conjecture puis d'en déduire le résultat désiré.
|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-2.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution alternative"
}
|
9fd345aa-b716-59b0-a714-8a815c0914e2
| 604,241
|
Let $P_{1} P_{2} \ldots P_{2021}$ be a convex polygon with 2021 vertices such that, for each vertex $P_{i}$, the 2018 diagonals emanating from $P_{i}$ divide the angle $\widehat{P}_{i}$ into 2019 equal angles.
Prove that $P_{1} P_{2} \ldots P_{2021}$ is a regular polygon, that is, a polygon where all angles have the same measure and all sides have the same length.
|
In the following, we set \( n=2019 \) and, for any vertex \( P_{i} \), we denote \( a_{i} \) as the angle \( \widehat{P}_{i} / n \). Let \( P_{k} \), \( P_{k+1} \), \( P_{k+2} \), \( P_{k+3} \), and \( P_{k+4} \) be four consecutive vertices, with the indices of the vertices considered modulo \( n+2 \).
The sum of the angles in a triangle is \( 180^{\circ} \). By considering the triangles \( P_{i} P_{i+1} P_{i+2} \), \( P_{i} P_{i+1} P_{i+3} \), and \( P_{i} P_{i+1} P_{i+4} \), we observe that
\[
\begin{aligned}
a_{i} + n a_{i+1} + a_{i+2} & = 180^{\circ} \\
2 a_{i} + (n-1) a_{i+1} + a_{i+3} & = 180^{\circ} \\
3 a_{i} + (n-2) a_{i+1} + a_{i+4} & = 180^{\circ}
\end{aligned}
\]
We will then subtract these equations two by two:
\(\triangleright (1)-(2)\) indicates that \( a_{i+1} + a_{i+2} = a_{i} + a_{i+3} \), which means \( a_{i+1} - a_{i} = a_{i+3} - a_{i+2} \);
\(\triangleright (2)-(3)\) indicates that \( a_{i+1} + a_{i+3} = a_{i} + a_{i+4} \), which means \( a_{i+1} - a_{i} = a_{i+4} - a_{i+3} \).
We observe that \( a_{i+4} - a_{i+3} = a_{i+3} - a_{i+2} \). The difference between two consecutive angles \( a_{j} \) and \( a_{j+1} \) is therefore equal to a constant \( \mathbf{c} \).
This means that \( a_{i+k} = a_{i} + k \mathbf{c} \) for all integers \( i \) and \( k \). In particular, \( a_{1} = a_{n+3} = a_{1} + (n+2) \mathbf{c} \), so \( \mathbf{c} = 0^{\circ} \). Thus, our polygon has all its vertices equal.
The triangle \( P_{i} P_{i+1} P_{i+2} \) is therefore isosceles at \( P_{i+1} \), so that \( P_{i} P_{i+1} = P_{i+1} P_{i+2} \). Since two consecutive sides are of the same length, our polygon has all its sides of the same length, and it is indeed a regular polygon.
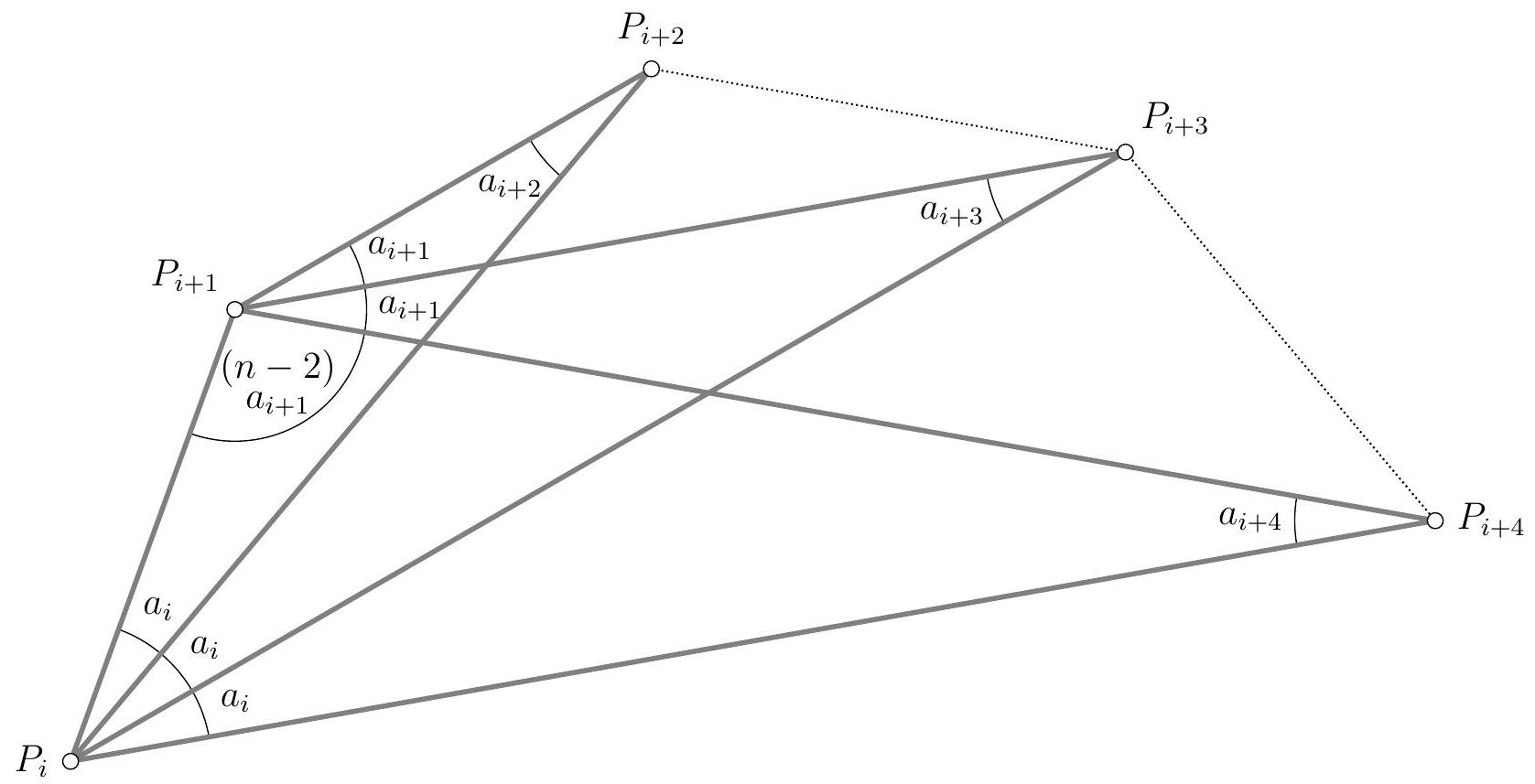
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $P_{1} P_{2} \ldots P_{2021}$ un polygone convexe à 2021 sommets tel que, pour chaque sommet $P_{i}$, les 2018 diagonales issues de $P_{i}$ divisent l'angle $\widehat{P}_{i}$ en 2019 angles égaux.
Démontrer que $P_{1} P_{2} \ldots P_{2021}$ est un polygone régulier, c'est-à-dire un polygone dont tous les angles ont même mesure et tous les côtés ont même longueur.
|
Dans la suite, on pose $n=2019$ et, pour tout sommet $P_{i}$, on note $a_{i}$ l'angle $\widehat{P}_{i} / n$. Soit alors $P_{k}$, $P_{k+1}, P_{k+2}, P_{k+3}$ et $P_{k+4}$ quatre sommets consécutifs, les indices des sommets étant considérés modulo $n+2$.
La somme des angles d'un triangle vaut $180^{\circ}$. En considérant respectivement les triangles $P_{i} P_{i+1} P_{i+2}, P_{i} P_{i+1} P_{i+3}$ et $P_{i} P_{i+1} P_{i+4}$, on constate que
$$
\begin{aligned}
a_{i}+n a_{i+1}+a_{i+2} & =180^{\circ} \\
2 a_{i}+(n-1) a_{i+1}+a_{i+3} & =180^{\circ} \\
3 a_{i}+(n-2) a_{i+1}+a_{i+4} & =180^{\circ}
\end{aligned}
$$
Nous allons alors soustraire deux à deux ces équations :
$\triangleright(11)-(2)$ indique que $a_{i+1}+a_{i+2}=a_{i}+a_{i+3}$, c'est-à-dire que $a_{i+1}-a_{i}=a_{i+3}-a_{i+2}$;
$\triangleright(2)-(3)$ indique que $a_{i+1}+a_{i+3}=a_{i}+a_{i+4}$, c'est-à-dire que $a_{i+1}-a_{i}=a_{i+4}-a_{i+3}$.
On constate donc que $a_{i+4}-a_{i+3}=a_{i+3}-a_{i+2}$. La différence entre deux angles $a_{j}$ et $a_{j+1}$ consécutifs est donc égale à une constante $\mathbf{c}$.
Cela signifie que $a_{i+k}=a_{i}+k \mathbf{c}$ pour tous les entiers $i$ et $k$. En particulier, $a_{1}=a_{n+3}=$ $a_{1}+(n+2) \mathbf{c}$, donc $\mathbf{c}=0^{\circ}$. Ainsi, notre polygone a tous ses sommets égaux.
Le triangle $P_{i} P_{i+1} P_{i+2}$ est donc isocèle en $P_{i+1}$, de sorte que $P_{i} P_{i+1}=P_{i+1} P_{i+2}$. Deux côtés consécutifs étant de même longueur, notre polygone a donc tous ses côtés de même longueur, et il s'agit bien d'un polygone régulier.

|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-2.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "## Solution de l'exercice 4"
}
|
e68d3c5f-f895-5a75-aeb1-b95d25645d46
| 604,259
|
Let $P_{1} P_{2} \ldots P_{2021}$ be a convex polygon with 2021 vertices such that, for each vertex $P_{i}$, the 2018 diagonals emanating from $P_{i}$ divide the angle $\widehat{P}_{i}$ into 2019 equal angles.
Prove that $P_{1} P_{2} \ldots P_{2021}$ is a regular polygon, that is, a polygon where all angles have the same measure and all sides have the same length.
|
$n^{\circ} 2$ As previously, we prove the equality (1). If we set $b_{i}=a_{i}-180^{\circ} /(n+2)$, this equality can be rewritten as $b_{i}+n b_{i+1}+b_{i+2}=0$.
The sequence $\left(b_{i}\right)_{i \geqslant 1}$ is therefore a linear recurrence. If we denote $r_{+}$ and $r_{-}$ the two roots of the polynomial $1+n X+X^{2}$, that is,
$$
r_{ \pm}=\frac{-n \pm \sqrt{n^{2}-4}}{2}
$$
there exist two numbers $\lambda_{+}$ and $\lambda_{-}$ such that
$$
b_{i}=\lambda_{+} r_{+}^{i}+\lambda_{-} r_{-}^{i}
$$
for all $i \geqslant 0$.
Since $n \geqslant 5$, we know that
$$
\left(n^{2}-4\right)-(n-2)^{2}=2(n-4)>0
$$
so that $r_{-} \leqslant-n / 2<-1<r_{+}<0$ and that we know $\left|r_{-}\right|>1>\left|r_{+}\right|$. Consequently, we know that, if $\lambda_{-} \neq 0$, the fraction $b_{i} /\left(\lambda_{-} r_{-}^{i}\right)$ tends to 1 as $i \rightarrow+\infty$. However, the sequence $\left(b_{i}\right)_{i \geqslant 1}$ is $(n+2)$-periodic. We deduce that $\lambda_{-}=0$.
Similarly, if $\lambda_{+} \neq 0$, the fraction $b_{i} /\left(\lambda_{+} r_{+}^{i}\right)$ tends to 1 as $i \rightarrow+\infty$, in contradiction with the $(n+2)$-periodic nature of the sequence $\left(b_{i}\right)_{i \geqslant 1}$. We deduce that $\lambda_{+}=0$, so that $b_{i}=0$ for all $i \geqslant 1$.
In conclusion, all the angles $a_{i}$ are equal, and we prove as previously that the sides of the polygon are equal as well.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $P_{1} P_{2} \ldots P_{2021}$ un polygone convexe à 2021 sommets tel que, pour chaque sommet $P_{i}$, les 2018 diagonales issues de $P_{i}$ divisent l'angle $\widehat{P}_{i}$ en 2019 angles égaux.
Démontrer que $P_{1} P_{2} \ldots P_{2021}$ est un polygone régulier, c'est-à-dire un polygone dont tous les angles ont même mesure et tous les côtés ont même longueur.
|
$n^{\circ} 2$ Comme précédemment, on démontre l'égalité (1). Si l'on pose $b_{i}=a_{i}-180^{\circ} /(n+2)$, cette égalité se réécrit comme $b_{i}+n b_{i+1}+b_{i+2}=0$.
La suite $\left(b_{i}\right)_{i \geqslant 1}$ est donc récurrente linéaire. Si l'on note $r_{+}$et $r_{-}$les deux racines du polynôme $1+n X+X^{2}$, c'est-à-dire
$$
r_{ \pm}=\frac{-n \pm \sqrt{n^{2}-4}}{2}
$$
il existe donc deux nombres $\lambda_{+}$et $\lambda_{-}$tels que
$$
b_{i}=\lambda_{+} r_{+}^{i}+\lambda_{-} r_{-}^{i}
$$
pour tout $i \geqslant 0$.
Puisque $n \geqslant 5$, on sait que
$$
\left(n^{2}-4\right)-(n-2)^{2}=2(n-4)>0
$$
donc que $r_{-} \leqslant-n / 2<-1<r_{+}<0$ et que on sait que $\left|r_{-}\right|>1>\left|r_{+}\right|$. Par conséquent, on sait que, si $\lambda_{-} \neq 0$, la fraction $b_{i} /\left(\lambda_{-} r_{-}^{i}\right)$ tend vers 1 quand $i \rightarrow+\infty$. Or, la suite $\left(b_{i}\right)_{i \geqslant 1}$ est $(n+2)$-périodique. On en déduit que $\lambda_{-}=0$.
De même, si $\lambda_{+} \neq 0$, la fraction $b_{i} /\left(\lambda_{+} r_{+}^{i}\right)$ tend vers 1 quand $i \rightarrow+\infty$, en contradiction avec le caractère $(n+2)$-périodique de la suite $\left(b_{i}\right)_{i \geqslant 1}$. On en déduit que $\lambda_{+}=0$, donc que $b_{i}=0$ pour tout $i \geqslant 1$.
En conclusion, tous les angles $a_{i}$ sont égaux, et on démontre comme précédemment que les côtés du polygone sont égaux eux aussi.
|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-2.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "\nSolution alternative"
}
|
e68d3c5f-f895-5a75-aeb1-b95d25645d46
| 604,259
|
Let $P_{1} P_{2} \ldots P_{2021}$ be a convex polygon with 2021 vertices such that, for each vertex $P_{i}$, the 2018 diagonals emanating from $P_{i}$ divide the angle $\widehat{P}_{i}$ into 2019 equal angles.
Prove that $P_{1} P_{2} \ldots P_{2021}$ is a regular polygon, that is, a polygon where all angles have the same measure and all sides have the same length.
|
$n^{\circ} 3$ As before, we prove the equality (1). By writing this equality for two consecutive integers $i$, and subtracting the two obtained equalities, we observe that
$$
a_{i}+(n-1) a_{i+1}-(n-1) a_{i+2}-a_{i+3}=0.
$$
The sequence $a_{i}$ is therefore a linear recurrence. This time, the roots of the polynomial
$$
1+(n-1) X-(n-1) X^{2}-X^{3}=(1-X)\left(1+n X+X^{2}\right)
$$
are $r_{\pm}$ and 1. Since $n \geqslant 5$, we know that
$$
\left(n^{2}-4\right)-(n-2)^{2}=2(n-4)>0
$$
so that $r_{-} \leqslant -n / 2 < -1 < r_{+} < 0 < 1$ and that $\left|r_{-}\right| > 1 > \left|r_{+}\right|$.
Therefore, there exist three numbers $\lambda_{+}, \lambda_{1}$, and $\lambda_{-}$ such that
$$
a_{i}=\lambda_{+} r_{+}^{i}+\lambda_{1}+\lambda_{-} r_{-}^{i}
$$
for all $i \in \mathbb{Z}$. As in the previous solution, we prove that $\lambda_{-}=0$. Similarly, if $\lambda_{+} \neq 0$, then $a_{i} / \left(\lambda_{+} r_{+}^{i}\right) \rightarrow 1$ as $i \rightarrow -\infty$, contradicting the periodicity of $\left(a_{i}\right)$. Thus, $\lambda_{+}=0.1$
[^0]In conclusion, all the angles $a_{i}$ are equal to $\lambda_{1}$, and we prove as before that the sides of the polygon are also equal.
Remark: This problem was proposed in 2003, at the First Year Mathematical Olympiads, in the Academy of Versailles, but with intermediate questions included. Out of the 623 candidates present in the academy, including two national laureates, none managed to solve this problem, which proved to be particularly difficult despite requiring few technical tools.
Comment from the markers: The problem, being difficult, was fully solved by only a very few students. Many students, however, managed to earn partial points by establishing interesting equations between the angles, or by showing that if all the angles of the polygon were equal, then all the sides of the polygon were also of the same length.
## Senior Problems
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $P_{1} P_{2} \ldots P_{2021}$ un polygone convexe à 2021 sommets tel que, pour chaque sommet $P_{i}$, les 2018 diagonales issues de $P_{i}$ divisent l'angle $\widehat{P}_{i}$ en 2019 angles égaux.
Démontrer que $P_{1} P_{2} \ldots P_{2021}$ est un polygone régulier, c'est-à-dire un polygone dont tous les angles ont même mesure et tous les côtés ont même longueur.
|
$n^{\circ} 3$ Comme précédemment, on démontre l'égalité (1). En écrivant cette égalité pour deux entiers $i$ consécutifs, et en soustrayant les deux égalités obtenues, on constate que
$$
a_{i}+(n-1) a_{i+1}-(n-1) a_{i+2}-a_{i+3}=0 .
$$
La suite $a_{i}$ est donc récurrente linéaire. Cette fois-ci, les racines du polynôme
$$
1+(n-1) X-(n-1) X^{2}-X^{3}=(1-X)\left(1+n X+X^{2}\right)
$$
sont $r_{ \pm}$et 1 . Puisque $n \geqslant 5$, on sait que
$$
\left(n^{2}-4\right)-(n-2)^{2}=2(n-4)>0
$$
donc que $r_{-} \leqslant-n / 2<-1<r_{+}<0<1$ et que on sait que $\left|r_{-}\right|>1>\left|r_{+}\right|$.
Il existe donc trois nombres $\lambda_{+}, \lambda_{1}$ et $\lambda_{-}$tels que
$$
a_{i}=\lambda_{+} r_{+}^{i}+\lambda_{1}+\lambda_{-} r_{-}^{i}
$$
pour tout $i \in \mathbb{Z}$. On démontre comme dans la solution précédente que $\lambda_{-}=0$. De même, si $\lambda_{+} \neq 0$, alors $a_{i} /\left(\lambda_{+} r_{+}^{i}\right) \rightarrow 1$ quand $i \rightarrow-\infty$, en contradiction avec le caractère périodique de $\left(a_{i}\right)$. Ainsi, $\lambda_{+}=0.1$
[^0]En conclusion, tous les angles $a_{i}$ sont égaux à $\lambda_{1}$, et on démontre comme précédemment que les côtés du polygone sont égaux eux aussi.
Remarque : Cet exercice avait été proposé en 2003, aux Olympiades mathématiques de première, dans l'académie de Versailles, mais en incluant des questions intermédiaires. Sur les 623 candidats présents dans l'académie, dont deux lauréats nationaux, aucun n'était parvenu à résoudre cet exercice, qui s'était donc révélé particulièrement difficile bien qu'abordable avec peu d'outils techniques.
Commentaire des correcteurs L'exercice, difficile, n'a été complètement résolu que par très peu d'élèves. Un grand nombre d'élèves ont tout de même réussi à obtenir des points partiels en établissant des équations intéressantes entre les angles, ou bien en montrant que, si tous les angles du polygone étaient égaux, alors tous les côtés du polygone étaient également de même longueur.
## Problèmes Senior
|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-2.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "\nSolution alternative"
}
|
e68d3c5f-f895-5a75-aeb1-b95d25645d46
| 604,259
|
Let $P_{1} P_{2} \ldots P_{2021}$ be a convex polygon with 2021 vertices such that, for each vertex $P_{i}$, the 2018 diagonals emanating from $P_{i}$ divide the angle $\widehat{P}_{i}$ into 2019 equal angles.
Prove that $P_{1} P_{2} \ldots P_{2021}$ is a regular polygon, that is, a polygon where all angles have the same measure and all sides have the same length.
|
In the following, we set \( n=2019 \) and, for any vertex \( P_{i} \), we denote \( a_{i} \) as the angle \( \widehat{P}_{i} / n \). Let \( P_{k} \), \( P_{k+1} \), \( P_{k+2} \), \( P_{k+3} \), and \( P_{k+4} \) be four consecutive vertices, with the indices of the vertices considered modulo \( n+2 \).
The sum of the angles in a triangle is \( 180^{\circ} \). By considering the triangles \( P_{i} P_{i+1} P_{i+2} \), \( P_{i} P_{i+1} P_{i+3} \), and \( P_{i} P_{i+1} P_{i+4} \), we observe that
\[
\begin{aligned}
a_{i} + n a_{i+1} + a_{i+2} & = 180^{\circ} \\
2 a_{i} + (n-1) a_{i+1} + a_{i+3} & = 180^{\circ} \\
3 a_{i} + (n-2) a_{i+1} + a_{i+4} & = 180^{\circ}
\end{aligned}
\]
We will then subtract these equations two by two:
\(\triangleright\) (1) - (2) indicates that \( a_{i+1} + a_{i+2} = a_{i} + a_{i+3} \), which means \( a_{i+1} - a_{i} = a_{i+3} - a_{i+2} \);
\(\triangleright\) (2) - (3) indicates that \( a_{i+1} + a_{i+3} = a_{i} + a_{i+4} \), which means \( a_{i+1} - a_{i} = a_{i+4} - a_{i+3} \).
We observe that \( a_{i+4} - a_{i+3} = a_{i+3} - a_{i+2} \). The difference between two consecutive angles \( a_{j} \) and \( a_{j+1} \) is therefore equal to a constant \(\mathbf{c}\).
This means that \( a_{i+k} = a_{i} + k \mathbf{c} \) for all integers \( i \) and \( k \). In particular, \( a_{1} = a_{n+3} = a_{1} + (n+2) \mathbf{c} \), so \(\mathbf{c} = 0^{\circ}\). Thus, our polygon has all its vertices equal.
The triangle \( P_{i} P_{i+1} P_{i+2} \) is therefore isosceles at \( P_{i+1} \), so that \( P_{i} P_{i+1} = P_{i+1} P_{i+2} \). Since two consecutive sides are of the same length, our polygon has all its sides of the same length, and it is indeed a regular polygon.
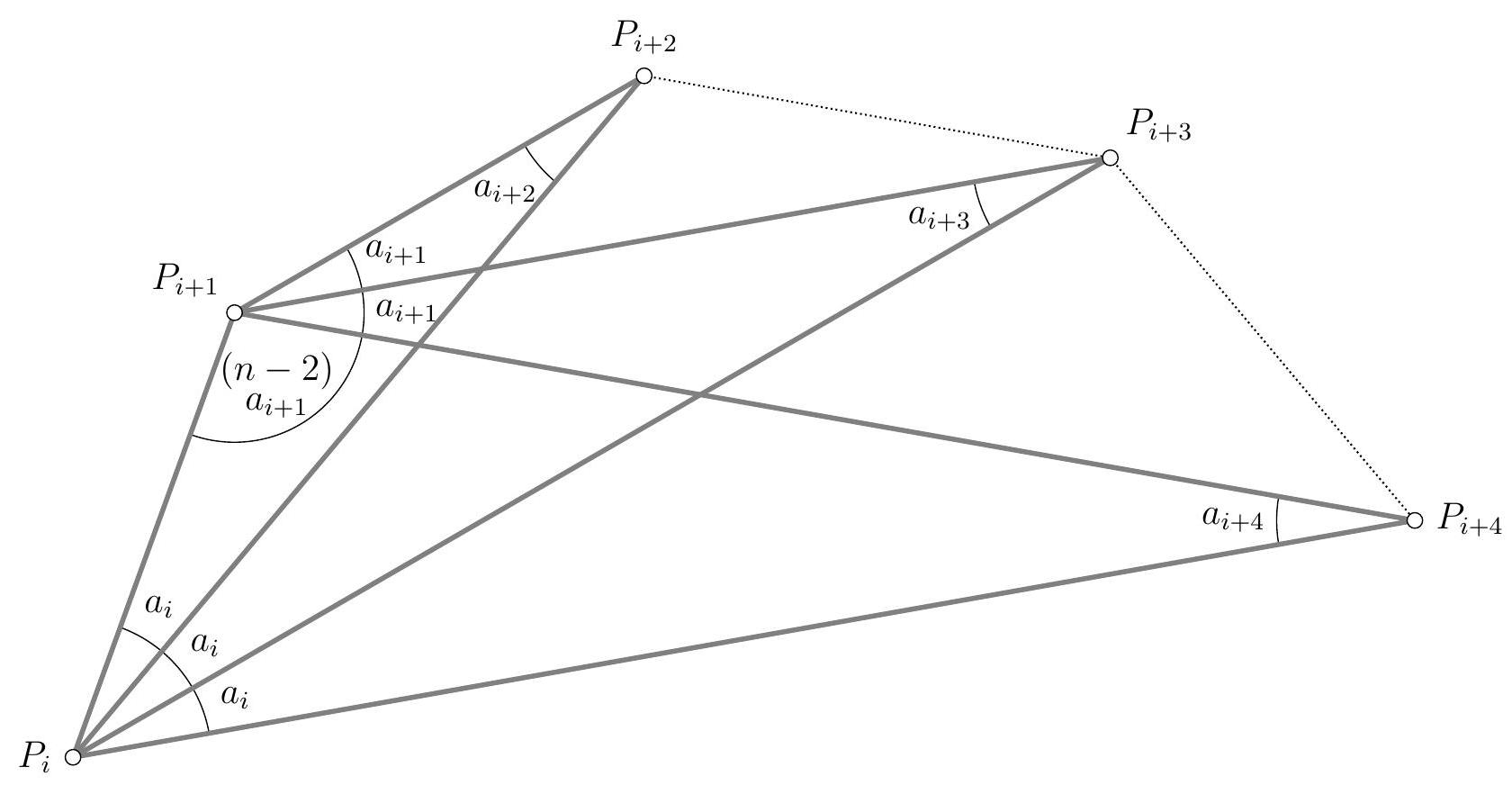
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $P_{1} P_{2} \ldots P_{2021}$ un polygone convexe à 2021 sommets tel que, pour chaque sommet $P_{i}$, les 2018 diagonales issues de $P_{i}$ divisent l'angle $\widehat{P}_{i}$ en 2019 angles égaux.
Démontrer que $P_{1} P_{2} \ldots P_{2021}$ est un polygone régulier, c'est-à-dire un polygone dont tous les angles ont même mesure et tous les côtés ont même longueur.
|
Dans la suite, on pose $n=2019$ et, pour tout sommet $P_{i}$, on note $a_{i}$ l'angle $\widehat{P}_{i} / n$. Soit alors $P_{k}$, $P_{k+1}, P_{k+2}, P_{k+3}$ et $P_{k+4}$ quatre sommets consécutifs, les indices des sommets étant considérés modulo $n+2$.
La somme des angles d'un triangle vaut $180^{\circ}$. En considérant respectivement les triangles $P_{i} P_{i+1} P_{i+2}, P_{i} P_{i+1} P_{i+3}$ et $P_{i} P_{i+1} P_{i+4}$, on constate que
$$
\begin{aligned}
a_{i}+n a_{i+1}+a_{i+2} & =180^{\circ} \\
2 a_{i}+(n-1) a_{i+1}+a_{i+3} & =180^{\circ} \\
3 a_{i}+(n-2) a_{i+1}+a_{i+4} & =180^{\circ}
\end{aligned}
$$
Nous allons alors soustraire deux à deux ces équations :
$\triangleright$ (1) - (2) indique que $a_{i+1}+a_{i+2}=a_{i}+a_{i+3}$, c'est-à-dire que $a_{i+1}-a_{i}=a_{i+3}-a_{i+2}$;
$\triangleright(2)-(3)$ indique que $a_{i+1}+a_{i+3}=a_{i}+a_{i+4}$, c'est-à-dire que $a_{i+1}-a_{i}=a_{i+4}-a_{i+3}$.
On constate donc que $a_{i+4}-a_{i+3}=a_{i+3}-a_{i+2}$. La différence entre deux angles $a_{j}$ et $a_{j+1}$ consécutifs est donc égale à une constante $\mathbf{c}$.
Cela signifie que $a_{i+k}=a_{i}+k \mathbf{c}$ pour tous les entiers $i$ et $k$. En particulier, $a_{1}=a_{n+3}=$ $a_{1}+(n+2) \mathbf{c}$, donc $\mathbf{c}=0^{\circ}$. Ainsi, notre polygone a tous ses sommets égaux.
Le triangle $P_{i} P_{i+1} P_{i+2}$ est donc isocèle en $P_{i+1}$, de sorte que $P_{i} P_{i+1}=P_{i+1} P_{i+2}$. Deux côtés consécutifs étant de même longueur, notre polygone a donc tous ses côtés de même longueur, et il s'agit bien d'un polygone régulier.

|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-2.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "## Solution de l'exercice 5"
}
|
e68d3c5f-f895-5a75-aeb1-b95d25645d46
| 604,259
|
Let $P_{1} P_{2} \ldots P_{2021}$ be a convex polygon with 2021 vertices such that, for each vertex $P_{i}$, the 2018 diagonals emanating from $P_{i}$ divide the angle $\widehat{P}_{i}$ into 2019 equal angles.
Prove that $P_{1} P_{2} \ldots P_{2021}$ is a regular polygon, that is, a polygon where all angles have the same measure and all sides have the same length.
|
$n^{\circ} 2$ As previously, we prove equality (1). If we set $b_{i}=a_{i}-180^{\circ} /(n+2)$, this equality can be rewritten as $b_{i}+n b_{i+1}+b_{i+2}=0$.
The sequence $\left(b_{i}\right)_{i \geqslant 1}$ is therefore a linear recurrence. If we denote $r_{+}$ and $r_{-}$ as the two roots of the polynomial $1+n X+X^{2}$, that is,
$$
r_{ \pm}=\frac{-n \pm \sqrt{n^{2}-4}}{2}
$$
there exist two numbers $\lambda_{+}$ and $\lambda_{-}$ such that
$$
b_{i}=\lambda_{+} r_{+}^{i}+\lambda_{-} r_{-}^{i}
$$
for all $i \geqslant 0$.
Since $n \geqslant 5$, we know that
$$
\left(n^{2}-4\right)-(n-2)^{2}=2(n-4)>0
$$
so that $r_{-} \leqslant-n / 2<-1<r_{+}<0$ and that we know $\left|r_{-}\right|>1>\left|r_{+}\right|$. Consequently, we know that, if $\lambda_{-} \neq 0$, the fraction $b_{i} /\left(\lambda_{-} r_{-}^{i}\right)$ tends to 1 as $i \rightarrow+\infty$. However, the sequence $\left(b_{i}\right)_{i \geqslant 1}$ is $(n+2)$-periodic. We deduce that $\lambda_{-}=0$.
Similarly, if $\lambda_{+} \neq 0$, the fraction $b_{i} /\left(\lambda_{+} r_{+}^{i}\right)$ tends to 1 as $i \rightarrow+\infty$, in contradiction with the $(n+2)$-periodic nature of the sequence $\left(b_{i}\right)_{i \geqslant 1}$. We deduce that $\lambda_{+}=0$, and thus that $b_{i}=0$ for all $i \geqslant 1$.
In conclusion, all the angles $a_{i}$ are equal, and we prove as previously that the sides of the polygon are equal as well.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $P_{1} P_{2} \ldots P_{2021}$ un polygone convexe à 2021 sommets tel que, pour chaque sommet $P_{i}$, les 2018 diagonales issues de $P_{i}$ divisent l'angle $\widehat{P}_{i}$ en 2019 angles égaux.
Démontrer que $P_{1} P_{2} \ldots P_{2021}$ est un polygone régulier, c'est-à-dire un polygone dont tous les angles ont même mesure et tous les côtés ont même longueur.
|
$n^{\circ} 2$ Comme précédemment, on démontre l'égalité (1). Si l'on pose $b_{i}=a_{i}-180^{\circ} /(n+2)$, cette égalité se réécrit comme $b_{i}+n b_{i+1}+b_{i+2}=0$.
La suite $\left(b_{i}\right)_{i \geqslant 1}$ est donc récurrente linéaire. Si l'on note $r_{+}$et $r_{-}$les deux racines du polynôme $1+n X+X^{2}$, c'est-à-dire
$$
r_{ \pm}=\frac{-n \pm \sqrt{n^{2}-4}}{2}
$$
il existe donc deux nombres $\lambda_{+}$et $\lambda_{-}$tels que
$$
b_{i}=\lambda_{+} r_{+}^{i}+\lambda_{-} r_{-}^{i}
$$
pour tout $i \geqslant 0$.
Puisque $n \geqslant 5$, on sait que
$$
\left(n^{2}-4\right)-(n-2)^{2}=2(n-4)>0
$$
donc que $r_{-} \leqslant-n / 2<-1<r_{+}<0$ et que on sait que $\left|r_{-}\right|>1>\left|r_{+}\right|$. Par conséquent, on sait que, si $\lambda_{-} \neq 0$, la fraction $b_{i} /\left(\lambda_{-} r_{-}^{i}\right)$ tend vers 1 quand $i \rightarrow+\infty$. Or, la suite $\left(b_{i}\right)_{i \geqslant 1}$ est $(n+2)$-périodique. On en déduit que $\lambda_{-}=0$.
De même, si $\lambda_{+} \neq 0$, la fraction $b_{i} /\left(\lambda_{+} r_{+}^{i}\right)$ tend vers 1 quand $i \rightarrow+\infty$, en contradiction avec le caractère $(n+2)$-périodique de la suite $\left(b_{i}\right)_{i \geqslant 1}$. On en déduit que $\lambda_{+}=0$, donc que $b_{i}=0$ pour tout $i \geqslant 1$.
En conclusion, tous les angles $a_{i}$ sont égaux, et on démontre comme précédemment que les côtés du polygone sont égaux eux aussi.
|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-2.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution alternative"
}
|
e68d3c5f-f895-5a75-aeb1-b95d25645d46
| 604,259
|
Let $P_{1} P_{2} \ldots P_{2021}$ be a convex polygon with 2021 vertices such that, for each vertex $P_{i}$, the 2018 diagonals emanating from $P_{i}$ divide the angle $\widehat{P}_{i}$ into 2019 equal angles.
Prove that $P_{1} P_{2} \ldots P_{2021}$ is a regular polygon, that is, a polygon where all angles have the same measure and all sides have the same length.
|
$n^{\circ} 3$ As previously, we prove the equality (1). By writing this equality for two consecutive integers $i$, and subtracting the two obtained equalities, we observe that
$$
a_{i}+(n-1) a_{i+1}-(n-1) a_{i+2}-a_{i+3}=0 .
$$
The sequence $a_{i}$ is therefore linearly recurrent. This time, the roots of the polynomial
$$
1+(n-1) X-(n-1) X^{2}-X^{3}=(1-X)\left(1+n X+X^{2}\right)
$$
are $r_{ \pm}$ and 1. Since $n \geqslant 5$, we know that
$$
\left(n^{2}-4\right)-(n-2)^{2}=2(n-4)>0
$$
so that $r_{-} \leqslant-n / 2<-1<r_{+}<0<1$ and that $\left|r_{-}\right|>1>\left|r_{+}\right|$.
There therefore exist three numbers $\lambda_{+}, \lambda_{1}$ and $\lambda_{-}$ such that
$$
a_{i}=\lambda_{+} r_{+}^{i}+\lambda_{1}+\lambda_{-} r_{-}^{i}
$$
for all $i \in \mathbb{Z}$. As in the previous solution, we prove that $\lambda_{-}=0$. Similarly, if $\lambda_{+} \neq 0$, then $a_{i} /\left(\lambda_{+} r_{+}^{i}\right) \rightarrow 1$ as $i \rightarrow-\infty$, in contradiction with the periodicity of $\left(a_{i}\right)$. Thus, $\lambda_{+}=0 .{ }^{2}$
2. One could also consider the periodicity of the sequence $a_{i}-\lambda_{1}$, but then we would fall back into the alternative solution $\mathrm{n}^{\circ} 2$.
In conclusion, all the angles $a_{i}$ are equal to $\lambda_{1}$, and we prove as previously that the sides of the polygon are equal as well.
Remark: This exercise was proposed in 2003, at the first-year Mathematical Olympiads, in the Academy of Versailles, but with intermediate questions included. Out of the 623 candidates present in the academy, including two national laureates, none managed to solve this exercise, which thus proved to be particularly difficult despite requiring few technical tools.
Comment from the graders: The exercise was solved by a large number of students. Almost all students managed to obtain at least partial points by establishing interesting equations between the angles associated with two or three consecutive vertices. However, here are several frequent errors:
$\triangleright$ A non-negligible portion of students stop after showing that all angles are equal. This, however, is not enough to show that the polygon is regular, as it is also necessary to show that all lengths are equal.
$\triangleright$ Some students provided the following reasoning: they start from the configuration of the regular polygon and show that it is not possible, by moving the vertices from this configuration while respecting the hypothesis of the statement, to obtain another polygon that satisfies the condition. However, this reasoning relies on continuity assumptions that have no basis, and therefore does not show that there are no other polygons that satisfy the property given by the statement. Often, the transformations proposed do not allow moving from a square to a non-square rhombus, although both quadrilaterals satisfy the condition of the statement.
$\triangleright$ Many students content themselves with treating the case of the pentagon instead of the 2021-gon and say that the result can be easily extended to the case of the 2021-gon. While a large part of their reasoning is indeed applicable to solving the case $n=2021$, one aspect of the problem is precisely to be able to fully generalize the reasoning on small polygons. Therefore, to be fully convincing, the proof should have been redone in the general case. Indeed, often the reasoning on the pentagon produced equations relating the angles to each other that were much simpler than the general case.
$\triangleright$ Some students content themselves with noting that there are many equations between the angles and that one therefore has a system with 2021 equations and 2021 unknowns, before asserting that such a system always admits a unique solution (here, the constant solution). However, it was necessary to specify the 2021 equations involved (too many students only note that there are more than 2021 equations) and show that these equations were independent of each other. The fact that a linear system of 2021 equations and 2021 unknowns admits a unique solution is only true in this context.
Other students, after stating the system, assert that "after calculations," the unique solution is given by all angles being equal. But this assertion is far from convincing without the calculations to support it.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $P_{1} P_{2} \ldots P_{2021}$ un polygone convexe à 2021 sommets tel que, pour chaque sommet $P_{i}$, les 2018 diagonales issues de $P_{i}$ divisent l'angle $\widehat{P}_{i}$ en 2019 angles égaux.
Démontrer que $P_{1} P_{2} \ldots P_{2021}$ est un polygone régulier, c'est-à-dire un polygone dont tous les angles ont même mesure et tous les côtés ont même longueur.
|
$n^{\circ} 3$ Comme précédemment, on démontre l'égalité (1). En écrivant cette égalité pour deux entiers $i$ consécutifs, et en soustrayant les deux égalités obtenues, on constate que
$$
a_{i}+(n-1) a_{i+1}-(n-1) a_{i+2}-a_{i+3}=0 .
$$
La suite $a_{i}$ est donc récurrente linéaire. Cette fois-ci, les racines du polynôme
$$
1+(n-1) X-(n-1) X^{2}-X^{3}=(1-X)\left(1+n X+X^{2}\right)
$$
sont $r_{ \pm}$et 1 . Puisque $n \geqslant 5$, on sait que
$$
\left(n^{2}-4\right)-(n-2)^{2}=2(n-4)>0
$$
donc que $r_{-} \leqslant-n / 2<-1<r_{+}<0<1$ et que on sait que $\left|r_{-}\right|>1>\left|r_{+}\right|$.
Il existe donc trois nombres $\lambda_{+}, \lambda_{1}$ et $\lambda_{-}$tels que
$$
a_{i}=\lambda_{+} r_{+}^{i}+\lambda_{1}+\lambda_{-} r_{-}^{i}
$$
pour tout $i \in \mathbb{Z}$. On démontre comme dans la solution précédente que $\lambda_{-}=0$. De même, si $\lambda_{+} \neq 0$, alors $a_{i} /\left(\lambda_{+} r_{+}^{i}\right) \rightarrow 1$ quand $i \rightarrow-\infty$, en contradiction avec le caractère périodique de $\left(a_{i}\right)$. Ainsi, $\lambda_{+}=0 .{ }^{2}$
2. On pourrait aussi considérer le caractère périodique de la suite $a_{i}-\lambda_{1}$, mais alors on retomberait dans la solution alternative $\mathrm{n}^{\circ} 2$.
En conclusion, tous les angles $a_{i}$ sont égaux à $\lambda_{1}$, et on démontre comme précédemment que les côtés du polygone sont égaux eux aussi.
Remarque : Cet exercice avait été proposé en 2003, aux Olympiades mathématiques de première, dans l'académie de Versailles, mais en incluant des questions intermédiaires. Sur les 623 candidats présents dans l'académie, dont deux lauréats nationaux, aucun n'était parvenu à résoudre cet exercice, qui s'était donc révélé particulièrement difficile bien qu'abordable avec peu d'outils techniques.
Commentaire des correcteurs L'exercice a été résolu par un grand nombre d'élèves. Pratiquement tous les élèves ont su obtenir au moins des points partiels en établissant des équations intéressantes entre les angles associés à deux ou trois sommets consécutifs. Voici cependant plusieurs erreurs rencontrées fréquemment:
$\triangleright$ Une partie non négligeable des élèves s'arrête après avoir montré que tous les angles sont égaux. Cela ne suffit pourtant pas à montrer que le polygone est régulier, puisqu'il faut aussi montrer que toutes les longueurs sont égales.
$\triangleright$ Quelques élèves ont donné le raisonnement suivant : ils partent de la configuration du polygone régulier et montrent qu'il n'est pas possible, en bougeant les sommets à partir de cette configuration de manière à respecter l'hypothèse de l'énoncé, d'obtenir un autre polygone respectant la condition. Cependant ce raisonnement repose sur des hypothèses de continuité qui n'ont aucune raison d'être, et ne permet donc pas de montrer qu'il n'existe pas d'autres polygones respectant la propriété donnée par l'énoncé. Bien souvent, les transformations proposées ne permettent pas de passer du carré au losange non carré, alors que les deux quadrilatères respectent la condition de l'énoncé.
$\triangleright$ Beaucoup d'élèves se contentent de traiter le cas du pentagone au lieu du 2021-gone et disent qu'on étend aisément le résultat pour le cas du 2021-gone. Si une grande partie de leurs raisonnement est effectivement utilisable pour la résolution du cas $n=2021$, l'un des aspects du problème est justement d'être capable de généraliser complètement le raisonnement sur des petits polygones. Il fallait donc, pour être parfaitement convaincant, effectuer de nouveau la preuve dans le cas général. En effet, bien souvent, le raisonnement sur le pentagone produisait des équations reliant les angles entre eux qui étaient beaucoup plus simples que le cas général.
$\triangleright$ Quelques élèves se contentent de signaler qu'il y a beaucoup d'équations entre les angles et qu'on a donc un système avec 2021 équations à 2021 inconnues, avant d'affirmer qu'un tel système admet toujours une unique solution (ici, la solution constante). Mais il fallait alors préciser les 2021 équations mises en jeu (trop d'élèves ne font que signaler qu'il y a bien plus que 2021 équations) et montrer que ces équations étaient indépendantes les unes des autres. Le fait qu'un système linéaire de 2021 équations à 2021 inconnues admet une unique solution n'est vrai que dans ce cadre.
D'autres élèves, après avoir énoncé le système, affirment que « après calculs », l'unique solution est donnée par des angles tous égaux. Mais cette affirmation est loin d'être convaincante sans les calculs à l'appui.
|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-2.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution alternative"
}
|
e68d3c5f-f895-5a75-aeb1-b95d25645d46
| 604,259
|
The sequences $\left(a_{n}\right)_{n \geqslant 0}$ and $\left(b_{n}\right)_{n \geqslant 0}$ are defined by
$$
\left\{\begin{array} { l l }
{ a _ { n } = 0 } & { \text { if } n = 0 ; } \\
{ a _ { n } = 2 a _ { \lfloor n / 2 \rfloor } + n } & { \text { if } n \geqslant 1 ; }
\end{array} \quad \text { and } \quad \left\{\begin{array}{ll}
b_{n}=0 & \text { if } n=0 ; \\
b_{n}=3 b_{\lfloor n / 3\rfloor}+n & \text { if } n \geqslant 1 .
\end{array}\right.\right.
$$
Prove that the sequence with general term $2^{a_{n}}-3^{b_{n}}$ changes sign infinitely often.
|
First, we show by induction on $n$ that $a_{n} \leqslant n\left\lfloor\log _{2}(2 n)\right\rfloor$ for all integers $n \geqslant 1$, with equality when $n$ is a power of 2. Indeed, for $n=1$, we have $a_{n}=1=n \log _{2}(2 n)$. Then, if $n \geqslant 2$,
$$
a_{n}=2 a_{\lfloor n / 2\rfloor}+n \leqslant 2\lfloor n / 2\rfloor\left\lfloor\log _{2}(2\lfloor n / 2\rfloor)\right\rfloor+n \leqslant n\left\lfloor\log _{2}(n)+1\right\rfloor=n\left\lfloor\log _{2}(2 n)\right\rfloor \text {, }
$$
with equality when $n / 2=\lfloor n / 2\rfloor$ and $n / 2$ is a power of 2.
Similarly, we show that $b_{n} \leqslant n\left\lfloor\log _{3}(3 n)\right\rfloor$ for all integers $n \geqslant 1$, with equality when $n$ is a power of 3. We already deduce, if $n$ is a power of 3, that
$$
2^{a_{n}}-3^{b_{n}}=2^{a_{n}}-(3 n)^{n} \leqslant(2 n)^{n}-(3 n)^{n}<0 .
$$
Conversely, let $k$ and $\ell$ be two non-zero natural numbers such that $2^{\ell}<3^{k} \leqslant 2^{\ell+1}$, and let $n=2^{\ell}$. Then $k \log _{2}(3) \leqslant \ell+1$, so
$$
\log _{2}(3) b_{n} \leqslant \log _{2}(3) n\left\lfloor\log _{3}(3 n)\right\rfloor=\log _{2}(3) k n \leqslant(\ell+1) n=a_{n}
$$
so that $2^{a_{n}}-3^{b_{n}}=2^{a_{n}}-2^{\log _{2}(3) b_{n}} \geqslant 0$. Since $2^{a_{n}} \neq 3^{b_{n}}$, as one is odd and the other is not, we deduce that $2^{a_{n}}-3^{b_{n}}>0$, which concludes this solution.
Remark: In fact, we could have shown that, if
$$
n=\sum_{k \geqslant 0} \alpha_{k} 2^{k}=\sum_{\ell \geqslant 0} \beta_{\ell} 3^{\ell},
$$
then
$$
a_{n}=\sum_{k \geqslant 0}(k+1) \alpha_{k} 2^{k} \text { and } b_{n}=\sum_{\ell \geqslant 0}(\ell+1) \beta_{\ell} 3^{\ell} .
$$
Remark: It would have been tempting to show that $2^{a_{n}}>3^{b_{n}}$ as soon as $n$ is a power of 2 or $n+1$ is a power of 3. However, this is not the case: by noting $\langle x\rangle$ the fractional part of a real number $x$, i.e., $\langle x\rangle=x-\lfloor x\rfloor$, we can in fact show that $2^{a_{n}}<3^{b_{n}}$ as soon as $\left\langle\log _{3}(n)\right\rangle<7 / 100$ or $\left\langle\log _{2}(n)\right\rangle>98 / 100$.
Examiner's Comment: This problem was difficult, and only five students solved it completely. In practice, many students had good ideas but stopped halfway, instead of stepping back to see how to generalize or exploit their discoveries. Thus,
$\triangleright$ Several students empirically noticed and proved that the value of $a_{n+1}-a_{n}$ depended on the 2-adic valuation of $n$, deriving horrible sums for the expression of $a_{n}$, whereas using a double-counting method, they could have obtained the rather cute expressions given above.
$\triangleright$ Many students empirically noticed that $a_{n}$ grew quickly when $n$ was a power of 2, and thus expressed their desire to prove that $2^{a_{n}}>3^{b_{n}}$ when $n$ was a power of 2. However, they stopped there, or simply verified that $a_{n}=n\left(1+\log _{2}(n)\right)$ when $n$ is a power of 2, but did not think to look for an upper bound for the term $b_{n}$ when $n$ is any number.
$\triangleright$ Several students, after successfully proving that $3^{b_{n}}>2^{a_{n}}$ when $n$ was a power of 3, conjectured and tried to prove that $2^{a_{n}}>3^{b_{n}}$ when $n$ was a power of 2. Unfortunately for them, this was the main (and particularly insidious!) difficulty of the problem, since this tempting conjecture was invalid, the first counterexample being $n=2^{8}$.
This is where it would have been useful to step back to see where the proof of this conjecture failed, before refining it to focus simultaneously on integers $n$ for which $a_{n}$ is "large" (i.e., $n$ is not much larger than a power of 2) and $b_{n}$ is "small" (i.e., $n$ is not much smaller than a power of 3). The students who had this idea all did very well.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Les suites $\left(a_{n}\right)_{n \geqslant 0}$ et $\left(b_{n}\right)_{n \geqslant 0}$ sont définies par
$$
\left\{\begin{array} { l l }
{ a _ { n } = 0 } & { \text { si } n = 0 ; } \\
{ a _ { n } = 2 a _ { \lfloor n / 2 \rfloor } + n } & { \text { si } n \geqslant 1 ; }
\end{array} \quad \text { et } \quad \left\{\begin{array}{ll}
b_{n}=0 & \text { si } n=0 ; \\
b_{n}=3 b_{\lfloor n / 3\rfloor}+n & \text { si } n \geqslant 1 .
\end{array}\right.\right.
$$
Démontrer que la suite de terme général $2^{a_{n}}-3^{b_{n}}$ change de signe infiniment souvent.
|
On montre tout d'abord, par récurrence sur $n$, que $a_{n} \leqslant n\left\lfloor\log _{2}(2 n)\right\rfloor$ pour tout entier $n \geqslant 1$, avec égalité lorsque $n$ est une puissance de 2 . En effet, pour $n=1$, on a bien $a_{n}=1=n \log _{2}(2 n)$. Puis, si $n \geqslant 2$,
$$
a_{n}=2 a_{\lfloor n / 2\rfloor}+n \leqslant 2\lfloor n / 2\rfloor\left\lfloor\log _{2}(2\lfloor n / 2\rfloor)\right\rfloor+n \leqslant n\left\lfloor\log _{2}(n)+1\right\rfloor=n\left\lfloor\log _{2}(2 n)\right\rfloor \text {, }
$$
avec égalité lorsque $n / 2=\lfloor n / 2\rfloor$ et $n / 2$ est une puissance de 2 .
On montre de même que $b_{n} \leqslant n\left\lfloor\log _{3}(3 n)\right\rfloor$ pour tout entier $n \geqslant 1$, avec égalité lorsque $n$ est une puissance de 3 . On en déduit déjà, si $n$ est une puissance de 3 , que
$$
2^{a_{n}}-3^{b_{n}}=2^{a_{n}}-(3 n)^{n} \leqslant(2 n)^{n}-(3 n)^{n}<0 .
$$
Réciproquement, soit $k$ et $\ell$ deux entiers naturels non nuls tels que $2^{\ell}<3^{k} \leqslant 2^{\ell+1}$, et soit $n=2^{\ell}$. Alors $k \log _{2}(3) \leqslant \ell+1$, donc
$$
\log _{2}(3) b_{n} \leqslant \log _{2}(3) n\left\lfloor\log _{3}(3 n)\right\rfloor=\log _{2}(3) k n \leqslant(\ell+1) n=a_{n}
$$
de sorte que $2^{a_{n}}-3^{b_{n}}=2^{a_{n}}-2^{\log _{2}(3) b_{n}} \geqslant 0$. Puisque $2^{a_{n}} \neq 3^{b_{n}}$, car l'un est impair et l'autre non, on en déduit que $2^{a_{n}}-3^{b_{n}}>0$, ce qui conclut cette solution.
Remarque: On pouvait en fait démontrer que, si
$$
n=\sum_{k \geqslant 0} \alpha_{k} 2^{k}=\sum_{\ell \geqslant 0} \beta_{\ell} 3^{\ell},
$$
alors
$$
a_{n}=\sum_{k \geqslant 0}(k+1) \alpha_{k} 2^{k} \text { et } b_{n}=\sum_{\ell \geqslant 0}(\ell+1) \beta_{\ell} 3^{\ell} .
$$
Remarque: Il eût été tentant de démontrer que $2^{a_{n}}>3^{b_{n}}$ dès lors que $n$ est une puissance de 2 ou que $n+1$ est une puissance de 3 . Cependant, il n'en est rien : en notant $\langle x\rangle$ la partie fractionnaire d'un réel $x$, c'est-à-dire $\langle x\rangle=x-\lfloor x\rfloor$, on peut en fait démontrer que $2^{a_{n}}<3^{b_{n}}$ dès lors que $\left\langle\log _{3}(n)\right\rangle<7 / 100$ ou que $\left\langle\log _{2}(n)\right\rangle>98 / 100$.
Commentaire des correcteurs Cet exercice était difficile, et seuls cinq élèves l'ont intégralement résolu. En pratique, de nombreux élèves ont eu de bonnes idées mais se sont arrêtés en cours de route, au lieu de prendre du recul pour voir comment généraliser ou exploiter leurs découvertes. Ainsi,
$\triangleright$ Plusieurs élèves ont remarqué empiriquement, puis démontré, que la valeur de $a_{n+1}-$ $a_{n}$ dépendait de la valuation 2-adique de $n$, en déduisant des sommes horribles pour l'expression de $a_{n}$, alors qu'en utiisant un double-comptage, ils auraient pu obtenir les expressions somme toute mignonnes obtenues ci-dessus.
$\triangleright$ De nombreux élèves ont remarqué empiriquement que $a_{n}$ croissait vite quand $n$ était une puissance de 2, et ont donc exprimé leur envie de démontrer que $2^{a_{n}}>3^{b_{n}}$ quand $n$ était une puissance de 2 . Cependant, ils se sont arrêtés là, ou bien se sont contentés de vérifier que $a_{n}=n\left(1+\log _{2}(n)\right)$ quand $n$ est une puissance de 2, mais n'ont pas pensé à rechercher de borne supérieure pour le terme $b_{n}$ quand $n$ est un nombre quelconque.
$\triangleright$ Plusieurs élèves, après avoir réussi à démontrer que $3^{b_{n}}>2^{a_{n}}$ lorsque $n$ était une puissance de 3 , ont conjecturé et cherché à démontrer que $2^{a_{n}}>3^{b_{n}}$ lorsque $n$ était une puissance de 2 . Malheureusement pour eux, là résidait la difficulté principale (et particulièrement sournoise!) du problème, puisque cette conjecture pourtant très tentante était invalide, le premier contre-exemple étant $n=2^{8}$.
C'est là qu'il aurait été utile de prendre du recul pour voir où la preuve de cette conjecture pêchait, avant de l'affiner pour se concentrer simultanément sur les entiers $n$ pour lesquels $a_{n}$ est « grand » (c'est-à-dire que $n$ n'est pas beaucoup plus grand qu'une puissance de 2) et $b_{n}$ est « petit » (c'est-à-dire que $n$ n'est pas beaucoup plus petit qu'une puissance de 3). Les élèves qui ont eu cette idée s'en sont tous tirés avec brio.
|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-2.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "\nSolution de l'exercice 6"
}
|
f7c7edb1-2ef4-573a-aed0-149fc6b2165d
| 604,352
|
Let $a, b, c$ and $d$ be four real numbers. Suppose there exists a permutation $(x, y, z, t)$ of the numbers $a, b, c$ and $d$ such that
$$
x \leqslant 2 a-b, y \leqslant 2 b-c, z \leqslant 2 c-d \text { and } t \leqslant 2 d-a .
$$
Prove that $a=b=c=d$.
|
To better exploit the first inequality, which we rewrite as $x + b \leqslant 2a$, it would be ideal for $x$ and $b$ to be maximal, or for $a$ to be minimal. Obviously, it is quite possible that neither $a$, nor $b$, nor $x$ is extremal. Nevertheless, since the variables play cyclic roles, we can still hope, at our choice, that $a$ is minimal, or that $b$ is maximal, or that $x$ is maximal. However, hoping that $b$ and $x$ would be simultaneously maximal would be too much to ask. Instead, we assume, without loss of generality, that $a$ is the smallest of the four real numbers. Under these conditions, $2a \leqslant b + x \leqslant 2a$, so $a = b$. But then $b$ is also the smallest of the four real numbers, so $b = c$, and we similarly prove that $c = d$.
$\underline{\text{Alternative Solution } n^{\circ} 1}$ By summing the four inequalities given in the problem, we obtain the inequality $x + y + z + t \leqslant a + b + c + d$. Since $(x, y, z, t)$ is a permutation of $(a, b, c, d)$, this last inequality is actually an equality, so each of the inequalities given in the problem is also an equality: $x = 2a - b$, $y = 2b - c$, $z = 2c - d$, and $t = 2d - a$.
By squaring each side and adding the resulting equalities, we observe that
$$
a^{2} + b^{2} + c^{2} + d^{2} = x^{2} + y^{2} + z^{2} + t^{2} = 5\left(a^{2} + b^{2} + c^{2} + d^{2}\right) - 4(ab + bc + cd + da)
$$
This means that $ab + bc + cd + da = a^{2} + b^{2} + c^{2} + d^{2}$, or equivalently,
$$
0 = 2\left(a^{2} + b^{2} + c^{2} + d^{2}\right) - 2(ab + bc + cd + da) = (a - b)^{2} + (b - c)^{2} + (c - d)^{2} + (d - a)^{2},
$$
so $a = b = c = d$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit $a, b, c$ et $d$ quatre nombres réels. On suppose qu'il existe une permutation $(x, y, z, t)$ des nombres $a, b, c$ et $d$ telle que
$$
x \leqslant 2 a-b, y \leqslant 2 b-c, z \leqslant 2 c-d \text { et } t \leqslant 2 d-a .
$$
Démontrer que $a=b=c=d$.
|
Pour mieux exploiter la première inégalité, que l'on réécrit comme $x+b \leqslant 2 a$, l'idéal serait que $x$ et $b$ soient maximaux, ou bien que $a$ soit minimal. Évidemment, il se pourrait très bien que ni $a$, ni $b$, ni $x$ ne soit extrémal. Néanmoins, puisque les variables jouent des rôles cycliques, on peut tout de même espérer, au choix, que $a$ soit minimal, ou que $b$ soit maximal, ou que $x$ soit maximal.
Cependant, espérer que $b$ et $x$ seraient simultanément maximaux serait trop demander. À la place, on se contente de supposer, sans perte de généralité, que $a$ est le plus petit des quatre nombres réels. Dans ces conditions, $2 a \leqslant b+x \leqslant 2 a$, donc $a=b$. Mais alors $b$ est aussi le plus petit des quatre nombres réels, donc $b=c$, et on démontre de même que $c=d$.
$\underline{\text { Solution alternative } n^{\circ} 1}$ En sommant les quatre inégalités de l'énoncé, on obtient l'inégalité $x+y+z+t \leqslant a+b+c+d$. Puisque $(x, y, z, t)$ est une permutation de $(a, b, c, d)$, cette dernière inégalité est en fait une égalité, donc chacune des inégalités de l'énoncé est également une égalité : $x=2 a-b, y=2 b-c, z=2 c-d$ et $t=2 d-a$.
En élevant chaque membre au carré et en additionnant les égalités ainsi obtenues, on constate alors que
$$
a^{2}+b^{2}+c^{2}+d^{2}=x^{2}+y^{2}+z^{2}+t^{2}=5\left(a^{2}+b^{2}+c^{2}+d^{2}\right)-4(a b+b c+c d+d a)
$$
Cela signifie que $a b+b c+c d+d a=a^{2}+b^{2}+c^{2}+d^{2}$, ou encore que
$$
0=2\left(a^{2}+b^{2}+c^{2}+d^{2}\right)-2(a b+b c+c d+d a)=(a-b)^{2}+(b-c)^{2}+(c-d)^{2}+(d-a)^{2},
$$
de sorte que $a=b=c=d$.
|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution de l'exercice 1"
}
|
2b455f2f-c2cd-5c0b-b96f-7c51234d0437
| 604,385
|
Let $ABC$ be a triangle with acute angles. We denote $D$ as the foot of the altitude from $A$ in triangle $ABC$, then $E$ as the midpoint of the segment $[AD]$, and $\omega$ as the circle with diameter $[AD]$. Next, let $X$ be the intersection point between $\omega$ and the line $(BE)$, such that $B$ and $X$ are on opposite sides of the line $(AD)$. Similarly, let $Y$ be the intersection point between $\omega$ and the line $(CE)$, such that $C$ and $Y$ are on opposite sides of the line $(AD)$. Finally, suppose there exists a point $Z$, other than $D$, lying on the line $(AD)$ and on both circumcircles of $BDX$ and $CDY$. Prove that $AB = AC$.
|
$n^{\circ} 1$ Let $\omega_{b}$ and $\omega_{c}$ be the circumcircles of $B D X Z$ and $C D Y Z$. The line $(D Z)$ is the radical axis of these two circles. Since $E$ lies on this radical axis, it has the same power with respect to the circles $\omega_{b}$ and $\omega_{c}$, which means that $E X \cdot E B = E Y \cdot E C$. Since $E$ is the center of the circle $\omega$, we deduce that $E X = E Y$, and therefore that $E B = E C$.
Consequently, the line $(A D)$, which is the perpendicular to $(B C)$ passing through $E$, is also the perpendicular bisector of $[B C]$. We conclude as expected that $A B = A C$.
Comment from the graders: One of the first difficulties of the exercise was to figure out how to draw the figure in a relevant way. Indeed, drawing an isosceles triangle right away risked giving false intuitions about the figure. This was detrimental to many students who, after drawing the figure for an isosceles triangle $A B C$ at $A$, claimed certain angle equalities without proving them because they appeared true on the figure. After drawing this first figure, it would have been better to draw a new figure by forgetting one of the hypotheses, for example, by constructing a side $A B$ slightly longer than the side $A C$; this new figure could then serve as an alternative support for reflection, to ensure not to be misled by one's own sketch. In general, this advice remains valid for all geometry exercises with a format similar to the statement.
It was then necessary to figure out how to exploit the hypothesis given by the statement. The inscribed angle theorem was the key here, and very few students noted the equality $\widehat{Z X B} = \widehat{Z D B} = 90^{\circ}$, which was the starting point of the reasoning. Most students who noted this equality managed to conclude the exercise.
Here are some elements found repeatedly in the proposed solutions:
$\triangleright$ Many students claim to provide a complete solution to the problem, but in reality, it did not work or had a significant gap. Most of the time, this is because an assertion is given without proof, perhaps because it appears visually on the figure (see the remark above). The assertion is often true, but proving it often amounts to proving the exercise.
One way to avoid this pitfall is to reread, check that all assertions are justified, and verify if all the hypotheses of the statement have been used! Some students claim to prove that the triangle $A B C$ is isosceles without ever mentioning the point $Z$ or noting that the point $E$ is defined as the midpoint of the segment $[A D]$.
In fact, drawing an alternative figure where one forgets such and such hypothesis (for example, the hypotheses that were not used) allows checking if what one is saying has a chance of being true.
$\triangleright$ Many students notice that the line $(A D)$ is the radical axis of two circles. This observation could lead to another way (rather effective) to solve the exercise. However, it is frustrating to see that most students who made this observation stopped at this observation without continuing their reasoning.
The interest in identifying a radical axis is to then look at the power of a well-chosen point on this axis with respect to the two circles concerned. Here, very few students point out that the point $E$ belongs to the radical axis and therefore has the same power with respect to the two given circles.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle dont les angles sont aigus. On note $D$ le pied de la hauteur issue de $A$ dans le triangle $A B C$, puis $E$ le milieu du segment $[A D]$, et $\omega$ le cercle de diamètre $[A D]$. Ensuite, soit $X$ le point d'intersection entre $\omega$ et la droite $(B E)$, tel que $B$ et $X$ soient situés de part et d'autre de la droite $(A D)$. De même, soit $Y$ le point d'intersection entre $\omega$ et la droite $(C E)$, tel que $C$ et $Y$ soient situés de part et d'autre de la droite $(A D)$. Enfin, on suppose qu'il existe un point $Z$, autre que $D$, appartenant à la droite $(A D)$ et aux deux cercles circonscrits à $B D X$ et à $C D Y$. Démontrer que $A B=A C$.
|
$n^{\circ} 1$ Notons $\omega_{b}$ et $\omega_{c}$ les cercles circonscrits à $B D X Z$ et à $C D Y Z$. La droite $(D Z)$ est l'axe radical de ces deux cercles. Puisque $E$ appartient à cet axe radical, il a mêmes puissances par rapport aux cercles $\omega_{b}$ et $\omega_{c}$, ce qui signifie que $E X \cdot E B=E Y \cdot E C$. Or, $E$ est le centre du cercle $\omega$. On en déduit que $E X=E Y$, et donc que $E B=E C$.
Par conséquent, la droite $(A D)$, qui est la perpendiculaire à $(B C)$ passant par $E$, est aussi la médiatrice de $[B C]$. On en conclut comme prévu que $A B=A C$.
Commentaire des correcteurs Une première difficulté de l'exercice était de trouver comment tracer sa figure de façon pertinente. En effet, tracer d'emblée un triangle isocèle risquait
de donner de fausses intuitions sur la figure. Cela a été dommageable pour des nombreux élèves qui, après avoir tracé la figure pour un triangle $A B C$ isocèle en $A$, ont affirmé sans les démontrer certaines égalités d'angles parce qu'elles apparaissaient comme vraies sur la figure. Après avoir tracé cette première figure, il aurait en fait fallu tracer une nouvelle figure obtenue en oubliant l'une des hypothèses, par exemple en construisant un côté $A B$ légèrement plus grand que le côté $A C$; cette nouvelle figure pouvant alors servir comme support de réflexion alternatif, pour être sûr de ne pas être trompé par son propre brouillon. De manière générale, ce conseil reste valide pour tous les exercices de géométrie ayant un format analogue à celui de l'énoncé.
Il fallait ensuite trouver comment exploiter l'hypothèse donnée par l'énoncé. Le théorème de l'angle inscrit était de mise ici, et très peu d'élèves ont relevé l'égalité $\widehat{Z X B}=\widehat{Z D B}=90^{\circ}$, qui était pourtant le point de départ du raisonnement. La plupart des élèves qui ont noté cette égalité sont parvenus à conclure l'exercice.
Voici quelques éléments trouvés de façon récurrente dans les réponses proposées :
$\triangleright$ Beaucoup d'élèves prétendent donner une solution complète du problème, mais qui en réalité ne fonctionnait pas ou comportait un trou important. La plupart du temps, cela vient du fait qu'une affirmation est donnée sans démonstration, sans doute parce qu'elle apparaît visuellement sur la figure (cf la remarque plus haut). L'affirmation est souvent vraie mais la démontrer revient souvent à démontrer l'exercice.
Une façon de ne pas tomber dans cet écueil est de se relire, de vérifier que toutes les affirmations sont justifiées, et de vérifier si toutes les hypothèses de l'énoncé ont été utilisées! Certains élèves affirment ainsi démontrer que le triangle $A B C$ est isocèle sans évoquer une seule fois le point $Z$ ou sans mentionner que le point $E$ est défini comme le milieu du segment $[A D]$.
De fait, tracer une figure alternative où l'on oublie telle ou telle hypothèse (par exemple les hypothèses que l'on n'a pas utilisées) permet de vérifier si ce que l'on raconte a une chance d'être vrai.
$\triangleright$ Beaucoup d'élèves remarquent que la droite $(A D)$ est l'axe radical de deux cercles. Cette remarque pouvait conduire à une autre façon (plutôt efficace) de résoudre l'exercice. Toutefois, il est frustrant de voir que la plupart des élèves ayant formulé cette remarque se sont arrêtés à cette remarque sans continuer leur raisonnement.
L'intérêt de repérer un axe radical est de pouvoir ensuite regarder la puissance d'un point bien choisi sur cet axe par rapport aux deux cercles concernés. Ici, très peu d'élèves signalent que le point $E$ appartenait à l'axe radical et a donc la même puissance par rapport aux deux cercles donnés.
|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution alternative"
}
|
84eb7049-35ce-5e20-ac4a-8bb5b81da5c0
| 604,427
|
Let $\left(F_{k}\right)_{k \geqslant 0}$ be the sequence defined by $F_{0}=0, F_{1}=1$, and $F_{k+2}=F_{k}+F_{k+1}$ for all integers $k \geqslant 0$. Let then $n \geqslant 1$ be an integer. Prove that there are exactly $F_{n+1}$ ways to order the numbers $1,2, \ldots, n$ to obtain an $n$-tuple $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ such that
$$
a_{1} \leqslant 2 a_{2} \leqslant 3 a_{3} \leqslant \ldots \leqslant n a_{n} .
$$
|
A permutation $\mathbf{a}=\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ of the integers $1,2, \ldots, n$ is said to be pretty if it satisfies the inequalities $a_{1} \leqslant 2 a_{2} \leqslant \ldots \leqslant n a_{n}$.
First, let $a$ be a pretty permutation. If there exists an integer $k$ for which $a_{k} \leqslant k-2$, we choose the minimal $k$. In this case, we know that $k \geqslant 2$ and that $a_{k-1} \geqslant k-2 \geqslant a_{k}$, so $a_{k-1} \geqslant a_{k}+1$. We conclude that
$$
(k-1) a_{k-1} \geqslant(k-1)\left(a_{k}+1\right)=k a_{k}+\left(k-a_{k}-1\right) \geqslant k a_{k}+1,
$$
and thus that $a$ is not pretty. Therefore, we conclude that $a_{k} \geqslant k-1$ for all $k \leqslant n$.
On the other hand, let $\ell$ be the integer such that $a_{\ell}=n$. Given the result obtained previously, an immediate downward induction on $k$ ensures that $a_{k}=k-1$ for all integers $k$ such that $\ell+1 \leqslant k \leqslant n$. Since
$$
\ell n=\ell a_{\ell} \leqslant(\ell+1) a_{\ell+1}=(\ell+1) \ell
$$
we conclude that $\ell \in\{n-1, n\}$.
Thus, for $a$ to be pretty, we have two choices a priori:
$\triangleright$ either $\ell=n$, in which case $a$ is indeed pretty if and only if the permutation $\left(a_{1}, a_{2}, \ldots, a_{n-1}\right)$ of the integers $1,2, \ldots, n-1$ is pretty;
$\triangleright$ or $\ell=n-1$, in which case $a_{n}=n-1$, and then $a$ is indeed pretty if the permutation $\left(a_{1}, a_{2}, \ldots, a_{n-2}\right)$ of the integers $1,2, \ldots, n-2$ is pretty.
Consequently, if we denote by $J_{n}$ the number of pretty permutations of $1,2, \ldots, n$, we note that $J_{n}=J_{n-1}+J_{n-2}$ as soon as $n \geqslant 3$. We conclude by verifying that $J_{1}=1=F_{2}$ and that $J_{2}=2=F_{3}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soit $\left(F_{k}\right)_{k \geqslant 0}$ la suite définie par $F_{0}=0, F_{1}=1$, et $F_{k+2}=F_{k}+F_{k+1}$ pour tout entier $k \geqslant 0$. Soit ensuite $n \geqslant 1$ un entier. Démontrer qu'il existe exactement $F_{n+1}$ façons d'ordonner les nombres $1,2, \ldots, n$ de manière à obtenir un $n$-uplet $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ tel que
$$
a_{1} \leqslant 2 a_{2} \leqslant 3 a_{3} \leqslant \ldots \leqslant n a_{n} .
$$
|
On dit qu'une permutation $\mathbf{a}=\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ des entiers $1,2, \ldots, n$ est jolie si elle satisfait les inégalités $a_{1} \leqslant 2 a_{2} \leqslant \ldots \leqslant n a_{n}$.
Tout d'abord, soit a une jolie permutation. S'il existe un entier $k$ pour lequel $a_{k} \leqslant k-2$, on choisit $k$ minimal. Dans ces conditions, on sait que $k \geqslant 2$ et que $a_{k-1} \geqslant k-2 \geqslant a_{k}$, de sorte que $a_{k-1} \geqslant a_{k}+1$. On en conclut que
$$
(k-1) a_{k-1} \geqslant(k-1)\left(a_{k}+1\right)=k a_{k}+\left(k-a_{k}-1\right) \geqslant k a_{k}+1,
$$
et donc que a n'est pas jolie. On en conclut donc que $a_{k} \geqslant k-1$ pour tout $k \leqslant n$.
D'autre part, soit $\ell$ l'entier tel que $a_{\ell}=n$. Au vu du résultat obtenu précédemment, une récurrence descendante immédiate sur $k$ nous assure que $a_{k}=k-1$ pour tout entier $k$ tel que $\ell+1 \leqslant k \leqslant n$. Puisque
$$
\ell n=\ell a_{\ell} \leqslant(\ell+1) a_{\ell+1}=(\ell+1) \ell
$$
on en conclut que $\ell \in\{n-1, n\}$.
Ainsi, pour que a soit jolie, on dispose a priori de deux choix :
$\triangleright$ soit $\ell=n$, auquel cas a est effectivement jolie si et seulement si la permutation $\left(a_{1}, a_{2}, \ldots, a_{n-1}\right)$ des entiers $1,2, \ldots, n-1$ est jolie;
$\triangleright$ soit $\ell=n-1$, auquel cas $a_{n}=n-1$, et alors a est effectivement jolie si la permutation $\left(a_{1}, a_{2}, \ldots, a_{n-2}\right)$ des entiers $1,2, \ldots, n-2$ est jolie.
Par conséquent, si on note $J_{n}$ le nombre de jolies permutations de $1,2, \ldots, n$, on remarque bien que $J_{n}=J_{n-1}+J_{n-2}$ dès lors que $n \geqslant 3$. On conclut en vérifiant que $J_{1}=1=F_{2}$ et que $J_{2}=2=F_{3}$ 。
|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "\nSolution de l'exercice 4"
}
|
028b99cd-e589-5cca-b96e-6a9a5e41b921
| 604,465
|
Let $\left(F_{k}\right)_{k \geqslant 0}$ be the sequence defined by $F_{0}=0, F_{1}=1$, and $F_{k+2}=F_{k}+F_{k+1}$ for all integers $k \geqslant 0$. Let then $n \geqslant 1$ be an integer. Prove that there are exactly $F_{n+1}$ ways to order the numbers $1,2, \ldots, n$ to obtain an $n$-tuple $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ such that
$$
a_{1} \leqslant 2 a_{2} \leqslant 3 a_{3} \leqslant \ldots \leqslant n a_{n} .
$$
|
$n^{\circ} 1$ As previously, we consider a permutation $a$ and the integer $\ell$ such that $a_{\ell}=n$. Since $n a_{k} \geqslant k a_{k} \geqslant \ell a_{\ell}=\ell n$ for all $k \geqslant \ell$, we know that $a$ induces a permutation of $1,2, \ldots, \ell-1$ and of $\ell, \ell+1, \ldots, n$.
If $\ell \leqslant n-1$, let $m$ be the unique integer such that $a_{m}=\ell$. Since $m \geqslant \ell$, we know that
$$
m \ell=m a_{m} \geqslant \ell a_{\ell}=\ell n
$$
thus $m=n$. But then $k a_{k}=\ell n$ for all integers $k$ such that $\ell \leqslant k \leqslant n$. We deduce in particular that $n-1$ divides $(n-1) a_{n-1}=\ell n$, and thus divides $\ell$ as well, which means that $\ell=n-1$. Now that we have established that $\ell \in\{n-1, n\}$, we conclude as previously.
Comment from the graders: This problem was difficult. Nevertheless, a good number of students had the good idea to try to find a recurrence relation on the number of permutations satisfying the statement and succeeded, by analyzing the recurrence relation, to understand the structure of the permutations satisfying the statement.
However, very few students managed to formalize this, in particular to show that the integer $\ell$ defined in the solution was indeed greater than or equal to $n-1$. Some used the fact that $n(n-2)<(n-1)^{2}$ to conclude in the general case. If this argument worked for $\ell=n-2$, it was unfortunately impossible to adapt it directly for arbitrary $\ell$.
Also be careful with the recurrence! Several students showed, if we denote by $k_{n}$ the number of permutations of $\{1, \ldots, n\}$ satisfying the statement, that $k_{n}=k_{n-1}+k_{n-2}$. They then performed a strong induction, initialized at $n=1$, to prove that $k_{n}=F_{n+1}$. Here, for $n=2$, the formula $k_{2}=k_{1}+k_{0}$ does not make sense because $k_{0}$ is not even defined. This inductive reasoning therefore did not allow proving that $k_{2}=F_{3}$, and it would have been necessary to treat this equality in the initialization of our recurrence. Here, to avoid this error, it would have been better to perform a double induction, which requires explicitly initializing at $n=1$ and $n=2$.
## Senior Problems
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soit $\left(F_{k}\right)_{k \geqslant 0}$ la suite définie par $F_{0}=0, F_{1}=1$, et $F_{k+2}=F_{k}+F_{k+1}$ pour tout entier $k \geqslant 0$. Soit ensuite $n \geqslant 1$ un entier. Démontrer qu'il existe exactement $F_{n+1}$ façons d'ordonner les nombres $1,2, \ldots, n$ de manière à obtenir un $n$-uplet $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ tel que
$$
a_{1} \leqslant 2 a_{2} \leqslant 3 a_{3} \leqslant \ldots \leqslant n a_{n} .
$$
|
$n^{\circ} 1$ Comme précédemment, on considère une permutation a puis l'entier $\ell$ tel que $a_{\ell}=n$. Puisque $n a_{k} \geqslant k a_{k} \geqslant \ell a_{\ell}=\ell$ n pour tout $k \geqslant \ell$, on sait que a induit une permutation de $1,2, \ldots, \ell-1$ et de $\ell, \ell+1, \ldots, n$.
Si $\ell \leqslant n-1$, soit $m$ l'unique entier tel que $a_{m}=\ell$. Puisque $m \geqslant \ell$, on sait que
$$
m \ell=m a_{m} \geqslant \ell a_{\ell}=\ell n
$$
donc que $m=n$. Mais alors $k a_{k}=\ell n$ pour tout entier $k$ tel que $\ell \leqslant k \leqslant n$. On en déduit en particulier que $n-1$ divise $(n-1) a_{n-1}=\ell n$, donc divise $\ell$ aussi, ce qui signifie que $\ell=n-1$. Maintenant acquis le fait que $\ell \in\{n-1, n\}$, on conclut comme précédemment.
Commentaire des correcteurs Cet exercice était difficile. Néanmoins, une bonne partie des élèves a eu la bonne idée d'essayer de trouver une relation de récurrence sur le nombre de permutations vérifiant l'énoncé et a réussi, en analysant la relation de récurrence, à comprendre la structure des permutations vérifiant l'énoncé.
Toutefois, très peu d'élèves ont réussi à formaliser cela, en particulier à montrer que l'entier $\ell$ défini dans la correction était bien supérieur ou égal à $n-1$. Certains ont utilisé le fait que $n(n-2)<(n-1)^{2}$ pour conclure dans le cas général. Si cet argument fonctionnait
pour $\ell=n-2$, il était malheureusement impossible de l'adapter directement pour des $\ell$ quelconques.
Attention aussi à la récurrence! Plusieurs élèves ont montré, si on note $k_{n}$ le nombre de permutations de $\{1, \ldots, n\}$ vérifiant l'énoncé, que $k_{n}=k_{n-1}+k_{n-2}$. Ils ont ensuite fait une récurrence forte, initialisée à $n=1$, pour prouver que $k_{n}=F_{n+1}$. Ici pour $n=2$, la formule $k_{2}=k_{1}+k_{0}$ n'a pas de sens car $k_{0}$ n'est même pas défini. Ce raisonnement par récurrence ne permettait donc pas de prouver que $k_{2}=F_{3}$, et il aurait fallu traiter cette égalité dans le cadre de l'initialisation de notre récurrence. Ici, pour éviter cette erreur, il valait mieux faire une récurrence double, qui nécessite explicitement d'initialiser à $n=1$ et $n=2$.
## Problèmes Senior
|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "\nSolution alternative"
}
|
028b99cd-e589-5cca-b96e-6a9a5e41b921
| 604,465
|
Let $\left(F_{k}\right)_{k \geqslant 0}$ be the sequence defined by $F_{0}=0, F_{1}=1$, and $F_{k+2}=F_{k}+F_{k+1}$ for all integers $k \geqslant 0$. Let then $n \geqslant 1$ be an integer. Prove that there are exactly $F_{n+1}$ ways to order the numbers $1,2, \ldots, n$ to obtain an $n$-tuple $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ such that
$$
a_{1} \leqslant 2 a_{2} \leqslant 3 a_{3} \leqslant \ldots \leqslant n a_{n}
$$
|
A permutation $\mathbf{a}=\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ of the integers $1,2, \ldots, n$ is said to be pretty if it satisfies the inequalities $a_{1} \leqslant 2 a_{2} \leqslant \ldots \leqslant n a_{n}$.
First, let a be a pretty permutation. If there exists an integer $k$ for which $a_{k} \leqslant k-2$, we choose the minimal $k$. In this case, we know that $k \geqslant 2$ and that $a_{k-1} \geqslant k-2 \geqslant a_{k}$, so that $a_{k-1} \geqslant a_{k}+1$. We conclude that
$$
(k-1) a_{k-1} \geqslant(k-1)\left(a_{k}+1\right)=k a_{k}+\left(k-a_{k}-1\right) \geqslant k a_{k}+1,
$$
and thus that a is not pretty. Therefore, we conclude that $a_{k} \geqslant k-1$ for all $k \leqslant n$.
On the other hand, let $\ell$ be the integer such that $a_{\ell}=n$. Given the result obtained previously, an immediate downward induction on $k$ ensures that $a_{k}=k-1$ for all integers $k$ such that $\ell+1 \leqslant k \leqslant n$. Since
$$
\ell n=\ell a_{\ell} \leqslant(\ell+1) a_{\ell+1}=(\ell+1) \ell
$$
we conclude that $\ell \in\{n-1, n\}$.
Thus, for a to be pretty, we have two choices a priori:
$\triangleright$ either $\ell=n$, in which case a is indeed pretty if and only if the permutation $\left(a_{1}, a_{2}, \ldots, a_{n-1}\right)$ of the integers $1,2, \ldots, n-1$ is pretty;
$\triangleright$ or $\ell=n-1$, in which case $a_{n}=n-1$, and then a is indeed pretty if the permutation $\left(a_{1}, a_{2}, \ldots, a_{n-2}\right)$ of the integers $1,2, \ldots, n-2$ is pretty.
Consequently, if we denote by $J_{n}$ the number of pretty permutations of $1,2, \ldots, n$, we note that $J_{n}=J_{n-1}+J_{n-2}$ as soon as $n \geqslant 3$. We conclude by verifying that $J_{1}=1=F_{2}$ and that $J_{2}=2=F_{3}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soit $\left(F_{k}\right)_{k \geqslant 0}$ la suite définie par $F_{0}=0, F_{1}=1$, et $F_{k+2}=F_{k}+F_{k+1}$ pour tout entier $k \geqslant 0$. Soit ensuite $n \geqslant 1$ un entier. Démontrer qu'il existe exactement $F_{n+1}$ façons d'ordonner les nombres $1,2, \ldots, n$ de manière à obtenir un $n$-uplet $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ tel que
$$
a_{1} \leqslant 2 a_{2} \leqslant 3 a_{3} \leqslant \ldots \leqslant n a_{n}
$$
|
On dit qu'une permutation $\mathbf{a}=\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ des entiers $1,2, \ldots, n$ est jolie si elle satisfait les inégalités $a_{1} \leqslant 2 a_{2} \leqslant \ldots \leqslant n a_{n}$.
Tout d'abord, soit a une jolie permutation. S'il existe un entier $k$ pour lequel $a_{k} \leqslant k-2$, on choisit $k$ minimal. Dans ces conditions, on sait que $k \geqslant 2$ et que $a_{k-1} \geqslant k-2 \geqslant a_{k}$, de sorte que $a_{k-1} \geqslant a_{k}+1$. On en conclut que
$$
(k-1) a_{k-1} \geqslant(k-1)\left(a_{k}+1\right)=k a_{k}+\left(k-a_{k}-1\right) \geqslant k a_{k}+1,
$$
et donc que a n'est pas jolie. On en conclut donc que $a_{k} \geqslant k-1$ pour tout $k \leqslant n$.
D'autre part, soit $\ell$ l'entier tel que $a_{\ell}=n$. Au vu du résultat obtenu précédemment, une récurrence descendante immédiate sur $k$ nous assure que $a_{k}=k-1$ pour tout entier $k$ tel que $\ell+1 \leqslant k \leqslant n$. Puisque
$$
\ell n=\ell a_{\ell} \leqslant(\ell+1) a_{\ell+1}=(\ell+1) \ell
$$
on en conclut que $\ell \in\{n-1, n\}$.
Ainsi, pour que a soit jolie, on dispose a priori de deux choix :
$\triangleright$ soit $\ell=n$, auquel cas a est effectivement jolie si et seulement si la permutation $\left(a_{1}, a_{2}, \ldots, a_{n-1}\right)$ des entiers $1,2, \ldots, n-1$ est jolie;
$\triangleright$ soit $\ell=n-1$, auquel cas $a_{n}=n-1$, et alors a est effectivement jolie si la permutation $\left(a_{1}, a_{2}, \ldots, a_{n-2}\right)$ des entiers $1,2, \ldots, n-2$ est jolie.
Par conséquent, si on note $J_{n}$ le nombre de jolies permutations de $1,2, \ldots, n$, on remarque bien que $J_{n}=J_{n-1}+J_{n-2}$ dès lors que $n \geqslant 3$. On conclut en vérifiant que $J_{1}=1=F_{2}$ et que $J_{2}=2=F_{3}$.
|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"problem_match": "\nExercice 8.",
"solution_match": "\nSolution de l'exercice 8"
}
|
743382e1-3a04-5d04-bc9f-2358a98f4163
| 604,578
|
Let $\left(F_{k}\right)_{k \geqslant 0}$ be the sequence defined by $F_{0}=0, F_{1}=1$, and $F_{k+2}=F_{k}+F_{k+1}$ for all integers $k \geqslant 0$. Let then $n \geqslant 1$ be an integer. Prove that there are exactly $F_{n+1}$ ways to order the numbers $1,2, \ldots, n$ to obtain an $n$-tuple $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ such that
$$
a_{1} \leqslant 2 a_{2} \leqslant 3 a_{3} \leqslant \ldots \leqslant n a_{n}
$$
|
$n^{\circ} 1$ As previously, we consider a permutation $a$ and the integer $\ell$ such that $a_{\ell}=n$. Since $n a_{k} \geqslant k a_{k} \geqslant \ell a_{\ell}=\ell n$ for all $k \geqslant \ell$, we know that $a$ induces a permutation of $1,2, \ldots, \ell-1$ and of $\ell, \ell+1, \ldots, n$.
If $\ell \leqslant n-1$, let $m$ be the unique integer such that $a_{m}=\ell$. Since $m \geqslant \ell$, we know that
$$
m \ell=m a_{m} \geqslant \ell a_{\ell}=\ell n
$$
thus $m=n$. But then $k a_{k}=\ell n$ for all integers $k$ such that $\ell \leqslant k \leqslant n$. We deduce in particular that $n-1$ divides $(n-1) a_{n-1}=\ell n$, and thus divides $\ell$ as well, which means that $\ell=n-1$. Now that we have established that $\ell \in\{n-1, n\}$, we conclude as previously.
Comment from the graders This problem was difficult. Nevertheless, a good number of students had the good idea to try to find a recurrence relation on the number of permutations satisfying the statement and succeeded, by analyzing the recurrence relation, to understand the structure of the permutations satisfying the statement.
However, very few students managed to formalize this, in particular to show that the integer $\ell$ defined in the solution was indeed greater than or equal to $n-1$. Some used the fact that $n(n-2)<(n-1)^{2}$ to conclude in the general case. While this argument worked for $\ell=n-2$, it was unfortunately impossible to adapt it directly for arbitrary $\ell$.
Also be careful with the recurrence! Several students showed, if we denote by $k_{n}$ the number of permutations of $\{1, \ldots, n\}$ satisfying the statement, that $k_{n}=k_{n-1}+k_{n-2}$. They then performed a strong induction, initialized at $n=1$, to prove that $k_{n}=F_{n+1}$. Here, for $n=2$, the formula $k_{2}=k_{1}+k_{0}$ does not make sense because $k_{0}$ is not even defined. This inductive reasoning therefore did not allow proving that $k_{2}=F_{3}$, and it would have been necessary to treat this equality in the initialization of our induction. Here, to avoid this error, it would have been better to perform a double induction, which requires explicitly initializing at $n=1$ and $n=2$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soit $\left(F_{k}\right)_{k \geqslant 0}$ la suite définie par $F_{0}=0, F_{1}=1$, et $F_{k+2}=F_{k}+F_{k+1}$ pour tout entier $k \geqslant 0$. Soit ensuite $n \geqslant 1$ un entier. Démontrer qu'il existe exactement $F_{n+1}$ façons d'ordonner les nombres $1,2, \ldots, n$ de manière à obtenir un $n$-uplet $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ tel que
$$
a_{1} \leqslant 2 a_{2} \leqslant 3 a_{3} \leqslant \ldots \leqslant n a_{n}
$$
|
$n^{\circ} 1$ Comme précédemment, on considère une permutation a puis l'entier $\ell$ tel que $a_{\ell}=n$. Puisque $n a_{k} \geqslant k a_{k} \geqslant \ell a_{\ell}=\ell$ n pour tout $k \geqslant \ell$, on sait que a induit une permutation de $1,2, \ldots, \ell-1$ et de $\ell, \ell+1, \ldots, n$.
Si $\ell \leqslant n-1$, soit $m$ l'unique entier tel que $a_{m}=\ell$. Puisque $m \geqslant \ell$, on sait que
$$
m \ell=m a_{m} \geqslant \ell a_{\ell}=\ell n
$$
donc que $m=n$. Mais alors $k a_{k}=\ell n$ pour tout entier $k$ tel que $\ell \leqslant k \leqslant n$. On en déduit en particulier que $n-1$ divise $(n-1) a_{n-1}=\ell n$, donc divise $\ell$ aussi, ce qui signifie que $\ell=n-1$. Maintenant acquis le fait que $\ell \in\{n-1, n\}$, on conclut comme précédemment.
Commentaire des correcteurs Cet exercice était difficile. Néanmoins, une bonne partie des élèves a eu la bonne idée d'essayer de trouver une relation de récurrence sur le nombre de permutations vérifiant l'énoncé et a réussi, en analysant la relation de récurrence, à comprendre la structure des permutations vérifiant l'énoncé.
Toutefois, très peu d'élèves ont réussi à formaliser cela, en particulier à montrer que l'entier $\ell$ défini dans la correction était bien supérieur ou égal à $n-1$. Certains ont utilisé le fait que $n(n-2)<(n-1)^{2}$ pour conclure dans le cas général. Si cet argument fonctionnait pour $\ell=n-2$, il était malheureusement impossible de l'adapter directement pour des $\ell$ quelconques.
Attention aussi à la récurrence! Plusieurs élèves ont montré, si on note $k_{n}$ le nombre de permutations de $\{1, \ldots, n\}$ vérifiant l'énoncé, que $k_{n}=k_{n-1}+k_{n-2}$. Ils ont ensuite fait une récurrence forte, initialisée à $n=1$, pour prouver que $k_{n}=F_{n+1}$. Ici pour $n=2$, la formule $k_{2}=k_{1}+k_{0}$ n'a pas de sens car $k_{0}$ n'est même pas défini. Ce raisonnement par récurrence ne permettait donc pas de prouver que $k_{2}=F_{3}$, et il aurait fallu traiter cette égalité dans le cadre de l'initialisation de notre récurrence. Ici, pour éviter cette erreur, il valait mieux faire une récurrence double, qui nécessite explicitement d'initialiser à $n=1$ et $n=2$.
|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"problem_match": "\nExercice 8.",
"solution_match": "\nSolution alternative"
}
|
743382e1-3a04-5d04-bc9f-2358a98f4163
| 604,578
|
Let $n$ be a natural number. Prove that the binary representation of the integer $n\left(2^{n}-1\right)$ contains exactly $n$ occurrences of the digit 1.
|
Let $s_{n}$ be the integer $n\left(2^{n}-1\right)$. Since $s_{0}=0$ and $s_{1}=1$, the statement is verified for $n \leqslant 1$. We therefore assume from now on that $n \geqslant 2$.
We then set $t=2^{n}-n$ and $s=n-1$, so that $n\left(2^{n}-1\right)=2^{n} s+t$ and $s+t=2^{n}-1$. By the binomial theorem, we know that $2^{n} \geqslant(1+1)^{n} \geqslant\binom{ n}{0}+\binom{n}{1}=n+1$. Thus, $s$ and $t$ are two natural numbers whose sum is $2^{n}-1$. Consequently, they can be written respectively as
$$
{\overline{a_{n-1} a_{n-2} \ldots a_{0}}}^{2} \text { and }{\overline{b_{n-1} b_{n-2} \ldots b_{0}}}^{2}
$$
in base 2, and we are assured that $a_{i}+b_{i}=1$ for all $i \leqslant n-1$.
Furthermore, since $t<2^{n}$, the base 2 representation of $2^{n} s+t$ starts with the $n$ digits of $s$ and ends with the $n$ digits of $t$. The integer $n\left(2^{n}-1\right)=2^{n} s+t$ is therefore written as
$$
{\overline{a_{n-1} a_{n-2} \ldots a_{0} b_{n-1} b_{n-2} \ldots b_{0}}}^{2}
$$
in base 2. The sum of these digits is therefore $\left(a_{0}+b_{0}\right)+\left(a_{1}+b_{1}\right)+\ldots+\left(a_{n-1}+b_{n-1}\right)=n$, which concludes the proof.
Grader's Comment This problem was difficult. The key was to recognize that the $k^{\text {th }}$ and $(n+k)^{\text {th }}$ digits of $n\left(2^{n}-1\right)$ were a 0 and a 1, which a systematic study of small cases (say, up to 8) could have helped to observe. The only student who noticed this phenomenon is also the only one who provided a complete solution.
Moreover, it is unfortunate that several students, having had the good idea of writing $2^{n}-1$ in base 2, then prematurely claimed that any number of the form $k\left(2^{n}-1\right)$ contains $n$ occurrences of the digit 1 when written in base 2: this is true only if $1 \leqslant k \leqslant 2^{n}$. Any proof intended to work for all integers $k$ was therefore doomed to fail, which was predictable by looking at the case where $n=1$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $n$ un entier naturel. Démontrer que l'écriture de l'entier $n\left(2^{n}-1\right)$ en base 2 compte exactement $n$ occurrences du chiffre 1.
|
Notons $s_{n}$ l'entier $n\left(2^{n}-1\right)$. Puisque $s_{0}=0$ et $s_{1}=1$, l'énoncé est bien vérifié lorsque $n \leqslant 1$. On suppose donc désormais que $n \geqslant 2$.
On pose alors $t=2^{n}-n$ et $s=n-1$, de sorte que $n\left(2^{n}-1\right)=2^{n} s+t$ et que $s+t=2^{n}-1$. En vertu du binôme de Newton, on sait que $2^{n} \geqslant(1+1)^{n} \geqslant\binom{ n}{0}+\binom{n}{1}=n+1$. Ainsi, $s$ et $t$ sont deux entiers naturels de somme $2^{n}-1$. Par conséquent, ils s'écrivent respectivement comme
$$
{\overline{a_{n-1} a_{n-2} \ldots a_{0}}}^{2} \text { et }{\overline{b_{n-1} b_{n-2} \ldots b_{0}}}^{2}
$$
en base 2 , et on est assuré que $a_{i}+b_{i}=1$ pour tout $i \leqslant n-1$.
En outre, comme $t<2^{n}$, l'écriture de $2^{n} s+t$ en base 2 commence avec les $n$ chiffres de $s$ puis se termine avec les $n$ chiffres de $t$. L'entier $n\left(2^{n}-1\right)=2^{n} s+t$ s'écrit donc
$$
{\overline{a_{n-1} a_{n-2} \ldots a_{0} b_{n-1} b_{n-2} \ldots b_{0}}}^{2}
$$
en base 2. La somme de ces chiffres vaut donc $\left(a_{0}+b_{0}\right)+\left(a_{1}+b_{1}\right)+\ldots+\left(a_{n-1}+b_{n-1}\right)=n$ , ce qui conclut.
Commentaire des correcteurs Cet exercice était difficile. Le point crucial consistait à repérer que les $k^{\text {ème }}$ et $(n+k)^{\text {ème }}$ chiffres de $n\left(2^{n}-1\right)$ étaient un 0 et un 1 , ce qu'une étude systématique des petits cas (disons, jusqu'à 8) aurait pu aider à constater. La seule élève qui a remarqué ce phénomène est également la seule qui a fourni une solution complète.
Par ailleurs, il est dommage que plusieurs élèves, ayant eu la bonne idée d'écrire $2^{n}-1$ en base 2, aient ensuite prématurément affirmé que tout nombre de la forme $k\left(2^{n}-1\right)$ contenait $n$ occurrences du chiffre 1 quand on l'écrivait en base 2 : ceci n'est vrai que si $1 \leqslant k \leqslant 2^{n}$. Toute preuve censée fonctionner pour tout entier $k$ était donc vouée à l'échec, ce qui était prévisible en regardant le cas où $n=1$.
|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"problem_match": "\nExercice 9.",
"solution_match": "\nSolution de l'exercice 9"
}
|
22bc0b41-eaa8-5215-8994-57ff8363c132
| 604,603
|
Let $ABC$ be a triangle. We denote $H_{A}$ as the foot of the altitude from $A$ in $\triangle ABC$, and $A^{\prime}$ as the midpoint of the segment $[BC]$. We then denote $Q_{A}$ as the symmetric point of $H_{A}$ with respect to $A^{\prime}$. We define the points $Q_{B}$ and $Q_{C}$ similarly. Finally, we denote $R$ as the intersection point, other than $Q_{A}$, of the circumcircles of triangles $Q_{A} Q_{B} C$ and $Q_{A} B Q_{C}$.
Prove that the lines $\left(Q_{A} R\right)$ and $(BC)$ are perpendicular.
|
Let $H$ be the orthocenter of $ABC$, $O$ the center of the circumcircle of $ABC$, and $R'$ the symmetric point of $H$ with respect to $O$. The orthogonal projections of $H$ and $O$ on $(BC)$ are $H_a$ and $A'$, so the orthogonal projection of $R'$ on $(BC)$ is $Q_A$. Similarly, the orthogonal projections of $R'$ on $(CA)$ and $(AB)$ are $Q_B$ and $Q_C$.
This means, among other things, that $\widehat{C Q_A R'} = \widehat{Q C_B R'} = 90^\circ$, so $Q_A$ and $Q_B$ belong to the circle with diameter $[CR']$. This circle therefore coincides with the circumcircle of $Q_A Q_B C$. Similarly, the points $Q_A$ and $Q_C$ belong to the circle with diameter $[BR']$, which coincides with the circumcircle of $Q_A B Q_C$. Consequently, the points $R$ and $R'$ are coincident, and $(Q_A R)$ is indeed perpendicular to $(BC)$.
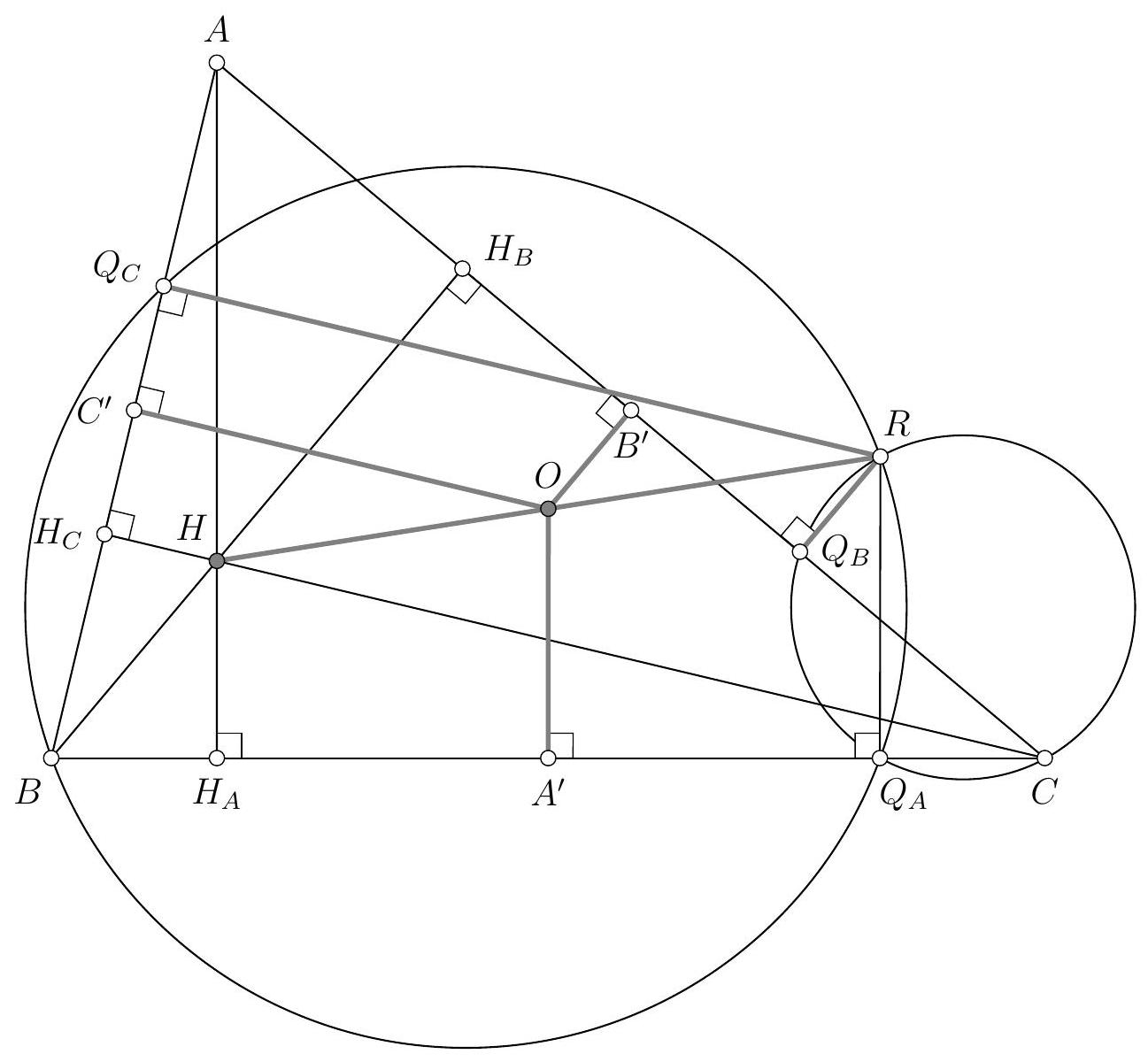
$\underline{\text{Alternative Solution } n^\circ 1}$ Below, we denote by $\Gamma_A, \Gamma_B$, and $\Gamma_C$ the circumcircles of $A Q_B Q_C$, $Q_A B Q_C$, and $Q_A Q_B C$, respectively. Since $R$ belongs to $\Gamma_B$ and $\Gamma_C$, we know that
\[
\left(Q_C A, Q_C R\right) = \left(Q_C B, Q_C R\right) = \left(Q_A B, Q_A R\right) = \left(Q_A C, Q_A R\right) = \left(Q_B C, Q_B R\right) = \left(Q_B A, Q_B R\right)
\]
This means that $R$ also belongs to $\Gamma_A$, and thus $A, B$, and $C$ play symmetric roles. With this observation, we introduce the circumcircle of $ABC$, which we denote by $\Omega$. In search of remarkable circles, we also notice that the right angles at $H_A, H_B$, and $H_C$ suggest drawing the circles $\Xi_A, \Xi_B$, and $\Xi_C$, with diameters $[BC]$, $[CA]$, and $[AB]$, respectively.
Finally, if we denote by $m$ the perpendicular bisector of $[BC]$, the problem asks us to prove that $(Q_A R)$ and $(A H_A)$ are symmetric with respect to $m$. We therefore focus more closely on the symmetry with axis $m$ and the circles for which $m$ is an axis of symmetry: these are the circles $\Omega, \Xi_A$, and, at least in appearance, $\Gamma_A$.
Lacking a proof that the center of the latter circle lies on $m$, we can attempt to prove that the radical axes of $\Gamma_A$ with $\Omega$ or $\Xi_A$ are parallel to $(BC)$. The first would then clearly be the line parallel to $(BC)$ passing through $A$, while the second appears to be the line $(B' C')$.
Since $B'$ is the midpoint of $[AC]$ and $[H_B Q_B]$, we know that $B' H_B \cdot B' C = B' Q_B \cdot B' A$, which means that $B'$ belongs to the radical axis of $\Gamma_A$ and $\Xi_A$. Similarly, $C'$ belongs to this radical axis, which is therefore coincident with $(B' C')$, so $\Gamma_A$ is indeed symmetric with respect to $m$.
Consequently, the circles $\Omega$ and $\Gamma_A$ intersect at a point $X$ which is none other than the symmetric point of $A$ with respect to $m$. Let us then denote by $R'$ the intersection of $(Q_A X)$ and $\Gamma_C$. We know that $\widehat{C Q_B R'} = \widehat{C Q_A R'} = 90^\circ$. Since we also have $\widehat{A X R'} = 90^\circ$, the point $R'$ is therefore diametrically opposite to $A$ in the circumcircle of $A Q_B X$. This proves that $R'$ belongs to $\Gamma_A$, and thus coincides with $R$, which concludes the proof.
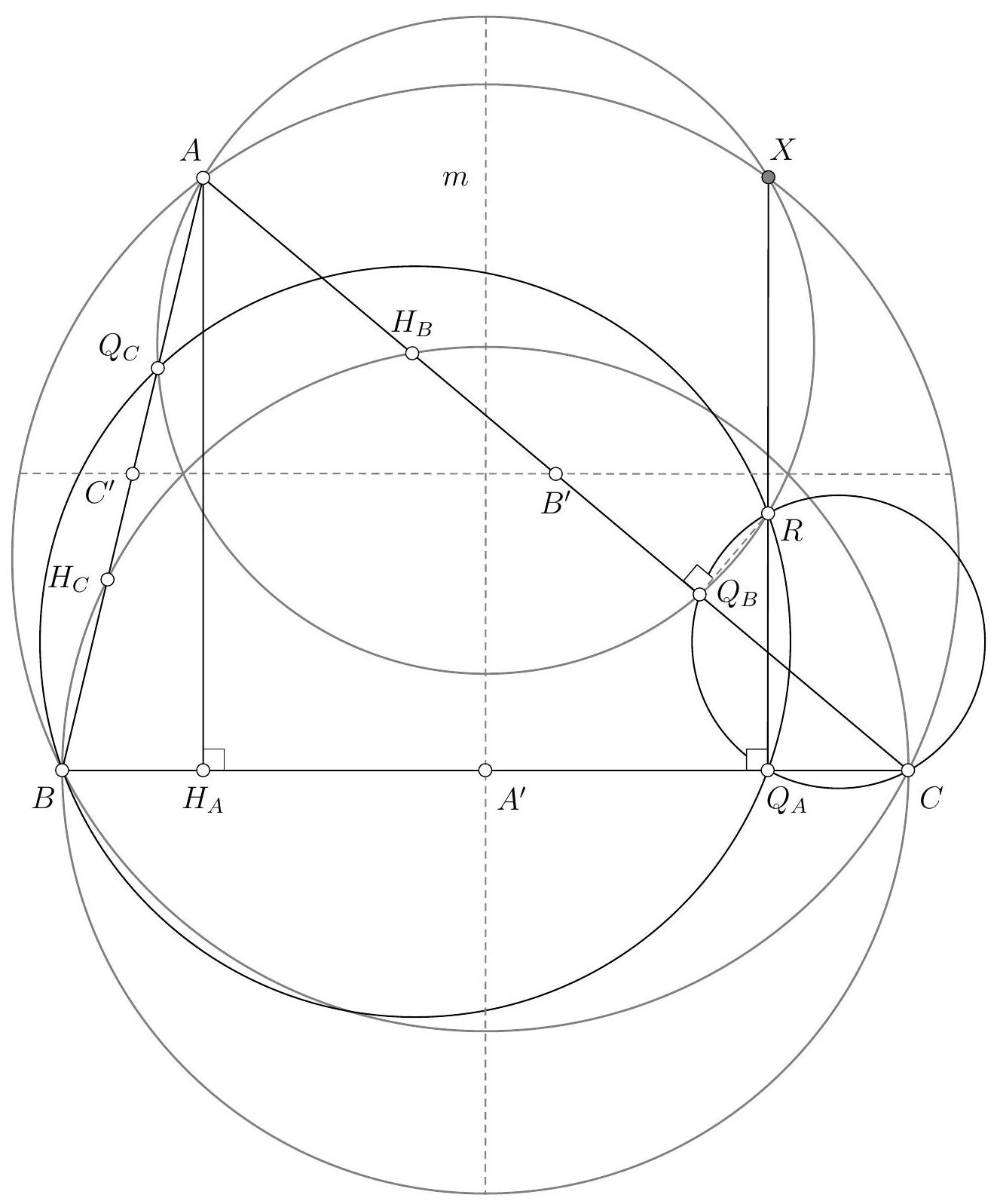
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle. On note $H_{A}$ le pied de la hauteur de $A B C$ issue de $A$, et $A^{\prime}$ le milieu du segment $[B C]$. On note ensuite $Q_{A}$ le symétrique de $H_{A}$ par rapport à $A^{\prime}$. On définit de même les points $Q_{B}$ et $Q_{C}$. Enfin, on note $R$ le point d'intersection, autre que $Q_{A}$, entre les cercles circonscrits aux triangles $Q_{A} Q_{B} C$ et $Q_{A} B Q_{C}$.
Démontrer que les droites $\left(Q_{A} R\right)$ et $(B C)$ sont perpendiculaires.
|
Soit $H$ l'orthocentre de $A B C, O$ le centre du cercle circonscrit à $A B C$, et $R^{\prime}$ le symétrique de $H$ par rapport à $O$. Les projetés orthogonaux de $H$ et $O \operatorname{sur}(B C)$ sont $H_{a}$ et $A^{\prime}$, donc le projeté orthogonal de $R^{\prime}$ sur $(B C)$ est $Q_{A}$. De même, les projetés orthogonaux de $R^{\prime}$ sur $(C A)$ et sur $(A B)$ sont $Q_{B}$ et $Q_{C}$.
Cela signifie entre autres que $\widehat{C Q_{A} R^{\prime}}=\widehat{Q C_{B} R^{\prime}}=90^{\circ}$, donc que $Q_{A}$ et $Q_{B}$ appartiennent au cercle de diamètre $\left[C R^{\prime}\right]$. Ce cercle coïncide donc avec le cercle circonscrit à $Q_{A} Q_{B} C$. De même, les points $Q_{A}$ et $Q_{C}$ appartiennent au cercle de diamètre [ $B R^{\prime}$ ], qui coïncide avec le cercle circonscrit à $Q_{A} B Q_{C}$. Par conséquent, les points $R$ et $R^{\prime}$ sont confondus, et ( $Q_{A} R$ ) est bien perpendiculaire à $(B C)$.

$\underline{\text { Solution alternative } n^{\circ} 1}$ Ci-dessous, on note $\Gamma_{A}, \Gamma_{B}$ et $\Gamma_{C}$ les cercles circonscrits respectifs à $A Q_{B} Q_{C}, Q_{A} B Q_{C}$ et $Q_{A} Q_{B} C$. Puisque $R$ appartient à $\Gamma_{B}$ et à $\Gamma_{C}$, on sait que
$$
\left(Q_{C} A, Q_{C} R\right)=\left(Q_{C} B, Q_{C} R\right)=\left(Q_{A} B, Q_{A} R\right)=\left(Q_{A} C, Q_{A} R\right)=\left(Q_{B} C, Q_{B} R\right)=\left(Q_{B} A, Q_{B} R\right)
$$
Cela signifie que $R$ appartient aussi à $\Gamma_{A}$, et donc que $A, B$ et $C$ jouent des rôles symétriques. Forts de ce constat, on introduit donc également le cercle circonscrit à $A B C$, que l'on note $\Omega$. Toujours à la recherche de cercles remarquables, on remarque alors que les angles droits en $H_{A}, H_{B}$ et $H_{C}$ suggèrent aussi de tracer les cercles $\Xi_{A}, \Xi_{B}$ et $\Xi_{C}$, de diamètres respectifs $[B C],[C A]$ et $[A B]$.
Enfin, si l'on note $m$ la médiatrice de $[B C]$, l'énoncé nous demande de démontrer que ( $Q_{A} R$ ) et $\left(A H_{A}\right)$ sont symétriques l'une de l'autre par rapport à $m$. On s'intéresse donc de plus près à la symétrie d'axe $m$ et aux cercles dont $m$ est un axe de symétrie : il s'agit des cercles $\Omega, \Xi_{A}$ et, ne serait-ce qu'en apparence, $\Gamma_{A}$.
À défaut de démontrer que le centre de ce dernier cercle se trouve sur $m$, on peut tenter de démontrer que les axes radicaux de $\Gamma_{A}$ avec $\Omega$ ou $\Xi_{A}$ sont parallèles à $(B C)$. Le premier serait alors manifestement la parallèle à $(B C)$ passant par $A$, tandis que le deuxième a l'air $d^{\prime}$ être la droite $\left(B^{\prime} C^{\prime}\right)$.
Comme $B^{\prime}$ est le milieu de $[A C]$ et de $\left[H_{B} Q_{B}\right.$, on sait que $B^{\prime} H_{B} \cdot B^{\prime} C=B^{\prime} Q_{B} \cdot B^{\prime} A$, ce qui signifie bien que $B^{\prime}$ appartient à l'axe radical de $\Gamma_{A}$ et $\Xi_{A}$. De même, $C^{\prime}$ appartient à cet axe radical, qui est donc confondu avec $\left(B^{\prime} C^{\prime}\right)$, de sorte que $\Gamma_{A}$ est bien symétrique par rapport à $m$.
Par conséquent, les cercles $\Omega$ et $\Gamma_{A}$ se rencontrent en un point $X$ qui n'est autre que le symétrique de $A$ par rapport à $m$. Notons alors $R^{\prime}$ le point d'intersection entre $\left(Q_{A} X\right)$ et $\Gamma_{C}$. On sait que $\widehat{C Q_{B} R^{\prime}}=\widehat{C Q_{A} R^{\prime}}=90^{\circ}$. Puisque l'on a également $\widehat{A X R^{\prime}}=90^{\circ}$, le point $R^{\prime}$ est donc diamétralement opposé à $A$ dans le cercle circonscrit à $A Q_{B} X$. Cela démontre que $R^{\prime}$ appartient à $\Gamma_{A}$, donc coïncide avec $R$, ce qui conclut.

|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"problem_match": "\nExercice 10.",
"solution_match": "\nSolution de l'exercice 10"
}
|
915f25ea-5c41-5ec3-b0e7-cc550df3f81b
| 604,618
|
Let $ABC$ be a triangle. We denote $H_{A}$ as the foot of the altitude from $A$ in $\triangle ABC$, and $A^{\prime}$ as the midpoint of the segment $[BC]$. We then denote $Q_{A}$ as the symmetric point of $H_{A}$ with respect to $A^{\prime}$. We define the points $Q_{B}$ and $Q_{C}$ similarly. Finally, we denote $R$ as the intersection point, other than $Q_{A}$, of the circumcircles of triangles $Q_{A} Q_{B} C$ and $Q_{A} B Q_{C}$.
Prove that the lines $\left(Q_{A} R\right)$ and $(BC)$ are perpendicular.
|
$n^{\circ} 2$ We resume the notations from the previous solution. Since the line $\left(Q_{A} R\right)$ is the radical axis of the circles $\Gamma_{B}$ and $\Gamma_{C}$, it is tempting to look for the radical axes of these two circles with another circle. For this purpose, we could consider the circle $\Gamma_{A}$, and observe as before that $R$ is the radical center of the three circles $\Gamma_{A}, \Gamma_{B}$, and $\Gamma_{C}$. Given this symmetry of roles, we also consider the circle $\Omega$, and denote by $Y$ the radical center of $\Gamma_{B}, \Gamma_{C}$, and $\Omega$.
It seems that $B A C Y$ is a parallelogram, and we therefore set out to prove this. To do so, we proceed as in the previous solution. Since $A^{\prime}$ is the midpoint of $[B C]$ and of $\left[H_{A} Q_{A}\right]$, it has the same power with respect to $\Gamma_{C}$ and $\Xi_{C}$. Similarly, $B^{\prime}$ has the same power with respect to $\Gamma_{C}$ and $\Xi_{C}$. We deduce that $\left(A^{\prime} B^{\prime}\right)$ is the radical axis of $\Gamma_{C}$ and $\Xi_{C}$. Since $(A B)$ is the radical axis of $\Xi_{C}$ and $\Omega$ and that $(A B)$ is parallel to $\left(A^{\prime} B^{\prime}\right)$, we deduce that $(A B)$ is parallel to the third radical axis $(C Y)$ between $\Gamma_{C}$ and $\Omega$. Similarly, $(A C)$ is parallel to $(B Y)$.
The symmetry with center $A^{\prime}$ therefore exchanges the line $\left(A H_{A}\right)$ with $\left(Y Q_{A}\right)$, that is, with $\left(Q_{A} R\right)$. The line $\left(Q_{A} R\right)$ is therefore indeed perpendicular to $(B C)$.
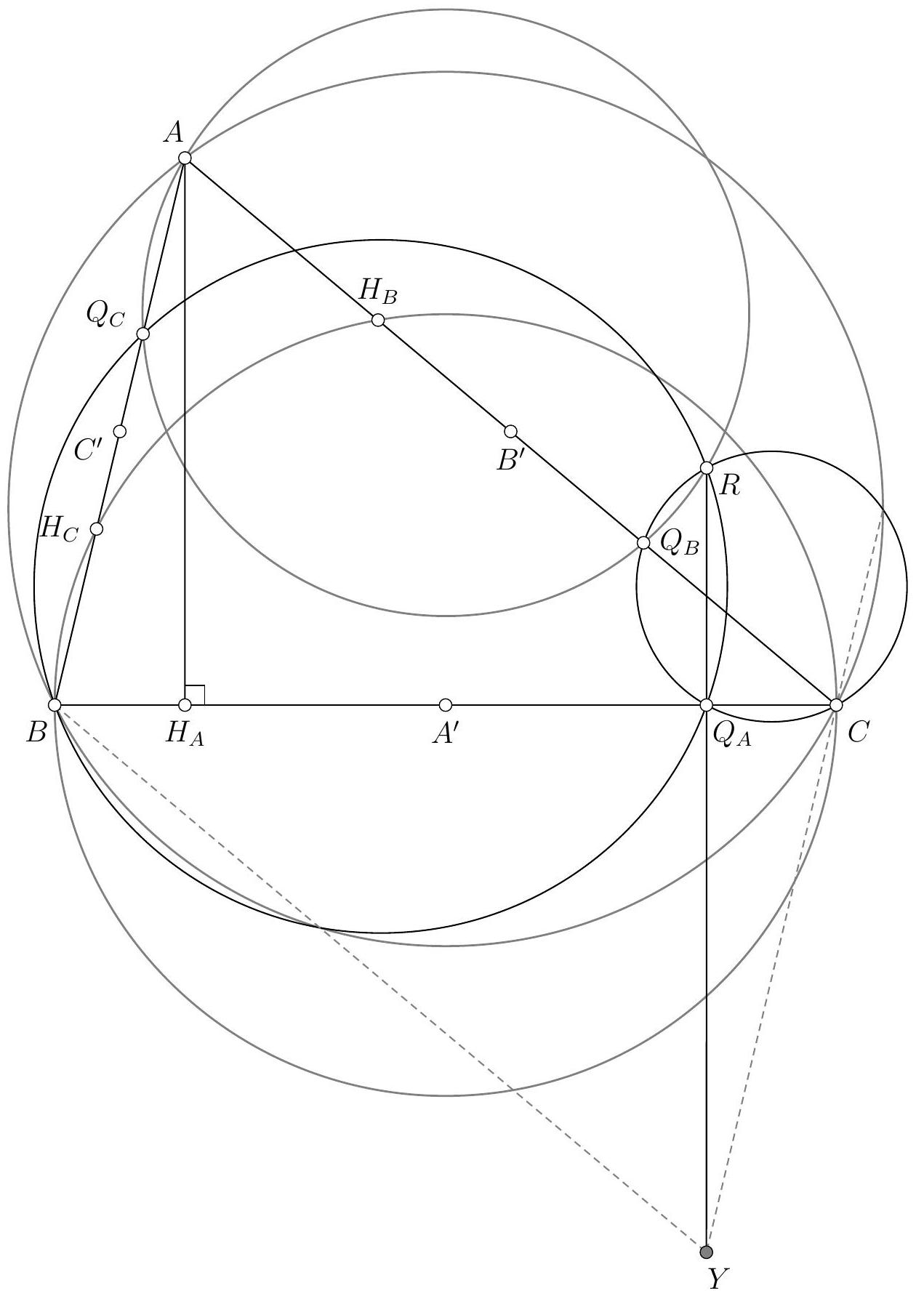
Graders' Comments Very few points were awarded on this problem, for which no student provided a complete solution. The graders nevertheless wish to commend the numerous attempts that were submitted, demonstrating a genuine effort to solve the problem.
Often, the relationships established around the points $H_{A}, H_{B}$, and $H_{C}$ were entirely correct, and we encourage students to remember these as they are true and applicable in many contexts. However, here they were not sufficient on their own to approach the solution and therefore did not earn points.
The problem required a bit of perspective on the definition of the points $Q_{A}, Q_{B}$, and $Q_{C}$. A few students managed to add symmetry to the problem by showing that the point $R$ defined also belongs to the circle $\Gamma_{C}$. It was by examining the many symmetries offered by the figure that it was possible to gain an intuition of the numerous properties of the point $R$, such as the fact that it is the symmetric of $H$ with respect to $O$.
Here are some recurring elements in the proposed solutions:
$\triangleright$ Some students identified the line $\left(Q_{A} R\right)$ as a radical axis. This is indeed the starting point of a possible approach. It would have been necessary to extend this radical axis to guess some of its properties or to introduce other interesting points lying on it, for example, the symmetric of point $A$ with respect to $A^{\prime}$.
$\triangleright$ Some students claimed to submit a complete solution but which in reality did not work. To avoid falling into this trap, it is important to reread and verify that each statement is true and justified. Another way to reread is to check that all the hypotheses of the problem statement have been used.
For example, the fact of having used the point $R$'s belonging to only one of the two circles should be a clue that one has been too hasty.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle. On note $H_{A}$ le pied de la hauteur de $A B C$ issue de $A$, et $A^{\prime}$ le milieu du segment $[B C]$. On note ensuite $Q_{A}$ le symétrique de $H_{A}$ par rapport à $A^{\prime}$. On définit de même les points $Q_{B}$ et $Q_{C}$. Enfin, on note $R$ le point d'intersection, autre que $Q_{A}$, entre les cercles circonscrits aux triangles $Q_{A} Q_{B} C$ et $Q_{A} B Q_{C}$.
Démontrer que les droites $\left(Q_{A} R\right)$ et $(B C)$ sont perpendiculaires.
|
$n^{\circ} 2$ On reprend les notations de la solution précédente. Puisque la droite $\left(Q_{A} R\right)$ est l'axe radical des cercles $\Gamma_{B}$ et $\Gamma_{C}$, il est tentant de rechercher les axes radicaux de ces deux cercles avec un autre cercle. À cette fin, on pourrait considérer le cercle $\Gamma_{A}$, et constater comme précédemment que $R$ est le centre radical des trois cercles $\Gamma_{A}, \Gamma_{B}$ et $\Gamma_{C}$. Au vu de cette symétrie des rôles, on considère également le cercle $\Omega$, et on note alors $Y$ le centre radical de $\Gamma_{B}, \Gamma_{C}$ et $\Omega$.
Il semble que $B A C Y$ soit un parallélogramme, et on entreprend donc de le démontrer. Pour ce faire, on procède comme dans la solution précédente. Puisque $A^{\prime}$ est le milieu de $[B C]$ et de $\left[H_{A} Q_{A}\right]$, il a même puissance par rapport à $\Gamma_{C}$ et $\Xi_{C}$. De même, $B^{\prime}$ a même puissance par rapport à $\Gamma_{C}$ et $\Xi_{C}$. On en déduit que $\left(A^{\prime} B^{\prime}\right)$ est l'axe radical de $\Gamma_{C}$ et $\Xi_{C}$. Puisque $(A B)$ est l'axe radical de $\Xi_{C}$ et $\Omega$ et que $(A B)$ est parallèle à $\left(A^{\prime} B^{\prime}\right)$, on en déduit que $(A B)$ est parallèle au troisième axe radical $(C Y)$ entre $\Gamma_{C}$ et $\Omega$. De même, $(A C)$ est parallèle à $(B Y)$.
La symétrie de centre $A^{\prime}$ échange donc la droite $\left(A H_{A}\right)$ avec $\left(Y Q_{A}\right)$, c'est-à-dire avec $\left(Q_{A} R\right)$. La droite $\left(Q_{A} R\right)$ est donc bien perpendiculaire à $(B C)$.

Commentaire des correcteurs Très peu de points ont été distribués sur cet exercice, pour lequel aucune élève n'a proposé de solution complète. Les correcteurs tiennent toutefois à saluer les nombreuses tentatives qui ont été rendues, témoignant d'un réel effort de recherche sur le problème.
Bien souvent, les relations établies autour des points $H_{A}, H_{B}$ et $H_{C}$ sont tout à fait correctes, et nous encourageons les élèves à les retenir car elles sont vraies et applicables dans de nombreux contextes. Toutefois ici, elles ne suffisaient pas à elles seules à se rapprocher de la solution et ne rapportaient donc pas de points.
L'exercice nécessitait un peu de recul sur la définition des points $Q_{A}, Q_{B}$ et $Q_{C}$. De rares élèves ont pu donc rajouté de la symétrie au problème en montrant que le point $R$ défini appartenait également au cercle $\Gamma_{C}$. C'est en examinant les nombreuses symétries offertes par la figure qu'il était possible d'acquérir l'intuition des nombreuses propriétés sur le point $R$, comme le fait qu'il s'agit du symétrique de $H$ par rapport à $O$.
Voici quelques éléments récurrents dans les solutions proposées:
$\triangleright$ Quelques élèves ont identifié la droite $\left(Q_{A} R\right)$ comme un axe radical. C'est en effet le point de départ d'une approche possible. Il aurait fallu prolonger cet axe radical pour en deviner quelques propriétés ou pour introduire d'autres points intéressants y appartenant, par exemple le symétrique du point $A$ par rapport à $A^{\prime}$.
$\triangleright$ Quelques élèves ont prétendu rendre une solution complète mais qui ne fonctionnait en réalité pas. Pour éviter de tomber dans cet écueil, il est important de se relire et de vérifier que chaque affirmation est vraie et justifiée. Une autre façon de se relire est de vérifier que toutes les hypothèses de l'énoncé ont été utilisées.
Par exemple, le fait de n'avoir utilisé l'appartenance du point $R$ qu'à un seul des deux cercles doit mettre sur la piste que l'on a été trop vite.
|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"problem_match": "\nExercice 10.",
"solution_match": "\nSolution alternative"
}
|
915f25ea-5c41-5ec3-b0e7-cc550df3f81b
| 604,618
|
Let $ABC$ be a triangle such that $90^{\circ}>\widehat{ABC}>\widehat{BCA}$. Let $D$ be the point on the segment $[BC]$ such that $2 \widehat{DAC}=\widehat{ABC}-\widehat{BCA}$. We denote $E$ as the intersection point, other than $A$, between $(AB)$ and the circumcircle of $ACD$, and $P$ as the intersection point between $(AB)$ and the angle bisector of $\widehat{BDE}$. Similarly, we denote $F$ as the intersection point, other than $A$, between $(AC)$ and the circumcircle of $ABD$, and $Q$ as the intersection point between $(AC)$ and the angle bisector of $\widehat{CDF}$.
Prove that $(AB)$ and $(PQ)$ are perpendicular.
|
As usual, we start with a figure that is sufficiently beautiful and large to serve as a support for reflection. For this purpose, we first construct a triangle $A'BC'$ isometric to $ABC$, such that $C'$ lies on the ray $[BA)$, then we draw the bisector of the angle $\widehat{CBA'}$, which we denote as $d$. We can then transfer the angle between the lines $(BC)$ and $d$ to $A$ to construct the ray $[AD)$.
Alternatively, the cocyclicity of points $A, B, D$, and $F$ ensures the equality
$$
\widehat{DBF} = \widehat{DAF} = \widehat{DAC} = \widehat{CBA'}/2
$$
Thus, $F$ is the intersection point of the lines $(AC)$ and $d$, and $D$ is the intersection point, other than $B$, of the line $(BC)$ with the circumcircle of $ABF$.
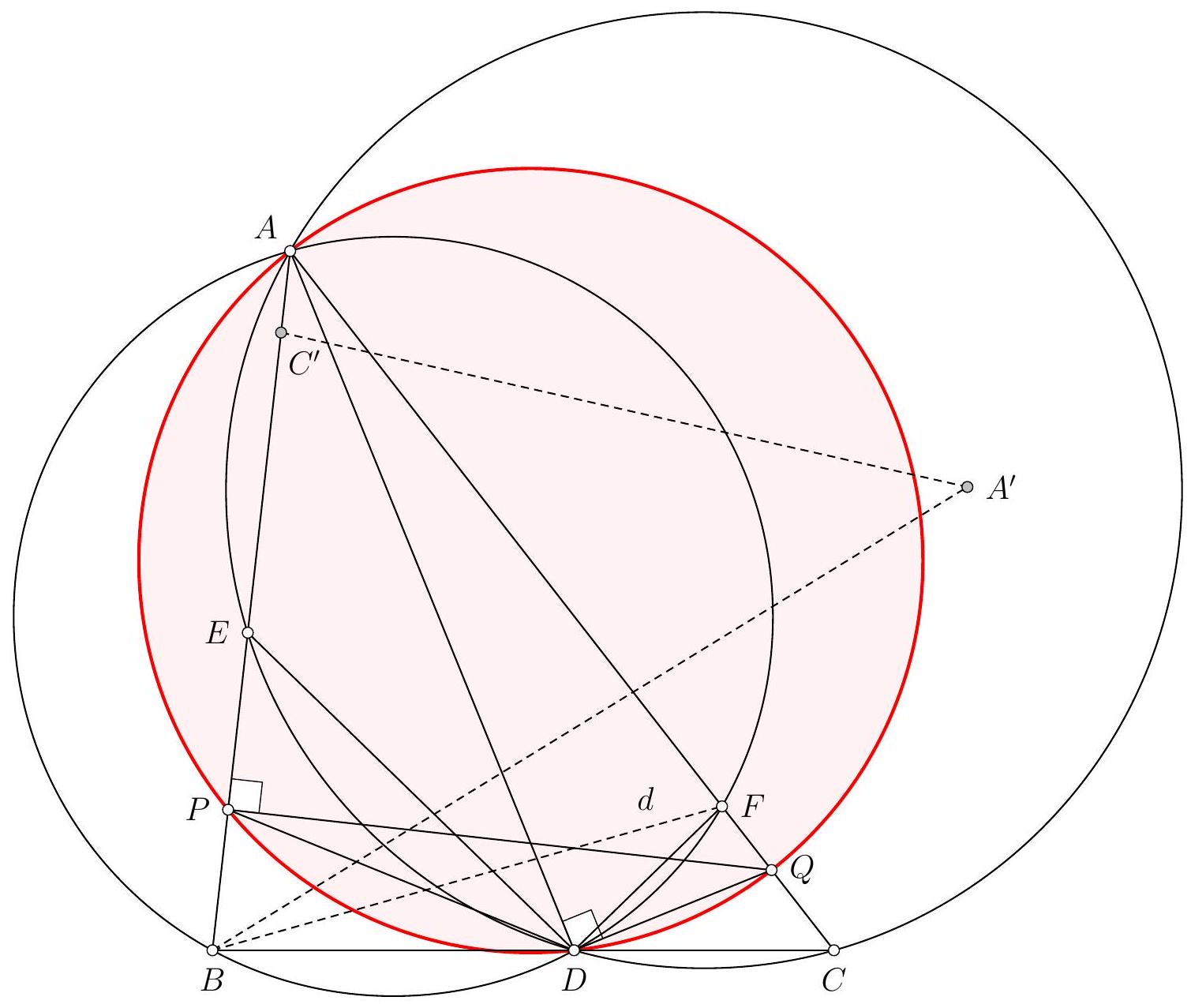
Given the statement, an angle chase is necessary. We set $x = \widehat{BCA}$ and $y = \widehat{DAC}$, and observe that
$$
2 \widehat{CDQ} = \widehat{CDF} = 180^\circ - \widehat{FDB} = \widehat{BAF} = \widehat{BAC} = 180^\circ - 2(x + y),
$$
so $\widehat{CDQ} = 90^\circ - (x + y)$. Similarly,
$$
2 \widehat{PDB} = \widehat{EDB} = 180^\circ - \widehat{CDE} = \widehat{EAC} = \widehat{BAC}
$$
so $\widehat{PDB} = 90^\circ - (x + y)$.
We continue our angle chase, from which we deduce that
$\widehat{QDA} = 180^\circ - \widehat{DAQ} - \widehat{AQD} = 180^\circ - y - (180^\circ - \widehat{DQC}) = (180^\circ - \widehat{CDQ} - \widehat{QCD}) - y = 90^\circ$.
Thus, we need to prove that $A, P, D$, and $Q$ are concyclic. We verify that
$$
\widehat{DPA} = 180^\circ - \widehat{BPD} = \widehat{PDB} + \widehat{DBP} = (90^\circ - x - y) + (x + 2y) = 90^\circ + y = 180^\circ - \widehat{AQD},
$$
which concludes the proof.
Comment from the graders The exercise had two difficulties:
$\triangleright$ The first difficulty was to draw the figure. It was certainly possible to solve the problem without an exact figure, but it is always good to focus on the exact construction of the figure because often, finding how to construct a figure with a complicated hypothesis is already starting to solve the exercise. Moreover, an exact figure allowed one to visually observe that the angle $\widehat{QDA}$ was a right angle, which was a crucial step in the proof.
$\triangleright$ The second difficulty was to express all the angles in the figure solely in terms of the angles $\widehat{CAB}$, $\widehat{ABC}$, and $\widehat{BCA}$. The few students who managed this work mostly solved the exercise immediately.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle tel que $90^{\circ}>\widehat{A B C}>\widehat{B C A}$. Soit $D$ le point sur le segment $[B C]$ tel que $2 \widehat{D A C}=\widehat{A B C}-\widehat{B C A}$. On note $E$ le point d'intersection, autre que $A$, entre $(A B)$ et le cercle circonscrit à $A C D$, puis $P$ le point d'intersection entre $(A B)$ et la bissectrice de $\widehat{B D E}$. De même, on note $F$ le point d'intersection, autre que $A$, entre $(A C)$ et le cercle circonscrit à $A B D$, puis $Q$ le point d'intersection entre $(A C)$ et la bissectrice de $\widehat{C D F}$.
Démontrer que $(A B)$ et $(P Q)$ sont perpendiculaires.
|
Comme d'habitude, on commence par une figure suffisamment belle et grande pour servir de support à la réflexion. À cette fin, on construit tout d'abord un triangle $A^{\prime} B C^{\prime}$ isométrique à $A B C$, tel que $C^{\prime}$ se trouve sur la demi-droite $[B A)$, puis on trace la bissectrice de l'angle $\widehat{C B A^{\prime}}$, que l'on note $d$. On peut alors reporter en $A$ l'angle en entre les droites $(B C)$ et $d$, pour construire la demi-droite $[A D)$.
Alternativement, la cocyclicité des points $A, B, D$ et $F$ nous assure de l'égalité
$$
\widehat{D B F}=\widehat{D A F}=\widehat{D A C}=\widehat{C B A^{\prime}} / 2
$$
Ainsi, $F$ est le point d'intersection des droites $(A C)$ et $d$, et $D$ est le point d'intersection, autre que $B$, de la droite $(B C)$ avec le cercle circonscrit à $A B F$.

Au vu de l'énoncé, une chasse aux angles s'impose. On pose donc $x=\widehat{B C A}$ et $y=\widehat{D A C}$, puis l'on constate que
$$
2 \widehat{C D Q}=\widehat{C D F}=180^{\circ}-\widehat{F D B}=\widehat{B A F}=\widehat{B A C}=180^{\circ}-2(x+y),
$$
de sorte que $\widehat{C D Q}=90^{\circ}-(x+y)$. De même,
$$
2 \widehat{P D B}=\widehat{E D B}=180^{\circ}-\widehat{C D E}=\widehat{E A C}=\widehat{B A C}
$$
de sorte que $\widehat{P D B}=90^{\circ}-(x+y)$.
On continue notre chasse aux angles, d'où l'on déduit que
$\widehat{Q D A}=180^{\circ}-\widehat{D A Q}-\widehat{A Q D}=180^{\circ}-y-\left(180^{\circ}-\widehat{D Q C}\right)=\left(180^{\circ}-\widehat{C D Q}-\widehat{Q C D}\right)-y=90^{\circ}$.
Il s'agit donc de démontrer que $A, P, D$ et $Q$ sont cocycliques. On vérifie alors que
$$
\widehat{D P A}=180^{\circ}-\widehat{B P D}=\widehat{P D B}+\widehat{D B P}=\left(90^{\circ}-x-y\right)+(x+2 y)=90^{\circ}+y=180^{\circ}-\widehat{A Q D},
$$
ce qui conclut.
Commentaire des correcteurs L'exercice comportait deux difficultés:
$\triangleright$ La première difficulté était de tracer la figure. Ici il était certes possible de résoudre le problème sans avoir une figure exacte, mais il est toujours bon de s'intéresser à a construction exacte de la figure car bien souvent, trouver comment construire une figure comportant une hypothèse compliquée, c'est déjà commencer à résoudre l'exercice. De plus, une figure exacte permettait de constater visuellement que l'angle $\widehat{Q D A}$ était droit, ce qui constituait une étape cruciale de la preuve.
$\triangleright$ La deuxième difficulté était d'exprimer tous les angles de la figures uniquement en fonction des angles $\widehat{C A B}, \widehat{A B C}$ et $\widehat{B C A}$. Les quelques élèves ayant réussi ce travail ont pour la plupart résolu l'exercice dans la foulée.
|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-4-Web.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
db23bc86-1c45-5597-8d2a-81dd140759bb
| 604,723
|
Let $ABC$ be an isosceles triangle at $A$, and let $D$ be a point on the segment $[BC]$ such that $BD \neq CD$. Let $P$ and $Q$ be the orthogonal projections of $D$ onto $(AB)$ and $(AC)$. Finally, let $E$ be the point of intersection, other than $A$, between the circumcircles of $ABC$ and $APQ$.
Prove that, if the lines $(EP)$, $(AC)$, and the perpendicular bisector of $[PQ]$ are concurrent, the triangle $ABC$ is right-angled at $A$.
|
A first reflex is to draw a figure where the triangle $ABC$ is isosceles right-angled, but without indicating that it is. Many symmetries then appear. Let $X$ be the intersection point of the lines $(AC)$ and $(EP)$, $\ell$ the perpendicular bisector of $[PQ]$, $O$ the center of the circumcircle of $ABC$, and $M$ the midpoint of $[BC]$: it is a matter of proving that $M=O$.
Since $PQX$ is isosceles at $X$, the symmetry with axis $\ell$ exchanges the lines $(AQ)$ and $(PE)$, so that $\widehat{AQP}=\widehat{QPE}$. Since $A, E, P$, and $Q$ are concyclic, the quadrilateral $AEPQ$ is therefore an isosceles trapezoid, which is easily verified since
$$
(AE, PQ) = (AE, AQ) + (AQ, PQ) = (PE, PQ) + (QA, QP) = 0^{\circ}
$$
The symmetry with axis $\ell$ therefore exchanges the points $A$ and $E$, and $\ell$ is in fact the perpendicular bisector of $[AE]$. It therefore contains, in particular, the centers $O$ and $O'$ of the circumcircles of $ABC$ and $AEPQ$.
Given the right angles at $P, Q$, and $M$, the latter circle is in fact the circle with diameter $[AD]$, and it contains $D$ and $M$. Moreover, $(AM)$ is the angle bisector of $\widehat{BAC}$, so $M$ is the South pole of $A$ in the triangle $APQ$, and $PQM$ is isosceles at $M$. Thus, $M$ lies on $\ell$.
In conclusion, $M$ and $O$ both belong to $(AM)$ and to $\ell$. Since $D \neq M$, we also know that $O'$, the midpoint of $[AD]$, is not on $(AM)$. Since $\ell$ contains $O'$, it is therefore not coincident with $(AM)$, and $M$ must coincide with $O$, which concludes.
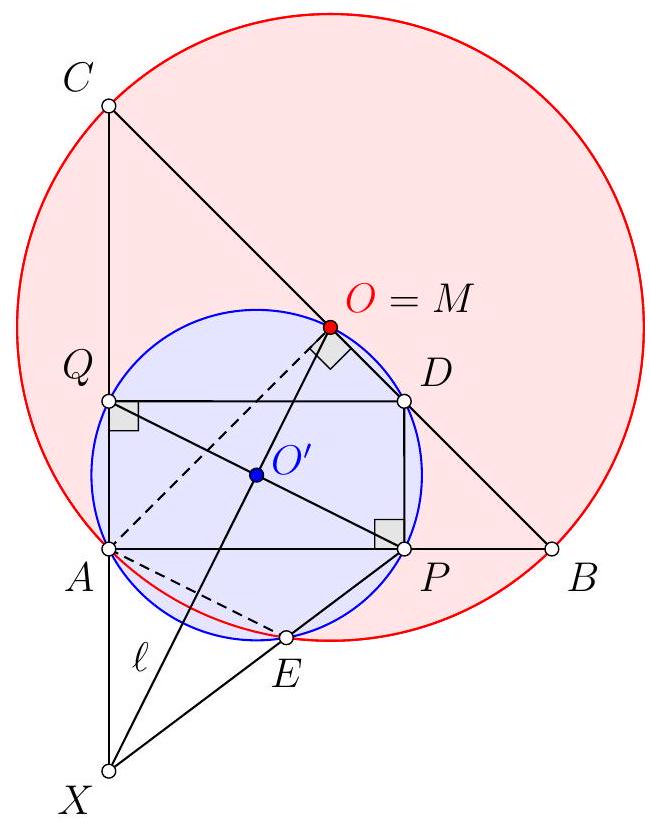
Comment from the graders: The exercise was very well done. Many students manage, through the development of simple ideas like angle chasing, to make significant progress in solving the problem, while some others force the use of very advanced results like Pascal's or Desargues' theorems but without obtaining significant results.
The figures provided are often very precise, and it was sometimes frustrating to see that the midpoint of the segment $[BC]$ belongs to the circle passing through the points $A, P$, and $Q$ appear on them without the student mentioning this midpoint in their attempt.
We noted a significant number of incorrect solutions. The errors are often due to the use of a property that is evident on the figure but not yet proven. Often, to avoid this pitfall, it is good to ask oneself if all the hypotheses of the statement have been used. Thus, several students believe they have solved the exercise without using either that the triangle $ABC$ is isosceles or that the point $E$ belongs to its circumcircle.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle isocèle en $A$, puis $D$ un point du segment $[B C]$ tel que $B D \neq C D$. Soit $P$ et $Q$ les projetés orthogonaux de $D$ sur $(A B)$ et $(A C)$. Enfin, soit $E$ le point d'intersection, autre que $A$, entre les cercles circonscrits à $A B C$ et $A P Q$.
Démontrer que, si les droites $(E P),(A C)$ et la médiatrice de $[P Q]$ sont concourantes, le triangle $A B C$ est rectangle en $A$.
|
Un premier réflexe est de dessiner une figure où le triangle $A B C$ est isocèle rectangle, mais sans indiquer qu'il l'est. De nombreuses symétries apparaissent alors. Notons $X$ le point d'intersection des droites $(A C)$, et $(E P), \ell$ la médiatrice de $[P Q]$, $O$ le centre du cercle circonscrit à $A B C$ et $M$ le milieu de $[B C]$ : il s'agit de démontrer que $M=O$.
Comme $P Q X$ est isocèle en $X$, la symétrie d'axe $\ell$ échange les droites $(A Q)$ et $(P E)$, de sorte que $\widehat{A Q P}=\widehat{Q P E}$. Puisque $A, E, P$ et $Q$ sont cocycliques, le quadrilatère $A E P Q$ est donc un trapèze isocèle, ce qui se vérifie aisément puisque
$$
(A E, P Q)=(A E, A Q)+(A Q, P Q)=(P E, P Q)+(Q A, Q P)=0^{\circ}
$$
La symétrie d'axe $\ell$ échange donc les points $A$ et $E$, et $\ell$ est en fait la médiatrice de $[A E]$. Elle contient donc, en particulier, les centres $O$ et $O^{\prime}$ des cercles circonscrits à $A B C$ et $A E P Q$.
Au vu des angles droits en $P, Q$ et $M$, ce dernier cercle est en fait le cercle de diamètre $[A D]$, et il contient $D$ et $M$. En outre, $(A M)$ est la bissectrice de $\widehat{B A C}$, donc $M$ est le pôle Sud de $A$ dans le triangle $A P Q$, et $P Q M$ est isocèle en $M$. Ainsi, $M$ appartient à $\ell$.
En conclusion, $M$ et $O$ appartiennent tous deux à $(A M)$ et à $\ell$. Puisque $D \neq M$, on sait aussi que $O^{\prime}$, le milieu de $[A D]$, n'est pas sur $(A M)$. Puisque $\ell$ contient $O^{\prime}$, elle n'est donc pas confondue avec ( $A M)$, et $M$ coïncide donc avec $O$, ce qui conclut.

Commentaire des correcteurs L'exercice a été très bien réussi. Beaucoup d'élèves arrivent, par le développement d'idées simples comme une chasse aux angles, à avancer significativement dans la résolution du problème, quand certains autres forcent l'utilisation de résultats très avancés comme le théorème de Pascal ou de Desargues mais sans en obtenir des résultats conséquents.
Les figures fournies sont souvent très précises et il a été parfois frustrant de voir apparaître sur celles-ci que le milieu du segment $[B C]$ appartient au cercle passant par les points $A, P$ et $Q$ sans que l'élève n'évoque ce milieu dans sa tentative.
Nous avons noté une quantité significative de solutions erronées. Les erreurs sont souvent dues à l'utilisation d'une propriété manifeste sur la figure mais qui n'est pas encore démontrée. Bien souvent, pour éviter cet écueil, il est bon de se demander si toutes les hypothèses de l'énoncé ont été utilisées. Ainsi, plusieurs élèves croient avoir résolu l'exercice sans avoir utilisé ni que le triangle $A B C$ est isocèle, ni que le point $E$ appartient à son cercle circonscrit.
|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-4-Web.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "\nSolution de l'exercice 6"
}
|
403e90a7-02ab-53c7-a444-bba7341f3b84
| 604,764
|
Let $n \geqslant 6$ be an integer. In the plane, we have arranged $n$ pairwise disjoint disks $D_{1}, D_{2}, \ldots, D_{n}$ with radii $r_{1} \geqslant r_{2} \geqslant \ldots \geqslant r_{n}$. For every integer $i \leqslant n$, consider a point $P_{i}$ inside the disk $D_{i}$. Finally, let $A$ be any point in the plane. Prove that
$$
A P_{1}+A P_{2}+\ldots+A P_{n} \geqslant r_{6}+r_{7}+\ldots+r_{n}
$$
|
Let $O_{i}$ be the center of the disk $D_{i}$. If $A$ coincides with one of the points $O_{i}$, the desired result is immediate. Otherwise, we sort the centers $O_{i}$ clockwise around $A$. These define six angles whose sum is $360^{\circ}$, so one of the angles, say $\widehat{O_{i} A O_{j}}$, is at most $60^{\circ}$. If we assume without loss of generality that $A O_{i} \geqslant A O_{j}$, the Law of Cosines (Al-Kashi's theorem) then indicates that
$$
\begin{aligned}
\left(r_{i}+r_{j}\right)^{2} & \leqslant O_{i} O_{j}^{2}=A O_{i}^{2}+A O_{j}^{2}-2 \cos \left(\widehat{O_{i} A O_{j}}\right) A O_{i} \cdot A O_{j} \leqslant A O_{i}^{2}-A O_{i} \cdot A O_{j}+A O_{j}^{2} \\
& \leqslant A O_{i}^{2} \leqslant\left(A P_{i}+r_{i}\right)^{2},
\end{aligned}
$$
so that $A P_{i} \geqslant r_{j} \geqslant r_{6}$.
We now proceed by induction on $n$. First, if $n=6$, the statement of the problem is a simple corollary of our lemma. Then, if $n \geqslant 7$, we apply our lemma to the disks $D_{1}, \ldots, D_{6}$. There exists an integer $i \leqslant 6$ such that $A P_{i} \geqslant r_{6}$. We now remove the disk $D_{i}$ and apply the induction hypothesis to the remaining $n-1$ disks, so that
$$
A P_{i}+\sum_{j \neq i} A P_{j} \geqslant r_{6}+\left(r_{7}+\ldots+r_{n}\right)
$$
which concludes the proof.
Comment from the graders: The proposed problem was very difficult and was only tackled by about twenty students. The graders were amazed to see that two students had solved it brilliantly.
Many students first made the relevant observation that one could always assume that $A P_{i}=A O_{i}-r_{i}$ when $A$ does not belong to $D_{i}$, where $O_{i}$ is the center of the disk $D_{i}$. However, the graders were surprised to find sometimes very complicated proofs for this result, which is quite simple and geometrically clear. Unfortunately, given the difficulty of the exercise, this observation did not earn any points, but it does not detract from its relevance. The key was therefore to find a stronger intermediate statement from which the desired conclusion could be deduced.
Several students thought about the case $n=6$, which was very good, but the two who rigorously treated this case are also the only two to have concluded the exercise. In general, asserting outright that "the worst situation is when the disks have the same radius and their centers form a regular hexagon centered at $A$" is a welcome heuristic, but it is not proven, and it is clear that this statement cannot earn any points until it is supported.
Similarly, several students tried to prove that when $A$ does not belong to any disk $D_{i}$, there exists such a disk for which $A P_{i} \geqslant r_{i}$. However, it was easy to construct a counterexample to this inequality, for example if $A$ and the points $P_{i}$ and $O_{i}$ are
aligned, with $A O_{i}=5^{i}, r_{i}=3 \times 5^{i-1}$ and $A P_{i}=2 \times 5^{i-1}$. Indeed, when formulating an idea for a lemma, it is very important to look for simple counterexamples to this lemma, which would invalidate it, and this in order to limit the time wasted trying to prove something false. Such a phase often allows, at little cost, to refine the formulation of the lemma, or to realize that the underlying idea is completely wrong; when it does not lead to anything, that is, when no counterexample has been found, one has more confidence in the lemma, and this is also encouraging, therefore positive.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $n \geqslant 6$ un entier. On a disposé, dans le plan, $n$ disques $D_{1}, D_{2}, \ldots, D_{n}$ deux à deux disjoints, de rayons $r_{1} \geqslant r_{2} \geqslant \ldots \geqslant r_{n}$. Pour tout entier $i \leqslant n$, on considère un point $P_{i}$ à l'intérieur du disque $D_{i}$. Enfin, soit $A$ un point quelconque du plan. Démontrer que
$$
A P_{1}+A P_{2}+\ldots+A P_{n} \geqslant r_{6}+r_{7}+\ldots+r_{n}
$$
|
Soit $O_{i}$ le centre du disque $D_{i}$. Si $A$ coïncide avec l'un des points $O_{i}$, le résultat désiré est immédiat. Sinon, on trie les centres $O_{i}$ dans le sens horaire autour de $A$. Ceux-ci définissent six angles de somme $360^{\circ}$, donc l'un des angles, disons $\widehat{O_{i} A O_{j}}$, vaut au plus $60^{\circ}$. Si l'on suppose sans perte de généralité que $A O_{i} \geqslant A O_{j}$, le théorème d'Al-Kashi indique alors que
$$
\begin{aligned}
\left(r_{i}+r_{j}\right)^{2} & \leqslant O_{i} O_{j}^{2}=A O_{i}^{2}+A O_{j}^{2}-2 \cos \left(\widehat{O_{i} A O_{j}}\right) A O_{i} \cdot A O_{j} \leqslant A O_{i}^{2}-A O_{i} \cdot A O_{j}+A O_{j}^{2} \\
& \leqslant A O_{i}^{2} \leqslant\left(A P_{i}+r_{i}\right)^{2},
\end{aligned}
$$
de sorte que $A P_{i} \geqslant r_{j} \geqslant r_{6}$.
On procède maintenant par récurrence sur $n$. Tout d'abord, si $n=6$, le résultat de l'énoncé est un simple corollaire de notre lemme. Puis, si $n \geqslant 7$, on applique notre lemme aux disques $D_{1}, \ldots, D_{6}$. Il existe donc un entier $i \leqslant 6$ tel que $A P_{i} \geqslant r_{6}$. On supprime maintenant le disque $D_{i}$ et on applique l'hypothèse de récurrence aux $n-1$ disques restants, de sorte que
$$
A P_{i}+\sum_{j \neq i} A P_{j} \geqslant r_{6}+\left(r_{7}+\ldots+r_{n}\right)
$$
ce qui conclut.
Commentaire des correcteurs Le problème proposé était très difficile, et il n'a été abordé que par une vingtaine d'élèves. Les correcteurs se sont émerveillés de constater que deux élèves l'avaient résolu avec brio.
De nombreux élèves ont tout d'abord formulé la remarque pertinente selon laquelle on pouvait toujours supposer que $A P_{i}=A O_{i}-r_{i}$ quand $A$ n'appartient pas à $D_{i}$, où $O_{i}$ est le centre du disque $D_{i}$. Toutefois, les correcteurs ont été surpris de découvrir des preuves parfois très compliquées pour ce résultat pourtant fort simple et géométriquement clair. Malheureusement, au vu de la difficulté de l'exercice, cette remarque ne rapportait aucun point, mais cela n'enlève rien à sa pertinence. La clé consistait donc à trouver un énoncé intermédiaire plus fort, dont on pourrait déduire la conclusion demandée.
Plusieurs élèves ont pensé à regarder le cas $n=6$, ce qui était très bien, mais les deux seuls qui ont traité ce cas rigoureusement sont aussi les deux seuls à avoir conclu l'exercice. De manière générale, affirmer tout de go que « la pire situation est celle où les disques sont de même rayon et où leurs centres forment un hexagone régulier de centre $A$ » repose sur une heuristique bienvenue, mais nullement prouvée, et il est clair que cette affirmation ne peut pas rapporter le moindre point tant qu'elle n'est pas étayée.
De même, plusieurs élèves ont cherché à démontrer que lorsque $A$ n'appartient à aucun disque $D_{i}$, il existait un tel disque pour lequel $A P_{i} \geqslant r_{i}$. Cependant, il était facile de construire un contre-exemple à cette inégalité, par exemple si $A$ et les points $P_{i}$ et $O_{i}$ sont
alignés, avec $A O_{i}=5^{i}, r_{i}=3 \times 5^{i-1}$ et $A P_{i}=2 \times 5^{i-1}$. De fait, lorsque l'on formule une idée de lemme, il est très important de rechercher des contre-exemples simples à ce lemme, qui seraient de nature à l'invalider, et ce dans le but de limiter le temps perdu à tenter de démontrer quelque chose de faux. Une telle phase permet souvent, à peu de frais, d'affiner la formulation du lemme, ou bien de se rendre compte que l'idée sous-jacente est complètement fausse; quand elle n'aboutit pas, c'est-à-dire quand on n'a pas trouvé de contre-exemple, on a plus confiance dans le lemme, et c'est là aussi encourageant, donc positif.
|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-4-Web.jsonl",
"problem_match": "\nExercice 7.",
"solution_match": "\nDémonstration."
}
|
a49e18a6-cb71-5ec8-a949-35e7f071b275
| 604,775
|
Let $A B C D E$ be a convex pentagon such that $\widehat{A B E}=\widehat{A C E}=\widehat{A D E}=90^{\circ}$ and $B C=C D$. Finally, let $K$ be a point on the ray $[A B]$ such that $A K=A D$, and let $L$ be a point on the ray $[E D)$ such that $E L=B E$. Prove that the points $B, D, K$ and $L$ lie on the same circle with center $C$.
|
Given the right angles at $B, C$, and $D$, the points $A, B, C, D$, and $E$ lie on the same semicircle with diameter $[A E]$. Since $B C = C D$, point $C$ is the South Pole of $A$ in triangle $A B D$. Therefore, $(A C)$ is the angle bisector of $\widehat{D A B}$, which means it is the perpendicular bisector of $[K D]$. Similarly, $(C E)$ is the perpendicular bisector of $[B L]$. This implies that $C L = B C = D C = C K$, which concludes the proof.
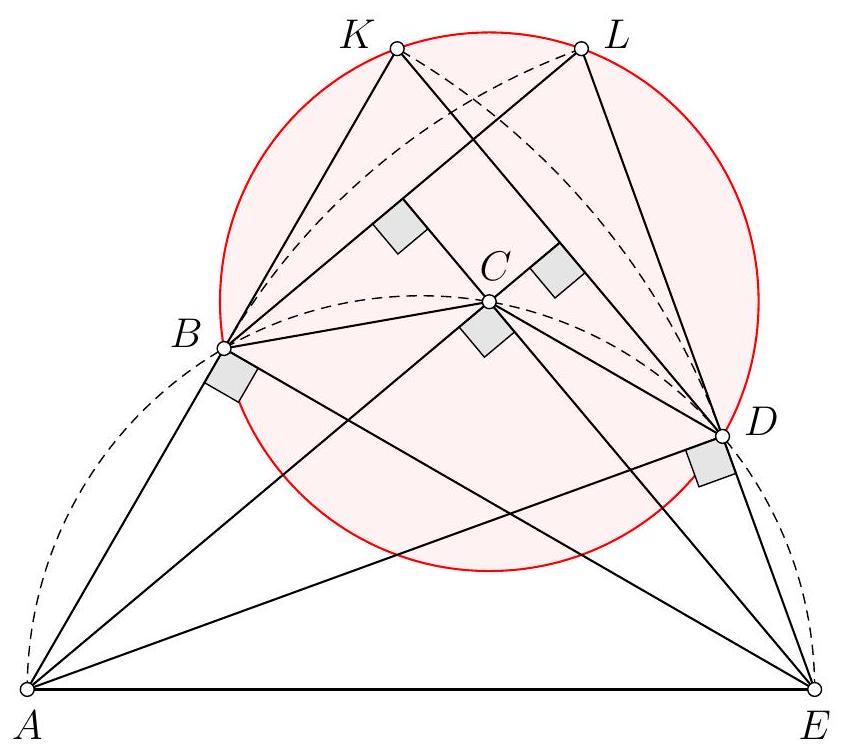
Comment from the graders: The problem was well approached. Many students managed to show that points $B, D, L$, and $K$ are concyclic. Once this step was achieved, most students attempted to show that $\widehat{B C D} = 2 \widehat{B K D}$ to apply the converse of the inscribed angle theorem.
Unfortunately, the angle equality alone is not sufficient to establish that point $C$ is the center of the circumcircle of triangle $B K D$. Indeed, any point $X$ on the arc $B D$ containing $C$ in the circumcircle of triangle $B C D$ also satisfies this angle equality.
It was necessary to invoke the hypothesis given in the problem statement, which is that $B C = C D$. The equalities $B C = C D$ and $\widehat{B C D} = 2 \widehat{B K D}$ were then sufficient to conclude, since on the perpendicular bisector of segment $[B D]$, there is only one point $X$ that satisfies $\widehat{B X D} = 2 \widehat{B K D}$. Since this property is satisfied by the center of the circumcircle of triangle $B K D$, such a point $X$ is indeed the center sought. This recurring error prevented many students from earning full points.
It is also worth noting that very few students recognized the South Pole configuration, which is present in many geometry problems and should therefore be remembered.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D E$ un pentagone convexe tel que $\widehat{A B E}=\widehat{A C E}=\widehat{A D E}=90^{\circ}$ et $B C=C D$. Enfin, soit $K$ un point sur la demi-droite $[A B]$ tel que $A K=A D$, et soit $L$ un point sur la demi-droite $[E D)$ tel que $E L=B E$. Démontrer que les points $B, D, K$ et $L$ appartiennent à un même cercle de centre $C$.
|
Au vu des angles droits dont on dispose en $B, C$ et $D$, les points $A$, $B, C, D$ et $E$ appartiennent à un même demi-cercle de diamètre $[A E]$. Comme $B C=C D$, le point $C$ est donc le pôle Sud issu de $A$ dans le triangle $A B D$. Ainsi, $(A C)$ est la bissectrice de $\widehat{D A B}$, c'est-à-dire la médiatrice de $[K D]$. De même, $(C E)$ est la médiatrice de $[B L]$. Cela signifie que $C L=B C=D C=C K$, ce qui conclut.

Commentaire des correcteurs Le problème a été bien abordé. Une bonne partie des élèves parvient à montrer que les points $B, D, L$ et $K$ sont cocycliques. Une fois cette étape franchie, la plupart des élèves tentent de montrer que $\widehat{B C D}=2 \widehat{B K D}$ pour appliquer une réciproque du théorème de l'angle au centre.
Malheureusement, l'égalité d'angle seule ne permet pas d'établir que le point $C$ est le centre du cercle circonscrit au triangle $B K D$. En effet, tout point $X$ sur l'arc $B D$ contenant $C$ dans le cercle circonscrit au triangle $B C D$ vérifie également cette égalité d'angle.
Il fallait encore invoquer l'hypothèse donnée par l'énoncé qui est que $B C=C D$. Les égalités $B C=C D$ et $\widehat{B C D}=2 \widehat{B K D}$ étaient alors suffisantes pour conclure, puisque sur la médiatrice du segment $[B D]$, il n'y a qu'un seul point $X$ vérifiant $\widehat{B X D}=2 \widehat{B K D}$, et comme cette propriété est vérifiée par le centre du cercle circonscrit au triangle $B K D$, un tel point $X$ est bien le centre recherché. Cette erreur récurrente a empêché de nombreux élèves d'avoir la totalité des points.
Mentionnons également que très peu d'élèves ont reconnu la configuration du pôle Sud, qui est pourtant présente dans de nombreux problèmes de géométrie et qui est donc à retenir.
|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Web-Test-5.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution de l'exercice 1"
}
|
93af54df-1369-5917-bbfb-60fde056b1c4
| 604,803
|
To prepare for the final POFM test of the year, Jean-Baptiste and Marie-Odile have collected 100 math problems and are now working on creating a revision schedule. Over the 100 days leading up to the POFM test, each of them will solve one problem per day. Let \( x \) be the number of problems Jean-Baptiste solves strictly before Marie-Odile, and \( y \) be the number of problems Marie-Odile solves strictly before Jean-Baptiste. Finally, we say that the revision schedule is fair if \( x = y \).
Prove that there are at least \( 100! \times \left(2^{50} + (50!)^2\right) \) fair schedules.
|
First, there are 100! ways to choose the order in which Jean-Baptiste will handle the problems. These 100! ways all play symmetric roles. Without loss of generality, we number the problems from 1 to 100, in the order Jean-Baptiste deals with them, and it is necessary to prove that there are at least \(2^{50}+(50!)^{2}\) permutations \(\sigma\) of the set \(\{1,2, \ldots, 100\}\) for which the sets \(\{k: \sigma(k)<k\}\) and \(\{k: \sigma(k)>k\}\) have the same cardinality. We will say that these permutations are fair.
First, we can construct \(2^{50}\) fair permutations as follows: given a subset \(X\) of \(\{1,2, \ldots, 50\}\), among the \(2^{50}\) possible subsets, we construct the permutation \(\sigma_{X}\) such that
\[
\sigma_{X}(2 k-1)=\left\{\begin{array}{ll}
2 k & \text { if } k \in X \\
2 k-1 & \text { if } k \notin X
\end{array} \text { and } \sigma_{X}(2 k)= \begin{cases}2 k-1 & \text { if } k \in X \\
2 k & \text { if } k \notin X .\end{cases}\right.
\]
For such a permutation, we observe that \(\sigma_{X}(k)<k\) if and only if \(k / 2 \in X\), and that \(\sigma_{X}(k)>k\) if and only if \((k+1) / 2 \in X\). Consequently, \(\sigma_{X}\) is fair.
We then construct \((50! )^{2}\) fair permutations as follows: given two permutations \(\tau\) and \(\pi\) of \(\{1,2, \ldots, 50\}\) among the \((50!)^{2}\) pairs of possible permutations, we construct the permutation \(\sigma_{\pi, \tau}\) such that
\[
\sigma_{\pi, \tau}(k)= \begin{cases}50+\pi(k) & \text { if } 1 \leqslant k \leqslant 50 \\ \tau(k-50) & \text { if } 51 \leqslant k \leqslant 100\end{cases}
\]
For such a permutation, we observe that \(\sigma_{\pi, \tau}(k)<k\) if and only if \(51 \leqslant k \leqslant 100\), and that \(\sigma_{X}(k)>k\) if and only if \(1 \leqslant k \leqslant 50\). Consequently, \(\sigma_{\pi, \tau}\) is fair.
Finally, we of course verify that two permutations \(\sigma_{X}\) and \(\sigma_{\pi, \tau}\) are never equal, since \(\sigma_{X}(1) \leqslant 2<51 \leqslant \sigma_{\pi, \tau}(1)\).
Examiner's Comment The problem was difficult and few students managed to make significant progress. Some tried to invoke possible meanings of \(100!, 2^{50}\), and \((50!)^{2}\) somewhat randomly, hoping it would work. It is important to remain rigorous: trying to interpret each of these quantities is obviously a good idea, but one must carefully examine the expression.
Here, the term 100! invites us to fix an initial permutation for one of the two people, for which there are 100! choices. Then, we wanted to find \(2^{50}+(50!)^{2}\) permutations. Here, the plus sign suggests that we need to find at least two types of permutations: ideally, one type with \((50!)^{2}\) permutations, and another with \(2^{50}\) permutations.
Some students, in their vague justifications, did not understand this and tried to show that there were \(2^{50}\) possibilities for something, and \((50!)^{2}\) for something else, which here would have given a product. Moreover, several students, once the two sets of permutations were created, did not verify that these sets were disjoint, which is necessary to conclude: it must obviously be done!
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Pour s'entraîner en prévision du dernier test POFM de l'année, Jean-Baptiste et Marie-Odile ont collecté 100 problèmes de mathématiques, et s'attellent désormais à la confection d'un programme de révisions. Pendant les 100 jours qui les séparent du test POFM, chacun devra traiter un problème par jour. On note $x$ le nombre de problèmes que Jean-Baptiste a traités strictement avant Marie-Odile, et $y$ le nombre de problèmes que Marie-Odile a traités strictement avant Jean-Baptiste. Enfin, on dit que le programme de révisions est équitable si $x=y$.
Démontrer qu'il existe au moins $100!\times\left(2^{50}+(50!)^{2}\right)$ programmes équitables.
|
Tout d'abord, il existe 100! manières de choisir l'ordre dans lequel Jean-Baptiste traitera les problèmes. Ces 100! manières jouent toutes des rôles symétriques. Sans perte de généralité, on numérote les problèmes de 1 à 100, dans l'ordre où Jean-Baptiste les traite, et il s'agit de démontrer qu'il existe au moins $2^{50}+(50!)^{2}$ permutations $\sigma$ de l'ensemble $\{1,2, \ldots, 100\}$ pour lesquelles les ensembles $\{k: \sigma(k)<k\}$ et $\{k: \sigma(k)>k\}$ ont même cardinal. On dira que ces permutations sont équitables.
Tout d'abord, on peut construire $2^{50}$ permutations équitables comme suit : étant donné un sous-ensemble $X$ de $\{1,2, \ldots, 50\}$, parmi les $2^{50}$ possibles, on construit la permutation $\sigma_{X}$ telle que
$$
\sigma_{X}(2 k-1)=\left\{\begin{array}{ll}
2 k & \text { si } k \in X \\
2 k-1 & \text { si } k \notin X
\end{array} \text { et } \sigma_{X}(2 k)= \begin{cases}2 k-1 & \text { si } k \in X \\
2 k & \text { si } k \notin X .\end{cases}\right.
$$
Pour une telle permutation, on constate que $\sigma_{X}(k)<k$ si et seulement $k / 2 \in X$, et que $\sigma_{X}(k)>k$ si et seulement si $(k+1) / 2 \in X$. Par conséquent, $\sigma_{X}$ est équitable.
On construit ensuite (50! $)^{2}$ permutations équitables comme suit : étant données deux permutations $\tau$ et $\pi$ de $\{1,2, \ldots, 50\}$ parmi les $(50!)^{2}$ paires de permutations possibles, on construit la permutation $\sigma_{\pi, \tau}$ telle que
$$
\sigma_{\pi, \tau}(k)= \begin{cases}50+\pi(k) & \text { si } 1 \leqslant k \leqslant 50 \\ \tau(k-50) & \text { si } 51 \leqslant k \leqslant 100\end{cases}
$$
Pour une telle permutation, on constate que $\sigma_{\pi, \tau}(k)<k$ si et seulement $51 \leqslant k \leqslant 100$, et que $\sigma_{X}(k)>k$ si et seulement si $1 \leqslant k \leqslant 50$. Par conséquent, $\sigma_{\pi, \tau}$ est équitable.
Enfin, on vérifie bien sûr que deux permutations $\sigma_{X}$ et $\sigma_{\pi, \tau}$ ne sont jamais égales, puisque $\sigma_{X}(1) \leqslant 2<51 \leqslant \sigma_{\pi, \tau}(1)$.
Commentaire des correcteurs L'exercice était difficile et peu d'élèves ont réussi à bien avancer dessus. Certains ont tenté d'invoquer parfois un peu au hasard des significations possibles de $100!, 2^{50}$ et $(50!)^{2}$ en espérant que cela fonctionnait. Il faut rester rigoureux : essayer d'interpréter chacune de ces quantités est évidemment une bonne idée, mais il faut bien regarder l'expression.
Ici, le terme 100! nous invitait à fixer une permutation initiale pour une des deux personnes, pour laquelle il y a 100! choix. Ensuite, on voulait trouver $2^{50}+(50!)^{2}$ permutations. Ici, le fait d'avoir un plus nous fait comprendre qu'il faut trouver deux types de permutations au moins : idéalement, un type avec (50!) $)^{2}$ permutations, et un autre avec $2^{50}$ permutations.
Certains élèves, dans leurs justifications très vagues, n'ont pas compris cela, et essayaient de montrer qu'il y avait $2^{50}$ possibilités pour quelque chose, puis (50!) ${ }^{2}$ pour autre chose, ce qui ici aurait donné un produit. Par ailleurs, plusieurs élèves, une fois les deux ensembles de permutations créés, n'ont pas vérifié que ces ensembles étaient disjoints, chose pourtant nécessaire pour conclure : il faut évidemment le faire!
|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Web-Test-5.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
383f7a65-4ba3-56f9-9e9b-7cc4b3f2af36
| 604,832
|
Let $ABCD$ be a convex quadrilateral where the angles at $B$ and $D$ are obtuse, and the angles at $A$ and $C$ are equal to each other. Let $E$ and $F$ be the reflections of $A$ with respect to $(BC)$ and $(CD)$. Let $K$ and $L$ be the points of intersection of $(BD)$ with $(AE)$ and $(AF)$. Prove that the circumcircles of triangles $BEK$ and $DFL$ are tangent to each other.
|
The most practical way to construct point $A$ is to first construct its symmetric point $A^{\prime}$ with respect to $(B D)$, since $A^{\prime}$ is cocyclic with $B, C$, and $D$. By doing so, we observe that $A^{\prime}$ seems to belong to the circumcircles of triangles $B E K$ and $D F L$, and an angle chase indeed shows that
$$
\begin{aligned}
\left(K E, K A^{\prime}\right) & =(K E, B C)+(B C, B D)+\left(B D, K A^{\prime}\right) \\
& =90^{\circ}+(B C, B D)+(K A, B D) \\
& =90^{\circ}+(B C, B D)+(K A, B C)+(B C, B D) \\
& =2(B C, B D) \\
\left(B E, B A^{\prime}\right) & =(B E, B C)+(B C, B D)+\left(B D, B A^{\prime}\right) \\
& =(B C, B A)+(B C, B D)+(B A, B D) \\
& =2(B C, B D) .
\end{aligned}
$$
This means that $A^{\prime}, B, K$, and $E$ lie on a circle $\omega_{b}$, and similarly, that $A^{\prime}, D, L$, and $F$ lie on a circle $\omega_{d}$. Let $t$ and $t^{\prime}$ be the tangents to $\omega_{b}$ and $\omega_{d}$ at $A^{\prime}$. Another angle chase shows that
$$
\begin{aligned}
(t, B D) & =\left(t, A^{\prime} B\right)+\left(A^{\prime} B, B D\right) \\
& =\left(K A^{\prime}, K B\right)+(B D, B A) \\
& =(K B, K A)+(B D, B A) \\
& =(B D, B C)+90^{\circ}+(B D, B A) \\
\left(t^{\prime}, B D\right) & =\left(t^{\prime}, A^{\prime} D\right)+\left(A^{\prime} D, B D\right) \\
& =\left(L A^{\prime}, L D\right)+(B D, A D) \\
& =(L D, L A)+(B D, A D) \\
& =(B D, D C)+90^{\circ}+(B D, A D) .
\end{aligned}
$$
Finally, we verify that
$$
\begin{aligned}
(B D, B C)+(B D, B A) & =(B D, B C)+(B D, A D)+(A D, A B) \\
& =(B D, B C)+(B D, A D)+(B C, C D) \\
& =(B D, D C)+(B D, A D),
\end{aligned}
$$
which concludes the proof.
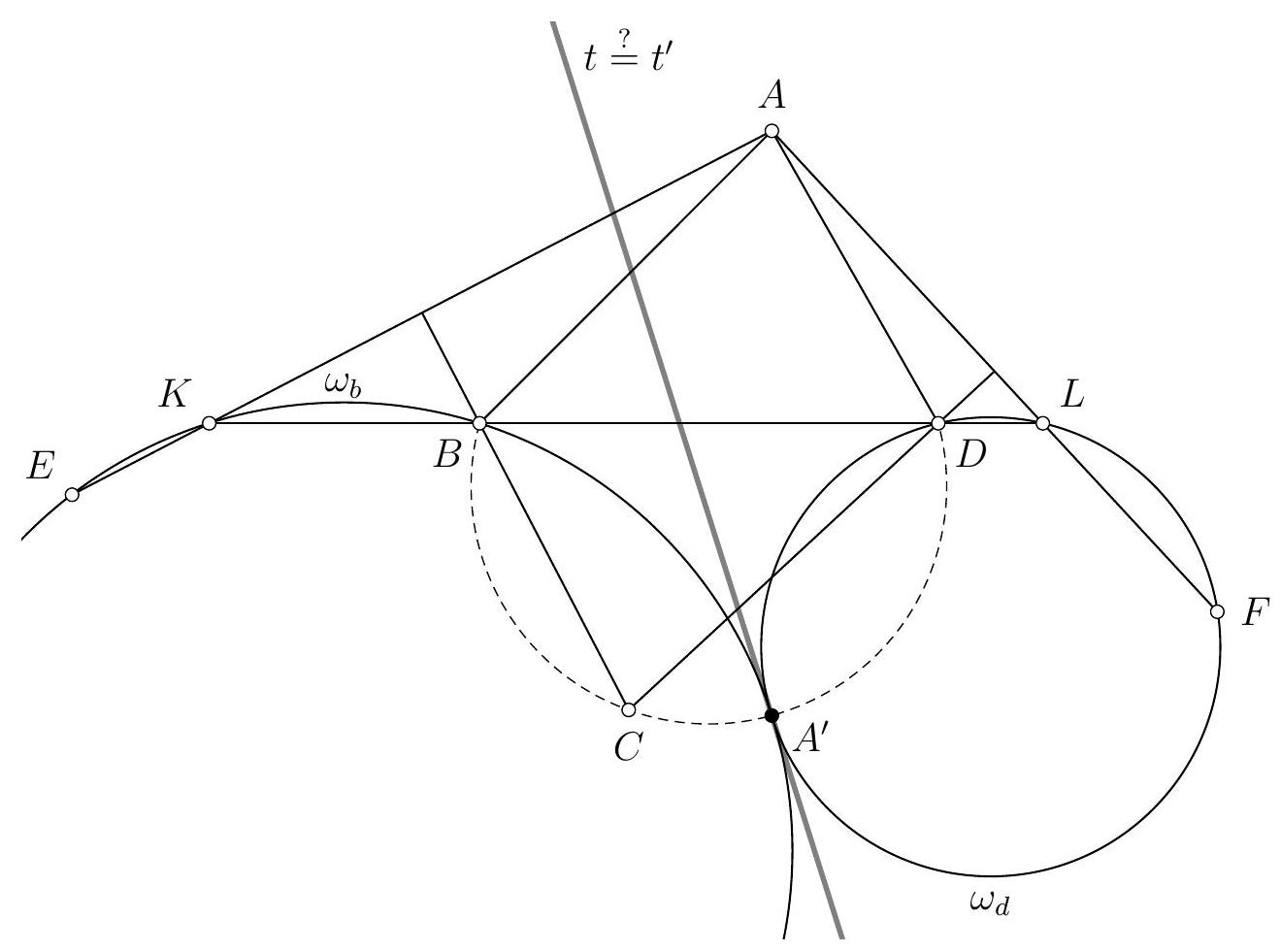
Comment from the graders: Only half of the students who took the test attempted this problem. It is very concerning to note that students' strategy when facing an Olympiad problem does not take into account the fact that the problems are ranked in increasing order of difficulty. Of course, students are encouraged to look at each of the problems on the test. However, unless a student has a very particular interest in a specific area of the Olympiads, to the point of being able to completely solve problems of any difficulty in that area, it is much more profitable to devote the majority of their time to the problem ranked as the easiest, regardless of its theme, since they are more likely to have interesting ideas.
It is naive to think that one can skip one of the four themes of the Olympiads, especially geometry, which has been the theme of a problem 1 or 4 in the International Olympiads 8 times in the last 10 years. The strategy of not reflecting on the geometry problem in this test to focus on the other two problems often backfired against the students, as problems 6 and 7 were very difficult and required many ideas to hope to obtain a significant number of points. We hope that students who have the opportunity will adjust their strategy for next year.
Regarding this problem, finding how to draw the exact figure was essential to get started. Indeed, looking for how to draw the exact figure pushed students to introduce additional points necessary for the subsequent steps. To construct a point $C$ such that $\widehat{B C D}=\widehat{B A D}$, one needed to find a particular point $X$ that satisfies $\widehat{B X D}=\widehat{B A D}$ but such that $X$ and $A$ are on opposite sides of the line $(B D)$, and then construct $C$ anywhere on the circle $\mathcal{C}_{B X D}$. This reasoning (which can be used whenever one is faced with an angle condition to realize with a ruler and compass) pushed to introduce the symmetric point of $A$ with respect to the line $(B D)$. Once the figure was completed, it was then legitimate to conjecture that this symmetric point was the desired point of tangency. This conjecture work was the most difficult part of the task, and often students who made this conjecture managed to completely prove it.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un quadrilatère convexe dont les angles en $B$ et en $D$ sont obtus, et dont les angles en $A$ et en $C$ sont égaux l'un à l'autre. Soit $E$ et $F$ les symétriques de $A$ par rapport à $(B C)$ et $(C D)$. Soit $K$ et $L$ les points d'intersection de $(B D)$ avec $(A E)$ et $(A F)$. Démontrer que les cercles circonscrits aux triangles $B E K$ et $D F L$ sont tangents l'un à l'autre.
|
La manière la plus pratique de construire le point $A$ est d'en construire tout d'abord son symétrique $A^{\prime}$ par rapport à $(B D)$, puisque $A^{\prime}$ est cocyclique avec $B, C$ et $D$. Ce faisant, on constate que $A^{\prime}$ semble appartenir aux deux cercles circonscrits aux triangles $B E K$ et $D F L$, et une chasse aux angles indique en effet que
$$
\begin{aligned}
\left(K E, K A^{\prime}\right) & =(K E, B C)+(B C, B D)+\left(B D, K A^{\prime}\right) \\
& =90^{\circ}+(B C, B D)+(K A, B D) \\
& =90^{\circ}+(B C, B D)+(K A, B C)+(B C, B D) \\
& =2(B C, B D) \\
\left(B E, B A^{\prime}\right) & =(B E, B C)+(B C, B D)+\left(B D, B A^{\prime}\right) \\
& =(B C, B A)+(B C, B D)+(B A, B D) \\
& =2(B C, B D) .
\end{aligned}
$$
Cela signifie bien que $A^{\prime}, B, K$ et $E$ appartiennent à un cercle $\omega_{b}$ et, de même, que $A^{\prime}, D, L$ et $F$ appartiennent à un cercle $\omega_{d}$.
Soit alors $t$ et $t^{\prime}$ les tangentes à $\omega_{b}$ et $\omega_{d}$ en $A^{\prime}$. Une nouvelle chasse aux angles indique que
$$
\begin{aligned}
(t, B D) & =\left(t, A^{\prime} B\right)+\left(A^{\prime} B, B D\right) \\
& =\left(K A^{\prime}, K B\right)+(B D, B A) \\
& =(K B, K A)+(B D, B A) \\
& =(B D, B C)+90^{\circ}+(B D, B A) \\
\left(t^{\prime}, B D\right) & =\left(t^{\prime}, A^{\prime} D\right)+\left(A^{\prime} D, B D\right) \\
& =\left(L A^{\prime}, L D\right)+(B D, A D) \\
& =(L D, L A)+(B D, A D) \\
& =(B D, D C)+90^{\circ}+(B D, A D) .
\end{aligned}
$$
On vérifie enfin que
$$
\begin{aligned}
(B D, B C)+(B D, B A) & =(B D, B C)+(B D, A D)+(A D, A B) \\
& =(B D, B C)+(B D, A D)+(B C, C D) \\
& =(B D, D C)+(B D, A D),
\end{aligned}
$$
ce qui conclut.

Commentaire des correcteurs Seule la moitié des élèves ayant pris part au test ont abordé cet exercice. Il est très préoccupant de constater que la stratégie des élèves face à un sujet d'Olympiade ne prend pas en compte le fait que les problèmes sont classés par ordre de difficulté croissante. On encourage bien sûr les élèves à regarder chacun des problèmes du sujet. Mais, à moins d'avoir une appétence très particulière pour un domaine des olympiades, au point d'être capable de résoudre complètement des problèmes de toute difficulté portant sur ce thème, il est bien plus rentable de consacrer la majeure partie de son temps au problème classé comme le plus facile, quel que soit son thème, puisqu'on a plus de chances d'y avoir des idées intéressantes.
Il est bien naïf de penser pouvoir faire l'impasse sur l'un des 4 thèmes des olympiades, en particulier la géométrie qui, ces 10 dernières années, a été 8 fois le thème d'un problème 1 ou 4 des Olympiades Internationales. La stratégie de ne pas réfléchir au problème de géométrie du présent test pour se consacrer aux deux autres problèmes s'est bien souvent retournée contre les élèves, puisque les problèmes 6 et 7 étaient très difficiles et demandaient de nombreuses idées pour espérer obtenir une quantité significative de points. Nous espérons donc que les élèves qui en ont l'occasion adapteront leur stratégie pour l'année prochaine.
Concernant ce problème, trouver comment tracer la figure exacte était essentiel pour démarrer. En effet, chercher comment tracer la figure exacte poussait à introduire des points supplémentaires nécessaires dans la suite. Pour construire un point $C$ tel que $\widehat{B C D}=\widehat{B A D}$, il fallait trouver un point $X$ particulier qui vérifie $\widehat{B X D}=\widehat{B A D}$ mais tel que $X$ et $A$ soient de part et d'autre de l'axe $(B D)$, puis construire $C$ quelconque sur le cercle $\mathcal{C}_{B X D}$. Ce raisonnement (qui peut être employé dès que l'on se retrouve face à une hypothèse d'angle à réaliser à la règle et au compas) poussait à introduire le symétrique du point $A$ par rapport à la droite $(B D)$. Une fois la figure complétée, il était alors légitime de conjecturer que ce symétrique était le point de tangence recherché. Ce travail de conjecture était la partie la plus difficile du travail, et bien souvent les élèves ayant fait cette conjecture ont réussi à la démontrer complètement.
|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Web-Test-5.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution de l'exercice 5"
}
|
87d7131b-fd0a-5ba2-9725-0a8c29ec49a1
| 604,856
|
Find the functions $f: \mathbb{N}_{\geqslant 1} \mapsto \mathbb{N}_{\geqslant 0}$ satisfying the following two conditions:
1. $f(x y)=f(x)+f(y)$ for all integers $x \geqslant 1$ and $y \geqslant 1$;
2. there exists an infinite number of integers $n \geqslant 1$ such that the equality $f(k)=f(n-k)$ holds for every integer $k$ such that $1 \leqslant k \leqslant n-1$.
We denote $\mathbb{N}_{\geqslant 0}$ the set of integers greater than or equal to 0, and $\mathbb{N}_{\geqslant 1}$ the set of integers greater than or equal to 1.
|
The sought functions are of the form $f: n \mapsto c v_{p}(n)$, where $c$ is a natural number, $p$ is a prime number, and $v_{p}(n)$ is the $p$-adic valuation of $n$. First, it is clear that these functions are indeed solutions to the problem.
Conversely, let $f$ be a non-zero solution to the problem. We say that an integer $n$ is $j o l i$ if the equality $f(k)=f(n-k)$ holds for all integers $k \leqslant 1$. Note that any divisor of a joli integer is joli. Indeed, if $d$ divides a joli integer $n=a d$, then
$$
f(k)=f(a k)-f(a)=f(n-a k)-f(a)=f(a(d-k))-f(a)=f(d-k)
$$
for all integers $k \leqslant d-1$.
Furthermore, condition 1 means that $f\left(\prod_{i} p_{i}^{\alpha_{i}}\right)=\sum_{i} \alpha_{i} f\left(p_{i}\right)$ for any prime factorization. Therefore, it is necessary to show that there is at most one prime $p$ for which $f(p)>0$. We then consider the smallest integer $p$ such that $f(p)>0$. The above formula indicates that $p$ is prime, and we set $c=f(p)$.
If there exists a joli integer $n \geqslant p$ that $p$ does not divide, let $n=p q+r$, with $q$ an integer and $1 \leqslant r \leqslant p-1$. Since $n$ is joli, we know that $f(r)=f(n-p q)=f(p q) \geqslant f(p)>0$, which contradicts the definition of $p$. Thus, every joli integer is of the form $a p^{b}$ with $b$ an integer and $1 \leqslant a \leqslant p-1$. Conversely, since there are infinitely many joli integers and $a$ can only take a finite number of values, every power of $p$ divides a joli integer, and is therefore joli itself.
Consequently, for any prime $q$ different from $p$, the integer $p^{q-1}$ is joli. Since $q$ divides $p^{q-1}-1$, we deduce in particular that $0=f(1)=f\left(p^{q-1}-1\right) \geqslant f(q)$, which concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Trouver les fonctions $f: \mathbb{N}_{\geqslant 1} \mapsto \mathbb{N}_{\geqslant 0}$ vérifiant les deux conditions suivantes :
1. $f(x y)=f(x)+f(y)$ pour tous les entiers $x \geqslant 1$ et $y \geqslant 1$;
2. il existe une infinité d'entiers $n \geqslant 1$ tels que l'égalité $f(k)=f(n-k)$ est vraie pour tout entier $k$ tel que $1 \leqslant k \leqslant n-1$.
On note $\mathbb{N}_{\geqslant 0}$ l'ensemble des entiers supérieurs ou égaux à 0 , et $\mathbb{N}_{\geqslant 1}$ l'ensemble des entiers supérieurs ou égauxà 1.
|
Les fonctions recherchées sont les fonctions de la forme $f: n \mapsto c v_{p}(n)$, où $c$ est un entier naturel, $p$ est un nombre premier, et $v_{p}(n)$ et la valuation $p$-adique de $n$. Tout d'abord, il est clair que ces fonctions sont bien solutions du problème.
Réciproquement, soit $f$ une solution non nulle du problème. On dit qu'un entier $n$ est $j o l i$ si l'égalité $f(k)=f(n-k)$ est vraie pour tout entier $k \leqslant 1$. Remarquons que tout diviseur d'un joli entier est joli. En effet, si $d$ divise un joli entier $n=a d$, alors
$$
f(k)=f(a k)-f(a)=f(n-a k)-f(a)=f(a(d-k))-f(a)=f(d-k)
$$
pour tout entier $k \leqslant d-1$.
En outre, la condition 1 signifie que $f\left(\prod_{i} p_{i}^{\alpha_{i}}\right)=\sum_{i} \alpha_{i} f\left(p_{i}\right)$ pour toute décomposition en produit de facteurs premiers. Il s'agit donc de démontrer qu'il existe au plus un nombre premier $p$ pour lequel $f(p)>0$. On considère alors le plus petit entier $p$ tel que $f(p)>0$. La formule ci-dessus indique que $p$ est premier, et on pose $c=f(p)$.
S'il existe un joli entier $n \geqslant p$ que $p$ ne divise pas, posons $n=p q+r$, avec $q$ entier et $1 \leqslant r \leqslant p-1$. Puisque $n$ est joli, on sait que $f(r)=f(n-p q)=f(p q) \geqslant f(p)>0$, en contradiction avec la définition de $p$. Ainsi, tout entier joli est de la forme $a p^{b}$ avec $b$ entier et $1 \leqslant a \leqslant p-1$. Réciproquement, puisqu'il existe une infinité d'entiers jolis et que $a$ ne peut prendre qu'un nombre fini de valeurs, toute puissance de $p$ divise un joli entier, et est donc elle-même jolie.
Par conséquent, pour tout nombre premier $q$ distinct de $p, l^{\prime}$ entier $p^{q-1}$ est joli. Puisque $q$ divise $p^{q-1}-1$, on en déduit en particulier que $0=f(1)=f\left(p^{q-1}-1\right) \geqslant f(q)$, ce qui conclut.
|
{
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Web-Test-5.jsonl",
"problem_match": "\nExercice 7.",
"solution_match": "\nSolution de l'exercice 7"
}
|
118cd944-815a-56fe-9c3d-1822b2ba6609
| 604,888
|
Let $ABCD$ be a parallelogram. The internal bisector of angle $\widehat{BAC}$ intersects the segment $[BC]$ at $E$, while its external bisector intersects the line $(CD)$ at $F$. Let $M$ be the midpoint of the segment $[AE]$.
Prove that the lines $(EF)$ and $(BM)$ are parallel.
|
Let $G$ be the intersection point of the lines $(A B)$ and $(E F)$. The problem reduces to proving that $(M B)$ is a midline of the triangle $A E G$, that is, that $B$ is the midpoint of $[A G]$.
Similarly, let $H$ be the intersection point of the lines $(A E)$ and $(C D)$. The homothety centered at $E$ that maps $(A B)$ to $(C D)$ maps the points $A, B$ and $G$ to $H, C$ and $F$. Equivalently, the problem reduces to proving that $C$ is the midpoint of $[H F]$.
Now, in terms of angles between lines,
$$
\begin{aligned}
(A C, A F) & =(A C, A E)+(A E, A F)=(A E, A B)+90^{\circ}=(A E, A B)+(A F, A E)=(A F, A B) \\
& =(F A, F C)
\end{aligned}
$$
which means that the triangle $A C F$ is isosceles at $C$. Similarly,
$$
(H A, H C)=(E A, C D)=(A E, A B)=(A C, A E)=(A C, A H)
$$
so $A C H$ is isosceles at $C$.
We conclude that $C F=C A=C H$, hence $C$ is indeed the midpoint of $[\mathrm{CH}]$.
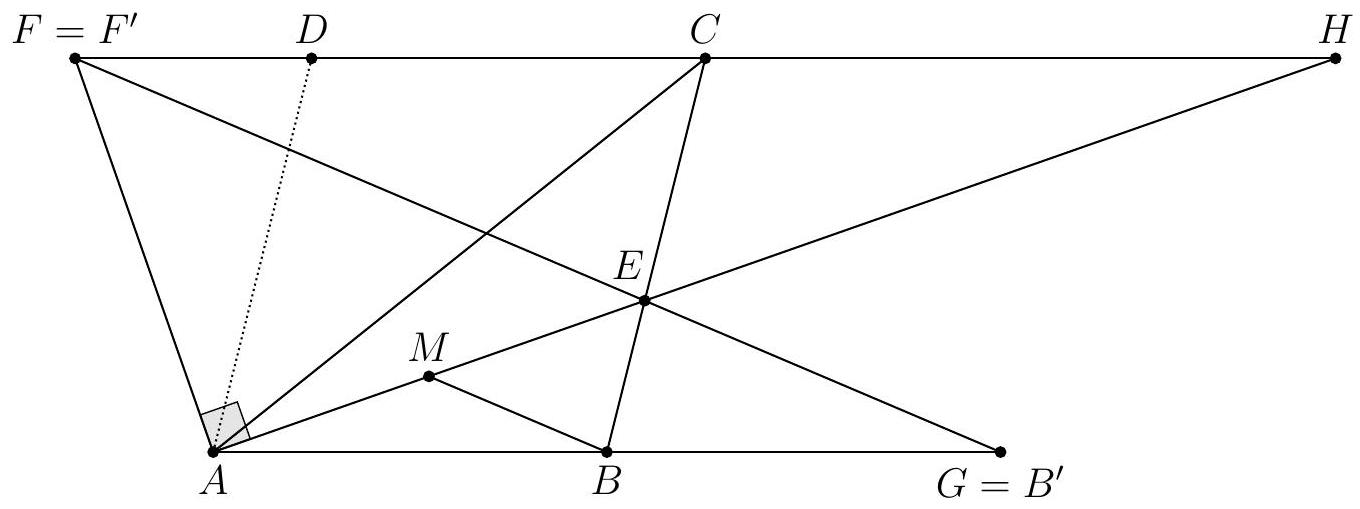
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un parallélogramme. La bissectrice intérieure de l'angle $\widehat{B A C}$ coupe le segment $[B C]$ en $E$ tandis que sa bissectrice extérieure coupe la droite ( $C D)$ en $F$. Soit $M$ le milieu du segment $[A E]$.
Démontrer que les droites $(E F)$ et $(B M)$ sont parallèles.
|
Soit $G$ le point d'intersection des droites $(A B)$ et $(E F)$. Le problème revient à démontrer que $(M B)$ est une droite des milieux du triangle $A E G$, c'est-à-dire que $B$ est le milieu de $[A G]$.
De même, soit $H$ le point d'intersection des droites $(A E)$ et $(C D)$. L'homothétie de centre $E$ qui envoie $(A B)$ sur $(C D)$ envoie les points $A, B$ et $G \operatorname{sur} H, C$ et $F$. De manière équivalente, le problème revient donc à démontrer que $C$ est le milieu de $[H F]$.
Or, en angles de droites,
$$
\begin{aligned}
(A C, A F) & =(A C, A E)+(A E, A F)=(A E, A B)+90^{\circ}=(A E, A B)+(A F, A E)=(A F, A B) \\
& =(F A, F C)
\end{aligned}
$$
ce qui signifie que le triangle $A C F$ est isocèle en $C$. De même,
$$
(H A, H C)=(E A, C D)=(A E, A B)=(A C, A E)=(A C, A H)
$$
donc $A C H$ est isocèle en $C$.
On en conclut que $C F=C A=C H$, donc que $C$ est bien le milieu de $[\mathrm{CH}]$.

|
{
"resource_path": "French/segmented/tests/fr-2021-2022-Corrigé-Web-Test-1.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution de l'exercice 1"
}
|
44986948-f061-54a8-b345-66a31bc177eb
| 604,910
|
Let $ABCD$ be a parallelogram. The internal bisector of angle $\widehat{BAC}$ intersects the segment $[BC]$ at $E$, while its external bisector intersects the line $(CD)$ at $F$. Let $M$ be the midpoint of the segment $[AE]$.
Prove that the lines $(EF)$ and $(BM)$ are parallel.
|
$n^{\circ} 1$ As in the previous solution, it is a matter of proving that $A B=B G$. Now, the angle bisector theorem indicates that $E B / E C=A B / A C$, and Thales' theorem indicates that $E B / E C=B G / C F$. We conclude that
$$
\frac{A B}{A C}=\frac{E B}{E C}=\frac{B G}{C F},
$$
It remains to prove that $C A=C F$, that is, that triangle $A C F$ is isosceles at $C$, which is directly deduced from the equalities of angles of lines
$$
\begin{aligned}
(A C, A F) & =(A C, A E)+(A E, A F)=(A E, A B)+90^{\circ}=(A E, A B)+(A F, A E)=(A F, A B) \\
& =(F A, F C) .
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un parallélogramme. La bissectrice intérieure de l'angle $\widehat{B A C}$ coupe le segment $[B C]$ en $E$ tandis que sa bissectrice extérieure coupe la droite ( $C D)$ en $F$. Soit $M$ le milieu du segment $[A E]$.
Démontrer que les droites $(E F)$ et $(B M)$ sont parallèles.
|
$n^{\circ} 1$ Comme dans la solution précédente, il s'agit de démontrer que $A B=B G$. Or, le théorème de la bissectrice indique que $E B / E C=A B / A C$, et le théorème de Thalès indique que $E B / E C=B G / C F$. On en conclut que
$$
\frac{A B}{A C}=\frac{E B}{E C}=\frac{B G}{C F},
$$
Il reste donc à démontrer que $C A=C F$, c'est-à-dire que le triangle $A C F$ est isocèle en $C$, ce qui se déduit directement des égalités d'angles de droites
$$
\begin{aligned}
(A C, A F) & =(A C, A E)+(A E, A F)=(A E, A B)+90^{\circ}=(A E, A B)+(A F, A E)=(A F, A B) \\
& =(F A, F C) .
\end{aligned}
$$
|
{
"resource_path": "French/segmented/tests/fr-2021-2022-Corrigé-Web-Test-1.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution alternative"
}
|
44986948-f061-54a8-b345-66a31bc177eb
| 604,910
|
Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be an increasing function such that $f(y)-f(x)<y-x$ for all real numbers $x$ and $y$ such that $y>x$. Let $\left(u_{n}\right)_{n \geqslant 0}$ be a sequence such that $u_{n+2}=f\left(u_{n+1}\right)-f\left(u_{n}\right)$ for all integers $n \geqslant 0$.
Prove that the sequence $\left(u_{n}\right)_{n \geqslant 0}$ converges to 0, that is, for all real $\varepsilon>0$, there exists an integer $N$ such that $\left|u_{n}\right| \leqslant \varepsilon$ for all integers $n \geqslant N$.
|
By replacing the function $f$ with the function $t \mapsto f(t)-f(0)$, which does not change the desired property, we assume that $f(0)=0$.
Furthermore, replacing the function $f$ with the function $t \mapsto -f(-t)$ and the sequence $\left(u_{n}\right)_{n \geqslant 0}$ with the sequence $\left(-u_{n}\right)_{n \geqslant 0}$ does not change the desired property either. Therefore, we can freely assume, without further ado, that a certain term $u_{n}$ is positive or non-negative. Below, these assumptions are marked with the symbol ( $\star$ ).
We now say that an integer $n$ is good if the terms $u_{n}$ and $u_{n+1}$ have the same sign and satisfy the inequality $\left|u_{n+1}\right| \leqslant\left|u_{n}\right|$. Moreover, we say that an integer $n$ is dominant if every integer $k \geqslant n$ satisfies the inequality $\left|u_{k}\right| \leqslant\left|u_{n}\right|$. Let's prove some intermediate results.
Lemma 1: Among three consecutive integers, at least one is good.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit $f: \mathbb{R} \rightarrow \mathbb{R}$ une fonction croissante telle que $f(y)-f(x)<y-x$ pour tous les réels $x$ et $y$ tels que $y>x$. Soit $\left(u_{n}\right)_{n \geqslant 0}$ une suite telle que $u_{n+2}=f\left(u_{n+1}\right)-f\left(u_{n}\right)$ pour tout entier $n \geqslant 0$.
Démontrer que la suite $\left(u_{n}\right)_{n \geqslant 0}$ converge vers 0 , c'est-à-dire que, pour tout réel $\varepsilon>0$, il existe un entier $N$ tel que $\left|u_{n}\right| \leqslant \varepsilon$ pour tout entier $n \geqslant N$.
|
Quitte à remplacer la fonction $f$ par la fonction $t \mapsto f(t)-f(0)$, ce qui ne change rien à la propriété désirée, on suppose que $f(0)=0$.
Par ailleurs, remplacer la fonction $f$ par la fonction $t \mapsto-f(-t)$ et la suite $\left(u_{n}\right)_{n \geqslant 0}$ par la suite $\left(-u_{n}\right)_{n \geqslant 0}$ ne change rien non plus à la propriété désirée. On pourra donc librement supposer, sans autre forme de procès, que tel ou tel terme $u_{n}$ est positif ou nul. Ci-dessous, ces suppositions sont marquées par le symbole ( $\star$ ).
On dit maintenant qu'un entier $n$ est bon si les termes $u_{n}$ et $u_{n+1}$ sont de même signe et vérifient l'inégalité $\left|u_{n+1}\right| \leqslant\left|u_{n}\right|$. Par ailleurs, on dit qu'un entier $n$ est dominant si tout entier $k \geqslant n$ satisfait l'inégalité $\left|u_{k}\right| \leqslant\left|u_{n}\right|$. Démontrons quelques résultats intermédiaires.
Lemme 1 : Parmi trois entiers consécutifs, au moins un est bon.
|
{
"resource_path": "French/segmented/tests/fr-2021-2022-Corrigé-Web-Test-1.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "\nSolution de l'exercice 4"
}
|
f8ff49df-828b-55bf-8d96-32a709224f75
| 604,991
|
Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be an increasing function such that $f(y)-f(x)<y-x$ for all real numbers $x$ and $y$ such that $y>x$. Let $\left(u_{n}\right)_{n \geqslant 0}$ be a sequence such that $u_{n+2}=f\left(u_{n+1}\right)-f\left(u_{n}\right)$ for all integers $n \geqslant 0$.
Prove that the sequence $\left(u_{n}\right)_{n \geqslant 0}$ converges to 0, that is, for all real $\varepsilon>0$, there exists an integer $N$ such that $\left|u_{n}\right| \leqslant \varepsilon$ for all integers $n \geqslant N$.
|
Let $n$ be a natural integer. If $u_{n}$ and $u_{n+1}$ have opposite signs, and assuming that $u_{n} \geqslant 0^{(*)}$, we observe that $u_{n} \geqslant 0 \geqslant u_{n+1}$, hence $u_{n+2}=f\left(u_{n+1}\right)-f\left(u_{n}\right) \leqslant 0$ has the same sign as $u_{n+1}$. Thus, we can choose $k=n$ or $k=n+1$ such that $u_{k}$ and $u_{k+1}$ have the same sign.
We then prove that one of the two integers $k$ or $k+1$ is good. Indeed, if $\left|u_{k+1}\right| \geqslant\left|u_{k}\right|$, and assuming that $u_{k} \geqslant 0^{(*)}$, we have $u_{k+1} \geqslant u_{k}$, and the term $u_{k+2}=f\left(u_{k+1}\right)-f\left(u_{k}\right)$ is between 0 and $u_{k+1}$, so that $k+1$ is good.
Lemma 2: For any good integer $m$, there exists an integer $n$, equal to $m+2$ or $m+3$, such that
$\triangleright n$ is good,
$\triangleright u_{m}$ and $u_{n}$ have opposite signs, and
$\triangleright\left|u_{k}\right| \leqslant\left|u_{m}\right|$ for any integer $k$ such that $m \leqslant k \leqslant n$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit $f: \mathbb{R} \rightarrow \mathbb{R}$ une fonction croissante telle que $f(y)-f(x)<y-x$ pour tous les réels $x$ et $y$ tels que $y>x$. Soit $\left(u_{n}\right)_{n \geqslant 0}$ une suite telle que $u_{n+2}=f\left(u_{n+1}\right)-f\left(u_{n}\right)$ pour tout entier $n \geqslant 0$.
Démontrer que la suite $\left(u_{n}\right)_{n \geqslant 0}$ converge vers 0 , c'est-à-dire que, pour tout réel $\varepsilon>0$, il existe un entier $N$ tel que $\left|u_{n}\right| \leqslant \varepsilon$ pour tout entier $n \geqslant N$.
|
Soit $n$ un entier naturel. Si $u_{n}$ et $u_{n+1}$ sont de signes opposés, et en supposant que $u_{n} \geqslant 0^{(*)}$, on constate que $u_{n} \geqslant 0 \geqslant u_{n+1}$, donc que $u_{n+2}=f\left(u_{n+1}\right)-f\left(u_{n}\right) \leqslant 0$ est de même signe que $u_{n+1}$. Ainsi, on peut choisir $k=n$ ou $k=n+1$ de sorte que $u_{k}$ et $u_{k+1}$ soient de même signe.
On démontre alors que l'un des deux entiers $k$ ou $k+1$ est bon. En effet, si $\left|u_{k+1}\right| \geqslant\left|u_{k}\right|$, et en supposant que $u_{k} \geqslant 0^{(*)}$, on a $u_{k+1} \geqslant u_{k}$, et le terme $u_{k+2}=f\left(u_{k+1}\right)-f\left(u_{k}\right)$ est compris entre 0 et $u_{k+1}$, de sorte que $k+1$ est bon.
Lemme 2: Pour tout bon entier $m$, il existe un entier $n$, égal à $m+2$ ou à $m+3$, tel que
$\triangleright n$ est bon,
$\triangleright u_{m}$ et $u_{n}$ sont de signes opposés, et
$\triangleright\left|u_{k}\right| \leqslant\left|u_{m}\right|$ pour tout entier $k$ tel que $m \leqslant k \leqslant n$.
|
{
"resource_path": "French/segmented/tests/fr-2021-2022-Corrigé-Web-Test-1.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "\nDémonstration."
}
|
f8ff49df-828b-55bf-8d96-32a709224f75
| 604,991
|
Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be an increasing function such that $f(y)-f(x)<y-x$ for all real numbers $x$ and $y$ such that $y>x$. Let $\left(u_{n}\right)_{n \geqslant 0}$ be a sequence such that $u_{n+2}=f\left(u_{n+1}\right)-f\left(u_{n}\right)$ for all integers $n \geqslant 0$.
Prove that the sequence $\left(u_{n}\right)_{n \geqslant 0}$ converges to 0, that is, for all real $\varepsilon>0$, there exists an integer $N$ such that $\left|u_{n}\right| \leqslant \varepsilon$ for all integers $n \geqslant N$.
|
Let $m$ be a good integer. Assuming that $u_{m} \geqslant 0{ }^{(*)}$, the inequality $0 \leqslant u_{m+1} \leqslant u_{m}$ ensures that $u_{m+2}=f\left(u_{m+1}\right)-f\left(u_{m}\right) \leqslant 0 \leqslant u_{m+1}$, and then $u_{m+3}=f\left(u_{m+2}\right)-f\left(u_{m+1}\right) \leqslant 0$. Thus, $u_{m+2}$ and $u_{m+3}$ have opposite signs to that of $u_{m}$, and one of the two integers $m+2$ or $m+3$ is good.
Finally, $0 \leqslant u_{m+1} \leqslant u_{m}, u_{m+2} \geqslant u_{m+1}-u_{m} \geqslant-u_{m}$ and $u_{m+3} \geqslant u_{m+2}-u_{m+1} \geqslant-u_{m}$, so that $u_{m+1}, u_{m+2}$ and $u_{m+3}$ are all three between $-u_{m}$ and $u_{m}$.
Lemma 3: Every good integer is dominant.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit $f: \mathbb{R} \rightarrow \mathbb{R}$ une fonction croissante telle que $f(y)-f(x)<y-x$ pour tous les réels $x$ et $y$ tels que $y>x$. Soit $\left(u_{n}\right)_{n \geqslant 0}$ une suite telle que $u_{n+2}=f\left(u_{n+1}\right)-f\left(u_{n}\right)$ pour tout entier $n \geqslant 0$.
Démontrer que la suite $\left(u_{n}\right)_{n \geqslant 0}$ converge vers 0 , c'est-à-dire que, pour tout réel $\varepsilon>0$, il existe un entier $N$ tel que $\left|u_{n}\right| \leqslant \varepsilon$ pour tout entier $n \geqslant N$.
|
Soit $m$ un bon entier. En supposant que $u_{m} \geqslant 0{ }^{(*)}$, l'inégalité $0 \leqslant u_{m+1} \leqslant u_{m}$ nous assure que $u_{m+2}=f\left(u_{m+1}\right)-f\left(u_{m}\right) \leqslant 0 \leqslant u_{m+1}$, puis $u_{m+3}=f\left(u_{m+2}\right)-f\left(u_{m+1}\right) \leqslant 0$. Ainsi, $u_{m+2}$ et $u_{m+3}$ sont de signe opposé à celui de $u_{m}$, et l'un des deux entiers $m+2$ ou $m+3$ est bon.
Enfin, $0 \leqslant u_{m+1} \leqslant u_{m}, u_{m+2} \geqslant u_{m+1}-u_{m} \geqslant-u_{m}$ et $u_{m+3} \geqslant u_{m+2}-u_{m+1} \geqslant-u_{m}$, de sorte que $u_{m+1}, u_{m+2}$ et $u_{m+3}$ sont tous trois compris entre $-u_{m}$ et $u_{m}$.
Lemme 3 : Tout bon entier est dominant.
|
{
"resource_path": "French/segmented/tests/fr-2021-2022-Corrigé-Web-Test-1.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "\nDémonstration."
}
|
f8ff49df-828b-55bf-8d96-32a709224f75
| 604,991
|
Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be an increasing function such that $f(y)-f(x)<y-x$ for all real numbers $x$ and $y$ such that $y>x$. Let $\left(u_{n}\right)_{n \geqslant 0}$ be a sequence such that $u_{n+2}=f\left(u_{n+1}\right)-f\left(u_{n}\right)$ for all integers $n \geqslant 0$.
Prove that the sequence $\left(u_{n}\right)_{n \geqslant 0}$ converges to 0, that is, for all real $\varepsilon>0$, there exists an integer $N$ such that $\left|u_{n}\right| \leqslant \varepsilon$ for all integers $n \geqslant N$.
|
For any good integer $m$, we denote $\psi(m)$ as the smallest good integer greater than or equal to $m+2$. Here, Lemma 2 and induction show that $\left|u_{m}\right| \geqslant\left|u_{\psi^{k}(m)}\right| \geqslant\left|u_{\ell}\right|$ for any integer $\ell$ such that $\psi^{k}(m) \leqslant \ell \leqslant \psi^{k+1}(m)$, so that $m$ is dominant.
Let $a$ be the smallest good integer. We assume that $u_{a} \geqslant 0{ }^{(*)}$. The sequence $\left(u_{\psi^{k}(a)}\right)_{k \geqslant 0}$ consists of terms that are alternately positive and negative, with their absolute values decreasing. Thus, the sequence $\left(u_{\psi^{2 k}(a)}\right)_{k \geqslant 0}$ is decreasing and has a limit $\ell \geqslant 0$, while the sequence $\left(u_{\psi^{2 k+1}(a)}\right)_{k \geqslant 0}$ is increasing and has $-\ell$ as its limit.
If $\ell=0$, since all integers $\psi^{k}(a)$ are dominant, the sequence $\left(u_{n}\right)_{n \geqslant 0}$ converges to 0. Otherwise, let $\varepsilon=\min \{\ell / 2-f(\ell / 2), \ell / 2+f(\ell / 2)-f(\ell)\}$. The statement tells us that $\varepsilon>0$, and also allows us to obtain the following result.
Lemma 4: Let $x$ and $y$ be two real numbers. If $x \leqslant \ell / 2$ and $y \geqslant \ell$, or if $x \leqslant 0$ and $y \geqslant \ell / 2$, then $f(y)-f(x) \leqslant y-x-\varepsilon$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit $f: \mathbb{R} \rightarrow \mathbb{R}$ une fonction croissante telle que $f(y)-f(x)<y-x$ pour tous les réels $x$ et $y$ tels que $y>x$. Soit $\left(u_{n}\right)_{n \geqslant 0}$ une suite telle que $u_{n+2}=f\left(u_{n+1}\right)-f\left(u_{n}\right)$ pour tout entier $n \geqslant 0$.
Démontrer que la suite $\left(u_{n}\right)_{n \geqslant 0}$ converge vers 0 , c'est-à-dire que, pour tout réel $\varepsilon>0$, il existe un entier $N$ tel que $\left|u_{n}\right| \leqslant \varepsilon$ pour tout entier $n \geqslant N$.
|
Pour tout bon entier $m$, on note $\psi(m)$ le plus petit bon entier supérieur ou égal à $m+2$. Ici, le lemme 2 et une récurrence montrent que $\left|u_{m}\right| \geqslant\left|u_{\psi^{k}(m)}\right| \geqslant\left|u_{\ell}\right|$ pour tout entier $\ell$ tel que $\psi^{k}(m) \leqslant \ell \leqslant \psi^{k+1}(m)$, de sorte que $m$ est dominant.
Soit $a$ le plus petit bon entier. On suppose que $u_{a} \geqslant 0{ }^{(*)}$. La suite $\left(u_{\psi^{k}(a)}\right)_{k \geqslant 0}$ est formée de termes alternativement positifs et négatifs, dont les valeurs absolues décroissent. Ainsi, la suite $\left(u_{\psi^{2 k}(a)}\right)_{k \geqslant 0}$ est décroissante, et admet une limite $\ell \geqslant 0$, tandis que la suite $\left(u_{\psi^{2 k+1}(a)}\right)_{k \geqslant 0}$ est croissante, et admet $-\ell$ pour limite.
Si $\ell=0$, puisque tous les entiers $\psi^{k}(a)$ sont dominants, la suite $\left(u_{n}\right)_{n \geqslant 0}$ converge bien vers 0 . Sinon, soit $\varepsilon=\min \{\ell / 2-f(\ell / 2), \ell / 2+f(\ell / 2)-f(\ell)\}$. L'énoncé nous indique que $\varepsilon>0$, et nous permet aussi d'obtenir le résultat suivant.
Lemme 4 : Soit $x$ et $y$ deux réels. Si $x \leqslant \ell / 2$ et $y \geqslant \ell$, ou bien si $x \leqslant 0$ et $y \geqslant \ell / 2$, alors $f(y)-f(x) \leqslant y-x-\varepsilon$.
|
{
"resource_path": "French/segmented/tests/fr-2021-2022-Corrigé-Web-Test-1.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "\nDémonstration."
}
|
f8ff49df-828b-55bf-8d96-32a709224f75
| 604,991
|
Martin hastily poured $n$ liters of water into $n$ bottles. As a result, some bottles are more filled than others. It is then that he remembers his mission was to put exactly one liter of water in each bottle before closing the cap. Since he hasn't closed the caps yet, there is still time to fix his mistakes.
To do this, he chooses a first bottle, pours part of its contents into another bottle if he wishes, and then caps this first bottle. He then chooses a second bottle (which could be the one into which he partially poured the first bottle, or not), pours part of its contents into another bottle (but not into the first bottle, which is already capped) if he wishes, and then caps it. He then proceeds similarly with a third bottle, and so on, until all the bottles are capped.
Prove that, if Martin astutely chooses the bottles he caps and those into which he partially pours, he will eventually fix his mistakes.
Note: the bottles are oversized and can each hold up to $n$ liters of water, which will prevent them from overflowing.
|
We will proceed by induction on $n$. First, if $n=1$, there is only one bottle containing one liter of water, so Martin has already won.
Then, if $n \geqslant 2$, Martin chooses the bottle $\mathrm{n}^{\circ} i$ that is the most filled, i.e., the one for which $x_{i}$ is maximal. We then observe that
$$
n=x_{1}+x_{2}+\ldots+x_{n} \leqslant x_{i}+x_{i}+\ldots+x_{i}=n x_{i}
$$
so that $x_{i} \geqslant 1$. If $x_{i}>1$, he partially empties it into another bottle until bottle $\mathrm{n}^{\circ} i$ contains only one liter of water, and then he seals it. He then needs to harmoniously distribute the remaining $n-1$ liters of water, which are in $n-1$ bottles, and the induction hypothesis ensures that he can indeed perform this distribution.
Comment from the graders This problem was generally well done. Unfortunately, some students misunderstood what was being asked, which prevented them from solving the problem. Others proposed a winning strategy for Martin, but demonstrating that this strategy worked still required a few lines of explanation: the goal is not just to have a correct solution, but also to convince the reader that it is correct and, more importantly, to convince the grader that the student understood that the solution was correct.
|
proof
|
Yes
|
Yes
|
proof
|
Logic and Puzzles
|
Martin a versé à la hâte $n$ litres d'eau dans $n$ bouteilles. Certaines bouteilles sont donc plus remplies que d'autres. C'est alors qu'il se rappelle que sa mission était de mettre exactement un litre d'eau dans chaque bouteille avant de refermer le bouchon de celle-ci. Comme il n'a pas encore refermé les bouchons, il est encore temps de réparer ses bêtises.
Pour ce faire, il choisit une première bouteille, verse une partie de son contenu dans une autre bouteille s'il le souhaite, puis bouche cette première bouteille. Il choisit ensuite une seconde bouteille (qui peut être celle dans laquelle il a partiellement vidé la première bouteille, ou pas), verse une partie de son contenu dans une autre bouteille (mais pas dans la première bouteille, qui est déjà bouchée) s'il le souhaite, puis la bouche. Puis il procède de même avec une troisième bouteille, et ainsi de suite, jusqu'à boucher toutes les bouteilles.
Démontrer que, si Martin choisit astucieusement les bouteilles dont il referme le bouchon et celles dans lesquelles il les vide partiellement, il finira bien par réparer ses bêtises.
Note : les bouteilles sont surdimensionnées, et pourraient chacune contenir jusqu'à n litres d'eau, ce qui les empêchera de déborder.
|
Nous allons procéder par récurrence sur $n$. Tout d'abord, si $n=1$, il y a une seule bouteille dans laquelle se trouve un litre d'eau, donc Martin a déjà gagné.
Puis, si $n \geqslant 2$, Martin choisit la bouteille $\mathrm{n}^{\circ} i$ la plus remplie, c'est-à-dire celle pour laquelle $x_{i}$ est maximal. On constate alors que
$$
n=x_{1}+x_{2}+\ldots+x_{n} \leqslant x_{i}+x_{i}+\ldots+x_{i}=n x_{i}
$$
de sorte que $x_{i} \geqslant 1$. Si $x_{i}>1$, il la vide donc partiellement dans une autre bouteille, jusqu'à ce que la bouteille $n^{\circ} i$ ne contienne plus qu'un litre d'eau, puis il la bouche. Il lui suffit alors de répartir harmonieusement les $n-1$ litres d'eau restants, qui se trouvent dans $n-1$ bouteilles, et l'hypothèse de récurrence lui assure qu'il pourra bien effectuer cette répartition.
Commentaire des correcteurs Ce problème a été très bien réussi dans l'ensemble. Quelques élèves ont malheureusement mal compris ce qui leur était demandé, ce qui les a empêchés de résoudre ce problème. D'autres ont proposé une stratégie gagnante pour Martin, mais démontrer que cette stratégie fonctionnait nécessitait néanmoins quelques lignes d'explication : le but n'est pas simplement d'avoir une solution correcte, mais aussi de convaincre le lecteur qu'elle est correcte et, plus encore, de convaincre le correcteur que l'élève a compris que la solution était correcte.
|
{
"resource_path": "French/segmented/tests/fr-2021-2022-Corrigé-Web-Test-2.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution de l'exercice 1"
}
|
a4bff101-6b10-5f9a-bded-cbc6a8b48a21
| 605,047
|
Let $ABC$ be a triangle and $\Omega$ its circumcircle. Let $D$ be the foot of the altitude from vertex $A$. The angle bisector from vertex $A$ intersects the segment $[BC]$ at point $P$ and intersects the circle $\Omega$ again at point $S$. Let $A'$ be the point diametrically opposite to vertex $A$ on the circle $\Omega$. Prove that the lines $(SD)$ and $(A'P)$ intersect on the circle $\Omega$.
|
Let $X$ be the point where the line $\left(A^{\prime} P\right)$ intersects the circle $\Omega$. We will prove that the points $D, S$, and $X$ are collinear.
Let $O$ be the center of $\Omega$. The point $S$ is the South pole of $A B C$ from $A$, so it lies on the perpendicular bisector of $[B C]$, which is the line $(O S)$. Therefore, the lines $(O S)$ and $(A D)$ are parallel, and the angles $\widehat{D A P}$ and $\widehat{O S A}$ are alternate interior angles. Furthermore, the triangle $A O S$ is isosceles at $O$. Thus, in terms of angles, we already know that
$$
\left(X A^{\prime}, X S\right)=\left(A A^{\prime}, A X\right)=(A O, A S)=(S A, S O)=(A P, A D)
$$
It remains to verify that
$$
(X P, X D)=\left(X A^{\prime}, X D\right)=(A P, A D)
$$
that is, the points $X, A, D$, and $P$ are concyclic. Since $\left[A A^{\prime}\right]$ is a diameter of $\Omega$, we know that $\widehat{A X P}=\widehat{A X A^{\prime}}=90^{\circ}=\widehat{A D P}$. Thus, the two points $D$ and $X$ lie on the circle with diameter $[A P]$, and the desired result follows immediately.
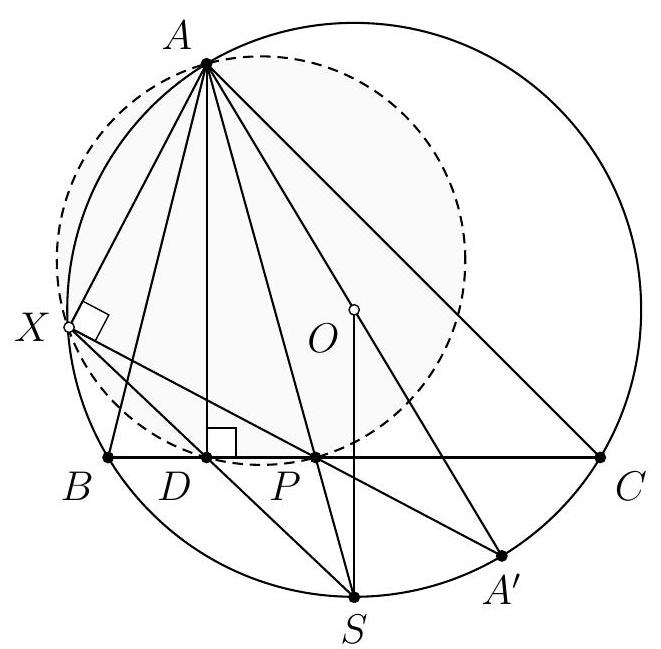
Comment from the graders: This problem was very poorly solved. The main difficulty was to think of proving an equivalent but different statement to the problem statement: showing that the second intersection point of the line $\left(A^{\prime} P\right)$ and the circle $\Omega$ lies on $(S D)$. This is indeed equivalent to the statement, as it ultimately involves showing that the three objects (two lines and a circle) are concurrent. Such a trick is sometimes called the "phantom point" trick and is extremely useful. Here, working with the intersection point of a line and a circle rather than the intersection point of two lines provided more angle equalities.
Such reasoning should not be confused with the "reasoning," which of course does not work, of assuming from the outset that the intersection point of the two lines is on the circle, i.e., precisely the result one wishes to prove. Many students thus assumed that the point $X$ of intersection of $(S D)$ and $\left(A^{\prime} P\right)$ was on $\Omega$, obtained an angle equality involving the point $X$ using the inscribed angle theorem, and concluded shortly thereafter that the point $I$ was on the circle by the converse of the inscribed angle theorem.
Understanding the difference between the two reasonings to avoid making such an error again is surely the best lesson one can take from this exercise.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $\Omega$ son cercle circonscrit. Soit $D$ le pied de la hauteur issue du sommet $A$. La bissectrice issue du sommet $A$ coupe le segment $[B C]$ au point $P$ et recoupe le cercle $\Omega$ au point $S$. Soit $A^{\prime}$ le point diamétralement opposé au sommet $A$ dans le cercle $\Omega$. Démontrer que les droites $(S D)$ et ( $A^{\prime} P$ ) se coupent sur le cercle $\Omega$.
|
Soit $X$ le point où la droite $\left(A^{\prime} P\right)$ recoupe le cercle $\Omega$. Nous allons démontrer que les points $D, S$ et $X$ sont alignés.
Soit $O$ le centre de $\Omega$. Le point $S$ n'est autre que le pôle Sud de $A B C$ issu de $A$, donc il appartient à la médiatrice de $[B C]$, qui n'est autre que la droite $(O S)$. Par conséquent, les droites $(O S)$ et $(A D)$ sont parallèles, et les angles $\widehat{D A P}$ et $\widehat{O S A}$ sont alternes-internes. En outre, le triangle $A O S$ est isocèle en $O$. Ainsi, en angles de droites, on sait déjà que
$$
\left(X A^{\prime}, X S\right)=\left(A A^{\prime}, A X\right)=(A O, A S)=(S A, S O)=(A P, A D)
$$
Il reste donc à vérifier que
$$
(X P, X D)=\left(X A^{\prime}, X D\right)=(A P, A D)
$$
c'est-à-dire que les points $X, A, D$ et $P$ sont cocycliques. Or, puisque $\left[A A^{\prime}\right]$ est un diamètre de $\Omega$, on sait que $\widehat{A X P}=\widehat{A X A^{\prime}}=90^{\circ}=\widehat{A D P}$. Ainsi, les deux points $D$ et $X$ appartiennent au cercle de diamètre $[A P]$, et le résultat désiré en découle immédiatement.

Commentaire des correcteurs Ce problème a été très peu réussi. La difficulté principale était de penser à montrer un énoncé différent mais équivalent à l'énoncé du problème : montrer que le second point d'intersection de la droite $\left(A^{\prime} P\right.$ ) et du cercle $\Omega$ appartient à $(S D)$. Ceci est bien équivalent à l'énoncé puisqu'il s'agit finalement de montrer que les trois objets (deux droites et un cercle) sont concourants. Une telle astuce est parfois appelée astuce du « point fantôme » et est extrêmement utile. Ici, travailler avec le point d'intersection d'une droite et d'un cercle plutôt que le point d'intersection de deux droites fournissait plus d'égalités d'angles.
Un tel raisonnement ne doit surtout pas être confondu avec le « raisonnement», qui ne marche bien sûr pas, consistant à supposer de prime abord que le point d'intersection des deux droites est sur le cercle, c'est-à-dire précisément le résultat que l'on souhaite démontrer. Beaucoup d'élèves ont ainsi supposé que le point $X$ d'intersection de $(S D)$ et $\left(A^{\prime} P\right)$ était sur $\Omega$, ont obtenu une égalité d'angles concernant le point $X$ avec le théorème de l'angle inscrit,
et ont conclu peu de temps après que le point $I$ était sur le cercle par la réciproque du théorème de l'angle inscrit.
Comprendre la différence entre les deux raisonnements pour ne plus refaire une telle erreur est sûrement la meilleure leçon que l'on peut tirer de cet exercice.
|
{
"resource_path": "French/segmented/tests/fr-2021-2022-Corrigé-Web-Test-2.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
0a8e334e-fa4d-5a35-a942-331b42010889
| 605,070
|
Let $n$ be a non-zero natural number. Anna has written $4 n+2$ distinct integers between 0 and $5^{n}$ inclusive. Prove that among the integers she has written, there exist three, say $a, b$ and $c$, such that $a<b<c$ and $c+2 a>3 b$.
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
|
Let $x_{1}<x_{2}<\ldots<x_{4 n+2}$ be the $4 n+2$ integers that Anna has written. We will prove that there exists an integer $k \leqslant 4 n$ such that $x_{4 n+2}+2 x_{k}>3 x_{k+1}$.
Indeed, in the contrary case, let $y_{k}=x_{4 n+2}-x_{k}$ for all integer $k$, so that
$$
3 y_{k+1}=3 x_{4 n+2}-3 x_{k+1} \leqslant 2 x_{4 n+2}-2 x_{k}=2 y_{k} .
$$
This means that $y_{k} \geqslant(3 / 2) y_{k+1}$ for all $k \leqslant 4 n$, and therefore that
$$
5^{n} \geqslant y_{1} \geqslant(3 / 2)^{4 n} y_{4 n+1} \geqslant(3 / 2)^{4 n}=(5+1 / 16)^{n},
$$
which is impossible.
Comment from the graders: This problem, whose solution indeed fits in a few lines, was far from easy and had many pitfalls. Typically, it was not very useful to look at the smallest gap, and often any intuition about a "worst case" turned out to be incorrect.
Even though the problem was relatively well solved, the solutions were often quite long, sometimes introducing variables that were not necessarily useful: we therefore invite even students who received the maximum score to read the solution carefully.
Moreover, there are many confusions between broad and strict inequalities: one must pay attention to this, as it can sometimes lead to incorrect solutions. Similarly, some transform inequalities into equalities at their whim: this is rarely rigorous and often leads to silly point losses. Finally, be careful about recurring calculation errors.
Here, a good approach to start was to question $a, b, c$: once $a$ is fixed, which $b$ and $c$ are most likely to give $2 a+c>3 b$? Asking and answering this question was already a step forward towards the solution and was obviously valued.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $n$ un entier naturel non nul. Anna a écrit $4 n+2$ entiers deux à deux distincts et compris entre 0 et $5^{n}$ inclus. Démontrer que, parmi les entiers qu'elle a écrits, il en existe trois, disons $a, b$ et $c$, tels que $a<b<c$ et $c+2 a>3 b$.
|
Soit $x_{1}<x_{2}<\ldots<x_{4 n+2}$ les $4 n+2$ entiers qu'Anna a écrits. Nous allons démontrer qu'il existe un entier $k \leqslant 4 n$ tel que $x_{4 n+2}+2 x_{k}>3 x_{k+1}$.
En effet, dans le cas contraire, posons $y_{k}=x_{4 n+2}-x_{k}$ pour tout entier $k$, de sorte que
$$
3 y_{k+1}=3 x_{4 n+2}-3 x_{k+1} \leqslant 2 x_{4 n+2}-2 x_{k}=2 y_{k} .
$$
Cela signifie que $y_{k} \geqslant(3 / 2) y_{k+1}$ pour tout $k \leqslant 4 n$, et donc que
$$
5^{n} \geqslant y_{1} \geqslant(3 / 2)^{4 n} y_{4 n+1} \geqslant(3 / 2)^{4 n}=(5+1 / 16)^{n},
$$
ce qui est impossible.
Commentaire des correcteurs Ce problème, dont la solution tient certes en quelques lignes, était loin d'être facile et comportait de nombreux pièges. Typiquement il était peu intéressant de regarder le plus petit écart, et souvent toute intuition sur un «pire cas » se révélait inexacte.
Même si le problème a été plutôt bien réussi, les solutions étaient souvent assez longues, en introduisant parfois des variables pas forcément utiles: nous invitons donc même les élèves ayant eu la note maximale à lire attentivement le corrigé.
De plus, il y a de nombreuses confusions entre inégalités larges et strictes : il faut faire attention à cela, qui peut mener parfois à des solutions incorrectes. De même, certains transforment des inégalités en égalités à leur bon vouloir : c'est rarement rigoureux et cela entraîne souvent des pertes bêtes de points. Attention, enfin, aux erreurs de calcul récurrentes.
Ici, une bonne piste pour commencer était de se questionner sur $a, b, c$ : une fois $a$ fixé, quels sont les $b$ et les $c$ qui auront le plus tendance à donner $2 a+c>3 b$ ? Se poser cette question et y répondre était déjà un pas en avant vers la solution et était évidemment valorisé.
|
{
"resource_path": "French/segmented/tests/fr-2021-2022-Corrigé-Web-Test-2.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution de l'exercice 5"
}
|
36557f15-8f60-5ca2-abe5-12f6ed015340
| 605,084
|
Let $A B C$ be a triangle with acute angles and let $D$ be a point inside the triangle $A B C$. The lines $(A D)$ and $(B D)$ intersect the circumcircle of triangle $A B C$ again at points $A_{1}$ and $B_{1}$, respectively. The circumcircle of triangle $B_{1} D A$ intersects the line $(A C)$ at point $P$. The circumcircle of triangle $A_{1} B D$ intersects the line $(B C)$ at point $Q$.
Prove that the quadrilateral $C P D Q$ is a parallelogram.
|
A hunt for angles of straight lines indicates that
$$
(Q D, C B)=(Q D, Q B)=\left(A_{1} D, A_{1} B\right)=\left(A_{1} A, A_{1} B\right)=(C A, C B),
$$
which means that the lines $(Q D)$ and $(A C)$ are parallel to each other. Similarly, we can prove that
$$
(P D, C A)=(P D, P A)=\left(B_{1} D, B_{1} A\right)=\left(B_{1} B, B_{1} A\right)=(C B, C A)
$$
which means that the lines $(P D)$ and $(B C)$ are parallel to each other. Therefore, the quadrilateral $C P D Q$ is a parallelogram.
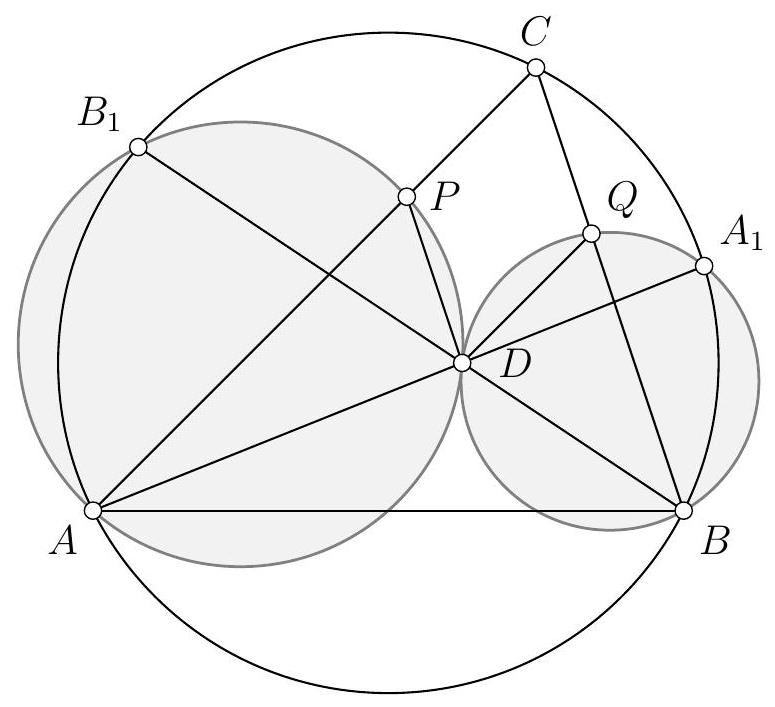
Examiner's Comment The exercise is very well solved.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle dont les angles sont aigus et soit $D$ un point situé à l'intérieur du triangle $A B C$. Les droites $(A D)$ et $(B D)$ recoupent le cercle circonscrit au triangle $A B C$ respectivement en les points $A_{1}$ et $B_{1}$. Le cercle circonscrit au triangle $B_{1} D A$ recoupe la droite $(A C)$ au point $P$. Le cercle circonscrit au triangle $A_{1} B D$ recoupe la droite $(B C)$ au point $Q$.
Démontrer que le quadrilatère $C P D Q$ est un parallélogramme.
|
Une chasse aux angles de droites indique que
$$
(Q D, C B)=(Q D, Q B)=\left(A_{1} D, A_{1} B\right)=\left(A_{1} A, A_{1} B\right)=(C A, C B),
$$
ce qui signifie que les droites $(Q D)$ et $(A C)$ sont parallèles l'une à l'autre. On démontre de même que
$$
(P D, C A)=(P D, P A)=\left(B_{1} D, B_{1} A\right)=\left(B_{1} B, B_{1} A\right)=(C B, C A)
$$
ce qui signifie que les droites $(P D)$ et $(B C)$ sont parallèles l'une à l'autre. Le quadrilatère $C P D Q$ est donc un parallélogramme.

Commentaire des correcteurs L'exercice est très bien résolu.
|
{
"resource_path": "French/segmented/tests/fr-2021-2022-Corrigé-Web-Test-3.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
d64c367c-3f7a-57ae-acc0-a3e77434b91e
| 605,159
|
Let $p$ and $q$ be two distinct prime numbers, such that $p<2q$ and $q<2p$. Prove that there exist two consecutive integers, one of which has $p$ as its largest prime factor and the other has $q$ as its largest prime factor.
|
Suppose without loss of generality that $p<q$. Bézout's theorem indicates that there exist integers $a$ and $b$ such that $a p + b q = 1$.
We can always replace such a pair $(a, b)$ with $(a \pm q, b \mp p)$. Consequently, if we seek a pair for which the value of $|a|$ is minimal, we know that $|a - q| \geqslant |a|$ and $|a| \leqslant |a + q|$, so that $|a| \leqslant q / 2 < p$.
Furthermore, since $|a p + b q| = 1 \leqslant p + q$, the integers $a$ and $b$ are of opposite signs, which means that the integers $n = |a| p$ and $m = |b| q$ are two consecutive integers.
Since $|a| < p$, the integer $n$ therefore has $p$ as its largest prime factor. Moreover, $m \leqslant n + 1 \leqslant p^2 \leqslant q^2$, so $m$ has $q$ as its largest prime factor. The integers $m$ and $n$ thus satisfy the constraints of the statement.
Grader's Comment: Only two students solved this particularly difficult problem. The idea was to find a number $n$, possibly negative, of the form $n = a p = b q - 1$, where $a$ and $b$ would have only small prime factors.
Two approaches were then a priori possible: either ensure that $a$ and $b$ would be powers of $p$ and $q$, in which case Fermat's little theorem could have been relevant, or ensure that they were small. However, as soon as one imposes that $a$ is a power of $p$ such that $a p \equiv 1 \pmod{q}$, one loses control over the factors of $b$. It was therefore necessary to choose $a$, $b$, and $n$ to be small, which required invoking Bézout's theorem.
A final difficulty was that one had to, if necessary, not hesitate to choose $n$ negative, and then take the absolute value.
Surprisingly, several students were content to look at what happened in some specific cases, for example $p=2$ and $q=3$, or even $p=3$ and $q=5$. Looking at small cases is always a good thing, but it is obviously essential to then consider the general case.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $p$ et $q$ deux nombres premiers distincts, tels que $p<2 q$ et $q<2 p$. Démontrer qu'il existe deux entiers consécutifs dont l'un a $p$ pour plus grand facteur premier et l'autre a $q$ pour plus grand facteur premier.
|
Supposons sans perte de généralité que $p<q$. Le théorème de Bézout indique qu'il existe des entiers $a$ et $b$ tels que $a p+b q=1$.
On peut toujours remplacer un tel couple $(a, b) \operatorname{par}(a \pm q, b \mp p)$. Par conséquent, si on cherche un couple pour lequel la valeur de $|a|$ est minimale, on sait que $|a-q| \geqslant|a|$ et $|a| \leqslant|a+q|$, de sorte que $|a| \leqslant q / 2<p$.
En outre, puisque $|a p+b q|=1 \leqslant p+q$, les entiers $a$ et $b$ sont de signes opposés, ce qui signifie que les entiers $n=|a| p$ et $m=|b| q$ sont deux entiers consécutifs.
Puisque $|a|<p$, l'entier $n$ a donc $p$ comme facteur premier maximal. En outre, $m \leqslant n+1 \leqslant$ $p^{2} \leqslant q^{2}$, donc $m$ a $q$ comme facteur premier maximal. Les entiers $m$ et $n$ satisfont donc les contraintes de l'énoncé.
Commentaire des correcteurs Seuls deux élèves ont résolu ce problème particulièrement difficile. L'idée était de trouver un nombre $n$, éventuellement négatif, de la forme $n=a p=$ $b q-1$, où $a$ et $b$ n'auraient que de petits facteurs premiers.
Deux approches étaient alors a priori possibles : soit s'assurer que $a$ et $b$ seraient des puissances de $p$ et de $q$, auquel cas le petit théorème de Fermat aurait pu être pertinent, soit s'assurer qu'ils étaient petits. Or, dès que l'on impose à $a$ d'être une puissance de $p$ telle que $a p \equiv 1(\bmod q)$, on n'a plus aucun contrôle sur les facteurs de $b$. Il convenait donc de choisir $a, b$ et $n$ petits, ce qui exigeait de faire appel au théorème de Bézout.
Une dernière difficulté était que l'on devait, au besoin, ne pas hésiter à chosir $n$ négatif, quitte à passer ensuite à la valeur absolue.
Enfin, de manière surprenante, plusieurs élèves se sont contentés de regarder ce qui se passait dans certains cas particuliers, par exemple $p=2$ et $q=3$, ou encore $p=3$ et $q=5$. Regarder des petits cas est toujours une excellente chose, mais il est évidemment indispensable de s'intéresser ensuite au cas général.
## Problèmes Senior
|
{
"resource_path": "French/segmented/tests/fr-2021-2022-Corrigé-Web-Test-3.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "\nSolution de l'exercice 4"
}
|
26a3a9a4-9600-53c9-974f-4d6e24a4a2da
| 605,182
|
Let $\mathcal{S}$ be an infinite set of non-zero natural numbers containing four integers $a, b, c, d$ that are pairwise distinct such that $\operatorname{pgcd}(a, b) \neq \operatorname{pgcd}(c, d)$. Prove that $\mathcal{S}$ contains three integers $x, y, z$ that are pairwise distinct such that $\operatorname{pgcd}(x, y)=\operatorname{pgcd}(y, z) \neq \operatorname{pgcd}(z, x)$.
|
Below, we denote $m \wedge n$ as the greatest common divisor of two integers $m$ and $n$. We consider the infinite colored graph whose vertices are the elements of $\mathcal{S}$, and where each pair of distinct vertices $(u, v)$ is connected by an edge of color $u \wedge v$.
Suppose that the integers $x, y, z$ do not exist. This means that every triangle is colored using either a single color or exactly three colors.

Now consider $u, v$, and $w$ as three elements of $\mathcal{S}$. Since $u, v$, and $w$ each have a finite number of divisors, the function $f: x \mapsto(u \wedge x, v \wedge x, w \wedge x)$ takes only a finite number of values. Among the infinity of elements of $\mathcal{S}$ distinct from $u, v$, and $w$, there exist two, say $s$ and $t$, such that $f(s)=f(t)$, i.e.,
$$
s \wedge u=t \wedge u, s \wedge v=t \wedge v \text{ and } s \wedge w=t \wedge w
$$
The triangles $(s, t, u), (s, t, v)$, and $(s, t, w)$ are therefore monochromatic, and since they share the edge $(s, t)$, they are of the same color, say $\mathcal{C}$. But then the triangles $(s, u, v)$ and $(s, u, w)$ each have two edges of color $\mathcal{C}$, making them monochromatic of color $\mathcal{C}$ as well, so $u \wedge v = u \wedge w$.
Thus, two edges sharing a common vertex are necessarily of the same color, and our graph is monochromatic. This means in particular that
$$
a \wedge b = c \wedge d
$$
contradicting the assumptions of the statement. Our initial assumption was therefore invalid, which concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $\mathcal{S}$ un ensemble infini d'entiers naturels non nuls contenant quatre entiers $a, b, c, d$ deux à deux distincts tels que $\operatorname{pgcd}(a, b) \neq \operatorname{pgcd}(c, d)$. Démontrer que $\mathcal{S}$ contient trois entiers $x, y, z$ deux à deux distincts tels que $\operatorname{pgcd}(x, y)=\operatorname{pgcd}(y, z) \neq \operatorname{pgcd}(z, x)$.
|
Ci-dessous, on note $m \wedge n$ le plus grand diviseur commun à deux entiers $m$ et $n$. On considère alors le graphe colorié infini dont les sommets sont les éléments de $\mathcal{S}$, et où chaque paire de sommets $(u, v)$ distincts l'un de l'autre est reliée par une arête de couleur $u \wedge v$.
Supposons que les entiers $x, y, z$ n'existent pas. Cela signifie que tout triangle est colorié en utilisant soit une seule couleur, soit exactement trois couleurs.

Soit maintenant $u, v$ et $w$ trois éléments de $\mathcal{S}$. Puisque $u, v$ et $w$ comptent chacun un nombre fini de diviseurs, la fonction $f: x \mapsto(u \wedge x, v \wedge x, w \wedge x)$ ne prend qu'un nombre fini de valeurs. Parmi l'infinité d'éléments de $\mathcal{S}$ distincts de $u, v$ et $w$, il en existe donc deux, disons $s$ et $t$, tels que $f(s)=f(t)$, c'est-à-dire que
$$
s \wedge u=t \wedge u, s \wedge v=t \wedge v \text { et } s \wedge w=t \wedge w
$$
Les triangles $(s, t, u),(s, t, v)$ et $(s, t, w)$ sont donc monochromes, et puisqu'ils partagent l'arête $(s, t)$, ils sont de la même couleur, disons $\mathcal{C}$. Mais alors les triangles $(s, u, v)$ et $(s, u, w)$ ont chacun deux arêtes de couleur $\mathcal{C}$, dont ils sont eux aussi monochromes de couleur $\mathcal{C}$, de sorte que $u \wedge v=u \wedge w$.

Ainsi, deux arêtes ayant un sommet commun sont nécessairement de la même couleur, et notre graphe est monochrome. Cela signifie en particulier que
$$
a \wedge b=c \wedge d
$$
en contradiction avec les hypothèses de l'énoncé. Notre hypothèse initiale était donc invalide, ce qui conclut.
|
{
"resource_path": "French/segmented/tests/fr-2021-2022-Corrigé-Web-Test-3.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution de l'exercice 5"
}
|
2f72ac8d-7f00-5f0f-bbfe-89a3d748b256
| 605,192
|
Let $\mathcal{S}$ be an infinite set of non-zero natural numbers containing four integers $a, b, c, d$ that are pairwise distinct such that $\operatorname{pgcd}(a, b) \neq \operatorname{pgcd}(c, d)$. Prove that $\mathcal{S}$ contains three integers $x, y, z$ that are pairwise distinct such that $\operatorname{pgcd}(x, y)=\operatorname{pgcd}(y, z) \neq \operatorname{pgcd}(z, x)$.
|
$n^{\circ} 1$ Let $k$ be the GCD of the elements of $\mathcal{S}$. If we divide each element of $\mathcal{S}$ by $k$, we obtain a set $\mathcal{S}^{\prime}$ that still satisfies the statement, and conversely, if $\mathcal{S}^{\prime}$ satisfies the statement, $\mathcal{S}$ also satisfies it. We can therefore replace $\mathcal{S}$ with $\mathcal{S}^{\prime}$, that is, we assume from now on that $k=1$.
Let $x$ and $y$ be two elements of $\mathcal{S}$ such that $x \wedge y \neq 1$. For example, we can choose $(x, y)=(a, b)$ or $(x, y)=(c, d)$. If $\mathcal{S}$ has an element $z$ that is coprime with $x$ and $y$, we have $x \wedge z=y \wedge z=1 \neq x \wedge y$, which is the desired result.
Otherwise, among the prime factors of $xy$, there is at least one, say $p$, that divides infinitely many elements of $\mathcal{S}$. Let $\mathcal{S}_{p}$ be the set of elements of $\mathcal{S}$ that are divisible by $p$. Since $k=1$, there exists an element $t$ of $\mathcal{S}$ that does not belong to $\mathcal{S}_{p}$. Since $\mathcal{S}_{p}$ is infinite, and since the function $n \mapsto t \wedge n$ takes only a finite number of values as $n$ varies, there exist two elements $u$ and $v$ of $\mathcal{S}_{p}$ such that $t \wedge u=t \wedge v$. Since $p$ divides $u \wedge v$ but not $u \wedge v$, we conclude that $t \wedge u=t \wedge v \neq u \wedge v$, which again gives the desired result.
Comment from the graders: The problem was quite discriminating: few students had interesting elements and were able to make significant progress without intuiting and finding the solution. Many students who did not succeed in advancing focused on $a, b, c$, and $d$. However, a key element for being able to advance was the infinitude of $S$. This is the most crucial hypothesis in the statement, and it is unfortunate that some papers nowhere used this fact, which is the most interesting part of the statement, and suggested applying the pigeonhole principle.
In a problem, even if it has an apparent arithmetic aspect, one should not necessarily limit oneself to this domain and the considerations directly related to it: the problem may lie at the interface between several domains. Here, some presented very combinatorial proofs, others more arithmetic: it is important not to limit oneself to one's first impression.
Moreover, more than one in five students did not submit a solution to the problem: in olympiads, the first problem is difficult, but the problems are in a gradual order. It is therefore risky to skip the first problem in the hope of doing better later.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $\mathcal{S}$ un ensemble infini d'entiers naturels non nuls contenant quatre entiers $a, b, c, d$ deux à deux distincts tels que $\operatorname{pgcd}(a, b) \neq \operatorname{pgcd}(c, d)$. Démontrer que $\mathcal{S}$ contient trois entiers $x, y, z$ deux à deux distincts tels que $\operatorname{pgcd}(x, y)=\operatorname{pgcd}(y, z) \neq \operatorname{pgcd}(z, x)$.
|
$n^{\circ} 1$ Soit $k$ le PGCD des éléments de $\mathcal{S}$. Si l'on divise chaque élément de $\mathcal{S}$ par $k$, on obtient un ensemble $\mathcal{S}^{\prime}$ qui vérifie toujours l'énoncé et, réciproquement, si $\mathcal{S}^{\prime}$ vérifie l'énoncé, $\mathcal{S}$ le vérifie aussi. On remplace donc $\mathcal{S}$ par $\mathcal{S}^{\prime}$, c'est-à-dire que l'on suppose désormais que $k=1$.
Soit $x$ et $y$ deux éléments de $\mathcal{S}$ tels que $x \wedge y \neq 1$. Il suffit, par exemple, de choisir $(x, y)=(a, b)$ ou $(x, y)=(c, d)$. Si $\mathcal{S}$ admet un élément $z$ premier avec $x$ et $y$, on a $x \wedge z=y \wedge z=1 \neq x \wedge y$, ce qui constitue le résultat souhaité.
Sinon, parmi les facteurs premiers de $x y$, il en existe au moins un, disons $p$, qui divise une infinité d'éléments de $\mathcal{S}$. Notons $\mathcal{S}_{p}$ l'ensemble des éléments de $\mathcal{S}$ qui sont divisibles par $p$. Puisque $k=1$, il existe un élément $t$ de $\mathcal{S}$ qui n'appartient pas à $\mathcal{S}_{p}$. Comme $\mathcal{S}_{p}$ est infini, et puisque la fonction $n \mapsto t \wedge n$ ne prend qu'un nombre fini de valeurs lorsque $n$ varie, il existe deux éléments $u$ et $v$ de $\mathcal{S}_{p}$ tels que $t \wedge u=t \wedge v$. Puisque $p$ divise $u \wedge v$ mais pas $u \wedge v$, on en conclut que $t \wedge u=t \wedge v \neq u \wedge v$, ce qui donne de nouveau le résultat souhaité.
Commentaire des correcteurs L'exercice a été assez discriminant : peu d'élèves ont eu des éléments intéressants et permettant de bien avancer sans avoir intuité et trouvé la solution. Beaucoup des élèves n'ayant pas réussi à avancer se sont focalisés sur $a, b, c$ et $d$. Cependant un élément était clé pour pouvoir avancer : l'infinité de $S$. C'est l'hypothèse la plus cruciale de l'énoncé, et il est dommage que certaines copies se retrouvent à n'utiliser nulle part ce fait, qui est pourtant le plus intéressant de l'énoncé, et incitait à appliquer le principe des tiroirs.
Dans un exercice, même si celui-ci a un aspect arithmétique apparent, il ne faut pas forcément se limiter à ce domaine et aux considérations qui y sont directement liées : l'exercice peut se situer à l'interface entre plusieurs domaines. Ici, certains ont présenté des preuves très combinatoires, d'autres plus arithmétiques:il est important de ne pas se limiter à sa première impression.
Par ailleurs, plus d'un élève sur cinq n'a pas rendu de copies au problème : en olympiades, le premier problème est difficile, mais les problèmes sont en ordre graduel. Il est donc dangereux de faire l'impasse sur le premier problème en espérant mieux réussir après.
|
{
"resource_path": "French/segmented/tests/fr-2021-2022-Corrigé-Web-Test-3.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution alternative"
}
|
2f72ac8d-7f00-5f0f-bbfe-89a3d748b256
| 605,192
|
Let $A, B, C$ and $D$ be four points on a circle $\Omega$. Let $E$ and $F$ be the points of intersection of the rays $[B A)$ and $[B C)$ with the tangent to $\Omega$ at $D$. Let $T$ be a point inside the triangle $A B C$ such that $(T E)$ is parallel to $(C D)$ and that $(T F)$ is parallel to $(A D)$. Finally, let $K$ be the point on the segment $[D F]$, other than $D$, such that $T D = T K$.
Prove that the lines $(A C), (D T)$ and $(B K)$ are concurrent.
|
Let $P$ and $Q$ be the points of intersection of the lines (TE) and (TF) with $(A C)$. Since $(E D)$ is tangent to $\Omega$, we know that
$$
(P A, P E)=(C A, C D)=(D A, D E)
$$
thus, the points $A, D, E$, and $P$ lie on the same circle $\alpha$. Similarly, we can show that the points $C, D, F$, and $Q$ lie on the same circle $\beta$.
This also means that
$$
(P Q, P E)=(P A, P E)=(D A, D E)=(F Q, F E)
$$
thus, the points $E, F, P$, and $Q$ lie on the same circle $\gamma$. Therefore, $T$ is the radical center of the three circles $\alpha, \beta$, and $\gamma$. We then focus on the radical axis of the circles $\alpha$ and $\beta$, which appears to be their common tangent at $D$. We denote $d$ and $d'$ as the tangents to $\alpha$ and $\beta$ at $D$, and verify that
$$
\left(d, d'\right)=(d, D E)+(D F, d')=(A D, A E)+(C F, C D)=(A D, A B)+(C B, C D)=0^{\circ},
$$
which means that the tangents $d$ and $d'$ are coincident. In particular, this common tangent contains $T$.
Consequently, and since the triangle $T D K$ is isosceles at $K$, we know that
$$
(T P, T K)=(P E, E D)+(E D, T K)=(D P, D T)+(T D, D K)=(D P, D K)
$$
which means that $P$ lies on the circumcircle of $D K T$. Similarly, we can show that $Q$ lies on this circumcircle, which we denote as $\tau$.
With all these relations of cocyclicity and tangency, we then have
$$
(K T, K D)=(D K, D T)=(D E, d)=(A E, A D)=(A B, A D)=(B D, D K)
$$
which means that the lines $(B D)$ and $(K T)$ are parallel. Similarly,
$$
\begin{aligned}
(K P, K D) & =(Q P, Q D)=(Q P, Q F)+(Q F, Q D)=(E P, E F)+(C F, C D) \\
& =(C D, K D)+(B C, C D)=(B C, K D)
\end{aligned}
$$
thus, $(K P)$ is parallel to $(B C)$. We can similarly show that $(K Q)$ is parallel to $(A B)$.
These parallel relations indicate that there exists a homothety that maps $A B C D$ to $Q K P T$, and the center of this homothety lies on the lines $(A Q)=(C P)=(A C)$, $(B K)$, and $(D T)$.
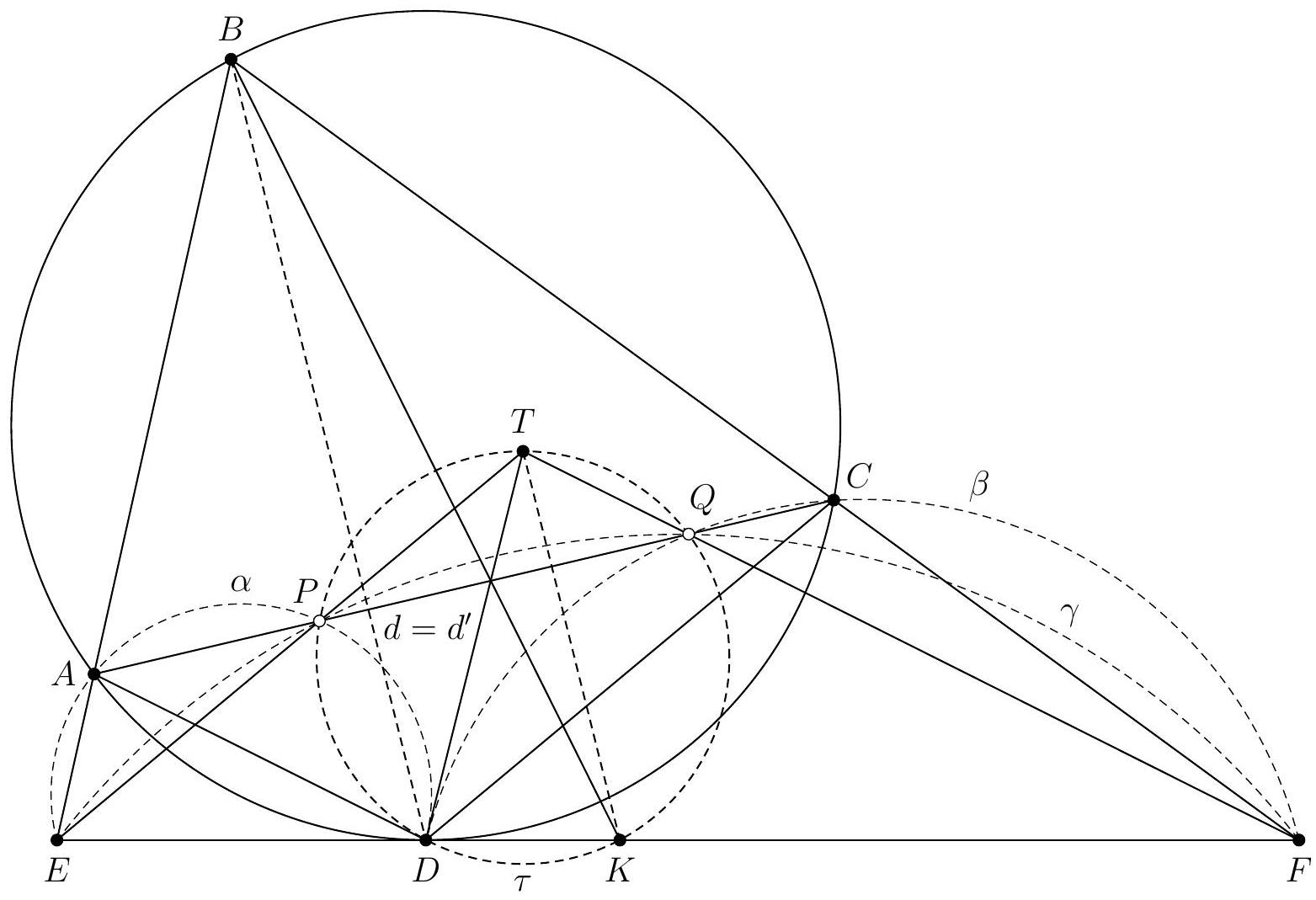
Comment from the graders: The exercise was very long. In each of the possible solutions, there were points to introduce and many relations to guess and then prove. Many students were able to start well on one or the other of the solutions and show the first relations. A handful of students managed to prove everything.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A, B, C$ et $D$ quatre points situés sur un cercle $\Omega$. Soit $E$ et $F$ les points d'intersection des demi-droites $[B A)$ et $[B C)$ avec la tangente à $\Omega$ en $D$. Soit $T$ un point, situé à l'intérieur du triangle $A B C$, tel que $(T E)$ soit parallèle à $(C D)$ et que $(T F)$ soit parallèle à $(A D)$. Enfin, soit $K$ le point du segment $[D F]$, autre que $D$, tel que $T D=T K$.
Démontrer que les droites $(A C),(D T)$ et $(B K)$ sont concourantes.
|
Soit $P$ et $Q$ les points d'intersection des droites (TE) et (TF) avec $(A C)$. Puisque $(E D)$ est tangente à $\Omega$, on sait que
$$
(P A, P E)=(C A, C D)=(D A, D E)
$$
donc que les points $A, D, E$ et $P$ sont appartiennent à un même cercle $\alpha$. On démontre de même que les points $C, D, F$ et $Q$ appartiennent à un même cercle $\beta$.
Cela signifie en outre que
$$
(P Q, P E)=(P A, P E)=(D A, D E)=(F Q, F E)
$$
donc que les points $E, F, P$ et $Q$ appartiennent à un même cercle $\gamma$. Ainsi, $T$ est le centre radical des trois cercles $\alpha, \beta$ et $\gamma$. On s'intéresse donc à l'axe radical des cercles $\alpha$ et $\beta$, qui semble être leur tangente commune en $D$. On note donc $d$ et $d^{\prime}$ les tangentes à $\alpha$ et à $\beta$ en $D$, et on vérifie que
$$
\left(d, d^{\prime}\right)=(d, D E)+\left(D F, d^{\prime}\right)=(A D, A E)+(C F, C D)=(A D, A B)+(C B, C D)=0^{\circ},
$$
ce qui signifie bien que les tangentes $d$ et $d^{\prime}$ sont confondues. En particulier, cette tangente commune contient $T$.
Par conséquent, et puisque le triangle $T D K$ est isocèle en $K$, on sait que
$$
(T P, T K)=(P E, E D)+(E D, T K)=(D P, D T)+(T D, D K)=(D P, D K)
$$
ce qui signifie que $P$ appartient au cercle circonscrit à $D K T$. On démontre de même que $Q$ appartient à ce cercle circonscrit, que l'on note $\tau$.
Forts de toutes ces relations de cocyclicité et de tangence, ensuite que
$$
(K T, K D)=(D K, D T)=(D E, d)=(A E, A D)=(A B, A D)=(B D, D K)
$$
ce qui signifie que les droites $(B D)$ et $(K T)$ sont parallèles. De manière analogue,
$$
\begin{aligned}
(K P, K D) & =(Q P, Q D)=(Q P, Q F)+(Q F, Q D)=(E P, E F)+(C F, C D) \\
& =(C D, K D)+(B C, C D)=(B C, K D)
\end{aligned}
$$
donc $(K P)$ est parallèle à $(B C)$. On démontre de même que $(K Q)$ est parallèle à $(A B)$.
Ces relations de parallélisme indique qu'il existe une homothétie qui envoie $A B C D$ sur $Q K P T$, et le centre de cette homothétie appartient bien aux droites $(A Q)=(C P)=(A C)$, $(B K)$ et $(D T)$.

Commentaire des correcteurs L'exercice était très long. Dans chacune des solutions possibles, il y avait des points à introduire et beaucoup de relations à deviner puis à démontrer. Beaucoup d'élèves ont bien su démarrer sur l'une ou l'autre des solutions et montrer les premières relations. Une poignée d'élèves est parvenue à tout démontrer.
|
{
"resource_path": "French/segmented/tests/fr-2021-2022-Corrigé-Web-Test-3.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "\nSolution de l'exercice 6"
}
|
d99dfa96-41ac-55ff-b23a-ed8cca861cb1
| 605,217
|
Let $ABCD$ be a parallelogram. A line $d$ passing through $C$ intersects lines $(AB)$ and $(AD)$ at $X$ and $Y$ respectively. The tangents at $X$ and $Y$ to the circumcircle of $AXY$ intersect at a point $T$, then line $(CT)$ intersects the circumcircle of $CDY$ at a point $P$.
Prove that points $A, B, D$, and $P$ are concyclic.
|
In the following, we denote $\mathcal{C}_{\mathcal{P}}$ as the circumcircle of a triangle $\mathcal{P}$.
Since $(T X)$ is tangent to $\mathcal{C}_{A X Y}$, an angle chase indicates that
$$
(X T, X Y)=(A X, A Y)=(D C, D Y)=(P C, P Y)=(P T, P Y)
$$
which means that $P$ belongs to $\mathcal{C}_{T X Y}$.
Similarly, since $(T Y)$ is tangent to $\mathcal{C}_{A X Y}$, an angle chase indicates that
$$
(P C, P X)=(P T, P X)=(Y T, Y X)=(A Y, A X)=(B C, B X),
$$
which means that $P$ belongs to $\mathcal{C}_{B C X}$.
We conclude that
$$
(B P, B A)=(B P, B X)=(C P, C X)=(C P, C Y)=(D P, D Y)=(D P, D A)
$$
which means that $P$ belongs to $\mathcal{C}_{A B D}$.
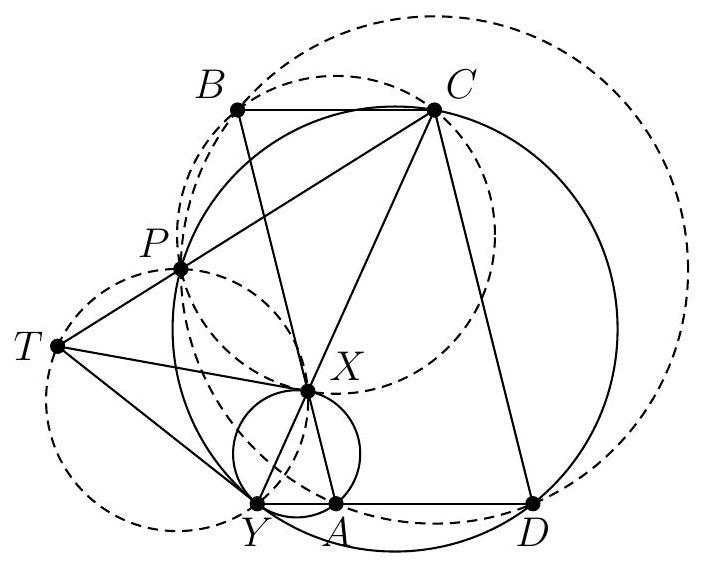
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un parallélogramme. Une droite $d$ passant par $C$ coupe respectivement les droites $(A B)$ et $(A D)$ en $X$ et en $Y$. Les tangentes en $X$ et en $Y$ au cercle circonscrit à $A X Y$ se coupent en un point $T$, puis la droite $(C T)$ recoupe le cercle circonscrit à $C D Y$ en un point $P$.
Démontrer que les points $A, B, D$ et $P$ sont cocycliques.
|
Dans la suite, on note $\mathcal{C}_{\mathcal{P}}$ le cercle circonscrit à un triangle $\mathcal{P}$.
Puisque $(T X)$ est tangente à $\mathcal{C}_{A X Y}$, une chasse aux angles indique que
$$
(X T, X Y)=(A X, A Y)=(D C, D Y)=(P C, P Y)=(P T, P Y)
$$
ce qui signifie que $P$ appartient à $\mathcal{C}_{T X Y}$.
De même, puisque $(T Y)$ est tangente à $\mathcal{C}_{A X Y}$, une chasse aux angles indique que
$$
(P C, P X)=(P T, P X)=(Y T, Y X)=(A Y, A X)=(B C, B X),
$$
ce qui signifie que $P$ appartient à $\mathcal{C}_{B C X}$.
On en conclut que
$$
(B P, B A)=(B P, B X)=(C P, C X)=(C P, C Y)=(D P, D Y)=(D P, D A)
$$
ce qui signifie que $P$ appartient à $\mathcal{C}_{A B D}$.

|
{
"resource_path": "French/segmented/tests/fr-2021-2022-Corrigé-Web-Test-3.jsonl",
"problem_match": "\nExercice 8.",
"solution_match": "\nSolution de l'exercice 8"
}
|
2bbb51ae-ac50-5271-bbad-59c77d55a6df
| 605,240
|
Let $ABCD$ be a parallelogram. A line $d$ passing through $C$ intersects lines $(AB)$ and $(AD)$ at $X$ and $Y$ respectively. The tangents at $X$ and $Y$ to the circumcircle of $AXY$ intersect at a point $T$, then line $(CT)$ intersects the circumcircle of $CDY$ at a point $P$.
Prove that points $A, B, D$, and $P$ are concyclic.
|
$n^{\circ} 1$ The figure suggests that $(T Y)$ is tangent to both circles $\mathcal{C}_{A X Y}$ and $\mathcal{C}_{C D Y P}$. We then verify that this is indeed the case, since
$$
(Y T, Y D)=(Y T, Y A)=(A Y, A X)=(D Y, D C)
$$
Thus, $T$ is the radical center of the three circles $\mathcal{C}_{A X Y}, \mathcal{C}_{C D Y P}$, and $\mathcal{C}_{P C X}$, and since the radical axis $(T X)$ of the circles $\mathcal{C}_{A X Y}$ and $\mathcal{C}_{P C X}$ is tangent to $\mathcal{C}_{A X Y}$, it is also tangent to $\mathcal{C}_{P C X}$.
We can then deduce that
$$
(P X, P C)=(X T, X C)=(X T, X Y)=(A X, A Y)=(B X, B C),
$$
so $B$ lies on $\mathcal{C}_{P C X}$, and that
$$
(X T, X P)=(C X, C P)=(C Y, C P)=(Y T, Y P)
$$
so $P$ lies on $\mathcal{C}_{T X Y}$.
We conclude as before that
$$
(B P, B A)=(B P, B X)=(C P, C X)=(C P, C Y)=(D P, D Y)=(D P, D A)
$$
which means that $P$ lies on $\mathcal{C}_{A B D}$.
Comment from the graders: The exercise was well approached: several students provided a complete solution and several students made significant progress. The most challenging part here was to notice the multitude of cocyclic points. A good figure was once again essential here to make conjectures and prove them.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un parallélogramme. Une droite $d$ passant par $C$ coupe respectivement les droites $(A B)$ et $(A D)$ en $X$ et en $Y$. Les tangentes en $X$ et en $Y$ au cercle circonscrit à $A X Y$ se coupent en un point $T$, puis la droite $(C T)$ recoupe le cercle circonscrit à $C D Y$ en un point $P$.
Démontrer que les points $A, B, D$ et $P$ sont cocycliques.
|
$n^{\circ} 1$ Le tracé de la figure suggère que $(T Y)$ est tangente aux deux cercles $\mathcal{C}_{A X Y}$ et $\mathcal{C}_{C D Y P}$. On vérifie alors que c'est bien le cas, puisque
$$
(Y T, Y D)=(Y T, Y A)=(A Y, A X)=(D Y, D C)
$$
Ainsi, $T$ est le centre radical des trois cercles $\mathcal{C}_{A X Y}, \mathcal{C}_{C D Y P}$ et $\mathcal{C}_{P C X}$, et puisque l'axe radical $(T X)$ des cercles $\mathcal{C}_{A X Y}$ et $\mathcal{C}_{P C X}$ est tangent à $\mathcal{C}_{A X Y}$, il est aussi tangent à $\mathcal{C}_{P C X}$.
On en déduit en particulier que
$$
(P X, P C)=(X T, X C)=(X T, X Y)=(A X, A Y)=(B X, B C),
$$
de sorte que $B$ appartient à $\mathcal{C}_{P C X}$, et que
$$
(X T, X P)=(C X, C P)=(C Y, C P)=(Y T, Y P)
$$
de sorte que $P$ appartient à $\mathcal{C}_{T X Y}$.
On en conclut comme précédemment que
$$
(B P, B A)=(B P, B X)=(C P, C X)=(C P, C Y)=(D P, D Y)=(D P, D A)
$$
ce qui signifie que $P$ appartient à $\mathcal{C}_{A B D}$.
Commentaire des correcteurs L'exercice a été bien abordé : plusieurs élèves ont proposé une solution complète et plusieurs élèves ont produit des avances significative. Le plus difficile ici était de remarquer la multitude de points cocycliques. Une bonne figure était encore une fois essentielle ici pour pouvoir effectuer des conjectures et les prouver.
|
{
"resource_path": "French/segmented/tests/fr-2021-2022-Corrigé-Web-Test-3.jsonl",
"problem_match": "\nExercice 8.",
"solution_match": "\nSolution alternative"
}
|
2bbb51ae-ac50-5271-bbad-59c77d55a6df
| 605,240
|
Let $ABCD$ be a rectangle. Let $\omega$ be the semicircle with diameter $[BC]$, such that point $A$ and the semicircle $\omega$ are on the same side relative to the segment $[BC]$. The circle centered at $B$ with radius $AB$ intersects the semicircle $\omega$ at point $E$. The line $(AE)$ intersects the semicircle $\omega$ at point $F$. Show that $AF = BF$.
|
First, the statement indicates that $B A=B E$, so triangle $A B E$ is isosceles at $B$. Furthermore, since $(A B)$ is tangent to $\omega$, we know that
$$
\widehat{E B A}=\widehat{E F B}=\widehat{A F B} .
$$
Since triangles $A B E$ and $A F B$ share the angle $\widehat{B A E}$, they are therefore similar. In particular, $A F B$ is isosceles at $F$, which means as desired that $A F=B F$.
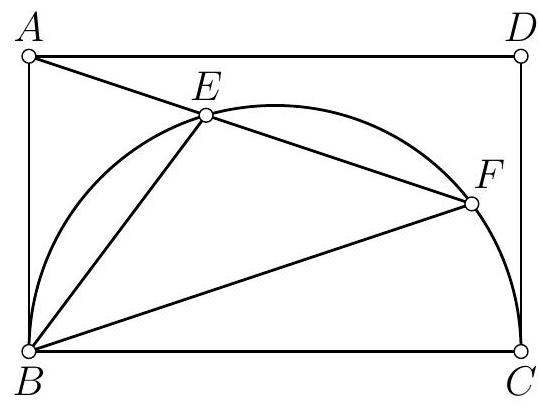
Graders' Comment The exercise is generally well solved. However, many students embarked on extensive angle hunts, introducing a lot of notation and new points. As the solution suggests, this was not necessary. Systematically, the equalities obtained by introducing the center of $\omega$ could be derived in one line by invoking the inscribed angle theorem or the tangent angle theorem, since $(A B)$ is tangent to the circle $\omega$.
Some attempts involved looking at the symmetries of the figure. This was a risky game since, the figure appearing symmetric, one could quickly assert that $F$ was on the perpendicular bisector of $[A B]$, which was equivalent to the statement. To avoid this pitfall, the proofreading step is very important and allows one to check if all the hypotheses of the statement have been used. Often, the unsuccessful attempts simply did not use the point $E$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un rectangle. Soit $\omega$ le demi-cercle de diamètre $[B C]$, de sorte que le point $A$ et le demi-cercle $\omega$ sont situés du même côté par rapport au segment $[B C]$. Le cercle de centre $B$ et de rayon $A B$ recoupe le demi-cercle $\omega$ au point $E$. La droite $(A E)$ recoupe le demi-cercle $\omega$ au point $F$. Montrer que $A F=B F$.
|
Tout d'abord, l'énoncé nous indique que $B A=B E$, de sorte que le triangle $A B E$ est isocèle en $B$. En outre, puisque $(A B)$ est tangente à $\omega$, on sait que
$$
\widehat{E B A}=\widehat{E F B}=\widehat{A F B} .
$$
Comme les triangles $A B E$ et $A F B$ ont l'angle $\widehat{B A E}$ en commun, ils sont donc semblables. En particulier, $A F B$ est isocèle en $F$, ce qui signifie comme souhaité que $A F=B F$.

Commentaire des correcteurs L'exercice est dans l'ensemble bien résolu. Toutefois, beaucoup d'élèves se sont lancés dans de grandes chasses aux angles, en introduisant beaucoup de notations et de nouveaux points. Comme le suggère le corrigé, cela n'était pas nécessaire. Systématiquement, les égalités obtenues autour de l'introduction du centre de $\omega$ pouvaient être retrouvées en une ligne en invoquant le théorème de l'angle inscrit ou le théorème de l'angle tangentiel, puisque $(A B)$ est tangent au cercle $\omega$.
Certaines tentatives consistaient à regarder les symétries de la figure. Il s'agissait d'un jeu dangereux puisque, la figure semblant symétrique, on pouvait rapidement affirmer que $F$ était sur la médiatrice de $[A B]$ alors que cela était équivalent à l'énoncé. Pour ne pas tomber dans ce piège, l'étape de relecture est très importante et permet de regarder si toutes les hypothèses de l'énoncé ont bien été utilisées. Bien souvent, les tentatives infructueuses n'utilisaient tout simplement pas le point $E$.
|
{
"resource_path": "French/segmented/tests/fr-2021-2022-Corrigé-Web-Test-4.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution de l'exercice 1"
}
|
c3077ce1-57ff-5a79-b575-683eb3637261
| 605,286
|
Let $\left(a_{n}\right)_{n \geqslant 1}$ be a sequence of non-zero natural numbers such that $a_{n+2 m}$ divides $a_{n}+a_{n+m}$ for all integers $m \geqslant 1$ and $n \geqslant 1$. Prove that this sequence is ultimately periodic, that is, there exist two integers $N \geqslant 1$ and $d \geqslant 1$ such that $a_{n}=a_{n+d}$ for all $n \geqslant N$.
|
Suppose there exists an integer $k \geqslant 9$ such that $a_{i}<a_{k}$ for all $i \leqslant k-1$. Under these conditions, and for any integer $i<k / 2$, we know that $a_{k-2 i}+a_{k-i}$ is a multiple of $a_{k}$ and that $a_{k-2 i}+a_{k-i}<2 a_{k}$, so that $a_{k-2 i}+a_{k-i}=a_{k}$. By choosing $i=1$, $i=2$ and $i=4$, we deduce that
$$
a_{k-8}+a_{k-4}=a_{k-4}+a_{k-2}=a_{k}=a_{k-2}+a_{k-1}
$$
so that $a_{k-8}=a_{k-2}$ and $a_{k-4}=a_{k-1}$. Induction on $\ell$ then shows that $a_{k-1}$ divides $a_{k-1-3 \ell}$ for all $\ell \leqslant(k-2) / 3$, so that $a_{k-1} \leqslant \max \left\{a_{1}, a_{2}, a_{3}\right\}$, and that $a_{k-2}$ divides $a_{k-2-6 \ell}$ for all $\ell \leqslant(k-3) / 6$, so that $a_{k-2} \leqslant \max \left\{a_{1}, a_{2}, \ldots, a_{6}\right\}$. We conclude that
$$
a_{k}=a_{k-1}+a_{k-2} \leqslant 2 \max \left\{a_{1}, a_{2}, \ldots, a_{6}\right\}
$$
Therefore, the sequence $\left(a_{n}\right)_{n \geqslant 1}$ is bounded.
Let $\lambda$ be the maximum value that the sequence $\left(a_{n}\right)_{n \geqslant 1}$ takes infinitely often, and let $\kappa \geqslant 0$ be an integer such that $a_{n} \leqslant \lambda$ for all $n \geqslant \kappa+1$. By ignoring the first $\kappa$ terms of the sequence, i.e., by replacing each term $a_{n}$ with the term $\hat{a}_{n}=a_{n+\kappa}$, which does not change the statement, we assume that $\kappa=0$, i.e., that $a_{n} \leqslant \lambda$ for all $n \geqslant 1$.
Consider the set $\mathcal{E}=\left\{k \geqslant 1: a_{k}=\lambda\right\}$, and three consecutive elements $k<\ell<m$ of $\mathcal{E}$. If $k \equiv \ell(\bmod 2)$, we know that $\lambda=a_{\ell}$ divides $a_{k}+a_{(k+\ell) / 2}=\lambda+a_{(k+\ell) / 2}$, so that $a_{(k+\ell) / 2}=\lambda$, which contradicts the fact that $k$ and $\ell$ were consecutive elements of $\mathcal{E}$.
We conclude that $k \not \equiv \ell(\bmod 2)$ and, similarly, that $\ell \not \equiv m(\bmod 2)$. But then $\lambda=a_{m}$ divides $a_{k}+a_{(k+m) / 2}=\lambda+a_{(k+m) / 2}$, so $a_{(k+m) / 2}=\lambda$, and $(k+m) / 2$ is an element of $\mathcal{E}$ between $k$ and $m$, so $(k+m) / 2=\ell$. This means that $\ell-k=m-\ell$ and, more generally, that the elements of $\mathcal{E}$ form an infinite arithmetic progression, with common difference $d$.
Finally, let $n \geqslant 1$ be any integer, and let $m \geqslant 1$ be an integer such that $m+n \in \mathcal{E}$. Then $\lambda=a_{m+n}$ divides $a_{n}+a_{m}$, and $m+n+d \in \mathcal{E}$, so $\lambda=a_{m+n+d}$ divides $a_{n+d}+a_{m}$. We conclude that $a_{n} \equiv-a_{m} \equiv a_{n+d}(\bmod \lambda)$. Since $a_{n}$ and $a_{n+d}$ are between 1 and $\lambda$, this means that $a_{n}=a_{n+d}$. Therefore, the sequence $\left(a_{n}\right)_{n \geqslant 1}$ is $d$-periodic, which concludes.
Comment from the graders: The problem was extremely difficult, and only one student scored points. Some students had good initial approaches but did not advance sufficiently. However, be careful of errors in basic arithmetic properties: just because $a$ divides $b+c$ does not mean that $a$ divides $\operatorname{GCD}(b, c)$, especially if $a=b+c$. Similarly, if $a$ divides $b-c$, we have $a \leqslant|b-c|$, but only if $b$ is different from $c$!
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $\left(a_{n}\right)_{n \geqslant 1}$ une suite d'entiers naturels non nuls telle que $a_{n+2 m}$ divise $a_{n}+a_{n+m}$ pour tous les entiers $m \geqslant 1$ et $n \geqslant 1$. Démontrer que cette suite est ultimement périodique, c'est-à-dire qu'il existe deux entiers $N \geqslant 1$ et $d \geqslant 1$ tels que $a_{n}=a_{n+d}$ pour tout $n \geqslant N$.
|
Supposons qu'il existe un entier $k \geqslant 9$ tel que $a_{i}<a_{k}$ pour tout $i \leqslant k-1$. Dans ces conditions, et pour tout entier $i<k / 2$, on sait que $a_{k-2 i}+a_{k-i}$ est un multiple de $a_{k}$ et que $a_{k-2 i}+a_{k-i}<2 a_{k}$, de sorte que $a_{k-2 i}+a_{k-i}=a_{k}$. En choisissant $i=1$, $i=2$ et $i=4$, on en déduit que
$$
a_{k-8}+a_{k-4}=a_{k-4}+a_{k-2}=a_{k}=a_{k-2}+a_{k-1}
$$
donc que $a_{k-8}=a_{k-2}$ et $a_{k-4}=a_{k-1}$.
Une récurrence sur $\ell$ indique alors que $a_{k-1}$ divise $a_{k-1-3 \ell}$ pour tout $\ell \leqslant(k-2) / 3$, de sorte que $a_{k-1} \leqslant \max \left\{a_{1}, a_{2}, a_{3}\right\}$, et que $a_{k-2}$ divise $a_{k-2-6 \ell}$ pour tout $\ell \leqslant(k-3) / 6$, de sorte que $a_{k-2} \leqslant \max \left\{a_{1}, a_{2}, \ldots, a_{6}\right\}$. On en conclut que
$$
a_{k}=a_{k-1}+a_{k-2} \leqslant 2 \max \left\{a_{1}, a_{2}, \ldots, a_{6}\right\}
$$
Par conséquent, la suite $\left(a_{n}\right)_{n \geqslant 1}$ est bornée.
Soit $\lambda$ la valeur maximale que prend infiniment souvent la suite $\left(a_{n}\right)_{n \geqslant 1}$, et soit $\kappa \geqslant 0$ un entier tel que $a_{n} \leqslant \lambda$ pour tout $n \geqslant \kappa+1$. Quitte à oublier les $\kappa$ premiers termes de la suite, c'est-à-dire à remplacer chaque terme $a_{n}$ par le terme $\hat{a}_{n}=a_{n+\kappa}$, ce qui ne change rien à l'énoncé, on suppose que $\kappa=0$, c'est-à-dire que $a_{n} \leqslant \lambda$ pour tout $n \geqslant 1$.
Considérons l'ensemble $\mathcal{E}=\left\{k \geqslant 1: a_{k}=\lambda\right\}$, puis trois éléments consécutifs $k<\ell<m$ de $\mathcal{E}$. Si $k \equiv \ell(\bmod 2)$, on sait que $\lambda=a_{\ell}$ divise $a_{k}+a_{(k+\ell) / 2}=\lambda+a_{(k+\ell) / 2}$, donc que $a_{(k+\ell) / 2}=\lambda$, en contradiction avec le fait que $k$ et $\ell$ étaient des éléments consécutifs de $\mathcal{E}$.
On en déduit que $k \not \equiv \ell(\bmod 2)$ et, de même, que $\ell \not \equiv m(\bmod 2)$. Mais alors $\lambda=a_{m}$ divise $a_{k}+a_{(k+m) / 2}=\lambda+a_{(k+m) / 2}$, donc $a_{(k+m) / 2}=\lambda$, et $(k+m) / 2$ est un élément de $\mathcal{E}$ compris entre $k$ et $m$, de sorte que $(k+m) / 2=\ell$. Cela signifie que $\ell-k=m-\ell$ et, plus généralement, que les éléments de $\mathcal{E}$ forment une progression arithmétique infinie, dont on note $d$ la raison.
Enfin, soit $n \geqslant 1$ un entier quelconque, puis soit $m \geqslant 1$ un entier tel que $m+n \in \mathcal{E}$. Alors $\lambda=a_{m+n}$ divise $a_{n}+a_{m}$, et $m+n+d \in \mathcal{E}$, donc $\lambda=a_{m+n+d}$ divise $a_{n+d}+a_{m}$. On en conclut que $a_{n} \equiv-a_{m} \equiv a_{n+d}(\bmod \lambda)$. Comme $a_{n}$ et $a_{n+d}$ sont compris entre 1 et $\lambda$, cela signifie que $a_{n}=a_{n+d}$. Par conséquent, la suite $\left(a_{n}\right)_{n \geqslant 1}$ est $d$-périodique, ce qui conclut.
Commentaire des correcteurs Le problème était extrêmement difficile, et un seul élève a obtenu des points. Des élèves ont eu de bons réflexes pour commencer mais n'ont pas réussi à avancer suffisamment. Attention cependant aux erreurs sur les propriétés arithmétique de base : ce n'est pas parce que $a$ divise $b+c$ que $a$ divise $\operatorname{PGCD}(b, c)$, surtout si $a=b+c$. De même, si $a$ divise $b-c$, on a certes $a \leqslant|b-c|$, mais uniquement à condition que $b$ soit différent de $c$ !
|
{
"resource_path": "French/segmented/tests/fr-2021-2022-Corrigé-Web-Test-4.jsonl",
"problem_match": "\nExercice 7.",
"solution_match": "\nSolution de l'exercice 7"
}
|
fa3326b5-6995-5194-b4d3-6c20dcbff1bd
| 605,350
|
Let $ABCD$ be a parallelogram such that $AC = BC$. Let $P$ be a point located on the extension of the segment $[AB]$ beyond $B$. Let $Q$ be the intersection point, other than $D$, between the segment $[PD]$ and the circumcircle of $ACD$. Let then $R$ be the intersection point, other than $P$, between the segment $[PC]$ and the circumcircle of $APQ$.
Prove that the lines $(AQ), (BR)$, and $(CD)$ are concurrent.
|
First, we observe that
$$
(R A, R C)=(R A, R P)=(Q A, Q P)=(Q A, Q D)=(C A, C D)=(A C, A B)=(B A, B C)
$$
which means that the points $A, B, C$ and $R$ are concyclic.
Similarly, if we denote $X$ as the intersection point of the lines $(A Q)$ and $(C D)$, we observe that
$$
(Q R, Q X)=(Q R, Q A)=(P R, P A)=(C R, C X)
$$
which means that the points $C, Q, R$ and $X$ are concyclic.
We conclude that
$$
(R C, R X)=(Q C, Q X)=(Q C, Q A)=(D C, D A)=(B A, B C)=(A C, A B)=(R C, R B)
$$
which means that, as announced, the points $B, R$ and $X$ are collinear.
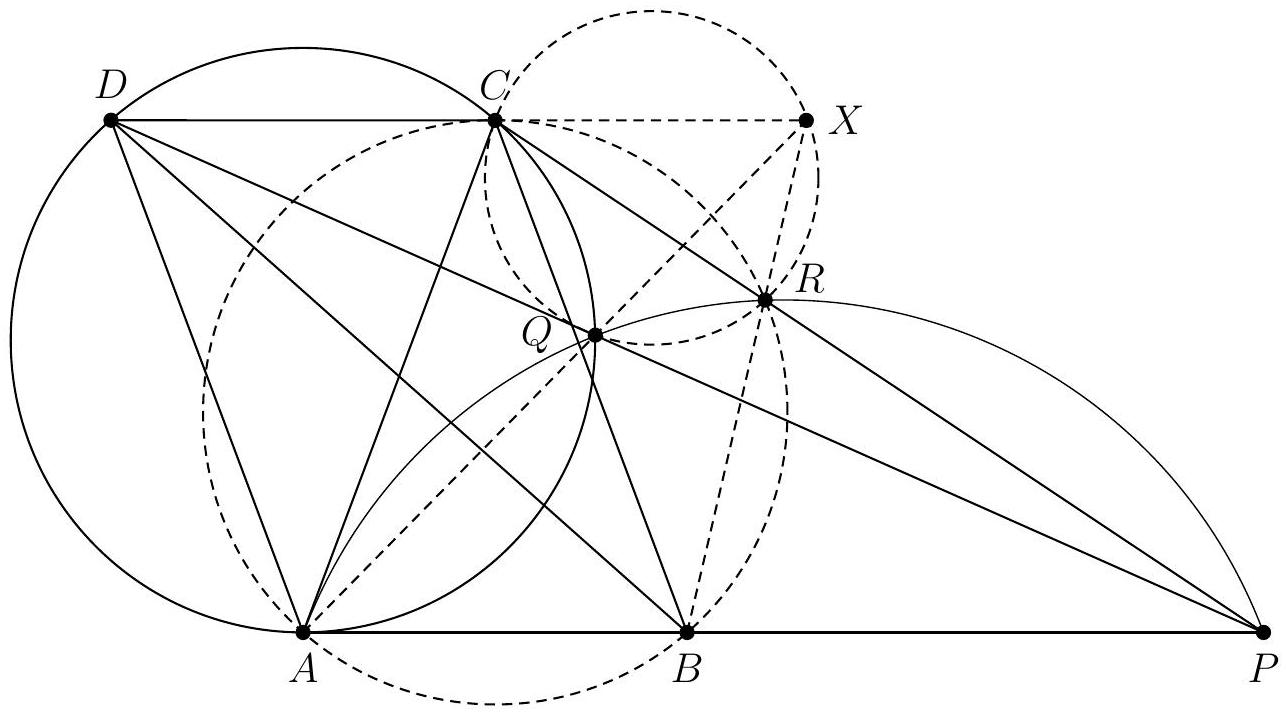
Graders' Comments: If no student solved the problem in its entirety, a few brave students developed very interesting ideas: approaching the problem from the perspective of radical axes, showing that certain points were concyclic, etc. All students who submitted an attempt showed initiative, drew a figure on which they could reasonably make conjectures (and on which graders could follow their reasoning) and started a reasoning process aimed at reaching the solution. Even if it did not always earn points, this kind of effort will allow these students to progress over time.
## Senior Statements
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un parallélogramme tel que $A C=B C$. Soit $P$ un point situé sur le prolongement du segment $[A B]$ au-delà de $B$. Soit $Q$ le point d'intersection, autre que $D$, entre le segment $[P D]$ et le cercle circonscrit à $A C D$. Soit ensuite $R$ le point d'intersection, autre que $P$, entre le segment $[P C]$ et le cercle circonscrit à $A P Q$.
Démontrer que les droites $(A Q),(B R)$ et $(C D)$ sont concourantes.
|
Tout d'abord, on constate que
$$
(R A, R C)=(R A, R P)=(Q A, Q P)=(Q A, Q D)=(C A, C D)=(A C, A B)=(B A, B C)
$$
ce qui signifie que les points $A, B, C$ et $R$ sont cocycliques.
De même, si l'on note $X$ le point d'intersection des droites $(A Q)$ et $(C D)$, on constate que
$$
(Q R, Q X)=(Q R, Q A)=(P R, P A)=(C R, C X)
$$
ce qui signifie que les points $C, Q, R$ et $X$ sont cocycliques.
On en conclut que
$$
(R C, R X)=(Q C, Q X)=(Q C, Q A)=(D C, D A)=(B A, B C)=(A C, A B)=(R C, R B)
$$
ce qui signifie que, comme annoncé, les points $B, R$ et $X$ sont alignés.

Commentaire des correcteurs Si l'exercice n'a été résolu en entier par aucun élève, quelques élèves courageux ont développé des idées très intéressantes : abordé le problème sous l'angle des axes radicaux, montré que des points étaient cocycliques etc...Tous les élèves qui ont rendu une tentative ont fait preuve d'initiative, ont tracé une figure sur laquelle ils pouvaient raisonnablement effectuer des conjectures (et sur laquelle les correcteurs ont pu suivre leur raisonnement) et ont démarré un raisonnement dans le but d'aller vers la solution. Même si cela ne rapportait pas toujours des points, c'est le genre d'effort qui permettra à ces élèves de progresser sur la durée.
## Énoncés Senior
|
{
"resource_path": "French/segmented/tests/fr-2021-2022-Corrigé-Web-Test-5.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "\nSolution de l'exercice 4"
}
|
82a24d9a-6993-521c-8166-5fa04af76e38
| 605,401
|
Let $ABCD$ be a parallelogram such that $AC = BC$. Let $P$ be a point located on the extension of the segment $[AB]$ beyond $B$. Let $Q$ be the intersection point, other than $D$, between the segment $[PD]$ and the circumcircle of $ACD$. Let then $R$ be the intersection point, other than $P$, between the segment $[PC]$ and the circumcircle of $APQ$.
Prove that the lines $(AQ), (BR)$, and $(CD)$ are concurrent.
|
First, we observe that
$$
(R A, R C)=(R A, R P)=(Q A, Q P)=(Q A, Q D)=(C A, C D)=(A C, A B)=(B A, B C),
$$
which means that the points $A, B, C$ and $R$ are concyclic.
Similarly, if we denote $X$ as the intersection point of the lines $(A Q)$ and $(C D)$, we observe that
$$
(Q R, Q X)=(Q R, Q A)=(P R, P A)=(C R, C X)
$$
which means that the points $C, Q, R$ and $X$ are concyclic.
We conclude that
$$
(R C, R X)=(Q C, Q X)=(Q C, Q A)=(D C, D A)=(B A, B C)=(A C, A B)=(R C, R B)
$$
which means that, as announced, the points $B, R$ and $X$ are collinear.
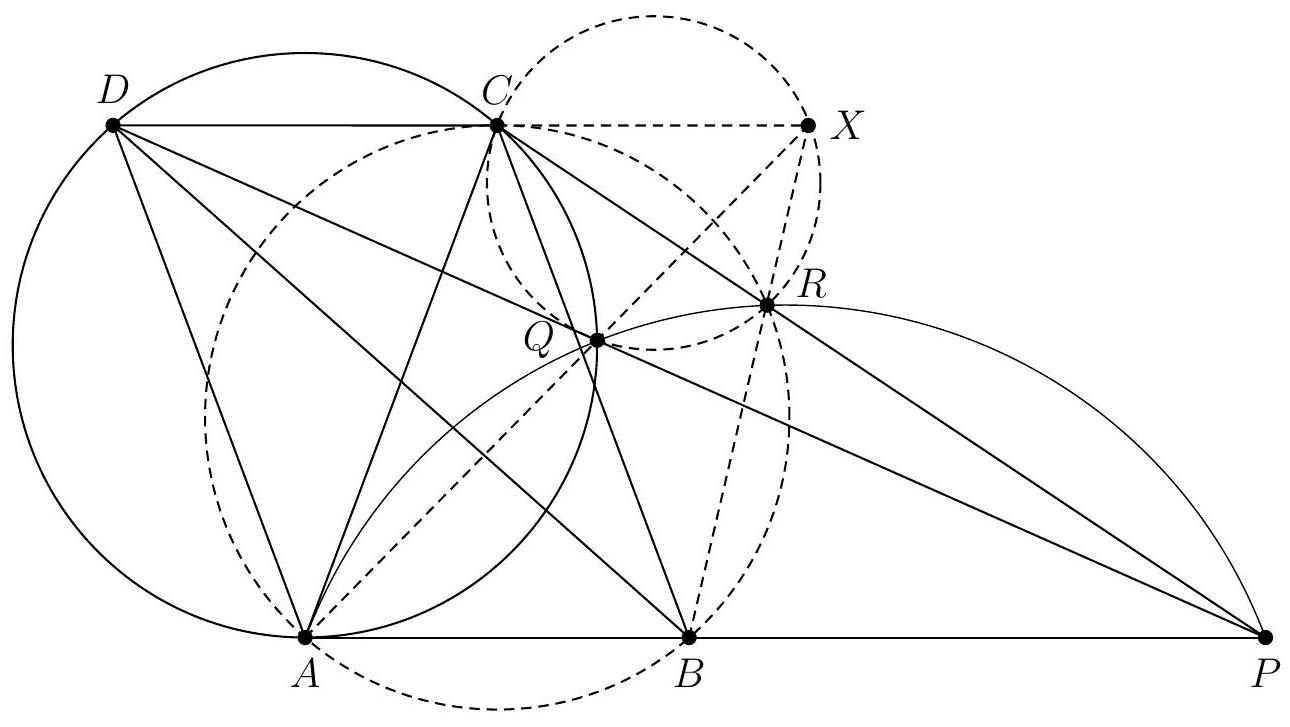
Graders' Comments: The exercise is quite well done. It is worth noting that many students attempted, with varying degrees of success, a dynamic geometry approach.
In such a problem, where it is necessary to show that three objects concur, it is always possible to make reasoning errors, for example, by using a property that appears on the figure but has not yet been proven, which generates a shortcut in the solution. Thus, several students ended up proving the statement without even using all the points in the figure. To avoid this danger, some students drew deliberately inaccurate figures (without losing cleanliness), on which, for example, the lines $(C D),(A Q)$ and $(B R)$ do not concur, in addition to their initial figure, to ensure they did not assume the concurrence of the three lines in their solution. These initiatives and the overall level of the students on the problem reassure us that the students are equipped to face international competition problems.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un parallélogramme tel que $A C=B C$. Soit $P$ un point situé sur le prolongement du segment $[A B]$ au-delà de $B$. Soit $Q$ le point d'intersection, autre que $D$, entre le segment $[P D]$ et le cercle circonscrit à $A C D$. Soit ensuite $R$ le point d'intersection, autre que $P$, entre le segment $[P C]$ et le cercle circonscrit à $A P Q$.
Démontrer que les droites $(A Q),(B R)$ et $(C D)$ sont concourantes.
|
Tout d'abord, on constate que
$$
(R A, R C)=(R A, R P)=(Q A, Q P)=(Q A, Q D)=(C A, C D)=(A C, A B)=(B A, B C),
$$
ce qui signifie que les points $A, B, C$ et $R$ sont cocycliques.
De même, si l'on note $X$ le point d'intersection des droites $(A Q)$ et ( $C D)$, on constate que
$$
(Q R, Q X)=(Q R, Q A)=(P R, P A)=(C R, C X)
$$
ce qui signifie que les points $C, Q, R$ et $X$ sont cocycliques.
On en conclut que
$$
(R C, R X)=(Q C, Q X)=(Q C, Q A)=(D C, D A)=(B A, B C)=(A C, A B)=(R C, R B)
$$
ce qui signifie que, comme annoncé, les points $B, R$ et $X$ sont alignés.

Commentaire des correcteurs L'exercice est plutôt bien réussi. Il est à noter que beaucoup d'élèves ont tenté, avec plus ou moins de succès, une approche avec de la géométrie dynamique.
Dans un tel problème, où il faut montrer que trois objets concourent, il est toujours possible de faire des erreurs de raisonnement, par exemple en utilisant une propriété qui est apparente sur la figure mais que l'on n'a pas encore démontrée et qui génère un raccourci dans la solution. Ainsi, plusieurs élèves se sont retrouvés à montrer l'énoncé sans même utiliser tous les points de la figure. Pour pallier ce danger, quelques élèves ont tracé des figures volontairement inexactes (sans pour autant perdre en propreté), sur lesquelles par exemple les droites $(C D),(A Q)$ et $(B R)$ ne sont pas concourantes, en plus de leur figure de départ, pour être sûr de ne pas supposer sans le vouloir la concourance des trois droites dans leur résolution. Ces initiatives et le niveau global des élèves sur le problème nous confortent dans l'idée que les élèves sont armés pour affronter les problèmes de compétitions internationales.
|
{
"resource_path": "French/segmented/tests/fr-2021-2022-Corrigé-Web-Test-5.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution de l'exercice 5"
}
|
82a24d9a-6993-521c-8166-5fa04af76e38
| 605,401
|
A hunter and an invisible rabbit play on an infinite square grid, that is, where each cell has four neighbors: left, right, up, and down. First, the hunter colors each cell of the grid, but can only use a finite number of colors. The rabbit then chooses a cell on the grid, which will be its starting point. It then begins to move: each minute, it tells the hunter the color of the cell it is on, and then moves to one of the four adjacent cells. Of course, since it is invisible, the only information the hunter has access to are the colors the rabbit announces each minute just before moving.
The hunter wins if, after a finite time,
$\triangleright$ he can identify the cell the rabbit initially chose, or if
$\triangleright$ the rabbit returns to a cell it had previously visited.
Does the hunter have a winning strategy?
|
Indeed, the hunter has a winning strategy, for example, the one given below. First, he identifies the grid with the set $\mathbb{Z}^{2}$, then associates each cell $\mathbf{c}=(x, y)$ with the triplet $\varphi(\mathbf{c})=(x, y, x+y)$.
Each time the rabbit moves, two components of the triplet $\varphi \mathbf{( c )}$ vary by $\pm 1$, and the third component does not change. Furthermore, knowing two of the coordinates of $\varphi(\mathbf{c})$ is enough to identify c. In particular, if there exists a finite set $E$ such that at any time, the rabbit is in a cell c such that at least two of the components of $\varphi(\mathbf{c})$ are in $E$, it is known that the rabbit is constrained to evolve within a finite set of cells, which will inevitably lead to its defeat and transformation into civet.
Therefore, at least two of the three components of $\varphi(\mathbf{c})$ will take an infinite number of values. If the hunter can identify, at a given moment, the values taken by these components, he will deduce the actual position of the rabbit and will have won.
By doing so, the hunter has reduced the problem to the following one-dimensional problem: given an invisible rabbit that moves along the axis $\mathbb{Z}$ by steps of $-1,0$ or +1 and is constrained to pass through an infinite number of integers, how can coloring $\mathbb{Z}$ using a finite number of colors allow the hunter to identify the initial position of the rabbit along this axis? Once such a coloring col: $\mathbb{Z} \rightarrow\{0,1, \ldots, \kappa-1\}$ using $\kappa$ colors numbered from 0 to $\kappa-1$ is established, the hunter only needs to use $\kappa^{3}$ colors, identified with the elements of the set $\{0,1, \ldots, \kappa-1\}^{3}$, and to color the cell $\mathbf{c}=(x, y)$ with the color $(\operatorname{col}(x), \operatorname{col}(y), \operatorname{col}(x+y))$.
To answer this new one-dimensional problem, the hunter colors $\mathbb{Z}$ using three colors, numbered from 1 to 3, and paints in color $c$ all integers $n$ such that $n \equiv c(\bmod 3)$. In this way, he knows at any time whether the rabbit is moving to the left or to the right.
Then he repaints with color 4 the integers, previously colored 3, that are of the form $3 \times(-3)^{n}$ with $n$ a natural number. Thus, he does not lose his previous information on the value of the cells modulo 3, nor on the value $(-1,0$ or +1) of the rabbit's movements. Consequently, if he ever manages to identify the rabbit's position at a given moment, he knows its position at any time during the game.
Finally, the rabbit will pass through two consecutive elements of the set $\mathcal{E}=\left\{3 \times(-3)^{n}: n \geqslant 0\right\}$. If these two elements are $3 \times(-3)^{n}$ and $3 \times(-3)^{n+2}$, the difference between them, in absolute value, is $8 \times 3^{n}$. If they are 3 and -9, this difference, in absolute value, is equal to 12. Therefore, after the rabbit has passed through two consecutive elements of $\mathcal{E}$, the hunter easily identifies these two elements and, based on the variations in the rabbit's position, the element of $\mathcal{E}$ where the rabbit has just arrived. He then deduces the initial position of the rabbit, which allows him to win the one-dimensional game, and thus win the original two-dimensional game.
|
proof
|
Yes
|
Yes
|
proof
|
Logic and Puzzles
|
Un chasseur et un lapin invisible jouent sur une grille infinie à maille carrée, c'est-à-dire où chaque case a quatre voisines : à gauche, à droite, en haut et en bas. Tout d'abord, le chasseur colorie chaque case de la grille, mais ne peut utiliser qu'un nombre fini de couleurs. Le lapin choisit ensuite une case de la grille, qui sera son point de départ. Il commence alors à se déplacer : chaque minute, il indique au chasseur la couleur de la case sur laquelle il se trouve, puis il se déplace sur une des quatre cases adjacentes. Évidemment, comme il est invisible, les seules informations auxquelles le chasseur a accès sont les couleurs que le lapin annonce chaque minute juste avant de se déplacer.
Le chasseur gagne si, au bout d'une durée finie,
$\triangleright$ il peut identifier la case que le lapin avait initialement choisie, ou bien si
$\triangleright$ le lapin revient en une case où il s'était déjà trouvé précédemment.
Le chasseur dispose-t-il d'une stratégie gagnante?
|
Le chasseur dispose en effet d'une stratégie gagnante, par exemple celle que nous donnons ci-dessous. Tout d'abord, il identifie la grille à l'ensemble $\mathbb{Z}^{2}$, puis il associe à chaque case $\mathbf{c}=(x, y)$ le triplet $\varphi(\mathbf{c})=(x, y, x+y)$.
Chaque fois que le lapin se déplace, deux composantes du triplet $\varphi \mathbf{( c )}$ varient de $\pm 1$, et la troisième composante ne change pas. En outre, connaître deux des coordonnées de $\varphi(\mathbf{c})$ suffit à identifier c. En particulier, s'il existe un ensemble fini $E$ tel que, à tout moment, le lapin se trouve en une case c telle que deux des composantes (au moins) de $\varphi(\mathbf{c})$ soient dans $E$, on sait que lapin est contraint d'évoluer dans un ensemble fini de cases, ce qui entraînera immanquablement sa défaite et sa transformation en civet.
On sait donc qu'au moins deux des trois composantes de $\varphi(\mathbf{c})$ prendront une infinité de valeurs. Si le chasseur parvient à identifier, à un instant donné, les valeurs prises par ces composantes, il en déduira la position réelle du lapin et aura donc gagné.
Ce faisant, le chasseur s'est ramené au problème unidimensionnel suivant : étant donné un lapin invisible qui se déplace sur l'axe $\mathbb{Z}$ par pas de $-1,0$ ou +1 et qui est contraint à passer par une infinité d'entiers, comment colorier $\mathbb{Z}$ en usant d'un nombre fini de couleurs peut-il permettre au chasseur d'identifier la position initiale du lapin le long de cet axe? Une fois un tel coloriage col: $\mathbb{Z} \rightarrow\{0,1, \ldots, \kappa-1\}$ utilisant $\kappa$ couleurs numérotées de 0 à $\kappa-1$, le chasseur n'aura plus qu'à utiliser $\kappa^{3}$ couleurs, identifiées aux éléments de l'ensemble $\{0,1, \ldots, \kappa-1\}^{3}$, et à colorier la case $\mathbf{c}=(x, y)$ avec la couleur $(\operatorname{col}(x), \operatorname{col}(y), \operatorname{col}(x+y))$.
Pour répondre à ce nouveau problème unidimensionnel, le chasseur colorie $\mathbb{Z}$ en utilisant trois couleurs, numérotées de 1 et à 3 , et peint en couleur $c$ tous les entiers $n$ tels que $n \equiv c(\bmod 3)$. De la sorte, il sait à tout instant si le lapin se déplace vers la gauche ou vers la droite.
Puis il repeint avec la couleur 4 les entiers, préalablement de couleur 3, qui sont de la forme $3 \times(-3)^{n}$ avec $n$ entier naturel. Ainsi, il ne perd pas son information précédente sur la valeur des cases modulo 3 , ni sur la valeur $(-1,0$ ou +1 ) des mouvements du lapin. Par conséquent, si jamais il arrive à identifier la position du lapin à un moment donné, il connaît sa position à tout moment du jeu.
Enfin, le lapin passera par deux éléments consécutifs de l'ensemble $\mathcal{E}=\left\{3 \times(-3)^{n}: n \geqslant 0\right\}$. Si ces deux éléments sont $3 \times(-3)^{n}$ et $3 \times(-3)^{n+2}$, la différence entre eux, en valeur absolue, est $8 \times 3^{n}$. Si ce sont 3 et -9 , cette différence, en valeur absolue, est égale à 12 . Par conséquent, après que le lapin est passé par deux éléments consécutifs de $\mathcal{E}$, le chasseur identifie aisément ces deux éléments et, en fonction des variations de position du lapin, l'élément de $\mathcal{E}$ en lequel le lapin vient d'arriver. Il en déduit alors la position initiale du lapin, ce qui lui permet de gagner le jeu unidimensionnel, donc de gagner le jeu bidimensionnel d'origine.
|
{
"resource_path": "French/segmented/tests/fr-2021-2022-Corrigé-Web-Test-5.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "\nSolution de l'exercice 6"
}
|
24039f5d-78f4-5b65-9d34-3bbdf5e0ad97
| 605,423
|
Let $n$ be an integer greater than or equal to 2, and let $a_{1}, a_{2}, \ldots, a_{n}$ be strictly positive real numbers such that $a_{1}+a_{2}+\ldots+a_{n}=1$. Prove that
$$
\sum_{k=1}^{n} \frac{a_{k}}{1-a_{k}}\left(a_{1}+a_{2}+\ldots+a_{k-1}\right)^{2}<\frac{1}{3}
$$
|
For any integer $k$, since $0<a_{k}<1$, we set $s_{k}=a_{1}+a_{2}+\ldots+a_{k}$ and $b_{k}=a_{k} s_{k-1}^{2} /\left(1-a_{k}\right)$, with the convention that $s_{0}=0$. We will prove the inequality
$$
b_{k}<\left(s_{k}^{3}-s_{k-1}^{3}\right) / 3
$$
This follows from the fact that
$$
\text { (1) } \begin{aligned}
& \Leftrightarrow 0<\left(1-a_{k}\right)\left(\left(s_{k-1}+a_{k}\right)^{3}-s_{k-1}^{3}\right)-3 a_{k} s_{k-1}^{2} \\
& \Leftrightarrow 0<\left(1-a_{k}\right) a_{k}\left(3 s_{k-1}^{2}+3 s_{k-1} a_{k}+a_{k}^{2}\right)-3 a_{k} s_{k-1}^{2} \\
& \Leftrightarrow 0<3 a_{k} s_{k-1}^{2}-3 a_{k}^{2} s_{k-1}^{2}+3\left(1-a_{k}\right) s_{k-1} a_{k}^{2}+\left(1-a_{k}\right) a_{k}^{3}-3 a_{k} s_{k-1}^{2} \\
& \Leftrightarrow 0<3\left(1-a_{k}-s_{k-1}\right) s_{k-1} a_{k}^{2}+\left(1-a_{k}\right) a_{k}^{3} \\
& \Leftrightarrow 0<3\left(1-s_{k}\right) s_{k-1} a_{k}^{2}+\left(1-a_{k}\right) a_{k}^{3},
\end{aligned}
$$
the last inequality being indeed correct. We conclude that
$$
b_{1}+b_{2}+\ldots+b_{n}<\left(s_{n}^{3}-s_{0}^{3}\right) / 3=1 / 3 .
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $n$ un entier supérieur ou égal à 2 , et soit $a_{1}, a_{2}, \ldots, a_{n}$ des réels strictement positifs tels que $a_{1}+a_{2}+\ldots+a_{n}=1$. Démontrer que
$$
\sum_{k=1}^{n} \frac{a_{k}}{1-a_{k}}\left(a_{1}+a_{2}+\ldots+a_{k-1}\right)^{2}<\frac{1}{3}
$$
|
Pour tout entier $k$, puisque $0<a_{k}<1$, on pose $s_{k}=a_{1}+a_{2}+\ldots+a_{k}$ et $b_{k}=a_{k} s_{k-1}^{2} /\left(1-a_{k}\right)$, avec la convention selon laquelle $s_{0}=0$. Nous allons démontrer l'inégalité
$$
b_{k}<\left(s_{k}^{3}-s_{k-1}^{3}\right) / 3
$$
Celle-ci découle du fait que
$$
\text { (1) } \begin{aligned}
& \Leftrightarrow 0<\left(1-a_{k}\right)\left(\left(s_{k-1}+a_{k}\right)^{3}-s_{k-1}^{3}\right)-3 a_{k} s_{k-1}^{2} \\
& \Leftrightarrow 0<\left(1-a_{k}\right) a_{k}\left(3 s_{k-1}^{2}+3 s_{k-1} a_{k}+a_{k}^{2}\right)-3 a_{k} s_{k-1}^{2} \\
& \Leftrightarrow 0<3 a_{k} s_{k-1}^{2}-3 a_{k}^{2} s_{k-1}^{2}+3\left(1-a_{k}\right) s_{k-1} a_{k}^{2}+\left(1-a_{k}\right) a_{k}^{3}-3 a_{k} s_{k-1}^{2} \\
& \Leftrightarrow 0<3\left(1-a_{k}-s_{k-1}\right) s_{k-1} a_{k}^{2}+\left(1-a_{k}\right) a_{k}^{3} \\
& \Leftrightarrow 0<3\left(1-s_{k}\right) s_{k-1} a_{k}^{2}+\left(1-a_{k}\right) a_{k}^{3},
\end{aligned}
$$
cette dernière inégalité étant effectivement correcte. On en conclut que
$$
b_{1}+b_{2}+\ldots+b_{n}<\left(s_{n}^{3}-s_{0}^{3}\right) / 3=1 / 3 .
$$
|
{
"resource_path": "French/segmented/tests/fr-2021-2022-Corrigé-Web-Test-5.jsonl",
"problem_match": "\nExercice 7.",
"solution_match": "\nSolution de l'exercice 7"
}
|
cec3d418-6b30-52fe-9526-8fe128a1001e
| 605,440
|
Let $ABC$ be a triangle and $\Gamma$ its circumcircle. Let $A_{1}$ be the midpoint of the arc $\widehat{BC}$ not containing $A$; $B_{1}$ the midpoint of the arc $\overparen{CA}$ not containing $B$; $C_{1}$ the midpoint of the arc $\overparen{AB}$ not containing $C$. Finally, let $A_{2}$ be the point such that $A B_{1} A_{2} C_{1}$ is a parallelogram; $B_{2}$ the point such that $B C_{1} B_{2} A_{1}$ is a parallelogram; $C_{2}$ the point such that $C A_{1} C_{2} B_{1}$ is a parallelogram.
Prove that the circumcircles of $ABC$ and $A_{2} B_{2} C_{2}$ are concentric.
|
First, we aim to prove that \( O A_{2} = O B_{2} \). Since \( A_{1} B_{2} = B C_{1} = A C_{1} = B_{1} A_{2} \) and \( A_{1} O = B_{1} O \), the equality \( O A_{2} = O B_{2} \) is equivalent to the fact that triangles \( O A_{1} B_{2} \) and \( O B_{1} A_{2} \) are isometric to each other, which means that \( \widehat{O A_{1} B} = \widehat{O B_{1} A_{2}} \).
We denote \(\alpha = \widehat{C A B}\), \(\beta = \widehat{A B C}\), and \(\gamma = \widehat{B C A}\) as the angles of the triangle. Here, given our parallelism and cocyclicity relations, it is more convenient to work with angles between lines. Thus, since \((C C_{1})\) is the bisector of angle \(\widehat{B C A}\), we observe that
\[
\begin{aligned}
\left(A_{1} O, A_{1} B_{2}\right) & = \left(A_{1} O, B C\right) + \left(B C, A_{1} B_{2}\right) \\
& = 90^{\circ} + \left(B C, B C_{1}\right) \\
& = 90^{\circ} + (B C, B A) + \left(B A, B C_{1}\right) \\
& = 90^{\circ} + \alpha + \gamma / 2 = (\alpha - \beta) / 2.
\end{aligned}
\]
This means that \(\widehat{O A_{1} B_{2}} = |\alpha - \beta| / 2\). Since \(A, B\), and \(C\) play symmetric roles, we deduce that \(\widehat{O B_{1} A_{2}} = |\beta - \alpha| / 2 = \widehat{O A_{1} B}\), hence \(O A_{2} = O B_{2}\). By symmetry, we even conclude that \(O B_{2} = O C_{2}\).
Next, we will directly calculate \(O A_{2}\) in terms of the angles \(\alpha, \beta, \gamma\) and the radius \(R = O A\). First, we note that \(\widehat{A O B_{1}} = \beta\), \(\widehat{C_{1} O A} = \gamma\), and \(\widehat{C_{1} O B_{1}} = \beta + \gamma = 180^{\circ} - \alpha\). Moreover, the condition on \(A_{2}\) means that \(A_{2} = (B_{1} + C_{1}) - A\), so
\[
\begin{aligned}
O A_{2}^{2} & = \overrightarrow{O A_{2}} \cdot \overrightarrow{O A_{2}} \\
& = \left(\overrightarrow{O B_{1}} + \overrightarrow{O C_{1}} - \overrightarrow{O A}\right) \cdot \left(\overrightarrow{O B_{1}} + \overrightarrow{O C_{1}} - \overrightarrow{O A}\right) \\
& = \overrightarrow{O B_{1}}^{2} + \overrightarrow{O C_{1}}^{2} + \overrightarrow{O A}^{2} + 2 \overrightarrow{O B_{1}} \cdot \overrightarrow{O C_{1}} - 2 \overrightarrow{O A} \cdot \overrightarrow{O B_{1}} - 2 \overrightarrow{O C_{1}} \cdot \overrightarrow{O A} \\
& = \left(3 + 2 \cos \left(180^{\circ} - \alpha\right) - 2 \cos (\beta) - 2 \cos (\gamma)\right) R^{2} \\
& = (3 - 2 \cos (\alpha) - 2 \cos (\beta) - 2 \cos (\gamma)) R^{2}.
\end{aligned}
\]
Since \(A, B\), and \(C\) play symmetric roles, we conclude that \(O A_{2}^{2} = O B_{2}^{2} = O C_{2}^{2}\).
**Comment from the Examiners:** The exercise was very poorly performed. Many students touched on the beginning of the solution by exploiting the length equalities from the parallelograms or angle equalities with the South poles, but very few thought to introduce the center \(O\) into their calculations or figures, even though it was the star of the exercise.
It is also frustrating to see students make statements like "there exists a transformation/similarity that maps the triangle/parallelogram to another" when the content of the statement is false and the conclusion of the statement does not help: no, the existence of a similarity that maps one triangle to another does not tell us anything about whether the centers of the circles are the same! It is even more frustrating to see that these are the only apparent arguments. Instead of trying simple things like angle chasing or length chasing, students persist in improvising arguments with concepts they do not master either the theory or the scope of. This is certainly not the way to progress in geometry.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $\Gamma$ son cercle circonscrit. Soit $A_{1}$ le milieu de l'arc $\widehat{B C}$ ne contenant pas $A ; B_{1}$ le milieu de l'arc $\overparen{C A}$ ne contenant pas $B ; C_{1}$ le milieu de l'arc $\overparen{A B}$ ne contenant pas $C$. Enfin, soit $A_{2}$ le point pour lequel $A B_{1} A_{2} C_{1}$ est un parallélogramme; $B_{2}$ le point pour lequel $B C_{1} B_{2} A_{1}$ est un parallélogramme; $C_{2}$ le point pour lequel $C A_{1} C_{2} B_{1}$ est un parallélogramme.
Démontrer que les cercles circonscrits à $A B C$ et à $A_{2} B_{2} C_{2}$ sont concentriques.
|
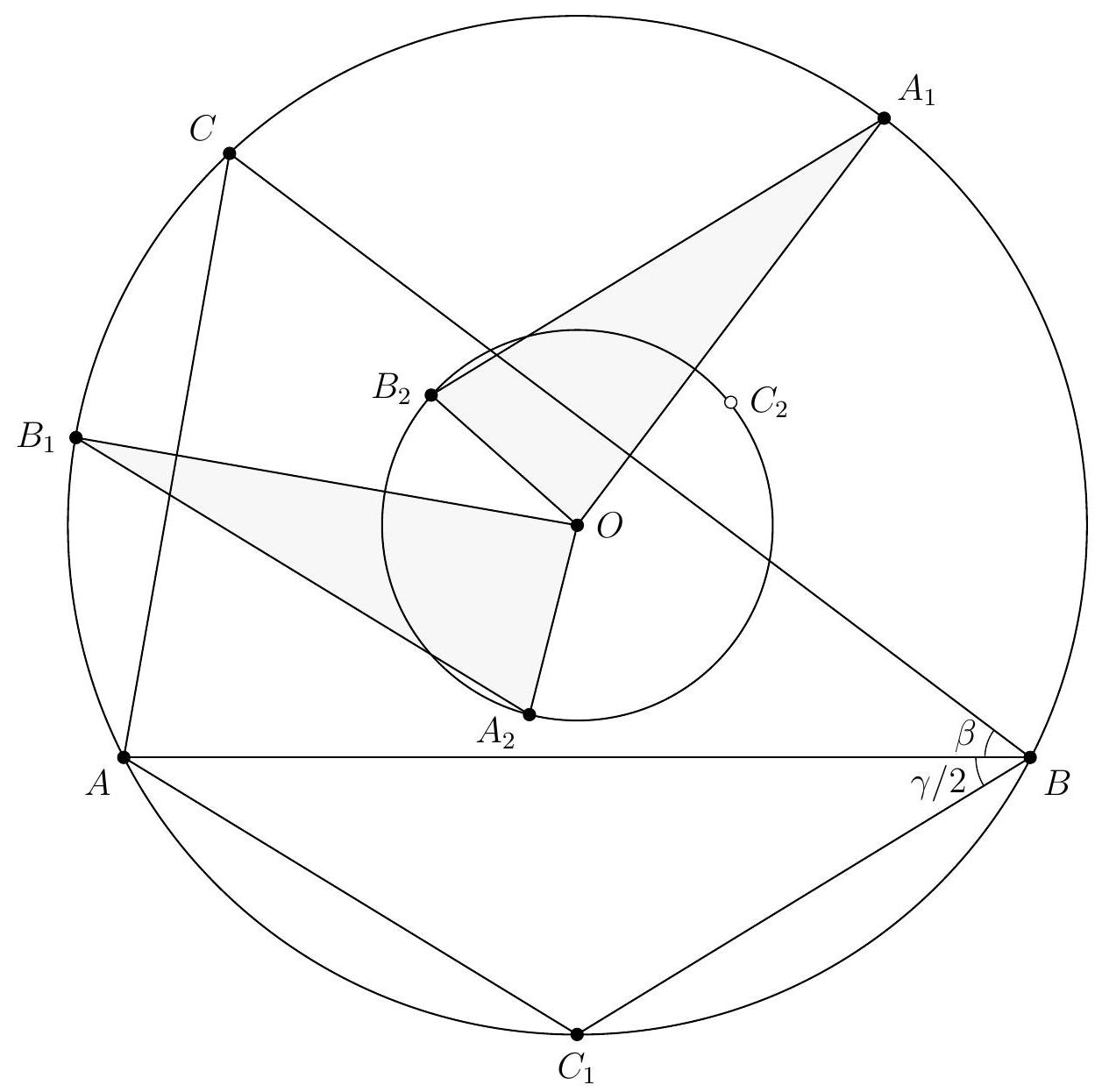
On cherche tout d'abord à démontrer que $O A_{2}=O B_{2}$. Puisque $A_{1} B_{2}=B C_{1}=A C_{1}=B_{1} A_{2}$ et que $A_{1} O=B_{1} O$, l'égalité $O A_{2}=O B_{2}$ équivaut au fait que les triangles $O A_{1} B_{2}$ et $O B_{1} A_{2}$ soient isométriques l'un de l'autre, c'est-à-dire au fait que $\widehat{O A_{1} B}=\widehat{O B_{1} A_{2}}$.
On note alors $\alpha=\widehat{C A B}, \beta=\widehat{A B C}$ et $\gamma=\widehat{B C A}$ les angles du triangle. Ici, vu nos relations de parallélisme et de cocyclicité, il sera plus agréable de travailler en angles de droites. Ainsi, comme ( $C C_{1}$ ) est la bissectrice de l'angle $\widehat{B C A}$, on constate que
$$
\begin{aligned}
\left(A_{1} O, A_{1} B_{2}\right) & =\left(A_{1} O, B C\right)+\left(B C, A_{1} B_{2}\right) \\
& =90^{\circ}+\left(B C, B C_{1}\right) \\
& =90^{\circ}+(B C, B A)+\left(B A, B C_{1}\right) \\
& =90^{\circ}+\alpha+\gamma / 2=(\alpha-\beta) / 2 .
\end{aligned}
$$
Cela signifie que $\widehat{O A_{1} B_{2}}=|\alpha-\beta| / 2$. Puisque $A, B$ et $C$ jouent des rôles symétriques, on en déduit que $\widehat{O B_{1} A_{2}}=|\beta-\alpha| / 2=\widehat{O A_{1} B}$, donc que $O A_{2}=O B_{2}$. Toujours par symétrie des rôles, on en conclut même que $O B_{2}=O C_{2}$.
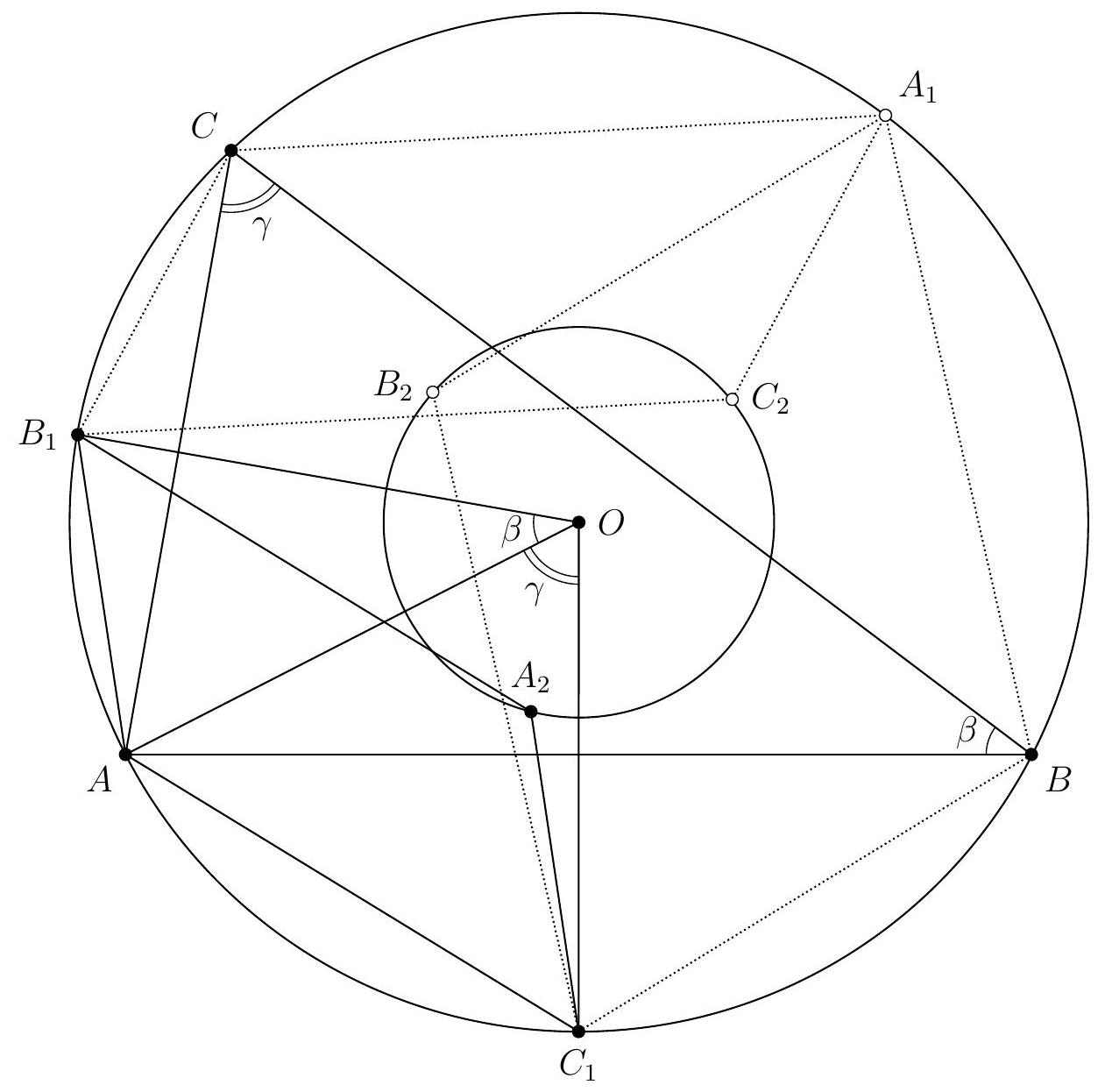
Nous allons calculer directement $O A_{2}$ en fonction des angles $\alpha, \beta, \gamma$ et du rayon $R=O A$. Pour ce faire, on remarque d'abord que $\widehat{A O B_{1}}=\beta, \widehat{C_{1} O A}=\gamma$ et $\widehat{C_{1} O B_{1}}=\beta+\gamma=180^{\circ}-\alpha$. En outre, la condition sur $A_{2}$ signifie que $A_{2}=\left(B_{1}+C_{1}\right)-A$, de sorte que
$$
\begin{aligned}
O A_{2}^{2} & =\overrightarrow{O A_{2}} \cdot \overrightarrow{O A_{2}} \\
& =\left(\overrightarrow{O B_{1}}+\overrightarrow{O C_{1}}-\overrightarrow{O A}\right) \cdot\left(\overrightarrow{O B_{1}}+\overrightarrow{O C_{1}}-\overrightarrow{O A}\right) \\
& ={\overrightarrow{O B_{1}}}^{2}+{\overrightarrow{O C_{1}}}^{2}+\overrightarrow{O A}^{2}+2 \overrightarrow{O B_{1}} \cdot \overrightarrow{O C_{1}}-2 \overrightarrow{O A} \cdot \overrightarrow{O B_{1}}-2 \overrightarrow{O C_{1}} \cdot \overrightarrow{O A} \\
& =\left(3+2 \cos \left(180^{\circ}-\alpha\right)-2 \cos (\beta)-2 \cos (\gamma)\right) R^{2} \\
& =(3-2 \cos (\alpha)-2 \cos (\beta)-2 \cos (\gamma)) R^{2} .
\end{aligned}
$$
Puisque $A, B$ et $C$ jouent des rôles symétriques, on en conclut que $O A_{2}^{2}=O B_{2}^{2}=O C_{2}^{2}$.
Commentaire des correcteurs L'exercice a été très peu réussi. Beaucoup d'élèves ont effleuré le début de la solution en exploitant les égalités de longueurs issues des parallélogrammes ou les égalités d'angles avec les pôles Sud, mais très très peu ont pensé à introduire le centre $O$ dans leurs calculs ou dans leur figure alors qu'il était la star de l'exercice.
Mentionnons également qu'il est agaçant de voir des élèves lancer des phrases du type « il existe une transformation/une similitude envoyant le triangle/le parallélogramme sur un autre » alors que le contenu de la phrase est faux et que l'issue de la phrase ne permet pas de conclure :non, l'existence d'une similitude envoyant un triangle sur un autre ne nous dit rien sur le fait que le centre des cercles est le même! Il est encore plus agaçant de voir que ces raisonnements sont les seuls apparents. Les élèves, au lieu d'essayer des choses simples
comme une chasse aux angles ou une chasse aux longueurs, s'entêtent à improviser des raisonnements avec des concepts dont ils ne maîtrisent ni la théorie ni la portée. Ce n'est certainement pas de cette façon que l'on progresse en géométrie.
|
{
"resource_path": "French/segmented/tests/fr-2022-2023-Corrige-Test-3.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "## Solution de l'exercice 3"
}
|
1bb5fb8c-64b1-5c8b-9f70-d1760b603317
| 605,476
|
Let $a_{1}, a_{2}, \ldots$ be strictly positive real numbers such that
$$
a_{n+1}^{2}+a_{n} a_{n+2} \leqslant a_{n}+a_{n+2}
$$
for all integers $n \geqslant 1$. Prove that $a_{2023} \leqslant 1$.
|
The given inequality and the one we are asked to prove suggest focusing on terms of the form $b_{n}=a_{n}-1$, because then the equation in the statement can be rewritten as
$$
b_{n+1}\left(b_{n+1}+2\right)+b_{n} b_{n+2} \leqslant 0,
$$
and we need to prove that $b_{2023} \leqslant 0$.
Let $n \geqslant 2$ be an integer for which $b_{n}>0$. Since $b_{n-1} b_{n+1} \leqslant -b_{n}\left(b_{n}+2\right)<0$, one of the two terms $b_{n-1}$ and $b_{n+1}$ is strictly positive, and the other is strictly negative. By setting $m=n-1$ in the case where $b_{n-1}>0$, and $m=n$ in the case where $b_{n+1}>0$, we now have an integer $m \geqslant 1$ for which $b_{m}>0$ and $b_{m+1}>0$. Under these conditions, and since $b_{m+2} \geqslant -1$, we know that
$$
b_{m} \geqslant b_{m}+b_{m} b_{m+2}+b_{m+1}\left(b_{m+1}+2\right) \geqslant b_{m+1}\left(b_{m+1}+2\right)>b_{m+1}
$$
Similarly, since $b_{m-1} \geqslant -1$, we know that
$$
b_{m+1} \geqslant b_{m+1}+b_{m-1} b_{m+1}+b_{m}\left(b_{m}+2\right) \geqslant b_{m}\left(b_{m}+2\right)>b_{m},
$$
which contradicts the inequality $b_{m}>b_{m+1}$ obtained previously.
We conclude that $b_{n} \leqslant 0$, that is, $a_{n} \leqslant 1$, for all integers $n \geqslant 2$, and in particular for $n=2023$.
Comment from the graders: The problem was relatively difficult, but was generally well done. Be careful not to get tangled up in the implications, to distinguish between the inequalities $<$ and $\leqslant$, and especially to be careful when dividing an inequality: the term by which you divide can be zero (in which case you are not allowed to divide) or negative (in which case the division changes the direction of the inequality).
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $a_{1}, a_{2}, \ldots$ des nombres réels strictement positifs tels que
$$
a_{n+1}^{2}+a_{n} a_{n+2} \leqslant a_{n}+a_{n+2}
$$
pour tout entier $n \geqslant 1$. Démontrer que $a_{2023} \leqslant 1$.
|
L'inégalité donnée dans l'énoncé et celle qu'il nous est demandé de démontrer suggèrent de s'intéresser aux termes de la forme $b_{n}=a_{n}-1$, car alors l'équation de l'énoncé se réécrit comme
$$
b_{n+1}\left(b_{n+1}+2\right)+b_{n} b_{n+2} \leqslant 0,
$$
et il s'agit de démontrer que $b_{2023} \leqslant 0$.
Soit $n \geqslant 2$ un entier éventuel pour lequel $b_{n}>0$. Puisque $b_{n-1} b_{n+1} \leqslant-b_{n}\left(b_{n}+2\right)<0, l^{\prime}$ un des deux termes $b_{n-1}$ et $b_{n+1}$ est strictement positif, et l'autre est strictement négatif. En posant $m=n-1$ dans le cas où $b_{n-1}>0$, et $m=n$ dans le cas où $b_{n+1}>0$, on dispose désormais d'un entier $m \geqslant 1$ pour lequel $b_{m}>0$ et $b_{m+1}>0$. Dans ces conditions, et puisque $b_{m+2} \geqslant-1$, on sait que
$$
b_{m} \geqslant b_{m}+b_{m} b_{m+2}+b_{m+1}\left(b_{m+1}+2\right) \geqslant b_{m+1}\left(b_{m+1}+2\right)>b_{m+1}
$$
De même, puisque $b_{m-1} \geqslant-1$, on sait que
$$
b_{m+1} \geqslant b_{m+1}+b_{m-1} b_{m+1}+b_{m}\left(b_{m}+2\right) \geqslant b_{m}\left(b_{m}+2\right)>b_{m},
$$
ce qui contredit l'inégalité $b_{m}>b_{m+1}$ obtenue précédemment.
On en conclut que $b_{n} \leqslant 0$, c'est-à-dire $a_{n} \leqslant 1$, pour tout entier $n \geqslant 2$, et notamment pour $n=2023$.
Commentaire des correcteurs Le problème était relativement difficile, mais a été plutôt bien réussi. Attention à ne pas s'emmêler dans les implications, à bien distinguer les inégalités $<$ et $\leqslant$, et surtout à faire attention attention lorsque l'on divise une inégalité : le terme par lequel on divise peut être nul (auquel cas on n'a pas le droit de diviser) ou négatif (auquel cas la division change le sens de l'inégalité).
|
{
"resource_path": "French/segmented/tests/fr-2022-2023-Corrige-Test-3.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution de l'exercice 5"
}
|
928b8654-5cfe-50e9-b02c-1640010f0eb4
| 605,495
|
Let $A, B, C, D$ be four points on a circle $\omega$ in that order. Let $P$ and $Q$ be two points on the line $(A B)$ such that the points $Q, A, B, P$ are collinear in that order, the circumcircle of $A D Q$ is tangent to the line $(A C)$, and the circumcircle of $B C P$ is tangent to the line $(B D)$. Let $M$ and $N$ be the midpoints of the segments $[B C]$ and $[A D]$, respectively.
Prove that the tangent to the circumcircle of $A N Q$ at $A$, the tangent to the circumcircle of $B M P$ at $B$, and the line $(C D)$ are concurrent.
|
Let $X$ be the potential intersection point whose existence we need to prove: we will look for alternative characterizations. For this purpose, and given the many tangency and cocyclicity relations we have, a hunt for angles is necessary.
For example, $(A Q, A D)=(A B, A D)=(C B, C D)$ and $(Q A, Q D)=(A C, A D)=(B C, B D)$. Therefore, there exists a direct similarity that maps $A Q D$ to $C B D$. This similarity also maps $N$ to the midpoint of $[C D]$, which we will denote as $R$. But then
$$
(A B, A X)=(A Q, A X)=(N Q, N A)=(R B, R C)=(R B, R X)
$$
which means that the points $A, B, X$, and $R$ are cocyclic.
We define the point $\hat{X}$ as the second intersection point of the circumcircle of $A B R$ with the line $(C D)$, and by repeating the previous calculation, we notice that
$$
(A Q, A \hat{X})=(A B, A \hat{X})=(R B, R \hat{X})=(R B, R C)=(N Q, N A)
$$
which means, as expected, that the line $(A \hat{X})$ is tangent to the circumcircle of $A N Q$. We similarly prove that $(B \hat{X})$ is tangent to the circumcircle of $B M P$, which concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A, B, C, D$ quatre points situés dans cet ordre sur un cercle $\omega$. Soit $P$ et $Q$ deux points situés sur la droite $(A B)$, de sorte que les points $Q, A, B, P$ soient alignés dans cet ordre, que le cercle circonscrit à $A D Q$ soit tangent à la droite ( $A C$ ), et que le cercle circonscrit à $B C P$ soit tangent à la droite $(B D)$. Soit $M$ et $N$ les milieux respectifs des segments $[B C]$ et $[A D]$.
Démontrer que la tangente en $A$ au cercle circonscrit à $A N Q$, la tangente en $B$ au cercle circonscrit à $B M P$ et la droite $(C D)$ sont concourantes.
|
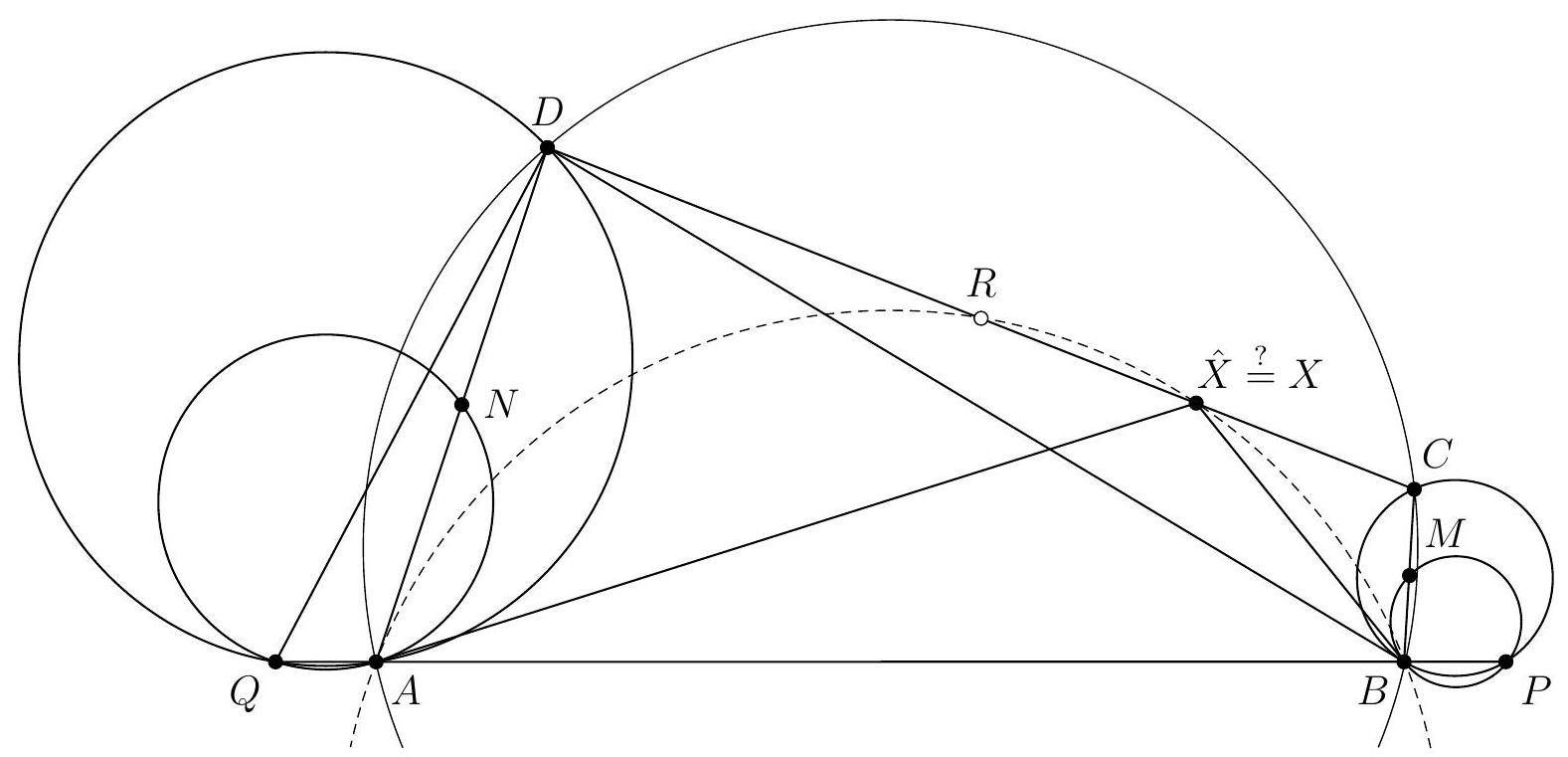
Soit $X$ le point d'intersection éventuel dont on doit démontrer l'existence : nous allons en chercher des caractérisations alternatives. Pour ce faire, et au vu des nombreuses relations de tangence et de cocyclicité dont on dispose, une chasse aux angles s'impose.
Par exemple, $(A Q, A D)=(A B, A D)=(C B, C D)$ et $(Q A, Q D)=(A C, A D)=(B C, B D)$. Il existe donc une similitude directe qui envoie $A Q D$ sur $C B D$. Celle-ci envoie également $N$ sur le milieu de $[C D]$, que l'on notera $R$. Mais alors
$$
(A B, A X)=(A Q, A X)=(N Q, N A)=(R B, R C)=(R B, R X)
$$
ce qui signifie que les points $A, B, X$ et $R$ sont cocycliques.
On définit donc le point $\hat{X}$ comme étant le second point d'intersection du cercle circonscrit à $A B R$ avec la droite $(C D)$, et en reprenant le calcul précédent, on remarque que
$$
(A Q, A \hat{X})=(A B, A \hat{X})=(R B, R \hat{X})=(R B, R C)=(N Q, N A)
$$
ce qui signifie comme prévu que la droite $(A \hat{X})$ est tangente au cercle circonscrit à $A N Q$. On démontre de même que $(B \hat{X})$ est tangente au cercle circonscrit à $B M P$, ce qui conclut.
|
{
"resource_path": "French/segmented/tests/fr-2022-2023-Corrige-Test-3.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "## Solution de l'exercice 6"
}
|
ae7949c4-642d-5c4b-930e-70e8e853be01
| 605,508
|
Let $A, B, C, D$ be four points on a circle $\omega$ in that order. Let $P$ and $Q$ be two points on the line $(A B)$ such that the points $Q, A, B, P$ are collinear in that order, the circumcircle of $A D Q$ is tangent to the line $(A C)$, and the circumcircle of $B C P$ is tangent to the line $(B D)$. Let $M$ and $N$ be the midpoints of the segments $[B C]$ and $[A D]$, respectively.
Prove that the tangent to the circumcircle of $A N Q$ at $A$, the tangent to the circumcircle of $B M P$ at $B$, and the line $(C D)$ are concurrent.
|
$n^{\circ} 1$ Once in a while, Cartesian coordinates can be used bluntly. Each point is identified by its coordinates, and we denote $O$ and $O_{2}$ as the centers of the circumcircles of $Q A D$ and $Q A N$. We choose the coordinate system such that $A=(0,0)$ and $B=(1,0)$, and we set $C=(x, y)$ and $D=(u, v), O=(s, t)$ and $O_{2}=\left(s_{2}, t_{2}\right)$. Thus, $N=(u / 2, v / 2), Q=(2 s, 0)$ and $s_{2}=s$.
The equalities $O C^{2}=O A^{2}+A C^{2}$ and $O A^{2}=O D^{2}$ can be rewritten as $s x+t y=0$ and $2(s u+t v)=$ $u^{2}+v^{2}$, so that
$$
s=\frac{u^{2}+v^{2}}{2 \delta} y
$$
where we have set $\delta=u y-v x$. Similarly, the equality $O_{2} A^{2}=O_{2} N^{2}$ can be rewritten as $4\left(u s+v t_{2}\right)=$ $u^{2}+v^{2}$, so that
$$
t_{2}=\frac{u^{2}+v^{2}-4 u s}{4 v} .
$$
Furthermore, let $Z=(z, w)$ be the point on $(C D)$ for which $(A Z)$ is tangent to the circumcircle of $A Q N$. The alignment of $Z$ with $C$ and $D$ indicates that there exists a real number $\lambda$ such that $Z=\lambda C+(1-\lambda) D$; the orthogonality of $(A X)$ with $\left(A O_{2}\right)$ indicates that $\overrightarrow{A O_{2}} \cdot \overrightarrow{A Z}=s z+t_{2} w=0$. We deduce that $s(\lambda x+u-\lambda u)+t_{2}(\lambda y+v-\lambda v)=0$, that is,
$$
\begin{aligned}
\lambda & =\frac{s u+t_{2} v}{s(u-x)+t_{2}(v-y)} \\
& =\frac{4 s u v+\left(u^{2}+v^{2}-4 u s\right) v}{4 s(u-x) v+\left(u^{2}+v^{2}-4 u s\right)(v-y)} \\
& =\frac{\left(u^{2}+v^{2}\right) v}{\left(u^{2}+v^{2}\right)(v-y)+4(u y-v x) s} \\
& =\frac{\left(u^{2}+v^{2}\right) v}{\left(u^{2}+v^{2}\right)(v-y)+2\left(u^{2}+v^{2}\right) y} \\
& =\frac{v}{v+y} .
\end{aligned}
$$
For symmetry reasons, the point $Z^{\prime}$ on $(C D)$ for which $\left(B Z^{\prime}\right)$ is tangent to the circumcircle of $B P M$ is also described by the relation $Z^{\prime}=\mu D+(1-\mu) C$, with $\mu=y /(v+y)$. But then $\lambda+\mu=1$, which means as expected that $Z=Z^{\prime}$.
Remark: In this second solution, we did not even use the cocyclicity of the points $A, B, C$ and $D$, which translates to the equality $v\left(x^{2}+y^{2}\right)+u y=v x+\left(u^{2}+v^{2}\right) y$. Thus, the cocyclicity hypothesis mentioned in the statement was mainly intended to make the problem more accessible.
Furthermore, an alternative characterization of the point $X$ that remains valid in this more general framework is as follows: if we denote $Y$ as the intersection of the lines $(A C)$ and $(B D)$, and $Z$ as the intersection of the lines $(A D)$ and $(B C)$, $X$ is actually the intersection of the lines $(Y Z)$ and $(C D)$. This characterization can be verified quite simply by calculating the coordinates of the points $Y$ and $Z$.
Comment from the graders: The problem was relatively well solved. Approaches using the law of sines and angle chasing were possible. However, far too many students introduce the centers of the circumcircles to translate the tangency hypotheses, which is often very inefficient compared to using the tangent angle theorem. Many students announce that they will attempt complicated transformations or introduce many new points before even trying angle chasing with the existing points. One should ALWAYS start by testing simple and feasible ideas rather than trying conceptual methods.
It is also a pity that not more students introduce the midpoint of $[C D]$, as the figure already has some midpoints and it is known that in the presence of midpoints of segments, introducing new midpoints can be very useful for obtaining angle equalities.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A, B, C, D$ quatre points situés dans cet ordre sur un cercle $\omega$. Soit $P$ et $Q$ deux points situés sur la droite $(A B)$, de sorte que les points $Q, A, B, P$ soient alignés dans cet ordre, que le cercle circonscrit à $A D Q$ soit tangent à la droite ( $A C$ ), et que le cercle circonscrit à $B C P$ soit tangent à la droite $(B D)$. Soit $M$ et $N$ les milieux respectifs des segments $[B C]$ et $[A D]$.
Démontrer que la tangente en $A$ au cercle circonscrit à $A N Q$, la tangente en $B$ au cercle circonscrit à $B M P$ et la droite $(C D)$ sont concourantes.
|
$n^{\circ} 1$ Une fois n'est pas coutume, on peut utiliser brutalement des coordonnées cartésiennes. On identifie chaque point à ses coordonnées, puis on note $O$ et $O_{2}$ les centres des cercles circonscrits à $Q A D$ et à $Q A N$. On choisit en outre le repère de sorte que $A=(0,0)$ et $B=(1,0)$, puis on pose $C=(x, y)$ et $D=(u, v), O=(s, t)$ et $O_{2}=\left(s_{2}, t_{2}\right)$. Ainsi, $N=(u / 2, v / 2), Q=(2 s, 0)$ et $s_{2}=s$.
Les égalités $O C^{2}=O A^{2}+A C^{2}$ et $O A^{2}=O D^{2}$ se réécrivent comme $s x+t y=0$ et $2(s u+t v)=$ $u^{2}+v^{2}$, de sorte que
$$
s=\frac{u^{2}+v^{2}}{2 \delta} y
$$
où l'on a posé $\delta=u y-v x$. De même, l'égalité $O_{2} A^{2}=O_{2} N^{2}$ se réécrit comme $4\left(u s+v t_{2}\right)=$ $u^{2}+v^{2}$, de sorte que
$$
t_{2}=\frac{u^{2}+v^{2}-4 u s}{4 v} .
$$
Par ailleurs, notons $Z=(z, w)$ le point de $(C D)$ pour lequel $(A Z)$ est tangente au cercle circonscrit à $A Q N$. L'alignement de $Z$ avec $C$ et $D$ indique qu'il existe un réel $\lambda$ tel que $Z=\lambda C+(1-\lambda) D$; l'orthogonalité de $(A X)$ avec $\left(A O_{2}\right)$ indique que $\overrightarrow{A O_{2}} \cdot \overrightarrow{A Z}=s z+t_{2} w=0$. On en déduit que $s(\lambda x+u-\lambda u)+t_{2}(\lambda y+v-\lambda v)=0$, c'est-à-dire
$$
\begin{aligned}
\lambda & =\frac{s u+t_{2} v}{s(u-x)+t_{2}(v-y)} \\
& =\frac{4 s u v+\left(u^{2}+v^{2}-4 u s\right) v}{4 s(u-x) v+\left(u^{2}+v^{2}-4 u s\right)(v-y)} \\
& =\frac{\left(u^{2}+v^{2}\right) v}{\left(u^{2}+v^{2}\right)(v-y)+4(u y-v x) s} \\
& =\frac{\left(u^{2}+v^{2}\right) v}{\left(u^{2}+v^{2}\right)(v-y)+2\left(u^{2}+v^{2}\right) y} \\
& =\frac{v}{v+y} .
\end{aligned}
$$
Pour des raisons de symétrie, le point $Z^{\prime}$ de $(C D)$ pour lequel $\left(B Z^{\prime}\right)$ est tangente au cercle circonscrit à $B P M$ est lui aussi décrit par la relation $Z^{\prime}=\mu D+(1-\mu) C$, avec $\mu=y /(v+y)$. Mais alors $\lambda+\mu=1$, ce qui signifie comme prévu que $Z=Z^{\prime}$.
Remarque: Dans cette deuxième solution, on n'a même pas utilisé la cocyclicité des points $A, B, C$ et $D$, qui se traduit par l'égalité $v\left(x^{2}+y^{2}\right)+u y=v x+\left(u^{2}+v^{2}\right) y$. Ainsi, l'hypothèse de cocyclicité mentionnée dans l'énoncé avait pour but principal de rendre le problème plus accessible.
Par ailleurs, une caractérisation alternative du point $X$ qui reste valide dans ce cadre plus général est la suivante : si l'on note $Y$ le point d'intersection des droites $(A C)$ et $(B D)$, puis $Z$ le point d'intersection des droites $(A D)$ et $(B C), X$ est en fait le point d'intersection des droites $(Y Z)$ et $(C D)$. Cette caractérisation se vérifie assez simplement en calculant les coordonnées des points $Y$ et $Z$.
Commentaire des correcteurs L'exercice a été relativement bien trouvé. Des approches à coup de loi des sinus et de chasse aux rapports étaient possibles. En revanche, beaucoup trop d'élèves introduisent encore les centre des cercles circonscrits pour traduire les hypothèses de tangence, alors que cela est souvent très inefficace comparé à l'usage du théorème de l'angle tangentiel. Beaucoup d'élèves annoncent vouloir tenter des transformations compliquées ou introduire beaucoup de nouveaux points avant même d'essayer une chasse aux angles avec les points existant déjà. Il faut TOUJOURS commencer par tester des idées simples et à sa portée plutôt que d'essayer des méthodes conceptuelles.
Il est également dommage de ne pas voir plus d'élèves introduire le milieu de $[C D$ ], alors que la figure présente déjà quelques milieux et que l'on sait qu'en présence de milieux de segments, introduire de nouveaux milieux peut s'avérer très utile pour obtenir des égalités d'angles.
|
{
"resource_path": "French/segmented/tests/fr-2022-2023-Corrige-Test-3.jsonl",
"problem_match": "\nExercice 6.",
"solution_match": "\nSolution alternative"
}
|
ae7949c4-642d-5c4b-930e-70e8e853be01
| 605,508
|
Let $n \geqslant 1$ be an integer. Morgane writes on the board, in base 10, the numbers $2023, 2023 \times 2, \ldots, 2023 \times n$. For every digit $c$ between 1 and 9, she then notes $\mathrm{d}_{c}(n)$ as the number of occurrences of the digit $c$ on the board. For example, if $n=3$, she writes the numbers 2023, 4046, and 6069, so $\mathrm{d}_{1}(3)=\mathrm{d}_{5}(3)=\mathrm{d}_{7}(3)=\mathrm{d}_{8}(3)=0, \mathrm{~d}_{3}(3)=\mathrm{d}_{9}(3)=1$, $\mathrm{d}_{2}(3)=\mathrm{d}_{4}(3)=2$ and $\mathrm{d}_{6}(3)=3$; these nine numbers thus take exactly four values.
Prove that there are infinitely many integers $n \geqslant 1$ for which the nine numbers $\mathrm{d}_{1}(n), \mathrm{d}_{2}(n), \ldots, \mathrm{d}_{9}(n)$ take exactly two values.
|
Let $k$ be a multiple of $\varphi(2023)$, and let $\ell = \left(10^k - 1\right) / 2023$. We will prove that $\ell$ is a solution. To do this, we introduce the set
$$
\Omega = \{2023 n : 1 \leqslant n \leqslant \ell\}
$$
The elements of $\Omega$ precisely describe the set of residues modulo $10^k - 1$ that are multiples of 2023, with each residue being obtained exactly once. Consequently, the function $\phi: x \mapsto 10x$, which defines a permutation of $\mathbb{Z} / (10^k - 1) \mathbb{Z}$, also defines a permutation of the set of residues that are multiples of 2023, and thus induces a permutation of $\Omega$ itself. Specifically, if we write the elements of $\Omega$ in base 10 with $k$ digits (padding with leading zeros if necessary), $\phi$ maps ${\overline{a_{k-1} a_{k-2} \ldots a_{1} a_{0}}}^{10}$ to $\overline{a_{k-2} a_{k-3} \ldots a_{1} a_{0} a_{k-1}}^{10}$.
For any digit $c$ and any integer $i$ such that $0 \leqslant i \leqslant k-1$, we denote by $\Omega(c, i)$ the set of elements of $\Omega$ whose digit $a_i$, with weight $10^i$, is equal to $c$; we abuse notation by setting $\Omega(c, k) = \Omega(c, 0)$. When $0 \leqslant i \leqslant k-1$, the bijection $\phi$ induces a bijection from $\Omega(c, i)$ to $\Omega(c, i+1)$. Thus, the sets $\Omega(c, 0), \Omega(c, 1), \ldots, \Omega(c, k-1)$ all have the same cardinality, and
$$
\mathrm{d}_c(\ell) = |\Omega(c, 0)| + |\Omega(c, 1)| + \cdots + |\Omega(c, k-1)| = k |\Omega(c, 0)|.
$$
Now, $\Omega(c, 0)$ consists of the numbers $2023 n$ for which $1 \leqslant n \leqslant \ell$ and $c \equiv 3n \pmod{10}$. Since $\ell \equiv -1/3 \equiv 3 \pmod{10}$, we deduce that $|\Omega(c, 0)|$ is $(\ell + 7) / 10$ if $c$ is 3, 6, or 9, and $(\ell - 3) / 10$ otherwise. This means that the cardinals $|\Omega(c, 0)|$ take exactly two values as $c$ varies from 1 to 9, and thus the integers $\mathrm{d}_c(\ell)$ also take exactly two values.
**Comment from the graders:** The problem was very difficult. Few students approached it, and among those who did, several made remarks about periodicity that were then difficult to validate. The idea was to ask why 2023 would work and to test small cases to find a conjecture to prove: the remarkable property for 2023 was being coprime with 10 and not ending in 1, so the first interesting small case was 3: it turns out that the solutions given by this small case are exactly the general solutions to the problem!
Another approach, more qualitative, was possible; it involved realizing that $2023 n$ had to be a power of 10 minus 1 to achieve a nearly uniform distribution of all digits from 1 to 9. Once the general form of the solutions was found, one could show that they were indeed solutions by counting the occurrences of each digit and showing that the digits of the numbers could be cyclically permuted.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $n \geqslant 1$ un entier. Morgane écrit au tableau, en base 10 , les nombres $2023,2023 \times 2, \ldots, 2023 \times n$. Pour tout chiffre $c$ compris entre 1 et 9 , elle note alors $\mathrm{d}_{c}(n)$ le nombre d'apparitions du chiffre $c$ sur le tableau. Par exemple, si $n=3$, elle écrit les nombres 2023, 4046 et 6069, donc $\mathrm{d}_{1}(3)=\mathrm{d}_{5}(3)=\mathrm{d}_{7}(3)=\mathrm{d}_{8}(3)=0, \mathrm{~d}_{3}(3)=\mathrm{d}_{9}(3)=1$, $\mathrm{d}_{2}(3)=\mathrm{d}_{4}(3)=2$ et $\mathrm{d}_{6}(3)=3$; ces neuf nombres prennent donc exactement quatre valeurs.
Démontrer qu'il existe une infinité d'entiers $n \geqslant 1$ pour lesquels les neuf nombres $\mathrm{d}_{1}(n), \mathrm{d}_{2}(n), \ldots, \mathrm{d}_{9}(n)$ prennent exactement deux valeurs.
|
Soit $k$ un multiple de $\varphi(2023)$, soit $\ell=\left(10^{k}-1\right) / 2023$. Nous allons démontrer que $\ell$ est une solution. Pour ce faire, on introduit l'ensemble
$$
\Omega=\{2023 n: 1 \leqslant n \leqslant \ell\}
$$
Les éléments de $\Omega$ décrivent précisément l'ensemble des résidus modulo $10^{k}-1$ qui sont des multiples de 2023, chaque résidu étant obtenu exactement une fois. Par conséquent, l'application $\phi: x \mapsto 10 x$, qui définit une permutation de $\mathbb{Z} /\left(10^{k}-1\right) \mathbb{Z}$, définit aussi une permutation de l'ensemble des résidus qui sont des multiples de 2023, et induit donc une permutation de $\Omega$ lui-même. Concrètement, si l'on écrit les éléments de $\Omega$ en base 10 avec $k$ chiffres (quitte à laisser des 0 en apparence inutiles sur la gauche), $\phi$ envoie ${\overline{a_{k-1} a_{k-2} \ldots a_{1} a_{0}}}^{10}$ sur $\overline{a_{k-2} a_{k-3} \ldots a_{1} a_{0} a_{k-1}}{ }^{10}$ 。
Pour tout chiffre $c$ et tout entier $i$ tel que $0 \leqslant i \leqslant k-1$, on note $\Omega(c, i)$ l'ensemble des éléments de $\Omega$ dont le chiffre $a_{i}$, de poids $10^{i}$, est égal à $c$; on pose abusivement $\Omega(c, k)=\Omega(c, 0)$. Lorsque $0 \leqslant i \leqslant k-1$, la bijection $\phi$ induit une bijection de $\Omega(c, i)$ vers $\Omega(c, i+1)$. Ainsi, les ensembles $\Omega(c, 0), \Omega(c, 1), \ldots, \Omega(c, k-1)$ sont tous de même cardinal, et
$$
\mathrm{d}_{c}(\ell)=|\Omega(c, 0)|+|\Omega(c, 1)|+\cdots+|\Omega(c, k-1)|=k|\Omega(c, 0)| .
$$
Or, $\Omega(c, 0)$ est formé des nombres $2023 n$ pour lesquels $1 \leqslant n \leqslant \ell$ et $c \equiv 3 n(\bmod 10)$. Puisque $\ell \equiv-1 / 3 \equiv 3(\bmod 10)$, on en déduit que $|\Omega(c, 0)|$ vaut $(\ell+7) / 10$ si $c$ vaut 3,6 ou 9 , et vaut $(\ell-3) / 10$ sinon. Cela signifie que les cardinaux $|\Omega(c, 0)|$ prennent exactement deux valeurs lorsque $c$ varie de 1 à 9 , et donc que les entiers $\mathrm{d}_{c}(\ell)$ prennent eux aussi deux valeurs.
Commentaire des correcteurs Le problème était très difficile. Peu d'élèves l'ont abordé et, parmi eux, plusieurs on formulé des remarques sur la périodicité qu'il était ensuite difficile de valoriser. L'idée était de se demander pourquoi 2023 marcherait et de tester des petits cas pour trouver une conjecture à prouver : la propriété remarquable pour 2023 était d'être premier avec 10 et de ne pas terminer par 1, donc le premier petit cas intéressant était 3 :il se trouve que les solutions que donne ce petit cas sont exactement des solutions générales au problème!
Une autre approche, plus qualitative, était possible; elle consistait à se dire qu'il fallait que $2023 n$ soit une puissance de 10 moins 1, pour avoir une répartition quasi-uniforme de tous les chiffres de 1 à 9 . Une fois la forme générale des solutions trouvées, on pouvait montrer qu'il s'agissait effectivement de solutions, en dénombrant les occurrences de chaque chiffre et en montrant qu'on pouvait permuter cycliquement les chiffres des nombres.
## Problèmes EGMO
|
{
"resource_path": "French/segmented/tests/fr-2022-2023-Corrige-Test-3.jsonl",
"problem_match": "\nExercice 7.",
"solution_match": "\nSolution de l'exercice 7"
}
|
32a4fdc4-fb7b-58b3-82bb-8d18bf56ac5c
| 605,532
|
Let $ABC$ be a triangle, and let $E$ be the midpoint of $[BC]$. Let $m$ be the perpendicular bisector of $[AC]$, and let $D$ be a point on $m$ such that the circumcircle of $ABD$ is tangent to $m$. Finally, let $K$ be the intersection point, other than $A$, between the circumcircle of $ABD$ and the line $(AC)$, and let $F$ be the midpoint of $[CK]$. Prove that the lines $(DE)$ and $(EF)$ are perpendicular.
|
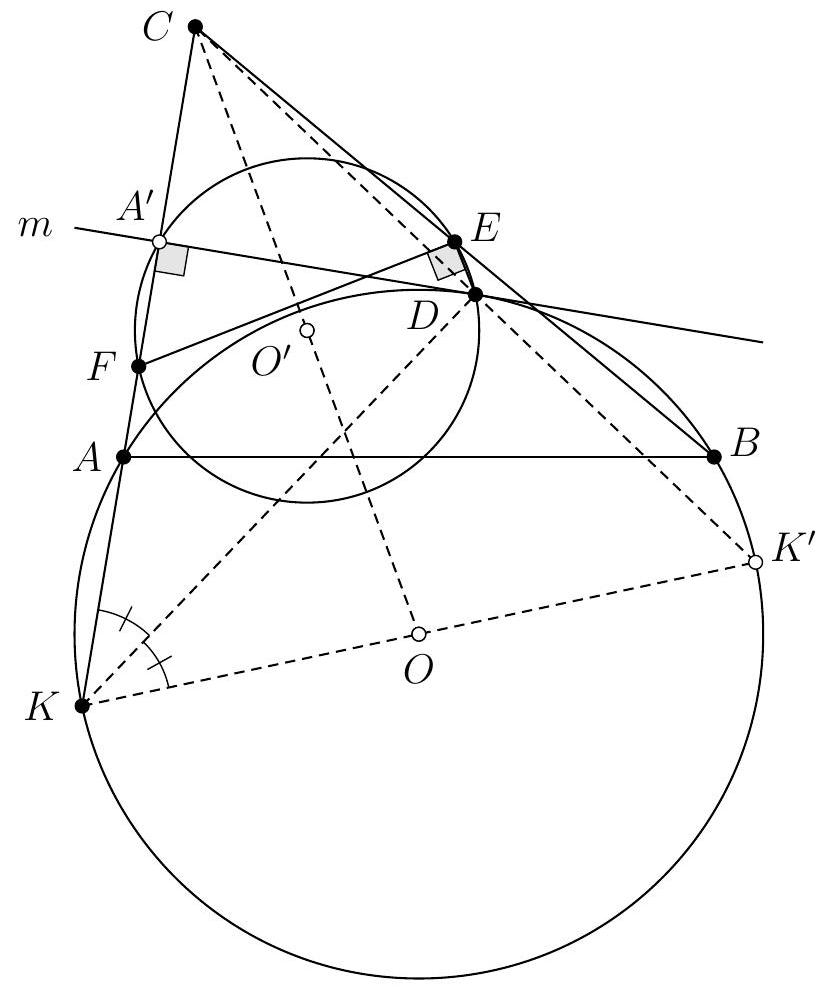
The first difficulty is to draw the figure: how to draw a point tangent to a line and passing through two given points? A common strategy in such cases is to reverse the drawing: start by placing points \(A, B\), and \(D\), then deduce the tangent \(m\) and the point \(C\).
Let \(\Omega\) and \(\Omega'\) be the circumcircles of \(ABD\) and \(DEF\), and \(O\) and \(O'\) their centers. Our hard-earned figure suggests that \(\Omega'\), \(m\), and \((AC)\) are concurrent. This is not surprising: indeed, it is to be shown that \(\mathcal{C}'\) is the circle with diameter \([FD]\), or that the midpoint of \([AC]\), which we will denote as \(A'\), belongs to \(\Omega'\).
Now, the three points \(A'\), \(E\), and \(F\) are the midpoints of the segments \([CA]\), \([CB]\), and \([CK]\), respectively. The circumcircle of these three points, which we wish to prove is \(\Omega'\), is therefore the image of \(\Omega\) under the homothety centered at \(C\) with a ratio of \(1/2\). Given the figure, it is therefore necessary to prove, if we denote \(K'\) as the symmetric point of \(K\) with respect to \(O\), that this homothety maps \(K'\) to \(D\), i.e., that \(D\) is the midpoint of \([K'C]\). By construction, we already know that \(\widehat{KDK'} = 90^\circ\).
We will now prove that \((KD)\) is the bisector of \(\widehat{CKK'}\), using angle chasing. First, since \(AKO\) is isosceles at \(O\) and \((AK)\) and \((DO)\) are perpendicular to \(m\), we know that
\[
(KC, KK') = (KA, KO) = (AO, AK) = (OA, OD)
\]
Furthermore, since \(m\) is tangent to \(\Omega\), we also know that
\[
(KC, KD) = (KA, KD) = (DA, DA') = (DA, CA) + 90^\circ = (DA, DO) + 90^\circ.
\]
Since \(ADO\) is isosceles at \(O\), we conclude as desired that
\[
2(KC, KD) = 2(DA, DO) = (DA, DO) + (AO, AD) = (OA, OD) = (KC, KK').
\]
Comment from the examiners: The problem was adequately addressed, with several copies reaching far and even concluding with simple observations about the figure, such as the right angle \(\widehat{KDC}\). Few students thought to introduce the point \(K'\) from the official solution; although introducing this point was not strictly necessary, all students who did so subsequently solved the problem and received excellent grades.
It can therefore be judicious to introduce new points, but many do so without a specific reason, simply to express an angle in a new way. Here, there are very strong reasons to want to introduce the point \(K'\), and it is necessary to convince oneself of the possible utility of a point before introducing it, at the risk of getting lost in unnecessary considerations.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle, et soit $E$ le milieu de $[B C]$. Soit $m$ la médiatrice de $[A C]$, et soit $D$ un point de $m$ tel que le cercle circonscrit à $A B D$ soit tangent à $m$. Enfin, soit $K$ le point d'intersection, autre que $A$, entre le cercle circonscrit à $A B D$ et la droite $(A C)$, et soit $F$ le milieu de $[C K]$. Démontrer que les droites $(D E)$ et $(E F)$ sont perpendiculaires.
|

Une première difficulté est de tracer la figure : comment tracer un point tangent à une droite et passant par deux points donnés? Une stratégie usuelle, en pareil cas, est d'inverser le tracé : on commence par placer les points $A, B$ et $D$, puis on en déduit la tangente $m$ et le point $C$.
Notons maintenant $\Omega$ et $\Omega^{\prime}$ les cercles circonscrits à $A B D$ et $D E F$, puis $O$ et $O^{\prime}$ leurs centres. Notre figure chèrement acquise suggère que $\Omega^{\prime}, m$ et $(A C)$ sont concourantes. Ce n'est pas là une surprise : en effet, il s'agit de démontrer que $\mathcal{C}^{\prime}$ est le cercle de diamètre $[F D]$, ou encore que le milieu de $[A C]$, que l'on notera $A^{\prime}$, appartient à $\Omega^{\prime}$.
Or, les trois points $A^{\prime}, E$ et $F$ sont les milieux respectifs des segments $[C A],[C B]$ et $[C K]$. Le cercle circonscrit à ces trois points, dont on souhaite démontrer qu'il s'agit de $\Omega^{\prime}$, est donc l'image de $\Omega$ par l'homothétie de centre $C$ et de rayon $1 / 2$. Au vu de la figure, il s'agit donc de démontrer, si l'on note $K^{\prime}$ le symétrique de $K$ par rapport à $O$, que cette homothétie envoie $K^{\prime}$ sur $D$, c'est-à-dire que $D$ est le milieu de $\left[K^{\prime} C\right]$. Or, par construction, on sait déjà que $\widehat{K D K^{\prime}}=90^{\circ}$.
On va donc maintenant démontrer que $(K D)$ est la bissectrice de $\widehat{C K K^{\prime}}$, grâce à une chasse aux angles. Tout d'abord, puisque $A K O$ est isocèle en $O$ et que $(A K)$ et $(D O)$ sont perpendiculaires à $m$, on sait que
$$
\left(K C, K K^{\prime}\right)=(K A, K O)=(A O, A K)=(O A, O D)
$$
D'autre part, puisque $m$ est tangente à $\Omega$, on sait également que
$$
(K C, K D)=(K A, K D)=\left(D A, D A^{\prime}\right)=(D A, C A)+90^{\circ}=(D A, D O)+90^{\circ} .
$$
Puisque $A D O$ est isocèle en $O$, on en conclut comme souhaité que
$$
2(K C, K D)=2(D A, D O)=(D A, D O)+(A O, A D)=(O A, O D)=\left(K C, K K^{\prime}\right)
$$
Commentaire des correcteurs Problème convenablement traité, avec plusieurs copies qui arrivent à aller loin voire à conclure avec des remarques simples sur la figure, comme l'angle droit $\widehat{K D C}$. Peu d'élèves ont pensé à introduire le point $K^{\prime}$ de la solution officielle; même si introduire ce point n'était pas strictement nécessaire, tous les élèves qui l'ont fait on ensuite résolu le problème et obtenu d'excellentes notes.
Il peut donc être judicieux d'introduire de nouveaux points mais beaucoup le font sans raison précise, simplement pour exprimer un angle d'une nouvelle façon. Ici, on a de très fortes raisons de vouloir introduire le point $K^{\prime}$, et il est nécessaire de se convaincre de la possible utilité d'un point avant de l'introduire, au risque de se perdre dans des considérations inutiles.
|
{
"resource_path": "French/segmented/tests/fr-2022-2023-Corrige-Test-3.jsonl",
"problem_match": "\nExercice 9.",
"solution_match": "## Solution de l'exercice 9"
}
|
47cb4d1a-f2f7-5b37-b4cc-709dd68d2665
| 605,554
|
Let $n \geqslant 2$ be an integer. Anna has written on the board $n$ integers $a_{1}, a_{2}, \ldots, a_{n}$, all distinct. She then notices that, no matter which $n-1$ of these integers are selected, their sum is divisible by $n$.
Prove that the sum of all $n$ integers is divisible by $n$.
|
Let $s$ be the sum of all integers. Selecting $n-1$ integers amounts to choosing the integer, say $a_{i}$, that we have not selected. The sum of our $n-1$ integers is then equal to $s-a_{i}$. Thus, Anna simply noticed that $a_{i} \equiv s(\bmod n)$.
Since this is true for any $i$, we deduce that $a_{1} \equiv a_{2} \equiv \ldots \equiv a_{n} \equiv s(\bmod n)$. We conclude that $s \equiv a_{1}+a_{2}+\cdots+a_{n} \equiv n s \equiv 0(\bmod n)$.
Examiner's Comment: The problem was generally well done, but a quarter of the students incorrectly wrote that "if $a$ does not divide $b$ or $c$, then $a$ does not divide $bc$." Such a result is only valid if $a$ is coprime with $b$ or $c$, and any student who stated it in a general (and therefore false) context saw their grade significantly drop. It is a pity to have relevant ideas on an exercise that requires imagination, only to go astray in this way.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $n \geqslant 2$ un entier. Anna a écrit au tableau $n$ entiers $a_{1}, a_{2}, \ldots, a_{n}$ deux à deux distincts. Elle remarque alors que, quelle que soit la manière de sélectionner $n-1$ de ces entiers, leur somme est divisible par $n$.
Démontrer que la somme de l'ensemble des $n$ entiers est divisible par $n$.
|
Soit $s$ la somme de tous les entiers. Sélectionner $n-1$ entiers revient à choisir l'entier, disons $a_{i}$, que l'on n'a pas sélectionné. La somme de nos $n-1$ entiers est alors égale à $s-a_{i}$. Ainsi, Anna a simplement remarqué que $a_{i} \equiv s(\bmod n)$.
Ceci étant valable pour tout $i$, on en déduit que $a_{1} \equiv a_{2} \equiv \ldots \equiv a_{n} \equiv s(\bmod n)$. On en conclut que $s \equiv a_{1}+a_{2}+\cdots+a_{n} \equiv n s \equiv 0(\bmod n)$.
Commentaire des correcteurs Le problème a été très réussi dans l'ensemble, mais un quart des élèves a écrit, à tort, que « si $a$ ne divise ni $b$ ni $c$, alors $a$ ne divise pas $b c$. » Ce genre de résultats n'est valide que si $a$ est premier avec $b$ ou $c$, et tout élève qui l'énonçait dans un cadre général (donc faux) a vu sa note fortement chuter. Il est dommage de réussir à avoir des idées pertinentes sur un exercice qui requiert de l'imagination, pour ensuite se fourvoyer de la sorte.
|
{
"resource_path": "French/segmented/tests/fr-2022-2023-Corrige-Test-4.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution de l'exercice 1"
}
|
994428fa-b170-512b-a1cd-746ba8b4d3a0
| 605,578
|
Let $a, b$ and $c$ be three strictly positive real numbers. Prove that
$$
4\left(a^{3}+b^{3}+c^{3}+3\right) \geqslant 3(a+1)(b+1)(c+1) .
$$
|
In this inequality, the terms in $a, b$, and $c$ are added to each other (and of degree 3) on the left-hand side, while they are multiplied with each other (and each of degree 1) on the right-hand side. A first idea is therefore to use the arithmetic-geometric inequality to end up, on both sides of the inequality, with two products of terms of degree 1, or two sums of terms of degree 3, each involving only one of the variables $a, b$, or $c$.
Thus, we observe that
$$
(a+1)(b+1)(c+1)=\sqrt[3]{(a+1)^{3}(b+1)^{3}(c+1)^{3}} \leqslant \frac{(a+1)^{3}+(b+1)^{3}+(c+1)^{3}}{3}
$$
Furthermore, this inequality is an equality when $a=b=c=1$, which is also an equality case for the inequality in the statement. We therefore very much hope that the inequality
$$
4\left(a^{3}+b^{3}+c^{3}+3\right) \geqslant(a+1)^{3}+(b+1)^{3}+(c+1)^{3}
$$
is valid, and we will try to prove it.
We therefore continue our wanderings and, since we have made all these efforts to separate the terms in the variables $a, b$, and $c$, we observe that it now suffices to prove that
$$
4\left(a^{3}+1\right) \geqslant(a+1)^{3}
$$
This is an inequality in a single variable, for which $a=1$ is an equality case, and which will be proven (or invalidated for certain values of $a$) with little effort.
Indeed, if we expand each term and insert them all into the left-hand side, the inequality can be rewritten as
$$
3 a^{3}-3 a^{2}-3 a+3 \geqslant 0
$$
Since we know that there is equality when $a=0$, and given the manifest symmetry between the terms of low degree and those of high degree, we factor the left-hand side as
$$
3 a^{3}-3 a^{2}-3 a+3=3(a-1)\left(a^{2}-1\right)=3(a-1)^{2}(a+1)
$$
which is clearly positive or zero, allowing us to conclude that the inequality in the statement is indeed valid.
Comment from the graders The problem was approached in a rather uneven manner. Half of the students thought of the arithmetic-geometric inequality, but several students failed to conclude from there; it is a pity that these students did not realize that, since $a, b$, and $c$ do not appear in any term of the sum, it was sufficient to prove the inequality without $b$ or $c$, especially since some seemed to think they had concluded by partially factoring.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $a, b$ et $c$ trois réels strictement positifs. Démontrer que
$$
4\left(a^{3}+b^{3}+c^{3}+3\right) \geqslant 3(a+1)(b+1)(c+1) .
$$
|
Dans cette inégalité, les termes en $a, b$ et $c$ sont additionnés les uns aux autres (et de degré 3) dans le membre de gauche, tandis qu'ils sont multipliés les uns aux autres (et chacun de degré 1) dans le membre de droite. Une première idée est donc d'utiliser l'inégalité arithmético-géométrique pour se retrouver, de part et d'autre de l'inégalité, avec deux produits de termes de degré 1 , ou bien deux sommes de termes de degré 3 faisant chacun intervenir une seule des variables $a, b$ ou $c$.
Ainsi, on constate que
$$
(a+1)(b+1)(c+1)=\sqrt[3]{(a+1)^{3}(b+1)^{3}(c+1)^{3}} \leqslant \frac{(a+1)^{3}+(b+1)^{3}+(c+1)^{3}}{3}
$$
En outre, cette inégalité a le bon goût d'être une égalité lorsque $a=b=c=1$, qui est également un cas d'égalité pour l'inégalité de l'énoncé. On espère donc très fort que l'inégalité
$$
4\left(a^{3}+b^{3}+c^{3}+3\right) \geqslant(a+1)^{3}+(b+1)^{3}+(c+1)^{3}
$$
est valide, et on va tenter de la démontrer.
On continue donc nos pérégrinations et, puisque l'on a fait tous ces efforts pour séparer les termes en les variables $a, b$ et $c$, on constate qu'il suffit désormais de démontrer que
$$
4\left(a^{3}+1\right) \geqslant(a+1)^{3}
$$
Il s'agit là d'une inégalité en une seule variable, dont $a=1$ est un cas d'égalité, et qui aura le bon goût d'être démontrée (ou invalidée pour certaines valeurs de $a$ ) sans trop d'efforts.
En effet, si on développe chaque terme et qu'on les insère tous dans le membre de gauche, l'inégalité se réécrit comme
$$
3 a^{3}-3 a^{2}-3 a+3 \geqslant 0
$$
Puisque l'on sait qu'il y a égalité lorsque $a=0$, et au vu de la symétrie manifeste entre les termes de petit degré et ceux de grand degré, on factorise le membre de gauche comme
$$
3 a^{3}-3 a^{2}-3 a+3=3(a-1)\left(a^{2}-1\right)=3(a-1)^{2}(a+1)
$$
ce qui est manifestement positif ou nul, et nous permet de conclure que l'inégalité de l'énoncé est effectivement valide.
Commentaire des correcteurs Le problème a été abordé de manière assez inégale. Une moitié des élèves a pensé à l'inégalité arithmético-géométrique, mais plusieurs élèves n'ont pas réussi à conclure à partir de là; il est dommage que ces élèves ne se soient pas rendus compte que, comme $a, b$ et $c$ n'apparaissent dans aucun terme de la somme, il suffisait de prouver l'inégalité sans $b$ ni $c$, surtout que certains ont l'air de penser avoir conclu en factorisant partiellement.
|
{
"resource_path": "French/segmented/tests/fr-2022-2023-Corrige-Test-4.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
1440a950-dd07-5543-9784-34ae25e35cd1
| 605,586
|
Alice has arranged 200 boxes in her living room. Each box contains a paper on which she has written a non-zero natural number; the 200 numbers are not necessarily distinct. Each minute, and as long as it is possible, Alice performs an action of the following form: she chooses three boxes, containing integers $a, b$, and $c$ such that $a+b=c$, and also chooses an arbitrary integer $k \geqslant 2$; she then replaces the integer $c$ with the integer $k \times c$. If she can no longer perform such an action, she stops definitively.
Prove that, regardless of the initial situation and Alice's choices, she will be forced to stop at some point.
|
Below, we will say that an integer changes if Alice replaces $c$ with an integer $k \times c$. She paints in blue the integers that change only a finite number of times, and in red those that change an infinite number of times. By construction, the initially minimal number can never change, so it is blue. We then assume, somewhat abusively, that there exists a red number.
At some point, Alice completely stops changing the blue numbers. Let $v$ be the value of the largest of them at that time. When a red number changes, its value increases by at least one. Therefore, there is a time from which each red number is at least $2 v + 1$, for example, when each red number has changed at least $2 v$ times.
At that time, the smallest red number is less than or equal to all other red numbers, and it is strictly greater than the sum of any two blue numbers. It will therefore never change its value again, and it should have been blue. This observation invalidates our assumption, which means that every number is blue and concludes the problem.
Comment from the graders The problem had a statement error. It was therefore difficult to make relevant observations on it.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Alice a disposé 200 boîtes dans son salon. Chaque boîte contient un papier sur lequel elle a écrit un entier naturel non nul; les 200 entiers ne sont pas nécessairement distincts. Chaque minute, et tant que c'est possible, Alice effectue une action de la forme suivante : elle choisit trois boîtes, contenant des entiers $a, b$ et $c$ tels que $a+b=c$, et choisit également un entier $k \geqslant 2$ arbitraire; elle remplace alors l'entier $c$ par l'entier $k \times c$. Si elle ne peut plus effectuer de telle action, elle s'arrête définitivement.
Démontrer que, quels que soient la situation initiale et les choix d'Alice, elle sera forcée de s'arrêter à un moment.
|
Ci-dessous, on dira qu'un entier change si Alice remplace $c$ par un entier $k \times c$. Elle peint en bleu les entiers qui ne changent qu'un nombre fini de fois, et en rouge ceux qui changent un nombre infini de fois. Par construction, le nombre initialement minimal ne pourra jamais changer, donc il est bleu. On suppose alors abusivement qu'il existe un nombre rouge.
À partir d'un certain temps, Alice cesse complètement de changer les nombres bleus. Soit $v$ la valeur du plus grand d'entre eux à ce moment-là. Quand un nombre rouge change, sa valeur augmente d'au moins un. Il y a donc un moment à partir duquel chaque nombre rouge vaut au moins $2 v+1$, par exemple quand chaque nombre rouge a changé au moins $2 v$ fois.
À ce moment-là, le plus petit nombre rouge est inférieur ou égal à tous les autres nombres rouges, et il est strictement supérieur à la somme de deux nombres bleus quelconques. Il ne pourra donc plus jamais changer de valeur, et il aurait dû être bleu. Ce constat invalide notre supposition, ce qui signifie que tout nombre est bleu et conclut le problème.
Commentaire des correcteurs Le problème comportait une erreur d'énoncé. Il était donc difficile de faire des observations pertinentes dessus.
|
{
"resource_path": "French/segmented/tests/fr-2022-2023-Corrige-Test-4.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
9c06f989-bf85-573e-9ed2-ac82df2d658a
| 605,592
|
Let $ABC$ be an isosceles triangle at $A$ with all angles acute, and let $D$ be a point on the segment $[BC]$. Let $\ell$ be the line parallel to $(BC)$ passing through $A$, and $X$ the point on $\ell$ such that $(XD)$ is perpendicular to $(BC)$, and $\Gamma$ the circle centered at $X$ passing through $D$. The circle $\Gamma$ intersects the segment $[AB]$ at a point $E$, and we denote by $Y$ the point on $\ell$ such that $(AB)$ is perpendicular to $(EY)$; similarly, $\Gamma$ intersects the segment $[AC]$ at a point $F$, and we denote by $Z$ the point on $\ell$ such that $(AC)$ is perpendicular to $(FZ)$.
Prove that the bisectors of the angles $\widehat{EYA}$ and $\widehat{FZA}$ intersect at a point on the line $(XD)$.
|
Let $T$ be the intersection point of the bisectors of $\widehat{E Y A}$ and $\widehat{F Z A}$, $U$ the intersection point of the lines $(E Y)$ and $(F Z)$, and $\mathcal{C}$ the circle with radius $[A U]$. Since the angles $\widehat{U E A}$ and $\widehat{A F U}$ are right angles, $E$ and $F$ belong to $\mathcal{C}$.
Furthermore, since $A B C$ is isosceles at $A$, the bisector of the angles $\widehat{B A C}$ and $\widehat{E A F}$ is also the altitude of $A B C$ from $A$. It is therefore perpendicular to the lines $(B C)$ and $\ell=(A X)$. Since $D X=E X=F X$, the point $X$ is the intersection of the external bisector of $\widehat{E A F}$ with the perpendicular bisector of $[E F]$, i.e., the North Pole of $A E F$ from $A$. This means in particular that $X$ belongs to the circumcircle of $A E F$, i.e., to $\mathcal{C}$.
Under these conditions, the angle $\widehat{U X A}$ is a right angle, so the triangles $U X Y$ and $U X Z$ are right-angled at $U$. Since the triangles $A F Z$ and $A E Y$ are right-angled at $E$ and $F$ and $A B C$ is isosceles at $A$, we know that
$$
\widehat{X Z U}=\widehat{A Z F}=90^{\circ}-\widehat{F A Z}=90^{\circ}-\widehat{A C B}=90^{\circ}-\widehat{C B A}=90^{\circ}-\widehat{Y A E}=\widehat{E Y A}=\widehat{Y U X} .
$$
Thus, the two right-angled triangles $U X Y$ and $U X Z$ are symmetric with respect to the line $(U X)$. The two bisectors $(T Y)$ and $(T Z)$ are also symmetric with respect to $(U X)$, so $T$ lies on $(U X)$.
Finally, by construction, the line $(D X)$ is perpendicular to the lines $(B C)$ and $\ell$, so it coincides with $(U X)$. Therefore, as required in the statement, it contains the point $T$.
Remark: When looking for a solution, it may be more natural to proceed in reverse order of the solution presented above, for example as follows:
1. We notice that the two triangles $T X Y$ and $T X Z$ appear to be symmetric, and we will have won if they are.
2. We prove that $\widehat{X Z T}=\widehat{T Y X}$, so it suffices to prove that $X Y=X Z$.
3. We notice that the problem would be analogous if we replaced our bisectors with the lines $(Y E)$ and $(Z F)$, which leads us to introduce the point $U$ and to try to prove that $(X U)$ is perpendicular to $\ell$.
4. We then identify two right angles joining $A$ to $U$, and a third one which we hope is right.
5. The existence of these right angles is characterized by belonging to a circle with radius $[A U]$, so it is a matter of proving that $E, X, A$, and $F$ are concyclic.
6. To prove that they are indeed concyclic, we recognize $X$ as the North Pole of $A E F$ from $A$, and we prove that it is indeed.
Comment from the graders: The problem, which is difficult, was fully solved by only one student. Many students managed to reduce the problem to showing that $X Y=X Z$, or an equivalent property. Such a reduction of the problem is always good to write.
However, too many students make reasoning errors that must be eliminated: lack of knowledge of the similarity criterion for two triangles, circular reasoning, or misreading of the figure (or the statement). These students then believe they can conclude the problem in a few lines without using some crucial hypotheses of the statement, which should lead them to reread and verify their proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle isocèle en $A$ dont tous les angles sont aigus, et soit $D$ un point situé sur le segment $[B C]$. Soit $\ell$ la droite parallèle à $(B C)$ passant par $A$, puis $X$ le point de $\ell$ pour lequel $(X D)$ est perpendiculaire à $(B C)$, et $\Gamma$ le cercle de centre $X$ passant par $D$. Le cercle $\Gamma$ coupe le segment $[A B]$ en un point $E$, et on note $Y$ le point de $\ell$ tel que $(A B)$ soit perpendiculaire à $(E Y)$; de même, $\Gamma$ coupe le segment $[A C]$ en un point $F$, et on note $Z$ le point de $\ell$ tel que $(A C)$ soit perpendiculaire à $(F Z)$.
Démonter que les bissectrices des angles $\widehat{E Y A}$ et $\widehat{F Z A}$ se coupent en un point de la droite ( $X D$ ).
|
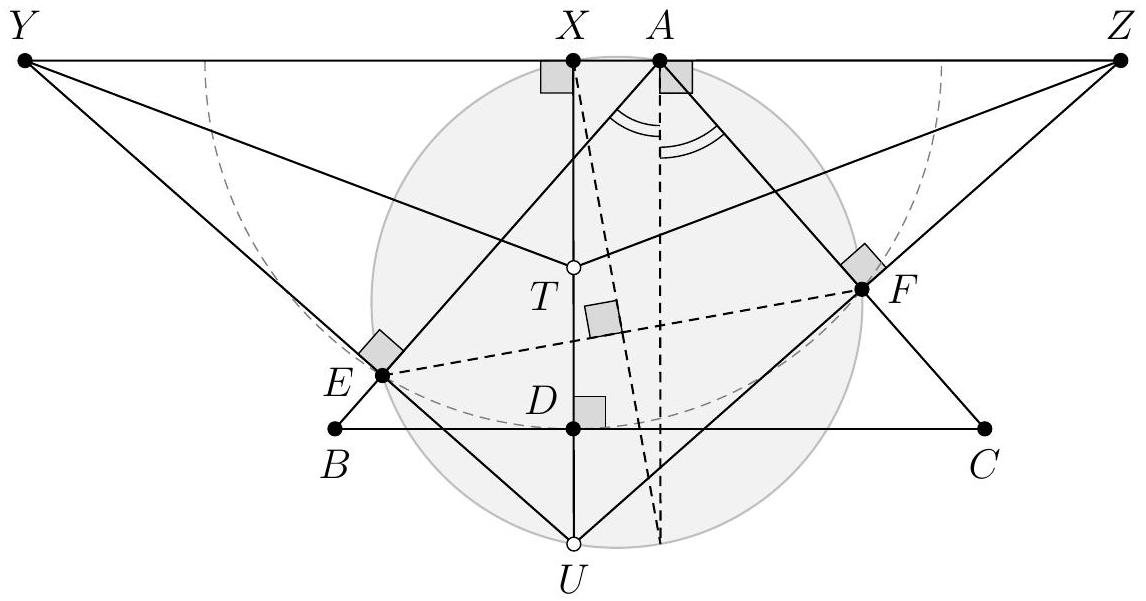
Notons $T$ le point d'intersection des bissectrices de $\widehat{E Y A}$ et $\widehat{F Z A}, U$ le point d'intersection des droites $(E Y)$ et $(F Z)$, et $\mathcal{C}$ le cercle de rayon $[A U]$. Puisque les angles $\widehat{U E A}$ et $\widehat{A F U}$ sont droits, $E$ et $F$ appartiennent à $\mathcal{C}$.
Par ailleurs, puisque $A B C$ est isocèle en $A$, la bissectrice des angles $\widehat{B A C}$ et $\widehat{E A F}$ est aussi la hauteur de $A B C$ issue de $A$. Elle est donc perpendiculaire aux droites $(B C)$ et $\ell=(A X)$. Comme $D X=E X=F X$, le point $X$ est donc le point d'intersection de la bissectrice extérieure de $\widehat{E A F}$ avec la médiatrice de $[E F]$, c'est-à-dire le pôle Nord de $A E F$ issu de $A$. Cela signifie en particulier que $X$ appartient au cercle circonscrit à $A E F$, c'est-à-dire à $\mathcal{C}$.
Dans ces conditions, l'angle $\widehat{U X A}$ est droit, donc les triangles $U X Y$ et $U X Z$ sont rectangles en $U$. Or, puisque les triangles $A F Z$ et $A E Y$ sont rectangles en $E$ et $F$ et que $A B C$ est isocèle en $A$, on sait que
$$
\widehat{X Z U}=\widehat{A Z F}=90^{\circ}-\widehat{F A Z}=90^{\circ}-\widehat{A C B}=90^{\circ}-\widehat{C B A}=90^{\circ}-\widehat{Y A E}=\widehat{E Y A}=\widehat{Y U X} .
$$
Ainsi, les deux triangles rectangles $U X Y$ et $U X Z$ sont symétriques l'un de l'autre par rapport à la droite $(U X)$. Les deux bissectrices $(T Y)$ et $(T Z)$ se retrouvent elles aussi symétriques l'une de l'autre par rapport à $(U X)$, donc $T$ appartient à $(U X)$.
Enfin, par construction, la droite $(D X)$ est perpendiculaire aux droites $(B C)$ et $\ell$, donc elle est confondue avec $(U X)$. On en conclut donc, comme demandé dans l'énoncé, qu'elle contient le point $T$.
Remarque: Lors de la recherche d'une solution, on pourra bien sûr trouver plus naturel de procéder à rebours de la solution présentée ci-dessus, par exemple en procédant comme suit:
1. On remarque que les deux triangles $T X Y$ et $T X Z$ semblent symétriques, et qu'on aura gagné s'ils le sont.
2. On démontre que $\widehat{X Z T}=\widehat{T Y X}$, de sorte qu'il suffit de démontrer que $X Y=X Z$.
3. On remarque que le problème serait analogue si on remplaçait nos bissectrices par les deux droites $(Y E)$ et $(Z F)$, ce qui nous pousse à introduire le point $U$ et à chercher à démontrer que $(X U)$ est perpendiculaire à $\ell$.
4. On repère alors deux angles droits joignant $A$ à $U$, et un troisième dont on espère justement qu'il est droit.
5. L'existence de ces angles droits se caractérisant par l'appartenance à un cercle de rayon [ $A U]$, il s'agit de démontrer que $E, X, A$ et $F$ sont cocycliques.
6. Pour démontrer qu'ils le sont effectivement, on reconnaît en $X$ le pôle Nord de $A E F$ issu de $A$, et on démontre qu'il l'est effectivement.
Commentaire des correcteurs Le problème, difficile, n'a été résolu entièrement que par un élève. Beaucoup d'élèves sont parvenus à réduire le problème au fait de montrer que $X Y=X Z$, ou à une propriété équivalente. Une telle réduction du problème est toujours bonne à écrire.
En revanche, trop d'élèves font des erreurs de raisonnements qu'il faut absolument gommer : méconnaissance du critère de similitude de deux triangles, raisonnements circulaires ou mauvaise lecture de le figure (voire de l'énoncé). Ces élèves croient alors conclure le problème en quelques lignes alors qu'ils n'ont pas utilisé certaines hypothèses cruciales de l'énoncé, ce qui devrait les amener à relire et vérifier leur preuve.
## Énoncés Senior
|
{
"resource_path": "French/segmented/tests/fr-2022-2023-Corrige-Test-4.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "## Solution de l'exercice 4"
}
|
de997333-7ca2-5630-91a8-18e5af6594b1
| 605,600
|
Let $ABC$ be a triangle with all angles acute. Let $F$ be the foot of the altitude from $A$ in $\triangle ABC$, and let $P$ be a point on the segment $[AF]$. We denote $D$ as the point on $(BC)$ such that $(PD)$ is parallel to $(AC)$, and then $X$ as the point where the circumcircle of $\triangle ABD$ and the circle centered at $D$ passing through $A$ intersect. Similarly, we denote $E$ as the point on $(BC)$ such that $(PE)$ is parallel to $(AB)$, and then $Y$ as the point where the circumcircle of $\triangle ACE$ and the circle centered at $E$ passing through $A$ intersect.
Prove that the points $B, C, X$, and $Y$ are concyclic.
|
In such a problem, the simplest approach is to try to eliminate as many points as possible that might prove less useful for the next steps. Here, for example, this is the case with point $P$, which serves only to construct points $D$ and $E$ as images of $B$ and $C$ through a homothety centered at $F$. Thus, $F E \times F C = F B \times F D$, and $F$ therefore has the same power with respect to the circumcircles of $A B D$ and $A C E$. These two circles therefore have $(A F)$ as their radical axis.
We then focus on the radical axes of these two circles with the potential circumcircle of $B X C Y$, that is, the lines $(B X)$ and $(C Y)$, and the radical center of these three circles. On the figure, this center seems to belong to the circles centered at $D$ and $E$ passing through $A$. This would mean that it is coincident with the reflection of $A$ across the line $(D E) = (B C)$; we denote this reflection by $A^{\prime}$.
A simple way to reuse the equality $D A = D X$ is to say that the arcs $\widehat{D A}$ and $\widehat{X D}$ have the same measure. Thus,
$$
(B X, B C) = (B X, B D) = (B D, B A) = (B C, B A) = \left(B A^{\prime}, B C\right)
$$
We similarly prove that $(C Y, C B) = \left(C A^{\prime}, C B\right)$, so the three lines $(A F)$, $(B X)$, and $(C Y)$ are indeed concurrent at $A^{\prime}$.
In particular, $A^{\prime}$ is the radical center of the circumcircles of $A B D X$, $A C E Y$, and $B C Y$, so $\left(A^{\prime} B\right) = (B X)$ is the radical axis of the circumcircles of $A B D X$ and $B C Y$. Since $X$ belongs to one of these circles, it also belongs to the other, which concludes the proof.
Comment from the graders: Many students solved this problem. Simply translating the hypotheses of cocyclicity or parallelism into angle equalities was not sufficient here to make significant progress. However, several parts of the problem were accessible and were often addressed in practice: showing that $F$ is on a radical axis by angle chasing, introducing the intersection of $(B X)$ and $(C Y)$ and translating the result to be proven into the membership of a certain point to a radical axis...
Finally, even in the face of a problem with a proof using such elementary arguments, some students attempted (with little success) very technical solutions: inversions, dynamic geometry... It is frustrating to see students deploy such an arsenal without arriving at an interesting relationship, especially when it is the only attempt they leave a written trace of. We implore students to try simple things for the first exercises.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle dont tous les angles sont aigus. Soit $F$ le pied de la hauteur de $A B C$ issue de $A$, et soit $P$ un point situé sur le segment $[A F]$. On note $D$ le point de ( $B C)$ tel que $(P D)$ soit parallèle à $(A C)$, puis $X$ le point où se recoupent le cercle circonscrit à $A B D$ et le cercle de centre $D$ passant par $A$. De même, on note $E$ le point de $(B C)$ tel que $(P E)$ soit parallèle à $(A B)$, puis $Y$ le point où se recoupent le cercle circonscrit à $A C E$ et le cercle de centre $E$ passant par $A$.
Démontrer que les points $B, C, X$ et $Y$ sont cocycliques.
|
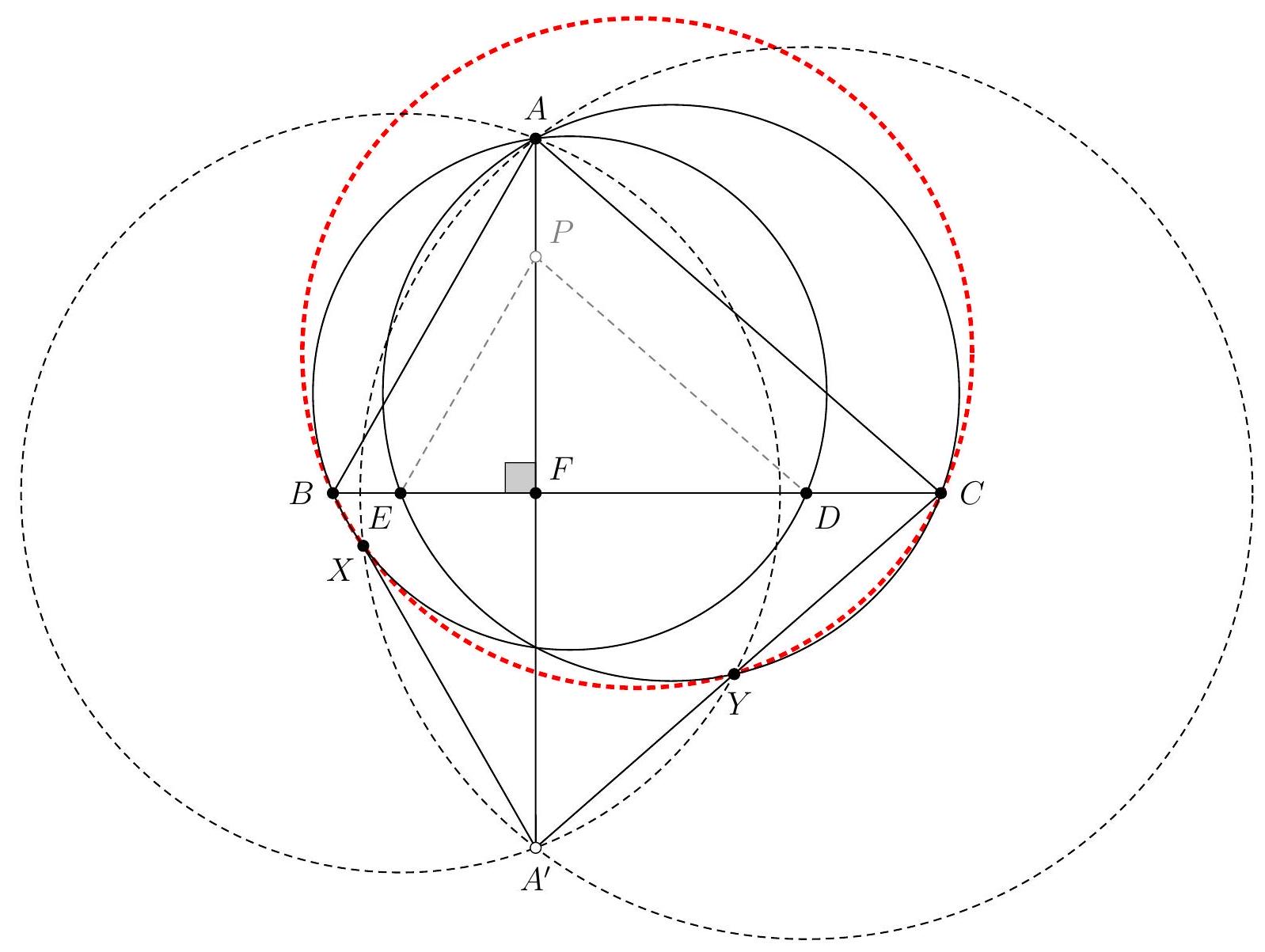
Dans un tel problème, le plus simple est d'essayer d'éliminer au mieux les points qui pourraient s'avérer peu utiles pour la suite. Ici, c'est par exemple le cas du point $P$, qui ne sert qu'à construire les points $D$ et $E$ en tant qu'images de $B$ et $C$ par une même homothétie de centre $F$. Ainsi, $F E \times F C=F B \times F D$, et $F$ a donc même puissance par rapport aux cercles circonscrits à $A B D$ et à $A C E$. Ces deux cercles ont donc $(A F)$ pour axe radical.
On s'intéresse donc aux axes radicaux de ces deux cercles avec l'éventuel cercle circonscrit à $B X C Y$, c'est-à-dire aux droites $(B X)$ et $(C Y)$, et au centre radical de ces trois cercles. Or, sur la figure, celui-ci semble appartenir aux cercles de centres $D$ et $E$ passant par $A$. Cela signifierait qu'il est confondu avec le symétrique de $A$ par rapport à la droite $(D E)=(B C)$; on note $A^{\prime}$ ce symétrique.
Une manière simple de réutiliser l'égalité $D A=D X$ consiste à dire que les arcs de cercle $\widehat{D A}$ et $\widehat{X D}$ ont même mesure. Ainsi,
$$
(B X, B C)=(B X, B D)=(B D, B A)=(B C, B A)=\left(B A^{\prime}, B C\right)
$$
On démontre de même que $(C Y, C B)=\left(C A^{\prime}, C B\right)$, de sorte que les trois droites $(A F),(B X)$ et $(C Y)$ sont bien concourantes en $A^{\prime}$.
En particulier, $A^{\prime}$ est le centre radical des cercles circonscrits à $A B D X$, à $A C E Y$ et à $B C Y$, donc $\left(A^{\prime} B\right)=(B X)$ est l'axe radical des cercles circonscrits à $A B D X$ et à $B C Y$. Puisque $X$ appartient à l'un de ces cercles, il appartient aussi à l'autre, ce qui conclut.
Commentaire des correcteurs De nombreux élèves ont résolu ce problème. Se contenter de traduire les hypothèses de cocyclicité ou de parallélisme par des égalités d'angles ne suffisait pas ici pour avancer significativement. Néanmoins, plusieurs parties du problème étaient abordables, et ont été souvent abordées en pratique : montrer que $F$ est sur un axe radical par chasse aux rapports, introduire le point d'intersection de $(B X)$ et $(C Y)$ et traduire le résultat à démontrer en appartenance d'un certain point à un axe radical...
Signalons enfin que, même devant un problème avec une preuve aux arguments aussi élémentaires, des élèves ont tenté (sans vraiment beaucoup de succès) des solutions très techniques : des inversions, de la géométrie dynamique... Il est frustrant de voir les élèves déployer un tel arsenal sans aboutir à une relation intéressante, surtout quand c'est la seule tentative dont ils laissent une trace écrite. On implore les élèves d'essayer des choses simples pour les premiers exercices.
|
{
"resource_path": "French/segmented/tests/fr-2022-2023-Corrige-Test-4.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "## Solution de l'exercice 5"
}
|
6f53d831-5386-53f3-95ce-f5061c93de3f
| 605,611
|
Let $ABC$ be a triangle such that $\widehat{CAB} < \widehat{ABC} < \widehat{BCA} < 90^{\circ}$. Let $\omega$ be the circumcircle of $ABC$, $\gamma_{a}$ the circle centered at $A$ with radius $[AC]$, and $\gamma_{b}$ the circle centered at $B$ with radius $[BC]$. Finally, let $D$ be the intersection point, other than $C$, between $\omega$ and $\gamma_{b}$, and let $E$ be the intersection point, other than $C$, between $\gamma_{a}$ and $\gamma_{b}$.
Prove that the points $A, D$, and $E$ are collinear.
|
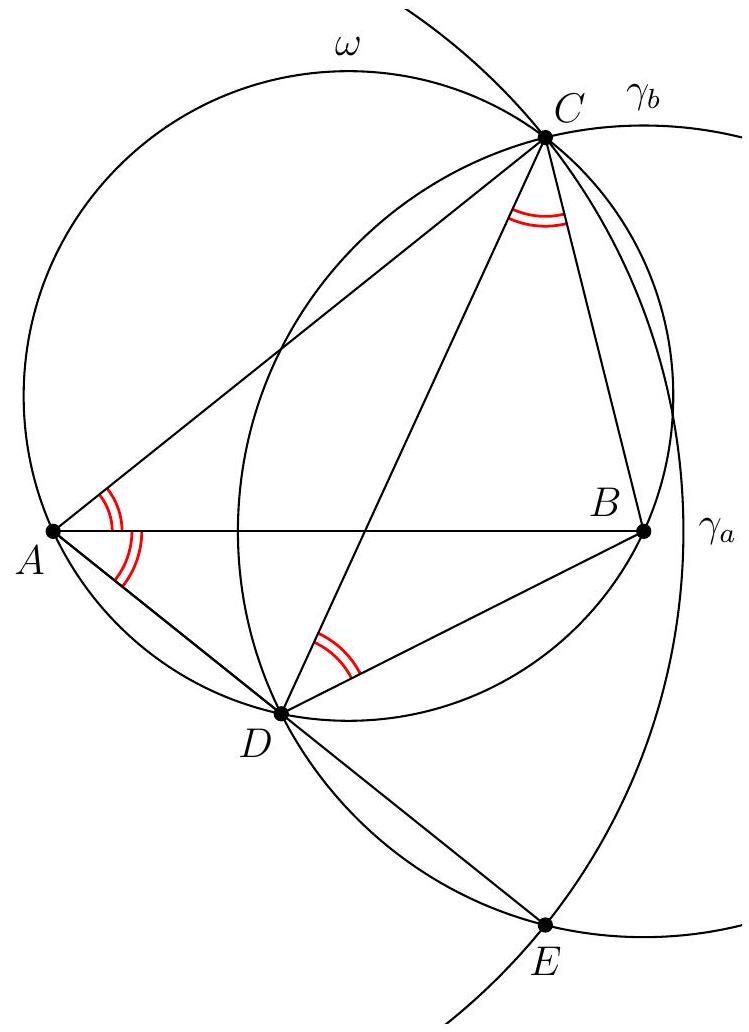
By construction, $(CE)$ is the radical axis of the circles $\gamma_a$ and $\gamma_b$, so $C$ and $E$ are symmetric with respect to $(AB)$. Furthermore, we know that $BC = BD = BE$. Therefore, we have multiple angle and length equalities, and the simplest way to obtain the desired alignment is probably to perform an angle chase.
We observe that
$$
\widehat{BAE} = \widehat{CAB} = \widehat{CDB} = \widehat{BCD} = 180^{\circ} - \widehat{DAB},
$$
which means that $D$, $A$, and $E$ are collinear.
Comment from the graders: Although successfully solved by a fair number of students, this problem caused quite a bit of damage for several reasons. First, many students used circular reasoning, for example, implicitly assuming that points $A$, $D$, and $E$ are collinear to deduce an angle equality and the collinearity of points $A$, $D$, and $E$. This issue persists despite warnings from previous tests. The solutions to avoid this problem are: draw a (slightly) incorrect figure to avoid being misled, clearly define your different angles, and justify each equality written.
The second problem also affects students who solved the problem: there is inefficient writing, in which students introduce many points and sometimes extend over several pages to show equalities that follow either from the symmetry of $C$ and $E$ or from the inscribed angle theorem. It is recommended to read the solution to understand how to proceed directly. Recognizing a South Pole here could also save time and improve clarity in writing.
Finally, many students tried to show that $\widehat{ADE} = 180^{\circ}$. Very few attempted to show instead that $\widehat{BAE} = \widehat{BAD}$ to ensure collinearity, which was the simplest approach here. Try all possibilities, and not just the naive method.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle tel que $\widehat{C A B}<\widehat{A B C}<\widehat{B C A}<90^{\circ}$. Soit $\omega$ le cercle circonscrit à $A B C, \gamma_{a}$ le cercle de centre $A$ et de rayon $[A C]$, et $\gamma_{b}$ le cercle de centre $B$ et de rayon $[B C]$. Enfin, soit $D$ le point d'intersection, autre que $C$, entre $\omega$ et $\gamma_{b}$, et soit $E$ le point d'intersection, autre que $C$, entre $\gamma_{a}$ et $\gamma_{b}$.
Démontrer que les points $A, D$ et $E$ sont alignés.
|

Par construction, $(C E)$ est l'axe radical des cercles $\gamma_{a}$ et $\gamma_{b}$, donc $C$ et $E$ sont symétriques l'un de l'autre par rapport à $(A B)$. En outre, on sait que $B C=B D=B E$. On dispose donc de multiples égalités d'angles et de longueurs, et la manière la plus simple d'obtenir l'alignement recherché est sans doute de procéder à une chasse aux angles.
On observe ainsi que
$$
\widehat{B A E}=\widehat{C A B}=\widehat{C D B}=\widehat{B C D}=180^{\circ}-\widehat{D A B},
$$
ce qui signifie bien que $D, A$ et $E$ sont alignés.
Commentaire des correcteurs Bien que réussi par d'assez nombreux élèves, ce problème a fait pas mal de dégâts, et ce pour plusieurs raisons. Tout d'abord, beaucoup d'élèves ont mis en œuvre des raisonnements circulaires, par exemple en supposant implicitement les points $A$, $D$ et $E$ alignés pour en déduire une égalité d'angles et l'alignement des points $A, D$ et $E$. Ce souci persiste malgré les mises en garde des précédents tests. Les solutions pour éviter ce problème sont : tracer une figure (un peu) fausse pour ne pas se faire avoir, bien définir ses différents angles, justifier chaque égalité écrite...
Le second problème concerne aussi des élèves ayant résolu le problème : on déplore une rédaction inefficace, dans laquelle les élèves introduisent beaucoup de points et s'étendent
parfois sur plusieurs pages pour montrer des égalités qui découlent soit de la symétrie de $C$ et $E$ soit du théorème de l'angle inscrit. On conseille de bien lire le corrigé pour comprendre comment procéder de façon directe. Reconnaître un pôle Sud ici pouvait également permettre de gagner du temps et de la clarté dans la rédaction.
Enfin, beaucoup d'élèves ont essayé de montrer que $\widehat{A D E}=180^{\circ}$. Très peu ont tenté de montrer plutôt que $\widehat{B A E}=\widehat{B A D}$ pour assurer l'alignement, ce qui était le plus simple ici. Essayez toutes les possibilités, et pas seulement la méthode naïve.
|
{
"resource_path": "French/segmented/tests/fr-2022-2023-Corrige-Test-5.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "## Solution de l'exercice 1"
}
|
b30a4b73-a95a-546e-9f9d-f079d68f5992
| 605,644
|
Let $n \geqslant 1$ be an integer. Bosphore has written the number 2 on the board $n$ times. He then performs, $n-1$ times in a row, the following operation: he chooses two numbers written on the board, which he calls $a$ and $b$, then erases them and writes the number $\sqrt{(a b+1) / 2}$ in their place. Finally, he calls $x$ the number written on the board after these $n-1$ operations, and $y$ the number $\sqrt{(n+3) / n}$.
a) Prove that $x \geqslant y$.
b) Prove that there are infinitely many integers $n \geqslant 1$ for which $x > y$ necessarily.
c) Prove that there are infinitely many integers $n \geqslant 1$ for which Bosphore can ensure that $x = y$.
|
In the following, let $x_{n}$ be the smallest real number $x$ that Bosphore can end up with starting from $n$ integers all equal to 2, and let $y_{n}=\sqrt{(n+3) / n}$. The goal is to prove that $x_{n} \geqslant y_{n}$, with equality an infinite number of times and strict inequality an infinite number of times. A study of small cases suggests the property $\mathcal{P}(n)$: "the inequality $x_{n} \geqslant y_{n}$ is indeed true, and $x_{n}=y_{n}$ if and only if $n$ is a power of 2."
Conversely, let $u$ and $v$ be the last two numbers he erases, just before writing $x$ on the board. If Bosphore's goal is to achieve the inequality $x \leqslant y$, it is in his interest for $u$ and $v$ to be as small as possible. Therefore, if there are $k$ numbers that, through repeated rewriting, have been transformed into the number $u$, and $\ell$ numbers that have been transformed into the number $v$, Bosphore will ensure that $u=x_{k}$ and $v=x_{\ell}$. This means that $x_{n}$ is the smallest of the numbers
$$
\sqrt{\frac{x_{1} x_{n-1}+1}{2}}, \sqrt{\frac{x_{2} x_{n-2}+1}{2}}, \ldots, \sqrt{\frac{x_{n-1} x_{1}+1}{2}}.
$$
We therefore set out to prove $\mathcal{P}(n)$ by induction on $n \geqslant 1$. First, $x_{1}=2=y_{1}$, so $\mathcal{P}(1)$ is true. Then, if $\mathcal{P}(1), \ldots, \mathcal{P}(n-1)$ are true, and for all integers $k$ and $\ell$ such that $1 \leqslant k \leqslant n-1$ and $1 \leqslant \ell \leqslant n-1$, we know that
$$
\sqrt{\frac{x_{k} x_{\ell}+1}{2}} \geqslant y_{k+\ell} \Leftrightarrow x_{k} x_{\ell} \geqslant 2 y_{k+\ell}^{2}-1
$$
Since $x_{k} \geqslant y_{k}$ and $x_{\ell} \geqslant y_{\ell}$, it suffices to prove that $y_{k} y_{\ell} \geqslant 2 y_{k+\ell}^{2}-1$.
If we set $\Delta=y_{k}^{2} y_{\ell}^{2}-\left(2 y_{k+\ell}^{2}-1\right)^{2}$, we verify that
$$
\begin{aligned}
k \ell(k+\ell)^{2} \Delta & =(k+3)(\ell+3)(k+\ell)^{2}-k \ell(k+\ell+6)^{2} \\
& =3(k+\ell+3)(k+\ell)^{2}-12 k \ell(k+\ell+3) \\
& =3(k+\ell+3)\left(k^{2}+2 k \ell+\ell^{2}-4 k \ell\right) \\
& =3(k+\ell+3)(k-\ell)^{2}.
\end{aligned}
$$
This ensures that $\Delta \geqslant 0$, and thus that $x_{k} x_{\ell} \geqslant y_{k} y_{\ell} \geqslant 2 y_{k+\ell}^{2}-1$. Moreover, the cases of equality occur exactly when $x_{k}=y_{k}, x_{\ell}=y_{\ell}$, and $\Delta=0$, i.e., when $k=\ell$ is a power of 2. In particular, the inequality
$$
\sqrt{\frac{x_{k} x_{\ell}+1}{2}} \geqslant y_{k+\ell}
$$
is necessarily satisfied, and it is an equality if and only if $k=\ell$ is a power of 2.
In conclusion:
a) Regardless of the value of $n$, there exist two integers $k$ and $\ell=n-k$ such that $x_{n}=\sqrt{\left(x_{k} x_{\ell}+1\right) / 2} \geqslant \sqrt{\left(y_{k} y_{\ell}+1\right) / 2} \geqslant y_{k+\ell}=y_{n}$.
b) If $n$ is not a power of 2, $k$ and $\ell$ are not equal to the same power of 2, so one of the three inequalities $x_{k} \geqslant y_{k}, x_{\ell} \geqslant y_{\ell}$, and $\sqrt{\left(y_{k} y_{\ell}+1\right) / 2} \geqslant y_{n}$ is strict, and $x_{n}>y_{n}$.
c) If $n$ is a power of 2, the inequality $x_{n} \leqslant \sqrt{\left(x_{n / 2}^{2}+1\right) / 2}=\sqrt{\left(y_{n / 2}^{2}+1\right) / 2}=y_{n}$ indicates that $x_{n}=y_{n}$.
Comment from the graders: The problem was rarely addressed. Some students directly formed an intuition of the result for part c) by observing that equality holds when $n$ is a power of 2. However, only one student really understood the issues of the problem and solved it.
Here, it was natural to use induction and to look at how the last two numbers were obtained. Some students assumed that each time they took the result of the previous test and performed the operation with one of the two initially written: this is not the only possibility.
## Senior Problems
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit $n \geqslant 1$ un entier. Bosphore a écrit $n$ fois le nombre 2 au tableau. Il effectue ensuite, $n-1$ fois d'affilée, l'opération suivante : il choisit deux nombres écrits au tableau, qu'il appelle $a$ et $b$, puis les efface et écrit le nombre $\sqrt{(a b+1) / 2}$ à la place. Enfin, il appelle $x$ le nombre écrit au tableau après ces $n-1$ opérations, et $y$ le nombre $\sqrt{(n+3) / n}$.
a) Démontrer que $x \geqslant y$.
b) Démontrer qu'il existe une infinité d'entiers $n \geqslant 1$ pour lesquels on a nécessairement $x>y$.
c) Démontrer qu'il existe une infinité d'entiers $n \geqslant 1$ pour lesquels Bosphore peut faire en sorte que $x=y$.
|
Dans la suite, notons $x_{n}$ le plus petit réel $x$ auquel peut aboutir Bosphore en partant de $n$ entiers égaux à 2 , et posons $y_{n}=\sqrt{(n+3) / n}$. Il s'agit de démontrer que $x_{n} \geqslant y_{n}$, avec égalité une infinité de fois et inégalité stricte une infinité de fois. Une étude des petits cas suggère la propriété $\mathcal{P}(n)$ suivante : «l'inégalité $x_{n} \geqslant y_{n}$ est bien vraie, et $x_{n}=y_{n}$ si et seulement $n$ est une puissance de $2 »$.
Réciproquement, soit $u$ et $v$ les deux derniers nombres qu'il efface, juste avant d'écrire $x$ au tableau. Si Bosphore a pour objectif d'aboutir à l'inégalité $x \leqslant y$, il a intérêt à ce que $u$ et $v$ soient aussi petits que possible. Par conséquent, s'il y a $k$ nombres qui, à force de réécritures, ont été transformés en le nombre $u$, et $\ell$ nombres qui ont été transformés en le nombre $v$, Bosphore fera en sorte que $u=x_{k}$ et $v=x_{\ell}$. Cela signifie en fait que $x_{n}$ est le plus petit des nombres
$$
\sqrt{\frac{x_{1} x_{n-1}+1}{2}}, \sqrt{\frac{x_{2} x_{n-2}+1}{2}}, \ldots, \sqrt{\frac{x_{n-1} x_{1}+1}{2}} .
$$
On entreprend donc de démontrer $\mathcal{P}(n)$ par récurrence sur $n \geqslant 1$. Tout d'abord, $x_{1}=2=y_{1}$, donc $\mathcal{P}(1)$ est vraie. Puis, si $\mathcal{P}(1), \ldots, \mathcal{P}(n-1)$ sont vraies, et pour tous entiers $k$ et $\ell$ tels que $1 \leqslant k \leqslant n-1$ et $1 \leqslant \ell \leqslant n-1$, on sait que
$$
\sqrt{\frac{x_{k} x_{\ell}+1}{2}} \geqslant y_{k+\ell} \Leftrightarrow x_{k} x_{\ell} \geqslant 2 y_{k+\ell}^{2}-1
$$
Puisque $x_{k} \geqslant y_{k}$ et $x_{\ell} \geqslant y_{\ell}$, il suffit donc de démontrer que $y_{k} y_{\ell} \geqslant 2 y_{k+\ell}^{2}-1$.
Si l'on pose $\Delta=y_{k}^{2} y_{\ell}^{2}-\left(2 y_{k+\ell}^{2}-1\right)^{2}$, on vérifie alors que
$$
\begin{aligned}
k \ell(k+\ell)^{2} \Delta & =(k+3)(\ell+3)(k+\ell)^{2}-k \ell(k+\ell+6)^{2} \\
& =3(k+\ell+3)(k+\ell)^{2}-12 k \ell(k+\ell+3) \\
& =3(k+\ell+3)\left(k^{2}+2 k \ell+\ell^{2}-4 k \ell\right) \\
& =3(k+\ell+3)(k-\ell)^{2} .
\end{aligned}
$$
Ceci nous assure que $\Delta \geqslant 0$, donc que $x_{k} x_{\ell} \geqslant y_{k} y_{\ell} \geqslant 2 y_{k+\ell}^{2}-1$. En outre, les cas d'égalité surviennent exactement lorsque $x_{k}=y_{k}, x_{\ell}=y_{\ell}$ et $\Delta=0$, c'est-à-dire lorsque $k=\ell$ est une puissance de 2. En particulier, l'inégalité
$$
\sqrt{\frac{x_{k} x_{\ell}+1}{2}} \geqslant y_{k+\ell}
$$
est nécessairement vérifiée, et il s'agit d'une égalité si et seulement si $k=\ell$ est une puissance de 2.
En conclusion :
a) Quelle que soit la valeur de $n$, il existe deux entiers $k$ et $\ell=n-k$ pour lesquels $x_{n}=\sqrt{\left(x_{k} x_{\ell}+1\right) / 2} \geqslant \sqrt{\left(y_{k} y_{\ell}+1\right) / 2} \geqslant y_{k+\ell}=y_{n}$.
b) Si $n$ n'est pas une puissance de $2, k$ et $\ell$ ne sont pas égaux à une même puissance de 2 , donc l'une des trois inégalités $x_{k} \geqslant y_{k}, x_{\ell} \geqslant y_{\ell}$ et $\sqrt{\left(y_{k} y_{\ell}+1\right) / 2} \geqslant y_{n}$ est stricte, et $x_{n}>y_{n}$.
c) Si $n$ est une puissance de 2, l'inégalité $x_{n} \leqslant \sqrt{\left(x_{n / 2}^{2}+1\right) / 2}=\sqrt{\left(y_{n / 2}^{2}+1\right) / 2}=y_{n}$ indique que $x_{n}=y_{n}$.
Commentaire des correcteurs Le problème a été peu abordé. Quelques élèves se sont directement forgés une intuition du résultat pour la question c) en constatant que l'on avait égalité lorsque $n$ est puissance de 2 . Toutefois, seul un élève a vraiment réussi à comprendre les enjeux du problème et le résoudre.
Ici, il était naturel de faire une récurrence et de regarder comment avait été obtenus les deux derniers nombres. Certains élèves ont supposé qu'à chaque fois on prenait le résultat du test précédent, et qu'on faisait l'opération avec un des 2 écrits au départ : ce n'est pas du tout la seule possibilité.
## Problèmes Senior
|
{
"resource_path": "French/segmented/tests/fr-2022-2023-Corrige-Test-5.jsonl",
"problem_match": "\nExercice 4.",
"solution_match": "\nSolution de l'exercice 4"
}
|
ae92fd51-743f-53f1-993a-5e29405eb0e8
| 605,676
|
For any integer $k \geqslant 0$, we denote $a_{k}$ as the first digit of the number $2^{k}$, written in base 10. For example, $a_{5}=3$ is the first digit of $2^{5}=32$.
Let $n \geqslant 1$ be an integer. Prove that, among the digits from 1 to 9, there is one that is equal to at most $n / 17$ of the $n$ digits $a_{0}, a_{1}, a_{2}, \ldots, a_{n-1}$.
|
Let $\mathrm{c}(k)$ be the number of times the digit $k$ appears among the digits $a_{0}, a_{1}, a_{2}, \ldots, a_{n-1}$. When $a_{i} \geqslant 2$, we know that $i \geqslant 1$ and that $a_{i-1}=\left\lfloor a_{i} / 2\right\rfloor$.
Thus, for any digit $k \leqslant 5$, $a_{i}=k$ if and only if $a_{i+1}=2 k$ or $a_{i+1}=2 k+1$, so that $\mathrm{c}(k) \geqslant \mathrm{c}(2 k)+\mathrm{c}(2 k+1)$. If we set $m=\min \{\mathrm{c}(k): 1 \leqslant k \leqslant 9\}$, we conclude in particular that
$$
\begin{array}{rlrl}
n & \geqslant \mathrm{c}(1)+\mathrm{c}(2)+\mathrm{c}(3)+\mathrm{c}(4)+\mathrm{c}(5)+\mathrm{c}(6)+\mathrm{c}(7)+\mathrm{c}(8)+\mathrm{c}(9) \\
& \geqslant \quad+2 \mathrm{c}(2)+2 \mathrm{c}(3)+\mathrm{c}(4)+\mathrm{c}(5)+\mathrm{c}(6)+\mathrm{c}(7)+\mathrm{c}(8)+\mathrm{c}(9) \\
& \geqslant \quad+3 \mathrm{c}(4)+3 \mathrm{c}(5)+3 \mathrm{c}(6)+3 \mathrm{c}(7)+\mathrm{c}(8)+\mathrm{c}(9) \\
& \geqslant \begin{aligned}
& +3 \mathrm{c}(5)+3 \mathrm{c}(6)+3 \mathrm{c}(7)+4 \mathrm{c}(8)+4 \mathrm{c}(9)
\end{aligned} \\
& \geqslant 17 \mathrm{~m} . &
\end{array}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Pour tout entier $k \geqslant 0$, on note $a_{k}$ le premier chiffre du nombre $2^{k}$, écrit en base 10. Par exemple, $a_{5}=3$ est le premier chiffre de $2^{5}=32$.
Soit $n \geqslant 1$ un entier. Démontrer que, parmi les chiffres de 1 à 9 , il y en a un qui est égal à au plus $n / 17$ des $n$ chiffres $a_{0}, a_{1}, a_{2}, \ldots, a_{n-1}$.
|
Soit $\mathrm{c}(k)$ le nombre de fois où le chiffre $k$ figure parmi les chiffres $a_{0}, a_{1}, a_{2}, \ldots, a_{n-1}$. Lorsque $a_{i} \geqslant 2$, on sait que $i \geqslant 1$ et que $a_{i-1}=\left\lfloor a_{i} / 2\right\rfloor$.
Ainsi, pour tout chiffre $k \leqslant 5$, on a $a_{i}=k$ si et seulement si $a_{i+1}=2 k$ ou $a_{i+1}=2 k+1$, de sorte que $\mathrm{c}(k) \geqslant \mathrm{c}(2 k)+\mathrm{c}(2 k+1)$. Si l'on pose $m=\min \{\mathrm{c}(k): 1 \leqslant k \leqslant 9\}$, on en conclut en particulier que
$$
\begin{array}{rlrl}
n & \geqslant \mathrm{c}(1)+\mathrm{c}(2)+\mathrm{c}(3)+\mathrm{c}(4)+\mathrm{c}(5)+\mathrm{c}(6)+\mathrm{c}(7)+\mathrm{c}(8)+\mathrm{c}(9) \\
& \geqslant \quad+2 \mathrm{c}(2)+2 \mathrm{c}(3)+\mathrm{c}(4)+\mathrm{c}(5)+\mathrm{c}(6)+\mathrm{c}(7)+\mathrm{c}(8)+\mathrm{c}(9) \\
& \geqslant \quad+3 \mathrm{c}(4)+3 \mathrm{c}(5)+3 \mathrm{c}(6)+3 \mathrm{c}(7)+\mathrm{c}(8)+\mathrm{c}(9) \\
& \geqslant \begin{aligned}
& +3 \mathrm{c}(5)+3 \mathrm{c}(6)+3 \mathrm{c}(7)+4 \mathrm{c}(8)+4 \mathrm{c}(9)
\end{aligned} \\
& \geqslant 17 \mathrm{~m} . &
\end{array}
$$
|
{
"resource_path": "French/segmented/tests/fr-2022-2023-Corrigé-Web-Test-1.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution de l'exercice 1"
}
|
ec962654-0473-5c23-8407-3c53f5558578
| 605,713
|
For any integer $k \geqslant 0$, we denote $a_{k}$ as the first digit of the number $2^{k}$, written in base 10. For example, $a_{5}=3$ is the first digit of $2^{5}=32$.
Let $n \geqslant 1$ be an integer. Prove that, among the digits from 1 to 9, there is one that is equal to at most $n / 17$ of the $n$ digits $a_{0}, a_{1}, a_{2}, \ldots, a_{n-1}$.
|
$n^{\circ} 1$ Let's resume the notations from the previous solution. For any event $\mathbf{E}$, we denote $\mathbf{1}_{\mathrm{E}}$ as the integer that equals 1 when $\mathbf{E}$ occurs, and 0 otherwise.
For any digit $k \leqslant 5$, we have
$$
\mathrm{c}(k)=\mathrm{c}(2 k)+\mathrm{c}(2 k+1)+\mathbf{1}_{a_{n-1}=k} .
$$
Similarly, since $a_{1}=1$, we know that
$$
1+c(5)+c(6)+c(7)+c(8)+c(9)=c(1)+1_{5 \leqslant a_{n-1} \leqslant 9}
$$
We then distinguish two cases.
$\triangleright$ If $a_{n-1}=1$, we find
$$
\begin{aligned}
c(1) & =c(5)+c(6)+c(7)+c(8)+c(9)+1 \geqslant 5 m+1 ; \\
c(2)+c(3) & =c(1)-1 \geqslant 5 m \\
c(4) & =c(8)+c(9) \geqslant 2 m .
\end{aligned}
$$
We deduce that $n \geqslant \sum_{k=1}^{9} \mathrm{c}(k) \geqslant 17 m+1$.
$\triangleright$ If $a_{n-1} \geqslant 2$, we find
$$
\begin{aligned}
c(1) & \geqslant c(5)+c(6)+c(7)+c(8)+c(9) \geqslant 5 m \\
c(2)+c(3) & =c(1) \geqslant 5 m \\
c(4) & =c(8)+c(9) \geqslant 2 m
\end{aligned}
$$
We deduce once again that $n \geqslant \sum_{k=1}^{9} \mathrm{c}(k) \geqslant 17 m+1$, which concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Pour tout entier $k \geqslant 0$, on note $a_{k}$ le premier chiffre du nombre $2^{k}$, écrit en base 10. Par exemple, $a_{5}=3$ est le premier chiffre de $2^{5}=32$.
Soit $n \geqslant 1$ un entier. Démontrer que, parmi les chiffres de 1 à 9 , il y en a un qui est égal à au plus $n / 17$ des $n$ chiffres $a_{0}, a_{1}, a_{2}, \ldots, a_{n-1}$.
|
$n^{\circ} 1$ Reprenons les notations de la solution précédente. Pour tout événement $\mathbf{E}$, on notera $\mathbf{1}_{\mathrm{E}}$ l'entier qui vaut 1 lorsque $\mathbf{E}$ se produit, et 0 sinon.
Pour tout chiffre $k \leqslant 5$, on a
$$
\mathrm{c}(k)=\mathrm{c}(2 k)+\mathrm{c}(2 k+1)+\mathbf{1}_{a_{n-1}=k} .
$$
De même, puisque $a_{1}=1$, on sait que
$$
1+c(5)+c(6)+c(7)+c(8)+c(9)=c(1)+1_{5 \leqslant a_{n-1} \leqslant 9}
$$
On distingue alors deux cas.
$\triangleright \operatorname{Si} a_{n-1}=1$, on trouve
$$
\begin{aligned}
c(1) & =c(5)+c(6)+c(7)+c(8)+c(9)+1 \geqslant 5 m+1 ; \\
c(2)+c(3) & =c(1)-1 \geqslant 5 m \\
c(4) & =c(8)+c(9) \geqslant 2 m .
\end{aligned}
$$
On en déduit que $n \geqslant \sum_{k=1}^{9} \mathrm{c}(k) \geqslant 17 m+1$.
$\triangleright \operatorname{Si} a_{n-1} \geqslant 2$, on trouve
$$
\begin{aligned}
c(1) & \geqslant c(5)+c(6)+c(7)+c(8)+c(9) \geqslant 5 m \\
c(2)+c(3) & =c(1) \geqslant 5 m \\
c(4) & =c(8)+c(9) \geqslant 2 m
\end{aligned}
$$
On en déduit là encore que $n \geqslant \sum_{k=1}^{9} \mathrm{c}(k) \geqslant 17 m+1$, ce qui conclut.
|
{
"resource_path": "French/segmented/tests/fr-2022-2023-Corrigé-Web-Test-1.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution alternative"
}
|
ec962654-0473-5c23-8407-3c53f5558578
| 605,713
|
Let $ABCD$ be a parallelogram and let $G$ be the centroid of triangle $ABD$. Let $P$ and $Q$ be points on the line $(BD)$ such that the lines $(GP)$ and $(PC)$ are perpendicular and the lines $(GQ)$ and $(QC)$ are perpendicular.
Prove that the line $(AG)$ is the bisector of the angle $\widehat{PAQ}$.
|
First, since $ABCD$ is a parallelogram, the median $(AG)$ of triangle $ABD$ and the diagonal $(AC)$ both pass through the midpoint $N$ of $[BD]$.
Since $CGP$ and $CGQ$ are right-angled at $P$ and $Q$, the points $P$ and $Q$ are the two points of intersection of $(BD)$ with the circle of diameter $[CG]$. Since this circle is drawn, we denote $M$ as its center, i.e., the midpoint of $[GC]$. In particular, the five points $A, G, N, M$, and $C$ are collinear.
The most reliable way to prove that $(AG)$ is the bisector of $\widehat{PAQ}$ is to invoke the South Pole theorem, i.e., to prove that $(AG)$ passes through the midpoint of the arc $\overparen{PQ}$ on the circumcircle of $APQ$.
We therefore proceed to draw the circumcircle of $APQ$, and we visually observe that it passes through $M$. Since $PM = QM$, it is indeed sufficient to prove that $A, Q, M$, and $P$ are concyclic. The figure strongly suggests invoking the power of $N$. Indeed, with respect to the circumcircle of $PCQG$, this power is $\overline{NP} \cdot \overline{NQ} = \overline{NG} \cdot \overline{NC}$. Moreover, we know that $N = (A + C) / 2$, that $M = (G + C) / 2$, and that $G = (2N + A) / 3$. We deduce that $\overline{NA} \cdot \overline{NM} = -3NG^2 = \overline{NG} \cdot \overline{NC} = \overline{NP} \cdot \overline{NQ}$.
This means that the points $A, Q, M$, and $P$ are indeed concyclic, and therefore that $M$ is the South Pole of $APQ$ from $A$, which concludes the proof.
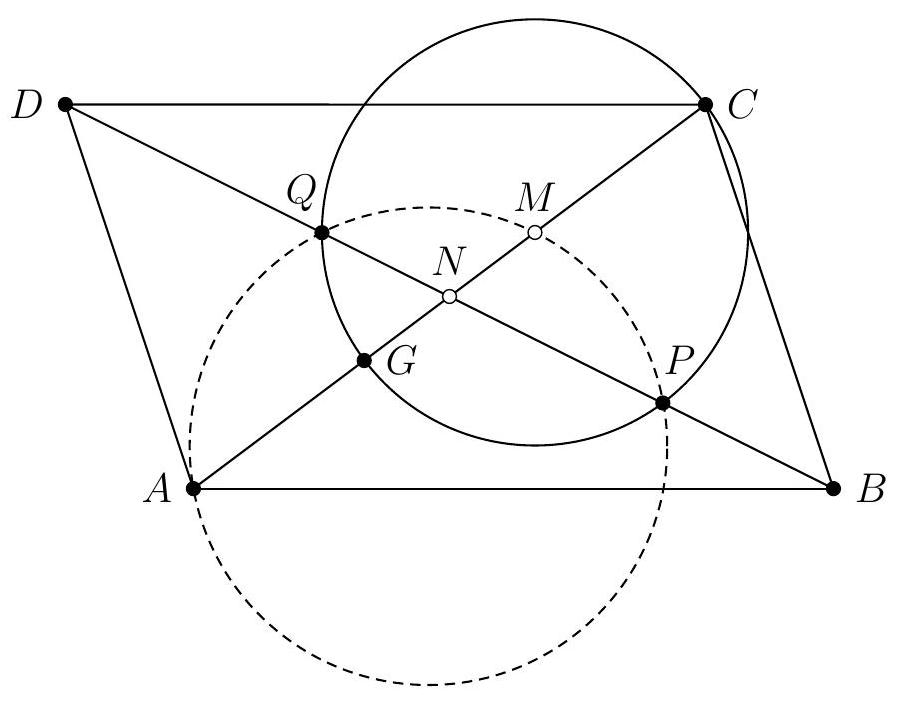
Comment from the graders: The problem was widely addressed, and the copies show a real effort on the part of the students to give themselves the means to progress. This can only be a cause for rejoicing.
Most students identified that the points $G, P, C$, and $Q$ are concyclic. Unfortunately, once this observation was made, very few students actually drew this new circle on their figure, although drawing the properties one demonstrates as one goes along is THE reflex to have in geometry. There is also a strong correlation between students who drew this circle on their figure (and who therefore needed to place its center) and students who went far in the problem. The introduction of the center of the circle with diameter $[CG]$ brought a lot of symmetry to the figure, which allowed for a significant approach to the solution.
Several students saw the South Pole configuration forming; all that remained was to prove a result of concyclicity. Surprisingly, a few students attempted length calculations using Ptolemy's characterization of cyclic quadrilaterals. This approach could be attempted, but not before looking at the criterion of the power of a point, which is much more practical to handle in the general case.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un parallélogramme et soit $G$ le centre de gravité du triangle $A B D$. Soit $P$ et $Q$ les points de la droite $(B D)$ tels que les droites $(G P)$ et $(P C)$ sont perpendiculaires et les droites $(G Q)$ et $(Q C)$ sont perpendiculaires.
Démontrer que la droite $(A G)$ est la bissectrice de l'angle $\widehat{P A Q}$.
|
Tout d'abord, puisque $A B C D$ est un parallélogramme, la médiane $(A G)$ du triangle $A B D$ et la diagonale $(A C)$ passent toutes deux par le milieu $N$ de $[B D]$.
Puisque $C G P$ et $C G Q$ sont rectangles en $P$ et en $Q$, les points $P$ et $Q$ sont les deux points d'intersection de $(B D)$ avec le cercle de diamètre $[C G]$. Puisque l'on trace ce cercle, on note donc $M$ son centre, c'est-à-dire le milieu de $[G C]$. En particulier, les cinq points $A, G, N, M$ et $C$ sont alignés.
Le moyen le plus sûr de démontrer que $(A G)$ est la bissectrice de $\widehat{P A Q}$ est alors d'invoquer le théorème du pôle Sud, c'est-à-dire de démontrer que $(A G)$ passe par le milieu de l'arc $\overparen{P Q}$ sur le cercle circonscrit à $A P Q$.
On entreprend donc de tracer le cercle circonscrit à $A P Q$, et on constate visuellement qu'il passe par $M$. Puisque $P M=Q M$, il suffit donc effectivement de démontrer que $A, Q, M$ et $P$ sont cocycliques. La figure suggère alors très fortement d'invoquer la puissance de $N$. En effet, par rapport au cercle circonscrit à $P C Q G$, cette puissance vaut $\overline{N P} \cdot \overline{N Q}=\overline{N G} \cdot \overline{N C}$. Par ailleurs, on sait que $N=(A+C) / 2$, que $M=(G+C) / 2$ et que $G=(2 N+A) / 3$. On en déduit que $\overline{N A} \cdot \overline{N M}=-3 N G^{2}=\overline{N G} \cdot \overline{N C}=\overline{N P} \cdot \overline{N Q}$.
Cela signifie bien que les points $A, Q, M$ et $P$ sont cocycliques, et donc que $M$ est le pôle Sud de $A P Q$ issu de $A$, ce qui conclut.

Commentaire des correcteurs Le problème a été beaucoup abordé, et les copies témoignent d'un réel effort de la part des élèves pour se donner les moyens d'avancer. On ne peut que s'en réjouir.
La plupart des élèves ont identifié que les points $G, P, C$ et $Q$ sont cocycliques. Malheureusement, une fois ce constat effectué, très peu d'élèves ont en fait tracé ce nouveau cercle sur leur figure, alors que faire apparaître sur sa figure les propriétés que l'on démontre au fur et à mesure est LE réflexe à avoir en géométrie. Il y a d'ailleurs une forte corrélation entre les élèves ayant tracé ce cercle sur leur figure (et qui ont donc eu besoin d'en placer le centre) et les élèves qui sont allés loin dans le problème. L'introduction du centre du cercle de diamètre $[C G]$ amenait beaucoup de symétrie dans la figure, ce qui permettait de beaucoup se rapprocher de la solution.
Plusieurs élèves ont vu la configuration du pôle Sud se dessiner; il ne leur restait plus qu'à démontrer un résultat de cocyclicité. Surprenamment, quelques élèves ont tenté des calculs de longueurs avec la caractérisation de Ptolémée des quadrilatères cycliques. Cette piste pouvait être tentée, mais pas avant d'avoir regardé le critère de la puissance d'un point, beaucoup plus pratique à manipuler dans le cas général.
|
{
"resource_path": "French/segmented/tests/fr-2022-2023-Corrigé-Web-Test-1.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
e62e421e-8394-5283-9e34-6186d490561b
| 605,733
|
Let $A, B, C, D$ and $E$ be five points located in this order on a circle $\Omega$, such that $(CD)$ is parallel to $(BE)$ and $(AB)$ is parallel to $(DE)$. Let $X, Y$ and $Z$ be the midpoints of the segments $[BD]$, $[CE]$ and $[AE]$ respectively.
Prove that the line $(AE)$ is tangent to the circumcircle of $XYZ$.
|
Let $O$ be the center of the circle $\Omega$. Whenever one focuses on drawing a figure including the circumcircle $\Gamma$ of $X Y Z$, it appears that $\Gamma$ is tangent to the three lines $(B D)$, $(C E)$, and $(A E)$, while its center seems to coincide with $O$. Therefore, we aim to prove the equalities of lengths $O X=O Y=O Z$, which will allow us to conclude that $(O Z)$ is a radius of $\Gamma$, and that the line $(A E)$, which is perpendicular to it, is indeed tangent to $\Gamma$.
If we denote $R$ as the radius of the circle $\Gamma$, the Pythagorean theorem indicates that
$$
O X^{2}=R^{2}-(B D)^{2} / 4, O Y^{2}=R^{2}-(C E)^{2} / 4 \text { and } O Z^{2}=R^{2}-(A E)^{2} / 4
$$
Thus, it is necessary to prove that $B D=C E=A E$.
Since $(C D)$ is parallel to $(B E)$ and the trapezoid $B C D E$ is inscribed in the circle $\Omega$, it is an isosceles trapezoid, so $B D=C E$. Similarly, since $(A B)$ is parallel to $(D E)$, the trapezoid $A B D E$, which is inscribed in $\Omega$, is also isosceles, and we conclude as desired that $A E=B D$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A, B, C, D$ et $E$ cinq points situés dans cet ordre sur un cercle $\Omega$, de sorte que $(C D)$ soit parallèle à $(B E)$ et que $(A B)$ soit parallèle à $(D E)$. Soit $X, Y$ et $Z$ les milieux respectifs des segments $[B D],[C E]$ et $[A E]$.
Démontrer que la droite $(A E)$ est tangente au cercle circonscrit à $X Y Z$.
|
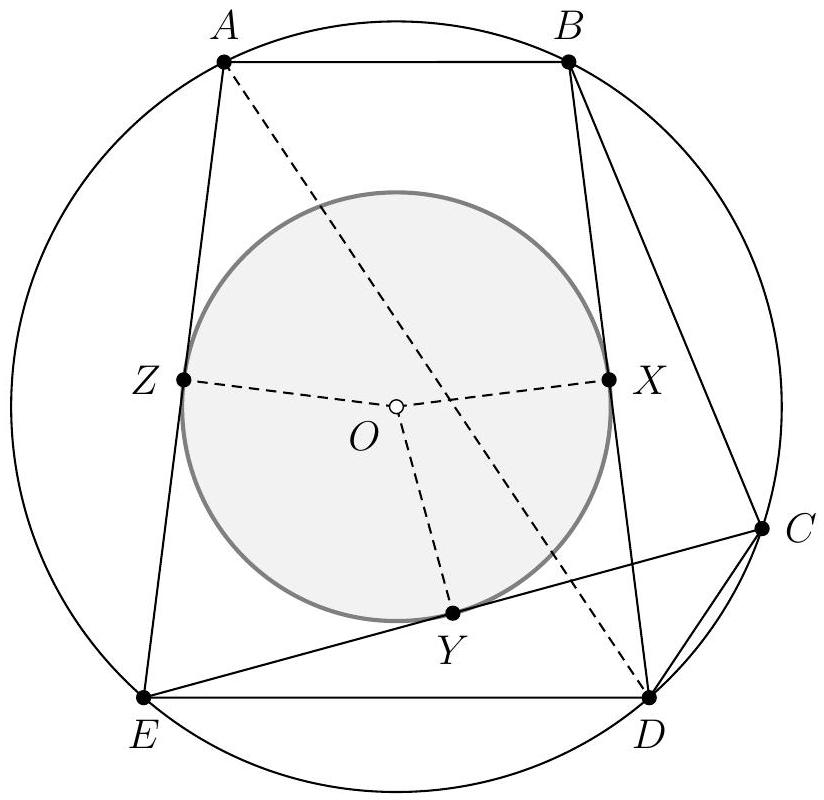
Soit $O$ le centre du cercle $\Omega$. Dès lors que l'on s'attache à tracer une figure incluant le cercle $\Gamma$ circonscrit à $X Y Z$, on constate que celui-ci semble tangent aux trois droites $(B D),(C E)$ et $(A E)$, tandis que son centre semble coïncider avec $O$. On entreprend donc de démontrer les égalités de longueurs $O X=O Y=O Z$, ce qui permettra de conclure que $(O Z)$ est un rayon de $\Gamma$, et que la droite $(A E)$, qui lui est perpendiculaire, est bien tangente à $\Gamma$.
Or, si l'on note $R$ le rayon du cercle $\Gamma$, le théorème de Pythagore indique que
$$
O X^{2}=R^{2}-(B D)^{2} / 4, O Y^{2}=R^{2}-(C E)^{2} / 4 \text { et } O Z^{2}=R^{2}-(A E)^{2} / 4
$$
Il s'agit donc de démontrer que $B D=C E=A E$.
Puisque $(C D)$ est parallèle à $(B E)$ et que le trapèze $B C D E$ est inscrit dans le cercle $\Omega$, il s'agit d'un trapèze isocèle, de sorte que $B D=C E$. De même, comme ( $A B$ ) est parallèle à $(D E)$, le trapèze $A B D E$, qui est inscrit dans $\Omega$, est lui aussi isocèle, et l'on conclut comme souhaité que $A E=B D$.
|
{
"resource_path": "French/segmented/tests/fr-2022-2023-Corrigé-Web-Test-2.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "## Solution de l'exercice 2"
}
|
b6fc4843-3490-5ef2-84bf-e013228cfc0c
| 605,792
|
Let $A, B, C, D$ and $E$ be five points located in this order on a circle $\Omega$, such that $(CD)$ is parallel to $(BE)$ and $(AB)$ is parallel to $(DE)$. Let $X, Y$ and $Z$ be the midpoints of the segments $[BD]$, $[CE]$ and $[AE]$ respectively.
Prove that the line $(AE)$ is tangent to the circumcircle of $XYZ$.
|
$n^{\circ} 1$ Here is another way to arrive at the equalities $B D=C E=A E$. These are equivalent to the angle equalities $\widehat{B O D}=\widehat{C O E}=\widehat{E O A}$. The parallelism of $(C D)$ and $(B E)$ then indicates that
$$
\widehat{B O D}=2 \widehat{B E D}=2\left(180^{\circ}-\widehat{E D C}\right)=\widehat{C O E},
$$
while the parallelism of $(A B)$ and $(D E)$ indicates as expected that
$$
\widehat{E O A}=2 \widehat{E D A}=2 \widehat{B A D}=\widehat{B O D}
$$
Examiner's Comment The problem admitted many solutions. All of them passed through the essential observation (which many students redemonstrated, sometimes through quite laborious reasoning) that the trapezoids $A B D E$ and $B E D C$ are isosceles. Once this observation was made, one could conclude by angle chasing or by involving the center of the circumcircle of $\Omega$, which, with a good figure, also appeared as the center of the circle passing through $X, Y$, and $Z$. The main difficulty encountered by students who did not solve the problem was not including the points $X, Y$, and $Z$ in their calculations.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A, B, C, D$ et $E$ cinq points situés dans cet ordre sur un cercle $\Omega$, de sorte que $(C D)$ soit parallèle à $(B E)$ et que $(A B)$ soit parallèle à $(D E)$. Soit $X, Y$ et $Z$ les milieux respectifs des segments $[B D],[C E]$ et $[A E]$.
Démontrer que la droite $(A E)$ est tangente au cercle circonscrit à $X Y Z$.
|
$n^{\circ} 1$ Voici une autre manière d'aboutir aux égalités $B D=C E=A E$. Celles-ci sont équivalentes aux égalités d'angles $\widehat{B O D}=\widehat{C O E}=\widehat{E O A}$. Le parallélisme de $(C D)$ et $(B E)$ indique alors que
$$
\widehat{B O D}=2 \widehat{B E D}=2\left(180^{\circ}-\widehat{E D C}\right)=\widehat{C O E},
$$
tandis que le parallélisme de $(A B)$ et $(D E)$ indique comme prévu que
$$
\widehat{E O A}=2 \widehat{E D A}=2 \widehat{B A D}=\widehat{B O D}
$$
Commentaire des correcteurs Le problème admettait de nombreuses solutions. Toutes passaient par la remarque essentielle (que beaucoup d'élèves ont redémontrée, parfois par
des raisonnement bien laborieux) que les trapèzes $A B D E$ et $B E D C$ sont isocèles. Une fois ce constat effectué, on pouvait conclure par chasse aux angles ou en faisant intervenir le centre du cercle circonscrit de $\Omega$ qui, avec une bonne figure, apparaissait également comme le centre du cercle passant par $X, Y$ et $Z$. La principale difficulté rencontrée par les élèves n'ayant pas réussi le problème est de ne pas avoir inclus les points $X, Y$ et $Z$ dans leurs calculs.
|
{
"resource_path": "French/segmented/tests/fr-2022-2023-Corrigé-Web-Test-2.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution alternative"
}
|
b6fc4843-3490-5ef2-84bf-e013228cfc0c
| 605,792
|
Let $x, y$ and $z$ be strictly positive real numbers such that $x y + y z + z x = 3$.
Prove that
$$
\frac{x+3}{y+z}+\frac{y+3}{z+x}+\frac{z+3}{x+y}+3 \geqslant 27 \frac{(\sqrt{x}+\sqrt{y}+\sqrt{z})^{2}}{(x+y+z)^{3}}
$$
|
Let $s=x+y+z$, and let $L$ and $R$ be the left and right sides of our inequality. We can rewrite $L$ as
$$
L=\frac{x+3}{y+z}+1+\frac{y+3}{z+x}+1+\frac{z+3}{x+y}+1=(s+3)\left(\frac{1}{y+z}+\frac{1}{z+x}+\frac{1}{x+y}\right).
$$
By the Cauchy-Schwarz inequality, applied to the vectors
$$
\left(\frac{1}{\sqrt{y+z}}, \frac{1}{\sqrt{z+x}}, \frac{1}{\sqrt{x+y}}\right) \text { and }(\sqrt{y+z}, \sqrt{z+x}, \sqrt{x+y})
$$
we have
$$
\left(\frac{1}{y+z}+\frac{1}{z+x}+\frac{1}{x+y}\right)(y+z+z+x+x+y) \geqslant(1+1+1)^{2}
$$
From this, we deduce that $L \geqslant 9(s+3) /(2 s)$.
Furthermore, the arithmetic-quadratic inequality, applied to the terms $\sqrt{x}, \sqrt{y}$, and $\sqrt{z}$, indicates that
$$
\frac{s}{3} \geqslant\left(\frac{\sqrt{x}+\sqrt{y}+\sqrt{z}}{3}\right)^{2}
$$
Thus, $(\sqrt{x}+\sqrt{y}+\sqrt{z})^{2} \leqslant 3(x+y+z)=3 s$ and $R \leqslant 81 / s^{2}$.
To show that $L \geqslant R$, it suffices to prove that $9(s+3) \times s^{2} \geqslant 81 \times 2 s$, which is equivalent to $s(s+3) \geqslant 18$, or $s \geqslant 3$. We conclude by using the turnstile lemma, which states that
$$
s^{2}=x^{2}+y^{2}+z^{2}+2(x y+y z+z x) \geqslant 3(x y+y z+z x) \geqslant 9
$$
which means $s \geqslant 3$.
Remark: The particular case of the Cauchy-Schwarz inequality that we used is also known as the bad students' inequality: here, applying the bad students' inequality to the fractions
$$
\frac{1^{2}}{y+z}, \frac{1^{2}}{z+x} \text { and } \frac{1^{2}}{x+y}
$$
indicates that
$$
\frac{1^{2}}{y+z}+\frac{1^{2}}{z+x}+\frac{1^{2}}{x+y} \geqslant \frac{(1+1+1)^{2}}{y+z+z+x+x+y}
$$
$\underline{\text { Alternative Solution } n^{\circ} 1}$ This time, we use the Nesbitt's inequality, which states that
$$
\frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y} \geqslant \frac{3}{2}
$$
and the bad students' inequality, which still indicates that
$$
\frac{1}{y+z}+\frac{1}{z+x}+\frac{1}{x+y} \geqslant \frac{9}{2 s}
$$
Thus,
$$
L \geqslant \frac{3}{2}+\frac{3 \times 9}{2 s}+3=9 \frac{s+3}{2 s}
$$
We then conclude the exercise in the same way as before.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $x, y$ et $z$ des réels strictement positifs tels que $x y+y z+z x=3$.
Démontrer que
$$
\frac{x+3}{y+z}+\frac{y+3}{z+x}+\frac{z+3}{x+y}+3 \geqslant 27 \frac{(\sqrt{x}+\sqrt{y}+\sqrt{z})^{2}}{(x+y+z)^{3}}
$$
|
Posons $s=x+y+z$, et soit $L$ et $R$ les membres de gauche et de droite de notre inégalité. On peut réécrire $L$ comme
$$
L=\frac{x+3}{y+z}+1+\frac{y+3}{z+x}+1+\frac{z+3}{x+y}+1=(s+3)\left(\frac{1}{y+z}+\frac{1}{z+x}+\frac{1}{x+y}\right) .
$$
Or, l'inégalité de Cauchy-Schwarz, appliquée aux vecteurs
$$
\left(\frac{1}{\sqrt{y+z}}, \frac{1}{\sqrt{z+x}}, \frac{1}{\sqrt{x+y}}\right) \text { et }(\sqrt{y+z}, \sqrt{z+x}, \sqrt{x+y})
$$
indique que
$$
\left(\frac{1}{y+z}+\frac{1}{z+x}+\frac{1}{x+y}\right)(y+z+z+x+x+y) \geqslant(1+1+1)^{2}
$$
On en déduit que $L \geqslant 9(s+3) /(2 s)$.
En outre, l'inégalité arithmético-quadratique, appliquée aux termes $\sqrt{x}, \sqrt{y}$ et $\sqrt{z}$, indique que
$$
\frac{s}{3} \geqslant\left(\frac{\sqrt{x}+\sqrt{y}+\sqrt{z}}{3}\right)^{2}
$$
Ainsi, $(\sqrt{x}+\sqrt{y}+\sqrt{z})^{2} \leqslant 3(x+y+z)=3 s$ et $R \leqslant 81 / s^{2}$.
Pour montrer que $L \geqslant R$, il suffit donc de démontrer que $9(s+3) \times s^{2} \geqslant 81 \times 2 s$, c'est-à-dire que $s(s+3) \geqslant 18$, ou encore que $s \geqslant 3$. On conclut alors en utilisant le lemme du tourniquet, qui indique que
$$
s^{2}=x^{2}+y^{2}+z^{2}+2(x y+y z+z x) \geqslant 3(x y+y z+z x) \geqslant 9
$$
c'est-à-dire que $s \geqslant 3$.
Remarque: Le cas particulier de l'inégalité de Cauchy-Schwarz que nous avons utilisé est aussi appelé inégalité des mauvais élèves: ici, appliquer l'inégalité des mauvais élèves aux fractions
$$
\frac{1^{2}}{y+z^{\prime}}, \frac{1^{2}}{z+x} \text { et } \frac{1^{2}}{x+y}
$$
nous indique que
$$
\frac{1^{2}}{y+z}+\frac{1^{2}}{z+x}+\frac{1^{2}}{x+y} \geqslant \frac{(1+1+1)^{2}}{y+z+z+x+x+y}
$$
$\underline{\text { Solution alternative } n^{\circ} 1}$ Cette fois-ci, on utilise d'une part l'inégalité de Nesbitt, qui indique que
$$
\frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y} \geqslant \frac{3}{2}
$$
et d'autre part l'inégalité des mauvais élèves, qui indique toujours que
$$
\frac{1}{y+z}+\frac{1}{z+x}+\frac{1}{x+y} \geqslant \frac{9}{2 s}
$$
Ainsi,
$$
L \geqslant \frac{3}{2}+\frac{3 \times 9}{2 s}+3=9 \frac{s+3}{2 s}
$$
On conclut alors l'exercice de la même façon que précédemment.
|
{
"resource_path": "French/segmented/tests/fr-2022-2023-Corrigé-Web-Test-2.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
9945e23e-2bdd-52a1-b896-49c7d275a73c
| 605,810
|
Let $x, y$ and $z$ be strictly positive real numbers such that $x y + y z + z x = 3$.
Prove that
$$
\frac{x+3}{y+z}+\frac{y+3}{z+x}+\frac{z+3}{x+y}+3 \geqslant 27 \frac{(\sqrt{x}+\sqrt{y}+\sqrt{z})^{2}}{(x+y+z)^{3}}
$$
|
$n^{\circ} 2$ Since the function $f: t \mapsto 1 / t$ is convex, we know that
$$
L=(s+3)(f(y+z)+f(z+x)+f(x+y)) \geqslant 3(s+3) f(2 s / 3)=9(s+3) /(2 s) .
$$
Similarly, the rearrangement inequality, applied to the terms $\sqrt{x}, \sqrt{y}$ and $\sqrt{z}$, indicates that
$$
R \leqslant 27 \frac{3 s}{s^{3}}=\frac{81}{s^{2}} .
$$
To show that $L \geqslant R$, it is therefore sufficient to prove that $3(s+3) \times s^{2} \geqslant 81 \times 2 s / 3$, that is, $s(s+3) \geqslant 18$, or again that $s \geqslant 3$.
We conclude by noting that the rearrangement inequality, applied to the terms $x$, $y$ and $z$, indicates that
$$
s^{2}=x^{2}+y^{2}+z^{2}+2(x y+y z+z x) \geqslant 3(x y+y z+z x) \geqslant 9,
$$
that is, $s \geqslant 3$.
Comment from the graders The exercise was quite approached but little successful. Indeed, many students try to expand everything, for example by calculating $(x+y+z)^{3}$ and then replacing all the 3's by $x y+y z+x z$. This approach is not necessarily the most natural: in an inequality problem, a more fruitful approach is often to use inequalities directly, while a 10-line calculation without a single inequality suggests changing direction. Here, trying many inequalities was a good idea: there were multiple ways to reach the result, for example by using the Cauchy-Schwarz, bad students, Nesbitt or convexity inequalities.
All these inequalities could advance the solution, provided that one had thought about the relevance of their use; for example, using the bad students' inequality by writing the numerator $x+3$ of the fraction $(x+3) /(y+z)$ as $\sqrt{x+3}^{2}=x+3$ is not very natural, as $\sqrt{x+3}$ plays no special role. If one is to use this inequality, it is better to split the fraction into 2, with two numerators equal to $x$ and 3, which can then be treated independently of each other.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $x, y$ et $z$ des réels strictement positifs tels que $x y+y z+z x=3$.
Démontrer que
$$
\frac{x+3}{y+z}+\frac{y+3}{z+x}+\frac{z+3}{x+y}+3 \geqslant 27 \frac{(\sqrt{x}+\sqrt{y}+\sqrt{z})^{2}}{(x+y+z)^{3}}
$$
|
$n^{\circ} 2$ Puisque la fonction $f: t \mapsto 1 / t$ est convexe, on sait que
$$
L=(s+3)(f(y+z)+f(z+x)+f(x+y)) \geqslant 3(s+3) f(2 s / 3)=9(s+3) /(2 s) .
$$
De même, l'inégalité du réordonnement, appliquée aux termes $\sqrt{x}, \sqrt{y}$ et $\sqrt{z}$, indique que
$$
R \leqslant 27 \frac{3 s}{s^{3}}=\frac{81}{s^{2}} .
$$
Pour montrer que $L \geqslant R$, il suffit donc de démontrer que $3(s+3) \times s^{2} \geqslant 81 \times 2 s / 3$, c'est-à-dire que $s(s+3) \geqslant 18$, ou encore que $s \geqslant 3$.
On conclut alors en remarquant que l'inégalité du réordonnement, appliquée aux termes $x$, $y$ et $z$, indique que
$$
s^{2}=x^{2}+y^{2}+z^{2}+2(x y+y z+z x) \geqslant 3(x y+y z+z x) \geqslant 9,
$$
c'est-à-dire que $s \geqslant 3$.
Commentaire des correcteurs L'exercice a été assez abordé mais peu réussi. En effet, de nombreux élèves tentent de tout développer, par exemple en calculant $(x+y+z)^{3}$ puis en remplaçant tous les 3 par $x y+y z+x z$. Cette approche n'est pas nécessairement la plus naturelle : dans un problème d'inégalité, une approche souvent plus fructueuse est d'utiliser directement des inégalités, tandis qu'un calcul de 10 lignes sans une seule inégalité suggère de changer de direction. Ici, ici tenter beaucoup d'inégalités était une bonne idée : il y avait de multiples manières d'aboutir au résultat, par exemple en utilisant les inégalités de Cauchy-Schwarz, des mauvais élèves, de Nesbitt ou de convexité.
Toutes ces inégalités permettaient d'avancer, sous réserve que l'on ait réfléchi à la pertinence de leur utilisation; par exemple, utiliser l'inégalité des mauvais élèves en écrivant le numérateur $x+3$ de la fraction $(x+3) /(y+z)$ comme $\sqrt{x+3}^{2}=x+3$ n'est pas très naturel, car $\sqrt{x+3}$ ne joue aucun rôle spécial. Quitte à utiliser cette inégalité, autant découper la fraction en 2 , avec deux numérateurs égaux à $x$ et à 3 , que l'on pourra éventuellement traiter indépendamment l'une de l'autre.
|
{
"resource_path": "French/segmented/tests/fr-2022-2023-Corrigé-Web-Test-2.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution alternative"
}
|
9945e23e-2bdd-52a1-b896-49c7d275a73c
| 605,810
|
Prove: If \( x, y, z \) are the lengths of the angle bisectors of a triangle with a perimeter of 6, then
$$
\frac{1}{x^2}+\frac{1}{y^2}+\frac{1}{z^2} \geq 1
$$
|
Consider the adjacent figure.
DP and DQ are the parallels through D to AB and
AC. Since $A D=x$ is the angle bisector of $\alpha$, AQDP is a rhombus, whose side length is denoted by $u$.
From the similarity of triangles PDC and QBD, it follows that $\frac{u}{c-u}=\frac{b-u}{u}$, from which we obtain $u=\frac{bc}{b+c}$.
Applying the Law of Cosines in triangle AQD leads to
\[
\begin{aligned}
x^{2}=2 u^{2}-2 u^{2} \cos (\pi-\alpha) & =2 u^{2}(1+\cos \alpha) \\
=2 u^{2}\left(1+\frac{b^{2}+c^{2}-a^{2}}{2 b c}\right)=2 u^{2} & \frac{(b+c)^{2}-a^{2}}{2 b c}= \\
& =\frac{b c}{(b+c)^{2}}(a+b+c)(-a+b+c)
\end{aligned}
\]
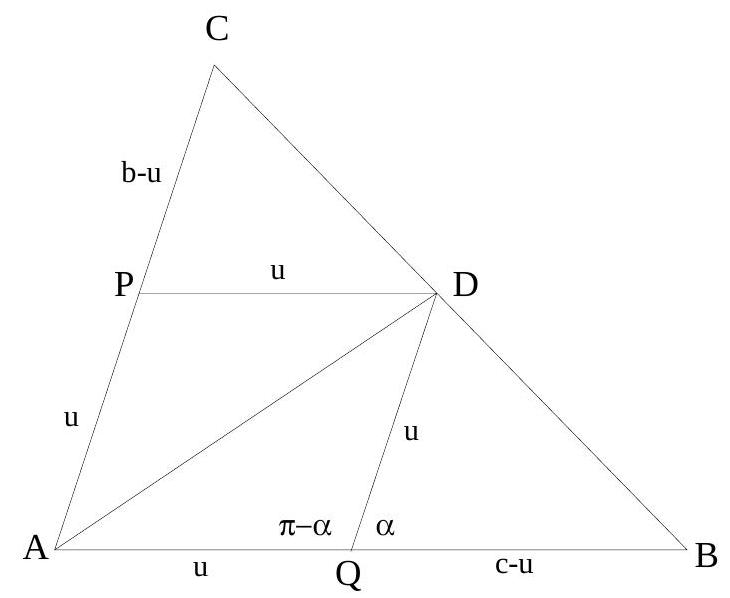
With $(b+c)^{2} \geq 4 b c$ and $a+b+c=6$, it follows that $x^{2} \leq 1.5(-a+b+c)$.
Similarly, we get $y^{2} \leq 1.5(a-b+c)$ and $z^{2} \leq 1.5(a+b-c)$.
From the inequality between the arithmetic and geometric means of three positive numbers, we get $\left(\frac{1}{x^{2}}+\frac{1}{y^{2}}+\frac{1}{z^{2}}\right)\left(x^{2}+y^{2}+z^{2}\right) \geq 9$ and from this, finally,
\[
\frac{1}{x^{2}}+\frac{1}{y^{2}}+\frac{1}{z^{2}} \geq \frac{9}{x^{2}+y^{2}+z^{2}} \geq \frac{9}{1.5 \cdot 6}=1
\]
where the equality sign holds only for $x=y=z$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Man beweise: Sind x, y, z die Längen der Winkelhalbierenden eines Dreiecks mit dem Umfang 6, dann gilt
$$
\frac{1}{\mathrm{x}^{2}}+\frac{1}{\mathrm{y}^{2}}+\frac{1}{\mathrm{z}^{2}} \geq 1
$$
|
Man beachte nebenstehende Figur.
DP und DQ sind die Parallelen durch D zu AB und
AC. Da $A D=x$ die Winkelhalbierende von $\alpha$ ist, ist AQDP eine Raute, deren Seitenlänge mit $u$ bezeichnet wurde.
Aus der Ähnlichkeit der Dreiecke PDC mit QBD folgt $\frac{\mathrm{u}}{\mathrm{c}-\mathrm{u}}=\frac{\mathrm{b}-\mathrm{u}}{\mathrm{u}}$, woraus man $u=\frac{b c}{b+c}$ erhält.
Der Kosinussatz im Dreieck AQD führt zu
$$
\begin{aligned}
\mathrm{x}^{2}=2 \mathrm{u}^{2}-2 \mathrm{u}^{2} \cos (\pi-\alpha) & =2 \mathrm{u}^{2}(1+\cos \alpha) \\
=2 u^{2}\left(1+\frac{b^{2}+c^{2}-a^{2}}{2 b c}\right)=2 u^{2} & \frac{(b+c)^{2}-a^{2}}{2 b c}= \\
& =\frac{b c}{(b+c)^{2}}(a+b+c)(-a+b+c)
\end{aligned}
$$

Mit $(b+c)^{2} \geq 4 b c$ und $a+b+c=6$ folgt $x^{2} \leq 1,5(-a+b+c)$.
Ähnlich ergibt sich $y^{2} \leq 1,5(a-b+c)$ und $z^{2} \leq 1,5(a+b-c)$.
Aus der Ungleichung zwischen dem arithmetischen und geometrischen Mittel dreier positiver Zahlen, ergibt sich $\left(\frac{1}{x^{2}}+\frac{1}{y^{2}}+\frac{1}{z^{2}}\right)\left(x^{2}+y^{2}+z^{2}\right) \geq 9$ und hieraus schließlich
$$
\frac{1}{x^{2}}+\frac{1}{y^{2}}+\frac{1}{z^{2}} \geq \frac{9}{x^{2}+y^{2}+z^{2}} \geq \frac{9}{1,5 \cdot 6}=1
$$
wobei das Gleichheitszeichen nur für $x=y=z$ gilt.
|
{
"resource_path": "Germany_TST/segmented/de-2002-loes_awkl1_02.jsonl",
"problem_match": "# Aufgabe 2",
"solution_match": "# Lösung\n"
}
|
0e78735c-283e-564f-b8b6-f77118c7cb02
| 605,988
|
In an acute-angled triangle $A B C$, a square with center $A_{1}$ is inscribed such that two vertices lie on $B C$ and one each on $A B$ and $A C$. Analogously, the squares with centers $B_{1}$ and $C_{1}$ are defined.
Prove that the lines $A A_{1}, B B_{1}$, and $C C_{1}$ have a common intersection point.
|
In addition to the given figure, we consider the square constructed outwardly over the side $AB$ with the center $C_{2}$. Since there is a central dilation that transforms the inscribed square with center $C_{1}$ into the outwardly constructed square, $C, C_{1}$, and $C_{2}$ lie on a straight line.
The height $h_{c}$ intersects $AB$ at $H_{c}$, and let $\left|A H_{c}\right|=p,\left|H_{c} B\right|=q$. Furthermore, let $M_{c}$ be the midpoint of $AB$ and $C^{\prime}$ be the intersection of $C C_{2}$ with $AB$. Finally, set $\left|A C^{\prime}\right|=c_{1}$ and $\left|C^{\prime} B\right|=c_{2}$. All subsegments of $AB$ exist due to the acute angles of triangle $ABC$. For the other sides of the triangle, corresponding points and segments are defined analogously.
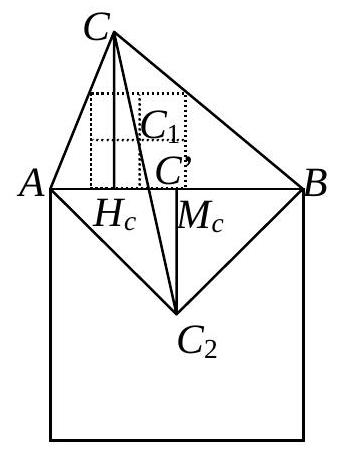
By the intercept theorems, $\frac{\left|H_{c} C^{\prime}\right|}{\left|C H_{c}\right|}=\frac{\left|C^{\prime} M_{c}\right|}{\left|M_{c} C_{2}\right|}$, i.e., $\frac{c_{1}-p}{h_{c}}=\frac{\frac{1}{2} c-c_{1}}{\frac{1}{2} c} \Rightarrow c_{1}=\frac{c\left(p+h_{c}\right)}{c+2 h_{c}}$.
Similarly, $c_{2}=\frac{c\left(q+h_{c}\right)}{c+2 h_{c}}$ and we obtain $\frac{c_{1}}{c_{2}}=\frac{\frac{p}{h_{c}}+1}{\frac{q}{h_{c}}+1}$. (For $\alpha=\beta$, $\frac{c_{1}}{c_{2}}=1$. )
The angles between the heights and the respective adjacent sides are cyclically denoted by $\gamma_{1}, \gamma_{2}$, $\alpha_{1}, \alpha_{2}$, and $\beta_{1}, \beta_{2}$. Then, $\alpha_{1}=\gamma_{2}\left(=90^{\circ}-\beta\right), \quad \beta_{1}=\alpha_{2}\left(=90^{\circ}-\gamma\right)$, and $\gamma_{1}=\beta_{2}\left(=90^{\circ}-\alpha\right)$. Furthermore, $\frac{p}{h_{c}}=\tan \gamma_{1}$ and $\frac{q}{h_{c}}=\tan \gamma_{2}$, so $\frac{c_{1}}{c_{2}}=\frac{\tan \gamma_{1}+1}{\tan \gamma_{2}+1}$. Similarly, $\frac{a_{1}}{a_{2}}=\frac{\tan \alpha_{1}+1}{\tan \alpha_{2}+1}$ and $\frac{b_{1}}{b_{2}}=\frac{\tan \beta_{1}+1}{\tan \beta_{2}+1}$. Therefore,
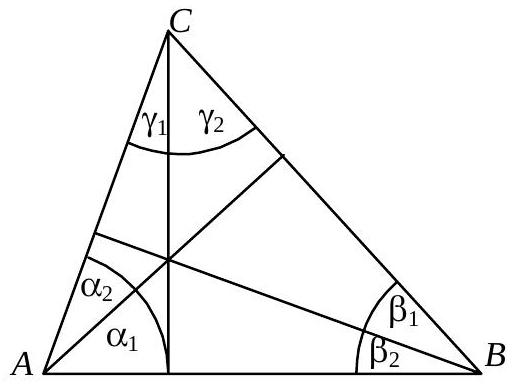
\[
\frac{a_{1}}{a_{2}} \cdot \frac{b_{1}}{b_{2}} \cdot \frac{c_{1}}{c_{2}}=\frac{\left(\tan \alpha_{1}+1\right)\left(\tan \beta_{1}+1\right)\left(\tan \gamma_{1}+1\right)}{\left(\tan \alpha_{2}+1\right)\left(\tan \beta_{2}+1\right)\left(\tan \gamma_{2}+1\right)}=\frac{\tan \alpha_{1}+1}{\tan \gamma_{2}+1} \cdot \frac{\tan \beta_{1}+1}{\tan \alpha_{2}+1} \cdot \frac{\tan \gamma_{1}+1}{\tan \beta_{2}+1}=1 \cdot 1 \cdot 1=1.
\]
By the converse of Ceva's theorem, the lines $A A^{\prime}=A A_{1}$, $B B^{\prime}=B B_{1}$, and $C C^{\prime}=C C_{1}$ intersect at a point.
Note: Some participants conjectured that the lines $A A_{1}$ etc. are the angle bisectors of the given triangle. This conjecture is false, as can be seen from a very acute, nearly right-angled triangle. Ceva's theorem is not necessary for the proof; there are other solution methods, such as using spiral dilations.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In ein spitzwinkliges Dreieck $A B C$ wird ein Quadrat mit Mittelpunkt $A_{1}$ so einbeschrieben, dass zwei Ecken auf $B C$ und je eine auf $A B$ bzw. $A C$ liegen. Analog sind die Quadrate mit den Mittelpunkten $B_{1}$ bzw. $C_{1}$ definiert.
Man beweise, dass die Geraden $A A_{1}, B B_{1}$ und $C C_{1}$ einen gemeinsamen Schnittpunkt haben.
|
Zusätzlich zur gegebenen Figur betrachten wir das nach außen errichtete Quadrat über der Seite $A B$ mit dem Mittelpunkt $C_{2}$. Da es eine zentrische Streckung gibt, welche das einbeschriebene Quadrat mit Mittelpunkt $C_{1}$ in das nach außen errichtete Quadrat überführt, liegen $C, C_{1}$ und $C_{2}$ auf einer Geraden.
Die Höhe $h_{c}$ schneidet $A B$ in $H_{c}$ und es sei $\left|A H_{c}\right|=p,\left|H_{c} B\right|=q$. Ferner sei $M_{c}$ der Mittelpunkt von $A B$ und $C^{\prime}$ der Schnittpunkt von $C C_{2}$ mit $A B$. Schließlich setzen wir $\left|A C^{\prime}\right|=c_{1}$ und $\left|C^{\prime} B\right|=c_{2}$. Alle Teilstrecken von $A B$ existieren wegen der Spitzwinkligkeit des Dreiecks $A B C$. Für die anderen Dreiecksseiten seien entsprechende

Punkte und Abschnitte analog definiert.
Nach den Strahlensätzen gilt $\frac{\left|H_{c} C^{\prime}\right|}{\left|C H_{c}\right|}=\frac{\left|C^{\prime} M_{c}\right|}{\left|M_{c} C_{2}\right|}$, d.h. $\frac{c_{1}-p}{h_{c}}=\frac{\frac{1}{2} c-c_{1}}{\frac{1}{2} c} \Rightarrow c_{1}=\frac{c\left(p+h_{c}\right)}{c+2 h_{c}}$.
Analog ist $c_{2}=\frac{c\left(q+h_{c}\right)}{c+2 h_{c}}$ und wir erhalten $\frac{c_{1}}{c_{2}}=\frac{\frac{p}{h_{c}}+1}{\frac{q}{h_{c}}+1}$. (Für $\alpha=\beta$ ist $\frac{c_{1}}{c_{2}}=1$. )
Die Winkel zwischen den Höhen und den jeweils anliegenden beiden Seiten seien zyklisch mit $\gamma_{1}, \gamma_{2}$ bzw. $\alpha_{1}, \alpha_{2}$ bzw. $\beta_{1}, \beta_{2}$ bezeichnet. Dann gilt $\alpha_{1}=\gamma_{2}\left(=90^{\circ}-\beta\right), \quad \beta_{1}=\alpha_{2}\left(=90^{\circ}-\gamma\right)$ und $\gamma_{1}=\beta_{2}\left(=90^{\circ}-\alpha\right)$. Ferner ist $\frac{p}{h_{c}}=\tan \gamma_{1}$ und $\frac{q}{h_{c}}=\tan \gamma_{2}$, also $\frac{c_{1}}{c_{2}}=\frac{\tan \gamma_{1}+1}{\tan \gamma_{2}+1}$. Analog gilt $\frac{a_{1}}{a_{2}}=\frac{\tan \alpha_{1}+1}{\tan \alpha_{2}+1}$ und $\frac{b_{1}}{b_{2}}=\frac{\tan \beta_{1}+1}{\tan \beta_{2}+1}$. Damit ist

$\frac{a_{1}}{a_{2}} \cdot \frac{b_{1}}{b_{2}} \cdot \frac{c_{1}}{c_{2}}=\frac{\left(\tan \alpha_{1}+1\right)\left(\tan \beta_{1}+1\right)\left(\tan \gamma_{1}+1\right)}{\left(\tan \alpha_{2}+1\right)\left(\tan \beta_{2}+1\right)\left(\tan \gamma_{2}+1\right)}=\frac{\tan \alpha_{1}+1}{\tan \gamma_{2}+1} \cdot \frac{\tan \beta_{1}+1}{\tan \alpha_{2}+1} \cdot \frac{\tan \gamma_{1}+1}{\tan \beta_{2}+1}=1 \cdot 1 \cdot 1=1$.
Nach der Umkehrung des Satzes von Ceva schneiden sich daher die Geraden $A A^{\prime}=A A_{1}$, $B B^{\prime}=B B_{1}$ und $C C^{\prime}=C C_{1}$ in einem Punkt.
Anmerkung: Einige Teilnehmer haben vermutet, die Geraden $A A_{1}$ etc. seien die Winkelhalbierenden des gegebenen Dreiecks. Diese Vermutung ist falsch, wie man an einem sehr spitzen, fast rechtwinkligen Dreieck sieht. Der Satz von Ceva ist zum Beweis nicht notwendig; es gibt andere Lösungsmöglichkeiten, z.B. mit Drehstreckungen.
|
{
"resource_path": "Germany_TST/segmented/de-2002-loes_awkl2_02.jsonl",
"problem_match": "# Aufgabe 2",
"solution_match": "# Lösung\n"
}
|
6688f26c-e360-5ecd-9887-9252e35cc833
| 606,012
|
Prove that there is no positive integer $n$ with the following property: For $k=1,2, \ldots, 9$ the leftmost digit - in decimal notation - of $(n+k)!$ is $k$.
|
We assume that there is a number $n$ with the required property. Then none of the factorials can be a power of ten, because from 3! onwards all factorials are divisible by 3 and the first factorials obviously do not have the required property. None of the numbers $n+2, \ldots, n+9$ can be a power of ten either, because otherwise the leading digit of two consecutive factorials in the considered sequence would be the same. Thus, there is a $j$ such that $10^{j}<n+2<\ldots<n+9<10^{j+1}$ (1). Because $(n+8)!$ ends with an 8 and $(n+9)!$ with a 9, there are natural numbers $a$ and $b$ with $9 \cdot 10^{a}<(n+9)!<10^{a+1}$ and $8 \cdot 10^{b}<(n+8)!<9 \cdot 10^{b}$, which leads to $10^{a-b}<n+9<\frac{5}{4} \cdot 10^{a-b}$.
From (1) it follows that $j=a-b$ and $10^{j}<n+2<\ldots<n+9<\frac{5}{4} \cdot 10^{j}$ (2).
Since $(n+1)!$ starts with a 1, there is an $m$ such that $10^{m}<(n+1)!<2 \cdot 10^{m}$, while from (2) it follows: $10^{3 j}<(n+2)(n+3)(n+4)<\left(\frac{5}{4}\right)^{3} \cdot 10^{3 j}$. Multiplying the last two inequalities yields $10^{3 j+m}<(n+4)!<2 \cdot \frac{125}{64} \cdot 10^{3 j+m}$, which can be weakened to $10^{3 j+m}<(n+4)!<4 \cdot 10^{3 j+m}$ because $\frac{250}{64}<4$. This implies that the number $(n+4)!$ would not start with 4, but with 1, 2, or 3 - in contradiction to the assumption.
Note: Most participants who attempted this or similar estimates were also successful. However, this problem sometimes led to very unclear presentations.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Man beweise, dass es keine positive ganze Zahl $n$ mit der folgenden Eigenschaft gibt: Für $k=1,2, \ldots, 9$ ist die - in dezimaler Schreibweise - linke Ziffer von $(n+k)$ ! gleich $k$.
|
Wir nehmen an, dass es eine Zahl $n$ mit der verlangten Eigenschaft gibt. Dann kann keine der Fakultäten eine Zehnerpotenz sein, weil ab 3! alle Fakultäten durch 3 teilbar sind und die ersten Fakultäten offensichtlich nicht die verlangte Eigenschaft haben. Es kann auch keine der Zahlen $n+2, \ldots, n+9$ eine Zehnerpotenz sein, weil sonst die Anfangsziffer zweier aufeinanderfolgender Fakultäten in der betrachteten Folge dieselbe wäre. Somit gibt es ein $j$ mit $10^{j}<n+2<\ldots<n+9<10^{j+1}$ (1). Weil $(n+8)$ ! mit einer 8 und $(n+9)$ ! mit einer 9 endet, gibt es natürliche Zahlen a und $b$ mit $9 \cdot 10^{a}<(n+9)!<10^{a+1}$ und $8 \cdot 10^{b}<(n+8)!<9 \cdot 10^{b}$, was auf $10^{a-b}<n+9<\frac{5}{4} \cdot 10^{a-b}$ führt.
Mit (1) folgt $j=a-b$ und $10^{j}<n+2<\ldots<n+9<\frac{5}{4} \cdot 10^{j}$ (2).
Da $(n+1)$ ! mit 1 anfängt, gibt es ein $m$ mit $10^{m}<(n+1)!<2 \cdot 10^{m}$, während aus (2) folgt: $10^{3 j}<(n+2)(n+3)(n+4)<\left(\frac{5}{4}\right)^{3} \cdot 10^{3 j}$. Multiplikation der beiden letzten Ungleichungen liefert $10^{3 j+m}<(n+4)!<2 \cdot \frac{125}{64} \cdot 10^{3 j+m}$, was wegen $\frac{250}{64}<4 \mathrm{zu} 10^{3 j+m}<(n+4)!<4 \cdot 10^{3 j+m}$ abgeschwächt werden kann. Daraus folgt, dass die Zahl $(n+4)$ ! nicht mit 4, sondern mit 1, 2 oder 3 beginnen würde - im Widerspruch zur Voraussetzung.
Anmerkung: Die meisten Teilnehmer, die sich auf diese oder ähnliche Abschätzungen eingelassen hatten, waren dann auch erfolgreich. Allerdings gab es gerade bei dieser Aufgabe z.T. sehr unübersichtliche Darstellungen.
|
{
"resource_path": "Germany_TST/segmented/de-2002-loes_awkl2_02.jsonl",
"problem_match": "# Aufgabe 3",
"solution_match": "# Lösung\n"
}
|
f55e2ffc-bf2f-5366-a713-b18f11a99472
| 606,021
|
Gegeben ist ein Dreieck ABC und ein Punkt M so, dass die Geraden MA, MB, MC die Geraden BC, CA, AB (in dieser Reihenfolge) in D, E beziehungsweise F schneiden.
Man beweise, dass es dann stets die Zahlen $\varepsilon_{1}, \varepsilon_{2}, \varepsilon_{3}$ aus $\{-1,1\}$ gibt, so dass gilt:
$\varepsilon_{1} \cdot \frac{M D}{A D}+\varepsilon_{2} \cdot \frac{M E}{B E}+\varepsilon_{3} \cdot \frac{M F}{C F}=1$
|
Punkt $M$ ( $M \notin\{A, B, C\})$ kann entweder auf einer der vorgegebenen Geraden, oder in einer der sieben Gebiete liegen, in denen die Ebene des Dreiecks ABC durch die Geraden $A B, B C, C A$ geteilt wird.
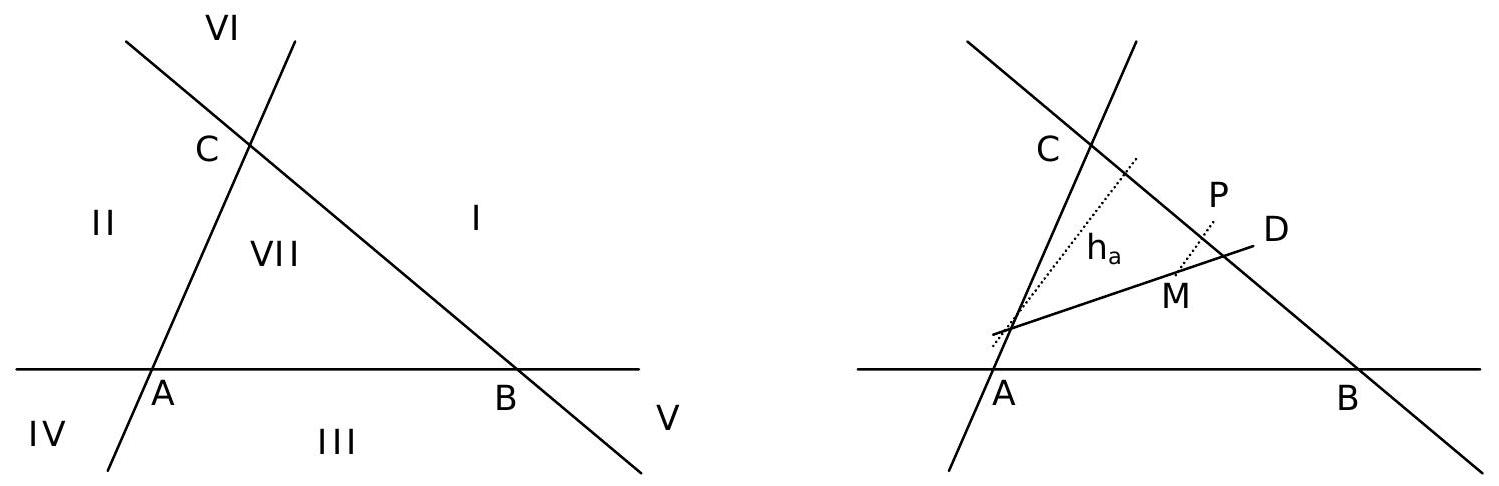
Es ist stets
$$
\begin{aligned}
& \frac{M D}{A D}=\frac{M P}{h_{a}}=\frac{0,5 \cdot M P \cdot B C}{0,5 \cdot h_{a} \cdot B C}=\frac{F(M B C)}{F(A B C)}, \\
& \text { (Strahlensatz) }
\end{aligned}
$$
wobei $P \in B C$ und $M P \perp B C$ und $F(X Y Z)$ der Inhalt des Dreiecks XYZ ist. Ähnliches gilt für die anderen Verhältnisse.
Liegt M im Inneren oder am Rande des Dreiecks $A B C$, dann ist also:
$$
\frac{M D}{A D}+\frac{M E}{B E}+\frac{M F}{C F}=\frac{F(M B C)}{F(A B C)}+\frac{F(M C A)}{F(A B C)}+\frac{F(M A B)}{F(A B C)}=1
$$
woraus $\varepsilon_{1}=\varepsilon_{2}=\varepsilon_{3}=1$ folgt.
Ähnliche Überlegungen führen auch dann ans Ziel, wenn M außerhalb des Dreiecks ABC liegt, nur dass $\varepsilon_{1}, \varepsilon_{2}$ bzw. $\varepsilon_{3}=-1$, falls $M$ im Bereich I, II bzw. III liegt. Sollte $M$ in den Bereichen IV, V bzw. VI liegen, dann sind genau zwei der $\varepsilon_{i}$ gleich -1 .
Etwas eleganter und straffer lässt sich der Beweis führen, falls man orientierte Strecken oder Flächen verwendet.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Gegeben ist ein Dreieck ABC und ein Punkt M so, dass die Geraden MA, MB, MC die Geraden BC, CA, AB (in dieser Reihenfolge) in D, E beziehungsweise F schneiden.
Man beweise, dass es dann stets die Zahlen $\varepsilon_{1}, \varepsilon_{2}, \varepsilon_{3}$ aus $\{-1,1\}$ gibt, so dass gilt:
$\varepsilon_{1} \cdot \frac{M D}{A D}+\varepsilon_{2} \cdot \frac{M E}{B E}+\varepsilon_{3} \cdot \frac{M F}{C F}=1$
|
Punkt $M$ ( $M \notin\{A, B, C\})$ kann entweder auf einer der vorgegebenen Geraden, oder in einer der sieben Gebiete liegen, in denen die Ebene des Dreiecks ABC durch die Geraden $A B, B C, C A$ geteilt wird.

Es ist stets
$$
\begin{aligned}
& \frac{M D}{A D}=\frac{M P}{h_{a}}=\frac{0,5 \cdot M P \cdot B C}{0,5 \cdot h_{a} \cdot B C}=\frac{F(M B C)}{F(A B C)}, \\
& \text { (Strahlensatz) }
\end{aligned}
$$
wobei $P \in B C$ und $M P \perp B C$ und $F(X Y Z)$ der Inhalt des Dreiecks XYZ ist. Ähnliches gilt für die anderen Verhältnisse.
Liegt M im Inneren oder am Rande des Dreiecks $A B C$, dann ist also:
$$
\frac{M D}{A D}+\frac{M E}{B E}+\frac{M F}{C F}=\frac{F(M B C)}{F(A B C)}+\frac{F(M C A)}{F(A B C)}+\frac{F(M A B)}{F(A B C)}=1
$$
woraus $\varepsilon_{1}=\varepsilon_{2}=\varepsilon_{3}=1$ folgt.
Ähnliche Überlegungen führen auch dann ans Ziel, wenn M außerhalb des Dreiecks ABC liegt, nur dass $\varepsilon_{1}, \varepsilon_{2}$ bzw. $\varepsilon_{3}=-1$, falls $M$ im Bereich I, II bzw. III liegt. Sollte $M$ in den Bereichen IV, V bzw. VI liegen, dann sind genau zwei der $\varepsilon_{i}$ gleich -1 .
Etwas eleganter und straffer lässt sich der Beweis führen, falls man orientierte Strecken oder Flächen verwendet.
|
{
"resource_path": "Germany_TST/segmented/de-2003-loes_awkl1_03.jsonl",
"problem_match": "# Aufgabe 2",
"solution_match": "# Lösung\n"
}
|
ce73bd2d-f40e-5fa6-8435-20580ae456f3
| 606,039
|
Let \( N \) be a natural number and \( x_{1}, x_{2}, \ldots, x_{n} \) be other natural numbers less than \( N \) such that the least common multiple of any two of these \( n \) numbers is greater than \( N \).
Prove that the sum of the reciprocals of these \( n \) numbers is always less than 2; that is,
$$
\frac{1}{x_{1}}+\frac{1}{x_{2}}+\cdots+\frac{1}{x_{n}}<2
$$
|
Since the least common multiple (LCM) of $x_i$ and $x_j$ is greater than N, there are no two numbers among $1, 2, \ldots, N$ that are multiples of both $x_i$ and $x_j$.
Among the multiples of the natural number $x$, there are two such that $kx \leq N < (k+1)x$, which implies $k \leq \frac{N}{x} < k+1$. The number of multiples of $x$ that are less than N is therefore the integer part of $\frac{N}{x}$, which is equal to $\left[\frac{N}{x}\right]$.
For the numbers $x_1, x_2, \ldots, x_n$, it follows that $\left[\frac{N}{x_1}\right] + \left[\frac{N}{x_2}\right] + \cdots + \left[\frac{N}{x_n}\right] < N$.
On the other hand, $\left[\frac{N}{x_i}\right] > \frac{N}{x_i} - 1$, and thus $\frac{N}{x_1} + \frac{N}{x_2} + \cdots + \frac{N}{x_n} - n < N$.
Since $n < N$, it follows that:
$\frac{N}{x_1} + \frac{N}{x_2} + \cdots + \frac{N}{x_n} < 2N$, which finally leads to $\frac{1}{x_1} + \frac{1}{x_2} + \cdots + \frac{1}{x_n} < 2$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Sei N eine natürliche Zahl und $\mathrm{x}_{1}, \mathrm{x}_{2}, \ldots, \mathrm{x}_{\mathrm{n}}$ weitere natürliche Zahlen kleiner als N und so, dass das kleinste gemeinsame Vielfache von beliebigen zwei dieser n Zahlen größer als N ist.
Man beweise, dass die Summe der Kehrwerte dieser n Zahlen stets kleiner 2 ist; also
$$
\frac{1}{x_{1}}+\frac{1}{x_{2}}+\cdots+\frac{1}{x_{n}}<2
$$
|
Da das kgV von $\mathrm{x}_{\mathrm{i}}$ und $\mathrm{x}_{\mathrm{j}}$ größer als N ist, gibt es unter den Zahlen $1,2, \ldots, \mathrm{~N}$ keine zwei, die sowohl Vielfache von $\mathrm{x}_{\mathrm{i}}$, als auch von $\mathrm{x}_{\mathrm{j}}$ sind.
Unter den Vielfachen der natürlichen Zahl $x$ gibt es zwei so, dass $k x \leq N<(k+1) x$, woraus $\mathrm{k} \leq \frac{N}{x}<\mathrm{k}+1$ folgt. Die Anzahl der Vielfachen von x , die kleiner N sind, ist demnach der ganzzahlige Teil von $\frac{N}{X}$, also gleich $\left[\frac{N}{x}\right]$.
Für die Zahlen $\mathrm{x}_{1}, \mathrm{x}_{2}, \ldots, \mathrm{x}_{\mathrm{n}}$ gilt folglich $\left[\frac{N}{x_{1}}\right]+\left[\frac{N}{x_{2}}\right]+\cdots+\left[\frac{N}{x_{n}}\right]<N$.
Andrerseits ist $\left[\frac{N}{x_{i}}\right]>\frac{N}{x_{i}}-1$ und demnach $\frac{N}{x_{1}}+\frac{N}{x_{2}}+\cdots+\frac{N}{x_{n}}-n<N$.
Da aber $\mathrm{n}<\mathrm{N}$ ist folgt:
$\frac{N}{x_{1}}+\frac{N}{x_{2}}+\cdots+\frac{N}{x_{n}}<2 N$, was schließlich zu $\frac{1}{x_{1}}+\frac{1}{x_{2}}+\cdots+\frac{1}{x_{n}}<2$ führt.
|
{
"resource_path": "Germany_TST/segmented/de-2003-loes_awkl1_03.jsonl",
"problem_match": "# Aufgabe 3",
"solution_match": "# Lösung\n"
}
|
b7be3b93-07dd-566f-bd32-264d6a59a5de
| 606,046
|
Let $B$ be any point on a circle $k_{1}$ and let $A$ be a point different from $B$ on the tangent to $k_{1}$ at $B$. Furthermore, let $C$ be a point outside $k_{1}$ with the property that the segment $A C$ intersects $k_{1}$ at two distinct points. Finally, let $k_{2}$ be the circle that touches the line $(A C)$ at $C$ and touches the circle $k_{1}$ at a point $D$ which lies on the opposite side of $(A C)$ from $B$.
Prove that the circumcenter of triangle $BCD$ lies on the circumcircle of triangle $A B C$.
|
We denote the centers of the circles $k_{1}$ and $k_{2}$ with $O_{1}$ and $O_{2}$, respectively. The solution assumes that $\angle C D B$ is obtuse (see Fig.); otherwise, some angles need to be swapped modulo $180^{\circ}$.
Let $P$ be the circumcenter of triangle BDC; then, by the central angle theorem,
$\angle B P C=2 \cdot\left(180^{\circ}-\angle C D B\right)=360^{\circ}-2 \cdot \angle C D B$ (1).
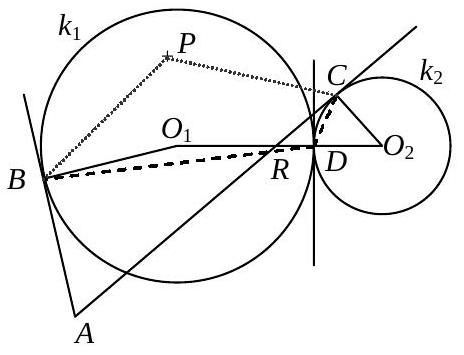
$P$ lies on the circumcircle of triangle $A B C$ if $A C P B$ is a cyclic quadrilateral; this is true if $\angle B P C=180^{\circ}-\angle C A B$.
To prove this, we calculate $\angle C D B$. Since $k_{1}$ and $k_{2}$ touch at $D$, $D$ lies on the segment $O_{1} O_{2}$ and we have $\angle C D B=180^{\circ}+\angle O_{1} D B-\angle O_{2} D C$ (2). Since $k_{1}$ touches the line ( $A B$ ), $\angle A B O_{1}=90^{\circ}$, so $\angle A B D+\angle D B O_{1}=90^{\circ}$. Since $B$ and $D$ lie on $k_{1}$, triangle $B D O_{1}$ is isosceles with $\angle O_{1} D B=\angle D B O_{1}$. Thus, $\angle O_{1} D B=90^{\circ}-\angle A B D$ (3). Since $k_{2}$ touches the line ( $A C$ ), $\angle A C O_{2}=90^{\circ}$, so $\angle A C D+\angle D C O_{2}=90^{\circ}$. Since $C$ and $D$ lie on $k_{2}$, triangle $\mathrm{CDO}_{2}$ is isosceles with $\angle \mathrm{O}_{2} D C=\angle D C O_{2}$. Thus, $\angle O_{2} D C=90^{\circ}-\angle A C D$ (4). Substituting (3) and (4) into (2) yields $\angle C D B=180^{\circ}+\left(90^{\circ}-\angle A B D\right)-\left(90^{\circ}-\angle A C D\right)=180^{\circ}-\angle A B D+\angle A C D$ (5).
Now consider the intersection point $R$ of $(A C)$ and ( $B D$ ) and deduce
$\angle A B D=\angle A B R=180^{\circ}-\angle R A B-\angle B R A=180^{\circ}-\angle C A B-\angle B R A$ and
$\angle A C D=\angle R C D=180^{\circ}-\angle C D R-\angle D R C=180^{\circ}-\angle C D B-\angle B R A$. From (5) we get
$\angle C D B=180^{\circ}+\angle C A B-\angle C D B$, so $2 \cdot \angle C D B=180^{\circ}+\angle C A B$. Substituting into (1) gives $\angle B P C=360^{\circ}-\left(180^{\circ}+\angle C A B\right)=180^{\circ}-\angle C A B$. This completes the proof.
Note: Since $k_{1}$ is intersected by the segment $A C$, $k_{2}$ cannot touch the line ( $\left.A C\right)$ from $A$ before intersecting with $k_{1}$. Also, $C$ cannot be chosen specially.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Es sei $B$ ein beliebiger Punkt auf einem Kreis $k_{1}$ und es sei $A$ ein von $B$ verschiedener Punkt auf der Tangente an $k_{1}$ in $B$. Ferner sei $C$ ein Punkt außerhalb von $k_{1}$ mit der Eigenschaft, dass die Strecke $A C$ den Kreis $k_{1}$ in zwei verschiedenen Punkten schneidet. Schließlich sei $k_{2}$ der Kreis, der die Gerade ( $A C$ ) in $C$ berührt und den Kreis $k_{1}$ in einem Punkt $D$ berührt, welcher auf der anderen Seite von ( $A C$ ) liegt wie $B$.
Man beweise, dass der Umkreismittelpunkt des Dreiecks BCD auf dem Umkreis des Dreiecks $A B C$ liegt.
|
Wir bezeichnen die Mittelpunkte der Kreise $k_{1}$ und $k_{2}$ mit $O_{1}$ bzw. $O_{2}$. Die Lösung setzt nun voraus, dass $\angle C D B$ stumpf ist (siehe Fig.); andernfalls sind lediglich einige Winkel modulo $180^{\circ}$ zu vertauschen.
Es sei $P$ der Umkreismittelpunkt des Dreiecks BDC; dann ist nach dem Satz vom Mittelpunktswinkel
$\angle B P C=2 \cdot\left(180^{\circ}-\angle C D B\right)=360^{\circ}-2 \cdot \angle C D B$ (1).

$P$ liegt dann auf dem Umkreis von Dreieck $A B C$, wenn $A C P B$ ein Sehnenviereck ist; dies gilt dann, wenn $\angle B P C=180^{\circ}-\angle C A B$ ist.
Um dies zu beweisen, berechnen wir $\angle C D B$. Da $k_{1}$ und $k_{2}$ sich in $D$ berühren, liegt $D$ auf der Strecke $O_{1} O_{2}$ und es gilt $\angle C D B=180^{\circ}+\angle O_{1} D B-\angle O_{2} D C$ (2). Da $k_{1}$ die Gerade ( $A B$ ) berührt, ist $\angle A B O_{1}=90^{\circ}$, also $\angle A B D+\angle D B O_{1}=90^{\circ}$. Da $B$ und $D$ auf $k_{1}$ liegen, ist das Dreieck $B D O_{1}$ gleichschenklig mit $\angle O_{1} D B=\angle D B O_{1}$. Somit ist $\angle O_{1} D B=90^{\circ}-\angle A B D$ (3). Da $k_{2}$ die Gerade ( $A C$ ) berührt, ist $\angle A C O_{2}=90^{\circ}$, also $\angle A C D+\angle D C O_{2}=90^{\circ}$. Da $C$ und $D$ auf $k_{2}$ liegen, ist das Dreieck $\mathrm{CDO}_{2}$ gleichschenklig mit $\angle \mathrm{O}_{2} D C=\angle D C O_{2}$. Somit ist $\angle O_{2} D C=90^{\circ}-\angle A C D$ (4). Einsetzen von (3) und (4) in (2) liefert $\angle C D B=180^{\circ}+\left(90^{\circ}-\angle A B D\right)-\left(90^{\circ}-\angle A C D\right)=180^{\circ}-\angle A B D+\angle A C D$ (5).
Nun betrachten wir den Schnittpunkt $R$ von $(A C)$ und ( $B D$ ) und folgern
$\angle A B D=\angle A B R=180^{\circ}-\angle R A B-\angle B R A=180^{\circ}-\angle C A B-\angle B R A$ sowie
$\angle A C D=\angle R C D=180^{\circ}-\angle C D R-\angle D R C=180^{\circ}-\angle C D B-\angle B R A$. Aus (5) ergibt sich
$\angle C D B=180^{\circ}+\angle C A B-\angle C D B$, also $2 \cdot \angle C D B=180^{\circ}+\angle C A B$. Einsetzen in (1) liefert $\angle B P C=360^{\circ}-\left(180^{\circ}+\angle C A B\right)=180^{\circ}-\angle C A B$. Damit ist alles gezeigt.
Anmerkung: Da $k_{1}$ von der Strecke $A C$ geschnitten wird, kann $k_{2}$ die Gerade ( $\left.A C\right)$ nicht - von $A$ aus vor dem Schnitt mit $k_{1}$ berühren. Auch darf $C$ nicht speziell gewählt werden.
|
{
"resource_path": "Germany_TST/segmented/de-2003-loes_awkl2_03.jsonl",
"problem_match": "# Aufgabe 2",
"solution_match": "# Lösung\n"
}
|
1391e3ff-30e7-53a5-ba08-c0b1dcc80013
| 606,061
|
In triangle $A B C$, $A D (D \in B C)$ is a median, $E$ is a point on $A C$, and $F$ is the intersection of $B E$ with $A D$.
Prove: If $\frac{B F}{F E}=\frac{B C}{A B}+1$, then $B E$ is an angle bisector.
|
Let $B^{\prime}, C^{\prime}, E^{\prime}$ be the projections of $B, C$, and $E$ onto the line $A D$. The right triangles $\triangle D B B^{\prime}$ and $\triangle D C C^{\prime}$ are congruent, since $D$ is the midpoint of $B C$ and the acute angles at $D$ are equal. This implies that $B B^{\prime}=C C^{\prime}$.
In the triangle $\triangle A C^{\prime} C$, $E E^{\prime}$ is parallel to $C C^{\prime}$, and thus
$$
\frac{A C}{A E}=\frac{C C^{\prime}}{E E^{\prime}}=\frac{B B^{\prime}}{E E^{\prime}}.
$$
The right triangles $\triangle B B^{\prime} F$ and $\triangle E E^{\prime} F$ are similar, as the angles at $F$ are equal. This implies $\frac{B B^{\prime}}{E E^{\prime}}=\frac{B F}{F E}$, which, together with the previous relationship, leads to $\frac{A C}{A E}=\frac{B F}{E F}$.
Replacing $\frac{B F}{E F}$ in the initial relationship with $\frac{A C}{A E}$, we get:
$\frac{B C}{A B}+1=\frac{A C}{A E}=\frac{B C+A B}{A B}$, which simplifies to $\frac{A C-A E}{A E}=\frac{B C}{A B}$ and finally to $\frac{E C}{A E}=\frac{B C}{A B}$.
According to the converse of the Angle Bisector Theorem, $B E=w_{\beta}$.
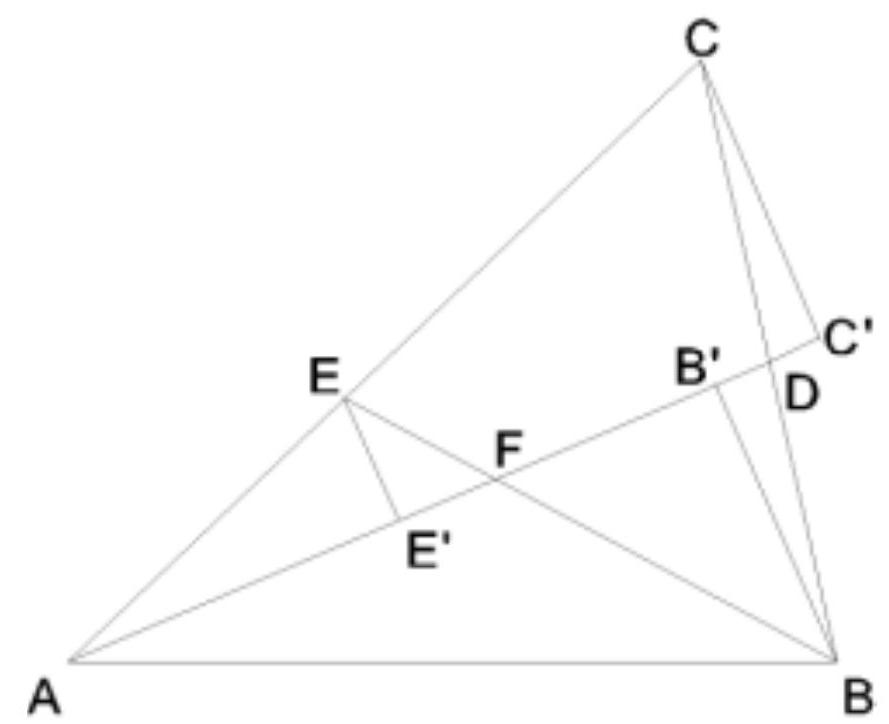
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Im Dreieck $A B C$ ist $A D(D \in B C)$ eine Seitenhalbierende, $E$ ein Punkt auf $A C$ und $F$ der Schnittpunkt von $B E$ mit $A D$.
Man beweise: Falls $\frac{B F}{F E}=\frac{B C}{A B}+1$, dann ist $B E$ eine Winkelhalbierende.
|
Seien $B^{\prime}, C^{\prime}, E^{\prime}$ die Projektionen von $B, C$ und $E$ auf die Gerade $A D$. Die rechtwinkligen Dreiecke $\triangle D B B^{\prime}$ und $\triangle D C C^{\prime}$ sind kongruent, da $D$ der Mittelpunkt von $B C$ ist und die spitzen Winkel bei $D$ gleich groß sind. Daraus folgt, dass $B B^{\prime}=C C^{\prime}$.
Im Dreieck $\triangle A C^{\prime} C$ ist $E E^{\prime}$ parallel zu $C C^{\prime}$ und folglich
$$
\frac{A C}{A E}=\frac{C C^{\prime}}{E E^{\prime}}=\frac{B B^{\prime}}{E E^{\prime}} .
$$
Die rechtwinkligen Dreiecke $\triangle B B^{\prime} F$ und $\triangle E E^{\prime} F$ sind ähnlich, da die Winkel bei $F$ gleich sind. Daraus folgt $\frac{B B^{\prime}}{E E^{\prime}}=\frac{B F}{F E}$, was zusammen mit der vorletzten Beziehung zu $\frac{A C}{A E}=\frac{B F}{E F}$ führt.

Ersetzt man nun $\frac{B F}{E F}$ in der Ausgangsbeziehung durch $\frac{A C}{A E}$, ergibt sich:
$\frac{B C}{A B}+1=\frac{A C}{A E}=\frac{B C+A B}{A B}$, was zu $\frac{A C-A E}{A E}=\frac{B C}{A B}$ und schließlich zu $\frac{E C}{A E}=\frac{B C}{A B}$ führt.
Gemäß der Umkehrung des Satzes der Winkelhalbierenden ist $B E=w_{\beta}$.
|
{
"resource_path": "Germany_TST/segmented/de-2004-loes_awkl1_04.jsonl",
"problem_match": "# Aufgabe 2",
"solution_match": "# Lösung\n"
}
|
7f0b37d4-6eee-54e5-8101-7a9bc49d0545
| 606,086
|
In the plane, there are $n$ closed disks $\mathrm{K}_{1}, \mathrm{~K}_{2}, \ldots ; \mathrm{K}_{\mathrm{n}}$ with the same radius $r$. Each point in the plane is contained in at most 2003 of these disks. Prove that each disk $K_{\mathrm{i}}$ intersects at most 14020 other disks.
|
We conduct a proof by contradiction. In addition to the assumption, we assume that a circular disk (w.l.o.g. let this be $K_{1}$) intersects at least 14021 other circular disks. The centers of these disks then obviously all lie within a circular disk of radius $2r$ around the center $M_{1}$ of $K_{1}$. If 2003 or more of the centers of these other disks were to lie within or on the boundary of $K_{1}$, then these disks would all contain $M_{1}$. Thus, $M_{1}$ would be contained in more than 2003 disks, since $M_{1}$ is also contained in $K_{1}$. Therefore, at least 14021 - 2002 $=12019$ centers of the other disks must lie in an annulus with inner radius $r$ and outer radius $2r$ around $M_{1}$. Dividing this annulus into 6 equal sectors with an internal angle of $60^{\circ}$, it follows by the pigeonhole principle that at least 2004 of these centers must lie in at least one sector.
In the diagram, this sector is shown with the midpoint $M$ of the segment $AB$. From $\left|A M_{1}\right|=\left|B M_{1}\right|=2r$ and $\angle A M_{1} B = 60^{\circ}$, it follows that $\triangle A B M_{1}$ is equilateral. Thus, $M D$ and $MC$ are its midlines, and it follows that
$|M A|=|M B|=|M C|=|M D|=r$. Therefore, the sector lies entirely within a circle around $M$ with radius $r$. Each of the at least 2004 disks with centers in this sector thus contains the point $M$. Hence, $M$ is contained in at least 2004 disks - a contradiction to the assumption.
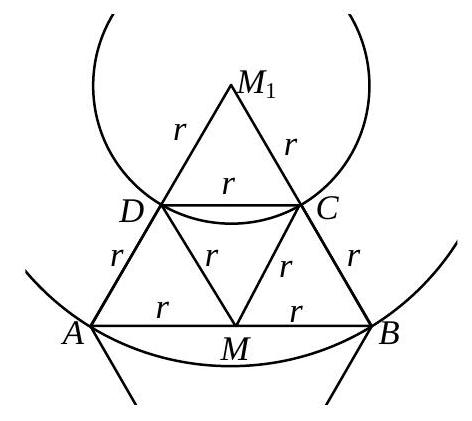
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
In der Ebene liegen n abgeschlossene Kreisscheiben $\mathrm{K}_{1}, \mathrm{~K}_{2}, \ldots ; \mathrm{K}_{\mathrm{n}}$ mit gleichem Radius r . Jeder Punkt der Ebene ist dabei in höchstens 2003 dieser Kreisscheiben enthalten. Man beweise, dass jede Kreisscheibe $K_{\mathrm{i}}$ höchstens 14020 andere Kreisscheiben schneidet.
|
Wir führen einen Beweis durch Widerspruch. Dazu nehmen wir zusätzlich zur Voraussetzung an, dass eine Kreisscheibe (oBdA sei dies $K_{1}$ ) mindestens 14021 andere Kreisscheiben schneidet. Die Mittelpunkte dieser Scheiben liegen dann offensichtlich alle in einer Kreisscheibe mit Radius $2 r$ um den Mittelpunkt $M_{1}$ von $K_{1}$. Lägen 2003 oder mehr der Mittelpunkte dieser anderen Kreisscheiben in oder auf dem Rand von $K_{1}$, so würden diese Scheiben alle $M_{1}$ enthalten. Damit würde $M_{1}$ in mehr als 2003 Kreisscheiben enthalten sein, da $M_{1}$ auch in $K_{1}$ enthalten ist. Also müssen mindestens 14021 - 2002 $=12019$ Mittelpunkte der anderen Kreisscheiben in einem Kreisring mit innerem Radius r und äußerem Radius $2 r$ um $M_{1}$ liegen. Teilen wir diesen Ring in 6 gleich große Sektoren mit Innenwinkel $60^{\circ}$, so liegen nach dem Schubfachprinzip in mindestens einem Sektor wenigstens 2004 dieser Mittelpunkte.
In der Zeichnung ist dieser Sektor mit dem Mittelpunkt $M$ der Strecke $A B$ dargestellt. Aus $\left|A M_{1}\right|=\left|B M_{1}\right|=2 r$ und $\angle A M_{1} B=$ $60^{\circ}$ folgt, dass $\triangle A B M_{1}$ gleichseitig ist. Also sind $M D$ und MC seine Mittelparallelen und es folgt
$|M A|=|M B|=|M C|=|M D|=r$. Daher liegt der Sektor vollständig in einem Kreis um M mit Radius r. Jede der wenigstens 2004 Kreisscheiben mit Mittelpunkten in diesem Sektor enthält also den Punkt M. Damit ist M aber in

wenigstens 2004 Kreisscheiben enthalten - ein Widerspruch zur Annahme.
|
{
"resource_path": "Germany_TST/segmented/de-2004-loes_awkl2_04.jsonl",
"problem_match": "# Aufgabe 1",
"solution_match": "# Lösung\n"
}
|
3a19e667-bf2d-5c6c-bf37-6229ab49e8d3
| 606,105
|
Given are $n$ real numbers $\mathrm{x}_{1}, \mathrm{x}_{2}, \ldots, \mathrm{x}_{\mathrm{n}}$ and $\mathrm{y}_{1}, \mathrm{y}_{2}, \ldots, \mathrm{y}_{\mathrm{n}}$. The elements of an $\mathrm{n} \times \mathrm{n}$ matrix A are defined as follows: ( $1 \leq \mathrm{i}, \mathrm{j} \leq \mathrm{n}$ )
$$
a_{i j}= \begin{cases}1 & \text { if } x_{i}+y_{j} \geq 0 \\ 0 & \text { if } x_{i}+y_{j}<0\end{cases}
$$
Furthermore, let B be an $\mathrm{n} \times \mathrm{n}$ matrix with elements 0 or 1, such that the sum of the elements in each row and each column of B is equal to the sum of the elements in the corresponding row or column of A.
Prove that then $\mathrm{A}=\mathrm{B}$ holds.
|
We assume that there is a matrix $B$ of the required type with $B \neq A$. Now we consider in $A$ only those elements $a_{ij}$ that differ from the corresponding elements $b_{ij}$. There must be at least one such element. All other elements of $A$ are deleted. Then, within each row and column, the number of remaining zeros is equal to the number of remaining ones, since these counts in $B$ are simply swapped for the same row or column sum. Thus, each number $x_i$ appears in the remaining arrangement just as often as a summand in a sum $x_i + y_j < 0$ as it does in a sum $x_i + y_j \geq 0$. The same applies to each number $y_j$.
Now we add up all sums $x_i + y_j < 0$ with $a_{ij} \neq b_{ij}$. The sum of these sums is necessarily $< 0$. Similarly, we add up all sums $x_i + y_j \geq 0$ with $a_{ij} \neq b_{ij}$. The sum of these sums is necessarily $\geq 0$. However, since each of the numbers $x_i$ and $y_j$ appears equally often in both sums, these sums must have the same value, which is a contradiction! Therefore, there can be no different elements in $A$ and $B$, and it follows that $A = B$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Gegeben seien jeweils n reelle Zahlen $\mathrm{x}_{1}, \mathrm{x}_{2}, \ldots, \mathrm{x}_{\mathrm{n}}$ bzw. $\mathrm{y}_{1}, \mathrm{y}_{2}, \ldots, \mathrm{y}_{\mathrm{n}}$. Die Elemente einer $\mathrm{n} \times \mathrm{n}$-Matrix A seien folgendermaßen definiert: ( $1 \leq \mathrm{i}, \mathrm{j} \leq \mathrm{n}$ )
$$
a_{i j}= \begin{cases}1 & \text { wenn } x_{i}+y_{j} \geq 0 \\ 0 & \text { wenn } x_{i}+y_{j}<0\end{cases}
$$
Weiter sei B eine $\mathrm{n} \times \mathrm{n}$-Matrix mit Elementen 0 oder 1, so dass die Summe der Elemente in jeder Zeile und jeder Spalte von B gleich der Summe der Elemente in der entsprechenden Zeile bzw. Spalte von A ist.
Man beweise, dass dann $\mathrm{A}=\mathrm{B}$ gilt.
|
Wir nehmen an, dass es eine Matrix $B$ der geforderten Art gebe mit $B \neq A$. Nun betrachten wir in A nur noch diejenigen Elemente $a_{i j}$, die sich von den entsprechenden Elementen $b_{i j}$ unterscheiden. Es muss mindestens ein solches Element geben. Alle anderen Elemente von A werden gestrichen. Dann ist innerhalb jeder Zeile bzw. Spalte die Anzahl der verbleibenden Nullen gleich der Anzahl der verbleibenden Einsen, da diese
Anzahlen in B bei gleicher Zeilen- bzw. Spaltensumme gerade vertauscht sind. Also tritt jede Zahl $x_{i}$ in der verbleibenden Anordnung genauso oft als Summand einer Summe $x_{i}+y_{j}<0$ auf wie als Summand einer Summe $x_{i}+y_{j} \geq 0$. Das Gleiche gilt für jede Zahl $y_{j}$.
Nun addieren wir alle Summen $x_{i}+y_{j}<0$ mit $a_{i j} \neq b_{i j}$. Die Summe dieser Summen ist zwangsläufig $<0$. Ebenso addieren wir alle Summen $x_{i}+y_{j} \geq 0$ mit $a_{i j} \neq b_{i j}$. Die Summe dieser Summen ist zwangsläufig $\geq 0$. Da aber jede der Zahlen $x_{i}$ und $y_{j}$ gleich häufig in beiden Summen auftritt, müssen diese Summen den gleichen Wert haben Widerspruch! Daher kann es keine verschiedenen Elemente in A und B geben und es gilt $A=B$.
|
{
"resource_path": "Germany_TST/segmented/de-2004-loes_awkl2_04.jsonl",
"problem_match": "# Aufgabe 2",
"solution_match": "# Lösung\n"
}
|
01501c18-50e0-57db-84b8-ac3df7a42b7d
| 606,113
|
Let $ABC$ be an isosceles triangle with $\overline{AC} = \overline{BC}$ and incenter $I$. Furthermore, let $P$ be a point inside $ABC$ on the circumcircle of triangle $BIA$. The parallels to $CA$ and $CB$ through $P$ intersect $AB$ at $D$ and $E$ respectively. The parallel to $AB$ through $P$ intersects $CA$ and $CB$ at $F$ and $G$ respectively.
Show that the lines $DF$ and $EG$ intersect on the circumcircle of triangle $ABC$.
|
Due to $\angle F P E=\angle F G B=180^{\circ}-\angle C B A=180^{\circ}-\angle B A C=180^{\circ}-\angle F A E$ (parallelism and isosceles property), FAEP is a cyclic quadrilateral. Similarly, GPDB is also a cyclic quadrilateral. Their two circumcircles intersect at P and another point, which we denote as S. Now it follows that $\angle E S P=\angle E A P=\angle B A P=180^{\circ}-\angle A P B-\angle P B A$ $=180^{\circ}-\angle A I B-\angle P B A=\angle B A I+\angle I B A-\angle P B A=2 \cdot \frac{1}{2} \angle C B A-\angle P B A=\angle C B P=\angle G B P$ $=\angle G S P$ (inscribed angles and symmetry). Therefore, S lies on the line EG; similarly, S, D, and F are collinear. Hence, S is the intersection of DF and EG. It remains to prove that this point lies on the circumcircle of ABC.
Indeed, we have
$\angle B S A=\angle P S A+\angle B S P=180^{\circ}-\angle A F P+180^{\circ}-\angle P G B=$ $\angle G F C+\angle C G F=180^{\circ}-\angle F C G=180^{\circ}-\angle A C B$. Thus, ASBC is a cyclic quadrilateral, which is what we needed to prove.
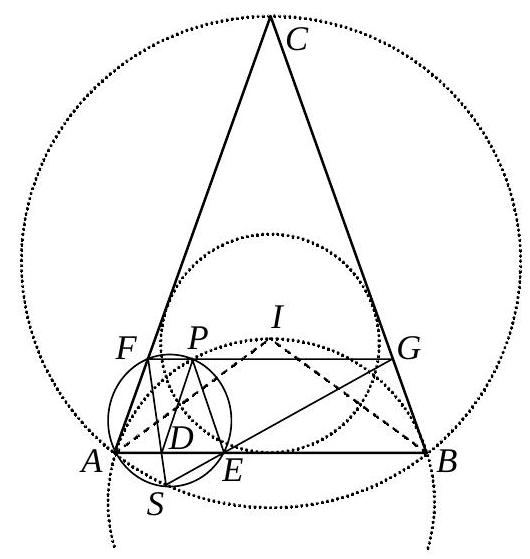
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Es sei $A B C$ ein gleichschenkliges Dreieck mit $\overline{A C}=\overline{B C}$ und Inkreismittelpunkt I. Ferner sei $P$ ein Punkt im Inneren von ABC auf dem Umkreis des Dreiecks BIA. Die Parallelen zu $C A$ und $C B$ durch $P$ schneiden $A B$ in $D$ bzw. E. Die Parallele zu AB durch P schneidet CA und $C B$ in $F$ bzw. G.
Man zeige, dass sich die Geraden DF und EG auf dem Umkreis des Dreiecks ABC schneiden.
|
Wegen $\angle F P E=\angle F G B=180^{\circ}-\angle C B A=180^{\circ}-\angle B A C=180^{\circ}-\angle F A E$ (Parallelität und Gleichschenkligkeit) ist FAEP ein Sehnenviereck. Analog erweist sich GPDB als Sehnenviereck. Ihre beiden Umkreise schneiden sich in P und einem weiteren Punkt, den wir mit S bezeichnen. Nun folgt weiter $\angle E S P=\angle E A P=\angle B A P=180^{\circ}-\angle A P B-\angle P B A$ $=180^{\circ}-\angle A I B-\angle P B A=\angle B A I+\angle I B A-\angle P B A=2 \cdot \frac{1}{2} \angle C B A-\angle P B A=\angle C B P=\angle G B P$ $=\angle G S P$ (Umfangswinkel und Symmetrie). Also liegt S auf der Geraden EG; entsprechend sind S, D und F kollinear. Deshalb ist S der Schnittpunkt von DF und EG. Es bleibt zu beweisen, dass dieser Punkt auf dem Umkreis von ABC liegt.
In der Tat gilt
$\angle B S A=\angle P S A+\angle B S P=180^{\circ}-\angle A F P+180^{\circ}-\angle P G B=$ $\angle G F C+\angle C G F=180^{\circ}-\angle F C G=180^{\circ}-\angle A C B$. Somit ist ASBC ein Sehnenviereck, was zu beweisen war.

|
{
"resource_path": "Germany_TST/segmented/de-2004-loes_awkl2_04.jsonl",
"problem_match": "# Aufgabe 3",
"solution_match": "\nLösung:"
}
|
71b62092-5445-510b-b9bd-1ad1fa5086f7
| 606,127
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.