problem
stringlengths 54
2.23k
| solution
stringlengths 134
24.1k
| answer
stringclasses 1
value | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 54
2.21k
| solution_raw
stringlengths 134
24.1k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 23.5k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
Prove: If $4^{n} \cdot 7=a^{2}+b^{2}+c^{2}+d^{2}$ with $n, a, b, c, d \in N \backslash\{0\}$, then none of the square numbers can be less than $4^{\mathrm{n}-1}$.
|
If $n=1$, then the claim is correct; the only solutions for $a, b, c, d$ are, apart from the order, the quadruples $(1,1,1,5)$, $(1,3,3,3)$, and $(2,2,2,4)$. For each $n \geq 1$, $4^{n} \cdot 7$ is divisible by 4. Since the square of a natural number can only have remainders of 0 or 1 when divided by 4, only numbers of the same residue class modulo 4 are possible for $a, b, c, d$.
If $a, b, c, d$ (all) are odd, then the right-hand side is divisible by 4, but not by 8, and certainly not by 16. In this case, only $\mathrm{n}=1$ is possible. If $n>1$, then the four numbers on the right-hand side must all be even.
Assuming the property that all square numbers exceed $4^{n-1}$ does not hold for all $n$, then there is a smallest $k (k \in \mathbb{N})$ for which it does not hold. Since it holds for $n=1$, $k$ must be greater than 1. Then, however (see above), $a, b, c, d$ are all even. One could therefore divide both sides by 4, and the property should not hold for $k-1$, which, due to the minimality of $k$, cannot be. The claim is therefore correct for all natural numbers $\mathrm{n}, \mathrm{n} \geq 1$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Man beweise: Ist $4^{n} \cdot 7=a^{2}+b^{2}+c^{2}+d^{2}$ mit $n, a, b, c, d \in N \backslash\{0\}$, dann kann keine der Quadratzahlen die Zahl $4^{\mathrm{n}-1}$ unterschreiten.
|
Ist $n=1$, dann ist die Behauptung richtig; die einzigen Lösungen für $a, b, c, d$ sind, abgesehen von der Reihenfolge, die Quadrupel $(1,1,1,5)$, $(1,3,3,3)$ und $(2,2,2,4)$. Für jedes $n \geq 1$ ist $4^{n} .7$ durch 4 teilbar. Da das Quadrat einer natürlichen Zahl bei der Division durch 4 nur die Reste 0 oder 1 haben kann, kommen für $a, b, c, d$ nur Zahlen gleicher Restklasse modulo 4 in Frage.
Sind a, b, c, d (alle) ungerade, dann ist die rechte Seite zwar durch 4, nicht aber durch 8 und erst recht nicht durch 16 teilbar. In diesem Fall kommt also nur $\mathrm{n}=1$ in Frage. Sollte $n>1$ sein, dann müssen die vier Zahlen auf der rechten Seite demnach alle gerade sein.
Vorausgesetzt die Eigenschaft, dass alle Quadratzahlen $4^{n-1}$ überschreiten, gilt nicht für alle $n$, dann gibt es ein kleinstes $k(k \in N)$ für das sie nicht gilt. Da sie für $n=1$ gilt, muss $k$ größer 1 sein. Dann sind aber (siehe oben) a, b, c, d alle gerade. Man könnte also beide Seiten durch 4 teilen und die Eigenschaft dürfte auch für k-1 nicht gelten, was aber wegen der Minimalität von $k$ nicht sein kann. Die Behauptung stimmt also für alle natürlichen Zahlen $\mathrm{n}, \mathrm{n} \geq 1$.
|
{
"resource_path": "Germany_TST/segmented/de-2005-loes_awkl1_05.jsonl",
"problem_match": "# Aufgabe 3",
"solution_match": "# Lösung\n"
}
|
a9e694d1-7503-5d59-a68b-4882c09af9c6
| 606,162
|
An infinite sequence $a_{0}, a_{1}, a_{2}, \ldots$ of real numbers satisfies the condition $a_{n}=\left|a_{n+1}-a_{n+2}\right|$ for all $n \geq 0$, where $a_{0}$ and $a_{1}$ are distinct positive numbers.
Can this sequence be bounded? The answer needs to be justified.
|
First, we prove that two consecutive terms can never be equal. From $a_{n}=a_{n+1}=c$ it would immediately follow that $a_{n-1}=0$ and $a_{n-2}=a_{n-3}=c \quad(n>2)$. Eventually, $a_{0}=a_{1}$ or $a_{0}=0$ and $a_{1}=0$ would have to be true, which is excluded. Therefore, $a_{n}>0$ for all n.
Solving the condition yields $a_{n+2}=a_{n+1}+a_{n}$ if $a_{n+2}>a_{n+1}$, and $a_{n+2}=a_{n+1}-a_{n}$ if $a_{n+2}<a_{n+1}$. From $a_{n+1}<a_{n}$ it follows that $a_{n+2}>a_{n}$ and $a_{n+2}>a_{n+1}$. Therefore, the subsequence $b_{0}, b_{1}, b_{2}, \ldots$ that is created by removing all terms that are smaller than their predecessor and successor is strictly monotonically increasing.
If we now show that $b_{m+1}-b_{m} \geq b_{m}-b_{m-1}$ for all $m \geq 2$, then we have an arithmetic sequence with a positive difference as a minorant for this subsequence, from which the unboundedness follows directly. For this, we set $b_{m+1}=a_{n+2}$, where $a_{n+2}>a_{n+1}$ should hold. For $a_{n+1}>a_{n}$, we have $b_{m}=a_{n+1}$ and $b_{m-1} \geq a_{n-1}$ (because either $b_{m-1}=a_{n-1}$ or $b_{m-1}=$ $a_{n}>a_{n-1}$ holds). Thus, $b_{m+1}-b_{m}=a_{n}=a_{n+1}-a_{n-1} \geq b_{m}-b_{m-1}$. For $a_{n+1}<a_{n}$, we have $b_{m}=a_{n}$ and $b_{m-1} \geq a_{n-1}$ (because either $b_{m-1}=a_{n-1}$ or $b_{m-1}=a_{n-2}>a_{n-1}$ holds). Thus, here $b_{m+1}-b_{m}=a_{n+1}=a_{n}-a_{n-1} \geq b_{m}-b_{m-1}$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Eine unendliche Folge $a_{0}, a_{1}, a_{2}, \ldots$ reeller Zahlen erfüllt die Bedingung $a_{n}=\left|a_{n+1}-a_{n+2}\right|$ für alle $n \geq 0$, wobei $a_{0}$ und $a_{1}$ verschiedene positive Zahlen sind.
Kann diese Folge beschränkt sein? Die Antwort ist zu begründen.
|
Zunächst beweisen wir, dass zwei aufeinander folgende Glieder niemals gleich sein können. Aus $a_{n}=a_{n+1}=c$ folgte nämlich sofort $a_{n-1}=0$ und $a_{n-2}=a_{n-3}=c \quad(n>2)$. Schließlich müsste $a_{0}=a_{1}$ oder $a_{0}=0$ bzw. $a_{1}=0$ sein, was ausgeschlossen ist. Daher gilt auch $a_{n}>0$ für alle n.
Auflösen der Bedingung liefert $a_{n+2}=a_{n+1}+a_{n}$ falls $a_{n+2}>a_{n+1}$ ist, sowie $a_{n+2}=a_{n+1}-a_{n}$ falls $a_{n+2}<a_{n+1}$ ist. Aus $a_{n+1}<a_{n}$ folgt also $a_{n+2}>a_{n}$ und $a_{n+2}>a_{n+1}$. Daher ist diejenige Teilfolge $b_{0}, b_{1}, b_{2}, \ldots$ streng monoton wachsend, die durch Weglassen aller Glieder entsteht, die kleiner als ihr Vorgänger und ihr Nachfolger sind.
Wenn wir nun zeigen, dass $b_{m+1}-b_{m} \geq b_{m}-b_{m-1}$ für alle $m \geq 2$ gilt, so haben wir für diese Teilfolge eine arithmetische Folge mit positiver Differenz als Minorante, woraus die Unbeschränktheit direkt folgt. Dazu setzen wir $b_{m+1}=a_{n+2}$, wobei $a_{n+2}>a_{n+1}$ gelten soll. Für $a_{n+1}>a_{n}$ haben wir $b_{m}=a_{n+1}$ und $b_{m-1} \geq a_{n-1}$ (weil entweder $b_{m-1}=a_{n-1}$ oder $b_{m-1}=$ $a_{n}>a_{n-1}$ gilt). So ist $b_{m+1}-b_{m}=a_{n}=a_{n+1}-a_{n-1} \geq b_{m}-b_{m-1}$. Für $a_{n+1}<a_{n}$ haben wir dagegen $b_{m}=a_{n}$ und $b_{m-1} \geq a_{n-1}$ (weil entweder $b_{m-1}=a_{n-1}$ oder $b_{m-1}=a_{n-2}>a_{n-1}$ gilt). So ist hier $b_{m+1}-b_{m}=a_{n+1}=a_{n}-a_{n-1} \geq b_{m}-b_{m-1}$.
|
{
"resource_path": "Germany_TST/segmented/de-2005-loes_awkl2_05.jsonl",
"problem_match": "# Aufgabe 1",
"solution_match": "# Lösung\n"
}
|
b02f8399-b9d3-5aef-8279-5275eb3ad9a8
| 606,174
|
Given a circle K and a line g, which have no common points.
Furthermore, let $\overline{AB}$ be the diameter of K that is orthogonal to g, with B being closer to g than $A$. Additionally, let C be any point on K, different from $A$ and $B$. The line AC intersects g at D; the line DE is tangent to K at E, where B and E lie on the same side of AC. Finally, BE intersects the line g at point F and AF intersects the circle K, other than at A, at point G.
Prove that the reflection of G with respect to the axis AB lies on the line CF.
|
We denote the second intersection of CF and K with H and the intersection of AB and g with X. Since $A B \perp g$, it suffices to show that $G H \| g$. This is the case if and only if $\angle A G H = \angle A F D$. The inscribed angle theorem and vertical angles yield $\angle A G H = \angle A C H = \angle D C F$; thus, we need to show that $\angle D C F = \angle A F D$. Since triangles DFC and ADF share an angle at D, it suffices to prove their (opposite) similarity. This is true if and only if $\frac{|D C|}{|D F|} = \frac{|D F|}{|D A|}$, i.e., $|D F|^2 = |D A| \cdot |D C|$ holds. According to the tangent-secant theorem, however, $|D E|^2 = |D A| \cdot |D C|$, so it remains to show that $|D E| = |D F|$, which is equivalent to $\angle D E F = \angle E F D$.
Since $\angle F X B = \angle A E B = 90^{\circ}$, AEXF is a cyclic quadrilateral and we have $\angle E F X = \angle E A B$. The equality of the angle between the chord and the tangent yields $\angle D E F = \angle E A B$, from which $\angle D E F = \angle E F D$ follows.
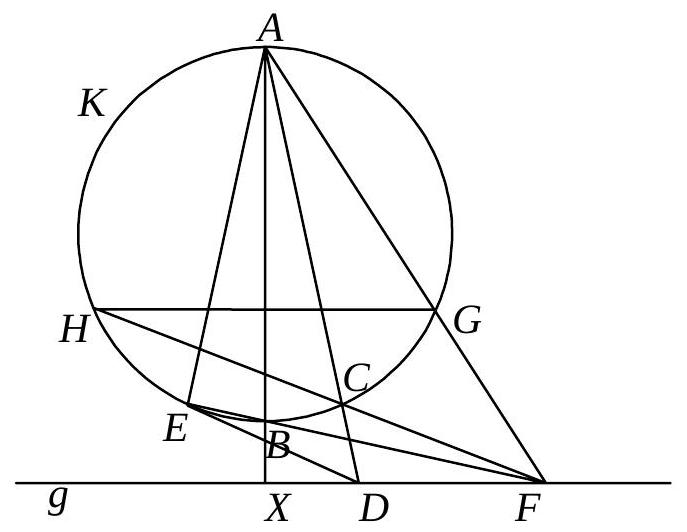
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Gegeben seien ein Kreis K und eine Gerade g , die keinen gemeinsamen Punkt haben.
Ferner sei $\overline{A B}$ der Durchmesser von K , der orthogonal zu g ist, wobei B näher an g liegt als $A$. Weiter sei ein beliebiger Punkt $C$, verschieden von $A$ und $B$, auf $K$ gegeben. Die Gerade AC schneidet g in D; die Gerade DE berührt K in E, wobei B und E auf derselben Seite von AC liegen. Schließlich schneidet BE die Gerade g im Punkt F und AF den Kreis K außer in A im Punkt G.
Man beweise, dass der Spiegelpunkt von G bezüglich der Achse AB auf der Geraden CF liegt.
|
Wir bezeichnen den zweiten Schnittpunkt von CF und K mit H sowie den Schnittpunkt von AB und g mit X . Wegen $A B \perp g$ reicht es zu zeigen, dass $G H \| g$. Dies ist genau dann der Fall, wenn $\angle A G H=\angle A F D$. Umfangswinkelsatz und Scheitelwinkel liefern $\angle A G H=\angle A C H=\angle D C F$; also muss $\angle D C F=\angle A F D$ gezeigt werden. Da die Dreiecke DFC und ADF bei D einen Winkel gemeinsam haben, braucht nur deren (gegensinnige) Ähnlichkeit nachgewiesen zu werden. Diese ist genau dann erfültt, wenn $\frac{|D C|}{|D F|}=\frac{|D F|}{|D A|}$,
d.h. $|D F|^{2}=|D A| \cdot|D C|$ gilt. Nach dem TangentenSekantensatz gilt allerdings $|D E|^{2}=|D A| \cdot|D C|$, so dass nur $|D E|=|D F|$ zu zeigen bleibt, was mit $\angle D E F=\angle E F D$ gleichbedeutend ist.
Wegen $\angle F X B=\angle A E B=90^{\circ}$ ist AEXF ein Sehnenviereck und es gilt $\angle E F X=\angle E A B$. Die Gleichheit der Sehnen-Tangentenwinkel liefert
$\angle D E F=\angle E A B$, woraus $\angle D E F=\angle E F D$ folgt.

|
{
"resource_path": "Germany_TST/segmented/de-2005-loes_awkl2_05.jsonl",
"problem_match": "# Aufgabe 2",
"solution_match": "# Lösung\n"
}
|
2b0b9b9a-f6e4-5d6c-a016-f6f0983772e9
| 606,184
|
Let $A, B, C, D, E, F$ be points on a circle with $A E \| B D$ and $B C \| D F$. By reflection across the line $C E$, the point $D$ is mapped to $X$. Show that $X$ is as far from the line $E F$ as $B$ is from $A C$.
|
All angles appearing below are to be understood as oriented and modulo $180^{\circ}$. This makes considerations of the relative positions of the involved points unnecessary. The feet of the perpendiculars from $B, X$ to $A C, E F$ are denoted by $P, Q$.
Strategy. Show the congruence of triangles $ABP$ and $EXQ$. (*)
From this, $BP = XQ$ will immediately follow, and thus the claim will be proven. The proof of (*) itself proceeds in three steps using a known congruence theorem.
I. Since $\varangle BPA \equiv \varangle EQX \equiv 90^{\circ}$, both triangles are right-angled.
II. Because $AE \| BD$, the cyclic quadrilateral $ABDE$ is an isosceles trapezoid, and thus $AB = DE$. Furthermore, $DE = XE$ by the construction of $X$, and therefore $AB = XE$, i.e., the hypotenuses are equal.
III. As before, we conclude from $BC \| DF$ that $BCDF$ is also an isosceles trapezoid. By repeated application of the inscribed angle theorem, we now get $\varangle DEC + \varangle CAB \equiv \varangle DAC + \varangle CAB \equiv \varangle DAB \equiv \varangle DFB \equiv \varangle CDF \equiv \varangle CEF \equiv \varangle CEX + \varangle XEF$. From $\varangle DEC \equiv \varangle CEX$, it follows that $\varangle CAB \equiv \varangle XEF$, or, in other words, $-\varangle PAB \equiv \varangle XEQ$.
Remark. Discussions of positional relationships have not been taken into account either positively or negatively in the evaluation.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Es seien $A, B, C, D, E, F$ Punkte auf einem Kreis mit $A E \| B D$ und $B C \| D F$. Durch Spiegelung an der Geraden $C E$ gehe der Punkt $D$ in $X$ über. Zeige, dass $X$ so weit von der Geraden $E F$ entfernt ist wie $B$ von $A C$.
|
Alle im folgenden auftretenden Winkel sind als orientiert und modulo $180^{\circ} \mathrm{zu}$ verstehen; dadurch wird eine Betrachtung der Lage der involvierten Punkte zueinander entbehrlich. Die Fußpunkte der Lote von $B, X$ auf $A C, E F$ seien mit $P, Q$ bezeichnet.
Strategie. Zeige die Kongruenz der Dreiecke ABP, EXQ. (*)
Hieraus wird sich sofort $B P=X Q$ und damit die Behauptung ergeben. Der Beweis von (*) selbst erfolgt vermittelst eines bekannten Kongruenzsatzes in drei Schritten.
I. Wegen $\varangle B P A \equiv \varangle E Q X \equiv 90^{\circ}$ sind beide Dreiecke rechtwinklig.
II. Da $A E \| B D$ ist das Sehnenviereck $A B D E$ ein gleichschenkeliges Trapez und demnach $A B=D E$. Weiterhin ist $D E=X E$ nach Konstruktion von $X$ und mithin $A B=X E$, d.h. die Hypotenusen stimmen überein.
III. Wie vorhin schließen wir aus $B C \| D F$, daß auch $B C D F$ ein gleichschenkliges Trapez ist. Durch wiederholte Verwendung des Peripheriewinkelsatzes erhalten wir nun $\varangle D E C+$ $\varangle C A B \equiv \varangle D A C+\varangle C A B \equiv \varangle D A B \equiv \varangle D F B \equiv \varangle C D F \equiv \varangle C E F \equiv \varangle C E X+\varangle X E F$. Infolge $\varangle D E C \equiv \varangle C E X$ ergibt sich hieraus $\varangle C A B \equiv \varangle X E F$, oder - anders formuliert $-\varangle P A B \equiv \varangle X E Q$.
Bemerkung. Diskussionen der Lagebeziehungen sind weder positiv noch negativ in die Bewertung eingegangen.
|
{
"resource_path": "Germany_TST/segmented/de-2006-loes_awkl1_06.jsonl",
"problem_match": "1. Aufgabe\n",
"solution_match": "\nLösung."
}
|
1f383e70-5f6a-5c36-866d-9d13a1e4421b
| 606,208
|
In a room, there are 2005 fruit crates, each containing one or more types of fruit, with each type of fruit being present in whole numbers.
a) Show that it is always possible to select 669 fruit crates that together contain at least one third of all the apples and at least one third of all the pears.
b) Can the crates in part a) always be chosen such that they also contain at least one third of all the peaches?
|
a) Let $N$ be a box containing a maximum number of apples, say $n$ pieces. It is set aside. We now consider all possibilities of dividing the remaining $2004 = 3 \cdot 668$ boxes into three piles, $A, B$, and $C$, each with 668 boxes. Let the total number of apples in these boxes be $a, b, c$. By starting with any such division and renaming the formed piles if necessary, we see that there are divisions with $a \leqq b \leqq c$. Among all these, we fix for the rest of the proof a division for which $c-a$ is minimal. If $c-a > n$, we could swap a box from $A$ with the maximum number of apples with a box from $C$ with the minimum number of apples and, due to the maximality of $n$, after possibly renaming the piles, we would obtain a contradiction to the minimality of $c-a$. Therefore, $c-a \leqq n$, so $a+n \geqq c \geqq b$, from which it immediately follows that
$$
a+n = \frac{(a+n) + (a+n) + a+n}{3} \geqq \frac{c+b+a+n}{3}
$$
If we ultimately decide to take the 669 boxes $A \cup \{N\}$, i.e., the boxes of pile $A$ together with the box $N$, we would have at least met the condition on the number of apples to be taken. This is of course also true for $B \cup \{N\}$ and $C \cup \{N\}$. Now, by the pigeonhole principle, let $T$ be one of these three piles that contains at least one-third of the pears occurring in them. Thus, the selection $T \cup \{N\}$ certainly meets the requirement for the number of pears to be chosen and is therefore as desired.
b) Here it suffices to provide a counterexample. Let one of the boxes contain nothing but an apple, another only a pear, and in the remaining 2003 boxes, let there be a peach each. If we wanted to meet the given conditions, we would have to select the box with the apple, the box with the pear, and 668 boxes with a peach, thus requiring a total of 670 boxes.
Remark. In part (a), it is instructive to consider the case where there are 1002 boxes each containing $2m$ apples but no pears, 1002 boxes each containing $2m$ pears but no apples, and one box, $(H)$, containing $m$ apples and $m$ pears, where $m$ stands for a possibly large natural number (e.g., 100000). One can easily convince oneself that box $H$ must be taken. This is still the case even if the described configuration is slightly modified, i.e., by changing the number of fruits (e.g., 1, 2, 3) in comparison to $m$. Most proposed algorithmic approaches of the form "Take boxes with the maximum number of fruits/apples/pears until ... and then always take boxes with the maximum number of ..." do not always lead to taking box $H$ in the described situations. Therefore, they do not solve the problem without further ado.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
In einem Raum stehen 2005 Obstkisten, von denen jede eine oder mehrere Sorten Obst enthält, von jeder Obstsorte ganzzahlig viele Früchte.
a) Man zeige, dass man stets 669 Obstkisten auswählen kann, die zusammen sowohl mindestens ein Drittel aller Äpfel als auch mindestens ein Drittel aller Birnen enthalten.
b) Können die Kisten in Teil a) stets so gewählt werden, dass sie außerdem mindestens ein Drittel aller Pfirsiche enthalten?
|
a) Es sei $N$ eine Kiste, die eine maximale Anzahl von Äpfeln enthält, sagen wir $n$ Stück. Sie werde zunächst beiseite gestellt. Wir betrachten nun alle Möglichkeiten, die verbleibenden $2004=3 \cdot 668$ Kisten in drei Haufen, $A, B$ und $C$ zu je 668 Kisten aufzuteilen. Die Gesamtzahl an Äpfeln in diesen Kisten sei $a, b, c$. Indem wir mit einer beliebigen solchen Aufteilung beginnen und die gebildeten Haufen gegebenenfalls umbenennen, sehen wir, daß es Aufteilungen mit $a \leqq$ $b \leqq c$ gibt. Unter allen diesen fixieren wir für den Rest der Beweisführung eine solche, für die $c-a$ minimal ist. Wäre nun $c-a>n$, so könnten wir eine Kiste aus $A$ mit darin maximaler Anzahl von Äpfeln gegen eine Kiste aus $C$ mit darin minimaler Anzahl vertauschen und erhielten infolge der Maximalität von $n$ nach eventueller Umbenennung der Haufen einen Widerspruch zur Minimalität von $c-a$. Demnach ist $c-a \leqq n$, also $a+n \geqq c \geqq b$, woraus sofort
$$
a+n=\frac{(a+n)+(a+n)+a+n}{3} \geqq \frac{c+b+a+n}{3}
$$
folgt. Sollten wir uns also letzten Endes entschließen, die 669 Kisten $A \cup\{N\}$ zu nehmen, d.h. die Kisten des Haufens $A$ zusammen mit der Kiste $N$, so hätten wir zumindest die Bedingung über die Anzahl der zu nehmenden Äpfel erfüllt. Dies gilt natürlich erst recht für $B \cup\{N\}$ und $C \cup\{N\}$. Nun sei (nach Schubfachprinzip) $T$ ein solcher der drei Haufen, der mindestens ein Drittel der in ihnen zusammen vorkommenden Birnen enthält. Damit erfüllt die Auswahl
$T \cup\{N\}$ sicher die Anforderung an die zu wählende Anzahl von Birnen und ist folglich nach obigem wie gewünscht.
b) Hier genügt die Angabe eines Gegenbeispiels. Es enthalte eine der Kisten nichts außer einem Apfel, eine weitere bloß eine Birne und in den übrigen 2003 Kisten möge jeweils ein Pfirsich liegen. Wollte man nun den gestellten Bedingungen genügen, müßte man die Kiste mit dem Apfel, die Kiste mit der Birne und 668 Kisten mit einem Pfirsich auswählen, bräuchte also insgesamt 670 Kisten.
Bemerkung. In Teilaufgabe (a) ist es instruktiv, den Fall zu betrachten, daß es 1002 Kisten mit jeweil $2 m$ Äpfeln aber keiner Birne, 1002 Kisten mit jeweils $2 m$ Birnen aber keinem Apfel und eine Kiste, $(H)$, mit $m$ Äpfeln und $m$ Birnen gibt, wobei $m$ für eine womöglich große natürliche Zahl (z.B. 100000) steht. Man überzeugt sich leicht, daß Kiste $H$ genommen werden muß. Dies ist auch dann noch der Fall, wenn die beschriebene Konfiguration geringfügig, d.h. um im Vergleich zu $m$ sehr kleine Anzahlen von Früchten (z.B. 1, 2, 3) geändert wird. Nun führen die meisten vorgeschlagenen algorithmischen Ansätze der Form „Man nehme solange Kisten mit maximal vielen Früchten/Äpfeln/Birnen, bis . . . und danach immer Kisten mit maximal vielen ..." nicht immer darauf, in den beschriebenen Situationen die Kiste $H$ zu nehmen. Daher lösen sie ohne weiteres die Aufgabe nicht.
|
{
"resource_path": "Germany_TST/segmented/de-2006-loes_awkl1_06.jsonl",
"problem_match": "2. Aufgabe\n",
"solution_match": "\nLösung."
}
|
d26f684a-e6af-5e0c-a6f2-f5efc03148ef
| 606,217
|
Can non-negative integers $a, b, c, d, e, f, g$, $h$ be found for every positive integer $n$ such that
$$
n=\frac{2^{a}-2^{b}}{2^{c}-2^{d}} \cdot \frac{2^{e}-2^{f}}{2^{g}-2^{h}}
$$
The answer needs to be justified.
Preliminary remark: In the following, let $n$ be odd. Without loss of generality, $a>b, c>d, e>f$, $g>h$. The condition equation is then equivalent to $n 2^{d+h-b-f}\left(2^{c-d}-1\right)\left(2^{g-h}-1\right)=$ $\left(2^{a-b}-1\right)\left(2^{e-f}-1\right)$. Since $n$ is odd, $d+h-b-f=0$, and one can set $d=h=b=f=0$ without loss of generality:
$$
n\left(2^{c}-1\right)\left(2^{g}-1\right)=\left(2^{a}-1\right)\left(2^{c}-1\right)
$$
|
The numbers of the form $n=19+64k$ with integer $k \geq 0$ cannot be represented. For $x>1$, $2^x-1$ gives a remainder of 3 when divided by 4, and for $x=1$ a remainder of 1. Only when an odd number of the variables $a, c, e, g$ have the value 1 can equation (*) be satisfied. If three of the variables have the value 1, the equation cannot hold because $n$ does not have the form $2^x-1$. Therefore, exactly one of the parentheses in $\left(^{*}\right)$ has the value 1. By appropriate considerations and case distinctions for remainders when divided by 8, 16, 32, 64, the values of the remaining parentheses can be determined and each can lead to a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Lassen sich für jede positive ganze Zahl $n$ nicht-negative ganze Zahlen $a, b, c, d, e, f, g$, $h$ mit
$$
n=\frac{2^{a}-2^{b}}{2^{c}-2^{d}} \cdot \frac{2^{e}-2^{f}}{2^{g}-2^{h}}
$$
finden? Die Antwort ist zu begründen.
Vorbemerkung: Im Folgenden sei $n$ ungerade. Ohne Einschränkung ist $a>b, c>d, e>f$, $g>h$. Die Bedingungsgleichung ist dann äquivalent zu $n 2^{d+h-b-f}\left(2^{c-d}-1\right)\left(2^{g-h}-1\right)=$ $\left(2^{a-b}-1\right)\left(2^{e-f}-1\right)$. Da $n$ ungerade ist, gilt $d+h-b-f=0$, und man kann ohne Einschränkung $d=h=b=f=0$ setzen:
$$
n\left(2^{c}-1\right)\left(2^{g}-1\right)=\left(2^{a}-1\right)\left(2^{c}-1\right)
$$
|
Die Zahlen der Form $n=19+64 k$ mit ganzzahligem $k \geqq 0$ lassen sich nicht darstellen. Für $x>1$ liefert $2^{x}-1$ Rest 3 bei Division durch 4, für $x=1$ Rest 1. Nur wenn eine ungerade Anzahl der Variablen $a, c, e, g$ Wert 1 hat, kann Gleichung (*) erfüllt sein. Haben drei der Variablen Wert 1, kann die Gleichung nicht gelten, da $n$ ncht die Form $2^{x}-1$ hat. Also hat genau eine der Klammern in $\left(^{*}\right)$ Wert 1. Durch entsprechende Überlegungen und Fallunterscheidungen zu Resten bei Division durch 8, 16, 32, 64 kann man die Werte der restlichen Klammern festlegen und jeweils zum Widerspruch führen.
|
{
"resource_path": "Germany_TST/segmented/de-2006-loes_awkl1_06.jsonl",
"problem_match": "3. Aufgabe\n",
"solution_match": "\n1. Lösung (skizziert):"
}
|
a3187b44-88d5-512e-9860-acdc3fce585e
| 604,162
|
Determine with proof all functions $f: \mathbb{R}^{+} \rightarrow \mathbb{R}^{+}$ with the property
$$
f(x) f(y)=2 f(x+y f(x))
$$
for all positive real numbers $x, y$.
|
Obviously, the function $f(x)=2$ for all $x \in \mathbb{R}^{+}$ satisfies the given functional equation. We will show that this is the only solution.
Lemma 1: For all $x \in \mathbb{R}^{+}$, $f(x) \geq 1$.
To prove this, assume $f(x)<1$ for some suitable $x$ and set $y=\frac{x}{1-f(x)}$. Then $x>0$ and it follows that $y=x+y f(x)$. From (I) we get $f(x) f(x+y f(x))=2 f(x+y f(x))$ and since $f(x+y f(x))>0$ it follows that $f(x)=2$, a contradiction!
Lemma 2: For all $x \in \mathbb{R}^{+}$, $f(x) \geq 2$.
To prove this, set $x=y$ in (I) and we get (II): $f^{2}(x)=2 f(x+x f(x))$. Suppose $f\left(x_{1}\right)<2$ for some suitable $x_{1}$. Then $f\left(x_{1}+x_{1} f\left(x_{1}\right)\right)=\frac{f^{2}\left(x_{1}\right)}{2}<f\left(x_{1}\right)$. With $x_{k+1}=x_{k}+x_{k} f\left(x_{k}\right)$ for $k=1,2, \ldots$ we get a monotonically decreasing sequence $\left(f\left(x_{1}\right)=a ; \frac{a^{2}}{2} ; \frac{a^{4}}{2^{3}} ; \ldots ; \frac{a^{2 t}}{2^{2 t-1}}, \ldots\right)$ of
function values. For $t>\frac{1}{2-2 \log _{2} a}$, the values of this sequence are less than 1, a contradiction!
Lemma 3: $f$ is monotonically increasing.
To prove this, assume there exist $s, \varepsilon>0$ such that $f(s)>f(s+\varepsilon)$. Substituting $x=s$ and $y=\frac{\varepsilon}{f(s)}$ into (I) gives $f(s) f\left(\frac{\varepsilon}{f(s)}\right)=2 f(s+\varepsilon)$, from which it follows that $f\left(\frac{\varepsilon}{f(s)}\right)<2$, a contradiction!
Lemma 4: If there exists a $z \in \mathbb{R}^{+}$ such that $f(z)>2$, then $f(x)>2$ for all $x \in \mathbb{R}^{+}$.
Again, substituting $x=z$ and $y=\frac{\varepsilon}{f(z)}$ into (I) gives $f(z) f\left(\frac{\varepsilon}{f(z)}\right)=2 f(z+\varepsilon)$, from which it follows with Lemma 2 that $f(z) \leq f(z+\varepsilon)$ for all $\varepsilon>0$. Therefore, there exists a $z_{0} \geq 0$ such that $f(z)>2$ for all $z>z_{0}$. Assume $z_{0}>0$. Then from (I) with $x=y=z_{0}-\varepsilon>0$ we get $f(x) f(y)=4$, and since $x+y f(x)=\left(z_{0}-\varepsilon\right)\left(1+f\left(z_{0}-\varepsilon\right)\right)=3\left(z_{0}-\varepsilon\right)$, for sufficiently small $\varepsilon$, we have $3\left(z_{0}-\varepsilon\right)>z_{0}$ and thus $2 f(x+y f(x))>4$, a contradiction!
Lemma 5: If $f(x)>2$ for all $x \in \mathbb{R}^{+}$, then $f$ is injective.
Assume there exist $s, \varepsilon>0$ such that $f(s)=f(s+\varepsilon)$. Substituting $x=s$ and $y=\frac{\varepsilon}{f(s)}$ into (I) gives $f(s) f\left(\frac{\varepsilon}{f(s)}\right)=2 f(s+\varepsilon)$, from which it follows that $f(s)<f(s+\varepsilon)$, a contradiction!
Main Proof: Due to the symmetry of the left side of (I), we also have $x+y f(x)=y+x f(y)$. For $y=1$ it follows that $f(x)=(f(1)-1) x+1=m x+1$. However, it is easily shown that no linear function can be a solution to (I).
Note: Since $\mathbb{D}=\mathbb{R}^{+}$, we cannot operate with $f(0)$. $f: \mathbb{R}^{+} \rightarrow \mathbb{R}^{+}$ does not mean that every positive real number must be a function value. Additional assumptions about $f$, such as continuity, are not allowed.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Man bestimme mit Beweis alle Funktionen $f: \mathbb{R}^{+} \rightarrow \mathbb{R}^{+}$mit der Eigenschaft
$$
f(x) f(y)=2 f(x+y f(x))
$$
für alle positiven reellen Zahlen $x, y$.
|
Offensichtlich erfüllt die Funktion $f(x)=2$ für alle $x \in \mathbb{R}^{+}$die gegebene Funktionalgleichung. Wir werden zeigen, dass dies die einzige Lösung ist.
Lemma 1: Für alle $x \in \mathbb{R}^{+}$gilt $f(x) \geq 1$.
Zum Beweis nehmen wir $f(x)<1$ für ein geeignetes $x$ an und setzen $y=\frac{x}{1-f(x)}$. Dann ist $x>0$ und es folgt $y=x+y f(x)$. Aus (I) erhalten wir $f(x) f(x+y f(x))=2 f(x+y f(x))$ und wegen $f(x+y f(x))>0$ folgt $f(x)=2$, Widerspruch!
Lemma 2: Für alle $x \in \mathbb{R}^{+}$gilt $f(x) \geq 2$.
Zum Beweis setzen wir in (I) $x=y$ und erhalten (II): $f^{2}(x)=2 f(x+x f(x))$. Sei $f\left(x_{1}\right)<2$ für ein geeignetes $x_{1}$. Dann ist $f\left(x_{1}+x_{1} f\left(x_{1}\right)\right)=\frac{f^{2}\left(x_{1}\right)}{2}<f\left(x_{1}\right)$. Mit $x_{k+1}=x_{k}+x_{k} f\left(x_{k}\right)$ für $k=1,2, \ldots$ entsteht eine monoton fallende Folge $\left(f\left(x_{1}\right)=a ; \frac{a^{2}}{2} ; \frac{a^{4}}{2^{3}} ; \ldots ; \frac{a^{2 t}}{2^{2 t-1}}, \ldots\right.$ ) von
Funktionswerten. Für $t>\frac{1}{2-2 \log _{2} a}$ sind die Werte dieser Folge kleiner als 1, Widerspruch!
Lemma 3: $f$ ist monoton steigend.
Zum Beweis nehmen wir an, es gibt $s, \varepsilon>0$ mit $f(s)>f(s+\varepsilon)$. Einsetzen von $x=s$ und $y=\frac{\varepsilon}{f(s)}$ in (I) liefert $f(s) f\left(\frac{\varepsilon}{f(s)}\right)=2 f(s+\varepsilon)$, woraus $f\left(\frac{\varepsilon}{f(s)}\right)<2$ folgt, Widerspruch!
Lemma 4: Wenn es ein $z \in \mathbb{R}^{+}$gibt mit $f(z)>2$, dann gilt $f(x)>2$ für alle $x \in \mathbb{R}^{+}$.
Wieder setzen wir $x=z$ und $y=\frac{\varepsilon}{f(z)}$ in (I) ein und haben $f(z) f\left(\frac{\varepsilon}{f(z)}\right)=2 f(z+\varepsilon)$, woraus jetzt mit Lemma 2 folgt: $f(z) \leq f(z+\varepsilon)$ für alle $\varepsilon>0$. Also existiert ein $z_{0} \geq 0$ mit $f(z)>2$ für alle $z>z_{0}$. Nehmen wir an, dass $z_{0}>0$ gilt. Dann folgt mit $x=y=z_{0}-\varepsilon>0$ aus (I) $f(x) f(y)=4$, und wegen $x+y f(x)=\left(z_{0}-\varepsilon\right)\left(1+f\left(z_{0}-\varepsilon\right)\right)=3\left(z_{0}-\varepsilon\right)$ gilt für hinreichend kleines $\varepsilon$, dass $3\left(z_{0}-\varepsilon\right)>z_{0}$ und daher $2 f(x+y f(x))>4$, Widerspruch!
Lemma 5: Wenn $f(x)>2$ für alle $x \in \mathbb{R}^{+}$, dann ist $f$ injektiv.
Angenommen, es gäbe $s, \varepsilon>0$ mit $f(s)=f(s+\varepsilon)$. Wir setzen $x=s$ und $y=\frac{\varepsilon}{f(s)}$ in (I) ein und haben $f(s) f\left(\frac{\varepsilon}{f(s)}\right)=2 f(s+\varepsilon)$, woraus nun $f(s)<f(s+\varepsilon)$ folgt, Widerspruch!
Hauptbeweis: Wegen der Symmetrie der linken Seite von (I) gilt auch $x+y f(x)=y+x f(y)$. Für $y=1$ folgt $f(x)=(f(1)-1) x+1=m x+1$. Durch Einsetzen wird jedoch leicht gezeigt, dass keine lineare Funktion Lösung von (I) sein kann.
Anmerkung: Wegen $\mathbb{D}=\mathbb{R}^{+}$darf nicht mit $f(0)$ operiert werden. $f: \mathbb{R}^{+} \rightarrow \mathbb{R}^{+}$bedeutet nicht, dass jede positive reelle Zahl Funktionswert sein muss. Zusätzliche Annahmen über $f$ wie z.B. Stetigkeit sind nicht zulässig.
|
{
"resource_path": "Germany_TST/segmented/de-2006-loes_awkl2_06.jsonl",
"problem_match": "# Aufgabe 1",
"solution_match": "\nLösung:"
}
|
9f8663c1-0506-5121-87e4-16bee955bba4
| 604,177
|
Given a triangle $ABC$ with $\overline{AB} + \overline{BC} = 3 \overline{AC}$. Its incircle has the center $I$ and touches the sides $AB$ at $D$ and $BC$ at $E$. Furthermore, let $K$ and $L$ be the reflection points of $D$ and $E$ with respect to $I$.
Prove that the quadrilateral $ACKL$ is a cyclic quadrilateral.
|
We denote the point of tangency of the incircle with $AC$ as $F$, the midpoint of $AC$ as $S$, the intersection of $w_{\beta}$ and the perpendicular bisector $m_{AC}$ as $P$, the reflection of $B$ over $I$ as $R$, the midpoint of $BI$ as $T$, and the equal segments on the triangle sides as $x, y$ and $z$ (see figure).
From $\overline{AB} + \overline{BC} = 3 \overline{AC}$ it follows that
$x + z + z + y = 3(x + y)$, thus (I) $z = x + y$. It is known that $P$ lies on the circumcircle of $ABC$. Therefore, $\angle CAP = \angle CBP = \angle PBA = \angle PCA = \frac{\beta}{2}$ and $\overline{AP} = \overline{CP}$. The triangles $ASP$ and $BEI$ are similar, and since $\overline{AS} = \frac{1}{2} \overline{AC} = \frac{x + y}{2} = \frac{z}{2} = \frac{1}{2} \overline{BE}$, with the notation $r$ for the inradius,
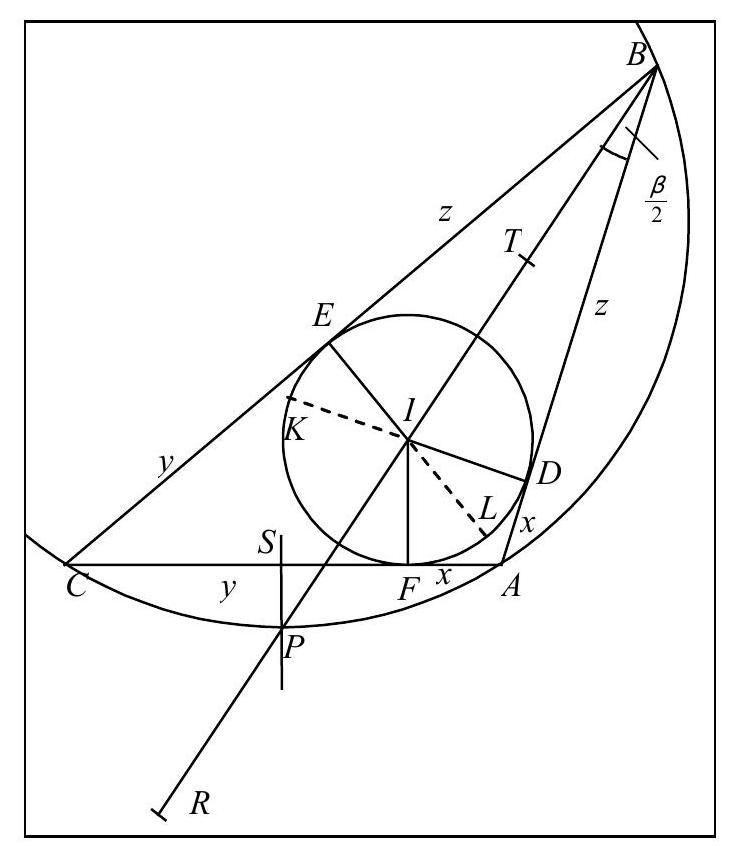
(II) $\overline{SP} = \frac{1}{2} \overline{EI} = \frac{r}{2}$ and $\overline{AP} = \frac{1}{2} \overline{BI}$.
For the area $F$ of triangle $ABC$, we have $F = rs = \sqrt{s(s-a)(s-b)(s-c)}$, where $s = \frac{a + b + c}{2} = x + y + z$. Therefore, $r(x + y + z) = \sqrt{(x + y + z)xyz}$ and with (I) it follows that $2rz = \sqrt{2zxyz} \Leftrightarrow 4r^2 = 2xy \Leftrightarrow 8r^2 = 4xy \Leftrightarrow 9r^2 + (x - y)^2 = r^2 + (x + y)^2 = r^2 + z^2$. Since $\angle BDI = 90^\circ$, (III) $\overline{BI}^2 = r^2 + z^2$. Because $PS \perp AC \perp FI$, we have $\overline{PI}^2 = \overline{SF}^2 + (\overline{PS} + \overline{FI})^2$.
But $\overline{SF} = \frac{1}{2} \overline{AC} - x = \frac{x + y}{2} - x = \frac{y - x}{2}$ and $\overline{FI} = r$. Therefore, and with (II), $\overline{PI}^2 = \left(\frac{y - x}{2}\right)^2 + \left(\frac{3}{2}r\right)^2 = \frac{(y - x)^2 + 9r^2}{4}$. With (III), it follows that $\overline{PI}^2 = \frac{1}{4} \overline{BI}^2$, thus $\overline{PI} = \frac{1}{2} \overline{BI}$. Therefore, (IV) $\overline{PI} = \overline{PA} = \overline{PC} = \overline{PR}$.
Additionally, $T$ is mapped to $P$ when reflected over $I$. Hence, $\overline{IT} = \overline{PI}$. $\overline{BI}$ is the diameter of the circle through $B, I, D$, and $E$ (right angles at $D$ and $E$). This circle has $T$ as its center. When this circle is reflected over $I$, $I$ is mapped to $I$, $T$ to $P$, $D$ to $K$, and $E$ to $L$, and the radius remains unchanged. With (IV), it follows that $A, L, I, K, C$, and $R$ lie on a circle centered at $P$; thus, $ACKL$ is a cyclic quadrilateral.
Note: Often, positional relationships or congruences were used without proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Gegeben sei ein Dreieck $A B C$ mit $\overline{A B}+\overline{B C}=3 \overline{A C}$. Sein Inkreis habe den Mittelpunkt $I$ und berühre die Seiten $A B$ in $D$ bzw. $B C$ in $E$. Weiter seien $K$ und $L$ die Spiegelpunkte von $D$ bzw. $E$ bezüglich $I$.
Man beweise, dass das Viereck $A C K L$ ein Sehnenviereck ist.
|
Zu den in der Aufgabenstellung genannten Punkten bezeichnen wir den Berührpunkt des Inkreises mit $A C$ mit $F$, den Mittelpunkt von AC mit $S$, den Schnittpunkt von $w_{\beta}$ und der Mittelsenkrechten $m_{A C}$ mit $P$, den Spiegelpunkt von $B$ an $I$ mit $R$, den Mittelpunkt von $B I$ mit $T$ und die paarweise gleichen Abschnitte auf den Dreiecksseiten mit $x, y$ bzw. $z$ (siehe Figur).
Aus $\overline{A B}+\overline{B C}=3 \overline{A C}$ folgt
$x+z+z+y=3(x+y)$, also (I) $z=x+y$. Bekanntlich liegt $P$ auf dem Umkreis von $A B C$. Daher gilt $\angle C A P=\angle C B P=\angle P B A=\angle P C A=\frac{\beta}{2}$ und $\overline{A P}=\overline{C P}$. Die Dreiecke $A S P$ und $B E I$ sind ähnlich, und wegen $\overline{A S}=\frac{1}{2} \overline{A C}=\frac{x+y}{2}=\frac{z}{2}=\frac{1}{2} \overline{B E}$ gilt mit der Bezeichnung $r$ für den Inkreisradius

(II) $\overline{S P}=\frac{1}{2} \overline{E I}=\frac{r}{2}$ sowie $\overline{A P}=\frac{1}{2} \overline{B I}$.
Für den Flächeninhalt $F$ des Dreiecks $A B C$ gilt $F=r s=\sqrt{s(s-a)(s-b)(s-c)}$, wobei $s=\frac{a+b+c}{2}=x+y+z$ ist. Daher ist $r(x+y+z)=\sqrt{(x+y+z) x y z}$ und mit (I) folgt $2 r z=\sqrt{2 z x y z} \Leftrightarrow 4 r^{2}=2 x y \Leftrightarrow 8 r^{2}=4 x y \Leftrightarrow 9 r^{2}+(x-y)^{2}=r^{2}+(x+y)^{2}=r^{2}+z^{2}$. Wegen $\angle B D I=90^{\circ}$ ist (III) $\overline{B I}^{2}=r^{2}+z^{2}$. Wegen $P S \perp A C \perp F I$ gilt $\overline{P I}^{2}=\overline{S F}^{2}+(\overline{P S}+\overline{F I})^{2}$.
Aber $\overline{S F}=\frac{1}{2} \overline{A C}-x=\frac{x+y}{2}-x=\frac{y-x}{2}$ und $\overline{F I}=r$. Daher und mit (II) ist $\overline{P I}^{2}=\left(\frac{y-x}{2}\right)^{2}+\left(\frac{3}{2} r\right)^{2}$ $=\frac{(y-x)^{2}+9 r^{2}}{4}$. Mit (III) folgt $\overline{P I}^{2}=\frac{1}{4} \overline{B I}^{2}$, also $\overline{P I}=\frac{1}{2} \overline{B I}$. So gilt (IV) $\overline{P I}=\overline{P A}=\overline{P C}=\overline{P R}$.
Außerdem wird $T$ bei Spiegelung an $I$ auf $P$ abgebildet. Daher ist auch $\overline{I T}=\overline{P I} . \overline{B I}$ ist der Durchmesser des Kreises durch $B, I, D$ und $E$ (rechte Winkel bei $D$ und $E$ ). Dieser Kreis hat $T$ als Mittelpunkt. Bei Spiegelung dieses Kreises an $I$ wird $I$ auf $I, T$ auf $P, D$ auf $K, E$ auf $L$ abgebildet und der Radius bleibt erhalten. Mit (IV) folgt, dass $A, L, I, K, C$ und $R$ auf einem Kreis um $P$ liegen; also ist $A C K L$ ein Sehnenviereck.
Anmerkung: Öfters wurden Lagebeziehungen oder Kongruenzen unbewiesen verwendet.
|
{
"resource_path": "Germany_TST/segmented/de-2006-loes_awkl2_06.jsonl",
"problem_match": "# Aufgabe 2",
"solution_match": "\nLösung:"
}
|
993900d5-c929-543f-9b14-a30bbe6090ce
| 604,190
|
We consider an $m \times n$-rectangle made up of $m n$ unit squares. Two of its unit squares are called adjacent if they share a common side, and a path is a sequence of unit squares in which any two consecutive elements are adjacent.
Each unit square of the rectangle can be either white or black. If all squares are colored, we have a coloring of the rectangle.
Let $N$ be the number of such colorings in which there is at least one black path from the left to the right side of the rectangle. Furthermore, let $M$ be the number of colorings in which there are at least two black paths from the left to the right side of the rectangle that do not share any square.
Prove that $N^{2} \geq M \cdot 2^{m n}$.
|
We will generalize the claim. To do this, we allow that the $m \times n$ rectangle is colored on both sides and that some of the unit squares are transparent. Such fields need only be colored on one side and then look the same on both sides. A non-transparent unit square, on the other hand, must be colored on both sides, though not necessarily with the same color.
Now let $A$ be the number of all such colorings of the top side, in which there is at least one black path from the left to the right side edge of the rectangle. Correspondingly, let $B$ be defined for the bottom side. Furthermore, let $C$ be the number of all colorings in which there are two black paths from the left to the right side edge of the rectangle, one on the top and one on the bottom, which do not contain a common transparent square. Finally, let $D$ be the number of all colorings of this rectangle. We will prove (I) $A \cdot B \geq C \cdot D$ and thus have shown the original claim as a special case, in which all fields are transparent. Here, $A=B=N, C=M, D=2^{m n}$. The proof of (I) is carried out by complete induction on the number $k$ of transparent fields. For $k=0$, we have $A=B=N \cdot 2^{m n}, C=N^{2}$, and $D=\left(2^{m n}\right)^{2}$, so equality holds in (I). Now we assume that the claim holds for $k$, and consider a rectangle with $k+1$ transparent fields. The numbers $A, B, C, D$ now apply to this rectangle. We choose a transparent unit square $t$ and make it opaque. For the resulting rectangle, let the respective numbers be denoted by $A^{\prime}, B^{\prime}, C^{\prime}, D^{\prime}$, and by the induction hypothesis, $A^{\prime} \cdot B^{\prime} \geq C^{\prime \prime} \cdot D^{\prime}$ holds.
Now it is obvious that $D^{\prime}=2 \cdot D$. For each coloring counted in $A$, there are exactly two colorings of $A^{\prime}$, namely distinguished by whether $t$ is colored black or white from below. Conversely, two colorings counted in $A^{\prime}$, which differ only in the color of the bottom side of a square, can be assigned one coloring counted in $A$. Thus, $A^{\prime}=2 \cdot A$ and correspondingly $B^{\prime}=2 \cdot B$. To prove (I) for $k+1$, it therefore suffices to show $C^{\prime} \geq 2 \cdot C$.
For this, let $t$ be transparent again. Since in $C$ only those colorings are counted that contain at least one black path on the top and one on the bottom, which do not intersect in a transparent square, $t$ can lie on at most one of these paths, w.l.o.g. on the top one. So if we make $t$ opaque and keep its color on top, we can color its bottom side black or white, so that both colorings are counted in $C^{\prime}$. Different colorings counted in $C$ always yield different pairs of colorings counted in $C^{\prime}$. This completes the proof.
[^0]
[^0]: Note: A proof by complete induction on one side of the board is delicate, as estimating the continuation of the paths often leads to counting errors. In most cases, possible cases were overlooked. The number of black fields in a black path can be greater than the width of the rectangle.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Wir betrachten ein $m \times n$-Rechteck aus $m n$ Einheitsquadraten. Zwei seiner Einheitsquadrate heißen benachbart, wenn sie eine gemeinsame Seitenkante haben, und ein Pfad ist eine Folge von Einheitsquadraten, in der je zwei aufeinander folgende Elemente benachbart sind.
Jedes Einheitsquadrat des Rechtecks kann entweder weiß oder schwarz gefärbt werden. Sind alle Quadrate gefärbt, so liegt eine Färbung des Rechtecks vor.
Es sei $N$ die Anzahl aller solcher Färbungen, bei denen es wenigstens einen schwarzen Pfad von der linken zur rechten Seitenkante des Rechtecks gibt. Ferner sei $M$ die Anzahl aller Färbungen, bei denen es wenigstens zwei schwarze Pfade von der linken zur rechten Seitenkante des Rechtecks gibt, die kein gemeinsames Quadrat enthalten.
Man beweise, dass $N^{2} \geq M \cdot 2^{m n}$.
|
Wir werden die Behauptung verallgemeinern. Dazu lassen wir zu, dass das $m \times n$ Rechteck auf beiden Seiten gefärbt wird und dass einige der Einheitsquadrate transparent sind. Solche Felder brauchen nur auf einer Seite gefärbt zu werden und sehen dann auf beiden Seiten gleich aus. Ein nicht transparentes Einheitsquadrat muss dagegen auf beiden Seiten gefärbt werden, allerdings nicht notwendigerweise mit der gleichen Farbe.
Nun sei $A$ die Anzahl aller solcher Färbungen der Oberseite, bei denen es wenigstens einen schwarzen Pfad von der linken zur rechten Seitenkante des Rechtecks gibt. Entsprechend sei $B$ für die Unterseite definiert. Ferner sei $C$ die Anzahl aller Färbungen, bei denen es zwei schwarze Pfade von der linken zur rechten Seitenkante des Rechtecks gibt, und zwar einen auf der Ober- und einen auf der Unterseite, die kein gemeinsames transparentes Quadrat enthalten. Schließlich sei $D$ die Anzahl aller Färbungen dieses Rechtecks. Wir werden (I) $A \cdot B \geq C \cdot D$ beweisen und haben damit die ursprüngliche Behauptung als Spezialfall gezeigt, in dem alle Felder transparent sind. Hier gilt nämlich $A=B=N, C=M, D=2^{m n}$. Den Beweis von (I) führen wir mit vollständiger Induktion nach der Anzahl $k$ der transparenten Felder. Für $k=0$ ist $A=B=N \cdot 2^{m n}, C=N^{2}$ und $D=\left(2^{m n}\right)^{2}$, so dass in (I) Gleichheit gilt. Nun nehmen wir an, dass die Behauptung für $k$ erfüllt ist, und betrachten ein Rechteck mit $k+1$ transparenten Feldern. Die Anzahlen $A, B, C, D$ gelten nun für dieses Rechteck. Wir wählen ein transparentes Einheitsquadrat $t$ und machen es undurchsichtig. Für das so entstandene Rechteck seien die jeweiligen Anzahlen mit $A^{\prime}, B^{\prime}, C^{\prime}, D^{\prime}$ bezeichnet und nach Induktionsannahme gilt $A^{\prime} \cdot B^{\prime} \geq C^{\prime \prime} \cdot D^{\prime}$.
Nun ist offensichtlich $D^{\prime}=2 \cdot D$. Für jede in $A$ gezählte Färbung existieren genau zwei Färbungen von $A^{\prime}$, nämlich dadurch unterschieden, dass $t$ von unten schwarz oder weiß gefärbt wird. Umgekehrt kann man zwei in $A^{\prime}$ gezählten Färbungen, die sich nur in der Farbe der Unterseite eines Quadrats unterscheiden, eine in $A$ gezählte Färbung zuordnen. Also ist $A^{\prime}=2 \cdot A$ und entsprechend $B^{\prime}=2 \cdot B$. Zum Beweis von (I) für $k+1$ genügt also der Nachweis von $C^{\prime} \geq 2 \cdot C$.
Dazu sei $t$ wieder transparent. Weil in $C$ nur solche Färbungen gezählt werden, die wenigstens einen schwarzen Pfad oben und unten enthalten, wobei diese sich nicht in einem transparenten Quadrat schneiden, kann $t$ höchstens auf einem dieser Pfade, oBdA auf dem oberen, liegen. Machen wir also $t$ undurchsichtig und behalten seine Farbe oben bei, können wir seine Unterseite schwarz oder weiß färben, so dass beide Färbungen in $C^{\prime}$ gezählt werden. Dabei liefern verschiedene in $C$ gezählte Färbungen stets verschiedene Paare von Färbungen, die in $C^{\prime}$ gezählt werden. Damit ist alles gezeigt.
[^0]
[^0]: Anmerkung: Ein Beweis mit vollständiger Induktion auf einer Brettseite ist heikel, da beim Abschätzen der Fortsetzungen der Pfade häufig Zählfehler auftreten. In der Regel wurden mögliche Fälle übersehen. Die Anzahl schwarzer Felder in einem schwarzen Pfad kann größer sein als die Breite des Rechtecks.
|
{
"resource_path": "Germany_TST/segmented/de-2006-loes_awkl2_06.jsonl",
"problem_match": "# Aufgabe 3",
"solution_match": "\nLösung:"
}
|
67c1e4df-f9e1-5295-9804-e04791c74db8
| 604,203
|
The point $P$ lies in the interior of triangle $ABC$ and satisfies
$$
\varangle B P C-\varangle B A C=\varangle C P A-\varangle C B A=\varangle A P B-\varangle A C B .
$$
Prove that then the following holds:
$$
\overline{P A} \cdot \overline{B C}=\overline{P B} \cdot \overline{A C}=\overline{P C} \cdot \overline{A B}
$$
First, one observes that $\varangle B P C=60^{\circ}+\alpha, \varangle C P A=60^{\circ}+\beta, \varangle A P B=60^{\circ}+\gamma$. By symmetry, it suffices to show one of the two claimed equations. (Hint: For an angle $\varangle X Y Z$ with $0^{\circ}<\varangle X Y Z<180^{\circ}$ in the mathematically positive direction, set $\varangle Z Y X:=$ $180^{\circ}-\varangle X Y Z$. With this convention, for example, for four pairwise distinct points $W, X, Y, Z$ on a circle, it always holds that $\varangle X Y Z=\varangle X W Z$ ).
|
The extensions of $A P, B P, C P$ meet the circumcircle of triangle $A B C$ again at $A^{\prime}, B^{\prime}, C^{\prime}$. Using the inscribed angle theorem and a simple angle sum argument, we find $\varangle B^{\prime} A^{\prime} C^{\prime}=\varangle B^{\prime} A^{\prime} A+\varangle A A^{\prime} C^{\prime}=\varangle B^{\prime} B A+\varangle A C C^{\prime}=\varangle B P C-\varangle B A C=60^{\circ}$. Similarly, $\varangle A^{\prime} C^{\prime} B^{\prime}=60^{\circ}$, and thus triangle $A^{\prime} B^{\prime} C^{\prime}$ is equilateral, i.e., $A^{\prime} B^{\prime}=B^{\prime} C^{\prime}=C^{\prime} A^{\prime}$. As usual, we have $A P B \sim B^{\prime} P A^{\prime}$ and $A P C \sim C^{\prime} P A^{\prime}$; this yields $\frac{A P}{A C}=\frac{C^{\prime} P}{C^{\prime} A^{\prime}}$ and $\frac{B P}{B C}=\frac{C^{\prime} P}{C^{\prime} B^{\prime}}$. In conjunction with the previous, this teaches us $\frac{A P}{A C}=\frac{B P}{B C}$ and thus indeed $A B \cdot P C=$ $A C \cdot P B$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Der Punkt $P$ liege im Inneren des Dreiecks $A B C$ und erfülle
$$
\varangle B P C-\varangle B A C=\varangle C P A-\varangle C B A=\varangle A P B-\varangle A C B .
$$
Man beweise, dass dann gilt:
$$
\overline{P A} \cdot \overline{B C}=\overline{P B} \cdot \overline{A C}=\overline{P C} \cdot \overline{A B}
$$
Zunächst überlegt man sich, daß $\varangle B P C=60^{\circ}+\alpha, \varangle C P A=60^{\circ}+\beta, \varangle A P B=60^{\circ}+\gamma$. Aus Symmetriegründen genügt es, eine der beiden behaupteten Gleichungen zu zeigen. (Hinweis: Für einen Winkel $\varangle X Y Z$ mit $0^{\circ}<\varangle X Y Z<180^{\circ}$ im mathematisch positiven Sinn setze $\varangle Z Y X:=$ $180^{\circ}-\varangle X Y Z$. Mit dieser Konvention gilt z. B. für vier paarweise verschiedene Punkte $W, X, Y, Z$ auf einer Kreislinie stets $\varangle X Y Z=\varangle X W Z$ ).
|
Die Verlängerungen von $A P, B P, C P$ mögen den Umkreis des Dreiecks $A B C$ erneut in $A^{\prime}, B^{\prime}, C^{\prime}$ treffen. Mit Hilfe des Peripheriewinkelsatzes und einem einfachen Winkelsummenargument finden wir $\varangle B^{\prime} A^{\prime} C^{\prime}=\varangle B^{\prime} A^{\prime} A+\varangle A A^{\prime} C^{\prime}=\varangle B^{\prime} B A+\varangle A C C^{\prime}=\varangle B P C-\varangle B A C=60^{\circ}$. Ebenso $\varangle A^{\prime} C^{\prime} B^{\prime}=60^{\circ}$ und folglich ist das Dreieck $A^{\prime} B^{\prime} C^{\prime}$ gleichseitig, d.h. $A^{\prime} B^{\prime}=B^{\prime} C^{\prime}=C^{\prime} A^{\prime}$. Wie üblich haben wir $A P B \sim B^{\prime} P A^{\prime}$ und $A P C \sim C^{\prime} P A^{\prime}$; hieraus ergibt sich $\frac{A P}{A C}=\frac{C^{\prime} P}{C^{\prime} A^{\prime}}$ und $\frac{B P}{B C}=\frac{C^{\prime} P}{C^{\prime} B^{\prime}}$. In Verbindung mit vorigem lehrt dies $\frac{A P}{A C}=\frac{B P}{B C}$ und somit in der Tat $A B \cdot P C=$ $A C \cdot P B$.
|
{
"resource_path": "Germany_TST/segmented/de-2007-loes_awkl1_07.jsonl",
"problem_match": "3. Aufgabe\n",
"solution_match": "\n1. Lösung."
}
|
40079e08-b3a3-58e3-a845-399290934788
| 604,285
|
The point $P$ lies in the interior of triangle $ABC$ and satisfies
$$
\varangle B P C-\varangle B A C=\varangle C P A-\varangle C B A=\varangle A P B-\varangle A C B .
$$
Prove that then the following holds:
$$
\overline{P A} \cdot \overline{B C}=\overline{P B} \cdot \overline{A C}=\overline{P C} \cdot \overline{A B}
$$
First, one observes that $\varangle B P C=60^{\circ}+\alpha, \varangle C P A=60^{\circ}+\beta, \varangle A P B=60^{\circ}+\gamma$. By symmetry, it suffices to show one of the two claimed equations. (Hint: For an angle $\varangle X Y Z$ with $0^{\circ}<\varangle X Y Z<180^{\circ}$ in the mathematically positive sense, set $\varangle Z Y X:=$ $180^{\circ}-\varangle X Y Z$. With this convention, for example, for four pairwise distinct points $W, X, Y, Z$ on a circle, it always holds that $\varangle X Y Z=\varangle X W Z$ ).
|
Choose point $J$ such that the triangles $A B C, P B J$ (equi-oriented) are similar. Then $\frac{A B}{B P}=\frac{B C}{B J}$ and $\varangle P B A=\varangle J B C$, which means that the triangles $A B P, C B J$ (equi-oriented) must also be similar. Consequently, $\varangle C J P=\varangle C J B-\varangle P J B=\left(60^{\circ}+\gamma\right)-\gamma=60^{\circ}$. Since $\varangle J P C=\varangle B P C-\varangle B P J=\left(60^{\circ}+\alpha\right)-\alpha=60^{\circ}$, triangle $P C J$ is equilateral and thus $P C=P J$. By the choice of $J$, we have $\frac{A B}{A C}=\frac{P B}{P J}$, and from this, using the previous result, we get $A C \cdot P B=A B \cdot P J=A B \cdot P C$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Der Punkt $P$ liege im Inneren des Dreiecks $A B C$ und erfülle
$$
\varangle B P C-\varangle B A C=\varangle C P A-\varangle C B A=\varangle A P B-\varangle A C B .
$$
Man beweise, dass dann gilt:
$$
\overline{P A} \cdot \overline{B C}=\overline{P B} \cdot \overline{A C}=\overline{P C} \cdot \overline{A B}
$$
Zunächst überlegt man sich, daß $\varangle B P C=60^{\circ}+\alpha, \varangle C P A=60^{\circ}+\beta, \varangle A P B=60^{\circ}+\gamma$. Aus Symmetriegründen genügt es, eine der beiden behaupteten Gleichungen zu zeigen. (Hinweis: Für einen Winkel $\varangle X Y Z$ mit $0^{\circ}<\varangle X Y Z<180^{\circ}$ im mathematisch positiven Sinn setze $\varangle Z Y X:=$ $180^{\circ}-\varangle X Y Z$. Mit dieser Konvention gilt z. B. für vier paarweise verschiedene Punkte $W, X, Y, Z$ auf einer Kreislinie stets $\varangle X Y Z=\varangle X W Z$ ).
|
Wähle den Punkt $J$ so, daß die Dreiecke $A B C, P B J$ (gleichorientiert) ähnlich sind. Sodann ist $\frac{A B}{B P}=\frac{B C}{B J}$ und $\varangle P B A=\varangle J B C$, weshalb auch die Dreiecke $A B P, C B J$ (gleichorientiert) ähnlich sein müssen. Folglich gilt $\varangle C J P=\varangle C J B-\varangle P J B=\left(60^{\circ}+\gamma\right)-\gamma=60^{\circ}$. Da auch $\varangle J P C=\varangle B P C-\varangle B P J=\left(60^{\circ}+\alpha\right)-\alpha=60^{\circ}$ ist das Dreieck $P C J$ gleichseitig und mithin $P C=P J$. Nach Wahl von $J$ haben wir $\frac{A B}{A C}=\frac{P B}{P J}$ und hieraus folgt mit Hilfe des vorigen wie gewünscht $A C \cdot P B=A B \cdot P J=A B \cdot P C$.
|
{
"resource_path": "Germany_TST/segmented/de-2007-loes_awkl1_07.jsonl",
"problem_match": "3. Aufgabe\n",
"solution_match": "\n2. Lösung."
}
|
40079e08-b3a3-58e3-a845-399290934788
| 604,285
|
The point $P$ lies in the interior of triangle $ABC$ and satisfies
$$
\varangle B P C-\varangle B A C=\varangle C P A-\varangle C B A=\varangle A P B-\varangle A C B .
$$
Prove that then the following holds:
$$
\overline{P A} \cdot \overline{B C}=\overline{P B} \cdot \overline{A C}=\overline{P C} \cdot \overline{A B}
$$
First, one observes that $\varangle B P C=60^{\circ}+\alpha, \varangle C P A=60^{\circ}+\beta, \varangle A P B=60^{\circ}+\gamma$. By symmetry, it suffices to show one of the two claimed equations. (Hint: For an angle $\varangle X Y Z$ with $0^{\circ}<\varangle X Y Z<180^{\circ}$ in the mathematically positive sense, set $\varangle Z Y X:=$ $180^{\circ}-\varangle X Y Z$. With this convention, for example, for four pairwise distinct points $W, X, Y, Z$ on a circle, it always holds that $\varangle X Y Z=\varangle X W Z$ ).
|
Over the segment $B P$, construct the equilateral triangle $B P T$. The intersection of $P T$ with $A B$ is called $G$. Additionally, on $A C$, choose the point $H$ such that $\varangle C P H=60^{\circ}$. Since $\varangle A P G=\gamma$ and $\varangle H P A=\beta$, it must be that $\varangle H P G+\varangle G A H=180^{\circ}$, meaning the quadrilateral $G A H P$ is inscribed in a circle. Therefore, $\varangle H G A=\varangle H P A=\beta$, from which it immediately follows that $G H \| B C$. For this reason, $\frac{A B}{A C}=\frac{B G}{C H} \quad$ (1). Furthermore, simple angle considerations show $\varangle H C P=$ $60^{\circ}-\varangle P B G=\varangle G B T$, which, together with $\varangle C P H=\varangle B T G\left[=60^{\circ}\right]$, teaches us the similarity of triangles $P C H$ and $T B G$. Thus, we have $\frac{B G}{C H}=\frac{B T}{C P} \quad$ (2). Since the triangle $BPT$ is equilateral by construction, in particular $B T=B P$. Together with (1) and (2), we obtain from this $\frac{A B}{A C}=\frac{B P}{C P}$ and thus indeed $A B \cdot P C=A C \cdot P B$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Der Punkt $P$ liege im Inneren des Dreiecks $A B C$ und erfülle
$$
\varangle B P C-\varangle B A C=\varangle C P A-\varangle C B A=\varangle A P B-\varangle A C B .
$$
Man beweise, dass dann gilt:
$$
\overline{P A} \cdot \overline{B C}=\overline{P B} \cdot \overline{A C}=\overline{P C} \cdot \overline{A B}
$$
Zunächst überlegt man sich, daß $\varangle B P C=60^{\circ}+\alpha, \varangle C P A=60^{\circ}+\beta, \varangle A P B=60^{\circ}+\gamma$. Aus Symmetriegründen genügt es, eine der beiden behaupteten Gleichungen zu zeigen. (Hinweis: Für einen Winkel $\varangle X Y Z$ mit $0^{\circ}<\varangle X Y Z<180^{\circ}$ im mathematisch positiven Sinn setze $\varangle Z Y X:=$ $180^{\circ}-\varangle X Y Z$. Mit dieser Konvention gilt z. B. für vier paarweise verschiedene Punkte $W, X, Y, Z$ auf einer Kreislinie stets $\varangle X Y Z=\varangle X W Z$ ).
|
Über der Strecke $B P$ werde das gleichseitige Dreieck $B P T$ errichtet. Der Schnittpunkt von $P T$ mit $A B$ heiße $G$. Außerdem werde auf $A C$ der Punkt $H$ mit $\varangle C P H=60^{\circ}$ gewählt. Wegen $\varangle A P G=\gamma$ und $\varangle H P A=\beta$ muss $\varangle H P G+\varangle G A H=180^{\circ}$ sein, d.h. das Viereck $G A H P$ ist einem Kreis einbeschrieben. Demnach $\varangle H G A=\varangle H P A=\beta$, woraus sofort $G H \| B C$ geschlossen wird. Aus diesem Grund gilt $\frac{A B}{A C}=\frac{B G}{C H} \quad$ (1). Ferner zeigen einfache Winkelbetrachtungen $\varangle H C P=$ $60^{\circ}-\varangle P B G=\varangle G B T$, was zusammen mit $\varangle C P H=\varangle B T G\left[=60^{\circ}\right]$ die Ähnlichkeit der Dreiecke $P C H$ und $T B G$ lehrt. Mithin haben wir $\frac{B G}{C H}=\frac{B T}{C P} \quad$ (2). Nachdem das Dreieck BPT nach Konstruktion gleichseitig ist, gilt insbsondere $B T=B P$. Zusammen mit (1) und (2) erhalten wir hieraus $\frac{A B}{A C}=\frac{B P}{C P}$ und damit in der Tat $A B \cdot P C=A C \cdot P B$.
|
{
"resource_path": "Germany_TST/segmented/de-2007-loes_awkl1_07.jsonl",
"problem_match": "3. Aufgabe\n",
"solution_match": "\n3. Lösung."
}
|
40079e08-b3a3-58e3-a845-399290934788
| 604,285
|
The point $P$ lies in the interior of triangle $ABC$ and satisfies
$$
\varangle B P C-\varangle B A C=\varangle C P A-\varangle C B A=\varangle A P B-\varangle A C B .
$$
Prove that then the following holds:
$$
\overline{P A} \cdot \overline{B C}=\overline{P B} \cdot \overline{A C}=\overline{P C} \cdot \overline{A B}
$$
First, one observes that $\varangle B P C=60^{\circ}+\alpha, \varangle C P A=60^{\circ}+\beta, \varangle A P B=60^{\circ}+\gamma$. By symmetry, it suffices to show one of the two claimed equations. (Hint: For an angle $\varangle X Y Z$ with $0^{\circ}<\varangle X Y Z<180^{\circ}$ in the mathematically positive sense, set $\varangle Z Y X:=$ $180^{\circ}-\varangle X Y Z$. With this convention, for example, for four pairwise distinct points $W, X, Y, Z$ on a circle, it always holds that $\varangle X Y Z=\varangle X W Z$ ).
|
Choose point $G$ such that the triangles $A G C, P B C$ (equally oriented) are similar. As seen in the second solution, the triangles $GBC$ and $A P C$ (equally oriented) are also similar. Furthermore, $\varangle B A G=\varangle C A G-\varangle C A B=\left(60^{\circ}+\alpha\right)-\alpha=60^{\circ}$ and similarly $\varangle G B A=60^{\circ}$. Therefore, triangle $A G B$ is equilateral and thus $A G=A B$. According to $A G C \sim P B C$, we have $P B: P C=A G: A C=A B: A C$. Therefore, as claimed, $A B \cdot P C=A C \cdot P B$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Der Punkt $P$ liege im Inneren des Dreiecks $A B C$ und erfülle
$$
\varangle B P C-\varangle B A C=\varangle C P A-\varangle C B A=\varangle A P B-\varangle A C B .
$$
Man beweise, dass dann gilt:
$$
\overline{P A} \cdot \overline{B C}=\overline{P B} \cdot \overline{A C}=\overline{P C} \cdot \overline{A B}
$$
Zunächst überlegt man sich, daß $\varangle B P C=60^{\circ}+\alpha, \varangle C P A=60^{\circ}+\beta, \varangle A P B=60^{\circ}+\gamma$. Aus Symmetriegründen genügt es, eine der beiden behaupteten Gleichungen zu zeigen. (Hinweis: Für einen Winkel $\varangle X Y Z$ mit $0^{\circ}<\varangle X Y Z<180^{\circ}$ im mathematisch positiven Sinn setze $\varangle Z Y X:=$ $180^{\circ}-\varangle X Y Z$. Mit dieser Konvention gilt z. B. für vier paarweise verschiedene Punkte $W, X, Y, Z$ auf einer Kreislinie stets $\varangle X Y Z=\varangle X W Z$ ).
|
Wähle den Punkt $G$ so, daß die Dreiecke $A G C, P B C$ (gleichorientiert) ähnlich sind. Wie in der zweiten Lösung sehen wir, daß dann auch die Dreiecke GBC und $A P C$ (gleichorientiert) ähnlich sind. Ferner ist $\varangle B A G=\varangle C A G-\varangle C A B=\left(60^{\circ}+\alpha\right)-\alpha=60^{\circ}$ und ebenso $\varangle G B A=60^{\circ}$. Das Dreieck $A G B$ ist also gleichseitig und mithin $A G=A B$. Nach $A G C \sim P B C$ haben wir also $P B: P C=A G: A C=A B: A C$. Daher wie behauptet $A B \cdot P C=A C \cdot P B$.
|
{
"resource_path": "Germany_TST/segmented/de-2007-loes_awkl1_07.jsonl",
"problem_match": "3. Aufgabe\n",
"solution_match": "\n4. Lösung."
}
|
40079e08-b3a3-58e3-a845-399290934788
| 604,285
|
The point $P$ lies in the interior of triangle $ABC$ and satisfies
$$
\varangle B P C-\varangle B A C=\varangle C P A-\varangle C B A=\varangle A P B-\varangle A C B .
$$
Prove that then the following holds:
$$
\overline{P A} \cdot \overline{B C}=\overline{P B} \cdot \overline{A C}=\overline{P C} \cdot \overline{A B}
$$
First, one observes that $\varangle B P C=60^{\circ}+\alpha, \varangle C P A=60^{\circ}+\beta, \varangle A P B=60^{\circ}+\gamma$. By symmetry, it suffices to show one of the two claimed equations. (Hint: For an angle $\varangle X Y Z$ with $0^{\circ}<\varangle X Y Z<180^{\circ}$ in the mathematically positive sense, set $\varangle Z Y X:=$ $180^{\circ}-\varangle X Y Z$. With this convention, for example, for four pairwise distinct points $W, X, Y, Z$ on a circle, it always holds that $\varangle X Y Z=\varangle X W Z$ ).
|
The feet of the perpendiculars from $P$ to the sides $BC, CA, AB$ are denoted as $X, Y, Z$ respectively. According to Thales' theorem, the quadrilaterals $PXCY, PYAZ, PZBX$ each have a circumcircle. We now find $\varangle ZXY = \varangle ZXP + \varangle PXY = \varangle ZBP + \varangle PCY = 60^{\circ}$ and similarly $\varangle XYZ = \varangle YZX = 60^{\circ}$. Therefore, the triangle $XYZ$ is equilateral. For the length of the side $XY$, we find by using the Law of Sines twice that $XY = PC \cdot \sin \gamma = \frac{AB \cdot PC}{2R}$, where $R$ is the radius of the circumcircle of triangle $ABC$. Similarly, $XZ = \frac{AC \cdot PB}{2R}$. From $XY = XZ$, it follows as required that $AB \cdot PC = AC \cdot PB$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Der Punkt $P$ liege im Inneren des Dreiecks $A B C$ und erfülle
$$
\varangle B P C-\varangle B A C=\varangle C P A-\varangle C B A=\varangle A P B-\varangle A C B .
$$
Man beweise, dass dann gilt:
$$
\overline{P A} \cdot \overline{B C}=\overline{P B} \cdot \overline{A C}=\overline{P C} \cdot \overline{A B}
$$
Zunächst überlegt man sich, daß $\varangle B P C=60^{\circ}+\alpha, \varangle C P A=60^{\circ}+\beta, \varangle A P B=60^{\circ}+\gamma$. Aus Symmetriegründen genügt es, eine der beiden behaupteten Gleichungen zu zeigen. (Hinweis: Für einen Winkel $\varangle X Y Z$ mit $0^{\circ}<\varangle X Y Z<180^{\circ}$ im mathematisch positiven Sinn setze $\varangle Z Y X:=$ $180^{\circ}-\varangle X Y Z$. Mit dieser Konvention gilt z. B. für vier paarweise verschiedene Punkte $W, X, Y, Z$ auf einer Kreislinie stets $\varangle X Y Z=\varangle X W Z$ ).
|
Die Fußpunkte der Lote von $P$ auf die Seiten $B C, C A, A B$ mögen $X, Y, Z$ genannte werden. Nach Satz von Thales besitzen die Vierecke $P X C Y, P Y A Z, P Z B X$ jeweils einen Umkreis. Wir finden nun $\varangle Z X Y=\varangle Z X P+\varangle P X Y=\varangle Z B P+\varangle P C Y=60^{\circ}$ und analog
$\varangle X Y Z=\varangle Y Z X=60^{\circ}$. Das Dreieck $X Y Z$ ist also gleichseitig. Für die Länge der Seite $X Y$ finden wir durch zweimalige Verwendung des Sinussatzes $X Y=P C \cdot \sin \gamma=\frac{A B \cdot P C}{2 R}$, wobei $R$ den Radius des Umkreises des Dreiecks $A B C$ bezeichnet. Ebenso $X Z=\frac{A C \cdot P B}{2 R}$. Aus $X Y=X Z$ folgt nunmehr wie verlangt $A B \cdot P C=A C \cdot P B$.
|
{
"resource_path": "Germany_TST/segmented/de-2007-loes_awkl1_07.jsonl",
"problem_match": "3. Aufgabe\n",
"solution_match": "\n5. Lösung."
}
|
40079e08-b3a3-58e3-a845-399290934788
| 604,285
|
The point $P$ lies in the interior of triangle $ABC$ and satisfies
$$
\varangle B P C-\varangle B A C=\varangle C P A-\varangle C B A=\varangle A P B-\varangle A C B .
$$
Prove that then the following holds:
$$
\overline{P A} \cdot \overline{B C}=\overline{P B} \cdot \overline{A C}=\overline{P C} \cdot \overline{A B}
$$
First, one observes that $\varangle B P C=60^{\circ}+\alpha, \varangle C P A=60^{\circ}+\beta, \varangle A P B=60^{\circ}+\gamma$. By symmetry, it suffices to show one of the two claimed equations. (Hint: For an angle $\varangle X Y Z$ with $0^{\circ}<\varangle X Y Z<180^{\circ}$ in the mathematically positive sense, set $\varangle Z Y X:=$ $180^{\circ}-\varangle X Y Z$. With this convention, for example, for four pairwise distinct points $W, X, Y, Z$ on a circle, it always holds that $\varangle X Y Z=\varangle X W Z$ ).
|
The circumcircle of triangle $A B P$ intersects $A C$ for the second time at $Q$. We obtain $\varangle B Q A=\varangle B P A=\gamma+60^{\circ}$ and from the exterior angle theorem $\varangle Q B C=60^{\circ}$. Furthermore, from $\varangle B P Q=180^{\circ}-\alpha$ and $\varangle C P B=60^{\circ}+\alpha$ we immediately get $\varangle Q P C=120^{\circ}$. Moreover, if we set $\varangle A B P=\varphi$, we immediately get $\varangle C Q P=\varphi$. By repeatedly using the Law of Sines, we now obtain
$$
\frac{P C}{P A}=\frac{P C}{C Q} \cdot \frac{C Q}{Q B} \cdot \frac{Q B}{A P}=\frac{\sin \varphi}{\sin 120^{\circ}} \cdot \frac{\sin 60^{\circ}}{\sin \gamma} \cdot \frac{\sin \alpha}{\sin \varphi}=\frac{\sin \alpha}{\sin \gamma}=\frac{B C}{A B}
$$
From this, it immediately follows that $A B \cdot P C=A P \cdot B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Der Punkt $P$ liege im Inneren des Dreiecks $A B C$ und erfülle
$$
\varangle B P C-\varangle B A C=\varangle C P A-\varangle C B A=\varangle A P B-\varangle A C B .
$$
Man beweise, dass dann gilt:
$$
\overline{P A} \cdot \overline{B C}=\overline{P B} \cdot \overline{A C}=\overline{P C} \cdot \overline{A B}
$$
Zunächst überlegt man sich, daß $\varangle B P C=60^{\circ}+\alpha, \varangle C P A=60^{\circ}+\beta, \varangle A P B=60^{\circ}+\gamma$. Aus Symmetriegründen genügt es, eine der beiden behaupteten Gleichungen zu zeigen. (Hinweis: Für einen Winkel $\varangle X Y Z$ mit $0^{\circ}<\varangle X Y Z<180^{\circ}$ im mathematisch positiven Sinn setze $\varangle Z Y X:=$ $180^{\circ}-\varangle X Y Z$. Mit dieser Konvention gilt z. B. für vier paarweise verschiedene Punkte $W, X, Y, Z$ auf einer Kreislinie stets $\varangle X Y Z=\varangle X W Z$ ).
|
Der Umkreis des Dreiecks $A B P$ schneide $A C$ zum zweiten Mal in $Q$. Wir erhalten $\varangle B Q A=\varangle B P A=\gamma+60^{\circ}$ und hieraus nach Außenwinkelsatz $\varangle Q B C=60^{\circ}$. Außerdem ergibt sich aus $\varangle B P Q=180^{\circ}-\alpha$ und $\varangle C P B=60^{\circ}+\alpha$ sofort $\varangle Q P C=120^{\circ}$. Ferner erhalten wir, wenn wir $\varangle A B P=\varphi$ setzen, sofort $\varangle C Q P=\varphi$. Durch mehrmalige Verwendung des Sinussatzes erhalten wir nun
$$
\frac{P C}{P A}=\frac{P C}{C Q} \cdot \frac{C Q}{Q B} \cdot \frac{Q B}{A P}=\frac{\sin \varphi}{\sin 120^{\circ}} \cdot \frac{\sin 60^{\circ}}{\sin \gamma} \cdot \frac{\sin \alpha}{\sin \varphi}=\frac{\sin \alpha}{\sin \gamma}=\frac{B C}{A B}
$$
Hieraus folgt sofort $A B \cdot P C=A P \cdot B C$.
|
{
"resource_path": "Germany_TST/segmented/de-2007-loes_awkl1_07.jsonl",
"problem_match": "3. Aufgabe\n",
"solution_match": "\n6. Lösung."
}
|
40079e08-b3a3-58e3-a845-399290934788
| 604,285
|
The point $P$ lies in the interior of triangle $ABC$ and satisfies
$$
\varangle B P C-\varangle B A C=\varangle C P A-\varangle C B A=\varangle A P B-\varangle A C B .
$$
Prove that then the following holds:
$$
\overline{P A} \cdot \overline{B C}=\overline{P B} \cdot \overline{A C}=\overline{P C} \cdot \overline{A B}
$$
First, one observes that $\varangle B P C=60^{\circ}+\alpha, \varangle C P A=60^{\circ}+\beta, \varangle A P B=60^{\circ}+\gamma$. By symmetry, it suffices to show one of the two claimed equations. (Hint: For an angle $\varangle X Y Z$ with $0^{\circ}<\varangle X Y Z<180^{\circ}$ in the mathematically positive direction, set $\varangle Z Y X:=$ $180^{\circ}-\varangle X Y Z$. With this convention, for example, for four pairwise distinct points $W, X, Y, Z$ on a circle, it always holds that $\varangle X Y Z=\varangle X W Z$ ).
|
Above the side $A B$, construct the equilateral triangle $A B Q$ inward. Simple angle considerations now show $\varangle Q A P=60^{\circ}-\varangle P A B=\varangle B C P$ and similarly $\varangle P B Q=\varangle P C A$. By introducing the intersection of $A C$ with $B Q$ as $T$ into the consideration, the quadrilateral $B C T P$ becomes a cyclic quadrilateral because $\varangle P B T=\varangle P B Q=\varangle P C A=\varangle P C T$. Consequently, $\varangle B T P=\varangle B C P=\varangle Q A P$, so $\varangle P T Q+\varangle Q A P=180^{\circ}$ and thus $P T Q A$ is also a cyclic quadrilateral. For this reason, $\varangle B Q P=\varangle T Q P=\varangle T A P=\varangle C A P$, and together with $\varangle P B Q=\varangle P C A$, the similarity of the triangles $B Q P, C A P$ follows. From this, $P C: A C=P B: B Q=P B: A B$, so as desired $A B \cdot P C=A C \cdot P B$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Der Punkt $P$ liege im Inneren des Dreiecks $A B C$ und erfülle
$$
\varangle B P C-\varangle B A C=\varangle C P A-\varangle C B A=\varangle A P B-\varangle A C B .
$$
Man beweise, dass dann gilt:
$$
\overline{P A} \cdot \overline{B C}=\overline{P B} \cdot \overline{A C}=\overline{P C} \cdot \overline{A B}
$$
Zunächst überlegt man sich, daß $\varangle B P C=60^{\circ}+\alpha, \varangle C P A=60^{\circ}+\beta, \varangle A P B=60^{\circ}+\gamma$. Aus Symmetriegründen genügt es, eine der beiden behaupteten Gleichungen zu zeigen. (Hinweis: Für einen Winkel $\varangle X Y Z$ mit $0^{\circ}<\varangle X Y Z<180^{\circ}$ im mathematisch positiven Sinn setze $\varangle Z Y X:=$ $180^{\circ}-\varangle X Y Z$. Mit dieser Konvention gilt z. B. für vier paarweise verschiedene Punkte $W, X, Y, Z$ auf einer Kreislinie stets $\varangle X Y Z=\varangle X W Z$ ).
|
Über der Seite $A B$ errichte man das gleichseitige Dreieck $A B Q$ nach innen. Einfache Winkelbetrachtungen zeigen nun $\varangle Q A P=60^{\circ}-\varangle P A B=\varangle B C P$ und ebenso $\varangle P B Q=\varangle P C A$. Indem wir also den Schnittpunkt von $A C$ mit $B Q$ als $T$ in die Überlegung einführen, wird das Viereck $B C T P$ wegen $\varangle P B T=\varangle P B Q=\varangle P C A=\varangle P C T$ ein Sehnenviereck sein. Folglich $\varangle B T P=\varangle B C P=\varangle Q A P$, also $\varangle P T Q+\varangle Q A P=180^{\circ}$ und somit ist auch $P T Q A$ ein Sehnenviereck. Aus diesem Grund gilt $\varangle B Q P=\varangle T Q P=\varangle T A P=\varangle C A P$, woraus in Verbindung mit $\varangle P B Q=\varangle P C A$ die Ähnlichkeit der Dreiecke $B Q P, C A P$ folgt. Hieraus erhellt $P C: A C=P B: B Q=P B: A B$, also wie gewünscht $A B \cdot P C=A C \cdot P B$.
|
{
"resource_path": "Germany_TST/segmented/de-2007-loes_awkl1_07.jsonl",
"problem_match": "3. Aufgabe\n",
"solution_match": "\n7. Lösung."
}
|
40079e08-b3a3-58e3-a845-399290934788
| 604,285
|
The point $P$ lies in the interior of triangle $ABC$ and satisfies
$$
\varangle B P C-\varangle B A C=\varangle C P A-\varangle C B A=\varangle A P B-\varangle A C B .
$$
Prove that then the following holds:
$$
\overline{P A} \cdot \overline{B C}=\overline{P B} \cdot \overline{A C}=\overline{P C} \cdot \overline{A B}
$$
First, one observes that $\varangle B P C=60^{\circ}+\alpha, \varangle C P A=60^{\circ}+\beta, \varangle A P B=60^{\circ}+\gamma$. By symmetry, it suffices to show one of the two claimed equations. (Hint: For an angle $\varangle X Y Z$ with $0^{\circ}<\varangle X Y Z<180^{\circ}$ in the mathematically positive direction, set $\varangle Z Y X:=$ $180^{\circ}-\varangle X Y Z$. With this convention, for example, for four pairwise distinct points $W, X, Y, Z$ on a circle, it always holds that $\varangle X Y Z=\varangle X W Z$ ).
|
Set $\varangle A C P=\gamma^{\prime}, \varangle P B C=\gamma^{\prime \prime}, \varangle P B A=\beta^{\prime \prime}$. By the Law of Sines, we have
$\frac{\sin \beta^{\prime \prime}}{\sin \gamma^{\prime}}=\frac{\sin \beta^{\prime \prime}}{A P} \cdot \frac{A P}{\sin \gamma^{\prime}}=\frac{\sin \left(60^{\circ}+\gamma\right)}{c} \cdot \frac{b}{\sin \left(60^{\circ}+\beta\right)}=\frac{\sin \left(60^{\circ}+\gamma\right)}{\sin \gamma} \cdot \frac{\sin \beta}{\sin \left(60^{\circ}+\beta\right)}=\frac{1+\sqrt{3} \cot \gamma}{1+\sqrt{3} \cot \beta}$.
Since $\beta^{\prime \prime}+\gamma^{\prime}=60^{\circ}$, we also have
$$
\frac{\sin \beta^{\prime \prime}}{\sin \gamma^{\prime}}=\frac{\sin \left(60^{\circ}-\gamma^{\prime}\right)}{\sin \gamma^{\prime}}=\frac{\sqrt{3}}{2} \cot \gamma^{\prime}-\frac{1}{2} .
$$
Combining these two equations, we get
$$
\cot \gamma^{\prime}=\frac{\sqrt{3}+\cot \beta+2 \cot \gamma}{1+\sqrt{3} \cot \beta}
$$
Furthermore,
$$
\frac{\sin \gamma^{\prime \prime}}{\sin \gamma^{\prime}}=\frac{\sin \left(\gamma-\gamma^{\prime}\right)}{\sin \gamma^{\prime}}=\sin \gamma \cot \gamma^{\prime}-\cos \gamma
$$
Substituting the previously found equation, we obtain
$$
\begin{gathered}
\frac{\sin \gamma^{\prime \prime}}{\sin \gamma^{\prime}}=\frac{(\sqrt{3} \sin \beta \sin \gamma+\cos \beta \sin \gamma+2 \sin \beta \cos \gamma)-(\sin \beta \cos \gamma+\sqrt{3} \cos \beta \cos \gamma)}{\sin \beta+\sqrt{3} \cos \beta} \\
=\frac{\sin \alpha+\sqrt{3} \cos \alpha}{\sin \beta+\sqrt{3} \cos \beta}=\frac{\sin \left(60^{\circ}+\alpha\right)}{\sin \left(60^{\circ}+\beta\right)}
\end{gathered}
$$
Therefore, by the Law of Sines,
$$
\frac{A P}{A C}=\frac{\sin \gamma^{\prime}}{\sin \left(\beta+60^{\circ}\right)}=\frac{\sin \gamma^{\prime \prime}}{\sin \left(\alpha+60^{\circ}\right)}=\frac{B P}{B C}
$$
i.e., as desired, $A P \cdot B C=B P \cdot A C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Der Punkt $P$ liege im Inneren des Dreiecks $A B C$ und erfülle
$$
\varangle B P C-\varangle B A C=\varangle C P A-\varangle C B A=\varangle A P B-\varangle A C B .
$$
Man beweise, dass dann gilt:
$$
\overline{P A} \cdot \overline{B C}=\overline{P B} \cdot \overline{A C}=\overline{P C} \cdot \overline{A B}
$$
Zunächst überlegt man sich, daß $\varangle B P C=60^{\circ}+\alpha, \varangle C P A=60^{\circ}+\beta, \varangle A P B=60^{\circ}+\gamma$. Aus Symmetriegründen genügt es, eine der beiden behaupteten Gleichungen zu zeigen. (Hinweis: Für einen Winkel $\varangle X Y Z$ mit $0^{\circ}<\varangle X Y Z<180^{\circ}$ im mathematisch positiven Sinn setze $\varangle Z Y X:=$ $180^{\circ}-\varangle X Y Z$. Mit dieser Konvention gilt z. B. für vier paarweise verschiedene Punkte $W, X, Y, Z$ auf einer Kreislinie stets $\varangle X Y Z=\varangle X W Z$ ).
|
Setze $\varangle A C P=\gamma^{\prime}, \varangle P B C=\gamma^{\prime \prime}, \varangle P B A=\beta^{\prime \prime}$. Nun ist nach Sinussatz
$\frac{\sin \beta^{\prime \prime}}{\sin \gamma^{\prime}}=\frac{\sin \beta^{\prime \prime}}{A P} \cdot \frac{A P}{\sin \gamma^{\prime}}=\frac{\sin \left(60^{\circ}+\gamma\right)}{c} \cdot \frac{b}{\sin \left(60^{\circ}+\beta\right)}=\frac{\sin \left(60^{\circ}+\gamma\right)}{\sin \gamma} \cdot \frac{\sin \beta}{\sin \left(60^{\circ}+\beta\right)}=\frac{1+\sqrt{3} \cot \gamma}{1+\sqrt{3} \cot \beta}$.
Da jedoch $\beta^{\prime \prime}+\gamma^{\prime}=60^{\circ}$ haben wir auch
$$
\frac{\sin \beta^{\prime \prime}}{\sin \gamma^{\prime}}=\frac{\sin \left(60^{\circ}-\gamma^{\prime}\right)}{\sin \gamma^{\prime}}=\frac{\sqrt{3}}{2} \cot \gamma^{\prime}-\frac{1}{2} .
$$
Diese beiden Gleichungen liefern zusammengenommen
$$
\cot \gamma^{\prime}=\frac{\sqrt{3}+\cot \beta+2 \cot \gamma}{1+\sqrt{3} \cot \beta}
$$
Weiterhin
$$
\frac{\sin \gamma^{\prime \prime}}{\sin \gamma^{\prime}}=\frac{\sin \left(\gamma-\gamma^{\prime}\right)}{\sin \gamma^{\prime}}=\sin \gamma \cot \gamma^{\prime}-\cos \gamma
$$
Hierin setzen wir die zuvor gefundene Gleichung ein und erhalten
$$
\begin{gathered}
\frac{\sin \gamma^{\prime \prime}}{\sin \gamma^{\prime}}=\frac{(\sqrt{3} \sin \beta \sin \gamma+\cos \beta \sin \gamma+2 \sin \beta \cos \gamma)-(\sin \beta \cos \gamma+\sqrt{3} \cos \beta \cos \gamma)}{\sin \beta+\sqrt{3} \cos \beta} \\
=\frac{\sin \alpha+\sqrt{3} \cos \alpha}{\sin \beta+\sqrt{3} \cos \beta}=\frac{\sin \left(60^{\circ}+\alpha\right)}{\sin \left(60^{\circ}+\beta\right)}
\end{gathered}
$$
Daher nach Sinussatz
$$
\frac{A P}{A C}=\frac{\sin \gamma^{\prime}}{\sin \left(\beta+60^{\circ}\right)}=\frac{\sin \gamma^{\prime \prime}}{\sin \left(\alpha+60^{\circ}\right)}=\frac{B P}{B C}
$$
d.h. wie gewünscht $A P \cdot B C=B P \cdot A C$.
|
{
"resource_path": "Germany_TST/segmented/de-2007-loes_awkl1_07.jsonl",
"problem_match": "3. Aufgabe\n",
"solution_match": "\n8. Lösung."
}
|
40079e08-b3a3-58e3-a845-399290934788
| 604,285
|
The point $P$ lies in the interior of triangle $ABC$ and satisfies
$$
\varangle B P C-\varangle B A C=\varangle C P A-\varangle C B A=\varangle A P B-\varangle A C B .
$$
Prove that then the following holds:
$$
\overline{P A} \cdot \overline{B C}=\overline{P B} \cdot \overline{A C}=\overline{P C} \cdot \overline{A B}
$$
First, one observes that $\varangle B P C=60^{\circ}+\alpha, \varangle C P A=60^{\circ}+\beta, \varangle A P B=60^{\circ}+\gamma$. By symmetry, it suffices to show one of the two claimed equations. (Hint: For an angle $\varangle X Y Z$ with $0^{\circ}<\varangle X Y Z<180^{\circ}$ in the mathematically positive direction, set $\varangle Z Y X:=$ $180^{\circ}-\varangle X Y Z$. With this convention, for example, for four pairwise distinct points $W, X, Y, Z$ on a circle, it always holds that $\varangle X Y Z=\varangle X W Z$ ).
|
The circumcircle of triangle $A P B$ meets the line $C P$ for the second time at $J$. Then, $\varangle A J P = \varangle A B P$. Together with $\varangle A B P + \varangle P C A = 60^{\circ}$, this teaches us that $\varangle C A J = 120^{\circ}$. Similarly, we see that $\varangle J B C = 120^{\circ}$. Thus, we have
$$
\frac{A C}{B C} = \frac{A C}{J C} \cdot \frac{J C}{B C} = \frac{\sin \varangle A J C}{\sin \varangle C A J} \cdot \frac{\sin \varangle J B C}{\sin \varangle C J B} = \frac{\sin \varangle A J P}{\sin \varangle P J B} = \frac{\sin \varangle A B P}{\sin \varangle P A B} = \frac{A P}{B P},
$$
i.e., as claimed, $A C \cdot B P = B C \cdot A P$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Der Punkt $P$ liege im Inneren des Dreiecks $A B C$ und erfülle
$$
\varangle B P C-\varangle B A C=\varangle C P A-\varangle C B A=\varangle A P B-\varangle A C B .
$$
Man beweise, dass dann gilt:
$$
\overline{P A} \cdot \overline{B C}=\overline{P B} \cdot \overline{A C}=\overline{P C} \cdot \overline{A B}
$$
Zunächst überlegt man sich, daß $\varangle B P C=60^{\circ}+\alpha, \varangle C P A=60^{\circ}+\beta, \varangle A P B=60^{\circ}+\gamma$. Aus Symmetriegründen genügt es, eine der beiden behaupteten Gleichungen zu zeigen. (Hinweis: Für einen Winkel $\varangle X Y Z$ mit $0^{\circ}<\varangle X Y Z<180^{\circ}$ im mathematisch positiven Sinn setze $\varangle Z Y X:=$ $180^{\circ}-\varangle X Y Z$. Mit dieser Konvention gilt z. B. für vier paarweise verschiedene Punkte $W, X, Y, Z$ auf einer Kreislinie stets $\varangle X Y Z=\varangle X W Z$ ).
|
Der Umkreis des Dreiecks $A P B$ treffe die Gerade $C P$ zum zweiten Mal in $J$. Sodann ist $\varangle A J P=\varangle A B P$. Zusammen mit $\varangle A B P+\varangle P C A=60^{\circ}$ lehrt dies $\varangle C A J=120^{\circ}$. Ebenso sehen wir $\varangle J B C=120^{\circ}$ ein. Damit haben wir
$$
\frac{A C}{B C}=\frac{A C}{J C} \cdot \frac{J C}{B C}=\frac{\sin \varangle A J C}{\sin \varangle C A J} \cdot \frac{\sin \varangle J B C}{\sin \varangle C J B}=\frac{\sin \varangle A J P}{\sin \varangle P J B}=\frac{\sin \varangle A B P}{\sin \varangle P A B}=\frac{A P}{B P},
$$
d.h. wie behauptet $A C \cdot B P=B C \cdot A P$.
|
{
"resource_path": "Germany_TST/segmented/de-2007-loes_awkl1_07.jsonl",
"problem_match": "3. Aufgabe\n",
"solution_match": "\n9. Lösung."
}
|
40079e08-b3a3-58e3-a845-399290934788
| 604,285
|
A sequence $a_{0}, a_{1}, a_{2}, \ldots$ of real numbers is recursively defined by
$$
a_{0}=-1, \quad \sum_{k=0}^{n} \frac{a_{n-k}}{k+1}=0 \quad \text { for } n \geq 1 .
$$
Prove that $a_{n}>0$ for all $n \geq 1$.
|
For $n=1$ we have $a_{1}+\frac{1}{2} a_{0}=0$, thus $a_{1}=\frac{1}{2}>0$. Now let $a_{i}>0$ for $1 \leq i<n$. From the given, it follows that $\sum_{k=1}^{n-1} \frac{a_{n-k}}{k+1}+\frac{a_{n}}{1}+\frac{a_{0}}{n+1}=0 \Leftrightarrow a_{n}=\frac{1}{n+1}-\sum_{k=1}^{n-1} \frac{a_{n-k}}{k+1}(*)$ and similarly $0=\sum_{k=0}^{n-1} \frac{a_{(n-1)-k}}{k+1}=\sum_{k=1}^{n} \frac{a_{n-k}}{k}=\sum_{k=1}^{n-1} \frac{a_{n-k}}{k}+\frac{a_{0}}{n} \Leftrightarrow \frac{1}{n}=\sum_{k=1}^{n-1} \frac{a_{n-k}}{k}$. This leads to $\frac{1}{n+1}=\sum_{k=1}^{n-1}\left(\frac{a_{n-k}}{k} \cdot \frac{n}{n+1}\right)$ and since $n>k \Leftrightarrow \frac{n}{n+1}>\frac{k}{k+1} \Leftrightarrow \frac{n}{k(n+1)}>\frac{1}{k+1}$, we have $\frac{1}{n+1}>\sum_{k=1}^{n-1} \frac{a_{n-k}}{k+1}$. With (*), it follows that $a_{n}>\sum_{k=1}^{n-1} \frac{a_{n-k}}{k+1}-\sum_{k=1}^{n-1} \frac{a_{n-k}}{k+1}=0$. By complete induction, $a_{n}>0$ for all $n \geq 1$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Eine $F$ olge $a_{0}, a_{1}, a_{2}, \ldots$ reeller Zahlen ist rekursiv definiert durch
$$
a_{0}=-1, \quad \sum_{k=0}^{n} \frac{a_{n-k}}{k+1}=0 \quad \text { für } n \geq 1 .
$$
$M$ an beweise, dass $a_{n}>0$ für alle $n \geq 1$ gilt.
|
Für $n=1$ gilt $a_{1}+\frac{1}{2} a_{0}=0$, also $a_{1}=\frac{1}{2}>0$. Nun gelte $a_{i}>0$ für $1 \leq i<n$. A us dem Gegebenen folgt $\sum_{k=1}^{n-1} \frac{a_{n-k}}{k+1}+\frac{a_{n}}{1}+\frac{a_{0}}{n+1}=0 \Leftrightarrow a_{n}=\frac{1}{n+1}-\sum_{k=1}^{n-1} \frac{a_{n-k}}{k+1}(*)$ und ebenso $0=\sum_{k=0}^{n-1} \frac{a_{(n-1)-k}}{k+1}=\sum_{k=1}^{n} \frac{a_{n-k}}{k}=\sum_{k=1}^{n-1} \frac{a_{n-k}}{k}+\frac{a_{0}}{n} \Leftrightarrow \frac{1}{n}=\sum_{k=1}^{n-1} \frac{a_{n-k}}{k}$. Dies führt auf $\frac{1}{n+1}=\sum_{k=1}^{n-1}\left(\frac{a_{n-k}}{k} \cdot \frac{n}{n+1}\right)$ und wegen $n>k \Leftrightarrow \frac{n}{n+1}>\frac{k}{k+1} \Leftrightarrow \frac{n}{k(n+1)}>\frac{1}{k+1}$ auf $\frac{1}{n+1}>\sum_{k=1}^{n-1} \frac{a_{n-k}}{k+1}$. Mit (*) ergibt sich $a_{n}>\sum_{k=1}^{n-1} \frac{a_{n-k}}{k+1}-\sum_{k=1}^{n-1} \frac{a_{n-k}}{k+1}=0$. Mit vollständiger Induktion gilt daher $a_{n}>0$ für alle $n \geq 1$.
|
{
"resource_path": "Germany_TST/segmented/de-2007-loes_awkl2_07.jsonl",
"problem_match": "# Aufgabe 1",
"solution_match": "\nLösung:"
}
|
8c78e168-996e-5a61-a249-42d918232326
| 604,349
|
For a convex pentagon $A B C D E$, the following holds
$$
\varangle B A C=\varangle C A D=\varangle D A E \quad \text { and } \quad \varangle C B A=\varangle D C A=\varangle E D A .
$$
The intersection of the diagonals BD and CE is denoted by $P$.
Prove that the line $A P$ passes through the midpoint of the side $C D$.
|
Due to two equal angles each, the triangles $A B C, A C D$ and $A D E$ are similar, and because of the position of the angles, $\frac{|B C|}{|C D|}=\frac{|C D|}{|D E|}$. Since $\varangle D C B=\varangle E D C$ (sum of two equal angles), the triangles $B C D$ and $C D E$ are also similar. This implies $\varangle B D C=\varangle C E D=: \varepsilon$ as well as $\varangle C B D=\varangle D C E=: \delta$. Therefore, the triangles $B C D$ and $D P C$ are similar, from which $\varangle A E P=\gamma-\varepsilon=\varangle A D P$ follows. Hence, $A P D E$ is a cyclic quadrilateral. Similarly, it follows that $A B C P$ is also a cyclic quadrilateral. The angles resulting from this are marked in the figure with vertices $A$ and $P$. In particular, this implies that the triangles $A F D$ and $P F D$ as well as $A C F$ and $P C F$ are similar, where $F$ is the intersection of $A P$ and $C D$. From these
similarities, it follows that $\frac{|D F|}{|F P|}=\frac{|A F|}{|D F|}$ and $\frac{|C F|}{|F P|}=\frac{|A F|}{|C F|}$, which yields $|A F| \cdot|F P|=|D F|^{2}$ on the one hand, and $|A F| \cdot|F P|=|C F|^{2}$ on the other. This results in $|C F|=|D F|$, which was to be proven.
Note: Another very elegant solution can be obtained by using Ceva's theorem in triangle $A C D$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Für ein konvexes Fünfeck $A B C D E$ gilt
$$
\varangle B A C=\varangle C A D=\varangle D A E \quad \text { sowie } \quad \varangle C B A=\varangle D C A=\varangle E D A .
$$
Der Schnittpunkt der Diagonalen BD und CE wird mit $P$ bezeichnet.
M an beweise, dass die Gerade $A P$ durch den Mittelpunkt der Seite $C D$ verläuft.
|
W egen jeweils zweier gleicher Winkel sind die Dreiecke $A B C, A C D$ und $A D E$ ähnlich und wegen der Lage der W inkel gilt $\frac{|B C|}{|C D|}=\frac{|C D|}{|D E|}$. W eil gilt $\varangle D C B=\varangle E D C$ (Summe zweier gleicher Winkel), sind auch die Dreiecke $B C D$ und $C D E$ ähnlich. Daraus folgt $\varangle B D C=\varangle C E D=: \varepsilon$ sowie $\varangle C B D=\varangle D C E=: \delta$. Somit sind die Dreiecke $B C D$ und $D P C$ ähnlich, woraus $\varangle A E P=\gamma-\varepsilon=\varangle A D P$ folgt. Daher ist $A P D E$ ein Sehnenviereck. Völlig analog folgt, dass auch $A B C P$ ein Sehnenviereck ist. In der Figur sind die sich daraus ergebenden Winkel mit den Scheiteln $A$ und $P$ eingetragen. Insbesondere folgt daraus, dass die Dreiecke $A F D$ und $P F D$ sowie $A C F$ und $P C F$ ähnlich sind, wobei $F$ der Schnittpunkt von $A P$ und $C D$ ist. A us diesen
Ähnlichkeiten folgt $\frac{|D F|}{|F P|}=\frac{|A F|}{|D F|}$ sowie $\frac{|C F|}{|F P|}=\frac{|A F|}{|C F|}$, woraus sich einerseits $|A F| \cdot|F P|=|D F|^{2}$, andererseits $|A F| \cdot|F P|=|C F|^{2}$ ergibt. Dies liefert $|C F|=|D F|$, was zu beweisen war.
Anmerkung: Eine weitere, sehr elegante Lösung ergibt sich bei Verwendung des Satzes von Ceva im Dreieck $A C D$.

|
{
"resource_path": "Germany_TST/segmented/de-2007-loes_awkl2_07.jsonl",
"problem_match": "# Aufgabe 2",
"solution_match": "\nLösung:"
}
|
80888802-aec3-5e28-aea7-ff3d2437497d
| 604,363
|
For every real number $x$ with $0<x<1$ let $y \in] 0 ; 1[$ be the number whose $n$-th decimal place is the $(2n)$-th decimal place of $x$. $M$ prove: If $x$ is rational, then $y$ is also rational.
|
A rational number has a terminating or a periodic decimal fraction expansion. A terminating decimal fraction expansion can be continued indefinitely by appending zeros and thus corresponds to a periodic decimal fraction expansion with a period length of 1.
In the following, we only consider the digits after a possible pre-period of length $v$. The first power of two greater than $v$ is denoted by $2^{s}$, and the period length of the decimal fraction by $d$.
Since there are only finitely many residue classes mod $d$, there exist two numbers $2^{t}$ and $2^{t+m}$ that yield the same remainder $r$ mod $d$, i.e., $2^{t} \equiv 2^{t+m} \bmod d$ with $m \geq 1$. This means that the $t$-th and the $(t+m)$-th decimal place of $y$ are the same.
However, it also follows that $2 \cdot 2^{t} \equiv 2 \cdot 2^{t+m} \bmod d \Leftrightarrow 2^{t+1} \equiv 2^{t+m+1} \operatorname{modd}$, i.e., the $(t+1)$-th and the $(t+m+1)$-th decimal place of $y$ are the same. Accordingly, all $(t+k)$-th and $(t+m+k)$-th decimal places of $y$ are the same $(0 \leq k \leq m)$. Therefore, $y$ is periodic with a period length of $m$.
$y$ can also have a pre-period - at most of length $s$.
These considerations are independent of the base $b \geq 2$ of the number system.
Note: A mere reference to the DIRICHLET drawer principle is not sufficient. An approach using Fermat's little theorem provides more precise information, for example, about the period length of $y$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Für jede reelle Zahl $x$ mit $0<x<1$ sei $y \in] 0 ; 1[$ diejenige Zahl, deren $n$-te Nachkommastelle die (2n)-te Nachkommastelle von $x$ ist. $M$ an beweise: Wenn $x$ rational ist, dann ist auch $y$ rational.
|
Eine rationale Zahl besitzt eine abbrechende oder eine periodische Dezimalbruchentwicklung. Eine abbrechende Dezimalbruchentwicklung lässt sich durch Anhängen von Nullen ins U nendliche fortsetzen und entspricht daher einer periodischen Dezimalbruchentwicklung mit der Periodenlänge 1.
Im Folgenden betrachten wir nur die Stellen hinter einer evtl. auftretenden
Vorperiode der Länge $v$. Die erste Zweierpotenz größer als $v$ sei mit $2^{s}$ bezeichnet, die P eriodenlänge des Dezimalbruchs mit $d$.
W eil es nur endlich viele Restklassen mod $d$ gibt, existieren zwei Zahlen $2^{t}$ und $2^{t+m}$, die den gleichen Rest $r$ mod $d$ lassen, d.h. $2^{t} \equiv 2^{t+m} \bmod d$ mit $m \geq 1$. Dies bedeutet, dass die $t$. und die $(t+m)$. Nachkommastelle von $y$ gleich sind.
Dann gilt aber auch $2 \cdot 2^{t} \equiv 2 \cdot 2^{t+m} \bmod d \Leftrightarrow 2^{t+1} \equiv 2^{t+m+1} \operatorname{modd}$, d.h. die ( $t+1$ ). und die $(t+m+1)$. Nachkommastelle von $y$ sind gleich. Entsprechend sind alle $(t+k)$. und $(t+m+k)$. Nachkommastellen von $y$ jeweils gleich $(0 \leq k \leq m)$. Daher ist $y$ periodisch mit der P eriodenlänge $m$.
A uch y kann eine Vorperiode - höchstens von der Länge $s$ - besitzen.
Diese Überlegungen sind unabhängig von der Basis $b \geq 2$ des Zahlsystems.
Anmerkung: Der bloße Hinweis auf das DIRICHLETsche Schubfachprinzip reicht nicht aus. Ein Zugang mit dem kleinen Satz von Fermat liefert genauere Informationen z.B. über die P eriodenlänge von $y$.
|
{
"resource_path": "Germany_TST/segmented/de-2007-loes_awkl2_07.jsonl",
"problem_match": "# Aufgabe 3",
"solution_match": "\nLösung:"
}
|
26f2cdcb-ded8-549a-adaa-1c20ced471cb
| 604,376
|
Show that in the decimal representation of $\sqrt[3]{3}$, there is a digit different from 2 between the 1000000th and 3141592nd decimal place.
|
If $\sqrt[3]{3}$ between the 1,000,000th and 3,141,592nd decimal place consisted only of the digit 2, then with $a=\left[10^{1000000} \sqrt[3]{3}\right]<10^{1000001}$, we would have $\left|\sqrt[3]{3}-(a+2 / 9) 10^{-1000000}\right|<10^{-3141592}$, or equivalently,
$$
\left|\sqrt[3]{3\left(9 \cdot 10^{1000000}\right)^{3}}-(9 a+2)\right|<9 \cdot 10^{-2141592}
$$
However, it is certain that $(9 a+2)^{3} \neq 3\left(9 \cdot 10^{1000000}\right)^{3}$, because the right side contains the prime factor 3 in a multiplicity not divisible by 3. Generally, for $m, n \in \mathbb{N}$ with $m \neq n^{3}$:
$$
|\sqrt[3]{m}-n| \geq \frac{\left|m-n^{3}\right|}{\sqrt[3]{m^{2}}+\sqrt[3]{m} n+n^{2}} \geq \frac{1}{3 \cdot(\max (\sqrt[3]{m}, n))^{2}}
$$
This implies, in contradiction to (1):
$$
\left|\sqrt[3]{3\left(9 \cdot 10^{1000000}\right)^{3}}-(9 a+2)\right|>\frac{1}{3\left(10^{1000001}\right)^{2}}>10^{-2000003}
$$
Remarks:
1. It could be assumed as known that $\sqrt[3]{3}$ is irrational.
2. Many participants tried to argue digit by digit that the digits of $\sqrt[3]{3}$, when raised to the third power, cannot all be zero, by considering $\sqrt[3]{3}$ in its decimal representation as a power series $\sqrt[3]{3}=1+a_{1} x+a_{2} x^{2}+\ldots$ with $a_{1}, a_{2}, \ldots \in\{0,1, \ldots, 9\}$ and $x=1 / 10$. Here, carry-overs can easily be overlooked: Indeed, $\sqrt[3]{3}=1.442 \ldots$, and $\left(1+4 x+4 x^{2}+2 x^{3}+\ldots\right)^{3}=1+12 x+60 x^{2}+166 x^{3}+\ldots$.
3. Some participants considered the binomial series $(1+x)^{1 / 3}=\sum_{k=0}^{\infty}\binom{1 / 3}{k} x^{k}$ with $\binom{1 / 3}{k}=\frac{1}{3} \cdot\left(\frac{1}{3}-1\right)\left(\frac{1}{3}-2\right) \cdots\left(\frac{1}{3}-k+1\right) / k!$ for $k \in \mathbb{N}_{0}$, which converges for $|x| \leq 1$, at the point $x=2$ - here the series does not converge.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Man zeige, dass es in der Dezimaldarstellung von $\sqrt[3]{3}$ zwischen der 1000000. und 3141592. Nachkommastelle eine von 2 verschiedene Ziffer gibt.
|
Hätte $\sqrt[3]{3}$ zwischen der 1000000. und 3141592. Nachkommastelle nur die Ziffer 2, wäre mit $a=\left[10^{1000000} \sqrt[3]{3}\right]<10^{1000001}$ also $\left|\sqrt[3]{3}-(a+2 / 9) 10^{-1000000}\right|<10^{-3141592}$ oder äquivalent
$$
\left|\sqrt[3]{3\left(9 \cdot 10^{1000000}\right)^{3}}-(9 a+2)\right|<9 \cdot 10^{-2141592}
$$
Nun ist sicher $(9 a+2)^{3} \neq 3\left(9 \cdot 10^{1000000}\right)^{3}$, da die rechte Seite den Primfaktor 3 in nicht durch 3 teilbarer Vielfachheit enthält. Allgemein gilt für $m, n \in \mathbb{N}$ mit $m \neq n^{3}$ :
$$
|\sqrt[3]{m}-n| \geq \frac{\left|m-n^{3}\right|}{\sqrt[3]{m^{2}}+\sqrt[3]{m} n+n^{2}} \geq \frac{1}{3 \cdot(\max (\sqrt[3]{m}, n))^{2}}
$$
Daraus folgt aber - im Widerspruch zu (1):
$$
\left|\sqrt[3]{3\left(9 \cdot 10^{1000000}\right)^{3}}-(9 a+2)\right|>\frac{1}{3\left(10^{1000001}\right)^{2}}>10^{-2000003}
$$
Bemerkungen:
1. Man konnte als bekannt voraussetzen, dass $\sqrt[3]{3}$ irrational ist.
2. Viele Teilnehmer haben versucht, ziffernweise zu argumentieren, dass die Ziffern von $\sqrt[3]{3}$ nach Erheben in die dritte Potenz nicht alle Null sein können, indem man $\sqrt[3]{3}$ in der Dezimaldarstellung als eine Potenzreihe $\sqrt[3]{3}=1+a_{1} x+a_{2} x^{2}+\ldots$ mit $a_{1}, a_{2}, \ldots \in\{0,1, \ldots, 9\}$ und $x=1 / 10$ betrachtet hat. Hier kann man leicht Überträge übersehen: Tatsächlich ist nämlich $\sqrt[3]{3}=1,442 \ldots$, und $\left(1+4 x+4 x^{2}+\right.$ $\left.2 x^{3}+\ldots\right)^{3}=1+12 x+60 x^{2}+166 x^{3}+\ldots$.
3. Manche Teilnehmer haben die binomischen Reihe $(1+x)^{1 / 3}=\sum_{k=0}^{\infty}\binom{1 / 3}{k} x^{k}$ mit $\binom{1 / 3}{k}=\frac{1}{3} \cdot\left(\frac{1}{3}-1\right)\left(\frac{1}{3}-2\right) \cdots\left(\frac{1}{3}-k+1\right) / k!$ für $k \in \mathbb{N}_{0}$, die für $|x| \leq 1$ konvergiert, an der Stelle $x=2$ betrachtet - hier konvergiert die Reihe nicht.
|
{
"resource_path": "Germany_TST/segmented/de-2008-loes_awkl1_08.jsonl",
"problem_match": "# Aufgabe 1",
"solution_match": "\nLösung:"
}
|
640c4c83-ed20-5979-9fef-2edaf238299c
| 604,389
|
Let $A B C D$ be an isosceles trapezoid with $A B \| C D$ and $\overline{B C}=\overline{A D}$. The line parallel to $A D$ through $B$ meets the perpendicular to $A D$ through $D$ at point $X$. Furthermore, the line parallel to $B D$ through $A$ meets the perpendicular to $B D$ through $D$ at point $Y$. Prove that the points $C, X, D$ and $Y$ lie on a common circle.
|
Let $M$ be the midpoint of the segment $A B$. The parallel through $M$ to $D Y$ meets $B D$ at $G$ and the parallel through $A$ to $B D$ at $H$. From $\overline{A M}=\overline{M B}$, we easily conclude $\overline{H M}=\overline{M G}$, and since $D Y \perp D B$ is assumed, the quadrilateral $D G H Y$ is a rectangle. Together, this teaches us $\overline{D M}=\overline{M Y}$, and in the same
way, we show $\overline{D M}=\overline{M X}$. Since the trapezoid $A B C D$ is isosceles, we further have $\overline{D M}=\overline{M C}$, and from the combination of the last three equations, it immediately follows that the four points $C, D, X, Y$ lie on a common circle around $M$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Es sei $A B C D$ ein gleichschenkliges Trapez mit $A B \| C D$ und $\overline{B C}=\overline{A D}$. Die Parallele zu $A D$ durch $B$ treffe die Senkrechte zu $A D$ durch $D$ im Punkt $X$. Ferner treffe die durch $A$ gezogene Parallele zu $B D$ die Senkrechte zu $B D$ durch $D$ im Punkt $Y$. Man beweise, dass die Punkte $C, X, D$ und $Y$ auf einem gemeinsamen Kreis liegen.
|
Es sei $M$ der Mittelpunkt der Strecke $A B$. Die durch $M$ gezogene Parallele zu $D Y$ treffe $B D$ in $G$ und die durch $A$ gezogene Parallele zu $B D$ in $H$. Aus $\overline{A M}=\overline{M B}$ schließt man leicht $\overline{H M}=\overline{M G}$, und da $D Y \perp D B$ vorausgesetzt ist, ist das Viereck $D G H Y$ ein Rechteck. Beides zusammen lehrt $\overline{D M}=\overline{M Y}$, und in gleicher
Weise zeigt man $\overline{D M}=\overline{M X}$. Da das Trapez $A B C D$ gleichschenklig ist, gilt ferner $\overline{D M}=\overline{M C}$, und aus der Kombination der drei letzten Gleichungen ergibt sich sofort, daß die vier Punkte $C, D, X, Y$ auf einem gemeinsamen Kreis um $M$ liegen.
|
{
"resource_path": "Germany_TST/segmented/de-2008-loes_awkl1_08.jsonl",
"problem_match": "# Aufgabe 2",
"solution_match": "\nErste Lösung."
}
|
62acfafd-6377-5a04-88e1-8b6e5afe989a
| 604,418
|
Let $A B C D$ be an isosceles trapezoid with $A B \| C D$ and $\overline{B C}=\overline{A D}$. The parallel to $A D$ through $B$ meets the perpendicular to $A D$ through $D$ at point $X$. Furthermore, the parallel to $B D$ through $A$ meets the perpendicular to $B D$ through $D$ at point $Y$. Prove that the points $C, X, D$ and $Y$ lie on a common circle.
|
Complete the triangle $D A B$ to a parallelogram $D A Z B$. By construction of $X$ and $Y$, these two points lie on $Z B$ and $Z A$, respectively, and it holds that $\varangle D X Z=\varangle Z Y D=90^{\circ}$. The Thales' theorem now yields that $X$ and $Y$ lie on the circle with diameter $D Z$. The center of this circle is simultaneously the midpoint of the segment $D Z$ and, since in parallelograms the diagonals bisect each other, it coincides with the midpoint of the segment $A B$. Given that the trapezoid $A B C D$ is assumed to be isosceles, it follows that $\overline{D M}=\overline{M C}$, which shows that the point $C$ also lies on the circle considered earlier.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Es sei $A B C D$ ein gleichschenkliges Trapez mit $A B \| C D$ und $\overline{B C}=\overline{A D}$. Die Parallele zu $A D$ durch $B$ treffe die Senkrechte zu $A D$ durch $D$ im Punkt $X$. Ferner treffe die durch $A$ gezogene Parallele zu $B D$ die Senkrechte zu $B D$ durch $D$ im Punkt $Y$. Man beweise, dass die Punkte $C, X, D$ und $Y$ auf einem gemeinsamen Kreis liegen.
|
Man ergänze das Dreieck $D A B$ zu einem Parallelogramm $D A Z B$. Nach Konstruktion von $X$ und $Y$ liegen diese beiden Punkte auf $Z B$ bzw. $Z A$, und es gilt $\varangle D X Z=\varangle Z Y D=90^{\circ}$. Der Satz des Thales liefert nunmehr, daß $X$ und $Y$ auf dem Kreis mit Durchmesser $D Z$ liegen. Der Mittelpunkt dieses Kreises ist gleichzeitig der Mittelpunkt der Strecke $D Z$ und, da sich in Parallelogrammen die Diagonalen gegenseitig halbieren, fällt dieser mit dem Mittelpunkt der Strecke $A B$ zusammen. Nachdem nun das Trapez $A B C D$ als gleichschenklig vorausgesetzt ist, gilt folglich $\overline{D M}=\overline{M C}$, womit gezeigt ist, daß auch der Punkt $C$ auf dem vorhin betrachteten Kreis liegt.
|
{
"resource_path": "Germany_TST/segmented/de-2008-loes_awkl1_08.jsonl",
"problem_match": "# Aufgabe 2",
"solution_match": "\nZweite Lösung."
}
|
62acfafd-6377-5a04-88e1-8b6e5afe989a
| 604,418
|
Let $A B C D$ be an isosceles trapezoid with $A B \| C D$ and $\overline{B C}=\overline{A D}$. The line parallel to $A D$ through $B$ meets the perpendicular to $A D$ through $D$ at point $X$. Furthermore, the line parallel to $B D$ through $A$ meets the perpendicular to $B D$ through $D$ at point $Y$. Prove that the points $C, X, D$ and $Y$ lie on a common circle.
|
Let $F=(A B D)$ be the area of triangle $A B D$. We draw a circle $\omega$ around $D$ with radius $\sqrt{2 F}$ and invert at this circle. Those familiar with the subject can easily see that $\overline{D X^{\prime}}=\overline{D A}$ and $\overline{D Y^{\prime}}=\overline{D B}$ hold, and from this, $(D X^{\prime} Y^{\prime})=F$ follows. Now let $C^{*}$ be the intersection of the line $D C$ and $X^{\prime} Y^{\prime}$, and let $H$ be the foot of the perpendicular dropped from $D$ to $A B$. The points $X^{\prime}, Y^{\prime}$ have distances $\overline{A H}, \overline{B H}$ from the line $C D$, and from this, $(D X^{\prime} Y^{\prime})=(D C^{*} Y^{\prime})-(D C^{*} X^{\prime})=\frac{1}{2} \overline{D C^{*}} \cdot(\overline{H B}-\overline{A H})=\frac{1}{2} \overline{D C^{*}} \cdot \overline{D C}$ follows. In connection with an already given equation, this yields $\overline{D C^{*}} \cdot \overline{D C}=2 F$, from which, using a small positional consideration, $C^{*}=C^{\prime}$ follows. Therefore, the three points $C^{\prime}, X^{\prime}, Y^{\prime}$ lie on a common line, and one can easily convince oneself that this line cannot pass through $D$. This implies the claim.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Es sei $A B C D$ ein gleichschenkliges Trapez mit $A B \| C D$ und $\overline{B C}=\overline{A D}$. Die Parallele zu $A D$ durch $B$ treffe die Senkrechte zu $A D$ durch $D$ im Punkt $X$. Ferner treffe die durch $A$ gezogene Parallele zu $B D$ die Senkrechte zu $B D$ durch $D$ im Punkt $Y$. Man beweise, dass die Punkte $C, X, D$ und $Y$ auf einem gemeinsamen Kreis liegen.
|
Es sei $F=(A B D)$ der Flächeninhalt des Dreiecks $A B D$. Wir ziehen um $D$ einen Kreis $\omega$ mit Radius $\sqrt{2 F}$ und invertieren an diesem. Kundige können sich leicht überlegen, daß $\overline{D X^{\prime}}=\overline{D A}$ sowie $\overline{D Y^{\prime}}=\overline{D B}$ gilt und daß hieraus $\left(D X^{\prime} Y^{\prime}\right)=F$ folgt. Es sei nun $C^{*}$ der Schnittpunkt der Geraden $D C$ und $X^{\prime} Y^{\prime}$ sowie $H$ der Fußpunkt des aus $D$ auf $A B$ gefällten Lotes. Nun haben die Punkte $X^{\prime}, Y^{\prime}$ von der Geraden $C D$ die Abstände $\overline{A H}, \overline{B H}$, und hieraus ergibt sich $\left(D X^{\prime} Y^{\prime}\right)=\left(D C^{*} Y^{\prime}\right)-\left(D C^{*} X^{\prime}\right)=\frac{1}{2} \overline{D C^{*}} \cdot(\overline{H B}-\overline{A H})=\frac{1}{2} \overline{D C^{*}} \cdot \overline{D C}$. Im Zusammenhang mit einer bereits angegebenen Gleichung folgt hieraus $\overline{D C^{*}} \cdot \overline{D C}=2 F$, woraus sich mit Hilfe einer kleinen Lagebetrachtung $C^{*}=C^{\prime}$ ergibt. Demnach liegen die drei Punkte $C^{\prime}, X^{\prime}, Y^{\prime}$ auf einer gemeinsamen Geraden, und von dieser überzeugt man sich leicht, daß sie nicht durch $D$ gehen kann. Dies impliziert die Behauptung.
|
{
"resource_path": "Germany_TST/segmented/de-2008-loes_awkl1_08.jsonl",
"problem_match": "# Aufgabe 2",
"solution_match": "\nDritte Lösung (skizziert, nach einer Idee von Andreas Gross)."
}
|
62acfafd-6377-5a04-88e1-8b6e5afe989a
| 604,418
|
Show that there exists an integer $a$ for which $a^{3}-36 a^{2}+51 a-97$ is a multiple of $3^{2008}$.
|
Define the polynomial $P(x)=x^{3}-36 x^{2}+51 x-97$. Starting from $P_{0}(x)=\frac{1}{81} P(9 x+1)=9 x^{3}-33 x^{2}-2 x-1$, define recursively polynomials $P_{k}(x)=$ $3 a_{k} x^{3}+3 b_{k} x^{2}+c_{k} x+d_{k}$ with integers $a_{k}, b_{k}, c_{k}, d_{k}$, where $c_{k}$ is not divisible by 3, and $P_{k+1}(x)=\frac{1}{3} P_{k}\left(3 x+\varepsilon_{k}\right)$ with $\varepsilon_{k} \in\{-1,0,1\}$ for all $k$ : Since $c_{k}$ is not divisible by 3, one can choose $\varepsilon_{k}$ such that $\varepsilon_{k} c_{k}+d_{k}$ is divisible by 3; then $\frac{1}{3} P_{k}\left(3 x+\varepsilon_{k}\right)=3 a_{k+1} x^{3}+3 b_{k+1} x^{2}+c_{k+1}+d_{k+1}$ with $a_{k+1}=9 a_{k}, b_{k+1}=9 \varepsilon_{k} a_{k}+3 b_{k}$, $c_{k+1}=3\left(3 \varepsilon_{k}^{2} a_{k}+2 \varepsilon_{k} b_{k}\right)+c_{k}, d_{k+1}=\varepsilon_{k}^{3} a_{k}+\varepsilon_{k}^{2} b_{k}+\left(\varepsilon_{k} c_{k}+d_{k}\right) / 3$, thus $c_{k+1}$ is also not divisible by 3.
If we set $x_{2004}=0$ and recursively $x_{k}=3 x_{k+1}+\varepsilon_{k}$, so $P_{k}\left(x_{k}\right)=3 P_{k}\left(x_{k+1}\right)$ for $k=2003, \ldots, 0$, then for $a=9 x_{0}+1$ the number $P(a)=81 \cdot 3^{2004} P_{2004}\left(x_{2004}\right)$ is a multiple of $3^{2008}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Man zeige, dass es eine ganze Zahl $a$ gibt, für die $a^{3}-36 a^{2}+51 a-97$ ein Vielfaches von $3^{2008}$ ist.
|
Definiere das Polynom $P(x)=x^{3}-36 x^{2}+51 x-97$. Ausgehend von $P_{0}(x)=\frac{1}{81} P(9 x+1)=9 x^{3}-33 x^{2}-2 x-1$, definiere rekursiv Polynome $P_{k}(x)=$ $3 a_{k} x^{3}+3 b_{k} x^{2}+c_{k} x+d_{k}$ mit ganzen Zahlen $a_{k}, b_{k}, c_{k}, d_{k}$, wobei $c_{k}$ nicht durch 3 teilbar ist, und $P_{k+1}(x)=\frac{1}{3} P_{k}\left(3 x+\varepsilon_{k}\right)$ mit $\varepsilon_{k} \in\{-1,0,1\}$ für alle $k$ : Da $c_{k}$ nicht durch 3 teilbar ist, kann man $\varepsilon_{k}$ so wählen, dass $\varepsilon_{k} c_{k}+d_{k}$ durch 3 teilbar ist; dann ist $\frac{1}{3} P_{k}\left(3 x+\varepsilon_{k}\right)=3 a_{k+1} x^{3}+3 b_{k+1} x^{2}+c_{k+1}+d_{k+1}$ mit $a_{k+1}=9 a_{k}, b_{k+1}=9 \varepsilon_{k} a_{k}+3 b_{k}$, $c_{k+1}=3\left(3 \varepsilon_{k}^{2} a_{k}+2 \varepsilon_{k} b_{k}\right)+c_{k}, d_{k+1}=\varepsilon_{k}^{3} a_{k}+\varepsilon_{k}^{2} b_{k}+\left(\varepsilon_{k} c_{k}+d_{k}\right) / 3$, somit ist auch $c_{k+1}$ nicht durch 3 teilbar.
Setzt man $x_{2004}=0$ und rekursiv $x_{k}=3 x_{k+1}+\varepsilon_{k}$, also $P_{k}\left(x_{k}\right)=3 P_{k}\left(x_{k+1}\right)$ für $k=2003, \ldots, 0$, so ist für $a=9 x_{0}+1$ die Zahl $P(a)=81 \cdot 3^{2004} P_{2004}\left(x_{2004}\right)$ ein Vielfaches von $3^{2008}$.
|
{
"resource_path": "Germany_TST/segmented/de-2008-loes_awkl1_08.jsonl",
"problem_match": "# Aufgabe 3",
"solution_match": "\n1. Lösung:"
}
|
57acea83-31cb-5e01-b41c-79f3c322f3e6
| 604,431
|
Show that there exists an integer $a$ for which $a^{3}-36 a^{2}+51 a-97$ is a multiple of $3^{2008}$.
|
Define the polynomial $P(x)=x^{3}-36 x^{2}+51 x-97$. For $k \geq 4$, integers $a_{k}$ are constructed inductively such that $a_{k} \equiv 1 \bmod 9$ and $3^{k} \mid P\left(a_{k}\right)$; the problem statement then satisfies $a=a_{2008}$:
Base case $k=4$: For $a_{4}=1$, $3^{4} \mid P\left(a_{4}\right)$.
Inductive step $k \rightarrow k+1$: For $k \geq 4$, $2 k-3 \geq k+1$ and $3 k-6 > k+1$, thus for all integers $x$:
\[
\begin{aligned}
P\left(x+3^{k-2}\right)-P(x) & \equiv 3^{k-1} x^{2}+3^{2 k-3} x+3^{3 k-6}-36\left(2 \cdot 3^{k-2} x+3^{2 k-4}\right)+51 \cdot 3^{k-2} \\
& \equiv 3^{k-1}\left(x^{2}-24 x+17\right) \bmod 3^{k+1}
\end{aligned}
\]
For $x \equiv 1 \bmod 9$, $x^{2}-24 x+17 \equiv 1-24+17 \equiv 3 \bmod 9$. Since $k \geq 4$, $x \equiv x+3^{k-2} \bmod 9$. Therefore, the difference $3^{k-1}\left(x^{2}-24 x+17\right)$ contains the prime factor 3 exactly $k$ times, so $P(u)$ for $u=a_{k}$ or $u=a_{k}+3^{k-2}$ or $u=a_{k}+2 \cdot 3^{k-2}$ is divisible by $3^{k+1}$, set $a_{k+1}$ to this value of $u$. By construction, $a_{k+1} \equiv 1 \bmod 9$.
Remarks:
1. Some participants tried to argue using the pigeonhole principle: If $P(m) \not \equiv P(n) \bmod 3^{2008}$ for $m \not \equiv n \bmod 3^{2008}$, there would necessarily be an $a$ with $P(a) \equiv 0 \bmod 3^{2008}$. However, the second solution shows that $P\left(x+3^{2006}\right) \equiv P(x) \bmod 3^{2008}$.
2. If $P$ is a polynomial with integer coefficients and $p$ is a prime, the equation $P(a) \equiv 0 \bmod p^{m}$ has a solution for all $m \geq 0$ if there is a $u$ with $P(u) \equiv 0 \bmod p$ and $P^{\prime}(u) \not \equiv 0 \bmod p$ (Hensel's Lemma, see E. J. Barbeau, Polynomials, Springer-Verlag New York 1989, page 100), where for a polynomial $P(x)=b_{n} x^{n}+\ldots b_{0}$, the derivative is $P^{\prime}(x)=n b_{n} x^{n-1}+\ldots+b_{1}$. For $P(x)=x^{3}-36 x^{2}+51 x-97$, however, $3 \mid P^{\prime}(a)$ for all $a$, so Hensel's Lemma is not applicable here. However, it leads to the goal for $Q(x)=P(3 x+1) / 27 = x^{3}-11 x^{2}-2 x-3$ at the point $u=0$.
3. The problem is not solvable for all polynomials: there are integers $a$ with $3 \mid 1+a+a^{2}$, but no integer with $9 \mid 1+a+a^{2}$.
4. The first values for the numbers $\varepsilon_{k}$ in the first solution are $1,0,0,1,-1$, $0,0,1,1,1,-1,-1,0,-1,1,-1,-1,0,1-$ thus no (obvious) regularity is discernible.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Man zeige, dass es eine ganze Zahl $a$ gibt, für die $a^{3}-36 a^{2}+51 a-97$ ein Vielfaches von $3^{2008}$ ist.
|
Definiere das Polynom $P(x)=x^{3}-36 x^{2}+51 x-97$. Für $k \geq 4$ werden induktiv ganze Zahlen $a_{k}$ mit $a_{k} \equiv 1 \bmod 9$ und $3^{k} \mid P\left(a_{k}\right)$ konstruiert; die Aufgabenstellung erfüllt dann $a=a_{2008}$ :
Verankerung $k=4$ : Für $a_{4}=1$ ist $3^{4} \mid P\left(a_{4}\right)$.
Induktionsschritt $k \rightarrow k+1$ : Für $k \geq 4$ ist $2 k-3 \geq k+1$ und $3 k-6>k+1$, also für
alle ganzzahligen $x$ :
$$
\begin{aligned}
P\left(x+3^{k-2}\right)-P(x) & \equiv 3^{k-1} x^{2}+3^{2 k-3} x+3^{3 k-6}-36\left(2 \cdot 3^{k-2} x+3^{2 k-4}\right)+51 \cdot 3^{k-2} \\
& \equiv 3^{k-1}\left(x^{2}-24 x+17\right) \bmod 3^{k+1}
\end{aligned}
$$
Für $x \equiv 1 \bmod 9$ ist $x^{2}-24 x+17 \equiv 1-24+17 \equiv 3 \bmod 9$. Wegen $k \geq 4$ ist auch $x \equiv x+3^{k-2} \bmod 9$. Daher enthält die Differenz $3^{k-1}\left(x^{2}-24 x+17\right)$ den Primfaktor 3 genau $k$-mal, also ist $P(u)$ für $u=a_{k}$ oder $u=a_{k}+3^{k-2}$ oder $u=a_{k}+2 \cdot 3^{k-2}$ durch $3^{k+1}$ teilbar, setze $a_{k+1}$ auf diesen Wert von $u$. Nach Konstruktion ist $a_{k+1} \equiv 1 \bmod 9$.
Bemerkungen:
1. Manche Teilnehmer versuchten, mittels Schubfachprinzip zu argumentieren: Wäre $P(m) \not \equiv P(n) \bmod 3^{2008}$ für $m \not \equiv n \bmod 3^{2008}$, gäbe es zwangsläufig auch ein $a \operatorname{mit} P(a) \equiv 0 \bmod 3^{2008}$. Die zweite Lösung zeigt aber, dass $P\left(x+3^{2006}\right) \equiv$ $P(x) \bmod 3^{2008}$.
2. Ist $P$ ein Polynom mit ganzzahligen Koeffizienten und $p$ eine Primzahl, hat die Gleichung $P(a) \equiv 0 \bmod p^{m}$ eine Lösung für alle $m \geq 0$, wenn es ein $u$ mit $P(u) \equiv 0 \bmod p$ und $P^{\prime}(u) \not \equiv 0 \bmod p$ gibt (Hensel-Lemma, siehe E. J. Barbeau, Polynomials, Springer-Verlag New York 1989, Seite 100), hierbei ist für ein Polynom $P(x)=b_{n} x^{n}+\ldots b_{0}$ die Ableitung $P^{\prime}(x)=n b_{n} x^{n-1}+\ldots+b_{1}$. Für $P(x)=x^{3}-36 x^{2}+51 x-97$ ist jedoch $3 \mid P^{\prime}(a)$ für alle $a$, so dass das HenselLemma hier nicht anwendbar ist. Es führt jedoch für $Q(x)=P(3 x+1) / 27=$ $x^{3}-11 x^{2}-2 x-3$ an der Stelle $u=0$ zum Ziel.
3. Die Aufgabe ist nicht für alle Polynome lösbar: es gibt zwar ganze Zahlen $a$ mit $3 \mid 1+a+a^{2}$, aber keine ganze Zahl mit $9 \mid 1+a+a^{2}$.
4. Die ersten Werte für die Zahlen $\varepsilon_{k}$ in der ersten Lösung lauten $1,0,0,1,-1$, $0,0,1,1,1,-1,-1,0,-1,1,-1,-1,0,1-$ es ist also keine (offensichtliche) Regelmäßigkeit erkennbar.
|
{
"resource_path": "Germany_TST/segmented/de-2008-loes_awkl1_08.jsonl",
"problem_match": "# Aufgabe 3",
"solution_match": "\n2. Lösung:"
}
|
57acea83-31cb-5e01-b41c-79f3c322f3e6
| 604,431
|
Given is a (general) trapezoid $A B C D$, whose diagonals intersect at point $P$. A point $Q$ lies between the parallels $A B$ and $D C$ such that $\varangle A Q B = \varangle C Q D$ holds and the line $B C$ lies between $P$ and $Q$.
Prove that $\varangle D Q P = \varangle B A Q$ holds.
|
Due to $A B \| C D$, the central dilation $\sigma$ at the intersection point $P$ of the diagonals with scaling factor $k=-\frac{|C D|}{|A B|}=-\frac{|C P|}{|A P|}=-\frac{|D P|}{|B P|}$ maps point $C$ to $A$ and $D$ to $B$. Let $Q^{\prime}$ be the image of $Q$ under $\boldsymbol{\sigma}$. Because
the triangle $D Q C$ is mapped to the triangle $B Q^{\prime} A$ under $\sigma$, both triangles are similar, and with the given condition, $\varangle A Q^{\prime} B = \varangle C Q D = \varangle A Q B$. Therefore, $A, B, Q$, and $Q^{\prime}$ lie on a circle, and it follows that $\varangle B A Q = \varangle B Q^{\prime} Q$. The triangle $B Q^{\prime} Q$ is mapped to the triangle $D Q Q^{\prime}$ under $\sigma$. Hence, these triangles are similar, and since $P, Q$, and $Q^{\prime}$ lie on a straight line, $\varangle B Q^{\prime} Q = \varangle D Q Q^{\prime} = \varangle D Q P$.
Thus, $\varangle B A Q = \varangle B Q^{\prime} Q = \varangle D Q P$, which is what we needed to prove.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Gegeben ist ein (allgemeines) Trapez $A B C D$, dessen Diagonalen sich im Punkt $P$ schneiden. Ein Punkt $Q$ liegt so zwischen den Parallelen $A B$ und $D C$, dass $\varangle A Q B=\varangle C Q D$ gilt und die Gerade $B C$ zwischen $P$ und $Q$ verläuft.
Man beweise, dass $\varangle D Q P=\varangle B A Q$ gilt.
|
Wegen $A B \| C D$ bildet die zentrische Streckung $\sigma$ am Schnittpunkt $P$ der Diagonalen mit Streckfaktor $k=-\frac{|C D|}{|A B|}=-\frac{|C P|}{|A P|}=-\frac{|D P|}{|B P|}$ den Punkt $C$ auf $A$ und $D$ auf $B$ ab. Es sei $Q^{\prime}$ der Bildpunkt von $Q$ unter $\boldsymbol{\sigma}$. Weil

das Dreieck $D Q C$ unter $\sigma$ auf das Dreieck $B Q^{\prime} A$ abgebildet wird, sind beide Dreiecke ähnlich und mit der Voraussetzung gilt $\varangle A Q^{\prime} B=\varangle C Q D=\varangle A Q B$. Somit liegen $A, B, Q$ und $Q^{\prime}$ auf einem Kreis und es gilt $\varangle B A Q=\varangle B Q^{\prime} Q$. Das Dreieck $B Q^{\prime} Q$ wird unter $\sigma$ auf das Dreieck $D Q Q^{\prime}$ abgebildet. Daher sind diese Dreiecke ähnlich und es folgt, da $P, Q$ und $Q^{\prime}$ auf einer Geraden liegen, $\varangle B Q^{\prime} Q=\varangle D Q Q^{\prime}=\varangle D Q P$.
Also ist $\varangle B A Q=\varangle B Q^{\prime} Q=\varangle D Q P$, was zu beweisen war.
|
{
"resource_path": "Germany_TST/segmented/de-2008-loes_awkl2_08.jsonl",
"problem_match": "# Aufgabe 2",
"solution_match": "\nLösung:"
}
|
d61cd368-7137-52ec-8be0-90a2d89bf159
| 604,466
|
A square is divided into $n>1$ rectangles such that the sides of the rectangles are parallel to the sides of the given square. Each line that is parallel to one of the sides of the square and intersects the interior of the square shall also run in the interior of at least one of the rectangles.
Prove that there is then always a rectangle in this division that has no point in common with the boundary of the square.
|
We prove the contraposition and assume that every rectangle in the partition has at least one point in common with the boundary of the square. According to the conditions, it then has at least one of its sides in common with the boundary of the square. Therefore, the boundary of the square can be uniquely assigned to the rectangles of the partition in segments. Two non-connected segments cannot belong to the same rectangle; otherwise, they would be opposite each other, and lines on the other sides of this rectangle would intersect the interior of the square without running inside a rectangle.
The number \( n \) of these segments thus matches the number \( n \) of the rectangles. At the \( n \) endpoints of the segments, two rectangles meet on the boundary of the square and have a corner there. Four additional corners of the rectangles coincide with the corners of the square, so that a total of \( 2n + 4 \) rectangle corners lie on the boundary of the square. Thus, \( 4n - (2n + 4) = 2n - 4 \) corners remain for the interior of the square. Now consider one of the \( n \) points on the boundary of the square where two rectangles meet. The line perpendicular to the respective side of the square through this point \( P \)

initially runs inside the square on one side of each of the two rectangles. For this line to run inside a rectangle within the square, it must intersect a side of a rectangle that is parallel to the side of the square from which we started. At this branching point \( Q \), the two rectangles, whose boundary the line was previously (these do not have to be the two rectangles with the corner point \( P \)), each have a corner point. Such a point \( Q \) exists for each starting point \( P \), and two different starting points cannot have the same branching point \( Q \). Therefore, at least \( 2n \) rectangle corners must lie in the interior of the square, contradicting the previously determined maximum number \( 2n - 4 \). Thus, there is always a rectangle that has no point in common with the boundary of the square.
Notes: The outer rectangle was only raised to a square so that the formulation of the solution is simpler. The frequently presented solutions involving the construction of impossible cases could easily leave gaps if arguments were made about the relative positions of rectangles or the course of paths.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Ein Quadrat wird so in $n>1$ Rechtecke zerlegt, dass die Seiten der Rechtecke parallel zu den Seiten des gegebenen Quadrats verlaufen. Jede Gerade, die parallel zu einer der Seiten des Quadrats verläuft und das Innere des Quadrats schneidet, soll dabei auch im Inneren wenigstens eines der Rechtecke verlaufen.
Man beweise, dass es dann in dieser Zerlegung stets ein Rechteck gibt, das keinen Punkt mit dem Rand des Quadrats gemeinsam hat.
|
Wir beweisen die Kontraposition und nehmen dazu an, dass jedes Rechteck der Zerlegung mindestens einen Punkt mit dem Rand des Quadrates gemeinsam hat. Nach den Voraussetzungen hat es dann wenigstens eine seiner Seiten mit dem Rand des Quadrates gemeinsam. Daher lässt sich der Rand des Quadrates abschnittweise eindeutig den Rechtecken der Zerlegung zuordnen. Zwei nicht zusammenhängende Abschnitte können nicht zu demselben Rechteck gehören; sie müssten sonst einander gegenüberliegen und auf den anderen Seiten dieses Rechtecks schneiden Geraden das Innere des Quadrates, ohne im Inneren eines Rechtecks zu verlaufen.
Die Anzahl $n$ dieser Abschnitte stimmt also mit der Anzahl $n$ der Rechtecke überein. In den $n$ Endpunkten der Abschnitte treffen auf dem Rand des Quadrates jeweils zwei Rechtecke zusammen und haben dort jeweils eine Ecke. Vier weitere Ecken der Rechtecke fallen mit den Ecken des Quadrates zusammen, so dass insgesamt $2 n+4$ Rechtecksecken auf dem Rand des Quadrates liegen. Somit verbleiben $4 n-(2 n+4)=2 n-4$ Ecken für das Innere des Quadrates. Nun betrachten wir einen der $n$ Punkte auf dem Rand des Quadrates, in denen zwei Rechtecke zusammenstoßen. Die Gerade senkrecht zur jeweiligen Quadratseite durch diesen Punkt $P$

verläuft im Inneren des Quadrats zunächst auf je einer Seite der beiden Rechtecke. Damit diese Gerade innerhalb des Quadrates auch im Inneren eines Rechtecks verlaufen kann, muss sie eine Rechtecksseite schneiden, die parallel zur Quadratseite verläuft, von der wir ausgegangen sind. In diesem Verzweigungspunkt $Q$ haben die zwei Rechtecke, deren Rand die Gerade vorher war (das müssen nicht mehr die beiden Rechtecke mit Eckpunkt $P$ sein), jeweils einen Eckpunkt. Ein solcher Punkt $Q$ existiert für jeden Ausgangspunkt $P$, und zwei verschiedene Ausgangspunkte können nicht denselben Verzweigungspunkt $Q$ haben. Daher müssen wenigstens $2 n$ Rechtecksecken im Inneren des Quadrates liegen, im Widerspruch zur oben bestimmten Höchstzahl $2 n-4$. Also gibt es stets ein Rechteck, das keinen Punkt mit dem Rand des Quadrats gemeinsam hat.
Anmerkungen: Das äußere Rechteck wurde nur deshalb zum Quadrat erhoben, damit die Abfassung der Lösung einfacher ist. Die häufig vorgelegten Lösungen über die Konstruktion von unmöglichen Fällen ließen leicht Lücken entstehen, wenn mit der gegenseitigen Lage von Rechtecken oder dem Verlauf von Pfaden argumentiert wurde.
|
{
"resource_path": "Germany_TST/segmented/de-2008-loes_awkl2_08.jsonl",
"problem_match": "# Aufgabe 3",
"solution_match": "\nLösung:"
}
|
b38da02f-5c3f-5824-9fd2-4d82c04d96c5
| 604,477
|
Let $p>7$ be a prime number that leaves a remainder of 1 when divided by 6. Set $m=2^{p}-1$. Prove that $2^{m-1}-1$ is divisible by $127 m$ without any remainder.
|
The solution consists of three steps:
1. $2^{m-1}-1$ is divisible by 127.
2. $2^{m-1}-1$ is divisible by $m$.
3. 127 and $m$ are coprime.
For 1: It holds that $2^{6} \equiv 1 \bmod 7$. From $p \equiv 1 \bmod 6$ it follows that $2^{p} \equiv 2 \bmod 7$, thus $7 \mid m-1$. With $2^{7} \equiv 1 \bmod 127$ it follows that $2^{m-1} \equiv 1 \bmod 127$.
For 2: It holds that $2^{p} \equiv 2 \bmod p$ (Fermat's little theorem), i.e., $p \mid m-1$. From $2^{p} \equiv 1 \bmod m$ it follows that $2^{m-1} \equiv 1 \bmod m$.
For 3: It holds that $2^{p} \equiv 1 \bmod 127$ if and only if $p$ is divisible by 7 (write $p=7 k+r$ with $0 \leq r<7$ and use $2^{7} \equiv 1 \bmod 127$). Since $p>7$, this is not the case, so $m$ is not divisible by 127, and since 127 is a prime number, 127 and $m$ are coprime.
Remarks: The relationship $\operatorname{ggT}\left(2^{a}-1,2^{b}-1\right)=2^{\operatorname{ggT}(a, b)}-1$ allows for a shortened solution. Instead of congruence arithmetic, the divisibility statement $a-b \mid a^{n}-b^{n}$ can be used in some cases. Some participants used an incorrect version of the Euler-Fermat theorem: it states $a^{\phi(m)} \equiv 1 \bmod m$ for $\operatorname{ggT}(a, m)=1$ but only for $m$ a prime number does $\phi(m)=m-1$ hold.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Es sei $p>7$ eine Primzahl, die bei Division durch 6 den Rest 1 lässt. Setze $m=2^{p}-1$. Man beweise, dass $2^{m-1}-1$ ohne Rest durch $127 m$ teilbar ist.
|
Die Lösung besteht aus drei Schritten:
1. $2^{m-1}-1$ ist durch 127 teilbar.
2. $2^{m-1}-1$ ist durch $m$ teilbar.
3. 127 und $m$ sind teilerfremd.
Zu 1: Es gilt $2^{6} \equiv 1 \bmod 7$. Aus $p \equiv 1 \bmod 6$ folgt $2^{p} \equiv 2 \bmod 7$, also $7 \mid m-1$. Mit $2^{7} \equiv 1 \bmod 127$ folgt daraus $2^{m-1} \equiv 1 \bmod 127$.
Zu 2 : Es gilt $2^{p} \equiv 2 \bmod p$ (kleiner Satz von Fermat), d. h. $p \mid m-1$. Aus $2^{p} \equiv 1 \bmod m$ folgt damit $2^{m-1} \equiv 1 \bmod m$.
Zu 3 : Es gilt $2^{p} \equiv 1 \bmod 127$ genau dann, wenn $p$ durch 7 teilbar ist (schreibe $p=7 k+r$ mit $0 \leq r<7$ und verwende $2^{7} \equiv 1 \bmod 127$ ). Wegen $p>7$ ist das nicht der Fall, also ist $m$ nicht durch 127 teilbar, und da 127 eine Primzahl ist, sind 127 und $m$ teilerfremd.
Bemerkungen: Die Beziehung $\operatorname{ggT}\left(2^{a}-1,2^{b}-1\right)=2^{\operatorname{ggT}(a, b)}-1$ erlaubt eine Verkürzung der Lösung. Statt Kongruenzrechnung kann teilweise auch die Teilbarkeitsaussage $a-b \mid a^{n}-b^{n}$ verwendet werden. Einige Teilnehmer verwendeten eine fehlerhafte Fassung des Satzes von Euler-Fermat: er lautet $a^{\phi(m)} \equiv 1 \bmod m$ für $\operatorname{ggT}(a, m)=1$ doch nur für $m$ Primzahl gilt $\phi(m)=m-1$.
|
{
"resource_path": "Germany_TST/segmented/de-2009-loes_awkl1_09.jsonl",
"problem_match": "# Aufgabe 1",
"solution_match": "\nLösung:"
}
|
2f782f0a-30c9-5309-987e-9b05fbe357de
| 604,490
|
The triangle $A B C$ is right-angled at $A$. Let $M$ be the midpoint of the segment $B C$. The point $D$ lies on the side $A C$ and satisfies $\overline{A D}=\overline{A M}$. The intersection point of the circumcircles of triangles $A M C$ and $B D C$, different from $C$, is called $P$. Prove that $C P$ bisects the angle at $C$ of triangle $A B C$.
|
The angle $\varangle P D C$ is on the one hand the adjacent angle of $\varangle A D P$, and on the other hand, it lies in the cyclic quadrilateral $B P D C$ opposite the angle $\varangle C B P$. Consequently, $\varangle A D P = \varangle C B P$. Similarly, the angle $\varangle C M P$ is the adjacent angle of $\varangle P M B$ and lies in the cyclic quadrilateral $A P M C$ opposite the angle $\varangle P A C$, so $\varangle P M B = \varangle P A C$. The triangles $P B M$ and $P D A$ thus agree in the interior angles at $B$ and $D$ as well as at $M$ and $A$, and furthermore, by assumption, $\overline{A D} = \overline{A M} = \overline{M B}$ (the last equality follows from Thales' theorem). According to the congruence theorem wsw, the triangles $P B M$ and $P D A$ are congruent, in particular, their heights from $P$ are of equal length. They are, however, the perpendiculars from $P$ to the triangle sides $C A$ and $C B$, so $P$ lies on the angle bisector.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Das Dreieck $A B C$ sei bei $A$ rechtwinklig. Es bezeichne $M$ den Mittelpunkt der Strecke $B C$. Der Punkt $D$ liege auf der Seite $A C$ und erfülle $\overline{A D}=\overline{A M}$. Der von $C$ verschiedene Schnittpunkt der Umkreise der Dreiecke $A M C$ und $B D C$ heiße $P$. Man beweise, dass $C P$ den bei $C$ gelegenen Winkel des Dreiecks $A B C$ halbiert.
|
: Der Winkel $\varangle P D C$ ist einerseits Nebenwinkel von $\varangle A D P$, andererseits liegt er im Sehnenviereck $B P D C$ dem Winkel $\varangle C B P$ gegenüber. Folglich $\varangle A D P=$ $\varangle C B P$. Analog ist der Winkel $\varangle C M P$ Nebenwinkel von $\varangle P M B$ und liegt im Sehnenviereck $A P M C$ dem Winkel $\varangle P A C$ gegenüber, also $\varangle P M B=\varangle P A C$. Die Dreiecke $P B M$ und $P D A$ stimmen somit in den Innenwinkeln bei $B$ und $D$ sowie bei $M$ und $A$ überein, außerdem ist nach Voraussetzung $\overline{A D}=\overline{A M}=\overline{M B}$ (die letzte Gleichheit ergibt sich aus dem Satz des Thales). Nach dem Kongruenzsatz wsw sind die Dreicke $P B M$ und $P D A$ kongruent, insbesondere sind ihre von $P$ ausgehenden Höhen gleich lang. Sie sind aber die Lote von $P$ auf die Dreiecksseiten $C A$ bzw. $C B$, also liegt $P$ auf der Winkelhalbierenden.
|
{
"resource_path": "Germany_TST/segmented/de-2009-loes_awkl1_09.jsonl",
"problem_match": "# Aufgabe 2",
"solution_match": "\nLösung 1"
}
|
084901ba-b404-5052-a09d-121dbf3ae9c2
| 604,503
|
The triangle $A B C$ is right-angled at $A$. Let $M$ be the midpoint of the segment $B C$. The point $D$ lies on the side $A C$ and satisfies $\overline{A D}=\overline{A M}$. The intersection point of the circumcircles of triangles $A M C$ and $B D C$, different from $C$, is called $P$. Prove that $C P$ bisects the angle at $C$ of triangle $A B C$.
|
(Sketch, after M. Krebs): Denote by $m_{X Y}$ the perpendicular bisector of the segment $X Y$. Then both $m_{C D}$ and $m_{C A}$, as well as $m_{C M}$ and $m_{C B}$, are pairs of parallel lines at a distance of $\frac{1}{4} \overline{B C}$, thus they form a rhombus. The midpoints $M_{1}, M_{2}$ of the two circumcircles mentioned in the problem are the intersection points of $m_{C A}$ with $m_{C M}$ and of $m_{C D}$ with $m_{C B}$, respectively. The line $(C P)$ is perpendicular to the connecting line $\left(M_{1} M_{2}\right)$, and is therefore parallel to the second diagonal in the rhombus. It is then easy to see that the second diagonal is parallel to the angle bisector.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Das Dreieck $A B C$ sei bei $A$ rechtwinklig. Es bezeichne $M$ den Mittelpunkt der Strecke $B C$. Der Punkt $D$ liege auf der Seite $A C$ und erfülle $\overline{A D}=\overline{A M}$. Der von $C$ verschiedene Schnittpunkt der Umkreise der Dreiecke $A M C$ und $B D C$ heiße $P$. Man beweise, dass $C P$ den bei $C$ gelegenen Winkel des Dreiecks $A B C$ halbiert.
|
(Skizze, nach M. Krebs): Bezeichne mit $m_{X Y}$ die Mittelsenkrechte der Strecke $X Y$. Dann sind sowohl $m_{C D}$ und $m_{C A}$ also auch $m_{C M}$ und $m_{C B}$ Paare paralleler Geraden im Abstand $\frac{1}{4} \overline{B C}$, also begrenzen sie eine Raute. Die Mittelpunkte $M_{1}, M_{2}$ der beiden in der Aufgabe genannten Umkreise sind die Schnittpunkte von $m_{C A}$ mit $m_{C M}$ bzw. von $m_{C D}$ mit $m_{C B}$. Die Gerade $(C P)$ steht senkrecht auf der Verbindungsgeraden $\left(M_{1} M_{2}\right)$, ist also parallel zur zweiten Diagonalen in der Raute. Man überlegt sich nun leicht, dass die zweite Diagonale parallel zur Winkelhalbierenden ist.
|
{
"resource_path": "Germany_TST/segmented/de-2009-loes_awkl1_09.jsonl",
"problem_match": "# Aufgabe 2",
"solution_match": "\nLösung 2"
}
|
084901ba-b404-5052-a09d-121dbf3ae9c2
| 604,503
|
Starting from a convex quadrilateral $A B C D$ without a pair of parallel sides, let $P$ and $Q$ be points inside $A B C D$ such that $P Q D A$ and $Q P B C$ are both cyclic quadrilaterals. We also assume that there is a point $E$ on the segment $P Q$ with the property that $\varangle P A E=\varangle E D Q$ and $\varangle E B P=\varangle Q C E$.
Prove that then $A B C D$ is also a cyclic quadrilateral.
|
Let $F$ be the intersection of the parallel to $AP$ through $E$ with $AD$. Then, because $\Varangle EFD = \Varangle PAD$, $EQDF$ is also a cyclic quadrilateral, and it follows that $\Varangle EFQ = \Varangle EDQ = \Varangle PAE$.
Thus, the triangles $APE$ and $FEQ$ are similar. For $\overline{PE} \neq \overline{EQ}$, they can be mapped onto each other by a central dilation from the intersection point $X$ of the lines $AD$ and $PQ$. For $\overline{PE} = \overline{EQ}$, they are mapped onto each other by a translation. (If $F$ does not lie between $A$ and $D$, the proof proceeds analogously.) For the intersection point $G$ of the parallel to $BP$ through $E$ with $BC$, it follows similarly that $EGCQ$ is a cyclic quadrilateral, from which the similarity of the triangles $BEP$ and $GQE$ follows. These are mapped onto each other by the same dilation or translation as before, because they share the sides $PE$ and $EQ$. Thus, $BC$ and $PQ$ also intersect at point $X$ or are parallel.
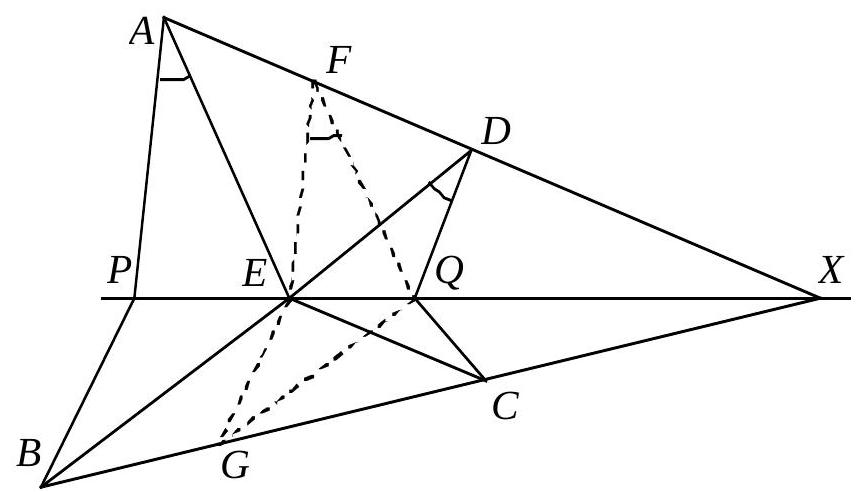
For $\overline{PE} \neq \overline{EQ}$, it follows from the assumption that
$\overline{XD} \cdot \overline{XA} = \overline{XQ} \cdot \overline{XP} = \overline{XC} \cdot \overline{XB}$, which implies that $ABCD$ is a cyclic quadrilateral. For
$\overline{PE} = \overline{EQ}$, $BCQP$ and $PQDA$ are two trapezoids with a common parallel; therefore, $ABCD$ is also a trapezoid and thus a cyclic quadrilateral.
Hint: Using the method of inversion in the unit circle around $E$ yields a particularly elegant proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Ausgehend von einem konvexen Viereck $A B C D$ ohne ein Paar paralleler Seiten seien $P$ und $Q$ Punkte innerhalb $A B C D$, so dass $P Q D A$ und $Q P B C$ beides Sehnenvierecke sind. Wir nehmen außerdem an, dass es einen Punkt $E$ auf der Strecke $P Q$ mit der Eigenschaft gibt, dass $\varangle P A E=\varangle E D Q$ und $\varangle E B P=\varangle Q C E$ ist.
Man beweise, dass dann $A B C D$ ebenfalls ein Sehnenviereck ist.
|
Es sei $F$ der Schnittpunkt der Parallelen zu $A P$ durch $E$ mit $A D$. Dann ist wegen $\Varangle E F D=\Varangle P A D$ auch $E Q D F$ ein Sehnenviereck und es folgt $\Varangle E F Q=\Varangle E D Q=\Varangle P A E$.
Somit sind die Dreiecke $A P E$ und $F E Q$ ähnlich. Für $\overline{P E} \neq \overline{E Q}$ lassen sie sich durch eine zentrische Streckung vom Schnittpunkt $X$ der Geraden $A D$ und $P Q$ aus aufeinander abbilden. Für $\overline{P E}=\overline{E Q}$ werden sie durch eine Verschiebung aufeinander abgebildet. (Falls $F$ nicht zwischen $A$ und $D$ liegt, verläuft der Beweis völlig analog.) Für den Schnittpunkt $G$ der
Parallelen zu BP durch $E$ mit $B C$ folgt entsprechend, dass EGCQ ein Sehnenviereck ist, woraus sich die Ähnlichkeit der Dreiecke BEP und GQE ergibt. Diese werden durch dieselbe Streckung bzw. Verschiebung wie vorher aufeinander abgebildet, weil sie die Seiten $P E$ bzw. $E Q$ gemeinsam haben. Somit schneiden sich $B C$ und $P Q$ ebenfalls im Punkt $X$ bzw. sind parallel.

Für $\overline{P E} \neq \overline{E Q}$ folgt aus der Voraussetzung
$\overline{X D} \cdot \overline{X A}=\overline{X Q} \cdot \overline{X P}=\overline{X C} \cdot \overline{X B}$, woraus sich ergibt, dass $A B C D$ ein Sehnenviereck ist. Für
$\overline{P E}=\overline{E Q}$ sind $B C Q P$ und $P Q D A$ zwei Trapeze mit einer gemeinsamen Parallelen; daher ist auch $A B C D$ ein Trapez und somit ein Sehnenviereck.
Hinweise: Mit der Methode der Inversion am Einheitskreis um $E$ ergibt sich ein besonders eleganter Beweis.
|
{
"resource_path": "Germany_TST/segmented/de-2009-loes_awkl2_09.jsonl",
"problem_match": "# Aufgabe 2",
"solution_match": "\nLösung:"
}
|
afb5f54a-ce33-501b-b4f0-d612d2d2597f
| 604,552
|
The quadrilateral $A B C D$ is a rhombus with an acute angle at $A$. The points $M$ and $N$ are located on the segments $A C$ and $B C$ such that $|D M|=|M N|$. Furthermore, let $P$ be the intersection of $A C$ and $D N$, and $R$ be the intersection of $A B$ and $D M$. Prove that $|R P|=|P D|$.
Note: For $M=A$ and $N=B$, $|D M|=|M N|$ holds, but $|R P| \neq|P D|$. Under the additional assumption that $M$ and $N$ lie in the interior of the segments $A C$ and $B C$, respectively, the claim is correct. Noticing this error does not count as a solution.
|
The case $N=B$ is excluded in the following. Then $D N$ is not orthogonal to $A C$, and $M$ is uniquely characterized as the intersection of the perpendicular bisector of $D N$ with $A C$. In triangle $D N C$, $A C$ is the angle bisector at $C$, and in any triangle, the angle bisector and the perpendicular bisector of the opposite side intersect on the corresponding arc of the circumcircle, so $D M N C$ is a cyclic quadrilateral, in particular $\varangle M D N=\varangle M C N$. Now $\varangle M D N=\varangle R D P$ and $\varangle M C N=\varangle A C B=\varangle B A C=\varangle R A P$, so by the inscribed angle theorem, $A R P D$ is also a cyclic quadrilateral. In its circumcircle, due to $\varangle R A P=\varangle B A C=\varangle C A D=\varangle P A D$, the chords $R P$ and $P D$ are of equal length (by the Law of Sines or the inscribed angle).
Remarks: This problem required a precise analysis of the relative positions of the various points. Often, the given argument was only applicable in certain cases, for example, in the context of the cyclic pentagon $M R B N P$ or MBRNP. Most attempts to solve the problem using coordinate geometry failed due to calculation errors. Relatively frequently, the cyclic quadrilateral $B N P M$ was also recognized.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Das Viereck $A B C D$ sei eine Raute mit spitzem Winkel bei $A$. Die Punkte $M$ und $N$ mögen so auf den Strecken $A C$ und $B C$ gelegen sein, dass $|D M|=|M N|$. Ferner sei $P$ der Schnittpunkt von $A C$ und $D N$ sowie $R$ der Schnittpunkt von $A B$ und $D M$. Man beweise, dass $|R P|=|P D|$.
Anmerkung: Für $M=A$ und $N=B$ gilt $|D M|=|M N|$, aber $|R P| \neq|P D|$. Unter der zusätzlichen Voraussetzung, dass $M$ bzw. $N$ im Inneren der Strecken $A C$ bzw. $B C$ liegen, ist die Behauptung jedoch korrekt. Den Fehler zu bemerken, zählte nicht als Lösung.
|
Der Fall $N=B$ sei im Folgenden ausgeschlossen. Dann ist $D N$ nicht orthogonal zu $A C$, und $M$ ist eindeutig charakterisiert als Schnittpunkt der Mittelsenkrechte von $D N$ mit $A C$. Im Dreieck $D N C$ ist $A C$ die Winkelhalbierende bei $C$, und in jedem Dreieck schneiden sich die Winkelhalbierende und die gegenüberliegende Mittelsenkrechte auf dem zugehörigen Umkreisbogen, also ist $D M N C$ ein Sehnenviereck, insbesondere ist $\varangle M D N=\varangle M C N$. Nun ist $\varangle M D N=\varangle R D P$ und $\varangle M C N=\varangle A C B=\varangle B A C=\varangle R A P$, also ist nach dem Satz vom Umfangswinkel auch $A R P D$ ein Sehnenviereck. In seinem Umkreis sind wegen $\varangle R A P=\varangle B A C=\varangle C A D=\varangle P A D$ die Sehnen $R P$ und $P D$ gleich lang (Sinussatz oder Umfangswinkel).
Bemerkungen: Diese Aufgabe erforderte eine genaue Analyse der relativen Lage der verschiedenen Punkte. Häufig war das angegebene Argument deshalb nur in bestimmten Fällen anwendbar, beispielsweise im Kontext des Sehnenfünfecks $M R B N P$ bzw. MBRNP. Die meisten Versuche, die Aufgabe durch Verwendung von Koordinaten rechnerisch zu lösen, scheiterten an Rechenfehlern. Relativ häufig wurde auch das Sehnenviereck $B N P M$ erkannt.
|
{
"resource_path": "Germany_TST/segmented/de-2010-loes_awkl1_10.jsonl",
"problem_match": "# Aufgabe 1",
"solution_match": "\nLösung:"
}
|
df988e3c-fa49-5735-a083-c557891c0f7e
| 604,575
|
Prove or disprove that for all positive real numbers $a, b$ and $c$ the inequality
$$
3 \leq \frac{4 a+b}{a+4 b}+\frac{4 b+c}{b+4 c}+\frac{4 c+a}{c+4 a}<\frac{33}{4}
$$
|
Proof of $3 \leq \frac{4 a+b}{a+4 b}+\frac{4 b+c}{b+4 c}+\frac{4 c+a}{c+4 a}$:
1. Variant: Multiplying by the main denominator and simplifying leads to the equivalent inequality $45 a b c \leq 7\left(a^{2} b+b^{2} c+c^{2} a\right)+8\left(a b^{2}+b c^{2}+c a^{2}\right)$. This follows from the inequality between the arithmetic and geometric mean (e.g., $a^{2} b+b^{2} c+c^{2} a \geq 3 \sqrt[3]{a^{2} b \cdot b^{2} c \cdot c^{2} a}=3 a b c$).
2. Variant: For $n \geq 1$ and real numbers $a_{1}, \ldots, a_{n}, b_{1}, \ldots, b_{n}$, the Cauchy-Schwarz inequality $\sqrt{a_{1}^{2}+\ldots+a_{n}^{2}} \sqrt{b_{1}^{2}+\ldots+b_{n}^{2}} \geq a_{1} b_{1}+\ldots+a_{n} b_{n}$ holds. For $n=3, a_{1}^{2}=\frac{4 a+b}{a+4 b}, a_{2}^{2}=\frac{4 b+c}{b+4 c}, a_{3}^{2}=\frac{4 c+a}{c+4 a}$, $b_{1}^{2}=(4 a+b)(a+4 b), b_{2}^{2}=(4 b+c)(b+4 c), b_{3}^{2}=(4 c+a)(c+4 a)$, we get
$$
\left(\frac{4 a+b}{a+4 b}+\frac{4 b+c}{b+4 c}+\frac{4 c+a}{c+4 a}\right)((4 a+b)(a+4 b)+(4 b+c)(b+4 c)+(4 c+a)(c+4 a)) \geq(5(a+b+c))^{2}
$$
The second factor is less than $\frac{25}{3}(a+b+c)^{2}$ because $2(a+b+c)^{2}-6(a b+b c+c a)=(a-b)^{2}+(b-c)^{2}+(c-a)^{2} \geq 0$, from which the claim follows.
Proof of $\frac{4 a+b}{a+4 b}+\frac{4 b+c}{b+4 c}+\frac{4 c+a}{c+4 a}<\frac{33}{4}$:
1. Variant: Multiplying by the main denominator and simplifying yields the equivalent (trivial) inequality $0<127 a b c+16\left(a^{2} b+b^{2} c+c^{2} a\right)$.
2. Variant: The inequality is equivalent to $\frac{b}{a+4 b}+\frac{c}{b+4 c}+\frac{a}{c+4 a}>\frac{1}{4}$; the latter holds because
$$
\frac{b}{a+4 b}+\frac{c}{b+4 c}+\frac{a}{c+4 a}>\frac{b}{4 a+4 b+4 c}+\frac{c}{4 a+4 b+4 c}+\frac{a}{4 a+4 b+4 c}=\frac{1}{4}
$$
Remarks: 1. The inequality is invariant under cyclic permutation of $a$ to $b$, $b$ to $c$, and $c$ to $a$, but not under arbitrary permutation of $a, b, c$. Therefore, one can assume without loss of generality that $a \geq b$ and $a \geq c$, but not $a \geq b \geq c$. Many solution approaches only worked under the latter assumption.
2. Some participants examined the limit for $a \rightarrow \infty$ with fixed $b$ and $c$ and estimated $\frac{4 b+c}{b+4 c}$. This is not a proof of the right inequality, as the sum for finite values of $a$ can be larger than for $a \rightarrow \infty$.
3. The number $\frac{33}{4}$ can be approximated arbitrarily closely for $a=1, b=\varepsilon, c=\varepsilon^{2}$ as $\varepsilon \rightarrow 0$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Man beweise oder widerlege, dass für alle positiven reellen Zahlen $a, b$ und $c$ die Ungleichung
$$
3 \leq \frac{4 a+b}{a+4 b}+\frac{4 b+c}{b+4 c}+\frac{4 c+a}{c+4 a}<\frac{33}{4}
$$
|
Beweis von $3 \leq \frac{4 a+b}{a+4 b}+\frac{4 b+c}{b+4 c}+\frac{4 c+a}{c+4 a}$ :
1. Variante: Multiplizieren mit Hauptnenner und Vereinfachen führt zur äquivalenten Ungleichung $45 a b c \leq 7\left(a^{2} b+b^{2} c+c^{2} a\right)+8\left(a b^{2}+b c^{2}+c a^{2}\right)$. Dies folgt aus der Ungleichung zwischen arithmetischem und geometrischem Mittel (z. B. $a^{2} b+b^{2} c+c^{2} a \geq 3 \sqrt[3]{a^{2} b \cdot b^{2} c \cdot c^{2} a}=3 a b c$ ).
2. Variante: Für $n \geq 1$ und reelle Zahlen $a_{1}, \ldots, a_{n}, b_{1}, \ldots, b_{n}$ gilt die Cauchy-Schwarz-Ungleichung $\sqrt{a_{1}^{2}+\ldots+a_{n}^{2}} \sqrt{b_{1}^{2}+\ldots+b_{n}^{2}} \geq a_{1} b_{1}+\ldots+a_{n} b_{n}$. Für $n=3, a_{1}^{2}=\frac{4 a+b}{a+4 b}, a_{2}^{2}=\frac{4 b+c}{b+4 c}, a_{3}^{2}=\frac{4 c+a}{c+4 a}$, $b_{1}^{2}=(4 a+b)(a+4 b), b_{2}^{2}=(4 b+c)(b+4 c), b_{3}^{2}=(4 c+a)(c+4 a)$ ergibt sich
$$
\left(\frac{4 a+b}{a+4 b}+\frac{4 b+c}{b+4 c}+\frac{4 c+a}{c+4 a}\right)((4 a+b)(a+4 b)+(4 b+c)(b+4 c)+(4 c+a)(c+4 a)) \geq(5(a+b+c))^{2}
$$
Der zweite Faktor ist wegen $2(a+b+c)^{2}-6(a b+b c+c a)=(a-b)^{2}+(b-c)^{2}+(c-a)^{2} \geq 0$ kleiner als $\frac{25}{3}(a+b+c)^{2}$, woraus die Behauptung folgt.
Beweis von $\frac{4 a+b}{a+4 b}+\frac{4 b+c}{b+4 c}+\frac{4 c+a}{c+4 a}<\frac{33}{4}$ :
1. Variante: Multiplizieren mit Hauptnenner und Vereinfachen liefert die äquivalente (triviale) Ungleichung $0<127 a b c+16\left(a^{2} b+b^{2} c+c^{2} a\right)$.
2. Variante: Die Ungleichung ist äquivalent $\mathrm{zu} \frac{b}{a+4 b}+\frac{c}{b+4 c}+\frac{a}{c+4 a}>\frac{1}{4}$; Letzteres gilt wegen
$$
\frac{b}{a+4 b}+\frac{c}{b+4 c}+\frac{a}{c+4 a}>\frac{b}{4 a+4 b+4 c}+\frac{c}{4 a+4 b+4 c}+\frac{a}{4 a+4 b+4 c}=\frac{1}{4}
$$
Bemerkungen: 1. Die Ungleichung geht zwar bei zyklischer Vertauschung $a$ nach $b, b$ nach $c, c$ nach $a$ in sich über, nicht aber bei beliebigem Permutatieren von $a, b, c$. Daher kann man zwar ohne Einschränkung $a \geq b$ und $a \geq c$ voraussetzen, nicht jedoch $a \geq b \geq c$. Viele Lösungsansätze funktionierten nur unter letzterer Voraussetzung.
2. Manche Teilnehmer untersuchten den Grenzwert für $a \rightarrow \infty$ bei festem $b$ und $c$ und schätzten dann $\frac{4 b+c}{b+4 c}$ ab. Das ist kein Beweis für die rechte Ungleichung, da die Summe für endliche Werte von $a$ größer als für $a \rightarrow \infty$ sein kann.
3. Die Zahl $\frac{33}{4}$ wird für $a=1, b=\varepsilon, c=\varepsilon^{2}$ für $\varepsilon \rightarrow 0$ beliebig angenähert.
|
{
"resource_path": "Germany_TST/segmented/de-2010-loes_awkl1_10.jsonl",
"problem_match": "# Aufgabe 2",
"solution_match": "\nLösung:"
}
|
ba872d0e-2b81-5b48-a2c4-209b7da7a4e6
| 604,589
|
Given a cyclic quadrilateral $A B C D$, whose diagonals $A C$ and $B D$ intersect at point $E$ and whose sides $A D$ and $B C$ lie on lines that intersect at point $F$. The midpoints of segments $A B$ and $C D$ are denoted by $G$ and $H$, respectively. Prove that the line $E F$ is tangent to the circle through $E, G$, and $H$ at $E$.
|
A central dilation with center $E$ and dilation factor 2 maps $G$ to $G^{\prime}$ and $H$ to $H^{\prime}$. Then (1) $\Varangle G H E=\Varangle G^{\prime} H^{\prime} E$. Since $\Varangle A B F=180^{\circ}-\Varangle C B A=\Varangle A D C$ and $\Varangle F A B=180^{\circ}-\Varangle B A D=\Varangle D C B$ (cyclic quadrilateral $A B C D$), the triangles $F B A$ and $F D C$ are similar and are mapped onto each other by a stretch reflection with center $F$ on the angle bisector of $\Varangle B F A$. In this mapping, in particular, $A \rightarrow C, B \rightarrow D, G \rightarrow H$ (midpoints!). Due to the definition of $H^{\prime}$, the diagonals $E H^{\prime}$ and $C D$ bisect each other; hence $D E C H^{\prime}$ is a parallelogram and it follows that $\Varangle H^{\prime} C D=\Varangle E D C=\Varangle B D C=\Varangle B A C=\Varangle B A E$. Similarly, $\Varangle C D H^{\prime}=\Varangle E B A$. Therefore, the triangles $A B E$ and $C D H^{\prime}$
are similar. Because of the similarity of $FBA$ and $FDC$, the quadrilaterals $FBEA$ and $FDH 'C$ are also similar, so that in the considered stretch reflection, $E$ is mapped to $H^{\prime}$. Therefore, the triangles $FGE$ and $FHH '$ are similar, and it follows (2) $\Varangle G E F=\Varangle H H^{\prime} F=\Varangle E H^{\prime} F$.
Let $C^{\prime}$ and $D^{\prime}$ be the preimages of $A$ and $B$, respectively, under the considered stretch reflection. Then, due to the similarity of the triangles $F C^{\prime} D^{\prime}$ and $F A B$ and because
$|F B| /\left|F D^{\prime}\right|=|F D| /|F B|$, the quadrilateral $D^{\prime} C^{\prime} B A$ is a cyclic quadrilateral similar to $B A D C$. Let the intersection of its diagonals be $G^{\prime \prime}$. Then $\Varangle G^{\prime \prime} A B=\Varangle C^{\prime} A B=\Varangle C^{\prime} D^{\prime} B=\Varangle A B D=\Varangle A B E$ and it follows that $G^{"} A \| B E$ and similarly $G " B \| A E$. Thus, $A G " B E$ is a parallelogram and by definition of $G^{\prime}$, $G^{\prime}=G^{\prime \prime}$. Consequently, $G^{\prime}$ is mapped to $E$ under the considered stretch reflection. Since $E$ is mapped to $H^{\prime}$, $G^{\prime}$ is mapped to $H^{\prime}$ under the double application. In this double application, the two reflections cancel each other out, leaving a central dilation at $F$. Therefore, $F, G^{\prime}$, and $H^{\prime}$ are collinear. This implies (3) $\Varangle F H^{\prime} E=\Varangle G^{\prime} H^{\prime} E$.
From (1), (2), and (3), it follows that $\Varangle G H E=\Varangle G^{\prime} H^{\prime} E=\Varangle F H^{\prime} E=\Varangle F E G$.
By the converse of the tangent-secant angle theorem, it follows that $FE$ is tangent to the circle through $E, G$, and $H$.
Hints: Other proof ideas use the polar and the theorem of the complete quadrilateral or inversion in the circle. Approaches using analytic geometry could only be awarded a few partial points.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Gegeben sei ein Sehnenviereck $A B C D$, dessen Diagonalen $A C$ und $B D$ sich im Punkt $E$ schneiden und dessen Seiten $A D$ und $B C$ auf Geraden liegen, die sich im Punkt $F$ schneiden. Die Mittelpunkte der Strecken $A B$ und $C D$ seien mit $G$ bzw. $H$ bezeichnet. Man beweise, dass die Gerade $E F$ in $E$ den Kreis durch $E, G$ und $H$ berührt.
|
Eine zentrische Streckung mit Zentrum $E$ und Streckfaktor 2 bildet $G$ auf $G^{\prime}$ und $H$ auf $H^{\prime}$ ab. Dann ist (1) $\Varangle G H E=\Varangle G^{\prime} H^{\prime} E$. Wegen $\Varangle A B F=180^{\circ}-\Varangle C B A=\Varangle A D C$ und $\Varangle F A B=180^{\circ}-\Varangle B A D=\Varangle D C B$ (Sehnenviereck $A B C D$ ) sind die Dreiecke $F B A$ und $F D C$ ähnlich und werden durch eine Streckspiegelung mit Zentrum $F$ an der Winkelhalbierenden von $\Varangle B F A$ aufeinander abgebildet. Bei dieser Abbildung gilt insbesondere $A \rightarrow C, B \rightarrow D, G \rightarrow H$ (Mittelpunkte!). Aufgrund der Definition von $H^{\prime}$ halbieren sich die Diagonalen $E H^{\prime}$ und $C D$; daher ist $D E C H^{\prime}$ ein Parallelogramm und es gilt $\Varangle H^{\prime} C D=\Varangle E D C=\Varangle B D C=\Varangle B A C=\Varangle B A E$. Analog gilt $\Varangle C D H^{\prime}=\Varangle E B A$. Damit sind die Dreiecke $A B E$ und $C D H^{\prime}$

ähnlich. Wegen der Ähnlichkeit von FBA und FDC sind auch die
Vierecke FBEA und FDH 'C ähnlich, so dass bei der betrachteten Streckspiegelung E auf $H^{\prime}$ abgebildet wird. Damit sind die Dreiecke FGE und FHH ' ähnlich, und es gilt (2) $\Varangle G E F=\Varangle H H^{\prime} F=\Varangle E H^{\prime} F$.
Es seien $C^{\prime}$ und $D^{\prime}$ die Urbilder von $A$ bzw. $B$ bei der betrachteten Streckspiegelung. Dann ist wegen der Ähnlichkeit der Dreiecke $F C^{\prime} D^{\prime}$ und $F A B$ sowie wegen
$|F B| /\left|F D^{\prime}\right|=|F D| /|F B|$ das Viereck $D^{\prime} C^{\prime} B A$ ein zu $B A D C$ ähnliches Sehnenviereck. Sein
Diagonalenschnittpunkt sei $G^{\prime \prime}$. Dann gilt $\Varangle G^{\prime \prime} A B=\Varangle C^{\prime} A B=\Varangle C^{\prime} D^{\prime} B=\Varangle A B D=\Varangle A B E$ und es folgt $G^{"} A \| B E$ sowie analog $G " B \| A E$. Also ist $A G " B E$ ein Parallelogramm und nach Definition von $G^{\prime}$ gilt $G^{\prime}=G^{\prime \prime}$. Folglich geht $G^{\prime}$ bei der betrachteten Streckspiegelung in $E$ über. Weil aber $E$ in $H^{\prime}$ übergeht, wird $G^{\prime}$ bei der zweifachen
Hintereinanderausführung in $H^{\prime}$ abgebildet. Bei dieser Hintereinanderausführung heben sich die beiden Spiegelungen auf und es bleibt eine zentrische Streckung an $F$. Deshalb sind $F, G^{\prime}$ und $H^{\prime}$ kollinear. Daraus folgt (3) $\Varangle F H^{\prime} E=\Varangle G^{\prime} H^{\prime} E$.
Aus (1), (2) und (3) folgt nun $\Varangle G H E=\Varangle G^{\prime} H^{\prime} E=\Varangle F H^{\prime} E=\Varangle F E G$.
Aus der Umkehrung des Sehnen-Tangentenwinkelsatzes ergibt sich daher, dass FE Tangente an den Kreis durch $E, G$ und $H$ ist.
Hinweise: Weitere Beweisideen verwenden die Polare und den Satz vom vollständigen Vierseit oder Inversion am Kreis. Ansätze mit analytischer Geometrie konnten nur mit wenigen Teilpunkten bedacht werden.
|
{
"resource_path": "Germany_TST/segmented/de-2010-loes_awkl2_10.jsonl",
"problem_match": "# Aufgabe 2",
"solution_match": "\nLösung:"
}
|
d54d7e45-39ae-5eaa-bfff-13321c9fe79f
| 604,627
|
Two circles $\Gamma$ and $\Gamma^{\prime}$ may intersect at two distinct points $A$ and $B$. A line through $B$ intersects $\Gamma$ and $\Gamma^{\prime}$ at $C$ and $D$ respectively, such that $B$ lies between $C$ and $D$. Another line through $B$ intersects $\Gamma$ and $\Gamma^{\prime}$ at $E$ and $F$ respectively, such that $E$ lies between $B$ and $F$. It is given that $|C D|=|E F|$. The interior of the segment $C F$ intersects $\Gamma$ and $\Gamma^{\prime}$ at $P$ and $Q$ respectively. Furthermore, let $M$ and $N$ be the midpoints of the arcs $P B$ and $B Q$ of $\Gamma$ and $\Gamma^{\prime}$, not containing $C$ and $F$ respectively. Prove that $C N M F$ is a cyclic quadrilateral.
|
(1) The triangles $A C D$ and $A E F$ are congruent in the same orientation: We work with oriented angles modulo $\pi$. It is $\varangle A D C=\varangle A D B=\varangle A F B=\varangle A F E$ and $\varangle D C A=\varangle B C A=\varangle B E A=\varangle F E A$ (the middle equality was used twice, applying the inscribed angle theorem). Since also by assumption $|C D|=|E F|$, the claim follows from the SAS congruence criterion.
(2) $A$ lies on the same side of the line $C D$ as $F$: The intersection area of the two circles contains the segment $B E$ and intersects the line $C D$ only at the point $B$.
(3) The triangles $C D Q$ and $E F P$ are congruent in the same orientation: As in (1), $\varangle Q D C=\varangle Q D B=\varangle Q F B=\varangle P F B$ etc.
(4) There is a rotation around $A$ that maps the points $C, D, Q$ to the points $E, F, P$: This follows from (1) and (3).
(5) $A$ lies on the same side of the line $B F$ as $C$: From (2) it follows that $A$ and $Q$ lie on the same side of the line $C D$, and together with (4) it follows that $A$ and $P$ lie on the same side of the line $E F=B F$, and thus also $A$ and $C$.
(6) $B A$ is the angle bisector of the interior angle of the triangle $B F C$ at $B$: Because of (1), the distances from $A$ to the extended sides are equal, and because of (2) and (5), it is an internal angle bisector.
(7) $C M$ is the angle bisector of the interior angle of the triangle $B F C$ at $C$: This follows from the inscribed angle theorem.
(8) Similarly, $F N$ is the angle bisector of the interior angle of the triangle $B F C$ at $F$. Let $I$ be the incenter of the triangle $B F C$.
(9) $M$ lies on the arc $B A$ of $\Gamma$ that does not contain $C$: From (2) and (5) it follows that the points on $\Gamma$ have the cyclic order $B, E, A, C$ or $B, P, C$ (same orientation). The oriented arcs $E A$ and $A C$ are equal in size after (4), so $\frac{1}{2} B C < B A$ and thus $B M = \frac{1}{2} B P < \frac{1}{2} B C < B A$.
(10) $N$ lies on the arc $A B$ of $\Gamma^{\prime}$ that does not contain $F$: analogous to (9).
(11) $I$ is an interior point of $C M$ and $F N$: $I$ lies on the line $A B$, so the claim follows from (9) or (10).
(12) $I$ is an interior point of $B A$: This follows from (9) or (10).
(13) It holds that $|C I| \cdot |I M| = |F I| \cdot |I N|$: By the chord theorem in $\Gamma$, $|C I| \cdot |I M| = |B I| \cdot |I A|$, and by the chord theorem in $\Gamma^{\prime}$, $|B I| \cdot |I A| = |F I| \cdot |I N|$.
(14) By the converse of the chord theorem, it follows from (11) and (13) that $C N M F$ is a cyclic quadrilateral.
Remarks: The partial results (1) or (3) were awarded 3 points, (7) or (8) 1 point.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zwei Kreise $\Gamma$ und $\Gamma^{\prime}$ mögen sich in den beiden voneinander verschiedenen Punkten $A$ und $B$ schneiden. Eine Gerade durch $B$ schneide $\Gamma$ und $\Gamma^{\prime}$ so in $C$ bzw. $D$, dass $B$ zwischen $C$ und $D$ liege. Eine weitere Gerade durch $B$ schneide $\Gamma$ und $\Gamma^{\prime}$ derart in $E$ bzw. $F$, dass $E$ zwischen $B$ und $F$ liege. Es möge sich ergeben, dass $|C D|=|E F|$ gilt. Das Innere der Strecke $C F$ treffe $\Gamma$ und $\Gamma^{\prime}$ ind $P$ bzw. $Q$. Weiterhin seien $M$ und $N$ die Mittelpunkte der $C$ bzw. $F$ nicht enthaltenden Bögen $P B$ bzw. $B Q$ von $\Gamma$ und $\Gamma^{\prime}$. Man beweise, dass $C N M F$ ein Sehnenviereck ist.
|
(1) Die Dreiecke $A C D$ und $A E F$ gleichsinnig kongruent: Wir arbeiten mit orientierten Winkeln modulo $\pi$. Es ist $\varangle A D C=\varangle A D B=\varangle A F B=\varangle A F E$ und $\varangle D C A=\varangle B C A=\varangle B E A=\varangle F E A$ (für das mittlere Gleichheitszeichen wurde beide Male der Satz vom Umfangswinkel benutzt). Da außerdem nach Voraussetzung $|C D|=|E F|$ gilt, folgt die Behauptung mit dem Kongruenzsatz wsw.
(2) $A$ liegt auf derselben Seite der Geraden $C D$ wie $F$ : Der Überlappungsbereich der beiden Kreise enthält die Strecke $B E$ und trifft die Gerade $C D$ nur im Punkt $B$.
(3) Die Dreiecke $C D Q$ und EFP sind gleichsinnig kongruent: Wie bei (1), $\varangle Q D C=\varangle Q D B=\varangle Q F B=$ $\varangle P F B$ usw.
(4) Es gibt eine Drehung um $A$, die die Punkte $C, D, Q$ in die Punkte $E, F, P$ überführt: folgt aus (1) und (3).
(5) $A$ liegt auf derselben Seite der Geraden $B F$ wie $C$ : Aus (2) folgt, dass $A$ und $Q$ auf derselben Seite der Geraden $C D$ liegen, und zusammen mit (4) ergibt sich, dass $A$ und $P$ auf derselben Seite der Geraden $E F=B F$ liegen, also auch $A$ und $C$.
(6) $B A$ ist die Winkelhalbierende des Innenwinkels des Dreiecks $B F C$ bei $B$ : Wegen (1) sind die Abstände von $A$ zu den verlängerten Seiten gleich, und wegen (2) und (5) handelt es sich um eine innere Winkelhalbierende.
(7) $C M$ ist die Winkelhalbierende des Innenwinkels des Dreiecks $B F C$ bei $C$ : Das folgt aus dem Umfangswinkelsatz.
(8) Analog ist $F N$ ist die Winkelhalbierende des Innenwinkels des Dreiecks $B F C$ bei $F$. Es sei $I$ der Inkreismittelpunkt des Dreiecks BFC.
(9) $M$ liegt auf dem $C$ nicht enthaltenden Kreisbogen $B A$ von $\Gamma$ : Aus (2) und (5) folgt, dass die Punkte auf $\Gamma$ die zyklische Reihenfolge $B, E, A, C$ bzw. $B, P, C$ (gleich orientiert) haben. Die orientierten Bögen $E A$ und $A C$ sind nach (4) gleich groß, also ist $\frac{1}{2} B C<B A$ und damit $B M=\frac{1}{2} B P<\frac{1}{2} B C<B A$.
(10) $N$ liegt auf dem $F$ nicht enthaltenden Kreisbogen $A B$ von $\Gamma^{\prime}$ : analog zu (9).
(11) $I$ ist ein innerer Punkt von $C M$ und $F N$ : $I$ liegt auf der Geraden $A B$, damit folgt die Behauptung aus (9) bzw. (10).
(12) $I$ ist ein innerer Punkt von $B A$ : folgt aus (9) oder (10).
(13) Es gilt $|C I| \cdot|I M|=|F I| \cdot|I N|$ : Nach dem Sehnensatz in $\Gamma$ ist $|C I| \cdot|I M|=|B I| \cdot|I A|$, nach dem Sehnensatz in $\Gamma^{\prime}$ ist $|B I| \cdot|I A|=|F I| \cdot|I N|$.
(14) Nach der Umkehrung des Sehnensatzes folgt mit (11) und (13), dass CNMF ein Sehnenviereck ist.
Bemerkungen: Die Teilergebnisse (1) oder (3) wurden mit 3 Punkten, (7) oder (8) mit 1 Punkt honoriert.
|
{
"resource_path": "Germany_TST/segmented/de-2011-loes_awkl1_11.jsonl",
"problem_match": "\nAufgabe 1 ",
"solution_match": "\nLösung:"
}
|
9a27442d-2aa7-527a-801e-75da3f27aceb
| 604,654
|
Let $n$ be a positive integer and $b$ the greatest integer less than $(\sqrt[3]{28}-3)^{-n}$. Prove that $b$ cannot be divisible by 6.
|
The complex number $\omega=\frac{-1+\sqrt{3} i}{2}$ is known to be a third root of unity and satisfies $\omega^{2}=\frac{-1-\sqrt{3} i}{2}$, $\omega^{3}=1$ and $\omega^{2}+\omega+1=0$, in particular,
$$
1+\omega^{j}+\omega^{2 j}= \begin{cases}3, & \text { if } j \text { is divisible by three } \\ 0 & \text { otherwise. }\end{cases}
$$
Set $r_{k}=\sqrt[3]{28} \omega^{k}-3$ for $k=0,1,2$. By definition of $b$, $\left|r_{0}^{-n}-b\right|<1$; since the real parts of $\omega$ and $\omega^{2}$ are negative, $\left|r_{1}\right|>1$ and $\left|r_{2}\right|>1$. Therefore,
$$
\left|b-\left(r_{0}^{-n}+r_{1}^{-n}+r_{2}^{-n}\right)\right|<\left|b-r_{0}^{-n}\right|+\left|r_{1}^{-n}\right|+\left|r_{2}^{-n}\right|<3 .
$$
Since $\left(\sqrt[3]{28} \omega^{k}\right)^{3}=28$,
$$
r_{k}^{-1}=\frac{1}{\sqrt[3]{28} \omega^{k}-3}=\frac{\left(\sqrt[3]{28} \omega^{k}\right)^{3}-3^{3}}{\sqrt[3]{28} \omega^{k}-3}=\sqrt[3]{28}^{2} \omega^{2 k}+3 \sqrt[3]{28} \omega^{k}+9
$$
Raising the polynomial $X^{2}+3 X+9$ to its $n$-th power, there exist integers $c_{0}, \ldots, c_{2 n}$ such that $\left(X^{2}+3 X+9\right)^{n}=c_{2 n} X^{2 n}+c_{2 n-1} X^{2 n-1}+\ldots+c_{0}$, where $c_{0}=9^{n}$ is odd. Substituting $X=\sqrt[3]{28} \omega^{k}$, we get $r_{k}^{-n}=\sum_{j=0}^{2 n} c_{j} \sqrt[3]{28}^{j} \omega^{k j}$; from this, using (1):
$$
r_{0}^{-n}+r_{1}^{-n}+r_{2}^{-n}=\sum_{j=0}^{2 n} c_{j} \sqrt[3]{28}^{j}\left(1+\omega^{j}+\omega^{2 j}\right)=3 \sum_{0 \leq \ell \leq 2 n / 3} c_{3 \ell} 28^{\ell}
$$
The sum is clearly a multiple of 3 and also odd, since the term $c_{3 \ell} 28^{\ell}$ is odd for $\ell=0$ and even for $\ell>0$. If $b$ were divisible by 6, the magnitude $\left|b-\left(r_{0}^{-n}+r_{1}^{-n}+r_{2}^{-n}\right)\right|$ would be at least 3, contradicting (2).
Remarks: 1. Some participants tried to numerically estimate the value of $(\sqrt[3]{28}-3)^{-1}$ and thus of $b$. This is a wrong approach because for all real numbers $m, M$ with $1<m<(\sqrt[3]{28}-3)^{-1}<M$, there exists a positive integer $n$ such that $M^{n}-m^{n}>6$.
2. Some thought that the "conjugate" of $\sqrt[3]{28}-3$ is $-\sqrt[3]{28}-3$. This only works for square roots, here one needs $\omega \sqrt[3]{28}-3$ and $\omega^{2} \sqrt[3]{28}-3$.
3. The sums $s_{n}=r_{0}^{-n}+r_{1}^{-n}+r_{2}^{-n}$ satisfy the linear recurrence $s_{t+3}=27 s_{t+2}+9 s_{t+1}+s_{t}$ for all $t$, since from $28=\left(r_{k}+3\right)^{3}$, i.e., $1=27 r_{k}+9 r_{k}^{2}+r_{k}^{3}$ and $r_{k}^{-t-3}=27 r_{k}^{-t-2}+9 r_{k}^{-t-1}+r_{k}^{-t}$, the recurrence follows by summing over $k=0,1,2$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Es sei $n$ eine positive ganze Zahl und $b$ die größte ganze Zahl, die kleiner als $(\sqrt[3]{28}-3)^{-n}$ ist. Man beweise, dass $b$ nicht durch 6 teilbar sein kann.
|
Die komplexe Zahl $\omega=\frac{-1+\sqrt{3} i}{2}$ ist bekanntlich eine dritte Einheitswurzel und erfüllt $\omega^{2}=\frac{-1-\sqrt{3} i}{2}$, $\omega^{3}=1$ und $\omega^{2}+\omega+1=0$, insbesondere gilt
$$
1+\omega^{j}+\omega^{2 j}= \begin{cases}3, & \text { falls } j \text { durch drei teilbar ist } \\ 0 & \text { sonst. }\end{cases}
$$
Setze $r_{k}=\sqrt[3]{28} \omega^{k}-3$ für $k=0,1,2$. Nach Definition von $b$ ist $\left|r_{0}^{-n}-b\right|<1$; da die Realteile von $\omega$ und $\omega^{2}$ negativ sind, gilt $\left|r_{1}\right|>1$ und $\left|r_{2}\right|>1$. Damit ist
$$
\left|b-\left(r_{0}^{-n}+r_{1}^{-n}+r_{2}^{-n}\right)\right|<\left|b-r_{0}^{-n}\right|+\left|r_{1}^{-n}\right|+\left|r_{2}^{-n}\right|<3 .
$$
Wegen $\left(\sqrt[3]{28} \omega^{k}\right)^{3}=28$ ist
$$
r_{k}^{-1}=\frac{1}{\sqrt[3]{28} \omega^{k}-3}=\frac{\left(\sqrt[3]{28} \omega^{k}\right)^{3}-3^{3}}{\sqrt[3]{28} \omega^{k}-3}=\sqrt[3]{28}^{2} \omega^{2 k}+3 \sqrt[3]{28} \omega^{k}+9
$$
Erhebt man das Polynom $X^{2}+3 X+9$ in seine $n$-te Potenz, gibt es ganze Zahlen $c_{0}, \ldots, c_{2 n}$ mit $\left(X^{2}+3 X+\right.$ $9)^{n}=c_{2 n} X^{2 n}+c_{2 n-1} X^{2 n-1}+\ldots+c_{0}$, hierbei ist $c_{0}=9^{n}$ ungerade. Durch Einsetzen $X=\sqrt[3]{28} \omega^{k}$ folgt $r_{k}^{-n}=\sum_{j=0}^{2 n} c_{j} \sqrt[3]{28}^{j} \omega^{k j}$; daraus ergibt sich mit (1):
$$
r_{0}^{-n}+r_{1}^{-n}+r_{2}^{-n}=\sum_{j=0}^{2 n} c_{j} \sqrt[3]{28}^{j}\left(1+\omega^{j}+\omega^{2 j}\right)=3 \sum_{0 \leq \ell \leq 2 n / 3} c_{3 \ell} 28^{\ell}
$$
Die Summe ist offenbar ein Vielfaches von 3 und außerdem ungerade, da der Summand $c_{3 \ell} 28^{\ell}$ für $\ell=0$ ungerade, für $\ell>0$ gerade ist. Wäre $b$ durch 6 teilbar, wäre der Betrag $\left|b-\left(r_{0}^{-n}+r_{1}^{-n}+r_{2}^{-n}\right)\right|$ mindestens 3 im Widerspruch zu (2).
Bemerkungen: 1. Manche Teilnehmer versuchten, den Wert von $(\sqrt[3]{28}-3)^{-1}$ und damit von $b$ numerisch abzuschätzen. Das ist ein Irrweg, weil für alle reellen Zahlen $m, M$ mit $1<m<(\sqrt[3]{28}-3)^{-1}<M$ eine positive ganze Zahl $n$ existiert mit $M^{n}-m^{n}>6$.
2. Manche dachten, zu $\sqrt[3]{28}-3$ sei $-\sqrt[3]{28}-3$ „konjugierte Zahl". Das funktioniert so nur bei Quadratwurzeln, hier benötigt man $\omega \sqrt[3]{28}-3$ und $\omega^{2} \sqrt[3]{28}-3$.
3. Die Summen $s_{n}=r_{0}^{-n}+r_{1}^{-n}+r_{2}^{-n}$ genügen der linearen Rekursion $s_{t+3}=27 s_{t+2}+9 s_{t+1}+s_{t}$ für alle $t$, da aus $28=\left(r_{k}+3\right)^{3}$, also $1=27 r_{k}+9 r_{k}^{2}+r_{k}^{3}$ und $r_{k}^{-t-3}=27 r_{k}^{-t-2}+9 r_{k}^{-t-1}+r_{k}^{-t}$ die Rekursion durch Summation über $k=0,1,2$ folgt.
|
{
"resource_path": "Germany_TST/segmented/de-2011-loes_awkl1_11.jsonl",
"problem_match": "# Aufgabe 2",
"solution_match": "\nLösung:"
}
|
b253197d-39f7-5a80-8ca8-19f7ddb92beb
| 604,666
|
Let $\mathbb{Q}^{+}$ denote the set of positive rational numbers. A function $f: \mathbb{Q}^{+} \rightarrow \mathbb{Q}^{+}$ is called elastic if for all $x, y \in \mathbb{Q}^{+}$ the inequality
$$
f(x)+f(y) \geq 4 f(x+y)
$$
holds.
(a) [5 points] Show: If $f: \mathbb{Q}^{+} \rightarrow \mathbb{Q}^{+}$ is elastic and $x, y, z$ are positive rational numbers, then $f(x)+$ $f(y)+f(z) \geq 8 f(x+y+z)$.
(b) [5 points] Is there an elastic function $f: \mathbb{Q}^{+} \rightarrow \mathbb{Q}^{+}$ together with positive rational numbers $x, y, z$, for which $f(x)+f(y)+f(z)<9 f(x+y+z)$ is true?
|
(a) It holds that
$$
4 f(x)+f(y)+f(z) \stackrel{(*)}{\geq} 4(f(x)+f(y+z)) \stackrel{(*)}{\geq} 16 f(x+y+z) .
$$
Adding to this the cyclically permuted versions $f(x)+4 f(y)+f(z) \geq \ldots$ and $f(x)+f(y)+4 f(z) \geq \ldots$, one obtains $6(f(x)+f(y)+f(z)) \geq 48 f(x+y+z)$ and after division by 6 the claim.
(b) Yes, there are such $f, x, y, z$. Consider the piecewise affine-linear function $f$ with the kink points $\left(2^{k}, 2^{-k}\right)$ for $k \in \mathbb{Z}$, explicitly: For each $k \in \mathbb{Z}$, let $f$ be defined on the interval $\left[2^{k}, 2^{k+1}[\right.$ by
$$
f(x)=-\frac{x}{2^{2 k+1}}+\frac{3}{2^{k+1}} \quad \text { for } 2^{k} \leq x<2^{k+1} .
$$
This defines $f$ for all $x \in \mathbb{Q}^{+}$. For all $x$, $f(2 x)=\frac{1}{2} f(x)$ holds, making (*) equivalent to the convexity inequality $\frac{1}{2}(f(x)+f(y)) \geq f\left(\frac{x+y}{2}\right)$. The function $f$ is convex, and thus also elastic. With $x=y=z=1$,
$$
f(x)+f(y)+f(z)=3<9 \cdot \frac{3}{8}=9 f(x+y+z) .
$$
Remark: Contrary to a frequently expressed claim, elastic functions are not necessarily monotonic, for example:
$$
f(x)= \begin{cases}\frac{1}{x^{2}} ; & x \neq 1 \\ 2 ; & x=1\end{cases}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Es bezeichne $\mathbb{Q}^{+}$die Menge der positiven rationalen Zahlen. Eine Funktion $f: \mathbb{Q}^{+} \rightarrow \mathbb{Q}^{+}$heiße elastisch, wenn für alle $x, y \in \mathbb{Q}^{+}$die Ungleichung
$$
f(x)+f(y) \geq 4 f(x+y)
$$
gilt.
(a) [5 Punkte] Man zeige: Ist $f: \mathbb{Q}^{+} \rightarrow \mathbb{Q}^{+}$elastisch und sind $x, y, z$ positive rationale Zahlen, so ist $f(x)+$ $f(y)+f(z) \geq 8 f(x+y+z)$.
(b) [5 Punkte] Gibt es eine elastische Funktion $f: \mathbb{Q}^{+} \rightarrow \mathbb{Q}^{+}$zusammen mit positiven rationalen Zahlen $x, y, z$, für die $f(x)+f(y)+f(z)<9 f(x+y+z)$ der Fall ist?
|
(a) Es gilt
$$
4 f(x)+f(y)+f(z) \stackrel{(*)}{\geq} 4(f(x)+f(y+z)) \stackrel{(*)}{\geq} 16 f(x+y+z) .
$$
Addiert man dazu die zyklisch vertauschten Versionen $f(x)+4 f(y)+f(z) \geq \ldots$ und $f(x)+f(y)+4 f(z) \geq \ldots$, erhält man $6(f(x)+f(y)+f(z)) \geq 48 f(x+y+z)$ und nach Division durch 6 die Behauptung.
(b) Ja, es gibt solche $f, x, y, z$. Betrachte die stückweise affin-lineare Funktion $f$ mit den Knickpunkten $\left(2^{k}, 2^{-k}\right)$ für $k \in \mathbb{Z}$, explizit: Für jedes $k \in \mathbb{Z}$ sei $f$ auf dem Intervall $\left[2^{k}, 2^{k+1}[\right.$ definiert durch
$$
f(x)=-\frac{x}{2^{2 k+1}}+\frac{3}{2^{k+1}} \quad \text { für } 2^{k} \leq x<2^{k+1} .
$$
Damit ist $f$ für alle $x \in \mathbb{Q}^{+}$definiert. Für alle $x$ gilt $f(2 x)=\frac{1}{2} f(x)$, damit wird (*) äquivalent zur Konvexitätsungleichung $\frac{1}{2}(f(x)+f(y)) \geq f\left(\frac{x+y}{2}\right)$. Die Funktion $f$ ist konvex, also auch elastisch. Mit $x=y=z=1$ gilt
$$
f(x)+f(y)+f(z)=3<9 \cdot \frac{3}{8}=9 f(x+y+z) .
$$
Bemerkung: Entgegen einer häufig geäußerten Behauptung sind elastische Funktionen nicht notwendigerweise monoton, Beispiel:
$$
f(x)= \begin{cases}\frac{1}{x^{2}} ; & x \neq 1 \\ 2 ; & x=1\end{cases}
$$
|
{
"resource_path": "Germany_TST/segmented/de-2011-loes_awkl1_11.jsonl",
"problem_match": "# Aufgabe 3",
"solution_match": "\nLösung:"
}
|
b4554154-cd52-55d5-8633-ac57c10a771d
| 604,678
|
A sequence $x_{1}, x_{2}, \ldots$ is defined by $x_{1}=1$ and $x_{2 k}=-x_{k}, x_{2 k-1}=(-1)^{k+1} x_{k}$ for all $k \geq 1$. Show that for all $n \geq 1$ it holds: $x_{1}+x_{2}+\ldots+x_{n} \geq 0$.
|
We denote $S_{n}=x_{1}+\ldots+x_{n}$ and conduct an induction proof. Calculation yields $x_{1}=1, x_{2}=-1, x_{3}=1, x_{4}=1$ and thus $S_{n} \geq 0$ for $1 \leq n \leq 4$.
Now we assume that $S_{k} \geq 0$ for all natural $k<n$, and claim $S_{n} \geq 0$.
To do this, we distinguish four cases.
Case 1: $n=4 m$. It holds that $S_{n}=\sum_{i=1}^{m}\left(x_{4 i-3}+x_{4 i-2}+x_{4 i-1}+x_{4 i}\right)=\sum_{i=1}^{m}\left(x_{2 i-1}-x_{2 i-1}-x_{2 i}-x_{2 i}\right)$
$=-2 \sum_{i=1}^{m} x_{2 i}=2 \sum_{i=1}^{m} x_{i}=2 S_{m} \geq 0$.
Case 2: $n=4 m+1$. It holds that $S_{n}=2 S_{m}+x_{4 m+1}=2 S_{m}+x_{2 m+1}=2 S_{m}+(-1)^{m} x_{m+1}$.
Case 2.1: $m$ is odd. Then $S_{m}$ is also odd, so $2 S_{m} \geq 2$ and $S_{n} \geq 1>0$.
Case 2.2: $m$ is even. It holds that $S_{n}=2 S_{m}+x_{m+1}=S_{m}+S_{m+1} \geq 0$.
Case 3: $n=4 m+2$. It holds that $S_{n}=S_{n-2}+x_{4 m+1}+x_{4 m+2}=S_{n-2}+x_{2 m+1}-x_{2 m+1}=S_{n-2} \geq 0$.
Case 4: $n=4 m+3$. It holds that $S_{n}=S_{n+1}-x_{n+1}=2 S_{m+1}+x_{2 m+2}=2 S_{m+1}-x_{m+1}=S_{m}+S_{m+1} \geq 0$.
Note: In this or other case distinctions, sometimes not all possibilities were covered or treated carefully enough. A balancing act such that each element ultimately generates an equal number of positive and negative successors and the claim follows because the first term is positive, is not sufficient.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Eine Folge $x_{1}, x_{2}, \ldots$ ist definiert durch $x_{1}=1$ und $x_{2 k}=-x_{k}, x_{2 k-1}=(-1)^{k+1} x_{k}$ für alle $k \geq 1$. Man zeige, dass für alle $n \geq 1$ gilt: $x_{1}+x_{2}+\ldots+x_{n} \geq 0$.
|
Wir bezeichnen $S_{n}=x_{1}+\ldots+x_{n}$ und führen einen Induktionsbeweis. Nachrechnen ergibt $x_{1}=1, x_{2}=-1, x_{3}=1, x_{4}=1$ und damit $S_{n} \geq 0$ für $1 \leq n \leq 4$.
Nun nehmen wir an, dass $S_{k} \geq 0$ für alle natürlichen $k<n$ gilt, und behaupten $S_{n} \geq 0$.
Dazu unterscheiden wir vier Fälle.
Fall 1: $n=4 m$. Es gilt $S_{n}=\sum_{i=1}^{m}\left(x_{4 i-3}+x_{4 i-2}+x_{4 i-1}+x_{4 i}\right)=\sum_{i=1}^{m}\left(x_{2 i-1}-x_{2 i-1}-x_{2 i}-x_{2 i}\right)$
$=-2 \sum_{i=1}^{m} x_{2 i}=2 \sum_{i=1}^{m} x_{i}=2 S_{m} \geq 0$.
Fall 2: $n=4 m+1$. Es gilt $S_{n}=2 S_{m}+x_{4 m+1}=2 S_{m}+x_{2 m+1}=2 S_{m}+(-1)^{m} x_{m+1}$.
Fall 2.1: $m$ ist ungerade. Dann ist auch $S_{m}$ ungerade, also $2 S_{m} \geq 2$ und $S_{n} \geq 1>0$.
Fall 2.2: $m$ ist gerade. Es gilt $S_{n}=2 S_{m}+x_{m+1}=S_{m}+S_{m+1} \geq 0$.
Fall 3: $n=4 m+2$. Es gilt $S_{n}=S_{n-2}+x_{4 m+1}+x_{4 m+2}=S_{n-2}+x_{2 m+1}-x_{2 m+1}=S_{n-2} \geq 0$.
Fall 4: $n=4 m+3$. Es gilt $S_{n}=S_{n+1}-x_{n+1}=2 S_{m+1}+x_{2 m+2}=2 S_{m+1}-x_{m+1}=S_{m}+S_{m+1} \geq 0$.
Hinweise: Bei dieser oder anderen Fallunterscheidungen wurden manchmal nicht alle Möglichkeiten abgedeckt oder sorgfältig genug behandelt. Eine Bilanzierung derart, dass jedes Element auf lange Sicht gleich viele positive und negative Nachfolger erzeugt und die Behauptung folgt, weil das erste Glied positiv ist, reicht nicht.
|
{
"resource_path": "Germany_TST/segmented/de-2011-loes_awkl2_11.jsonl",
"problem_match": "# Aufgabe 1",
"solution_match": "\nLösung:"
}
|
992d5767-fefb-5120-bf73-f3b7628311ad
| 604,689
|
Given a convex pentagon $A B C D E$ with the properties $B C \| A E$ and $\overline{A B}=\overline{A E}$. Furthermore, let $F$ be a point on the segment $A E$ such that $\overline{A B}=\overline{B C}+\overline{A F}$ and $\Varangle C B A=\Varangle F D C$ are satisfied. Finally, let $M$ be the midpoint of the segment $C F$ and $O$ be the circumcenter of the triangle $B C D$.
Prove: If $D M \perp M O$, then $\Varangle F D C=2 \cdot \Varangle A D B$.
|
From the conditions, it follows that $\overline{F E}=\overline{A E}-\overline{A F}=\overline{A B}-(\overline{A B}-\overline{B C})=\overline{B C}$.
Therefore, $B C E F$ is a parallelogram, whose diagonals $C F$ and $B E$ bisect each other at $M$.
Due to the point symmetry about $M$, $\Varangle C B E=\Varangle A E B$, and since $A B E$ is an isosceles triangle, $\Varangle A E B=\Varangle E B A$. Thus, $E B$ is the angle bisector of $\Varangle C B A$. It follows that $\Varangle F D C=\Varangle C B A=2 \cdot \Varangle A E B$, so it remains to show that $\Varangle A E B=\Varangle A D B$.
Let $D^{\prime}$ be the reflection of $D$ about $M$. Since $D M \perp M O$, it follows that
$\overline{O D^{\prime}}=\overline{O D}=\overline{O B}=\overline{O C}$ and $D^{\prime} B C D$ is a cyclic quadrilateral. Therefore, $\Varangle B D C=\Varangle B D^{\prime} C$, and since $B C D E F D^{\prime}$ is even a point-symmetric hexagon about $M$, it follows further that $\Varangle E D F=\Varangle B D^{\prime} C=\Varangle B D C$. Thus, $\Varangle E D B=\Varangle F D C$, while on the other hand, $\Varangle B A E=180^{\circ}-2 \cdot \Varangle A E B=180^{\circ}-\Varangle F D C$ holds. Therefore, $A B D E$ is a cyclic quadrilateral, and the claim follows from the inscribed angle theorem.
Hint: There were several incomplete but largely correct solutions. The problem, although solvable using elementary methods, appeared cumbersome due to the abundance of information and difficulties in creating a satisfactory sketch.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Gegeben sei ein konvexes Fünfeck $A B C D E$ mit den Eigenschaften $B C \| A E$ und $\overline{A B}=\overline{A E}$. Weiter sei $F$ ein Punkt auf der Strecke $A E$, so dass $\overline{A B}=\overline{B C}+\overline{A F}$ sowie $\Varangle C B A=\Varangle F D C$ erfüllt ist. Schließlich sei $M$ der Mittelpunkt der Strecke $C F$ und $O$ der Umkreismittelpunkt des Dreiecks $B C D$.
Man beweise: Wenn $D M \perp M O$, dann gilt $\Varangle F D C=2 \cdot \Varangle A D B$.
|
Aus den Bedingungen folgt $\overline{F E}=\overline{A E}-\overline{A F}=\overline{A B}-(\overline{A B}-\overline{B C})=\overline{B C}$.
Daher ist $B C E F$ ein Parallelogramm, dessen beide Diagonalen $C F$ und $B E$ einander in $M$ halbieren.
Wegen der Punktsymmetrie an M gilt $\Varangle C B E=\Varangle A E B$, und da $A B E$ ein gleichschenkliges Dreieck ist, gilt $\Varangle A E B=\Varangle E B A$. Also ist $E B$ die Winkelhalbierende von $\Varangle C B A$. Es folgt $\Varangle F D C=\Varangle C B A=2 \cdot \Varangle A E B$, so dass nur noch $\Varangle A E B=\Varangle A D B$ zu zeigen ist.
Es sei $D^{\prime}$ der Spiegelpunkt von $D$ an $M$. Wegen $D M \perp M O$ ist dann

$\overline{O D^{\prime}}=\overline{O D}=\overline{O B}=\overline{O C}$ und $D^{\prime} B C D$ ist ein Sehnenviereck. Deshalb ist $\Varangle B D C=\Varangle B D^{\prime} C$, und weil $B C D E F D^{\prime}$ sogar ein zu $M$ punktsymmetrisches Sechseck ist, folgt weiter $\Varangle E D F=\Varangle B D^{\prime} C=\Varangle B D C$. Also ist $\Varangle E D B=\Varangle F D C$, während andererseits $\Varangle B A E=180^{\circ}-2 \cdot \Varangle A E B=180^{\circ}-\Varangle F D C$ gilt. Somit ist $A B D E$ ein Sehnenviereck, und die Behauptung folgt aus dem Umfangswinkelsatz.
Hinweis: Hier gab es mehrere unvollständige, aber wenig falsche Lösungen. Die Aufgabe war zwar elementar zu lösen, wirkte aber sperrig durch die Fülle der Informationen und Schwierigkeiten bei der Anfertigung einer befriedigenden Skizze.
|
{
"resource_path": "Germany_TST/segmented/de-2011-loes_awkl2_11.jsonl",
"problem_match": "# Aufgabe 2",
"solution_match": "\nLösung:"
}
|
6e45d354-4edc-57a5-9d2d-47cd61c27c02
| 604,703
|
The corners and edges of a regular $n$-gon are numbered clockwise from 1 to $n$ such that edge number $i$ follows corner number $i$ ($1 \leq i \leq n$).
Now, the corners are labeled with non-negative integers $e_{i}$ and the edges with non-negative integers $k_{i}$ such that the following conditions hold:
(1) The $n$-tuple $\left(e_{1}, e_{2}, \ldots, e_{n}\right)$ is a permutation of the $n$-tuple $\left(k_{1}, k_{2}, \ldots, k_{n}\right)$.
(2) For every $i \in \mathbb{N}$ with $1 \leq i \leq n$, it holds that $k_{i}=\left|e_{i+1}-e_{i}\right|$, where $e_{n+1}=e_{1}$.
a) Prove that for all natural numbers $n, n \geq 3$, such $n$-tuples exist that are different from $(0, \ldots, 0)$.
b) Determine for each positive natural number $m$ the smallest natural number $n$ with the following property: In the $n$-tuples $\left(e_{1}, e_{2}, \ldots, e_{n}\right)$ and $\left(k_{1}, k_{2}, \ldots, k_{n}\right)$, all natural numbers from 0 to $m$ appear.
|
a) A possible example for $n \geq 3$ is $e_{1}=e_{2}=1, e_{i}=0$ for $3 \leq i \leq n$. This implies $k_{2}=k_{n}=1$ and $k_{i}=0$ otherwise. Clearly, all conditions are satisfied.
b) We prove that $n=m+2$ always holds. The proof is in two steps.
i) It holds that $n \geq m+2$: Because the number 0 appears in $\left(k_{1}, k_{2}, \ldots, k_{n}\right)$, two elements of $\left(e_{1}, e_{2}, \ldots, e_{n}\right)$ must be equal. Since each of the $m+1$ natural numbers from 0 to $m$ must appear at least once, it follows that $n \geq m+2$.
ii) We provide an example for $n=m+2 \geq 3$: Let $\left(e_{1}, e_{2}, \ldots, e_{n}\right)=(0, m, 1, m-1, \ldots)$. In the $n$-tuple, the numbers alternate and decrease by 1 until the difference is 0, so that $e_{n-1}=e_{n}$. Thus, each natural number from 0 to $m$ appears exactly once, and the number $e_{n}$ appears exactly twice. The absolute values of the differences appear from $m$ downwards to 0 exactly once; the difference $\left|e_{n}-0\right|=e_{n}$ appears twice because $e_{n}<m$. This shows properties (1) and (2).
Hint: For part a), 3 points were awarded, and for part b), 7 points were awarded. Neither the example for a) nor the example for b) are the only possible ones.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Die Ecken und Kanten eines regulären $n$-Ecks seien im Uhrzeigersinn jeweils so von 1 bis $n$ nummeriert, dass die Kante Nr. $i$ auf die Ecke Nr. $i$ folgt ( $1 \leq i \leq n$ ).
Nun werden die Ecken mit nichtnegativen ganzen Zahlen $e_{i}$ und die Kanten mit nichtnegativen ganzen Zahlen $k_{i}$ so belegt, dass gilt:
(1) Das $n$-Tupel $\left(e_{1}, e_{2}, \ldots, e_{n}\right)$ ist eine Permutation des $n$-Tupels $\left(k_{1}, k_{2}, \ldots, k_{n}\right)$.
(2) Für jedes $i \in \mathbb{N}$ mit $1 \leq i \leq n$ gilt $k_{i}=\left|e_{i+1}-e_{i}\right|$, wobei $e_{n+1}=e_{1}$ ist.
a) Man beweise, dass für alle natürlichen Zahlen $n, n \geq 3$, solche $n$-Tupel existieren, die von $(0, \ldots, 0)$ verschieden sind.
b) Man bestimme zu jeder positiven natürlichen Zahl $m$ die kleinste natürliche Zahl $n$ mit folgender Eigenschaft: In den $n$-Tupeln $\left(e_{1}, e_{2}, \ldots, e_{n}\right)$ und $\left(k_{1}, k_{2}, \ldots, k_{n}\right)$ kommen jeweils alle natürlichen Zahlen von 0 bis $m$ vor.
|
a) Ein mögliches Beispiel für $n \geq 3$ ist $e_{1}=e_{2}=1, e_{i}=0$ für $3 \leq i \leq n$. Dies bedingt $k_{2}=k_{n}=1$ und $k_{i}=0$ sonst. Offensichtlich sind alle Bedingungen erfüllt.
b) Wir beweisen, dass stets $n=m+2$ gilt. Der Beweis erfolgt in zwei Schritten.
i) Es gilt $n \geq m+2$ : Weil die Zahl 0 in $\left(k_{1}, k_{2}, \ldots, k_{n}\right)$ vorkommt, müssen zwei Elemente von $\left(e_{1}, e_{2}, \ldots, e_{n}\right)$ gleich sein. Da außerdem jede der $m+1$ natürlichen Zahlen von 0 bis $m$ wenigstens einmal vorkommen muss, folgt $n \geq m+2$.
ii) Wir geben ein Beispiel für $n=m+2 \geq 3$ : Es sei $\left(e_{1}, e_{2}, \ldots, e_{n}\right)=(0, m, 1, m-1, \ldots)$. In dem $n$-Tupel werden die Zahlen alternierend bis zur Differenz 0 absteigend fortgesetzt, so dass $e_{n-1}=e_{n}$ gilt. Damit tritt jede natürliche Zahl von 0 bis $m$ genau einmal, die Zahl $e_{n}$ genau zweimal auf. Die Beträge der Differenzen treten von $m$ abwärts bis zur 0 offensichtlich je einmal auf; die Differenz $\left|e_{n}-0\right|=e_{n}$ tritt zweimal auf, weil $e_{n}<m$ ist. Damit sind die Eigenschaften (1) und (2) gezeigt.
Hinweis: Für Teil a) wurden 3 P . und für Teil b) 7 P . vergeben. Weder das Beispiel für a) noch das Beispiel für b) sind die einzig möglichen.
|
{
"resource_path": "Germany_TST/segmented/de-2011-loes_awkl2_11.jsonl",
"problem_match": "# Aufgabe 3",
"solution_match": "\nLösung:"
}
|
96e1ce1f-3196-5c38-97b9-318441a0cd6b
| 604,715
|
Let $\Gamma$ be the circumcircle of the isosceles triangle $ABC$ with $C$ as the vertex. Inside the side $\overline{BC}$, there lies a point $M$. There exists a point $N$ on the ray $AM$ such that $M$ is between $A$ and $N$ and $|AN|=|AC|$. The circumcircle of triangle $CMN$ intersects $\Gamma$ at two distinct points $C$ and $P$. The lines $AB$ and $CP$ intersect at a point $Q$. Prove that $\measuredangle BMQ = \measuredangle QMN$.
|
The idea for the solution is based on the observation that the requirement $|A N|=|A C|=|B C|$ remains unchanged if $A$ and $C$ as well as $N$ and $B$ are swapped. This suggests that one should also consider the circumcircle of triangle $A M B$. The second intersection point of the circumcircles of $A M B$ and $C M N$ can ultimately be identified as the incenter of $A M C$.
Let $I$ be the incenter of triangle $A M C$. It is known that $\measuredangle M I C=\frac{\pi}{2}+\frac{1}{2} \measuredangle M A C=\frac{\pi}{2}+\frac{1}{2} \measuredangle N A C$, and since triangle $A N C$ is isosceles at $A$, $\measuredangle N A C=\pi-2 \measuredangle C N A$, so $\measuredangle M I C=\pi-\measuredangle C N A=\pi-\measuredangle C N M$. Since $I$ and $N$ lie in different half-planes with respect to the line $C M$, it follows from the cyclic quadrilateral theorem that $I M N C$ is a cyclic quadrilateral, i.e., that $I$ lies on the circumcircle of $C M N$. Due to the symmetry mentioned at the beginning, $I$ also lies on the circumcircle of $A B M$. Since $I$ as the incenter is an interior point of triangle $A M C$, in particular $I \neq M$, and thus the line $I M$ is the radical axis of the circumcircles of $A B M$ and $C M N$. Since the line $A B$ is the radical axis of the circumcircles of $A B C$ and $A B M$ and the line $C P$ is the radical axis of the circumcircles of $A B C$ and $C M N$, the lines $I M, A B$, and $C P$ intersect at a point. This point is defined as $Q$, i.e., $Q$ lies on the angle bisector $I M$ of angle $C M A$, but this is identical to the angle bisector of angle $B M N$, so $\measuredangle B M Q=\measuredangle Q M N$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Es sei $\Gamma$ der Umkreis des bei $C$ gleichschenkligen Dreiecks $A B C$. Im Inneren der Seite $\overline{B C}$ liege der Punkt $M$. Es gebe einen Punkt $N$ auf dem Strahl $A M$, für den $M$ zwischen $A$ und $N$ liegt und der $|A N|=|A C|$ erfüllt. Der Umkreis des Dreiecks $C M N$ schneide $\Gamma$ in den beiden verschiedenen Punkten $C$ und $P$. Die Geraden $A B$ und $C P$ mögen sich in einem Punkt $Q$ treffen. Man beweise, dass $\measuredangle B M Q=\measuredangle Q M N$.
|
Die Idee zur Lösung geht von der Beobachtung aus, dass die Forderung $|A N|=|A C|=|B C|$ unverändert bleibt, wenn man $A$ und $C$ sowie $N$ und $B$ miteinander vertauscht. Dies legt nahe, dass man auch den Umkreis des Dreiecks $A M B$ betrachten sollte. Der zweite Schnittpunkt der Umkreise von $A M B$ und $C M N$ lässt sich schließlich als Inkreismittelpunkt von $A M C$ identifizieren.
Es sei $I$ der Inkreismittelpunkt des Dreiecks $A M C$. Bekanntlich ist $\measuredangle M I C=\frac{\pi}{2}+\frac{1}{2} \measuredangle M A C=\frac{\pi}{2}+\frac{1}{2} \measuredangle N A C$, und weil das Dreieck $A N C$ bei $A$ gleichschenklig ist, ist $\measuredangle N A C=\pi-2 \measuredangle C N A$, also ist $\measuredangle M I C=\pi-\measuredangle C N A=$ $\pi-\measuredangle C N M$, und weil $I$ und $N$ bezüglich der Geraden $C M$ in verschiedenen Halbebenen liegen, folgt aus dem Satz vom Sehnenviereck, dass $I M N C$ ein Sehnenviereck ist, d. h., dass $I$ auf dem Umkreis von $C M N$ liegt. Auf Grund der eingangs angesprochenen Symmetrie liegt $I$ auch auf dem Umkreis von $A B M$. Da $I$ als Inkreismittelpunkt ein innerer Punkt des Dreiecks $A M C$ ist, ist insbesondere $I \neq M$, und damit ist die Gerade $I M$ die Potenzgerade der Umkreise von $A B M$ und $C M N$. Da weiterhin die Gerade $A B$ die Potenzgerade der Umkreise von $A B C$ und $A B M$ und die Gerade $C P$ die Potenzgerade der Umkreise von $A B C$ und $C M N$ ist, schneiden sich die Geraden $I M, A B$ und $C P$ in einem Punkt. Dieser Punkt ist nach Definition $Q$, d.h. $Q$ liegt auf der Winkelhalbierenden $I M$ des Winkels $C M A$, aber diese ist identisch mit der Winkelhalbierenden des Winkels $B M N$, folglich ist $\measuredangle B M Q=\measuredangle Q M N$.
|
{
"resource_path": "Germany_TST/segmented/de-2012-loes_awkl1_12.jsonl",
"problem_match": "\nAufgabe 2 ",
"solution_match": "\nLösung:"
}
|
b9685e49-fadd-5ee4-8a00-7701bb95904c
| 604,742
|
For nine different positive integers $d_{1}, d_{2}, \ldots, d_{9}$, consider the polynomial $P(n)=\left(n+d_{1}\right)\left(n+d_{2}\right) \cdot \ldots \cdot\left(n+d_{9}\right)$.
Show that there exists an integer $N$ with the following property:
For all integers $n \geq N$, the number $P(n)$ is divisible by a prime number greater than 20.
|
We can assume according to the problem statement that $N>0$ and $d_{1}<d_{2}<\ldots<d_{9}$. Then $k=d_{9}-d_{1}=\max _{1 \leq q<r \leq 9}\left(d_{r}-d_{q}\right)$. Let $z \in \mathbb{N}$ be chosen such that $2^{z}>k$.
Claim: With $N=2^{z} \cdot 3^{z} \cdot 5^{z} \cdot 7^{z} \cdot 11^{z} \cdot 13^{z} \cdot 17^{z} \cdot 19^{z}$, a solution for $N$ is found.
Proof: We assume that for $n \geq N$ none of the factors of $P(n)$ has a prime factor greater than 20 and consider first $n+d_{1}=2^{e_{1}^{(1)}} \cdot 3^{e_{2}^{(1)}} \cdot \ldots \cdot 19^{e_{8}^{(1)}}$. Since $n \geq N$, there must be at least one $e_{j}^{(1)}$ with $e_{j}^{(1)} \geq z$ $(1 \leq j \leq 8)$. The corresponding prime factor is $p$. Thus, $n+d_{1}$ is divisible by $p^{e_{j}^{(1)}}$. Since $p^{e_{j}^{(1)}} \geq 2^{\ell_{j}^{(1)}} \geq 2^{z}>k=\max _{1 \leq q<r \leq 9}\left(d_{r}-d_{q}\right)$, none of the other numbers $n+d_{i}$ is divisible by $p^{e_{j}^{(1)}}$ $(2 \leq i \leq 9)$, because otherwise $d_{i}-d_{1}$ would be divisible by $p_{j}^{e_{j}^{(1)}}$. Therefore, $e_{j}^{(1)}=\max _{1 \leq i \leq 9}\left(e_{j}^{(i)}\right)$. Now consider $n+d_{2}$. Since $d_{2}>d_{1}$, there must be at least one $e_{j}^{(2)}$ with $e_{j}^{(2)}>e_{j}^{(1)}$ and $e_{j}^{(2)} \geq z$. Hence, $n+d_{2}$ also has a maximal $e_{j}^{(2)}$ with respect to all factors. This applies correspondingly to the other factors $n+d_{i}$.
Since there are only 8 prime factors less than 20 for the 9 factors of the polynomial, a contradiction arises by the pigeonhole principle. Therefore, an additional prime factor must occur, by which $P(n)$ is divisible.
Hints: The $N$ given here is not the only possible one. Often, the proofs were not rigorous enough. For example, one argued with the addition of more and more prime numbers as $n$ becomes larger.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Für neun verschiedene positive ganze Zahlen $d_{1}, d_{2}, \ldots, d_{9}$ betrachten wir das Polynom $P(n)=\left(n+d_{1}\right)\left(n+d_{2}\right) \cdot \ldots \cdot\left(n+d_{9}\right)$.
Man zeige, dass eine ganze Zahl $N$ mit folgender Eigenschaft existiert:
Für alle ganzen Zahlen $n \geq N$ ist die Zahl $P(n)$ durch eine Primzahl größer als 20 teilbar.
|
Wir können der Aufgabenstellung gemäß $N>0$ und $d_{1}<d_{2}<\ldots<d_{9}$ annehmen. Dann ist $k=d_{9}-d_{1}=\max _{1 \leq q<r \leq 9}\left(d_{r}-d_{q}\right)$. Es sei $z \in \mathbb{N}$ so gewählt, dass $2^{z}>k$.
Behauptung: Mit $N=2^{z} \cdot 3^{z} \cdot 5^{z} \cdot 7^{z} \cdot 11^{z} \cdot 13^{z} \cdot 17^{z} \cdot 19^{z}$ ist eine Lösung für $N$ gefunden.
Beweis: Wir nehmen an, dass für $n \geq N$ keiner der Faktoren von $P(n)$ einen Primfaktor größer als 20 besitzt und betrachten zunächst $n+d_{1}=2^{e_{1}^{(1)}} \cdot 3^{e_{2}^{(1)}} \cdot \ldots \cdot 19^{e_{8}^{(1)}}$. Wegen $n \geq N$ muss es dann wenigstens ein $e_{j}^{(1)}$ mit $e_{j}^{(1)} \geq z$ geben $(1 \leq j \leq 8)$. Der zugehörige Primfaktor sei $p$. Somit ist $n+d_{1}$ durch $p^{e_{j}^{(1)}}$ teilbar. Wegen $p^{e_{j}^{(1)}} \geq 2^{\ell_{j}^{(1)}} \geq 2^{z}>k=\max _{1 \leq q<r \leq 9}\left(d_{r}-d_{q}\right)$ ist keine weitere der Zahlen $n+d_{i}$ durch $p^{e_{j}^{(1)}}$ teilbar $(2 \leq i \leq 9)$, weil sonst $d_{i}-d_{1}$ durch $p_{j}^{e_{j}^{(1)}}$ teilbar wäre. Es ist also $e_{j}^{(1)}=\max _{1 \leq i \leq 9}\left(e_{j}^{(i)}\right)$. Betrachten wir nun $n+d_{2}$, so finden wird dort wegen $d_{2}>d_{1}$ wenigstens ein $e_{j}^{(2)}$ mit $e_{j}^{(2)}>e_{j}^{(1)}$ sowie $e_{j}^{(2)} \geq z$. Daher besitzt auch $n+d_{2}$ ein im Bezug auf alle Faktoren maximales $e_{j}^{(2)}$. Dies gilt entsprechend für die anderen Faktoren $n+d_{i}$.
Da es für die 9 Faktoren des Polynoms jedoch nur 8 Primfaktoren kleiner als 20 gibt, entsteht hier nach dem Schubfachprinzip ein Widerspruch. Daher muss ein weiterer Primfaktor auftreten, durch den $P(n)$ teilbar ist.
Hinweise: Das hier angegebene $N$ ist nicht das einzig mögliche. Häufig waren Beweise nicht streng genug. Man argumentierte etwa mit immer mehr dazukommenden Primzahlen, wenn $n$ immer größer wird.
|
{
"resource_path": "Germany_TST/segmented/de-2012-loes_awkl2_12.jsonl",
"problem_match": "# Aufgabe 1",
"solution_match": "\nLösung:"
}
|
642ab8b0-5ae5-561e-8da3-14a565e205e0
| 604,769
|
Let $A B C$ be an acute-angled triangle with circumcenter $O$. Furthermore, let $k$ be a circle with the following properties:
(1) The center $K$ of $k$ lies in the interior of the side $B C$.
(2) $k$ touches $A B$ at $B^{\prime}$ and $A C$ at $C^{\prime}$.
(3) $O$ lies on the shorter of the two arc segments $B^{\prime} C^{\prime}$ of $k$.
Prove: The circumcircle of $A B C$ and $k$ intersect at two distinct points.
|
The point $O^{\prime}$ is the image point of $O$ under reflection across the line $B C$. $S$ is the intersection of $K O^{\prime}$ with the circumcircle $u$ (see figure).
According to the central angle theorem, $\Varangle B O C=2 \alpha$. Since $C^{\prime}$ and $B^{\prime}$ lie inside the segments $A C$ and $A B$ respectively, and $O$ lies inside the triangle $A B C$ due to its acute angles, $\Varangle B^{\prime} O C^{\prime}>2 \alpha$. In the quadrilateral $A B^{\prime} K C^{\prime}$, we have: $360^{\circ}=2 \cdot 90^{\circ}+\alpha+\Varangle C^{\prime} K B^{\prime}$, because the angles at the points of tangency $C^{\prime}$ and $B^{\prime}$ are right angles. It follows that $\Varangle C^{\prime} K B^{\prime}=180^{\circ}-\alpha$.
Thus, in the cyclic quadrilateral $B^{\prime} O^{\prime} C^{\prime} O$:
$\Varangle B^{\prime} O C^{\prime}=180^{\circ}-\Varangle C^{\prime} O^{\prime} B^{\prime}=180^{\circ}-\frac{1}{2} \Varangle C^{\prime} K B^{\prime}$
$=\frac{1}{2}\left(180^{\circ}+\alpha\right)$. Therefore, $\frac{1}{2}\left(180^{\circ}+\alpha\right)>2 \alpha$ and hence
$\alpha<60^{\circ}$.
In the cyclic quadrilateral $A B S C$, it follows that $\Varangle C S B=180^{\circ}-\alpha>120^{\circ}$.
Due to the axial symmetry across $B C$, $B O^{\prime} C O$ is a kite, and we have:
$\Varangle C O^{\prime} B=\Varangle B O C=2 \alpha<120^{\circ}$. Thus, $\Varangle C S B>\Varangle C O^{\prime} B$.
Since $S$ lies on $u$, $\Varangle C S B$ is a circumferential angle over the chord $B C$. From the last inequality, it follows that $O^{\prime}$ lies outside of $u$. Because the axis of reflection $B C$ is a diameter of $k$, $O^{\prime}$ lies on $k$. Therefore, there are points $O$ and $O^{\prime}$ on $k$, one inside and one outside of $u$. This leads to the claim.
Hint: The claim does not hold for every acute triangle, which significantly complicates the approach to the problem. A simple solution is possible using inversion with respect to $u$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Es sei $A B C$ ein spitzwinkliges Dreieck mit dem Umkreismittelpunkt $O$. Ferner sei $k$ ein Kreis mit folgenden Eigenschaften:
(1) Der Mittelpunkt $K$ von $k$ liegt im Inneren der Seite $B C$.
(2) $k$ berührt $A B$ in $B^{\prime}$ und $A C$ in $C^{\prime}$.
(3) $O$ liegt auf dem kürzeren der beiden Bogenstücke $B^{\prime} C^{\prime}$ von $k$.
Man beweise: Der Umkreis von $A B C$ und $k$ schneiden einander in zwei verschiedenen Punkten.
|
Der Punkt $O^{\prime}$ ist Bildpunkt von $O$ bei der Spiegelung an der Geraden $B C$. $S$ ist der Schnittpunkt von $K O^{\prime}$ mit dem Umkreis $u$ (siehe Figur).
Nach dem Satz vom Mittelpunktswinkel ist $\Varangle B O C=2 \alpha$. Weil $C^{\prime}$ und $B^{\prime}$ im Inneren der Strecken $A C$ bzw. $A B$ liegen und $O$ wegen der Spitzwinkligkeit innerhalb von $A B C$ liegt, ist $\Varangle B^{\prime} O C^{\prime}>2 \alpha$. Im Viereck $A B^{\prime} K C^{\prime}$ gilt: $360^{\circ}=2 \cdot 90^{\circ}+\alpha+\Varangle C^{\prime} K B^{\prime}$, da die Winkel in den Berührpunkten $C^{\prime}$ und $B^{\prime}$ Rechte sind. Es folgt $\Varangle C^{\prime} K B^{\prime}=180^{\circ}-\alpha$.
Damit gilt im Sehnenviereck $B^{\prime} O^{\prime} C^{\prime} O$ :
$\Varangle B^{\prime} O C^{\prime}=180^{\circ}-\Varangle C^{\prime} O^{\prime} B^{\prime}=180^{\circ}-\frac{1}{2} \Varangle C^{\prime} K B^{\prime}$
$=\frac{1}{2}\left(180^{\circ}+\alpha\right)$. Somit ist $\frac{1}{2}\left(180^{\circ}+\alpha\right)>2 \alpha$ und daher

$\alpha<60^{\circ}$.
Im Sehnenviereck $A B S C$ folgt daraus $\Varangle C S B=180^{\circ}-\alpha>120^{\circ}$.
Aufgrund der Achsensymmetrie an $B C$ ist $B O^{\prime} C O$ ein Drachenviereck und es gilt:
$\Varangle C O^{\prime} B=\Varangle B O C=2 \alpha<120^{\circ}$. Also ist $\Varangle C S B>\Varangle C O^{\prime} B$.
Da $S$ auf $u$ liegt, ist $\Varangle C S B$ ein Umfangswinkel über der Sehne $B C$. Aus der letzten Ungleichung folgt dann, dass $O^{\prime}$ außerhalb von $u$ liegt. Weil die Spiegelachse $B C$ Durchmesser von $k$ ist, liegt $O^{\prime}$ auf $k$. Somit gibt es mit $O$ und $O^{\prime}$ je einen Punkt auf $k$, der innerhalb bzw. außerhalb von $u$ liegt. Daraus folgt die Behauptung.
Hinweis: Die Behauptung gilt nicht für jedes spitzwinklige Dreieck, was den Zugang zu der Aufgabe deutlich erschwert hat. Eine einfache Lösung ist unter Verwendung von Inversion an $u$ möglich.
|
{
"resource_path": "Germany_TST/segmented/de-2012-loes_awkl2_12.jsonl",
"problem_match": "# Aufgabe 2",
"solution_match": "\nLösung:"
}
|
ced7b11f-1064-5d85-b822-57f4102c81a0
| 604,780
|
Let $n$ be an odd natural number and $x$ and $y$ be two rational numbers such that
$$
x^{n}+2 y=y^{n}+2 x
$$
Show that $x=y$.
|
We first consider
( $\boxtimes$) Let $n \geqslant 3$ be an odd natural number. Furthermore, let $a, b$, and $c$ be three integers such that
$$
a^{n-1}+a^{n-2} b+\ldots+b^{n-1}=2 c^{n-1}
$$
Then $a=b=c=0$.
If this were false for some $n$, we could choose a counterexample $(a, b, c)$ for which the expression $|a|+|b|+|c|$ takes its smallest positive value. If both $a$ and $b$ were odd, the left side would be the sum of an odd number of odd summands and thus odd, while the right side is even. Therefore, at least one of the numbers $a$ and $b$ must be even. If, for example, $a$ is even, the left side has the same parity as $b^{n-1}$, and the right side is even, so $b$ must also be even. Similarly, one sees that $a$ must be even if $b$ is assumed to be even. Therefore, both $a$ and $b$ are even. Consequently, the left side is divisible by $2^{n-1}$ and thus, in particular, by 4, which implies that $c^{n-1}$ and hence $c$ is also even. If we now introduce three integers $a^{\prime}, b^{\prime}$, and $c^{\prime}$ with $a=2 a^{\prime}, b=2 b^{\prime}$, and $c=2 c^{\prime}$, then first
$$
a^{\prime n-1}+a^{\prime n-2} b^{\prime}+\ldots+b^{\prime n-1}=2 c^{\prime n-1}
$$
and secondly
$$
0<\left|a^{\prime}\right|+\left|b^{\prime}\right|+\left|c^{\prime}\right|<|a|+|b|+|c| .
$$
The triple $\left(a^{\prime}, b^{\prime}, c^{\prime}\right)$ thus contradicts the choice of $(a, b, c)$, and $(\boxtimes)$ is proved.
We now turn to the actual problem. In the case $n=1$, the claim is trivial, and from now on we focus only on the case $n \geqslant 3$. Let $x$ and $y$ be two rational numbers such that $x^{n}+2 x=y^{n}+2 y$. By bringing everything to one side and then factoring, we obtain
$$
(x-y)\left(x^{n-1}+x^{n-2} y+\ldots+y^{n-1}-2\right)=0
$$
If $x$ and $y$ were different, which we will assume from now on, then
$$
x^{n-1}+x^{n-2} y+\ldots+y^{n-1}=2
$$
must hold. Since any two rational numbers can be brought to a common denominator, there exist three integers $a, b$, and $c$ with $c \neq 0, x=a / c$, and $y=b / c$. Substituting these fractions into (1) and then multiplying by $c^{n-1}$, we get
$$
a^{n-1}+a^{n-2} b+\ldots+b^{n-1}=2 c^{n-1}
$$
From $(\boxtimes)$ it follows, in particular, that $c=0$. This contradiction shows that $x$ and $y$ must indeed be equal, thus solving the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Es sei $n$ eine ungerade natürliche Zahl und $x$ und $y$ seien zwei rationale Zahlen mit
$$
x^{n}+2 y=y^{n}+2 x
$$
Man zeige, dass $x=y$.
|
Wir überlegen uns zuerst
( $\boxtimes)$ Es sei $n \geqslant 3$ eine ungerade natürliche Zahl. Weiterhin seien $a, b$ und $c$ drei ganze Zahlen mit
$$
a^{n-1}+a^{n-2} b+\ldots+b^{n-1}=2 c^{n-1}
$$
Sodann ist $a=b=c=0$.
Wenn dies bei einem gewissen $n$ falsch wäre, könnten wir zu diesem ein Gegenbeispiel ( $a, b, c$ ) wählen, bei dem der Ausdruck $|a|+|b|+|c|$ seinen kleinstmöglichen positiven Wert annimmt. Wären $a$ und $b$ beide ungerade, so wäre die linke Seite die Summe einer ungeraden Anzahl ungerader Summanden und mithin selbst ungerade, während die rechte Seite gerade ist. Also ist mindestens eine der beiden Zahlen $a$ und $b$ gerade. Ist etwa $a$ gerade, so hat die linke Seite dieselbe Parität wie $b^{n-1}$ und die rechte Seite ist gerade, sodass $b$ ebenfalls gerade ist. Ebenso sieht man, dass $a$ gerade sein muss, falls $b$ als gerade vorausgesetzt wird. Insgesamt sind also $a$ und $b$ beide gerade. Folglich ist die linke Seite durch $2^{n-1}$ und damit insbesondere durch 4 teilbar, womit sich $c^{n-1}$ und demnach auch $c$ als gerade erwiesen hat. Führt man nun drei ganze Zahlen $a^{\prime}, b^{\prime}$ und $c^{\prime}$ mit $a=2 a^{\prime}, b=2 b^{\prime}$ und $c=2 c^{\prime}$ in die Betrachtung ein, so ist erstens
$$
a^{\prime n-1}+a^{\prime n-2} b^{\prime}+\ldots+b^{\prime n-1}=2 c^{\prime n-1}
$$
und zweitens
$$
0<\left|a^{\prime}\right|+\left|b^{\prime}\right|+\left|c^{\prime}\right|<|a|+|b|+|c| .
$$
Das Tripel $\left(a^{\prime}, b^{\prime}, c^{\prime}\right)$ widerspricht also der Wahl von $(a, b, c)$ und damit ist $(\boxtimes)$ bewiesen.
Wir wenden und nunmehr der eigentlichen Aufgabe zu. $\operatorname{Im}$ Fall $n=1$ ist die Behauptung trivial und wir konzentrieren uns von jetzt an nur noch auf den Fall $n \geqslant 3$. Es seien $x$ und $y$ zwei rationale Zahlen mit $x^{n}+2 x=y^{n}+2 y$. Indem wir alles auf eine Seite bringen und anschließend faktorisieren, erhalten wir
$$
(x-y)\left(x^{n-1}+x^{n-2} y+\ldots+y^{n-1}-2\right)=0
$$
Wenn $x$ und $y$ also verschieden wären, was wir von jetzt an annehmen wollen, müsste
$$
x^{n-1}+x^{n-2} y+\ldots+y^{n-1}=2
$$
sein. Da man je zwei rationale Zahlen auf einen gemeinsamen Nenner bringen kann, gibt es drei ganze Zahlen $a, b$ und $c$ mit $c \neq 0, x=a / c$ und $y=b / c$. Wer diese Brüche in (1) einsetzt und daraufhin mit $c^{n-1}$ multipliziert, erhält
$$
a^{n-1}+a^{n-2} b+\ldots+b^{n-1}=2 c^{n-1}
$$
Aus $(\boxtimes)$ folgt nun allerdings insbesondere $c=0$. Dieser Widerspruch zeigt, dass $x$ und $y$ doch gleich sein müssen, womit die Aufgabe gelöst ist.
|
{
"resource_path": "Germany_TST/segmented/de-2013-loes_awkl_13.jsonl",
"problem_match": "1. Aufgabe.",
"solution_match": "\nLösung."
}
|
8aaa97e4-6526-5d50-8ea4-25f18eb7ff67
| 604,807
|
Let $A B C$ be an acute-angled triangle with circumcircle $\omega$. Prove that there exists a point $J$ with the following property: If $X$ is an interior point of $A B C$, the rays $A X$, $B X$ and $C X$ intersect the circle $w$ again at points $A_{1}, B_{1}$ and $C_{1}$, and the points $A_{2}$, $B_{2}$ and $C_{2}$ are symmetric to $A_{1}, B_{1}$ and $C_{1}$ with respect to the midpoints of the segments $\overline{B C}, \overline{C^{\prime} A}$ and $\overline{A B}$, respectively, then the four points $A_{2}, B_{2}, C_{2}$ and $J$ lie on a common circle.
|
We show that the point $J$, usually denoted as $H$, the orthocenter of triangle $ABC$, has the described property. For this, let $a$ be the line through $A$ parallel to $BC$, and the lines $b$ and $c$ are defined analogously. No two of the three lines $a, b$, and $c$ are parallel, and therefore, the intersection point $A'$ of $b$ with $c$ and the two analogously defined points $B'$ and $C'$ exist.
The quadrilateral $A' C J B$ has right angles at $B$ and $C$ and is therefore a cyclic quadrilateral. Since the reflection at the midpoint of the segment $\overline{BC}$ maps point $A$ to $A'$ and swaps $B$ with $C$, it transforms $\omega$ into the circumcircle of the just found cyclic quadrilateral. Consequently, $A_2$ lies on this circle, and $\Lambda' A_2$ is parallel to $AX$.
Let the centroid of triangle $ABC$ be $S$. The central dilation $\sigma$ with center $S$ and factor $-2$ maps $A$ to $A'$; the image of $X$ is denoted by $X'$. Then, the lines $AX$ and $A'X''$ are parallel, and therefore, $X'$ lies on the line $A'A_2$. Similar arguments can be made by replacing $A$ with $B$ and $C$, and we learn in total: The three lines $A'A_2, B'B_2$, and $C''C_2$ intersect at $X'$.
If $X' = J$, the points $A_2, B_2$, and $C_2$ coincide with $J$, and the claim is trivial. From now on, let $X' \neq J$.
Since $\varangle A'CJ = 90^\circ$, the segment $\overline{A'J}$ is, by Thales' theorem, a diameter of the circumcircle of the quadrilateral $A'CJB$. Again, by Thales' theorem, $\varangle JA_2A' = 90^\circ$ and therefore also $\varangle JA_2X' = 90^\circ$. Thus, the point $A_2$ lies, once again by Thales' theorem, on the circle with diameter $JX^{-1}$. For similar reasons, the points $B_2$ and $C_2$ also lie on this circle, and in particular, we have now found a circle on which all four points $A_2, B_2, C_2$, and $J$ lie.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Es sei $A B C$ ein spitzwinkliges Dreieck mit Umkreis $\omega$. Man beweise, dass es einen Punkt $J$ mit der folgenden Eigenschaft gibt: Ist $X$ cin innerer Punkt von $A B C$, treffen die Strahlen $A X$, $B X$ und $C X$ den Kreis $w$ erneut in den Punkten $A_{1}, B_{1}$ und $C_{1}$ und liegen die Punkte $A_{2}$, $B_{2}$ und $C_{2}$ symmetrisch zu $A_{1}, B_{1}$ und $C_{1}$ bezüglich der Mittelpunkte der Strecken $\overline{B C}, \overline{C^{\prime} A}$ beziehungsweise $\overline{A B}$, so liegen die vier Punkte $A_{2}, B_{2}, C_{2}$ und $J$ auf einem gemeinsamen Kreis.
|
Wir zeigen, dass der normalerweise $H$ genannte Höhenschnittpunkt $J$ des Dreiecks $A B C$ die beschriebene Eigenschaft aufweisi. Hierzu sei a die durch $A$ gezogene Parallele zu $B C$ und dic Geraden $b$ und $c$ seien analog definiert. Keine zwei der drei Geraden $a, b$ und $c$ sind parallel und folglich existieren der Schnittpunkt $A^{\prime}$ von $b$ mit $c$ sowie die beiden analog definierten Punkte $B^{\prime}$ und $C^{\prime}$.
Das Viereck $A^{\prime} C J B$ besitzt bei $B$ und $C$ rechte Winkel und ist daher ein Sehnenviereck. Da die Spiegelung am Mittelpunkt der Strecke $\overline{B C}$ den Punkt $A$ auf $A^{\prime}$ abbildet und $B$ mit $C$ vertauscht, führt sie $\omega$ in den Umkreis des gerade gefundenen Sehnenvierecks über. Demnach liegt $A_{2}$ auf diesom Krcis und $\Lambda^{\prime} A_{2}$ ist zu $A X$ parallel.
Der Schwerpunkt des Dreiecks $A B C$ heiße $S$. Die zentrische Streckung $\sigma$ mit Zentrum $S$ und Faktor -2 bildet $A$ auf $A^{\prime}$ ab; der Bildpunkt von $X$ heiBe $X^{\prime}$. Sodann sind die beiden Geraden $A X$ und $A^{\prime} X^{\prime \prime}$ parallel und daher liegt $X^{\prime}$ auf der Geraden $A^{\prime} A_{2}$. Ähnliche Argumente lassen sich auch mit $B$ und $C$ an der Stelle von $A$ ausführen und wir lernen insgesamt: Die drei Geraden $A^{\prime} A_{2}, B^{\prime} B_{2}$ und $C^{\prime \prime} C_{2}$ schneiden sich in $X^{\prime}$.

Falls $X^{\prime}=J$ fallen auch die Punkte $A_{2}, B_{2}$ und $C_{2}$ mit $J$ zusammen und die Behauptung ist trivial. Von nun ab sei daher $X^{\prime} \neq J$.
Wegen $\varangle A^{\prime} C J=90^{\circ}$ ist die Strecke $\overline{A^{\prime} J}$ nach Satz des Thales ein Durchmesser des Umkreises des Viereck $A^{\prime} C J B$. Wieder um nach Satz des Thales ist daher $\varangle J A_{2} A^{\prime}=90^{\circ}$ und folglich auch $\varangle J A_{2} X^{\prime}=90^{\circ}$. Der Punkt $A_{2}$ liegt demnach, abermals nach Satz des 'l'haces, auf dem Kreis mit Durchmesser $J X^{-1}$. Aus analogen Gründen liegen auch die beiden Punkte $B_{2}$ und $C_{2}$ auf diesem Kreis und insbesondere haben wir nunmehr einen Kreis gefunden, auf dem alle vier der Punkte $A_{2}, B_{2}, C_{2}$ und $J$ liegen.
|
{
"resource_path": "Germany_TST/segmented/de-2013-loes_awkl_13.jsonl",
"problem_match": "3. Aufgabe\n",
"solution_match": "\nLösung."
}
|
15d92758-f190-52e5-bd08-8832b79f6028
| 604,835
|
The central bank of Sikinia mints coins worth 11 and 12 Kulotnik. During a burglary, 11 Sicilian thieves cracked a safe and looted coins with a total value of 5940 Kulotnik. They try for a while to fairly divide the loot among themselves - so that everyone gets the same amount - but they can't manage it; after a while, their leader claims to have figured out that it is indeed impossible.
Prove that they did not loot any coin worth 12 Kulotnik.
|
The thieves may have looted $a$ coins worth 11 Kulotnik and $b$ coins worth 12 Kulotnik. Here, $a$ and $b$ are two non-negative integers with
$$
11 a + 12 b = 5940 = 11 \cdot 540 = 12 \cdot 495
$$
We now assume $b > 0$ and try to find a fair distribution of the loot among the thieves.
From (1), we have $11 a = 12 \cdot (495 - b)$, meaning $11 a$ is divisible by 12. Since 11 and 12 are coprime, $a$ must also be a multiple of 12. Therefore, the thieves can distribute the looted 11-Kulotnik coins into $\frac{a}{12}$ bags, each containing $12 \cdot 11 = 132$ Kulotnik. Similarly, (1) implies the equation $12 b = 11 \cdot (540 - a)$, so $12 b$ is divisible by 11. As before, this shows that $b$ is also divisible by 11. Since we assumed $b > 0$, each of the thieves can take one coin worth 12 Kulotnik, and the number $b - 11$ of the remaining 12-Kulotnik coins is still divisible by 11, allowing them to be distributed into $\frac{b}{11} - 1$ bags, each containing $11 \cdot 12 = 132$ Kulotnik.
Since
$$
5940 - 11 \cdot 12 = 5808 = 132 \cdot 44
$$
the undistributed remainder of the loot is now in $44 = 11 \cdot 4$ bags, each containing 132 Kulotnik. If each of the 11 thieves takes 4 of these bags, they will have fairly divided the loot. However, since their leader proved that this is impossible, our assumption $b > 0$ must be false: In other words, there was indeed no coin worth 12 Kulotnik in the safe.
Remark. Some participants came up with very creative nicknames for the thieves: bank robbers, pirates, gangsters, bandits, criminals, offenders, thieves.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Die Zentralbank von Sikinien prägt Münzen im Wert von 11 und 12 Kulotnik. Bei einem Einbruch haben 11 sikinische Ganoven einen Tresor geknackt und Münzen im Gesamtwert von 5940 Kulotnik erbeutet. Sie versuchen für eine Weile, die Beute gerecht unter sich aufzuteilen - also so, dass jeder gleich viel erhält - aber es will ihnen nicht gelingen; nach einer Weile behauptet ihr Anführer, sich überlegt zu haben, dass dies tatsächlich nicht möglich ist.
Man beweise, dass sie keine Münze im Wert von 12 Kulotnik erbeutet haben.
|
Die Ganoven mögen $a$ Münzen im Wert von 11 Kulotnik und $b$ Münzen im Wert von 12 Kulotnik erbeutet haben. Dabei sind $a$ und $b$ zwei nichtnegative ganze Zahlen mit
$$
11 a+12 b=5940=11 \cdot 540=12 \cdot 495
$$
Wir nehmen nun $b>0$ an und versuchen, eine gerechte Aufteilung der Beute auf die Ganoven zu finden.
Nach (1) ist $11 a=12 \cdot(495-b)$, d.h. $11 a$ ist durch 12 teilbar. Nachdem 11 und 12 teilerfremd sind, ist folglich auch $a$ ein Vielfaches von 12 und demnach können die Ganoven die erbeuteten 11-Kulotnik-Stücke in $\frac{a}{12}$ Säckchen verteilen, von denen jedes $12 \cdot 11=132$ Kulotnik enthält. Analog impliziert (1) die Gleichung $12 b=11 \cdot(540-a)$ und mithin ist $12 b$ durch 11 teilbar. Wie vorhin zeigt dies, dass auch $b$ durch 11 teilbar ist. Da wir $b>0$ angenommen haben, kann sich jeder der Ganoven eine Münze im Wert von 12 Kulotnik nehmen, und die Anzahl $b-11$ der übrigen 12-Kulotnik-Stücke ist immer noch durch 11 teilbar, weshalb sich diese in $\frac{b}{11}-1$ Säckchen aufteilen lassen, die ebenfalls je $11 \cdot 12=132$ Kulotnik enthalten.
Wegen
$$
5940-11 \cdot 12=5808=132 \cdot 44
$$
befindet sich der noch nicht verteilte Rest der Beute nunmehr in $44=11 \cdot 4$ Säckchen zu je 132 Kulotnik. Wenn sich nun jeder der 11 Ganoven 4 dieser Säckchen nimmt haben sie insgesamt die Beute gerecht geteilt. Doch da ihr Anführer beweisen konnte, dass dies gar nicht möglich ist, muss unsere Annahme $b>0$ falsch gewesen sein: Anders ausgedrückt lag tatsächlich keine Münze im Wert von 12 Kulotnik im Tresor.
Bemerkung. Manche Teilnehmer ersannen für die Ganoven äußerst findige Spitznamen: Bankräuber, Piraten, Gangster, Banditen, Gauner, Kriminelle, Straftäter, Diebe.
|
{
"resource_path": "Germany_TST/segmented/de-2014-loes_awkl_14.jsonl",
"problem_match": "\nAufgabe 1.",
"solution_match": "\nLösung."
}
|
f00e08e2-bfd5-531a-ad4c-85ed78a2b169
| 604,890
|
Let $A B C D$ be a convex cyclic quadrilateral with $|A D|=|B D|$. Its diagonals $\overline{A C}$ and $\overline{B D}$ intersect at $E$. The incenter of triangle $BCE$ is denoted by $I$. The circumcircle of triangle $BIE$ intersects the interior of the segment $\overline{A E}$ at point $N$.
Prove that
$$
|A N| \cdot|N C|=|C D| \cdot|B N|
$$
|
If we set $\varphi = \angle DAB$, then $\angle ABD = \varphi$ must also hold, as triangle $ABD$ is assumed to be isosceles. This implies $\angle BDA = 180^\circ - 2\varphi$, and using the inscribed angle theorem, we get $\angle BCE = \angle BCA = 180^\circ - 2\varphi$.
Next, we want to express the angle $\angle BIE$ in terms of $\varphi$: Since the lines $BI$ and $EI$ are angle bisectors in triangle $BCE$, we have
$$
\angle BIE = 180^\circ - (\angle IEB + \angle EBI) = 90^\circ + \frac{1}{2}(180^\circ - \angle CEB + \angle EBC) = 90^\circ + \frac{1}{2} \angle BCE,
$$
which, combined with the previous result,
$$
\angle BIE = 90^\circ + \frac{1}{2}(180^\circ - 2\varphi) = 180^\circ - \varphi
$$
yields.
Since $BIEN$ is a convex cyclic quadrilateral, this implies $\angle CNB = \varphi$. By the inscribed angle theorem over the chord $\overline{AD}$, $\angle ACD = \varphi$ also holds, so $CD \parallel BN$ must be true.
Now, extend the segment $\overline{BN}$ beyond $N$ until it intersects the circumcircle of quadrilateral $ABCD$ again at $Q$. Applying the inscribed angle theorem over the chord $\overline{BD}$, we get $\angle DQB = \varphi$, which implies $CN \parallel QD$.
Since both pairs of opposite sides of quadrilateral $CNQD$ are parallel, it must be a parallelogram. Therefore, $|CD| = |NQ|$, and substituting this into the equation derived from the intersecting chords theorem,
$$
|AN| \cdot |NC| = |BN| \cdot |NQ|
$$
proves the claim.
Remark. One can prove that the two circles in the figure are tangent to each other.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Es sei $A B C D$ ein konvexes Sehnenviereck mit $|A D|=|B D|$. Seine Diagonalen $\overline{A C}$ und $\overline{B D}$ mögen sich in E schneiden. Der Mittelpunkt des Inkreises des Dreiecks BCE heiße I. Der Umkreis des Dreiecks BIE schneide das Innere der Strecke $\overline{A E}$ im Punkt $N$.
Man beweise, dass
$$
|A N| \cdot|N C|=|C D| \cdot|B N|
$$
|
Setzt man $\varphi=\Varangle D A B$, so muss auch $\Varangle A B D=\varphi$ sein, denn das Dreieck $A B D$ wurde als gleichschenklig vorausgesetzt. Hieraus ergibt sich $\Varangle B D A=180^{\circ}-2 \varphi$ und mit Hilfe des Peripheriewinkelsatzes folgt $\Varangle B C E=\Varangle B C A=180^{\circ}-2 \varphi$.

Als nächstes wollen wir den Winkel $B I E$ durch $\varphi$ ausdrücken: Da die Geraden $B I$ und $E I$ Winkelhalbierende im Dreieck $B C E$ sind, ist
$$
\Varangle B I E=180^{\circ}-(\Varangle I E B+\Varangle E B I)=90^{\circ}+\frac{1}{2}\left(180^{\circ}-\Varangle C E B+\Varangle E B C\right)=90^{\circ}+\frac{1}{2} \Varangle B C E,
$$
was mit vorigem verbunden
$$
\Varangle B I E=90^{\circ}+\frac{1}{2}\left(180^{\circ}-2 \varphi\right)=180^{\circ}-\varphi
$$
liefert.
Nachdem BIEN ein konvexes Sehnenviereck ist, impliziert dies $\Varangle C N B=\varphi$. Da nach Peripheriewinkelsatz über der Sehne $\overline{A D}$ auch $\Varangle A C D=\varphi$ gilt, muss demnach $C D \| B N$ sein.
Man verlängere nun die Strecke $\overline{B N}$ über $N$ hinaus, bis sie den Umkreis des Vierecks $A B C D$ erneut in $Q$ schneidet. Indem wir den Peripheriewinkelsatz über der Sehne $\overline{B D}$ anwenden, erhalten wir $\Varangle D Q B=\varphi$, was wiederum $C N \| Q D$ nach sich zieht.
Da die beiden Paare gegenüberliegender Seiten des Vierecks $C N Q D$ also jeweils parallel sind, muss es sich bei diesem um ein Parallelogramm handeln. Mithin ist $|C D|=|N Q|$ und sobald man dies in die aus dem Sehnensatz folgende Gleichung
$$
|A N| \cdot|N C|=|B N| \cdot|N Q|
$$
einträgt hat man die Behauptung bewiesen.
Bemerkung. Man kann beweisen, dass sich in der Figur die beiden Kreise berühren.
|
{
"resource_path": "Germany_TST/segmented/de-2014-loes_awkl_14.jsonl",
"problem_match": "\nAufgabe 2.",
"solution_match": "\nLösung."
}
|
2cc4f31a-40b0-5fd6-9323-fe46b782598d
| 604,900
|
Let $a_{1} \leqslant a_{2} \leqslant \ldots$ be a monotonically increasing sequence of positive integers. A positive integer $n$ is called reliable if there exists a positive integer index $i$ such that $n=\frac{i}{a_{i}}$.
Prove: If 2013 is reliable, then 20 is also reliable.
|
If 2013 is reliable, there is a positive integer index $i$ with $i=2013 a_{i} \geqslant 20 a_{i}$. In particular, the set $S$ of all positive integers $s$ for which $s \geqslant 20 a_{s}$ holds is not empty. Thus, $S$ contains a smallest element $j$, and this satisfies on the one hand
$$
j \geqslant 20 a_{j}
$$
and on the other hand $(j-1) \notin S$. The latter means that either $j=1$ must be true, or $j>1$ and $j-1<20 a_{j-1}$. Due to $a_{j} \geqslant 1$, it follows from (2) that $j \geqslant 20$, which excludes the first of these alternatives; therefore, $j \leqslant 20 a_{j-1}$ must hold, and in conjunction with (2) we obtain the chain of inequalities
$$
j \geqslant 20 a_{j} \geqslant 20 a_{j-1} \geqslant j .
$$
This can only hold if equality prevails everywhere. Since $j=20 a_{j}$, the index $j$ attests that 20 is reliable as claimed.
Remark. Nothing changes if the numbers 2013 and 20 in the problem statement are replaced by any two positive integers $r$ and $s$ with $r>s$.
## Solutions to the 2nd Selection Exam 2013/2014
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Es sei $a_{1} \leqslant a_{2} \leqslant \ldots$ eine monoton steigende Folge positiver ganzer Zahlen. Eine positive ganze Zahl $n$ heißt verlässlich, wenn es einen positiven ganzzahligen Index i mit $n=\frac{i}{a_{i}}$ gibt.
Man beweise: Wenn 2013 verlässlich ist, dann ist auch 20 verlässlich.
|
Wenn 2013 verlässlich ist, gibt es einen positiven ganzzahligen Index $i$ mit $i=2013 a_{i} \geqslant$ $20 a_{i}$. Insbesondere ist die Menge $S$ aller positiven ganzen Zahlen $s$, für die $s \geqslant 20 a_{s}$ gilt, nicht leer. Somit enthält $S$ ein kleinstes Element $j$, und dieses erfüllt einerseits
$$
j \geqslant 20 a_{j}
$$
und andererseits $(j-1) \notin S$. Letzteres bedeutet, dass entweder $j=1$ sein muss, oder $j>1$ und $j-1<20 a_{j-1}$. Wegen $a_{j} \geqslant 1$ folgt aus (2) jedoch $j \geqslant 20$, was die erste dieser beiden Alternativen ausschließt; demnach muss $j \leqslant 20 a_{j-1}$ sein und in Verbindung mit (2) erhalten wir die Ungleichungskette
$$
j \geqslant 20 a_{j} \geqslant 20 a_{j-1} \geqslant j .
$$
Diese kann nicht anders bestehen als dass überall Gleichheit gilt. Wegen $j=20 a_{j}$ bezeugt der Index $j$, dass 20 wie behauptet verlässlich ist.
Bemerkung. Es ändert sich nichts, wenn man in der Aufgabenstellung die Zahlen 2013 und 20 durch zwei beliebige positive ganze Zahlen $r$ und $s$ mit $r>s$ ersetzt.
## Lösungen zur 2. Auswahlklausur 2013/2014
|
{
"resource_path": "Germany_TST/segmented/de-2014-loes_awkl_14.jsonl",
"problem_match": "\nAufgabe 3.",
"solution_match": "\nLösung."
}
|
1e981594-1696-5ec1-9326-fe6f0801fbb2
| 604,912
|
In a scalene triangle $ABC$, let the interior angles be denoted as $\alpha, \beta, \gamma$ as usual. Furthermore, let the intersection of the angle bisector of $\alpha$ and $BC$ be denoted as $D$, and the intersection of the angle bisector of $\beta$ and $AC$ be denoted as $E$.
Now, a rhombus is inscribed in the quadrilateral $ABDE$ such that all vertices of the rhombus lie on different sides of the quadrilateral. In this rhombus, let the non-obtuse interior angles be denoted as $\varphi$. Prove that $\varphi \leq \max (\alpha, \beta)$ holds.
|
The corners of the rhombus are named $K(K \in A E), L$ $(L \in A B), M(M \in B D)$, and $N(N \in D E)$. Let $d(X, Y Z)$ denote the distance of a point $X$ from a line $Y Z$. Since $D$ and $E$ lie on the respective angle bisectors, we have $d(D, A B)=d(D, A C)$, $d(E, A B)=d(E, B C)$, and $d(D, B C)=d(E, A C)=0$, from which $d(D, A C)+d(D, B C)=d(D, A B)$ and $d(E, A C)+d(E, B C)=d(E, A B)$ follow.
Since $N$ lies on the segment $D E$ and because in the equation $d(X, A C)+d(X, B C)=d(X, A B)$, if $X$ moves along the segment $D E$, all terms change only linearly, it follows from the two upper relations also for $N$:
from the two upper relations also for $N$:
$d(N, A C)+d(N, B C)=d(N, A B)(1)$.
With the notations of the figure, we have $d(N, A C)=s \cdot \sin \mu$ and $d(N, B C)=s \cdot \sin v$. Since the rhombus $K L M N$ lies entirely in one of the half-planes with respect to $A B$, we obtain from its parallelogram property
$d(N, A B)=d(N, A B)+d(L, A B)=d(K, A B)+d(M, A B)=s(\sin \delta+\sin \varepsilon)$.
With (1), it follows that $\sin \mu+\sin v=\sin \delta+\sin \varepsilon$ (2).
From the assumption $\varphi>\max (\alpha, \beta)$, we would directly get $\mu=\alpha-\varphi+\delta<\delta$ and analogously $v<\varepsilon$ because $\mu+\varphi=\angle C K L=\alpha+\delta$. Since $K L \| M N$, we have $\beta=\delta+v$, so $\delta<\beta<90^{\circ}$. Similarly, it follows that $\varepsilon<90^{\circ}$. Thus, we get $\sin \mu<\sin \delta$ and $\sin v<\sin \varepsilon$, in contradiction to (2). Therefore, $\varphi \leq \max (\alpha, \beta)$.
Hint: A pure angle chase does not lead to the goal. The position of the rhombus is not uniquely determined, contrary to the opinion of some participants. Equality holds only for $\alpha=\beta$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In einem spitzwinkligen Dreieck $A B C$ seien die Innenwinkel $\alpha, \beta, \gamma$ wie üblich bezeichnet. Ferner seien der Schnittpunkt der Winkelhalbierenden von $\alpha$ und $B C$ mit $D$ sowie der Schnittpunkt der Winkelhalbierenden von $\beta$ und $A C$ mit $E$ bezeichnet.
Nun wird dem Viereck $A B D E$ eine Raute so einbeschrieben, dass alle Eckpunkte dieser Raute auf verschiedenen Seiten des Vierecks liegen. In dieser Raute seien die nicht-stumpfen Innenwinkel mit $\varphi$ bezeichnet. Man beweise, dass $\varphi \leq \max (\alpha, \beta)$ gilt.
|
Die Ecken der Raute werden mit $K(K \in A E), L$ $(L \in A B), M(M \in B D)$ und $N(N \in D E)$ benannt. Mit $d(X, Y Z)$ sei der Abstand eines Punktes $X$ von einer Geraden $Y Z$ bezeichnet. Weil $D$ und $E$ auf den jeweiligen Winkelhalbierenden liegen, gilt $d(D, A B)=d(D, A C)$, $d(E, A B)=d(E, B C)$ und $d(D, B C)=d(E, A C)=0$, woraus $d(D, A C)+d(D, B C)=d(D, A B)$ und $d(E, A C)+d(E, B C)=d(E, A B)$ folgt.
Weil $N$ auf der Strecke $D E$ liegt und weil sich in der Gleichung $d(X, A C)+d(X, B C)=d(X, A B)$, wenn $X$ längs der Strecke $D E$ wandert, alle Terme nur linear ändern, folgt

aus den beiden oberen Beziehungen auch für $N$ :
$d(N, A C)+d(N, B C)=d(N, A B)(1)$.
Mit den Bezeichnungen der Figur gilt $d(N, A C)=s \cdot \sin \mu$ und $d(N, B C)=s \cdot \sin v$. Weil die Raute $K L M N$ ganz in einer der Halbebenen bezüglich $A B$ liegt, erhalten wir aus ihrer Parallelogrammeigenschaft
$d(N, A B)=d(N, A B)+d(L, A B)=d(K, A B)+d(M, A B)=s(\sin \delta+\sin \varepsilon)$.
Mit (1) folgt $\sin \mu+\sin v=\sin \delta+\sin \varepsilon$ (2).
Aus der Annahme $\varphi>\max (\alpha, \beta)$ würde wegen $\mu+\varphi=\Varangle C K L=\alpha+\delta$ direkt $\mu=\alpha-\varphi+\delta<\delta$ und analog $v<\varepsilon$ folgen. Wegen $K L \| M N$ gilt $\beta=\delta+v$, also $\delta<\beta<90^{\circ}$. Entsprechend folgt $\varepsilon<90^{\circ}$. So erhalten wir $\sin \mu<\sin \delta$ und $\sin v<\sin \varepsilon$, im Widerspruch zu (2). Also gilt $\varphi \leq \max (\alpha, \beta)$.
Hinweis: Eine reine Winkeljagd führt nicht zum Ziel. Die Lage der Raute ist - entgegen der Meinung einiger Teilnehmer - nicht eindeutig bestimmt. Gleichheit gilt nur für $\alpha=\beta$.
|
{
"resource_path": "Germany_TST/segmented/de-2014-loes_awkl_14.jsonl",
"problem_match": "# Aufgabe 3",
"solution_match": "\nLösung:"
}
|
d48118fc-f744-5527-af63-12b45717d060
| 604,947
|
Let $A B C$ be an acute-angled triangle with $|A B| \neq|A C|$. The midpoints of the sides $\overline{A B}$ and $\overline{A C}$ are $D$ and $E$, respectively. The circumcircles of triangles $B C D$ and $B C E$ intersect the circumcircle of triangle $A D E$ at $P$ and $Q$, respectively, where $P \neq D$ and $Q \neq E$.
Prove that $|A P|=|A Q|$.
|
Without restriction, let $|A C|>|A B|$. Since $D$ and $E$ are the midpoints of the sides $\overline{A B}$ and $\overline{A C}$, by the intercept theorem, $D E$ is parallel to $B C$. In the case $E=P$ or $D=Q$, $C E D B$ would be a cyclic quadrilateral with parallel sides $B C$ and $D E$, thus an isosceles trapezoid with $|B D|=|E C|$, and therefore $|A B|=|A C|$, which is excluded. If it can be shown that the (non-degenerate) triangles $A P C$ and $B Q A$ are similar, the claim follows, since due to $\angle P Q A=\measuredangle P D A=180^{\circ}-\measuredangle B D P=\measuredangle P C B=\measuredangle P C A+\gamma=\measuredangle B A Q+\measuredangle A E D=\measuredangle D P Q+\measuredangle A P D=$ $\measuredangle A P Q$ (using the inscribed angle theorem), the triangle $A P Q$ is isosceles with $|A P|=|A Q|$. - Proof that triangles $A P C$ and $B Q A$ are similar: First, by the inscribed angle theorem,
$$
\measuredangle D Q B=360^{\circ}-\measuredangle E Q D-\measuredangle B Q E=\measuredangle D A E+\measuredangle E C B=\alpha+\gamma=180^{\circ}-\beta=180^{\circ}-\measuredangle E D A=\measuredangle A P E,
$$
$\measuredangle E P C=\measuredangle D P C-\measuredangle D P E=\left(180^{\circ}-\beta\right)-\alpha=\gamma=\measuredangle A E D=\measuredangle A Q D$.
From this, the similarity of triangles $A P C$ and $B Q A$ follows:
1. Proof: Let $Q^{\prime}$ be the uniquely determined point on the same side of $A C$ as $P$, such that triangle $A Q^{\prime} C$ is similar to triangle $B Q A$. Since $D$ and $E$ are the midpoints of the sides $\overline{A B}$ and $\overline{A C}$, the sub-triangles $A Q^{\prime} E$ and $B Q D$ as well as $C E Q^{\prime}$ and $A D Q$ are also similar. Therefore, $Q^{\prime}$ lies on the circumcircles of $A E P$ and $C E P$, which intersect at $E$ and $P$. $Q^{\prime}=E$ is excluded because $Q \neq D$. Thus, $Q^{\prime}=P$, and the triangles $A P C$ and $B Q A$ are similar. 2. Proof: By the sine rule in $A D Q$ and $B Q D$, $|A Q|:|A D|=\sin \measuredangle Q D A: \sin \measuredangle A Q D,|B Q|:|B D|=$ $\sin \measuredangle B D Q: \sin \measuredangle D Q B$. With $\measuredangle B D Q=180^{\circ}-\measuredangle Q D A$, it follows that $|A Q|:|B Q|=\sin \measuredangle D Q B: \sin \measuredangle A Q D$. Similarly, $|C P|:|P A|=\sin \measuredangle A P E: \sin \measuredangle E P C$. Due to (1) and (2), $A P C$ and $B Q A$ are similar by the criterion sws.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Es sei $A B C$ ein spitzwinkliges Dreieck mit $|A B| \neq|A C|$. Die Mittelpunkte der Seiten $\overline{A B}$ und $\overline{A C}$ seien $D$ beziehungsweise $E$. Die Umkreise der Dreiecke $B C D$ und $B C E$ mögen den Umkreis des Dreiecks $A D E$ in $P$ beziehungsweise $Q$ schneiden, wobei $P \neq D$ und $Q \neq E$.
Man beweise, dass $|A P|=|A Q|$.
|
Ohne Einschränkung sei $|A C|>|A B|$. Da $D$ und $E$ Mitten der Seiten $\overline{A B}$ und $\overline{A C}$ sind, ist nach Strahlensatz $D E$ parallel zu $B C$. Im Falle $E=P$ oder $D=Q$ wäre $C E D B$ Sehnenviereck mit parallelen Seiten $B C$ und $D E$, also gleichschenkliges Trapez mit $|B D|=|E C|$, somit $|A B|=|A C|$, was aber ausgeschlossen ist. Kann man zeigen, dass die (nicht ausgearteten) Dreiecke $A P C$ und $B Q A$ ähnlich sind, folgt die Behauptung, da wegen $\angle P Q A=\measuredangle P D A=180^{\circ}-\measuredangle B D P=\measuredangle P C B=\measuredangle P C A+\gamma=\measuredangle B A Q+\measuredangle A E D=\measuredangle D P Q+\measuredangle A P D=$ $\measuredangle A P Q$ (unter Benutzung des Umfangswinkelsatzes) das Dreieck $A P Q$ gleichschenklig ist mit $|A P|=|A Q| .-$ Beweis, dass Dreiecke $A P C$ und $B Q A$ ähnlich sind: Zunächst gilt mit Umfangswinkelsatz
$$
\measuredangle D Q B=360^{\circ}-\measuredangle E Q D-\measuredangle B Q E=\measuredangle D A E+\measuredangle E C B=\alpha+\gamma=180^{\circ}-\beta=180^{\circ}-\measuredangle E D A=\measuredangle A P E,
$$
$\measuredangle E P C=\measuredangle D P C-\measuredangle D P E=\left(180^{\circ}-\beta\right)-\alpha=\gamma=\measuredangle A E D=\measuredangle A Q D$.
Hieraus folgt die Ähnlichkeit der Dreiecke $A P C$ und $B Q A$ :
1. Beweis: Es sei $Q^{\prime}$ der eindeutig bestimmte Punkt auf derselben Seite von $A C$ wie $P$, so dass Dreieck $A Q^{\prime} C$ ähnlich zu Dreieck $B Q A$ ist. Da $D$ und $E$ Mitten der Seiten $\overline{A B}$ und $\overline{A C}$ sind, sind auch die Teildreiecke $A Q^{\prime} E$ und $B Q D$ sowie $C E Q^{\prime}$ und $A D Q$ ähnlich. Damit liegt $Q^{\prime}$ wegen (1) und (2), also $\measuredangle A P E=\measuredangle B Q D=\measuredangle A Q^{\prime} E$ und $\measuredangle E P C=\measuredangle D Q A=\measuredangle E Q^{\prime} C$, auf den Umkreisen von $A E P$ und $C E P$, die sich in $E$ und $P$ schneiden. $Q^{\prime}=E$ ist wegen $Q \neq D$ ausgeschlossen. Damit ist $Q^{\prime}=P$, und die Dreiecke $A P C$ und $B Q A$ sind ähnlich. 2. Beweis: Mit Sinussatz in $A D Q$ und $B Q D$ gilt $|A Q|:|A D|=\sin \measuredangle Q D A: \sin \measuredangle A Q D,|B Q|:|B D|=$ $\sin \measuredangle B D Q: \sin \measuredangle D Q B$. Mit $\measuredangle B D Q=180^{\circ}-\measuredangle Q D A$ folgt $|A Q|:|B Q|=\sin \measuredangle D Q B: \sin \measuredangle A Q D$. Analog ist $|C P|:|P A|=\sin \measuredangle A P E: \sin \measuredangle E P C$. Wegen (1) und (2) sind $A P C$ und $B Q A$ ähnlich nach Merkmal sws.
|
{
"resource_path": "Germany_TST/segmented/de-2015-loes_awkl_15.jsonl",
"problem_match": "# Aufgabe 3",
"solution_match": "\n1. Lösung:"
}
|
01cf24cf-07b1-52ac-bac2-d3e02cec01d2
| 604,977
|
Let $A B C$ be an acute-angled triangle with $|A B| \neq|A C|$. The midpoints of the sides $\overline{A B}$ and $\overline{A C}$ are $D$ and $E$, respectively. The circumcircles of triangles $B C D$ and $B C E$ intersect the circumcircle of triangle $A D E$ at $P$ and $Q$, respectively, where $P \neq D$ and $Q \neq E$.
Prove that $|A P|=|A Q|$.
|
One inverts at a circle with center $A$ and radius 1. The image point of a point $X$ is denoted by $X^{\prime}$. Since $D$ and $E$ are the midpoints of the sides $\overline{A B}$ and $\overline{A C}$, $B^{\prime}$ and $C^{\prime}$ are the midpoints of the sides $\overline{A D^{\prime}}$ and $\overline{A E^{\prime}}$. The inversion maps the circumcircle of triangle $A D E$ to the line $D^{\prime} E^{\prime}$, so $P^{\prime} \neq D^{\prime}$ and $Q^{\prime} \neq E^{\prime}$ are the second intersection points of the circumcircles of triangles $B^{\prime} C^{\prime} D^{\prime}$ and $B^{\prime} C^{\prime} E^{\prime}$ with the line $D^{\prime} E^{\prime}$. Since the lines $D^{\prime} E^{\prime}$ and $B^{\prime} C^{\prime}$ are parallel, the circumcircles of triangles $B^{\prime} C^{\prime} D^{\prime}$ and $B^{\prime} C^{\prime} E^{\prime}$ are symmetric with respect to the perpendicular bisector of the segment $\overline{B^{\prime} C^{\prime}}$, in particular, the points $Q^{\prime}$, $B^{\prime}$, and $P^{\prime}$ map to $E^{\prime}$, $C^{\prime}$, and $D^{\prime}$, respectively. Therefore, $\left|P^{\prime} C^{\prime}\right|=\left|B^{\prime} D^{\prime}\right|=\left|A B^{\prime}\right|$ (since $B^{\prime}$ is the midpoint of $\overline{A D^{\prime}}$) and $\left|B^{\prime} Q^{\prime}\right|=\left|C^{\prime} E^{\prime}\right|=\left|A C^{\prime}\right|$ (since $C^{\prime}$ is the midpoint of $\overline{A E^{\prime}}$) and $\measuredangle Q^{\prime} B^{\prime} D^{\prime}=\measuredangle P^{\prime} C^{\prime} E^{\prime}$. It follows that $\measuredangle A B^{\prime} Q^{\prime}=180^{\circ}-\measuredangle Q^{\prime} B^{\prime} D^{\prime}=180^{\circ}-\measuredangle P^{\prime} C^{\prime} E^{\prime}=\measuredangle A C^{\prime} P^{\prime}$. Thus, triangles $A P^{\prime} C^{\prime}$ and $A Q^{\prime} B^{\prime}$ are congruent by the SAS congruence criterion. Therefore, $\left|A P^{\prime}\right|=\left|A Q^{\prime}\right|$ and $|A P|=1 /\left|A P^{\prime}\right|=1 /\left|A Q^{\prime}\right|=|A Q|$.
## Solutions to the 2nd Selection Test 2014/2015
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Es sei $A B C$ ein spitzwinkliges Dreieck mit $|A B| \neq|A C|$. Die Mittelpunkte der Seiten $\overline{A B}$ und $\overline{A C}$ seien $D$ beziehungsweise $E$. Die Umkreise der Dreiecke $B C D$ und $B C E$ mögen den Umkreis des Dreiecks $A D E$ in $P$ beziehungsweise $Q$ schneiden, wobei $P \neq D$ und $Q \neq E$.
Man beweise, dass $|A P|=|A Q|$.
|
Man invertiere an einem Kreis mit Mittelpunkt $A$ und Radius 1. Der Bildpunkt eines Punkts $X$ sei mit $X^{\prime}$ bezeichnet. Da $D$ und $E$ die Mitten der Seiten $\overline{A B}$ und $\overline{A C}$ sind, sind $B^{\prime}$ und $C^{\prime}$ die Mitten der Seiten $\overline{A D^{\prime}}$ und $\overline{A E^{\prime}}$. Die Inversion bildet den Umkreis des Dreiecks $A D E$ auf die Gerade $D^{\prime} E^{\prime}$ ab, damit sind $P^{\prime} \neq D^{\prime}$ und $Q^{\prime} \neq E^{\prime}$ die zweiten Schnittpunkte der Umkreise der Dreiecke $B^{\prime} C^{\prime} D^{\prime}$ und $B^{\prime} C^{\prime} E^{\prime}$ mit der Geraden $D^{\prime} E^{\prime}$. Da die Geraden $D^{\prime} E^{\prime}$ und $B^{\prime} C^{\prime}$ parallel sind, liegen die Umkreise der Dreiecke $B^{\prime} C^{\prime} D^{\prime}$ und $B^{\prime} C^{\prime} E^{\prime}$ symmetrisch zur Mittelsenkrechten der Strecke $\overline{B^{\prime} C^{\prime}}$, insbesondere gehen die Punkte $Q^{\prime}$ bzw. $B^{\prime}$ bzw. $P^{\prime}$ in $E^{\prime}$ bzw. $C^{\prime}$ bzw. $D^{\prime}$ über. Damit ist $\left|P^{\prime} C^{\prime}\right|=\left|B^{\prime} D^{\prime}\right|=\left|A B^{\prime}\right|$ (da $B^{\prime}$ Mitte von $\overline{A D^{\prime}}$ ) sowie $\left|B^{\prime} Q^{\prime}\right|=\left|C^{\prime} E^{\prime}\right|=\left|A C^{\prime}\right|$ (da $C^{\prime}$ Mitte von $\overline{A E^{\prime}}$ ) und $\measuredangle Q^{\prime} B^{\prime} D^{\prime}=\measuredangle P^{\prime} C^{\prime} E^{\prime}$. Daraus folgt $\measuredangle A B^{\prime} Q^{\prime}=180^{\circ}-\measuredangle Q^{\prime} B^{\prime} D^{\prime}=180^{\circ}-\measuredangle P^{\prime} C^{\prime} E^{\prime}=\measuredangle A C^{\prime} P^{\prime}$. Damit sind die Dreiecke $A P^{\prime} C^{\prime}$ und $A Q^{\prime} B^{\prime}$ nach Kongruenzsatz sws kongruent. Somit ist $\left|A P^{\prime}\right|=\left|A Q^{\prime}\right|$ und $|A P|=1 /\left|A P^{\prime}\right|=1 /\left|A Q^{\prime}\right|=|A Q|$.
## Lösungen zur 2. Auswahlklausur 2014/2015
|
{
"resource_path": "Germany_TST/segmented/de-2015-loes_awkl_15.jsonl",
"problem_match": "# Aufgabe 3",
"solution_match": "\n2. Lösung (mit Inversion am Kreis):"
}
|
01cf24cf-07b1-52ac-bac2-d3e02cec01d2
| 604,977
|
Let $ABC$ be an acute-angled triangle with circumcircle $k$ and incenter $I$. The perpendicular to $CI$ through $I$ intersects the side $BC$ at $U$ and $k$ at $V$, where $V$ and $A$ lie on opposite sides of $BC$. The parallel to $AI$ through $U$ intersects $AV$ at point $X$.
Prove: If the lines $XI$ and $AI$ are perpendicular to each other, then $XI$ intersects the side $AC$ at its midpoint $M$.
|
In the figure, $M$ is initially only the intersection of $X I$ and $A C$. $N$ is the intersection of $X U$ and $A B$, and $Y$ is the intersection of $X I$ and $A B$. The half interior angles of triangle $A B C$ are denoted by $\alpha, \beta$ and $\gamma$ respectively. Since $\angle U I C=90^{\circ}$, it follows that $\angle C U I=\alpha+\beta$ and therefore $\angle B N U=\angle B A I=\angle B I U=\alpha$, so the points $B, U, I$ and $N$ lie on a circle. Therefore, $\overline{\Pi U}=\overline{I N}$ (chords corresponding to $\beta$) and since $X \perp N U$, it follows that $\overline{N X}=\overline{X U}$. Applying the intercept theorem leads to $\frac{\overline{V X}}{\overline{V A}}=\frac{\overline{X U}}{\overline{A I}}=\frac{\overline{N X}}{\overline{A I}}=\frac{\overline{Y X}}{\overline{Y I}}$, from which $Y V \| A I$ follows. Thus, $\angle B Y V=\alpha=\angle B N$, so
the points $B, V, I$ and $Y$ lie on a circle. Therefore, $\angle V B I=\angle V Y I=90^{\circ}$. Since the bisectors of the interior and exterior angles at a vertex in a triangle are always perpendicular, $B V$ is the bisector of the exterior angle at $B$. In the cyclic quadrilateral $A B V C$ (circumcircle of $A B C$), we recognize that $\angle V A C=\angle V B C=\alpha+\gamma$ and $\angle A C V=180^{\circ}-\angle V B A=180^{\circ}-(\alpha+2 \beta+\gamma)=\alpha+\gamma$, so $\angle V A C=\angle A C V$. Thus, triangle $A V C$ is isosceles with the apex at $V$. To show that $M$ is the midpoint of $A C$, it suffices to prove that $\angle V M C=90^{\circ}$. For this, we use in the cyclic quadrilaterals $B V I Y$ and $A B V C$ that $\angle V I M=180^{\circ}-\angle Y I V=\angle V B Y=\angle V B A=180^{\circ}-\angle A C V$, so $V C M I$ is also a cyclic quadrilateral. This yields $\angle V M C=\angle V I C=90^{\circ}$.
Hint: Some participants attempted a chase of angles, which, however, remains unsuccessful without a chase of cyclic quadrilaterals. Analytical approaches could not be successfully completed.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Es sei $A B C$ ein spitzwinkliges Dreieck mit dem Umkreis $k$ und dem Inkreismittelpunkt $I$. Die Orthogonale zu $C I$ durch I schneide die Seite $B C$ in $U$ und $k$ in $V$, wobei $V$ und $A$ auf verschiedenen Seiten von $B C$ liegen. Die Parallele zu $A I$ durch $U$ schneide $A V$ im Punkt $X$.
Man beweise: Wenn die Geraden $X I$ und $A I$ orthogonal zueinander sind, dann schneidet $X I$ die Seite $A C$ in ihrem Mittelpunkt $M$.
|
In der Figur ist $M$ zunächst nur der Schnittpunkt von $X I$ und $A C . N$ ist der Schnittpunkt von $X U$ und $A B$ und $Y$ der Schnittpunkt von $X I$ und $A B$. Die halben Innenwinkel des Dreiecks $A B C$ sind mit $\alpha, \beta$ bzw. $\gamma$ bezeichnet. Wegen $\Varangle U I C=90^{\circ}$ ist $\Varangle C U I=\alpha+\beta$ und daher $\Varangle B N U=\Varangle B A I=\Varangle B I U=\alpha$, so dass die Punkte $B, U, I$ und $N$ auf einem Kreis liegen. Deshalb gilt $\overline{\Pi U}=\overline{I N}$ (Sehnen $\mathrm{zu} \beta$ ) und wegen $X \perp N U$ folgt $\overline{N X}=\overline{X U}$. Anwendung der Strahlensätze führt auf $\frac{\overline{V X}}{\overline{V A}}=\frac{\overline{X U}}{\overline{A I}}=\frac{\overline{N X}}{\overline{A I}}=\frac{\overline{Y X}}{\overline{Y I}}$, woraus $Y V \| A I$ folgt. Also ist auch $\Varangle B Y V=\alpha=\Varangle B N$, so

dass die Punkte $B, V, I$ und $Y$ auf einem Kreis
liegen. Daher ist $\Varangle V B I=\Varangle V Y I=90^{\circ}$. Da die Halbierenden von Innen- und Außenwinkel an einer Ecke im Dreieck stets orthogonal sind, ist $B V$ die Halbierende des Außenwinkels bei $B$. Im Sehnenviereck $A B V C$ (Umkreis von $A B C$ ) erkennen wir daher $\Varangle V A C=\Varangle V B C=\alpha+\gamma$ und $\Varangle A C V=180^{\circ}-\Varangle V B A=180^{\circ}-(\alpha+2 \beta+\gamma)=\alpha+\gamma$, also $\Varangle V A C=\Varangle A C V$. Das Dreieck $A V C$ ist somit gleichschenklig mit der Spitze $V$. Um nun zu zeigen, dass $M$ der Mittelpunkt von $A C$ ist, reicht der Nachweis von $\varangle V M C=90^{\circ}$. Dazu verwenden wir in den Sehnenvierecken $B V I Y$ und $A B V C$, dass $\Varangle V I M=180^{\circ}-\Varangle Y I V=\Varangle V B Y=\Varangle V B A=180^{\circ}-\Varangle A C V$ ist, so dass auch $V C M I$ ein Sehnenviereck ist. Dies liefert $\Varangle V M C=\Varangle V I C=90^{\circ}$.
Hinweis: Einige Teilnehmer haben eine Winkeljagd versucht, die jedoch ohne eine Jagd nach Sehnenvierecken erfolglos bleibt. Analytische Ansätze konnten nicht erfolgreich abgeschlossen werden.
|
{
"resource_path": "Germany_TST/segmented/de-2015-loes_awkl_15.jsonl",
"problem_match": "# Aufgabe 2",
"solution_match": "\nLösung:"
}
|
c942d596-b971-5028-9149-9e1af9066add
| 605,009
|
Let $ABC$ be a right triangle with $\varangle ACB = \gamma = 90^{\circ}$. Furthermore, let $H$ be the foot of the altitude from $C$ to $AB$.
Now, we choose a point $D$ inside the triangle $HBC$ such that $CH$ bisects the segment $AD$, and denote the intersection of $CH$ and $BD$ by $P$. We construct the semicircle $k$ with $BD$ as its diameter, which is intersected by $BC$. A line through $P$ is tangent to $k$ at the point $Q$. Prove that the lines $CQ$ and $AD$ always intersect on $k$.
|
Let $K$ be the foot of the perpendicular from $D$ to $AB$ and $T$ the intersection of $AD$ with $k$. Since $\varangle A T B = \varangle A C B = 90^{\circ}$, $T$ also lies on the circumcircle of $ABC$. Because $C H \| D K$, it follows that $|A H| = |H K|$.
To prove that $C, Q$, and $T$ are collinear, we consider the intersection $Q'$ of $CT$ with $k$ and need only show that $P Q' k$ is tangent, or that $\varangle P Q' D = \varangle Q' B D$.
Since $B T Q' D$ is a cyclic quadrilateral and the triangles $A H C$ and $H K C$ are congruent, we have
$\varangle Q' B D = \varangle Q' T D = \varangle C T A = \varangle C B A = \varangle A C H = \varangle H C K$. Therefore, the right triangles $C H K$ and $B Q' D$ are similar, which implies $|H K| / |C K| = |Q' D| / |B D|$, hence $|H K| \cdot |B D| = |C K| \cdot |Q' D|$ (1). Since $P H \| D K$, we have $|P D| / |B D| = |H K| / |B K|$, thus $|P D| \cdot |B K| = |H K| \cdot |B D|$ (2). Comparing (1) and (2) leads to $|P D| \cdot |B K| = |C K| \cdot |Q' D|$ and thus $|P D| / |Q' D| = |C K| / |B K|$. Therefore, and because $\varangle C K A = \varangle K A C = \varangle B D Q'$, the triangles $C K B$ and $P D Q'$ are similar. Hence, $\varangle P Q' D = \varangle C B A = \varangle Q' B D$, which is what we needed to show.
Hint: A pure angle chase does not lead to the goal; however, there are other proof possibilities, such as utilizing a suitable homothety with center $B$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Es sei $A B C$ ein rechtwinkliges Dreieck mit $\varangle A C B=\gamma=90^{\circ}$. Ferner sei $H$ der Fußpunkt der Höhe von $C$ auf $A B$.
Nun wählen wir einen Punkt $D$ so im Inneren des Dreiecks $H B C$, dass $C H$ die Strecke $A D$ halbiert, und bezeichnen den Schnittpunkt von $C H$ und $B D$ mit $P$. Über der Strecke $B D$ als Durchmesser errichten wir denjenigen Halbkreis $k$, der von $B C$ geschnitten wird. Eine Gerade durch $P$ berührt $k$ im Punkt $Q$. Man beweise, dass sich die Geraden $C Q$ und $A D$ stets auf $k$ schneiden.
|
Wie in der Figur sei $K$ der Fußpunkt des Lotes von $D$ auf $A B$ und $T$ der Schnittpunkt von $A D$ mit $k$. Wegen $\varangle A T B=\varangle A C B=90^{\circ}$ liegt $T$ auch auf dem Umkreis von $A B C$. Wegen $C H \| D K$ gilt $|A H|=|H K|$.

Um nachzuweisen, dass $C, Q$ und $T$ kollinear sind, betrachten wir den Schnittpunkt $Q^{\prime}$ von $C T$ mit $k$ und müssen nur zeigen, dass $P Q^{\prime} k$ berührt, bzw. dass $\varangle P Q^{\prime} D=\varangle Q^{\prime} B D$ ist.
Weil $B T Q^{\prime} D$ ein Sehnenviereck ist und die Dreiecke $A H C$ und $H K C$ kongruent sind, gilt
$\varangle Q^{\prime} B D=\varangle Q ' T D=\varangle C T A=\varangle C B A=\varangle A C H=\varangle H C K$. Also sind die rechtwinkligen Dreiecke $C H K$ und $B Q^{\prime} D$ ähnlich, woraus $|H K| /|C K|=\left|Q^{\prime} D\right| /|B D|$ folgt, also $|H K| \cdot|B D|=|C K| \cdot\left|Q^{\prime} D\right|$ (1). Wegen $P H \| D K$ gilt $|P D| /|B D|=|H K| /|B K|$, also $|P D| \cdot|B K|=|H K| \cdot|B D|$ (2). Der Vergleich von (1) und (2) führt auf $|P D| \cdot|B K|=|C K| \cdot\left|Q^{\prime} D\right|$ und somit $|P D| /\left|Q^{\prime} D\right|=|C K| /|B K|$. Deswegen und weil $\varangle C K A=\varangle K A C=\varangle B D Q^{\prime}$ ist, sind die Dreiecke $C K B$ und $P D Q^{\prime}$ ähnlich. Daher gilt $\varangle P Q^{\prime} D=\varangle C B A=\varangle Q^{\prime} B D$, was zu zeigen war.
Hinweis: Eine reine Winkeljagd führt nicht zu Ziel; allerdings gibt es andere Beweismöglichkeiten, wie etwa Ausnutzen einer geeigneten Drehstreckung mit Zentrum $B$.
|
{
"resource_path": "Germany_TST/segmented/de-2016-loes_awkl_16.jsonl",
"problem_match": "# Aufgabe 2",
"solution_match": "\nLösung:"
}
|
6d9731b5-b408-5056-82d8-4d954474b4f3
| 605,051
|
Let $ABCD$ be a convex quadrilateral. The diagonal $BD$ bisects the angle $\measuredangle CBA$. The circumcircle of triangle $ABC$ intersects the segments $\overline{CD}$ and $\overline{DA}$ at the interior points $P$ and $Q$, respectively. The line through point $D$ parallel to the line $AC$ intersects the lines $BA$ and $BC$ at the points $R$ and $S$, respectively. Prove that the four points $P, Q, R$, and $S$ lie on a common circle.
|
Step 1: Since $\measuredangle B R D = \measuredangle B A C = \measuredangle B P C = \pi - \measuredangle D P B$, $B P D R$ is a cyclic quadrilateral. Similarly, it can be shown that $B S D Q$ is also a cyclic quadrilateral. Step 2: Let $X$ be defined as the intersection of $B D$ with the circumcircle of triangle $A B C$. Then, $\measuredangle D P X = \pi - \measuredangle X P C = \measuredangle C B X = 1 / 2 \measuredangle C B A$. Since from Step 1, $\measuredangle D P R = \measuredangle D B R = 1 / 2 \measuredangle D B A$ also holds, $X$ lies on $P R$. Similarly, it can be shown that $X$ also lies on $Q S$. Step 3: We combine these insights and calculate (using the chord theorem) $|P X| \cdot |X R| = |B X| \cdot |X D| = |Q X| \cdot |X S|$. Using the converse of the chord theorem, the claim follows.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Es sei $A B C D$ ein konvexes Viereck. Die Diagonale $B D$ halbiere den Winkel $\measuredangle C B A$. Der Umkreis des Dreiecks $A B C$ schneide die Strecken $\overline{C D}$ und $\overline{D A}$ in den inneren Punkten $P$ bzw. $Q$. Die durch den Punkt $D$ verlaufende Parallele zur Geraden $A C$ schneide die Geraden $B A$ und $B C$ in den Punkten $R$ bzw. $S$. Man beweise, dass die vier Punkte $P, Q, R$ und $S$ auf einem gemeinsamen Kreis liegen.
|
Schritt 1: Wegen $\measuredangle B R D=\measuredangle B A C=\measuredangle B P C=\pi-\measuredangle D P B$ ist $B P D R$ ein Sehnenviereck. Analog zeigt man, dass auch $B S D Q$ ein Sehnenviereck ist. Schritt 2: Es sei $X$ definiert als der Schnittpunkt von $B D$ mit dem Umkreis des Dreiecks $A B C$. Dann gilt $\measuredangle D P X=\pi-\measuredangle X P C=\measuredangle C B X=1 / 2 \measuredangle C B A$. Da nach Schritt 1 auch $\measuredangle D P R=\measuredangle D B R=1 / 2 \measuredangle D B A$ gilt, liegt $X$ auf $P R$. Analog zeigt man, dass $X$ auch auf $Q S$ liegt. Schritt 3: Wir kombinieren die Erkenntnisse und rechnen (mithilfe des Sehnensatzes) $|P X| \cdot|X R|=|B X| \cdot|X D|=|Q X| \cdot|X S|$. Mit der Umkehrung des Sehnensatzes folgt nun die Behauptung.

|
{
"resource_path": "Germany_TST/segmented/de-2017-loes_awkl_17.jsonl",
"problem_match": "2. Aufgabe.",
"solution_match": "\nLösung."
}
|
4a12a68c-8900-5977-a005-93c3b9f2210b
| 605,077
|
Let $n$ be a positive integer that is coprime to 6. We color the vertices of a regular $n$-gon with three colors such that for each color, the number of vertices colored with it is odd.
Prove that there always exists an isosceles triangle whose vertices belong to the vertices of the $n$-gon and are all colored differently.
|
Let $a_{1}, a_{2}, a_{3}$ be the numbers of isosceles triangles whose vertices contain exactly 1, 2, and 3 colors, respectively. We assume that $a_{3}=0$. The colors are red, green, and blue, where $r, g$, and $b$ denote the (odd) number of vertices colored with each respective color. We now determine the number $a$ of pairs $(\Delta, v)$, where $\Delta$ is an isosceles triangle with more than one vertex color and $v$ is a side of this triangle whose endpoints are colored differently, in two ways.
Due to $a_{3}=0$, the vertices of such a triangle must be colored with exactly two colors, one of which belongs to two vertices that are endpoints of a side $v$. Thus, each triangle contributes two pairs, and it follows that $a=2 a_{2}$.
For any two vertices $A$ and $B$, there are exactly three different vertices $C$ that form an isosceles triangle with $A$ and $B$: either $A B=A C$ or $A B=B C$ or $A C=B C$. None of these possibilities can coincide, otherwise $A B C$ would be equilateral and $n$ would be divisible by 3. $A C=B C$ exists because $n$ is odd, and thus the perpendicular bisector of $A B$ passes through exactly one other vertex. Therefore, starting from two differently colored vertices $A$ and $B$, we have $a=3(r g+g b+b r)$. This term is odd by assumption, in contradiction to $a=2 a_{2}$. Hence, $a_{3} \neq 0$ must hold.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Es sei $n$ eine positive ganze Zahl, die teilerfremd zu 6 ist. Wir färben die Ecken eines regulären $n$-Ecks so mit drei Farben, dass für jede Farbe die Anzahl der mit ihr gefärbten Ecken ungerade ist.
Man beweise, dass es dann stets ein gleichschenkliges Dreieck gibt, dessen Ecken zu den Ecken des $n$ Ecks gehören und alle verschieden gefärbt sind.
|
Es seien $a_{1}, a_{2}, a_{3}$ die Anzahlen der gleichschenkligen Dreiecke, in deren Eckpunkten genau 1, 2 bzw. 3 Farben vorkommen. Wir nehmen an, dass $a_{3}=0$ gelte. Die Farben seien rot, grün und blau, wobei $r, g$ und $b$ die (ungerade) Anzahl der jeweils so gefärbten Ecken bezeichnet. Wir bestimmen nun auf zwei Arten die Anzahl $a$ der Paare ( $\Delta, v$ ), wobei $\Delta$ ein gleichschenkliges Dreieck mit mehr als einer Eckenfarbe und $v$ eine Seitenkante dieses Dreiecks ist, deren Endpunkte mit verschiedenen Farben belegt sind.
Wegen $a_{3}=0$ müssen die Eckpunkte eines solchen Dreiecks mit genau zwei Farben belegt sein, von denen eine zu zwei Ecken gehört, die jeweils Endpunkte einer Seitenkante $v$ sind. Also trägt jedes Dreieck zwei Paare bei und es ist $a=2 a_{2}$.
Zu je zwei Eckpunkten $A$ und $B$ gibt genau drei verschiedene Eckpunkte $C$, die mit $A$ und $B$ ein gleichschenkliges Dreieck bilden: entweder ist $A B=A C$ oder $A B=B C$ oder $A C=B C$. Dabei können keine dieser Möglichkeiten zusammenfallen, weil sonst $A B C$ gleichseitig und $n$ durch 3 teilbar wäre. $A C=B C$ existiert, weil $n$ ungerade ist und daher die Mittelsenkrechte von $A B$ durch genau einen weiteren Eckpunkt verläuft. Daher gilt, ausgehend von zwei verschieden gefärbten Eckpunkten $A$ und $B$, dass $a=3(r g+g b+b r)$ ist. Dieser Term ist nach Voraussetzung ungerade, im Widerspruch zu $a=2 a_{2}$. Daher muss $a_{3} \neq 0$ gelten.
[^0]
|
{
"resource_path": "Germany_TST/segmented/de-2017-loes_awkl_17.jsonl",
"problem_match": "# Aufgabe 2",
"solution_match": "\nLösung:"
}
|
d709d4d7-31dc-5206-b9d3-79626c309e4e
| 605,110
|
Let $ABC$ be a triangle with $AB = AC \neq BC$. Furthermore, let $I$ be the incenter of $ABC$.
The line $BI$ intersects $AC$ at point $D$, and the perpendicular to $AC$ through $D$ intersects $AI$ at point $E$. Prove that the reflection of $I$ over the line $AC$ lies on the circumcircle of triangle $BDE$.
|
First, we prove the following lemma (already using the appropriate notation for the problem): The perpendicular bisector of a side $B I I^{\prime}$ and the angle bisector through the third vertex $D$ intersect on the circumcircle of any non-isosceles triangle $B I^{\prime} D$. ("South Pole Theorem") Proof of the lemma: Let $M$ be the center of the circumcircle of $B I^{\prime} D$ and $S$ the intersection point of the angle bisector with the circumcircle, different from $D$. Then $\angle B M I I^{\prime}$, as a central angle, is twice as large as $\angle B D I^{\prime}$, and $\angle S D I^{\prime}$ is half as large as $\angle B D I^{\prime}$. Since the perpendicular bisector of $B I^{\prime}$ bisects both arcs of the circumcircle corresponding to this chord, it must pass through $S$.
Corollary: Let the other intersection point of the perpendicular bisector of $B I^{\prime}$ with the circumcircle be $E$. Then, according to the lemma, $D$ lies on the Thales circle over $E S$, and $\angle E D S = 90^{\circ}$. Therefore, $D E$ is the external angle bisector of $\angle B D I^{\prime}$. The converse also holds: If for a point $E$ on the external angle bisector of $\angle B D I^{\prime}$, $B E = E I^{\prime}$ also holds, then $E$ lies on the circumcircle of $B I^{\prime} D$.
For the main proof, we denote the reflection point of $I$ as $I^{\prime}$ and the second intersection point of $A I$ with the circumcircle of triangle $A B D$ as $D^{\prime}$. Since $A D^{\prime}$ is the angle bisector of $\angle B A D$, $D^{\prime}$ is the midpoint of the arc $B D$, and thus $D D^{\prime} = B D^{\prime} = C D^{\prime}$.
Using the inscribed angle theorem for the chord $A D$ and appropriate angle bisectors, we get $\angle D D^{\prime} E = \angle D D^{\prime} A = \angle D B A = \angle C B I = \angle I C B$. Since $D^{\prime}$, due to the equal distances, is the circumcenter of triangle $B C D$, we have $\angle E D D^{\prime} = 90^{\circ} - \angle D^{\prime} D C = \angle C B D = \angle C B I$, and thus the triangles $E D^{\prime} D$ and $I B C$ are similar. This implies $\frac{B C}{C I} = \frac{B C}{C I} = \frac{D D^{\prime}}{D^{\prime} E} = \frac{B D^{\prime}}{D^{\prime} E}$.
Furthermore, $\angle I^{\prime} C B = \angle A C B + \angle I^{\prime} C A = \angle A C B + \angle A C I = \angle A C B + \angle C B D = \angle B D A = \angle B D^{\prime} E$, and therefore the triangles $B C I^{\prime}$ and $B D^{\prime} E$ are similar, as are $B C D^{\prime}$ and $B I^{\prime} E$, because the rotation-dilation centered at $B$ that maps $B C I^{\prime}$ to $B D^{\prime} E$ also maps $C D^{\prime}$ to $I^{\prime} E$.
Since $B C D^{\prime}$ is isosceles, $B E = E I^{\prime}$ also holds.
Now, $D E \perp A C$, and by the corollary, $E$ lies on the circumcircle of triangle $B I^{\prime} D$.
Note: There are many other solution approaches to this problem, but none of them can be solved with simple angle chasing. All analytical solution attempts failed due to the increasingly complex terms. In the sketch, $M I^{\prime}$ and $D S$ intersect at $C$; this is indeed always the case.
[^0]: Note: Many solution approaches using a procedure to color new points appropriately contained gaps because loops or multiple assignments were not fully investigated.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Es sei $A B C$ ein Dreieck mit $A B=A C \neq B C$. Ferner sei $I$ der Inkreismittelpunkt von $A B C$.
Die Gerade $B I$ schneidet $A C$ im Punkt $D$, und die Orthogonale zu $A C$ durch $D$ schneidet $A I$ im Punkt $E$. Man beweise, dass der Spiegelpunkt von $I$ bei Spiegelung an der Achse $A C$ auf dem Umkreis des Dreiecks BDE liegt.
|
Zunächst beweisen wir (schon mit den zur Aufgabe passenden Bezeichnungen) folgendes Lemma: Die Mittelsenkrechte einer Seite $B I I^{\prime}$ und die Winkelhalbierende durch den dritten Eckpunkt $D$ schneiden sich auf dem Umkreis jedes nicht gleichschenkligen Dreiecks $B I^{\prime} D$. („Südpolsatz") Beweis des Lemmas: Es sei $M$ der Mittelpunkt des Umkreises von $B I^{\prime} D$ und $S$ der von $D$ verschiedene Schnittpunkt der Winkelhalbierenden mit dem Umkreis. Dann ist $\square B M I I^{\prime}$ als Mittelpunktswinkel doppelt so groß wie $\square B D I^{\prime}$ und $\square S D I^{\prime}$ halb so groß wie $\square B D I^{\prime}$. Da aber die Mittelsenkrechte von $B I^{\prime}$ beide Bögen des Umkreises zu dieser Sehne halbiert, muss sie durch $S$ gehen.
Korollar: Der andere Schnittpunkt der Mittelsenkrechten von $B I$ ' mit dem Umkreis sei $E$. Dann liegt nach dem Lemma $D$ auf dem Thaleskreis über $E S$ und es ist $\square E D S=90^{\circ}$ Somit ist $D E$ die äußere Winkelhalbierende von $\square B D I^{\prime}$. Die Umkehrung gilt ebenfalls: Wenn für den Punkt $E$ auf der äußeren Winkelhalbierenden von $\square B D I^{\prime}$ auch $B E=E I '$ gilt, dann liegt $E$ auf dem Umkreis von $B I^{\prime} D$.

Für den Hauptbeweis bezeichnen wir den Spiegelpunkt von $I$ mit $I^{\prime}$ und den zweiten Schnittpunkt von $A I$ und dem Umkreis des Dreiecks $A B D$ mit $D^{\prime}$. Weil $A D^{\prime}$ die Winkelhalbierende von $\square B A D$ ist, liegt $D^{\prime}$ in der Mitte des Bogens $B D$ und so gilt $D D^{\prime}=B D^{\prime}=C D^{\prime}$.
Unter Verwendung des Umfangswinkelsatzes über der Sehne $A D$ sowie geeigneter Winkelhalbierender erhalten wir $\square D D^{\prime} E=\square D D^{\prime} A=\square D B A=\square C B I=\square I C B$. Weil $D^{\prime}$ wegen der gleichen Abstände der Umkreismittelpunkt des Dreiecks $B C D$ ist, gilt $\square E D D^{\prime}=90^{\circ}-\square D^{\prime} D C=\square C B D=\square C B I$, also sind wegen $\square C B I=\square I C B$ die Dreiecke $E D^{\prime} D$ und $I B C$ ähnlich. Daraus folgt $\frac{B C}{C I}=\frac{B C}{C I}=\frac{D D^{\prime}}{D^{\prime} E}=\frac{B D^{\prime}}{D^{\prime} E}$.
Außerdem gilt $\square I^{\prime} C B=\square A C B+\square I^{\prime} C A=\square A C B+\square A C I=\square A C B+\square C B D=\square B D A=\square B D^{\prime} E$, und daher sind die Dreiecke $B C I^{\prime}$ und $B D^{\prime} E$ ähnlich, ebenso sind $B C D^{\prime}$ und $B I^{\prime} E$ ähnliche Dreiecke, denn bei der Drehstreckung um $B$, die $B C I^{\prime}$ in $B D^{\prime} E$ überführt, geht $C D^{\prime}$ in $I^{\prime} E$ über.
Weil aber $B C D^{\prime}$ gleichschenklig ist, gilt auch $B E=E I^{\prime}$.
Nun ist $D E \perp A C$, und nach dem Korollar liegt $E$ auf dem Umkreis des Dreiecks $B I^{\prime} D$. .
Hinweis: Es gibt viele weitere Lösungswege zu diesem Problem, die jedoch alle nicht mit einer einfachen Winkeljagd auskommen. Sämtliche analytischen Lösungsansätze waren wegen der immer komplexer werdenden Terme zum Scheitern verurteilt. In der Skizze schneiden sich MI* und $D S$ in $C$; dies ist tatsächlich immer so.
[^0]: Hinweis: Viele Lösungsansätze über eine Prozedur, mit der man immer neue Punkte geeignet färbt, enthielten Lücken, weil Schleifen oder Mehrfachbelegungen nicht vollständig untersucht worden sind.
|
{
"resource_path": "Germany_TST/segmented/de-2017-loes_awkl_17.jsonl",
"problem_match": "# Aufgabe 3",
"solution_match": "\nLösung:"
}
|
af83330b-225e-5418-810d-084fe309d909
| 605,122
|
A rectangle $\mathcal{R}$ with odd integer side lengths is divided into rectangles, all of which have integer side lengths. Prove that for at least one of these rectangles, the distances to each of the four sides of $\mathcal{R}$ are all even or all odd.
|
We divide $\mathcal{R}$ into unit squares and color some of these unit squares in red or blue, as shown in the following illustration.
Since $\mathcal{R}$ has odd side lengths by assumption, all four corner squares of $\mathcal{R}$ are colored blue, and there are more colored than uncolored squares in total. Therefore, at least one of the rectangles $\mathcal{R}_{1}, \ldots, \mathcal{R}_{k}$ into which $\mathcal{R}$ is divided must also contain more colored than uncolored squares, let $\mathcal{R}_{i}$ be such a rectangle. Then $\mathcal{R}_{i}$ has odd side lengths and all four corner squares of $\mathcal{R}_{i}$ are colored. This implies that all four corner squares of $\mathcal{R}_{i}$ must have the same color. If they are blue, $\mathcal{R}_{i}$ has even distances to all four sides of $\mathcal{R}$; if they are red, $\mathcal{R}_{i}$ has odd distances to all four sides of $\mathcal{R}$. In either case, $\mathcal{R}_{i}$ satisfies the required condition.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Ein Rechteck $\mathcal{R}$ mit ungeraden ganzzahligen Seitenlängen ist in Rechtecke unterteilt, die alle ganzahlige Seitenlängen haben. Man beweise, dass für mindestens eines dieser Rechtecke die Abstände zu jeder der vier Seiten von $\mathcal{R}$ alle gerade oder alle ungerade sind.
|
Wir unterteilen $\mathcal{R}$ in Einheitsquadrate und färben einige dieser Einheitsquadrate in rot oder blau ein, entsprechend der folgenden Illustration.

Da $\mathcal{R}$ laut Voraussetzung ungerade Seitenlängen hat, sind alle vier Eckfelder von $\mathcal{R}$ blau gefärbt, und es gibt insgesamt mehr gefäbte als ungefärbte Felder. Somit enthält auch mindestens eines der Rechtecke $\mathcal{R}_{1}, \ldots, \mathcal{R}_{k}$, in die $\mathcal{R}$ unterteilt wurde, mehr gefärbte als ungefärbte Felder, sei $\mathcal{R}_{i}$ ein solches. Dann hat $\mathcal{R}_{i}$ ungerade Seitenlängen und alle vier Eckfelder von $\mathcal{R}_{i}$ sind gefärbt. Daraus folgt, dass alle vier Eckfelder von $\mathcal{R}_{i}$ dieselbe Farbe tragen müssen. Falls sie blau sind, hat $\mathcal{R}_{i}$ gerade Abstände zu allen vier Seiten von $\mathcal{R}$; falls sie rot sind hat $\mathcal{R}_{i}$ ungerade Abstände zu allen vier Seiten von $\mathcal{R}$. In jedem Fall erfüllt $\mathcal{R}_{i}$ die geforderte Bedingung.
|
{
"resource_path": "Germany_TST/segmented/de-2018-loes_awkl_18.jsonl",
"problem_match": "\nAufgabe 1.",
"solution_match": "\nLösung."
}
|
592bdc7d-903a-5cb7-9736-e1a52a939e81
| 605,131
|
Let $d$ be a positive integer and $\left(a_{i}\right)_{i=1,2,3, \ldots}$ be a sequence of positive integers. We assume that the following two conditions are satisfied:
- Every positive integer appears exactly once in the sequence.
- For all indices $i \geq 10^{100}$, $\left|a_{i+1}-a_{i}\right| \leq 2 d$.
Prove that there exist infinitely many indices $j$ for which $\left|a_{j}-j\right|<d$.
|
Assume the claim is not satisfied. Then there exists an index $N>10^{100}$ such that for all $i \geq N$ either $a_{i} \leq i-d$ or $a_{i} \geq i+d$ holds. In the first case, because $i \geq N>10^{100}$, according to the second condition on the sequence, we also have
$$
a_{i+1} \leq a_{i}+2 d \leq i-d+2 d=(i+1)+(d-1)
$$
so it must be that $a_{i+1} \leq(i+1)-d$. By induction, it follows that $a_{i} \leq j-d$ for all $j \geq i$.
Thus, we have shown:
(A) Either $a_{i} \geq i+d$ for all $i \geq N$, or
(B) there exists an $M \geq N$ such that $a_{i} \leq i-d$ for all $i \geq M$.
First, assume (A) is satisfied. The numbers $1, \ldots, N$ must, according to the first condition on the sequence, all appear in the sequence. However, $a_{i} \geq i+d > i \geq N$ for all $i \geq N$, meaning there are only the $N-1$ sequence terms $a_{1}, \ldots, a_{N-1}$ that can take on any of these values. By the pigeonhole principle, a contradiction arises.
Now, assume (B) is satisfied. Let $k=\max \left\{M, a_{1}, \ldots, a_{M}\right\}$. Then the $k$ sequence terms $a_{1}, \ldots, a_{k}$ are all less than $k$, because for $i=1, \ldots M-1$ we have $a_{i} \leq$ $\max \left\{a_{1}, \ldots, a_{M-1}\right\} \leq k$ and for $i=M, \ldots, k$ we have $a_{i} \leq i-d < i \leq k$. These $k$ numbers are thus all in the set $\{1,2, \ldots, k-1\}$. By the pigeonhole principle, there exist two indices $1 \leq i<j \leq k$ with $a_{i}=a_{j}$, which contradicts the first condition on the sequence.
Since we have obtained a contradiction in each case, the claim holds.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Es sei eine positive ganze Zahl $d$ und eine Folge $\left(a_{i}\right)_{i=1,2,3, \ldots}$ positiver ganzer Zahlen gegeben. Wir nehmen an, dass folgende zwei Bedingungen erfüllt sind:
- Jede positive ganze Zahl taucht genau einmal in der Folge auf.
- Für alle Indizes $i \geq 10^{100}$ gilt $\left|a_{i+1}-a_{i}\right| \leq 2 d$.
Man beweise, dass unendlich viele Indizes $j$ existieren, für die $\left|a_{j}-j\right|<d$ gilt.
|
Angenommen, die Behauptung wäre nicht erfüllt. Dann existiert ein Index $N>10^{100}$, sodass für alle $i \geq N$ entweder $a_{i} \leq i-d$ oder $a_{i} \geq i+d$ gilt. Im ersten Fall gilt wegen $i \geq N>10^{100}$ laut der zweiten Voraussetzung an die Folge auch
$$
a_{i+1} \leq a_{i}+2 d \leq i-d+2 d=(i+1)+(d-1)
$$
es muss also $a_{i+1} \leq(i+1)-d$ gelten. Induktiv folgt damit $a_{i} \leq j-d$ für alle $j \geq i$.
Damit haben wir gezeigt:
(A) Entweder es gilt $a_{i} \geq i+d$ für alle $i \geq N$, oder
(B) es existiert ein $M \geq N$, sodass $a_{i} \leq i-d$ für alle $i \geq M$ gilt.
Nehmen wir zunächst an, (A) sei erfüllt. Die Zahlen $1, \ldots, N$ müssen laut der ersten Voraussetzung an die Folge alle einmal in der Folge auftauchen. Nun gilt jedoch $a_{i} \geq i+d>i \geq N$ für alle $i \geq N$, das heißt es gibt nur die $N-1$ Folgenglieder $a_{1}, \ldots, a_{N-1}$, die einen dieser Werte annehmen können. Nach dem Schubfachprinzip ergibt sich ein Widerspruch.
Nehmen wir nun an, (B) sei erfüllt. Es sei $k=\max \left\{M, a_{1}, \ldots, a_{M}\right\}$. Dann sind die $k$ Folgenglieder $a_{1}, \ldots, a_{k}$ alle kleiner als $k$, denn für $i=1, \ldots M-1$ gilt $a_{i} \leq$ $\max \left\{a_{1}, \ldots, a_{M-1}\right\} \leq k$ und für $i=M, \ldots, k$ gilt $a_{i} \leq i-d<i \leq k$. Diese $k$ Zahlen liegen damit alle in der Menge $\{1,2, \ldots, k-1\}$. Nach dem Schubfachprinzip existieren daher zwei Indizes $1 \leq i<j \leq k$ mit $a_{i}=a_{j}$, was er ersten Voraussetzung an die Folge widerspricht.
Da wir in jedem Fall einen Widerspruch erhalten haben, gilt die Behauptung.
|
{
"resource_path": "Germany_TST/segmented/de-2018-loes_awkl_18.jsonl",
"problem_match": "\nAufgabe 2.",
"solution_match": "\nLösung."
}
|
68ea8886-5411-5820-ab08-c59c550f203d
| 605,140
|
Let $ABC$ be a triangle. The excircle $\omega$ opposite to point $A$ touches the segment $\overline{BC}$ and the rays $AC$ and $AB$ at points $D$, $E$, and $F$, respectively. The circumcircle of triangle $AEF$ intersects the line $BC$ at points $P$ and $Q$. Finally, let $M$ be the midpoint of the segment $\overline{AD}$. Prove that $\omega$ and the circumcircle of triangle $MPQ$ are tangent.
|
Let $J$ be the center of the incircle $\omega$. Then $J E \perp A E$ and $J F \perp A F$, so the Thales circle $\Omega$ of $\overline{A J}$ passes through $E$ and $F$, and thus also through $P$ and $Q$. The ray $A D$ intersects $\Omega$ and $\omega$ again at $N$ and $T$ respectively.

Then $J N$ is the perpendicular from $J$ to $D T$, so $N$ is the midpoint of the segment $\overline{D T}$. By the chord theorem, we have
$$
|D M| \cdot |D T| = \frac{1}{2} \cdot |D A| \cdot |D T| = |D A| \cdot |D N| = |D P| \cdot |D Q|
$$
Thus, by the converse of the chord theorem, the point $T$ lies on the circumcircle of triangle $M P Q$. Now consider the image point of $N$ under inversion with respect to the circle $\omega$, denoted by $Z$. Since the Thales circles over $\overline{J D}$ and $\overline{J T}$ both pass through the point $N$, $Z$ lies on the images of these circles, which are the tangents through $D$ and $T$ to $\omega$. The points $B, C, P$, and $Q$ also lie on the first of these lines. Furthermore, $N$ lies on the circle $\Omega$, which inverts to the line $E F$, so $Z$ also lies on the line $E F$. Therefore, by the secant theorem,
$$
|Z T|^{2} = |Z E| \cdot |Z F| = |Z P| \cdot |Z Q|,
$$
and by the converse of the secant theorem, $Z T$ is also tangent to the circumcircle of triangle $M P Q$. This proves that this circle and $\omega$ touch at the point $T$.
## Solutions to the 2nd Selection Exam 2017/2018
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Es sei $A B C$ ein Dreieck. Der dem Punkt $A$ gegenüberliegende Ankreis $\omega$ berühre die Strecke $\overline{B C}$ sowie die Strahlen $A C$ und $A B$ in den Punkten $D, E$ bzw. $F$. Der Umkreis des Dreiecks $A E F$ schneide die Gerade $B C$ in den Punkten $P$ und $Q$. Schließlich sei $M$ der Mittelpunkt der Strecke $\overline{A D}$. Man beweise, dass sich $\omega$ und der Umkreis des Dreiecks $M P Q$ berühren
|
Es sei $J$ der Mittelpunkt des Ankreises $\omega$. Dann gilt $J E \perp A E$ und $J F \perp$ $A F$, der Thaleskreis $\Omega$ von $\overline{A J}$ verläuft also durch $E$ und $F$, und damit auch durch $P$ und $Q$. Der Strahl $A D$ schneide $\Omega$ und $\omega$ erneut in $N$ bzw. $T$.

Dann ist $J N$ die Lotgerade von $J$ auf $D T$, also ist $N$ der Mittelpunkt der Strecke $\overline{D T}$. Damit gilt laut dem Sehnensatz
$$
|D M| \cdot|D T|=1 / 2 \cdot|D A| \cdot|D T|=|D A| \cdot|D N|=|D P| \cdot|D Q|
$$
der Punkt $T$ liegt nach der Umkehrung des Sehnensatzes also auf dem Umkreis des Dreiecks $M P Q$. Wir betrachten nun den Bildpunkt von $N$ bei Inversion am Kreis $\omega$, dieser sei mit $Z$ bezeichnet. Da die Thaleskreise über $\overline{J D}$ und $\overline{J T}$ beide durch den Punkt $N$ verlaufen, liegt $Z$ auf den Bildern dieser Kreise, also den Tangenten durch $D$ und $T$ an $\omega$. Auf ersterer Geraden liegen auch $B, C, P$ und $Q$. Ferner liegt $N$ auf dem Kreis $\Omega$, der bei der betrachteten Inversion in die Gerade $E F$ übergeht, also liegt auch $Z$ auf der Geraden $E F$. Damit gilt nach dem Sekantensatz
$$
|Z T|^{2}=|Z E| \cdot|Z F|=|Z P| \cdot|Z Q|,
$$
nach der Umkehrung des Sekantensatzes tangiert $Z T$ daher auch den Umkreis des Dreiecks $M P Q$. Damit haben wir beweisen, dass sich dieser Kreis und $\omega$ im Punkt $T$ berühren.
## Lösungen zur 2. Auswahlklausur 2017/2018
|
{
"resource_path": "Germany_TST/segmented/de-2018-loes_awkl_18.jsonl",
"problem_match": "\nAufgabe 3.",
"solution_match": "\nLösung."
}
|
9d657773-6629-5c0e-a9d9-2e7c1bf1dcbd
| 605,151
|
Let $a_{1}, a_{2}, \ldots, a_{n}, k$ and $M$ be positive integers with the properties
$$
\frac{1}{a_{1}}+\frac{1}{a_{2}}+\ldots+\frac{1}{a_{n}}=k \quad \text { and } \quad a_{1} a_{2} \ldots a_{n}=M .
$$
Prove: For $M>1$, the polynomial
$$
P(x)=M(x+1)^{k}-\left(x+a_{1}\right)\left(x+a_{2}\right) \ldots\left(x+a_{n}\right)
$$
has no positive solutions.
|
We show $P(x)<0$ for all $x>0$, i.e., $M(x+1)^{k}<\left(x+a_{1}\right) \ldots\left(x+a_{n}\right) \Leftrightarrow$ $a_{1} a_{2} \ldots a_{n}(x+1)^{\frac{1}{a_{1}}+\frac{1}{a_{2}}+\ldots+\frac{1}{a_{n}}}<\left(x+a_{1}\right) \ldots\left(x+a_{n}\right) \Leftrightarrow \prod_{i=1}^{n} a_{i}(x+1)^{\frac{1}{a_{i}}}<\prod_{i=1}^{n}\left(x+a_{i}\right)$.
To do this, we show that for each $i\left((1 \leq i \leq n)\right.$ the relation $a_{i}(x+1)^{\frac{1}{a_{i}}} \leq x+a_{i}(1)$ holds and for at least one $i$ even $a_{i}(x+1)^{\frac{1}{a_{i}}}<x+a_{i}$ is true. The claim then follows by multiplication for all $i$.
From the AM-GM inequality for the numbers $x+1,1,1, \ldots, 1\left(a_{i}-1\right.$ summands 1$)$, we get $\frac{x+a_{i}}{a_{i}} \geq \sqrt[a]{x+1}$, which, after multiplication by $a_{i}$, precisely yields (1). The equality sign holds exactly for $a_{i}=1$, which cannot be true for all $i$, because then $M=1$, contradicting the assumption $M>1$. Since all transformations are valid for the given values, everything is shown.
Hint: Further proof approaches using the Bernoulli inequality, the binomial theorem, Jensen's inequality, or analysis are possible. The term "solution" in the problem statement, of course, stands synonymously for "root".
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Es seien $a_{1}, a_{2}, \ldots, a_{n}, k$ und $M$ positive ganze Zahlen mit den Eigenschaften
$$
\frac{1}{a_{1}}+\frac{1}{a_{2}}+\ldots+\frac{1}{a_{n}}=k \quad \text { und } \quad a_{1} a_{2} \ldots a_{n}=M .
$$
Man beweise: Für $M>1$ hat das Polynom
$$
P(x)=M(x+1)^{k}-\left(x+a_{1}\right)\left(x+a_{2}\right) \ldots\left(x+a_{n}\right)
$$
keine positiven Lösungen.
|
Wir zeigen $P(x)<0$ für alle $x>0$, also $M(x+1)^{k}<\left(x+a_{1}\right) \ldots\left(x+a_{n}\right) \Leftrightarrow$ $a_{1} a_{2} \ldots a_{n}(x+1)^{\frac{1}{a_{1}}+\frac{1}{a_{2}}+\ldots+\frac{1}{a_{n}}}<\left(x+a_{1}\right) \ldots\left(x+a_{n}\right) \Leftrightarrow \prod_{i=1}^{n} a_{i}(x+1)^{\frac{1}{a_{i}}}<\prod_{i=1}^{n}\left(x+a_{i}\right)$.
Dazu zeigen wir, dass für jedes $i\left((1 \leq i \leq n)\right.$ die Beziehung $a_{i}(x+1)^{\frac{1}{a_{i}}} \leq x+a_{i}(1)$ gilt und für wenigstens ein $i$ sogar $a_{i}(x+1)^{\frac{1}{a_{i}}}<x+a_{i}$ ist. Die Behauptung folgt dann durch Multiplikation für alle $i$.
Aus der AM-GM-Ungleichung für die Zahlen $x+1,1,1, \ldots, 1\left(a_{i}-1\right.$ Summanden 1$)$ folgt $\frac{x+a_{i}}{a_{i}} \geq \sqrt[a]{x+1}$, was nach Multiplikation mit $a_{i}$ gerade (1) ergibt. Das Gleichheitszeichen gilt genau für $a_{i}=1$, was nicht für alle $i$ sein kann, denn dann wäre $M=1$, im Widerspruch zur Voraussetzung $M>1$. Da für die gegebenen Werte alle Umformungen erlaubt sind, ist alles gezeigt.
Hinweis: Weitere Beweisansätze über die Bernoulli-Ungleichung, den binomischen Satz, die Jensensche Ungleichung oder Analysis sind möglich. Der Begriff „Lösung" in der Aufgabenstellung steht natürlich synonym zu „Nullstelle".
|
{
"resource_path": "Germany_TST/segmented/de-2018-loes_awkl_18.jsonl",
"problem_match": "# Aufgabe 1",
"solution_match": "\nLösung:"
}
|
ba6b2424-fce8-5de4-99aa-7690f9a3b5b4
| 605,162
|
Let $A B C D E$ be a convex pentagon with the properties
$$
\overline{A B}=\overline{B C}=\overline{C D}, \angle B A E=\angle D C B \text { and } \angle E D C=\angle C B A .
$$
Prove that the perpendicular from $E$ to $B C$ passes through the intersection of $A C$ and $B D$.
|
Due to the conditions, $\triangle A B C$ and $\triangle B C D$ are isosceles. Therefore, the perpendicular bisector of $A C$ passes through $B$ and the perpendicular bisector of $B D$ passes through $C$. Both intersect at point $I$ (see figure).
Because $B D \perp C I$ and $A C \perp B I$, $A C$ and $B D$ intersect at the orthocenter of triangle $B C I$, and it follows that $I H \perp B C$. If we can show that $E I \perp B C$, the claim follows because there can only be one perpendicular to $B C$ through $I$. Since $B I$ and $C I$ are also angle bisectors of $\angle C B A$ and $\angle D C B$ respectively, it follows that $\overline{I A}=\overline{I C}$ and $\overline{I B}=\overline{I D}$. Because $\overline{A B}=\overline{B C}=\overline{C D}$, the triangles $A B I, B C I$, and $C D I$ are congruent. Therefore, $\angle B A I=\angle I C B=\frac{1}{2} \angle D C B=\frac{1}{2} \angle B A E$, so $I A$ is the angle bisector of $\angle B A E$. Similarly, $I D$ is the angle bisector of $\angle E D C$.
The composition of the reflections in $A I, B I, C I, D I$, and $E I$ is a reflection with fixed points $E$ and $I$. Therefore, $I$ also lies on the angle bisector of $\angle A E D$.
Now, $\angle A E D=540^{\circ}-2 \angle C B A-2 \angle B A E$, and thus in quadrilateral $A B I E$:
$\angle B I E=360^{\circ}-\angle B A E-\angle I B A-\angle A E I=360^{\circ}-\angle B A E-\frac{1}{2} \angle C B A-\left(270^{\circ}-\angle C B A-\angle B A E\right)$
$=90^{\circ}+\frac{1}{2} \angle C B A=90^{\circ}+\angle C B I$. By the exterior angle theorem, it follows that $E I \perp B C$. ㅁ.
Hint: There are other solution paths using the intersection points of the extensions of suitable sides, using trigonometry, or (usually very laborious) analytic geometry. Errors partly arose from using the claim in the proof, such as not distinguishing between the lines $E T$ and $I T$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Es sei $A B C D E$ ein konvexes Fünfeck mit den Eigenschaften
$$
\overline{A B}=\overline{B C}=\overline{C D}, \angle B A E=\angle D C B \text { und } \angle E D C=\angle C B A .
$$
Man beweise, dass die Lotgerade von $E$ auf $B C$ durch den Schnittpunkt von $A C$ und $B D$ verläuft.
|
Wegen der Voraussetzungen sind $\triangle A B C$ und $\triangle B C D$ gleichschenklig. Daher geht die Mittelsenkrechte zu $A C$ durch $B$ und die Mittelsenkrechte zu $B D$ durch $C$. Beide schneiden sich im Punkt $I$ (siehe Figur).
Wegen $B D \perp C I$ und $A C \perp B I$ schneiden sich $A C$ und $B D$ im Höhenschnittpunkt des Dreiecks $B C I$ und es folgt $I H \perp B C$. Wenn wir nun zeigen können, dass $E I \perp B C$ ist, folgt die Behauptung, weil es durch $I$ nur eine Orthogonale zu $B C$ geben kann. Weil $B I$ und $C I$ auch Winkelhalbierende von $\angle C B A$ bzw. $\angle D C B$ sind, folgt $\overline{I A}=\overline{I C}$ sowie $\overline{I B}=\overline{I D}$. Wegen $\overline{A B}=\overline{B C}=\overline{C D}$ sind die Dreiecke $A B I, B C I$ und $C D I$ kongruent. Daher ist $\angle B A I=\angle I C B=\frac{1}{2} \angle D C B=\frac{1}{2} \angle B A E$, so dass $I A$ Winkelhalbierende von $\angle B A E$ ist. Analog gilt, dass $I D$ Winkelhalbierende von $\angle E D C$ ist.
Die Verkettung der Achsenspiegelungen an $A I, B I, C I, D I$ und $E I$ ist eine Achsenspiegelung mit den Fixpunkten $E$ und $I$. Daher liegt $I$ auch auf der Winkelhalbierenden von $\angle A E D$.
Nun gilt $\angle A E D=540^{\circ}-2 \angle C B A-2 \angle B A E$, und damit folgt im Viereck $A B I E$ :
$\angle B I E=360^{\circ}-\angle B A E-\angle I B A-\angle A E I=360^{\circ}-\angle B A E-\frac{1}{2} \angle C B A-\left(270^{\circ}-\angle C B A-\angle B A E\right)$
$=90^{\circ}+\frac{1}{2} \angle C B A=90^{\circ}+\angle C B I$. Mit dem Außenwinkelsatz folgt $E I \perp B C$. ㅁ.
Hinweis: Es gibt andere Lösungswege über die Schnittpunkte der Verlängerungen geeigneter Seiten, mithilfe von
Trigonometrie oder (in der Regel sehr aufwändig) analytischer Geometrie. Fehler entstanden z.T. durch Verwendung der Behauptung im Beweis, etwa durch Nicht-Unterscheiden der Geraden $E T$ und IT.
|
{
"resource_path": "Germany_TST/segmented/de-2018-loes_awkl_18.jsonl",
"problem_match": "# Aufgabe 2",
"solution_match": "\nLösung:"
}
|
b6114224-ba45-54d4-a4ca-a85e5d6a390e
| 605,173
|
Determine all integers $n \geq 2$ with the following property:
For any not necessarily distinct integers $m_{1}, m_{2}, \ldots, m_{n}$, whose sum is not divisible by $n$, there exists an index $i(1 \leq i \leq n)$, such that none of the numbers
$$
m_{i}, m_{i}+m_{i+1}, m_{i}+m_{i+1}+m_{i+2}, \ldots, m_{i}+m_{i+1}+\ldots+m_{i+n-1}
$$
is divisible by $n$. (Here, $m_{i}=m_{i-n}$ for $i>n$.)
|
The sought numbers are exactly the prime numbers.
Part Proof 1: No non-prime number satisfies all conditions.
Let $n=a \cdot b$ with $1<a, b<n$ be a decomposition of $n$ into two proper divisors. We choose $m_{i}=a$ for $1 \leq i<n$ and $m_{n}=0$. Then the sum $m_{1}+m_{2}+\ldots+m_{n}=(n-1) a$ is obviously not divisible by $n$, since neither factor is divisible by $n$.
Now we choose for any index $i$ the index $j=\left\{\begin{array}{ll}b & \text { for } 1 \leq i \leq n-b \\ b+1 & \text { for } n-b<i \leq n\end{array}\right.$ and obtain $m_{i}+m_{i+1}+\ldots+m_{i+j-1}=a \cdot b=n \equiv 0 \bmod n$. With this counterexample, the part proof is complete.
Part Proof 2: Every prime number satisfies all conditions.
Let $n$ now be a prime number. For a proof by contradiction, assume that for the numbers $m_{1}, m_{2}, \ldots, m_{n}$, whose sum is not divisible by $n$, there is a number $j(1 \leq j \leq n)$ for every index $i(1 \leq i \leq n)$ such that the sum $m_{l}+m_{i+1}+\ldots+m_{i+j-1}$ is divisible by $n$. Here, even $j \neq n$ holds, because the sum of all $m_{i}$ is not divisible by $n$.
Now we construct for $0 \leq k \leq n-1$ a finite sequence of integers $i_{0}, i_{1}, \ldots, i_{n}$ with $i_{k+1}-i_{k} \leq n-1$ (1), by choosing $m_{i_{k}+1}+m_{i_{k}+2}+\ldots+m_{i_{k+1}} \equiv 0 \bmod n$. The starting index $i_{0}$ is arbitrary and the new index $i_{k+1}$ is the smallest possible after $i_{k}$ when proceeding cyclically $\bmod n$.
By the pigeonhole principle, there are two different numbers $i_{r}$ and $i_{s}$ in the sequence of these $n+1$ indices with $0 \leq r<s \leq n$ that are congruent $\bmod n$. With them, $\sum_{j=r}^{s-1}\left(m_{i_{j}+1}+m_{i_{j+2}}+\ldots+m_{i_{j+1}}\right) \equiv 0 \bmod n$ holds, because this is true for each bracketed sum.
On the other hand, from $i_{s} \equiv i_{r} \bmod n$, it follows that there is a positive integer $d$ with $i_{s}-i_{r}=d \cdot n$. Due to (1), $i_{s}-i_{r} \leq(n-1) n$, so $d \leq n-1$ follows. Then $\sum_{j=r}^{s-1}\left(m_{i_{j}+1}+m_{i_{j+2}}+\ldots+m_{i_{j+1}}\right)=d\left(m_{1}+m_{2}+\ldots+m_{n}\right)$
cannot be a multiple of $n$, because $n$ is prime and neither $d$ nor $m_{1}+m_{2}+\ldots+m_{n}$ are multiples of $n$ - contradiction! $\square$
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Man bestimme alle ganzen Zahlen $n \geq 2$ mit der folgenden Eigenschaft:
Für beliebige, nicht notwendigerweise verschiedene ganze Zahlen $m_{1}, m_{2}, \ldots, m_{n}$, deren Summe nicht durch $n$ teilbar ist, existiert ein Index $i(1 \leq i \leq n)$, so dass keine der Zahlen
$$
m_{i}, m_{i}+m_{i+1}, m_{i}+m_{i+1}+m_{i+2}, \ldots, m_{i}+m_{i+1}+\ldots+m_{i+n-1}
$$
durch $n$ teilbar ist. (Dabei sei $m_{i}=m_{i-n}$ für $i>n$.)
|
Bei den gesuchten Zahlen handelt es sich genau um die Primzahlen.
Teilbeweis 1: Keine Nichtprimzahl crfüllt allc Voraussctzungen.
Es sei $n=a \cdot b$ mit $1<a, b<n$ eine Zerlegung von $n$ in zwei echte Teiler. Wir wählen $m_{i}=a$ für $1 \leq i<n$ sowie $m_{n}=0$. Dann ist die Summe $m_{1}+m_{2}+\ldots+m_{n}=(n-1) a$ offensichtlich nicht durch $n$ teilbar, da beide Faktoren nicht durch $n$ teilbar sind.
Nun wählen wir zu einem beliebigen Index $i$ den Index $j=\left\{\begin{array}{ll}b & \text { für } 1 \leq i \leq n-b \\ b+1 & \text { für } n-b<i \leq n\end{array}\right.$ und erhalten $m_{i}+m_{i+1}+\ldots+m_{i+j-1}=a \cdot b=n \equiv 0 \bmod n$. Mit diesem Gegenbeispiel ist der Teilbeweis abgeschlossen.
Teilbeweis 2: Jede Primzahl erfüllt alle Voraussetzungen.
Es sei nun $n$ eine Primzahl. Für einen Widerspruchsbeweis nehmen wir an, dass es für die Zahlen $m_{1}, m_{2}, \ldots, m_{n}$, deren Summe nicht durch $n$ teilbar ist, zu jedem Index $i(1 \leq i \leq n)$ eine Zahl $j(1 \leq j \leq n)$ gibt, so dass die Summe $m_{l}+m_{i+1}+\ldots+m_{i+j-1}$ durch $n$ teilbar ist. Dabei gilt sogar $j \neq n$, denn die Summe aller $m_{i}$ ist nicht durch $n$ teilbar.
Nun konstruieren wir für $0 \leq k \leq n-1$ eine endliche Folge ganzer Zahlen $i_{0}, i_{1}, \ldots, i_{n}$ mit $i_{k+1}-i_{k} \leq n-1$ (1), indem wir $m_{i_{k}+1}+m_{i_{k}+2}+\ldots+m_{i_{k+1}} \equiv 0 \bmod n$ wählen. Der Startindex $i_{0}$ ist beliebig und der neue Index $i_{k+1}$ sei der jeweils kleinstmögliche nach $i_{k}$ beim zyklischen Weitergehen $\bmod n$.
Nach dem Schubfachprinzip gibt es in der Folge dieser $n+1$ Indizes zwei verschiedene Zahlen $i_{r}$ und $i_{s}$ mit $0 \leq r<s \leq n$, die $\bmod n$ kongruent sind. Mit ihnen gilt $\sum_{j=r}^{s-1}\left(m_{i_{j}+1}+m_{i_{j+2}}+\ldots+m_{i_{j+1}}\right) \equiv 0 \bmod n$, weil dies für jede Klammersumme gilt.
Andererseits folgt aus $i_{s} \equiv i_{r} \bmod n$, dass es eine positive ganze Zahl $d$ gibt mit $i_{s}-i_{r}=d \cdot n$. Wegen (1)
ist $i_{s}-i_{r} \leq(n-1) n$, so dass $d \leq n-1$ folgt. Dann kann $\sum_{j=r}^{s-1}\left(m_{i_{j}+1}+m_{i_{j+2}}+\ldots+m_{i_{j+1}}\right)=d\left(m_{1}+m_{2}+\ldots+m_{n}\right)$
aber kein Vielfaches von $n$ sein, denn $n$ ist prim und weder $d$ noch $m_{1}+m_{2}+\ldots+m_{n}$ sind Vielfache von $n$ - Widerspruch! $\square$
|
{
"resource_path": "Germany_TST/segmented/de-2018-loes_awkl_18.jsonl",
"problem_match": "# Aufgabe 3",
"solution_match": "\nLösung:"
}
|
ec86aa3f-55db-58a1-8a7c-fab4fddcc646
| 605,185
|
In an isosceles triangle $ABC$ with $|AB|=|AC|$, let $M$ be the midpoint of $BC$. Further, let $P$ be a point such that $PA$ is parallel to $BC$ and $|PB|<|PC|$ holds. Additionally, let $X$ and $Y$ be points on the lines $(PB)$ and $(PC)$, respectively, such that $B$ lies on the segment $PX$, $C$ lies on the segment $PY$, and $\measuredangle MX P = \measuredangle PY M$ holds. Prove that $APXY$ is a cyclic quadrilateral.
|
We denote the intersection of (AM) and the perpendicular to (PC) at point $Y$ with $Z$ and note that $Z$ lies in the half-plane with respect to $(BC)$ that is different from the one containing $A$ and $P$.
Since $\measuredangle P A Z=\measuredangle P Y Z=90^{\circ}$, $A P Z Y$ is a cyclic quadrilateral. Similarly, because $\measuredangle Z M C=\measuredangle C Y Z=90^{\circ}$, $C M Z Y$ is also a cyclic quadrilateral, from which $\measuredangle C Z M=\measuredangle C Y M$ (1) follows. With the condition from the problem, we get $\measuredangle C Y M=\measuredangle M X B$ (2), and due to the axial symmetry with respect to $(A Z)$, $\measuredangle C Z M=\measuredangle M Z B$ (3). (1), (2), and (3) yield $\measuredangle M X B=\measuredangle M Z B$. Therefore, $B X Z M$ is also a cyclic quadrilateral and $\measuredangle Z X B=180^{\circ}-\measuredangle B M Z=90^{\circ}$. Since $\measuredangle Z X P=\measuredangle Z X B=90^{\circ}$, point $X$ lies on the
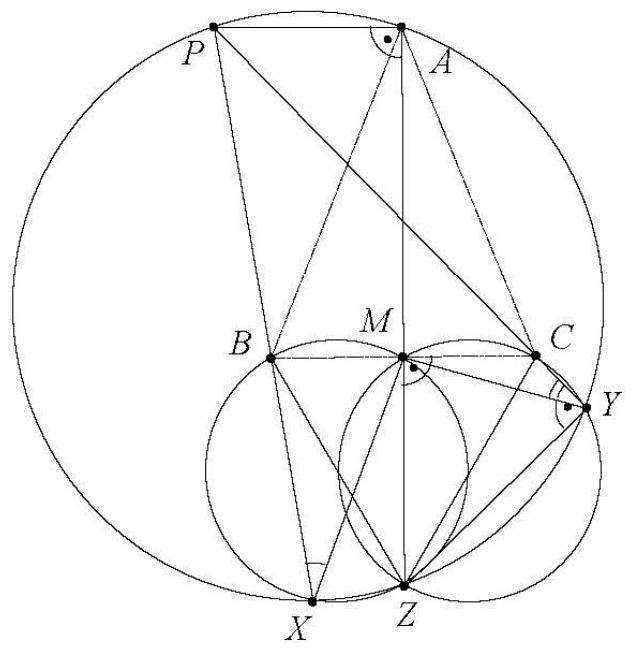
circumcircle of the cyclic quadrilateral $A P Z Y$. Thus, the four points $A, P, X$, and $Y$ also form a cyclic quadrilateral. $\square$
Hint: A pure angle chase does not lead to the solution here, nor does coordinate geometry. However, there are other solution paths, such as inversion or the introduction of other auxiliary points besides $Z$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In einem gleichschenkligen Dreieck $A B C$ mit $|A B|=|A C|$ sei $M$ der Mittelpunkt von $B C$. Weiter sei $P$ ein Punkt, für den $P A$ parallel zu $B C$ ist und $|P B|<|P C|$ gilt. Ferner seien $X$ bzw. $Y$ je ein Punkt auf der Geraden $(P B)$ bzw. $(P C)$, so dass $B$ auf der Strecke $P X$ liegt, $C$ auf der Strecke $P Y$ liegt und $\measuredangle M X P=\measuredangle P Y M$ gilt. Man beweise, dass $A P X Y$ ein Sehnenviereck ist.
|
Wir bezeichnen den Schnittpunkt von (AM) und der Senkrechten zu (PC) im Punkt $Y$ mit $Z$ und bemerken, dass $Z$ in der bezüglich $(B C)$ anderen Halbebene liegt wie $A$ und $P$.
Wegen $\measuredangle P A Z=\measuredangle P Y Z=90^{\circ}$ ist $A P Z Y$ ein
Sehnenviereck. Ebenso ist wegen $\measuredangle Z M C=\measuredangle C Y Z=90^{\circ}$ auch $C M Z Y$ ein
Sehnenviereck, woraus $\measuredangle C Z M=\measuredangle C Y M$ (1) folgt. Mit der Bedingung aus der Aufgabe ergibt sich $\measuredangle C Y M=\measuredangle M X B(2)$, und wegen der Achsensymmetrie zu $(A Z)$ ist $\measuredangle C Z M=\measuredangle M Z B$ (3). (1), (2) und (3) liefern $\measuredangle M X B=\measuredangle M Z B$. Also ist $B X Z M$ ebenfalls ein Sehnenviereck und es gilt $\measuredangle Z X B=180^{\circ}-\measuredangle B M Z=90^{\circ}$. Weil nun $\measuredangle Z X P=\measuredangle Z X B=90^{\circ}$ ist, liegt der Punkt $X$ auf dem

Umkreis des Sehnenvierecks $A P Z Y$. Somit bilden auch die vier Punkte $A, P, X$ und $Y$ ein Sehnenviereck. $\square$
Hinweis: Eine reine Winkeljagd führt hier nicht zum Ziel, ebenso wie Koordinatengeometrie. Dagegen gibt es weitere Lösungswege etwa über Inversion oder die Einführung anderer Hilfspunkte als Z.
|
{
"resource_path": "Germany_TST/segmented/de-2019-loes_awkl_19.jsonl",
"problem_match": "# Aufgabe 2",
"solution_match": "\nLösung:"
}
|
66530449-cd6a-53a7-89e0-a8b2ca7ac8e8
| 605,206
|
Given is a positive integer $n$ and a game board consisting of $n+1$ square fields arranged side by side, numbered from 0 to $n$ from left to right. At the beginning of the game, $n$ game pieces are located on field number 0, and the other fields are empty.
A patient player now chooses for each move a field with $k \neq 0$ pieces and moves one of them at most $k$ fields to the right. The piece must remain on the board. His goal is to move all $n$ pieces to field number $n$ with a sequence of such moves.
Prove that the player cannot achieve this goal in fewer than $\left\lceil\frac{n}{1}\right\rceil+\left\lceil\frac{n}{2}\right\rceil+\left\lceil\frac{n}{3}\right\rceil+\ldots+\left\lceil\frac{n}{n}\right\rceil$ moves. (Here, $\lceil x\rceil$ denotes the smallest integer not less than $x$.)
|
The game pieces are indistinguishable and all have the same starting and target field. Therefore, a patient player can invent a rule that tells him which of the pieces on the selected field he should move.
A possible rule is obtained by firmly numbering the pieces from 1 to $n$ and in each move, after selecting the field, moving the piece with the highest number there.
Assume he moves the piece with the number $k(1 \leq k \leq n)$ to the right in this way. Then there cannot have been more than $k$ pieces on the selected field, because their numbers are at most equal to $k$. Thus, piece $k$ is moved at most $k$ fields to the right each time. Since it is moved a total of exactly $n$ fields, at least $\left\lceil\frac{n}{k}\right\rceil$ moves are required. This holds for all $k$ with $1 \leq k \leq n$. Summing over $k$ yields the minimum number of required game moves according to the problem statement. $\square$
Hint: A proof by complete induction is just as doomed to fail as considerations of seemingly "optimal" strategies whose optimality can only be locally convincingly justified.
It can be shown that the exact value of the given term can only be achieved for $n=1,2,3,4,5,7$.
## Solutions to the 2nd Selection Test 2018/2019
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Gegeben ist eine positive ganze Zahl $n$ und ein Spielbrett, das aus $n+1$ nebeneinander angeordneten quadratischen Feldern besteht, die von links nach rechts von 0 bis $n$ nummeriert sind. Zu Beginn des Spiels befinden $\operatorname{sich} n$ Spielsteine auf dem Feld Nr. 0 und die anderen Felder sind leer.
Ein geduldiger Spieler wählt nun für jeden Zug ein Feld mit $k \neq 0$ Steinen und rückt einen davon um höchstens $k$ Felder nach rechts. Dabei muss der Stein auf dem Spielbrett bleiben. Sein Ziel ist es, mit einer Folge solcher Züge alle $n$ Steine auf das Feld Nr. $n$ zu befördern.
Man beweise, dass der Spieler dieses Ziel nicht mit weniger als $\left\lceil\frac{n}{1}\right\rceil+\left\lceil\frac{n}{2}\right\rceil+\left\lceil\frac{n}{3}\right\rceil+\ldots+\left\lceil\frac{n}{n}\right\rceil$ Zügen erreichen kann. (Dabei bezeichnet $\lceil x\rceil$ die kleinste ganze Zahl, die nicht kleiner als $x$ ist.)
|
Die Spielsteine sind ununterscheidbar und haben alle dasselbe Start- und Zielfeld. Daher kann der geduldige Spieler eine Vorschrift erfinden, die ihm angibt, welchen der Steine auf dem jeweils ausgewählten Feld er ziehen soll.
Eine mögliche Vorschrift erhält er, indem er die Steine fest von 1 bis $n$ nummeriert und in jedem Zug nach der Auswahl des Feldes den dort befindlichen Stein mit der höchsten Nummer bewegt.
Angenommen, er zieht auf diese Weise den Stein mit der Nummer $k(1 \leq k \leq n)$ nach rechts. Dann können auf dem dafür ausgewählten Feld nicht mehr als $k$ Steine gelegen haben, weil ihre Nummern höchstens gleich $k$ sind. Also wird Stein $k$ um jeweils höchstens $k$ Felder nach rechts bewegt. Weil er aber insgesamt um genau $n$ Felder bewegt wird, sind dafür wenigstens $\left\lceil\frac{n}{k}\right\rceil$ Züge erforderlich. Dies gilt für alle $k$ mit $1 \leq k \leq n$. Aufsummieren über $k$ liefert die Mindestanzahl der erforderlichen Spielzüge gemäß der Aufgabenstellung. $\square$
Hinweis: Ein Beweis mit vollständiger Induktion ist ebenso zum Scheitern verurteilt wie Betrachtungen scheinbar „optimaler" Strategien, deren Optimalität nur lokal einsichtig begründet werden kann.
Man kann zeigen, dass der genaue Wert des angegebenen Terms nur für $n=1,2,3,4,5,7$ erreicht werden kann.
## Lösungen zur 2. Auswahlklausur 2018/2019
|
{
"resource_path": "Germany_TST/segmented/de-2019-loes_awkl_19.jsonl",
"problem_match": "# Aufgabe 3",
"solution_match": "\nLösung:"
}
|
7a937299-e205-5110-bcb8-0ed25dece459
| 605,220
|
Decide whether there exists a set $M$ of positive integers that has the following property: For every positive rational number $r<1$ there exists exactly one finite subset $S$ of $M$ such that $\sum_{s \in S} 1 / s=r$, that is, the sum of the reciprocals of all elements of $S$ is equal to $r$.
|
Such a set does not exist, which we will show using a proof by contradiction. Assume that $S$ has the given property. Clearly, $M$ is then infinite, and we may assume without loss of generality that $1 \notin M$. We denote the elements of $M$ in increasing order by $m_{1}<m_{2}<m_{3}<\ldots$. Case 1: It holds that $m_{i} \geq 2 m_{i-1}$ for all $i \geq 2$. Then $m_{i} \geq 2^{i-1} m_{1}$ for all $i \geq 1$, and it follows that
$$
r^{*}:=\sum_{i=1}^{\infty} \frac{1}{m_{i}} \leq \sum_{i=0}^{\infty} \frac{1}{2^{i} m_{1}}=\frac{2}{m_{1}},
$$
that is, if $m_{1} \geq 3$ or $m_{i}>2 m_{i-1}$ for at least one $i$ is satisfied, then $r^{*}<1$. In this case, $M$ does not satisfy the condition given in the problem text if $s \in\left(r^{*}, 1\right)$ is chosen. Therefore, $m_{1}=2$ and $m_{i}=2 m_{i-1}$ for all $i$ must hold, so $M$ consists exactly of the powers of two greater than 1. Since $1 / 3=\sum_{i=2}^{\infty} 2^{-i}$ cannot be written as a finite sum of reciprocals of powers of two, a contradiction also arises in this case.
Case 2: There exists an $i>1$ such that $m_{i}<2 m_{i-1}$. We consider
$$
r:=\frac{1}{m_{i-1}}-\frac{1}{m_{i}}<\frac{1}{m_{i}}.
$$
By assumption, there exists a finite subset $S \subset M$ such that $\sum_{s \in S} 1 / s=r$ holds. Since $s<1 / m_{i}$, it follows that $m_{i} \notin S$. Thus, $S_{1}=S \cup\left\{m_{i}\right\}$ and $S_{2}=\left\{m_{i-1}\right\}$ are two different finite subsets of $M$ such that the sums of the reciprocals of $S_{1}$ and $S_{2}$ yield the value $1 / m_{i-1}$, which is a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Entscheiden Sie, ob es eine Menge $M$ positiver ganzer Zahlen gibt, die folgende Eigenschaft hat: Für jede positive rationale Zahl $r<1$ existiert genau eine endliche Teilmenge $S$ von $M$, sodass $\sum_{s \in S} 1 / s=r$ gilt, das heißt die Summe der Kehrwerte aller Elemente von $S$ ist gleich $r$.
|
Eine solche Menge existiert nicht, was wir mithilfe eines Widerpsruchsbeweises zeigen werden. Angenommen, $S$ hat die angegebene Eigenschaft. Offenbar ist $M$ dann unendlich, und wir dürfen ohne Beschränkung der Allgemeinheit annehmen, dass $1 \notin M$. Wir bezeichnen die Elemente von $M$ der Größe nach geordnet mit $m_{1}<m_{2}<m_{3}<\ldots$. Fall 1: Es gilt $m_{i} \geq 2 m_{i-1}$ für alle $i \geq 2$. Dann gilt $m_{i} \geq 2^{i-1} m_{1}$ für alle $i \geq 1$, und es folgt
$$
r^{*}:=\sum_{i=1}^{\infty} \frac{1}{m_{i}} \leq \sum_{i=0}^{\infty} \frac{1}{2^{i} m_{1}}=\frac{2}{m_{1}},
$$
das heißt falls $m_{1} \geq 3$ oder $m_{i}>2 m_{i-1}$ für mindestens ein $i$ erfüllt ist, dann gilt $r^{*}<1$. In diesem Fall erfüllt $M$ jedoch entgegen der Annahme nicht die im Aufgabentext angegebene Bedingung, falls $s \in\left(r^{*}, 1\right)$ gewählt wird. Somit muss $m_{1}=2$ und $m_{i}=2 m_{i-1}$ für alle $i$ gelten, also besteht $M$ genau aus den Zweierpotenzen größer als 1 . Da sich $1 / 3=\sum_{i=2}^{\infty} 2^{-i}$ aber nicht als endliche Summe von Kehrwerten von Zweierpotenzen schreiben lässt, ergibt sich auch in diesem Fall ein Widerspruch.
Fall 2: Es existiert ein $i>1$, sodass $m_{i}<2 m_{i-1}$. Wir betrachten
$$
r:=\frac{1}{m_{i-1}}-\frac{1}{m_{i}}<\frac{1}{m_{i}} .
$$
Nach Annahme existiert eine endliche Teilmenge $S \subset M$, sodass $\sum_{s \in S} 1 / s=r$ gilt. Wegen $s<1 / m_{i}$ gilt $m_{i} \notin S$. Damit sind aber $S_{1}=S \cup\left\{m_{i}\right\}$ und $S_{2}=\left\{m_{i-1}\right\}$ zwei verschiedene endliche Teilmengen von $M$, sodass die Summen der Kehrwerte von $S_{1}$ und $S_{2}$ den Wert $1 / m_{i-1}$ ergeben, was ein Widerspruch ist.
|
{
"resource_path": "Germany_TST/segmented/de-2019-loes_awkl_19.jsonl",
"problem_match": "\nAufgabe 2.",
"solution_match": "\nLösung."
}
|
0e3b98e7-7f1d-5cb8-bf4f-179458ec383b
| 605,242
|
We consider a triangle $ABC$ and a point $P$ in its interior. The reflection points of $P$ across the sides $\overline{BC}, \overline{CA}$, and $\overline{AB}$ are denoted by $A_{1}, B_{1}$, and $C_{1}$, respectively. Furthermore, let $\Omega$ be the circumcircle of triangle $A_{1} B_{1} C_{1}$, and let $A_{2}, B_{2}$, and $C_{2}$ be the second intersection points of the lines $A_{1} P, B_{1} P$, and $C_{1} P$ with $\Omega$. Prove that the three lines $A A_{2}, B B_{2}$, and $C C_{2}$ intersect on $\Omega$.
|
We are working with directed angles modulo $180^{\circ}$.
In this sketch, $T$ corresponds to the point $P$.
Step 1: First, we observe that $C A$ and $C B$ are the perpendicular bisectors of the segments $\overline{P B_{1}}$ and $\overline{P A_{1}}$, so $C$ is the circumcenter of triangle $P A_{1} B_{1}$, and it follows that
$$
\measuredangle A_{1} C B = \frac{1}{2} \measuredangle A_{1} C P = \measuredangle A_{1} B_{1} P = \measuredangle A_{1} B_{1} B_{2} = \measuredangle A_{1} C_{2} B_{2}.
$$
Step 2: Analogously to Step 1, it follows that $\measuredangle A_{1} B C = \measuredangle A_{1} B_{2} C_{2}$, so triangles $A_{1} B C$ and $A_{1} B_{2} C_{2}$ are similar.
Step 3: Using the similarity just proven, we have
$$
\measuredangle C A_{1} B = \measuredangle C_{2} A_{1} B_{2} \quad \text{and} \quad \frac{\left|\overline{A_{1} C}\right|}{\left|\overline{A_{1} B}\right|} = \frac{\left|\overline{A_{1} C_{2}}\right|}{\left|\overline{A_{1} B_{2}}\right|}
$$
and thus also
$$
\measuredangle B_{2} A_{1} B = \measuredangle C_{2} A_{1} C \quad \text{and} \quad \frac{\left|\overline{A_{1} B_{2}}\right|}{\left|\overline{A_{1} B}\right|} = \frac{\left|\overline{A_{1} C_{2}}\right|}{\left|\overline{A_{1} C}\right|}
$$
so triangles $A_{1} B_{2} B$ and $A_{1} C_{2} C$ are also similar.
Step 4: Let $K$ be the intersection of $C_{2} C$ with $\Omega$. Then $180^{\circ} - \measuredangle A_{1} B_{2} K = \measuredangle A_{1} C_{2} K = \measuredangle A_{1} C_{2} C = \measuredangle A_{1} B_{2} B$, so $K$ lies on the line $B B_{2}$. Similarly, one can show that $K$ also lies on the line $A A_{2}$, which completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Wir betrachten ein Dreieck $A B C$ und einen Punkt $P$ in dessen Inneren. Die Spiegelpunkte von $P$ an den Seiten $\overline{B C}, \overline{C A}$ und $\overline{A B}$ seien mit $A_{1}, B_{1}$ und $C_{1}$ bezeichnet. Ferner sei $\Omega$ der Umkreis des Dreiecks $A_{1} B_{1} C_{1}$ und schließlich seien $A_{2}, B_{2}$ und $C_{2}$ die zweiten Schnittpunkte der Geraden $A_{1} P, B_{1} P$ und $C_{1} P$ mit $\Omega$. Beweisen Sie, dass sich die drei Geraden $A A_{2}, B B_{2}$ und $C C_{2}$ auf $\Omega$ schneiden.
|
Wir arbeiten mit gerichteten Winkeln modulo $180^{\circ}$.
In dieser Skizze entspricht $T$ dem Punkt $P$.

Schritt 1: Zunächst stellen wir fest, dass es sich bei $C A$ und $C B$ um die Mittelsenkrechten der Strecken $\overline{P B_{1}}$ und $\overline{P A_{1}}$ handelt, also ist $C$ der Umkreismittelpunkt des Dreiecks $P A_{1} B_{1}$ und es folgt
$$
\measuredangle A_{1} C B=\frac{1}{2} \measuredangle A_{1} C P=\measuredangle A_{1} B_{1} P=\measuredangle A_{1} B_{1} B_{2}=\measuredangle A_{1} C_{2} B_{2} .
$$
Schritt 2: Analog wie in Schritt 1 folgt, dass $\measuredangle A_{1} B C=\measuredangle A_{1} B_{2} C_{2}$, also sind die Dreiecke $A_{1} B C$ und $A_{1} B_{2} C_{2}$ ähnlich.
Schritt 3: Unter Benutzung der soeben bewiesenen Ähnlichkeit folgt
$$
\measuredangle C A_{1} B=\measuredangle C_{2} A_{1} B_{2} \quad \text { und } \quad \frac{\left|\overline{A_{1} C}\right|}{\left|\overline{A_{1} B}\right|}=\frac{\left|\overline{A_{1} C_{2}}\right|}{\left|\overline{A_{1} B_{2}}\right|}
$$
und somit auch
$$
\measuredangle B_{2} A_{1} B=\measuredangle C_{2} A_{1} C \quad \text { und } \quad \frac{\left|\overline{A_{1} B_{2}}\right|}{\left|\overline{A_{1} B}\right|}=\frac{\left|\overline{A_{1} C_{2}}\right|}{\left|\overline{A_{1} C}\right|}
$$
also sind auch die Dreiecke $A_{1} B_{2} B$ und $A_{1} C_{2} C$ ähnlich.
Schritt 4: Es sei $K$ der Schnittpunkt von $C_{2} C$ mit $\Omega$. Dann gilt $180^{\circ}-\measuredangle A_{1} B_{2} K=$ $\measuredangle A_{1} C_{2} K=\measuredangle A_{1} C_{2} C=\measuredangle A_{1} B_{2} B$, also liegt $K$ auf der Geraden $B B_{2}$. Analog kann man zeigen, dass $K$ auch auf der Geraden $A A_{2}$ liegt, was den Beweis beendet.
|
{
"resource_path": "Germany_TST/segmented/de-2019-loes_awkl_19.jsonl",
"problem_match": "\nAufgabe 3.",
"solution_match": "\nLösung."
}
|
c8b67762-3731-513b-9cdb-2d9e526312ef
| 605,253
|
The real numbers $r_{1}, r_{2}, \ldots, r_{2019}$ satisfy the conditions
$r_{1}+r_{2}+\ldots+r_{2019}=0$ (1) and $r_{1}^{2}+r_{2}^{2}+\ldots+r_{2019}^{2}=1$ (2).
Let $a=\min \left(r_{1}, r_{2}, \ldots, r_{2019}\right)$ and $b=\max \left(r_{1}, r_{2}, \ldots, r_{2019}\right)$. Prove: $a b \leq \frac{-1}{2019}$.
|
Again, starting from $b>0$ and $a<0$, we consider the following convex point set $C$ in the $\mathrm{x}-\mathrm{y}$ plane:
(i) The lower boundary of $C$ is the parabola $y=x^{2}$ in the range $a \leq x \leq b$.
(ii) The upper boundary of $C$ is the line $g: y=(a+b)x-ab$ in the range $a \leq x \leq b$.
Each of the points $(u_{i}, u_{i}^{2})$ lies on the lower boundary of $C$. Therefore, the centroid $S$ of these 2019 points, each with equal mass, also lies within $C$. It holds that $S=\left(\frac{1}{2019} \sum_{i=1}^{2019} u_{i}, \frac{1}{2019} \sum_{i=1}^{2019} u_{i}^{2}\right)=\left(0, \frac{1}{2019}\right)$. For $g$, at the point $x=0$, $y=-ab$ holds. $S$ must not lie above the upper boundary, from which the claim follows.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Die reellen Zahlen $r_{1}, r_{2}, \ldots, r_{2019}$ erfüllen die Bedingungen
$r_{1}+r_{2}+\ldots+r_{2019}=0$ (1) sowie $r_{1}^{2}+r_{2}^{2}+\ldots+r_{2019}^{2}=1$ (2).
Es sei $a=\min \left(r_{1}, r_{2}, \ldots, r_{2019}\right)$ und $b=\max \left(r_{1}, r_{2}, \ldots, r_{2019}\right)$. Man beweise: $a b \leq \frac{-1}{2019}$.
|
Wiederum ausgehend von $b>0$ und $a<0$ betrachten wir die folgende konvexe Punktmenge $C$ in der $\mathrm{x}-\mathrm{y}$-Ebene:
(i) Der untere Rand von $C$ ist die Parabel $y=x^{2}$ im Bereich $a \leq x \leq b$.
(ii) Der obere Rand von $C$ ist die Gerade $g: y=(a+b) x-a b$ im Bereich $a \leq x \leq b$.
Jeder der Punkte ( $u_{i}, u_{i}^{2}$ ) liegt auf dem unteren Rand von $C$. Daher liegt der Schwerpunkt $S$ dieser 2019 Punkte, die mit gleicher Masse versehen seien, ebenfalls in C. Es gilt $S=\left(\frac{1}{2019} \sum_{i 1}^{2019} u_{i}, \frac{1}{2019} \sum_{i 1}^{2019} u_{i}^{2}\right)=\left(0, \frac{1}{2019}\right)$. Für $g$ gilt an der Stelle $x=0$, dass $y=-a b$ ist. $S$ darf nicht oberhalb der oberen Begrenzung liegen, woraus die Behauptung folgt.
|
{
"resource_path": "Germany_TST/segmented/de-2020-loes_awkl_20.jsonl",
"problem_match": "\nAufgabe 1:",
"solution_match": "\n2. Lösung:"
}
|
17c4a01a-e61a-5493-aa02-b6caf2e74f73
| 605,266
|
Given a triangle $ABC$. A circle $k$ passes through $A$, intersects the sides $\overline{AB}$ and $\overline{AC}$ again at points $D$ and $E$ respectively, and intersects the side $\overline{BC}$ at points $F$ and $G$, where $F$ lies between $B$ and $G$. The tangent to the circle through $B, D$, and $F$ at $F$ and the tangent to the circle through $C, E$, and $G$ at $G$ intersect at a point $T$. We assume that $A \neq T$. Prove that the lines $AT$ and $BC$ are parallel.
|
According to the secant-tangent angle theorem for the chord $\overline{F B}$, it holds (see figure) $\angle T F B=180^{\circ}-\angle B D F=\angle F D A$. In the cyclic quadrilateral $A D F G$, therefore, $\angle F D A=180^{\circ}-\angle A G F=\angle C G A$ (small arcs), analogously $\angle T G B=180^{\circ}-\angle C G T=\angle G E C$ and $\angle G E C=\angle C F A$ (cyclic quadrilateral $A F G E$, large arcs). Thus, $\angle T F B=\angle C G A$ (1), from which $\angle G F T=\angle A G B$ follows, and $\angle T G B=\angle C F A$ (2).
Therefore, the triangles $A F G$ and $T F G$ are congruent by ASA, so their heights on the common side $\overline{F G}$ are equal, which proves the claim.
Variant: From (1) and (2), it directly follows that $\angle A F T=\angle A G T$. This means, by the converse of the cyclic quadrilateral theorem, that $T$ lies on $k$. With $\angle T A F=\angle T G F=\angle G F A$, the parallelism of $\overline{T A}$ and $\overline{F G}$ follows.
Note: For some claims, a positional consideration is necessary, the absence of which would have resulted in a point deduction.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Gegeben sei ein Dreieck $A B C$. Ein Kreis $k$ geht durch $A$, schneidet die Seiten $\overline{A B}$ und $\overline{A C}$ nochmals in den Punkten $D$ bzw. $E$ und schneidet die Seite $\overline{B C}$ in den Punkten $F$ und $G$, wobei $F$ zwischen $B$ und $G$ liegt. Die Tangente an den Kreis durch $B, D$ und $F$ in $F$ und die Tangente an den Kreis durch $C, E$ und $G$ in $G$ schneiden sich in einem Punkt $T$. Wir nehmen an, dass $A \neq T$ gilt. Man beweise, dass die Geraden $A T$ und $B C$ parallel sind.

|
Nach dem Sehnen-Tangentenwinkelsatz für die Sehne $\overline{F B}$ gilt (siehe Figur) $\angle T F B=180^{\circ}-\angle B D F=\angle F D A$. Im Sehnenviereck $A D F G$ gilt daher $\angle F D A=180^{\circ}-\angle A G F=\angle C G A$ (kleine Bögen), analog ist $\angle T G B=180^{\circ}-\angle C G T=\angle G E C$ und $\angle G E C=\angle C F A$ (Sehnenviereck $A F G E$, große Bögen). Also gilt $\angle T F B=\angle C G A$ (1), woraus $\angle G F T=\angle A G B$ folgt, und $\angle T G B=\angle C F A$ (2).
Damit sind die Dreiecke $A F G$ und $T F G$ nach wsw kongruent, somit ihre Höhen auf der gemeinsamen Seite $\overline{F G}$ gleich, woraus die Behauptung folgt.
Variante: Aus (1) und (2) folgt direkt, dass $\angle A F T=\angle A G T$ gilt. Dies bedeutet nach der Umkehrung des Satzes vom Sehnenviereck, dass $T$ auf $k$ liegt. Mit $\angle T A F=\angle T G F=\angle G F A$ folgt die Parallelität von $\overline{T A}$ und $\overline{F G}$.
Hinweis: Für einige Behauptungen ist eine Lagebetrachtung erforderlich, deren Fehlen einen Punktabzug zur Folge hatte.
|
{
"resource_path": "Germany_TST/segmented/de-2020-loes_awkl_20.jsonl",
"problem_match": "\nAufgabe 2:",
"solution_match": "\nLösung:"
}
|
01708ca0-b3d0-51ea-adc0-88534bc773e2
| 605,297
|
Let $m$ and $n$ be two positive integers. Prove that the integer $m^{2}+\left\lceil\frac{4 m^{2}}{n}\right\rceil$ is not a perfect square.
(Here, $\lceil x\rceil$ denotes the smallest integer not less than $x$.)
|
For an indirect proof, we assume that there is a $k \in \mathbb{N}$ such that $m^{2}+\left\lceil\frac{4 m^{2}}{n}\right\rceil=(m+k)^{2}$, i.e., $\left\lceil\frac{(2 m)^{2}}{n}\right\rceil=(2 m+k) k$. Clearly, $k \geq 1$. Thus, the equation $\left\lceil\frac{c^{2}}{n}\right\rceil=(c+k) k(1)$ has a positive integer solution $(c, k)$ with even $c$. Ignoring the parity of $c$, we consider such a solution of (1) with minimal $k$. From $\frac{c^{2}}{n}>\left\lceil\frac{c^{2}}{n}\right\rceil-1=c k+k^{2}-1 \geq c k$ and $\frac{(c-k)(c+k)}{n}<\frac{c^{2}}{n} \leq\left\lceil\frac{c^{2}}{n}\right\rceil=(c+k) k$, we deduce $c>n k>n-k$, so that $c=k n+r$ with a suitable $0<r<k$ holds. Substituting this into (1) yields $\left\lceil\frac{c^{2}}{n}\right\rceil=\left\lceil\frac{(n k+r)^{2}}{n}\right\rceil=k^{2} n+2 k r+\left\lceil\frac{r^{2}}{n}\right\rceil$ and $(c+k) k=(k n+r+k) k=k^{2} n+2 k r+k(k-r)$, so that $\left\lceil\frac{r^{2}}{n}\right\rceil=k(k-r)$ (2) follows. This provides another positive integer solution of (1) with $c^{\prime}=r$ and $k^{\prime}=k-r<k$, which contradicts the minimality of $k$.
Variant: Let $m^{2}+\left\lceil\frac{4 m^{2}}{n}\right\rceil=c^{2}$ for a positive integer $c>m$, from which
$c^{2}-1<m^{2}+\frac{4 m^{2}}{n} \leq c^{2}$ and thus $0 \leq c^{2} n-m^{2}(m+4)<n$ (3) follows. We substitute $d=c^{2} n-m^{2}(n+4), x=c+m$ and $y=c-m$, obtaining $c=\frac{x+y}{2}$ and $m=\frac{x-y}{2}$, and rewrite (3) as: $\left(\frac{x+y}{2}\right)^{2} n-\left(\frac{x-y}{2}\right)^{2}(n+4)=d$ or $x^{2}-(n+2) x y+y^{2}+d=0$ with $0 \leq d<n$. We choose for fixed $n$ and $d$ an integer solution pair $(x, y)$ for which $x+y$ is minimal. Due to the symmetry of (4), we can assume $x \geq y \geq 1$. As above, another solution $(z, y)$ can also be found here, for which $z<x$ - contradiction!
Hint: Those who know "Vieta jumping" can also apply this method here wonderfully. This problem was the hardest in the exam and was not fully solved by any participant. Relatively common errors: rational squares were confused with integer squares, the upper with the lower Gaussian bracket, factors were extracted from the Gaussian bracket, or calculations with residue classes were performed with it.
## Solutions to the 2nd Selection Exam 2019/2020
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Es seien $m$ und $n$ zwei positive ganze Zahlen. Man beweise, dass die ganze Zahl $m^{2}+\left\lceil\frac{4 m^{2}}{n}\right\rceil$ keine Quadratzahl ist.
(Dabei bezeichnet $\lceil x\rceil$ die kleinste ganze Zahl, die nicht kleiner als $x$ ist.)
|
Für einen indirekten Beweis nehmen wir an, dass es ein $k \in \mathbb{N}$ gibt mit $m^{2}+\left\lceil\frac{4 m^{2}}{n}\right\rceil=(m+k)^{2}$, d.h. $\left\lceil\frac{(2 m)^{2}}{n}\right\rceil=(2 m+k) k$. Offensichtlich ist $k \geq 1$. Also hat die Gleichung $\left\lceil\frac{c^{2}}{n}\right\rceil=(c+k) k(1)$ eine positive ganzzahlige Lösung $(c, k)$ mit geradem $c$. Ohne auf die Parität von $c$ zu achten, betrachten wir eine solche Lösung von (1) mit minimalem $k$. Aus $\frac{c^{2}}{n}>\left\lceil\frac{c^{2}}{n}\right\rceil-1=c k+k^{2}-1 \geq c k$ und $\frac{(c-k)(c+k)}{n}<\frac{c^{2}}{n} \leq\left\lceil\frac{c^{2}}{n}\right\rceil=(c+k) k$ entnehmen wir $c>n k>n-k$, so dass $c=k n+r$ mit geeignetem $0<r<k$ gilt. Dies in (1) eingesetzt liefert $\left\lceil\frac{c^{2}}{n}\right\rceil=\left\lceil\frac{(n k+r)^{2}}{n}\right\rceil=k^{2} n+2 k r+\left\lceil\frac{r^{2}}{n}\right\rceil$ und $(c+k) k=(k n+r+k) k=k^{2} n+2 k r+k(k-r)$, so dass $\left\lceil\frac{r^{2}}{n}\right\rceil=k(k-r)$ (2) folgt. Dies liefert eine andere positive ganzzahlige Lösung von (1) mit $c^{\prime}=r$ und $k^{\prime}=k-r<k$, was der Minimalität von $k$ widerspricht.
Variante: Es sei $m^{2}+\left\lceil\frac{4 m^{2}}{n}\right\rceil=c^{2}$ für eine positive ganze Zahl $c>m$, woraus
$c^{2}-1<m^{2}+\frac{4 m^{2}}{n} \leq c^{2}$ und daraus $0 \leq c^{2} n-m^{2}(m+4)<n$ (3) folgt. Wir substituieren $d=c^{2} n-m^{2}(n+4), x=c+m$ und $y=c-m$, erhalten $c=\frac{x+y}{2}$ sowie $m=\frac{x-y}{2}$ und schreiben (3) damit um: $\left(\frac{x+y}{2}\right)^{2} n-\left(\frac{x-y}{2}\right)^{2}(n+4)=d$ bzw. $x^{2}-(n+2) x y+y^{2}+d=0$ mit $0 \leq d<n$. Wir wählen für festes $n$ und $d$ ein ganzzahliges Lösungspaar $(x, y)$, für das $x+y$ minimal ist. Wegen der Symmetrie von (4) können wir dabei $x \geq y \geq 1$ annehmen. Wie oben läst sich auch hier eine weitere Lösung $(z, y)$ finden, für die $z<x$ ist - Widerspruch!
Hinweis: Wer „Vieta jumping" kennt, kann auch diese Methode hier wunderbar anwenden. Diese Aufgabe war die schwerste der Klausur und wurde von keinem Teilnehmer vollständig gelöst. Relativ häufig auftretende Fehler: rationale Quadratzahlen wurden mit ganzen Quadratzahlen verwechselt, ebenso die obere mit der unteren Gaußklammer verwechselt, aus der Gaußklammer wurden Faktoren herausgezogen oder mit ihr wurde Restklassenrechnung betrieben.
## Lösungen zur 2. Auswahlklausur 2019/2020
|
{
"resource_path": "Germany_TST/segmented/de-2020-loes_awkl_20.jsonl",
"problem_match": "\nAufgabe 3:",
"solution_match": "\nLösung:"
}
|
d8d8c7dc-ccc5-5b51-b2fa-d194d5287f19
| 605,305
|
A pirate wants to divide a treasure consisting of 1000 gold coins, each weighing at least 1 g and together exactly 2 kg, into two parts, each of which may deviate from 1 kg in mass by at most 1 g. Prove that this is possible.
|
Let the masses of the 1000 coins in grams, in ascending order, be denoted by $m_{1} \leq m_{2} \leq \cdots \leq m_{1000}$. We will now prove by induction on $\ell=1, \ldots, 1000$ the following statement.
Lemma. For all $1 \leq \ell \leq 1000$ and every real number $0 \leq x \leq 2+\sum_{i=1}^{\ell} m_{i}$, there exists a (potentially empty) subset $I \subset\{1,2, \ldots, \ell\}$ such that $\sum_{i \in I} m_{i} \in[x-2, x]$.
It holds that $x_{1} \leq 2000 / 1000=2$, so the base case $\ell=1$ is clear: if $x<2$, we can choose $I=\emptyset$, otherwise $I=\{1\}$ works.
For the induction step $\left(\ell \rightarrow \ell+1\right.$, where $\ell \leq 999$), we see that for $x \leq \sum_{i=1}^{\ell} m_{i}$, there is nothing to show. Since we can replace any set $I$ by $I \cup\{\ell+1\}$, the claim is also true for $m_{\ell+1} \leq x \leq m_{\ell+1}+\sum_{i=1}^{\ell} m_{i}=\sum_{i=1}^{\ell+1} m_{i}$. The induction step is thus completed, except if $2+\sum_{i=1}^{\ell} m_{i}<m_{\ell+1}$. In this case, it follows that $m_{i}>2+\ell$ for all $\ell+1 \leq i \leq 1000$, which implies the following inequality.
$$
2000=\sum_{i=1}^{1000} m_{i}=\sum_{i=1}^{\ell} m_{i}+\sum_{i=\ell+1}^{1000} m_{i}>\ell+(1000-\ell)(2+\ell)=2000+999 \ell-\ell^{2}
$$
Thus, $\ell>999$, a contradiction, which completes the proof of the lemma.
We now apply the lemma to $\ell=1000$ and $x=1001$. This shows that there exists a subset $I \subset\{1,2, \ldots, 1000\}$ such that $\sum_{i \in I} x_{i} \in[999,1001]$. Since $\sum_{i=1}^{1000} m_{i}=$ 2000, it also follows that $\sum_{i \in\{1, \ldots, 1000\} \backslash I} x_{i} \in[999,1001]$, and the partition of the coins corresponding to the decomposition
$$
\{1, \ldots, 1000\}=I \cup(\{1, \ldots, 1000\} \backslash I)
$$
satisfies the claim.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Ein Pirat möchte einen Schatz, bestehend aus 1000 Goldmünzen, die jeweils mindestens 1 g und zusammen genau 2 kg wiegen, in zwei Teile aufteilen, die in ihrer Masse jeweils um höchstens 1 g von 1 kg abweichen. Beweisen Sie, dass dies möglich ist.
|
Die Massen der 1000 Münzen in Gramm, in aufsteigender Reihenfolge geordnet, seien mit $m_{1} \leq m_{2} \leq \cdots \leq m_{1000}$ bezeichnet. Wir beweisen nun zunächst mit vollständiger Induktion nach $\ell=1, \ldots, 1000$ die folgende Aussage.
Lemma. Für alle $1 \leq \ell \leq 1000$ und jede reelle Zahl $0 \leq x \leq 2+\sum_{i=1}^{\ell} m_{i}$ existiert eine (potentiell leere) Teilmenge $I \subset\{1,2, \ldots, \ell\}$, sodass $\sum_{i \in I} m_{i} \in[x-2, x]$ gilt.
Es gilt $x_{1} \leq 2000 / 1000=2$, also ist der Induktionsanfang $\ell=1$ klar: falls $x<2$, können wir $I=\emptyset$ wählen, ansonsten funktioniert $I=\{1\}$.
Für den Induktionsschritt $\left(\ell \rightarrow \ell+1\right.$, wobei $\ell \leq 999$ ) sehen wir, dass für $x \leq \sum_{i=1}^{\ell} m_{i}$ nichts zu zeigen ist. Da wir jede Menge $I$ durch $I \cup\{\ell+1\}$ ersetzen können, ist die Behauptung auch für $m_{\ell+1} \leq x \leq m_{\ell+1}+\sum_{i=1}^{\ell} m_{i}=\sum_{i=1}^{\ell+1} m_{i}$ erfüllt. Der Induktionssschritt ist also beendet, außer es gilt $2+\sum_{i=1}^{\ell} m_{i}<m_{\ell+1}$. In diesem Fall folgt $m_{i}>2+\ell$ für alle $\ell+1 \leq i \leq 1000$, was folgende Umgleichung impliziert.
$$
2000=\sum_{i=1}^{1000} m_{i}=\sum_{i=1}^{\ell} m_{i}+\sum_{i=\ell+1}^{1000} m_{i}>\ell+(1000-\ell)(2+\ell)=2000+999 \ell-\ell^{2}
$$
Damit folgt $\ell>999$, ein Widerspruch, was den Beweis des Lemmas abschließt.
Wir wenden das Lemma nun auf $\ell=1000$ und $x=1001$ an. Dadurch wird ersichtlich, dass eine Teilmenge $I \subset\{1,2, \ldots, 1000\}$ existiert, für die $\sum_{i \in I} x_{i} \in[999,1001]$ gilt. Wegen $\sum_{i=1}^{1000} m_{i}=$ 2000 gilt auch $\sum_{i \in\{1, \ldots, 1000\} \backslash I} x_{i} \in[999,1001]$, und die Aufteilung der Münzen, die der Zerlegung
$$
\{1, \ldots, 1000\}=I \cup(\{1, \ldots, 1000\} \backslash I)
$$
entspricht, erfüllt die Behauptung.
|
{
"resource_path": "Germany_TST/segmented/de-2020-loes_awkl_20.jsonl",
"problem_match": "\nAufgabe 1.",
"solution_match": "\n1. Lösung (Vollständige Induktion)."
}
|
d7df1a11-2928-56a0-a04f-a168f1ddd509
| 605,319
|
A pirate wants to divide a treasure consisting of 1000 gold coins, each weighing at least 1 g and together exactly 2 kg, into two parts, each of which may deviate from 1 kg in mass by at most 1 g. Prove that this is possible.
|
We use the same notation as in the first solution. The pirate distributes the coins according to the following procedure: He places all the coins, in descending order of their masses (starting with the heaviest coin with mass \( m_{1000} \)), one by one onto two piles \( H_{1} \) and \( H_{2} \), placing each coin on the pile that is lighter at that moment; in case of a tie, he chooses any pile.
We claim that neither of the two piles will ever weigh more than 1001 grams.
Suppose, after adding the \( k \)-th coin with mass \( m_{1001-k} \), one of the piles does weigh more than 1001 grams. Before this step, the total weight of both piles was \( \sum_{i=1002-k}^{1000} m_{i} \) grams, and since the coin was placed on the lighter pile, it follows that
\[
\begin{aligned}
m_{1001-k} + \frac{1}{2} \sum_{i=1002-k}^{1000} m_{i} & > 1001 \\
m_{1001-k} + \frac{1}{2} \sum_{i=1}^{1000} m_{i} & > 1001 + \frac{1}{2} \sum_{i=1}^{1001-k} m_{i} \\
\frac{1}{2} m_{1001-k} + 1000 & > 1001 + \frac{1}{2} \sum_{i=1}^{1000-k} m_{i} \\
m_{1001-k} & > 2 + \sum_{i=1}^{1000-k} m_{i} \geq 2 + 1000 - k = 1002 - k
\end{aligned}
\]
Thus, it follows that
\[
\begin{aligned}
2000 = \sum_{i=1}^{1000} m_{i} & = \left( \sum_{i=1}^{1000-k} m_{i} \right) + \left( \sum_{i=1001-k}^{1000} m_{i} \right) \\
& \geq 1000 - k + k \cdot m_{1001-k} \\
& > 1000 - k + k(1002 - k)
\end{aligned}
\]
Therefore, \( f(k) = -k^2 + 1001k - 1000 < 0 \), which is a contradiction because \( f(k) = (k-1)(1000-k) \) and \( 1 \leq k \leq 1000 \).
Thus, the claim is true, and even after distributing the lightest coin with mass \( m_{1} \), neither pile weighs more than 1001 grams. Since they together weigh 2000 grams, each pile must weigh at least 999 grams, and we have found the required distribution.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Ein Pirat möchte einen Schatz, bestehend aus 1000 Goldmünzen, die jeweils mindestens 1 g und zusammen genau 2 kg wiegen, in zwei Teile aufteilen, die in ihrer Masse jeweils um höchstens 1 g von 1 kg abweichen. Beweisen Sie, dass dies möglich ist.
|
Wir verwenden die gleiche Notation wie in der ersten Lösung. Der Pirat verteilt die Münzen nach folgendem Verfahren: Er legt alle Münzen, in absteigender Reihenfolge ihrer Massen (also beginnend mit der schwersten Münze mit Masse $m_{1000}$ ), nach und nach auf zwei Haufen $H_{1}$ und $H_{2}$, wobei er jede Münze auf denjenigen Haufen legt, der zu diesem Zeitpunkt leichter ist; bei eine Gleichgewicht wählt er einen beliebigen Haufen aus.
Wir behaupten, dass keiner der beiden Haufen jemals mehr als 1001 Gramm wiegt.
Angenommen, nach dem Hinzulegen der kten Münze mit Masse $m_{1001-k}$ ist doch einer der Haufen schwerer als 1001 Gramm. Vor diesem Schritt wogen beide Haufen zusammen $\sum_{i=1002-k}^{1000} m_{i}$
Gramm, und da die Münze auf den leichteren Haufen gelegt wurde, folgt
$$
\begin{aligned}
m_{1001-k}+\frac{1}{2} \sum_{i=1002-k}^{1000} m_{i} & >1001 \\
m_{1001-k}+\frac{1}{2} \sum_{i=1}^{1000} m_{i} & >1001+\frac{1}{2} \sum_{i=1}^{1001-k} m_{i} \\
\frac{1}{2} m_{1001-k}+1000 & >1001+\frac{1}{2} \sum_{i=1}^{1000-k} m_{i} \\
m_{1001-k} & >2+\sum_{i=1}^{1000-k} m_{i} \geq 2+1000-k=1002-k
\end{aligned}
$$
Damit folgt nun
$$
\begin{aligned}
2000=\sum_{i=1}^{1000} m_{i} & =\left(\sum_{i=1}^{1000-k} m_{i}\right)+\left(\sum_{i=1001-k}^{1000} m_{i}\right) \\
& \geq 1000-k+k \cdot m_{1001-k} \\
& >1000-k+k(1002-k)
\end{aligned}
$$
also folgt $f(k)=-k^{2}+1001 k-1000<0$, was wegen $f(k)=(k-1)(1000-k)$ und $1 \leq k \leq 1000$ jedoch ein Widerspruch ist.
Also stimmt die Behauptung, und auch nach dem Verteilen der leichtesten Münze mit Masse $m_{1}$ wiegen beide Haufen nicht mehr als 1001 Gramm. Da sie zusammen 2000 Gramm wiegen, muss damit jeder Haufen mindestens 999 Gramm wiegen, und wir haben eine Verteilung wie gefordert gefunden.
|
{
"resource_path": "Germany_TST/segmented/de-2020-loes_awkl_20.jsonl",
"problem_match": "\nAufgabe 1.",
"solution_match": "\n2. Lösung (Greedy-Algorithmus)."
}
|
d7df1a11-2928-56a0-a04f-a168f1ddd509
| 605,319
|
A pirate wants to divide a treasure consisting of 1000 gold coins, each weighing at least 1 g and together exactly 2 kg, into two parts, each of which may deviate from 1 kg in mass by at most 1 g. Prove that this is possible.
|
We use the same notation as in the first solution. Since $m_{1000} \geq 2 > 1$, it follows that $m_{1} + \cdots + m_{999} < 1999$, and the 1000 sums
$$
0, m_{1}, m_{1} + m_{2}, \ldots, m_{1} + m_{2} + \cdots + m_{999}
$$
each lie in exactly one of the 1000 drawers
$$
\begin{gathered}
{[0,1) \cup [1000,1001),} \\
{[1,2) \cup [1001,1002),} \\
\ldots, \\
{[998,999) \cup [1998,1999),} \\
{[999,1000)}
\end{gathered}
$$
If one of the sums lies in the last drawer $[999,1000)$, we are done. Otherwise, two sums lie in the same drawer $[k, k+1) \cup [1000+k, 1001+k)$ (for some fixed $0 \leq k \leq 998$). Since by assumption $m_{i} \geq 1$, one of the sums lies in the interval $[k, k+1)$ and the other in $[1000+k, 1001+k)$, the difference $m_{i+1} + m_{i+2} + \cdots + m_{j}$ of the two sums thus lies in the interval $(999,1001)$ and provides the desired distribution.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Ein Pirat möchte einen Schatz, bestehend aus 1000 Goldmünzen, die jeweils mindestens 1 g und zusammen genau 2 kg wiegen, in zwei Teile aufteilen, die in ihrer Masse jeweils um höchstens 1 g von 1 kg abweichen. Beweisen Sie, dass dies möglich ist.
|
Wir verwenden wieder die gleiche Notation wie in der ersten Lösung. Wegen $m_{1000} \geq 2>1$ gilt $m_{1}+\cdots+m_{999}<1999$, und die 1000 Summen
$$
0, m_{1}, m_{1}+m_{2}, \ldots, m_{1}+m_{2}+\cdots+m_{999}
$$
liegen jeweils in genau einem der 1000 Schubfächer
$$
\begin{gathered}
{[0,1) \cup[1000,1001),} \\
{[1,2) \cup[1001,1002),} \\
\ldots, \\
{[998,999) \cup[1998,1999),} \\
{[999,1000)}
\end{gathered}
$$
Falls eine der Summen im letzten Schubfach $[999,1000)$ liegt, sind wir fertig, ansonsten liegen zwei Summen im gleichen Schubfach $[k, k+1) \cup[1000+k, 1001+k$ ) (für ein festes $0 \leq k \leq 998$ ). Da nach Voraussetzung $m_{i} \geq 1$ gilt, liegt eine der Summen im Intervall $[k, k+1)$ und die andere in $[1000+k, 1001+k)$, die Differenz $m_{i+1}+m_{i+2}+\cdots+m_{j}$ der beiden Summen liegt somit im Intervall $(999,1001)$ und liefert daher eine Verteilung wie gewünscht.
|
{
"resource_path": "Germany_TST/segmented/de-2020-loes_awkl_20.jsonl",
"problem_match": "\nAufgabe 1.",
"solution_match": "\n3. Lösung (Schubfachprinzip)."
}
|
d7df1a11-2928-56a0-a04f-a168f1ddd509
| 605,319
|
Let $\triangle ABC$ have circumcircle $\Omega$, and let points $A_1, B_1$, and $C_1$ lie on the sides $\overline{BC}, \overline{CA}$, and $\overline{AB}$, respectively, such that the three lines $AA_1, BB_1$, and $CC_1$ intersect at a point $P$.
It is to be shown that at most two of the three reflection points of $P$ when reflected over $A_1$, $B_1$, or $C_1$ lie outside $\Omega$.
|
Due to $\measuredangle B P C+\measuredangle C P A+\measuredangle A P B=360^{\circ}=\left(180^{\circ}-\measuredangle B A C\right)+\left(180^{\circ}-\measuredangle C B A\right)+$ $\left(180^{\circ}-\measuredangle A C B\right)$, we can assume without loss of generality that $\measuredangle A P B \leq$ $180^{\circ}-\measuredangle A C B$. Since $P$ lies inside the triangle $A B C$, $\angle A P B>\measuredangle A C B$, which implies $\measuredangle A P B \in\left[\measuredangle A C B, 180^{\circ}-\measuredangle A C B\right]$ and thus $\sin \measuredangle A P B \geq \sin \measuredangle A C B$.
Let $A_{2}, B_{2}$, and $C_{2}$ be the reflection points described in the problem, and $A_{3}, B_{3}$, and $C_{3}$ be the second intersection points of the lines $A P, B P$, and $C P$ with $\Omega$. We will now prove that at least one of the ratios $\frac{\left|\overline{P A_{1}}\right|}{\left|\overline{A_{1} A_{3}}\right|}$ and $\frac{\left|\overline{P B_{1}}\right|}{\left|\overline{B_{1} B_{3}}\right|}$ is not greater than 1, which implies the claim.
To do this, we calculate using the Law of Sines,
$$
\frac{\left|\overline{P A_{1}}\right|}{\left|\overline{A_{1} A_{3}}\right|}=\frac{\left|\overline{P A_{1}}\right|}{\left|\overline{A_{1} B}\right|} \cdot \frac{\left|\overline{A_{1} B}\right|}{\left|\overline{A_{1} A_{3}}\right|} \stackrel{(*)}{=} \frac{\sin \measuredangle C B P}{\sin \measuredangle A P B} \cdot \frac{\left|\overline{A_{1} A}\right|}{\left|\overline{A_{1} C}\right|}=\frac{\sin \measuredangle C B P}{\sin \measuredangle A P B} \cdot \frac{\sin \measuredangle A C B}{\sin \measuredangle P A C},
$$
where in step (*) we used the equation $\left|\overline{A_{1} B}\right| \cdot\left|\overline{A_{1} C}\right|=\left|\overline{A_{1} A}\right| \cdot\left|\overline{A_{1} A_{3}}\right|$, which follows from the Power of a Point theorem. Similarly, we can show
$$
\frac{\left|\overline{P B_{1}}\right|}{\left|\overline{B_{1} B_{3}}\right|}=\frac{\sin \measuredangle P A C}{\sin \measuredangle A P B} \cdot \frac{\sin \measuredangle A C B}{\sin \measuredangle C B P},
$$
and by multiplying both equations, we finally get
$$
\frac{\left|\overline{P A_{1}}\right|}{\left|\overline{A_{1} A_{3}}\right|} \cdot \frac{\left|\overline{P B_{1}}\right|}{\left|\overline{B_{1} B_{3}}\right|}=\frac{(\sin \measuredangle A C B)^{2}}{(\sin \measuredangle A P B)^{2}} \leq 1,
$$
which implies the claim.
Note: Many of the participants solved the (much simpler) problem where $P$ is reflected over the three sides of the triangle instead of the points $A_{1}, B_{1}$, and $C_{1}$, and showed that at least one of the resulting reflection points does not lie outside the triangle.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Es seien ein Dreieck $A B C$ mit Umkreis $\Omega$ sowie Punkte $A_{1}, B_{1}$ und $C_{1}$ auf den Dreiecksseiten $\overline{B C}, \overline{C A}$ und $\overline{A B}$ gegeben, sodass die drei Geraden $A A_{1}, B B_{1}$ und $C C_{1}$ einen Punkt $P$ gemeinsam haben.
Es ist zu zeigen, dass höchstens zwei der drei Spiegelpunkte von $P$ bei Punktspiegelung an $A_{1}$, $B_{1}$, bzw. $C_{1}$ außerhalb von $\Omega$ liegen.
|
Wegen $\measuredangle B P C+\measuredangle C P A+\measuredangle A P B=360^{\circ}=\left(180^{\circ}-\measuredangle B A C\right)+\left(180^{\circ}-\measuredangle C B A\right)+$ $\left(180^{\circ}-\measuredangle A C B\right)$ dürfen wir ohne Beschränkung der Allgemeinheit annehmen, dass $\measuredangle A P B \leq$ $180^{\circ}-\measuredangle A C B$ gilt. Da $P$ im Inneren des Dreiecks $A B C$ liegt, gilt $\angle A P B>\measuredangle A C B$, woraus $\measuredangle A P B \in\left[\measuredangle A C B, 180^{\circ}-\measuredangle A C B\right]$ und damit $\sin \measuredangle A P B \geq \sin \measuredangle A C B$ folgt.
Es seien $A_{2}, B_{2}$ und $C_{2}$ die im Aufgabentext beschriebenen Spiegelpunkte, sowie $A_{3}, B_{3}$ und $C_{3}$ die zweiten Schnittpunkte der Geraden $A P, B P$ und $C P$ mit $\Omega$. Wir werden nun beweisen, dass mindestens eines der Verhältnisse $\frac{\left|\overline{P A_{1}}\right|}{\left|\overline{A_{1} A_{3}}\right|}$ und $\frac{\left|\overline{P B_{1}}\right|}{\left|\overline{B_{1} B_{3}}\right|}$ nicht größer als 1 ist, woraus die Behauptung folgt.

Dazu rechnen wir unter Ausnutzung des Sinussatzes,
$$
\frac{\left|\overline{P A_{1}}\right|}{\left|\overline{A_{1} A_{3}}\right|}=\frac{\left|\overline{P A_{1}}\right|}{\left|\overline{A_{1} B}\right|} \cdot \frac{\left|\overline{A_{1} B}\right|}{\left|\overline{A_{1} A_{3}}\right|} \stackrel{(*)}{=} \frac{\sin \measuredangle C B P}{\sin \measuredangle A P B} \cdot \frac{\left|\overline{A_{1} A}\right|}{\left|\overline{A_{1} C}\right|}=\frac{\sin \measuredangle C B P}{\sin \measuredangle A P B} \cdot \frac{\sin \measuredangle A C B}{\sin \measuredangle P A C},
$$
wobei wir im Schritt (*) die Gleichung $\left|\overline{A_{1} B}\right| \cdot\left|\overline{A_{1} C}\right|=\left|\overline{A_{1} A}\right| \cdot\left|\overline{A_{1} A_{3}}\right|$ verwendet haben, die aus dem Sehnensatz folgt. Analog zeigt man nun auch
$$
\frac{\left|\overline{P B_{1}}\right|}{\left|\overline{B_{1} B_{3}}\right|}=\frac{\sin \measuredangle P A C}{\sin \measuredangle A P B} \cdot \frac{\sin \measuredangle A C B}{\sin \measuredangle C B P},
$$
und durch Multiplikation beider Gleichungen folgt schlieBlich
$$
\frac{\left|\overline{P A_{1}}\right|}{\left|\overline{A_{1} A_{3}}\right|} \cdot \frac{\left|\overline{P B_{1}}\right|}{\left|\overline{B_{1} B_{3}}\right|}=\frac{(\sin \measuredangle A C B)^{2}}{(\sin \measuredangle A P B)^{2}} \leq 1,
$$
was die Behauptung impliziert.
Anmerkung: Viele der Teilnehmenden haben statt der eigentlich gestellten Aufgabe das (deutlich einfachere) Problem gelöst, in dem $P$ an den drei Seiten des Dreiecks statt an den Punkten $A_{1}, B_{1}$, und $C_{1}$ gespiegelt wird, und gezeigt, dass mindestens einer der resultierenden Spiegelpunkte nicht außerhalb des Dreiecks liegt.
|
{
"resource_path": "Germany_TST/segmented/de-2020-loes_awkl_20.jsonl",
"problem_match": "\nAufgabe 2.",
"solution_match": "\nLösung."
}
|
eb057453-8f25-5930-ab0d-22125579108a
| 605,346
|
Let $\varepsilon>0$ be given. Show that there exist integers $a, b$, and $c$, not all zero, such that the inequality $|a \sqrt{2}+b \sqrt{3}+c \sqrt{5}|<\varepsilon$ is satisfied.
Furthermore, prove that in every triple $(a, b, c) \neq(0,0,0)$ of integers for which this inequality holds, at least one of the absolute values $|a|,|b|,|c|$ is greater than $\varepsilon^{-1 / 3} / \sqrt{30}$.
|
In the first proof of the first part, for a real number $x$, let $[x]$ be the greatest integer not greater than $x$ (Gauss bracket), and the number $\langle x\rangle:=x-[x] \in[0,1)$ is referred to as the fractional part of $x$.
We choose an integer $n>\sqrt{2} \varepsilon^{-1}$. By the pigeonhole principle, there exist different indices $i, j \in\{0,1, \ldots, n\}$, such that $\langle i \sqrt{6}\rangle$ and $\langle j \sqrt{6}\rangle$ lie in the same of the $n$ intervals
$$
\left[0, \frac{1}{n}\right),\left[\frac{1}{n}, \frac{2}{n}\right), \ldots,\left[\frac{n-1}{n}, 1\right)
$$
Then there exists an integer $a$ such that $|a-(i \sqrt{6}-j \sqrt{6})|<1 / n$. This implies, by multiplying with $\sqrt{2}$, for $b:=2(j-i)$, the inequality $|a \sqrt{2}+b \sqrt{3}|<\sqrt{2} / n<\varepsilon$, which, with $c=0$, leads to the inequality in the problem statement.
The second proof avoids the pigeonhole principle: Since $0<\sqrt{6}-2<1$, we find a positive integer $k$ such that $X=(\sqrt{6}-2)^{k} \in(0, \varepsilon / \sqrt{3})$. Clearly, there exist non-zero integers $a_{0}, b_{0}$ such that $X=a_{0} \sqrt{6}+b_{0}$. We set $a=3 a_{0}, b=b_{0}, c=0$, then $|a \sqrt{2}+b \sqrt{3}+c \sqrt{5}|=\left|\sqrt{3}\left(a_{0} \sqrt{3} \sqrt{2}+b_{0}\right)\right|=\sqrt{3} X<\varepsilon$.
Note: It is also possible to derive this part of the problem in a few lines from Dirichlet's approximation theorem or Minkowski's lattice point theorem. However, during the correction, it was emphasized that these theorems were cited exactly.
For the (more difficult) second part of the problem, we assume that $a, b$ and $c$ satisfy the inequality. We first calculate that the following expression is an integer.
$$
\begin{aligned}
Z & :=(a \sqrt{2}+b \sqrt{3}+c \sqrt{5})(a \sqrt{2}-b \sqrt{3}-c \sqrt{5})(a \sqrt{2}+b \sqrt{3}-c \sqrt{5})(a \sqrt{2}-b \sqrt{3}+c \sqrt{5}) \\
& =\left(2 a^{2}-\left(3 b^{2}+2 \sqrt{15} b c+5 c^{2}\right)\right)\left(2 a^{2}-\left(3 b^{2}-2 \sqrt{15} b c+5 c^{2}\right)\right) \\
& =\left(2 a^{2}-3 b^{2}-5 c^{2}\right)^{2}-60 b^{2} c^{2}
\end{aligned}
$$
This number is non-zero, because otherwise 60 would be the square of a rational number, which is not the case due to the unique prime factorization of positive integers. Thus, $|Z| \geq 1$. On the other hand, $|Z|$ can be bounded from above as follows
$$
\begin{aligned}
|Z| & <|a \sqrt{2}+b \sqrt{3}+c \sqrt{5}| \cdot(|a| \sqrt{2}+|b| \sqrt{3}+|c| \sqrt{5})^{3} \\
& <\varepsilon\left((2+3+5)^{\frac{1}{2}} \cdot\left(a^{2}+b^{2}+c^{2}\right)^{\frac{1}{2}}\right)^{3} \\
& <\left(\varepsilon^{1 / 3} \sqrt{10} \cdot \sqrt{3} \cdot \max (|a|,|b|,|c|)\right)^{3}
\end{aligned}
$$
where we used the Cauchy-Schwarz inequality in the second step. After rearrangement, the claim follows.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Es sei $\varepsilon>0$ gegeben. Zeigen Sie, dass es ganze Zahlen $a, b$ und $c$ gibt, die nicht alle 0 sind, sodass die Ungleichung $|a \sqrt{2}+b \sqrt{3}+c \sqrt{5}|<\varepsilon$ erfüllt ist.
Beweisen Sie außerdem, dass in jedem Tripel $(a, b, c) \neq(0,0,0)$ ganzer Zahlen, für das diese Ungleichung gilt, mindestens einer der Absolutbeträge $|a|,|b|,|c|$ größer als $\varepsilon^{-1 / 3} / \sqrt{30}$ ist.
|
Im ersten Beweis des ersten Teils bezeichnen wir für eine reelle Zahl $x$ sei $[x]$ die größte ganze Zahl, die nicht größer als $x$ ist (Gauß-Klammer), die Zahl $\langle x\rangle:=x-[x] \in[0,1)$ wird als als gebrochener Anteil von $x$ bezeichnet.
Wir wählen eine ganze Zahl $n>\sqrt{2} \varepsilon^{-1}$. Nach dem Schubfachprinzip existieren verschiedene Indizes $i, j \in\{0,1, d \ldots, n\}$, sodass $\langle i \sqrt{6}\rangle$ und $\langle j \sqrt{6}\rangle$ im gleichen der $n$ Intervalle
$$
\left[0, \frac{1}{n}\right),\left[\frac{1}{n}, \frac{2}{n}\right), \ldots,\left[\frac{n-1}{n}, 1\right)
$$
liegen. Dann existiert eine ganze Zahl $a$, sodass $|a-(i \sqrt{6}-j \sqrt{6})|<1 / n$ gilt. Daraus folgt durch Multiplikation mit $\sqrt{2}$, für $b:=2(j-i)$, die Ungleichung $|a \sqrt{2}+b \sqrt{3}|<\sqrt{2} / n<\varepsilon$, was mit $c=0$ auf die Ungleichung im Aufgabentext führt.
Der zweite Beweis kommt ohne das Schubfachprinzip aus: Wegen $0<\sqrt{6}-2<1$ finden wir eine positive ganze Zahl $k$, sodass $X=(\sqrt{6}-2)^{k} \in(0, \varepsilon / \sqrt{3})$. Offenbar gibt es von 0 verschiedene ganze Zahlen $a_{0}, b_{0}$, sodass $X=a_{0} \sqrt{6}+b_{0}$. Wir setzen nun $a=3 a_{0}, b=b_{0}, c=0$, dann gilt $|a \sqrt{2}+b \sqrt{3}+c \sqrt{5}|=\left|\sqrt{3}\left(a_{0} \sqrt{3} \sqrt{2}+b_{0}\right)\right|=\sqrt{3} X<\varepsilon$.
Anmerkung: es ist auch möglich, diesen Teil der Aufgabe in wenigen Zeilen aus dem Dirichletschen Approximationssatz oder dem Gitterpunktsatz von Minkowski herzuleiten. Bei der Korrektur wurde aber Wert darauf gelegt, dass diese Sätze genau zitiert wurden.
Für den (schwierigeren) zweiten Teil der Aufgabe nehmen wir an, dass $a, b$ und $c$ die Ungleichung erfüllen. Wir berechnen zunächst, dass es sich beim folgenden Ausdruck um eine ganze Zahl handelt.
$$
\begin{aligned}
Z & :=(a \sqrt{2}+b \sqrt{3}+c \sqrt{5})(a \sqrt{2}-b \sqrt{3}-c \sqrt{5})(a \sqrt{2}+b \sqrt{3}-c \sqrt{5})(a \sqrt{2}-b \sqrt{3}+c \sqrt{5}) \\
& =\left(2 a^{2}-\left(3 b^{2}+2 \sqrt{15} b c+5 c^{2}\right)\right)\left(2 a^{2}-\left(3 b^{2}-2 \sqrt{15} b c+5 c^{2}\right)\right) \\
& =\left(2 a^{2}-3 b^{2}-5 c^{2}\right)^{2}-60 b^{2} c^{2}
\end{aligned}
$$
Diese Zahl ist von 0 verschieden, denn ansonsten wäre 60 das Quadrat einer rationalen Zahl, was aufgrund der eindeutigen Primfaktorzerlegung positiver ganzer Zahlen aber nicht der Fall ist. Damit gilt $|Z| \geq 1$. Andererseits lässt sich $|Z|$ wie folgt nach oben abschätzen
$$
\begin{aligned}
|Z| & <|a \sqrt{2}+b \sqrt{3}+c \sqrt{5}| \cdot(|a| \sqrt{2}+|b| \sqrt{3}+|c| \sqrt{5})^{3} \\
& <\varepsilon\left((2+3+5)^{\frac{1}{2}} \cdot\left(a^{2}+b^{2}+c^{2}\right)^{\frac{1}{2}}\right)^{3} \\
& <\left(\varepsilon^{1 / 3} \sqrt{10} \cdot \sqrt{3} \cdot \max (|a|,|b|,|c|)\right)^{3}
\end{aligned}
$$
wobei wir im zweiten Schritt die Ungleichung von Cauchy-Schwarz verwendet haben. Nach Umstellung folgt die Behauptung.
|
{
"resource_path": "Germany_TST/segmented/de-2020-loes_awkl_20.jsonl",
"problem_match": "\nAufgabe 3.",
"solution_match": "\nLösung."
}
|
24d549b7-7650-5d27-b835-4b0f79002783
| 605,355
|
Let $ABCD$ be a convex parallelogram that is acute-angled at $A$. The reflection points of $A$ across the lines $BC$ and $CD$ are denoted by $P$ and $Q$, respectively. Moreover, the line $BD$ intersects the segments $\overline{AP}$ and $\overline{AQ}$ internally at the points $R$ and $S$, respectively.
Prove that the circumcircles of triangles $BRP$ and $DQS$ touch each other.
|
We consider the reflection point $Z$ of $A$ when reflected across $BD$. We will prove that the two circles mentioned in the problem statement touch at $Z$.
First, because $\measuredangle B Z R = \measuredangle R A B = \measuredangle B P R$ and by the converse of the inscribed angle theorem, it is clear that $Z$ lies on the circumcircle $\omega_{1}$ of $B R P$. Similarly, one can show that $Z$ also lies on the circumcircle $\omega_{2}$ of $D Q S$. The tangent-chord angle of the chord $Z B$ of $\omega_{1}$ is $\angle Z R B = \measuredangle B R A$. Since $A R$ is perpendicular to $B C$ and thus also to $A D$, this angle has the size $90^{\circ} - \angle A D B$. Similarly, one can show that the tangent-chord angle of the chord $Z D$ of $\omega_{2}$ is $90^{\circ} - \angle D B A$. The sum of these two angles is now $180^{\circ} - \measuredangle A D B - \angle D B A = \angle B A D = \angle D Z B$, which shows that the tangents to $\omega_{1}$ and $\omega_{2}$ at point $Z$ coincide. Therefore, the two circles indeed touch each other.
[^0]
# Selection Competition for the International Mathematical Olympiad 2021
Example Solutions and Hints for the 2nd Selection Test
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Es sei $A B C D$ ein konvexes Parallelogramm, das bei $A$ spitzwinklig ist. Die Spiegelpunkte von $A$ an den Geraden $B C$ und $C D$ seien mit $P$ bzw. $Q$ bezeichnet. Außerdem schneidet die Gerade $B D$ die Strecken $\overline{A P}$ und $\overline{A Q}$ im Inneren in den Punkten $R$ bzw. $S$.
Beweisen Sie, dass sich die Umkreise der Dreiecke $B R P$ und $D Q S$ berühren.
|
Wir betrachten den Spiegelpunkt $Z$ von $A$ bei Spiegelung an $B D$. Wir werden beweisen, dass sich die beiden in der Aufgabenstellung erwähnten Kreise in $Z$ berühren.

Zunächst ist wegen $\measuredangle B Z R=\measuredangle R A B=\measuredangle B P R$ und der Umkrehrung des Peripheriewinkelsatzes klar, dass $Z$ auf dem Umkreis $\omega_{1}$ von $B R P$ liegt. Analog zeigt man, dass $Z$ auch auf dem Umkreis $\omega_{2}$ von $D Q S$ liegt. Der Sehnen-Tangentenwinkel der Sehne $Z B$ von $\omega_{1}$ ist $\angle Z R B=\measuredangle B R A$. Da $A R$ auf $B C$ und damit auch auf $A D$ senkrecht steht, hat dieser Winkel die Größe $90^{\circ}-\angle A D B$. Analog zeigt man, dass der Sehnen-Tangentenwinkel der Sehne $Z D$ von $\omega_{2}$ gleich $90^{\circ}-\angle D B A$ ist. Die Summe dieser beiden Winkel beträgt nun $180^{\circ}-\measuredangle A D B-\angle D B A=\angle B A D=\angle D Z B$, was zeigt, dass die Tangenten an $\omega_{1}$ und $\omega_{2}$ im Punkt $Z$ übereinstimmen. Somit berühren sich beide Kreise wirklich.
[^0]
# Auswahlwettbewerb zur Internationalen Mathematik-Olympiade 2021
Beispiellösungen und Hinweise zur 2. Auswahlklausur
|
{
"resource_path": "Germany_TST/segmented/de-2021-2021_IMO_Auswahlklausuren_Lsg_HP.jsonl",
"problem_match": "\nAufgabe 3.",
"solution_match": "\nLösung."
}
|
5f34678b-fd95-5e1c-bc5d-95ed5c8d1663
| 605,378
|
Prove that for any nonnegative integer $z$ there is a unique ordered pair $(m, n)$ of positive integers $m, n$ such that $2 z=(m+n)^{2}-m-3 n$ (1) holds.
|
Rewriting (1) yields $2 z=(m+n-1)^{2}+m-n-1=2 m-2+(m+n-1)(m+n-1-1)$, from which $z+1=m+\frac{(m+n-1)(m+n-2)}{2}$ follows. We set $m+n-1=k$ and obtain $z+1=m+\frac{k(k-1)}{2}(2)$, where $0<m \leq k$ and $k \in \mathbb{Z}, k \geq 1$ holds. Additionally, $\frac{k(k-1)}{2} \in \mathbb{Z}$.
Obviously, for every positive integer $z+1$ there is exactly one $k$ with
$\frac{k(k-1)}{2}<z+1 \leq \frac{k(k-1)}{2}+k=\frac{(k+1) k}{2}$.
Then $m=z+1-\frac{k(k-1)}{2}$ and $n=k+1-m$ are uniquely determined positive integers such that (2) provides a unique representation of every positive integer $z+1$ and thus of every non-negative integer $z$ by $m$ and $n$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Beweisen Sie, dass es für jede beliebige nichtnegative ganze Zahl $z$ genau ein geordnetes Paar $(m, n)$ positiver ganzer Zahlen $m, n$ gibt, so dass $2 z=(m+n)^{2}-m-3 n$ (1) gilt.
|
Umformen von (1) ergibt $2 z=(m+n-1)^{2}+m-n-1=2 m-2+(m+n-1)(m+n-1-1)$, woraus $z+1=m+\frac{(m+n-1)(m+n-2)}{2}$ folgt. Wir setzen $m+n-1=k$ und erhalten $z+1=m+\frac{k(k-1)}{2}(2)$, wobei $0<m \leq k$ und $k \in \mathbb{Z}, k \geq 1$ gilt. Außerdem ist $\frac{k(k-1)}{2} \in \mathbb{Z}$.
Offensichtlich gibt es zu jeder positiven ganzen Zahl $z+1$ genau ein $k$ mit
$\frac{k(k-1)}{2}<z+1 \leq \frac{k(k-1)}{2}+k=\frac{(k+1) k}{2}$.
Dann sind auch $m=z+1-\frac{k(k-1)}{2}$ und $n=k+1-m$ eindeutig bestimmte positive ganze
Zahlen, so dass (2) eine eindeutige Darstellung jeder positiven ganzen Zahl $z+1$ und damit jeder nichtnegativen ganzen Zahl $z$ durch $m$ und $n$ liefert.
|
{
"resource_path": "Germany_TST/segmented/de-2021-2021_IMO_Auswahlklausuren_Lsg_HP.jsonl",
"problem_match": "# Aufgabe 1",
"solution_match": "# Erste Lösung:"
}
|
31de23c7-cfa2-5026-a21a-3db7c64f45f8
| 605,391
|
Prove that for any nonnegative integer $z$ there is a unique ordered pair $(m, n)$ of positive integers $m, n$ such that $2 z=(m+n)^{2}-m-3 n$ (1) holds.
|
Rewriting (1) yields $2 z=(m+n)(m+n-1)-2 n$. We notice that the right-hand side is always even and set $m+n=k$. For a constant $k(k \geq 2)$, $n$ can take the values $1,2, \ldots, k-1$, so that the right-hand side yields different even numbers from $k(k-1)-2$ to $k(k-1)-2(k-1)=(k-1)(k-2)$. For $k=2,3, \ldots$, this results in a complete, disjoint partition of the set of all non-negative even integers. The number $2 z$ therefore lies in exactly one interval determined by $k$ at a position determined by $n$, which uniquely determines $m$ as well.
Hints: The proof can also be conducted using mathematical induction. The appearance of the triangular numbers $\frac{k(k-1)}{2}$ allows for a beautiful geometric representation of the different intervals in which $2 z$ can lie.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Beweisen Sie, dass es für jede beliebige nichtnegative ganze Zahl $z$ genau ein geordnetes Paar $(m, n)$ positiver ganzer Zahlen $m, n$ gibt, so dass $2 z=(m+n)^{2}-m-3 n$ (1) gilt.
|
Umformen von (1) ergibt $2 z=(m+n)(m+n-1)-2 n$. Wir bemerken, dass die rechte Seite stets gerade ist und setzen $m+n=k$. Für konstantes $k(k \geq 2)$ kann $n$ die Werte $1,2, \ldots, k-1$ annehmen, so dass die rechte Seite jeweils verschiedene gerade Zahlen von $k(k-1)-2$ bis $k(k-1)-2(k-1)=(k-1)(k-2)$ liefert. Für $k=2,3, \ldots$ entsteht so eine vollständige, disjunkte Zerlegung der Menge aller nichtnegativer gerader ganzer Zahlen. Die Zahl $2 z$ liegt daher in genau einem durch $k$ bestimmten Intervall an einer durch $n$ bestimmten Stelle, womit dafür auch $m$ eindeutig bestimmt ist. .
Hinweise: Der Beweis lässt sich auch mit vollständiger Induktion führen. Das Auftauchen der Dreieckszahlen $\frac{k(k-1)}{2}$ erlaubt eine schöne geometrische Darstellung der verschiedenen Intervalle, in denen $2 z$ liegen kann.
|
{
"resource_path": "Germany_TST/segmented/de-2021-2021_IMO_Auswahlklausuren_Lsg_HP.jsonl",
"problem_match": "# Aufgabe 1",
"solution_match": "# Zweite Lösung:"
}
|
31de23c7-cfa2-5026-a21a-3db7c64f45f8
| 605,391
|
In an isosceles triangle $ABC$ with $\overline{BC} = \overline{CA}$, let $D$ be a point inside the side $AB$ such that $\overline{AD} < \overline{DB}$. Furthermore, let $P$ and $Q$ be two points inside the sides $BC$ and $CA$, respectively, such that $\angle DPB = \angle AQD = 90^\circ$. The perpendicular bisector of $PQ$ intersects $CQ$ at point $E$, and the circumcircles of triangles $ABC$ and $QPC$ intersect at another point $F$ besides $C$.
Prove: If $P$, $E$, and $F$ are collinear, then $\angle ACB = 90^\circ$.
## NATIONAL <br> MATHEMATICS COMPETITIONS
Education & Talent
|
We denote the perpendicular bisector of the segment $P Q$ by $m$ and the circle $Q P C F$ by $k$. Because $D P \perp B C$ and $D Q \perp A C$, $D$ also lies on $k$ and $C D$ is even the diameter of $k$. The segments $Q E$ and $P E$ are symmetric with respect to $m$; simultaneously, $m$ is also the axis of symmetry of $k$. Therefore, the chords $C Q$ and $F P$ are symmetric to $m$, and thus $C$ and $F$ are symmetric (by assumption, $P, E$, and $F$ are collinear!). Hence, the perpendicular bisector of $C F$ coincides with $m$; it follows that $m$ passes through the circumcenter $O$ of $A B C$.
Now consider the midpoint $M$ of the segment $A B$. Because $C M \perp D M$, $M$ also lies on $k$. Since $\angle A C M = \angle M C B$, it follows from the inscribed angle theorem that the chords $M P$ and $M Q$ of $k$ are of equal length. This shows that $m$ passes through $M$. Since both $O$ and $M$ lie on $m$ and on $C M$, it follows that $O = M$ and thus $\angle A C B = 90^{\circ}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In einem gleichschenkligen Dreieck $A B C$ mit $\overline{B C}=\overline{C A}$ sei $D$ ein Punkt im Inneren der Seite $A B$, für den $\overline{A D}<\overline{D B}$ gilt. Weiter seien $P$ und $Q$ zwei Punkte im Inneren der Seiten $B C$ bzw. $C A$, so dass $\angle D P B=\angle A Q D=90^{\circ}$ gilt. Die Mittelsenkrechte von $P Q$ schneide $C Q$ im Punkt $E$, und die Umkreise der Dreiecke $A B C$ und $Q P C$ schneiden sich außer in $C$ in einem weiteren Punkt $F$.
Beweisen Sie: Wenn $P, E$ und $F$ kollinear sind, dann gilt $\angle A C B=90^{\circ}$.
## BUNDESWEITE <br> MATHEMATIK-WETTBEWERBE
Bildung \& Begabung
|
Wir bezeichnen die Mittelsenkrechte der Strecke $P Q$ mit $m$ und den Kreis $Q P C F$ mit $k$. Wegen $D P \perp B C$ und $D Q \perp A C$ liegt auch $D$ auf $k$ und $C D$ ist sogar Durchmesser von $k$. Die Strecken $Q E$ und $P E$ liegen symmetrisch zu $m$; gleichzeitig ist $m$ auch Symmetrieachse von $k$. Daher sind die Sehnen $C Q$ und $F P$ symmetrisch zu $m$, also auch $C$ und $F$ (nach
Voraussetzung sind $P, E$ und $F$ kollinear!). Somit stimmt die Mittelsenkrechte von $C F$ mit $m$ überein; es folgt, dass $m$ durch den Umkreismittelpunkt $O$ von $A B C$ verläuft.
Nun betrachten wir den Mittelpunkt $M$ der Strecke $A B$. Wegen $C M \perp D M$ liegt $M$ auch
auf $k$. Wegen $\angle A C M=\angle M C B$ folgt aus dem Umfangswinkelsatz, dass die Sehnen $M P$ und $M Q$ von $k$ gleich lang sind. Damit ist aber gezeigt, dass $m$ durch $M$ verläuft. Da sowohl $O$ als auch $M$ auf $m$ und auf $C M$ liegen, folgt $O=M$ und damit $\angle A C B=90^{\circ}$.
|
{
"resource_path": "Germany_TST/segmented/de-2021-2021_IMO_Auswahlklausuren_Lsg_HP.jsonl",
"problem_match": "# Aufgabe 2",
"solution_match": "# Erste Lösung:"
}
|
086dbbe8-1baf-54ef-8e12-32efe76ee765
| 605,414
|
In an isosceles triangle $ABC$ with $\overline{BC} = \overline{CA}$, let $D$ be a point inside the side $AB$ such that $\overline{AD} < \overline{DB}$. Furthermore, let $P$ and $Q$ be two points inside the sides $BC$ and $CA$, respectively, such that $\angle DPB = \angle AQD = 90^\circ$. The perpendicular bisector of $PQ$ intersects $CQ$ at point $E$, and the circumcircles of triangles $ABC$ and $QPC$ intersect at another point $F$ besides $C$.
Prove: If $P$, $E$, and $F$ are collinear, then $\angle ACB = 90^\circ$.
## NATIONAL <br> MATHEMATICS COMPETITIONS
Education & Talent
|
As outlined in the first solution, we find that the points $P, C, F, Q, D$, and the midpoint $M$ of $AB$ lie on the circle $k$ with diameter $CD$, and that the perpendicular bisector $m$ of $PQ$ passes through $M$.
Let $G$ be the intersection of $BF$ and $CM$, and let $\alpha = \angle FBA$. Since $E$ lies on $m$, since $P, E$, and $F$ are collinear,

and since $CFAB$ and $CFQP$ are cyclic quadrilaterals, it follows that $\angle PQC = \angle PQE = \angle EPQ = \angle FPQ = \angle FCQ = \angle FCA = \angle FBA = \alpha$.
Furthermore, $\angle FEM = \angle FEQ + \angle QEM = 2\alpha + (90^\circ - \alpha) = 90^\circ + \alpha$. Similarly, using exterior angles, $\angle FGM = 90^\circ + \alpha$; hence, $MGFE$ is a cyclic quadrilateral.
It follows that $\angle CGE = \angle MFE = \angle MFP = \angle MCP$. Therefore, $GE \parallel BC$ and thus we obtain $\angle EAF = \angle CAF = \angle CBF = \angle EGF$, so that $GEFA$ is also a cyclic quadrilateral. This implies $\angle ACB = \angle AFB = \angle AFG = 180^\circ - \angle GMA = 90^\circ$, which is what we needed to show.
Hints: The converse of the statement to be proven also holds; therefore, it is important to distinguish between the premise and the conclusion to avoid circular reasoning. A proof using the intercept theorem is also possible, whereas approaches using spiral similarity did not lead to a solution.
## NATIONAL <br> MATHEMATICS COMPETITIONS
Education & Talent
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In einem gleichschenkligen Dreieck $A B C$ mit $\overline{B C}=\overline{C A}$ sei $D$ ein Punkt im Inneren der Seite $A B$, für den $\overline{A D}<\overline{D B}$ gilt. Weiter seien $P$ und $Q$ zwei Punkte im Inneren der Seiten $B C$ bzw. $C A$, so dass $\angle D P B=\angle A Q D=90^{\circ}$ gilt. Die Mittelsenkrechte von $P Q$ schneide $C Q$ im Punkt $E$, und die Umkreise der Dreiecke $A B C$ und $Q P C$ schneiden sich außer in $C$ in einem weiteren Punkt $F$.
Beweisen Sie: Wenn $P, E$ und $F$ kollinear sind, dann gilt $\angle A C B=90^{\circ}$.
## BUNDESWEITE <br> MATHEMATIK-WETTBEWERBE
Bildung \& Begabung
|
Wie in der ersten Lösung ausgeführt, stellen wir fest, dass die Punkte $P, C, F, Q, D$ und der Mittelpunkt $M$ von $A B$ auf dem Kreis $k$ mit Durchmesser $C D$ liegen, und dass die Mittelsenkrechte $m$ von $P Q$ durch $M$ verläuft.
Es sei $G$ der Schnittpunkt von $B F$ und $C M$ und wir bezeichnen $\alpha=\angle F B A$. Weil $E$ auf $m$ liegt, weil $P, E$ und $F$ kollinear sind,

und weil $C F A B$ und $C F Q P$ Sehnenvierecke sind, folgt $\angle P Q C=\angle P Q E=\angle E P Q=\angle F P Q=\angle F C Q=\angle F C A=\angle F B A=\alpha$.
Weiter gilt $\angle F E M=\angle F E Q+\angle Q E M=2 \alpha+\left(90^{\circ}-\alpha\right)=90^{\circ}+\alpha$. Ebenfalls mit Außenwinkeln gilt $\angle F G M=90^{\circ}+\alpha$; daher ist $M G E F$ ein Sehnenviereck.
Es folgt $\angle C G E=\angle M F E=\angle M F P=\angle M C P$. Also ist $G E \| B C$ und damit erhalten wir $\angle E A F=\angle C A F=\angle C B F=\angle E G F$, so dass $G E F A$ ebenfalls ein Sehnenviereck ist. Daraus folgt $\angle A C B=\angle A F B=\angle A F G=180^{\circ}-\angle G M A=90^{\circ}$, was zu zeigen war.
Hinweise: Es gilt auch die Umkehrung der zu beweisenden Aussage; daher ist auf die Unterscheidung von Voraussetzung und Behauptung zu achten, um Zirkelschlüsse zu vermeiden. Ein Beweis mit Strahlensatz ist ebenfalls möglich, dagegen führten Ansätze mit Drehstreckung (,„spiral similarity") nicht zum Ziel.
## BUNDESWEITE <br> MATHEMATIK-WETTBEWERBE
Bildung \& Begabung
|
{
"resource_path": "Germany_TST/segmented/de-2021-2021_IMO_Auswahlklausuren_Lsg_HP.jsonl",
"problem_match": "# Aufgabe 2",
"solution_match": "# Zweite Lösung:"
}
|
086dbbe8-1baf-54ef-8e12-32efe76ee765
| 605,414
|
The greatest common divisor of two positive integers $m$ and $n$ is denoted by $\operatorname{ggT}(m, n)$.
Let there be an infinite set $S$ of positive integers such that there exist four pairwise distinct numbers $v, w, x, y \in S$ for which $\operatorname{ggT}(v, w) \neq \operatorname{ggT}(x, y)$ holds.
Prove that there exist three pairwise distinct numbers $a, b, c \in S$ such that $\operatorname{ggT}(a, b) = \operatorname{ggT}(a, c) \neq \operatorname{ggT}(b, c)$ holds.
|
In the following, we call a three-element subset $\{s, t, u\} \subset S$ a balanced triangle if the set $\{\mathrm{ggT}(s, t), \operatorname{ggT}(s, u), \operatorname{ggT}(t, u)\}$ has exactly two different elements. It is to be shown that there exists a balanced triangle.
Lemma. For pairwise different numbers $a, b, c, d \in S$, such that $\operatorname{ggT}(a, b)=\operatorname{ggT}(a, c) \neq \operatorname{ggT}(a, d)$ and $\operatorname{ggT}(b, d)=\operatorname{ggT}(c, d)$, the set $\{a, b, c, d\}$ contains a balanced triangle.
Proof. If $\operatorname{ggT}(a, b)=\operatorname{ggT}(b, d)$, then $\{a, b, d\}$ is a balanced triangle. Otherwise, either $\operatorname{ggT}(a, d) \neq \operatorname{ggT}(a, b)$ or $\operatorname{ggT}(a, d) \neq \operatorname{ggT}(b, d)$, so $\{a, b, c\}$ or $\{b, c, d\}$ is a balanced triangle.
For each element $a \in S$, let $S_{a}=\{\operatorname{ggT}(a, s) \mid s \in S, s \neq a\}$. Since this set contains only divisors of $a$, it is finite. From the assumption, we can choose $a \in S$ such that $S_{a}$ has at least two elements, otherwise $\operatorname{ggT}(v, w)=\operatorname{ggT}(w, x)=\operatorname{ggT}(x, y)$ would hold.
By the pigeonhole principle, we find an infinite subset $T \subset S$ such that $\operatorname{ggT}(a, t)$ is the same value $g$ for all $t \in T$. Now we choose a $d \in S \backslash(T \cup\{a\})$ such that $\operatorname{ggT}(a, d) \neq g$, which must exist due to $\left|S_{a}\right|>1$. Since $S_{d}$ is also finite, we find by the pigeonhole principle two different elements $b, c \in T$ such that $\operatorname{ggT}(b, d)=\operatorname{ggT}(c, d)$. Then $a, b, c, d$ satisfy the conditions of the lemma, so indeed there exists a balanced triangle.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Der größte gemeinsame Teiler zweier positiver ganzer Zahlen $m$ und $n$ sei mit $\operatorname{ggT}(m, n)$ bezeichnet.
Es sei eine unendliche Menge $S$ positiver ganzer Zahlen gegeben, sodass es vier paarweise verschiedene Zahlen $v, w, x, y \in S$ gibt, für die $\operatorname{ggT}(v, w) \neq \operatorname{ggT}(x, y)$ gilt.
Beweisen Sie, dass es drei paarweise verschiedene Zahlen $a, b, c \in S$ gibt, für die $\operatorname{ggT}(a, b)=$ $\operatorname{ggT}(a, c) \neq \operatorname{ggT}(b, c)$ gilt.
|
Im folgenden nennen wir eine dreielementige Teilmenge $\{s, t, u\} \subset S$ ein ausgewogenes Dreieck, falls die Menge $\{\mathrm{ggT}(s, t), \operatorname{ggT}(s, u), \operatorname{ggT}(t, u)\}$ genau zwei verschiedene Elemente hat. Es ist zu zeigen, dass es ein ausgewogenes Dreieck gibt.
Lemma. Für paarweise verschiedene Zahlen $a, b, c, d \in S$, sodass $\operatorname{ggT}(a, b)=\operatorname{ggT}(a, c) \neq$ $\operatorname{ggT}(a, d)$ und $\operatorname{ggT}(b, d)=\operatorname{ggT}(c, d)$ gilt, enthält die Menge $\{a, b, c, d\}$ ein ausgewogenes Dreieck.
Beweis. Falls $\operatorname{ggT}(a, b)=\operatorname{ggT}(b, d)$, dann ist $\{a, b, d\}$ ein ausgewogenes Dreieck. Ansonsten gilt entweder $\operatorname{ggT}(a, d) \neq \operatorname{ggT}(a, b)$ oder $\operatorname{ggT}(a, d) \neq \operatorname{ggT}(b, d)$, also ist $\{a, b, c\}$ oder $\{b, c, d\}$ ein ausgewogenes Dreieck.

Für jedes Element $a \in S$ sei $S_{a}=\{\operatorname{ggT}(a, s) \mid s \in S, s \neq a\}$. Da diese Menge nur Teiler von $a$ enthält, ist sie endlich. Aus der Voraussetzung folgt, dass wir $a \in S$ so wählen können, dass $S_{a}$ mindestens zwei Elemente enthält, da ansonsten $\operatorname{ggT}(v, w)=\operatorname{ggT}(w, x)=\operatorname{ggT}(x, y)$ gelten würde.
Nach dem Schubfachprinzip finden wir eine unendliche Teilmenge $T \subset S$, sodass $\operatorname{ggT}(a, t)$ der gleiche Wert $g$ ist für alle $t \in T$. Nun wählen wir ein $d \in S \backslash(T \cup\{a\})$ sodass $\operatorname{ggT}(a, d) \neq g$, das wegen $\left|S_{a}\right|>1$ existieren muss. Da auch $S_{d}$ endlich ist, finden wir nach dem Schubfachprinzip zwei verschiedene Elemente $b, c \in T$ sodass $\operatorname{ggT}(b, d)=\operatorname{ggT}(c, d)$ gilt. Dann erfüllen $a, b, c, d$ die Voraussetzungen des Lemmas, also existiert in der Tat ein ausgewogenes Dreieck.
|
{
"resource_path": "Germany_TST/segmented/de-2022-2022_IMO_Auswahlklausuren_Lsg_HP.jsonl",
"problem_match": "\nAufgabe 1.",
"solution_match": "\nErste Lösung."
}
|
0cc9e428-d294-58ff-b2f6-88282a8ebee0
| 605,447
|
The greatest common divisor of two positive integers $m$ and $n$ is denoted by $\operatorname{ggT}(m, n)$.
Let there be an infinite set $S$ of positive integers such that there exist four pairwise distinct numbers $v, w, x, y \in S$ for which $\operatorname{ggT}(v, w) \neq \operatorname{ggT}(x, y)$ holds.
Prove that there exist three pairwise distinct numbers $a, b, c \in S$ such that $\operatorname{ggT}(a, b) = \operatorname{ggT}(a, c) \neq \operatorname{ggT}(b, c)$ holds.
|
We may assume w.l.o.g. that no integer $g>1$ divides all numbers in $S$, since otherwise we could choose the largest such number $g$ and replace $S$ with the set $S^{\prime}=\{s / g \mid s \in S\}$: If the claim holds for $S^{\prime}$, then it also holds for $S$.
## NATIONAL <br> MATHEMATICS COMPETITIONS
Education & Talent
Assume for a prime $p$ the subset $S_{p} \subset S$ of all numbers divisible by $p$ is infinitely large, then we choose $a \in S \backslash S_{p}$, which is possible due to the preliminary consideration. Since the numbers $\operatorname{gcd}(a, s)$ for $s \in S_{p}$ are divisors of $c$, by the pigeonhole principle there exist different $b, c \in S_{p}$ with $\operatorname{gcd}(a, b)=\operatorname{gcd}(a, c)$. Since $b, c$ are both divisible by $p$, it follows that $\operatorname{gcd}(b, c) \neq \operatorname{gcd}(a, c)$, thus proving the claim.
Therefore, we may assume that each prime divides only finitely many elements of $S$. Due to the assumption, we can now find numbers $b, c \in S$ that are not coprime. There are only finitely many primes that divide $b$ or $c$, so $S$ also contains only finitely many elements that are not coprime to $b$ or $c$. Thus, because $|S|=\infty$, we can choose an element $a \in S$ that is coprime to both $b$ and $c$. Then $a, b, c$ satisfy the claim.
Note: It is possible to construct arbitrarily large finite sets such that the corresponding statement does not hold, e.g., by choosing for different primes $p_{1}, p_{2}, \ldots, p_{r}$ with product $N=p_{1} \cdots p_{r}$ the set $S=\left\{N / p_{i} \mid i=1, \ldots, r\right\}$. Then $\operatorname{gcd}(x, y), x, y \in S$ are all different, so the assumption holds, but not the claim from the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Der größte gemeinsame Teiler zweier positiver ganzer Zahlen $m$ und $n$ sei mit $\operatorname{ggT}(m, n)$ bezeichnet.
Es sei eine unendliche Menge $S$ positiver ganzer Zahlen gegeben, sodass es vier paarweise verschiedene Zahlen $v, w, x, y \in S$ gibt, für die $\operatorname{ggT}(v, w) \neq \operatorname{ggT}(x, y)$ gilt.
Beweisen Sie, dass es drei paarweise verschiedene Zahlen $a, b, c \in S$ gibt, für die $\operatorname{ggT}(a, b)=$ $\operatorname{ggT}(a, c) \neq \operatorname{ggT}(b, c)$ gilt.
|
Wir dürfen o.B.d.A. voraussetzen, dass keine ganze Zahl $g>1$ alle Zahlen aus $S$ teilt, da wir sonst die größte derartige Zahl $g$ wählen und $S$ durch die Menge $S^{\prime}=\{s / g \mid s \in S\}$ ersetzen könnten: Falls die Behauptung für $S^{\prime}$ gilt, dann auch für $S$.
## BUNDESWEITE <br> MATHEMATIK-WETTBEWERBE
Bildung \& Begabung
Angenommen für eine Primzahl $p$ wäre die Teilmenge $S_{p} \subset S$ aller durch $p$ teilbaren Zahlen unendlich groß, dann wählen wir $a \in S \backslash S_{p}$, was wegen der Vorüberlegung möglich ist. Da die Zahlen $\operatorname{ggT}(a, s)$ für $s \in S_{p}$ Teiler von $c$ sind, gibt es nach dem Schubfachprinzip verschiedene $b, c \in S_{p}$ mit $\operatorname{ggT}(a, b)=\operatorname{ggT}(a, c)$. Da $b, c$ beide durch $p$ teilbar sind, folgt auch $\operatorname{ggT}(b, c) \neq$ $\operatorname{ggT}(a, c)$, also die Behauptung.
Somit dürfen wir annehmen, dass jede Primzahl nur endlich viele Elemente aus $S$ teilt. Wegen der Voraussetzung finden wir nun aber Zahlen $b, c \in S$, die nicht teilerfremd sind. Es gibt nur endlich viele Primzahlen, die $b$ oder $c$ teilen, also enthält $S$ auch nur endlich viele Elemente, die nicht zu $b$ oder $c$ teilerfremd sind. Somit können wir wegen $|S|=\infty$ ein Element $a \in S$ wählen, dass zu $b$ und $c$ teilerfremd ist. Dann erfüllen $a, b, c$ die Behauptung.
Anmerkung: Es ist möglich, beliebig große endliche Mengen konstruieren, sodass die entsprechende Aussage nicht gilt, z.B. indem man für verschiedene Primzahlen $p_{1}, p_{2}, \ldots, p_{r}$ mit Produkt $N=p_{1} \cdots p_{r}$ die Menge $S=\left\{N / p_{i} \mid i=1, \ldots, r\right\}$ wählt. Dann sind ggT $(x, y), x, y \in S$ alle verschieden, also gilt die Voraussetzung, aber nicht die Behauptung aus der Aufgabe.
|
{
"resource_path": "Germany_TST/segmented/de-2022-2022_IMO_Auswahlklausuren_Lsg_HP.jsonl",
"problem_match": "\nAufgabe 1.",
"solution_match": "\nZweite Lösung."
}
|
0cc9e428-d294-58ff-b2f6-88282a8ebee0
| 605,447
|
Let $ABCD$ be a parallelogram with $|AC|=|BC|$. A point $P$ is chosen on the ray $AB$ such that $B$ lies between $A$ and $P$. The circumcircle of triangle $ACD$ and the segment $PD$ intersect at a point $Q$ other than $D$. The circumcircle of triangle $APQ$ and the segment $PC$ intersect at a point $R$ other than $P$.
Prove that the three lines $CD$, $AQ$, and $BR$ intersect at a single point.
|
We worked with directed angles modulo 180 degrees. Initially, we recognize that from the condition $|A C|=|B C|$, it immediately follows that the angles $\angle B A C$, $\angle C B A$, $\angle D C A$, and $\angle A D C$ are all equal.
It suffices to show that the intersection point $S$ of the lines $A Q$ and $C D$ lies on the line $B R$. Since $\angle C S Q = \angle P A Q = \angle C R Q$, $C S R Q$ is a cyclic quadrilateral. Since $\angle C R A = 180^{\circ} - \angle A R P = 180^{\circ} - \angle A Q P = \angle D Q A = \angle D C A = \angle C B A$, $A B R C$ is also a cyclic quadrilateral. Therefore, $\angle S R C = \angle S Q C = \angle A D C = \angle B A C = \angle B R P$, which indeed implies that $P, R$, and $S$ lie on a straight line.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Es sei $A B C D$ ein Parallelogramm mit $|A C|=|B C|$. Ein Punkt $P$ sei auf dem Strahl $A B$ gewählt, sodass $B$ zwischen $A$ und $P$ liegt. Der Umkreis des Dreiecks $A C D$ und die Strecke $P D$ haben außer dem Punkt $D$ noch den Punkt $Q$ gemeinsam. Der Umkreis des Dreiecks $A P Q$ und die Strecke $P C$ haben außer dem Punkt $P$ noch den Punkt $R$ gemeinsam.
Beweisen Sie, dass sich die drei Geraden $C D, A Q$ und $B R$ in einem Punkt schneiden.
|
Wir arbeiteten mit gerichteten Winkeln modulo 180 Grad. Zunächst erkennen wir, dass aus der Voraussetzung $|A C|=|B C|$ unmittelbar folgt, dass die Winkel $\angle B A C$, $\angle C B A, \angle D C A$ und $\angle A D C$ allesamt gleich groß sind.

Es genügt zu zeigen, dass der Schnittpunkt $S$ der Geraden $A Q$ und $C D$ auf der Geraden $B R$ liegt. Wegen $\angle C S Q=\angle P A Q=\angle C R Q$ ist $C S R Q$ ein Sehnenviereck. Wegen $\angle C R A=180^{\circ}-$ $\angle A R P=180^{\circ}-\angle A Q P=\angle D Q A=\angle D C A=\angle C B A$ ist auch $A B R C$ ein Sehnenviereck. Also gilt $\angle S R C=\angle S Q C=\angle A D C=\angle B A C=\angle B R P$, woraus in der Tat folgt, dass $P, R$ und $S$ auf einer Geraden liegen.
|
{
"resource_path": "Germany_TST/segmented/de-2022-2022_IMO_Auswahlklausuren_Lsg_HP.jsonl",
"problem_match": "\nAufgabe 2.",
"solution_match": "\nErste Lösung."
}
|
8676d1fa-347c-54c2-a245-7ca99e66e7af
| 605,463
|
Let $ABCD$ be a parallelogram with $|AC|=|BC|$. A point $P$ is chosen on the ray $AB$ such that $B$ lies between $A$ and $P$. The circumcircle of triangle $ACD$ and the segment $PD$ intersect at a point $Q$ other than $D$. The circumcircle of triangle $APQ$ and the segment $PC$ intersect at a point $R$ other than $P$.
Prove that the three lines $CD$, $AQ$, and $BR$ intersect at a single point.
|
As shown in the first solution, to prove that $A B R C$ is a cyclic quadrilateral, we consider the intersection point $E$ of the lines $A D$ and $B R$. Then, $\angle E A P = \angle C B A = \angle B A C = \angle E R P$, which means that $E$ lies on the circumcircle of the cyclic quadrilateral $A P R Q$.
## NATIONAL <br> MATHEMATICS COMPETITIONS
Education & Talent
Now, $\angle C E R = \angle A P R = 180^{\circ} - \angle D C R$, so $E$ also lies on the circumcircle of triangle $R C D$. The pairwise radical axes of the circumcircles of $A C D$, $A P R$, and $R C D$ are thus the lines $C D$, $A Q$, and $R E = R B$, so they intersect at a single point. This implies the claim.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Es sei $A B C D$ ein Parallelogramm mit $|A C|=|B C|$. Ein Punkt $P$ sei auf dem Strahl $A B$ gewählt, sodass $B$ zwischen $A$ und $P$ liegt. Der Umkreis des Dreiecks $A C D$ und die Strecke $P D$ haben außer dem Punkt $D$ noch den Punkt $Q$ gemeinsam. Der Umkreis des Dreiecks $A P Q$ und die Strecke $P C$ haben außer dem Punkt $P$ noch den Punkt $R$ gemeinsam.
Beweisen Sie, dass sich die drei Geraden $C D, A Q$ und $B R$ in einem Punkt schneiden.
|
Wie in der ersten Lösung zeigt man, dass $A B R C$ ein Sehnenviereck ist. Wir betrachten den Schnittpunkt $E$ der Geraden $A D$ und $B R$. Dann gilt $\angle E A P=\angle C B A=\angle B A C=$ $\measuredangle E R P$, also liegt $E$ auf dem Umkreis des Sehnenvierecks $A P R Q$.
## BUNDESWEITE <br> MATHEMATIK-WETTBEWERBE
Bildung \& Begabung

Nun gilt $\angle C E R=\angle A P R=180^{\circ}-\angle D C R$, also liegt $E$ auch auf dem Umkreis des Dreiecks $R C D$. Die paarweisen Potenzgeraden der Umkreise von $A C D, A P R$ und $R C D$ sind somit die Geraden $C D, A Q, R E=R B$, also schneiden sie sich in einem Punkt. Dies impliziert die Behauptung.
|
{
"resource_path": "Germany_TST/segmented/de-2022-2022_IMO_Auswahlklausuren_Lsg_HP.jsonl",
"problem_match": "\nAufgabe 2.",
"solution_match": "\nZweite Lösung."
}
|
8676d1fa-347c-54c2-a245-7ca99e66e7af
| 605,463
|
Let $ABCD$ be a parallelogram with $|AC|=|BC|$. A point $P$ is chosen on the ray $AB$ such that $B$ lies between $A$ and $P$. The circumcircle of triangle $ACD$ and the segment $PD$ intersect at a point $Q$ other than $D$. The circumcircle of triangle $APQ$ and the segment $PC$ intersect at a point $R$ other than $P$.
Prove that the three lines $CD$, $AQ$, and $BR$ intersect at a single point.
|
From $\angle Q A C=\measuredangle Q D C=\angle Q P A$ it follows from the converse of the tangent-secant angle theorem that the line $A C$ is tangent to the circumcircle of the cyclic quadrilateral $A P R Q$. Due to the given condition, $A B$ is also tangent to the circumcircle of the cyclic quadrilateral $A Q C D$, so the angles $\angle A D Q$ and $\angle P A Q$ are equal. This implies $\angle A C Q=\angle A D Q=\angle P A Q=\angle C R Q$, so $A C$ is also tangent to the circumcircle of the triangle $C Q R$.
The intersection point $M$ of the lines $R Q$ and $A C$ thus satisfies the secant-tangent theorem $|M A|^{2}=|M Q| \cdot|M R|=|M C|^{2}$, so $M$ is the midpoint of the segment $A C$, and thus also the midpoint of the segment $B D$.
Pappus's theorem, applied to the collinear points $A, B, P$ and $R, Q, M$, implies that the intersection point $S$ of the lines $A Q$ and $B R$, $C$ (as the intersection of the lines $A M$ and $P R$), and $D$ (as the intersection of the lines $B M$ and $P Q$) lie on a straight line, which is the statement to be proven.
## NATIONAL <br> MATHEMATICS COMPETITIONS
Education & Talent
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Es sei $A B C D$ ein Parallelogramm mit $|A C|=|B C|$. Ein Punkt $P$ sei auf dem Strahl $A B$ gewählt, sodass $B$ zwischen $A$ und $P$ liegt. Der Umkreis des Dreiecks $A C D$ und die Strecke $P D$ haben außer dem Punkt $D$ noch den Punkt $Q$ gemeinsam. Der Umkreis des Dreiecks $A P Q$ und die Strecke $P C$ haben außer dem Punkt $P$ noch den Punkt $R$ gemeinsam.
Beweisen Sie, dass sich die drei Geraden $C D, A Q$ und $B R$ in einem Punkt schneiden.
|
Da $\angle Q A C=\measuredangle Q D C=\angle Q P A$ folgt mit der Umkehrung des Sehnen-Tangenten-Winkel-Satzes, dass die Gerade $A C$ den Umkreis des Sehnenvierecks $A P R Q$ tangiert. Wegen der Voraussetzung tangiert $A B$ auch den Umkreis des Sehnenvierecks $A Q C D$, also sind die Winkel $\angle A D Q$ und $\angle P A Q$ gleich groß. Damit folgt aber $\angle A C Q=\angle A D Q=\angle P A Q=\angle C R Q$, also tangiert $A C$ auch den Umkreis des Dreiecks $C Q R$.

Der Schnittpunkt $M$ der Geraden $R Q$ und $A C$ erfüllt damit nach dem Sekanten-TangentenSatz $|M A|^{2}=|M Q| \cdot|M R|=|M C|^{2}$, also ist $M$ der Mittelpunkt der Strecke $A C$, also auch der Mittelpunkt der Strecke $B D$.
Der Satz von Pappos, angewandt auf die jeweils kollinearen Punkte $A, B, P$ und $R, Q, M$ impliziert nun, dass der Schnittpunkt $S$ der Geraden $A Q$ und $B R, C$ (als Schnittpunkt der Geraden $A M$ und $P R$ ), sowie $D$ (als Schnittpunkt der Geraden $B M$ und $P Q$ ) auf einer Geraden liegen, was der zu zeigenden Aussage entspricht.
## BUNDESWEITE <br> MATHEMATIK-WETTBEWERBE
Bildung \& Begabung
|
{
"resource_path": "Germany_TST/segmented/de-2022-2022_IMO_Auswahlklausuren_Lsg_HP.jsonl",
"problem_match": "\nAufgabe 2.",
"solution_match": "\nDritte Lösung."
}
|
8676d1fa-347c-54c2-a245-7ca99e66e7af
| 605,463
|
For a fixed positive integer $m$, let $A$ be a subset of $\left\{0,1,2, \ldots, 5^{m}\right\}$, consisting of $4 m+$ elements.
Prove that there are always three numbers $a, b, c$ in $A$ such that $a<b<c$ and $c+2 a>3 b$ holds.
|
We assume that there are $4 m+2$ elements $x_{0}<x_{1}<\ldots<x_{4 m+1}$ from $\left\{0,1,2, \ldots, 5^{m}\right\}$ for which the claim is not satisfied. Then, in particular, $x_{4 m+1}+2 x_{i} \leq 3 x_{i+1}$ for all $i=0,1, \ldots, 4 m-1$. Rearranging gives $x_{4 m+1}-x_{i} \geq \frac{3}{2}\left(x_{4 m+1}-x_{i+1}\right)$.
A simple induction yields $x_{4 m+1}-x_{i} \geq\left(\frac{3}{2}\right)^{4 m-i}\left(x_{4 m+1}-x_{4 m}\right)$.
Now, $i=0$ leads to $x_{4 m+1}-x_{0} \geq\left(\frac{1}{2}\right)^{4 m}\left(x_{4 m+1}-x_{4 m}\right)=\left(\frac{81}{16}\right)^{m}\left(x_{4 m+1}-x_{4 m}\right)>5^{m} \cdot 1$,
Contradiction! ㅁ
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Für eine feste positive ganze Zahl $m$ sei $A$ eine Teilmenge von $\left\{0,1,2, \ldots, 5^{m}\right\}$, die aus $4 m+$ Elementen besteht.
Beweisen Sie, dass es in $A$ stets drei Zahlen $a, b, c$ gibt, für die $a<b<c$ und $c+2 a>3 b$ gil
|
Wir nehmen an, dass es $4 m+2$ Elemente $x_{0}<x_{1}<\ldots<x_{4 m+1}$ aus $\left\{0,1,2, \ldots, 5^{m}\right\}$ gibt, für welche die Behauptung nicht erfullt ist. Dann gilt insbesondere $x_{4 m+1}+2 x_{i} \leq 3 x_{i+1}$ für alle $i=0,1, \ldots, 4 m-1$. Umformen ergibt $x_{4 m+1}-x_{i} \geq \frac{3}{2}\left(x_{4 m+1}-x_{i+1}\right)$.
Ein einfacher Induktionsschluss liefert daraus $x_{4 m+1}-x_{i} \geq\left(\frac{3}{2}\right)^{4 m-i}\left(x_{4 m+1}-x_{4 m}\right)$.
Hier führt nun $i=0$ auf $x_{4 m+1}-x_{0} \geq\left(\frac{1}{2}\right)^{4 m}\left(x_{4 m+1}-x_{4 m}\right)=\left(\frac{81}{16}\right)^{m}\left(x_{4 m+1}-x_{4 m}\right)>5^{m} \cdot 1$,
Widerspruch! ㅁ
|
{
"resource_path": "Germany_TST/segmented/de-2022-2022_IMO_Auswahlklausuren_Lsg_HP.jsonl",
"problem_match": "# Aufgabe 1",
"solution_match": "# Erste Lösung:"
}
|
908f898e-5889-590e-94f0-ddb093bebdee
| 605,502
|
For a fixed positive integer $m$, let $A$ be a subset of $\left\{0,1,2, \ldots, 5^{m}\right\}$, consisting of $4 m+$ elements.
Prove that there are always three numbers $a, b, c$ in $A$ such that $a<b<c$ and $c+2 a>3 b$ holds.
|
We denote the largest element of $A$ by $c$. For $k=0, \ldots, 4 m-1$ we define $A_{k}=\left\{x \in A \left\lvert\,\left(1-\left(\frac{2}{3}\right)^{k}\right) c \leq x<\left(1-\left(\frac{2}{3}\right)^{k+1}\right) c\right.\right\}$.
Since $\left(1-\left(\frac{2}{3}\right)^{4 m}\right) c=c-\left(\frac{16}{81}\right)^{m!} c>c-\left(\frac{1}{5}\right)^{m!} c \geq c-1$, the sets $A_{0}, A_{1}, \ldots, A_{4 m-1}$ form a partition of $A \backslash\{c\}$. Because $A \backslash\{c\}$ consists of $4 m+1$ elements, by the pigeonhole principle, there must exist a set $A_{k}$ that contains at least two elements. We denote two of the numbers from $A_{k}$ as $a$ and $b$ such that $a<b<c$. Then, $c+2 a \geq c+2\left(1-\left(\frac{2}{3}\right)^{k}\right) c=\left(3-2\left(\frac{2}{3}\right)^{k}\right) c=3\left(1-\left(\frac{2}{3}\right)^{k+1}\right) c>3 b$, as required. $\square$
Hints: Clearly, the size of $A$ in the claim cannot be reduced to $4 m+$, as the example $A=\{0,2,3,4,5\}$ for $m=1$ shows. A common error was to manipulate or replace the elements of $A$ without checking whether the conclusions drawn from them are valid for the original set $A$.
## NATIONAL <br> MATHEMATICS COMPETITIONS
Education & Talent
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Für eine feste positive ganze Zahl $m$ sei $A$ eine Teilmenge von $\left\{0,1,2, \ldots, 5^{m}\right\}$, die aus $4 m+$ Elementen besteht.
Beweisen Sie, dass es in $A$ stets drei Zahlen $a, b, c$ gibt, für die $a<b<c$ und $c+2 a>3 b$ gil
|
Wir bezeichnen das gröBte Element von $A$ mit $c$. Für $k=0, \ldots, 4 m-1$ definieren wir $A_{k}=\left\{x \in A \left\lvert\,\left(1-\left(\frac{2}{3}\right)^{k}\right) c \leq x<\left(1-\left(\frac{2}{3}\right)^{k+1}\right) c\right.\right\}$.
Wegen $\left(1-\left(\frac{2}{3}\right)^{4 m}\right) c=c-\left(\frac{16}{81}\right)^{m i n} c>c-\left(\frac{1}{5}\right)^{m!} c \geq c-1$ bilden die Mengen $A_{0}, A_{1}, \ldots, A_{4 m-1}$ eine Zerlegung von $A \backslash\{c\}$. Weil $A \backslash\{c\}$ aus $4 m+1$ Elementen besteht, muss nach dem Schubfachprinzip eine Menge $A_{k}$ existieren, die aus wenigstens zwei Elementen besteht. Wi bezeichnen zwei der Zahlen aus $A_{k}$ so mit $a$ und $b$, dass $a<b<c$ gilt. Dann ist $c+2 a \geq c+2\left(1-\left(\frac{2}{3}\right)^{k}\right) c=\left(3-2\left(\frac{2}{3}\right)^{k}\right) c=3\left(1-\left(\frac{2}{3}\right)^{k+1}\right) c>3 b$, wie verlangt. $\square$
Hinweise: Offensichtlich lässt sich in der Behauptung die Mächtigkeit von $A$ nicht auf $4 m+$ verkleinern, wie für $m=1$ das Beispiel $A=\{0,2,3,4,5\}$ zeigt. Ein gelegentlich auftretender Fehler bestand darin, die Elemente von $A$ zu manipulieren oder zu ersetzen, ohne dabei zu überprüfen, ob die daraus gezogenen Schlussfolgerungen für die ursprüngliche Menge $A$ gültig sind.
## BUNDESWEITE <br> MATHEMATIK-WETTBEWERBE
Bildung \& Begabung
|
{
"resource_path": "Germany_TST/segmented/de-2022-2022_IMO_Auswahlklausuren_Lsg_HP.jsonl",
"problem_match": "# Aufgabe 1",
"solution_match": "# Zweite Lösung:"
}
|
908f898e-5889-590e-94f0-ddb093bebdee
| 605,502
|
Prove that for every integer $n$ greater than 1 ,
$$
\sigma(n) \phi(n) \leq n^{2}-1
$$
When does equality hold?
|
Note that
$$
\sigma(m n) \phi(m n)=\sigma(m) \phi(m) \sigma(n) \phi(n) \leq\left(m^{2}-1\right)\left(n^{2}-1\right)=(m n)^{2}-\left(m^{2}+n^{2}-1\right)<(m n)^{2}-1
$$
for any pair of relatively prime positive integers $(m, n)$ other than $(1,1)$. Now, for $p$ a prime and $k$ a positive integer, $\sigma\left(p^{k}\right)=1+p+\cdots+p^{k}=\frac{p^{k+1}-1}{p-1}$ and $\phi\left(p^{k}\right)=p^{k}-\frac{1}{p} \cdot p^{k}=(p-1) p^{k-1}$. Thus,
$$
\sigma\left(p^{k}\right) \phi\left(p^{k}\right)=\frac{p^{k+1}-1}{p-1} \cdot(p-1) p^{k-1}=\left(p^{k+1}-1\right) p^{k-1}=p^{2 k}-p^{k-1} \leq p^{2 k}-1
$$
with equality where $k=1$. It follows that equality holds in the given inequality if and only if $n$ is prime.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that for every integer $n$ greater than 1 ,
$$
\sigma(n) \phi(n) \leq n^{2}-1
$$
When does equality hold?
|
Note that
$$
\sigma(m n) \phi(m n)=\sigma(m) \phi(m) \sigma(n) \phi(n) \leq\left(m^{2}-1\right)\left(n^{2}-1\right)=(m n)^{2}-\left(m^{2}+n^{2}-1\right)<(m n)^{2}-1
$$
for any pair of relatively prime positive integers $(m, n)$ other than $(1,1)$. Now, for $p$ a prime and $k$ a positive integer, $\sigma\left(p^{k}\right)=1+p+\cdots+p^{k}=\frac{p^{k+1}-1}{p-1}$ and $\phi\left(p^{k}\right)=p^{k}-\frac{1}{p} \cdot p^{k}=(p-1) p^{k-1}$. Thus,
$$
\sigma\left(p^{k}\right) \phi\left(p^{k}\right)=\frac{p^{k+1}-1}{p-1} \cdot(p-1) p^{k-1}=\left(p^{k+1}-1\right) p^{k-1}=p^{2 k}-p^{k-1} \leq p^{2 k}-1
$$
with equality where $k=1$. It follows that equality holds in the given inequality if and only if $n$ is prime.
|
{
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team1-solutions.jsonl",
"problem_match": "\n3. [25]",
"solution_match": "\nSolution. "
}
|
6c52eed7-7b2c-50c3-b017-9fa87897ec70
| 608,225
|
Prove the identity
$$
\sum_{d \mid n} \tau(d)^{3}=\left(\sum_{d \mid n} \tau(d)\right)^{2}
$$
|
Note that $\tau^{3}$ is multiplicative; in light of the convolution property just shown, it follows that both sides of the posed equality are multiplicative. Thus, it would suffice to prove the claim for $n$ a power of a prime. So, write $n=p^{k}$ where $p$ is a prime and $k$ is a nonnegative integer. Then
$$
\begin{aligned}
& \sum_{d \mid n} \tau(d)^{3}=\sum_{i=0}^{k} \tau\left(p^{i}\right)^{3}=\sum_{i=0}^{k}(i+1)^{3} \\
& \quad=1^{3}+\cdots+(k+1)^{3}=\frac{(k+1)^{2}(k+2)^{2}}{4}=\left(\frac{(k+1)(k+2)}{2}\right)^{2} \\
& \quad=\left(\sum_{i=0}^{k} \tau\left(p^{i}\right)\right)^{2}=\left(\sum_{d \mid n} \tau(d)\right)^{2}
\end{aligned}
$$
as required.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove the identity
$$
\sum_{d \mid n} \tau(d)^{3}=\left(\sum_{d \mid n} \tau(d)\right)^{2}
$$
|
Note that $\tau^{3}$ is multiplicative; in light of the convolution property just shown, it follows that both sides of the posed equality are multiplicative. Thus, it would suffice to prove the claim for $n$ a power of a prime. So, write $n=p^{k}$ where $p$ is a prime and $k$ is a nonnegative integer. Then
$$
\begin{aligned}
& \sum_{d \mid n} \tau(d)^{3}=\sum_{i=0}^{k} \tau\left(p^{i}\right)^{3}=\sum_{i=0}^{k}(i+1)^{3} \\
& \quad=1^{3}+\cdots+(k+1)^{3}=\frac{(k+1)^{2}(k+2)^{2}}{4}=\left(\frac{(k+1)(k+2)}{2}\right)^{2} \\
& \quad=\left(\sum_{i=0}^{k} \tau\left(p^{i}\right)\right)^{2}=\left(\sum_{d \mid n} \tau(d)\right)^{2}
\end{aligned}
$$
as required.
|
{
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team1-solutions.jsonl",
"problem_match": "\n5. [30]",
"solution_match": "\nSolution. "
}
|
2a4f9fee-83fa-53ce-9873-3ee979b04fda
| 608,226
|
Show that for positive integers $n$,
$$
\sum_{d \mid n} \phi(d)=n
$$
|
Both sides are multiplicative functions of $n$, the right side trivially and the left because for relatively prime positive integers $n$ and $n^{\prime}$,
$$
\left(\sum_{d \mid n} \phi(d)\right)\left(\sum_{d^{\prime} \mid n^{\prime}} \phi\left(d^{\prime}\right)\right)=\sum_{d\left|n, d^{\prime}\right| n^{\prime}} \phi(d) \phi\left(d^{\prime}\right),
$$
and $\phi(d) \phi\left(d^{\prime}\right)=\phi\left(d d^{\prime}\right)$. The identity is then easy to check; since $\phi\left(p^{k}\right)=p^{k-1}(p-1)$ for positive integers $k$ and $\phi(1)=1$, we have $\phi(1)+\phi(p)+\cdots+\phi\left(p^{k}\right)=1+(p-1)+\left(p^{2}-p\right)+\cdots+\left(p^{k}-p^{k-1}\right)=p^{k}$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Show that for positive integers $n$,
$$
\sum_{d \mid n} \phi(d)=n
$$
|
Both sides are multiplicative functions of $n$, the right side trivially and the left because for relatively prime positive integers $n$ and $n^{\prime}$,
$$
\left(\sum_{d \mid n} \phi(d)\right)\left(\sum_{d^{\prime} \mid n^{\prime}} \phi\left(d^{\prime}\right)\right)=\sum_{d\left|n, d^{\prime}\right| n^{\prime}} \phi(d) \phi\left(d^{\prime}\right),
$$
and $\phi(d) \phi\left(d^{\prime}\right)=\phi\left(d d^{\prime}\right)$. The identity is then easy to check; since $\phi\left(p^{k}\right)=p^{k-1}(p-1)$ for positive integers $k$ and $\phi(1)=1$, we have $\phi(1)+\phi(p)+\cdots+\phi\left(p^{k}\right)=1+(p-1)+\left(p^{2}-p\right)+\cdots+\left(p^{k}-p^{k-1}\right)=p^{k}$, as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team1-solutions.jsonl",
"problem_match": "\n6. [25]",
"solution_match": "\nSolution. "
}
|
f1d5add7-4b1e-5273-9ed7-770854649b1b
| 608,227
|
Show that for positive integers $n$,
$$
\sum_{d \mid n} \frac{\mu(d)}{d}=\frac{\phi(n)}{n}
$$
|
On the grounds of the previous problem, Möbius inversion with $f(k)=\phi(k)$ and $g(k)=k$ gives:
$$
\phi(n)=f(n)=\sum_{d \mid n} g(d) \mu\left(\frac{n}{d}\right)=\sum_{d^{\prime} \mid n} g\left(\frac{n}{d^{\prime}}\right) \mu\left(d^{\prime}\right)=\sum_{d^{\prime} \mid n} \frac{n}{d^{\prime}} \mu\left(d^{\prime}\right)
$$
Alternatively, one uses the convolution of the functions $f(k)=n$ and $g(k)=\frac{\mu(d)}{d}$. The strategy is the same as the previous convolution proof. For $n=p^{k}$ with $k$ a positive integer, we have $\phi(n)=p^{k}-p^{k-1}$, while the series reduces to $p^{k} \cdot \mu(1)+p^{k} \cdot \mu(p) / p=p^{k}-p^{k-1}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Show that for positive integers $n$,
$$
\sum_{d \mid n} \frac{\mu(d)}{d}=\frac{\phi(n)}{n}
$$
|
On the grounds of the previous problem, Möbius inversion with $f(k)=\phi(k)$ and $g(k)=k$ gives:
$$
\phi(n)=f(n)=\sum_{d \mid n} g(d) \mu\left(\frac{n}{d}\right)=\sum_{d^{\prime} \mid n} g\left(\frac{n}{d^{\prime}}\right) \mu\left(d^{\prime}\right)=\sum_{d^{\prime} \mid n} \frac{n}{d^{\prime}} \mu\left(d^{\prime}\right)
$$
Alternatively, one uses the convolution of the functions $f(k)=n$ and $g(k)=\frac{\mu(d)}{d}$. The strategy is the same as the previous convolution proof. For $n=p^{k}$ with $k$ a positive integer, we have $\phi(n)=p^{k}-p^{k-1}$, while the series reduces to $p^{k} \cdot \mu(1)+p^{k} \cdot \mu(p) / p=p^{k}-p^{k-1}$.
|
{
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team1-solutions.jsonl",
"problem_match": "\n7. [25]",
"solution_match": "\nSolution. "
}
|
51af65b5-a913-52cd-abb0-7a7e65c0ee44
| 608,228
|
Let $A B C D$ be a cyclic quadrilateral, and let $P$ be the intersection of its two diagonals. Points $R, S, T$, and $U$ are feet of the perpendiculars from $P$ to sides $A B, B C, C D$, and $A D$, respectively. Show that quadrilateral $R S T U$ is bicentric if and only if $A C \perp B D$. (Note that a quadrilateral is called inscriptible if it has an incircle; a quadrilateral is called bicentric if it is both cyclic and inscriptible.)
|
First we show that $R S T U$ is always inscriptible. Note that in addition to $A B C D$, we have cyclic quadrilaterals $A R P U$ and $B S P R$. Thus,
$$
\angle P R U=\angle P A U=\angle C A D=\angle C B D=\angle S B P=\angle S R P
$$
and it follows that $P$ lies on the bisector of $\angle S R U$. Analogously, $P$ lies on the bisectors of $\angle T S R$ and $\angle U T S$, so is equidistant from lines $U R, R S, S T$, and $T U$, and $R S T U$ is inscriptible having incenter $P$. Now we show that $R S T U$ is cyclic if and only if the diagonals of $A B C D$ are orthogonal. We have
$$
\begin{aligned}
& \angle A P B=\pi-\angle B A P-\angle P B A=\pi-\angle R A P-\angle P B R=\pi-\angle R U P-\angle P S R \\
& \quad=\pi-\frac{1}{2}(\angle R U T+\angle T S R)
\end{aligned}
$$
It follows that $\angle A P B=\frac{\pi}{2}$ if and only if $\angle R U T+\angle T S R=\pi$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic quadrilateral, and let $P$ be the intersection of its two diagonals. Points $R, S, T$, and $U$ are feet of the perpendiculars from $P$ to sides $A B, B C, C D$, and $A D$, respectively. Show that quadrilateral $R S T U$ is bicentric if and only if $A C \perp B D$. (Note that a quadrilateral is called inscriptible if it has an incircle; a quadrilateral is called bicentric if it is both cyclic and inscriptible.)

|
First we show that $R S T U$ is always inscriptible. Note that in addition to $A B C D$, we have cyclic quadrilaterals $A R P U$ and $B S P R$. Thus,
$$
\angle P R U=\angle P A U=\angle C A D=\angle C B D=\angle S B P=\angle S R P
$$
and it follows that $P$ lies on the bisector of $\angle S R U$. Analogously, $P$ lies on the bisectors of $\angle T S R$ and $\angle U T S$, so is equidistant from lines $U R, R S, S T$, and $T U$, and $R S T U$ is inscriptible having incenter $P$. Now we show that $R S T U$ is cyclic if and only if the diagonals of $A B C D$ are orthogonal. We have
$$
\begin{aligned}
& \angle A P B=\pi-\angle B A P-\angle P B A=\pi-\angle R A P-\angle P B R=\pi-\angle R U P-\angle P S R \\
& \quad=\pi-\frac{1}{2}(\angle R U T+\angle T S R)
\end{aligned}
$$
It follows that $\angle A P B=\frac{\pi}{2}$ if and only if $\angle R U T+\angle T S R=\pi$, as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team1-solutions.jsonl",
"problem_match": "\n12. [30]",
"solution_match": "\nSolution. "
}
|
0645a1be-e803-551a-bcd9-1d3e0936b76a
| 608,233
|
Show that $P A I B$ is cyclic by proving that $\angle I A P$ is supplementary to $\angle P B I$.
|
Note that $I$ lies on the angle bisectors of the angles of quadrilateral $A B C D$. So writing $\angle D A B=2 \alpha, \angle A B C=2 \beta, \angle B C D=2 \gamma$, and $\angle C D A=2 \delta$, we have
$$
\begin{aligned}
\angle I A P+\angle P B I & =\angle I A B+\angle B A P+\angle P B A+\angle A B I \\
& =\angle I A B+\angle C D I+\angle I C D+\angle A B I \\
& =\alpha+\beta+\gamma+\delta .
\end{aligned}
$$
We are done because the angles in quadrilateral $A B C D$ add up to $360^{\circ}$.

|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Show that $P A I B$ is cyclic by proving that $\angle I A P$ is supplementary to $\angle P B I$.
|
Note that $I$ lies on the angle bisectors of the angles of quadrilateral $A B C D$. So writing $\angle D A B=2 \alpha, \angle A B C=2 \beta, \angle B C D=2 \gamma$, and $\angle C D A=2 \delta$, we have
$$
\begin{aligned}
\angle I A P+\angle P B I & =\angle I A B+\angle B A P+\angle P B A+\angle A B I \\
& =\angle I A B+\angle C D I+\angle I C D+\angle A B I \\
& =\alpha+\beta+\gamma+\delta .
\end{aligned}
$$
We are done because the angles in quadrilateral $A B C D$ add up to $360^{\circ}$.

|
{
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team2-solutions.jsonl",
"problem_match": "\n1. $[\\mathbf{3 0}]$",
"solution_match": "\nSolution. "
}
|
5619124d-1fe3-5ad9-8c26-52f9db297576
| 608,246
|
Show that $A B+C D=A D+B C$. Use the above to conclude that for some positive number $\alpha$,
$$
\begin{array}{ll}
A B=\alpha \cdot\left(\frac{A I}{C I}+\frac{B I}{D I}\right) & B C=\alpha \cdot\left(\frac{B I}{D I}+\frac{C I}{A I}\right) \\
C D=\alpha \cdot\left(\frac{C I}{A I}+\frac{D I}{B I}\right) & D A=\alpha \cdot\left(\frac{D I}{B I}+\frac{A I}{C I}\right) .
\end{array}
$$
|
Draw in the points of tangency $P, Q, R$, and $S$, of the incircle with sides $A B, B C, C D$, and $A D$, as shown. Then we have equal tangents $A P=A S, B P=B Q, C Q=C R$, and $D R=D S$. Then
$$
A B+C D=A P+B P+C R+D R=A S+(B Q+C Q)+D S=B C+A D
$$
Using the result of problem 3, we set $B C=x \cdot B I \cdot C I$ and $A D=x \cdot A I \cdot D I$ for some $x$, and $A B=y \cdot A I \cdot B I$ and $C D=y \cdot C I \cdot D I$ for some $y$. Now because $A B+C D=B C+A D$, we obtain
$$
y(A I \cdot B I+C I \cdot D I)=x(B I \cdot C I+A I \cdot D I)
$$
So it follows that the ratio $A B: B C: C D: D A$ is uniquely determined. One easily checks that the posed ratio satisfies the three required relations.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Show that $A B+C D=A D+B C$. Use the above to conclude that for some positive number $\alpha$,
$$
\begin{array}{ll}
A B=\alpha \cdot\left(\frac{A I}{C I}+\frac{B I}{D I}\right) & B C=\alpha \cdot\left(\frac{B I}{D I}+\frac{C I}{A I}\right) \\
C D=\alpha \cdot\left(\frac{C I}{A I}+\frac{D I}{B I}\right) & D A=\alpha \cdot\left(\frac{D I}{B I}+\frac{A I}{C I}\right) .
\end{array}
$$
|
Draw in the points of tangency $P, Q, R$, and $S$, of the incircle with sides $A B, B C, C D$, and $A D$, as shown. Then we have equal tangents $A P=A S, B P=B Q, C Q=C R$, and $D R=D S$. Then
$$
A B+C D=A P+B P+C R+D R=A S+(B Q+C Q)+D S=B C+A D
$$
Using the result of problem 3, we set $B C=x \cdot B I \cdot C I$ and $A D=x \cdot A I \cdot D I$ for some $x$, and $A B=y \cdot A I \cdot B I$ and $C D=y \cdot C I \cdot D I$ for some $y$. Now because $A B+C D=B C+A D$, we obtain
$$
y(A I \cdot B I+C I \cdot D I)=x(B I \cdot C I+A I \cdot D I)
$$
So it follows that the ratio $A B: B C: C D: D A$ is uniquely determined. One easily checks that the posed ratio satisfies the three required relations.

|
{
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team2-solutions.jsonl",
"problem_match": "\n4. [25]",
"solution_match": "\nSolution. "
}
|
c90e9ed8-fc06-5dc6-88b0-81d60c91b7c3
| 608,249
|
Let the incircle of $A B C D$ be tangent to sides $A B, B C, C D$, and $A D$ at points $P, Q, R$, and $S$, respectively. Show that $A B C D$ is cyclic if and only if $P R \perp Q S$.
|
Let the diagonals of $P Q R S$ intersect at $T$. Because $\overline{A P}$ and $\overline{A S}$ are tangent to $\omega$ at $P$ and $S$, we may write $\alpha=\angle A S P=\angle S P A=\angle S Q P$ and $\beta=\angle C Q R=\angle Q R C=\angle Q P R$. Then $\angle P T Q=\pi-\alpha-\beta$. On the other hand, $\angle P A S=\pi-2 \alpha$ and $\angle R C Q=\pi-2 \beta$, so that $A B C D$ is cyclic if and only if
$$
\pi=\angle B A D+\angle D C B=2 \pi-2 \alpha-2 \beta
$$
or simply
$$
\pi / 2=\pi-\alpha-\beta=\angle P T Q
$$
as desired.
A brief review of cyclic Quadrilaterals.
The following discussion of cyclic quadrilaterals is included for reference. Any of the results given here may be cited without proof in your writeups.
A cyclic quadrilateral is a quadrilateral whose four vertices lie on a circle called the circumcircle (the circle is unique if it exists.) If a quadrilateral has a circumcircle, then the center of this circumcircle is called the circumcenter of the quadrilateral. For a convex quadrilateral $A B C D$, the following are equivalent:
- Quadrilateral $A B C D$ is cyclic;
- $\angle A B D=\angle A C D$ (or $\angle B C A=\angle B D A$, etc.);
- Angles $\angle A B C$ and $\angle C D A$ are supplementary, that is, $m \angle A B C+m \angle C D A=180^{\circ}$ (or angles $\angle B C D$ and $\angle B A D$ are supplementary);
Cyclic quadrilaterals have a number of interesting properties. A cyclic quadrilateral $A B C D$ satisfies
$$
A C \cdot B D=A B \cdot C D+A D \cdot B C
$$
a result known as Ptolemy's theorem. Another result, typically called Power of a Point, asserts that given a circle $\omega$, a point $P$ anywhere in the plane of $\omega$, and a line $\ell$ through $P$ intersecting $\omega$ at points $A$ and $B$, the value of $A P \cdot B P$ is independent of $\ell$; i.e., if a second line $\ell^{\prime}$ through $P$ intersects $\omega$ at $A^{\prime}$ and $B^{\prime}$, then $A P \cdot B P=A^{\prime} P \cdot B^{\prime} P$. This second theorem is proved via similar triangles. Say $P$ lies outside of $\omega$, that $\ell$ and $\ell^{\prime}$ are as before and that $A$ and $A^{\prime}$ lie on segments $B P$ and $B^{\prime} P$ respectively. Then triangle $A A^{\prime} P$ is similar to triangle $B^{\prime} B P$ because the triangles share an angle at $P$ and we have
$$
m \angle A A^{\prime} P=180^{\circ}-m \angle B^{\prime} A^{\prime} A=m \angle A B B^{\prime}=m \angle P B B^{\prime}
$$
The case where $A=B$ is valid and describes the tangents to $\omega$. A similar proof works for $P$ inside $\omega$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let the incircle of $A B C D$ be tangent to sides $A B, B C, C D$, and $A D$ at points $P, Q, R$, and $S$, respectively. Show that $A B C D$ is cyclic if and only if $P R \perp Q S$.
|
Let the diagonals of $P Q R S$ intersect at $T$. Because $\overline{A P}$ and $\overline{A S}$ are tangent to $\omega$ at $P$ and $S$, we may write $\alpha=\angle A S P=\angle S P A=\angle S Q P$ and $\beta=\angle C Q R=\angle Q R C=\angle Q P R$. Then $\angle P T Q=\pi-\alpha-\beta$. On the other hand, $\angle P A S=\pi-2 \alpha$ and $\angle R C Q=\pi-2 \beta$, so that $A B C D$ is cyclic if and only if
$$
\pi=\angle B A D+\angle D C B=2 \pi-2 \alpha-2 \beta
$$
or simply
$$
\pi / 2=\pi-\alpha-\beta=\angle P T Q
$$
as desired.
A brief review of cyclic Quadrilaterals.
The following discussion of cyclic quadrilaterals is included for reference. Any of the results given here may be cited without proof in your writeups.
A cyclic quadrilateral is a quadrilateral whose four vertices lie on a circle called the circumcircle (the circle is unique if it exists.) If a quadrilateral has a circumcircle, then the center of this circumcircle is called the circumcenter of the quadrilateral. For a convex quadrilateral $A B C D$, the following are equivalent:
- Quadrilateral $A B C D$ is cyclic;
- $\angle A B D=\angle A C D$ (or $\angle B C A=\angle B D A$, etc.);
- Angles $\angle A B C$ and $\angle C D A$ are supplementary, that is, $m \angle A B C+m \angle C D A=180^{\circ}$ (or angles $\angle B C D$ and $\angle B A D$ are supplementary);
Cyclic quadrilaterals have a number of interesting properties. A cyclic quadrilateral $A B C D$ satisfies
$$
A C \cdot B D=A B \cdot C D+A D \cdot B C
$$
a result known as Ptolemy's theorem. Another result, typically called Power of a Point, asserts that given a circle $\omega$, a point $P$ anywhere in the plane of $\omega$, and a line $\ell$ through $P$ intersecting $\omega$ at points $A$ and $B$, the value of $A P \cdot B P$ is independent of $\ell$; i.e., if a second line $\ell^{\prime}$ through $P$ intersects $\omega$ at $A^{\prime}$ and $B^{\prime}$, then $A P \cdot B P=A^{\prime} P \cdot B^{\prime} P$. This second theorem is proved via similar triangles. Say $P$ lies outside of $\omega$, that $\ell$ and $\ell^{\prime}$ are as before and that $A$ and $A^{\prime}$ lie on segments $B P$ and $B^{\prime} P$ respectively. Then triangle $A A^{\prime} P$ is similar to triangle $B^{\prime} B P$ because the triangles share an angle at $P$ and we have
$$
m \angle A A^{\prime} P=180^{\circ}-m \angle B^{\prime} A^{\prime} A=m \angle A B B^{\prime}=m \angle P B B^{\prime}
$$
The case where $A=B$ is valid and describes the tangents to $\omega$. A similar proof works for $P$ inside $\omega$.
|
{
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team2-solutions.jsonl",
"problem_match": "\n6. [40]",
"solution_match": "\nSolution. "
}
|
add6b298-cda3-513e-a7cc-1c9c9cd15dd6
| 608,251
|
Let $S$ be a set of 5 points in the 2 -dimensional lattice. Show that we can always choose a pair of points in $S$ whose midpoint is also a lattice point.
|
Consider the parities of the coordinates. There are four possibilities: (odd, odd), (odd, even), (even, odd), (even, even). By the pigeonhole principle, two of the points must have the same parity in both coordinates (i.e., they are congruent in mod 2). Then, the midpoint of these two points must be a lattice point.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $S$ be a set of 5 points in the 2 -dimensional lattice. Show that we can always choose a pair of points in $S$ whose midpoint is also a lattice point.
|
Consider the parities of the coordinates. There are four possibilities: (odd, odd), (odd, even), (even, odd), (even, even). By the pigeonhole principle, two of the points must have the same parity in both coordinates (i.e., they are congruent in mod 2). Then, the midpoint of these two points must be a lattice point.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team1-solutions.jsonl",
"problem_match": "\n5. [10]",
"solution_match": "\nSolution: "
}
|
8d0f20b1-b5e0-51c7-bdc0-b251547ddad1
| 608,344
|
Show that for positive integers $n$ and $d$,
$$
(n-1) 2^{d}+1 \leq f(n, d) \leq(n-1) n^{d}+1 .
$$
|
Note that taking the set of points to be a multiset does not affect $f(n, d)$ as adding multiples of $n$ to any of the coordinate values does not change the result. The lower bound is obtained by considering the multiset consisting of $n-1$ copies of each of the $2^{d}$ 0,1 -vectors of length $d$, as it contains no submultiset of size $n$ whose centroid is also a lattice point. By the pigeonhole principle, any multiset of $(n-1) n^{d}+1$ lattice points must contain $n$ points whose coordinates are congruent modulo $n$. The centroid of these $n$ points is also a lattice point, thus proving the upper bound.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Show that for positive integers $n$ and $d$,
$$
(n-1) 2^{d}+1 \leq f(n, d) \leq(n-1) n^{d}+1 .
$$
|
Note that taking the set of points to be a multiset does not affect $f(n, d)$ as adding multiples of $n$ to any of the coordinate values does not change the result. The lower bound is obtained by considering the multiset consisting of $n-1$ copies of each of the $2^{d}$ 0,1 -vectors of length $d$, as it contains no submultiset of size $n$ whose centroid is also a lattice point. By the pigeonhole principle, any multiset of $(n-1) n^{d}+1$ lattice points must contain $n$ points whose coordinates are congruent modulo $n$. The centroid of these $n$ points is also a lattice point, thus proving the upper bound.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team1-solutions.jsonl",
"problem_match": "\n7. [35]",
"solution_match": "\nSolution: "
}
|
7d83a828-839b-5cf8-9487-05a70790f8f9
| 608,346
|
Show that for positive integers $n_{1}, n_{2}$ and $d$,
$$
f\left(n_{1} n_{2}, d\right) \leq f\left(n_{1}, d\right)+n_{1}\left(f\left(n_{2}, d\right)-1\right)
$$
|
Given a multiset of $f\left(n_{1}, d\right)+n_{1}\left(f\left(n_{2}, d\right)-1\right)$ lattice points, we may select $l=f\left(n_{2}, d\right)$ pairwise disjoint submultisets $S_{1}, S_{2}, \ldots, S_{l}$, each consisting of $n_{1}$ points, whose centroid is a lattice point. Let $\varphi$ map each multiset $S_{i}$ to its centroid $g_{i}$. By the definition of $f\left(n_{2}, d\right)$, there exists a submultiset $T \subset\left\{g_{1}, g_{2}, \ldots, g_{l}\right\}$ satisfying $|T|=n_{2}$ whose centroid is a lattice point. Then $\bigcup_{i \in T} \varphi^{-1}\left(g_{i}\right)$ is a multiset of $n_{1} n_{2}$ lattice points whose centroid is also a lattice point.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Show that for positive integers $n_{1}, n_{2}$ and $d$,
$$
f\left(n_{1} n_{2}, d\right) \leq f\left(n_{1}, d\right)+n_{1}\left(f\left(n_{2}, d\right)-1\right)
$$
|
Given a multiset of $f\left(n_{1}, d\right)+n_{1}\left(f\left(n_{2}, d\right)-1\right)$ lattice points, we may select $l=f\left(n_{2}, d\right)$ pairwise disjoint submultisets $S_{1}, S_{2}, \ldots, S_{l}$, each consisting of $n_{1}$ points, whose centroid is a lattice point. Let $\varphi$ map each multiset $S_{i}$ to its centroid $g_{i}$. By the definition of $f\left(n_{2}, d\right)$, there exists a submultiset $T \subset\left\{g_{1}, g_{2}, \ldots, g_{l}\right\}$ satisfying $|T|=n_{2}$ whose centroid is a lattice point. Then $\bigcup_{i \in T} \varphi^{-1}\left(g_{i}\right)$ is a multiset of $n_{1} n_{2}$ lattice points whose centroid is also a lattice point.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team1-solutions.jsonl",
"problem_match": "\n8. [40]",
"solution_match": "\nSolution: "
}
|
7f8f1745-fcbd-5265-9383-0cde8e03fc79
| 608,347
|
On the circumcircle of $A B C$, let $A^{\prime}$ be the midpoint of arc $B C$ (not containing $A$ ).
(a) $[\mathbf{1 0}]$ Show that $A, I, A^{\prime}$ are collinear.
(b) $[\mathbf{2 0}]$ Show that $A^{\prime}$ is the circumcenter of BIC.
|
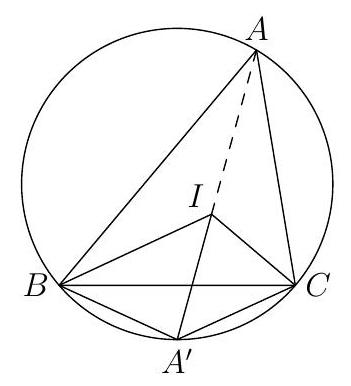
(a) Since $A^{\prime}$ bisectors the arc $B C$, the two arcs $A^{\prime} B$ and $A^{\prime} C$ are equal, and so $\angle B A A^{\prime}=$ $\angle C A A^{\prime}$. Thus, $A^{\prime}$ lies on the angle bisector of $B A C$. Since $I$ also lies on the angle bisector of $B A C$, we see that $A, I, A^{\prime}$ are collinear.
(b) We have
$$
\angle C I A^{\prime}=\angle A^{\prime} A C+\angle I C A=\angle A^{\prime} A B+\angle I C B=\angle A^{\prime} C B+\angle I C B=\angle I C A^{\prime} .
$$
Therefore, $A^{\prime} I=A^{\prime} C$. By similar arguments, $A^{\prime} I=A^{\prime} B$. So, $A^{\prime}$ is equidistant from $B, I, C$, and thus is its circumcenter.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
On the circumcircle of $A B C$, let $A^{\prime}$ be the midpoint of arc $B C$ (not containing $A$ ).
(a) $[\mathbf{1 0}]$ Show that $A, I, A^{\prime}$ are collinear.
(b) $[\mathbf{2 0}]$ Show that $A^{\prime}$ is the circumcenter of BIC.
|

(a) Since $A^{\prime}$ bisectors the arc $B C$, the two arcs $A^{\prime} B$ and $A^{\prime} C$ are equal, and so $\angle B A A^{\prime}=$ $\angle C A A^{\prime}$. Thus, $A^{\prime}$ lies on the angle bisector of $B A C$. Since $I$ also lies on the angle bisector of $B A C$, we see that $A, I, A^{\prime}$ are collinear.
(b) We have
$$
\angle C I A^{\prime}=\angle A^{\prime} A C+\angle I C A=\angle A^{\prime} A B+\angle I C B=\angle A^{\prime} C B+\angle I C B=\angle I C A^{\prime} .
$$
Therefore, $A^{\prime} I=A^{\prime} C$. By similar arguments, $A^{\prime} I=A^{\prime} B$. So, $A^{\prime}$ is equidistant from $B, I, C$, and thus is its circumcenter.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team1-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\n## Solution:\n\n"
}
|
76b08b8c-1eaf-5c78-870f-07b5a56e47ab
| 608,349
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.