problem
stringlengths 54
2.23k
| solution
stringlengths 134
24.1k
| answer
stringclasses 1
value | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 54
2.21k
| solution_raw
stringlengths 134
24.1k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 23.5k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
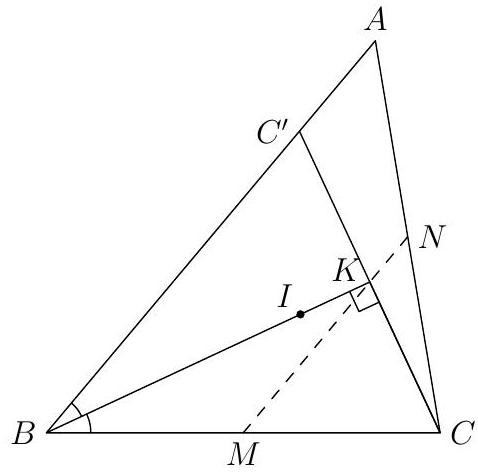
Let $K$ be as in the previous problem. Let $M$ be the midpoint of $B C$ and $N$ the midpoint of $A C$. Show that $K$ lies on line $M N$.
|
Since $I, K, E, C$ are concyclic, we have $\angle I K C=\angle I E C=90^{\circ}$. Let $C^{\prime}$ be the reflection of $C$ across $B I$, then $C^{\prime}$ must lie on $A B$. Then, $K$ is the midpoint of $C C^{\prime}$. Consider a dilation centered at $C$ with factor $\frac{1}{2}$. Since $C^{\prime}$ lies on $A B$, it follows that $K$ lies on $M N$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $K$ be as in the previous problem. Let $M$ be the midpoint of $B C$ and $N$ the midpoint of $A C$. Show that $K$ lies on line $M N$.
|
Since $I, K, E, C$ are concyclic, we have $\angle I K C=\angle I E C=90^{\circ}$. Let $C^{\prime}$ be the reflection of $C$ across $B I$, then $C^{\prime}$ must lie on $A B$. Then, $K$ is the midpoint of $C C^{\prime}$. Consider a dilation centered at $C$ with factor $\frac{1}{2}$. Since $C^{\prime}$ lies on $A B$, it follows that $K$ lies on $M N$.

|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team1-solutions.jsonl",
"problem_match": "\n12. [40]",
"solution_match": "\nSolution: "
}
|
feef6375-04d8-54e6-ac85-b345e979ac0c
| 608,351
|
Let $M$ be the midpoint of $B C$, and $T$ diametrically opposite to $D$ on the incircle of $A B C$. Show that $D T, A M, E F$ are concurrent.
|
If $A B=A C$, then the result is clear as $A M$ and $D T$ coincide. So, assume that $A B \neq A C$.
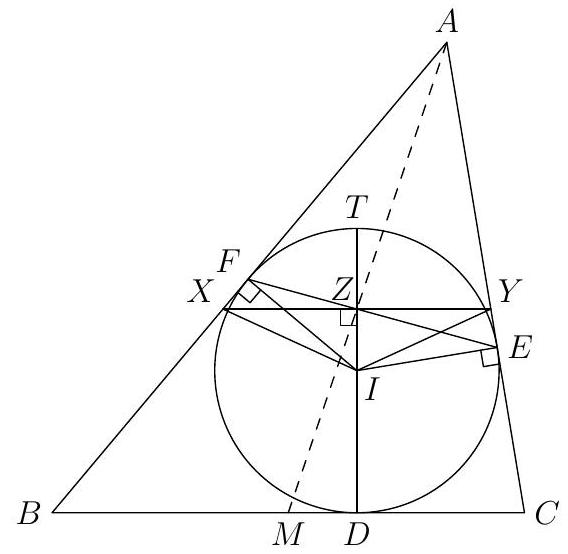
Let lines $D T$ and $E F$ meet at $Z$. Construct a line through $Z$ parallel to $B C$, and let it meet $A B$ and $A C$ at $X$ and $Y$, respectively. We have $\angle X Z I=90^{\circ}$, and $\angle X F I=90^{\circ}$. Therefore, $F, Z, I, X$ are concyclic, and thus $\angle I X Z=\angle I F Z$. By similar arguments, we also have $\angle I Y Z=\angle I E Z$. Thus, triangles $I F E$ and $I X Y$ are similar. Since $I E=I F$, we must also have $I X=I Y$. Since $I Z$ is an altitude of the isosceles triangle $I X Y, Z$ is the midpoint of $X Y$.
Since $X Y$ and $B C$ are parallel, there is a dilation centered at $A$ that sends $X Y$ to $B C$. So it must send the midpoint $Z$ to the midpoint $M$. Therefore, $A, Z, M$ are collinear. It follows that $D T, A M, E F$ are concurrent.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $M$ be the midpoint of $B C$, and $T$ diametrically opposite to $D$ on the incircle of $A B C$. Show that $D T, A M, E F$ are concurrent.
|
If $A B=A C$, then the result is clear as $A M$ and $D T$ coincide. So, assume that $A B \neq A C$.

Let lines $D T$ and $E F$ meet at $Z$. Construct a line through $Z$ parallel to $B C$, and let it meet $A B$ and $A C$ at $X$ and $Y$, respectively. We have $\angle X Z I=90^{\circ}$, and $\angle X F I=90^{\circ}$. Therefore, $F, Z, I, X$ are concyclic, and thus $\angle I X Z=\angle I F Z$. By similar arguments, we also have $\angle I Y Z=\angle I E Z$. Thus, triangles $I F E$ and $I X Y$ are similar. Since $I E=I F$, we must also have $I X=I Y$. Since $I Z$ is an altitude of the isosceles triangle $I X Y, Z$ is the midpoint of $X Y$.
Since $X Y$ and $B C$ are parallel, there is a dilation centered at $A$ that sends $X Y$ to $B C$. So it must send the midpoint $Z$ to the midpoint $M$. Therefore, $A, Z, M$ are collinear. It follows that $D T, A M, E F$ are concurrent.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team1-solutions.jsonl",
"problem_match": "\n13. [40]",
"solution_match": "\nSolution: "
}
|
ba595b09-5f66-5359-b370-fbe7cd8a4e63
| 608,352
|
Let $P$ be a point inside the incircle of $A B C$. Let lines $D P, E P, F P$ meet the incircle again at $D^{\prime}, E^{\prime}, F^{\prime}$. Show that $A D^{\prime}, B E^{\prime}, C F^{\prime}$ are concurrent.
|
Using the trigonometric version of Ceva's theorem, it suffices to prove that
$$
\frac{\sin \angle B A D^{\prime}}{\sin \angle D^{\prime} A C} \cdot \frac{\sin \angle C B E^{\prime}}{\sin \angle E^{\prime} B A} \cdot \frac{\sin \angle A C F^{\prime}}{\sin \angle F^{\prime} C B}=1 .
$$
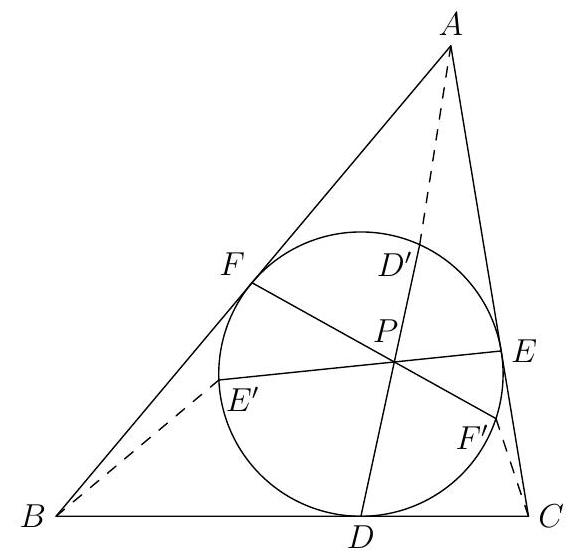
Using sine law, we have
$$
\sin \angle B A D^{\prime}=\frac{F D^{\prime}}{A D^{\prime}} \cdot \sin \angle A F D^{\prime}=\frac{F D^{\prime}}{A D^{\prime}} \cdot \sin \angle F D D^{\prime}
$$
Let $r$ be the inradius of $A B C$. Using the extended sine law, we have $F D^{\prime}=2 r \sin \angle F D D^{\prime}$. Therefore,
$$
\sin \angle B A D^{\prime}=\frac{2 r}{A D^{\prime}} \cdot \sin ^{2} \angle F D D^{\prime}
$$
Do this for all the factors in ( $\dagger$ ), and we get
$$
\frac{\sin \angle B A D^{\prime}}{\sin \angle D^{\prime} A C} \cdot \frac{\sin \angle C B E^{\prime}}{\sin \angle E^{\prime} B A} \cdot \frac{\sin \angle A C F^{\prime}}{\sin \angle F^{\prime} C B}=\left(\frac{\sin \angle F D D^{\prime}}{\sin \angle D^{\prime} D E} \cdot \frac{\sin \angle D E E^{\prime}}{\sin \angle E^{\prime} E F} \cdot \frac{\sin \angle E F F^{\prime}}{\sin \angle F^{\prime} F D}\right)^{2}
$$
Since $D D^{\prime}, E E^{\prime}, F F^{\prime}$ are concurrent, the above expression equals to 1 by using trig Ceva on triangle $D E F$. The result follows.
Remark: This result is known as Steinbart Theorem. Beware that its converse is not completely true. For more information and discussion, see Darij Grinberg's paper "Variations of the Steinbart Theorem" at http://de.geocities.com/darij_grinberg/.
## Glossary and some possibly useful facts
- A set of points is collinear if they lie on a common line. A set of lines is concurrent if they pass through a common point. A set of points are concyclic if they lie on a common circle.
- Given $A B C$ a triangle, the three angle bisectors are concurrent at the incenter of the triangle. The incenter is the center of the incircle, which is the unique circle inscribed in $A B C$, tangent to all three sides.
- Ceva's theorem states that given $A B C$ a triangle, and points $X, Y, Z$ on sides $B C, C A, A B$, respectively, the lines $A X, B Y, C Z$ are concurrent if and only if
$$
\frac{B X}{X B} \cdot \frac{C Y}{Y A} \cdot \frac{A Z}{Z B}=1
$$
- "Trig" Ceva states that given $A B C$ a triangle, and points $X, Y, Z$ inside the triangle, the lines $A X, B Y, C Z$ are concurrent if and only if
$$
\frac{\sin \angle B A X}{\sin \angle X A C} \cdot \frac{\sin \angle C B Y}{\sin \angle Y B A} \cdot \frac{\sin \angle A C Z}{\sin \angle Z C B}=1 .
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $P$ be a point inside the incircle of $A B C$. Let lines $D P, E P, F P$ meet the incircle again at $D^{\prime}, E^{\prime}, F^{\prime}$. Show that $A D^{\prime}, B E^{\prime}, C F^{\prime}$ are concurrent.
|
Using the trigonometric version of Ceva's theorem, it suffices to prove that
$$
\frac{\sin \angle B A D^{\prime}}{\sin \angle D^{\prime} A C} \cdot \frac{\sin \angle C B E^{\prime}}{\sin \angle E^{\prime} B A} \cdot \frac{\sin \angle A C F^{\prime}}{\sin \angle F^{\prime} C B}=1 .
$$

Using sine law, we have
$$
\sin \angle B A D^{\prime}=\frac{F D^{\prime}}{A D^{\prime}} \cdot \sin \angle A F D^{\prime}=\frac{F D^{\prime}}{A D^{\prime}} \cdot \sin \angle F D D^{\prime}
$$
Let $r$ be the inradius of $A B C$. Using the extended sine law, we have $F D^{\prime}=2 r \sin \angle F D D^{\prime}$. Therefore,
$$
\sin \angle B A D^{\prime}=\frac{2 r}{A D^{\prime}} \cdot \sin ^{2} \angle F D D^{\prime}
$$
Do this for all the factors in ( $\dagger$ ), and we get
$$
\frac{\sin \angle B A D^{\prime}}{\sin \angle D^{\prime} A C} \cdot \frac{\sin \angle C B E^{\prime}}{\sin \angle E^{\prime} B A} \cdot \frac{\sin \angle A C F^{\prime}}{\sin \angle F^{\prime} C B}=\left(\frac{\sin \angle F D D^{\prime}}{\sin \angle D^{\prime} D E} \cdot \frac{\sin \angle D E E^{\prime}}{\sin \angle E^{\prime} E F} \cdot \frac{\sin \angle E F F^{\prime}}{\sin \angle F^{\prime} F D}\right)^{2}
$$
Since $D D^{\prime}, E E^{\prime}, F F^{\prime}$ are concurrent, the above expression equals to 1 by using trig Ceva on triangle $D E F$. The result follows.
Remark: This result is known as Steinbart Theorem. Beware that its converse is not completely true. For more information and discussion, see Darij Grinberg's paper "Variations of the Steinbart Theorem" at http://de.geocities.com/darij_grinberg/.
## Glossary and some possibly useful facts
- A set of points is collinear if they lie on a common line. A set of lines is concurrent if they pass through a common point. A set of points are concyclic if they lie on a common circle.
- Given $A B C$ a triangle, the three angle bisectors are concurrent at the incenter of the triangle. The incenter is the center of the incircle, which is the unique circle inscribed in $A B C$, tangent to all three sides.
- Ceva's theorem states that given $A B C$ a triangle, and points $X, Y, Z$ on sides $B C, C A, A B$, respectively, the lines $A X, B Y, C Z$ are concurrent if and only if
$$
\frac{B X}{X B} \cdot \frac{C Y}{Y A} \cdot \frac{A Z}{Z B}=1
$$
- "Trig" Ceva states that given $A B C$ a triangle, and points $X, Y, Z$ inside the triangle, the lines $A X, B Y, C Z$ are concurrent if and only if
$$
\frac{\sin \angle B A X}{\sin \angle X A C} \cdot \frac{\sin \angle C B Y}{\sin \angle Y B A} \cdot \frac{\sin \angle A C Z}{\sin \angle Z C B}=1 .
$$
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team1-solutions.jsonl",
"problem_match": "\n14. [40]",
"solution_match": "\nSolution: "
}
|
4a863bc9-62a7-57b2-b2ca-6c0a84b4a26b
| 608,353
|
(Distributive law) Prove that $(x \oplus y) \odot z=x \odot z \oplus y \odot z$ for all $x, y, z \in \mathbb{R} \cup\{\infty\}$.
|
This is equivalent to proving that
$$
\min (x, y)+z=\min (x+z, y+z) .
$$
Consider two cases. If $x \leq y$, then $L H S=x+z$ and $R H S=x+z$. If $x>y$, then $L H S=y+z$ and $R H S=y+z$. It follows that $L H S=R H S$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
(Distributive law) Prove that $(x \oplus y) \odot z=x \odot z \oplus y \odot z$ for all $x, y, z \in \mathbb{R} \cup\{\infty\}$.
|
This is equivalent to proving that
$$
\min (x, y)+z=\min (x+z, y+z) .
$$
Consider two cases. If $x \leq y$, then $L H S=x+z$ and $R H S=x+z$. If $x>y$, then $L H S=y+z$ and $R H S=y+z$. It follows that $L H S=R H S$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team2-solutions.jsonl",
"problem_match": "\n1. [10]",
"solution_match": "\nSolution: "
}
|
c7b6ebe6-8ebf-5617-ad07-4eda696fd2a0
| 608,354
|
By a tropical polynomial we mean a function of the form
$$
p(x)=a_{n} \odot x^{n} \oplus a_{n-1} \odot x^{n-1} \oplus \cdots \oplus a_{1} \odot x \oplus a_{0}
$$
where exponentiation is as defined in the previous problem.
Let $p$ be a tropical polynomial. Prove that
$$
p\left(\frac{x+y}{2}\right) \geq \frac{p(x)+p(y)}{2}
$$
for all $x, y \in \mathbb{R} \cup\{\infty\}$. (This means that all tropical polynomials are concave.)
|
First, note that for any $x_{1}, \ldots, x_{n}, y_{1}, \ldots, y_{n}$, we have
$$
\min \left\{x_{1}+y_{1}, x_{2}+y_{2}, \ldots, x_{n}+y_{n}\right\} \geq \min \left\{x_{1}, x_{2}, \ldots, x_{n}\right\}+\min \left\{y_{1}, y_{2}, \ldots, y_{n}\right\} .
$$
Indeed, suppose that $x_{m}+y_{m}=\min _{i}\left\{x_{i}+y_{i}\right\}$, then $x_{m} \geq \min _{i} x_{i}$ and $y_{m} \geq \min _{i} y_{i}$, and so $\min _{i}\left\{x_{i}+y_{i}\right\}=x_{m}+y_{m} \geq \min _{i} x_{i}+\min _{i} y_{i}$.
Now, let us write a tropical polynomial in a more familiar notation. We have
$$
p(x)=\min _{0 \leq k \leq n}\left\{a_{k}+k x\right\} .
$$
So
$$
\begin{aligned}
p\left(\frac{x+y}{2}\right) & =\min _{0 \leq k \leq n}\left\{a_{k}+k\left(\frac{x+y}{2}\right)\right\} \\
& =\frac{1}{2} \min _{0 \leq k \leq n}\left\{\left(a_{k}+k x\right)+\left(a_{k}+k y\right)\right\} \\
& \geq \frac{1}{2}\left(\min _{0 \leq k \leq n}\left\{a_{k}+k x\right\}+\min _{0 \leq k \leq n}\left\{a_{k}+k y\right\}\right) \\
& =\frac{1}{2}(p(x)+p(y)) .
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
By a tropical polynomial we mean a function of the form
$$
p(x)=a_{n} \odot x^{n} \oplus a_{n-1} \odot x^{n-1} \oplus \cdots \oplus a_{1} \odot x \oplus a_{0}
$$
where exponentiation is as defined in the previous problem.
Let $p$ be a tropical polynomial. Prove that
$$
p\left(\frac{x+y}{2}\right) \geq \frac{p(x)+p(y)}{2}
$$
for all $x, y \in \mathbb{R} \cup\{\infty\}$. (This means that all tropical polynomials are concave.)
|
First, note that for any $x_{1}, \ldots, x_{n}, y_{1}, \ldots, y_{n}$, we have
$$
\min \left\{x_{1}+y_{1}, x_{2}+y_{2}, \ldots, x_{n}+y_{n}\right\} \geq \min \left\{x_{1}, x_{2}, \ldots, x_{n}\right\}+\min \left\{y_{1}, y_{2}, \ldots, y_{n}\right\} .
$$
Indeed, suppose that $x_{m}+y_{m}=\min _{i}\left\{x_{i}+y_{i}\right\}$, then $x_{m} \geq \min _{i} x_{i}$ and $y_{m} \geq \min _{i} y_{i}$, and so $\min _{i}\left\{x_{i}+y_{i}\right\}=x_{m}+y_{m} \geq \min _{i} x_{i}+\min _{i} y_{i}$.
Now, let us write a tropical polynomial in a more familiar notation. We have
$$
p(x)=\min _{0 \leq k \leq n}\left\{a_{k}+k x\right\} .
$$
So
$$
\begin{aligned}
p\left(\frac{x+y}{2}\right) & =\min _{0 \leq k \leq n}\left\{a_{k}+k\left(\frac{x+y}{2}\right)\right\} \\
& =\frac{1}{2} \min _{0 \leq k \leq n}\left\{\left(a_{k}+k x\right)+\left(a_{k}+k y\right)\right\} \\
& \geq \frac{1}{2}\left(\min _{0 \leq k \leq n}\left\{a_{k}+k x\right\}+\min _{0 \leq k \leq n}\left\{a_{k}+k y\right\}\right) \\
& =\frac{1}{2}(p(x)+p(y)) .
\end{aligned}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team2-solutions.jsonl",
"problem_match": "\n3. [35]",
"solution_match": "\nSolution: "
}
|
f22cf218-a735-5e30-ab3a-e7f013561692
| 608,356
|
(Fundamental Theorem of Algebra) Let $p$ be a tropical polynomial:
$$
p(x)=a_{n} \odot x^{n} \oplus a_{n-1} \odot x^{n-1} \oplus \cdots \oplus a_{1} \odot x \oplus a_{0}, \quad a_{n} \neq \infty
$$
Prove that we can find $r_{1}, r_{2}, \ldots, r_{n} \in \mathbb{R} \cup\{\infty\}$ so that
$$
p(x)=a_{n} \odot\left(x \oplus r_{1}\right) \odot\left(x \oplus r_{2}\right) \odot \cdots \odot\left(x \oplus r_{n}\right)
$$
for all $x$.
|
Again, we have
$$
p(x)=\min _{0 \leq k \leq n}\left\{a_{k}+k x\right\} .
$$
So the graph of $y=p(x)$ can be drawn as follows: first, draw all the lines $y=a_{k}+k x$, $k=0,1, \ldots, n$, then trace out the lowest broken line, which then is the graph of $y=p(x)$.
So $p(x)$ is piecewise linear and continuous, and has slopes from the set $\{0,1,2, \ldots, n\}$. We know from the previous problem that $p(x)$ is concave, and so its slope must be decreasing (this can also be observed simply from the drawing of the graph of $y=p(x)$ ). Then, let $r_{k}$ denote the $x$-coordinate of the leftmost kink such that the slope of the graph is less than $k$ to the right of this kink. Then, $r_{n} \leq r_{n-1} \leq \cdots \leq r_{1}$, and for $r_{k-1} \leq x \leq r_{k}$, the graph of $p$ is linear with slope $k$. Note that is if possible that $r_{k-1}=r_{k}$, if no segment of $p$ has slope $k$. Also, since $a_{n} \neq \infty$, the leftmost piece of $p(x)$ must have slope $n$, and thus $r_{n}$ exists, and thus all $r_{i}$ exist.
Now, compare $p(x)$ with
$$
\begin{aligned}
q(x) & =a_{n} \odot\left(x \oplus r_{1}\right) \odot\left(x \oplus r_{2}\right) \odot \cdots \odot\left(x \oplus r_{n}\right) \\
& =a_{n}+\min \left(x, r_{1}\right)+\min \left(x, r_{2}\right)+\cdots+\min \left(x, r_{n}\right) .
\end{aligned}
$$
For $r_{k-1} \leq x \leq r_{k}$, the slope of $q(x)$ is $k$, and for $x \leq r_{n}$ the slope of $q$ is $n$ and for $x \geq r_{1}$ the slope of $q$ is 0 . So $q$ is piecewise linear, and of course it is continuous. It follows that the graph of $q$ coincides with that of $p$ up to a translation. By taking any $x<r_{n}$, we see that $q(x)=a_{n}+n x=p(x)$, we see that the graphs of $p$ and $q$ coincide, and thus they must be the same function.
## Juggling [125]
A juggling sequence of length $n$ is a sequence $j(\cdot)$ of $n$ nonnegative integers, usually written as a string
$$
j(0) j(1) \ldots j(n-1)
$$
such that the mapping $f: \mathbb{Z} \rightarrow \mathbb{Z}$ defined by
$$
f(t)=t+j(\bar{t})
$$
is a permutation of the integers. Here $\bar{t}$ denotes the remainder of $t$ when divided by $n$. In this case, we say that $f$ is the corresponding juggling pattern.
For a juggling pattern $f$ (or its corresponding juggling sequence), we say that it has $b$ balls if the permutation induces $b$ infinite orbits on the set of integers. Equivalently, $b$ is the maximum number such that we can find a set of $b$ integers $\left\{t_{1}, t_{2}, \ldots, t_{b}\right\}$ so that the sets $\left\{t_{i}, f\left(t_{i}\right), f\left(f\left(t_{i}\right)\right), f\left(f\left(f\left(t_{i}\right)\right)\right), \ldots\right\}$ are all infinite and mutually disjoint (i.e. non-overlapping) for $i=1,2, \ldots, b$. (This definition will become clear in a second.)
Now is probably a good time to pause and think about what all this has to do with juggling. Imagine that we are juggling a number of balls, and at time $t$, we toss a ball from our hand up to a height $j(\bar{t})$. This ball stays up in the air for $j(\bar{t})$ units of time, so that it comes back to our hand at time $f(t)=t+j(\bar{t})$. Then, the juggling pattern presents a simplified model of how balls are juggled (for instance, we ignore information such as which hand we use to toss the ball). A throw height of 0 (i.e., $j(\bar{t})=0$ and $f(t)=t$ ) represents that no thrown takes place at time $t$, which could correspond to an empty hand. Then, $b$ is simply the minimum number of balls needed to carry out the juggling.
The following graphical representation may be helpful to you. On a horizontal line, an curve is drawn from $t$ to $f(t)$. For instance, the following diagram depicts the juggling sequence 441 (or the juggling sequences 414 and 144). Then $b$ is simply the number of contiguous "paths" drawn, which is 3 in this case.
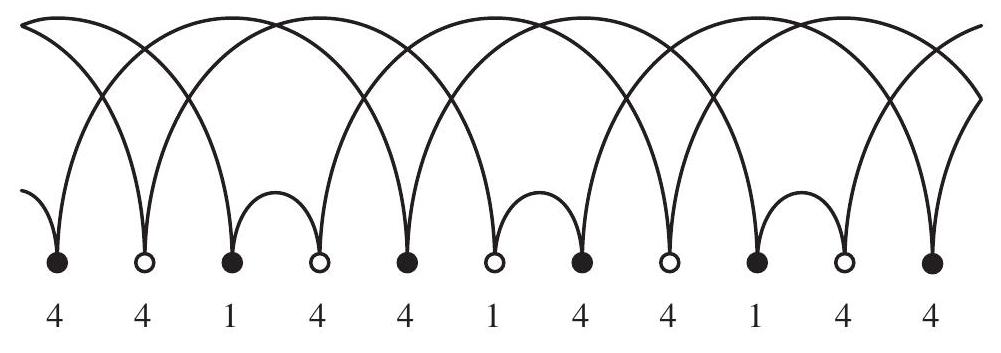
Figure 1: Juggling diagram of 441.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
(Fundamental Theorem of Algebra) Let $p$ be a tropical polynomial:
$$
p(x)=a_{n} \odot x^{n} \oplus a_{n-1} \odot x^{n-1} \oplus \cdots \oplus a_{1} \odot x \oplus a_{0}, \quad a_{n} \neq \infty
$$
Prove that we can find $r_{1}, r_{2}, \ldots, r_{n} \in \mathbb{R} \cup\{\infty\}$ so that
$$
p(x)=a_{n} \odot\left(x \oplus r_{1}\right) \odot\left(x \oplus r_{2}\right) \odot \cdots \odot\left(x \oplus r_{n}\right)
$$
for all $x$.
|
Again, we have
$$
p(x)=\min _{0 \leq k \leq n}\left\{a_{k}+k x\right\} .
$$
So the graph of $y=p(x)$ can be drawn as follows: first, draw all the lines $y=a_{k}+k x$, $k=0,1, \ldots, n$, then trace out the lowest broken line, which then is the graph of $y=p(x)$.
So $p(x)$ is piecewise linear and continuous, and has slopes from the set $\{0,1,2, \ldots, n\}$. We know from the previous problem that $p(x)$ is concave, and so its slope must be decreasing (this can also be observed simply from the drawing of the graph of $y=p(x)$ ). Then, let $r_{k}$ denote the $x$-coordinate of the leftmost kink such that the slope of the graph is less than $k$ to the right of this kink. Then, $r_{n} \leq r_{n-1} \leq \cdots \leq r_{1}$, and for $r_{k-1} \leq x \leq r_{k}$, the graph of $p$ is linear with slope $k$. Note that is if possible that $r_{k-1}=r_{k}$, if no segment of $p$ has slope $k$. Also, since $a_{n} \neq \infty$, the leftmost piece of $p(x)$ must have slope $n$, and thus $r_{n}$ exists, and thus all $r_{i}$ exist.
Now, compare $p(x)$ with
$$
\begin{aligned}
q(x) & =a_{n} \odot\left(x \oplus r_{1}\right) \odot\left(x \oplus r_{2}\right) \odot \cdots \odot\left(x \oplus r_{n}\right) \\
& =a_{n}+\min \left(x, r_{1}\right)+\min \left(x, r_{2}\right)+\cdots+\min \left(x, r_{n}\right) .
\end{aligned}
$$
For $r_{k-1} \leq x \leq r_{k}$, the slope of $q(x)$ is $k$, and for $x \leq r_{n}$ the slope of $q$ is $n$ and for $x \geq r_{1}$ the slope of $q$ is 0 . So $q$ is piecewise linear, and of course it is continuous. It follows that the graph of $q$ coincides with that of $p$ up to a translation. By taking any $x<r_{n}$, we see that $q(x)=a_{n}+n x=p(x)$, we see that the graphs of $p$ and $q$ coincide, and thus they must be the same function.
## Juggling [125]
A juggling sequence of length $n$ is a sequence $j(\cdot)$ of $n$ nonnegative integers, usually written as a string
$$
j(0) j(1) \ldots j(n-1)
$$
such that the mapping $f: \mathbb{Z} \rightarrow \mathbb{Z}$ defined by
$$
f(t)=t+j(\bar{t})
$$
is a permutation of the integers. Here $\bar{t}$ denotes the remainder of $t$ when divided by $n$. In this case, we say that $f$ is the corresponding juggling pattern.
For a juggling pattern $f$ (or its corresponding juggling sequence), we say that it has $b$ balls if the permutation induces $b$ infinite orbits on the set of integers. Equivalently, $b$ is the maximum number such that we can find a set of $b$ integers $\left\{t_{1}, t_{2}, \ldots, t_{b}\right\}$ so that the sets $\left\{t_{i}, f\left(t_{i}\right), f\left(f\left(t_{i}\right)\right), f\left(f\left(f\left(t_{i}\right)\right)\right), \ldots\right\}$ are all infinite and mutually disjoint (i.e. non-overlapping) for $i=1,2, \ldots, b$. (This definition will become clear in a second.)
Now is probably a good time to pause and think about what all this has to do with juggling. Imagine that we are juggling a number of balls, and at time $t$, we toss a ball from our hand up to a height $j(\bar{t})$. This ball stays up in the air for $j(\bar{t})$ units of time, so that it comes back to our hand at time $f(t)=t+j(\bar{t})$. Then, the juggling pattern presents a simplified model of how balls are juggled (for instance, we ignore information such as which hand we use to toss the ball). A throw height of 0 (i.e., $j(\bar{t})=0$ and $f(t)=t$ ) represents that no thrown takes place at time $t$, which could correspond to an empty hand. Then, $b$ is simply the minimum number of balls needed to carry out the juggling.
The following graphical representation may be helpful to you. On a horizontal line, an curve is drawn from $t$ to $f(t)$. For instance, the following diagram depicts the juggling sequence 441 (or the juggling sequences 414 and 144). Then $b$ is simply the number of contiguous "paths" drawn, which is 3 in this case.

Figure 1: Juggling diagram of 441.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team2-solutions.jsonl",
"problem_match": "\n4. [40]",
"solution_match": "\nSolution: "
}
|
02605877-1d7b-58a4-9b5e-e0de91f7ce4f
| 608,357
|
Suppose that $j(0) j(1) \cdots j(n-1)$ is a valid juggling sequence. For $i=0,1, \ldots, n-1$, Let $a_{i}$ denote the remainder of $j(i)+i$ when divided by $n$. Prove that $\left(a_{0}, a_{1}, \ldots, a_{n-1}\right)$ is a permutation of $(0,1, \ldots, n-1)$.
|
Suppose that $a_{i}=j(i)+i-b_{i} n$, where $b_{i}$ is an integer. Note that $f\left(i-b_{i} n\right)=$ $i-b_{i} n+j(i)=a_{i}$. Since $\left\{i-b_{i} n \mid i=0,1, \ldots, n-1\right\}$ contains $n$ distinct integers (as their residue $\bmod n$ are all distinct), and $f$ is a permutation, we see that after applying the map $f$, the resulting set $\left\{a_{0}, a_{1}, \ldots, a_{n-1}\right\}$ is a set of $n$ distinct integers. Since $0 \leq a_{i}<n$ from definition, we see that ( $a_{0}, a_{1}, \ldots, a_{n-1}$ ) is a permutation of $(0,1, \ldots, n-1)$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Suppose that $j(0) j(1) \cdots j(n-1)$ is a valid juggling sequence. For $i=0,1, \ldots, n-1$, Let $a_{i}$ denote the remainder of $j(i)+i$ when divided by $n$. Prove that $\left(a_{0}, a_{1}, \ldots, a_{n-1}\right)$ is a permutation of $(0,1, \ldots, n-1)$.
|
Suppose that $a_{i}=j(i)+i-b_{i} n$, where $b_{i}$ is an integer. Note that $f\left(i-b_{i} n\right)=$ $i-b_{i} n+j(i)=a_{i}$. Since $\left\{i-b_{i} n \mid i=0,1, \ldots, n-1\right\}$ contains $n$ distinct integers (as their residue $\bmod n$ are all distinct), and $f$ is a permutation, we see that after applying the map $f$, the resulting set $\left\{a_{0}, a_{1}, \ldots, a_{n-1}\right\}$ is a set of $n$ distinct integers. Since $0 \leq a_{i}<n$ from definition, we see that ( $a_{0}, a_{1}, \ldots, a_{n-1}$ ) is a permutation of $(0,1, \ldots, n-1)$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team2-solutions.jsonl",
"problem_match": "\n6. [40]",
"solution_match": "\nSolution: "
}
|
e0446597-b63f-5e37-acf0-4ac458034e07
| 608,359
|
Prove that the number of balls $b$ in a juggling sequence $j(0) j(1) \cdots j(n-1)$ is simply the average
$$
b=\frac{j(0)+j(1)+\cdots+j(n-1)}{n} .
$$
|
Consider the corresponding juggling diagram. Say the length of an curve from $t$ to $f(t)$ is $f(t)-t$. Let us draw only the curves whose left endpoint lies inside $[0, M n-1]$. For every single ball, the sum of the lengths of the arrows drawn corresponding to that ball is between $M n-J$ and $M n+J$, where $J=\max \{j(0), j(1), \ldots, j(n-1)\}$. It follows that the sum of the lengths of the arrows drawn is between $b(M n-J)$ and $b(M n+J)$. Since the arrow drawn at $t$ has length $j(\bar{t})$, the sum of the lengths of the arrows drawn is $M(j(0)+j(1)+\cdots+j(n-1))$. It follows that
$$
b(M n-J) \leq M(j(0)+j(1)+\cdots+j(n-1)) \leq b(M n+J)
$$
Dividing by $M n$, we get
$$
b\left(1-\frac{J}{n M}\right) \leq \frac{j(0)+j(1)+\cdots+j(n-1)}{n} \leq b\left(1+\frac{J}{n M}\right)
$$
Since we can take $M$ to be arbitrarily large, we must have
$$
b=\frac{j(0)+j(1)+\cdots+j(n-1)}{n}
$$
as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Prove that the number of balls $b$ in a juggling sequence $j(0) j(1) \cdots j(n-1)$ is simply the average
$$
b=\frac{j(0)+j(1)+\cdots+j(n-1)}{n} .
$$
|
Consider the corresponding juggling diagram. Say the length of an curve from $t$ to $f(t)$ is $f(t)-t$. Let us draw only the curves whose left endpoint lies inside $[0, M n-1]$. For every single ball, the sum of the lengths of the arrows drawn corresponding to that ball is between $M n-J$ and $M n+J$, where $J=\max \{j(0), j(1), \ldots, j(n-1)\}$. It follows that the sum of the lengths of the arrows drawn is between $b(M n-J)$ and $b(M n+J)$. Since the arrow drawn at $t$ has length $j(\bar{t})$, the sum of the lengths of the arrows drawn is $M(j(0)+j(1)+\cdots+j(n-1))$. It follows that
$$
b(M n-J) \leq M(j(0)+j(1)+\cdots+j(n-1)) \leq b(M n+J)
$$
Dividing by $M n$, we get
$$
b\left(1-\frac{J}{n M}\right) \leq \frac{j(0)+j(1)+\cdots+j(n-1)}{n} \leq b\left(1+\frac{J}{n M}\right)
$$
Since we can take $M$ to be arbitrarily large, we must have
$$
b=\frac{j(0)+j(1)+\cdots+j(n-1)}{n}
$$
as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team2-solutions.jsonl",
"problem_match": "\n8. [40]",
"solution_match": "\nSolution: "
}
|
52161c7e-715f-5464-a88f-9258867fbf3f
| 608,361
|
Show that the converse of the previous statement is false by providing a non-juggling sequence $j(0) j(1) j(2)$ of length 3 where the average $\frac{1}{3}(j(0)+j(1)+j(2))$ is an integer. Show that your example works.
|
One such example is 210 . This is not a juggling sequence since $f(0)=f(1)=2$.
## Incircles [180]
In the following problems, $A B C$ is a triangle with incenter $I$. Let $D, E, F$ denote the points where the incircle of $A B C$ touches sides $B C, C A, A B$, respectively.
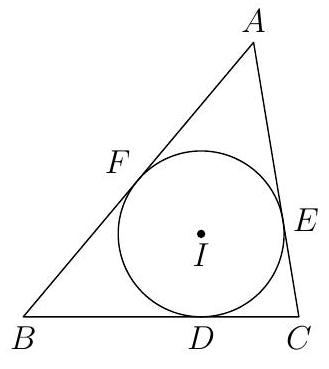
At the end of this section you can find some terminology and theorems that may be helpful to you.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Show that the converse of the previous statement is false by providing a non-juggling sequence $j(0) j(1) j(2)$ of length 3 where the average $\frac{1}{3}(j(0)+j(1)+j(2))$ is an integer. Show that your example works.
|
One such example is 210 . This is not a juggling sequence since $f(0)=f(1)=2$.
## Incircles [180]
In the following problems, $A B C$ is a triangle with incenter $I$. Let $D, E, F$ denote the points where the incircle of $A B C$ touches sides $B C, C A, A B$, respectively.

At the end of this section you can find some terminology and theorems that may be helpful to you.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team2-solutions.jsonl",
"problem_match": "\n9. [5]",
"solution_match": "\nSolution: "
}
|
74ec490a-ee87-5504-b291-8a1983e85d2e
| 608,362
|
Show that the incenter of triangle $A E F$ lies on the incircle of $A B C$.
|
Let segment $A I$ meet the incircle at $A_{1}$. Let us show that $A_{1}$ is the incenter of $A E F$.
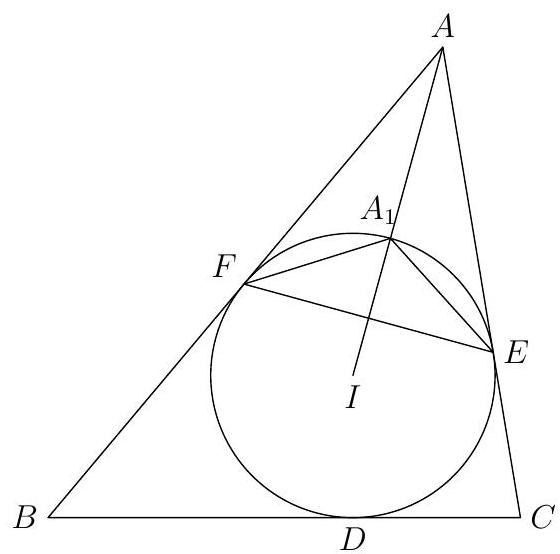
Since $A E=A F$ and $A A^{\prime}$ is the angle bisector of $\angle E A F$, we find that $A_{1} E=A_{1} F$. Using tangent-chord, we see that $\angle A F A_{1}=\angle A_{1} E F=\angle A_{1} F E$. Therefore, $A_{1}$ lies on the angle bisector of $\angle A F E$. Since $A_{1}$ also lies on the angle bisector of $\angle E A F, A_{1}$ must be the incenter of $A E F$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Show that the incenter of triangle $A E F$ lies on the incircle of $A B C$.
|
Let segment $A I$ meet the incircle at $A_{1}$. Let us show that $A_{1}$ is the incenter of $A E F$.

Since $A E=A F$ and $A A^{\prime}$ is the angle bisector of $\angle E A F$, we find that $A_{1} E=A_{1} F$. Using tangent-chord, we see that $\angle A F A_{1}=\angle A_{1} E F=\angle A_{1} F E$. Therefore, $A_{1}$ lies on the angle bisector of $\angle A F E$. Since $A_{1}$ also lies on the angle bisector of $\angle E A F, A_{1}$ must be the incenter of $A E F$, as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team2-solutions.jsonl",
"problem_match": "\n12. [35]",
"solution_match": "\nSolution: "
}
|
fcce9c1e-d0a0-5ad4-9d09-df3a092790c4
| 608,365
|
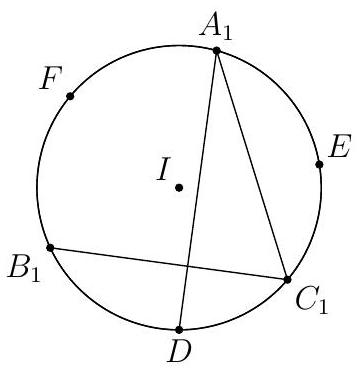
Let $A_{1}, B_{1}, C_{1}$ be the incenters of triangle $A E F, B D F, C D E$, respectively. Show that $A_{1} D, B_{1} E, C_{1} F$ all pass through the orthocenter of $A_{1} B_{1} C_{1}$.
|
Using the result from the previous problem, we see that $A_{1}, B_{1}, C_{1}$ are respectively the midpoints of the $\operatorname{arc} F E, F D, D F$ of the incircle. We have
$$
\begin{aligned}
\angle D A_{1} C_{1}+\angle B_{1} C_{1} A_{1} & =\frac{1}{2} \angle D I C_{1}+\frac{1}{2} \angle B_{1} I F+\frac{1}{2} \angle F I A_{1} \\
& =\frac{1}{4}(\angle E I D+\angle D I F+\angle F I E) \\
& =\frac{1}{4} \cdot 360^{\circ} \\
& =90^{\circ} .
\end{aligned}
$$
It follows that $A_{1} D$ is perpendicular to $B_{1} C_{1}$, and thus $A_{1} D$ passes through the orthocenter of $A_{1} B_{1} C_{1}$. Similarly, $A_{1} D, B_{1} E, C_{1} F$ all pass through the orthocenter of $A_{1} B_{1} C_{1}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A_{1}, B_{1}, C_{1}$ be the incenters of triangle $A E F, B D F, C D E$, respectively. Show that $A_{1} D, B_{1} E, C_{1} F$ all pass through the orthocenter of $A_{1} B_{1} C_{1}$.
|
Using the result from the previous problem, we see that $A_{1}, B_{1}, C_{1}$ are respectively the midpoints of the $\operatorname{arc} F E, F D, D F$ of the incircle. We have

$$
\begin{aligned}
\angle D A_{1} C_{1}+\angle B_{1} C_{1} A_{1} & =\frac{1}{2} \angle D I C_{1}+\frac{1}{2} \angle B_{1} I F+\frac{1}{2} \angle F I A_{1} \\
& =\frac{1}{4}(\angle E I D+\angle D I F+\angle F I E) \\
& =\frac{1}{4} \cdot 360^{\circ} \\
& =90^{\circ} .
\end{aligned}
$$
It follows that $A_{1} D$ is perpendicular to $B_{1} C_{1}$, and thus $A_{1} D$ passes through the orthocenter of $A_{1} B_{1} C_{1}$. Similarly, $A_{1} D, B_{1} E, C_{1} F$ all pass through the orthocenter of $A_{1} B_{1} C_{1}$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team2-solutions.jsonl",
"problem_match": "\n13. [35]",
"solution_match": "\nSolution: "
}
|
4521613b-f650-5ace-9e0c-1c09492b1068
| 608,366
|
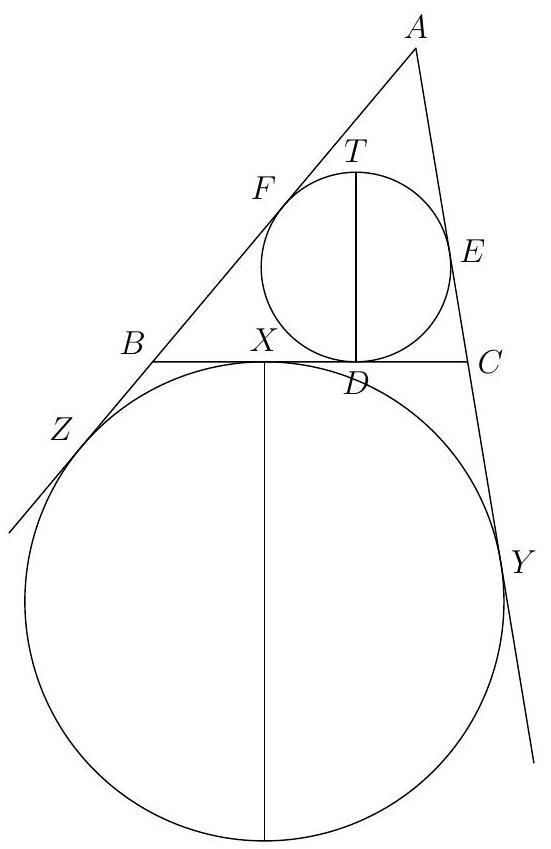
Let $X$ be the point on side $B C$ such that $B X=C D$. Show that the excircle $A B C$ opposite of vertex $A$ touches segment $B C$ at $X$.
|
Let the excircle touch lines $B C, A C$ and $A B$ at $X^{\prime}, Y$ and $Z$, respectively. Using the equal tangent property repeatedly, we have
$$
B X^{\prime}-X^{\prime} C=B Z-C Y=(E Y-C Y)-(F Z-B Z)=C E-B F=C D-B D .
$$
It follows that $B X^{\prime}=C D$, and thus $X^{\prime}=X$. So the excircle touches $B C$ at $X$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $X$ be the point on side $B C$ such that $B X=C D$. Show that the excircle $A B C$ opposite of vertex $A$ touches segment $B C$ at $X$.
|
Let the excircle touch lines $B C, A C$ and $A B$ at $X^{\prime}, Y$ and $Z$, respectively. Using the equal tangent property repeatedly, we have
$$
B X^{\prime}-X^{\prime} C=B Z-C Y=(E Y-C Y)-(F Z-B Z)=C E-B F=C D-B D .
$$
It follows that $B X^{\prime}=C D$, and thus $X^{\prime}=X$. So the excircle touches $B C$ at $X$.

|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team2-solutions.jsonl",
"problem_match": "\n14. [40]",
"solution_match": "\nSolution: "
}
|
f72e89a8-28bf-5bc5-8740-243dd8ba5e75
| 608,367
|
Let $X$ be as in the previous problem. Let $T$ be the point diametrically opposite to $D$ on on the incircle of $A B C$. Show that $A, T, X$ are collinear.
|
Consider a dilation centered at $A$ that carries the incircle to the excircle. This dilation must send the diameter $D T$ to some the diameter of excircle that is perpendicular to $B C$. The only such diameter is the one goes through $X$. It follows that $T$ gets carried to $X$. Therefore, $A, T, X$ are collinear.
## Glossary and some possibly useful facts
- A set of points is collinear if they lie on a common line. A set of lines is concurrent if they pass through a common point.
- Given $A B C$ a triangle, the three angle bisectors are concurrent at the incenter of the triangle. The incenter is the center of the incircle, which is the unique circle inscribed in $A B C$, tangent to all three sides.
- The excircles of a triangle $A B C$ are the three circles on the exterior the triangle but tangent to all three lines $A B, B C, C A$.
- The orthocenter of a triangle is the point of concurrency of the three altitudes.
- Ceva's theorem states that given $A B C$ a triangle, and points $X, Y, Z$ on sides $B C, C A, A B$, respectively, the lines $A X, B Y, C Z$ are concurrent if and only if
$$
\frac{B X}{X B} \cdot \frac{C Y}{Y A} \cdot \frac{A Z}{Z B}=1
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $X$ be as in the previous problem. Let $T$ be the point diametrically opposite to $D$ on on the incircle of $A B C$. Show that $A, T, X$ are collinear.
|
Consider a dilation centered at $A$ that carries the incircle to the excircle. This dilation must send the diameter $D T$ to some the diameter of excircle that is perpendicular to $B C$. The only such diameter is the one goes through $X$. It follows that $T$ gets carried to $X$. Therefore, $A, T, X$ are collinear.
## Glossary and some possibly useful facts
- A set of points is collinear if they lie on a common line. A set of lines is concurrent if they pass through a common point.
- Given $A B C$ a triangle, the three angle bisectors are concurrent at the incenter of the triangle. The incenter is the center of the incircle, which is the unique circle inscribed in $A B C$, tangent to all three sides.
- The excircles of a triangle $A B C$ are the three circles on the exterior the triangle but tangent to all three lines $A B, B C, C A$.
- The orthocenter of a triangle is the point of concurrency of the three altitudes.
- Ceva's theorem states that given $A B C$ a triangle, and points $X, Y, Z$ on sides $B C, C A, A B$, respectively, the lines $A X, B Y, C Z$ are concurrent if and only if
$$
\frac{B X}{X B} \cdot \frac{C Y}{Y A} \cdot \frac{A Z}{Z B}=1
$$
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team2-solutions.jsonl",
"problem_match": "\n15. [40]",
"solution_match": "\nSolution: "
}
|
0b3a2597-7f6b-5328-8fda-b767d1ac045d
| 608,368
|
Say that $\frac{a}{b}$ is a positive rational number in simplest form, with $a \neq 1$. Further, say that $n$ is an integer such that:
$$
\frac{1}{n}>\frac{a}{b}>\frac{1}{n+1}
$$
Show that when $\frac{a}{b}-\frac{1}{n+1}$ is written in simplest form, its numerator is smaller than $a$.
|
$\quad \frac{a}{b}-\frac{1}{n+1}=\frac{a(n+1)-b}{b(n+1)}$. Therefore, when we write it in simplest form, its numerator will be at most $a(n+1)-b$. We claim that $a(n+1)-b<a$. Indeed, this is the same as $a n-b<0 \Longleftrightarrow a n<b \Longleftrightarrow \frac{b}{a}>n$, which is given.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Say that $\frac{a}{b}$ is a positive rational number in simplest form, with $a \neq 1$. Further, say that $n$ is an integer such that:
$$
\frac{1}{n}>\frac{a}{b}>\frac{1}{n+1}
$$
Show that when $\frac{a}{b}-\frac{1}{n+1}$ is written in simplest form, its numerator is smaller than $a$.
|
$\quad \frac{a}{b}-\frac{1}{n+1}=\frac{a(n+1)-b}{b(n+1)}$. Therefore, when we write it in simplest form, its numerator will be at most $a(n+1)-b$. We claim that $a(n+1)-b<a$. Indeed, this is the same as $a n-b<0 \Longleftrightarrow a n<b \Longleftrightarrow \frac{b}{a}>n$, which is given.
|
{
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-team-solutions.jsonl",
"problem_match": "\n4. ",
"solution_match": "\nSolution: "
}
|
c1e35a4b-2e23-5782-b52c-aa52691b5560
| 608,456
|
Now, using information from problems 4 and 5 , prove that the following method to decompose any positive rational number will always terminate:
Step 1. Start with the fraction $\frac{a}{b}$. Let $t_{1}$ be the largest unit fraction $\frac{1}{n}$ which is less than or equal to $\frac{a}{b}$.
Step 2. If we have already chosen $t_{1}$ through $t_{k}$, and if $t_{1}+t_{2}+\ldots+t_{k}$ is still less than $\frac{a}{b}$, then let $t_{k+1}$ be the largest unit fraction less than both $t_{k}$ and $\frac{a}{b}$.
Step 3. If $t_{1}+\ldots+t_{k+1}$ equals $\frac{a}{b}$, the decomposition is found. Otherwise, repeat step 2 .
Why does this method never result in an infinite sequence of $t_{i}$ ?
|
Let $\frac{a_{k}}{b_{k}}=\frac{a}{b}-t_{1}-\ldots-t_{k}$, where $\frac{a_{k}}{b_{k}}$ is a fraction in simplest terms. Initially, this algorithm will have $t_{1}=1, t_{2}=\frac{1}{2}, t_{3}=\frac{1}{3}$, etc. until $\frac{a_{k}}{b_{k}}<\frac{1}{k+1}$. This will eventually happen by problem 5 , since there exists a $k$ such that $\frac{1}{1}+\ldots+\frac{1}{k+1}>\frac{a_{k}}{b_{k}}$. At that point, there is some $n$ with $\frac{1}{n}<t_{k}$ such that $\frac{1}{n}>\frac{a_{k}}{b_{k}}>\frac{1}{n+1}$. In this case, $t_{k+1}=\frac{1}{n+1}$.
Suppose that there exists $n_{k}$ such that $\frac{1}{n_{k}}>\frac{a_{k}}{b_{k}}>\frac{1}{n_{k}+1}$ for some $k$. Then we have $t_{k+1}=\frac{1}{n_{k}+1}$ and $\frac{a_{k+1}}{b_{k+1}}<\frac{1}{n_{k}\left(n_{k}+1\right)}$. This shows that once we have found $n_{k}$ such that $\frac{1}{n_{k}}>\frac{a_{k}}{b_{k}}>\frac{1}{n_{k}+1}$ and $\frac{1}{n_{k}} \leq t_{k}$, we no longer have to worry about $t_{k+1}$ being less than $t_{k}$, since $t_{k+1}=\frac{1}{n_{k}+1}<\frac{1}{n_{k}}<$ $t_{k}$, and also $n_{k+1} \geq n_{k}\left(n_{k}+1\right)$ while $\frac{1}{n_{k}\left(n_{k}+1\right)} \leq \frac{1}{n_{k}+1}=t_{k+1}$.
On the other hand, once we have found such an $n_{k}$, the sequence $\left\{a_{k}\right\}$ must be decreasing by problem 4. Since the $a_{k}$ are all integers, we eventually have to get to 0 (as there is no infinite decreasing sequence of positive integers). Therefore, after some finite number of steps the algorithm terminates with $a_{k+1}=0$, so $0=\frac{a_{k}}{b_{k}}=\frac{a}{b}-t_{1}-\ldots-t_{k}$, so $\frac{a}{b}=t_{1}+\ldots+t_{k}$, which is what we wanted.
## Juicy Numbers [100]
A juicy number is an integer $j>1$ for which there is a sequence $a_{1}<a_{2}<\ldots<a_{k}$ of positive integers such that $a_{k}=j$ and such that the sum of the reciprocals of all the $a_{i}$ is 1 . For example, 6 is a juicy number because $\frac{1}{2}+\frac{1}{3}+\frac{1}{6}=1$, but 2 is not juicy.
In this part, you will investigate some of the properties of juicy numbers. Remember that if you do not solve a question, you can still use its result on later questions.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Now, using information from problems 4 and 5 , prove that the following method to decompose any positive rational number will always terminate:
Step 1. Start with the fraction $\frac{a}{b}$. Let $t_{1}$ be the largest unit fraction $\frac{1}{n}$ which is less than or equal to $\frac{a}{b}$.
Step 2. If we have already chosen $t_{1}$ through $t_{k}$, and if $t_{1}+t_{2}+\ldots+t_{k}$ is still less than $\frac{a}{b}$, then let $t_{k+1}$ be the largest unit fraction less than both $t_{k}$ and $\frac{a}{b}$.
Step 3. If $t_{1}+\ldots+t_{k+1}$ equals $\frac{a}{b}$, the decomposition is found. Otherwise, repeat step 2 .
Why does this method never result in an infinite sequence of $t_{i}$ ?
|
Let $\frac{a_{k}}{b_{k}}=\frac{a}{b}-t_{1}-\ldots-t_{k}$, where $\frac{a_{k}}{b_{k}}$ is a fraction in simplest terms. Initially, this algorithm will have $t_{1}=1, t_{2}=\frac{1}{2}, t_{3}=\frac{1}{3}$, etc. until $\frac{a_{k}}{b_{k}}<\frac{1}{k+1}$. This will eventually happen by problem 5 , since there exists a $k$ such that $\frac{1}{1}+\ldots+\frac{1}{k+1}>\frac{a_{k}}{b_{k}}$. At that point, there is some $n$ with $\frac{1}{n}<t_{k}$ such that $\frac{1}{n}>\frac{a_{k}}{b_{k}}>\frac{1}{n+1}$. In this case, $t_{k+1}=\frac{1}{n+1}$.
Suppose that there exists $n_{k}$ such that $\frac{1}{n_{k}}>\frac{a_{k}}{b_{k}}>\frac{1}{n_{k}+1}$ for some $k$. Then we have $t_{k+1}=\frac{1}{n_{k}+1}$ and $\frac{a_{k+1}}{b_{k+1}}<\frac{1}{n_{k}\left(n_{k}+1\right)}$. This shows that once we have found $n_{k}$ such that $\frac{1}{n_{k}}>\frac{a_{k}}{b_{k}}>\frac{1}{n_{k}+1}$ and $\frac{1}{n_{k}} \leq t_{k}$, we no longer have to worry about $t_{k+1}$ being less than $t_{k}$, since $t_{k+1}=\frac{1}{n_{k}+1}<\frac{1}{n_{k}}<$ $t_{k}$, and also $n_{k+1} \geq n_{k}\left(n_{k}+1\right)$ while $\frac{1}{n_{k}\left(n_{k}+1\right)} \leq \frac{1}{n_{k}+1}=t_{k+1}$.
On the other hand, once we have found such an $n_{k}$, the sequence $\left\{a_{k}\right\}$ must be decreasing by problem 4. Since the $a_{k}$ are all integers, we eventually have to get to 0 (as there is no infinite decreasing sequence of positive integers). Therefore, after some finite number of steps the algorithm terminates with $a_{k+1}=0$, so $0=\frac{a_{k}}{b_{k}}=\frac{a}{b}-t_{1}-\ldots-t_{k}$, so $\frac{a}{b}=t_{1}+\ldots+t_{k}$, which is what we wanted.
## Juicy Numbers [100]
A juicy number is an integer $j>1$ for which there is a sequence $a_{1}<a_{2}<\ldots<a_{k}$ of positive integers such that $a_{k}=j$ and such that the sum of the reciprocals of all the $a_{i}$ is 1 . For example, 6 is a juicy number because $\frac{1}{2}+\frac{1}{3}+\frac{1}{6}=1$, but 2 is not juicy.
In this part, you will investigate some of the properties of juicy numbers. Remember that if you do not solve a question, you can still use its result on later questions.
|
{
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-team-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\nSolution: "
}
|
81161faf-9a32-5ded-b80f-e40b1a3d0f23
| 608,458
|
Let $p$ be a prime. Given a sequence of positive integers $b_{1}$ through $b_{n}$, exactly one of which is divisible by $p$, show that when
$$
\frac{1}{b_{1}}+\frac{1}{b_{2}}+\ldots+\frac{1}{b_{n}}
$$
is written as a fraction in lowest terms, then its denominator is divisible by $p$. Use this fact to explain why no prime $p$ is ever juicy.
|
We can assume that $b_{n}$ is the term divisible by $p$ (i.e. $b_{n}=k p$ ) since the order of addition doesn't matter. We can then write
$$
\frac{1}{b_{1}}+\frac{1}{b_{2}}+\ldots+\frac{1}{b_{n-1}}=\frac{a}{b}
$$
where $b$ is not divisible by $p$ (since none of the $b_{i}$ are). But then $\frac{a}{b}+\frac{1}{k p}=\frac{k p a+b}{k p b}$. Since $b$ is not divisible by $p, k p a+b$ is not divisible by $p$, so we cannot remove the factor of $p$ from the denominator. In particular, $p$ cannot be juicy as 1 can be written as $\frac{1}{1}$, which has a denominator not divisible by $p$, whereas being juicy means we have a sum $\frac{1}{b_{1}}+\ldots+\frac{1}{b_{n}}=1$, where $b_{1}<b_{2}<\ldots<b_{n}=p$, and so in particular none of the $b_{i}$ with $i<n$ are divisible by p.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $p$ be a prime. Given a sequence of positive integers $b_{1}$ through $b_{n}$, exactly one of which is divisible by $p$, show that when
$$
\frac{1}{b_{1}}+\frac{1}{b_{2}}+\ldots+\frac{1}{b_{n}}
$$
is written as a fraction in lowest terms, then its denominator is divisible by $p$. Use this fact to explain why no prime $p$ is ever juicy.
|
We can assume that $b_{n}$ is the term divisible by $p$ (i.e. $b_{n}=k p$ ) since the order of addition doesn't matter. We can then write
$$
\frac{1}{b_{1}}+\frac{1}{b_{2}}+\ldots+\frac{1}{b_{n-1}}=\frac{a}{b}
$$
where $b$ is not divisible by $p$ (since none of the $b_{i}$ are). But then $\frac{a}{b}+\frac{1}{k p}=\frac{k p a+b}{k p b}$. Since $b$ is not divisible by $p, k p a+b$ is not divisible by $p$, so we cannot remove the factor of $p$ from the denominator. In particular, $p$ cannot be juicy as 1 can be written as $\frac{1}{1}$, which has a denominator not divisible by $p$, whereas being juicy means we have a sum $\frac{1}{b_{1}}+\ldots+\frac{1}{b_{n}}=1$, where $b_{1}<b_{2}<\ldots<b_{n}=p$, and so in particular none of the $b_{i}$ with $i<n$ are divisible by p.
|
{
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-team-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nSolution: "
}
|
f2742ee7-a8ba-564b-b6ad-f9bb46bdca42
| 608,461
|
Let $n \geq 3$ be a positive integer. A triangulation of a convex $n$-gon is a set of $n-3$ of its diagonals which do not intersect in the interior of the polygon. Along with the $n$ sides, these diagonals separate the polygon into $n-2$ disjoint triangles. Any triangulation can be viewed as a graph: the vertices of the graph are the corners of the polygon, and the $n$ sides and $n-3$ diagonals are the edges.
For a fixed $n$-gon, different triangulations correspond to different graphs. Prove that all of these graphs have the same chromatic number.
|
We will show that all triangulations have chromatic number 3, by induction on $n$. As a base case, if $n=3$, a triangle has chromatic number 3. Now, given a triangulation of an $n$-gon for $n>3$, every edge is either a side or a diagonal of the polygon. There are $n$ sides and only $n-3$ diagonals in the edge-set, so the Pigeonhole Principle guarentees a triangle with two side edges. These two sides must be adjacent, so we can remove this triangle to leave a triangulation of an ( $n-1$ )-gon, which has chromatic number 3 by the inductive hypothesis. Adding the last triangle adds only one new vertex with two neighbors, so we can color this vertex with one of the three colors not used on its neighbors.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n \geq 3$ be a positive integer. A triangulation of a convex $n$-gon is a set of $n-3$ of its diagonals which do not intersect in the interior of the polygon. Along with the $n$ sides, these diagonals separate the polygon into $n-2$ disjoint triangles. Any triangulation can be viewed as a graph: the vertices of the graph are the corners of the polygon, and the $n$ sides and $n-3$ diagonals are the edges.
For a fixed $n$-gon, different triangulations correspond to different graphs. Prove that all of these graphs have the same chromatic number.
|
We will show that all triangulations have chromatic number 3, by induction on $n$. As a base case, if $n=3$, a triangle has chromatic number 3. Now, given a triangulation of an $n$-gon for $n>3$, every edge is either a side or a diagonal of the polygon. There are $n$ sides and only $n-3$ diagonals in the edge-set, so the Pigeonhole Principle guarentees a triangle with two side edges. These two sides must be adjacent, so we can remove this triangle to leave a triangulation of an ( $n-1$ )-gon, which has chromatic number 3 by the inductive hypothesis. Adding the last triangle adds only one new vertex with two neighbors, so we can color this vertex with one of the three colors not used on its neighbors.
|
{
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-team1-solutions.jsonl",
"problem_match": "\n1. [8]",
"solution_match": "\nSolution: "
}
|
9209b951-07aa-5f5a-aa65-a6c8d2eed284
| 608,547
|
A graph is finite if it has a finite number of vertices.
(a) $[6]$ Let $G$ be a finite graph in which every vertex has degree $k$. Prove that the chromatic number of $G$ is at most $k+1$.
|
We find a good coloring with $k+1$ colors. Order the vertices and color them one by one. Since each vertex has at most $k$ neighbors, one of the $k+1$ colors has not been used on a neighbor, so there is always a good color for that vertex. In fact, we have shows that any graph in which every vertex has degree at most $k$ can be colored with $k+1$ colors.
(b) [10] In terms of $n$, what is the minimum number of edges a finite graph with chromatic number $n$ could have? Prove your answer.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A graph is finite if it has a finite number of vertices.
(a) $[6]$ Let $G$ be a finite graph in which every vertex has degree $k$. Prove that the chromatic number of $G$ is at most $k+1$.
|
We find a good coloring with $k+1$ colors. Order the vertices and color them one by one. Since each vertex has at most $k$ neighbors, one of the $k+1$ colors has not been used on a neighbor, so there is always a good color for that vertex. In fact, we have shows that any graph in which every vertex has degree at most $k$ can be colored with $k+1$ colors.
(b) [10] In terms of $n$, what is the minimum number of edges a finite graph with chromatic number $n$ could have? Prove your answer.
|
{
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-team1-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nSolution: "
}
|
d3aa505e-c42f-522c-8773-0f5c0ecfa3c6
| 608,549
|
The size of a finite graph is the number of vertices in the graph.
(a) [15] Show that, for any $n>2$, and any positive integer $N$, there are finite graphs with size at least $N$ and with chromatic number $n$ such that removing any vertex (and all its incident edges) from the graph decreases its chromatic number.
|
Let $k>1$ be an odd number, and let $G$ be a graph with $k$ vertices arranged in a circle, with each vertex connected to its two neighbors. If $n=3$, these graphs can be arbitrarily large, and are the graphs we need. If $n>3$, let $H$ be a complete graph on $n-3$ vertices, and let $J$ be the graph created by adding an edge from every vertex in $G$ to every vertex in $H$. Then $n-3$ colors are needed to color $H$ and another 3 are
needed to color $G$, so $n$ colors is both necessary and sufficient for a good coloring of $J$. Now, say a vertex is removed from $J$. There are two cases:
If the vertex was removed from $G$, then the remaining vertices in $G$ can be colored with 2 colors, because the cycle has been broken. A set of $n-3$ different colors can be used to color $H$, so only $n-1$ colors are needed to color the reduced graph. On the other hand, if the vertex was removed from $H$, then $n-4$ colors are used to color $H$ and 3 used to color $G$. So removing any vertex decreases the chromatic number of $J$.
(b) [15] Show that, for any positive integers $n$ and $r$, there exists a positive integer $N$ such that for any finite graph having size at least $N$ and chromatic number equal to $n$, it is possible to remove $r$ vertices (and all their incident edges) in such a way that the remaining vertices form a graph with chromatic number at least $n-1$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
The size of a finite graph is the number of vertices in the graph.
(a) [15] Show that, for any $n>2$, and any positive integer $N$, there are finite graphs with size at least $N$ and with chromatic number $n$ such that removing any vertex (and all its incident edges) from the graph decreases its chromatic number.
|
Let $k>1$ be an odd number, and let $G$ be a graph with $k$ vertices arranged in a circle, with each vertex connected to its two neighbors. If $n=3$, these graphs can be arbitrarily large, and are the graphs we need. If $n>3$, let $H$ be a complete graph on $n-3$ vertices, and let $J$ be the graph created by adding an edge from every vertex in $G$ to every vertex in $H$. Then $n-3$ colors are needed to color $H$ and another 3 are
needed to color $G$, so $n$ colors is both necessary and sufficient for a good coloring of $J$. Now, say a vertex is removed from $J$. There are two cases:
If the vertex was removed from $G$, then the remaining vertices in $G$ can be colored with 2 colors, because the cycle has been broken. A set of $n-3$ different colors can be used to color $H$, so only $n-1$ colors are needed to color the reduced graph. On the other hand, if the vertex was removed from $H$, then $n-4$ colors are used to color $H$ and 3 used to color $G$. So removing any vertex decreases the chromatic number of $J$.
(b) [15] Show that, for any positive integers $n$ and $r$, there exists a positive integer $N$ such that for any finite graph having size at least $N$ and chromatic number equal to $n$, it is possible to remove $r$ vertices (and all their incident edges) in such a way that the remaining vertices form a graph with chromatic number at least $n-1$.
|
{
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-team1-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\nSolution: "
}
|
4c32fb52-d72e-5247-8e7d-2c86e33933ce
| 608,551
|
For any set of graphs $G_{1}, G_{2}, \ldots, G_{n}$ all having the same set of vertices $V$, define their overlap, denoted $G_{1} \cup G_{2} \cup \cdots \cup G_{n}$, to be the graph having vertex set $V$ for which two vertices are adjacent in the overlap if and only if they are adjacent in at least one of the graphs $G_{i}$.
(a) $[\mathbf{1 0}]$ Let $G$ and $H$ be graphs having the same vertex set and let $a$ be the chromatic number of $G$ and $b$ the chromatic number of $H$. Find, in terms of $a$ and $b$, the largest possible chromatic number of $G \cup H$. Prove your answer.
|
[NOTE: This problem differs from the problem statement in the test as administered at the 2009 HMMT. The reader is encouraged to try it before reading the solution.]
The bound on $k$ follows from iterating part (a).
Let $G$ be a graph with chromatic number $n$. Consider a coloring of $G$ using $n$ colors labeled $1,2, \ldots, n$. For $i$ from 1 to $\left\lceil\log _{2}(n)\right\rceil$, define $G_{i}$ to be the graph on the vertices of $G$ for which two vertices are connected by an edge if and only if the $i$ th digit from the right in the binary expansions of their colors do not match. Clearly each of the graphs $G_{i}$ have chromatic number at most 2 , by coloring each node with the $i$ th digit of the binary expansion of their color in $G$. Moreover, each edge occurs in some $G_{i}$, since if two vertices match in every digit they are not connected by an edge. Therefore $G_{1} \cup G_{2} \cup \cdots \cup G_{\left\lceil\log _{2}(n)\right\rceil}=G$, and so we have found such a decomposition of $G$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
For any set of graphs $G_{1}, G_{2}, \ldots, G_{n}$ all having the same set of vertices $V$, define their overlap, denoted $G_{1} \cup G_{2} \cup \cdots \cup G_{n}$, to be the graph having vertex set $V$ for which two vertices are adjacent in the overlap if and only if they are adjacent in at least one of the graphs $G_{i}$.
(a) $[\mathbf{1 0}]$ Let $G$ and $H$ be graphs having the same vertex set and let $a$ be the chromatic number of $G$ and $b$ the chromatic number of $H$. Find, in terms of $a$ and $b$, the largest possible chromatic number of $G \cup H$. Prove your answer.
|
[NOTE: This problem differs from the problem statement in the test as administered at the 2009 HMMT. The reader is encouraged to try it before reading the solution.]
The bound on $k$ follows from iterating part (a).
Let $G$ be a graph with chromatic number $n$. Consider a coloring of $G$ using $n$ colors labeled $1,2, \ldots, n$. For $i$ from 1 to $\left\lceil\log _{2}(n)\right\rceil$, define $G_{i}$ to be the graph on the vertices of $G$ for which two vertices are connected by an edge if and only if the $i$ th digit from the right in the binary expansions of their colors do not match. Clearly each of the graphs $G_{i}$ have chromatic number at most 2 , by coloring each node with the $i$ th digit of the binary expansion of their color in $G$. Moreover, each edge occurs in some $G_{i}$, since if two vertices match in every digit they are not connected by an edge. Therefore $G_{1} \cup G_{2} \cup \cdots \cup G_{\left\lceil\log _{2}(n)\right\rceil}=G$, and so we have found such a decomposition of $G$.
|
{
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-team1-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\nSolution: "
}
|
c986e895-05b9-57e5-9545-8506f0ac8175
| 608,552
|
Let $n$ be a positive integer. Let $V_{n}$ be the set of all sequences of 0 's and 1's of length $n$. Define $G_{n}$ to be the graph having vertex set $V_{n}$, such that two sequences are adjacent in $G_{n}$ if and only if they differ in either 1 or 2 places. For instance, if $n=3$, the sequences $(1,0,0)$, $(1,1,0)$, and $(1,1,1)$ are mutually adjacent, but $(1,0,0)$ is not adjacent to $(0,1,1)$.
Show that, if $n+1$ is not a power of 2 , then the chromatic number of $G_{n}$ is at least $n+2$.
|
We will assume that there is a coloring with $n+1$ colors and derive a contradiction. For each string $s$, let $T_{s}$ be the set consisting of all strings that differ from $s$ in at most 1 place. Thus $T_{s}$ has size $n+1$ and all vertices in $T_{s}$ are adjacent. In particular, if there is an $(n+1)$-coloring, then each color is used exactly once in $T_{s}$. Let $c$ be one of the colors that we used. We will determine how many vertices are colored with $c$. We will do this by counting in two ways.
Let $k$ be the number of vertices colored with color $c$. Each such vertex is part of $T_{s}$ for exactly $n+1$ values of $s$. On the other hand, each $T_{s}$ contains exactly one vertex with color $c$. It follows that $k(n+1)=2^{n}$. In particular, since $k$ is an integer, $n+1$ divides $2^{n}$. This is a contradiction since $n+1$ is now a power of 2 by assumption, so actually there can be no $n+1$-coloring, as claimed.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ be a positive integer. Let $V_{n}$ be the set of all sequences of 0 's and 1's of length $n$. Define $G_{n}$ to be the graph having vertex set $V_{n}$, such that two sequences are adjacent in $G_{n}$ if and only if they differ in either 1 or 2 places. For instance, if $n=3$, the sequences $(1,0,0)$, $(1,1,0)$, and $(1,1,1)$ are mutually adjacent, but $(1,0,0)$ is not adjacent to $(0,1,1)$.
Show that, if $n+1$ is not a power of 2 , then the chromatic number of $G_{n}$ is at least $n+2$.
|
We will assume that there is a coloring with $n+1$ colors and derive a contradiction. For each string $s$, let $T_{s}$ be the set consisting of all strings that differ from $s$ in at most 1 place. Thus $T_{s}$ has size $n+1$ and all vertices in $T_{s}$ are adjacent. In particular, if there is an $(n+1)$-coloring, then each color is used exactly once in $T_{s}$. Let $c$ be one of the colors that we used. We will determine how many vertices are colored with $c$. We will do this by counting in two ways.
Let $k$ be the number of vertices colored with color $c$. Each such vertex is part of $T_{s}$ for exactly $n+1$ values of $s$. On the other hand, each $T_{s}$ contains exactly one vertex with color $c$. It follows that $k(n+1)=2^{n}$. In particular, since $k$ is an integer, $n+1$ divides $2^{n}$. This is a contradiction since $n+1$ is now a power of 2 by assumption, so actually there can be no $n+1$-coloring, as claimed.
|
{
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-team1-solutions.jsonl",
"problem_match": "\n7. [20]",
"solution_match": "\nSolution: "
}
|
b03af06a-5be7-5de0-a23e-be2950b63b84
| 608,553
|
Let $n \geq 3$ be a positive integer. A triangulation of a convex $n$-gon is a set of $n-3$ of its diagonals which do not intersect in the interior of the polygon. Along with the $n$ sides, these diagonals separate the polygon into $n-2$ disjoint triangles. Any triangulation can be viewed as a graph: the vertices of the graph are the corners of the polygon, and the $n$ sides and $n-3$ diagonals are the edges.
For a fixed $n$-gon, different triangulations correspond to different graphs. Prove that all of these graphs have the same chromatic number.
|
We will show that all triangulations have chromatic number 3, by induction on $n$. As a base case, if $n=3$, a triangle has chromatic number 3 . Now, given a triangulation of an $n$-gon for $n>3$, every edge is either a side or a diagonal of the polygon. There are $n$ sides and only $n-3$ diagonals in the edge-set, so the Pigeonhole Principle guarentees a triangle with two side edges. These two sides must be adjacent, so we can remove this triangle to leave a triangulation of an $n-1$-gon, which has chromatic number 3 by the inductive hypothesis. Adding the last triangle adds only one new vertex with two neighbors, so we can color this vertex with one of the three colors not used on its neighbors.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n \geq 3$ be a positive integer. A triangulation of a convex $n$-gon is a set of $n-3$ of its diagonals which do not intersect in the interior of the polygon. Along with the $n$ sides, these diagonals separate the polygon into $n-2$ disjoint triangles. Any triangulation can be viewed as a graph: the vertices of the graph are the corners of the polygon, and the $n$ sides and $n-3$ diagonals are the edges.
For a fixed $n$-gon, different triangulations correspond to different graphs. Prove that all of these graphs have the same chromatic number.
|
We will show that all triangulations have chromatic number 3, by induction on $n$. As a base case, if $n=3$, a triangle has chromatic number 3 . Now, given a triangulation of an $n$-gon for $n>3$, every edge is either a side or a diagonal of the polygon. There are $n$ sides and only $n-3$ diagonals in the edge-set, so the Pigeonhole Principle guarentees a triangle with two side edges. These two sides must be adjacent, so we can remove this triangle to leave a triangulation of an $n-1$-gon, which has chromatic number 3 by the inductive hypothesis. Adding the last triangle adds only one new vertex with two neighbors, so we can color this vertex with one of the three colors not used on its neighbors.
|
{
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-team2-solutions.jsonl",
"problem_match": "\n3. [8]",
"solution_match": "\nSolution: "
}
|
9209b951-07aa-5f5a-aa65-a6c8d2eed284
| 608,547
|
Let $G$ be a finite graph in which every vertex has degree less than or equal to $k$. Prove that the chromatic number of $G$ is less than or equal to $k+1$.
|
Using a greedy algorithm we find a good coloring with $k+1$ colors. Order the vertices and color them one by one - since each vertex has at most $k$ neighbors, one of the $k+1$ colors has not been used on a neighbor, so there is always a good color for that vertex. In fact, we have shows that any graph in which every vertex has degree at most $k$ can be colored with $k+1$ colors.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $G$ be a finite graph in which every vertex has degree less than or equal to $k$. Prove that the chromatic number of $G$ is less than or equal to $k+1$.
|
Using a greedy algorithm we find a good coloring with $k+1$ colors. Order the vertices and color them one by one - since each vertex has at most $k$ neighbors, one of the $k+1$ colors has not been used on a neighbor, so there is always a good color for that vertex. In fact, we have shows that any graph in which every vertex has degree at most $k$ can be colored with $k+1$ colors.
|
{
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-team2-solutions.jsonl",
"problem_match": "\n4. [10]",
"solution_match": "\nSolution: "
}
|
2be76ca6-e1d3-5719-8f03-84f317e8a835
| 608,557
|
(a) [5] If a single vertex (and all its incident edges) is removed from a finite graph, show that the graph's chromatic number cannot decrease by more than 1.
|
Suppose the chromatic number of the graph was $C$, and removing a single vertex resulted in a graph with chromatic number at most $C-2$. Then we can color the remaining graph with at most $C-2$ colors. Replacing the vertex and its edges, we can then choose any color not already used to form a coloring of the original graph using at most $C-1$ colors, contradicting the fact that $C$ is the chromatic number of the graph.
(b) [15] Show that, for any $n>2$, there are infinitely many graphs with chromatic number $n$ such that removing any vertex (and all its incident edges) from the graph decreases its chromatic number.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
(a) [5] If a single vertex (and all its incident edges) is removed from a finite graph, show that the graph's chromatic number cannot decrease by more than 1.
|
Suppose the chromatic number of the graph was $C$, and removing a single vertex resulted in a graph with chromatic number at most $C-2$. Then we can color the remaining graph with at most $C-2$ colors. Replacing the vertex and its edges, we can then choose any color not already used to form a coloring of the original graph using at most $C-1$ colors, contradicting the fact that $C$ is the chromatic number of the graph.
(b) [15] Show that, for any $n>2$, there are infinitely many graphs with chromatic number $n$ such that removing any vertex (and all its incident edges) from the graph decreases its chromatic number.
|
{
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-team2-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\nSolution: "
}
|
023b49a0-6ac7-5f2e-bcde-5ffcd40b9526
| 608,559
|
You are trying to sink a submarine. Every second, you launch a missile at a point of your choosing on the $x$-axis. If the submarine is at that point at that time, you sink it. A firing sequence is a sequence of real numbers that specify where you will fire at each second. For example, the firing sequence $2,3,5,6, \ldots$ means that you will fire at 2 after one second, 3 after two seconds, 5 after three seconds, 6 after four seconds, and so on.
(a) [5] Suppose that the submarine starts at the origin and travels along the positive $x$-axis with an (unknown) positive integer velocity. Show that there is a firing sequence that is guaranteed to hit the submarine eventually.
|
The firing sequence $1,4,9, \ldots, n^{2}, \ldots$ works. If the velocity of the submarine is $v$, then after $v$ seconds it will be at $x=v^{2}$, the same location where the mine explodes at time $v$.
(b) [10] Suppose now that the submarine starts at an unknown integer point on the non-negative $x$-axis and again travels with an unknown positive integer velocity. Show that there is still a firing sequence that is guaranteed to hit the submarine eventually.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
You are trying to sink a submarine. Every second, you launch a missile at a point of your choosing on the $x$-axis. If the submarine is at that point at that time, you sink it. A firing sequence is a sequence of real numbers that specify where you will fire at each second. For example, the firing sequence $2,3,5,6, \ldots$ means that you will fire at 2 after one second, 3 after two seconds, 5 after three seconds, 6 after four seconds, and so on.
(a) [5] Suppose that the submarine starts at the origin and travels along the positive $x$-axis with an (unknown) positive integer velocity. Show that there is a firing sequence that is guaranteed to hit the submarine eventually.
|
The firing sequence $1,4,9, \ldots, n^{2}, \ldots$ works. If the velocity of the submarine is $v$, then after $v$ seconds it will be at $x=v^{2}$, the same location where the mine explodes at time $v$.
(b) [10] Suppose now that the submarine starts at an unknown integer point on the non-negative $x$-axis and again travels with an unknown positive integer velocity. Show that there is still a firing sequence that is guaranteed to hit the submarine eventually.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-team1-solutions.jsonl",
"problem_match": "\n1. ",
"solution_match": "\nSolution: "
}
|
f6571ba6-9250-5547-86ab-7b530d2324ab
| 608,702
|
You are trying to sink a submarine. Every second, you launch a missile at a point of your choosing on the $x$-axis. If the submarine is at that point at that time, you sink it. A firing sequence is a sequence of real numbers that specify where you will fire at each second. For example, the firing sequence $2,3,5,6, \ldots$ means that you will fire at 2 after one second, 3 after two seconds, 5 after three seconds, 6 after four seconds, and so on.
(a) [5] Suppose that the submarine starts at the origin and travels along the positive $x$-axis with an (unknown) positive integer velocity. Show that there is a firing sequence that is guaranteed to hit the submarine eventually.
|
Represent the submarine's motion by an ordered pair ( $a, b$ ), where $a$ is the starting point of the submarine and $b$ is its velocity. We want to find a way to map each positive integer to a possible ordered pair so that every ordered pair is covered. This way, if we fire at $b_{n} n+a_{n}$ at time $n$, where $\left(a_{n}, b_{n}\right)$ is the point that $n$ maps to, then we will eventually hit the submarine. (Keep in mind that $b_{n} n+a_{n}$ would be the location of the submarine at time $n$.) There are many such ways to map the positive integers to possible points; here is one way:
$$
\begin{aligned}
& 1 \rightarrow(1,1), 2 \rightarrow(2,1), 3 \rightarrow(1,2), 4 \rightarrow(3,1), 5 \rightarrow(2,2), 6 \rightarrow(1,3), 7 \rightarrow(4,1), 8 \rightarrow(3,2), \\
& 9 \rightarrow(2,3), 10 \rightarrow(1,4), 11 \rightarrow(5,1), 12 \rightarrow(4,2), 13 \rightarrow(3,3), 14 \rightarrow(2,4), 15 \rightarrow(1,5), \ldots
\end{aligned}
$$
(The path of points trace out diagonal lines that sweep every lattice point in the coordinate plane.) Since we cover every point, we will eventually hit the submarine.
Remark: The mapping shown above is known as a bijection between the positive integers and ordered pairs of integers $(a, b)$ where $b>0$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
You are trying to sink a submarine. Every second, you launch a missile at a point of your choosing on the $x$-axis. If the submarine is at that point at that time, you sink it. A firing sequence is a sequence of real numbers that specify where you will fire at each second. For example, the firing sequence $2,3,5,6, \ldots$ means that you will fire at 2 after one second, 3 after two seconds, 5 after three seconds, 6 after four seconds, and so on.
(a) [5] Suppose that the submarine starts at the origin and travels along the positive $x$-axis with an (unknown) positive integer velocity. Show that there is a firing sequence that is guaranteed to hit the submarine eventually.
|
Represent the submarine's motion by an ordered pair ( $a, b$ ), where $a$ is the starting point of the submarine and $b$ is its velocity. We want to find a way to map each positive integer to a possible ordered pair so that every ordered pair is covered. This way, if we fire at $b_{n} n+a_{n}$ at time $n$, where $\left(a_{n}, b_{n}\right)$ is the point that $n$ maps to, then we will eventually hit the submarine. (Keep in mind that $b_{n} n+a_{n}$ would be the location of the submarine at time $n$.) There are many such ways to map the positive integers to possible points; here is one way:
$$
\begin{aligned}
& 1 \rightarrow(1,1), 2 \rightarrow(2,1), 3 \rightarrow(1,2), 4 \rightarrow(3,1), 5 \rightarrow(2,2), 6 \rightarrow(1,3), 7 \rightarrow(4,1), 8 \rightarrow(3,2), \\
& 9 \rightarrow(2,3), 10 \rightarrow(1,4), 11 \rightarrow(5,1), 12 \rightarrow(4,2), 13 \rightarrow(3,3), 14 \rightarrow(2,4), 15 \rightarrow(1,5), \ldots
\end{aligned}
$$
(The path of points trace out diagonal lines that sweep every lattice point in the coordinate plane.) Since we cover every point, we will eventually hit the submarine.
Remark: The mapping shown above is known as a bijection between the positive integers and ordered pairs of integers $(a, b)$ where $b>0$.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-team1-solutions.jsonl",
"problem_match": "\n1. ",
"solution_match": "\nSolution: "
}
|
f6571ba6-9250-5547-86ab-7b530d2324ab
| 608,702
|
Call a positive integer in base $10 k$-good if we can split it into two integers y and z , such that y is all digits on the left and z is all digits on the right, and such that $y=k \cdot z$. For example, 2010 is 2 -good because we can split it into 20 and 10 and $20=2 \cdot 10.20010$ is also 2 -good, because we can split it into 20 and 010 . In addition, it is 20 -good, because we can split it into 200 and 10 .
Show that there exists a 48 -good perfect square.
|
We wish to find integers $a, z$ such that $48 z \cdot 10^{a}+z=z\left(48 \cdot 10^{a}+1\right)$ a perfect square, where $z<10^{a}$. This would prove that there exists a 48 -good perfect square because we are pulling off the last $a$ digits of the number and get two integers $48 z$ and $z$. To make $z$ small by keeping the product a perfect square, we'd like $48 \cdot 10^{a}+1$ to be divisible by some reasonably large square. Take $a=42=\varphi(49)$. By Euler's theorem, $10^{42} \equiv 1(\bmod 49)$, so $48 \cdot 10^{a}+1$ is a multiple of 49 . Then we can take $z=\frac{48 \cdot 10^{a}+1}{49}$. (Clearly $z<10^{a}$, so we're fine.) Then we have $z\left(48 \cdot 10^{a}+1\right)=\left(\frac{48 \cdot 10^{42}+1}{7}\right)^{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Call a positive integer in base $10 k$-good if we can split it into two integers y and z , such that y is all digits on the left and z is all digits on the right, and such that $y=k \cdot z$. For example, 2010 is 2 -good because we can split it into 20 and 10 and $20=2 \cdot 10.20010$ is also 2 -good, because we can split it into 20 and 010 . In addition, it is 20 -good, because we can split it into 200 and 10 .
Show that there exists a 48 -good perfect square.
|
We wish to find integers $a, z$ such that $48 z \cdot 10^{a}+z=z\left(48 \cdot 10^{a}+1\right)$ a perfect square, where $z<10^{a}$. This would prove that there exists a 48 -good perfect square because we are pulling off the last $a$ digits of the number and get two integers $48 z$ and $z$. To make $z$ small by keeping the product a perfect square, we'd like $48 \cdot 10^{a}+1$ to be divisible by some reasonably large square. Take $a=42=\varphi(49)$. By Euler's theorem, $10^{42} \equiv 1(\bmod 49)$, so $48 \cdot 10^{a}+1$ is a multiple of 49 . Then we can take $z=\frac{48 \cdot 10^{a}+1}{49}$. (Clearly $z<10^{a}$, so we're fine.) Then we have $z\left(48 \cdot 10^{a}+1\right)=\left(\frac{48 \cdot 10^{42}+1}{7}\right)^{2}$.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-team1-solutions.jsonl",
"problem_match": "\n3. [15]",
"solution_match": "\nSolution: "
}
|
5065997c-3ad9-5b3f-b25b-da8714042a13
| 608,704
|
Let
$$
\begin{gathered}
e^{x}+e^{y}=A \\
x e^{x}+y e^{y}=B \\
x^{2} e^{x}+y^{2} e^{y}=C \\
x^{3} e^{x}+y^{3} e^{y}=D \\
x^{4} e^{x}+y^{4} e^{y}=E .
\end{gathered}
$$
Prove that if $A, B, C$, and $D$ are all rational, then so is $E$.
|
We can express $x+y$ in two ways:
$$
\begin{aligned}
& x+y=\frac{A D-B C}{A C-B^{2}} \\
& x+y=\frac{A E-C^{2}}{A D-B C}
\end{aligned}
$$
(We have to be careful if $A C-B^{2}$ or $A D-B C$ is zero. We'll deal with that case later.) It is easy to check that these equations hold by substituting the expressions for $A, B, C, D$, and $E$. Setting these two expressions for $x+y$ equal to each other, we get
$$
\frac{A D-B C}{A C-B^{2}}=\frac{A E-C^{2}}{A D-B C}
$$
which we can easily solve for $E$ as a rational function of $A, B, C$, and $D$. Therefore if $A, B, C$, and $D$ are all rational, then $E$ will be rational as well.
Now, we have to check what happens if $A C-B^{2}=0$ or $A D-B C=0$. If $A C-B^{2}=0$, then writing down the expressions for $A, B$, and $C$ gives us that $(x-y)^{2} e^{x+y}=0$, meaning that $x=y$. If $x=y$, and $x \neq 0, A$ and $D$ are also non-zero, and $\frac{B}{A}=\frac{E}{D}=x$. Since $\frac{B}{A}$ is rational and $D$ is rational, this implies that $E$ is rational. If $x=y=0$, then $E=0$ and so is certainly rational.
We finally must check what happens if $A D-B C=0$. Since $A D-B C=(x+y)\left(A C-B^{2}\right)$, either $A C-B^{2}=0$ (a case we have already dealt with), or $x+y=0$. But if $x+y=0$ then $A E-C^{2}=0$, which implies that $E=\frac{C^{2}}{A}$ (we know that $A \neq 0$ because $e^{x}$ and $e^{y}$ are both positive). Since $A$ and $C$ are rational, this implies that $E$ is also rational.
So, we have shown $E$ to be rational in all cases, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let
$$
\begin{gathered}
e^{x}+e^{y}=A \\
x e^{x}+y e^{y}=B \\
x^{2} e^{x}+y^{2} e^{y}=C \\
x^{3} e^{x}+y^{3} e^{y}=D \\
x^{4} e^{x}+y^{4} e^{y}=E .
\end{gathered}
$$
Prove that if $A, B, C$, and $D$ are all rational, then so is $E$.
|
We can express $x+y$ in two ways:
$$
\begin{aligned}
& x+y=\frac{A D-B C}{A C-B^{2}} \\
& x+y=\frac{A E-C^{2}}{A D-B C}
\end{aligned}
$$
(We have to be careful if $A C-B^{2}$ or $A D-B C$ is zero. We'll deal with that case later.) It is easy to check that these equations hold by substituting the expressions for $A, B, C, D$, and $E$. Setting these two expressions for $x+y$ equal to each other, we get
$$
\frac{A D-B C}{A C-B^{2}}=\frac{A E-C^{2}}{A D-B C}
$$
which we can easily solve for $E$ as a rational function of $A, B, C$, and $D$. Therefore if $A, B, C$, and $D$ are all rational, then $E$ will be rational as well.
Now, we have to check what happens if $A C-B^{2}=0$ or $A D-B C=0$. If $A C-B^{2}=0$, then writing down the expressions for $A, B$, and $C$ gives us that $(x-y)^{2} e^{x+y}=0$, meaning that $x=y$. If $x=y$, and $x \neq 0, A$ and $D$ are also non-zero, and $\frac{B}{A}=\frac{E}{D}=x$. Since $\frac{B}{A}$ is rational and $D$ is rational, this implies that $E$ is rational. If $x=y=0$, then $E=0$ and so is certainly rational.
We finally must check what happens if $A D-B C=0$. Since $A D-B C=(x+y)\left(A C-B^{2}\right)$, either $A C-B^{2}=0$ (a case we have already dealt with), or $x+y=0$. But if $x+y=0$ then $A E-C^{2}=0$, which implies that $E=\frac{C^{2}}{A}$ (we know that $A \neq 0$ because $e^{x}$ and $e^{y}$ are both positive). Since $A$ and $C$ are rational, this implies that $E$ is also rational.
So, we have shown $E$ to be rational in all cases, as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-team1-solutions.jsonl",
"problem_match": "\n4. [20]",
"solution_match": "\nSolution: "
}
|
674e14e7-d621-576d-ac7c-b65538ba4595
| 608,705
|
Show that, for every positive integer $n$, there exists a monic polynomial of degree $n$ with integer coefficients such that the coefficients are decreasing and the roots of the polynomial are all integers.
|
We claim we can find values $a$ and $b$ such that $p(x)=(x-a)(x+b)^{n}$ is a polynomial of degree $n+1$ that satisfies these constraints. We show that its coefficients are decreasing by finding a general formula for the coefficient of $x^{k}$.
The coefficient of $x^{k}$ is $b^{k}\binom{n}{k}-a b^{k-1}\binom{n}{k-1}$, which can be seen by expanding out $(x+b)^{n}$ and then multiplying by $(x-a)$. Then we must prove that
$$
b^{k+1}\binom{n}{k+1}-a b^{k}\binom{n}{k}<b^{k}\binom{n}{k}-a b^{k-1}\binom{n}{k-1}
$$
or
$$
a b^{k-1}\left(b\binom{n}{k}-\binom{n}{k-1}\right)>b^{k}\left(b\binom{n}{k+1}-\binom{n}{k}\right) .
$$
Choose $b>\max \left(\frac{\binom{n}{k}}{\binom{n}{k-1}}\right)$ in order to make sure the right-hand term in each product on each side of the inequality sign is positive (we'll be dividing by it, so this makes things much easier), and choose $a>\max \left(\frac{b\left(b\binom{n}{k+1}-\binom{n}{k}\right)}{b\binom{n}{k}-\binom{n}{k-1}}\right)$ to make sure the inequality always holds. Since there are only finite values that $k$ can take on given a fixed $n$ (namely, integers between 0 and $n$ inclusive), we can always find values of $a$ and $b$ that satisfy these constraints.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Show that, for every positive integer $n$, there exists a monic polynomial of degree $n$ with integer coefficients such that the coefficients are decreasing and the roots of the polynomial are all integers.
|
We claim we can find values $a$ and $b$ such that $p(x)=(x-a)(x+b)^{n}$ is a polynomial of degree $n+1$ that satisfies these constraints. We show that its coefficients are decreasing by finding a general formula for the coefficient of $x^{k}$.
The coefficient of $x^{k}$ is $b^{k}\binom{n}{k}-a b^{k-1}\binom{n}{k-1}$, which can be seen by expanding out $(x+b)^{n}$ and then multiplying by $(x-a)$. Then we must prove that
$$
b^{k+1}\binom{n}{k+1}-a b^{k}\binom{n}{k}<b^{k}\binom{n}{k}-a b^{k-1}\binom{n}{k-1}
$$
or
$$
a b^{k-1}\left(b\binom{n}{k}-\binom{n}{k-1}\right)>b^{k}\left(b\binom{n}{k+1}-\binom{n}{k}\right) .
$$
Choose $b>\max \left(\frac{\binom{n}{k}}{\binom{n}{k-1}}\right)$ in order to make sure the right-hand term in each product on each side of the inequality sign is positive (we'll be dividing by it, so this makes things much easier), and choose $a>\max \left(\frac{b\left(b\binom{n}{k+1}-\binom{n}{k}\right)}{b\binom{n}{k}-\binom{n}{k-1}}\right)$ to make sure the inequality always holds. Since there are only finite values that $k$ can take on given a fixed $n$ (namely, integers between 0 and $n$ inclusive), we can always find values of $a$ and $b$ that satisfy these constraints.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-team1-solutions.jsonl",
"problem_match": "\n5. [20]",
"solution_match": "\nSolution: "
}
|
862deaac-74cb-57c7-8a81-672b516a2898
| 608,706
|
Let $S$ be a convex set in the plane with a finite area $a$. Prove that either $a=0$ or $S$ is bounded. Note: a set is bounded if it is contained in a circle of finite radius. Note: a set is convex if, whenever two points $A$ and $B$ are in the set, the line segment between them is also in the set.
|
If all points in $S$ lie on a straight line, then $a=0$.
Otherwise we may pick three points $A, B$, and $C$ that are not collinear. Let $\omega$ be the incircle of $\triangle A B C$, with $I$ its center and $r$ its radius. Since $S$ is convex, $S$ must contain $\omega$.

Suppose $S$ also contains a point $X$ at a distance $d$ from $I$, with $d>R$. We will show that $d \leq \sqrt{r^{2}+\frac{a^{2}}{r^{2}}}$, which implies that the $S$ is bounded since all points are contained within the circle centered at $I$ of radius $\sqrt{r^{2}+\frac{a^{2}}{r^{2}}}$.
Let $Y$ and $Z$ be on $\omega$ such that $\overline{X Y}$ and $\overline{X Z}$ are tangents to $\omega$. Because $S$ is convex, it must contain kite $I Y X Z$, whose area we can compute in terms of $d$ and $r$.
Let $M$ be the midpoint of $\overline{Y Z}$. Since $\triangle I Y X \sim \triangle I M Y$, we know that $\frac{I M}{I Y}=\frac{I Y}{I X}$, that is, $I M=$ $\frac{(I Y)^{2}}{I X}=\frac{r^{2}}{d}$. Then $M Y=\sqrt{r^{2}-\frac{r^{4}}{d^{2}}}=r \sqrt{1-\left(\frac{r}{d}\right)^{2}}=\frac{1}{2} Y Z$.
The area of $I Y X Z$ is $\frac{1}{2}(Y Z)(I X)=r d \sqrt{1-\left(\frac{r}{d}\right)^{2}}=r \sqrt{d^{2}-r^{2}}$. This must be less than or equal to $a$, the area of $S$. This yields $a^{2} \geq r^{2} d^{2}-r^{4}$ or $d^{2} \leq r^{2}+\frac{a^{2}}{r^{2}}$. It follows that $d \leq \sqrt{r^{2}+\frac{a^{2}}{r^{2}}}$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $S$ be a convex set in the plane with a finite area $a$. Prove that either $a=0$ or $S$ is bounded. Note: a set is bounded if it is contained in a circle of finite radius. Note: a set is convex if, whenever two points $A$ and $B$ are in the set, the line segment between them is also in the set.
|
If all points in $S$ lie on a straight line, then $a=0$.
Otherwise we may pick three points $A, B$, and $C$ that are not collinear. Let $\omega$ be the incircle of $\triangle A B C$, with $I$ its center and $r$ its radius. Since $S$ is convex, $S$ must contain $\omega$.

Suppose $S$ also contains a point $X$ at a distance $d$ from $I$, with $d>R$. We will show that $d \leq \sqrt{r^{2}+\frac{a^{2}}{r^{2}}}$, which implies that the $S$ is bounded since all points are contained within the circle centered at $I$ of radius $\sqrt{r^{2}+\frac{a^{2}}{r^{2}}}$.
Let $Y$ and $Z$ be on $\omega$ such that $\overline{X Y}$ and $\overline{X Z}$ are tangents to $\omega$. Because $S$ is convex, it must contain kite $I Y X Z$, whose area we can compute in terms of $d$ and $r$.
Let $M$ be the midpoint of $\overline{Y Z}$. Since $\triangle I Y X \sim \triangle I M Y$, we know that $\frac{I M}{I Y}=\frac{I Y}{I X}$, that is, $I M=$ $\frac{(I Y)^{2}}{I X}=\frac{r^{2}}{d}$. Then $M Y=\sqrt{r^{2}-\frac{r^{4}}{d^{2}}}=r \sqrt{1-\left(\frac{r}{d}\right)^{2}}=\frac{1}{2} Y Z$.
The area of $I Y X Z$ is $\frac{1}{2}(Y Z)(I X)=r d \sqrt{1-\left(\frac{r}{d}\right)^{2}}=r \sqrt{d^{2}-r^{2}}$. This must be less than or equal to $a$, the area of $S$. This yields $a^{2} \geq r^{2} d^{2}-r^{4}$ or $d^{2} \leq r^{2}+\frac{a^{2}}{r^{2}}$. It follows that $d \leq \sqrt{r^{2}+\frac{a^{2}}{r^{2}}}$, as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-team1-solutions.jsonl",
"problem_match": "\n6. [20]",
"solution_match": "\nSolution: "
}
|
a4f58ff0-16aa-5abb-aa8d-d6d96ead86ac
| 608,707
|
A knight moves on a two-dimensional grid. From any square, it can move 2 units in one axisparallel direction, then move 1 unit in an orthogonal direction, the way a regular knight moves in a game of chess. The knight starts at the origin. As it moves, it keeps track of a number $t$, which is initially 0 . When the knight lands at the point $(a, b)$, the number is changed from $x$ to $a x+b$.
Show that, for any integers $a$ and $b$, it is possible for the knight to land at the points $(1, a)$ and $(-1, a)$ with $t$ equal to $b$.
|
For convenience, we will refer to $(a, b)$ as $[a x+b]$, the function it represents. This will make it easier to follow the trajectory of $t$ over a given sequence of moves.
Suppose we start at $[x+1]$ with $t=a$. Taking the path $[x+1] \rightarrow[-x] \rightarrow[x-1] \rightarrow[-x] \rightarrow[x+1]$ will yield $t=a+2$. So we can go from $t=a$ to $t=a+2$ at $[x+1]$.
We can also move until we get to $[-3]$, then go $[-3] \rightarrow[x-1]$ to end up with $t=-4$ at $[x-1]$. But going $[x-1] \rightarrow[3 x] \rightarrow[x-1]$ means we can go from $t=a$ to $t=3 a-1$ at $x-1$. Since we can start with $t=-4$, this means we can therefore get arbitrarily small even and odd numbers at $[x-1]$, hence also $[3 x]$, hence also at $[x+1]$.
This implies we can get any value of $t$ we want at $[x+1]$, so we can also get any value of $t$ we want at $[-x],[x-1],[-x-2],[x-3]$, etc., as well as $[-x+2],[x+3],[-x+4],[x+5]$, etc. We can do a similar thing starting at $[-x+1]$ to get from $t=a$ to $t=a+2$, and use the $[-x-1] \rightarrow[-3 x] \rightarrow[-x-1]$ loop to get arbitrarily small integers of both parities. So we can get any value of $t$ we want at all points of the form $[ \pm x+k]$ for any integer $k$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
A knight moves on a two-dimensional grid. From any square, it can move 2 units in one axisparallel direction, then move 1 unit in an orthogonal direction, the way a regular knight moves in a game of chess. The knight starts at the origin. As it moves, it keeps track of a number $t$, which is initially 0 . When the knight lands at the point $(a, b)$, the number is changed from $x$ to $a x+b$.
Show that, for any integers $a$ and $b$, it is possible for the knight to land at the points $(1, a)$ and $(-1, a)$ with $t$ equal to $b$.
|
For convenience, we will refer to $(a, b)$ as $[a x+b]$, the function it represents. This will make it easier to follow the trajectory of $t$ over a given sequence of moves.
Suppose we start at $[x+1]$ with $t=a$. Taking the path $[x+1] \rightarrow[-x] \rightarrow[x-1] \rightarrow[-x] \rightarrow[x+1]$ will yield $t=a+2$. So we can go from $t=a$ to $t=a+2$ at $[x+1]$.
We can also move until we get to $[-3]$, then go $[-3] \rightarrow[x-1]$ to end up with $t=-4$ at $[x-1]$. But going $[x-1] \rightarrow[3 x] \rightarrow[x-1]$ means we can go from $t=a$ to $t=3 a-1$ at $x-1$. Since we can start with $t=-4$, this means we can therefore get arbitrarily small even and odd numbers at $[x-1]$, hence also $[3 x]$, hence also at $[x+1]$.
This implies we can get any value of $t$ we want at $[x+1]$, so we can also get any value of $t$ we want at $[-x],[x-1],[-x-2],[x-3]$, etc., as well as $[-x+2],[x+3],[-x+4],[x+5]$, etc. We can do a similar thing starting at $[-x+1]$ to get from $t=a$ to $t=a+2$, and use the $[-x-1] \rightarrow[-3 x] \rightarrow[-x-1]$ loop to get arbitrarily small integers of both parities. So we can get any value of $t$ we want at all points of the form $[ \pm x+k]$ for any integer $k$.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-team1-solutions.jsonl",
"problem_match": "\n8. [30]",
"solution_match": "\nSolution: "
}
|
a82f2bea-bcbb-5b71-ba15-f22ba21b547f
| 608,709
|
Let $p(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\ldots+a_{0}$ be a polynomial with complex coefficients such that $a_{i} \neq 0$ for all $i$. Prove that $|r| \leq 2 \max _{i=0}^{n-1}\left|\frac{a_{i-1}}{a_{i}}\right|$ for all roots $r$ of all such polynomials $p$. Here we let $|z|$ denote the absolute value of the complex number $z$.
|
If $r$ is a root, then $-a_{n} r^{n}=a_{n-1} r^{n-1}+\ldots+a_{0}$. By the Triangle Inequality, $\left|-a_{n} r^{n}\right| \leq$ $\left|a_{n-1} r^{n-1}\right|+\ldots+\left|a_{0}\right|$. Rearranging this inequality yields $\left|a_{n} r^{n}\right|-\left|a_{n-1} r^{n-1}\right|-\ldots-\left|a_{0}\right| \leq 0$.
Now suppose $|r|=k \max \left|\frac{a_{i-1}}{a_{i}}\right|$. Applying this over values of $i$ ranging from $m+1$ to $n$ (assuming $m+1 \leq n$ ), we get $\left|a_{m} r^{m}\right| \leq \frac{\left|a_{n} r^{n}\right|}{k^{n-m}}$. This, along with the above equation, yields:
$$
\left|a_{n} r^{n}\right| \cdot\left(1-\frac{1}{k}-\frac{1}{k^{2}}-\frac{1}{k^{3}}-\ldots-\frac{1}{k^{n}}\right)=0
$$
This is only true when $a_{n}=0, r=0$, or $\left(1-\frac{1}{k}-\frac{1}{k^{2}}-\ldots\right)=0$. The first option is impossible by the constraints in the problem. The second option implies $k=0$. The third option implies that $k<2$; otherwise ( $1-\frac{1}{k}-\frac{1}{k^{2}}-\ldots-\frac{1}{k^{n}}$ ) would always remain positive. Either way, $|r| \leq 2 \max _{i=0}^{n-1}\left|\frac{a_{i-1}}{a_{i}}\right|$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $p(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\ldots+a_{0}$ be a polynomial with complex coefficients such that $a_{i} \neq 0$ for all $i$. Prove that $|r| \leq 2 \max _{i=0}^{n-1}\left|\frac{a_{i-1}}{a_{i}}\right|$ for all roots $r$ of all such polynomials $p$. Here we let $|z|$ denote the absolute value of the complex number $z$.
|
If $r$ is a root, then $-a_{n} r^{n}=a_{n-1} r^{n-1}+\ldots+a_{0}$. By the Triangle Inequality, $\left|-a_{n} r^{n}\right| \leq$ $\left|a_{n-1} r^{n-1}\right|+\ldots+\left|a_{0}\right|$. Rearranging this inequality yields $\left|a_{n} r^{n}\right|-\left|a_{n-1} r^{n-1}\right|-\ldots-\left|a_{0}\right| \leq 0$.
Now suppose $|r|=k \max \left|\frac{a_{i-1}}{a_{i}}\right|$. Applying this over values of $i$ ranging from $m+1$ to $n$ (assuming $m+1 \leq n$ ), we get $\left|a_{m} r^{m}\right| \leq \frac{\left|a_{n} r^{n}\right|}{k^{n-m}}$. This, along with the above equation, yields:
$$
\left|a_{n} r^{n}\right| \cdot\left(1-\frac{1}{k}-\frac{1}{k^{2}}-\frac{1}{k^{3}}-\ldots-\frac{1}{k^{n}}\right)=0
$$
This is only true when $a_{n}=0, r=0$, or $\left(1-\frac{1}{k}-\frac{1}{k^{2}}-\ldots\right)=0$. The first option is impossible by the constraints in the problem. The second option implies $k=0$. The third option implies that $k<2$; otherwise ( $1-\frac{1}{k}-\frac{1}{k^{2}}-\ldots-\frac{1}{k^{n}}$ ) would always remain positive. Either way, $|r| \leq 2 \max _{i=0}^{n-1}\left|\frac{a_{i-1}}{a_{i}}\right|$.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-team1-solutions.jsonl",
"problem_match": "\n9. [30]",
"solution_match": "\nSolution: "
}
|
a15af981-8572-50e0-9712-11c1efd29f70
| 608,710
|
Alice and Barbara play a game on a blackboard. At the start, zero is written on the board. Alice goes first, and the players alternate turns. On her turn, each player replaces $x$ - the number written on the board - with any real number $y$, subject to the constraint that $0<y-x<1$.
(a) [10] If the first player to write a number greater than or equal to 2010 wins, determine, with proof, who has the winning strategy.
(b) [10] If the first player to write a number greater than or equal to 2010 on her 2011th turn or later wins (if a player writes a number greater than or equal to 2010 on her 2010th turn or earlier, she loses immediately), determine, with proof, who has the winning strategy.
|
Each turn of the game is equivalent to adding a number between 0 and 1 to the number on the board.
(a) Barbara has the winning strategy: whenever Alice adds $z$ to the number on the board, Barbara adds $1-z$. After Barbara's $i$ th turn, the number on the board will be $i$. Therefore, after Barbara's 2009th turn, Alice will be forced to write a number between 2009 and 2010, after which Barbara can write 2010 and win the game.
(b) Alice has the winning strategy: she writes any number $a$ on her first turn, and, after that, whenever Barbara adds $z$ to the number on the board, Alice adds $1-z$. After Alice's $i$ th turn, the number on the board will be $(i-1)+a$, so after Alice's 2010th turn, the number will be $2009+a$. Since Barbara cannot write a number greater than or equal to 2010 on her 2010 th turn, she will be forced to write a number between $2009+a$ and 2010 , after which Alice can write 2010 and win the game.
|
proof
|
Yes
|
Yes
|
proof
|
Logic and Puzzles
|
Alice and Barbara play a game on a blackboard. At the start, zero is written on the board. Alice goes first, and the players alternate turns. On her turn, each player replaces $x$ - the number written on the board - with any real number $y$, subject to the constraint that $0<y-x<1$.
(a) [10] If the first player to write a number greater than or equal to 2010 wins, determine, with proof, who has the winning strategy.
(b) [10] If the first player to write a number greater than or equal to 2010 on her 2011th turn or later wins (if a player writes a number greater than or equal to 2010 on her 2010th turn or earlier, she loses immediately), determine, with proof, who has the winning strategy.
|
Each turn of the game is equivalent to adding a number between 0 and 1 to the number on the board.
(a) Barbara has the winning strategy: whenever Alice adds $z$ to the number on the board, Barbara adds $1-z$. After Barbara's $i$ th turn, the number on the board will be $i$. Therefore, after Barbara's 2009th turn, Alice will be forced to write a number between 2009 and 2010, after which Barbara can write 2010 and win the game.
(b) Alice has the winning strategy: she writes any number $a$ on her first turn, and, after that, whenever Barbara adds $z$ to the number on the board, Alice adds $1-z$. After Alice's $i$ th turn, the number on the board will be $(i-1)+a$, so after Alice's 2010th turn, the number will be $2009+a$. Since Barbara cannot write a number greater than or equal to 2010 on her 2010 th turn, she will be forced to write a number between $2009+a$ and 2010 , after which Alice can write 2010 and win the game.
|
{
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-team1-solutions.jsonl",
"problem_match": "\n1. [20]",
"solution_match": "\nSolution: "
}
|
d32b998b-007e-5cc5-8c11-5736a5e2d372
| 608,864
|
Let $n$ be a positive integer, and let $a_{1}, a_{2}, \ldots, a_{n}$ be a set of positive integers such that $a_{1}=2$ and $a_{m}=\varphi\left(a_{m+1}\right)$ for all $1 \leq m \leq n-1$, where, for all positive integers $k, \varphi(k)$ denotes the number of positive integers less than or equal to $k$ that are relatively prime to $k$. Prove that $a_{n} \geq 2^{n-1}$.
|
We first note that $\varphi(s)<s$ for all positive integers $s \geq 2$, so $a_{m}>2$ for all $m>1$.
For integers $s>2$, let $A_{s}$ be the set of all positive integers $x \leq s$ such that $\operatorname{gcd}(s, x)=1$. Since $\operatorname{gcd}(s, x)=\operatorname{gcd}(s, s-x)$ for all $x$, if $a$ is a positive integer in $A_{s}$, so is $s-a$. Moreover, if $a$ is in $A_{s}$, $a$ and $s-a$ are different since $\operatorname{gcd}\left(s, \frac{s}{2}\right)=\frac{s}{2}>1$, meaning $\frac{s}{2}$ is not in $A_{s}$. Hence we may evenly pair
up the elements of $A_{s}$ that sum to $s$, so $\varphi(s)$, the number of elements of $A_{s}$, must be even. It follows that $a_{m}$ is even for all $m \leq n-1$.
If $t>2$ is even, $A_{t}$ will not contain any even number, so $\varphi(t) \leq \frac{t}{2}$. We may conclude that $a_{m} \geq 2 a_{m-1}$ for all $m \leq n-1$, so $a_{n} \geq a_{n-1} \geq 2^{n-2} a_{1}=2^{n-1}$, as desired.
Finally, note that such a set exists for all $n$ by letting $a_{i}=2^{i}$ for all $i$.
## Complex Numbers [35]
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n$ be a positive integer, and let $a_{1}, a_{2}, \ldots, a_{n}$ be a set of positive integers such that $a_{1}=2$ and $a_{m}=\varphi\left(a_{m+1}\right)$ for all $1 \leq m \leq n-1$, where, for all positive integers $k, \varphi(k)$ denotes the number of positive integers less than or equal to $k$ that are relatively prime to $k$. Prove that $a_{n} \geq 2^{n-1}$.
|
We first note that $\varphi(s)<s$ for all positive integers $s \geq 2$, so $a_{m}>2$ for all $m>1$.
For integers $s>2$, let $A_{s}$ be the set of all positive integers $x \leq s$ such that $\operatorname{gcd}(s, x)=1$. Since $\operatorname{gcd}(s, x)=\operatorname{gcd}(s, s-x)$ for all $x$, if $a$ is a positive integer in $A_{s}$, so is $s-a$. Moreover, if $a$ is in $A_{s}$, $a$ and $s-a$ are different since $\operatorname{gcd}\left(s, \frac{s}{2}\right)=\frac{s}{2}>1$, meaning $\frac{s}{2}$ is not in $A_{s}$. Hence we may evenly pair
up the elements of $A_{s}$ that sum to $s$, so $\varphi(s)$, the number of elements of $A_{s}$, must be even. It follows that $a_{m}$ is even for all $m \leq n-1$.
If $t>2$ is even, $A_{t}$ will not contain any even number, so $\varphi(t) \leq \frac{t}{2}$. We may conclude that $a_{m} \geq 2 a_{m-1}$ for all $m \leq n-1$, so $a_{n} \geq a_{n-1} \geq 2^{n-2} a_{1}=2^{n-1}$, as desired.
Finally, note that such a set exists for all $n$ by letting $a_{i}=2^{i}$ for all $i$.
## Complex Numbers [35]
|
{
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-team1-solutions.jsonl",
"problem_match": "\n3. [15]",
"solution_match": "\nSolution: "
}
|
dc9d83c3-6456-536a-8a70-121f29d469bf
| 608,866
|
Let $a$ and $b$ be positive real numbers. Define two sequences of real numbers $\left\{a_{n}\right\}$ and $\left\{b_{n}\right\}$ for all positive integers $n$ by $(a+b i)^{n}=a_{n}+b_{n} i$. Prove that
$$
\frac{\left|a_{n+1}\right|+\left|b_{n+1}\right|}{\left|a_{n}\right|+\left|b_{n}\right|} \geq \frac{a^{2}+b^{2}}{a+b}
$$
for all positive integers $n$.
|
Let $z=a+b i$. It is easy to see that what we are asked to show is equivalent to
$$
\frac{\left|z^{n+1}+\bar{z}^{n+1}\right|+\left|z^{n+1}-\bar{z}^{n+1}\right|}{\left|z^{n}+\bar{z}^{n}\right|+\left|z^{n}-\bar{z}^{n}\right|} \geq \frac{2 z \bar{z}}{|z+\bar{z}|+|z-\bar{z}|}
$$
Cross-multiplying, we see that it suffices to show
$$
\begin{gathered}
\left|z^{n+2}+z^{n+1} \bar{z}+z \bar{z}^{n+1}+\bar{z}^{n+2}\right|+\left|z^{n+2}-z^{n+1} \bar{z}+z \bar{z}^{n+1}-\bar{z}^{n+2}\right| \\
+\left|z^{n+2}+z^{n+1} \bar{z}-z \bar{z}^{n+1}-\bar{z}^{n+2}\right|+\left|z^{n+2}-z^{n+1} \bar{z}-z \bar{z}^{n+1}+\bar{z}^{n+2}\right| \\
\geq 2\left|z^{n+1} \bar{z}+z \bar{z}^{n+1}\right|+2\left|z^{n+1} \bar{z}-z \bar{z}^{n+1}\right|
\end{gathered}
$$
However, by the triangle inequality,
$$
\left|z^{n+2}+z^{n+1} \bar{z}+z \bar{z}^{n+1}+\bar{z}^{n+2}\right|+\left|z^{n+2}-z^{n+1} \bar{z}-z \bar{z}^{n+1}+\bar{z}^{n+2}\right| \geq 2\left|z^{n+1} \bar{z}+z \bar{z}^{n+1}\right|
$$
and
$$
\left|z^{n+2}-z^{n+1} \bar{z}+z \bar{z}^{n+1}-\bar{z}^{n+2}\right|+\left|z^{n+2}+z^{n+1} \bar{z}-z \bar{z}^{n+1}-\bar{z}^{n+2}\right| \geq 2\left|z^{n+1} \bar{z}-z \bar{z}^{n+1}\right|
$$
This completes the proof.
Remark: more computationally intensive trigonometric solutions are also possible by reducing the problem to maximizing and minimizing the values of the sine and cosine functions.
## Coin Flipping [75]
In a one-player game, the player begins with $4 m$ fair coins. On each of $m$ turns, the player takes 4 unused coins, flips 3 of them randomly to heads or tails, and then selects whether the 4 th one is heads or tails (these four coins are then considered used). After $m$ turns, when the sides of all $4 m$ coins have been determined, if half the coins are heads and half are tails, the player wins; otherwise, the player loses.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $a$ and $b$ be positive real numbers. Define two sequences of real numbers $\left\{a_{n}\right\}$ and $\left\{b_{n}\right\}$ for all positive integers $n$ by $(a+b i)^{n}=a_{n}+b_{n} i$. Prove that
$$
\frac{\left|a_{n+1}\right|+\left|b_{n+1}\right|}{\left|a_{n}\right|+\left|b_{n}\right|} \geq \frac{a^{2}+b^{2}}{a+b}
$$
for all positive integers $n$.
|
Let $z=a+b i$. It is easy to see that what we are asked to show is equivalent to
$$
\frac{\left|z^{n+1}+\bar{z}^{n+1}\right|+\left|z^{n+1}-\bar{z}^{n+1}\right|}{\left|z^{n}+\bar{z}^{n}\right|+\left|z^{n}-\bar{z}^{n}\right|} \geq \frac{2 z \bar{z}}{|z+\bar{z}|+|z-\bar{z}|}
$$
Cross-multiplying, we see that it suffices to show
$$
\begin{gathered}
\left|z^{n+2}+z^{n+1} \bar{z}+z \bar{z}^{n+1}+\bar{z}^{n+2}\right|+\left|z^{n+2}-z^{n+1} \bar{z}+z \bar{z}^{n+1}-\bar{z}^{n+2}\right| \\
+\left|z^{n+2}+z^{n+1} \bar{z}-z \bar{z}^{n+1}-\bar{z}^{n+2}\right|+\left|z^{n+2}-z^{n+1} \bar{z}-z \bar{z}^{n+1}+\bar{z}^{n+2}\right| \\
\geq 2\left|z^{n+1} \bar{z}+z \bar{z}^{n+1}\right|+2\left|z^{n+1} \bar{z}-z \bar{z}^{n+1}\right|
\end{gathered}
$$
However, by the triangle inequality,
$$
\left|z^{n+2}+z^{n+1} \bar{z}+z \bar{z}^{n+1}+\bar{z}^{n+2}\right|+\left|z^{n+2}-z^{n+1} \bar{z}-z \bar{z}^{n+1}+\bar{z}^{n+2}\right| \geq 2\left|z^{n+1} \bar{z}+z \bar{z}^{n+1}\right|
$$
and
$$
\left|z^{n+2}-z^{n+1} \bar{z}+z \bar{z}^{n+1}-\bar{z}^{n+2}\right|+\left|z^{n+2}+z^{n+1} \bar{z}-z \bar{z}^{n+1}-\bar{z}^{n+2}\right| \geq 2\left|z^{n+1} \bar{z}-z \bar{z}^{n+1}\right|
$$
This completes the proof.
Remark: more computationally intensive trigonometric solutions are also possible by reducing the problem to maximizing and minimizing the values of the sine and cosine functions.
## Coin Flipping [75]
In a one-player game, the player begins with $4 m$ fair coins. On each of $m$ turns, the player takes 4 unused coins, flips 3 of them randomly to heads or tails, and then selects whether the 4 th one is heads or tails (these four coins are then considered used). After $m$ turns, when the sides of all $4 m$ coins have been determined, if half the coins are heads and half are tails, the player wins; otherwise, the player loses.
|
{
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-team1-solutions.jsonl",
"problem_match": "\n5. [20]",
"solution_match": "\nSolution: "
}
|
b1ad2137-5602-597f-94c3-05460857e439
| 608,868
|
Prove that whenever the player must choose the side of a coin, the optimal strategy is to choose heads if more coins have been determined tails than heads and to choose tails if more coins have been determined heads than tails.
|
Let $q_{n}(k)$ be the probability that, with $n$ turns left and $|H-T|=k$, the player wins playing the optimal strategy. Note that $k$ is always even. We prove by induction on $n$ that with $n$ turns left in the game, this is the optimal strategy, and that $q_{n}(k) \geq q_{n}(k+2)$.
Base Case: $n=1$, if there is one more turn in the game, then clearly if we flip 3 coins and get $|H-T| \geq 3$ then our play does not matter. If we get $|H-T|=1$ then the optimal strategy is to pick the side so that $|H-T|=0$. So this is the optimal strategy.
Now $q_{1}(0)=\frac{3}{4}, q_{1}(2)=\frac{1}{2}, q_{1}(4)=\frac{1}{8}$ and $q_{1}(2 k)=0$ for $k \geq 3$. So $q_{1}(k) \geq q_{1}(k+2)$ for all $k$.
Induction Step: Assume the induction hypothesis for $n-1$ turns left in the game. With $n$ turns left in the game, since $q_{n-1}(k)$ decreases when $k=|H-T|$ increases, a larger value of $|H-T|$ is never more desirable. So picking the side of the coin that minimizes $|H-T|$ is the optimal strategy.
Now for $k \geq 2, q_{n}(2 k)=\frac{1}{8} q_{n-1}(2 k-4)+\frac{3}{8} q_{n-1}(2 k-2)+\frac{3}{8} q_{n-1}(2 k)+\frac{1}{8} q_{n-1}(2 k+2)$, and it is clear, by the induction hypothesis that $q_{n}(2 k) \geq q_{n}(2 k+2)$ for all $k \geq 2$. Similar computations make it clear that $q_{n}(0) \geq q_{n}(2) \geq q_{n}(4)$. This completes the induction step.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Prove that whenever the player must choose the side of a coin, the optimal strategy is to choose heads if more coins have been determined tails than heads and to choose tails if more coins have been determined heads than tails.
|
Let $q_{n}(k)$ be the probability that, with $n$ turns left and $|H-T|=k$, the player wins playing the optimal strategy. Note that $k$ is always even. We prove by induction on $n$ that with $n$ turns left in the game, this is the optimal strategy, and that $q_{n}(k) \geq q_{n}(k+2)$.
Base Case: $n=1$, if there is one more turn in the game, then clearly if we flip 3 coins and get $|H-T| \geq 3$ then our play does not matter. If we get $|H-T|=1$ then the optimal strategy is to pick the side so that $|H-T|=0$. So this is the optimal strategy.
Now $q_{1}(0)=\frac{3}{4}, q_{1}(2)=\frac{1}{2}, q_{1}(4)=\frac{1}{8}$ and $q_{1}(2 k)=0$ for $k \geq 3$. So $q_{1}(k) \geq q_{1}(k+2)$ for all $k$.
Induction Step: Assume the induction hypothesis for $n-1$ turns left in the game. With $n$ turns left in the game, since $q_{n-1}(k)$ decreases when $k=|H-T|$ increases, a larger value of $|H-T|$ is never more desirable. So picking the side of the coin that minimizes $|H-T|$ is the optimal strategy.
Now for $k \geq 2, q_{n}(2 k)=\frac{1}{8} q_{n-1}(2 k-4)+\frac{3}{8} q_{n-1}(2 k-2)+\frac{3}{8} q_{n-1}(2 k)+\frac{1}{8} q_{n-1}(2 k+2)$, and it is clear, by the induction hypothesis that $q_{n}(2 k) \geq q_{n}(2 k+2)$ for all $k \geq 2$. Similar computations make it clear that $q_{n}(0) \geq q_{n}(2) \geq q_{n}(4)$. This completes the induction step.
|
{
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-team1-solutions.jsonl",
"problem_match": "\n6. [10]",
"solution_match": "\nSolution: "
}
|
1e23ca93-63a3-5162-a427-8fb1c55a6757
| 608,869
|
Let $T$ denote the number of coins determined tails and $H$ denote the number of coins determined heads at the end of the game. Let $p_{m}(k)$ be the probability that $|T-H|=k$ after a game with $4 m$ coins, assuming that the player follows the optimal strategy outlined in problem 6. Clearly $p_{m}(k)=0$ if $k$ is an odd integer, so we need only consider the case when $k$ is an even integer. (By definition, $p_{0}(0)=1$ and $p_{0}(k)=0$ for $\left.k \geq 1\right)$. Prove that $p_{m}(0) \geq p_{m+1}(0)$ for all nonnegative integers $m$.
|
First solution. Using the sequences $q_{n}(k)$ defined above, it is clear that $q_{n+1}(0)=\frac{3}{4} q_{n}(0)+\frac{1}{4} q_{n}(2) \leq$ $q_{n}(0)$. So $q_{n+1}(0) \leq q_{n}(0)$. Now note that for $k=0, p_{n}(k)=q_{n}(k)$, because they are both equal to the probability that after $n$ turns of the optimal strategy $|H-T|=0$ (this is only true for $k=0$ ). It follows that $p_{n+1}(0) \leq p_{n}(0)$.
Second solution. When we play the game with $n+1$ turns, there is a $\frac{3}{4}$ chance that after 1 turn $|H-T|=0$ and a $\frac{1}{4}$ chance that $|H-T|=2$.
Now suppose we play the game, and get 2 tails and 1 heads on the first turn. Consider the following two strategies for the rest of the game.
Strategy A: We pick the fourth coin to be heads, and play the optimal strategy for the other $n$ turns. Our probability of winning is $p_{n}(0)$.
Strategy B: We pick the fourth coin to be heads with probability $\frac{3}{4}$ and tails with probability $\frac{1}{4}$, then proceed with the optimal strategy for the rest of the game. This is equivalent to throwing the first 3 coins over again and applying the optimal strategy. Our probability of winning is $p_{n+1}(0)$.
By the theorem in the previous problem, Strategy A is the optimal strategy, and thus our probability of winning employing Strategy B does not exceed our probability of wining employing Strategy A. So $p_{n}(0) \geq p_{n+1}(0)$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $T$ denote the number of coins determined tails and $H$ denote the number of coins determined heads at the end of the game. Let $p_{m}(k)$ be the probability that $|T-H|=k$ after a game with $4 m$ coins, assuming that the player follows the optimal strategy outlined in problem 6. Clearly $p_{m}(k)=0$ if $k$ is an odd integer, so we need only consider the case when $k$ is an even integer. (By definition, $p_{0}(0)=1$ and $p_{0}(k)=0$ for $\left.k \geq 1\right)$. Prove that $p_{m}(0) \geq p_{m+1}(0)$ for all nonnegative integers $m$.
|
First solution. Using the sequences $q_{n}(k)$ defined above, it is clear that $q_{n+1}(0)=\frac{3}{4} q_{n}(0)+\frac{1}{4} q_{n}(2) \leq$ $q_{n}(0)$. So $q_{n+1}(0) \leq q_{n}(0)$. Now note that for $k=0, p_{n}(k)=q_{n}(k)$, because they are both equal to the probability that after $n$ turns of the optimal strategy $|H-T|=0$ (this is only true for $k=0$ ). It follows that $p_{n+1}(0) \leq p_{n}(0)$.
Second solution. When we play the game with $n+1$ turns, there is a $\frac{3}{4}$ chance that after 1 turn $|H-T|=0$ and a $\frac{1}{4}$ chance that $|H-T|=2$.
Now suppose we play the game, and get 2 tails and 1 heads on the first turn. Consider the following two strategies for the rest of the game.
Strategy A: We pick the fourth coin to be heads, and play the optimal strategy for the other $n$ turns. Our probability of winning is $p_{n}(0)$.
Strategy B: We pick the fourth coin to be heads with probability $\frac{3}{4}$ and tails with probability $\frac{1}{4}$, then proceed with the optimal strategy for the rest of the game. This is equivalent to throwing the first 3 coins over again and applying the optimal strategy. Our probability of winning is $p_{n+1}(0)$.
By the theorem in the previous problem, Strategy A is the optimal strategy, and thus our probability of winning employing Strategy B does not exceed our probability of wining employing Strategy A. So $p_{n}(0) \geq p_{n+1}(0)$.
|
{
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-team1-solutions.jsonl",
"problem_match": "\n7. [15]",
"solution_match": "\nSolution:\n"
}
|
64c4d865-1bfc-57af-9c0b-032ab4639ed3
| 608,870
|
We would now like to examine the behavior of $p_{m}(k)$ as $m$ becomes arbitrarily large; specifically, we would like to discern whether $\lim _{m \rightarrow \infty} p_{m}(0)$ exists and, if it does, to determine its value. Let $\lim _{m \rightarrow \infty} p_{m}(k)=A_{k}$.
(a) [5] Prove that $\frac{2}{3} p_{m}(k) \geq p_{m}(k+2)$ for all $m$ and $k$.
(b) [10] Prove that $A_{0}$ exists and that $A_{0}>0$. Feel free to assume the result of analysis that a non-increasing sequence of real numbers that is bounded below by a constant converges to a limit that is greater than or equal to $c$.
|
(a) We proceed by induction.
Base Case: When $n=1$, we get $\frac{2}{3} p_{1}(0)=\frac{2}{3} \cdot \frac{3}{4}=\frac{1}{2}>\frac{1}{4}=p_{1}(2)$. And since $p_{1}(2 k)=0$ for $k \geq 2$, we get $\frac{2}{3} p_{1}(k) \geq p_{1}(k+2)$ for all $k$.
Induction Step: Assume that $\frac{2}{3} p_{i}(k) \geq p_{i}(k+2)$ for all $i \leq n$. This clearly implies $\frac{2}{3} p_{n+1}(k) \geq$ $p_{n+1}(k+2)$ for all $k \geq 4$ by the formula (c) from the previous problem.
Now, for $k=2$,
$$
\begin{aligned}
\frac{2}{3} p_{n+1}(2) & =\frac{2}{3}\left(\frac{1}{4} p_{n}(0)+\frac{3}{8} p_{n}(2)+\frac{3}{8} p_{n}(4)+\frac{1}{8} p_{n}(6)\right) \\
& \geq \frac{1}{12} p_{n}(0)+p_{n+1}(4) \\
& \geq p_{n+1}(4)
\end{aligned}
$$
by the formula (b) from the previous problem and our induction hypothesis. For $k=0$, we write out formula (a) from the previous problem.
$$
\begin{aligned}
\frac{2}{3} p_{n+1}(0) & =\frac{2}{3}\left(\frac{3}{4} p_{n}(0)+\frac{1}{2} p_{n}(2)+\frac{1}{8} p_{n}(4)\right) \\
& \geq \frac{1}{4} p_{n}(0)+\frac{3}{8} p_{n}(2)+\frac{1}{2} p_{n}(4)+\frac{1}{8} p_{n}(6)
\end{aligned}
$$
by our induction hypothesis. But $p_{n+1}(2)=\frac{1}{4} p_{n}(0)+\frac{3}{8} p_{n}(2)+\frac{3}{8} p_{n}(4)+\frac{1}{8} p_{n}(6)$, which is clearly less than the last line above. Thus $\frac{2}{3} p_{n+1}(0) \geq p_{n+1}(2)$. This completes the induction step.
Remark: This is nowhere near the strongest bound. We intentionally asked for a bound strong enough to be helpful in part b, but not strong enough to help with other problems. The strongest bound is $p_{n}(0) \geq \frac{2+\sqrt{5}}{2} p_{n}(2)$ and $p_{n}(2 k) \geq(2+\sqrt{5}) p_{n}(2 k+2)$ for $k \geq 1$. This is intuitive because $A_{0}=\frac{2+\sqrt{5}}{2} A_{2}$ and for $k \geq 1, A_{2 k}=(2+\sqrt{5}) A_{2 k+2}$.
(b) For any $n$ and $k, p_{n}(2 k) \leq\left(\frac{2}{3}\right)^{k} p_{n}(0)$. Now
$$
1=\sum_{k=0}^{\infty} p_{n}(2 k) \leq p_{n}(0) \sum_{k=0}^{\infty}\left(\frac{2}{3}\right)^{k}=3 p_{n}(0)
$$
So $p_{n}(0) \geq \frac{1}{3}$ for all $n$. This means $p_{n}(0)$ is a non-increasing sequence that is bounded below by $\frac{1}{3}$. So $A_{0}$ exists and $A_{0} \geq \frac{1}{3}>0$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
We would now like to examine the behavior of $p_{m}(k)$ as $m$ becomes arbitrarily large; specifically, we would like to discern whether $\lim _{m \rightarrow \infty} p_{m}(0)$ exists and, if it does, to determine its value. Let $\lim _{m \rightarrow \infty} p_{m}(k)=A_{k}$.
(a) [5] Prove that $\frac{2}{3} p_{m}(k) \geq p_{m}(k+2)$ for all $m$ and $k$.
(b) [10] Prove that $A_{0}$ exists and that $A_{0}>0$. Feel free to assume the result of analysis that a non-increasing sequence of real numbers that is bounded below by a constant converges to a limit that is greater than or equal to $c$.
|
(a) We proceed by induction.
Base Case: When $n=1$, we get $\frac{2}{3} p_{1}(0)=\frac{2}{3} \cdot \frac{3}{4}=\frac{1}{2}>\frac{1}{4}=p_{1}(2)$. And since $p_{1}(2 k)=0$ for $k \geq 2$, we get $\frac{2}{3} p_{1}(k) \geq p_{1}(k+2)$ for all $k$.
Induction Step: Assume that $\frac{2}{3} p_{i}(k) \geq p_{i}(k+2)$ for all $i \leq n$. This clearly implies $\frac{2}{3} p_{n+1}(k) \geq$ $p_{n+1}(k+2)$ for all $k \geq 4$ by the formula (c) from the previous problem.
Now, for $k=2$,
$$
\begin{aligned}
\frac{2}{3} p_{n+1}(2) & =\frac{2}{3}\left(\frac{1}{4} p_{n}(0)+\frac{3}{8} p_{n}(2)+\frac{3}{8} p_{n}(4)+\frac{1}{8} p_{n}(6)\right) \\
& \geq \frac{1}{12} p_{n}(0)+p_{n+1}(4) \\
& \geq p_{n+1}(4)
\end{aligned}
$$
by the formula (b) from the previous problem and our induction hypothesis. For $k=0$, we write out formula (a) from the previous problem.
$$
\begin{aligned}
\frac{2}{3} p_{n+1}(0) & =\frac{2}{3}\left(\frac{3}{4} p_{n}(0)+\frac{1}{2} p_{n}(2)+\frac{1}{8} p_{n}(4)\right) \\
& \geq \frac{1}{4} p_{n}(0)+\frac{3}{8} p_{n}(2)+\frac{1}{2} p_{n}(4)+\frac{1}{8} p_{n}(6)
\end{aligned}
$$
by our induction hypothesis. But $p_{n+1}(2)=\frac{1}{4} p_{n}(0)+\frac{3}{8} p_{n}(2)+\frac{3}{8} p_{n}(4)+\frac{1}{8} p_{n}(6)$, which is clearly less than the last line above. Thus $\frac{2}{3} p_{n+1}(0) \geq p_{n+1}(2)$. This completes the induction step.
Remark: This is nowhere near the strongest bound. We intentionally asked for a bound strong enough to be helpful in part b, but not strong enough to help with other problems. The strongest bound is $p_{n}(0) \geq \frac{2+\sqrt{5}}{2} p_{n}(2)$ and $p_{n}(2 k) \geq(2+\sqrt{5}) p_{n}(2 k+2)$ for $k \geq 1$. This is intuitive because $A_{0}=\frac{2+\sqrt{5}}{2} A_{2}$ and for $k \geq 1, A_{2 k}=(2+\sqrt{5}) A_{2 k+2}$.
(b) For any $n$ and $k, p_{n}(2 k) \leq\left(\frac{2}{3}\right)^{k} p_{n}(0)$. Now
$$
1=\sum_{k=0}^{\infty} p_{n}(2 k) \leq p_{n}(0) \sum_{k=0}^{\infty}\left(\frac{2}{3}\right)^{k}=3 p_{n}(0)
$$
So $p_{n}(0) \geq \frac{1}{3}$ for all $n$. This means $p_{n}(0)$ is a non-increasing sequence that is bounded below by $\frac{1}{3}$. So $A_{0}$ exists and $A_{0} \geq \frac{1}{3}>0$.
|
{
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-team1-solutions.jsonl",
"problem_match": "\n9. [15]",
"solution_match": "\n## Solution:\n\n"
}
|
369eec27-12b5-55ab-a87f-908e5bf35220
| 608,872
|
Let $A B C$ be a non-isosceles, non-right triangle, let $\omega$ be its circumcircle, and let $O$ be its circumcenter. Let $M$ be the midpoint of segment $B C$. Let the circumcircle of triangle $A O M$ intersect $\omega$ again at $D$. If $H$ is the orthocenter of triangle $A B C$, prove that $\angle D A H=\angle M A O$.
|
First solution.
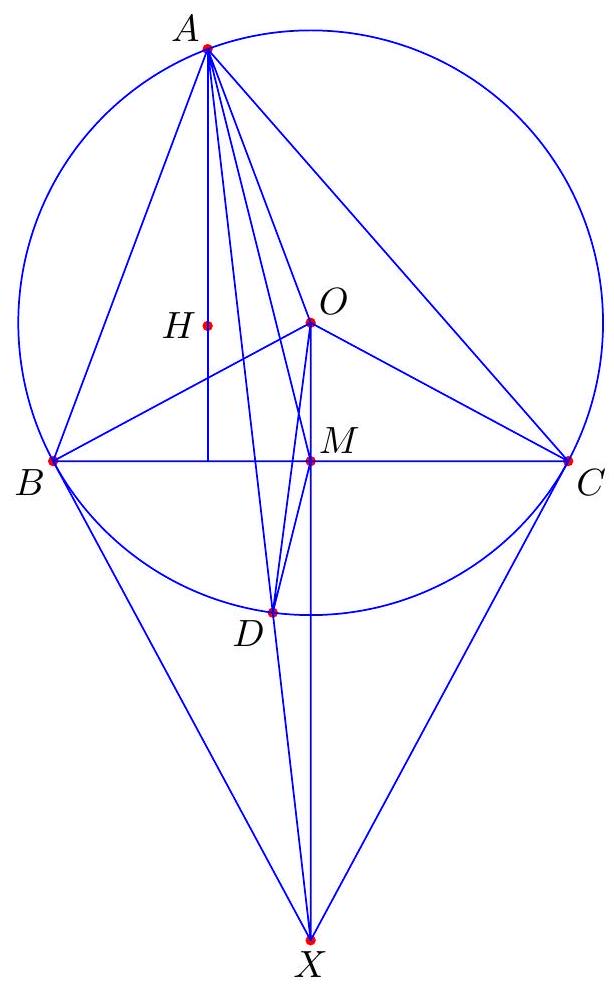
Let $X$ be the intersection of the line tangent to $\omega$ at $B$ with the line tangent to $\omega$ at $C$. Note that $\triangle O M C \sim \triangle O C X$ since $\angle O M C=\angle O C X=\frac{\pi}{2}$. Hence $\frac{O M}{O C}=\frac{O C}{O X}$, or, equivalently, $\frac{O M}{O A}=\frac{O A}{O X}$. By SAS similarity, it follows that $\triangle O A M \sim \triangle O X A$. Therefore, $\angle O A M=\angle O X A$.
We claim now that $\angle O A D=\angle O A X$. By the similarity $\triangle O A M \sim O X A$, we have that $\angle O A X=$ $\angle O M A$. Since $A O M D$ is a cyclic quadrilateral, we have that $\angle O M A=\angle O D A$. Since $O A=O D$, we have that $\angle O D A=\angle O A D$. Combining these equations tells us that $\angle O A X=\angle O A D$, so $A, D$, and $X$ are collinear.
Finally, since both $A H$ and $O X$ are perpendicular to $B C$, it follows that $A H \| O X$, so $\angle D A H=$ $\angle D X O=\angle A X O=\angle M A O$, as desired.
Second solution.
Let $Y$ be the intersection of $B C$ with the line tangent to $\omega$ at $A$. Then the circumcircle of triangle $A O M$ has diameter $O Y$, so $A D$ is perpendicular to $O Y$ because the radical axis of two circles is perpendicular to the line between their centers. Since $Y$ is on the polar of $A$, it follows that $A$ is on the polar of $Y$, so $A D \perp O X$ implies that $A D$ is the polar of $Y$, i.e. $A D$ is the symmedian from $A$ in triangle $A B C$. Hence $A D$ and $A M$ are isogonal. Since $A H$ and $A O$ are also isogonal, the desired conclusion follows immediately.
Remark: with sufficient perserverance, angle-chasing solutions involving only the points given in the diagram may also be devised.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a non-isosceles, non-right triangle, let $\omega$ be its circumcircle, and let $O$ be its circumcenter. Let $M$ be the midpoint of segment $B C$. Let the circumcircle of triangle $A O M$ intersect $\omega$ again at $D$. If $H$ is the orthocenter of triangle $A B C$, prove that $\angle D A H=\angle M A O$.
|
First solution.

Let $X$ be the intersection of the line tangent to $\omega$ at $B$ with the line tangent to $\omega$ at $C$. Note that $\triangle O M C \sim \triangle O C X$ since $\angle O M C=\angle O C X=\frac{\pi}{2}$. Hence $\frac{O M}{O C}=\frac{O C}{O X}$, or, equivalently, $\frac{O M}{O A}=\frac{O A}{O X}$. By SAS similarity, it follows that $\triangle O A M \sim \triangle O X A$. Therefore, $\angle O A M=\angle O X A$.
We claim now that $\angle O A D=\angle O A X$. By the similarity $\triangle O A M \sim O X A$, we have that $\angle O A X=$ $\angle O M A$. Since $A O M D$ is a cyclic quadrilateral, we have that $\angle O M A=\angle O D A$. Since $O A=O D$, we have that $\angle O D A=\angle O A D$. Combining these equations tells us that $\angle O A X=\angle O A D$, so $A, D$, and $X$ are collinear.
Finally, since both $A H$ and $O X$ are perpendicular to $B C$, it follows that $A H \| O X$, so $\angle D A H=$ $\angle D X O=\angle A X O=\angle M A O$, as desired.
Second solution.
Let $Y$ be the intersection of $B C$ with the line tangent to $\omega$ at $A$. Then the circumcircle of triangle $A O M$ has diameter $O Y$, so $A D$ is perpendicular to $O Y$ because the radical axis of two circles is perpendicular to the line between their centers. Since $Y$ is on the polar of $A$, it follows that $A$ is on the polar of $Y$, so $A D \perp O X$ implies that $A D$ is the polar of $Y$, i.e. $A D$ is the symmedian from $A$ in triangle $A B C$. Hence $A D$ and $A M$ are isogonal. Since $A H$ and $A O$ are also isogonal, the desired conclusion follows immediately.
Remark: with sufficient perserverance, angle-chasing solutions involving only the points given in the diagram may also be devised.
|
{
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-team1-solutions.jsonl",
"problem_match": "\n11. [20]",
"solution_match": "\nSolution:\n"
}
|
6aaae126-64aa-5919-9480-d176256fddfc
| 608,874
|
Denote $\{1,2, \ldots, n\}$ by $[n]$, and let $S$ be the set of all permutations of [ $n$ ]. Call a subset $T$ of $S$ good if every permutation $\sigma$ in $S$ may be written as $t_{1} t_{2}$ for elements $t_{1}$ and $t_{2}$ of $T$, where the product of two permutations is defined to be their composition. Call a subset of $U$ of $S$ extremely good if every permutation $\sigma$ in $S$ may be written as $s^{-1} u s$ for elements $s$ of $S$ and $u$ of $U$. Let $\tau$ be the smallest value of $|T| /|S|$ for all good subsets $T$, and let $v$ be the smallest value of $|U| /|S|$ for all extremely good subsets $U$. Prove that $\sqrt{v} \geq \tau$.
|
Denote $\{1,2, \ldots, n\}$ by $[n]$, and let $S$ be the set of all permutations of $[n]$. Call a subset $T$ of $S$ good if every permutation $\sigma$ in $S$ may be written as $t_{1} t_{2}$ for elements $t_{1}$ and $t_{2}$ of $T$, where the product of two permutations is defined to be their composition. Call a subset of $U$ of $S$ extremely good if every permutation $\sigma$ in $S$ may be written as $s^{-1} u s$ for elements $s$ of $S$ and $u$ of $U$. Let $\tau$ be
the smallest value of $|T| /|S|$ for all good subsets $T$, and let $v$ be the smallest value of $|U| /|S|$ for all extremely good subsets $U$. Prove that $\sqrt{v} \geq \tau$.
Call an element $t \in S$ an involution if and only if $t^{2}$ is the identity permutation. We claim that the set of all involutions in $S$ constitutes a good subset of $S$. The proof is simple. Let $s$ be an arbitrary permutation in $S$. Note that $s$ may be decomposed into a product of disjoint cycles of length at least 2 , and suppose that there are $m$ such cycles in its decomposition. For $1 \leq i \leq m$, let $l_{i}$ denote the length of the $i$ th cycle, so that $s$ may be written as
$$
\left(a_{1,1} a_{1,2} \ldots a_{1, l_{1}}\right)\left(a_{2,1} a_{2,2} \ldots a_{2, l_{2}}\right) \ldots\left(a_{m, 1} a_{m, 2} \ldots a_{m, l_{m}}\right)
$$
for some pairwise distinct elements
$$
a_{1,1}, a_{1,2}, \ldots, a_{1, l_{1}}, a_{2,1}, a_{2,2}, \ldots, a_{2, l_{2}}, \ldots, a_{m, 1}, a_{m, 2}, \ldots, a_{m, l_{m}}
$$
of $[n]$. Consider the permutations $q$ and $r$ defined by $q\left(a_{i, j}\right)=a_{i, l_{i}+1-j}$ for all $1 \leq j \leq l_{i}$ and $r\left(a_{i, 1}\right)=a_{i, 1}$ and $r\left(a_{i, k}\right)=a_{i, l_{i}+2-k}$ for all $2 \leq k \leq l_{i}$, for all $1 \leq i \leq m$, and by $q(x)=r(x)=x$ for all $x \in[n]$ otherwise. Since $q, r \in S, q^{2}=r^{2}=1$, and $r q=s$, it follows that the set of all involutions in $S$ is indeed good, as desired.
For all integer partitions $\lambda$ of $n$, let $f^{\lambda}$ denote the number of standard Young tableaux of shape $\lambda$. By the Robinson-Schensted-Knuth correspondence, the permutations of [ $n$ ] are in bijection with pairs of standard Young tableaux of the same shape in such a way that the involutions of $[n]$ are in bijection with pairs of identical standard Young tableaux. In other words, the number of permutations of $[n]$ is equal to the number of pairs of identically shaped standard Young tableaux whose shape is a partition of $n$, and the number of involutions of $[n]$ is equal to the number of standard Young tableaux whose shape is a partition of $n$. Hence $n!=\sum_{\lambda}\left(f^{\lambda}\right)^{2}$ and $\tau \leq \sum_{\lambda} \frac{f^{\lambda}}{n!}$, where both sums range over all partitions $\lambda$ of $n$.
For all elements $u \in S$, define the conjugacy class of $u$ to be the set of elements that may be written in the form $s^{-1} u s$ for some $s \in S$. It is easy to see that for all $u, u^{\prime} \in S$, the conjugacy classes of $u$ and $u^{\prime}$ are either identical or disjoint. It follows that $S$ may be partitioned into disjoint conjugacy classes and that any extremely good subset of $S$ must contain at least one element from each distinct conjugacy class. We claim that the number of distinct conjuguacy classes of $S$ is at least the number of integer partitions of $n$. It turns out that the two numbers are in fact equal, but such a result is not necessary for the purposes of this problem. Let $u$ be an arbitrary permutation in $S$. Recall that $u$ may be written as
$$
\left(a_{1,1} a_{1,2} \ldots a_{1, l_{1}}\right)\left(a_{2,1} a_{2,2} \ldots a_{2, l_{2}}\right) \ldots\left(a_{m, 1} a_{m, 2} \ldots a_{m, l_{m}}\right)
$$
for some pairwise distinct elements
$$
a_{1,1}, a_{1,2}, \ldots, a_{1, l_{1}}, a_{2,1}, a_{2,2}, \ldots, a_{2, l_{2}}, \ldots, a_{m, 1}, a_{m, 2}, \ldots, a_{m, l_{m}}
$$
of $[n]$. Associate to the conjugacy class of $u$ the partition $n=l_{w_{1}}+l_{w_{2}}+\ldots+l_{w_{m}}+1+\ldots+1$, where $w_{1}, w_{2}, \ldots, w_{m}$ is a partition of $1,2, \ldots, m$ such that $w_{1} \geq w_{2} \geq \ldots \geq w_{m}$ and the 1 's represent all the fixed points of $s$. Now note that if $s$ is any permutation in $S, s^{-1} u s$ may be written in the form
$$
s^{-1}\left(a_{1,1} a_{1,2} \ldots a_{1, l_{1}}\right) s s^{-1}\left(a_{2,1} a_{2,2} \ldots a_{2, l_{2}}\right) s \ldots s^{-1}\left(a_{m, 1} a_{m, 2} \ldots a_{m, l_{m}}\right) s
$$
which may be written as
$$
\left(b_{1,1} b_{1,2} \ldots b_{1, l_{1}}\right)\left(b_{2,1} b_{2,2} \ldots b_{2, l_{2}}\right) \ldots\left(b_{m, 1} b_{m, 2} \ldots b_{m, l_{m}}\right)
$$
for some pairwise distinct elements
$$
b_{1,1}, b_{1,2}, \ldots, b_{1, l_{1}}, b_{2,1}, b_{2,2}, \ldots, b_{2, l_{2}}, \ldots, b_{m, 1}, b_{m, 2}, \ldots, b_{m, l_{m}}
$$
of $[n]$ because multiplying by $s^{-1}$ on the left and by $s$ on the right is equivalent to re-indexing the letters $1,2, \ldots, n$. Hence if partitions of $n$ are associated to all conjugacy classes of $S$ analogously, the
same partition that is associated to $u$ is associated to $s^{-1} u s$ for all $s \in S$. Since exactly one partition is associated to each conjugacy class, it follows that the number of conjugacy classes cannot exceed the number of partitions, as desired.
To conclude, we need only observe that $v \geq \sum_{\lambda} \frac{1}{n!}$ by our above claim, for then
$$
n!\sqrt{v}=\sqrt{n!\sum_{\lambda} 1}=\sqrt{\left(\sum_{\lambda}\left(f^{\lambda}\right)^{2}\right)\left(\sum_{\lambda} 1\right)} \geq \sum_{\lambda} f^{\lambda} \geq n!\tau
$$
by the Cauchy-Schwarz inequality, and this completes the proof.
Remark: more computationally intensive solutions that do not use Young tableaux but instead calculate the number of involutions explicitly and make use of the generating function for the number of integer partitions are also possible.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Denote $\{1,2, \ldots, n\}$ by $[n]$, and let $S$ be the set of all permutations of [ $n$ ]. Call a subset $T$ of $S$ good if every permutation $\sigma$ in $S$ may be written as $t_{1} t_{2}$ for elements $t_{1}$ and $t_{2}$ of $T$, where the product of two permutations is defined to be their composition. Call a subset of $U$ of $S$ extremely good if every permutation $\sigma$ in $S$ may be written as $s^{-1} u s$ for elements $s$ of $S$ and $u$ of $U$. Let $\tau$ be the smallest value of $|T| /|S|$ for all good subsets $T$, and let $v$ be the smallest value of $|U| /|S|$ for all extremely good subsets $U$. Prove that $\sqrt{v} \geq \tau$.
|
Denote $\{1,2, \ldots, n\}$ by $[n]$, and let $S$ be the set of all permutations of $[n]$. Call a subset $T$ of $S$ good if every permutation $\sigma$ in $S$ may be written as $t_{1} t_{2}$ for elements $t_{1}$ and $t_{2}$ of $T$, where the product of two permutations is defined to be their composition. Call a subset of $U$ of $S$ extremely good if every permutation $\sigma$ in $S$ may be written as $s^{-1} u s$ for elements $s$ of $S$ and $u$ of $U$. Let $\tau$ be
the smallest value of $|T| /|S|$ for all good subsets $T$, and let $v$ be the smallest value of $|U| /|S|$ for all extremely good subsets $U$. Prove that $\sqrt{v} \geq \tau$.
Call an element $t \in S$ an involution if and only if $t^{2}$ is the identity permutation. We claim that the set of all involutions in $S$ constitutes a good subset of $S$. The proof is simple. Let $s$ be an arbitrary permutation in $S$. Note that $s$ may be decomposed into a product of disjoint cycles of length at least 2 , and suppose that there are $m$ such cycles in its decomposition. For $1 \leq i \leq m$, let $l_{i}$ denote the length of the $i$ th cycle, so that $s$ may be written as
$$
\left(a_{1,1} a_{1,2} \ldots a_{1, l_{1}}\right)\left(a_{2,1} a_{2,2} \ldots a_{2, l_{2}}\right) \ldots\left(a_{m, 1} a_{m, 2} \ldots a_{m, l_{m}}\right)
$$
for some pairwise distinct elements
$$
a_{1,1}, a_{1,2}, \ldots, a_{1, l_{1}}, a_{2,1}, a_{2,2}, \ldots, a_{2, l_{2}}, \ldots, a_{m, 1}, a_{m, 2}, \ldots, a_{m, l_{m}}
$$
of $[n]$. Consider the permutations $q$ and $r$ defined by $q\left(a_{i, j}\right)=a_{i, l_{i}+1-j}$ for all $1 \leq j \leq l_{i}$ and $r\left(a_{i, 1}\right)=a_{i, 1}$ and $r\left(a_{i, k}\right)=a_{i, l_{i}+2-k}$ for all $2 \leq k \leq l_{i}$, for all $1 \leq i \leq m$, and by $q(x)=r(x)=x$ for all $x \in[n]$ otherwise. Since $q, r \in S, q^{2}=r^{2}=1$, and $r q=s$, it follows that the set of all involutions in $S$ is indeed good, as desired.
For all integer partitions $\lambda$ of $n$, let $f^{\lambda}$ denote the number of standard Young tableaux of shape $\lambda$. By the Robinson-Schensted-Knuth correspondence, the permutations of [ $n$ ] are in bijection with pairs of standard Young tableaux of the same shape in such a way that the involutions of $[n]$ are in bijection with pairs of identical standard Young tableaux. In other words, the number of permutations of $[n]$ is equal to the number of pairs of identically shaped standard Young tableaux whose shape is a partition of $n$, and the number of involutions of $[n]$ is equal to the number of standard Young tableaux whose shape is a partition of $n$. Hence $n!=\sum_{\lambda}\left(f^{\lambda}\right)^{2}$ and $\tau \leq \sum_{\lambda} \frac{f^{\lambda}}{n!}$, where both sums range over all partitions $\lambda$ of $n$.
For all elements $u \in S$, define the conjugacy class of $u$ to be the set of elements that may be written in the form $s^{-1} u s$ for some $s \in S$. It is easy to see that for all $u, u^{\prime} \in S$, the conjugacy classes of $u$ and $u^{\prime}$ are either identical or disjoint. It follows that $S$ may be partitioned into disjoint conjugacy classes and that any extremely good subset of $S$ must contain at least one element from each distinct conjugacy class. We claim that the number of distinct conjuguacy classes of $S$ is at least the number of integer partitions of $n$. It turns out that the two numbers are in fact equal, but such a result is not necessary for the purposes of this problem. Let $u$ be an arbitrary permutation in $S$. Recall that $u$ may be written as
$$
\left(a_{1,1} a_{1,2} \ldots a_{1, l_{1}}\right)\left(a_{2,1} a_{2,2} \ldots a_{2, l_{2}}\right) \ldots\left(a_{m, 1} a_{m, 2} \ldots a_{m, l_{m}}\right)
$$
for some pairwise distinct elements
$$
a_{1,1}, a_{1,2}, \ldots, a_{1, l_{1}}, a_{2,1}, a_{2,2}, \ldots, a_{2, l_{2}}, \ldots, a_{m, 1}, a_{m, 2}, \ldots, a_{m, l_{m}}
$$
of $[n]$. Associate to the conjugacy class of $u$ the partition $n=l_{w_{1}}+l_{w_{2}}+\ldots+l_{w_{m}}+1+\ldots+1$, where $w_{1}, w_{2}, \ldots, w_{m}$ is a partition of $1,2, \ldots, m$ such that $w_{1} \geq w_{2} \geq \ldots \geq w_{m}$ and the 1 's represent all the fixed points of $s$. Now note that if $s$ is any permutation in $S, s^{-1} u s$ may be written in the form
$$
s^{-1}\left(a_{1,1} a_{1,2} \ldots a_{1, l_{1}}\right) s s^{-1}\left(a_{2,1} a_{2,2} \ldots a_{2, l_{2}}\right) s \ldots s^{-1}\left(a_{m, 1} a_{m, 2} \ldots a_{m, l_{m}}\right) s
$$
which may be written as
$$
\left(b_{1,1} b_{1,2} \ldots b_{1, l_{1}}\right)\left(b_{2,1} b_{2,2} \ldots b_{2, l_{2}}\right) \ldots\left(b_{m, 1} b_{m, 2} \ldots b_{m, l_{m}}\right)
$$
for some pairwise distinct elements
$$
b_{1,1}, b_{1,2}, \ldots, b_{1, l_{1}}, b_{2,1}, b_{2,2}, \ldots, b_{2, l_{2}}, \ldots, b_{m, 1}, b_{m, 2}, \ldots, b_{m, l_{m}}
$$
of $[n]$ because multiplying by $s^{-1}$ on the left and by $s$ on the right is equivalent to re-indexing the letters $1,2, \ldots, n$. Hence if partitions of $n$ are associated to all conjugacy classes of $S$ analogously, the
same partition that is associated to $u$ is associated to $s^{-1} u s$ for all $s \in S$. Since exactly one partition is associated to each conjugacy class, it follows that the number of conjugacy classes cannot exceed the number of partitions, as desired.
To conclude, we need only observe that $v \geq \sum_{\lambda} \frac{1}{n!}$ by our above claim, for then
$$
n!\sqrt{v}=\sqrt{n!\sum_{\lambda} 1}=\sqrt{\left(\sum_{\lambda}\left(f^{\lambda}\right)^{2}\right)\left(\sum_{\lambda} 1\right)} \geq \sum_{\lambda} f^{\lambda} \geq n!\tau
$$
by the Cauchy-Schwarz inequality, and this completes the proof.
Remark: more computationally intensive solutions that do not use Young tableaux but instead calculate the number of involutions explicitly and make use of the generating function for the number of integer partitions are also possible.
|
{
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-team1-solutions.jsonl",
"problem_match": "\n15. [55]",
"solution_match": "\nSolution: "
}
|
25e8060e-7286-5b87-8577-4b8440888f8f
| 608,878
|
(a) [20] Alice and Barbara play a game on a blackboard. At the start, zero is written on the board. The players alternate turns. On her turn, each player replaces $x$ - the number written on the board - with any real number $y$, subject to the constraint that $0<y-x<1$. The first player to write a number greater than or equal to 2010 wins. If Alice goes first, determine, with proof, who has the winning strategy.
(b) [20] Alice and Barbara play a game on a blackboard. At the start, zero is written on the board. The players alternate turns. On her turn, each player replaces $x$ - the number written on the board - with any real number $y$, subject to the constraint that $y-x \in(0,1)$. The first player to write a number greater than or equal to 2010 on her 2011th turn or later wins. If a player writes a number greater than or equal to 2010 on her 2010th turn or before, she loses immediately. If Alice goes first, determine, with proof, who has the winning strategy.
|
Each turn of the game is equivalent to adding a number between 0 and 1 to the number on the board.
(a) Barbara has the winning strategy: whenever Alice adds $z$ to the number on the board, Barbara adds $1-z$. After Barbara's $i$ th turn, the number on the board will be $i$. Therefore, after Barbara's 2009th turn, Alice will be forced to write a number between 2009 and 2010, after which Barbara can write 2010 and win the game.
(b) Alice has the winning strategy: she writes any number $a$ on her first turn, and, after that, whenever Barbara adds $z$ to the number on the board, Alice adds $1-z$. After Alice's $i$ th turn, the number on the board will be $(i-1)+a$, so after Alice's 2010th turn, the number will be $2009+a$. Since Barbara cannot write a number greater than or equal to 2010 on her 2010th turn, she will be forced to write a number between $2009+a$ and 2010, after which Alice can write 2010 and win the game.
## The Euler Totient Function [40]
The problems in this section require complete proofs.
Euler's totient function, denoted by $\varphi$, is a function whose domain is the set of positive integers. It is especially important in number theory, so it is often discussed on the radio or on national TV. (Just kidding). But what is it, exactly? For all positive integers $k, \varphi(k)$ is defined to be the number of positive integers less than or equal to $k$ that are relatively prime to $k$. It turns out that $\varphi$ is what you would call a multiplicative function, which means that if $a$ and $b$ are relatively prime positive integers, $\varphi(a b)=\varphi(a) \varphi(b)$. Unfortunately, the proof of this result is highly nontrivial. However, there is much more than that to $\varphi$, as you are about to discover!
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
(a) [20] Alice and Barbara play a game on a blackboard. At the start, zero is written on the board. The players alternate turns. On her turn, each player replaces $x$ - the number written on the board - with any real number $y$, subject to the constraint that $0<y-x<1$. The first player to write a number greater than or equal to 2010 wins. If Alice goes first, determine, with proof, who has the winning strategy.
(b) [20] Alice and Barbara play a game on a blackboard. At the start, zero is written on the board. The players alternate turns. On her turn, each player replaces $x$ - the number written on the board - with any real number $y$, subject to the constraint that $y-x \in(0,1)$. The first player to write a number greater than or equal to 2010 on her 2011th turn or later wins. If a player writes a number greater than or equal to 2010 on her 2010th turn or before, she loses immediately. If Alice goes first, determine, with proof, who has the winning strategy.
|
Each turn of the game is equivalent to adding a number between 0 and 1 to the number on the board.
(a) Barbara has the winning strategy: whenever Alice adds $z$ to the number on the board, Barbara adds $1-z$. After Barbara's $i$ th turn, the number on the board will be $i$. Therefore, after Barbara's 2009th turn, Alice will be forced to write a number between 2009 and 2010, after which Barbara can write 2010 and win the game.
(b) Alice has the winning strategy: she writes any number $a$ on her first turn, and, after that, whenever Barbara adds $z$ to the number on the board, Alice adds $1-z$. After Alice's $i$ th turn, the number on the board will be $(i-1)+a$, so after Alice's 2010th turn, the number will be $2009+a$. Since Barbara cannot write a number greater than or equal to 2010 on her 2010th turn, she will be forced to write a number between $2009+a$ and 2010, after which Alice can write 2010 and win the game.
## The Euler Totient Function [40]
The problems in this section require complete proofs.
Euler's totient function, denoted by $\varphi$, is a function whose domain is the set of positive integers. It is especially important in number theory, so it is often discussed on the radio or on national TV. (Just kidding). But what is it, exactly? For all positive integers $k, \varphi(k)$ is defined to be the number of positive integers less than or equal to $k$ that are relatively prime to $k$. It turns out that $\varphi$ is what you would call a multiplicative function, which means that if $a$ and $b$ are relatively prime positive integers, $\varphi(a b)=\varphi(a) \varphi(b)$. Unfortunately, the proof of this result is highly nontrivial. However, there is much more than that to $\varphi$, as you are about to discover!
|
{
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-team2-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\nSolution: "
}
|
070ac05f-3a9d-54fb-b8a1-e142d8807172
| 608,883
|
Let $n$ be a positive integer such that $n>2$. Prove that $\varphi(n)$ is even.
|
Let $A_{n}$ be the set of all positive integers $x \leq n$ such that $\operatorname{gcd}(n, x)=1$. Since $\operatorname{gcd}(n, x)=$ $\operatorname{gcd}(n, n-x)$ for all $x$, if $a$ is a positive integer in $A_{n}$, so is $n-a$. Moreover, if $a$ is in $A_{n}, a$ and $n-a$ are different since $\operatorname{gcd}\left(n, \frac{n}{2}\right)=\frac{n}{2}>1$, meaning $\frac{n}{2}$ is not in $A_{n}$. Hence we may evenly pair up the elements of $A_{n}$ that sum to $n$, so $\varphi(n)$, the number of elements of $A_{n}$, must be even, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n$ be a positive integer such that $n>2$. Prove that $\varphi(n)$ is even.
|
Let $A_{n}$ be the set of all positive integers $x \leq n$ such that $\operatorname{gcd}(n, x)=1$. Since $\operatorname{gcd}(n, x)=$ $\operatorname{gcd}(n, n-x)$ for all $x$, if $a$ is a positive integer in $A_{n}$, so is $n-a$. Moreover, if $a$ is in $A_{n}, a$ and $n-a$ are different since $\operatorname{gcd}\left(n, \frac{n}{2}\right)=\frac{n}{2}>1$, meaning $\frac{n}{2}$ is not in $A_{n}$. Hence we may evenly pair up the elements of $A_{n}$ that sum to $n$, so $\varphi(n)$, the number of elements of $A_{n}$, must be even, as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-team2-solutions.jsonl",
"problem_match": "\n6. [10]",
"solution_match": "\nSolution: "
}
|
3d2c868d-040b-5f95-8049-83a435b407a5
| 608,884
|
Let $n$ be an even positive integer. Prove that $\varphi(n) \leq \frac{n}{2}$.
|
Again, let $A_{n}$ be the set of all positive integers $x \leq n$ such that $\operatorname{gcd}(n, x)=1$. Since $n$ is even, no element of $A_{n}$ may be even, and, by definition, every element of $A_{n}$ must be at most $n$. It follows that $\varphi(n)$, the number of elements of $A_{n}$, must be at most $\frac{n}{2}$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n$ be an even positive integer. Prove that $\varphi(n) \leq \frac{n}{2}$.
|
Again, let $A_{n}$ be the set of all positive integers $x \leq n$ such that $\operatorname{gcd}(n, x)=1$. Since $n$ is even, no element of $A_{n}$ may be even, and, by definition, every element of $A_{n}$ must be at most $n$. It follows that $\varphi(n)$, the number of elements of $A_{n}$, must be at most $\frac{n}{2}$, as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-team2-solutions.jsonl",
"problem_match": "\n7. [10]",
"solution_match": "\nSolution: "
}
|
def7aca7-59d4-5db9-8d51-4e1b50201dc4
| 608,885
|
Let $A B C$ be a non-isosceles, non-right triangle, let $\omega$ be its circumcircle, and let $O$ be its circumcenter. Let $M$ be the midpoint of segment $B C$. Let the tangents to $\omega$ at $B$ and $C$ intersect at $X$. Prove that $\angle O A M=\angle O X A$. (Hint: use SAS similarity).
|
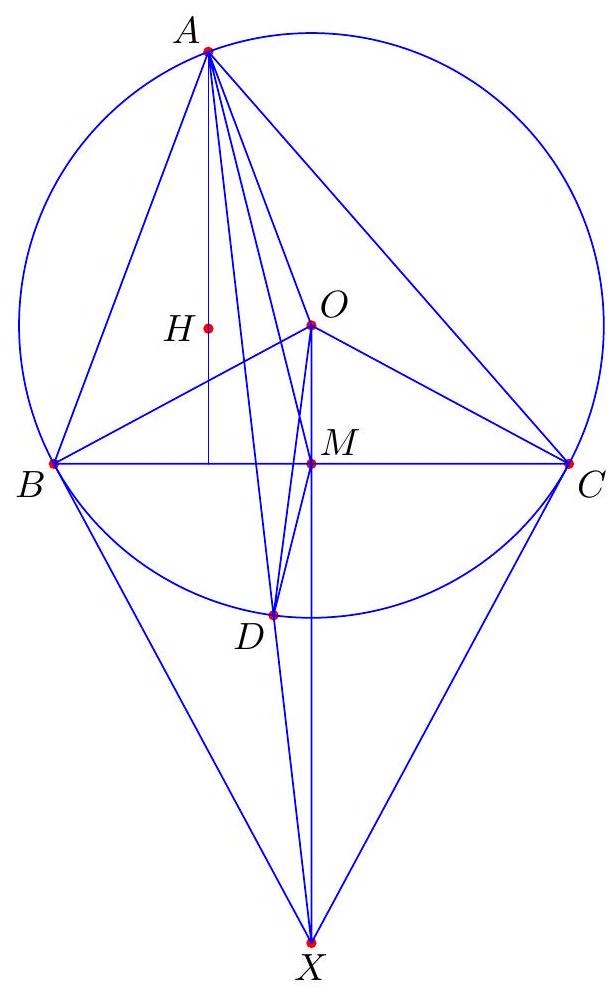
Note that $\triangle O M C \sim \triangle O C X$ since $\angle O M C=\angle O C X=\frac{\pi}{2}$. Hence $\frac{O M}{O C}=\frac{O C}{O X}$, or, equivalently, $\frac{O M}{O A}=\frac{O A}{O X}$. By SAS similarity, it follows that $\triangle O A M \sim \triangle O X A$. Therefore, $\angle O A M=\angle O X A$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a non-isosceles, non-right triangle, let $\omega$ be its circumcircle, and let $O$ be its circumcenter. Let $M$ be the midpoint of segment $B C$. Let the tangents to $\omega$ at $B$ and $C$ intersect at $X$. Prove that $\angle O A M=\angle O X A$. (Hint: use SAS similarity).
|

Note that $\triangle O M C \sim \triangle O C X$ since $\angle O M C=\angle O C X=\frac{\pi}{2}$. Hence $\frac{O M}{O C}=\frac{O C}{O X}$, or, equivalently, $\frac{O M}{O A}=\frac{O A}{O X}$. By SAS similarity, it follows that $\triangle O A M \sim \triangle O X A$. Therefore, $\angle O A M=\angle O X A$.
|
{
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-team2-solutions.jsonl",
"problem_match": "\n9. [25]",
"solution_match": "\n## Solution:\n\n"
}
|
303b11a8-d888-5d1f-be01-d0ad69462d6f
| 608,887
|
Let $A B C$ be a triangle with $A B<A C$. Let the angle bisector of $\angle A$ and the perpendicular bisector of $B C$ intersect at $D$. Then let $E$ and $F$ be points on $A B$ and $A C$ such that $D E$ and $D F$ are perpendicular to $A B$ and $A C$, respectively. Prove that $B E=C F$.
|
see below Note that $D E, D F$ are the distances from $D$ to $A B, A C$, respectively, and because $A D$ is the angle bisector of $\angle B A C$, we have $D E=D F$. Also, $D B=D C$ because $D$ is on the perpendicular bisector of $B C$. Finally, $\angle D E B=\angle D F C=90^{\circ}$, so it follows that $D E B \cong D F C$, and $B E=C F$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $A B<A C$. Let the angle bisector of $\angle A$ and the perpendicular bisector of $B C$ intersect at $D$. Then let $E$ and $F$ be points on $A B$ and $A C$ such that $D E$ and $D F$ are perpendicular to $A B$ and $A C$, respectively. Prove that $B E=C F$.
|
see below Note that $D E, D F$ are the distances from $D$ to $A B, A C$, respectively, and because $A D$ is the angle bisector of $\angle B A C$, we have $D E=D F$. Also, $D B=D C$ because $D$ is on the perpendicular bisector of $B C$. Finally, $\angle D E B=\angle D F C=90^{\circ}$, so it follows that $D E B \cong D F C$, and $B E=C F$.
|
{
"resource_path": "HarvardMIT/segmented/en-152-2012-feb-team1-solutions.jsonl",
"problem_match": "\n1. [20]",
"solution_match": "\nAnswer: "
}
|
3bf733eb-d163-5ca3-8967-0f6e6872ea54
| 609,025
|
Alice and Bob are playing a game of Token Tag, played on an $8 \times 8$ chessboard. At the beginning of the game, Bob places a token for each player on the board. After this, in every round, Alice moves her token, then Bob moves his token. If at any point in a round the two tokens are on the same square, Alice immediately wins. If Alice has not won by the end of 2012 rounds, then Bob wins.
(a) Suppose that a token can legally move to any horizontally or vertically adjacent square. Show that Bob has a winning strategy for this game.
(b) Suppose instead that a token can legally move to any horizontally, vertically, or diagonally adjacent square. Show that Alice has a winning strategy for this game.
|
see below For part (a), color the checkerboard in the standard way so that half of the squares are black and the other half are white. Bob's winning strategy is to place the two coins on the same color, so that Alice must always move her coin on to a square with the opposite color as the square containing Bob's coin.
For part (b), consider any starting configuration. By considering only the column that the tokens are in, it is easy to see that Alice can get to the same column as Bob (immediately after her move) in 7 rounds. (This is just a game on a $1 \times 8$ chessboard.) Following this, Alice can stay on the same column as Bob each turn, while getting to the same row as him. This too also takes at most 7 rounds. Thus, Alice can catch Bob in $14<2012$ rounds from any starting position.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Alice and Bob are playing a game of Token Tag, played on an $8 \times 8$ chessboard. At the beginning of the game, Bob places a token for each player on the board. After this, in every round, Alice moves her token, then Bob moves his token. If at any point in a round the two tokens are on the same square, Alice immediately wins. If Alice has not won by the end of 2012 rounds, then Bob wins.
(a) Suppose that a token can legally move to any horizontally or vertically adjacent square. Show that Bob has a winning strategy for this game.
(b) Suppose instead that a token can legally move to any horizontally, vertically, or diagonally adjacent square. Show that Alice has a winning strategy for this game.
|
see below For part (a), color the checkerboard in the standard way so that half of the squares are black and the other half are white. Bob's winning strategy is to place the two coins on the same color, so that Alice must always move her coin on to a square with the opposite color as the square containing Bob's coin.
For part (b), consider any starting configuration. By considering only the column that the tokens are in, it is easy to see that Alice can get to the same column as Bob (immediately after her move) in 7 rounds. (This is just a game on a $1 \times 8$ chessboard.) Following this, Alice can stay on the same column as Bob each turn, while getting to the same row as him. This too also takes at most 7 rounds. Thus, Alice can catch Bob in $14<2012$ rounds from any starting position.
|
{
"resource_path": "HarvardMIT/segmented/en-152-2012-feb-team1-solutions.jsonl",
"problem_match": "\n3. [20]",
"solution_match": "\nAnswer: "
}
|
ae77341b-0cdb-5e31-a752-f3ef4eb1c97f
| 609,027
|
Let $A B C$ be a triangle with $A B<A C$. Let $M$ be the midpoint of $B C$. Line $l$ is drawn through $M$ so that it is perpendicular to $A M$, and intersects line $A B$ at point $X$ and line $A C$ at point $Y$. Prove that $\angle B A C=90^{\circ}$ if and only if quadrilateral $X B Y C$ is cyclic.
|
see below
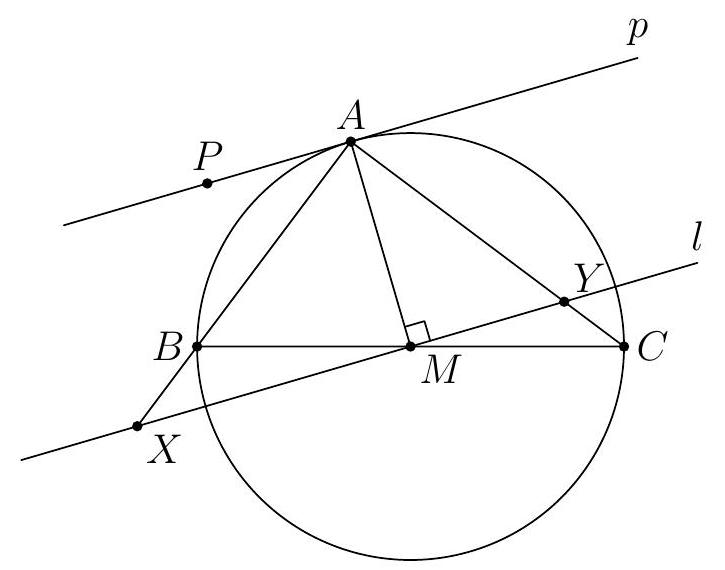
First, note that $X B Y C$ cyclic is equivalent to $\measuredangle B X M=\measuredangle A C B$. However, note that $\measuredangle B X M=$ $90^{\circ}-\measuredangle B A M$, so $X B Y C$ cyclic is in turn equivalent to $\measuredangle B A M+\measuredangle A C B=90^{\circ}$.
Let the line tangent to the circumcircle of $\triangle A B C$ at $A$ be $p$, and let $P$ be an arbitrary point on $p$ on the same side of $A M$ as $B$. Note that $\measuredangle P A B=\measuredangle A C B$. If $\measuredangle A C B=90^{\circ}-\measuredangle B A M$ we have $l \perp A M$ and thus the circumcenter $O$ of $\triangle A B C$ lies on $A M$. Since $A B<A C$, we must have $O=M$, and $\measuredangle B A C=90^{\circ}$. Conversely, if $\measuredangle B A C=90^{\circ}, \measuredangle P A M=90^{\circ}$, and it follows that $\measuredangle A C B=90^{\circ}-\measuredangle B A M$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $A B<A C$. Let $M$ be the midpoint of $B C$. Line $l$ is drawn through $M$ so that it is perpendicular to $A M$, and intersects line $A B$ at point $X$ and line $A C$ at point $Y$. Prove that $\angle B A C=90^{\circ}$ if and only if quadrilateral $X B Y C$ is cyclic.
|
see below

First, note that $X B Y C$ cyclic is equivalent to $\measuredangle B X M=\measuredangle A C B$. However, note that $\measuredangle B X M=$ $90^{\circ}-\measuredangle B A M$, so $X B Y C$ cyclic is in turn equivalent to $\measuredangle B A M+\measuredangle A C B=90^{\circ}$.
Let the line tangent to the circumcircle of $\triangle A B C$ at $A$ be $p$, and let $P$ be an arbitrary point on $p$ on the same side of $A M$ as $B$. Note that $\measuredangle P A B=\measuredangle A C B$. If $\measuredangle A C B=90^{\circ}-\measuredangle B A M$ we have $l \perp A M$ and thus the circumcenter $O$ of $\triangle A B C$ lies on $A M$. Since $A B<A C$, we must have $O=M$, and $\measuredangle B A C=90^{\circ}$. Conversely, if $\measuredangle B A C=90^{\circ}, \measuredangle P A M=90^{\circ}$, and it follows that $\measuredangle A C B=90^{\circ}-\measuredangle B A M$.
|
{
"resource_path": "HarvardMIT/segmented/en-152-2012-feb-team1-solutions.jsonl",
"problem_match": "\n4. [20]",
"solution_match": "\nAnswer: "
}
|
4b23b136-0505-5842-945a-dc2d201eaf04
| 609,028
|
It has recently been discovered that the right triangle with vertices $(0,0),(0,2012)$, and $(2012,0)$ is a giant pond that is home to many frogs. Frogs have the special ability that, if they are at a lattice point $(x, y)$, they can hop to any of the three lattice points $(x+1, y+1),(x-2, y+1)$, and $(x+1, y-2)$, assuming the given lattice point lies in or on the boundary of the triangle.
Frog Jeff starts at the corner $(0,0)$, while Frog Kenny starts at the corner $(0,2012)$. Show that the set of points that Jeff can reach is equal in size to the set of points that Kenny can reach.
|
see below
We transform the triangle as follows: map each lattice point $(x, y)$ to the point
$$
x(1,0)+y(1 / 2, \sqrt{3} / 2)=(x+y / 2, y \sqrt{3} / 2) .
$$
This transforms the right triangle into an equilateral triangle as shown above.
Now, the three allowed movements
$$
\begin{aligned}
& (x, y) \mapsto(x+1, y+1), \\
& (x, y) \mapsto(x-2, y+1), \\
& (x, y) \mapsto(x+1, y-2)
\end{aligned}
$$
become the movements
$$
\begin{aligned}
(x, y) & \mapsto(x+3 / 2, y+\sqrt{3} / 2), \\
(x, y) & \mapsto(x-3 / 2, y+\sqrt{3} / 2), \\
(x, y) & \mapsto(x, y-\sqrt{3})
\end{aligned}
$$
That is, each step is a movement of $\sqrt{3}$ in any of these three directions, which are separated by $120^{\circ}$ angles. The pond is now completely symmetrical with respect to $120^{\circ}$ rotations, so it does not matter which vertex you start at. The lower left vertex corresponds to the original point $(0,0)$, and the top vertex corresponds to the original point $(0,2012)$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
It has recently been discovered that the right triangle with vertices $(0,0),(0,2012)$, and $(2012,0)$ is a giant pond that is home to many frogs. Frogs have the special ability that, if they are at a lattice point $(x, y)$, they can hop to any of the three lattice points $(x+1, y+1),(x-2, y+1)$, and $(x+1, y-2)$, assuming the given lattice point lies in or on the boundary of the triangle.
Frog Jeff starts at the corner $(0,0)$, while Frog Kenny starts at the corner $(0,2012)$. Show that the set of points that Jeff can reach is equal in size to the set of points that Kenny can reach.
|
see below

We transform the triangle as follows: map each lattice point $(x, y)$ to the point
$$
x(1,0)+y(1 / 2, \sqrt{3} / 2)=(x+y / 2, y \sqrt{3} / 2) .
$$
This transforms the right triangle into an equilateral triangle as shown above.
Now, the three allowed movements
$$
\begin{aligned}
& (x, y) \mapsto(x+1, y+1), \\
& (x, y) \mapsto(x-2, y+1), \\
& (x, y) \mapsto(x+1, y-2)
\end{aligned}
$$
become the movements
$$
\begin{aligned}
(x, y) & \mapsto(x+3 / 2, y+\sqrt{3} / 2), \\
(x, y) & \mapsto(x-3 / 2, y+\sqrt{3} / 2), \\
(x, y) & \mapsto(x, y-\sqrt{3})
\end{aligned}
$$
That is, each step is a movement of $\sqrt{3}$ in any of these three directions, which are separated by $120^{\circ}$ angles. The pond is now completely symmetrical with respect to $120^{\circ}$ rotations, so it does not matter which vertex you start at. The lower left vertex corresponds to the original point $(0,0)$, and the top vertex corresponds to the original point $(0,2012)$.
|
{
"resource_path": "HarvardMIT/segmented/en-152-2012-feb-team1-solutions.jsonl",
"problem_match": "\n6. [30]",
"solution_match": "\nAnswer: "
}
|
580f7dad-3eaa-55ae-81c5-6fc597585fa3
| 609,030
|
For integer $n, m \geq 1$, let $A(n, m)$ denote the number of functions $f:\{1,2, \ldots, n\} \rightarrow\{1,2, \ldots, m\}$ such that $f(j)-f(i) \leq j-i$ for all $1 \leq i<j \leq n$, and let $B(n, m)$ denote the number of functions $g:\{0,1, \ldots, 2 n+m\} \rightarrow\{0,1, \ldots, m\}$ such that $g(0)=0, g(2 n+m)=m$, and $|g(i)-g(i-1)|=1$ for all $1 \leq i \leq 2 n+m$. Prove that $A(n, m)=B(n, m)$.
|
see below We first note that the condition for $f$ is equivalent to $i-f(i) \leq j-f(j)$ for all $1 \leq i<j \leq n$. Letting $f^{\prime}(x)=x-f(x)$, we see this is equivalent to saying that $f^{\prime}$ is decreasing. Thus, we only need that $f^{\prime}(x) \leq f^{\prime}(x+1)$; in other words, we only require the statement to be true for $j=i+1$.
Fix $m, n$. For any function $g$ satisfying the conditions for $B$, we construct a function $f$ satisfying the conditions for $A$ as follows. For a given function $g$ and $1 \leq i \leq 2 n+m$, say that $g$ has a up step at $i$ if $g(i)-g(i-1)=1$, and say it has a down step at $i$ otherwise. We see that $g$ must be composed of $m+n$ up steps and $n$ down steps. Let $i_{1}, i_{2}, \ldots, i_{n}$ be the indices for which down steps occur, in ascending order. Let $f$ be the function such that $f(j)=(m+1)-g\left(i_{j}\right)$ for $1 \leq j \leq n$. By our argument in the first paragraph, it suffices to show that $f(k)-f(k-1) \leq 1$ for $1<k \leq n$, or that $g\left(i_{k-1}\right)-1 \leq g\left(i_{k}\right)$. If this were not the case for some $k$, then there would be at least 1 down step in between $i_{k-1}$ and $i_{k}$, a contradiction, so the condition indeed holds.
We now claim that this construction is a bijection. For injectivity, note that for any two distinct $g, g^{\prime}$, there exists a $k$ for which the values of $g\left(i_{k}\right), g^{\prime}\left(i_{k}^{\prime}\right)$ are distinct, in which case the functions $f, f^{\prime}$ must be distinct. For surjectivity, consider any suitable $f$. Let $f^{\prime}$ be the function such that $f^{\prime}(k)=(m+1)-f(k)$ for all $1 \leq k \leq n$. (The range of this function is still $\{1,2, \ldots, m\}$.) Then, we can find a $g$ as follows: for each $1 \leq k \leq n$ in sequence, have $g$ make up steps until it reaches the value $f^{\prime}(k)$, then take one down step. This is always possible, as $f^{\prime}(k+1)-f^{\prime}(k) \leq 1$. Thus, our claim is true, and our proof is complete.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
For integer $n, m \geq 1$, let $A(n, m)$ denote the number of functions $f:\{1,2, \ldots, n\} \rightarrow\{1,2, \ldots, m\}$ such that $f(j)-f(i) \leq j-i$ for all $1 \leq i<j \leq n$, and let $B(n, m)$ denote the number of functions $g:\{0,1, \ldots, 2 n+m\} \rightarrow\{0,1, \ldots, m\}$ such that $g(0)=0, g(2 n+m)=m$, and $|g(i)-g(i-1)|=1$ for all $1 \leq i \leq 2 n+m$. Prove that $A(n, m)=B(n, m)$.
|
see below We first note that the condition for $f$ is equivalent to $i-f(i) \leq j-f(j)$ for all $1 \leq i<j \leq n$. Letting $f^{\prime}(x)=x-f(x)$, we see this is equivalent to saying that $f^{\prime}$ is decreasing. Thus, we only need that $f^{\prime}(x) \leq f^{\prime}(x+1)$; in other words, we only require the statement to be true for $j=i+1$.
Fix $m, n$. For any function $g$ satisfying the conditions for $B$, we construct a function $f$ satisfying the conditions for $A$ as follows. For a given function $g$ and $1 \leq i \leq 2 n+m$, say that $g$ has a up step at $i$ if $g(i)-g(i-1)=1$, and say it has a down step at $i$ otherwise. We see that $g$ must be composed of $m+n$ up steps and $n$ down steps. Let $i_{1}, i_{2}, \ldots, i_{n}$ be the indices for which down steps occur, in ascending order. Let $f$ be the function such that $f(j)=(m+1)-g\left(i_{j}\right)$ for $1 \leq j \leq n$. By our argument in the first paragraph, it suffices to show that $f(k)-f(k-1) \leq 1$ for $1<k \leq n$, or that $g\left(i_{k-1}\right)-1 \leq g\left(i_{k}\right)$. If this were not the case for some $k$, then there would be at least 1 down step in between $i_{k-1}$ and $i_{k}$, a contradiction, so the condition indeed holds.
We now claim that this construction is a bijection. For injectivity, note that for any two distinct $g, g^{\prime}$, there exists a $k$ for which the values of $g\left(i_{k}\right), g^{\prime}\left(i_{k}^{\prime}\right)$ are distinct, in which case the functions $f, f^{\prime}$ must be distinct. For surjectivity, consider any suitable $f$. Let $f^{\prime}$ be the function such that $f^{\prime}(k)=(m+1)-f(k)$ for all $1 \leq k \leq n$. (The range of this function is still $\{1,2, \ldots, m\}$.) Then, we can find a $g$ as follows: for each $1 \leq k \leq n$ in sequence, have $g$ make up steps until it reaches the value $f^{\prime}(k)$, then take one down step. This is always possible, as $f^{\prime}(k+1)-f^{\prime}(k) \leq 1$. Thus, our claim is true, and our proof is complete.
|
{
"resource_path": "HarvardMIT/segmented/en-152-2012-feb-team1-solutions.jsonl",
"problem_match": "\n8. [30]",
"solution_match": "\nAnswer: "
}
|
c5108443-caa7-5f84-b08c-36a47081bb48
| 609,032
|
For any positive integer $n$, let $N=\varphi(1)+\varphi(2)+\ldots+\varphi(n)$. Show that there exists a sequence
$$
a_{1}, a_{2}, \ldots, a_{N}
$$
containing exactly $\varphi(k)$ instances of $k$ for all positive integers $k \leq n$ such that
$$
\frac{1}{a_{1} a_{2}}+\frac{1}{a_{2} a_{3}}+\cdots+\frac{1}{a_{N} a_{1}}=1 .
$$
|
see below We write all fractions of the form $b / a$, where $a$ and $b$ are relatively prime, and $0 \leq b \leq a \leq n$, in ascending order. For instance, for $n=5$, this is the sequence
$$
\frac{0}{1}, \frac{1}{5}, \frac{1}{4}, \frac{1}{3}, \frac{2}{5}, \frac{1}{2}, \frac{3}{5}, \frac{2}{3}, \frac{3}{4}, \frac{4}{5}, \frac{1}{1}
$$
This sequence is known as the Farey sequence.
Now, if we look at the the sequence of the denominators of the fractions, we see that $k$ appears $\varphi(k)$ times when $k>1$, although 1 appears twice. Thus, there are $N+1$ elements in the Farey sequence. Let the Farey sequence be
$$
\frac{b_{1}}{a_{1}}, \frac{b_{2}}{a_{2}}, \ldots, \frac{b_{N+1}}{a_{N+1}}
$$
Now, $a_{N+1}=1$, so the sequence $a_{1}, a_{2}, \ldots, a_{N}$ contains $\varphi(k)$ instances of $k$ for every $1 \leq k \leq n$. We claim that this sequence also satisfies
$$
\frac{1}{a_{1} a_{2}}+\frac{1}{a_{2} a_{3}}+\cdots+\frac{1}{a_{N} a_{1}}=1 .
$$
Since $a_{1}=a_{N+1}=1$, we have
$$
\frac{1}{a_{1} a_{2}}+\frac{1}{a_{2} a_{3}}+\cdots+\frac{1}{a_{N} a_{1}}=\frac{1}{a_{1} a_{2}}+\frac{1}{a_{2} a_{3}}+\cdots+\frac{1}{a_{N} a_{N+1}} .
$$
Now, it will suffice to show that $\frac{1}{a_{i} a_{i+1}}=\frac{b_{i+1}}{a_{i+1}}-\frac{b_{i}}{a_{i}}$. Once we have shown this, the above sum will telescope to $\frac{b_{N+1}}{a_{N+1}}-\frac{b_{1}}{a_{1}}=1-0=1$.
To see why $\frac{1}{a_{i} a_{i+1}}=\frac{b_{i+1}}{a_{i+1}}-\frac{b_{i}}{a_{i}}$ holds, we note that this is equivalent to $1=b_{i+1} a_{i}-b_{i} a_{i+1}$. We can prove this fact geometrically: consider the triangle in the plane with vertices $(0,0),\left(a_{i}, b_{i}\right)$, and
$\left(a_{i+1}, b_{i+1}\right)$. This triangle contains these three boundary points, but it contains no other boundary or interior points since $a_{i}$ and $a_{i+1}$ are relatively prime to $b_{i}$ and $b_{i+1}$, respectively, and since no other fraction with denominator at most $n$ lies between $\frac{b_{i}}{a_{i}}$ and $\frac{b_{i+1}}{a_{i+1}}$. Thus, by Pick's theorem, this triangle has area $1 / 2$. But the area of the triangle can also be computed as the cross product $\frac{1}{2}\left(b_{i+1} a_{i}-b_{i} a_{i+1}\right)$; hence $b_{i+1} a_{i}-b_{i} a_{i+1}=1$ and we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For any positive integer $n$, let $N=\varphi(1)+\varphi(2)+\ldots+\varphi(n)$. Show that there exists a sequence
$$
a_{1}, a_{2}, \ldots, a_{N}
$$
containing exactly $\varphi(k)$ instances of $k$ for all positive integers $k \leq n$ such that
$$
\frac{1}{a_{1} a_{2}}+\frac{1}{a_{2} a_{3}}+\cdots+\frac{1}{a_{N} a_{1}}=1 .
$$
|
see below We write all fractions of the form $b / a$, where $a$ and $b$ are relatively prime, and $0 \leq b \leq a \leq n$, in ascending order. For instance, for $n=5$, this is the sequence
$$
\frac{0}{1}, \frac{1}{5}, \frac{1}{4}, \frac{1}{3}, \frac{2}{5}, \frac{1}{2}, \frac{3}{5}, \frac{2}{3}, \frac{3}{4}, \frac{4}{5}, \frac{1}{1}
$$
This sequence is known as the Farey sequence.
Now, if we look at the the sequence of the denominators of the fractions, we see that $k$ appears $\varphi(k)$ times when $k>1$, although 1 appears twice. Thus, there are $N+1$ elements in the Farey sequence. Let the Farey sequence be
$$
\frac{b_{1}}{a_{1}}, \frac{b_{2}}{a_{2}}, \ldots, \frac{b_{N+1}}{a_{N+1}}
$$
Now, $a_{N+1}=1$, so the sequence $a_{1}, a_{2}, \ldots, a_{N}$ contains $\varphi(k)$ instances of $k$ for every $1 \leq k \leq n$. We claim that this sequence also satisfies
$$
\frac{1}{a_{1} a_{2}}+\frac{1}{a_{2} a_{3}}+\cdots+\frac{1}{a_{N} a_{1}}=1 .
$$
Since $a_{1}=a_{N+1}=1$, we have
$$
\frac{1}{a_{1} a_{2}}+\frac{1}{a_{2} a_{3}}+\cdots+\frac{1}{a_{N} a_{1}}=\frac{1}{a_{1} a_{2}}+\frac{1}{a_{2} a_{3}}+\cdots+\frac{1}{a_{N} a_{N+1}} .
$$
Now, it will suffice to show that $\frac{1}{a_{i} a_{i+1}}=\frac{b_{i+1}}{a_{i+1}}-\frac{b_{i}}{a_{i}}$. Once we have shown this, the above sum will telescope to $\frac{b_{N+1}}{a_{N+1}}-\frac{b_{1}}{a_{1}}=1-0=1$.
To see why $\frac{1}{a_{i} a_{i+1}}=\frac{b_{i+1}}{a_{i+1}}-\frac{b_{i}}{a_{i}}$ holds, we note that this is equivalent to $1=b_{i+1} a_{i}-b_{i} a_{i+1}$. We can prove this fact geometrically: consider the triangle in the plane with vertices $(0,0),\left(a_{i}, b_{i}\right)$, and
$\left(a_{i+1}, b_{i+1}\right)$. This triangle contains these three boundary points, but it contains no other boundary or interior points since $a_{i}$ and $a_{i+1}$ are relatively prime to $b_{i}$ and $b_{i+1}$, respectively, and since no other fraction with denominator at most $n$ lies between $\frac{b_{i}}{a_{i}}$ and $\frac{b_{i+1}}{a_{i+1}}$. Thus, by Pick's theorem, this triangle has area $1 / 2$. But the area of the triangle can also be computed as the cross product $\frac{1}{2}\left(b_{i+1} a_{i}-b_{i} a_{i+1}\right)$; hence $b_{i+1} a_{i}-b_{i} a_{i+1}=1$ and we are done.
|
{
"resource_path": "HarvardMIT/segmented/en-152-2012-feb-team1-solutions.jsonl",
"problem_match": "\n9. [40]",
"solution_match": "\nAnswer: "
}
|
9218b143-acac-5f81-91de-5380ba0c8510
| 609,033
|
For positive odd integer $n$, let $f(n)$ denote the number of matrices $A$ satisfying the following conditions:
- $A$ is $n \times n$.
- Each row and column contains each of $1,2, \ldots, n$ exactly once in some order.
- $A^{T}=A$. (That is, the element in row $i$ and column $j$ is equal to the one in row $j$ and column $i$, for all $1 \leq i, j \leq n$.)
Prove that $f(n) \geq \frac{n!(n-1)!}{\varphi(n)}$.
|
see below We first note that main diagonal (the squares with row number equal to column number) is a permutation of $1,2, \ldots, n$. This is because each number $i(1 \leq i \leq n)$ appears an even number of times off the main diagonal, so must appear an odd number of times on the main diagonal. Thus, we may assume that the main diagonal's values are $1,2, \ldots, n$ in that order. Call any matrix satifsying this condition and the problem conditions good. Let $g(n)$ denote the number of good matrices. It now remains to show that $g(n) \geq \frac{(n-1)!}{\varphi(n)}$.
Now, consider a round-robin tournament with $n$ teams, labeled from 1 through $n$, with the matches spread over $n$ days such that on day $i$, all teams except team $i$ play exactly one match (so there are $\frac{n-1}{2}$ pairings), and at the end of $n$ days, each pair of teams has played exactly once. We consider two such tournaments distinct if there is some pairing of teams $i, j$ which occurs on different days in the tournaments. We claim that the tournaments are in bijection with the good matrices.
Proof of Claim: Given any good matrix $A$, we construct a tournament by making day $k$ have matches between team $i$ and $j$ for each $i, j$ such that $A_{i, j}=k$, besides $(i, j)=(k, k)$. Every pair will play some day, and since each column and row contains exactly one value of each number, no team will play more than once a day. Furthermore, given two distinct good matrices, there exists a value (off the main diagonal) on which they differ; this value corresponds to the same pair playing on different dates, so the corresponding tournaments must be distinct. For the other direction, take any tournament. Make a matrix $A$ with the main diagonal as $1,2, \ldots, n$, and for each $k$, set $A_{i, j}=k$ for each $i, j$ such that teams $i, j$ play each other on day $k$. This gives a good matrix. Similarly, given any two distinct tournaments, there exists a team pair $i, j$ which play each other on different days; this corresponds to a differing value on the corresponding good matrices.
It now suffices to exhibit $\frac{(n-1)!}{\varphi(n)}$ distinct tournaments. (It may be helpful here to think of the days in the tournament as an unordered collection of sets of pairings, with the order implictly imposed by the team not present in the set of pairings.) For our construction, consider a regular $n$-gon with center $O$. Label the points as $A_{1}, A_{2}, \ldots, A_{n}$ as an arbitrary permutation (so there are $n$ ! possible labelings). The team $k$ will be represented by $A_{k}$. For each $k$, consider the line $A_{k} O$. The remaining $n-1$ vertices can be paired into $\frac{n-1}{2}$ groups which are perpendicular to this line; use these pairings for day $k$. Of course, this doesn't generate $n$ ! distinct tournaments- but how many does it make?
Consider any permutation of labels. Starting from an arbitrary point, let the points of the polygon be $A_{\pi(1)}, A_{\pi(2)}, \ldots, A_{\pi(n)}$ in clockwise order. Letting $\pi(0)=\pi(n)$ and $\pi(n+1)=\pi(1)$, we note that $\pi(i-1)$ and $\pi(i+1)$ play each other on day $\pi(i)$. We then see that any other permutation of labels representing the same tournament must have $A_{\pi(i-1)} A_{\pi(i)}=A_{\pi(i)} A_{\pi(i+1)}$ for all $i$. Thus, if $A_{\pi(1)}$ is $k$ vertices clockwise of $A_{\pi(0)}$, then $A_{\pi(2)}$ is $k$ vertices clockwise of $A_{\pi(1)}$, and so on all the way up to $A_{\pi(n-1)}$ being $k$ vertices clockwise of $A_{\pi(n)}$. This is only possible if $k$ is relatively prime to $n$,so there are $\varphi(n)$ choices of $k$. There are $n$ choices of the place to put $A_{\pi(1)}$, giving $n \varphi(n)$ choices of permutations meeting this condition. It is clear that each permutation meeting this condition provides the same tournament, so the $n$ ! permutations can be partitioned into equivalence classes of size $n \varphi(n)$ each. Thus, there are $\frac{n!}{n \varphi(n)}$ distinct equivalence classes, and we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
For positive odd integer $n$, let $f(n)$ denote the number of matrices $A$ satisfying the following conditions:
- $A$ is $n \times n$.
- Each row and column contains each of $1,2, \ldots, n$ exactly once in some order.
- $A^{T}=A$. (That is, the element in row $i$ and column $j$ is equal to the one in row $j$ and column $i$, for all $1 \leq i, j \leq n$.)
Prove that $f(n) \geq \frac{n!(n-1)!}{\varphi(n)}$.
|
see below We first note that main diagonal (the squares with row number equal to column number) is a permutation of $1,2, \ldots, n$. This is because each number $i(1 \leq i \leq n)$ appears an even number of times off the main diagonal, so must appear an odd number of times on the main diagonal. Thus, we may assume that the main diagonal's values are $1,2, \ldots, n$ in that order. Call any matrix satifsying this condition and the problem conditions good. Let $g(n)$ denote the number of good matrices. It now remains to show that $g(n) \geq \frac{(n-1)!}{\varphi(n)}$.
Now, consider a round-robin tournament with $n$ teams, labeled from 1 through $n$, with the matches spread over $n$ days such that on day $i$, all teams except team $i$ play exactly one match (so there are $\frac{n-1}{2}$ pairings), and at the end of $n$ days, each pair of teams has played exactly once. We consider two such tournaments distinct if there is some pairing of teams $i, j$ which occurs on different days in the tournaments. We claim that the tournaments are in bijection with the good matrices.
Proof of Claim: Given any good matrix $A$, we construct a tournament by making day $k$ have matches between team $i$ and $j$ for each $i, j$ such that $A_{i, j}=k$, besides $(i, j)=(k, k)$. Every pair will play some day, and since each column and row contains exactly one value of each number, no team will play more than once a day. Furthermore, given two distinct good matrices, there exists a value (off the main diagonal) on which they differ; this value corresponds to the same pair playing on different dates, so the corresponding tournaments must be distinct. For the other direction, take any tournament. Make a matrix $A$ with the main diagonal as $1,2, \ldots, n$, and for each $k$, set $A_{i, j}=k$ for each $i, j$ such that teams $i, j$ play each other on day $k$. This gives a good matrix. Similarly, given any two distinct tournaments, there exists a team pair $i, j$ which play each other on different days; this corresponds to a differing value on the corresponding good matrices.
It now suffices to exhibit $\frac{(n-1)!}{\varphi(n)}$ distinct tournaments. (It may be helpful here to think of the days in the tournament as an unordered collection of sets of pairings, with the order implictly imposed by the team not present in the set of pairings.) For our construction, consider a regular $n$-gon with center $O$. Label the points as $A_{1}, A_{2}, \ldots, A_{n}$ as an arbitrary permutation (so there are $n$ ! possible labelings). The team $k$ will be represented by $A_{k}$. For each $k$, consider the line $A_{k} O$. The remaining $n-1$ vertices can be paired into $\frac{n-1}{2}$ groups which are perpendicular to this line; use these pairings for day $k$. Of course, this doesn't generate $n$ ! distinct tournaments- but how many does it make?
Consider any permutation of labels. Starting from an arbitrary point, let the points of the polygon be $A_{\pi(1)}, A_{\pi(2)}, \ldots, A_{\pi(n)}$ in clockwise order. Letting $\pi(0)=\pi(n)$ and $\pi(n+1)=\pi(1)$, we note that $\pi(i-1)$ and $\pi(i+1)$ play each other on day $\pi(i)$. We then see that any other permutation of labels representing the same tournament must have $A_{\pi(i-1)} A_{\pi(i)}=A_{\pi(i)} A_{\pi(i+1)}$ for all $i$. Thus, if $A_{\pi(1)}$ is $k$ vertices clockwise of $A_{\pi(0)}$, then $A_{\pi(2)}$ is $k$ vertices clockwise of $A_{\pi(1)}$, and so on all the way up to $A_{\pi(n-1)}$ being $k$ vertices clockwise of $A_{\pi(n)}$. This is only possible if $k$ is relatively prime to $n$,so there are $\varphi(n)$ choices of $k$. There are $n$ choices of the place to put $A_{\pi(1)}$, giving $n \varphi(n)$ choices of permutations meeting this condition. It is clear that each permutation meeting this condition provides the same tournament, so the $n$ ! permutations can be partitioned into equivalence classes of size $n \varphi(n)$ each. Thus, there are $\frac{n!}{n \varphi(n)}$ distinct equivalence classes, and we are done.
|
{
"resource_path": "HarvardMIT/segmented/en-152-2012-feb-team1-solutions.jsonl",
"problem_match": "\n10. [40]",
"solution_match": "\nAnswer: "
}
|
3de34c61-602e-5d73-bb99-11f9362b7f23
| 609,034
|
Let $A B C$ be a triangle with $A B<A C$. Let the angle bisector of $\angle A$ and the perpendicular bisector of $B C$ intersect at $D$. Then let $E$ and $F$ be points on $A B$ and $A C$ such that $D E$ and $D F$ are perpendicular to $A B$ and $A C$, respectively. Prove that $B E=C F$.
|
see below Note that $D E, D F$ are the distances from $D$ to $A B, A C$, respectively, and because $A D$ is the angle bisector of $\angle B A C$, we have $D E=D F$. Also, $D B=D C$ because $D$ is on the perpendicular bisector of $B C$. Finally, $\angle D E B=\angle D F C=90^{\circ}$, so it follows that $D E B \cong D F C$, and $B E=C F$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $A B<A C$. Let the angle bisector of $\angle A$ and the perpendicular bisector of $B C$ intersect at $D$. Then let $E$ and $F$ be points on $A B$ and $A C$ such that $D E$ and $D F$ are perpendicular to $A B$ and $A C$, respectively. Prove that $B E=C F$.
|
see below Note that $D E, D F$ are the distances from $D$ to $A B, A C$, respectively, and because $A D$ is the angle bisector of $\angle B A C$, we have $D E=D F$. Also, $D B=D C$ because $D$ is on the perpendicular bisector of $B C$. Finally, $\angle D E B=\angle D F C=90^{\circ}$, so it follows that $D E B \cong D F C$, and $B E=C F$.
|
{
"resource_path": "HarvardMIT/segmented/en-152-2012-feb-team2-solutions.jsonl",
"problem_match": "\n6. [20]",
"solution_match": "\nAnswer: "
}
|
3bf733eb-d163-5ca3-8967-0f6e6872ea54
| 609,025
|
Alice and Bob are playing a game of Token Tag, played on an $8 \times 8$ chessboard. At the beginning of the game, Bob places a token for each player on the board. After this, in every round, Alice moves her token, then Bob moves his token. If at any point in a round the two tokens are on the same square, Alice immediately wins. If Alice has not won by the end of 2012 rounds, then Bob wins.
(a) Suppose that a token can legally move to any horizontally or vertically adjacent square. Show that Bob has a winning strategy for this game.
(b) Suppose instead that a token can legally move to any horizontally, vertically, or diagonally adjacent square. Show that Alice has a winning strategy for this game.
|
see below For part (a), color the checkerboard in the standard way so that half of the squares are black and the other half are white. Bob's winning strategy is to place the two coins on the same color, so that Alice must always move her coin on to a square with the opposite color as the square containing Bob's coin.
For part (b), consider any starting configuration. By considering only the column that the tokens are in, it is easy to see that Alice can get to the same column as Bob (immediately after her move) in 7 rounds. (This is just a game on a $1 \times 8$ chessboard.) Following this, Alice can stay on the same column as Bob each turn, while getting to the same row as him. This too also takes at most 7 rounds. Thus, Alice can catch Bob in $14<2012$ rounds from any starting position.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Alice and Bob are playing a game of Token Tag, played on an $8 \times 8$ chessboard. At the beginning of the game, Bob places a token for each player on the board. After this, in every round, Alice moves her token, then Bob moves his token. If at any point in a round the two tokens are on the same square, Alice immediately wins. If Alice has not won by the end of 2012 rounds, then Bob wins.
(a) Suppose that a token can legally move to any horizontally or vertically adjacent square. Show that Bob has a winning strategy for this game.
(b) Suppose instead that a token can legally move to any horizontally, vertically, or diagonally adjacent square. Show that Alice has a winning strategy for this game.
|
see below For part (a), color the checkerboard in the standard way so that half of the squares are black and the other half are white. Bob's winning strategy is to place the two coins on the same color, so that Alice must always move her coin on to a square with the opposite color as the square containing Bob's coin.
For part (b), consider any starting configuration. By considering only the column that the tokens are in, it is easy to see that Alice can get to the same column as Bob (immediately after her move) in 7 rounds. (This is just a game on a $1 \times 8$ chessboard.) Following this, Alice can stay on the same column as Bob each turn, while getting to the same row as him. This too also takes at most 7 rounds. Thus, Alice can catch Bob in $14<2012$ rounds from any starting position.
|
{
"resource_path": "HarvardMIT/segmented/en-152-2012-feb-team2-solutions.jsonl",
"problem_match": "\n8. [20]",
"solution_match": "\nAnswer: "
}
|
ae77341b-0cdb-5e31-a752-f3ef4eb1c97f
| 609,027
|
Let $A B C$ be a triangle with $A B<A C$. Let $M$ be the midpoint of $B C$. Line $l$ is drawn through $M$ so that it is perpendicular to $A M$, and intersects line $A B$ at point $X$ and line $A C$ at point $Y$. Prove that $\angle B A C=90^{\circ}$ if and only if quadrilateral $X B Y C$ is cyclic.
|
see below
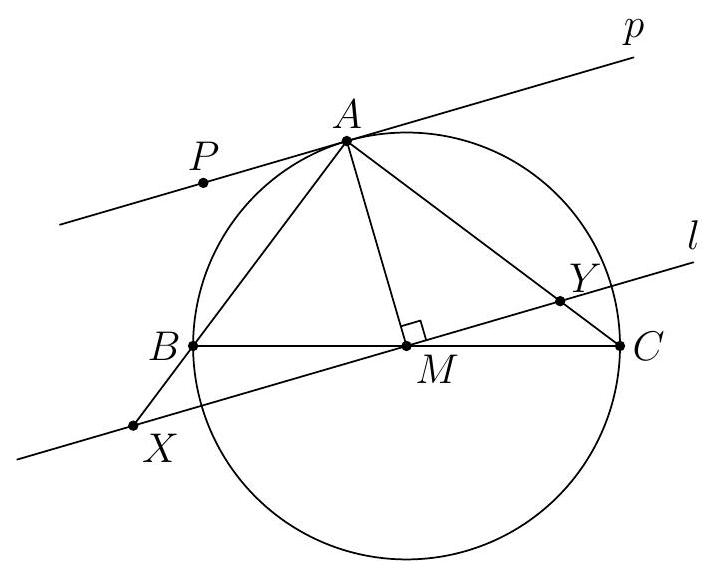
First, note that $X B Y C$ cyclic is equivalent to $\measuredangle B X M=\measuredangle A C B$. However, note that $\measuredangle B X M=$ $90^{\circ}-\measuredangle B A M$, so $X B Y C$ cyclic is in turn equivalent to $\measuredangle B A M+\measuredangle A C B=90^{\circ}$.
Let the line tangent to the circumcircle of $\triangle A B C$ at $A$ be $p$, and let $P$ be an arbitrary point on $p$ on the same side of $A M$ as $B$. Note that $\measuredangle P A B=\measuredangle A C B$. If $\measuredangle A C B=90^{\circ}-\measuredangle B A M$ we have $l \perp A M$ and thus the circumcenter $O$ of $\triangle A B C$ lies on $A M$. Since $A B<A C$, we must have $O=M$, and $\measuredangle B A C=90^{\circ}$. Conversely, if $\measuredangle B A C=90^{\circ}, \measuredangle P A M=90^{\circ}$, and it follows that $\measuredangle A C B=90^{\circ}-\measuredangle B A M$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $A B<A C$. Let $M$ be the midpoint of $B C$. Line $l$ is drawn through $M$ so that it is perpendicular to $A M$, and intersects line $A B$ at point $X$ and line $A C$ at point $Y$. Prove that $\angle B A C=90^{\circ}$ if and only if quadrilateral $X B Y C$ is cyclic.
|
see below

First, note that $X B Y C$ cyclic is equivalent to $\measuredangle B X M=\measuredangle A C B$. However, note that $\measuredangle B X M=$ $90^{\circ}-\measuredangle B A M$, so $X B Y C$ cyclic is in turn equivalent to $\measuredangle B A M+\measuredangle A C B=90^{\circ}$.
Let the line tangent to the circumcircle of $\triangle A B C$ at $A$ be $p$, and let $P$ be an arbitrary point on $p$ on the same side of $A M$ as $B$. Note that $\measuredangle P A B=\measuredangle A C B$. If $\measuredangle A C B=90^{\circ}-\measuredangle B A M$ we have $l \perp A M$ and thus the circumcenter $O$ of $\triangle A B C$ lies on $A M$. Since $A B<A C$, we must have $O=M$, and $\measuredangle B A C=90^{\circ}$. Conversely, if $\measuredangle B A C=90^{\circ}, \measuredangle P A M=90^{\circ}$, and it follows that $\measuredangle A C B=90^{\circ}-\measuredangle B A M$.
|
{
"resource_path": "HarvardMIT/segmented/en-152-2012-feb-team2-solutions.jsonl",
"problem_match": "\n9. [20]",
"solution_match": "\nAnswer: "
}
|
4b23b136-0505-5842-945a-dc2d201eaf04
| 609,028
|
Let triangle $A B C$ satisfy $2 B C=A B+A C$ and have incenter $I$ and circumcircle $\omega$. Let $D$ be the intersection of $A I$ and $\omega$ (with $A, D$ distinct). Prove that $I$ is the midpoint of $A D$.
|
N/A Since $A D$ is an angle bisector, $D$ is the midpoint of $\operatorname{arc} B C$ opposite $A$ on $\omega$. It is well-known that $B, I$, and $C$ lie on a circle centered at $D$. Thus $B D=D C=D I$. Applying Ptolemy's theorem to cyclic quadrilateral $A B D C$, we get
$A B \cdot D C+A C \cdot B D=A D \cdot B C=A D \cdot(A B+A C) / 2$
Using $B D=D C$ we have immediately that $A D=2 B D=2 D I$ so $I$ is the midpoint of $A D$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let triangle $A B C$ satisfy $2 B C=A B+A C$ and have incenter $I$ and circumcircle $\omega$. Let $D$ be the intersection of $A I$ and $\omega$ (with $A, D$ distinct). Prove that $I$ is the midpoint of $A D$.
|
N/A Since $A D$ is an angle bisector, $D$ is the midpoint of $\operatorname{arc} B C$ opposite $A$ on $\omega$. It is well-known that $B, I$, and $C$ lie on a circle centered at $D$. Thus $B D=D C=D I$. Applying Ptolemy's theorem to cyclic quadrilateral $A B D C$, we get
$A B \cdot D C+A C \cdot B D=A D \cdot B C=A D \cdot(A B+A C) / 2$
Using $B D=D C$ we have immediately that $A D=2 B D=2 D I$ so $I$ is the midpoint of $A D$ as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-162-2013-feb-team-solutions.jsonl",
"problem_match": "\n6. [25]",
"solution_match": "\nAnswer: "
}
|
f3245381-9563-5378-a6c8-5b5f4867ac20
| 609,138
|
Let triangle $A B C$ satisfy $2 B C=A B+A C$ and have incenter $I$ and circumcircle $\omega$. Let $D$ be the intersection of $A I$ and $\omega$ (with $A, D$ distinct). Prove that $I$ is the midpoint of $A D$.
|
Let $P$ and $Q$ be the midpoints of $A B$ and $A C$, and take the point $E$ on segment $B C$ such that $B E=B P$. Note that $C E=A B-B E=A B-B P=\frac{A B+A C}{2}-\frac{A B}{2}=\frac{A C}{2}=C Q$, so triangles $B P E$ and $C Q E$ are isosceles. In addition, $\frac{B E}{E C}=\frac{A B / 2}{A C / 2}=\frac{A B}{A C}$, so by the angle bisector theorem, $A E$ bisects $\angle C A B$, whence $E$ must lie on the bisector of $\angle A$.
Since triangles $B P E$ and $C Q E$ are isosceles, the bisectors of angles $B$ and $C$ are the perpendicular bisectors of segments $P E$ and $E Q$, respectively. Thus, the circumcenter of $\triangle P Q E$ is $I$, so the perpendicular bisector of $P Q$ meets the bisector of $\angle A$ at $I$.
Furthermore, since $\angle D A B=\angle C A D$, arcs $\widehat{B D}$ and $\widehat{D C}$ have the same measure, so $B D=D C$, whence the perpendicular bisector of $B C$ meets the bisector of $\angle A$ at $D$. A homothety centered at $A$ with factor $1 / 2$ maps $B C$ to $P Q$, and so maps $D$ to $I$. Thus, $D$ is the midpoint of $A I$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let triangle $A B C$ satisfy $2 B C=A B+A C$ and have incenter $I$ and circumcircle $\omega$. Let $D$ be the intersection of $A I$ and $\omega$ (with $A, D$ distinct). Prove that $I$ is the midpoint of $A D$.
|
Let $P$ and $Q$ be the midpoints of $A B$ and $A C$, and take the point $E$ on segment $B C$ such that $B E=B P$. Note that $C E=A B-B E=A B-B P=\frac{A B+A C}{2}-\frac{A B}{2}=\frac{A C}{2}=C Q$, so triangles $B P E$ and $C Q E$ are isosceles. In addition, $\frac{B E}{E C}=\frac{A B / 2}{A C / 2}=\frac{A B}{A C}$, so by the angle bisector theorem, $A E$ bisects $\angle C A B$, whence $E$ must lie on the bisector of $\angle A$.
Since triangles $B P E$ and $C Q E$ are isosceles, the bisectors of angles $B$ and $C$ are the perpendicular bisectors of segments $P E$ and $E Q$, respectively. Thus, the circumcenter of $\triangle P Q E$ is $I$, so the perpendicular bisector of $P Q$ meets the bisector of $\angle A$ at $I$.
Furthermore, since $\angle D A B=\angle C A D$, arcs $\widehat{B D}$ and $\widehat{D C}$ have the same measure, so $B D=D C$, whence the perpendicular bisector of $B C$ meets the bisector of $\angle A$ at $D$. A homothety centered at $A$ with factor $1 / 2$ maps $B C$ to $P Q$, and so maps $D$ to $I$. Thus, $D$ is the midpoint of $A I$.
|
{
"resource_path": "HarvardMIT/segmented/en-162-2013-feb-team-solutions.jsonl",
"problem_match": "\n6. [25]",
"solution_match": "\nSolution 2: "
}
|
f3245381-9563-5378-a6c8-5b5f4867ac20
| 609,138
|
Let triangle $A B C$ satisfy $2 B C=A B+A C$ and have incenter $I$ and circumcircle $\omega$. Let $D$ be the intersection of $A I$ and $\omega$ (with $A, D$ distinct). Prove that $I$ is the midpoint of $A D$.
|
Let $a=B C, b=C A$, and $c=A B$, let $r$ and $R$ denote the lengths of the inradius and circumradius of $\triangle A B C$, respectively, let $E$ be the intersection of segments $A D$ and $B C$, and let $O$ be the circumcenter of $\triangle A B C . I$ is the midpoint of chord $A D$ if and only if $O I \perp A D$, which is true if and only if $O A^{2}=O I^{2}+A I^{2}$. By Euler's distance formula, $O I^{2}=R(R-2 r)$, and by Stewart's theorem and the angle bisector theorem we can find $A I^{2}=\left(\frac{b+c}{a+b+c}\right)^{2} b c\left(1-\left(\frac{a}{b+c}\right)^{2}\right)=\frac{b c}{3}$. Thus, it remains to show that $6 R r=b c$.
Now, we use the combine the well-known formulas $\frac{a b c}{4 K}=R$ and $K=r s$ to get $a b c=4 R r s$, where $K$ is the area of $\triangle A B C$ and $s$ is its semiperimeter. We have $b c=\operatorname{Rr} \frac{4 s}{a}=\operatorname{Rr} \frac{2 a+2(b+c)}{a}=\operatorname{Rr} \frac{2 a+2(2 a)}{a}=6 R r$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let triangle $A B C$ satisfy $2 B C=A B+A C$ and have incenter $I$ and circumcircle $\omega$. Let $D$ be the intersection of $A I$ and $\omega$ (with $A, D$ distinct). Prove that $I$ is the midpoint of $A D$.
|
Let $a=B C, b=C A$, and $c=A B$, let $r$ and $R$ denote the lengths of the inradius and circumradius of $\triangle A B C$, respectively, let $E$ be the intersection of segments $A D$ and $B C$, and let $O$ be the circumcenter of $\triangle A B C . I$ is the midpoint of chord $A D$ if and only if $O I \perp A D$, which is true if and only if $O A^{2}=O I^{2}+A I^{2}$. By Euler's distance formula, $O I^{2}=R(R-2 r)$, and by Stewart's theorem and the angle bisector theorem we can find $A I^{2}=\left(\frac{b+c}{a+b+c}\right)^{2} b c\left(1-\left(\frac{a}{b+c}\right)^{2}\right)=\frac{b c}{3}$. Thus, it remains to show that $6 R r=b c$.
Now, we use the combine the well-known formulas $\frac{a b c}{4 K}=R$ and $K=r s$ to get $a b c=4 R r s$, where $K$ is the area of $\triangle A B C$ and $s$ is its semiperimeter. We have $b c=\operatorname{Rr} \frac{4 s}{a}=\operatorname{Rr} \frac{2 a+2(b+c)}{a}=\operatorname{Rr} \frac{2 a+2(2 a)}{a}=6 R r$, as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-162-2013-feb-team-solutions.jsonl",
"problem_match": "\n6. [25]",
"solution_match": "\nSolution 3: "
}
|
f3245381-9563-5378-a6c8-5b5f4867ac20
| 609,138
|
There are $n$ children and $n$ toys such that each child has a strict preference ordering on the toys. We want to distribute the toys: say a distribution $A$ dominates a distribution $B \neq A$ if in $A$, each child receives at least as preferable of an toy as in $B$. Prove that if some distribution is not dominated by any other, then at least one child gets his/her favorite toy in that distribution.
|
N/A Suppose we have a distribution $A$ assigning each child $C_{i}, i=1,2, \ldots, n$, toy $T_{i}$, such that no child $C_{i}$ gets their top preference $T_{i}^{\prime} \neq T_{i}$. Then, pick an arbitrary child $C_{1}$ and construct the sequence of children $C_{i_{1}}, C_{i_{2}}, C_{i_{3}}, \ldots$ where $i_{1}=1$ and $C_{i_{k+1}}$ was assigned the favorite toy $T_{i_{k}}^{\prime}$ of the last child $C_{i_{k}}$. Eventually, some $C_{i_{k}}=C_{i_{1}}$; at this point, just pass the toys around this cycle so that each of these children gets their favorite toy. Clearly the resulting distribution dominates the original, so we're done.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
There are $n$ children and $n$ toys such that each child has a strict preference ordering on the toys. We want to distribute the toys: say a distribution $A$ dominates a distribution $B \neq A$ if in $A$, each child receives at least as preferable of an toy as in $B$. Prove that if some distribution is not dominated by any other, then at least one child gets his/her favorite toy in that distribution.
|
N/A Suppose we have a distribution $A$ assigning each child $C_{i}, i=1,2, \ldots, n$, toy $T_{i}$, such that no child $C_{i}$ gets their top preference $T_{i}^{\prime} \neq T_{i}$. Then, pick an arbitrary child $C_{1}$ and construct the sequence of children $C_{i_{1}}, C_{i_{2}}, C_{i_{3}}, \ldots$ where $i_{1}=1$ and $C_{i_{k+1}}$ was assigned the favorite toy $T_{i_{k}}^{\prime}$ of the last child $C_{i_{k}}$. Eventually, some $C_{i_{k}}=C_{i_{1}}$; at this point, just pass the toys around this cycle so that each of these children gets their favorite toy. Clearly the resulting distribution dominates the original, so we're done.
|
{
"resource_path": "HarvardMIT/segmented/en-162-2013-feb-team-solutions.jsonl",
"problem_match": "\n7. [30]",
"solution_match": "\nAnswer: "
}
|
08f141c7-c618-5a66-aead-4b11779b81fd
| 609,139
|
Let points $A$ and $B$ be on circle $\omega$ centered at $O$. Suppose that $\omega_{A}$ and $\omega_{B}$ are circles not containing $O$ which are internally tangent to $\omega$ at $A$ and $B$, respectively. Let $\omega_{A}$ and $\omega_{B}$ intersect at $C$ and $D$ such that $D$ is inside triangle $A B C$. Suppose that line $B C$ meets $\omega$ again at $E$ and let line $E A$ intersect $\omega_{A}$ at $F$. If $F C \perp C D$, prove that $O, C$, and $D$ are collinear.
|
N/A Let $H=C A \cap \omega$, and $G=B H \cap \omega_{B}$. There are homotheties centered at A and B taking $\omega_{A} \rightarrow \omega$ and $\omega_{B} \rightarrow \omega$ that take $A: F \mapsto E, A: C \mapsto H, B: C \mapsto E$ and $B: G \mapsto H$. In particular $C F\|E H\| C G$, so $C, F, G$ are collinear, lying on a line perpendicular to $D C$.
Because of the right angles at $C, D F$ and $D G$ are diameters of $\omega_{A}, \omega_{B}$, respectively. Also, we have that the ratio of the sizes of $\omega_{A}$ and $\omega_{B}$, under the two homotheties above, is $C F / E H \cdot E H / C G=C F / C G$. Therefore, $D F / D G=C F / C G$, but then $\triangle D C F$ and $\triangle D C G$ are both right triangles which share one side and have hypotenuse and other side in proportion; it is obvious now that the two circles $\omega_{A}$ and $\omega_{B}$ are congruent.
Therefore, $O$ has the same distance to $A$ and $B$, and so the same distances to the centers of the two circles as well. As a result, $O$ lies on the radical axis $C D$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let points $A$ and $B$ be on circle $\omega$ centered at $O$. Suppose that $\omega_{A}$ and $\omega_{B}$ are circles not containing $O$ which are internally tangent to $\omega$ at $A$ and $B$, respectively. Let $\omega_{A}$ and $\omega_{B}$ intersect at $C$ and $D$ such that $D$ is inside triangle $A B C$. Suppose that line $B C$ meets $\omega$ again at $E$ and let line $E A$ intersect $\omega_{A}$ at $F$. If $F C \perp C D$, prove that $O, C$, and $D$ are collinear.
|
N/A Let $H=C A \cap \omega$, and $G=B H \cap \omega_{B}$. There are homotheties centered at A and B taking $\omega_{A} \rightarrow \omega$ and $\omega_{B} \rightarrow \omega$ that take $A: F \mapsto E, A: C \mapsto H, B: C \mapsto E$ and $B: G \mapsto H$. In particular $C F\|E H\| C G$, so $C, F, G$ are collinear, lying on a line perpendicular to $D C$.
Because of the right angles at $C, D F$ and $D G$ are diameters of $\omega_{A}, \omega_{B}$, respectively. Also, we have that the ratio of the sizes of $\omega_{A}$ and $\omega_{B}$, under the two homotheties above, is $C F / E H \cdot E H / C G=C F / C G$. Therefore, $D F / D G=C F / C G$, but then $\triangle D C F$ and $\triangle D C G$ are both right triangles which share one side and have hypotenuse and other side in proportion; it is obvious now that the two circles $\omega_{A}$ and $\omega_{B}$ are congruent.
Therefore, $O$ has the same distance to $A$ and $B$, and so the same distances to the centers of the two circles as well. As a result, $O$ lies on the radical axis $C D$ as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-162-2013-feb-team-solutions.jsonl",
"problem_match": "\n8. [35]",
"solution_match": "\nAnswer: "
}
|
7fa48052-da58-5d0d-9008-99a5d05611cb
| 609,140
|
Chim Tu has a large rectangular table. On it, there are finitely many pieces of paper with nonoverlapping interiors, each one in the shape of a convex polygon. At each step, Chim Tu is allowed to slide one piece of paper in a straight line such that its interior does not touch any other piece of paper during the slide. Can Chim Tu always slide all the pieces of paper off the table in finitely many steps?
|
N/A Let the pieces of paper be $P_{1}, P_{2}, \ldots, P_{n}$ in the Cartesian plane. It suffices to show that for any constant distance $D$, they can be slid so that each pairwise distance is at least $D$. Then, we can apply this using $D$ equal to the diameter of the rectangle, sliding all but at most one of the pieces of paper off the table, and then slide this last one off arbitrarily.
We show in particular that there is always a polygon $P_{i}$ which can be slid arbitrarily far to the right (i.e. in the positive $x$-direction). For each $P_{i}$ let $B_{i}$ be a bottommost (i.e. lowest $y$-coordinate) point on the boundary of $P_{i}$. Define a point $Q$ to be exposed if the ray starting at $Q$ in the positive $x$ direction meets the interior of no piece of paper.
Consider the set of all exposed $B_{i}$; this set is nonempty because certainly the bottommost of all the $B_{i}$ is exposed. Of this set, let $B_{k}$ be the exposed $B_{i}$ with maximal $y$-coordinate, and if there are more than one such, choose the one with maximal $x$-coordinate. We claim that the corresponding $P_{k}$ can be slid arbitrarily far to the right.
Suppose for the sake of contradiction that there is some polygon blocking this path. To be precise, if $A_{k}$ is the highest point of $P_{k}$, then the region $R$ formed by the right-side boundary of $P_{k}$ and the rays pointing in the positive $x$ direction from $A_{k}$ and $B_{k}$, must contain interior point(s) of some set of polygon(s) $P_{j}$ in its interior. All of their bottommost points $B_{j}$ must lie in $R$, since none of them can have boundary intersecting the ray from $B_{k}$, by the construction of $B_{k}$.
Because $B_{k}$ was chosen to be rightmost out of all the exposed $B_{i}$ with that $y$-coordinate, it must be that all of the $B_{j}$ corresponding to the blocking $P_{j}$ have larger $y$-coordinate. Now, choose of these the one with smallest $y$-coordinate - it must be exposed, and it has strictly higher $y$-coordinate than $B_{k}$, contradiction. It follows that the interior of $R$ intersects no pieces of paper.
Now, for a fixed $D$ such that $D$ is at least the largest distance between any two points of two polygons, we can shift this exposed piece of paper $n D$ to the right, the next one of the remaining pieces $(n-1) D$, and so on, so that the pairwise distances between pieces of paper, even when projected onto the $x$-axis, are at least $D$ each. We're done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Chim Tu has a large rectangular table. On it, there are finitely many pieces of paper with nonoverlapping interiors, each one in the shape of a convex polygon. At each step, Chim Tu is allowed to slide one piece of paper in a straight line such that its interior does not touch any other piece of paper during the slide. Can Chim Tu always slide all the pieces of paper off the table in finitely many steps?
|
N/A Let the pieces of paper be $P_{1}, P_{2}, \ldots, P_{n}$ in the Cartesian plane. It suffices to show that for any constant distance $D$, they can be slid so that each pairwise distance is at least $D$. Then, we can apply this using $D$ equal to the diameter of the rectangle, sliding all but at most one of the pieces of paper off the table, and then slide this last one off arbitrarily.
We show in particular that there is always a polygon $P_{i}$ which can be slid arbitrarily far to the right (i.e. in the positive $x$-direction). For each $P_{i}$ let $B_{i}$ be a bottommost (i.e. lowest $y$-coordinate) point on the boundary of $P_{i}$. Define a point $Q$ to be exposed if the ray starting at $Q$ in the positive $x$ direction meets the interior of no piece of paper.
Consider the set of all exposed $B_{i}$; this set is nonempty because certainly the bottommost of all the $B_{i}$ is exposed. Of this set, let $B_{k}$ be the exposed $B_{i}$ with maximal $y$-coordinate, and if there are more than one such, choose the one with maximal $x$-coordinate. We claim that the corresponding $P_{k}$ can be slid arbitrarily far to the right.
Suppose for the sake of contradiction that there is some polygon blocking this path. To be precise, if $A_{k}$ is the highest point of $P_{k}$, then the region $R$ formed by the right-side boundary of $P_{k}$ and the rays pointing in the positive $x$ direction from $A_{k}$ and $B_{k}$, must contain interior point(s) of some set of polygon(s) $P_{j}$ in its interior. All of their bottommost points $B_{j}$ must lie in $R$, since none of them can have boundary intersecting the ray from $B_{k}$, by the construction of $B_{k}$.
Because $B_{k}$ was chosen to be rightmost out of all the exposed $B_{i}$ with that $y$-coordinate, it must be that all of the $B_{j}$ corresponding to the blocking $P_{j}$ have larger $y$-coordinate. Now, choose of these the one with smallest $y$-coordinate - it must be exposed, and it has strictly higher $y$-coordinate than $B_{k}$, contradiction. It follows that the interior of $R$ intersects no pieces of paper.
Now, for a fixed $D$ such that $D$ is at least the largest distance between any two points of two polygons, we can shift this exposed piece of paper $n D$ to the right, the next one of the remaining pieces $(n-1) D$, and so on, so that the pairwise distances between pieces of paper, even when projected onto the $x$-axis, are at least $D$ each. We're done.
|
{
"resource_path": "HarvardMIT/segmented/en-162-2013-feb-team-solutions.jsonl",
"problem_match": "\n10. [40]",
"solution_match": "\nAnswer: "
}
|
89832a30-ee99-5449-8c89-e0aeb9a30e05
| 609,142
|
Let $\mathcal{S}$ be a set of size $n$, and $k$ be a positive integer. For each $1 \leq i \leq k n$, there is a subset $S_{i} \subset \mathcal{S}$ such that $\left|S_{i}\right|=2$. Furthermore, for each $e \in \mathcal{S}$, there are exactly $2 k$ values of $i$ such that $e \in S_{i}$. Show that it is possible to choose one element from $S_{i}$ for each $1 \leq i \leq k n$ such that every element of $\mathcal{S}$ is chosen exactly $k$ times.
|
N/A Consider the undirected graph $G=(\mathcal{S}, E)$ where the elements of $\mathcal{S}$ are the vertices, and for each $1 \leq i \leq k n$, there is an edge between the two elements of $S_{i}$. (Note that there might be multiedges if two subsets are the same, but there are no self-loops.) Consider any connected component $C$ of $G$, which must be a $2 k$-regular graph, and because $2 k$ is even, $C$ has an Eulerian circuit. Pick an orientation of the circuit, and hence a direction for each edge in $C$. Then, for each $i$ such that the edge corresponding to $S_{i}$ is in $C$, pick the element that is pointed to by that edge. Since the circuit goes into each vertex of $C k$ times, each element in $C$ is picked exactly $k$ times as desired. Repeating for each connected component finishes the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $\mathcal{S}$ be a set of size $n$, and $k$ be a positive integer. For each $1 \leq i \leq k n$, there is a subset $S_{i} \subset \mathcal{S}$ such that $\left|S_{i}\right|=2$. Furthermore, for each $e \in \mathcal{S}$, there are exactly $2 k$ values of $i$ such that $e \in S_{i}$. Show that it is possible to choose one element from $S_{i}$ for each $1 \leq i \leq k n$ such that every element of $\mathcal{S}$ is chosen exactly $k$ times.
|
N/A Consider the undirected graph $G=(\mathcal{S}, E)$ where the elements of $\mathcal{S}$ are the vertices, and for each $1 \leq i \leq k n$, there is an edge between the two elements of $S_{i}$. (Note that there might be multiedges if two subsets are the same, but there are no self-loops.) Consider any connected component $C$ of $G$, which must be a $2 k$-regular graph, and because $2 k$ is even, $C$ has an Eulerian circuit. Pick an orientation of the circuit, and hence a direction for each edge in $C$. Then, for each $i$ such that the edge corresponding to $S_{i}$ is in $C$, pick the element that is pointed to by that edge. Since the circuit goes into each vertex of $C k$ times, each element in $C$ is picked exactly $k$ times as desired. Repeating for each connected component finishes the problem.
|
{
"resource_path": "HarvardMIT/segmented/en-164-tournaments-2013-hmic-solutions.jsonl",
"problem_match": "\n1. [5]",
"solution_match": "\nAnswer: "
}
|
873d6fc1-99ed-5b7c-87eb-700725e84fb3
| 609,143
|
A subset $U \subset \mathbb{R}$ is open if for any $x \in U$, there exist real numbers $a, b$ such that $x \in(a, b) \subset U$. Suppose $S \subset \mathbb{R}$ has the property that any open set intersecting $(0,1)$ also intersects $S$. Let $T$ be a countable collection of open sets containing $S$. Prove that the intersection of all of the sets of $T$ is not a countable subset of $\mathbb{R}$.
(A set $\Gamma$ is countable if there exists a bijective function $f: \Gamma \rightarrow \mathbb{Z}$.)
|
N/A If $S$ is uncountable then we're done, so assume $S$ is countable. We may also assume that the supersets are a chain $V_{1} \supset V_{2} \supset V_{3} \supset \cdots$ by taking intersections.
We will use the following fact from point set topology:
If $K_{1} \supset K_{2} \supset \cdots$ is a sequence of nonempty compact sets, then their intersection is nonempty.
Now, we construct an uncountable family of such sequences $K_{1} \supset K_{2} \supset \cdots$ such that $K_{i}$ is a nontrivial (i.e. $[a, b]$ with $b>a$ ) closed interval contained in $V_{i}$, and any two such sequences have disjoint intersection. The construction proceeds as follows. At each step, we choose out of countably many options one closed interval $K_{i+1} \subset K_{i}$.
To choose $K_{1}$, we claim that there exist countably many disjoint closed intervals in $V_{1}$. To do this, choose an open interval in $V_{1}$ of length at most $1 / 2$, and take some closed interval inside it. In the remainder of $(0,1)$, which has measure at least $1 / 2$ and where $V_{1}$ is still dense, choose another open interval of length at most $1 / 4$, and a closed interval inside it. This process can be repeated indefinitely to find a countably infinite family of nontrivial disjoint closed intervals in $V_{1}$. Choose one of them to be $K_{1}$.
Now, inductively apply this construction on $K_{i}$ to find countably many choices for $K_{i+1}$, all disjoint. As a result, we get a total of $\mathbb{N}^{\mathbb{N}}$, i.e. uncountably many, choices of sequences $K_{i}$ satisfying the given properties. Any pair of sequences eventually have disjoint $K_{i}$ after some point, so no two intersections will intersect. Thus we can choose a point out of the intersection of each $K_{i}$ sequence to find uncountably many points in the intersection of all the $V_{i}$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Other
|
A subset $U \subset \mathbb{R}$ is open if for any $x \in U$, there exist real numbers $a, b$ such that $x \in(a, b) \subset U$. Suppose $S \subset \mathbb{R}$ has the property that any open set intersecting $(0,1)$ also intersects $S$. Let $T$ be a countable collection of open sets containing $S$. Prove that the intersection of all of the sets of $T$ is not a countable subset of $\mathbb{R}$.
(A set $\Gamma$ is countable if there exists a bijective function $f: \Gamma \rightarrow \mathbb{Z}$.)
|
N/A If $S$ is uncountable then we're done, so assume $S$ is countable. We may also assume that the supersets are a chain $V_{1} \supset V_{2} \supset V_{3} \supset \cdots$ by taking intersections.
We will use the following fact from point set topology:
If $K_{1} \supset K_{2} \supset \cdots$ is a sequence of nonempty compact sets, then their intersection is nonempty.
Now, we construct an uncountable family of such sequences $K_{1} \supset K_{2} \supset \cdots$ such that $K_{i}$ is a nontrivial (i.e. $[a, b]$ with $b>a$ ) closed interval contained in $V_{i}$, and any two such sequences have disjoint intersection. The construction proceeds as follows. At each step, we choose out of countably many options one closed interval $K_{i+1} \subset K_{i}$.
To choose $K_{1}$, we claim that there exist countably many disjoint closed intervals in $V_{1}$. To do this, choose an open interval in $V_{1}$ of length at most $1 / 2$, and take some closed interval inside it. In the remainder of $(0,1)$, which has measure at least $1 / 2$ and where $V_{1}$ is still dense, choose another open interval of length at most $1 / 4$, and a closed interval inside it. This process can be repeated indefinitely to find a countably infinite family of nontrivial disjoint closed intervals in $V_{1}$. Choose one of them to be $K_{1}$.
Now, inductively apply this construction on $K_{i}$ to find countably many choices for $K_{i+1}$, all disjoint. As a result, we get a total of $\mathbb{N}^{\mathbb{N}}$, i.e. uncountably many, choices of sequences $K_{i}$ satisfying the given properties. Any pair of sequences eventually have disjoint $K_{i}$ after some point, so no two intersections will intersect. Thus we can choose a point out of the intersection of each $K_{i}$ sequence to find uncountably many points in the intersection of all the $V_{i}$, as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-164-tournaments-2013-hmic-solutions.jsonl",
"problem_match": "\n4. [10]",
"solution_match": "\nAnswer: "
}
|
30969139-9047-56c0-8f90-3b0bab5bd3fd
| 609,146
|
Let $\omega$ be a circle, and let $A$ and $B$ be two points in its interior. Prove that there exists a circle passing through $A$ and $B$ that is contained in the interior of $\omega$.
|
N/A WLOG, suppose $O A \geq O B$. Let $\omega^{\prime}$ be the circle of radius $O A$ centered at $O$. We have that $B$ lies inside $\omega^{\prime}$. Thus, it is possible to scale $\omega^{\prime}$ down about the point $A$ to get a circle $\omega^{\prime \prime}$ passing through both $A$ and $B$. Since $\omega^{\prime \prime}$ lies inside $\omega^{\prime}$ and $\omega^{\prime}$ lies inside $\omega, \omega^{\prime \prime}$ lies inside $\omega$.
Alternative solution 1: WLOG, suppose $O A \geq O B$. Since $O A \geq O B$, the perpendicular bisector of $A B$ intersects segment $O A$ at some point $C$. We claim that the circle $\omega^{\prime}$ passing through $A$ and $B$ and centered at $C$ lies entirely in $\omega$. Let $x=O A$ and $y=A C=B C$. Note that $y$ is the length of the radius of $\omega^{\prime}$. By definition, any point $P$ contained in $\omega^{\prime}$ is of distance at most $y$ from $C$. Applying the triangle inequality to $O C P$, we see that $O P \leq O C+C P \leq(x-y)+y=x$, so $P$ lies in $\omega$. Since $P$ was arbitrary, it follows that $\omega^{\prime}$ lies entirely in $\omega$.
Alternative solution 2: Draw line $A B$, and let it intersect $\omega$ at $A^{\prime}$ and $B^{\prime}$, where $A$ and $A^{\prime}$ are on the same side of $B$. Choose $X$ inside the segment $A B$ so that $A^{\prime} X / A X=B^{\prime} X / B X$; such a point exists by the intermediate value theorem. Notice that $X$ is the center of a dilation taking $A^{\prime} B^{\prime}$ to $A B$ - the same dilation carries $\omega$ to $\omega^{\prime}$ which goes through $A$ and $B$. Since $\omega^{\prime}$ is $\omega$ dilated with respect to a point in its interior, it's clear that $\omega^{\prime}$ must be contained entirely within $\omega$, and so we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\omega$ be a circle, and let $A$ and $B$ be two points in its interior. Prove that there exists a circle passing through $A$ and $B$ that is contained in the interior of $\omega$.
|
N/A WLOG, suppose $O A \geq O B$. Let $\omega^{\prime}$ be the circle of radius $O A$ centered at $O$. We have that $B$ lies inside $\omega^{\prime}$. Thus, it is possible to scale $\omega^{\prime}$ down about the point $A$ to get a circle $\omega^{\prime \prime}$ passing through both $A$ and $B$. Since $\omega^{\prime \prime}$ lies inside $\omega^{\prime}$ and $\omega^{\prime}$ lies inside $\omega, \omega^{\prime \prime}$ lies inside $\omega$.
Alternative solution 1: WLOG, suppose $O A \geq O B$. Since $O A \geq O B$, the perpendicular bisector of $A B$ intersects segment $O A$ at some point $C$. We claim that the circle $\omega^{\prime}$ passing through $A$ and $B$ and centered at $C$ lies entirely in $\omega$. Let $x=O A$ and $y=A C=B C$. Note that $y$ is the length of the radius of $\omega^{\prime}$. By definition, any point $P$ contained in $\omega^{\prime}$ is of distance at most $y$ from $C$. Applying the triangle inequality to $O C P$, we see that $O P \leq O C+C P \leq(x-y)+y=x$, so $P$ lies in $\omega$. Since $P$ was arbitrary, it follows that $\omega^{\prime}$ lies entirely in $\omega$.
Alternative solution 2: Draw line $A B$, and let it intersect $\omega$ at $A^{\prime}$ and $B^{\prime}$, where $A$ and $A^{\prime}$ are on the same side of $B$. Choose $X$ inside the segment $A B$ so that $A^{\prime} X / A X=B^{\prime} X / B X$; such a point exists by the intermediate value theorem. Notice that $X$ is the center of a dilation taking $A^{\prime} B^{\prime}$ to $A B$ - the same dilation carries $\omega$ to $\omega^{\prime}$ which goes through $A$ and $B$. Since $\omega^{\prime}$ is $\omega$ dilated with respect to a point in its interior, it's clear that $\omega^{\prime}$ must be contained entirely within $\omega$, and so we are done.
|
{
"resource_path": "HarvardMIT/segmented/en-172-2014-feb-team-solutions.jsonl",
"problem_match": "\n1. [10]",
"solution_match": "\nAnswer: "
}
|
08dfce9b-dba1-5b85-9629-10ed09393c9d
| 609,276
|
For integers $m, n \geq 1$, let $A(n, m)$ be the number of sequences $\left(a_{1}, \cdots, a_{n m}\right)$ of integers satisfying the following two properties:
(a) Each integer $k$ with $1 \leq k \leq n$ occurs exactly $m$ times in the sequence $\left(a_{1}, \cdots, a_{n m}\right)$.
(b) If $i, j$, and $k$ are integers such that $1 \leq i \leq n m$ and $1 \leq j \leq k \leq n$, then $j$ occurs in the sequence $\left(a_{1}, \cdots, a_{i}\right)$ at least as many times as $k$ does.
For example, if $n=2$ and $m=5$, a possible sequence is $\left(a_{1}, \cdots, a_{10}\right)=(1,1,2,1,2,2,1,2,1,2)$. On the other hand, the sequence $\left(a_{1}, \cdots, a_{10}\right)=(1,2,1,2,2,1,1,1,2,2)$ does not satisfy property (2) for $i=5, j=1$, and $k=2$.
Prove that $A(n, m)=A(m, n)$.
|
N/A Solution 1: We show that $A(n, m)$ is equal to the the number of standard Young tableaux with $n$ rows and $m$ columns (i.e. fillings of an $n \times m$ matrix with the numbers $1,2, \ldots, n m$ so that numbers are increasing in each row and column). Consider the procedure where every time a $k$ appears in the sequences, you add a number to the leftmost empty spot of the $k$-th row. Doing this procedure will result in a valid standard Young tableau. The entries are increasing along every row because new elements are added from left to right. The elements are also increasing along every column. This is because the condition about the sequences implies that there will always be at least as many elements in row $i$ as there are in row $j$ for $i<j$. At the end of this procedure, the Young Tableaux has been filled because each of the $n$ numbers have been added $m$ times.
Now, consider a $n \times m$ standard Young tableau. If the number $p$ is in row $k$, you add a $k$ to the sequence. This will produce a valid sequence. To see this, suppose that $p$ appears in the entry $(x, y)$. Then all of the entries $(q, y)$ where $q<x$ have already been added to the sequence because they must contain entries less than $p$. Thus, the numbers 1 through $x-1$ have all already been added at least $y$ times Then, when we process $p$, we are adding the $y$-th $x$, which is valid. At the end of this procedure, $n$ numbers have been added $m$ times to the sequence.
The two procedures given above are inverses of each other. Thus, $A(n, m)$ is equal to the number of $n \times m$ standard Young tableaux. For every $n \times m$ Tableaux, we can transpose it to form an $m \times n$ tableau. The number of such tableaux is $A(m, n)$. Thus, $A(n, m)=A(m, n)$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
For integers $m, n \geq 1$, let $A(n, m)$ be the number of sequences $\left(a_{1}, \cdots, a_{n m}\right)$ of integers satisfying the following two properties:
(a) Each integer $k$ with $1 \leq k \leq n$ occurs exactly $m$ times in the sequence $\left(a_{1}, \cdots, a_{n m}\right)$.
(b) If $i, j$, and $k$ are integers such that $1 \leq i \leq n m$ and $1 \leq j \leq k \leq n$, then $j$ occurs in the sequence $\left(a_{1}, \cdots, a_{i}\right)$ at least as many times as $k$ does.
For example, if $n=2$ and $m=5$, a possible sequence is $\left(a_{1}, \cdots, a_{10}\right)=(1,1,2,1,2,2,1,2,1,2)$. On the other hand, the sequence $\left(a_{1}, \cdots, a_{10}\right)=(1,2,1,2,2,1,1,1,2,2)$ does not satisfy property (2) for $i=5, j=1$, and $k=2$.
Prove that $A(n, m)=A(m, n)$.
|
N/A Solution 1: We show that $A(n, m)$ is equal to the the number of standard Young tableaux with $n$ rows and $m$ columns (i.e. fillings of an $n \times m$ matrix with the numbers $1,2, \ldots, n m$ so that numbers are increasing in each row and column). Consider the procedure where every time a $k$ appears in the sequences, you add a number to the leftmost empty spot of the $k$-th row. Doing this procedure will result in a valid standard Young tableau. The entries are increasing along every row because new elements are added from left to right. The elements are also increasing along every column. This is because the condition about the sequences implies that there will always be at least as many elements in row $i$ as there are in row $j$ for $i<j$. At the end of this procedure, the Young Tableaux has been filled because each of the $n$ numbers have been added $m$ times.
Now, consider a $n \times m$ standard Young tableau. If the number $p$ is in row $k$, you add a $k$ to the sequence. This will produce a valid sequence. To see this, suppose that $p$ appears in the entry $(x, y)$. Then all of the entries $(q, y)$ where $q<x$ have already been added to the sequence because they must contain entries less than $p$. Thus, the numbers 1 through $x-1$ have all already been added at least $y$ times Then, when we process $p$, we are adding the $y$-th $x$, which is valid. At the end of this procedure, $n$ numbers have been added $m$ times to the sequence.
The two procedures given above are inverses of each other. Thus, $A(n, m)$ is equal to the number of $n \times m$ standard Young tableaux. For every $n \times m$ Tableaux, we can transpose it to form an $m \times n$ tableau. The number of such tableaux is $A(m, n)$. Thus, $A(n, m)=A(m, n)$.
|
{
"resource_path": "HarvardMIT/segmented/en-172-2014-feb-team-solutions.jsonl",
"problem_match": "\n9. [35]",
"solution_match": "\nAnswer: "
}
|
57d35eec-1316-58ed-b78f-2e7fed5d088f
| 609,283
|
For integers $m, n \geq 1$, let $A(n, m)$ be the number of sequences $\left(a_{1}, \cdots, a_{n m}\right)$ of integers satisfying the following two properties:
(a) Each integer $k$ with $1 \leq k \leq n$ occurs exactly $m$ times in the sequence $\left(a_{1}, \cdots, a_{n m}\right)$.
(b) If $i, j$, and $k$ are integers such that $1 \leq i \leq n m$ and $1 \leq j \leq k \leq n$, then $j$ occurs in the sequence $\left(a_{1}, \cdots, a_{i}\right)$ at least as many times as $k$ does.
For example, if $n=2$ and $m=5$, a possible sequence is $\left(a_{1}, \cdots, a_{10}\right)=(1,1,2,1,2,2,1,2,1,2)$. On the other hand, the sequence $\left(a_{1}, \cdots, a_{10}\right)=(1,2,1,2,2,1,1,1,2,2)$ does not satisfy property (2) for $i=5, j=1$, and $k=2$.
Prove that $A(n, m)=A(m, n)$.
|
We can also form a direct bijection to show $A(n, m)=A(m, n)$, as follows. Suppose that $a=\left(a_{1}, \ldots, a_{m n}\right)$ is a sequence satisfying properties 1 and 2 . We will define a sequence $f(a)=$ $\left(b_{1}, \ldots, b_{n m}\right)$ satisfying the same properties 1 and 2 , but with $m$ and $n$ switched.
The bijection $f$ is simple: just define $b_{i}$, for $1 \leq i \leq n m$, to be equal to the number of $j$ with $1 \leq j \leq i$ such that $a_{j}=a_{i}$. In other words, to obtain $f(a)$ from $a$, replace the $k$ th occurrence of each number with the number $k$. For example, if $n=2$ and $m=5$, then $f(1,1,2,1,2,2,1,2,1,2)=$ $(1,2,1,3,2,3,4,4,5,5)$.
First, it is clear that $f(a)$ satisfies property 1 with $m$ and $n$ switched. Indeed, it follows directly from the definition of $f$ that for each pair $\left(k_{1}, k_{2}\right)$ with $1 \leq k_{1} \leq n$ and $1 \leq k_{2} \leq m$, there is exactly one index $i$ for which $\left(a_{i}, b_{i}\right)=\left(k_{1}, k_{2}\right)$. This implies the desired result.
Second, we show that $f(a)$ satisfies property 2 with $m$ and $n$ switched. For this, suppose that $i, j, k$ are integers with $1 \leq i \leq n m$ and $1 \leq j \leq k \leq m$. Then, the number of times that $k$ appears in the sequence $\left(b_{1}, \ldots, b_{i}\right)$ is exactly equal to the number of integers $\ell$ with $1 \leq \ell \leq n$ such that $\ell$ appears at least $k$ times in the sequence $\left(a_{1}, \ldots, a_{i}\right)$. Similarly, the number of times that $j$ appears in the sequence $\left(b_{1}, \ldots, b_{i}\right)$ is exactly equal to the number of integers $\ell$ with $1 \leq j \leq n$ such that $\ell$ appears at least $j$
times in the sequence $\left(a_{1}, \ldots, a_{i}\right)$. In particular, the number $j$ appears in the sequence $\left(b_{1}, \ldots, b_{i}\right)$ at least as many times as $k$ does.
Now, we show that $f$ is a bijection. We claim that $f$ is actually an involution; that is, $f(f(a))=a$. (Note in particular that this implies that $f$ is a bijection, and its inverse is itself.)
Fix an index $i$ with $1 \leq i \leq m n$. Let $\ell=a_{i}$ and $k=b_{i}$; then, $k$ is the number of times that the term $\ell$ appears in the sequence $\left(a_{1}, \ldots, a_{i}\right)$. It is enough to show that $\ell$ is the number of times that the term $k$ appears in the sequence $\left(b_{1}, \ldots, b_{i}\right)$. First, note that by definition of $f$, the number of times $k$ appears in the sequence $\left(b_{1}, \ldots, b_{i}\right)$ is equal to the number of integers $j$ such that the sequence $\left(a_{1}, \ldots, a_{i}\right)$ contains the number $j$ at least $k$ times.
Now, $\ell$ occurs exactly $k$ times in the sequence $\left(a_{1}, \ldots, a_{i}\right)$. So by property 2 , each $j$ with $j \leq \ell$ appears at least $k$ times in the sequence $\left(a_{1}, \ldots, a_{i}\right)$. Furthermore, each $j$ with $j>\ell$ appears at most $k-1$ times in the sequence $\left(a_{1}, \ldots, a_{i-1}\right)$ and thus appears at most $k-1$ times in the sequence $\left(a_{1}, \ldots, a_{i}\right)$ as well (because $a_{i}=\ell$ ). Therefore, the number of integers $j$ such that the sequence ( $a_{1}, \ldots, a_{i}$ ) contains the number $j$ at least $k$ times is exactly equal to $\ell$. This shows the desired result.
Note: The bijections given in solutions 1 and 2 can actually be shown to be the same.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
For integers $m, n \geq 1$, let $A(n, m)$ be the number of sequences $\left(a_{1}, \cdots, a_{n m}\right)$ of integers satisfying the following two properties:
(a) Each integer $k$ with $1 \leq k \leq n$ occurs exactly $m$ times in the sequence $\left(a_{1}, \cdots, a_{n m}\right)$.
(b) If $i, j$, and $k$ are integers such that $1 \leq i \leq n m$ and $1 \leq j \leq k \leq n$, then $j$ occurs in the sequence $\left(a_{1}, \cdots, a_{i}\right)$ at least as many times as $k$ does.
For example, if $n=2$ and $m=5$, a possible sequence is $\left(a_{1}, \cdots, a_{10}\right)=(1,1,2,1,2,2,1,2,1,2)$. On the other hand, the sequence $\left(a_{1}, \cdots, a_{10}\right)=(1,2,1,2,2,1,1,1,2,2)$ does not satisfy property (2) for $i=5, j=1$, and $k=2$.
Prove that $A(n, m)=A(m, n)$.
|
We can also form a direct bijection to show $A(n, m)=A(m, n)$, as follows. Suppose that $a=\left(a_{1}, \ldots, a_{m n}\right)$ is a sequence satisfying properties 1 and 2 . We will define a sequence $f(a)=$ $\left(b_{1}, \ldots, b_{n m}\right)$ satisfying the same properties 1 and 2 , but with $m$ and $n$ switched.
The bijection $f$ is simple: just define $b_{i}$, for $1 \leq i \leq n m$, to be equal to the number of $j$ with $1 \leq j \leq i$ such that $a_{j}=a_{i}$. In other words, to obtain $f(a)$ from $a$, replace the $k$ th occurrence of each number with the number $k$. For example, if $n=2$ and $m=5$, then $f(1,1,2,1,2,2,1,2,1,2)=$ $(1,2,1,3,2,3,4,4,5,5)$.
First, it is clear that $f(a)$ satisfies property 1 with $m$ and $n$ switched. Indeed, it follows directly from the definition of $f$ that for each pair $\left(k_{1}, k_{2}\right)$ with $1 \leq k_{1} \leq n$ and $1 \leq k_{2} \leq m$, there is exactly one index $i$ for which $\left(a_{i}, b_{i}\right)=\left(k_{1}, k_{2}\right)$. This implies the desired result.
Second, we show that $f(a)$ satisfies property 2 with $m$ and $n$ switched. For this, suppose that $i, j, k$ are integers with $1 \leq i \leq n m$ and $1 \leq j \leq k \leq m$. Then, the number of times that $k$ appears in the sequence $\left(b_{1}, \ldots, b_{i}\right)$ is exactly equal to the number of integers $\ell$ with $1 \leq \ell \leq n$ such that $\ell$ appears at least $k$ times in the sequence $\left(a_{1}, \ldots, a_{i}\right)$. Similarly, the number of times that $j$ appears in the sequence $\left(b_{1}, \ldots, b_{i}\right)$ is exactly equal to the number of integers $\ell$ with $1 \leq j \leq n$ such that $\ell$ appears at least $j$
times in the sequence $\left(a_{1}, \ldots, a_{i}\right)$. In particular, the number $j$ appears in the sequence $\left(b_{1}, \ldots, b_{i}\right)$ at least as many times as $k$ does.
Now, we show that $f$ is a bijection. We claim that $f$ is actually an involution; that is, $f(f(a))=a$. (Note in particular that this implies that $f$ is a bijection, and its inverse is itself.)
Fix an index $i$ with $1 \leq i \leq m n$. Let $\ell=a_{i}$ and $k=b_{i}$; then, $k$ is the number of times that the term $\ell$ appears in the sequence $\left(a_{1}, \ldots, a_{i}\right)$. It is enough to show that $\ell$ is the number of times that the term $k$ appears in the sequence $\left(b_{1}, \ldots, b_{i}\right)$. First, note that by definition of $f$, the number of times $k$ appears in the sequence $\left(b_{1}, \ldots, b_{i}\right)$ is equal to the number of integers $j$ such that the sequence $\left(a_{1}, \ldots, a_{i}\right)$ contains the number $j$ at least $k$ times.
Now, $\ell$ occurs exactly $k$ times in the sequence $\left(a_{1}, \ldots, a_{i}\right)$. So by property 2 , each $j$ with $j \leq \ell$ appears at least $k$ times in the sequence $\left(a_{1}, \ldots, a_{i}\right)$. Furthermore, each $j$ with $j>\ell$ appears at most $k-1$ times in the sequence $\left(a_{1}, \ldots, a_{i-1}\right)$ and thus appears at most $k-1$ times in the sequence $\left(a_{1}, \ldots, a_{i}\right)$ as well (because $a_{i}=\ell$ ). Therefore, the number of integers $j$ such that the sequence ( $a_{1}, \ldots, a_{i}$ ) contains the number $j$ at least $k$ times is exactly equal to $\ell$. This shows the desired result.
Note: The bijections given in solutions 1 and 2 can actually be shown to be the same.
|
{
"resource_path": "HarvardMIT/segmented/en-172-2014-feb-team-solutions.jsonl",
"problem_match": "\n9. [35]",
"solution_match": "\nSolution 2: "
}
|
57d35eec-1316-58ed-b78f-2e7fed5d088f
| 609,283
|
Consider a regular $n$-gon with $n>3$, and call a line acceptable if it passes through the interior of this $n$-gon. Draw $m$ different acceptable lines, so that the $n$-gon is divided into several smaller polygons.
(a) Prove that there exists an $m$, depending only on $n$, such that any collection of $m$ acceptable lines results in one of the smaller polygons having 3 or 4 sides.
(b) Find the smallest possible $m$ which guarantees that at least one of the smaller polygons will have 3 or 4 sides.
|
N/A We will prove that if $m \geq n-4$, then there is guaranteed to be a smaller polygon with 3 or 4 sides, while if $m \leq n-5$, there might not be a polygon with 3 or 4 sides. This will solve both parts of the problem.
Given a configuration of lines, let $P_{1}, \ldots, P_{k}$ be all of the resulting smaller polygons. Let $E\left(P_{i}\right)$ be the number of edges in polygon $P_{i}$, and let $E=E\left(P_{1}\right)+\cdots+E\left(P_{k}\right)$. First, note that whenever a new polygon is formed, it must have been because a larger polygon was split into two smaller polygons by a line passing through it. When this happens, $k$ increases by 1 and $E$ increases by at most 4 (it might be less than 4 if the line passes through vertices of the larger polygon). Therefore, if adding an acceptable line increases the number of polygons by $a$, then $E$ increases by at most $4 a$.
Now, assume $m \geq n-4$. At the beginning, we have $k=1$ and $E=n$. If the number of polygons at the end is $p+1$, then $E \leq n+4 p$, so the average number of edges per polygon is less than or equal to $\frac{n+4 p}{1+p}$. Now, note that each acceptable line introduces at least one new polygon, so $p \geq m \geq n-4$. Also, note that as $p$ increases, $\frac{n+4 p}{1+p}$ strictly decreases, so it is maximized at $p=n-4$, where $\frac{n+4 p}{1+p}=$ $\frac{5 n-16}{n-3}=5-\frac{1}{n-3}<5$. Therefore, the average number of edges per polygon is less than 5 , so there must exist a polygon with either 3 or 4 edges, as desired.
We will now show that if $m \leq n-5$, then we can draw $m$ acceptable lines in a regular $n$-gon $A_{1} A_{2} \ldots A_{n}$ such that there are no polygons with 3 or 4 sides. Let $M_{1}$ be the midpoint of $A_{3} A_{4}$, $M_{2}$ be the midpoint of $A_{4} A_{5}, \ldots, M_{n-5}$ be the midpoint of $A_{n-3} A_{n-4}$. Let the $m$ acceptable lines be $A_{1} M_{1}, A_{1} M_{2}, \ldots, A_{1} M_{m}$. We can see that all resulting polygons have 5 sides or more, so we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Consider a regular $n$-gon with $n>3$, and call a line acceptable if it passes through the interior of this $n$-gon. Draw $m$ different acceptable lines, so that the $n$-gon is divided into several smaller polygons.
(a) Prove that there exists an $m$, depending only on $n$, such that any collection of $m$ acceptable lines results in one of the smaller polygons having 3 or 4 sides.
(b) Find the smallest possible $m$ which guarantees that at least one of the smaller polygons will have 3 or 4 sides.
|
N/A We will prove that if $m \geq n-4$, then there is guaranteed to be a smaller polygon with 3 or 4 sides, while if $m \leq n-5$, there might not be a polygon with 3 or 4 sides. This will solve both parts of the problem.
Given a configuration of lines, let $P_{1}, \ldots, P_{k}$ be all of the resulting smaller polygons. Let $E\left(P_{i}\right)$ be the number of edges in polygon $P_{i}$, and let $E=E\left(P_{1}\right)+\cdots+E\left(P_{k}\right)$. First, note that whenever a new polygon is formed, it must have been because a larger polygon was split into two smaller polygons by a line passing through it. When this happens, $k$ increases by 1 and $E$ increases by at most 4 (it might be less than 4 if the line passes through vertices of the larger polygon). Therefore, if adding an acceptable line increases the number of polygons by $a$, then $E$ increases by at most $4 a$.
Now, assume $m \geq n-4$. At the beginning, we have $k=1$ and $E=n$. If the number of polygons at the end is $p+1$, then $E \leq n+4 p$, so the average number of edges per polygon is less than or equal to $\frac{n+4 p}{1+p}$. Now, note that each acceptable line introduces at least one new polygon, so $p \geq m \geq n-4$. Also, note that as $p$ increases, $\frac{n+4 p}{1+p}$ strictly decreases, so it is maximized at $p=n-4$, where $\frac{n+4 p}{1+p}=$ $\frac{5 n-16}{n-3}=5-\frac{1}{n-3}<5$. Therefore, the average number of edges per polygon is less than 5 , so there must exist a polygon with either 3 or 4 edges, as desired.
We will now show that if $m \leq n-5$, then we can draw $m$ acceptable lines in a regular $n$-gon $A_{1} A_{2} \ldots A_{n}$ such that there are no polygons with 3 or 4 sides. Let $M_{1}$ be the midpoint of $A_{3} A_{4}$, $M_{2}$ be the midpoint of $A_{4} A_{5}, \ldots, M_{n-5}$ be the midpoint of $A_{n-3} A_{n-4}$. Let the $m$ acceptable lines be $A_{1} M_{1}, A_{1} M_{2}, \ldots, A_{1} M_{m}$. We can see that all resulting polygons have 5 sides or more, so we are done.
|
{
"resource_path": "HarvardMIT/segmented/en-174-tournaments-2014-hmic-solutions.jsonl",
"problem_match": "\n1. [20]",
"solution_match": "\nAnswer: "
}
|
c3629e2f-fec6-53bb-8633-7e4ed65c4ddb
| 609,285
|
Fix positive integers $m$ and $n$. Suppose that $a_{1}, a_{2}, \ldots, a_{m}$ are reals, and that pairwise distinct vectors $v_{1}, \ldots, v_{m} \in \mathbb{R}^{n}$ satisfy
$$
\sum_{j \neq i} a_{j} \frac{v_{j}-v_{i}}{\left\|v_{j}-v_{i}\right\|^{3}}=0
$$
for $i=1,2, \ldots, m$.
Prove that
$$
\sum_{1 \leq i<j \leq m} \frac{a_{i} a_{j}}{\left\|v_{j}-v_{i}\right\|}=0
$$
|
N/A Since $v_{i} \cdot\left(v_{j}-v_{i}\right)+v_{j} \cdot\left(v_{i}-v_{j}\right)=-\left\|v_{j}-v_{i}\right\|^{2}$ for any $1 \leq i<j \leq m$, we have
$$
0=\sum_{i=1}^{m} a_{i} v_{i} \cdot 0=\sum_{i=1}^{m} a_{i} v_{i} \sum_{j \neq i} a_{j} \frac{v_{j}-v_{i}}{\left\|v_{j}-v_{i}\right\|^{3}}=-\sum_{1 \leq i<j \leq m} \frac{a_{i} a_{j}}{\left\|v_{j}-v_{i}\right\|}
$$
as desired.
Alternative Solution. Fix $a_{1}, \ldots, a_{m}$, and define $f:\left(\mathbb{R}^{n}\right)^{m} \rightarrow \mathbb{R}$ by
$$
f\left(x_{1}, \ldots, x_{m}\right)=\sum_{1 \leq i<j \leq m} \frac{a_{i} a_{j}}{\left\|x_{j}-x_{i}\right\|}
$$
Now if we view $f\left(x_{1}, \ldots, x_{m}\right)$ individually as a function in $x_{k}$ ( $k$ fixed), then the problem condition for $i=k$ says precisely that the gradient of $f$ with respect to $x_{k}$ (but of course, multiplied by $a_{k}$ ) evaluated at $\left(v_{1}, \ldots, v_{m}\right)$ is 0 .
Finally, the multivariate chain rule shows that $F(t):=f\left(t v_{1}, \ldots, t v_{m}\right)=\frac{1}{t} f\left(v_{1}, \ldots, v_{m}\right)$ must satisfy $F^{\prime}(1)=0$. Yet $F^{\prime}(1)=-\frac{1}{1^{2}} f\left(v_{1}, \ldots, v_{m}\right)$, so we have $f\left(v_{1}, \ldots, v_{m}\right)=0$, as desired.
Comment. This is (sort of) an energy minimization problem from physics (more precisely, minimizing electrostatic or gravitational potential).
Comment. It would be interesting to determine all differentiable $A: \mathbb{R}^{+} \rightarrow \mathbb{R}$ such that the problem still holds when the terms are replaced by $\frac{v_{j}-v_{i}}{\left\|v_{j}-v_{i}\right\|} A^{\prime}\left(\left\|v_{j}-v_{i}\right\|\right)$ and $A\left(\left\|v_{j}-v_{i}\right\|\right)$. (Here $A(t)=1 / t$, which has a nice physical interpretation, but that's not important.) The obvious examples are $A(t)=c t^{s}$ for constant $c$ and real $s$ (where both solutions easily carry through). But there may be others where instead of defining $F(t)$ through the scaling transformation $\left(v_{1}, \ldots, v_{m}\right) \rightarrow\left(t v_{1}, \ldots, t v_{m}\right)$, there's a subtler translation.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Fix positive integers $m$ and $n$. Suppose that $a_{1}, a_{2}, \ldots, a_{m}$ are reals, and that pairwise distinct vectors $v_{1}, \ldots, v_{m} \in \mathbb{R}^{n}$ satisfy
$$
\sum_{j \neq i} a_{j} \frac{v_{j}-v_{i}}{\left\|v_{j}-v_{i}\right\|^{3}}=0
$$
for $i=1,2, \ldots, m$.
Prove that
$$
\sum_{1 \leq i<j \leq m} \frac{a_{i} a_{j}}{\left\|v_{j}-v_{i}\right\|}=0
$$
|
N/A Since $v_{i} \cdot\left(v_{j}-v_{i}\right)+v_{j} \cdot\left(v_{i}-v_{j}\right)=-\left\|v_{j}-v_{i}\right\|^{2}$ for any $1 \leq i<j \leq m$, we have
$$
0=\sum_{i=1}^{m} a_{i} v_{i} \cdot 0=\sum_{i=1}^{m} a_{i} v_{i} \sum_{j \neq i} a_{j} \frac{v_{j}-v_{i}}{\left\|v_{j}-v_{i}\right\|^{3}}=-\sum_{1 \leq i<j \leq m} \frac{a_{i} a_{j}}{\left\|v_{j}-v_{i}\right\|}
$$
as desired.
Alternative Solution. Fix $a_{1}, \ldots, a_{m}$, and define $f:\left(\mathbb{R}^{n}\right)^{m} \rightarrow \mathbb{R}$ by
$$
f\left(x_{1}, \ldots, x_{m}\right)=\sum_{1 \leq i<j \leq m} \frac{a_{i} a_{j}}{\left\|x_{j}-x_{i}\right\|}
$$
Now if we view $f\left(x_{1}, \ldots, x_{m}\right)$ individually as a function in $x_{k}$ ( $k$ fixed), then the problem condition for $i=k$ says precisely that the gradient of $f$ with respect to $x_{k}$ (but of course, multiplied by $a_{k}$ ) evaluated at $\left(v_{1}, \ldots, v_{m}\right)$ is 0 .
Finally, the multivariate chain rule shows that $F(t):=f\left(t v_{1}, \ldots, t v_{m}\right)=\frac{1}{t} f\left(v_{1}, \ldots, v_{m}\right)$ must satisfy $F^{\prime}(1)=0$. Yet $F^{\prime}(1)=-\frac{1}{1^{2}} f\left(v_{1}, \ldots, v_{m}\right)$, so we have $f\left(v_{1}, \ldots, v_{m}\right)=0$, as desired.
Comment. This is (sort of) an energy minimization problem from physics (more precisely, minimizing electrostatic or gravitational potential).
Comment. It would be interesting to determine all differentiable $A: \mathbb{R}^{+} \rightarrow \mathbb{R}$ such that the problem still holds when the terms are replaced by $\frac{v_{j}-v_{i}}{\left\|v_{j}-v_{i}\right\|} A^{\prime}\left(\left\|v_{j}-v_{i}\right\|\right)$ and $A\left(\left\|v_{j}-v_{i}\right\|\right)$. (Here $A(t)=1 / t$, which has a nice physical interpretation, but that's not important.) The obvious examples are $A(t)=c t^{s}$ for constant $c$ and real $s$ (where both solutions easily carry through). But there may be others where instead of defining $F(t)$ through the scaling transformation $\left(v_{1}, \ldots, v_{m}\right) \rightarrow\left(t v_{1}, \ldots, t v_{m}\right)$, there's a subtler translation.
|
{
"resource_path": "HarvardMIT/segmented/en-174-tournaments-2014-hmic-solutions.jsonl",
"problem_match": "\n3. [30]",
"solution_match": "\nAnswer: "
}
|
98081316-9d68-5923-b5ba-b1d9c607e33a
| 609,287
|
Let $n$ be a positive integer, and let $A$ and $B$ be $n \times n$ matrices with complex entries such that $A^{2}=B^{2}$. Show that there exists an $n \times n$ invertible matrix $S$ with complex entries that satisfies $S(A B-B A)=(B A-A B) S$.
|
N/A Let $X=A+B$ and $Y=A-B$, so $X Y=B A-A B$ and $Y X=A B-B A$. Note that $X Y=-Y X$.
It suffices (actually is equivalent) to show that $A B-B A$ and $B A-A B$ have the same Jordan forms. In other words, we need to show that for any complex number $\lambda$, the Jordan $\lambda$-block decompositions of $A B-B A$ and $B A-A B$ are the same.
However, the $\lambda$-decomposition of a matrix $M$ is uniquely determined by the infinite (eventually constant) sequence $\left(\operatorname{dim} \operatorname{ker}(M-\lambda I)^{1}, \operatorname{dim} \operatorname{ker}(M-\lambda I)^{2}, \ldots\right)$, so we only have to show that $\operatorname{dim} \operatorname{ker}(X Y-$ $\lambda I)^{k}=\operatorname{dim} \operatorname{ker}(Y X-\lambda I)^{k}$ for all positive integers $k$ and complex numbers $\lambda$.
For $\lambda=0$, this follows trivially from $X Y=-Y X$ : we have $(X Y)^{k} v=0$ if and only if $(Y X)^{k} v=0$.
Now suppose $\lambda \neq 0$, and define the (matrix) polynomial $p(T)=(T-\lambda I)^{k}$. Let $V_{1}=\left\{v \in \mathbb{C}^{n}\right.$ : $p(X Y) v=0\}$, and $V_{2}=\left\{v \in \mathbb{C}^{n}: p(Y X) v=0\right\}$. Note that if $v \in V_{1}$, then $0=[Y p(X Y)] v=$ $[p(Y X) Y] v=p(Y X)[Y v]$, so $Y v \in V_{2}$. Furthermore, if $v \neq 0$, then $Y v \neq 0$, or else $p(X Y) v=$ $p(0) v=(-\lambda I)^{k} v \neq 0$ (since $(X Y)^{j} v=0$ for all $j \geq 1$ ), contradiction. Viewing $Y$ (more precisely, $v \rightarrow Y v)$ as a linear map from $V_{1}$ to $V_{2}$, we have $\operatorname{dim} V_{1}=\operatorname{dim} Y V_{1}+\operatorname{dim} \operatorname{ker} Y=\operatorname{dim} Y V_{1} \leq \operatorname{dim} V_{2}$ (alternatively, if $v_{1}, \ldots, v_{r}$ is a basis of $V_{1}$, then $Y v_{1}, \ldots, Y v_{r}$ are linearly independent in $V_{2}$ ). By symmetry, $\operatorname{dim} V_{1}=\operatorname{dim} V_{2}$, and we're done.
Comment. If $A, B$ are additionally real, then we can also choose $S$ to be real (not just complex). Indeed, note that if $S=P+Q i$ for real $P, Q$, then since $A, B$ are real, it suffices to find $c \in \mathbb{R}$ such that $\operatorname{det}(P+c Q) \neq 0$. However, $\operatorname{det}(P+x Q)$ is a polynomial in $x$ that is not identically zero (it is nonzero for $x=i$ ), so it has finitely many (complex, and thus real) roots. Thus the desired $c$ clearly exists.
Comment. Note that $A(A B-B A)=(B A-A B) A$, since $A^{2} B=B^{3}=B A^{2}$. (The same holds for $A \rightarrow B$.) Thus the problem is easy unless all linear combinations of $A, B$ are noninvertible. However, it seems difficult to finish without analyzing generalized eigenvectors as above.
Comment. See this paper by Ross Lippert and Gilbert Strang for a general analysis of the Jordan forms of $M N$ and $N M$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $n$ be a positive integer, and let $A$ and $B$ be $n \times n$ matrices with complex entries such that $A^{2}=B^{2}$. Show that there exists an $n \times n$ invertible matrix $S$ with complex entries that satisfies $S(A B-B A)=(B A-A B) S$.
|
N/A Let $X=A+B$ and $Y=A-B$, so $X Y=B A-A B$ and $Y X=A B-B A$. Note that $X Y=-Y X$.
It suffices (actually is equivalent) to show that $A B-B A$ and $B A-A B$ have the same Jordan forms. In other words, we need to show that for any complex number $\lambda$, the Jordan $\lambda$-block decompositions of $A B-B A$ and $B A-A B$ are the same.
However, the $\lambda$-decomposition of a matrix $M$ is uniquely determined by the infinite (eventually constant) sequence $\left(\operatorname{dim} \operatorname{ker}(M-\lambda I)^{1}, \operatorname{dim} \operatorname{ker}(M-\lambda I)^{2}, \ldots\right)$, so we only have to show that $\operatorname{dim} \operatorname{ker}(X Y-$ $\lambda I)^{k}=\operatorname{dim} \operatorname{ker}(Y X-\lambda I)^{k}$ for all positive integers $k$ and complex numbers $\lambda$.
For $\lambda=0$, this follows trivially from $X Y=-Y X$ : we have $(X Y)^{k} v=0$ if and only if $(Y X)^{k} v=0$.
Now suppose $\lambda \neq 0$, and define the (matrix) polynomial $p(T)=(T-\lambda I)^{k}$. Let $V_{1}=\left\{v \in \mathbb{C}^{n}\right.$ : $p(X Y) v=0\}$, and $V_{2}=\left\{v \in \mathbb{C}^{n}: p(Y X) v=0\right\}$. Note that if $v \in V_{1}$, then $0=[Y p(X Y)] v=$ $[p(Y X) Y] v=p(Y X)[Y v]$, so $Y v \in V_{2}$. Furthermore, if $v \neq 0$, then $Y v \neq 0$, or else $p(X Y) v=$ $p(0) v=(-\lambda I)^{k} v \neq 0$ (since $(X Y)^{j} v=0$ for all $j \geq 1$ ), contradiction. Viewing $Y$ (more precisely, $v \rightarrow Y v)$ as a linear map from $V_{1}$ to $V_{2}$, we have $\operatorname{dim} V_{1}=\operatorname{dim} Y V_{1}+\operatorname{dim} \operatorname{ker} Y=\operatorname{dim} Y V_{1} \leq \operatorname{dim} V_{2}$ (alternatively, if $v_{1}, \ldots, v_{r}$ is a basis of $V_{1}$, then $Y v_{1}, \ldots, Y v_{r}$ are linearly independent in $V_{2}$ ). By symmetry, $\operatorname{dim} V_{1}=\operatorname{dim} V_{2}$, and we're done.
Comment. If $A, B$ are additionally real, then we can also choose $S$ to be real (not just complex). Indeed, note that if $S=P+Q i$ for real $P, Q$, then since $A, B$ are real, it suffices to find $c \in \mathbb{R}$ such that $\operatorname{det}(P+c Q) \neq 0$. However, $\operatorname{det}(P+x Q)$ is a polynomial in $x$ that is not identically zero (it is nonzero for $x=i$ ), so it has finitely many (complex, and thus real) roots. Thus the desired $c$ clearly exists.
Comment. Note that $A(A B-B A)=(B A-A B) A$, since $A^{2} B=B^{3}=B A^{2}$. (The same holds for $A \rightarrow B$.) Thus the problem is easy unless all linear combinations of $A, B$ are noninvertible. However, it seems difficult to finish without analyzing generalized eigenvectors as above.
Comment. See this paper by Ross Lippert and Gilbert Strang for a general analysis of the Jordan forms of $M N$ and $N M$.
|
{
"resource_path": "HarvardMIT/segmented/en-174-tournaments-2014-hmic-solutions.jsonl",
"problem_match": "\n5. [40]",
"solution_match": "\nAnswer: "
}
|
10b2eb53-9cce-53fb-8f57-95593471c5fa
| 609,288
|
Let $P$ be a (non-self-intersecting) polygon in the plane. Let $C_{1}, \ldots, C_{n}$ be circles in the plane whose interiors cover the interior of $P$. For $1 \leq i \leq n$, let $r_{i}$ be the radius of $C_{i}$. Prove that there is a single circle of radius $r_{1}+\cdots+r_{n}$ whose interior covers the interior of $P$.
|
N/A If $n=1$, we are done. Suppose $n>1$. Since $P$ is connected, there must be a point $x$ on the plane which lies in the interiors of two circles, say $C_{i}, C_{j}$. Let $O_{i}, O_{j}$, respectively, be the centers of $C_{i}, C_{j}$. Since $O_{i} O_{j}<r_{i}+r_{j}$, we can choose $O$ to be a point on segment $O_{i} O_{j}$ such that $O_{i} O \leq r_{j}$ and $O_{j} O \leq r_{i}$. Replace the two circles $C_{i}$ and $C_{j}$ with the circle $C$ centered at $O$ of radius $r_{i}+r_{j}$. Note that $C$ covers both $C_{i}$ and $C_{j}$. Induct to finish.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $P$ be a (non-self-intersecting) polygon in the plane. Let $C_{1}, \ldots, C_{n}$ be circles in the plane whose interiors cover the interior of $P$. For $1 \leq i \leq n$, let $r_{i}$ be the radius of $C_{i}$. Prove that there is a single circle of radius $r_{1}+\cdots+r_{n}$ whose interior covers the interior of $P$.
|
N/A If $n=1$, we are done. Suppose $n>1$. Since $P$ is connected, there must be a point $x$ on the plane which lies in the interiors of two circles, say $C_{i}, C_{j}$. Let $O_{i}, O_{j}$, respectively, be the centers of $C_{i}, C_{j}$. Since $O_{i} O_{j}<r_{i}+r_{j}$, we can choose $O$ to be a point on segment $O_{i} O_{j}$ such that $O_{i} O \leq r_{j}$ and $O_{j} O \leq r_{i}$. Replace the two circles $C_{i}$ and $C_{j}$ with the circle $C$ centered at $O$ of radius $r_{i}+r_{j}$. Note that $C$ covers both $C_{i}$ and $C_{j}$. Induct to finish.
|
{
"resource_path": "HarvardMIT/segmented/en-182-2015-feb-team-solutions.jsonl",
"problem_match": "\n2. [10]",
"solution_match": "\nAnswer: "
}
|
0f6a6a77-f7c3-54bb-ab18-ba5f2f6fae63
| 609,418
|
Let $z=a+b i$ be a complex number with integer real and imaginary parts $a, b \in \mathbb{Z}$, where $i=\sqrt{-1}$ (i.e. $z$ is a Gaussian integer). If $p$ is an odd prime number, show that the real part of $z^{p}-z$ is an integer divisible by $p$.
|
N/A Solution 1. We directly compute/expand
$$
\begin{aligned}
\operatorname{Re}\left(z^{p}-z\right) & =\operatorname{Re}\left((a+b i)^{p}-(a+b i)\right) \\
& =\left[a^{p}-\binom{p}{2} a^{p-2} b^{2}+\binom{p}{4} a^{p-4} b^{4}-\cdots\right]-a .
\end{aligned}
$$
Since $\binom{p}{i}$ is divisible by $p$ for all $i=2,4,6, \ldots($ since $1 \leq i \leq p-1)$, we have
$$
\left[a^{p}-\binom{p}{2} a^{p-2} b^{2}+\binom{p}{4} a^{p-4} b^{4}-\cdots\right]-a \equiv a^{p}-a \equiv 0 \quad(\bmod p)
$$
by Fermat's little theorem. Thus $p$ divides the real part of $z^{p}-z$.
Remark. The fact that $\binom{p}{i}$ is divisible by $p$ (for $1 \leq i \leq p-1$ ) is essentially equivalent to the polynomial congruence $(r X+s Y)^{p} \equiv r X^{p}+s Y^{p}(\bmod p)$ (here the coefficients are taken modulo $p$ ), a fundamental result often called that 'Frobenius endomorphism'.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $z=a+b i$ be a complex number with integer real and imaginary parts $a, b \in \mathbb{Z}$, where $i=\sqrt{-1}$ (i.e. $z$ is a Gaussian integer). If $p$ is an odd prime number, show that the real part of $z^{p}-z$ is an integer divisible by $p$.
|
N/A Solution 1. We directly compute/expand
$$
\begin{aligned}
\operatorname{Re}\left(z^{p}-z\right) & =\operatorname{Re}\left((a+b i)^{p}-(a+b i)\right) \\
& =\left[a^{p}-\binom{p}{2} a^{p-2} b^{2}+\binom{p}{4} a^{p-4} b^{4}-\cdots\right]-a .
\end{aligned}
$$
Since $\binom{p}{i}$ is divisible by $p$ for all $i=2,4,6, \ldots($ since $1 \leq i \leq p-1)$, we have
$$
\left[a^{p}-\binom{p}{2} a^{p-2} b^{2}+\binom{p}{4} a^{p-4} b^{4}-\cdots\right]-a \equiv a^{p}-a \equiv 0 \quad(\bmod p)
$$
by Fermat's little theorem. Thus $p$ divides the real part of $z^{p}-z$.
Remark. The fact that $\binom{p}{i}$ is divisible by $p$ (for $1 \leq i \leq p-1$ ) is essentially equivalent to the polynomial congruence $(r X+s Y)^{p} \equiv r X^{p}+s Y^{p}(\bmod p)$ (here the coefficients are taken modulo $p$ ), a fundamental result often called that 'Frobenius endomorphism'.
|
{
"resource_path": "HarvardMIT/segmented/en-182-2015-feb-team-solutions.jsonl",
"problem_match": "\n3. [15]",
"solution_match": "\nAnswer: "
}
|
64147744-507b-5976-83a5-aa133e5b4646
| 609,419
|
Let $z=a+b i$ be a complex number with integer real and imaginary parts $a, b \in \mathbb{Z}$, where $i=\sqrt{-1}$ (i.e. $z$ is a Gaussian integer). If $p$ is an odd prime number, show that the real part of $z^{p}-z$ is an integer divisible by $p$.
|
From the Frobenius endomorphism,
$$
z^{p}=(a+b i)^{p} \equiv a^{p}+(b i)^{p}=a^{p} \pm b^{p} i \equiv a \pm b i \quad(\bmod p \cdot \mathbb{Z}[i])
$$
where we're using congruence of Gaussian integers (so that $u \equiv v(\bmod p)$ if and only if $\frac{u-v}{p}$ is a Gaussian integer). This is equivalent to the simultaneous congruence of the real and imaginary parts modulo $p$, so the real part of $z^{p}$ is congruent to $a$, the real part of $z$. So indeed $p$ divides the real part of $z^{p}-z$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $z=a+b i$ be a complex number with integer real and imaginary parts $a, b \in \mathbb{Z}$, where $i=\sqrt{-1}$ (i.e. $z$ is a Gaussian integer). If $p$ is an odd prime number, show that the real part of $z^{p}-z$ is an integer divisible by $p$.
|
From the Frobenius endomorphism,
$$
z^{p}=(a+b i)^{p} \equiv a^{p}+(b i)^{p}=a^{p} \pm b^{p} i \equiv a \pm b i \quad(\bmod p \cdot \mathbb{Z}[i])
$$
where we're using congruence of Gaussian integers (so that $u \equiv v(\bmod p)$ if and only if $\frac{u-v}{p}$ is a Gaussian integer). This is equivalent to the simultaneous congruence of the real and imaginary parts modulo $p$, so the real part of $z^{p}$ is congruent to $a$, the real part of $z$. So indeed $p$ divides the real part of $z^{p}-z$.
|
{
"resource_path": "HarvardMIT/segmented/en-182-2015-feb-team-solutions.jsonl",
"problem_match": "\n3. [15]",
"solution_match": "\nSolution 2. "
}
|
64147744-507b-5976-83a5-aa133e5b4646
| 609,419
|
(Convex) quadrilateral $A B C D$ with $B C=C D$ is inscribed in circle $\Omega$; the diagonals of $A B C D$ meet at $X$. Suppose $A D<A B$, the circumcircle of triangle $B C X$ intersects segment $A B$ at a point $Y \neq B$, and ray $\overrightarrow{C Y}$ meets $\Omega$ again at a point $Z \neq C$. Prove that ray $\overrightarrow{D Y}$ bisects angle $Z D B$.
(We have only included the conditions $A D<A B$ and that $Z$ lies on ray $\overrightarrow{C Y}$ for everyone's convenience. With slight modifications, the problem holds in general. But we will only grade your team's solution in this special case.)
|
N/A This is mostly just angle chasing. The conditions $A D<A B$ (or $\angle A B D<\angle A D B$ ) and the assumption $Z \in \overrightarrow{C Y}$ are not crucial, as long as we're careful with configurations (for example, $D Y$ may only be an external angle bisector of $\angle Z D B$ in some cases), 1 but it's the easiest to visualize. In this case $Y$ and $Z$ lie between $A$ and $B$, on the respective segment/arc. We'll prove $Y$ is the incenter of $\triangle Z D B$; it will follow that ray $\overrightarrow{D Y}$ indeed (internally) bisects $\angle Z D B$. It suffices to prove the following two facts:
- $B Y$ is the internal angle bisector of $\angle D B Z 2^{2}$
- $Z Y$ is the internal angle bisector of $\angle B Z D$, since $C B=C D$. Indeed (more explicitly), arcs $B C$ and $C D$ are equal, so $\angle B Z C=\angle C Z D$, i.e. $Y Z$ bisects $\angle B Z D$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
(Convex) quadrilateral $A B C D$ with $B C=C D$ is inscribed in circle $\Omega$; the diagonals of $A B C D$ meet at $X$. Suppose $A D<A B$, the circumcircle of triangle $B C X$ intersects segment $A B$ at a point $Y \neq B$, and ray $\overrightarrow{C Y}$ meets $\Omega$ again at a point $Z \neq C$. Prove that ray $\overrightarrow{D Y}$ bisects angle $Z D B$.
(We have only included the conditions $A D<A B$ and that $Z$ lies on ray $\overrightarrow{C Y}$ for everyone's convenience. With slight modifications, the problem holds in general. But we will only grade your team's solution in this special case.)
|
N/A This is mostly just angle chasing. The conditions $A D<A B$ (or $\angle A B D<\angle A D B$ ) and the assumption $Z \in \overrightarrow{C Y}$ are not crucial, as long as we're careful with configurations (for example, $D Y$ may only be an external angle bisector of $\angle Z D B$ in some cases), 1 but it's the easiest to visualize. In this case $Y$ and $Z$ lie between $A$ and $B$, on the respective segment/arc. We'll prove $Y$ is the incenter of $\triangle Z D B$; it will follow that ray $\overrightarrow{D Y}$ indeed (internally) bisects $\angle Z D B$. It suffices to prove the following two facts:
- $B Y$ is the internal angle bisector of $\angle D B Z 2^{2}$
- $Z Y$ is the internal angle bisector of $\angle B Z D$, since $C B=C D$. Indeed (more explicitly), arcs $B C$ and $C D$ are equal, so $\angle B Z C=\angle C Z D$, i.e. $Y Z$ bisects $\angle B Z D$.
|
{
"resource_path": "HarvardMIT/segmented/en-182-2015-feb-team-solutions.jsonl",
"problem_match": "\n4. [15]",
"solution_match": "\nAnswer: "
}
|
1439955e-3895-51a1-a75e-688b21603d52
| 609,420
|
$\$$ indy has $\$ 100$ in pennies (worth $\$ 0.01$ each), nickels (worth $\$ 0.05$ each), dimes (worth $\$ 0.10$ each), and quarters (worth $\$ 0.25$ each). Prove that she can split her coins into two piles, each with total value exactly $\$ 50$.
|
N/A Solution 1. First, observe that if there are pennies in the mix, there must be a multiple of 5 pennies $($ since $5,10,25 \equiv 0(\bmod 5)$ ), so we can treat each group of 5 pennies as nickels and reduce the problem to the case of no pennies, treated below.
Indeed, suppose there are no pennies and that we are solving the problem with only quarters, dimes, and nickels. So we have $25 q+10 d+5 n=10000$ (or equivalently, $5 q+2 d+n=2000$ ), where $q$ is the number of quarters, $d$ is the number of dimes, and $n$ is the number of nickels. Notice that if $q \geq 200$, $d \geq 500$, or $n \geq 1000$, then we can just take a subset of 200 quarters, 500 dimes, or 1000 nickels, respectively, and make that our first pile and the remaining coins our second pile.
Thus, we can assume that $q \leq 199, d \leq 499, n \leq 999$. Now if there are only quarters and dimes, we have $5 q+2 d<1000+1000=2000$, so there must be nickels in the mix. By similar reasoning, there must be dimes and quarters in the mix.
So to make our first pile, we throw all the quarters in that pile. The total money in the pile is at most $\$ 49.75$, so now,
- if possible, we keep adding in dimes until we get an amount equal to or greater than $\$ 50$. If it is $\$ 50$, then we are done. Otherwise, it must be $\$ 50.05$ since the total money value before the last dime is either $\$ 49.90$ or $\$ 49.95$. In that case, we take out the last dime and replace it with a nickel, giving us $\$ 50$.
- if not possible (i.e. we run out of dimes before reaching $\$ 50$ ), then all the quarters and dimes have been used up, so we only have nickels left. Of course, our money value now has a hundredth's place of 5 or 0 and is less than $\$ 50$, so we simply keep adding nickels until we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
$\$$ indy has $\$ 100$ in pennies (worth $\$ 0.01$ each), nickels (worth $\$ 0.05$ each), dimes (worth $\$ 0.10$ each), and quarters (worth $\$ 0.25$ each). Prove that she can split her coins into two piles, each with total value exactly $\$ 50$.
|
N/A Solution 1. First, observe that if there are pennies in the mix, there must be a multiple of 5 pennies $($ since $5,10,25 \equiv 0(\bmod 5)$ ), so we can treat each group of 5 pennies as nickels and reduce the problem to the case of no pennies, treated below.
Indeed, suppose there are no pennies and that we are solving the problem with only quarters, dimes, and nickels. So we have $25 q+10 d+5 n=10000$ (or equivalently, $5 q+2 d+n=2000$ ), where $q$ is the number of quarters, $d$ is the number of dimes, and $n$ is the number of nickels. Notice that if $q \geq 200$, $d \geq 500$, or $n \geq 1000$, then we can just take a subset of 200 quarters, 500 dimes, or 1000 nickels, respectively, and make that our first pile and the remaining coins our second pile.
Thus, we can assume that $q \leq 199, d \leq 499, n \leq 999$. Now if there are only quarters and dimes, we have $5 q+2 d<1000+1000=2000$, so there must be nickels in the mix. By similar reasoning, there must be dimes and quarters in the mix.
So to make our first pile, we throw all the quarters in that pile. The total money in the pile is at most $\$ 49.75$, so now,
- if possible, we keep adding in dimes until we get an amount equal to or greater than $\$ 50$. If it is $\$ 50$, then we are done. Otherwise, it must be $\$ 50.05$ since the total money value before the last dime is either $\$ 49.90$ or $\$ 49.95$. In that case, we take out the last dime and replace it with a nickel, giving us $\$ 50$.
- if not possible (i.e. we run out of dimes before reaching $\$ 50$ ), then all the quarters and dimes have been used up, so we only have nickels left. Of course, our money value now has a hundredth's place of 5 or 0 and is less than $\$ 50$, so we simply keep adding nickels until we are done.
|
{
"resource_path": "HarvardMIT/segmented/en-182-2015-feb-team-solutions.jsonl",
"problem_match": "\n6. [30]",
"solution_match": "\nAnswer: "
}
|
6aae88e8-fa93-5217-823c-b0fbdc24853f
| 609,421
|
$\$$ indy has $\$ 100$ in pennies (worth $\$ 0.01$ each), nickels (worth $\$ 0.05$ each), dimes (worth $\$ 0.10$ each), and quarters (worth $\$ 0.25$ each). Prove that she can split her coins into two piles, each with total value exactly $\$ 50$.
|
First, observe that if there are pennies in the mix, there must be a multiple of 5 pennies (since $5,10,25 \equiv 0(\bmod 5)$ ), so we can treat each group of 5 pennies as nickels and reduce the problem to the case of no pennies, treated below. Similarly, we can treat each group of 2 nickels as dimes, and reduce the problem to the case of at most one nickel. We have two cases:
Case 1. There are no nickels. Then, either the dimes alone total to at least $\$ 50$, in which case $\$$ indy can form a pile with $\$ 50$ worth of dimes and a pile with the rest of the money, or the quarters alone total to at least $\$ 50$, in which case $\$$ indy can form a pile with $\$ 50$ worth of quarters and a pile with the rest of the money.
Case 2. There is exactly one nickel. By examining the value of the money modulo $\$ 0.25$, we find that there must be at least two dimes. Then, we treat the nickel and two dimes as a quarter, and reduce the problem to the previously solved case.
Remark. There are probably many other solutions/algorithms for this specific problem. For example, many teams did casework based on the parities of $q, d, n$, after "getting rid of pennies".
Remark. It would certainly be interesting to investigate the natural generalizations of this problem (see e.g. the knapsack problem and partition problem). For instance, it's true that given a set of
positive integers ranging from 1 to $n$ with sum no less than $2 n$ !, there exists a subset of them summing up to exactly $n!$. (See here and here for discussion on two AoPS blogs.)
Remark. The problem author (Carl Lian) says the problem comes from algebraic geometry!
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
$\$$ indy has $\$ 100$ in pennies (worth $\$ 0.01$ each), nickels (worth $\$ 0.05$ each), dimes (worth $\$ 0.10$ each), and quarters (worth $\$ 0.25$ each). Prove that she can split her coins into two piles, each with total value exactly $\$ 50$.
|
First, observe that if there are pennies in the mix, there must be a multiple of 5 pennies (since $5,10,25 \equiv 0(\bmod 5)$ ), so we can treat each group of 5 pennies as nickels and reduce the problem to the case of no pennies, treated below. Similarly, we can treat each group of 2 nickels as dimes, and reduce the problem to the case of at most one nickel. We have two cases:
Case 1. There are no nickels. Then, either the dimes alone total to at least $\$ 50$, in which case $\$$ indy can form a pile with $\$ 50$ worth of dimes and a pile with the rest of the money, or the quarters alone total to at least $\$ 50$, in which case $\$$ indy can form a pile with $\$ 50$ worth of quarters and a pile with the rest of the money.
Case 2. There is exactly one nickel. By examining the value of the money modulo $\$ 0.25$, we find that there must be at least two dimes. Then, we treat the nickel and two dimes as a quarter, and reduce the problem to the previously solved case.
Remark. There are probably many other solutions/algorithms for this specific problem. For example, many teams did casework based on the parities of $q, d, n$, after "getting rid of pennies".
Remark. It would certainly be interesting to investigate the natural generalizations of this problem (see e.g. the knapsack problem and partition problem). For instance, it's true that given a set of
positive integers ranging from 1 to $n$ with sum no less than $2 n$ !, there exists a subset of them summing up to exactly $n!$. (See here and here for discussion on two AoPS blogs.)
Remark. The problem author (Carl Lian) says the problem comes from algebraic geometry!
|
{
"resource_path": "HarvardMIT/segmented/en-182-2015-feb-team-solutions.jsonl",
"problem_match": "\n6. [30]",
"solution_match": "\nSolution 2. "
}
|
6aae88e8-fa93-5217-823c-b0fbdc24853f
| 609,421
|
Let $f:[0,1] \rightarrow \mathbb{C}$ be a nonconstant complex-valued function on the real interval $[0,1]$. Prove that there exists $\epsilon>0$ (possibly depending on $f$ ) such that for any polynomial $P$ with complex coefficients, there exists a complex number $z$ with $|z| \leq 1$ such that $|f(|z|)-P(z)| \geq \epsilon$.
|
N/A Here's a brief summary of how we'll proceed: Use a suitably-centered high-degree roots of unity filter, or alternatively integrate over suitably-centered circles ("continuous roots of unity filter").
We claim we can choose $\epsilon(f)=\max \left(\left|f\left(x_{1}\right)-f\left(x_{2}\right)\right|\right) / 2$. Fix $P$ and suppose for the sake of contradiction that for all $z$ with $|z| \leq 1$ it is the case that $|f(z)-P(z)|<\epsilon$. We can write $z=r e^{i \theta}$ so that
$$
\left|f(r)-P\left(r e^{i \theta}\right)\right|<\epsilon
$$
Let $p$ be a prime larger than $\operatorname{deg}(P)$ and set $\theta=0,2 \pi / p, 4 \pi / p, \ldots$ in the above. Averaging, and using triangle inequality,
$$
\left|f(r)-\frac{1}{p} \sum_{k=0}^{p-1} P\left(r e^{2 \pi i k / p}\right)\right|<\epsilon
$$
The sum inside the absolute value is a roots of unity filter; since $p>\operatorname{deg}(P)$ it is simply the constant term of $P$ - denote this value by $p_{0}$. Thus for all $r$,
$$
\left|f(r)-p_{0}\right|<\epsilon
$$
Setting $r=x_{1}, x_{2}$ and applying triangle inequality gives the desired contradiction.
Remark. This is more or less a concrete instance of Runge's approximation theorem from complex analysis. However, do not be intimidated by the fancy names here: in fact, the key ingredient behind this more general theorem (namely, or simila, ${ }^{3}$ ) uses the same core idea of the "continuous roots of unity filter".
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $f:[0,1] \rightarrow \mathbb{C}$ be a nonconstant complex-valued function on the real interval $[0,1]$. Prove that there exists $\epsilon>0$ (possibly depending on $f$ ) such that for any polynomial $P$ with complex coefficients, there exists a complex number $z$ with $|z| \leq 1$ such that $|f(|z|)-P(z)| \geq \epsilon$.
|
N/A Here's a brief summary of how we'll proceed: Use a suitably-centered high-degree roots of unity filter, or alternatively integrate over suitably-centered circles ("continuous roots of unity filter").
We claim we can choose $\epsilon(f)=\max \left(\left|f\left(x_{1}\right)-f\left(x_{2}\right)\right|\right) / 2$. Fix $P$ and suppose for the sake of contradiction that for all $z$ with $|z| \leq 1$ it is the case that $|f(z)-P(z)|<\epsilon$. We can write $z=r e^{i \theta}$ so that
$$
\left|f(r)-P\left(r e^{i \theta}\right)\right|<\epsilon
$$
Let $p$ be a prime larger than $\operatorname{deg}(P)$ and set $\theta=0,2 \pi / p, 4 \pi / p, \ldots$ in the above. Averaging, and using triangle inequality,
$$
\left|f(r)-\frac{1}{p} \sum_{k=0}^{p-1} P\left(r e^{2 \pi i k / p}\right)\right|<\epsilon
$$
The sum inside the absolute value is a roots of unity filter; since $p>\operatorname{deg}(P)$ it is simply the constant term of $P$ - denote this value by $p_{0}$. Thus for all $r$,
$$
\left|f(r)-p_{0}\right|<\epsilon
$$
Setting $r=x_{1}, x_{2}$ and applying triangle inequality gives the desired contradiction.
Remark. This is more or less a concrete instance of Runge's approximation theorem from complex analysis. However, do not be intimidated by the fancy names here: in fact, the key ingredient behind this more general theorem (namely, or simila, ${ }^{3}$ ) uses the same core idea of the "continuous roots of unity filter".
|
{
"resource_path": "HarvardMIT/segmented/en-182-2015-feb-team-solutions.jsonl",
"problem_match": "\n7. [35]",
"solution_match": "\nAnswer: "
}
|
aebe92e0-e81d-5266-9729-fe8f966efbe6
| 609,422
|
Let $S$ be the set of positive integers $n$ such that the inequality
$$
\phi(n) \cdot \tau(n) \geq \sqrt{\frac{n^{3}}{3}}
$$
holds, where $\phi(n)$ is the number of positive integers $k \leq n$ that are relatively prime to $n$, and $\tau(n)$ is the number of positive divisors of $n$. Prove that $S$ is finite.
|
N/A
Proof. Let $S$ be the set of all positive integers $n$ such that
$$
\phi(n) \cdot \tau(n) \geq \sqrt{\frac{n^{3}}{3}}
$$
Define a function $\Phi$ on all positive integers $n$ by
$$
\Phi(n)=\frac{\phi(n)^{2} \cdot \tau(n)^{2}}{n^{3}}
$$
An important observation is that $\Phi$ has the property that for every relatively prime positive integers $m, n$, we have $\Phi(m n)=\Phi(m) \Phi(n)$.
Define another function $\psi$ on all ordered-pairs ( $a, p$ ) of positive integer $a$ and prime number $p$ as follows:
$$
\psi(a, p):=\frac{(a+1)^{2}(1-1 / p)^{2}}{p^{a}}
$$
If we express $n$ in its canonical form as $n=\prod_{i=1}^{k} p_{i}^{a_{i}}$, then we have
$$
\Phi(n)=\prod_{i=1}^{k} \psi\left(a_{i}, p_{i}\right)
$$
Therefore, $S$ is actually the set of all $n=\prod_{i=1}^{k} p_{i}^{a_{i}}$ such that
$$
\prod_{i=1}^{k} \psi\left(a_{i}, p_{i}\right) \geq \frac{1}{3}
$$
It is straightforward to establish the following: for every prime $p$ and positive integer $a$,
- if $p \geq 11$, then $\psi(a, p)<\frac{1}{3}$;
- if $p=5$ and $a \geq 2$, then $\psi(a, p)<\frac{1}{3}$;
- if $p=3$ and $a \geq 3$, then $\psi(a, p)<\frac{1}{3}$;
- if $p=2$ and $a \geq 5$, then $\psi(a, p)<\frac{1}{3}$;
- $\psi(a, p)$ is always less than $\frac{1}{\sqrt{3}}$ unless $(a, p)=(1,3)$ where $\psi(1,3)=\frac{16}{27}$.
The data above shows that in the case $n=p^{a}$, in which there is only one prime dividing $n$, there are at most 8 possible $n$ in $S: 2^{1}, 2^{2}, 2^{3}, 2^{4}, 3^{1}, 3^{2}, 5^{1}, 7^{1}$. If $n$ is divisible by at least two distinct primes,
then one of them must be $3^{1}$ and $3^{1}$ fully divides $n$ (that is, $3^{2} \nmid n$ ). In the latter case $n=3 \cdot n_{0}$. Write $n_{0}=\prod_{j=1}^{l} q_{j}^{b_{j}}$. In order for $\Phi(n) \geq \frac{1}{3}$, we require
$$
\prod_{j=1}^{l} \psi\left(b_{j}, q_{j}\right) \geq \frac{9}{16}
$$
This is only possible when $(b, q)=(2,2)$, where $n=12$. Also, note that when $n=1, \Phi(1)=1$, so $1 \in S$. Hence, there are at most 10 (a finite number of) possible values of $n$ in $S$.
Remark 0.1. This problem was proposed by Pakawut Jiradilok.
Remark 0.2 . By explicit calculations, there are in fact exactly ten elements in $S: 1,2,3,4,5,7,8,9,12,16$.
Remark 0.3. To only get a finite bound, one does not need to be nearly as careful as we are in the above proof.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $S$ be the set of positive integers $n$ such that the inequality
$$
\phi(n) \cdot \tau(n) \geq \sqrt{\frac{n^{3}}{3}}
$$
holds, where $\phi(n)$ is the number of positive integers $k \leq n$ that are relatively prime to $n$, and $\tau(n)$ is the number of positive divisors of $n$. Prove that $S$ is finite.
|
N/A
Proof. Let $S$ be the set of all positive integers $n$ such that
$$
\phi(n) \cdot \tau(n) \geq \sqrt{\frac{n^{3}}{3}}
$$
Define a function $\Phi$ on all positive integers $n$ by
$$
\Phi(n)=\frac{\phi(n)^{2} \cdot \tau(n)^{2}}{n^{3}}
$$
An important observation is that $\Phi$ has the property that for every relatively prime positive integers $m, n$, we have $\Phi(m n)=\Phi(m) \Phi(n)$.
Define another function $\psi$ on all ordered-pairs ( $a, p$ ) of positive integer $a$ and prime number $p$ as follows:
$$
\psi(a, p):=\frac{(a+1)^{2}(1-1 / p)^{2}}{p^{a}}
$$
If we express $n$ in its canonical form as $n=\prod_{i=1}^{k} p_{i}^{a_{i}}$, then we have
$$
\Phi(n)=\prod_{i=1}^{k} \psi\left(a_{i}, p_{i}\right)
$$
Therefore, $S$ is actually the set of all $n=\prod_{i=1}^{k} p_{i}^{a_{i}}$ such that
$$
\prod_{i=1}^{k} \psi\left(a_{i}, p_{i}\right) \geq \frac{1}{3}
$$
It is straightforward to establish the following: for every prime $p$ and positive integer $a$,
- if $p \geq 11$, then $\psi(a, p)<\frac{1}{3}$;
- if $p=5$ and $a \geq 2$, then $\psi(a, p)<\frac{1}{3}$;
- if $p=3$ and $a \geq 3$, then $\psi(a, p)<\frac{1}{3}$;
- if $p=2$ and $a \geq 5$, then $\psi(a, p)<\frac{1}{3}$;
- $\psi(a, p)$ is always less than $\frac{1}{\sqrt{3}}$ unless $(a, p)=(1,3)$ where $\psi(1,3)=\frac{16}{27}$.
The data above shows that in the case $n=p^{a}$, in which there is only one prime dividing $n$, there are at most 8 possible $n$ in $S: 2^{1}, 2^{2}, 2^{3}, 2^{4}, 3^{1}, 3^{2}, 5^{1}, 7^{1}$. If $n$ is divisible by at least two distinct primes,
then one of them must be $3^{1}$ and $3^{1}$ fully divides $n$ (that is, $3^{2} \nmid n$ ). In the latter case $n=3 \cdot n_{0}$. Write $n_{0}=\prod_{j=1}^{l} q_{j}^{b_{j}}$. In order for $\Phi(n) \geq \frac{1}{3}$, we require
$$
\prod_{j=1}^{l} \psi\left(b_{j}, q_{j}\right) \geq \frac{9}{16}
$$
This is only possible when $(b, q)=(2,2)$, where $n=12$. Also, note that when $n=1, \Phi(1)=1$, so $1 \in S$. Hence, there are at most 10 (a finite number of) possible values of $n$ in $S$.
Remark 0.1. This problem was proposed by Pakawut Jiradilok.
Remark 0.2 . By explicit calculations, there are in fact exactly ten elements in $S: 1,2,3,4,5,7,8,9,12,16$.
Remark 0.3. To only get a finite bound, one does not need to be nearly as careful as we are in the above proof.
|
{
"resource_path": "HarvardMIT/segmented/en-184-tournaments-2015-hmic-solutions.jsonl",
"problem_match": "\n1. [20]",
"solution_match": "\nAnswer: "
}
|
e9952d28-53a2-52d7-a278-797134dda564
| 609,426
|
Let $m, n$ be positive integers with $m \geq n$. Let $S$ be the set of pairs $(a, b)$ of relatively prime positive integers such that $a, b \leq m$ and $a+b>m$.
For each pair $(a, b) \in S$, consider the nonnegative integer solution $(u, v)$ to the equation $a u-b v=n$ chosen with $v \geq 0$ minimal, and let $I(a, b)$ denote the (open) interval $(v / a, u / b)$.
Prove that $I(a, b) \subseteq(0,1)$ for every $(a, b) \in S$, and that any fixed irrational number $\alpha \in(0,1)$ lies in $I(a, b)$ for exactly $n$ distinct pairs $(a, b) \in S$.
|
N/A
Proof. The fact that $I(a, b) \subseteq(0,1)$ follows from the small-ness of $n \leq m<a+b$ : the smallest solution $(u, v)$ has $0 \leq v \leq a-1$, so $u=\frac{n+b v}{a}<\frac{(a+b)+b(a-1)}{a}=b+1$ forces $1 \leq u \leq b$.
For the main part of the problem, it suffices (actually, is equivalent) to show that
(i) 0,1 each appear exactly $n$ times as endpoints of intervals $I(a, b)$; and
(ii) each reduced rational $p / q \in(0,1)$ appears an equal (possibly zero, if $q$ is large) number of times as left and right endpoints of intervals $I(a, b)$.
We prove these separately as follows:
(i) 0 is a (left) endpoint precisely when $v / a=0$, or equivalently $(a, b) \in S$ has $a \mid n$ (look at $v$ mod $a)$. Since $n \leq m$, we get $\phi(d)$ good pairs $(d, b) \in S$ for fixed $d \mid n$. Indeed, for any coprime residue class modulo $d$, there's exactly one representative $b$ with $b \leq m<b+d$. (Conceptually, it may be enlightening to think of $S$ as part of the Euclidean algorithm tree generated by $(1,1)$.)
Thus 0 occurs as an endpoint $\sum_{d \mid n} \phi(d)=n$ times. Similarly, 1 is an endpoint precisely when $u=b$, or equivalently $(a, b) \in S$ has $b \mid n$ (look at $u \bmod b)$. By the same reasoning as before, we get $n$ right endpoint occurrences of 1 .
(ii) Fix $p / q \in(0,1)$ with $p, q$ coprime, so $q \geq 2$. We want to show that $v_{1} / a_{1}=p / q$ occurs for the same number of $\left(a_{1}, b_{1}\right) \in S$ as $u_{2} / b_{2}=p / q$ occurs for $\left(a_{2}, b_{2}\right) \in S$. (In fact, we will show that the number of occurrences of the former in $\left(x, b_{1}\right) \in S$ equals the number of the latter in $\left(a_{2}, x\right) \in S$.) The former occurs precisely when $1 \leq a_{1} \leq m, q \mid a_{1}$, and (given the first two conditions) $v_{1} \equiv p\left(a_{1} / q\right)\left(\bmod a_{1}\right)$. Given the first two conditions, the third is equivalent to $-n b_{1}^{-1} \equiv$ $p\left(a_{1} / q\right)\left(\bmod a_{1}\right)$, or $b_{1}\left(a_{1} / q\right) \equiv-n p^{-1}\left(\bmod a_{1}\right)$. This is equivalent to having $\left(a_{1} / q\right) \mid n$ and $b_{1} \equiv\left(-n /\left(a_{1} / q\right)\right) p^{-1}(\bmod q)$.
Similarly, the latter occurs precisely when $1 \leq b_{2} \leq m, q\left|b_{2},\left(b_{2} / q\right)\right| n$, and $a_{2} \equiv\left(n /\left(b_{2} / q\right)\right) p^{-1}$ $(\bmod q)$.
As hinted at before, if we consider the occurrences for a fixed value $x=a_{1}=b_{2}$, then the number of permitted residue classes $b_{1}\left(\bmod a_{1}=x\right)($ in the former $)$ is the same as the number of permitted residue classes $a_{2}\left(\bmod b_{2}=x\right)$ (in the latter): $y(\bmod x)$ is permitted in the former if and only if $-y(\bmod x)$ is permitted in the latter; note that $(y, x)=1$ if and only if $(-y, x)=1$.
Remark 0.4. This problem was proposed by Victor Wang.
Remark 0.5. This problem was inspired by ISL 2013 N7. Note that the $n=1$ case gives the famous Farey fractions sequence (for fractions of denominator at most $m$ ).
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $m, n$ be positive integers with $m \geq n$. Let $S$ be the set of pairs $(a, b)$ of relatively prime positive integers such that $a, b \leq m$ and $a+b>m$.
For each pair $(a, b) \in S$, consider the nonnegative integer solution $(u, v)$ to the equation $a u-b v=n$ chosen with $v \geq 0$ minimal, and let $I(a, b)$ denote the (open) interval $(v / a, u / b)$.
Prove that $I(a, b) \subseteq(0,1)$ for every $(a, b) \in S$, and that any fixed irrational number $\alpha \in(0,1)$ lies in $I(a, b)$ for exactly $n$ distinct pairs $(a, b) \in S$.
|
N/A
Proof. The fact that $I(a, b) \subseteq(0,1)$ follows from the small-ness of $n \leq m<a+b$ : the smallest solution $(u, v)$ has $0 \leq v \leq a-1$, so $u=\frac{n+b v}{a}<\frac{(a+b)+b(a-1)}{a}=b+1$ forces $1 \leq u \leq b$.
For the main part of the problem, it suffices (actually, is equivalent) to show that
(i) 0,1 each appear exactly $n$ times as endpoints of intervals $I(a, b)$; and
(ii) each reduced rational $p / q \in(0,1)$ appears an equal (possibly zero, if $q$ is large) number of times as left and right endpoints of intervals $I(a, b)$.
We prove these separately as follows:
(i) 0 is a (left) endpoint precisely when $v / a=0$, or equivalently $(a, b) \in S$ has $a \mid n$ (look at $v$ mod $a)$. Since $n \leq m$, we get $\phi(d)$ good pairs $(d, b) \in S$ for fixed $d \mid n$. Indeed, for any coprime residue class modulo $d$, there's exactly one representative $b$ with $b \leq m<b+d$. (Conceptually, it may be enlightening to think of $S$ as part of the Euclidean algorithm tree generated by $(1,1)$.)
Thus 0 occurs as an endpoint $\sum_{d \mid n} \phi(d)=n$ times. Similarly, 1 is an endpoint precisely when $u=b$, or equivalently $(a, b) \in S$ has $b \mid n$ (look at $u \bmod b)$. By the same reasoning as before, we get $n$ right endpoint occurrences of 1 .
(ii) Fix $p / q \in(0,1)$ with $p, q$ coprime, so $q \geq 2$. We want to show that $v_{1} / a_{1}=p / q$ occurs for the same number of $\left(a_{1}, b_{1}\right) \in S$ as $u_{2} / b_{2}=p / q$ occurs for $\left(a_{2}, b_{2}\right) \in S$. (In fact, we will show that the number of occurrences of the former in $\left(x, b_{1}\right) \in S$ equals the number of the latter in $\left(a_{2}, x\right) \in S$.) The former occurs precisely when $1 \leq a_{1} \leq m, q \mid a_{1}$, and (given the first two conditions) $v_{1} \equiv p\left(a_{1} / q\right)\left(\bmod a_{1}\right)$. Given the first two conditions, the third is equivalent to $-n b_{1}^{-1} \equiv$ $p\left(a_{1} / q\right)\left(\bmod a_{1}\right)$, or $b_{1}\left(a_{1} / q\right) \equiv-n p^{-1}\left(\bmod a_{1}\right)$. This is equivalent to having $\left(a_{1} / q\right) \mid n$ and $b_{1} \equiv\left(-n /\left(a_{1} / q\right)\right) p^{-1}(\bmod q)$.
Similarly, the latter occurs precisely when $1 \leq b_{2} \leq m, q\left|b_{2},\left(b_{2} / q\right)\right| n$, and $a_{2} \equiv\left(n /\left(b_{2} / q\right)\right) p^{-1}$ $(\bmod q)$.
As hinted at before, if we consider the occurrences for a fixed value $x=a_{1}=b_{2}$, then the number of permitted residue classes $b_{1}\left(\bmod a_{1}=x\right)($ in the former $)$ is the same as the number of permitted residue classes $a_{2}\left(\bmod b_{2}=x\right)$ (in the latter): $y(\bmod x)$ is permitted in the former if and only if $-y(\bmod x)$ is permitted in the latter; note that $(y, x)=1$ if and only if $(-y, x)=1$.
Remark 0.4. This problem was proposed by Victor Wang.
Remark 0.5. This problem was inspired by ISL 2013 N7. Note that the $n=1$ case gives the famous Farey fractions sequence (for fractions of denominator at most $m$ ).
|
{
"resource_path": "HarvardMIT/segmented/en-184-tournaments-2015-hmic-solutions.jsonl",
"problem_match": "\n2. [25]",
"solution_match": "\n## Answer: "
}
|
9b7b6c7a-3c22-5ab8-9f40-f0804ab9cca7
| 609,427
|
Let $\omega=e^{2 \pi i / 5}$ be a primitive fifth root of unity. Prove that there do not exist integers $a, b, c, d, k$ with $k>1$ such that
$$
\left(a+b \omega+c \omega^{2}+d \omega^{3}\right)^{k}=1+\omega
$$
|
N/A
Proof. Let $\zeta=\omega=e^{2 \pi i / 5}$ be a primitive fifth root of unity. If $x=a+b \zeta+c \zeta^{2}+d \zeta^{3}(a, b, c, d \in \mathbb{Z})$, then from $\zeta+\zeta^{-1}=\frac{\sqrt{5}-1}{2}$ and $\zeta^{2}+\zeta^{-2}=\zeta^{3}+\zeta^{-3}=-\frac{\sqrt{5}+1}{2}$, we deduce $|x|^{2}=\left(a^{2}+b^{2}+c^{2}+d^{2}\right)+$ $\frac{\sqrt{5}-1}{2}(a b+b c+c d)-\frac{\sqrt{5}+1}{2}(a c+b d+a d) \in \mathbb{Z}[\phi]$, where $\phi=\frac{1+\sqrt{5}}{2}$.
But $|x|^{2 k}=|1+\zeta|^{2}=2+\phi^{-1}=\phi^{2}$, so $\phi^{2 / k}=|x|^{2} \in \mathbb{Z}[\phi]$. It follows that $|x|^{2}$ has norm $\phi^{2 / k} \bar{\phi}^{2 / k}$ in $\mathbb{Z}[\phi]$, and so must be a positive unit. Yet by the lemma below, the positive units are precisely the integer powers of $\phi$, so $k>1$ forces $k=2$.
However, there must exist $f, g \in \mathbb{Z}[t]$ such that $f(t)^{k}=1+t+g(t)\left(t^{4}+t^{3}+t^{2}+t+1\right)($ if $f(\zeta)=x$, then the minimal polynomial of $\zeta$ over $\mathbb{Q}$ must divide $\left.f(t)^{k}-1-t\right)$, whence $f(1)^{k} \equiv 2(\bmod 5)$, so $2 \nmid k$, contradiction.
(Alternatively, $k=2$ would force $a^{2}+b^{2}+c^{2}+d^{2}-a b-b c-c d=0$, which can only occur if $a=b=c=d=0 ـ^{2}$
Lemma 0.2. The positive units of $\mathbb{Z}[\phi]$ are precisely the integer powers of $\phi$. (In other words, ${ }^{3} \phi$ is the fundamental unit of $\mathbb{Q}(\sqrt{5})$.)
Proof. To prove this, one can either use Pell equation theory, or reason more directly as follows: a unit $m+n \phi>1$ must be at least $\phi$. (Sketch: unit is equivalent to norm $\pm 1$, and so its conjugate $m+n \bar{\phi}=\frac{ \pm 1}{m+n \phi}$ lies in $(-1,1)$, so $n \sqrt{5}=n(\phi-\bar{\phi})>0$ forces $n$ positive, and then $-1<m+n \bar{\phi}$ forces $m>-n \bar{\phi}-1=\frac{n}{\phi}-1>-1$. Hence $m+n \phi \geq 0+1 \phi=\phi$, as desired.) If it's not a positive power of $\phi$, then for some $\ell>0, \frac{m+n \phi}{\phi^{\ell}}$ is a unit lying in $(1, \phi)$, contradiction.
Remark 0.12. This problem was proposed by Carl Lian.
Remark 0.13. The "morally correct" (purely algebraic) way to think about about the above solution is via the tower of (number field) extensions
$$
\mathbb{Q}(\zeta) / \mathbb{Q}(\sqrt{5}) / \mathbb{Q}
$$
Instead of thinking in terms of complex absolute value $|\cdot|$, it is better to reason in terms of the norm $N_{\mathbb{Q}(\zeta) / \mathbb{Q}(\sqrt{5})}(\cdot): \mathbb{Q}(\zeta) \rightarrow \mathbb{Q}(\sqrt{5})$ (which happens to be the same as looking at the square of complex absolute value, in our case), which maps algebraic integers to algebraic integers; the norm of $x^{k}=1+\zeta$ over $\mathbb{Q}(\sqrt{5})$ is $\phi^{2}$, and $\phi$ is the fundamental unit of $\mathbb{Q}(\sqrt{5})$. Then one proceeds as in the above solution.
[^1]
[^0]: ${ }^{1}$ The reason for choosing the threshold $3 n$ will become clear.
[^1]: ${ }^{2}$ On a silly note, this inspired HMMT November 2013 General Problem 7.
${ }^{3}$ since $\mathbb{Z}[\phi]$ is the ring of integers of $\mathbb{Q}(\sqrt{ } 5)$
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $\omega=e^{2 \pi i / 5}$ be a primitive fifth root of unity. Prove that there do not exist integers $a, b, c, d, k$ with $k>1$ such that
$$
\left(a+b \omega+c \omega^{2}+d \omega^{3}\right)^{k}=1+\omega
$$
|
N/A
Proof. Let $\zeta=\omega=e^{2 \pi i / 5}$ be a primitive fifth root of unity. If $x=a+b \zeta+c \zeta^{2}+d \zeta^{3}(a, b, c, d \in \mathbb{Z})$, then from $\zeta+\zeta^{-1}=\frac{\sqrt{5}-1}{2}$ and $\zeta^{2}+\zeta^{-2}=\zeta^{3}+\zeta^{-3}=-\frac{\sqrt{5}+1}{2}$, we deduce $|x|^{2}=\left(a^{2}+b^{2}+c^{2}+d^{2}\right)+$ $\frac{\sqrt{5}-1}{2}(a b+b c+c d)-\frac{\sqrt{5}+1}{2}(a c+b d+a d) \in \mathbb{Z}[\phi]$, where $\phi=\frac{1+\sqrt{5}}{2}$.
But $|x|^{2 k}=|1+\zeta|^{2}=2+\phi^{-1}=\phi^{2}$, so $\phi^{2 / k}=|x|^{2} \in \mathbb{Z}[\phi]$. It follows that $|x|^{2}$ has norm $\phi^{2 / k} \bar{\phi}^{2 / k}$ in $\mathbb{Z}[\phi]$, and so must be a positive unit. Yet by the lemma below, the positive units are precisely the integer powers of $\phi$, so $k>1$ forces $k=2$.
However, there must exist $f, g \in \mathbb{Z}[t]$ such that $f(t)^{k}=1+t+g(t)\left(t^{4}+t^{3}+t^{2}+t+1\right)($ if $f(\zeta)=x$, then the minimal polynomial of $\zeta$ over $\mathbb{Q}$ must divide $\left.f(t)^{k}-1-t\right)$, whence $f(1)^{k} \equiv 2(\bmod 5)$, so $2 \nmid k$, contradiction.
(Alternatively, $k=2$ would force $a^{2}+b^{2}+c^{2}+d^{2}-a b-b c-c d=0$, which can only occur if $a=b=c=d=0 ـ^{2}$
Lemma 0.2. The positive units of $\mathbb{Z}[\phi]$ are precisely the integer powers of $\phi$. (In other words, ${ }^{3} \phi$ is the fundamental unit of $\mathbb{Q}(\sqrt{5})$.)
Proof. To prove this, one can either use Pell equation theory, or reason more directly as follows: a unit $m+n \phi>1$ must be at least $\phi$. (Sketch: unit is equivalent to norm $\pm 1$, and so its conjugate $m+n \bar{\phi}=\frac{ \pm 1}{m+n \phi}$ lies in $(-1,1)$, so $n \sqrt{5}=n(\phi-\bar{\phi})>0$ forces $n$ positive, and then $-1<m+n \bar{\phi}$ forces $m>-n \bar{\phi}-1=\frac{n}{\phi}-1>-1$. Hence $m+n \phi \geq 0+1 \phi=\phi$, as desired.) If it's not a positive power of $\phi$, then for some $\ell>0, \frac{m+n \phi}{\phi^{\ell}}$ is a unit lying in $(1, \phi)$, contradiction.
Remark 0.12. This problem was proposed by Carl Lian.
Remark 0.13. The "morally correct" (purely algebraic) way to think about about the above solution is via the tower of (number field) extensions
$$
\mathbb{Q}(\zeta) / \mathbb{Q}(\sqrt{5}) / \mathbb{Q}
$$
Instead of thinking in terms of complex absolute value $|\cdot|$, it is better to reason in terms of the norm $N_{\mathbb{Q}(\zeta) / \mathbb{Q}(\sqrt{5})}(\cdot): \mathbb{Q}(\zeta) \rightarrow \mathbb{Q}(\sqrt{5})$ (which happens to be the same as looking at the square of complex absolute value, in our case), which maps algebraic integers to algebraic integers; the norm of $x^{k}=1+\zeta$ over $\mathbb{Q}(\sqrt{5})$ is $\phi^{2}$, and $\phi$ is the fundamental unit of $\mathbb{Q}(\sqrt{5})$. Then one proceeds as in the above solution.
[^1]
[^0]: ${ }^{1}$ The reason for choosing the threshold $3 n$ will become clear.
[^1]: ${ }^{2}$ On a silly note, this inspired HMMT November 2013 General Problem 7.
${ }^{3}$ since $\mathbb{Z}[\phi]$ is the ring of integers of $\mathbb{Q}(\sqrt{ } 5)$
|
{
"resource_path": "HarvardMIT/segmented/en-184-tournaments-2015-hmic-solutions.jsonl",
"problem_match": "\n5. [40]",
"solution_match": "\nAnswer: "
}
|
5744243a-5824-50c7-a7cf-f1b23c6e4a2b
| 609,430
|
Let $a$ and $b$ be integers (not necessarily positive). Prove that $a^{3}+5 b^{3} \neq 2016$.
|
Since cubes are 0 or $\pm 1$ modulo 9 , by inspection we see that we must have $a^{3} \equiv b^{3} \equiv 0(\bmod 3)$ for this to be possible. Thus $a, b$ are divisible by 3 . But then we get $3^{3} \mid 2016$, which is a contradiction.
One can also solve the problem in the same manner by taking modulo 7 exist, since all cubes are 0 or $\pm 1$ modulo 7 . The proof can be copied literally, noting that $7 \mid 2016$ but $7^{3} \nmid 2016$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a$ and $b$ be integers (not necessarily positive). Prove that $a^{3}+5 b^{3} \neq 2016$.
|
Since cubes are 0 or $\pm 1$ modulo 9 , by inspection we see that we must have $a^{3} \equiv b^{3} \equiv 0(\bmod 3)$ for this to be possible. Thus $a, b$ are divisible by 3 . But then we get $3^{3} \mid 2016$, which is a contradiction.
One can also solve the problem in the same manner by taking modulo 7 exist, since all cubes are 0 or $\pm 1$ modulo 7 . The proof can be copied literally, noting that $7 \mid 2016$ but $7^{3} \nmid 2016$.
|
{
"resource_path": "HarvardMIT/segmented/en-192-2016-feb-team-solutions.jsonl",
"problem_match": "\n1. [25]",
"solution_match": "\nProposed by: Evan Chen\n"
}
|
9a64ef28-c393-5de8-8f2c-1a929fdae483
| 609,561
|
Fix positive integers $r>s$, and let $F$ be an infinite family of sets, each of size $r$, no two of which share fewer than $s$ elements. Prove that there exists a set of size $r-1$ that shares at least $s$ elements with each set in $F$.
|
Say a set $S$-meets $F$ if it shares at least $s$ elements with each set in $F$. Suppose no such set of size (at most) $r-1$ exists. (Each $S \in F s$-meets $F$ by the problem hypothesis.)
Let $T$ be a maximal set such that $T \subseteq S$ for infinitely many $S \in F$, which form $F^{\prime} \subseteq F$ (such $T$ exists, since the empty set works). Clearly $|T|<r$, so by assumption, $T$ does not $s$-meet $F$, and there exists $U \in F$ with $|U \cap T| \leq s-1$. But $U s$-meets $F^{\prime}$, so by pigeonhole, there must exist $u \in U \backslash T$ belonging to infinitely many $S \in F^{\prime}$, contradicting the maximality of $T$.
Comment. Let $X$ be an infinite set, and $a_{1}, \ldots, a_{2 r-2-s}$ elements not in $X$. Then $F=\{B \cup\{x\}$ : $\left.B \subseteq\left\{a_{1}, \ldots, a_{2 r-2-s}\right\},|B|=r-1, x \in X\right\}$ shows we cannot replace $r-1$ with any smaller number.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Fix positive integers $r>s$, and let $F$ be an infinite family of sets, each of size $r$, no two of which share fewer than $s$ elements. Prove that there exists a set of size $r-1$ that shares at least $s$ elements with each set in $F$.
|
Say a set $S$-meets $F$ if it shares at least $s$ elements with each set in $F$. Suppose no such set of size (at most) $r-1$ exists. (Each $S \in F s$-meets $F$ by the problem hypothesis.)
Let $T$ be a maximal set such that $T \subseteq S$ for infinitely many $S \in F$, which form $F^{\prime} \subseteq F$ (such $T$ exists, since the empty set works). Clearly $|T|<r$, so by assumption, $T$ does not $s$-meet $F$, and there exists $U \in F$ with $|U \cap T| \leq s-1$. But $U s$-meets $F^{\prime}$, so by pigeonhole, there must exist $u \in U \backslash T$ belonging to infinitely many $S \in F^{\prime}$, contradicting the maximality of $T$.
Comment. Let $X$ be an infinite set, and $a_{1}, \ldots, a_{2 r-2-s}$ elements not in $X$. Then $F=\{B \cup\{x\}$ : $\left.B \subseteq\left\{a_{1}, \ldots, a_{2 r-2-s}\right\},|B|=r-1, x \in X\right\}$ shows we cannot replace $r-1$ with any smaller number.
|
{
"resource_path": "HarvardMIT/segmented/en-192-2016-feb-team-solutions.jsonl",
"problem_match": "\n9. [40]",
"solution_match": "\nSolution 1. "
}
|
9a830738-8525-58eb-891a-c8fbc42c2ac4
| 41,984
|
Fix positive integers $r>s$, and let $F$ be an infinite family of sets, each of size $r$, no two of which share fewer than $s$ elements. Prove that there exists a set of size $r-1$ that shares at least $s$ elements with each set in $F$.
|
We can also use a more indirect approach (where the use of contradiction is actually essential).
Fix $S \in F$ and $a \in S$. By assumption, $S \backslash\{a\}$ does not $s$-meet $F$, so there exists $S^{\prime} \in F$ such that $S^{\prime}$ contains at most $s-1$ elements of $S \backslash\{a\}$, whence $S \cap S^{\prime}$ is an $s$-set containing $a$. We will derive a contradiction from the following lemma:
Lemma. Let $F, G$ be families of $r$-sets such that any $f \in F$ and $g \in G$ share at least $s$ elements. Then there exists a finite set $H$ such that for any $f \in F$ and $g \in G,|f \cap g \cap H| \geq s$.
Proof. Suppose not, and take a counterexample with $r+s$ minimal; then $F, G$ must be infinite and $r>s>0$.
Take arbitrary $f_{0} \in F$ and $g_{0} \in G$; then the finite set $X=f_{0} \cup g_{0}$ meets $F, G$. For every subset $Y \subseteq X$, let $F_{Y}=\{S \in F: S \cap X=Y\}$; analogously define $G_{Y}$. Then the $F_{Y}, G_{Y}$ partition $F, G$, respectively. For any $F_{Y}$ and $y \in Y$, define $F_{Y}(y)=\left\{S \backslash\{y\}: S \in F_{Y}\right\}$.
Now fix subsets $Y, Z \subseteq X$. If one of $F_{Y}, G_{Z}$ is empty, define $H_{Y, Z}=\emptyset$.
Otherwise, if $Y, Z$ are disjoint, take arbitrary $y \in Y, z \in Z$. By the minimality assumption, there exists finite $H_{Y, Z}$ such that for any $f \in F_{Y}(y)$ and $g \in G_{Z}(z),\left|f \cap g \cap H_{Y, Z}\right| \geq s$.
If $Y, Z$ share an element $a$, and $s=1$, take $H_{Y, Z}=\{a\}$. Otherwise, if $s \geq 2$, we find again by minimality a finite $H_{Y, Z}(a)$ such that for $f \in F_{Y}(a)$ and $g \in G_{Z}(a),\left|f \cap g \cap H_{Y, Z}\right| \geq s-1$; then take $H_{Y, Z}=H_{Y, Z}(a) \cup\{a\}$.
Finally, we see that $H=\bigcup_{Y, Z \subseteq X} H_{Y, Z}$ shares at least $s$ elements with each $f \cap g$ (by construction), contradicting our assumption.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Fix positive integers $r>s$, and let $F$ be an infinite family of sets, each of size $r$, no two of which share fewer than $s$ elements. Prove that there exists a set of size $r-1$ that shares at least $s$ elements with each set in $F$.
|
We can also use a more indirect approach (where the use of contradiction is actually essential).
Fix $S \in F$ and $a \in S$. By assumption, $S \backslash\{a\}$ does not $s$-meet $F$, so there exists $S^{\prime} \in F$ such that $S^{\prime}$ contains at most $s-1$ elements of $S \backslash\{a\}$, whence $S \cap S^{\prime}$ is an $s$-set containing $a$. We will derive a contradiction from the following lemma:
Lemma. Let $F, G$ be families of $r$-sets such that any $f \in F$ and $g \in G$ share at least $s$ elements. Then there exists a finite set $H$ such that for any $f \in F$ and $g \in G,|f \cap g \cap H| \geq s$.
Proof. Suppose not, and take a counterexample with $r+s$ minimal; then $F, G$ must be infinite and $r>s>0$.
Take arbitrary $f_{0} \in F$ and $g_{0} \in G$; then the finite set $X=f_{0} \cup g_{0}$ meets $F, G$. For every subset $Y \subseteq X$, let $F_{Y}=\{S \in F: S \cap X=Y\}$; analogously define $G_{Y}$. Then the $F_{Y}, G_{Y}$ partition $F, G$, respectively. For any $F_{Y}$ and $y \in Y$, define $F_{Y}(y)=\left\{S \backslash\{y\}: S \in F_{Y}\right\}$.
Now fix subsets $Y, Z \subseteq X$. If one of $F_{Y}, G_{Z}$ is empty, define $H_{Y, Z}=\emptyset$.
Otherwise, if $Y, Z$ are disjoint, take arbitrary $y \in Y, z \in Z$. By the minimality assumption, there exists finite $H_{Y, Z}$ such that for any $f \in F_{Y}(y)$ and $g \in G_{Z}(z),\left|f \cap g \cap H_{Y, Z}\right| \geq s$.
If $Y, Z$ share an element $a$, and $s=1$, take $H_{Y, Z}=\{a\}$. Otherwise, if $s \geq 2$, we find again by minimality a finite $H_{Y, Z}(a)$ such that for $f \in F_{Y}(a)$ and $g \in G_{Z}(a),\left|f \cap g \cap H_{Y, Z}\right| \geq s-1$; then take $H_{Y, Z}=H_{Y, Z}(a) \cup\{a\}$.
Finally, we see that $H=\bigcup_{Y, Z \subseteq X} H_{Y, Z}$ shares at least $s$ elements with each $f \cap g$ (by construction), contradicting our assumption.
|
{
"resource_path": "HarvardMIT/segmented/en-192-2016-feb-team-solutions.jsonl",
"problem_match": "\n9. [40]",
"solution_match": "\nSolution 2. "
}
|
9a830738-8525-58eb-891a-c8fbc42c2ac4
| 41,984
|
Let $A B C$ be a triangle with incenter $I$ whose incircle is tangent to $\overline{B C}, \overline{C A}, \overline{A B}$ at $D, E, F$. Point $P$ lies on $\overline{E F}$ such that $\overline{D P} \perp \overline{E F}$. Ray $B P$ meets $\overline{A C}$ at $Y$ and ray $C P$ meets $\overline{A B}$ at $Z$. Point $Q$ is selected on the circumcircle of $\triangle A Y Z$ so that $\overline{A Q} \perp \overline{B C}$.
Prove that $P, I, Q$ are collinear.
|
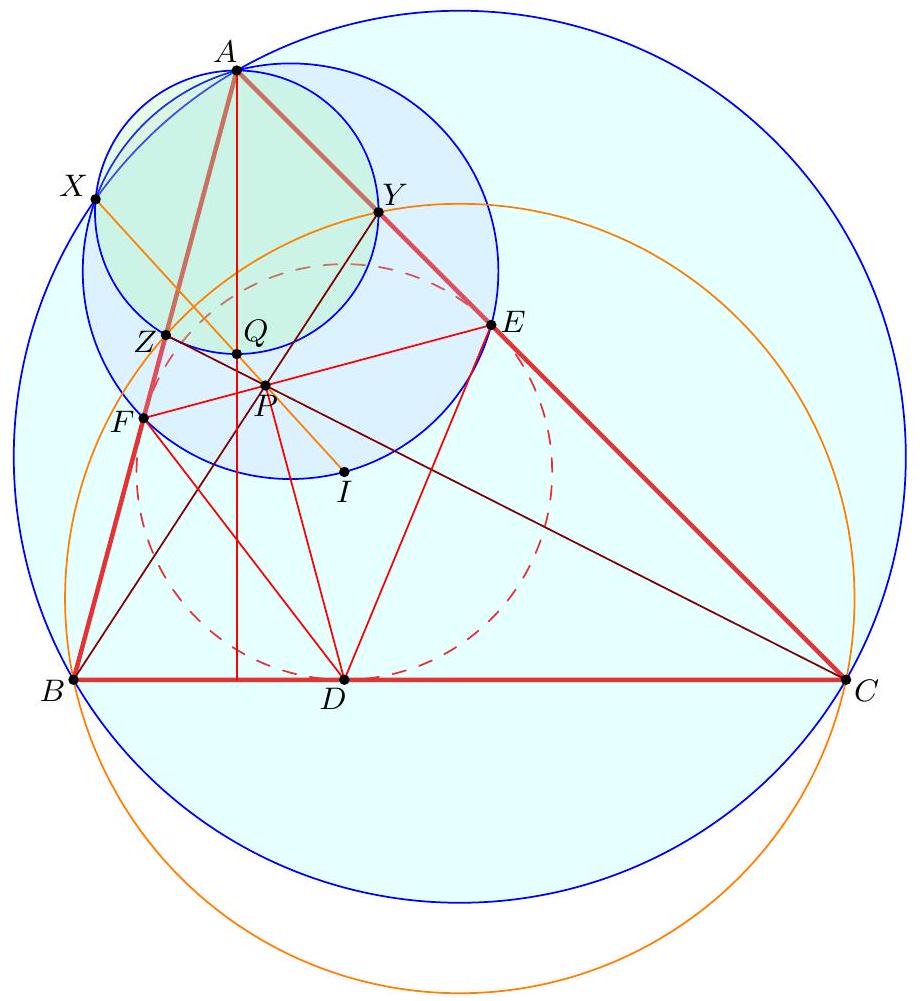
The proof proceeds through a series of seven lemmas.
Lemma 1. Lines $D P$ and $E F$ are the internal and external angle bisectors of $\angle B P C$.
Proof. Since $D E F$ the cevian triangle of $A B C$ with respect to its Gregonne point, we have that
$$
-1=(\overline{E F} \cap \overline{B C}, D ; B, C)
$$
Then since $\angle D P F=90^{\circ}$ we see $P$ is on the Apollonian circle of $B C$ through $D$. So the conclusion follows.
Lemma 2. Triangles $B P F$ and $C E P$ are similar.
Proof. Invoking the angle bisector theorem with the previous lemma gives
$$
\frac{B P}{B F}=\frac{B P}{B D}=\frac{C P}{C D}=\frac{C P}{C E}
$$
But $\angle B F P=\angle C E P$, so $\triangle B F P \sim \triangle C E P$.
Lemma 3. Quadrilateral $B Z Y C$ is cyclic; in particular, line $Y Z$ is the antiparallel of line $B C$ through $\angle B A C$.
Proof. Remark that $\angle Y B Z=\angle P B F=\angle E C P=\angle Y C Z$.
Lemma 4. The circumcircles of triangles $A Y Z, A E F, A B C$ are concurrent at a point $X$ such that $\triangle X B F \sim \triangle X C E$.
Proof. Note that line $E F$ is the angle bisector of $\angle B P Z=\angle C P Y$. Thus
$$
\frac{Z F}{F B}=\frac{Z P}{P B}=\frac{Y P}{P C}=\frac{Y E}{E C}
$$
Then, if we let $X$ be the Miquel point of quadrilateral $Z Y C B$, it follows that the spiral similarity mapping segment $B Z$ to segment $C Y$ maps $E$ to $F$; therefore the circumcircle of $\triangle A E F$ must pass through $X$ too.
Lemma 5. Ray $X P$ bisects $\angle F X E$.
Proof. The assertion amounts to
$$
\frac{X F}{X E}=\frac{B F}{E C}=\frac{F P}{P E}
$$
The first equality follows from the spiral similarity $\triangle B F X \sim \triangle C E X$, while the second is from $\triangle B F P \sim \triangle C E P$. So the proof is complete by the converse of angle bisector theorem.
Lemma 6. Points $X, P, I$ are collinear.
Proof. On one hand, $\angle F X I=\angle F A I=\frac{1}{2} \angle A$. On the other hand, $\angle F X P=\frac{1}{2} \angle F X E=\frac{1}{2} \angle A$. Hence, $X, Y, I$ collinear.
Lemma 7. Points $X, Q, I$ are collinear.
Proof. On one hand, $\angle A X Q=90^{\circ}$, because we established earlier that line $Y Z$ was antiparallel to line $B C$ through $\angle A$, hence $A Q \perp B C$ means exactly that $\angle A Z Q=A Y Q=90^{\circ}$. On the other hand, $\angle A X I=90^{\circ}$ according to the fact that $X$ lies on the circle with diameter $A I$. This completes the proof of the lemma.
Finally, combining the final two lemmas solves the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incenter $I$ whose incircle is tangent to $\overline{B C}, \overline{C A}, \overline{A B}$ at $D, E, F$. Point $P$ lies on $\overline{E F}$ such that $\overline{D P} \perp \overline{E F}$. Ray $B P$ meets $\overline{A C}$ at $Y$ and ray $C P$ meets $\overline{A B}$ at $Z$. Point $Q$ is selected on the circumcircle of $\triangle A Y Z$ so that $\overline{A Q} \perp \overline{B C}$.
Prove that $P, I, Q$ are collinear.
|

The proof proceeds through a series of seven lemmas.
Lemma 1. Lines $D P$ and $E F$ are the internal and external angle bisectors of $\angle B P C$.
Proof. Since $D E F$ the cevian triangle of $A B C$ with respect to its Gregonne point, we have that
$$
-1=(\overline{E F} \cap \overline{B C}, D ; B, C)
$$
Then since $\angle D P F=90^{\circ}$ we see $P$ is on the Apollonian circle of $B C$ through $D$. So the conclusion follows.
Lemma 2. Triangles $B P F$ and $C E P$ are similar.
Proof. Invoking the angle bisector theorem with the previous lemma gives
$$
\frac{B P}{B F}=\frac{B P}{B D}=\frac{C P}{C D}=\frac{C P}{C E}
$$
But $\angle B F P=\angle C E P$, so $\triangle B F P \sim \triangle C E P$.
Lemma 3. Quadrilateral $B Z Y C$ is cyclic; in particular, line $Y Z$ is the antiparallel of line $B C$ through $\angle B A C$.
Proof. Remark that $\angle Y B Z=\angle P B F=\angle E C P=\angle Y C Z$.
Lemma 4. The circumcircles of triangles $A Y Z, A E F, A B C$ are concurrent at a point $X$ such that $\triangle X B F \sim \triangle X C E$.
Proof. Note that line $E F$ is the angle bisector of $\angle B P Z=\angle C P Y$. Thus
$$
\frac{Z F}{F B}=\frac{Z P}{P B}=\frac{Y P}{P C}=\frac{Y E}{E C}
$$
Then, if we let $X$ be the Miquel point of quadrilateral $Z Y C B$, it follows that the spiral similarity mapping segment $B Z$ to segment $C Y$ maps $E$ to $F$; therefore the circumcircle of $\triangle A E F$ must pass through $X$ too.
Lemma 5. Ray $X P$ bisects $\angle F X E$.
Proof. The assertion amounts to
$$
\frac{X F}{X E}=\frac{B F}{E C}=\frac{F P}{P E}
$$
The first equality follows from the spiral similarity $\triangle B F X \sim \triangle C E X$, while the second is from $\triangle B F P \sim \triangle C E P$. So the proof is complete by the converse of angle bisector theorem.
Lemma 6. Points $X, P, I$ are collinear.
Proof. On one hand, $\angle F X I=\angle F A I=\frac{1}{2} \angle A$. On the other hand, $\angle F X P=\frac{1}{2} \angle F X E=\frac{1}{2} \angle A$. Hence, $X, Y, I$ collinear.
Lemma 7. Points $X, Q, I$ are collinear.
Proof. On one hand, $\angle A X Q=90^{\circ}$, because we established earlier that line $Y Z$ was antiparallel to line $B C$ through $\angle A$, hence $A Q \perp B C$ means exactly that $\angle A Z Q=A Y Q=90^{\circ}$. On the other hand, $\angle A X I=90^{\circ}$ according to the fact that $X$ lies on the circle with diameter $A I$. This completes the proof of the lemma.
Finally, combining the final two lemmas solves the problem.
|
{
"resource_path": "HarvardMIT/segmented/en-192-2016-feb-team-solutions.jsonl",
"problem_match": "\n10. [50]",
"solution_match": "\nProposed by: Evan Chen\n"
}
|
2ebe0fb2-58c1-5d3b-8060-9e6784d060a5
| 609,569
|
Let $A B C$ be an acute triangle with circumcenter $O$, orthocenter $H$, and circumcircle $\Omega$. Let $M$ be the midpoint of $A H$ and $N$ the midpoint of $B H$. Assume the points $M, N, O, H$ are distinct and lie on a circle $\omega$. Prove that the circles $\omega$ and $\Omega$ are internally tangent to each other.
|
Let $R$ be the circumradius of $\triangle A B C$. Recall that the circumcircle of $\triangle H B C$ has radius equal to $R$. By a homothety at $H$ with factor 2 at $H$, it follows that $\triangle H M N$ has circumradius $R / 2$. Thus $\omega$ has circumradius $R / 2$, and since $O$ lies on $\omega$ the conclusion follows.
Remark. This problem is a slight modification of a proposal by Dhroova Aiylam.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with circumcenter $O$, orthocenter $H$, and circumcircle $\Omega$. Let $M$ be the midpoint of $A H$ and $N$ the midpoint of $B H$. Assume the points $M, N, O, H$ are distinct and lie on a circle $\omega$. Prove that the circles $\omega$ and $\Omega$ are internally tangent to each other.
|
Let $R$ be the circumradius of $\triangle A B C$. Recall that the circumcircle of $\triangle H B C$ has radius equal to $R$. By a homothety at $H$ with factor 2 at $H$, it follows that $\triangle H M N$ has circumradius $R / 2$. Thus $\omega$ has circumradius $R / 2$, and since $O$ lies on $\omega$ the conclusion follows.
Remark. This problem is a slight modification of a proposal by Dhroova Aiylam.
|
{
"resource_path": "HarvardMIT/segmented/en-194-tournaments-2016-hmic-solutions.jsonl",
"problem_match": "\n2. [7]",
"solution_match": "\n## Proposed by: Evan Chen\n\n"
}
|
87668061-3fe2-554b-a8e6-e42177162c1c
| 609,571
|
Denote by $\mathbb{N}$ the positive integers. Let $f: \mathbb{N} \rightarrow \mathbb{N}$ be a function such that, for any $w, x, y, z \in \mathbb{N}$,
$$
f(f(f(z))) f(w x f(y f(z)))=z^{2} f(x f(y)) f(w)
$$
Show that $f(n!) \geq n$ ! for every positive integer $n$.
|
If $f\left(z_{1}\right)=f\left(z_{2}\right)$, then plugging in $\left(w, x, y, z_{1}\right)$ and $\left(w, x, y, z_{2}\right)$ yields $z_{1}=z_{2}$. Thus, $f$ is injective. Substitution of $(z, w)$ with $(1, f(f(1)))$ in the main equation yields
$$
f(f(f(1)) x f(y f(1)))=f(x f(y))
$$
Because $f$ is injective, we have
$$
f(y f(1)) \cdot f(f(1))=f(y), \forall y \in \mathbb{N}
$$
We can easily show by induction that
$$
f(y)=f\left(y f(1)^{n}\right) f(f(1))^{n}, \forall n \in \mathbb{N}
$$
Thus, $f(f(1))^{n} \mid f(y), \forall n \in \mathbb{N}$ which implies that $f(f(1))=1$. Using this equality in $(*)$ yields $f(1)=1$. Substitution of $(y, z)$ with $(1,1)$ in the main equation yields $f(x y)=f(x) f(y)$.
So,
$$
f(n!)=f\left(\prod_{i=1}^{n} i\right)=\prod_{i=1}^{n} f(i)
$$
By injectivity, each $f(i)$ in this product is a distinct positive integer, so their product is at least $\prod_{i=1}^{n} i=n!$, as desired.
Remark 1. The equation condition of $f$ in the problem is actually equivalent to the following two conditions combined:
$$
\begin{aligned}
& \text { (C1) } f(x y)=f(x) f(y), \forall x, y \in \mathbb{N} \text {, and } \\
& \text { (C2) } f(f(f(x)))=x, \forall x \in \mathbb{N}
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Denote by $\mathbb{N}$ the positive integers. Let $f: \mathbb{N} \rightarrow \mathbb{N}$ be a function such that, for any $w, x, y, z \in \mathbb{N}$,
$$
f(f(f(z))) f(w x f(y f(z)))=z^{2} f(x f(y)) f(w)
$$
Show that $f(n!) \geq n$ ! for every positive integer $n$.
|
If $f\left(z_{1}\right)=f\left(z_{2}\right)$, then plugging in $\left(w, x, y, z_{1}\right)$ and $\left(w, x, y, z_{2}\right)$ yields $z_{1}=z_{2}$. Thus, $f$ is injective. Substitution of $(z, w)$ with $(1, f(f(1)))$ in the main equation yields
$$
f(f(f(1)) x f(y f(1)))=f(x f(y))
$$
Because $f$ is injective, we have
$$
f(y f(1)) \cdot f(f(1))=f(y), \forall y \in \mathbb{N}
$$
We can easily show by induction that
$$
f(y)=f\left(y f(1)^{n}\right) f(f(1))^{n}, \forall n \in \mathbb{N}
$$
Thus, $f(f(1))^{n} \mid f(y), \forall n \in \mathbb{N}$ which implies that $f(f(1))=1$. Using this equality in $(*)$ yields $f(1)=1$. Substitution of $(y, z)$ with $(1,1)$ in the main equation yields $f(x y)=f(x) f(y)$.
So,
$$
f(n!)=f\left(\prod_{i=1}^{n} i\right)=\prod_{i=1}^{n} f(i)
$$
By injectivity, each $f(i)$ in this product is a distinct positive integer, so their product is at least $\prod_{i=1}^{n} i=n!$, as desired.
Remark 1. The equation condition of $f$ in the problem is actually equivalent to the following two conditions combined:
$$
\begin{aligned}
& \text { (C1) } f(x y)=f(x) f(y), \forall x, y \in \mathbb{N} \text {, and } \\
& \text { (C2) } f(f(f(x)))=x, \forall x \in \mathbb{N}
\end{aligned}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-194-tournaments-2016-hmic-solutions.jsonl",
"problem_match": "\n3. [8]",
"solution_match": "\nProposed by: Pakawut Jiradilok\n"
}
|
c4d4191e-6647-5faa-bedc-a0e7cd5b43b3
| 609,572
|
Let $P$ be an odd-degree integer-coefficient polynomial. Suppose that $x P(x)=y P(y)$ for infinitely many pairs $x, y$ of integers with $x \neq y$. Prove that the equation $P(x)=0$ has an integer root.
|
Proof. Let $n$ be the (odd) degree of $P$. Suppose, for contradiction, that $P$ has no integer roots, and let $Q(x)=x P(x)=a_{n} x^{n+1}+a_{n-1} x^{n}+\cdots+a_{0} x^{1}$. WLOG $a_{n}>0$, so there exists $M>0$ such that $Q(M)<Q(M+1)<\cdots$ and $Q(-M)<Q(-M-1)<\cdots$ (as $n+1$ is even).
There exist finitely many solutions $(t, y)$ for any fixed $t$, so infinitely many solutions $(x, y)$ with $|x|,|y| \geq$ $M$. By definition of $M$, there WLOG exist infinitely many solutions with $|x| \geq M$ and $y \geq-x>0$ (otherwise replace $P(t)$ with $P(-t)$ ).
Equivalently, there exist infinitely many $(t, k)$ with $t \geq M$ and $k \geq 0$ such that
$$
0=Q(t+k)-Q(-t)=a_{n}\left[(t+k)^{n+1}-(-t)^{n+1}\right]+\cdots+a_{0}\left[(t+k)^{1}-(-t)^{1}\right] .
$$
If $k \neq 0$, then $Q(x+k)-Q(-x)$ has constant term $Q(k)-Q(0)=k P(k) \neq 0$, and if $k=0$, then $Q(x+k)-Q(-x)=2\left(a_{0} x^{1}+a_{2} x^{3}+\cdots+a_{n-1} x^{n}\right)$ has $x^{1}$ coefficient nonzero (otherwise $\left.P(0)=0\right)$, so no fixed $k$ yields infinitely many solutions.
Hence for any $N \geq 0$, there exist $k=k_{N} \geq N$ and $t=t_{N} \geq M$ such that $0=Q(t+k)-Q(-t)$. But then the triangle inequality yields
$$
\underbrace{a_{n}\left[(t+k)^{n+1}-(-t)^{n+1}\right]}_{=\sum_{i=0}^{n-1}-a_{i}\left[(t+k)^{i+1}-(-t)^{i}\right]} \leq 2(t+k)^{n}\left(\left|a_{n-1}\right|+\cdots+\left|a_{0}\right|\right) .
$$
But $(t+k)^{n+1}-t^{n+1} \geq(t+k)^{n+1}-t \cdot(t+k)^{n}=k \cdot(t+k)^{n} 1$ so $a_{n} k_{N} \leq 2\left(\left|a_{n-1}\right|+\cdots+\left|a_{0}\right|\right)$ for all $N$. Since $k_{N} \geq N$, this gives a contradiction for sufficiently large $N$.
[^0]Remark 2. Another way to finish after the triangle inequality estimate (1) is to observe that $(t+$ $k)^{n+1}-(-t)^{n+1}=(t+k)^{n+1}-t^{n+1} \geq t^{n} \cdot k+k^{n+1}$ (by binomial expansion), so $\frac{k_{N}\left(t_{N}^{n}+k_{N}^{n}\right)}{\left(t_{N}+k_{N}\right)^{n}}$ (which by Holder's inequality is at least $\frac{k_{N}}{2^{n-1}} \geq \frac{N}{2^{n-1}}$ ) is bounded above (independently of $N$ ), contradiction. (Here we use Holder's inequality to deduce $(1+1)^{n-1}\left(a^{n}+b^{n}\right) \geq(a+b)^{n}$ for positive reals $a, b$.)
Remark 3. The statement is vacuous for even-degree polynomials. The case of degree 3 polynomials was given as ISL 2002 A3.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $P$ be an odd-degree integer-coefficient polynomial. Suppose that $x P(x)=y P(y)$ for infinitely many pairs $x, y$ of integers with $x \neq y$. Prove that the equation $P(x)=0$ has an integer root.
|
Proof. Let $n$ be the (odd) degree of $P$. Suppose, for contradiction, that $P$ has no integer roots, and let $Q(x)=x P(x)=a_{n} x^{n+1}+a_{n-1} x^{n}+\cdots+a_{0} x^{1}$. WLOG $a_{n}>0$, so there exists $M>0$ such that $Q(M)<Q(M+1)<\cdots$ and $Q(-M)<Q(-M-1)<\cdots$ (as $n+1$ is even).
There exist finitely many solutions $(t, y)$ for any fixed $t$, so infinitely many solutions $(x, y)$ with $|x|,|y| \geq$ $M$. By definition of $M$, there WLOG exist infinitely many solutions with $|x| \geq M$ and $y \geq-x>0$ (otherwise replace $P(t)$ with $P(-t)$ ).
Equivalently, there exist infinitely many $(t, k)$ with $t \geq M$ and $k \geq 0$ such that
$$
0=Q(t+k)-Q(-t)=a_{n}\left[(t+k)^{n+1}-(-t)^{n+1}\right]+\cdots+a_{0}\left[(t+k)^{1}-(-t)^{1}\right] .
$$
If $k \neq 0$, then $Q(x+k)-Q(-x)$ has constant term $Q(k)-Q(0)=k P(k) \neq 0$, and if $k=0$, then $Q(x+k)-Q(-x)=2\left(a_{0} x^{1}+a_{2} x^{3}+\cdots+a_{n-1} x^{n}\right)$ has $x^{1}$ coefficient nonzero (otherwise $\left.P(0)=0\right)$, so no fixed $k$ yields infinitely many solutions.
Hence for any $N \geq 0$, there exist $k=k_{N} \geq N$ and $t=t_{N} \geq M$ such that $0=Q(t+k)-Q(-t)$. But then the triangle inequality yields
$$
\underbrace{a_{n}\left[(t+k)^{n+1}-(-t)^{n+1}\right]}_{=\sum_{i=0}^{n-1}-a_{i}\left[(t+k)^{i+1}-(-t)^{i}\right]} \leq 2(t+k)^{n}\left(\left|a_{n-1}\right|+\cdots+\left|a_{0}\right|\right) .
$$
But $(t+k)^{n+1}-t^{n+1} \geq(t+k)^{n+1}-t \cdot(t+k)^{n}=k \cdot(t+k)^{n} 1$ so $a_{n} k_{N} \leq 2\left(\left|a_{n-1}\right|+\cdots+\left|a_{0}\right|\right)$ for all $N$. Since $k_{N} \geq N$, this gives a contradiction for sufficiently large $N$.
[^0]Remark 2. Another way to finish after the triangle inequality estimate (1) is to observe that $(t+$ $k)^{n+1}-(-t)^{n+1}=(t+k)^{n+1}-t^{n+1} \geq t^{n} \cdot k+k^{n+1}$ (by binomial expansion), so $\frac{k_{N}\left(t_{N}^{n}+k_{N}^{n}\right)}{\left(t_{N}+k_{N}\right)^{n}}$ (which by Holder's inequality is at least $\frac{k_{N}}{2^{n-1}} \geq \frac{N}{2^{n-1}}$ ) is bounded above (independently of $N$ ), contradiction. (Here we use Holder's inequality to deduce $(1+1)^{n-1}\left(a^{n}+b^{n}\right) \geq(a+b)^{n}$ for positive reals $a, b$.)
Remark 3. The statement is vacuous for even-degree polynomials. The case of degree 3 polynomials was given as ISL 2002 A3.
|
{
"resource_path": "HarvardMIT/segmented/en-194-tournaments-2016-hmic-solutions.jsonl",
"problem_match": "\n4. [10]",
"solution_match": "\nProposed by: Victor Wang\n"
}
|
40ee68ac-60d9-5ed9-acb6-80595d957dd1
| 609,573
|
Let $S=\left\{a_{1}, \ldots, a_{n}\right\}$ be a finite set of positive integers of size $n \geq 1$, and let $T$ be the set of all positive integers that can be expressed as sums of perfect powers (including 1) of distinct numbers in $S$, meaning
$$
T=\left\{\sum_{i=1}^{n} a_{i}^{e_{i}} \mid e_{1}, e_{2}, \ldots, e_{n} \geq 0\right\}
$$
Show that there is a positive integer $N$ (only depending on $n$ ) such that $T$ contains no arithmetic progression of length $N$.
|
Answer: N/A
In general we can assume that each $a_{i}>1$, since replacing $a_{i}=1$ by some large integer $a$ creates a set $T$ containing the original $T$ as a subset (by setting $e_{i}=0$ ).
We proceed by induction on $n$. For the base case $n=1$, an arithmetic progression of length at least 3 would give $a_{1}^{e_{1}}+a_{1}^{e_{3}}=2 a_{1}^{e_{2}}$ where $e_{3}>e_{2}>e_{1}$. But $a_{1}^{e_{3}} \geq 2 a_{1}^{e_{2}}$, so this is impossible. Thus our result holds for $n=1$.
Assume the result is true for some $n-1$, and let $A_{n-1}$ be a number such that the longest progression when $|S|=n-1$ has length less than $A_{n-1}$. Let $M$ be a large integer that we will choose later. Take an arithmetic progression of length $2 M+1$, calling the terms $b_{1}, b_{2}, \ldots, b_{2 M+1}$. Note that $b_{2 M+1} \leq$ $2 b_{M+1}$, since $b$ is a sequence of positive integers. For each term from $b_{M+1}$ to $b_{2 M+1}$ assign to it the maximum power that is part of the sum. Call this value $c\left(b_{i}\right)$. More explicitly, if $b_{i}=\sum_{j=1}^{n} a_{j}^{e_{j}}$, then $c\left(b_{i}\right)=\max \left(a_{1}^{e_{1}}, a_{2}^{e_{2}}, \ldots, a_{n}^{e_{n}}\right)$.
Since $\frac{b_{M+1}}{n} \leq c\left(b_{i}\right) \leq b_{2 M+1} \leq 2 b_{M+1}$ for $M+1 \leq i \leq 2 M+1$, there are at most $\sum_{j=1}^{n}\left(\log _{a_{i}} 2 n+1\right) \leq$ $n\left(\log _{2} 2 n+1\right)$ different values of $c\left(b_{i}\right)$. By Van der Waerden's Theorem, there exists a value of $M$ such that coloring an arithmetic progression of length $M$ with $n\left(\log _{2} 2 n+1\right)$ colors yields a monochromatic arithmetic progression of length $A_{n-1}$. In particular, we can take $M=W\left(A_{n-1}, n\left(\log _{2} 2 n+1\right)\right)$, where $W(n, k)$ denotes the Van der Waerden number. So, we color $b_{M+1}, \ldots, b_{2 M+1}$ by their $c\left(b_{i}\right)$. Subtracting the common perfect power from each term of the monochromatic arithmetic progression obtained gives an arithmetic progression of $A_{n-1}$ integers expressible as the sum of perfect powers of distinct numbers in $S \backslash a_{j}$. By the inductive hypothesis, this is a contradiction. So no arithmetic progression of length $2 M+1$ can be contained in $T$, and we can take $A_{n}=2 M+1$.
By induction, we thus have such an $A_{n}$ for all $n$.
[^0]: ${ }^{1}$ However, the mean value theorem estimate $(t+k)^{n+1}-t^{n+1} \geq k \cdot(n+1) t^{n}$ will not suffice a priori, if $k$ happens to be much larger than $t$. Of course, it is easy to prove that $k$ cannot be too much larger than $t$ (even before finishing the problem); the execution would just take slightly longer.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $S=\left\{a_{1}, \ldots, a_{n}\right\}$ be a finite set of positive integers of size $n \geq 1$, and let $T$ be the set of all positive integers that can be expressed as sums of perfect powers (including 1) of distinct numbers in $S$, meaning
$$
T=\left\{\sum_{i=1}^{n} a_{i}^{e_{i}} \mid e_{1}, e_{2}, \ldots, e_{n} \geq 0\right\}
$$
Show that there is a positive integer $N$ (only depending on $n$ ) such that $T$ contains no arithmetic progression of length $N$.
|
Answer: N/A
In general we can assume that each $a_{i}>1$, since replacing $a_{i}=1$ by some large integer $a$ creates a set $T$ containing the original $T$ as a subset (by setting $e_{i}=0$ ).
We proceed by induction on $n$. For the base case $n=1$, an arithmetic progression of length at least 3 would give $a_{1}^{e_{1}}+a_{1}^{e_{3}}=2 a_{1}^{e_{2}}$ where $e_{3}>e_{2}>e_{1}$. But $a_{1}^{e_{3}} \geq 2 a_{1}^{e_{2}}$, so this is impossible. Thus our result holds for $n=1$.
Assume the result is true for some $n-1$, and let $A_{n-1}$ be a number such that the longest progression when $|S|=n-1$ has length less than $A_{n-1}$. Let $M$ be a large integer that we will choose later. Take an arithmetic progression of length $2 M+1$, calling the terms $b_{1}, b_{2}, \ldots, b_{2 M+1}$. Note that $b_{2 M+1} \leq$ $2 b_{M+1}$, since $b$ is a sequence of positive integers. For each term from $b_{M+1}$ to $b_{2 M+1}$ assign to it the maximum power that is part of the sum. Call this value $c\left(b_{i}\right)$. More explicitly, if $b_{i}=\sum_{j=1}^{n} a_{j}^{e_{j}}$, then $c\left(b_{i}\right)=\max \left(a_{1}^{e_{1}}, a_{2}^{e_{2}}, \ldots, a_{n}^{e_{n}}\right)$.
Since $\frac{b_{M+1}}{n} \leq c\left(b_{i}\right) \leq b_{2 M+1} \leq 2 b_{M+1}$ for $M+1 \leq i \leq 2 M+1$, there are at most $\sum_{j=1}^{n}\left(\log _{a_{i}} 2 n+1\right) \leq$ $n\left(\log _{2} 2 n+1\right)$ different values of $c\left(b_{i}\right)$. By Van der Waerden's Theorem, there exists a value of $M$ such that coloring an arithmetic progression of length $M$ with $n\left(\log _{2} 2 n+1\right)$ colors yields a monochromatic arithmetic progression of length $A_{n-1}$. In particular, we can take $M=W\left(A_{n-1}, n\left(\log _{2} 2 n+1\right)\right)$, where $W(n, k)$ denotes the Van der Waerden number. So, we color $b_{M+1}, \ldots, b_{2 M+1}$ by their $c\left(b_{i}\right)$. Subtracting the common perfect power from each term of the monochromatic arithmetic progression obtained gives an arithmetic progression of $A_{n-1}$ integers expressible as the sum of perfect powers of distinct numbers in $S \backslash a_{j}$. By the inductive hypothesis, this is a contradiction. So no arithmetic progression of length $2 M+1$ can be contained in $T$, and we can take $A_{n}=2 M+1$.
By induction, we thus have such an $A_{n}$ for all $n$.
[^0]: ${ }^{1}$ However, the mean value theorem estimate $(t+k)^{n+1}-t^{n+1} \geq k \cdot(n+1) t^{n}$ will not suffice a priori, if $k$ happens to be much larger than $t$. Of course, it is easy to prove that $k$ cannot be too much larger than $t$ (even before finishing the problem); the execution would just take slightly longer.
|
{
"resource_path": "HarvardMIT/segmented/en-194-tournaments-2016-hmic-solutions.jsonl",
"problem_match": "\n5. [12]",
"solution_match": "\nProposed by: Yang Liu\n"
}
|
2a0284c8-f503-5c0c-9a9c-341af8804c79
| 609,574
|
Let $P(x), Q(x)$ be nonconstant polynomials with real number coefficients. Prove that if
$$
\lfloor P(y)\rfloor=\lfloor Q(y)\rfloor
$$
for all real numbers $y$, then $P(x)=Q(x)$ for all real numbers $x$.
|
## Answer:
By the condition, we know that $|P(x)-Q(x)| \leq 1$ for all $x$. This can only hold if $P(x)-Q(x)$ is a constant polynomial. Now take a constant $c$ such that $P(x)=Q(x)+c$. Without loss of generality, we can assume that $c \geq 0$. Assume that $c>0$. By continuity, if $\operatorname{deg} P=\operatorname{deg} Q>0$, we can select an integer $r$ and a real number $x_{0}$ such that $Q\left(x_{0}\right)+c=r$. Then $\left\lfloor P\left(x_{0}\right)\right\rfloor=\left\lfloor Q\left(x_{0}\right)+c\right\rfloor=r$. On the other hand, $\left\lfloor Q\left(x_{0}\right)\right\rfloor=\lfloor r-c\rfloor<r$ as $r$ was an integer. This is a contradiction. Therefore, $c=0$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $P(x), Q(x)$ be nonconstant polynomials with real number coefficients. Prove that if
$$
\lfloor P(y)\rfloor=\lfloor Q(y)\rfloor
$$
for all real numbers $y$, then $P(x)=Q(x)$ for all real numbers $x$.
|
## Answer:
By the condition, we know that $|P(x)-Q(x)| \leq 1$ for all $x$. This can only hold if $P(x)-Q(x)$ is a constant polynomial. Now take a constant $c$ such that $P(x)=Q(x)+c$. Without loss of generality, we can assume that $c \geq 0$. Assume that $c>0$. By continuity, if $\operatorname{deg} P=\operatorname{deg} Q>0$, we can select an integer $r$ and a real number $x_{0}$ such that $Q\left(x_{0}\right)+c=r$. Then $\left\lfloor P\left(x_{0}\right)\right\rfloor=\left\lfloor Q\left(x_{0}\right)+c\right\rfloor=r$. On the other hand, $\left\lfloor Q\left(x_{0}\right)\right\rfloor=\lfloor r-c\rfloor<r$ as $r$ was an integer. This is a contradiction. Therefore, $c=0$ as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-team-solutions.jsonl",
"problem_match": "\n1. [15]",
"solution_match": "\nProposed by: Alexander Katz\n\n"
}
|
86955f0d-cfd1-5d7f-b523-91bc03443683
| 609,703
|
A polyhedron has $7 n$ faces. Show that there exist $n+1$ of the polyhedron's faces that all have the same number of edges.
|
Let $V, E$, and $F$ denote the number of vertices, edges, and faces respectively. Let $a_{k}$ denote the number of faces with $k$ sides, and let $M$ be the maximum number of sides any face has.
Suppose that $a_{k} \leq n$ for all $k$ and that $M>8$. Note that each edge is part of exactly two faces, and each vertex is part of at least three faces. It follows that
$$
\begin{aligned}
& \sum_{k=3}^{M} a_{k}=F \\
& \sum_{k=3}^{M} \frac{k a_{k}}{2}=E \\
& \sum_{k=3}^{M} \frac{k a_{k}}{3} \geq V
\end{aligned}
$$
and in particular
$$
\sum_{k=3}^{M} a_{k}\left(1-\frac{k}{2}+\frac{k}{3}\right) \geq F-E+V=2
$$
by Euler's formula. But on the other hand, $a_{k} \leq n$ by assumption, so
$$
\begin{aligned}
2 & \leq \sum_{k=3}^{M} a_{k}\left(1-\frac{k}{6}\right) \\
& \leq \sum_{k=3}^{M} n\left(1-\frac{k}{6}\right) \\
& =\sum_{k=3}^{8} n\left(1-\frac{k}{6}\right)+\sum_{k=9}^{M} n\left(1-\frac{k}{6}\right) \\
& \leq \frac{1}{2} n-\frac{1}{2} n(M-8)
\end{aligned}
$$
where the last step follows from the fact that $1-\frac{k}{6} \leq-\frac{1}{2}$ for $k \geq 9$. Thus
$$
2 \leq \frac{9}{2} n-\frac{1}{2} n M \Longrightarrow M \leq \frac{\frac{9}{2} n-2}{\frac{1}{2} n}<9
$$
contradicting the fact that $M>8$. It follows that $M \leq 8$, and as each face has at least 3 edges, the result follows directly from Pigeonhole.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A polyhedron has $7 n$ faces. Show that there exist $n+1$ of the polyhedron's faces that all have the same number of edges.
|
Let $V, E$, and $F$ denote the number of vertices, edges, and faces respectively. Let $a_{k}$ denote the number of faces with $k$ sides, and let $M$ be the maximum number of sides any face has.
Suppose that $a_{k} \leq n$ for all $k$ and that $M>8$. Note that each edge is part of exactly two faces, and each vertex is part of at least three faces. It follows that
$$
\begin{aligned}
& \sum_{k=3}^{M} a_{k}=F \\
& \sum_{k=3}^{M} \frac{k a_{k}}{2}=E \\
& \sum_{k=3}^{M} \frac{k a_{k}}{3} \geq V
\end{aligned}
$$
and in particular
$$
\sum_{k=3}^{M} a_{k}\left(1-\frac{k}{2}+\frac{k}{3}\right) \geq F-E+V=2
$$
by Euler's formula. But on the other hand, $a_{k} \leq n$ by assumption, so
$$
\begin{aligned}
2 & \leq \sum_{k=3}^{M} a_{k}\left(1-\frac{k}{6}\right) \\
& \leq \sum_{k=3}^{M} n\left(1-\frac{k}{6}\right) \\
& =\sum_{k=3}^{8} n\left(1-\frac{k}{6}\right)+\sum_{k=9}^{M} n\left(1-\frac{k}{6}\right) \\
& \leq \frac{1}{2} n-\frac{1}{2} n(M-8)
\end{aligned}
$$
where the last step follows from the fact that $1-\frac{k}{6} \leq-\frac{1}{2}$ for $k \geq 9$. Thus
$$
2 \leq \frac{9}{2} n-\frac{1}{2} n M \Longrightarrow M \leq \frac{\frac{9}{2} n-2}{\frac{1}{2} n}<9
$$
contradicting the fact that $M>8$. It follows that $M \leq 8$, and as each face has at least 3 edges, the result follows directly from Pigeonhole.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-team-solutions.jsonl",
"problem_match": "\n3. [30]",
"solution_match": "\nProposed by: Alexander Katz\n"
}
|
6555959c-ac05-5744-9509-483f87469bfd
| 609,704
|
Let $w=w_{1} w_{2} \ldots w_{n}$ be a word. Define a substring of $w$ to be a word of the form $w_{i} w_{i+1} \ldots w_{j-1} w_{j}$, for some pair of positive integers $1 \leq i \leq j \leq n$. Show that $w$ has at most $n$ distinct palindromic substrings.
For example, aaaaa has 5 distinct palindromic substrings, and abcata has 5 ( $a, b, c, t, a t a)$.
|
For each palindrome substring appearing in $w$, consider only the leftmost position in which is appears. I claim that now, no two substrings share the same right endpoint. If some two do, then you can reflect the smaller one about the center of the larger one to move the smaller one left.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $w=w_{1} w_{2} \ldots w_{n}$ be a word. Define a substring of $w$ to be a word of the form $w_{i} w_{i+1} \ldots w_{j-1} w_{j}$, for some pair of positive integers $1 \leq i \leq j \leq n$. Show that $w$ has at most $n$ distinct palindromic substrings.
For example, aaaaa has 5 distinct palindromic substrings, and abcata has 5 ( $a, b, c, t, a t a)$.
|
For each palindrome substring appearing in $w$, consider only the leftmost position in which is appears. I claim that now, no two substrings share the same right endpoint. If some two do, then you can reflect the smaller one about the center of the larger one to move the smaller one left.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-team-solutions.jsonl",
"problem_match": "\n4. [35]",
"solution_match": "\nProposed by: Yang Liu\n"
}
|
f95c28f0-9ae8-5d9d-8426-69204cff1831
| 609,705
|
Let $A B C$ be an acute triangle. The altitudes $B E$ and $C F$ intersect at the orthocenter $H$, and point $O$ denotes the circumcenter. Point $P$ is chosen so that $\angle A P H=\angle O P E=90^{\circ}$, and point $Q$ is chosen so that $\angle A Q H=\angle O Q F=90^{\circ}$. Lines $E P$ and $F Q$ meet at point $T$. Prove that points $A, T, O$ are collinear.
|
Observe that $T$ is the radical center of the circles with diameter $O E, O F, A H$. So $T$ lies on the radical axis of $(O E),(O F)$ which is the altitude from $O$ to $E F$, hence passing through $A$.
So $A T O$ are collinear, done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle. The altitudes $B E$ and $C F$ intersect at the orthocenter $H$, and point $O$ denotes the circumcenter. Point $P$ is chosen so that $\angle A P H=\angle O P E=90^{\circ}$, and point $Q$ is chosen so that $\angle A Q H=\angle O Q F=90^{\circ}$. Lines $E P$ and $F Q$ meet at point $T$. Prove that points $A, T, O$ are collinear.
|
Observe that $T$ is the radical center of the circles with diameter $O E, O F, A H$. So $T$ lies on the radical axis of $(O E),(O F)$ which is the altitude from $O$ to $E F$, hence passing through $A$.
So $A T O$ are collinear, done.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-team-solutions.jsonl",
"problem_match": "\n5. [35]",
"solution_match": "\n## Proposed by: Evan Chen\n\n"
}
|
1e7085ef-fc78-5f7a-aa36-14516f8faf7a
| 609,706
|
Let $r$ be a positive integer. Show that if a graph $G$ has no cycles of length at most $2 r$, then it has at most $|V|^{2016}$ cycles of length exactly $2016 r$, where $|V|$ denotes the number of vertices in the graph $G$.
|
The key idea is that there is at most 1 path of length $r$ between any pair of vertices, or else you get a cycle of length $\leq 2 r$. Now, start at any vertex ( $|V|$ choices) and walk 2015 times. There's at most $|V|^{2016}$ ways to do this by the previous argument. Now you have to go from the end to the start, and there's only one way to do this. So we're done.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $r$ be a positive integer. Show that if a graph $G$ has no cycles of length at most $2 r$, then it has at most $|V|^{2016}$ cycles of length exactly $2016 r$, where $|V|$ denotes the number of vertices in the graph $G$.
|
The key idea is that there is at most 1 path of length $r$ between any pair of vertices, or else you get a cycle of length $\leq 2 r$. Now, start at any vertex ( $|V|$ choices) and walk 2015 times. There's at most $|V|^{2016}$ ways to do this by the previous argument. Now you have to go from the end to the start, and there's only one way to do this. So we're done.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-team-solutions.jsonl",
"problem_match": "\n6. [40]",
"solution_match": "\nProposed by: Yang Liu\n"
}
|
a2c60ac5-07c3-530a-b820-f75c07870b0d
| 609,707
|
Let $p$ be a prime. A complete residue class modulo $p$ is a set containing at least one element equivalent to $k(\bmod p)$ for all $k$.
(a) (20) Show that there exists an $n$ such that the $n$th row of Pascal's triangle forms a complete residue class modulo $p$.
(b) (25) Show that there exists an $n \leq p^{2}$ such that the $n$th row of Pascal's triangle forms a complete residue class modulo $p$.
|
We use the following theorem of Lucas:
Theorem. Given a prime $p$ and nonnegative integers $a, b$ written in base $p$ as $a={\overline{a_{n}} a_{n-1} \ldots a_{0}}_{p}$ and $b=\overline{b_{n} b_{n-1} \ldots b_{0}}$ respectively, where $0 \leq a_{i}, b_{i} \leq p-1$ for $0 \leq i \leq n$, we have
$$
\binom{a}{b}=\prod_{i=0}^{n}\binom{a_{i}}{b_{i}} \quad(\bmod p)
$$
Now, let $n=(p-1) \times p+(p-2)=p^{2}-2$. For $k=p q+r$ with $0 \leq q, r \leq p-1$, applying Lucas's theorem gives
$$
\binom{n}{k} \equiv\binom{p-1}{q}\binom{p-2}{r} \quad(\bmod p)
$$
Note that
$$
\binom{p-1}{q}=\prod_{i=1}^{q} \frac{p-i}{i} \equiv(-1)^{q} \quad(\bmod p)
$$
and
$$
\binom{p-2}{r}=\prod_{i=1}^{r} \frac{p-1-i}{i} \equiv(-1)^{r} \frac{(r+1)!}{r!}=(-1)^{r}(r+1) \quad(\bmod p)
$$
So for $2 \leq i \leq p$ we can take $k=(p+1)(i-1)$ and obtain $\binom{n}{k} \equiv i(\bmod p)$, while for $i=1$ we can take $k=0$. Thus this row satisfies the desired property.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $p$ be a prime. A complete residue class modulo $p$ is a set containing at least one element equivalent to $k(\bmod p)$ for all $k$.
(a) (20) Show that there exists an $n$ such that the $n$th row of Pascal's triangle forms a complete residue class modulo $p$.
(b) (25) Show that there exists an $n \leq p^{2}$ such that the $n$th row of Pascal's triangle forms a complete residue class modulo $p$.
|
We use the following theorem of Lucas:
Theorem. Given a prime $p$ and nonnegative integers $a, b$ written in base $p$ as $a={\overline{a_{n}} a_{n-1} \ldots a_{0}}_{p}$ and $b=\overline{b_{n} b_{n-1} \ldots b_{0}}$ respectively, where $0 \leq a_{i}, b_{i} \leq p-1$ for $0 \leq i \leq n$, we have
$$
\binom{a}{b}=\prod_{i=0}^{n}\binom{a_{i}}{b_{i}} \quad(\bmod p)
$$
Now, let $n=(p-1) \times p+(p-2)=p^{2}-2$. For $k=p q+r$ with $0 \leq q, r \leq p-1$, applying Lucas's theorem gives
$$
\binom{n}{k} \equiv\binom{p-1}{q}\binom{p-2}{r} \quad(\bmod p)
$$
Note that
$$
\binom{p-1}{q}=\prod_{i=1}^{q} \frac{p-i}{i} \equiv(-1)^{q} \quad(\bmod p)
$$
and
$$
\binom{p-2}{r}=\prod_{i=1}^{r} \frac{p-1-i}{i} \equiv(-1)^{r} \frac{(r+1)!}{r!}=(-1)^{r}(r+1) \quad(\bmod p)
$$
So for $2 \leq i \leq p$ we can take $k=(p+1)(i-1)$ and obtain $\binom{n}{k} \equiv i(\bmod p)$, while for $i=1$ we can take $k=0$. Thus this row satisfies the desired property.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-team-solutions.jsonl",
"problem_match": "\n7. [45]",
"solution_match": "\nProposed by: Alexander Katz\n"
}
|
093bb7db-5106-54ac-8a0c-2a407b8b6877
| 609,708
|
Does there exist an irrational number $\alpha>1$ such that
$$
\left\lfloor\alpha^{n}\right\rfloor \equiv 0 \quad(\bmod 2017)
$$
for all integers $n \geq 1$ ?
|
Answer: Yes
Let $\alpha>1$ and $0<\beta<1$ be the roots of $x^{2}-4035 x+2017$. Then note that $\left\lfloor\alpha^{n}\right\rfloor=\alpha^{n}+\beta^{n}-1$. Let $x_{n}=\alpha^{n}+\beta^{n}$ for all nonnegative integers $n$. It's easy to verify that $x_{n}=4035 x_{n-1}-2017 x_{n-2} \equiv x_{n-1}$ $(\bmod 2017)$ so since $x_{1}=4035 \equiv 1(\bmod 2017)$ we have that $x_{n} \equiv 1(\bmod 2017)$ for all $n$. Thus $\alpha$ satisfies the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Does there exist an irrational number $\alpha>1$ such that
$$
\left\lfloor\alpha^{n}\right\rfloor \equiv 0 \quad(\bmod 2017)
$$
for all integers $n \geq 1$ ?
|
Answer: Yes
Let $\alpha>1$ and $0<\beta<1$ be the roots of $x^{2}-4035 x+2017$. Then note that $\left\lfloor\alpha^{n}\right\rfloor=\alpha^{n}+\beta^{n}-1$. Let $x_{n}=\alpha^{n}+\beta^{n}$ for all nonnegative integers $n$. It's easy to verify that $x_{n}=4035 x_{n-1}-2017 x_{n-2} \equiv x_{n-1}$ $(\bmod 2017)$ so since $x_{1}=4035 \equiv 1(\bmod 2017)$ we have that $x_{n} \equiv 1(\bmod 2017)$ for all $n$. Thus $\alpha$ satisfies the problem.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-team-solutions.jsonl",
"problem_match": "\n8. [45]",
"solution_match": "\nProposed by: Sam Korsky\n"
}
|
8ff45023-b05b-5ffa-af99-55c410ff1848
| 609,709
|
Let $n$ be a positive odd integer greater than 2 , and consider a regular $n$-gon $\mathcal{G}$ in the plane centered at the origin. Let a subpolygon $\mathcal{G}^{\prime}$ be a polygon with at least 3 vertices whose vertex set is a subset of that of $\mathcal{G}$. Say $\mathcal{G}^{\prime}$ is well-centered if its centroid is the origin. Also, say $\mathcal{G}^{\prime}$ is decomposable if its vertex set can be written as the disjoint union of regular polygons with at least 3 vertices. Show that all well-centered subpolygons are decomposable if and only if $n$ has at most two distinct prime divisors.
|
$\Rightarrow$, i.e. $n$ has $\geq 3$ prime divisors: Let $n=\prod p_{i}^{e_{i}}$. Note it suffices to only consider regular $p_{i}$-gons. Label the vertices of the $n$-gon $0,1, \ldots, n-1$. Let $S=\left\{\frac{x n}{p_{1}}: 0 \leq x \leq p_{1}-1\right\}$, and let $S_{j}=S+\frac{j n}{p_{3}}$ for $0 \leq j \leq p_{3}-2 .\left(S+a=\{s+a: s \in S\}\right.$.) Then let $S_{p_{3}-1}=\left\{\frac{x n}{p_{2}}: 0 \leq x \leq p_{2}-1\right\}+\frac{\left(p_{3}-1\right) n}{p_{3}}$. Finally, let $S^{\prime}=\left\{\frac{x n}{p_{3}}: 0 \leq x \leq p_{3}-1\right\}$. Then I claim
$$
\left(\bigsqcup_{i=0}^{p_{3}-1} S_{i}\right) \backslash S^{\prime}
$$
is well-centered but not decomposable. Well-centered follows from the construction: I only added and subtracted off regular polygons. To show that its decomposable, consider $\frac{n}{p_{1}}$. Clearly this is in the set, but isn't in $S^{\prime}$. I claim that $\frac{n}{p_{1}}$ isn't in any more regular $p_{i}$-gons. For $i \geq 4$, this means that $\frac{n}{p_{1}}+\frac{n}{p_{i}}$ is in some set. But this is a contradiction, as we can easily check that all points we added in are multiples of $p_{i}^{e_{i}}$, while $\frac{n}{p_{i}}$ isn't.
For $i=1$, note that 0 was removed by $S^{\prime}$. For $i=2$, note that the only multiples of $p_{3}^{e_{3}}$ that are in some $S_{j}$ are $0, \frac{n}{p_{1}}, \ldots, \frac{\left(p_{1}-1\right) n}{p_{1}}$. In particular, $\frac{n}{p_{1}}+\frac{n}{p_{2}}$ isn't in any $S_{j}$. So it suffices to consider the case $i=3$, but it is easy to show that $\frac{n}{p_{1}}+\frac{\left(p_{3}-1\right) n}{p_{3}}$ isn't in any $S_{i}$. So we're done.
$\Leftarrow$, i.e. $n$ has $\leq 2$ prime divisors: This part seems to require knowledge of cyclotomic polynomials. These will easily give a solution in the case $n=p^{a}$. Now, instead turn to the case $n=p^{a} q^{b}$. The next lemma is the key ingredient to the solution.
Lemma: Every well-centered subpolygon can be gotten by adding in and subtracting off regular polygons.
Note that this is weaker than the problem claim, as the problem claims that adding in polygons is enough.
Proof. It is easy to verify that $\phi_{n}(x)=\frac{\left(x^{n}-1\right)\left(x^{\frac{n}{p q}}-1\right)}{\left(x^{\frac{n}{p}}-1\right)\left(x^{\frac{n}{q}}-1\right)}$. Therefore, it suffices to check that there exist integer polynomials $c(x), d(x)$ such that
$$
\frac{x^{n}-1}{x^{\frac{n}{p}}-1} \cdot c(x)+\frac{x^{n}-1}{x^{\frac{n}{q}}-1} \cdot d(x)=\frac{\left(x^{n}-1\right)\left(x^{\frac{n}{p q}}-1\right)}{\left(x^{\frac{n}{p}}-1\right)\left(x^{\frac{n}{q}}-1\right)}
$$
Rearranging means that we want
$$
\left(x^{\frac{n}{q}}-1\right) \cdot c(x)+\left(x^{\frac{n}{p}}-1\right) \cdot d(x)=x^{\frac{n}{p q}}-1 .
$$
But now, since $\underset{\substack{s n}}{\operatorname{gcd}}(n / p, n / q) \underset{\substack{s n}}{=n / p q}$, there exist positive integers $s, t$ such that $\frac{s n}{q}-\frac{t n}{p}=\frac{n}{p q}$. Now choose $c(x)=\frac{x^{\frac{s n}{q}}-1}{x^{\frac{n}{q}}-1}, d(x)=\frac{x^{\frac{s n}{q}}-x^{\frac{n}{p q}}}{x^{\frac{n}{p}}-1}$ to finish.
Now we can finish combinatorially. Say we need subtraction, and at some point we subtract off a $p$-gon. All the points in the $p$-gon must have been added at some point. If any of them was added from a $p$-gon, we could just cancel both $p$-gons. If they all came from a $q$-gon, then the sum of those $p q$-gons would be a $p q$-gon, which could have been instead written as the sum of $q p$-gons. So we don't need subtraction either way. This completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $n$ be a positive odd integer greater than 2 , and consider a regular $n$-gon $\mathcal{G}$ in the plane centered at the origin. Let a subpolygon $\mathcal{G}^{\prime}$ be a polygon with at least 3 vertices whose vertex set is a subset of that of $\mathcal{G}$. Say $\mathcal{G}^{\prime}$ is well-centered if its centroid is the origin. Also, say $\mathcal{G}^{\prime}$ is decomposable if its vertex set can be written as the disjoint union of regular polygons with at least 3 vertices. Show that all well-centered subpolygons are decomposable if and only if $n$ has at most two distinct prime divisors.
|
$\Rightarrow$, i.e. $n$ has $\geq 3$ prime divisors: Let $n=\prod p_{i}^{e_{i}}$. Note it suffices to only consider regular $p_{i}$-gons. Label the vertices of the $n$-gon $0,1, \ldots, n-1$. Let $S=\left\{\frac{x n}{p_{1}}: 0 \leq x \leq p_{1}-1\right\}$, and let $S_{j}=S+\frac{j n}{p_{3}}$ for $0 \leq j \leq p_{3}-2 .\left(S+a=\{s+a: s \in S\}\right.$.) Then let $S_{p_{3}-1}=\left\{\frac{x n}{p_{2}}: 0 \leq x \leq p_{2}-1\right\}+\frac{\left(p_{3}-1\right) n}{p_{3}}$. Finally, let $S^{\prime}=\left\{\frac{x n}{p_{3}}: 0 \leq x \leq p_{3}-1\right\}$. Then I claim
$$
\left(\bigsqcup_{i=0}^{p_{3}-1} S_{i}\right) \backslash S^{\prime}
$$
is well-centered but not decomposable. Well-centered follows from the construction: I only added and subtracted off regular polygons. To show that its decomposable, consider $\frac{n}{p_{1}}$. Clearly this is in the set, but isn't in $S^{\prime}$. I claim that $\frac{n}{p_{1}}$ isn't in any more regular $p_{i}$-gons. For $i \geq 4$, this means that $\frac{n}{p_{1}}+\frac{n}{p_{i}}$ is in some set. But this is a contradiction, as we can easily check that all points we added in are multiples of $p_{i}^{e_{i}}$, while $\frac{n}{p_{i}}$ isn't.
For $i=1$, note that 0 was removed by $S^{\prime}$. For $i=2$, note that the only multiples of $p_{3}^{e_{3}}$ that are in some $S_{j}$ are $0, \frac{n}{p_{1}}, \ldots, \frac{\left(p_{1}-1\right) n}{p_{1}}$. In particular, $\frac{n}{p_{1}}+\frac{n}{p_{2}}$ isn't in any $S_{j}$. So it suffices to consider the case $i=3$, but it is easy to show that $\frac{n}{p_{1}}+\frac{\left(p_{3}-1\right) n}{p_{3}}$ isn't in any $S_{i}$. So we're done.
$\Leftarrow$, i.e. $n$ has $\leq 2$ prime divisors: This part seems to require knowledge of cyclotomic polynomials. These will easily give a solution in the case $n=p^{a}$. Now, instead turn to the case $n=p^{a} q^{b}$. The next lemma is the key ingredient to the solution.
Lemma: Every well-centered subpolygon can be gotten by adding in and subtracting off regular polygons.
Note that this is weaker than the problem claim, as the problem claims that adding in polygons is enough.
Proof. It is easy to verify that $\phi_{n}(x)=\frac{\left(x^{n}-1\right)\left(x^{\frac{n}{p q}}-1\right)}{\left(x^{\frac{n}{p}}-1\right)\left(x^{\frac{n}{q}}-1\right)}$. Therefore, it suffices to check that there exist integer polynomials $c(x), d(x)$ such that
$$
\frac{x^{n}-1}{x^{\frac{n}{p}}-1} \cdot c(x)+\frac{x^{n}-1}{x^{\frac{n}{q}}-1} \cdot d(x)=\frac{\left(x^{n}-1\right)\left(x^{\frac{n}{p q}}-1\right)}{\left(x^{\frac{n}{p}}-1\right)\left(x^{\frac{n}{q}}-1\right)}
$$
Rearranging means that we want
$$
\left(x^{\frac{n}{q}}-1\right) \cdot c(x)+\left(x^{\frac{n}{p}}-1\right) \cdot d(x)=x^{\frac{n}{p q}}-1 .
$$
But now, since $\underset{\substack{s n}}{\operatorname{gcd}}(n / p, n / q) \underset{\substack{s n}}{=n / p q}$, there exist positive integers $s, t$ such that $\frac{s n}{q}-\frac{t n}{p}=\frac{n}{p q}$. Now choose $c(x)=\frac{x^{\frac{s n}{q}}-1}{x^{\frac{n}{q}}-1}, d(x)=\frac{x^{\frac{s n}{q}}-x^{\frac{n}{p q}}}{x^{\frac{n}{p}}-1}$ to finish.
Now we can finish combinatorially. Say we need subtraction, and at some point we subtract off a $p$-gon. All the points in the $p$-gon must have been added at some point. If any of them was added from a $p$-gon, we could just cancel both $p$-gons. If they all came from a $q$-gon, then the sum of those $p q$-gons would be a $p q$-gon, which could have been instead written as the sum of $q p$-gons. So we don't need subtraction either way. This completes the proof.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-team-solutions.jsonl",
"problem_match": "\n9. [65]",
"solution_match": "\nProposed by: Yang Liu\n"
}
|
c5797b53-1979-507e-aeba-2194d3565419
| 609,710
|
Let $L B C$ be a fixed triangle with $L B=L C$, and let $A$ be a variable point on arc $L B$ of its circumcircle. Let $I$ be the incenter of $\triangle A B C$ and $\overline{A K}$ the altitude from $A$. The circumcircle of $\triangle I K L$ intersects lines $K A$ and $B C$ again at $U \neq K$ and $V \neq K$. Finally, let $T$ be the projection of $I$ onto line $U V$. Prove that the line through $T$ and the midpoint of $\overline{I K}$ passes through a fixed point as $A$ varies.
|
## Answer:
Let $M$ be the midpoint of arc $B C$ not containing $L$ and let $D$ be the point where the incircle of triangle $A B C$ touches $B C$. Also let $N$ be the projection from $I$ to $A K$. We claim that $M$ is the desired fixed point.
By Simson's Theorem on triangle $K U V$ and point $I$ we have that points $T, D, N$ are collinear and since quadrilateral $N K D I$ is a rectangle we have that line $D N$ passes through the midpoint of $I K$. Thus it suffices to show that $M$ lies on line $D N$.
Now, let $I_{a}, I_{b}, I_{c}$ be the $A, B, C$-excenters of triangle $A B C$ respectively. Then $I$ is the orthocenter of triangle $I_{a} I_{b} I_{c}$ and $A B C$ is the Cevian triangle of $I$ with respect to triangle $I_{a} I_{b} I_{c}$. It's also well-known that $M$ is the midpoint of $I I_{a}$.
Let $D^{\prime}$ be the reflection of $I$ over $B C$ and let $N^{\prime}$ be the reflection of $I$ over $A K$. Clearly $K$ is the midpoint of $D^{\prime} N^{\prime}$. If we could prove that $I_{a}, D^{\prime}, K, N^{\prime}$ were collinear then by taking a homothety centered at $I$ with ratio $\frac{1}{2}$ we would have that points $M, D, N$ were collinear as desired. Thus it suffices to show that points $I_{a}, D^{\prime}, K$ are collinear.
Let lines $B C$ and $I_{b} I_{c}$ intersect at $R$ and let lines $A I$ and $B C$ intersect at $S$. Then it's well-known that ( $I_{b}, I_{c} ; A, R$ ) is harmonic and projecting from $C$ we have that $\left(I_{a}, I ; S, A\right)$ is harmonic. But $K S \perp K A$ which means that $K S$ bisects angle $\angle I K I_{a}$. But it's clear by the definition of $D^{\prime}$ that $K S$ bisects angle $\angle I K D^{\prime}$ which implies that points $I_{a}, K, D^{\prime}$ are collinear as desired. This completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $L B C$ be a fixed triangle with $L B=L C$, and let $A$ be a variable point on arc $L B$ of its circumcircle. Let $I$ be the incenter of $\triangle A B C$ and $\overline{A K}$ the altitude from $A$. The circumcircle of $\triangle I K L$ intersects lines $K A$ and $B C$ again at $U \neq K$ and $V \neq K$. Finally, let $T$ be the projection of $I$ onto line $U V$. Prove that the line through $T$ and the midpoint of $\overline{I K}$ passes through a fixed point as $A$ varies.
|
## Answer:
Let $M$ be the midpoint of arc $B C$ not containing $L$ and let $D$ be the point where the incircle of triangle $A B C$ touches $B C$. Also let $N$ be the projection from $I$ to $A K$. We claim that $M$ is the desired fixed point.
By Simson's Theorem on triangle $K U V$ and point $I$ we have that points $T, D, N$ are collinear and since quadrilateral $N K D I$ is a rectangle we have that line $D N$ passes through the midpoint of $I K$. Thus it suffices to show that $M$ lies on line $D N$.
Now, let $I_{a}, I_{b}, I_{c}$ be the $A, B, C$-excenters of triangle $A B C$ respectively. Then $I$ is the orthocenter of triangle $I_{a} I_{b} I_{c}$ and $A B C$ is the Cevian triangle of $I$ with respect to triangle $I_{a} I_{b} I_{c}$. It's also well-known that $M$ is the midpoint of $I I_{a}$.
Let $D^{\prime}$ be the reflection of $I$ over $B C$ and let $N^{\prime}$ be the reflection of $I$ over $A K$. Clearly $K$ is the midpoint of $D^{\prime} N^{\prime}$. If we could prove that $I_{a}, D^{\prime}, K, N^{\prime}$ were collinear then by taking a homothety centered at $I$ with ratio $\frac{1}{2}$ we would have that points $M, D, N$ were collinear as desired. Thus it suffices to show that points $I_{a}, D^{\prime}, K$ are collinear.
Let lines $B C$ and $I_{b} I_{c}$ intersect at $R$ and let lines $A I$ and $B C$ intersect at $S$. Then it's well-known that ( $I_{b}, I_{c} ; A, R$ ) is harmonic and projecting from $C$ we have that $\left(I_{a}, I ; S, A\right)$ is harmonic. But $K S \perp K A$ which means that $K S$ bisects angle $\angle I K I_{a}$. But it's clear by the definition of $D^{\prime}$ that $K S$ bisects angle $\angle I K D^{\prime}$ which implies that points $I_{a}, K, D^{\prime}$ are collinear as desired. This completes the proof.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-team-solutions.jsonl",
"problem_match": "\n10. [65]",
"solution_match": "\nProposed by: Sam Korsky\n\n"
}
|
3323c1f2-e60e-5153-91d5-c3e6f92e8620
| 609,711
|
Let $S=\{1,2 \ldots, n\}$ for some positive integer $n$, and let $A$ be an $n$-by- $n$ matrix having as entries only ones and zeros. Define an infinite sequence $\left\{x_{i}\right\}_{i \geq 0}$ to be strange if:
- $x_{i} \in S$ for all $i$,
- $a_{x_{k} x_{k+1}}=1$ for all $k$, where $a_{i j}$ denotes the element in the $i^{\text {th }}$ row and $j^{\text {th }}$ column of $A$.
Prove that the set of strange sequences is empty if and only if $A$ is nilpotent, i.e. $A^{m}=0$ for some integer $m$.
|
Answer:
Consider the directed graph $G$ on $n$ labeled vertices whose adjacency matrix is $A$. Then, observe that a strange sequence is simply an infinite path on $G$. Since powers of the adjacency matrix count paths, if $A$ is nilpotent, there exists no infinite path. If $A$ is not nilpotent, a cycle must exist, so we're done.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $S=\{1,2 \ldots, n\}$ for some positive integer $n$, and let $A$ be an $n$-by- $n$ matrix having as entries only ones and zeros. Define an infinite sequence $\left\{x_{i}\right\}_{i \geq 0}$ to be strange if:
- $x_{i} \in S$ for all $i$,
- $a_{x_{k} x_{k+1}}=1$ for all $k$, where $a_{i j}$ denotes the element in the $i^{\text {th }}$ row and $j^{\text {th }}$ column of $A$.
Prove that the set of strange sequences is empty if and only if $A$ is nilpotent, i.e. $A^{m}=0$ for some integer $m$.
|
Answer:
Consider the directed graph $G$ on $n$ labeled vertices whose adjacency matrix is $A$. Then, observe that a strange sequence is simply an infinite path on $G$. Since powers of the adjacency matrix count paths, if $A$ is nilpotent, there exists no infinite path. If $A$ is not nilpotent, a cycle must exist, so we're done.
|
{
"resource_path": "HarvardMIT/segmented/en-204-tournaments-2017-hmic-solutions.jsonl",
"problem_match": "\n2. [7]",
"solution_match": "\nProposed by: Henrik Boecken\n"
}
|
ed798be6-6485-5981-8c9b-3d98a6966e04
| 609,713
|
Let $G$ be a weighted bipartite graph $A \cup B$, with $|A|=|B|=n$. In other words, each edge in the graph is assigned a positive integer value, called its weight. Also, define the weight of a perfect matching in $G$ to be the sum of the weights of the edges in the matching.
Let $G^{\prime}$ be the graph with vertex set $A \cup B$, and contains the edge $e$ if and only if $e$ is part of some minimum weight perfect matching in $G$.
Show that all perfect matchings in $G^{\prime}$ have the same weight.
|
Let $m$ denote the minimum weight of a matching in $G$. Let $G^{\prime \prime}$ be the (multi)graph formed by taking the union of all minimum weight perfect matchings, but keeping edges multiple times. Note that $G^{\prime \prime}$ is regular. Now, assume that some perfect matching in $G^{\prime}$ (equivalently $G^{\prime \prime}$ ) has weight $M>m$. Delete this matching from $G^{\prime \prime}$, and call the resulting graph $H . H$ is still regular, so it can be decomposed into a union of perfect matchings. Now using pigeonhole directly gives us a contradiction.
To show that all regular bipartite graphs can be decomposed into a union of perfect matchings, use Hall's marriage lemma to take out one perfect matching and use induction.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $G$ be a weighted bipartite graph $A \cup B$, with $|A|=|B|=n$. In other words, each edge in the graph is assigned a positive integer value, called its weight. Also, define the weight of a perfect matching in $G$ to be the sum of the weights of the edges in the matching.
Let $G^{\prime}$ be the graph with vertex set $A \cup B$, and contains the edge $e$ if and only if $e$ is part of some minimum weight perfect matching in $G$.
Show that all perfect matchings in $G^{\prime}$ have the same weight.
|
Let $m$ denote the minimum weight of a matching in $G$. Let $G^{\prime \prime}$ be the (multi)graph formed by taking the union of all minimum weight perfect matchings, but keeping edges multiple times. Note that $G^{\prime \prime}$ is regular. Now, assume that some perfect matching in $G^{\prime}$ (equivalently $G^{\prime \prime}$ ) has weight $M>m$. Delete this matching from $G^{\prime \prime}$, and call the resulting graph $H . H$ is still regular, so it can be decomposed into a union of perfect matchings. Now using pigeonhole directly gives us a contradiction.
To show that all regular bipartite graphs can be decomposed into a union of perfect matchings, use Hall's marriage lemma to take out one perfect matching and use induction.
|
{
"resource_path": "HarvardMIT/segmented/en-204-tournaments-2017-hmic-solutions.jsonl",
"problem_match": "\n4. [9]",
"solution_match": "\nProposed by: Yang Liu\n"
}
|
8e09df0a-ecf3-5fe7-a4fd-e68073562231
| 609,715
|
Let $S$ be the set $\{-1,1\}^{n}$, that is, $n$-tuples such that each coordinate is either -1 or 1 . For
$$
s=\left(s_{1}, s_{2}, \ldots, s_{n}\right), t=\left(t_{1}, t_{2}, \ldots, t_{n}\right) \in\{-1,1\}^{n}
$$
define $s \odot t=\left(s_{1} t_{1}, s_{2} t_{2}, \ldots, s_{n} t_{n}\right)$.
Let $c$ be a positive constant, and let $f: S \rightarrow\{-1,1\}$ be a function such that there are at least $(1-c) \cdot 2^{2 n}$ pairs $(s, t)$ with $s, t \in S$ such that $f(s \odot t)=f(s) f(t)$. Show that there exists a function $f^{\prime}$ such that $f^{\prime}(s \odot t)=f^{\prime}(s) f^{\prime}(t)$ for all $s, t \in S$ and $f(s)=f^{\prime}(s)$ for at least $(1-10 c) \cdot 2^{n}$ values of $s \in S$.
|
We use finite fourier analysis, which we explain the setup for below. For a subset $T \subseteq S$, define the function $\chi_{T}: S \rightarrow\{-1,1\}$ to satisfy $\chi_{T}(s)=\prod_{t \in T} s_{t}$. Note that $\chi_{T}(s \odot t)=\chi_{T}(s) \chi_{T}(t)$ for all $s, t \in S$. Therefore, we should show that there exists a subset $T$ such that taking $f^{\prime}=\chi_{T}$ satisfies the constraint. This subset $T$ also has to exist, as the $\chi_{T}$ are all the multiplicative functions from $S \rightarrow\{-1,1\}$. Also, for two functions $f, g: S \rightarrow \mathbb{R}$ define
$$
\langle f, g\rangle=\frac{1}{2^{n}} \sum_{s \in S} f(s) g(s)
$$
Now we claim a few facts below that are easy to verify. One, for any subsets $T_{1}, T_{2} \in S$ we have that
$$
\left\langle\chi_{T_{1}}, \chi_{T_{2}}\right\rangle=\left\{\begin{array}{l}
0 \text { if } T_{1} \neq T_{2} \\
1 \text { if } T_{1}=T_{2}
\end{array}\right.
$$
We will refer to this claim as orthogonality. Also, note that for any function $f: S \rightarrow \mathbb{R}$, we can write
$$
f=\sum_{T \subseteq S}\left\langle f, \chi_{T}\right\rangle \chi_{T}
$$
This is called expressing $f$ by its Fourier basis. By the given condition, we have that
$$
\sum_{s, t \in S} f(s \odot t) f(s) f(t)=1-2 c
$$
Expanding the left-hand side in terms of the Fourier basis, we get that
$$
\begin{gathered}
1-2 c=\frac{1}{2^{2 n}} \sum_{s, t \in S} f(s \odot t) f(s) f(t)=\frac{1}{2^{2 n}} \sum_{T_{1}, T_{2}, T_{3} \subseteq S} \sum_{s, t \in S}\left\langle f, \chi_{T_{1}}\right\rangle\left\langle f, \chi_{T_{2}}\right\rangle\left\langle f, \chi_{T_{3}}\right\rangle_{\chi_{1}}(s) \chi_{T_{1}}(t) \chi_{T_{2}}(s) \chi_{T_{3}}(t) \\
=\sum_{T_{1}, T_{2}, T_{3} \subseteq S}\left\langle f, \chi_{T_{1}}\right\rangle\left\langle f, \chi_{T_{2}}\right\rangle\left\langle f, \chi_{T_{3}}\right\rangle\left\langle\chi_{T_{1}}, \chi_{T_{2}}\right\rangle\left\langle\chi_{T_{1}}, \chi_{T_{3}}\right\rangle=\sum_{T \subseteq S}\left\langle f, \chi_{T}\right\rangle^{3}
\end{gathered}
$$
by orthogonality. Also note by orthogonality that
$$
1=\langle f, f\rangle=\left\langle\sum_{T_{1} \subseteq S}\left\langle f, T_{1}\right\rangle \chi_{T_{1}}(s), \sum_{T_{2} \subseteq S}\left\langle f, T_{2}\right\rangle \chi_{T_{2}}(s)\right\rangle=\sum_{T \subseteq S}\left\langle f, \chi_{T}\right\rangle^{2}
$$
Finally, from above we have that
$$
1-2 c=\sum_{T \subseteq S}\left\langle f, \chi_{T}\right\rangle^{3} \leq\left(\max _{T \subseteq S}\left\langle f, \chi_{T}\right\rangle\right) \sum_{T \subseteq S}\left\langle f, \chi_{T}\right\rangle^{2}=\max _{T \subseteq S}\left\langle f, \chi_{T}\right\rangle
$$
This last equation implies that some $\chi_{T}$ and $f$ agree on $(1-c) \cdot 2^{n}$ values, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $S$ be the set $\{-1,1\}^{n}$, that is, $n$-tuples such that each coordinate is either -1 or 1 . For
$$
s=\left(s_{1}, s_{2}, \ldots, s_{n}\right), t=\left(t_{1}, t_{2}, \ldots, t_{n}\right) \in\{-1,1\}^{n}
$$
define $s \odot t=\left(s_{1} t_{1}, s_{2} t_{2}, \ldots, s_{n} t_{n}\right)$.
Let $c$ be a positive constant, and let $f: S \rightarrow\{-1,1\}$ be a function such that there are at least $(1-c) \cdot 2^{2 n}$ pairs $(s, t)$ with $s, t \in S$ such that $f(s \odot t)=f(s) f(t)$. Show that there exists a function $f^{\prime}$ such that $f^{\prime}(s \odot t)=f^{\prime}(s) f^{\prime}(t)$ for all $s, t \in S$ and $f(s)=f^{\prime}(s)$ for at least $(1-10 c) \cdot 2^{n}$ values of $s \in S$.
|
We use finite fourier analysis, which we explain the setup for below. For a subset $T \subseteq S$, define the function $\chi_{T}: S \rightarrow\{-1,1\}$ to satisfy $\chi_{T}(s)=\prod_{t \in T} s_{t}$. Note that $\chi_{T}(s \odot t)=\chi_{T}(s) \chi_{T}(t)$ for all $s, t \in S$. Therefore, we should show that there exists a subset $T$ such that taking $f^{\prime}=\chi_{T}$ satisfies the constraint. This subset $T$ also has to exist, as the $\chi_{T}$ are all the multiplicative functions from $S \rightarrow\{-1,1\}$. Also, for two functions $f, g: S \rightarrow \mathbb{R}$ define
$$
\langle f, g\rangle=\frac{1}{2^{n}} \sum_{s \in S} f(s) g(s)
$$
Now we claim a few facts below that are easy to verify. One, for any subsets $T_{1}, T_{2} \in S$ we have that
$$
\left\langle\chi_{T_{1}}, \chi_{T_{2}}\right\rangle=\left\{\begin{array}{l}
0 \text { if } T_{1} \neq T_{2} \\
1 \text { if } T_{1}=T_{2}
\end{array}\right.
$$
We will refer to this claim as orthogonality. Also, note that for any function $f: S \rightarrow \mathbb{R}$, we can write
$$
f=\sum_{T \subseteq S}\left\langle f, \chi_{T}\right\rangle \chi_{T}
$$
This is called expressing $f$ by its Fourier basis. By the given condition, we have that
$$
\sum_{s, t \in S} f(s \odot t) f(s) f(t)=1-2 c
$$
Expanding the left-hand side in terms of the Fourier basis, we get that
$$
\begin{gathered}
1-2 c=\frac{1}{2^{2 n}} \sum_{s, t \in S} f(s \odot t) f(s) f(t)=\frac{1}{2^{2 n}} \sum_{T_{1}, T_{2}, T_{3} \subseteq S} \sum_{s, t \in S}\left\langle f, \chi_{T_{1}}\right\rangle\left\langle f, \chi_{T_{2}}\right\rangle\left\langle f, \chi_{T_{3}}\right\rangle_{\chi_{1}}(s) \chi_{T_{1}}(t) \chi_{T_{2}}(s) \chi_{T_{3}}(t) \\
=\sum_{T_{1}, T_{2}, T_{3} \subseteq S}\left\langle f, \chi_{T_{1}}\right\rangle\left\langle f, \chi_{T_{2}}\right\rangle\left\langle f, \chi_{T_{3}}\right\rangle\left\langle\chi_{T_{1}}, \chi_{T_{2}}\right\rangle\left\langle\chi_{T_{1}}, \chi_{T_{3}}\right\rangle=\sum_{T \subseteq S}\left\langle f, \chi_{T}\right\rangle^{3}
\end{gathered}
$$
by orthogonality. Also note by orthogonality that
$$
1=\langle f, f\rangle=\left\langle\sum_{T_{1} \subseteq S}\left\langle f, T_{1}\right\rangle \chi_{T_{1}}(s), \sum_{T_{2} \subseteq S}\left\langle f, T_{2}\right\rangle \chi_{T_{2}}(s)\right\rangle=\sum_{T \subseteq S}\left\langle f, \chi_{T}\right\rangle^{2}
$$
Finally, from above we have that
$$
1-2 c=\sum_{T \subseteq S}\left\langle f, \chi_{T}\right\rangle^{3} \leq\left(\max _{T \subseteq S}\left\langle f, \chi_{T}\right\rangle\right) \sum_{T \subseteq S}\left\langle f, \chi_{T}\right\rangle^{2}=\max _{T \subseteq S}\left\langle f, \chi_{T}\right\rangle
$$
This last equation implies that some $\chi_{T}$ and $f$ agree on $(1-c) \cdot 2^{n}$ values, as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-204-tournaments-2017-hmic-solutions.jsonl",
"problem_match": "\n5. [11]",
"solution_match": "\n## Proposed by: Yang Liu\n\n"
}
|
65efb92e-316c-5d1f-9730-05a5306cbb3e
| 609,716
|
In an $n \times n$ square array of $1 \times 1$ cells, at least one cell is colored pink. Show that you can always divide the square into rectangles along cell borders such that each rectangle contains exactly one pink cell.
|
We claim that the statement is true for arbitrary rectangles. We proceed by induction on the number of marked cells. Our base case is $k=1$ marked cell, in which case the original rectangle works.
To prove it for $k$ marked cells, we split the rectangle into two smaller rectangles, both of which contains at least one marked cell. By induction, we can divide the two smaller rectangles into rectangles with exactly one marked cell. Combining these two sets of rectangles gives a way to divide our original rectangle into rectangles with exactly one marked cell, completing the induction.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
In an $n \times n$ square array of $1 \times 1$ cells, at least one cell is colored pink. Show that you can always divide the square into rectangles along cell borders such that each rectangle contains exactly one pink cell.
|
We claim that the statement is true for arbitrary rectangles. We proceed by induction on the number of marked cells. Our base case is $k=1$ marked cell, in which case the original rectangle works.
To prove it for $k$ marked cells, we split the rectangle into two smaller rectangles, both of which contains at least one marked cell. By induction, we can divide the two smaller rectangles into rectangles with exactly one marked cell. Combining these two sets of rectangles gives a way to divide our original rectangle into rectangles with exactly one marked cell, completing the induction.
|
{
"resource_path": "HarvardMIT/segmented/en-212-2018-feb-team-solutions.jsonl",
"problem_match": "\n1. [20]",
"solution_match": "\nProposed by: Kevin Sun\n"
}
|
e90f61a3-bea3-522f-9c74-58fee49dae86
| 609,846
|
Let $n \geq 2$ be a positive integer. A subset of positive integers $S$ is said to be comprehensive if for every integer $0 \leq x<n$, there is a subset of $S$ whose sum has remainder $x$ when divided by $n$. Note that the empty set has sum 0 . Show that if a set $S$ is comprehensive, then there is some (not necessarily proper) subset of $S$ with at most $n-1$ elements which is also comprehensive.
|
We will show that if $|S| \geq n$, we can remove one element from $S$ and still have a comprehensive set. Doing this repeatedly will always allow us to find a comprehensive subset of size at most $n-1$.
Write $S=\left\{s_{1}, s_{2}, \ldots, s_{k}\right\}$ for some $k \geq n$. Now start with the empty set and add in the elements $s_{i}$ in order. During this process, we will keep track of all possible remainders of sums of any subset.
If $T$ is the set of current remainders at any time, and we add an element $s_{i}$, the set of remainders will be $T \cup\left\{t+s_{i} \mid t \in T\right\}$. In particular, the set of remainders only depends on the previous set of remainders and the element we add in.
At the beginning of our process, the set of possible remainders is $\{0\}$ for the empty set. Since we assumed that $S$ is comprehensive, the final set is $\{0,1, \ldots, n\}$. The number of elements changes from 1 to $n-1$. However, since we added $k \geq n$ elements, at least one element did not change the size of our remainder set. This implies that adding this element did not contribute to making any new remainders and $S$ is still comprehensive without this element, proving our claim.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n \geq 2$ be a positive integer. A subset of positive integers $S$ is said to be comprehensive if for every integer $0 \leq x<n$, there is a subset of $S$ whose sum has remainder $x$ when divided by $n$. Note that the empty set has sum 0 . Show that if a set $S$ is comprehensive, then there is some (not necessarily proper) subset of $S$ with at most $n-1$ elements which is also comprehensive.
|
We will show that if $|S| \geq n$, we can remove one element from $S$ and still have a comprehensive set. Doing this repeatedly will always allow us to find a comprehensive subset of size at most $n-1$.
Write $S=\left\{s_{1}, s_{2}, \ldots, s_{k}\right\}$ for some $k \geq n$. Now start with the empty set and add in the elements $s_{i}$ in order. During this process, we will keep track of all possible remainders of sums of any subset.
If $T$ is the set of current remainders at any time, and we add an element $s_{i}$, the set of remainders will be $T \cup\left\{t+s_{i} \mid t \in T\right\}$. In particular, the set of remainders only depends on the previous set of remainders and the element we add in.
At the beginning of our process, the set of possible remainders is $\{0\}$ for the empty set. Since we assumed that $S$ is comprehensive, the final set is $\{0,1, \ldots, n\}$. The number of elements changes from 1 to $n-1$. However, since we added $k \geq n$ elements, at least one element did not change the size of our remainder set. This implies that adding this element did not contribute to making any new remainders and $S$ is still comprehensive without this element, proving our claim.
|
{
"resource_path": "HarvardMIT/segmented/en-212-2018-feb-team-solutions.jsonl",
"problem_match": "\n6. [35]",
"solution_match": "\nProposed by: Allen Liu\n"
}
|
f3fd4674-bdfd-5144-b4b1-22cb0af08833
| 609,850
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.