problem
stringlengths 54
2.23k
| solution
stringlengths 134
24.1k
| answer
stringclasses 1
value | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 54
2.21k
| solution_raw
stringlengths 134
24.1k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 23.5k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
Let $a_{1}, a_{2}, \ldots, a_{n}$ be distinct positive integers, $n \geq 3$. Prove that there exist distinct indices $i$ and $j$ such that $a_{i}+a_{j}$ does not divide any of the numbers $3 a_{1}, 3 a_{2}, \ldots, 3 a_{n}$.
|
Without loss of generality, let $0<a_{1}<a_{2}<\cdots<a_{n}$. One can also assume that $a_{1}, a_{2}, \ldots, a_{n}$ are coprime. Otherwise division by their greatest common divisor reduces the question to the new sequence whose terms are coprime integers. Suppose that the claim is false. Then for each $i<n$ there exists a $j$ such that $a_{n}+a_{i}$ divides $3 a_{j}$. If $a_{n}+a_{i}$ is not divisible by 3 then $a_{n}+a_{i}$ divides $a_{j}$ which is impossible as $0<a_{j} \leq a_{n}<a_{n}+a_{i}$. Thus $a_{n}+a_{i}$ is a multiple of 3 for $i=1, \ldots, n-1$, so that $a_{1}, a_{2}, \ldots, a_{n-1}$ are all congruent (to $-a_{n}$ ) modulo 3 . Now $a_{n}$ is not divisible by 3 or else so would be all remaining $a_{i}$ 's, meaning that $a_{1}, a_{2}, \ldots, a_{n}$ are not coprime. Hence $a_{n} \equiv r(\bmod 3)$ where $r \in\{1,2\}$, and $a_{i} \equiv 3-r(\bmod 3)$ for all $i=1, \ldots, n-1$. Consider a sum $a_{n-1}+a_{i}$ where $1 \leq i \leq n-2$. There is at least one such sum as $n \geq 3$. Let $j$ be an index such that $a_{n-1}+a_{i}$ divides $3 a_{j}$. Observe that $a_{n-1}+a_{i}$ is not divisible by 3 since $a_{n-1}+a_{i} \equiv 2 a_{i} \not \equiv 0(\bmod 3)$. It follows that $a_{n-1}+a_{i}$ divides $a_{j}$, in particular $a_{n-1}+a_{i} \leq a_{j}$. Hence $a_{n-1}<a_{j} \leq a_{n}$, implying $j=n$. So $a_{n}$ is divisible by all sums $a_{n-1}+a_{i}, 1 \leq i \leq n-2$. In particular $a_{n-1}+a_{i} \leq a_{n}$ for $i=1, \ldots, n-2$. Let $j$ be such that $a_{n}+a_{n-1}$ divides $3 a_{j}$. If $j \leq n-2$ then $a_{n}+a_{n-1} \leq 3 a_{j}<a_{j}+2 a_{n-1}$. This yields $a_{n}<a_{n-1}+a_{j}$; however $a_{n-1}+a_{j} \leq a_{n}$ for $j \leq n-2$. Therefore $j=n-1$ or $j=n$. For $j=n-1$ we obtain $3 a_{n-1}=k\left(a_{n}+a_{n-1}\right)$ with $k$ an integer, and it is straightforward that $k=1\left(k \leq 0\right.$ and $k \geq 3$ contradict $0<a_{n-1}<a_{n} ; k=2$ leads to $\left.a_{n-1}=2 a_{n}>a_{n-1}\right)$. Thus $3 a_{n-1}=a_{n}+a_{n-1}$, i. e. $a_{n}=2 a_{n-1}$. Similarly, if $j=n$ then $3 a_{n}=k\left(a_{n}+a_{n-1}\right)$ for some integer $k$, and only $k=2$ is possible. Hence $a_{n}=2 a_{n-1}$ holds true in both cases remaining, $j=n-1$ and $j=n$. Now $a_{n}=2 a_{n-1}$ implies that the sum $a_{n-1}+a_{1}$ is strictly between $a_{n} / 2$ and $a_{n}$. But $a_{n-1}$ and $a_{1}$ are distinct as $n \geq 3$, so it follows from the above that $a_{n-1}+a_{1}$ divides $a_{n}$. This provides the desired contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a_{1}, a_{2}, \ldots, a_{n}$ be distinct positive integers, $n \geq 3$. Prove that there exist distinct indices $i$ and $j$ such that $a_{i}+a_{j}$ does not divide any of the numbers $3 a_{1}, 3 a_{2}, \ldots, 3 a_{n}$.
|
Without loss of generality, let $0<a_{1}<a_{2}<\cdots<a_{n}$. One can also assume that $a_{1}, a_{2}, \ldots, a_{n}$ are coprime. Otherwise division by their greatest common divisor reduces the question to the new sequence whose terms are coprime integers. Suppose that the claim is false. Then for each $i<n$ there exists a $j$ such that $a_{n}+a_{i}$ divides $3 a_{j}$. If $a_{n}+a_{i}$ is not divisible by 3 then $a_{n}+a_{i}$ divides $a_{j}$ which is impossible as $0<a_{j} \leq a_{n}<a_{n}+a_{i}$. Thus $a_{n}+a_{i}$ is a multiple of 3 for $i=1, \ldots, n-1$, so that $a_{1}, a_{2}, \ldots, a_{n-1}$ are all congruent (to $-a_{n}$ ) modulo 3 . Now $a_{n}$ is not divisible by 3 or else so would be all remaining $a_{i}$ 's, meaning that $a_{1}, a_{2}, \ldots, a_{n}$ are not coprime. Hence $a_{n} \equiv r(\bmod 3)$ where $r \in\{1,2\}$, and $a_{i} \equiv 3-r(\bmod 3)$ for all $i=1, \ldots, n-1$. Consider a sum $a_{n-1}+a_{i}$ where $1 \leq i \leq n-2$. There is at least one such sum as $n \geq 3$. Let $j$ be an index such that $a_{n-1}+a_{i}$ divides $3 a_{j}$. Observe that $a_{n-1}+a_{i}$ is not divisible by 3 since $a_{n-1}+a_{i} \equiv 2 a_{i} \not \equiv 0(\bmod 3)$. It follows that $a_{n-1}+a_{i}$ divides $a_{j}$, in particular $a_{n-1}+a_{i} \leq a_{j}$. Hence $a_{n-1}<a_{j} \leq a_{n}$, implying $j=n$. So $a_{n}$ is divisible by all sums $a_{n-1}+a_{i}, 1 \leq i \leq n-2$. In particular $a_{n-1}+a_{i} \leq a_{n}$ for $i=1, \ldots, n-2$. Let $j$ be such that $a_{n}+a_{n-1}$ divides $3 a_{j}$. If $j \leq n-2$ then $a_{n}+a_{n-1} \leq 3 a_{j}<a_{j}+2 a_{n-1}$. This yields $a_{n}<a_{n-1}+a_{j}$; however $a_{n-1}+a_{j} \leq a_{n}$ for $j \leq n-2$. Therefore $j=n-1$ or $j=n$. For $j=n-1$ we obtain $3 a_{n-1}=k\left(a_{n}+a_{n-1}\right)$ with $k$ an integer, and it is straightforward that $k=1\left(k \leq 0\right.$ and $k \geq 3$ contradict $0<a_{n-1}<a_{n} ; k=2$ leads to $\left.a_{n-1}=2 a_{n}>a_{n-1}\right)$. Thus $3 a_{n-1}=a_{n}+a_{n-1}$, i. e. $a_{n}=2 a_{n-1}$. Similarly, if $j=n$ then $3 a_{n}=k\left(a_{n}+a_{n-1}\right)$ for some integer $k$, and only $k=2$ is possible. Hence $a_{n}=2 a_{n-1}$ holds true in both cases remaining, $j=n-1$ and $j=n$. Now $a_{n}=2 a_{n-1}$ implies that the sum $a_{n-1}+a_{1}$ is strictly between $a_{n} / 2$ and $a_{n}$. But $a_{n-1}$ and $a_{1}$ are distinct as $n \geq 3$, so it follows from the above that $a_{n-1}+a_{1}$ divides $a_{n}$. This provides the desired contradiction.
|
{
"resource_path": "IMO/segmented/en-IMO2008SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
f03dd5f1-48c6-547d-a4c2-734976ede07a
| 23,781
|
Let $a_{0}, a_{1}, a_{2}, \ldots$ be a sequence of positive integers such that the greatest common divisor of any two consecutive terms is greater than the preceding term; in symbols, $\operatorname{gcd}\left(a_{i}, a_{i+1}\right)>a_{i-1}$. Prove that $a_{n} \geq 2^{n}$ for all $n \geq 0$.
|
Since $a_{i} \geq \operatorname{gcd}\left(a_{i}, a_{i+1}\right)>a_{i-1}$, the sequence is strictly increasing. In particular $a_{0} \geq 1, a_{1} \geq 2$. For each $i \geq 1$ we also have $a_{i+1}-a_{i} \geq \operatorname{gcd}\left(a_{i}, a_{i+1}\right)>a_{i-1}$, and consequently $a_{i+1} \geq a_{i}+a_{i-1}+1$. Hence $a_{2} \geq 4$ and $a_{3} \geq 7$. The equality $a_{3}=7$ would force equalities in the previous estimates, leading to $\operatorname{gcd}\left(a_{2}, a_{3}\right)=\operatorname{gcd}(4,7)>a_{1}=2$, which is false. Thus $a_{3} \geq 8$; the result is valid for $n=0,1,2,3$. These are the base cases for a proof by induction. Take an $n \geq 3$ and assume that $a_{i} \geq 2^{i}$ for $i=0,1, \ldots, n$. We must show that $a_{n+1} \geq 2^{n+1}$. Let $\operatorname{gcd}\left(a_{n}, a_{n+1}\right)=d$. We know that $d>a_{n-1}$. The induction claim is reached immediately in the following cases: $$ \begin{array}{ll} \text { if } \quad a_{n+1} \geq 4 d & \text { then } a_{n+1}>4 a_{n-1} \geq 4 \cdot 2^{n-1}=2^{n+1} \\ \text { if } \quad a_{n} \geq 3 d & \text { then } a_{n+1} \geq a_{n}+d \geq 4 d>4 a_{n-1} \geq 4 \cdot 2^{n-1}=2^{n+1} \\ \text { if } \quad a_{n}=d & \text { then } a_{n+1} \geq a_{n}+d=2 a_{n} \geq 2 \cdot 2^{n}=2^{n+1} \end{array} $$ The only remaining possibility is that $a_{n}=2 d$ and $a_{n+1}=3 d$, which we assume for the sequel. So $a_{n+1}=\frac{3}{2} a_{n}$. Let now $\operatorname{gcd}\left(a_{n-1}, a_{n}\right)=d^{\prime}$; then $d^{\prime}>a_{n-2}$. Write $a_{n}=m d^{\prime} \quad(m$ an integer $)$. Keeping in mind that $d^{\prime} \leq a_{n-1}<d$ and $a_{n}=2 d$, we get that $m \geq 3$. Also $a_{n-1}<d=\frac{1}{2} m d^{\prime}$, $a_{n+1}=\frac{3}{2} m d^{\prime}$. Again we single out the cases which imply the induction claim immediately: $$ \begin{aligned} & \text { if } m \geq 6 \quad \text { then } a_{n+1}=\frac{3}{2} m d^{\prime} \geq 9 d^{\prime}>9 a_{n-2} \geq 9 \cdot 2^{n-2}>2^{n+1} \\ & \text { if } 3 \leq m \leq 4 \text { then } a_{n-1}<\frac{1}{2} \cdot 4 d^{\prime} \text {, and hence } a_{n-1}=d^{\prime} \\ & \qquad a_{n+1}=\frac{3}{2} m a_{n-1} \geq \frac{3}{2} \cdot 3 a_{n-1} \geq \frac{9}{2} \cdot 2^{n-1}>2^{n+1} . \end{aligned} $$ So we are left with the case $m=5$, which means that $a_{n}=5 d^{\prime}, a_{n+1}=\frac{15}{2} d^{\prime}, a_{n-1}<d=\frac{5}{2} d^{\prime}$. The last relation implies that $a_{n-1}$ is either $d^{\prime}$ or $2 d^{\prime}$. Anyway, $a_{n-1} \mid 2 d^{\prime}$. The same pattern repeats once more. We denote $\operatorname{gcd}\left(a_{n-2}, a_{n-1}\right)=d^{\prime \prime}$; then $d^{\prime \prime}>a_{n-3}$. Because $d^{\prime \prime}$ is a divisor of $a_{n-1}$, hence also of $2 d^{\prime}$, we may write $2 d^{\prime}=m^{\prime} d^{\prime \prime}$ ( $m^{\prime}$ an integer). Since $d^{\prime \prime} \leq a_{n-2}<d^{\prime}$, we get $m^{\prime} \geq 3$. Also, $a_{n-2}<d^{\prime}=\frac{1}{2} m^{\prime} d^{\prime \prime}, a_{n+1}=\frac{15}{2} d^{\prime}=\frac{15}{4} m^{\prime} d^{\prime \prime}$. As before, we consider the cases: $$ \begin{aligned} & \text { if } m^{\prime} \geq 5 \quad \text { then } a_{n+1}=\frac{15}{4} m^{\prime} d^{\prime \prime} \geq \frac{75}{4} d^{\prime \prime}>\frac{75}{4} a_{n-3} \geq \frac{75}{4} \cdot 2^{n-3}>2^{n+1} \\ & \text { if } 3 \leq m^{\prime} \leq 4 \text { then } a_{n-2}<\frac{1}{2} \cdot 4 d^{\prime \prime} \text {, and hence } a_{n-2}=d^{\prime \prime} \\ & \qquad a_{n+1}=\frac{15}{4} m^{\prime} a_{n-2} \geq \frac{15}{4} \cdot 3 a_{n-2} \geq \frac{45}{4} \cdot 2^{n-2}>2^{n+1} . \end{aligned} $$ Both of them have produced the induction claim. But now there are no cases left. Induction is complete; the inequality $a_{n} \geq 2^{n}$ holds for all $n$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a_{0}, a_{1}, a_{2}, \ldots$ be a sequence of positive integers such that the greatest common divisor of any two consecutive terms is greater than the preceding term; in symbols, $\operatorname{gcd}\left(a_{i}, a_{i+1}\right)>a_{i-1}$. Prove that $a_{n} \geq 2^{n}$ for all $n \geq 0$.
|
Since $a_{i} \geq \operatorname{gcd}\left(a_{i}, a_{i+1}\right)>a_{i-1}$, the sequence is strictly increasing. In particular $a_{0} \geq 1, a_{1} \geq 2$. For each $i \geq 1$ we also have $a_{i+1}-a_{i} \geq \operatorname{gcd}\left(a_{i}, a_{i+1}\right)>a_{i-1}$, and consequently $a_{i+1} \geq a_{i}+a_{i-1}+1$. Hence $a_{2} \geq 4$ and $a_{3} \geq 7$. The equality $a_{3}=7$ would force equalities in the previous estimates, leading to $\operatorname{gcd}\left(a_{2}, a_{3}\right)=\operatorname{gcd}(4,7)>a_{1}=2$, which is false. Thus $a_{3} \geq 8$; the result is valid for $n=0,1,2,3$. These are the base cases for a proof by induction. Take an $n \geq 3$ and assume that $a_{i} \geq 2^{i}$ for $i=0,1, \ldots, n$. We must show that $a_{n+1} \geq 2^{n+1}$. Let $\operatorname{gcd}\left(a_{n}, a_{n+1}\right)=d$. We know that $d>a_{n-1}$. The induction claim is reached immediately in the following cases: $$ \begin{array}{ll} \text { if } \quad a_{n+1} \geq 4 d & \text { then } a_{n+1}>4 a_{n-1} \geq 4 \cdot 2^{n-1}=2^{n+1} \\ \text { if } \quad a_{n} \geq 3 d & \text { then } a_{n+1} \geq a_{n}+d \geq 4 d>4 a_{n-1} \geq 4 \cdot 2^{n-1}=2^{n+1} \\ \text { if } \quad a_{n}=d & \text { then } a_{n+1} \geq a_{n}+d=2 a_{n} \geq 2 \cdot 2^{n}=2^{n+1} \end{array} $$ The only remaining possibility is that $a_{n}=2 d$ and $a_{n+1}=3 d$, which we assume for the sequel. So $a_{n+1}=\frac{3}{2} a_{n}$. Let now $\operatorname{gcd}\left(a_{n-1}, a_{n}\right)=d^{\prime}$; then $d^{\prime}>a_{n-2}$. Write $a_{n}=m d^{\prime} \quad(m$ an integer $)$. Keeping in mind that $d^{\prime} \leq a_{n-1}<d$ and $a_{n}=2 d$, we get that $m \geq 3$. Also $a_{n-1}<d=\frac{1}{2} m d^{\prime}$, $a_{n+1}=\frac{3}{2} m d^{\prime}$. Again we single out the cases which imply the induction claim immediately: $$ \begin{aligned} & \text { if } m \geq 6 \quad \text { then } a_{n+1}=\frac{3}{2} m d^{\prime} \geq 9 d^{\prime}>9 a_{n-2} \geq 9 \cdot 2^{n-2}>2^{n+1} \\ & \text { if } 3 \leq m \leq 4 \text { then } a_{n-1}<\frac{1}{2} \cdot 4 d^{\prime} \text {, and hence } a_{n-1}=d^{\prime} \\ & \qquad a_{n+1}=\frac{3}{2} m a_{n-1} \geq \frac{3}{2} \cdot 3 a_{n-1} \geq \frac{9}{2} \cdot 2^{n-1}>2^{n+1} . \end{aligned} $$ So we are left with the case $m=5$, which means that $a_{n}=5 d^{\prime}, a_{n+1}=\frac{15}{2} d^{\prime}, a_{n-1}<d=\frac{5}{2} d^{\prime}$. The last relation implies that $a_{n-1}$ is either $d^{\prime}$ or $2 d^{\prime}$. Anyway, $a_{n-1} \mid 2 d^{\prime}$. The same pattern repeats once more. We denote $\operatorname{gcd}\left(a_{n-2}, a_{n-1}\right)=d^{\prime \prime}$; then $d^{\prime \prime}>a_{n-3}$. Because $d^{\prime \prime}$ is a divisor of $a_{n-1}$, hence also of $2 d^{\prime}$, we may write $2 d^{\prime}=m^{\prime} d^{\prime \prime}$ ( $m^{\prime}$ an integer). Since $d^{\prime \prime} \leq a_{n-2}<d^{\prime}$, we get $m^{\prime} \geq 3$. Also, $a_{n-2}<d^{\prime}=\frac{1}{2} m^{\prime} d^{\prime \prime}, a_{n+1}=\frac{15}{2} d^{\prime}=\frac{15}{4} m^{\prime} d^{\prime \prime}$. As before, we consider the cases: $$ \begin{aligned} & \text { if } m^{\prime} \geq 5 \quad \text { then } a_{n+1}=\frac{15}{4} m^{\prime} d^{\prime \prime} \geq \frac{75}{4} d^{\prime \prime}>\frac{75}{4} a_{n-3} \geq \frac{75}{4} \cdot 2^{n-3}>2^{n+1} \\ & \text { if } 3 \leq m^{\prime} \leq 4 \text { then } a_{n-2}<\frac{1}{2} \cdot 4 d^{\prime \prime} \text {, and hence } a_{n-2}=d^{\prime \prime} \\ & \qquad a_{n+1}=\frac{15}{4} m^{\prime} a_{n-2} \geq \frac{15}{4} \cdot 3 a_{n-2} \geq \frac{45}{4} \cdot 2^{n-2}>2^{n+1} . \end{aligned} $$ Both of them have produced the induction claim. But now there are no cases left. Induction is complete; the inequality $a_{n} \geq 2^{n}$ holds for all $n$.
|
{
"resource_path": "IMO/segmented/en-IMO2008SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
d7fa9e77-3f94-5a54-85c5-c151b794b2e5
| 23,783
|
Let $n$ be a positive integer. Show that the numbers $$ \left(\begin{array}{c} 2^{n}-1 \\ 0 \end{array}\right), \quad\left(\begin{array}{c} 2^{n}-1 \\ 1 \end{array}\right), \quad\left(\begin{array}{c} 2^{n}-1 \\ 2 \end{array}\right), \quad \ldots, \quad\left(\begin{array}{c} 2^{n}-1 \\ 2^{n-1}-1 \end{array}\right) $$ are congruent modulo $2^{n}$ to $1,3,5, \ldots, 2^{n}-1$ in some order.
|
We again proceed by induction, writing for brevity $N=2^{n-1}$ and keeping notation $a_{k}=\left(\begin{array}{c}N-1 \\ k\end{array}\right), b_{m}=\left(\begin{array}{c}2 N-1 \\ m\end{array}\right)$. Assume that the result holds for the sequence $\left(a_{0}, a_{1}, a_{2}, \ldots, a_{N / 2-1}\right)$. In view of the symmetry $a_{N-1-k}=a_{k}$ this sequence is a permutation of $\left(a_{0}, a_{2}, a_{4}, \ldots, a_{N-2}\right)$. So the induction hypothesis says that this latter sequence, taken $(\bmod N)$, is a permutation of $(1,3,5, \ldots, N-1)$. Similarly, the induction claim is that $\left(b_{0}, b_{2}, b_{4}, \ldots, b_{2 N-2}\right)$, taken $(\bmod 2 N)$, is a permutation of $(1,3,5, \ldots, 2 N-1)$. In place of the congruence relations (2) we now use the following ones, $$ b_{4 i} \equiv a_{2 i} \quad(\bmod N) \quad \text { and } \quad b_{4 i+2} \equiv b_{4 i}+N \quad(\bmod 2 N) . $$ Given this, the conclusion is immediate: the first formula of (5) together with the induction hypothesis tells us that $\left(b_{0}, b_{4}, b_{8}, \ldots, b_{2 N-4}\right)(\bmod N)$ is a permutation of $(1,3,5, \ldots, N-1)$. Then the second formula of $(5)$ shows that $\left(b_{2}, b_{6}, b_{10}, \ldots, b_{2 N-2}\right)(\bmod N)$ is exactly the same permutation; moreover, this formula distinguishes $(\bmod 2 N)$ each $b_{4 i}$ from $b_{4 i+2}$. Consequently, these two sequences combined represent $(\bmod 2 N)$ a permutation of the sequence $(1,3,5, \ldots, N-1, N+1, N+3, N+5, \ldots, N+N-1)$, and this is precisely the induction claim. Now we prove formulas (5); we begin with the second one. Since $b_{m+1}=b_{m} \cdot \frac{2 N-m-1}{m+1}$, $$ b_{4 i+2}=b_{4 i} \cdot \frac{2 N-4 i-1}{4 i+1} \cdot \frac{2 N-4 i-2}{4 i+2}=b_{4 i} \cdot \frac{2 N-4 i-1}{4 i+1} \cdot \frac{N-2 i-1}{2 i+1} . $$ The desired congruence $b_{4 i+2} \equiv b_{4 i}+N$ may be multiplied by the odd number $(4 i+1)(2 i+1)$, giving rise to a chain of successively equivalent congruences: $$ \begin{aligned} b_{4 i}(2 N-4 i-1)(N-2 i-1) & \equiv\left(b_{4 i}+N\right)(4 i+1)(2 i+1) & & (\bmod 2 N), \\ b_{4 i}(2 i+1-N) & \equiv\left(b_{4 i}+N\right)(2 i+1) & & (\bmod 2 N), \\ \left(b_{4 i}+2 i+1\right) N & \equiv 0 & & (\bmod 2 N) ; \end{aligned} $$ and the last one is satisfied, as $b_{4 i}$ is odd. This settles the second relation in (5). The first one is proved by induction on $i$. It holds for $i=0$. Assume $b_{4 i} \equiv a_{2 i}(\bmod 2 N)$ and consider $i+1$ : $$ b_{4 i+4}=b_{4 i+2} \cdot \frac{2 N-4 i-3}{4 i+3} \cdot \frac{2 N-4 i-4}{4 i+4} ; \quad a_{2 i+2}=a_{2 i} \cdot \frac{N-2 i-1}{2 i+1} \cdot \frac{N-2 i-2}{2 i+2} . $$ Both expressions have the fraction $\frac{N-2 i-2}{2 i+2}$ as the last factor. Since $2 i+2<N=2^{n-1}$, this fraction reduces to $\ell / m$ with $\ell$ and $m$ odd. In showing that $b_{4 i+4} \equiv a_{2 i+2}(\bmod 2 N)$, we may ignore this common factor $\ell / m$. Clearing other odd denominators reduces the claim to $$ b_{4 i+2}(2 N-4 i-3)(2 i+1) \equiv a_{2 i}(N-2 i-1)(4 i+3) \quad(\bmod 2 N) $$ By the inductive assumption (saying that $b_{4 i} \equiv a_{2 i}(\bmod 2 N)$ ) and by the second relation of (5), this is equivalent to $$ \left(b_{4 i}+N\right)(2 i+1) \equiv b_{4 i}(2 i+1-N) \quad(\bmod 2 N) $$ a congruence which we have already met in the preceding proof a few lines above. This completes induction (on $i$ ) and the proof of (5), hence also the whole solution. Comment. One can avoid the words congruent modulo in the problem statement by rephrasing the assertion into: Show that these numbers leave distinct remainders in division by $2^{n}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n$ be a positive integer. Show that the numbers $$ \left(\begin{array}{c} 2^{n}-1 \\ 0 \end{array}\right), \quad\left(\begin{array}{c} 2^{n}-1 \\ 1 \end{array}\right), \quad\left(\begin{array}{c} 2^{n}-1 \\ 2 \end{array}\right), \quad \ldots, \quad\left(\begin{array}{c} 2^{n}-1 \\ 2^{n-1}-1 \end{array}\right) $$ are congruent modulo $2^{n}$ to $1,3,5, \ldots, 2^{n}-1$ in some order.
|
We again proceed by induction, writing for brevity $N=2^{n-1}$ and keeping notation $a_{k}=\left(\begin{array}{c}N-1 \\ k\end{array}\right), b_{m}=\left(\begin{array}{c}2 N-1 \\ m\end{array}\right)$. Assume that the result holds for the sequence $\left(a_{0}, a_{1}, a_{2}, \ldots, a_{N / 2-1}\right)$. In view of the symmetry $a_{N-1-k}=a_{k}$ this sequence is a permutation of $\left(a_{0}, a_{2}, a_{4}, \ldots, a_{N-2}\right)$. So the induction hypothesis says that this latter sequence, taken $(\bmod N)$, is a permutation of $(1,3,5, \ldots, N-1)$. Similarly, the induction claim is that $\left(b_{0}, b_{2}, b_{4}, \ldots, b_{2 N-2}\right)$, taken $(\bmod 2 N)$, is a permutation of $(1,3,5, \ldots, 2 N-1)$. In place of the congruence relations (2) we now use the following ones, $$ b_{4 i} \equiv a_{2 i} \quad(\bmod N) \quad \text { and } \quad b_{4 i+2} \equiv b_{4 i}+N \quad(\bmod 2 N) . $$ Given this, the conclusion is immediate: the first formula of (5) together with the induction hypothesis tells us that $\left(b_{0}, b_{4}, b_{8}, \ldots, b_{2 N-4}\right)(\bmod N)$ is a permutation of $(1,3,5, \ldots, N-1)$. Then the second formula of $(5)$ shows that $\left(b_{2}, b_{6}, b_{10}, \ldots, b_{2 N-2}\right)(\bmod N)$ is exactly the same permutation; moreover, this formula distinguishes $(\bmod 2 N)$ each $b_{4 i}$ from $b_{4 i+2}$. Consequently, these two sequences combined represent $(\bmod 2 N)$ a permutation of the sequence $(1,3,5, \ldots, N-1, N+1, N+3, N+5, \ldots, N+N-1)$, and this is precisely the induction claim. Now we prove formulas (5); we begin with the second one. Since $b_{m+1}=b_{m} \cdot \frac{2 N-m-1}{m+1}$, $$ b_{4 i+2}=b_{4 i} \cdot \frac{2 N-4 i-1}{4 i+1} \cdot \frac{2 N-4 i-2}{4 i+2}=b_{4 i} \cdot \frac{2 N-4 i-1}{4 i+1} \cdot \frac{N-2 i-1}{2 i+1} . $$ The desired congruence $b_{4 i+2} \equiv b_{4 i}+N$ may be multiplied by the odd number $(4 i+1)(2 i+1)$, giving rise to a chain of successively equivalent congruences: $$ \begin{aligned} b_{4 i}(2 N-4 i-1)(N-2 i-1) & \equiv\left(b_{4 i}+N\right)(4 i+1)(2 i+1) & & (\bmod 2 N), \\ b_{4 i}(2 i+1-N) & \equiv\left(b_{4 i}+N\right)(2 i+1) & & (\bmod 2 N), \\ \left(b_{4 i}+2 i+1\right) N & \equiv 0 & & (\bmod 2 N) ; \end{aligned} $$ and the last one is satisfied, as $b_{4 i}$ is odd. This settles the second relation in (5). The first one is proved by induction on $i$. It holds for $i=0$. Assume $b_{4 i} \equiv a_{2 i}(\bmod 2 N)$ and consider $i+1$ : $$ b_{4 i+4}=b_{4 i+2} \cdot \frac{2 N-4 i-3}{4 i+3} \cdot \frac{2 N-4 i-4}{4 i+4} ; \quad a_{2 i+2}=a_{2 i} \cdot \frac{N-2 i-1}{2 i+1} \cdot \frac{N-2 i-2}{2 i+2} . $$ Both expressions have the fraction $\frac{N-2 i-2}{2 i+2}$ as the last factor. Since $2 i+2<N=2^{n-1}$, this fraction reduces to $\ell / m$ with $\ell$ and $m$ odd. In showing that $b_{4 i+4} \equiv a_{2 i+2}(\bmod 2 N)$, we may ignore this common factor $\ell / m$. Clearing other odd denominators reduces the claim to $$ b_{4 i+2}(2 N-4 i-3)(2 i+1) \equiv a_{2 i}(N-2 i-1)(4 i+3) \quad(\bmod 2 N) $$ By the inductive assumption (saying that $b_{4 i} \equiv a_{2 i}(\bmod 2 N)$ ) and by the second relation of (5), this is equivalent to $$ \left(b_{4 i}+N\right)(2 i+1) \equiv b_{4 i}(2 i+1-N) \quad(\bmod 2 N) $$ a congruence which we have already met in the preceding proof a few lines above. This completes induction (on $i$ ) and the proof of (5), hence also the whole solution. Comment. One can avoid the words congruent modulo in the problem statement by rephrasing the assertion into: Show that these numbers leave distinct remainders in division by $2^{n}$.
|
{
"resource_path": "IMO/segmented/en-IMO2008SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
b91b5db5-2122-5bcc-9b5b-46f432124596
| 23,785
|
Prove that there exist infinitely many positive integers $n$ such that $n^{2}+1$ has a prime divisor greater than $2 n+\sqrt{2 n}$.
|
Let $p \equiv 1(\bmod 8)$ be a prime. The congruence $x^{2} \equiv-1(\bmod p)$ has two solutions in $[1, p-1]$ whose sum is $p$. If $n$ is the smaller one of them then $p$ divides $n^{2}+1$ and $n \leq(p-1) / 2$. We show that $p>2 n+\sqrt{10 n}$. Let $n=(p-1) / 2-\ell$ where $\ell \geq 0$. Then $n^{2} \equiv-1(\bmod p)$ gives $$ \left(\frac{p-1}{2}-\ell\right)^{2} \equiv-1 \quad(\bmod p) \quad \text { or } \quad(2 \ell+1)^{2}+4 \equiv 0 \quad(\bmod p) $$ Thus $(2 \ell+1)^{2}+4=r p$ for some $r \geq 0$. As $(2 \ell+1)^{2} \equiv 1 \equiv p(\bmod 8)$, we have $r \equiv 5(\bmod 8)$, so that $r \geq 5$. Hence $(2 \ell+1)^{2}+4 \geq 5 p$, implying $\ell \geq(\sqrt{5 p-4}-1) / 2$. Set $\sqrt{5 p-4}=u$ for clarity; then $\ell \geq(u-1) / 2$. Therefore $$ n=\frac{p-1}{2}-\ell \leq \frac{1}{2}(p-u) $$ Combined with $p=\left(u^{2}+4\right) / 5$, this leads to $u^{2}-5 u-10 n+4 \geq 0$. Solving this quadratic inequality with respect to $u \geq 0$ gives $u \geq(5+\sqrt{40 n+9}) / 2$. So the estimate $n \leq(p-u) / 2$ leads to $$ p \geq 2 n+u \geq 2 n+\frac{1}{2}(5+\sqrt{40 n+9})>2 n+\sqrt{10 n} $$ Since there are infinitely many primes of the form $8 k+1$, it follows easily that there are also infinitely many $n$ with the stated property. Comment. By considering the prime factorization of the product $\prod_{n=1}^{N}\left(n^{2}+1\right)$, it can be obtained that its greatest prime divisor is at least $c N \log N$. This could improve the statement as $p>n \log n$. However, the proof applies some advanced information about the distribution of the primes of the form $4 k+1$, which is inappropriate for high schools contests.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that there exist infinitely many positive integers $n$ such that $n^{2}+1$ has a prime divisor greater than $2 n+\sqrt{2 n}$.
|
Let $p \equiv 1(\bmod 8)$ be a prime. The congruence $x^{2} \equiv-1(\bmod p)$ has two solutions in $[1, p-1]$ whose sum is $p$. If $n$ is the smaller one of them then $p$ divides $n^{2}+1$ and $n \leq(p-1) / 2$. We show that $p>2 n+\sqrt{10 n}$. Let $n=(p-1) / 2-\ell$ where $\ell \geq 0$. Then $n^{2} \equiv-1(\bmod p)$ gives $$ \left(\frac{p-1}{2}-\ell\right)^{2} \equiv-1 \quad(\bmod p) \quad \text { or } \quad(2 \ell+1)^{2}+4 \equiv 0 \quad(\bmod p) $$ Thus $(2 \ell+1)^{2}+4=r p$ for some $r \geq 0$. As $(2 \ell+1)^{2} \equiv 1 \equiv p(\bmod 8)$, we have $r \equiv 5(\bmod 8)$, so that $r \geq 5$. Hence $(2 \ell+1)^{2}+4 \geq 5 p$, implying $\ell \geq(\sqrt{5 p-4}-1) / 2$. Set $\sqrt{5 p-4}=u$ for clarity; then $\ell \geq(u-1) / 2$. Therefore $$ n=\frac{p-1}{2}-\ell \leq \frac{1}{2}(p-u) $$ Combined with $p=\left(u^{2}+4\right) / 5$, this leads to $u^{2}-5 u-10 n+4 \geq 0$. Solving this quadratic inequality with respect to $u \geq 0$ gives $u \geq(5+\sqrt{40 n+9}) / 2$. So the estimate $n \leq(p-u) / 2$ leads to $$ p \geq 2 n+u \geq 2 n+\frac{1}{2}(5+\sqrt{40 n+9})>2 n+\sqrt{10 n} $$ Since there are infinitely many primes of the form $8 k+1$, it follows easily that there are also infinitely many $n$ with the stated property. Comment. By considering the prime factorization of the product $\prod_{n=1}^{N}\left(n^{2}+1\right)$, it can be obtained that its greatest prime divisor is at least $c N \log N$. This could improve the statement as $p>n \log n$. However, the proof applies some advanced information about the distribution of the primes of the form $4 k+1$, which is inappropriate for high schools contests.
|
{
"resource_path": "IMO/segmented/en-IMO2008SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
60bbe692-050c-55a3-87f4-ce460a1e63cf
| 23,791
|
EST Let $a, b, c$ be positive real numbers such that $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=a+b+c$. Prove that $$ \frac{1}{(2 a+b+c)^{2}}+\frac{1}{(2 b+c+a)^{2}}+\frac{1}{(2 c+a+b)^{2}} \leq \frac{3}{16} $$
|
Equivalently, we prove the homogenized inequality $$ \frac{(a+b+c)^{2}}{(2 a+b+c)^{2}}+\frac{(a+b+c)^{2}}{(a+2 b+c)^{2}}+\frac{(a+b+c)^{2}}{(a+b+2 c)^{2}} \leq \frac{3}{16}(a+b+c)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right) $$ for all positive real numbers $a, b, c$. Without loss of generality we choose $a+b+c=1$. Thus, the problem is equivalent to prove for all $a, b, c>0$, fulfilling this condition, the inequality $$ \frac{1}{(1+a)^{2}}+\frac{1}{(1+b)^{2}}+\frac{1}{(1+c)^{2}} \leq \frac{3}{16}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right) . $$ Applying Jensen's inequality to the function $f(x)=\frac{x}{(1+x)^{2}}$, which is concave for $0 \leq x \leq 2$ and increasing for $0 \leq x \leq 1$, we obtain $$ \alpha \frac{a}{(1+a)^{2}}+\beta \frac{b}{(1+b)^{2}}+\gamma \frac{c}{(1+c)^{2}} \leq(\alpha+\beta+\gamma) \frac{A}{(1+A)^{2}}, \quad \text { where } \quad A=\frac{\alpha a+\beta b+\gamma c}{\alpha+\beta+\gamma} $$ Choosing $\alpha=\frac{1}{a}, \beta=\frac{1}{b}$, and $\gamma=\frac{1}{c}$, we can apply the harmonic-arithmetic-mean inequality $$ A=\frac{3}{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}} \leq \frac{a+b+c}{3}=\frac{1}{3}<1 $$ Finally we prove (5): $$ \begin{aligned} \frac{1}{(1+a)^{2}}+\frac{1}{(1+b)^{2}}+\frac{1}{(1+c)^{2}} & \leq\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right) \frac{A}{(1+A)^{2}} \\ & \leq\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right) \frac{\frac{1}{3}}{\left(1+\frac{1}{3}\right)^{2}}=\frac{3}{16}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right) . \end{aligned} $$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
EST Let $a, b, c$ be positive real numbers such that $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=a+b+c$. Prove that $$ \frac{1}{(2 a+b+c)^{2}}+\frac{1}{(2 b+c+a)^{2}}+\frac{1}{(2 c+a+b)^{2}} \leq \frac{3}{16} $$
|
Equivalently, we prove the homogenized inequality $$ \frac{(a+b+c)^{2}}{(2 a+b+c)^{2}}+\frac{(a+b+c)^{2}}{(a+2 b+c)^{2}}+\frac{(a+b+c)^{2}}{(a+b+2 c)^{2}} \leq \frac{3}{16}(a+b+c)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right) $$ for all positive real numbers $a, b, c$. Without loss of generality we choose $a+b+c=1$. Thus, the problem is equivalent to prove for all $a, b, c>0$, fulfilling this condition, the inequality $$ \frac{1}{(1+a)^{2}}+\frac{1}{(1+b)^{2}}+\frac{1}{(1+c)^{2}} \leq \frac{3}{16}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right) . $$ Applying Jensen's inequality to the function $f(x)=\frac{x}{(1+x)^{2}}$, which is concave for $0 \leq x \leq 2$ and increasing for $0 \leq x \leq 1$, we obtain $$ \alpha \frac{a}{(1+a)^{2}}+\beta \frac{b}{(1+b)^{2}}+\gamma \frac{c}{(1+c)^{2}} \leq(\alpha+\beta+\gamma) \frac{A}{(1+A)^{2}}, \quad \text { where } \quad A=\frac{\alpha a+\beta b+\gamma c}{\alpha+\beta+\gamma} $$ Choosing $\alpha=\frac{1}{a}, \beta=\frac{1}{b}$, and $\gamma=\frac{1}{c}$, we can apply the harmonic-arithmetic-mean inequality $$ A=\frac{3}{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}} \leq \frac{a+b+c}{3}=\frac{1}{3}<1 $$ Finally we prove (5): $$ \begin{aligned} \frac{1}{(1+a)^{2}}+\frac{1}{(1+b)^{2}}+\frac{1}{(1+c)^{2}} & \leq\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right) \frac{A}{(1+A)^{2}} \\ & \leq\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right) \frac{\frac{1}{3}}{\left(1+\frac{1}{3}\right)^{2}}=\frac{3}{16}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right) . \end{aligned} $$
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
a73c6797-9383-5a5f-b6ac-acddb31cb51d
| 23,797
|
BLR Let $a, b, c$ be positive real numbers such that $a b+b c+c a \leq 3 a b c$. Prove that $$ \sqrt{\frac{a^{2}+b^{2}}{a+b}}+\sqrt{\frac{b^{2}+c^{2}}{b+c}}+\sqrt{\frac{c^{2}+a^{2}}{c+a}}+3 \leq \sqrt{2}(\sqrt{a+b}+\sqrt{b+c}+\sqrt{c+a}) . $$
|
Starting with the terms of the right-hand side, the quadratic-arithmetic-mean inequality yields $$ \begin{aligned} \sqrt{2} \sqrt{a+b} & =2 \sqrt{\frac{a b}{a+b}} \sqrt{\frac{1}{2}\left(2+\frac{a^{2}+b^{2}}{a b}\right)} \\ & \geq 2 \sqrt{\frac{a b}{a+b}} \cdot \frac{1}{2}\left(\sqrt{2}+\sqrt{\frac{a^{2}+b^{2}}{a b}}\right)=\sqrt{\frac{2 a b}{a+b}}+\sqrt{\frac{a^{2}+b^{2}}{a+b}} \end{aligned} $$ and, analogously, $$ \sqrt{2} \sqrt{b+c} \geq \sqrt{\frac{2 b c}{b+c}}+\sqrt{\frac{b^{2}+c^{2}}{b+c}}, \quad \sqrt{2} \sqrt{c+a} \geq \sqrt{\frac{2 c a}{c+a}}+\sqrt{\frac{c^{2}+a^{2}}{c+a}} . $$ Applying the inequality between the arithmetic mean and the squared harmonic mean will finish the proof: $$ \sqrt{\frac{2 a b}{a+b}}+\sqrt{\frac{2 b c}{b+c}}+\sqrt{\frac{2 c a}{c+a}} \geq 3 \cdot \sqrt{\frac{3}{\sqrt{\frac{a+b}{2 a b}}^{2}+\sqrt{\frac{b+c}{2 b c}}^{2}+\sqrt{\frac{c+a}{2 c a}}}}{ }^{2}=3 \cdot \sqrt{\frac{3 a b c}{a b+b c+c a}} \geq 3 . $$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
BLR Let $a, b, c$ be positive real numbers such that $a b+b c+c a \leq 3 a b c$. Prove that $$ \sqrt{\frac{a^{2}+b^{2}}{a+b}}+\sqrt{\frac{b^{2}+c^{2}}{b+c}}+\sqrt{\frac{c^{2}+a^{2}}{c+a}}+3 \leq \sqrt{2}(\sqrt{a+b}+\sqrt{b+c}+\sqrt{c+a}) . $$
|
Starting with the terms of the right-hand side, the quadratic-arithmetic-mean inequality yields $$ \begin{aligned} \sqrt{2} \sqrt{a+b} & =2 \sqrt{\frac{a b}{a+b}} \sqrt{\frac{1}{2}\left(2+\frac{a^{2}+b^{2}}{a b}\right)} \\ & \geq 2 \sqrt{\frac{a b}{a+b}} \cdot \frac{1}{2}\left(\sqrt{2}+\sqrt{\frac{a^{2}+b^{2}}{a b}}\right)=\sqrt{\frac{2 a b}{a+b}}+\sqrt{\frac{a^{2}+b^{2}}{a+b}} \end{aligned} $$ and, analogously, $$ \sqrt{2} \sqrt{b+c} \geq \sqrt{\frac{2 b c}{b+c}}+\sqrt{\frac{b^{2}+c^{2}}{b+c}}, \quad \sqrt{2} \sqrt{c+a} \geq \sqrt{\frac{2 c a}{c+a}}+\sqrt{\frac{c^{2}+a^{2}}{c+a}} . $$ Applying the inequality between the arithmetic mean and the squared harmonic mean will finish the proof: $$ \sqrt{\frac{2 a b}{a+b}}+\sqrt{\frac{2 b c}{b+c}}+\sqrt{\frac{2 c a}{c+a}} \geq 3 \cdot \sqrt{\frac{3}{\sqrt{\frac{a+b}{2 a b}}^{2}+\sqrt{\frac{b+c}{2 b c}}^{2}+\sqrt{\frac{c+a}{2 c a}}}}{ }^{2}=3 \cdot \sqrt{\frac{3 a b c}{a b+b c+c a}} \geq 3 . $$
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
e2be455b-8da8-50e5-9b06-2dc82c23b267
| 23,802
|
BLR Let $f$ be any function that maps the set of real numbers into the set of real numbers. Prove that there exist real numbers $x$ and $y$ such that $$ f(x-f(y))>y f(x)+x $$
|
Assume that $$ f(x-f(y)) \leq y f(x)+x \quad \text { for all real } x, y $$ Let $a=f(0)$. Setting $y=0$ in (1) gives $f(x-a) \leq x$ for all real $x$ and, equivalently, $$ f(y) \leq y+a \quad \text { for all real } y $$ Setting $x=f(y)$ in (1) yields in view of (2) $$ a=f(0) \leq y f(f(y))+f(y) \leq y f(f(y))+y+a . $$ This implies $0 \leq y(f(f(y))+1)$ and thus $$ f(f(y)) \geq-1 \quad \text { for all } y>0 $$ From (2) and (3) we obtain $-1 \leq f(f(y)) \leq f(y)+a$ for all $y>0$, so $$ f(y) \geq-a-1 \quad \text { for all } y>0 $$ Now we show that $$ f(x) \leq 0 \quad \text { for all real } x $$ Assume the contrary, i.e. there is some $x$ such that $f(x)>0$. Take any $y$ such that $$ y<x-a \quad \text { and } \quad y<\frac{-a-x-1}{f(x)} $$ Then in view of (2) $$ x-f(y) \geq x-(y+a)>0 $$ and with (1) and (4) we obtain $$ y f(x)+x \geq f(x-f(y)) \geq-a-1, $$ whence $$ y \geq \frac{-a-x-1}{f(x)} $$ contrary to our choice of $y$. Thereby, we have established (5). Setting $x=0$ in (5) leads to $a=f(0) \leq 0$ and (2) then yields $$ f(x) \leq x \quad \text { for all real } x $$ Now choose $y$ such that $y>0$ and $y>-f(-1)-1$ and set $x=f(y)-1$. From (11), (5) and (6) we obtain $$ f(-1)=f(x-f(y)) \leq y f(x)+x=y f(f(y)-1)+f(y)-1 \leq y(f(y)-1)-1 \leq-y-1, $$ i.e. $y \leq-f(-1)-1$, a contradiction to the choice of $y$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
BLR Let $f$ be any function that maps the set of real numbers into the set of real numbers. Prove that there exist real numbers $x$ and $y$ such that $$ f(x-f(y))>y f(x)+x $$
|
Assume that $$ f(x-f(y)) \leq y f(x)+x \quad \text { for all real } x, y $$ Let $a=f(0)$. Setting $y=0$ in (1) gives $f(x-a) \leq x$ for all real $x$ and, equivalently, $$ f(y) \leq y+a \quad \text { for all real } y $$ Setting $x=f(y)$ in (1) yields in view of (2) $$ a=f(0) \leq y f(f(y))+f(y) \leq y f(f(y))+y+a . $$ This implies $0 \leq y(f(f(y))+1)$ and thus $$ f(f(y)) \geq-1 \quad \text { for all } y>0 $$ From (2) and (3) we obtain $-1 \leq f(f(y)) \leq f(y)+a$ for all $y>0$, so $$ f(y) \geq-a-1 \quad \text { for all } y>0 $$ Now we show that $$ f(x) \leq 0 \quad \text { for all real } x $$ Assume the contrary, i.e. there is some $x$ such that $f(x)>0$. Take any $y$ such that $$ y<x-a \quad \text { and } \quad y<\frac{-a-x-1}{f(x)} $$ Then in view of (2) $$ x-f(y) \geq x-(y+a)>0 $$ and with (1) and (4) we obtain $$ y f(x)+x \geq f(x-f(y)) \geq-a-1, $$ whence $$ y \geq \frac{-a-x-1}{f(x)} $$ contrary to our choice of $y$. Thereby, we have established (5). Setting $x=0$ in (5) leads to $a=f(0) \leq 0$ and (2) then yields $$ f(x) \leq x \quad \text { for all real } x $$ Now choose $y$ such that $y>0$ and $y>-f(-1)-1$ and set $x=f(y)-1$. From (11), (5) and (6) we obtain $$ f(-1)=f(x-f(y)) \leq y f(x)+x=y f(f(y)-1)+f(y)-1 \leq y(f(y)-1)-1 \leq-y-1, $$ i.e. $y \leq-f(-1)-1$, a contradiction to the choice of $y$.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
9f3220b8-540f-5e38-ade0-a83e2871a5cd
| 23,804
|
BLR Let $f$ be any function that maps the set of real numbers into the set of real numbers. Prove that there exist real numbers $x$ and $y$ such that $$ f(x-f(y))>y f(x)+x $$
|
Assume that $$ f(x-f(y)) \leq y f(x)+x \quad \text { for all real } x, y $$ Let $a=f(0)$. Setting $y=0$ in (7) gives $f(x-a) \leq x$ for all real $x$ and, equivalently, $$ f(y) \leq y+a \quad \text { for all real } y $$ Now we show that $$ f(z) \geq 0 \quad \text { for all } z \geq 1 $$ Let $z \geq 1$ be fixed, set $b=f(z)$ and assume that $b<0$. Setting $x=w+b$ and $y=z$ in (7) gives $$ f(w)-z f(w+b) \leq w+b \quad \text { for all real } w $$ Applying (10) to $w, w+b, \ldots, w+(n-1) b$, where $n=1,2, \ldots$, leads to $$ \begin{gathered} f(w)-z^{n} f(w+n b)=(f(w)-z f(w+b))+z(f(w+b)-z f(w+2 b)) \\ +\cdots+z^{n-1}(f(w+(n-1) b)-z f(w+n b)) \\ \leq(w+b)+z(w+2 b)+\cdots+z^{n-1}(w+n b) \end{gathered} $$ From (8) we obtain $$ f(w+n b) \leq w+n b+a $$ and, thus, we have for all positive integers $n$ $$ f(w) \leq\left(1+z+\cdots+z^{n-1}+z^{n}\right) w+\left(1+2 z+\cdots+n z^{n-1}+n z^{n}\right) b+z^{n} a . $$ With $w=0$ we get $$ a \leq\left(1+2 z+\cdots+n z^{n-1}+n z^{n}\right) b+a z^{n} . $$ In view of the assumption $b<0$ we find some $n$ such that $$ a>(n b+a) z^{n} $$ because the right hand side tends to $-\infty$ as $n \rightarrow \infty$. Now (12) and (13) give the desired contradiction and (9) is established. In addition, we have for $z=1$ the strict inequality $$ f(1)>0 \text {. } $$ Indeed, assume that $f(1)=0$. Then setting $w=-1$ and $z=1$ in (11) leads to $$ f(-1) \leq-(n+1)+a $$ which is false if $n$ is sufficiently large. To complete the proof we set $t=\min \{-a,-2 / f(1)\}$. Setting $x=1$ and $y=t$ in (7) gives $$ f(1-f(t)) \leq t f(1)+1 \leq-2+1=-1 . $$ On the other hand, by (8) and the choice of $t$ we have $f(t) \leq t+a \leq 0$ and hence $1-f(t) \geq 1$. The inequality (9) yields $$ f(1-f(t)) \geq 0 $$ which contradicts (15).
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
BLR Let $f$ be any function that maps the set of real numbers into the set of real numbers. Prove that there exist real numbers $x$ and $y$ such that $$ f(x-f(y))>y f(x)+x $$
|
Assume that $$ f(x-f(y)) \leq y f(x)+x \quad \text { for all real } x, y $$ Let $a=f(0)$. Setting $y=0$ in (7) gives $f(x-a) \leq x$ for all real $x$ and, equivalently, $$ f(y) \leq y+a \quad \text { for all real } y $$ Now we show that $$ f(z) \geq 0 \quad \text { for all } z \geq 1 $$ Let $z \geq 1$ be fixed, set $b=f(z)$ and assume that $b<0$. Setting $x=w+b$ and $y=z$ in (7) gives $$ f(w)-z f(w+b) \leq w+b \quad \text { for all real } w $$ Applying (10) to $w, w+b, \ldots, w+(n-1) b$, where $n=1,2, \ldots$, leads to $$ \begin{gathered} f(w)-z^{n} f(w+n b)=(f(w)-z f(w+b))+z(f(w+b)-z f(w+2 b)) \\ +\cdots+z^{n-1}(f(w+(n-1) b)-z f(w+n b)) \\ \leq(w+b)+z(w+2 b)+\cdots+z^{n-1}(w+n b) \end{gathered} $$ From (8) we obtain $$ f(w+n b) \leq w+n b+a $$ and, thus, we have for all positive integers $n$ $$ f(w) \leq\left(1+z+\cdots+z^{n-1}+z^{n}\right) w+\left(1+2 z+\cdots+n z^{n-1}+n z^{n}\right) b+z^{n} a . $$ With $w=0$ we get $$ a \leq\left(1+2 z+\cdots+n z^{n-1}+n z^{n}\right) b+a z^{n} . $$ In view of the assumption $b<0$ we find some $n$ such that $$ a>(n b+a) z^{n} $$ because the right hand side tends to $-\infty$ as $n \rightarrow \infty$. Now (12) and (13) give the desired contradiction and (9) is established. In addition, we have for $z=1$ the strict inequality $$ f(1)>0 \text {. } $$ Indeed, assume that $f(1)=0$. Then setting $w=-1$ and $z=1$ in (11) leads to $$ f(-1) \leq-(n+1)+a $$ which is false if $n$ is sufficiently large. To complete the proof we set $t=\min \{-a,-2 / f(1)\}$. Setting $x=1$ and $y=t$ in (7) gives $$ f(1-f(t)) \leq t f(1)+1 \leq-2+1=-1 . $$ On the other hand, by (8) and the choice of $t$ we have $f(t) \leq t+a \leq 0$ and hence $1-f(t) \geq 1$. The inequality (9) yields $$ f(1-f(t)) \geq 0 $$ which contradicts (15).
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
9f3220b8-540f-5e38-ade0-a83e2871a5cd
| 23,804
|
USA Suppose that $s_{1}, s_{2}, s_{3}, \ldots$ is a strictly increasing sequence of positive integers such that the subsequences $$ s_{s_{1}}, s_{s_{2}}, s_{s_{3}}, \ldots \quad \text { and } \quad s_{s_{1}+1}, s_{s_{2}+1}, s_{s_{3}+1}, \ldots $$ are both arithmetic progressions. Prove that $s_{1}, s_{2}, s_{3}, \ldots$ is itself an arithmetic progression.
|
Let $D$ be the common difference of the progression $s_{s_{1}}, s_{s_{2}}, \ldots$. Let for $n=$ 1, 2, ... $$ d_{n}=s_{n+1}-s_{n} $$ We have to prove that $d_{n}$ is constant. First we show that the numbers $d_{n}$ are bounded. Indeed, by supposition $d_{n} \geq 1$ for all $n$. Thus, we have for all $n$ $$ d_{n}=s_{n+1}-s_{n} \leq d_{s_{n}}+d_{s_{n}+1}+\cdots+d_{s_{n+1}-1}=s_{s_{n+1}}-s_{s_{n}}=D . $$ The boundedness implies that there exist $$ m=\min \left\{d_{n}: n=1,2, \ldots\right\} \quad \text { and } \quad M=\max \left\{d_{n}: n=1,2, \ldots\right\} $$ It suffices to show that $m=M$. Assume that $m<M$. Choose $n$ such that $d_{n}=m$. Considering a telescoping sum of $m=d_{n}=s_{n+1}-s_{n}$ items not greater than $M$ leads to $$ D=s_{s_{n+1}}-s_{s_{n}}=s_{s_{n}+m}-s_{s_{n}}=d_{s_{n}}+d_{s_{n}+1}+\cdots+d_{s_{n}+m-1} \leq m M $$ and equality holds if and only if all items of the sum are equal to $M$. Now choose $n$ such that $d_{n}=M$. In the same way, considering a telescoping sum of $M$ items not less than $m$ we obtain $$ D=s_{s_{n+1}}-s_{s_{n}}=s_{s_{n}+M}-s_{s_{n}}=d_{s_{n}}+d_{s_{n}+1}+\cdots+d_{s_{n}+M-1} \geq M m $$ and equality holds if and only if all items of the sum are equal to $m$. The inequalities (1) and (2) imply that $D=M m$ and that $$ \begin{aligned} d_{s_{n}}=d_{s_{n}+1}=\cdots=d_{s_{n+1}-1}=M & \text { if } d_{n}=m, \\ d_{s_{n}}=d_{s_{n}+1}=\cdots=d_{s_{n+1}-1}=m & \text { if } d_{n}=M . \end{aligned} $$ Hence, $d_{n}=m$ implies $d_{s_{n}}=M$. Note that $s_{n} \geq s_{1}+(n-1) \geq n$ for all $n$ and moreover $s_{n}>n$ if $d_{n}=n$, because in the case $s_{n}=n$ we would have $m=d_{n}=d_{s_{n}}=M$ in contradiction to the assumption $m<M$. In the same way $d_{n}=M$ implies $d_{s_{n}}=m$ and $s_{n}>n$. Consequently, there is a strictly increasing sequence $n_{1}, n_{2}, \ldots$ such that $$ d_{s_{n_{1}}}=M, \quad d_{s_{n_{2}}}=m, \quad d_{s_{n_{3}}}=M, \quad d_{s_{n_{4}}}=m, \quad \ldots $$ The sequence $d_{s_{1}}, d_{s_{2}}, \ldots$ is the sequence of pairwise differences of $s_{s_{1}+1}, s_{s_{2}+1}, \ldots$ and $s_{s_{1}}, s_{s_{2}}, \ldots$, hence also an arithmetic progression. Thus $m=M$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
USA Suppose that $s_{1}, s_{2}, s_{3}, \ldots$ is a strictly increasing sequence of positive integers such that the subsequences $$ s_{s_{1}}, s_{s_{2}}, s_{s_{3}}, \ldots \quad \text { and } \quad s_{s_{1}+1}, s_{s_{2}+1}, s_{s_{3}+1}, \ldots $$ are both arithmetic progressions. Prove that $s_{1}, s_{2}, s_{3}, \ldots$ is itself an arithmetic progression.
|
Let $D$ be the common difference of the progression $s_{s_{1}}, s_{s_{2}}, \ldots$. Let for $n=$ 1, 2, ... $$ d_{n}=s_{n+1}-s_{n} $$ We have to prove that $d_{n}$ is constant. First we show that the numbers $d_{n}$ are bounded. Indeed, by supposition $d_{n} \geq 1$ for all $n$. Thus, we have for all $n$ $$ d_{n}=s_{n+1}-s_{n} \leq d_{s_{n}}+d_{s_{n}+1}+\cdots+d_{s_{n+1}-1}=s_{s_{n+1}}-s_{s_{n}}=D . $$ The boundedness implies that there exist $$ m=\min \left\{d_{n}: n=1,2, \ldots\right\} \quad \text { and } \quad M=\max \left\{d_{n}: n=1,2, \ldots\right\} $$ It suffices to show that $m=M$. Assume that $m<M$. Choose $n$ such that $d_{n}=m$. Considering a telescoping sum of $m=d_{n}=s_{n+1}-s_{n}$ items not greater than $M$ leads to $$ D=s_{s_{n+1}}-s_{s_{n}}=s_{s_{n}+m}-s_{s_{n}}=d_{s_{n}}+d_{s_{n}+1}+\cdots+d_{s_{n}+m-1} \leq m M $$ and equality holds if and only if all items of the sum are equal to $M$. Now choose $n$ such that $d_{n}=M$. In the same way, considering a telescoping sum of $M$ items not less than $m$ we obtain $$ D=s_{s_{n+1}}-s_{s_{n}}=s_{s_{n}+M}-s_{s_{n}}=d_{s_{n}}+d_{s_{n}+1}+\cdots+d_{s_{n}+M-1} \geq M m $$ and equality holds if and only if all items of the sum are equal to $m$. The inequalities (1) and (2) imply that $D=M m$ and that $$ \begin{aligned} d_{s_{n}}=d_{s_{n}+1}=\cdots=d_{s_{n+1}-1}=M & \text { if } d_{n}=m, \\ d_{s_{n}}=d_{s_{n}+1}=\cdots=d_{s_{n+1}-1}=m & \text { if } d_{n}=M . \end{aligned} $$ Hence, $d_{n}=m$ implies $d_{s_{n}}=M$. Note that $s_{n} \geq s_{1}+(n-1) \geq n$ for all $n$ and moreover $s_{n}>n$ if $d_{n}=n$, because in the case $s_{n}=n$ we would have $m=d_{n}=d_{s_{n}}=M$ in contradiction to the assumption $m<M$. In the same way $d_{n}=M$ implies $d_{s_{n}}=m$ and $s_{n}>n$. Consequently, there is a strictly increasing sequence $n_{1}, n_{2}, \ldots$ such that $$ d_{s_{n_{1}}}=M, \quad d_{s_{n_{2}}}=m, \quad d_{s_{n_{3}}}=M, \quad d_{s_{n_{4}}}=m, \quad \ldots $$ The sequence $d_{s_{1}}, d_{s_{2}}, \ldots$ is the sequence of pairwise differences of $s_{s_{1}+1}, s_{s_{2}+1}, \ldots$ and $s_{s_{1}}, s_{s_{2}}, \ldots$, hence also an arithmetic progression. Thus $m=M$.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
b46e876c-1af1-527c-a2b1-3b2bf24e7682
| 23,808
|
USA Suppose that $s_{1}, s_{2}, s_{3}, \ldots$ is a strictly increasing sequence of positive integers such that the subsequences $$ s_{s_{1}}, s_{s_{2}}, s_{s_{3}}, \ldots \quad \text { and } \quad s_{s_{1}+1}, s_{s_{2}+1}, s_{s_{3}+1}, \ldots $$ are both arithmetic progressions. Prove that $s_{1}, s_{2}, s_{3}, \ldots$ is itself an arithmetic progression.
|
Let the integers $D$ and $E$ be the common differences of the progressions $s_{s_{1}}, s_{s_{2}}, \ldots$ and $s_{s_{1}+1}, s_{s_{2}+1}, \ldots$, respectively. Let briefly $A=s_{s_{1}}-D$ and $B=s_{s_{1}+1}-E$. Then, for all positive integers $n$, $$ s_{s_{n}}=A+n D, \quad s_{s_{n}+1}=B+n E $$ Since the sequence $s_{1}, s_{2}, \ldots$ is strictly increasing, we have for all positive integers $n$ $$ s_{s_{n}}<s_{s_{n}+1} \leq s_{s_{n+1}} $$ which implies $$ A+n D<B+n E \leq A+(n+1) D $$ and thereby $$ 0<B-A+n(E-D) \leq D $$ which implies $D-E=0$ and thus $$ 0 \leq B-A \leq D $$ Let $m=\min \left\{s_{n+1}-s_{n}: n=1,2, \ldots\right\}$. Then $$ B-A=\left(s_{s_{1}+1}-E\right)-\left(s_{s_{1}}-D\right)=s_{s_{1}+1}-s_{s_{1}} \geq m $$ and $$ D=A+\left(s_{1}+1\right) D-\left(A+s_{1} D\right)=s_{s_{s_{1}+1}}-s_{s_{s_{1}}}=s_{B+D}-s_{A+D} \geq m(B-A) $$ From (3) we consider two cases. Case 1. $B-A=D$. Then, for each positive integer $n, s_{s_{n}+1}=B+n D=A+(n+1) D=s_{s_{n+1}}$, hence $s_{n+1}=s_{n}+1$ and $s_{1}, s_{2}, \ldots$ is an arithmetic progression with common difference 1 . Case 2. $B-A<D$. Choose some positive integer $N$ such that $s_{N+1}-s_{N}=m$. Then $$ \begin{aligned} m(A-B+D-1) & =m((A+(N+1) D)-(B+N D+1)) \\ & \leq s_{A+(N+1) D}-s_{B+N D+1}=s_{s_{s_{N+1}}}-s_{s_{s_{N}+1}+1} \\ & =\left(A+s_{N+1} D\right)-\left(B+\left(s_{N}+1\right) D\right)=\left(s_{N+1}-s_{N}\right) D+A-B-D \\ & =m D+A-B-D, \end{aligned} $$ i.e., $$ (B-A-m)+(D-m(B-A)) \leq 0 $$ The inequalities (4)-(6) imply that $$ B-A=m \quad \text { and } \quad D=m(B-A) $$ Assume that there is some positive integer $n$ such that $s_{n+1}>s_{n}+m$. Then $\left.m(m+1) \leq m\left(s_{n+1}-s_{n}\right) \leq s_{s_{n+1}}-s_{s_{n}}=(A+(n+1) D)-(A+n D)\right)=D=m(B-A)=m^{2}$, a contradiction. Hence $s_{1}, s_{2}, \ldots$ is an arithmetic progression with common difference $m$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
USA Suppose that $s_{1}, s_{2}, s_{3}, \ldots$ is a strictly increasing sequence of positive integers such that the subsequences $$ s_{s_{1}}, s_{s_{2}}, s_{s_{3}}, \ldots \quad \text { and } \quad s_{s_{1}+1}, s_{s_{2}+1}, s_{s_{3}+1}, \ldots $$ are both arithmetic progressions. Prove that $s_{1}, s_{2}, s_{3}, \ldots$ is itself an arithmetic progression.
|
Let the integers $D$ and $E$ be the common differences of the progressions $s_{s_{1}}, s_{s_{2}}, \ldots$ and $s_{s_{1}+1}, s_{s_{2}+1}, \ldots$, respectively. Let briefly $A=s_{s_{1}}-D$ and $B=s_{s_{1}+1}-E$. Then, for all positive integers $n$, $$ s_{s_{n}}=A+n D, \quad s_{s_{n}+1}=B+n E $$ Since the sequence $s_{1}, s_{2}, \ldots$ is strictly increasing, we have for all positive integers $n$ $$ s_{s_{n}}<s_{s_{n}+1} \leq s_{s_{n+1}} $$ which implies $$ A+n D<B+n E \leq A+(n+1) D $$ and thereby $$ 0<B-A+n(E-D) \leq D $$ which implies $D-E=0$ and thus $$ 0 \leq B-A \leq D $$ Let $m=\min \left\{s_{n+1}-s_{n}: n=1,2, \ldots\right\}$. Then $$ B-A=\left(s_{s_{1}+1}-E\right)-\left(s_{s_{1}}-D\right)=s_{s_{1}+1}-s_{s_{1}} \geq m $$ and $$ D=A+\left(s_{1}+1\right) D-\left(A+s_{1} D\right)=s_{s_{s_{1}+1}}-s_{s_{s_{1}}}=s_{B+D}-s_{A+D} \geq m(B-A) $$ From (3) we consider two cases. Case 1. $B-A=D$. Then, for each positive integer $n, s_{s_{n}+1}=B+n D=A+(n+1) D=s_{s_{n+1}}$, hence $s_{n+1}=s_{n}+1$ and $s_{1}, s_{2}, \ldots$ is an arithmetic progression with common difference 1 . Case 2. $B-A<D$. Choose some positive integer $N$ such that $s_{N+1}-s_{N}=m$. Then $$ \begin{aligned} m(A-B+D-1) & =m((A+(N+1) D)-(B+N D+1)) \\ & \leq s_{A+(N+1) D}-s_{B+N D+1}=s_{s_{s_{N+1}}}-s_{s_{s_{N}+1}+1} \\ & =\left(A+s_{N+1} D\right)-\left(B+\left(s_{N}+1\right) D\right)=\left(s_{N+1}-s_{N}\right) D+A-B-D \\ & =m D+A-B-D, \end{aligned} $$ i.e., $$ (B-A-m)+(D-m(B-A)) \leq 0 $$ The inequalities (4)-(6) imply that $$ B-A=m \quad \text { and } \quad D=m(B-A) $$ Assume that there is some positive integer $n$ such that $s_{n+1}>s_{n}+m$. Then $\left.m(m+1) \leq m\left(s_{n+1}-s_{n}\right) \leq s_{s_{n+1}}-s_{s_{n}}=(A+(n+1) D)-(A+n D)\right)=D=m(B-A)=m^{2}$, a contradiction. Hence $s_{1}, s_{2}, \ldots$ is an arithmetic progression with common difference $m$.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
b46e876c-1af1-527c-a2b1-3b2bf24e7682
| 23,808
|
RUS Let $n$ be a positive integer. Given a sequence $\varepsilon_{1}, \ldots, \varepsilon_{n-1}$ with $\varepsilon_{i}=0$ or $\varepsilon_{i}=1$ for each $i=1, \ldots, n-1$, the sequences $a_{0}, \ldots, a_{n}$ and $b_{0}, \ldots, b_{n}$ are constructed by the following rules: $$ \begin{gathered} a_{0}=b_{0}=1, \quad a_{1}=b_{1}=7, \\ a_{i+1}=\left\{\begin{array}{ll} 2 a_{i-1}+3 a_{i}, & \text { if } \varepsilon_{i}=0, \\ 3 a_{i-1}+a_{i}, & \text { if } \varepsilon_{i}=1, \end{array} \text { for each } i=1, \ldots, n-1,\right. \\ b_{i+1}=\left\{\begin{array}{ll} 2 b_{i-1}+3 b_{i}, & \text { if } \varepsilon_{n-i}=0, \\ 3 b_{i-1}+b_{i}, & \text { if } \varepsilon_{n-i}=1, \end{array} \text { for each } i=1, \ldots, n-1 .\right. \end{gathered} $$ Prove that $a_{n}=b_{n}$.
|
For a binary word $w=\sigma_{1} \ldots \sigma_{n}$ of length $n$ and a letter $\sigma \in\{0,1\}$ let $w \sigma=$ $\sigma_{1} \ldots \sigma_{n} \sigma$ and $\sigma w=\sigma \sigma_{1} \ldots \sigma_{n}$. Moreover let $\bar{w}=\sigma_{n} \ldots \sigma_{1}$ and let $\emptyset$ be the empty word (of length 0 and with $\bar{\emptyset}=\emptyset$ ). Let $(u, v)$ be a pair of two real numbers. For binary words $w$ we define recursively the numbers $(u, v)^{w}$ as follows: $$ \begin{gathered} (u, v)^{\emptyset}=v, \quad(u, v)^{0}=2 u+3 v, \quad(u, v)^{1}=3 u+v, \\ (u, v)^{w \sigma \varepsilon}= \begin{cases}3(u, v)^{w}+3(u, v)^{w \sigma}, & \text { if } \varepsilon=0, \\ 3(u, v)^{w}+(u, v)^{w \sigma}, & \text { if } \varepsilon=1\end{cases} \end{gathered} $$ It easily follows by induction on the length of $w$ that for all real numbers $u_{1}, v_{1}, u_{2}, v_{2}, \lambda_{1}$ and $\lambda_{2}$ $$ \left(\lambda_{1} u_{1}+\lambda_{2} u_{2}, \lambda_{1} v_{1}+\lambda_{2} v_{2}\right)^{w}=\lambda_{1}\left(u_{1}, v_{1}\right)^{w}+\lambda_{2}\left(u_{2}, v_{2}\right)^{w} $$ and that for $\varepsilon \in\{0,1\}$ $$ (u, v)^{\varepsilon w}=\left(v,(u, v)^{\varepsilon}\right)^{w} . $$ Obviously, for $n \geq 1$ and $w=\varepsilon_{1} \ldots \varepsilon_{n-1}$, we have $a_{n}=(1,7)^{w}$ and $b_{n}=(1,7)^{\bar{w}}$. Thus it is sufficient to prove that $$ (1,7)^{w}=(1,7)^{\bar{w}} $$ for each binary word $w$. We proceed by induction on the length of $w$. The assertion is obvious if $w$ has length 0 or 1 . Now let $w \sigma \varepsilon$ be a binary word of length $n \geq 2$ and suppose that the assertion is true for all binary words of length at most $n-1$. Note that $(2,1)^{\sigma}=7=(1,7)^{\emptyset}$ for $\sigma \in\{0,1\},(1,7)^{0}=23$, and $(1,7)^{1}=10$. First let $\varepsilon=0$. Then in view of the induction hypothesis and the equalities (1) and (2), we obtain $$ \begin{aligned} &(1,7)^{w \sigma 0}=2(1,7)^{w}+3(1,7)^{w \sigma}=2(1,7)^{\bar{w}}+3(1,7)^{\sigma \bar{w}}=2(2,1)^{\sigma \bar{w}}+3(1,7)^{\sigma \bar{w}} \\ &=(7,23)^{\sigma \bar{w}}=(1,7)^{0 \sigma \bar{w}} \end{aligned} $$ Now let $\varepsilon=1$. Analogously, we obtain $$ \begin{aligned} &(1,7)^{w \sigma 1}=3(1,7)^{w}+(1,7)^{w \sigma}=3(1,7)^{\bar{w}}+(1,7)^{\sigma \bar{w}}=3(2,1)^{\sigma \bar{w}}+(1,7)^{\sigma \bar{w}} \\ &=(7,10)^{\sigma \bar{w}}=(1,7)^{1 \sigma \bar{w}} \end{aligned} $$ Thus the induction step is complete, (3) and hence also $a_{n}=b_{n}$ are proved. Comment. The original solution uses the relation $$ (1,7)^{\alpha \beta w}=\left((1,7)^{w},(1,7)^{\beta w}\right)^{\alpha}, \quad \alpha, \beta \in\{0,1\} $$ which can be proved by induction on the length of $w$. Then (3) also follows by induction on the length of $w$ : $$ (1,7)^{\alpha \beta w}=\left((1,7)^{w},(1,7)^{\beta w}\right)^{\alpha}=\left((1,7)^{\bar{w}},(1,7)^{\bar{w} \beta}\right)^{\alpha}=(1,7)^{\bar{w} \beta \alpha} . $$ Here $w$ may be the empty word.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
RUS Let $n$ be a positive integer. Given a sequence $\varepsilon_{1}, \ldots, \varepsilon_{n-1}$ with $\varepsilon_{i}=0$ or $\varepsilon_{i}=1$ for each $i=1, \ldots, n-1$, the sequences $a_{0}, \ldots, a_{n}$ and $b_{0}, \ldots, b_{n}$ are constructed by the following rules: $$ \begin{gathered} a_{0}=b_{0}=1, \quad a_{1}=b_{1}=7, \\ a_{i+1}=\left\{\begin{array}{ll} 2 a_{i-1}+3 a_{i}, & \text { if } \varepsilon_{i}=0, \\ 3 a_{i-1}+a_{i}, & \text { if } \varepsilon_{i}=1, \end{array} \text { for each } i=1, \ldots, n-1,\right. \\ b_{i+1}=\left\{\begin{array}{ll} 2 b_{i-1}+3 b_{i}, & \text { if } \varepsilon_{n-i}=0, \\ 3 b_{i-1}+b_{i}, & \text { if } \varepsilon_{n-i}=1, \end{array} \text { for each } i=1, \ldots, n-1 .\right. \end{gathered} $$ Prove that $a_{n}=b_{n}$.
|
For a binary word $w=\sigma_{1} \ldots \sigma_{n}$ of length $n$ and a letter $\sigma \in\{0,1\}$ let $w \sigma=$ $\sigma_{1} \ldots \sigma_{n} \sigma$ and $\sigma w=\sigma \sigma_{1} \ldots \sigma_{n}$. Moreover let $\bar{w}=\sigma_{n} \ldots \sigma_{1}$ and let $\emptyset$ be the empty word (of length 0 and with $\bar{\emptyset}=\emptyset$ ). Let $(u, v)$ be a pair of two real numbers. For binary words $w$ we define recursively the numbers $(u, v)^{w}$ as follows: $$ \begin{gathered} (u, v)^{\emptyset}=v, \quad(u, v)^{0}=2 u+3 v, \quad(u, v)^{1}=3 u+v, \\ (u, v)^{w \sigma \varepsilon}= \begin{cases}3(u, v)^{w}+3(u, v)^{w \sigma}, & \text { if } \varepsilon=0, \\ 3(u, v)^{w}+(u, v)^{w \sigma}, & \text { if } \varepsilon=1\end{cases} \end{gathered} $$ It easily follows by induction on the length of $w$ that for all real numbers $u_{1}, v_{1}, u_{2}, v_{2}, \lambda_{1}$ and $\lambda_{2}$ $$ \left(\lambda_{1} u_{1}+\lambda_{2} u_{2}, \lambda_{1} v_{1}+\lambda_{2} v_{2}\right)^{w}=\lambda_{1}\left(u_{1}, v_{1}\right)^{w}+\lambda_{2}\left(u_{2}, v_{2}\right)^{w} $$ and that for $\varepsilon \in\{0,1\}$ $$ (u, v)^{\varepsilon w}=\left(v,(u, v)^{\varepsilon}\right)^{w} . $$ Obviously, for $n \geq 1$ and $w=\varepsilon_{1} \ldots \varepsilon_{n-1}$, we have $a_{n}=(1,7)^{w}$ and $b_{n}=(1,7)^{\bar{w}}$. Thus it is sufficient to prove that $$ (1,7)^{w}=(1,7)^{\bar{w}} $$ for each binary word $w$. We proceed by induction on the length of $w$. The assertion is obvious if $w$ has length 0 or 1 . Now let $w \sigma \varepsilon$ be a binary word of length $n \geq 2$ and suppose that the assertion is true for all binary words of length at most $n-1$. Note that $(2,1)^{\sigma}=7=(1,7)^{\emptyset}$ for $\sigma \in\{0,1\},(1,7)^{0}=23$, and $(1,7)^{1}=10$. First let $\varepsilon=0$. Then in view of the induction hypothesis and the equalities (1) and (2), we obtain $$ \begin{aligned} &(1,7)^{w \sigma 0}=2(1,7)^{w}+3(1,7)^{w \sigma}=2(1,7)^{\bar{w}}+3(1,7)^{\sigma \bar{w}}=2(2,1)^{\sigma \bar{w}}+3(1,7)^{\sigma \bar{w}} \\ &=(7,23)^{\sigma \bar{w}}=(1,7)^{0 \sigma \bar{w}} \end{aligned} $$ Now let $\varepsilon=1$. Analogously, we obtain $$ \begin{aligned} &(1,7)^{w \sigma 1}=3(1,7)^{w}+(1,7)^{w \sigma}=3(1,7)^{\bar{w}}+(1,7)^{\sigma \bar{w}}=3(2,1)^{\sigma \bar{w}}+(1,7)^{\sigma \bar{w}} \\ &=(7,10)^{\sigma \bar{w}}=(1,7)^{1 \sigma \bar{w}} \end{aligned} $$ Thus the induction step is complete, (3) and hence also $a_{n}=b_{n}$ are proved. Comment. The original solution uses the relation $$ (1,7)^{\alpha \beta w}=\left((1,7)^{w},(1,7)^{\beta w}\right)^{\alpha}, \quad \alpha, \beta \in\{0,1\} $$ which can be proved by induction on the length of $w$. Then (3) also follows by induction on the length of $w$ : $$ (1,7)^{\alpha \beta w}=\left((1,7)^{w},(1,7)^{\beta w}\right)^{\alpha}=\left((1,7)^{\bar{w}},(1,7)^{\bar{w} \beta}\right)^{\alpha}=(1,7)^{\bar{w} \beta \alpha} . $$ Here $w$ may be the empty word.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
9af54c97-0a0e-5c1f-9b35-8d54e05ea24c
| 23,819
|
NLD Five identical empty buckets of 2-liter capacity stand at the vertices of a regular pentagon. Cinderella and her wicked Stepmother go through a sequence of rounds: At the beginning of every round, the Stepmother takes one liter of water from the nearby river and distributes it arbitrarily over the five buckets. Then Cinderella chooses a pair of neighboring buckets, empties them into the river, and puts them back. Then the next round begins. The Stepmother's goal is to make one of these buckets overflow. Cinderella's goal is to prevent this. Can the wicked Stepmother enforce a bucket overflow?
|
No, the Stepmother cannot enforce a bucket overflow and Cinderella can keep playing forever. Throughout we denote the five buckets by $B_{0}, B_{1}, B_{2}, B_{3}$, and $B_{4}$, where $B_{k}$ is adjacent to bucket $B_{k-1}$ and $B_{k+1}(k=0,1,2,3,4)$ and all indices are taken modulo 5 . Cinderella enforces that the following three conditions are satisfied at the beginning of every round: (1) Two adjacent buckets (say $B_{1}$ and $B_{2}$ ) are empty. (2) The two buckets standing next to these adjacent buckets (here $B_{0}$ and $B_{3}$ ) have total contents at most 1. (3) The remaining bucket (here $B_{4}$ ) has contents at most 1 . These conditions clearly hold at the beginning of the first round, when all buckets are empty. Assume that Cinderella manages to maintain them until the beginning of the $r$-th round $(r \geq 1)$. Denote by $x_{k}(k=0,1,2,3,4)$ the contents of bucket $B_{k}$ at the beginning of this round and by $y_{k}$ the corresponding contents after the Stepmother has distributed her liter of water in this round. By the conditions, we can assume $x_{1}=x_{2}=0, x_{0}+x_{3} \leq 1$ and $x_{4} \leq 1$. Then, since the Stepmother adds one liter, we conclude $y_{0}+y_{1}+y_{2}+y_{3} \leq 2$. This inequality implies $y_{0}+y_{2} \leq 1$ or $y_{1}+y_{3} \leq 1$. For reasons of symmetry, we only consider the second case. Then Cinderella empties buckets $B_{0}$ and $B_{4}$. At the beginning of the next round $B_{0}$ and $B_{4}$ are empty (condition (1) is fulfilled), due to $y_{1}+y_{3} \leq 1$ condition (2) is fulfilled and finally since $x_{2}=0$ we also must have $y_{2} \leq 1$ (condition (3) is fulfilled). Therefore, Cinderella can indeed manage to maintain the three conditions (1)-(3) also at the beginning of the $(r+1)$-th round. By induction, she thus manages to maintain them at the beginning of every round. In particular she manages to keep the contents of every single bucket at most 1 liter. Therefore, the buckets of 2-liter capacity will never overflow.
|
proof
|
Yes
|
Yes
|
proof
|
Logic and Puzzles
|
NLD Five identical empty buckets of 2-liter capacity stand at the vertices of a regular pentagon. Cinderella and her wicked Stepmother go through a sequence of rounds: At the beginning of every round, the Stepmother takes one liter of water from the nearby river and distributes it arbitrarily over the five buckets. Then Cinderella chooses a pair of neighboring buckets, empties them into the river, and puts them back. Then the next round begins. The Stepmother's goal is to make one of these buckets overflow. Cinderella's goal is to prevent this. Can the wicked Stepmother enforce a bucket overflow?
|
No, the Stepmother cannot enforce a bucket overflow and Cinderella can keep playing forever. Throughout we denote the five buckets by $B_{0}, B_{1}, B_{2}, B_{3}$, and $B_{4}$, where $B_{k}$ is adjacent to bucket $B_{k-1}$ and $B_{k+1}(k=0,1,2,3,4)$ and all indices are taken modulo 5 . Cinderella enforces that the following three conditions are satisfied at the beginning of every round: (1) Two adjacent buckets (say $B_{1}$ and $B_{2}$ ) are empty. (2) The two buckets standing next to these adjacent buckets (here $B_{0}$ and $B_{3}$ ) have total contents at most 1. (3) The remaining bucket (here $B_{4}$ ) has contents at most 1 . These conditions clearly hold at the beginning of the first round, when all buckets are empty. Assume that Cinderella manages to maintain them until the beginning of the $r$-th round $(r \geq 1)$. Denote by $x_{k}(k=0,1,2,3,4)$ the contents of bucket $B_{k}$ at the beginning of this round and by $y_{k}$ the corresponding contents after the Stepmother has distributed her liter of water in this round. By the conditions, we can assume $x_{1}=x_{2}=0, x_{0}+x_{3} \leq 1$ and $x_{4} \leq 1$. Then, since the Stepmother adds one liter, we conclude $y_{0}+y_{1}+y_{2}+y_{3} \leq 2$. This inequality implies $y_{0}+y_{2} \leq 1$ or $y_{1}+y_{3} \leq 1$. For reasons of symmetry, we only consider the second case. Then Cinderella empties buckets $B_{0}$ and $B_{4}$. At the beginning of the next round $B_{0}$ and $B_{4}$ are empty (condition (1) is fulfilled), due to $y_{1}+y_{3} \leq 1$ condition (2) is fulfilled and finally since $x_{2}=0$ we also must have $y_{2} \leq 1$ (condition (3) is fulfilled). Therefore, Cinderella can indeed manage to maintain the three conditions (1)-(3) also at the beginning of the $(r+1)$-th round. By induction, she thus manages to maintain them at the beginning of every round. In particular she manages to keep the contents of every single bucket at most 1 liter. Therefore, the buckets of 2-liter capacity will never overflow.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
5a2c767c-0a44-5f31-bcc8-50c0bc507e2b
| 23,826
|
AUT For any integer $n \geq 2$, we compute the integer $h(n)$ by applying the following procedure to its decimal representation. Let $r$ be the rightmost digit of $n$. (1) If $r=0$, then the decimal representation of $h(n)$ results from the decimal representation of $n$ by removing this rightmost digit 0 . (2) If $1 \leq r \leq 9$ we split the decimal representation of $n$ into a maximal right part $R$ that solely consists of digits not less than $r$ and into a left part $L$ that either is empty or ends with a digit strictly smaller than $r$. Then the decimal representation of $h(n)$ consists of the decimal representation of $L$, followed by two copies of the decimal representation of $R-1$. For instance, for the number $n=17,151,345,543$, we will have $L=17,151, R=345,543$ and $h(n)=17,151,345,542,345,542$. Prove that, starting with an arbitrary integer $n \geq 2$, iterated application of $h$ produces the integer 1 after finitely many steps.
|
We identify integers $n \geq 2$ with the digit-strings, briefly strings, of their decimal representation and extend the definition of $h$ to all non-empty strings with digits from 0 to 9. We recursively define ten functions $f_{0}, \ldots, f_{9}$ that map some strings into integers for $k=$ $9,8, \ldots, 1,0$. The function $f_{9}$ is only defined on strings $x$ (including the empty string $\varepsilon$ ) that entirely consist of nines. If $x$ consists of $m$ nines, then $f_{9}(x)=m+1, m=0,1, \ldots$ For $k \leq 8$, the domain of $f_{k}(x)$ is the set of all strings consisting only of digits that are $\geq k$. We write $x$ in the form $x_{0} k x_{1} k x_{2} k \ldots x_{m-1} k x_{m}$ where the strings $x_{s}$ only consist of digits $\geq k+1$. Note that some of these strings might equal the empty string $\varepsilon$ and that $m=0$ is possible, i.e. the digit $k$ does not appear in $x$. Then we define $$ f_{k}(x)=\sum_{s=0}^{m} 4^{f_{k+1}\left(x_{s}\right)} $$ We will use the following obvious fact: Fact 1. If $x$ does not contain digits smaller than $k$, then $f_{i}(x)=4^{f_{i+1}(x)}$ for all $i=0, \ldots, k-1$. In particular, $f_{i}(\varepsilon)=4^{9-i}$ for all $i=0,1, \ldots, 9$. Moreover, by induction on $k=9,8, \ldots, 0$ it follows easily: Fact 2. If the nonempty string $x$ does not contain digits smaller than $k$, then $f_{i}(x)>f_{i}(\varepsilon)$ for all $i=0, \ldots, k$. We will show the essential fact: Fact 3. $f_{0}(n)>f_{0}(h(n))$. Then the empty string will necessarily be reached after a finite number of applications of $h$. But starting from a string without leading zeros, $\varepsilon$ can only be reached via the strings $1 \rightarrow 00 \rightarrow 0 \rightarrow \varepsilon$. Hence also the number 1 will appear after a finite number of applications of $h$. Proof of Fact 3. If the last digit $r$ of $n$ is 0 , then we write $n=x_{0} 0 \ldots 0 x_{m-1} 0 \varepsilon$ where the $x_{i}$ do not contain the digit 0 . Then $h(n)=x_{0} 0 \ldots 0 x_{m-1}$ and $f_{0}(n)-f_{0}(h(n))=f_{0}(\varepsilon)>0$. So let the last digit $r$ of $n$ be at least 1 . Let $L=y k$ and $R=z r$ be the corresponding left and right parts where $y$ is some string, $k \leq r-1$ and the string $z$ consists only of digits not less than $r$. Then $n=y k z r$ and $h(n)=y k z(r-1) z(r-1)$. Let $d(y)$ be the smallest digit of $y$. We consider two cases which do not exclude each other. Case 1. $d(y) \geq k$. Then $$ f_{k}(n)-f_{k}(h(n))=f_{k}(z r)-f_{k}(z(r-1) z(r-1)) . $$ In view of Fact 1 this difference is positive if and only if $$ f_{r-1}(z r)-f_{r-1}(z(r-1) z(r-1))>0 $$ We have, using Fact 2, $$ f_{r-1}(z r)=4^{f_{r}(z r)}=4^{f_{r}(z)+4^{f_{r+1}(z)}} \geq 4 \cdot 4^{f_{r}(z)}>4^{f_{r}(z)}+4^{f_{r}(z)}+4^{f_{r}(z)}=f_{r-1}(z(r-1) z(r-1)) . $$ Here we use the additional definition $f_{10}(\varepsilon)=0$ if $r=9$. Consequently, $f_{k}(n)-f_{k}(h(n))>0$ and according to Fact $1, f_{0}(n)-f_{0}(h(n))>0$. Case 2. $d(y) \leq k$. We prove by induction on $d(y)=k, k-1, \ldots, 0$ that $f_{i}(n)-f_{i}(h(n))>0$ for all $i=0, \ldots, d(y)$. By Fact 1, it suffices to do so for $i=d(y)$. The initialization $d(y)=k$ was already treated in Case 1. Let $t=d(y)<k$. Write $y$ in the form utv where $v$ does not contain digits $\leq t$. Then, in view of the induction hypothesis, $$ f_{t}(n)-f_{t}(h(n))=f_{t}(v k z r)-f_{t}(v k z(r-1) z(r-1))=4^{f_{t+1}(v k z r)}-4^{f_{t+1}(v k z(r-1) z(r-1))}>0 $$ Thus the inequality $f_{d(y)}(n)-f_{d(y)}(h(n))>0$ is established and from Fact 1 it follows that $f_{0}(n)-f_{0}(h(n))>0$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
AUT For any integer $n \geq 2$, we compute the integer $h(n)$ by applying the following procedure to its decimal representation. Let $r$ be the rightmost digit of $n$. (1) If $r=0$, then the decimal representation of $h(n)$ results from the decimal representation of $n$ by removing this rightmost digit 0 . (2) If $1 \leq r \leq 9$ we split the decimal representation of $n$ into a maximal right part $R$ that solely consists of digits not less than $r$ and into a left part $L$ that either is empty or ends with a digit strictly smaller than $r$. Then the decimal representation of $h(n)$ consists of the decimal representation of $L$, followed by two copies of the decimal representation of $R-1$. For instance, for the number $n=17,151,345,543$, we will have $L=17,151, R=345,543$ and $h(n)=17,151,345,542,345,542$. Prove that, starting with an arbitrary integer $n \geq 2$, iterated application of $h$ produces the integer 1 after finitely many steps.
|
We identify integers $n \geq 2$ with the digit-strings, briefly strings, of their decimal representation and extend the definition of $h$ to all non-empty strings with digits from 0 to 9. We recursively define ten functions $f_{0}, \ldots, f_{9}$ that map some strings into integers for $k=$ $9,8, \ldots, 1,0$. The function $f_{9}$ is only defined on strings $x$ (including the empty string $\varepsilon$ ) that entirely consist of nines. If $x$ consists of $m$ nines, then $f_{9}(x)=m+1, m=0,1, \ldots$ For $k \leq 8$, the domain of $f_{k}(x)$ is the set of all strings consisting only of digits that are $\geq k$. We write $x$ in the form $x_{0} k x_{1} k x_{2} k \ldots x_{m-1} k x_{m}$ where the strings $x_{s}$ only consist of digits $\geq k+1$. Note that some of these strings might equal the empty string $\varepsilon$ and that $m=0$ is possible, i.e. the digit $k$ does not appear in $x$. Then we define $$ f_{k}(x)=\sum_{s=0}^{m} 4^{f_{k+1}\left(x_{s}\right)} $$ We will use the following obvious fact: Fact 1. If $x$ does not contain digits smaller than $k$, then $f_{i}(x)=4^{f_{i+1}(x)}$ for all $i=0, \ldots, k-1$. In particular, $f_{i}(\varepsilon)=4^{9-i}$ for all $i=0,1, \ldots, 9$. Moreover, by induction on $k=9,8, \ldots, 0$ it follows easily: Fact 2. If the nonempty string $x$ does not contain digits smaller than $k$, then $f_{i}(x)>f_{i}(\varepsilon)$ for all $i=0, \ldots, k$. We will show the essential fact: Fact 3. $f_{0}(n)>f_{0}(h(n))$. Then the empty string will necessarily be reached after a finite number of applications of $h$. But starting from a string without leading zeros, $\varepsilon$ can only be reached via the strings $1 \rightarrow 00 \rightarrow 0 \rightarrow \varepsilon$. Hence also the number 1 will appear after a finite number of applications of $h$. Proof of Fact 3. If the last digit $r$ of $n$ is 0 , then we write $n=x_{0} 0 \ldots 0 x_{m-1} 0 \varepsilon$ where the $x_{i}$ do not contain the digit 0 . Then $h(n)=x_{0} 0 \ldots 0 x_{m-1}$ and $f_{0}(n)-f_{0}(h(n))=f_{0}(\varepsilon)>0$. So let the last digit $r$ of $n$ be at least 1 . Let $L=y k$ and $R=z r$ be the corresponding left and right parts where $y$ is some string, $k \leq r-1$ and the string $z$ consists only of digits not less than $r$. Then $n=y k z r$ and $h(n)=y k z(r-1) z(r-1)$. Let $d(y)$ be the smallest digit of $y$. We consider two cases which do not exclude each other. Case 1. $d(y) \geq k$. Then $$ f_{k}(n)-f_{k}(h(n))=f_{k}(z r)-f_{k}(z(r-1) z(r-1)) . $$ In view of Fact 1 this difference is positive if and only if $$ f_{r-1}(z r)-f_{r-1}(z(r-1) z(r-1))>0 $$ We have, using Fact 2, $$ f_{r-1}(z r)=4^{f_{r}(z r)}=4^{f_{r}(z)+4^{f_{r+1}(z)}} \geq 4 \cdot 4^{f_{r}(z)}>4^{f_{r}(z)}+4^{f_{r}(z)}+4^{f_{r}(z)}=f_{r-1}(z(r-1) z(r-1)) . $$ Here we use the additional definition $f_{10}(\varepsilon)=0$ if $r=9$. Consequently, $f_{k}(n)-f_{k}(h(n))>0$ and according to Fact $1, f_{0}(n)-f_{0}(h(n))>0$. Case 2. $d(y) \leq k$. We prove by induction on $d(y)=k, k-1, \ldots, 0$ that $f_{i}(n)-f_{i}(h(n))>0$ for all $i=0, \ldots, d(y)$. By Fact 1, it suffices to do so for $i=d(y)$. The initialization $d(y)=k$ was already treated in Case 1. Let $t=d(y)<k$. Write $y$ in the form utv where $v$ does not contain digits $\leq t$. Then, in view of the induction hypothesis, $$ f_{t}(n)-f_{t}(h(n))=f_{t}(v k z r)-f_{t}(v k z(r-1) z(r-1))=4^{f_{t+1}(v k z r)}-4^{f_{t+1}(v k z(r-1) z(r-1))}>0 $$ Thus the inequality $f_{d(y)}(n)-f_{d(y)}(h(n))>0$ is established and from Fact 1 it follows that $f_{0}(n)-f_{0}(h(n))>0$.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
7856a4bd-65ff-55f4-94f5-a034424aeeb8
| 23,833
|
RUS Let $A B C$ be a triangle with circumcenter $O$. The points $P$ and $Q$ are interior points of the sides $C A$ and $A B$, respectively. The circle $k$ passes through the midpoints of the segments $B P$, $C Q$, and $P Q$. Prove that if the line $P Q$ is tangent to circle $k$ then $O P=O Q$.
|
Let $K, L, M, B^{\prime}, C^{\prime}$ be the midpoints of $B P, C Q, P Q, C A$, and $A B$, respectively (see Figure 1). Since $C A \| L M$, we have $\angle L M P=\angle Q P A$. Since $k$ touches the segment $P Q$ at $M$, we find $\angle L M P=\angle L K M$. Thus $\angle Q P A=\angle L K M$. Similarly it follows from $A B \| M K$ that $\angle P Q A=\angle K L M$. Therefore, triangles $A P Q$ and $M K L$ are similar, hence $$ \frac{A P}{A Q}=\frac{M K}{M L}=\frac{\frac{Q B}{2}}{\frac{P C}{2}}=\frac{Q B}{P C} $$ Now (1) is equivalent to $A P \cdot P C=A Q \cdot Q B$ which means that the power of points $P$ and $Q$ with respect to the circumcircle of $\triangle A B C$ are equal, hence $O P=O Q$. 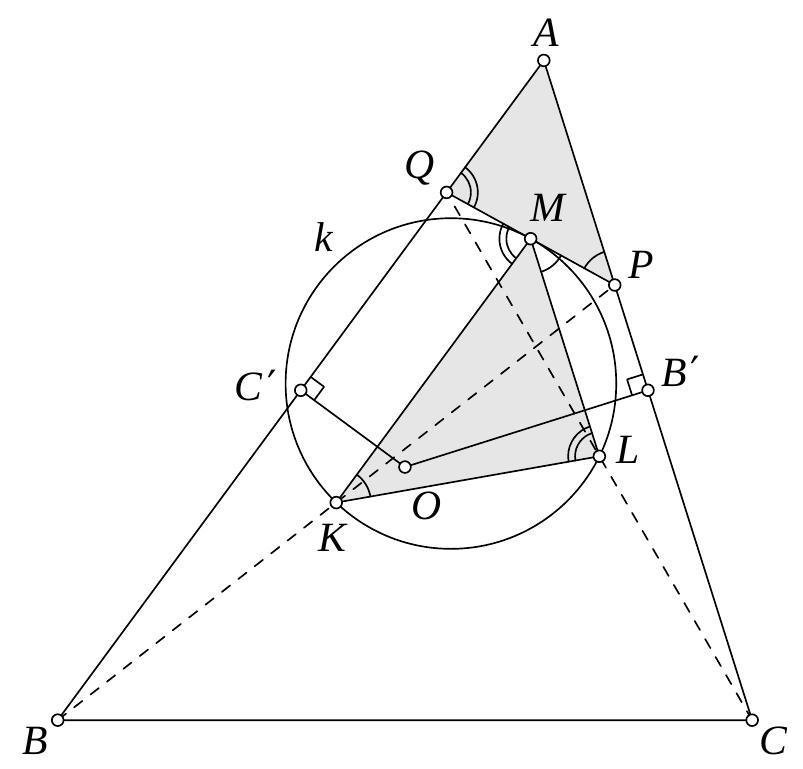 Figure 1 Comment. The last argument can also be established by the following calculation: $$ \begin{aligned} O P^{2}-O Q^{2} & =O B^{\prime 2}+B^{\prime} P^{2}-O C^{2}-C^{\prime} Q^{2} \\ & =\left(O A^{2}-A B^{2}\right)+B^{\prime} P^{2}-\left(O A^{2}-A C^{\prime 2}\right)-C^{\prime} Q^{2} \\ & =\left(A C^{\prime 2}-C^{\prime} Q^{2}\right)-\left(A B^{\prime 2}-B^{\prime} P^{2}\right) \\ & =\left(A C^{\prime}-C^{\prime} Q\right)\left(A C^{\prime}+C^{\prime} Q\right)-\left(A B^{\prime}-B^{\prime} P\right)\left(A B^{\prime}+B^{\prime} P\right) \\ & =A Q \cdot Q B-A P \cdot P C . \end{aligned} $$ With (1), we conclude $O P^{2}-O Q^{2}=0$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
RUS Let $A B C$ be a triangle with circumcenter $O$. The points $P$ and $Q$ are interior points of the sides $C A$ and $A B$, respectively. The circle $k$ passes through the midpoints of the segments $B P$, $C Q$, and $P Q$. Prove that if the line $P Q$ is tangent to circle $k$ then $O P=O Q$.
|
Let $K, L, M, B^{\prime}, C^{\prime}$ be the midpoints of $B P, C Q, P Q, C A$, and $A B$, respectively (see Figure 1). Since $C A \| L M$, we have $\angle L M P=\angle Q P A$. Since $k$ touches the segment $P Q$ at $M$, we find $\angle L M P=\angle L K M$. Thus $\angle Q P A=\angle L K M$. Similarly it follows from $A B \| M K$ that $\angle P Q A=\angle K L M$. Therefore, triangles $A P Q$ and $M K L$ are similar, hence $$ \frac{A P}{A Q}=\frac{M K}{M L}=\frac{\frac{Q B}{2}}{\frac{P C}{2}}=\frac{Q B}{P C} $$ Now (1) is equivalent to $A P \cdot P C=A Q \cdot Q B$ which means that the power of points $P$ and $Q$ with respect to the circumcircle of $\triangle A B C$ are equal, hence $O P=O Q$.  Figure 1 Comment. The last argument can also be established by the following calculation: $$ \begin{aligned} O P^{2}-O Q^{2} & =O B^{\prime 2}+B^{\prime} P^{2}-O C^{2}-C^{\prime} Q^{2} \\ & =\left(O A^{2}-A B^{2}\right)+B^{\prime} P^{2}-\left(O A^{2}-A C^{\prime 2}\right)-C^{\prime} Q^{2} \\ & =\left(A C^{\prime 2}-C^{\prime} Q^{2}\right)-\left(A B^{\prime 2}-B^{\prime} P^{2}\right) \\ & =\left(A C^{\prime}-C^{\prime} Q\right)\left(A C^{\prime}+C^{\prime} Q\right)-\left(A B^{\prime}-B^{\prime} P\right)\left(A B^{\prime}+B^{\prime} P\right) \\ & =A Q \cdot Q B-A P \cdot P C . \end{aligned} $$ With (1), we conclude $O P^{2}-O Q^{2}=0$, as desired.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
c5cceecb-6a01-5daf-8a14-7206df5b793c
| 23,841
|
RUS Let $A B C$ be a triangle with circumcenter $O$. The points $P$ and $Q$ are interior points of the sides $C A$ and $A B$, respectively. The circle $k$ passes through the midpoints of the segments $B P$, $C Q$, and $P Q$. Prove that if the line $P Q$ is tangent to circle $k$ then $O P=O Q$.
|
Again, denote by $K, L, M$ the midpoints of segments $B P, C Q$, and $P Q$, respectively. Let $O, S, T$ be the circumcenters of triangles $A B C, K L M$, and $A P Q$, respectively (see Figure 2). Note that $M K$ and $L M$ are the midlines in triangles $B P Q$ and $C P Q$, respectively, so $\overrightarrow{M K}=\frac{1}{2} \overrightarrow{Q B}$ and $\overrightarrow{M L}=\frac{1}{2} \overrightarrow{P C}$. Denote by $\operatorname{pr}_{l}(\vec{v})$ the projection of vector $\vec{v}$ onto line $l$. Then $\operatorname{pr}_{A B}(\overrightarrow{O T})=\operatorname{pr}_{A B}(\overrightarrow{O A}-\overrightarrow{T A})=\frac{1}{2} \overrightarrow{B A}-\frac{1}{2} \overrightarrow{Q A}=\frac{1}{2} \overrightarrow{B Q}=\overrightarrow{K M}$ and $\operatorname{pr}_{A B}(\overrightarrow{S M})=\operatorname{pr}_{M K}(\overrightarrow{S M})=$ $\frac{1}{2} \overrightarrow{K M}=\frac{1}{2} \operatorname{pr}_{A B}(\overrightarrow{O T})$. Analogously we get $\operatorname{pr}_{C A}(\overrightarrow{S M})=\frac{1}{2} \operatorname{pr}_{C A}(\overrightarrow{O T})$. Since $A B$ and $C A$ are not parallel, this implies that $\overrightarrow{S M}=\frac{1}{2} \overrightarrow{O T}$. 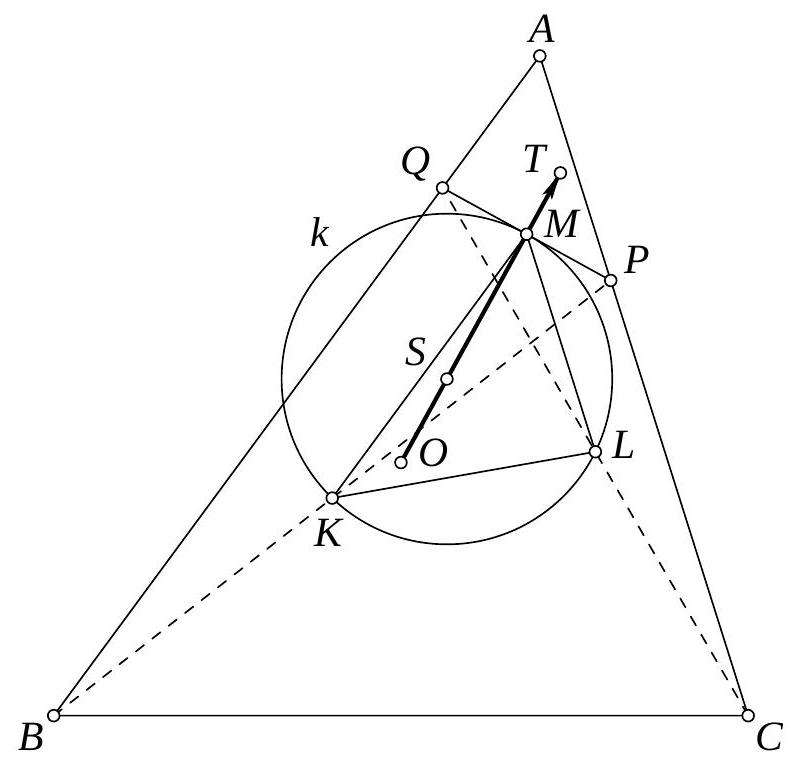 Figure 2 Now, since the circle $k$ touches $P Q$ at $M$, we get $S M \perp P Q$, hence $O T \perp P Q$. Since $T$ is equidistant from $P$ and $Q$, the line $O T$ is a perpendicular bisector of segment $P Q$, and hence $O$ is equidistant from $P$ and $Q$ which finishes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
RUS Let $A B C$ be a triangle with circumcenter $O$. The points $P$ and $Q$ are interior points of the sides $C A$ and $A B$, respectively. The circle $k$ passes through the midpoints of the segments $B P$, $C Q$, and $P Q$. Prove that if the line $P Q$ is tangent to circle $k$ then $O P=O Q$.
|
Again, denote by $K, L, M$ the midpoints of segments $B P, C Q$, and $P Q$, respectively. Let $O, S, T$ be the circumcenters of triangles $A B C, K L M$, and $A P Q$, respectively (see Figure 2). Note that $M K$ and $L M$ are the midlines in triangles $B P Q$ and $C P Q$, respectively, so $\overrightarrow{M K}=\frac{1}{2} \overrightarrow{Q B}$ and $\overrightarrow{M L}=\frac{1}{2} \overrightarrow{P C}$. Denote by $\operatorname{pr}_{l}(\vec{v})$ the projection of vector $\vec{v}$ onto line $l$. Then $\operatorname{pr}_{A B}(\overrightarrow{O T})=\operatorname{pr}_{A B}(\overrightarrow{O A}-\overrightarrow{T A})=\frac{1}{2} \overrightarrow{B A}-\frac{1}{2} \overrightarrow{Q A}=\frac{1}{2} \overrightarrow{B Q}=\overrightarrow{K M}$ and $\operatorname{pr}_{A B}(\overrightarrow{S M})=\operatorname{pr}_{M K}(\overrightarrow{S M})=$ $\frac{1}{2} \overrightarrow{K M}=\frac{1}{2} \operatorname{pr}_{A B}(\overrightarrow{O T})$. Analogously we get $\operatorname{pr}_{C A}(\overrightarrow{S M})=\frac{1}{2} \operatorname{pr}_{C A}(\overrightarrow{O T})$. Since $A B$ and $C A$ are not parallel, this implies that $\overrightarrow{S M}=\frac{1}{2} \overrightarrow{O T}$.  Figure 2 Now, since the circle $k$ touches $P Q$ at $M$, we get $S M \perp P Q$, hence $O T \perp P Q$. Since $T$ is equidistant from $P$ and $Q$, the line $O T$ is a perpendicular bisector of segment $P Q$, and hence $O$ is equidistant from $P$ and $Q$ which finishes the proof.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
c5cceecb-6a01-5daf-8a14-7206df5b793c
| 23,841
|
IRN Let $A B C$ be a triangle. The incircle of $A B C$ touches the sides $A B$ and $A C$ at the points $Z$ and $Y$, respectively. Let $G$ be the point where the lines $B Y$ and $C Z$ meet, and let $R$ and $S$ be points such that the two quadrilaterals $B C Y R$ and $B C S Z$ are parallelograms. Prove that $G R=G S$.
|
Denote by $k$ the incircle and by $k_{a}$ the excircle opposite to $A$ of triangle $A B C$. Let $k$ and $k_{a}$ touch the side $B C$ at the points $X$ and $T$, respectively, let $k_{a}$ touch the lines $A B$ and $A C$ at the points $P$ and $Q$, respectively. We use several times the fact that opposing sides of a parallelogram are of equal length, that points of contact of the excircle and incircle to a side of a triangle lie symmetric with respect to the midpoint of this side and that segments on two tangents to a circle defined by the points of contact and their point of intersection have the same length. So we conclude $$ \begin{gathered} Z P=Z B+B P=X B+B T=B X+C X=Z S \text { and } \\ C Q=C T=B X=B Z=C S . \end{gathered} $$  So for each of the points $Z, C$, their distances to $S$ equal the length of a tangent segment from this point to $k_{a}$. It is well-known, that all points with this property lie on the line $Z C$, which is the radical axis of $S$ and $k_{a}$. Similar arguments yield that $B Y$ is the radical axis of $R$ and $k_{a}$. So the point of intersection of $Z C$ and $B Y$, which is $G$ by definition, is the radical center of $R, S$ and $k_{a}$, from which the claim $G R=G S$ follows immediately.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
IRN Let $A B C$ be a triangle. The incircle of $A B C$ touches the sides $A B$ and $A C$ at the points $Z$ and $Y$, respectively. Let $G$ be the point where the lines $B Y$ and $C Z$ meet, and let $R$ and $S$ be points such that the two quadrilaterals $B C Y R$ and $B C S Z$ are parallelograms. Prove that $G R=G S$.
|
Denote by $k$ the incircle and by $k_{a}$ the excircle opposite to $A$ of triangle $A B C$. Let $k$ and $k_{a}$ touch the side $B C$ at the points $X$ and $T$, respectively, let $k_{a}$ touch the lines $A B$ and $A C$ at the points $P$ and $Q$, respectively. We use several times the fact that opposing sides of a parallelogram are of equal length, that points of contact of the excircle and incircle to a side of a triangle lie symmetric with respect to the midpoint of this side and that segments on two tangents to a circle defined by the points of contact and their point of intersection have the same length. So we conclude $$ \begin{gathered} Z P=Z B+B P=X B+B T=B X+C X=Z S \text { and } \\ C Q=C T=B X=B Z=C S . \end{gathered} $$  So for each of the points $Z, C$, their distances to $S$ equal the length of a tangent segment from this point to $k_{a}$. It is well-known, that all points with this property lie on the line $Z C$, which is the radical axis of $S$ and $k_{a}$. Similar arguments yield that $B Y$ is the radical axis of $R$ and $k_{a}$. So the point of intersection of $Z C$ and $B Y$, which is $G$ by definition, is the radical center of $R, S$ and $k_{a}$, from which the claim $G R=G S$ follows immediately.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
6828e6f5-b5d7-5bf5-ab2b-4bf89ccee0af
| 23,846
|
IRN Let $A B C$ be a triangle. The incircle of $A B C$ touches the sides $A B$ and $A C$ at the points $Z$ and $Y$, respectively. Let $G$ be the point where the lines $B Y$ and $C Z$ meet, and let $R$ and $S$ be points such that the two quadrilaterals $B C Y R$ and $B C S Z$ are parallelograms. Prove that $G R=G S$.
|
Denote $x=A Z=A Y, y=B Z=B X, z=C X=C Y, p=Z G, q=G C$. Several lengthy calculations (Menelaos' theorem in triangle $A Z C$, law of Cosines in triangles $A B C$ and $A Z C$ and Stewart's theorem in triangle $Z C S$ ) give four equations for $p, q, \cos \alpha$ and $G S$ in terms of $x, y$, and $z$ that can be resolved for $G S$. The result is symmetric in $y$ and $z$, so $G R=G S$. More in detail this means: The line $B Y$ intersects the sides of triangle $A Z C$, so Menelaos' theorem yields $\frac{p}{q} \cdot \frac{z}{x} \cdot \frac{x+y}{y}=1$, hence $$ \frac{p}{q}=\frac{x y}{y z+z x} . $$ Since we only want to show that the term for $G S$ is symmetric in $y$ and $z$, we abbreviate terms that are symmetric in $y$ and $z$ by capital letters, starting with $N=x y+y z+z x$. So (1) implies $$ \frac{p}{p+q}=\frac{x y}{x y+y z+z x}=\frac{x y}{N} \quad \text { and } \quad \frac{q}{p+q}=\frac{y z+z x}{x y+y z+z x}=\frac{y z+z x}{N} . $$ Now the law of Cosines in triangle $A B C$ yields $$ \cos \alpha=\frac{(x+y)^{2}+(x+z)^{2}-(y+z)^{2}}{2(x+y)(x+z)}=\frac{2 x^{2}+2 x y+2 x z-2 y z}{2(x+y)(x+z)}=1-\frac{2 y z}{(x+y)(x+z)} . $$ We use this result to apply the law of Cosines in triangle $A Z C$ : $$ \begin{aligned} (p+q)^{2} & =x^{2}+(x+z)^{2}-2 x(x+z) \cos \alpha \\ & =x^{2}+(x+z)^{2}-2 x(x+z) \cdot\left(1-\frac{2 y z}{(x+y)(x+z)}\right) \\ & =z^{2}+\frac{4 x y z}{x+y} . \end{aligned} $$ Now in triangle $Z C S$ the segment $G S$ is a cevian, so with StEWART's theorem we have $p y^{2}+q(y+z)^{2}=(p+q)\left(G S^{2}+p q\right)$, hence $$ G S^{2}=\frac{p}{p+q} \cdot y^{2}+\frac{q}{p+q} \cdot(y+z)^{2}-\frac{p}{p+q} \cdot \frac{q}{p+q} \cdot(p+q)^{2} . $$ Replacing the $p$ 's and $q$ 's herein by (2) and (3) yields $$ \begin{aligned} G S^{2} & =\frac{x y}{N} y^{2}+\frac{y z+z x}{N}(y+z)^{2}-\frac{x y}{N} \cdot \frac{y z+z x}{N} \cdot\left(z^{2}+\frac{4 x y z}{x+y}\right) \\ & =\frac{x y^{3}}{N}+\underbrace{\frac{y z(y+z)^{2}}{N}}_{M_{1}}+\frac{z x(y+z)^{2}}{N}-\frac{x y z^{3}(x+y)}{N^{2}}-\underbrace{\frac{4 x^{2} y^{2} z^{2}}{N^{2}}}_{M_{2}} \\ & =\frac{x y^{3}+z x(y+z)^{2}}{N}-\frac{x y z^{3}(x+y)}{N^{2}}+M_{1}-M_{2} \\ & =\underbrace{\frac{x\left(y^{3}+y^{2} z+y z^{2}+z^{3}\right)}{N}}_{M_{3}}+\frac{x y z^{2} N}{N^{2}}-\frac{x y z^{3}(x+y)}{N^{2}}+M_{1}-M_{2} \\ & =\frac{x^{2} y^{2} z^{2}+x y^{2} z^{3}+x^{2} y z^{3}-x^{2} y z^{3}-x y^{2} z^{3}}{N^{2}}+M_{1}-M_{2}+M_{3} \\ & =\frac{x^{2} y^{2} z^{2}}{N^{2}}+M_{1}-M_{2}+M_{3}, \end{aligned} $$ a term that is symmetric in $y$ and $z$, indeed. Comment. $G$ is known as GERGONnE's point of $\triangle A B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
IRN Let $A B C$ be a triangle. The incircle of $A B C$ touches the sides $A B$ and $A C$ at the points $Z$ and $Y$, respectively. Let $G$ be the point where the lines $B Y$ and $C Z$ meet, and let $R$ and $S$ be points such that the two quadrilaterals $B C Y R$ and $B C S Z$ are parallelograms. Prove that $G R=G S$.
|
Denote $x=A Z=A Y, y=B Z=B X, z=C X=C Y, p=Z G, q=G C$. Several lengthy calculations (Menelaos' theorem in triangle $A Z C$, law of Cosines in triangles $A B C$ and $A Z C$ and Stewart's theorem in triangle $Z C S$ ) give four equations for $p, q, \cos \alpha$ and $G S$ in terms of $x, y$, and $z$ that can be resolved for $G S$. The result is symmetric in $y$ and $z$, so $G R=G S$. More in detail this means: The line $B Y$ intersects the sides of triangle $A Z C$, so Menelaos' theorem yields $\frac{p}{q} \cdot \frac{z}{x} \cdot \frac{x+y}{y}=1$, hence $$ \frac{p}{q}=\frac{x y}{y z+z x} . $$ Since we only want to show that the term for $G S$ is symmetric in $y$ and $z$, we abbreviate terms that are symmetric in $y$ and $z$ by capital letters, starting with $N=x y+y z+z x$. So (1) implies $$ \frac{p}{p+q}=\frac{x y}{x y+y z+z x}=\frac{x y}{N} \quad \text { and } \quad \frac{q}{p+q}=\frac{y z+z x}{x y+y z+z x}=\frac{y z+z x}{N} . $$ Now the law of Cosines in triangle $A B C$ yields $$ \cos \alpha=\frac{(x+y)^{2}+(x+z)^{2}-(y+z)^{2}}{2(x+y)(x+z)}=\frac{2 x^{2}+2 x y+2 x z-2 y z}{2(x+y)(x+z)}=1-\frac{2 y z}{(x+y)(x+z)} . $$ We use this result to apply the law of Cosines in triangle $A Z C$ : $$ \begin{aligned} (p+q)^{2} & =x^{2}+(x+z)^{2}-2 x(x+z) \cos \alpha \\ & =x^{2}+(x+z)^{2}-2 x(x+z) \cdot\left(1-\frac{2 y z}{(x+y)(x+z)}\right) \\ & =z^{2}+\frac{4 x y z}{x+y} . \end{aligned} $$ Now in triangle $Z C S$ the segment $G S$ is a cevian, so with StEWART's theorem we have $p y^{2}+q(y+z)^{2}=(p+q)\left(G S^{2}+p q\right)$, hence $$ G S^{2}=\frac{p}{p+q} \cdot y^{2}+\frac{q}{p+q} \cdot(y+z)^{2}-\frac{p}{p+q} \cdot \frac{q}{p+q} \cdot(p+q)^{2} . $$ Replacing the $p$ 's and $q$ 's herein by (2) and (3) yields $$ \begin{aligned} G S^{2} & =\frac{x y}{N} y^{2}+\frac{y z+z x}{N}(y+z)^{2}-\frac{x y}{N} \cdot \frac{y z+z x}{N} \cdot\left(z^{2}+\frac{4 x y z}{x+y}\right) \\ & =\frac{x y^{3}}{N}+\underbrace{\frac{y z(y+z)^{2}}{N}}_{M_{1}}+\frac{z x(y+z)^{2}}{N}-\frac{x y z^{3}(x+y)}{N^{2}}-\underbrace{\frac{4 x^{2} y^{2} z^{2}}{N^{2}}}_{M_{2}} \\ & =\frac{x y^{3}+z x(y+z)^{2}}{N}-\frac{x y z^{3}(x+y)}{N^{2}}+M_{1}-M_{2} \\ & =\underbrace{\frac{x\left(y^{3}+y^{2} z+y z^{2}+z^{3}\right)}{N}}_{M_{3}}+\frac{x y z^{2} N}{N^{2}}-\frac{x y z^{3}(x+y)}{N^{2}}+M_{1}-M_{2} \\ & =\frac{x^{2} y^{2} z^{2}+x y^{2} z^{3}+x^{2} y z^{3}-x^{2} y z^{3}-x y^{2} z^{3}}{N^{2}}+M_{1}-M_{2}+M_{3} \\ & =\frac{x^{2} y^{2} z^{2}}{N^{2}}+M_{1}-M_{2}+M_{3}, \end{aligned} $$ a term that is symmetric in $y$ and $z$, indeed. Comment. $G$ is known as GERGONnE's point of $\triangle A B C$.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
6828e6f5-b5d7-5bf5-ab2b-4bf89ccee0af
| 23,846
|
UNK Given a cyclic quadrilateral $A B C D$, let the diagonals $A C$ and $B D$ meet at $E$ and the lines $A D$ and $B C$ meet at $F$. The midpoints of $A B$ and $C D$ are $G$ and $H$, respectively. Show that $E F$ is tangent at $E$ to the circle through the points $E, G$, and $H$.
|
It suffices to show that $\angle H E F=\angle H G E$ (see Figure 1), since in circle $E G H$ the angle over the chord $E H$ at $G$ equals the angle between the tangent at $E$ and $E H$. First, $\angle B A D=180^{\circ}-\angle D C B=\angle F C D$. Since triangles $F A B$ and $F C D$ have also a common interior angle at $F$, they are similar.  Figure 1 Denote by $\mathcal{T}$ the transformation consisting of a reflection at the bisector of $\angle D F C$ followed by a dilation with center $F$ and factor of $\frac{F A}{F C}$. Then $\mathcal{T}$ maps $F$ to $F, C$ to $A, D$ to $B$, and $H$ to $G$. To see this, note that $\triangle F C A \sim \triangle F D B$, so $\frac{F A}{F C}=\frac{F B}{F D}$. Moreover, as $\angle A D B=\angle A C B$, the image of the line $D E$ under $\mathcal{T}$ is parallel to $A C$ (and passes through $B$ ) and similarly the image of $C E$ is parallel to $D B$ and passes through $A$. Hence $E$ is mapped to the point $X$ which is the fourth vertex of the parallelogram $B E A X$. Thus, in particular $\angle H E F=\angle F X G$. As $G$ is the midpoint of the diagonal $A B$ of the parallelogram $B E A X$, it is also the midpoint of $E X$. In particular, $E, G, X$ are collinear, and $E X=2 \cdot E G$. Denote by $Y$ the fourth vertex of the parallelogram $D E C Y$. By an analogous reasoning as before, it follows that $\mathcal{T}$ maps $Y$ to $E$, thus $E, H, Y$ are collinear with $E Y=2 \cdot E H$. Therefore, by the intercept theorem, $H G \| X Y$. From the construction of $\mathcal{T}$ it is clear that the lines $F X$ and $F E$ are symmetric with respect to the bisector of $\angle D F C$, as are $F Y$ and $F E$. Thus, $F, X, Y$ are collinear, which together with $H G \| X Y$ implies $\angle F X E=\angle H G E$. This completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
UNK Given a cyclic quadrilateral $A B C D$, let the diagonals $A C$ and $B D$ meet at $E$ and the lines $A D$ and $B C$ meet at $F$. The midpoints of $A B$ and $C D$ are $G$ and $H$, respectively. Show that $E F$ is tangent at $E$ to the circle through the points $E, G$, and $H$.
|
It suffices to show that $\angle H E F=\angle H G E$ (see Figure 1), since in circle $E G H$ the angle over the chord $E H$ at $G$ equals the angle between the tangent at $E$ and $E H$. First, $\angle B A D=180^{\circ}-\angle D C B=\angle F C D$. Since triangles $F A B$ and $F C D$ have also a common interior angle at $F$, they are similar.  Figure 1 Denote by $\mathcal{T}$ the transformation consisting of a reflection at the bisector of $\angle D F C$ followed by a dilation with center $F$ and factor of $\frac{F A}{F C}$. Then $\mathcal{T}$ maps $F$ to $F, C$ to $A, D$ to $B$, and $H$ to $G$. To see this, note that $\triangle F C A \sim \triangle F D B$, so $\frac{F A}{F C}=\frac{F B}{F D}$. Moreover, as $\angle A D B=\angle A C B$, the image of the line $D E$ under $\mathcal{T}$ is parallel to $A C$ (and passes through $B$ ) and similarly the image of $C E$ is parallel to $D B$ and passes through $A$. Hence $E$ is mapped to the point $X$ which is the fourth vertex of the parallelogram $B E A X$. Thus, in particular $\angle H E F=\angle F X G$. As $G$ is the midpoint of the diagonal $A B$ of the parallelogram $B E A X$, it is also the midpoint of $E X$. In particular, $E, G, X$ are collinear, and $E X=2 \cdot E G$. Denote by $Y$ the fourth vertex of the parallelogram $D E C Y$. By an analogous reasoning as before, it follows that $\mathcal{T}$ maps $Y$ to $E$, thus $E, H, Y$ are collinear with $E Y=2 \cdot E H$. Therefore, by the intercept theorem, $H G \| X Y$. From the construction of $\mathcal{T}$ it is clear that the lines $F X$ and $F E$ are symmetric with respect to the bisector of $\angle D F C$, as are $F Y$ and $F E$. Thus, $F, X, Y$ are collinear, which together with $H G \| X Y$ implies $\angle F X E=\angle H G E$. This completes the proof.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
20fe1e8e-83bb-5c01-b87c-3669155cf234
| 23,849
|
UNK Given a cyclic quadrilateral $A B C D$, let the diagonals $A C$ and $B D$ meet at $E$ and the lines $A D$ and $B C$ meet at $F$. The midpoints of $A B$ and $C D$ are $G$ and $H$, respectively. Show that $E F$ is tangent at $E$ to the circle through the points $E, G$, and $H$.
|
We use the following Lemma (Gauß). Let $A B C D$ be a quadrilateral. Let $A B$ and $C D$ intersect at $P$, and $B C$ and $D A$ intersect at $Q$. Then the midpoints $K, L, M$ of $A C, B D$, and $P Q$, respectively, are collinear. Proof: Let us consider the points $Z$ that fulfill the equation $$ (A B Z)+(C D Z)=(B C Z)+(D A Z) $$ where $(R S T)$ denotes the oriented area of the triangle $R S T$ (see Figure 2). 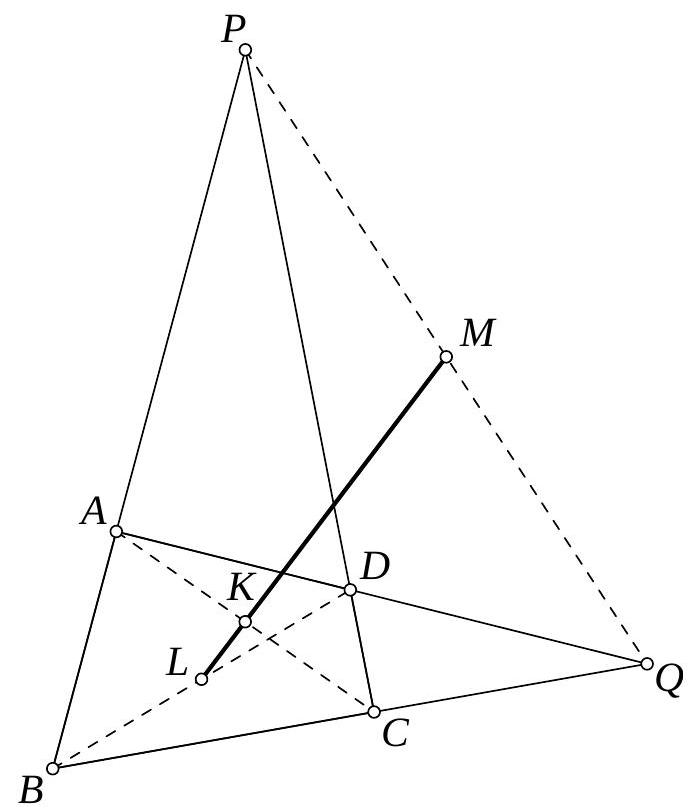 Figure 2 As (1) is linear in $Z$, it can either characterize a line, or be contradictory, or be trivially fulfilled for all $Z$ in the plane. If (1) was fulfilled for all $Z$, then it would hold for $Z=A, Z=B$, which gives $(C D A)=(B C A),(C D B)=(D A B)$, respectively, i.e. the diagonals of $A B C D$ would bisect each other, thus $A B C D$ would be a parallelogram. This contradicts the hypothesis that $A D$ and $B C$ intersect. Since $E, F, G$ fulfill (1), it is the equation of a line which completes the proof of the lemma. Now consider the parallelograms $E A X B$ and $E C Y D$ (see Figure 1). Then $G, H$ are the midpoints of $E X, E Y$, respectively. Let $M$ be the midpoint of $E F$. By applying the Lemma to the (re-entrant) quadrilateral $A D B C$, it is evident that $G, H$, and $M$ are collinear. A dilation by a factor of 2 with center $E$ shows that $X, Y, F$ are collinear. Since $A X \| D E$ and $B X \| C E$, we have pairwise equal interior angles in the quadrilaterals $F D E C$ and $F B X A$. Since we have also $\angle E B A=\angle D C A=\angle C D Y$, the quadrilaterals are similar. Thus, $\angle F X A=\angle C E F$. Clearly the parallelograms $E C Y D$ and $E B X A$ are similar, too, thus $\angle E X A=\angle C E Y$. Consequently, $\angle F X E=\angle F X A-\angle E X A=\angle C E F-\angle C E Y=\angle Y E F$. By the converse of the tangent-chord angle theorem $E F$ is tangent to the circle $X E Y$. A dilation by a factor of $\frac{1}{2}$ completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
UNK Given a cyclic quadrilateral $A B C D$, let the diagonals $A C$ and $B D$ meet at $E$ and the lines $A D$ and $B C$ meet at $F$. The midpoints of $A B$ and $C D$ are $G$ and $H$, respectively. Show that $E F$ is tangent at $E$ to the circle through the points $E, G$, and $H$.
|
We use the following Lemma (Gauß). Let $A B C D$ be a quadrilateral. Let $A B$ and $C D$ intersect at $P$, and $B C$ and $D A$ intersect at $Q$. Then the midpoints $K, L, M$ of $A C, B D$, and $P Q$, respectively, are collinear. Proof: Let us consider the points $Z$ that fulfill the equation $$ (A B Z)+(C D Z)=(B C Z)+(D A Z) $$ where $(R S T)$ denotes the oriented area of the triangle $R S T$ (see Figure 2).  Figure 2 As (1) is linear in $Z$, it can either characterize a line, or be contradictory, or be trivially fulfilled for all $Z$ in the plane. If (1) was fulfilled for all $Z$, then it would hold for $Z=A, Z=B$, which gives $(C D A)=(B C A),(C D B)=(D A B)$, respectively, i.e. the diagonals of $A B C D$ would bisect each other, thus $A B C D$ would be a parallelogram. This contradicts the hypothesis that $A D$ and $B C$ intersect. Since $E, F, G$ fulfill (1), it is the equation of a line which completes the proof of the lemma. Now consider the parallelograms $E A X B$ and $E C Y D$ (see Figure 1). Then $G, H$ are the midpoints of $E X, E Y$, respectively. Let $M$ be the midpoint of $E F$. By applying the Lemma to the (re-entrant) quadrilateral $A D B C$, it is evident that $G, H$, and $M$ are collinear. A dilation by a factor of 2 with center $E$ shows that $X, Y, F$ are collinear. Since $A X \| D E$ and $B X \| C E$, we have pairwise equal interior angles in the quadrilaterals $F D E C$ and $F B X A$. Since we have also $\angle E B A=\angle D C A=\angle C D Y$, the quadrilaterals are similar. Thus, $\angle F X A=\angle C E F$. Clearly the parallelograms $E C Y D$ and $E B X A$ are similar, too, thus $\angle E X A=\angle C E Y$. Consequently, $\angle F X E=\angle F X A-\angle E X A=\angle C E F-\angle C E Y=\angle Y E F$. By the converse of the tangent-chord angle theorem $E F$ is tangent to the circle $X E Y$. A dilation by a factor of $\frac{1}{2}$ completes the proof.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
20fe1e8e-83bb-5c01-b87c-3669155cf234
| 23,849
|
UNK Given a cyclic quadrilateral $A B C D$, let the diagonals $A C$ and $B D$ meet at $E$ and the lines $A D$ and $B C$ meet at $F$. The midpoints of $A B$ and $C D$ are $G$ and $H$, respectively. Show that $E F$ is tangent at $E$ to the circle through the points $E, G$, and $H$.
|
As in $$ \left(\frac{\boldsymbol{e}-\boldsymbol{f}}{2}\right)^{2}=\left(\frac{\boldsymbol{e}+\boldsymbol{f}}{2}-\frac{\boldsymbol{a}+\boldsymbol{b}}{2}\right)\left(\frac{\boldsymbol{e}+\boldsymbol{f}}{2}-\frac{\boldsymbol{c}+\boldsymbol{d}}{2}\right) $$ or equivalently $$ 4 \boldsymbol{e f}-(\boldsymbol{e}+\boldsymbol{f})(\boldsymbol{a}+\boldsymbol{b}+\boldsymbol{c}+\boldsymbol{d})+(\boldsymbol{a}+\boldsymbol{b})(\boldsymbol{c}+\boldsymbol{d})=0 $$ With $R$ as the circumradius of $A B C D$, we obtain for the powers $\mathcal{P}(E)$ and $\mathcal{P}(F)$ of $E$ and $F$, respectively, with respect to the circumcircle $$ \begin{aligned} & \mathcal{P}(E)=(\boldsymbol{e}-\boldsymbol{a})(\boldsymbol{e}-\boldsymbol{c})=(\boldsymbol{e}-\boldsymbol{b})(\boldsymbol{e}-\boldsymbol{d})=\boldsymbol{e}^{2}-R^{2} \\ & \mathcal{P}(F)=(\boldsymbol{f}-\boldsymbol{a})(\boldsymbol{f}-\boldsymbol{d})=(\boldsymbol{f}-\boldsymbol{b})(\boldsymbol{f}-\boldsymbol{c})=\boldsymbol{f}^{2}-R^{2} \end{aligned} $$ hence $$ \begin{aligned} & (\boldsymbol{e}-\boldsymbol{a})(\boldsymbol{e}-\boldsymbol{c})=\boldsymbol{e}^{2}-R^{2} \\ & (\boldsymbol{e}-\boldsymbol{b})(\boldsymbol{e}-\boldsymbol{d})=\boldsymbol{e}^{2}-R^{2} \\ & (\boldsymbol{f}-\boldsymbol{a})(\boldsymbol{f}-\boldsymbol{d})=\boldsymbol{f}^{2}-R^{2} \\ & (\boldsymbol{f}-\boldsymbol{b})(\boldsymbol{f}-\boldsymbol{c})=\boldsymbol{f}^{2}-R^{2} \end{aligned} $$ Since $F$ lies on the polar to $E$ with respect to the circumcircle, we have $$ 4 \boldsymbol{e} \boldsymbol{f}=4 R^{2} $$ Adding up (3) to (7) yields (2), as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
UNK Given a cyclic quadrilateral $A B C D$, let the diagonals $A C$ and $B D$ meet at $E$ and the lines $A D$ and $B C$ meet at $F$. The midpoints of $A B$ and $C D$ are $G$ and $H$, respectively. Show that $E F$ is tangent at $E$ to the circle through the points $E, G$, and $H$.
|
As in $$ \left(\frac{\boldsymbol{e}-\boldsymbol{f}}{2}\right)^{2}=\left(\frac{\boldsymbol{e}+\boldsymbol{f}}{2}-\frac{\boldsymbol{a}+\boldsymbol{b}}{2}\right)\left(\frac{\boldsymbol{e}+\boldsymbol{f}}{2}-\frac{\boldsymbol{c}+\boldsymbol{d}}{2}\right) $$ or equivalently $$ 4 \boldsymbol{e f}-(\boldsymbol{e}+\boldsymbol{f})(\boldsymbol{a}+\boldsymbol{b}+\boldsymbol{c}+\boldsymbol{d})+(\boldsymbol{a}+\boldsymbol{b})(\boldsymbol{c}+\boldsymbol{d})=0 $$ With $R$ as the circumradius of $A B C D$, we obtain for the powers $\mathcal{P}(E)$ and $\mathcal{P}(F)$ of $E$ and $F$, respectively, with respect to the circumcircle $$ \begin{aligned} & \mathcal{P}(E)=(\boldsymbol{e}-\boldsymbol{a})(\boldsymbol{e}-\boldsymbol{c})=(\boldsymbol{e}-\boldsymbol{b})(\boldsymbol{e}-\boldsymbol{d})=\boldsymbol{e}^{2}-R^{2} \\ & \mathcal{P}(F)=(\boldsymbol{f}-\boldsymbol{a})(\boldsymbol{f}-\boldsymbol{d})=(\boldsymbol{f}-\boldsymbol{b})(\boldsymbol{f}-\boldsymbol{c})=\boldsymbol{f}^{2}-R^{2} \end{aligned} $$ hence $$ \begin{aligned} & (\boldsymbol{e}-\boldsymbol{a})(\boldsymbol{e}-\boldsymbol{c})=\boldsymbol{e}^{2}-R^{2} \\ & (\boldsymbol{e}-\boldsymbol{b})(\boldsymbol{e}-\boldsymbol{d})=\boldsymbol{e}^{2}-R^{2} \\ & (\boldsymbol{f}-\boldsymbol{a})(\boldsymbol{f}-\boldsymbol{d})=\boldsymbol{f}^{2}-R^{2} \\ & (\boldsymbol{f}-\boldsymbol{b})(\boldsymbol{f}-\boldsymbol{c})=\boldsymbol{f}^{2}-R^{2} \end{aligned} $$ Since $F$ lies on the polar to $E$ with respect to the circumcircle, we have $$ 4 \boldsymbol{e} \boldsymbol{f}=4 R^{2} $$ Adding up (3) to (7) yields (2), as desired.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
20fe1e8e-83bb-5c01-b87c-3669155cf234
| 23,849
|
POL Let $P$ be a polygon that is convex and symmetric to some point $O$. Prove that for some parallelogram $R$ satisfying $P \subset R$ we have $$ \frac{|R|}{|P|} \leq \sqrt{2} $$ where $|R|$ and $|P|$ denote the area of the sets $R$ and $P$, respectively.
|
We construct the parallelograms $R_{1}, R_{2}$ and $R_{3}$ in the same way as in  Figure 2 Recall that affine one-to-one maps of the plane preserve the ratio of areas of subsets of the plane. On the other hand, every parallelogram can be transformed with an affine map onto a square. It follows that without loss of generality we may assume that $R_{1}$ is a square (see Figure 2). Then $R_{2}$, whose vertices are the midpoints of the sides of $R_{1}$, is a square too, and $R_{3}$, whose sides are parallel to the diagonals of $R_{1}$, is a rectangle. Let $a>0, b \geq 0$ and $c \geq 0$ be the distances introduced in Figure 2. Then $\left|R_{1}\right|=2 a^{2}$ and $\left|R_{3}\right|=(a+2 b)(a+2 c)$. Points $A, A^{\prime}, B$ and $B^{\prime}$ are in the convex polygon $P$. Hence the square $A B A^{\prime} B^{\prime}$ is a subset of $P$. Moreover, each of the sides of the rectangle $R_{3}$ contains a point of $P$, otherwise $R_{3}$ would not be minimal. It follows that $$ |P| \geq a^{2}+2 \cdot \frac{a b}{2}+2 \cdot \frac{a c}{2}=a(a+b+c) $$ Now assume that both $\frac{\left|R_{1}\right|}{|P|}>\sqrt{2}$ and $\frac{\left|R_{3}\right|}{|P|}>\sqrt{2}$, then $$ 2 a^{2}=\left|R_{1}\right|>\sqrt{2} \cdot|P| \geq \sqrt{2} \cdot a(a+b+c) $$ and $$ (a+2 b)(a+2 c)=\left|R_{3}\right|>\sqrt{2} \cdot|P| \geq \sqrt{2} \cdot a(a+b+c) $$ All numbers concerned are positive, so after multiplying these inequalities we get $$ 2 a^{2}(a+2 b)(a+2 c)>2 a^{2}(a+b+c)^{2} $$ But the arithmetic-geometric-mean inequality implies the contradictory result $$ 2 a^{2}(a+2 b)(a+2 c) \leq 2 a^{2}\left(\frac{(a+2 b)+(a+2 c)}{2}\right)^{2}=2 a^{2}(a+b+c)^{2} $$ Hence $\frac{\left|R_{1}\right|}{|P|} \leq \sqrt{2}$ or $\frac{\left|R_{3}\right|}{|P|} \leq \sqrt{2}$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
POL Let $P$ be a polygon that is convex and symmetric to some point $O$. Prove that for some parallelogram $R$ satisfying $P \subset R$ we have $$ \frac{|R|}{|P|} \leq \sqrt{2} $$ where $|R|$ and $|P|$ denote the area of the sets $R$ and $P$, respectively.
|
We construct the parallelograms $R_{1}, R_{2}$ and $R_{3}$ in the same way as in  Figure 2 Recall that affine one-to-one maps of the plane preserve the ratio of areas of subsets of the plane. On the other hand, every parallelogram can be transformed with an affine map onto a square. It follows that without loss of generality we may assume that $R_{1}$ is a square (see Figure 2). Then $R_{2}$, whose vertices are the midpoints of the sides of $R_{1}$, is a square too, and $R_{3}$, whose sides are parallel to the diagonals of $R_{1}$, is a rectangle. Let $a>0, b \geq 0$ and $c \geq 0$ be the distances introduced in Figure 2. Then $\left|R_{1}\right|=2 a^{2}$ and $\left|R_{3}\right|=(a+2 b)(a+2 c)$. Points $A, A^{\prime}, B$ and $B^{\prime}$ are in the convex polygon $P$. Hence the square $A B A^{\prime} B^{\prime}$ is a subset of $P$. Moreover, each of the sides of the rectangle $R_{3}$ contains a point of $P$, otherwise $R_{3}$ would not be minimal. It follows that $$ |P| \geq a^{2}+2 \cdot \frac{a b}{2}+2 \cdot \frac{a c}{2}=a(a+b+c) $$ Now assume that both $\frac{\left|R_{1}\right|}{|P|}>\sqrt{2}$ and $\frac{\left|R_{3}\right|}{|P|}>\sqrt{2}$, then $$ 2 a^{2}=\left|R_{1}\right|>\sqrt{2} \cdot|P| \geq \sqrt{2} \cdot a(a+b+c) $$ and $$ (a+2 b)(a+2 c)=\left|R_{3}\right|>\sqrt{2} \cdot|P| \geq \sqrt{2} \cdot a(a+b+c) $$ All numbers concerned are positive, so after multiplying these inequalities we get $$ 2 a^{2}(a+2 b)(a+2 c)>2 a^{2}(a+b+c)^{2} $$ But the arithmetic-geometric-mean inequality implies the contradictory result $$ 2 a^{2}(a+2 b)(a+2 c) \leq 2 a^{2}\left(\frac{(a+2 b)+(a+2 c)}{2}\right)^{2}=2 a^{2}(a+b+c)^{2} $$ Hence $\frac{\left|R_{1}\right|}{|P|} \leq \sqrt{2}$ or $\frac{\left|R_{3}\right|}{|P|} \leq \sqrt{2}$, as desired.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
3d41bf6a-5947-5da9-878f-16b039aa4cf8
| 23,853
|
UKR Let the sides $A D$ and $B C$ of the quadrilateral $A B C D$ (such that $A B$ is not parallel to $C D$ ) intersect at point $P$. Points $O_{1}$ and $O_{2}$ are the circumcenters and points $H_{1}$ and $H_{2}$ are the orthocenters of triangles $A B P$ and $D C P$, respectively. Denote the midpoints of segments $O_{1} H_{1}$ and $O_{2} H_{2}$ by $E_{1}$ and $E_{2}$, respectively. Prove that the perpendicular from $E_{1}$ on $C D$, the perpendicular from $E_{2}$ on $A B$ and the line $H_{1} H_{2}$ are concurrent.
|
We keep triangle $A B P$ fixed and move the line $C D$ parallel to itself uniformly, i.e. linearly dependent on a single parameter $\lambda$ (see Figure 1). Then the points $C$ and $D$ also move uniformly. Hence, the points $O_{2}, H_{2}$ and $E_{2}$ move uniformly, too. Therefore also the perpendicular from $E_{2}$ on $A B$ moves uniformly. Obviously, the points $O_{1}, H_{1}, E_{1}$ and the perpendicular from $E_{1}$ on $C D$ do not move at all. Hence, the intersection point $S$ of these two perpendiculars moves uniformly. Since $H_{1}$ does not move, while $H_{2}$ and $S$ move uniformly along parallel lines (both are perpendicular to $C D$ ), it is sufficient to prove their collinearity for two different positions of $C D$.  Figure 1 Let $C D$ pass through either point $A$ or point $B$. Note that by hypothesis these two cases are different. We will consider the case $A \in C D$, i.e. $A=D$. So we have to show that the perpendiculars from $E_{1}$ on $A C$ and from $E_{2}$ on $A B$ intersect on the altitude $A H$ of triangle $A B C$ (see Figure 2).  Figure 2 To this end, we consider the midpoints $A_{1}, B_{1}, C_{1}$ of $B C, C A, A B$, respectively. As $E_{1}$ is the center of Feuerbach's circle (nine-point circle) of $\triangle A B P$, we have $E_{1} C_{1}=E_{1} H$. Similarly, $E_{2} B_{1}=E_{2} H$. Note further that a point $X$ lies on the perpendicular from $E_{1}$ on $A_{1} C_{1}$ if and only if $$ X C_{1}^{2}-X A_{1}^{2}=E_{1} C_{1}^{2}-E_{1} A_{1}^{2} $$ Similarly, the perpendicular from $E_{2}$ on $A_{1} B_{1}$ is characterized by $$ X A_{1}^{2}-X B_{1}^{2}=E_{2} A_{1}^{2}-E_{2} B_{1}^{2} $$ The line $H_{1} H_{2}$, which is perpendicular to $B_{1} C_{1}$ and contains $A$, is given by $$ X B_{1}^{2}-X C_{1}^{2}=A B_{1}^{2}-A C_{1}^{2} $$ The three lines are concurrent if and only if $$ \begin{aligned} 0 & =X C_{1}^{2}-X A_{1}^{2}+X A_{1}^{2}-X B_{1}^{2}+X B_{1}^{2}-X C_{1}^{2} \\ & =E_{1} C_{1}^{2}-E_{1} A_{1}^{2}+E_{2} A_{1}^{2}-E_{2} B_{1}^{2}+A B_{1}^{2}-A C_{1}^{2} \\ & =-E_{1} A_{1}^{2}+E_{2} A_{1}^{2}+E_{1} H^{2}-E_{2} H^{2}+A B_{1}^{2}-A C_{1}^{2} \end{aligned} $$ i.e. it suffices to show that $$ E_{1} A_{1}^{2}-E_{2} A_{1}^{2}-E_{1} H^{2}+E_{2} H^{2}=\frac{A C^{2}-A B^{2}}{4} $$ We have $$ \frac{A C^{2}-A B^{2}}{4}=\frac{H C^{2}-H B^{2}}{4}=\frac{(H C+H B)(H C-H B)}{4}=\frac{H A_{1} \cdot B C}{2} $$ Let $F_{1}, F_{2}$ be the projections of $E_{1}, E_{2}$ on $B C$. Obviously, these are the midpoints of $H P_{1}$, $H P_{2}$, where $P_{1}, P_{2}$ are the midpoints of $P B$ and $P C$ respectively. Then $$ \begin{aligned} & E_{1} A_{1}^{2}-E_{2} A_{1}^{2}-E_{1} H^{2}+E_{2} H^{2} \\ & =F_{1} A_{1}^{2}-F_{1} H^{2}-F_{2} A_{1}^{2}+F_{2} H^{2} \\ & =\left(F_{1} A_{1}-F_{1} H\right)\left(F_{1} A_{1}+F_{1} H\right)-\left(F_{2} A_{1}-F_{2} H\right)\left(F_{2} A_{1}+F_{2} H\right) \\ & =A_{1} H \cdot\left(A_{1} P_{1}-A_{1} P_{2}\right) \\ & =\frac{A_{1} H \cdot B C}{2} \\ & =\frac{A C^{2}-A B^{2}}{4} \end{aligned} $$ which proves the claim.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
UKR Let the sides $A D$ and $B C$ of the quadrilateral $A B C D$ (such that $A B$ is not parallel to $C D$ ) intersect at point $P$. Points $O_{1}$ and $O_{2}$ are the circumcenters and points $H_{1}$ and $H_{2}$ are the orthocenters of triangles $A B P$ and $D C P$, respectively. Denote the midpoints of segments $O_{1} H_{1}$ and $O_{2} H_{2}$ by $E_{1}$ and $E_{2}$, respectively. Prove that the perpendicular from $E_{1}$ on $C D$, the perpendicular from $E_{2}$ on $A B$ and the line $H_{1} H_{2}$ are concurrent.
|
We keep triangle $A B P$ fixed and move the line $C D$ parallel to itself uniformly, i.e. linearly dependent on a single parameter $\lambda$ (see Figure 1). Then the points $C$ and $D$ also move uniformly. Hence, the points $O_{2}, H_{2}$ and $E_{2}$ move uniformly, too. Therefore also the perpendicular from $E_{2}$ on $A B$ moves uniformly. Obviously, the points $O_{1}, H_{1}, E_{1}$ and the perpendicular from $E_{1}$ on $C D$ do not move at all. Hence, the intersection point $S$ of these two perpendiculars moves uniformly. Since $H_{1}$ does not move, while $H_{2}$ and $S$ move uniformly along parallel lines (both are perpendicular to $C D$ ), it is sufficient to prove their collinearity for two different positions of $C D$.  Figure 1 Let $C D$ pass through either point $A$ or point $B$. Note that by hypothesis these two cases are different. We will consider the case $A \in C D$, i.e. $A=D$. So we have to show that the perpendiculars from $E_{1}$ on $A C$ and from $E_{2}$ on $A B$ intersect on the altitude $A H$ of triangle $A B C$ (see Figure 2).  Figure 2 To this end, we consider the midpoints $A_{1}, B_{1}, C_{1}$ of $B C, C A, A B$, respectively. As $E_{1}$ is the center of Feuerbach's circle (nine-point circle) of $\triangle A B P$, we have $E_{1} C_{1}=E_{1} H$. Similarly, $E_{2} B_{1}=E_{2} H$. Note further that a point $X$ lies on the perpendicular from $E_{1}$ on $A_{1} C_{1}$ if and only if $$ X C_{1}^{2}-X A_{1}^{2}=E_{1} C_{1}^{2}-E_{1} A_{1}^{2} $$ Similarly, the perpendicular from $E_{2}$ on $A_{1} B_{1}$ is characterized by $$ X A_{1}^{2}-X B_{1}^{2}=E_{2} A_{1}^{2}-E_{2} B_{1}^{2} $$ The line $H_{1} H_{2}$, which is perpendicular to $B_{1} C_{1}$ and contains $A$, is given by $$ X B_{1}^{2}-X C_{1}^{2}=A B_{1}^{2}-A C_{1}^{2} $$ The three lines are concurrent if and only if $$ \begin{aligned} 0 & =X C_{1}^{2}-X A_{1}^{2}+X A_{1}^{2}-X B_{1}^{2}+X B_{1}^{2}-X C_{1}^{2} \\ & =E_{1} C_{1}^{2}-E_{1} A_{1}^{2}+E_{2} A_{1}^{2}-E_{2} B_{1}^{2}+A B_{1}^{2}-A C_{1}^{2} \\ & =-E_{1} A_{1}^{2}+E_{2} A_{1}^{2}+E_{1} H^{2}-E_{2} H^{2}+A B_{1}^{2}-A C_{1}^{2} \end{aligned} $$ i.e. it suffices to show that $$ E_{1} A_{1}^{2}-E_{2} A_{1}^{2}-E_{1} H^{2}+E_{2} H^{2}=\frac{A C^{2}-A B^{2}}{4} $$ We have $$ \frac{A C^{2}-A B^{2}}{4}=\frac{H C^{2}-H B^{2}}{4}=\frac{(H C+H B)(H C-H B)}{4}=\frac{H A_{1} \cdot B C}{2} $$ Let $F_{1}, F_{2}$ be the projections of $E_{1}, E_{2}$ on $B C$. Obviously, these are the midpoints of $H P_{1}$, $H P_{2}$, where $P_{1}, P_{2}$ are the midpoints of $P B$ and $P C$ respectively. Then $$ \begin{aligned} & E_{1} A_{1}^{2}-E_{2} A_{1}^{2}-E_{1} H^{2}+E_{2} H^{2} \\ & =F_{1} A_{1}^{2}-F_{1} H^{2}-F_{2} A_{1}^{2}+F_{2} H^{2} \\ & =\left(F_{1} A_{1}-F_{1} H\right)\left(F_{1} A_{1}+F_{1} H\right)-\left(F_{2} A_{1}-F_{2} H\right)\left(F_{2} A_{1}+F_{2} H\right) \\ & =A_{1} H \cdot\left(A_{1} P_{1}-A_{1} P_{2}\right) \\ & =\frac{A_{1} H \cdot B C}{2} \\ & =\frac{A C^{2}-A B^{2}}{4} \end{aligned} $$ which proves the claim.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
7a6160f3-da01-5a0f-9a2c-32b5ca3bc350
| 23,857
|
UKR Let the sides $A D$ and $B C$ of the quadrilateral $A B C D$ (such that $A B$ is not parallel to $C D$ ) intersect at point $P$. Points $O_{1}$ and $O_{2}$ are the circumcenters and points $H_{1}$ and $H_{2}$ are the orthocenters of triangles $A B P$ and $D C P$, respectively. Denote the midpoints of segments $O_{1} H_{1}$ and $O_{2} H_{2}$ by $E_{1}$ and $E_{2}$, respectively. Prove that the perpendicular from $E_{1}$ on $C D$, the perpendicular from $E_{2}$ on $A B$ and the line $H_{1} H_{2}$ are concurrent.
|
Let the perpendicular from $E_{1}$ on $C D$ meet $P H_{1}$ at $X$, and the perpendicular from $E_{2}$ on $A B$ meet $P H_{2}$ at $Y$ (see Figure 3). Let $\varphi$ be the intersection angle of $A B$ and $C D$. Denote by $M, N$ the midpoints of $P H_{1}, P H_{2}$ respectively.  Figure 3 We will prove now that triangles $E_{1} X M$ and $E_{2} Y N$ have equal angles at $E_{1}, E_{2}$, and supplementary angles at $X, Y$. In the following, angles are understood as oriented, and equalities of angles modulo $180^{\circ}$. Let $\alpha=\angle H_{2} P D, \psi=\angle D P C, \beta=\angle C P H_{1}$. Then $\alpha+\psi+\beta=\varphi, \angle E_{1} X H_{1}=\angle H_{2} Y E_{2}=\varphi$, thus $\angle M X E_{1}+\angle N Y E_{2}=180^{\circ}$. By considering the Feuerbach circle of $\triangle A B P$ whose center is $E_{1}$ and which goes through $M$, we have $\angle E_{1} M H_{1}=\psi+2 \beta$. Analogous considerations with the Feuerbach circle of $\triangle D C P$ yield $\angle H_{2} N E_{2}=\psi+2 \alpha$. Hence indeed $\angle X E_{1} M=\varphi-(\psi+2 \beta)=(\psi+2 \alpha)-\varphi=\angle Y E_{2} N$. It follows now that $$ \frac{X M}{M E_{1}}=\frac{Y N}{N E_{2}} $$ Furthermore, $M E_{1}$ is half the circumradius of $\triangle A B P$, while $P H_{1}$ is the distance of $P$ to the orthocenter of that triangle, which is twice the circumradius times the cosine of $\psi$. Together with analogous reasoning for $\triangle D C P$ we have $$ \frac{M E_{1}}{P H_{1}}=\frac{1}{4 \cos \psi}=\frac{N E_{2}}{P H_{2}} $$ By multiplication, $$ \frac{X M}{P H_{1}}=\frac{Y N}{P H_{2}} $$ and therefore $$ \frac{P X}{X H_{1}}=\frac{H_{2} Y}{Y P} $$ Let $E_{1} X, E_{2} Y$ meet $H_{1} H_{2}$ in $R, S$ respectively. Applying the intercept theorem to the parallels $E_{1} X, P H_{2}$ and center $H_{1}$ gives $$ \frac{H_{2} R}{R H_{1}}=\frac{P X}{X H_{1}} $$ while with parallels $E_{2} Y, P H_{1}$ and center $H_{2}$ we obtain $$ \frac{H_{2} S}{S H_{1}}=\frac{H_{2} Y}{Y P} $$ Combination of the last three equalities yields that $R$ and $S$ coincide.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
UKR Let the sides $A D$ and $B C$ of the quadrilateral $A B C D$ (such that $A B$ is not parallel to $C D$ ) intersect at point $P$. Points $O_{1}$ and $O_{2}$ are the circumcenters and points $H_{1}$ and $H_{2}$ are the orthocenters of triangles $A B P$ and $D C P$, respectively. Denote the midpoints of segments $O_{1} H_{1}$ and $O_{2} H_{2}$ by $E_{1}$ and $E_{2}$, respectively. Prove that the perpendicular from $E_{1}$ on $C D$, the perpendicular from $E_{2}$ on $A B$ and the line $H_{1} H_{2}$ are concurrent.
|
Let the perpendicular from $E_{1}$ on $C D$ meet $P H_{1}$ at $X$, and the perpendicular from $E_{2}$ on $A B$ meet $P H_{2}$ at $Y$ (see Figure 3). Let $\varphi$ be the intersection angle of $A B$ and $C D$. Denote by $M, N$ the midpoints of $P H_{1}, P H_{2}$ respectively.  Figure 3 We will prove now that triangles $E_{1} X M$ and $E_{2} Y N$ have equal angles at $E_{1}, E_{2}$, and supplementary angles at $X, Y$. In the following, angles are understood as oriented, and equalities of angles modulo $180^{\circ}$. Let $\alpha=\angle H_{2} P D, \psi=\angle D P C, \beta=\angle C P H_{1}$. Then $\alpha+\psi+\beta=\varphi, \angle E_{1} X H_{1}=\angle H_{2} Y E_{2}=\varphi$, thus $\angle M X E_{1}+\angle N Y E_{2}=180^{\circ}$. By considering the Feuerbach circle of $\triangle A B P$ whose center is $E_{1}$ and which goes through $M$, we have $\angle E_{1} M H_{1}=\psi+2 \beta$. Analogous considerations with the Feuerbach circle of $\triangle D C P$ yield $\angle H_{2} N E_{2}=\psi+2 \alpha$. Hence indeed $\angle X E_{1} M=\varphi-(\psi+2 \beta)=(\psi+2 \alpha)-\varphi=\angle Y E_{2} N$. It follows now that $$ \frac{X M}{M E_{1}}=\frac{Y N}{N E_{2}} $$ Furthermore, $M E_{1}$ is half the circumradius of $\triangle A B P$, while $P H_{1}$ is the distance of $P$ to the orthocenter of that triangle, which is twice the circumradius times the cosine of $\psi$. Together with analogous reasoning for $\triangle D C P$ we have $$ \frac{M E_{1}}{P H_{1}}=\frac{1}{4 \cos \psi}=\frac{N E_{2}}{P H_{2}} $$ By multiplication, $$ \frac{X M}{P H_{1}}=\frac{Y N}{P H_{2}} $$ and therefore $$ \frac{P X}{X H_{1}}=\frac{H_{2} Y}{Y P} $$ Let $E_{1} X, E_{2} Y$ meet $H_{1} H_{2}$ in $R, S$ respectively. Applying the intercept theorem to the parallels $E_{1} X, P H_{2}$ and center $H_{1}$ gives $$ \frac{H_{2} R}{R H_{1}}=\frac{P X}{X H_{1}} $$ while with parallels $E_{2} Y, P H_{1}$ and center $H_{2}$ we obtain $$ \frac{H_{2} S}{S H_{1}}=\frac{H_{2} Y}{Y P} $$ Combination of the last three equalities yields that $R$ and $S$ coincide.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
7a6160f3-da01-5a0f-9a2c-32b5ca3bc350
| 23,857
|
IRN Let $A B C$ be a triangle with incenter $I$ and let $X, Y$ and $Z$ be the incenters of the triangles $B I C, C I A$ and $A I B$, respectively. Let the triangle $X Y Z$ be equilateral. Prove that $A B C$ is equilateral too.
|
$A Z, A I$ and $A Y$ divide $\angle B A C$ into four equal angles; denote them by $\alpha$. In the same way we have four equal angles $\beta$ at $B$ and four equal angles $\gamma$ at $C$. Obviously $\alpha+\beta+\gamma=\frac{180^{\circ}}{4}=45^{\circ}$; and $0^{\circ}<\alpha, \beta, \gamma<45^{\circ}$.  Easy calculations in various triangles yield $\angle B I C=180^{\circ}-2 \beta-2 \gamma=180^{\circ}-\left(90^{\circ}-2 \alpha\right)=$ $90^{\circ}+2 \alpha$, hence (for $X$ is the incenter of triangle $B C I$, so $I X$ bisects $\angle B I C$ ) we have $\angle X I C=$ $\angle B I X=\frac{1}{2} \angle B I C=45^{\circ}+\alpha$ and with similar aguments $\angle C I Y=\angle Y I A=45^{\circ}+\beta$ and $\angle A I Z=\angle Z I B=45^{\circ}+\gamma$. Furthermore, we have $\angle X I Y=\angle X I C+\angle C I Y=\left(45^{\circ}+\alpha\right)+$ $\left(45^{\circ}+\beta\right)=135^{\circ}-\gamma, \angle Y I Z=135^{\circ}-\alpha$, and $\angle Z I X=135^{\circ}-\beta$. Now we calculate the lengths of $I X, I Y$ and $I Z$ in terms of $\alpha, \beta$ and $\gamma$. The perpendicular from $I$ on $C X$ has length $I X \cdot \sin \angle C X I=I X \cdot \sin \left(90^{\circ}+\beta\right)=I X \cdot \cos \beta$. But $C I$ bisects $\angle Y C X$, so the perpendicular from $I$ on $C Y$ has the same length, and we conclude $$ I X \cdot \cos \beta=I Y \cdot \cos \alpha $$ To make calculations easier we choose a length unit that makes $I X=\cos \alpha$. Then $I Y=\cos \beta$ and with similar arguments $I Z=\cos \gamma$. Since $X Y Z$ is equilateral we have $Z X=Z Y$. The law of Cosines in triangles $X Y I, Y Z I$ yields $$ \begin{aligned} & Z X^{2}=Z Y^{2} \\ \Longrightarrow & I Z^{2}+I X^{2}-2 \cdot I Z \cdot I X \cdot \cos \angle Z I X=I Z^{2}+I Y^{2}-2 \cdot I Z \cdot I Y \cdot \cos \angle Y I Z \\ \Longrightarrow & I X^{2}-I Y^{2}=2 \cdot I Z \cdot(I X \cdot \cos \angle Z I X-I Y \cdot \cos \angle Y I Z) \\ \Longrightarrow & \underbrace{\cos ^{2} \alpha-\cos ^{2} \beta}_{\text {L.H.S. }}=\underbrace{2 \cdot \cos \gamma \cdot\left(\cos \alpha \cdot \cos \left(135^{\circ}-\beta\right)-\cos \beta \cdot \cos \left(135^{\circ}-\alpha\right)\right)}_{\text {R.H.S. }} . \end{aligned} $$ A transformation of the left-hand side (L.H.S.) yields $$ \begin{aligned} \text { L.H.S. } & =\cos ^{2} \alpha \cdot\left(\sin ^{2} \beta+\cos ^{2} \beta\right)-\cos ^{2} \beta \cdot\left(\sin ^{2} \alpha+\cos ^{2} \alpha\right) \\ & =\cos ^{2} \alpha \cdot \sin ^{2} \beta-\cos ^{2} \beta \cdot \sin ^{2} \alpha \end{aligned} $$ $$ \begin{aligned} & =(\cos \alpha \cdot \sin \beta+\cos \beta \cdot \sin \alpha) \cdot(\cos \alpha \cdot \sin \beta-\cos \beta \cdot \sin \alpha) \\ & =\sin (\beta+\alpha) \cdot \sin (\beta-\alpha)=\sin \left(45^{\circ}-\gamma\right) \cdot \sin (\beta-\alpha) \end{aligned} $$ whereas a transformation of the right-hand side (R.H.S.) leads to $$ \begin{aligned} \text { R.H.S. } & =2 \cdot \cos \gamma \cdot\left(\cos \alpha \cdot\left(-\cos \left(45^{\circ}+\beta\right)\right)-\cos \beta \cdot\left(-\cos \left(45^{\circ}+\alpha\right)\right)\right) \\ & =2 \cdot \frac{\sqrt{2}}{2} \cdot \cos \gamma \cdot(\cos \alpha \cdot(\sin \beta-\cos \beta)+\cos \beta \cdot(\cos \alpha-\sin \alpha)) \\ & =\sqrt{2} \cdot \cos \gamma \cdot(\cos \alpha \cdot \sin \beta-\cos \beta \cdot \sin \alpha) \\ & =\sqrt{2} \cdot \cos \gamma \cdot \sin (\beta-\alpha) \end{aligned} $$ Equating L.H.S. and R.H.S. we obtain $$ \begin{aligned} & \sin \left(45^{\circ}-\gamma\right) \cdot \sin (\beta-\alpha)=\sqrt{2} \cdot \cos \gamma \cdot \sin (\beta-\alpha) \\ \Longrightarrow & \sin (\beta-\alpha) \cdot\left(\sqrt{2} \cdot \cos \gamma-\sin \left(45^{\circ}-\gamma\right)\right)=0 \\ \Longrightarrow & \alpha=\beta \quad \text { or } \quad \sqrt{2} \cdot \cos \gamma=\sin \left(45^{\circ}-\gamma\right) . \end{aligned} $$ But $\gamma<45^{\circ}$; so $\sqrt{2} \cdot \cos \gamma>\cos \gamma>\cos 45^{\circ}=\sin 45^{\circ}>\sin \left(45^{\circ}-\gamma\right)$. This leaves $\alpha=\beta$. With similar reasoning we have $\alpha=\gamma$, which means triangle $A B C$ must be equilateral.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
IRN Let $A B C$ be a triangle with incenter $I$ and let $X, Y$ and $Z$ be the incenters of the triangles $B I C, C I A$ and $A I B$, respectively. Let the triangle $X Y Z$ be equilateral. Prove that $A B C$ is equilateral too.
|
$A Z, A I$ and $A Y$ divide $\angle B A C$ into four equal angles; denote them by $\alpha$. In the same way we have four equal angles $\beta$ at $B$ and four equal angles $\gamma$ at $C$. Obviously $\alpha+\beta+\gamma=\frac{180^{\circ}}{4}=45^{\circ}$; and $0^{\circ}<\alpha, \beta, \gamma<45^{\circ}$.  Easy calculations in various triangles yield $\angle B I C=180^{\circ}-2 \beta-2 \gamma=180^{\circ}-\left(90^{\circ}-2 \alpha\right)=$ $90^{\circ}+2 \alpha$, hence (for $X$ is the incenter of triangle $B C I$, so $I X$ bisects $\angle B I C$ ) we have $\angle X I C=$ $\angle B I X=\frac{1}{2} \angle B I C=45^{\circ}+\alpha$ and with similar aguments $\angle C I Y=\angle Y I A=45^{\circ}+\beta$ and $\angle A I Z=\angle Z I B=45^{\circ}+\gamma$. Furthermore, we have $\angle X I Y=\angle X I C+\angle C I Y=\left(45^{\circ}+\alpha\right)+$ $\left(45^{\circ}+\beta\right)=135^{\circ}-\gamma, \angle Y I Z=135^{\circ}-\alpha$, and $\angle Z I X=135^{\circ}-\beta$. Now we calculate the lengths of $I X, I Y$ and $I Z$ in terms of $\alpha, \beta$ and $\gamma$. The perpendicular from $I$ on $C X$ has length $I X \cdot \sin \angle C X I=I X \cdot \sin \left(90^{\circ}+\beta\right)=I X \cdot \cos \beta$. But $C I$ bisects $\angle Y C X$, so the perpendicular from $I$ on $C Y$ has the same length, and we conclude $$ I X \cdot \cos \beta=I Y \cdot \cos \alpha $$ To make calculations easier we choose a length unit that makes $I X=\cos \alpha$. Then $I Y=\cos \beta$ and with similar arguments $I Z=\cos \gamma$. Since $X Y Z$ is equilateral we have $Z X=Z Y$. The law of Cosines in triangles $X Y I, Y Z I$ yields $$ \begin{aligned} & Z X^{2}=Z Y^{2} \\ \Longrightarrow & I Z^{2}+I X^{2}-2 \cdot I Z \cdot I X \cdot \cos \angle Z I X=I Z^{2}+I Y^{2}-2 \cdot I Z \cdot I Y \cdot \cos \angle Y I Z \\ \Longrightarrow & I X^{2}-I Y^{2}=2 \cdot I Z \cdot(I X \cdot \cos \angle Z I X-I Y \cdot \cos \angle Y I Z) \\ \Longrightarrow & \underbrace{\cos ^{2} \alpha-\cos ^{2} \beta}_{\text {L.H.S. }}=\underbrace{2 \cdot \cos \gamma \cdot\left(\cos \alpha \cdot \cos \left(135^{\circ}-\beta\right)-\cos \beta \cdot \cos \left(135^{\circ}-\alpha\right)\right)}_{\text {R.H.S. }} . \end{aligned} $$ A transformation of the left-hand side (L.H.S.) yields $$ \begin{aligned} \text { L.H.S. } & =\cos ^{2} \alpha \cdot\left(\sin ^{2} \beta+\cos ^{2} \beta\right)-\cos ^{2} \beta \cdot\left(\sin ^{2} \alpha+\cos ^{2} \alpha\right) \\ & =\cos ^{2} \alpha \cdot \sin ^{2} \beta-\cos ^{2} \beta \cdot \sin ^{2} \alpha \end{aligned} $$ $$ \begin{aligned} & =(\cos \alpha \cdot \sin \beta+\cos \beta \cdot \sin \alpha) \cdot(\cos \alpha \cdot \sin \beta-\cos \beta \cdot \sin \alpha) \\ & =\sin (\beta+\alpha) \cdot \sin (\beta-\alpha)=\sin \left(45^{\circ}-\gamma\right) \cdot \sin (\beta-\alpha) \end{aligned} $$ whereas a transformation of the right-hand side (R.H.S.) leads to $$ \begin{aligned} \text { R.H.S. } & =2 \cdot \cos \gamma \cdot\left(\cos \alpha \cdot\left(-\cos \left(45^{\circ}+\beta\right)\right)-\cos \beta \cdot\left(-\cos \left(45^{\circ}+\alpha\right)\right)\right) \\ & =2 \cdot \frac{\sqrt{2}}{2} \cdot \cos \gamma \cdot(\cos \alpha \cdot(\sin \beta-\cos \beta)+\cos \beta \cdot(\cos \alpha-\sin \alpha)) \\ & =\sqrt{2} \cdot \cos \gamma \cdot(\cos \alpha \cdot \sin \beta-\cos \beta \cdot \sin \alpha) \\ & =\sqrt{2} \cdot \cos \gamma \cdot \sin (\beta-\alpha) \end{aligned} $$ Equating L.H.S. and R.H.S. we obtain $$ \begin{aligned} & \sin \left(45^{\circ}-\gamma\right) \cdot \sin (\beta-\alpha)=\sqrt{2} \cdot \cos \gamma \cdot \sin (\beta-\alpha) \\ \Longrightarrow & \sin (\beta-\alpha) \cdot\left(\sqrt{2} \cdot \cos \gamma-\sin \left(45^{\circ}-\gamma\right)\right)=0 \\ \Longrightarrow & \alpha=\beta \quad \text { or } \quad \sqrt{2} \cdot \cos \gamma=\sin \left(45^{\circ}-\gamma\right) . \end{aligned} $$ But $\gamma<45^{\circ}$; so $\sqrt{2} \cdot \cos \gamma>\cos \gamma>\cos 45^{\circ}=\sin 45^{\circ}>\sin \left(45^{\circ}-\gamma\right)$. This leaves $\alpha=\beta$. With similar reasoning we have $\alpha=\gamma$, which means triangle $A B C$ must be equilateral.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
1ba8bd45-a773-5f24-ba88-799b99f38e84
| 23,860
|
BGR Let $A B C D$ be a circumscribed quadrilateral. Let $g$ be a line through $A$ which meets the segment $B C$ in $M$ and the line $C D$ in $N$. Denote by $I_{1}, I_{2}$, and $I_{3}$ the incenters of $\triangle A B M$, $\triangle M N C$, and $\triangle N D A$, respectively. Show that the orthocenter of $\triangle I_{1} I_{2} I_{3}$ lies on $g$.
|
Let $k_{1}, k_{2}$ and $k_{3}$ be the incircles of triangles $A B M, M N C$, and $N D A$, respectively (see Figure 1). We shall show that the tangent $h$ from $C$ to $k_{1}$ which is different from $C B$ is also tangent to $k_{3}$.  Figure 1 To this end, let $X$ denote the point of intersection of $g$ and $h$. Then $A B C X$ and $A B C D$ are circumscribed quadrilaterals, whence $$ C D-C X=(A B+C D)-(A B+C X)=(B C+A D)-(B C+A X)=A D-A X $$ i.e. $$ A X+C D=C X+A D $$ which in turn reveals that the quadrilateral $A X C D$ is also circumscribed. Thus $h$ touches indeed the circle $k_{3}$. Moreover, we find that $\angle I_{3} C I_{1}=\angle I_{3} C X+\angle X C I_{1}=\frac{1}{2}(\angle D C X+\angle X C B)=\frac{1}{2} \angle D C B=$ $\frac{1}{2}\left(180^{\circ}-\angle M C N\right)=180^{\circ}-\angle M I_{2} N=\angle I_{3} I_{2} I_{1}$, from which we conclude that $C, I_{1}, I_{2}, I_{3}$ are concyclic. Let now $L_{1}$ and $L_{3}$ be the reflection points of $C$ with respect to the lines $I_{2} I_{3}$ and $I_{1} I_{2}$ respectively. Since $I_{1} I_{2}$ is the angle bisector of $\angle N M C$, it follows that $L_{3}$ lies on $g$. By analogous reasoning, $L_{1}$ lies on $g$. Let $H$ be the orthocenter of $\triangle I_{1} I_{2} I_{3}$. We have $\angle I_{2} L_{3} I_{1}=\angle I_{1} C I_{2}=\angle I_{1} I_{3} I_{2}=180^{\circ}-\angle I_{1} H I_{2}$, which entails that the quadrilateral $I_{2} H I_{1} L_{3}$ is cyclic. Analogously, $I_{3} H L_{1} I_{2}$ is cyclic. Then, working with oriented angles modulo $180^{\circ}$, we have $$ \angle L_{3} H I_{2}=\angle L_{3} I_{1} I_{2}=\angle I_{2} I_{1} C=\angle I_{2} I_{3} C=\angle L_{1} I_{3} I_{2}=\angle L_{1} H I_{2}, $$ whence $L_{1}, L_{3}$, and $H$ are collinear. By $L_{1} \neq L_{3}$, the claim follows. Comment. The last part of the argument essentially reproves the following fact: The Simson line of a point $P$ lying on the circumcircle of a triangle $A B C$ with respect to that triangle bisects the line segment connecting $P$ with the orthocenter of $A B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
BGR Let $A B C D$ be a circumscribed quadrilateral. Let $g$ be a line through $A$ which meets the segment $B C$ in $M$ and the line $C D$ in $N$. Denote by $I_{1}, I_{2}$, and $I_{3}$ the incenters of $\triangle A B M$, $\triangle M N C$, and $\triangle N D A$, respectively. Show that the orthocenter of $\triangle I_{1} I_{2} I_{3}$ lies on $g$.
|
Let $k_{1}, k_{2}$ and $k_{3}$ be the incircles of triangles $A B M, M N C$, and $N D A$, respectively (see Figure 1). We shall show that the tangent $h$ from $C$ to $k_{1}$ which is different from $C B$ is also tangent to $k_{3}$.  Figure 1 To this end, let $X$ denote the point of intersection of $g$ and $h$. Then $A B C X$ and $A B C D$ are circumscribed quadrilaterals, whence $$ C D-C X=(A B+C D)-(A B+C X)=(B C+A D)-(B C+A X)=A D-A X $$ i.e. $$ A X+C D=C X+A D $$ which in turn reveals that the quadrilateral $A X C D$ is also circumscribed. Thus $h$ touches indeed the circle $k_{3}$. Moreover, we find that $\angle I_{3} C I_{1}=\angle I_{3} C X+\angle X C I_{1}=\frac{1}{2}(\angle D C X+\angle X C B)=\frac{1}{2} \angle D C B=$ $\frac{1}{2}\left(180^{\circ}-\angle M C N\right)=180^{\circ}-\angle M I_{2} N=\angle I_{3} I_{2} I_{1}$, from which we conclude that $C, I_{1}, I_{2}, I_{3}$ are concyclic. Let now $L_{1}$ and $L_{3}$ be the reflection points of $C$ with respect to the lines $I_{2} I_{3}$ and $I_{1} I_{2}$ respectively. Since $I_{1} I_{2}$ is the angle bisector of $\angle N M C$, it follows that $L_{3}$ lies on $g$. By analogous reasoning, $L_{1}$ lies on $g$. Let $H$ be the orthocenter of $\triangle I_{1} I_{2} I_{3}$. We have $\angle I_{2} L_{3} I_{1}=\angle I_{1} C I_{2}=\angle I_{1} I_{3} I_{2}=180^{\circ}-\angle I_{1} H I_{2}$, which entails that the quadrilateral $I_{2} H I_{1} L_{3}$ is cyclic. Analogously, $I_{3} H L_{1} I_{2}$ is cyclic. Then, working with oriented angles modulo $180^{\circ}$, we have $$ \angle L_{3} H I_{2}=\angle L_{3} I_{1} I_{2}=\angle I_{2} I_{1} C=\angle I_{2} I_{3} C=\angle L_{1} I_{3} I_{2}=\angle L_{1} H I_{2}, $$ whence $L_{1}, L_{3}$, and $H$ are collinear. By $L_{1} \neq L_{3}$, the claim follows. Comment. The last part of the argument essentially reproves the following fact: The Simson line of a point $P$ lying on the circumcircle of a triangle $A B C$ with respect to that triangle bisects the line segment connecting $P$ with the orthocenter of $A B C$.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
7732359a-2c21-5dc5-9b4c-448027da2258
| 23,863
|
BGR Let $A B C D$ be a circumscribed quadrilateral. Let $g$ be a line through $A$ which meets the segment $B C$ in $M$ and the line $C D$ in $N$. Denote by $I_{1}, I_{2}$, and $I_{3}$ the incenters of $\triangle A B M$, $\triangle M N C$, and $\triangle N D A$, respectively. Show that the orthocenter of $\triangle I_{1} I_{2} I_{3}$ lies on $g$.
|
We start by proving that $C, I_{1}, I_{2}$, and $I_{3}$ are concyclic.  Figure 2 To this end, notice first that $I_{2}, M, I_{1}$ are collinear, as are $N, I_{2}, I_{3}$ (see Figure 2). Denote by $\alpha, \beta, \gamma, \delta$ the internal angles of $A B C D$. By considerations in triangle $C M N$, it follows that $\angle I_{3} I_{2} I_{1}=\frac{\gamma}{2}$. We will show that $\angle I_{3} C I_{1}=\frac{\gamma}{2}$, too. Denote by $I$ the incenter of $A B C D$. Clearly, $I_{1} \in B I, I_{3} \in D I, \angle I_{1} A I_{3}=\frac{\alpha}{2}$. Using the abbreviation $[X, Y Z]$ for the distance from point $X$ to the line $Y Z$, we have because of $\angle B A I_{1}=\angle I A I_{3}$ and $\angle I_{1} A I=\angle I_{3} A D$ that $$ \frac{\left[I_{1}, A B\right]}{\left[I_{1}, A I\right]}=\frac{\left[I_{3}, A I\right]}{\left[I_{3}, A D\right]} $$ Furthermore, consideration of the angle sums in $A I B, B I C, C I D$ and $D I A$ implies $\angle A I B+$ $\angle C I D=\angle B I C+\angle D I A=180^{\circ}$, from which we see $$ \frac{\left[I_{1}, A I\right]}{\left[I_{3}, C I\right]}=\frac{I_{1} I}{I_{3} I}=\frac{\left[I_{1}, C I\right]}{\left[I_{3}, A I\right]} . $$ Because of $\left[I_{1}, A B\right]=\left[I_{1}, B C\right],\left[I_{3}, A D\right]=\left[I_{3}, C D\right]$, multiplication yields $$ \frac{\left[I_{1}, B C\right]}{\left[I_{3}, C I\right]}=\frac{\left[I_{1}, C I\right]}{\left[I_{3}, C D\right]} . $$ By $\angle D C I=\angle I C B=\gamma / 2$ it follows that $\angle I_{1} C B=\angle I_{3} C I$ which concludes the proof of the above statement. Let the perpendicular from $I_{1}$ on $I_{2} I_{3}$ intersect $g$ at $Z$. Then $\angle M I_{1} Z=90^{\circ}-\angle I_{3} I_{2} I_{1}=$ $90^{\circ}-\gamma / 2=\angle M C I_{2}$. Since we have also $\angle Z M I_{1}=\angle I_{2} M C$, triangles $M Z I_{1}$ and $M I_{2} C$ are similar. From this one easily proves that also $M I_{2} Z$ and $M C I_{1}$ are similar. Because $C, I_{1}, I_{2}$, and $I_{3}$ are concyclic, $\angle M Z I_{2}=\angle M I_{1} C=\angle N I_{3} C$, thus $N I_{2} Z$ and $N C I_{3}$ are similar, hence $N C I_{2}$ and $N I_{3} Z$ are similar. We conclude $\angle Z I_{3} I_{2}=\angle I_{2} C N=90^{\circ}-\gamma / 2$, hence $I_{1} I_{2} \perp Z I_{3}$. This completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
BGR Let $A B C D$ be a circumscribed quadrilateral. Let $g$ be a line through $A$ which meets the segment $B C$ in $M$ and the line $C D$ in $N$. Denote by $I_{1}, I_{2}$, and $I_{3}$ the incenters of $\triangle A B M$, $\triangle M N C$, and $\triangle N D A$, respectively. Show that the orthocenter of $\triangle I_{1} I_{2} I_{3}$ lies on $g$.
|
We start by proving that $C, I_{1}, I_{2}$, and $I_{3}$ are concyclic.  Figure 2 To this end, notice first that $I_{2}, M, I_{1}$ are collinear, as are $N, I_{2}, I_{3}$ (see Figure 2). Denote by $\alpha, \beta, \gamma, \delta$ the internal angles of $A B C D$. By considerations in triangle $C M N$, it follows that $\angle I_{3} I_{2} I_{1}=\frac{\gamma}{2}$. We will show that $\angle I_{3} C I_{1}=\frac{\gamma}{2}$, too. Denote by $I$ the incenter of $A B C D$. Clearly, $I_{1} \in B I, I_{3} \in D I, \angle I_{1} A I_{3}=\frac{\alpha}{2}$. Using the abbreviation $[X, Y Z]$ for the distance from point $X$ to the line $Y Z$, we have because of $\angle B A I_{1}=\angle I A I_{3}$ and $\angle I_{1} A I=\angle I_{3} A D$ that $$ \frac{\left[I_{1}, A B\right]}{\left[I_{1}, A I\right]}=\frac{\left[I_{3}, A I\right]}{\left[I_{3}, A D\right]} $$ Furthermore, consideration of the angle sums in $A I B, B I C, C I D$ and $D I A$ implies $\angle A I B+$ $\angle C I D=\angle B I C+\angle D I A=180^{\circ}$, from which we see $$ \frac{\left[I_{1}, A I\right]}{\left[I_{3}, C I\right]}=\frac{I_{1} I}{I_{3} I}=\frac{\left[I_{1}, C I\right]}{\left[I_{3}, A I\right]} . $$ Because of $\left[I_{1}, A B\right]=\left[I_{1}, B C\right],\left[I_{3}, A D\right]=\left[I_{3}, C D\right]$, multiplication yields $$ \frac{\left[I_{1}, B C\right]}{\left[I_{3}, C I\right]}=\frac{\left[I_{1}, C I\right]}{\left[I_{3}, C D\right]} . $$ By $\angle D C I=\angle I C B=\gamma / 2$ it follows that $\angle I_{1} C B=\angle I_{3} C I$ which concludes the proof of the above statement. Let the perpendicular from $I_{1}$ on $I_{2} I_{3}$ intersect $g$ at $Z$. Then $\angle M I_{1} Z=90^{\circ}-\angle I_{3} I_{2} I_{1}=$ $90^{\circ}-\gamma / 2=\angle M C I_{2}$. Since we have also $\angle Z M I_{1}=\angle I_{2} M C$, triangles $M Z I_{1}$ and $M I_{2} C$ are similar. From this one easily proves that also $M I_{2} Z$ and $M C I_{1}$ are similar. Because $C, I_{1}, I_{2}$, and $I_{3}$ are concyclic, $\angle M Z I_{2}=\angle M I_{1} C=\angle N I_{3} C$, thus $N I_{2} Z$ and $N C I_{3}$ are similar, hence $N C I_{2}$ and $N I_{3} Z$ are similar. We conclude $\angle Z I_{3} I_{2}=\angle I_{2} C N=90^{\circ}-\gamma / 2$, hence $I_{1} I_{2} \perp Z I_{3}$. This completes the proof.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
7732359a-2c21-5dc5-9b4c-448027da2258
| 23,863
|
AUS A social club has $n$ members. They have the membership numbers $1,2, \ldots, n$, respectively. From time to time members send presents to other members, including items they have already received as presents from other members. In order to avoid the embarrassing situation that a member might receive a present that he or she has sent to other members, the club adds the following rule to its statutes at one of its annual general meetings: "A member with membership number $a$ is permitted to send a present to a member with membership number $b$ if and only if $a(b-1)$ is a multiple of $n$." Prove that, if each member follows this rule, none will receive a present from another member that he or she has already sent to other members. Alternative formulation: Let $G$ be a directed graph with $n$ vertices $v_{1}, v_{2}, \ldots, v_{n}$, such that there is an edge going from $v_{a}$ to $v_{b}$ if and only if $a$ and $b$ are distinct and $a(b-1)$ is a multiple of $n$. Prove that this graph does not contain a directed cycle.
|
Suppose there is an edge from $v_{i}$ to $v_{j}$. Then $i(j-1)=i j-i=k n$ for some integer $k$, which implies $i=i j-k n$. If $\operatorname{gcd}(i, n)=d$ and $\operatorname{gcd}(j, n)=e$, then $e$ divides $i j-k n=i$ and thus $e$ also divides $d$. Hence, if there is an edge from $v_{i}$ to $v_{j}$, then $\operatorname{gcd}(j, n) \mid \operatorname{gcd}(i, n)$. If there is a cycle in $G$, say $v_{i_{1}} \rightarrow v_{i_{2}} \rightarrow \cdots \rightarrow v_{i_{r}} \rightarrow v_{i_{1}}$, then we have $$ \operatorname{gcd}\left(i_{1}, n\right)\left|\operatorname{gcd}\left(i_{r}, n\right)\right| \operatorname{gcd}\left(i_{r-1}, n\right)|\ldots| \operatorname{gcd}\left(i_{2}, n\right) \mid \operatorname{gcd}\left(i_{1}, n\right) $$ which implies that all these greatest common divisors must be equal, say be equal to $t$. Now we pick any of the $i_{k}$, without loss of generality let it be $i_{1}$. Then $i_{r}\left(i_{1}-1\right)$ is a multiple of $n$ and hence also (by dividing by $t$ ), $i_{1}-1$ is a multiple of $\frac{n}{t}$. Since $i_{1}$ and $i_{1}-1$ are relatively prime, also $t$ and $\frac{n}{t}$ are relatively prime. So, by the Chinese remainder theorem, the value of $i_{1}$ is uniquely determined modulo $n=t \cdot \frac{n}{t}$ by the value of $t$. But, as $i_{1}$ was chosen arbitrarily among the $i_{k}$, this implies that all the $i_{k}$ have to be equal, a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
AUS A social club has $n$ members. They have the membership numbers $1,2, \ldots, n$, respectively. From time to time members send presents to other members, including items they have already received as presents from other members. In order to avoid the embarrassing situation that a member might receive a present that he or she has sent to other members, the club adds the following rule to its statutes at one of its annual general meetings: "A member with membership number $a$ is permitted to send a present to a member with membership number $b$ if and only if $a(b-1)$ is a multiple of $n$." Prove that, if each member follows this rule, none will receive a present from another member that he or she has already sent to other members. Alternative formulation: Let $G$ be a directed graph with $n$ vertices $v_{1}, v_{2}, \ldots, v_{n}$, such that there is an edge going from $v_{a}$ to $v_{b}$ if and only if $a$ and $b$ are distinct and $a(b-1)$ is a multiple of $n$. Prove that this graph does not contain a directed cycle.
|
Suppose there is an edge from $v_{i}$ to $v_{j}$. Then $i(j-1)=i j-i=k n$ for some integer $k$, which implies $i=i j-k n$. If $\operatorname{gcd}(i, n)=d$ and $\operatorname{gcd}(j, n)=e$, then $e$ divides $i j-k n=i$ and thus $e$ also divides $d$. Hence, if there is an edge from $v_{i}$ to $v_{j}$, then $\operatorname{gcd}(j, n) \mid \operatorname{gcd}(i, n)$. If there is a cycle in $G$, say $v_{i_{1}} \rightarrow v_{i_{2}} \rightarrow \cdots \rightarrow v_{i_{r}} \rightarrow v_{i_{1}}$, then we have $$ \operatorname{gcd}\left(i_{1}, n\right)\left|\operatorname{gcd}\left(i_{r}, n\right)\right| \operatorname{gcd}\left(i_{r-1}, n\right)|\ldots| \operatorname{gcd}\left(i_{2}, n\right) \mid \operatorname{gcd}\left(i_{1}, n\right) $$ which implies that all these greatest common divisors must be equal, say be equal to $t$. Now we pick any of the $i_{k}$, without loss of generality let it be $i_{1}$. Then $i_{r}\left(i_{1}-1\right)$ is a multiple of $n$ and hence also (by dividing by $t$ ), $i_{1}-1$ is a multiple of $\frac{n}{t}$. Since $i_{1}$ and $i_{1}-1$ are relatively prime, also $t$ and $\frac{n}{t}$ are relatively prime. So, by the Chinese remainder theorem, the value of $i_{1}$ is uniquely determined modulo $n=t \cdot \frac{n}{t}$ by the value of $t$. But, as $i_{1}$ was chosen arbitrarily among the $i_{k}$, this implies that all the $i_{k}$ have to be equal, a contradiction.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
05606ebf-f6c2-526d-b5fb-89fdeafb344d
| 23,867
|
AUS A social club has $n$ members. They have the membership numbers $1,2, \ldots, n$, respectively. From time to time members send presents to other members, including items they have already received as presents from other members. In order to avoid the embarrassing situation that a member might receive a present that he or she has sent to other members, the club adds the following rule to its statutes at one of its annual general meetings: "A member with membership number $a$ is permitted to send a present to a member with membership number $b$ if and only if $a(b-1)$ is a multiple of $n$." Prove that, if each member follows this rule, none will receive a present from another member that he or she has already sent to other members. Alternative formulation: Let $G$ be a directed graph with $n$ vertices $v_{1}, v_{2}, \ldots, v_{n}$, such that there is an edge going from $v_{a}$ to $v_{b}$ if and only if $a$ and $b$ are distinct and $a(b-1)$ is a multiple of $n$. Prove that this graph does not contain a directed cycle.
|
If $a, b, c$ are integers such that $a b-a$ and $b c-b$ are multiples of $n$, then also $a c-a=a(b c-b)+(a b-a)-(a b-a) c$ is a multiple of $n$. This implies that if there is an edge from $v_{a}$ to $v_{b}$ and an edge from $v_{b}$ to $v_{c}$, then there also must be an edge from $v_{a}$ to $v_{c}$. Therefore, if there are any cycles at all, the smallest cycle must have length 2. But suppose the vertices $v_{a}$ and $v_{b}$ form such a cycle, i. e., $a b-a$ and $a b-b$ are both multiples of $n$. Then $a-b$ is also a multiple of $n$, which can only happen if $a=b$, which is impossible.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
AUS A social club has $n$ members. They have the membership numbers $1,2, \ldots, n$, respectively. From time to time members send presents to other members, including items they have already received as presents from other members. In order to avoid the embarrassing situation that a member might receive a present that he or she has sent to other members, the club adds the following rule to its statutes at one of its annual general meetings: "A member with membership number $a$ is permitted to send a present to a member with membership number $b$ if and only if $a(b-1)$ is a multiple of $n$." Prove that, if each member follows this rule, none will receive a present from another member that he or she has already sent to other members. Alternative formulation: Let $G$ be a directed graph with $n$ vertices $v_{1}, v_{2}, \ldots, v_{n}$, such that there is an edge going from $v_{a}$ to $v_{b}$ if and only if $a$ and $b$ are distinct and $a(b-1)$ is a multiple of $n$. Prove that this graph does not contain a directed cycle.
|
If $a, b, c$ are integers such that $a b-a$ and $b c-b$ are multiples of $n$, then also $a c-a=a(b c-b)+(a b-a)-(a b-a) c$ is a multiple of $n$. This implies that if there is an edge from $v_{a}$ to $v_{b}$ and an edge from $v_{b}$ to $v_{c}$, then there also must be an edge from $v_{a}$ to $v_{c}$. Therefore, if there are any cycles at all, the smallest cycle must have length 2. But suppose the vertices $v_{a}$ and $v_{b}$ form such a cycle, i. e., $a b-a$ and $a b-b$ are both multiples of $n$. Then $a-b$ is also a multiple of $n$, which can only happen if $a=b$, which is impossible.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
05606ebf-f6c2-526d-b5fb-89fdeafb344d
| 23,867
|
AUS A social club has $n$ members. They have the membership numbers $1,2, \ldots, n$, respectively. From time to time members send presents to other members, including items they have already received as presents from other members. In order to avoid the embarrassing situation that a member might receive a present that he or she has sent to other members, the club adds the following rule to its statutes at one of its annual general meetings: "A member with membership number $a$ is permitted to send a present to a member with membership number $b$ if and only if $a(b-1)$ is a multiple of $n$." Prove that, if each member follows this rule, none will receive a present from another member that he or she has already sent to other members. Alternative formulation: Let $G$ be a directed graph with $n$ vertices $v_{1}, v_{2}, \ldots, v_{n}$, such that there is an edge going from $v_{a}$ to $v_{b}$ if and only if $a$ and $b$ are distinct and $a(b-1)$ is a multiple of $n$. Prove that this graph does not contain a directed cycle.
|
Suppose there was a cycle $v_{i_{1}} \rightarrow v_{i_{2}} \rightarrow \cdots \rightarrow v_{i_{r}} \rightarrow v_{i_{1}}$. Then $i_{1}\left(i_{2}-1\right)$ is a multiple of $n$, i.e., $i_{1} \equiv i_{1} i_{2} \bmod n$. Continuing in this manner, we get $i_{1} \equiv i_{1} i_{2} \equiv$ $i_{1} i_{2} i_{3} \equiv i_{1} i_{2} i_{3} \ldots i_{r} \bmod n$. But the same holds for all $i_{k}$, i. e., $i_{k} \equiv i_{1} i_{2} i_{3} \ldots i_{r} \bmod n$. Hence $i_{1} \equiv i_{2} \equiv \cdots \equiv i_{r} \bmod n$, which means $i_{1}=i_{2}=\cdots=i_{r}$, a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
AUS A social club has $n$ members. They have the membership numbers $1,2, \ldots, n$, respectively. From time to time members send presents to other members, including items they have already received as presents from other members. In order to avoid the embarrassing situation that a member might receive a present that he or she has sent to other members, the club adds the following rule to its statutes at one of its annual general meetings: "A member with membership number $a$ is permitted to send a present to a member with membership number $b$ if and only if $a(b-1)$ is a multiple of $n$." Prove that, if each member follows this rule, none will receive a present from another member that he or she has already sent to other members. Alternative formulation: Let $G$ be a directed graph with $n$ vertices $v_{1}, v_{2}, \ldots, v_{n}$, such that there is an edge going from $v_{a}$ to $v_{b}$ if and only if $a$ and $b$ are distinct and $a(b-1)$ is a multiple of $n$. Prove that this graph does not contain a directed cycle.
|
Suppose there was a cycle $v_{i_{1}} \rightarrow v_{i_{2}} \rightarrow \cdots \rightarrow v_{i_{r}} \rightarrow v_{i_{1}}$. Then $i_{1}\left(i_{2}-1\right)$ is a multiple of $n$, i.e., $i_{1} \equiv i_{1} i_{2} \bmod n$. Continuing in this manner, we get $i_{1} \equiv i_{1} i_{2} \equiv$ $i_{1} i_{2} i_{3} \equiv i_{1} i_{2} i_{3} \ldots i_{r} \bmod n$. But the same holds for all $i_{k}$, i. e., $i_{k} \equiv i_{1} i_{2} i_{3} \ldots i_{r} \bmod n$. Hence $i_{1} \equiv i_{2} \equiv \cdots \equiv i_{r} \bmod n$, which means $i_{1}=i_{2}=\cdots=i_{r}$, a contradiction.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
05606ebf-f6c2-526d-b5fb-89fdeafb344d
| 23,867
|
AUS A social club has $n$ members. They have the membership numbers $1,2, \ldots, n$, respectively. From time to time members send presents to other members, including items they have already received as presents from other members. In order to avoid the embarrassing situation that a member might receive a present that he or she has sent to other members, the club adds the following rule to its statutes at one of its annual general meetings: "A member with membership number $a$ is permitted to send a present to a member with membership number $b$ if and only if $a(b-1)$ is a multiple of $n$." Prove that, if each member follows this rule, none will receive a present from another member that he or she has already sent to other members. Alternative formulation: Let $G$ be a directed graph with $n$ vertices $v_{1}, v_{2}, \ldots, v_{n}$, such that there is an edge going from $v_{a}$ to $v_{b}$ if and only if $a$ and $b$ are distinct and $a(b-1)$ is a multiple of $n$. Prove that this graph does not contain a directed cycle.
|
Let $n=k$ be the smallest value of $n$ for which the corresponding graph has a cycle. We show that $k$ is a prime power. If $k$ is not a prime power, it can be written as a product $k=d e$ of relatively prime integers greater than 1. Reducing all the numbers modulo $d$ yields a single vertex or a cycle in the corresponding graph on $d$ vertices, because if $a(b-1) \equiv 0 \bmod k$ then this equation also holds modulo $d$. But since the graph on $d$ vertices has no cycles, by the minimality of $k$, we must have that all the indices of the cycle are congruent modulo $d$. The same holds modulo $e$ and hence also modulo $k=d e$. But then all the indices are equal, which is a contradiction. Thus $k$ must be a prime power $k=p^{m}$. There are no edges ending at $v_{k}$, so $v_{k}$ is not contained in any cycle. All edges not starting at $v_{k}$ end at a vertex belonging to a non-multiple of $p$, and all edges starting at a non-multiple of $p$ must end at $v_{1}$. But there is no edge starting at $v_{1}$. Hence there is no cycle.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
AUS A social club has $n$ members. They have the membership numbers $1,2, \ldots, n$, respectively. From time to time members send presents to other members, including items they have already received as presents from other members. In order to avoid the embarrassing situation that a member might receive a present that he or she has sent to other members, the club adds the following rule to its statutes at one of its annual general meetings: "A member with membership number $a$ is permitted to send a present to a member with membership number $b$ if and only if $a(b-1)$ is a multiple of $n$." Prove that, if each member follows this rule, none will receive a present from another member that he or she has already sent to other members. Alternative formulation: Let $G$ be a directed graph with $n$ vertices $v_{1}, v_{2}, \ldots, v_{n}$, such that there is an edge going from $v_{a}$ to $v_{b}$ if and only if $a$ and $b$ are distinct and $a(b-1)$ is a multiple of $n$. Prove that this graph does not contain a directed cycle.
|
Let $n=k$ be the smallest value of $n$ for which the corresponding graph has a cycle. We show that $k$ is a prime power. If $k$ is not a prime power, it can be written as a product $k=d e$ of relatively prime integers greater than 1. Reducing all the numbers modulo $d$ yields a single vertex or a cycle in the corresponding graph on $d$ vertices, because if $a(b-1) \equiv 0 \bmod k$ then this equation also holds modulo $d$. But since the graph on $d$ vertices has no cycles, by the minimality of $k$, we must have that all the indices of the cycle are congruent modulo $d$. The same holds modulo $e$ and hence also modulo $k=d e$. But then all the indices are equal, which is a contradiction. Thus $k$ must be a prime power $k=p^{m}$. There are no edges ending at $v_{k}$, so $v_{k}$ is not contained in any cycle. All edges not starting at $v_{k}$ end at a vertex belonging to a non-multiple of $p$, and all edges starting at a non-multiple of $p$ must end at $v_{1}$. But there is no edge starting at $v_{1}$. Hence there is no cycle.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
05606ebf-f6c2-526d-b5fb-89fdeafb344d
| 23,867
|
AUS A social club has $n$ members. They have the membership numbers $1,2, \ldots, n$, respectively. From time to time members send presents to other members, including items they have already received as presents from other members. In order to avoid the embarrassing situation that a member might receive a present that he or she has sent to other members, the club adds the following rule to its statutes at one of its annual general meetings: "A member with membership number $a$ is permitted to send a present to a member with membership number $b$ if and only if $a(b-1)$ is a multiple of $n$." Prove that, if each member follows this rule, none will receive a present from another member that he or she has already sent to other members. Alternative formulation: Let $G$ be a directed graph with $n$ vertices $v_{1}, v_{2}, \ldots, v_{n}$, such that there is an edge going from $v_{a}$ to $v_{b}$ if and only if $a$ and $b$ are distinct and $a(b-1)$ is a multiple of $n$. Prove that this graph does not contain a directed cycle.
|
Suppose there was a cycle $v_{i_{1}} \rightarrow v_{i_{2}} \rightarrow \cdots \rightarrow v_{i_{r}} \rightarrow v_{i_{1}}$. Let $q=p^{m}$ be a prime power dividing $n$. We claim that either $i_{1} \equiv i_{2} \equiv \cdots \equiv i_{r} \equiv 0 \bmod q$ or $i_{1} \equiv i_{2} \equiv \cdots \equiv i_{r} \equiv$ $1 \bmod q$. Suppose that there is an $i_{s}$ not divisible by $q$. Then, as $i_{s}\left(i_{s+1}-1\right)$ is a multiple of $q, i_{s+1} \equiv$ $1 \bmod p$. Similarly, we conclude $i_{s+2} \equiv 1 \bmod p$ and so on. So none of the labels is divisible by $p$, but since $i_{s}\left(i_{s+1}-1\right)$ is a multiple of $q=p^{m}$ for all $s$, all $i_{s+1}$ are congruent to 1 modulo $q$. This proves the claim. Now, as all the labels are congruent modulo all the prime powers dividing $n$, they must all be equal by the Chinese remainder theorem. This is a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
AUS A social club has $n$ members. They have the membership numbers $1,2, \ldots, n$, respectively. From time to time members send presents to other members, including items they have already received as presents from other members. In order to avoid the embarrassing situation that a member might receive a present that he or she has sent to other members, the club adds the following rule to its statutes at one of its annual general meetings: "A member with membership number $a$ is permitted to send a present to a member with membership number $b$ if and only if $a(b-1)$ is a multiple of $n$." Prove that, if each member follows this rule, none will receive a present from another member that he or she has already sent to other members. Alternative formulation: Let $G$ be a directed graph with $n$ vertices $v_{1}, v_{2}, \ldots, v_{n}$, such that there is an edge going from $v_{a}$ to $v_{b}$ if and only if $a$ and $b$ are distinct and $a(b-1)$ is a multiple of $n$. Prove that this graph does not contain a directed cycle.
|
Suppose there was a cycle $v_{i_{1}} \rightarrow v_{i_{2}} \rightarrow \cdots \rightarrow v_{i_{r}} \rightarrow v_{i_{1}}$. Let $q=p^{m}$ be a prime power dividing $n$. We claim that either $i_{1} \equiv i_{2} \equiv \cdots \equiv i_{r} \equiv 0 \bmod q$ or $i_{1} \equiv i_{2} \equiv \cdots \equiv i_{r} \equiv$ $1 \bmod q$. Suppose that there is an $i_{s}$ not divisible by $q$. Then, as $i_{s}\left(i_{s+1}-1\right)$ is a multiple of $q, i_{s+1} \equiv$ $1 \bmod p$. Similarly, we conclude $i_{s+2} \equiv 1 \bmod p$ and so on. So none of the labels is divisible by $p$, but since $i_{s}\left(i_{s+1}-1\right)$ is a multiple of $q=p^{m}$ for all $s$, all $i_{s+1}$ are congruent to 1 modulo $q$. This proves the claim. Now, as all the labels are congruent modulo all the prime powers dividing $n$, they must all be equal by the Chinese remainder theorem. This is a contradiction.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
05606ebf-f6c2-526d-b5fb-89fdeafb344d
| 23,867
|
PER A positive integer $N$ is called balanced, if $N=1$ or if $N$ can be written as a product of an even number of not necessarily distinct primes. Given positive integers $a$ and $b$, consider the polynomial $P$ defined by $P(x)=(x+a)(x+b)$. (a) Prove that there exist distinct positive integers $a$ and $b$ such that all the numbers $P(1), P(2)$, $\ldots, P(50)$ are balanced. (b) Prove that if $P(n)$ is balanced for all positive integers $n$, then $a=b$.
|
Define a function $f$ on the set of positive integers by $f(n)=0$ if $n$ is balanced and $f(n)=1$ otherwise. Clearly, $f(n m) \equiv f(n)+f(m) \bmod 2$ for all positive integers $n, m$. (a) Now for each positive integer $n$ consider the binary sequence $(f(n+1), f(n+2), \ldots, f(n+$ $50)$ ). As there are only $2^{50}$ different such sequences there are two different positive integers $a$ and $b$ such that $$ (f(a+1), f(a+2), \ldots, f(a+50))=(f(b+1), f(b+2), \ldots, f(b+50)) $$ But this implies that for the polynomial $P(x)=(x+a)(x+b)$ all the numbers $P(1), P(2)$, $\ldots, P(50)$ are balanced, since for all $1 \leq k \leq 50$ we have $f(P(k)) \equiv f(a+k)+f(b+k) \equiv$ $2 f(a+k) \equiv 0 \bmod 2$. (b) Now suppose $P(n)$ is balanced for all positive integers $n$ and $a<b$. Set $n=k(b-a)-a$ for sufficiently large $k$, such that $n$ is positive. Then $P(n)=k(k+1)(b-a)^{2}$, and this number can only be balanced, if $f(k)=f(k+1)$ holds. Thus, the sequence $f(k)$ must become constant for sufficiently large $k$. But this is not possible, as for every prime $p$ we have $f(p)=1$ and for every square $t^{2}$ we have $f\left(t^{2}\right)=0$. Hence $a=b$. Comment. Given a positive integer $k$, a computer search for the pairs of positive integers $(a, b)$, for which $P(1), P(2), \ldots, P(k)$ are all balanced yields the following results with minimal sum $a+b$ and $a<b$ : | $k$ | 3 | 4 | 5 | 10 | 20 | | :--- | :---: | :---: | :---: | :---: | :---: | | $(a, b)$ | $(2,4)$ | $(6,11)$ | $(8,14)$ | $(20,34)$ | $(1751,3121)$ | Therefore, trying to find $a$ and $b$ in part (a) of the problem cannot be done by elementary calculations.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
PER A positive integer $N$ is called balanced, if $N=1$ or if $N$ can be written as a product of an even number of not necessarily distinct primes. Given positive integers $a$ and $b$, consider the polynomial $P$ defined by $P(x)=(x+a)(x+b)$. (a) Prove that there exist distinct positive integers $a$ and $b$ such that all the numbers $P(1), P(2)$, $\ldots, P(50)$ are balanced. (b) Prove that if $P(n)$ is balanced for all positive integers $n$, then $a=b$.
|
Define a function $f$ on the set of positive integers by $f(n)=0$ if $n$ is balanced and $f(n)=1$ otherwise. Clearly, $f(n m) \equiv f(n)+f(m) \bmod 2$ for all positive integers $n, m$. (a) Now for each positive integer $n$ consider the binary sequence $(f(n+1), f(n+2), \ldots, f(n+$ $50)$ ). As there are only $2^{50}$ different such sequences there are two different positive integers $a$ and $b$ such that $$ (f(a+1), f(a+2), \ldots, f(a+50))=(f(b+1), f(b+2), \ldots, f(b+50)) $$ But this implies that for the polynomial $P(x)=(x+a)(x+b)$ all the numbers $P(1), P(2)$, $\ldots, P(50)$ are balanced, since for all $1 \leq k \leq 50$ we have $f(P(k)) \equiv f(a+k)+f(b+k) \equiv$ $2 f(a+k) \equiv 0 \bmod 2$. (b) Now suppose $P(n)$ is balanced for all positive integers $n$ and $a<b$. Set $n=k(b-a)-a$ for sufficiently large $k$, such that $n$ is positive. Then $P(n)=k(k+1)(b-a)^{2}$, and this number can only be balanced, if $f(k)=f(k+1)$ holds. Thus, the sequence $f(k)$ must become constant for sufficiently large $k$. But this is not possible, as for every prime $p$ we have $f(p)=1$ and for every square $t^{2}$ we have $f\left(t^{2}\right)=0$. Hence $a=b$. Comment. Given a positive integer $k$, a computer search for the pairs of positive integers $(a, b)$, for which $P(1), P(2), \ldots, P(k)$ are all balanced yields the following results with minimal sum $a+b$ and $a<b$ : | $k$ | 3 | 4 | 5 | 10 | 20 | | :--- | :---: | :---: | :---: | :---: | :---: | | $(a, b)$ | $(2,4)$ | $(6,11)$ | $(8,14)$ | $(20,34)$ | $(1751,3121)$ | Therefore, trying to find $a$ and $b$ in part (a) of the problem cannot be done by elementary calculations.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
6a626b37-9446-5db5-8518-f9a5f24b034c
| 23,876
|
EST Let $f$ be a non-constant function from the set of positive integers into the set of positive integers, such that $a-b$ divides $f(a)-f(b)$ for all distinct positive integers $a, b$. Prove that there exist infinitely many primes $p$ such that $p$ divides $f(c)$ for some positive integer $c$.
|
Denote by $v_{p}(a)$ the exponent of the prime $p$ in the prime decomposition of $a$. Assume that there are only finitely many primes $p_{1}, p_{2}, \ldots, p_{m}$ that divide some function value produced of $f$. There are infinitely many positive integers $a$ such that $v_{p_{i}}(a)>v_{p_{i}}(f(1))$ for all $i=1,2, \ldots, m$, e.g. $a=\left(p_{1} p_{2} \ldots p_{m}\right)^{\alpha}$ with $\alpha$ sufficiently large. Pick any such $a$. The condition of the problem then yields $a \mid(f(a+1)-f(1))$. Assume $f(a+1) \neq f(1)$. Then we must have $v_{p_{i}}(f(a+1)) \neq$ $v_{p_{i}}(f(1))$ for at least one $i$. This yields $v_{p_{i}}(f(a+1)-f(1))=\min \left\{v_{p_{i}}(f(a+1)), v_{p_{i}}(f(1))\right\} \leq$ $v_{p_{1}}(f(1))<v_{p_{i}}(a)$. But this contradicts the fact that $a \mid(f(a+1)-f(1))$. Hence we must have $f(a+1)=f(1)$ for all such $a$. Now, for any positive integer $b$ and all such $a$, we have $(a+1-b) \mid(f(a+1)-f(b))$, i.e., $(a+1-b) \mid(f(1)-f(b))$. Since this is true for infinitely many positive integers $a$ we must have $f(b)=f(1)$. Hence $f$ is a constant function, a contradiction. Therefore, our initial assumption was false and there are indeed infinitely many primes $p$ dividing $f(c)$ for some positive integer c.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
EST Let $f$ be a non-constant function from the set of positive integers into the set of positive integers, such that $a-b$ divides $f(a)-f(b)$ for all distinct positive integers $a, b$. Prove that there exist infinitely many primes $p$ such that $p$ divides $f(c)$ for some positive integer $c$.
|
Denote by $v_{p}(a)$ the exponent of the prime $p$ in the prime decomposition of $a$. Assume that there are only finitely many primes $p_{1}, p_{2}, \ldots, p_{m}$ that divide some function value produced of $f$. There are infinitely many positive integers $a$ such that $v_{p_{i}}(a)>v_{p_{i}}(f(1))$ for all $i=1,2, \ldots, m$, e.g. $a=\left(p_{1} p_{2} \ldots p_{m}\right)^{\alpha}$ with $\alpha$ sufficiently large. Pick any such $a$. The condition of the problem then yields $a \mid(f(a+1)-f(1))$. Assume $f(a+1) \neq f(1)$. Then we must have $v_{p_{i}}(f(a+1)) \neq$ $v_{p_{i}}(f(1))$ for at least one $i$. This yields $v_{p_{i}}(f(a+1)-f(1))=\min \left\{v_{p_{i}}(f(a+1)), v_{p_{i}}(f(1))\right\} \leq$ $v_{p_{1}}(f(1))<v_{p_{i}}(a)$. But this contradicts the fact that $a \mid(f(a+1)-f(1))$. Hence we must have $f(a+1)=f(1)$ for all such $a$. Now, for any positive integer $b$ and all such $a$, we have $(a+1-b) \mid(f(a+1)-f(b))$, i.e., $(a+1-b) \mid(f(1)-f(b))$. Since this is true for infinitely many positive integers $a$ we must have $f(b)=f(1)$. Hence $f$ is a constant function, a contradiction. Therefore, our initial assumption was false and there are indeed infinitely many primes $p$ dividing $f(c)$ for some positive integer c.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
412fa83a-6033-56ad-aad5-98e9164a6d58
| 23,878
|
EST Let $f$ be a non-constant function from the set of positive integers into the set of positive integers, such that $a-b$ divides $f(a)-f(b)$ for all distinct positive integers $a, b$. Prove that there exist infinitely many primes $p$ such that $p$ divides $f(c)$ for some positive integer $c$.
|
Assume that there are only finitely many primes $p_{1}, p_{2}, \ldots, p_{m}$ that divide some function value of $f$. Since $f$ is not identically 1 , we must have $m \geq 1$. Then there exist non-negative integers $\alpha_{1}, \ldots, \alpha_{m}$ such that $$ f(1)=p_{1}^{\alpha_{1}} p_{2}^{\alpha_{2}} \ldots p_{m}^{\alpha_{m}} $$ We can pick a positive integer $r$ such that $f(r) \neq f(1)$. Let $$ M=1+p_{1}^{\alpha_{1}+1} p_{2}^{\alpha_{2}+1} \ldots p_{m}^{\alpha_{m}+1} \cdot(f(r)+r) $$ Then for all $i \in\{1, \ldots, m\}$ we have that $p_{i}^{\alpha_{i}+1}$ divides $M-1$ and hence by the condition of the problem also $f(M)-f(1)$. This implies that $f(M)$ is divisible by $p_{i}^{\alpha_{i}}$ but not by $p_{i}^{\alpha_{i}+1}$ for all $i$ and therefore $f(M)=f(1)$. Hence $$ \begin{aligned} M-r & >p_{1}^{\alpha_{1}+1} p_{2}^{\alpha_{2}+1} \ldots p_{m}^{\alpha_{m}+1} \cdot(f(r)+r)-r \\ & \geq p_{1}^{\alpha_{1}+1} p_{2}^{\alpha_{2}+1} \ldots p_{m}^{\alpha_{m}+1}+(f(r)+r)-r \\ & >p_{1}^{\alpha_{1}} p_{2}^{\alpha_{2}} \ldots p_{m}^{\alpha_{m}}+f(r) \\ & \geq|f(M)-f(r)| . \end{aligned} $$ But since $M-r$ divides $f(M)-f(r)$ this can only be true if $f(r)=f(M)=f(1)$, which contradicts the choice of $r$. Comment. In the case that $f$ is a polynomial with integer coefficients the result is well-known, see e.g. W. Schwarz, Einführung in die Methoden der Primzahltheorie, 1969.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
EST Let $f$ be a non-constant function from the set of positive integers into the set of positive integers, such that $a-b$ divides $f(a)-f(b)$ for all distinct positive integers $a, b$. Prove that there exist infinitely many primes $p$ such that $p$ divides $f(c)$ for some positive integer $c$.
|
Assume that there are only finitely many primes $p_{1}, p_{2}, \ldots, p_{m}$ that divide some function value of $f$. Since $f$ is not identically 1 , we must have $m \geq 1$. Then there exist non-negative integers $\alpha_{1}, \ldots, \alpha_{m}$ such that $$ f(1)=p_{1}^{\alpha_{1}} p_{2}^{\alpha_{2}} \ldots p_{m}^{\alpha_{m}} $$ We can pick a positive integer $r$ such that $f(r) \neq f(1)$. Let $$ M=1+p_{1}^{\alpha_{1}+1} p_{2}^{\alpha_{2}+1} \ldots p_{m}^{\alpha_{m}+1} \cdot(f(r)+r) $$ Then for all $i \in\{1, \ldots, m\}$ we have that $p_{i}^{\alpha_{i}+1}$ divides $M-1$ and hence by the condition of the problem also $f(M)-f(1)$. This implies that $f(M)$ is divisible by $p_{i}^{\alpha_{i}}$ but not by $p_{i}^{\alpha_{i}+1}$ for all $i$ and therefore $f(M)=f(1)$. Hence $$ \begin{aligned} M-r & >p_{1}^{\alpha_{1}+1} p_{2}^{\alpha_{2}+1} \ldots p_{m}^{\alpha_{m}+1} \cdot(f(r)+r)-r \\ & \geq p_{1}^{\alpha_{1}+1} p_{2}^{\alpha_{2}+1} \ldots p_{m}^{\alpha_{m}+1}+(f(r)+r)-r \\ & >p_{1}^{\alpha_{1}} p_{2}^{\alpha_{2}} \ldots p_{m}^{\alpha_{m}}+f(r) \\ & \geq|f(M)-f(r)| . \end{aligned} $$ But since $M-r$ divides $f(M)-f(r)$ this can only be true if $f(r)=f(M)=f(1)$, which contradicts the choice of $r$. Comment. In the case that $f$ is a polynomial with integer coefficients the result is well-known, see e.g. W. Schwarz, Einführung in die Methoden der Primzahltheorie, 1969.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
412fa83a-6033-56ad-aad5-98e9164a6d58
| 23,878
|
HUN Let $P(x)$ be a non-constant polynomial with integer coefficients. Prove that there is no function $T$ from the set of integers into the set of integers such that the number of integers $x$ with $T^{n}(x)=x$ is equal to $P(n)$ for every $n \geq 1$, where $T^{n}$ denotes the $n$-fold application of $T$.
|
Assume there is a polynomial $P$ of degree at least 1 with the desired property for a given function $T$. Let $A(n)$ denote the set of all $x \in \mathbb{Z}$ such that $T^{n}(x)=x$ and let $B(n)$ denote the set of all $x \in \mathbb{Z}$ for which $T^{n}(x)=x$ and $T^{k}(x) \neq x$ for all $1 \leq k<n$. Both sets are finite under the assumption made. For each $x \in A(n)$ there is a smallest $k \geq 1$ such that $T^{k}(x)=x$, i.e., $x \in B(k)$. Let $d=\operatorname{gcd}(k, n)$. There are positive integers $r, s$ such that $r k-s n=d$ and hence $x=T^{r k}(x)=T^{s n+d}(x)=T^{d}\left(T^{s n}(x)\right)=T^{d}(x)$. The minimality of $k$ implies $d=k$, i.e., $k \mid n$. On the other hand one clearly has $B(k) \subset A(n)$ if $k \mid n$ and thus we have $A(n)=\bigcup_{d \mid n} B(d)$ as a disjoint union and hence $$ |A(n)|=\sum_{d \mid n}|B(d)| $$ Furthermore, for every $x \in B(n)$ the elements $x, T^{1}(x), T^{2}(x), \ldots, T^{n-1}(x)$ are $n$ distinct elements of $B(n)$. The fact that they are in $A(n)$ is obvious. If for some $k<n$ and some $0 \leq i<n$ we had $T^{k}\left(T^{i}(x)\right)=T^{i}(x)$, i.e. $\quad T^{k+i}(x)=T^{i}(x)$, that would imply $x=T^{n}(x)=T^{n-i}\left(T^{i}(x)\right)=T^{n-i}\left(T^{k+i}(x)\right)=T^{k}\left(T^{n}(x)\right)=T^{k}(x)$ contradicting the minimality of $n$. Thus $T^{i}(x) \in B(n)$ and $T^{i}(x) \neq T^{j}(x)$ for $0 \leq i<j \leq n-1$. So indeed, $T$ permutes the elements of $B(n)$ in (disjoint) cycles of length $n$ and in particular one has $n||B(n)|$. Now let $P(x)=\sum_{i=0}^{k} a_{i} x^{i}, a_{i} \in \mathbb{Z}, k \geq 1, a_{k} \neq 0$ and suppose that $|A(n)|=P(n)$ for all $n \geq 1$. Let $p$ be any prime. Then $$ p^{2}| | B\left(p^{2}\right)\left|=\left|A\left(p^{2}\right)\right|-|A(p)|=a_{1}\left(p^{2}-p\right)+a_{2}\left(p^{4}-p^{2}\right)+\ldots\right. $$ Hence $p \mid a_{1}$ and since this is true for all primes we must have $a_{1}=0$. Now consider any two different primes $p$ and $q$. Since $a_{1}=0$ we have that $$ \left|A\left(p^{2} q\right)\right|-|A(p q)|=a_{2}\left(p^{4} q^{2}-p^{2} q^{2}\right)+a_{3}\left(p^{6} q^{3}-p^{3} q^{3}\right)+\ldots $$ is a multiple of $p^{2} q$. But we also have $$ p^{2} q| | B\left(p^{2} q\right)\left|=\left|A\left(p^{2} q\right)\right|-|A(p q)|-\left|B\left(p^{2}\right)\right|\right. $$ This implies $$ p^{2} q| | B\left(p^{2}\right)\left|=\left|A\left(p^{2}\right)\right|-|A(p)|=a_{2}\left(p^{4}-p^{2}\right)+a_{3}\left(p^{6}-p^{3}\right)+\cdots+a_{k}\left(p^{2 k}-p^{k}\right)\right. $$ Since this is true for every prime $q$ we must have $a_{2}\left(p^{4}-p^{2}\right)+a_{3}\left(p^{6}-p^{3}\right)+\cdots+a_{k}\left(p^{2 k}-p^{k}\right)=0$ for every prime $p$. Since this expression is a polynomial in $p$ of degree $2 k$ (because $a_{k} \neq 0$ ) this is a contradiction, as such a polynomial can have at most $2 k$ zeros. Comment. The last contradiction can also be reached via $$ a_{k}=\lim _{p \rightarrow \infty} \frac{1}{p^{2 k}}\left(a_{2}\left(p^{4}-p^{2}\right)+a_{3}\left(p^{6}-p^{3}\right)+\cdots+a_{k}\left(p^{2 k}-p^{k}\right)\right)=0 . $$
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
HUN Let $P(x)$ be a non-constant polynomial with integer coefficients. Prove that there is no function $T$ from the set of integers into the set of integers such that the number of integers $x$ with $T^{n}(x)=x$ is equal to $P(n)$ for every $n \geq 1$, where $T^{n}$ denotes the $n$-fold application of $T$.
|
Assume there is a polynomial $P$ of degree at least 1 with the desired property for a given function $T$. Let $A(n)$ denote the set of all $x \in \mathbb{Z}$ such that $T^{n}(x)=x$ and let $B(n)$ denote the set of all $x \in \mathbb{Z}$ for which $T^{n}(x)=x$ and $T^{k}(x) \neq x$ for all $1 \leq k<n$. Both sets are finite under the assumption made. For each $x \in A(n)$ there is a smallest $k \geq 1$ such that $T^{k}(x)=x$, i.e., $x \in B(k)$. Let $d=\operatorname{gcd}(k, n)$. There are positive integers $r, s$ such that $r k-s n=d$ and hence $x=T^{r k}(x)=T^{s n+d}(x)=T^{d}\left(T^{s n}(x)\right)=T^{d}(x)$. The minimality of $k$ implies $d=k$, i.e., $k \mid n$. On the other hand one clearly has $B(k) \subset A(n)$ if $k \mid n$ and thus we have $A(n)=\bigcup_{d \mid n} B(d)$ as a disjoint union and hence $$ |A(n)|=\sum_{d \mid n}|B(d)| $$ Furthermore, for every $x \in B(n)$ the elements $x, T^{1}(x), T^{2}(x), \ldots, T^{n-1}(x)$ are $n$ distinct elements of $B(n)$. The fact that they are in $A(n)$ is obvious. If for some $k<n$ and some $0 \leq i<n$ we had $T^{k}\left(T^{i}(x)\right)=T^{i}(x)$, i.e. $\quad T^{k+i}(x)=T^{i}(x)$, that would imply $x=T^{n}(x)=T^{n-i}\left(T^{i}(x)\right)=T^{n-i}\left(T^{k+i}(x)\right)=T^{k}\left(T^{n}(x)\right)=T^{k}(x)$ contradicting the minimality of $n$. Thus $T^{i}(x) \in B(n)$ and $T^{i}(x) \neq T^{j}(x)$ for $0 \leq i<j \leq n-1$. So indeed, $T$ permutes the elements of $B(n)$ in (disjoint) cycles of length $n$ and in particular one has $n||B(n)|$. Now let $P(x)=\sum_{i=0}^{k} a_{i} x^{i}, a_{i} \in \mathbb{Z}, k \geq 1, a_{k} \neq 0$ and suppose that $|A(n)|=P(n)$ for all $n \geq 1$. Let $p$ be any prime. Then $$ p^{2}| | B\left(p^{2}\right)\left|=\left|A\left(p^{2}\right)\right|-|A(p)|=a_{1}\left(p^{2}-p\right)+a_{2}\left(p^{4}-p^{2}\right)+\ldots\right. $$ Hence $p \mid a_{1}$ and since this is true for all primes we must have $a_{1}=0$. Now consider any two different primes $p$ and $q$. Since $a_{1}=0$ we have that $$ \left|A\left(p^{2} q\right)\right|-|A(p q)|=a_{2}\left(p^{4} q^{2}-p^{2} q^{2}\right)+a_{3}\left(p^{6} q^{3}-p^{3} q^{3}\right)+\ldots $$ is a multiple of $p^{2} q$. But we also have $$ p^{2} q| | B\left(p^{2} q\right)\left|=\left|A\left(p^{2} q\right)\right|-|A(p q)|-\left|B\left(p^{2}\right)\right|\right. $$ This implies $$ p^{2} q| | B\left(p^{2}\right)\left|=\left|A\left(p^{2}\right)\right|-|A(p)|=a_{2}\left(p^{4}-p^{2}\right)+a_{3}\left(p^{6}-p^{3}\right)+\cdots+a_{k}\left(p^{2 k}-p^{k}\right)\right. $$ Since this is true for every prime $q$ we must have $a_{2}\left(p^{4}-p^{2}\right)+a_{3}\left(p^{6}-p^{3}\right)+\cdots+a_{k}\left(p^{2 k}-p^{k}\right)=0$ for every prime $p$. Since this expression is a polynomial in $p$ of degree $2 k$ (because $a_{k} \neq 0$ ) this is a contradiction, as such a polynomial can have at most $2 k$ zeros. Comment. The last contradiction can also be reached via $$ a_{k}=\lim _{p \rightarrow \infty} \frac{1}{p^{2 k}}\left(a_{2}\left(p^{4}-p^{2}\right)+a_{3}\left(p^{6}-p^{3}\right)+\cdots+a_{k}\left(p^{2 k}-p^{k}\right)\right)=0 . $$
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
fc11f218-c1fe-53d1-9fbf-214a9acdf573
| 23,886
|
HUN Let $P(x)$ be a non-constant polynomial with integer coefficients. Prove that there is no function $T$ from the set of integers into the set of integers such that the number of integers $x$ with $T^{n}(x)=x$ is equal to $P(n)$ for every $n \geq 1$, where $T^{n}$ denotes the $n$-fold application of $T$.
|
As in the first solution define $A(n)$ and $B(n)$ and assume that a polynomial $P$ with the required property exists. This again implies that $|A(n)|$ and $|B(n)|$ is finite for all positive integers $n$ and that $$ P(n)=|A(n)|=\sum_{d \mid n}|B(d)| \quad \text { and } \quad n||B(n)| . $$ Now, for any two distinct primes $p$ and $q$, we have $$ P(0) \equiv P(p q) \equiv|B(1)|+|B(p)|+|B(q)|+|B(p q)| \equiv|B(1)|+|B(p)| \quad \bmod q $$ Thus, for any fixed $p$, the expression $P(0)-|B(1)|-|B(p)|$ is divisible by arbitrarily large primes $q$ which means that $P(0)=|B(1)|+|B(p)|=P(p)$ for any prime $p$. This implies that the polynomial $P$ is constant, a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
HUN Let $P(x)$ be a non-constant polynomial with integer coefficients. Prove that there is no function $T$ from the set of integers into the set of integers such that the number of integers $x$ with $T^{n}(x)=x$ is equal to $P(n)$ for every $n \geq 1$, where $T^{n}$ denotes the $n$-fold application of $T$.
|
As in the first solution define $A(n)$ and $B(n)$ and assume that a polynomial $P$ with the required property exists. This again implies that $|A(n)|$ and $|B(n)|$ is finite for all positive integers $n$ and that $$ P(n)=|A(n)|=\sum_{d \mid n}|B(d)| \quad \text { and } \quad n||B(n)| . $$ Now, for any two distinct primes $p$ and $q$, we have $$ P(0) \equiv P(p q) \equiv|B(1)|+|B(p)|+|B(q)|+|B(p q)| \equiv|B(1)|+|B(p)| \quad \bmod q $$ Thus, for any fixed $p$, the expression $P(0)-|B(1)|-|B(p)|$ is divisible by arbitrarily large primes $q$ which means that $P(0)=|B(1)|+|B(p)|=P(p)$ for any prime $p$. This implies that the polynomial $P$ is constant, a contradiction.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
fc11f218-c1fe-53d1-9fbf-214a9acdf573
| 23,886
|
TUR Let $k$ be a positive integer. Show that if there exists a sequence $a_{0}, a_{1}, \ldots$ of integers satisfying the condition $$ a_{n}=\frac{a_{n-1}+n^{k}}{n} \quad \text { for all } n \geq 1 $$ then $k-2$ is divisible by 3 .
|
Part $A$. For each positive integer $k$, there exists a polynomial $P_{k}$ of degree $k-1$ with integer coefficients, i. e., $P_{k} \in \mathbb{Z}[x]$, and an integer $q_{k}$ such that the polynomial identity $$ x P_{k}(x)=x^{k}+P_{k}(x-1)+q_{k} $$ is satisfied. To prove this, for fixed $k$ we write $$ P_{k}(x)=b_{k-1} x^{k-1}+\cdots+b_{1} x+b_{0} $$ and determine the coefficients $b_{k-1}, b_{k-2}, \ldots, b_{0}$ and the number $q_{k}$ successively. Obviously, we have $b_{k-1}=1$. For $m=k-1, k-2, \ldots, 1$, comparing the coefficients of $x^{m}$ in the identity $\left(I_{k}\right)$ results in an expression of $b_{m-1}$ as an integer linear combination of $b_{k-1}, \ldots, b_{m}$, and finally $q_{k}=-P_{k}(-1)$. Part $B$. Let $k$ be a positive integer, and let $a_{0}, a_{1}, \ldots$ be a sequence of real numbers satisfying the recursion given in the problem. This recursion can be written as $$ a_{n}-P_{k}(n)=\frac{a_{n-1}-P_{k}(n-1)}{n}-\frac{q_{k}}{n} \quad \text { for all } n \geq 1 $$ which by induction gives $$ a_{n}-P_{k}(n)=\frac{a_{0}-P_{k}(0)}{n!}-q_{k} \sum_{i=0}^{n-1} \frac{i!}{n!} \text { for all } n \geq 1 $$ Therefore, the numbers $a_{n}$ are integers for all $n \geq 1$ only if $$ a_{0}=P_{k}(0) \quad \text { and } \quad q_{k}=0 $$ Part $C$. Multiplying the identity $\left(I_{k}\right)$ by $x^{2}+x$ and subtracting the identities $\left(I_{k+1}\right),\left(I_{k+2}\right)$ and $q_{k} x^{2}=q_{k} x^{2}$ therefrom, we obtain $$ x T_{k}(x)=T_{k}(x-1)+2 x\left(P_{k}(x-1)+q_{k}\right)-\left(q_{k+2}+q_{k+1}+q_{k}\right), $$ where the polynomials $T_{k} \in \mathbb{Z}[x]$ are defined by $T_{k}(x)=\left(x^{2}+x\right) P_{k}(x)-P_{k+1}(x)-P_{k+2}(x)-q_{k} x$. Thus $$ x T_{k}(x) \equiv T_{k}(x-1)+q_{k+2}+q_{k+1}+q_{k} \bmod 2, \quad k=1,2, \ldots $$ Comparing the degrees, we easily see that this is only possible if $T_{k}$ is the zero polynomial modulo 2 , and $$ q_{k+2} \equiv q_{k+1}+q_{k} \bmod 2 \quad \text { for } k=1,2, \ldots $$ Since $q_{1}=-1$ and $q_{2}=0$, these congruences finish the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
TUR Let $k$ be a positive integer. Show that if there exists a sequence $a_{0}, a_{1}, \ldots$ of integers satisfying the condition $$ a_{n}=\frac{a_{n-1}+n^{k}}{n} \quad \text { for all } n \geq 1 $$ then $k-2$ is divisible by 3 .
|
Part $A$. For each positive integer $k$, there exists a polynomial $P_{k}$ of degree $k-1$ with integer coefficients, i. e., $P_{k} \in \mathbb{Z}[x]$, and an integer $q_{k}$ such that the polynomial identity $$ x P_{k}(x)=x^{k}+P_{k}(x-1)+q_{k} $$ is satisfied. To prove this, for fixed $k$ we write $$ P_{k}(x)=b_{k-1} x^{k-1}+\cdots+b_{1} x+b_{0} $$ and determine the coefficients $b_{k-1}, b_{k-2}, \ldots, b_{0}$ and the number $q_{k}$ successively. Obviously, we have $b_{k-1}=1$. For $m=k-1, k-2, \ldots, 1$, comparing the coefficients of $x^{m}$ in the identity $\left(I_{k}\right)$ results in an expression of $b_{m-1}$ as an integer linear combination of $b_{k-1}, \ldots, b_{m}$, and finally $q_{k}=-P_{k}(-1)$. Part $B$. Let $k$ be a positive integer, and let $a_{0}, a_{1}, \ldots$ be a sequence of real numbers satisfying the recursion given in the problem. This recursion can be written as $$ a_{n}-P_{k}(n)=\frac{a_{n-1}-P_{k}(n-1)}{n}-\frac{q_{k}}{n} \quad \text { for all } n \geq 1 $$ which by induction gives $$ a_{n}-P_{k}(n)=\frac{a_{0}-P_{k}(0)}{n!}-q_{k} \sum_{i=0}^{n-1} \frac{i!}{n!} \text { for all } n \geq 1 $$ Therefore, the numbers $a_{n}$ are integers for all $n \geq 1$ only if $$ a_{0}=P_{k}(0) \quad \text { and } \quad q_{k}=0 $$ Part $C$. Multiplying the identity $\left(I_{k}\right)$ by $x^{2}+x$ and subtracting the identities $\left(I_{k+1}\right),\left(I_{k+2}\right)$ and $q_{k} x^{2}=q_{k} x^{2}$ therefrom, we obtain $$ x T_{k}(x)=T_{k}(x-1)+2 x\left(P_{k}(x-1)+q_{k}\right)-\left(q_{k+2}+q_{k+1}+q_{k}\right), $$ where the polynomials $T_{k} \in \mathbb{Z}[x]$ are defined by $T_{k}(x)=\left(x^{2}+x\right) P_{k}(x)-P_{k+1}(x)-P_{k+2}(x)-q_{k} x$. Thus $$ x T_{k}(x) \equiv T_{k}(x-1)+q_{k+2}+q_{k+1}+q_{k} \bmod 2, \quad k=1,2, \ldots $$ Comparing the degrees, we easily see that this is only possible if $T_{k}$ is the zero polynomial modulo 2 , and $$ q_{k+2} \equiv q_{k+1}+q_{k} \bmod 2 \quad \text { for } k=1,2, \ldots $$ Since $q_{1}=-1$ and $q_{2}=0$, these congruences finish the proof.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
5ae93e5d-28f0-53d2-8986-fc945349a002
| 23,890
|
TUR Let $k$ be a positive integer. Show that if there exists a sequence $a_{0}, a_{1}, \ldots$ of integers satisfying the condition $$ a_{n}=\frac{a_{n-1}+n^{k}}{n} \quad \text { for all } n \geq 1 $$ then $k-2$ is divisible by 3 .
|
Part $A$ and $B$. Let $k$ be a positive integer, and suppose there is a sequence $a_{0}, a_{1}, \ldots$ as required. We prove: There exists a polynomial $P \in \mathbb{Z}[x]$, i. e., with integer coefficients, such that $a_{n}=P(n), n=0,1, \ldots$, and $\quad x P(x)=x^{k}+P(x-1)$. To prove this, we write $\quad P(x)=b_{k-1} x^{k-1}+\cdots+b_{1} x+b_{0} \quad$ and determine the coefficients $b_{k-1}, b_{k-2}, \ldots, b_{0}$ successively such that $$ x P(x)-x^{k}-P(x-1)=q, $$ where $q=q_{k}$ is an integer. Comparing the coefficients of $x^{m}$ results in an expression of $b_{m-1}$ as an integer linear combination of $b_{k-1}, \ldots, b_{m}$. Defining $c_{n}=a_{n}-P(n)$, we get $$ \begin{aligned} P(n)+c_{n} & =\frac{P(n-1)+c_{n-1}+n^{k}}{n}, \quad \text { i.e., } \\ q+n c_{n} & =c_{n-1}, \end{aligned} $$ hence $$ c_{n}=\frac{c_{0}}{n!}-q \cdot \frac{0!+1!+\cdots+(n-1)!}{n!} $$ We conclude $\lim _{n \rightarrow \infty} c_{n}=0$, which, using $c_{n} \in \mathbb{Z}$, implies $c_{n}=0$ for sufficiently large $n$. Therefore, we get $q=0$ and $c_{n}=0, n=0,1, \ldots$. Part C. Suppose that $q=q_{k}=0$, i. e. $x P(x)=x^{k}+P(x-1)$. To consider this identity for arguments $x \in \mathbb{F}_{4}$, we write $\mathbb{F}_{4}=\{0,1, \alpha, \alpha+1\}$. Then we get $$ \begin{aligned} \alpha P_{k}(\alpha) & =\alpha^{k}+P_{k}(\alpha+1) \quad \text { and } \\ (\alpha+1) P_{k}(\alpha+1) & =(\alpha+1)^{k}+P_{k}(\alpha), \end{aligned} $$ hence $$ \begin{aligned} P_{k}(\alpha) & =1 \cdot P_{k}(\alpha)=(\alpha+1) \alpha P_{k}(\alpha) \\ & =(\alpha+1) P_{k}(\alpha+1)+(\alpha+1) \alpha^{k} \\ & =P_{k}(\alpha)+(\alpha+1)^{k}+(\alpha+1) \alpha^{k} . \end{aligned} $$ Now, $(\alpha+1)^{k-1}=\alpha^{k}$ implies $k \equiv 2 \bmod 3$. Comment 1. For $k=2$, the sequence given by $a_{n}=n+1, n=0,1, \ldots$, satisfies the conditions of the problem. Comment 2. The first few polynomials $P_{k}$ and integers $q_{k}$ are $$ \begin{aligned} & P_{1}(x)=1, \quad q_{1}=-1, \\ & P_{2}(x)=x+1, \quad q_{2}=0, \\ & P_{3}(x)=x^{2}+x-1, \quad q_{3}=1, \\ & P_{4}(x)=x^{3}+x^{2}-2 x-1, \quad q_{4}=-1, \\ & P_{5}(x)=x^{4}+x^{3}-3 x^{2}+5, \quad q_{5}=-2, \\ & P_{6}(x)=x^{5}+x^{4}-4 x^{3}+2 x^{2}+10 x-5, \quad q_{6}=9, \\ & q_{7}=-9, \quad q_{8}=-50, \quad q_{9}=267, \quad q_{10}=-413, \quad q_{11}=-2180 . \end{aligned} $$ A lookup in the On-Line Encyclopedia of Integer Sequences (A000587) reveals that the sequence $q_{1},-q_{2}, q_{3},-q_{4}, q_{5}, \ldots$ is known as Uppuluri-CARPENTER numbers. The result that $q_{k}=0$ implies $k \equiv 2 \bmod 3$ is contained in Murty, Summer: On the $p$-adic series $\sum_{n=0}^{\infty} n^{k} \cdot n$ !. CRM Proc. and Lecture Notes 36, 2004. As shown by Alexander (Non-Vanishing of Uppuluri-Carpenter Numbers, Preprint 2006), Uppuluri-Carpenter numbers are zero at most twice. Comment 3. The numbers $q_{k}$ can be written in terms of the Stirling numbers of the second kind. To show this, we fix the notation such that $$ \begin{aligned} x^{k}= & S_{k-1, k-1} x(x-1) \cdots(x-k+1) \\ & +S_{k-1, k-2} x(x-1) \cdots(x-k+2) \\ & +\cdots+S_{k-1,0} x \end{aligned} $$ e.g., $S_{2,2}=1, S_{2,1}=3, S_{2,0}=1$, and we define $$ \Omega_{k}=S_{k-1, k-1}-S_{k-1, k-2}+-\cdots $$ Replacing $x$ by $-x$ in (*) results in $$ \begin{aligned} x^{k}= & S_{k-1, k-1} x(x+1) \cdots(x+k-1) \\ & -S_{k-1, k-2} x(x+1) \cdots(x+k-2) \\ & +-\cdots \pm S_{k-1,0} x \end{aligned} $$ Defining $$ \begin{aligned} P(x)= & S_{k-1, k-1}(x+1) \cdots(x+k-1) \\ & +\left(S_{k-1, k-1}-S_{k-1, k-2}\right)(x+1) \cdots(x+k-2) \\ & +\left(S_{k-1, k-1}-S_{k-1, k-2}+S_{k-1, k-3}\right)(x+1) \cdots(x+k-3) \\ & +\cdots+\Omega_{k} \end{aligned} $$ we obtain $$ \begin{aligned} x P(x)-P(x-1)= & S_{k-1, k-1} x(x+1) \cdots(x+k-1) \\ & -S_{k-1, k-2} x(x+1) \cdots(x+k-2) \\ & +-\cdots \pm S_{k-1,0} x-\Omega_{k} \\ = & x^{k}-\Omega_{k} \end{aligned} $$ hence $q_{k}=-\Omega_{k}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
TUR Let $k$ be a positive integer. Show that if there exists a sequence $a_{0}, a_{1}, \ldots$ of integers satisfying the condition $$ a_{n}=\frac{a_{n-1}+n^{k}}{n} \quad \text { for all } n \geq 1 $$ then $k-2$ is divisible by 3 .
|
Part $A$ and $B$. Let $k$ be a positive integer, and suppose there is a sequence $a_{0}, a_{1}, \ldots$ as required. We prove: There exists a polynomial $P \in \mathbb{Z}[x]$, i. e., with integer coefficients, such that $a_{n}=P(n), n=0,1, \ldots$, and $\quad x P(x)=x^{k}+P(x-1)$. To prove this, we write $\quad P(x)=b_{k-1} x^{k-1}+\cdots+b_{1} x+b_{0} \quad$ and determine the coefficients $b_{k-1}, b_{k-2}, \ldots, b_{0}$ successively such that $$ x P(x)-x^{k}-P(x-1)=q, $$ where $q=q_{k}$ is an integer. Comparing the coefficients of $x^{m}$ results in an expression of $b_{m-1}$ as an integer linear combination of $b_{k-1}, \ldots, b_{m}$. Defining $c_{n}=a_{n}-P(n)$, we get $$ \begin{aligned} P(n)+c_{n} & =\frac{P(n-1)+c_{n-1}+n^{k}}{n}, \quad \text { i.e., } \\ q+n c_{n} & =c_{n-1}, \end{aligned} $$ hence $$ c_{n}=\frac{c_{0}}{n!}-q \cdot \frac{0!+1!+\cdots+(n-1)!}{n!} $$ We conclude $\lim _{n \rightarrow \infty} c_{n}=0$, which, using $c_{n} \in \mathbb{Z}$, implies $c_{n}=0$ for sufficiently large $n$. Therefore, we get $q=0$ and $c_{n}=0, n=0,1, \ldots$. Part C. Suppose that $q=q_{k}=0$, i. e. $x P(x)=x^{k}+P(x-1)$. To consider this identity for arguments $x \in \mathbb{F}_{4}$, we write $\mathbb{F}_{4}=\{0,1, \alpha, \alpha+1\}$. Then we get $$ \begin{aligned} \alpha P_{k}(\alpha) & =\alpha^{k}+P_{k}(\alpha+1) \quad \text { and } \\ (\alpha+1) P_{k}(\alpha+1) & =(\alpha+1)^{k}+P_{k}(\alpha), \end{aligned} $$ hence $$ \begin{aligned} P_{k}(\alpha) & =1 \cdot P_{k}(\alpha)=(\alpha+1) \alpha P_{k}(\alpha) \\ & =(\alpha+1) P_{k}(\alpha+1)+(\alpha+1) \alpha^{k} \\ & =P_{k}(\alpha)+(\alpha+1)^{k}+(\alpha+1) \alpha^{k} . \end{aligned} $$ Now, $(\alpha+1)^{k-1}=\alpha^{k}$ implies $k \equiv 2 \bmod 3$. Comment 1. For $k=2$, the sequence given by $a_{n}=n+1, n=0,1, \ldots$, satisfies the conditions of the problem. Comment 2. The first few polynomials $P_{k}$ and integers $q_{k}$ are $$ \begin{aligned} & P_{1}(x)=1, \quad q_{1}=-1, \\ & P_{2}(x)=x+1, \quad q_{2}=0, \\ & P_{3}(x)=x^{2}+x-1, \quad q_{3}=1, \\ & P_{4}(x)=x^{3}+x^{2}-2 x-1, \quad q_{4}=-1, \\ & P_{5}(x)=x^{4}+x^{3}-3 x^{2}+5, \quad q_{5}=-2, \\ & P_{6}(x)=x^{5}+x^{4}-4 x^{3}+2 x^{2}+10 x-5, \quad q_{6}=9, \\ & q_{7}=-9, \quad q_{8}=-50, \quad q_{9}=267, \quad q_{10}=-413, \quad q_{11}=-2180 . \end{aligned} $$ A lookup in the On-Line Encyclopedia of Integer Sequences (A000587) reveals that the sequence $q_{1},-q_{2}, q_{3},-q_{4}, q_{5}, \ldots$ is known as Uppuluri-CARPENTER numbers. The result that $q_{k}=0$ implies $k \equiv 2 \bmod 3$ is contained in Murty, Summer: On the $p$-adic series $\sum_{n=0}^{\infty} n^{k} \cdot n$ !. CRM Proc. and Lecture Notes 36, 2004. As shown by Alexander (Non-Vanishing of Uppuluri-Carpenter Numbers, Preprint 2006), Uppuluri-Carpenter numbers are zero at most twice. Comment 3. The numbers $q_{k}$ can be written in terms of the Stirling numbers of the second kind. To show this, we fix the notation such that $$ \begin{aligned} x^{k}= & S_{k-1, k-1} x(x-1) \cdots(x-k+1) \\ & +S_{k-1, k-2} x(x-1) \cdots(x-k+2) \\ & +\cdots+S_{k-1,0} x \end{aligned} $$ e.g., $S_{2,2}=1, S_{2,1}=3, S_{2,0}=1$, and we define $$ \Omega_{k}=S_{k-1, k-1}-S_{k-1, k-2}+-\cdots $$ Replacing $x$ by $-x$ in (*) results in $$ \begin{aligned} x^{k}= & S_{k-1, k-1} x(x+1) \cdots(x+k-1) \\ & -S_{k-1, k-2} x(x+1) \cdots(x+k-2) \\ & +-\cdots \pm S_{k-1,0} x \end{aligned} $$ Defining $$ \begin{aligned} P(x)= & S_{k-1, k-1}(x+1) \cdots(x+k-1) \\ & +\left(S_{k-1, k-1}-S_{k-1, k-2}\right)(x+1) \cdots(x+k-2) \\ & +\left(S_{k-1, k-1}-S_{k-1, k-2}+S_{k-1, k-3}\right)(x+1) \cdots(x+k-3) \\ & +\cdots+\Omega_{k} \end{aligned} $$ we obtain $$ \begin{aligned} x P(x)-P(x-1)= & S_{k-1, k-1} x(x+1) \cdots(x+k-1) \\ & -S_{k-1, k-2} x(x+1) \cdots(x+k-2) \\ & +-\cdots \pm S_{k-1,0} x-\Omega_{k} \\ = & x^{k}-\Omega_{k} \end{aligned} $$ hence $q_{k}=-\Omega_{k}$.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
5ae93e5d-28f0-53d2-8986-fc945349a002
| 23,890
|
MNG Let $a$ and $b$ be distinct integers greater than 1 . Prove that there exists a positive integer $n$ such that $\left(a^{n}-1\right)\left(b^{n}-1\right)$ is not a perfect square.
|
At first we notice that $$ \begin{aligned} (1-\alpha)^{\frac{1}{2}}(1-\beta)^{\frac{1}{2}} & =\left(1-\frac{1}{2} \cdot \alpha-\frac{1}{8} \cdot \alpha^{2}-\cdots\right)\left(1-\frac{1}{2} \cdot \beta-\frac{1}{8} \cdot \beta^{2}-\cdots\right) \\ & =\sum_{k, \ell \geq 0} c_{k, \ell} \cdot \alpha^{k} \beta^{\ell} \quad \text { for all } \alpha, \beta \in(0,1) \end{aligned} $$ where $c_{0,0}=1$ and $c_{k, \ell}$ are certain coefficients. For an indirect proof, we suppose that $x_{n}=\sqrt{\left(a^{n}-1\right)\left(b^{n}-1\right)} \in \mathbb{Z}$ for all positive integers $n$. Replacing $a$ by $a^{2}$ and $b$ by $b^{2}$ if necessary, we may assume that $a$ and $b$ are perfect squares, hence $\sqrt{a b}$ is an integer. At first we shall assume that $a^{\mu} \neq b^{\nu}$ for all positive integers $\mu, \nu$. We have $$ x_{n}=(\sqrt{a b})^{n}\left(1-\frac{1}{a^{n}}\right)^{\frac{1}{2}}\left(1-\frac{1}{b^{n}}\right)^{\frac{1}{2}}=\sum_{k, \ell \geq 0} c_{k, \ell}\left(\frac{\sqrt{a b}}{a^{k} b^{\ell}}\right)^{n} . $$ Choosing $k_{0}$ and $\ell_{0}$ such that $a^{k_{0}}>\sqrt{a b}, b^{\ell_{0}}>\sqrt{a b}$, we define the polynomial $$ P(x)=\prod_{k=0, \ell=0}^{k_{0}-1, \ell_{0}-1}\left(a^{k} b^{\ell} x-\sqrt{a b}\right)=: \sum_{i=0}^{k_{0} \cdot \ell_{0}} d_{i} x^{i} $$ with integer coefficients $d_{i}$. By our assumption, the zeros $$ \frac{\sqrt{a b}}{a^{k} b^{\ell}}, \quad k=0, \ldots, k_{0}-1, \quad \ell=0, \ldots, \ell_{0}-1 $$ of $P$ are pairwise distinct. Furthermore, we consider the integer sequence $$ y_{n}=\sum_{i=0}^{k_{0} \cdot \ell_{0}} d_{i} x_{n+i}, \quad n=1,2, \ldots $$ By the theory of linear recursions, we obtain $$ y_{n}=\sum_{\substack{k, \ell \geq 0 \\ k \geq k_{0} \text { or } \ell \geq \ell_{0}}} e_{k, \ell}\left(\frac{\sqrt{a b}}{a^{k} b^{\ell}}\right)^{n}, \quad n=1,2, \ldots $$ with real numbers $e_{k, \ell}$. We have $$ \left|y_{n}\right| \leq \sum_{\substack{k, \ell \geq 0 \\ k \geq k_{0} \text { or } \ell \geq \ell_{0}}}\left|e_{k, \ell}\right|\left(\frac{\sqrt{a b}}{a^{k} b^{\ell}}\right)^{n}=: M_{n} . $$ Because the series in (4) is obtained by a finite linear combination of the absolutely convergent series (1), we conclude that in particular $M_{1}<\infty$. Since $$ \frac{\sqrt{a b}}{a^{k} b^{\ell}} \leq \lambda:=\max \left\{\frac{\sqrt{a b}}{a^{k_{0}}}, \frac{\sqrt{a b}}{b^{\ell_{0}}}\right\} \quad \text { for all } k, \ell \geq 0 \text { such that } k \geq k_{0} \text { or } \ell \geq \ell_{0} $$ we get the estimates $M_{n+1} \leq \lambda M_{n}, n=1,2, \ldots$ Our choice of $k_{0}$ and $\ell_{0}$ ensures $\lambda<1$, which implies $M_{n} \rightarrow 0$ and consequently $y_{n} \rightarrow 0$ as $n \rightarrow \infty$. It follows that $y_{n}=0$ for all sufficiently large $n$. So, equation (3) reduces to $\sum_{i=0}^{k_{0} \cdot \ell_{0}} d_{i} x_{n+i}=0$. Using the theory of linear recursions again, for sufficiently large $n$ we have $$ x_{n}=\sum_{k=0, \ell=0}^{k_{0}-1, \ell_{0}-1} f_{k, \ell}\left(\frac{\sqrt{a b}}{a^{k} b^{\ell}}\right)^{n} $$ for certain real numbers $f_{k, \ell}$. Comparing with (2), we see that $f_{k, \ell}=c_{k, \ell}$ for all $k, \ell \geq 0$ with $k<k_{0}, \ell<\ell_{0}$, and $c_{k, \ell}=0$ if $k \geq k_{0}$ or $\ell \geq \ell_{0}$, since we assumed that $a^{\mu} \neq b^{\nu}$ for all positive integers $\mu, \nu$. In view of (1), this means $$ (1-\alpha)^{\frac{1}{2}}(1-\beta)^{\frac{1}{2}}=\sum_{k=0, \ell=0}^{k_{0}-1, \ell_{0}-1} c_{k, \ell} \cdot \alpha^{k} \beta^{\ell} $$ for all real numbers $\alpha, \beta \in(0,1)$. We choose $k^{*}<k_{0}$ maximal such that there is some $i$ with $c_{k^{*}, i} \neq 0$. Squaring (5) and comparing coefficients of $\alpha^{2 k^{*}} \beta^{2 i^{*}}$, where $i^{*}$ is maximal with $c_{k^{*}, i^{*}} \neq 0$, we see that $k^{*}=0$. This means that the right hand side of (5) is independent of $\alpha$, which is clearly impossible. We are left with the case that $a^{\mu}=b^{\nu}$ for some positive integers $\mu$ and $\nu$. We may assume that $\mu$ and $\nu$ are relatively prime. Then there is some positive integer $c$ such that $a=c^{\nu}$ and $b=c^{\mu}$. Now starting with the expansion (2), i. e., $$ x_{n}=\sum_{j \geq 0} g_{j}\left(\frac{\sqrt{c^{\mu+\nu}}}{c^{j}}\right)^{n} $$ for certain coefficients $g_{j}$, and repeating the arguments above, we see that $g_{j}=0$ for sufficiently large $j$, say $j>j_{0}$. But this means that $$ \left(1-x^{\mu}\right)^{\frac{1}{2}}\left(1-x^{\nu}\right)^{\frac{1}{2}}=\sum_{j=0}^{j_{0}} g_{j} x^{j} $$ for all real numbers $x \in(0,1)$. Squaring, we see that $$ \left(1-x^{\mu}\right)\left(1-x^{\nu}\right) $$ is the square of a polynomial in $x$. In particular, all its zeros are of order at least 2 , which implies $\mu=\nu$ by looking at roots of unity. So we obtain $\mu=\nu=1$, i. e., $a=b$, a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
MNG Let $a$ and $b$ be distinct integers greater than 1 . Prove that there exists a positive integer $n$ such that $\left(a^{n}-1\right)\left(b^{n}-1\right)$ is not a perfect square.
|
At first we notice that $$ \begin{aligned} (1-\alpha)^{\frac{1}{2}}(1-\beta)^{\frac{1}{2}} & =\left(1-\frac{1}{2} \cdot \alpha-\frac{1}{8} \cdot \alpha^{2}-\cdots\right)\left(1-\frac{1}{2} \cdot \beta-\frac{1}{8} \cdot \beta^{2}-\cdots\right) \\ & =\sum_{k, \ell \geq 0} c_{k, \ell} \cdot \alpha^{k} \beta^{\ell} \quad \text { for all } \alpha, \beta \in(0,1) \end{aligned} $$ where $c_{0,0}=1$ and $c_{k, \ell}$ are certain coefficients. For an indirect proof, we suppose that $x_{n}=\sqrt{\left(a^{n}-1\right)\left(b^{n}-1\right)} \in \mathbb{Z}$ for all positive integers $n$. Replacing $a$ by $a^{2}$ and $b$ by $b^{2}$ if necessary, we may assume that $a$ and $b$ are perfect squares, hence $\sqrt{a b}$ is an integer. At first we shall assume that $a^{\mu} \neq b^{\nu}$ for all positive integers $\mu, \nu$. We have $$ x_{n}=(\sqrt{a b})^{n}\left(1-\frac{1}{a^{n}}\right)^{\frac{1}{2}}\left(1-\frac{1}{b^{n}}\right)^{\frac{1}{2}}=\sum_{k, \ell \geq 0} c_{k, \ell}\left(\frac{\sqrt{a b}}{a^{k} b^{\ell}}\right)^{n} . $$ Choosing $k_{0}$ and $\ell_{0}$ such that $a^{k_{0}}>\sqrt{a b}, b^{\ell_{0}}>\sqrt{a b}$, we define the polynomial $$ P(x)=\prod_{k=0, \ell=0}^{k_{0}-1, \ell_{0}-1}\left(a^{k} b^{\ell} x-\sqrt{a b}\right)=: \sum_{i=0}^{k_{0} \cdot \ell_{0}} d_{i} x^{i} $$ with integer coefficients $d_{i}$. By our assumption, the zeros $$ \frac{\sqrt{a b}}{a^{k} b^{\ell}}, \quad k=0, \ldots, k_{0}-1, \quad \ell=0, \ldots, \ell_{0}-1 $$ of $P$ are pairwise distinct. Furthermore, we consider the integer sequence $$ y_{n}=\sum_{i=0}^{k_{0} \cdot \ell_{0}} d_{i} x_{n+i}, \quad n=1,2, \ldots $$ By the theory of linear recursions, we obtain $$ y_{n}=\sum_{\substack{k, \ell \geq 0 \\ k \geq k_{0} \text { or } \ell \geq \ell_{0}}} e_{k, \ell}\left(\frac{\sqrt{a b}}{a^{k} b^{\ell}}\right)^{n}, \quad n=1,2, \ldots $$ with real numbers $e_{k, \ell}$. We have $$ \left|y_{n}\right| \leq \sum_{\substack{k, \ell \geq 0 \\ k \geq k_{0} \text { or } \ell \geq \ell_{0}}}\left|e_{k, \ell}\right|\left(\frac{\sqrt{a b}}{a^{k} b^{\ell}}\right)^{n}=: M_{n} . $$ Because the series in (4) is obtained by a finite linear combination of the absolutely convergent series (1), we conclude that in particular $M_{1}<\infty$. Since $$ \frac{\sqrt{a b}}{a^{k} b^{\ell}} \leq \lambda:=\max \left\{\frac{\sqrt{a b}}{a^{k_{0}}}, \frac{\sqrt{a b}}{b^{\ell_{0}}}\right\} \quad \text { for all } k, \ell \geq 0 \text { such that } k \geq k_{0} \text { or } \ell \geq \ell_{0} $$ we get the estimates $M_{n+1} \leq \lambda M_{n}, n=1,2, \ldots$ Our choice of $k_{0}$ and $\ell_{0}$ ensures $\lambda<1$, which implies $M_{n} \rightarrow 0$ and consequently $y_{n} \rightarrow 0$ as $n \rightarrow \infty$. It follows that $y_{n}=0$ for all sufficiently large $n$. So, equation (3) reduces to $\sum_{i=0}^{k_{0} \cdot \ell_{0}} d_{i} x_{n+i}=0$. Using the theory of linear recursions again, for sufficiently large $n$ we have $$ x_{n}=\sum_{k=0, \ell=0}^{k_{0}-1, \ell_{0}-1} f_{k, \ell}\left(\frac{\sqrt{a b}}{a^{k} b^{\ell}}\right)^{n} $$ for certain real numbers $f_{k, \ell}$. Comparing with (2), we see that $f_{k, \ell}=c_{k, \ell}$ for all $k, \ell \geq 0$ with $k<k_{0}, \ell<\ell_{0}$, and $c_{k, \ell}=0$ if $k \geq k_{0}$ or $\ell \geq \ell_{0}$, since we assumed that $a^{\mu} \neq b^{\nu}$ for all positive integers $\mu, \nu$. In view of (1), this means $$ (1-\alpha)^{\frac{1}{2}}(1-\beta)^{\frac{1}{2}}=\sum_{k=0, \ell=0}^{k_{0}-1, \ell_{0}-1} c_{k, \ell} \cdot \alpha^{k} \beta^{\ell} $$ for all real numbers $\alpha, \beta \in(0,1)$. We choose $k^{*}<k_{0}$ maximal such that there is some $i$ with $c_{k^{*}, i} \neq 0$. Squaring (5) and comparing coefficients of $\alpha^{2 k^{*}} \beta^{2 i^{*}}$, where $i^{*}$ is maximal with $c_{k^{*}, i^{*}} \neq 0$, we see that $k^{*}=0$. This means that the right hand side of (5) is independent of $\alpha$, which is clearly impossible. We are left with the case that $a^{\mu}=b^{\nu}$ for some positive integers $\mu$ and $\nu$. We may assume that $\mu$ and $\nu$ are relatively prime. Then there is some positive integer $c$ such that $a=c^{\nu}$ and $b=c^{\mu}$. Now starting with the expansion (2), i. e., $$ x_{n}=\sum_{j \geq 0} g_{j}\left(\frac{\sqrt{c^{\mu+\nu}}}{c^{j}}\right)^{n} $$ for certain coefficients $g_{j}$, and repeating the arguments above, we see that $g_{j}=0$ for sufficiently large $j$, say $j>j_{0}$. But this means that $$ \left(1-x^{\mu}\right)^{\frac{1}{2}}\left(1-x^{\nu}\right)^{\frac{1}{2}}=\sum_{j=0}^{j_{0}} g_{j} x^{j} $$ for all real numbers $x \in(0,1)$. Squaring, we see that $$ \left(1-x^{\mu}\right)\left(1-x^{\nu}\right) $$ is the square of a polynomial in $x$. In particular, all its zeros are of order at least 2 , which implies $\mu=\nu$ by looking at roots of unity. So we obtain $\mu=\nu=1$, i. e., $a=b$, a contradiction.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
f0dc3174-b1e6-5d35-abc5-44b2fe93711a
| 23,893
|
MNG Let $a$ and $b$ be distinct integers greater than 1 . Prove that there exists a positive integer $n$ such that $\left(a^{n}-1\right)\left(b^{n}-1\right)$ is not a perfect square.
|
We set $a^{2}=A, b^{2}=B$, and $z_{n}=\sqrt{\left(A^{n}-1\right)\left(B^{n}-1\right)}$. Let us assume that $z_{n}$ is an integer for $n=1,2, \ldots$. Without loss of generality, we may suppose that $b<a$. We determine an integer $k \geq 2$ such that $b^{k-1} \leq a<b^{k}$, and define a sequence $\gamma_{1}, \gamma_{2}, \ldots$ of rational numbers such that $$ 2 \gamma_{1}=1 \quad \text { and } \quad 2 \gamma_{n+1}=\sum_{i=1}^{n} \gamma_{i} \gamma_{n-i} \text { for } n=1,2, \ldots $$ It could easily be shown that $\gamma_{n}=\frac{1 \cdot 1 \cdot 3 . .(2 n-3)}{2 \cdot 4 \cdot 6 \cdot \ldots 2 n}$, for instance by reading VANDERMONDEs convolution as an equation between polynomials, but we shall have no use for this fact. Using Landaus $O$-Notation in the usual way, we have $$ \begin{aligned} & \left\{(a b)^{n}-\gamma_{1}\left(\frac{a}{b}\right)^{n}-\gamma_{2}\left(\frac{a}{b^{3}}\right)^{n}-\cdots-\gamma_{k}\left(\frac{a}{b^{2 k-1}}\right)^{n}+O\left(\frac{b}{a}\right)^{n}\right\}^{2} \\ & =A^{n} B^{n}-2 \gamma_{1} A^{n}-\sum_{i=2}^{k}\left(2 \gamma_{i}-\sum_{j=1}^{i-1} \gamma_{j} \gamma_{i-j}\right)\left(\frac{A}{B^{i-1}}\right)^{n}+O\left(\frac{A}{B^{k}}\right)^{n}+O\left(B^{n}\right) \\ & =A^{n} B^{n}-A^{n}+O\left(B^{n}\right) \end{aligned} $$ whence $$ z_{n}=(a b)^{n}-\gamma_{1}\left(\frac{a}{b}\right)^{n}-\gamma_{2}\left(\frac{a}{b^{3}}\right)^{n}-\cdots-\gamma_{k}\left(\frac{a}{b^{2 k-1}}\right)^{n}+O\left(\frac{b}{a}\right)^{n} $$ Now choose rational numbers $r_{1}, r_{2}, \ldots, r_{k+1}$ such that $$ (x-a b) \cdot\left(x-\frac{a}{b}\right) \ldots\left(x-\frac{a}{b^{2 k-1}}\right)=x^{k+1}-r_{1} x^{k}+-\cdots \pm r_{k+1} $$ and then a natural number $M$ for which $M r_{1}, M r_{2}, \ldots M r_{k+1}$ are integers. For known reasons, $$ M\left(z_{n+k+1}-r_{1} z_{n+k}+-\cdots \pm r_{k+1} z_{n}\right)=O\left(\frac{b}{a}\right)^{n} $$ for all $n \in \mathbb{N}$ and thus there is a natural number $N$ which is so large, that $$ z_{n+k+1}=r_{1} z_{n+k}-r_{2} z_{n+k-1}+-\cdots \mp r_{k+1} z_{n} $$ holds for all $n \geqslant N$. Now the theory of linear recursions reveals that there are some rational numbers $\delta_{0}, \delta_{1}, \delta_{2}, \ldots, \delta_{k}$ such that $$ z_{n}=\delta_{0}(a b)^{n}-\delta_{1}\left(\frac{a}{b}\right)^{n}-\delta_{2}\left(\frac{a}{b^{3}}\right)^{n}-\cdots-\delta_{k}\left(\frac{a}{b^{2 k-1}}\right)^{n} $$ for sufficiently large $n$, where $\delta_{0}>0$ as $z_{n}>0$. As before, one obtains $$ \begin{aligned} & A^{n} B^{n}-A^{n}-B^{n}+1=z_{n}^{2} \\ & =\left\{\delta_{0}(a b)^{n}-\delta_{1}\left(\frac{a}{b}\right)^{n}-\delta_{2}\left(\frac{a}{b^{3}}\right)^{n}-\cdots-\delta_{k}\left(\frac{a}{b^{2 k-1}}\right)^{n}\right\}^{2} \\ & =\delta_{0}^{2} A^{n} B^{n}-2 \delta_{0} \delta_{1} A^{n}-\sum_{i=2}^{i=k}\left(2 \delta_{0} \delta_{i}-\sum_{j=1}^{j=i-1} \delta_{j} \delta_{i-j}\right)\left(\frac{A}{B^{i-1}}\right)^{n}+O\left(\frac{A}{B^{k}}\right)^{n} \end{aligned} $$ Easy asymptotic calculations yield $\delta_{0}=1, \delta_{1}=\frac{1}{2}, \delta_{i}=\frac{1}{2} \sum_{j=1}^{j=i-1} \delta_{j} \delta_{i-j}$ for $i=2,3, \ldots, k-2$, and then $a=b^{k-1}$. It follows that $k>2$ and there is some $P \in \mathbb{Q}[X]$ for which $(X-1)\left(X^{k-1}-1\right)=$ $P(X)^{2}$. But this cannot occur, for instance as $X^{k-1}-1$ has no double zeros. Thus our assumption that $z_{n}$ was an integer for $n=1,2, \ldots$ turned out to be wrong, which solves the problem. Original formulation of the problem. $a, b$ are positive integers such that $a \cdot b$ is not a square of an integer. Prove that there exists a (infinitely many) positive integer $n$ such that ( $\left.a^{n}-1\right)\left(b^{n}-1\right)$ is not a square of an integer.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
MNG Let $a$ and $b$ be distinct integers greater than 1 . Prove that there exists a positive integer $n$ such that $\left(a^{n}-1\right)\left(b^{n}-1\right)$ is not a perfect square.
|
We set $a^{2}=A, b^{2}=B$, and $z_{n}=\sqrt{\left(A^{n}-1\right)\left(B^{n}-1\right)}$. Let us assume that $z_{n}$ is an integer for $n=1,2, \ldots$. Without loss of generality, we may suppose that $b<a$. We determine an integer $k \geq 2$ such that $b^{k-1} \leq a<b^{k}$, and define a sequence $\gamma_{1}, \gamma_{2}, \ldots$ of rational numbers such that $$ 2 \gamma_{1}=1 \quad \text { and } \quad 2 \gamma_{n+1}=\sum_{i=1}^{n} \gamma_{i} \gamma_{n-i} \text { for } n=1,2, \ldots $$ It could easily be shown that $\gamma_{n}=\frac{1 \cdot 1 \cdot 3 . .(2 n-3)}{2 \cdot 4 \cdot 6 \cdot \ldots 2 n}$, for instance by reading VANDERMONDEs convolution as an equation between polynomials, but we shall have no use for this fact. Using Landaus $O$-Notation in the usual way, we have $$ \begin{aligned} & \left\{(a b)^{n}-\gamma_{1}\left(\frac{a}{b}\right)^{n}-\gamma_{2}\left(\frac{a}{b^{3}}\right)^{n}-\cdots-\gamma_{k}\left(\frac{a}{b^{2 k-1}}\right)^{n}+O\left(\frac{b}{a}\right)^{n}\right\}^{2} \\ & =A^{n} B^{n}-2 \gamma_{1} A^{n}-\sum_{i=2}^{k}\left(2 \gamma_{i}-\sum_{j=1}^{i-1} \gamma_{j} \gamma_{i-j}\right)\left(\frac{A}{B^{i-1}}\right)^{n}+O\left(\frac{A}{B^{k}}\right)^{n}+O\left(B^{n}\right) \\ & =A^{n} B^{n}-A^{n}+O\left(B^{n}\right) \end{aligned} $$ whence $$ z_{n}=(a b)^{n}-\gamma_{1}\left(\frac{a}{b}\right)^{n}-\gamma_{2}\left(\frac{a}{b^{3}}\right)^{n}-\cdots-\gamma_{k}\left(\frac{a}{b^{2 k-1}}\right)^{n}+O\left(\frac{b}{a}\right)^{n} $$ Now choose rational numbers $r_{1}, r_{2}, \ldots, r_{k+1}$ such that $$ (x-a b) \cdot\left(x-\frac{a}{b}\right) \ldots\left(x-\frac{a}{b^{2 k-1}}\right)=x^{k+1}-r_{1} x^{k}+-\cdots \pm r_{k+1} $$ and then a natural number $M$ for which $M r_{1}, M r_{2}, \ldots M r_{k+1}$ are integers. For known reasons, $$ M\left(z_{n+k+1}-r_{1} z_{n+k}+-\cdots \pm r_{k+1} z_{n}\right)=O\left(\frac{b}{a}\right)^{n} $$ for all $n \in \mathbb{N}$ and thus there is a natural number $N$ which is so large, that $$ z_{n+k+1}=r_{1} z_{n+k}-r_{2} z_{n+k-1}+-\cdots \mp r_{k+1} z_{n} $$ holds for all $n \geqslant N$. Now the theory of linear recursions reveals that there are some rational numbers $\delta_{0}, \delta_{1}, \delta_{2}, \ldots, \delta_{k}$ such that $$ z_{n}=\delta_{0}(a b)^{n}-\delta_{1}\left(\frac{a}{b}\right)^{n}-\delta_{2}\left(\frac{a}{b^{3}}\right)^{n}-\cdots-\delta_{k}\left(\frac{a}{b^{2 k-1}}\right)^{n} $$ for sufficiently large $n$, where $\delta_{0}>0$ as $z_{n}>0$. As before, one obtains $$ \begin{aligned} & A^{n} B^{n}-A^{n}-B^{n}+1=z_{n}^{2} \\ & =\left\{\delta_{0}(a b)^{n}-\delta_{1}\left(\frac{a}{b}\right)^{n}-\delta_{2}\left(\frac{a}{b^{3}}\right)^{n}-\cdots-\delta_{k}\left(\frac{a}{b^{2 k-1}}\right)^{n}\right\}^{2} \\ & =\delta_{0}^{2} A^{n} B^{n}-2 \delta_{0} \delta_{1} A^{n}-\sum_{i=2}^{i=k}\left(2 \delta_{0} \delta_{i}-\sum_{j=1}^{j=i-1} \delta_{j} \delta_{i-j}\right)\left(\frac{A}{B^{i-1}}\right)^{n}+O\left(\frac{A}{B^{k}}\right)^{n} \end{aligned} $$ Easy asymptotic calculations yield $\delta_{0}=1, \delta_{1}=\frac{1}{2}, \delta_{i}=\frac{1}{2} \sum_{j=1}^{j=i-1} \delta_{j} \delta_{i-j}$ for $i=2,3, \ldots, k-2$, and then $a=b^{k-1}$. It follows that $k>2$ and there is some $P \in \mathbb{Q}[X]$ for which $(X-1)\left(X^{k-1}-1\right)=$ $P(X)^{2}$. But this cannot occur, for instance as $X^{k-1}-1$ has no double zeros. Thus our assumption that $z_{n}$ was an integer for $n=1,2, \ldots$ turned out to be wrong, which solves the problem. Original formulation of the problem. $a, b$ are positive integers such that $a \cdot b$ is not a square of an integer. Prove that there exists a (infinitely many) positive integer $n$ such that ( $\left.a^{n}-1\right)\left(b^{n}-1\right)$ is not a square of an integer.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
f0dc3174-b1e6-5d35-abc5-44b2fe93711a
| 23,893
|
PER A positive integer $N$ is called balanced, if $N=1$ or if $N$ can be written as a product of an even number of not necessarily distinct primes. Given positive integers $a$ and $b$, consider the polynomial $P$ defined by $P(x)=(x+a)(x+b)$. (a) Prove that there exist distinct positive integers $a$ and $b$ such that all the numbers $P(1), P(2)$, ..., $P(50)$ are balanced. (b) Prove that if $P(n)$ is balanced for all positive integers $n$, then $a=b$.
|
Define a function $f$ on the set of positive integers by $f(n)=0$ if $n$ is balanced and $f(n)=1$ otherwise. Clearly, $f(n m) \equiv f(n)+f(m) \bmod 2$ for all positive integers $n, m$. (a) Now for each positive integer $n$ consider the binary sequence $(f(n+1), f(n+2), \ldots, f(n+$ $50)$ ). As there are only $2^{50}$ different such sequences there are two different positive integers $a$ and $b$ such that $$ (f(a+1), f(a+2), \ldots, f(a+50))=(f(b+1), f(b+2), \ldots, f(b+50)) $$ But this implies that for the polynomial $P(x)=(x+a)(x+b)$ all the numbers $P(1), P(2)$, $\ldots, P(50)$ are balanced, since for all $1 \leq k \leq 50$ we have $f(P(k)) \equiv f(a+k)+f(b+k) \equiv$ $2 f(a+k) \equiv 0 \bmod 2$. (b) Now suppose $P(n)$ is balanced for all positive integers $n$ and $a<b$. Set $n=k(b-a)-a$ for sufficiently large $k$, such that $n$ is positive. Then $P(n)=k(k+1)(b-a)^{2}$, and this number can only be balanced, if $f(k)=f(k+1)$ holds. Thus, the sequence $f(k)$ must become constant for sufficiently large $k$. But this is not possible, as for every prime $p$ we have $f(p)=1$ and for every square $t^{2}$ we have $f\left(t^{2}\right)=0$. Hence $a=b$. Comment. Given a positive integer $k$, a computer search for the pairs of positive integers $(a, b)$, for which $P(1), P(2), \ldots, P(k)$ are all balanced yields the following results with minimal sum $a+b$ and $a<b$ : | $k$ | 3 | 4 | 5 | 10 | 20 | | :--- | :---: | :---: | :---: | :---: | :---: | | $(a, b)$ | $(2,4)$ | $(6,11)$ | $(8,14)$ | $(20,34)$ | $(1751,3121)$ | Therefore, trying to find $a$ and $b$ in part (a) of the problem cannot be done by elementary calculations.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
PER A positive integer $N$ is called balanced, if $N=1$ or if $N$ can be written as a product of an even number of not necessarily distinct primes. Given positive integers $a$ and $b$, consider the polynomial $P$ defined by $P(x)=(x+a)(x+b)$. (a) Prove that there exist distinct positive integers $a$ and $b$ such that all the numbers $P(1), P(2)$, ..., $P(50)$ are balanced. (b) Prove that if $P(n)$ is balanced for all positive integers $n$, then $a=b$.
|
Define a function $f$ on the set of positive integers by $f(n)=0$ if $n$ is balanced and $f(n)=1$ otherwise. Clearly, $f(n m) \equiv f(n)+f(m) \bmod 2$ for all positive integers $n, m$. (a) Now for each positive integer $n$ consider the binary sequence $(f(n+1), f(n+2), \ldots, f(n+$ $50)$ ). As there are only $2^{50}$ different such sequences there are two different positive integers $a$ and $b$ such that $$ (f(a+1), f(a+2), \ldots, f(a+50))=(f(b+1), f(b+2), \ldots, f(b+50)) $$ But this implies that for the polynomial $P(x)=(x+a)(x+b)$ all the numbers $P(1), P(2)$, $\ldots, P(50)$ are balanced, since for all $1 \leq k \leq 50$ we have $f(P(k)) \equiv f(a+k)+f(b+k) \equiv$ $2 f(a+k) \equiv 0 \bmod 2$. (b) Now suppose $P(n)$ is balanced for all positive integers $n$ and $a<b$. Set $n=k(b-a)-a$ for sufficiently large $k$, such that $n$ is positive. Then $P(n)=k(k+1)(b-a)^{2}$, and this number can only be balanced, if $f(k)=f(k+1)$ holds. Thus, the sequence $f(k)$ must become constant for sufficiently large $k$. But this is not possible, as for every prime $p$ we have $f(p)=1$ and for every square $t^{2}$ we have $f\left(t^{2}\right)=0$. Hence $a=b$. Comment. Given a positive integer $k$, a computer search for the pairs of positive integers $(a, b)$, for which $P(1), P(2), \ldots, P(k)$ are all balanced yields the following results with minimal sum $a+b$ and $a<b$ : | $k$ | 3 | 4 | 5 | 10 | 20 | | :--- | :---: | :---: | :---: | :---: | :---: | | $(a, b)$ | $(2,4)$ | $(6,11)$ | $(8,14)$ | $(20,34)$ | $(1751,3121)$ | Therefore, trying to find $a$ and $b$ in part (a) of the problem cannot be done by elementary calculations.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
3968ebc2-4de1-5b92-8005-544540d2c10c
| 23,903
|
Let the real numbers $a, b, c, d$ satisfy the relations $a+b+c+d=6$ and $a^{2}+b^{2}+c^{2}+d^{2}=12$. Prove that $$ 36 \leq 4\left(a^{3}+b^{3}+c^{3}+d^{3}\right)-\left(a^{4}+b^{4}+c^{4}+d^{4}\right) \leq 48 $$ (Ukraine)
|
Observe that $$ \begin{gathered} 4\left(a^{3}+b^{3}+c^{3}+d^{3}\right)-\left(a^{4}+b^{4}+c^{4}+d^{4}\right)=-\left((a-1)^{4}+(b-1)^{4}+(c-1)^{4}+(d-1)^{4}\right) \\ +6\left(a^{2}+b^{2}+c^{2}+d^{2}\right)-4(a+b+c+d)+4 \\ =-\left((a-1)^{4}+(b-1)^{4}+(c-1)^{4}+(d-1)^{4}\right)+52 \end{gathered} $$ Now, introducing $x=a-1, y=b-1, z=c-1, t=d-1$, we need to prove the inequalities $$ 16 \geq x^{4}+y^{4}+z^{4}+t^{4} \geq 4 $$ under the constraint $$ x^{2}+y^{2}+z^{2}+t^{2}=\left(a^{2}+b^{2}+c^{2}+d^{2}\right)-2(a+b+c+d)+4=4 $$ (we will not use the value of $x+y+z+t$ though it can be found). Now the rightmost inequality in (1) follows from the power mean inequality: $$ x^{4}+y^{4}+z^{4}+t^{4} \geq \frac{\left(x^{2}+y^{2}+z^{2}+t^{2}\right)^{2}}{4}=4 . $$ For the other one, expanding the brackets we note that $$ \left(x^{2}+y^{2}+z^{2}+t^{2}\right)^{2}=\left(x^{4}+y^{4}+z^{4}+t^{4}\right)+q $$ where $q$ is a nonnegative number, so $$ x^{4}+y^{4}+z^{4}+t^{4} \leq\left(x^{2}+y^{2}+z^{2}+t^{2}\right)^{2}=16 $$ and we are done. Comment 1. The estimates are sharp; the lower and upper bounds are attained at $(3,1,1,1)$ and $(0,2,2,2)$, respectively. Comment 2. After the change of variables, one can finish the solution in several different ways. The latter estimate, for instance, it can be performed by moving the variables - since we need only the second of the two shifted conditions.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let the real numbers $a, b, c, d$ satisfy the relations $a+b+c+d=6$ and $a^{2}+b^{2}+c^{2}+d^{2}=12$. Prove that $$ 36 \leq 4\left(a^{3}+b^{3}+c^{3}+d^{3}\right)-\left(a^{4}+b^{4}+c^{4}+d^{4}\right) \leq 48 $$ (Ukraine)
|
Observe that $$ \begin{gathered} 4\left(a^{3}+b^{3}+c^{3}+d^{3}\right)-\left(a^{4}+b^{4}+c^{4}+d^{4}\right)=-\left((a-1)^{4}+(b-1)^{4}+(c-1)^{4}+(d-1)^{4}\right) \\ +6\left(a^{2}+b^{2}+c^{2}+d^{2}\right)-4(a+b+c+d)+4 \\ =-\left((a-1)^{4}+(b-1)^{4}+(c-1)^{4}+(d-1)^{4}\right)+52 \end{gathered} $$ Now, introducing $x=a-1, y=b-1, z=c-1, t=d-1$, we need to prove the inequalities $$ 16 \geq x^{4}+y^{4}+z^{4}+t^{4} \geq 4 $$ under the constraint $$ x^{2}+y^{2}+z^{2}+t^{2}=\left(a^{2}+b^{2}+c^{2}+d^{2}\right)-2(a+b+c+d)+4=4 $$ (we will not use the value of $x+y+z+t$ though it can be found). Now the rightmost inequality in (1) follows from the power mean inequality: $$ x^{4}+y^{4}+z^{4}+t^{4} \geq \frac{\left(x^{2}+y^{2}+z^{2}+t^{2}\right)^{2}}{4}=4 . $$ For the other one, expanding the brackets we note that $$ \left(x^{2}+y^{2}+z^{2}+t^{2}\right)^{2}=\left(x^{4}+y^{4}+z^{4}+t^{4}\right)+q $$ where $q$ is a nonnegative number, so $$ x^{4}+y^{4}+z^{4}+t^{4} \leq\left(x^{2}+y^{2}+z^{2}+t^{2}\right)^{2}=16 $$ and we are done. Comment 1. The estimates are sharp; the lower and upper bounds are attained at $(3,1,1,1)$ and $(0,2,2,2)$, respectively. Comment 2. After the change of variables, one can finish the solution in several different ways. The latter estimate, for instance, it can be performed by moving the variables - since we need only the second of the two shifted conditions.
|
{
"resource_path": "IMO/segmented/en-IMO2010SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
79dbdecd-5305-5157-abee-9d2bf9daf56c
| 23,908
|
Let the real numbers $a, b, c, d$ satisfy the relations $a+b+c+d=6$ and $a^{2}+b^{2}+c^{2}+d^{2}=12$. Prove that $$ 36 \leq 4\left(a^{3}+b^{3}+c^{3}+d^{3}\right)-\left(a^{4}+b^{4}+c^{4}+d^{4}\right) \leq 48 $$ (Ukraine)
|
First, we claim that $0 \leq a, b, c, d \leq 3$. Actually, we have $$ a+b+c=6-d, \quad a^{2}+b^{2}+c^{2}=12-d^{2} $$ hence the power mean inequality $$ a^{2}+b^{2}+c^{2} \geq \frac{(a+b+c)^{2}}{3} $$ rewrites as $$ 12-d^{2} \geq \frac{(6-d)^{2}}{3} \quad \Longleftrightarrow \quad 2 d(d-3) \leq 0 $$ which implies the desired inequalities for $d$; since the conditions are symmetric, we also have the same estimate for the other variables. Now, to prove the rightmost inequality, we use the obvious inequality $x^{2}(x-2)^{2} \geq 0$ for each real $x$; this inequality rewrites as $4 x^{3}-x^{4} \leq 4 x^{2}$. It follows that $$ \left(4 a^{3}-a^{4}\right)+\left(4 b^{3}-b^{4}\right)+\left(4 c^{3}-c^{4}\right)+\left(4 d^{3}-d^{4}\right) \leq 4\left(a^{2}+b^{2}+c^{2}+d^{2}\right)=48 $$ as desired. Now we prove the leftmost inequality in an analogous way. For each $x \in[0,3]$, we have $(x+1)(x-1)^{2}(x-3) \leq 0$ which is equivalent to $4 x^{3}-x^{4} \geq 2 x^{2}+4 x-3$. This implies that $\left(4 a^{3}-a^{4}\right)+\left(4 b^{3}-b^{4}\right)+\left(4 c^{3}-c^{4}\right)+\left(4 d^{3}-d^{4}\right) \geq 2\left(a^{2}+b^{2}+c^{2}+d^{2}\right)+4(a+b+c+d)-12=36$, as desired. Comment. It is easy to guess the extremal points $(0,2,2,2)$ and $(3,1,1,1)$ for this inequality. This provides a method of finding the polynomials used in Solution 2. Namely, these polynomials should have the form $x^{4}-4 x^{3}+a x^{2}+b x+c$; moreover, the former polynomial should have roots at 2 (with an even multiplicity) and 0 , while the latter should have roots at 1 (with an even multiplicity) and 3 . These conditions determine the polynomials uniquely.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let the real numbers $a, b, c, d$ satisfy the relations $a+b+c+d=6$ and $a^{2}+b^{2}+c^{2}+d^{2}=12$. Prove that $$ 36 \leq 4\left(a^{3}+b^{3}+c^{3}+d^{3}\right)-\left(a^{4}+b^{4}+c^{4}+d^{4}\right) \leq 48 $$ (Ukraine)
|
First, we claim that $0 \leq a, b, c, d \leq 3$. Actually, we have $$ a+b+c=6-d, \quad a^{2}+b^{2}+c^{2}=12-d^{2} $$ hence the power mean inequality $$ a^{2}+b^{2}+c^{2} \geq \frac{(a+b+c)^{2}}{3} $$ rewrites as $$ 12-d^{2} \geq \frac{(6-d)^{2}}{3} \quad \Longleftrightarrow \quad 2 d(d-3) \leq 0 $$ which implies the desired inequalities for $d$; since the conditions are symmetric, we also have the same estimate for the other variables. Now, to prove the rightmost inequality, we use the obvious inequality $x^{2}(x-2)^{2} \geq 0$ for each real $x$; this inequality rewrites as $4 x^{3}-x^{4} \leq 4 x^{2}$. It follows that $$ \left(4 a^{3}-a^{4}\right)+\left(4 b^{3}-b^{4}\right)+\left(4 c^{3}-c^{4}\right)+\left(4 d^{3}-d^{4}\right) \leq 4\left(a^{2}+b^{2}+c^{2}+d^{2}\right)=48 $$ as desired. Now we prove the leftmost inequality in an analogous way. For each $x \in[0,3]$, we have $(x+1)(x-1)^{2}(x-3) \leq 0$ which is equivalent to $4 x^{3}-x^{4} \geq 2 x^{2}+4 x-3$. This implies that $\left(4 a^{3}-a^{4}\right)+\left(4 b^{3}-b^{4}\right)+\left(4 c^{3}-c^{4}\right)+\left(4 d^{3}-d^{4}\right) \geq 2\left(a^{2}+b^{2}+c^{2}+d^{2}\right)+4(a+b+c+d)-12=36$, as desired. Comment. It is easy to guess the extremal points $(0,2,2,2)$ and $(3,1,1,1)$ for this inequality. This provides a method of finding the polynomials used in Solution 2. Namely, these polynomials should have the form $x^{4}-4 x^{3}+a x^{2}+b x+c$; moreover, the former polynomial should have roots at 2 (with an even multiplicity) and 0 , while the latter should have roots at 1 (with an even multiplicity) and 3 . These conditions determine the polynomials uniquely.
|
{
"resource_path": "IMO/segmented/en-IMO2010SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
79dbdecd-5305-5157-abee-9d2bf9daf56c
| 23,908
|
Let the real numbers $a, b, c, d$ satisfy the relations $a+b+c+d=6$ and $a^{2}+b^{2}+c^{2}+d^{2}=12$. Prove that $$ 36 \leq 4\left(a^{3}+b^{3}+c^{3}+d^{3}\right)-\left(a^{4}+b^{4}+c^{4}+d^{4}\right) \leq 48 $$ (Ukraine)
|
First, expanding $48=4\left(a^{2}+b^{2}+c^{2}+d^{2}\right)$ and applying the AM-GM inequality, we have $$ \begin{aligned} a^{4}+b^{4}+c^{4}+d^{4}+48 & =\left(a^{4}+4 a^{2}\right)+\left(b^{4}+4 b^{2}\right)+\left(c^{4}+4 c^{2}\right)+\left(d^{4}+4 d^{2}\right) \\ & \geq 2\left(\sqrt{a^{4} \cdot 4 a^{2}}+\sqrt{b^{4} \cdot 4 b^{2}}+\sqrt{c^{4} \cdot 4 c^{2}}+\sqrt{d^{4} \cdot 4 d^{2}}\right) \\ & =4\left(\left|a^{3}\right|+\left|b^{3}\right|+\left|c^{3}\right|+\left|d^{3}\right|\right) \geq 4\left(a^{3}+b^{3}+c^{3}+d^{3}\right) \end{aligned} $$ which establishes the rightmost inequality. To prove the leftmost inequality, we first show that $a, b, c, d \in[0,3]$ as in the previous solution. Moreover, we can assume that $0 \leq a \leq b \leq c \leq d$. Then we have $a+b \leq b+c \leq$ $\frac{2}{3}(b+c+d) \leq \frac{2}{3} \cdot 6=4$. Next, we show that $4 b-b^{2} \leq 4 c-c^{2}$. Actually, this inequality rewrites as $(c-b)(b+c-4) \leq 0$, which follows from the previous estimate. The inequality $4 a-a^{2} \leq 4 b-b^{2}$ can be proved analogously. Further, the inequalities $a \leq b \leq c$ together with $4 a-a^{2} \leq 4 b-b^{2} \leq 4 c-c^{2}$ allow us to apply the Chebyshev inequality obtaining $$ \begin{aligned} a^{2}\left(4 a-a^{2}\right)+b^{2}\left(4 b-b^{2}\right)+c^{2}\left(4 c-c^{2}\right) & \geq \frac{1}{3}\left(a^{2}+b^{2}+c^{2}\right)\left(4(a+b+c)-\left(a^{2}+b^{2}+c^{2}\right)\right) \\ & =\frac{\left(12-d^{2}\right)\left(4(6-d)-\left(12-d^{2}\right)\right)}{3} . \end{aligned} $$ This implies that $$ \begin{aligned} \left(4 a^{3}-a^{4}\right) & +\left(4 b^{3}-b^{4}\right)+\left(4 c^{3}-c^{4}\right)+\left(4 d^{3}-d^{4}\right) \geq \frac{\left(12-d^{2}\right)\left(d^{2}-4 d+12\right)}{3}+4 d^{3}-d^{4} \\ & =\frac{144-48 d+16 d^{3}-4 d^{4}}{3}=36+\frac{4}{3}(3-d)(d-1)\left(d^{2}-3\right) \end{aligned} $$ Finally, we have $d^{2} \geq \frac{1}{4}\left(a^{2}+b^{2}+c^{2}+d^{2}\right)=3$ (which implies $d>1$ ); so, the expression $\frac{4}{3}(3-d)(d-1)\left(d^{2}-3\right)$ in the right-hand part of $(2)$ is nonnegative, and the desired inequality is proved. Comment. The rightmost inequality is easier than the leftmost one. In particular, Solutions 2 and 3 show that only the condition $a^{2}+b^{2}+c^{2}+d^{2}=12$ is needed for the former one.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let the real numbers $a, b, c, d$ satisfy the relations $a+b+c+d=6$ and $a^{2}+b^{2}+c^{2}+d^{2}=12$. Prove that $$ 36 \leq 4\left(a^{3}+b^{3}+c^{3}+d^{3}\right)-\left(a^{4}+b^{4}+c^{4}+d^{4}\right) \leq 48 $$ (Ukraine)
|
First, expanding $48=4\left(a^{2}+b^{2}+c^{2}+d^{2}\right)$ and applying the AM-GM inequality, we have $$ \begin{aligned} a^{4}+b^{4}+c^{4}+d^{4}+48 & =\left(a^{4}+4 a^{2}\right)+\left(b^{4}+4 b^{2}\right)+\left(c^{4}+4 c^{2}\right)+\left(d^{4}+4 d^{2}\right) \\ & \geq 2\left(\sqrt{a^{4} \cdot 4 a^{2}}+\sqrt{b^{4} \cdot 4 b^{2}}+\sqrt{c^{4} \cdot 4 c^{2}}+\sqrt{d^{4} \cdot 4 d^{2}}\right) \\ & =4\left(\left|a^{3}\right|+\left|b^{3}\right|+\left|c^{3}\right|+\left|d^{3}\right|\right) \geq 4\left(a^{3}+b^{3}+c^{3}+d^{3}\right) \end{aligned} $$ which establishes the rightmost inequality. To prove the leftmost inequality, we first show that $a, b, c, d \in[0,3]$ as in the previous solution. Moreover, we can assume that $0 \leq a \leq b \leq c \leq d$. Then we have $a+b \leq b+c \leq$ $\frac{2}{3}(b+c+d) \leq \frac{2}{3} \cdot 6=4$. Next, we show that $4 b-b^{2} \leq 4 c-c^{2}$. Actually, this inequality rewrites as $(c-b)(b+c-4) \leq 0$, which follows from the previous estimate. The inequality $4 a-a^{2} \leq 4 b-b^{2}$ can be proved analogously. Further, the inequalities $a \leq b \leq c$ together with $4 a-a^{2} \leq 4 b-b^{2} \leq 4 c-c^{2}$ allow us to apply the Chebyshev inequality obtaining $$ \begin{aligned} a^{2}\left(4 a-a^{2}\right)+b^{2}\left(4 b-b^{2}\right)+c^{2}\left(4 c-c^{2}\right) & \geq \frac{1}{3}\left(a^{2}+b^{2}+c^{2}\right)\left(4(a+b+c)-\left(a^{2}+b^{2}+c^{2}\right)\right) \\ & =\frac{\left(12-d^{2}\right)\left(4(6-d)-\left(12-d^{2}\right)\right)}{3} . \end{aligned} $$ This implies that $$ \begin{aligned} \left(4 a^{3}-a^{4}\right) & +\left(4 b^{3}-b^{4}\right)+\left(4 c^{3}-c^{4}\right)+\left(4 d^{3}-d^{4}\right) \geq \frac{\left(12-d^{2}\right)\left(d^{2}-4 d+12\right)}{3}+4 d^{3}-d^{4} \\ & =\frac{144-48 d+16 d^{3}-4 d^{4}}{3}=36+\frac{4}{3}(3-d)(d-1)\left(d^{2}-3\right) \end{aligned} $$ Finally, we have $d^{2} \geq \frac{1}{4}\left(a^{2}+b^{2}+c^{2}+d^{2}\right)=3$ (which implies $d>1$ ); so, the expression $\frac{4}{3}(3-d)(d-1)\left(d^{2}-3\right)$ in the right-hand part of $(2)$ is nonnegative, and the desired inequality is proved. Comment. The rightmost inequality is easier than the leftmost one. In particular, Solutions 2 and 3 show that only the condition $a^{2}+b^{2}+c^{2}+d^{2}=12$ is needed for the former one.
|
{
"resource_path": "IMO/segmented/en-IMO2010SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
79dbdecd-5305-5157-abee-9d2bf9daf56c
| 23,908
|
A sequence $x_{1}, x_{2}, \ldots$ is defined by $x_{1}=1$ and $x_{2 k}=-x_{k}, x_{2 k-1}=(-1)^{k+1} x_{k}$ for all $k \geq 1$. Prove that $x_{1}+x_{2}+\cdots+x_{n} \geq 0$ for all $n \geq 1$. (Austria)
|
We start with some observations. First, from the definition of $x_{i}$ it follows that for each positive integer $k$ we have $$ x_{4 k-3}=x_{2 k-1}=-x_{4 k-2} \quad \text { and } \quad x_{4 k-1}=x_{4 k}=-x_{2 k}=x_{k} $$ Hence, denoting $S_{n}=\sum_{i=1}^{n} x_{i}$, we have $$ \begin{gathered} S_{4 k}=\sum_{i=1}^{k}\left(\left(x_{4 k-3}+x_{4 k-2}\right)+\left(x_{4 k-1}+x_{4 k}\right)\right)=\sum_{i=1}^{k}\left(0+2 x_{k}\right)=2 S_{k}, \\ S_{4 k+2}=S_{4 k}+\left(x_{4 k+1}+x_{4 k+2}\right)=S_{4 k} . \end{gathered} $$ Observe also that $S_{n}=\sum_{i=1}^{n} x_{i} \equiv \sum_{i=1}^{n} 1=n(\bmod 2)$. Now we prove by induction on $k$ that $S_{i} \geq 0$ for all $i \leq 4 k$. The base case is valid since $x_{1}=x_{3}=x_{4}=1, x_{2}=-1$. For the induction step, assume that $S_{i} \geq 0$ for all $i \leq 4 k$. Using the relations (1)-(3), we obtain $$ S_{4 k+4}=2 S_{k+1} \geq 0, \quad S_{4 k+2}=S_{4 k} \geq 0, \quad S_{4 k+3}=S_{4 k+2}+x_{4 k+3}=\frac{S_{4 k+2}+S_{4 k+4}}{2} \geq 0 $$ So, we are left to prove that $S_{4 k+1} \geq 0$. If $k$ is odd, then $S_{4 k}=2 S_{k} \geq 0$; since $k$ is odd, $S_{k}$ is odd as well, so we have $S_{4 k} \geq 2$ and hence $S_{4 k+1}=S_{4 k}+x_{4 k+1} \geq 1$. Conversely, if $k$ is even, then we have $x_{4 k+1}=x_{2 k+1}=x_{k+1}$, hence $S_{4 k+1}=S_{4 k}+x_{4 k+1}=$ $2 S_{k}+x_{k+1}=S_{k}+S_{k+1} \geq 0$. The step is proved.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
A sequence $x_{1}, x_{2}, \ldots$ is defined by $x_{1}=1$ and $x_{2 k}=-x_{k}, x_{2 k-1}=(-1)^{k+1} x_{k}$ for all $k \geq 1$. Prove that $x_{1}+x_{2}+\cdots+x_{n} \geq 0$ for all $n \geq 1$. (Austria)
|
We start with some observations. First, from the definition of $x_{i}$ it follows that for each positive integer $k$ we have $$ x_{4 k-3}=x_{2 k-1}=-x_{4 k-2} \quad \text { and } \quad x_{4 k-1}=x_{4 k}=-x_{2 k}=x_{k} $$ Hence, denoting $S_{n}=\sum_{i=1}^{n} x_{i}$, we have $$ \begin{gathered} S_{4 k}=\sum_{i=1}^{k}\left(\left(x_{4 k-3}+x_{4 k-2}\right)+\left(x_{4 k-1}+x_{4 k}\right)\right)=\sum_{i=1}^{k}\left(0+2 x_{k}\right)=2 S_{k}, \\ S_{4 k+2}=S_{4 k}+\left(x_{4 k+1}+x_{4 k+2}\right)=S_{4 k} . \end{gathered} $$ Observe also that $S_{n}=\sum_{i=1}^{n} x_{i} \equiv \sum_{i=1}^{n} 1=n(\bmod 2)$. Now we prove by induction on $k$ that $S_{i} \geq 0$ for all $i \leq 4 k$. The base case is valid since $x_{1}=x_{3}=x_{4}=1, x_{2}=-1$. For the induction step, assume that $S_{i} \geq 0$ for all $i \leq 4 k$. Using the relations (1)-(3), we obtain $$ S_{4 k+4}=2 S_{k+1} \geq 0, \quad S_{4 k+2}=S_{4 k} \geq 0, \quad S_{4 k+3}=S_{4 k+2}+x_{4 k+3}=\frac{S_{4 k+2}+S_{4 k+4}}{2} \geq 0 $$ So, we are left to prove that $S_{4 k+1} \geq 0$. If $k$ is odd, then $S_{4 k}=2 S_{k} \geq 0$; since $k$ is odd, $S_{k}$ is odd as well, so we have $S_{4 k} \geq 2$ and hence $S_{4 k+1}=S_{4 k}+x_{4 k+1} \geq 1$. Conversely, if $k$ is even, then we have $x_{4 k+1}=x_{2 k+1}=x_{k+1}$, hence $S_{4 k+1}=S_{4 k}+x_{4 k+1}=$ $2 S_{k}+x_{k+1}=S_{k}+S_{k+1} \geq 0$. The step is proved.
|
{
"resource_path": "IMO/segmented/en-IMO2010SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
0dd5eeab-6fae-58fa-90bb-5426165954f5
| 23,917
|
A sequence $x_{1}, x_{2}, \ldots$ is defined by $x_{1}=1$ and $x_{2 k}=-x_{k}, x_{2 k-1}=(-1)^{k+1} x_{k}$ for all $k \geq 1$. Prove that $x_{1}+x_{2}+\cdots+x_{n} \geq 0$ for all $n \geq 1$. (Austria)
|
We will use the notation of $S_{n}$ and the relations (1)-(3) from the previous solution. Assume the contrary and consider the minimal $n$ such that $S_{n+1}<0$; surely $n \geq 1$, and from $S_{n} \geq 0$ we get $S_{n}=0, x_{n+1}=-1$. Hence, we are especially interested in the set $M=\left\{n: S_{n}=0\right\}$; our aim is to prove that $x_{n+1}=1$ whenever $n \in M$ thus coming to a contradiction. For this purpose, we first describe the set $M$ inductively. We claim that (i) $M$ consists only of even numbers, (ii) $2 \in M$, and (iii) for every even $n \geq 4$ we have $n \in M \Longleftrightarrow[n / 4] \in M$. Actually, (i) holds since $S_{n} \equiv n(\bmod 2)$, (ii) is straightforward, while (iii) follows from the relations $S_{4 k+2}=S_{4 k}=2 S_{k}$. Now, we are left to prove that $x_{n+1}=1$ if $n \in M$. We use the induction on $n$. The base case is $n=2$, that is, the minimal element of $M$; here we have $x_{3}=1$, as desired. For the induction step, consider some $4 \leq n \in M$ and let $m=[n / 4] \in M$; then $m$ is even, and $x_{m+1}=1$ by the induction hypothesis. We prove that $x_{n+1}=x_{m+1}=1$. If $n=4 m$ then we have $x_{n+1}=x_{2 m+1}=x_{m+1}$ since $m$ is even; otherwise, $n=4 m+2$, and $x_{n+1}=-x_{2 m+2}=x_{m+1}$, as desired. The proof is complete. Comment. Using the inductive definition of set $M$, one can describe it explicitly. Namely, $M$ consists exactly of all positive integers not containing digits 1 and 3 in their 4 -base representation.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
A sequence $x_{1}, x_{2}, \ldots$ is defined by $x_{1}=1$ and $x_{2 k}=-x_{k}, x_{2 k-1}=(-1)^{k+1} x_{k}$ for all $k \geq 1$. Prove that $x_{1}+x_{2}+\cdots+x_{n} \geq 0$ for all $n \geq 1$. (Austria)
|
We will use the notation of $S_{n}$ and the relations (1)-(3) from the previous solution. Assume the contrary and consider the minimal $n$ such that $S_{n+1}<0$; surely $n \geq 1$, and from $S_{n} \geq 0$ we get $S_{n}=0, x_{n+1}=-1$. Hence, we are especially interested in the set $M=\left\{n: S_{n}=0\right\}$; our aim is to prove that $x_{n+1}=1$ whenever $n \in M$ thus coming to a contradiction. For this purpose, we first describe the set $M$ inductively. We claim that (i) $M$ consists only of even numbers, (ii) $2 \in M$, and (iii) for every even $n \geq 4$ we have $n \in M \Longleftrightarrow[n / 4] \in M$. Actually, (i) holds since $S_{n} \equiv n(\bmod 2)$, (ii) is straightforward, while (iii) follows from the relations $S_{4 k+2}=S_{4 k}=2 S_{k}$. Now, we are left to prove that $x_{n+1}=1$ if $n \in M$. We use the induction on $n$. The base case is $n=2$, that is, the minimal element of $M$; here we have $x_{3}=1$, as desired. For the induction step, consider some $4 \leq n \in M$ and let $m=[n / 4] \in M$; then $m$ is even, and $x_{m+1}=1$ by the induction hypothesis. We prove that $x_{n+1}=x_{m+1}=1$. If $n=4 m$ then we have $x_{n+1}=x_{2 m+1}=x_{m+1}$ since $m$ is even; otherwise, $n=4 m+2$, and $x_{n+1}=-x_{2 m+2}=x_{m+1}$, as desired. The proof is complete. Comment. Using the inductive definition of set $M$, one can describe it explicitly. Namely, $M$ consists exactly of all positive integers not containing digits 1 and 3 in their 4 -base representation.
|
{
"resource_path": "IMO/segmented/en-IMO2010SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
0dd5eeab-6fae-58fa-90bb-5426165954f5
| 23,917
|
Suppose that $f$ and $g$ are two functions defined on the set of positive integers and taking positive integer values. Suppose also that the equations $f(g(n))=f(n)+1$ and $g(f(n))=$ $g(n)+1$ hold for all positive integers. Prove that $f(n)=g(n)$ for all positive integer $n$. (Germany)
|
Throughout the solution, by $\mathbb{N}$ we denote the set of all positive integers. For any function $h: \mathbb{N} \rightarrow \mathbb{N}$ and for any positive integer $k$, define $h^{k}(x)=\underbrace{h(h(\ldots h}_{k}(x) \ldots)$ ) (in particular, $\left.h^{0}(x)=x\right)$. Observe that $f\left(g^{k}(x)\right)=f\left(g^{k-1}(x)\right)+1=\cdots=f(x)+k$ for any positive integer $k$, and similarly $g\left(f^{k}(x)\right)=g(x)+k$. Now let $a$ and $b$ are the minimal values attained by $f$ and $g$, respectively; say $f\left(n_{f}\right)=a, g\left(n_{g}\right)=b$. Then we have $f\left(g^{k}\left(n_{f}\right)\right)=a+k, g\left(f^{k}\left(n_{g}\right)\right)=b+k$, so the function $f$ attains all values from the set $N_{f}=\{a, a+1, \ldots\}$, while $g$ attains all the values from the set $N_{g}=\{b, b+1, \ldots\}$. Next, note that $f(x)=f(y)$ implies $g(x)=g(f(x))-1=g(f(y))-1=g(y)$; surely, the converse implication also holds. Now, we say that $x$ and $y$ are similar (and write $x \sim y$ ) if $f(x)=f(y)$ (equivalently, $g(x)=g(y)$ ). For every $x \in \mathbb{N}$, we define $[x]=\{y \in \mathbb{N}: x \sim y\}$; surely, $y_{1} \sim y_{2}$ for all $y_{1}, y_{2} \in[x]$, so $[x]=[y]$ whenever $y \in[x]$. Now we investigate the structure of the sets $[x]$. Claim 1. Suppose that $f(x) \sim f(y)$; then $x \sim y$, that is, $f(x)=f(y)$. Consequently, each class $[x]$ contains at most one element from $N_{f}$, as well as at most one element from $N_{g}$. Proof. If $f(x) \sim f(y)$, then we have $g(x)=g(f(x))-1=g(f(y))-1=g(y)$, so $x \sim y$. The second statement follows now from the sets of values of $f$ and $g$. Next, we clarify which classes do not contain large elements. Claim 2. For any $x \in \mathbb{N}$, we have $[x] \subseteq\{1,2, \ldots, b-1\}$ if and only if $f(x)=a$. Analogously, $[x] \subseteq\{1,2, \ldots, a-1\}$ if and only if $g(x)=b$. Proof. We will prove that $[x] \nsubseteq\{1,2, \ldots, b-1\} \Longleftrightarrow f(x)>a$; the proof of the second statement is similar. Note that $f(x)>a$ implies that there exists some $y$ satisfying $f(y)=f(x)-1$, so $f(g(y))=$ $f(y)+1=f(x)$, and hence $x \sim g(y) \geq b$. Conversely, if $b \leq c \sim x$ then $c=g(y)$ for some $y \in \mathbb{N}$, which in turn follows $f(x)=f(g(y))=f(y)+1 \geq a+1$, and hence $f(x)>a$. Claim 2 implies that there exists exactly one class contained in $\{1, \ldots, a-1\}$ (that is, the class $\left[n_{g}\right]$ ), as well as exactly one class contained in $\{1, \ldots, b-1\}$ (the class $\left[n_{f}\right]$ ). Assume for a moment that $a \leq b$; then $\left[n_{g}\right]$ is contained in $\{1, \ldots, b-1\}$ as well, hence it coincides with $\left[n_{g}\right]$. So, we get that $$ f(x)=a \Longleftrightarrow g(x)=b \Longleftrightarrow x \sim n_{f} \sim n_{g} . $$ Claim 3. $a=b$. Proof. By Claim 2, we have $[a] \neq\left[n_{f}\right]$, so $[a]$ should contain some element $a^{\prime} \geq b$ by Claim 2 again. If $a \neq a^{\prime}$, then $[a]$ contains two elements $\geq a$ which is impossible by Claim 1. Therefore, $a=a^{\prime} \geq b$. Similarly, $b \geq a$. Now we are ready to prove the problem statement. First, we establish the following Claim 4. For every integer $d \geq 0, f^{d+1}\left(n_{f}\right)=g^{d+1}\left(n_{f}\right)=a+d$. Proof. Induction on $d$. For $d=0$, the statement follows from (1) and Claim 3. Next, for $d>1$ from the induction hypothesis we have $f^{d+1}\left(n_{f}\right)=f\left(f^{d}\left(n_{f}\right)\right)=f\left(g^{d}\left(n_{f}\right)\right)=f\left(n_{f}\right)+d=a+d$. The equality $g^{d+1}\left(n_{f}\right)=a+d$ is analogous. Finally, for each $x \in \mathbb{N}$, we have $f(x)=a+d$ for some $d \geq 0$, so $f(x)=f\left(g^{d}\left(n_{f}\right)\right)$ and hence $x \sim g^{d}\left(n_{f}\right)$. It follows that $g(x)=g\left(g^{d}\left(n_{f}\right)\right)=g^{d+1}\left(n_{f}\right)=a+d=f(x)$ by Claim 4 .
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Suppose that $f$ and $g$ are two functions defined on the set of positive integers and taking positive integer values. Suppose also that the equations $f(g(n))=f(n)+1$ and $g(f(n))=$ $g(n)+1$ hold for all positive integers. Prove that $f(n)=g(n)$ for all positive integer $n$. (Germany)
|
Throughout the solution, by $\mathbb{N}$ we denote the set of all positive integers. For any function $h: \mathbb{N} \rightarrow \mathbb{N}$ and for any positive integer $k$, define $h^{k}(x)=\underbrace{h(h(\ldots h}_{k}(x) \ldots)$ ) (in particular, $\left.h^{0}(x)=x\right)$. Observe that $f\left(g^{k}(x)\right)=f\left(g^{k-1}(x)\right)+1=\cdots=f(x)+k$ for any positive integer $k$, and similarly $g\left(f^{k}(x)\right)=g(x)+k$. Now let $a$ and $b$ are the minimal values attained by $f$ and $g$, respectively; say $f\left(n_{f}\right)=a, g\left(n_{g}\right)=b$. Then we have $f\left(g^{k}\left(n_{f}\right)\right)=a+k, g\left(f^{k}\left(n_{g}\right)\right)=b+k$, so the function $f$ attains all values from the set $N_{f}=\{a, a+1, \ldots\}$, while $g$ attains all the values from the set $N_{g}=\{b, b+1, \ldots\}$. Next, note that $f(x)=f(y)$ implies $g(x)=g(f(x))-1=g(f(y))-1=g(y)$; surely, the converse implication also holds. Now, we say that $x$ and $y$ are similar (and write $x \sim y$ ) if $f(x)=f(y)$ (equivalently, $g(x)=g(y)$ ). For every $x \in \mathbb{N}$, we define $[x]=\{y \in \mathbb{N}: x \sim y\}$; surely, $y_{1} \sim y_{2}$ for all $y_{1}, y_{2} \in[x]$, so $[x]=[y]$ whenever $y \in[x]$. Now we investigate the structure of the sets $[x]$. Claim 1. Suppose that $f(x) \sim f(y)$; then $x \sim y$, that is, $f(x)=f(y)$. Consequently, each class $[x]$ contains at most one element from $N_{f}$, as well as at most one element from $N_{g}$. Proof. If $f(x) \sim f(y)$, then we have $g(x)=g(f(x))-1=g(f(y))-1=g(y)$, so $x \sim y$. The second statement follows now from the sets of values of $f$ and $g$. Next, we clarify which classes do not contain large elements. Claim 2. For any $x \in \mathbb{N}$, we have $[x] \subseteq\{1,2, \ldots, b-1\}$ if and only if $f(x)=a$. Analogously, $[x] \subseteq\{1,2, \ldots, a-1\}$ if and only if $g(x)=b$. Proof. We will prove that $[x] \nsubseteq\{1,2, \ldots, b-1\} \Longleftrightarrow f(x)>a$; the proof of the second statement is similar. Note that $f(x)>a$ implies that there exists some $y$ satisfying $f(y)=f(x)-1$, so $f(g(y))=$ $f(y)+1=f(x)$, and hence $x \sim g(y) \geq b$. Conversely, if $b \leq c \sim x$ then $c=g(y)$ for some $y \in \mathbb{N}$, which in turn follows $f(x)=f(g(y))=f(y)+1 \geq a+1$, and hence $f(x)>a$. Claim 2 implies that there exists exactly one class contained in $\{1, \ldots, a-1\}$ (that is, the class $\left[n_{g}\right]$ ), as well as exactly one class contained in $\{1, \ldots, b-1\}$ (the class $\left[n_{f}\right]$ ). Assume for a moment that $a \leq b$; then $\left[n_{g}\right]$ is contained in $\{1, \ldots, b-1\}$ as well, hence it coincides with $\left[n_{g}\right]$. So, we get that $$ f(x)=a \Longleftrightarrow g(x)=b \Longleftrightarrow x \sim n_{f} \sim n_{g} . $$ Claim 3. $a=b$. Proof. By Claim 2, we have $[a] \neq\left[n_{f}\right]$, so $[a]$ should contain some element $a^{\prime} \geq b$ by Claim 2 again. If $a \neq a^{\prime}$, then $[a]$ contains two elements $\geq a$ which is impossible by Claim 1. Therefore, $a=a^{\prime} \geq b$. Similarly, $b \geq a$. Now we are ready to prove the problem statement. First, we establish the following Claim 4. For every integer $d \geq 0, f^{d+1}\left(n_{f}\right)=g^{d+1}\left(n_{f}\right)=a+d$. Proof. Induction on $d$. For $d=0$, the statement follows from (1) and Claim 3. Next, for $d>1$ from the induction hypothesis we have $f^{d+1}\left(n_{f}\right)=f\left(f^{d}\left(n_{f}\right)\right)=f\left(g^{d}\left(n_{f}\right)\right)=f\left(n_{f}\right)+d=a+d$. The equality $g^{d+1}\left(n_{f}\right)=a+d$ is analogous. Finally, for each $x \in \mathbb{N}$, we have $f(x)=a+d$ for some $d \geq 0$, so $f(x)=f\left(g^{d}\left(n_{f}\right)\right)$ and hence $x \sim g^{d}\left(n_{f}\right)$. It follows that $g(x)=g\left(g^{d}\left(n_{f}\right)\right)=g^{d+1}\left(n_{f}\right)=a+d=f(x)$ by Claim 4 .
|
{
"resource_path": "IMO/segmented/en-IMO2010SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
49dbb33a-8b85-5846-ba5d-03d9a7ec90a1
| 23,922
|
Suppose that $f$ and $g$ are two functions defined on the set of positive integers and taking positive integer values. Suppose also that the equations $f(g(n))=f(n)+1$ and $g(f(n))=$ $g(n)+1$ hold for all positive integers. Prove that $f(n)=g(n)$ for all positive integer $n$. (Germany)
|
We start with the same observations, introducing the relation $\sim$ and proving Claim 1 from the previous solution. Note that $f(a)>a$ since otherwise we have $f(a)=a$ and hence $g(a)=g(f(a))=g(a)+1$, which is false. Claim 2'. $a=b$. Proof. We can assume that $a \leq b$. Since $f(a) \geq a+1$, there exists some $x \in \mathbb{N}$ such that $f(a)=f(x)+1$, which is equivalent to $f(a)=f(g(x))$ and $a \sim g(x)$. Since $g(x) \geq b \geq a$, by Claim 1 we have $a=g(x) \geq b$, which together with $a \leq b$ proves the Claim. Now, almost the same method allows to find the values $f(a)$ and $g(a)$. Claim 3'. $f(a)=g(a)=a+1$. Proof. Assume the contrary; then $f(a) \geq a+2$, hence there exist some $x, y \in \mathbb{N}$ such that $f(x)=f(a)-2$ and $f(y)=g(x)($ as $g(x) \geq a=b)$. Now we get $f(a)=f(x)+2=f\left(g^{2}(x)\right)$, so $a \sim g^{2}(x) \geq a$, and by Claim 1 we get $a=g^{2}(x)=g(f(y))=1+g(y) \geq 1+a$; this is impossible. The equality $g(a)=a+1$ is similar. Now, we are prepared for the proof of the problem statement. First, we prove it for $n \geq a$. Claim 4'. For each integer $x \geq a$, we have $f(x)=g(x)=x+1$. Proof. Induction on $x$. The base case $x=a$ is provided by Claim $3^{\prime}$, while the induction step follows from $f(x+1)=f(g(x))=f(x)+1=(x+1)+1$ and the similar computation for $g(x+1)$. Finally, for an arbitrary $n \in \mathbb{N}$ we have $g(n) \geq a$, so by Claim $4^{\prime}$ we have $f(n)+1=$ $f(g(n))=g(n)+1$, hence $f(n)=g(n)$. Comment. It is not hard now to describe all the functions $f: \mathbb{N} \rightarrow \mathbb{N}$ satisfying the property $f(f(n))=$ $f(n)+1$. For each such function, there exists $n_{0} \in \mathbb{N}$ such that $f(n)=n+1$ for all $n \geq n_{0}$, while for each $n<n_{0}, f(n)$ is an arbitrary number greater than of equal to $n_{0}$ (these numbers may be different for different $n<n_{0}$ ).
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Suppose that $f$ and $g$ are two functions defined on the set of positive integers and taking positive integer values. Suppose also that the equations $f(g(n))=f(n)+1$ and $g(f(n))=$ $g(n)+1$ hold for all positive integers. Prove that $f(n)=g(n)$ for all positive integer $n$. (Germany)
|
We start with the same observations, introducing the relation $\sim$ and proving Claim 1 from the previous solution. Note that $f(a)>a$ since otherwise we have $f(a)=a$ and hence $g(a)=g(f(a))=g(a)+1$, which is false. Claim 2'. $a=b$. Proof. We can assume that $a \leq b$. Since $f(a) \geq a+1$, there exists some $x \in \mathbb{N}$ such that $f(a)=f(x)+1$, which is equivalent to $f(a)=f(g(x))$ and $a \sim g(x)$. Since $g(x) \geq b \geq a$, by Claim 1 we have $a=g(x) \geq b$, which together with $a \leq b$ proves the Claim. Now, almost the same method allows to find the values $f(a)$ and $g(a)$. Claim 3'. $f(a)=g(a)=a+1$. Proof. Assume the contrary; then $f(a) \geq a+2$, hence there exist some $x, y \in \mathbb{N}$ such that $f(x)=f(a)-2$ and $f(y)=g(x)($ as $g(x) \geq a=b)$. Now we get $f(a)=f(x)+2=f\left(g^{2}(x)\right)$, so $a \sim g^{2}(x) \geq a$, and by Claim 1 we get $a=g^{2}(x)=g(f(y))=1+g(y) \geq 1+a$; this is impossible. The equality $g(a)=a+1$ is similar. Now, we are prepared for the proof of the problem statement. First, we prove it for $n \geq a$. Claim 4'. For each integer $x \geq a$, we have $f(x)=g(x)=x+1$. Proof. Induction on $x$. The base case $x=a$ is provided by Claim $3^{\prime}$, while the induction step follows from $f(x+1)=f(g(x))=f(x)+1=(x+1)+1$ and the similar computation for $g(x+1)$. Finally, for an arbitrary $n \in \mathbb{N}$ we have $g(n) \geq a$, so by Claim $4^{\prime}$ we have $f(n)+1=$ $f(g(n))=g(n)+1$, hence $f(n)=g(n)$. Comment. It is not hard now to describe all the functions $f: \mathbb{N} \rightarrow \mathbb{N}$ satisfying the property $f(f(n))=$ $f(n)+1$. For each such function, there exists $n_{0} \in \mathbb{N}$ such that $f(n)=n+1$ for all $n \geq n_{0}$, while for each $n<n_{0}, f(n)$ is an arbitrary number greater than of equal to $n_{0}$ (these numbers may be different for different $n<n_{0}$ ).
|
{
"resource_path": "IMO/segmented/en-IMO2010SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
49dbb33a-8b85-5846-ba5d-03d9a7ec90a1
| 23,922
|
Let $a_{1}, \ldots, a_{r}$ be positive real numbers. For $n>r$, we inductively define $$ a_{n}=\max _{1 \leq k \leq n-1}\left(a_{k}+a_{n-k}\right) $$ Prove that there exist positive integers $\ell \leq r$ and $N$ such that $a_{n}=a_{n-\ell}+a_{\ell}$ for all $n \geq N$. (Iran)
|
First, from the problem conditions we have that each $a_{n}(n>r)$ can be expressed as $a_{n}=a_{j_{1}}+a_{j_{2}}$ with $j_{1}, j_{2}<n, j_{1}+j_{2}=n$. If, say, $j_{1}>r$ then we can proceed in the same way with $a_{j_{1}}$, and so on. Finally, we represent $a_{n}$ in a form $$ \begin{gathered} a_{n}=a_{i_{1}}+\cdots+a_{i_{k}}, \\ 1 \leq i_{j} \leq r, \quad i_{1}+\cdots+i_{k}=n . \end{gathered} $$ Moreover, if $a_{i_{1}}$ and $a_{i_{2}}$ are the numbers in (2) obtained on the last step, then $i_{1}+i_{2}>r$. Hence we can adjust (3) as $$ 1 \leq i_{j} \leq r, \quad i_{1}+\cdots+i_{k}=n, \quad i_{1}+i_{2}>r . $$ On the other hand, suppose that the indices $i_{1}, \ldots, i_{k}$ satisfy the conditions (4). Then, denoting $s_{j}=i_{1}+\cdots+i_{j}$, from (1) we have $$ a_{n}=a_{s_{k}} \geq a_{s_{k-1}}+a_{i_{k}} \geq a_{s_{k-2}}+a_{i_{k-1}}+a_{i_{k}} \geq \cdots \geq a_{i_{1}}+\cdots+a_{i_{k}} $$ Summarizing these observations we get the following Claim. For every $n>r$, we have $$ a_{n}=\max \left\{a_{i_{1}}+\cdots+a_{i_{k}}: \text { the collection }\left(i_{1}, \ldots, i_{k}\right) \text { satisfies }(4)\right\} $$ Now we denote $$ s=\max _{1 \leq i \leq r} \frac{a_{i}}{i} $$ and fix some index $\ell \leq r$ such that $s=\frac{a_{\ell}}{\ell}$. Consider some $n \geq r^{2} \ell+2 r$ and choose an expansion of $a_{n}$ in the form (2), (4). Then we have $n=i_{1}+\cdots+i_{k} \leq r k$, so $k \geq n / r \geq r \ell+2$. Suppose that none of the numbers $i_{3}, \ldots, i_{k}$ equals $\ell$. Then by the pigeonhole principle there is an index $1 \leq j \leq r$ which appears among $i_{3}, \ldots, i_{k}$ at least $\ell$ times, and surely $j \neq \ell$. Let us delete these $\ell$ occurrences of $j$ from $\left(i_{1}, \ldots, i_{k}\right)$, and add $j$ occurrences of $\ell$ instead, obtaining a sequence $\left(i_{1}, i_{2}, i_{3}^{\prime}, \ldots, i_{k^{\prime}}^{\prime}\right)$ also satisfying (4). By Claim, we have $$ a_{i_{1}}+\cdots+a_{i_{k}}=a_{n} \geq a_{i_{1}}+a_{i_{2}}+a_{i_{3}^{\prime}}+\cdots+a_{i_{k^{\prime}}^{\prime}} $$ or, after removing the coinciding terms, $\ell a_{j} \geq j a_{\ell}$, so $\frac{a_{\ell}}{\ell} \leq \frac{a_{j}}{j}$. By the definition of $\ell$, this means that $\ell a_{j}=j a_{\ell}$, hence $$ a_{n}=a_{i_{1}}+a_{i_{2}}+a_{i_{3}^{\prime}}+\cdots+a_{i_{k^{\prime}}^{\prime}} $$ Thus, for every $n \geq r^{2} \ell+2 r$ we have found a representation of the form (2), (4) with $i_{j}=\ell$ for some $j \geq 3$. Rearranging the indices we may assume that $i_{k}=\ell$. Finally, observe that in this representation, the indices $\left(i_{1}, \ldots, i_{k-1}\right)$ satisfy the conditions (4) with $n$ replaced by $n-\ell$. Thus, from the Claim we get $$ a_{n-\ell}+a_{\ell} \geq\left(a_{i_{1}}+\cdots+a_{i_{k-1}}\right)+a_{\ell}=a_{n} $$ which by (1) implies $$ a_{n}=a_{n-\ell}+a_{\ell} \quad \text { for each } n \geq r^{2} \ell+2 r $$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $a_{1}, \ldots, a_{r}$ be positive real numbers. For $n>r$, we inductively define $$ a_{n}=\max _{1 \leq k \leq n-1}\left(a_{k}+a_{n-k}\right) $$ Prove that there exist positive integers $\ell \leq r$ and $N$ such that $a_{n}=a_{n-\ell}+a_{\ell}$ for all $n \geq N$. (Iran)
|
First, from the problem conditions we have that each $a_{n}(n>r)$ can be expressed as $a_{n}=a_{j_{1}}+a_{j_{2}}$ with $j_{1}, j_{2}<n, j_{1}+j_{2}=n$. If, say, $j_{1}>r$ then we can proceed in the same way with $a_{j_{1}}$, and so on. Finally, we represent $a_{n}$ in a form $$ \begin{gathered} a_{n}=a_{i_{1}}+\cdots+a_{i_{k}}, \\ 1 \leq i_{j} \leq r, \quad i_{1}+\cdots+i_{k}=n . \end{gathered} $$ Moreover, if $a_{i_{1}}$ and $a_{i_{2}}$ are the numbers in (2) obtained on the last step, then $i_{1}+i_{2}>r$. Hence we can adjust (3) as $$ 1 \leq i_{j} \leq r, \quad i_{1}+\cdots+i_{k}=n, \quad i_{1}+i_{2}>r . $$ On the other hand, suppose that the indices $i_{1}, \ldots, i_{k}$ satisfy the conditions (4). Then, denoting $s_{j}=i_{1}+\cdots+i_{j}$, from (1) we have $$ a_{n}=a_{s_{k}} \geq a_{s_{k-1}}+a_{i_{k}} \geq a_{s_{k-2}}+a_{i_{k-1}}+a_{i_{k}} \geq \cdots \geq a_{i_{1}}+\cdots+a_{i_{k}} $$ Summarizing these observations we get the following Claim. For every $n>r$, we have $$ a_{n}=\max \left\{a_{i_{1}}+\cdots+a_{i_{k}}: \text { the collection }\left(i_{1}, \ldots, i_{k}\right) \text { satisfies }(4)\right\} $$ Now we denote $$ s=\max _{1 \leq i \leq r} \frac{a_{i}}{i} $$ and fix some index $\ell \leq r$ such that $s=\frac{a_{\ell}}{\ell}$. Consider some $n \geq r^{2} \ell+2 r$ and choose an expansion of $a_{n}$ in the form (2), (4). Then we have $n=i_{1}+\cdots+i_{k} \leq r k$, so $k \geq n / r \geq r \ell+2$. Suppose that none of the numbers $i_{3}, \ldots, i_{k}$ equals $\ell$. Then by the pigeonhole principle there is an index $1 \leq j \leq r$ which appears among $i_{3}, \ldots, i_{k}$ at least $\ell$ times, and surely $j \neq \ell$. Let us delete these $\ell$ occurrences of $j$ from $\left(i_{1}, \ldots, i_{k}\right)$, and add $j$ occurrences of $\ell$ instead, obtaining a sequence $\left(i_{1}, i_{2}, i_{3}^{\prime}, \ldots, i_{k^{\prime}}^{\prime}\right)$ also satisfying (4). By Claim, we have $$ a_{i_{1}}+\cdots+a_{i_{k}}=a_{n} \geq a_{i_{1}}+a_{i_{2}}+a_{i_{3}^{\prime}}+\cdots+a_{i_{k^{\prime}}^{\prime}} $$ or, after removing the coinciding terms, $\ell a_{j} \geq j a_{\ell}$, so $\frac{a_{\ell}}{\ell} \leq \frac{a_{j}}{j}$. By the definition of $\ell$, this means that $\ell a_{j}=j a_{\ell}$, hence $$ a_{n}=a_{i_{1}}+a_{i_{2}}+a_{i_{3}^{\prime}}+\cdots+a_{i_{k^{\prime}}^{\prime}} $$ Thus, for every $n \geq r^{2} \ell+2 r$ we have found a representation of the form (2), (4) with $i_{j}=\ell$ for some $j \geq 3$. Rearranging the indices we may assume that $i_{k}=\ell$. Finally, observe that in this representation, the indices $\left(i_{1}, \ldots, i_{k-1}\right)$ satisfy the conditions (4) with $n$ replaced by $n-\ell$. Thus, from the Claim we get $$ a_{n-\ell}+a_{\ell} \geq\left(a_{i_{1}}+\cdots+a_{i_{k-1}}\right)+a_{\ell}=a_{n} $$ which by (1) implies $$ a_{n}=a_{n-\ell}+a_{\ell} \quad \text { for each } n \geq r^{2} \ell+2 r $$ as desired.
|
{
"resource_path": "IMO/segmented/en-IMO2010SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
7f97f493-46bc-5567-9b4a-71985dfc60fb
| 23,926
|
Let $a_{1}, \ldots, a_{r}$ be positive real numbers. For $n>r$, we inductively define $$ a_{n}=\max _{1 \leq k \leq n-1}\left(a_{k}+a_{n-k}\right) $$ Prove that there exist positive integers $\ell \leq r$ and $N$ such that $a_{n}=a_{n-\ell}+a_{\ell}$ for all $n \geq N$. (Iran)
|
As in the previous solution, we involve the expansion (2), (3), and we fix some index $1 \leq \ell \leq r$ such that $$ \frac{a_{\ell}}{\ell}=s=\max _{1 \leq i \leq r} \frac{a_{i}}{i} $$ Now, we introduce the sequence $\left(b_{n}\right)$ as $b_{n}=a_{n}-s n$; then $b_{\ell}=0$. We prove by induction on $n$ that $b_{n} \leq 0$, and $\left(b_{n}\right)$ satisfies the same recurrence relation as $\left(a_{n}\right)$. The base cases $n \leq r$ follow from the definition of $s$. Now, for $n>r$ from the induction hypothesis we have $$ b_{n}=\max _{1 \leq k \leq n-1}\left(a_{k}+a_{n-k}\right)-n s=\max _{1 \leq k \leq n-1}\left(b_{k}+b_{n-k}+n s\right)-n s=\max _{1 \leq k \leq n-1}\left(b_{k}+b_{n-k}\right) \leq 0 $$ as required. Now, if $b_{k}=0$ for all $1 \leq k \leq r$, then $b_{n}=0$ for all $n$, hence $a_{n}=s n$, and the statement is trivial. Otherwise, define $$ M=\max _{1 \leq i \leq r}\left|b_{i}\right|, \quad \varepsilon=\min \left\{\left|b_{i}\right|: 1 \leq i \leq r, b_{i}<0\right\} $$ Then for $n>r$ we obtain $$ b_{n}=\max _{1 \leq k \leq n-1}\left(b_{k}+b_{n-k}\right) \geq b_{\ell}+b_{n-\ell}=b_{n-\ell} $$ so $$ 0 \geq b_{n} \geq b_{n-\ell} \geq b_{n-2 \ell} \geq \cdots \geq-M $$ Thus, in view of the expansion (2), (3) applied to the sequence $\left(b_{n}\right)$, we get that each $b_{n}$ is contained in a set $$ T=\left\{b_{i_{1}}+b_{i_{2}}+\cdots+b_{i_{k}}: i_{1}, \ldots, i_{k} \leq r\right\} \cap[-M, 0] $$ We claim that this set is finite. Actually, for any $x \in T$, let $x=b_{i_{1}}+\cdots+b_{i_{k}}\left(i_{1}, \ldots, i_{k} \leq r\right)$. Then among $b_{i_{j}}$ 's there are at most $\frac{M}{\varepsilon}$ nonzero terms (otherwise $x<\frac{M}{\varepsilon} \cdot(-\varepsilon)<-M$ ). Thus $x$ can be expressed in the same way with $k \leq \frac{M}{\varepsilon}$, and there is only a finite number of such sums. Finally, for every $t=1,2, \ldots, \ell$ we get that the sequence $$ b_{r+t}, b_{r+t+\ell}, b_{r+t+2 \ell}, \ldots $$ is non-decreasing and attains the finite number of values; therefore it is constant from some index. Thus, the sequence $\left(b_{n}\right)$ is periodic with period $\ell$ from some index $N$, which means that $$ b_{n}=b_{n-\ell}=b_{n-\ell}+b_{\ell} \quad \text { for all } n>N+\ell $$ and hence $$ a_{n}=b_{n}+n s=\left(b_{n-\ell}+(n-\ell) s\right)+\left(b_{\ell}+\ell s\right)=a_{n-\ell}+a_{\ell} \quad \text { for all } n>N+\ell \text {, } $$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $a_{1}, \ldots, a_{r}$ be positive real numbers. For $n>r$, we inductively define $$ a_{n}=\max _{1 \leq k \leq n-1}\left(a_{k}+a_{n-k}\right) $$ Prove that there exist positive integers $\ell \leq r$ and $N$ such that $a_{n}=a_{n-\ell}+a_{\ell}$ for all $n \geq N$. (Iran)
|
As in the previous solution, we involve the expansion (2), (3), and we fix some index $1 \leq \ell \leq r$ such that $$ \frac{a_{\ell}}{\ell}=s=\max _{1 \leq i \leq r} \frac{a_{i}}{i} $$ Now, we introduce the sequence $\left(b_{n}\right)$ as $b_{n}=a_{n}-s n$; then $b_{\ell}=0$. We prove by induction on $n$ that $b_{n} \leq 0$, and $\left(b_{n}\right)$ satisfies the same recurrence relation as $\left(a_{n}\right)$. The base cases $n \leq r$ follow from the definition of $s$. Now, for $n>r$ from the induction hypothesis we have $$ b_{n}=\max _{1 \leq k \leq n-1}\left(a_{k}+a_{n-k}\right)-n s=\max _{1 \leq k \leq n-1}\left(b_{k}+b_{n-k}+n s\right)-n s=\max _{1 \leq k \leq n-1}\left(b_{k}+b_{n-k}\right) \leq 0 $$ as required. Now, if $b_{k}=0$ for all $1 \leq k \leq r$, then $b_{n}=0$ for all $n$, hence $a_{n}=s n$, and the statement is trivial. Otherwise, define $$ M=\max _{1 \leq i \leq r}\left|b_{i}\right|, \quad \varepsilon=\min \left\{\left|b_{i}\right|: 1 \leq i \leq r, b_{i}<0\right\} $$ Then for $n>r$ we obtain $$ b_{n}=\max _{1 \leq k \leq n-1}\left(b_{k}+b_{n-k}\right) \geq b_{\ell}+b_{n-\ell}=b_{n-\ell} $$ so $$ 0 \geq b_{n} \geq b_{n-\ell} \geq b_{n-2 \ell} \geq \cdots \geq-M $$ Thus, in view of the expansion (2), (3) applied to the sequence $\left(b_{n}\right)$, we get that each $b_{n}$ is contained in a set $$ T=\left\{b_{i_{1}}+b_{i_{2}}+\cdots+b_{i_{k}}: i_{1}, \ldots, i_{k} \leq r\right\} \cap[-M, 0] $$ We claim that this set is finite. Actually, for any $x \in T$, let $x=b_{i_{1}}+\cdots+b_{i_{k}}\left(i_{1}, \ldots, i_{k} \leq r\right)$. Then among $b_{i_{j}}$ 's there are at most $\frac{M}{\varepsilon}$ nonzero terms (otherwise $x<\frac{M}{\varepsilon} \cdot(-\varepsilon)<-M$ ). Thus $x$ can be expressed in the same way with $k \leq \frac{M}{\varepsilon}$, and there is only a finite number of such sums. Finally, for every $t=1,2, \ldots, \ell$ we get that the sequence $$ b_{r+t}, b_{r+t+\ell}, b_{r+t+2 \ell}, \ldots $$ is non-decreasing and attains the finite number of values; therefore it is constant from some index. Thus, the sequence $\left(b_{n}\right)$ is periodic with period $\ell$ from some index $N$, which means that $$ b_{n}=b_{n-\ell}=b_{n-\ell}+b_{\ell} \quad \text { for all } n>N+\ell $$ and hence $$ a_{n}=b_{n}+n s=\left(b_{n-\ell}+(n-\ell) s\right)+\left(b_{\ell}+\ell s\right)=a_{n-\ell}+a_{\ell} \quad \text { for all } n>N+\ell \text {, } $$ as desired.
|
{
"resource_path": "IMO/segmented/en-IMO2010SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
7f97f493-46bc-5567-9b4a-71985dfc60fb
| 23,926
|
Given six positive numbers $a, b, c, d, e, f$ such that $a<b<c<d<e<f$. Let $a+c+e=S$ and $b+d+f=T$. Prove that $$ 2 S T>\sqrt{3(S+T)(S(b d+b f+d f)+T(a c+a e+c e))} $$ (South Korea)
|
Let $$ U=\frac{1}{2}\left((e-a)^{2}+(c-a)^{2}+(e-c)^{2}\right)=S^{2}-3(a c+a e+c e) $$ and $$ V=\frac{1}{2}\left((f-b)^{2}+(f-d)^{2}+(d-b)^{2}\right)=T^{2}-3(b d+b f+d f) $$ Then $$ \begin{aligned} & \text { (L.H.S. })^{2}-(\text { R.H.S. })^{2}=(2 S T)^{2}-(S+T)(S \cdot 3(b d+b f+d f)+T \cdot 3(a c+a e+c e))= \\ & \quad=4 S^{2} T^{2}-(S+T)\left(S\left(T^{2}-V\right)+T\left(S^{2}-U\right)\right)=(S+T)(S V+T U)-S T(T-S)^{2} \end{aligned} $$ and the statement is equivalent with $$ (S+T)(S V+T U)>S T(T-S)^{2} $$ By the Cauchy-Schwarz inequality, $$ (S+T)(T U+S V) \geq(\sqrt{S \cdot T U}+\sqrt{T \cdot S V})^{2}=S T(\sqrt{U}+\sqrt{V})^{2} $$ Estimate the quantities $\sqrt{U}$ and $\sqrt{V}$ by the QM-AM inequality with the positive terms $(e-c)^{2}$ and $(d-b)^{2}$ being omitted: $$ \begin{aligned} \sqrt{U}+\sqrt{V} & >\sqrt{\frac{(e-a)^{2}+(c-a)^{2}}{2}}+\sqrt{\frac{(f-b)^{2}+(f-d)^{2}}{2}} \\ & >\frac{(e-a)+(c-a)}{2}+\frac{(f-b)+(f-d)}{2}=\left(f-\frac{d}{2}-\frac{b}{2}\right)+\left(\frac{e}{2}+\frac{c}{2}-a\right) \\ & =(T-S)+\frac{3}{2}(e-d)+\frac{3}{2}(c-b)>T-S . \end{aligned} $$ The estimates (5) and (6) prove (4) and hence the statement.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Given six positive numbers $a, b, c, d, e, f$ such that $a<b<c<d<e<f$. Let $a+c+e=S$ and $b+d+f=T$. Prove that $$ 2 S T>\sqrt{3(S+T)(S(b d+b f+d f)+T(a c+a e+c e))} $$ (South Korea)
|
Let $$ U=\frac{1}{2}\left((e-a)^{2}+(c-a)^{2}+(e-c)^{2}\right)=S^{2}-3(a c+a e+c e) $$ and $$ V=\frac{1}{2}\left((f-b)^{2}+(f-d)^{2}+(d-b)^{2}\right)=T^{2}-3(b d+b f+d f) $$ Then $$ \begin{aligned} & \text { (L.H.S. })^{2}-(\text { R.H.S. })^{2}=(2 S T)^{2}-(S+T)(S \cdot 3(b d+b f+d f)+T \cdot 3(a c+a e+c e))= \\ & \quad=4 S^{2} T^{2}-(S+T)\left(S\left(T^{2}-V\right)+T\left(S^{2}-U\right)\right)=(S+T)(S V+T U)-S T(T-S)^{2} \end{aligned} $$ and the statement is equivalent with $$ (S+T)(S V+T U)>S T(T-S)^{2} $$ By the Cauchy-Schwarz inequality, $$ (S+T)(T U+S V) \geq(\sqrt{S \cdot T U}+\sqrt{T \cdot S V})^{2}=S T(\sqrt{U}+\sqrt{V})^{2} $$ Estimate the quantities $\sqrt{U}$ and $\sqrt{V}$ by the QM-AM inequality with the positive terms $(e-c)^{2}$ and $(d-b)^{2}$ being omitted: $$ \begin{aligned} \sqrt{U}+\sqrt{V} & >\sqrt{\frac{(e-a)^{2}+(c-a)^{2}}{2}}+\sqrt{\frac{(f-b)^{2}+(f-d)^{2}}{2}} \\ & >\frac{(e-a)+(c-a)}{2}+\frac{(f-b)+(f-d)}{2}=\left(f-\frac{d}{2}-\frac{b}{2}\right)+\left(\frac{e}{2}+\frac{c}{2}-a\right) \\ & =(T-S)+\frac{3}{2}(e-d)+\frac{3}{2}(c-b)>T-S . \end{aligned} $$ The estimates (5) and (6) prove (4) and hence the statement.
|
{
"resource_path": "IMO/segmented/en-IMO2010SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
78fb861e-021d-5c1d-9d30-0539860b513d
| 23,930
|
Given six positive numbers $a, b, c, d, e, f$ such that $a<b<c<d<e<f$. Let $a+c+e=S$ and $b+d+f=T$. Prove that $$ 2 S T>\sqrt{3(S+T)(S(b d+b f+d f)+T(a c+a e+c e))} $$ (South Korea)
|
We introduce the expressions $\sigma$ and $\tau$ as in the previous solutions. The idea of the solution is to change the values of variables $a, \ldots, f$ keeping the left-hand side unchanged and increasing the right-hand side; it will lead to a simpler inequality which can be proved in a direct way. Namely, we change the variables (i) keeping the (non-strict) inequalities $a \leq b \leq c \leq d \leq$ $e \leq f$; (ii) keeping the values of sums $S$ and $T$ unchanged; and finally (iii) increasing the values of $\sigma$ and $\tau$. Then the left-hand side of (1) remains unchanged, while the right-hand side increases. Hence, the inequality (1) (and even a non-strict version of (1)) for the changed values would imply the same (strict) inequality for the original values. First, we find the sufficient conditions for (ii) and (iii) to be satisfied. Lemma. Let $x, y, z>0$; denote $U(x, y, z)=x+y+z, v(x, y, z)=x y+x z+y z$. Suppose that $x^{\prime}+y^{\prime}=x+y$ but $|x-y| \geq\left|x^{\prime}-y^{\prime}\right| ;$ then we have $U\left(x^{\prime}, y^{\prime}, z\right)=U(x, y, z)$ and $v\left(x^{\prime}, y^{\prime}, z\right) \geq$ $v(x, y, z)$ with equality achieved only when $|x-y|=\left|x^{\prime}-y^{\prime}\right|$. Proof. The first equality is obvious. For the second, we have $$ \begin{aligned} v\left(x^{\prime}, y^{\prime}, z\right)=z\left(x^{\prime}+y^{\prime}\right)+x^{\prime} y^{\prime} & =z\left(x^{\prime}+y^{\prime}\right)+\frac{\left(x^{\prime}+y^{\prime}\right)^{2}-\left(x^{\prime}-y^{\prime}\right)^{2}}{4} \\ & \geq z(x+y)+\frac{(x+y)^{2}-(x-y)^{2}}{4}=v(x, y, z) \end{aligned} $$ with the equality achieved only for $\left(x^{\prime}-y^{\prime}\right)^{2}=(x-y)^{2} \Longleftrightarrow\left|x^{\prime}-y^{\prime}\right|=|x-y|$, as desired. Now, we apply Lemma several times making the following changes. For each change, we denote the new values by the same letters to avoid cumbersome notations. 1. Let $k=\frac{d-c}{2}$. Replace $(b, c, d, e)$ by $(b+k, c+k, d-k, e-k)$. After the change we have $a<b<c=d<e<f$, the values of $S, T$ remain unchanged, but $\sigma, \tau$ strictly increase by Lemma. 2. Let $\ell=\frac{e-d}{2}$. Replace $(c, d, e, f)$ by $(c+\ell, d+\ell, e-\ell, f-\ell)$. After the change we have $a<b<c=d=e<f$, the values of $S, T$ remain unchanged, but $\sigma, \tau$ strictly increase by the Lemma. 3. Finally, let $m=\frac{c-b}{3}$. Replace $(a, b, c, d, e, f)$ by $(a+2 m, b+2 m, c-m, d-m, e-m, f-m)$. After the change, we have $a<b=c=d=e<f$ and $S, T$ are unchanged. To check (iii), we observe that our change can be considered as a composition of two changes: $(a, b, c, d) \rightarrow$ $(a+m, b+m, c-m, d-m)$ and $(a, b, e, f) \rightarrow(a+m, b+m, e-m, f-m)$. It is easy to see that each of these two consecutive changes satisfy the conditions of the Lemma, hence the values of $\sigma$ and $\tau$ increase. Finally, we come to the situation when $a<b=c=d=e<f$, and we need to prove the inequality $$ \begin{aligned} 2(a+2 b)(2 b+f) & \geq \sqrt{3(a+4 b+f)\left((a+2 b)\left(b^{2}+2 b f\right)+(2 b+f)\left(2 a b+b^{2}\right)\right)} \\ & =\sqrt{3 b(a+4 b+f) \cdot((a+2 b)(b+2 f)+(2 b+f)(2 a+b))} \end{aligned} $$ Now, observe that $$ 2 \cdot 2(a+2 b)(2 b+f)=3 b(a+4 b+f)+((a+2 b)(b+2 f)+(2 a+b)(2 b+f)) $$ Hence (4) rewrites as $$ \begin{aligned} 3 b(a+4 b+f) & +((a+2 b)(b+2 f)+(2 a+b)(2 b+f)) \\ & \geq 2 \sqrt{3 b(a+4 b+f) \cdot((a+2 b)(b+2 f)+(2 b+f)(2 a+b))} \end{aligned} $$ which is simply the AM-GM inequality. Comment 3. Here, we also can find all the cases of equality. Actually, it is easy to see that if some two numbers among $b, c, d, e$ are distinct then one can use Lemma to increase the right-hand side of (1). Further, if $b=c=d=e$, then we need equality in (4); this means that we apply AM-GM to equal numbers, that is, $$ 3 b(a+4 b+f)=(a+2 b)(b+2 f)+(2 a+b)(2 b+f) $$ which leads to the same equality as in Comment 1.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Given six positive numbers $a, b, c, d, e, f$ such that $a<b<c<d<e<f$. Let $a+c+e=S$ and $b+d+f=T$. Prove that $$ 2 S T>\sqrt{3(S+T)(S(b d+b f+d f)+T(a c+a e+c e))} $$ (South Korea)
|
We introduce the expressions $\sigma$ and $\tau$ as in the previous solutions. The idea of the solution is to change the values of variables $a, \ldots, f$ keeping the left-hand side unchanged and increasing the right-hand side; it will lead to a simpler inequality which can be proved in a direct way. Namely, we change the variables (i) keeping the (non-strict) inequalities $a \leq b \leq c \leq d \leq$ $e \leq f$; (ii) keeping the values of sums $S$ and $T$ unchanged; and finally (iii) increasing the values of $\sigma$ and $\tau$. Then the left-hand side of (1) remains unchanged, while the right-hand side increases. Hence, the inequality (1) (and even a non-strict version of (1)) for the changed values would imply the same (strict) inequality for the original values. First, we find the sufficient conditions for (ii) and (iii) to be satisfied. Lemma. Let $x, y, z>0$; denote $U(x, y, z)=x+y+z, v(x, y, z)=x y+x z+y z$. Suppose that $x^{\prime}+y^{\prime}=x+y$ but $|x-y| \geq\left|x^{\prime}-y^{\prime}\right| ;$ then we have $U\left(x^{\prime}, y^{\prime}, z\right)=U(x, y, z)$ and $v\left(x^{\prime}, y^{\prime}, z\right) \geq$ $v(x, y, z)$ with equality achieved only when $|x-y|=\left|x^{\prime}-y^{\prime}\right|$. Proof. The first equality is obvious. For the second, we have $$ \begin{aligned} v\left(x^{\prime}, y^{\prime}, z\right)=z\left(x^{\prime}+y^{\prime}\right)+x^{\prime} y^{\prime} & =z\left(x^{\prime}+y^{\prime}\right)+\frac{\left(x^{\prime}+y^{\prime}\right)^{2}-\left(x^{\prime}-y^{\prime}\right)^{2}}{4} \\ & \geq z(x+y)+\frac{(x+y)^{2}-(x-y)^{2}}{4}=v(x, y, z) \end{aligned} $$ with the equality achieved only for $\left(x^{\prime}-y^{\prime}\right)^{2}=(x-y)^{2} \Longleftrightarrow\left|x^{\prime}-y^{\prime}\right|=|x-y|$, as desired. Now, we apply Lemma several times making the following changes. For each change, we denote the new values by the same letters to avoid cumbersome notations. 1. Let $k=\frac{d-c}{2}$. Replace $(b, c, d, e)$ by $(b+k, c+k, d-k, e-k)$. After the change we have $a<b<c=d<e<f$, the values of $S, T$ remain unchanged, but $\sigma, \tau$ strictly increase by Lemma. 2. Let $\ell=\frac{e-d}{2}$. Replace $(c, d, e, f)$ by $(c+\ell, d+\ell, e-\ell, f-\ell)$. After the change we have $a<b<c=d=e<f$, the values of $S, T$ remain unchanged, but $\sigma, \tau$ strictly increase by the Lemma. 3. Finally, let $m=\frac{c-b}{3}$. Replace $(a, b, c, d, e, f)$ by $(a+2 m, b+2 m, c-m, d-m, e-m, f-m)$. After the change, we have $a<b=c=d=e<f$ and $S, T$ are unchanged. To check (iii), we observe that our change can be considered as a composition of two changes: $(a, b, c, d) \rightarrow$ $(a+m, b+m, c-m, d-m)$ and $(a, b, e, f) \rightarrow(a+m, b+m, e-m, f-m)$. It is easy to see that each of these two consecutive changes satisfy the conditions of the Lemma, hence the values of $\sigma$ and $\tau$ increase. Finally, we come to the situation when $a<b=c=d=e<f$, and we need to prove the inequality $$ \begin{aligned} 2(a+2 b)(2 b+f) & \geq \sqrt{3(a+4 b+f)\left((a+2 b)\left(b^{2}+2 b f\right)+(2 b+f)\left(2 a b+b^{2}\right)\right)} \\ & =\sqrt{3 b(a+4 b+f) \cdot((a+2 b)(b+2 f)+(2 b+f)(2 a+b))} \end{aligned} $$ Now, observe that $$ 2 \cdot 2(a+2 b)(2 b+f)=3 b(a+4 b+f)+((a+2 b)(b+2 f)+(2 a+b)(2 b+f)) $$ Hence (4) rewrites as $$ \begin{aligned} 3 b(a+4 b+f) & +((a+2 b)(b+2 f)+(2 a+b)(2 b+f)) \\ & \geq 2 \sqrt{3 b(a+4 b+f) \cdot((a+2 b)(b+2 f)+(2 b+f)(2 a+b))} \end{aligned} $$ which is simply the AM-GM inequality. Comment 3. Here, we also can find all the cases of equality. Actually, it is easy to see that if some two numbers among $b, c, d, e$ are distinct then one can use Lemma to increase the right-hand side of (1). Further, if $b=c=d=e$, then we need equality in (4); this means that we apply AM-GM to equal numbers, that is, $$ 3 b(a+4 b+f)=(a+2 b)(b+2 f)+(2 a+b)(2 b+f) $$ which leads to the same equality as in Comment 1.
|
{
"resource_path": "IMO/segmented/en-IMO2010SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
78fb861e-021d-5c1d-9d30-0539860b513d
| 23,930
|
$n \geq 4$ players participated in a tennis tournament. Any two players have played exactly one game, and there was no tie game. We call a company of four players bad if one player was defeated by the other three players, and each of these three players won a game and lost another game among themselves. Suppose that there is no bad company in this tournament. Let $w_{i}$ and $\ell_{i}$ be respectively the number of wins and losses of the $i$ th player. Prove that $$ \sum_{i=1}^{n}\left(w_{i}-\ell_{i}\right)^{3} \geq 0 $$ (South Korea)
|
For any tournament $T$ satisfying the problem condition, denote by $S(T)$ sum under consideration, namely $$ S(T)=\sum_{i=1}^{n}\left(w_{i}-\ell_{i}\right)^{3} $$ First, we show that the statement holds if a tournament $T$ has only 4 players. Actually, let $A=\left(a_{1}, a_{2}, a_{3}, a_{4}\right)$ be the number of wins of the players; we may assume that $a_{1} \geq a_{2} \geq a_{3} \geq a_{4}$. We have $a_{1}+a_{2}+a_{3}+a_{4}=\binom{4}{2}=6$, hence $a_{4} \leq 1$. If $a_{4}=0$, then we cannot have $a_{1}=a_{2}=a_{3}=2$, otherwise the company of all players is bad. Hence we should have $A=(3,2,1,0)$, and $S(T)=3^{3}+1^{3}+(-1)^{3}+(-3)^{3}=0$. On the other hand, if $a_{4}=1$, then only two possibilities, $A=(3,1,1,1)$ and $A=(2,2,1,1)$ can take place. In the former case we have $S(T)=3^{3}+3 \cdot(-2)^{3}>0$, while in the latter one $S(T)=1^{3}+1^{3}+(-1)^{3}+(-1)^{3}=0$, as desired. Now we turn to the general problem. Consider a tournament $T$ with no bad companies and enumerate the players by the numbers from 1 to $n$. For every 4 players $i_{1}, i_{2}, i_{3}, i_{4}$ consider a "sub-tournament" $T_{i_{1} i_{2} i_{3} i_{4}}$ consisting of only these players and the games which they performed with each other. By the abovementioned, we have $S\left(T_{i_{1} i_{2} i_{3} i_{4}}\right) \geq 0$. Our aim is to prove that $$ S(T)=\sum_{i_{1}, i_{2}, i_{3}, i_{4}} S\left(T_{i_{1} i_{2} i_{3} i_{4}}\right) $$ where the sum is taken over all 4 -tuples of distinct numbers from the set $\{1, \ldots, n\}$. This way the problem statement will be established. We interpret the number $\left(w_{i}-\ell_{i}\right)^{3}$ as following. For $i \neq j$, let $\varepsilon_{i j}=1$ if the $i$ th player wins against the $j$ th one, and $\varepsilon_{i j}=-1$ otherwise. Then $$ \left(w_{i}-\ell_{i}\right)^{3}=\left(\sum_{j \neq i} \varepsilon_{i j}\right)^{3}=\sum_{j_{1}, j_{2}, j_{3} \neq i} \varepsilon_{i j_{1}} \varepsilon_{i j_{2}} \varepsilon_{i j_{3}} . $$ Hence, $$ S(T)=\sum_{i \notin\left\{j_{1}, j_{2}, j_{3}\right\}} \varepsilon_{i j_{1}} \varepsilon_{i j_{2}} \varepsilon_{i j_{3}} $$ To simplify this expression, consider all the terms in this sum where two indices are equal. If, for instance, $j_{1}=j_{2}$, then the term contains $\varepsilon_{i j_{1}}^{2}=1$, so we can replace this term by $\varepsilon_{i j_{3}}$. Make such replacements for each such term; obviously, after this change each term of the form $\varepsilon_{i j_{3}}$ will appear $P(T)$ times, hence $$ S(T)=\sum_{\left|\left\{i, j_{1}, j_{2}, j_{3}\right\}\right|=4} \varepsilon_{i j_{1}} \varepsilon_{i j_{2}} \varepsilon_{i j_{3}}+P(T) \sum_{i \neq j} \varepsilon_{i j}=S_{1}(T)+P(T) S_{2}(T) $$ We show that $S_{2}(T)=0$ and hence $S(T)=S_{1}(T)$ for each tournament. Actually, note that $\varepsilon_{i j}=-\varepsilon_{j i}$, and the whole sum can be split into such pairs. Since the sum in each pair is 0 , so is $S_{2}(T)$. Thus the desired equality (2) rewrites as $$ S_{1}(T)=\sum_{i_{1}, i_{2}, i_{3}, i_{4}} S_{1}\left(T_{i_{1} i_{2} i_{3} i_{4}}\right) $$ Now, if all the numbers $j_{1}, j_{2}, j_{3}$ are distinct, then the set $\left\{i, j_{1}, j_{2}, j_{3}\right\}$ is contained in exactly one 4 -tuple, hence the term $\varepsilon_{i j_{1}} \varepsilon_{i j_{2}} \varepsilon_{i j_{3}}$ appears in the right-hand part of (3) exactly once, as well as in the left-hand part. Clearly, there are no other terms in both parts, so the equality is established.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
$n \geq 4$ players participated in a tennis tournament. Any two players have played exactly one game, and there was no tie game. We call a company of four players bad if one player was defeated by the other three players, and each of these three players won a game and lost another game among themselves. Suppose that there is no bad company in this tournament. Let $w_{i}$ and $\ell_{i}$ be respectively the number of wins and losses of the $i$ th player. Prove that $$ \sum_{i=1}^{n}\left(w_{i}-\ell_{i}\right)^{3} \geq 0 $$ (South Korea)
|
For any tournament $T$ satisfying the problem condition, denote by $S(T)$ sum under consideration, namely $$ S(T)=\sum_{i=1}^{n}\left(w_{i}-\ell_{i}\right)^{3} $$ First, we show that the statement holds if a tournament $T$ has only 4 players. Actually, let $A=\left(a_{1}, a_{2}, a_{3}, a_{4}\right)$ be the number of wins of the players; we may assume that $a_{1} \geq a_{2} \geq a_{3} \geq a_{4}$. We have $a_{1}+a_{2}+a_{3}+a_{4}=\binom{4}{2}=6$, hence $a_{4} \leq 1$. If $a_{4}=0$, then we cannot have $a_{1}=a_{2}=a_{3}=2$, otherwise the company of all players is bad. Hence we should have $A=(3,2,1,0)$, and $S(T)=3^{3}+1^{3}+(-1)^{3}+(-3)^{3}=0$. On the other hand, if $a_{4}=1$, then only two possibilities, $A=(3,1,1,1)$ and $A=(2,2,1,1)$ can take place. In the former case we have $S(T)=3^{3}+3 \cdot(-2)^{3}>0$, while in the latter one $S(T)=1^{3}+1^{3}+(-1)^{3}+(-1)^{3}=0$, as desired. Now we turn to the general problem. Consider a tournament $T$ with no bad companies and enumerate the players by the numbers from 1 to $n$. For every 4 players $i_{1}, i_{2}, i_{3}, i_{4}$ consider a "sub-tournament" $T_{i_{1} i_{2} i_{3} i_{4}}$ consisting of only these players and the games which they performed with each other. By the abovementioned, we have $S\left(T_{i_{1} i_{2} i_{3} i_{4}}\right) \geq 0$. Our aim is to prove that $$ S(T)=\sum_{i_{1}, i_{2}, i_{3}, i_{4}} S\left(T_{i_{1} i_{2} i_{3} i_{4}}\right) $$ where the sum is taken over all 4 -tuples of distinct numbers from the set $\{1, \ldots, n\}$. This way the problem statement will be established. We interpret the number $\left(w_{i}-\ell_{i}\right)^{3}$ as following. For $i \neq j$, let $\varepsilon_{i j}=1$ if the $i$ th player wins against the $j$ th one, and $\varepsilon_{i j}=-1$ otherwise. Then $$ \left(w_{i}-\ell_{i}\right)^{3}=\left(\sum_{j \neq i} \varepsilon_{i j}\right)^{3}=\sum_{j_{1}, j_{2}, j_{3} \neq i} \varepsilon_{i j_{1}} \varepsilon_{i j_{2}} \varepsilon_{i j_{3}} . $$ Hence, $$ S(T)=\sum_{i \notin\left\{j_{1}, j_{2}, j_{3}\right\}} \varepsilon_{i j_{1}} \varepsilon_{i j_{2}} \varepsilon_{i j_{3}} $$ To simplify this expression, consider all the terms in this sum where two indices are equal. If, for instance, $j_{1}=j_{2}$, then the term contains $\varepsilon_{i j_{1}}^{2}=1$, so we can replace this term by $\varepsilon_{i j_{3}}$. Make such replacements for each such term; obviously, after this change each term of the form $\varepsilon_{i j_{3}}$ will appear $P(T)$ times, hence $$ S(T)=\sum_{\left|\left\{i, j_{1}, j_{2}, j_{3}\right\}\right|=4} \varepsilon_{i j_{1}} \varepsilon_{i j_{2}} \varepsilon_{i j_{3}}+P(T) \sum_{i \neq j} \varepsilon_{i j}=S_{1}(T)+P(T) S_{2}(T) $$ We show that $S_{2}(T)=0$ and hence $S(T)=S_{1}(T)$ for each tournament. Actually, note that $\varepsilon_{i j}=-\varepsilon_{j i}$, and the whole sum can be split into such pairs. Since the sum in each pair is 0 , so is $S_{2}(T)$. Thus the desired equality (2) rewrites as $$ S_{1}(T)=\sum_{i_{1}, i_{2}, i_{3}, i_{4}} S_{1}\left(T_{i_{1} i_{2} i_{3} i_{4}}\right) $$ Now, if all the numbers $j_{1}, j_{2}, j_{3}$ are distinct, then the set $\left\{i, j_{1}, j_{2}, j_{3}\right\}$ is contained in exactly one 4 -tuple, hence the term $\varepsilon_{i j_{1}} \varepsilon_{i j_{2}} \varepsilon_{i j_{3}}$ appears in the right-hand part of (3) exactly once, as well as in the left-hand part. Clearly, there are no other terms in both parts, so the equality is established.
|
{
"resource_path": "IMO/segmented/en-IMO2010SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
89c31809-5b69-54af-af95-5794ef201dfb
| 23,951
|
$n \geq 4$ players participated in a tennis tournament. Any two players have played exactly one game, and there was no tie game. We call a company of four players bad if one player was defeated by the other three players, and each of these three players won a game and lost another game among themselves. Suppose that there is no bad company in this tournament. Let $w_{i}$ and $\ell_{i}$ be respectively the number of wins and losses of the $i$ th player. Prove that $$ \sum_{i=1}^{n}\left(w_{i}-\ell_{i}\right)^{3} \geq 0 $$ (South Korea)
|
Similarly to the first solution, we call the subsets of players as companies, and the $k$-element subsets will be called as $k$-companies. In any company of the players, call a player the local champion of the company if he defeated all other members of the company. Similarly, if a player lost all his games against the others in the company then call him the local loser of the company. Obviously every company has at most one local champion and at most one local loser. By the condition of the problem, whenever a 4-company has a local loser, then this company has a local champion as well. Suppose that $k$ is some positive integer, and let us count all cases when a player is the local champion of some $k$-company. The $i$ th player won against $w_{i}$ other player. To be the local champion of a $k$-company, he must be a member of the company, and the other $k-1$ members must be chosen from those whom he defeated. Therefore, the $i$ th player is the local champion of $\binom{w_{i}}{k-1} k$-companies. Hence, the total number of local champions of all $k$-companies is $\sum_{i=1}^{n}\binom{w_{i}}{k-1}$. Similarly, the total number of local losers of the $k$-companies is $\sum_{i=1}^{n}\binom{\ell_{i}}{k-1}$. Now apply this for $k=2,3$ and 4. Since every game has a winner and a loser, we have $\sum_{i=1}^{n} w_{i}=\sum_{i=1}^{n} \ell_{i}=\binom{n}{2}$, and hence $$ \sum_{i=1}^{n}\left(w_{i}-\ell_{i}\right)=0 $$ In every 3-company, either the players defeated one another in a cycle or the company has both a local champion and a local loser. Therefore, the total number of local champions and local losers in the 3-companies is the same, $\sum_{i=1}^{n}\binom{w_{i}}{2}=\sum_{i=1}^{n}\binom{\ell_{i}}{2}$. So we have $$ \sum_{i=1}^{n}\left(\binom{w_{i}}{2}-\binom{\ell_{i}}{2}\right)=0 $$ In every 4-company, by the problem's condition, the number of local losers is less than or equal to the number of local champions. Then the same holds for the total numbers of local champions and local losers in all 4-companies, so $\sum_{i=1}^{n}\binom{w_{i}}{3} \geq \sum_{i=1}^{n}\binom{\ell_{i}}{3}$. Hence, $$ \sum_{i=1}^{n}\left(\binom{w_{i}}{3}-\binom{\ell_{i}}{3}\right) \geq 0 $$ Now we establish the problem statement (1) as a linear combination of (4), (5) and (6). It is easy check that $$ (x-y)^{3}=24\left(\binom{x}{3}-\binom{y}{3}\right)+24\left(\binom{x}{2}-\binom{y}{2}\right)-\left(3(x+y)^{2}-4\right)(x-y) $$ Apply this identity to $x=w_{1}$ and $y=\ell_{i}$. Since every player played $n-1$ games, we have $w_{i}+\ell_{i}=n-1$, and thus $$ \left(w_{i}-\ell_{i}\right)^{3}=24\left(\binom{w_{i}}{3}-\binom{\ell_{i}}{3}\right)+24\left(\binom{w_{i}}{2}-\binom{\ell_{i}}{2}\right)-\left(3(n-1)^{2}-4\right)\left(w_{i}-\ell_{i}\right) $$ Then $$ \sum_{i=1}^{n}\left(w_{i}-\ell_{i}\right)^{3}=24 \underbrace{\sum_{i=1}^{n}\left(\binom{w_{i}}{3}-\binom{\ell_{i}}{3}\right)}_{\geq 0}+24 \underbrace{\sum_{i=1}^{n}\left(\binom{w_{i}}{2}-\binom{\ell_{i}}{2}\right)}_{0}-\left(3(n-1)^{2}-4\right) \underbrace{\sum_{i=1}^{n}\left(w_{i}-\ell_{i}\right)}_{0} \geq 0 $$
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
$n \geq 4$ players participated in a tennis tournament. Any two players have played exactly one game, and there was no tie game. We call a company of four players bad if one player was defeated by the other three players, and each of these three players won a game and lost another game among themselves. Suppose that there is no bad company in this tournament. Let $w_{i}$ and $\ell_{i}$ be respectively the number of wins and losses of the $i$ th player. Prove that $$ \sum_{i=1}^{n}\left(w_{i}-\ell_{i}\right)^{3} \geq 0 $$ (South Korea)
|
Similarly to the first solution, we call the subsets of players as companies, and the $k$-element subsets will be called as $k$-companies. In any company of the players, call a player the local champion of the company if he defeated all other members of the company. Similarly, if a player lost all his games against the others in the company then call him the local loser of the company. Obviously every company has at most one local champion and at most one local loser. By the condition of the problem, whenever a 4-company has a local loser, then this company has a local champion as well. Suppose that $k$ is some positive integer, and let us count all cases when a player is the local champion of some $k$-company. The $i$ th player won against $w_{i}$ other player. To be the local champion of a $k$-company, he must be a member of the company, and the other $k-1$ members must be chosen from those whom he defeated. Therefore, the $i$ th player is the local champion of $\binom{w_{i}}{k-1} k$-companies. Hence, the total number of local champions of all $k$-companies is $\sum_{i=1}^{n}\binom{w_{i}}{k-1}$. Similarly, the total number of local losers of the $k$-companies is $\sum_{i=1}^{n}\binom{\ell_{i}}{k-1}$. Now apply this for $k=2,3$ and 4. Since every game has a winner and a loser, we have $\sum_{i=1}^{n} w_{i}=\sum_{i=1}^{n} \ell_{i}=\binom{n}{2}$, and hence $$ \sum_{i=1}^{n}\left(w_{i}-\ell_{i}\right)=0 $$ In every 3-company, either the players defeated one another in a cycle or the company has both a local champion and a local loser. Therefore, the total number of local champions and local losers in the 3-companies is the same, $\sum_{i=1}^{n}\binom{w_{i}}{2}=\sum_{i=1}^{n}\binom{\ell_{i}}{2}$. So we have $$ \sum_{i=1}^{n}\left(\binom{w_{i}}{2}-\binom{\ell_{i}}{2}\right)=0 $$ In every 4-company, by the problem's condition, the number of local losers is less than or equal to the number of local champions. Then the same holds for the total numbers of local champions and local losers in all 4-companies, so $\sum_{i=1}^{n}\binom{w_{i}}{3} \geq \sum_{i=1}^{n}\binom{\ell_{i}}{3}$. Hence, $$ \sum_{i=1}^{n}\left(\binom{w_{i}}{3}-\binom{\ell_{i}}{3}\right) \geq 0 $$ Now we establish the problem statement (1) as a linear combination of (4), (5) and (6). It is easy check that $$ (x-y)^{3}=24\left(\binom{x}{3}-\binom{y}{3}\right)+24\left(\binom{x}{2}-\binom{y}{2}\right)-\left(3(x+y)^{2}-4\right)(x-y) $$ Apply this identity to $x=w_{1}$ and $y=\ell_{i}$. Since every player played $n-1$ games, we have $w_{i}+\ell_{i}=n-1$, and thus $$ \left(w_{i}-\ell_{i}\right)^{3}=24\left(\binom{w_{i}}{3}-\binom{\ell_{i}}{3}\right)+24\left(\binom{w_{i}}{2}-\binom{\ell_{i}}{2}\right)-\left(3(n-1)^{2}-4\right)\left(w_{i}-\ell_{i}\right) $$ Then $$ \sum_{i=1}^{n}\left(w_{i}-\ell_{i}\right)^{3}=24 \underbrace{\sum_{i=1}^{n}\left(\binom{w_{i}}{3}-\binom{\ell_{i}}{3}\right)}_{\geq 0}+24 \underbrace{\sum_{i=1}^{n}\left(\binom{w_{i}}{2}-\binom{\ell_{i}}{2}\right)}_{0}-\left(3(n-1)^{2}-4\right) \underbrace{\sum_{i=1}^{n}\left(w_{i}-\ell_{i}\right)}_{0} \geq 0 $$
|
{
"resource_path": "IMO/segmented/en-IMO2010SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
89c31809-5b69-54af-af95-5794ef201dfb
| 23,951
|
Let $P_{1}, \ldots, P_{s}$ be arithmetic progressions of integers, the following conditions being satisfied: (i) each integer belongs to at least one of them; (ii) each progression contains a number which does not belong to other progressions. Denote by $n$ the least common multiple of steps of these progressions; let $n=p_{1}^{\alpha_{1}} \ldots p_{k}^{\alpha_{k}}$ be its prime factorization. Prove that $$ s \geq 1+\sum_{i=1}^{k} \alpha_{i}\left(p_{i}-1\right) $$ (Germany)
|
We start with introducing some notation. For positive integer $r$, we denote $[r]=\{1,2, \ldots, r\}$. Next, we say that a set of progressions $\mathcal{P}=\left\{P_{1}, \ldots, P_{s}\right\}$ cover $\mathbb{Z}$ if each integer belongs to some of them; we say that this covering is minimal if no proper subset of $\mathcal{P}$ covers $\mathbb{Z}$. Obviously, each covering contains a minimal subcovering. Next, for a minimal covering $\left\{P_{1}, \ldots, P_{s}\right\}$ and for every $1 \leq i \leq s$, let $d_{i}$ be the step of progression $P_{i}$, and $h_{i}$ be some number which is contained in $P_{i}$ but in none of the other progressions. We assume that $n>1$, otherwise the problem is trivial. This implies $d_{i}>1$, otherwise the progression $P_{i}$ covers all the numbers, and $n=1$. We will prove a more general statement, namely the following Claim. Assume that the progressions $P_{1}, \ldots, P_{s}$ and number $n=p_{1}^{\alpha_{1}} \ldots p_{k}^{\alpha_{k}}>1$ are chosen as in the problem statement. Moreover, choose some nonempty set of indices $I=\left\{i_{1}, \ldots, i_{t}\right\} \subseteq[k]$ and some positive integer $\beta_{i} \leq \alpha_{i}$ for every $i \in I$. Consider the set of indices $$ T=\left\{j: 1 \leq j \leq s, \text { and } p_{i}^{\alpha_{i}-\beta_{i}+1} \mid d_{j} \text { for some } i \in I\right\} $$ Then $$ |T| \geq 1+\sum_{i \in I} \beta_{i}\left(p_{i}-1\right) $$ Observe that the Claim for $I=[k]$ and $\beta_{i}=\alpha_{i}$ implies the problem statement, since the left-hand side in (2) is not greater than $s$. Hence, it suffices to prove the Claim. 1. First, we prove the Claim assuming that all $d_{j}$ 's are prime numbers. If for some $1 \leq i \leq k$ we have at least $p_{i}$ progressions with the step $p_{i}$, then they do not intersect and hence cover all the integers; it means that there are no other progressions, and $n=p_{i}$; the Claim is trivial in this case. Now assume that for every $1 \leq i \leq k$, there are not more than $p_{i}-1$ progressions with step $p_{i}$; each such progression covers the numbers with a fixed residue modulo $p_{i}$, therefore there exists a residue $q_{i} \bmod p_{i}$ which is not touched by these progressions. By the Chinese Remainder Theorem, there exists a number $q$ such that $q \equiv q_{i}\left(\bmod p_{i}\right)$ for all $1 \leq i \leq k$; this number cannot be covered by any progression with step $p_{i}$, hence it is not covered at all. A contradiction. 2. Now, we assume that the general Claim is not valid, and hence we consider a counterexample $\left\{P_{1}, \ldots, P_{s}\right\}$ for the Claim; we can choose it to be minimal in the following sense: - the number $n$ is minimal possible among all the counterexamples; - the sum $\sum_{i} d_{i}$ is minimal possible among all the counterexamples having the chosen value of $n$. As was mentioned above, not all numbers $d_{i}$ are primes; hence we can assume that $d_{1}$ is composite, say $p_{1} \mid d_{1}$ and $d_{1}^{\prime}=\frac{d_{1}}{p_{1}}>1$. Consider a progression $P_{1}^{\prime}$ having the step $d_{1}^{\prime}$, and containing $P_{1}$. We will focus on two coverings constructed as follows. (i) Surely, the progressions $P_{1}^{\prime}, P_{2}, \ldots, P_{s}$ cover $\mathbb{Z}$, though this covering in not necessarily minimal. So, choose some minimal subcovering $\mathcal{P}^{\prime}$ in it; surely $P_{1}^{\prime} \in \mathcal{P}^{\prime}$ since $h_{1}$ is not covered by $P_{2}, \ldots, P_{s}$, so we may assume that $\mathcal{P}^{\prime}=\left\{P_{1}^{\prime}, P_{2}, \ldots, P_{s^{\prime}}\right\}$ for some $s^{\prime} \leq s$. Furthermore, the period of the covering $\mathcal{P}^{\prime}$ can appear to be less than $n$; so we denote this period by $$ n^{\prime}=p_{1}^{\alpha_{1}-\sigma_{1}} \ldots p_{k}^{\alpha_{k}-\sigma_{k}}=\text { l.c.m. }\left(d_{1}^{\prime}, d_{2}, \ldots, d_{s^{\prime}}\right) $$ Observe that for each $P_{j} \notin \mathcal{P}^{\prime}$, we have $h_{j} \in P_{1}^{\prime}$, otherwise $h_{j}$ would not be covered by $\mathcal{P}$. (ii) On the other hand, each nonempty set of the form $R_{i}=P_{i} \cap P_{1}^{\prime}(1 \leq i \leq s)$ is also a progression with a step $r_{i}=$ l.c.m. $\left(d_{i}, d_{1}^{\prime}\right)$, and such sets cover $P_{1}^{\prime}$. Scaling these progressions with the ratio $1 / d_{1}^{\prime}$, we obtain the progressions $Q_{i}$ with steps $q_{i}=r_{i} / d_{1}^{\prime}$ which cover $\mathbb{Z}$. Now we choose a minimal subcovering $\mathcal{Q}$ of this covering; again we should have $Q_{1} \in \mathcal{Q}$ by the reasons of $h_{1}$. Now, denote the period of $\mathcal{Q}$ by $$ n^{\prime \prime}=\text { l.c.m. }\left\{q_{i}: Q_{i} \in \mathcal{Q}\right\}=\frac{\text { l.c.m. }\left\{r_{i}: Q_{i} \in \mathcal{Q}\right\}}{d_{1}^{\prime}}=\frac{p_{1}^{\gamma_{1}} \ldots p_{k}^{\gamma_{k}}}{d_{1}^{\prime}} $$ Note that if $h_{j} \in P_{1}^{\prime}$, then the image of $h_{j}$ under the scaling can be covered by $Q_{j}$ only; so, in this case we have $Q_{j} \in \mathcal{Q}$. Our aim is to find the desired number of progressions in coverings $\mathcal{P}$ and $\mathcal{Q}$. First, we have $n \geq n^{\prime}$, and the sum of the steps in $\mathcal{P}^{\prime}$ is less than that in $\mathcal{P}$; hence the Claim is valid for $\mathcal{P}^{\prime}$. We apply it to the set of indices $I^{\prime}=\left\{i \in I: \beta_{i}>\sigma_{i}\right\}$ and the exponents $\beta_{i}^{\prime}=\beta_{i}-\sigma_{i}$; hence the set under consideration is $$ T^{\prime}=\left\{j: 1 \leq j \leq s^{\prime}, \text { and } p_{i}^{\left(\alpha_{i}-\sigma_{i}\right)-\beta_{i}^{\prime}+1}=p_{i}^{\alpha_{i}-\beta_{i}+1} \mid d_{j} \text { for some } i \in I^{\prime}\right\} \subseteq T \cap\left[s^{\prime}\right], $$ and we obtain that $$ \left|T \cap\left[s^{\prime}\right]\right| \geq\left|T^{\prime}\right| \geq 1+\sum_{i \in I^{\prime}}\left(\beta_{i}-\sigma_{i}\right)\left(p_{i}-1\right)=1+\sum_{i \in I}\left(\beta_{i}-\sigma_{i}\right)_{+}\left(p_{i}-1\right) $$ where $(x)_{+}=\max \{x, 0\}$; the latter equality holds as for $i \notin I^{\prime}$ we have $\beta_{i} \leq \sigma_{i}$. Observe that $x=(x-y)_{+}+\min \{x, y\}$ for all $x, y$. So, if we find at least $$ G=\sum_{i \in I} \min \left\{\beta_{i}, \sigma_{i}\right\}\left(p_{i}-1\right) $$ indices in $T \cap\left\{s^{\prime}+1, \ldots, s\right\}$, then we would have $$ |T|=\left|T \cap\left[s^{\prime}\right]\right|+\left|T \cap\left\{s^{\prime}+1, \ldots, s\right\}\right| \geq 1+\sum_{i \in I}\left(\left(\beta_{i}-\sigma_{i}\right)_{+}+\min \left\{\beta_{i}, \sigma_{i}\right\}\right)\left(p_{i}-1\right)=1+\sum_{i \in I} \beta_{i}\left(p_{i}-1\right) $$ thus leading to a contradiction with the choice of $\mathcal{P}$. We will find those indices among the indices of progressions in $\mathcal{Q}$. 3. Now denote $I^{\prime \prime}=\left\{i \in I: \sigma_{i}>0\right\}$ and consider some $i \in I^{\prime \prime}$; then $p_{i}^{\alpha_{i}} \nmid n^{\prime}$. On the other hand, there exists an index $j(i)$ such that $p_{i}^{\alpha_{i}} \mid d_{j(i)}$; this means that $d_{j(i)} \backslash n^{\prime}$ and hence $P_{j(i)}$ cannot appear in $\mathcal{P}^{\prime}$, so $j(i)>s^{\prime}$. Moreover, we have observed before that in this case $h_{j(i)} \in P_{1}^{\prime}$, hence $Q_{j(i)} \in \mathcal{Q}$. This means that $q_{j(i)} \mid n^{\prime \prime}$, therefore $\gamma_{i}=\alpha_{i}$ for each $i \in I^{\prime \prime}$ (recall here that $q_{i}=r_{i} / d_{1}^{\prime}$ and hence $\left.d_{j(i)}\left|r_{j(i)}\right| d_{1}^{\prime} n^{\prime \prime}\right)$. Let $d_{1}^{\prime}=p_{1}^{\tau_{1}} \ldots p_{k}^{\tau_{k}}$. Then $n^{\prime \prime}=p_{1}^{\gamma_{1}-\tau_{1}} \ldots p_{k}^{\gamma_{i}-\tau_{i}}$. Now, if $i \in I^{\prime \prime}$, then for every $\beta$ the condition $p_{i}^{\left(\gamma_{i}-\tau_{i}\right)-\beta+1} \mid q_{j}$ is equivalent to $p_{i}^{\alpha_{i}-\beta+1} \mid r_{j}$. Note that $n^{\prime \prime} \leq n / d_{1}^{\prime}<n$, hence we can apply the Claim to the covering $\mathcal{Q}$. We perform this with the set of indices $I^{\prime \prime}$ and the exponents $\beta_{i}^{\prime \prime}=\min \left\{\beta_{i}, \sigma_{i}\right\}>0$. So, the set under consideration is $$ \begin{aligned} T^{\prime \prime} & =\left\{j: Q_{j} \in \mathcal{Q}, \text { and } p_{i}^{\left(\gamma_{i}-\tau_{i}\right)-\min \left\{\beta_{i}, \sigma_{i}\right\}+1} \mid q_{j} \text { for some } i \in I^{\prime \prime}\right\} \\ & =\left\{j: Q_{j} \in \mathcal{Q}, \text { and } p_{i}^{\alpha_{i}-\min \left\{\beta_{i}, \sigma_{i}\right\}+1} \mid r_{j} \text { for some } i \in I^{\prime \prime}\right\}, \end{aligned} $$ and we obtain $\left|T^{\prime \prime}\right| \geq 1+G$. Finally, we claim that $T^{\prime \prime} \subseteq T \cap\left(\{1\} \cup\left\{s^{\prime}+1, \ldots, s\right\}\right)$; then we will obtain $\left|T \cap\left\{s^{\prime}+1, \ldots, s\right\}\right| \geq G$, which is exactly what we need. To prove this, consider any $j \in T^{\prime \prime}$. Observe first that $\alpha_{i}-\min \left\{\beta_{i}, \sigma_{i}\right\}+1>\alpha_{i}-\sigma_{i} \geq \tau_{i}$, hence from $p_{i}^{\alpha_{i}-\min \left\{\beta_{i}, \sigma_{i}\right\}+1} \mid r_{j}=$ l.c.m. $\left(d_{1}^{\prime}, d_{j}\right)$ we have $p_{i}^{\alpha_{i}-\min \left\{\beta_{i}, \sigma_{i}\right\}+1} \mid d_{j}$, which means that $j \in T$. Next, the exponent of $p_{i}$ in $d_{j}$ is greater than that in $n^{\prime}$, which means that $P_{j} \notin \mathcal{P}^{\prime}$. This may appear only if $j=1$ or $j>s^{\prime}$, as desired. This completes the proof. Comment 2. A grid analogue of the Claim is also valid. It reads as following. Claim. Assume that the grid $N$ is covered by subgrids $L_{1}, L_{2}, \ldots, L_{s}$ so that (ii') each subgrid contains a point which is not covered by other subgrids; (iii) for each coordinate axis, there exists a subgrid $L_{i}$ orthogonal to this axis. Choose some set of indices $I=\left\{i_{1}, \ldots, i_{t}\right\} \subset[k]$, and consider the set of indices $$ T=\left\{j: 1 \leq j \leq s \text {, and } L_{j} \text { is orthogonal to the } i \text { th axis for some } i \in I\right\} $$ Then $$ |T| \geq 1+\sum_{i \in I}\left(n_{i}-1\right) $$ This Claim may be proved almost in the same way as in Solution 1.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $P_{1}, \ldots, P_{s}$ be arithmetic progressions of integers, the following conditions being satisfied: (i) each integer belongs to at least one of them; (ii) each progression contains a number which does not belong to other progressions. Denote by $n$ the least common multiple of steps of these progressions; let $n=p_{1}^{\alpha_{1}} \ldots p_{k}^{\alpha_{k}}$ be its prime factorization. Prove that $$ s \geq 1+\sum_{i=1}^{k} \alpha_{i}\left(p_{i}-1\right) $$ (Germany)
|
We start with introducing some notation. For positive integer $r$, we denote $[r]=\{1,2, \ldots, r\}$. Next, we say that a set of progressions $\mathcal{P}=\left\{P_{1}, \ldots, P_{s}\right\}$ cover $\mathbb{Z}$ if each integer belongs to some of them; we say that this covering is minimal if no proper subset of $\mathcal{P}$ covers $\mathbb{Z}$. Obviously, each covering contains a minimal subcovering. Next, for a minimal covering $\left\{P_{1}, \ldots, P_{s}\right\}$ and for every $1 \leq i \leq s$, let $d_{i}$ be the step of progression $P_{i}$, and $h_{i}$ be some number which is contained in $P_{i}$ but in none of the other progressions. We assume that $n>1$, otherwise the problem is trivial. This implies $d_{i}>1$, otherwise the progression $P_{i}$ covers all the numbers, and $n=1$. We will prove a more general statement, namely the following Claim. Assume that the progressions $P_{1}, \ldots, P_{s}$ and number $n=p_{1}^{\alpha_{1}} \ldots p_{k}^{\alpha_{k}}>1$ are chosen as in the problem statement. Moreover, choose some nonempty set of indices $I=\left\{i_{1}, \ldots, i_{t}\right\} \subseteq[k]$ and some positive integer $\beta_{i} \leq \alpha_{i}$ for every $i \in I$. Consider the set of indices $$ T=\left\{j: 1 \leq j \leq s, \text { and } p_{i}^{\alpha_{i}-\beta_{i}+1} \mid d_{j} \text { for some } i \in I\right\} $$ Then $$ |T| \geq 1+\sum_{i \in I} \beta_{i}\left(p_{i}-1\right) $$ Observe that the Claim for $I=[k]$ and $\beta_{i}=\alpha_{i}$ implies the problem statement, since the left-hand side in (2) is not greater than $s$. Hence, it suffices to prove the Claim. 1. First, we prove the Claim assuming that all $d_{j}$ 's are prime numbers. If for some $1 \leq i \leq k$ we have at least $p_{i}$ progressions with the step $p_{i}$, then they do not intersect and hence cover all the integers; it means that there are no other progressions, and $n=p_{i}$; the Claim is trivial in this case. Now assume that for every $1 \leq i \leq k$, there are not more than $p_{i}-1$ progressions with step $p_{i}$; each such progression covers the numbers with a fixed residue modulo $p_{i}$, therefore there exists a residue $q_{i} \bmod p_{i}$ which is not touched by these progressions. By the Chinese Remainder Theorem, there exists a number $q$ such that $q \equiv q_{i}\left(\bmod p_{i}\right)$ for all $1 \leq i \leq k$; this number cannot be covered by any progression with step $p_{i}$, hence it is not covered at all. A contradiction. 2. Now, we assume that the general Claim is not valid, and hence we consider a counterexample $\left\{P_{1}, \ldots, P_{s}\right\}$ for the Claim; we can choose it to be minimal in the following sense: - the number $n$ is minimal possible among all the counterexamples; - the sum $\sum_{i} d_{i}$ is minimal possible among all the counterexamples having the chosen value of $n$. As was mentioned above, not all numbers $d_{i}$ are primes; hence we can assume that $d_{1}$ is composite, say $p_{1} \mid d_{1}$ and $d_{1}^{\prime}=\frac{d_{1}}{p_{1}}>1$. Consider a progression $P_{1}^{\prime}$ having the step $d_{1}^{\prime}$, and containing $P_{1}$. We will focus on two coverings constructed as follows. (i) Surely, the progressions $P_{1}^{\prime}, P_{2}, \ldots, P_{s}$ cover $\mathbb{Z}$, though this covering in not necessarily minimal. So, choose some minimal subcovering $\mathcal{P}^{\prime}$ in it; surely $P_{1}^{\prime} \in \mathcal{P}^{\prime}$ since $h_{1}$ is not covered by $P_{2}, \ldots, P_{s}$, so we may assume that $\mathcal{P}^{\prime}=\left\{P_{1}^{\prime}, P_{2}, \ldots, P_{s^{\prime}}\right\}$ for some $s^{\prime} \leq s$. Furthermore, the period of the covering $\mathcal{P}^{\prime}$ can appear to be less than $n$; so we denote this period by $$ n^{\prime}=p_{1}^{\alpha_{1}-\sigma_{1}} \ldots p_{k}^{\alpha_{k}-\sigma_{k}}=\text { l.c.m. }\left(d_{1}^{\prime}, d_{2}, \ldots, d_{s^{\prime}}\right) $$ Observe that for each $P_{j} \notin \mathcal{P}^{\prime}$, we have $h_{j} \in P_{1}^{\prime}$, otherwise $h_{j}$ would not be covered by $\mathcal{P}$. (ii) On the other hand, each nonempty set of the form $R_{i}=P_{i} \cap P_{1}^{\prime}(1 \leq i \leq s)$ is also a progression with a step $r_{i}=$ l.c.m. $\left(d_{i}, d_{1}^{\prime}\right)$, and such sets cover $P_{1}^{\prime}$. Scaling these progressions with the ratio $1 / d_{1}^{\prime}$, we obtain the progressions $Q_{i}$ with steps $q_{i}=r_{i} / d_{1}^{\prime}$ which cover $\mathbb{Z}$. Now we choose a minimal subcovering $\mathcal{Q}$ of this covering; again we should have $Q_{1} \in \mathcal{Q}$ by the reasons of $h_{1}$. Now, denote the period of $\mathcal{Q}$ by $$ n^{\prime \prime}=\text { l.c.m. }\left\{q_{i}: Q_{i} \in \mathcal{Q}\right\}=\frac{\text { l.c.m. }\left\{r_{i}: Q_{i} \in \mathcal{Q}\right\}}{d_{1}^{\prime}}=\frac{p_{1}^{\gamma_{1}} \ldots p_{k}^{\gamma_{k}}}{d_{1}^{\prime}} $$ Note that if $h_{j} \in P_{1}^{\prime}$, then the image of $h_{j}$ under the scaling can be covered by $Q_{j}$ only; so, in this case we have $Q_{j} \in \mathcal{Q}$. Our aim is to find the desired number of progressions in coverings $\mathcal{P}$ and $\mathcal{Q}$. First, we have $n \geq n^{\prime}$, and the sum of the steps in $\mathcal{P}^{\prime}$ is less than that in $\mathcal{P}$; hence the Claim is valid for $\mathcal{P}^{\prime}$. We apply it to the set of indices $I^{\prime}=\left\{i \in I: \beta_{i}>\sigma_{i}\right\}$ and the exponents $\beta_{i}^{\prime}=\beta_{i}-\sigma_{i}$; hence the set under consideration is $$ T^{\prime}=\left\{j: 1 \leq j \leq s^{\prime}, \text { and } p_{i}^{\left(\alpha_{i}-\sigma_{i}\right)-\beta_{i}^{\prime}+1}=p_{i}^{\alpha_{i}-\beta_{i}+1} \mid d_{j} \text { for some } i \in I^{\prime}\right\} \subseteq T \cap\left[s^{\prime}\right], $$ and we obtain that $$ \left|T \cap\left[s^{\prime}\right]\right| \geq\left|T^{\prime}\right| \geq 1+\sum_{i \in I^{\prime}}\left(\beta_{i}-\sigma_{i}\right)\left(p_{i}-1\right)=1+\sum_{i \in I}\left(\beta_{i}-\sigma_{i}\right)_{+}\left(p_{i}-1\right) $$ where $(x)_{+}=\max \{x, 0\}$; the latter equality holds as for $i \notin I^{\prime}$ we have $\beta_{i} \leq \sigma_{i}$. Observe that $x=(x-y)_{+}+\min \{x, y\}$ for all $x, y$. So, if we find at least $$ G=\sum_{i \in I} \min \left\{\beta_{i}, \sigma_{i}\right\}\left(p_{i}-1\right) $$ indices in $T \cap\left\{s^{\prime}+1, \ldots, s\right\}$, then we would have $$ |T|=\left|T \cap\left[s^{\prime}\right]\right|+\left|T \cap\left\{s^{\prime}+1, \ldots, s\right\}\right| \geq 1+\sum_{i \in I}\left(\left(\beta_{i}-\sigma_{i}\right)_{+}+\min \left\{\beta_{i}, \sigma_{i}\right\}\right)\left(p_{i}-1\right)=1+\sum_{i \in I} \beta_{i}\left(p_{i}-1\right) $$ thus leading to a contradiction with the choice of $\mathcal{P}$. We will find those indices among the indices of progressions in $\mathcal{Q}$. 3. Now denote $I^{\prime \prime}=\left\{i \in I: \sigma_{i}>0\right\}$ and consider some $i \in I^{\prime \prime}$; then $p_{i}^{\alpha_{i}} \nmid n^{\prime}$. On the other hand, there exists an index $j(i)$ such that $p_{i}^{\alpha_{i}} \mid d_{j(i)}$; this means that $d_{j(i)} \backslash n^{\prime}$ and hence $P_{j(i)}$ cannot appear in $\mathcal{P}^{\prime}$, so $j(i)>s^{\prime}$. Moreover, we have observed before that in this case $h_{j(i)} \in P_{1}^{\prime}$, hence $Q_{j(i)} \in \mathcal{Q}$. This means that $q_{j(i)} \mid n^{\prime \prime}$, therefore $\gamma_{i}=\alpha_{i}$ for each $i \in I^{\prime \prime}$ (recall here that $q_{i}=r_{i} / d_{1}^{\prime}$ and hence $\left.d_{j(i)}\left|r_{j(i)}\right| d_{1}^{\prime} n^{\prime \prime}\right)$. Let $d_{1}^{\prime}=p_{1}^{\tau_{1}} \ldots p_{k}^{\tau_{k}}$. Then $n^{\prime \prime}=p_{1}^{\gamma_{1}-\tau_{1}} \ldots p_{k}^{\gamma_{i}-\tau_{i}}$. Now, if $i \in I^{\prime \prime}$, then for every $\beta$ the condition $p_{i}^{\left(\gamma_{i}-\tau_{i}\right)-\beta+1} \mid q_{j}$ is equivalent to $p_{i}^{\alpha_{i}-\beta+1} \mid r_{j}$. Note that $n^{\prime \prime} \leq n / d_{1}^{\prime}<n$, hence we can apply the Claim to the covering $\mathcal{Q}$. We perform this with the set of indices $I^{\prime \prime}$ and the exponents $\beta_{i}^{\prime \prime}=\min \left\{\beta_{i}, \sigma_{i}\right\}>0$. So, the set under consideration is $$ \begin{aligned} T^{\prime \prime} & =\left\{j: Q_{j} \in \mathcal{Q}, \text { and } p_{i}^{\left(\gamma_{i}-\tau_{i}\right)-\min \left\{\beta_{i}, \sigma_{i}\right\}+1} \mid q_{j} \text { for some } i \in I^{\prime \prime}\right\} \\ & =\left\{j: Q_{j} \in \mathcal{Q}, \text { and } p_{i}^{\alpha_{i}-\min \left\{\beta_{i}, \sigma_{i}\right\}+1} \mid r_{j} \text { for some } i \in I^{\prime \prime}\right\}, \end{aligned} $$ and we obtain $\left|T^{\prime \prime}\right| \geq 1+G$. Finally, we claim that $T^{\prime \prime} \subseteq T \cap\left(\{1\} \cup\left\{s^{\prime}+1, \ldots, s\right\}\right)$; then we will obtain $\left|T \cap\left\{s^{\prime}+1, \ldots, s\right\}\right| \geq G$, which is exactly what we need. To prove this, consider any $j \in T^{\prime \prime}$. Observe first that $\alpha_{i}-\min \left\{\beta_{i}, \sigma_{i}\right\}+1>\alpha_{i}-\sigma_{i} \geq \tau_{i}$, hence from $p_{i}^{\alpha_{i}-\min \left\{\beta_{i}, \sigma_{i}\right\}+1} \mid r_{j}=$ l.c.m. $\left(d_{1}^{\prime}, d_{j}\right)$ we have $p_{i}^{\alpha_{i}-\min \left\{\beta_{i}, \sigma_{i}\right\}+1} \mid d_{j}$, which means that $j \in T$. Next, the exponent of $p_{i}$ in $d_{j}$ is greater than that in $n^{\prime}$, which means that $P_{j} \notin \mathcal{P}^{\prime}$. This may appear only if $j=1$ or $j>s^{\prime}$, as desired. This completes the proof. Comment 2. A grid analogue of the Claim is also valid. It reads as following. Claim. Assume that the grid $N$ is covered by subgrids $L_{1}, L_{2}, \ldots, L_{s}$ so that (ii') each subgrid contains a point which is not covered by other subgrids; (iii) for each coordinate axis, there exists a subgrid $L_{i}$ orthogonal to this axis. Choose some set of indices $I=\left\{i_{1}, \ldots, i_{t}\right\} \subset[k]$, and consider the set of indices $$ T=\left\{j: 1 \leq j \leq s \text {, and } L_{j} \text { is orthogonal to the } i \text { th axis for some } i \in I\right\} $$ Then $$ |T| \geq 1+\sum_{i \in I}\left(n_{i}-1\right) $$ This Claim may be proved almost in the same way as in Solution 1.
|
{
"resource_path": "IMO/segmented/en-IMO2010SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
eadc714d-13a7-5bb9-b0fe-0d9955b98c0c
| 23,959
|
Let $A B C$ be an acute triangle with $D, E, F$ the feet of the altitudes lying on $B C, C A, A B$ respectively. One of the intersection points of the line $E F$ and the circumcircle is $P$. The lines $B P$ and $D F$ meet at point $Q$. Prove that $A P=A Q$. (United Kingdom)
|
The line $E F$ intersects the circumcircle at two points. Depending on the choice of $P$, there are two different cases to consider. Case 1: The point $P$ lies on the ray $E F$ (see Fig. 1). Let $\angle C A B=\alpha, \angle A B C=\beta$ and $\angle B C A=\gamma$. The quadrilaterals $B C E F$ and $C A F D$ are cyclic due to the right angles at $D, E$ and $F$. So, $$ \begin{aligned} & \angle B D F=180^{\circ}-\angle F D C=\angle C A F=\alpha, \\ & \angle A F E=180^{\circ}-\angle E F B=\angle B C E=\gamma, \\ & \angle D F B=180^{\circ}-\angle A F D=\angle D C A=\gamma . \end{aligned} $$ Since $P$ lies on the arc $A B$ of the circumcircle, $\angle P B A<\angle B C A=\gamma$. Hence, we have $$ \angle P B D+\angle B D F=\angle P B A+\angle A B D+\angle B D F<\gamma+\beta+\alpha=180^{\circ}, $$ and the point $Q$ must lie on the extensions of $B P$ and $D F$ beyond the points $P$ and $F$, respectively. From the cyclic quadrilateral $A P B C$ we get $$ \angle Q P A=180^{\circ}-\angle A P B=\angle B C A=\gamma=\angle D F B=\angle Q F A . $$ Hence, the quadrilateral $A Q P F$ is cyclic. Then $\angle A Q P=180^{\circ}-\angle P F A=\angle A F E=\gamma$. We obtained that $\angle A Q P=\angle Q P A=\gamma$, so the triangle $A Q P$ is isosceles, $A P=A Q$.  Fig. 1  Fig. 2 Case 2: The point $P$ lies on the ray $F E$ (see Fig. 2). In this case the point $Q$ lies inside the segment $F D$. Similarly to the first case, we have $$ \angle Q P A=\angle B C A=\gamma=\angle D F B=180^{\circ}-\angle A F Q $$ Hence, the quadrilateral $A F Q P$ is cyclic. Then $\angle A Q P=\angle A F P=\angle A F E=\gamma=\angle Q P A$. The triangle $A Q P$ is isosceles again, $\angle A Q P=\angle Q P A$ and thus $A P=A Q$. Comment. Using signed angles, the two possible configurations can be handled simultaneously, without investigating the possible locations of $P$ and $Q$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with $D, E, F$ the feet of the altitudes lying on $B C, C A, A B$ respectively. One of the intersection points of the line $E F$ and the circumcircle is $P$. The lines $B P$ and $D F$ meet at point $Q$. Prove that $A P=A Q$. (United Kingdom)
|
The line $E F$ intersects the circumcircle at two points. Depending on the choice of $P$, there are two different cases to consider. Case 1: The point $P$ lies on the ray $E F$ (see Fig. 1). Let $\angle C A B=\alpha, \angle A B C=\beta$ and $\angle B C A=\gamma$. The quadrilaterals $B C E F$ and $C A F D$ are cyclic due to the right angles at $D, E$ and $F$. So, $$ \begin{aligned} & \angle B D F=180^{\circ}-\angle F D C=\angle C A F=\alpha, \\ & \angle A F E=180^{\circ}-\angle E F B=\angle B C E=\gamma, \\ & \angle D F B=180^{\circ}-\angle A F D=\angle D C A=\gamma . \end{aligned} $$ Since $P$ lies on the arc $A B$ of the circumcircle, $\angle P B A<\angle B C A=\gamma$. Hence, we have $$ \angle P B D+\angle B D F=\angle P B A+\angle A B D+\angle B D F<\gamma+\beta+\alpha=180^{\circ}, $$ and the point $Q$ must lie on the extensions of $B P$ and $D F$ beyond the points $P$ and $F$, respectively. From the cyclic quadrilateral $A P B C$ we get $$ \angle Q P A=180^{\circ}-\angle A P B=\angle B C A=\gamma=\angle D F B=\angle Q F A . $$ Hence, the quadrilateral $A Q P F$ is cyclic. Then $\angle A Q P=180^{\circ}-\angle P F A=\angle A F E=\gamma$. We obtained that $\angle A Q P=\angle Q P A=\gamma$, so the triangle $A Q P$ is isosceles, $A P=A Q$.  Fig. 1  Fig. 2 Case 2: The point $P$ lies on the ray $F E$ (see Fig. 2). In this case the point $Q$ lies inside the segment $F D$. Similarly to the first case, we have $$ \angle Q P A=\angle B C A=\gamma=\angle D F B=180^{\circ}-\angle A F Q $$ Hence, the quadrilateral $A F Q P$ is cyclic. Then $\angle A Q P=\angle A F P=\angle A F E=\gamma=\angle Q P A$. The triangle $A Q P$ is isosceles again, $\angle A Q P=\angle Q P A$ and thus $A P=A Q$. Comment. Using signed angles, the two possible configurations can be handled simultaneously, without investigating the possible locations of $P$ and $Q$.
|
{
"resource_path": "IMO/segmented/en-IMO2010SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
86bb79f8-d1cd-5a17-a404-b47ee43770f0
| 23,964
|
Let $A B C$ be an acute triangle with $D, E, F$ the feet of the altitudes lying on $B C, C A, A B$ respectively. One of the intersection points of the line $E F$ and the circumcircle is $P$. The lines $B P$ and $D F$ meet at point $Q$. Prove that $A P=A Q$. (United Kingdom)
|
For arbitrary points $X, Y$ on the circumcircle, denote by $\widehat{X Y}$ the central angle of the arc $X Y$. Let $P$ and $P^{\prime}$ be the two points where the line $E F$ meets the circumcircle; let $P$ lie on the $\operatorname{arc} A B$ and let $P^{\prime}$ lie on the $\operatorname{arc} C A$. Let $B P$ and $B P^{\prime}$ meet the line $D F$ and $Q$ and $Q^{\prime}$, respectively (see Fig. 3). We will prove that $A P=A P^{\prime}=A Q=A Q^{\prime}$.  Fig. 3 Like in the first solution, we have $\angle A F E=\angle B F P=\angle D F B=\angle B C A=\gamma$ from the cyclic quadrilaterals $B C E F$ and $C A F D$. By $\overparen{P B}+\overparen{P^{\prime} A}=2 \angle A F P^{\prime}=2 \gamma=2 \angle B C A=\overparen{A P}+\overparen{P B}$, we have $$ \overline{A P}=\widetilde{P^{\prime} A}, \quad \angle P B A=\angle A B P^{\prime} \quad \text { and } \quad A P=A P^{\prime} $$ Due to $\overparen{A P}=\widehat{P^{\prime}} A$, the lines $B P$ and $B Q^{\prime}$ are symmetrical about line $A B$. Similarly, by $\angle B F P=\angle Q^{\prime} F B$, the lines $F P$ and $F Q^{\prime}$ are symmetrical about $A B$. It follows that also the points $P$ and $P^{\prime}$ are symmetrical to $Q^{\prime}$ and $Q$, respectively. Therefore, $$ A P=A Q^{\prime} \quad \text { and } \quad A P^{\prime}=A Q $$ The relations (1) and (2) together prove $A P=A P^{\prime}=A Q=A Q^{\prime}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with $D, E, F$ the feet of the altitudes lying on $B C, C A, A B$ respectively. One of the intersection points of the line $E F$ and the circumcircle is $P$. The lines $B P$ and $D F$ meet at point $Q$. Prove that $A P=A Q$. (United Kingdom)
|
For arbitrary points $X, Y$ on the circumcircle, denote by $\widehat{X Y}$ the central angle of the arc $X Y$. Let $P$ and $P^{\prime}$ be the two points where the line $E F$ meets the circumcircle; let $P$ lie on the $\operatorname{arc} A B$ and let $P^{\prime}$ lie on the $\operatorname{arc} C A$. Let $B P$ and $B P^{\prime}$ meet the line $D F$ and $Q$ and $Q^{\prime}$, respectively (see Fig. 3). We will prove that $A P=A P^{\prime}=A Q=A Q^{\prime}$.  Fig. 3 Like in the first solution, we have $\angle A F E=\angle B F P=\angle D F B=\angle B C A=\gamma$ from the cyclic quadrilaterals $B C E F$ and $C A F D$. By $\overparen{P B}+\overparen{P^{\prime} A}=2 \angle A F P^{\prime}=2 \gamma=2 \angle B C A=\overparen{A P}+\overparen{P B}$, we have $$ \overline{A P}=\widetilde{P^{\prime} A}, \quad \angle P B A=\angle A B P^{\prime} \quad \text { and } \quad A P=A P^{\prime} $$ Due to $\overparen{A P}=\widehat{P^{\prime}} A$, the lines $B P$ and $B Q^{\prime}$ are symmetrical about line $A B$. Similarly, by $\angle B F P=\angle Q^{\prime} F B$, the lines $F P$ and $F Q^{\prime}$ are symmetrical about $A B$. It follows that also the points $P$ and $P^{\prime}$ are symmetrical to $Q^{\prime}$ and $Q$, respectively. Therefore, $$ A P=A Q^{\prime} \quad \text { and } \quad A P^{\prime}=A Q $$ The relations (1) and (2) together prove $A P=A P^{\prime}=A Q=A Q^{\prime}$.
|
{
"resource_path": "IMO/segmented/en-IMO2010SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
86bb79f8-d1cd-5a17-a404-b47ee43770f0
| 23,964
|
Point $P$ lies inside triangle $A B C$. Lines $A P, B P, C P$ meet the circumcircle of $A B C$ again at points $K, L, M$, respectively. The tangent to the circumcircle at $C$ meets line $A B$ at $S$. Prove that $S C=S P$ if and only if $M K=M L$.
|
We assume that $C A>C B$, so point $S$ lies on the ray $A B$. From the similar triangles $\triangle P K M \sim \triangle P C A$ and $\triangle P L M \sim \triangle P C B$ we get $\frac{P M}{K M}=\frac{P A}{C A}$ and $\frac{L M}{P M}=\frac{C B}{P B}$. Multiplying these two equalities, we get $$ \frac{L M}{K M}=\frac{C B}{C A} \cdot \frac{P A}{P B} $$ Hence, the relation $M K=M L$ is equivalent to $\frac{C B}{C A}=\frac{P B}{P A}$. Denote by $E$ the foot of the bisector of angle $B$ in triangle $A B C$. Recall that the locus of points $X$ for which $\frac{X A}{X B}=\frac{C A}{C B}$ is the Apollonius circle $\Omega$ with the center $Q$ on the line $A B$, and this circle passes through $C$ and $E$. Hence, we have $M K=M L$ if and only if $P$ lies on $\Omega$, that is $Q P=Q C$.  Fig. 1 Now we prove that $S=Q$, thus establishing the problem statement. We have $\angle C E S=$ $\angle C A E+\angle A C E=\angle B C S+\angle E C B=\angle E C S$, so $S C=S E$. Hence, the point $S$ lies on $A B$ as well as on the perpendicular bisector of $C E$ and therefore coincides with $Q$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Point $P$ lies inside triangle $A B C$. Lines $A P, B P, C P$ meet the circumcircle of $A B C$ again at points $K, L, M$, respectively. The tangent to the circumcircle at $C$ meets line $A B$ at $S$. Prove that $S C=S P$ if and only if $M K=M L$.
|
We assume that $C A>C B$, so point $S$ lies on the ray $A B$. From the similar triangles $\triangle P K M \sim \triangle P C A$ and $\triangle P L M \sim \triangle P C B$ we get $\frac{P M}{K M}=\frac{P A}{C A}$ and $\frac{L M}{P M}=\frac{C B}{P B}$. Multiplying these two equalities, we get $$ \frac{L M}{K M}=\frac{C B}{C A} \cdot \frac{P A}{P B} $$ Hence, the relation $M K=M L$ is equivalent to $\frac{C B}{C A}=\frac{P B}{P A}$. Denote by $E$ the foot of the bisector of angle $B$ in triangle $A B C$. Recall that the locus of points $X$ for which $\frac{X A}{X B}=\frac{C A}{C B}$ is the Apollonius circle $\Omega$ with the center $Q$ on the line $A B$, and this circle passes through $C$ and $E$. Hence, we have $M K=M L$ if and only if $P$ lies on $\Omega$, that is $Q P=Q C$.  Fig. 1 Now we prove that $S=Q$, thus establishing the problem statement. We have $\angle C E S=$ $\angle C A E+\angle A C E=\angle B C S+\angle E C B=\angle E C S$, so $S C=S E$. Hence, the point $S$ lies on $A B$ as well as on the perpendicular bisector of $C E$ and therefore coincides with $Q$.
|
{
"resource_path": "IMO/segmented/en-IMO2010SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
f594fbe1-808e-55f5-b9af-43d8f777a340
| 23,968
|
Point $P$ lies inside triangle $A B C$. Lines $A P, B P, C P$ meet the circumcircle of $A B C$ again at points $K, L, M$, respectively. The tangent to the circumcircle at $C$ meets line $A B$ at $S$. Prove that $S C=S P$ if and only if $M K=M L$.
|
As in the previous solution, we assume that $S$ lies on the ray $A B$. 1. Let $P$ be an arbitrary point inside both the circumcircle $\omega$ of the triangle $A B C$ and the angle $A S C$, the points $K, L, M$ defined as in the problem. We claim that $S P=S C$ implies $M K=M L$. Let $E$ and $F$ be the points of intersection of the line $S P$ with $\omega$, point $E$ lying on the segment $S P$ (see Fig. 2).  Fig. 2 We have $S P^{2}=S C^{2}=S A \cdot S B$, so $\frac{S P}{S B}=\frac{S A}{S P}$, and hence $\triangle P S A \sim \triangle B S P$. Then $\angle B P S=\angle S A P$. Since $2 \angle B P S=\overparen{B E}+\overparen{L F}$ and $2 \angle S A P=\overparen{B E}+\overparen{E K}$ we have $$ \overparen{L F}=\overparen{E K} $$ On the other hand, from $\angle S P C=\angle S C P$ we have $\widehat{E C}+\widehat{M F}=\widehat{E C}+\widehat{E M}$, or $$ \widetilde{M F}=\overparen{E M} . $$ From (1) and (2) we get $\widehat{M F L}=\widehat{M F}+\widehat{F L}=\widehat{M E}+\widehat{E K}=\widehat{M E K}$ and hence $M K=M L$. The claim is proved. 2. We are left to prove the converse. So, assume that $M K=M L$, and introduce the points $E$ and $F$ as above. We have $S C^{2}=S E \cdot S F$; hence, there exists a point $P^{\prime}$ lying on the segment $E F$ such that $S P^{\prime}=S C$ (see Fig. 3).  Fig. 3 Assume that $P \neq P^{\prime}$. Let the lines $A P^{\prime}, B P^{\prime}, C P^{\prime}$ meet $\omega$ again at points $K^{\prime}, L^{\prime}, M^{\prime}$ respectively. Now, if $P^{\prime}$ lies on the segment $P F$ then by the first part of the solution we have $\widehat{M^{\prime} F L^{\prime}}=\widehat{M^{\prime} E K^{\prime}}$. On the other hand, we have $\widehat{M F L}>\widehat{M^{\prime} F L^{\prime}}=\widehat{M^{\prime} E K^{\prime}}>\widehat{M E K}$, therefore $\widehat{M F L}>\widehat{M E K}$ which contradicts $M K=M L$. Similarly, if point $P^{\prime}$ lies on the segment $E P$ then we get $\widehat{M F L}<\widehat{M E K}$ which is impossible. Therefore, the points $P$ and $P^{\prime}$ coincide and hence $S P=S P^{\prime}=S C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Point $P$ lies inside triangle $A B C$. Lines $A P, B P, C P$ meet the circumcircle of $A B C$ again at points $K, L, M$, respectively. The tangent to the circumcircle at $C$ meets line $A B$ at $S$. Prove that $S C=S P$ if and only if $M K=M L$.
|
As in the previous solution, we assume that $S$ lies on the ray $A B$. 1. Let $P$ be an arbitrary point inside both the circumcircle $\omega$ of the triangle $A B C$ and the angle $A S C$, the points $K, L, M$ defined as in the problem. We claim that $S P=S C$ implies $M K=M L$. Let $E$ and $F$ be the points of intersection of the line $S P$ with $\omega$, point $E$ lying on the segment $S P$ (see Fig. 2).  Fig. 2 We have $S P^{2}=S C^{2}=S A \cdot S B$, so $\frac{S P}{S B}=\frac{S A}{S P}$, and hence $\triangle P S A \sim \triangle B S P$. Then $\angle B P S=\angle S A P$. Since $2 \angle B P S=\overparen{B E}+\overparen{L F}$ and $2 \angle S A P=\overparen{B E}+\overparen{E K}$ we have $$ \overparen{L F}=\overparen{E K} $$ On the other hand, from $\angle S P C=\angle S C P$ we have $\widehat{E C}+\widehat{M F}=\widehat{E C}+\widehat{E M}$, or $$ \widetilde{M F}=\overparen{E M} . $$ From (1) and (2) we get $\widehat{M F L}=\widehat{M F}+\widehat{F L}=\widehat{M E}+\widehat{E K}=\widehat{M E K}$ and hence $M K=M L$. The claim is proved. 2. We are left to prove the converse. So, assume that $M K=M L$, and introduce the points $E$ and $F$ as above. We have $S C^{2}=S E \cdot S F$; hence, there exists a point $P^{\prime}$ lying on the segment $E F$ such that $S P^{\prime}=S C$ (see Fig. 3).  Fig. 3 Assume that $P \neq P^{\prime}$. Let the lines $A P^{\prime}, B P^{\prime}, C P^{\prime}$ meet $\omega$ again at points $K^{\prime}, L^{\prime}, M^{\prime}$ respectively. Now, if $P^{\prime}$ lies on the segment $P F$ then by the first part of the solution we have $\widehat{M^{\prime} F L^{\prime}}=\widehat{M^{\prime} E K^{\prime}}$. On the other hand, we have $\widehat{M F L}>\widehat{M^{\prime} F L^{\prime}}=\widehat{M^{\prime} E K^{\prime}}>\widehat{M E K}$, therefore $\widehat{M F L}>\widehat{M E K}$ which contradicts $M K=M L$. Similarly, if point $P^{\prime}$ lies on the segment $E P$ then we get $\widehat{M F L}<\widehat{M E K}$ which is impossible. Therefore, the points $P$ and $P^{\prime}$ coincide and hence $S P=S P^{\prime}=S C$.
|
{
"resource_path": "IMO/segmented/en-IMO2010SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
f594fbe1-808e-55f5-b9af-43d8f777a340
| 23,968
|
Point $P$ lies inside triangle $A B C$. Lines $A P, B P, C P$ meet the circumcircle of $A B C$ again at points $K, L, M$, respectively. The tangent to the circumcircle at $C$ meets line $A B$ at $S$. Prove that $S C=S P$ if and only if $M K=M L$.
|
We present a different proof of the converse direction, that is, $M K=M L \Rightarrow$ $S P=S C$. As in the previous solutions we assume that $C A>C B$, and the line $S P$ meets $\omega$ at $E$ and $F$. From $M L=M K$ we get $\widehat{M E K}=\widehat{M F L}$. Now we claim that $\widehat{M E}=\widehat{M F}$ and $\widehat{E K}=\widehat{F L}$. To the contrary, suppose first that $\widehat{M E}>\widehat{M F}$; then $\widehat{E K}=\widehat{M E K}-\widehat{M E}<\widehat{M F L}-\widehat{M F}=$ $\overparen{F L}$. Now, the inequality $\overparen{M E}>\overparen{M F}$ implies $2 \angle S C M=\overparen{E C}+\overparen{M E}>\overparen{E C}+\overparen{M F}=2 \angle S P C$ and hence $S P>S C$. On the other hand, the inequality $\overparen{E K}<\overparen{F L}$ implies $2 \angle S P K=$ $\overparen{E K}+\widetilde{A F}<\overparen{F L}+\widetilde{A F}=2 \angle A B L$, hence $$ \angle S P A=180^{\circ}-\angle S P K>180^{\circ}-\angle A B L=\angle S B P . $$  Fig. 4 Consider the point $A^{\prime}$ on the ray $S A$ for which $\angle S P A^{\prime}=\angle S B P$; in our case, this point lies on the segment $S A$ (see Fig. 4). Then $\triangle S B P \sim \triangle S P A^{\prime}$ and $S P^{2}=S B \cdot S A^{\prime}<S B \cdot S A=S C^{2}$. Therefore, $S P<S C$ which contradicts $S P>S C$. Similarly, one can prove that the inequality $\widehat{M E}<\widehat{M F}$ is also impossible. So, we get $\widehat{M E}=\widehat{M F}$ and therefore $2 \angle S C M=\widehat{E C}+\widehat{M E}=\widehat{E C}+\widehat{M F}=2 \angle S P C$, which implies $S C=S P$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Point $P$ lies inside triangle $A B C$. Lines $A P, B P, C P$ meet the circumcircle of $A B C$ again at points $K, L, M$, respectively. The tangent to the circumcircle at $C$ meets line $A B$ at $S$. Prove that $S C=S P$ if and only if $M K=M L$.
|
We present a different proof of the converse direction, that is, $M K=M L \Rightarrow$ $S P=S C$. As in the previous solutions we assume that $C A>C B$, and the line $S P$ meets $\omega$ at $E$ and $F$. From $M L=M K$ we get $\widehat{M E K}=\widehat{M F L}$. Now we claim that $\widehat{M E}=\widehat{M F}$ and $\widehat{E K}=\widehat{F L}$. To the contrary, suppose first that $\widehat{M E}>\widehat{M F}$; then $\widehat{E K}=\widehat{M E K}-\widehat{M E}<\widehat{M F L}-\widehat{M F}=$ $\overparen{F L}$. Now, the inequality $\overparen{M E}>\overparen{M F}$ implies $2 \angle S C M=\overparen{E C}+\overparen{M E}>\overparen{E C}+\overparen{M F}=2 \angle S P C$ and hence $S P>S C$. On the other hand, the inequality $\overparen{E K}<\overparen{F L}$ implies $2 \angle S P K=$ $\overparen{E K}+\widetilde{A F}<\overparen{F L}+\widetilde{A F}=2 \angle A B L$, hence $$ \angle S P A=180^{\circ}-\angle S P K>180^{\circ}-\angle A B L=\angle S B P . $$  Fig. 4 Consider the point $A^{\prime}$ on the ray $S A$ for which $\angle S P A^{\prime}=\angle S B P$; in our case, this point lies on the segment $S A$ (see Fig. 4). Then $\triangle S B P \sim \triangle S P A^{\prime}$ and $S P^{2}=S B \cdot S A^{\prime}<S B \cdot S A=S C^{2}$. Therefore, $S P<S C$ which contradicts $S P>S C$. Similarly, one can prove that the inequality $\widehat{M E}<\widehat{M F}$ is also impossible. So, we get $\widehat{M E}=\widehat{M F}$ and therefore $2 \angle S C M=\widehat{E C}+\widehat{M E}=\widehat{E C}+\widehat{M F}=2 \angle S P C$, which implies $S C=S P$.
|
{
"resource_path": "IMO/segmented/en-IMO2010SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
f594fbe1-808e-55f5-b9af-43d8f777a340
| 23,968
|
Let $A_{1} A_{2} \ldots A_{n}$ be a convex polygon. Point $P$ inside this polygon is chosen so that its projections $P_{1}, \ldots, P_{n}$ onto lines $A_{1} A_{2}, \ldots, A_{n} A_{1}$ respectively lie on the sides of the polygon. Prove that for arbitrary points $X_{1}, \ldots, X_{n}$ on sides $A_{1} A_{2}, \ldots, A_{n} A_{1}$ respectively, $$ \max \left\{\frac{X_{1} X_{2}}{P_{1} P_{2}}, \ldots, \frac{X_{n} X_{1}}{P_{n} P_{1}}\right\} \geq 1 $$ (Armenia)
|
Denote $P_{n+1}=P_{1}, X_{n+1}=X_{1}, A_{n+1}=A_{1}$. Lemma. Let point $Q$ lies inside $A_{1} A_{2} \ldots A_{n}$. Then it is contained in at least one of the circumcircles of triangles $X_{1} A_{2} X_{2}, \ldots, X_{n} A_{1} X_{1}$. Proof. If $Q$ lies in one of the triangles $X_{1} A_{2} X_{2}, \ldots, X_{n} A_{1} X_{1}$, the claim is obvious. Otherwise $Q$ lies inside the polygon $X_{1} X_{2} \ldots X_{n}$ (see Fig. 1). Then we have $$ \begin{aligned} & \left(\angle X_{1} A_{2} X_{2}+\angle X_{1} Q X_{2}\right)+\cdots+\left(\angle X_{n} A_{1} X_{1}+\angle X_{n} Q X_{1}\right) \\ & \quad=\left(\angle X_{1} A_{1} X_{2}+\cdots+\angle X_{n} A_{1} X_{1}\right)+\left(\angle X_{1} Q X_{2}+\cdots+\angle X_{n} Q X_{1}\right)=(n-2) \pi+2 \pi=n \pi \end{aligned} $$ hence there exists an index $i$ such that $\angle X_{i} A_{i+1} X_{i+1}+\angle X_{i} Q X_{i+1} \geq \frac{\pi n}{n}=\pi$. Since the quadrilateral $Q X_{i} A_{i+1} X_{i+1}$ is convex, this means exactly that $Q$ is contained the circumcircle of $\triangle X_{i} A_{i+1} X_{i+1}$, as desired. Now we turn to the solution. Applying lemma, we get that $P$ lies inside the circumcircle of triangle $X_{i} A_{i+1} X_{i+1}$ for some $i$. Consider the circumcircles $\omega$ and $\Omega$ of triangles $P_{i} A_{i+1} P_{i+1}$ and $X_{i} A_{i+1} X_{i+1}$ respectively (see Fig. 2); let $r$ and $R$ be their radii. Then we get $2 r=A_{i+1} P \leq 2 R$ (since $P$ lies inside $\Omega$ ), hence $$ P_{i} P_{i+1}=2 r \sin \angle P_{i} A_{i+1} P_{i+1} \leq 2 R \sin \angle X_{i} A_{i+1} X_{i+1}=X_{i} X_{i+1} $$ QED.  Fig. 1  Fig. 2
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A_{1} A_{2} \ldots A_{n}$ be a convex polygon. Point $P$ inside this polygon is chosen so that its projections $P_{1}, \ldots, P_{n}$ onto lines $A_{1} A_{2}, \ldots, A_{n} A_{1}$ respectively lie on the sides of the polygon. Prove that for arbitrary points $X_{1}, \ldots, X_{n}$ on sides $A_{1} A_{2}, \ldots, A_{n} A_{1}$ respectively, $$ \max \left\{\frac{X_{1} X_{2}}{P_{1} P_{2}}, \ldots, \frac{X_{n} X_{1}}{P_{n} P_{1}}\right\} \geq 1 $$ (Armenia)
|
Denote $P_{n+1}=P_{1}, X_{n+1}=X_{1}, A_{n+1}=A_{1}$. Lemma. Let point $Q$ lies inside $A_{1} A_{2} \ldots A_{n}$. Then it is contained in at least one of the circumcircles of triangles $X_{1} A_{2} X_{2}, \ldots, X_{n} A_{1} X_{1}$. Proof. If $Q$ lies in one of the triangles $X_{1} A_{2} X_{2}, \ldots, X_{n} A_{1} X_{1}$, the claim is obvious. Otherwise $Q$ lies inside the polygon $X_{1} X_{2} \ldots X_{n}$ (see Fig. 1). Then we have $$ \begin{aligned} & \left(\angle X_{1} A_{2} X_{2}+\angle X_{1} Q X_{2}\right)+\cdots+\left(\angle X_{n} A_{1} X_{1}+\angle X_{n} Q X_{1}\right) \\ & \quad=\left(\angle X_{1} A_{1} X_{2}+\cdots+\angle X_{n} A_{1} X_{1}\right)+\left(\angle X_{1} Q X_{2}+\cdots+\angle X_{n} Q X_{1}\right)=(n-2) \pi+2 \pi=n \pi \end{aligned} $$ hence there exists an index $i$ such that $\angle X_{i} A_{i+1} X_{i+1}+\angle X_{i} Q X_{i+1} \geq \frac{\pi n}{n}=\pi$. Since the quadrilateral $Q X_{i} A_{i+1} X_{i+1}$ is convex, this means exactly that $Q$ is contained the circumcircle of $\triangle X_{i} A_{i+1} X_{i+1}$, as desired. Now we turn to the solution. Applying lemma, we get that $P$ lies inside the circumcircle of triangle $X_{i} A_{i+1} X_{i+1}$ for some $i$. Consider the circumcircles $\omega$ and $\Omega$ of triangles $P_{i} A_{i+1} P_{i+1}$ and $X_{i} A_{i+1} X_{i+1}$ respectively (see Fig. 2); let $r$ and $R$ be their radii. Then we get $2 r=A_{i+1} P \leq 2 R$ (since $P$ lies inside $\Omega$ ), hence $$ P_{i} P_{i+1}=2 r \sin \angle P_{i} A_{i+1} P_{i+1} \leq 2 R \sin \angle X_{i} A_{i+1} X_{i+1}=X_{i} X_{i+1} $$ QED.  Fig. 1  Fig. 2
|
{
"resource_path": "IMO/segmented/en-IMO2010SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
f3412c2c-109b-5716-a539-d7721ef5d278
| 23,973
|
Let $A_{1} A_{2} \ldots A_{n}$ be a convex polygon. Point $P$ inside this polygon is chosen so that its projections $P_{1}, \ldots, P_{n}$ onto lines $A_{1} A_{2}, \ldots, A_{n} A_{1}$ respectively lie on the sides of the polygon. Prove that for arbitrary points $X_{1}, \ldots, X_{n}$ on sides $A_{1} A_{2}, \ldots, A_{n} A_{1}$ respectively, $$ \max \left\{\frac{X_{1} X_{2}}{P_{1} P_{2}}, \ldots, \frac{X_{n} X_{1}}{P_{n} P_{1}}\right\} \geq 1 $$ (Armenia)
|
As in We will prove a bit stronger inequality, namely $$ \max \left\{\frac{X_{1} X_{2}}{P_{1} P_{2}} \cos \alpha_{1}, \ldots, \frac{X_{n} X_{1}}{P_{n} P_{1}} \cos \alpha_{n}\right\} \geq 1 $$ where $\alpha_{i}(1 \leq i \leq n)$ is the angle between lines $X_{i} X_{i+1}$ and $P_{i} P_{i+1}$. We denote $\beta_{i}=\angle A_{i} P_{i} P_{i-1}$ and $\gamma_{i}=\angle A_{i+1} P_{i} P_{i+1}$ for all $1 \leq i \leq n$. Suppose that for some $1 \leq i \leq n$, point $X_{i}$ lies on the segment $A_{i} P_{i}$, while point $X_{i+1}$ lies on the segment $P_{i+1} A_{i+2}$. Then the projection of the segment $X_{i} X_{i+1}$ onto the line $P_{i} P_{i+1}$ contains segment $P_{i} P_{i+1}$, since $\gamma_{i}$ and $\beta_{i+1}$ are acute angles (see Fig. 3). Therefore, $X_{i} X_{i+1} \cos \alpha_{i} \geq$ $P_{i} P_{i+1}$, and in this case the statement is proved. So, the only case left is when point $X_{i}$ lies on segment $P_{i} A_{i+1}$ for all $1 \leq i \leq n$ (the case when each $X_{i}$ lies on segment $A_{i} P_{i}$ is completely analogous). Now, assume to the contrary that the inequality $$ X_{i} X_{i+1} \cos \alpha_{i}<P_{i} P_{i+1} $$ holds for every $1 \leq i \leq n$. Let $Y_{i}$ and $Y_{i+1}^{\prime}$ be the projections of $X_{i}$ and $X_{i+1}$ onto $P_{i} P_{i+1}$. Then inequality (1) means exactly that $Y_{i} Y_{i+1}^{\prime}<P_{i} P_{i+1}$, or $P_{i} Y_{i}>P_{i+1} Y_{i+1}^{\prime}$ (again since $\gamma_{i}$ and $\beta_{i+1}$ are acute; see Fig. 4). Hence, we have $$ X_{i} P_{i} \cos \gamma_{i}>X_{i+1} P_{i+1} \cos \beta_{i+1}, \quad 1 \leq i \leq n $$ Multiplying these inequalities, we get $$ \cos \gamma_{1} \cos \gamma_{2} \cdots \cos \gamma_{n}>\cos \beta_{1} \cos \beta_{2} \cdots \cos \beta_{n} $$ On the other hand, the sines theorem applied to triangle $P P_{i} P_{i+1}$ provides $$ \frac{P P_{i}}{P P_{i+1}}=\frac{\sin \left(\frac{\pi}{2}-\beta_{i+1}\right)}{\sin \left(\frac{\pi}{2}-\gamma_{i}\right)}=\frac{\cos \beta_{i+1}}{\cos \gamma_{i}} $$ Multiplying these equalities we get $$ 1=\frac{\cos \beta_{2}}{\cos \gamma_{1}} \cdot \frac{\cos \beta_{3}}{\cos \gamma_{2}} \cdots \frac{\cos \beta_{1}}{\cos \gamma_{n}} $$ which contradicts (2).  Fig. 3 Fig. 4
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A_{1} A_{2} \ldots A_{n}$ be a convex polygon. Point $P$ inside this polygon is chosen so that its projections $P_{1}, \ldots, P_{n}$ onto lines $A_{1} A_{2}, \ldots, A_{n} A_{1}$ respectively lie on the sides of the polygon. Prove that for arbitrary points $X_{1}, \ldots, X_{n}$ on sides $A_{1} A_{2}, \ldots, A_{n} A_{1}$ respectively, $$ \max \left\{\frac{X_{1} X_{2}}{P_{1} P_{2}}, \ldots, \frac{X_{n} X_{1}}{P_{n} P_{1}}\right\} \geq 1 $$ (Armenia)
|
As in We will prove a bit stronger inequality, namely $$ \max \left\{\frac{X_{1} X_{2}}{P_{1} P_{2}} \cos \alpha_{1}, \ldots, \frac{X_{n} X_{1}}{P_{n} P_{1}} \cos \alpha_{n}\right\} \geq 1 $$ where $\alpha_{i}(1 \leq i \leq n)$ is the angle between lines $X_{i} X_{i+1}$ and $P_{i} P_{i+1}$. We denote $\beta_{i}=\angle A_{i} P_{i} P_{i-1}$ and $\gamma_{i}=\angle A_{i+1} P_{i} P_{i+1}$ for all $1 \leq i \leq n$. Suppose that for some $1 \leq i \leq n$, point $X_{i}$ lies on the segment $A_{i} P_{i}$, while point $X_{i+1}$ lies on the segment $P_{i+1} A_{i+2}$. Then the projection of the segment $X_{i} X_{i+1}$ onto the line $P_{i} P_{i+1}$ contains segment $P_{i} P_{i+1}$, since $\gamma_{i}$ and $\beta_{i+1}$ are acute angles (see Fig. 3). Therefore, $X_{i} X_{i+1} \cos \alpha_{i} \geq$ $P_{i} P_{i+1}$, and in this case the statement is proved. So, the only case left is when point $X_{i}$ lies on segment $P_{i} A_{i+1}$ for all $1 \leq i \leq n$ (the case when each $X_{i}$ lies on segment $A_{i} P_{i}$ is completely analogous). Now, assume to the contrary that the inequality $$ X_{i} X_{i+1} \cos \alpha_{i}<P_{i} P_{i+1} $$ holds for every $1 \leq i \leq n$. Let $Y_{i}$ and $Y_{i+1}^{\prime}$ be the projections of $X_{i}$ and $X_{i+1}$ onto $P_{i} P_{i+1}$. Then inequality (1) means exactly that $Y_{i} Y_{i+1}^{\prime}<P_{i} P_{i+1}$, or $P_{i} Y_{i}>P_{i+1} Y_{i+1}^{\prime}$ (again since $\gamma_{i}$ and $\beta_{i+1}$ are acute; see Fig. 4). Hence, we have $$ X_{i} P_{i} \cos \gamma_{i}>X_{i+1} P_{i+1} \cos \beta_{i+1}, \quad 1 \leq i \leq n $$ Multiplying these inequalities, we get $$ \cos \gamma_{1} \cos \gamma_{2} \cdots \cos \gamma_{n}>\cos \beta_{1} \cos \beta_{2} \cdots \cos \beta_{n} $$ On the other hand, the sines theorem applied to triangle $P P_{i} P_{i+1}$ provides $$ \frac{P P_{i}}{P P_{i+1}}=\frac{\sin \left(\frac{\pi}{2}-\beta_{i+1}\right)}{\sin \left(\frac{\pi}{2}-\gamma_{i}\right)}=\frac{\cos \beta_{i+1}}{\cos \gamma_{i}} $$ Multiplying these equalities we get $$ 1=\frac{\cos \beta_{2}}{\cos \gamma_{1}} \cdot \frac{\cos \beta_{3}}{\cos \gamma_{2}} \cdots \frac{\cos \beta_{1}}{\cos \gamma_{n}} $$ which contradicts (2).  Fig. 3 Fig. 4
|
{
"resource_path": "IMO/segmented/en-IMO2010SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
f3412c2c-109b-5716-a539-d7721ef5d278
| 23,973
|
Let $I$ be the incenter of a triangle $A B C$ and $\Gamma$ be its circumcircle. Let the line $A I$ intersect $\Gamma$ at a point $D \neq A$. Let $F$ and $E$ be points on side $B C$ and $\operatorname{arc} B D C$ respectively such that $\angle B A F=\angle C A E<\frac{1}{2} \angle B A C$. Finally, let $G$ be the midpoint of the segment $I F$. Prove that the lines $D G$ and $E I$ intersect on $\Gamma$. (Hong Kong)
|
Let $X$ be the second point of intersection of line $E I$ with $\Gamma$, and $L$ be the foot of the bisector of angle $B A C$. Let $G^{\prime}$ and $T$ be the points of intersection of segment $D X$ with lines $I F$ and $A F$, respectively. We are to prove that $G=G^{\prime}$, or $I G^{\prime}=G^{\prime} F$. By the Menelaus theorem applied to triangle $A I F$ and line $D X$, it means that we need the relation $$ 1=\frac{G^{\prime} F}{I G^{\prime}}=\frac{T F}{A T} \cdot \frac{A D}{I D}, \quad \text { or } \quad \frac{T F}{A T}=\frac{I D}{A D} $$ Let the line $A F$ intersect $\Gamma$ at point $K \neq A$ (see Fig. 1); since $\angle B A K=\angle C A E$ we have $\widehat{B K}=\widehat{C E}$, hence $K E \| B C$. Notice that $\angle I A T=\angle D A K=\angle E A D=\angle E X D=\angle I X T$, so the points $I, A, X, T$ are concyclic. Hence we have $\angle I T A=\angle I X A=\angle E X A=\angle E K A$, so $I T\|K E\| B C$. Therefore we obtain $\frac{T F}{A T}=\frac{I L}{A I}$. Since $C I$ is the bisector of $\angle A C L$, we get $\frac{I L}{A I}=\frac{C L}{A C}$. Furthermore, $\angle D C L=\angle D C B=$ $\angle D A B=\angle C A D=\frac{1}{2} \angle B A C$, hence the triangles $D C L$ and $D A C$ are similar; therefore we get $\frac{C L}{A C}=\frac{D C}{A D}$. Finally, it is known that the midpoint $D$ of $\operatorname{arc} B C$ is equidistant from points $I$, $B, C$, hence $\frac{D C}{A D}=\frac{I D}{A D}$. Summarizing all these equalities, we get $$ \frac{T F}{A T}=\frac{I L}{A I}=\frac{C L}{A C}=\frac{D C}{A D}=\frac{I D}{A D} $$ as desired.  Fig. 1  Fig. 2 Comment. The equality $\frac{A I}{I L}=\frac{A D}{D I}$ is known and can be obtained in many different ways. For instance, one can consider the inversion with center $D$ and radius $D C=D I$. This inversion takes $\widehat{B A C}$ to the segment $B C$, so point $A$ goes to $L$. Hence $\frac{I L}{D I}=\frac{A I}{A D}$, which is the desired equality.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $I$ be the incenter of a triangle $A B C$ and $\Gamma$ be its circumcircle. Let the line $A I$ intersect $\Gamma$ at a point $D \neq A$. Let $F$ and $E$ be points on side $B C$ and $\operatorname{arc} B D C$ respectively such that $\angle B A F=\angle C A E<\frac{1}{2} \angle B A C$. Finally, let $G$ be the midpoint of the segment $I F$. Prove that the lines $D G$ and $E I$ intersect on $\Gamma$. (Hong Kong)
|
Let $X$ be the second point of intersection of line $E I$ with $\Gamma$, and $L$ be the foot of the bisector of angle $B A C$. Let $G^{\prime}$ and $T$ be the points of intersection of segment $D X$ with lines $I F$ and $A F$, respectively. We are to prove that $G=G^{\prime}$, or $I G^{\prime}=G^{\prime} F$. By the Menelaus theorem applied to triangle $A I F$ and line $D X$, it means that we need the relation $$ 1=\frac{G^{\prime} F}{I G^{\prime}}=\frac{T F}{A T} \cdot \frac{A D}{I D}, \quad \text { or } \quad \frac{T F}{A T}=\frac{I D}{A D} $$ Let the line $A F$ intersect $\Gamma$ at point $K \neq A$ (see Fig. 1); since $\angle B A K=\angle C A E$ we have $\widehat{B K}=\widehat{C E}$, hence $K E \| B C$. Notice that $\angle I A T=\angle D A K=\angle E A D=\angle E X D=\angle I X T$, so the points $I, A, X, T$ are concyclic. Hence we have $\angle I T A=\angle I X A=\angle E X A=\angle E K A$, so $I T\|K E\| B C$. Therefore we obtain $\frac{T F}{A T}=\frac{I L}{A I}$. Since $C I$ is the bisector of $\angle A C L$, we get $\frac{I L}{A I}=\frac{C L}{A C}$. Furthermore, $\angle D C L=\angle D C B=$ $\angle D A B=\angle C A D=\frac{1}{2} \angle B A C$, hence the triangles $D C L$ and $D A C$ are similar; therefore we get $\frac{C L}{A C}=\frac{D C}{A D}$. Finally, it is known that the midpoint $D$ of $\operatorname{arc} B C$ is equidistant from points $I$, $B, C$, hence $\frac{D C}{A D}=\frac{I D}{A D}$. Summarizing all these equalities, we get $$ \frac{T F}{A T}=\frac{I L}{A I}=\frac{C L}{A C}=\frac{D C}{A D}=\frac{I D}{A D} $$ as desired.  Fig. 1  Fig. 2 Comment. The equality $\frac{A I}{I L}=\frac{A D}{D I}$ is known and can be obtained in many different ways. For instance, one can consider the inversion with center $D$ and radius $D C=D I$. This inversion takes $\widehat{B A C}$ to the segment $B C$, so point $A$ goes to $L$. Hence $\frac{I L}{D I}=\frac{A I}{A D}$, which is the desired equality.
|
{
"resource_path": "IMO/segmented/en-IMO2010SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
d75255d9-c670-513f-a193-75954170fc58
| 23,977
|
Let $I$ be the incenter of a triangle $A B C$ and $\Gamma$ be its circumcircle. Let the line $A I$ intersect $\Gamma$ at a point $D \neq A$. Let $F$ and $E$ be points on side $B C$ and $\operatorname{arc} B D C$ respectively such that $\angle B A F=\angle C A E<\frac{1}{2} \angle B A C$. Finally, let $G$ be the midpoint of the segment $I F$. Prove that the lines $D G$ and $E I$ intersect on $\Gamma$. (Hong Kong)
|
As in the previous solution, we introduce the points $X, T$ and $K$ and note that it suffice to prove the equality $$ \frac{T F}{A T}=\frac{D I}{A D} \quad \Longleftrightarrow \quad \frac{T F+A T}{A T}=\frac{D I+A D}{A D} \quad \Longleftrightarrow \quad \frac{A T}{A D}=\frac{A F}{D I+A D} $$ Since $\angle F A D=\angle E A I$ and $\angle T D A=\angle X D A=\angle X E A=\angle I E A$, we get that the triangles $A T D$ and $A I E$ are similar, therefore $\frac{A T}{A D}=\frac{A I}{A E}$. Next, we also use the relation $D B=D C=D I$. Let $J$ be the point on the extension of segment $A D$ over point $D$ such that $D J=D I=D C$ (see Fig. 2). Then $\angle D J C=$ $\angle J C D=\frac{1}{2}(\pi-\angle J D C)=\frac{1}{2} \angle A D C=\frac{1}{2} \angle A B C=\angle A B I$. Moreover, $\angle B A I=\angle J A C$, hence triangles $A B I$ and $A J C$ are similar, so $\frac{A B}{A J}=\frac{A I}{A C}$, or $A B \cdot A C=A J \cdot A I=(D I+A D) \cdot A I$. On the other hand, we get $\angle A B F=\angle A B C=\angle A E C$ and $\angle B A F=\angle C A E$, so triangles $A B F$ and $A E C$ are also similar, which implies $\frac{A F}{A C}=\frac{A B}{A E}$, or $A B \cdot A C=A F \cdot A E$. Summarizing we get $$ (D I+A D) \cdot A I=A B \cdot A C=A F \cdot A E \quad \Rightarrow \quad \frac{A I}{A E}=\frac{A F}{A D+D I} \quad \Rightarrow \quad \frac{A T}{A D}=\frac{A F}{A D+D I} $$ as desired. Comment. In fact, point $J$ is an excenter of triangle $A B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $I$ be the incenter of a triangle $A B C$ and $\Gamma$ be its circumcircle. Let the line $A I$ intersect $\Gamma$ at a point $D \neq A$. Let $F$ and $E$ be points on side $B C$ and $\operatorname{arc} B D C$ respectively such that $\angle B A F=\angle C A E<\frac{1}{2} \angle B A C$. Finally, let $G$ be the midpoint of the segment $I F$. Prove that the lines $D G$ and $E I$ intersect on $\Gamma$. (Hong Kong)
|
As in the previous solution, we introduce the points $X, T$ and $K$ and note that it suffice to prove the equality $$ \frac{T F}{A T}=\frac{D I}{A D} \quad \Longleftrightarrow \quad \frac{T F+A T}{A T}=\frac{D I+A D}{A D} \quad \Longleftrightarrow \quad \frac{A T}{A D}=\frac{A F}{D I+A D} $$ Since $\angle F A D=\angle E A I$ and $\angle T D A=\angle X D A=\angle X E A=\angle I E A$, we get that the triangles $A T D$ and $A I E$ are similar, therefore $\frac{A T}{A D}=\frac{A I}{A E}$. Next, we also use the relation $D B=D C=D I$. Let $J$ be the point on the extension of segment $A D$ over point $D$ such that $D J=D I=D C$ (see Fig. 2). Then $\angle D J C=$ $\angle J C D=\frac{1}{2}(\pi-\angle J D C)=\frac{1}{2} \angle A D C=\frac{1}{2} \angle A B C=\angle A B I$. Moreover, $\angle B A I=\angle J A C$, hence triangles $A B I$ and $A J C$ are similar, so $\frac{A B}{A J}=\frac{A I}{A C}$, or $A B \cdot A C=A J \cdot A I=(D I+A D) \cdot A I$. On the other hand, we get $\angle A B F=\angle A B C=\angle A E C$ and $\angle B A F=\angle C A E$, so triangles $A B F$ and $A E C$ are also similar, which implies $\frac{A F}{A C}=\frac{A B}{A E}$, or $A B \cdot A C=A F \cdot A E$. Summarizing we get $$ (D I+A D) \cdot A I=A B \cdot A C=A F \cdot A E \quad \Rightarrow \quad \frac{A I}{A E}=\frac{A F}{A D+D I} \quad \Rightarrow \quad \frac{A T}{A D}=\frac{A F}{A D+D I} $$ as desired. Comment. In fact, point $J$ is an excenter of triangle $A B C$.
|
{
"resource_path": "IMO/segmented/en-IMO2010SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
d75255d9-c670-513f-a193-75954170fc58
| 23,977
|
Three circular arcs $\gamma_{1}, \gamma_{2}$, and $\gamma_{3}$ connect the points $A$ and $C$. These arcs lie in the same half-plane defined by line $A C$ in such a way that arc $\gamma_{2}$ lies between the arcs $\gamma_{1}$ and $\gamma_{3}$. Point $B$ lies on the segment $A C$. Let $h_{1}, h_{2}$, and $h_{3}$ be three rays starting at $B$, lying in the same half-plane, $h_{2}$ being between $h_{1}$ and $h_{3}$. For $i, j=1,2,3$, denote by $V_{i j}$ the point of intersection of $h_{i}$ and $\gamma_{j}$ (see the Figure below). Denote by $\widehat{V_{i j} V_{k j}} \widehat{V_{k \ell} V_{i \ell}}$ the curved quadrilateral, whose sides are the segments $V_{i j} V_{i \ell}, V_{k j} V_{k \ell}$ and $\operatorname{arcs} V_{i j} V_{k j}$ and $V_{i \ell} V_{k \ell}$. We say that this quadrilateral is circumscribed if there exists a circle touching these two segments and two arcs. Prove that if the curved quadrilaterals $\sqrt{V_{11} V_{21}} \sqrt{22} V_{12}, \sqrt{V_{12} V_{22}} \sqrt{23} V_{13}, \sqrt{V_{21} V_{31}} \sqrt{V_{32} V_{22}}$ are circumscribed, then the curved quadrilateral $\sqrt{V_{22} V_{32}} \sqrt{33} V_{23}$ is circumscribed, too.  Fig. 1 (Hungary)
|
Denote by $O_{i}$ and $R_{i}$ the center and the radius of $\gamma_{i}$, respectively. Denote also by $H$ the half-plane defined by $A C$ which contains the whole configuration. For every point $P$ in the half-plane $H$, denote by $d(P)$ the distance between $P$ and line $A C$. Furthermore, for any $r>0$, denote by $\Omega(P, r)$ the circle with center $P$ and radius $r$. Lemma 1. For every $1 \leq i<j \leq 3$, consider those circles $\Omega(P, r)$ in the half-plane $H$ which are tangent to $h_{i}$ and $h_{j}$. (a) The locus of the centers of these circles is the angle bisector $\beta_{i j}$ between $h_{i}$ and $h_{j}$. (b) There is a constant $u_{i j}$ such that $r=u_{i j} \cdot d(P)$ for all such circles. Proof. Part (a) is obvious. To prove part (b), notice that the circles which are tangent to $h_{i}$ and $h_{j}$ are homothetic with the common homothety center $B$ (see Fig. 2). Then part (b) also becomes trivial. Lemma 2. For every $1 \leq i<j \leq 3$, consider those circles $\Omega(P, r)$ in the half-plane $H$ which are externally tangent to $\gamma_{i}$ and internally tangent to $\gamma_{j}$. (a) The locus of the centers of these circles is an ellipse $\operatorname{arc} \varepsilon_{i j}$ with end-points $A$ and $C$. (b) There is a constant $v_{i j}$ such that $r=v_{i j} \cdot d(P)$ for all such circles. Proof. (a) Notice that the circle $\Omega(P, r)$ is externally tangent to $\gamma_{i}$ and internally tangent to $\gamma_{j}$ if and only if $O_{i} P=R_{i}+r$ and $O_{j}=R_{j}-r$. Therefore, for each such circle we have $$ O_{i} P+O_{j} P=O_{i} A+O_{j} A=O_{i} C+O_{j} C=R_{i}+R_{j} $$ Such points lie on an ellipse with foci $O_{i}$ and $O_{j}$; the diameter of this ellipse is $R_{i}+R_{j}$, and it passes through the points $A$ and $C$. Let $\varepsilon_{i j}$ be that arc $A C$ of the ellipse which runs inside the half plane $H$ (see Fig. 3.) This ellipse arc lies between the arcs $\gamma_{i}$ and $\gamma_{j}$. Therefore, if some point $P$ lies on $\varepsilon_{i j}$, then $O_{i} P>R_{i}$ and $O_{j} P<R_{j}$. Now, we choose $r=O_{i} P-R_{i}=R_{j}-O_{j} P>0$; then the  circle $\Omega(P, r)$ touches $\gamma_{i}$ externally and touches $\gamma_{j}$ internally, so $P$ belongs to the locus under investigation. (b) Let $\vec{\rho}=\overrightarrow{A P}, \vec{\rho}_{i}=\overrightarrow{A O_{i}}$, and $\vec{\rho}_{j}=\overrightarrow{A O_{j}}$; let $d_{i j}=O_{i} O_{j}$, and let $\vec{v}$ be a unit vector orthogonal to $A C$ and directed toward $H$. Then we have $\left|\vec{\rho}_{i}\right|=R_{i},\left|\vec{\rho}_{j}\right|=R_{j},\left|\overrightarrow{O_{i} P}\right|=$ $\left|\vec{\rho}-\vec{\rho}_{i}\right|=R_{i}+r,\left|\overrightarrow{O_{j} P}\right|=\left|\vec{\rho}-\vec{\rho}_{j}\right|=R_{j}-r$, hence $$ \begin{gathered} \left(\vec{\rho}-\vec{\rho}_{i}\right)^{2}-\left(\vec{\rho}-\vec{\rho}_{j}\right)^{2}=\left(R_{i}+r\right)^{2}-\left(R_{j}-r\right)^{2}, \\ \left(\vec{\rho}_{i}^{2}-\vec{\rho}_{j}^{2}\right)+2 \vec{\rho} \cdot\left(\vec{\rho}_{j}-\vec{\rho}_{i}\right)=\left(R_{i}^{2}-R_{j}^{2}\right)+2 r\left(R_{i}+R_{j}\right), \\ d_{i j} \cdot d(P)=d_{i j} \vec{v} \cdot \vec{\rho}=\left(\vec{\rho}_{j}-\vec{\rho}_{i}\right) \cdot \vec{\rho}=r\left(R_{i}+R_{j}\right) . \end{gathered} $$ Therefore, $$ r=\frac{d_{i j}}{R_{i}+R_{j}} \cdot d(P) $$ and the value $v_{i j}=\frac{d_{i j}}{R_{i}+R_{j}}$ does not depend on $P$. Lemma 3. The curved quadrilateral $\mathcal{Q}_{i j}=\sqrt{i, j V_{i+1, j}} V_{i+1, j+1} V_{i, j+1}$ is circumscribed if and only if $u_{i, i+1}=v_{j, j+1}$. Proof. First suppose that the curved quadrilateral $\mathcal{Q}_{i j}$ is circumscribed and $\Omega(P, r)$ is its inscribed circle. By Lemma 1 and Lemma 2 we have $r=u_{i, i+1} \cdot d(P)$ and $r=v_{j, j+1} \cdot d(P)$ as well. Hence, $u_{i, i+1}=v_{j, j+1}$. To prove the opposite direction, suppose $u_{i, i+1}=v_{j, j+1}$. Let $P$ be the intersection of the angle bisector $\beta_{i, i+1}$ and the ellipse arc $\varepsilon_{j, j+1}$. Choose $r=u_{i, i+1} \cdot d(P)=v_{j, j+1} \cdot d(P)$. Then the circle $\Omega(P, r)$ is tangent to the half lines $h_{i}$ and $h_{i+1}$ by Lemma 1 , and it is tangent to the $\operatorname{arcs} \gamma_{j}$ and $\gamma_{j+1}$ by Lemma 2. Hence, the curved quadrilateral $\mathcal{Q}_{i j}$ is circumscribed. By Lemma 3, the statement of the problem can be reformulated to an obvious fact: If the equalities $u_{12}=v_{12}, u_{12}=v_{23}$, and $u_{23}=v_{12}$ hold, then $u_{23}=v_{23}$ holds as well. Comment 1. Lemma 2(b) (together with the easy Lemma 1(b)) is the key tool in this solution. If one finds this fact, then the solution can be finished in many ways. That is, one can find a circle touching three of $h_{2}, h_{3}, \gamma_{2}$, and $\gamma_{3}$, and then prove that it is tangent to the fourth one in either synthetic or analytical way. Both approaches can be successful. Here we present some discussion about this key Lemma. 1. In the solution above we chose an analytic proof for Lemma 2(b) because we expect that most students will use coordinates or vectors to examine the locus of the centers, and these approaches are less case-sensitive. Here we outline a synthetic proof. We consider only the case when $P$ does not lie in the line $O_{i} O_{j}$. The other case can be obtained as a limit case, or computed in a direct way. Let $S$ be the internal homothety center between the circles of $\gamma_{i}$ and $\gamma_{j}$, lying on $O_{i} O_{j}$; this point does not depend on $P$. Let $U$ and $V$ be the points of tangency of circle $\sigma=\Omega(P, r)$ with $\gamma_{i}$ and $\gamma_{j}$, respectively (then $r=P U=P V$ ); in other words, points $U$ and $V$ are the intersection points of rays $O_{i} P, O_{j} P$ with arcs $\gamma_{i}, \gamma_{j}$ respectively (see Fig. 4). Due to the theorem on three homothety centers (or just to the Menelaus theorem applied to triangle $O_{i} O_{j} P$ ), the points $U, V$ and $S$ are collinear. Let $T$ be the intersection point of line $A C$ and the common tangent to $\sigma$ and $\gamma_{i}$ at $U$; then $T$ is the radical center of $\sigma, \gamma_{i}$ and $\gamma_{j}$, hence $T V$ is the common tangent to $\sigma$ and $\gamma_{j}$. Let $Q$ be the projection of $P$ onto the line $A C$. By the right angles, the points $U, V$ and $Q$ lie on the circle with diameter $P T$. From this fact and the equality $P U=P V$ we get $\angle U Q P=\angle U V P=$ $\angle V U P=\angle S U O_{i}$. Since $O_{i} S \| P Q$, we have $\angle S O_{i} U=\angle Q P U$. Hence, the triangles $S O_{i} U$ and $U P Q$ are similar and thus $\frac{r}{d(P)}=\frac{P U}{P Q}=\frac{O_{i} S}{O_{i} U}=\frac{O_{i} S}{R_{i}}$; the last expression is constant since $S$ is a constant point.  Fig. 4  Fig. 5 2. Using some known facts about conics, the same statement can be proved in a very short way. Denote by $\ell$ the directrix of ellipse of $\varepsilon_{i j}$ related to the focus $O_{j}$; since $\varepsilon_{i j}$ is symmetrical about $O_{i} O_{j}$, we have $\ell \| A C$. Recall that for each point $P \in \varepsilon_{i j}$, we have $P O_{j}=\epsilon \cdot d_{\ell}(P)$, where $d_{\ell}(P)$ is the distance from $P$ to $\ell$, and $\epsilon$ is the eccentricity of $\varepsilon_{i j}$ (see Fig. 5). Now we have $$ r=R_{j}-\left(R_{j}-r\right)=A O_{j}-P O_{j}=\epsilon\left(d_{\ell}(A)-d_{\ell}(P)\right)=\epsilon(d(P)-d(A))=\epsilon \cdot d(P), $$ and $\epsilon$ does not depend on $P$. Comment 2. One can find a spatial interpretations of the problem and the solution. For every point $(x, y)$ and radius $r>0$, represent the circle $\Omega((x, y), r)$ by the point $(x, y, r)$ in space. This point is the apex of the cone with base circle $\Omega((x, y), r)$ and height $r$. According to Lemma 1 , the circles which are tangent to $h_{i}$ and $h_{j}$ correspond to the points of a half line $\beta_{i j}^{\prime}$, starting at $B$. Now we translate Lemma 2. Take some $1 \leq i<j \leq 3$, and consider those circles which are internally tangent to $\gamma_{j}$. It is easy to see that the locus of the points which represent these circles is a subset of a cone, containing $\gamma_{j}$. Similarly, the circles which are externally tangent to $\gamma_{i}$ correspond to the points on the extension of another cone, which has its apex on the opposite side of the base plane $\Pi$. (See Fig. 6; for this illustration, the $z$-coordinates were multiplied by 2.) The two cones are symmetric to each other (they have the same aperture, and their axes are parallel). As is well-known, it follows that the common points of the two cones are co-planar. So the intersection of the two cones is a a conic section - which is an ellipse, according to Lemma 2(a). The points which represent the circles touching $\gamma_{i}$ and $\gamma_{j}$ is an ellipse arc $\varepsilon_{i j}^{\prime}$ with end-points $A$ and $C$.  Fig. 6  Fig. 7 Thus, the curved quadrilateral $\mathcal{Q}_{i j}$ is circumscribed if and only if $\beta_{i, i+1}^{\prime}$ and $\varepsilon_{j, j+1}^{\prime}$ intersect, i.e. if they are coplanar. If three of the four curved quadrilaterals are circumscribed, it means that $\varepsilon_{12}^{\prime}, \varepsilon_{23}^{\prime}$, $\beta_{12}^{\prime}$ and $\beta_{23}^{\prime}$ lie in the same plane $\Sigma$, and the fourth intersection comes to existence, too (see Fig. 7).  A connection between mathematics and real life: the Palace of Creativity "Shabyt" ("Inspiration") in Astana
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Three circular arcs $\gamma_{1}, \gamma_{2}$, and $\gamma_{3}$ connect the points $A$ and $C$. These arcs lie in the same half-plane defined by line $A C$ in such a way that arc $\gamma_{2}$ lies between the arcs $\gamma_{1}$ and $\gamma_{3}$. Point $B$ lies on the segment $A C$. Let $h_{1}, h_{2}$, and $h_{3}$ be three rays starting at $B$, lying in the same half-plane, $h_{2}$ being between $h_{1}$ and $h_{3}$. For $i, j=1,2,3$, denote by $V_{i j}$ the point of intersection of $h_{i}$ and $\gamma_{j}$ (see the Figure below). Denote by $\widehat{V_{i j} V_{k j}} \widehat{V_{k \ell} V_{i \ell}}$ the curved quadrilateral, whose sides are the segments $V_{i j} V_{i \ell}, V_{k j} V_{k \ell}$ and $\operatorname{arcs} V_{i j} V_{k j}$ and $V_{i \ell} V_{k \ell}$. We say that this quadrilateral is circumscribed if there exists a circle touching these two segments and two arcs. Prove that if the curved quadrilaterals $\sqrt{V_{11} V_{21}} \sqrt{22} V_{12}, \sqrt{V_{12} V_{22}} \sqrt{23} V_{13}, \sqrt{V_{21} V_{31}} \sqrt{V_{32} V_{22}}$ are circumscribed, then the curved quadrilateral $\sqrt{V_{22} V_{32}} \sqrt{33} V_{23}$ is circumscribed, too.  Fig. 1 (Hungary)
|
Denote by $O_{i}$ and $R_{i}$ the center and the radius of $\gamma_{i}$, respectively. Denote also by $H$ the half-plane defined by $A C$ which contains the whole configuration. For every point $P$ in the half-plane $H$, denote by $d(P)$ the distance between $P$ and line $A C$. Furthermore, for any $r>0$, denote by $\Omega(P, r)$ the circle with center $P$ and radius $r$. Lemma 1. For every $1 \leq i<j \leq 3$, consider those circles $\Omega(P, r)$ in the half-plane $H$ which are tangent to $h_{i}$ and $h_{j}$. (a) The locus of the centers of these circles is the angle bisector $\beta_{i j}$ between $h_{i}$ and $h_{j}$. (b) There is a constant $u_{i j}$ such that $r=u_{i j} \cdot d(P)$ for all such circles. Proof. Part (a) is obvious. To prove part (b), notice that the circles which are tangent to $h_{i}$ and $h_{j}$ are homothetic with the common homothety center $B$ (see Fig. 2). Then part (b) also becomes trivial. Lemma 2. For every $1 \leq i<j \leq 3$, consider those circles $\Omega(P, r)$ in the half-plane $H$ which are externally tangent to $\gamma_{i}$ and internally tangent to $\gamma_{j}$. (a) The locus of the centers of these circles is an ellipse $\operatorname{arc} \varepsilon_{i j}$ with end-points $A$ and $C$. (b) There is a constant $v_{i j}$ such that $r=v_{i j} \cdot d(P)$ for all such circles. Proof. (a) Notice that the circle $\Omega(P, r)$ is externally tangent to $\gamma_{i}$ and internally tangent to $\gamma_{j}$ if and only if $O_{i} P=R_{i}+r$ and $O_{j}=R_{j}-r$. Therefore, for each such circle we have $$ O_{i} P+O_{j} P=O_{i} A+O_{j} A=O_{i} C+O_{j} C=R_{i}+R_{j} $$ Such points lie on an ellipse with foci $O_{i}$ and $O_{j}$; the diameter of this ellipse is $R_{i}+R_{j}$, and it passes through the points $A$ and $C$. Let $\varepsilon_{i j}$ be that arc $A C$ of the ellipse which runs inside the half plane $H$ (see Fig. 3.) This ellipse arc lies between the arcs $\gamma_{i}$ and $\gamma_{j}$. Therefore, if some point $P$ lies on $\varepsilon_{i j}$, then $O_{i} P>R_{i}$ and $O_{j} P<R_{j}$. Now, we choose $r=O_{i} P-R_{i}=R_{j}-O_{j} P>0$; then the  circle $\Omega(P, r)$ touches $\gamma_{i}$ externally and touches $\gamma_{j}$ internally, so $P$ belongs to the locus under investigation. (b) Let $\vec{\rho}=\overrightarrow{A P}, \vec{\rho}_{i}=\overrightarrow{A O_{i}}$, and $\vec{\rho}_{j}=\overrightarrow{A O_{j}}$; let $d_{i j}=O_{i} O_{j}$, and let $\vec{v}$ be a unit vector orthogonal to $A C$ and directed toward $H$. Then we have $\left|\vec{\rho}_{i}\right|=R_{i},\left|\vec{\rho}_{j}\right|=R_{j},\left|\overrightarrow{O_{i} P}\right|=$ $\left|\vec{\rho}-\vec{\rho}_{i}\right|=R_{i}+r,\left|\overrightarrow{O_{j} P}\right|=\left|\vec{\rho}-\vec{\rho}_{j}\right|=R_{j}-r$, hence $$ \begin{gathered} \left(\vec{\rho}-\vec{\rho}_{i}\right)^{2}-\left(\vec{\rho}-\vec{\rho}_{j}\right)^{2}=\left(R_{i}+r\right)^{2}-\left(R_{j}-r\right)^{2}, \\ \left(\vec{\rho}_{i}^{2}-\vec{\rho}_{j}^{2}\right)+2 \vec{\rho} \cdot\left(\vec{\rho}_{j}-\vec{\rho}_{i}\right)=\left(R_{i}^{2}-R_{j}^{2}\right)+2 r\left(R_{i}+R_{j}\right), \\ d_{i j} \cdot d(P)=d_{i j} \vec{v} \cdot \vec{\rho}=\left(\vec{\rho}_{j}-\vec{\rho}_{i}\right) \cdot \vec{\rho}=r\left(R_{i}+R_{j}\right) . \end{gathered} $$ Therefore, $$ r=\frac{d_{i j}}{R_{i}+R_{j}} \cdot d(P) $$ and the value $v_{i j}=\frac{d_{i j}}{R_{i}+R_{j}}$ does not depend on $P$. Lemma 3. The curved quadrilateral $\mathcal{Q}_{i j}=\sqrt{i, j V_{i+1, j}} V_{i+1, j+1} V_{i, j+1}$ is circumscribed if and only if $u_{i, i+1}=v_{j, j+1}$. Proof. First suppose that the curved quadrilateral $\mathcal{Q}_{i j}$ is circumscribed and $\Omega(P, r)$ is its inscribed circle. By Lemma 1 and Lemma 2 we have $r=u_{i, i+1} \cdot d(P)$ and $r=v_{j, j+1} \cdot d(P)$ as well. Hence, $u_{i, i+1}=v_{j, j+1}$. To prove the opposite direction, suppose $u_{i, i+1}=v_{j, j+1}$. Let $P$ be the intersection of the angle bisector $\beta_{i, i+1}$ and the ellipse arc $\varepsilon_{j, j+1}$. Choose $r=u_{i, i+1} \cdot d(P)=v_{j, j+1} \cdot d(P)$. Then the circle $\Omega(P, r)$ is tangent to the half lines $h_{i}$ and $h_{i+1}$ by Lemma 1 , and it is tangent to the $\operatorname{arcs} \gamma_{j}$ and $\gamma_{j+1}$ by Lemma 2. Hence, the curved quadrilateral $\mathcal{Q}_{i j}$ is circumscribed. By Lemma 3, the statement of the problem can be reformulated to an obvious fact: If the equalities $u_{12}=v_{12}, u_{12}=v_{23}$, and $u_{23}=v_{12}$ hold, then $u_{23}=v_{23}$ holds as well. Comment 1. Lemma 2(b) (together with the easy Lemma 1(b)) is the key tool in this solution. If one finds this fact, then the solution can be finished in many ways. That is, one can find a circle touching three of $h_{2}, h_{3}, \gamma_{2}$, and $\gamma_{3}$, and then prove that it is tangent to the fourth one in either synthetic or analytical way. Both approaches can be successful. Here we present some discussion about this key Lemma. 1. In the solution above we chose an analytic proof for Lemma 2(b) because we expect that most students will use coordinates or vectors to examine the locus of the centers, and these approaches are less case-sensitive. Here we outline a synthetic proof. We consider only the case when $P$ does not lie in the line $O_{i} O_{j}$. The other case can be obtained as a limit case, or computed in a direct way. Let $S$ be the internal homothety center between the circles of $\gamma_{i}$ and $\gamma_{j}$, lying on $O_{i} O_{j}$; this point does not depend on $P$. Let $U$ and $V$ be the points of tangency of circle $\sigma=\Omega(P, r)$ with $\gamma_{i}$ and $\gamma_{j}$, respectively (then $r=P U=P V$ ); in other words, points $U$ and $V$ are the intersection points of rays $O_{i} P, O_{j} P$ with arcs $\gamma_{i}, \gamma_{j}$ respectively (see Fig. 4). Due to the theorem on three homothety centers (or just to the Menelaus theorem applied to triangle $O_{i} O_{j} P$ ), the points $U, V$ and $S$ are collinear. Let $T$ be the intersection point of line $A C$ and the common tangent to $\sigma$ and $\gamma_{i}$ at $U$; then $T$ is the radical center of $\sigma, \gamma_{i}$ and $\gamma_{j}$, hence $T V$ is the common tangent to $\sigma$ and $\gamma_{j}$. Let $Q$ be the projection of $P$ onto the line $A C$. By the right angles, the points $U, V$ and $Q$ lie on the circle with diameter $P T$. From this fact and the equality $P U=P V$ we get $\angle U Q P=\angle U V P=$ $\angle V U P=\angle S U O_{i}$. Since $O_{i} S \| P Q$, we have $\angle S O_{i} U=\angle Q P U$. Hence, the triangles $S O_{i} U$ and $U P Q$ are similar and thus $\frac{r}{d(P)}=\frac{P U}{P Q}=\frac{O_{i} S}{O_{i} U}=\frac{O_{i} S}{R_{i}}$; the last expression is constant since $S$ is a constant point.  Fig. 4  Fig. 5 2. Using some known facts about conics, the same statement can be proved in a very short way. Denote by $\ell$ the directrix of ellipse of $\varepsilon_{i j}$ related to the focus $O_{j}$; since $\varepsilon_{i j}$ is symmetrical about $O_{i} O_{j}$, we have $\ell \| A C$. Recall that for each point $P \in \varepsilon_{i j}$, we have $P O_{j}=\epsilon \cdot d_{\ell}(P)$, where $d_{\ell}(P)$ is the distance from $P$ to $\ell$, and $\epsilon$ is the eccentricity of $\varepsilon_{i j}$ (see Fig. 5). Now we have $$ r=R_{j}-\left(R_{j}-r\right)=A O_{j}-P O_{j}=\epsilon\left(d_{\ell}(A)-d_{\ell}(P)\right)=\epsilon(d(P)-d(A))=\epsilon \cdot d(P), $$ and $\epsilon$ does not depend on $P$. Comment 2. One can find a spatial interpretations of the problem and the solution. For every point $(x, y)$ and radius $r>0$, represent the circle $\Omega((x, y), r)$ by the point $(x, y, r)$ in space. This point is the apex of the cone with base circle $\Omega((x, y), r)$ and height $r$. According to Lemma 1 , the circles which are tangent to $h_{i}$ and $h_{j}$ correspond to the points of a half line $\beta_{i j}^{\prime}$, starting at $B$. Now we translate Lemma 2. Take some $1 \leq i<j \leq 3$, and consider those circles which are internally tangent to $\gamma_{j}$. It is easy to see that the locus of the points which represent these circles is a subset of a cone, containing $\gamma_{j}$. Similarly, the circles which are externally tangent to $\gamma_{i}$ correspond to the points on the extension of another cone, which has its apex on the opposite side of the base plane $\Pi$. (See Fig. 6; for this illustration, the $z$-coordinates were multiplied by 2.) The two cones are symmetric to each other (they have the same aperture, and their axes are parallel). As is well-known, it follows that the common points of the two cones are co-planar. So the intersection of the two cones is a a conic section - which is an ellipse, according to Lemma 2(a). The points which represent the circles touching $\gamma_{i}$ and $\gamma_{j}$ is an ellipse arc $\varepsilon_{i j}^{\prime}$ with end-points $A$ and $C$.  Fig. 6  Fig. 7 Thus, the curved quadrilateral $\mathcal{Q}_{i j}$ is circumscribed if and only if $\beta_{i, i+1}^{\prime}$ and $\varepsilon_{j, j+1}^{\prime}$ intersect, i.e. if they are coplanar. If three of the four curved quadrilaterals are circumscribed, it means that $\varepsilon_{12}^{\prime}, \varepsilon_{23}^{\prime}$, $\beta_{12}^{\prime}$ and $\beta_{23}^{\prime}$ lie in the same plane $\Sigma$, and the fourth intersection comes to existence, too (see Fig. 7).  A connection between mathematics and real life: the Palace of Creativity "Shabyt" ("Inspiration") in Astana
|
{
"resource_path": "IMO/segmented/en-IMO2010SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
5a5359d1-549a-5639-a53c-eef831e65d8c
| 23,986
|
Prove that for every positive integer $n$, the set $\{2,3,4, \ldots, 3 n+1\}$ can be partitioned into $n$ triples in such a way that the numbers from each triple are the lengths of the sides of some obtuse triangle.
|
Throughout the solution, we denote by $[a, b]$ the set $\{a, a+1, \ldots, b\}$. We say that $\{a, b, c\}$ is an obtuse triple if $a, b, c$ are the sides of some obtuse triangle. We prove by induction on $n$ that there exists a partition of $[2,3 n+1]$ into $n$ obtuse triples $A_{i}$ $(2 \leq i \leq n+1)$ having the form $A_{i}=\left\{i, a_{i}, b_{i}\right\}$. For the base case $n=1$, one can simply set $A_{2}=\{2,3,4\}$. For the induction step, we need the following simple lemma. Lemma. Suppose that the numbers $a<b<c$ form an obtuse triple, and let $x$ be any positive number. Then the triple $\{a, b+x, c+x\}$ is also obtuse. Proof. The numbers $a<b+x<c+x$ are the sides of a triangle because $(c+x)-(b+x)=$ $c-b<a$. This triangle is obtuse since $(c+x)^{2}-(b+x)^{2}=(c-b)(c+b+2 x)>(c-b)(c+b)>a^{2}$. Now we turn to the induction step. Let $n>1$ and put $t=\lfloor n / 2\rfloor<n$. By the induction hypothesis, there exists a partition of the set $[2,3 t+1]$ into $t$ obtuse triples $A_{i}^{\prime}=\left\{i, a_{i}^{\prime}, b_{i}^{\prime}\right\}$ $(i \in[2, t+1])$. For the same values of $i$, define $A_{i}=\left\{i, a_{i}^{\prime}+(n-t), b_{i}^{\prime}+(n-t)\right\}$. The constructed triples are obviously disjoint, and they are obtuse by the lemma. Moreover, we have $$ \bigcup_{i=2}^{t+1} A_{i}=[2, t+1] \cup[n+2, n+2 t+1] $$ Next, for each $i \in[t+2, n+1]$, define $A_{i}=\{i, n+t+i, 2 n+i\}$. All these sets are disjoint, and $$ \bigcup_{i=t+2}^{n+1} A_{i}=[t+2, n+1] \cup[n+2 t+2,2 n+t+1] \cup[2 n+t+2,3 n+1] $$ so $$ \bigcup_{i=2}^{n+1} A_{i}=[2,3 n+1] $$ Thus, we are left to prove that the triple $A_{i}$ is obtuse for each $i \in[t+2, n+1]$. Since $(2 n+i)-(n+t+i)=n-t<t+2 \leq i$, the elements of $A_{i}$ are the sides of a triangle. Next, we have $(2 n+i)^{2}-(n+t+i)^{2}=(n-t)(3 n+t+2 i) \geq \frac{n}{2} \cdot(3 n+3(t+1)+1)>\frac{n}{2} \cdot \frac{9 n}{2} \geq(n+1)^{2} \geq i^{2}$, so this triangle is obtuse. The proof is completed.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Prove that for every positive integer $n$, the set $\{2,3,4, \ldots, 3 n+1\}$ can be partitioned into $n$ triples in such a way that the numbers from each triple are the lengths of the sides of some obtuse triangle.
|
Throughout the solution, we denote by $[a, b]$ the set $\{a, a+1, \ldots, b\}$. We say that $\{a, b, c\}$ is an obtuse triple if $a, b, c$ are the sides of some obtuse triangle. We prove by induction on $n$ that there exists a partition of $[2,3 n+1]$ into $n$ obtuse triples $A_{i}$ $(2 \leq i \leq n+1)$ having the form $A_{i}=\left\{i, a_{i}, b_{i}\right\}$. For the base case $n=1$, one can simply set $A_{2}=\{2,3,4\}$. For the induction step, we need the following simple lemma. Lemma. Suppose that the numbers $a<b<c$ form an obtuse triple, and let $x$ be any positive number. Then the triple $\{a, b+x, c+x\}$ is also obtuse. Proof. The numbers $a<b+x<c+x$ are the sides of a triangle because $(c+x)-(b+x)=$ $c-b<a$. This triangle is obtuse since $(c+x)^{2}-(b+x)^{2}=(c-b)(c+b+2 x)>(c-b)(c+b)>a^{2}$. Now we turn to the induction step. Let $n>1$ and put $t=\lfloor n / 2\rfloor<n$. By the induction hypothesis, there exists a partition of the set $[2,3 t+1]$ into $t$ obtuse triples $A_{i}^{\prime}=\left\{i, a_{i}^{\prime}, b_{i}^{\prime}\right\}$ $(i \in[2, t+1])$. For the same values of $i$, define $A_{i}=\left\{i, a_{i}^{\prime}+(n-t), b_{i}^{\prime}+(n-t)\right\}$. The constructed triples are obviously disjoint, and they are obtuse by the lemma. Moreover, we have $$ \bigcup_{i=2}^{t+1} A_{i}=[2, t+1] \cup[n+2, n+2 t+1] $$ Next, for each $i \in[t+2, n+1]$, define $A_{i}=\{i, n+t+i, 2 n+i\}$. All these sets are disjoint, and $$ \bigcup_{i=t+2}^{n+1} A_{i}=[t+2, n+1] \cup[n+2 t+2,2 n+t+1] \cup[2 n+t+2,3 n+1] $$ so $$ \bigcup_{i=2}^{n+1} A_{i}=[2,3 n+1] $$ Thus, we are left to prove that the triple $A_{i}$ is obtuse for each $i \in[t+2, n+1]$. Since $(2 n+i)-(n+t+i)=n-t<t+2 \leq i$, the elements of $A_{i}$ are the sides of a triangle. Next, we have $(2 n+i)^{2}-(n+t+i)^{2}=(n-t)(3 n+t+2 i) \geq \frac{n}{2} \cdot(3 n+3(t+1)+1)>\frac{n}{2} \cdot \frac{9 n}{2} \geq(n+1)^{2} \geq i^{2}$, so this triangle is obtuse. The proof is completed.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
297d05b9-3e19-5dda-8bd7-5cbcfee0bb60
| 24,016
|
Let $f$ be a function from the set of real numbers to itself that satisfies $$ f(x+y) \leq y f(x)+f(f(x)) $$ for all real numbers $x$ and $y$. Prove that $f(x)=0$ for all $x \leq 0$.
|
Substituting $y=t-x$, we rewrite (II) as $$ f(t) \leq t f(x)-x f(x)+f(f(x)) . $$ Consider now some real numbers $a, b$ and use (2) with $t=f(a), x=b$ as well as with $t=f(b)$, $x=a$. We get $$ \begin{aligned} & f(f(a))-f(f(b)) \leq f(a) f(b)-b f(b), \\ & f(f(b))-f(f(a)) \leq f(a) f(b)-a f(a) . \end{aligned} $$ Adding these two inequalities yields $$ 2 f(a) f(b) \geq a f(a)+b f(b) . $$ Now, substitute $b=2 f(a)$ to obtain $2 f(a) f(b) \geq a f(a)+2 f(a) f(b)$, or $a f(a) \leq 0$. So, we get $$ f(a) \geq 0 \text { for all } a<0 \text {. } $$ Now suppose $f(x)>0$ for some real number $x$. From (21) we immediately get that for every $t<\frac{x f(x)-f(f(x))}{f(x)}$ we have $f(t)<0$. This contradicts (3); therefore $$ f(x) \leq 0 \quad \text { for all real } x $$ and by (3) again we get $f(x)=0$ for all $x<0$. We are left to find $f(0)$. Setting $t=x<0$ in (2) we get $$ 0 \leq 0-0+f(0), $$ so $f(0) \geq 0$. Combining this with (4) we obtain $f(0)=0$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $f$ be a function from the set of real numbers to itself that satisfies $$ f(x+y) \leq y f(x)+f(f(x)) $$ for all real numbers $x$ and $y$. Prove that $f(x)=0$ for all $x \leq 0$.
|
Substituting $y=t-x$, we rewrite (II) as $$ f(t) \leq t f(x)-x f(x)+f(f(x)) . $$ Consider now some real numbers $a, b$ and use (2) with $t=f(a), x=b$ as well as with $t=f(b)$, $x=a$. We get $$ \begin{aligned} & f(f(a))-f(f(b)) \leq f(a) f(b)-b f(b), \\ & f(f(b))-f(f(a)) \leq f(a) f(b)-a f(a) . \end{aligned} $$ Adding these two inequalities yields $$ 2 f(a) f(b) \geq a f(a)+b f(b) . $$ Now, substitute $b=2 f(a)$ to obtain $2 f(a) f(b) \geq a f(a)+2 f(a) f(b)$, or $a f(a) \leq 0$. So, we get $$ f(a) \geq 0 \text { for all } a<0 \text {. } $$ Now suppose $f(x)>0$ for some real number $x$. From (21) we immediately get that for every $t<\frac{x f(x)-f(f(x))}{f(x)}$ we have $f(t)<0$. This contradicts (3); therefore $$ f(x) \leq 0 \quad \text { for all real } x $$ and by (3) again we get $f(x)=0$ for all $x<0$. We are left to find $f(0)$. Setting $t=x<0$ in (2) we get $$ 0 \leq 0-0+f(0), $$ so $f(0) \geq 0$. Combining this with (4) we obtain $f(0)=0$.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
6194ac57-b640-5345-95d1-eee7519e67a7
| 24,019
|
Let $f$ be a function from the set of real numbers to itself that satisfies $$ f(x+y) \leq y f(x)+f(f(x)) $$ for all real numbers $x$ and $y$. Prove that $f(x)=0$ for all $x \leq 0$.
|
We will also use the condition of the problem in form (2)). For clarity we divide the argument into four steps. Step 1. We begin by proving that $f$ attains nonpositive values only. Assume that there exist some real number $z$ with $f(z)>0$. Substituting $x=z$ into (2) and setting $A=f(z)$, $B=-z f(z)-f(f(z))$ we get $f(t) \leq A t+B$ for all real $t$. Hence, if for any positive real number $t$ we substitute $x=-t, y=t$ into (11), we get $$ \begin{aligned} f(0) & \leq t f(-t)+f(f(-t)) \leq t(-A t+B)+A f(-t)+B \\ & \leq-t(A t-B)+A(-A t+B)+B=-A t^{2}-\left(A^{2}-B\right) t+(A+1) B . \end{aligned} $$ But surely this cannot be true if we take $t$ to be large enough. This contradiction proves that we have indeed $f(x) \leq 0$ for all real numbers $x$. Note that for this reason (11) entails $$ f(x+y) \leq y f(x) $$ for all real numbers $x$ and $y$. Step 2. We proceed by proving that $f$ has at least one zero. If $f(0)=0$, we are done. Otherwise, in view of Step 1 we get $f(0)<0$. Observe that (5) tells us now $f(y) \leq y f(0)$ for all real numbers $y$. Thus we can specify a positive real number $a$ that is so large that $f(a)^{2}>-f(0)$. Put $b=f(a)$ and substitute $x=b$ and $y=-b$ into (5); we learn $-b^{2}<f(0) \leq-b f(b)$, i.e. $b<f(b)$. Now we apply (2) to $x=b$ and $t=f(b)$, which yields $$ f(f(b)) \leq(f(b)-b) f(b)+f(f(b)), $$ i.e. $f(b) \geq 0$. So in view of Step $1, b$ is a zero of $f$. Step 3. Next we show that if $f(a)=0$ and $b<a$, then $f(b)=0$ as well. To see this, we just substitute $x=b$ and $y=a-b$ into (5), thus getting $f(b) \geq 0$, which suffices by Step 1 . Step 4. By Step 3, the solution of the problem is reduced to showing $f(0)=0$. Pick any zero $r$ of $f$ and substitute $x=r$ and $y=-1$ into (1). Because of $f(r)=f(r-1)=0$ this gives $f(0) \geq 0$ and hence $f(0)=0$ by Step 1 again. Comment 1. Both of these solutions also show $f(x) \leq 0$ for all real numbers $x$. As one can see from Solution 1, this task gets much easier if one already knows that $f$ takes nonnegative values for sufficiently small arguments. Another way of arriving at this statement, suggested by the proposer, is as follows: Put $a=f(0)$ and substitute $x=0$ into (1). This gives $f(y) \leq a y+f(a)$ for all real numbers $y$. Thus if for any real number $x$ we plug $y=a-x$ into (1), we obtain $$ f(a) \leq(a-x) f(x)+f(f(x)) \leq(a-x) f(x)+a f(x)+f(a) $$ and hence $0 \leq(2 a-x) f(x)$. In particular, if $x<2 a$, then $f(x) \geq 0$. Having reached this point, one may proceed almost exactly as in the first solution to deduce $f(x) \leq 0$ for all $x$. Afterwards the problem can be solved in a few lines as shown in steps 3 and 4 of the second solution. Comment 2. The original problem also contained the question whether a nonzero function satisfying the problem condition exists. Here we present a family of such functions. Notice first that if $g:(0, \infty) \longrightarrow[0, \infty)$ denotes any function such that $$ g(x+y) \geq y g(x) $$ for all positive real numbers $x$ and $y$, then the function $f$ given by $$ f(x)= \begin{cases}-g(x) & \text { if } x>0 \\ 0 & \text { if } x \leq 0\end{cases} $$ automatically satisfies (11). Indeed, we have $f(x) \leq 0$ and hence also $f(f(x))=0$ for all real numbers $x$. So (11) reduces to (5); moreover, this inequality is nontrivial only if $x$ and $y$ are positive. In this last case it is provided by (6). Now it is not hard to come up with a nonzero function $g$ obeying (6). E.g. $g(z)=C e^{z}$ (where $C$ is a positive constant) fits since the inequality $e^{y}>y$ holds for all (positive) real numbers $y$. One may also consider the function $g(z)=e^{z}-1$; in this case, we even have that $f$ is continuous.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $f$ be a function from the set of real numbers to itself that satisfies $$ f(x+y) \leq y f(x)+f(f(x)) $$ for all real numbers $x$ and $y$. Prove that $f(x)=0$ for all $x \leq 0$.
|
We will also use the condition of the problem in form (2)). For clarity we divide the argument into four steps. Step 1. We begin by proving that $f$ attains nonpositive values only. Assume that there exist some real number $z$ with $f(z)>0$. Substituting $x=z$ into (2) and setting $A=f(z)$, $B=-z f(z)-f(f(z))$ we get $f(t) \leq A t+B$ for all real $t$. Hence, if for any positive real number $t$ we substitute $x=-t, y=t$ into (11), we get $$ \begin{aligned} f(0) & \leq t f(-t)+f(f(-t)) \leq t(-A t+B)+A f(-t)+B \\ & \leq-t(A t-B)+A(-A t+B)+B=-A t^{2}-\left(A^{2}-B\right) t+(A+1) B . \end{aligned} $$ But surely this cannot be true if we take $t$ to be large enough. This contradiction proves that we have indeed $f(x) \leq 0$ for all real numbers $x$. Note that for this reason (11) entails $$ f(x+y) \leq y f(x) $$ for all real numbers $x$ and $y$. Step 2. We proceed by proving that $f$ has at least one zero. If $f(0)=0$, we are done. Otherwise, in view of Step 1 we get $f(0)<0$. Observe that (5) tells us now $f(y) \leq y f(0)$ for all real numbers $y$. Thus we can specify a positive real number $a$ that is so large that $f(a)^{2}>-f(0)$. Put $b=f(a)$ and substitute $x=b$ and $y=-b$ into (5); we learn $-b^{2}<f(0) \leq-b f(b)$, i.e. $b<f(b)$. Now we apply (2) to $x=b$ and $t=f(b)$, which yields $$ f(f(b)) \leq(f(b)-b) f(b)+f(f(b)), $$ i.e. $f(b) \geq 0$. So in view of Step $1, b$ is a zero of $f$. Step 3. Next we show that if $f(a)=0$ and $b<a$, then $f(b)=0$ as well. To see this, we just substitute $x=b$ and $y=a-b$ into (5), thus getting $f(b) \geq 0$, which suffices by Step 1 . Step 4. By Step 3, the solution of the problem is reduced to showing $f(0)=0$. Pick any zero $r$ of $f$ and substitute $x=r$ and $y=-1$ into (1). Because of $f(r)=f(r-1)=0$ this gives $f(0) \geq 0$ and hence $f(0)=0$ by Step 1 again. Comment 1. Both of these solutions also show $f(x) \leq 0$ for all real numbers $x$. As one can see from Solution 1, this task gets much easier if one already knows that $f$ takes nonnegative values for sufficiently small arguments. Another way of arriving at this statement, suggested by the proposer, is as follows: Put $a=f(0)$ and substitute $x=0$ into (1). This gives $f(y) \leq a y+f(a)$ for all real numbers $y$. Thus if for any real number $x$ we plug $y=a-x$ into (1), we obtain $$ f(a) \leq(a-x) f(x)+f(f(x)) \leq(a-x) f(x)+a f(x)+f(a) $$ and hence $0 \leq(2 a-x) f(x)$. In particular, if $x<2 a$, then $f(x) \geq 0$. Having reached this point, one may proceed almost exactly as in the first solution to deduce $f(x) \leq 0$ for all $x$. Afterwards the problem can be solved in a few lines as shown in steps 3 and 4 of the second solution. Comment 2. The original problem also contained the question whether a nonzero function satisfying the problem condition exists. Here we present a family of such functions. Notice first that if $g:(0, \infty) \longrightarrow[0, \infty)$ denotes any function such that $$ g(x+y) \geq y g(x) $$ for all positive real numbers $x$ and $y$, then the function $f$ given by $$ f(x)= \begin{cases}-g(x) & \text { if } x>0 \\ 0 & \text { if } x \leq 0\end{cases} $$ automatically satisfies (11). Indeed, we have $f(x) \leq 0$ and hence also $f(f(x))=0$ for all real numbers $x$. So (11) reduces to (5); moreover, this inequality is nontrivial only if $x$ and $y$ are positive. In this last case it is provided by (6). Now it is not hard to come up with a nonzero function $g$ obeying (6). E.g. $g(z)=C e^{z}$ (where $C$ is a positive constant) fits since the inequality $e^{y}>y$ holds for all (positive) real numbers $y$. One may also consider the function $g(z)=e^{z}-1$; in this case, we even have that $f$ is continuous.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
6194ac57-b640-5345-95d1-eee7519e67a7
| 24,019
|
Let $a, b$, and $c$ be positive real numbers satisfying $\min (a+b, b+c, c+a)>\sqrt{2}$ and $a^{2}+b^{2}+c^{2}=3$. Prove that $$ \frac{a}{(b+c-a)^{2}}+\frac{b}{(c+a-b)^{2}}+\frac{c}{(a+b-c)^{2}} \geq \frac{3}{(a b c)^{2}} $$
|
The condition $b+c>\sqrt{2}$ implies $b^{2}+c^{2}>1$, so $a^{2}=3-\left(b^{2}+c^{2}\right)<2$, i.e. $a<\sqrt{2}<b+c$. Hence we have $b+c-a>0$, and also $c+a-b>0$ and $a+b-c>0$ for similar reasons. We will use the variant of HÖLDER's inequality $$ \frac{x_{1}^{p+1}}{y_{1}^{p}}+\frac{x_{1}^{p+1}}{y_{1}^{p}}+\ldots+\frac{x_{n}^{p+1}}{y_{n}^{p}} \geq \frac{\left(x_{1}+x_{2}+\ldots+x_{n}\right)^{p+1}}{\left(y_{1}+y_{2}+\ldots+y_{n}\right)^{p}} $$ which holds for all positive real numbers $p, x_{1}, x_{2}, \ldots, x_{n}, y_{1}, y_{2}, \ldots, y_{n}$. Applying it to the left-hand side of (11) with $p=2$ and $n=3$, we get $$ \sum \frac{a}{(b+c-a)^{2}}=\sum \frac{\left(a^{2}\right)^{3}}{a^{5}(b+c-a)^{2}} \geq \frac{\left(a^{2}+b^{2}+c^{2}\right)^{3}}{\left(\sum a^{5 / 2}(b+c-a)\right)^{2}}=\frac{27}{\left(\sum a^{5 / 2}(b+c-a)\right)^{2}} . $$ To estimate the denominator of the right-hand part, we use an instance of SCHUR's inequality, namely $$ \sum a^{3 / 2}(a-b)(a-c) \geq 0 $$ which can be rewritten as $$ \sum a^{5 / 2}(b+c-a) \leq a b c(\sqrt{a}+\sqrt{b}+\sqrt{c}) . $$ Moreover, by the inequality between the arithmetic mean and the fourth power mean we also have $$ \left(\frac{\sqrt{a}+\sqrt{b}+\sqrt{c}}{3}\right)^{4} \leq \frac{a^{2}+b^{2}+c^{2}}{3}=1 $$ i.e., $\sqrt{a}+\sqrt{b}+\sqrt{c} \leq 3$. Hence, (2) yields $$ \sum \frac{a}{(b+c-a)^{2}} \geq \frac{27}{(a b c(\sqrt{a}+\sqrt{b}+\sqrt{c}))^{2}} \geq \frac{3}{a^{2} b^{2} c^{2}} $$ thus solving the problem. Comment. In this solution, one may also start from the following version of HÖLDER's inequality $$ \left(\sum_{i=1}^{n} a_{i}^{3}\right)\left(\sum_{i=1}^{n} b_{i}^{3}\right)\left(\sum_{i=1}^{n} c_{i}^{3}\right) \geq\left(\sum_{i=1}^{n} a_{i} b_{i} c_{i}\right)^{3} $$ applied as $$ \sum \frac{a}{(b+c-a)^{2}} \cdot \sum a^{3}(b+c-a) \cdot \sum a^{2}(b+c-a) \geq 27 $$ After doing that, one only needs the slightly better known instances $$ \sum a^{3}(b+c-a) \leq(a+b+c) a b c \quad \text { and } \quad \sum a^{2}(b+c-a) \leq 3 a b c $$ of Schur's Inequality.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b$, and $c$ be positive real numbers satisfying $\min (a+b, b+c, c+a)>\sqrt{2}$ and $a^{2}+b^{2}+c^{2}=3$. Prove that $$ \frac{a}{(b+c-a)^{2}}+\frac{b}{(c+a-b)^{2}}+\frac{c}{(a+b-c)^{2}} \geq \frac{3}{(a b c)^{2}} $$
|
The condition $b+c>\sqrt{2}$ implies $b^{2}+c^{2}>1$, so $a^{2}=3-\left(b^{2}+c^{2}\right)<2$, i.e. $a<\sqrt{2}<b+c$. Hence we have $b+c-a>0$, and also $c+a-b>0$ and $a+b-c>0$ for similar reasons. We will use the variant of HÖLDER's inequality $$ \frac{x_{1}^{p+1}}{y_{1}^{p}}+\frac{x_{1}^{p+1}}{y_{1}^{p}}+\ldots+\frac{x_{n}^{p+1}}{y_{n}^{p}} \geq \frac{\left(x_{1}+x_{2}+\ldots+x_{n}\right)^{p+1}}{\left(y_{1}+y_{2}+\ldots+y_{n}\right)^{p}} $$ which holds for all positive real numbers $p, x_{1}, x_{2}, \ldots, x_{n}, y_{1}, y_{2}, \ldots, y_{n}$. Applying it to the left-hand side of (11) with $p=2$ and $n=3$, we get $$ \sum \frac{a}{(b+c-a)^{2}}=\sum \frac{\left(a^{2}\right)^{3}}{a^{5}(b+c-a)^{2}} \geq \frac{\left(a^{2}+b^{2}+c^{2}\right)^{3}}{\left(\sum a^{5 / 2}(b+c-a)\right)^{2}}=\frac{27}{\left(\sum a^{5 / 2}(b+c-a)\right)^{2}} . $$ To estimate the denominator of the right-hand part, we use an instance of SCHUR's inequality, namely $$ \sum a^{3 / 2}(a-b)(a-c) \geq 0 $$ which can be rewritten as $$ \sum a^{5 / 2}(b+c-a) \leq a b c(\sqrt{a}+\sqrt{b}+\sqrt{c}) . $$ Moreover, by the inequality between the arithmetic mean and the fourth power mean we also have $$ \left(\frac{\sqrt{a}+\sqrt{b}+\sqrt{c}}{3}\right)^{4} \leq \frac{a^{2}+b^{2}+c^{2}}{3}=1 $$ i.e., $\sqrt{a}+\sqrt{b}+\sqrt{c} \leq 3$. Hence, (2) yields $$ \sum \frac{a}{(b+c-a)^{2}} \geq \frac{27}{(a b c(\sqrt{a}+\sqrt{b}+\sqrt{c}))^{2}} \geq \frac{3}{a^{2} b^{2} c^{2}} $$ thus solving the problem. Comment. In this solution, one may also start from the following version of HÖLDER's inequality $$ \left(\sum_{i=1}^{n} a_{i}^{3}\right)\left(\sum_{i=1}^{n} b_{i}^{3}\right)\left(\sum_{i=1}^{n} c_{i}^{3}\right) \geq\left(\sum_{i=1}^{n} a_{i} b_{i} c_{i}\right)^{3} $$ applied as $$ \sum \frac{a}{(b+c-a)^{2}} \cdot \sum a^{3}(b+c-a) \cdot \sum a^{2}(b+c-a) \geq 27 $$ After doing that, one only needs the slightly better known instances $$ \sum a^{3}(b+c-a) \leq(a+b+c) a b c \quad \text { and } \quad \sum a^{2}(b+c-a) \leq 3 a b c $$ of Schur's Inequality.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
f34b556a-ffc3-59b1-998f-48c062ab630f
| 24,023
|
Let $a, b$, and $c$ be positive real numbers satisfying $\min (a+b, b+c, c+a)>\sqrt{2}$ and $a^{2}+b^{2}+c^{2}=3$. Prove that $$ \frac{a}{(b+c-a)^{2}}+\frac{b}{(c+a-b)^{2}}+\frac{c}{(a+b-c)^{2}} \geq \frac{3}{(a b c)^{2}} $$
|
As in $$ a^{5}+b^{5}+c^{5} \geq 3 $$ which is weaker than the given one. Due to the symmetry we may assume that $a \geq b \geq c$. In view of (3)), it suffices to prove the inequality $$ \sum \frac{a^{3} b^{2} c^{2}}{(b+c-a)^{2}} \geq \sum a^{5} $$ or, moving all the terms into the left-hand part, $$ \sum \frac{a^{3}}{(b+c-a)^{2}}\left((b c)^{2}-(a(b+c-a))^{2}\right) \geq 0 $$ Note that the signs of the expressions $(y z)^{2}-(x(y+z-x))^{2}$ and $y z-x(y+z-x)=(x-y)(x-z)$ are the same for every positive $x, y, z$ satisfying the triangle inequality. So the terms in (4) corresponding to $a$ and $c$ are nonnegative, and hence it is sufficient to prove that the sum of the terms corresponding to $a$ and $b$ is nonnegative. Equivalently, we need the relation $$ \frac{a^{3}}{(b+c-a)^{2}}(a-b)(a-c)(b c+a(b+c-a)) \geq \frac{b^{3}}{(a+c-b)^{2}}(a-b)(b-c)(a c+b(a+c-b)) $$ Obviously, we have $$ a^{3} \geq b^{3} \geq 0, \quad 0<b+c-a \leq a+c-b, \quad \text { and } \quad a-c \geq b-c \geq 0 $$ hence it suffices to prove that $$ \frac{a b+a c+b c-a^{2}}{b+c-a} \geq \frac{a b+a c+b c-b^{2}}{c+a-b} . $$ Since all the denominators are positive, it is equivalent to $$ (c+a-b)\left(a b+a c+b c-a^{2}\right)-\left(a b+a c+b c-b^{2}\right)(b+c-a) \geq 0 $$ or $$ (a-b)\left(2 a b-a^{2}-b^{2}+a c+b c\right) \geq 0 . $$ Since $a \geq b$, the last inequality follows from $$ c(a+b)>(a-b)^{2} $$ which holds since $c>a-b \geq 0$ and $a+b>a-b \geq 0$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b$, and $c$ be positive real numbers satisfying $\min (a+b, b+c, c+a)>\sqrt{2}$ and $a^{2}+b^{2}+c^{2}=3$. Prove that $$ \frac{a}{(b+c-a)^{2}}+\frac{b}{(c+a-b)^{2}}+\frac{c}{(a+b-c)^{2}} \geq \frac{3}{(a b c)^{2}} $$
|
As in $$ a^{5}+b^{5}+c^{5} \geq 3 $$ which is weaker than the given one. Due to the symmetry we may assume that $a \geq b \geq c$. In view of (3)), it suffices to prove the inequality $$ \sum \frac{a^{3} b^{2} c^{2}}{(b+c-a)^{2}} \geq \sum a^{5} $$ or, moving all the terms into the left-hand part, $$ \sum \frac{a^{3}}{(b+c-a)^{2}}\left((b c)^{2}-(a(b+c-a))^{2}\right) \geq 0 $$ Note that the signs of the expressions $(y z)^{2}-(x(y+z-x))^{2}$ and $y z-x(y+z-x)=(x-y)(x-z)$ are the same for every positive $x, y, z$ satisfying the triangle inequality. So the terms in (4) corresponding to $a$ and $c$ are nonnegative, and hence it is sufficient to prove that the sum of the terms corresponding to $a$ and $b$ is nonnegative. Equivalently, we need the relation $$ \frac{a^{3}}{(b+c-a)^{2}}(a-b)(a-c)(b c+a(b+c-a)) \geq \frac{b^{3}}{(a+c-b)^{2}}(a-b)(b-c)(a c+b(a+c-b)) $$ Obviously, we have $$ a^{3} \geq b^{3} \geq 0, \quad 0<b+c-a \leq a+c-b, \quad \text { and } \quad a-c \geq b-c \geq 0 $$ hence it suffices to prove that $$ \frac{a b+a c+b c-a^{2}}{b+c-a} \geq \frac{a b+a c+b c-b^{2}}{c+a-b} . $$ Since all the denominators are positive, it is equivalent to $$ (c+a-b)\left(a b+a c+b c-a^{2}\right)-\left(a b+a c+b c-b^{2}\right)(b+c-a) \geq 0 $$ or $$ (a-b)\left(2 a b-a^{2}-b^{2}+a c+b c\right) \geq 0 . $$ Since $a \geq b$, the last inequality follows from $$ c(a+b)>(a-b)^{2} $$ which holds since $c>a-b \geq 0$ and $a+b>a-b \geq 0$.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
f34b556a-ffc3-59b1-998f-48c062ab630f
| 24,023
|
Let $n$ be a positive integer and let $W=\ldots x_{-1} x_{0} x_{1} x_{2} \ldots$ be an infinite periodic word consisting of the letters $a$ and $b$. Suppose that the minimal period $N$ of $W$ is greater than $2^{n}$. A finite nonempty word $U$ is said to appear in $W$ if there exist indices $k \leq \ell$ such that $U=x_{k} x_{k+1} \ldots x_{\ell}$. A finite word $U$ is called ubiquitous if the four words $U a, U b, a U$, and $b U$ all appear in $W$. Prove that there are at least $n$ ubiquitous finite nonempty words.
|
Throughout the solution, all the words are nonempty. For any word $R$ of length $m$, we call the number of indices $i \in\{1,2, \ldots, N\}$ for which $R$ coincides with the subword $x_{i+1} x_{i+2} \ldots x_{i+m}$ of $W$ the multiplicity of $R$ and denote it by $\mu(R)$. Thus a word $R$ appears in $W$ if and only if $\mu(R)>0$. Since each occurrence of a word in $W$ is both succeeded by either the letter $a$ or the letter $b$ and similarly preceded by one of those two letters, we have $$ \mu(R)=\mu(R a)+\mu(R b)=\mu(a R)+\mu(b R) $$ for all words $R$. We claim that the condition that $N$ is in fact the minimal period of $W$ guarantees that each word of length $N$ has multiplicity 1 or 0 depending on whether it appears or not. Indeed, if the words $x_{i+1} x_{i+2} \ldots x_{i+N}$ and $x_{j+1} \ldots x_{j+N}$ are equal for some $1 \leq i<j \leq N$, then we have $x_{i+a}=x_{j+a}$ for every integer $a$, and hence $j-i$ is also a period. Moreover, since $N>2^{n}$, at least one of the two words $a$ and $b$ has a multiplicity that is strictly larger than $2^{n-1}$. For each $k=0,1, \ldots, n-1$, let $U_{k}$ be a subword of $W$ whose multiplicity is strictly larger than $2^{k}$ and whose length is maximal subject to this property. Note that such a word exists in view of the two observations made in the two previous paragraphs. Fix some index $k \in\{0,1, \ldots, n-1\}$. Since the word $U_{k} b$ is longer than $U_{k}$, its multiplicity can be at most $2^{k}$, so in particular $\mu\left(U_{k} b\right)<\mu\left(U_{k}\right)$. Therefore, the word $U_{k} a$ has to appear by (11). For a similar reason, the words $U_{k} b, a U_{k}$, and $b U_{k}$ have to appear as well. Hence, the word $U_{k}$ is ubiquitous. Moreover, if the multiplicity of $U_{k}$ were strictly greater than $2^{k+1}$, then by (1) at least one of the two words $U_{k} a$ and $U_{k} b$ would have multiplicity greater than $2^{k}$ and would thus violate the maximality condition imposed on $U_{k}$. So we have $\mu\left(U_{0}\right) \leq 2<\mu\left(U_{1}\right) \leq 4<\ldots \leq 2^{n-1}<\mu\left(U_{n-1}\right)$, which implies in particular that the words $U_{0}, U_{1}, \ldots, U_{n-1}$ have to be distinct. As they have been proved to be ubiquitous as well, the problem is solved. Comment 1. There is an easy construction for obtaining ubiquitous words from appearing words whose multiplicity is at least two. Starting with any such word $U$ we may simply extend one of its occurrences in $W$ forwards and backwards as long as its multiplicity remains fixed, thus arriving at a word that one might call the ubiquitous prolongation $p(U)$ of $U$. There are several variants of the argument in the second half of the solution using the concept of prolongation. For instance, one may just take all ubiquitous words $U_{1}, U_{2}, \ldots, U_{\ell}$ ordered by increasing multiplicity and then prove for $i \in\{1,2, \ldots, \ell\}$ that $\mu\left(U_{i}\right) \leq 2^{i}$. Indeed, assume that $i$ is a minimal counterexample to this statement; then by the arguments similar to those presented above, the ubiquitous prolongation of one of the words $U_{i} a, U_{i} b, a U_{i}$ or $b U_{i}$ violates the definition of $U_{i}$. Now the multiplicity of one of the two letters $a$ and $b$ is strictly greater than $2^{n-1}$, so passing to ubiquitous prolongations once more we obtain $2^{n-1}<\mu\left(U_{\ell}\right) \leq 2^{\ell}$, which entails $\ell \geq n$, as needed. Comment 2. The bound $n$ for the number of ubiquitous subwords in the problem statement is not optimal, but it is close to an optimal one in the following sense. There is a universal constant $C>0$ such that for each positive integer $n$ there exists an infinite periodic word $W$ whose minimal period is greater than $2^{n}$ but for which there exist fewer than $C n$ ubiquitous words.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ be a positive integer and let $W=\ldots x_{-1} x_{0} x_{1} x_{2} \ldots$ be an infinite periodic word consisting of the letters $a$ and $b$. Suppose that the minimal period $N$ of $W$ is greater than $2^{n}$. A finite nonempty word $U$ is said to appear in $W$ if there exist indices $k \leq \ell$ such that $U=x_{k} x_{k+1} \ldots x_{\ell}$. A finite word $U$ is called ubiquitous if the four words $U a, U b, a U$, and $b U$ all appear in $W$. Prove that there are at least $n$ ubiquitous finite nonempty words.
|
Throughout the solution, all the words are nonempty. For any word $R$ of length $m$, we call the number of indices $i \in\{1,2, \ldots, N\}$ for which $R$ coincides with the subword $x_{i+1} x_{i+2} \ldots x_{i+m}$ of $W$ the multiplicity of $R$ and denote it by $\mu(R)$. Thus a word $R$ appears in $W$ if and only if $\mu(R)>0$. Since each occurrence of a word in $W$ is both succeeded by either the letter $a$ or the letter $b$ and similarly preceded by one of those two letters, we have $$ \mu(R)=\mu(R a)+\mu(R b)=\mu(a R)+\mu(b R) $$ for all words $R$. We claim that the condition that $N$ is in fact the minimal period of $W$ guarantees that each word of length $N$ has multiplicity 1 or 0 depending on whether it appears or not. Indeed, if the words $x_{i+1} x_{i+2} \ldots x_{i+N}$ and $x_{j+1} \ldots x_{j+N}$ are equal for some $1 \leq i<j \leq N$, then we have $x_{i+a}=x_{j+a}$ for every integer $a$, and hence $j-i$ is also a period. Moreover, since $N>2^{n}$, at least one of the two words $a$ and $b$ has a multiplicity that is strictly larger than $2^{n-1}$. For each $k=0,1, \ldots, n-1$, let $U_{k}$ be a subword of $W$ whose multiplicity is strictly larger than $2^{k}$ and whose length is maximal subject to this property. Note that such a word exists in view of the two observations made in the two previous paragraphs. Fix some index $k \in\{0,1, \ldots, n-1\}$. Since the word $U_{k} b$ is longer than $U_{k}$, its multiplicity can be at most $2^{k}$, so in particular $\mu\left(U_{k} b\right)<\mu\left(U_{k}\right)$. Therefore, the word $U_{k} a$ has to appear by (11). For a similar reason, the words $U_{k} b, a U_{k}$, and $b U_{k}$ have to appear as well. Hence, the word $U_{k}$ is ubiquitous. Moreover, if the multiplicity of $U_{k}$ were strictly greater than $2^{k+1}$, then by (1) at least one of the two words $U_{k} a$ and $U_{k} b$ would have multiplicity greater than $2^{k}$ and would thus violate the maximality condition imposed on $U_{k}$. So we have $\mu\left(U_{0}\right) \leq 2<\mu\left(U_{1}\right) \leq 4<\ldots \leq 2^{n-1}<\mu\left(U_{n-1}\right)$, which implies in particular that the words $U_{0}, U_{1}, \ldots, U_{n-1}$ have to be distinct. As they have been proved to be ubiquitous as well, the problem is solved. Comment 1. There is an easy construction for obtaining ubiquitous words from appearing words whose multiplicity is at least two. Starting with any such word $U$ we may simply extend one of its occurrences in $W$ forwards and backwards as long as its multiplicity remains fixed, thus arriving at a word that one might call the ubiquitous prolongation $p(U)$ of $U$. There are several variants of the argument in the second half of the solution using the concept of prolongation. For instance, one may just take all ubiquitous words $U_{1}, U_{2}, \ldots, U_{\ell}$ ordered by increasing multiplicity and then prove for $i \in\{1,2, \ldots, \ell\}$ that $\mu\left(U_{i}\right) \leq 2^{i}$. Indeed, assume that $i$ is a minimal counterexample to this statement; then by the arguments similar to those presented above, the ubiquitous prolongation of one of the words $U_{i} a, U_{i} b, a U_{i}$ or $b U_{i}$ violates the definition of $U_{i}$. Now the multiplicity of one of the two letters $a$ and $b$ is strictly greater than $2^{n-1}$, so passing to ubiquitous prolongations once more we obtain $2^{n-1}<\mu\left(U_{\ell}\right) \leq 2^{\ell}$, which entails $\ell \geq n$, as needed. Comment 2. The bound $n$ for the number of ubiquitous subwords in the problem statement is not optimal, but it is close to an optimal one in the following sense. There is a universal constant $C>0$ such that for each positive integer $n$ there exists an infinite periodic word $W$ whose minimal period is greater than $2^{n}$ but for which there exist fewer than $C n$ ubiquitous words.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
12555155-6bee-5b98-a20c-5e132bcb6a8d
| 24,036
|
Let $A B C$ be an acute triangle. Let $\omega$ be a circle whose center $L$ lies on the side $B C$. Suppose that $\omega$ is tangent to $A B$ at $B^{\prime}$ and to $A C$ at $C^{\prime}$. Suppose also that the circumcenter $O$ of the triangle $A B C$ lies on the shorter $\operatorname{arc} B^{\prime} C^{\prime}$ of $\omega$. Prove that the circumcircle of $A B C$ and $\omega$ meet at two points.
|
The point $B^{\prime}$, being the perpendicular foot of $L$, is an interior point of side $A B$. Analogously, $C^{\prime}$ lies in the interior of $A C$. The point $O$ is located inside the triangle $A B^{\prime} C^{\prime}$, hence $\angle C O B<\angle C^{\prime} O B^{\prime}$.  Let $\alpha=\angle C A B$. The angles $\angle C A B$ and $\angle C^{\prime} O B^{\prime}$ are inscribed into the two circles with centers $O$ and $L$, respectively, so $\angle C O B=2 \angle C A B=2 \alpha$ and $2 \angle C^{\prime} O B^{\prime}=360^{\circ}-\angle C^{\prime} L B^{\prime}$. From the kite $A B^{\prime} L C^{\prime}$ we have $\angle C^{\prime} L B^{\prime}=180^{\circ}-\angle C^{\prime} A B^{\prime}=180^{\circ}-\alpha$. Combining these, we get $$ 2 \alpha=\angle C O B<\angle C^{\prime} O B^{\prime}=\frac{360^{\circ}-\angle C^{\prime} L B^{\prime}}{2}=\frac{360^{\circ}-\left(180^{\circ}-\alpha\right)}{2}=90^{\circ}+\frac{\alpha}{2}, $$ So $$ \alpha<60^{\circ} \text {. } $$ Let $O^{\prime}$ be the reflection of $O$ in the line $B C$. In the quadrilateral $A B O^{\prime} C$ we have $$ \angle C O^{\prime} B+\angle C A B=\angle C O B+\angle C A B=2 \alpha+\alpha<180^{\circ}, $$ so the point $O^{\prime}$ is outside the circle $A B C$. Hence, $O$ and $O^{\prime}$ are two points of $\omega$ such that one of them lies inside the circumcircle, while the other one is located outside. Therefore, the two circles intersect. Comment. There are different ways of reducing the statement of the problem to the case $\alpha<60^{\circ}$. E.g., since the point $O$ lies in the interior of the isosceles triangle $A B^{\prime} C^{\prime}$, we have $O A<A B^{\prime}$. So, if $A B^{\prime} \leq 2 L B^{\prime}$ then $O A<2 L O$, which means that $\omega$ intersects the circumcircle of $A B C$. Hence the only interesting case is $A B^{\prime}>2 L B^{\prime}$, and this condition implies $\angle C A B=2 \angle B^{\prime} A L<2 \cdot 30^{\circ}=60^{\circ}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle. Let $\omega$ be a circle whose center $L$ lies on the side $B C$. Suppose that $\omega$ is tangent to $A B$ at $B^{\prime}$ and to $A C$ at $C^{\prime}$. Suppose also that the circumcenter $O$ of the triangle $A B C$ lies on the shorter $\operatorname{arc} B^{\prime} C^{\prime}$ of $\omega$. Prove that the circumcircle of $A B C$ and $\omega$ meet at two points.
|
The point $B^{\prime}$, being the perpendicular foot of $L$, is an interior point of side $A B$. Analogously, $C^{\prime}$ lies in the interior of $A C$. The point $O$ is located inside the triangle $A B^{\prime} C^{\prime}$, hence $\angle C O B<\angle C^{\prime} O B^{\prime}$.  Let $\alpha=\angle C A B$. The angles $\angle C A B$ and $\angle C^{\prime} O B^{\prime}$ are inscribed into the two circles with centers $O$ and $L$, respectively, so $\angle C O B=2 \angle C A B=2 \alpha$ and $2 \angle C^{\prime} O B^{\prime}=360^{\circ}-\angle C^{\prime} L B^{\prime}$. From the kite $A B^{\prime} L C^{\prime}$ we have $\angle C^{\prime} L B^{\prime}=180^{\circ}-\angle C^{\prime} A B^{\prime}=180^{\circ}-\alpha$. Combining these, we get $$ 2 \alpha=\angle C O B<\angle C^{\prime} O B^{\prime}=\frac{360^{\circ}-\angle C^{\prime} L B^{\prime}}{2}=\frac{360^{\circ}-\left(180^{\circ}-\alpha\right)}{2}=90^{\circ}+\frac{\alpha}{2}, $$ So $$ \alpha<60^{\circ} \text {. } $$ Let $O^{\prime}$ be the reflection of $O$ in the line $B C$. In the quadrilateral $A B O^{\prime} C$ we have $$ \angle C O^{\prime} B+\angle C A B=\angle C O B+\angle C A B=2 \alpha+\alpha<180^{\circ}, $$ so the point $O^{\prime}$ is outside the circle $A B C$. Hence, $O$ and $O^{\prime}$ are two points of $\omega$ such that one of them lies inside the circumcircle, while the other one is located outside. Therefore, the two circles intersect. Comment. There are different ways of reducing the statement of the problem to the case $\alpha<60^{\circ}$. E.g., since the point $O$ lies in the interior of the isosceles triangle $A B^{\prime} C^{\prime}$, we have $O A<A B^{\prime}$. So, if $A B^{\prime} \leq 2 L B^{\prime}$ then $O A<2 L O$, which means that $\omega$ intersects the circumcircle of $A B C$. Hence the only interesting case is $A B^{\prime}>2 L B^{\prime}$, and this condition implies $\angle C A B=2 \angle B^{\prime} A L<2 \cdot 30^{\circ}=60^{\circ}$.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
5eb68f04-2fef-5952-bd3d-4c56aeb49551
| 24,043
|
Let $A_{1} A_{2} A_{3} A_{4}$ be a non-cyclic quadrilateral. Let $O_{1}$ and $r_{1}$ be the circumcenter and the circumradius of the triangle $A_{2} A_{3} A_{4}$. Define $O_{2}, O_{3}, O_{4}$ and $r_{2}, r_{3}, r_{4}$ in a similar way. Prove that $$ \frac{1}{O_{1} A_{1}^{2}-r_{1}^{2}}+\frac{1}{O_{2} A_{2}^{2}-r_{2}^{2}}+\frac{1}{O_{3} A_{3}^{2}-r_{3}^{2}}+\frac{1}{O_{4} A_{4}^{2}-r_{4}^{2}}=0 $$
|
Introduce a Cartesian coordinate system in the plane. Every circle has an equation of the form $p(x, y)=x^{2}+y^{2}+l(x, y)=0$, where $l(x, y)$ is a polynomial of degree at most 1 . For any point $A=\left(x_{A}, y_{A}\right)$ we have $p\left(x_{A}, y_{A}\right)=d^{2}-r^{2}$, where $d$ is the distance from $A$ to the center of the circle and $r$ is the radius of the circle. For each $i$ in $\{1,2,3,4\}$ let $p_{i}(x, y)=x^{2}+y^{2}+l_{i}(x, y)=0$ be the equation of the circle with center $O_{i}$ and radius $r_{i}$ and let $d_{i}$ be the distance from $A_{i}$ to $O_{i}$. Consider the equation $$ \sum_{i=1}^{4} \frac{p_{i}(x, y)}{d_{i}^{2}-r_{i}^{2}}=1 $$ Since the coordinates of the points $A_{1}, A_{2}, A_{3}$, and $A_{4}$ satisfy (1) but these four points do not lie on a circle or on an line, equation (1) defines neither a circle, nor a line. Hence, the equation is an identity and the coefficient of the quadratic term $x^{2}+y^{2}$ also has to be zero, i.e. $$ \sum_{i=1}^{4} \frac{1}{d_{i}^{2}-r_{i}^{2}}=0 $$ Comment. Using the determinant form of the equation of the circle through three given points, the same solution can be formulated as follows. For $i=1,2,3,4$ let $\left(u_{i}, v_{i}\right)$ be the coordinates of $A_{i}$ and define $$ \Delta=\left|\begin{array}{llll} u_{1}^{2}+v_{1}^{2} & u_{1} & v_{1} & 1 \\ u_{2}^{2}+v_{2}^{2} & u_{2} & v_{2} & 1 \\ u_{3}^{2}+v_{3}^{2} & u_{3} & v_{3} & 1 \\ u_{4}^{2}+v_{4}^{2} & u_{4} & v_{4} & 1 \end{array}\right| \quad \text { and } \quad \Delta_{i}=\left|\begin{array}{lll} u_{i+1} & v_{i+1} & 1 \\ u_{i+2} & v_{i+2} & 1 \\ u_{i+3} & v_{i+3} & 1 \end{array}\right| $$ where $i+1, i+2$, and $i+3$ have to be read modulo 4 as integers in the set $\{1,2,3,4\}$. Expanding $\left|\begin{array}{llll}u_{1} & v_{1} & 1 & 1 \\ u_{2} & v_{2} & 1 & 1 \\ u_{3} & v_{3} & 1 & 1 \\ u_{4} & v_{4} & 1 & 1\end{array}\right|=0$ along the third column, we get $\Delta_{1}-\Delta_{2}+\Delta_{3}-\Delta_{4}=0$. The circle through $A_{i+1}, A_{i+2}$, and $A_{i+3}$ is given by the equation $$ \frac{1}{\Delta_{i}}\left|\begin{array}{cccc} x^{2}+y^{2} & x & y & 1 \\ u_{i+1}^{2}+v_{i+1}^{2} & u_{i+1} & v_{i+1} & 1 \\ u_{i+2}^{2}+v_{i+2}^{2} & u_{i+2} & v_{i+2} & 1 \\ u_{i+3}^{2}+v_{i+3}^{2} & u_{i+3} & v_{i+3} & 1 \end{array}\right|=0 $$ On the left-hand side, the coefficient of $x^{2}+y^{2}$ is equal to 1 . Substituting $\left(u_{i}, v_{i}\right)$ for $(x, y)$ in (2) we obtain the power of point $A_{i}$ with respect to the circle through $A_{i+1}, A_{i+2}$, and $A_{i+3}$ : $$ d_{i}^{2}-r_{i}^{2}=\frac{1}{\Delta_{i}}\left|\begin{array}{cccc} u_{i}^{2}+v_{i}^{2} & u_{i} & v_{i} & 1 \\ u_{i+1}^{2}+v_{i+1}^{2} & u_{i+1} & v_{i+1} & 1 \\ u_{i+2}^{2}+v_{i+2}^{2} & u_{i+2} & v_{i+2} & 1 \\ u_{i+3}^{2}+v_{i+3}^{2} & u_{i+3} & v_{i+3} & 1 \end{array}\right|=(-1)^{i+1} \frac{\Delta}{\Delta_{i}} $$ Thus, we have $$ \sum_{i=1}^{4} \frac{1}{d_{i}^{2}-r_{i}^{2}}=\frac{\Delta_{1}-\Delta_{2}+\Delta_{3}-\Delta_{4}}{\Delta}=0 $$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A_{1} A_{2} A_{3} A_{4}$ be a non-cyclic quadrilateral. Let $O_{1}$ and $r_{1}$ be the circumcenter and the circumradius of the triangle $A_{2} A_{3} A_{4}$. Define $O_{2}, O_{3}, O_{4}$ and $r_{2}, r_{3}, r_{4}$ in a similar way. Prove that $$ \frac{1}{O_{1} A_{1}^{2}-r_{1}^{2}}+\frac{1}{O_{2} A_{2}^{2}-r_{2}^{2}}+\frac{1}{O_{3} A_{3}^{2}-r_{3}^{2}}+\frac{1}{O_{4} A_{4}^{2}-r_{4}^{2}}=0 $$
|
Introduce a Cartesian coordinate system in the plane. Every circle has an equation of the form $p(x, y)=x^{2}+y^{2}+l(x, y)=0$, where $l(x, y)$ is a polynomial of degree at most 1 . For any point $A=\left(x_{A}, y_{A}\right)$ we have $p\left(x_{A}, y_{A}\right)=d^{2}-r^{2}$, where $d$ is the distance from $A$ to the center of the circle and $r$ is the radius of the circle. For each $i$ in $\{1,2,3,4\}$ let $p_{i}(x, y)=x^{2}+y^{2}+l_{i}(x, y)=0$ be the equation of the circle with center $O_{i}$ and radius $r_{i}$ and let $d_{i}$ be the distance from $A_{i}$ to $O_{i}$. Consider the equation $$ \sum_{i=1}^{4} \frac{p_{i}(x, y)}{d_{i}^{2}-r_{i}^{2}}=1 $$ Since the coordinates of the points $A_{1}, A_{2}, A_{3}$, and $A_{4}$ satisfy (1) but these four points do not lie on a circle or on an line, equation (1) defines neither a circle, nor a line. Hence, the equation is an identity and the coefficient of the quadratic term $x^{2}+y^{2}$ also has to be zero, i.e. $$ \sum_{i=1}^{4} \frac{1}{d_{i}^{2}-r_{i}^{2}}=0 $$ Comment. Using the determinant form of the equation of the circle through three given points, the same solution can be formulated as follows. For $i=1,2,3,4$ let $\left(u_{i}, v_{i}\right)$ be the coordinates of $A_{i}$ and define $$ \Delta=\left|\begin{array}{llll} u_{1}^{2}+v_{1}^{2} & u_{1} & v_{1} & 1 \\ u_{2}^{2}+v_{2}^{2} & u_{2} & v_{2} & 1 \\ u_{3}^{2}+v_{3}^{2} & u_{3} & v_{3} & 1 \\ u_{4}^{2}+v_{4}^{2} & u_{4} & v_{4} & 1 \end{array}\right| \quad \text { and } \quad \Delta_{i}=\left|\begin{array}{lll} u_{i+1} & v_{i+1} & 1 \\ u_{i+2} & v_{i+2} & 1 \\ u_{i+3} & v_{i+3} & 1 \end{array}\right| $$ where $i+1, i+2$, and $i+3$ have to be read modulo 4 as integers in the set $\{1,2,3,4\}$. Expanding $\left|\begin{array}{llll}u_{1} & v_{1} & 1 & 1 \\ u_{2} & v_{2} & 1 & 1 \\ u_{3} & v_{3} & 1 & 1 \\ u_{4} & v_{4} & 1 & 1\end{array}\right|=0$ along the third column, we get $\Delta_{1}-\Delta_{2}+\Delta_{3}-\Delta_{4}=0$. The circle through $A_{i+1}, A_{i+2}$, and $A_{i+3}$ is given by the equation $$ \frac{1}{\Delta_{i}}\left|\begin{array}{cccc} x^{2}+y^{2} & x & y & 1 \\ u_{i+1}^{2}+v_{i+1}^{2} & u_{i+1} & v_{i+1} & 1 \\ u_{i+2}^{2}+v_{i+2}^{2} & u_{i+2} & v_{i+2} & 1 \\ u_{i+3}^{2}+v_{i+3}^{2} & u_{i+3} & v_{i+3} & 1 \end{array}\right|=0 $$ On the left-hand side, the coefficient of $x^{2}+y^{2}$ is equal to 1 . Substituting $\left(u_{i}, v_{i}\right)$ for $(x, y)$ in (2) we obtain the power of point $A_{i}$ with respect to the circle through $A_{i+1}, A_{i+2}$, and $A_{i+3}$ : $$ d_{i}^{2}-r_{i}^{2}=\frac{1}{\Delta_{i}}\left|\begin{array}{cccc} u_{i}^{2}+v_{i}^{2} & u_{i} & v_{i} & 1 \\ u_{i+1}^{2}+v_{i+1}^{2} & u_{i+1} & v_{i+1} & 1 \\ u_{i+2}^{2}+v_{i+2}^{2} & u_{i+2} & v_{i+2} & 1 \\ u_{i+3}^{2}+v_{i+3}^{2} & u_{i+3} & v_{i+3} & 1 \end{array}\right|=(-1)^{i+1} \frac{\Delta}{\Delta_{i}} $$ Thus, we have $$ \sum_{i=1}^{4} \frac{1}{d_{i}^{2}-r_{i}^{2}}=\frac{\Delta_{1}-\Delta_{2}+\Delta_{3}-\Delta_{4}}{\Delta}=0 $$
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
46fc2f14-c1b1-5b1a-be5e-864bf3768bed
| 24,045
|
Let $A B C D$ be a convex quadrilateral whose sides $A D$ and $B C$ are not parallel. Suppose that the circles with diameters $A B$ and $C D$ meet at points $E$ and $F$ inside the quadrilateral. Let $\omega_{E}$ be the circle through the feet of the perpendiculars from $E$ to the lines $A B, B C$, and $C D$. Let $\omega_{F}$ be the circle through the feet of the perpendiculars from $F$ to the lines $C D, D A$, and $A B$. Prove that the midpoint of the segment $E F$ lies on the line through the two intersection points of $\omega_{E}$ and $\omega_{F}$.
|
Denote by $P, Q, R$, and $S$ the projections of $E$ on the lines $D A, A B, B C$, and $C D$ respectively. The points $P$ and $Q$ lie on the circle with diameter $A E$, so $\angle Q P E=\angle Q A E$; analogously, $\angle Q R E=\angle Q B E$. So $\angle Q P E+\angle Q R E=\angle Q A E+\angle Q B E=90^{\circ}$. By similar reasons, we have $\angle S P E+\angle S R E=90^{\circ}$, hence we get $\angle Q P S+\angle Q R S=90^{\circ}+90^{\circ}=180^{\circ}$, and the quadrilateral $P Q R S$ is inscribed in $\omega_{E}$. Analogously, all four projections of $F$ onto the sides of $A B C D$ lie on $\omega_{F}$. Denote by $K$ the meeting point of the lines $A D$ and $B C$. Due to the arguments above, there is no loss of generality in assuming that $A$ lies on segment $D K$. Suppose that $\angle C K D \geq 90^{\circ}$; then the circle with diameter $C D$ covers the whole quadrilateral $A B C D$, so the points $E, F$ cannot lie inside this quadrilateral. Hence our assumption is wrong. Therefore, the lines EP and $B C$ intersect at some point $P^{\prime}$, while the lines $E R$ and $A D$ intersect at some point $R^{\prime}$.  Figure 1 We claim that the points $P^{\prime}$ and $R^{\prime}$ also belong to $\omega_{E}$. Since the points $R, E, Q, B$ are concyclic, $\angle Q R K=\angle Q E B=90^{\circ}-\angle Q B E=\angle Q A E=\angle Q P E$. So $\angle Q R K=\angle Q P P^{\prime}$, which means that the point $P^{\prime}$ lies on $\omega_{E}$. Analogously, $R^{\prime}$ also lies on $\omega_{E}$. In the same manner, denote by $M$ and $N$ the projections of $F$ on the lines $A D$ and $B C$ respectively, and let $M^{\prime}=F M \cap B C, N^{\prime}=F N \cap A D$. By the same arguments, we obtain that the points $M^{\prime}$ and $N^{\prime}$ belong to $\omega_{F}$.  Figure 2 Now we concentrate on Figure 2, where all unnecessary details are removed. Let $U=N N^{\prime} \cap$ $P P^{\prime}, V=M M^{\prime} \cap R R^{\prime}$. Due to the right angles at $N$ and $P$, the points $N, N^{\prime}, P, P^{\prime}$ are concyclic, so $U N \cdot U N^{\prime}=U P \cdot U P^{\prime}$ which means that $U$ belongs to the radical axis $g$ of the circles $\omega_{E}$ and $\omega_{F}$. Analogously, $V$ also belongs to $g$. Finally, since $E U F V$ is a parallelogram, the radical axis $U V$ of $\omega_{E}$ and $\omega_{F}$ bisects $E F$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral whose sides $A D$ and $B C$ are not parallel. Suppose that the circles with diameters $A B$ and $C D$ meet at points $E$ and $F$ inside the quadrilateral. Let $\omega_{E}$ be the circle through the feet of the perpendiculars from $E$ to the lines $A B, B C$, and $C D$. Let $\omega_{F}$ be the circle through the feet of the perpendiculars from $F$ to the lines $C D, D A$, and $A B$. Prove that the midpoint of the segment $E F$ lies on the line through the two intersection points of $\omega_{E}$ and $\omega_{F}$.
|
Denote by $P, Q, R$, and $S$ the projections of $E$ on the lines $D A, A B, B C$, and $C D$ respectively. The points $P$ and $Q$ lie on the circle with diameter $A E$, so $\angle Q P E=\angle Q A E$; analogously, $\angle Q R E=\angle Q B E$. So $\angle Q P E+\angle Q R E=\angle Q A E+\angle Q B E=90^{\circ}$. By similar reasons, we have $\angle S P E+\angle S R E=90^{\circ}$, hence we get $\angle Q P S+\angle Q R S=90^{\circ}+90^{\circ}=180^{\circ}$, and the quadrilateral $P Q R S$ is inscribed in $\omega_{E}$. Analogously, all four projections of $F$ onto the sides of $A B C D$ lie on $\omega_{F}$. Denote by $K$ the meeting point of the lines $A D$ and $B C$. Due to the arguments above, there is no loss of generality in assuming that $A$ lies on segment $D K$. Suppose that $\angle C K D \geq 90^{\circ}$; then the circle with diameter $C D$ covers the whole quadrilateral $A B C D$, so the points $E, F$ cannot lie inside this quadrilateral. Hence our assumption is wrong. Therefore, the lines EP and $B C$ intersect at some point $P^{\prime}$, while the lines $E R$ and $A D$ intersect at some point $R^{\prime}$.  Figure 1 We claim that the points $P^{\prime}$ and $R^{\prime}$ also belong to $\omega_{E}$. Since the points $R, E, Q, B$ are concyclic, $\angle Q R K=\angle Q E B=90^{\circ}-\angle Q B E=\angle Q A E=\angle Q P E$. So $\angle Q R K=\angle Q P P^{\prime}$, which means that the point $P^{\prime}$ lies on $\omega_{E}$. Analogously, $R^{\prime}$ also lies on $\omega_{E}$. In the same manner, denote by $M$ and $N$ the projections of $F$ on the lines $A D$ and $B C$ respectively, and let $M^{\prime}=F M \cap B C, N^{\prime}=F N \cap A D$. By the same arguments, we obtain that the points $M^{\prime}$ and $N^{\prime}$ belong to $\omega_{F}$.  Figure 2 Now we concentrate on Figure 2, where all unnecessary details are removed. Let $U=N N^{\prime} \cap$ $P P^{\prime}, V=M M^{\prime} \cap R R^{\prime}$. Due to the right angles at $N$ and $P$, the points $N, N^{\prime}, P, P^{\prime}$ are concyclic, so $U N \cdot U N^{\prime}=U P \cdot U P^{\prime}$ which means that $U$ belongs to the radical axis $g$ of the circles $\omega_{E}$ and $\omega_{F}$. Analogously, $V$ also belongs to $g$. Finally, since $E U F V$ is a parallelogram, the radical axis $U V$ of $\omega_{E}$ and $\omega_{F}$ bisects $E F$.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
0a35403d-1a1f-5207-b3e3-4be4c572e112
| 24,049
|
Let $A B C$ be an acute triangle with circumcircle $\Omega$. Let $B_{0}$ be the midpoint of $A C$ and let $C_{0}$ be the midpoint of $A B$. Let $D$ be the foot of the altitude from $A$, and let $G$ be the centroid of the triangle $A B C$. Let $\omega$ be a circle through $B_{0}$ and $C_{0}$ that is tangent to the circle $\Omega$ at a point $X \neq A$. Prove that the points $D, G$, and $X$ are collinear.
|
If $A B=A C$, then the statement is trivial. So without loss of generality we may assume $A B<A C$. Denote the tangents to $\Omega$ at points $A$ and $X$ by $a$ and $x$, respectively. Let $\Omega_{1}$ be the circumcircle of triangle $A B_{0} C_{0}$. The circles $\Omega$ and $\Omega_{1}$ are homothetic with center $A$, so they are tangent at $A$, and $a$ is their radical axis. Now, the lines $a, x$, and $B_{0} C_{0}$ are the three radical axes of the circles $\Omega, \Omega_{1}$, and $\omega$. Since $a \nmid B_{0} C_{0}$, these three lines are concurrent at some point $W$. The points $A$ and $D$ are symmetric with respect to the line $B_{0} C_{0}$; hence $W X=W A=W D$. This means that $W$ is the center of the circumcircle $\gamma$ of triangle $A D X$. Moreover, we have $\angle W A O=\angle W X O=90^{\circ}$, where $O$ denotes the center of $\Omega$. Hence $\angle A W X+\angle A O X=180^{\circ}$.  Denote by $T$ the second intersection point of $\Omega$ and the line $D X$. Note that $O$ belongs to $\Omega_{1}$. Using the circles $\gamma$ and $\Omega$, we find $\angle D A T=\angle A D X-\angle A T D=\frac{1}{2}\left(360^{\circ}-\angle A W X\right)-\frac{1}{2} \angle A O X=$ $180^{\circ}-\frac{1}{2}(\angle A W X+\angle A O X)=90^{\circ}$. So, $A D \perp A T$, and hence $A T \| B C$. Thus, $A T C B$ is an isosceles trapezoid inscribed in $\Omega$. Denote by $A_{0}$ the midpoint of $B C$, and consider the image of $A T C B$ under the homothety $h$ with center $G$ and factor $-\frac{1}{2}$. We have $h(A)=A_{0}, h(B)=B_{0}$, and $h(C)=C_{0}$. From the symmetry about $B_{0} C_{0}$, we have $\angle T C B=\angle C B A=\angle B_{0} C_{0} A=\angle D C_{0} B_{0}$. Using $A T \| D A_{0}$, we conclude $h(T)=D$. Hence the points $D, G$, and $T$ are collinear, and $X$ lies on the same line.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with circumcircle $\Omega$. Let $B_{0}$ be the midpoint of $A C$ and let $C_{0}$ be the midpoint of $A B$. Let $D$ be the foot of the altitude from $A$, and let $G$ be the centroid of the triangle $A B C$. Let $\omega$ be a circle through $B_{0}$ and $C_{0}$ that is tangent to the circle $\Omega$ at a point $X \neq A$. Prove that the points $D, G$, and $X$ are collinear.
|
If $A B=A C$, then the statement is trivial. So without loss of generality we may assume $A B<A C$. Denote the tangents to $\Omega$ at points $A$ and $X$ by $a$ and $x$, respectively. Let $\Omega_{1}$ be the circumcircle of triangle $A B_{0} C_{0}$. The circles $\Omega$ and $\Omega_{1}$ are homothetic with center $A$, so they are tangent at $A$, and $a$ is their radical axis. Now, the lines $a, x$, and $B_{0} C_{0}$ are the three radical axes of the circles $\Omega, \Omega_{1}$, and $\omega$. Since $a \nmid B_{0} C_{0}$, these three lines are concurrent at some point $W$. The points $A$ and $D$ are symmetric with respect to the line $B_{0} C_{0}$; hence $W X=W A=W D$. This means that $W$ is the center of the circumcircle $\gamma$ of triangle $A D X$. Moreover, we have $\angle W A O=\angle W X O=90^{\circ}$, where $O$ denotes the center of $\Omega$. Hence $\angle A W X+\angle A O X=180^{\circ}$.  Denote by $T$ the second intersection point of $\Omega$ and the line $D X$. Note that $O$ belongs to $\Omega_{1}$. Using the circles $\gamma$ and $\Omega$, we find $\angle D A T=\angle A D X-\angle A T D=\frac{1}{2}\left(360^{\circ}-\angle A W X\right)-\frac{1}{2} \angle A O X=$ $180^{\circ}-\frac{1}{2}(\angle A W X+\angle A O X)=90^{\circ}$. So, $A D \perp A T$, and hence $A T \| B C$. Thus, $A T C B$ is an isosceles trapezoid inscribed in $\Omega$. Denote by $A_{0}$ the midpoint of $B C$, and consider the image of $A T C B$ under the homothety $h$ with center $G$ and factor $-\frac{1}{2}$. We have $h(A)=A_{0}, h(B)=B_{0}$, and $h(C)=C_{0}$. From the symmetry about $B_{0} C_{0}$, we have $\angle T C B=\angle C B A=\angle B_{0} C_{0} A=\angle D C_{0} B_{0}$. Using $A T \| D A_{0}$, we conclude $h(T)=D$. Hence the points $D, G$, and $T$ are collinear, and $X$ lies on the same line.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
4dbe1f6d-66cf-5c45-81e0-9392bad3f07d
| 24,051
|
Let $A B C$ be an acute triangle with circumcircle $\Omega$. Let $B_{0}$ be the midpoint of $A C$ and let $C_{0}$ be the midpoint of $A B$. Let $D$ be the foot of the altitude from $A$, and let $G$ be the centroid of the triangle $A B C$. Let $\omega$ be a circle through $B_{0}$ and $C_{0}$ that is tangent to the circle $\Omega$ at a point $X \neq A$. Prove that the points $D, G$, and $X$ are collinear.
|
We define the points $A_{0}, O$, and $W$ as in the previous solution and we concentrate on the case $A B<A C$. Let $Q$ be the perpendicular projection of $A_{0}$ on $B_{0} C_{0}$. Since $\angle W A O=\angle W Q O=\angle O X W=90^{\circ}$, the five points $A, W, X, O$, and $Q$ lie on a common circle. Furthermore, the reflections with respect to $B_{0} C_{0}$ and $O W$ map $A$ to $D$ and $X$, respectively. For these reasons, we have $$ \angle W Q D=\angle A Q W=\angle A X W=\angle W A X=\angle W Q X . $$ Thus the three points $Q, D$, and $X$ lie on a common line, say $\ell$.  To complete the argument, we note that the homothety centered at $G$ sending the triangle $A B C$ to the triangle $A_{0} B_{0} C_{0}$ maps the altitude $A D$ to the altitude $A_{0} Q$. Therefore it maps $D$ to $Q$, so the points $D, G$, and $Q$ are collinear. Hence $G$ lies on $\ell$ as well. Comment. There are various other ways to prove the collinearity of $Q, D$, and $X$ obtained in the middle part of Solution 2. Introduce for instance the point $J$ where the lines $A W$ and $B C$ intersect. Then the four points $A, D, X$, and $J$ lie at the same distance from $W$, so the quadrilateral $A D X J$ is cyclic. In combination with the fact that $A W X Q$ is cyclic as well, this implies $$ \angle J D X=\angle J A X=\angle W A X=\angle W Q X $$ Since $B C \| W Q$, it follows that $Q, D$, and $X$ are indeed collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with circumcircle $\Omega$. Let $B_{0}$ be the midpoint of $A C$ and let $C_{0}$ be the midpoint of $A B$. Let $D$ be the foot of the altitude from $A$, and let $G$ be the centroid of the triangle $A B C$. Let $\omega$ be a circle through $B_{0}$ and $C_{0}$ that is tangent to the circle $\Omega$ at a point $X \neq A$. Prove that the points $D, G$, and $X$ are collinear.
|
We define the points $A_{0}, O$, and $W$ as in the previous solution and we concentrate on the case $A B<A C$. Let $Q$ be the perpendicular projection of $A_{0}$ on $B_{0} C_{0}$. Since $\angle W A O=\angle W Q O=\angle O X W=90^{\circ}$, the five points $A, W, X, O$, and $Q$ lie on a common circle. Furthermore, the reflections with respect to $B_{0} C_{0}$ and $O W$ map $A$ to $D$ and $X$, respectively. For these reasons, we have $$ \angle W Q D=\angle A Q W=\angle A X W=\angle W A X=\angle W Q X . $$ Thus the three points $Q, D$, and $X$ lie on a common line, say $\ell$.  To complete the argument, we note that the homothety centered at $G$ sending the triangle $A B C$ to the triangle $A_{0} B_{0} C_{0}$ maps the altitude $A D$ to the altitude $A_{0} Q$. Therefore it maps $D$ to $Q$, so the points $D, G$, and $Q$ are collinear. Hence $G$ lies on $\ell$ as well. Comment. There are various other ways to prove the collinearity of $Q, D$, and $X$ obtained in the middle part of Solution 2. Introduce for instance the point $J$ where the lines $A W$ and $B C$ intersect. Then the four points $A, D, X$, and $J$ lie at the same distance from $W$, so the quadrilateral $A D X J$ is cyclic. In combination with the fact that $A W X Q$ is cyclic as well, this implies $$ \angle J D X=\angle J A X=\angle W A X=\angle W Q X $$ Since $B C \| W Q$, it follows that $Q, D$, and $X$ are indeed collinear.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
4dbe1f6d-66cf-5c45-81e0-9392bad3f07d
| 24,051
|
Let $A B C$ be a triangle with incenter $I$ and circumcircle $\omega$. Let $D$ and $E$ be the second intersection points of $\omega$ with the lines $A I$ and $B I$, respectively. The chord $D E$ meets $A C$ at a point $F$, and $B C$ at a point $G$. Let $P$ be the intersection point of the line through $F$ parallel to $A D$ and the line through $G$ parallel to $B E$. Suppose that the tangents to $\omega$ at $A$ and at $B$ meet at a point $K$. Prove that the three lines $A E, B D$, and $K P$ are either parallel or concurrent.
|
Since $$ \angle I A F=\angle D A C=\angle B A D=\angle B E D=\angle I E F $$ the quadrilateral $A I F E$ is cyclic. Denote its circumcircle by $\omega_{1}$. Similarly, the quadrilateral $B D G I$ is cyclic; denote its circumcircle by $\omega_{2}$. The line $A E$ is the radical axis of $\omega$ and $\omega_{1}$, and the line $B D$ is the radical axis of $\omega$ and $\omega_{2}$. Let $t$ be the radical axis of $\omega_{1}$ and $\omega_{2}$. These three lines meet at the radical center of the three circles, or they are parallel to each other. We will show that $t$ is in fact the line $P K$. Let $L$ be the second intersection point of $\omega_{1}$ and $\omega_{2}$, so $t=I L$. (If the two circles are tangent to each other then $L=I$ and $t$ is the common tangent.)  Let the line $t$ meet the circumcircles of the triangles $A B L$ and $F G L$ at $K^{\prime} \neq L$ and $P^{\prime} \neq L$, respectively. Using oriented angles we have $$ \angle\left(A B, B K^{\prime}\right)=\angle\left(A L, L K^{\prime}\right)=\angle(A L, L I)=\angle(A E, E I)=\angle(A E, E B)=\angle(A B, B K) \text {, } $$ so $B K^{\prime} \| B K$. Similarly we have $A K^{\prime} \| A K$, and therefore $K^{\prime}=K$. Next, we have $$ \angle\left(P^{\prime} F, F G\right)=\angle\left(P^{\prime} L, L G\right)=\angle(I L, L G)=\angle(I D, D G)=\angle(A D, D E)=\angle(P F, F G), $$ hence $P^{\prime} F \| P F$ and similarly $P^{\prime} G \| P G$. Therefore $P^{\prime}=P$. This means that $t$ passes through $K$ and $P$, which finishes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incenter $I$ and circumcircle $\omega$. Let $D$ and $E$ be the second intersection points of $\omega$ with the lines $A I$ and $B I$, respectively. The chord $D E$ meets $A C$ at a point $F$, and $B C$ at a point $G$. Let $P$ be the intersection point of the line through $F$ parallel to $A D$ and the line through $G$ parallel to $B E$. Suppose that the tangents to $\omega$ at $A$ and at $B$ meet at a point $K$. Prove that the three lines $A E, B D$, and $K P$ are either parallel or concurrent.
|
Since $$ \angle I A F=\angle D A C=\angle B A D=\angle B E D=\angle I E F $$ the quadrilateral $A I F E$ is cyclic. Denote its circumcircle by $\omega_{1}$. Similarly, the quadrilateral $B D G I$ is cyclic; denote its circumcircle by $\omega_{2}$. The line $A E$ is the radical axis of $\omega$ and $\omega_{1}$, and the line $B D$ is the radical axis of $\omega$ and $\omega_{2}$. Let $t$ be the radical axis of $\omega_{1}$ and $\omega_{2}$. These three lines meet at the radical center of the three circles, or they are parallel to each other. We will show that $t$ is in fact the line $P K$. Let $L$ be the second intersection point of $\omega_{1}$ and $\omega_{2}$, so $t=I L$. (If the two circles are tangent to each other then $L=I$ and $t$ is the common tangent.)  Let the line $t$ meet the circumcircles of the triangles $A B L$ and $F G L$ at $K^{\prime} \neq L$ and $P^{\prime} \neq L$, respectively. Using oriented angles we have $$ \angle\left(A B, B K^{\prime}\right)=\angle\left(A L, L K^{\prime}\right)=\angle(A L, L I)=\angle(A E, E I)=\angle(A E, E B)=\angle(A B, B K) \text {, } $$ so $B K^{\prime} \| B K$. Similarly we have $A K^{\prime} \| A K$, and therefore $K^{\prime}=K$. Next, we have $$ \angle\left(P^{\prime} F, F G\right)=\angle\left(P^{\prime} L, L G\right)=\angle(I L, L G)=\angle(I D, D G)=\angle(A D, D E)=\angle(P F, F G), $$ hence $P^{\prime} F \| P F$ and similarly $P^{\prime} G \| P G$. Therefore $P^{\prime}=P$. This means that $t$ passes through $K$ and $P$, which finishes the proof.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
d94f1d2f-fd83-5cdb-9179-c70d1e01cefa
| 24,055
|
Let $A B C$ be a triangle with incenter $I$ and circumcircle $\omega$. Let $D$ and $E$ be the second intersection points of $\omega$ with the lines $A I$ and $B I$, respectively. The chord $D E$ meets $A C$ at a point $F$, and $B C$ at a point $G$. Let $P$ be the intersection point of the line through $F$ parallel to $A D$ and the line through $G$ parallel to $B E$. Suppose that the tangents to $\omega$ at $A$ and at $B$ meet at a point $K$. Prove that the three lines $A E, B D$, and $K P$ are either parallel or concurrent.
|
Let $M$ be the intersection point of the tangents to $\omega$ at $D$ and $E$, and let the lines $A E$ and $B D$ meet at $T$; if $A E$ and $B D$ are parallel, then let $T$ be their common ideal point. It is well-known that the points $K$ and $M$ lie on the line $T I$ (as a consequence of PASCAL's theorem, applied to the inscribed degenerate hexagons $A A D B B E$ and $A D D B E E)$. The lines $A D$ and $B E$ are the angle bisectors of the angles $\angle C A B$ and $\angle A B C$, respectively, so $D$ and $E$ are the midpoints of the $\operatorname{arcs} B C$ and $C A$ of the circle $\omega$, respectively. Hence, $D M$ is parallel to $B C$ and $E M$ is parallel to $A C$. Apply PASCAL's theorem to the degenerate hexagon $C A D D E B$. By the theorem, the points $C A \cap D E=F, A D \cap E B=I$ and the common ideal point of lines $D M$ and $B C$ are collinear, therefore $F I$ is parallel to $B C$ and $D M$. Analogously, the line $G I$ is parallel to $A C$ and $E M$.  Now consider the homothety with scale factor $-\frac{F G}{E D}$ which takes $E$ to $G$ and $D$ to $F$. Since the triangles $E D M$ and $G F I$ have parallel sides, the homothety takes $M$ to $I$. Similarly, since the triangles $D E I$ and $F G P$ have parallel sides, the homothety takes $I$ to $P$. Hence, the points M, I, $P$ and the homothety center $H$ must lie on the same line. Therefore, the point $P$ also lies on the line $T K I M$. Comment. One may prove that $I F \| B C$ and $I G \| A C$ in a more elementary way. Since $\angle A D E=$ $\angle E D C$ and $\angle D E B=\angle C E D$, the points $I$ and $C$ are symmetric about $D E$. Moreover, since the $\operatorname{arcs} A E$ and $E C$ are equal and the arcs $C D$ and $D B$ are equal, we have $\angle C F G=\angle F G C$, so the triangle $C F G$ is isosceles. Hence, the quadrilateral $I F C G$ is a rhombus.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incenter $I$ and circumcircle $\omega$. Let $D$ and $E$ be the second intersection points of $\omega$ with the lines $A I$ and $B I$, respectively. The chord $D E$ meets $A C$ at a point $F$, and $B C$ at a point $G$. Let $P$ be the intersection point of the line through $F$ parallel to $A D$ and the line through $G$ parallel to $B E$. Suppose that the tangents to $\omega$ at $A$ and at $B$ meet at a point $K$. Prove that the three lines $A E, B D$, and $K P$ are either parallel or concurrent.
|
Let $M$ be the intersection point of the tangents to $\omega$ at $D$ and $E$, and let the lines $A E$ and $B D$ meet at $T$; if $A E$ and $B D$ are parallel, then let $T$ be their common ideal point. It is well-known that the points $K$ and $M$ lie on the line $T I$ (as a consequence of PASCAL's theorem, applied to the inscribed degenerate hexagons $A A D B B E$ and $A D D B E E)$. The lines $A D$ and $B E$ are the angle bisectors of the angles $\angle C A B$ and $\angle A B C$, respectively, so $D$ and $E$ are the midpoints of the $\operatorname{arcs} B C$ and $C A$ of the circle $\omega$, respectively. Hence, $D M$ is parallel to $B C$ and $E M$ is parallel to $A C$. Apply PASCAL's theorem to the degenerate hexagon $C A D D E B$. By the theorem, the points $C A \cap D E=F, A D \cap E B=I$ and the common ideal point of lines $D M$ and $B C$ are collinear, therefore $F I$ is parallel to $B C$ and $D M$. Analogously, the line $G I$ is parallel to $A C$ and $E M$.  Now consider the homothety with scale factor $-\frac{F G}{E D}$ which takes $E$ to $G$ and $D$ to $F$. Since the triangles $E D M$ and $G F I$ have parallel sides, the homothety takes $M$ to $I$. Similarly, since the triangles $D E I$ and $F G P$ have parallel sides, the homothety takes $I$ to $P$. Hence, the points M, I, $P$ and the homothety center $H$ must lie on the same line. Therefore, the point $P$ also lies on the line $T K I M$. Comment. One may prove that $I F \| B C$ and $I G \| A C$ in a more elementary way. Since $\angle A D E=$ $\angle E D C$ and $\angle D E B=\angle C E D$, the points $I$ and $C$ are symmetric about $D E$. Moreover, since the $\operatorname{arcs} A E$ and $E C$ are equal and the arcs $C D$ and $D B$ are equal, we have $\angle C F G=\angle F G C$, so the triangle $C F G$ is isosceles. Hence, the quadrilateral $I F C G$ is a rhombus.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
d94f1d2f-fd83-5cdb-9179-c70d1e01cefa
| 24,055
|
Let $A B C$ be a triangle with $A B=A C$, and let $D$ be the midpoint of $A C$. The angle bisector of $\angle B A C$ intersects the circle through $D, B$, and $C$ in a point $E$ inside the triangle $A B C$. The line $B D$ intersects the circle through $A, E$, and $B$ in two points $B$ and $F$. The lines $A F$ and $B E$ meet at a point $I$, and the lines $C I$ and $B D$ meet at a point $K$. Show that $I$ is the incenter of triangle $K A B$.
|
Let $D^{\prime}$ be the midpoint of the segment $A B$, and let $M$ be the midpoint of $B C$. By symmetry at line $A M$, the point $D^{\prime}$ has to lie on the circle $B C D$. Since the $\operatorname{arcs} D^{\prime} E$ and $E D$ of that circle are equal, we have $\angle A B I=\angle D^{\prime} B E=\angle E B D=I B K$, so $I$ lies on the angle bisector of $\angle A B K$. For this reason it suffices to prove in the sequel that the ray $A I$ bisects the angle $\angle B A K$. From $$ \angle D F A=180^{\circ}-\angle B F A=180^{\circ}-\angle B E A=\angle M E B=\frac{1}{2} \angle C E B=\frac{1}{2} \angle C D B $$ we derive $\angle D F A=\angle D A F$ so the triangle $A F D$ is isosceles with $A D=D F$.  Applying MenELaUs's theorem to the triangle $A D F$ with respect to the line $C I K$, and applying the angle bisector theorem to the triangle $A B F$, we infer $$ 1=\frac{A C}{C D} \cdot \frac{D K}{K F} \cdot \frac{F I}{I A}=2 \cdot \frac{D K}{K F} \cdot \frac{B F}{A B}=2 \cdot \frac{D K}{K F} \cdot \frac{B F}{2 \cdot A D}=\frac{D K}{K F} \cdot \frac{B F}{A D} $$ and therefore $$ \frac{B D}{A D}=\frac{B F+F D}{A D}=\frac{B F}{A D}+1=\frac{K F}{D K}+1=\frac{D F}{D K}=\frac{A D}{D K} $$ It follows that the triangles $A D K$ and $B D A$ are similar, hence $\angle D A K=\angle A B D$. Then $$ \angle I A B=\angle A F D-\angle A B D=\angle D A F-\angle D A K=\angle K A I $$ shows that the point $K$ is indeed lying on the angle bisector of $\angle B A K$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $A B=A C$, and let $D$ be the midpoint of $A C$. The angle bisector of $\angle B A C$ intersects the circle through $D, B$, and $C$ in a point $E$ inside the triangle $A B C$. The line $B D$ intersects the circle through $A, E$, and $B$ in two points $B$ and $F$. The lines $A F$ and $B E$ meet at a point $I$, and the lines $C I$ and $B D$ meet at a point $K$. Show that $I$ is the incenter of triangle $K A B$.
|
Let $D^{\prime}$ be the midpoint of the segment $A B$, and let $M$ be the midpoint of $B C$. By symmetry at line $A M$, the point $D^{\prime}$ has to lie on the circle $B C D$. Since the $\operatorname{arcs} D^{\prime} E$ and $E D$ of that circle are equal, we have $\angle A B I=\angle D^{\prime} B E=\angle E B D=I B K$, so $I$ lies on the angle bisector of $\angle A B K$. For this reason it suffices to prove in the sequel that the ray $A I$ bisects the angle $\angle B A K$. From $$ \angle D F A=180^{\circ}-\angle B F A=180^{\circ}-\angle B E A=\angle M E B=\frac{1}{2} \angle C E B=\frac{1}{2} \angle C D B $$ we derive $\angle D F A=\angle D A F$ so the triangle $A F D$ is isosceles with $A D=D F$.  Applying MenELaUs's theorem to the triangle $A D F$ with respect to the line $C I K$, and applying the angle bisector theorem to the triangle $A B F$, we infer $$ 1=\frac{A C}{C D} \cdot \frac{D K}{K F} \cdot \frac{F I}{I A}=2 \cdot \frac{D K}{K F} \cdot \frac{B F}{A B}=2 \cdot \frac{D K}{K F} \cdot \frac{B F}{2 \cdot A D}=\frac{D K}{K F} \cdot \frac{B F}{A D} $$ and therefore $$ \frac{B D}{A D}=\frac{B F+F D}{A D}=\frac{B F}{A D}+1=\frac{K F}{D K}+1=\frac{D F}{D K}=\frac{A D}{D K} $$ It follows that the triangles $A D K$ and $B D A$ are similar, hence $\angle D A K=\angle A B D$. Then $$ \angle I A B=\angle A F D-\angle A B D=\angle D A F-\angle D A K=\angle K A I $$ shows that the point $K$ is indeed lying on the angle bisector of $\angle B A K$.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
236e30c8-9224-5717-a0a7-dc078527b028
| 24,059
|
Let $A B C$ be a triangle with $A B=A C$, and let $D$ be the midpoint of $A C$. The angle bisector of $\angle B A C$ intersects the circle through $D, B$, and $C$ in a point $E$ inside the triangle $A B C$. The line $B D$ intersects the circle through $A, E$, and $B$ in two points $B$ and $F$. The lines $A F$ and $B E$ meet at a point $I$, and the lines $C I$ and $B D$ meet at a point $K$. Show that $I$ is the incenter of triangle $K A B$.
|
It can be shown in the same way as in the first solution that $I$ lies on the angle bisector of $\angle A B K$. Here we restrict ourselves to proving that $K I$ bisects $\angle A K B$.  Denote the circumcircle of triangle $B C D$ and its center by $\omega_{1}$ and by $O_{1}$, respectively. Since the quadrilateral $A B F E$ is cyclic, we have $\angle D F E=\angle B A E=\angle D A E$. By the same reason, we have $\angle E A F=\angle E B F=\angle A B E=\angle A F E$. Therefore $\angle D A F=\angle D F A$, and hence $D F=D A=D C$. So triangle $A F C$ is inscribed in a circle $\omega_{2}$ with center $D$. Denote the circumcircle of triangle $A B D$ by $\omega_{3}$, and let its center be $O_{3}$. Since the arcs $B E$ and $E C$ of circle $\omega_{1}$ are equal, and the triangles $A D E$ and $F D E$ are congruent, we have $\angle A O_{1} B=2 \angle B D E=\angle B D A$, so $O_{1}$ lies on $\omega_{3}$. Hence $\angle O_{3} O_{1} D=\angle O_{3} D O_{1}$. The line $B D$ is the radical axis of $\omega_{1}$ and $\omega_{3}$. Point $C$ belongs to the radical axis of $\omega_{1}$ and $\omega_{2}$, and $I$ also belongs to it since $A I \cdot I F=B I \cdot I E$. Hence $K=B D \cap C I$ is the radical center of $\omega_{1}$, $\omega_{2}$, and $\omega_{3}$, and $A K$ is the radical axis of $\omega_{2}$ and $\omega_{3}$. Now, the radical axes $A K, B K$ and $I K$ are perpendicular to the central lines $O_{3} D, O_{3} O_{1}$ and $O_{1} D$, respectively. By $\angle O_{3} O_{1} D=\angle O_{3} D O_{1}$, we get that $K I$ is the angle bisector of $\angle A K B$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $A B=A C$, and let $D$ be the midpoint of $A C$. The angle bisector of $\angle B A C$ intersects the circle through $D, B$, and $C$ in a point $E$ inside the triangle $A B C$. The line $B D$ intersects the circle through $A, E$, and $B$ in two points $B$ and $F$. The lines $A F$ and $B E$ meet at a point $I$, and the lines $C I$ and $B D$ meet at a point $K$. Show that $I$ is the incenter of triangle $K A B$.
|
It can be shown in the same way as in the first solution that $I$ lies on the angle bisector of $\angle A B K$. Here we restrict ourselves to proving that $K I$ bisects $\angle A K B$.  Denote the circumcircle of triangle $B C D$ and its center by $\omega_{1}$ and by $O_{1}$, respectively. Since the quadrilateral $A B F E$ is cyclic, we have $\angle D F E=\angle B A E=\angle D A E$. By the same reason, we have $\angle E A F=\angle E B F=\angle A B E=\angle A F E$. Therefore $\angle D A F=\angle D F A$, and hence $D F=D A=D C$. So triangle $A F C$ is inscribed in a circle $\omega_{2}$ with center $D$. Denote the circumcircle of triangle $A B D$ by $\omega_{3}$, and let its center be $O_{3}$. Since the arcs $B E$ and $E C$ of circle $\omega_{1}$ are equal, and the triangles $A D E$ and $F D E$ are congruent, we have $\angle A O_{1} B=2 \angle B D E=\angle B D A$, so $O_{1}$ lies on $\omega_{3}$. Hence $\angle O_{3} O_{1} D=\angle O_{3} D O_{1}$. The line $B D$ is the radical axis of $\omega_{1}$ and $\omega_{3}$. Point $C$ belongs to the radical axis of $\omega_{1}$ and $\omega_{2}$, and $I$ also belongs to it since $A I \cdot I F=B I \cdot I E$. Hence $K=B D \cap C I$ is the radical center of $\omega_{1}$, $\omega_{2}$, and $\omega_{3}$, and $A K$ is the radical axis of $\omega_{2}$ and $\omega_{3}$. Now, the radical axes $A K, B K$ and $I K$ are perpendicular to the central lines $O_{3} D, O_{3} O_{1}$ and $O_{1} D$, respectively. By $\angle O_{3} O_{1} D=\angle O_{3} D O_{1}$, we get that $K I$ is the angle bisector of $\angle A K B$.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
236e30c8-9224-5717-a0a7-dc078527b028
| 24,059
|
Let $A B C$ be a triangle with $A B=A C$, and let $D$ be the midpoint of $A C$. The angle bisector of $\angle B A C$ intersects the circle through $D, B$, and $C$ in a point $E$ inside the triangle $A B C$. The line $B D$ intersects the circle through $A, E$, and $B$ in two points $B$ and $F$. The lines $A F$ and $B E$ meet at a point $I$, and the lines $C I$ and $B D$ meet at a point $K$. Show that $I$ is the incenter of triangle $K A B$.
|
Again, let $M$ be the midpoint of $B C$. As in the previous solutions, we can deduce $\angle A B I=\angle I B K$. We show that the point $I$ lies on the angle bisector of $\angle K A B$. Let $G$ be the intersection point of the circles $A F C$ and $B C D$, different from $C$. The lines $C G, A F$, and $B E$ are the radical axes of the three circles $A G F C, C D B$, and $A B F E$, so $I=A F \cap B E$ is the radical center of the three circles and $C G$ also passes through $I$.  The angle between line $D E$ and the tangent to the circle $B C D$ at $E$ is equal to $\angle E B D=$ $\angle E A F=\angle A B E=\angle A F E$. As the tangent at $E$ is perpendicular to $A M$, the line $D E$ is perpendicular to $A F$. The triangle $A F E$ is isosceles, so $D E$ is the perpendicular bisector of $A F$ and thus $A D=D F$. Hence, the point $D$ is the center of the circle $A F C$, and this circle passes through $M$ as well since $\angle A M C=90^{\circ}$. Let $B^{\prime}$ be the reflection of $B$ in the point $D$, so $A B C B^{\prime}$ is a parallelogram. Since $D C=D G$ we have $\angle G C D=\angle D B C=\angle K B^{\prime} A$. Hence, the quadrilateral $A K C B^{\prime}$ is cyclic and thus $\angle C A K=\angle C B^{\prime} K=\angle A B D=2 \angle M A I$. Then $$ \angle I A B=\angle M A B-\angle M A I=\frac{1}{2} \angle C A B-\frac{1}{2} \angle C A K=\frac{1}{2} \angle K A B $$ and therefore $A I$ is the angle bisector of $\angle K A B$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $A B=A C$, and let $D$ be the midpoint of $A C$. The angle bisector of $\angle B A C$ intersects the circle through $D, B$, and $C$ in a point $E$ inside the triangle $A B C$. The line $B D$ intersects the circle through $A, E$, and $B$ in two points $B$ and $F$. The lines $A F$ and $B E$ meet at a point $I$, and the lines $C I$ and $B D$ meet at a point $K$. Show that $I$ is the incenter of triangle $K A B$.
|
Again, let $M$ be the midpoint of $B C$. As in the previous solutions, we can deduce $\angle A B I=\angle I B K$. We show that the point $I$ lies on the angle bisector of $\angle K A B$. Let $G$ be the intersection point of the circles $A F C$ and $B C D$, different from $C$. The lines $C G, A F$, and $B E$ are the radical axes of the three circles $A G F C, C D B$, and $A B F E$, so $I=A F \cap B E$ is the radical center of the three circles and $C G$ also passes through $I$.  The angle between line $D E$ and the tangent to the circle $B C D$ at $E$ is equal to $\angle E B D=$ $\angle E A F=\angle A B E=\angle A F E$. As the tangent at $E$ is perpendicular to $A M$, the line $D E$ is perpendicular to $A F$. The triangle $A F E$ is isosceles, so $D E$ is the perpendicular bisector of $A F$ and thus $A D=D F$. Hence, the point $D$ is the center of the circle $A F C$, and this circle passes through $M$ as well since $\angle A M C=90^{\circ}$. Let $B^{\prime}$ be the reflection of $B$ in the point $D$, so $A B C B^{\prime}$ is a parallelogram. Since $D C=D G$ we have $\angle G C D=\angle D B C=\angle K B^{\prime} A$. Hence, the quadrilateral $A K C B^{\prime}$ is cyclic and thus $\angle C A K=\angle C B^{\prime} K=\angle A B D=2 \angle M A I$. Then $$ \angle I A B=\angle M A B-\angle M A I=\frac{1}{2} \angle C A B-\frac{1}{2} \angle C A K=\frac{1}{2} \angle K A B $$ and therefore $A I$ is the angle bisector of $\angle K A B$.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
236e30c8-9224-5717-a0a7-dc078527b028
| 24,059
|
Let $A B C D E F$ be a convex hexagon all of whose sides are tangent to a circle $\omega$ with center $O$. Suppose that the circumcircle of triangle $A C E$ is concentric with $\omega$. Let $J$ be the foot of the perpendicular from $B$ to $C D$. Suppose that the perpendicular from $B$ to $D F$ intersects the line $E O$ at a point $K$. Let $L$ be the foot of the perpendicular from $K$ to $D E$. Prove that $D J=D L$.
|
Since $\omega$ and the circumcircle of triangle $A C E$ are concentric, the tangents from $A$, $C$, and $E$ to $\omega$ have equal lengths; that means that $A B=B C, C D=D E$, and $E F=F A$. Moreover, we have $\angle B C D=\angle D E F=\angle F A B$.  Consider the rotation around point $D$ mapping $C$ to $E$; let $B^{\prime}$ and $L^{\prime}$ be the images of the points $B$ and $J$, respectively, under this rotation. Then one has $D J=D L^{\prime}$ and $B^{\prime} L^{\prime} \perp D E$; moreover, the triangles $B^{\prime} E D$ and $B C D$ are congruent. Since $\angle D E O<90^{\circ}$, the lines $E O$ and $B^{\prime} L^{\prime}$ intersect at some point $K^{\prime}$. We intend to prove that $K^{\prime} B \perp D F$; this would imply $K=K^{\prime}$, therefore $L=L^{\prime}$, which proves the problem statement. Analogously, consider the rotation around $F$ mapping $A$ to $E$; let $B^{\prime \prime}$ be the image of $B$ under this rotation. Then the triangles $F A B$ and $F E B^{\prime \prime}$ are congruent. We have $E B^{\prime \prime}=A B=B C=$ $E B^{\prime}$ and $\angle F E B^{\prime \prime}=\angle F A B=\angle B C D=\angle D E B^{\prime}$, so the points $B^{\prime}$ and $B^{\prime \prime}$ are symmetrical with respect to the angle bisector $E O$ of $\angle D E F$. So, from $K^{\prime} B^{\prime} \perp D E$ we get $K^{\prime} B^{\prime \prime} \perp E F$. From these two relations we obtain $$ K^{\prime} D^{2}-K^{\prime} E^{2}=B^{\prime} D^{2}-B^{\prime} E^{2} \quad \text { and } \quad K^{\prime} E^{2}-K^{\prime} F^{2}=B^{\prime \prime} E^{2}-B^{\prime \prime} F^{2} $$ Adding these equalities and taking into account that $B^{\prime} E=B^{\prime \prime} E$ we obtain $$ K^{\prime} D^{2}-K^{\prime} F^{2}=B^{\prime} D^{2}-B^{\prime \prime} F^{2}=B D^{2}-B F^{2}, $$ which means exactly that $K^{\prime} B \perp D F$. Comment. There are several variations of this solution. For instance, let us consider the intersection point $M$ of the lines $B J$ and $O C$. Define the point $K^{\prime}$ as the reflection of $M$ in the line $D O$. Then one has $$ D K^{\prime 2}-D B^{2}=D M^{2}-D B^{2}=C M^{2}-C B^{2} . $$ Next, consider the rotation around $O$ which maps $C M$ to $E K^{\prime}$. Let $P$ be the image of $B$ under this rotation; so $P$ lies on $E D$. Then $E F \perp K^{\prime} P$, so $$ C M^{2}-C B^{2}=E K^{\prime 2}-E P^{2}=F K^{\prime 2}-F P^{2}=F K^{\prime 2}-F B^{2}, $$ since the triangles $F E P$ and $F A B$ are congruent.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D E F$ be a convex hexagon all of whose sides are tangent to a circle $\omega$ with center $O$. Suppose that the circumcircle of triangle $A C E$ is concentric with $\omega$. Let $J$ be the foot of the perpendicular from $B$ to $C D$. Suppose that the perpendicular from $B$ to $D F$ intersects the line $E O$ at a point $K$. Let $L$ be the foot of the perpendicular from $K$ to $D E$. Prove that $D J=D L$.
|
Since $\omega$ and the circumcircle of triangle $A C E$ are concentric, the tangents from $A$, $C$, and $E$ to $\omega$ have equal lengths; that means that $A B=B C, C D=D E$, and $E F=F A$. Moreover, we have $\angle B C D=\angle D E F=\angle F A B$.  Consider the rotation around point $D$ mapping $C$ to $E$; let $B^{\prime}$ and $L^{\prime}$ be the images of the points $B$ and $J$, respectively, under this rotation. Then one has $D J=D L^{\prime}$ and $B^{\prime} L^{\prime} \perp D E$; moreover, the triangles $B^{\prime} E D$ and $B C D$ are congruent. Since $\angle D E O<90^{\circ}$, the lines $E O$ and $B^{\prime} L^{\prime}$ intersect at some point $K^{\prime}$. We intend to prove that $K^{\prime} B \perp D F$; this would imply $K=K^{\prime}$, therefore $L=L^{\prime}$, which proves the problem statement. Analogously, consider the rotation around $F$ mapping $A$ to $E$; let $B^{\prime \prime}$ be the image of $B$ under this rotation. Then the triangles $F A B$ and $F E B^{\prime \prime}$ are congruent. We have $E B^{\prime \prime}=A B=B C=$ $E B^{\prime}$ and $\angle F E B^{\prime \prime}=\angle F A B=\angle B C D=\angle D E B^{\prime}$, so the points $B^{\prime}$ and $B^{\prime \prime}$ are symmetrical with respect to the angle bisector $E O$ of $\angle D E F$. So, from $K^{\prime} B^{\prime} \perp D E$ we get $K^{\prime} B^{\prime \prime} \perp E F$. From these two relations we obtain $$ K^{\prime} D^{2}-K^{\prime} E^{2}=B^{\prime} D^{2}-B^{\prime} E^{2} \quad \text { and } \quad K^{\prime} E^{2}-K^{\prime} F^{2}=B^{\prime \prime} E^{2}-B^{\prime \prime} F^{2} $$ Adding these equalities and taking into account that $B^{\prime} E=B^{\prime \prime} E$ we obtain $$ K^{\prime} D^{2}-K^{\prime} F^{2}=B^{\prime} D^{2}-B^{\prime \prime} F^{2}=B D^{2}-B F^{2}, $$ which means exactly that $K^{\prime} B \perp D F$. Comment. There are several variations of this solution. For instance, let us consider the intersection point $M$ of the lines $B J$ and $O C$. Define the point $K^{\prime}$ as the reflection of $M$ in the line $D O$. Then one has $$ D K^{\prime 2}-D B^{2}=D M^{2}-D B^{2}=C M^{2}-C B^{2} . $$ Next, consider the rotation around $O$ which maps $C M$ to $E K^{\prime}$. Let $P$ be the image of $B$ under this rotation; so $P$ lies on $E D$. Then $E F \perp K^{\prime} P$, so $$ C M^{2}-C B^{2}=E K^{\prime 2}-E P^{2}=F K^{\prime 2}-F P^{2}=F K^{\prime 2}-F B^{2}, $$ since the triangles $F E P$ and $F A B$ are congruent.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
efdcfd06-42a9-5f09-9432-08043adf4236
| 24,064
|
Let $A B C$ be an acute triangle with circumcircle $\omega$. Let $t$ be a tangent line to $\omega$. Let $t_{a}, t_{b}$, and $t_{c}$ be the lines obtained by reflecting $t$ in the lines $B C, C A$, and $A B$, respectively. Show that the circumcircle of the triangle determined by the lines $t_{a}, t_{b}$, and $t_{c}$ is tangent to the circle $\omega$.
|
Denote by $T$ the point of tangency of $t$ and $\omega$. Let $A^{\prime}=t_{b} \cap t_{c}, B^{\prime}=t_{a} \cap t_{c}$, $C^{\prime}=t_{a} \cap t_{b}$. Introduce the point $A^{\prime \prime}$ on $\omega$ such that $T A=A A^{\prime \prime}\left(A^{\prime \prime} \neq T\right.$ unless $T A$ is a diameter). Define the points $B^{\prime \prime}$ and $C^{\prime \prime}$ in a similar way. Since the points $C$ and $B$ are the midpoints of arcs $T C^{\prime \prime}$ and $T B^{\prime \prime}$, respectively, we have $$ \begin{aligned} \angle\left(t, B^{\prime \prime} C^{\prime \prime}\right) & =\angle\left(t, T C^{\prime \prime}\right)+\angle\left(T C^{\prime \prime}, B^{\prime \prime} C^{\prime \prime}\right)=2 \angle(t, T C)+2 \angle\left(T C^{\prime \prime}, B C^{\prime \prime}\right) \\ & =2(\angle(t, T C)+\angle(T C, B C))=2 \angle(t, B C)=\angle\left(t, t_{a}\right) . \end{aligned} $$ It follows that $t_{a}$ and $B^{\prime \prime} C^{\prime \prime}$ are parallel. Similarly, $t_{b} \| A^{\prime \prime} C^{\prime \prime}$ and $t_{c} \| A^{\prime \prime} B^{\prime \prime}$. Thus, either the triangles $A^{\prime} B^{\prime} C^{\prime}$ and $A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}$ are homothetic, or they are translates of each other. Now we will prove that they are in fact homothetic, and that the center $K$ of the homothety belongs to $\omega$. It would then follow that their circumcircles are also homothetic with respect to $K$ and are therefore tangent at this point, as desired. We need the two following claims. Claim 1. The point of intersection $X$ of the lines $B^{\prime \prime} C$ and $B C^{\prime \prime}$ lies on $t_{a}$. Proof. Actually, the points $X$ and $T$ are symmetric about the line $B C$, since the lines $C T$ and $C B^{\prime \prime}$ are symmetric about this line, as are the lines $B T$ and $B C^{\prime \prime}$. Claim 2. The point of intersection $I$ of the lines $B B^{\prime}$ and $C C^{\prime}$ lies on the circle $\omega$. Proof. We consider the case that $t$ is not parallel to the sides of $A B C$; the other cases may be regarded as limit cases. Let $D=t \cap B C, E=t \cap A C$, and $F=t \cap A B$. Due to symmetry, the line $D B$ is one of the angle bisectors of the lines $B^{\prime} D$ and $F D$; analogously, the line $F B$ is one of the angle bisectors of the lines $B^{\prime} F$ and $D F$. So $B$ is either the incenter or one of the excenters of the triangle $B^{\prime} D F$. In any case we have $\angle(B D, D F)+\angle(D F, F B)+$ $\angle\left(B^{\prime} B, B^{\prime} D\right)=90^{\circ}$, so $$ \angle\left(B^{\prime} B, B^{\prime} C^{\prime}\right)=\angle\left(B^{\prime} B, B^{\prime} D\right)=90^{\circ}-\angle(B C, D F)-\angle(D F, B A)=90^{\circ}-\angle(B C, A B) \text {. } $$ Analogously, we get $\angle\left(C^{\prime} C, B^{\prime} C^{\prime}\right)=90^{\circ}-\angle(B C, A C)$. Hence, $$ \angle(B I, C I)=\angle\left(B^{\prime} B, B^{\prime} C^{\prime}\right)+\angle\left(B^{\prime} C^{\prime}, C^{\prime} C\right)=\angle(B C, A C)-\angle(B C, A B)=\angle(A B, A C), $$ which means exactly that the points $A, B, I, C$ are concyclic. Now we can complete the proof. Let $K$ be the second intersection point of $B^{\prime} B^{\prime \prime}$ and $\omega$. Applying PASCAL's theorem to hexagon $K B^{\prime \prime} C I B C^{\prime \prime}$ we get that the points $B^{\prime}=K B^{\prime \prime} \cap I B$ and $X=B^{\prime \prime} C \cap B C^{\prime \prime}$ are collinear with the intersection point $S$ of $C I$ and $C^{\prime \prime} K$. So $S=$ $C I \cap B^{\prime} X=C^{\prime}$, and the points $C^{\prime}, C^{\prime \prime}, K$ are collinear. Thus $K$ is the intersection point of $B^{\prime} B^{\prime \prime}$ and $C^{\prime} C^{\prime \prime}$ which implies that $K$ is the center of the homothety mapping $A^{\prime} B^{\prime} C^{\prime}$ to $A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}$, and it belongs to $\omega$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with circumcircle $\omega$. Let $t$ be a tangent line to $\omega$. Let $t_{a}, t_{b}$, and $t_{c}$ be the lines obtained by reflecting $t$ in the lines $B C, C A$, and $A B$, respectively. Show that the circumcircle of the triangle determined by the lines $t_{a}, t_{b}$, and $t_{c}$ is tangent to the circle $\omega$.
|
Denote by $T$ the point of tangency of $t$ and $\omega$. Let $A^{\prime}=t_{b} \cap t_{c}, B^{\prime}=t_{a} \cap t_{c}$, $C^{\prime}=t_{a} \cap t_{b}$. Introduce the point $A^{\prime \prime}$ on $\omega$ such that $T A=A A^{\prime \prime}\left(A^{\prime \prime} \neq T\right.$ unless $T A$ is a diameter). Define the points $B^{\prime \prime}$ and $C^{\prime \prime}$ in a similar way. Since the points $C$ and $B$ are the midpoints of arcs $T C^{\prime \prime}$ and $T B^{\prime \prime}$, respectively, we have $$ \begin{aligned} \angle\left(t, B^{\prime \prime} C^{\prime \prime}\right) & =\angle\left(t, T C^{\prime \prime}\right)+\angle\left(T C^{\prime \prime}, B^{\prime \prime} C^{\prime \prime}\right)=2 \angle(t, T C)+2 \angle\left(T C^{\prime \prime}, B C^{\prime \prime}\right) \\ & =2(\angle(t, T C)+\angle(T C, B C))=2 \angle(t, B C)=\angle\left(t, t_{a}\right) . \end{aligned} $$ It follows that $t_{a}$ and $B^{\prime \prime} C^{\prime \prime}$ are parallel. Similarly, $t_{b} \| A^{\prime \prime} C^{\prime \prime}$ and $t_{c} \| A^{\prime \prime} B^{\prime \prime}$. Thus, either the triangles $A^{\prime} B^{\prime} C^{\prime}$ and $A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}$ are homothetic, or they are translates of each other. Now we will prove that they are in fact homothetic, and that the center $K$ of the homothety belongs to $\omega$. It would then follow that their circumcircles are also homothetic with respect to $K$ and are therefore tangent at this point, as desired. We need the two following claims. Claim 1. The point of intersection $X$ of the lines $B^{\prime \prime} C$ and $B C^{\prime \prime}$ lies on $t_{a}$. Proof. Actually, the points $X$ and $T$ are symmetric about the line $B C$, since the lines $C T$ and $C B^{\prime \prime}$ are symmetric about this line, as are the lines $B T$ and $B C^{\prime \prime}$. Claim 2. The point of intersection $I$ of the lines $B B^{\prime}$ and $C C^{\prime}$ lies on the circle $\omega$. Proof. We consider the case that $t$ is not parallel to the sides of $A B C$; the other cases may be regarded as limit cases. Let $D=t \cap B C, E=t \cap A C$, and $F=t \cap A B$. Due to symmetry, the line $D B$ is one of the angle bisectors of the lines $B^{\prime} D$ and $F D$; analogously, the line $F B$ is one of the angle bisectors of the lines $B^{\prime} F$ and $D F$. So $B$ is either the incenter or one of the excenters of the triangle $B^{\prime} D F$. In any case we have $\angle(B D, D F)+\angle(D F, F B)+$ $\angle\left(B^{\prime} B, B^{\prime} D\right)=90^{\circ}$, so $$ \angle\left(B^{\prime} B, B^{\prime} C^{\prime}\right)=\angle\left(B^{\prime} B, B^{\prime} D\right)=90^{\circ}-\angle(B C, D F)-\angle(D F, B A)=90^{\circ}-\angle(B C, A B) \text {. } $$ Analogously, we get $\angle\left(C^{\prime} C, B^{\prime} C^{\prime}\right)=90^{\circ}-\angle(B C, A C)$. Hence, $$ \angle(B I, C I)=\angle\left(B^{\prime} B, B^{\prime} C^{\prime}\right)+\angle\left(B^{\prime} C^{\prime}, C^{\prime} C\right)=\angle(B C, A C)-\angle(B C, A B)=\angle(A B, A C), $$ which means exactly that the points $A, B, I, C$ are concyclic. Now we can complete the proof. Let $K$ be the second intersection point of $B^{\prime} B^{\prime \prime}$ and $\omega$. Applying PASCAL's theorem to hexagon $K B^{\prime \prime} C I B C^{\prime \prime}$ we get that the points $B^{\prime}=K B^{\prime \prime} \cap I B$ and $X=B^{\prime \prime} C \cap B C^{\prime \prime}$ are collinear with the intersection point $S$ of $C I$ and $C^{\prime \prime} K$. So $S=$ $C I \cap B^{\prime} X=C^{\prime}$, and the points $C^{\prime}, C^{\prime \prime}, K$ are collinear. Thus $K$ is the intersection point of $B^{\prime} B^{\prime \prime}$ and $C^{\prime} C^{\prime \prime}$ which implies that $K$ is the center of the homothety mapping $A^{\prime} B^{\prime} C^{\prime}$ to $A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}$, and it belongs to $\omega$.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
ecbd624d-a30e-5a61-9f4f-12e3e0bf3d5c
| 24,067
|
Let $A B C$ be an acute triangle with circumcircle $\omega$. Let $t$ be a tangent line to $\omega$. Let $t_{a}, t_{b}$, and $t_{c}$ be the lines obtained by reflecting $t$ in the lines $B C, C A$, and $A B$, respectively. Show that the circumcircle of the triangle determined by the lines $t_{a}, t_{b}$, and $t_{c}$ is tangent to the circle $\omega$.
|
Define the points $T, A^{\prime}, B^{\prime}$, and $C^{\prime}$ in the same way as in the previous solution. Let $X, Y$, and $Z$ be the symmetric images of $T$ about the lines $B C, C A$, and $A B$, respectively. Note that the projections of $T$ on these lines form a Simson line of $T$ with respect to $A B C$, therefore the points $X, Y, Z$ are also collinear. Moreover, we have $X \in B^{\prime} C^{\prime}, Y \in C^{\prime} A^{\prime}$, $Z \in A^{\prime} B^{\prime}$. Denote $\alpha=\angle(t, T C)=\angle(B T, B C)$. Using the symmetry in the lines $A C$ and $B C$, we get $$ \angle(B C, B X)=\angle(B T, B C)=\alpha \quad \text { and } \quad \angle\left(X C, X C^{\prime}\right)=\angle(t, T C)=\angle\left(Y C, Y C^{\prime}\right)=\alpha . $$ Since $\angle\left(X C, X C^{\prime}\right)=\angle\left(Y C, Y C^{\prime}\right)$, the points $X, Y, C, C^{\prime}$ lie on some circle $\omega_{c}$. Define the circles $\omega_{a}$ and $\omega_{b}$ analogously. Let $\omega^{\prime}$ be the circumcircle of triangle $A^{\prime} B^{\prime} C^{\prime}$. Now, applying Miquel's theorem to the four lines $A^{\prime} B^{\prime}, A^{\prime} C^{\prime}, B^{\prime} C^{\prime}$, and $X Y$, we obtain that the circles $\omega^{\prime}, \omega_{a}, \omega_{b}, \omega_{c}$ intersect at some point $K$. We will show that $K$ lies on $\omega$, and that the tangent lines to $\omega$ and $\omega^{\prime}$ at this point coincide; this implies the problem statement. Due to symmetry, we have $X B=T B=Z B$, so the point $B$ is the midpoint of one of the $\operatorname{arcs} X Z$ of circle $\omega_{b}$. Therefore $\angle(K B, K X)=\angle(X Z, X B)$. Analogously, $\angle(K X, K C)=$ $\angle(X C, X Y)$. Adding these equalities and using the symmetry in the line $B C$ we get $$ \angle(K B, K C)=\angle(X Z, X B)+\angle(X C, X Z)=\angle(X C, X B)=\angle(T B, T C) . $$ Therefore, $K$ lies on $\omega$. Next, let $k$ be the tangent line to $\omega$ at $K$. We have $$ \begin{aligned} \angle\left(k, K C^{\prime}\right) & =\angle(k, K C)+\angle\left(K C, K C^{\prime}\right)=\angle(K B, B C)+\angle\left(X C, X C^{\prime}\right) \\ & =(\angle(K B, B X)-\angle(B C, B X))+\alpha=\angle\left(K B^{\prime}, B^{\prime} X\right)-\alpha+\alpha=\angle\left(K B^{\prime}, B^{\prime} C^{\prime}\right), \end{aligned} $$ which means exactly that $k$ is tangent to $\omega^{\prime}$.  Comment. There exist various solutions combining the ideas from the two solutions presented above. For instance, one may define the point $X$ as the reflection of $T$ with respect to the line $B C$, and then introduce the point $K$ as the second intersection point of the circumcircles of $B B^{\prime} X$ and $C C^{\prime} X$. Using the fact that $B B^{\prime}$ and $C C^{\prime}$ are the bisectors of $\angle\left(A^{\prime} B^{\prime}, B^{\prime} C^{\prime}\right)$ and $\angle\left(A^{\prime} C^{\prime}, B^{\prime} C^{\prime}\right)$ one can show successively that $K \in \omega, K \in \omega^{\prime}$, and that the tangents to $\omega$ and $\omega^{\prime}$ at $K$ coincide.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with circumcircle $\omega$. Let $t$ be a tangent line to $\omega$. Let $t_{a}, t_{b}$, and $t_{c}$ be the lines obtained by reflecting $t$ in the lines $B C, C A$, and $A B$, respectively. Show that the circumcircle of the triangle determined by the lines $t_{a}, t_{b}$, and $t_{c}$ is tangent to the circle $\omega$.
|
Define the points $T, A^{\prime}, B^{\prime}$, and $C^{\prime}$ in the same way as in the previous solution. Let $X, Y$, and $Z$ be the symmetric images of $T$ about the lines $B C, C A$, and $A B$, respectively. Note that the projections of $T$ on these lines form a Simson line of $T$ with respect to $A B C$, therefore the points $X, Y, Z$ are also collinear. Moreover, we have $X \in B^{\prime} C^{\prime}, Y \in C^{\prime} A^{\prime}$, $Z \in A^{\prime} B^{\prime}$. Denote $\alpha=\angle(t, T C)=\angle(B T, B C)$. Using the symmetry in the lines $A C$ and $B C$, we get $$ \angle(B C, B X)=\angle(B T, B C)=\alpha \quad \text { and } \quad \angle\left(X C, X C^{\prime}\right)=\angle(t, T C)=\angle\left(Y C, Y C^{\prime}\right)=\alpha . $$ Since $\angle\left(X C, X C^{\prime}\right)=\angle\left(Y C, Y C^{\prime}\right)$, the points $X, Y, C, C^{\prime}$ lie on some circle $\omega_{c}$. Define the circles $\omega_{a}$ and $\omega_{b}$ analogously. Let $\omega^{\prime}$ be the circumcircle of triangle $A^{\prime} B^{\prime} C^{\prime}$. Now, applying Miquel's theorem to the four lines $A^{\prime} B^{\prime}, A^{\prime} C^{\prime}, B^{\prime} C^{\prime}$, and $X Y$, we obtain that the circles $\omega^{\prime}, \omega_{a}, \omega_{b}, \omega_{c}$ intersect at some point $K$. We will show that $K$ lies on $\omega$, and that the tangent lines to $\omega$ and $\omega^{\prime}$ at this point coincide; this implies the problem statement. Due to symmetry, we have $X B=T B=Z B$, so the point $B$ is the midpoint of one of the $\operatorname{arcs} X Z$ of circle $\omega_{b}$. Therefore $\angle(K B, K X)=\angle(X Z, X B)$. Analogously, $\angle(K X, K C)=$ $\angle(X C, X Y)$. Adding these equalities and using the symmetry in the line $B C$ we get $$ \angle(K B, K C)=\angle(X Z, X B)+\angle(X C, X Z)=\angle(X C, X B)=\angle(T B, T C) . $$ Therefore, $K$ lies on $\omega$. Next, let $k$ be the tangent line to $\omega$ at $K$. We have $$ \begin{aligned} \angle\left(k, K C^{\prime}\right) & =\angle(k, K C)+\angle\left(K C, K C^{\prime}\right)=\angle(K B, B C)+\angle\left(X C, X C^{\prime}\right) \\ & =(\angle(K B, B X)-\angle(B C, B X))+\alpha=\angle\left(K B^{\prime}, B^{\prime} X\right)-\alpha+\alpha=\angle\left(K B^{\prime}, B^{\prime} C^{\prime}\right), \end{aligned} $$ which means exactly that $k$ is tangent to $\omega^{\prime}$.  Comment. There exist various solutions combining the ideas from the two solutions presented above. For instance, one may define the point $X$ as the reflection of $T$ with respect to the line $B C$, and then introduce the point $K$ as the second intersection point of the circumcircles of $B B^{\prime} X$ and $C C^{\prime} X$. Using the fact that $B B^{\prime}$ and $C C^{\prime}$ are the bisectors of $\angle\left(A^{\prime} B^{\prime}, B^{\prime} C^{\prime}\right)$ and $\angle\left(A^{\prime} C^{\prime}, B^{\prime} C^{\prime}\right)$ one can show successively that $K \in \omega, K \in \omega^{\prime}$, and that the tangents to $\omega$ and $\omega^{\prime}$ at $K$ coincide.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
ecbd624d-a30e-5a61-9f4f-12e3e0bf3d5c
| 24,067
|
For any integer $d>0$, let $f(d)$ be the smallest positive integer that has exactly $d$ positive divisors (so for example we have $f(1)=1, f(5)=16$, and $f(6)=12$ ). Prove that for every integer $k \geq 0$ the number $f\left(2^{k}\right)$ divides $f\left(2^{k+1}\right)$.
|
For any positive integer $n$, let $d(n)$ be the number of positive divisors of $n$. Let $n=\prod_{p} p^{a(p)}$ be the prime factorization of $n$ where $p$ ranges over the prime numbers, the integers $a(p)$ are nonnegative and all but finitely many $a(p)$ are zero. Then we have $d(n)=\prod_{p}(a(p)+1)$. Thus, $d(n)$ is a power of 2 if and only if for every prime $p$ there is a nonnegative integer $b(p)$ with $a(p)=2^{b(p)}-1=1+2+2^{2}+\cdots+2^{b(p)-1}$. We then have $$ n=\prod_{p} \prod_{i=0}^{b(p)-1} p^{2^{i}}, \quad \text { and } \quad d(n)=2^{k} \quad \text { with } \quad k=\sum_{p} b(p) $$ Let $\mathcal{S}$ be the set of all numbers of the form $p^{2^{r}}$ with $p$ prime and $r$ a nonnegative integer. Then we deduce that $d(n)$ is a power of 2 if and only if $n$ is the product of the elements of some finite subset $\mathcal{T}$ of $\mathcal{S}$ that satisfies the following condition: for all $t \in \mathcal{T}$ and $s \in \mathcal{S}$ with $s \mid t$ we have $s \in \mathcal{T}$. Moreover, if $d(n)=2^{k}$ then the corresponding set $\mathcal{T}$ has $k$ elements. Note that the set $\mathcal{T}_{k}$ consisting of the smallest $k$ elements from $\mathcal{S}$ obviously satisfies the condition above. Thus, given $k$, the smallest $n$ with $d(n)=2^{k}$ is the product of the elements of $\mathcal{T}_{k}$. This $n$ is $f\left(2^{k}\right)$. Since obviously $\mathcal{T}_{k} \subset \mathcal{T}_{k+1}$, it follows that $f\left(2^{k}\right) \mid f\left(2^{k+1}\right)$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For any integer $d>0$, let $f(d)$ be the smallest positive integer that has exactly $d$ positive divisors (so for example we have $f(1)=1, f(5)=16$, and $f(6)=12$ ). Prove that for every integer $k \geq 0$ the number $f\left(2^{k}\right)$ divides $f\left(2^{k+1}\right)$.
|
For any positive integer $n$, let $d(n)$ be the number of positive divisors of $n$. Let $n=\prod_{p} p^{a(p)}$ be the prime factorization of $n$ where $p$ ranges over the prime numbers, the integers $a(p)$ are nonnegative and all but finitely many $a(p)$ are zero. Then we have $d(n)=\prod_{p}(a(p)+1)$. Thus, $d(n)$ is a power of 2 if and only if for every prime $p$ there is a nonnegative integer $b(p)$ with $a(p)=2^{b(p)}-1=1+2+2^{2}+\cdots+2^{b(p)-1}$. We then have $$ n=\prod_{p} \prod_{i=0}^{b(p)-1} p^{2^{i}}, \quad \text { and } \quad d(n)=2^{k} \quad \text { with } \quad k=\sum_{p} b(p) $$ Let $\mathcal{S}$ be the set of all numbers of the form $p^{2^{r}}$ with $p$ prime and $r$ a nonnegative integer. Then we deduce that $d(n)$ is a power of 2 if and only if $n$ is the product of the elements of some finite subset $\mathcal{T}$ of $\mathcal{S}$ that satisfies the following condition: for all $t \in \mathcal{T}$ and $s \in \mathcal{S}$ with $s \mid t$ we have $s \in \mathcal{T}$. Moreover, if $d(n)=2^{k}$ then the corresponding set $\mathcal{T}$ has $k$ elements. Note that the set $\mathcal{T}_{k}$ consisting of the smallest $k$ elements from $\mathcal{S}$ obviously satisfies the condition above. Thus, given $k$, the smallest $n$ with $d(n)=2^{k}$ is the product of the elements of $\mathcal{T}_{k}$. This $n$ is $f\left(2^{k}\right)$. Since obviously $\mathcal{T}_{k} \subset \mathcal{T}_{k+1}$, it follows that $f\left(2^{k}\right) \mid f\left(2^{k+1}\right)$.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
56d29187-44f6-502f-a67c-d0600d92543f
| 24,072
|
For any integer $d>0$, let $f(d)$ be the smallest positive integer that has exactly $d$ positive divisors (so for example we have $f(1)=1, f(5)=16$, and $f(6)=12$ ). Prove that for every integer $k \geq 0$ the number $f\left(2^{k}\right)$ divides $f\left(2^{k+1}\right)$.
|
This is an alternative to the second part of the $$ m=p^{2^{b(p)}}>q^{2^{b(q)-1}}=\ell . $$ To see this, note first that $\ell$ divides $f\left(2^{k}\right)$. With the first part of Solution 1 one can see that the integer $n=f\left(2^{k}\right) m / \ell$ also satisfies $d(n)=2^{k}$. By the definition of $f\left(2^{k}\right)$ this implies that $n \geq f\left(2^{k}\right)$ so $m \geq \ell$. Since $p \neq q$ the inequality (1) follows. Let the prime factorization of $f\left(2^{k+1}\right)$ be given by $f\left(2^{k+1}\right)=\prod_{p} p^{r(p)}$ with $r(p)=2^{s(p)}-1$. Since we have $\sum_{p} s(p)=k+1>k=\sum_{p} b(p)$ there is a prime $p$ with $s(p)>b(p)$. For any prime $q \neq p$ with $b(q)>0$ we apply inequality (1) twice and get $$ q^{2^{s(q)}}>p^{2^{s(p)-1}} \geq p^{2^{b(p)}}>q^{2^{b(q)-1}} $$ which implies $s(q) \geq b(q)$. It follows that $s(q) \geq b(q)$ for all primes $q$, so $f\left(2^{k}\right) \mid f\left(2^{k+1}\right)$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For any integer $d>0$, let $f(d)$ be the smallest positive integer that has exactly $d$ positive divisors (so for example we have $f(1)=1, f(5)=16$, and $f(6)=12$ ). Prove that for every integer $k \geq 0$ the number $f\left(2^{k}\right)$ divides $f\left(2^{k+1}\right)$.
|
This is an alternative to the second part of the $$ m=p^{2^{b(p)}}>q^{2^{b(q)-1}}=\ell . $$ To see this, note first that $\ell$ divides $f\left(2^{k}\right)$. With the first part of Solution 1 one can see that the integer $n=f\left(2^{k}\right) m / \ell$ also satisfies $d(n)=2^{k}$. By the definition of $f\left(2^{k}\right)$ this implies that $n \geq f\left(2^{k}\right)$ so $m \geq \ell$. Since $p \neq q$ the inequality (1) follows. Let the prime factorization of $f\left(2^{k+1}\right)$ be given by $f\left(2^{k+1}\right)=\prod_{p} p^{r(p)}$ with $r(p)=2^{s(p)}-1$. Since we have $\sum_{p} s(p)=k+1>k=\sum_{p} b(p)$ there is a prime $p$ with $s(p)>b(p)$. For any prime $q \neq p$ with $b(q)>0$ we apply inequality (1) twice and get $$ q^{2^{s(q)}}>p^{2^{s(p)-1}} \geq p^{2^{b(p)}}>q^{2^{b(q)-1}} $$ which implies $s(q) \geq b(q)$. It follows that $s(q) \geq b(q)$ for all primes $q$, so $f\left(2^{k}\right) \mid f\left(2^{k+1}\right)$.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
56d29187-44f6-502f-a67c-d0600d92543f
| 24,072
|
Consider a polynomial $P(x)=\left(x+d_{1}\right)\left(x+d_{2}\right) \cdot \ldots \cdot\left(x+d_{9}\right)$, where $d_{1}, d_{2}, \ldots, d_{9}$ are nine distinct integers. Prove that there exists an integer $N$ such that for all integers $x \geq N$ the number $P(x)$ is divisible by a prime number greater than 20 .
|
Note that the statement of the problem is invariant under translations of $x$; hence without loss of generality we may suppose that the numbers $d_{1}, d_{2}, \ldots, d_{9}$ are positive. The key observation is that there are only eight primes below 20, while $P(x)$ involves more than eight factors. We shall prove that $N=d^{8}$ satisfies the desired property, where $d=\max \left\{d_{1}, d_{2}, \ldots, d_{9}\right\}$. Suppose for the sake of contradiction that there is some integer $x \geq N$ such that $P(x)$ is composed of primes below 20 only. Then for every index $i \in\{1,2, \ldots, 9\}$ the number $x+d_{i}$ can be expressed as product of powers of the first 8 primes. Since $x+d_{i}>x \geq d^{8}$ there is some prime power $f_{i}>d$ that divides $x+d_{i}$. Invoking the pigeonhole principle we see that there are two distinct indices $i$ and $j$ such that $f_{i}$ and $f_{j}$ are powers of the same prime number. For reasons of symmetry, we may suppose that $f_{i} \leq f_{j}$. Now both of the numbers $x+d_{i}$ and $x+d_{j}$ are divisible by $f_{i}$ and hence so is their difference $d_{i}-d_{j}$. But as $$ 0<\left|d_{i}-d_{j}\right| \leq \max \left(d_{i}, d_{j}\right) \leq d<f_{i} $$ this is impossible. Thereby the problem is solved.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Consider a polynomial $P(x)=\left(x+d_{1}\right)\left(x+d_{2}\right) \cdot \ldots \cdot\left(x+d_{9}\right)$, where $d_{1}, d_{2}, \ldots, d_{9}$ are nine distinct integers. Prove that there exists an integer $N$ such that for all integers $x \geq N$ the number $P(x)$ is divisible by a prime number greater than 20 .
|
Note that the statement of the problem is invariant under translations of $x$; hence without loss of generality we may suppose that the numbers $d_{1}, d_{2}, \ldots, d_{9}$ are positive. The key observation is that there are only eight primes below 20, while $P(x)$ involves more than eight factors. We shall prove that $N=d^{8}$ satisfies the desired property, where $d=\max \left\{d_{1}, d_{2}, \ldots, d_{9}\right\}$. Suppose for the sake of contradiction that there is some integer $x \geq N$ such that $P(x)$ is composed of primes below 20 only. Then for every index $i \in\{1,2, \ldots, 9\}$ the number $x+d_{i}$ can be expressed as product of powers of the first 8 primes. Since $x+d_{i}>x \geq d^{8}$ there is some prime power $f_{i}>d$ that divides $x+d_{i}$. Invoking the pigeonhole principle we see that there are two distinct indices $i$ and $j$ such that $f_{i}$ and $f_{j}$ are powers of the same prime number. For reasons of symmetry, we may suppose that $f_{i} \leq f_{j}$. Now both of the numbers $x+d_{i}$ and $x+d_{j}$ are divisible by $f_{i}$ and hence so is their difference $d_{i}-d_{j}$. But as $$ 0<\left|d_{i}-d_{j}\right| \leq \max \left(d_{i}, d_{j}\right) \leq d<f_{i} $$ this is impossible. Thereby the problem is solved.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
f7812fb8-b690-5c0a-b729-656c222f5928
| 24,076
|
Consider a polynomial $P(x)=\left(x+d_{1}\right)\left(x+d_{2}\right) \cdot \ldots \cdot\left(x+d_{9}\right)$, where $d_{1}, d_{2}, \ldots, d_{9}$ are nine distinct integers. Prove that there exists an integer $N$ such that for all integers $x \geq N$ the number $P(x)$ is divisible by a prime number greater than 20 .
|
Observe that for each index $i \in\{1,2, \ldots, 9\}$ the product $$ D_{i}=\prod_{1 \leq j \leq 9, j \neq i}\left|d_{i}-d_{j}\right| $$ is positive. We claim that $N=\max \left\{D_{1}-d_{1}, D_{2}-d_{2}, \ldots, D_{9}-d_{9}\right\}+1$ satisfies the statement of the problem. Suppose there exists an integer $x \geq N$ such that all primes dividing $P(x)$ are smaller than 20. For each index $i$ we reduce the fraction $\left(x+d_{i}\right) / D_{i}$ to lowest terms. Since $x+d_{i}>D_{i}$ the numerator of the fraction we thereby get cannot be 1 , and hence it has to be divisible by some prime number $p_{i}<20$. By the pigeonhole principle, there are a prime number $p$ and two distinct indices $i$ and $j$ such that $p_{i}=p_{j}=p$. Let $p^{\alpha_{i}}$ and $p^{\alpha_{j}}$ be the greatest powers of $p$ dividing $x+d_{i}$ and $x+d_{j}$, respectively. Due to symmetry we may suppose $\alpha_{i} \leq \alpha_{j}$. But now $p^{\alpha_{i}}$ divides $d_{i}-d_{j}$ and hence also $D_{i}$, which means that all occurrences of $p$ in the numerator of the fraction $\left(x+d_{i}\right) / D_{i}$ cancel out, contrary to the choice of $p=p_{i}$. This contradiction proves our claim.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Consider a polynomial $P(x)=\left(x+d_{1}\right)\left(x+d_{2}\right) \cdot \ldots \cdot\left(x+d_{9}\right)$, where $d_{1}, d_{2}, \ldots, d_{9}$ are nine distinct integers. Prove that there exists an integer $N$ such that for all integers $x \geq N$ the number $P(x)$ is divisible by a prime number greater than 20 .
|
Observe that for each index $i \in\{1,2, \ldots, 9\}$ the product $$ D_{i}=\prod_{1 \leq j \leq 9, j \neq i}\left|d_{i}-d_{j}\right| $$ is positive. We claim that $N=\max \left\{D_{1}-d_{1}, D_{2}-d_{2}, \ldots, D_{9}-d_{9}\right\}+1$ satisfies the statement of the problem. Suppose there exists an integer $x \geq N$ such that all primes dividing $P(x)$ are smaller than 20. For each index $i$ we reduce the fraction $\left(x+d_{i}\right) / D_{i}$ to lowest terms. Since $x+d_{i}>D_{i}$ the numerator of the fraction we thereby get cannot be 1 , and hence it has to be divisible by some prime number $p_{i}<20$. By the pigeonhole principle, there are a prime number $p$ and two distinct indices $i$ and $j$ such that $p_{i}=p_{j}=p$. Let $p^{\alpha_{i}}$ and $p^{\alpha_{j}}$ be the greatest powers of $p$ dividing $x+d_{i}$ and $x+d_{j}$, respectively. Due to symmetry we may suppose $\alpha_{i} \leq \alpha_{j}$. But now $p^{\alpha_{i}}$ divides $d_{i}-d_{j}$ and hence also $D_{i}$, which means that all occurrences of $p$ in the numerator of the fraction $\left(x+d_{i}\right) / D_{i}$ cancel out, contrary to the choice of $p=p_{i}$. This contradiction proves our claim.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
f7812fb8-b690-5c0a-b729-656c222f5928
| 24,076
|
Consider a polynomial $P(x)=\left(x+d_{1}\right)\left(x+d_{2}\right) \cdot \ldots \cdot\left(x+d_{9}\right)$, where $d_{1}, d_{2}, \ldots, d_{9}$ are nine distinct integers. Prove that there exists an integer $N$ such that for all integers $x \geq N$ the number $P(x)$ is divisible by a prime number greater than 20 .
|
Given a nonzero integer $N$ as well as a prime number $p$ we write $v_{p}(N)$ for the exponent with which $p$ occurs in the prime factorization of $|N|$. Evidently, if the statement of the problem were not true, then there would exist an infinite sequence $\left(x_{n}\right)$ of positive integers tending to infinity such that for each $n \in \mathbb{Z}_{+}$the integer $P\left(x_{n}\right)$ is not divisible by any prime number $>20$. Observe that the numbers $-d_{1},-d_{2}, \ldots,-d_{9}$ do not appear in this sequence. Now clearly there exists a prime $p_{1}<20$ for which the sequence $v_{p_{1}}\left(x_{n}+d_{1}\right)$ is not bounded; thinning out the sequence $\left(x_{n}\right)$ if necessary we may even suppose that $$ v_{p_{1}}\left(x_{n}+d_{1}\right) \longrightarrow \infty . $$ Repeating this argument eight more times we may similarly choose primes $p_{2}, \ldots, p_{9}<20$ and suppose that our sequence $\left(x_{n}\right)$ has been thinned out to such an extent that $v_{p_{i}}\left(x_{n}+d_{i}\right) \longrightarrow \infty$ holds for $i=2, \ldots, 9$ as well. In view of the pigeonhole principle, there are distinct indices $i$ and $j$ as well as a prime $p<20$ such that $p_{i}=p_{j}=p$. Setting $k=v_{p}\left(d_{i}-d_{j}\right)$ there now has to be some $n$ for which both $v_{p}\left(x_{n}+d_{i}\right)$ and $v_{p}\left(x_{n}+d_{j}\right)$ are greater than $k$. But now the numbers $x_{n}+d_{i}$ and $x_{n}+d_{j}$ are divisible by $p^{k+1}$ whilst their difference $d_{i}-d_{j}$ is not - a contradiction. Comment. This problem is supposed to be a relatively easy one, so one might consider adding the hypothesis that the numbers $d_{1}, d_{2}, \ldots, d_{9}$ be positive. Then certain merely technical issues are not going to arise while the main ideas required to solve the problems remain the same. Let $n \geq 1$ be an odd integer. Determine all functions $f$ from the set of integers to itself such that for all integers $x$ and $y$ the difference $f(x)-f(y)$ divides $x^{n}-y^{n}$. Answer. All functions $f$ of the form $f(x)=\varepsilon x^{d}+c$, where $\varepsilon$ is in $\{1,-1\}$, the integer $d$ is a positive divisor of $n$, and $c$ is an integer.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Consider a polynomial $P(x)=\left(x+d_{1}\right)\left(x+d_{2}\right) \cdot \ldots \cdot\left(x+d_{9}\right)$, where $d_{1}, d_{2}, \ldots, d_{9}$ are nine distinct integers. Prove that there exists an integer $N$ such that for all integers $x \geq N$ the number $P(x)$ is divisible by a prime number greater than 20 .
|
Given a nonzero integer $N$ as well as a prime number $p$ we write $v_{p}(N)$ for the exponent with which $p$ occurs in the prime factorization of $|N|$. Evidently, if the statement of the problem were not true, then there would exist an infinite sequence $\left(x_{n}\right)$ of positive integers tending to infinity such that for each $n \in \mathbb{Z}_{+}$the integer $P\left(x_{n}\right)$ is not divisible by any prime number $>20$. Observe that the numbers $-d_{1},-d_{2}, \ldots,-d_{9}$ do not appear in this sequence. Now clearly there exists a prime $p_{1}<20$ for which the sequence $v_{p_{1}}\left(x_{n}+d_{1}\right)$ is not bounded; thinning out the sequence $\left(x_{n}\right)$ if necessary we may even suppose that $$ v_{p_{1}}\left(x_{n}+d_{1}\right) \longrightarrow \infty . $$ Repeating this argument eight more times we may similarly choose primes $p_{2}, \ldots, p_{9}<20$ and suppose that our sequence $\left(x_{n}\right)$ has been thinned out to such an extent that $v_{p_{i}}\left(x_{n}+d_{i}\right) \longrightarrow \infty$ holds for $i=2, \ldots, 9$ as well. In view of the pigeonhole principle, there are distinct indices $i$ and $j$ as well as a prime $p<20$ such that $p_{i}=p_{j}=p$. Setting $k=v_{p}\left(d_{i}-d_{j}\right)$ there now has to be some $n$ for which both $v_{p}\left(x_{n}+d_{i}\right)$ and $v_{p}\left(x_{n}+d_{j}\right)$ are greater than $k$. But now the numbers $x_{n}+d_{i}$ and $x_{n}+d_{j}$ are divisible by $p^{k+1}$ whilst their difference $d_{i}-d_{j}$ is not - a contradiction. Comment. This problem is supposed to be a relatively easy one, so one might consider adding the hypothesis that the numbers $d_{1}, d_{2}, \ldots, d_{9}$ be positive. Then certain merely technical issues are not going to arise while the main ideas required to solve the problems remain the same. Let $n \geq 1$ be an odd integer. Determine all functions $f$ from the set of integers to itself such that for all integers $x$ and $y$ the difference $f(x)-f(y)$ divides $x^{n}-y^{n}$. Answer. All functions $f$ of the form $f(x)=\varepsilon x^{d}+c$, where $\varepsilon$ is in $\{1,-1\}$, the integer $d$ is a positive divisor of $n$, and $c$ is an integer.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
f7812fb8-b690-5c0a-b729-656c222f5928
| 24,076
|
Let $f$ be a function from the set of integers to the set of positive integers. Suppose that for any two integers $m$ and $n$, the difference $f(m)-f(n)$ is divisible by $f(m-n)$. Prove that for all integers $m, n$ with $f(m) \leq f(n)$ the number $f(n)$ is divisible by $f(m)$.
|
Suppose that $x$ and $y$ are two integers with $f(x)<f(y)$. We will show that $f(x) \mid f(y)$. By taking $m=x$ and $n=y$ we see that $$ f(x-y)|| f(x)-f(y) \mid=f(y)-f(x)>0 $$ so $f(x-y) \leq f(y)-f(x)<f(y)$. Hence the number $d=f(x)-f(x-y)$ satisfies $$ -f(y)<-f(x-y)<d<f(x)<f(y) . $$ Taking $m=x$ and $n=x-y$ we see that $f(y) \mid d$, so we deduce $d=0$, or in other words $f(x)=f(x-y)$. Taking $m=x$ and $n=y$ we see that $f(x)=f(x-y) \mid f(x)-f(y)$, which implies $f(x) \mid f(y)$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $f$ be a function from the set of integers to the set of positive integers. Suppose that for any two integers $m$ and $n$, the difference $f(m)-f(n)$ is divisible by $f(m-n)$. Prove that for all integers $m, n$ with $f(m) \leq f(n)$ the number $f(n)$ is divisible by $f(m)$.
|
Suppose that $x$ and $y$ are two integers with $f(x)<f(y)$. We will show that $f(x) \mid f(y)$. By taking $m=x$ and $n=y$ we see that $$ f(x-y)|| f(x)-f(y) \mid=f(y)-f(x)>0 $$ so $f(x-y) \leq f(y)-f(x)<f(y)$. Hence the number $d=f(x)-f(x-y)$ satisfies $$ -f(y)<-f(x-y)<d<f(x)<f(y) . $$ Taking $m=x$ and $n=x-y$ we see that $f(y) \mid d$, so we deduce $d=0$, or in other words $f(x)=f(x-y)$. Taking $m=x$ and $n=y$ we see that $f(x)=f(x-y) \mid f(x)-f(y)$, which implies $f(x) \mid f(y)$.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
89bd7113-84bb-5d41-b917-e5b1a9be2294
| 24,086
|
Let $f$ be a function from the set of integers to the set of positive integers. Suppose that for any two integers $m$ and $n$, the difference $f(m)-f(n)$ is divisible by $f(m-n)$. Prove that for all integers $m, n$ with $f(m) \leq f(n)$ the number $f(n)$ is divisible by $f(m)$.
|
We split the solution into a sequence of claims; in each claim, the letters $m$ and $n$ denote arbitrary integers. Claim 1. $f(n) \mid f(m n)$. Proof. Since trivially $f(n) \mid f(1 \cdot n)$ and $f(n) \mid f((k+1) n)-f(k n)$ for all integers $k$, this is easily seen by using induction on $m$ in both directions. Claim 2. $f(n) \mid f(0)$ and $f(n)=f(-n)$. Proof. The first part follows by plugging $m=0$ into Claim 1. Using Claim 1 twice with $m=-1$, we get $f(n)|f(-n)| f(n)$, from which the second part follows. From Claim 1, we get $f(1) \mid f(n)$ for all integers $n$, so $f(1)$ is the minimal value attained by $f$. Next, from Claim 2, the function $f$ can attain only a finite number of values since all these values divide $f(0)$. Now we prove the statement of the problem by induction on the number $N_{f}$ of values attained by $f$. In the base case $N_{f} \leq 2$, we either have $f(0) \neq f(1)$, in which case these two numbers are the only values attained by $f$ and the statement is clear, or we have $f(0)=f(1)$, in which case we have $f(1)|f(n)| f(0)$ for all integers $n$, so $f$ is constant and the statement is obvious again. For the induction step, assume that $N_{f} \geq 3$, and let $a$ be the least positive integer with $f(a)>f(1)$. Note that such a number exists due to the symmetry of $f$ obtained in Claim 2. Claim 3. $f(n) \neq f(1)$ if and only if $a \mid n$. Proof. Since $f(1)=\cdots=f(a-1)<f(a)$, the claim follows from the fact that $$ f(n)=f(1) \Longleftrightarrow f(n+a)=f(1) . $$ So it suffices to prove this fact. Assume that $f(n)=f(1)$. Then $f(n+a) \mid f(a)-f(-n)=f(a)-f(n)>0$, so $f(n+a) \leq$ $f(a)-f(n)<f(a)$; in particular the difference $f(n+a)-f(n)$ is stricly smaller than $f(a)$. Furthermore, this difference is divisible by $f(a)$ and nonnegative since $f(n)=f(1)$ is the least value attained by $f$. So we have $f(n+a)-f(n)=0$, as desired. For the converse direction we only need to remark that $f(n+a)=f(1)$ entails $f(-n-a)=f(1)$, and hence $f(n)=f(-n)=f(1)$ by the forward implication. We return to the induction step. So let us take two arbitrary integers $m$ and $n$ with $f(m) \leq f(n)$. If $a \nmid m$, then we have $f(m)=f(1) \mid f(n)$. On the other hand, suppose that $a \mid m$; then by Claim $3 a \mid n$ as well. Now define the function $g(x)=f(a x)$. Clearly, $g$ satisfies the conditions of the problem, but $N_{g}<N_{f}-1$, since $g$ does not attain $f(1)$. Hence, by the induction hypothesis, $f(m)=g(m / a) \mid g(n / a)=f(n)$, as desired. Comment. After the fact that $f$ attains a finite number of values has been established, there are several ways of finishing the solution. For instance, let $f(0)=b_{1}>b_{2}>\cdots>b_{k}$ be all these values. One may show (essentially in the same way as in Claim 3) that the set $S_{i}=\left\{n: f(n) \geq b_{i}\right\}$ consists exactly of all numbers divisible by some integer $a_{i} \geq 0$. One obviously has $a_{i} \mid a_{i-1}$, which implies $f\left(a_{i}\right) \mid f\left(a_{i-1}\right)$ by Claim 1. So, $b_{k}\left|b_{k-1}\right| \cdots \mid b_{1}$, thus proving the problem statement. Moreover, now it is easy to describe all functions satisfying the conditions of the problem. Namely, all these functions can be constructed as follows. Consider a sequence of nonnegative integers $a_{1}, a_{2}, \ldots, a_{k}$ and another sequence of positive integers $b_{1}, b_{2}, \ldots, b_{k}$ such that $\left|a_{k}\right|=1, a_{i} \neq a_{j}$ and $b_{i} \neq b_{j}$ for all $1 \leq i<j \leq k$, and $a_{i} \mid a_{i-1}$ and $b_{i} \mid b_{i-1}$ for all $i=2, \ldots, k$. Then one may introduce the function $$ f(n)=b_{i(n)}, \quad \text { where } \quad i(n)=\min \left\{i: a_{i} \mid n\right\} $$ These are all the functions which satisfy the conditions of the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $f$ be a function from the set of integers to the set of positive integers. Suppose that for any two integers $m$ and $n$, the difference $f(m)-f(n)$ is divisible by $f(m-n)$. Prove that for all integers $m, n$ with $f(m) \leq f(n)$ the number $f(n)$ is divisible by $f(m)$.
|
We split the solution into a sequence of claims; in each claim, the letters $m$ and $n$ denote arbitrary integers. Claim 1. $f(n) \mid f(m n)$. Proof. Since trivially $f(n) \mid f(1 \cdot n)$ and $f(n) \mid f((k+1) n)-f(k n)$ for all integers $k$, this is easily seen by using induction on $m$ in both directions. Claim 2. $f(n) \mid f(0)$ and $f(n)=f(-n)$. Proof. The first part follows by plugging $m=0$ into Claim 1. Using Claim 1 twice with $m=-1$, we get $f(n)|f(-n)| f(n)$, from which the second part follows. From Claim 1, we get $f(1) \mid f(n)$ for all integers $n$, so $f(1)$ is the minimal value attained by $f$. Next, from Claim 2, the function $f$ can attain only a finite number of values since all these values divide $f(0)$. Now we prove the statement of the problem by induction on the number $N_{f}$ of values attained by $f$. In the base case $N_{f} \leq 2$, we either have $f(0) \neq f(1)$, in which case these two numbers are the only values attained by $f$ and the statement is clear, or we have $f(0)=f(1)$, in which case we have $f(1)|f(n)| f(0)$ for all integers $n$, so $f$ is constant and the statement is obvious again. For the induction step, assume that $N_{f} \geq 3$, and let $a$ be the least positive integer with $f(a)>f(1)$. Note that such a number exists due to the symmetry of $f$ obtained in Claim 2. Claim 3. $f(n) \neq f(1)$ if and only if $a \mid n$. Proof. Since $f(1)=\cdots=f(a-1)<f(a)$, the claim follows from the fact that $$ f(n)=f(1) \Longleftrightarrow f(n+a)=f(1) . $$ So it suffices to prove this fact. Assume that $f(n)=f(1)$. Then $f(n+a) \mid f(a)-f(-n)=f(a)-f(n)>0$, so $f(n+a) \leq$ $f(a)-f(n)<f(a)$; in particular the difference $f(n+a)-f(n)$ is stricly smaller than $f(a)$. Furthermore, this difference is divisible by $f(a)$ and nonnegative since $f(n)=f(1)$ is the least value attained by $f$. So we have $f(n+a)-f(n)=0$, as desired. For the converse direction we only need to remark that $f(n+a)=f(1)$ entails $f(-n-a)=f(1)$, and hence $f(n)=f(-n)=f(1)$ by the forward implication. We return to the induction step. So let us take two arbitrary integers $m$ and $n$ with $f(m) \leq f(n)$. If $a \nmid m$, then we have $f(m)=f(1) \mid f(n)$. On the other hand, suppose that $a \mid m$; then by Claim $3 a \mid n$ as well. Now define the function $g(x)=f(a x)$. Clearly, $g$ satisfies the conditions of the problem, but $N_{g}<N_{f}-1$, since $g$ does not attain $f(1)$. Hence, by the induction hypothesis, $f(m)=g(m / a) \mid g(n / a)=f(n)$, as desired. Comment. After the fact that $f$ attains a finite number of values has been established, there are several ways of finishing the solution. For instance, let $f(0)=b_{1}>b_{2}>\cdots>b_{k}$ be all these values. One may show (essentially in the same way as in Claim 3) that the set $S_{i}=\left\{n: f(n) \geq b_{i}\right\}$ consists exactly of all numbers divisible by some integer $a_{i} \geq 0$. One obviously has $a_{i} \mid a_{i-1}$, which implies $f\left(a_{i}\right) \mid f\left(a_{i-1}\right)$ by Claim 1. So, $b_{k}\left|b_{k-1}\right| \cdots \mid b_{1}$, thus proving the problem statement. Moreover, now it is easy to describe all functions satisfying the conditions of the problem. Namely, all these functions can be constructed as follows. Consider a sequence of nonnegative integers $a_{1}, a_{2}, \ldots, a_{k}$ and another sequence of positive integers $b_{1}, b_{2}, \ldots, b_{k}$ such that $\left|a_{k}\right|=1, a_{i} \neq a_{j}$ and $b_{i} \neq b_{j}$ for all $1 \leq i<j \leq k$, and $a_{i} \mid a_{i-1}$ and $b_{i} \mid b_{i-1}$ for all $i=2, \ldots, k$. Then one may introduce the function $$ f(n)=b_{i(n)}, \quad \text { where } \quad i(n)=\min \left\{i: a_{i} \mid n\right\} $$ These are all the functions which satisfy the conditions of the problem.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
89bd7113-84bb-5d41-b917-e5b1a9be2294
| 24,086
|
Let $P(x)$ and $Q(x)$ be two polynomials with integer coefficients such that no nonconstant polynomial with rational coefficients divides both $P(x)$ and $Q(x)$. Suppose that for every positive integer $n$ the integers $P(n)$ and $Q(n)$ are positive, and $2^{Q(n)}-1$ divides $3^{P(n)}-1$. Prove that $Q(x)$ is a constant polynomial.
|
First we show that there exists an integer $d$ such that for all positive integers $n$ we have $\operatorname{gcd}(P(n), Q(n)) \leq d$. Since $P(x)$ and $Q(x)$ are coprime (over the polynomials with rational coefficients), EuCLID's algorithm provides some polynomials $R_{0}(x), S_{0}(x)$ with rational coefficients such that $P(x) R_{0}(x)-$ $Q(x) S_{0}(x)=1$. Multiplying by a suitable positive integer $d$, we obtain polynomials $R(x)=$ $d \cdot R_{0}(x)$ and $S(x)=d \cdot S_{0}(x)$ with integer coefficients for which $P(x) R(x)-Q(x) S(x)=d$. Then we have $\operatorname{gcd}(P(n), Q(n)) \leq d$ for any integer $n$. To prove the problem statement, suppose that $Q(x)$ is not constant. Then the sequence $Q(n)$ is not bounded and we can choose a positive integer $m$ for which $$ M=2^{Q(m)}-1 \geq 3^{\max \{P(1), P(2), \ldots, P(d)\}} $$ Since $M=2^{Q(n)}-1 \mid 3^{P(n)}-1$, we have $2,3 \not M$. Let $a$ and $b$ be the multiplicative orders of 2 and 3 modulo $M$, respectively. Obviously, $a=Q(m)$ since the lower powers of 2 do not reach $M$. Since $M$ divides $3^{P(m)}-1$, we have $b \mid P(m)$. Then $\operatorname{gcd}(a, b) \leq \operatorname{gcd}(P(m), Q(m)) \leq d$. Since the expression $a x$ - by attains all integer values divisible by $\operatorname{gcd}(a, b)$ when $x$ and $y$ run over all nonnegative integer values, there exist some nonnegative integers $x, y$ such that $1 \leq m+a x-b y \leq d$. By $Q(m+a x) \equiv Q(m)(\bmod a)$ we have $$ 2^{Q(m+a x)} \equiv 2^{Q(m)} \equiv 1 \quad(\bmod M) $$ and therefore $$ M\left|2^{Q(m+a x)}-1\right| 3^{P(m+a x)}-1 . $$ Then, by $P(m+a x-b y) \equiv P(m+a x)(\bmod b)$ we have $$ 3^{P(m+a x-b y)} \equiv 3^{P(m+a x)} \equiv 1 \quad(\bmod M) $$ Since $P(m+a x-b y)>0$ this implies $M \leq 3^{P(m+a x-b y)}-1$. But $P(m+a x-b y)$ is listed among $P(1), P(2), \ldots, P(d)$, so $$ M<3^{P(m+a x-b y)} \leq 3^{\max \{P(1), P(2), \ldots, P(d)\}} $$ which contradicts (1). Comment. We present another variant of the solution above. Denote the degree of $P$ by $k$ and its leading coefficient by $p$. Consider any positive integer $n$ and let $a=Q(n)$. Again, denote by $b$ the multiplicative order of 3 modulo $2^{a}-1$. Since $2^{a}-1 \mid 3^{P(n)}-1$, we have $b \mid P(n)$. Moreover, since $2^{Q(n+a t)}-1 \mid 3^{P(n+a t)}-1$ and $a=Q(n) \mid Q(n+a t)$ for each positive integer $t$, we have $2^{a}-1 \mid 3^{P(n+a t)}-1$, hence $b \mid P(n+a t)$ as well. Therefore, $b$ divides $\operatorname{gcd}\{P(n+a t): t \geq 0\}$; hence it also divides the number $$ \sum_{i=0}^{k}(-1)^{k-i}\left(\begin{array}{c} k \\ i \end{array}\right) P(n+a i)=p \cdot k ! \cdot a^{k} $$ Finally, we get $b \mid \operatorname{gcd}\left(P(n), k ! \cdot p \cdot Q(n)^{k}\right)$, which is bounded by the same arguments as in the beginning of the solution. So $3^{b}-1$ is bounded, and hence $2^{Q(n)}-1$ is bounded as well.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $P(x)$ and $Q(x)$ be two polynomials with integer coefficients such that no nonconstant polynomial with rational coefficients divides both $P(x)$ and $Q(x)$. Suppose that for every positive integer $n$ the integers $P(n)$ and $Q(n)$ are positive, and $2^{Q(n)}-1$ divides $3^{P(n)}-1$. Prove that $Q(x)$ is a constant polynomial.
|
First we show that there exists an integer $d$ such that for all positive integers $n$ we have $\operatorname{gcd}(P(n), Q(n)) \leq d$. Since $P(x)$ and $Q(x)$ are coprime (over the polynomials with rational coefficients), EuCLID's algorithm provides some polynomials $R_{0}(x), S_{0}(x)$ with rational coefficients such that $P(x) R_{0}(x)-$ $Q(x) S_{0}(x)=1$. Multiplying by a suitable positive integer $d$, we obtain polynomials $R(x)=$ $d \cdot R_{0}(x)$ and $S(x)=d \cdot S_{0}(x)$ with integer coefficients for which $P(x) R(x)-Q(x) S(x)=d$. Then we have $\operatorname{gcd}(P(n), Q(n)) \leq d$ for any integer $n$. To prove the problem statement, suppose that $Q(x)$ is not constant. Then the sequence $Q(n)$ is not bounded and we can choose a positive integer $m$ for which $$ M=2^{Q(m)}-1 \geq 3^{\max \{P(1), P(2), \ldots, P(d)\}} $$ Since $M=2^{Q(n)}-1 \mid 3^{P(n)}-1$, we have $2,3 \not M$. Let $a$ and $b$ be the multiplicative orders of 2 and 3 modulo $M$, respectively. Obviously, $a=Q(m)$ since the lower powers of 2 do not reach $M$. Since $M$ divides $3^{P(m)}-1$, we have $b \mid P(m)$. Then $\operatorname{gcd}(a, b) \leq \operatorname{gcd}(P(m), Q(m)) \leq d$. Since the expression $a x$ - by attains all integer values divisible by $\operatorname{gcd}(a, b)$ when $x$ and $y$ run over all nonnegative integer values, there exist some nonnegative integers $x, y$ such that $1 \leq m+a x-b y \leq d$. By $Q(m+a x) \equiv Q(m)(\bmod a)$ we have $$ 2^{Q(m+a x)} \equiv 2^{Q(m)} \equiv 1 \quad(\bmod M) $$ and therefore $$ M\left|2^{Q(m+a x)}-1\right| 3^{P(m+a x)}-1 . $$ Then, by $P(m+a x-b y) \equiv P(m+a x)(\bmod b)$ we have $$ 3^{P(m+a x-b y)} \equiv 3^{P(m+a x)} \equiv 1 \quad(\bmod M) $$ Since $P(m+a x-b y)>0$ this implies $M \leq 3^{P(m+a x-b y)}-1$. But $P(m+a x-b y)$ is listed among $P(1), P(2), \ldots, P(d)$, so $$ M<3^{P(m+a x-b y)} \leq 3^{\max \{P(1), P(2), \ldots, P(d)\}} $$ which contradicts (1). Comment. We present another variant of the solution above. Denote the degree of $P$ by $k$ and its leading coefficient by $p$. Consider any positive integer $n$ and let $a=Q(n)$. Again, denote by $b$ the multiplicative order of 3 modulo $2^{a}-1$. Since $2^{a}-1 \mid 3^{P(n)}-1$, we have $b \mid P(n)$. Moreover, since $2^{Q(n+a t)}-1 \mid 3^{P(n+a t)}-1$ and $a=Q(n) \mid Q(n+a t)$ for each positive integer $t$, we have $2^{a}-1 \mid 3^{P(n+a t)}-1$, hence $b \mid P(n+a t)$ as well. Therefore, $b$ divides $\operatorname{gcd}\{P(n+a t): t \geq 0\}$; hence it also divides the number $$ \sum_{i=0}^{k}(-1)^{k-i}\left(\begin{array}{c} k \\ i \end{array}\right) P(n+a i)=p \cdot k ! \cdot a^{k} $$ Finally, we get $b \mid \operatorname{gcd}\left(P(n), k ! \cdot p \cdot Q(n)^{k}\right)$, which is bounded by the same arguments as in the beginning of the solution. So $3^{b}-1$ is bounded, and hence $2^{Q(n)}-1$ is bounded as well.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
75dd30ce-22c5-5cf3-a613-64b50ecaa899
| 24,089
|
Let $p$ be an odd prime number. For every integer $a$, define the number $$ S_{a}=\frac{a}{1}+\frac{a^{2}}{2}+\cdots+\frac{a^{p-1}}{p-1} $$ Let $m$ and $n$ be integers such that $$ S_{3}+S_{4}-3 S_{2}=\frac{m}{n} $$ Prove that $p$ divides $m$.
|
For rational numbers $p_{1} / q_{1}$ and $p_{2} / q_{2}$ with the denominators $q_{1}, q_{2}$ not divisible by $p$, we write $p_{1} / q_{1} \equiv p_{2} / q_{2}(\bmod p)$ if the numerator $p_{1} q_{2}-p_{2} q_{1}$ of their difference is divisible by $p$. We start with finding an explicit formula for the residue of $S_{a}$ modulo $p$. Note first that for every $k=1, \ldots, p-1$ the number $\left(\begin{array}{l}p \\ k\end{array}\right)$ is divisible by $p$, and $$ \frac{1}{p}\left(\begin{array}{l} p \\ k \end{array}\right)=\frac{(p-1)(p-2) \cdots(p-k+1)}{k !} \equiv \frac{(-1) \cdot(-2) \cdots(-k+1)}{k !}=\frac{(-1)^{k-1}}{k} \quad(\bmod p) $$ Therefore, we have $$ S_{a}=-\sum_{k=1}^{p-1} \frac{(-a)^{k}(-1)^{k-1}}{k} \equiv-\sum_{k=1}^{p-1}(-a)^{k} \cdot \frac{1}{p}\left(\begin{array}{l} p \\ k \end{array}\right) \quad(\bmod p) $$ The number on the right-hand side is integer. Using the binomial formula we express it as $$ -\sum_{k=1}^{p-1}(-a)^{k} \cdot \frac{1}{p}\left(\begin{array}{l} p \\ k \end{array}\right)=-\frac{1}{p}\left(-1-(-a)^{p}+\sum_{k=0}^{p}(-a)^{k}\left(\begin{array}{l} p \\ k \end{array}\right)\right)=\frac{(a-1)^{p}-a^{p}+1}{p} $$ since $p$ is odd. So, we have $$ S_{a} \equiv \frac{(a-1)^{p}-a^{p}+1}{p} \quad(\bmod p) $$ Finally, using the obtained formula we get $$ \begin{aligned} S_{3}+S_{4}-3 S_{2} & \equiv \frac{\left(2^{p}-3^{p}+1\right)+\left(3^{p}-4^{p}+1\right)-3\left(1^{p}-2^{p}+1\right)}{p} \\ & =\frac{4 \cdot 2^{p}-4^{p}-4}{p}=-\frac{\left(2^{p}-2\right)^{2}}{p} \quad(\bmod p) . \end{aligned} $$ By Fermat's theorem, $p \mid 2^{p}-2$, so $p^{2} \mid\left(2^{p}-2\right)^{2}$ and hence $S_{3}+S_{4}-3 S_{2} \equiv 0(\bmod p)$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $p$ be an odd prime number. For every integer $a$, define the number $$ S_{a}=\frac{a}{1}+\frac{a^{2}}{2}+\cdots+\frac{a^{p-1}}{p-1} $$ Let $m$ and $n$ be integers such that $$ S_{3}+S_{4}-3 S_{2}=\frac{m}{n} $$ Prove that $p$ divides $m$.
|
For rational numbers $p_{1} / q_{1}$ and $p_{2} / q_{2}$ with the denominators $q_{1}, q_{2}$ not divisible by $p$, we write $p_{1} / q_{1} \equiv p_{2} / q_{2}(\bmod p)$ if the numerator $p_{1} q_{2}-p_{2} q_{1}$ of their difference is divisible by $p$. We start with finding an explicit formula for the residue of $S_{a}$ modulo $p$. Note first that for every $k=1, \ldots, p-1$ the number $\left(\begin{array}{l}p \\ k\end{array}\right)$ is divisible by $p$, and $$ \frac{1}{p}\left(\begin{array}{l} p \\ k \end{array}\right)=\frac{(p-1)(p-2) \cdots(p-k+1)}{k !} \equiv \frac{(-1) \cdot(-2) \cdots(-k+1)}{k !}=\frac{(-1)^{k-1}}{k} \quad(\bmod p) $$ Therefore, we have $$ S_{a}=-\sum_{k=1}^{p-1} \frac{(-a)^{k}(-1)^{k-1}}{k} \equiv-\sum_{k=1}^{p-1}(-a)^{k} \cdot \frac{1}{p}\left(\begin{array}{l} p \\ k \end{array}\right) \quad(\bmod p) $$ The number on the right-hand side is integer. Using the binomial formula we express it as $$ -\sum_{k=1}^{p-1}(-a)^{k} \cdot \frac{1}{p}\left(\begin{array}{l} p \\ k \end{array}\right)=-\frac{1}{p}\left(-1-(-a)^{p}+\sum_{k=0}^{p}(-a)^{k}\left(\begin{array}{l} p \\ k \end{array}\right)\right)=\frac{(a-1)^{p}-a^{p}+1}{p} $$ since $p$ is odd. So, we have $$ S_{a} \equiv \frac{(a-1)^{p}-a^{p}+1}{p} \quad(\bmod p) $$ Finally, using the obtained formula we get $$ \begin{aligned} S_{3}+S_{4}-3 S_{2} & \equiv \frac{\left(2^{p}-3^{p}+1\right)+\left(3^{p}-4^{p}+1\right)-3\left(1^{p}-2^{p}+1\right)}{p} \\ & =\frac{4 \cdot 2^{p}-4^{p}-4}{p}=-\frac{\left(2^{p}-2\right)^{2}}{p} \quad(\bmod p) . \end{aligned} $$ By Fermat's theorem, $p \mid 2^{p}-2$, so $p^{2} \mid\left(2^{p}-2\right)^{2}$ and hence $S_{3}+S_{4}-3 S_{2} \equiv 0(\bmod p)$.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
d3721836-b6c5-576e-810a-84482c61fee5
| 24,092
|
Let $p$ be an odd prime number. For every integer $a$, define the number $$ S_{a}=\frac{a}{1}+\frac{a^{2}}{2}+\cdots+\frac{a^{p-1}}{p-1} $$ Let $m$ and $n$ be integers such that $$ S_{3}+S_{4}-3 S_{2}=\frac{m}{n} $$ Prove that $p$ divides $m$.
|
One may solve the problem without finding an explicit formula for $S_{a}$. It is enough to find the following property. Lemma. For every integer $a$, we have $S_{a+1} \equiv S_{-a}(\bmod p)$. Proof. We expand $S_{a+1}$ using the binomial formula as $$ S_{a+1}=\sum_{k=1}^{p-1} \frac{1}{k} \sum_{j=0}^{k}\left(\begin{array}{l} k \\ j \end{array}\right) a^{j}=\sum_{k=1}^{p-1}\left(\frac{1}{k}+\sum_{j=1}^{k} a^{j} \cdot \frac{1}{k}\left(\begin{array}{l} k \\ j \end{array}\right)\right)=\sum_{k=1}^{p-1} \frac{1}{k}+\sum_{j=1}^{p-1} a^{j} \sum_{k=j}^{p-1} \frac{1}{k}\left(\begin{array}{l} k \\ j \end{array}\right) a^{k} . $$ Note that $\frac{1}{k}+\frac{1}{p-k}=\frac{p}{k(p-k)} \equiv 0(\bmod p)$ for all $1 \leq k \leq p-1$; hence the first sum vanishes modulo $p$. For the second sum, we use the relation $\frac{1}{k}\left(\begin{array}{c}k \\ j\end{array}\right)=\frac{1}{j}\left(\begin{array}{c}k-1 \\ j-1\end{array}\right)$ to obtain $$ S_{a+1} \equiv \sum_{j=1}^{p-1} \frac{a^{j}}{j} \sum_{k=1}^{p-1}\left(\begin{array}{c} k-1 \\ j-1 \end{array}\right) \quad(\bmod p) $$ Finally, from the relation $$ \sum_{k=1}^{p-1}\left(\begin{array}{l} k-1 \\ j-1 \end{array}\right)=\left(\begin{array}{c} p-1 \\ j \end{array}\right)=\frac{(p-1)(p-2) \ldots(p-j)}{j !} \equiv(-1)^{j} \quad(\bmod p) $$ we obtain $$ S_{a+1} \equiv \sum_{j=1}^{p-1} \frac{a^{j}(-1)^{j}}{j !}=S_{-a} $$ Now we turn to the problem. Using the lemma we get $$ S_{3}-3 S_{2} \equiv S_{-2}-3 S_{2}=\sum_{\substack{1 \leq k \leq p-1 \\ k \text { is even }}} \frac{-2 \cdot 2^{k}}{k}+\sum_{\substack{1 \leq k \leq p-1 \\ k \text { is odd }}} \frac{-4 \cdot 2^{k}}{k}(\bmod p) . $$ The first sum in (11) expands as $$ \sum_{\ell=1}^{(p-1) / 2} \frac{-2 \cdot 2^{2 \ell}}{2 \ell}=-\sum_{\ell=1}^{(p-1) / 2} \frac{4^{\ell}}{\ell} $$ Next, using Fermat's theorem, we expand the second sum in (11) as $$ -\sum_{\ell=1}^{(p-1) / 2} \frac{2^{2 \ell+1}}{2 \ell-1} \equiv-\sum_{\ell=1}^{(p-1) / 2} \frac{2^{p+2 \ell}}{p+2 \ell-1}=-\sum_{m=(p+1) / 2}^{p-1} \frac{2 \cdot 4^{m}}{2 m}=-\sum_{m=(p+1) / 2}^{p-1} \frac{4^{m}}{m}(\bmod p) $$ (here we set $m=\ell+\frac{p-1}{2}$ ). Hence, $$ S_{3}-3 S_{2} \equiv-\sum_{\ell=1}^{(p-1) / 2} \frac{4^{\ell}}{\ell}-\sum_{m=(p+1) / 2}^{p-1} \frac{4^{m}}{m}=-S_{4} \quad(\bmod p) $$ Let $k$ be a positive integer and set $n=2^{k}+1$. Prove that $n$ is a prime number if and only if the following holds: there is a permutation $a_{1}, \ldots, a_{n-1}$ of the numbers $1,2, \ldots, n-1$ and a sequence of integers $g_{1}, g_{2}, \ldots, g_{n-1}$ such that $n$ divides $g_{i}^{a_{i}}-a_{i+1}$ for every $i \in\{1,2, \ldots, n-1\}$, where we set $a_{n}=a_{1}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $p$ be an odd prime number. For every integer $a$, define the number $$ S_{a}=\frac{a}{1}+\frac{a^{2}}{2}+\cdots+\frac{a^{p-1}}{p-1} $$ Let $m$ and $n$ be integers such that $$ S_{3}+S_{4}-3 S_{2}=\frac{m}{n} $$ Prove that $p$ divides $m$.
|
One may solve the problem without finding an explicit formula for $S_{a}$. It is enough to find the following property. Lemma. For every integer $a$, we have $S_{a+1} \equiv S_{-a}(\bmod p)$. Proof. We expand $S_{a+1}$ using the binomial formula as $$ S_{a+1}=\sum_{k=1}^{p-1} \frac{1}{k} \sum_{j=0}^{k}\left(\begin{array}{l} k \\ j \end{array}\right) a^{j}=\sum_{k=1}^{p-1}\left(\frac{1}{k}+\sum_{j=1}^{k} a^{j} \cdot \frac{1}{k}\left(\begin{array}{l} k \\ j \end{array}\right)\right)=\sum_{k=1}^{p-1} \frac{1}{k}+\sum_{j=1}^{p-1} a^{j} \sum_{k=j}^{p-1} \frac{1}{k}\left(\begin{array}{l} k \\ j \end{array}\right) a^{k} . $$ Note that $\frac{1}{k}+\frac{1}{p-k}=\frac{p}{k(p-k)} \equiv 0(\bmod p)$ for all $1 \leq k \leq p-1$; hence the first sum vanishes modulo $p$. For the second sum, we use the relation $\frac{1}{k}\left(\begin{array}{c}k \\ j\end{array}\right)=\frac{1}{j}\left(\begin{array}{c}k-1 \\ j-1\end{array}\right)$ to obtain $$ S_{a+1} \equiv \sum_{j=1}^{p-1} \frac{a^{j}}{j} \sum_{k=1}^{p-1}\left(\begin{array}{c} k-1 \\ j-1 \end{array}\right) \quad(\bmod p) $$ Finally, from the relation $$ \sum_{k=1}^{p-1}\left(\begin{array}{l} k-1 \\ j-1 \end{array}\right)=\left(\begin{array}{c} p-1 \\ j \end{array}\right)=\frac{(p-1)(p-2) \ldots(p-j)}{j !} \equiv(-1)^{j} \quad(\bmod p) $$ we obtain $$ S_{a+1} \equiv \sum_{j=1}^{p-1} \frac{a^{j}(-1)^{j}}{j !}=S_{-a} $$ Now we turn to the problem. Using the lemma we get $$ S_{3}-3 S_{2} \equiv S_{-2}-3 S_{2}=\sum_{\substack{1 \leq k \leq p-1 \\ k \text { is even }}} \frac{-2 \cdot 2^{k}}{k}+\sum_{\substack{1 \leq k \leq p-1 \\ k \text { is odd }}} \frac{-4 \cdot 2^{k}}{k}(\bmod p) . $$ The first sum in (11) expands as $$ \sum_{\ell=1}^{(p-1) / 2} \frac{-2 \cdot 2^{2 \ell}}{2 \ell}=-\sum_{\ell=1}^{(p-1) / 2} \frac{4^{\ell}}{\ell} $$ Next, using Fermat's theorem, we expand the second sum in (11) as $$ -\sum_{\ell=1}^{(p-1) / 2} \frac{2^{2 \ell+1}}{2 \ell-1} \equiv-\sum_{\ell=1}^{(p-1) / 2} \frac{2^{p+2 \ell}}{p+2 \ell-1}=-\sum_{m=(p+1) / 2}^{p-1} \frac{2 \cdot 4^{m}}{2 m}=-\sum_{m=(p+1) / 2}^{p-1} \frac{4^{m}}{m}(\bmod p) $$ (here we set $m=\ell+\frac{p-1}{2}$ ). Hence, $$ S_{3}-3 S_{2} \equiv-\sum_{\ell=1}^{(p-1) / 2} \frac{4^{\ell}}{\ell}-\sum_{m=(p+1) / 2}^{p-1} \frac{4^{m}}{m}=-S_{4} \quad(\bmod p) $$ Let $k$ be a positive integer and set $n=2^{k}+1$. Prove that $n$ is a prime number if and only if the following holds: there is a permutation $a_{1}, \ldots, a_{n-1}$ of the numbers $1,2, \ldots, n-1$ and a sequence of integers $g_{1}, g_{2}, \ldots, g_{n-1}$ such that $n$ divides $g_{i}^{a_{i}}-a_{i+1}$ for every $i \in\{1,2, \ldots, n-1\}$, where we set $a_{n}=a_{1}$.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
d3721836-b6c5-576e-810a-84482c61fee5
| 24,092
|
Let $a, b$, and $c$ be positive real numbers satisfying $\min (a+b, b+c, c+a)>\sqrt{2}$ and $a^{2}+b^{2}+c^{2}=3$. Prove that $$ \frac{a}{(b+c-a)^{2}}+\frac{b}{(c+a-b)^{2}}+\frac{c}{(a+b-c)^{2}} \geq \frac{3}{(a b c)^{2}} $$ Throughout both solutions, we denote the sums of the form $f(a, b, c)+f(b, c, a)+f(c, a, b)$ by $\sum f(a, b, c)$.
|
The condition $b+c>\sqrt{2}$ implies $b^{2}+c^{2}>1$, so $a^{2}=3-\left(b^{2}+c^{2}\right)<2$, i.e. $a<\sqrt{2}<b+c$. Hence we have $b+c-a>0$, and also $c+a-b>0$ and $a+b-c>0$ for similar reasons. We will use the variant of HÖLDER's inequality $$ \frac{x_{1}^{p+1}}{y_{1}^{p}}+\frac{x_{1}^{p+1}}{y_{1}^{p}}+\ldots+\frac{x_{n}^{p+1}}{y_{n}^{p}} \geq \frac{\left(x_{1}+x_{2}+\ldots+x_{n}\right)^{p+1}}{\left(y_{1}+y_{2}+\ldots+y_{n}\right)^{p}} $$ which holds for all positive real numbers $p, x_{1}, x_{2}, \ldots, x_{n}, y_{1}, y_{2}, \ldots, y_{n}$. Applying it to the left-hand side of (11) with $p=2$ and $n=3$, we get $$ \sum \frac{a}{(b+c-a)^{2}}=\sum \frac{\left(a^{2}\right)^{3}}{a^{5}(b+c-a)^{2}} \geq \frac{\left(a^{2}+b^{2}+c^{2}\right)^{3}}{\left(\sum a^{5 / 2}(b+c-a)\right)^{2}}=\frac{27}{\left(\sum a^{5 / 2}(b+c-a)\right)^{2}} . $$ To estimate the denominator of the right-hand part, we use an instance of SCHUR's inequality, namely $$ \sum a^{3 / 2}(a-b)(a-c) \geq 0 $$ which can be rewritten as $$ \sum a^{5 / 2}(b+c-a) \leq a b c(\sqrt{a}+\sqrt{b}+\sqrt{c}) . $$ Moreover, by the inequality between the arithmetic mean and the fourth power mean we also have $$ \left(\frac{\sqrt{a}+\sqrt{b}+\sqrt{c}}{3}\right)^{4} \leq \frac{a^{2}+b^{2}+c^{2}}{3}=1 $$ i.e., $\sqrt{a}+\sqrt{b}+\sqrt{c} \leq 3$. Hence, (2) yields $$ \sum \frac{a}{(b+c-a)^{2}} \geq \frac{27}{(a b c(\sqrt{a}+\sqrt{b}+\sqrt{c}))^{2}} \geq \frac{3}{a^{2} b^{2} c^{2}} $$ thus solving the problem. Comment. In this solution, one may also start from the following version of HÖLDER's inequality $$ \left(\sum_{i=1}^{n} a_{i}^{3}\right)\left(\sum_{i=1}^{n} b_{i}^{3}\right)\left(\sum_{i=1}^{n} c_{i}^{3}\right) \geq\left(\sum_{i=1}^{n} a_{i} b_{i} c_{i}\right)^{3} $$ applied as $$ \sum \frac{a}{(b+c-a)^{2}} \cdot \sum a^{3}(b+c-a) \cdot \sum a^{2}(b+c-a) \geq 27 $$ After doing that, one only needs the slightly better known instances $$ \sum a^{3}(b+c-a) \leq(a+b+c) a b c \quad \text { and } \quad \sum a^{2}(b+c-a) \leq 3 a b c $$ of Schur's Inequality.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b$, and $c$ be positive real numbers satisfying $\min (a+b, b+c, c+a)>\sqrt{2}$ and $a^{2}+b^{2}+c^{2}=3$. Prove that $$ \frac{a}{(b+c-a)^{2}}+\frac{b}{(c+a-b)^{2}}+\frac{c}{(a+b-c)^{2}} \geq \frac{3}{(a b c)^{2}} $$ Throughout both solutions, we denote the sums of the form $f(a, b, c)+f(b, c, a)+f(c, a, b)$ by $\sum f(a, b, c)$.
|
The condition $b+c>\sqrt{2}$ implies $b^{2}+c^{2}>1$, so $a^{2}=3-\left(b^{2}+c^{2}\right)<2$, i.e. $a<\sqrt{2}<b+c$. Hence we have $b+c-a>0$, and also $c+a-b>0$ and $a+b-c>0$ for similar reasons. We will use the variant of HÖLDER's inequality $$ \frac{x_{1}^{p+1}}{y_{1}^{p}}+\frac{x_{1}^{p+1}}{y_{1}^{p}}+\ldots+\frac{x_{n}^{p+1}}{y_{n}^{p}} \geq \frac{\left(x_{1}+x_{2}+\ldots+x_{n}\right)^{p+1}}{\left(y_{1}+y_{2}+\ldots+y_{n}\right)^{p}} $$ which holds for all positive real numbers $p, x_{1}, x_{2}, \ldots, x_{n}, y_{1}, y_{2}, \ldots, y_{n}$. Applying it to the left-hand side of (11) with $p=2$ and $n=3$, we get $$ \sum \frac{a}{(b+c-a)^{2}}=\sum \frac{\left(a^{2}\right)^{3}}{a^{5}(b+c-a)^{2}} \geq \frac{\left(a^{2}+b^{2}+c^{2}\right)^{3}}{\left(\sum a^{5 / 2}(b+c-a)\right)^{2}}=\frac{27}{\left(\sum a^{5 / 2}(b+c-a)\right)^{2}} . $$ To estimate the denominator of the right-hand part, we use an instance of SCHUR's inequality, namely $$ \sum a^{3 / 2}(a-b)(a-c) \geq 0 $$ which can be rewritten as $$ \sum a^{5 / 2}(b+c-a) \leq a b c(\sqrt{a}+\sqrt{b}+\sqrt{c}) . $$ Moreover, by the inequality between the arithmetic mean and the fourth power mean we also have $$ \left(\frac{\sqrt{a}+\sqrt{b}+\sqrt{c}}{3}\right)^{4} \leq \frac{a^{2}+b^{2}+c^{2}}{3}=1 $$ i.e., $\sqrt{a}+\sqrt{b}+\sqrt{c} \leq 3$. Hence, (2) yields $$ \sum \frac{a}{(b+c-a)^{2}} \geq \frac{27}{(a b c(\sqrt{a}+\sqrt{b}+\sqrt{c}))^{2}} \geq \frac{3}{a^{2} b^{2} c^{2}} $$ thus solving the problem. Comment. In this solution, one may also start from the following version of HÖLDER's inequality $$ \left(\sum_{i=1}^{n} a_{i}^{3}\right)\left(\sum_{i=1}^{n} b_{i}^{3}\right)\left(\sum_{i=1}^{n} c_{i}^{3}\right) \geq\left(\sum_{i=1}^{n} a_{i} b_{i} c_{i}\right)^{3} $$ applied as $$ \sum \frac{a}{(b+c-a)^{2}} \cdot \sum a^{3}(b+c-a) \cdot \sum a^{2}(b+c-a) \geq 27 $$ After doing that, one only needs the slightly better known instances $$ \sum a^{3}(b+c-a) \leq(a+b+c) a b c \quad \text { and } \quad \sum a^{2}(b+c-a) \leq 3 a b c $$ of Schur's Inequality.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
a1a21019-5dae-55b2-a9d5-9c2cb44ee729
| 24,109
|
Let $a, b$, and $c$ be positive real numbers satisfying $\min (a+b, b+c, c+a)>\sqrt{2}$ and $a^{2}+b^{2}+c^{2}=3$. Prove that $$ \frac{a}{(b+c-a)^{2}}+\frac{b}{(c+a-b)^{2}}+\frac{c}{(a+b-c)^{2}} \geq \frac{3}{(a b c)^{2}} $$ Throughout both solutions, we denote the sums of the form $f(a, b, c)+f(b, c, a)+f(c, a, b)$ by $\sum f(a, b, c)$.
|
As in $$ a^{5}+b^{5}+c^{5} \geq 3 $$ which is weaker than the given one. Due to the symmetry we may assume that $a \geq b \geq c$. In view of (3)), it suffices to prove the inequality $$ \sum \frac{a^{3} b^{2} c^{2}}{(b+c-a)^{2}} \geq \sum a^{5} $$ or, moving all the terms into the left-hand part, $$ \sum \frac{a^{3}}{(b+c-a)^{2}}\left((b c)^{2}-(a(b+c-a))^{2}\right) \geq 0 $$ Note that the signs of the expressions $(y z)^{2}-(x(y+z-x))^{2}$ and $y z-x(y+z-x)=(x-y)(x-z)$ are the same for every positive $x, y, z$ satisfying the triangle inequality. So the terms in (4) corresponding to $a$ and $c$ are nonnegative, and hence it is sufficient to prove that the sum of the terms corresponding to $a$ and $b$ is nonnegative. Equivalently, we need the relation $$ \frac{a^{3}}{(b+c-a)^{2}}(a-b)(a-c)(b c+a(b+c-a)) \geq \frac{b^{3}}{(a+c-b)^{2}}(a-b)(b-c)(a c+b(a+c-b)) $$ Obviously, we have $$ a^{3} \geq b^{3} \geq 0, \quad 0<b+c-a \leq a+c-b, \quad \text { and } \quad a-c \geq b-c \geq 0 $$ hence it suffices to prove that $$ \frac{a b+a c+b c-a^{2}}{b+c-a} \geq \frac{a b+a c+b c-b^{2}}{c+a-b} . $$ Since all the denominators are positive, it is equivalent to $$ (c+a-b)\left(a b+a c+b c-a^{2}\right)-\left(a b+a c+b c-b^{2}\right)(b+c-a) \geq 0 $$ or $$ (a-b)\left(2 a b-a^{2}-b^{2}+a c+b c\right) \geq 0 . $$ Since $a \geq b$, the last inequality follows from $$ c(a+b)>(a-b)^{2} $$ which holds since $c>a-b \geq 0$ and $a+b>a-b \geq 0$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b$, and $c$ be positive real numbers satisfying $\min (a+b, b+c, c+a)>\sqrt{2}$ and $a^{2}+b^{2}+c^{2}=3$. Prove that $$ \frac{a}{(b+c-a)^{2}}+\frac{b}{(c+a-b)^{2}}+\frac{c}{(a+b-c)^{2}} \geq \frac{3}{(a b c)^{2}} $$ Throughout both solutions, we denote the sums of the form $f(a, b, c)+f(b, c, a)+f(c, a, b)$ by $\sum f(a, b, c)$.
|
As in $$ a^{5}+b^{5}+c^{5} \geq 3 $$ which is weaker than the given one. Due to the symmetry we may assume that $a \geq b \geq c$. In view of (3)), it suffices to prove the inequality $$ \sum \frac{a^{3} b^{2} c^{2}}{(b+c-a)^{2}} \geq \sum a^{5} $$ or, moving all the terms into the left-hand part, $$ \sum \frac{a^{3}}{(b+c-a)^{2}}\left((b c)^{2}-(a(b+c-a))^{2}\right) \geq 0 $$ Note that the signs of the expressions $(y z)^{2}-(x(y+z-x))^{2}$ and $y z-x(y+z-x)=(x-y)(x-z)$ are the same for every positive $x, y, z$ satisfying the triangle inequality. So the terms in (4) corresponding to $a$ and $c$ are nonnegative, and hence it is sufficient to prove that the sum of the terms corresponding to $a$ and $b$ is nonnegative. Equivalently, we need the relation $$ \frac{a^{3}}{(b+c-a)^{2}}(a-b)(a-c)(b c+a(b+c-a)) \geq \frac{b^{3}}{(a+c-b)^{2}}(a-b)(b-c)(a c+b(a+c-b)) $$ Obviously, we have $$ a^{3} \geq b^{3} \geq 0, \quad 0<b+c-a \leq a+c-b, \quad \text { and } \quad a-c \geq b-c \geq 0 $$ hence it suffices to prove that $$ \frac{a b+a c+b c-a^{2}}{b+c-a} \geq \frac{a b+a c+b c-b^{2}}{c+a-b} . $$ Since all the denominators are positive, it is equivalent to $$ (c+a-b)\left(a b+a c+b c-a^{2}\right)-\left(a b+a c+b c-b^{2}\right)(b+c-a) \geq 0 $$ or $$ (a-b)\left(2 a b-a^{2}-b^{2}+a c+b c\right) \geq 0 . $$ Since $a \geq b$, the last inequality follows from $$ c(a+b)>(a-b)^{2} $$ which holds since $c>a-b \geq 0$ and $a+b>a-b \geq 0$.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
a1a21019-5dae-55b2-a9d5-9c2cb44ee729
| 24,109
|
Let $\mathcal{S}$ be a finite set of at least two points in the plane. Assume that no three points of $\mathcal{S}$ are collinear. By a windmill we mean a process as follows. Start with a line $\ell$ going through a point $P \in \mathcal{S}$. Rotate $\ell$ clockwise around the pivot $P$ until the line contains another point $Q$ of $\mathcal{S}$. The point $Q$ now takes over as the new pivot. This process continues indefinitely, with the pivot always being a point from $\mathcal{S}$. Show that for a suitable $P \in \mathcal{S}$ and a suitable starting line $\ell$ containing $P$, the resulting windmill will visit each point of $\mathcal{S}$ as a pivot infinitely often.
|
Give the rotating line an orientation and distinguish its sides as the oranje side and the blue side. Notice that whenever the pivot changes from some point $T$ to another point $U$, after the change, $T$ is on the same side as $U$ was before. Therefore, the number of elements of $\mathcal{S}$ on the oranje side and the number of those on the blue side remain the same throughout the whole process (except for those moments when the line contains two points).  First consider the case that $|\mathcal{S}|=2 n+1$ is odd. We claim that through any point $T \in \mathcal{S}$, there is a line that has $n$ points on each side. To see this, choose an oriented line through $T$ containing no other point of $\mathcal{S}$ and suppose that it has $n+r$ points on its oranje side. If $r=0$ then we have established the claim, so we may assume that $r \neq 0$. As the line rotates through $180^{\circ}$ around $T$, the number of points of $\mathcal{S}$ on its oranje side changes by 1 whenever the line passes through a point; after $180^{\circ}$, the number of points on the oranje side is $n-r$. Therefore there is an intermediate stage at which the oranje side, and thus also the blue side, contains $n$ points. Now select the point $P$ arbitrarily, and choose a line through $P$ that has $n$ points of $\mathcal{S}$ on each side to be the initial state of the windmill. We will show that during a rotation over $180^{\circ}$, the line of the windmill visits each point of $\mathcal{S}$ as a pivot. To see this, select any point $T$ of $\mathcal{S}$ and select a line $\ell$ through $T$ that separates $\mathcal{S}$ into equal halves. The point $T$ is the unique point of $\mathcal{S}$ through which a line in this direction can separate the points of $\mathcal{S}$ into equal halves (parallel translation would disturb the balance). Therefore, when the windmill line is parallel to $\ell$, it must be $\ell$ itself, and so pass through $T$. Next suppose that $|\mathcal{S}|=2 n$. Similarly to the odd case, for every $T \in \mathcal{S}$ there is an oriented line through $T$ with $n-1$ points on its oranje side and $n$ points on its blue side. Select such an oriented line through an arbitrary $P$ to be the initial state of the windmill. We will now show that during a rotation over $360^{\circ}$, the line of the windmill visits each point of $\mathcal{S}$ as a pivot. To see this, select any point $T$ of $\mathcal{S}$ and an oriented line $\ell$ through $T$ that separates $\mathcal{S}$ into two subsets with $n-1$ points on its oranje and $n$ points on its blue side. Again, parallel translation would change the numbers of points on the two sides, so when the windmill line is parallel to $\ell$ with the same orientation, the windmill line must pass through $T$. Comment. One may shorten this solution in the following way. Suppose that $|\mathcal{S}|=2 n+1$. Consider any line $\ell$ that separates $\mathcal{S}$ into equal halves; this line is unique given its direction and contains some point $T \in \mathcal{S}$. Consider the windmill starting from this line. When the line has made a rotation of $180^{\circ}$, it returns to the same location but the oranje side becomes blue and vice versa. So, for each point there should have been a moment when it appeared as pivot, as this is the only way for a point to pass from on side to the other. Now suppose that $|\mathcal{S}|=2 n$. Consider a line having $n-1$ and $n$ points on the two sides; it contains some point $T$. Consider the windmill starting from this line. After having made a rotation of $180^{\circ}$, the windmill line contains some different point $R$, and each point different from $T$ and $R$ has changed the color of its side. So, the windmill should have passed through all the points. ## $\mathrm{C} 4$ Determine the greatest positive integer $k$ that satisfies the following property: The set of positive integers can be partitioned into $k$ subsets $A_{1}, A_{2}, \ldots, A_{k}$ such that for all integers $n \geq 15$ and all $i \in\{1,2, \ldots, k\}$ there exist two distinct elements of $A_{i}$ whose sum is $n$. Answer. The greatest such number $k$ is 3 .
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\mathcal{S}$ be a finite set of at least two points in the plane. Assume that no three points of $\mathcal{S}$ are collinear. By a windmill we mean a process as follows. Start with a line $\ell$ going through a point $P \in \mathcal{S}$. Rotate $\ell$ clockwise around the pivot $P$ until the line contains another point $Q$ of $\mathcal{S}$. The point $Q$ now takes over as the new pivot. This process continues indefinitely, with the pivot always being a point from $\mathcal{S}$. Show that for a suitable $P \in \mathcal{S}$ and a suitable starting line $\ell$ containing $P$, the resulting windmill will visit each point of $\mathcal{S}$ as a pivot infinitely often.
|
Give the rotating line an orientation and distinguish its sides as the oranje side and the blue side. Notice that whenever the pivot changes from some point $T$ to another point $U$, after the change, $T$ is on the same side as $U$ was before. Therefore, the number of elements of $\mathcal{S}$ on the oranje side and the number of those on the blue side remain the same throughout the whole process (except for those moments when the line contains two points).  First consider the case that $|\mathcal{S}|=2 n+1$ is odd. We claim that through any point $T \in \mathcal{S}$, there is a line that has $n$ points on each side. To see this, choose an oriented line through $T$ containing no other point of $\mathcal{S}$ and suppose that it has $n+r$ points on its oranje side. If $r=0$ then we have established the claim, so we may assume that $r \neq 0$. As the line rotates through $180^{\circ}$ around $T$, the number of points of $\mathcal{S}$ on its oranje side changes by 1 whenever the line passes through a point; after $180^{\circ}$, the number of points on the oranje side is $n-r$. Therefore there is an intermediate stage at which the oranje side, and thus also the blue side, contains $n$ points. Now select the point $P$ arbitrarily, and choose a line through $P$ that has $n$ points of $\mathcal{S}$ on each side to be the initial state of the windmill. We will show that during a rotation over $180^{\circ}$, the line of the windmill visits each point of $\mathcal{S}$ as a pivot. To see this, select any point $T$ of $\mathcal{S}$ and select a line $\ell$ through $T$ that separates $\mathcal{S}$ into equal halves. The point $T$ is the unique point of $\mathcal{S}$ through which a line in this direction can separate the points of $\mathcal{S}$ into equal halves (parallel translation would disturb the balance). Therefore, when the windmill line is parallel to $\ell$, it must be $\ell$ itself, and so pass through $T$. Next suppose that $|\mathcal{S}|=2 n$. Similarly to the odd case, for every $T \in \mathcal{S}$ there is an oriented line through $T$ with $n-1$ points on its oranje side and $n$ points on its blue side. Select such an oriented line through an arbitrary $P$ to be the initial state of the windmill. We will now show that during a rotation over $360^{\circ}$, the line of the windmill visits each point of $\mathcal{S}$ as a pivot. To see this, select any point $T$ of $\mathcal{S}$ and an oriented line $\ell$ through $T$ that separates $\mathcal{S}$ into two subsets with $n-1$ points on its oranje and $n$ points on its blue side. Again, parallel translation would change the numbers of points on the two sides, so when the windmill line is parallel to $\ell$ with the same orientation, the windmill line must pass through $T$. Comment. One may shorten this solution in the following way. Suppose that $|\mathcal{S}|=2 n+1$. Consider any line $\ell$ that separates $\mathcal{S}$ into equal halves; this line is unique given its direction and contains some point $T \in \mathcal{S}$. Consider the windmill starting from this line. When the line has made a rotation of $180^{\circ}$, it returns to the same location but the oranje side becomes blue and vice versa. So, for each point there should have been a moment when it appeared as pivot, as this is the only way for a point to pass from on side to the other. Now suppose that $|\mathcal{S}|=2 n$. Consider a line having $n-1$ and $n$ points on the two sides; it contains some point $T$. Consider the windmill starting from this line. After having made a rotation of $180^{\circ}$, the windmill line contains some different point $R$, and each point different from $T$ and $R$ has changed the color of its side. So, the windmill should have passed through all the points. ## $\mathrm{C} 4$ Determine the greatest positive integer $k$ that satisfies the following property: The set of positive integers can be partitioned into $k$ subsets $A_{1}, A_{2}, \ldots, A_{k}$ such that for all integers $n \geq 15$ and all $i \in\{1,2, \ldots, k\}$ there exist two distinct elements of $A_{i}$ whose sum is $n$. Answer. The greatest such number $k$ is 3 .
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
74859399-d3fb-5cd5-8218-b2ce12d76bb0
| 24,119
|
Let $A B C$ be an acute triangle. Let $\omega$ be a circle whose center $L$ lies on the side $B C$. Suppose that $\omega$ is tangent to $A B$ at $B^{\prime}$ and to $A C$ at $C^{\prime}$. Suppose also that the circumcenter $O$ of the triangle $A B C$ lies on the shorter arc $B^{\prime} C^{\prime}$ of $\omega$. Prove that the circumcircle of $A B C$ and $\omega$ meet at two points.
|
The point $B^{\prime}$, being the perpendicular foot of $L$, is an interior point of side $A B$. Analogously, $C^{\prime}$ lies in the interior of $A C$. The point $O$ is located inside the triangle $A B^{\prime} C^{\prime}$, hence $\angle C O B<\angle C^{\prime} O B^{\prime}$.  Let $\alpha=\angle C A B$. The angles $\angle C A B$ and $\angle C^{\prime} O B^{\prime}$ are inscribed into the two circles with centers $O$ and $L$, respectively, so $\angle C O B=2 \angle C A B=2 \alpha$ and $2 \angle C^{\prime} O B^{\prime}=360^{\circ}-\angle C^{\prime} L B^{\prime}$. From the kite $A B^{\prime} L C^{\prime}$ we have $\angle C^{\prime} L B^{\prime}=180^{\circ}-\angle C^{\prime} A B^{\prime}=180^{\circ}-\alpha$. Combining these, we get $$ 2 \alpha=\angle C O B<\angle C^{\prime} O B^{\prime}=\frac{360^{\circ}-\angle C^{\prime} L B^{\prime}}{2}=\frac{360^{\circ}-\left(180^{\circ}-\alpha\right)}{2}=90^{\circ}+\frac{\alpha}{2}, $$ So $$ \alpha<60^{\circ} \text {. } $$ Let $O^{\prime}$ be the reflection of $O$ in the line $B C$. In the quadrilateral $A B O^{\prime} C$ we have $$ \angle C O^{\prime} B+\angle C A B=\angle C O B+\angle C A B=2 \alpha+\alpha<180^{\circ}, $$ so the point $O^{\prime}$ is outside the circle $A B C$. Hence, $O$ and $O^{\prime}$ are two points of $\omega$ such that one of them lies inside the circumcircle, while the other one is located outside. Therefore, the two circles intersect. Comment. There are different ways of reducing the statement of the problem to the case $\alpha<60^{\circ}$. E.g., since the point $O$ lies in the interior of the isosceles triangle $A B^{\prime} C^{\prime}$, we have $O A<A B^{\prime}$. So, if $A B^{\prime} \leq 2 L B^{\prime}$ then $O A<2 L O$, which means that $\omega$ intersects the circumcircle of $A B C$. Hence the only interesting case is $A B^{\prime}>2 L B^{\prime}$, and this condition implies $\angle C A B=2 \angle B^{\prime} A L<2 \cdot 30^{\circ}=60^{\circ}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle. Let $\omega$ be a circle whose center $L$ lies on the side $B C$. Suppose that $\omega$ is tangent to $A B$ at $B^{\prime}$ and to $A C$ at $C^{\prime}$. Suppose also that the circumcenter $O$ of the triangle $A B C$ lies on the shorter arc $B^{\prime} C^{\prime}$ of $\omega$. Prove that the circumcircle of $A B C$ and $\omega$ meet at two points.
|
The point $B^{\prime}$, being the perpendicular foot of $L$, is an interior point of side $A B$. Analogously, $C^{\prime}$ lies in the interior of $A C$. The point $O$ is located inside the triangle $A B^{\prime} C^{\prime}$, hence $\angle C O B<\angle C^{\prime} O B^{\prime}$.  Let $\alpha=\angle C A B$. The angles $\angle C A B$ and $\angle C^{\prime} O B^{\prime}$ are inscribed into the two circles with centers $O$ and $L$, respectively, so $\angle C O B=2 \angle C A B=2 \alpha$ and $2 \angle C^{\prime} O B^{\prime}=360^{\circ}-\angle C^{\prime} L B^{\prime}$. From the kite $A B^{\prime} L C^{\prime}$ we have $\angle C^{\prime} L B^{\prime}=180^{\circ}-\angle C^{\prime} A B^{\prime}=180^{\circ}-\alpha$. Combining these, we get $$ 2 \alpha=\angle C O B<\angle C^{\prime} O B^{\prime}=\frac{360^{\circ}-\angle C^{\prime} L B^{\prime}}{2}=\frac{360^{\circ}-\left(180^{\circ}-\alpha\right)}{2}=90^{\circ}+\frac{\alpha}{2}, $$ So $$ \alpha<60^{\circ} \text {. } $$ Let $O^{\prime}$ be the reflection of $O$ in the line $B C$. In the quadrilateral $A B O^{\prime} C$ we have $$ \angle C O^{\prime} B+\angle C A B=\angle C O B+\angle C A B=2 \alpha+\alpha<180^{\circ}, $$ so the point $O^{\prime}$ is outside the circle $A B C$. Hence, $O$ and $O^{\prime}$ are two points of $\omega$ such that one of them lies inside the circumcircle, while the other one is located outside. Therefore, the two circles intersect. Comment. There are different ways of reducing the statement of the problem to the case $\alpha<60^{\circ}$. E.g., since the point $O$ lies in the interior of the isosceles triangle $A B^{\prime} C^{\prime}$, we have $O A<A B^{\prime}$. So, if $A B^{\prime} \leq 2 L B^{\prime}$ then $O A<2 L O$, which means that $\omega$ intersects the circumcircle of $A B C$. Hence the only interesting case is $A B^{\prime}>2 L B^{\prime}$, and this condition implies $\angle C A B=2 \angle B^{\prime} A L<2 \cdot 30^{\circ}=60^{\circ}$.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
163c24c5-dd6d-5437-bdd4-83ae2f36c982
| 24,130
|
Let $A B C$ be an acute triangle with circumcircle $\omega$. Let $t$ be a tangent line to $\omega$. Let $t_{a}, t_{b}$, and $t_{c}$ be the lines obtained by reflecting $t$ in the lines $B C, C A$, and $A B$, respectively. Show that the circumcircle of the triangle determined by the lines $t_{a}, t_{b}$, and $t_{c}$ is tangent to the circle $\omega$. To avoid a large case distinction, we will use the notion of oriented angles. Namely, for two lines $\ell$ and $m$, we denote by $\angle(\ell, m)$ the angle by which one may rotate $\ell$ anticlockwise to obtain a line parallel to $m$. Thus, all oriented angles are considered modulo $180^{\circ}$. 
|
Denote by $T$ the point of tangency of $t$ and $\omega$. Let $A^{\prime}=t_{b} \cap t_{c}, B^{\prime}=t_{a} \cap t_{c}$, $C^{\prime}=t_{a} \cap t_{b}$. Introduce the point $A^{\prime \prime}$ on $\omega$ such that $T A=A A^{\prime \prime}\left(A^{\prime \prime} \neq T\right.$ unless $T A$ is a diameter). Define the points $B^{\prime \prime}$ and $C^{\prime \prime}$ in a similar way. Since the points $C$ and $B$ are the midpoints of arcs $T C^{\prime \prime}$ and $T B^{\prime \prime}$, respectively, we have $$ \begin{aligned} \angle\left(t, B^{\prime \prime} C^{\prime \prime}\right) & =\angle\left(t, T C^{\prime \prime}\right)+\angle\left(T C^{\prime \prime}, B^{\prime \prime} C^{\prime \prime}\right)=2 \angle(t, T C)+2 \angle\left(T C^{\prime \prime}, B C^{\prime \prime}\right) \\ & =2(\angle(t, T C)+\angle(T C, B C))=2 \angle(t, B C)=\angle\left(t, t_{a}\right) . \end{aligned} $$ It follows that $t_{a}$ and $B^{\prime \prime} C^{\prime \prime}$ are parallel. Similarly, $t_{b} \| A^{\prime \prime} C^{\prime \prime}$ and $t_{c} \| A^{\prime \prime} B^{\prime \prime}$. Thus, either the triangles $A^{\prime} B^{\prime} C^{\prime}$ and $A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}$ are homothetic, or they are translates of each other. Now we will prove that they are in fact homothetic, and that the center $K$ of the homothety belongs to $\omega$. It would then follow that their circumcircles are also homothetic with respect to $K$ and are therefore tangent at this point, as desired. We need the two following claims. Claim 1. The point of intersection $X$ of the lines $B^{\prime \prime} C$ and $B C^{\prime \prime}$ lies on $t_{a}$. Proof. Actually, the points $X$ and $T$ are symmetric about the line $B C$, since the lines $C T$ and $C B^{\prime \prime}$ are symmetric about this line, as are the lines $B T$ and $B C^{\prime \prime}$. Claim 2. The point of intersection $I$ of the lines $B B^{\prime}$ and $C C^{\prime}$ lies on the circle $\omega$. Proof. We consider the case that $t$ is not parallel to the sides of $A B C$; the other cases may be regarded as limit cases. Let $D=t \cap B C, E=t \cap A C$, and $F=t \cap A B$. Due to symmetry, the line $D B$ is one of the angle bisectors of the lines $B^{\prime} D$ and $F D$; analogously, the line $F B$ is one of the angle bisectors of the lines $B^{\prime} F$ and $D F$. So $B$ is either the incenter or one of the excenters of the triangle $B^{\prime} D F$. In any case we have $\angle(B D, D F)+\angle(D F, F B)+$ $\angle\left(B^{\prime} B, B^{\prime} D\right)=90^{\circ}$, so $$ \angle\left(B^{\prime} B, B^{\prime} C^{\prime}\right)=\angle\left(B^{\prime} B, B^{\prime} D\right)=90^{\circ}-\angle(B C, D F)-\angle(D F, B A)=90^{\circ}-\angle(B C, A B) \text {. } $$ Analogously, we get $\angle\left(C^{\prime} C, B^{\prime} C^{\prime}\right)=90^{\circ}-\angle(B C, A C)$. Hence, $$ \angle(B I, C I)=\angle\left(B^{\prime} B, B^{\prime} C^{\prime}\right)+\angle\left(B^{\prime} C^{\prime}, C^{\prime} C\right)=\angle(B C, A C)-\angle(B C, A B)=\angle(A B, A C), $$ which means exactly that the points $A, B, I, C$ are concyclic. Now we can complete the proof. Let $K$ be the second intersection point of $B^{\prime} B^{\prime \prime}$ and $\omega$. Applying PASCAL's theorem to hexagon $K B^{\prime \prime} C I B C^{\prime \prime}$ we get that the points $B^{\prime}=K B^{\prime \prime} \cap I B$ and $X=B^{\prime \prime} C \cap B C^{\prime \prime}$ are collinear with the intersection point $S$ of $C I$ and $C^{\prime \prime} K$. So $S=$ $C I \cap B^{\prime} X=C^{\prime}$, and the points $C^{\prime}, C^{\prime \prime}, K$ are collinear. Thus $K$ is the intersection point of $B^{\prime} B^{\prime \prime}$ and $C^{\prime} C^{\prime \prime}$ which implies that $K$ is the center of the homothety mapping $A^{\prime} B^{\prime} C^{\prime}$ to $A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}$, and it belongs to $\omega$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with circumcircle $\omega$. Let $t$ be a tangent line to $\omega$. Let $t_{a}, t_{b}$, and $t_{c}$ be the lines obtained by reflecting $t$ in the lines $B C, C A$, and $A B$, respectively. Show that the circumcircle of the triangle determined by the lines $t_{a}, t_{b}$, and $t_{c}$ is tangent to the circle $\omega$. To avoid a large case distinction, we will use the notion of oriented angles. Namely, for two lines $\ell$ and $m$, we denote by $\angle(\ell, m)$ the angle by which one may rotate $\ell$ anticlockwise to obtain a line parallel to $m$. Thus, all oriented angles are considered modulo $180^{\circ}$. 
|
Denote by $T$ the point of tangency of $t$ and $\omega$. Let $A^{\prime}=t_{b} \cap t_{c}, B^{\prime}=t_{a} \cap t_{c}$, $C^{\prime}=t_{a} \cap t_{b}$. Introduce the point $A^{\prime \prime}$ on $\omega$ such that $T A=A A^{\prime \prime}\left(A^{\prime \prime} \neq T\right.$ unless $T A$ is a diameter). Define the points $B^{\prime \prime}$ and $C^{\prime \prime}$ in a similar way. Since the points $C$ and $B$ are the midpoints of arcs $T C^{\prime \prime}$ and $T B^{\prime \prime}$, respectively, we have $$ \begin{aligned} \angle\left(t, B^{\prime \prime} C^{\prime \prime}\right) & =\angle\left(t, T C^{\prime \prime}\right)+\angle\left(T C^{\prime \prime}, B^{\prime \prime} C^{\prime \prime}\right)=2 \angle(t, T C)+2 \angle\left(T C^{\prime \prime}, B C^{\prime \prime}\right) \\ & =2(\angle(t, T C)+\angle(T C, B C))=2 \angle(t, B C)=\angle\left(t, t_{a}\right) . \end{aligned} $$ It follows that $t_{a}$ and $B^{\prime \prime} C^{\prime \prime}$ are parallel. Similarly, $t_{b} \| A^{\prime \prime} C^{\prime \prime}$ and $t_{c} \| A^{\prime \prime} B^{\prime \prime}$. Thus, either the triangles $A^{\prime} B^{\prime} C^{\prime}$ and $A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}$ are homothetic, or they are translates of each other. Now we will prove that they are in fact homothetic, and that the center $K$ of the homothety belongs to $\omega$. It would then follow that their circumcircles are also homothetic with respect to $K$ and are therefore tangent at this point, as desired. We need the two following claims. Claim 1. The point of intersection $X$ of the lines $B^{\prime \prime} C$ and $B C^{\prime \prime}$ lies on $t_{a}$. Proof. Actually, the points $X$ and $T$ are symmetric about the line $B C$, since the lines $C T$ and $C B^{\prime \prime}$ are symmetric about this line, as are the lines $B T$ and $B C^{\prime \prime}$. Claim 2. The point of intersection $I$ of the lines $B B^{\prime}$ and $C C^{\prime}$ lies on the circle $\omega$. Proof. We consider the case that $t$ is not parallel to the sides of $A B C$; the other cases may be regarded as limit cases. Let $D=t \cap B C, E=t \cap A C$, and $F=t \cap A B$. Due to symmetry, the line $D B$ is one of the angle bisectors of the lines $B^{\prime} D$ and $F D$; analogously, the line $F B$ is one of the angle bisectors of the lines $B^{\prime} F$ and $D F$. So $B$ is either the incenter or one of the excenters of the triangle $B^{\prime} D F$. In any case we have $\angle(B D, D F)+\angle(D F, F B)+$ $\angle\left(B^{\prime} B, B^{\prime} D\right)=90^{\circ}$, so $$ \angle\left(B^{\prime} B, B^{\prime} C^{\prime}\right)=\angle\left(B^{\prime} B, B^{\prime} D\right)=90^{\circ}-\angle(B C, D F)-\angle(D F, B A)=90^{\circ}-\angle(B C, A B) \text {. } $$ Analogously, we get $\angle\left(C^{\prime} C, B^{\prime} C^{\prime}\right)=90^{\circ}-\angle(B C, A C)$. Hence, $$ \angle(B I, C I)=\angle\left(B^{\prime} B, B^{\prime} C^{\prime}\right)+\angle\left(B^{\prime} C^{\prime}, C^{\prime} C\right)=\angle(B C, A C)-\angle(B C, A B)=\angle(A B, A C), $$ which means exactly that the points $A, B, I, C$ are concyclic. Now we can complete the proof. Let $K$ be the second intersection point of $B^{\prime} B^{\prime \prime}$ and $\omega$. Applying PASCAL's theorem to hexagon $K B^{\prime \prime} C I B C^{\prime \prime}$ we get that the points $B^{\prime}=K B^{\prime \prime} \cap I B$ and $X=B^{\prime \prime} C \cap B C^{\prime \prime}$ are collinear with the intersection point $S$ of $C I$ and $C^{\prime \prime} K$. So $S=$ $C I \cap B^{\prime} X=C^{\prime}$, and the points $C^{\prime}, C^{\prime \prime}, K$ are collinear. Thus $K$ is the intersection point of $B^{\prime} B^{\prime \prime}$ and $C^{\prime} C^{\prime \prime}$ which implies that $K$ is the center of the homothety mapping $A^{\prime} B^{\prime} C^{\prime}$ to $A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}$, and it belongs to $\omega$.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
38f970d3-8957-575f-b25f-e6c28a6add8a
| 24,131
|
Let $A B C$ be an acute triangle with circumcircle $\omega$. Let $t$ be a tangent line to $\omega$. Let $t_{a}, t_{b}$, and $t_{c}$ be the lines obtained by reflecting $t$ in the lines $B C, C A$, and $A B$, respectively. Show that the circumcircle of the triangle determined by the lines $t_{a}, t_{b}$, and $t_{c}$ is tangent to the circle $\omega$. To avoid a large case distinction, we will use the notion of oriented angles. Namely, for two lines $\ell$ and $m$, we denote by $\angle(\ell, m)$ the angle by which one may rotate $\ell$ anticlockwise to obtain a line parallel to $m$. Thus, all oriented angles are considered modulo $180^{\circ}$. 
|
Define the points $T, A^{\prime}, B^{\prime}$, and $C^{\prime}$ in the same way as in the previous solution. Let $X, Y$, and $Z$ be the symmetric images of $T$ about the lines $B C, C A$, and $A B$, respectively. Note that the projections of $T$ on these lines form a Simson line of $T$ with respect to $A B C$, therefore the points $X, Y, Z$ are also collinear. Moreover, we have $X \in B^{\prime} C^{\prime}, Y \in C^{\prime} A^{\prime}$, $Z \in A^{\prime} B^{\prime}$. Denote $\alpha=\angle(t, T C)=\angle(B T, B C)$. Using the symmetry in the lines $A C$ and $B C$, we get $$ \angle(B C, B X)=\angle(B T, B C)=\alpha \quad \text { and } \quad \angle\left(X C, X C^{\prime}\right)=\angle(t, T C)=\angle\left(Y C, Y C^{\prime}\right)=\alpha . $$ Since $\angle\left(X C, X C^{\prime}\right)=\angle\left(Y C, Y C^{\prime}\right)$, the points $X, Y, C, C^{\prime}$ lie on some circle $\omega_{c}$. Define the circles $\omega_{a}$ and $\omega_{b}$ analogously. Let $\omega^{\prime}$ be the circumcircle of triangle $A^{\prime} B^{\prime} C^{\prime}$. Now, applying Miquel's theorem to the four lines $A^{\prime} B^{\prime}, A^{\prime} C^{\prime}, B^{\prime} C^{\prime}$, and $X Y$, we obtain that the circles $\omega^{\prime}, \omega_{a}, \omega_{b}, \omega_{c}$ intersect at some point $K$. We will show that $K$ lies on $\omega$, and that the tangent lines to $\omega$ and $\omega^{\prime}$ at this point coincide; this implies the problem statement. Due to symmetry, we have $X B=T B=Z B$, so the point $B$ is the midpoint of one of the $\operatorname{arcs} X Z$ of circle $\omega_{b}$. Therefore $\angle(K B, K X)=\angle(X Z, X B)$. Analogously, $\angle(K X, K C)=$ $\angle(X C, X Y)$. Adding these equalities and using the symmetry in the line $B C$ we get $$ \angle(K B, K C)=\angle(X Z, X B)+\angle(X C, X Z)=\angle(X C, X B)=\angle(T B, T C) . $$ Therefore, $K$ lies on $\omega$. Next, let $k$ be the tangent line to $\omega$ at $K$. We have $$ \begin{aligned} \angle\left(k, K C^{\prime}\right) & =\angle(k, K C)+\angle\left(K C, K C^{\prime}\right)=\angle(K B, B C)+\angle\left(X C, X C^{\prime}\right) \\ & =(\angle(K B, B X)-\angle(B C, B X))+\alpha=\angle\left(K B^{\prime}, B^{\prime} X\right)-\alpha+\alpha=\angle\left(K B^{\prime}, B^{\prime} C^{\prime}\right), \end{aligned} $$ which means exactly that $k$ is tangent to $\omega^{\prime}$.  Comment. There exist various solutions combining the ideas from the two solutions presented above. For instance, one may define the point $X$ as the reflection of $T$ with respect to the line $B C$, and then introduce the point $K$ as the second intersection point of the circumcircles of $B B^{\prime} X$ and $C C^{\prime} X$. Using the fact that $B B^{\prime}$ and $C C^{\prime}$ are the bisectors of $\angle\left(A^{\prime} B^{\prime}, B^{\prime} C^{\prime}\right)$ and $\angle\left(A^{\prime} C^{\prime}, B^{\prime} C^{\prime}\right)$ one can show successively that $K \in \omega, K \in \omega^{\prime}$, and that the tangents to $\omega$ and $\omega^{\prime}$ at $K$ coincide.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with circumcircle $\omega$. Let $t$ be a tangent line to $\omega$. Let $t_{a}, t_{b}$, and $t_{c}$ be the lines obtained by reflecting $t$ in the lines $B C, C A$, and $A B$, respectively. Show that the circumcircle of the triangle determined by the lines $t_{a}, t_{b}$, and $t_{c}$ is tangent to the circle $\omega$. To avoid a large case distinction, we will use the notion of oriented angles. Namely, for two lines $\ell$ and $m$, we denote by $\angle(\ell, m)$ the angle by which one may rotate $\ell$ anticlockwise to obtain a line parallel to $m$. Thus, all oriented angles are considered modulo $180^{\circ}$. 
|
Define the points $T, A^{\prime}, B^{\prime}$, and $C^{\prime}$ in the same way as in the previous solution. Let $X, Y$, and $Z$ be the symmetric images of $T$ about the lines $B C, C A$, and $A B$, respectively. Note that the projections of $T$ on these lines form a Simson line of $T$ with respect to $A B C$, therefore the points $X, Y, Z$ are also collinear. Moreover, we have $X \in B^{\prime} C^{\prime}, Y \in C^{\prime} A^{\prime}$, $Z \in A^{\prime} B^{\prime}$. Denote $\alpha=\angle(t, T C)=\angle(B T, B C)$. Using the symmetry in the lines $A C$ and $B C$, we get $$ \angle(B C, B X)=\angle(B T, B C)=\alpha \quad \text { and } \quad \angle\left(X C, X C^{\prime}\right)=\angle(t, T C)=\angle\left(Y C, Y C^{\prime}\right)=\alpha . $$ Since $\angle\left(X C, X C^{\prime}\right)=\angle\left(Y C, Y C^{\prime}\right)$, the points $X, Y, C, C^{\prime}$ lie on some circle $\omega_{c}$. Define the circles $\omega_{a}$ and $\omega_{b}$ analogously. Let $\omega^{\prime}$ be the circumcircle of triangle $A^{\prime} B^{\prime} C^{\prime}$. Now, applying Miquel's theorem to the four lines $A^{\prime} B^{\prime}, A^{\prime} C^{\prime}, B^{\prime} C^{\prime}$, and $X Y$, we obtain that the circles $\omega^{\prime}, \omega_{a}, \omega_{b}, \omega_{c}$ intersect at some point $K$. We will show that $K$ lies on $\omega$, and that the tangent lines to $\omega$ and $\omega^{\prime}$ at this point coincide; this implies the problem statement. Due to symmetry, we have $X B=T B=Z B$, so the point $B$ is the midpoint of one of the $\operatorname{arcs} X Z$ of circle $\omega_{b}$. Therefore $\angle(K B, K X)=\angle(X Z, X B)$. Analogously, $\angle(K X, K C)=$ $\angle(X C, X Y)$. Adding these equalities and using the symmetry in the line $B C$ we get $$ \angle(K B, K C)=\angle(X Z, X B)+\angle(X C, X Z)=\angle(X C, X B)=\angle(T B, T C) . $$ Therefore, $K$ lies on $\omega$. Next, let $k$ be the tangent line to $\omega$ at $K$. We have $$ \begin{aligned} \angle\left(k, K C^{\prime}\right) & =\angle(k, K C)+\angle\left(K C, K C^{\prime}\right)=\angle(K B, B C)+\angle\left(X C, X C^{\prime}\right) \\ & =(\angle(K B, B X)-\angle(B C, B X))+\alpha=\angle\left(K B^{\prime}, B^{\prime} X\right)-\alpha+\alpha=\angle\left(K B^{\prime}, B^{\prime} C^{\prime}\right), \end{aligned} $$ which means exactly that $k$ is tangent to $\omega^{\prime}$.  Comment. There exist various solutions combining the ideas from the two solutions presented above. For instance, one may define the point $X$ as the reflection of $T$ with respect to the line $B C$, and then introduce the point $K$ as the second intersection point of the circumcircles of $B B^{\prime} X$ and $C C^{\prime} X$. Using the fact that $B B^{\prime}$ and $C C^{\prime}$ are the bisectors of $\angle\left(A^{\prime} B^{\prime}, B^{\prime} C^{\prime}\right)$ and $\angle\left(A^{\prime} C^{\prime}, B^{\prime} C^{\prime}\right)$ one can show successively that $K \in \omega, K \in \omega^{\prime}$, and that the tangents to $\omega$ and $\omega^{\prime}$ at $K$ coincide.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
38f970d3-8957-575f-b25f-e6c28a6add8a
| 24,131
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.