problem
stringlengths 54
2.23k
| solution
stringlengths 134
24.1k
| answer
stringclasses 1
value | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 54
2.21k
| solution_raw
stringlengths 134
24.1k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 23.5k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
Let $a_{2}, \ldots, a_{n}$ be $n-1$ positive real numbers, where $n \geq 3$, such that $a_{2} a_{3} \cdots a_{n}=1$. Prove that $$ \left(1+a_{2}\right)^{2}\left(1+a_{3}\right)^{3} \cdots\left(1+a_{n}\right)^{n}>n^{n} . $$
|
The substitution $a_{2}=\frac{x_{2}}{x_{1}}, a_{3}=\frac{x_{3}}{x_{2}}, \ldots, a_{n}=\frac{x_{1}}{x_{n-1}}$ transforms the original problem into the inequality $$ \left(x_{1}+x_{2}\right)^{2}\left(x_{2}+x_{3}\right)^{3} \cdots\left(x_{n-1}+x_{1}\right)^{n}>n^{n} x_{1}^{2} x_{2}^{3} \cdots x_{n-1}^{n} $$ for all $x_{1}, \ldots, x_{n-1}>0$. To prove this, we use the AM-GM inequality for each factor of the left-hand side as follows: $$ \begin{array}{rlcl} \left(x_{1}+x_{2}\right)^{2} & & & \geq 2^{2} x_{1} x_{2} \\ \left(x_{2}+x_{3}\right)^{3} & = & \left(2\left(\frac{x_{2}}{2}\right)+x_{3}\right)^{3} & \geq 3^{3}\left(\frac{x_{2}}{2}\right)^{2} x_{3} \\ \left(x_{3}+x_{4}\right)^{4} & = & \left(3\left(\frac{x_{3}}{3}\right)+x_{4}\right)^{4} & \geq 4^{4}\left(\frac{x_{3}}{3}\right)^{3} x_{4} \\ & \vdots & \vdots & \vdots \end{array} $$ Multiplying these inequalities together gives $\left({ }^{*}\right)$, with inequality sign $\geq$ instead of $>$. However for the equality to occur it is necessary that $x_{1}=x_{2}, x_{2}=2 x_{3}, \ldots, x_{n-1}=(n-1) x_{1}$, implying $x_{1}=(n-1) ! x_{1}$. This is impossible since $x_{1}>0$ and $n \geq 3$. Therefore the inequality is strict. Comment. One can avoid the substitution $a_{i}=x_{i} / x_{i-1}$. Apply the weighted AM-GM inequality to each factor $\left(1+a_{k}\right)^{k}$, with the same weights like above, to obtain $$ \left(1+a_{k}\right)^{k}=\left((k-1) \frac{1}{k-1}+a_{k}\right)^{k} \geq \frac{k^{k}}{(k-1)^{k-1}} a_{k} $$ Multiplying all these inequalities together gives $$ \left(1+a_{2}\right)^{2}\left(1+a_{3}\right)^{3} \cdots\left(1+a_{n}\right)^{n} \geq n^{n} a_{2} a_{3} \cdots a_{n}=n^{n} . $$ The same argument as in the proof above shows that the equality cannot be attained.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a_{2}, \ldots, a_{n}$ be $n-1$ positive real numbers, where $n \geq 3$, such that $a_{2} a_{3} \cdots a_{n}=1$. Prove that $$ \left(1+a_{2}\right)^{2}\left(1+a_{3}\right)^{3} \cdots\left(1+a_{n}\right)^{n}>n^{n} . $$
|
The substitution $a_{2}=\frac{x_{2}}{x_{1}}, a_{3}=\frac{x_{3}}{x_{2}}, \ldots, a_{n}=\frac{x_{1}}{x_{n-1}}$ transforms the original problem into the inequality $$ \left(x_{1}+x_{2}\right)^{2}\left(x_{2}+x_{3}\right)^{3} \cdots\left(x_{n-1}+x_{1}\right)^{n}>n^{n} x_{1}^{2} x_{2}^{3} \cdots x_{n-1}^{n} $$ for all $x_{1}, \ldots, x_{n-1}>0$. To prove this, we use the AM-GM inequality for each factor of the left-hand side as follows: $$ \begin{array}{rlcl} \left(x_{1}+x_{2}\right)^{2} & & & \geq 2^{2} x_{1} x_{2} \\ \left(x_{2}+x_{3}\right)^{3} & = & \left(2\left(\frac{x_{2}}{2}\right)+x_{3}\right)^{3} & \geq 3^{3}\left(\frac{x_{2}}{2}\right)^{2} x_{3} \\ \left(x_{3}+x_{4}\right)^{4} & = & \left(3\left(\frac{x_{3}}{3}\right)+x_{4}\right)^{4} & \geq 4^{4}\left(\frac{x_{3}}{3}\right)^{3} x_{4} \\ & \vdots & \vdots & \vdots \end{array} $$ Multiplying these inequalities together gives $\left({ }^{*}\right)$, with inequality sign $\geq$ instead of $>$. However for the equality to occur it is necessary that $x_{1}=x_{2}, x_{2}=2 x_{3}, \ldots, x_{n-1}=(n-1) x_{1}$, implying $x_{1}=(n-1) ! x_{1}$. This is impossible since $x_{1}>0$ and $n \geq 3$. Therefore the inequality is strict. Comment. One can avoid the substitution $a_{i}=x_{i} / x_{i-1}$. Apply the weighted AM-GM inequality to each factor $\left(1+a_{k}\right)^{k}$, with the same weights like above, to obtain $$ \left(1+a_{k}\right)^{k}=\left((k-1) \frac{1}{k-1}+a_{k}\right)^{k} \geq \frac{k^{k}}{(k-1)^{k-1}} a_{k} $$ Multiplying all these inequalities together gives $$ \left(1+a_{2}\right)^{2}\left(1+a_{3}\right)^{3} \cdots\left(1+a_{n}\right)^{n} \geq n^{n} a_{2} a_{3} \cdots a_{n}=n^{n} . $$ The same argument as in the proof above shows that the equality cannot be attained.
|
{
"resource_path": "IMO/segmented/en-IMO2012SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
dbf5c9a1-f1fa-5160-9b65-96aa3f10b76e
| 24,144
|
Let $f$ and $g$ be two nonzero polynomials with integer coefficients and $\operatorname{deg} f>\operatorname{deg} g$. Suppose that for infinitely many primes $p$ the polynomial $p f+g$ has a rational root. Prove that $f$ has a rational root.
|
Since $\operatorname{deg} f>\operatorname{deg} g$, we have $|g(x) / f(x)|<1$ for sufficiently large $x$; more precisely, there is a real number $R$ such that $|g(x) / f(x)|<1$ for all $x$ with $|x|>R$. Then for all such $x$ and all primes $p$ we have $$ |p f(x)+g(x)| \geq|f(x)|\left(p-\frac{|g(x)|}{|f(x)|}\right)>0 $$ Hence all real roots of the polynomials $p f+g$ lie in the interval $[-R, R]$. Let $f(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{0}$ and $g(x)=b_{m} x^{m}+b_{m-1} x^{m-1}+\cdots+b_{0}$ where $n>m, a_{n} \neq 0$ and $b_{m} \neq 0$. Upon replacing $f(x)$ and $g(x)$ by $a_{n}^{n-1} f\left(x / a_{n}\right)$ and $a_{n}^{n-1} g\left(x / a_{n}\right)$ respectively, we reduce the problem to the case $a_{n}=1$. In other words one can assume that $f$ is monic. Then the leading coefficient of $p f+g$ is $p$, and if $r=u / v$ is a rational root of $p f+g$ with $(u, v)=1$ and $v>0$, then either $v=1$ or $v=p$. First consider the case when $v=1$ infinitely many times. If $v=1$ then $|u| \leq R$, so there are only finitely many possibilities for the integer $u$. Therefore there exist distinct primes $p$ and $q$ for which we have the same value of $u$. Then the polynomials $p f+g$ and $q f+g$ share this root, implying $f(u)=g(u)=0$. So in this case $f$ and $g$ have an integer root in common. Now suppose that $v=p$ infinitely many times. By comparing the exponent of $p$ in the denominators of $p f(u / p)$ and $g(u / p)$ we get $m=n-1$ and $p f(u / p)+g(u / p)=0$ reduces to an equation of the form $$ \left(u^{n}+a_{n-1} p u^{n-1}+\ldots+a_{0} p^{n}\right)+\left(b_{n-1} u^{n-1}+b_{n-2} p u^{n-2}+\ldots+b_{0} p^{n-1}\right)=0 . $$ The equation above implies that $u^{n}+b_{n-1} u^{n-1}$ is divisible by $p$ and hence, since $(u, p)=1$, we have $u+b_{n-1}=p k$ with some integer $k$. On the other hand all roots of $p f+g$ lie in the interval $[-R, R]$, so that $$ \begin{gathered} \frac{\left|p k-b_{n-1}\right|}{p}=\frac{|u|}{p}<R, \\ |k|<R+\frac{\left|b_{n-1}\right|}{p}<R+\left|b_{n-1}\right| . \end{gathered} $$ Therefore the integer $k$ can attain only finitely many values. Hence there exists an integer $k$ such that the number $\frac{p k-b_{n-1}}{p}=k-\frac{b_{n-1}}{p}$ is a root of $p f+g$ for infinitely many primes $p$. For these primes we have $$ f\left(k-b_{n-1} \frac{1}{p}\right)+\frac{1}{p} g\left(k-b_{n-1} \frac{1}{p}\right)=0 . $$ So the equation $$ f\left(k-b_{n-1} x\right)+x g\left(k-b_{n-1} x\right)=0 $$ has infinitely many solutions of the form $x=1 / p$. Since the left-hand side is a polynomial, this implies that (1) is a polynomial identity, so it holds for all real $x$. In particular, by substituting $x=0$ in (1) we get $f(k)=0$. Thus the integer $k$ is a root of $f$. In summary the monic polynomial $f$ obtained after the initial reduction always has an integer root. Therefore the original polynomial $f$ has a rational root.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $f$ and $g$ be two nonzero polynomials with integer coefficients and $\operatorname{deg} f>\operatorname{deg} g$. Suppose that for infinitely many primes $p$ the polynomial $p f+g$ has a rational root. Prove that $f$ has a rational root.
|
Since $\operatorname{deg} f>\operatorname{deg} g$, we have $|g(x) / f(x)|<1$ for sufficiently large $x$; more precisely, there is a real number $R$ such that $|g(x) / f(x)|<1$ for all $x$ with $|x|>R$. Then for all such $x$ and all primes $p$ we have $$ |p f(x)+g(x)| \geq|f(x)|\left(p-\frac{|g(x)|}{|f(x)|}\right)>0 $$ Hence all real roots of the polynomials $p f+g$ lie in the interval $[-R, R]$. Let $f(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{0}$ and $g(x)=b_{m} x^{m}+b_{m-1} x^{m-1}+\cdots+b_{0}$ where $n>m, a_{n} \neq 0$ and $b_{m} \neq 0$. Upon replacing $f(x)$ and $g(x)$ by $a_{n}^{n-1} f\left(x / a_{n}\right)$ and $a_{n}^{n-1} g\left(x / a_{n}\right)$ respectively, we reduce the problem to the case $a_{n}=1$. In other words one can assume that $f$ is monic. Then the leading coefficient of $p f+g$ is $p$, and if $r=u / v$ is a rational root of $p f+g$ with $(u, v)=1$ and $v>0$, then either $v=1$ or $v=p$. First consider the case when $v=1$ infinitely many times. If $v=1$ then $|u| \leq R$, so there are only finitely many possibilities for the integer $u$. Therefore there exist distinct primes $p$ and $q$ for which we have the same value of $u$. Then the polynomials $p f+g$ and $q f+g$ share this root, implying $f(u)=g(u)=0$. So in this case $f$ and $g$ have an integer root in common. Now suppose that $v=p$ infinitely many times. By comparing the exponent of $p$ in the denominators of $p f(u / p)$ and $g(u / p)$ we get $m=n-1$ and $p f(u / p)+g(u / p)=0$ reduces to an equation of the form $$ \left(u^{n}+a_{n-1} p u^{n-1}+\ldots+a_{0} p^{n}\right)+\left(b_{n-1} u^{n-1}+b_{n-2} p u^{n-2}+\ldots+b_{0} p^{n-1}\right)=0 . $$ The equation above implies that $u^{n}+b_{n-1} u^{n-1}$ is divisible by $p$ and hence, since $(u, p)=1$, we have $u+b_{n-1}=p k$ with some integer $k$. On the other hand all roots of $p f+g$ lie in the interval $[-R, R]$, so that $$ \begin{gathered} \frac{\left|p k-b_{n-1}\right|}{p}=\frac{|u|}{p}<R, \\ |k|<R+\frac{\left|b_{n-1}\right|}{p}<R+\left|b_{n-1}\right| . \end{gathered} $$ Therefore the integer $k$ can attain only finitely many values. Hence there exists an integer $k$ such that the number $\frac{p k-b_{n-1}}{p}=k-\frac{b_{n-1}}{p}$ is a root of $p f+g$ for infinitely many primes $p$. For these primes we have $$ f\left(k-b_{n-1} \frac{1}{p}\right)+\frac{1}{p} g\left(k-b_{n-1} \frac{1}{p}\right)=0 . $$ So the equation $$ f\left(k-b_{n-1} x\right)+x g\left(k-b_{n-1} x\right)=0 $$ has infinitely many solutions of the form $x=1 / p$. Since the left-hand side is a polynomial, this implies that (1) is a polynomial identity, so it holds for all real $x$. In particular, by substituting $x=0$ in (1) we get $f(k)=0$. Thus the integer $k$ is a root of $f$. In summary the monic polynomial $f$ obtained after the initial reduction always has an integer root. Therefore the original polynomial $f$ has a rational root.
|
{
"resource_path": "IMO/segmented/en-IMO2012SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
aa5d752a-c297-5ca0-89c2-2366a5fde362
| 24,147
|
Let $f$ and $g$ be two nonzero polynomials with integer coefficients and $\operatorname{deg} f>\operatorname{deg} g$. Suppose that for infinitely many primes $p$ the polynomial $p f+g$ has a rational root. Prove that $f$ has a rational root.
|
Analogously to the first solution, there exists a real number $R$ such that the complex roots of all polynomials of the form $p f+g$ lie in the disk $|z| \leq R$. For each prime $p$ such that $p f+g$ has a rational root, by GAUSs' lemma $p f+g$ is the product of two integer polynomials, one with degree 1 and the other with degree $\operatorname{deg} f-1$. Since $p$ is a prime, the leading coefficient of one of these factors divides the leading coefficient of $f$. Denote that factor by $h_{p}$. By narrowing the set of the primes used we can assume that all polynomials $h_{p}$ have the same degree and the same leading coefficient. Their complex roots lie in the disk $|z| \leq R$, hence VIETA's formulae imply that all coefficients of all polynomials $h_{p}$ form a bounded set. Since these coefficients are integers, there are only finitely many possible polynomials $h_{p}$. Hence there is a polynomial $h$ such that $h_{p}=h$ for infinitely many primes $p$. Finally, if $p$ and $q$ are distinct primes with $h_{p}=h_{q}=h$ then $h$ divides $(p-q) f$. Since $\operatorname{deg} h=1$ or $\operatorname{deg} h=\operatorname{deg} f-1$, in both cases $f$ has a rational root. Comment. Clearly the polynomial $h$ is a common factor of $f$ and $g$. If $\operatorname{deg} h=1$ then $f$ and $g$ share a rational root. Otherwise $\operatorname{deg} h=\operatorname{deg} f-1$ forces $\operatorname{deg} g=\operatorname{deg} f-1$ and $g$ divides $f$ over the rationals.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $f$ and $g$ be two nonzero polynomials with integer coefficients and $\operatorname{deg} f>\operatorname{deg} g$. Suppose that for infinitely many primes $p$ the polynomial $p f+g$ has a rational root. Prove that $f$ has a rational root.
|
Analogously to the first solution, there exists a real number $R$ such that the complex roots of all polynomials of the form $p f+g$ lie in the disk $|z| \leq R$. For each prime $p$ such that $p f+g$ has a rational root, by GAUSs' lemma $p f+g$ is the product of two integer polynomials, one with degree 1 and the other with degree $\operatorname{deg} f-1$. Since $p$ is a prime, the leading coefficient of one of these factors divides the leading coefficient of $f$. Denote that factor by $h_{p}$. By narrowing the set of the primes used we can assume that all polynomials $h_{p}$ have the same degree and the same leading coefficient. Their complex roots lie in the disk $|z| \leq R$, hence VIETA's formulae imply that all coefficients of all polynomials $h_{p}$ form a bounded set. Since these coefficients are integers, there are only finitely many possible polynomials $h_{p}$. Hence there is a polynomial $h$ such that $h_{p}=h$ for infinitely many primes $p$. Finally, if $p$ and $q$ are distinct primes with $h_{p}=h_{q}=h$ then $h$ divides $(p-q) f$. Since $\operatorname{deg} h=1$ or $\operatorname{deg} h=\operatorname{deg} f-1$, in both cases $f$ has a rational root. Comment. Clearly the polynomial $h$ is a common factor of $f$ and $g$. If $\operatorname{deg} h=1$ then $f$ and $g$ share a rational root. Otherwise $\operatorname{deg} h=\operatorname{deg} f-1$ forces $\operatorname{deg} g=\operatorname{deg} f-1$ and $g$ divides $f$ over the rationals.
|
{
"resource_path": "IMO/segmented/en-IMO2012SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
aa5d752a-c297-5ca0-89c2-2366a5fde362
| 24,147
|
Let $f$ and $g$ be two nonzero polynomials with integer coefficients and $\operatorname{deg} f>\operatorname{deg} g$. Suppose that for infinitely many primes $p$ the polynomial $p f+g$ has a rational root. Prove that $f$ has a rational root.
|
Like in the first solution, there is a real number $R$ such that the real roots of all polynomials of the form $p f+g$ lie in the interval $[-R, R]$. Let $p_{1}<p_{2}<\cdots$ be an infinite sequence of primes so that for every index $k$ the polynomial $p_{k} f+g$ has a rational root $r_{k}$. The sequence $r_{1}, r_{2}, \ldots$ is bounded, so it has a convergent subsequence $r_{k_{1}}, r_{k_{2}}, \ldots$ Now replace the sequences $\left(p_{1}, p_{2}, \ldots\right)$ and $\left(r_{1}, r_{2}, \ldots\right)$ by $\left(p_{k_{1}}, p_{k_{2}}, \ldots\right)$ and $\left(r_{k_{1}}, r_{k_{2}}, \ldots\right)$; after this we can assume that the sequence $r_{1}, r_{2}, \ldots$ is convergent. Let $\alpha=\lim _{k \rightarrow \infty} r_{k}$. We show that $\alpha$ is a rational root of $f$. Over the interval $[-R, R]$, the polynomial $g$ is bounded, $|g(x)| \leq M$ with some fixed $M$. Therefore $$ \left|f\left(r_{k}\right)\right|=\left|f\left(r_{k}\right)-\frac{p_{k} f\left(r_{k}\right)+g\left(r_{k}\right)}{p_{k}}\right|=\frac{\left|g\left(r_{k}\right)\right|}{p_{k}} \leq \frac{M}{p_{k}} \rightarrow 0, $$ and $$ f(\alpha)=f\left(\lim _{k \rightarrow \infty} r_{k}\right)=\lim _{k \rightarrow \infty} f\left(r_{k}\right)=0 $$ So $\alpha$ is a root of $f$ indeed. Now let $u_{k}, v_{k}$ be relative prime integers for which $r_{k}=\frac{u_{k}}{v_{k}}$. Let $a$ be the leading coefficient of $f$, let $b=f(0)$ and $c=g(0)$ be the constant terms of $f$ and $g$, respectively. The leading coefficient of the polynomial $p_{k} f+g$ is $p_{k} a$, its constant term is $p_{k} b+c$. So $v_{k}$ divides $p_{k} a$ and $u_{k}$ divides $p_{k} b+c$. Let $p_{k} b+c=u_{k} e_{k}$ (if $p_{k} b+c=u_{k}=0$ then let $e_{k}=1$ ). We prove that $\alpha$ is rational by using the following fact. Let $\left(p_{n}\right)$ and $\left(q_{n}\right)$ be sequences of integers such that the sequence $\left(p_{n} / q_{n}\right)$ converges. If $\left(p_{n}\right)$ or $\left(q_{n}\right)$ is bounded then $\lim \left(p_{n} / q_{n}\right)$ is rational. Case 1: There is an infinite subsequence $\left(k_{n}\right)$ of indices such that $v_{k_{n}}$ divides $a$. Then $\left(v_{k_{n}}\right)$ is bounded, so $\alpha=\lim _{n \rightarrow \infty}\left(u_{k_{n}} / v_{k_{n}}\right)$ is rational. Case 2: There is an infinite subsequence $\left(k_{n}\right)$ of indices such that $v_{k_{n}}$ does not divide $a$. For such indices we have $v_{k_{n}}=p_{k_{n}} d_{k_{n}}$ where $d_{k_{n}}$ is a divisor of $a$. Then $$ \alpha=\lim _{n \rightarrow \infty} \frac{u_{k_{n}}}{v_{k_{n}}}=\lim _{n \rightarrow \infty} \frac{p_{k_{n}} b+c}{p_{k_{n}} d_{k_{n}} e_{k_{n}}}=\lim _{n \rightarrow \infty} \frac{b}{d_{k_{n}} e_{k_{n}}}+\lim _{n \rightarrow \infty} \frac{c}{p_{k_{n}} d_{k_{n}} e_{k_{n}}}=\lim _{n \rightarrow \infty} \frac{b}{d_{k_{n}} e_{k_{n}}} . $$ Because the numerator $b$ in the last limit is bounded, $\alpha$ is rational.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $f$ and $g$ be two nonzero polynomials with integer coefficients and $\operatorname{deg} f>\operatorname{deg} g$. Suppose that for infinitely many primes $p$ the polynomial $p f+g$ has a rational root. Prove that $f$ has a rational root.
|
Like in the first solution, there is a real number $R$ such that the real roots of all polynomials of the form $p f+g$ lie in the interval $[-R, R]$. Let $p_{1}<p_{2}<\cdots$ be an infinite sequence of primes so that for every index $k$ the polynomial $p_{k} f+g$ has a rational root $r_{k}$. The sequence $r_{1}, r_{2}, \ldots$ is bounded, so it has a convergent subsequence $r_{k_{1}}, r_{k_{2}}, \ldots$ Now replace the sequences $\left(p_{1}, p_{2}, \ldots\right)$ and $\left(r_{1}, r_{2}, \ldots\right)$ by $\left(p_{k_{1}}, p_{k_{2}}, \ldots\right)$ and $\left(r_{k_{1}}, r_{k_{2}}, \ldots\right)$; after this we can assume that the sequence $r_{1}, r_{2}, \ldots$ is convergent. Let $\alpha=\lim _{k \rightarrow \infty} r_{k}$. We show that $\alpha$ is a rational root of $f$. Over the interval $[-R, R]$, the polynomial $g$ is bounded, $|g(x)| \leq M$ with some fixed $M$. Therefore $$ \left|f\left(r_{k}\right)\right|=\left|f\left(r_{k}\right)-\frac{p_{k} f\left(r_{k}\right)+g\left(r_{k}\right)}{p_{k}}\right|=\frac{\left|g\left(r_{k}\right)\right|}{p_{k}} \leq \frac{M}{p_{k}} \rightarrow 0, $$ and $$ f(\alpha)=f\left(\lim _{k \rightarrow \infty} r_{k}\right)=\lim _{k \rightarrow \infty} f\left(r_{k}\right)=0 $$ So $\alpha$ is a root of $f$ indeed. Now let $u_{k}, v_{k}$ be relative prime integers for which $r_{k}=\frac{u_{k}}{v_{k}}$. Let $a$ be the leading coefficient of $f$, let $b=f(0)$ and $c=g(0)$ be the constant terms of $f$ and $g$, respectively. The leading coefficient of the polynomial $p_{k} f+g$ is $p_{k} a$, its constant term is $p_{k} b+c$. So $v_{k}$ divides $p_{k} a$ and $u_{k}$ divides $p_{k} b+c$. Let $p_{k} b+c=u_{k} e_{k}$ (if $p_{k} b+c=u_{k}=0$ then let $e_{k}=1$ ). We prove that $\alpha$ is rational by using the following fact. Let $\left(p_{n}\right)$ and $\left(q_{n}\right)$ be sequences of integers such that the sequence $\left(p_{n} / q_{n}\right)$ converges. If $\left(p_{n}\right)$ or $\left(q_{n}\right)$ is bounded then $\lim \left(p_{n} / q_{n}\right)$ is rational. Case 1: There is an infinite subsequence $\left(k_{n}\right)$ of indices such that $v_{k_{n}}$ divides $a$. Then $\left(v_{k_{n}}\right)$ is bounded, so $\alpha=\lim _{n \rightarrow \infty}\left(u_{k_{n}} / v_{k_{n}}\right)$ is rational. Case 2: There is an infinite subsequence $\left(k_{n}\right)$ of indices such that $v_{k_{n}}$ does not divide $a$. For such indices we have $v_{k_{n}}=p_{k_{n}} d_{k_{n}}$ where $d_{k_{n}}$ is a divisor of $a$. Then $$ \alpha=\lim _{n \rightarrow \infty} \frac{u_{k_{n}}}{v_{k_{n}}}=\lim _{n \rightarrow \infty} \frac{p_{k_{n}} b+c}{p_{k_{n}} d_{k_{n}} e_{k_{n}}}=\lim _{n \rightarrow \infty} \frac{b}{d_{k_{n}} e_{k_{n}}}+\lim _{n \rightarrow \infty} \frac{c}{p_{k_{n}} d_{k_{n}} e_{k_{n}}}=\lim _{n \rightarrow \infty} \frac{b}{d_{k_{n}} e_{k_{n}}} . $$ Because the numerator $b$ in the last limit is bounded, $\alpha$ is rational.
|
{
"resource_path": "IMO/segmented/en-IMO2012SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
aa5d752a-c297-5ca0-89c2-2366a5fde362
| 24,147
|
Let $f: \mathbb{N} \rightarrow \mathbb{N}$ be a function, and let $f^{m}$ be $f$ applied $m$ times. Suppose that for every $n \in \mathbb{N}$ there exists a $k \in \mathbb{N}$ such that $f^{2 k}(n)=n+k$, and let $k_{n}$ be the smallest such $k$. Prove that the sequence $k_{1}, k_{2}, \ldots$ is unbounded.
|
We restrict attention to the set $$ S=\left\{1, f(1), f^{2}(1), \ldots\right\} $$ Observe that $S$ is unbounded because for every number $n$ in $S$ there exists a $k>0$ such that $f^{2 k}(n)=n+k$ is in $S$. Clearly $f$ maps $S$ into itself; moreover $f$ is injective on $S$. Indeed if $f^{i}(1)=f^{j}(1)$ with $i \neq j$ then the values $f^{m}(1)$ start repeating periodically from some point on, and $S$ would be finite. Define $g: S \rightarrow S$ by $g(n)=f^{2 k_{n}}(n)=n+k_{n}$. We prove that $g$ is injective too. Suppose that $g(a)=g(b)$ with $a<b$. Then $a+k_{a}=f^{2 k_{a}}(a)=f^{2 k_{b}}(b)=b+k_{b}$ implies $k_{a}>k_{b}$. So, since $f$ is injective on $S$, we obtain $$ f^{2\left(k_{a}-k_{b}\right)}(a)=b=a+\left(k_{a}-k_{b}\right) . $$ However this contradicts the minimality of $k_{a}$ as $0<k_{a}-k_{b}<k_{a}$. Let $T$ be the set of elements of $S$ that are not of the form $g(n)$ with $n \in S$. Note that $1 \in T$ by $g(n)>n$ for $n \in S$, so $T$ is non-empty. For each $t \in T$ denote $C_{t}=\left\{t, g(t), g^{2}(t), \ldots\right\}$; call $C_{t}$ the chain starting at $t$. Observe that distinct chains are disjoint because $g$ is injective. Each $n \in S \backslash T$ has the form $n=g\left(n^{\prime}\right)$ with $n^{\prime}<n, n^{\prime} \in S$. Repeated applications of the same observation show that $n \in C_{t}$ for some $t \in T$, i. e. $S$ is the disjoint union of the chains $C_{t}$. If $f^{n}(1)$ is in the chain $C_{t}$ starting at $t=f^{n_{t}}(1)$ then $n=n_{t}+2 a_{1}+\cdots+2 a_{j}$ with $$ f^{n}(1)=g^{j}\left(f^{n_{t}}(1)\right)=f^{2 a_{j}}\left(f^{2 a_{j-1}}\left(\cdots f^{2 a_{1}}\left(f^{n_{t}}(1)\right)\right)\right)=f^{n_{t}}(1)+a_{1}+\cdots+a_{j} . $$ Hence $$ f^{n}(1)=f^{n_{t}}(1)+\frac{n-n_{t}}{2}=t+\frac{n-n_{t}}{2} . $$ Now we show that $T$ is infinite. We argue by contradiction. Suppose that there are only finitely many chains $C_{t_{1}}, \ldots, C_{t_{r}}$, starting at $t_{1}<\cdots<t_{r}$. Fix $N$. If $f^{n}(1)$ with $1 \leq n \leq N$ is in $C_{t}$ then $f^{n}(1)=t+\frac{n-n_{t}}{2} \leq t_{r}+\frac{N}{2}$ by (1). But then the $N+1$ distinct natural numbers $1, f(1), \ldots, f^{N}(1)$ are all less than $t_{r}+\frac{N}{2}$ and hence $N+1 \leq t_{r}+\frac{N}{2}$. This is a contradiction if $N$ is sufficiently large, and hence $T$ is infinite. To complete the argument, choose any $k$ in $\mathbb{N}$ and consider the $k+1$ chains starting at the first $k+1$ numbers in $T$. Let $t$ be the greatest one among these numbers. Then each of the chains in question contains a number not exceeding $t$, and at least one of them does not contain any number among $t+1, \ldots, t+k$. So there is a number $n$ in this chain such that $g(n)-n>k$, i. e. $k_{n}>k$. In conclusion $k_{1}, k_{2}, \ldots$ is unbounded.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $f: \mathbb{N} \rightarrow \mathbb{N}$ be a function, and let $f^{m}$ be $f$ applied $m$ times. Suppose that for every $n \in \mathbb{N}$ there exists a $k \in \mathbb{N}$ such that $f^{2 k}(n)=n+k$, and let $k_{n}$ be the smallest such $k$. Prove that the sequence $k_{1}, k_{2}, \ldots$ is unbounded.
|
We restrict attention to the set $$ S=\left\{1, f(1), f^{2}(1), \ldots\right\} $$ Observe that $S$ is unbounded because for every number $n$ in $S$ there exists a $k>0$ such that $f^{2 k}(n)=n+k$ is in $S$. Clearly $f$ maps $S$ into itself; moreover $f$ is injective on $S$. Indeed if $f^{i}(1)=f^{j}(1)$ with $i \neq j$ then the values $f^{m}(1)$ start repeating periodically from some point on, and $S$ would be finite. Define $g: S \rightarrow S$ by $g(n)=f^{2 k_{n}}(n)=n+k_{n}$. We prove that $g$ is injective too. Suppose that $g(a)=g(b)$ with $a<b$. Then $a+k_{a}=f^{2 k_{a}}(a)=f^{2 k_{b}}(b)=b+k_{b}$ implies $k_{a}>k_{b}$. So, since $f$ is injective on $S$, we obtain $$ f^{2\left(k_{a}-k_{b}\right)}(a)=b=a+\left(k_{a}-k_{b}\right) . $$ However this contradicts the minimality of $k_{a}$ as $0<k_{a}-k_{b}<k_{a}$. Let $T$ be the set of elements of $S$ that are not of the form $g(n)$ with $n \in S$. Note that $1 \in T$ by $g(n)>n$ for $n \in S$, so $T$ is non-empty. For each $t \in T$ denote $C_{t}=\left\{t, g(t), g^{2}(t), \ldots\right\}$; call $C_{t}$ the chain starting at $t$. Observe that distinct chains are disjoint because $g$ is injective. Each $n \in S \backslash T$ has the form $n=g\left(n^{\prime}\right)$ with $n^{\prime}<n, n^{\prime} \in S$. Repeated applications of the same observation show that $n \in C_{t}$ for some $t \in T$, i. e. $S$ is the disjoint union of the chains $C_{t}$. If $f^{n}(1)$ is in the chain $C_{t}$ starting at $t=f^{n_{t}}(1)$ then $n=n_{t}+2 a_{1}+\cdots+2 a_{j}$ with $$ f^{n}(1)=g^{j}\left(f^{n_{t}}(1)\right)=f^{2 a_{j}}\left(f^{2 a_{j-1}}\left(\cdots f^{2 a_{1}}\left(f^{n_{t}}(1)\right)\right)\right)=f^{n_{t}}(1)+a_{1}+\cdots+a_{j} . $$ Hence $$ f^{n}(1)=f^{n_{t}}(1)+\frac{n-n_{t}}{2}=t+\frac{n-n_{t}}{2} . $$ Now we show that $T$ is infinite. We argue by contradiction. Suppose that there are only finitely many chains $C_{t_{1}}, \ldots, C_{t_{r}}$, starting at $t_{1}<\cdots<t_{r}$. Fix $N$. If $f^{n}(1)$ with $1 \leq n \leq N$ is in $C_{t}$ then $f^{n}(1)=t+\frac{n-n_{t}}{2} \leq t_{r}+\frac{N}{2}$ by (1). But then the $N+1$ distinct natural numbers $1, f(1), \ldots, f^{N}(1)$ are all less than $t_{r}+\frac{N}{2}$ and hence $N+1 \leq t_{r}+\frac{N}{2}$. This is a contradiction if $N$ is sufficiently large, and hence $T$ is infinite. To complete the argument, choose any $k$ in $\mathbb{N}$ and consider the $k+1$ chains starting at the first $k+1$ numbers in $T$. Let $t$ be the greatest one among these numbers. Then each of the chains in question contains a number not exceeding $t$, and at least one of them does not contain any number among $t+1, \ldots, t+k$. So there is a number $n$ in this chain such that $g(n)-n>k$, i. e. $k_{n}>k$. In conclusion $k_{1}, k_{2}, \ldots$ is unbounded.
|
{
"resource_path": "IMO/segmented/en-IMO2012SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
f88d1469-5556-5b12-abec-818b6abf3a76
| 24,155
|
Several positive integers are written in a row. Iteratively, Alice chooses two adjacent numbers $x$ and $y$ such that $x>y$ and $x$ is to the left of $y$, and replaces the pair $(x, y)$ by either $(y+1, x)$ or $(x-1, x)$. Prove that she can perform only finitely many such iterations.
|
Note first that the allowed operation does not change the maximum $M$ of the initial sequence. Let $a_{1}, a_{2}, \ldots, a_{n}$ be the numbers obtained at some point of the process. Consider the sum $$ S=a_{1}+2 a_{2}+\cdots+n a_{n} $$ We claim that $S$ increases by a positive integer amount with every operation. Let the operation replace the pair ( $\left.a_{i}, a_{i+1}\right)$ by a pair $\left(c, a_{i}\right)$, where $a_{i}>a_{i+1}$ and $c=a_{i+1}+1$ or $c=a_{i}-1$. Then the new and the old value of $S$ differ by $d=\left(i c+(i+1) a_{i}\right)-\left(i a_{i}+(i+1) a_{i+1}\right)=a_{i}-a_{i+1}+i\left(c-a_{i+1}\right)$. The integer $d$ is positive since $a_{i}-a_{i+1} \geq 1$ and $c-a_{i+1} \geq 0$. On the other hand $S \leq(1+2+\cdots+n) M$ as $a_{i} \leq M$ for all $i=1, \ldots, n$. Since $S$ increases by at least 1 at each step and never exceeds the constant $(1+2+\cdots+n) M$, the process stops after a finite number of iterations.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Several positive integers are written in a row. Iteratively, Alice chooses two adjacent numbers $x$ and $y$ such that $x>y$ and $x$ is to the left of $y$, and replaces the pair $(x, y)$ by either $(y+1, x)$ or $(x-1, x)$. Prove that she can perform only finitely many such iterations.
|
Note first that the allowed operation does not change the maximum $M$ of the initial sequence. Let $a_{1}, a_{2}, \ldots, a_{n}$ be the numbers obtained at some point of the process. Consider the sum $$ S=a_{1}+2 a_{2}+\cdots+n a_{n} $$ We claim that $S$ increases by a positive integer amount with every operation. Let the operation replace the pair ( $\left.a_{i}, a_{i+1}\right)$ by a pair $\left(c, a_{i}\right)$, where $a_{i}>a_{i+1}$ and $c=a_{i+1}+1$ or $c=a_{i}-1$. Then the new and the old value of $S$ differ by $d=\left(i c+(i+1) a_{i}\right)-\left(i a_{i}+(i+1) a_{i+1}\right)=a_{i}-a_{i+1}+i\left(c-a_{i+1}\right)$. The integer $d$ is positive since $a_{i}-a_{i+1} \geq 1$ and $c-a_{i+1} \geq 0$. On the other hand $S \leq(1+2+\cdots+n) M$ as $a_{i} \leq M$ for all $i=1, \ldots, n$. Since $S$ increases by at least 1 at each step and never exceeds the constant $(1+2+\cdots+n) M$, the process stops after a finite number of iterations.
|
{
"resource_path": "IMO/segmented/en-IMO2012SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
54b5b6f8-a696-5e45-9f93-233d11b8f1a8
| 24,161
|
Several positive integers are written in a row. Iteratively, Alice chooses two adjacent numbers $x$ and $y$ such that $x>y$ and $x$ is to the left of $y$, and replaces the pair $(x, y)$ by either $(y+1, x)$ or $(x-1, x)$. Prove that she can perform only finitely many such iterations.
|
Like in the first solution note that the operations do not change the maximum $M$ of the initial sequence. Now consider the reverse lexicographical order for $n$-tuples of integers. We say that $\left(x_{1}, \ldots, x_{n}\right)<\left(y_{1}, \ldots, y_{n}\right)$ if $x_{n}<y_{n}$, or if $x_{n}=y_{n}$ and $x_{n-1}<y_{n-1}$, or if $x_{n}=y_{n}$, $x_{n-1}=y_{n-1}$ and $x_{n-2}<y_{n-2}$, etc. Each iteration creates a sequence that is greater than the previous one with respect to this order, and no sequence occurs twice during the process. On the other hand there are finitely many possible sequences because their terms are always positive integers not exceeding $M$. Hence the process cannot continue forever.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Several positive integers are written in a row. Iteratively, Alice chooses two adjacent numbers $x$ and $y$ such that $x>y$ and $x$ is to the left of $y$, and replaces the pair $(x, y)$ by either $(y+1, x)$ or $(x-1, x)$. Prove that she can perform only finitely many such iterations.
|
Like in the first solution note that the operations do not change the maximum $M$ of the initial sequence. Now consider the reverse lexicographical order for $n$-tuples of integers. We say that $\left(x_{1}, \ldots, x_{n}\right)<\left(y_{1}, \ldots, y_{n}\right)$ if $x_{n}<y_{n}$, or if $x_{n}=y_{n}$ and $x_{n-1}<y_{n-1}$, or if $x_{n}=y_{n}$, $x_{n-1}=y_{n-1}$ and $x_{n-2}<y_{n-2}$, etc. Each iteration creates a sequence that is greater than the previous one with respect to this order, and no sequence occurs twice during the process. On the other hand there are finitely many possible sequences because their terms are always positive integers not exceeding $M$. Hence the process cannot continue forever.
|
{
"resource_path": "IMO/segmented/en-IMO2012SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
54b5b6f8-a696-5e45-9f93-233d11b8f1a8
| 24,161
|
Several positive integers are written in a row. Iteratively, Alice chooses two adjacent numbers $x$ and $y$ such that $x>y$ and $x$ is to the left of $y$, and replaces the pair $(x, y)$ by either $(y+1, x)$ or $(x-1, x)$. Prove that she can perform only finitely many such iterations.
|
Let the current numbers be $a_{1}, a_{2}, \ldots, a_{n}$. Define the score $s_{i}$ of $a_{i}$ as the number of $a_{j}$ 's that are less than $a_{i}$. Call the sequence $s_{1}, s_{2}, \ldots, s_{n}$ the score sequence of $a_{1}, a_{2}, \ldots, a_{n}$. Let us say that a sequence $x_{1}, \ldots, x_{n}$ dominates a sequence $y_{1}, \ldots, y_{n}$ if the first index $i$ with $x_{i} \neq y_{i}$ is such that $x_{i}<y_{i}$. We show that after each operation the new score sequence dominates the old one. Score sequences do not repeat, and there are finitely many possibilities for them, no more than $(n-1)^{n}$. Hence the process will terminate. Consider an operation that replaces $(x, y)$ by $(a, x)$, with $a=y+1$ or $a=x-1$. Suppose that $x$ was originally at position $i$. For each $j<i$ the score $s_{j}$ does not increase with the change because $y \leq a$ and $x \leq x$. If $s_{j}$ decreases for some $j<i$ then the new score sequence dominates the old one. Assume that $s_{j}$ stays the same for all $j<i$ and consider $s_{i}$. Since $x>y$ and $y \leq a \leq x$, we see that $s_{i}$ decreases by at least 1 . This concludes the proof. Comment. All three proofs work if $x$ and $y$ are not necessarily adjacent, and if the pair $(x, y)$ is replaced by any pair $(a, x)$, with $a$ an integer satisfying $y \leq a \leq x$. There is nothing special about the "weights" $1,2, \ldots, n$ in the definition of $S=\sum_{i=1}^{n} i a_{i}$ from the first solution. For any sequence $w_{1}<w_{2}<\cdots<w_{n}$ of positive integers, the sum $\sum_{i=1}^{n} w_{i} a_{i}$ increases by at least 1 with each operation. Consider the same problem, but letting Alice replace the pair $(x, y)$ by $(a, x)$, where $a$ is any positive integer less than $x$. The same conclusion holds in this version, i. e. the process stops eventually. The solution using the reverse lexicographical order works without any change. The first solution would require a special set of weights like $w_{i}=M^{i}$ for $i=1, \ldots, n$. Comment. The first and the second solutions provide upper bounds for the number of possible operations, respectively of order $M n^{2}$ and $M^{n}$ where $M$ is the maximum of the original sequence. The upper bound $(n-1)^{n}$ in the third solution does not depend on $M$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Several positive integers are written in a row. Iteratively, Alice chooses two adjacent numbers $x$ and $y$ such that $x>y$ and $x$ is to the left of $y$, and replaces the pair $(x, y)$ by either $(y+1, x)$ or $(x-1, x)$. Prove that she can perform only finitely many such iterations.
|
Let the current numbers be $a_{1}, a_{2}, \ldots, a_{n}$. Define the score $s_{i}$ of $a_{i}$ as the number of $a_{j}$ 's that are less than $a_{i}$. Call the sequence $s_{1}, s_{2}, \ldots, s_{n}$ the score sequence of $a_{1}, a_{2}, \ldots, a_{n}$. Let us say that a sequence $x_{1}, \ldots, x_{n}$ dominates a sequence $y_{1}, \ldots, y_{n}$ if the first index $i$ with $x_{i} \neq y_{i}$ is such that $x_{i}<y_{i}$. We show that after each operation the new score sequence dominates the old one. Score sequences do not repeat, and there are finitely many possibilities for them, no more than $(n-1)^{n}$. Hence the process will terminate. Consider an operation that replaces $(x, y)$ by $(a, x)$, with $a=y+1$ or $a=x-1$. Suppose that $x$ was originally at position $i$. For each $j<i$ the score $s_{j}$ does not increase with the change because $y \leq a$ and $x \leq x$. If $s_{j}$ decreases for some $j<i$ then the new score sequence dominates the old one. Assume that $s_{j}$ stays the same for all $j<i$ and consider $s_{i}$. Since $x>y$ and $y \leq a \leq x$, we see that $s_{i}$ decreases by at least 1 . This concludes the proof. Comment. All three proofs work if $x$ and $y$ are not necessarily adjacent, and if the pair $(x, y)$ is replaced by any pair $(a, x)$, with $a$ an integer satisfying $y \leq a \leq x$. There is nothing special about the "weights" $1,2, \ldots, n$ in the definition of $S=\sum_{i=1}^{n} i a_{i}$ from the first solution. For any sequence $w_{1}<w_{2}<\cdots<w_{n}$ of positive integers, the sum $\sum_{i=1}^{n} w_{i} a_{i}$ increases by at least 1 with each operation. Consider the same problem, but letting Alice replace the pair $(x, y)$ by $(a, x)$, where $a$ is any positive integer less than $x$. The same conclusion holds in this version, i. e. the process stops eventually. The solution using the reverse lexicographical order works without any change. The first solution would require a special set of weights like $w_{i}=M^{i}$ for $i=1, \ldots, n$. Comment. The first and the second solutions provide upper bounds for the number of possible operations, respectively of order $M n^{2}$ and $M^{n}$ where $M$ is the maximum of the original sequence. The upper bound $(n-1)^{n}$ in the third solution does not depend on $M$.
|
{
"resource_path": "IMO/segmented/en-IMO2012SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
54b5b6f8-a696-5e45-9f93-233d11b8f1a8
| 24,161
|
The columns and the rows of a $3 n \times 3 n$ square board are numbered $1,2, \ldots, 3 n$. Every square $(x, y)$ with $1 \leq x, y \leq 3 n$ is colored asparagus, byzantium or citrine according as the modulo 3 remainder of $x+y$ is 0,1 or 2 respectively. One token colored asparagus, byzantium or citrine is placed on each square, so that there are $3 n^{2}$ tokens of each color. Suppose that one can permute the tokens so that each token is moved to a distance of at most $d$ from its original position, each asparagus token replaces a byzantium token, each byzantium token replaces a citrine token, and each citrine token replaces an asparagus token. Prove that it is possible to permute the tokens so that each token is moved to a distance of at most $d+2$ from its original position, and each square contains a token with the same color as the square.
|
Without loss of generality it suffices to prove that the A-tokens can be moved to distinct $\mathrm{A}$-squares in such a way that each $\mathrm{A}$-token is moved to a distance at most $d+2$ from its original place. This means we need a perfect matching between the $3 n^{2} \mathrm{~A}$-squares and the $3 n^{2}$ A-tokens such that the distance in each pair of the matching is at most $d+2$. To find the matching, we construct a bipartite graph. The A-squares will be the vertices in one class of the graph; the vertices in the other class will be the A-tokens. Split the board into $3 \times 1$ horizontal triminos; then each trimino contains exactly one Asquare. Take a permutation $\pi$ of the tokens which moves A-tokens to B-tokens, B-tokens to C-tokens, and C-tokens to A-tokens, in each case to a distance at most $d$. For each A-square $S$, and for each A-token $T$, connect $S$ and $T$ by an edge if $T, \pi(T)$ or $\pi^{-1}(T)$ is on the trimino containing $S$. We allow multiple edges; it is even possible that the same square and the same token are connected with three edges. Obviously the lengths of the edges in the graph do not exceed $d+2$. By length of an edge we mean the distance between the A-square and the A-token it connects. Each A-token $T$ is connected with the three A-squares whose triminos contain $T, \pi(T)$ and $\pi^{-1}(T)$. Therefore in the graph all tokens are of degree 3. We show that the same is true for the A-squares. Let $S$ be an arbitrary A-square, and let $T_{1}, T_{2}, T_{3}$ be the three tokens on the trimino containing $S$. For $i=1,2,3$, if $T_{i}$ is an A-token, then $S$ is connected with $T_{i}$; if $T_{i}$ is a B-token then $S$ is connected with $\pi^{-1}\left(T_{i}\right)$; finally, if $T_{i}$ is a C-token then $S$ is connected with $\pi\left(T_{i}\right)$. Hence in the graph the A-squares also are of degree 3. Since the A-squares are of degree 3 , from every set $\mathcal{S}$ of A-squares exactly $3|\mathcal{S}|$ edges start. These edges end in at least $|\mathcal{S}|$ tokens because the A-tokens also are of degree 3. Hence every set $\mathcal{S}$ of A-squares has at least $|\mathcal{S}|$ neighbors among the A-tokens. Therefore, by HALL's marriage theorem, the graph contains a perfect matching between the two vertex classes. So there is a perfect matching between the A-squares and A-tokens with edges no longer than $d+2$. It follows that the tokens can be permuted as specified in the problem statement. Comment 1. In the original problem proposal the board was infinite and there were only two colors. Having $n$ colors for some positive integer $n$ was an option; we chose $n=3$. Moreover, we changed the board to a finite one to avoid dealing with infinite graphs (although Hall's theorem works in the infinite case as well). With only two colors Hall's theorem is not needed. In this case we split the board into $2 \times 1$ dominos, and in the resulting graph all vertices are of degree 2. The graph consists of disjoint cycles with even length and infinite paths, so the existence of the matching is trivial. Having more than three colors would make the problem statement more complicated, because we need a matching between every two color classes of tokens. However, this would not mean a significant increase in difficulty. Comment 2. According to Wikipedia, the color asparagus (hexadecimal code \#87A96B) is a tone of green that is named after the vegetable. Crayola created this color in 1993 as one of the 16 to be named in the Name The Color Contest. Byzantium (\#702963) is a dark tone of purple. Its first recorded use as a color name in English was in 1926. Citrine (\#E4D00A) is variously described as yellow, greenish-yellow, brownish-yellow or orange. The first known use of citrine as a color name in English was in the 14th century.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
The columns and the rows of a $3 n \times 3 n$ square board are numbered $1,2, \ldots, 3 n$. Every square $(x, y)$ with $1 \leq x, y \leq 3 n$ is colored asparagus, byzantium or citrine according as the modulo 3 remainder of $x+y$ is 0,1 or 2 respectively. One token colored asparagus, byzantium or citrine is placed on each square, so that there are $3 n^{2}$ tokens of each color. Suppose that one can permute the tokens so that each token is moved to a distance of at most $d$ from its original position, each asparagus token replaces a byzantium token, each byzantium token replaces a citrine token, and each citrine token replaces an asparagus token. Prove that it is possible to permute the tokens so that each token is moved to a distance of at most $d+2$ from its original position, and each square contains a token with the same color as the square.
|
Without loss of generality it suffices to prove that the A-tokens can be moved to distinct $\mathrm{A}$-squares in such a way that each $\mathrm{A}$-token is moved to a distance at most $d+2$ from its original place. This means we need a perfect matching between the $3 n^{2} \mathrm{~A}$-squares and the $3 n^{2}$ A-tokens such that the distance in each pair of the matching is at most $d+2$. To find the matching, we construct a bipartite graph. The A-squares will be the vertices in one class of the graph; the vertices in the other class will be the A-tokens. Split the board into $3 \times 1$ horizontal triminos; then each trimino contains exactly one Asquare. Take a permutation $\pi$ of the tokens which moves A-tokens to B-tokens, B-tokens to C-tokens, and C-tokens to A-tokens, in each case to a distance at most $d$. For each A-square $S$, and for each A-token $T$, connect $S$ and $T$ by an edge if $T, \pi(T)$ or $\pi^{-1}(T)$ is on the trimino containing $S$. We allow multiple edges; it is even possible that the same square and the same token are connected with three edges. Obviously the lengths of the edges in the graph do not exceed $d+2$. By length of an edge we mean the distance between the A-square and the A-token it connects. Each A-token $T$ is connected with the three A-squares whose triminos contain $T, \pi(T)$ and $\pi^{-1}(T)$. Therefore in the graph all tokens are of degree 3. We show that the same is true for the A-squares. Let $S$ be an arbitrary A-square, and let $T_{1}, T_{2}, T_{3}$ be the three tokens on the trimino containing $S$. For $i=1,2,3$, if $T_{i}$ is an A-token, then $S$ is connected with $T_{i}$; if $T_{i}$ is a B-token then $S$ is connected with $\pi^{-1}\left(T_{i}\right)$; finally, if $T_{i}$ is a C-token then $S$ is connected with $\pi\left(T_{i}\right)$. Hence in the graph the A-squares also are of degree 3. Since the A-squares are of degree 3 , from every set $\mathcal{S}$ of A-squares exactly $3|\mathcal{S}|$ edges start. These edges end in at least $|\mathcal{S}|$ tokens because the A-tokens also are of degree 3. Hence every set $\mathcal{S}$ of A-squares has at least $|\mathcal{S}|$ neighbors among the A-tokens. Therefore, by HALL's marriage theorem, the graph contains a perfect matching between the two vertex classes. So there is a perfect matching between the A-squares and A-tokens with edges no longer than $d+2$. It follows that the tokens can be permuted as specified in the problem statement. Comment 1. In the original problem proposal the board was infinite and there were only two colors. Having $n$ colors for some positive integer $n$ was an option; we chose $n=3$. Moreover, we changed the board to a finite one to avoid dealing with infinite graphs (although Hall's theorem works in the infinite case as well). With only two colors Hall's theorem is not needed. In this case we split the board into $2 \times 1$ dominos, and in the resulting graph all vertices are of degree 2. The graph consists of disjoint cycles with even length and infinite paths, so the existence of the matching is trivial. Having more than three colors would make the problem statement more complicated, because we need a matching between every two color classes of tokens. However, this would not mean a significant increase in difficulty. Comment 2. According to Wikipedia, the color asparagus (hexadecimal code \#87A96B) is a tone of green that is named after the vegetable. Crayola created this color in 1993 as one of the 16 to be named in the Name The Color Contest. Byzantium (\#702963) is a dark tone of purple. Its first recorded use as a color name in English was in 1926. Citrine (\#E4D00A) is variously described as yellow, greenish-yellow, brownish-yellow or orange. The first known use of citrine as a color name in English was in the 14th century.
|
{
"resource_path": "IMO/segmented/en-IMO2012SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
c3f95224-caf8-522c-bc7b-603c743ed466
| 24,176
|
Let $k$ and $n$ be fixed positive integers. In the liar's guessing game, Amy chooses integers $x$ and $N$ with $1 \leq x \leq N$. She tells Ben what $N$ is, but not what $x$ is. Ben may then repeatedly ask Amy whether $x \in S$ for arbitrary sets $S$ of integers. Amy will always answer with yes or no, but she might lie. The only restriction is that she can lie at most $k$ times in a row. After he has asked as many questions as he wants, Ben must specify a set of at most $n$ positive integers. If $x$ is in this set he wins; otherwise, he loses. Prove that: a) If $n \geq 2^{k}$ then Ben can always win. b) For sufficiently large $k$ there exist $n \geq 1.99^{k}$ such that Ben cannot guarantee a win.
|
Consider an answer $A \in\{y e s, n o\}$ to a question of the kind "Is $x$ in the set $S$ ?" We say that $A$ is inconsistent with a number $i$ if $A=y e s$ and $i \notin S$, or if $A=n o$ and $i \in S$. Observe that an answer inconsistent with the target number $x$ is a lie. a) Suppose that Ben has determined a set $T$ of size $m$ that contains $x$. This is true initially with $m=N$ and $T=\{1,2, \ldots, N\}$. For $m>2^{k}$ we show how Ben can find a number $y \in T$ that is different from $x$. By performing this step repeatedly he can reduce $T$ to be of size $2^{k} \leq n$ and thus win. Since only the size $m>2^{k}$ of $T$ is relevant, assume that $T=\left\{0,1, \ldots, 2^{k}, \ldots, m-1\right\}$. Ben begins by asking repeatedly whether $x$ is $2^{k}$. If Amy answers no $k+1$ times in a row, one of these answers is truthful, and so $x \neq 2^{k}$. Otherwise Ben stops asking about $2^{k}$ at the first answer yes. He then asks, for each $i=1, \ldots, k$, if the binary representation of $x$ has a 0 in the $i$ th digit. Regardless of what the $k$ answers are, they are all inconsistent with a certain number $y \in\left\{0,1, \ldots, 2^{k}-1\right\}$. The preceding answer yes about $2^{k}$ is also inconsistent with $y$. Hence $y \neq x$. Otherwise the last $k+1$ answers are not truthful, which is impossible. Either way, Ben finds a number in $T$ that is different from $x$, and the claim is proven. b) We prove that if $1<\lambda<2$ and $n=\left\lfloor(2-\lambda) \lambda^{k+1}\right\rfloor-1$ then Ben cannot guarantee a win. To complete the proof, then it suffices to take $\lambda$ such that $1.99<\lambda<2$ and $k$ large enough so that $$ n=\left\lfloor(2-\lambda) \lambda^{k+1}\right\rfloor-1 \geq 1.99^{k} $$ Consider the following strategy for Amy. First she chooses $N=n+1$ and $x \in\{1,2, \ldots, n+1\}$ arbitrarily. After every answer of hers Amy determines, for each $i=1,2, \ldots, n+1$, the number $m_{i}$ of consecutive answers she has given by that point that are inconsistent with $i$. To decide on her next answer, she then uses the quantity $$ \phi=\sum_{i=1}^{n+1} \lambda^{m_{i}} $$ No matter what Ben's next question is, Amy chooses the answer which minimizes $\phi$. We claim that with this strategy $\phi$ will always stay less than $\lambda^{k+1}$. Consequently no exponent $m_{i}$ in $\phi$ will ever exceed $k$, hence Amy will never give more than $k$ consecutive answers inconsistent with some $i$. In particular this applies to the target number $x$, so she will never lie more than $k$ times in a row. Thus, given the claim, Amy's strategy is legal. Since the strategy does not depend on $x$ in any way, Ben can make no deductions about $x$, and therefore he cannot guarantee a win. It remains to show that $\phi<\lambda^{k+1}$ at all times. Initially each $m_{i}$ is 0 , so this condition holds in the beginning due to $1<\lambda<2$ and $n=\left\lfloor(2-\lambda) \lambda^{k+1}\right\rfloor-1$. Suppose that $\phi<\lambda^{k+1}$ at some point, and Ben has just asked if $x \in S$ for some set $S$. According as Amy answers yes or no, the new value of $\phi$ becomes $$ \phi_{1}=\sum_{i \in S} 1+\sum_{i \notin S} \lambda^{m_{i}+1} \quad \text { or } \quad \phi_{2}=\sum_{i \in S} \lambda^{m_{i}+1}+\sum_{i \notin S} 1 $$ Since Amy chooses the option minimizing $\phi$, the new $\phi$ will equal $\min \left(\phi_{1}, \phi_{2}\right)$. Now we have $$ \min \left(\phi_{1}, \phi_{2}\right) \leq \frac{1}{2}\left(\phi_{1}+\phi_{2}\right)=\frac{1}{2}\left(\sum_{i \in S}\left(1+\lambda^{m_{i}+1}\right)+\sum_{i \notin S}\left(\lambda^{m_{i}+1}+1\right)\right)=\frac{1}{2}(\lambda \phi+n+1) $$ Because $\phi<\lambda^{k+1}$, the assumptions $\lambda<2$ and $n=\left\lfloor(2-\lambda) \lambda^{k+1}\right\rfloor-1$ lead to $$ \min \left(\phi_{1}, \phi_{2}\right)<\frac{1}{2}\left(\lambda^{k+2}+(2-\lambda) \lambda^{k+1}\right)=\lambda^{k+1} $$ The claim follows, which completes the solution. Comment. Given a fixed $k$, let $f(k)$ denote the minimum value of $n$ for which Ben can guarantee a victory. The problem asks for a proof that for large $k$ $$ 1.99^{k} \leq f(k) \leq 2^{k} $$ A computer search shows that $f(k)=2,3,4,7,11,17$ for $k=1,2,3,4,5,6$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $k$ and $n$ be fixed positive integers. In the liar's guessing game, Amy chooses integers $x$ and $N$ with $1 \leq x \leq N$. She tells Ben what $N$ is, but not what $x$ is. Ben may then repeatedly ask Amy whether $x \in S$ for arbitrary sets $S$ of integers. Amy will always answer with yes or no, but she might lie. The only restriction is that she can lie at most $k$ times in a row. After he has asked as many questions as he wants, Ben must specify a set of at most $n$ positive integers. If $x$ is in this set he wins; otherwise, he loses. Prove that: a) If $n \geq 2^{k}$ then Ben can always win. b) For sufficiently large $k$ there exist $n \geq 1.99^{k}$ such that Ben cannot guarantee a win.
|
Consider an answer $A \in\{y e s, n o\}$ to a question of the kind "Is $x$ in the set $S$ ?" We say that $A$ is inconsistent with a number $i$ if $A=y e s$ and $i \notin S$, or if $A=n o$ and $i \in S$. Observe that an answer inconsistent with the target number $x$ is a lie. a) Suppose that Ben has determined a set $T$ of size $m$ that contains $x$. This is true initially with $m=N$ and $T=\{1,2, \ldots, N\}$. For $m>2^{k}$ we show how Ben can find a number $y \in T$ that is different from $x$. By performing this step repeatedly he can reduce $T$ to be of size $2^{k} \leq n$ and thus win. Since only the size $m>2^{k}$ of $T$ is relevant, assume that $T=\left\{0,1, \ldots, 2^{k}, \ldots, m-1\right\}$. Ben begins by asking repeatedly whether $x$ is $2^{k}$. If Amy answers no $k+1$ times in a row, one of these answers is truthful, and so $x \neq 2^{k}$. Otherwise Ben stops asking about $2^{k}$ at the first answer yes. He then asks, for each $i=1, \ldots, k$, if the binary representation of $x$ has a 0 in the $i$ th digit. Regardless of what the $k$ answers are, they are all inconsistent with a certain number $y \in\left\{0,1, \ldots, 2^{k}-1\right\}$. The preceding answer yes about $2^{k}$ is also inconsistent with $y$. Hence $y \neq x$. Otherwise the last $k+1$ answers are not truthful, which is impossible. Either way, Ben finds a number in $T$ that is different from $x$, and the claim is proven. b) We prove that if $1<\lambda<2$ and $n=\left\lfloor(2-\lambda) \lambda^{k+1}\right\rfloor-1$ then Ben cannot guarantee a win. To complete the proof, then it suffices to take $\lambda$ such that $1.99<\lambda<2$ and $k$ large enough so that $$ n=\left\lfloor(2-\lambda) \lambda^{k+1}\right\rfloor-1 \geq 1.99^{k} $$ Consider the following strategy for Amy. First she chooses $N=n+1$ and $x \in\{1,2, \ldots, n+1\}$ arbitrarily. After every answer of hers Amy determines, for each $i=1,2, \ldots, n+1$, the number $m_{i}$ of consecutive answers she has given by that point that are inconsistent with $i$. To decide on her next answer, she then uses the quantity $$ \phi=\sum_{i=1}^{n+1} \lambda^{m_{i}} $$ No matter what Ben's next question is, Amy chooses the answer which minimizes $\phi$. We claim that with this strategy $\phi$ will always stay less than $\lambda^{k+1}$. Consequently no exponent $m_{i}$ in $\phi$ will ever exceed $k$, hence Amy will never give more than $k$ consecutive answers inconsistent with some $i$. In particular this applies to the target number $x$, so she will never lie more than $k$ times in a row. Thus, given the claim, Amy's strategy is legal. Since the strategy does not depend on $x$ in any way, Ben can make no deductions about $x$, and therefore he cannot guarantee a win. It remains to show that $\phi<\lambda^{k+1}$ at all times. Initially each $m_{i}$ is 0 , so this condition holds in the beginning due to $1<\lambda<2$ and $n=\left\lfloor(2-\lambda) \lambda^{k+1}\right\rfloor-1$. Suppose that $\phi<\lambda^{k+1}$ at some point, and Ben has just asked if $x \in S$ for some set $S$. According as Amy answers yes or no, the new value of $\phi$ becomes $$ \phi_{1}=\sum_{i \in S} 1+\sum_{i \notin S} \lambda^{m_{i}+1} \quad \text { or } \quad \phi_{2}=\sum_{i \in S} \lambda^{m_{i}+1}+\sum_{i \notin S} 1 $$ Since Amy chooses the option minimizing $\phi$, the new $\phi$ will equal $\min \left(\phi_{1}, \phi_{2}\right)$. Now we have $$ \min \left(\phi_{1}, \phi_{2}\right) \leq \frac{1}{2}\left(\phi_{1}+\phi_{2}\right)=\frac{1}{2}\left(\sum_{i \in S}\left(1+\lambda^{m_{i}+1}\right)+\sum_{i \notin S}\left(\lambda^{m_{i}+1}+1\right)\right)=\frac{1}{2}(\lambda \phi+n+1) $$ Because $\phi<\lambda^{k+1}$, the assumptions $\lambda<2$ and $n=\left\lfloor(2-\lambda) \lambda^{k+1}\right\rfloor-1$ lead to $$ \min \left(\phi_{1}, \phi_{2}\right)<\frac{1}{2}\left(\lambda^{k+2}+(2-\lambda) \lambda^{k+1}\right)=\lambda^{k+1} $$ The claim follows, which completes the solution. Comment. Given a fixed $k$, let $f(k)$ denote the minimum value of $n$ for which Ben can guarantee a victory. The problem asks for a proof that for large $k$ $$ 1.99^{k} \leq f(k) \leq 2^{k} $$ A computer search shows that $f(k)=2,3,4,7,11,17$ for $k=1,2,3,4,5,6$.
|
{
"resource_path": "IMO/segmented/en-IMO2012SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
2fea8430-ecf3-5002-8082-2ae72d0ea929
| 24,178
|
There are given $2^{500}$ points on a circle labeled $1,2, \ldots, 2^{500}$ in some order. Prove that one can choose 100 pairwise disjoint chords joining some of these points so that the 100 sums of the pairs of numbers at the endpoints of the chosen chords are equal.
|
The proof is based on the following general fact. Lemma. In a graph $G$ each vertex $v$ has degree $d_{v}$. Then $G$ contains an independent set $S$ of vertices such that $|S| \geq f(G)$ where $$ f(G)=\sum_{v \in G} \frac{1}{d_{v}+1} $$ Proof. Induction on $n=|G|$. The base $n=1$ is clear. For the inductive step choose a vertex $v_{0}$ in $G$ of minimum degree $d$. Delete $v_{0}$ and all of its neighbors $v_{1}, \ldots, v_{d}$ and also all edges with endpoints $v_{0}, v_{1}, \ldots, v_{d}$. This gives a new graph $G^{\prime}$. By the inductive assumption $G^{\prime}$ contains an independent set $S^{\prime}$ of vertices such that $\left|S^{\prime}\right| \geq f\left(G^{\prime}\right)$. Since no vertex in $S^{\prime}$ is a neighbor of $v_{0}$ in $G$, the set $S=S^{\prime} \cup\left\{v_{0}\right\}$ is independent in $G$. Let $d_{v}^{\prime}$ be the degree of a vertex $v$ in $G^{\prime}$. Clearly $d_{v}^{\prime} \leq d_{v}$ for every such vertex $v$, and also $d_{v_{i}} \geq d$ for all $i=0,1, \ldots, d$ by the minimal choice of $v_{0}$. Therefore $$ f\left(G^{\prime}\right)=\sum_{v \in G^{\prime}} \frac{1}{d_{v}^{\prime}+1} \geq \sum_{v \in G^{\prime}} \frac{1}{d_{v}+1}=f(G)-\sum_{i=0}^{d} \frac{1}{d_{v_{i}}+1} \geq f(G)-\frac{d+1}{d+1}=f(G)-1 . $$ Hence $|S|=\left|S^{\prime}\right|+1 \geq f\left(G^{\prime}\right)+1 \geq f(G)$, and the induction is complete. We pass on to our problem. For clarity denote $n=2^{499}$ and draw all chords determined by the given $2 n$ points. Color each chord with one of the colors $3,4, \ldots, 4 n-1$ according to the sum of the numbers at its endpoints. Chords with a common endpoint have different colors. For each color $c$ consider the following graph $G_{c}$. Its vertices are the chords of color $c$, and two chords are neighbors in $G_{c}$ if they intersect. Let $f\left(G_{c}\right)$ have the same meaning as in the lemma for all graphs $G_{c}$. Every chord $\ell$ divides the circle into two arcs, and one of them contains $m(\ell) \leq n-1$ given points. (In particular $m(\ell)=0$ if $\ell$ joins two consecutive points.) For each $i=0,1, \ldots, n-2$ there are $2 n$ chords $\ell$ with $m(\ell)=i$. Such a chord has degree at most $i$ in the respective graph. Indeed let $A_{1}, \ldots, A_{i}$ be all points on either arc determined by a chord $\ell$ with $m(\ell)=i$ and color $c$. Every $A_{j}$ is an endpoint of at most 1 chord colored $c, j=1, \ldots, i$. Hence at most $i$ chords of color $c$ intersect $\ell$. It follows that for each $i=0,1, \ldots, n-2$ the $2 n$ chords $\ell$ with $m(\ell)=i$ contribute at least $\frac{2 n}{i+1}$ to the sum $\sum_{c} f\left(G_{c}\right)$. Summation over $i=0,1, \ldots, n-2$ gives $$ \sum_{c} f\left(G_{c}\right) \geq 2 n \sum_{i=1}^{n-1} \frac{1}{i} $$ Because there are $4 n-3$ colors in all, averaging yields a color $c$ such that $$ f\left(G_{c}\right) \geq \frac{2 n}{4 n-3} \sum_{i=1}^{n-1} \frac{1}{i}>\frac{1}{2} \sum_{i=1}^{n-1} \frac{1}{i} $$ By the lemma there are at least $\frac{1}{2} \sum_{i=1}^{n-1} \frac{1}{i}$ pairwise disjoint chords of color $c$, i. e. with the same sum $c$ of the pairs of numbers at their endpoints. It remains to show that $\frac{1}{2} \sum_{i=1}^{n-1} \frac{1}{i} \geq 100$ for $n=2^{499}$. Indeed we have $$ \sum_{i=1}^{n-1} \frac{1}{i}>\sum_{i=1}^{2^{400}} \frac{1}{i}=1+\sum_{k=1}^{400} \sum_{i=2^{k-1+1}}^{2^{k}} \frac{1}{i}>1+\sum_{k=1}^{400} \frac{2^{k-1}}{2^{k}}=201>200 $$ This completes the solution.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
There are given $2^{500}$ points on a circle labeled $1,2, \ldots, 2^{500}$ in some order. Prove that one can choose 100 pairwise disjoint chords joining some of these points so that the 100 sums of the pairs of numbers at the endpoints of the chosen chords are equal.
|
The proof is based on the following general fact. Lemma. In a graph $G$ each vertex $v$ has degree $d_{v}$. Then $G$ contains an independent set $S$ of vertices such that $|S| \geq f(G)$ where $$ f(G)=\sum_{v \in G} \frac{1}{d_{v}+1} $$ Proof. Induction on $n=|G|$. The base $n=1$ is clear. For the inductive step choose a vertex $v_{0}$ in $G$ of minimum degree $d$. Delete $v_{0}$ and all of its neighbors $v_{1}, \ldots, v_{d}$ and also all edges with endpoints $v_{0}, v_{1}, \ldots, v_{d}$. This gives a new graph $G^{\prime}$. By the inductive assumption $G^{\prime}$ contains an independent set $S^{\prime}$ of vertices such that $\left|S^{\prime}\right| \geq f\left(G^{\prime}\right)$. Since no vertex in $S^{\prime}$ is a neighbor of $v_{0}$ in $G$, the set $S=S^{\prime} \cup\left\{v_{0}\right\}$ is independent in $G$. Let $d_{v}^{\prime}$ be the degree of a vertex $v$ in $G^{\prime}$. Clearly $d_{v}^{\prime} \leq d_{v}$ for every such vertex $v$, and also $d_{v_{i}} \geq d$ for all $i=0,1, \ldots, d$ by the minimal choice of $v_{0}$. Therefore $$ f\left(G^{\prime}\right)=\sum_{v \in G^{\prime}} \frac{1}{d_{v}^{\prime}+1} \geq \sum_{v \in G^{\prime}} \frac{1}{d_{v}+1}=f(G)-\sum_{i=0}^{d} \frac{1}{d_{v_{i}}+1} \geq f(G)-\frac{d+1}{d+1}=f(G)-1 . $$ Hence $|S|=\left|S^{\prime}\right|+1 \geq f\left(G^{\prime}\right)+1 \geq f(G)$, and the induction is complete. We pass on to our problem. For clarity denote $n=2^{499}$ and draw all chords determined by the given $2 n$ points. Color each chord with one of the colors $3,4, \ldots, 4 n-1$ according to the sum of the numbers at its endpoints. Chords with a common endpoint have different colors. For each color $c$ consider the following graph $G_{c}$. Its vertices are the chords of color $c$, and two chords are neighbors in $G_{c}$ if they intersect. Let $f\left(G_{c}\right)$ have the same meaning as in the lemma for all graphs $G_{c}$. Every chord $\ell$ divides the circle into two arcs, and one of them contains $m(\ell) \leq n-1$ given points. (In particular $m(\ell)=0$ if $\ell$ joins two consecutive points.) For each $i=0,1, \ldots, n-2$ there are $2 n$ chords $\ell$ with $m(\ell)=i$. Such a chord has degree at most $i$ in the respective graph. Indeed let $A_{1}, \ldots, A_{i}$ be all points on either arc determined by a chord $\ell$ with $m(\ell)=i$ and color $c$. Every $A_{j}$ is an endpoint of at most 1 chord colored $c, j=1, \ldots, i$. Hence at most $i$ chords of color $c$ intersect $\ell$. It follows that for each $i=0,1, \ldots, n-2$ the $2 n$ chords $\ell$ with $m(\ell)=i$ contribute at least $\frac{2 n}{i+1}$ to the sum $\sum_{c} f\left(G_{c}\right)$. Summation over $i=0,1, \ldots, n-2$ gives $$ \sum_{c} f\left(G_{c}\right) \geq 2 n \sum_{i=1}^{n-1} \frac{1}{i} $$ Because there are $4 n-3$ colors in all, averaging yields a color $c$ such that $$ f\left(G_{c}\right) \geq \frac{2 n}{4 n-3} \sum_{i=1}^{n-1} \frac{1}{i}>\frac{1}{2} \sum_{i=1}^{n-1} \frac{1}{i} $$ By the lemma there are at least $\frac{1}{2} \sum_{i=1}^{n-1} \frac{1}{i}$ pairwise disjoint chords of color $c$, i. e. with the same sum $c$ of the pairs of numbers at their endpoints. It remains to show that $\frac{1}{2} \sum_{i=1}^{n-1} \frac{1}{i} \geq 100$ for $n=2^{499}$. Indeed we have $$ \sum_{i=1}^{n-1} \frac{1}{i}>\sum_{i=1}^{2^{400}} \frac{1}{i}=1+\sum_{k=1}^{400} \sum_{i=2^{k-1+1}}^{2^{k}} \frac{1}{i}>1+\sum_{k=1}^{400} \frac{2^{k-1}}{2^{k}}=201>200 $$ This completes the solution.
|
{
"resource_path": "IMO/segmented/en-IMO2012SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
99ef8db9-945c-5776-8c22-da704bff3e05
| 24,181
|
In the triangle $A B C$ the point $J$ is the center of the excircle opposite to $A$. This excircle is tangent to the side $B C$ at $M$, and to the lines $A B$ and $A C$ at $K$ and $L$ respectively. The lines $L M$ and $B J$ meet at $F$, and the lines $K M$ and $C J$ meet at $G$. Let $S$ be the point of intersection of the lines $A F$ and $B C$, and let $T$ be the point of intersection of the lines $A G$ and $B C$. Prove that $M$ is the midpoint of $S T$.
|
Let $\alpha=\angle C A B, \beta=\angle A B C$ and $\gamma=\angle B C A$. The line $A J$ is the bisector of $\angle C A B$, so $\angle J A K=\angle J A L=\frac{\alpha}{2}$. By $\angle A K J=\angle A L J=90^{\circ}$ the points $K$ and $L$ lie on the circle $\omega$ with diameter $A J$. The triangle $K B M$ is isosceles as $B K$ and $B M$ are tangents to the excircle. Since $B J$ is the bisector of $\angle K B M$, we have $\angle M B J=90^{\circ}-\frac{\beta}{2}$ and $\angle B M K=\frac{\beta}{2}$. Likewise $\angle M C J=90^{\circ}-\frac{\gamma}{2}$ and $\angle C M L=\frac{\gamma}{2}$. Also $\angle B M F=\angle C M L$, therefore $$ \angle L F J=\angle M B J-\angle B M F=\left(90^{\circ}-\frac{\beta}{2}\right)-\frac{\gamma}{2}=\frac{\alpha}{2}=\angle L A J . $$ Hence $F$ lies on the circle $\omega$. (By the angle computation, $F$ and $A$ are on the same side of $B C$.) Analogously, $G$ also lies on $\omega$. Since $A J$ is a diameter of $\omega$, we obtain $\angle A F J=\angle A G J=90^{\circ}$. 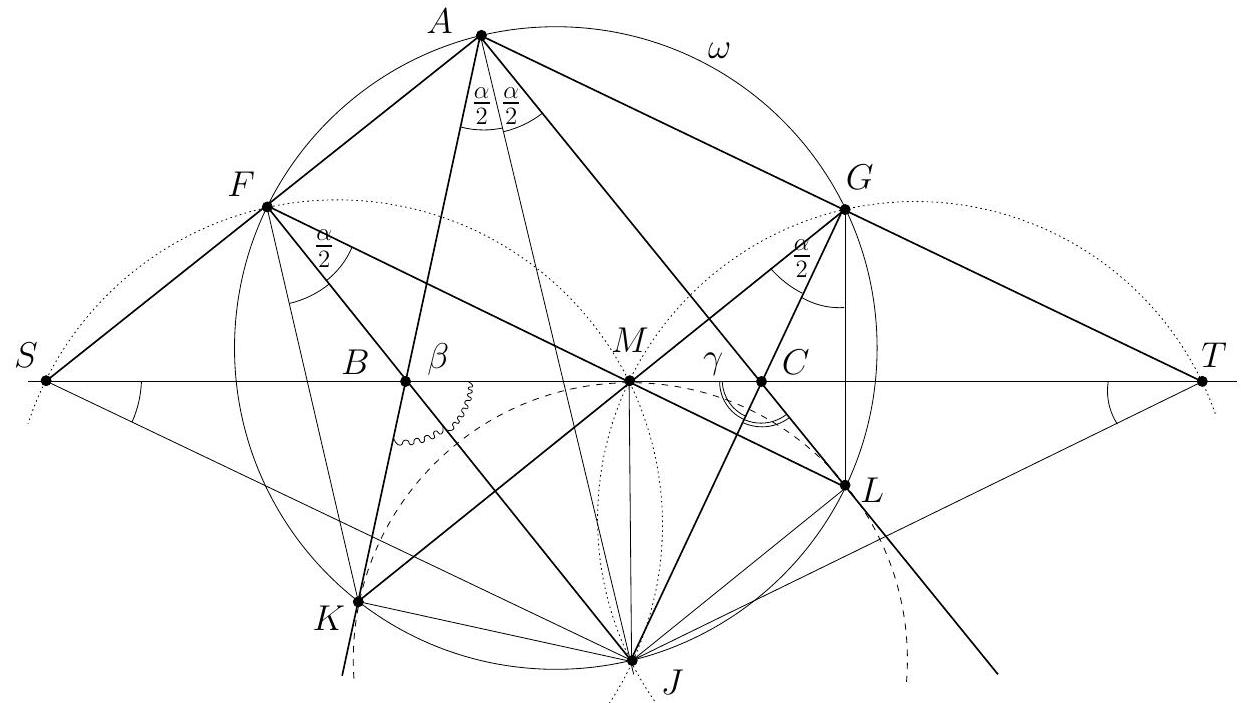 The lines $A B$ and $B C$ are symmetric with respect to the external bisector $B F$. Because $A F \perp B F$ and $K M \perp B F$, the segments $S M$ and $A K$ are symmetric with respect to $B F$, hence $S M=A K$. By symmetry $T M=A L$. Since $A K$ and $A L$ are equal as tangents to the excircle, it follows that $S M=T M$, and the proof is complete. Comment. After discovering the circle $A F K J L G$, there are many other ways to complete the solution. For instance, from the cyclic quadrilaterals $J M F S$ and $J M G T$ one can find $\angle T S J=\angle S T J=\frac{\alpha}{2}$. Another possibility is to use the fact that the lines $A S$ and $G M$ are parallel (both are perpendicular to the external angle bisector $B J$ ), so $\frac{M S}{M T}=\frac{A G}{G T}=1$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In the triangle $A B C$ the point $J$ is the center of the excircle opposite to $A$. This excircle is tangent to the side $B C$ at $M$, and to the lines $A B$ and $A C$ at $K$ and $L$ respectively. The lines $L M$ and $B J$ meet at $F$, and the lines $K M$ and $C J$ meet at $G$. Let $S$ be the point of intersection of the lines $A F$ and $B C$, and let $T$ be the point of intersection of the lines $A G$ and $B C$. Prove that $M$ is the midpoint of $S T$.
|
Let $\alpha=\angle C A B, \beta=\angle A B C$ and $\gamma=\angle B C A$. The line $A J$ is the bisector of $\angle C A B$, so $\angle J A K=\angle J A L=\frac{\alpha}{2}$. By $\angle A K J=\angle A L J=90^{\circ}$ the points $K$ and $L$ lie on the circle $\omega$ with diameter $A J$. The triangle $K B M$ is isosceles as $B K$ and $B M$ are tangents to the excircle. Since $B J$ is the bisector of $\angle K B M$, we have $\angle M B J=90^{\circ}-\frac{\beta}{2}$ and $\angle B M K=\frac{\beta}{2}$. Likewise $\angle M C J=90^{\circ}-\frac{\gamma}{2}$ and $\angle C M L=\frac{\gamma}{2}$. Also $\angle B M F=\angle C M L$, therefore $$ \angle L F J=\angle M B J-\angle B M F=\left(90^{\circ}-\frac{\beta}{2}\right)-\frac{\gamma}{2}=\frac{\alpha}{2}=\angle L A J . $$ Hence $F$ lies on the circle $\omega$. (By the angle computation, $F$ and $A$ are on the same side of $B C$.) Analogously, $G$ also lies on $\omega$. Since $A J$ is a diameter of $\omega$, we obtain $\angle A F J=\angle A G J=90^{\circ}$.  The lines $A B$ and $B C$ are symmetric with respect to the external bisector $B F$. Because $A F \perp B F$ and $K M \perp B F$, the segments $S M$ and $A K$ are symmetric with respect to $B F$, hence $S M=A K$. By symmetry $T M=A L$. Since $A K$ and $A L$ are equal as tangents to the excircle, it follows that $S M=T M$, and the proof is complete. Comment. After discovering the circle $A F K J L G$, there are many other ways to complete the solution. For instance, from the cyclic quadrilaterals $J M F S$ and $J M G T$ one can find $\angle T S J=\angle S T J=\frac{\alpha}{2}$. Another possibility is to use the fact that the lines $A S$ and $G M$ are parallel (both are perpendicular to the external angle bisector $B J$ ), so $\frac{M S}{M T}=\frac{A G}{G T}=1$.
|
{
"resource_path": "IMO/segmented/en-IMO2012SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
af8ca3ab-1067-5f94-b043-bcc229327c29
| 24,185
|
Let $A B C D$ be a cyclic quadrilateral whose diagonals $A C$ and $B D$ meet at $E$. The extensions of the sides $A D$ and $B C$ beyond $A$ and $B$ meet at $F$. Let $G$ be the point such that $E C G D$ is a parallelogram, and let $H$ be the image of $E$ under reflection in $A D$. Prove that $D, H, F, G$ are concyclic.
|
We show first that the triangles $F D G$ and $F B E$ are similar. Since $A B C D$ is cyclic, the triangles $E A B$ and $E D C$ are similar, as well as $F A B$ and $F C D$. The parallelogram $E C G D$ yields $G D=E C$ and $\angle C D G=\angle D C E$; also $\angle D C E=\angle D C A=\angle D B A$ by inscribed angles. Therefore $$ \begin{gathered} \angle F D G=\angle F D C+\angle C D G=\angle F B A+\angle A B D=\angle F B E, \\ \frac{G D}{E B}=\frac{C E}{E B}=\frac{C D}{A B}=\frac{F D}{F B} . \end{gathered} $$ It follows that $F D G$ and $F B E$ are similar, and so $\angle F G D=\angle F E B$. 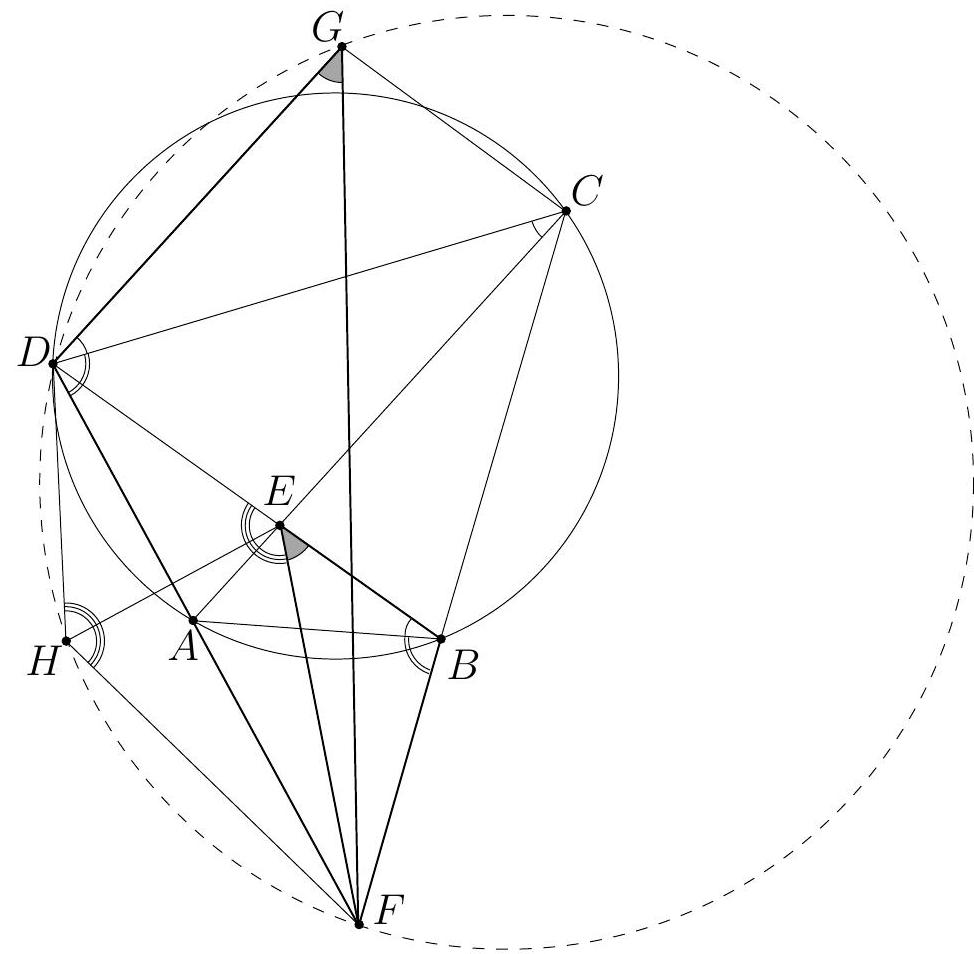 Since $H$ is the reflection of $E$ with respect to $F D$, we conclude that $$ \angle F H D=\angle F E D=180^{\circ}-\angle F E B=180^{\circ}-\angle F G D . $$ This proves that $D, H, F, G$ are concyclic. Comment. Points $E$ and $G$ are always in the half-plane determined by the line $F D$ that contains $B$ and $C$, but $H$ is always in the other half-plane. In particular, $D H F G$ is cyclic if and only if $\angle F H D+\angle F G D=180^{\circ}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic quadrilateral whose diagonals $A C$ and $B D$ meet at $E$. The extensions of the sides $A D$ and $B C$ beyond $A$ and $B$ meet at $F$. Let $G$ be the point such that $E C G D$ is a parallelogram, and let $H$ be the image of $E$ under reflection in $A D$. Prove that $D, H, F, G$ are concyclic.
|
We show first that the triangles $F D G$ and $F B E$ are similar. Since $A B C D$ is cyclic, the triangles $E A B$ and $E D C$ are similar, as well as $F A B$ and $F C D$. The parallelogram $E C G D$ yields $G D=E C$ and $\angle C D G=\angle D C E$; also $\angle D C E=\angle D C A=\angle D B A$ by inscribed angles. Therefore $$ \begin{gathered} \angle F D G=\angle F D C+\angle C D G=\angle F B A+\angle A B D=\angle F B E, \\ \frac{G D}{E B}=\frac{C E}{E B}=\frac{C D}{A B}=\frac{F D}{F B} . \end{gathered} $$ It follows that $F D G$ and $F B E$ are similar, and so $\angle F G D=\angle F E B$.  Since $H$ is the reflection of $E$ with respect to $F D$, we conclude that $$ \angle F H D=\angle F E D=180^{\circ}-\angle F E B=180^{\circ}-\angle F G D . $$ This proves that $D, H, F, G$ are concyclic. Comment. Points $E$ and $G$ are always in the half-plane determined by the line $F D$ that contains $B$ and $C$, but $H$ is always in the other half-plane. In particular, $D H F G$ is cyclic if and only if $\angle F H D+\angle F G D=180^{\circ}$.
|
{
"resource_path": "IMO/segmented/en-IMO2012SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
acb9a374-c904-58cf-b986-5cbd4475ab71
| 24,187
|
In an acute triangle $A B C$ the points $D, E$ and $F$ are the feet of the altitudes through $A$, $B$ and $C$ respectively. The incenters of the triangles $A E F$ and $B D F$ are $I_{1}$ and $I_{2}$ respectively; the circumcenters of the triangles $A C I_{1}$ and $B C I_{2}$ are $O_{1}$ and $O_{2}$ respectively. Prove that $I_{1} I_{2}$ and $O_{1} O_{2}$ are parallel.
|
Let $\angle C A B=\alpha, \angle A B C=\beta, \angle B C A=\gamma$. We start by showing that $A, B, I_{1}$ and $I_{2}$ are concyclic. Since $A I_{1}$ and $B I_{2}$ bisect $\angle C A B$ and $\angle A B C$, their extensions beyond $I_{1}$ and $I_{2}$ meet at the incenter $I$ of the triangle. The points $E$ and $F$ are on the circle with diameter $B C$, so $\angle A E F=\angle A B C$ and $\angle A F E=\angle A C B$. Hence the triangles $A E F$ and $A B C$ are similar with ratio of similitude $\frac{A E}{A B}=\cos \alpha$. Because $I_{1}$ and $I$ are their incenters, we obtain $I_{1} A=I A \cos \alpha$ and $I I_{1}=I A-I_{1} A=2 I A \sin ^{2} \frac{\alpha}{2}$. By symmetry $I I_{2}=2 I B \sin ^{2} \frac{\beta}{2}$. The law of sines in the triangle $A B I$ gives $I A \sin \frac{\alpha}{2}=I B \sin \frac{\beta}{2}$. Hence $$ I I_{1} \cdot I A=2\left(I A \sin \frac{\alpha}{2}\right)^{2}=2\left(I B \sin \frac{\beta}{2}\right)^{2}=I I_{2} \cdot I B $$ Therefore $A, B, I_{1}$ and $I_{2}$ are concyclic, as claimed. 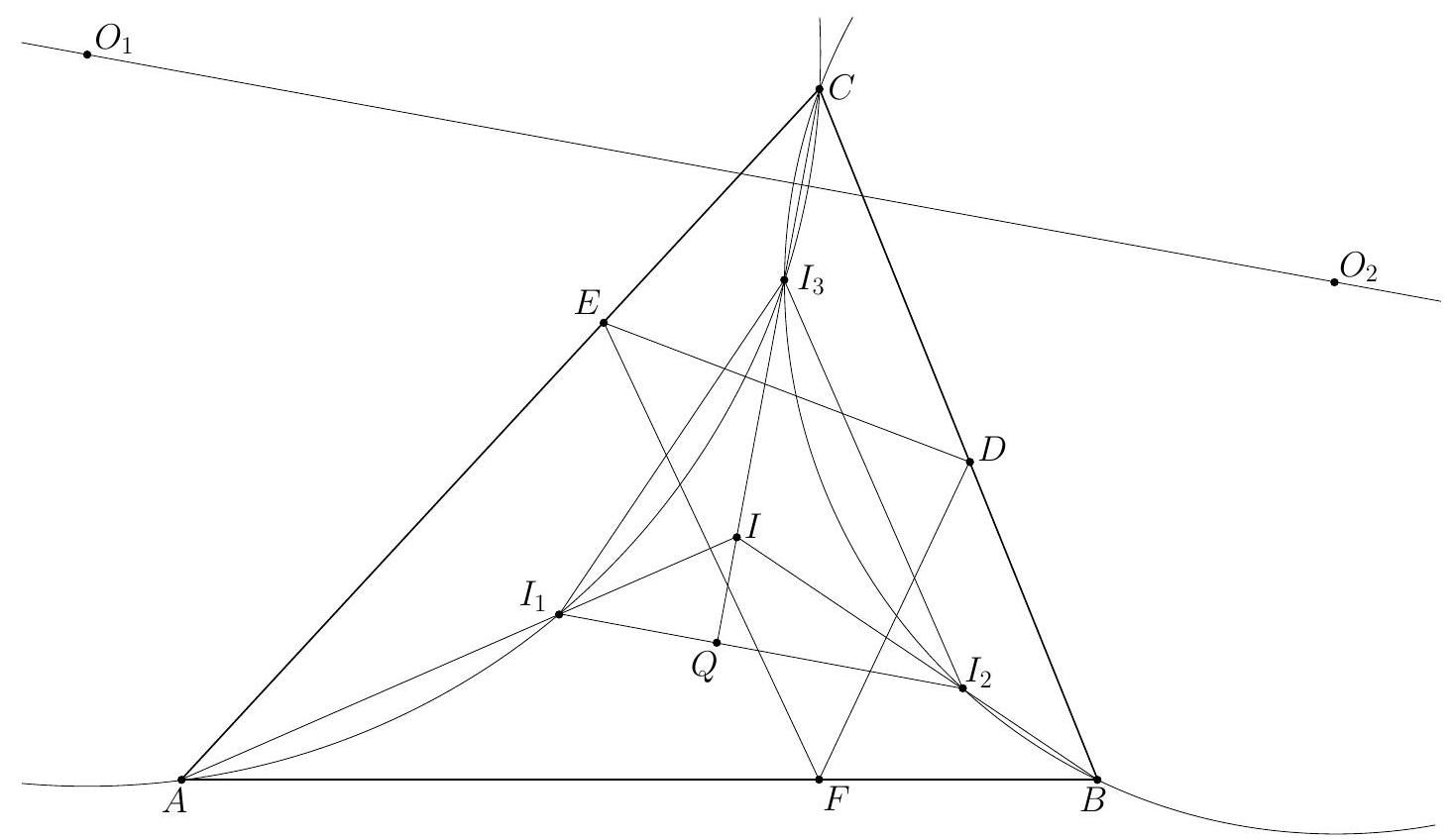 In addition $I I_{1} \cdot I A=I I_{2} \cdot I B$ implies that $I$ has the same power with respect to the circles $\left(A C I_{1}\right),\left(B C I_{2}\right)$ and $\left(A B I_{1} I_{2}\right)$. Then $C I$ is the radical axis of $\left(A C I_{1}\right)$ and $\left(B C I_{2}\right)$; in particular $C I$ is perpendicular to the line of centers $O_{1} O_{2}$. Now it suffices to prove that $C I \perp I_{1} I_{2}$. Let $C I$ meet $I_{1} I_{2}$ at $Q$, then it is enough to check that $\angle I I_{1} Q+\angle I_{1} I Q=90^{\circ}$. Since $\angle I_{1} I Q$ is external for the triangle $A C I$, we have $$ \angle I I_{1} Q+\angle I_{1} I Q=\angle I I_{1} Q+(\angle A C I+\angle C A I)=\angle I I_{1} I_{2}+\angle A C I+\angle C A I . $$ It remains to note that $\angle I I_{1} I_{2}=\frac{\beta}{2}$ from the cyclic quadrilateral $A B I_{1} I_{2}$, and $\angle A C I=\frac{\gamma}{2}$, $\angle C A I=\frac{\alpha}{2}$. Therefore $\angle I I_{1} Q+\angle I_{1} I Q=\frac{\alpha}{2}+\frac{\beta}{2}+\frac{\gamma}{2}=90^{\circ}$, completing the proof. Comment. It follows from the first part of the solution that the common point $I_{3} \neq C$ of the circles $\left(A C I_{1}\right)$ and $\left(B C I_{2}\right)$ is the incenter of the triangle $C D E$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In an acute triangle $A B C$ the points $D, E$ and $F$ are the feet of the altitudes through $A$, $B$ and $C$ respectively. The incenters of the triangles $A E F$ and $B D F$ are $I_{1}$ and $I_{2}$ respectively; the circumcenters of the triangles $A C I_{1}$ and $B C I_{2}$ are $O_{1}$ and $O_{2}$ respectively. Prove that $I_{1} I_{2}$ and $O_{1} O_{2}$ are parallel.
|
Let $\angle C A B=\alpha, \angle A B C=\beta, \angle B C A=\gamma$. We start by showing that $A, B, I_{1}$ and $I_{2}$ are concyclic. Since $A I_{1}$ and $B I_{2}$ bisect $\angle C A B$ and $\angle A B C$, their extensions beyond $I_{1}$ and $I_{2}$ meet at the incenter $I$ of the triangle. The points $E$ and $F$ are on the circle with diameter $B C$, so $\angle A E F=\angle A B C$ and $\angle A F E=\angle A C B$. Hence the triangles $A E F$ and $A B C$ are similar with ratio of similitude $\frac{A E}{A B}=\cos \alpha$. Because $I_{1}$ and $I$ are their incenters, we obtain $I_{1} A=I A \cos \alpha$ and $I I_{1}=I A-I_{1} A=2 I A \sin ^{2} \frac{\alpha}{2}$. By symmetry $I I_{2}=2 I B \sin ^{2} \frac{\beta}{2}$. The law of sines in the triangle $A B I$ gives $I A \sin \frac{\alpha}{2}=I B \sin \frac{\beta}{2}$. Hence $$ I I_{1} \cdot I A=2\left(I A \sin \frac{\alpha}{2}\right)^{2}=2\left(I B \sin \frac{\beta}{2}\right)^{2}=I I_{2} \cdot I B $$ Therefore $A, B, I_{1}$ and $I_{2}$ are concyclic, as claimed.  In addition $I I_{1} \cdot I A=I I_{2} \cdot I B$ implies that $I$ has the same power with respect to the circles $\left(A C I_{1}\right),\left(B C I_{2}\right)$ and $\left(A B I_{1} I_{2}\right)$. Then $C I$ is the radical axis of $\left(A C I_{1}\right)$ and $\left(B C I_{2}\right)$; in particular $C I$ is perpendicular to the line of centers $O_{1} O_{2}$. Now it suffices to prove that $C I \perp I_{1} I_{2}$. Let $C I$ meet $I_{1} I_{2}$ at $Q$, then it is enough to check that $\angle I I_{1} Q+\angle I_{1} I Q=90^{\circ}$. Since $\angle I_{1} I Q$ is external for the triangle $A C I$, we have $$ \angle I I_{1} Q+\angle I_{1} I Q=\angle I I_{1} Q+(\angle A C I+\angle C A I)=\angle I I_{1} I_{2}+\angle A C I+\angle C A I . $$ It remains to note that $\angle I I_{1} I_{2}=\frac{\beta}{2}$ from the cyclic quadrilateral $A B I_{1} I_{2}$, and $\angle A C I=\frac{\gamma}{2}$, $\angle C A I=\frac{\alpha}{2}$. Therefore $\angle I I_{1} Q+\angle I_{1} I Q=\frac{\alpha}{2}+\frac{\beta}{2}+\frac{\gamma}{2}=90^{\circ}$, completing the proof. Comment. It follows from the first part of the solution that the common point $I_{3} \neq C$ of the circles $\left(A C I_{1}\right)$ and $\left(B C I_{2}\right)$ is the incenter of the triangle $C D E$.
|
{
"resource_path": "IMO/segmented/en-IMO2012SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
6b5691a3-205f-5705-92a1-ce59bd706da3
| 24,190
|
Let $A B C$ be a triangle with $A B \neq A C$ and circumcenter $O$. The bisector of $\angle B A C$ intersects $B C$ at $D$. Let $E$ be the reflection of $D$ with respect to the midpoint of $B C$. The lines through $D$ and $E$ perpendicular to $B C$ intersect the lines $A O$ and $A D$ at $X$ and $Y$ respectively. Prove that the quadrilateral $B X C Y$ is cyclic.
|
The bisector of $\angle B A C$ and the perpendicular bisector of $B C$ meet at $P$, the midpoint of the minor arc $\widehat{B C}$ (they are different lines as $A B \neq A C$ ). In particular $O P$ is perpendicular to $B C$ and intersects it at $M$, the midpoint of $B C$. Denote by $Y^{\prime}$ the reflexion of $Y$ with respect to $O P$. Since $\angle B Y C=\angle B Y^{\prime} C$, it suffices to prove that $B X C Y^{\prime}$ is cyclic.  We have $$ \angle X A P=\angle O P A=\angle E Y P \text {. } $$ The first equality holds because $O A=O P$, and the second one because $E Y$ and $O P$ are both perpendicular to $B C$ and hence parallel. But $\left\{Y, Y^{\prime}\right\}$ and $\{E, D\}$ are pairs of symmetric points with respect to $O P$, it follows that $\angle E Y P=\angle D Y^{\prime} P$ and hence $$ \angle X A P=\angle D Y^{\prime} P=\angle X Y^{\prime} P . $$ The last equation implies that $X A Y^{\prime} P$ is cyclic. By the powers of $D$ with respect to the circles $\left(X A Y^{\prime} P\right)$ and $(A B P C)$ we obtain $$ X D \cdot D Y^{\prime}=A D \cdot D P=B D \cdot D C $$ It follows that $B X C Y^{\prime}$ is cyclic, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $A B \neq A C$ and circumcenter $O$. The bisector of $\angle B A C$ intersects $B C$ at $D$. Let $E$ be the reflection of $D$ with respect to the midpoint of $B C$. The lines through $D$ and $E$ perpendicular to $B C$ intersect the lines $A O$ and $A D$ at $X$ and $Y$ respectively. Prove that the quadrilateral $B X C Y$ is cyclic.
|
The bisector of $\angle B A C$ and the perpendicular bisector of $B C$ meet at $P$, the midpoint of the minor arc $\widehat{B C}$ (they are different lines as $A B \neq A C$ ). In particular $O P$ is perpendicular to $B C$ and intersects it at $M$, the midpoint of $B C$. Denote by $Y^{\prime}$ the reflexion of $Y$ with respect to $O P$. Since $\angle B Y C=\angle B Y^{\prime} C$, it suffices to prove that $B X C Y^{\prime}$ is cyclic.  We have $$ \angle X A P=\angle O P A=\angle E Y P \text {. } $$ The first equality holds because $O A=O P$, and the second one because $E Y$ and $O P$ are both perpendicular to $B C$ and hence parallel. But $\left\{Y, Y^{\prime}\right\}$ and $\{E, D\}$ are pairs of symmetric points with respect to $O P$, it follows that $\angle E Y P=\angle D Y^{\prime} P$ and hence $$ \angle X A P=\angle D Y^{\prime} P=\angle X Y^{\prime} P . $$ The last equation implies that $X A Y^{\prime} P$ is cyclic. By the powers of $D$ with respect to the circles $\left(X A Y^{\prime} P\right)$ and $(A B P C)$ we obtain $$ X D \cdot D Y^{\prime}=A D \cdot D P=B D \cdot D C $$ It follows that $B X C Y^{\prime}$ is cyclic, as desired.
|
{
"resource_path": "IMO/segmented/en-IMO2012SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
24b96a84-9749-5f22-b8fc-56de276e0453
| 24,192
|
Let $A B C$ be a triangle with $\angle B C A=90^{\circ}$, and let $C_{0}$ be the foot of the altitude from $C$. Choose a point $X$ in the interior of the segment $C C_{0}$, and let $K, L$ be the points on the segments $A X, B X$ for which $B K=B C$ and $A L=A C$ respectively. Denote by $M$ the intersection of $A L$ and $B K$. Show that $M K=M L$.
|
Let $C^{\prime}$ be the reflection of $C$ in the line $A B$, and let $\omega_{1}$ and $\omega_{2}$ be the circles with centers $A$ and $B$, passing through $L$ and $K$ respectively. Since $A C^{\prime}=A C=A L$ and $B C^{\prime}=B C=B K$, both $\omega_{1}$ and $\omega_{2}$ pass through $C$ and $C^{\prime}$. By $\angle B C A=90^{\circ}, A C$ is tangent to $\omega_{2}$ at $C$, and $B C$ is tangent to $\omega_{1}$ at $C$. Let $K_{1} \neq K$ be the second intersection of $A X$ and $\omega_{2}$, and let $L_{1} \neq L$ be the second intersection of $B X$ and $\omega_{1}$. 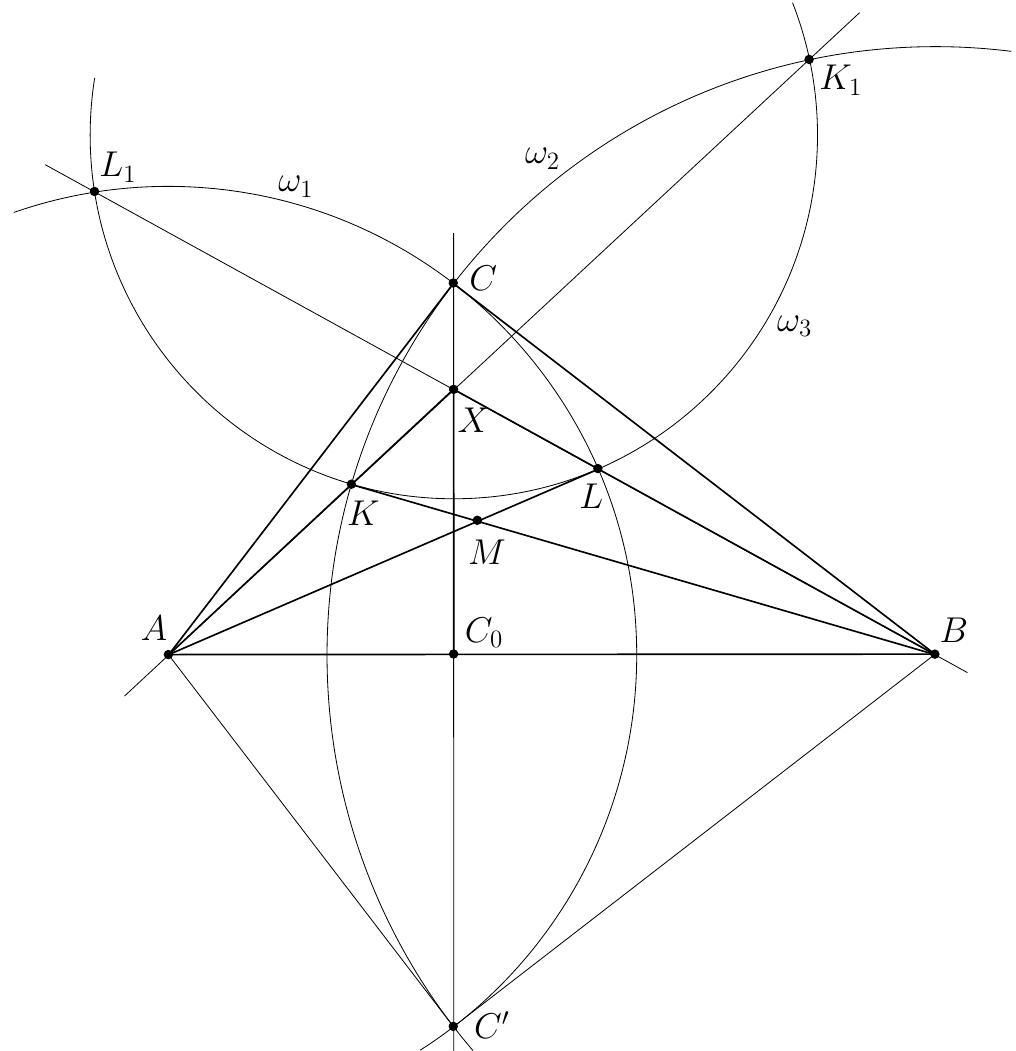 By the powers of $X$ with respect to $\omega_{2}$ and $\omega_{1}$, $$ X K \cdot X K_{1}=X C \cdot X C^{\prime}=X L \cdot X L_{1}, $$ so the points $K_{1}, L, K, L_{1}$ lie on a circle $\omega_{3}$. The power of $A$ with respect to $\omega_{2}$ gives $$ A L^{2}=A C^{2}=A K \cdot A K_{1}, $$ indicating that $A L$ is tangent to $\omega_{3}$ at $L$. Analogously, $B K$ is tangent to $\omega_{3}$ at $K$. Hence $M K$ and $M L$ are the two tangents from $M$ to $\omega_{3}$ and therefore $M K=M L$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $\angle B C A=90^{\circ}$, and let $C_{0}$ be the foot of the altitude from $C$. Choose a point $X$ in the interior of the segment $C C_{0}$, and let $K, L$ be the points on the segments $A X, B X$ for which $B K=B C$ and $A L=A C$ respectively. Denote by $M$ the intersection of $A L$ and $B K$. Show that $M K=M L$.
|
Let $C^{\prime}$ be the reflection of $C$ in the line $A B$, and let $\omega_{1}$ and $\omega_{2}$ be the circles with centers $A$ and $B$, passing through $L$ and $K$ respectively. Since $A C^{\prime}=A C=A L$ and $B C^{\prime}=B C=B K$, both $\omega_{1}$ and $\omega_{2}$ pass through $C$ and $C^{\prime}$. By $\angle B C A=90^{\circ}, A C$ is tangent to $\omega_{2}$ at $C$, and $B C$ is tangent to $\omega_{1}$ at $C$. Let $K_{1} \neq K$ be the second intersection of $A X$ and $\omega_{2}$, and let $L_{1} \neq L$ be the second intersection of $B X$ and $\omega_{1}$.  By the powers of $X$ with respect to $\omega_{2}$ and $\omega_{1}$, $$ X K \cdot X K_{1}=X C \cdot X C^{\prime}=X L \cdot X L_{1}, $$ so the points $K_{1}, L, K, L_{1}$ lie on a circle $\omega_{3}$. The power of $A$ with respect to $\omega_{2}$ gives $$ A L^{2}=A C^{2}=A K \cdot A K_{1}, $$ indicating that $A L$ is tangent to $\omega_{3}$ at $L$. Analogously, $B K$ is tangent to $\omega_{3}$ at $K$. Hence $M K$ and $M L$ are the two tangents from $M$ to $\omega_{3}$ and therefore $M K=M L$.
|
{
"resource_path": "IMO/segmented/en-IMO2012SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
e5ddc390-6451-54a6-9e44-3b9fa2444ac4
| 24,195
|
Let $A B C$ be a triangle with circumcenter $O$ and incenter $I$. The points $D, E$ and $F$ on the sides $B C, C A$ and $A B$ respectively are such that $B D+B F=C A$ and $C D+C E=A B$. The circumcircles of the triangles $B F D$ and $C D E$ intersect at $P \neq D$. Prove that $O P=O I$.
|
By Miquel's theorem the circles $(A E F)=\omega_{A},(B F D)=\omega_{B}$ and $(C D E)=\omega_{C}$ have a common point, for arbitrary points $D, E$ and $F$ on $B C, C A$ and $A B$. So $\omega_{A}$ passes through the common point $P \neq D$ of $\omega_{B}$ and $\omega_{C}$. Let $\omega_{A}, \omega_{B}$ and $\omega_{C}$ meet the bisectors $A I, B I$ and $C I$ at $A \neq A^{\prime}, B \neq B^{\prime}$ and $C \neq C^{\prime}$ respectively. The key observation is that $A^{\prime}, B^{\prime}$ and $C^{\prime}$ do not depend on the particular choice of $D, E$ and $F$, provided that $B D+B F=C A, C D+C E=A B$ and $A E+A F=B C$ hold true (the last equality follows from the other two). For a proof we need the following fact. Lemma. Given is an angle with vertex $A$ and measure $\alpha$. A circle $\omega$ through $A$ intersects the angle bisector at $L$ and sides of the angle at $X$ and $Y$. Then $A X+A Y=2 A L \cos \frac{\alpha}{2}$. Proof. Note that $L$ is the midpoint of $\operatorname{arc} \widehat{X L Y}$ in $\omega$ and set $X L=Y L=u, X Y=v$. By PtOLEMY's theorem $A X \cdot Y L+A Y \cdot X L=A L \cdot X Y$, which rewrites as $(A X+A Y) u=A L \cdot v$. Since $\angle L X Y=\frac{\alpha}{2}$ and $\angle X L Y=180^{\circ}-\alpha$, we have $v=2 \cos \frac{\alpha}{2} u$ by the law of sines, and the claim follows. 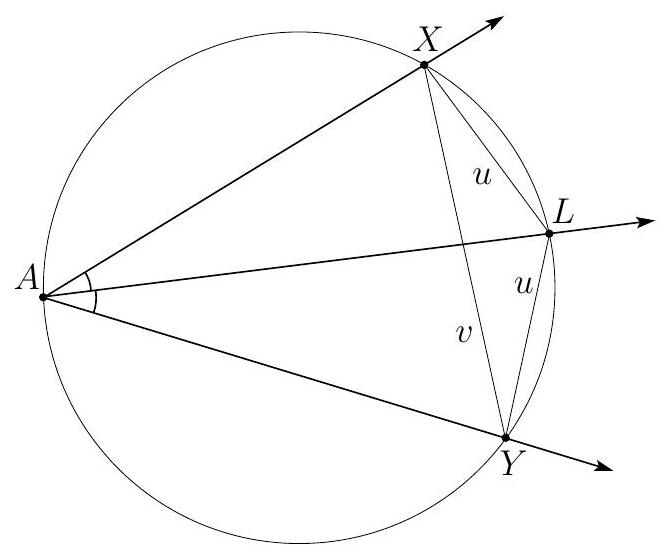 Apply the lemma to $\angle B A C=\alpha$ and the circle $\omega=\omega_{A}$, which intersects $A I$ at $A^{\prime}$. This gives $2 A A^{\prime} \cos \frac{\alpha}{2}=A E+A F=B C$; by symmetry analogous relations hold for $B B^{\prime}$ and $C C^{\prime}$. It follows that $A^{\prime}, B^{\prime}$ and $C^{\prime}$ are independent of the choice of $D, E$ and $F$, as stated. We use the lemma two more times with $\angle B A C=\alpha$. Let $\omega$ be the circle with diameter $A I$. Then $X$ and $Y$ are the tangency points of the incircle of $A B C$ with $A B$ and $A C$, and hence $A X=A Y=\frac{1}{2}(A B+A C-B C)$. So the lemma yields $2 A I \cos \frac{\alpha}{2}=A B+A C-B C$. Next, if $\omega$ is the circumcircle of $A B C$ and $A I$ intersects $\omega$ at $M \neq A$ then $\{X, Y\}=\{B, C\}$, and so $2 A M \cos \frac{\alpha}{2}=A B+A C$ by the lemma. To summarize, $$ 2 A A^{\prime} \cos \frac{\alpha}{2}=B C, \quad 2 A I \cos \frac{\alpha}{2}=A B+A C-B C, \quad 2 A M \cos \frac{\alpha}{2}=A B+A C $$ These equalities imply $A A^{\prime}+A I=A M$, hence the segments $A M$ and $I A^{\prime}$ have a common midpoint. It follows that $I$ and $A^{\prime}$ are equidistant from the circumcenter $O$. By symmetry $O I=O A^{\prime}=O B^{\prime}=O C^{\prime}$, so $I, A^{\prime}, B^{\prime}, C^{\prime}$ are on a circle centered at $O$. To prove $O P=O I$, now it suffices to show that $I, A^{\prime}, B^{\prime}, C^{\prime}$ and $P$ are concyclic. Clearly one can assume $P \neq I, A^{\prime}, B^{\prime}, C^{\prime}$. We use oriented angles to avoid heavy case distinction. The oriented angle between the lines $l$ and $m$ is denoted by $\angle(l, m)$. We have $\angle(l, m)=-\angle(m, l)$ and $\angle(l, m)+\angle(m, n)=\angle(l, n)$ for arbitrary lines $l, m$ and $n$. Four distinct non-collinear points $U, V, X, Y$ are concyclic if and only if $\angle(U X, V X)=\angle(U Y, V Y)$. 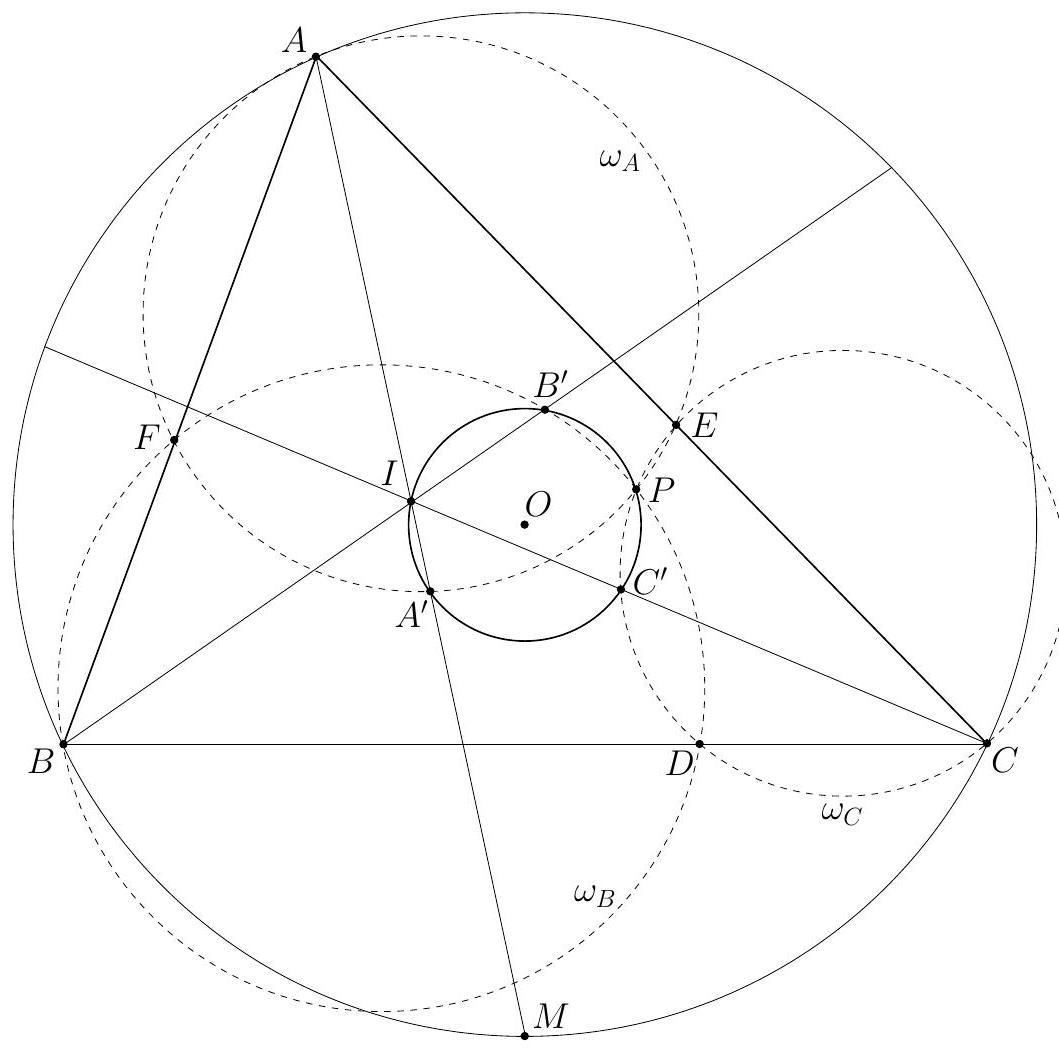 Suppose for the moment that $A^{\prime}, B^{\prime}, P, I$ are distinct and noncollinear; then it is enough to check the equality $\angle\left(A^{\prime} P, B^{\prime} P\right)=\angle\left(A^{\prime} I, B^{\prime} I\right)$. Because $A, F, P, A^{\prime}$ are on the circle $\omega_{A}$, we have $\angle\left(A^{\prime} P, F P\right)=\angle\left(A^{\prime} A, F A\right)=\angle\left(A^{\prime} I, A B\right)$. Likewise $\angle\left(B^{\prime} P, F P\right)=\angle\left(B^{\prime} I, A B\right)$. Therefore $$ \angle\left(A^{\prime} P, B^{\prime} P\right)=\angle\left(A^{\prime} P, F P\right)+\angle\left(F P, B^{\prime} P\right)=\angle\left(A^{\prime} I, A B\right)-\angle\left(B^{\prime} I, A B\right)=\angle\left(A^{\prime} I, B^{\prime} I\right) \text {. } $$ Here we assumed that $P \neq F$. If $P=F$ then $P \neq D, E$ and the conclusion follows similarly (use $\angle\left(A^{\prime} F, B^{\prime} F\right)=\angle\left(A^{\prime} F, E F\right)+\angle(E F, D F)+\angle\left(D F, B^{\prime} F\right)$ and inscribed angles in $\left.\omega_{A}, \omega_{B}, \omega_{C}\right)$. There is no loss of generality in assuming $A^{\prime}, B^{\prime}, P, I$ distinct and noncollinear. If $A B C$ is an equilateral triangle then the equalities $\left(^{*}\right)$ imply that $A^{\prime}, B^{\prime}, C^{\prime}, I, O$ and $P$ coincide, so $O P=O I$. Otherwise at most one of $A^{\prime}, B^{\prime}, C^{\prime}$ coincides with $I$. If say $C^{\prime}=I$ then $O I \perp C I$ by the previous reasoning. It follows that $A^{\prime}, B^{\prime} \neq I$ and hence $A^{\prime} \neq B^{\prime}$. Finally $A^{\prime}, B^{\prime}$ and $I$ are noncollinear because $I, A^{\prime}, B^{\prime}, C^{\prime}$ are concyclic. Comment. The proposer remarks that the locus $\gamma$ of the points $P$ is an arc of the circle $\left(A^{\prime} B^{\prime} C^{\prime} I\right)$. The reflection $I^{\prime}$ of $I$ in $O$ belongs to $\gamma$; it is obtained by choosing $D, E$ and $F$ to be the tangency points of the three excircles with their respective sides. The rest of the circle $\left(A^{\prime} B^{\prime} C^{\prime} I\right)$, except $I$, can be included in $\gamma$ by letting $D, E$ and $F$ vary on the extensions of the sides and assuming signed lengths. For instance if $B$ is between $C$ and $D$ then the length $B D$ must be taken with a negative sign. The incenter $I$ corresponds to the limit case where $D$ tends to infinity.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circumcenter $O$ and incenter $I$. The points $D, E$ and $F$ on the sides $B C, C A$ and $A B$ respectively are such that $B D+B F=C A$ and $C D+C E=A B$. The circumcircles of the triangles $B F D$ and $C D E$ intersect at $P \neq D$. Prove that $O P=O I$.
|
By Miquel's theorem the circles $(A E F)=\omega_{A},(B F D)=\omega_{B}$ and $(C D E)=\omega_{C}$ have a common point, for arbitrary points $D, E$ and $F$ on $B C, C A$ and $A B$. So $\omega_{A}$ passes through the common point $P \neq D$ of $\omega_{B}$ and $\omega_{C}$. Let $\omega_{A}, \omega_{B}$ and $\omega_{C}$ meet the bisectors $A I, B I$ and $C I$ at $A \neq A^{\prime}, B \neq B^{\prime}$ and $C \neq C^{\prime}$ respectively. The key observation is that $A^{\prime}, B^{\prime}$ and $C^{\prime}$ do not depend on the particular choice of $D, E$ and $F$, provided that $B D+B F=C A, C D+C E=A B$ and $A E+A F=B C$ hold true (the last equality follows from the other two). For a proof we need the following fact. Lemma. Given is an angle with vertex $A$ and measure $\alpha$. A circle $\omega$ through $A$ intersects the angle bisector at $L$ and sides of the angle at $X$ and $Y$. Then $A X+A Y=2 A L \cos \frac{\alpha}{2}$. Proof. Note that $L$ is the midpoint of $\operatorname{arc} \widehat{X L Y}$ in $\omega$ and set $X L=Y L=u, X Y=v$. By PtOLEMY's theorem $A X \cdot Y L+A Y \cdot X L=A L \cdot X Y$, which rewrites as $(A X+A Y) u=A L \cdot v$. Since $\angle L X Y=\frac{\alpha}{2}$ and $\angle X L Y=180^{\circ}-\alpha$, we have $v=2 \cos \frac{\alpha}{2} u$ by the law of sines, and the claim follows.  Apply the lemma to $\angle B A C=\alpha$ and the circle $\omega=\omega_{A}$, which intersects $A I$ at $A^{\prime}$. This gives $2 A A^{\prime} \cos \frac{\alpha}{2}=A E+A F=B C$; by symmetry analogous relations hold for $B B^{\prime}$ and $C C^{\prime}$. It follows that $A^{\prime}, B^{\prime}$ and $C^{\prime}$ are independent of the choice of $D, E$ and $F$, as stated. We use the lemma two more times with $\angle B A C=\alpha$. Let $\omega$ be the circle with diameter $A I$. Then $X$ and $Y$ are the tangency points of the incircle of $A B C$ with $A B$ and $A C$, and hence $A X=A Y=\frac{1}{2}(A B+A C-B C)$. So the lemma yields $2 A I \cos \frac{\alpha}{2}=A B+A C-B C$. Next, if $\omega$ is the circumcircle of $A B C$ and $A I$ intersects $\omega$ at $M \neq A$ then $\{X, Y\}=\{B, C\}$, and so $2 A M \cos \frac{\alpha}{2}=A B+A C$ by the lemma. To summarize, $$ 2 A A^{\prime} \cos \frac{\alpha}{2}=B C, \quad 2 A I \cos \frac{\alpha}{2}=A B+A C-B C, \quad 2 A M \cos \frac{\alpha}{2}=A B+A C $$ These equalities imply $A A^{\prime}+A I=A M$, hence the segments $A M$ and $I A^{\prime}$ have a common midpoint. It follows that $I$ and $A^{\prime}$ are equidistant from the circumcenter $O$. By symmetry $O I=O A^{\prime}=O B^{\prime}=O C^{\prime}$, so $I, A^{\prime}, B^{\prime}, C^{\prime}$ are on a circle centered at $O$. To prove $O P=O I$, now it suffices to show that $I, A^{\prime}, B^{\prime}, C^{\prime}$ and $P$ are concyclic. Clearly one can assume $P \neq I, A^{\prime}, B^{\prime}, C^{\prime}$. We use oriented angles to avoid heavy case distinction. The oriented angle between the lines $l$ and $m$ is denoted by $\angle(l, m)$. We have $\angle(l, m)=-\angle(m, l)$ and $\angle(l, m)+\angle(m, n)=\angle(l, n)$ for arbitrary lines $l, m$ and $n$. Four distinct non-collinear points $U, V, X, Y$ are concyclic if and only if $\angle(U X, V X)=\angle(U Y, V Y)$.  Suppose for the moment that $A^{\prime}, B^{\prime}, P, I$ are distinct and noncollinear; then it is enough to check the equality $\angle\left(A^{\prime} P, B^{\prime} P\right)=\angle\left(A^{\prime} I, B^{\prime} I\right)$. Because $A, F, P, A^{\prime}$ are on the circle $\omega_{A}$, we have $\angle\left(A^{\prime} P, F P\right)=\angle\left(A^{\prime} A, F A\right)=\angle\left(A^{\prime} I, A B\right)$. Likewise $\angle\left(B^{\prime} P, F P\right)=\angle\left(B^{\prime} I, A B\right)$. Therefore $$ \angle\left(A^{\prime} P, B^{\prime} P\right)=\angle\left(A^{\prime} P, F P\right)+\angle\left(F P, B^{\prime} P\right)=\angle\left(A^{\prime} I, A B\right)-\angle\left(B^{\prime} I, A B\right)=\angle\left(A^{\prime} I, B^{\prime} I\right) \text {. } $$ Here we assumed that $P \neq F$. If $P=F$ then $P \neq D, E$ and the conclusion follows similarly (use $\angle\left(A^{\prime} F, B^{\prime} F\right)=\angle\left(A^{\prime} F, E F\right)+\angle(E F, D F)+\angle\left(D F, B^{\prime} F\right)$ and inscribed angles in $\left.\omega_{A}, \omega_{B}, \omega_{C}\right)$. There is no loss of generality in assuming $A^{\prime}, B^{\prime}, P, I$ distinct and noncollinear. If $A B C$ is an equilateral triangle then the equalities $\left(^{*}\right)$ imply that $A^{\prime}, B^{\prime}, C^{\prime}, I, O$ and $P$ coincide, so $O P=O I$. Otherwise at most one of $A^{\prime}, B^{\prime}, C^{\prime}$ coincides with $I$. If say $C^{\prime}=I$ then $O I \perp C I$ by the previous reasoning. It follows that $A^{\prime}, B^{\prime} \neq I$ and hence $A^{\prime} \neq B^{\prime}$. Finally $A^{\prime}, B^{\prime}$ and $I$ are noncollinear because $I, A^{\prime}, B^{\prime}, C^{\prime}$ are concyclic. Comment. The proposer remarks that the locus $\gamma$ of the points $P$ is an arc of the circle $\left(A^{\prime} B^{\prime} C^{\prime} I\right)$. The reflection $I^{\prime}$ of $I$ in $O$ belongs to $\gamma$; it is obtained by choosing $D, E$ and $F$ to be the tangency points of the three excircles with their respective sides. The rest of the circle $\left(A^{\prime} B^{\prime} C^{\prime} I\right)$, except $I$, can be included in $\gamma$ by letting $D, E$ and $F$ vary on the extensions of the sides and assuming signed lengths. For instance if $B$ is between $C$ and $D$ then the length $B D$ must be taken with a negative sign. The incenter $I$ corresponds to the limit case where $D$ tends to infinity.
|
{
"resource_path": "IMO/segmented/en-IMO2012SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8fba148b-9684-50d0-a43a-b14da6989935
| 24,198
|
Let $A B C$ be a triangle with circumcircle $\omega$ and $\ell$ a line without common points with $\omega$. Denote by $P$ the foot of the perpendicular from the center of $\omega$ to $\ell$. The side-lines $B C, C A, A B$ intersect $\ell$ at the points $X, Y, Z$ different from $P$. Prove that the circumcircles of the triangles $A X P, B Y P$ and $C Z P$ have a common point different from $P$ or are mutually tangent at $P$.
|
First we prove that there is an inversion in space that takes $\ell$ and $\omega$ to parallel circles on a sphere. Let $Q R$ be the diameter of $\omega$ whose extension beyond $Q$ passes through $P$. Let $\Pi$ be the plane carrying our objects. In space, choose a point $O$ such that the line $Q O$ is perpendicular to $\Pi$ and $\angle P O R=90^{\circ}$, and apply an inversion with pole $O$ (the radius of the inversion does not matter). For any object $\mathcal{T}$ denote by $\mathcal{T}^{\prime}$ the image of $\mathcal{T}$ under this inversion. The inversion takes the plane $\Pi$ to a sphere $\Pi^{\prime}$. The lines in $\Pi$ are taken to circles through $O$, and the circles in $\Pi$ also are taken to circles on $\Pi^{\prime}$. 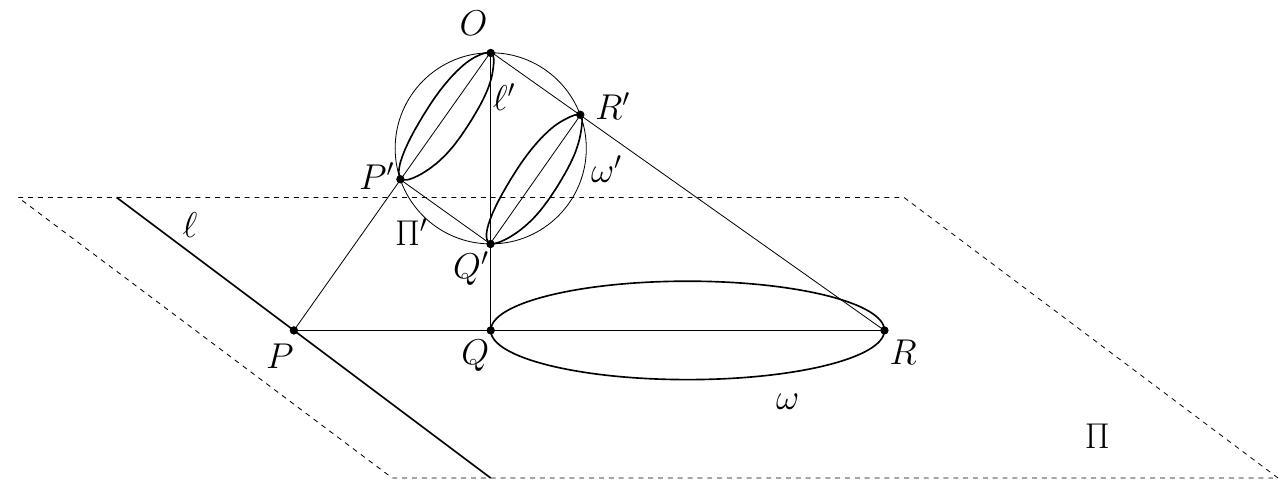 Since the line $\ell$ and the circle $\omega$ are perpendicular to the plane $O P Q$, the circles $\ell^{\prime}$ and $\omega^{\prime}$ also are perpendicular to this plane. Hence, the planes of the circles $\ell^{\prime}$ and $\omega^{\prime}$ are parallel. Now consider the circles $A^{\prime} X^{\prime} P^{\prime}, B^{\prime} Y^{\prime} P^{\prime}$ and $C^{\prime} Z^{\prime} P^{\prime}$. We want to prove that either they have a common point (on $\Pi^{\prime}$ ), different from $P^{\prime}$, or they are tangent to each other.  The point $X^{\prime}$ is the second intersection of the circles $B^{\prime} C^{\prime} O$ and $\ell^{\prime}$, other than $O$. Hence, the lines $O X^{\prime}$ and $B^{\prime} C^{\prime}$ are coplanar. Moreover, they lie in the parallel planes of $\ell^{\prime}$ and $\omega^{\prime}$. Therefore, $O X^{\prime}$ and $B^{\prime} C^{\prime}$ are parallel. Analogously, $O Y^{\prime}$ and $O Z^{\prime}$ are parallel to $A^{\prime} C^{\prime}$ and $A^{\prime} B^{\prime}$. Let $A_{1}$ be the second intersection of the circles $A^{\prime} X^{\prime} P^{\prime}$ and $\omega^{\prime}$, other than $A^{\prime}$. The segments $A^{\prime} A_{1}$ and $P^{\prime} X^{\prime}$ are coplanar, and therefore parallel. Now we know that $B^{\prime} C^{\prime}$ and $A^{\prime} A_{1}$ are parallel to $O X^{\prime}$ and $X^{\prime} P^{\prime}$ respectively, but these two segments are perpendicular because $O P^{\prime}$ is a diameter in $\ell^{\prime}$. We found that $A^{\prime} A_{1}$ and $B^{\prime} C^{\prime}$ are perpendicular, hence $A^{\prime} A_{1}$ is the altitude in the triangle $A^{\prime} B^{\prime} C^{\prime}$, starting from $A$. Analogously, let $B_{1}$ and $C_{1}$ be the second intersections of $\omega^{\prime}$ with the circles $B^{\prime} P^{\prime} Y^{\prime}$ and $C^{\prime} P^{\prime} Z^{\prime}$, other than $B^{\prime}$ and $C^{\prime}$ respectively. Then $B^{\prime} B_{1}$ and $C^{\prime} C_{1}$ are the other two altitudes in the triangle $A^{\prime} B^{\prime} C^{\prime}$. Let $H$ be the orthocenter of the triangle $A^{\prime} B^{\prime} C^{\prime}$. Let $W$ be the second intersection of the line $P^{\prime} H$ with the sphere $\Pi^{\prime}$, other than $P^{\prime}$. The point $W$ lies on the sphere $\Pi^{\prime}$, in the plane of the circle $A^{\prime} P^{\prime} X^{\prime}$, so $W$ lies on the circle $A^{\prime} P^{\prime} X^{\prime}$. Similarly, $W$ lies on the circles $B^{\prime} P^{\prime} Y^{\prime}$ and $C^{\prime} P^{\prime} Z^{\prime}$ as well; indeed $W$ is the second common point of the three circles. If the line $P^{\prime} H$ is tangent to the sphere then $W$ coincides with $P^{\prime}$, and $P^{\prime} H$ is the common tangent of the three circles.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circumcircle $\omega$ and $\ell$ a line without common points with $\omega$. Denote by $P$ the foot of the perpendicular from the center of $\omega$ to $\ell$. The side-lines $B C, C A, A B$ intersect $\ell$ at the points $X, Y, Z$ different from $P$. Prove that the circumcircles of the triangles $A X P, B Y P$ and $C Z P$ have a common point different from $P$ or are mutually tangent at $P$.
|
First we prove that there is an inversion in space that takes $\ell$ and $\omega$ to parallel circles on a sphere. Let $Q R$ be the diameter of $\omega$ whose extension beyond $Q$ passes through $P$. Let $\Pi$ be the plane carrying our objects. In space, choose a point $O$ such that the line $Q O$ is perpendicular to $\Pi$ and $\angle P O R=90^{\circ}$, and apply an inversion with pole $O$ (the radius of the inversion does not matter). For any object $\mathcal{T}$ denote by $\mathcal{T}^{\prime}$ the image of $\mathcal{T}$ under this inversion. The inversion takes the plane $\Pi$ to a sphere $\Pi^{\prime}$. The lines in $\Pi$ are taken to circles through $O$, and the circles in $\Pi$ also are taken to circles on $\Pi^{\prime}$.  Since the line $\ell$ and the circle $\omega$ are perpendicular to the plane $O P Q$, the circles $\ell^{\prime}$ and $\omega^{\prime}$ also are perpendicular to this plane. Hence, the planes of the circles $\ell^{\prime}$ and $\omega^{\prime}$ are parallel. Now consider the circles $A^{\prime} X^{\prime} P^{\prime}, B^{\prime} Y^{\prime} P^{\prime}$ and $C^{\prime} Z^{\prime} P^{\prime}$. We want to prove that either they have a common point (on $\Pi^{\prime}$ ), different from $P^{\prime}$, or they are tangent to each other.  The point $X^{\prime}$ is the second intersection of the circles $B^{\prime} C^{\prime} O$ and $\ell^{\prime}$, other than $O$. Hence, the lines $O X^{\prime}$ and $B^{\prime} C^{\prime}$ are coplanar. Moreover, they lie in the parallel planes of $\ell^{\prime}$ and $\omega^{\prime}$. Therefore, $O X^{\prime}$ and $B^{\prime} C^{\prime}$ are parallel. Analogously, $O Y^{\prime}$ and $O Z^{\prime}$ are parallel to $A^{\prime} C^{\prime}$ and $A^{\prime} B^{\prime}$. Let $A_{1}$ be the second intersection of the circles $A^{\prime} X^{\prime} P^{\prime}$ and $\omega^{\prime}$, other than $A^{\prime}$. The segments $A^{\prime} A_{1}$ and $P^{\prime} X^{\prime}$ are coplanar, and therefore parallel. Now we know that $B^{\prime} C^{\prime}$ and $A^{\prime} A_{1}$ are parallel to $O X^{\prime}$ and $X^{\prime} P^{\prime}$ respectively, but these two segments are perpendicular because $O P^{\prime}$ is a diameter in $\ell^{\prime}$. We found that $A^{\prime} A_{1}$ and $B^{\prime} C^{\prime}$ are perpendicular, hence $A^{\prime} A_{1}$ is the altitude in the triangle $A^{\prime} B^{\prime} C^{\prime}$, starting from $A$. Analogously, let $B_{1}$ and $C_{1}$ be the second intersections of $\omega^{\prime}$ with the circles $B^{\prime} P^{\prime} Y^{\prime}$ and $C^{\prime} P^{\prime} Z^{\prime}$, other than $B^{\prime}$ and $C^{\prime}$ respectively. Then $B^{\prime} B_{1}$ and $C^{\prime} C_{1}$ are the other two altitudes in the triangle $A^{\prime} B^{\prime} C^{\prime}$. Let $H$ be the orthocenter of the triangle $A^{\prime} B^{\prime} C^{\prime}$. Let $W$ be the second intersection of the line $P^{\prime} H$ with the sphere $\Pi^{\prime}$, other than $P^{\prime}$. The point $W$ lies on the sphere $\Pi^{\prime}$, in the plane of the circle $A^{\prime} P^{\prime} X^{\prime}$, so $W$ lies on the circle $A^{\prime} P^{\prime} X^{\prime}$. Similarly, $W$ lies on the circles $B^{\prime} P^{\prime} Y^{\prime}$ and $C^{\prime} P^{\prime} Z^{\prime}$ as well; indeed $W$ is the second common point of the three circles. If the line $P^{\prime} H$ is tangent to the sphere then $W$ coincides with $P^{\prime}$, and $P^{\prime} H$ is the common tangent of the three circles.
|
{
"resource_path": "IMO/segmented/en-IMO2012SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
937ab71a-c1fc-5258-888e-3c9cc0bb2eb3
| 24,203
|
Let $x$ and $y$ be positive integers. If $x^{2^{n}}-1$ is divisible by $2^{n} y+1$ for every positive integer $n$, prove that $x=1$.
|
First we prove the following fact: For every positive integer $y$ there exist infinitely many primes $p \equiv 3(\bmod 4)$ such that $p$ divides some number of the form $2^{n} y+1$. Clearly it is enough to consider the case $y$ odd. Let $$ 2 y+1=p_{1}^{e_{1}} \cdots p_{r}^{e_{r}} $$ be the prime factorization of $2 y+1$. Suppose on the contrary that there are finitely many primes $p_{r+1}, \ldots, p_{r+s} \equiv 3(\bmod 4)$ that divide some number of the form $2^{n} y+1$ but do not divide $2 y+1$. We want to find an $n$ such that $p_{i}^{e_{i}} \| 2^{n} y+1$ for $1 \leq i \leq r$ and $p_{i} \nmid 2^{n} y+1$ for $r+1 \leq i \leq r+s$. For this it suffices to take $$ n=1+\varphi\left(p_{1}^{e_{1}+1} \cdots p_{r}^{e_{r}+1} p_{r+1}^{1} \cdots p_{r+s}^{1}\right) $$ because then $$ 2^{n} y+1 \equiv 2 y+1 \quad\left(\bmod p_{1}^{e_{1}+1} \cdots p_{r}^{e_{r}+1} p_{r+1}^{1} \cdots p_{r+s}^{1}\right) $$ The last congruence means that $p_{1}^{e_{1}}, \ldots, p_{r}^{e_{r}}$ divide exactly $2^{n} y+1$ and no prime $p_{r+1}, \ldots, p_{r+s}$ divides $2^{n} y+1$. It follows that the prime factorization of $2^{n} y+1$ consists of the prime powers $p_{1}^{e_{1}}, \ldots, p_{r}^{e_{r}}$ and powers of primes $\equiv 1(\bmod 4)$. Because $y$ is odd, we obtain $$ 2^{n} y+1 \equiv p_{1}^{e_{1}} \cdots p_{r}^{e_{r}} \equiv 2 y+1 \equiv 3 \quad(\bmod 4) $$ This is a contradiction since $n>1$, and so $2^{n} y+1 \equiv 1(\bmod 4)$. Now we proceed to the problem. If $p$ is a prime divisor of $2^{n} y+1$ the problem statement implies that $x^{d} \equiv 1(\bmod p)$ for $d=2^{n}$. By FERMAT's little theorem the same congruence holds for $d=p-1$, so it must also hold for $d=\left(2^{n}, p-1\right)$. For $p \equiv 3(\bmod 4)$ we have $\left(2^{n}, p-1\right)=2$, therefore in this case $x^{2} \equiv 1(\bmod p)$. In summary, we proved that every prime $p \equiv 3(\bmod 4)$ that divides some number of the form $2^{n} y+1$ also divides $x^{2}-1$. This is possible only if $x=1$, otherwise by the above $x^{2}-1$ would be a positive integer with infinitely many prime factors. Comment. For each $x$ and each odd prime $p$ the maximal power of $p$ dividing $x^{2^{n}}-1$ for some $n$ is bounded and hence the same must be true for the numbers $2^{n} y+1$. We infer that $p^{2}$ divides $2^{p-1}-1$ for each prime divisor $p$ of $2^{n} y+1$. However trying to reach a contradiction with this conclusion alone seems hopeless, since it is not even known if there are infinitely many primes $p$ without this property.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $x$ and $y$ be positive integers. If $x^{2^{n}}-1$ is divisible by $2^{n} y+1$ for every positive integer $n$, prove that $x=1$.
|
First we prove the following fact: For every positive integer $y$ there exist infinitely many primes $p \equiv 3(\bmod 4)$ such that $p$ divides some number of the form $2^{n} y+1$. Clearly it is enough to consider the case $y$ odd. Let $$ 2 y+1=p_{1}^{e_{1}} \cdots p_{r}^{e_{r}} $$ be the prime factorization of $2 y+1$. Suppose on the contrary that there are finitely many primes $p_{r+1}, \ldots, p_{r+s} \equiv 3(\bmod 4)$ that divide some number of the form $2^{n} y+1$ but do not divide $2 y+1$. We want to find an $n$ such that $p_{i}^{e_{i}} \| 2^{n} y+1$ for $1 \leq i \leq r$ and $p_{i} \nmid 2^{n} y+1$ for $r+1 \leq i \leq r+s$. For this it suffices to take $$ n=1+\varphi\left(p_{1}^{e_{1}+1} \cdots p_{r}^{e_{r}+1} p_{r+1}^{1} \cdots p_{r+s}^{1}\right) $$ because then $$ 2^{n} y+1 \equiv 2 y+1 \quad\left(\bmod p_{1}^{e_{1}+1} \cdots p_{r}^{e_{r}+1} p_{r+1}^{1} \cdots p_{r+s}^{1}\right) $$ The last congruence means that $p_{1}^{e_{1}}, \ldots, p_{r}^{e_{r}}$ divide exactly $2^{n} y+1$ and no prime $p_{r+1}, \ldots, p_{r+s}$ divides $2^{n} y+1$. It follows that the prime factorization of $2^{n} y+1$ consists of the prime powers $p_{1}^{e_{1}}, \ldots, p_{r}^{e_{r}}$ and powers of primes $\equiv 1(\bmod 4)$. Because $y$ is odd, we obtain $$ 2^{n} y+1 \equiv p_{1}^{e_{1}} \cdots p_{r}^{e_{r}} \equiv 2 y+1 \equiv 3 \quad(\bmod 4) $$ This is a contradiction since $n>1$, and so $2^{n} y+1 \equiv 1(\bmod 4)$. Now we proceed to the problem. If $p$ is a prime divisor of $2^{n} y+1$ the problem statement implies that $x^{d} \equiv 1(\bmod p)$ for $d=2^{n}$. By FERMAT's little theorem the same congruence holds for $d=p-1$, so it must also hold for $d=\left(2^{n}, p-1\right)$. For $p \equiv 3(\bmod 4)$ we have $\left(2^{n}, p-1\right)=2$, therefore in this case $x^{2} \equiv 1(\bmod p)$. In summary, we proved that every prime $p \equiv 3(\bmod 4)$ that divides some number of the form $2^{n} y+1$ also divides $x^{2}-1$. This is possible only if $x=1$, otherwise by the above $x^{2}-1$ would be a positive integer with infinitely many prime factors. Comment. For each $x$ and each odd prime $p$ the maximal power of $p$ dividing $x^{2^{n}}-1$ for some $n$ is bounded and hence the same must be true for the numbers $2^{n} y+1$. We infer that $p^{2}$ divides $2^{p-1}-1$ for each prime divisor $p$ of $2^{n} y+1$. However trying to reach a contradiction with this conclusion alone seems hopeless, since it is not even known if there are infinitely many primes $p$ without this property.
|
{
"resource_path": "IMO/segmented/en-IMO2012SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
7db2a453-b6b9-553d-a59f-8037909daa3d
| 24,224
|
Prove that for every prime $p>100$ and every integer $r$ there exist two integers $a$ and $b$ such that $p$ divides $a^{2}+b^{5}-r$.
|
Throughout the solution, all congruence relations are meant modulo $p$. Fix $p$, and let $\mathcal{P}=\{0,1, \ldots, p-1\}$ be the set of residue classes modulo $p$. For every $r \in \mathcal{P}$, let $S_{r}=\left\{(a, b) \in \mathcal{P} \times \mathcal{P}: a^{2}+b^{5} \equiv r\right\}$, and let $s_{r}=\left|S_{r}\right|$. Our aim is to prove $s_{r}>0$ for all $r \in \mathcal{P}$. We will use the well-known fact that for every residue class $r \in \mathcal{P}$ and every positive integer $k$, there are at most $k$ values $x \in \mathcal{P}$ such that $x^{k} \equiv r$. Lemma. Let $N$ be the number of quadruples $(a, b, c, d) \in \mathcal{P}^{4}$ for which $a^{2}+b^{5} \equiv c^{2}+d^{5}$. Then $$ N=\sum_{r \in \mathcal{P}} s_{r}^{2} $$ and $$ N \leq p\left(p^{2}+4 p-4\right) $$ Proof. (a) For each residue class $r$ there exist exactly $s_{r}$ pairs $(a, b)$ with $a^{2}+b^{5} \equiv r$ and $s_{r}$ pairs $(c, d)$ with $c^{2}+d^{5} \equiv r$. So there are $s_{r}^{2}$ quadruples with $a^{2}+b^{5} \equiv c^{2}+d^{5} \equiv r$. Taking the sum over all $r \in \mathcal{P}$, the statement follows. (b) Choose an arbitrary pair $(b, d) \in \mathcal{P}$ and look for the possible values of $a, c$. 1. Suppose that $b^{5} \equiv d^{5}$, and let $k$ be the number of such pairs $(b, d)$. The value $b$ can be chosen in $p$ different ways. For $b \equiv 0$ only $d=0$ has this property; for the nonzero values of $b$ there are at most 5 possible values for $d$. So we have $k \leq 1+5(p-1)=5 p-4$. The values $a$ and $c$ must satisfy $a^{2} \equiv c^{2}$, so $a \equiv \pm c$, and there are exactly $2 p-1$ such pairs $(a, c)$. 2. Now suppose $b^{5} \not \equiv d^{5}$. In this case $a$ and $c$ must be distinct. By $(a-c)(a+c)=d^{5}-b^{5}$, the value of $a-c$ uniquely determines $a+c$ and thus $a$ and $c$ as well. Hence, there are $p-1$ suitable pairs $(a, c)$. Thus, for each of the $k$ pairs $(b, d)$ with $b^{5} \equiv d^{5}$ there are $2 p-1$ pairs $(a, c)$, and for each of the other $p^{2}-k$ pairs $(b, d)$ there are $p-1$ pairs $(a, c)$. Hence, $$ N=k(2 p-1)+\left(p^{2}-k\right)(p-1)=p^{2}(p-1)+k p \leq p^{2}(p-1)+(5 p-4) p=p\left(p^{2}+4 p-4\right) $$ To prove the statement of the problem, suppose that $S_{r}=\emptyset$ for some $r \in \mathcal{P}$; obviously $r \not \equiv 0$. Let $T=\left\{x^{10}: x \in \mathcal{P} \backslash\{0\}\right\}$ be the set of nonzero 10th powers modulo $p$. Since each residue class is the 10 th power of at most 10 elements in $\mathcal{P}$, we have $|T| \geq \frac{p-1}{10} \geq 4$ by $p>100$. For every $t \in T$, we have $S_{t r}=\emptyset$. Indeed, if $(x, y) \in S_{t r}$ and $t \equiv z^{10}$ then $$ \left(z^{-5} x\right)^{2}+\left(z^{-2} y\right)^{5} \equiv t^{-1}\left(x^{2}+y^{5}\right) \equiv r $$ so $\left(z^{-5} x, z^{-2} y\right) \in S_{r}$. So, there are at least $\frac{p-1}{10} \geq 4$ empty sets among $S_{1}, \ldots, S_{p-1}$, and there are at most $p-4$ nonzero values among $s_{0}, s_{2}, \ldots, s_{p-1}$. Then by the AM-QM inequality we obtain $$ N=\sum_{r \in \mathcal{P} \backslash r T} s_{r}^{2} \geq \frac{1}{p-4}\left(\sum_{r \in \mathcal{P} \backslash r T} s_{r}\right)^{2}=\frac{|\mathcal{P} \times \mathcal{P}|^{2}}{p-4}=\frac{p^{4}}{p-4}>p\left(p^{2}+4 p-4\right), $$ which is impossible by the lemma.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that for every prime $p>100$ and every integer $r$ there exist two integers $a$ and $b$ such that $p$ divides $a^{2}+b^{5}-r$.
|
Throughout the solution, all congruence relations are meant modulo $p$. Fix $p$, and let $\mathcal{P}=\{0,1, \ldots, p-1\}$ be the set of residue classes modulo $p$. For every $r \in \mathcal{P}$, let $S_{r}=\left\{(a, b) \in \mathcal{P} \times \mathcal{P}: a^{2}+b^{5} \equiv r\right\}$, and let $s_{r}=\left|S_{r}\right|$. Our aim is to prove $s_{r}>0$ for all $r \in \mathcal{P}$. We will use the well-known fact that for every residue class $r \in \mathcal{P}$ and every positive integer $k$, there are at most $k$ values $x \in \mathcal{P}$ such that $x^{k} \equiv r$. Lemma. Let $N$ be the number of quadruples $(a, b, c, d) \in \mathcal{P}^{4}$ for which $a^{2}+b^{5} \equiv c^{2}+d^{5}$. Then $$ N=\sum_{r \in \mathcal{P}} s_{r}^{2} $$ and $$ N \leq p\left(p^{2}+4 p-4\right) $$ Proof. (a) For each residue class $r$ there exist exactly $s_{r}$ pairs $(a, b)$ with $a^{2}+b^{5} \equiv r$ and $s_{r}$ pairs $(c, d)$ with $c^{2}+d^{5} \equiv r$. So there are $s_{r}^{2}$ quadruples with $a^{2}+b^{5} \equiv c^{2}+d^{5} \equiv r$. Taking the sum over all $r \in \mathcal{P}$, the statement follows. (b) Choose an arbitrary pair $(b, d) \in \mathcal{P}$ and look for the possible values of $a, c$. 1. Suppose that $b^{5} \equiv d^{5}$, and let $k$ be the number of such pairs $(b, d)$. The value $b$ can be chosen in $p$ different ways. For $b \equiv 0$ only $d=0$ has this property; for the nonzero values of $b$ there are at most 5 possible values for $d$. So we have $k \leq 1+5(p-1)=5 p-4$. The values $a$ and $c$ must satisfy $a^{2} \equiv c^{2}$, so $a \equiv \pm c$, and there are exactly $2 p-1$ such pairs $(a, c)$. 2. Now suppose $b^{5} \not \equiv d^{5}$. In this case $a$ and $c$ must be distinct. By $(a-c)(a+c)=d^{5}-b^{5}$, the value of $a-c$ uniquely determines $a+c$ and thus $a$ and $c$ as well. Hence, there are $p-1$ suitable pairs $(a, c)$. Thus, for each of the $k$ pairs $(b, d)$ with $b^{5} \equiv d^{5}$ there are $2 p-1$ pairs $(a, c)$, and for each of the other $p^{2}-k$ pairs $(b, d)$ there are $p-1$ pairs $(a, c)$. Hence, $$ N=k(2 p-1)+\left(p^{2}-k\right)(p-1)=p^{2}(p-1)+k p \leq p^{2}(p-1)+(5 p-4) p=p\left(p^{2}+4 p-4\right) $$ To prove the statement of the problem, suppose that $S_{r}=\emptyset$ for some $r \in \mathcal{P}$; obviously $r \not \equiv 0$. Let $T=\left\{x^{10}: x \in \mathcal{P} \backslash\{0\}\right\}$ be the set of nonzero 10th powers modulo $p$. Since each residue class is the 10 th power of at most 10 elements in $\mathcal{P}$, we have $|T| \geq \frac{p-1}{10} \geq 4$ by $p>100$. For every $t \in T$, we have $S_{t r}=\emptyset$. Indeed, if $(x, y) \in S_{t r}$ and $t \equiv z^{10}$ then $$ \left(z^{-5} x\right)^{2}+\left(z^{-2} y\right)^{5} \equiv t^{-1}\left(x^{2}+y^{5}\right) \equiv r $$ so $\left(z^{-5} x, z^{-2} y\right) \in S_{r}$. So, there are at least $\frac{p-1}{10} \geq 4$ empty sets among $S_{1}, \ldots, S_{p-1}$, and there are at most $p-4$ nonzero values among $s_{0}, s_{2}, \ldots, s_{p-1}$. Then by the AM-QM inequality we obtain $$ N=\sum_{r \in \mathcal{P} \backslash r T} s_{r}^{2} \geq \frac{1}{p-4}\left(\sum_{r \in \mathcal{P} \backslash r T} s_{r}\right)^{2}=\frac{|\mathcal{P} \times \mathcal{P}|^{2}}{p-4}=\frac{p^{4}}{p-4}>p\left(p^{2}+4 p-4\right), $$ which is impossible by the lemma.
|
{
"resource_path": "IMO/segmented/en-IMO2012SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
e8dd8b3c-3663-5137-a677-7055bcf29e6e
| 24,229
|
Prove that for every prime $p>100$ and every integer $r$ there exist two integers $a$ and $b$ such that $p$ divides $a^{2}+b^{5}-r$.
|
If $5 \nmid p-1$, then all modulo $p$ residue classes are complete fifth powers and the statement is trivial. So assume that $p=10 k+1$ where $k \geq 10$. Let $g$ be a primitive root modulo $p$. We will use the following facts: (F1) If some residue class $x$ is not quadratic then $x^{(p-1) / 2} \equiv-1(\bmod p)$. (F2) For every integer $d$, as a simple corollary of the summation formula for geometric progressions, $$ \sum_{i=0}^{2 k-1} g^{5 d i} \equiv\left\{\begin{array}{ll} 2 k & \text { if } 2 k \mid d \\ 0 & \text { if } 2 k \not \nless d \end{array} \quad(\bmod p)\right. $$ Suppose that, contrary to the statement, some modulo $p$ residue class $r$ cannot be expressed as $a^{2}+b^{5}$. Of course $r \not \equiv 0(\bmod p)$. By $(\mathrm{F} 1)$ we have $\left(r-b^{5}\right)^{(p-1) / 2}=\left(r-b^{5}\right)^{5 k} \equiv-1(\bmod p)$ for all residue classes $b$. For $t=1,2 \ldots, k-1$ consider the sums $$ S(t)=\sum_{i=0}^{2 k-1}\left(r-g^{5 i}\right)^{5 k} g^{5 t i} $$ By the indirect assumption and (F2), $$ S(t)=\sum_{i=0}^{2 k-1}\left(r-\left(g^{i}\right)^{5}\right)^{5 k} g^{5 t i} \equiv \sum_{i=0}^{2 k-1}(-1) g^{5 t i} \equiv-\sum_{i=0}^{2 k-1} g^{5 t i} \equiv 0 \quad(\bmod p) $$ because $2 k$ cannot divide $t$. On the other hand, by the binomial theorem, $$ \begin{aligned} S(t) & =\sum_{i=0}^{2 k-1}\left(\sum_{j=0}^{5 k}\left(\begin{array}{c} 5 k \\ j \end{array}\right) r^{5 k-j}\left(-g^{5 i}\right)^{j}\right) g^{5 t i}=\sum_{j=0}^{5 k}(-1)^{j}\left(\begin{array}{c} 5 k \\ j \end{array}\right) r^{5 k-j}\left(\sum_{i=0}^{2 k-1} g^{5(j+t) i}\right) \equiv \\ & \equiv \sum_{j=0}^{5 k}(-1)^{j}\left(\begin{array}{c} 5 k \\ j \end{array}\right) r^{5 k-j}\left\{\begin{array}{ll} 2 k & \text { if } 2 k \mid j+t \\ 0 & \text { if } 2 k \not j j+t \end{array}(\bmod p) .\right. \end{aligned} $$ Since $1 \leq j+t<6 k$, the number $2 k$ divides $j+t$ only for $j=2 k-t$ and $j=4 k-t$. Hence, $$ \begin{gathered} 0 \equiv S(t) \equiv(-1)^{t}\left(\left(\begin{array}{c} 5 k \\ 2 k-t \end{array}\right) r^{3 k+t}+\left(\begin{array}{c} 5 k \\ 4 k-t \end{array}\right) r^{k+t}\right) \cdot 2 k \quad(\bmod p), \\ \left(\begin{array}{c} 5 k \\ 2 k-t \end{array}\right) r^{2 k}+\left(\begin{array}{c} 5 k \\ 4 k-t \end{array}\right) \equiv 0 \quad(\bmod p) . \end{gathered} $$ Taking this for $t=1,2$ and eliminating $r$, we get $$ \begin{aligned} 0 & \equiv\left(\begin{array}{c} 5 k \\ 2 k-2 \end{array}\right)\left(\left(\begin{array}{c} 5 k \\ 2 k-1 \end{array}\right) r^{2 k}+\left(\begin{array}{c} 5 k \\ 4 k-1 \end{array}\right)\right)-\left(\begin{array}{c} 5 k \\ 2 k-1 \end{array}\right)\left(\left(\begin{array}{c} 5 k \\ 2 k-2 \end{array}\right) r^{2 k}+\left(\begin{array}{c} 5 k \\ 4 k-2 \end{array}\right)\right) \\ & =\left(\begin{array}{c} 5 k \\ 2 k-2 \end{array}\right)\left(\begin{array}{c} 5 k \\ 4 k-1 \end{array}\right)-\left(\begin{array}{c} 5 k \\ 2 k-1 \end{array}\right)\left(\begin{array}{c} 5 k \\ 4 k-2 \end{array}\right) \\ & =\frac{(5 k) !^{2}}{(2 k-1) !(3 k+2) !(4 k-1) !(k+2) !}((2 k-1)(k+2)-(3 k+2)(4 k-1)) \\ & =\frac{-(5 k) !^{2} \cdot 2 k(5 k+1)}{(2 k-1) !(3 k+2) !(4 k-1) !(k+2) !}(\bmod p) . \end{aligned} $$ But in the last expression none of the numbers is divisible by $p=10 k+1$, a contradiction. Comment 1. The argument in the second solution is valid whenever $k \geq 3$, that is for all primes $p=10 k+1$ except $p=11$. This is an exceptional case when the statement is not true; $r=7$ cannot be expressed as desired. Comment 2. The statement is true in a more general setting: for every positive integer $n$, for all sufficiently large $p$, each residue class modulo $p$ can be expressed as $a^{2}+b^{n}$. Choosing $t=3$ would allow using the Cauchy-Davenport theorem (together with some analysis on the case of equality). In the literature more general results are known. For instance, the statement easily follows from the Hasse-Weil bound.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that for every prime $p>100$ and every integer $r$ there exist two integers $a$ and $b$ such that $p$ divides $a^{2}+b^{5}-r$.
|
If $5 \nmid p-1$, then all modulo $p$ residue classes are complete fifth powers and the statement is trivial. So assume that $p=10 k+1$ where $k \geq 10$. Let $g$ be a primitive root modulo $p$. We will use the following facts: (F1) If some residue class $x$ is not quadratic then $x^{(p-1) / 2} \equiv-1(\bmod p)$. (F2) For every integer $d$, as a simple corollary of the summation formula for geometric progressions, $$ \sum_{i=0}^{2 k-1} g^{5 d i} \equiv\left\{\begin{array}{ll} 2 k & \text { if } 2 k \mid d \\ 0 & \text { if } 2 k \not \nless d \end{array} \quad(\bmod p)\right. $$ Suppose that, contrary to the statement, some modulo $p$ residue class $r$ cannot be expressed as $a^{2}+b^{5}$. Of course $r \not \equiv 0(\bmod p)$. By $(\mathrm{F} 1)$ we have $\left(r-b^{5}\right)^{(p-1) / 2}=\left(r-b^{5}\right)^{5 k} \equiv-1(\bmod p)$ for all residue classes $b$. For $t=1,2 \ldots, k-1$ consider the sums $$ S(t)=\sum_{i=0}^{2 k-1}\left(r-g^{5 i}\right)^{5 k} g^{5 t i} $$ By the indirect assumption and (F2), $$ S(t)=\sum_{i=0}^{2 k-1}\left(r-\left(g^{i}\right)^{5}\right)^{5 k} g^{5 t i} \equiv \sum_{i=0}^{2 k-1}(-1) g^{5 t i} \equiv-\sum_{i=0}^{2 k-1} g^{5 t i} \equiv 0 \quad(\bmod p) $$ because $2 k$ cannot divide $t$. On the other hand, by the binomial theorem, $$ \begin{aligned} S(t) & =\sum_{i=0}^{2 k-1}\left(\sum_{j=0}^{5 k}\left(\begin{array}{c} 5 k \\ j \end{array}\right) r^{5 k-j}\left(-g^{5 i}\right)^{j}\right) g^{5 t i}=\sum_{j=0}^{5 k}(-1)^{j}\left(\begin{array}{c} 5 k \\ j \end{array}\right) r^{5 k-j}\left(\sum_{i=0}^{2 k-1} g^{5(j+t) i}\right) \equiv \\ & \equiv \sum_{j=0}^{5 k}(-1)^{j}\left(\begin{array}{c} 5 k \\ j \end{array}\right) r^{5 k-j}\left\{\begin{array}{ll} 2 k & \text { if } 2 k \mid j+t \\ 0 & \text { if } 2 k \not j j+t \end{array}(\bmod p) .\right. \end{aligned} $$ Since $1 \leq j+t<6 k$, the number $2 k$ divides $j+t$ only for $j=2 k-t$ and $j=4 k-t$. Hence, $$ \begin{gathered} 0 \equiv S(t) \equiv(-1)^{t}\left(\left(\begin{array}{c} 5 k \\ 2 k-t \end{array}\right) r^{3 k+t}+\left(\begin{array}{c} 5 k \\ 4 k-t \end{array}\right) r^{k+t}\right) \cdot 2 k \quad(\bmod p), \\ \left(\begin{array}{c} 5 k \\ 2 k-t \end{array}\right) r^{2 k}+\left(\begin{array}{c} 5 k \\ 4 k-t \end{array}\right) \equiv 0 \quad(\bmod p) . \end{gathered} $$ Taking this for $t=1,2$ and eliminating $r$, we get $$ \begin{aligned} 0 & \equiv\left(\begin{array}{c} 5 k \\ 2 k-2 \end{array}\right)\left(\left(\begin{array}{c} 5 k \\ 2 k-1 \end{array}\right) r^{2 k}+\left(\begin{array}{c} 5 k \\ 4 k-1 \end{array}\right)\right)-\left(\begin{array}{c} 5 k \\ 2 k-1 \end{array}\right)\left(\left(\begin{array}{c} 5 k \\ 2 k-2 \end{array}\right) r^{2 k}+\left(\begin{array}{c} 5 k \\ 4 k-2 \end{array}\right)\right) \\ & =\left(\begin{array}{c} 5 k \\ 2 k-2 \end{array}\right)\left(\begin{array}{c} 5 k \\ 4 k-1 \end{array}\right)-\left(\begin{array}{c} 5 k \\ 2 k-1 \end{array}\right)\left(\begin{array}{c} 5 k \\ 4 k-2 \end{array}\right) \\ & =\frac{(5 k) !^{2}}{(2 k-1) !(3 k+2) !(4 k-1) !(k+2) !}((2 k-1)(k+2)-(3 k+2)(4 k-1)) \\ & =\frac{-(5 k) !^{2} \cdot 2 k(5 k+1)}{(2 k-1) !(3 k+2) !(4 k-1) !(k+2) !}(\bmod p) . \end{aligned} $$ But in the last expression none of the numbers is divisible by $p=10 k+1$, a contradiction. Comment 1. The argument in the second solution is valid whenever $k \geq 3$, that is for all primes $p=10 k+1$ except $p=11$. This is an exceptional case when the statement is not true; $r=7$ cannot be expressed as desired. Comment 2. The statement is true in a more general setting: for every positive integer $n$, for all sufficiently large $p$, each residue class modulo $p$ can be expressed as $a^{2}+b^{n}$. Choosing $t=3$ would allow using the Cauchy-Davenport theorem (together with some analysis on the case of equality). In the literature more general results are known. For instance, the statement easily follows from the Hasse-Weil bound.
|
{
"resource_path": "IMO/segmented/en-IMO2012SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
e8dd8b3c-3663-5137-a677-7055bcf29e6e
| 24,229
|
The columns and the rows of a $3 n \times 3 n$ square board are numbered $1,2, \ldots, 3 n$. Every square $(x, y)$ with $1 \leq x, y \leq 3 n$ is colored asparagus, byzantium or citrine according as the modulo 3 remainder of $x+y$ is 0 , 1 or 2 respectively. One token colored asparagus, byzantium or citrine is placed on each square, so that there are $3 n^{2}$ tokens of each color. Suppose that one can permute the tokens so that each token is moved to a distance of at most $d$ from its original position, each asparagus token replaces a byzantium token, each byzantium token replaces a citrine token, and each citrine token replaces an asparagus token. Prove that it is possible to permute the tokens so that each token is moved to a distance of at most $d+2$ from its original position, and each square contains a token with the same color as the square.
|
Without loss of generality it suffices to prove that the A-tokens can be moved to distinct $\mathrm{A}$-squares in such a way that each $\mathrm{A}$-token is moved to a distance at most $d+2$ from its original place. This means we need a perfect matching between the $3 n^{2} \mathrm{~A}$-squares and the $3 n^{2}$ A-tokens such that the distance in each pair of the matching is at most $d+2$. To find the matching, we construct a bipartite graph. The A-squares will be the vertices in one class of the graph; the vertices in the other class will be the A-tokens. Split the board into $3 \times 1$ horizontal triminos; then each trimino contains exactly one Asquare. Take a permutation $\pi$ of the tokens which moves A-tokens to B-tokens, B-tokens to C-tokens, and C-tokens to A-tokens, in each case to a distance at most $d$. For each A-square $S$, and for each A-token $T$, connect $S$ and $T$ by an edge if $T, \pi(T)$ or $\pi^{-1}(T)$ is on the trimino containing $S$. We allow multiple edges; it is even possible that the same square and the same token are connected with three edges. Obviously the lengths of the edges in the graph do not exceed $d+2$. By length of an edge we mean the distance between the A-square and the A-token it connects. Each A-token $T$ is connected with the three A-squares whose triminos contain $T, \pi(T)$ and $\pi^{-1}(T)$. Therefore in the graph all tokens are of degree 3. We show that the same is true for the A-squares. Let $S$ be an arbitrary A-square, and let $T_{1}, T_{2}, T_{3}$ be the three tokens on the trimino containing $S$. For $i=1,2,3$, if $T_{i}$ is an A-token, then $S$ is connected with $T_{i}$; if $T_{i}$ is a B-token then $S$ is connected with $\pi^{-1}\left(T_{i}\right)$; finally, if $T_{i}$ is a C-token then $S$ is connected with $\pi\left(T_{i}\right)$. Hence in the graph the A-squares also are of degree 3. Since the A-squares are of degree 3 , from every set $\mathcal{S}$ of A-squares exactly $3|\mathcal{S}|$ edges start. These edges end in at least $|\mathcal{S}|$ tokens because the A-tokens also are of degree 3. Hence every set $\mathcal{S}$ of A-squares has at least $|\mathcal{S}|$ neighbors among the A-tokens. Therefore, by HALL's marriage theorem, the graph contains a perfect matching between the two vertex classes. So there is a perfect matching between the A-squares and A-tokens with edges no longer than $d+2$. It follows that the tokens can be permuted as specified in the problem statement. Comment 1. In the original problem proposal the board was infinite and there were only two colors. Having $n$ colors for some positive integer $n$ was an option; we chose $n=3$. Moreover, we changed the board to a finite one to avoid dealing with infinite graphs (although Hall's theorem works in the infinite case as well). With only two colors Hall's theorem is not needed. In this case we split the board into $2 \times 1$ dominos, and in the resulting graph all vertices are of degree 2. The graph consists of disjoint cycles with even length and infinite paths, so the existence of the matching is trivial. Having more than three colors would make the problem statement more complicated, because we need a matching between every two color classes of tokens. However, this would not mean a significant increase in difficulty. Comment 2. According to Wikipedia, the color asparagus (hexadecimal code \#87A96B) is a tone of green that is named after the vegetable. Crayola created this color in 1993 as one of the 16 to be named in the Name The Color Contest. Byzantium (\#702963) is a dark tone of purple. Its first recorded use as a color name in English was in 1926. Citrine (\#E4D00A) is variously described as yellow, greenish-yellow, brownish-yellow or orange. The first known use of citrine as a color name in English was in the 14th century.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
The columns and the rows of a $3 n \times 3 n$ square board are numbered $1,2, \ldots, 3 n$. Every square $(x, y)$ with $1 \leq x, y \leq 3 n$ is colored asparagus, byzantium or citrine according as the modulo 3 remainder of $x+y$ is 0 , 1 or 2 respectively. One token colored asparagus, byzantium or citrine is placed on each square, so that there are $3 n^{2}$ tokens of each color. Suppose that one can permute the tokens so that each token is moved to a distance of at most $d$ from its original position, each asparagus token replaces a byzantium token, each byzantium token replaces a citrine token, and each citrine token replaces an asparagus token. Prove that it is possible to permute the tokens so that each token is moved to a distance of at most $d+2$ from its original position, and each square contains a token with the same color as the square.
|
Without loss of generality it suffices to prove that the A-tokens can be moved to distinct $\mathrm{A}$-squares in such a way that each $\mathrm{A}$-token is moved to a distance at most $d+2$ from its original place. This means we need a perfect matching between the $3 n^{2} \mathrm{~A}$-squares and the $3 n^{2}$ A-tokens such that the distance in each pair of the matching is at most $d+2$. To find the matching, we construct a bipartite graph. The A-squares will be the vertices in one class of the graph; the vertices in the other class will be the A-tokens. Split the board into $3 \times 1$ horizontal triminos; then each trimino contains exactly one Asquare. Take a permutation $\pi$ of the tokens which moves A-tokens to B-tokens, B-tokens to C-tokens, and C-tokens to A-tokens, in each case to a distance at most $d$. For each A-square $S$, and for each A-token $T$, connect $S$ and $T$ by an edge if $T, \pi(T)$ or $\pi^{-1}(T)$ is on the trimino containing $S$. We allow multiple edges; it is even possible that the same square and the same token are connected with three edges. Obviously the lengths of the edges in the graph do not exceed $d+2$. By length of an edge we mean the distance between the A-square and the A-token it connects. Each A-token $T$ is connected with the three A-squares whose triminos contain $T, \pi(T)$ and $\pi^{-1}(T)$. Therefore in the graph all tokens are of degree 3. We show that the same is true for the A-squares. Let $S$ be an arbitrary A-square, and let $T_{1}, T_{2}, T_{3}$ be the three tokens on the trimino containing $S$. For $i=1,2,3$, if $T_{i}$ is an A-token, then $S$ is connected with $T_{i}$; if $T_{i}$ is a B-token then $S$ is connected with $\pi^{-1}\left(T_{i}\right)$; finally, if $T_{i}$ is a C-token then $S$ is connected with $\pi\left(T_{i}\right)$. Hence in the graph the A-squares also are of degree 3. Since the A-squares are of degree 3 , from every set $\mathcal{S}$ of A-squares exactly $3|\mathcal{S}|$ edges start. These edges end in at least $|\mathcal{S}|$ tokens because the A-tokens also are of degree 3. Hence every set $\mathcal{S}$ of A-squares has at least $|\mathcal{S}|$ neighbors among the A-tokens. Therefore, by HALL's marriage theorem, the graph contains a perfect matching between the two vertex classes. So there is a perfect matching between the A-squares and A-tokens with edges no longer than $d+2$. It follows that the tokens can be permuted as specified in the problem statement. Comment 1. In the original problem proposal the board was infinite and there were only two colors. Having $n$ colors for some positive integer $n$ was an option; we chose $n=3$. Moreover, we changed the board to a finite one to avoid dealing with infinite graphs (although Hall's theorem works in the infinite case as well). With only two colors Hall's theorem is not needed. In this case we split the board into $2 \times 1$ dominos, and in the resulting graph all vertices are of degree 2. The graph consists of disjoint cycles with even length and infinite paths, so the existence of the matching is trivial. Having more than three colors would make the problem statement more complicated, because we need a matching between every two color classes of tokens. However, this would not mean a significant increase in difficulty. Comment 2. According to Wikipedia, the color asparagus (hexadecimal code \#87A96B) is a tone of green that is named after the vegetable. Crayola created this color in 1993 as one of the 16 to be named in the Name The Color Contest. Byzantium (\#702963) is a dark tone of purple. Its first recorded use as a color name in English was in 1926. Citrine (\#E4D00A) is variously described as yellow, greenish-yellow, brownish-yellow or orange. The first known use of citrine as a color name in English was in the 14th century.
|
{
"resource_path": "IMO/segmented/en-IMO2012SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
6207754e-333b-5c04-8ac7-6c2d8de0c414
| 24,233
|
Let $n$ be a positive integer and let $a_{1}, \ldots, a_{n-1}$ be arbitrary real numbers. Define the sequences $u_{0}, \ldots, u_{n}$ and $v_{0}, \ldots, v_{n}$ inductively by $u_{0}=u_{1}=v_{0}=v_{1}=1$, and $$ u_{k+1}=u_{k}+a_{k} u_{k-1}, \quad v_{k+1}=v_{k}+a_{n-k} v_{k-1} \quad \text { for } k=1, \ldots, n-1 . $$ Prove that $u_{n}=v_{n}$. (France)
|
We prove by induction on $k$ that $$ u_{k}=\sum_{\substack{0<i_{1}<\ldots<i_{t}<k \\ i_{j}+1-i_{j} \geqslant 2}} a_{i_{1}} \ldots a_{i_{t}} $$ Note that we have one trivial summand equal to 1 (which corresponds to $t=0$ and the empty sequence, whose product is 1 ). For $k=0,1$ the sum on the right-hand side only contains the empty product, so (1) holds due to $u_{0}=u_{1}=1$. For $k \geqslant 1$, assuming the result is true for $0,1, \ldots, k$, we have $$ \begin{aligned} u_{k+1} & =\sum_{\substack{0<i_{1}<\ldots<i_{t}<k, i_{j+1}-i_{j} \geqslant 2}} a_{i_{1}} \ldots a_{i_{t}}+\sum_{\substack{0<i_{1}<\ldots<i_{t}<k-1, i_{j+1}-i_{j} \geqslant 2}} a_{i_{1}} \ldots a_{i_{t}} \cdot a_{k} \\ & =\sum_{\substack{0<i_{1}<\ldots<i_{t}<k+1, i_{j+1}-i_{j} \geqslant 2, k \notin\left\{i_{1}, \ldots, i_{t}\right\}}} a_{i_{1}} \ldots a_{i_{t}}+\sum_{\substack{0<i_{1}<\ldots<i_{t}<k+1, i_{j+1}-i_{j} \geqslant 2, k \in\left\{i_{1}, \ldots, i_{t}\right\}}} a_{i_{1}} \ldots a_{i_{t}} \\ & =\sum_{\substack{0<i_{1}<\ldots<i_{t}<k+1, i_{j+1}-i_{j} \geqslant 2}} a_{i_{1}} \ldots a_{i_{t}}, \end{aligned} $$ as required. Applying (1) to the sequence $b_{1}, \ldots, b_{n}$ given by $b_{k}=a_{n-k}$ for $1 \leqslant k \leqslant n$, we get $$ v_{k}=\sum_{\substack{0<i_{1}<\ldots<i_{t}<k, i_{j+1}-i_{j} \geqslant 2}} b_{i_{1}} \ldots b_{i_{t}}=\sum_{\substack{n>i_{1}>\ldots>i_{t}>n-k \\ i_{j}-i_{j+1} \geqslant 2}} a_{i_{1}} \ldots a_{i_{t}} $$ For $k=n$ the expressions (1) and (2) coincide, so indeed $u_{n}=v_{n}$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $n$ be a positive integer and let $a_{1}, \ldots, a_{n-1}$ be arbitrary real numbers. Define the sequences $u_{0}, \ldots, u_{n}$ and $v_{0}, \ldots, v_{n}$ inductively by $u_{0}=u_{1}=v_{0}=v_{1}=1$, and $$ u_{k+1}=u_{k}+a_{k} u_{k-1}, \quad v_{k+1}=v_{k}+a_{n-k} v_{k-1} \quad \text { for } k=1, \ldots, n-1 . $$ Prove that $u_{n}=v_{n}$. (France)
|
We prove by induction on $k$ that $$ u_{k}=\sum_{\substack{0<i_{1}<\ldots<i_{t}<k \\ i_{j}+1-i_{j} \geqslant 2}} a_{i_{1}} \ldots a_{i_{t}} $$ Note that we have one trivial summand equal to 1 (which corresponds to $t=0$ and the empty sequence, whose product is 1 ). For $k=0,1$ the sum on the right-hand side only contains the empty product, so (1) holds due to $u_{0}=u_{1}=1$. For $k \geqslant 1$, assuming the result is true for $0,1, \ldots, k$, we have $$ \begin{aligned} u_{k+1} & =\sum_{\substack{0<i_{1}<\ldots<i_{t}<k, i_{j+1}-i_{j} \geqslant 2}} a_{i_{1}} \ldots a_{i_{t}}+\sum_{\substack{0<i_{1}<\ldots<i_{t}<k-1, i_{j+1}-i_{j} \geqslant 2}} a_{i_{1}} \ldots a_{i_{t}} \cdot a_{k} \\ & =\sum_{\substack{0<i_{1}<\ldots<i_{t}<k+1, i_{j+1}-i_{j} \geqslant 2, k \notin\left\{i_{1}, \ldots, i_{t}\right\}}} a_{i_{1}} \ldots a_{i_{t}}+\sum_{\substack{0<i_{1}<\ldots<i_{t}<k+1, i_{j+1}-i_{j} \geqslant 2, k \in\left\{i_{1}, \ldots, i_{t}\right\}}} a_{i_{1}} \ldots a_{i_{t}} \\ & =\sum_{\substack{0<i_{1}<\ldots<i_{t}<k+1, i_{j+1}-i_{j} \geqslant 2}} a_{i_{1}} \ldots a_{i_{t}}, \end{aligned} $$ as required. Applying (1) to the sequence $b_{1}, \ldots, b_{n}$ given by $b_{k}=a_{n-k}$ for $1 \leqslant k \leqslant n$, we get $$ v_{k}=\sum_{\substack{0<i_{1}<\ldots<i_{t}<k, i_{j+1}-i_{j} \geqslant 2}} b_{i_{1}} \ldots b_{i_{t}}=\sum_{\substack{n>i_{1}>\ldots>i_{t}>n-k \\ i_{j}-i_{j+1} \geqslant 2}} a_{i_{1}} \ldots a_{i_{t}} $$ For $k=n$ the expressions (1) and (2) coincide, so indeed $u_{n}=v_{n}$.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
2897d01e-463c-58ce-aa94-21023bc20f75
| 24,239
|
Let $n$ be a positive integer and let $a_{1}, \ldots, a_{n-1}$ be arbitrary real numbers. Define the sequences $u_{0}, \ldots, u_{n}$ and $v_{0}, \ldots, v_{n}$ inductively by $u_{0}=u_{1}=v_{0}=v_{1}=1$, and $$ u_{k+1}=u_{k}+a_{k} u_{k-1}, \quad v_{k+1}=v_{k}+a_{n-k} v_{k-1} \quad \text { for } k=1, \ldots, n-1 . $$ Prove that $u_{n}=v_{n}$. (France)
|
Define recursively a sequence of multivariate polynomials by $$ P_{0}=P_{1}=1, \quad P_{k+1}\left(x_{1}, \ldots, x_{k}\right)=P_{k}\left(x_{1}, \ldots, x_{k-1}\right)+x_{k} P_{k-1}\left(x_{1}, \ldots, x_{k-2}\right), $$ so $P_{n}$ is a polynomial in $n-1$ variables for each $n \geqslant 1$. Two easy inductive arguments show that $$ u_{n}=P_{n}\left(a_{1}, \ldots, a_{n-1}\right), \quad v_{n}=P_{n}\left(a_{n-1}, \ldots, a_{1}\right) $$ so we need to prove $P_{n}\left(x_{1}, \ldots, x_{n-1}\right)=P_{n}\left(x_{n-1}, \ldots, x_{1}\right)$ for every positive integer $n$. The cases $n=1,2$ are trivial, and the cases $n=3,4$ follow from $P_{3}(x, y)=1+x+y$ and $P_{4}(x, y, z)=$ $1+x+y+z+x z$. Now we proceed by induction, assuming that $n \geqslant 5$ and the claim hold for all smaller cases. Using $F(a, b)$ as an abbreviation for $P_{|a-b|+1}\left(x_{a}, \ldots, x_{b}\right)$ (where the indices $a, \ldots, b$ can be either in increasing or decreasing order), $$ \begin{aligned} F(n, 1) & =F(n, 2)+x_{1} F(n, 3)=F(2, n)+x_{1} F(3, n) \\ & =\left(F(2, n-1)+x_{n} F(2, n-2)\right)+x_{1}\left(F(3, n-1)+x_{n} F(3, n-2)\right) \\ & =\left(F(n-1,2)+x_{1} F(n-1,3)\right)+x_{n}\left(F(n-2,2)+x_{1} F(n-2,3)\right) \\ & =F(n-1,1)+x_{n} F(n-2,1)=F(1, n-1)+x_{n} F(1, n-2) \\ & =F(1, n), \end{aligned} $$ as we wished to show.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $n$ be a positive integer and let $a_{1}, \ldots, a_{n-1}$ be arbitrary real numbers. Define the sequences $u_{0}, \ldots, u_{n}$ and $v_{0}, \ldots, v_{n}$ inductively by $u_{0}=u_{1}=v_{0}=v_{1}=1$, and $$ u_{k+1}=u_{k}+a_{k} u_{k-1}, \quad v_{k+1}=v_{k}+a_{n-k} v_{k-1} \quad \text { for } k=1, \ldots, n-1 . $$ Prove that $u_{n}=v_{n}$. (France)
|
Define recursively a sequence of multivariate polynomials by $$ P_{0}=P_{1}=1, \quad P_{k+1}\left(x_{1}, \ldots, x_{k}\right)=P_{k}\left(x_{1}, \ldots, x_{k-1}\right)+x_{k} P_{k-1}\left(x_{1}, \ldots, x_{k-2}\right), $$ so $P_{n}$ is a polynomial in $n-1$ variables for each $n \geqslant 1$. Two easy inductive arguments show that $$ u_{n}=P_{n}\left(a_{1}, \ldots, a_{n-1}\right), \quad v_{n}=P_{n}\left(a_{n-1}, \ldots, a_{1}\right) $$ so we need to prove $P_{n}\left(x_{1}, \ldots, x_{n-1}\right)=P_{n}\left(x_{n-1}, \ldots, x_{1}\right)$ for every positive integer $n$. The cases $n=1,2$ are trivial, and the cases $n=3,4$ follow from $P_{3}(x, y)=1+x+y$ and $P_{4}(x, y, z)=$ $1+x+y+z+x z$. Now we proceed by induction, assuming that $n \geqslant 5$ and the claim hold for all smaller cases. Using $F(a, b)$ as an abbreviation for $P_{|a-b|+1}\left(x_{a}, \ldots, x_{b}\right)$ (where the indices $a, \ldots, b$ can be either in increasing or decreasing order), $$ \begin{aligned} F(n, 1) & =F(n, 2)+x_{1} F(n, 3)=F(2, n)+x_{1} F(3, n) \\ & =\left(F(2, n-1)+x_{n} F(2, n-2)\right)+x_{1}\left(F(3, n-1)+x_{n} F(3, n-2)\right) \\ & =\left(F(n-1,2)+x_{1} F(n-1,3)\right)+x_{n}\left(F(n-2,2)+x_{1} F(n-2,3)\right) \\ & =F(n-1,1)+x_{n} F(n-2,1)=F(1, n-1)+x_{n} F(1, n-2) \\ & =F(1, n), \end{aligned} $$ as we wished to show.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
2897d01e-463c-58ce-aa94-21023bc20f75
| 24,239
|
Let $n$ be a positive integer and let $a_{1}, \ldots, a_{n-1}$ be arbitrary real numbers. Define the sequences $u_{0}, \ldots, u_{n}$ and $v_{0}, \ldots, v_{n}$ inductively by $u_{0}=u_{1}=v_{0}=v_{1}=1$, and $$ u_{k+1}=u_{k}+a_{k} u_{k-1}, \quad v_{k+1}=v_{k}+a_{n-k} v_{k-1} \quad \text { for } k=1, \ldots, n-1 . $$ Prove that $u_{n}=v_{n}$. (France)
|
Using matrix notation, we can rewrite the recurrence relation as $$ \left(\begin{array}{c} u_{k+1} \\ u_{k+1}-u_{k} \end{array}\right)=\left(\begin{array}{c} u_{k}+a_{k} u_{k-1} \\ a_{k} u_{k-1} \end{array}\right)=\left(\begin{array}{cc} 1+a_{k} & -a_{k} \\ a_{k} & -a_{k} \end{array}\right)\left(\begin{array}{c} u_{k} \\ u_{k}-u_{k-1} \end{array}\right) $$ for $1 \leqslant k \leqslant n-1$, and similarly $$ \left(v_{k+1} ; v_{k}-v_{k+1}\right)=\left(v_{k}+a_{n-k} v_{k-1} ;-a_{n-k} v_{k-1}\right)=\left(v_{k} ; v_{k-1}-v_{k}\right)\left(\begin{array}{cc} 1+a_{n-k} & -a_{n-k} \\ a_{n-k} & -a_{n-k} \end{array}\right) $$ for $1 \leqslant k \leqslant n-1$. Hence, introducing the $2 \times 2$ matrices $A_{k}=\left(\begin{array}{cc}1+a_{k} & -a_{k} \\ a_{k} & -a_{k}\end{array}\right)$ we have $$ \left(\begin{array}{c} u_{k+1} \\ u_{k+1}-u_{k} \end{array}\right)=A_{k}\left(\begin{array}{c} u_{k} \\ u_{k}-u_{k-1} \end{array}\right) \quad \text { and } \quad\left(v_{k+1} ; v_{k}-v_{k+1}\right)=\left(v_{k} ; v_{k-1}-v_{k}\right) A_{n-k} . $$ for $1 \leqslant k \leqslant n-1$. Since $\left(\begin{array}{c}u_{1} \\ u_{1}-u_{0}\end{array}\right)=\left(\begin{array}{l}1 \\ 0\end{array}\right)$ and $\left(v_{1} ; v_{0}-v_{1}\right)=(1 ; 0)$, we get $$ \left(\begin{array}{c} u_{n} \\ u_{n}-u_{n-1} \end{array}\right)=A_{n-1} A_{n-2} \cdots A_{1} \cdot\left(\begin{array}{l} 1 \\ 0 \end{array}\right) \quad \text { and } \quad\left(v_{n} ; v_{n-1}-v_{n}\right)=(1 ; 0) \cdot A_{n-1} A_{n-2} \cdots A_{1} \text {. } $$ It follows that $$ \left(u_{n}\right)=(1 ; 0)\left(\begin{array}{c} u_{n} \\ u_{n}-u_{n-1} \end{array}\right)=(1 ; 0) \cdot A_{n-1} A_{n-2} \cdots A_{1} \cdot\left(\begin{array}{l} 1 \\ 0 \end{array}\right)=\left(v_{n} ; v_{n-1}-v_{n}\right)\left(\begin{array}{l} 1 \\ 0 \end{array}\right)=\left(v_{n}\right) . $$ Comment 1. These sequences are related to the Fibonacci sequence; when $a_{1}=\cdots=a_{n-1}=1$, we have $u_{k}=v_{k}=F_{k+1}$, the $(k+1)$ st Fibonacci number. Also, for every positive integer $k$, the polynomial $P_{k}\left(x_{1}, \ldots, x_{k-1}\right)$ from Solution 2 is the sum of $F_{k+1}$ monomials. Comment 2. One may notice that the condition is equivalent to $$ \frac{u_{k+1}}{u_{k}}=1+\frac{a_{k}}{1+\frac{a_{k-1}}{1+\ldots+\frac{a_{2}}{1+a_{1}}}} \quad \text { and } \quad \frac{v_{k+1}}{v_{k}}=1+\frac{a_{n-k}}{1+\frac{a_{n-k+1}}{1+\ldots+\frac{a_{n-2}}{1+a_{n-1}}}} $$ so the problem claims that the corresponding continued fractions for $u_{n} / u_{n-1}$ and $v_{n} / v_{n-1}$ have the same numerator. Comment 3. An alternative variant of the problem is the following. Let $n$ be a positive integer and let $a_{1}, \ldots, a_{n-1}$ be arbitrary real numbers. Define the sequences $u_{0}, \ldots, u_{n}$ and $v_{0}, \ldots, v_{n}$ inductively by $u_{0}=v_{0}=0, u_{1}=v_{1}=1$, and $$ u_{k+1}=a_{k} u_{k}+u_{k-1}, \quad v_{k+1}=a_{n-k} v_{k}+v_{k-1} \quad \text { for } k=1, \ldots, n-1 $$ Prove that $u_{n}=v_{n}$. All three solutions above can be reformulated to prove this statement; one may prove $$ u_{n}=v_{n}=\sum_{\substack{0=i_{0}<i_{1}<\ldots<i_{t}=n, i_{j+1}-i_{j} \text { is odd }}} a_{i_{1}} \ldots a_{i_{t-1}} \quad \text { for } n>0 $$ or observe that $$ \left(\begin{array}{c} u_{k+1} \\ u_{k} \end{array}\right)=\left(\begin{array}{cc} a_{k} & 1 \\ 1 & 0 \end{array}\right)\left(\begin{array}{c} u_{k} \\ u_{k-1} \end{array}\right) \quad \text { and } \quad\left(v_{k+1} ; v_{k}\right)=\left(v_{k} ; v_{k-1}\right)\left(\begin{array}{cc} a_{k} & 1 \\ 1 & 0 \end{array}\right) . $$ Here we have $$ \frac{u_{k+1}}{u_{k}}=a_{k}+\frac{1}{a_{k-1}+\frac{1}{a_{k-2}+\ldots+\frac{1}{a_{1}}}}=\left[a_{k} ; a_{k-1}, \ldots, a_{1}\right] $$ and $$ \frac{v_{k+1}}{v_{k}}=a_{n-k}+\frac{1}{a_{n-k+1}+\frac{1}{a_{n-k+2}+\ldots+\frac{1}{a_{n-1}}}}=\left[a_{n-k} ; a_{n-k+1}, \ldots, a_{n-1}\right] $$ so this alternative statement is equivalent to the known fact that the continued fractions $\left[a_{n-1} ; a_{n-2}, \ldots, a_{1}\right]$ and $\left[a_{1} ; a_{2}, \ldots, a_{n-1}\right]$ have the same numerator.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $n$ be a positive integer and let $a_{1}, \ldots, a_{n-1}$ be arbitrary real numbers. Define the sequences $u_{0}, \ldots, u_{n}$ and $v_{0}, \ldots, v_{n}$ inductively by $u_{0}=u_{1}=v_{0}=v_{1}=1$, and $$ u_{k+1}=u_{k}+a_{k} u_{k-1}, \quad v_{k+1}=v_{k}+a_{n-k} v_{k-1} \quad \text { for } k=1, \ldots, n-1 . $$ Prove that $u_{n}=v_{n}$. (France)
|
Using matrix notation, we can rewrite the recurrence relation as $$ \left(\begin{array}{c} u_{k+1} \\ u_{k+1}-u_{k} \end{array}\right)=\left(\begin{array}{c} u_{k}+a_{k} u_{k-1} \\ a_{k} u_{k-1} \end{array}\right)=\left(\begin{array}{cc} 1+a_{k} & -a_{k} \\ a_{k} & -a_{k} \end{array}\right)\left(\begin{array}{c} u_{k} \\ u_{k}-u_{k-1} \end{array}\right) $$ for $1 \leqslant k \leqslant n-1$, and similarly $$ \left(v_{k+1} ; v_{k}-v_{k+1}\right)=\left(v_{k}+a_{n-k} v_{k-1} ;-a_{n-k} v_{k-1}\right)=\left(v_{k} ; v_{k-1}-v_{k}\right)\left(\begin{array}{cc} 1+a_{n-k} & -a_{n-k} \\ a_{n-k} & -a_{n-k} \end{array}\right) $$ for $1 \leqslant k \leqslant n-1$. Hence, introducing the $2 \times 2$ matrices $A_{k}=\left(\begin{array}{cc}1+a_{k} & -a_{k} \\ a_{k} & -a_{k}\end{array}\right)$ we have $$ \left(\begin{array}{c} u_{k+1} \\ u_{k+1}-u_{k} \end{array}\right)=A_{k}\left(\begin{array}{c} u_{k} \\ u_{k}-u_{k-1} \end{array}\right) \quad \text { and } \quad\left(v_{k+1} ; v_{k}-v_{k+1}\right)=\left(v_{k} ; v_{k-1}-v_{k}\right) A_{n-k} . $$ for $1 \leqslant k \leqslant n-1$. Since $\left(\begin{array}{c}u_{1} \\ u_{1}-u_{0}\end{array}\right)=\left(\begin{array}{l}1 \\ 0\end{array}\right)$ and $\left(v_{1} ; v_{0}-v_{1}\right)=(1 ; 0)$, we get $$ \left(\begin{array}{c} u_{n} \\ u_{n}-u_{n-1} \end{array}\right)=A_{n-1} A_{n-2} \cdots A_{1} \cdot\left(\begin{array}{l} 1 \\ 0 \end{array}\right) \quad \text { and } \quad\left(v_{n} ; v_{n-1}-v_{n}\right)=(1 ; 0) \cdot A_{n-1} A_{n-2} \cdots A_{1} \text {. } $$ It follows that $$ \left(u_{n}\right)=(1 ; 0)\left(\begin{array}{c} u_{n} \\ u_{n}-u_{n-1} \end{array}\right)=(1 ; 0) \cdot A_{n-1} A_{n-2} \cdots A_{1} \cdot\left(\begin{array}{l} 1 \\ 0 \end{array}\right)=\left(v_{n} ; v_{n-1}-v_{n}\right)\left(\begin{array}{l} 1 \\ 0 \end{array}\right)=\left(v_{n}\right) . $$ Comment 1. These sequences are related to the Fibonacci sequence; when $a_{1}=\cdots=a_{n-1}=1$, we have $u_{k}=v_{k}=F_{k+1}$, the $(k+1)$ st Fibonacci number. Also, for every positive integer $k$, the polynomial $P_{k}\left(x_{1}, \ldots, x_{k-1}\right)$ from Solution 2 is the sum of $F_{k+1}$ monomials. Comment 2. One may notice that the condition is equivalent to $$ \frac{u_{k+1}}{u_{k}}=1+\frac{a_{k}}{1+\frac{a_{k-1}}{1+\ldots+\frac{a_{2}}{1+a_{1}}}} \quad \text { and } \quad \frac{v_{k+1}}{v_{k}}=1+\frac{a_{n-k}}{1+\frac{a_{n-k+1}}{1+\ldots+\frac{a_{n-2}}{1+a_{n-1}}}} $$ so the problem claims that the corresponding continued fractions for $u_{n} / u_{n-1}$ and $v_{n} / v_{n-1}$ have the same numerator. Comment 3. An alternative variant of the problem is the following. Let $n$ be a positive integer and let $a_{1}, \ldots, a_{n-1}$ be arbitrary real numbers. Define the sequences $u_{0}, \ldots, u_{n}$ and $v_{0}, \ldots, v_{n}$ inductively by $u_{0}=v_{0}=0, u_{1}=v_{1}=1$, and $$ u_{k+1}=a_{k} u_{k}+u_{k-1}, \quad v_{k+1}=a_{n-k} v_{k}+v_{k-1} \quad \text { for } k=1, \ldots, n-1 $$ Prove that $u_{n}=v_{n}$. All three solutions above can be reformulated to prove this statement; one may prove $$ u_{n}=v_{n}=\sum_{\substack{0=i_{0}<i_{1}<\ldots<i_{t}=n, i_{j+1}-i_{j} \text { is odd }}} a_{i_{1}} \ldots a_{i_{t-1}} \quad \text { for } n>0 $$ or observe that $$ \left(\begin{array}{c} u_{k+1} \\ u_{k} \end{array}\right)=\left(\begin{array}{cc} a_{k} & 1 \\ 1 & 0 \end{array}\right)\left(\begin{array}{c} u_{k} \\ u_{k-1} \end{array}\right) \quad \text { and } \quad\left(v_{k+1} ; v_{k}\right)=\left(v_{k} ; v_{k-1}\right)\left(\begin{array}{cc} a_{k} & 1 \\ 1 & 0 \end{array}\right) . $$ Here we have $$ \frac{u_{k+1}}{u_{k}}=a_{k}+\frac{1}{a_{k-1}+\frac{1}{a_{k-2}+\ldots+\frac{1}{a_{1}}}}=\left[a_{k} ; a_{k-1}, \ldots, a_{1}\right] $$ and $$ \frac{v_{k+1}}{v_{k}}=a_{n-k}+\frac{1}{a_{n-k+1}+\frac{1}{a_{n-k+2}+\ldots+\frac{1}{a_{n-1}}}}=\left[a_{n-k} ; a_{n-k+1}, \ldots, a_{n-1}\right] $$ so this alternative statement is equivalent to the known fact that the continued fractions $\left[a_{n-1} ; a_{n-2}, \ldots, a_{1}\right]$ and $\left[a_{1} ; a_{2}, \ldots, a_{n-1}\right]$ have the same numerator.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
2897d01e-463c-58ce-aa94-21023bc20f75
| 24,239
|
Prove that in any set of 2000 distinct real numbers there exist two pairs $a>b$ and $c>d$ with $a \neq c$ or $b \neq d$, such that $$ \left|\frac{a-b}{c-d}-1\right|<\frac{1}{100000} $$ (Lithuania)
|
For any set $S$ of $n=2000$ distinct real numbers, let $D_{1} \leqslant D_{2} \leqslant \cdots \leqslant D_{m}$ be the distances between them, displayed with their multiplicities. Here $m=n(n-1) / 2$. By rescaling the numbers, we may assume that the smallest distance $D_{1}$ between two elements of $S$ is $D_{1}=1$. Let $D_{1}=1=y-x$ for $x, y \in S$. Evidently $D_{m}=v-u$ is the difference between the largest element $v$ and the smallest element $u$ of $S$. If $D_{i+1} / D_{i}<1+10^{-5}$ for some $i=1,2, \ldots, m-1$ then the required inequality holds, because $0 \leqslant D_{i+1} / D_{i}-1<10^{-5}$. Otherwise, the reverse inequality $$ \frac{D_{i+1}}{D_{i}} \geqslant 1+\frac{1}{10^{5}} $$ holds for each $i=1,2, \ldots, m-1$, and therefore $$ v-u=D_{m}=\frac{D_{m}}{D_{1}}=\frac{D_{m}}{D_{m-1}} \cdots \frac{D_{3}}{D_{2}} \cdot \frac{D_{2}}{D_{1}} \geqslant\left(1+\frac{1}{10^{5}}\right)^{m-1} . $$ From $m-1=n(n-1) / 2-1=1000 \cdot 1999-1>19 \cdot 10^{5}$, together with the fact that for all $n \geqslant 1$, $\left(1+\frac{1}{n}\right)^{n} \geqslant 1+\left(\begin{array}{l}n \\ 1\end{array}\right) \cdot \frac{1}{n}=2$, we get $$ \left(1+\frac{1}{10^{5}}\right)^{19 \cdot 10^{5}}=\left(\left(1+\frac{1}{10^{5}}\right)^{10^{5}}\right)^{19} \geqslant 2^{19}=2^{9} \cdot 2^{10}>500 \cdot 1000>2 \cdot 10^{5}, $$ and so $v-u=D_{m}>2 \cdot 10^{5}$. Since the distance of $x$ to at least one of the numbers $u, v$ is at least $(u-v) / 2>10^{5}$, we have $$ |x-z|>10^{5} . $$ for some $z \in\{u, v\}$. Since $y-x=1$, we have either $z>y>x$ (if $z=v$ ) or $y>x>z$ (if $z=u$ ). If $z>y>x$, selecting $a=z, b=y, c=z$ and $d=x$ (so that $b \neq d$ ), we obtain $$ \left|\frac{a-b}{c-d}-1\right|=\left|\frac{z-y}{z-x}-1\right|=\left|\frac{x-y}{z-x}\right|=\frac{1}{z-x}<10^{-5} . $$ Otherwise, if $y>x>z$, we may choose $a=y, b=z, c=x$ and $d=z$ (so that $a \neq c$ ), and obtain $$ \left|\frac{a-b}{c-d}-1\right|=\left|\frac{y-z}{x-z}-1\right|=\left|\frac{y-x}{x-z}\right|=\frac{1}{x-z}<10^{-5} $$ The desired result follows. Comment. As the solution shows, the numbers 2000 and $\frac{1}{100000}$ appearing in the statement of the problem may be replaced by any $n \in \mathbb{Z}_{>0}$ and $\delta>0$ satisfying $$ \delta(1+\delta)^{n(n-1) / 2-1}>2 $$
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Prove that in any set of 2000 distinct real numbers there exist two pairs $a>b$ and $c>d$ with $a \neq c$ or $b \neq d$, such that $$ \left|\frac{a-b}{c-d}-1\right|<\frac{1}{100000} $$ (Lithuania)
|
For any set $S$ of $n=2000$ distinct real numbers, let $D_{1} \leqslant D_{2} \leqslant \cdots \leqslant D_{m}$ be the distances between them, displayed with their multiplicities. Here $m=n(n-1) / 2$. By rescaling the numbers, we may assume that the smallest distance $D_{1}$ between two elements of $S$ is $D_{1}=1$. Let $D_{1}=1=y-x$ for $x, y \in S$. Evidently $D_{m}=v-u$ is the difference between the largest element $v$ and the smallest element $u$ of $S$. If $D_{i+1} / D_{i}<1+10^{-5}$ for some $i=1,2, \ldots, m-1$ then the required inequality holds, because $0 \leqslant D_{i+1} / D_{i}-1<10^{-5}$. Otherwise, the reverse inequality $$ \frac{D_{i+1}}{D_{i}} \geqslant 1+\frac{1}{10^{5}} $$ holds for each $i=1,2, \ldots, m-1$, and therefore $$ v-u=D_{m}=\frac{D_{m}}{D_{1}}=\frac{D_{m}}{D_{m-1}} \cdots \frac{D_{3}}{D_{2}} \cdot \frac{D_{2}}{D_{1}} \geqslant\left(1+\frac{1}{10^{5}}\right)^{m-1} . $$ From $m-1=n(n-1) / 2-1=1000 \cdot 1999-1>19 \cdot 10^{5}$, together with the fact that for all $n \geqslant 1$, $\left(1+\frac{1}{n}\right)^{n} \geqslant 1+\left(\begin{array}{l}n \\ 1\end{array}\right) \cdot \frac{1}{n}=2$, we get $$ \left(1+\frac{1}{10^{5}}\right)^{19 \cdot 10^{5}}=\left(\left(1+\frac{1}{10^{5}}\right)^{10^{5}}\right)^{19} \geqslant 2^{19}=2^{9} \cdot 2^{10}>500 \cdot 1000>2 \cdot 10^{5}, $$ and so $v-u=D_{m}>2 \cdot 10^{5}$. Since the distance of $x$ to at least one of the numbers $u, v$ is at least $(u-v) / 2>10^{5}$, we have $$ |x-z|>10^{5} . $$ for some $z \in\{u, v\}$. Since $y-x=1$, we have either $z>y>x$ (if $z=v$ ) or $y>x>z$ (if $z=u$ ). If $z>y>x$, selecting $a=z, b=y, c=z$ and $d=x$ (so that $b \neq d$ ), we obtain $$ \left|\frac{a-b}{c-d}-1\right|=\left|\frac{z-y}{z-x}-1\right|=\left|\frac{x-y}{z-x}\right|=\frac{1}{z-x}<10^{-5} . $$ Otherwise, if $y>x>z$, we may choose $a=y, b=z, c=x$ and $d=z$ (so that $a \neq c$ ), and obtain $$ \left|\frac{a-b}{c-d}-1\right|=\left|\frac{y-z}{x-z}-1\right|=\left|\frac{y-x}{x-z}\right|=\frac{1}{x-z}<10^{-5} $$ The desired result follows. Comment. As the solution shows, the numbers 2000 and $\frac{1}{100000}$ appearing in the statement of the problem may be replaced by any $n \in \mathbb{Z}_{>0}$ and $\delta>0$ satisfying $$ \delta(1+\delta)^{n(n-1) / 2-1}>2 $$
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
31eab867-d2db-5957-9e34-31878e1b7dec
| 24,244
|
Let $\mathbb{Q}_{>0}$ be the set of positive rational numbers. Let $f: \mathbb{Q}_{>0} \rightarrow \mathbb{R}$ be a function satisfying the conditions $$ f(x) f(y) \geqslant f(x y) \text { and } f(x+y) \geqslant f(x)+f(y) $$ for all $x, y \in \mathbb{Q}_{>0}$. Given that $f(a)=a$ for some rational $a>1$, prove that $f(x)=x$ for all $x \in \mathbb{Q}_{>0}$. (Bulgaria)
|
Denote by $\mathbb{Z}_{>0}$ the set of positive integers. Plugging $x=1, y=a$ into (1) we get $f(1) \geqslant 1$. Next, by an easy induction on $n$ we get from (2) that $$ f(n x) \geqslant n f(x) \text { for all } n \in \mathbb{Z}_{>0} \text { and } x \in \mathbb{Q}_{>0} $$ In particular, we have $$ f(n) \geqslant n f(1) \geqslant n \quad \text { for all } n \in \mathbb{Z}_{>0} $$ From (1) again we have $f(m / n) f(n) \geqslant f(m)$, so $f(q)>0$ for all $q \in \mathbb{Q}_{>0}$. Now, (2) implies that $f$ is strictly increasing; this fact together with (4) yields $$ f(x) \geqslant f(\lfloor x\rfloor) \geqslant\lfloor x\rfloor>x-1 \quad \text { for all } x \geqslant 1 $$ By an easy induction we get from (1) that $f(x)^{n} \geqslant f\left(x^{n}\right)$, so $$ f(x)^{n} \geqslant f\left(x^{n}\right)>x^{n}-1 \quad \Longrightarrow \quad f(x) \geqslant \sqrt[n]{x^{n}-1} \text { for all } x>1 \text { and } n \in \mathbb{Z}_{>0} $$ This yields $$ f(x) \geqslant x \text { for every } x>1 \text {. } $$ (Indeed, if $x>y>1$ then $x^{n}-y^{n}=(x-y)\left(x^{n-1}+x^{n-2} y+\cdots+y^{n}\right)>n(x-y)$, so for a large $n$ we have $x^{n}-1>y^{n}$ and thus $f(x)>y$.) Now, (1) and (5) give $a^{n}=f(a)^{n} \geqslant f\left(a^{n}\right) \geqslant a^{n}$, so $f\left(a^{n}\right)=a^{n}$. Now, for $x>1$ let us choose $n \in \mathbb{Z}_{>0}$ such that $a^{n}-x>1$. Then by (2) and (5) we get $$ a^{n}=f\left(a^{n}\right) \geqslant f(x)+f\left(a^{n}-x\right) \geqslant x+\left(a^{n}-x\right)=a^{n} $$ and therefore $f(x)=x$ for $x>1$. Finally, for every $x \in \mathbb{Q}_{>0}$ and every $n \in \mathbb{Z}_{>0}$, from (1) and (3) we get $$ n f(x)=f(n) f(x) \geqslant f(n x) \geqslant n f(x) $$ which gives $f(n x)=n f(x)$. Therefore $f(m / n)=f(m) / n=m / n$ for all $m, n \in \mathbb{Z}_{>0}$. Comment. The condition $f(a)=a>1$ is essential. Indeed, for $b \geqslant 1$ the function $f(x)=b x^{2}$ satisfies (1) and (2) for all $x, y \in \mathbb{Q}_{>0}$, and it has a unique fixed point $1 / b \leqslant 1$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $\mathbb{Q}_{>0}$ be the set of positive rational numbers. Let $f: \mathbb{Q}_{>0} \rightarrow \mathbb{R}$ be a function satisfying the conditions $$ f(x) f(y) \geqslant f(x y) \text { and } f(x+y) \geqslant f(x)+f(y) $$ for all $x, y \in \mathbb{Q}_{>0}$. Given that $f(a)=a$ for some rational $a>1$, prove that $f(x)=x$ for all $x \in \mathbb{Q}_{>0}$. (Bulgaria)
|
Denote by $\mathbb{Z}_{>0}$ the set of positive integers. Plugging $x=1, y=a$ into (1) we get $f(1) \geqslant 1$. Next, by an easy induction on $n$ we get from (2) that $$ f(n x) \geqslant n f(x) \text { for all } n \in \mathbb{Z}_{>0} \text { and } x \in \mathbb{Q}_{>0} $$ In particular, we have $$ f(n) \geqslant n f(1) \geqslant n \quad \text { for all } n \in \mathbb{Z}_{>0} $$ From (1) again we have $f(m / n) f(n) \geqslant f(m)$, so $f(q)>0$ for all $q \in \mathbb{Q}_{>0}$. Now, (2) implies that $f$ is strictly increasing; this fact together with (4) yields $$ f(x) \geqslant f(\lfloor x\rfloor) \geqslant\lfloor x\rfloor>x-1 \quad \text { for all } x \geqslant 1 $$ By an easy induction we get from (1) that $f(x)^{n} \geqslant f\left(x^{n}\right)$, so $$ f(x)^{n} \geqslant f\left(x^{n}\right)>x^{n}-1 \quad \Longrightarrow \quad f(x) \geqslant \sqrt[n]{x^{n}-1} \text { for all } x>1 \text { and } n \in \mathbb{Z}_{>0} $$ This yields $$ f(x) \geqslant x \text { for every } x>1 \text {. } $$ (Indeed, if $x>y>1$ then $x^{n}-y^{n}=(x-y)\left(x^{n-1}+x^{n-2} y+\cdots+y^{n}\right)>n(x-y)$, so for a large $n$ we have $x^{n}-1>y^{n}$ and thus $f(x)>y$.) Now, (1) and (5) give $a^{n}=f(a)^{n} \geqslant f\left(a^{n}\right) \geqslant a^{n}$, so $f\left(a^{n}\right)=a^{n}$. Now, for $x>1$ let us choose $n \in \mathbb{Z}_{>0}$ such that $a^{n}-x>1$. Then by (2) and (5) we get $$ a^{n}=f\left(a^{n}\right) \geqslant f(x)+f\left(a^{n}-x\right) \geqslant x+\left(a^{n}-x\right)=a^{n} $$ and therefore $f(x)=x$ for $x>1$. Finally, for every $x \in \mathbb{Q}_{>0}$ and every $n \in \mathbb{Z}_{>0}$, from (1) and (3) we get $$ n f(x)=f(n) f(x) \geqslant f(n x) \geqslant n f(x) $$ which gives $f(n x)=n f(x)$. Therefore $f(m / n)=f(m) / n=m / n$ for all $m, n \in \mathbb{Z}_{>0}$. Comment. The condition $f(a)=a>1$ is essential. Indeed, for $b \geqslant 1$ the function $f(x)=b x^{2}$ satisfies (1) and (2) for all $x, y \in \mathbb{Q}_{>0}$, and it has a unique fixed point $1 / b \leqslant 1$.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
bf6369d6-abe3-51ff-90a3-ad2af844ae85
| 24,248
|
Let $n$ be a positive integer, and consider a sequence $a_{1}, a_{2}, \ldots, a_{n}$ of positive integers. Extend it periodically to an infinite sequence $a_{1}, a_{2}, \ldots$ by defining $a_{n+i}=a_{i}$ for all $i \geqslant 1$. If $$ a_{1} \leqslant a_{2} \leqslant \cdots \leqslant a_{n} \leqslant a_{1}+n $$ and $$ a_{a_{i}} \leqslant n+i-1 \quad \text { for } i=1,2, \ldots, n $$ prove that $$ a_{1}+\cdots+a_{n} \leqslant n^{2} . $$ (Germany)
|
First, we claim that $$ a_{i} \leqslant n+i-1 \quad \text { for } i=1,2, \ldots, n \text {. } $$ Assume contrariwise that $i$ is the smallest counterexample. From $a_{n} \geqslant a_{n-1} \geqslant \cdots \geqslant a_{i} \geqslant n+i$ and $a_{a_{i}} \leqslant n+i-1$, taking into account the periodicity of our sequence, it follows that $$ a_{i} \text { cannot be congruent to } i, i+1, \ldots, n-1 \text {, or } n(\bmod n) \text {. } $$ Thus our assumption that $a_{i} \geqslant n+i$ implies the stronger statement that $a_{i} \geqslant 2 n+1$, which by $a_{1}+n \geqslant a_{n} \geqslant a_{i}$ gives $a_{1} \geqslant n+1$. The minimality of $i$ then yields $i=1$, and (4) becomes contradictory. This establishes our first claim. In particular we now know that $a_{1} \leqslant n$. If $a_{n} \leqslant n$, then $a_{1} \leqslant \cdots \leqslant \cdots a_{n} \leqslant n$ and the desired inequality holds trivially. Otherwise, consider the number $t$ with $1 \leqslant t \leqslant n-1$ such that $$ a_{1} \leqslant a_{2} \leqslant \ldots \leqslant a_{t} \leqslant n<a_{t+1} \leqslant \ldots \leqslant a_{n} $$ Since $1 \leqslant a_{1} \leqslant n$ and $a_{a_{1}} \leqslant n$ by (2), we have $a_{1} \leqslant t$ and hence $a_{n} \leqslant n+t$. Therefore if for each positive integer $i$ we let $b_{i}$ be the number of indices $j \in\{t+1, \ldots, n\}$ satisfying $a_{j} \geqslant n+i$, we have $$ b_{1} \geqslant b_{2} \geqslant \ldots \geqslant b_{t} \geqslant b_{t+1}=0 $$ Next we claim that $a_{i}+b_{i} \leqslant n$ for $1 \leqslant i \leqslant t$. Indeed, by $n+i-1 \geqslant a_{a_{i}}$ and $a_{i} \leqslant n$, each $j$ with $a_{j} \geqslant n+i$ (thus $a_{j}>a_{a_{i}}$ ) belongs to $\left\{a_{i}+1, \ldots, n\right\}$, and for this reason $b_{i} \leqslant n-a_{i}$. It follows from the definition of the $b_{i} \mathrm{~s}$ and (5) that $$ a_{t+1}+\ldots+a_{n} \leqslant n(n-t)+b_{1}+\ldots+b_{t} . $$ Adding $a_{1}+\ldots+a_{t}$ to both sides and using that $a_{i}+b_{i} \leqslant n$ for $1 \leqslant i \leqslant t$, we get $$ a_{1}+a_{2}+\cdots+a_{n} \leqslant n(n-t)+n t=n^{2} $$ as we wished to prove.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n$ be a positive integer, and consider a sequence $a_{1}, a_{2}, \ldots, a_{n}$ of positive integers. Extend it periodically to an infinite sequence $a_{1}, a_{2}, \ldots$ by defining $a_{n+i}=a_{i}$ for all $i \geqslant 1$. If $$ a_{1} \leqslant a_{2} \leqslant \cdots \leqslant a_{n} \leqslant a_{1}+n $$ and $$ a_{a_{i}} \leqslant n+i-1 \quad \text { for } i=1,2, \ldots, n $$ prove that $$ a_{1}+\cdots+a_{n} \leqslant n^{2} . $$ (Germany)
|
First, we claim that $$ a_{i} \leqslant n+i-1 \quad \text { for } i=1,2, \ldots, n \text {. } $$ Assume contrariwise that $i$ is the smallest counterexample. From $a_{n} \geqslant a_{n-1} \geqslant \cdots \geqslant a_{i} \geqslant n+i$ and $a_{a_{i}} \leqslant n+i-1$, taking into account the periodicity of our sequence, it follows that $$ a_{i} \text { cannot be congruent to } i, i+1, \ldots, n-1 \text {, or } n(\bmod n) \text {. } $$ Thus our assumption that $a_{i} \geqslant n+i$ implies the stronger statement that $a_{i} \geqslant 2 n+1$, which by $a_{1}+n \geqslant a_{n} \geqslant a_{i}$ gives $a_{1} \geqslant n+1$. The minimality of $i$ then yields $i=1$, and (4) becomes contradictory. This establishes our first claim. In particular we now know that $a_{1} \leqslant n$. If $a_{n} \leqslant n$, then $a_{1} \leqslant \cdots \leqslant \cdots a_{n} \leqslant n$ and the desired inequality holds trivially. Otherwise, consider the number $t$ with $1 \leqslant t \leqslant n-1$ such that $$ a_{1} \leqslant a_{2} \leqslant \ldots \leqslant a_{t} \leqslant n<a_{t+1} \leqslant \ldots \leqslant a_{n} $$ Since $1 \leqslant a_{1} \leqslant n$ and $a_{a_{1}} \leqslant n$ by (2), we have $a_{1} \leqslant t$ and hence $a_{n} \leqslant n+t$. Therefore if for each positive integer $i$ we let $b_{i}$ be the number of indices $j \in\{t+1, \ldots, n\}$ satisfying $a_{j} \geqslant n+i$, we have $$ b_{1} \geqslant b_{2} \geqslant \ldots \geqslant b_{t} \geqslant b_{t+1}=0 $$ Next we claim that $a_{i}+b_{i} \leqslant n$ for $1 \leqslant i \leqslant t$. Indeed, by $n+i-1 \geqslant a_{a_{i}}$ and $a_{i} \leqslant n$, each $j$ with $a_{j} \geqslant n+i$ (thus $a_{j}>a_{a_{i}}$ ) belongs to $\left\{a_{i}+1, \ldots, n\right\}$, and for this reason $b_{i} \leqslant n-a_{i}$. It follows from the definition of the $b_{i} \mathrm{~s}$ and (5) that $$ a_{t+1}+\ldots+a_{n} \leqslant n(n-t)+b_{1}+\ldots+b_{t} . $$ Adding $a_{1}+\ldots+a_{t}$ to both sides and using that $a_{i}+b_{i} \leqslant n$ for $1 \leqslant i \leqslant t$, we get $$ a_{1}+a_{2}+\cdots+a_{n} \leqslant n(n-t)+n t=n^{2} $$ as we wished to prove.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8c4bd8e5-7a6f-569d-8632-92af8e74c0e3
| 24,250
|
Let $n$ be a positive integer, and consider a sequence $a_{1}, a_{2}, \ldots, a_{n}$ of positive integers. Extend it periodically to an infinite sequence $a_{1}, a_{2}, \ldots$ by defining $a_{n+i}=a_{i}$ for all $i \geqslant 1$. If $$ a_{1} \leqslant a_{2} \leqslant \cdots \leqslant a_{n} \leqslant a_{1}+n $$ and $$ a_{a_{i}} \leqslant n+i-1 \quad \text { for } i=1,2, \ldots, n $$ prove that $$ a_{1}+\cdots+a_{n} \leqslant n^{2} . $$ (Germany)
|
In the first quadrant of an infinite grid, consider the increasing "staircase" obtained by shading in dark the bottom $a_{i}$ cells of the $i$ th column for $1 \leqslant i \leqslant n$. We will prove that there are at most $n^{2}$ dark cells. To do it, consider the $n \times n$ square $S$ in the first quadrant with a vertex at the origin. Also consider the $n \times n$ square directly to the left of $S$. Starting from its lower left corner, shade in light the leftmost $a_{j}$ cells of the $j$ th row for $1 \leqslant j \leqslant n$. Equivalently, the light shading is obtained by reflecting the dark shading across the line $x=y$ and translating it $n$ units to the left. The figure below illustrates this construction for the sequence $6,6,6,7,7,7,8,12,12,14$.  We claim that there is no cell in $S$ which is both dark and light. Assume, contrariwise, that there is such a cell in column $i$. Consider the highest dark cell in column $i$ which is inside $S$. Since it is above a light cell and inside $S$, it must be light as well. There are two cases: Case 1. $a_{i} \leqslant n$ If $a_{i} \leqslant n$ then this dark and light cell is $\left(i, a_{i}\right)$, as highlighted in the figure. However, this is the $(n+i)$-th cell in row $a_{i}$, and we only shaded $a_{a_{i}}<n+i$ light cells in that row, a contradiction. Case 2. $a_{i} \geqslant n+1$ If $a_{i} \geqslant n+1$, this dark and light cell is $(i, n)$. This is the $(n+i)$-th cell in row $n$ and we shaded $a_{n} \leqslant a_{1}+n$ light cells in this row, so we must have $i \leqslant a_{1}$. But $a_{1} \leqslant a_{a_{1}} \leqslant n$ by (1) and (2), so $i \leqslant a_{1}$ implies $a_{i} \leqslant a_{a_{1}} \leqslant n$, contradicting our assumption. We conclude that there are no cells in $S$ which are both dark and light. It follows that the number of shaded cells in $S$ is at most $n^{2}$. Finally, observe that if we had a light cell to the right of $S$, then by symmetry we would have a dark cell above $S$, and then the cell $(n, n)$ would be dark and light. It follows that the number of light cells in $S$ equals the number of dark cells outside of $S$, and therefore the number of shaded cells in $S$ equals $a_{1}+\cdots+a_{n}$. The desired result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n$ be a positive integer, and consider a sequence $a_{1}, a_{2}, \ldots, a_{n}$ of positive integers. Extend it periodically to an infinite sequence $a_{1}, a_{2}, \ldots$ by defining $a_{n+i}=a_{i}$ for all $i \geqslant 1$. If $$ a_{1} \leqslant a_{2} \leqslant \cdots \leqslant a_{n} \leqslant a_{1}+n $$ and $$ a_{a_{i}} \leqslant n+i-1 \quad \text { for } i=1,2, \ldots, n $$ prove that $$ a_{1}+\cdots+a_{n} \leqslant n^{2} . $$ (Germany)
|
In the first quadrant of an infinite grid, consider the increasing "staircase" obtained by shading in dark the bottom $a_{i}$ cells of the $i$ th column for $1 \leqslant i \leqslant n$. We will prove that there are at most $n^{2}$ dark cells. To do it, consider the $n \times n$ square $S$ in the first quadrant with a vertex at the origin. Also consider the $n \times n$ square directly to the left of $S$. Starting from its lower left corner, shade in light the leftmost $a_{j}$ cells of the $j$ th row for $1 \leqslant j \leqslant n$. Equivalently, the light shading is obtained by reflecting the dark shading across the line $x=y$ and translating it $n$ units to the left. The figure below illustrates this construction for the sequence $6,6,6,7,7,7,8,12,12,14$.  We claim that there is no cell in $S$ which is both dark and light. Assume, contrariwise, that there is such a cell in column $i$. Consider the highest dark cell in column $i$ which is inside $S$. Since it is above a light cell and inside $S$, it must be light as well. There are two cases: Case 1. $a_{i} \leqslant n$ If $a_{i} \leqslant n$ then this dark and light cell is $\left(i, a_{i}\right)$, as highlighted in the figure. However, this is the $(n+i)$-th cell in row $a_{i}$, and we only shaded $a_{a_{i}}<n+i$ light cells in that row, a contradiction. Case 2. $a_{i} \geqslant n+1$ If $a_{i} \geqslant n+1$, this dark and light cell is $(i, n)$. This is the $(n+i)$-th cell in row $n$ and we shaded $a_{n} \leqslant a_{1}+n$ light cells in this row, so we must have $i \leqslant a_{1}$. But $a_{1} \leqslant a_{a_{1}} \leqslant n$ by (1) and (2), so $i \leqslant a_{1}$ implies $a_{i} \leqslant a_{a_{1}} \leqslant n$, contradicting our assumption. We conclude that there are no cells in $S$ which are both dark and light. It follows that the number of shaded cells in $S$ is at most $n^{2}$. Finally, observe that if we had a light cell to the right of $S$, then by symmetry we would have a dark cell above $S$, and then the cell $(n, n)$ would be dark and light. It follows that the number of light cells in $S$ equals the number of dark cells outside of $S$, and therefore the number of shaded cells in $S$ equals $a_{1}+\cdots+a_{n}$. The desired result follows.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8c4bd8e5-7a6f-569d-8632-92af8e74c0e3
| 24,250
|
Let $n$ be a positive integer, and consider a sequence $a_{1}, a_{2}, \ldots, a_{n}$ of positive integers. Extend it periodically to an infinite sequence $a_{1}, a_{2}, \ldots$ by defining $a_{n+i}=a_{i}$ for all $i \geqslant 1$. If $$ a_{1} \leqslant a_{2} \leqslant \cdots \leqslant a_{n} \leqslant a_{1}+n $$ and $$ a_{a_{i}} \leqslant n+i-1 \quad \text { for } i=1,2, \ldots, n $$ prove that $$ a_{1}+\cdots+a_{n} \leqslant n^{2} . $$ (Germany)
|
As in For $1 \leqslant i<j \leqslant n$ we have $a_{i} \leqslant a_{j}$ and $i<j$, so $c_{i} \leqslant c_{j}$. Also $a_{n} \leqslant a_{1}+n$ and $n<1+n$ imply $c_{n} \leqslant c_{1}+n$. Finally, the definitions imply that $c_{c_{i}} \in\left\{a_{a_{i}}, a_{i}, a_{i}-n, i\right\}$ so $c_{c_{i}} \leqslant n+i-1$ by (2) and (3). This establishes (1) and (2) for $c_{1}, c_{2}, \ldots$. Our new sequence has the additional property that $$ c_{i} \geqslant i \quad \text { for } i=1,2, \ldots, n $$ which allows us to construct the following visualization: Consider $n$ equally spaced points on a circle, sequentially labelled $1,2, \ldots, n(\bmod n)$, so point $k$ is also labelled $n+k$. We draw arrows from vertex $i$ to vertices $i+1, \ldots, c_{i}$ for $1 \leqslant i \leqslant n$, keeping in mind that $c_{i} \geqslant i$ by (6). Since $c_{i} \leqslant n+i-1$ by (3), no arrow will be drawn twice, and there is no arrow from a vertex to itself. The total number of arrows is $$ \text { number of arrows }=\sum_{i=1}^{n}\left(c_{i}-i\right)=\sum_{i=1}^{n} c_{i}-\left(\begin{array}{c} n+1 \\ 2 \end{array}\right) $$ Now we show that we never draw both arrows $i \rightarrow j$ and $j \rightarrow i$ for $1 \leqslant i<j \leqslant n$. Assume contrariwise. This means, respectively, that $$ i<j \leqslant c_{i} \quad \text { and } \quad j<n+i \leqslant c_{j} \text {. } $$ We have $n+i \leqslant c_{j} \leqslant c_{1}+n$ by (1), so $i \leqslant c_{1}$. Since $c_{1} \leqslant n$ by (3), this implies that $c_{i} \leqslant c_{c_{1}} \leqslant n$ using (1) and (3). But then, using (1) again, $j \leqslant c_{i} \leqslant n$ implies $c_{j} \leqslant c_{c_{i}}$, which combined with $n+i \leqslant c_{j}$ gives us that $n+i \leqslant c_{c_{i}}$. This contradicts (2). This means that the number of arrows is at most $\left(\begin{array}{l}n \\ 2\end{array}\right)$, which implies that $$ \sum_{i=1}^{n} c_{i} \leqslant\left(\begin{array}{l} n \\ 2 \end{array}\right)+\left(\begin{array}{c} n+1 \\ 2 \end{array}\right)=n^{2} $$ Recalling that $a_{i} \leqslant c_{i}$ for $1 \leqslant i \leqslant n$, the desired inequality follows. Comment 1. We sketch an alternative proof by induction. Begin by verifying the initial case $n=1$ and the simple cases when $a_{1}=1, a_{1}=n$, or $a_{n} \leqslant n$. Then, as in Solution 1 , consider the index $t$ such that $a_{1} \leqslant \cdots \leqslant a_{t} \leqslant n<a_{t+1} \leqslant \cdots \leqslant a_{n}$. Observe again that $a_{1} \leqslant t$. Define the sequence $d_{1}, \ldots, d_{n-1}$ by $$ d_{i}= \begin{cases}a_{i+1}-1 & \text { if } i \leqslant t-1 \\ a_{i+1}-2 & \text { if } i \geqslant t\end{cases} $$ and extend it periodically modulo $n-1$. One may verify that this sequence also satisfies the hypotheses of the problem. The induction hypothesis then gives $d_{1}+\cdots+d_{n-1} \leqslant(n-1)^{2}$, which implies that $$ \sum_{i=1}^{n} a_{i}=a_{1}+\sum_{i=2}^{t}\left(d_{i-1}+1\right)+\sum_{i=t+1}^{n}\left(d_{i-1}+2\right) \leqslant t+(t-1)+2(n-t)+(n-1)^{2}=n^{2} $$ Comment 2. One unusual feature of this problem is that there are many different sequences for which equality holds. The discovery of such optimal sequences is not difficult, and it is useful in guiding the steps of a proof. In fact, Solution 2 gives a complete description of the optimal sequences. Start with any lattice path $P$ from the lower left to the upper right corner of the $n \times n$ square $S$ using only steps up and right, such that the total number of steps along the left and top edges of $S$ is at least $n$. Shade the cells of $S$ below $P$ dark, and the cells of $S$ above $P$ light. Now reflect the light shape across the line $x=y$ and shift it up $n$ units, and shade it dark. As Solution 2 shows, the dark region will then correspond to an optimal sequence, and every optimal sequence arises in this way.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n$ be a positive integer, and consider a sequence $a_{1}, a_{2}, \ldots, a_{n}$ of positive integers. Extend it periodically to an infinite sequence $a_{1}, a_{2}, \ldots$ by defining $a_{n+i}=a_{i}$ for all $i \geqslant 1$. If $$ a_{1} \leqslant a_{2} \leqslant \cdots \leqslant a_{n} \leqslant a_{1}+n $$ and $$ a_{a_{i}} \leqslant n+i-1 \quad \text { for } i=1,2, \ldots, n $$ prove that $$ a_{1}+\cdots+a_{n} \leqslant n^{2} . $$ (Germany)
|
As in For $1 \leqslant i<j \leqslant n$ we have $a_{i} \leqslant a_{j}$ and $i<j$, so $c_{i} \leqslant c_{j}$. Also $a_{n} \leqslant a_{1}+n$ and $n<1+n$ imply $c_{n} \leqslant c_{1}+n$. Finally, the definitions imply that $c_{c_{i}} \in\left\{a_{a_{i}}, a_{i}, a_{i}-n, i\right\}$ so $c_{c_{i}} \leqslant n+i-1$ by (2) and (3). This establishes (1) and (2) for $c_{1}, c_{2}, \ldots$. Our new sequence has the additional property that $$ c_{i} \geqslant i \quad \text { for } i=1,2, \ldots, n $$ which allows us to construct the following visualization: Consider $n$ equally spaced points on a circle, sequentially labelled $1,2, \ldots, n(\bmod n)$, so point $k$ is also labelled $n+k$. We draw arrows from vertex $i$ to vertices $i+1, \ldots, c_{i}$ for $1 \leqslant i \leqslant n$, keeping in mind that $c_{i} \geqslant i$ by (6). Since $c_{i} \leqslant n+i-1$ by (3), no arrow will be drawn twice, and there is no arrow from a vertex to itself. The total number of arrows is $$ \text { number of arrows }=\sum_{i=1}^{n}\left(c_{i}-i\right)=\sum_{i=1}^{n} c_{i}-\left(\begin{array}{c} n+1 \\ 2 \end{array}\right) $$ Now we show that we never draw both arrows $i \rightarrow j$ and $j \rightarrow i$ for $1 \leqslant i<j \leqslant n$. Assume contrariwise. This means, respectively, that $$ i<j \leqslant c_{i} \quad \text { and } \quad j<n+i \leqslant c_{j} \text {. } $$ We have $n+i \leqslant c_{j} \leqslant c_{1}+n$ by (1), so $i \leqslant c_{1}$. Since $c_{1} \leqslant n$ by (3), this implies that $c_{i} \leqslant c_{c_{1}} \leqslant n$ using (1) and (3). But then, using (1) again, $j \leqslant c_{i} \leqslant n$ implies $c_{j} \leqslant c_{c_{i}}$, which combined with $n+i \leqslant c_{j}$ gives us that $n+i \leqslant c_{c_{i}}$. This contradicts (2). This means that the number of arrows is at most $\left(\begin{array}{l}n \\ 2\end{array}\right)$, which implies that $$ \sum_{i=1}^{n} c_{i} \leqslant\left(\begin{array}{l} n \\ 2 \end{array}\right)+\left(\begin{array}{c} n+1 \\ 2 \end{array}\right)=n^{2} $$ Recalling that $a_{i} \leqslant c_{i}$ for $1 \leqslant i \leqslant n$, the desired inequality follows. Comment 1. We sketch an alternative proof by induction. Begin by verifying the initial case $n=1$ and the simple cases when $a_{1}=1, a_{1}=n$, or $a_{n} \leqslant n$. Then, as in Solution 1 , consider the index $t$ such that $a_{1} \leqslant \cdots \leqslant a_{t} \leqslant n<a_{t+1} \leqslant \cdots \leqslant a_{n}$. Observe again that $a_{1} \leqslant t$. Define the sequence $d_{1}, \ldots, d_{n-1}$ by $$ d_{i}= \begin{cases}a_{i+1}-1 & \text { if } i \leqslant t-1 \\ a_{i+1}-2 & \text { if } i \geqslant t\end{cases} $$ and extend it periodically modulo $n-1$. One may verify that this sequence also satisfies the hypotheses of the problem. The induction hypothesis then gives $d_{1}+\cdots+d_{n-1} \leqslant(n-1)^{2}$, which implies that $$ \sum_{i=1}^{n} a_{i}=a_{1}+\sum_{i=2}^{t}\left(d_{i-1}+1\right)+\sum_{i=t+1}^{n}\left(d_{i-1}+2\right) \leqslant t+(t-1)+2(n-t)+(n-1)^{2}=n^{2} $$ Comment 2. One unusual feature of this problem is that there are many different sequences for which equality holds. The discovery of such optimal sequences is not difficult, and it is useful in guiding the steps of a proof. In fact, Solution 2 gives a complete description of the optimal sequences. Start with any lattice path $P$ from the lower left to the upper right corner of the $n \times n$ square $S$ using only steps up and right, such that the total number of steps along the left and top edges of $S$ is at least $n$. Shade the cells of $S$ below $P$ dark, and the cells of $S$ above $P$ light. Now reflect the light shape across the line $x=y$ and shift it up $n$ units, and shade it dark. As Solution 2 shows, the dark region will then correspond to an optimal sequence, and every optimal sequence arises in this way.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8c4bd8e5-7a6f-569d-8632-92af8e74c0e3
| 24,250
|
A crazy physicist discovered a new kind of particle which he called an imon, after some of them mysteriously appeared in his lab. Some pairs of imons in the lab can be entangled, and each imon can participate in many entanglement relations. The physicist has found a way to perform the following two kinds of operations with these particles, one operation at a time. (i) If some imon is entangled with an odd number of other imons in the lab, then the physicist can destroy it. (ii) At any moment, he may double the whole family of imons in his lab by creating a copy $I^{\prime}$ of each imon $I$. During this procedure, the two copies $I^{\prime}$ and $J^{\prime}$ become entangled if and only if the original imons $I$ and $J$ are entangled, and each copy $I^{\prime}$ becomes entangled with its original imon $I$; no other entanglements occur or disappear at this moment. Prove that the physicist may apply a sequence of such operations resulting in a family of imons, no two of which are entangled. (Japan)
|
Let us consider a graph with the imons as vertices, and two imons being connected if and only if they are entangled. Recall that a proper coloring of a graph $G$ is a coloring of its vertices in several colors so that every two connected vertices have different colors. Lemma. Assume that a graph $G$ admits a proper coloring in $n$ colors $(n>1)$. Then one may perform a sequence of operations resulting in a graph which admits a proper coloring in $n-1$ colors. Proof. Let us apply repeatedly operation $(i)$ to any appropriate vertices while it is possible. Since the number of vertices decreases, this process finally results in a graph where all the degrees are even. Surely this graph also admits a proper coloring in $n$ colors $1, \ldots, n$; let us fix this coloring. Now apply the operation (ii) to this graph. A proper coloring of the resulting graph in $n$ colors still exists: one may preserve the colors of the original vertices and color the vertex $I^{\prime}$ in a color $k+1(\bmod n)$ if the vertex $I$ has color $k$. Then two connected original vertices still have different colors, and so do their two connected copies. On the other hand, the vertices $I$ and $I^{\prime}$ have different colors since $n>1$. All the degrees of the vertices in the resulting graph are odd, so one may apply operation $(i)$ to delete consecutively all the vertices of color $n$ one by one; no two of them are connected by an edge, so their degrees do not change during the process. Thus, we obtain a graph admitting a proper coloring in $n-1$ colors, as required. The lemma is proved. Now, assume that a graph $G$ has $n$ vertices; then it admits a proper coloring in $n$ colors. Applying repeatedly the lemma we finally obtain a graph admitting a proper coloring in one color, that is - a graph with no edges, as required.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A crazy physicist discovered a new kind of particle which he called an imon, after some of them mysteriously appeared in his lab. Some pairs of imons in the lab can be entangled, and each imon can participate in many entanglement relations. The physicist has found a way to perform the following two kinds of operations with these particles, one operation at a time. (i) If some imon is entangled with an odd number of other imons in the lab, then the physicist can destroy it. (ii) At any moment, he may double the whole family of imons in his lab by creating a copy $I^{\prime}$ of each imon $I$. During this procedure, the two copies $I^{\prime}$ and $J^{\prime}$ become entangled if and only if the original imons $I$ and $J$ are entangled, and each copy $I^{\prime}$ becomes entangled with its original imon $I$; no other entanglements occur or disappear at this moment. Prove that the physicist may apply a sequence of such operations resulting in a family of imons, no two of which are entangled. (Japan)
|
Let us consider a graph with the imons as vertices, and two imons being connected if and only if they are entangled. Recall that a proper coloring of a graph $G$ is a coloring of its vertices in several colors so that every two connected vertices have different colors. Lemma. Assume that a graph $G$ admits a proper coloring in $n$ colors $(n>1)$. Then one may perform a sequence of operations resulting in a graph which admits a proper coloring in $n-1$ colors. Proof. Let us apply repeatedly operation $(i)$ to any appropriate vertices while it is possible. Since the number of vertices decreases, this process finally results in a graph where all the degrees are even. Surely this graph also admits a proper coloring in $n$ colors $1, \ldots, n$; let us fix this coloring. Now apply the operation (ii) to this graph. A proper coloring of the resulting graph in $n$ colors still exists: one may preserve the colors of the original vertices and color the vertex $I^{\prime}$ in a color $k+1(\bmod n)$ if the vertex $I$ has color $k$. Then two connected original vertices still have different colors, and so do their two connected copies. On the other hand, the vertices $I$ and $I^{\prime}$ have different colors since $n>1$. All the degrees of the vertices in the resulting graph are odd, so one may apply operation $(i)$ to delete consecutively all the vertices of color $n$ one by one; no two of them are connected by an edge, so their degrees do not change during the process. Thus, we obtain a graph admitting a proper coloring in $n-1$ colors, as required. The lemma is proved. Now, assume that a graph $G$ has $n$ vertices; then it admits a proper coloring in $n$ colors. Applying repeatedly the lemma we finally obtain a graph admitting a proper coloring in one color, that is - a graph with no edges, as required.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
71bc752f-d3cd-5624-bfa6-1f23bc410c03
| 24,273
|
Let $n$ be a positive integer, and let $A$ be a subset of $\{1, \ldots, n\}$. An $A$-partition of $n$ into $k$ parts is a representation of $n$ as a sum $n=a_{1}+\cdots+a_{k}$, where the parts $a_{1}, \ldots, a_{k}$ belong to $A$ and are not necessarily distinct. The number of different parts in such a partition is the number of (distinct) elements in the set $\left\{a_{1}, a_{2}, \ldots, a_{k}\right\}$. We say that an $A$-partition of $n$ into $k$ parts is optimal if there is no $A$-partition of $n$ into $r$ parts with $r<k$. Prove that any optimal $A$-partition of $n$ contains at most $\sqrt[3]{6 n}$ different parts. (Germany)
|
If there are no $A$-partitions of $n$, the result is vacuously true. Otherwise, let $k_{\min }$ be the minimum number of parts in an $A$-partition of $n$, and let $n=a_{1}+\cdots+a_{k_{\min }}$ be an optimal partition. Denote by $s$ the number of different parts in this partition, so we can write $S=\left\{a_{1}, \ldots, a_{k_{\min }}\right\}=\left\{b_{1}, \ldots, b_{s}\right\}$ for some pairwise different numbers $b_{1}<\cdots<b_{s}$ in $A$. If $s>\sqrt[3]{6 n}$, we will prove that there exist subsets $X$ and $Y$ of $S$ such that $|X|<|Y|$ and $\sum_{x \in X} x=\sum_{y \in Y} y$. Then, deleting the elements of $Y$ from our partition and adding the elements of $X$ to it, we obtain an $A$-partition of $n$ into less than $k_{\text {min }}$ parts, which is the desired contradiction. For each positive integer $k \leqslant s$, we consider the $k$-element subset $$ S_{1,0}^{k}:=\left\{b_{1}, \ldots, b_{k}\right\} $$ as well as the following $k$-element subsets $S_{i, j}^{k}$ of $S$ : $$ S_{i, j}^{k}:=\left\{b_{1}, \ldots, b_{k-i}, b_{k-i+j+1}, b_{s-i+2}, \ldots, b_{s}\right\}, \quad i=1, \ldots, k, \quad j=1, \ldots, s-k $$ Pictorially, if we represent the elements of $S$ by a sequence of dots in increasing order, and represent a subset of $S$ by shading in the appropriate dots, we have:  Denote by $\Sigma_{i, j}^{k}$ the sum of elements in $S_{i, j}^{k}$. Clearly, $\Sigma_{1,0}^{k}$ is the minimum sum of a $k$-element subset of $S$. Next, for all appropriate indices $i$ and $j$ we have $$ \Sigma_{i, j}^{k}=\Sigma_{i, j+1}^{k}+b_{k-i+j+1}-b_{k-i+j+2}<\Sigma_{i, j+1}^{k} \quad \text { and } \quad \sum_{i, s-k}^{k}=\sum_{i+1,1}^{k}+b_{k-i}-b_{k-i+1}<\Sigma_{i+1,1}^{k} \text {. } $$ Therefore $$ 1 \leqslant \Sigma_{1,0}^{k}<\Sigma_{1,1}^{k}<\Sigma_{1,2}^{k}<\cdots<\Sigma_{1, s-k}^{k}<\Sigma_{2,1}^{k}<\cdots<\Sigma_{2, s-k}^{k}<\Sigma_{3,1}^{k}<\cdots<\Sigma_{k, s-k}^{k} \leqslant n . $$ To see this in the picture, we start with the $k$ leftmost points marked. At each step, we look for the rightmost point which can move to the right, and move it one unit to the right. We continue until the $k$ rightmost points are marked. As we do this, the corresponding sums clearly increase. For each $k$ we have found $k(s-k)+1$ different integers of the form $\Sigma_{i, j}^{k}$ between 1 and $n$. As we vary $k$, the total number of integers we are considering is $$ \sum_{k=1}^{s}(k(s-k)+1)=s \cdot \frac{s(s+1)}{2}-\frac{s(s+1)(2 s+1)}{6}+s=\frac{s\left(s^{2}+5\right)}{6}>\frac{s^{3}}{6}>n . $$ Since they are between 1 and $n$, at least two of these integers are equal. Consequently, there exist $1 \leqslant k<k^{\prime} \leqslant s$ and $X=S_{i, j}^{k}$ as well as $Y=S_{i^{\prime}, j^{\prime}}^{k^{\prime}}$ such that $$ \sum_{x \in X} x=\sum_{y \in Y} y, \quad \text { but } \quad|X|=k<k^{\prime}=|Y| $$ as required. The result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ be a positive integer, and let $A$ be a subset of $\{1, \ldots, n\}$. An $A$-partition of $n$ into $k$ parts is a representation of $n$ as a sum $n=a_{1}+\cdots+a_{k}$, where the parts $a_{1}, \ldots, a_{k}$ belong to $A$ and are not necessarily distinct. The number of different parts in such a partition is the number of (distinct) elements in the set $\left\{a_{1}, a_{2}, \ldots, a_{k}\right\}$. We say that an $A$-partition of $n$ into $k$ parts is optimal if there is no $A$-partition of $n$ into $r$ parts with $r<k$. Prove that any optimal $A$-partition of $n$ contains at most $\sqrt[3]{6 n}$ different parts. (Germany)
|
If there are no $A$-partitions of $n$, the result is vacuously true. Otherwise, let $k_{\min }$ be the minimum number of parts in an $A$-partition of $n$, and let $n=a_{1}+\cdots+a_{k_{\min }}$ be an optimal partition. Denote by $s$ the number of different parts in this partition, so we can write $S=\left\{a_{1}, \ldots, a_{k_{\min }}\right\}=\left\{b_{1}, \ldots, b_{s}\right\}$ for some pairwise different numbers $b_{1}<\cdots<b_{s}$ in $A$. If $s>\sqrt[3]{6 n}$, we will prove that there exist subsets $X$ and $Y$ of $S$ such that $|X|<|Y|$ and $\sum_{x \in X} x=\sum_{y \in Y} y$. Then, deleting the elements of $Y$ from our partition and adding the elements of $X$ to it, we obtain an $A$-partition of $n$ into less than $k_{\text {min }}$ parts, which is the desired contradiction. For each positive integer $k \leqslant s$, we consider the $k$-element subset $$ S_{1,0}^{k}:=\left\{b_{1}, \ldots, b_{k}\right\} $$ as well as the following $k$-element subsets $S_{i, j}^{k}$ of $S$ : $$ S_{i, j}^{k}:=\left\{b_{1}, \ldots, b_{k-i}, b_{k-i+j+1}, b_{s-i+2}, \ldots, b_{s}\right\}, \quad i=1, \ldots, k, \quad j=1, \ldots, s-k $$ Pictorially, if we represent the elements of $S$ by a sequence of dots in increasing order, and represent a subset of $S$ by shading in the appropriate dots, we have:  Denote by $\Sigma_{i, j}^{k}$ the sum of elements in $S_{i, j}^{k}$. Clearly, $\Sigma_{1,0}^{k}$ is the minimum sum of a $k$-element subset of $S$. Next, for all appropriate indices $i$ and $j$ we have $$ \Sigma_{i, j}^{k}=\Sigma_{i, j+1}^{k}+b_{k-i+j+1}-b_{k-i+j+2}<\Sigma_{i, j+1}^{k} \quad \text { and } \quad \sum_{i, s-k}^{k}=\sum_{i+1,1}^{k}+b_{k-i}-b_{k-i+1}<\Sigma_{i+1,1}^{k} \text {. } $$ Therefore $$ 1 \leqslant \Sigma_{1,0}^{k}<\Sigma_{1,1}^{k}<\Sigma_{1,2}^{k}<\cdots<\Sigma_{1, s-k}^{k}<\Sigma_{2,1}^{k}<\cdots<\Sigma_{2, s-k}^{k}<\Sigma_{3,1}^{k}<\cdots<\Sigma_{k, s-k}^{k} \leqslant n . $$ To see this in the picture, we start with the $k$ leftmost points marked. At each step, we look for the rightmost point which can move to the right, and move it one unit to the right. We continue until the $k$ rightmost points are marked. As we do this, the corresponding sums clearly increase. For each $k$ we have found $k(s-k)+1$ different integers of the form $\Sigma_{i, j}^{k}$ between 1 and $n$. As we vary $k$, the total number of integers we are considering is $$ \sum_{k=1}^{s}(k(s-k)+1)=s \cdot \frac{s(s+1)}{2}-\frac{s(s+1)(2 s+1)}{6}+s=\frac{s\left(s^{2}+5\right)}{6}>\frac{s^{3}}{6}>n . $$ Since they are between 1 and $n$, at least two of these integers are equal. Consequently, there exist $1 \leqslant k<k^{\prime} \leqslant s$ and $X=S_{i, j}^{k}$ as well as $Y=S_{i^{\prime}, j^{\prime}}^{k^{\prime}}$ such that $$ \sum_{x \in X} x=\sum_{y \in Y} y, \quad \text { but } \quad|X|=k<k^{\prime}=|Y| $$ as required. The result follows.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
d5a4443a-9d8d-5a77-80b9-35b9504a33c0
| 24,277
|
Let $n$ be a positive integer, and let $A$ be a subset of $\{1, \ldots, n\}$. An $A$-partition of $n$ into $k$ parts is a representation of $n$ as a sum $n=a_{1}+\cdots+a_{k}$, where the parts $a_{1}, \ldots, a_{k}$ belong to $A$ and are not necessarily distinct. The number of different parts in such a partition is the number of (distinct) elements in the set $\left\{a_{1}, a_{2}, \ldots, a_{k}\right\}$. We say that an $A$-partition of $n$ into $k$ parts is optimal if there is no $A$-partition of $n$ into $r$ parts with $r<k$. Prove that any optimal $A$-partition of $n$ contains at most $\sqrt[3]{6 n}$ different parts. (Germany)
|
Assume, to the contrary, that the statement is false, and choose the minimum number $n$ for which it fails. So there exists a set $A \subseteq\{1, \ldots, n\}$ together with an optimal $A$ partition $n=a_{1}+\cdots+a_{k_{\min }}$ of $n$ refuting our statement, where, of course, $k_{\min }$ is the minimum number of parts in an $A$-partition of $n$. Again, we define $S=\left\{a_{1}, \ldots, a_{k_{\min }}\right\}=\left\{b_{1}, \ldots, b_{s}\right\}$ with $b_{1}<\cdots<b_{s}$; by our assumption we have $s>\sqrt[3]{6 n}>1$. Without loss of generality we assume that $a_{k_{\min }}=b_{s}$. Let us distinguish two cases. Case 1. $b_{s} \geqslant \frac{s(s-1)}{2}+1$. Consider the partition $n-b_{s}=a_{1}+\cdots+a_{k_{\min }-1}$, which is clearly a minimum $A$-partition of $n-b_{s}$ with at least $s-1 \geqslant 1$ different parts. Now, from $n<\frac{s^{3}}{6}$ we obtain $$ n-b_{s} \leqslant n-\frac{s(s-1)}{2}-1<\frac{s^{3}}{6}-\frac{s(s-1)}{2}-1<\frac{(s-1)^{3}}{6} $$ so $s-1>\sqrt[3]{6\left(n-b_{s}\right)}$, which contradicts the choice of $n$. Case 2. $b_{s} \leqslant \frac{s(s-1)}{2}$. Set $b_{0}=0, \Sigma_{0,0}=0$, and $\Sigma_{i, j}=b_{1}+\cdots+b_{i-1}+b_{j}$ for $1 \leqslant i \leqslant j<s$. There are $\frac{s(s-1)}{2}+1>b_{s}$ such sums; so at least two of them, say $\Sigma_{i, j}$ and $\Sigma_{i^{\prime}, j^{\prime}}$, are congruent modulo $b_{s}$ (where $(i, j) \neq\left(i^{\prime}, j^{\prime}\right)$ ). This means that $\Sigma_{i, j}-\Sigma_{i^{\prime}, j^{\prime}}=r b_{s}$ for some integer $r$. Notice that for $i \leqslant j<k<s$ we have $$ 0<\Sigma_{i, k}-\Sigma_{i, j}=b_{k}-b_{j}<b_{s} $$ so the indices $i$ and $i^{\prime}$ are distinct, and we may assume that $i>i^{\prime}$. Next, we observe that $\Sigma_{i, j}-\Sigma_{i^{\prime}, j^{\prime}}=\left(b_{i^{\prime}}-b_{j^{\prime}}\right)+b_{j}+b_{i^{\prime}+1}+\cdots+b_{i-1}$ and $b_{i^{\prime}} \leqslant b_{j^{\prime}}$ imply $$ -b_{s}<-b_{j^{\prime}}<\Sigma_{i, j}-\Sigma_{i^{\prime}, j^{\prime}}<\left(i-i^{\prime}\right) b_{s}, $$ so $0 \leqslant r \leqslant i-i^{\prime}-1$. Thus, we may remove the $i$ terms of $\Sigma_{i, j}$ in our $A$-partition, and replace them by the $i^{\prime}$ terms of $\Sigma_{i^{\prime}, j^{\prime}}$ and $r$ terms equal to $b_{s}$, for a total of $r+i^{\prime}<i$ terms. The result is an $A$-partition of $n$ into a smaller number of parts, a contradiction. Comment. The original proposal also contained a second part, showing that the estimate appearing in the problem has the correct order of magnitude: For every positive integer $n$, there exist a set $A$ and an optimal $A$-partition of $n$ that contains $\lfloor\sqrt[3]{2 n}\rfloor$ different parts. The Problem Selection Committee removed this statement from the problem, since it seems to be less suitable for the competiton; but for completeness we provide an outline of its proof here. Let $k=\lfloor\sqrt[3]{2 n}\rfloor-1$. The statement is trivial for $n<4$, so we assume $n \geqslant 4$ and hence $k \geqslant 1$. Let $h=\left\lfloor\frac{n-1}{k}\right\rfloor$. Notice that $h \geqslant \frac{n}{k}-1$. Now let $A=\{1, \ldots, h\}$, and set $a_{1}=h, a_{2}=h-1, \ldots, a_{k}=h-k+1$, and $a_{k+1}=n-\left(a_{1}+\cdots+a_{k}\right)$. It is not difficult to prove that $a_{k}>a_{k+1} \geqslant 1$, which shows that $$ n=a_{1}+\ldots+a_{k+1} $$ is an $A$-partition of $n$ into $k+1$ different parts. Since $k h<n$, any $A$-partition of $n$ has at least $k+1$ parts. Therefore our $A$-partition is optimal, and it has $\lfloor\sqrt[3]{2 n}\rfloor$ distinct parts, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ be a positive integer, and let $A$ be a subset of $\{1, \ldots, n\}$. An $A$-partition of $n$ into $k$ parts is a representation of $n$ as a sum $n=a_{1}+\cdots+a_{k}$, where the parts $a_{1}, \ldots, a_{k}$ belong to $A$ and are not necessarily distinct. The number of different parts in such a partition is the number of (distinct) elements in the set $\left\{a_{1}, a_{2}, \ldots, a_{k}\right\}$. We say that an $A$-partition of $n$ into $k$ parts is optimal if there is no $A$-partition of $n$ into $r$ parts with $r<k$. Prove that any optimal $A$-partition of $n$ contains at most $\sqrt[3]{6 n}$ different parts. (Germany)
|
Assume, to the contrary, that the statement is false, and choose the minimum number $n$ for which it fails. So there exists a set $A \subseteq\{1, \ldots, n\}$ together with an optimal $A$ partition $n=a_{1}+\cdots+a_{k_{\min }}$ of $n$ refuting our statement, where, of course, $k_{\min }$ is the minimum number of parts in an $A$-partition of $n$. Again, we define $S=\left\{a_{1}, \ldots, a_{k_{\min }}\right\}=\left\{b_{1}, \ldots, b_{s}\right\}$ with $b_{1}<\cdots<b_{s}$; by our assumption we have $s>\sqrt[3]{6 n}>1$. Without loss of generality we assume that $a_{k_{\min }}=b_{s}$. Let us distinguish two cases. Case 1. $b_{s} \geqslant \frac{s(s-1)}{2}+1$. Consider the partition $n-b_{s}=a_{1}+\cdots+a_{k_{\min }-1}$, which is clearly a minimum $A$-partition of $n-b_{s}$ with at least $s-1 \geqslant 1$ different parts. Now, from $n<\frac{s^{3}}{6}$ we obtain $$ n-b_{s} \leqslant n-\frac{s(s-1)}{2}-1<\frac{s^{3}}{6}-\frac{s(s-1)}{2}-1<\frac{(s-1)^{3}}{6} $$ so $s-1>\sqrt[3]{6\left(n-b_{s}\right)}$, which contradicts the choice of $n$. Case 2. $b_{s} \leqslant \frac{s(s-1)}{2}$. Set $b_{0}=0, \Sigma_{0,0}=0$, and $\Sigma_{i, j}=b_{1}+\cdots+b_{i-1}+b_{j}$ for $1 \leqslant i \leqslant j<s$. There are $\frac{s(s-1)}{2}+1>b_{s}$ such sums; so at least two of them, say $\Sigma_{i, j}$ and $\Sigma_{i^{\prime}, j^{\prime}}$, are congruent modulo $b_{s}$ (where $(i, j) \neq\left(i^{\prime}, j^{\prime}\right)$ ). This means that $\Sigma_{i, j}-\Sigma_{i^{\prime}, j^{\prime}}=r b_{s}$ for some integer $r$. Notice that for $i \leqslant j<k<s$ we have $$ 0<\Sigma_{i, k}-\Sigma_{i, j}=b_{k}-b_{j}<b_{s} $$ so the indices $i$ and $i^{\prime}$ are distinct, and we may assume that $i>i^{\prime}$. Next, we observe that $\Sigma_{i, j}-\Sigma_{i^{\prime}, j^{\prime}}=\left(b_{i^{\prime}}-b_{j^{\prime}}\right)+b_{j}+b_{i^{\prime}+1}+\cdots+b_{i-1}$ and $b_{i^{\prime}} \leqslant b_{j^{\prime}}$ imply $$ -b_{s}<-b_{j^{\prime}}<\Sigma_{i, j}-\Sigma_{i^{\prime}, j^{\prime}}<\left(i-i^{\prime}\right) b_{s}, $$ so $0 \leqslant r \leqslant i-i^{\prime}-1$. Thus, we may remove the $i$ terms of $\Sigma_{i, j}$ in our $A$-partition, and replace them by the $i^{\prime}$ terms of $\Sigma_{i^{\prime}, j^{\prime}}$ and $r$ terms equal to $b_{s}$, for a total of $r+i^{\prime}<i$ terms. The result is an $A$-partition of $n$ into a smaller number of parts, a contradiction. Comment. The original proposal also contained a second part, showing that the estimate appearing in the problem has the correct order of magnitude: For every positive integer $n$, there exist a set $A$ and an optimal $A$-partition of $n$ that contains $\lfloor\sqrt[3]{2 n}\rfloor$ different parts. The Problem Selection Committee removed this statement from the problem, since it seems to be less suitable for the competiton; but for completeness we provide an outline of its proof here. Let $k=\lfloor\sqrt[3]{2 n}\rfloor-1$. The statement is trivial for $n<4$, so we assume $n \geqslant 4$ and hence $k \geqslant 1$. Let $h=\left\lfloor\frac{n-1}{k}\right\rfloor$. Notice that $h \geqslant \frac{n}{k}-1$. Now let $A=\{1, \ldots, h\}$, and set $a_{1}=h, a_{2}=h-1, \ldots, a_{k}=h-k+1$, and $a_{k+1}=n-\left(a_{1}+\cdots+a_{k}\right)$. It is not difficult to prove that $a_{k}>a_{k+1} \geqslant 1$, which shows that $$ n=a_{1}+\ldots+a_{k+1} $$ is an $A$-partition of $n$ into $k+1$ different parts. Since $k h<n$, any $A$-partition of $n$ has at least $k+1$ parts. Therefore our $A$-partition is optimal, and it has $\lfloor\sqrt[3]{2 n}\rfloor$ distinct parts, as desired.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
d5a4443a-9d8d-5a77-80b9-35b9504a33c0
| 24,277
|
Let $r$ be a positive integer, and let $a_{0}, a_{1}, \ldots$ be an infinite sequence of real numbers. Assume that for all nonnegative integers $m$ and $s$ there exists a positive integer $n \in[m+1, m+r]$ such that $$ a_{m}+a_{m+1}+\cdots+a_{m+s}=a_{n}+a_{n+1}+\cdots+a_{n+s} $$ Prove that the sequence is periodic, i. e. there exists some $p \geqslant 1$ such that $a_{n+p}=a_{n}$ for all $n \geqslant 0$.
|
For every indices $m \leqslant n$ we will denote $S(m, n)=a_{m}+a_{m+1}+\cdots+a_{n-1}$; thus $S(n, n)=0$. Let us start with the following lemma. Lemma. Let $b_{0}, b_{1}, \ldots$ be an infinite sequence. Assume that for every nonnegative integer $m$ there exists a nonnegative integer $n \in[m+1, m+r]$ such that $b_{m}=b_{n}$. Then for every indices $k \leqslant \ell$ there exists an index $t \in[\ell, \ell+r-1]$ such that $b_{t}=b_{k}$. Moreover, there are at most $r$ distinct numbers among the terms of $\left(b_{i}\right)$. Proof. To prove the first claim, let us notice that there exists an infinite sequence of indices $k_{1}=k, k_{2}, k_{3}, \ldots$ such that $b_{k_{1}}=b_{k_{2}}=\cdots=b_{k}$ and $k_{i}<k_{i+1} \leqslant k_{i}+r$ for all $i \geqslant 1$. This sequence is unbounded from above, thus it hits each segment of the form $[\ell, \ell+r-1]$ with $\ell \geqslant k$, as required. To prove the second claim, assume, to the contrary, that there exist $r+1$ distinct numbers $b_{i_{1}}, \ldots, b_{i_{r+1}}$. Let us apply the first claim to $k=i_{1}, \ldots, i_{r+1}$ and $\ell=\max \left\{i_{1}, \ldots, i_{r+1}\right\}$; we obtain that for every $j \in\{1, \ldots, r+1\}$ there exists $t_{j} \in[s, s+r-1]$ such that $b_{t_{j}}=b_{i_{j}}$. Thus the segment $[s, s+r-1]$ should contain $r+1$ distinct integers, which is absurd. Setting $s=0$ in the problem condition, we see that the sequence $\left(a_{i}\right)$ satisfies the condition of the lemma, thus it attains at most $r$ distinct values. Denote by $A_{i}$ the ordered $r$-tuple $\left(a_{i}, \ldots, a_{i+r-1}\right)$; then among $A_{i}$ 's there are at most $r^{r}$ distinct tuples, so for every $k \geqslant 0$ two of the tuples $A_{k}, A_{k+1}, \ldots, A_{k+r^{r}}$ are identical. This means that there exists a positive integer $p \leqslant r^{r}$ such that the equality $A_{d}=A_{d+p}$ holds infinitely many times. Let $D$ be the set of indices $d$ satisfying this relation. Now we claim that $D$ coincides with the set of all nonnegative integers. Since $D$ is unbounded, it suffices to show that $d \in D$ whenever $d+1 \in D$. For that, denote $b_{k}=S(k, p+k)$. The sequence $b_{0}, b_{1}, \ldots$ satisfies the lemma conditions, so there exists an index $t \in[d+1, d+r]$ such that $S(t, t+p)=S(d, d+p)$. This last relation rewrites as $S(d, t)=S(d+p, t+p)$. Since $A_{d+1}=A_{d+p+1}$, we have $S(d+1, t)=S(d+p+1, t+p)$, therefore we obtain $$ a_{d}=S(d, t)-S(d+1, t)=S(d+p, t+p)-S(d+p+1, t+p)=a_{d+p} $$ and thus $A_{d}=A_{d+p}$, as required. Finally, we get $A_{d}=A_{d+p}$ for all $d$, so in particular $a_{d}=a_{d+p}$ for all $d$, QED. Comment 1. In the present proof, the upper bound for the minimal period length is $r^{r}$. This bound is not sharp; for instance, one may improve it to $(r-1)^{r}$ for $r \geqslant 3$.. On the other hand, this minimal length may happen to be greater than $r$. For instance, it is easy to check that the sequence with period $(3,-3,3,-3,3,-1,-1,-1)$ satisfies the problem condition for $r=7$. Comment 2. The conclusion remains true even if the problem condition only holds for every $s \geqslant N$ for some positive integer $N$. To show that, one can act as follows. Firstly, the sums of the form $S(i, i+N)$ attain at most $r$ values, as well as the sums of the form $S(i, i+N+1)$. Thus the terms $a_{i}=S(i, i+N+1)-$ $S(i+1, i+N+1)$ attain at most $r^{2}$ distinct values. Then, among the tuples $A_{k}, A_{k+N}, \ldots, A_{k+r^{2 r} N}$ two are identical, so for some $p \leqslant r^{2 r}$ the set $D=\left\{d: A_{d}=A_{d+N p}\right\}$ is infinite. The further arguments apply almost literally, with $p$ being replaced by $N p$. After having proved that such a sequence is also necessarily periodic, one may reduce the bound for the minimal period length to $r^{r}$ - essentially by verifying that the sequence satisfies the original version of the condition.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $r$ be a positive integer, and let $a_{0}, a_{1}, \ldots$ be an infinite sequence of real numbers. Assume that for all nonnegative integers $m$ and $s$ there exists a positive integer $n \in[m+1, m+r]$ such that $$ a_{m}+a_{m+1}+\cdots+a_{m+s}=a_{n}+a_{n+1}+\cdots+a_{n+s} $$ Prove that the sequence is periodic, i. e. there exists some $p \geqslant 1$ such that $a_{n+p}=a_{n}$ for all $n \geqslant 0$.
|
For every indices $m \leqslant n$ we will denote $S(m, n)=a_{m}+a_{m+1}+\cdots+a_{n-1}$; thus $S(n, n)=0$. Let us start with the following lemma. Lemma. Let $b_{0}, b_{1}, \ldots$ be an infinite sequence. Assume that for every nonnegative integer $m$ there exists a nonnegative integer $n \in[m+1, m+r]$ such that $b_{m}=b_{n}$. Then for every indices $k \leqslant \ell$ there exists an index $t \in[\ell, \ell+r-1]$ such that $b_{t}=b_{k}$. Moreover, there are at most $r$ distinct numbers among the terms of $\left(b_{i}\right)$. Proof. To prove the first claim, let us notice that there exists an infinite sequence of indices $k_{1}=k, k_{2}, k_{3}, \ldots$ such that $b_{k_{1}}=b_{k_{2}}=\cdots=b_{k}$ and $k_{i}<k_{i+1} \leqslant k_{i}+r$ for all $i \geqslant 1$. This sequence is unbounded from above, thus it hits each segment of the form $[\ell, \ell+r-1]$ with $\ell \geqslant k$, as required. To prove the second claim, assume, to the contrary, that there exist $r+1$ distinct numbers $b_{i_{1}}, \ldots, b_{i_{r+1}}$. Let us apply the first claim to $k=i_{1}, \ldots, i_{r+1}$ and $\ell=\max \left\{i_{1}, \ldots, i_{r+1}\right\}$; we obtain that for every $j \in\{1, \ldots, r+1\}$ there exists $t_{j} \in[s, s+r-1]$ such that $b_{t_{j}}=b_{i_{j}}$. Thus the segment $[s, s+r-1]$ should contain $r+1$ distinct integers, which is absurd. Setting $s=0$ in the problem condition, we see that the sequence $\left(a_{i}\right)$ satisfies the condition of the lemma, thus it attains at most $r$ distinct values. Denote by $A_{i}$ the ordered $r$-tuple $\left(a_{i}, \ldots, a_{i+r-1}\right)$; then among $A_{i}$ 's there are at most $r^{r}$ distinct tuples, so for every $k \geqslant 0$ two of the tuples $A_{k}, A_{k+1}, \ldots, A_{k+r^{r}}$ are identical. This means that there exists a positive integer $p \leqslant r^{r}$ such that the equality $A_{d}=A_{d+p}$ holds infinitely many times. Let $D$ be the set of indices $d$ satisfying this relation. Now we claim that $D$ coincides with the set of all nonnegative integers. Since $D$ is unbounded, it suffices to show that $d \in D$ whenever $d+1 \in D$. For that, denote $b_{k}=S(k, p+k)$. The sequence $b_{0}, b_{1}, \ldots$ satisfies the lemma conditions, so there exists an index $t \in[d+1, d+r]$ such that $S(t, t+p)=S(d, d+p)$. This last relation rewrites as $S(d, t)=S(d+p, t+p)$. Since $A_{d+1}=A_{d+p+1}$, we have $S(d+1, t)=S(d+p+1, t+p)$, therefore we obtain $$ a_{d}=S(d, t)-S(d+1, t)=S(d+p, t+p)-S(d+p+1, t+p)=a_{d+p} $$ and thus $A_{d}=A_{d+p}$, as required. Finally, we get $A_{d}=A_{d+p}$ for all $d$, so in particular $a_{d}=a_{d+p}$ for all $d$, QED. Comment 1. In the present proof, the upper bound for the minimal period length is $r^{r}$. This bound is not sharp; for instance, one may improve it to $(r-1)^{r}$ for $r \geqslant 3$.. On the other hand, this minimal length may happen to be greater than $r$. For instance, it is easy to check that the sequence with period $(3,-3,3,-3,3,-1,-1,-1)$ satisfies the problem condition for $r=7$. Comment 2. The conclusion remains true even if the problem condition only holds for every $s \geqslant N$ for some positive integer $N$. To show that, one can act as follows. Firstly, the sums of the form $S(i, i+N)$ attain at most $r$ values, as well as the sums of the form $S(i, i+N+1)$. Thus the terms $a_{i}=S(i, i+N+1)-$ $S(i+1, i+N+1)$ attain at most $r^{2}$ distinct values. Then, among the tuples $A_{k}, A_{k+N}, \ldots, A_{k+r^{2 r} N}$ two are identical, so for some $p \leqslant r^{2 r}$ the set $D=\left\{d: A_{d}=A_{d+N p}\right\}$ is infinite. The further arguments apply almost literally, with $p$ being replaced by $N p$. After having proved that such a sequence is also necessarily periodic, one may reduce the bound for the minimal period length to $r^{r}$ - essentially by verifying that the sequence satisfies the original version of the condition.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
b8ad4543-dc88-52fe-93a5-1c7b2ecfa89e
| 24,281
|
In some country several pairs of cities are connected by direct two-way flights. It is possible to go from any city to any other by a sequence of flights. The distance between two cities is defined to be the least possible number of flights required to go from one of them to the other. It is known that for any city there are at most 100 cities at distance exactly three from it. Prove that there is no city such that more than 2550 other cities have distance exactly four from it. (Russia)
|
Let us denote by $d(a, b)$ the distance between the cities $a$ and $b$, and by $$ S_{i}(a)=\{c: d(a, c)=i\} $$ the set of cities at distance exactly $i$ from city $a$. Assume that for some city $x$ the set $D=S_{4}(x)$ has size at least 2551 . Let $A=S_{1}(x)$. A subset $A^{\prime}$ of $A$ is said to be substantial, if every city in $D$ can be reached from $x$ with four flights while passing through some member of $A^{\prime}$; in other terms, every city in $D$ has distance 3 from some member of $A^{\prime}$, or $D \subseteq \bigcup_{a \in A^{\prime}} S_{3}(a)$. For instance, $A$ itself is substantial. Now let us fix some substantial subset $A^{*}$ of $A$ having the minimal cardinality $m=\left|A^{*}\right|$. Since $$ m(101-m) \leqslant 50 \cdot 51=2550 $$ there has to be a city $a \in A^{*}$ such that $\left|S_{3}(a) \cap D\right| \geqslant 102-m$. As $\left|S_{3}(a)\right| \leqslant 100$, we obtain that $S_{3}(a)$ may contain at most $100-(102-m)=m-2$ cities $c$ with $d(c, x) \leqslant 3$. Let us denote by $T=\left\{c \in S_{3}(a): d(x, c) \leqslant 3\right\}$ the set of all such cities, so $|T| \leqslant m-2$. Now, to get a contradiction, we will construct $m-1$ distinct elements in $T$, corresponding to $m-1$ elements of the set $A_{a}=A^{*} \backslash\{a\}$. Firstly, due to the minimality of $A^{*}$, for each $y \in A_{a}$ there exists some city $d_{y} \in D$ which can only be reached with four flights from $x$ by passing through $y$. So, there is a way to get from $x$ to $d_{y}$ along $x-y-b_{y}-c_{y}-d_{y}$ for some cities $b_{y}$ and $c_{y}$; notice that $d\left(x, b_{y}\right)=2$ and $d\left(x, c_{y}\right)=3$ since this path has the minimal possible length. Now we claim that all $2(m-1)$ cities of the form $b_{y}, c_{y}$ with $y \in A_{a}$ are distinct. Indeed, no $b_{y}$ may coincide with any $c_{z}$ since their distances from $x$ are different. On the other hand, if one had $b_{y}=b_{z}$ for $y \neq z$, then there would exist a path of length 4 from $x$ to $d_{z}$ via $y$, namely $x-y-b_{z}-c_{z}-d_{z}$; this is impossible by the choice of $d_{z}$. Similarly, $c_{y} \neq c_{z}$ for $y \neq z$. So, it suffices to prove that for every $y \in A_{a}$, one of the cities $b_{y}$ and $c_{y}$ has distance 3 from $a$ (and thus belongs to $T$ ). For that, notice that $d(a, y) \leqslant 2$ due to the path $a-x-y$, while $d\left(a, d_{y}\right) \geqslant d\left(x, d_{y}\right)-d(x, a)=3$. Moreover, $d\left(a, d_{y}\right) \neq 3$ by the choice of $d_{y}$; thus $d\left(a, d_{y}\right)>3$. Finally, in the sequence $d(a, y), d\left(a, b_{y}\right), d\left(a, c_{y}\right), d\left(a, d_{y}\right)$ the neighboring terms differ by at most 1 , the first term is less than 3 , and the last one is greater than 3 ; thus there exists one which is equal to 3 , as required. Comment 1. The upper bound 2550 is sharp. This can be seen by means of various examples; one of them is the "Roman Empire": it has one capital, called "Rome", that is connected to 51 semicapitals by internally disjoint paths of length 3. Moreover, each of these semicapitals is connected to 50 rural cities by direct flights. Comment 2. Observe that, under the conditions of the problem, there exists no bound for the size of $S_{1}(x)$ or $S_{2}(x)$. Comment 3. The numbers 100 and 2550 appearing in the statement of the problem may be replaced by $n$ and $\left\lfloor\frac{(n+1)^{2}}{4}\right\rfloor$ for any positive integer $n$. Still more generally, one can also replace the pair $(3,4)$ of distances under consideration by any pair $(r, s)$ of positive integers satisfying $r<s \leqslant \frac{3}{2} r$. To adapt the above proof to this situation, one takes $A=S_{s-r}(x)$ and defines the concept of substantiality as before. Then one takes $A^{*}$ to be a minimal substantial subset of $A$, and for each $y \in A^{*}$ one fixes an element $d_{y} \in S_{s}(x)$ which is only reachable from $x$ by a path of length $s$ by passing through $y$. As before, it suffices to show that for distinct $a, y \in A^{*}$ and a path $y=y_{0}-y_{1}-\ldots-y_{r}=d_{y}$, at least one of the cities $y_{0}, \ldots, y_{r-1}$ has distance $r$ from $a$. This can be done as above; the relation $s \leqslant \frac{3}{2} r$ is used here to show that $d\left(a, y_{0}\right) \leqslant r$. Moreover, the estimate $\left[\frac{(n+1)^{2}}{4}\right\rfloor$ is also sharp for every positive integer $n$ and every positive integers $r, s$ with $r<s \leqslant \frac{3}{2} r$. This may be shown by an example similar to that in the previous comment.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
In some country several pairs of cities are connected by direct two-way flights. It is possible to go from any city to any other by a sequence of flights. The distance between two cities is defined to be the least possible number of flights required to go from one of them to the other. It is known that for any city there are at most 100 cities at distance exactly three from it. Prove that there is no city such that more than 2550 other cities have distance exactly four from it. (Russia)
|
Let us denote by $d(a, b)$ the distance between the cities $a$ and $b$, and by $$ S_{i}(a)=\{c: d(a, c)=i\} $$ the set of cities at distance exactly $i$ from city $a$. Assume that for some city $x$ the set $D=S_{4}(x)$ has size at least 2551 . Let $A=S_{1}(x)$. A subset $A^{\prime}$ of $A$ is said to be substantial, if every city in $D$ can be reached from $x$ with four flights while passing through some member of $A^{\prime}$; in other terms, every city in $D$ has distance 3 from some member of $A^{\prime}$, or $D \subseteq \bigcup_{a \in A^{\prime}} S_{3}(a)$. For instance, $A$ itself is substantial. Now let us fix some substantial subset $A^{*}$ of $A$ having the minimal cardinality $m=\left|A^{*}\right|$. Since $$ m(101-m) \leqslant 50 \cdot 51=2550 $$ there has to be a city $a \in A^{*}$ such that $\left|S_{3}(a) \cap D\right| \geqslant 102-m$. As $\left|S_{3}(a)\right| \leqslant 100$, we obtain that $S_{3}(a)$ may contain at most $100-(102-m)=m-2$ cities $c$ with $d(c, x) \leqslant 3$. Let us denote by $T=\left\{c \in S_{3}(a): d(x, c) \leqslant 3\right\}$ the set of all such cities, so $|T| \leqslant m-2$. Now, to get a contradiction, we will construct $m-1$ distinct elements in $T$, corresponding to $m-1$ elements of the set $A_{a}=A^{*} \backslash\{a\}$. Firstly, due to the minimality of $A^{*}$, for each $y \in A_{a}$ there exists some city $d_{y} \in D$ which can only be reached with four flights from $x$ by passing through $y$. So, there is a way to get from $x$ to $d_{y}$ along $x-y-b_{y}-c_{y}-d_{y}$ for some cities $b_{y}$ and $c_{y}$; notice that $d\left(x, b_{y}\right)=2$ and $d\left(x, c_{y}\right)=3$ since this path has the minimal possible length. Now we claim that all $2(m-1)$ cities of the form $b_{y}, c_{y}$ with $y \in A_{a}$ are distinct. Indeed, no $b_{y}$ may coincide with any $c_{z}$ since their distances from $x$ are different. On the other hand, if one had $b_{y}=b_{z}$ for $y \neq z$, then there would exist a path of length 4 from $x$ to $d_{z}$ via $y$, namely $x-y-b_{z}-c_{z}-d_{z}$; this is impossible by the choice of $d_{z}$. Similarly, $c_{y} \neq c_{z}$ for $y \neq z$. So, it suffices to prove that for every $y \in A_{a}$, one of the cities $b_{y}$ and $c_{y}$ has distance 3 from $a$ (and thus belongs to $T$ ). For that, notice that $d(a, y) \leqslant 2$ due to the path $a-x-y$, while $d\left(a, d_{y}\right) \geqslant d\left(x, d_{y}\right)-d(x, a)=3$. Moreover, $d\left(a, d_{y}\right) \neq 3$ by the choice of $d_{y}$; thus $d\left(a, d_{y}\right)>3$. Finally, in the sequence $d(a, y), d\left(a, b_{y}\right), d\left(a, c_{y}\right), d\left(a, d_{y}\right)$ the neighboring terms differ by at most 1 , the first term is less than 3 , and the last one is greater than 3 ; thus there exists one which is equal to 3 , as required. Comment 1. The upper bound 2550 is sharp. This can be seen by means of various examples; one of them is the "Roman Empire": it has one capital, called "Rome", that is connected to 51 semicapitals by internally disjoint paths of length 3. Moreover, each of these semicapitals is connected to 50 rural cities by direct flights. Comment 2. Observe that, under the conditions of the problem, there exists no bound for the size of $S_{1}(x)$ or $S_{2}(x)$. Comment 3. The numbers 100 and 2550 appearing in the statement of the problem may be replaced by $n$ and $\left\lfloor\frac{(n+1)^{2}}{4}\right\rfloor$ for any positive integer $n$. Still more generally, one can also replace the pair $(3,4)$ of distances under consideration by any pair $(r, s)$ of positive integers satisfying $r<s \leqslant \frac{3}{2} r$. To adapt the above proof to this situation, one takes $A=S_{s-r}(x)$ and defines the concept of substantiality as before. Then one takes $A^{*}$ to be a minimal substantial subset of $A$, and for each $y \in A^{*}$ one fixes an element $d_{y} \in S_{s}(x)$ which is only reachable from $x$ by a path of length $s$ by passing through $y$. As before, it suffices to show that for distinct $a, y \in A^{*}$ and a path $y=y_{0}-y_{1}-\ldots-y_{r}=d_{y}$, at least one of the cities $y_{0}, \ldots, y_{r-1}$ has distance $r$ from $a$. This can be done as above; the relation $s \leqslant \frac{3}{2} r$ is used here to show that $d\left(a, y_{0}\right) \leqslant r$. Moreover, the estimate $\left[\frac{(n+1)^{2}}{4}\right\rfloor$ is also sharp for every positive integer $n$ and every positive integers $r, s$ with $r<s \leqslant \frac{3}{2} r$. This may be shown by an example similar to that in the previous comment.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
aaf3ded0-8d1e-50a6-b19d-49c7ba50442e
| 24,284
|
Let $A B C$ be an acute-angled triangle with orthocenter $H$, and let $W$ be a point on side $B C$. Denote by $M$ and $N$ the feet of the altitudes from $B$ and $C$, respectively. Denote by $\omega_{1}$ the circumcircle of $B W N$, and let $X$ be the point on $\omega_{1}$ which is diametrically opposite to $W$. Analogously, denote by $\omega_{2}$ the circumcircle of $C W M$, and let $Y$ be the point on $\omega_{2}$ which is diametrically opposite to $W$. Prove that $X, Y$ and $H$ are collinear. (Thaliand)
|
Let $L$ be the foot of the altitude from $A$, and let $Z$ be the second intersection point of circles $\omega_{1}$ and $\omega_{2}$, other than $W$. We show that $X, Y, Z$ and $H$ lie on the same line. Due to $\angle B N C=\angle B M C=90^{\circ}$, the points $B, C, N$ and $M$ are concyclic; denote their circle by $\omega_{3}$. Observe that the line $W Z$ is the radical axis of $\omega_{1}$ and $\omega_{2}$; similarly, $B N$ is the radical axis of $\omega_{1}$ and $\omega_{3}$, and $C M$ is the radical axis of $\omega_{2}$ and $\omega_{3}$. Hence $A=B N \cap C M$ is the radical center of the three circles, and therefore $W Z$ passes through $A$. Since $W X$ and $W Y$ are diameters in $\omega_{1}$ and $\omega_{2}$, respectively, we have $\angle W Z X=\angle W Z Y=90^{\circ}$, so the points $X$ and $Y$ lie on the line through $Z$, perpendicular to $W Z$.  The quadrilateral $B L H N$ is cyclic, because it has two opposite right angles. From the power of $A$ with respect to the circles $\omega_{1}$ and $B L H N$ we find $A L \cdot A H=A B \cdot A N=A W \cdot A Z$. If $H$ lies on the line $A W$ then this implies $H=Z$ immediately. Otherwise, by $\frac{A Z}{A H}=\frac{A L}{A W}$ the triangles $A H Z$ and $A W L$ are similar. Then $\angle H Z A=\angle W L A=90^{\circ}$, so the point $H$ also lies on the line $X Y Z$. Comment. The original proposal also included a second statement: Let $P$ be the point on $\omega_{1}$ such that $W P$ is parallel to $C N$, and let $Q$ be the point on $\omega_{2}$ such that $W Q$ is parallel to $B M$. Prove that $P, Q$ and $H$ are collinear if and only if $B W=C W$ or $A W \perp B C$. The Problem Selection Committee considered the first part more suitable for the competition.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute-angled triangle with orthocenter $H$, and let $W$ be a point on side $B C$. Denote by $M$ and $N$ the feet of the altitudes from $B$ and $C$, respectively. Denote by $\omega_{1}$ the circumcircle of $B W N$, and let $X$ be the point on $\omega_{1}$ which is diametrically opposite to $W$. Analogously, denote by $\omega_{2}$ the circumcircle of $C W M$, and let $Y$ be the point on $\omega_{2}$ which is diametrically opposite to $W$. Prove that $X, Y$ and $H$ are collinear. (Thaliand)
|
Let $L$ be the foot of the altitude from $A$, and let $Z$ be the second intersection point of circles $\omega_{1}$ and $\omega_{2}$, other than $W$. We show that $X, Y, Z$ and $H$ lie on the same line. Due to $\angle B N C=\angle B M C=90^{\circ}$, the points $B, C, N$ and $M$ are concyclic; denote their circle by $\omega_{3}$. Observe that the line $W Z$ is the radical axis of $\omega_{1}$ and $\omega_{2}$; similarly, $B N$ is the radical axis of $\omega_{1}$ and $\omega_{3}$, and $C M$ is the radical axis of $\omega_{2}$ and $\omega_{3}$. Hence $A=B N \cap C M$ is the radical center of the three circles, and therefore $W Z$ passes through $A$. Since $W X$ and $W Y$ are diameters in $\omega_{1}$ and $\omega_{2}$, respectively, we have $\angle W Z X=\angle W Z Y=90^{\circ}$, so the points $X$ and $Y$ lie on the line through $Z$, perpendicular to $W Z$.  The quadrilateral $B L H N$ is cyclic, because it has two opposite right angles. From the power of $A$ with respect to the circles $\omega_{1}$ and $B L H N$ we find $A L \cdot A H=A B \cdot A N=A W \cdot A Z$. If $H$ lies on the line $A W$ then this implies $H=Z$ immediately. Otherwise, by $\frac{A Z}{A H}=\frac{A L}{A W}$ the triangles $A H Z$ and $A W L$ are similar. Then $\angle H Z A=\angle W L A=90^{\circ}$, so the point $H$ also lies on the line $X Y Z$. Comment. The original proposal also included a second statement: Let $P$ be the point on $\omega_{1}$ such that $W P$ is parallel to $C N$, and let $Q$ be the point on $\omega_{2}$ such that $W Q$ is parallel to $B M$. Prove that $P, Q$ and $H$ are collinear if and only if $B W=C W$ or $A W \perp B C$. The Problem Selection Committee considered the first part more suitable for the competition.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
5715da49-f17c-5d8e-b1e8-72507c7ded03
| 24,293
|
Let $\omega$ be the circumcircle of a triangle $A B C$. Denote by $M$ and $N$ the midpoints of the sides $A B$ and $A C$, respectively, and denote by $T$ the midpoint of the $\operatorname{arc} B C$ of $\omega$ not containing $A$. The circumcircles of the triangles $A M T$ and $A N T$ intersect the perpendicular bisectors of $A C$ and $A B$ at points $X$ and $Y$, respectively; assume that $X$ and $Y$ lie inside the triangle $A B C$. The lines $M N$ and $X Y$ intersect at $K$. Prove that $K A=K T$. (Iran)
|
Let $O$ be the center of $\omega$, thus $O=M Y \cap N X$. Let $\ell$ be the perpendicular bisector of $A T$ (it also passes through $O$ ). Denote by $r$ the operation of reflection about $\ell$. Since $A T$ is the angle bisector of $\angle B A C$, the line $r(A B)$ is parallel to $A C$. Since $O M \perp A B$ and $O N \perp A C$, this means that the line $r(O M)$ is parallel to the line $O N$ and passes through $O$, so $r(O M)=O N$. Finally, the circumcircle $\gamma$ of the triangle $A M T$ is symmetric about $\ell$, so $r(\gamma)=\gamma$. Thus the point $M$ maps to the common point of $O N$ with the arc $A M T$ of $\gamma$ - that is, $r(M)=X$. Similarly, $r(N)=Y$. Thus, we get $r(M N)=X Y$, and the common point $K$ of $M N$ nd $X Y$ lies on $\ell$. This means exactly that $K A=K T$. 
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\omega$ be the circumcircle of a triangle $A B C$. Denote by $M$ and $N$ the midpoints of the sides $A B$ and $A C$, respectively, and denote by $T$ the midpoint of the $\operatorname{arc} B C$ of $\omega$ not containing $A$. The circumcircles of the triangles $A M T$ and $A N T$ intersect the perpendicular bisectors of $A C$ and $A B$ at points $X$ and $Y$, respectively; assume that $X$ and $Y$ lie inside the triangle $A B C$. The lines $M N$ and $X Y$ intersect at $K$. Prove that $K A=K T$. (Iran)
|
Let $O$ be the center of $\omega$, thus $O=M Y \cap N X$. Let $\ell$ be the perpendicular bisector of $A T$ (it also passes through $O$ ). Denote by $r$ the operation of reflection about $\ell$. Since $A T$ is the angle bisector of $\angle B A C$, the line $r(A B)$ is parallel to $A C$. Since $O M \perp A B$ and $O N \perp A C$, this means that the line $r(O M)$ is parallel to the line $O N$ and passes through $O$, so $r(O M)=O N$. Finally, the circumcircle $\gamma$ of the triangle $A M T$ is symmetric about $\ell$, so $r(\gamma)=\gamma$. Thus the point $M$ maps to the common point of $O N$ with the arc $A M T$ of $\gamma$ - that is, $r(M)=X$. Similarly, $r(N)=Y$. Thus, we get $r(M N)=X Y$, and the common point $K$ of $M N$ nd $X Y$ lies on $\ell$. This means exactly that $K A=K T$. 
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
f90081d2-e176-5b6d-a2f0-1c6edf488e14
| 24,295
|
Let $\omega$ be the circumcircle of a triangle $A B C$. Denote by $M$ and $N$ the midpoints of the sides $A B$ and $A C$, respectively, and denote by $T$ the midpoint of the $\operatorname{arc} B C$ of $\omega$ not containing $A$. The circumcircles of the triangles $A M T$ and $A N T$ intersect the perpendicular bisectors of $A C$ and $A B$ at points $X$ and $Y$, respectively; assume that $X$ and $Y$ lie inside the triangle $A B C$. The lines $M N$ and $X Y$ intersect at $K$. Prove that $K A=K T$. (Iran)
|
Let $L$ be the second common point of the line $A C$ with the circumcircle $\gamma$ of the triangle $A M T$. From the cyclic quadrilaterals $A B T C$ and $A M T L$ we get $\angle B T C=180^{\circ}-$ $\angle B A C=\angle M T L$, which implies $\angle B T M=\angle C T L$. Since $A T$ is an angle bisector in these quadrilaterals, we have $B T=T C$ and $M T=T L$. Thus the triangles $B T M$ and $C T L$ are congruent, so $C L=B M=A M$. Let $X^{\prime}$ be the common point of the line $N X$ with the external bisector of $\angle B A C$; notice that it lies outside the triangle $A B C$. Then we have $\angle T A X^{\prime}=90^{\circ}$ and $X^{\prime} A=X^{\prime} C$, so we get $\angle X^{\prime} A M=90^{\circ}+\angle B A C / 2=180^{\circ}-\angle X^{\prime} A C=180^{\circ}-\angle X^{\prime} C A=\angle X^{\prime} C L$. Thus the triangles $X^{\prime} A M$ and $X^{\prime} C L$ are congruent, and therefore $$ \angle M X^{\prime} L=\angle A X^{\prime} C+\left(\angle C X^{\prime} L-\angle A X^{\prime} M\right)=\angle A X^{\prime} C=180^{\circ}-2 \angle X^{\prime} A C=\angle B A C=\angle M A L . $$ This means that $X^{\prime}$ lies on $\gamma$. Thus we have $\angle T X N=\angle T X X^{\prime}=\angle T A X^{\prime}=90^{\circ}$, so $T X \| A C$. Then $\angle X T A=\angle T A C=$ $\angle T A M$, so the cyclic quadrilateral MATX is an isosceles trapezoid. Similarly, $N A T Y$ is an isosceles trapezoid, so again the lines $M N$ and $X Y$ are the reflections of each other about the perpendicular bisector of $A T$. Thus $K$ belongs to this perpendicular bisector. 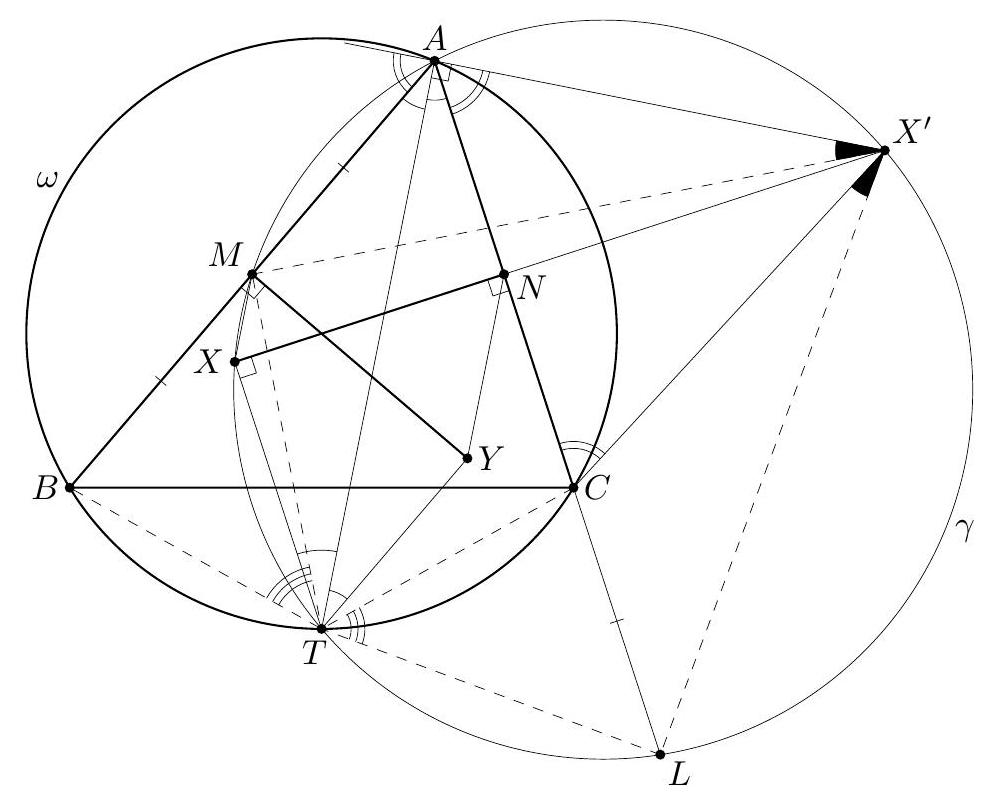 Comment. There are several different ways of showing that the points $X$ and $M$ are symmetrical with respect to $\ell$. For instance, one can show that the quadrilaterals $A M O N$ and $T X O Y$ are congruent. We chose Solution 1 as a simple way of doing it. On the other hand, Solution 2 shows some other interesting properties of the configuration. Let us define $Y^{\prime}$, analogously to $X^{\prime}$, as the common point of $M Y$ and the external bisector of $\angle B A C$. One may easily see that in general the lines $M N$ and $X^{\prime} Y^{\prime}$ (which is the external bisector of $\angle B A C$ ) do not intersect on the perpendicular bisector of $A T$. Thus, any solution should involve some argument using the choice of the intersection points $X$ and $Y$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\omega$ be the circumcircle of a triangle $A B C$. Denote by $M$ and $N$ the midpoints of the sides $A B$ and $A C$, respectively, and denote by $T$ the midpoint of the $\operatorname{arc} B C$ of $\omega$ not containing $A$. The circumcircles of the triangles $A M T$ and $A N T$ intersect the perpendicular bisectors of $A C$ and $A B$ at points $X$ and $Y$, respectively; assume that $X$ and $Y$ lie inside the triangle $A B C$. The lines $M N$ and $X Y$ intersect at $K$. Prove that $K A=K T$. (Iran)
|
Let $L$ be the second common point of the line $A C$ with the circumcircle $\gamma$ of the triangle $A M T$. From the cyclic quadrilaterals $A B T C$ and $A M T L$ we get $\angle B T C=180^{\circ}-$ $\angle B A C=\angle M T L$, which implies $\angle B T M=\angle C T L$. Since $A T$ is an angle bisector in these quadrilaterals, we have $B T=T C$ and $M T=T L$. Thus the triangles $B T M$ and $C T L$ are congruent, so $C L=B M=A M$. Let $X^{\prime}$ be the common point of the line $N X$ with the external bisector of $\angle B A C$; notice that it lies outside the triangle $A B C$. Then we have $\angle T A X^{\prime}=90^{\circ}$ and $X^{\prime} A=X^{\prime} C$, so we get $\angle X^{\prime} A M=90^{\circ}+\angle B A C / 2=180^{\circ}-\angle X^{\prime} A C=180^{\circ}-\angle X^{\prime} C A=\angle X^{\prime} C L$. Thus the triangles $X^{\prime} A M$ and $X^{\prime} C L$ are congruent, and therefore $$ \angle M X^{\prime} L=\angle A X^{\prime} C+\left(\angle C X^{\prime} L-\angle A X^{\prime} M\right)=\angle A X^{\prime} C=180^{\circ}-2 \angle X^{\prime} A C=\angle B A C=\angle M A L . $$ This means that $X^{\prime}$ lies on $\gamma$. Thus we have $\angle T X N=\angle T X X^{\prime}=\angle T A X^{\prime}=90^{\circ}$, so $T X \| A C$. Then $\angle X T A=\angle T A C=$ $\angle T A M$, so the cyclic quadrilateral MATX is an isosceles trapezoid. Similarly, $N A T Y$ is an isosceles trapezoid, so again the lines $M N$ and $X Y$ are the reflections of each other about the perpendicular bisector of $A T$. Thus $K$ belongs to this perpendicular bisector.  Comment. There are several different ways of showing that the points $X$ and $M$ are symmetrical with respect to $\ell$. For instance, one can show that the quadrilaterals $A M O N$ and $T X O Y$ are congruent. We chose Solution 1 as a simple way of doing it. On the other hand, Solution 2 shows some other interesting properties of the configuration. Let us define $Y^{\prime}$, analogously to $X^{\prime}$, as the common point of $M Y$ and the external bisector of $\angle B A C$. One may easily see that in general the lines $M N$ and $X^{\prime} Y^{\prime}$ (which is the external bisector of $\angle B A C$ ) do not intersect on the perpendicular bisector of $A T$. Thus, any solution should involve some argument using the choice of the intersection points $X$ and $Y$.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
f90081d2-e176-5b6d-a2f0-1c6edf488e14
| 24,295
|
In a triangle $A B C$, let $D$ and $E$ be the feet of the angle bisectors of angles $A$ and $B$, respectively. A rhombus is inscribed into the quadrilateral $A E D B$ (all vertices of the rhombus lie on different sides of $A E D B$ ). Let $\varphi$ be the non-obtuse angle of the rhombus. Prove that $\varphi \leqslant \max \{\angle B A C, \angle A B C\}$. (Serbia)
|
Let $K, L, M$, and $N$ be the vertices of the rhombus lying on the sides $A E, E D, D B$, and $B A$, respectively. Denote by $d(X, Y Z)$ the distance from a point $X$ to a line $Y Z$. Since $D$ and $E$ are the feet of the bisectors, we have $d(D, A B)=d(D, A C), d(E, A B)=d(E, B C)$, and $d(D, B C)=d(E, A C)=0$, which implies $$ d(D, A C)+d(D, B C)=d(D, A B) \quad \text { and } \quad d(E, A C)+d(E, B C)=d(E, A B) $$ Since $L$ lies on the segment $D E$ and the relation $d(X, A C)+d(X, B C)=d(X, A B)$ is linear in $X$ inside the triangle, these two relations imply $$ d(L, A C)+d(L, B C)=d(L, A B) . $$ Denote the angles as in the figure below, and denote $a=K L$. Then we have $d(L, A C)=a \sin \mu$ and $d(L, B C)=a \sin \nu$. Since $K L M N$ is a parallelogram lying on one side of $A B$, we get $$ d(L, A B)=d(L, A B)+d(N, A B)=d(K, A B)+d(M, A B)=a(\sin \delta+\sin \varepsilon) $$ Thus the condition (1) reads $$ \sin \mu+\sin \nu=\sin \delta+\sin \varepsilon $$  If one of the angles $\alpha$ and $\beta$ is non-acute, then the desired inequality is trivial. So we assume that $\alpha, \beta<\pi / 2$. It suffices to show then that $\psi=\angle N K L \leqslant \max \{\alpha, \beta\}$. Assume, to the contrary, that $\psi>\max \{\alpha, \beta\}$. Since $\mu+\psi=\angle C K N=\alpha+\delta$, by our assumption we obtain $\mu=(\alpha-\psi)+\delta<\delta$. Similarly, $\nu<\varepsilon$. Next, since $K N \| M L$, we have $\beta=\delta+\nu$, so $\delta<\beta<\pi / 2$. Similarly, $\varepsilon<\pi / 2$. Finally, by $\mu<\delta<\pi / 2$ and $\nu<\varepsilon<\pi / 2$, we obtain $$ \sin \mu<\sin \delta \quad \text { and } \quad \sin \nu<\sin \varepsilon $$ This contradicts (2). Comment. One can see that the equality is achieved if $\alpha=\beta$ for every rhombus inscribed into the quadrilateral $A E D B$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In a triangle $A B C$, let $D$ and $E$ be the feet of the angle bisectors of angles $A$ and $B$, respectively. A rhombus is inscribed into the quadrilateral $A E D B$ (all vertices of the rhombus lie on different sides of $A E D B$ ). Let $\varphi$ be the non-obtuse angle of the rhombus. Prove that $\varphi \leqslant \max \{\angle B A C, \angle A B C\}$. (Serbia)
|
Let $K, L, M$, and $N$ be the vertices of the rhombus lying on the sides $A E, E D, D B$, and $B A$, respectively. Denote by $d(X, Y Z)$ the distance from a point $X$ to a line $Y Z$. Since $D$ and $E$ are the feet of the bisectors, we have $d(D, A B)=d(D, A C), d(E, A B)=d(E, B C)$, and $d(D, B C)=d(E, A C)=0$, which implies $$ d(D, A C)+d(D, B C)=d(D, A B) \quad \text { and } \quad d(E, A C)+d(E, B C)=d(E, A B) $$ Since $L$ lies on the segment $D E$ and the relation $d(X, A C)+d(X, B C)=d(X, A B)$ is linear in $X$ inside the triangle, these two relations imply $$ d(L, A C)+d(L, B C)=d(L, A B) . $$ Denote the angles as in the figure below, and denote $a=K L$. Then we have $d(L, A C)=a \sin \mu$ and $d(L, B C)=a \sin \nu$. Since $K L M N$ is a parallelogram lying on one side of $A B$, we get $$ d(L, A B)=d(L, A B)+d(N, A B)=d(K, A B)+d(M, A B)=a(\sin \delta+\sin \varepsilon) $$ Thus the condition (1) reads $$ \sin \mu+\sin \nu=\sin \delta+\sin \varepsilon $$  If one of the angles $\alpha$ and $\beta$ is non-acute, then the desired inequality is trivial. So we assume that $\alpha, \beta<\pi / 2$. It suffices to show then that $\psi=\angle N K L \leqslant \max \{\alpha, \beta\}$. Assume, to the contrary, that $\psi>\max \{\alpha, \beta\}$. Since $\mu+\psi=\angle C K N=\alpha+\delta$, by our assumption we obtain $\mu=(\alpha-\psi)+\delta<\delta$. Similarly, $\nu<\varepsilon$. Next, since $K N \| M L$, we have $\beta=\delta+\nu$, so $\delta<\beta<\pi / 2$. Similarly, $\varepsilon<\pi / 2$. Finally, by $\mu<\delta<\pi / 2$ and $\nu<\varepsilon<\pi / 2$, we obtain $$ \sin \mu<\sin \delta \quad \text { and } \quad \sin \nu<\sin \varepsilon $$ This contradicts (2). Comment. One can see that the equality is achieved if $\alpha=\beta$ for every rhombus inscribed into the quadrilateral $A E D B$.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
df98375e-81c8-5ca4-a27d-655ffb8b3333
| 24,298
|
Let $A B C$ be a triangle with $\angle B>\angle C$. Let $P$ and $Q$ be two different points on line $A C$ such that $\angle P B A=\angle Q B A=\angle A C B$ and $A$ is located between $P$ and $C$. Suppose that there exists an interior point $D$ of segment $B Q$ for which $P D=P B$. Let the ray $A D$ intersect the circle $A B C$ at $R \neq A$. Prove that $Q B=Q R$. (Georgia)
|
Denote by $\omega$ the circumcircle of the triangle $A B C$, and let $\angle A C B=\gamma$. Note that the condition $\gamma<\angle C B A$ implies $\gamma<90^{\circ}$. Since $\angle P B A=\gamma$, the line $P B$ is tangent to $\omega$, so $P A \cdot P C=P B^{2}=P D^{2}$. By $\frac{P A}{P D}=\frac{P D}{P C}$ the triangles $P A D$ and $P D C$ are similar, and $\angle A D P=\angle D C P$. Next, since $\angle A B Q=\angle A C B$, the triangles $A B C$ and $A Q B$ are also similar. Then $\angle A Q B=$ $\angle A B C=\angle A R C$, which means that the points $D, R, C$, and $Q$ are concyclic. Therefore $\angle D R Q=$ $\angle D C Q=\angle A D P$. 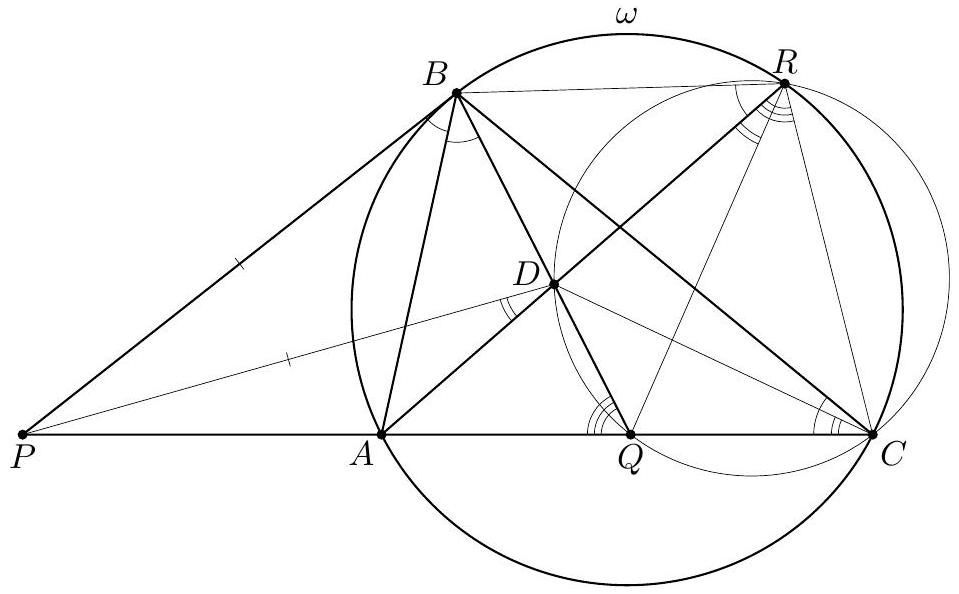 Figure 1 Now from $\angle A R B=\angle A C B=\gamma$ and $\angle P D B=\angle P B D=2 \gamma$ we get $$ \angle Q B R=\angle A D B-\angle A R B=\angle A D P+\angle P D B-\angle A R B=\angle D R Q+\gamma=\angle Q R B $$ so the triangle $Q R B$ is isosceles, which yields $Q B=Q R$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $\angle B>\angle C$. Let $P$ and $Q$ be two different points on line $A C$ such that $\angle P B A=\angle Q B A=\angle A C B$ and $A$ is located between $P$ and $C$. Suppose that there exists an interior point $D$ of segment $B Q$ for which $P D=P B$. Let the ray $A D$ intersect the circle $A B C$ at $R \neq A$. Prove that $Q B=Q R$. (Georgia)
|
Denote by $\omega$ the circumcircle of the triangle $A B C$, and let $\angle A C B=\gamma$. Note that the condition $\gamma<\angle C B A$ implies $\gamma<90^{\circ}$. Since $\angle P B A=\gamma$, the line $P B$ is tangent to $\omega$, so $P A \cdot P C=P B^{2}=P D^{2}$. By $\frac{P A}{P D}=\frac{P D}{P C}$ the triangles $P A D$ and $P D C$ are similar, and $\angle A D P=\angle D C P$. Next, since $\angle A B Q=\angle A C B$, the triangles $A B C$ and $A Q B$ are also similar. Then $\angle A Q B=$ $\angle A B C=\angle A R C$, which means that the points $D, R, C$, and $Q$ are concyclic. Therefore $\angle D R Q=$ $\angle D C Q=\angle A D P$.  Figure 1 Now from $\angle A R B=\angle A C B=\gamma$ and $\angle P D B=\angle P B D=2 \gamma$ we get $$ \angle Q B R=\angle A D B-\angle A R B=\angle A D P+\angle P D B-\angle A R B=\angle D R Q+\gamma=\angle Q R B $$ so the triangle $Q R B$ is isosceles, which yields $Q B=Q R$.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8298a6d4-654e-5002-bdb8-0ca7aeaf0ddd
| 24,301
|
Let $A B C$ be a triangle with $\angle B>\angle C$. Let $P$ and $Q$ be two different points on line $A C$ such that $\angle P B A=\angle Q B A=\angle A C B$ and $A$ is located between $P$ and $C$. Suppose that there exists an interior point $D$ of segment $B Q$ for which $P D=P B$. Let the ray $A D$ intersect the circle $A B C$ at $R \neq A$. Prove that $Q B=Q R$. (Georgia)
|
Again, denote by $\omega$ the circumcircle of the triangle $A B C$. Denote $\angle A C B=\gamma$. Since $\angle P B A=\gamma$, the line $P B$ is tangent to $\omega$. Let $E$ be the second intersection point of $B Q$ with $\omega$. If $V^{\prime}$ is any point on the ray $C E$ beyond $E$, then $\angle B E V^{\prime}=180^{\circ}-\angle B E C=180^{\circ}-\angle B A C=\angle P A B$; together with $\angle A B Q=$ $\angle P B A$ this shows firstly, that the rays $B A$ and $C E$ intersect at some point $V$, and secondly that the triangle $V E B$ is similar to the triangle $P A B$. Thus we have $\angle B V E=\angle B P A$. Next, $\angle A E V=\angle B E V-\gamma=\angle P A B-\angle A B Q=\angle A Q B$; so the triangles $P B Q$ and $V A E$ are also similar. Let $P H$ be an altitude in the isosceles triangle $P B D$; then $B H=H D$. Let $G$ be the intersection point of $P H$ and $A B$. By the symmetry with respect to $P H$, we have $\angle B D G=\angle D B G=\gamma=$ $\angle B E A$; thus $D G \| A E$ and hence $\frac{B G}{G A}=\frac{B D}{D E}$. Thus the points $G$ and $D$ correspond to each other in the similar triangles $P A B$ and $V E B$, so $\angle D V B=\angle G P B=90^{\circ}-\angle P B Q=90^{\circ}-\angle V A E$. Thus $V D \perp A E$. Let $T$ be the common point of $V D$ and $A E$, and let $D S$ be an altitude in the triangle $B D R$. The points $S$ and $T$ are the feet of corresponding altitudes in the similar triangles $A D E$ and $B D R$, so $\frac{B S}{S R}=\frac{A T}{T E}$. On the other hand, the points $T$ and $H$ are feet of corresponding altitudes in the similar triangles $V A E$ and $P B Q$, so $\frac{A T}{T E}=\frac{B H}{H Q}$. Thus $\frac{B S}{S R}=\frac{A T}{T E}=\frac{B H}{H Q}$, and the triangles $B H S$ and $B Q R$ are similar. Finally, $S H$ is a median in the right-angled triangle $S B D$; so $B H=H S$, and hence $B Q=Q R$. 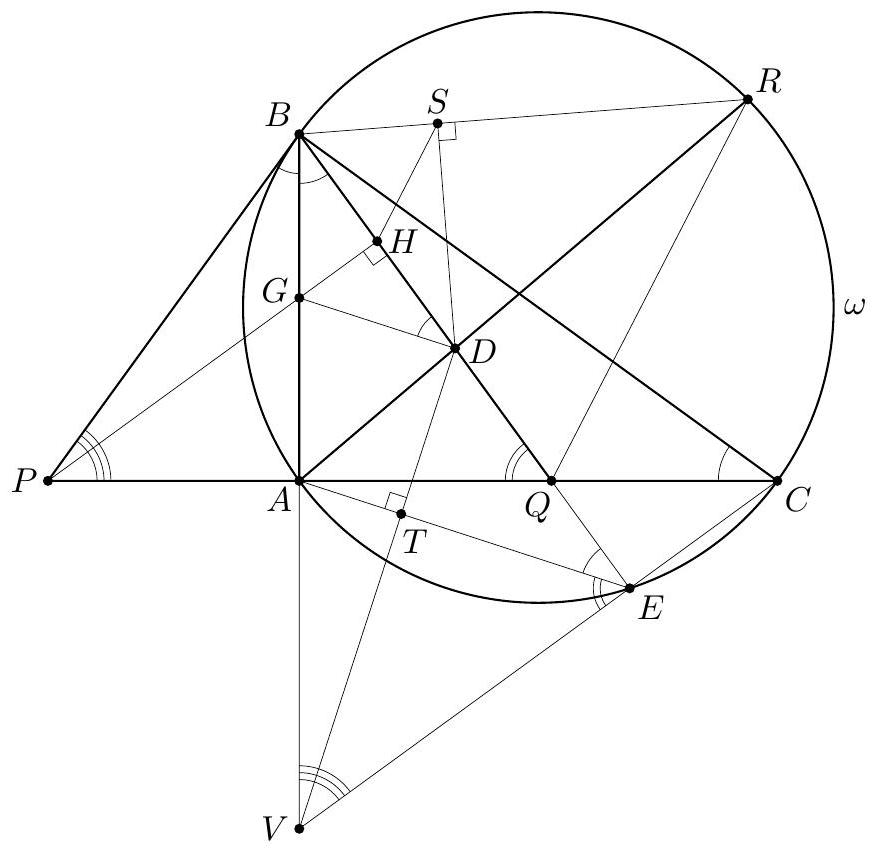 Figure 2
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $\angle B>\angle C$. Let $P$ and $Q$ be two different points on line $A C$ such that $\angle P B A=\angle Q B A=\angle A C B$ and $A$ is located between $P$ and $C$. Suppose that there exists an interior point $D$ of segment $B Q$ for which $P D=P B$. Let the ray $A D$ intersect the circle $A B C$ at $R \neq A$. Prove that $Q B=Q R$. (Georgia)
|
Again, denote by $\omega$ the circumcircle of the triangle $A B C$. Denote $\angle A C B=\gamma$. Since $\angle P B A=\gamma$, the line $P B$ is tangent to $\omega$. Let $E$ be the second intersection point of $B Q$ with $\omega$. If $V^{\prime}$ is any point on the ray $C E$ beyond $E$, then $\angle B E V^{\prime}=180^{\circ}-\angle B E C=180^{\circ}-\angle B A C=\angle P A B$; together with $\angle A B Q=$ $\angle P B A$ this shows firstly, that the rays $B A$ and $C E$ intersect at some point $V$, and secondly that the triangle $V E B$ is similar to the triangle $P A B$. Thus we have $\angle B V E=\angle B P A$. Next, $\angle A E V=\angle B E V-\gamma=\angle P A B-\angle A B Q=\angle A Q B$; so the triangles $P B Q$ and $V A E$ are also similar. Let $P H$ be an altitude in the isosceles triangle $P B D$; then $B H=H D$. Let $G$ be the intersection point of $P H$ and $A B$. By the symmetry with respect to $P H$, we have $\angle B D G=\angle D B G=\gamma=$ $\angle B E A$; thus $D G \| A E$ and hence $\frac{B G}{G A}=\frac{B D}{D E}$. Thus the points $G$ and $D$ correspond to each other in the similar triangles $P A B$ and $V E B$, so $\angle D V B=\angle G P B=90^{\circ}-\angle P B Q=90^{\circ}-\angle V A E$. Thus $V D \perp A E$. Let $T$ be the common point of $V D$ and $A E$, and let $D S$ be an altitude in the triangle $B D R$. The points $S$ and $T$ are the feet of corresponding altitudes in the similar triangles $A D E$ and $B D R$, so $\frac{B S}{S R}=\frac{A T}{T E}$. On the other hand, the points $T$ and $H$ are feet of corresponding altitudes in the similar triangles $V A E$ and $P B Q$, so $\frac{A T}{T E}=\frac{B H}{H Q}$. Thus $\frac{B S}{S R}=\frac{A T}{T E}=\frac{B H}{H Q}$, and the triangles $B H S$ and $B Q R$ are similar. Finally, $S H$ is a median in the right-angled triangle $S B D$; so $B H=H S$, and hence $B Q=Q R$.  Figure 2
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8298a6d4-654e-5002-bdb8-0ca7aeaf0ddd
| 24,301
|
Let $A B C$ be a triangle with $\angle B>\angle C$. Let $P$ and $Q$ be two different points on line $A C$ such that $\angle P B A=\angle Q B A=\angle A C B$ and $A$ is located between $P$ and $C$. Suppose that there exists an interior point $D$ of segment $B Q$ for which $P D=P B$. Let the ray $A D$ intersect the circle $A B C$ at $R \neq A$. Prove that $Q B=Q R$. (Georgia)
|
Denote by $\omega$ and $O$ the circumcircle of the triangle $A B C$ and its center, respectively. From the condition $\angle P B A=\angle B C A$ we know that $B P$ is tangent to $\omega$. Let $E$ be the second point of intersection of $\omega$ and $B D$. Due to the isosceles triangle $B D P$, the tangent of $\omega$ at $E$ is parallel to $D P$ and consequently it intersects $B P$ at some point $L$. Of course, $P D \| L E$. Let $M$ be the midpoint of $B E$, and let $H$ be the midpoint of $B R$. Notice that $\angle A E B=\angle A C B=\angle A B Q=\angle A B E$, so $A$ lies on the perpendicular bisector of $B E$; thus the points $L, A, M$, and $O$ are collinear. Let $\omega_{1}$ be the circle with diameter $B O$. Let $Q^{\prime}=H O \cap B E$; since $H O$ is the perpendicular bisector of $B R$, the statement of the problem is equivalent to $Q^{\prime}=Q$. Consider the following sequence of projections (see Fig. 3). 1. Project the line $B E$ to the line $L B$ through the center $A$. (This maps $Q$ to $P$.) 2. Project the line $L B$ to $B E$ in parallel direction with $L E$. $(P \mapsto D$.) 3. Project the line $B E$ to the circle $\omega$ through its point $A .(D \mapsto R$.) 4. Scale $\omega$ by the ratio $\frac{1}{2}$ from the point $B$ to the circle $\omega_{1} .(R \mapsto H$. 5. Project $\omega_{1}$ to the line $B E$ through its point $O$. $\left(H \mapsto Q^{\prime}\right.$.) We prove that the composition of these transforms, which maps the line $B E$ to itself, is the identity. To achieve this, it suffices to show three fixed points. An obvious fixed point is $B$ which is fixed by all the transformations above. Another fixed point is $M$, its path being $M \mapsto L \mapsto$ $E \mapsto E \mapsto M \mapsto M$. 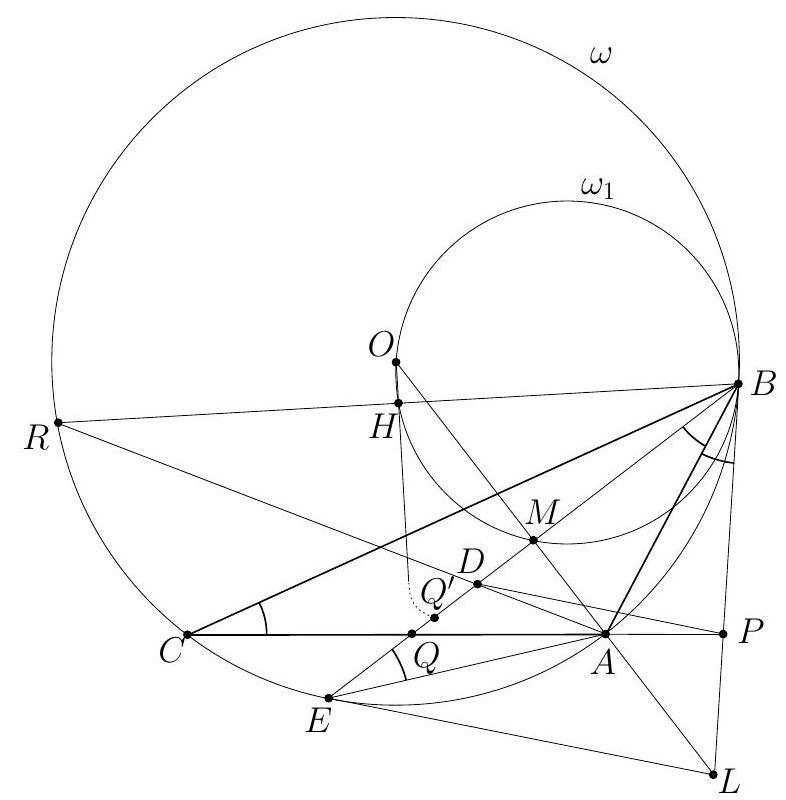 Figure 3 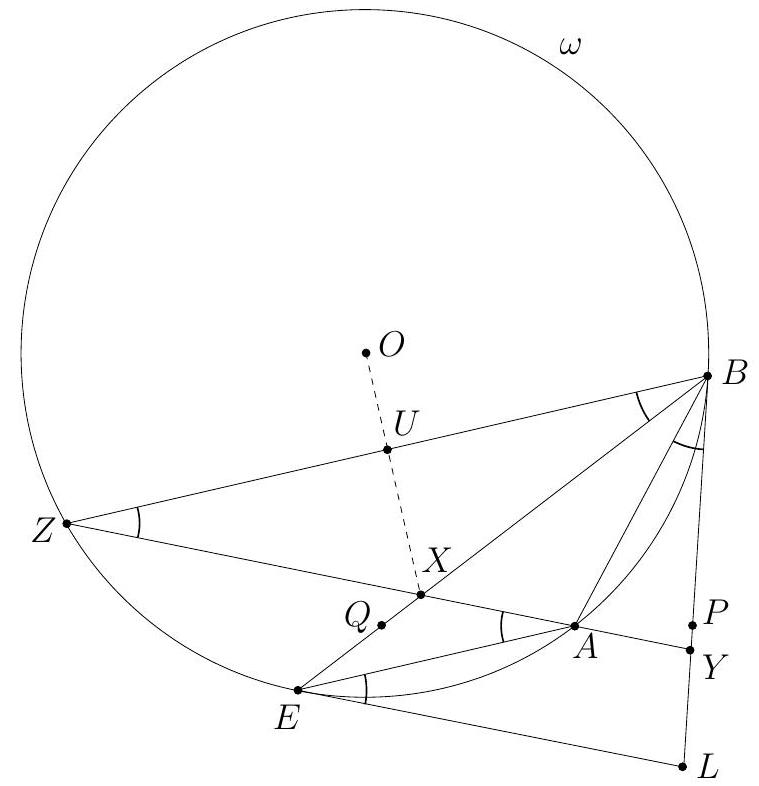 Figure 4 In order to show a third fixed point, draw a line parallel with $L E$ through $A$; let that line intersect $B E, L B$ and $\omega$ at $X, Y$ and $Z \neq A$, respectively (see Fig. 4). We show that $X$ is a fixed point. The images of $X$ at the first three transformations are $X \mapsto Y \mapsto X \mapsto Z$. From $\angle X B Z=\angle E A Z=\angle A E L=\angle L B A=\angle B Z X$ we can see that the triangle $X B Z$ is isosceles. Let $U$ be the midpoint of $B Z$; then the last two transformations do $Z \mapsto U \mapsto X$, and the point $X$ is fixed. Comment. Verifying that the point $E$ is fixed seems more natural at first, but it appears to be less straightforward. Here we outline a possible proof. Let the images of $E$ at the first three transforms above be $F, G$ and $I$. After comparing the angles depicted in Fig. 5 (noticing that the quadrilateral $A F B G$ is cyclic) we can observe that the tangent $L E$ of $\omega$ is parallel to $B I$. Then, similarly to the above reasons, the point $E$ is also fixed. 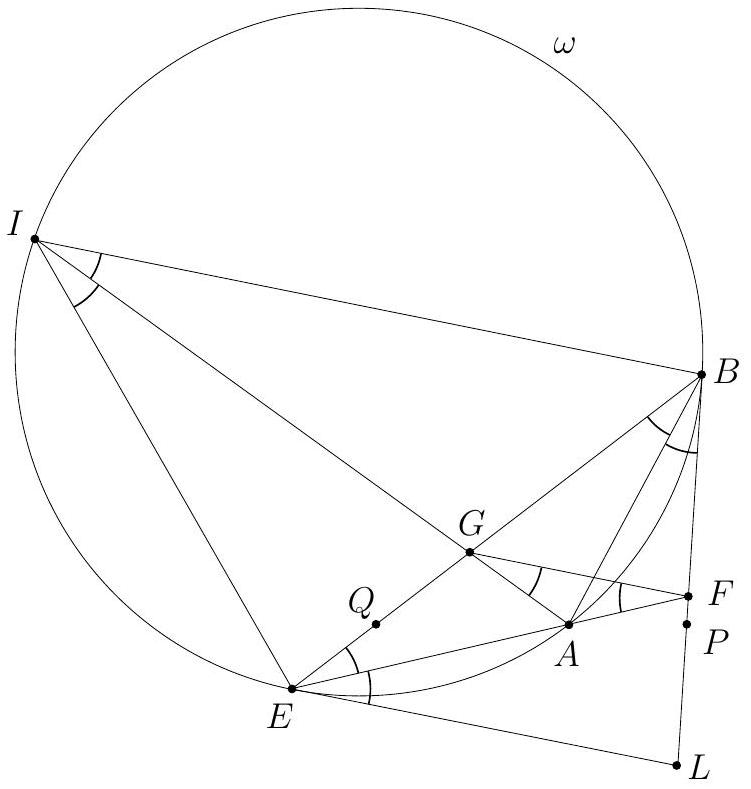 Figure 5
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $\angle B>\angle C$. Let $P$ and $Q$ be two different points on line $A C$ such that $\angle P B A=\angle Q B A=\angle A C B$ and $A$ is located between $P$ and $C$. Suppose that there exists an interior point $D$ of segment $B Q$ for which $P D=P B$. Let the ray $A D$ intersect the circle $A B C$ at $R \neq A$. Prove that $Q B=Q R$. (Georgia)
|
Denote by $\omega$ and $O$ the circumcircle of the triangle $A B C$ and its center, respectively. From the condition $\angle P B A=\angle B C A$ we know that $B P$ is tangent to $\omega$. Let $E$ be the second point of intersection of $\omega$ and $B D$. Due to the isosceles triangle $B D P$, the tangent of $\omega$ at $E$ is parallel to $D P$ and consequently it intersects $B P$ at some point $L$. Of course, $P D \| L E$. Let $M$ be the midpoint of $B E$, and let $H$ be the midpoint of $B R$. Notice that $\angle A E B=\angle A C B=\angle A B Q=\angle A B E$, so $A$ lies on the perpendicular bisector of $B E$; thus the points $L, A, M$, and $O$ are collinear. Let $\omega_{1}$ be the circle with diameter $B O$. Let $Q^{\prime}=H O \cap B E$; since $H O$ is the perpendicular bisector of $B R$, the statement of the problem is equivalent to $Q^{\prime}=Q$. Consider the following sequence of projections (see Fig. 3). 1. Project the line $B E$ to the line $L B$ through the center $A$. (This maps $Q$ to $P$.) 2. Project the line $L B$ to $B E$ in parallel direction with $L E$. $(P \mapsto D$.) 3. Project the line $B E$ to the circle $\omega$ through its point $A .(D \mapsto R$.) 4. Scale $\omega$ by the ratio $\frac{1}{2}$ from the point $B$ to the circle $\omega_{1} .(R \mapsto H$. 5. Project $\omega_{1}$ to the line $B E$ through its point $O$. $\left(H \mapsto Q^{\prime}\right.$.) We prove that the composition of these transforms, which maps the line $B E$ to itself, is the identity. To achieve this, it suffices to show three fixed points. An obvious fixed point is $B$ which is fixed by all the transformations above. Another fixed point is $M$, its path being $M \mapsto L \mapsto$ $E \mapsto E \mapsto M \mapsto M$.  Figure 3  Figure 4 In order to show a third fixed point, draw a line parallel with $L E$ through $A$; let that line intersect $B E, L B$ and $\omega$ at $X, Y$ and $Z \neq A$, respectively (see Fig. 4). We show that $X$ is a fixed point. The images of $X$ at the first three transformations are $X \mapsto Y \mapsto X \mapsto Z$. From $\angle X B Z=\angle E A Z=\angle A E L=\angle L B A=\angle B Z X$ we can see that the triangle $X B Z$ is isosceles. Let $U$ be the midpoint of $B Z$; then the last two transformations do $Z \mapsto U \mapsto X$, and the point $X$ is fixed. Comment. Verifying that the point $E$ is fixed seems more natural at first, but it appears to be less straightforward. Here we outline a possible proof. Let the images of $E$ at the first three transforms above be $F, G$ and $I$. After comparing the angles depicted in Fig. 5 (noticing that the quadrilateral $A F B G$ is cyclic) we can observe that the tangent $L E$ of $\omega$ is parallel to $B I$. Then, similarly to the above reasons, the point $E$ is also fixed.  Figure 5
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8298a6d4-654e-5002-bdb8-0ca7aeaf0ddd
| 24,301
|
Let $A B C D E F$ be a convex hexagon with $A B=D E, B C=E F, C D=F A$, and $\angle A-\angle D=\angle C-\angle F=\angle E-\angle B$. Prove that the diagonals $A D, B E$, and $C F$ are concurrent. (Ukraine)
|
Let $x=A B=D E, y=C D=F A, z=E F=B C$. Consider the points $P, Q$, and $R$ such that the quadrilaterals $C D E P, E F A Q$, and $A B C R$ are parallelograms. We compute $$ \begin{aligned} \angle P E Q & =\angle F E Q+\angle D E P-\angle E=\left(180^{\circ}-\angle F\right)+\left(180^{\circ}-\angle D\right)-\angle E \\ & =360^{\circ}-\angle D-\angle E-\angle F=\frac{1}{2}(\angle A+\angle B+\angle C-\angle D-\angle E-\angle F)=\theta / 2 \end{aligned} $$ Similarly, $\angle Q A R=\angle R C P=\theta / 2$. 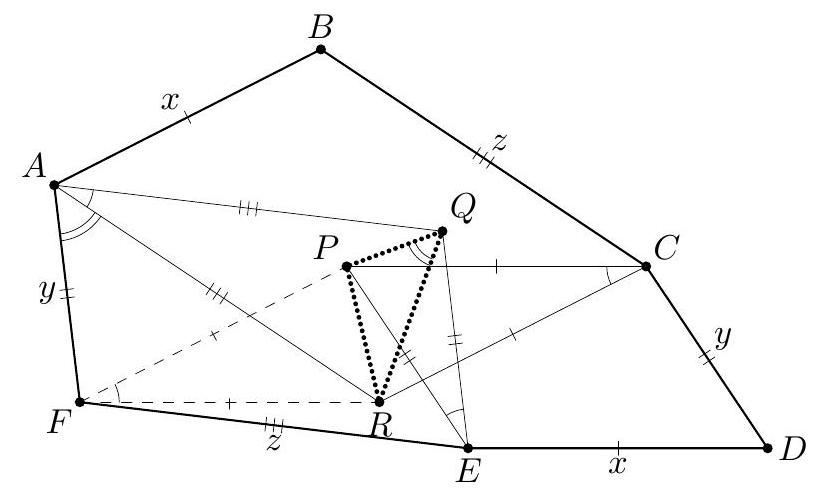 If $\theta=0$, since $\triangle R C P$ is isosceles, $R=P$. Therefore $A B\|R C=P C\| E D$, so $A B D E$ is a parallelogram. Similarly, $B C E F$ and $C D F A$ are parallelograms. It follows that $A D, B E$ and $C F$ meet at their common midpoint. Now assume $\theta>0$. Since $\triangle P E Q, \triangle Q A R$, and $\triangle R C P$ are isosceles and have the same angle at the apex, we have $\triangle P E Q \sim \triangle Q A R \sim \triangle R C P$ with ratios of similarity $y: z: x$. Thus $\triangle P Q R$ is similar to the triangle with sidelengths $y, z$, and $x$. Next, notice that $$ \frac{R Q}{Q P}=\frac{z}{y}=\frac{R A}{A F} $$ and, using directed angles between rays, $$ \begin{aligned} \not(R Q, Q P) & =\Varangle(R Q, Q E)+\Varangle(Q E, Q P) \\ & =\Varangle(R Q, Q E)+\Varangle(R A, R Q)=\Varangle(R A, Q E)=\Varangle(R A, A F) . \end{aligned} $$ Thus $\triangle P Q R \sim \triangle F A R$. Since $F A=y$ and $A R=z$, (1) then implies that $F R=x$. Similarly $F P=x$. Therefore $C R F P$ is a rhombus. We conclude that $C F$ is the perpendicular bisector of $P R$. Similarly, $B E$ is the perpendicular bisector of $P Q$ and $A D$ is the perpendicular bisector of $Q R$. It follows that $A D, B E$, and $C F$ are concurrent at the circumcenter of $P Q R$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D E F$ be a convex hexagon with $A B=D E, B C=E F, C D=F A$, and $\angle A-\angle D=\angle C-\angle F=\angle E-\angle B$. Prove that the diagonals $A D, B E$, and $C F$ are concurrent. (Ukraine)
|
Let $x=A B=D E, y=C D=F A, z=E F=B C$. Consider the points $P, Q$, and $R$ such that the quadrilaterals $C D E P, E F A Q$, and $A B C R$ are parallelograms. We compute $$ \begin{aligned} \angle P E Q & =\angle F E Q+\angle D E P-\angle E=\left(180^{\circ}-\angle F\right)+\left(180^{\circ}-\angle D\right)-\angle E \\ & =360^{\circ}-\angle D-\angle E-\angle F=\frac{1}{2}(\angle A+\angle B+\angle C-\angle D-\angle E-\angle F)=\theta / 2 \end{aligned} $$ Similarly, $\angle Q A R=\angle R C P=\theta / 2$.  If $\theta=0$, since $\triangle R C P$ is isosceles, $R=P$. Therefore $A B\|R C=P C\| E D$, so $A B D E$ is a parallelogram. Similarly, $B C E F$ and $C D F A$ are parallelograms. It follows that $A D, B E$ and $C F$ meet at their common midpoint. Now assume $\theta>0$. Since $\triangle P E Q, \triangle Q A R$, and $\triangle R C P$ are isosceles and have the same angle at the apex, we have $\triangle P E Q \sim \triangle Q A R \sim \triangle R C P$ with ratios of similarity $y: z: x$. Thus $\triangle P Q R$ is similar to the triangle with sidelengths $y, z$, and $x$. Next, notice that $$ \frac{R Q}{Q P}=\frac{z}{y}=\frac{R A}{A F} $$ and, using directed angles between rays, $$ \begin{aligned} \not(R Q, Q P) & =\Varangle(R Q, Q E)+\Varangle(Q E, Q P) \\ & =\Varangle(R Q, Q E)+\Varangle(R A, R Q)=\Varangle(R A, Q E)=\Varangle(R A, A F) . \end{aligned} $$ Thus $\triangle P Q R \sim \triangle F A R$. Since $F A=y$ and $A R=z$, (1) then implies that $F R=x$. Similarly $F P=x$. Therefore $C R F P$ is a rhombus. We conclude that $C F$ is the perpendicular bisector of $P R$. Similarly, $B E$ is the perpendicular bisector of $P Q$ and $A D$ is the perpendicular bisector of $Q R$. It follows that $A D, B E$, and $C F$ are concurrent at the circumcenter of $P Q R$.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
284d1131-5193-5a97-9cfc-06f9b25a34ef
| 24,306
|
Let $A B C D E F$ be a convex hexagon with $A B=D E, B C=E F, C D=F A$, and $\angle A-\angle D=\angle C-\angle F=\angle E-\angle B$. Prove that the diagonals $A D, B E$, and $C F$ are concurrent. (Ukraine)
|
Let $X=C D \cap E F, Y=E F \cap A B, Z=A B \cap C D, X^{\prime}=F A \cap B C, Y^{\prime}=$ $B C \cap D E$, and $Z^{\prime}=D E \cap F A$. From $\angle A+\angle B+\angle C=360^{\circ}+\theta / 2$ we get $\angle A+\angle B>180^{\circ}$ and $\angle B+\angle C>180^{\circ}$, so $Z$ and $X^{\prime}$ are respectively on the opposite sides of $B C$ and $A B$ from the hexagon. Similar conclusions hold for $X, Y, Y^{\prime}$, and $Z^{\prime}$. Then $$ \angle Y Z X=\angle B+\angle C-180^{\circ}=\angle E+\angle F-180^{\circ}=\angle Y^{\prime} Z^{\prime} X^{\prime}, $$ and similarly $\angle Z X Y=\angle Z^{\prime} X^{\prime} Y^{\prime}$ and $\angle X Y Z=\angle X^{\prime} Y^{\prime} Z^{\prime}$, so $\triangle X Y Z \sim \triangle X^{\prime} Y^{\prime} Z^{\prime}$. Thus there is a rotation $R$ which sends $\triangle X Y Z$ to a triangle with sides parallel to $\triangle X^{\prime} Y^{\prime} Z^{\prime}$. Since $A B=D E$ we have $R(\overrightarrow{A B})=\overrightarrow{D E}$. Similarly, $R(\overrightarrow{C D})=\overrightarrow{F A}$ and $R(\overrightarrow{E F})=\overrightarrow{B C}$. Therefore $$ \overrightarrow{0}=\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C D}+\overrightarrow{D E}+\overrightarrow{E F}+\overrightarrow{F A}=(\overrightarrow{A B}+\overrightarrow{C D}+\overrightarrow{E F})+R(\overrightarrow{A B}+\overrightarrow{C D}+\overrightarrow{E F}) $$ If $R$ is a rotation by $180^{\circ}$, then any two opposite sides of our hexagon are equal and parallel, so the three diagonals meet at their common midpoint. Otherwise, we must have $$ \overrightarrow{A B}+\overrightarrow{C D}+\overrightarrow{E F}=\overrightarrow{0} $$ or else we would have two vectors with different directions whose sum is $\overrightarrow{0}$.  This allows us to consider a triangle $L M N$ with $\overrightarrow{L M}=\overrightarrow{E F}, \overrightarrow{M N}=\overrightarrow{A B}$, and $\overrightarrow{N L}=\overrightarrow{C D}$. Let $O$ be the circumcenter of $\triangle L M N$ and consider the points $O_{1}, O_{2}, O_{3}$ such that $\triangle A O_{1} B, \triangle C O_{2} D$, and $\triangle E O_{3} F$ are translations of $\triangle M O N, \triangle N O L$, and $\triangle L O M$, respectively. Since $F O_{3}$ and $A O_{1}$ are translations of $M O$, quadrilateral $A F O_{3} O_{1}$ is a parallelogram and $O_{3} O_{1}=F A=C D=N L$. Similarly, $O_{1} O_{2}=L M$ and $O_{2} O_{3}=M N$. Therefore $\triangle O_{1} O_{2} O_{3} \cong \triangle L M N$. Moreover, by means of the rotation $R$ one may check that these triangles have the same orientation. Let $T$ be the circumcenter of $\triangle O_{1} O_{2} O_{3}$. We claim that $A D, B E$, and $C F$ meet at $T$. Let us show that $C, T$, and $F$ are collinear. Notice that $C O_{2}=O_{2} T=T O_{3}=O_{3} F$ since they are all equal to the circumradius of $\triangle L M N$. Therefore $\triangle T O_{3} F$ and $\triangle C O_{2} T$ are isosceles. Using directed angles between rays again, we get $$ \Varangle\left(T F, T O_{3}\right)=\Varangle\left(F O_{3}, F T\right) \quad \text { and } \quad \Varangle\left(T O_{2}, T C\right)=\Varangle\left(C T, C O_{2}\right) \text {. } $$ Also, $T$ and $O$ are the circumcenters of the congruent triangles $\triangle O_{1} O_{2} O_{3}$ and $\triangle L M N$ so we have $\Varangle\left(T O_{3}, T O_{2}\right)=\Varangle(O N, O M)$. Since $C_{2}$ and $F O_{3}$ are translations of $N O$ and $M O$ respectively, this implies $$ \Varangle\left(T O_{3}, T O_{2}\right)=\Varangle\left(C O_{2}, F O_{3}\right) . $$ Adding the three equations in (2) and (3) gives $$ \Varangle(T F, T C)=\Varangle(C T, F T)=-\not(T F, T C) $$ which implies that $T$ is on $C F$. Analogous arguments show that it is on $A D$ and $B E$ also. The desired result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D E F$ be a convex hexagon with $A B=D E, B C=E F, C D=F A$, and $\angle A-\angle D=\angle C-\angle F=\angle E-\angle B$. Prove that the diagonals $A D, B E$, and $C F$ are concurrent. (Ukraine)
|
Let $X=C D \cap E F, Y=E F \cap A B, Z=A B \cap C D, X^{\prime}=F A \cap B C, Y^{\prime}=$ $B C \cap D E$, and $Z^{\prime}=D E \cap F A$. From $\angle A+\angle B+\angle C=360^{\circ}+\theta / 2$ we get $\angle A+\angle B>180^{\circ}$ and $\angle B+\angle C>180^{\circ}$, so $Z$ and $X^{\prime}$ are respectively on the opposite sides of $B C$ and $A B$ from the hexagon. Similar conclusions hold for $X, Y, Y^{\prime}$, and $Z^{\prime}$. Then $$ \angle Y Z X=\angle B+\angle C-180^{\circ}=\angle E+\angle F-180^{\circ}=\angle Y^{\prime} Z^{\prime} X^{\prime}, $$ and similarly $\angle Z X Y=\angle Z^{\prime} X^{\prime} Y^{\prime}$ and $\angle X Y Z=\angle X^{\prime} Y^{\prime} Z^{\prime}$, so $\triangle X Y Z \sim \triangle X^{\prime} Y^{\prime} Z^{\prime}$. Thus there is a rotation $R$ which sends $\triangle X Y Z$ to a triangle with sides parallel to $\triangle X^{\prime} Y^{\prime} Z^{\prime}$. Since $A B=D E$ we have $R(\overrightarrow{A B})=\overrightarrow{D E}$. Similarly, $R(\overrightarrow{C D})=\overrightarrow{F A}$ and $R(\overrightarrow{E F})=\overrightarrow{B C}$. Therefore $$ \overrightarrow{0}=\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C D}+\overrightarrow{D E}+\overrightarrow{E F}+\overrightarrow{F A}=(\overrightarrow{A B}+\overrightarrow{C D}+\overrightarrow{E F})+R(\overrightarrow{A B}+\overrightarrow{C D}+\overrightarrow{E F}) $$ If $R$ is a rotation by $180^{\circ}$, then any two opposite sides of our hexagon are equal and parallel, so the three diagonals meet at their common midpoint. Otherwise, we must have $$ \overrightarrow{A B}+\overrightarrow{C D}+\overrightarrow{E F}=\overrightarrow{0} $$ or else we would have two vectors with different directions whose sum is $\overrightarrow{0}$.  This allows us to consider a triangle $L M N$ with $\overrightarrow{L M}=\overrightarrow{E F}, \overrightarrow{M N}=\overrightarrow{A B}$, and $\overrightarrow{N L}=\overrightarrow{C D}$. Let $O$ be the circumcenter of $\triangle L M N$ and consider the points $O_{1}, O_{2}, O_{3}$ such that $\triangle A O_{1} B, \triangle C O_{2} D$, and $\triangle E O_{3} F$ are translations of $\triangle M O N, \triangle N O L$, and $\triangle L O M$, respectively. Since $F O_{3}$ and $A O_{1}$ are translations of $M O$, quadrilateral $A F O_{3} O_{1}$ is a parallelogram and $O_{3} O_{1}=F A=C D=N L$. Similarly, $O_{1} O_{2}=L M$ and $O_{2} O_{3}=M N$. Therefore $\triangle O_{1} O_{2} O_{3} \cong \triangle L M N$. Moreover, by means of the rotation $R$ one may check that these triangles have the same orientation. Let $T$ be the circumcenter of $\triangle O_{1} O_{2} O_{3}$. We claim that $A D, B E$, and $C F$ meet at $T$. Let us show that $C, T$, and $F$ are collinear. Notice that $C O_{2}=O_{2} T=T O_{3}=O_{3} F$ since they are all equal to the circumradius of $\triangle L M N$. Therefore $\triangle T O_{3} F$ and $\triangle C O_{2} T$ are isosceles. Using directed angles between rays again, we get $$ \Varangle\left(T F, T O_{3}\right)=\Varangle\left(F O_{3}, F T\right) \quad \text { and } \quad \Varangle\left(T O_{2}, T C\right)=\Varangle\left(C T, C O_{2}\right) \text {. } $$ Also, $T$ and $O$ are the circumcenters of the congruent triangles $\triangle O_{1} O_{2} O_{3}$ and $\triangle L M N$ so we have $\Varangle\left(T O_{3}, T O_{2}\right)=\Varangle(O N, O M)$. Since $C_{2}$ and $F O_{3}$ are translations of $N O$ and $M O$ respectively, this implies $$ \Varangle\left(T O_{3}, T O_{2}\right)=\Varangle\left(C O_{2}, F O_{3}\right) . $$ Adding the three equations in (2) and (3) gives $$ \Varangle(T F, T C)=\Varangle(C T, F T)=-\not(T F, T C) $$ which implies that $T$ is on $C F$. Analogous arguments show that it is on $A D$ and $B E$ also. The desired result follows.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
284d1131-5193-5a97-9cfc-06f9b25a34ef
| 24,306
|
Let $A B C D E F$ be a convex hexagon with $A B=D E, B C=E F, C D=F A$, and $\angle A-\angle D=\angle C-\angle F=\angle E-\angle B$. Prove that the diagonals $A D, B E$, and $C F$ are concurrent. (Ukraine)
|
Place the hexagon on the complex plane, with $A$ at the origin and vertices labelled clockwise. Now $A, B, C, D, E, F$ represent the corresponding complex numbers. Also consider the complex numbers $a, b, c, a^{\prime}, b^{\prime}, c^{\prime}$ given by $B-A=a, D-C=b, F-E=c, E-D=a^{\prime}$, $A-F=b^{\prime}$, and $C-B=c^{\prime}$. Let $k=|a| /|b|$. From $a / b^{\prime}=-k e^{i \angle A}$ and $a^{\prime} / b=-k e^{i \angle D}$ we get that $\left(a^{\prime} / a\right)\left(b^{\prime} / b\right)=e^{-i \theta}$ and similarly $\left(b^{\prime} / b\right)\left(c^{\prime} / c\right)=e^{-i \theta}$ and $\left(c^{\prime} / c\right)\left(a^{\prime} / a\right)=e^{-i \theta}$. It follows that $a^{\prime}=a r$, $b^{\prime}=b r$, and $c^{\prime}=c r$ for a complex number $r$ with $|r|=1$, as shown below. 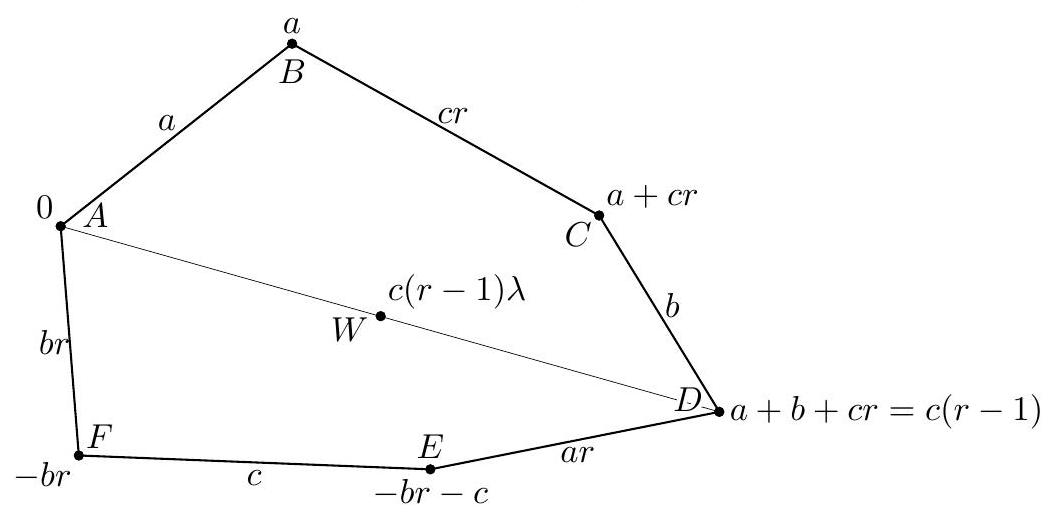 We have $$ 0=a+c r+b+a r+c+b r=(a+b+c)(1+r) . $$ If $r=-1$, then the hexagon is centrally symmetric and its diagonals intersect at its center of symmetry. Otherwise $$ a+b+c=0 \text {. } $$ Therefore $$ A=0, \quad B=a, \quad C=a+c r, \quad D=c(r-1), \quad E=-b r-c, \quad F=-b r . $$ Now consider a point $W$ on $A D$ given by the complex number $c(r-1) \lambda$, where $\lambda$ is a real number with $0<\lambda<1$. Since $D \neq A$, we have $r \neq 1$, so we can define $s=1 /(r-1)$. From $r \bar{r}=|r|^{2}=1$ we get $$ 1+s=\frac{r}{r-1}=\frac{r}{r-r \bar{r}}=\frac{1}{1-\bar{r}}=-\bar{s} . $$ Now, $$ \begin{aligned} W \text { is on } B E & \Longleftrightarrow c(r-1) \lambda-a\|a-(-b r-c)=b(r-1) \Longleftrightarrow c \lambda-a s\| b \\ & \Longleftrightarrow-a \lambda-b \lambda-a s\|b \Longleftrightarrow a(\lambda+s)\| b . \end{aligned} $$ One easily checks that $r \neq \pm 1$ implies that $\lambda+s \neq 0$ since $s$ is not real. On the other hand, $$ \begin{aligned} W \text { on } C F & \Longleftrightarrow c(r-1) \lambda+b r\|-b r-(a+c r)=a(r-1) \Longleftrightarrow c \lambda+b(1+s)\| a \\ & \Longleftrightarrow-a \lambda-b \lambda-b \bar{s}\|a \Longleftrightarrow b(\lambda+\bar{s})\| a \Longleftrightarrow b \| a(\lambda+s), \end{aligned} $$ where in the last step we use that $(\lambda+s)(\lambda+\bar{s})=|\lambda+s|^{2} \in \mathbb{R}_{>0}$. We conclude that $A D \cap B E=$ $C F \cap B E$, and the desired result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D E F$ be a convex hexagon with $A B=D E, B C=E F, C D=F A$, and $\angle A-\angle D=\angle C-\angle F=\angle E-\angle B$. Prove that the diagonals $A D, B E$, and $C F$ are concurrent. (Ukraine)
|
Place the hexagon on the complex plane, with $A$ at the origin and vertices labelled clockwise. Now $A, B, C, D, E, F$ represent the corresponding complex numbers. Also consider the complex numbers $a, b, c, a^{\prime}, b^{\prime}, c^{\prime}$ given by $B-A=a, D-C=b, F-E=c, E-D=a^{\prime}$, $A-F=b^{\prime}$, and $C-B=c^{\prime}$. Let $k=|a| /|b|$. From $a / b^{\prime}=-k e^{i \angle A}$ and $a^{\prime} / b=-k e^{i \angle D}$ we get that $\left(a^{\prime} / a\right)\left(b^{\prime} / b\right)=e^{-i \theta}$ and similarly $\left(b^{\prime} / b\right)\left(c^{\prime} / c\right)=e^{-i \theta}$ and $\left(c^{\prime} / c\right)\left(a^{\prime} / a\right)=e^{-i \theta}$. It follows that $a^{\prime}=a r$, $b^{\prime}=b r$, and $c^{\prime}=c r$ for a complex number $r$ with $|r|=1$, as shown below.  We have $$ 0=a+c r+b+a r+c+b r=(a+b+c)(1+r) . $$ If $r=-1$, then the hexagon is centrally symmetric and its diagonals intersect at its center of symmetry. Otherwise $$ a+b+c=0 \text {. } $$ Therefore $$ A=0, \quad B=a, \quad C=a+c r, \quad D=c(r-1), \quad E=-b r-c, \quad F=-b r . $$ Now consider a point $W$ on $A D$ given by the complex number $c(r-1) \lambda$, where $\lambda$ is a real number with $0<\lambda<1$. Since $D \neq A$, we have $r \neq 1$, so we can define $s=1 /(r-1)$. From $r \bar{r}=|r|^{2}=1$ we get $$ 1+s=\frac{r}{r-1}=\frac{r}{r-r \bar{r}}=\frac{1}{1-\bar{r}}=-\bar{s} . $$ Now, $$ \begin{aligned} W \text { is on } B E & \Longleftrightarrow c(r-1) \lambda-a\|a-(-b r-c)=b(r-1) \Longleftrightarrow c \lambda-a s\| b \\ & \Longleftrightarrow-a \lambda-b \lambda-a s\|b \Longleftrightarrow a(\lambda+s)\| b . \end{aligned} $$ One easily checks that $r \neq \pm 1$ implies that $\lambda+s \neq 0$ since $s$ is not real. On the other hand, $$ \begin{aligned} W \text { on } C F & \Longleftrightarrow c(r-1) \lambda+b r\|-b r-(a+c r)=a(r-1) \Longleftrightarrow c \lambda+b(1+s)\| a \\ & \Longleftrightarrow-a \lambda-b \lambda-b \bar{s}\|a \Longleftrightarrow b(\lambda+\bar{s})\| a \Longleftrightarrow b \| a(\lambda+s), \end{aligned} $$ where in the last step we use that $(\lambda+s)(\lambda+\bar{s})=|\lambda+s|^{2} \in \mathbb{R}_{>0}$. We conclude that $A D \cap B E=$ $C F \cap B E$, and the desired result follows.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
284d1131-5193-5a97-9cfc-06f9b25a34ef
| 24,306
|
Let the excircle of the triangle $A B C$ lying opposite to $A$ touch its side $B C$ at the point $A_{1}$. Define the points $B_{1}$ and $C_{1}$ analogously. Suppose that the circumcentre of the triangle $A_{1} B_{1} C_{1}$ lies on the circumcircle of the triangle $A B C$. Prove that the triangle $A B C$ is right-angled. (Russia)
|
Denote the circumcircles of the triangles $A B C$ and $A_{1} B_{1} C_{1}$ by $\Omega$ and $\Gamma$, respectively. Denote the midpoint of the arc $C B$ of $\Omega$ containing $A$ by $A_{0}$, and define $B_{0}$ as well as $C_{0}$ analogously. By our hypothesis the centre $Q$ of $\Gamma$ lies on $\Omega$. Lemma. One has $A_{0} B_{1}=A_{0} C_{1}$. Moreover, the points $A, A_{0}, B_{1}$, and $C_{1}$ are concyclic. Finally, the points $A$ and $A_{0}$ lie on the same side of $B_{1} C_{1}$. Similar statements hold for $B$ and $C$. Proof. Let us consider the case $A=A_{0}$ first. Then the triangle $A B C$ is isosceles at $A$, which implies $A B_{1}=A C_{1}$ while the remaining assertions of the Lemma are obvious. So let us suppose $A \neq A_{0}$ from now on. By the definition of $A_{0}$, we have $A_{0} B=A_{0} C$. It is also well known and easy to show that $B C_{1}=$ $C B_{1}$. Next, we have $\angle C_{1} B A_{0}=\angle A B A_{0}=\angle A C A_{0}=\angle B_{1} C A_{0}$. Hence the triangles $A_{0} B C_{1}$ and $A_{0} C B_{1}$ are congruent. This implies $A_{0} C_{1}=A_{0} B_{1}$, establishing the first part of the Lemma. It also follows that $\angle A_{0} C_{1} A=\angle A_{0} B_{1} A$, as these are exterior angles at the corresponding vertices $C_{1}$ and $B_{1}$ of the congruent triangles $A_{0} B C_{1}$ and $A_{0} C B_{1}$. For that reason the points $A, A_{0}, B_{1}$, and $C_{1}$ are indeed the vertices of some cyclic quadrilateral two opposite sides of which are $A A_{0}$ and $B_{1} C_{1}$. Now we turn to the solution. Evidently the points $A_{1}, B_{1}$, and $C_{1}$ lie interior to some semicircle arc of $\Gamma$, so the triangle $A_{1} B_{1} C_{1}$ is obtuse-angled. Without loss of generality, we will assume that its angle at $B_{1}$ is obtuse. Thus $Q$ and $B_{1}$ lie on different sides of $A_{1} C_{1}$; obviously, the same holds for the points $B$ and $B_{1}$. So, the points $Q$ and $B$ are on the same side of $A_{1} C_{1}$. Notice that the perpendicular bisector of $A_{1} C_{1}$ intersects $\Omega$ at two points lying on different sides of $A_{1} C_{1}$. By the first statement from the Lemma, both points $B_{0}$ and $Q$ are among these points of intersection; since they share the same side of $A_{1} C_{1}$, they coincide (see Figure 1). 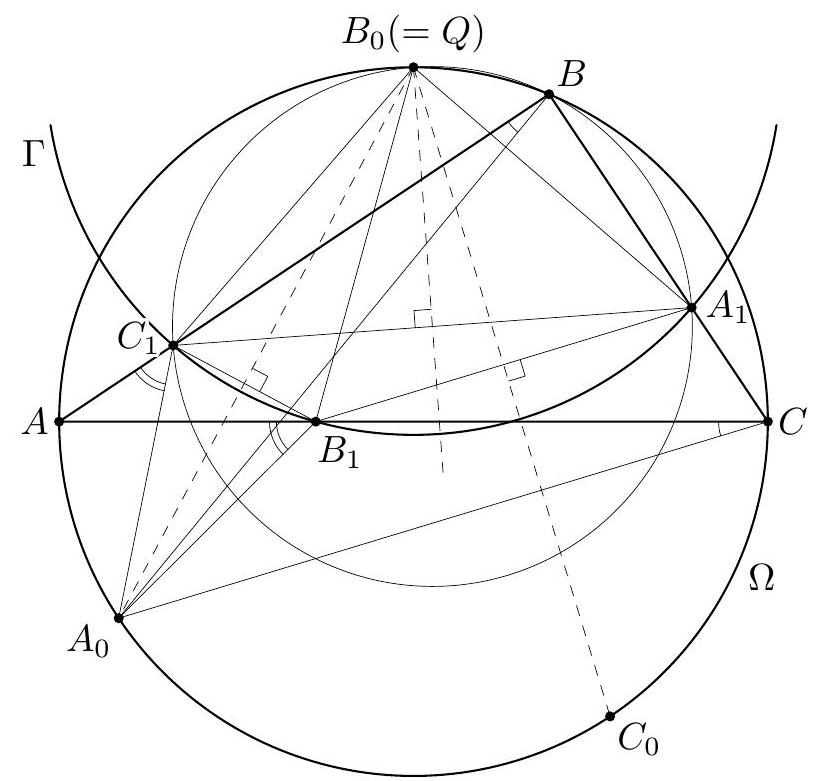 Figure 1 Now, by the first part of the Lemma again, the lines $Q A_{0}$ and $Q C_{0}$ are the perpendicular bisectors of $B_{1} C_{1}$ and $A_{1} B_{1}$, respectively. Thus $$ \angle C_{1} B_{0} A_{1}=\angle C_{1} B_{0} B_{1}+\angle B_{1} B_{0} A_{1}=2 \angle A_{0} B_{0} B_{1}+2 \angle B_{1} B_{0} C_{0}=2 \angle A_{0} B_{0} C_{0}=180^{\circ}-\angle A B C $$ recalling that $A_{0}$ and $C_{0}$ are the midpoints of the arcs $C B$ and $B A$, respectively. On the other hand, by the second part of the Lemma we have $$ \angle C_{1} B_{0} A_{1}=\angle C_{1} B A_{1}=\angle A B C . $$ From the last two equalities, we get $\angle A B C=90^{\circ}$, whereby the problem is solved.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let the excircle of the triangle $A B C$ lying opposite to $A$ touch its side $B C$ at the point $A_{1}$. Define the points $B_{1}$ and $C_{1}$ analogously. Suppose that the circumcentre of the triangle $A_{1} B_{1} C_{1}$ lies on the circumcircle of the triangle $A B C$. Prove that the triangle $A B C$ is right-angled. (Russia)
|
Denote the circumcircles of the triangles $A B C$ and $A_{1} B_{1} C_{1}$ by $\Omega$ and $\Gamma$, respectively. Denote the midpoint of the arc $C B$ of $\Omega$ containing $A$ by $A_{0}$, and define $B_{0}$ as well as $C_{0}$ analogously. By our hypothesis the centre $Q$ of $\Gamma$ lies on $\Omega$. Lemma. One has $A_{0} B_{1}=A_{0} C_{1}$. Moreover, the points $A, A_{0}, B_{1}$, and $C_{1}$ are concyclic. Finally, the points $A$ and $A_{0}$ lie on the same side of $B_{1} C_{1}$. Similar statements hold for $B$ and $C$. Proof. Let us consider the case $A=A_{0}$ first. Then the triangle $A B C$ is isosceles at $A$, which implies $A B_{1}=A C_{1}$ while the remaining assertions of the Lemma are obvious. So let us suppose $A \neq A_{0}$ from now on. By the definition of $A_{0}$, we have $A_{0} B=A_{0} C$. It is also well known and easy to show that $B C_{1}=$ $C B_{1}$. Next, we have $\angle C_{1} B A_{0}=\angle A B A_{0}=\angle A C A_{0}=\angle B_{1} C A_{0}$. Hence the triangles $A_{0} B C_{1}$ and $A_{0} C B_{1}$ are congruent. This implies $A_{0} C_{1}=A_{0} B_{1}$, establishing the first part of the Lemma. It also follows that $\angle A_{0} C_{1} A=\angle A_{0} B_{1} A$, as these are exterior angles at the corresponding vertices $C_{1}$ and $B_{1}$ of the congruent triangles $A_{0} B C_{1}$ and $A_{0} C B_{1}$. For that reason the points $A, A_{0}, B_{1}$, and $C_{1}$ are indeed the vertices of some cyclic quadrilateral two opposite sides of which are $A A_{0}$ and $B_{1} C_{1}$. Now we turn to the solution. Evidently the points $A_{1}, B_{1}$, and $C_{1}$ lie interior to some semicircle arc of $\Gamma$, so the triangle $A_{1} B_{1} C_{1}$ is obtuse-angled. Without loss of generality, we will assume that its angle at $B_{1}$ is obtuse. Thus $Q$ and $B_{1}$ lie on different sides of $A_{1} C_{1}$; obviously, the same holds for the points $B$ and $B_{1}$. So, the points $Q$ and $B$ are on the same side of $A_{1} C_{1}$. Notice that the perpendicular bisector of $A_{1} C_{1}$ intersects $\Omega$ at two points lying on different sides of $A_{1} C_{1}$. By the first statement from the Lemma, both points $B_{0}$ and $Q$ are among these points of intersection; since they share the same side of $A_{1} C_{1}$, they coincide (see Figure 1).  Figure 1 Now, by the first part of the Lemma again, the lines $Q A_{0}$ and $Q C_{0}$ are the perpendicular bisectors of $B_{1} C_{1}$ and $A_{1} B_{1}$, respectively. Thus $$ \angle C_{1} B_{0} A_{1}=\angle C_{1} B_{0} B_{1}+\angle B_{1} B_{0} A_{1}=2 \angle A_{0} B_{0} B_{1}+2 \angle B_{1} B_{0} C_{0}=2 \angle A_{0} B_{0} C_{0}=180^{\circ}-\angle A B C $$ recalling that $A_{0}$ and $C_{0}$ are the midpoints of the arcs $C B$ and $B A$, respectively. On the other hand, by the second part of the Lemma we have $$ \angle C_{1} B_{0} A_{1}=\angle C_{1} B A_{1}=\angle A B C . $$ From the last two equalities, we get $\angle A B C=90^{\circ}$, whereby the problem is solved.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
978a7792-e68c-5860-9e5e-1836d7a742d7
| 24,311
|
Let the excircle of the triangle $A B C$ lying opposite to $A$ touch its side $B C$ at the point $A_{1}$. Define the points $B_{1}$ and $C_{1}$ analogously. Suppose that the circumcentre of the triangle $A_{1} B_{1} C_{1}$ lies on the circumcircle of the triangle $A B C$. Prove that the triangle $A B C$ is right-angled. (Russia)
|
Let $Q$ again denote the centre of the circumcircle of the triangle $A_{1} B_{1} C_{1}$, that lies on the circumcircle $\Omega$ of the triangle $A B C$. We first consider the case where $Q$ coincides with one of the vertices of $A B C$, say $Q=B$. Then $B C_{1}=B A_{1}$ and consequently the triangle $A B C$ is isosceles at $B$. Moreover we have $B C_{1}=B_{1} C$ in any triangle, and hence $B B_{1}=B C_{1}=B_{1} C$; similarly, $B B_{1}=B_{1} A$. It follows that $B_{1}$ is the centre of $\Omega$ and that the triangle $A B C$ has a right angle at $B$. So from now on we may suppose $Q \notin\{A, B, C\}$. We start with the following well known fact. Lemma. Let $X Y Z$ and $X^{\prime} Y^{\prime} Z^{\prime}$ be two triangles with $X Y=X^{\prime} Y^{\prime}$ and $Y Z=Y^{\prime} Z^{\prime}$. (i) If $X Z \neq X^{\prime} Z^{\prime}$ and $\angle Y Z X=\angle Y^{\prime} Z^{\prime} X^{\prime}$, then $\angle Z X Y+\angle Z^{\prime} X^{\prime} Y^{\prime}=180^{\circ}$. (ii) If $\angle Y Z X+\angle X^{\prime} Z^{\prime} Y^{\prime}=180^{\circ}$, then $\angle Z X Y=\angle Y^{\prime} X^{\prime} Z^{\prime}$. Proof. For both parts, we may move the triangle $X Y Z$ through the plane until $Y=Y^{\prime}$ and $Z=Z^{\prime}$. Possibly after reflecting one of the two triangles about $Y Z$, we may also suppose that $X$ and $X^{\prime}$ lie on the same side of $Y Z$ if we are in case (i) and on different sides if we are in case (ii). In both cases, the points $X, Z$, and $X^{\prime}$ are collinear due to the angle condition (see Fig. 2). Moreover we have $X \neq X^{\prime}$, because in case (i) we assumed $X Z \neq X^{\prime} Z^{\prime}$ and in case (ii) these points even lie on different sides of $Y Z$. Thus the triangle $X X^{\prime} Y$ is isosceles at $Y$. The claim now follows by considering the equal angles at its base.  Figure 2(i)  Figure 2(ii) Relabeling the vertices of the triangle $A B C$ if necessary we may suppose that $Q$ lies in the interior of the arc $A B$ of $\Omega$ not containing $C$. We will sometimes use tacitly that the six triangles $Q B A_{1}, Q A_{1} C, Q C B_{1}, Q B_{1} A, Q C_{1} A$, and $Q B C_{1}$ have the same orientation. As $Q$ cannot be the circumcentre of the triangle $A B C$, it is impossible that $Q A=Q B=Q C$ and thus we may also suppose that $Q C \neq Q B$. Now the above Lemma $(i)$ is applicable to the triangles $Q B_{1} C$ and $Q C_{1} B$, since $Q B_{1}=Q C_{1}$ and $B_{1} C=C_{1} B$, while $\angle B_{1} C Q=\angle C_{1} B Q$ holds as both angles appear over the same side of the chord $Q A$ in $\Omega$ (see Fig. 3). So we get $$ \angle C Q B_{1}+\angle B Q C_{1}=180^{\circ} . $$ We claim that $Q C=Q A$. To see this, let us assume for the sake of a contradiction that $Q C \neq Q A$. Then arguing similarly as before but now with the triangles $Q A_{1} C$ and $Q C_{1} A$ we get $$ \angle A_{1} Q C+\angle C_{1} Q A=180^{\circ} \text {. } $$ Adding this equation to (1), we get $\angle A_{1} Q B_{1}+\angle B Q A=360^{\circ}$, which is absurd as both summands lie in the interval $\left(0^{\circ}, 180^{\circ}\right)$. This proves $Q C=Q A$; so the triangles $Q A_{1} C$ and $Q C_{1} A$ are congruent their sides being equal, which in turn yields $$ \angle A_{1} Q C=\angle C_{1} Q A \text {. } $$ Finally our Lemma (ii) is applicable to the triangles $Q A_{1} B$ and $Q B_{1} A$. Indeed we have $Q A_{1}=Q B_{1}$ and $A_{1} B=B_{1} A$ as usual, and the angle condition $\angle A_{1} B Q+\angle Q A B_{1}=180^{\circ}$ holds as $A$ and $B$ lie on different sides of the chord $Q C$ in $\Omega$. Consequently we have $$ \angle B Q A_{1}=\angle B_{1} Q A \text {. } $$ From (1) and (3) we get $$ \left(\angle B_{1} Q C+\angle B_{1} Q A\right)+\left(\angle C_{1} Q B-\angle B Q A_{1}\right)=180^{\circ} \text {, } $$ i.e. $\angle C Q A+\angle A_{1} Q C_{1}=180^{\circ}$. In light of (2) this may be rewritten as $2 \angle C Q A=180^{\circ}$ and as $Q$ lies on $\Omega$ this implies that the triangle $A B C$ has a right angle at $B$. 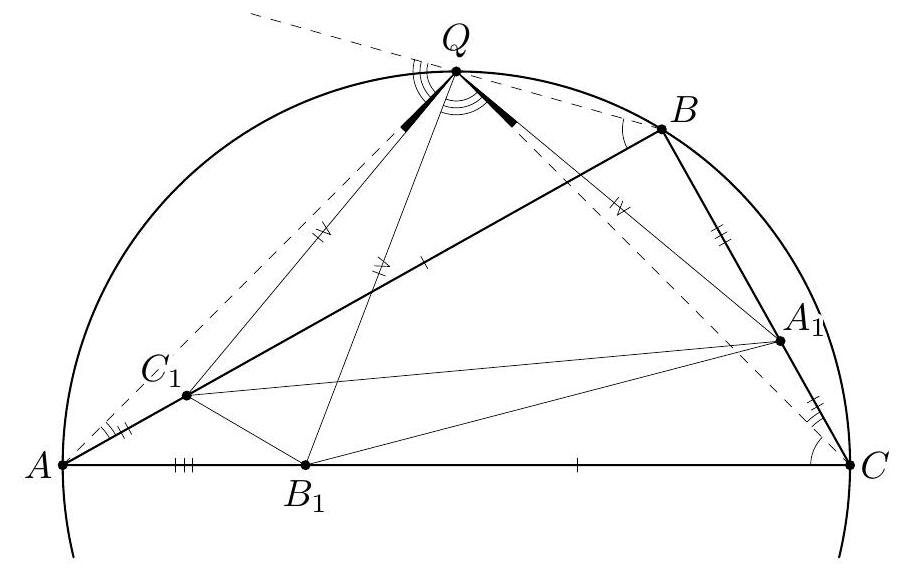 Figure 3 Comment 1. One may also check that $Q$ is in the interior of $\Omega$ if and only if the triangle $A B C$ is acute-angled. Comment 2. The original proposal asked to prove the converse statement as well: if the triangle $A B C$ is right-angled, then the point $Q$ lies on its circumcircle. The Problem Selection Committee thinks that the above simplified version is more suitable for the competition.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let the excircle of the triangle $A B C$ lying opposite to $A$ touch its side $B C$ at the point $A_{1}$. Define the points $B_{1}$ and $C_{1}$ analogously. Suppose that the circumcentre of the triangle $A_{1} B_{1} C_{1}$ lies on the circumcircle of the triangle $A B C$. Prove that the triangle $A B C$ is right-angled. (Russia)
|
Let $Q$ again denote the centre of the circumcircle of the triangle $A_{1} B_{1} C_{1}$, that lies on the circumcircle $\Omega$ of the triangle $A B C$. We first consider the case where $Q$ coincides with one of the vertices of $A B C$, say $Q=B$. Then $B C_{1}=B A_{1}$ and consequently the triangle $A B C$ is isosceles at $B$. Moreover we have $B C_{1}=B_{1} C$ in any triangle, and hence $B B_{1}=B C_{1}=B_{1} C$; similarly, $B B_{1}=B_{1} A$. It follows that $B_{1}$ is the centre of $\Omega$ and that the triangle $A B C$ has a right angle at $B$. So from now on we may suppose $Q \notin\{A, B, C\}$. We start with the following well known fact. Lemma. Let $X Y Z$ and $X^{\prime} Y^{\prime} Z^{\prime}$ be two triangles with $X Y=X^{\prime} Y^{\prime}$ and $Y Z=Y^{\prime} Z^{\prime}$. (i) If $X Z \neq X^{\prime} Z^{\prime}$ and $\angle Y Z X=\angle Y^{\prime} Z^{\prime} X^{\prime}$, then $\angle Z X Y+\angle Z^{\prime} X^{\prime} Y^{\prime}=180^{\circ}$. (ii) If $\angle Y Z X+\angle X^{\prime} Z^{\prime} Y^{\prime}=180^{\circ}$, then $\angle Z X Y=\angle Y^{\prime} X^{\prime} Z^{\prime}$. Proof. For both parts, we may move the triangle $X Y Z$ through the plane until $Y=Y^{\prime}$ and $Z=Z^{\prime}$. Possibly after reflecting one of the two triangles about $Y Z$, we may also suppose that $X$ and $X^{\prime}$ lie on the same side of $Y Z$ if we are in case (i) and on different sides if we are in case (ii). In both cases, the points $X, Z$, and $X^{\prime}$ are collinear due to the angle condition (see Fig. 2). Moreover we have $X \neq X^{\prime}$, because in case (i) we assumed $X Z \neq X^{\prime} Z^{\prime}$ and in case (ii) these points even lie on different sides of $Y Z$. Thus the triangle $X X^{\prime} Y$ is isosceles at $Y$. The claim now follows by considering the equal angles at its base.  Figure 2(i)  Figure 2(ii) Relabeling the vertices of the triangle $A B C$ if necessary we may suppose that $Q$ lies in the interior of the arc $A B$ of $\Omega$ not containing $C$. We will sometimes use tacitly that the six triangles $Q B A_{1}, Q A_{1} C, Q C B_{1}, Q B_{1} A, Q C_{1} A$, and $Q B C_{1}$ have the same orientation. As $Q$ cannot be the circumcentre of the triangle $A B C$, it is impossible that $Q A=Q B=Q C$ and thus we may also suppose that $Q C \neq Q B$. Now the above Lemma $(i)$ is applicable to the triangles $Q B_{1} C$ and $Q C_{1} B$, since $Q B_{1}=Q C_{1}$ and $B_{1} C=C_{1} B$, while $\angle B_{1} C Q=\angle C_{1} B Q$ holds as both angles appear over the same side of the chord $Q A$ in $\Omega$ (see Fig. 3). So we get $$ \angle C Q B_{1}+\angle B Q C_{1}=180^{\circ} . $$ We claim that $Q C=Q A$. To see this, let us assume for the sake of a contradiction that $Q C \neq Q A$. Then arguing similarly as before but now with the triangles $Q A_{1} C$ and $Q C_{1} A$ we get $$ \angle A_{1} Q C+\angle C_{1} Q A=180^{\circ} \text {. } $$ Adding this equation to (1), we get $\angle A_{1} Q B_{1}+\angle B Q A=360^{\circ}$, which is absurd as both summands lie in the interval $\left(0^{\circ}, 180^{\circ}\right)$. This proves $Q C=Q A$; so the triangles $Q A_{1} C$ and $Q C_{1} A$ are congruent their sides being equal, which in turn yields $$ \angle A_{1} Q C=\angle C_{1} Q A \text {. } $$ Finally our Lemma (ii) is applicable to the triangles $Q A_{1} B$ and $Q B_{1} A$. Indeed we have $Q A_{1}=Q B_{1}$ and $A_{1} B=B_{1} A$ as usual, and the angle condition $\angle A_{1} B Q+\angle Q A B_{1}=180^{\circ}$ holds as $A$ and $B$ lie on different sides of the chord $Q C$ in $\Omega$. Consequently we have $$ \angle B Q A_{1}=\angle B_{1} Q A \text {. } $$ From (1) and (3) we get $$ \left(\angle B_{1} Q C+\angle B_{1} Q A\right)+\left(\angle C_{1} Q B-\angle B Q A_{1}\right)=180^{\circ} \text {, } $$ i.e. $\angle C Q A+\angle A_{1} Q C_{1}=180^{\circ}$. In light of (2) this may be rewritten as $2 \angle C Q A=180^{\circ}$ and as $Q$ lies on $\Omega$ this implies that the triangle $A B C$ has a right angle at $B$.  Figure 3 Comment 1. One may also check that $Q$ is in the interior of $\Omega$ if and only if the triangle $A B C$ is acute-angled. Comment 2. The original proposal asked to prove the converse statement as well: if the triangle $A B C$ is right-angled, then the point $Q$ lies on its circumcircle. The Problem Selection Committee thinks that the above simplified version is more suitable for the competition.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
978a7792-e68c-5860-9e5e-1836d7a742d7
| 24,311
|
Prove that for any pair of positive integers $k$ and $n$ there exist $k$ positive integers $m_{1}, m_{2}, \ldots, m_{k}$ such that $$ 1+\frac{2^{k}-1}{n}=\left(1+\frac{1}{m_{1}}\right)\left(1+\frac{1}{m_{2}}\right) \cdots\left(1+\frac{1}{m_{k}}\right) . $$ (Japan)
|
We proceed by induction on $k$. For $k=1$ the statement is trivial. Assuming we have proved it for $k=j-1$, we now prove it for $k=j$. Case 1. $n=2 t-1$ for some positive integer $t$. Observe that $$ 1+\frac{2^{j}-1}{2 t-1}=\frac{2\left(t+2^{j-1}-1\right)}{2 t} \cdot \frac{2 t}{2 t-1}=\left(1+\frac{2^{j-1}-1}{t}\right)\left(1+\frac{1}{2 t-1}\right) . $$ By the induction hypothesis we can find $m_{1}, \ldots, m_{j-1}$ such that $$ 1+\frac{2^{j-1}-1}{t}=\left(1+\frac{1}{m_{1}}\right)\left(1+\frac{1}{m_{2}}\right) \cdots\left(1+\frac{1}{m_{j-1}}\right) $$ so setting $m_{j}=2 t-1$ gives the desired expression. Case 2. $n=2 t$ for some positive integer $t$. Now we have $$ 1+\frac{2^{j}-1}{2 t}=\frac{2 t+2^{j}-1}{2 t+2^{j}-2} \cdot \frac{2 t+2^{j}-2}{2 t}=\left(1+\frac{1}{2 t+2^{j}-2}\right)\left(1+\frac{2^{j-1}-1}{t}\right) $$ noting that $2 t+2^{j}-2>0$. Again, we use that $$ 1+\frac{2^{j-1}-1}{t}=\left(1+\frac{1}{m_{1}}\right)\left(1+\frac{1}{m_{2}}\right) \cdots\left(1+\frac{1}{m_{j-1}}\right) . $$ Setting $m_{j}=2 t+2^{j}-2$ then gives the desired expression.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that for any pair of positive integers $k$ and $n$ there exist $k$ positive integers $m_{1}, m_{2}, \ldots, m_{k}$ such that $$ 1+\frac{2^{k}-1}{n}=\left(1+\frac{1}{m_{1}}\right)\left(1+\frac{1}{m_{2}}\right) \cdots\left(1+\frac{1}{m_{k}}\right) . $$ (Japan)
|
We proceed by induction on $k$. For $k=1$ the statement is trivial. Assuming we have proved it for $k=j-1$, we now prove it for $k=j$. Case 1. $n=2 t-1$ for some positive integer $t$. Observe that $$ 1+\frac{2^{j}-1}{2 t-1}=\frac{2\left(t+2^{j-1}-1\right)}{2 t} \cdot \frac{2 t}{2 t-1}=\left(1+\frac{2^{j-1}-1}{t}\right)\left(1+\frac{1}{2 t-1}\right) . $$ By the induction hypothesis we can find $m_{1}, \ldots, m_{j-1}$ such that $$ 1+\frac{2^{j-1}-1}{t}=\left(1+\frac{1}{m_{1}}\right)\left(1+\frac{1}{m_{2}}\right) \cdots\left(1+\frac{1}{m_{j-1}}\right) $$ so setting $m_{j}=2 t-1$ gives the desired expression. Case 2. $n=2 t$ for some positive integer $t$. Now we have $$ 1+\frac{2^{j}-1}{2 t}=\frac{2 t+2^{j}-1}{2 t+2^{j}-2} \cdot \frac{2 t+2^{j}-2}{2 t}=\left(1+\frac{1}{2 t+2^{j}-2}\right)\left(1+\frac{2^{j-1}-1}{t}\right) $$ noting that $2 t+2^{j}-2>0$. Again, we use that $$ 1+\frac{2^{j-1}-1}{t}=\left(1+\frac{1}{m_{1}}\right)\left(1+\frac{1}{m_{2}}\right) \cdots\left(1+\frac{1}{m_{j-1}}\right) . $$ Setting $m_{j}=2 t+2^{j}-2$ then gives the desired expression.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
2a70e3f6-e55f-5422-88d5-ae4955f3bb55
| 24,321
|
Prove that for any pair of positive integers $k$ and $n$ there exist $k$ positive integers $m_{1}, m_{2}, \ldots, m_{k}$ such that $$ 1+\frac{2^{k}-1}{n}=\left(1+\frac{1}{m_{1}}\right)\left(1+\frac{1}{m_{2}}\right) \cdots\left(1+\frac{1}{m_{k}}\right) . $$ (Japan)
|
Consider the base 2 expansions of the residues of $n-1$ and $-n$ modulo $2^{k}$ : $$ \begin{aligned} n-1 & \equiv 2^{a_{1}}+2^{a_{2}}+\cdots+2^{a_{r}}\left(\bmod 2^{k}\right) & & \text { where } 0 \leqslant a_{1}<a_{2}<\ldots<a_{r} \leqslant k-1 \\ -n & \equiv 2^{b_{1}}+2^{b_{2}}+\cdots+2^{b_{s}}\left(\bmod 2^{k}\right) & & \text { where } 0 \leqslant b_{1}<b_{2}<\ldots<b_{s} \leqslant k-1 . \end{aligned} $$ Since $-1 \equiv 2^{0}+2^{1}+\cdots+2^{k-1}\left(\bmod 2^{k}\right)$, we have $\left\{a_{1}, \ldots, a_{r}\right\} \cup\left\{b_{1} \ldots, b_{s}\right\}=\{0,1, \ldots, k-1\}$ and $r+s=k$. Write $$ \begin{aligned} & S_{p}=2^{a_{p}}+2^{a_{p+1}}+\cdots+2^{a_{r}} \quad \text { for } 1 \leqslant p \leqslant r, \\ & T_{q}=2^{b_{1}}+2^{b_{2}}+\cdots+2^{b_{q}} \quad \text { for } 1 \leqslant q \leqslant s . \end{aligned} $$ Also set $S_{r+1}=T_{0}=0$. Notice that $S_{1}+T_{s}=2^{k}-1$ and $n+T_{s} \equiv 0\left(\bmod 2^{k}\right)$. We have $$ \begin{aligned} 1+\frac{2^{k}-1}{n} & =\frac{n+S_{1}+T_{s}}{n}=\frac{n+S_{1}+T_{s}}{n+T_{s}} \cdot \frac{n+T_{s}}{n} \\ & =\prod_{p=1}^{r} \frac{n+S_{p}+T_{s}}{n+S_{p+1}+T_{s}} \cdot \prod_{q=1}^{s} \frac{n+T_{q}}{n+T_{q-1}} \\ & =\prod_{p=1}^{r}\left(1+\frac{2^{a_{p}}}{n+S_{p+1}+T_{s}}\right) \cdot \prod_{q=1}^{s}\left(1+\frac{2^{b_{q}}}{n+T_{q-1}}\right), \end{aligned} $$ so if we define $$ m_{p}=\frac{n+S_{p+1}+T_{s}}{2^{a_{p}}} \quad \text { for } 1 \leqslant p \leqslant r \quad \text { and } \quad m_{r+q}=\frac{n+T_{q-1}}{2^{b_{q}}} \quad \text { for } 1 \leqslant q \leqslant s $$ the desired equality holds. It remains to check that every $m_{i}$ is an integer. For $1 \leqslant p \leqslant r$ we have $$ n+S_{p+1}+T_{s} \equiv n+T_{s} \equiv 0 \quad\left(\bmod 2^{a_{p}}\right) $$ and for $1 \leqslant q \leqslant r$ we have $$ n+T_{q-1} \equiv n+T_{s} \equiv 0 \quad\left(\bmod 2^{b_{q}}\right) . $$ The desired result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that for any pair of positive integers $k$ and $n$ there exist $k$ positive integers $m_{1}, m_{2}, \ldots, m_{k}$ such that $$ 1+\frac{2^{k}-1}{n}=\left(1+\frac{1}{m_{1}}\right)\left(1+\frac{1}{m_{2}}\right) \cdots\left(1+\frac{1}{m_{k}}\right) . $$ (Japan)
|
Consider the base 2 expansions of the residues of $n-1$ and $-n$ modulo $2^{k}$ : $$ \begin{aligned} n-1 & \equiv 2^{a_{1}}+2^{a_{2}}+\cdots+2^{a_{r}}\left(\bmod 2^{k}\right) & & \text { where } 0 \leqslant a_{1}<a_{2}<\ldots<a_{r} \leqslant k-1 \\ -n & \equiv 2^{b_{1}}+2^{b_{2}}+\cdots+2^{b_{s}}\left(\bmod 2^{k}\right) & & \text { where } 0 \leqslant b_{1}<b_{2}<\ldots<b_{s} \leqslant k-1 . \end{aligned} $$ Since $-1 \equiv 2^{0}+2^{1}+\cdots+2^{k-1}\left(\bmod 2^{k}\right)$, we have $\left\{a_{1}, \ldots, a_{r}\right\} \cup\left\{b_{1} \ldots, b_{s}\right\}=\{0,1, \ldots, k-1\}$ and $r+s=k$. Write $$ \begin{aligned} & S_{p}=2^{a_{p}}+2^{a_{p+1}}+\cdots+2^{a_{r}} \quad \text { for } 1 \leqslant p \leqslant r, \\ & T_{q}=2^{b_{1}}+2^{b_{2}}+\cdots+2^{b_{q}} \quad \text { for } 1 \leqslant q \leqslant s . \end{aligned} $$ Also set $S_{r+1}=T_{0}=0$. Notice that $S_{1}+T_{s}=2^{k}-1$ and $n+T_{s} \equiv 0\left(\bmod 2^{k}\right)$. We have $$ \begin{aligned} 1+\frac{2^{k}-1}{n} & =\frac{n+S_{1}+T_{s}}{n}=\frac{n+S_{1}+T_{s}}{n+T_{s}} \cdot \frac{n+T_{s}}{n} \\ & =\prod_{p=1}^{r} \frac{n+S_{p}+T_{s}}{n+S_{p+1}+T_{s}} \cdot \prod_{q=1}^{s} \frac{n+T_{q}}{n+T_{q-1}} \\ & =\prod_{p=1}^{r}\left(1+\frac{2^{a_{p}}}{n+S_{p+1}+T_{s}}\right) \cdot \prod_{q=1}^{s}\left(1+\frac{2^{b_{q}}}{n+T_{q-1}}\right), \end{aligned} $$ so if we define $$ m_{p}=\frac{n+S_{p+1}+T_{s}}{2^{a_{p}}} \quad \text { for } 1 \leqslant p \leqslant r \quad \text { and } \quad m_{r+q}=\frac{n+T_{q-1}}{2^{b_{q}}} \quad \text { for } 1 \leqslant q \leqslant s $$ the desired equality holds. It remains to check that every $m_{i}$ is an integer. For $1 \leqslant p \leqslant r$ we have $$ n+S_{p+1}+T_{s} \equiv n+T_{s} \equiv 0 \quad\left(\bmod 2^{a_{p}}\right) $$ and for $1 \leqslant q \leqslant r$ we have $$ n+T_{q-1} \equiv n+T_{s} \equiv 0 \quad\left(\bmod 2^{b_{q}}\right) . $$ The desired result follows.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
2a70e3f6-e55f-5422-88d5-ae4955f3bb55
| 24,321
|
Prove that there exist infinitely many positive integers $n$ such that the largest prime divisor of $n^{4}+n^{2}+1$ is equal to the largest prime divisor of $(n+1)^{4}+(n+1)^{2}+1$. (Belgium)
|
Let $p_{n}$ be the largest prime divisor of $n^{4}+n^{2}+1$ and let $q_{n}$ be the largest prime divisor of $n^{2}+n+1$. Then $p_{n}=q_{n^{2}}$, and from $$ n^{4}+n^{2}+1=\left(n^{2}+1\right)^{2}-n^{2}=\left(n^{2}-n+1\right)\left(n^{2}+n+1\right)=\left((n-1)^{2}+(n-1)+1\right)\left(n^{2}+n+1\right) $$ it follows that $p_{n}=\max \left\{q_{n}, q_{n-1}\right\}$ for $n \geqslant 2$. Keeping in mind that $n^{2}-n+1$ is odd, we have $$ \operatorname{gcd}\left(n^{2}+n+1, n^{2}-n+1\right)=\operatorname{gcd}\left(2 n, n^{2}-n+1\right)=\operatorname{gcd}\left(n, n^{2}-n+1\right)=1 . $$ Therefore $q_{n} \neq q_{n-1}$. To prove the result, it suffices to show that the set $$ S=\left\{n \in \mathbb{Z}_{\geqslant 2} \mid q_{n}>q_{n-1} \text { and } q_{n}>q_{n+1}\right\} $$ is infinite, since for each $n \in S$ one has $$ p_{n}=\max \left\{q_{n}, q_{n-1}\right\}=q_{n}=\max \left\{q_{n}, q_{n+1}\right\}=p_{n+1} . $$ Suppose on the contrary that $S$ is finite. Since $q_{2}=7<13=q_{3}$ and $q_{3}=13>7=q_{4}$, the set $S$ is non-empty. Since it is finite, we can consider its largest element, say $m$. Note that it is impossible that $q_{m}>q_{m+1}>q_{m+2}>\ldots$ because all these numbers are positive integers, so there exists a $k \geqslant m$ such that $q_{k}<q_{k+1}$ (recall that $q_{k} \neq q_{k+1}$ ). Next observe that it is impossible to have $q_{k}<q_{k+1}<q_{k+2}<\ldots$, because $q_{(k+1)^{2}}=p_{k+1}=\max \left\{q_{k}, q_{k+1}\right\}=q_{k+1}$, so let us take the smallest $\ell \geqslant k+1$ such that $q_{\ell}>q_{\ell+1}$. By the minimality of $\ell$ we have $q_{\ell-1}<q_{\ell}$, so $\ell \in S$. Since $\ell \geqslant k+1>k \geqslant m$, this contradicts the maximality of $m$, and hence $S$ is indeed infinite. Comment. Once the factorization of $n^{4}+n^{2}+1$ is found and the set $S$ is introduced, the problem is mainly about ruling out the case that $$ q_{k}<q_{k+1}<q_{k+2}<\ldots $$ might hold for some $k \in \mathbb{Z}_{>0}$. In the above solution, this is done by observing $q_{(k+1)^{2}}=\max \left(q_{k}, q_{k+1}\right)$. Alternatively one may notice that (1) implies that $q_{j+2}-q_{j} \geqslant 6$ for $j \geqslant k+1$, since every prime greater than 3 is congruent to -1 or 1 modulo 6 . Then there is some integer $C \geqslant 0$ such that $q_{n} \geqslant 3 n-C$ for all $n \geqslant k$. Now let the integer $t$ be sufficiently large (e.g. $t=\max \{k+1, C+3\}$ ) and set $p=q_{t-1} \geqslant 2 t$. Then $p \mid(t-1)^{2}+(t-1)+1$ implies that $p \mid(p-t)^{2}+(p-t)+1$, so $p$ and $q_{p-t}$ are prime divisors of $(p-t)^{2}+(p-t)+1$. But $p-t>t-1 \geqslant k$, so $q_{p-t}>q_{t-1}=p$ and $p \cdot q_{p-t}>p^{2}>(p-t)^{2}+(p-t)+1$, a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that there exist infinitely many positive integers $n$ such that the largest prime divisor of $n^{4}+n^{2}+1$ is equal to the largest prime divisor of $(n+1)^{4}+(n+1)^{2}+1$. (Belgium)
|
Let $p_{n}$ be the largest prime divisor of $n^{4}+n^{2}+1$ and let $q_{n}$ be the largest prime divisor of $n^{2}+n+1$. Then $p_{n}=q_{n^{2}}$, and from $$ n^{4}+n^{2}+1=\left(n^{2}+1\right)^{2}-n^{2}=\left(n^{2}-n+1\right)\left(n^{2}+n+1\right)=\left((n-1)^{2}+(n-1)+1\right)\left(n^{2}+n+1\right) $$ it follows that $p_{n}=\max \left\{q_{n}, q_{n-1}\right\}$ for $n \geqslant 2$. Keeping in mind that $n^{2}-n+1$ is odd, we have $$ \operatorname{gcd}\left(n^{2}+n+1, n^{2}-n+1\right)=\operatorname{gcd}\left(2 n, n^{2}-n+1\right)=\operatorname{gcd}\left(n, n^{2}-n+1\right)=1 . $$ Therefore $q_{n} \neq q_{n-1}$. To prove the result, it suffices to show that the set $$ S=\left\{n \in \mathbb{Z}_{\geqslant 2} \mid q_{n}>q_{n-1} \text { and } q_{n}>q_{n+1}\right\} $$ is infinite, since for each $n \in S$ one has $$ p_{n}=\max \left\{q_{n}, q_{n-1}\right\}=q_{n}=\max \left\{q_{n}, q_{n+1}\right\}=p_{n+1} . $$ Suppose on the contrary that $S$ is finite. Since $q_{2}=7<13=q_{3}$ and $q_{3}=13>7=q_{4}$, the set $S$ is non-empty. Since it is finite, we can consider its largest element, say $m$. Note that it is impossible that $q_{m}>q_{m+1}>q_{m+2}>\ldots$ because all these numbers are positive integers, so there exists a $k \geqslant m$ such that $q_{k}<q_{k+1}$ (recall that $q_{k} \neq q_{k+1}$ ). Next observe that it is impossible to have $q_{k}<q_{k+1}<q_{k+2}<\ldots$, because $q_{(k+1)^{2}}=p_{k+1}=\max \left\{q_{k}, q_{k+1}\right\}=q_{k+1}$, so let us take the smallest $\ell \geqslant k+1$ such that $q_{\ell}>q_{\ell+1}$. By the minimality of $\ell$ we have $q_{\ell-1}<q_{\ell}$, so $\ell \in S$. Since $\ell \geqslant k+1>k \geqslant m$, this contradicts the maximality of $m$, and hence $S$ is indeed infinite. Comment. Once the factorization of $n^{4}+n^{2}+1$ is found and the set $S$ is introduced, the problem is mainly about ruling out the case that $$ q_{k}<q_{k+1}<q_{k+2}<\ldots $$ might hold for some $k \in \mathbb{Z}_{>0}$. In the above solution, this is done by observing $q_{(k+1)^{2}}=\max \left(q_{k}, q_{k+1}\right)$. Alternatively one may notice that (1) implies that $q_{j+2}-q_{j} \geqslant 6$ for $j \geqslant k+1$, since every prime greater than 3 is congruent to -1 or 1 modulo 6 . Then there is some integer $C \geqslant 0$ such that $q_{n} \geqslant 3 n-C$ for all $n \geqslant k$. Now let the integer $t$ be sufficiently large (e.g. $t=\max \{k+1, C+3\}$ ) and set $p=q_{t-1} \geqslant 2 t$. Then $p \mid(t-1)^{2}+(t-1)+1$ implies that $p \mid(p-t)^{2}+(p-t)+1$, so $p$ and $q_{p-t}$ are prime divisors of $(p-t)^{2}+(p-t)+1$. But $p-t>t-1 \geqslant k$, so $q_{p-t}>q_{t-1}=p$ and $p \cdot q_{p-t}>p^{2}>(p-t)^{2}+(p-t)+1$, a contradiction.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
24ea2c7c-a9be-5b50-8fb0-c1ed96ebe988
| 24,324
|
Determine whether there exists an infinite sequence of nonzero digits $a_{1}, a_{2}, a_{3}, \ldots$ and a positive integer $N$ such that for every integer $k>N$, the number $\overline{a_{k} a_{k-1} \ldots a_{1}}$ is a perfect square. (Iran)
|
Assume that $a_{1}, a_{2}, a_{3}, \ldots$ is such a sequence. For each positive integer $k$, let $y_{k}=$ $\overline{a_{k} a_{k-1} \ldots a_{1}}$. By the assumption, for each $k>N$ there exists a positive integer $x_{k}$ such that $y_{k}=x_{k}^{2}$. I. For every $n$, let $5^{\gamma_{n}}$ be the greatest power of 5 dividing $x_{n}$. Let us show first that $2 \gamma_{n} \geqslant n$ for every positive integer $n>N$. Assume, to the contrary, that there exists a positive integer $n>N$ such that $2 \gamma_{n}<n$, which yields $$ y_{n+1}=\overline{a_{n+1} a_{n} \ldots a_{1}}=10^{n} a_{n+1}+\overline{a_{n} a_{n-1} \ldots a_{1}}=10^{n} a_{n+1}+y_{n}=5^{2 \gamma_{n}}\left(2^{n} 5^{n-2 \gamma_{n}} a_{n+1}+\frac{y_{n}}{5^{2 \gamma_{n}}}\right) . $$ Since $5 \nmid y_{n} / 5^{2 \gamma_{n}}$, we obtain $\gamma_{n+1}=\gamma_{n}<n<n+1$. By the same arguments we obtain that $\gamma_{n}=\gamma_{n+1}=\gamma_{n+2}=\ldots$. Denote this common value by $\gamma$. Now, for each $k \geqslant n$ we have $$ \left(x_{k+1}-x_{k}\right)\left(x_{k+1}+x_{k}\right)=x_{k+1}^{2}-x_{k}^{2}=y_{k+1}-y_{k}=a_{k+1} \cdot 10^{k} . $$ One of the numbers $x_{k+1}-x_{k}$ and $x_{k+1}+x_{k}$ is not divisible by $5^{\gamma+1}$ since otherwise one would have $5^{\gamma+1} \mid\left(\left(x_{k+1}-x_{k}\right)+\left(x_{k+1}+x_{k}\right)\right)=2 x_{k+1}$. On the other hand, we have $5^{k} \mid\left(x_{k+1}-x_{k}\right)\left(x_{k+1}+x_{k}\right)$, so $5^{k-\gamma}$ divides one of these two factors. Thus we get $$ 5^{k-\gamma} \leqslant \max \left\{x_{k+1}-x_{k}, x_{k+1}+x_{k}\right\}<2 x_{k+1}=2 \sqrt{y_{k+1}}<2 \cdot 10^{(k+1) / 2} $$ which implies $5^{2 k}<4 \cdot 5^{2 \gamma} \cdot 10^{k+1}$, or $(5 / 2)^{k}<40 \cdot 5^{2 \gamma}$. The last inequality is clearly false for sufficiently large values of $k$. This contradiction shows that $2 \gamma_{n} \geqslant n$ for all $n>N$. II. Consider now any integer $k>\max \{N / 2,2\}$. Since $2 \gamma_{2 k+1} \geqslant 2 k+1$ and $2 \gamma_{2 k+2} \geqslant 2 k+2$, we have $\gamma_{2 k+1} \geqslant k+1$ and $\gamma_{2 k+2} \geqslant k+1$. So, from $y_{2 k+2}=a_{2 k+2} \cdot 10^{2 k+1}+y_{2 k+1}$ we obtain $5^{2 k+2} \mid y_{2 k+2}-y_{2 k+1}=a_{2 k+2} \cdot 10^{2 k+1}$ and thus $5 \mid a_{2 k+2}$, which implies $a_{2 k+2}=5$. Therefore, $$ \left(x_{2 k+2}-x_{2 k+1}\right)\left(x_{2 k+2}+x_{2 k+1}\right)=x_{2 k+2}^{2}-x_{2 k+1}^{2}=y_{2 k+2}-y_{2 k+1}=5 \cdot 10^{2 k+1}=2^{2 k+1} \cdot 5^{2 k+2} . $$ Setting $A_{k}=x_{2 k+2} / 5^{k+1}$ and $B_{k}=x_{2 k+1} / 5^{k+1}$, which are integers, we obtain $$ \left(A_{k}-B_{k}\right)\left(A_{k}+B_{k}\right)=2^{2 k+1} . $$ Both $A_{k}$ and $B_{k}$ are odd, since otherwise $y_{2 k+2}$ or $y_{2 k+1}$ would be a multiple of 10 which is false by $a_{1} \neq 0$; so one of the numbers $A_{k}-B_{k}$ and $A_{k}+B_{k}$ is not divisible by 4 . Therefore (1) yields $A_{k}-B_{k}=2$ and $A_{k}+B_{k}=2^{2 k}$, hence $A_{k}=2^{2 k-1}+1$ and thus $$ x_{2 k+2}=5^{k+1} A_{k}=10^{k+1} \cdot 2^{k-2}+5^{k+1}>10^{k+1}, $$ since $k \geqslant 2$. This implies that $y_{2 k+2}>10^{2 k+2}$ which contradicts the fact that $y_{2 k+2}$ contains $2 k+2$ digits. The desired result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Determine whether there exists an infinite sequence of nonzero digits $a_{1}, a_{2}, a_{3}, \ldots$ and a positive integer $N$ such that for every integer $k>N$, the number $\overline{a_{k} a_{k-1} \ldots a_{1}}$ is a perfect square. (Iran)
|
Assume that $a_{1}, a_{2}, a_{3}, \ldots$ is such a sequence. For each positive integer $k$, let $y_{k}=$ $\overline{a_{k} a_{k-1} \ldots a_{1}}$. By the assumption, for each $k>N$ there exists a positive integer $x_{k}$ such that $y_{k}=x_{k}^{2}$. I. For every $n$, let $5^{\gamma_{n}}$ be the greatest power of 5 dividing $x_{n}$. Let us show first that $2 \gamma_{n} \geqslant n$ for every positive integer $n>N$. Assume, to the contrary, that there exists a positive integer $n>N$ such that $2 \gamma_{n}<n$, which yields $$ y_{n+1}=\overline{a_{n+1} a_{n} \ldots a_{1}}=10^{n} a_{n+1}+\overline{a_{n} a_{n-1} \ldots a_{1}}=10^{n} a_{n+1}+y_{n}=5^{2 \gamma_{n}}\left(2^{n} 5^{n-2 \gamma_{n}} a_{n+1}+\frac{y_{n}}{5^{2 \gamma_{n}}}\right) . $$ Since $5 \nmid y_{n} / 5^{2 \gamma_{n}}$, we obtain $\gamma_{n+1}=\gamma_{n}<n<n+1$. By the same arguments we obtain that $\gamma_{n}=\gamma_{n+1}=\gamma_{n+2}=\ldots$. Denote this common value by $\gamma$. Now, for each $k \geqslant n$ we have $$ \left(x_{k+1}-x_{k}\right)\left(x_{k+1}+x_{k}\right)=x_{k+1}^{2}-x_{k}^{2}=y_{k+1}-y_{k}=a_{k+1} \cdot 10^{k} . $$ One of the numbers $x_{k+1}-x_{k}$ and $x_{k+1}+x_{k}$ is not divisible by $5^{\gamma+1}$ since otherwise one would have $5^{\gamma+1} \mid\left(\left(x_{k+1}-x_{k}\right)+\left(x_{k+1}+x_{k}\right)\right)=2 x_{k+1}$. On the other hand, we have $5^{k} \mid\left(x_{k+1}-x_{k}\right)\left(x_{k+1}+x_{k}\right)$, so $5^{k-\gamma}$ divides one of these two factors. Thus we get $$ 5^{k-\gamma} \leqslant \max \left\{x_{k+1}-x_{k}, x_{k+1}+x_{k}\right\}<2 x_{k+1}=2 \sqrt{y_{k+1}}<2 \cdot 10^{(k+1) / 2} $$ which implies $5^{2 k}<4 \cdot 5^{2 \gamma} \cdot 10^{k+1}$, or $(5 / 2)^{k}<40 \cdot 5^{2 \gamma}$. The last inequality is clearly false for sufficiently large values of $k$. This contradiction shows that $2 \gamma_{n} \geqslant n$ for all $n>N$. II. Consider now any integer $k>\max \{N / 2,2\}$. Since $2 \gamma_{2 k+1} \geqslant 2 k+1$ and $2 \gamma_{2 k+2} \geqslant 2 k+2$, we have $\gamma_{2 k+1} \geqslant k+1$ and $\gamma_{2 k+2} \geqslant k+1$. So, from $y_{2 k+2}=a_{2 k+2} \cdot 10^{2 k+1}+y_{2 k+1}$ we obtain $5^{2 k+2} \mid y_{2 k+2}-y_{2 k+1}=a_{2 k+2} \cdot 10^{2 k+1}$ and thus $5 \mid a_{2 k+2}$, which implies $a_{2 k+2}=5$. Therefore, $$ \left(x_{2 k+2}-x_{2 k+1}\right)\left(x_{2 k+2}+x_{2 k+1}\right)=x_{2 k+2}^{2}-x_{2 k+1}^{2}=y_{2 k+2}-y_{2 k+1}=5 \cdot 10^{2 k+1}=2^{2 k+1} \cdot 5^{2 k+2} . $$ Setting $A_{k}=x_{2 k+2} / 5^{k+1}$ and $B_{k}=x_{2 k+1} / 5^{k+1}$, which are integers, we obtain $$ \left(A_{k}-B_{k}\right)\left(A_{k}+B_{k}\right)=2^{2 k+1} . $$ Both $A_{k}$ and $B_{k}$ are odd, since otherwise $y_{2 k+2}$ or $y_{2 k+1}$ would be a multiple of 10 which is false by $a_{1} \neq 0$; so one of the numbers $A_{k}-B_{k}$ and $A_{k}+B_{k}$ is not divisible by 4 . Therefore (1) yields $A_{k}-B_{k}=2$ and $A_{k}+B_{k}=2^{2 k}$, hence $A_{k}=2^{2 k-1}+1$ and thus $$ x_{2 k+2}=5^{k+1} A_{k}=10^{k+1} \cdot 2^{k-2}+5^{k+1}>10^{k+1}, $$ since $k \geqslant 2$. This implies that $y_{2 k+2}>10^{2 k+2}$ which contradicts the fact that $y_{2 k+2}$ contains $2 k+2$ digits. The desired result follows.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
f3c46ef2-501f-5236-9e6e-5eb8155b9c53
| 24,327
|
Determine whether there exists an infinite sequence of nonzero digits $a_{1}, a_{2}, a_{3}, \ldots$ and a positive integer $N$ such that for every integer $k>N$, the number $\overline{a_{k} a_{k-1} \ldots a_{1}}$ is a perfect square. (Iran)
|
Again, we assume that a sequence $a_{1}, a_{2}, a_{3}, \ldots$ satisfies the problem conditions, introduce the numbers $x_{k}$ and $y_{k}$ as in the previous solution, and notice that $$ y_{k+1}-y_{k}=\left(x_{k+1}-x_{k}\right)\left(x_{k+1}+x_{k}\right)=10^{k} a_{k+1} $$ for all $k>N$. Consider any such $k$. Since $a_{1} \neq 0$, the numbers $x_{k}$ and $x_{k+1}$ are not multiples of 10 , and therefore the numbers $p_{k}=x_{k+1}-x_{k}$ and $q_{k}=x_{k+1}+x_{k}$ cannot be simultaneously multiples of 20 , and hence one of them is not divisible either by 4 or by 5 . In view of (2), this means that the other one is divisible by either $5^{k}$ or by $2^{k-1}$. Notice also that $p_{k}$ and $q_{k}$ have the same parity, so both are even. On the other hand, we have $x_{k+1}^{2}=x_{k}^{2}+10^{k} a_{k+1} \geqslant x_{k}^{2}+10^{k}>2 x_{k}^{2}$, so $x_{k+1} / x_{k}>\sqrt{2}$, which implies that $$ 1<\frac{q_{k}}{p_{k}}=1+\frac{2}{x_{k+1} / x_{k}-1}<1+\frac{2}{\sqrt{2}-1}<6 . $$ Thus, if one of the numbers $p_{k}$ and $q_{k}$ is divisible by $5^{k}$, then we have $$ 10^{k+1}>10^{k} a_{k+1}=p_{k} q_{k} \geqslant \frac{\left(5^{k}\right)^{2}}{6} $$ and hence $(5 / 2)^{k}<60$ which is false for sufficiently large $k$. So, assuming that $k$ is large, we get that $2^{k-1}$ divides one of the numbers $p_{k}$ and $q_{k}$. Hence $$ \left\{p_{k}, q_{k}\right\}=\left\{2^{k-1} \cdot 5^{r_{k}} b_{k}, 2 \cdot 5^{k-r_{k}} c_{k}\right\} \quad \text { with nonnegative integers } b_{k}, c_{k}, r_{k} \text { such that } b_{k} c_{k}=a_{k+1} \text {. } $$ Moreover, from (3) we get $$ 6>\frac{2^{k-1} \cdot 5^{r_{k}} b_{k}}{2 \cdot 5^{k-r_{k}} c_{k}} \geqslant \frac{1}{36} \cdot\left(\frac{2}{5}\right)^{k} \cdot 5^{2 r_{k}} \quad \text { and } \quad 6>\frac{2 \cdot 5^{k-r_{k}} c_{k}}{2^{k-1} \cdot 5^{r_{k}} b_{k}} \geqslant \frac{4}{9} \cdot\left(\frac{5}{2}\right)^{k} \cdot 5^{-2 r_{k}} $$ SO $$ \alpha k+c_{1}<r_{k}<\alpha k+c_{2} \quad \text { for } \alpha=\frac{1}{2} \log _{5}\left(\frac{5}{2}\right)<1 \text { and some constants } c_{2}>c_{1} \text {. } $$ Consequently, for $C=c_{2}-c_{1}+1-\alpha>0$ we have $$ (k+1)-r_{k+1} \leqslant k-r_{k}+C . $$ Next, we will use the following easy lemma. Lemma. Let $s$ be a positive integer. Then $5^{s+2^{s}} \equiv 5^{s}\left(\bmod 10^{s}\right)$. Proof. Euler's theorem gives $5^{2^{s}} \equiv 1\left(\bmod 2^{s}\right)$, so $5^{s+2^{s}}-5^{s}=5^{s}\left(5^{2^{s}}-1\right)$ is divisible by $2^{s}$ and $5^{s}$. Now, for every large $k$ we have $$ x_{k+1}=\frac{p_{k}+q_{k}}{2}=5^{r_{k}} \cdot 2^{k-2} b_{k}+5^{k-r_{k}} c_{k} \equiv 5^{k-r_{k}} c_{k} \quad\left(\bmod 10^{r_{k}}\right) $$ since $r_{k} \leqslant k-2$ by $(4)$; hence $y_{k+1} \equiv 5^{2\left(k-r_{k}\right)} c_{k}^{2}\left(\bmod 10^{r_{k}}\right)$. Let us consider some large integer $s$, and choose the minimal $k$ such that $2\left(k-r_{k}\right) \geqslant s+2^{s}$; it exists by (4). Set $d=2\left(k-r_{k}\right)-\left(s+2^{s}\right)$. By (4) we have $2^{s}<2\left(k-r_{k}\right)<\left(\frac{2}{\alpha}-2\right) r_{k}-\frac{2 c_{1}}{\alpha}$; if $s$ is large this implies $r_{k}>s$, so (6) also holds modulo $10^{s}$. Then (6) and the lemma give $$ y_{k+1} \equiv 5^{2\left(k-r_{k}\right)} c_{k}^{2}=5^{s+2^{s}} \cdot 5^{d} c_{k}^{2} \equiv 5^{s} \cdot 5^{d} c_{k}^{2} \quad\left(\bmod 10^{s}\right) . $$ By (5) and the minimality of $k$ we have $d \leqslant 2 C$, so $5^{d} c_{k}^{2} \leqslant 5^{2 C} \cdot 81=D$. Using $5^{4}<10^{3}$ we obtain $$ 5^{s} \cdot 5^{d} c_{k}^{2}<10^{3 s / 4} D<10^{s-1} $$ for sufficiently large $s$. This, together with (7), shows that the sth digit from the right in $y_{k+1}$, which is $a_{s}$, is zero. This contradicts the problem condition.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Determine whether there exists an infinite sequence of nonzero digits $a_{1}, a_{2}, a_{3}, \ldots$ and a positive integer $N$ such that for every integer $k>N$, the number $\overline{a_{k} a_{k-1} \ldots a_{1}}$ is a perfect square. (Iran)
|
Again, we assume that a sequence $a_{1}, a_{2}, a_{3}, \ldots$ satisfies the problem conditions, introduce the numbers $x_{k}$ and $y_{k}$ as in the previous solution, and notice that $$ y_{k+1}-y_{k}=\left(x_{k+1}-x_{k}\right)\left(x_{k+1}+x_{k}\right)=10^{k} a_{k+1} $$ for all $k>N$. Consider any such $k$. Since $a_{1} \neq 0$, the numbers $x_{k}$ and $x_{k+1}$ are not multiples of 10 , and therefore the numbers $p_{k}=x_{k+1}-x_{k}$ and $q_{k}=x_{k+1}+x_{k}$ cannot be simultaneously multiples of 20 , and hence one of them is not divisible either by 4 or by 5 . In view of (2), this means that the other one is divisible by either $5^{k}$ or by $2^{k-1}$. Notice also that $p_{k}$ and $q_{k}$ have the same parity, so both are even. On the other hand, we have $x_{k+1}^{2}=x_{k}^{2}+10^{k} a_{k+1} \geqslant x_{k}^{2}+10^{k}>2 x_{k}^{2}$, so $x_{k+1} / x_{k}>\sqrt{2}$, which implies that $$ 1<\frac{q_{k}}{p_{k}}=1+\frac{2}{x_{k+1} / x_{k}-1}<1+\frac{2}{\sqrt{2}-1}<6 . $$ Thus, if one of the numbers $p_{k}$ and $q_{k}$ is divisible by $5^{k}$, then we have $$ 10^{k+1}>10^{k} a_{k+1}=p_{k} q_{k} \geqslant \frac{\left(5^{k}\right)^{2}}{6} $$ and hence $(5 / 2)^{k}<60$ which is false for sufficiently large $k$. So, assuming that $k$ is large, we get that $2^{k-1}$ divides one of the numbers $p_{k}$ and $q_{k}$. Hence $$ \left\{p_{k}, q_{k}\right\}=\left\{2^{k-1} \cdot 5^{r_{k}} b_{k}, 2 \cdot 5^{k-r_{k}} c_{k}\right\} \quad \text { with nonnegative integers } b_{k}, c_{k}, r_{k} \text { such that } b_{k} c_{k}=a_{k+1} \text {. } $$ Moreover, from (3) we get $$ 6>\frac{2^{k-1} \cdot 5^{r_{k}} b_{k}}{2 \cdot 5^{k-r_{k}} c_{k}} \geqslant \frac{1}{36} \cdot\left(\frac{2}{5}\right)^{k} \cdot 5^{2 r_{k}} \quad \text { and } \quad 6>\frac{2 \cdot 5^{k-r_{k}} c_{k}}{2^{k-1} \cdot 5^{r_{k}} b_{k}} \geqslant \frac{4}{9} \cdot\left(\frac{5}{2}\right)^{k} \cdot 5^{-2 r_{k}} $$ SO $$ \alpha k+c_{1}<r_{k}<\alpha k+c_{2} \quad \text { for } \alpha=\frac{1}{2} \log _{5}\left(\frac{5}{2}\right)<1 \text { and some constants } c_{2}>c_{1} \text {. } $$ Consequently, for $C=c_{2}-c_{1}+1-\alpha>0$ we have $$ (k+1)-r_{k+1} \leqslant k-r_{k}+C . $$ Next, we will use the following easy lemma. Lemma. Let $s$ be a positive integer. Then $5^{s+2^{s}} \equiv 5^{s}\left(\bmod 10^{s}\right)$. Proof. Euler's theorem gives $5^{2^{s}} \equiv 1\left(\bmod 2^{s}\right)$, so $5^{s+2^{s}}-5^{s}=5^{s}\left(5^{2^{s}}-1\right)$ is divisible by $2^{s}$ and $5^{s}$. Now, for every large $k$ we have $$ x_{k+1}=\frac{p_{k}+q_{k}}{2}=5^{r_{k}} \cdot 2^{k-2} b_{k}+5^{k-r_{k}} c_{k} \equiv 5^{k-r_{k}} c_{k} \quad\left(\bmod 10^{r_{k}}\right) $$ since $r_{k} \leqslant k-2$ by $(4)$; hence $y_{k+1} \equiv 5^{2\left(k-r_{k}\right)} c_{k}^{2}\left(\bmod 10^{r_{k}}\right)$. Let us consider some large integer $s$, and choose the minimal $k$ such that $2\left(k-r_{k}\right) \geqslant s+2^{s}$; it exists by (4). Set $d=2\left(k-r_{k}\right)-\left(s+2^{s}\right)$. By (4) we have $2^{s}<2\left(k-r_{k}\right)<\left(\frac{2}{\alpha}-2\right) r_{k}-\frac{2 c_{1}}{\alpha}$; if $s$ is large this implies $r_{k}>s$, so (6) also holds modulo $10^{s}$. Then (6) and the lemma give $$ y_{k+1} \equiv 5^{2\left(k-r_{k}\right)} c_{k}^{2}=5^{s+2^{s}} \cdot 5^{d} c_{k}^{2} \equiv 5^{s} \cdot 5^{d} c_{k}^{2} \quad\left(\bmod 10^{s}\right) . $$ By (5) and the minimality of $k$ we have $d \leqslant 2 C$, so $5^{d} c_{k}^{2} \leqslant 5^{2 C} \cdot 81=D$. Using $5^{4}<10^{3}$ we obtain $$ 5^{s} \cdot 5^{d} c_{k}^{2}<10^{3 s / 4} D<10^{s-1} $$ for sufficiently large $s$. This, together with (7), shows that the sth digit from the right in $y_{k+1}$, which is $a_{s}$, is zero. This contradicts the problem condition.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
f3c46ef2-501f-5236-9e6e-5eb8155b9c53
| 24,327
|
Let $\mathbb{Q}_{>0}$ be the set of positive rational numbers. Let $f: \mathbb{Q}_{>0} \rightarrow \mathbb{R}$ be a function satisfying the conditions $$ \begin{aligned} & f(x) f(y) \geqslant f(x y) \\ & f(x+y) \geqslant f(x)+f(y) \end{aligned} $$ for all $x, y \in \mathbb{Q}_{>0}$. Given that $f(a)=a$ for some rational $a>1$, prove that $f(x)=x$ for all $x \in \mathbb{Q}_{>0}$. (Bulgaria)
|
Denote by $\mathbb{Z}_{>0}$ the set of positive integers. Plugging $x=1, y=a$ into (1) we get $f(1) \geqslant 1$. Next, by an easy induction on $n$ we get from (2) that $$ f(n x) \geqslant n f(x) \text { for all } n \in \mathbb{Z}_{>0} \text { and } x \in \mathbb{Q}_{>0} $$ In particular, we have $$ f(n) \geqslant n f(1) \geqslant n \quad \text { for all } n \in \mathbb{Z}_{>0} $$ From (1) again we have $f(m / n) f(n) \geqslant f(m)$, so $f(q)>0$ for all $q \in \mathbb{Q}_{>0}$. Now, (2) implies that $f$ is strictly increasing; this fact together with (4) yields $$ f(x) \geqslant f(\lfloor x\rfloor) \geqslant\lfloor x\rfloor>x-1 \quad \text { for all } x \geqslant 1 $$ By an easy induction we get from (1) that $f(x)^{n} \geqslant f\left(x^{n}\right)$, so $$ f(x)^{n} \geqslant f\left(x^{n}\right)>x^{n}-1 \quad \Longrightarrow \quad f(x) \geqslant \sqrt[n]{x^{n}-1} \text { for all } x>1 \text { and } n \in \mathbb{Z}_{>0} $$ This yields $$ f(x) \geqslant x \text { for every } x>1 \text {. } $$ (Indeed, if $x>y>1$ then $x^{n}-y^{n}=(x-y)\left(x^{n-1}+x^{n-2} y+\cdots+y^{n}\right)>n(x-y)$, so for a large $n$ we have $x^{n}-1>y^{n}$ and thus $f(x)>y$.) Now, (1) and (5) give $a^{n}=f(a)^{n} \geqslant f\left(a^{n}\right) \geqslant a^{n}$, so $f\left(a^{n}\right)=a^{n}$. Now, for $x>1$ let us choose $n \in \mathbb{Z}_{>0}$ such that $a^{n}-x>1$. Then by (2) and (5) we get $$ a^{n}=f\left(a^{n}\right) \geqslant f(x)+f\left(a^{n}-x\right) \geqslant x+\left(a^{n}-x\right)=a^{n} $$ and therefore $f(x)=x$ for $x>1$. Finally, for every $x \in \mathbb{Q}_{>0}$ and every $n \in \mathbb{Z}_{>0}$, from (1) and (3) we get $$ n f(x)=f(n) f(x) \geqslant f(n x) \geqslant n f(x) $$ which gives $f(n x)=n f(x)$. Therefore $f(m / n)=f(m) / n=m / n$ for all $m, n \in \mathbb{Z}_{>0}$. Comment. The condition $f(a)=a>1$ is essential. Indeed, for $b \geqslant 1$ the function $f(x)=b x^{2}$ satisfies (1) and (2) for all $x, y \in \mathbb{Q}_{>0}$, and it has a unique fixed point $1 / b \leqslant 1$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $\mathbb{Q}_{>0}$ be the set of positive rational numbers. Let $f: \mathbb{Q}_{>0} \rightarrow \mathbb{R}$ be a function satisfying the conditions $$ \begin{aligned} & f(x) f(y) \geqslant f(x y) \\ & f(x+y) \geqslant f(x)+f(y) \end{aligned} $$ for all $x, y \in \mathbb{Q}_{>0}$. Given that $f(a)=a$ for some rational $a>1$, prove that $f(x)=x$ for all $x \in \mathbb{Q}_{>0}$. (Bulgaria)
|
Denote by $\mathbb{Z}_{>0}$ the set of positive integers. Plugging $x=1, y=a$ into (1) we get $f(1) \geqslant 1$. Next, by an easy induction on $n$ we get from (2) that $$ f(n x) \geqslant n f(x) \text { for all } n \in \mathbb{Z}_{>0} \text { and } x \in \mathbb{Q}_{>0} $$ In particular, we have $$ f(n) \geqslant n f(1) \geqslant n \quad \text { for all } n \in \mathbb{Z}_{>0} $$ From (1) again we have $f(m / n) f(n) \geqslant f(m)$, so $f(q)>0$ for all $q \in \mathbb{Q}_{>0}$. Now, (2) implies that $f$ is strictly increasing; this fact together with (4) yields $$ f(x) \geqslant f(\lfloor x\rfloor) \geqslant\lfloor x\rfloor>x-1 \quad \text { for all } x \geqslant 1 $$ By an easy induction we get from (1) that $f(x)^{n} \geqslant f\left(x^{n}\right)$, so $$ f(x)^{n} \geqslant f\left(x^{n}\right)>x^{n}-1 \quad \Longrightarrow \quad f(x) \geqslant \sqrt[n]{x^{n}-1} \text { for all } x>1 \text { and } n \in \mathbb{Z}_{>0} $$ This yields $$ f(x) \geqslant x \text { for every } x>1 \text {. } $$ (Indeed, if $x>y>1$ then $x^{n}-y^{n}=(x-y)\left(x^{n-1}+x^{n-2} y+\cdots+y^{n}\right)>n(x-y)$, so for a large $n$ we have $x^{n}-1>y^{n}$ and thus $f(x)>y$.) Now, (1) and (5) give $a^{n}=f(a)^{n} \geqslant f\left(a^{n}\right) \geqslant a^{n}$, so $f\left(a^{n}\right)=a^{n}$. Now, for $x>1$ let us choose $n \in \mathbb{Z}_{>0}$ such that $a^{n}-x>1$. Then by (2) and (5) we get $$ a^{n}=f\left(a^{n}\right) \geqslant f(x)+f\left(a^{n}-x\right) \geqslant x+\left(a^{n}-x\right)=a^{n} $$ and therefore $f(x)=x$ for $x>1$. Finally, for every $x \in \mathbb{Q}_{>0}$ and every $n \in \mathbb{Z}_{>0}$, from (1) and (3) we get $$ n f(x)=f(n) f(x) \geqslant f(n x) \geqslant n f(x) $$ which gives $f(n x)=n f(x)$. Therefore $f(m / n)=f(m) / n=m / n$ for all $m, n \in \mathbb{Z}_{>0}$. Comment. The condition $f(a)=a>1$ is essential. Indeed, for $b \geqslant 1$ the function $f(x)=b x^{2}$ satisfies (1) and (2) for all $x, y \in \mathbb{Q}_{>0}$, and it has a unique fixed point $1 / b \leqslant 1$.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
eb2eac58-4526-5c8d-9a1e-0c86b6e11373
| 24,341
|
Let $r$ be a positive integer, and let $a_{0}, a_{1}, \ldots$ be an infinite sequence of real numbers. Assume that for all nonnegative integers $m$ and $s$ there exists a positive integer $n \in[m+1, m+r]$ such that $$ a_{m}+a_{m+1}+\cdots+a_{m+s}=a_{n}+a_{n+1}+\cdots+a_{n+s} $$ Prove that the sequence is periodic, i. e. there exists some $p \geqslant 1$ such that $a_{n+p}=a_{n}$ for all $n \geqslant 0$. (India)
|
For every indices $m \leqslant n$ we will denote $S(m, n)=a_{m}+a_{m+1}+\cdots+a_{n-1}$; thus $S(n, n)=0$. Let us start with the following lemma. Lemma. Let $b_{0}, b_{1}, \ldots$ be an infinite sequence. Assume that for every nonnegative integer $m$ there exists a nonnegative integer $n \in[m+1, m+r]$ such that $b_{m}=b_{n}$. Then for every indices $k \leqslant \ell$ there exists an index $t \in[\ell, \ell+r-1]$ such that $b_{t}=b_{k}$. Moreover, there are at most $r$ distinct numbers among the terms of $\left(b_{i}\right)$. Proof. To prove the first claim, let us notice that there exists an infinite sequence of indices $k_{1}=k, k_{2}, k_{3}, \ldots$ such that $b_{k_{1}}=b_{k_{2}}=\cdots=b_{k}$ and $k_{i}<k_{i+1} \leqslant k_{i}+r$ for all $i \geqslant 1$. This sequence is unbounded from above, thus it hits each segment of the form $[\ell, \ell+r-1]$ with $\ell \geqslant k$, as required. To prove the second claim, assume, to the contrary, that there exist $r+1$ distinct numbers $b_{i_{1}}, \ldots, b_{i_{r+1}}$. Let us apply the first claim to $k=i_{1}, \ldots, i_{r+1}$ and $\ell=\max \left\{i_{1}, \ldots, i_{r+1}\right\}$; we obtain that for every $j \in\{1, \ldots, r+1\}$ there exists $t_{j} \in[s, s+r-1]$ such that $b_{t_{j}}=b_{i_{j}}$. Thus the segment $[s, s+r-1]$ should contain $r+1$ distinct integers, which is absurd. Setting $s=0$ in the problem condition, we see that the sequence $\left(a_{i}\right)$ satisfies the condition of the lemma, thus it attains at most $r$ distinct values. Denote by $A_{i}$ the ordered $r$-tuple $\left(a_{i}, \ldots, a_{i+r-1}\right)$; then among $A_{i}$ 's there are at most $r^{r}$ distinct tuples, so for every $k \geqslant 0$ two of the tuples $A_{k}, A_{k+1}, \ldots, A_{k+r^{r}}$ are identical. This means that there exists a positive integer $p \leqslant r^{r}$ such that the equality $A_{d}=A_{d+p}$ holds infinitely many times. Let $D$ be the set of indices $d$ satisfying this relation. Now we claim that $D$ coincides with the set of all nonnegative integers. Since $D$ is unbounded, it suffices to show that $d \in D$ whenever $d+1 \in D$. For that, denote $b_{k}=S(k, p+k)$. The sequence $b_{0}, b_{1}, \ldots$ satisfies the lemma conditions, so there exists an index $t \in[d+1, d+r]$ such that $S(t, t+p)=S(d, d+p)$. This last relation rewrites as $S(d, t)=S(d+p, t+p)$. Since $A_{d+1}=A_{d+p+1}$, we have $S(d+1, t)=S(d+p+1, t+p)$, therefore we obtain $$ a_{d}=S(d, t)-S(d+1, t)=S(d+p, t+p)-S(d+p+1, t+p)=a_{d+p} $$ and thus $A_{d}=A_{d+p}$, as required. Finally, we get $A_{d}=A_{d+p}$ for all $d$, so in particular $a_{d}=a_{d+p}$ for all $d$, QED. Comment 1. In the present proof, the upper bound for the minimal period length is $r^{r}$. This bound is not sharp; for instance, one may improve it to $(r-1)^{r}$ for $r \geqslant 3$.. On the other hand, this minimal length may happen to be greater than $r$. For instance, it is easy to check that the sequence with period $(3,-3,3,-3,3,-1,-1,-1)$ satisfies the problem condition for $r=7$. Comment 2. The conclusion remains true even if the problem condition only holds for every $s \geqslant N$ for some positive integer $N$. To show that, one can act as follows. Firstly, the sums of the form $S(i, i+N)$ attain at most $r$ values, as well as the sums of the form $S(i, i+N+1)$. Thus the terms $a_{i}=S(i, i+N+1)-$ $S(i+1, i+N+1)$ attain at most $r^{2}$ distinct values. Then, among the tuples $A_{k}, A_{k+N}, \ldots, A_{k+r^{2 r} N}$ two are identical, so for some $p \leqslant r^{2 r}$ the set $D=\left\{d: A_{d}=A_{d+N p}\right\}$ is infinite. The further arguments apply almost literally, with $p$ being replaced by $N p$. After having proved that such a sequence is also necessarily periodic, one may reduce the bound for the minimal period length to $r^{r}$ - essentially by verifying that the sequence satisfies the original version of the condition.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $r$ be a positive integer, and let $a_{0}, a_{1}, \ldots$ be an infinite sequence of real numbers. Assume that for all nonnegative integers $m$ and $s$ there exists a positive integer $n \in[m+1, m+r]$ such that $$ a_{m}+a_{m+1}+\cdots+a_{m+s}=a_{n}+a_{n+1}+\cdots+a_{n+s} $$ Prove that the sequence is periodic, i. e. there exists some $p \geqslant 1$ such that $a_{n+p}=a_{n}$ for all $n \geqslant 0$. (India)
|
For every indices $m \leqslant n$ we will denote $S(m, n)=a_{m}+a_{m+1}+\cdots+a_{n-1}$; thus $S(n, n)=0$. Let us start with the following lemma. Lemma. Let $b_{0}, b_{1}, \ldots$ be an infinite sequence. Assume that for every nonnegative integer $m$ there exists a nonnegative integer $n \in[m+1, m+r]$ such that $b_{m}=b_{n}$. Then for every indices $k \leqslant \ell$ there exists an index $t \in[\ell, \ell+r-1]$ such that $b_{t}=b_{k}$. Moreover, there are at most $r$ distinct numbers among the terms of $\left(b_{i}\right)$. Proof. To prove the first claim, let us notice that there exists an infinite sequence of indices $k_{1}=k, k_{2}, k_{3}, \ldots$ such that $b_{k_{1}}=b_{k_{2}}=\cdots=b_{k}$ and $k_{i}<k_{i+1} \leqslant k_{i}+r$ for all $i \geqslant 1$. This sequence is unbounded from above, thus it hits each segment of the form $[\ell, \ell+r-1]$ with $\ell \geqslant k$, as required. To prove the second claim, assume, to the contrary, that there exist $r+1$ distinct numbers $b_{i_{1}}, \ldots, b_{i_{r+1}}$. Let us apply the first claim to $k=i_{1}, \ldots, i_{r+1}$ and $\ell=\max \left\{i_{1}, \ldots, i_{r+1}\right\}$; we obtain that for every $j \in\{1, \ldots, r+1\}$ there exists $t_{j} \in[s, s+r-1]$ such that $b_{t_{j}}=b_{i_{j}}$. Thus the segment $[s, s+r-1]$ should contain $r+1$ distinct integers, which is absurd. Setting $s=0$ in the problem condition, we see that the sequence $\left(a_{i}\right)$ satisfies the condition of the lemma, thus it attains at most $r$ distinct values. Denote by $A_{i}$ the ordered $r$-tuple $\left(a_{i}, \ldots, a_{i+r-1}\right)$; then among $A_{i}$ 's there are at most $r^{r}$ distinct tuples, so for every $k \geqslant 0$ two of the tuples $A_{k}, A_{k+1}, \ldots, A_{k+r^{r}}$ are identical. This means that there exists a positive integer $p \leqslant r^{r}$ such that the equality $A_{d}=A_{d+p}$ holds infinitely many times. Let $D$ be the set of indices $d$ satisfying this relation. Now we claim that $D$ coincides with the set of all nonnegative integers. Since $D$ is unbounded, it suffices to show that $d \in D$ whenever $d+1 \in D$. For that, denote $b_{k}=S(k, p+k)$. The sequence $b_{0}, b_{1}, \ldots$ satisfies the lemma conditions, so there exists an index $t \in[d+1, d+r]$ such that $S(t, t+p)=S(d, d+p)$. This last relation rewrites as $S(d, t)=S(d+p, t+p)$. Since $A_{d+1}=A_{d+p+1}$, we have $S(d+1, t)=S(d+p+1, t+p)$, therefore we obtain $$ a_{d}=S(d, t)-S(d+1, t)=S(d+p, t+p)-S(d+p+1, t+p)=a_{d+p} $$ and thus $A_{d}=A_{d+p}$, as required. Finally, we get $A_{d}=A_{d+p}$ for all $d$, so in particular $a_{d}=a_{d+p}$ for all $d$, QED. Comment 1. In the present proof, the upper bound for the minimal period length is $r^{r}$. This bound is not sharp; for instance, one may improve it to $(r-1)^{r}$ for $r \geqslant 3$.. On the other hand, this minimal length may happen to be greater than $r$. For instance, it is easy to check that the sequence with period $(3,-3,3,-3,3,-1,-1,-1)$ satisfies the problem condition for $r=7$. Comment 2. The conclusion remains true even if the problem condition only holds for every $s \geqslant N$ for some positive integer $N$. To show that, one can act as follows. Firstly, the sums of the form $S(i, i+N)$ attain at most $r$ values, as well as the sums of the form $S(i, i+N+1)$. Thus the terms $a_{i}=S(i, i+N+1)-$ $S(i+1, i+N+1)$ attain at most $r^{2}$ distinct values. Then, among the tuples $A_{k}, A_{k+N}, \ldots, A_{k+r^{2 r} N}$ two are identical, so for some $p \leqslant r^{2 r}$ the set $D=\left\{d: A_{d}=A_{d+N p}\right\}$ is infinite. The further arguments apply almost literally, with $p$ being replaced by $N p$. After having proved that such a sequence is also necessarily periodic, one may reduce the bound for the minimal period length to $r^{r}$ - essentially by verifying that the sequence satisfies the original version of the condition.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8126ad29-9547-5ea9-96cb-3f1387e9a872
| 24,360
|
Let $A B C D E F$ be a convex hexagon with $A B=D E, B C=E F, C D=F A$, and $\angle A-\angle D=\angle C-\angle F=\angle E-\angle B$. Prove that the diagonals $A D, B E$, and $C F$ are concurrent. (Ukraine) In all three solutions, we denote $\theta=\angle A-\angle D=\angle C-\angle F=\angle E-\angle B$ and assume without loss of generality that $\theta \geqslant 0$.
|
Let $x=A B=D E, y=C D=F A, z=E F=B C$. Consider the points $P, Q$, and $R$ such that the quadrilaterals $C D E P, E F A Q$, and $A B C R$ are parallelograms. We compute $$ \begin{aligned} \angle P E Q & =\angle F E Q+\angle D E P-\angle E=\left(180^{\circ}-\angle F\right)+\left(180^{\circ}-\angle D\right)-\angle E \\ & =360^{\circ}-\angle D-\angle E-\angle F=\frac{1}{2}(\angle A+\angle B+\angle C-\angle D-\angle E-\angle F)=\theta / 2 \end{aligned} $$ Similarly, $\angle Q A R=\angle R C P=\theta / 2$.  If $\theta=0$, since $\triangle R C P$ is isosceles, $R=P$. Therefore $A B\|R C=P C\| E D$, so $A B D E$ is a parallelogram. Similarly, $B C E F$ and $C D F A$ are parallelograms. It follows that $A D, B E$ and $C F$ meet at their common midpoint. Now assume $\theta>0$. Since $\triangle P E Q, \triangle Q A R$, and $\triangle R C P$ are isosceles and have the same angle at the apex, we have $\triangle P E Q \sim \triangle Q A R \sim \triangle R C P$ with ratios of similarity $y: z: x$. Thus $\triangle P Q R$ is similar to the triangle with sidelengths $y, z$, and $x$. Next, notice that $$ \frac{R Q}{Q P}=\frac{z}{y}=\frac{R A}{A F} $$ and, using directed angles between rays, $$ \begin{aligned} \not(R Q, Q P) & =\Varangle(R Q, Q E)+\Varangle(Q E, Q P) \\ & =\Varangle(R Q, Q E)+\Varangle(R A, R Q)=\Varangle(R A, Q E)=\Varangle(R A, A F) . \end{aligned} $$ Thus $\triangle P Q R \sim \triangle F A R$. Since $F A=y$ and $A R=z$, (1) then implies that $F R=x$. Similarly $F P=x$. Therefore $C R F P$ is a rhombus. We conclude that $C F$ is the perpendicular bisector of $P R$. Similarly, $B E$ is the perpendicular bisector of $P Q$ and $A D$ is the perpendicular bisector of $Q R$. It follows that $A D, B E$, and $C F$ are concurrent at the circumcenter of $P Q R$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D E F$ be a convex hexagon with $A B=D E, B C=E F, C D=F A$, and $\angle A-\angle D=\angle C-\angle F=\angle E-\angle B$. Prove that the diagonals $A D, B E$, and $C F$ are concurrent. (Ukraine) In all three solutions, we denote $\theta=\angle A-\angle D=\angle C-\angle F=\angle E-\angle B$ and assume without loss of generality that $\theta \geqslant 0$.
|
Let $x=A B=D E, y=C D=F A, z=E F=B C$. Consider the points $P, Q$, and $R$ such that the quadrilaterals $C D E P, E F A Q$, and $A B C R$ are parallelograms. We compute $$ \begin{aligned} \angle P E Q & =\angle F E Q+\angle D E P-\angle E=\left(180^{\circ}-\angle F\right)+\left(180^{\circ}-\angle D\right)-\angle E \\ & =360^{\circ}-\angle D-\angle E-\angle F=\frac{1}{2}(\angle A+\angle B+\angle C-\angle D-\angle E-\angle F)=\theta / 2 \end{aligned} $$ Similarly, $\angle Q A R=\angle R C P=\theta / 2$.  If $\theta=0$, since $\triangle R C P$ is isosceles, $R=P$. Therefore $A B\|R C=P C\| E D$, so $A B D E$ is a parallelogram. Similarly, $B C E F$ and $C D F A$ are parallelograms. It follows that $A D, B E$ and $C F$ meet at their common midpoint. Now assume $\theta>0$. Since $\triangle P E Q, \triangle Q A R$, and $\triangle R C P$ are isosceles and have the same angle at the apex, we have $\triangle P E Q \sim \triangle Q A R \sim \triangle R C P$ with ratios of similarity $y: z: x$. Thus $\triangle P Q R$ is similar to the triangle with sidelengths $y, z$, and $x$. Next, notice that $$ \frac{R Q}{Q P}=\frac{z}{y}=\frac{R A}{A F} $$ and, using directed angles between rays, $$ \begin{aligned} \not(R Q, Q P) & =\Varangle(R Q, Q E)+\Varangle(Q E, Q P) \\ & =\Varangle(R Q, Q E)+\Varangle(R A, R Q)=\Varangle(R A, Q E)=\Varangle(R A, A F) . \end{aligned} $$ Thus $\triangle P Q R \sim \triangle F A R$. Since $F A=y$ and $A R=z$, (1) then implies that $F R=x$. Similarly $F P=x$. Therefore $C R F P$ is a rhombus. We conclude that $C F$ is the perpendicular bisector of $P R$. Similarly, $B E$ is the perpendicular bisector of $P Q$ and $A D$ is the perpendicular bisector of $Q R$. It follows that $A D, B E$, and $C F$ are concurrent at the circumcenter of $P Q R$.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
a0424ac6-0630-5911-81e9-41e5ed3445c1
| 24,366
|
Let $A B C D E F$ be a convex hexagon with $A B=D E, B C=E F, C D=F A$, and $\angle A-\angle D=\angle C-\angle F=\angle E-\angle B$. Prove that the diagonals $A D, B E$, and $C F$ are concurrent. (Ukraine) In all three solutions, we denote $\theta=\angle A-\angle D=\angle C-\angle F=\angle E-\angle B$ and assume without loss of generality that $\theta \geqslant 0$.
|
Let $X=C D \cap E F, Y=E F \cap A B, Z=A B \cap C D, X^{\prime}=F A \cap B C, Y^{\prime}=$ $B C \cap D E$, and $Z^{\prime}=D E \cap F A$. From $\angle A+\angle B+\angle C=360^{\circ}+\theta / 2$ we get $\angle A+\angle B>180^{\circ}$ and $\angle B+\angle C>180^{\circ}$, so $Z$ and $X^{\prime}$ are respectively on the opposite sides of $B C$ and $A B$ from the hexagon. Similar conclusions hold for $X, Y, Y^{\prime}$, and $Z^{\prime}$. Then $$ \angle Y Z X=\angle B+\angle C-180^{\circ}=\angle E+\angle F-180^{\circ}=\angle Y^{\prime} Z^{\prime} X^{\prime}, $$ and similarly $\angle Z X Y=\angle Z^{\prime} X^{\prime} Y^{\prime}$ and $\angle X Y Z=\angle X^{\prime} Y^{\prime} Z^{\prime}$, so $\triangle X Y Z \sim \triangle X^{\prime} Y^{\prime} Z^{\prime}$. Thus there is a rotation $R$ which sends $\triangle X Y Z$ to a triangle with sides parallel to $\triangle X^{\prime} Y^{\prime} Z^{\prime}$. Since $A B=D E$ we have $R(\overrightarrow{A B})=\overrightarrow{D E}$. Similarly, $R(\overrightarrow{C D})=\overrightarrow{F A}$ and $R(\overrightarrow{E F})=\overrightarrow{B C}$. Therefore $$ \overrightarrow{0}=\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C D}+\overrightarrow{D E}+\overrightarrow{E F}+\overrightarrow{F A}=(\overrightarrow{A B}+\overrightarrow{C D}+\overrightarrow{E F})+R(\overrightarrow{A B}+\overrightarrow{C D}+\overrightarrow{E F}) $$ If $R$ is a rotation by $180^{\circ}$, then any two opposite sides of our hexagon are equal and parallel, so the three diagonals meet at their common midpoint. Otherwise, we must have $$ \overrightarrow{A B}+\overrightarrow{C D}+\overrightarrow{E F}=\overrightarrow{0} $$ or else we would have two vectors with different directions whose sum is $\overrightarrow{0}$.  This allows us to consider a triangle $L M N$ with $\overrightarrow{L M}=\overrightarrow{E F}, \overrightarrow{M N}=\overrightarrow{A B}$, and $\overrightarrow{N L}=\overrightarrow{C D}$. Let $O$ be the circumcenter of $\triangle L M N$ and consider the points $O_{1}, O_{2}, O_{3}$ such that $\triangle A O_{1} B, \triangle C O_{2} D$, and $\triangle E O_{3} F$ are translations of $\triangle M O N, \triangle N O L$, and $\triangle L O M$, respectively. Since $F O_{3}$ and $A O_{1}$ are translations of $M O$, quadrilateral $A F O_{3} O_{1}$ is a parallelogram and $O_{3} O_{1}=F A=C D=N L$. Similarly, $O_{1} O_{2}=L M$ and $O_{2} O_{3}=M N$. Therefore $\triangle O_{1} O_{2} O_{3} \cong \triangle L M N$. Moreover, by means of the rotation $R$ one may check that these triangles have the same orientation. Let $T$ be the circumcenter of $\triangle O_{1} O_{2} O_{3}$. We claim that $A D, B E$, and $C F$ meet at $T$. Let us show that $C, T$, and $F$ are collinear. Notice that $C O_{2}=O_{2} T=T O_{3}=O_{3} F$ since they are all equal to the circumradius of $\triangle L M N$. Therefore $\triangle T O_{3} F$ and $\triangle C O_{2} T$ are isosceles. Using directed angles between rays again, we get $$ \Varangle\left(T F, T O_{3}\right)=\Varangle\left(F O_{3}, F T\right) \quad \text { and } \quad \Varangle\left(T O_{2}, T C\right)=\Varangle\left(C T, C O_{2}\right) \text {. } $$ Also, $T$ and $O$ are the circumcenters of the congruent triangles $\triangle O_{1} O_{2} O_{3}$ and $\triangle L M N$ so we have $\Varangle\left(T O_{3}, T O_{2}\right)=\Varangle(O N, O M)$. Since $C_{2}$ and $F O_{3}$ are translations of $N O$ and $M O$ respectively, this implies $$ \Varangle\left(T O_{3}, T O_{2}\right)=\Varangle\left(C O_{2}, F O_{3}\right) . $$ Adding the three equations in (2) and (3) gives $$ \Varangle(T F, T C)=\Varangle(C T, F T)=-\not(T F, T C) $$ which implies that $T$ is on $C F$. Analogous arguments show that it is on $A D$ and $B E$ also. The desired result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D E F$ be a convex hexagon with $A B=D E, B C=E F, C D=F A$, and $\angle A-\angle D=\angle C-\angle F=\angle E-\angle B$. Prove that the diagonals $A D, B E$, and $C F$ are concurrent. (Ukraine) In all three solutions, we denote $\theta=\angle A-\angle D=\angle C-\angle F=\angle E-\angle B$ and assume without loss of generality that $\theta \geqslant 0$.
|
Let $X=C D \cap E F, Y=E F \cap A B, Z=A B \cap C D, X^{\prime}=F A \cap B C, Y^{\prime}=$ $B C \cap D E$, and $Z^{\prime}=D E \cap F A$. From $\angle A+\angle B+\angle C=360^{\circ}+\theta / 2$ we get $\angle A+\angle B>180^{\circ}$ and $\angle B+\angle C>180^{\circ}$, so $Z$ and $X^{\prime}$ are respectively on the opposite sides of $B C$ and $A B$ from the hexagon. Similar conclusions hold for $X, Y, Y^{\prime}$, and $Z^{\prime}$. Then $$ \angle Y Z X=\angle B+\angle C-180^{\circ}=\angle E+\angle F-180^{\circ}=\angle Y^{\prime} Z^{\prime} X^{\prime}, $$ and similarly $\angle Z X Y=\angle Z^{\prime} X^{\prime} Y^{\prime}$ and $\angle X Y Z=\angle X^{\prime} Y^{\prime} Z^{\prime}$, so $\triangle X Y Z \sim \triangle X^{\prime} Y^{\prime} Z^{\prime}$. Thus there is a rotation $R$ which sends $\triangle X Y Z$ to a triangle with sides parallel to $\triangle X^{\prime} Y^{\prime} Z^{\prime}$. Since $A B=D E$ we have $R(\overrightarrow{A B})=\overrightarrow{D E}$. Similarly, $R(\overrightarrow{C D})=\overrightarrow{F A}$ and $R(\overrightarrow{E F})=\overrightarrow{B C}$. Therefore $$ \overrightarrow{0}=\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C D}+\overrightarrow{D E}+\overrightarrow{E F}+\overrightarrow{F A}=(\overrightarrow{A B}+\overrightarrow{C D}+\overrightarrow{E F})+R(\overrightarrow{A B}+\overrightarrow{C D}+\overrightarrow{E F}) $$ If $R$ is a rotation by $180^{\circ}$, then any two opposite sides of our hexagon are equal and parallel, so the three diagonals meet at their common midpoint. Otherwise, we must have $$ \overrightarrow{A B}+\overrightarrow{C D}+\overrightarrow{E F}=\overrightarrow{0} $$ or else we would have two vectors with different directions whose sum is $\overrightarrow{0}$.  This allows us to consider a triangle $L M N$ with $\overrightarrow{L M}=\overrightarrow{E F}, \overrightarrow{M N}=\overrightarrow{A B}$, and $\overrightarrow{N L}=\overrightarrow{C D}$. Let $O$ be the circumcenter of $\triangle L M N$ and consider the points $O_{1}, O_{2}, O_{3}$ such that $\triangle A O_{1} B, \triangle C O_{2} D$, and $\triangle E O_{3} F$ are translations of $\triangle M O N, \triangle N O L$, and $\triangle L O M$, respectively. Since $F O_{3}$ and $A O_{1}$ are translations of $M O$, quadrilateral $A F O_{3} O_{1}$ is a parallelogram and $O_{3} O_{1}=F A=C D=N L$. Similarly, $O_{1} O_{2}=L M$ and $O_{2} O_{3}=M N$. Therefore $\triangle O_{1} O_{2} O_{3} \cong \triangle L M N$. Moreover, by means of the rotation $R$ one may check that these triangles have the same orientation. Let $T$ be the circumcenter of $\triangle O_{1} O_{2} O_{3}$. We claim that $A D, B E$, and $C F$ meet at $T$. Let us show that $C, T$, and $F$ are collinear. Notice that $C O_{2}=O_{2} T=T O_{3}=O_{3} F$ since they are all equal to the circumradius of $\triangle L M N$. Therefore $\triangle T O_{3} F$ and $\triangle C O_{2} T$ are isosceles. Using directed angles between rays again, we get $$ \Varangle\left(T F, T O_{3}\right)=\Varangle\left(F O_{3}, F T\right) \quad \text { and } \quad \Varangle\left(T O_{2}, T C\right)=\Varangle\left(C T, C O_{2}\right) \text {. } $$ Also, $T$ and $O$ are the circumcenters of the congruent triangles $\triangle O_{1} O_{2} O_{3}$ and $\triangle L M N$ so we have $\Varangle\left(T O_{3}, T O_{2}\right)=\Varangle(O N, O M)$. Since $C_{2}$ and $F O_{3}$ are translations of $N O$ and $M O$ respectively, this implies $$ \Varangle\left(T O_{3}, T O_{2}\right)=\Varangle\left(C O_{2}, F O_{3}\right) . $$ Adding the three equations in (2) and (3) gives $$ \Varangle(T F, T C)=\Varangle(C T, F T)=-\not(T F, T C) $$ which implies that $T$ is on $C F$. Analogous arguments show that it is on $A D$ and $B E$ also. The desired result follows.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
a0424ac6-0630-5911-81e9-41e5ed3445c1
| 24,366
|
Let $A B C D E F$ be a convex hexagon with $A B=D E, B C=E F, C D=F A$, and $\angle A-\angle D=\angle C-\angle F=\angle E-\angle B$. Prove that the diagonals $A D, B E$, and $C F$ are concurrent. (Ukraine) In all three solutions, we denote $\theta=\angle A-\angle D=\angle C-\angle F=\angle E-\angle B$ and assume without loss of generality that $\theta \geqslant 0$.
|
Place the hexagon on the complex plane, with $A$ at the origin and vertices labelled clockwise. Now $A, B, C, D, E, F$ represent the corresponding complex numbers. Also consider the complex numbers $a, b, c, a^{\prime}, b^{\prime}, c^{\prime}$ given by $B-A=a, D-C=b, F-E=c, E-D=a^{\prime}$, $A-F=b^{\prime}$, and $C-B=c^{\prime}$. Let $k=|a| /|b|$. From $a / b^{\prime}=-k e^{i \angle A}$ and $a^{\prime} / b=-k e^{i \angle D}$ we get that $\left(a^{\prime} / a\right)\left(b^{\prime} / b\right)=e^{-i \theta}$ and similarly $\left(b^{\prime} / b\right)\left(c^{\prime} / c\right)=e^{-i \theta}$ and $\left(c^{\prime} / c\right)\left(a^{\prime} / a\right)=e^{-i \theta}$. It follows that $a^{\prime}=a r$, $b^{\prime}=b r$, and $c^{\prime}=c r$ for a complex number $r$ with $|r|=1$, as shown below.  We have $$ 0=a+c r+b+a r+c+b r=(a+b+c)(1+r) . $$ If $r=-1$, then the hexagon is centrally symmetric and its diagonals intersect at its center of symmetry. Otherwise $$ a+b+c=0 \text {. } $$ Therefore $$ A=0, \quad B=a, \quad C=a+c r, \quad D=c(r-1), \quad E=-b r-c, \quad F=-b r . $$ Now consider a point $W$ on $A D$ given by the complex number $c(r-1) \lambda$, where $\lambda$ is a real number with $0<\lambda<1$. Since $D \neq A$, we have $r \neq 1$, so we can define $s=1 /(r-1)$. From $r \bar{r}=|r|^{2}=1$ we get $$ 1+s=\frac{r}{r-1}=\frac{r}{r-r \bar{r}}=\frac{1}{1-\bar{r}}=-\bar{s} . $$ Now, $$ \begin{aligned} W \text { is on } B E & \Longleftrightarrow c(r-1) \lambda-a\|a-(-b r-c)=b(r-1) \Longleftrightarrow c \lambda-a s\| b \\ & \Longleftrightarrow-a \lambda-b \lambda-a s\|b \Longleftrightarrow a(\lambda+s)\| b . \end{aligned} $$ One easily checks that $r \neq \pm 1$ implies that $\lambda+s \neq 0$ since $s$ is not real. On the other hand, $$ \begin{aligned} W \text { on } C F & \Longleftrightarrow c(r-1) \lambda+b r\|-b r-(a+c r)=a(r-1) \Longleftrightarrow c \lambda+b(1+s)\| a \\ & \Longleftrightarrow-a \lambda-b \lambda-b \bar{s}\|a \Longleftrightarrow b(\lambda+\bar{s})\| a \Longleftrightarrow b \| a(\lambda+s), \end{aligned} $$ where in the last step we use that $(\lambda+s)(\lambda+\bar{s})=|\lambda+s|^{2} \in \mathbb{R}_{>0}$. We conclude that $A D \cap B E=$ $C F \cap B E$, and the desired result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D E F$ be a convex hexagon with $A B=D E, B C=E F, C D=F A$, and $\angle A-\angle D=\angle C-\angle F=\angle E-\angle B$. Prove that the diagonals $A D, B E$, and $C F$ are concurrent. (Ukraine) In all three solutions, we denote $\theta=\angle A-\angle D=\angle C-\angle F=\angle E-\angle B$ and assume without loss of generality that $\theta \geqslant 0$.
|
Place the hexagon on the complex plane, with $A$ at the origin and vertices labelled clockwise. Now $A, B, C, D, E, F$ represent the corresponding complex numbers. Also consider the complex numbers $a, b, c, a^{\prime}, b^{\prime}, c^{\prime}$ given by $B-A=a, D-C=b, F-E=c, E-D=a^{\prime}$, $A-F=b^{\prime}$, and $C-B=c^{\prime}$. Let $k=|a| /|b|$. From $a / b^{\prime}=-k e^{i \angle A}$ and $a^{\prime} / b=-k e^{i \angle D}$ we get that $\left(a^{\prime} / a\right)\left(b^{\prime} / b\right)=e^{-i \theta}$ and similarly $\left(b^{\prime} / b\right)\left(c^{\prime} / c\right)=e^{-i \theta}$ and $\left(c^{\prime} / c\right)\left(a^{\prime} / a\right)=e^{-i \theta}$. It follows that $a^{\prime}=a r$, $b^{\prime}=b r$, and $c^{\prime}=c r$ for a complex number $r$ with $|r|=1$, as shown below.  We have $$ 0=a+c r+b+a r+c+b r=(a+b+c)(1+r) . $$ If $r=-1$, then the hexagon is centrally symmetric and its diagonals intersect at its center of symmetry. Otherwise $$ a+b+c=0 \text {. } $$ Therefore $$ A=0, \quad B=a, \quad C=a+c r, \quad D=c(r-1), \quad E=-b r-c, \quad F=-b r . $$ Now consider a point $W$ on $A D$ given by the complex number $c(r-1) \lambda$, where $\lambda$ is a real number with $0<\lambda<1$. Since $D \neq A$, we have $r \neq 1$, so we can define $s=1 /(r-1)$. From $r \bar{r}=|r|^{2}=1$ we get $$ 1+s=\frac{r}{r-1}=\frac{r}{r-r \bar{r}}=\frac{1}{1-\bar{r}}=-\bar{s} . $$ Now, $$ \begin{aligned} W \text { is on } B E & \Longleftrightarrow c(r-1) \lambda-a\|a-(-b r-c)=b(r-1) \Longleftrightarrow c \lambda-a s\| b \\ & \Longleftrightarrow-a \lambda-b \lambda-a s\|b \Longleftrightarrow a(\lambda+s)\| b . \end{aligned} $$ One easily checks that $r \neq \pm 1$ implies that $\lambda+s \neq 0$ since $s$ is not real. On the other hand, $$ \begin{aligned} W \text { on } C F & \Longleftrightarrow c(r-1) \lambda+b r\|-b r-(a+c r)=a(r-1) \Longleftrightarrow c \lambda+b(1+s)\| a \\ & \Longleftrightarrow-a \lambda-b \lambda-b \bar{s}\|a \Longleftrightarrow b(\lambda+\bar{s})\| a \Longleftrightarrow b \| a(\lambda+s), \end{aligned} $$ where in the last step we use that $(\lambda+s)(\lambda+\bar{s})=|\lambda+s|^{2} \in \mathbb{R}_{>0}$. We conclude that $A D \cap B E=$ $C F \cap B E$, and the desired result follows.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
a0424ac6-0630-5911-81e9-41e5ed3445c1
| 24,366
|
Determine whether there exists an infinite sequence of nonzero digits $a_{1}, a_{2}, a_{3}, \ldots$ and a positive integer $N$ such that for every integer $k>N$, the number $\overline{a_{k} a_{k-1} \ldots a_{1}}$ is a perfect square. (Iran) Answer. No.
|
Assume that $a_{1}, a_{2}, a_{3}, \ldots$ is such a sequence. For each positive integer $k$, let $y_{k}=$ $\overline{a_{k} a_{k-1} \ldots a_{1}}$. By the assumption, for each $k>N$ there exists a positive integer $x_{k}$ such that $y_{k}=x_{k}^{2}$. I. For every $n$, let $5^{\gamma_{n}}$ be the greatest power of 5 dividing $x_{n}$. Let us show first that $2 \gamma_{n} \geqslant n$ for every positive integer $n>N$. Assume, to the contrary, that there exists a positive integer $n>N$ such that $2 \gamma_{n}<n$, which yields $$ y_{n+1}=\overline{a_{n+1} a_{n} \ldots a_{1}}=10^{n} a_{n+1}+\overline{a_{n} a_{n-1} \ldots a_{1}}=10^{n} a_{n+1}+y_{n}=5^{2 \gamma_{n}}\left(2^{n} 5^{n-2 \gamma_{n}} a_{n+1}+\frac{y_{n}}{5^{2 \gamma_{n}}}\right) . $$ Since $5 \nmid y_{n} / 5^{2 \gamma_{n}}$, we obtain $\gamma_{n+1}=\gamma_{n}<n<n+1$. By the same arguments we obtain that $\gamma_{n}=\gamma_{n+1}=\gamma_{n+2}=\ldots$. Denote this common value by $\gamma$. Now, for each $k \geqslant n$ we have $$ \left(x_{k+1}-x_{k}\right)\left(x_{k+1}+x_{k}\right)=x_{k+1}^{2}-x_{k}^{2}=y_{k+1}-y_{k}=a_{k+1} \cdot 10^{k} . $$ One of the numbers $x_{k+1}-x_{k}$ and $x_{k+1}+x_{k}$ is not divisible by $5^{\gamma+1}$ since otherwise one would have $5^{\gamma+1} \mid\left(\left(x_{k+1}-x_{k}\right)+\left(x_{k+1}+x_{k}\right)\right)=2 x_{k+1}$. On the other hand, we have $5^{k} \mid\left(x_{k+1}-x_{k}\right)\left(x_{k+1}+x_{k}\right)$, so $5^{k-\gamma}$ divides one of these two factors. Thus we get $$ 5^{k-\gamma} \leqslant \max \left\{x_{k+1}-x_{k}, x_{k+1}+x_{k}\right\}<2 x_{k+1}=2 \sqrt{y_{k+1}}<2 \cdot 10^{(k+1) / 2} $$ which implies $5^{2 k}<4 \cdot 5^{2 \gamma} \cdot 10^{k+1}$, or $(5 / 2)^{k}<40 \cdot 5^{2 \gamma}$. The last inequality is clearly false for sufficiently large values of $k$. This contradiction shows that $2 \gamma_{n} \geqslant n$ for all $n>N$. II. Consider now any integer $k>\max \{N / 2,2\}$. Since $2 \gamma_{2 k+1} \geqslant 2 k+1$ and $2 \gamma_{2 k+2} \geqslant 2 k+2$, we have $\gamma_{2 k+1} \geqslant k+1$ and $\gamma_{2 k+2} \geqslant k+1$. So, from $y_{2 k+2}=a_{2 k+2} \cdot 10^{2 k+1}+y_{2 k+1}$ we obtain $5^{2 k+2} \mid y_{2 k+2}-y_{2 k+1}=a_{2 k+2} \cdot 10^{2 k+1}$ and thus $5 \mid a_{2 k+2}$, which implies $a_{2 k+2}=5$. Therefore, $$ \left(x_{2 k+2}-x_{2 k+1}\right)\left(x_{2 k+2}+x_{2 k+1}\right)=x_{2 k+2}^{2}-x_{2 k+1}^{2}=y_{2 k+2}-y_{2 k+1}=5 \cdot 10^{2 k+1}=2^{2 k+1} \cdot 5^{2 k+2} . $$ Setting $A_{k}=x_{2 k+2} / 5^{k+1}$ and $B_{k}=x_{2 k+1} / 5^{k+1}$, which are integers, we obtain $$ \left(A_{k}-B_{k}\right)\left(A_{k}+B_{k}\right)=2^{2 k+1} . $$ Both $A_{k}$ and $B_{k}$ are odd, since otherwise $y_{2 k+2}$ or $y_{2 k+1}$ would be a multiple of 10 which is false by $a_{1} \neq 0$; so one of the numbers $A_{k}-B_{k}$ and $A_{k}+B_{k}$ is not divisible by 4 . Therefore (1) yields $A_{k}-B_{k}=2$ and $A_{k}+B_{k}=2^{2 k}$, hence $A_{k}=2^{2 k-1}+1$ and thus $$ x_{2 k+2}=5^{k+1} A_{k}=10^{k+1} \cdot 2^{k-2}+5^{k+1}>10^{k+1}, $$ since $k \geqslant 2$. This implies that $y_{2 k+2}>10^{2 k+2}$ which contradicts the fact that $y_{2 k+2}$ contains $2 k+2$ digits. The desired result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Determine whether there exists an infinite sequence of nonzero digits $a_{1}, a_{2}, a_{3}, \ldots$ and a positive integer $N$ such that for every integer $k>N$, the number $\overline{a_{k} a_{k-1} \ldots a_{1}}$ is a perfect square. (Iran) Answer. No.
|
Assume that $a_{1}, a_{2}, a_{3}, \ldots$ is such a sequence. For each positive integer $k$, let $y_{k}=$ $\overline{a_{k} a_{k-1} \ldots a_{1}}$. By the assumption, for each $k>N$ there exists a positive integer $x_{k}$ such that $y_{k}=x_{k}^{2}$. I. For every $n$, let $5^{\gamma_{n}}$ be the greatest power of 5 dividing $x_{n}$. Let us show first that $2 \gamma_{n} \geqslant n$ for every positive integer $n>N$. Assume, to the contrary, that there exists a positive integer $n>N$ such that $2 \gamma_{n}<n$, which yields $$ y_{n+1}=\overline{a_{n+1} a_{n} \ldots a_{1}}=10^{n} a_{n+1}+\overline{a_{n} a_{n-1} \ldots a_{1}}=10^{n} a_{n+1}+y_{n}=5^{2 \gamma_{n}}\left(2^{n} 5^{n-2 \gamma_{n}} a_{n+1}+\frac{y_{n}}{5^{2 \gamma_{n}}}\right) . $$ Since $5 \nmid y_{n} / 5^{2 \gamma_{n}}$, we obtain $\gamma_{n+1}=\gamma_{n}<n<n+1$. By the same arguments we obtain that $\gamma_{n}=\gamma_{n+1}=\gamma_{n+2}=\ldots$. Denote this common value by $\gamma$. Now, for each $k \geqslant n$ we have $$ \left(x_{k+1}-x_{k}\right)\left(x_{k+1}+x_{k}\right)=x_{k+1}^{2}-x_{k}^{2}=y_{k+1}-y_{k}=a_{k+1} \cdot 10^{k} . $$ One of the numbers $x_{k+1}-x_{k}$ and $x_{k+1}+x_{k}$ is not divisible by $5^{\gamma+1}$ since otherwise one would have $5^{\gamma+1} \mid\left(\left(x_{k+1}-x_{k}\right)+\left(x_{k+1}+x_{k}\right)\right)=2 x_{k+1}$. On the other hand, we have $5^{k} \mid\left(x_{k+1}-x_{k}\right)\left(x_{k+1}+x_{k}\right)$, so $5^{k-\gamma}$ divides one of these two factors. Thus we get $$ 5^{k-\gamma} \leqslant \max \left\{x_{k+1}-x_{k}, x_{k+1}+x_{k}\right\}<2 x_{k+1}=2 \sqrt{y_{k+1}}<2 \cdot 10^{(k+1) / 2} $$ which implies $5^{2 k}<4 \cdot 5^{2 \gamma} \cdot 10^{k+1}$, or $(5 / 2)^{k}<40 \cdot 5^{2 \gamma}$. The last inequality is clearly false for sufficiently large values of $k$. This contradiction shows that $2 \gamma_{n} \geqslant n$ for all $n>N$. II. Consider now any integer $k>\max \{N / 2,2\}$. Since $2 \gamma_{2 k+1} \geqslant 2 k+1$ and $2 \gamma_{2 k+2} \geqslant 2 k+2$, we have $\gamma_{2 k+1} \geqslant k+1$ and $\gamma_{2 k+2} \geqslant k+1$. So, from $y_{2 k+2}=a_{2 k+2} \cdot 10^{2 k+1}+y_{2 k+1}$ we obtain $5^{2 k+2} \mid y_{2 k+2}-y_{2 k+1}=a_{2 k+2} \cdot 10^{2 k+1}$ and thus $5 \mid a_{2 k+2}$, which implies $a_{2 k+2}=5$. Therefore, $$ \left(x_{2 k+2}-x_{2 k+1}\right)\left(x_{2 k+2}+x_{2 k+1}\right)=x_{2 k+2}^{2}-x_{2 k+1}^{2}=y_{2 k+2}-y_{2 k+1}=5 \cdot 10^{2 k+1}=2^{2 k+1} \cdot 5^{2 k+2} . $$ Setting $A_{k}=x_{2 k+2} / 5^{k+1}$ and $B_{k}=x_{2 k+1} / 5^{k+1}$, which are integers, we obtain $$ \left(A_{k}-B_{k}\right)\left(A_{k}+B_{k}\right)=2^{2 k+1} . $$ Both $A_{k}$ and $B_{k}$ are odd, since otherwise $y_{2 k+2}$ or $y_{2 k+1}$ would be a multiple of 10 which is false by $a_{1} \neq 0$; so one of the numbers $A_{k}-B_{k}$ and $A_{k}+B_{k}$ is not divisible by 4 . Therefore (1) yields $A_{k}-B_{k}=2$ and $A_{k}+B_{k}=2^{2 k}$, hence $A_{k}=2^{2 k-1}+1$ and thus $$ x_{2 k+2}=5^{k+1} A_{k}=10^{k+1} \cdot 2^{k-2}+5^{k+1}>10^{k+1}, $$ since $k \geqslant 2$. This implies that $y_{2 k+2}>10^{2 k+2}$ which contradicts the fact that $y_{2 k+2}$ contains $2 k+2$ digits. The desired result follows.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
a5963f82-34c4-5e1d-9505-8998a32f0708
| 24,377
|
Determine whether there exists an infinite sequence of nonzero digits $a_{1}, a_{2}, a_{3}, \ldots$ and a positive integer $N$ such that for every integer $k>N$, the number $\overline{a_{k} a_{k-1} \ldots a_{1}}$ is a perfect square. (Iran) Answer. No.
|
Again, we assume that a sequence $a_{1}, a_{2}, a_{3}, \ldots$ satisfies the problem conditions, introduce the numbers $x_{k}$ and $y_{k}$ as in the previous solution, and notice that $$ y_{k+1}-y_{k}=\left(x_{k+1}-x_{k}\right)\left(x_{k+1}+x_{k}\right)=10^{k} a_{k+1} $$ for all $k>N$. Consider any such $k$. Since $a_{1} \neq 0$, the numbers $x_{k}$ and $x_{k+1}$ are not multiples of 10 , and therefore the numbers $p_{k}=x_{k+1}-x_{k}$ and $q_{k}=x_{k+1}+x_{k}$ cannot be simultaneously multiples of 20 , and hence one of them is not divisible either by 4 or by 5 . In view of (2), this means that the other one is divisible by either $5^{k}$ or by $2^{k-1}$. Notice also that $p_{k}$ and $q_{k}$ have the same parity, so both are even. On the other hand, we have $x_{k+1}^{2}=x_{k}^{2}+10^{k} a_{k+1} \geqslant x_{k}^{2}+10^{k}>2 x_{k}^{2}$, so $x_{k+1} / x_{k}>\sqrt{2}$, which implies that $$ 1<\frac{q_{k}}{p_{k}}=1+\frac{2}{x_{k+1} / x_{k}-1}<1+\frac{2}{\sqrt{2}-1}<6 . $$ Thus, if one of the numbers $p_{k}$ and $q_{k}$ is divisible by $5^{k}$, then we have $$ 10^{k+1}>10^{k} a_{k+1}=p_{k} q_{k} \geqslant \frac{\left(5^{k}\right)^{2}}{6} $$ and hence $(5 / 2)^{k}<60$ which is false for sufficiently large $k$. So, assuming that $k$ is large, we get that $2^{k-1}$ divides one of the numbers $p_{k}$ and $q_{k}$. Hence $$ \left\{p_{k}, q_{k}\right\}=\left\{2^{k-1} \cdot 5^{r_{k}} b_{k}, 2 \cdot 5^{k-r_{k}} c_{k}\right\} \quad \text { with nonnegative integers } b_{k}, c_{k}, r_{k} \text { such that } b_{k} c_{k}=a_{k+1} \text {. } $$ Moreover, from (3) we get $$ 6>\frac{2^{k-1} \cdot 5^{r_{k}} b_{k}}{2 \cdot 5^{k-r_{k}} c_{k}} \geqslant \frac{1}{36} \cdot\left(\frac{2}{5}\right)^{k} \cdot 5^{2 r_{k}} \quad \text { and } \quad 6>\frac{2 \cdot 5^{k-r_{k}} c_{k}}{2^{k-1} \cdot 5^{r_{k}} b_{k}} \geqslant \frac{4}{9} \cdot\left(\frac{5}{2}\right)^{k} \cdot 5^{-2 r_{k}} $$ SO $$ \alpha k+c_{1}<r_{k}<\alpha k+c_{2} \quad \text { for } \alpha=\frac{1}{2} \log _{5}\left(\frac{5}{2}\right)<1 \text { and some constants } c_{2}>c_{1} \text {. } $$ Consequently, for $C=c_{2}-c_{1}+1-\alpha>0$ we have $$ (k+1)-r_{k+1} \leqslant k-r_{k}+C . $$ Next, we will use the following easy lemma. Lemma. Let $s$ be a positive integer. Then $5^{s+2^{s}} \equiv 5^{s}\left(\bmod 10^{s}\right)$. Proof. Euler's theorem gives $5^{2^{s}} \equiv 1\left(\bmod 2^{s}\right)$, so $5^{s+2^{s}}-5^{s}=5^{s}\left(5^{2^{s}}-1\right)$ is divisible by $2^{s}$ and $5^{s}$. Now, for every large $k$ we have $$ x_{k+1}=\frac{p_{k}+q_{k}}{2}=5^{r_{k}} \cdot 2^{k-2} b_{k}+5^{k-r_{k}} c_{k} \equiv 5^{k-r_{k}} c_{k} \quad\left(\bmod 10^{r_{k}}\right) $$ since $r_{k} \leqslant k-2$ by $(4)$; hence $y_{k+1} \equiv 5^{2\left(k-r_{k}\right)} c_{k}^{2}\left(\bmod 10^{r_{k}}\right)$. Let us consider some large integer $s$, and choose the minimal $k$ such that $2\left(k-r_{k}\right) \geqslant s+2^{s}$; it exists by (4). Set $d=2\left(k-r_{k}\right)-\left(s+2^{s}\right)$. By (4) we have $2^{s}<2\left(k-r_{k}\right)<\left(\frac{2}{\alpha}-2\right) r_{k}-\frac{2 c_{1}}{\alpha}$; if $s$ is large this implies $r_{k}>s$, so (6) also holds modulo $10^{s}$. Then (6) and the lemma give $$ y_{k+1} \equiv 5^{2\left(k-r_{k}\right)} c_{k}^{2}=5^{s+2^{s}} \cdot 5^{d} c_{k}^{2} \equiv 5^{s} \cdot 5^{d} c_{k}^{2} \quad\left(\bmod 10^{s}\right) . $$ By (5) and the minimality of $k$ we have $d \leqslant 2 C$, so $5^{d} c_{k}^{2} \leqslant 5^{2 C} \cdot 81=D$. Using $5^{4}<10^{3}$ we obtain $$ 5^{s} \cdot 5^{d} c_{k}^{2}<10^{3 s / 4} D<10^{s-1} $$ for sufficiently large $s$. This, together with (7), shows that the sth digit from the right in $y_{k+1}$, which is $a_{s}$, is zero. This contradicts the problem condition.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Determine whether there exists an infinite sequence of nonzero digits $a_{1}, a_{2}, a_{3}, \ldots$ and a positive integer $N$ such that for every integer $k>N$, the number $\overline{a_{k} a_{k-1} \ldots a_{1}}$ is a perfect square. (Iran) Answer. No.
|
Again, we assume that a sequence $a_{1}, a_{2}, a_{3}, \ldots$ satisfies the problem conditions, introduce the numbers $x_{k}$ and $y_{k}$ as in the previous solution, and notice that $$ y_{k+1}-y_{k}=\left(x_{k+1}-x_{k}\right)\left(x_{k+1}+x_{k}\right)=10^{k} a_{k+1} $$ for all $k>N$. Consider any such $k$. Since $a_{1} \neq 0$, the numbers $x_{k}$ and $x_{k+1}$ are not multiples of 10 , and therefore the numbers $p_{k}=x_{k+1}-x_{k}$ and $q_{k}=x_{k+1}+x_{k}$ cannot be simultaneously multiples of 20 , and hence one of them is not divisible either by 4 or by 5 . In view of (2), this means that the other one is divisible by either $5^{k}$ or by $2^{k-1}$. Notice also that $p_{k}$ and $q_{k}$ have the same parity, so both are even. On the other hand, we have $x_{k+1}^{2}=x_{k}^{2}+10^{k} a_{k+1} \geqslant x_{k}^{2}+10^{k}>2 x_{k}^{2}$, so $x_{k+1} / x_{k}>\sqrt{2}$, which implies that $$ 1<\frac{q_{k}}{p_{k}}=1+\frac{2}{x_{k+1} / x_{k}-1}<1+\frac{2}{\sqrt{2}-1}<6 . $$ Thus, if one of the numbers $p_{k}$ and $q_{k}$ is divisible by $5^{k}$, then we have $$ 10^{k+1}>10^{k} a_{k+1}=p_{k} q_{k} \geqslant \frac{\left(5^{k}\right)^{2}}{6} $$ and hence $(5 / 2)^{k}<60$ which is false for sufficiently large $k$. So, assuming that $k$ is large, we get that $2^{k-1}$ divides one of the numbers $p_{k}$ and $q_{k}$. Hence $$ \left\{p_{k}, q_{k}\right\}=\left\{2^{k-1} \cdot 5^{r_{k}} b_{k}, 2 \cdot 5^{k-r_{k}} c_{k}\right\} \quad \text { with nonnegative integers } b_{k}, c_{k}, r_{k} \text { such that } b_{k} c_{k}=a_{k+1} \text {. } $$ Moreover, from (3) we get $$ 6>\frac{2^{k-1} \cdot 5^{r_{k}} b_{k}}{2 \cdot 5^{k-r_{k}} c_{k}} \geqslant \frac{1}{36} \cdot\left(\frac{2}{5}\right)^{k} \cdot 5^{2 r_{k}} \quad \text { and } \quad 6>\frac{2 \cdot 5^{k-r_{k}} c_{k}}{2^{k-1} \cdot 5^{r_{k}} b_{k}} \geqslant \frac{4}{9} \cdot\left(\frac{5}{2}\right)^{k} \cdot 5^{-2 r_{k}} $$ SO $$ \alpha k+c_{1}<r_{k}<\alpha k+c_{2} \quad \text { for } \alpha=\frac{1}{2} \log _{5}\left(\frac{5}{2}\right)<1 \text { and some constants } c_{2}>c_{1} \text {. } $$ Consequently, for $C=c_{2}-c_{1}+1-\alpha>0$ we have $$ (k+1)-r_{k+1} \leqslant k-r_{k}+C . $$ Next, we will use the following easy lemma. Lemma. Let $s$ be a positive integer. Then $5^{s+2^{s}} \equiv 5^{s}\left(\bmod 10^{s}\right)$. Proof. Euler's theorem gives $5^{2^{s}} \equiv 1\left(\bmod 2^{s}\right)$, so $5^{s+2^{s}}-5^{s}=5^{s}\left(5^{2^{s}}-1\right)$ is divisible by $2^{s}$ and $5^{s}$. Now, for every large $k$ we have $$ x_{k+1}=\frac{p_{k}+q_{k}}{2}=5^{r_{k}} \cdot 2^{k-2} b_{k}+5^{k-r_{k}} c_{k} \equiv 5^{k-r_{k}} c_{k} \quad\left(\bmod 10^{r_{k}}\right) $$ since $r_{k} \leqslant k-2$ by $(4)$; hence $y_{k+1} \equiv 5^{2\left(k-r_{k}\right)} c_{k}^{2}\left(\bmod 10^{r_{k}}\right)$. Let us consider some large integer $s$, and choose the minimal $k$ such that $2\left(k-r_{k}\right) \geqslant s+2^{s}$; it exists by (4). Set $d=2\left(k-r_{k}\right)-\left(s+2^{s}\right)$. By (4) we have $2^{s}<2\left(k-r_{k}\right)<\left(\frac{2}{\alpha}-2\right) r_{k}-\frac{2 c_{1}}{\alpha}$; if $s$ is large this implies $r_{k}>s$, so (6) also holds modulo $10^{s}$. Then (6) and the lemma give $$ y_{k+1} \equiv 5^{2\left(k-r_{k}\right)} c_{k}^{2}=5^{s+2^{s}} \cdot 5^{d} c_{k}^{2} \equiv 5^{s} \cdot 5^{d} c_{k}^{2} \quad\left(\bmod 10^{s}\right) . $$ By (5) and the minimality of $k$ we have $d \leqslant 2 C$, so $5^{d} c_{k}^{2} \leqslant 5^{2 C} \cdot 81=D$. Using $5^{4}<10^{3}$ we obtain $$ 5^{s} \cdot 5^{d} c_{k}^{2}<10^{3 s / 4} D<10^{s-1} $$ for sufficiently large $s$. This, together with (7), shows that the sth digit from the right in $y_{k+1}$, which is $a_{s}$, is zero. This contradicts the problem condition.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
a5963f82-34c4-5e1d-9505-8998a32f0708
| 24,377
|
Let $z_{0}<z_{1}<z_{2}<\cdots$ be an infinite sequence of positive integers. Prove that there exists a unique integer $n \geqslant 1$ such that $$ z_{n}<\frac{z_{0}+z_{1}+\cdots+z_{n}}{n} \leqslant z_{n+1} $$ (Austria)
|
For $n=1,2, \ldots$ define $$ d_{n}=\left(z_{0}+z_{1}+\cdots+z_{n}\right)-n z_{n} $$ The sign of $d_{n}$ indicates whether the first inequality in (1) holds; i.e., it is satisfied if and only if $d_{n}>0$. Notice that $$ n z_{n+1}-\left(z_{0}+z_{1}+\cdots+z_{n}\right)=(n+1) z_{n+1}-\left(z_{0}+z_{1}+\cdots+z_{n}+z_{n+1}\right)=-d_{n+1} $$ so the second inequality in (1) is equivalent to $d_{n+1} \leqslant 0$. Therefore, we have to prove that there is a unique index $n \geqslant 1$ that satisfies $d_{n}>0 \geqslant d_{n+1}$. By its definition the sequence $d_{1}, d_{2}, \ldots$ consists of integers and we have $$ d_{1}=\left(z_{0}+z_{1}\right)-1 \cdot z_{1}=z_{0}>0 $$ From $d_{n+1}-d_{n}=\left(\left(z_{0}+\cdots+z_{n}+z_{n+1}\right)-(n+1) z_{n+1}\right)-\left(\left(z_{0}+\cdots+z_{n}\right)-n z_{n}\right)=n\left(z_{n}-z_{n+1}\right)<0$ we can see that $d_{n+1}<d_{n}$ and thus the sequence strictly decreases. Hence, we have a decreasing sequence $d_{1}>d_{2}>\ldots$ of integers such that its first element $d_{1}$ is positive. The sequence must drop below 0 at some point, and thus there is a unique index $n$, that is the index of the last positive term, satisfying $d_{n}>0 \geqslant d_{n+1}$. Comment. Omitting the assumption that $z_{1}, z_{2}, \ldots$ are integers allows the numbers $d_{n}$ to be all positive. In such cases the desired $n$ does not exist. This happens for example if $z_{n}=2-\frac{1}{2^{n}}$ for all integers $n \geqslant 0$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $z_{0}<z_{1}<z_{2}<\cdots$ be an infinite sequence of positive integers. Prove that there exists a unique integer $n \geqslant 1$ such that $$ z_{n}<\frac{z_{0}+z_{1}+\cdots+z_{n}}{n} \leqslant z_{n+1} $$ (Austria)
|
For $n=1,2, \ldots$ define $$ d_{n}=\left(z_{0}+z_{1}+\cdots+z_{n}\right)-n z_{n} $$ The sign of $d_{n}$ indicates whether the first inequality in (1) holds; i.e., it is satisfied if and only if $d_{n}>0$. Notice that $$ n z_{n+1}-\left(z_{0}+z_{1}+\cdots+z_{n}\right)=(n+1) z_{n+1}-\left(z_{0}+z_{1}+\cdots+z_{n}+z_{n+1}\right)=-d_{n+1} $$ so the second inequality in (1) is equivalent to $d_{n+1} \leqslant 0$. Therefore, we have to prove that there is a unique index $n \geqslant 1$ that satisfies $d_{n}>0 \geqslant d_{n+1}$. By its definition the sequence $d_{1}, d_{2}, \ldots$ consists of integers and we have $$ d_{1}=\left(z_{0}+z_{1}\right)-1 \cdot z_{1}=z_{0}>0 $$ From $d_{n+1}-d_{n}=\left(\left(z_{0}+\cdots+z_{n}+z_{n+1}\right)-(n+1) z_{n+1}\right)-\left(\left(z_{0}+\cdots+z_{n}\right)-n z_{n}\right)=n\left(z_{n}-z_{n+1}\right)<0$ we can see that $d_{n+1}<d_{n}$ and thus the sequence strictly decreases. Hence, we have a decreasing sequence $d_{1}>d_{2}>\ldots$ of integers such that its first element $d_{1}$ is positive. The sequence must drop below 0 at some point, and thus there is a unique index $n$, that is the index of the last positive term, satisfying $d_{n}>0 \geqslant d_{n+1}$. Comment. Omitting the assumption that $z_{1}, z_{2}, \ldots$ are integers allows the numbers $d_{n}$ to be all positive. In such cases the desired $n$ does not exist. This happens for example if $z_{n}=2-\frac{1}{2^{n}}$ for all integers $n \geqslant 0$.
|
{
"resource_path": "IMO/segmented/en-IMO2014SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
2c792ad4-d568-58ee-abea-397b3a19aa53
| 24,386
|
Define the function $f:(0,1) \rightarrow(0,1)$ by $$ f(x)= \begin{cases}x+\frac{1}{2} & \text { if } x<\frac{1}{2} \\ x^{2} & \text { if } x \geqslant \frac{1}{2}\end{cases} $$ Let $a$ and $b$ be two real numbers such that $0<a<b<1$. We define the sequences $a_{n}$ and $b_{n}$ by $a_{0}=a, b_{0}=b$, and $a_{n}=f\left(a_{n-1}\right), b_{n}=f\left(b_{n-1}\right)$ for $n>0$. Show that there exists a positive integer $n$ such that $$ \left(a_{n}-a_{n-1}\right)\left(b_{n}-b_{n-1}\right)<0 . $$ (Denmark)
|
Note that $$ f(x)-x=\frac{1}{2}>0 $$ if $x<\frac{1}{2}$ and $$ f(x)-x=x^{2}-x<0 $$ if $x \geqslant \frac{1}{2}$. So if we consider $(0,1)$ as being divided into the two subintervals $I_{1}=\left(0, \frac{1}{2}\right)$ and $I_{2}=\left[\frac{1}{2}, 1\right)$, the inequality $$ \left(a_{n}-a_{n-1}\right)\left(b_{n}-b_{n-1}\right)=\left(f\left(a_{n-1}\right)-a_{n-1}\right)\left(f\left(b_{n-1}\right)-b_{n-1}\right)<0 $$ holds if and only if $a_{n-1}$ and $b_{n-1}$ lie in distinct subintervals. Let us now assume, to the contrary, that $a_{k}$ and $b_{k}$ always lie in the same subinterval. Consider the distance $d_{k}=\left|a_{k}-b_{k}\right|$. If both $a_{k}$ and $b_{k}$ lie in $I_{1}$, then $$ d_{k+1}=\left|a_{k+1}-b_{k+1}\right|=\left|a_{k}+\frac{1}{2}-b_{k}-\frac{1}{2}\right|=d_{k} $$ If, on the other hand, $a_{k}$ and $b_{k}$ both lie in $I_{2}$, then $\min \left(a_{k}, b_{k}\right) \geqslant \frac{1}{2}$ and $\max \left(a_{k}, b_{k}\right)=$ $\min \left(a_{k}, b_{k}\right)+d_{k} \geqslant \frac{1}{2}+d_{k}$, which implies $$ d_{k+1}=\left|a_{k+1}-b_{k+1}\right|=\left|a_{k}^{2}-b_{k}^{2}\right|=\left|\left(a_{k}-b_{k}\right)\left(a_{k}+b_{k}\right)\right| \geqslant\left|a_{k}-b_{k}\right|\left(\frac{1}{2}+\frac{1}{2}+d_{k}\right)=d_{k}\left(1+d_{k}\right) \geqslant d_{k} $$ This means that the difference $d_{k}$ is non-decreasing, and in particular $d_{k} \geqslant d_{0}>0$ for all $k$. We can even say more. If $a_{k}$ and $b_{k}$ lie in $I_{2}$, then $$ d_{k+2} \geqslant d_{k+1} \geqslant d_{k}\left(1+d_{k}\right) \geqslant d_{k}\left(1+d_{0}\right) $$ If $a_{k}$ and $b_{k}$ both lie in $I_{1}$, then $a_{k+1}$ and $b_{k+1}$ both lie in $I_{2}$, and so we have $$ d_{k+2} \geqslant d_{k+1}\left(1+d_{k+1}\right) \geqslant d_{k+1}\left(1+d_{0}\right)=d_{k}\left(1+d_{0}\right) $$ In either case, $d_{k+2} \geqslant d_{k}\left(1+d_{0}\right)$, and inductively we get $$ d_{2 m} \geqslant d_{0}\left(1+d_{0}\right)^{m} $$ For sufficiently large $m$, the right-hand side is greater than 1 , but since $a_{2 m}, b_{2 m}$ both lie in $(0,1)$, we must have $d_{2 m}<1$, a contradiction. Thus there must be a positive integer $n$ such that $a_{n-1}$ and $b_{n-1}$ do not lie in the same subinterval, which proves the desired statement.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Define the function $f:(0,1) \rightarrow(0,1)$ by $$ f(x)= \begin{cases}x+\frac{1}{2} & \text { if } x<\frac{1}{2} \\ x^{2} & \text { if } x \geqslant \frac{1}{2}\end{cases} $$ Let $a$ and $b$ be two real numbers such that $0<a<b<1$. We define the sequences $a_{n}$ and $b_{n}$ by $a_{0}=a, b_{0}=b$, and $a_{n}=f\left(a_{n-1}\right), b_{n}=f\left(b_{n-1}\right)$ for $n>0$. Show that there exists a positive integer $n$ such that $$ \left(a_{n}-a_{n-1}\right)\left(b_{n}-b_{n-1}\right)<0 . $$ (Denmark)
|
Note that $$ f(x)-x=\frac{1}{2}>0 $$ if $x<\frac{1}{2}$ and $$ f(x)-x=x^{2}-x<0 $$ if $x \geqslant \frac{1}{2}$. So if we consider $(0,1)$ as being divided into the two subintervals $I_{1}=\left(0, \frac{1}{2}\right)$ and $I_{2}=\left[\frac{1}{2}, 1\right)$, the inequality $$ \left(a_{n}-a_{n-1}\right)\left(b_{n}-b_{n-1}\right)=\left(f\left(a_{n-1}\right)-a_{n-1}\right)\left(f\left(b_{n-1}\right)-b_{n-1}\right)<0 $$ holds if and only if $a_{n-1}$ and $b_{n-1}$ lie in distinct subintervals. Let us now assume, to the contrary, that $a_{k}$ and $b_{k}$ always lie in the same subinterval. Consider the distance $d_{k}=\left|a_{k}-b_{k}\right|$. If both $a_{k}$ and $b_{k}$ lie in $I_{1}$, then $$ d_{k+1}=\left|a_{k+1}-b_{k+1}\right|=\left|a_{k}+\frac{1}{2}-b_{k}-\frac{1}{2}\right|=d_{k} $$ If, on the other hand, $a_{k}$ and $b_{k}$ both lie in $I_{2}$, then $\min \left(a_{k}, b_{k}\right) \geqslant \frac{1}{2}$ and $\max \left(a_{k}, b_{k}\right)=$ $\min \left(a_{k}, b_{k}\right)+d_{k} \geqslant \frac{1}{2}+d_{k}$, which implies $$ d_{k+1}=\left|a_{k+1}-b_{k+1}\right|=\left|a_{k}^{2}-b_{k}^{2}\right|=\left|\left(a_{k}-b_{k}\right)\left(a_{k}+b_{k}\right)\right| \geqslant\left|a_{k}-b_{k}\right|\left(\frac{1}{2}+\frac{1}{2}+d_{k}\right)=d_{k}\left(1+d_{k}\right) \geqslant d_{k} $$ This means that the difference $d_{k}$ is non-decreasing, and in particular $d_{k} \geqslant d_{0}>0$ for all $k$. We can even say more. If $a_{k}$ and $b_{k}$ lie in $I_{2}$, then $$ d_{k+2} \geqslant d_{k+1} \geqslant d_{k}\left(1+d_{k}\right) \geqslant d_{k}\left(1+d_{0}\right) $$ If $a_{k}$ and $b_{k}$ both lie in $I_{1}$, then $a_{k+1}$ and $b_{k+1}$ both lie in $I_{2}$, and so we have $$ d_{k+2} \geqslant d_{k+1}\left(1+d_{k+1}\right) \geqslant d_{k+1}\left(1+d_{0}\right)=d_{k}\left(1+d_{0}\right) $$ In either case, $d_{k+2} \geqslant d_{k}\left(1+d_{0}\right)$, and inductively we get $$ d_{2 m} \geqslant d_{0}\left(1+d_{0}\right)^{m} $$ For sufficiently large $m$, the right-hand side is greater than 1 , but since $a_{2 m}, b_{2 m}$ both lie in $(0,1)$, we must have $d_{2 m}<1$, a contradiction. Thus there must be a positive integer $n$ such that $a_{n-1}$ and $b_{n-1}$ do not lie in the same subinterval, which proves the desired statement.
|
{
"resource_path": "IMO/segmented/en-IMO2014SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
bccf5959-a6d2-538a-96b6-3bb974e3ef40
| 24,389
|
Let $n$ points be given inside a rectangle $R$ such that no two of them lie on a line parallel to one of the sides of $R$. The rectangle $R$ is to be dissected into smaller rectangles with sides parallel to the sides of $R$ in such a way that none of these rectangles contains any of the given points in its interior. Prove that we have to dissect $R$ into at least $n+1$ smaller rectangles. (Serbia)
|
Let $k$ be the number of rectangles in the dissection. The set of all points that are corners of one of the rectangles can be divided into three disjoint subsets: - $A$, which consists of the four corners of the original rectangle $R$, each of which is the corner of exactly one of the smaller rectangles, - $B$, which contains points where exactly two of the rectangles have a common corner (T-junctions, see the figure below), - $C$, which contains points where four of the rectangles have a common corner (crossings, see the figure below).  Figure 1: A T-junction and a crossing We denote the number of points in $B$ by $b$ and the number of points in $C$ by $c$. Since each of the $k$ rectangles has exactly four corners, we get $$ 4 k=4+2 b+4 c $$ It follows that $2 b \leqslant 4 k-4$, so $b \leqslant 2 k-2$. Each of the $n$ given points has to lie on a side of one of the smaller rectangles (but not of the original rectangle $R$ ). If we extend this side as far as possible along borders between rectangles, we obtain a line segment whose ends are T-junctions. Note that every point in $B$ can only be an endpoint of at most one such segment containing one of the given points, since it is stated that no two of them lie on a common line parallel to the sides of $R$. This means that $$ b \geqslant 2 n $$ Combining our two inequalities for $b$, we get $$ 2 k-2 \geqslant b \geqslant 2 n $$ thus $k \geqslant n+1$, which is what we wanted to prove.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ points be given inside a rectangle $R$ such that no two of them lie on a line parallel to one of the sides of $R$. The rectangle $R$ is to be dissected into smaller rectangles with sides parallel to the sides of $R$ in such a way that none of these rectangles contains any of the given points in its interior. Prove that we have to dissect $R$ into at least $n+1$ smaller rectangles. (Serbia)
|
Let $k$ be the number of rectangles in the dissection. The set of all points that are corners of one of the rectangles can be divided into three disjoint subsets: - $A$, which consists of the four corners of the original rectangle $R$, each of which is the corner of exactly one of the smaller rectangles, - $B$, which contains points where exactly two of the rectangles have a common corner (T-junctions, see the figure below), - $C$, which contains points where four of the rectangles have a common corner (crossings, see the figure below).  Figure 1: A T-junction and a crossing We denote the number of points in $B$ by $b$ and the number of points in $C$ by $c$. Since each of the $k$ rectangles has exactly four corners, we get $$ 4 k=4+2 b+4 c $$ It follows that $2 b \leqslant 4 k-4$, so $b \leqslant 2 k-2$. Each of the $n$ given points has to lie on a side of one of the smaller rectangles (but not of the original rectangle $R$ ). If we extend this side as far as possible along borders between rectangles, we obtain a line segment whose ends are T-junctions. Note that every point in $B$ can only be an endpoint of at most one such segment containing one of the given points, since it is stated that no two of them lie on a common line parallel to the sides of $R$. This means that $$ b \geqslant 2 n $$ Combining our two inequalities for $b$, we get $$ 2 k-2 \geqslant b \geqslant 2 n $$ thus $k \geqslant n+1$, which is what we wanted to prove.
|
{
"resource_path": "IMO/segmented/en-IMO2014SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8079784e-778a-5265-bf1a-7b396d8da355
| 24,403
|
Let $n$ points be given inside a rectangle $R$ such that no two of them lie on a line parallel to one of the sides of $R$. The rectangle $R$ is to be dissected into smaller rectangles with sides parallel to the sides of $R$ in such a way that none of these rectangles contains any of the given points in its interior. Prove that we have to dissect $R$ into at least $n+1$ smaller rectangles. (Serbia)
|
Let $k$ denote the number of rectangles. In the following, we refer to the directions of the sides of $R$ as 'horizontal' and 'vertical' respectively. Our goal is to prove the inequality $k \geqslant n+1$ for fixed $n$. Equivalently, we can prove the inequality $n \leqslant k-1$ for each $k$, which will be done by induction on $k$. For $k=1$, the statement is trivial. Now assume that $k>1$. If none of the line segments that form the borders between the rectangles is horizontal, then we have $k-1$ vertical segments dividing $R$ into $k$ rectangles. On each of them, there can only be one of the $n$ points, so $n \leqslant k-1$, which is exactly what we want to prove. Otherwise, consider the lowest horizontal line $h$ that contains one or more of these line segments. Let $R^{\prime}$ be the rectangle that results when everything that lies below $h$ is removed from $R$ (see the example in the figure below). The rectangles that lie entirely below $h$ form blocks of rectangles separated by vertical line segments. Suppose there are $r$ blocks and $k_{i}$ rectangles in the $i^{\text {th }}$ block. The left and right border of each block has to extend further upwards beyond $h$. Thus we can move any points that lie on these borders upwards, so that they now lie inside $R^{\prime}$. This can be done without violating the conditions, one only needs to make sure that they do not get to lie on a common horizontal line with one of the other given points. All other borders between rectangles in the $i^{\text {th }}$ block have to lie entirely below $h$. There are $k_{i}-1$ such line segments, each of which can contain at most one of the given points. Finally, there can be one point that lies on $h$. All other points have to lie in $R^{\prime}$ (after moving some of them as explained in the previous paragraph).  Figure 2: Illustration of the inductive argument We see that $R^{\prime}$ is divided into $k-\sum_{i=1}^{r} k_{i}$ rectangles. Applying the induction hypothesis to $R^{\prime}$, we find that there are at most $$ \left(k-\sum_{i=1}^{r} k_{i}\right)-1+\sum_{i=1}^{r}\left(k_{i}-1\right)+1=k-r $$ points. Since $r \geqslant 1$, this means that $n \leqslant k-1$, which completes our induction.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ points be given inside a rectangle $R$ such that no two of them lie on a line parallel to one of the sides of $R$. The rectangle $R$ is to be dissected into smaller rectangles with sides parallel to the sides of $R$ in such a way that none of these rectangles contains any of the given points in its interior. Prove that we have to dissect $R$ into at least $n+1$ smaller rectangles. (Serbia)
|
Let $k$ denote the number of rectangles. In the following, we refer to the directions of the sides of $R$ as 'horizontal' and 'vertical' respectively. Our goal is to prove the inequality $k \geqslant n+1$ for fixed $n$. Equivalently, we can prove the inequality $n \leqslant k-1$ for each $k$, which will be done by induction on $k$. For $k=1$, the statement is trivial. Now assume that $k>1$. If none of the line segments that form the borders between the rectangles is horizontal, then we have $k-1$ vertical segments dividing $R$ into $k$ rectangles. On each of them, there can only be one of the $n$ points, so $n \leqslant k-1$, which is exactly what we want to prove. Otherwise, consider the lowest horizontal line $h$ that contains one or more of these line segments. Let $R^{\prime}$ be the rectangle that results when everything that lies below $h$ is removed from $R$ (see the example in the figure below). The rectangles that lie entirely below $h$ form blocks of rectangles separated by vertical line segments. Suppose there are $r$ blocks and $k_{i}$ rectangles in the $i^{\text {th }}$ block. The left and right border of each block has to extend further upwards beyond $h$. Thus we can move any points that lie on these borders upwards, so that they now lie inside $R^{\prime}$. This can be done without violating the conditions, one only needs to make sure that they do not get to lie on a common horizontal line with one of the other given points. All other borders between rectangles in the $i^{\text {th }}$ block have to lie entirely below $h$. There are $k_{i}-1$ such line segments, each of which can contain at most one of the given points. Finally, there can be one point that lies on $h$. All other points have to lie in $R^{\prime}$ (after moving some of them as explained in the previous paragraph).  Figure 2: Illustration of the inductive argument We see that $R^{\prime}$ is divided into $k-\sum_{i=1}^{r} k_{i}$ rectangles. Applying the induction hypothesis to $R^{\prime}$, we find that there are at most $$ \left(k-\sum_{i=1}^{r} k_{i}\right)-1+\sum_{i=1}^{r}\left(k_{i}-1\right)+1=k-r $$ points. Since $r \geqslant 1$, this means that $n \leqslant k-1$, which completes our induction.
|
{
"resource_path": "IMO/segmented/en-IMO2014SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8079784e-778a-5265-bf1a-7b396d8da355
| 24,403
|
Let $M$ be a set of $n \geqslant 4$ points in the plane, no three of which are collinear. Initially these points are connected with $n$ segments so that each point in $M$ is the endpoint of exactly two segments. Then, at each step, one may choose two segments $A B$ and $C D$ sharing a common interior point and replace them by the segments $A C$ and $B D$ if none of them is present at this moment. Prove that it is impossible to perform $n^{3} / 4$ or more such moves. (Russia)
|
A line is said to be red if it contains two points of $M$. As no three points of $M$ are collinear, each red line determines a unique pair of points of $M$. Moreover, there are precisely $\binom{n}{2}<\frac{n^{2}}{2}$ red lines. By the value of a segment we mean the number of red lines intersecting it in its interior, and the value of a set of segments is defined to be the sum of the values of its elements. We will prove that $(i)$ the value of the initial set of segments is smaller than $n^{3} / 2$ and that (ii) each step decreases the value of the set of segments present by at least 2 . Since such a value can never be negative, these two assertions imply the statement of the problem. To show $(i)$ we just need to observe that each segment has a value that is smaller than $n^{2} / 2$. Thus the combined value of the $n$ initial segments is indeed below $n \cdot n^{2} / 2=n^{3} / 2$. It remains to establish (ii). Suppose that at some moment we have two segments $A B$ and $C D$ sharing an interior point $S$, and that at the next moment we have the two segments $A C$ and $B D$ instead. Let $X_{A B}$ denote the set of red lines intersecting the segment $A B$ in its interior and let the sets $X_{A C}, X_{B D}$, and $X_{C D}$ be defined similarly. We are to prove that $\left|X_{A C}\right|+\left|X_{B D}\right|+2 \leqslant\left|X_{A B}\right|+\left|X_{C D}\right|$. As a first step in this direction, we claim that $$ \left|X_{A C} \cup X_{B D}\right|+2 \leqslant\left|X_{A B} \cup X_{C D}\right| . $$ Indeed, if $g$ is a red line intersecting, e.g. the segment $A C$ in its interior, then it has to intersect the triangle $A C S$ once again, either in the interior of its side $A S$, or in the interior of its side $C S$, or at $S$, meaning that it belongs to $X_{A B}$ or to $X_{C D}$ (see Figure 1). Moreover, the red lines $A B$ and $C D$ contribute to $X_{A B} \cup X_{C D}$ but not to $X_{A C} \cup X_{B D}$. Thereby (1) is proved.  Figure 1  Figure 2  Figure 3 Similarly but more easily one obtains $$ \left|X_{A C} \cap X_{B D}\right| \leqslant\left|X_{A B} \cap X_{C D}\right| $$ Indeed, a red line $h$ appearing in $X_{A C} \cap X_{B D}$ belongs, for similar reasons as above, also to $X_{A B} \cap X_{C D}$. To make the argument precise, one may just distinguish the cases $S \in h$ (see Figure 2) and $S \notin h$ (see Figure 3). Thereby (2) is proved. Adding (1) and (2) we obtain the desired conclusion, thus completing the solution of this problem. Comment 1. There is a problem belonging to the folklore, in the solution of which one may use the same kind of operation: Given $n$ red and $n$ green points in the plane, prove that one may draw $n$ nonintersecting segments each of which connects a red point with a green point. A standard approach to this problem consists in taking $n$ arbitrary segments connecting the red points with the green points, and to perform the same operation as in the above proposal whenever an intersection occurs. Now each time one performs such a step, the total length of the segments that are present decreases due to the triangle inequality. So, as there are only finitely many possibilities for the set of segments present, the process must end at some stage. In the above proposal, however, considering the sum of the Euclidean lengths of the segment that are present does not seem to help much, for even though it shows that the process must necessarily terminate after some finite number of steps, it does not seem to easily yield any upper bound on the number of these steps that grows polynomially with $n$. One may regard the concept of the value of a segment introduced in the above solution as an appropriately discretised version of Euclidean length suitable for obtaining such a bound. The Problem Selection Committee still believes the problem to be sufficiently original for the competition. Comment 2. There are some other essentially equivalent ways of presenting the same solution. E.g., put $M=\left\{A_{1}, A_{2}, \ldots, A_{n}\right\}$, denote the set of segments present at any moment by $\left\{e_{1}, e_{2}, \ldots, e_{n}\right\}$, and called a triple $(i, j, k)$ of indices with $i \neq j$ intersecting, if the line $A_{i} A_{j}$ intersects the segment $e_{k}$. It may then be shown that the number $S$ of intersecting triples satisfies $0 \leqslant S<n^{3}$ at the beginning and decreases by at least 4 in each step. Comment 3. It is not difficult to construct an example where $c n^{2}$ moves are possible (for some absolute constant $c>0$ ). It would be interesting to say more about the gap between $c n^{2}$ and $c n^{3}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $M$ be a set of $n \geqslant 4$ points in the plane, no three of which are collinear. Initially these points are connected with $n$ segments so that each point in $M$ is the endpoint of exactly two segments. Then, at each step, one may choose two segments $A B$ and $C D$ sharing a common interior point and replace them by the segments $A C$ and $B D$ if none of them is present at this moment. Prove that it is impossible to perform $n^{3} / 4$ or more such moves. (Russia)
|
A line is said to be red if it contains two points of $M$. As no three points of $M$ are collinear, each red line determines a unique pair of points of $M$. Moreover, there are precisely $\binom{n}{2}<\frac{n^{2}}{2}$ red lines. By the value of a segment we mean the number of red lines intersecting it in its interior, and the value of a set of segments is defined to be the sum of the values of its elements. We will prove that $(i)$ the value of the initial set of segments is smaller than $n^{3} / 2$ and that (ii) each step decreases the value of the set of segments present by at least 2 . Since such a value can never be negative, these two assertions imply the statement of the problem. To show $(i)$ we just need to observe that each segment has a value that is smaller than $n^{2} / 2$. Thus the combined value of the $n$ initial segments is indeed below $n \cdot n^{2} / 2=n^{3} / 2$. It remains to establish (ii). Suppose that at some moment we have two segments $A B$ and $C D$ sharing an interior point $S$, and that at the next moment we have the two segments $A C$ and $B D$ instead. Let $X_{A B}$ denote the set of red lines intersecting the segment $A B$ in its interior and let the sets $X_{A C}, X_{B D}$, and $X_{C D}$ be defined similarly. We are to prove that $\left|X_{A C}\right|+\left|X_{B D}\right|+2 \leqslant\left|X_{A B}\right|+\left|X_{C D}\right|$. As a first step in this direction, we claim that $$ \left|X_{A C} \cup X_{B D}\right|+2 \leqslant\left|X_{A B} \cup X_{C D}\right| . $$ Indeed, if $g$ is a red line intersecting, e.g. the segment $A C$ in its interior, then it has to intersect the triangle $A C S$ once again, either in the interior of its side $A S$, or in the interior of its side $C S$, or at $S$, meaning that it belongs to $X_{A B}$ or to $X_{C D}$ (see Figure 1). Moreover, the red lines $A B$ and $C D$ contribute to $X_{A B} \cup X_{C D}$ but not to $X_{A C} \cup X_{B D}$. Thereby (1) is proved.  Figure 1  Figure 2  Figure 3 Similarly but more easily one obtains $$ \left|X_{A C} \cap X_{B D}\right| \leqslant\left|X_{A B} \cap X_{C D}\right| $$ Indeed, a red line $h$ appearing in $X_{A C} \cap X_{B D}$ belongs, for similar reasons as above, also to $X_{A B} \cap X_{C D}$. To make the argument precise, one may just distinguish the cases $S \in h$ (see Figure 2) and $S \notin h$ (see Figure 3). Thereby (2) is proved. Adding (1) and (2) we obtain the desired conclusion, thus completing the solution of this problem. Comment 1. There is a problem belonging to the folklore, in the solution of which one may use the same kind of operation: Given $n$ red and $n$ green points in the plane, prove that one may draw $n$ nonintersecting segments each of which connects a red point with a green point. A standard approach to this problem consists in taking $n$ arbitrary segments connecting the red points with the green points, and to perform the same operation as in the above proposal whenever an intersection occurs. Now each time one performs such a step, the total length of the segments that are present decreases due to the triangle inequality. So, as there are only finitely many possibilities for the set of segments present, the process must end at some stage. In the above proposal, however, considering the sum of the Euclidean lengths of the segment that are present does not seem to help much, for even though it shows that the process must necessarily terminate after some finite number of steps, it does not seem to easily yield any upper bound on the number of these steps that grows polynomially with $n$. One may regard the concept of the value of a segment introduced in the above solution as an appropriately discretised version of Euclidean length suitable for obtaining such a bound. The Problem Selection Committee still believes the problem to be sufficiently original for the competition. Comment 2. There are some other essentially equivalent ways of presenting the same solution. E.g., put $M=\left\{A_{1}, A_{2}, \ldots, A_{n}\right\}$, denote the set of segments present at any moment by $\left\{e_{1}, e_{2}, \ldots, e_{n}\right\}$, and called a triple $(i, j, k)$ of indices with $i \neq j$ intersecting, if the line $A_{i} A_{j}$ intersects the segment $e_{k}$. It may then be shown that the number $S$ of intersecting triples satisfies $0 \leqslant S<n^{3}$ at the beginning and decreases by at least 4 in each step. Comment 3. It is not difficult to construct an example where $c n^{2}$ moves are possible (for some absolute constant $c>0$ ). It would be interesting to say more about the gap between $c n^{2}$ and $c n^{3}$.
|
{
"resource_path": "IMO/segmented/en-IMO2014SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
ec23ba44-964e-5419-be24-cdd20cff987e
| 24,425
|
There are $n$ circles drawn on a piece of paper in such a way that any two circles intersect in two points, and no three circles pass through the same point. Turbo the snail slides along the circles in the following fashion. Initially he moves on one of the circles in clockwise direction. Turbo always keeps sliding along the current circle until he reaches an intersection with another circle. Then he continues his journey on this new circle and also changes the direction of moving, i.e. from clockwise to anticlockwise or vice versa. Suppose that Turbo's path entirely covers all circles. Prove that $n$ must be odd.
|
Replace every cross (i.e. intersection of two circles) by two small circle arcs that indicate the direction in which the snail should leave the cross (see Figure 1.1). Notice that the placement of the small arcs does not depend on the direction of moving on the curves; no matter which direction the snail is moving on the circle arcs, he will follow the same curves (see Figure 1.2). In this way we have a set of curves, that are the possible paths of the snail. Call these curves snail orbits or just orbits. Every snail orbit is a simple closed curve that has no intersection with any other orbit.  Figure 1.1  Figure 1.2 We prove the following, more general statement. (*) In any configuration of $n$ circles such that no two of them are tangent, the number of snail orbits has the same parity as the number $n$. (Note that it is not assumed that all circle pairs intersect.) This immediately solves the problem. Let us introduce the following operation that will be called flipping a cross. At a cross, remove the two small arcs of the orbits, and replace them by the other two arcs. Hence, when the snail arrives at a flipped cross, he will continue on the other circle as before, but he will preserve the orientation in which he goes along the circle arcs (see Figure 2).  Figure 2 Consider what happens to the number of orbits when a cross is flipped. Denote by $a, b, c$, and $d$ the four arcs that meet at the cross such that $a$ and $b$ belong to the same circle. Before the flipping $a$ and $b$ were connected to $c$ and $d$, respectively, and after the flipping $a$ and $b$ are connected to $d$ and $c$, respectively. The orbits passing through the cross are closed curves, so each of the $\operatorname{arcs} a, b, c$, and $d$ is connected to another one by orbits outside the cross. We distinguish three cases. Case 1: $a$ is connected to $b$ and $c$ is connected to $d$ by the orbits outside the cross (see Figure 3.1). We show that this case is impossible. Remove the two small arcs at the cross, connect $a$ to $b$, and connect $c$ to $d$ at the cross. Let $\gamma$ be the new closed curve containing $a$ and $b$, and let $\delta$ be the new curve that connects $c$ and $d$. These two curves intersect at the cross. So one of $c$ and $d$ is inside $\gamma$ and the other one is outside $\gamma$. Then the two closed curves have to meet at least one more time, but this is a contradiction, since no orbit can intersect itself.  Figure 3.1  Figure 3.2  Figure 3.3 Case 2: $a$ is connected to $c$ and $b$ is connected to $d$ (see Figure 3.2). Before the flipping $a$ and $c$ belong to one orbit and $b$ and $d$ belong to another orbit. Flipping the cross merges the two orbits into a single orbit. Hence, the number of orbits decreases by 1. Case 3: $a$ is connected to $d$ and $b$ is connected to $c$ (see Figure 3.3). Before the flipping the arcs $a, b, c$, and $d$ belong to a single orbit. Flipping the cross splits that orbit in two. The number of orbits increases by 1. As can be seen, every flipping decreases or increases the number of orbits by one, thus changes its parity. Now flip every cross, one by one. Since every pair of circles has 0 or 2 intersections, the number of crosses is even. Therefore, when all crosses have been flipped, the original parity of the number of orbits is restored. So it is sufficient to prove (*) for the new configuration, where all crosses are flipped. Of course also in this new configuration the (modified) orbits are simple closed curves not intersecting each other. Orient the orbits in such a way that the snail always moves anticlockwise along the circle arcs. Figure 4 shows the same circles as in Figure 1 after flipping all crosses and adding orientation. (Note that this orientation may be different from the orientation of the orbit as a planar curve; the orientation of every orbit may be negative as well as positive, like the middle orbit in Figure 4.) If the snail moves around an orbit, the total angle change in his moving direction, the total curvature, is either $+2 \pi$ or $-2 \pi$, depending on the orientation of the orbit. Let $P$ and $N$ be the number of orbits with positive and negative orientation, respectively. Then the total curvature of all orbits is $(P-N) \cdot 2 \pi$.  Figure 4  Figure 5 Double-count the total curvature of all orbits. Along every circle the total curvature is $2 \pi$. At every cross, the two turnings make two changes with some angles having the same absolute value but opposite signs, as depicted in Figure 5. So the changes in the direction at the crosses cancel out. Hence, the total curvature is $n \cdot 2 \pi$. Now we have $(P-N) \cdot 2 \pi=n \cdot 2 \pi$, so $P-N=n$. The number of (modified) orbits is $P+N$, that has a same parity as $P-N=n$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
There are $n$ circles drawn on a piece of paper in such a way that any two circles intersect in two points, and no three circles pass through the same point. Turbo the snail slides along the circles in the following fashion. Initially he moves on one of the circles in clockwise direction. Turbo always keeps sliding along the current circle until he reaches an intersection with another circle. Then he continues his journey on this new circle and also changes the direction of moving, i.e. from clockwise to anticlockwise or vice versa. Suppose that Turbo's path entirely covers all circles. Prove that $n$ must be odd.
|
Replace every cross (i.e. intersection of two circles) by two small circle arcs that indicate the direction in which the snail should leave the cross (see Figure 1.1). Notice that the placement of the small arcs does not depend on the direction of moving on the curves; no matter which direction the snail is moving on the circle arcs, he will follow the same curves (see Figure 1.2). In this way we have a set of curves, that are the possible paths of the snail. Call these curves snail orbits or just orbits. Every snail orbit is a simple closed curve that has no intersection with any other orbit.  Figure 1.1  Figure 1.2 We prove the following, more general statement. (*) In any configuration of $n$ circles such that no two of them are tangent, the number of snail orbits has the same parity as the number $n$. (Note that it is not assumed that all circle pairs intersect.) This immediately solves the problem. Let us introduce the following operation that will be called flipping a cross. At a cross, remove the two small arcs of the orbits, and replace them by the other two arcs. Hence, when the snail arrives at a flipped cross, he will continue on the other circle as before, but he will preserve the orientation in which he goes along the circle arcs (see Figure 2).  Figure 2 Consider what happens to the number of orbits when a cross is flipped. Denote by $a, b, c$, and $d$ the four arcs that meet at the cross such that $a$ and $b$ belong to the same circle. Before the flipping $a$ and $b$ were connected to $c$ and $d$, respectively, and after the flipping $a$ and $b$ are connected to $d$ and $c$, respectively. The orbits passing through the cross are closed curves, so each of the $\operatorname{arcs} a, b, c$, and $d$ is connected to another one by orbits outside the cross. We distinguish three cases. Case 1: $a$ is connected to $b$ and $c$ is connected to $d$ by the orbits outside the cross (see Figure 3.1). We show that this case is impossible. Remove the two small arcs at the cross, connect $a$ to $b$, and connect $c$ to $d$ at the cross. Let $\gamma$ be the new closed curve containing $a$ and $b$, and let $\delta$ be the new curve that connects $c$ and $d$. These two curves intersect at the cross. So one of $c$ and $d$ is inside $\gamma$ and the other one is outside $\gamma$. Then the two closed curves have to meet at least one more time, but this is a contradiction, since no orbit can intersect itself.  Figure 3.1  Figure 3.2  Figure 3.3 Case 2: $a$ is connected to $c$ and $b$ is connected to $d$ (see Figure 3.2). Before the flipping $a$ and $c$ belong to one orbit and $b$ and $d$ belong to another orbit. Flipping the cross merges the two orbits into a single orbit. Hence, the number of orbits decreases by 1. Case 3: $a$ is connected to $d$ and $b$ is connected to $c$ (see Figure 3.3). Before the flipping the arcs $a, b, c$, and $d$ belong to a single orbit. Flipping the cross splits that orbit in two. The number of orbits increases by 1. As can be seen, every flipping decreases or increases the number of orbits by one, thus changes its parity. Now flip every cross, one by one. Since every pair of circles has 0 or 2 intersections, the number of crosses is even. Therefore, when all crosses have been flipped, the original parity of the number of orbits is restored. So it is sufficient to prove (*) for the new configuration, where all crosses are flipped. Of course also in this new configuration the (modified) orbits are simple closed curves not intersecting each other. Orient the orbits in such a way that the snail always moves anticlockwise along the circle arcs. Figure 4 shows the same circles as in Figure 1 after flipping all crosses and adding orientation. (Note that this orientation may be different from the orientation of the orbit as a planar curve; the orientation of every orbit may be negative as well as positive, like the middle orbit in Figure 4.) If the snail moves around an orbit, the total angle change in his moving direction, the total curvature, is either $+2 \pi$ or $-2 \pi$, depending on the orientation of the orbit. Let $P$ and $N$ be the number of orbits with positive and negative orientation, respectively. Then the total curvature of all orbits is $(P-N) \cdot 2 \pi$.  Figure 4  Figure 5 Double-count the total curvature of all orbits. Along every circle the total curvature is $2 \pi$. At every cross, the two turnings make two changes with some angles having the same absolute value but opposite signs, as depicted in Figure 5. So the changes in the direction at the crosses cancel out. Hence, the total curvature is $n \cdot 2 \pi$. Now we have $(P-N) \cdot 2 \pi=n \cdot 2 \pi$, so $P-N=n$. The number of (modified) orbits is $P+N$, that has a same parity as $P-N=n$.
|
{
"resource_path": "IMO/segmented/en-IMO2014SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
c4ce9bce-6fee-580f-b640-58afe14418ae
| 24,430
|
The points $P$ and $Q$ are chosen on the side $B C$ of an acute-angled triangle $A B C$ so that $\angle P A B=\angle A C B$ and $\angle Q A C=\angle C B A$. The points $M$ and $N$ are taken on the rays $A P$ and $A Q$, respectively, so that $A P=P M$ and $A Q=Q N$. Prove that the lines $B M$ and $C N$ intersect on the circumcircle of the triangle $A B C$. (Georgia)
|
Denote by $S$ the intersection point of the lines $B M$ and $C N$. Let moreover $\beta=\angle Q A C=\angle C B A$ and $\gamma=\angle P A B=\angle A C B$. From these equalities it follows that the triangles $A B P$ and $C A Q$ are similar (see Figure 1). Therefore we obtain $$ \frac{B P}{P M}=\frac{B P}{P A}=\frac{A Q}{Q C}=\frac{N Q}{Q C} $$ Moreover, $$ \angle B P M=\beta+\gamma=\angle C Q N $$ Hence the triangles $B P M$ and $N Q C$ are similar. This gives $\angle B M P=\angle N C Q$, so the triangles $B P M$ and $B S C$ are also similar. Thus we get $$ \angle C S B=\angle B P M=\beta+\gamma=180^{\circ}-\angle B A C, $$ which completes the solution. 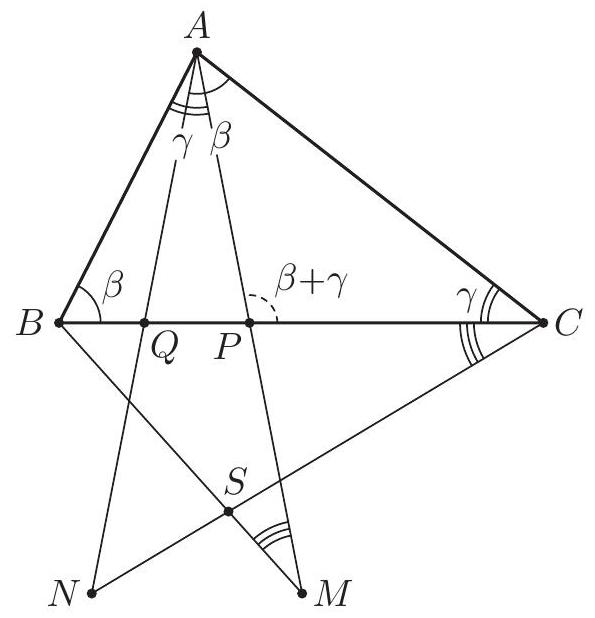 Figure 1 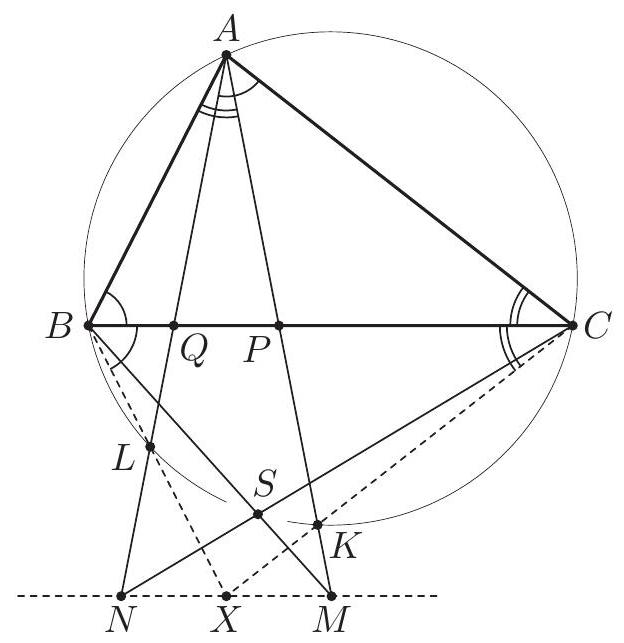 Figure 2
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The points $P$ and $Q$ are chosen on the side $B C$ of an acute-angled triangle $A B C$ so that $\angle P A B=\angle A C B$ and $\angle Q A C=\angle C B A$. The points $M$ and $N$ are taken on the rays $A P$ and $A Q$, respectively, so that $A P=P M$ and $A Q=Q N$. Prove that the lines $B M$ and $C N$ intersect on the circumcircle of the triangle $A B C$. (Georgia)
|
Denote by $S$ the intersection point of the lines $B M$ and $C N$. Let moreover $\beta=\angle Q A C=\angle C B A$ and $\gamma=\angle P A B=\angle A C B$. From these equalities it follows that the triangles $A B P$ and $C A Q$ are similar (see Figure 1). Therefore we obtain $$ \frac{B P}{P M}=\frac{B P}{P A}=\frac{A Q}{Q C}=\frac{N Q}{Q C} $$ Moreover, $$ \angle B P M=\beta+\gamma=\angle C Q N $$ Hence the triangles $B P M$ and $N Q C$ are similar. This gives $\angle B M P=\angle N C Q$, so the triangles $B P M$ and $B S C$ are also similar. Thus we get $$ \angle C S B=\angle B P M=\beta+\gamma=180^{\circ}-\angle B A C, $$ which completes the solution.  Figure 1  Figure 2
|
{
"resource_path": "IMO/segmented/en-IMO2014SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
0e088bcc-2942-52ac-8c66-7c7396f35b33
| 24,435
|
The points $P$ and $Q$ are chosen on the side $B C$ of an acute-angled triangle $A B C$ so that $\angle P A B=\angle A C B$ and $\angle Q A C=\angle C B A$. The points $M$ and $N$ are taken on the rays $A P$ and $A Q$, respectively, so that $A P=P M$ and $A Q=Q N$. Prove that the lines $B M$ and $C N$ intersect on the circumcircle of the triangle $A B C$. (Georgia)
|
As in the previous solution, denote by $S$ the intersection point of the lines $B M$ and $N C$. Let moreover the circumcircle of the triangle $A B C$ intersect the lines $A P$ and $A Q$ again at $K$ and $L$, respectively (see Figure 2). Note that $\angle L B C=\angle L A C=\angle C B A$ and similarly $\angle K C B=\angle K A B=\angle B C A$. It implies that the lines $B L$ and $C K$ meet at a point $X$, being symmetric to the point $A$ with respect to the line $B C$. Since $A P=P M$ and $A Q=Q N$, it follows that $X$ lies on the line $M N$. Therefore, using Pascal's theorem for the hexagon $A L B S C K$, we infer that $S$ lies on the circumcircle of the triangle $A B C$, which finishes the proof. Comment. Both solutions can be modified to obtain a more general result, with the equalities $$ A P=P M \quad \text { and } \quad A Q=Q N $$ replaced by $$ \frac{A P}{P M}=\frac{Q N}{A Q} $$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The points $P$ and $Q$ are chosen on the side $B C$ of an acute-angled triangle $A B C$ so that $\angle P A B=\angle A C B$ and $\angle Q A C=\angle C B A$. The points $M$ and $N$ are taken on the rays $A P$ and $A Q$, respectively, so that $A P=P M$ and $A Q=Q N$. Prove that the lines $B M$ and $C N$ intersect on the circumcircle of the triangle $A B C$. (Georgia)
|
As in the previous solution, denote by $S$ the intersection point of the lines $B M$ and $N C$. Let moreover the circumcircle of the triangle $A B C$ intersect the lines $A P$ and $A Q$ again at $K$ and $L$, respectively (see Figure 2). Note that $\angle L B C=\angle L A C=\angle C B A$ and similarly $\angle K C B=\angle K A B=\angle B C A$. It implies that the lines $B L$ and $C K$ meet at a point $X$, being symmetric to the point $A$ with respect to the line $B C$. Since $A P=P M$ and $A Q=Q N$, it follows that $X$ lies on the line $M N$. Therefore, using Pascal's theorem for the hexagon $A L B S C K$, we infer that $S$ lies on the circumcircle of the triangle $A B C$, which finishes the proof. Comment. Both solutions can be modified to obtain a more general result, with the equalities $$ A P=P M \quad \text { and } \quad A Q=Q N $$ replaced by $$ \frac{A P}{P M}=\frac{Q N}{A Q} $$
|
{
"resource_path": "IMO/segmented/en-IMO2014SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
0e088bcc-2942-52ac-8c66-7c7396f35b33
| 24,435
|
Let $A B C$ be a triangle. The points $K, L$, and $M$ lie on the segments $B C, C A$, and $A B$, respectively, such that the lines $A K, B L$, and $C M$ intersect in a common point. Prove that it is possible to choose two of the triangles $A L M, B M K$, and $C K L$ whose inradii sum up to at least the inradius of the triangle $A B C$. (Estonia)
|
Denote $$ a=\frac{B K}{K C}, \quad b=\frac{C L}{L A}, \quad c=\frac{A M}{M B} . $$ By Ceva's theorem, $a b c=1$, so we may, without loss of generality, assume that $a \geqslant 1$. Then at least one of the numbers $b$ or $c$ is not greater than 1 . Therefore at least one of the pairs $(a, b)$, $(b, c)$ has its first component not less than 1 and the second one not greater than 1 . Without loss of generality, assume that $1 \leqslant a$ and $b \leqslant 1$. Therefore, we obtain $b c \leqslant 1$ and $1 \leqslant c a$, or equivalently $$ \frac{A M}{M B} \leqslant \frac{L A}{C L} \quad \text { and } \quad \frac{M B}{A M} \leqslant \frac{B K}{K C} . $$ The first inequality implies that the line passing through $M$ and parallel to $B C$ intersects the segment $A L$ at a point $X$ (see Figure 1). Therefore the inradius of the triangle $A L M$ is not less than the inradius $r_{1}$ of triangle $A M X$. Similarly, the line passing through $M$ and parallel to $A C$ intersects the segment $B K$ at a point $Y$, so the inradius of the triangle $B M K$ is not less than the inradius $r_{2}$ of the triangle $B M Y$. Thus, to complete our solution, it is enough to show that $r_{1}+r_{2} \geqslant r$, where $r$ is the inradius of the triangle $A B C$. We prove that in fact $r_{1}+r_{2}=r$. 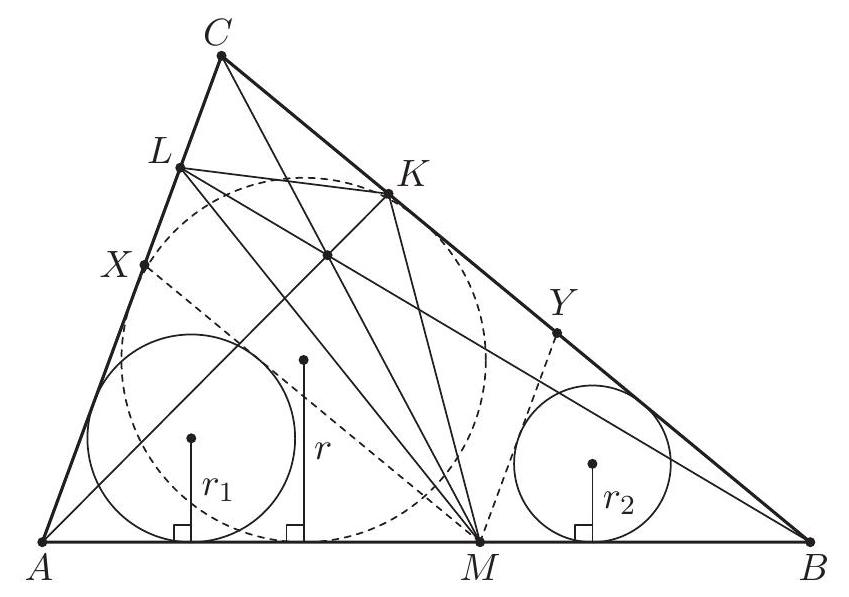 Figure 1 Since $M X \| B C$, the dilation with centre $A$ that takes $M$ to $B$ takes the incircle of the triangle $A M X$ to the incircle of the triangle $A B C$. Therefore $$ \frac{r_{1}}{r}=\frac{A M}{A B}, \quad \text { and similarly } \quad \frac{r_{2}}{r}=\frac{M B}{A B} . $$ Adding these equalities gives $r_{1}+r_{2}=r$, as required. Comment. Alternatively, one can use Desargues' theorem instead of Ceva's theorem, as follows: The lines $A B, B C, C A$ dissect the plane into seven regions. One of them is bounded, and amongst the other six, three are two-sided and three are three-sided. Now define the points $P=B C \cap L M$, $Q=C A \cap M K$, and $R=A B \cap K L$ (in the projective plane). By Desargues' theorem, the points $P$, $Q, R$ lie on a common line $\ell$. This line intersects only unbounded regions. If we now assume (without loss of generality) that $P, Q$ and $R$ lie on $\ell$ in that order, then one of the segments $P Q$ or $Q R$ lies inside a two-sided region. If, for example, this segment is $P Q$, then the triangles $A L M$ and $B M K$ will satisfy the statement of the problem for the same reason.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle. The points $K, L$, and $M$ lie on the segments $B C, C A$, and $A B$, respectively, such that the lines $A K, B L$, and $C M$ intersect in a common point. Prove that it is possible to choose two of the triangles $A L M, B M K$, and $C K L$ whose inradii sum up to at least the inradius of the triangle $A B C$. (Estonia)
|
Denote $$ a=\frac{B K}{K C}, \quad b=\frac{C L}{L A}, \quad c=\frac{A M}{M B} . $$ By Ceva's theorem, $a b c=1$, so we may, without loss of generality, assume that $a \geqslant 1$. Then at least one of the numbers $b$ or $c$ is not greater than 1 . Therefore at least one of the pairs $(a, b)$, $(b, c)$ has its first component not less than 1 and the second one not greater than 1 . Without loss of generality, assume that $1 \leqslant a$ and $b \leqslant 1$. Therefore, we obtain $b c \leqslant 1$ and $1 \leqslant c a$, or equivalently $$ \frac{A M}{M B} \leqslant \frac{L A}{C L} \quad \text { and } \quad \frac{M B}{A M} \leqslant \frac{B K}{K C} . $$ The first inequality implies that the line passing through $M$ and parallel to $B C$ intersects the segment $A L$ at a point $X$ (see Figure 1). Therefore the inradius of the triangle $A L M$ is not less than the inradius $r_{1}$ of triangle $A M X$. Similarly, the line passing through $M$ and parallel to $A C$ intersects the segment $B K$ at a point $Y$, so the inradius of the triangle $B M K$ is not less than the inradius $r_{2}$ of the triangle $B M Y$. Thus, to complete our solution, it is enough to show that $r_{1}+r_{2} \geqslant r$, where $r$ is the inradius of the triangle $A B C$. We prove that in fact $r_{1}+r_{2}=r$.  Figure 1 Since $M X \| B C$, the dilation with centre $A$ that takes $M$ to $B$ takes the incircle of the triangle $A M X$ to the incircle of the triangle $A B C$. Therefore $$ \frac{r_{1}}{r}=\frac{A M}{A B}, \quad \text { and similarly } \quad \frac{r_{2}}{r}=\frac{M B}{A B} . $$ Adding these equalities gives $r_{1}+r_{2}=r$, as required. Comment. Alternatively, one can use Desargues' theorem instead of Ceva's theorem, as follows: The lines $A B, B C, C A$ dissect the plane into seven regions. One of them is bounded, and amongst the other six, three are two-sided and three are three-sided. Now define the points $P=B C \cap L M$, $Q=C A \cap M K$, and $R=A B \cap K L$ (in the projective plane). By Desargues' theorem, the points $P$, $Q, R$ lie on a common line $\ell$. This line intersects only unbounded regions. If we now assume (without loss of generality) that $P, Q$ and $R$ lie on $\ell$ in that order, then one of the segments $P Q$ or $Q R$ lies inside a two-sided region. If, for example, this segment is $P Q$, then the triangles $A L M$ and $B M K$ will satisfy the statement of the problem for the same reason.
|
{
"resource_path": "IMO/segmented/en-IMO2014SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
60b7bfad-4c9c-5163-9bd8-bd89ed63c13c
| 24,439
|
Let $\Omega$ and $O$ be the circumcircle and the circumcentre of an acute-angled triangle $A B C$ with $A B>B C$. The angle bisector of $\angle A B C$ intersects $\Omega$ at $M \neq B$. Let $\Gamma$ be the circle with diameter $B M$. The angle bisectors of $\angle A O B$ and $\angle B O C$ intersect $\Gamma$ at points $P$ and $Q$, respectively. The point $R$ is chosen on the line $P Q$ so that $B R=M R$. Prove that $B R \| A C$. (Russia)
|
Let $K$ be the midpoint of $B M$, i.e., the centre of $\Gamma$. Notice that $A B \neq B C$ implies $K \neq O$. Clearly, the lines $O M$ and $O K$ are the perpendicular bisectors of $A C$ and $B M$, respectively. Therefore, $R$ is the intersection point of $P Q$ and $O K$. Let $N$ be the second point of intersection of $\Gamma$ with the line $O M$. Since $B M$ is a diameter of $\Gamma$, the lines $B N$ and $A C$ are both perpendicular to $O M$. Hence $B N \| A C$, and it suffices to prove that $B N$ passes through $R$. Our plan for doing this is to interpret the lines $B N, O K$, and $P Q$ as the radical axes of three appropriate circles. Let $\omega$ be the circle with diameter $B O$. Since $\angle B N O=\angle B K O=90^{\circ}$, the points $N$ and $K$ lie on $\omega$. Next we show that the points $O, K, P$, and $Q$ are concyclic. To this end, let $D$ and $E$ be the midpoints of $B C$ and $A B$, respectively. Clearly, $D$ and $E$ lie on the rays $O Q$ and $O P$, respectively. By our assumptions about the triangle $A B C$, the points $B, E, O, K$, and $D$ lie in this order on $\omega$. It follows that $\angle E O R=\angle E B K=\angle K B D=\angle K O D$, so the line $K O$ externally bisects the angle $P O Q$. Since the point $K$ is the centre of $\Gamma$, it also lies on the perpendicular bisector of $P Q$. So $K$ coincides with the midpoint of the $\operatorname{arc} P O Q$ of the circumcircle $\gamma$ of triangle $P O Q$. Thus the lines $O K, B N$, and $P Q$ are pairwise radical axes of the circles $\omega, \gamma$, and $\Gamma$. Hence they are concurrent at $R$, as required. 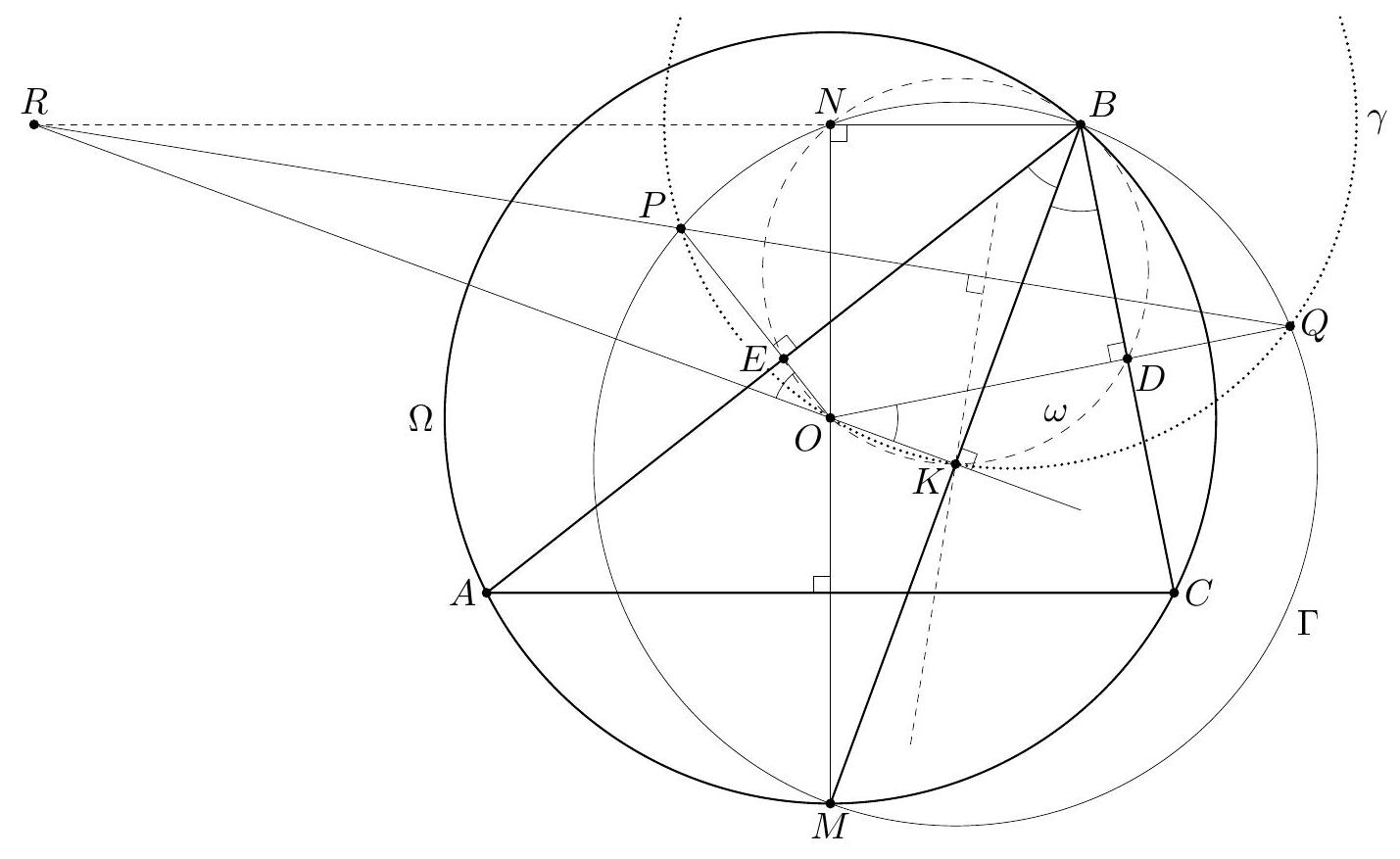
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\Omega$ and $O$ be the circumcircle and the circumcentre of an acute-angled triangle $A B C$ with $A B>B C$. The angle bisector of $\angle A B C$ intersects $\Omega$ at $M \neq B$. Let $\Gamma$ be the circle with diameter $B M$. The angle bisectors of $\angle A O B$ and $\angle B O C$ intersect $\Gamma$ at points $P$ and $Q$, respectively. The point $R$ is chosen on the line $P Q$ so that $B R=M R$. Prove that $B R \| A C$. (Russia)
|
Let $K$ be the midpoint of $B M$, i.e., the centre of $\Gamma$. Notice that $A B \neq B C$ implies $K \neq O$. Clearly, the lines $O M$ and $O K$ are the perpendicular bisectors of $A C$ and $B M$, respectively. Therefore, $R$ is the intersection point of $P Q$ and $O K$. Let $N$ be the second point of intersection of $\Gamma$ with the line $O M$. Since $B M$ is a diameter of $\Gamma$, the lines $B N$ and $A C$ are both perpendicular to $O M$. Hence $B N \| A C$, and it suffices to prove that $B N$ passes through $R$. Our plan for doing this is to interpret the lines $B N, O K$, and $P Q$ as the radical axes of three appropriate circles. Let $\omega$ be the circle with diameter $B O$. Since $\angle B N O=\angle B K O=90^{\circ}$, the points $N$ and $K$ lie on $\omega$. Next we show that the points $O, K, P$, and $Q$ are concyclic. To this end, let $D$ and $E$ be the midpoints of $B C$ and $A B$, respectively. Clearly, $D$ and $E$ lie on the rays $O Q$ and $O P$, respectively. By our assumptions about the triangle $A B C$, the points $B, E, O, K$, and $D$ lie in this order on $\omega$. It follows that $\angle E O R=\angle E B K=\angle K B D=\angle K O D$, so the line $K O$ externally bisects the angle $P O Q$. Since the point $K$ is the centre of $\Gamma$, it also lies on the perpendicular bisector of $P Q$. So $K$ coincides with the midpoint of the $\operatorname{arc} P O Q$ of the circumcircle $\gamma$ of triangle $P O Q$. Thus the lines $O K, B N$, and $P Q$ are pairwise radical axes of the circles $\omega, \gamma$, and $\Gamma$. Hence they are concurrent at $R$, as required. 
|
{
"resource_path": "IMO/segmented/en-IMO2014SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
b4dd3c45-87b7-592c-a09c-bc8d4b00dbbc
| 24,442
|
Consider a fixed circle $\Gamma$ with three fixed points $A, B$, and $C$ on it. Also, let us fix a real number $\lambda \in(0,1)$. For a variable point $P \notin\{A, B, C\}$ on $\Gamma$, let $M$ be the point on the segment $C P$ such that $C M=\lambda \cdot C P$. Let $Q$ be the second point of intersection of the circumcircles of the triangles $A M P$ and $B M C$. Prove that as $P$ varies, the point $Q$ lies on a fixed circle. (United Kingdom)
|
Throughout the solution, we denote by $\Varangle(a, b)$ the directed angle between the lines $a$ and $b$. Let $D$ be the point on the segment $A B$ such that $B D=\lambda \cdot B A$. We will show that either $Q=D$, or $\Varangle(D Q, Q B)=\Varangle(A B, B C)$; this would mean that the point $Q$ varies over the constant circle through $D$ tangent to $B C$ at $B$, as required. Denote the circumcircles of the triangles $A M P$ and $B M C$ by $\omega_{A}$ and $\omega_{B}$, respectively. The lines $A P, B C$, and $M Q$ are pairwise radical axes of the circles $\Gamma, \omega_{A}$, and $\omega_{B}$, thus either they are parallel, or they share a common point $X$. Assume that these lines are parallel (see Figure 1). Then the segments $A P, Q M$, and $B C$ have a common perpendicular bisector; the reflection in this bisector maps the segment $C P$ to $B A$, and maps $M$ to $Q$. Therefore, in this case $Q$ lies on $A B$, and $B Q / A B=C M / C P=$ $B D / A B$; so we have $Q=D$. 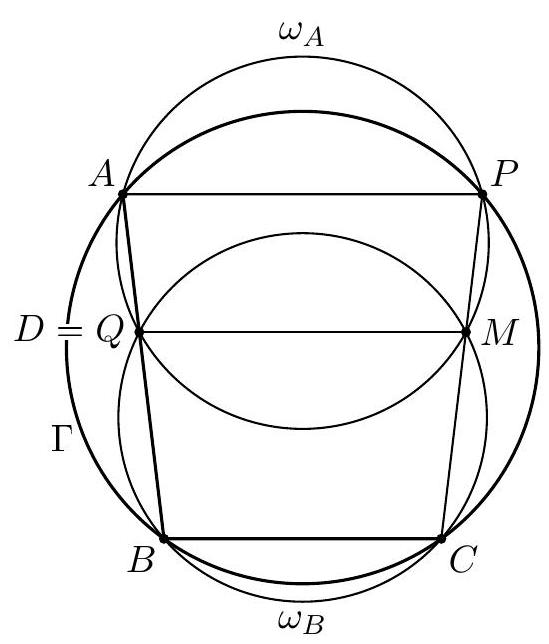 Figure 1  Figure 2 Now assume that the lines $A P, Q M$, and $B C$ are concurrent at some point $X$ (see Figure 2). Notice that the points $A, B, Q$, and $X$ lie on a common circle $\Omega$ by Miquel's theorem applied to the triangle $X P C$. Let us denote by $Y$ the symmetric image of $X$ about the perpendicular bisector of $A B$. Clearly, $Y$ lies on $\Omega$, and the triangles $Y A B$ and $\triangle X B A$ are congruent. Moreover, the triangle $X P C$ is similar to the triangle $X B A$, so it is also similar to the triangle $Y A B$. Next, the points $D$ and $M$ correspond to each other in similar triangles $Y A B$ and $X P C$, since $B D / B A=C M / C P=\lambda$. Moreover, the triangles $Y A B$ and $X P C$ are equi-oriented, so $\Varangle(M X, X P)=\Varangle(D Y, Y A)$. On the other hand, since the points $A, Q, X$, and $Y$ lie on $\Omega$, we have $\Varangle(Q Y, Y A)=\Varangle(M X, X P)$. Therefore, $\Varangle(Q Y, Y A)=\Varangle(D Y, Y A)$, so the points $Y, D$, and $Q$ are collinear. Finally, we have $\Varangle(D Q, Q B)=\Varangle(Y Q, Q B)=\Varangle(Y A, A B)=\Varangle(A B, B X)=\Varangle(A B, B C)$, as desired. Comment. In the original proposal, $\lambda$ was supposed to be an arbitrary real number distinct from 0 and 1, and the point $M$ was defined by $\overrightarrow{C M}=\lambda \cdot \overrightarrow{C P}$. The Problem Selection Committee decided to add the restriction $\lambda \in(0,1)$ in order to avoid a large case distinction.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Consider a fixed circle $\Gamma$ with three fixed points $A, B$, and $C$ on it. Also, let us fix a real number $\lambda \in(0,1)$. For a variable point $P \notin\{A, B, C\}$ on $\Gamma$, let $M$ be the point on the segment $C P$ such that $C M=\lambda \cdot C P$. Let $Q$ be the second point of intersection of the circumcircles of the triangles $A M P$ and $B M C$. Prove that as $P$ varies, the point $Q$ lies on a fixed circle. (United Kingdom)
|
Throughout the solution, we denote by $\Varangle(a, b)$ the directed angle between the lines $a$ and $b$. Let $D$ be the point on the segment $A B$ such that $B D=\lambda \cdot B A$. We will show that either $Q=D$, or $\Varangle(D Q, Q B)=\Varangle(A B, B C)$; this would mean that the point $Q$ varies over the constant circle through $D$ tangent to $B C$ at $B$, as required. Denote the circumcircles of the triangles $A M P$ and $B M C$ by $\omega_{A}$ and $\omega_{B}$, respectively. The lines $A P, B C$, and $M Q$ are pairwise radical axes of the circles $\Gamma, \omega_{A}$, and $\omega_{B}$, thus either they are parallel, or they share a common point $X$. Assume that these lines are parallel (see Figure 1). Then the segments $A P, Q M$, and $B C$ have a common perpendicular bisector; the reflection in this bisector maps the segment $C P$ to $B A$, and maps $M$ to $Q$. Therefore, in this case $Q$ lies on $A B$, and $B Q / A B=C M / C P=$ $B D / A B$; so we have $Q=D$.  Figure 1  Figure 2 Now assume that the lines $A P, Q M$, and $B C$ are concurrent at some point $X$ (see Figure 2). Notice that the points $A, B, Q$, and $X$ lie on a common circle $\Omega$ by Miquel's theorem applied to the triangle $X P C$. Let us denote by $Y$ the symmetric image of $X$ about the perpendicular bisector of $A B$. Clearly, $Y$ lies on $\Omega$, and the triangles $Y A B$ and $\triangle X B A$ are congruent. Moreover, the triangle $X P C$ is similar to the triangle $X B A$, so it is also similar to the triangle $Y A B$. Next, the points $D$ and $M$ correspond to each other in similar triangles $Y A B$ and $X P C$, since $B D / B A=C M / C P=\lambda$. Moreover, the triangles $Y A B$ and $X P C$ are equi-oriented, so $\Varangle(M X, X P)=\Varangle(D Y, Y A)$. On the other hand, since the points $A, Q, X$, and $Y$ lie on $\Omega$, we have $\Varangle(Q Y, Y A)=\Varangle(M X, X P)$. Therefore, $\Varangle(Q Y, Y A)=\Varangle(D Y, Y A)$, so the points $Y, D$, and $Q$ are collinear. Finally, we have $\Varangle(D Q, Q B)=\Varangle(Y Q, Q B)=\Varangle(Y A, A B)=\Varangle(A B, B X)=\Varangle(A B, B C)$, as desired. Comment. In the original proposal, $\lambda$ was supposed to be an arbitrary real number distinct from 0 and 1, and the point $M$ was defined by $\overrightarrow{C M}=\lambda \cdot \overrightarrow{C P}$. The Problem Selection Committee decided to add the restriction $\lambda \in(0,1)$ in order to avoid a large case distinction.
|
{
"resource_path": "IMO/segmented/en-IMO2014SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
84beaef8-6bf1-5df5-b158-c88fc99db1c6
| 24,445
|
Consider a fixed circle $\Gamma$ with three fixed points $A, B$, and $C$ on it. Also, let us fix a real number $\lambda \in(0,1)$. For a variable point $P \notin\{A, B, C\}$ on $\Gamma$, let $M$ be the point on the segment $C P$ such that $C M=\lambda \cdot C P$. Let $Q$ be the second point of intersection of the circumcircles of the triangles $A M P$ and $B M C$. Prove that as $P$ varies, the point $Q$ lies on a fixed circle. (United Kingdom)
|
As in the previous solution, we introduce the radical centre $X=A P \cap B C \cap M Q$ of the circles $\omega_{A}, \omega_{B}$, and $\Gamma$. Next, we also notice that the points $A, Q, B$, and $X$ lie on a common circle $\Omega$. If the point $P$ lies on the arc $B A C$ of $\Gamma$, then the point $X$ is outside $\Gamma$, thus the point $Q$ belongs to the ray $X M$, and therefore the points $P, A$, and $Q$ lie on the same side of $B C$. Otherwise, if $P$ lies on the arc $B C$ not containing $A$, then $X$ lies inside $\Gamma$, so $M$ and $Q$ lie on different sides of $B C$; thus again $Q$ and $A$ lie on the same side of $B C$. So, in each case the points $Q$ and $A$ lie on the same side of $B C$.  Figure 3 Now we prove that the ratio $$ \frac{Q B}{\sin \angle Q B C}=\frac{Q B}{Q X} \cdot \frac{Q X}{\sin \angle Q B X} $$ is constant. Since the points $A, Q, B$, and $X$ are concyclic, we have $$ \frac{Q X}{\sin \angle Q B X}=\frac{A X}{\sin \angle A B C} $$ Next, since the points $B, Q, M$, and $C$ are concyclic, the triangles $X B Q$ and $X M C$ are similar, so $$ \frac{Q B}{Q X}=\frac{C M}{C X}=\lambda \cdot \frac{C P}{C X} $$ Analogously, the triangles $X C P$ and $X A B$ are also similar, so $$ \frac{C P}{C X}=\frac{A B}{A X} $$ Therefore, we obtain $$ \frac{Q B}{\sin \angle Q B C}=\lambda \cdot \frac{A B}{A X} \cdot \frac{A X}{\sin \angle A B C}=\lambda \cdot \frac{A B}{\sin \angle A B C} $$ so this ratio is indeed constant. Thus the circle passing through $Q$ and tangent to $B C$ at $B$ is also constant, and $Q$ varies over this fixed circle. Comment. It is not hard to guess that the desired circle should be tangent to $B C$ at $B$. Indeed, the second paragraph of this solution shows that this circle lies on one side of $B C$; on the other hand, in the limit case $P=B$, the point $Q$ also coincides with $B$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Consider a fixed circle $\Gamma$ with three fixed points $A, B$, and $C$ on it. Also, let us fix a real number $\lambda \in(0,1)$. For a variable point $P \notin\{A, B, C\}$ on $\Gamma$, let $M$ be the point on the segment $C P$ such that $C M=\lambda \cdot C P$. Let $Q$ be the second point of intersection of the circumcircles of the triangles $A M P$ and $B M C$. Prove that as $P$ varies, the point $Q$ lies on a fixed circle. (United Kingdom)
|
As in the previous solution, we introduce the radical centre $X=A P \cap B C \cap M Q$ of the circles $\omega_{A}, \omega_{B}$, and $\Gamma$. Next, we also notice that the points $A, Q, B$, and $X$ lie on a common circle $\Omega$. If the point $P$ lies on the arc $B A C$ of $\Gamma$, then the point $X$ is outside $\Gamma$, thus the point $Q$ belongs to the ray $X M$, and therefore the points $P, A$, and $Q$ lie on the same side of $B C$. Otherwise, if $P$ lies on the arc $B C$ not containing $A$, then $X$ lies inside $\Gamma$, so $M$ and $Q$ lie on different sides of $B C$; thus again $Q$ and $A$ lie on the same side of $B C$. So, in each case the points $Q$ and $A$ lie on the same side of $B C$.  Figure 3 Now we prove that the ratio $$ \frac{Q B}{\sin \angle Q B C}=\frac{Q B}{Q X} \cdot \frac{Q X}{\sin \angle Q B X} $$ is constant. Since the points $A, Q, B$, and $X$ are concyclic, we have $$ \frac{Q X}{\sin \angle Q B X}=\frac{A X}{\sin \angle A B C} $$ Next, since the points $B, Q, M$, and $C$ are concyclic, the triangles $X B Q$ and $X M C$ are similar, so $$ \frac{Q B}{Q X}=\frac{C M}{C X}=\lambda \cdot \frac{C P}{C X} $$ Analogously, the triangles $X C P$ and $X A B$ are also similar, so $$ \frac{C P}{C X}=\frac{A B}{A X} $$ Therefore, we obtain $$ \frac{Q B}{\sin \angle Q B C}=\lambda \cdot \frac{A B}{A X} \cdot \frac{A X}{\sin \angle A B C}=\lambda \cdot \frac{A B}{\sin \angle A B C} $$ so this ratio is indeed constant. Thus the circle passing through $Q$ and tangent to $B C$ at $B$ is also constant, and $Q$ varies over this fixed circle. Comment. It is not hard to guess that the desired circle should be tangent to $B C$ at $B$. Indeed, the second paragraph of this solution shows that this circle lies on one side of $B C$; on the other hand, in the limit case $P=B$, the point $Q$ also coincides with $B$.
|
{
"resource_path": "IMO/segmented/en-IMO2014SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
84beaef8-6bf1-5df5-b158-c88fc99db1c6
| 24,445
|
Consider a fixed circle $\Gamma$ with three fixed points $A, B$, and $C$ on it. Also, let us fix a real number $\lambda \in(0,1)$. For a variable point $P \notin\{A, B, C\}$ on $\Gamma$, let $M$ be the point on the segment $C P$ such that $C M=\lambda \cdot C P$. Let $Q$ be the second point of intersection of the circumcircles of the triangles $A M P$ and $B M C$. Prove that as $P$ varies, the point $Q$ lies on a fixed circle. (United Kingdom)
|
Let us perform an inversion centred at $C$. Denote by $X^{\prime}$ the image of a point $X$ under this inversion. The circle $\Gamma$ maps to the line $\Gamma^{\prime}$ passing through the constant points $A^{\prime}$ and $B^{\prime}$, and containing the variable point $P^{\prime}$. By the problem condition, the point $M$ varies over the circle $\gamma$ which is the homothetic image of $\Gamma$ with centre $C$ and coefficient $\lambda$. Thus $M^{\prime}$ varies over the constant line $\gamma^{\prime} \| A^{\prime} B^{\prime}$ which is the homothetic image of $A^{\prime} B^{\prime}$ with centre $C$ and coefficient $1 / \lambda$, and $M=\gamma^{\prime} \cap C P^{\prime}$. Next, the circumcircles $\omega_{A}$ and $\omega_{B}$ of the triangles $A M P$ and $B M C$ map to the circumcircle $\omega_{A}^{\prime}$ of the triangle $A^{\prime} M^{\prime} P^{\prime}$ and to the line $B^{\prime} M^{\prime}$, respectively; the point $Q$ thus maps to the second point of intersection of $B^{\prime} M^{\prime}$ with $\omega_{A}^{\prime}$ (see Figure 4).  Figure 4 Let $J$ be the (constant) common point of the lines $\gamma^{\prime}$ and $C A^{\prime}$, and let $\ell$ be the (constant) line through $J$ parallel to $C B^{\prime}$. Let $V$ be the common point of the lines $\ell$ and $B^{\prime} M^{\prime}$. Applying Pappus' theorem to the triples $\left(C, J, A^{\prime}\right)$ and $\left(V, B^{\prime}, M^{\prime}\right)$ we get that the points $C B^{\prime} \cap J V$, $J M^{\prime} \cap A^{\prime} B^{\prime}$, and $C M^{\prime} \cap A^{\prime} V$ are collinear. The first two of these points are ideal, hence so is the third, which means that $C M^{\prime} \| A^{\prime} V$. Now we have $\Varangle\left(Q^{\prime} A^{\prime}, A^{\prime} P^{\prime}\right)=\Varangle\left(Q^{\prime} M^{\prime}, M^{\prime} P^{\prime}\right)=\angle\left(V M^{\prime}, A^{\prime} V\right)$, which means that the triangles $B^{\prime} Q^{\prime} A^{\prime}$ and $B^{\prime} A^{\prime} V$ are similar, and $\left(B^{\prime} A^{\prime}\right)^{2}=B^{\prime} Q^{\prime} \cdot B^{\prime} V$. Thus $Q^{\prime}$ is the image of $V$ under the second (fixed) inversion with centre $B^{\prime}$ and radius $B^{\prime} A^{\prime}$. Since $V$ varies over the constant line $\ell, Q^{\prime}$ varies over some constant circle $\Theta$. Thus, applying the first inversion back we get that $Q$ also varies over some fixed circle. One should notice that this last circle is not a line; otherwise $\Theta$ would contain $C$, and thus $\ell$ would contain the image of $C$ under the second inversion. This is impossible, since $C B^{\prime} \| \ell$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Consider a fixed circle $\Gamma$ with three fixed points $A, B$, and $C$ on it. Also, let us fix a real number $\lambda \in(0,1)$. For a variable point $P \notin\{A, B, C\}$ on $\Gamma$, let $M$ be the point on the segment $C P$ such that $C M=\lambda \cdot C P$. Let $Q$ be the second point of intersection of the circumcircles of the triangles $A M P$ and $B M C$. Prove that as $P$ varies, the point $Q$ lies on a fixed circle. (United Kingdom)
|
Let us perform an inversion centred at $C$. Denote by $X^{\prime}$ the image of a point $X$ under this inversion. The circle $\Gamma$ maps to the line $\Gamma^{\prime}$ passing through the constant points $A^{\prime}$ and $B^{\prime}$, and containing the variable point $P^{\prime}$. By the problem condition, the point $M$ varies over the circle $\gamma$ which is the homothetic image of $\Gamma$ with centre $C$ and coefficient $\lambda$. Thus $M^{\prime}$ varies over the constant line $\gamma^{\prime} \| A^{\prime} B^{\prime}$ which is the homothetic image of $A^{\prime} B^{\prime}$ with centre $C$ and coefficient $1 / \lambda$, and $M=\gamma^{\prime} \cap C P^{\prime}$. Next, the circumcircles $\omega_{A}$ and $\omega_{B}$ of the triangles $A M P$ and $B M C$ map to the circumcircle $\omega_{A}^{\prime}$ of the triangle $A^{\prime} M^{\prime} P^{\prime}$ and to the line $B^{\prime} M^{\prime}$, respectively; the point $Q$ thus maps to the second point of intersection of $B^{\prime} M^{\prime}$ with $\omega_{A}^{\prime}$ (see Figure 4).  Figure 4 Let $J$ be the (constant) common point of the lines $\gamma^{\prime}$ and $C A^{\prime}$, and let $\ell$ be the (constant) line through $J$ parallel to $C B^{\prime}$. Let $V$ be the common point of the lines $\ell$ and $B^{\prime} M^{\prime}$. Applying Pappus' theorem to the triples $\left(C, J, A^{\prime}\right)$ and $\left(V, B^{\prime}, M^{\prime}\right)$ we get that the points $C B^{\prime} \cap J V$, $J M^{\prime} \cap A^{\prime} B^{\prime}$, and $C M^{\prime} \cap A^{\prime} V$ are collinear. The first two of these points are ideal, hence so is the third, which means that $C M^{\prime} \| A^{\prime} V$. Now we have $\Varangle\left(Q^{\prime} A^{\prime}, A^{\prime} P^{\prime}\right)=\Varangle\left(Q^{\prime} M^{\prime}, M^{\prime} P^{\prime}\right)=\angle\left(V M^{\prime}, A^{\prime} V\right)$, which means that the triangles $B^{\prime} Q^{\prime} A^{\prime}$ and $B^{\prime} A^{\prime} V$ are similar, and $\left(B^{\prime} A^{\prime}\right)^{2}=B^{\prime} Q^{\prime} \cdot B^{\prime} V$. Thus $Q^{\prime}$ is the image of $V$ under the second (fixed) inversion with centre $B^{\prime}$ and radius $B^{\prime} A^{\prime}$. Since $V$ varies over the constant line $\ell, Q^{\prime}$ varies over some constant circle $\Theta$. Thus, applying the first inversion back we get that $Q$ also varies over some fixed circle. One should notice that this last circle is not a line; otherwise $\Theta$ would contain $C$, and thus $\ell$ would contain the image of $C$ under the second inversion. This is impossible, since $C B^{\prime} \| \ell$.
|
{
"resource_path": "IMO/segmented/en-IMO2014SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
84beaef8-6bf1-5df5-b158-c88fc99db1c6
| 24,445
|
Let $A B C D$ be a convex quadrilateral with $\angle B=\angle D=90^{\circ}$. Point $H$ is the foot of the perpendicular from $A$ to $B D$. The points $S$ and $T$ are chosen on the sides $A B$ and $A D$, respectively, in such a way that $H$ lies inside triangle $S C T$ and $$ \angle S H C-\angle B S C=90^{\circ}, \quad \angle T H C-\angle D T C=90^{\circ} . $$ Prove that the circumcircle of triangle $S H T$ is tangent to the line $B D$. (Iran)
|
Let the line passing through $C$ and perpendicular to the line $S C$ intersect the line $A B$ at $Q$ (see Figure 1). Then $$ \angle S Q C=90^{\circ}-\angle B S C=180^{\circ}-\angle S H C, $$ which implies that the points $C, H, S$, and $Q$ lie on a common circle. Moreover, since $S Q$ is a diameter of this circle, we infer that the circumcentre $K$ of triangle $S H C$ lies on the line $A B$. Similarly, we prove that the circumcentre $L$ of triangle $C H T$ lies on the line $A D$. 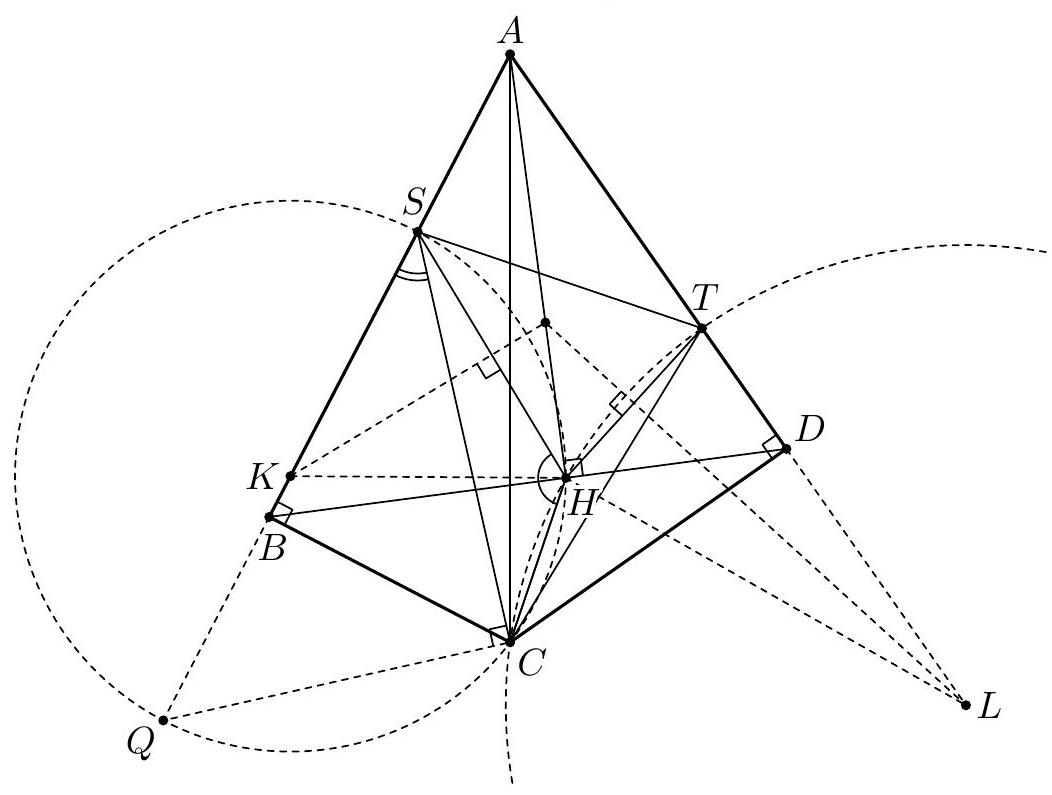 Figure 1 In order to prove that the circumcircle of triangle $S H T$ is tangent to $B D$, it suffices to show that the perpendicular bisectors of $H S$ and $H T$ intersect on the line $A H$. However, these two perpendicular bisectors coincide with the angle bisectors of angles $A K H$ and $A L H$. Therefore, in order to complete the solution, it is enough (by the bisector theorem) to show that $$ \frac{A K}{K H}=\frac{A L}{L H} $$ We present two proofs of this equality. First proof. Let the lines $K L$ and $H C$ intersect at $M$ (see Figure 2). Since $K H=K C$ and $L H=L C$, the points $H$ and $C$ are symmetric to each other with respect to the line $K L$. Therefore $M$ is the midpoint of $H C$. Denote by $O$ the circumcentre of quadrilateral $A B C D$. Then $O$ is the midpoint of $A C$. Therefore we have $O M \| A H$ and hence $O M \perp B D$. This together with the equality $O B=O D$ implies that $O M$ is the perpendicular bisector of $B D$ and therefore $B M=D M$. Since $C M \perp K L$, the points $B, C, M$, and $K$ lie on a common circle with diameter $K C$. Similarly, the points $L, C, M$, and $D$ lie on a circle with diameter $L C$. Thus, using the sine law, we obtain $$ \frac{A K}{A L}=\frac{\sin \angle A L K}{\sin \angle A K L}=\frac{D M}{C L} \cdot \frac{C K}{B M}=\frac{C K}{C L}=\frac{K H}{L H} $$ which finishes the proof of (1). 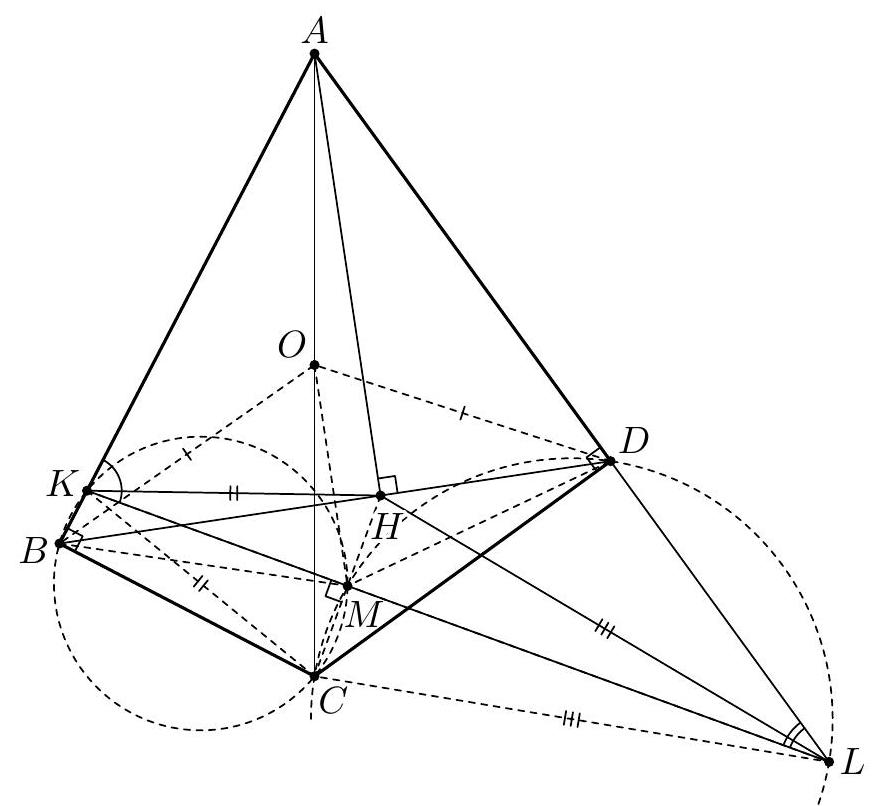 Figure 2 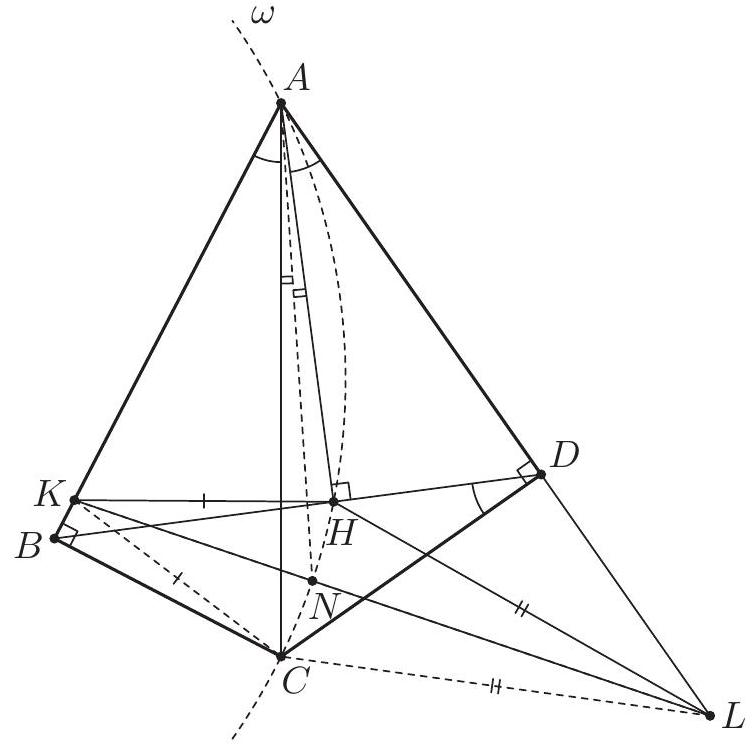 Figure 3 Second proof. If the points $A, H$, and $C$ are collinear, then $A K=A L$ and $K H=L H$, so the equality (1) follows. Assume therefore that the points $A, H$, and $C$ do not lie in a line and consider the circle $\omega$ passing through them (see Figure 3). Since the quadrilateral $A B C D$ is cyclic, $$ \angle B A C=\angle B D C=90^{\circ}-\angle A D H=\angle H A D . $$ Let $N \neq A$ be the intersection point of the circle $\omega$ and the angle bisector of $\angle C A H$. Then $A N$ is also the angle bisector of $\angle B A D$. Since $H$ and $C$ are symmetric to each other with respect to the line $K L$ and $H N=N C$, it follows that both $N$ and the centre of $\omega$ lie on the line $K L$. This means that the circle $\omega$ is an Apollonius circle of the points $K$ and $L$. This immediately yields (1). Comment. Either proof can be used to obtain the following generalised result: Let $A B C D$ be a convex quadrilateral and let $H$ be a point in its interior with $\angle B A C=\angle D A H$. The points $S$ and $T$ are chosen on the sides $A B$ and $A D$, respectively, in such a way that $H$ lies inside triangle SCT and $$ \angle S H C-\angle B S C=90^{\circ}, \quad \angle T H C-\angle D T C=90^{\circ} . $$ Then the circumcentre of triangle SHT lies on the line AH (and moreover the circumcentre of triangle SCT lies on $A C$ ).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral with $\angle B=\angle D=90^{\circ}$. Point $H$ is the foot of the perpendicular from $A$ to $B D$. The points $S$ and $T$ are chosen on the sides $A B$ and $A D$, respectively, in such a way that $H$ lies inside triangle $S C T$ and $$ \angle S H C-\angle B S C=90^{\circ}, \quad \angle T H C-\angle D T C=90^{\circ} . $$ Prove that the circumcircle of triangle $S H T$ is tangent to the line $B D$. (Iran)
|
Let the line passing through $C$ and perpendicular to the line $S C$ intersect the line $A B$ at $Q$ (see Figure 1). Then $$ \angle S Q C=90^{\circ}-\angle B S C=180^{\circ}-\angle S H C, $$ which implies that the points $C, H, S$, and $Q$ lie on a common circle. Moreover, since $S Q$ is a diameter of this circle, we infer that the circumcentre $K$ of triangle $S H C$ lies on the line $A B$. Similarly, we prove that the circumcentre $L$ of triangle $C H T$ lies on the line $A D$.  Figure 1 In order to prove that the circumcircle of triangle $S H T$ is tangent to $B D$, it suffices to show that the perpendicular bisectors of $H S$ and $H T$ intersect on the line $A H$. However, these two perpendicular bisectors coincide with the angle bisectors of angles $A K H$ and $A L H$. Therefore, in order to complete the solution, it is enough (by the bisector theorem) to show that $$ \frac{A K}{K H}=\frac{A L}{L H} $$ We present two proofs of this equality. First proof. Let the lines $K L$ and $H C$ intersect at $M$ (see Figure 2). Since $K H=K C$ and $L H=L C$, the points $H$ and $C$ are symmetric to each other with respect to the line $K L$. Therefore $M$ is the midpoint of $H C$. Denote by $O$ the circumcentre of quadrilateral $A B C D$. Then $O$ is the midpoint of $A C$. Therefore we have $O M \| A H$ and hence $O M \perp B D$. This together with the equality $O B=O D$ implies that $O M$ is the perpendicular bisector of $B D$ and therefore $B M=D M$. Since $C M \perp K L$, the points $B, C, M$, and $K$ lie on a common circle with diameter $K C$. Similarly, the points $L, C, M$, and $D$ lie on a circle with diameter $L C$. Thus, using the sine law, we obtain $$ \frac{A K}{A L}=\frac{\sin \angle A L K}{\sin \angle A K L}=\frac{D M}{C L} \cdot \frac{C K}{B M}=\frac{C K}{C L}=\frac{K H}{L H} $$ which finishes the proof of (1).  Figure 2  Figure 3 Second proof. If the points $A, H$, and $C$ are collinear, then $A K=A L$ and $K H=L H$, so the equality (1) follows. Assume therefore that the points $A, H$, and $C$ do not lie in a line and consider the circle $\omega$ passing through them (see Figure 3). Since the quadrilateral $A B C D$ is cyclic, $$ \angle B A C=\angle B D C=90^{\circ}-\angle A D H=\angle H A D . $$ Let $N \neq A$ be the intersection point of the circle $\omega$ and the angle bisector of $\angle C A H$. Then $A N$ is also the angle bisector of $\angle B A D$. Since $H$ and $C$ are symmetric to each other with respect to the line $K L$ and $H N=N C$, it follows that both $N$ and the centre of $\omega$ lie on the line $K L$. This means that the circle $\omega$ is an Apollonius circle of the points $K$ and $L$. This immediately yields (1). Comment. Either proof can be used to obtain the following generalised result: Let $A B C D$ be a convex quadrilateral and let $H$ be a point in its interior with $\angle B A C=\angle D A H$. The points $S$ and $T$ are chosen on the sides $A B$ and $A D$, respectively, in such a way that $H$ lies inside triangle SCT and $$ \angle S H C-\angle B S C=90^{\circ}, \quad \angle T H C-\angle D T C=90^{\circ} . $$ Then the circumcentre of triangle SHT lies on the line AH (and moreover the circumcentre of triangle SCT lies on $A C$ ).
|
{
"resource_path": "IMO/segmented/en-IMO2014SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
b3fc136c-acc7-502c-86b6-a672c53031a7
| 24,450
|
Let $A B C$ be a fixed acute-angled triangle. Consider some points $E$ and $F$ lying on the sides $A C$ and $A B$, respectively, and let $M$ be the midpoint of $E F$. Let the perpendicular bisector of $E F$ intersect the line $B C$ at $K$, and let the perpendicular bisector of $M K$ intersect the lines $A C$ and $A B$ at $S$ and $T$, respectively. We call the pair $(E, F)$ interesting, if the quadrilateral $K S A T$ is cyclic. Suppose that the pairs $\left(E_{1}, F_{1}\right)$ and $\left(E_{2}, F_{2}\right)$ are interesting. Prove that $$ \frac{E_{1} E_{2}}{A B}=\frac{F_{1} F_{2}}{A C} . $$
|
For any interesting pair $(E, F)$, we will say that the corresponding triangle $E F K$ is also interesting. Let $E F K$ be an interesting triangle. Firstly, we prove that $\angle K E F=\angle K F E=\angle A$, which also means that the circumcircle $\omega_{1}$ of the triangle $A E F$ is tangent to the lines $K E$ and $K F$. Denote by $\omega$ the circle passing through the points $K, S, A$, and $T$. Let the line $A M$ intersect the line $S T$ and the circle $\omega$ (for the second time) at $N$ and $L$, respectively (see Figure 1). Since $E F \| T S$ and $M$ is the midpoint of $E F, N$ is the midpoint of $S T$. Moreover, since $K$ and $M$ are symmetric to each other with respect to the line $S T$, we have $\angle K N S=\angle M N S=$ $\angle L N T$. Thus the points $K$ and $L$ are symmetric to each other with respect to the perpendicular bisector of $S T$. Therefore $K L \| S T$. Let $G$ be the point symmetric to $K$ with respect to $N$. Then $G$ lies on the line $E F$, and we may assume that it lies on the ray $M F$. One has $$ \angle K G E=\angle K N S=\angle S N M=\angle K L A=180^{\circ}-\angle K S A $$ (if $K=L$, then the angle $K L A$ is understood to be the angle between $A L$ and the tangent to $\omega$ at $L$ ). This means that the points $K, G, E$, and $S$ are concyclic. Now, since $K S G T$ is a parallelogram, we obtain $\angle K E F=\angle K S G=180^{\circ}-\angle T K S=\angle A$. Since $K E=K F$, we also have $\angle K F E=\angle K E F=\angle A$. After having proved this fact, one may finish the solution by different methods. 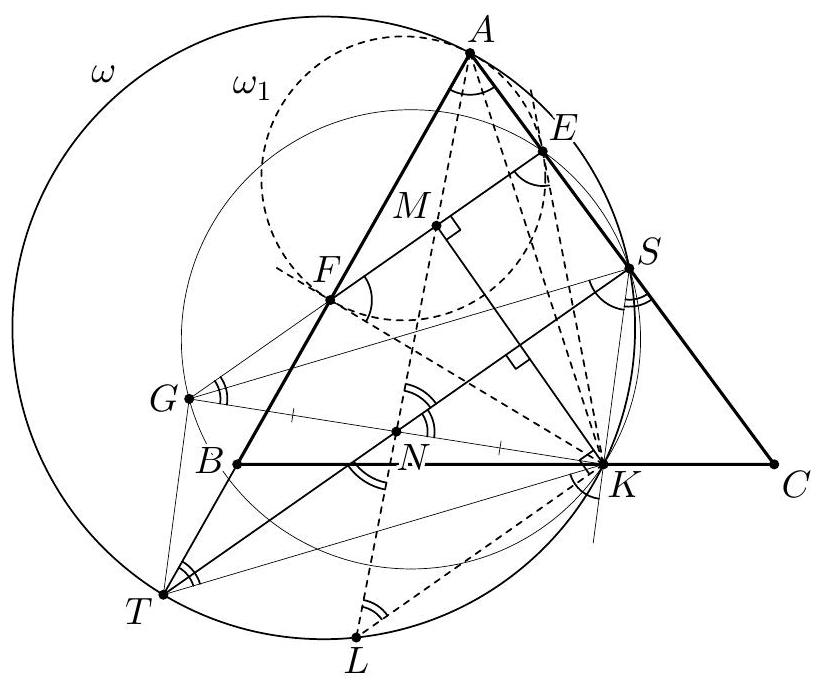 Figure 1 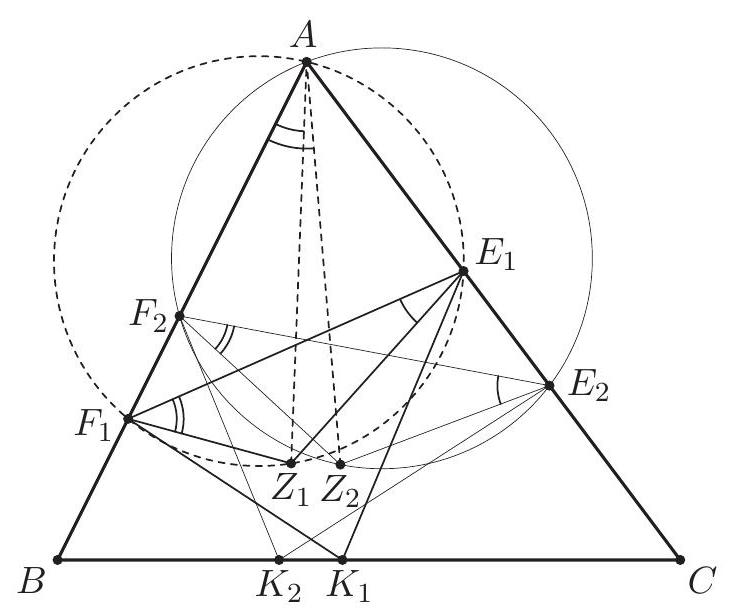 Figure 2 First method. We have just proved that all interesting triangles are similar to each other. This allows us to use the following lemma. Lemma. Let $A B C$ be an arbitrary triangle. Choose two points $E_{1}$ and $E_{2}$ on the side $A C$, two points $F_{1}$ and $F_{2}$ on the side $A B$, and two points $K_{1}$ and $K_{2}$ on the side $B C$, in a way that the triangles $E_{1} F_{1} K_{1}$ and $E_{2} F_{2} K_{2}$ are similar. Then the six circumcircles of the triangles $A E_{i} F_{i}$, $B F_{i} K_{i}$, and $C E_{i} K_{i}(i=1,2)$ meet at a common point $Z$. Moreover, $Z$ is the centre of the spiral similarity that takes the triangle $E_{1} F_{1} K_{1}$ to the triangle $E_{2} F_{2} K_{2}$. Proof. Firstly, notice that for each $i=1,2$, the circumcircles of the triangles $A E_{i} F_{i}, B F_{i} K_{i}$, and $C K_{i} E_{i}$ have a common point $Z_{i}$ by Miquel's theorem. Moreover, we have $\Varangle\left(Z_{i} F_{i}, Z_{i} E_{i}\right)=\Varangle(A B, C A), \quad \Varangle\left(Z_{i} K_{i}, Z_{i} F_{i}\right)=\Varangle(B C, A B), \quad \Varangle\left(Z_{i} E_{i}, Z_{i} K_{i}\right)=\Varangle(C A, B C)$. This yields that the points $Z_{1}$ and $Z_{2}$ correspond to each other in similar triangles $E_{1} F_{1} K_{1}$ and $E_{2} F_{2} K_{2}$. Thus, if they coincide, then this common point is indeed the desired centre of a spiral similarity. Finally, in order to show that $Z_{1}=Z_{2}$, one may notice that $\Varangle\left(A B, A Z_{1}\right)=\Varangle\left(E_{1} F_{1}, E_{1} Z_{1}\right)=$ $\Varangle\left(E_{2} F_{2}, E_{2} Z_{2}\right)=\Varangle\left(A B, A Z_{2}\right)$ (see Figure 2). Similarly, one has $\Varangle\left(B C, B Z_{1}\right)=\Varangle\left(B C, B Z_{2}\right)$ and $\Varangle\left(C A, C Z_{1}\right)=\Varangle\left(C A, C Z_{2}\right)$. This yields $Z_{1}=Z_{2}$. Now, let $P$ and $Q$ be the feet of the perpendiculars from $B$ and $C$ onto $A C$ and $A B$, respectively, and let $R$ be the midpoint of $B C$ (see Figure 3). Then $R$ is the circumcentre of the cyclic quadrilateral $B C P Q$. Thus we obtain $\angle A P Q=\angle B$ and $\angle R P C=\angle C$, which yields $\angle Q P R=\angle A$. Similarly, we show that $\angle P Q R=\angle A$. Thus, all interesting triangles are similar to the triangle $P Q R$. 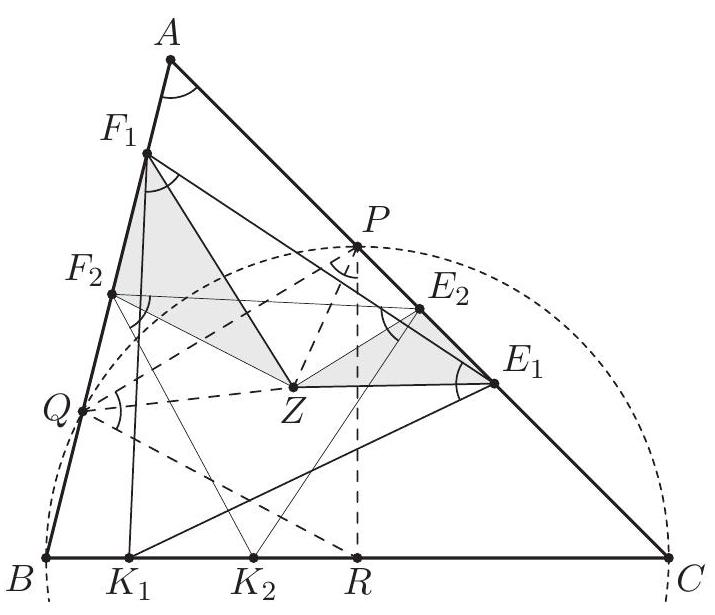 Figure 3 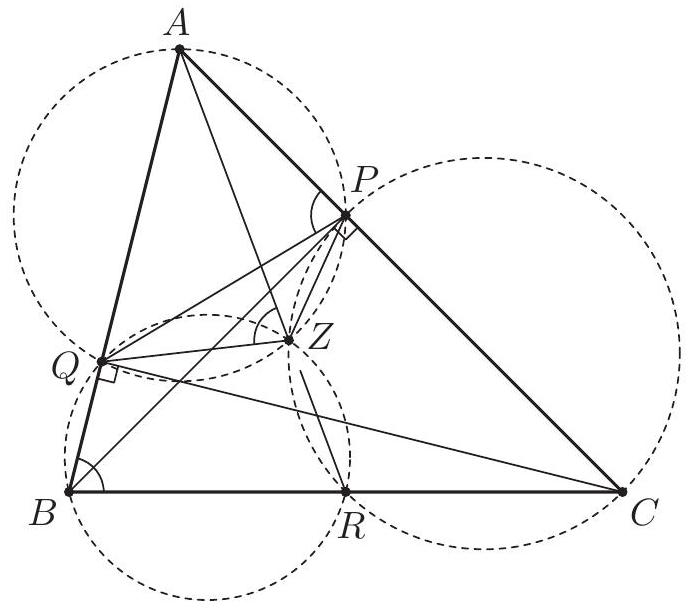 Figure 4 Denote now by $Z$ the common point of the circumcircles of $A P Q, B Q R$, and $C P R$. Let $E_{1} F_{1} K_{1}$ and $E_{2} F_{2} K_{2}$ be two interesting triangles. By the lemma, $Z$ is the centre of any spiral similarity taking one of the triangles $E_{1} F_{1} K_{1}, E_{2} F_{2} K_{2}$, and $P Q R$ to some other of them. Therefore the triangles $Z E_{1} E_{2}$ and $Z F_{1} F_{2}$ are similar, as well as the triangles $Z E_{1} F_{1}$ and $Z P Q$. Hence $$ \frac{E_{1} E_{2}}{F_{1} F_{2}}=\frac{Z E_{1}}{Z F_{1}}=\frac{Z P}{Z Q} $$ Moreover, the equalities $\angle A Z Q=\angle A P Q=\angle A B C=180^{\circ}-\angle Q Z R$ show that the point $Z$ lies on the line $A R$ (see Figure 4). Therefore the triangles $A Z P$ and $A C R$ are similar, as well as the triangles $A Z Q$ and $A B R$. This yields $$ \frac{Z P}{Z Q}=\frac{Z P}{R C} \cdot \frac{R B}{Z Q}=\frac{A Z}{A C} \cdot \frac{A B}{A Z}=\frac{A B}{A C} $$ which completes the solution. Second method. Now we will start from the fact that $\omega_{1}$ is tangent to the lines $K E$ and $K F$ (see Figure 5). We prove that if $(E, F)$ is an interesting pair, then $$ \frac{A E}{A B}+\frac{A F}{A C}=2 \cos \angle A $$ Let $Y$ be the intersection point of the segments $B E$ and $C F$. The points $B, K$, and $C$ are collinear, hence applying PASCAL's theorem to the degenerated hexagon AFFYEE, we infer that $Y$ lies on the circle $\omega_{1}$. Denote by $Z$ the second intersection point of the circumcircle of the triangle $B F Y$ with the line $B C$ (see Figure 6). By Miquel's theorem, the points $C, Z, Y$, and $E$ are concyclic. Therefore we obtain $$ B F \cdot A B+C E \cdot A C=B Y \cdot B E+C Y \cdot C F=B Z \cdot B C+C Z \cdot B C=B C^{2} $$ On the other hand, $B C^{2}=A B^{2}+A C^{2}-2 A B \cdot A C \cos \angle A$, by the cosine law. Hence $$ (A B-A F) \cdot A B+(A C-A E) \cdot A C=A B^{2}+A C^{2}-2 A B \cdot A C \cos \angle A, $$ which simplifies to the desired equality (1). Let now $\left(E_{1}, F_{1}\right)$ and $\left(E_{2}, F_{2}\right)$ be two interesting pairs of points. Then we get $$ \frac{A E_{1}}{A B}+\frac{A F_{1}}{A C}=\frac{A E_{2}}{A B}+\frac{A F_{2}}{A C} $$ which gives the desired result. 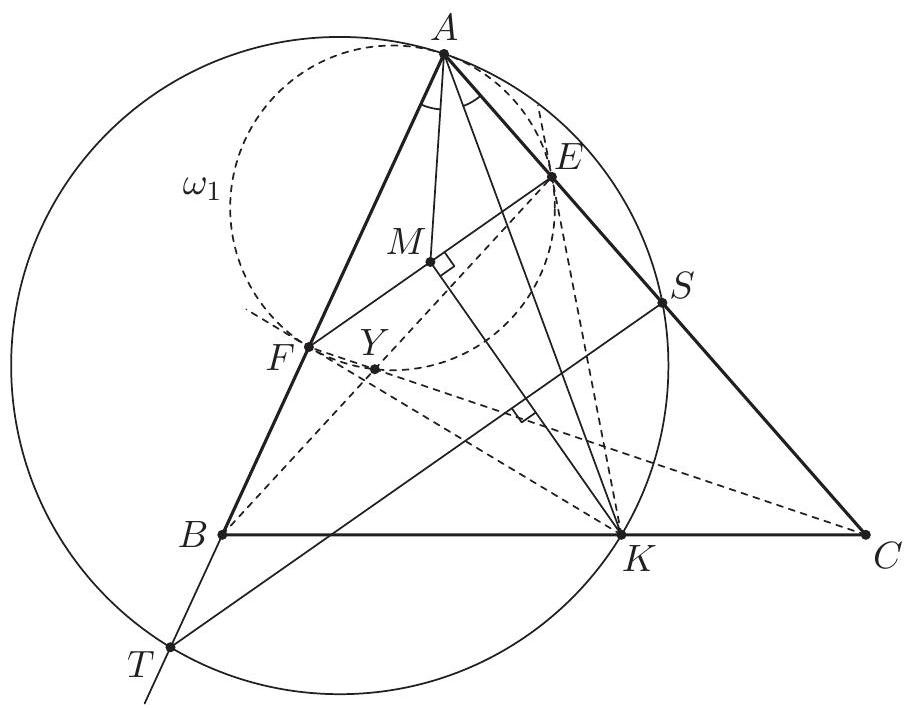 Figure 5 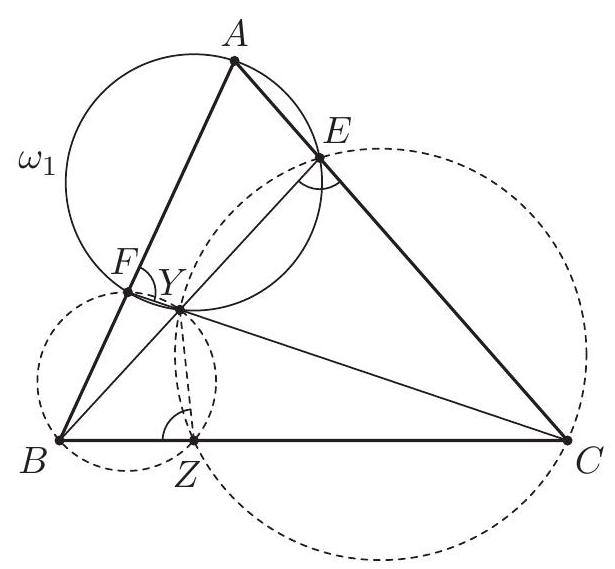 Figure 6 Third method. Again, we make use of the fact that all interesting triangles are similar (and equi-oriented). Let us put the picture onto a complex plane such that $A$ is at the origin, and identify each point with the corresponding complex number. Let $E F K$ be any interesting triangle. The equalities $\angle K E F=\angle K F E=\angle A$ yield that the ratio $\nu=\frac{K-E}{F-E}$ is the same for all interesting triangles. This in turn means that the numbers $E$, $F$, and $K$ satisfy the linear equation $$ K=\mu E+\nu F, \quad \text { where } \quad \mu=1-\nu $$ Now let us choose the points $X$ and $Y$ on the rays $A B$ and $A C$, respectively, so that $\angle C X A=\angle A Y B=\angle A=\angle K E F$ (see Figure 7). Then each of the triangles $A X C$ and $Y A B$ is similar to any interesting triangle, which also means that $$ C=\mu A+\nu X=\nu X \quad \text { and } \quad B=\mu Y+\nu A=\mu Y . $$ Moreover, one has $X / Y=\overline{C / B}$. Since the points $E, F$, and $K$ lie on $A C, A B$, and $B C$, respectively, one gets $$ E=\rho Y, \quad F=\sigma X, \quad \text { and } \quad K=\lambda B+(1-\lambda) C $$ for some real $\rho, \sigma$, and $\lambda$. In view of (3), the equation (2) now reads $\lambda B+(1-\lambda) C=K=$ $\mu E+\nu F=\rho B+\sigma C$, or $$ (\lambda-\rho) B=(\sigma+\lambda-1) C $$ Since the nonzero complex numbers $B$ and $C$ have different arguments, the coefficients in the brackets vanish, so $\rho=\lambda$ and $\sigma=1-\lambda$. Therefore, $$ \frac{E}{Y}+\frac{F}{X}=\rho+\sigma=1 $$ Now, if $\left(E_{1}, F_{1}\right)$ and $\left(E_{2}, F_{2}\right)$ are two distinct interesting pairs, one may apply (4) to both pairs. Subtracting, we get $$ \frac{E_{1}-E_{2}}{Y}=\frac{F_{2}-F_{1}}{X}, \quad \text { so } \quad \frac{E_{1}-E_{2}}{F_{2}-F_{1}}=\frac{Y}{X}=\frac{\bar{B}}{\bar{C}} $$ Taking absolute values provides the required result.  Figure 7 Comment 1. One may notice that the triangle $P Q R$ is also interesting. Comment 2. In order to prove that $\angle K E F=\angle K F E=\angle A$, one may also use the following well-known fact: Let $A E F$ be a triangle with $A E \neq A F$, and let $K$ be the common point of the symmedian taken from $A$ and the perpendicular bisector of $E F$. Then the lines $K E$ and $K F$ are tangent to the circumcircle $\omega_{1}$ of the triangle $A E F$. In this case, however, one needs to deal with the case $A E=A F$ separately.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a fixed acute-angled triangle. Consider some points $E$ and $F$ lying on the sides $A C$ and $A B$, respectively, and let $M$ be the midpoint of $E F$. Let the perpendicular bisector of $E F$ intersect the line $B C$ at $K$, and let the perpendicular bisector of $M K$ intersect the lines $A C$ and $A B$ at $S$ and $T$, respectively. We call the pair $(E, F)$ interesting, if the quadrilateral $K S A T$ is cyclic. Suppose that the pairs $\left(E_{1}, F_{1}\right)$ and $\left(E_{2}, F_{2}\right)$ are interesting. Prove that $$ \frac{E_{1} E_{2}}{A B}=\frac{F_{1} F_{2}}{A C} . $$
|
For any interesting pair $(E, F)$, we will say that the corresponding triangle $E F K$ is also interesting. Let $E F K$ be an interesting triangle. Firstly, we prove that $\angle K E F=\angle K F E=\angle A$, which also means that the circumcircle $\omega_{1}$ of the triangle $A E F$ is tangent to the lines $K E$ and $K F$. Denote by $\omega$ the circle passing through the points $K, S, A$, and $T$. Let the line $A M$ intersect the line $S T$ and the circle $\omega$ (for the second time) at $N$ and $L$, respectively (see Figure 1). Since $E F \| T S$ and $M$ is the midpoint of $E F, N$ is the midpoint of $S T$. Moreover, since $K$ and $M$ are symmetric to each other with respect to the line $S T$, we have $\angle K N S=\angle M N S=$ $\angle L N T$. Thus the points $K$ and $L$ are symmetric to each other with respect to the perpendicular bisector of $S T$. Therefore $K L \| S T$. Let $G$ be the point symmetric to $K$ with respect to $N$. Then $G$ lies on the line $E F$, and we may assume that it lies on the ray $M F$. One has $$ \angle K G E=\angle K N S=\angle S N M=\angle K L A=180^{\circ}-\angle K S A $$ (if $K=L$, then the angle $K L A$ is understood to be the angle between $A L$ and the tangent to $\omega$ at $L$ ). This means that the points $K, G, E$, and $S$ are concyclic. Now, since $K S G T$ is a parallelogram, we obtain $\angle K E F=\angle K S G=180^{\circ}-\angle T K S=\angle A$. Since $K E=K F$, we also have $\angle K F E=\angle K E F=\angle A$. After having proved this fact, one may finish the solution by different methods.  Figure 1  Figure 2 First method. We have just proved that all interesting triangles are similar to each other. This allows us to use the following lemma. Lemma. Let $A B C$ be an arbitrary triangle. Choose two points $E_{1}$ and $E_{2}$ on the side $A C$, two points $F_{1}$ and $F_{2}$ on the side $A B$, and two points $K_{1}$ and $K_{2}$ on the side $B C$, in a way that the triangles $E_{1} F_{1} K_{1}$ and $E_{2} F_{2} K_{2}$ are similar. Then the six circumcircles of the triangles $A E_{i} F_{i}$, $B F_{i} K_{i}$, and $C E_{i} K_{i}(i=1,2)$ meet at a common point $Z$. Moreover, $Z$ is the centre of the spiral similarity that takes the triangle $E_{1} F_{1} K_{1}$ to the triangle $E_{2} F_{2} K_{2}$. Proof. Firstly, notice that for each $i=1,2$, the circumcircles of the triangles $A E_{i} F_{i}, B F_{i} K_{i}$, and $C K_{i} E_{i}$ have a common point $Z_{i}$ by Miquel's theorem. Moreover, we have $\Varangle\left(Z_{i} F_{i}, Z_{i} E_{i}\right)=\Varangle(A B, C A), \quad \Varangle\left(Z_{i} K_{i}, Z_{i} F_{i}\right)=\Varangle(B C, A B), \quad \Varangle\left(Z_{i} E_{i}, Z_{i} K_{i}\right)=\Varangle(C A, B C)$. This yields that the points $Z_{1}$ and $Z_{2}$ correspond to each other in similar triangles $E_{1} F_{1} K_{1}$ and $E_{2} F_{2} K_{2}$. Thus, if they coincide, then this common point is indeed the desired centre of a spiral similarity. Finally, in order to show that $Z_{1}=Z_{2}$, one may notice that $\Varangle\left(A B, A Z_{1}\right)=\Varangle\left(E_{1} F_{1}, E_{1} Z_{1}\right)=$ $\Varangle\left(E_{2} F_{2}, E_{2} Z_{2}\right)=\Varangle\left(A B, A Z_{2}\right)$ (see Figure 2). Similarly, one has $\Varangle\left(B C, B Z_{1}\right)=\Varangle\left(B C, B Z_{2}\right)$ and $\Varangle\left(C A, C Z_{1}\right)=\Varangle\left(C A, C Z_{2}\right)$. This yields $Z_{1}=Z_{2}$. Now, let $P$ and $Q$ be the feet of the perpendiculars from $B$ and $C$ onto $A C$ and $A B$, respectively, and let $R$ be the midpoint of $B C$ (see Figure 3). Then $R$ is the circumcentre of the cyclic quadrilateral $B C P Q$. Thus we obtain $\angle A P Q=\angle B$ and $\angle R P C=\angle C$, which yields $\angle Q P R=\angle A$. Similarly, we show that $\angle P Q R=\angle A$. Thus, all interesting triangles are similar to the triangle $P Q R$.  Figure 3  Figure 4 Denote now by $Z$ the common point of the circumcircles of $A P Q, B Q R$, and $C P R$. Let $E_{1} F_{1} K_{1}$ and $E_{2} F_{2} K_{2}$ be two interesting triangles. By the lemma, $Z$ is the centre of any spiral similarity taking one of the triangles $E_{1} F_{1} K_{1}, E_{2} F_{2} K_{2}$, and $P Q R$ to some other of them. Therefore the triangles $Z E_{1} E_{2}$ and $Z F_{1} F_{2}$ are similar, as well as the triangles $Z E_{1} F_{1}$ and $Z P Q$. Hence $$ \frac{E_{1} E_{2}}{F_{1} F_{2}}=\frac{Z E_{1}}{Z F_{1}}=\frac{Z P}{Z Q} $$ Moreover, the equalities $\angle A Z Q=\angle A P Q=\angle A B C=180^{\circ}-\angle Q Z R$ show that the point $Z$ lies on the line $A R$ (see Figure 4). Therefore the triangles $A Z P$ and $A C R$ are similar, as well as the triangles $A Z Q$ and $A B R$. This yields $$ \frac{Z P}{Z Q}=\frac{Z P}{R C} \cdot \frac{R B}{Z Q}=\frac{A Z}{A C} \cdot \frac{A B}{A Z}=\frac{A B}{A C} $$ which completes the solution. Second method. Now we will start from the fact that $\omega_{1}$ is tangent to the lines $K E$ and $K F$ (see Figure 5). We prove that if $(E, F)$ is an interesting pair, then $$ \frac{A E}{A B}+\frac{A F}{A C}=2 \cos \angle A $$ Let $Y$ be the intersection point of the segments $B E$ and $C F$. The points $B, K$, and $C$ are collinear, hence applying PASCAL's theorem to the degenerated hexagon AFFYEE, we infer that $Y$ lies on the circle $\omega_{1}$. Denote by $Z$ the second intersection point of the circumcircle of the triangle $B F Y$ with the line $B C$ (see Figure 6). By Miquel's theorem, the points $C, Z, Y$, and $E$ are concyclic. Therefore we obtain $$ B F \cdot A B+C E \cdot A C=B Y \cdot B E+C Y \cdot C F=B Z \cdot B C+C Z \cdot B C=B C^{2} $$ On the other hand, $B C^{2}=A B^{2}+A C^{2}-2 A B \cdot A C \cos \angle A$, by the cosine law. Hence $$ (A B-A F) \cdot A B+(A C-A E) \cdot A C=A B^{2}+A C^{2}-2 A B \cdot A C \cos \angle A, $$ which simplifies to the desired equality (1). Let now $\left(E_{1}, F_{1}\right)$ and $\left(E_{2}, F_{2}\right)$ be two interesting pairs of points. Then we get $$ \frac{A E_{1}}{A B}+\frac{A F_{1}}{A C}=\frac{A E_{2}}{A B}+\frac{A F_{2}}{A C} $$ which gives the desired result.  Figure 5  Figure 6 Third method. Again, we make use of the fact that all interesting triangles are similar (and equi-oriented). Let us put the picture onto a complex plane such that $A$ is at the origin, and identify each point with the corresponding complex number. Let $E F K$ be any interesting triangle. The equalities $\angle K E F=\angle K F E=\angle A$ yield that the ratio $\nu=\frac{K-E}{F-E}$ is the same for all interesting triangles. This in turn means that the numbers $E$, $F$, and $K$ satisfy the linear equation $$ K=\mu E+\nu F, \quad \text { where } \quad \mu=1-\nu $$ Now let us choose the points $X$ and $Y$ on the rays $A B$ and $A C$, respectively, so that $\angle C X A=\angle A Y B=\angle A=\angle K E F$ (see Figure 7). Then each of the triangles $A X C$ and $Y A B$ is similar to any interesting triangle, which also means that $$ C=\mu A+\nu X=\nu X \quad \text { and } \quad B=\mu Y+\nu A=\mu Y . $$ Moreover, one has $X / Y=\overline{C / B}$. Since the points $E, F$, and $K$ lie on $A C, A B$, and $B C$, respectively, one gets $$ E=\rho Y, \quad F=\sigma X, \quad \text { and } \quad K=\lambda B+(1-\lambda) C $$ for some real $\rho, \sigma$, and $\lambda$. In view of (3), the equation (2) now reads $\lambda B+(1-\lambda) C=K=$ $\mu E+\nu F=\rho B+\sigma C$, or $$ (\lambda-\rho) B=(\sigma+\lambda-1) C $$ Since the nonzero complex numbers $B$ and $C$ have different arguments, the coefficients in the brackets vanish, so $\rho=\lambda$ and $\sigma=1-\lambda$. Therefore, $$ \frac{E}{Y}+\frac{F}{X}=\rho+\sigma=1 $$ Now, if $\left(E_{1}, F_{1}\right)$ and $\left(E_{2}, F_{2}\right)$ are two distinct interesting pairs, one may apply (4) to both pairs. Subtracting, we get $$ \frac{E_{1}-E_{2}}{Y}=\frac{F_{2}-F_{1}}{X}, \quad \text { so } \quad \frac{E_{1}-E_{2}}{F_{2}-F_{1}}=\frac{Y}{X}=\frac{\bar{B}}{\bar{C}} $$ Taking absolute values provides the required result.  Figure 7 Comment 1. One may notice that the triangle $P Q R$ is also interesting. Comment 2. In order to prove that $\angle K E F=\angle K F E=\angle A$, one may also use the following well-known fact: Let $A E F$ be a triangle with $A E \neq A F$, and let $K$ be the common point of the symmedian taken from $A$ and the perpendicular bisector of $E F$. Then the lines $K E$ and $K F$ are tangent to the circumcircle $\omega_{1}$ of the triangle $A E F$. In this case, however, one needs to deal with the case $A E=A F$ separately.
|
{
"resource_path": "IMO/segmented/en-IMO2014SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
42ed01d3-45e6-5914-8d89-8b8f665e1bfe
| 24,452
|
Let $A B C$ be a triangle with circumcircle $\Omega$ and incentre $I$. Let the line passing through $I$ and perpendicular to $C I$ intersect the segment $B C$ and the $\operatorname{arc} B C($ not containing $A)$ of $\Omega$ at points $U$ and $V$, respectively. Let the line passing through $U$ and parallel to $A I$ intersect $A V$ at $X$, and let the line passing through $V$ and parallel to $A I$ intersect $A B$ at $Y$. Let $W$ and $Z$ be the midpoints of $A X$ and $B C$, respectively. Prove that if the points $I, X$, and $Y$ are collinear, then the points $I, W$, and $Z$ are also collinear.
|
We start with some general observations. Set $\alpha=\angle A / 2, \beta=\angle B / 2, \gamma=\angle C / 2$. Then obviously $\alpha+\beta+\gamma=90^{\circ}$. Since $\angle U I C=90^{\circ}$, we obtain $\angle I U C=\alpha+\beta$. Therefore $\angle B I V=\angle I U C-\angle I B C=\alpha=\angle B A I=\angle B Y V$, which implies that the points $B, Y, I$, and $V$ lie on a common circle (see Figure 1). Assume now that the points $I, X$ and $Y$ are collinear. We prove that $\angle Y I A=90^{\circ}$. Let the line $X U$ intersect $A B$ at $N$. Since the lines $A I, U X$, and $V Y$ are parallel, we get $$ \frac{N X}{A I}=\frac{Y N}{Y A}=\frac{V U}{V I}=\frac{X U}{A I} $$ implying $N X=X U$. Moreover, $\angle B I U=\alpha=\angle B N U$. This implies that the quadrilateral BUIN is cyclic, and since $B I$ is the angle bisector of $\angle U B N$, we infer that $N I=U I$. Thus in the isosceles triangle $N I U$, the point $X$ is the midpoint of the base $N U$. This gives $\angle I X N=90^{\circ}$, i.e., $\angle Y I A=90^{\circ}$.  Figure 1 Let $S$ be the midpoint of the segment $V C$. Let moreover $T$ be the intersection point of the lines $A X$ and $S I$, and set $x=\angle B A V=\angle B C V$. Since $\angle C I A=90^{\circ}+\beta$ and $S I=S C$, we obtain $$ \angle T I A=180^{\circ}-\angle A I S=90^{\circ}-\beta-\angle C I S=90^{\circ}-\beta-\gamma-x=\alpha-x=\angle T A I, $$ which implies that $T I=T A$. Therefore, since $\angle X I A=90^{\circ}$, the point $T$ is the midpoint of $A X$, i.e., $T=W$. To complete our solution, it remains to show that the intersection point of the lines $I S$ and $B C$ coincide with the midpoint of the segment $B C$. But since $S$ is the midpoint of the segment $V C$, it suffices to show that the lines $B V$ and $I S$ are parallel. Since the quadrilateral $B Y I V$ is cyclic, $\angle V B I=\angle V Y I=\angle Y I A=90^{\circ}$. This implies that $B V$ is the external angle bisector of the angle $A B C$, which yields $\angle V A C=\angle V C A$. Therefore $2 \alpha-x=2 \gamma+x$, which gives $\alpha=\gamma+x$. Hence $\angle S C I=\alpha$, so $\angle V S I=2 \alpha$. On the other hand, $\angle B V C=180^{\circ}-\angle B A C=180^{\circ}-2 \alpha$, which implies that the lines $B V$ and $I S$ are parallel. This completes the solution.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circumcircle $\Omega$ and incentre $I$. Let the line passing through $I$ and perpendicular to $C I$ intersect the segment $B C$ and the $\operatorname{arc} B C($ not containing $A)$ of $\Omega$ at points $U$ and $V$, respectively. Let the line passing through $U$ and parallel to $A I$ intersect $A V$ at $X$, and let the line passing through $V$ and parallel to $A I$ intersect $A B$ at $Y$. Let $W$ and $Z$ be the midpoints of $A X$ and $B C$, respectively. Prove that if the points $I, X$, and $Y$ are collinear, then the points $I, W$, and $Z$ are also collinear.
|
We start with some general observations. Set $\alpha=\angle A / 2, \beta=\angle B / 2, \gamma=\angle C / 2$. Then obviously $\alpha+\beta+\gamma=90^{\circ}$. Since $\angle U I C=90^{\circ}$, we obtain $\angle I U C=\alpha+\beta$. Therefore $\angle B I V=\angle I U C-\angle I B C=\alpha=\angle B A I=\angle B Y V$, which implies that the points $B, Y, I$, and $V$ lie on a common circle (see Figure 1). Assume now that the points $I, X$ and $Y$ are collinear. We prove that $\angle Y I A=90^{\circ}$. Let the line $X U$ intersect $A B$ at $N$. Since the lines $A I, U X$, and $V Y$ are parallel, we get $$ \frac{N X}{A I}=\frac{Y N}{Y A}=\frac{V U}{V I}=\frac{X U}{A I} $$ implying $N X=X U$. Moreover, $\angle B I U=\alpha=\angle B N U$. This implies that the quadrilateral BUIN is cyclic, and since $B I$ is the angle bisector of $\angle U B N$, we infer that $N I=U I$. Thus in the isosceles triangle $N I U$, the point $X$ is the midpoint of the base $N U$. This gives $\angle I X N=90^{\circ}$, i.e., $\angle Y I A=90^{\circ}$.  Figure 1 Let $S$ be the midpoint of the segment $V C$. Let moreover $T$ be the intersection point of the lines $A X$ and $S I$, and set $x=\angle B A V=\angle B C V$. Since $\angle C I A=90^{\circ}+\beta$ and $S I=S C$, we obtain $$ \angle T I A=180^{\circ}-\angle A I S=90^{\circ}-\beta-\angle C I S=90^{\circ}-\beta-\gamma-x=\alpha-x=\angle T A I, $$ which implies that $T I=T A$. Therefore, since $\angle X I A=90^{\circ}$, the point $T$ is the midpoint of $A X$, i.e., $T=W$. To complete our solution, it remains to show that the intersection point of the lines $I S$ and $B C$ coincide with the midpoint of the segment $B C$. But since $S$ is the midpoint of the segment $V C$, it suffices to show that the lines $B V$ and $I S$ are parallel. Since the quadrilateral $B Y I V$ is cyclic, $\angle V B I=\angle V Y I=\angle Y I A=90^{\circ}$. This implies that $B V$ is the external angle bisector of the angle $A B C$, which yields $\angle V A C=\angle V C A$. Therefore $2 \alpha-x=2 \gamma+x$, which gives $\alpha=\gamma+x$. Hence $\angle S C I=\alpha$, so $\angle V S I=2 \alpha$. On the other hand, $\angle B V C=180^{\circ}-\angle B A C=180^{\circ}-2 \alpha$, which implies that the lines $B V$ and $I S$ are parallel. This completes the solution.
|
{
"resource_path": "IMO/segmented/en-IMO2014SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8ebd9764-56dc-5260-a3e5-5c089b943ac7
| 24,456
|
A coin is called a Cape Town coin if its value is $1 / n$ for some positive integer $n$. Given a collection of Cape Town coins of total value at most $99+\frac{1}{2}$, prove that it is possible to split this collection into at most 100 groups each of total value at most 1. (Luxembourg)
|
We will show that for every positive integer $N$ any collection of Cape Town coins of total value at most $N-\frac{1}{2}$ can be split into $N$ groups each of total value at most 1 . The problem statement is a particular case for $N=100$. We start with some preparations. If several given coins together have a total value also of the form $\frac{1}{k}$ for a positive integer $k$, then we may merge them into one new coin. Clearly, if the resulting collection can be split in the required way then the initial collection can also be split. After each such merging, the total number of coins decreases, thus at some moment we come to a situation when no more merging is possible. At this moment, for every even $k$ there is at most one coin of value $\frac{1}{k}$ (otherwise two such coins may be merged), and for every odd $k>1$ there are at most $k-1$ coins of value $\frac{1}{k}$ (otherwise $k$ such coins may also be merged). Now, clearly, each coin of value 1 should form a single group; if there are $d$ such coins then we may remove them from the collection and replace $N$ by $N-d$. So from now on we may assume that there are no coins of value 1. Finally, we may split all the coins in the following way. For each $k=1,2, \ldots, N$ we put all the coins of values $\frac{1}{2 k-1}$ and $\frac{1}{2 k}$ into a group $G_{k}$; the total value of $G_{k}$ does not exceed $$ (2 k-2) \cdot \frac{1}{2 k-1}+\frac{1}{2 k}<1 $$ It remains to distribute the "small" coins of values which are less than $\frac{1}{2 N}$; we will add them one by one. In each step, take any remaining small coin. The total value of coins in the groups at this moment is at most $N-\frac{1}{2}$, so there exists a group of total value at most $\frac{1}{N}\left(N-\frac{1}{2}\right)=1-\frac{1}{2 N}$; thus it is possible to put our small coin into this group. Acting so, we will finally distribute all the coins. Comment 1. The algorithm may be modified, at least the step where one distributes the coins of values $\geqslant \frac{1}{2 N}$. One different way is to put into $G_{k}$ all the coins of values $\frac{1}{(2 k-1) 2^{s}}$ for all integer $s \geqslant 0$. One may easily see that their total value also does not exceed 1. Comment 2. The original proposal also contained another part, suggesting to show that a required splitting may be impossible if the total value of coins is at most 100 . There are many examples of such a collection, e.g. one may take 98 coins of value 1 , one coin of value $\frac{1}{2}$, two coins of value $\frac{1}{3}$, and four coins of value $\frac{1}{5}$. The Problem Selection Committee thinks that this part is less suitable for the competition.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A coin is called a Cape Town coin if its value is $1 / n$ for some positive integer $n$. Given a collection of Cape Town coins of total value at most $99+\frac{1}{2}$, prove that it is possible to split this collection into at most 100 groups each of total value at most 1. (Luxembourg)
|
We will show that for every positive integer $N$ any collection of Cape Town coins of total value at most $N-\frac{1}{2}$ can be split into $N$ groups each of total value at most 1 . The problem statement is a particular case for $N=100$. We start with some preparations. If several given coins together have a total value also of the form $\frac{1}{k}$ for a positive integer $k$, then we may merge them into one new coin. Clearly, if the resulting collection can be split in the required way then the initial collection can also be split. After each such merging, the total number of coins decreases, thus at some moment we come to a situation when no more merging is possible. At this moment, for every even $k$ there is at most one coin of value $\frac{1}{k}$ (otherwise two such coins may be merged), and for every odd $k>1$ there are at most $k-1$ coins of value $\frac{1}{k}$ (otherwise $k$ such coins may also be merged). Now, clearly, each coin of value 1 should form a single group; if there are $d$ such coins then we may remove them from the collection and replace $N$ by $N-d$. So from now on we may assume that there are no coins of value 1. Finally, we may split all the coins in the following way. For each $k=1,2, \ldots, N$ we put all the coins of values $\frac{1}{2 k-1}$ and $\frac{1}{2 k}$ into a group $G_{k}$; the total value of $G_{k}$ does not exceed $$ (2 k-2) \cdot \frac{1}{2 k-1}+\frac{1}{2 k}<1 $$ It remains to distribute the "small" coins of values which are less than $\frac{1}{2 N}$; we will add them one by one. In each step, take any remaining small coin. The total value of coins in the groups at this moment is at most $N-\frac{1}{2}$, so there exists a group of total value at most $\frac{1}{N}\left(N-\frac{1}{2}\right)=1-\frac{1}{2 N}$; thus it is possible to put our small coin into this group. Acting so, we will finally distribute all the coins. Comment 1. The algorithm may be modified, at least the step where one distributes the coins of values $\geqslant \frac{1}{2 N}$. One different way is to put into $G_{k}$ all the coins of values $\frac{1}{(2 k-1) 2^{s}}$ for all integer $s \geqslant 0$. One may easily see that their total value also does not exceed 1. Comment 2. The original proposal also contained another part, suggesting to show that a required splitting may be impossible if the total value of coins is at most 100 . There are many examples of such a collection, e.g. one may take 98 coins of value 1 , one coin of value $\frac{1}{2}$, two coins of value $\frac{1}{3}$, and four coins of value $\frac{1}{5}$. The Problem Selection Committee thinks that this part is less suitable for the competition.
|
{
"resource_path": "IMO/segmented/en-IMO2014SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
9f3b252b-5a5a-5729-aefe-bfb16ba78c92
| 24,467
|
Let $n>1$ be a given integer. Prove that infinitely many terms of the sequence $\left(a_{k}\right)_{k \geqslant 1}$, defined by $$ a_{k}=\left\lfloor\frac{n^{k}}{k}\right\rfloor $$ are odd. (For a real number $x,\lfloor x\rfloor$ denotes the largest integer not exceeding $x$.) (Hong Kong)
|
If $n$ is odd, let $k=n^{m}$ for $m=1,2, \ldots$. Then $a_{k}=n^{n^{m}-m}$, which is odd for each $m$. Henceforth, assume that $n$ is even, say $n=2 t$ for some integer $t \geqslant 1$. Then, for any $m \geqslant 2$, the integer $n^{2^{m}}-2^{m}=2^{m}\left(2^{2^{m}-m} \cdot t^{2^{m}}-1\right)$ has an odd prime divisor $p$, since $2^{m}-m>1$. Then, for $k=p \cdot 2^{m}$, we have $$ n^{k}=\left(n^{2^{m}}\right)^{p} \equiv\left(2^{m}\right)^{p}=\left(2^{p}\right)^{m} \equiv 2^{m} $$ where the congruences are taken modulo $p\left(\right.$ recall that $2^{p} \equiv 2(\bmod p)$, by Fermat's little theorem). Also, from $n^{k}-2^{m}<n^{k}<n^{k}+2^{m}(p-1)$, we see that the fraction $\frac{n^{k}}{k}$ lies strictly between the consecutive integers $\frac{n^{k}-2^{m}}{p \cdot 2^{m}}$ and $\frac{n^{k}+2^{m}(p-1)}{p \cdot 2^{m}}$, which gives $$ \left\lfloor\frac{n^{k}}{k}\right\rfloor=\frac{n^{k}-2^{m}}{p \cdot 2^{m}} $$ We finally observe that $\frac{n^{k}-2^{m}}{p \cdot 2^{m}}=\frac{\frac{n^{k}}{2^{m}}-1}{p}$ is an odd integer, since the integer $\frac{n^{k}}{2^{m}}-1$ is odd (recall that $k>m$ ). Note that for different values of $m$, we get different values of $k$, due to the different powers of 2 in the prime factorisation of $k$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n>1$ be a given integer. Prove that infinitely many terms of the sequence $\left(a_{k}\right)_{k \geqslant 1}$, defined by $$ a_{k}=\left\lfloor\frac{n^{k}}{k}\right\rfloor $$ are odd. (For a real number $x,\lfloor x\rfloor$ denotes the largest integer not exceeding $x$.) (Hong Kong)
|
If $n$ is odd, let $k=n^{m}$ for $m=1,2, \ldots$. Then $a_{k}=n^{n^{m}-m}$, which is odd for each $m$. Henceforth, assume that $n$ is even, say $n=2 t$ for some integer $t \geqslant 1$. Then, for any $m \geqslant 2$, the integer $n^{2^{m}}-2^{m}=2^{m}\left(2^{2^{m}-m} \cdot t^{2^{m}}-1\right)$ has an odd prime divisor $p$, since $2^{m}-m>1$. Then, for $k=p \cdot 2^{m}$, we have $$ n^{k}=\left(n^{2^{m}}\right)^{p} \equiv\left(2^{m}\right)^{p}=\left(2^{p}\right)^{m} \equiv 2^{m} $$ where the congruences are taken modulo $p\left(\right.$ recall that $2^{p} \equiv 2(\bmod p)$, by Fermat's little theorem). Also, from $n^{k}-2^{m}<n^{k}<n^{k}+2^{m}(p-1)$, we see that the fraction $\frac{n^{k}}{k}$ lies strictly between the consecutive integers $\frac{n^{k}-2^{m}}{p \cdot 2^{m}}$ and $\frac{n^{k}+2^{m}(p-1)}{p \cdot 2^{m}}$, which gives $$ \left\lfloor\frac{n^{k}}{k}\right\rfloor=\frac{n^{k}-2^{m}}{p \cdot 2^{m}} $$ We finally observe that $\frac{n^{k}-2^{m}}{p \cdot 2^{m}}=\frac{\frac{n^{k}}{2^{m}}-1}{p}$ is an odd integer, since the integer $\frac{n^{k}}{2^{m}}-1$ is odd (recall that $k>m$ ). Note that for different values of $m$, we get different values of $k$, due to the different powers of 2 in the prime factorisation of $k$.
|
{
"resource_path": "IMO/segmented/en-IMO2014SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
e64f743a-f9ea-5299-b3f9-cb0d4fb92a0f
| 24,470
|
Let $n>1$ be a given integer. Prove that infinitely many terms of the sequence $\left(a_{k}\right)_{k \geqslant 1}$, defined by $$ a_{k}=\left\lfloor\frac{n^{k}}{k}\right\rfloor $$ are odd. (For a real number $x,\lfloor x\rfloor$ denotes the largest integer not exceeding $x$.) (Hong Kong)
|
Treat the (trivial) case when $n$ is odd as in Now assume that $n$ is even and $n>2$. Let $p$ be a prime divisor of $n-1$. Proceed by induction on $i$ to prove that $p^{i+1}$ is a divisor of $n^{p^{i}}-1$ for every $i \geqslant 0$. The case $i=0$ is true by the way in which $p$ is chosen. Suppose the result is true for some $i \geqslant 0$. The factorisation $$ n^{p^{i+1}}-1=\left(n^{p^{i}}-1\right)\left[n^{p^{i}(p-1)}+n^{p^{i}(p-2)}+\cdots+n^{p^{i}}+1\right], $$ together with the fact that each of the $p$ terms between the square brackets is congruent to 1 modulo $p$, implies that the result is also true for $i+1$. Hence $\left\lfloor\frac{n^{p^{i}}}{p^{i}}\right\rfloor=\frac{n^{p^{i}}-1}{p^{i}}$, an odd integer for each $i \geqslant 1$. Finally, we consider the case $n=2$. We observe that $3 \cdot 4^{i}$ is a divisor of $2^{3 \cdot 4^{i}}-4^{i}$ for every $i \geqslant 1$ : Trivially, $4^{i}$ is a divisor of $2^{3 \cdot 4^{i}}-4^{i}$, since $3 \cdot 4^{i}>2 i$. Furthermore, since $2^{3 \cdot 4^{i}}$ and $4^{i}$ are both congruent to 1 modulo 3, we have $3 \mid 2^{3 \cdot 4^{i}}-4^{i}$. Hence, $\left\lfloor\frac{2^{3 \cdot 4^{i}}}{3 \cdot 4^{i}}\right\rfloor=\frac{2^{3 \cdot 4^{i}}-4^{i}}{3 \cdot 4^{i}}=\frac{2^{3 \cdot 4^{i}-2 i}-1}{3}$, which is odd for every $i \geqslant 1$. Comment. The case $n$ even and $n>2$ can also be solved by recursively defining the sequence $\left(k_{i}\right)_{i \geqslant 1}$ by $k_{1}=1$ and $k_{i+1}=n^{k_{i}}-1$ for $i \geqslant 1$. Then $\left(k_{i}\right)$ is strictly increasing and it follows (by induction on $i$ ) that $k_{i} \mid n^{k_{i}}-1$ for all $i \geqslant 1$, so the $k_{i}$ are as desired. The case $n=2$ can also be solved as follows: Let $i \geqslant 2$. By Bertrand's postulate, there exists a prime number $p$ such that $2^{2^{i}-1}<p \cdot 2^{i}<2^{2^{i}}$. This gives $$ p \cdot 2^{i}<2^{2^{i}}<2 p \cdot 2^{i} . $$ Also, we have that $p \cdot 2^{i}$ is a divisor of $2^{p \cdot 2^{i}}-2^{2^{i}}$, hence, using (1), we get that $$ \left\lfloor\frac{2^{p \cdot 2^{i}}}{p \cdot 2^{i}}\right\rfloor=\frac{2^{p \cdot 2^{i}}-2^{2^{i}}+p \cdot 2^{i}}{p \cdot 2^{i}}=\frac{2^{p \cdot 2^{i}-i}-2^{2^{i}-i}+p}{p} $$ which is an odd integer.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n>1$ be a given integer. Prove that infinitely many terms of the sequence $\left(a_{k}\right)_{k \geqslant 1}$, defined by $$ a_{k}=\left\lfloor\frac{n^{k}}{k}\right\rfloor $$ are odd. (For a real number $x,\lfloor x\rfloor$ denotes the largest integer not exceeding $x$.) (Hong Kong)
|
Treat the (trivial) case when $n$ is odd as in Now assume that $n$ is even and $n>2$. Let $p$ be a prime divisor of $n-1$. Proceed by induction on $i$ to prove that $p^{i+1}$ is a divisor of $n^{p^{i}}-1$ for every $i \geqslant 0$. The case $i=0$ is true by the way in which $p$ is chosen. Suppose the result is true for some $i \geqslant 0$. The factorisation $$ n^{p^{i+1}}-1=\left(n^{p^{i}}-1\right)\left[n^{p^{i}(p-1)}+n^{p^{i}(p-2)}+\cdots+n^{p^{i}}+1\right], $$ together with the fact that each of the $p$ terms between the square brackets is congruent to 1 modulo $p$, implies that the result is also true for $i+1$. Hence $\left\lfloor\frac{n^{p^{i}}}{p^{i}}\right\rfloor=\frac{n^{p^{i}}-1}{p^{i}}$, an odd integer for each $i \geqslant 1$. Finally, we consider the case $n=2$. We observe that $3 \cdot 4^{i}$ is a divisor of $2^{3 \cdot 4^{i}}-4^{i}$ for every $i \geqslant 1$ : Trivially, $4^{i}$ is a divisor of $2^{3 \cdot 4^{i}}-4^{i}$, since $3 \cdot 4^{i}>2 i$. Furthermore, since $2^{3 \cdot 4^{i}}$ and $4^{i}$ are both congruent to 1 modulo 3, we have $3 \mid 2^{3 \cdot 4^{i}}-4^{i}$. Hence, $\left\lfloor\frac{2^{3 \cdot 4^{i}}}{3 \cdot 4^{i}}\right\rfloor=\frac{2^{3 \cdot 4^{i}}-4^{i}}{3 \cdot 4^{i}}=\frac{2^{3 \cdot 4^{i}-2 i}-1}{3}$, which is odd for every $i \geqslant 1$. Comment. The case $n$ even and $n>2$ can also be solved by recursively defining the sequence $\left(k_{i}\right)_{i \geqslant 1}$ by $k_{1}=1$ and $k_{i+1}=n^{k_{i}}-1$ for $i \geqslant 1$. Then $\left(k_{i}\right)$ is strictly increasing and it follows (by induction on $i$ ) that $k_{i} \mid n^{k_{i}}-1$ for all $i \geqslant 1$, so the $k_{i}$ are as desired. The case $n=2$ can also be solved as follows: Let $i \geqslant 2$. By Bertrand's postulate, there exists a prime number $p$ such that $2^{2^{i}-1}<p \cdot 2^{i}<2^{2^{i}}$. This gives $$ p \cdot 2^{i}<2^{2^{i}}<2 p \cdot 2^{i} . $$ Also, we have that $p \cdot 2^{i}$ is a divisor of $2^{p \cdot 2^{i}}-2^{2^{i}}$, hence, using (1), we get that $$ \left\lfloor\frac{2^{p \cdot 2^{i}}}{p \cdot 2^{i}}\right\rfloor=\frac{2^{p \cdot 2^{i}}-2^{2^{i}}+p \cdot 2^{i}}{p \cdot 2^{i}}=\frac{2^{p \cdot 2^{i}-i}-2^{2^{i}-i}+p}{p} $$ which is an odd integer.
|
{
"resource_path": "IMO/segmented/en-IMO2014SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
e64f743a-f9ea-5299-b3f9-cb0d4fb92a0f
| 24,470
|
Let $n>1$ be a given integer. Prove that infinitely many terms of the sequence $\left(a_{k}\right)_{k \geqslant 1}$, defined by $$ a_{k}=\left\lfloor\frac{n^{k}}{k}\right\rfloor $$ are odd. (For a real number $x,\lfloor x\rfloor$ denotes the largest integer not exceeding $x$.) (Hong Kong)
|
Treat the (trivial) case when $n$ is odd as in Let $n$ be even, and let $p$ be a prime divisor of $n+1$. Define the sequence $\left(a_{i}\right)_{i \geqslant 1}$ by $$ a_{i}=\min \left\{a \in \mathbb{Z}_{>0}: 2^{i} \text { divides } a p+1\right\} $$ Recall that there exists $a$ with $1 \leqslant a<2^{i}$ such that $a p \equiv-1\left(\bmod 2^{i}\right)$, so each $a_{i}$ satisfies $1 \leqslant a_{i}<2^{i}$. This implies that $a_{i} p+1<p \cdot 2^{i}$. Also, $a_{i} \rightarrow \infty$ as $i \rightarrow \infty$, whence there are infinitely many $i$ such that $a_{i}<a_{i+1}$. From now on, we restrict ourselves only to these $i$. Notice that $p$ is a divisor of $n^{p}+1$, which, in turn, divides $n^{p \cdot 2^{i}}-1$. It follows that $p \cdot 2^{i}$ is a divisor of $n^{p \cdot 2^{i}}-\left(a_{i} p+1\right)$, and we consequently see that the integer $\left\lfloor\frac{n^{p \cdot 2^{i}}}{p \cdot 2^{i}}\right\rfloor=\frac{n^{p \cdot 2^{i}}-\left(a_{i} p+1\right)}{p \cdot 2^{i}}$ is odd, since $2^{i+1}$ divides $n^{p \cdot 2^{i}}$, but not $a_{i} p+1$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n>1$ be a given integer. Prove that infinitely many terms of the sequence $\left(a_{k}\right)_{k \geqslant 1}$, defined by $$ a_{k}=\left\lfloor\frac{n^{k}}{k}\right\rfloor $$ are odd. (For a real number $x,\lfloor x\rfloor$ denotes the largest integer not exceeding $x$.) (Hong Kong)
|
Treat the (trivial) case when $n$ is odd as in Let $n$ be even, and let $p$ be a prime divisor of $n+1$. Define the sequence $\left(a_{i}\right)_{i \geqslant 1}$ by $$ a_{i}=\min \left\{a \in \mathbb{Z}_{>0}: 2^{i} \text { divides } a p+1\right\} $$ Recall that there exists $a$ with $1 \leqslant a<2^{i}$ such that $a p \equiv-1\left(\bmod 2^{i}\right)$, so each $a_{i}$ satisfies $1 \leqslant a_{i}<2^{i}$. This implies that $a_{i} p+1<p \cdot 2^{i}$. Also, $a_{i} \rightarrow \infty$ as $i \rightarrow \infty$, whence there are infinitely many $i$ such that $a_{i}<a_{i+1}$. From now on, we restrict ourselves only to these $i$. Notice that $p$ is a divisor of $n^{p}+1$, which, in turn, divides $n^{p \cdot 2^{i}}-1$. It follows that $p \cdot 2^{i}$ is a divisor of $n^{p \cdot 2^{i}}-\left(a_{i} p+1\right)$, and we consequently see that the integer $\left\lfloor\frac{n^{p \cdot 2^{i}}}{p \cdot 2^{i}}\right\rfloor=\frac{n^{p \cdot 2^{i}}-\left(a_{i} p+1\right)}{p \cdot 2^{i}}$ is odd, since $2^{i+1}$ divides $n^{p \cdot 2^{i}}$, but not $a_{i} p+1$.
|
{
"resource_path": "IMO/segmented/en-IMO2014SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
e64f743a-f9ea-5299-b3f9-cb0d4fb92a0f
| 24,470
|
Let $a_{1}<a_{2}<\cdots<a_{n}$ be pairwise coprime positive integers with $a_{1}$ being prime and $a_{1} \geqslant n+2$. On the segment $I=\left[0, a_{1} a_{2} \cdots a_{n}\right]$ of the real line, mark all integers that are divisible by at least one of the numbers $a_{1}, \ldots, a_{n}$. These points split $I$ into a number of smaller segments. Prove that the sum of the squares of the lengths of these segments is divisible by $a_{1}$. (Serbia)
|
The conventions from the first paragraph of the first solution are still in force. We shall prove the following more general statement: ( $\boxplus$ ) Let $p$ denote a prime number, let $p=a_{1}<a_{2}<\cdots<a_{n}$ be $n$ pairwise coprime positive integers, and let $d$ be an integer with $1 \leqslant d \leqslant p-n$. Mark all integers that are divisible by at least one of the numbers $a_{1}, \ldots, a_{n}$ on the interval $I=\left[0, a_{1} a_{2} \cdots a_{n}\right]$ of the real line. These points split I into a number of smaller segments, say of lengths $b_{1}, \ldots, b_{k}$. Then the sum $\sum_{i=1}^{k}\binom{b_{i}}{d}$ is divisible by $p$. Applying ( $\boxplus$ ) to $d=1$ and $d=2$ and using the equation $x^{2}=2\binom{x}{2}+\binom{x}{1}$, one easily gets the statement of the problem. To prove $(\boxplus)$ itself, we argue by induction on $n$. The base case $n=1$ follows from the known fact that the binomial coefficient $\binom{p}{d}$ is divisible by $p$ whenever $1 \leqslant d \leqslant p-1$. Let us now assume that $n \geqslant 2$, and that the statement is known whenever $n-1$ rather than $n$ coprime integers are given together with some integer $d \in[1, p-n+1]$. Suppose that the numbers $p=a_{1}<a_{2}<\cdots<a_{n}$ and $d$ are as above. Write $A^{\prime}=\prod_{i=1}^{n-1} a_{i}$ and $A=A^{\prime} a_{n}$. Mark the points on the real axis divisible by one of the numbers $a_{1}, \ldots, a_{n-1}$ green and those divisible by $a_{n}$ red. The green points divide $\left[0, A^{\prime}\right]$ into certain sub-intervals, say $J_{1}, J_{2}, \ldots$, and $J_{\ell}$. To translate intervals we use the notation $[a, b]+m=[a+m, b+m]$ whenever $a, b, m \in \mathbb{Z}$. For each $i \in\{1,2, \ldots, \ell\}$ let $\mathcal{F}_{i}$ be the family of intervals into which the red points partition the intervals $J_{i}, J_{i}+A^{\prime}, \ldots$, and $J_{i}+\left(a_{n}-1\right) A^{\prime}$. We are to prove that $$ \sum_{i=1}^{\ell} \sum_{X \in \mathcal{F}_{i}}\binom{|X|}{d} $$ is divisible by $p$. Let us fix any index $i$ with $1 \leqslant i \leqslant \ell$ for a while. Since the numbers $A^{\prime}$ and $a_{n}$ are coprime by hypothesis, the numbers $0, A^{\prime}, \ldots,\left(a_{n}-1\right) A^{\prime}$ form a complete system of residues modulo $a_{n}$. Moreover, we have $\left|J_{i}\right| \leqslant p<a_{n}$, as in particular all multiples of $p$ are green. So each of the intervals $J_{i}, J_{i}+A^{\prime}, \ldots$, and $J_{i}+\left(a_{n}-1\right) A^{\prime}$ contains at most one red point. More precisely, for each $j \in\left\{1, \ldots,\left|J_{i}\right|-1\right\}$ there is exactly one amongst those intervals containing a red point splitting it into an interval of length $j$ followed by an interval of length $\left|J_{i}\right|-j$, while the remaining $a_{n}-\left|J_{i}\right|+1$ such intervals have no red points in their interiors. For these reasons $$ \begin{aligned} \sum_{X \in \mathcal{F}_{i}}\binom{|X|}{d} & =2\left(\binom{1}{d}+\cdots+\binom{\left|J_{i}\right|-1}{d}\right)+\left(a_{n}-\left|J_{i}\right|+1\right)\binom{\left|J_{i}\right|}{d} \\ & =2\binom{\left|J_{i}\right|}{d+1}+\left(a_{n}-d+1\right)\binom{\left|J_{i}\right|}{d}-(d+1)\binom{\left|J_{i}\right|}{d+1} \\ & =(1-d)\binom{\left|J_{i}\right|}{d+1}+\left(a_{n}-d+1\right)\binom{\left|J_{i}\right|}{d} . \end{aligned} $$ So it remains to prove that $$ (1-d) \sum_{i=1}^{\ell}\binom{\left|J_{i}\right|}{d+1}+\left(a_{n}-d+1\right) \sum_{i=1}^{\ell}\binom{\left|J_{i}\right|}{d} $$ is divisible by $p$. By the induction hypothesis, however, it is even true that both summands are divisible by $p$, for $1 \leqslant d<d+1 \leqslant p-(n-1)$. This completes the proof of ( $\boxplus$ ) and hence the solution of the problem. Comment 2. The statement ( $\boxplus$ ) can also be proved by the method of the first solution, using the weights $w(x)=\binom{x-2}{d-2}$. This page is intentionally left blank
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a_{1}<a_{2}<\cdots<a_{n}$ be pairwise coprime positive integers with $a_{1}$ being prime and $a_{1} \geqslant n+2$. On the segment $I=\left[0, a_{1} a_{2} \cdots a_{n}\right]$ of the real line, mark all integers that are divisible by at least one of the numbers $a_{1}, \ldots, a_{n}$. These points split $I$ into a number of smaller segments. Prove that the sum of the squares of the lengths of these segments is divisible by $a_{1}$. (Serbia)
|
The conventions from the first paragraph of the first solution are still in force. We shall prove the following more general statement: ( $\boxplus$ ) Let $p$ denote a prime number, let $p=a_{1}<a_{2}<\cdots<a_{n}$ be $n$ pairwise coprime positive integers, and let $d$ be an integer with $1 \leqslant d \leqslant p-n$. Mark all integers that are divisible by at least one of the numbers $a_{1}, \ldots, a_{n}$ on the interval $I=\left[0, a_{1} a_{2} \cdots a_{n}\right]$ of the real line. These points split I into a number of smaller segments, say of lengths $b_{1}, \ldots, b_{k}$. Then the sum $\sum_{i=1}^{k}\binom{b_{i}}{d}$ is divisible by $p$. Applying ( $\boxplus$ ) to $d=1$ and $d=2$ and using the equation $x^{2}=2\binom{x}{2}+\binom{x}{1}$, one easily gets the statement of the problem. To prove $(\boxplus)$ itself, we argue by induction on $n$. The base case $n=1$ follows from the known fact that the binomial coefficient $\binom{p}{d}$ is divisible by $p$ whenever $1 \leqslant d \leqslant p-1$. Let us now assume that $n \geqslant 2$, and that the statement is known whenever $n-1$ rather than $n$ coprime integers are given together with some integer $d \in[1, p-n+1]$. Suppose that the numbers $p=a_{1}<a_{2}<\cdots<a_{n}$ and $d$ are as above. Write $A^{\prime}=\prod_{i=1}^{n-1} a_{i}$ and $A=A^{\prime} a_{n}$. Mark the points on the real axis divisible by one of the numbers $a_{1}, \ldots, a_{n-1}$ green and those divisible by $a_{n}$ red. The green points divide $\left[0, A^{\prime}\right]$ into certain sub-intervals, say $J_{1}, J_{2}, \ldots$, and $J_{\ell}$. To translate intervals we use the notation $[a, b]+m=[a+m, b+m]$ whenever $a, b, m \in \mathbb{Z}$. For each $i \in\{1,2, \ldots, \ell\}$ let $\mathcal{F}_{i}$ be the family of intervals into which the red points partition the intervals $J_{i}, J_{i}+A^{\prime}, \ldots$, and $J_{i}+\left(a_{n}-1\right) A^{\prime}$. We are to prove that $$ \sum_{i=1}^{\ell} \sum_{X \in \mathcal{F}_{i}}\binom{|X|}{d} $$ is divisible by $p$. Let us fix any index $i$ with $1 \leqslant i \leqslant \ell$ for a while. Since the numbers $A^{\prime}$ and $a_{n}$ are coprime by hypothesis, the numbers $0, A^{\prime}, \ldots,\left(a_{n}-1\right) A^{\prime}$ form a complete system of residues modulo $a_{n}$. Moreover, we have $\left|J_{i}\right| \leqslant p<a_{n}$, as in particular all multiples of $p$ are green. So each of the intervals $J_{i}, J_{i}+A^{\prime}, \ldots$, and $J_{i}+\left(a_{n}-1\right) A^{\prime}$ contains at most one red point. More precisely, for each $j \in\left\{1, \ldots,\left|J_{i}\right|-1\right\}$ there is exactly one amongst those intervals containing a red point splitting it into an interval of length $j$ followed by an interval of length $\left|J_{i}\right|-j$, while the remaining $a_{n}-\left|J_{i}\right|+1$ such intervals have no red points in their interiors. For these reasons $$ \begin{aligned} \sum_{X \in \mathcal{F}_{i}}\binom{|X|}{d} & =2\left(\binom{1}{d}+\cdots+\binom{\left|J_{i}\right|-1}{d}\right)+\left(a_{n}-\left|J_{i}\right|+1\right)\binom{\left|J_{i}\right|}{d} \\ & =2\binom{\left|J_{i}\right|}{d+1}+\left(a_{n}-d+1\right)\binom{\left|J_{i}\right|}{d}-(d+1)\binom{\left|J_{i}\right|}{d+1} \\ & =(1-d)\binom{\left|J_{i}\right|}{d+1}+\left(a_{n}-d+1\right)\binom{\left|J_{i}\right|}{d} . \end{aligned} $$ So it remains to prove that $$ (1-d) \sum_{i=1}^{\ell}\binom{\left|J_{i}\right|}{d+1}+\left(a_{n}-d+1\right) \sum_{i=1}^{\ell}\binom{\left|J_{i}\right|}{d} $$ is divisible by $p$. By the induction hypothesis, however, it is even true that both summands are divisible by $p$, for $1 \leqslant d<d+1 \leqslant p-(n-1)$. This completes the proof of ( $\boxplus$ ) and hence the solution of the problem. Comment 2. The statement ( $\boxplus$ ) can also be proved by the method of the first solution, using the weights $w(x)=\binom{x-2}{d-2}$. This page is intentionally left blank
|
{
"resource_path": "IMO/segmented/en-IMO2014SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
cf13e524-d6aa-5b4b-a7ad-494c0372135b
| 24,478
|
Let $c \geqslant 1$ be an integer. Define a sequence of positive integers by $a_{1}=c$ and $$ a_{n+1}=a_{n}^{3}-4 c \cdot a_{n}^{2}+5 c^{2} \cdot a_{n}+c $$ for all $n \geqslant 1$. Prove that for each integer $n \geqslant 2$ there exists a prime number $p$ dividing $a_{n}$ but none of the numbers $a_{1}, \ldots, a_{n-1}$. (Austria)
|
Let us define $x_{0}=0$ and $x_{n}=a_{n} / c$ for all integers $n \geqslant 1$. It is easy to see that the sequence $\left(x_{n}\right)$ thus obtained obeys the recursive law $$ x_{n+1}=c^{2}\left(x_{n}^{3}-4 x_{n}^{2}+5 x_{n}\right)+1 $$ for all integers $n \geqslant 0$. In particular, all of its terms are positive integers; notice that $x_{1}=1$ and $x_{2}=2 c^{2}+1$. Since $$ x_{n+1}=c^{2} x_{n}\left(x_{n}-2\right)^{2}+c^{2} x_{n}+1>x_{n} $$ holds for all integers $n \geqslant 0$, it is also strictly increasing. Since $x_{n+1}$ is by (1) coprime to $c$ for any $n \geqslant 0$, it suffices to prove that for each $n \geqslant 2$ there exists a prime number $p$ dividing $x_{n}$ but none of the numbers $x_{1}, \ldots, x_{n-1}$. Let us begin by establishing three preliminary claims. Claim 1. If $i \equiv j(\bmod m)$ holds for some integers $i, j \geqslant 0$ and $m \geqslant 1$, then $x_{i} \equiv x_{j}\left(\bmod x_{m}\right)$ holds as well. Proof. Evidently, it suffices to show $x_{i+m} \equiv x_{i}\left(\bmod x_{m}\right)$ for all integers $i \geqslant 0$ and $m \geqslant 1$. For this purpose we may argue for fixed $m$ by induction on $i$ using $x_{0}=0$ in the base case $i=0$. Now, if we have $x_{i+m} \equiv x_{i}\left(\bmod x_{m}\right)$ for some integer $i$, then the recursive equation (1) yields $$ x_{i+m+1} \equiv c^{2}\left(x_{i+m}^{3}-4 x_{i+m}^{2}+5 x_{i+m}\right)+1 \equiv c^{2}\left(x_{i}^{3}-4 x_{i}^{2}+5 x_{i}\right)+1 \equiv x_{i+1} \quad\left(\bmod x_{m}\right), $$ which completes the induction. Claim 2. If the integers $i, j \geqslant 2$ and $m \geqslant 1$ satisfy $i \equiv j(\bmod m)$, then $x_{i} \equiv x_{j}\left(\bmod x_{m}^{2}\right)$ holds as well. Proof. Again it suffices to prove $x_{i+m} \equiv x_{i}\left(\bmod x_{m}^{2}\right)$ for all integers $i \geqslant 2$ and $m \geqslant 1$. As above, we proceed for fixed $m$ by induction on $i$. The induction step is again easy using (1), but this time the base case $i=2$ requires some calculation. Set $L=5 c^{2}$. By (1) we have $x_{m+1} \equiv L x_{m}+1\left(\bmod x_{m}^{2}\right)$, and hence $$ \begin{aligned} x_{m+1}^{3}-4 x_{m+1}^{2}+5 x_{m+1} & \equiv\left(L x_{m}+1\right)^{3}-4\left(L x_{m}+1\right)^{2}+5\left(L x_{m}+1\right) \\ & \equiv\left(3 L x_{m}+1\right)-4\left(2 L x_{m}+1\right)+5\left(L x_{m}+1\right) \equiv 2 \quad\left(\bmod x_{m}^{2}\right) \end{aligned} $$ which in turn gives indeed $x_{m+2} \equiv 2 c^{2}+1 \equiv x_{2}\left(\bmod x_{m}^{2}\right)$. Claim 3. For each integer $n \geqslant 2$, we have $x_{n}>x_{1} \cdot x_{2} \cdots x_{n-2}$. Proof. The cases $n=2$ and $n=3$ are clear. Arguing inductively, we assume now that the claim holds for some $n \geqslant 3$. Recall that $x_{2} \geqslant 3$, so by monotonicity and (2) we get $x_{n} \geqslant x_{3} \geqslant x_{2}\left(x_{2}-2\right)^{2}+x_{2}+1 \geqslant 7$. It follows that $$ x_{n+1}>x_{n}^{3}-4 x_{n}^{2}+5 x_{n}>7 x_{n}^{2}-4 x_{n}^{2}>x_{n}^{2}>x_{n} x_{n-1} $$ which by the induction hypothesis yields $x_{n+1}>x_{1} \cdot x_{2} \cdots x_{n-1}$, as desired. Now we direct our attention to the problem itself: let any integer $n \geqslant 2$ be given. By Claim 3 there exists a prime number $p$ appearing with a higher exponent in the prime factorisation of $x_{n}$ than in the prime factorisation of $x_{1} \cdots x_{n-2}$. In particular, $p \mid x_{n}$, and it suffices to prove that $p$ divides none of $x_{1}, \ldots, x_{n-1}$. Otherwise let $k \in\{1, \ldots, n-1\}$ be minimal such that $p$ divides $x_{k}$. Since $x_{n-1}$ and $x_{n}$ are coprime by (1) and $x_{1}=1$, we actually have $2 \leqslant k \leqslant n-2$. Write $n=q k+r$ with some integers $q \geqslant 0$ and $0 \leqslant r<k$. By Claim 1 we have $x_{n} \equiv x_{r}\left(\bmod x_{k}\right)$, whence $p \mid x_{r}$. Due to the minimality of $k$ this entails $r=0$, i.e. $k \mid n$. Thus from Claim 2 we infer $$ x_{n} \equiv x_{k} \quad\left(\bmod x_{k}^{2}\right) . $$ Now let $\alpha \geqslant 1$ be maximal with the property $p^{\alpha} \mid x_{k}$. Then $x_{k}^{2}$ is divisible by $p^{\alpha+1}$ and by our choice of $p$ so is $x_{n}$. So by the previous congruence $x_{k}$ is a multiple of $p^{\alpha+1}$ as well, contrary to our choice of $\alpha$. This is the final contradiction concluding the solution.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $c \geqslant 1$ be an integer. Define a sequence of positive integers by $a_{1}=c$ and $$ a_{n+1}=a_{n}^{3}-4 c \cdot a_{n}^{2}+5 c^{2} \cdot a_{n}+c $$ for all $n \geqslant 1$. Prove that for each integer $n \geqslant 2$ there exists a prime number $p$ dividing $a_{n}$ but none of the numbers $a_{1}, \ldots, a_{n-1}$. (Austria)
|
Let us define $x_{0}=0$ and $x_{n}=a_{n} / c$ for all integers $n \geqslant 1$. It is easy to see that the sequence $\left(x_{n}\right)$ thus obtained obeys the recursive law $$ x_{n+1}=c^{2}\left(x_{n}^{3}-4 x_{n}^{2}+5 x_{n}\right)+1 $$ for all integers $n \geqslant 0$. In particular, all of its terms are positive integers; notice that $x_{1}=1$ and $x_{2}=2 c^{2}+1$. Since $$ x_{n+1}=c^{2} x_{n}\left(x_{n}-2\right)^{2}+c^{2} x_{n}+1>x_{n} $$ holds for all integers $n \geqslant 0$, it is also strictly increasing. Since $x_{n+1}$ is by (1) coprime to $c$ for any $n \geqslant 0$, it suffices to prove that for each $n \geqslant 2$ there exists a prime number $p$ dividing $x_{n}$ but none of the numbers $x_{1}, \ldots, x_{n-1}$. Let us begin by establishing three preliminary claims. Claim 1. If $i \equiv j(\bmod m)$ holds for some integers $i, j \geqslant 0$ and $m \geqslant 1$, then $x_{i} \equiv x_{j}\left(\bmod x_{m}\right)$ holds as well. Proof. Evidently, it suffices to show $x_{i+m} \equiv x_{i}\left(\bmod x_{m}\right)$ for all integers $i \geqslant 0$ and $m \geqslant 1$. For this purpose we may argue for fixed $m$ by induction on $i$ using $x_{0}=0$ in the base case $i=0$. Now, if we have $x_{i+m} \equiv x_{i}\left(\bmod x_{m}\right)$ for some integer $i$, then the recursive equation (1) yields $$ x_{i+m+1} \equiv c^{2}\left(x_{i+m}^{3}-4 x_{i+m}^{2}+5 x_{i+m}\right)+1 \equiv c^{2}\left(x_{i}^{3}-4 x_{i}^{2}+5 x_{i}\right)+1 \equiv x_{i+1} \quad\left(\bmod x_{m}\right), $$ which completes the induction. Claim 2. If the integers $i, j \geqslant 2$ and $m \geqslant 1$ satisfy $i \equiv j(\bmod m)$, then $x_{i} \equiv x_{j}\left(\bmod x_{m}^{2}\right)$ holds as well. Proof. Again it suffices to prove $x_{i+m} \equiv x_{i}\left(\bmod x_{m}^{2}\right)$ for all integers $i \geqslant 2$ and $m \geqslant 1$. As above, we proceed for fixed $m$ by induction on $i$. The induction step is again easy using (1), but this time the base case $i=2$ requires some calculation. Set $L=5 c^{2}$. By (1) we have $x_{m+1} \equiv L x_{m}+1\left(\bmod x_{m}^{2}\right)$, and hence $$ \begin{aligned} x_{m+1}^{3}-4 x_{m+1}^{2}+5 x_{m+1} & \equiv\left(L x_{m}+1\right)^{3}-4\left(L x_{m}+1\right)^{2}+5\left(L x_{m}+1\right) \\ & \equiv\left(3 L x_{m}+1\right)-4\left(2 L x_{m}+1\right)+5\left(L x_{m}+1\right) \equiv 2 \quad\left(\bmod x_{m}^{2}\right) \end{aligned} $$ which in turn gives indeed $x_{m+2} \equiv 2 c^{2}+1 \equiv x_{2}\left(\bmod x_{m}^{2}\right)$. Claim 3. For each integer $n \geqslant 2$, we have $x_{n}>x_{1} \cdot x_{2} \cdots x_{n-2}$. Proof. The cases $n=2$ and $n=3$ are clear. Arguing inductively, we assume now that the claim holds for some $n \geqslant 3$. Recall that $x_{2} \geqslant 3$, so by monotonicity and (2) we get $x_{n} \geqslant x_{3} \geqslant x_{2}\left(x_{2}-2\right)^{2}+x_{2}+1 \geqslant 7$. It follows that $$ x_{n+1}>x_{n}^{3}-4 x_{n}^{2}+5 x_{n}>7 x_{n}^{2}-4 x_{n}^{2}>x_{n}^{2}>x_{n} x_{n-1} $$ which by the induction hypothesis yields $x_{n+1}>x_{1} \cdot x_{2} \cdots x_{n-1}$, as desired. Now we direct our attention to the problem itself: let any integer $n \geqslant 2$ be given. By Claim 3 there exists a prime number $p$ appearing with a higher exponent in the prime factorisation of $x_{n}$ than in the prime factorisation of $x_{1} \cdots x_{n-2}$. In particular, $p \mid x_{n}$, and it suffices to prove that $p$ divides none of $x_{1}, \ldots, x_{n-1}$. Otherwise let $k \in\{1, \ldots, n-1\}$ be minimal such that $p$ divides $x_{k}$. Since $x_{n-1}$ and $x_{n}$ are coprime by (1) and $x_{1}=1$, we actually have $2 \leqslant k \leqslant n-2$. Write $n=q k+r$ with some integers $q \geqslant 0$ and $0 \leqslant r<k$. By Claim 1 we have $x_{n} \equiv x_{r}\left(\bmod x_{k}\right)$, whence $p \mid x_{r}$. Due to the minimality of $k$ this entails $r=0$, i.e. $k \mid n$. Thus from Claim 2 we infer $$ x_{n} \equiv x_{k} \quad\left(\bmod x_{k}^{2}\right) . $$ Now let $\alpha \geqslant 1$ be maximal with the property $p^{\alpha} \mid x_{k}$. Then $x_{k}^{2}$ is divisible by $p^{\alpha+1}$ and by our choice of $p$ so is $x_{n}$. So by the previous congruence $x_{k}$ is a multiple of $p^{\alpha+1}$ as well, contrary to our choice of $\alpha$. This is the final contradiction concluding the solution.
|
{
"resource_path": "IMO/segmented/en-IMO2014SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
eabf672f-0c77-57e5-a544-43997596c54b
| 24,481
|
For every real number $x$, let $\|x\|$ denote the distance between $x$ and the nearest integer. Prove that for every pair $(a, b)$ of positive integers there exist an odd prime $p$ and a positive integer $k$ satisfying $$ \left\|\frac{a}{p^{k}}\right\|+\left\|\frac{b}{p^{k}}\right\|+\left\|\frac{a+b}{p^{k}}\right\|=1 . $$ (Hungary)
|
Notice first that $\left\lfloor x+\frac{1}{2}\right\rfloor$ is an integer nearest to $x$, so $\|x\|=\left\lfloor\left.\left\lfloor x+\frac{1}{2}\right\rfloor-x \right\rvert\,\right.$. Thus we have $$ \left\lfloor x+\frac{1}{2}\right\rfloor=x \pm\|x\| . $$ For every rational number $r$ and every prime number $p$, denote by $v_{p}(r)$ the exponent of $p$ in the prime factorisation of $r$. Recall the notation $(2 n-1)!$ for the product of all odd positive integers not exceeding $2 n-1$, i.e., $(2 n-1)!!=1 \cdot 3 \cdots(2 n-1)$. Lemma. For every positive integer $n$ and every odd prime $p$, we have $$ v_{p}((2 n-1)!!)=\sum_{k=1}^{\infty}\left\lfloor\frac{n}{p^{k}}+\frac{1}{2}\right\rfloor . $$ Proof. For every positive integer $k$, let us count the multiples of $p^{k}$ among the factors $1,3, \ldots$, $2 n-1$. If $\ell$ is an arbitrary integer, the number $(2 \ell-1) p^{k}$ is listed above if and only if $$ 0<(2 \ell-1) p^{k} \leqslant 2 n \quad \Longleftrightarrow \quad \frac{1}{2}<\ell \leqslant \frac{n}{p^{k}}+\frac{1}{2} \quad \Longleftrightarrow \quad 1 \leqslant \ell \leqslant\left\lfloor\frac{n}{p^{k}}+\frac{1}{2}\right\rfloor $$ Hence, the number of multiples of $p^{k}$ among the factors is precisely $m_{k}=\left\lfloor\frac{n}{p^{k}}+\frac{1}{2}\right\rfloor$. Thus we obtain $$ v_{p}((2 n-1)!!)=\sum_{i=1}^{n} v_{p}(2 i-1)=\sum_{i=1}^{n} \sum_{k=1}^{v_{p}(2 i-1)} 1=\sum_{k=1}^{\infty} \sum_{\ell=1}^{m_{k}} 1=\sum_{k=1}^{\infty}\left\lfloor\frac{n}{p^{k}}+\frac{1}{2}\right\rfloor $$ In order to prove the problem statement, consider the rational number $$ N=\frac{(2 a+2 b-1)!!}{(2 a-1)!!\cdot(2 b-1)!!}=\frac{(2 a+1)(2 a+3) \cdots(2 a+2 b-1)}{1 \cdot 3 \cdots(2 b-1)} $$ Obviously, $N>1$, so there exists a prime $p$ with $v_{p}(N)>0$. Since $N$ is a fraction of two odd numbers, $p$ is odd. By our lemma, $$ 0<v_{p}(N)=\sum_{k=1}^{\infty}\left(\left\lfloor\frac{a+b}{p^{k}}+\frac{1}{2}\right\rfloor-\left\lfloor\frac{a}{p^{k}}+\frac{1}{2}\right\rfloor-\left\lfloor\frac{b}{p^{k}}+\frac{1}{2}\right\rfloor\right) . $$ Therefore, there exists some positive integer $k$ such that the integer number $$ d_{k}=\left\lfloor\frac{a+b}{p^{k}}+\frac{1}{2}\right\rfloor-\left\lfloor\frac{a}{p^{k}}+\frac{1}{2}\right\rfloor-\left\lfloor\frac{b}{p^{k}}+\frac{1}{2}\right\rfloor $$ is positive, so $d_{k} \geqslant 1$. By (2) we have $$ 1 \leqslant d_{k}=\frac{a+b}{p^{k}}-\frac{a}{p^{k}}-\frac{b}{p^{k}} \pm\left\|\frac{a+b}{p^{k}}\right\| \pm\left\|\frac{a}{p^{k}}\right\| \pm\left\|\frac{b}{p^{k}}\right\|= \pm\left\|\frac{a+b}{p^{k}}\right\| \pm\left\|\frac{a}{p^{k}}\right\| \pm\left\|\frac{b}{p^{k}}\right\| $$ Since $\|x\|<\frac{1}{2}$ for every rational $x$ with odd denominator, the relation (3) can only be satisfied if all three signs on the right-hand side are positive and $d_{k}=1$. Thus we get $$ \left\|\frac{a}{p^{k}}\right\|+\left\|\frac{b}{p^{k}}\right\|+\left\|\frac{a+b}{p^{k}}\right\|=d_{k}=1, $$ as required. Comment 1. There are various choices for the number $N$ in the solution. Here we sketch such a version. Let $x$ and $y$ be two rational numbers with odd denominators. It is easy to see that the condition $\|x\|+\|y\|+\|x+y\|=1$ is satisfied if and only if $$ \text { either } \quad\{x\}<\frac{1}{2}, \quad\{y\}<\frac{1}{2}, \quad\{x+y\}>\frac{1}{2}, \quad \text { or } \quad\{x\}>\frac{1}{2}, \quad\{y\}>\frac{1}{2}, \quad\{x+y\}<\frac{1}{2}, $$ where $\{x\}$ denotes the fractional part of $x$. In the context of our problem, the first condition seems easier to deal with. Also, one may notice that $$ \{x\}<\frac{1}{2} \Longleftrightarrow \varkappa(x)=0 \quad \text { and } \quad\{x\} \geqslant \frac{1}{2} \Longleftrightarrow \varkappa(x)=1, $$ where $$ \varkappa(x)=\lfloor 2 x\rfloor-2\lfloor x\rfloor . $$ Now it is natural to consider the number $$ M=\frac{\binom{2 a+2 b}{a+b}}{\binom{2 a}{a}\binom{2 b}{b}} $$ since $$ v_{p}(M)=\sum_{k=1}^{\infty}\left(\varkappa\left(\frac{2(a+b)}{p^{k}}\right)-\varkappa\left(\frac{2 a}{p^{k}}\right)-\varkappa\left(\frac{2 b}{p^{k}}\right)\right) . $$ One may see that $M>1$, and that $v_{2}(M) \leqslant 0$. Thus, there exist an odd prime $p$ and a positive integer $k$ with $$ \varkappa\left(\frac{2(a+b)}{p^{k}}\right)-\varkappa\left(\frac{2 a}{p^{k}}\right)-\varkappa\left(\frac{2 b}{p^{k}}\right)>0 . $$ In view of (4), the last inequality yields $$ \left\{\frac{a}{p^{k}}\right\}<\frac{1}{2}, \quad\left\{\frac{b}{p^{k}}\right\}<\frac{1}{2}, \quad \text { and } \quad\left\{\frac{a+b}{p^{k}}\right\}>\frac{1}{2} $$ which is what we wanted to obtain. Comment 2. Once one tries to prove the existence of suitable $p$ and $k$ satisfying (5), it seems somehow natural to suppose that $a \leqslant b$ and to add the restriction $p^{k}>a$. In this case the inequalities (5) can be rewritten as $$ 2 a<p^{k}, \quad 2 m p^{k}<2 b<(2 m+1) p^{k}, \quad \text { and } \quad(2 m+1) p^{k}<2(a+b)<(2 m+2) p^{k} $$ for some positive integer $m$. This means exactly that one of the numbers $2 a+1,2 a+3, \ldots, 2 a+2 b-1$ is divisible by some number of the form $p^{k}$ which is greater than $2 a$. Using more advanced techniques, one can show that such a number $p^{k}$ exists even with $k=1$. This was shown in 2004 by Laishram and Shorey; the methods used for this proof are elementary but still quite involved. In fact, their result generalises a theorem by SyLvester which states that for every pair of integers $(n, k)$ with $n \geqslant k \geqslant 1$, the product $(n+1)(n+2) \cdots(n+k)$ is divisible by some prime $p>k$. We would like to mention here that Sylvester's theorem itself does not seem to suffice for solving the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For every real number $x$, let $\|x\|$ denote the distance between $x$ and the nearest integer. Prove that for every pair $(a, b)$ of positive integers there exist an odd prime $p$ and a positive integer $k$ satisfying $$ \left\|\frac{a}{p^{k}}\right\|+\left\|\frac{b}{p^{k}}\right\|+\left\|\frac{a+b}{p^{k}}\right\|=1 . $$ (Hungary)
|
Notice first that $\left\lfloor x+\frac{1}{2}\right\rfloor$ is an integer nearest to $x$, so $\|x\|=\left\lfloor\left.\left\lfloor x+\frac{1}{2}\right\rfloor-x \right\rvert\,\right.$. Thus we have $$ \left\lfloor x+\frac{1}{2}\right\rfloor=x \pm\|x\| . $$ For every rational number $r$ and every prime number $p$, denote by $v_{p}(r)$ the exponent of $p$ in the prime factorisation of $r$. Recall the notation $(2 n-1)!$ for the product of all odd positive integers not exceeding $2 n-1$, i.e., $(2 n-1)!!=1 \cdot 3 \cdots(2 n-1)$. Lemma. For every positive integer $n$ and every odd prime $p$, we have $$ v_{p}((2 n-1)!!)=\sum_{k=1}^{\infty}\left\lfloor\frac{n}{p^{k}}+\frac{1}{2}\right\rfloor . $$ Proof. For every positive integer $k$, let us count the multiples of $p^{k}$ among the factors $1,3, \ldots$, $2 n-1$. If $\ell$ is an arbitrary integer, the number $(2 \ell-1) p^{k}$ is listed above if and only if $$ 0<(2 \ell-1) p^{k} \leqslant 2 n \quad \Longleftrightarrow \quad \frac{1}{2}<\ell \leqslant \frac{n}{p^{k}}+\frac{1}{2} \quad \Longleftrightarrow \quad 1 \leqslant \ell \leqslant\left\lfloor\frac{n}{p^{k}}+\frac{1}{2}\right\rfloor $$ Hence, the number of multiples of $p^{k}$ among the factors is precisely $m_{k}=\left\lfloor\frac{n}{p^{k}}+\frac{1}{2}\right\rfloor$. Thus we obtain $$ v_{p}((2 n-1)!!)=\sum_{i=1}^{n} v_{p}(2 i-1)=\sum_{i=1}^{n} \sum_{k=1}^{v_{p}(2 i-1)} 1=\sum_{k=1}^{\infty} \sum_{\ell=1}^{m_{k}} 1=\sum_{k=1}^{\infty}\left\lfloor\frac{n}{p^{k}}+\frac{1}{2}\right\rfloor $$ In order to prove the problem statement, consider the rational number $$ N=\frac{(2 a+2 b-1)!!}{(2 a-1)!!\cdot(2 b-1)!!}=\frac{(2 a+1)(2 a+3) \cdots(2 a+2 b-1)}{1 \cdot 3 \cdots(2 b-1)} $$ Obviously, $N>1$, so there exists a prime $p$ with $v_{p}(N)>0$. Since $N$ is a fraction of two odd numbers, $p$ is odd. By our lemma, $$ 0<v_{p}(N)=\sum_{k=1}^{\infty}\left(\left\lfloor\frac{a+b}{p^{k}}+\frac{1}{2}\right\rfloor-\left\lfloor\frac{a}{p^{k}}+\frac{1}{2}\right\rfloor-\left\lfloor\frac{b}{p^{k}}+\frac{1}{2}\right\rfloor\right) . $$ Therefore, there exists some positive integer $k$ such that the integer number $$ d_{k}=\left\lfloor\frac{a+b}{p^{k}}+\frac{1}{2}\right\rfloor-\left\lfloor\frac{a}{p^{k}}+\frac{1}{2}\right\rfloor-\left\lfloor\frac{b}{p^{k}}+\frac{1}{2}\right\rfloor $$ is positive, so $d_{k} \geqslant 1$. By (2) we have $$ 1 \leqslant d_{k}=\frac{a+b}{p^{k}}-\frac{a}{p^{k}}-\frac{b}{p^{k}} \pm\left\|\frac{a+b}{p^{k}}\right\| \pm\left\|\frac{a}{p^{k}}\right\| \pm\left\|\frac{b}{p^{k}}\right\|= \pm\left\|\frac{a+b}{p^{k}}\right\| \pm\left\|\frac{a}{p^{k}}\right\| \pm\left\|\frac{b}{p^{k}}\right\| $$ Since $\|x\|<\frac{1}{2}$ for every rational $x$ with odd denominator, the relation (3) can only be satisfied if all three signs on the right-hand side are positive and $d_{k}=1$. Thus we get $$ \left\|\frac{a}{p^{k}}\right\|+\left\|\frac{b}{p^{k}}\right\|+\left\|\frac{a+b}{p^{k}}\right\|=d_{k}=1, $$ as required. Comment 1. There are various choices for the number $N$ in the solution. Here we sketch such a version. Let $x$ and $y$ be two rational numbers with odd denominators. It is easy to see that the condition $\|x\|+\|y\|+\|x+y\|=1$ is satisfied if and only if $$ \text { either } \quad\{x\}<\frac{1}{2}, \quad\{y\}<\frac{1}{2}, \quad\{x+y\}>\frac{1}{2}, \quad \text { or } \quad\{x\}>\frac{1}{2}, \quad\{y\}>\frac{1}{2}, \quad\{x+y\}<\frac{1}{2}, $$ where $\{x\}$ denotes the fractional part of $x$. In the context of our problem, the first condition seems easier to deal with. Also, one may notice that $$ \{x\}<\frac{1}{2} \Longleftrightarrow \varkappa(x)=0 \quad \text { and } \quad\{x\} \geqslant \frac{1}{2} \Longleftrightarrow \varkappa(x)=1, $$ where $$ \varkappa(x)=\lfloor 2 x\rfloor-2\lfloor x\rfloor . $$ Now it is natural to consider the number $$ M=\frac{\binom{2 a+2 b}{a+b}}{\binom{2 a}{a}\binom{2 b}{b}} $$ since $$ v_{p}(M)=\sum_{k=1}^{\infty}\left(\varkappa\left(\frac{2(a+b)}{p^{k}}\right)-\varkappa\left(\frac{2 a}{p^{k}}\right)-\varkappa\left(\frac{2 b}{p^{k}}\right)\right) . $$ One may see that $M>1$, and that $v_{2}(M) \leqslant 0$. Thus, there exist an odd prime $p$ and a positive integer $k$ with $$ \varkappa\left(\frac{2(a+b)}{p^{k}}\right)-\varkappa\left(\frac{2 a}{p^{k}}\right)-\varkappa\left(\frac{2 b}{p^{k}}\right)>0 . $$ In view of (4), the last inequality yields $$ \left\{\frac{a}{p^{k}}\right\}<\frac{1}{2}, \quad\left\{\frac{b}{p^{k}}\right\}<\frac{1}{2}, \quad \text { and } \quad\left\{\frac{a+b}{p^{k}}\right\}>\frac{1}{2} $$ which is what we wanted to obtain. Comment 2. Once one tries to prove the existence of suitable $p$ and $k$ satisfying (5), it seems somehow natural to suppose that $a \leqslant b$ and to add the restriction $p^{k}>a$. In this case the inequalities (5) can be rewritten as $$ 2 a<p^{k}, \quad 2 m p^{k}<2 b<(2 m+1) p^{k}, \quad \text { and } \quad(2 m+1) p^{k}<2(a+b)<(2 m+2) p^{k} $$ for some positive integer $m$. This means exactly that one of the numbers $2 a+1,2 a+3, \ldots, 2 a+2 b-1$ is divisible by some number of the form $p^{k}$ which is greater than $2 a$. Using more advanced techniques, one can show that such a number $p^{k}$ exists even with $k=1$. This was shown in 2004 by Laishram and Shorey; the methods used for this proof are elementary but still quite involved. In fact, their result generalises a theorem by SyLvester which states that for every pair of integers $(n, k)$ with $n \geqslant k \geqslant 1$, the product $(n+1)(n+2) \cdots(n+k)$ is divisible by some prime $p>k$. We would like to mention here that Sylvester's theorem itself does not seem to suffice for solving the problem.
|
{
"resource_path": "IMO/segmented/en-IMO2014SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
fb2fce79-44ed-55dd-80a7-bbf3322fc3c5
| 24,485
|
Let $z_{0}<z_{1}<z_{2}<\cdots$ be an infinite sequence of positive integers. Prove that there exists a unique integer $n \geqslant 1$ such that $$ z_{n}<\frac{z_{0}+z_{1}+\cdots+z_{n}}{n} \leqslant z_{n+1} . $$ (Austria)
|
For $n=1,2, \ldots$ define $$ d_{n}=\left(z_{0}+z_{1}+\cdots+z_{n}\right)-n z_{n} $$ The sign of $d_{n}$ indicates whether the first inequality in (1) holds; i.e., it is satisfied if and only if $d_{n}>0$. Notice that $$ n z_{n+1}-\left(z_{0}+z_{1}+\cdots+z_{n}\right)=(n+1) z_{n+1}-\left(z_{0}+z_{1}+\cdots+z_{n}+z_{n+1}\right)=-d_{n+1} $$ so the second inequality in (1) is equivalent to $d_{n+1} \leqslant 0$. Therefore, we have to prove that there is a unique index $n \geqslant 1$ that satisfies $d_{n}>0 \geqslant d_{n+1}$. By its definition the sequence $d_{1}, d_{2}, \ldots$ consists of integers and we have $$ d_{1}=\left(z_{0}+z_{1}\right)-1 \cdot z_{1}=z_{0}>0 $$ From $d_{n+1}-d_{n}=\left(\left(z_{0}+\cdots+z_{n}+z_{n+1}\right)-(n+1) z_{n+1}\right)-\left(\left(z_{0}+\cdots+z_{n}\right)-n z_{n}\right)=n\left(z_{n}-z_{n+1}\right)<0$ we can see that $d_{n+1}<d_{n}$ and thus the sequence strictly decreases. Hence, we have a decreasing sequence $d_{1}>d_{2}>\ldots$ of integers such that its first element $d_{1}$ is positive. The sequence must drop below 0 at some point, and thus there is a unique index $n$, that is the index of the last positive term, satisfying $d_{n}>0 \geqslant d_{n+1}$. Comment. Omitting the assumption that $z_{1}, z_{2}, \ldots$ are integers allows the numbers $d_{n}$ to be all positive. In such cases the desired $n$ does not exist. This happens for example if $z_{n}=2-\frac{1}{2^{n}}$ for all integers $n \geqslant 0$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $z_{0}<z_{1}<z_{2}<\cdots$ be an infinite sequence of positive integers. Prove that there exists a unique integer $n \geqslant 1$ such that $$ z_{n}<\frac{z_{0}+z_{1}+\cdots+z_{n}}{n} \leqslant z_{n+1} . $$ (Austria)
|
For $n=1,2, \ldots$ define $$ d_{n}=\left(z_{0}+z_{1}+\cdots+z_{n}\right)-n z_{n} $$ The sign of $d_{n}$ indicates whether the first inequality in (1) holds; i.e., it is satisfied if and only if $d_{n}>0$. Notice that $$ n z_{n+1}-\left(z_{0}+z_{1}+\cdots+z_{n}\right)=(n+1) z_{n+1}-\left(z_{0}+z_{1}+\cdots+z_{n}+z_{n+1}\right)=-d_{n+1} $$ so the second inequality in (1) is equivalent to $d_{n+1} \leqslant 0$. Therefore, we have to prove that there is a unique index $n \geqslant 1$ that satisfies $d_{n}>0 \geqslant d_{n+1}$. By its definition the sequence $d_{1}, d_{2}, \ldots$ consists of integers and we have $$ d_{1}=\left(z_{0}+z_{1}\right)-1 \cdot z_{1}=z_{0}>0 $$ From $d_{n+1}-d_{n}=\left(\left(z_{0}+\cdots+z_{n}+z_{n+1}\right)-(n+1) z_{n+1}\right)-\left(\left(z_{0}+\cdots+z_{n}\right)-n z_{n}\right)=n\left(z_{n}-z_{n+1}\right)<0$ we can see that $d_{n+1}<d_{n}$ and thus the sequence strictly decreases. Hence, we have a decreasing sequence $d_{1}>d_{2}>\ldots$ of integers such that its first element $d_{1}$ is positive. The sequence must drop below 0 at some point, and thus there is a unique index $n$, that is the index of the last positive term, satisfying $d_{n}>0 \geqslant d_{n+1}$. Comment. Omitting the assumption that $z_{1}, z_{2}, \ldots$ are integers allows the numbers $d_{n}$ to be all positive. In such cases the desired $n$ does not exist. This happens for example if $z_{n}=2-\frac{1}{2^{n}}$ for all integers $n \geqslant 0$.
|
{
"resource_path": "IMO/segmented/en-IMO2014SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
2fe4f98f-be96-5a6e-b6ac-1ac3b9bce9a8
| 24,487
|
Let $A B C$ be a fixed acute-angled triangle. Consider some points $E$ and $F$ lying on the sides $A C$ and $A B$, respectively, and let $M$ be the midpoint of $E F$. Let the perpendicular bisector of $E F$ intersect the line $B C$ at $K$, and let the perpendicular bisector of $M K$ intersect the lines $A C$ and $A B$ at $S$ and $T$, respectively. We call the pair $(E, F)$ interesting, if the quadrilateral $K S A T$ is cyclic. Suppose that the pairs $\left(E_{1}, F_{1}\right)$ and $\left(E_{2}, F_{2}\right)$ are interesting. Prove that $$ \frac{E_{1} E_{2}}{A B}=\frac{F_{1} F_{2}}{A C} $$ (Iran)
|
For any interesting pair $(E, F)$, we will say that the corresponding triangle $E F K$ is also interesting. Let $E F K$ be an interesting triangle. Firstly, we prove that $\angle K E F=\angle K F E=\angle A$, which also means that the circumcircle $\omega_{1}$ of the triangle $A E F$ is tangent to the lines $K E$ and $K F$. Denote by $\omega$ the circle passing through the points $K, S, A$, and $T$. Let the line $A M$ intersect the line $S T$ and the circle $\omega$ (for the second time) at $N$ and $L$, respectively (see Figure 1). Since $E F \| T S$ and $M$ is the midpoint of $E F, N$ is the midpoint of $S T$. Moreover, since $K$ and $M$ are symmetric to each other with respect to the line $S T$, we have $\angle K N S=\angle M N S=$ $\angle L N T$. Thus the points $K$ and $L$ are symmetric to each other with respect to the perpendicular bisector of $S T$. Therefore $K L \| S T$. Let $G$ be the point symmetric to $K$ with respect to $N$. Then $G$ lies on the line $E F$, and we may assume that it lies on the ray $M F$. One has $$ \angle K G E=\angle K N S=\angle S N M=\angle K L A=180^{\circ}-\angle K S A $$ (if $K=L$, then the angle $K L A$ is understood to be the angle between $A L$ and the tangent to $\omega$ at $L$ ). This means that the points $K, G, E$, and $S$ are concyclic. Now, since $K S G T$ is a parallelogram, we obtain $\angle K E F=\angle K S G=180^{\circ}-\angle T K S=\angle A$. Since $K E=K F$, we also have $\angle K F E=\angle K E F=\angle A$. After having proved this fact, one may finish the solution by different methods.  Figure 1  Figure 2 First method. We have just proved that all interesting triangles are similar to each other. This allows us to use the following lemma. Lemma. Let $A B C$ be an arbitrary triangle. Choose two points $E_{1}$ and $E_{2}$ on the side $A C$, two points $F_{1}$ and $F_{2}$ on the side $A B$, and two points $K_{1}$ and $K_{2}$ on the side $B C$, in a way that the triangles $E_{1} F_{1} K_{1}$ and $E_{2} F_{2} K_{2}$ are similar. Then the six circumcircles of the triangles $A E_{i} F_{i}$, $B F_{i} K_{i}$, and $C E_{i} K_{i}(i=1,2)$ meet at a common point $Z$. Moreover, $Z$ is the centre of the spiral similarity that takes the triangle $E_{1} F_{1} K_{1}$ to the triangle $E_{2} F_{2} K_{2}$. Proof. Firstly, notice that for each $i=1,2$, the circumcircles of the triangles $A E_{i} F_{i}, B F_{i} K_{i}$, and $C K_{i} E_{i}$ have a common point $Z_{i}$ by Miquel's theorem. Moreover, we have $\Varangle\left(Z_{i} F_{i}, Z_{i} E_{i}\right)=\Varangle(A B, C A), \quad \Varangle\left(Z_{i} K_{i}, Z_{i} F_{i}\right)=\Varangle(B C, A B), \quad \Varangle\left(Z_{i} E_{i}, Z_{i} K_{i}\right)=\Varangle(C A, B C)$. This yields that the points $Z_{1}$ and $Z_{2}$ correspond to each other in similar triangles $E_{1} F_{1} K_{1}$ and $E_{2} F_{2} K_{2}$. Thus, if they coincide, then this common point is indeed the desired centre of a spiral similarity. Finally, in order to show that $Z_{1}=Z_{2}$, one may notice that $\Varangle\left(A B, A Z_{1}\right)=\Varangle\left(E_{1} F_{1}, E_{1} Z_{1}\right)=$ $\Varangle\left(E_{2} F_{2}, E_{2} Z_{2}\right)=\Varangle\left(A B, A Z_{2}\right)$ (see Figure 2). Similarly, one has $\Varangle\left(B C, B Z_{1}\right)=\Varangle\left(B C, B Z_{2}\right)$ and $\Varangle\left(C A, C Z_{1}\right)=\Varangle\left(C A, C Z_{2}\right)$. This yields $Z_{1}=Z_{2}$. Now, let $P$ and $Q$ be the feet of the perpendiculars from $B$ and $C$ onto $A C$ and $A B$, respectively, and let $R$ be the midpoint of $B C$ (see Figure 3). Then $R$ is the circumcentre of the cyclic quadrilateral $B C P Q$. Thus we obtain $\angle A P Q=\angle B$ and $\angle R P C=\angle C$, which yields $\angle Q P R=\angle A$. Similarly, we show that $\angle P Q R=\angle A$. Thus, all interesting triangles are similar to the triangle $P Q R$.  Figure 3  Figure 4 Denote now by $Z$ the common point of the circumcircles of $A P Q, B Q R$, and $C P R$. Let $E_{1} F_{1} K_{1}$ and $E_{2} F_{2} K_{2}$ be two interesting triangles. By the lemma, $Z$ is the centre of any spiral similarity taking one of the triangles $E_{1} F_{1} K_{1}, E_{2} F_{2} K_{2}$, and $P Q R$ to some other of them. Therefore the triangles $Z E_{1} E_{2}$ and $Z F_{1} F_{2}$ are similar, as well as the triangles $Z E_{1} F_{1}$ and $Z P Q$. Hence $$ \frac{E_{1} E_{2}}{F_{1} F_{2}}=\frac{Z E_{1}}{Z F_{1}}=\frac{Z P}{Z Q} $$ Moreover, the equalities $\angle A Z Q=\angle A P Q=\angle A B C=180^{\circ}-\angle Q Z R$ show that the point $Z$ lies on the line $A R$ (see Figure 4). Therefore the triangles $A Z P$ and $A C R$ are similar, as well as the triangles $A Z Q$ and $A B R$. This yields $$ \frac{Z P}{Z Q}=\frac{Z P}{R C} \cdot \frac{R B}{Z Q}=\frac{A Z}{A C} \cdot \frac{A B}{A Z}=\frac{A B}{A C} $$ which completes the solution. Second method. Now we will start from the fact that $\omega_{1}$ is tangent to the lines $K E$ and $K F$ (see Figure 5). We prove that if $(E, F)$ is an interesting pair, then $$ \frac{A E}{A B}+\frac{A F}{A C}=2 \cos \angle A $$ Let $Y$ be the intersection point of the segments $B E$ and $C F$. The points $B, K$, and $C$ are collinear, hence applying PASCAL's theorem to the degenerated hexagon AFFYEE, we infer that $Y$ lies on the circle $\omega_{1}$. Denote by $Z$ the second intersection point of the circumcircle of the triangle $B F Y$ with the line $B C$ (see Figure 6). By Miquel's theorem, the points $C, Z, Y$, and $E$ are concyclic. Therefore we obtain $$ B F \cdot A B+C E \cdot A C=B Y \cdot B E+C Y \cdot C F=B Z \cdot B C+C Z \cdot B C=B C^{2} $$ On the other hand, $B C^{2}=A B^{2}+A C^{2}-2 A B \cdot A C \cos \angle A$, by the cosine law. Hence $$ (A B-A F) \cdot A B+(A C-A E) \cdot A C=A B^{2}+A C^{2}-2 A B \cdot A C \cos \angle A, $$ which simplifies to the desired equality (1). Let now $\left(E_{1}, F_{1}\right)$ and $\left(E_{2}, F_{2}\right)$ be two interesting pairs of points. Then we get $$ \frac{A E_{1}}{A B}+\frac{A F_{1}}{A C}=\frac{A E_{2}}{A B}+\frac{A F_{2}}{A C} $$ which gives the desired result.  Figure 5  Figure 6 Third method. Again, we make use of the fact that all interesting triangles are similar (and equi-oriented). Let us put the picture onto a complex plane such that $A$ is at the origin, and identify each point with the corresponding complex number. Let $E F K$ be any interesting triangle. The equalities $\angle K E F=\angle K F E=\angle A$ yield that the ratio $\nu=\frac{K-E}{F-E}$ is the same for all interesting triangles. This in turn means that the numbers $E$, $F$, and $K$ satisfy the linear equation $$ K=\mu E+\nu F, \quad \text { where } \quad \mu=1-\nu $$ Now let us choose the points $X$ and $Y$ on the rays $A B$ and $A C$, respectively, so that $\angle C X A=\angle A Y B=\angle A=\angle K E F$ (see Figure 7). Then each of the triangles $A X C$ and $Y A B$ is similar to any interesting triangle, which also means that $$ C=\mu A+\nu X=\nu X \quad \text { and } \quad B=\mu Y+\nu A=\mu Y . $$ Moreover, one has $X / Y=\overline{C / B}$. Since the points $E, F$, and $K$ lie on $A C, A B$, and $B C$, respectively, one gets $$ E=\rho Y, \quad F=\sigma X, \quad \text { and } \quad K=\lambda B+(1-\lambda) C $$ for some real $\rho, \sigma$, and $\lambda$. In view of (3), the equation (2) now reads $\lambda B+(1-\lambda) C=K=$ $\mu E+\nu F=\rho B+\sigma C$, or $$ (\lambda-\rho) B=(\sigma+\lambda-1) C $$ Since the nonzero complex numbers $B$ and $C$ have different arguments, the coefficients in the brackets vanish, so $\rho=\lambda$ and $\sigma=1-\lambda$. Therefore, $$ \frac{E}{Y}+\frac{F}{X}=\rho+\sigma=1 $$ Now, if $\left(E_{1}, F_{1}\right)$ and $\left(E_{2}, F_{2}\right)$ are two distinct interesting pairs, one may apply (4) to both pairs. Subtracting, we get $$ \frac{E_{1}-E_{2}}{Y}=\frac{F_{2}-F_{1}}{X}, \quad \text { so } \quad \frac{E_{1}-E_{2}}{F_{2}-F_{1}}=\frac{Y}{X}=\frac{\bar{B}}{\bar{C}} $$ Taking absolute values provides the required result.  Figure 7 Comment 1. One may notice that the triangle $P Q R$ is also interesting. Comment 2. In order to prove that $\angle K E F=\angle K F E=\angle A$, one may also use the following well-known fact: Let $A E F$ be a triangle with $A E \neq A F$, and let $K$ be the common point of the symmedian taken from $A$ and the perpendicular bisector of $E F$. Then the lines $K E$ and $K F$ are tangent to the circumcircle $\omega_{1}$ of the triangle $A E F$. In this case, however, one needs to deal with the case $A E=A F$ separately.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a fixed acute-angled triangle. Consider some points $E$ and $F$ lying on the sides $A C$ and $A B$, respectively, and let $M$ be the midpoint of $E F$. Let the perpendicular bisector of $E F$ intersect the line $B C$ at $K$, and let the perpendicular bisector of $M K$ intersect the lines $A C$ and $A B$ at $S$ and $T$, respectively. We call the pair $(E, F)$ interesting, if the quadrilateral $K S A T$ is cyclic. Suppose that the pairs $\left(E_{1}, F_{1}\right)$ and $\left(E_{2}, F_{2}\right)$ are interesting. Prove that $$ \frac{E_{1} E_{2}}{A B}=\frac{F_{1} F_{2}}{A C} $$ (Iran)
|
For any interesting pair $(E, F)$, we will say that the corresponding triangle $E F K$ is also interesting. Let $E F K$ be an interesting triangle. Firstly, we prove that $\angle K E F=\angle K F E=\angle A$, which also means that the circumcircle $\omega_{1}$ of the triangle $A E F$ is tangent to the lines $K E$ and $K F$. Denote by $\omega$ the circle passing through the points $K, S, A$, and $T$. Let the line $A M$ intersect the line $S T$ and the circle $\omega$ (for the second time) at $N$ and $L$, respectively (see Figure 1). Since $E F \| T S$ and $M$ is the midpoint of $E F, N$ is the midpoint of $S T$. Moreover, since $K$ and $M$ are symmetric to each other with respect to the line $S T$, we have $\angle K N S=\angle M N S=$ $\angle L N T$. Thus the points $K$ and $L$ are symmetric to each other with respect to the perpendicular bisector of $S T$. Therefore $K L \| S T$. Let $G$ be the point symmetric to $K$ with respect to $N$. Then $G$ lies on the line $E F$, and we may assume that it lies on the ray $M F$. One has $$ \angle K G E=\angle K N S=\angle S N M=\angle K L A=180^{\circ}-\angle K S A $$ (if $K=L$, then the angle $K L A$ is understood to be the angle between $A L$ and the tangent to $\omega$ at $L$ ). This means that the points $K, G, E$, and $S$ are concyclic. Now, since $K S G T$ is a parallelogram, we obtain $\angle K E F=\angle K S G=180^{\circ}-\angle T K S=\angle A$. Since $K E=K F$, we also have $\angle K F E=\angle K E F=\angle A$. After having proved this fact, one may finish the solution by different methods.  Figure 1  Figure 2 First method. We have just proved that all interesting triangles are similar to each other. This allows us to use the following lemma. Lemma. Let $A B C$ be an arbitrary triangle. Choose two points $E_{1}$ and $E_{2}$ on the side $A C$, two points $F_{1}$ and $F_{2}$ on the side $A B$, and two points $K_{1}$ and $K_{2}$ on the side $B C$, in a way that the triangles $E_{1} F_{1} K_{1}$ and $E_{2} F_{2} K_{2}$ are similar. Then the six circumcircles of the triangles $A E_{i} F_{i}$, $B F_{i} K_{i}$, and $C E_{i} K_{i}(i=1,2)$ meet at a common point $Z$. Moreover, $Z$ is the centre of the spiral similarity that takes the triangle $E_{1} F_{1} K_{1}$ to the triangle $E_{2} F_{2} K_{2}$. Proof. Firstly, notice that for each $i=1,2$, the circumcircles of the triangles $A E_{i} F_{i}, B F_{i} K_{i}$, and $C K_{i} E_{i}$ have a common point $Z_{i}$ by Miquel's theorem. Moreover, we have $\Varangle\left(Z_{i} F_{i}, Z_{i} E_{i}\right)=\Varangle(A B, C A), \quad \Varangle\left(Z_{i} K_{i}, Z_{i} F_{i}\right)=\Varangle(B C, A B), \quad \Varangle\left(Z_{i} E_{i}, Z_{i} K_{i}\right)=\Varangle(C A, B C)$. This yields that the points $Z_{1}$ and $Z_{2}$ correspond to each other in similar triangles $E_{1} F_{1} K_{1}$ and $E_{2} F_{2} K_{2}$. Thus, if they coincide, then this common point is indeed the desired centre of a spiral similarity. Finally, in order to show that $Z_{1}=Z_{2}$, one may notice that $\Varangle\left(A B, A Z_{1}\right)=\Varangle\left(E_{1} F_{1}, E_{1} Z_{1}\right)=$ $\Varangle\left(E_{2} F_{2}, E_{2} Z_{2}\right)=\Varangle\left(A B, A Z_{2}\right)$ (see Figure 2). Similarly, one has $\Varangle\left(B C, B Z_{1}\right)=\Varangle\left(B C, B Z_{2}\right)$ and $\Varangle\left(C A, C Z_{1}\right)=\Varangle\left(C A, C Z_{2}\right)$. This yields $Z_{1}=Z_{2}$. Now, let $P$ and $Q$ be the feet of the perpendiculars from $B$ and $C$ onto $A C$ and $A B$, respectively, and let $R$ be the midpoint of $B C$ (see Figure 3). Then $R$ is the circumcentre of the cyclic quadrilateral $B C P Q$. Thus we obtain $\angle A P Q=\angle B$ and $\angle R P C=\angle C$, which yields $\angle Q P R=\angle A$. Similarly, we show that $\angle P Q R=\angle A$. Thus, all interesting triangles are similar to the triangle $P Q R$.  Figure 3  Figure 4 Denote now by $Z$ the common point of the circumcircles of $A P Q, B Q R$, and $C P R$. Let $E_{1} F_{1} K_{1}$ and $E_{2} F_{2} K_{2}$ be two interesting triangles. By the lemma, $Z$ is the centre of any spiral similarity taking one of the triangles $E_{1} F_{1} K_{1}, E_{2} F_{2} K_{2}$, and $P Q R$ to some other of them. Therefore the triangles $Z E_{1} E_{2}$ and $Z F_{1} F_{2}$ are similar, as well as the triangles $Z E_{1} F_{1}$ and $Z P Q$. Hence $$ \frac{E_{1} E_{2}}{F_{1} F_{2}}=\frac{Z E_{1}}{Z F_{1}}=\frac{Z P}{Z Q} $$ Moreover, the equalities $\angle A Z Q=\angle A P Q=\angle A B C=180^{\circ}-\angle Q Z R$ show that the point $Z$ lies on the line $A R$ (see Figure 4). Therefore the triangles $A Z P$ and $A C R$ are similar, as well as the triangles $A Z Q$ and $A B R$. This yields $$ \frac{Z P}{Z Q}=\frac{Z P}{R C} \cdot \frac{R B}{Z Q}=\frac{A Z}{A C} \cdot \frac{A B}{A Z}=\frac{A B}{A C} $$ which completes the solution. Second method. Now we will start from the fact that $\omega_{1}$ is tangent to the lines $K E$ and $K F$ (see Figure 5). We prove that if $(E, F)$ is an interesting pair, then $$ \frac{A E}{A B}+\frac{A F}{A C}=2 \cos \angle A $$ Let $Y$ be the intersection point of the segments $B E$ and $C F$. The points $B, K$, and $C$ are collinear, hence applying PASCAL's theorem to the degenerated hexagon AFFYEE, we infer that $Y$ lies on the circle $\omega_{1}$. Denote by $Z$ the second intersection point of the circumcircle of the triangle $B F Y$ with the line $B C$ (see Figure 6). By Miquel's theorem, the points $C, Z, Y$, and $E$ are concyclic. Therefore we obtain $$ B F \cdot A B+C E \cdot A C=B Y \cdot B E+C Y \cdot C F=B Z \cdot B C+C Z \cdot B C=B C^{2} $$ On the other hand, $B C^{2}=A B^{2}+A C^{2}-2 A B \cdot A C \cos \angle A$, by the cosine law. Hence $$ (A B-A F) \cdot A B+(A C-A E) \cdot A C=A B^{2}+A C^{2}-2 A B \cdot A C \cos \angle A, $$ which simplifies to the desired equality (1). Let now $\left(E_{1}, F_{1}\right)$ and $\left(E_{2}, F_{2}\right)$ be two interesting pairs of points. Then we get $$ \frac{A E_{1}}{A B}+\frac{A F_{1}}{A C}=\frac{A E_{2}}{A B}+\frac{A F_{2}}{A C} $$ which gives the desired result.  Figure 5  Figure 6 Third method. Again, we make use of the fact that all interesting triangles are similar (and equi-oriented). Let us put the picture onto a complex plane such that $A$ is at the origin, and identify each point with the corresponding complex number. Let $E F K$ be any interesting triangle. The equalities $\angle K E F=\angle K F E=\angle A$ yield that the ratio $\nu=\frac{K-E}{F-E}$ is the same for all interesting triangles. This in turn means that the numbers $E$, $F$, and $K$ satisfy the linear equation $$ K=\mu E+\nu F, \quad \text { where } \quad \mu=1-\nu $$ Now let us choose the points $X$ and $Y$ on the rays $A B$ and $A C$, respectively, so that $\angle C X A=\angle A Y B=\angle A=\angle K E F$ (see Figure 7). Then each of the triangles $A X C$ and $Y A B$ is similar to any interesting triangle, which also means that $$ C=\mu A+\nu X=\nu X \quad \text { and } \quad B=\mu Y+\nu A=\mu Y . $$ Moreover, one has $X / Y=\overline{C / B}$. Since the points $E, F$, and $K$ lie on $A C, A B$, and $B C$, respectively, one gets $$ E=\rho Y, \quad F=\sigma X, \quad \text { and } \quad K=\lambda B+(1-\lambda) C $$ for some real $\rho, \sigma$, and $\lambda$. In view of (3), the equation (2) now reads $\lambda B+(1-\lambda) C=K=$ $\mu E+\nu F=\rho B+\sigma C$, or $$ (\lambda-\rho) B=(\sigma+\lambda-1) C $$ Since the nonzero complex numbers $B$ and $C$ have different arguments, the coefficients in the brackets vanish, so $\rho=\lambda$ and $\sigma=1-\lambda$. Therefore, $$ \frac{E}{Y}+\frac{F}{X}=\rho+\sigma=1 $$ Now, if $\left(E_{1}, F_{1}\right)$ and $\left(E_{2}, F_{2}\right)$ are two distinct interesting pairs, one may apply (4) to both pairs. Subtracting, we get $$ \frac{E_{1}-E_{2}}{Y}=\frac{F_{2}-F_{1}}{X}, \quad \text { so } \quad \frac{E_{1}-E_{2}}{F_{2}-F_{1}}=\frac{Y}{X}=\frac{\bar{B}}{\bar{C}} $$ Taking absolute values provides the required result.  Figure 7 Comment 1. One may notice that the triangle $P Q R$ is also interesting. Comment 2. In order to prove that $\angle K E F=\angle K F E=\angle A$, one may also use the following well-known fact: Let $A E F$ be a triangle with $A E \neq A F$, and let $K$ be the common point of the symmedian taken from $A$ and the perpendicular bisector of $E F$. Then the lines $K E$ and $K F$ are tangent to the circumcircle $\omega_{1}$ of the triangle $A E F$. In this case, however, one needs to deal with the case $A E=A F$ separately.
|
{
"resource_path": "IMO/segmented/en-IMO2014SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
27c2e55c-3d3b-576f-965a-50ff6b890edc
| 24,528
|
Let $A B C$ be a fixed acute-angled triangle. Consider some points $E$ and $F$ lying on the sides $A C$ and $A B$, respectively, and let $M$ be the midpoint of $E F$. Let the perpendicular bisector of $E F$ intersect the line $B C$ at $K$, and let the perpendicular bisector of $M K$ intersect the lines $A C$ and $A B$ at $S$ and $T$, respectively. We call the pair $(E, F)$ interesting, if the quadrilateral $K S A T$ is cyclic. Suppose that the pairs $\left(E_{1}, F_{1}\right)$ and $\left(E_{2}, F_{2}\right)$ are interesting. Prove that $$ \frac{E_{1} E_{2}}{A B}=\frac{F_{1} F_{2}}{A C} $$ (Iran)
|
Let $(E, F)$ be an interesting pair. This time we prove that $$ \frac{A M}{A K}=\cos \angle A $$ As in Solution 1, we introduce the circle $\omega$ passing through the points $K, S$, $A$, and $T$, together with the points $N$ and $L$ at which the line $A M$ intersect the line $S T$ and the circle $\omega$ for the second time, respectively. Let moreover $O$ be the centre of $\omega$ (see Figures 8 and 9). As in Solution 1, we note that $N$ is the midpoint of $S T$ and show that $K L \| S T$, which implies $\angle F A M=\angle E A K$.  Figure 8 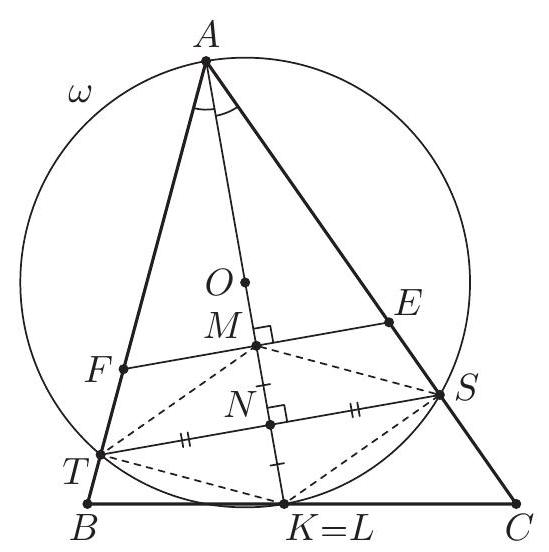 Figure 9 Suppose now that $K \neq L$ (see Figure 8). Then $K L \| S T$, and consequently the lines $K M$ and $K L$ are perpendicular. It implies that the lines $L O$ and $K M$ meet at a point $X$ lying on the circle $\omega$. Since the lines $O N$ and $X M$ are both perpendicular to the line $S T$, they are parallel to each other, and hence $\angle L O N=\angle L X K=\angle M A K$. On the other hand, $\angle O L N=\angle M K A$, so we infer that triangles $N O L$ and $M A K$ are similar. This yields $$ \frac{A M}{A K}=\frac{O N}{O L}=\frac{O N}{O T}=\cos \angle T O N=\cos \angle A $$ If, on the other hand, $K=L$, then the points $A, M, N$, and $K$ lie on a common line, and this line is the perpendicular bisector of $S T$ (see Figure 9). This implies that $A K$ is a diameter of $\omega$, which yields $A M=2 O K-2 N K=2 O N$. So also in this case we obtain $$ \frac{A M}{A K}=\frac{2 O N}{2 O T}=\cos \angle T O N=\cos \angle A $$ Thus (5) is proved. Let $P$ and $Q$ be the feet of the perpendiculars from $B$ and $C$ onto $A C$ and $A B$, respectively (see Figure 10). We claim that the point $M$ lies on the line $P Q$. Consider now the composition of the dilatation with factor $\cos \angle A$ and centre $A$, and the reflection with respect to the angle bisector of $\angle B A C$. This transformation is a similarity that takes $B, C$, and $K$ to $P, Q$, and $M$, respectively. Since $K$ lies on the line $B C$, the point $M$ lies on the line $P Q$.  Figure 10 Suppose that $E \neq P$. Then also $F \neq Q$, and by Menelaus' theorem, we obtain $$ \frac{A Q}{F Q} \cdot \frac{F M}{E M} \cdot \frac{E P}{A P}=1 $$ Using the similarity of the triangles $A P Q$ and $A B C$, we infer that $$ \frac{E P}{F Q}=\frac{A P}{A Q}=\frac{A B}{A C}, \quad \text { and hence } \quad \frac{E P}{A B}=\frac{F Q}{A C} $$ The last equality holds obviously also in case $E=P$, because then $F=Q$. Moreover, since the line $P Q$ intersects the segment $E F$, we infer that the point $E$ lies on the segment $A P$ if and only if the point $F$ lies outside of the segment $A Q$. Let now $\left(E_{1}, F_{1}\right)$ and $\left(E_{2}, F_{2}\right)$ be two interesting pairs. Then we obtain $$ \frac{E_{1} P}{A B}=\frac{F_{1} Q}{A C} \quad \text { and } \quad \frac{E_{2} P}{A B}=\frac{F_{2} Q}{A C} . $$ If $P$ lies between the points $E_{1}$ and $E_{2}$, we add the equalities above, otherwise we subtract them. In any case we obtain $$ \frac{E_{1} E_{2}}{A B}=\frac{F_{1} F_{2}}{A C} $$ which completes the solution.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a fixed acute-angled triangle. Consider some points $E$ and $F$ lying on the sides $A C$ and $A B$, respectively, and let $M$ be the midpoint of $E F$. Let the perpendicular bisector of $E F$ intersect the line $B C$ at $K$, and let the perpendicular bisector of $M K$ intersect the lines $A C$ and $A B$ at $S$ and $T$, respectively. We call the pair $(E, F)$ interesting, if the quadrilateral $K S A T$ is cyclic. Suppose that the pairs $\left(E_{1}, F_{1}\right)$ and $\left(E_{2}, F_{2}\right)$ are interesting. Prove that $$ \frac{E_{1} E_{2}}{A B}=\frac{F_{1} F_{2}}{A C} $$ (Iran)
|
Let $(E, F)$ be an interesting pair. This time we prove that $$ \frac{A M}{A K}=\cos \angle A $$ As in Solution 1, we introduce the circle $\omega$ passing through the points $K, S$, $A$, and $T$, together with the points $N$ and $L$ at which the line $A M$ intersect the line $S T$ and the circle $\omega$ for the second time, respectively. Let moreover $O$ be the centre of $\omega$ (see Figures 8 and 9). As in Solution 1, we note that $N$ is the midpoint of $S T$ and show that $K L \| S T$, which implies $\angle F A M=\angle E A K$.  Figure 8  Figure 9 Suppose now that $K \neq L$ (see Figure 8). Then $K L \| S T$, and consequently the lines $K M$ and $K L$ are perpendicular. It implies that the lines $L O$ and $K M$ meet at a point $X$ lying on the circle $\omega$. Since the lines $O N$ and $X M$ are both perpendicular to the line $S T$, they are parallel to each other, and hence $\angle L O N=\angle L X K=\angle M A K$. On the other hand, $\angle O L N=\angle M K A$, so we infer that triangles $N O L$ and $M A K$ are similar. This yields $$ \frac{A M}{A K}=\frac{O N}{O L}=\frac{O N}{O T}=\cos \angle T O N=\cos \angle A $$ If, on the other hand, $K=L$, then the points $A, M, N$, and $K$ lie on a common line, and this line is the perpendicular bisector of $S T$ (see Figure 9). This implies that $A K$ is a diameter of $\omega$, which yields $A M=2 O K-2 N K=2 O N$. So also in this case we obtain $$ \frac{A M}{A K}=\frac{2 O N}{2 O T}=\cos \angle T O N=\cos \angle A $$ Thus (5) is proved. Let $P$ and $Q$ be the feet of the perpendiculars from $B$ and $C$ onto $A C$ and $A B$, respectively (see Figure 10). We claim that the point $M$ lies on the line $P Q$. Consider now the composition of the dilatation with factor $\cos \angle A$ and centre $A$, and the reflection with respect to the angle bisector of $\angle B A C$. This transformation is a similarity that takes $B, C$, and $K$ to $P, Q$, and $M$, respectively. Since $K$ lies on the line $B C$, the point $M$ lies on the line $P Q$.  Figure 10 Suppose that $E \neq P$. Then also $F \neq Q$, and by Menelaus' theorem, we obtain $$ \frac{A Q}{F Q} \cdot \frac{F M}{E M} \cdot \frac{E P}{A P}=1 $$ Using the similarity of the triangles $A P Q$ and $A B C$, we infer that $$ \frac{E P}{F Q}=\frac{A P}{A Q}=\frac{A B}{A C}, \quad \text { and hence } \quad \frac{E P}{A B}=\frac{F Q}{A C} $$ The last equality holds obviously also in case $E=P$, because then $F=Q$. Moreover, since the line $P Q$ intersects the segment $E F$, we infer that the point $E$ lies on the segment $A P$ if and only if the point $F$ lies outside of the segment $A Q$. Let now $\left(E_{1}, F_{1}\right)$ and $\left(E_{2}, F_{2}\right)$ be two interesting pairs. Then we obtain $$ \frac{E_{1} P}{A B}=\frac{F_{1} Q}{A C} \quad \text { and } \quad \frac{E_{2} P}{A B}=\frac{F_{2} Q}{A C} . $$ If $P$ lies between the points $E_{1}$ and $E_{2}$, we add the equalities above, otherwise we subtract them. In any case we obtain $$ \frac{E_{1} E_{2}}{A B}=\frac{F_{1} F_{2}}{A C} $$ which completes the solution.
|
{
"resource_path": "IMO/segmented/en-IMO2014SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
27c2e55c-3d3b-576f-965a-50ff6b890edc
| 24,528
|
Let $A B C$ be a triangle with circumcircle $\Omega$ and incentre $I$. Let the line passing through $I$ and perpendicular to $C I$ intersect the segment $B C$ and the $\operatorname{arc} B C$ (not containing $A$ ) of $\Omega$ at points $U$ and $V$, respectively. Let the line passing through $U$ and parallel to $A I$ intersect $A V$ at $X$, and let the line passing through $V$ and parallel to $A I$ intersect $A B$ at $Y$. Let $W$ and $Z$ be the midpoints of $A X$ and $B C$, respectively. Prove that if the points $I, X$, and $Y$ are collinear, then the points $I, W$, and $Z$ are also collinear.
|
We start with some general observations. Set $\alpha=\angle A / 2, \beta=\angle B / 2, \gamma=\angle C / 2$. Then obviously $\alpha+\beta+\gamma=90^{\circ}$. Since $\angle U I C=90^{\circ}$, we obtain $\angle I U C=\alpha+\beta$. Therefore $\angle B I V=\angle I U C-\angle I B C=\alpha=\angle B A I=\angle B Y V$, which implies that the points $B, Y, I$, and $V$ lie on a common circle (see Figure 1). Assume now that the points $I, X$ and $Y$ are collinear. We prove that $\angle Y I A=90^{\circ}$. Let the line $X U$ intersect $A B$ at $N$. Since the lines $A I, U X$, and $V Y$ are parallel, we get $$ \frac{N X}{A I}=\frac{Y N}{Y A}=\frac{V U}{V I}=\frac{X U}{A I} $$ implying $N X=X U$. Moreover, $\angle B I U=\alpha=\angle B N U$. This implies that the quadrilateral BUIN is cyclic, and since $B I$ is the angle bisector of $\angle U B N$, we infer that $N I=U I$. Thus in the isosceles triangle $N I U$, the point $X$ is the midpoint of the base $N U$. This gives $\angle I X N=90^{\circ}$, i.e., $\angle Y I A=90^{\circ}$.  Figure 1 Let $S$ be the midpoint of the segment $V C$. Let moreover $T$ be the intersection point of the lines $A X$ and $S I$, and set $x=\angle B A V=\angle B C V$. Since $\angle C I A=90^{\circ}+\beta$ and $S I=S C$, we obtain $$ \angle T I A=180^{\circ}-\angle A I S=90^{\circ}-\beta-\angle C I S=90^{\circ}-\beta-\gamma-x=\alpha-x=\angle T A I, $$ which implies that $T I=T A$. Therefore, since $\angle X I A=90^{\circ}$, the point $T$ is the midpoint of $A X$, i.e., $T=W$. To complete our solution, it remains to show that the intersection point of the lines $I S$ and $B C$ coincide with the midpoint of the segment $B C$. But since $S$ is the midpoint of the segment $V C$, it suffices to show that the lines $B V$ and $I S$ are parallel. Since the quadrilateral $B Y I V$ is cyclic, $\angle V B I=\angle V Y I=\angle Y I A=90^{\circ}$. This implies that $B V$ is the external angle bisector of the angle $A B C$, which yields $\angle V A C=\angle V C A$. Therefore $2 \alpha-x=2 \gamma+x$, which gives $\alpha=\gamma+x$. Hence $\angle S C I=\alpha$, so $\angle V S I=2 \alpha$. On the other hand, $\angle B V C=180^{\circ}-\angle B A C=180^{\circ}-2 \alpha$, which implies that the lines $B V$ and $I S$ are parallel. This completes the solution.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circumcircle $\Omega$ and incentre $I$. Let the line passing through $I$ and perpendicular to $C I$ intersect the segment $B C$ and the $\operatorname{arc} B C$ (not containing $A$ ) of $\Omega$ at points $U$ and $V$, respectively. Let the line passing through $U$ and parallel to $A I$ intersect $A V$ at $X$, and let the line passing through $V$ and parallel to $A I$ intersect $A B$ at $Y$. Let $W$ and $Z$ be the midpoints of $A X$ and $B C$, respectively. Prove that if the points $I, X$, and $Y$ are collinear, then the points $I, W$, and $Z$ are also collinear.
|
We start with some general observations. Set $\alpha=\angle A / 2, \beta=\angle B / 2, \gamma=\angle C / 2$. Then obviously $\alpha+\beta+\gamma=90^{\circ}$. Since $\angle U I C=90^{\circ}$, we obtain $\angle I U C=\alpha+\beta$. Therefore $\angle B I V=\angle I U C-\angle I B C=\alpha=\angle B A I=\angle B Y V$, which implies that the points $B, Y, I$, and $V$ lie on a common circle (see Figure 1). Assume now that the points $I, X$ and $Y$ are collinear. We prove that $\angle Y I A=90^{\circ}$. Let the line $X U$ intersect $A B$ at $N$. Since the lines $A I, U X$, and $V Y$ are parallel, we get $$ \frac{N X}{A I}=\frac{Y N}{Y A}=\frac{V U}{V I}=\frac{X U}{A I} $$ implying $N X=X U$. Moreover, $\angle B I U=\alpha=\angle B N U$. This implies that the quadrilateral BUIN is cyclic, and since $B I$ is the angle bisector of $\angle U B N$, we infer that $N I=U I$. Thus in the isosceles triangle $N I U$, the point $X$ is the midpoint of the base $N U$. This gives $\angle I X N=90^{\circ}$, i.e., $\angle Y I A=90^{\circ}$.  Figure 1 Let $S$ be the midpoint of the segment $V C$. Let moreover $T$ be the intersection point of the lines $A X$ and $S I$, and set $x=\angle B A V=\angle B C V$. Since $\angle C I A=90^{\circ}+\beta$ and $S I=S C$, we obtain $$ \angle T I A=180^{\circ}-\angle A I S=90^{\circ}-\beta-\angle C I S=90^{\circ}-\beta-\gamma-x=\alpha-x=\angle T A I, $$ which implies that $T I=T A$. Therefore, since $\angle X I A=90^{\circ}$, the point $T$ is the midpoint of $A X$, i.e., $T=W$. To complete our solution, it remains to show that the intersection point of the lines $I S$ and $B C$ coincide with the midpoint of the segment $B C$. But since $S$ is the midpoint of the segment $V C$, it suffices to show that the lines $B V$ and $I S$ are parallel. Since the quadrilateral $B Y I V$ is cyclic, $\angle V B I=\angle V Y I=\angle Y I A=90^{\circ}$. This implies that $B V$ is the external angle bisector of the angle $A B C$, which yields $\angle V A C=\angle V C A$. Therefore $2 \alpha-x=2 \gamma+x$, which gives $\alpha=\gamma+x$. Hence $\angle S C I=\alpha$, so $\angle V S I=2 \alpha$. On the other hand, $\angle B V C=180^{\circ}-\angle B A C=180^{\circ}-2 \alpha$, which implies that the lines $B V$ and $I S$ are parallel. This completes the solution.
|
{
"resource_path": "IMO/segmented/en-IMO2014SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
04f73200-e7e3-5c9a-8a53-5a0f603dc0cb
| 24,532
|
Suppose that a sequence $a_{1}, a_{2}, \ldots$ of positive real numbers satisfies $$ a_{k+1} \geqslant \frac{k a_{k}}{a_{k}^{2}+(k-1)} $$ for every positive integer $k$. Prove that $a_{1}+a_{2}+\cdots+a_{n} \geqslant n$ for every $n \geqslant 2$.
|
From the constraint (1), it can be seen that $$ \frac{k}{a_{k+1}} \leqslant \frac{a_{k}^{2}+(k-1)}{a_{k}}=a_{k}+\frac{k-1}{a_{k}} $$ and so $$ a_{k} \geqslant \frac{k}{a_{k+1}}-\frac{k-1}{a_{k}} . $$ Summing up the above inequality for $k=1, \ldots, m$, we obtain $$ a_{1}+a_{2}+\cdots+a_{m} \geqslant\left(\frac{1}{a_{2}}-\frac{0}{a_{1}}\right)+\left(\frac{2}{a_{3}}-\frac{1}{a_{2}}\right)+\cdots+\left(\frac{m}{a_{m+1}}-\frac{m-1}{a_{m}}\right)=\frac{m}{a_{m+1}} $$ Now we prove the problem statement by induction on $n$. The case $n=2$ can be done by applying (1) to $k=1$ : $$ a_{1}+a_{2} \geqslant a_{1}+\frac{1}{a_{1}} \geqslant 2 $$ For the induction step, assume that the statement is true for some $n \geqslant 2$. If $a_{n+1} \geqslant 1$, then the induction hypothesis yields $$ \left(a_{1}+\cdots+a_{n}\right)+a_{n+1} \geqslant n+1 $$ Otherwise, if $a_{n+1}<1$ then apply (2) as $$ \left(a_{1}+\cdots+a_{n}\right)+a_{n+1} \geqslant \frac{n}{a_{n+1}}+a_{n+1}=\frac{n-1}{a_{n+1}}+\left(\frac{1}{a_{n+1}}+a_{n+1}\right)>(n-1)+2 $$ That completes the solution. Comment 1. It can be seen easily that having equality in the statement requires $a_{1}=a_{2}=1$ in the base case $n=2$, and $a_{n+1}=1$ in (3). So the equality $a_{1}+\cdots+a_{n}=n$ is possible only in the trivial case $a_{1}=\cdots=a_{n}=1$. Comment 2. After obtaining (2), there are many ways to complete the solution. We outline three such possibilities. - With defining $s_{n}=a_{1}+\cdots+a_{n}$, the induction step can be replaced by $$ s_{n+1}=s_{n}+a_{n+1} \geqslant s_{n}+\frac{n}{s_{n}} \geqslant n+1 $$ because the function $x \mapsto x+\frac{n}{x}$ increases on $[n, \infty)$. - By applying the AM-GM inequality to the numbers $a_{1}+\cdots+a_{k}$ and $k a_{k+1}$, we can conclude $$ a_{1}+\cdots+a_{k}+k a_{k+1} \geqslant 2 k $$ and sum it up for $k=1, \ldots, n-1$. - We can derive the symmetric estimate $$ \sum_{1 \leqslant i<j \leqslant n} a_{i} a_{j}=\sum_{j=2}^{n}\left(a_{1}+\cdots+a_{j-1}\right) a_{j} \geqslant \sum_{j=2}^{n}(j-1)=\frac{n(n-1)}{2} $$ and combine it with the AM-QM inequality.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Suppose that a sequence $a_{1}, a_{2}, \ldots$ of positive real numbers satisfies $$ a_{k+1} \geqslant \frac{k a_{k}}{a_{k}^{2}+(k-1)} $$ for every positive integer $k$. Prove that $a_{1}+a_{2}+\cdots+a_{n} \geqslant n$ for every $n \geqslant 2$.
|
From the constraint (1), it can be seen that $$ \frac{k}{a_{k+1}} \leqslant \frac{a_{k}^{2}+(k-1)}{a_{k}}=a_{k}+\frac{k-1}{a_{k}} $$ and so $$ a_{k} \geqslant \frac{k}{a_{k+1}}-\frac{k-1}{a_{k}} . $$ Summing up the above inequality for $k=1, \ldots, m$, we obtain $$ a_{1}+a_{2}+\cdots+a_{m} \geqslant\left(\frac{1}{a_{2}}-\frac{0}{a_{1}}\right)+\left(\frac{2}{a_{3}}-\frac{1}{a_{2}}\right)+\cdots+\left(\frac{m}{a_{m+1}}-\frac{m-1}{a_{m}}\right)=\frac{m}{a_{m+1}} $$ Now we prove the problem statement by induction on $n$. The case $n=2$ can be done by applying (1) to $k=1$ : $$ a_{1}+a_{2} \geqslant a_{1}+\frac{1}{a_{1}} \geqslant 2 $$ For the induction step, assume that the statement is true for some $n \geqslant 2$. If $a_{n+1} \geqslant 1$, then the induction hypothesis yields $$ \left(a_{1}+\cdots+a_{n}\right)+a_{n+1} \geqslant n+1 $$ Otherwise, if $a_{n+1}<1$ then apply (2) as $$ \left(a_{1}+\cdots+a_{n}\right)+a_{n+1} \geqslant \frac{n}{a_{n+1}}+a_{n+1}=\frac{n-1}{a_{n+1}}+\left(\frac{1}{a_{n+1}}+a_{n+1}\right)>(n-1)+2 $$ That completes the solution. Comment 1. It can be seen easily that having equality in the statement requires $a_{1}=a_{2}=1$ in the base case $n=2$, and $a_{n+1}=1$ in (3). So the equality $a_{1}+\cdots+a_{n}=n$ is possible only in the trivial case $a_{1}=\cdots=a_{n}=1$. Comment 2. After obtaining (2), there are many ways to complete the solution. We outline three such possibilities. - With defining $s_{n}=a_{1}+\cdots+a_{n}$, the induction step can be replaced by $$ s_{n+1}=s_{n}+a_{n+1} \geqslant s_{n}+\frac{n}{s_{n}} \geqslant n+1 $$ because the function $x \mapsto x+\frac{n}{x}$ increases on $[n, \infty)$. - By applying the AM-GM inequality to the numbers $a_{1}+\cdots+a_{k}$ and $k a_{k+1}$, we can conclude $$ a_{1}+\cdots+a_{k}+k a_{k+1} \geqslant 2 k $$ and sum it up for $k=1, \ldots, n-1$. - We can derive the symmetric estimate $$ \sum_{1 \leqslant i<j \leqslant n} a_{i} a_{j}=\sum_{j=2}^{n}\left(a_{1}+\cdots+a_{j-1}\right) a_{j} \geqslant \sum_{j=2}^{n}(j-1)=\frac{n(n-1)}{2} $$ and combine it with the AM-QM inequality.
|
{
"resource_path": "IMO/segmented/en-IMO2015SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
3ee6aa17-c294-50b3-8743-8a8ea3d65fe7
| 24,549
|
Let $n$ be a fixed integer with $n \geqslant 2$. We say that two polynomials $P$ and $Q$ with real coefficients are block-similar if for each $i \in\{1,2, \ldots, n\}$ the sequences $$ \begin{aligned} & P(2015 i), P(2015 i-1), \ldots, P(2015 i-2014) \quad \text { and } \\ & Q(2015 i), Q(2015 i-1), \ldots, Q(2015 i-2014) \end{aligned} $$ are permutations of each other. (a) Prove that there exist distinct block-similar polynomials of degree $n+1$. (b) Prove that there do not exist distinct block-similar polynomials of degree $n$.
|
We provide an alternative argument for part (b). Assume again that there exist two distinct block-similar polynomials $P(x)$ and $Q(x)$ of degree $n$. Let $R(x)=P(x)-Q(x)$ and $S(x)=P(x)+Q(x)$. For brevity, we also denote the segment $[(i-1) k+1, i k]$ by $I_{i}$, and the set $\{(i-1) k+1,(i-1) k+2, \ldots, i k\}$ of all integer points in $I_{i}$ by $Z_{i}$. Step 1. We prove that $R(x)$ has exactly one root in each segment $I_{i}, i=1,2, \ldots, n$, and all these roots are simple. Indeed, take any $i \in\{1,2, \ldots, n\}$ and choose some points $p^{-}, p^{+} \in Z_{i}$ so that $$ P\left(p^{-}\right)=\min _{x \in Z_{i}} P(x) \quad \text { and } \quad P\left(p^{+}\right)=\max _{x \in Z_{i}} P(x) $$ Since the sequences of values of $P$ and $Q$ in $Z_{i}$ are permutations of each other, we have $R\left(p^{-}\right)=P\left(p^{-}\right)-Q\left(p^{-}\right) \leqslant 0$ and $R\left(p^{+}\right)=P\left(p^{+}\right)-Q\left(p^{+}\right) \geqslant 0$. Since $R(x)$ is continuous, there exists at least one root of $R(x)$ between $p^{-}$and $p^{+}$- thus in $I_{i}$. So, $R(x)$ has at least one root in each of the $n$ disjoint segments $I_{i}$ with $i=1,2, \ldots, n$. Since $R(x)$ is nonzero and its degree does not exceed $n$, it should have exactly one root in each of these segments, and all these roots are simple, as required.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $n$ be a fixed integer with $n \geqslant 2$. We say that two polynomials $P$ and $Q$ with real coefficients are block-similar if for each $i \in\{1,2, \ldots, n\}$ the sequences $$ \begin{aligned} & P(2015 i), P(2015 i-1), \ldots, P(2015 i-2014) \quad \text { and } \\ & Q(2015 i), Q(2015 i-1), \ldots, Q(2015 i-2014) \end{aligned} $$ are permutations of each other. (a) Prove that there exist distinct block-similar polynomials of degree $n+1$. (b) Prove that there do not exist distinct block-similar polynomials of degree $n$.
|
We provide an alternative argument for part (b). Assume again that there exist two distinct block-similar polynomials $P(x)$ and $Q(x)$ of degree $n$. Let $R(x)=P(x)-Q(x)$ and $S(x)=P(x)+Q(x)$. For brevity, we also denote the segment $[(i-1) k+1, i k]$ by $I_{i}$, and the set $\{(i-1) k+1,(i-1) k+2, \ldots, i k\}$ of all integer points in $I_{i}$ by $Z_{i}$. Step 1. We prove that $R(x)$ has exactly one root in each segment $I_{i}, i=1,2, \ldots, n$, and all these roots are simple. Indeed, take any $i \in\{1,2, \ldots, n\}$ and choose some points $p^{-}, p^{+} \in Z_{i}$ so that $$ P\left(p^{-}\right)=\min _{x \in Z_{i}} P(x) \quad \text { and } \quad P\left(p^{+}\right)=\max _{x \in Z_{i}} P(x) $$ Since the sequences of values of $P$ and $Q$ in $Z_{i}$ are permutations of each other, we have $R\left(p^{-}\right)=P\left(p^{-}\right)-Q\left(p^{-}\right) \leqslant 0$ and $R\left(p^{+}\right)=P\left(p^{+}\right)-Q\left(p^{+}\right) \geqslant 0$. Since $R(x)$ is continuous, there exists at least one root of $R(x)$ between $p^{-}$and $p^{+}$- thus in $I_{i}$. So, $R(x)$ has at least one root in each of the $n$ disjoint segments $I_{i}$ with $i=1,2, \ldots, n$. Since $R(x)$ is nonzero and its degree does not exceed $n$, it should have exactly one root in each of these segments, and all these roots are simple, as required.
|
{
"resource_path": "IMO/segmented/en-IMO2015SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
0028f802-fa59-5e69-9f4c-86637eb1f436
| 24,568
|
In Lineland there are $n \geqslant 1$ towns, arranged along a road running from left to right. Each town has a left bulldozer (put to the left of the town and facing left) and a right bulldozer (put to the right of the town and facing right). The sizes of the $2 n$ bulldozers are distinct. Every time when a right and a left bulldozer confront each other, the larger bulldozer pushes the smaller one off the road. On the other hand, the bulldozers are quite unprotected at their rears; so, if a bulldozer reaches the rear-end of another one, the first one pushes the second one off the road, regardless of their sizes. Let $A$ and $B$ be two towns, with $B$ being to the right of $A$. We say that town $A$ can sweep town $B$ away if the right bulldozer of $A$ can move over to $B$ pushing off all bulldozers it meets. Similarly, $B$ can sweep $A$ away if the left bulldozer of $B$ can move to $A$ pushing off all bulldozers of all towns on its way. Prove that there is exactly one town which cannot be swept away by any other one. (Estonia)
|
Let $T_{1}, T_{2}, \ldots, T_{n}$ be the towns enumerated from left to right. Observe first that, if town $T_{i}$ can sweep away town $T_{j}$, then $T_{i}$ also can sweep away every town located between $T_{i}$ and $T_{j}$. We prove the problem statement by strong induction on $n$. The base case $n=1$ is trivial. For the induction step, we first observe that the left bulldozer in $T_{1}$ and the right bulldozer in $T_{n}$ are completely useless, so we may forget them forever. Among the other $2 n-2$ bulldozers, we choose the largest one. Without loss of generality, it is the right bulldozer of some town $T_{k}$ with $k<n$. Surely, with this large bulldozer $T_{k}$ can sweep away all the towns to the right of it. Moreover, none of these towns can sweep $T_{k}$ away; so they also cannot sweep away any town to the left of $T_{k}$. Thus, if we remove the towns $T_{k+1}, T_{k+2}, \ldots, T_{n}$, none of the remaining towns would change its status of being (un)sweepable away by the others. Applying the induction hypothesis to the remaining towns, we find a unique town among $T_{1}, T_{2}, \ldots, T_{k}$ which cannot be swept away. By the above reasons, it is also the unique such town in the initial situation. Thus the induction step is established.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
In Lineland there are $n \geqslant 1$ towns, arranged along a road running from left to right. Each town has a left bulldozer (put to the left of the town and facing left) and a right bulldozer (put to the right of the town and facing right). The sizes of the $2 n$ bulldozers are distinct. Every time when a right and a left bulldozer confront each other, the larger bulldozer pushes the smaller one off the road. On the other hand, the bulldozers are quite unprotected at their rears; so, if a bulldozer reaches the rear-end of another one, the first one pushes the second one off the road, regardless of their sizes. Let $A$ and $B$ be two towns, with $B$ being to the right of $A$. We say that town $A$ can sweep town $B$ away if the right bulldozer of $A$ can move over to $B$ pushing off all bulldozers it meets. Similarly, $B$ can sweep $A$ away if the left bulldozer of $B$ can move to $A$ pushing off all bulldozers of all towns on its way. Prove that there is exactly one town which cannot be swept away by any other one. (Estonia)
|
Let $T_{1}, T_{2}, \ldots, T_{n}$ be the towns enumerated from left to right. Observe first that, if town $T_{i}$ can sweep away town $T_{j}$, then $T_{i}$ also can sweep away every town located between $T_{i}$ and $T_{j}$. We prove the problem statement by strong induction on $n$. The base case $n=1$ is trivial. For the induction step, we first observe that the left bulldozer in $T_{1}$ and the right bulldozer in $T_{n}$ are completely useless, so we may forget them forever. Among the other $2 n-2$ bulldozers, we choose the largest one. Without loss of generality, it is the right bulldozer of some town $T_{k}$ with $k<n$. Surely, with this large bulldozer $T_{k}$ can sweep away all the towns to the right of it. Moreover, none of these towns can sweep $T_{k}$ away; so they also cannot sweep away any town to the left of $T_{k}$. Thus, if we remove the towns $T_{k+1}, T_{k+2}, \ldots, T_{n}$, none of the remaining towns would change its status of being (un)sweepable away by the others. Applying the induction hypothesis to the remaining towns, we find a unique town among $T_{1}, T_{2}, \ldots, T_{k}$ which cannot be swept away. By the above reasons, it is also the unique such town in the initial situation. Thus the induction step is established.
|
{
"resource_path": "IMO/segmented/en-IMO2015SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
ec35c816-a210-56e0-b52f-41c63ab44cc3
| 24,573
|
In Lineland there are $n \geqslant 1$ towns, arranged along a road running from left to right. Each town has a left bulldozer (put to the left of the town and facing left) and a right bulldozer (put to the right of the town and facing right). The sizes of the $2 n$ bulldozers are distinct. Every time when a right and a left bulldozer confront each other, the larger bulldozer pushes the smaller one off the road. On the other hand, the bulldozers are quite unprotected at their rears; so, if a bulldozer reaches the rear-end of another one, the first one pushes the second one off the road, regardless of their sizes. Let $A$ and $B$ be two towns, with $B$ being to the right of $A$. We say that town $A$ can sweep town $B$ away if the right bulldozer of $A$ can move over to $B$ pushing off all bulldozers it meets. Similarly, $B$ can sweep $A$ away if the left bulldozer of $B$ can move to $A$ pushing off all bulldozers of all towns on its way. Prove that there is exactly one town which cannot be swept away by any other one. (Estonia)
|
We start with the same enumeration and the same observation as in Clearly, there is no town which can sweep $T_{n}$ away from the right. Then we may choose the leftmost town $T_{k}$ which cannot be swept away from the right. One can observe now that no town $T_{i}$ with $i>k$ may sweep away some town $T_{j}$ with $j<k$, for otherwise $T_{i}$ would be able to sweep $T_{k}$ away as well. Now we prove two claims, showing together that $T_{k}$ is the unique town which cannot be swept away, and thus establishing the problem statement. Claim 1. $T_{k}$ also cannot be swept away from the left. Proof. Let $T_{m}$ be some town to the left of $T_{k}$. By the choice of $T_{k}$, town $T_{m}$ can be swept away from the right by some town $T_{p}$ with $p>m$. As we have already observed, $p$ cannot be greater than $k$. On the other hand, $T_{m}$ cannot sweep $T_{p}$ away, so a fortiori it cannot sweep $T_{k}$ away. Claim 2. Any town $T_{m}$ with $m \neq k$ can be swept away by some other town. Proof. If $m<k$, then $T_{m}$ can be swept away from the right due to the choice of $T_{k}$. In the remaining case we have $m>k$. Let $T_{p}$ be a town among $T_{k}, T_{k+1}, \ldots, T_{m-1}$ having the largest right bulldozer. We claim that $T_{p}$ can sweep $T_{m}$ away. If this is not the case, then $r_{p}<\ell_{q}$ for some $q$ with $p<q \leqslant m$. But this means that $\ell_{q}$ is greater than all the numbers $r_{i}$ with $k \leqslant i \leqslant m-1$, so $T_{q}$ can sweep $T_{k}$ away. This contradicts the choice of $T_{k}$. Comment 1. One may employ the same ideas within the inductive approach. Here we sketch such a solution. Assume that the problem statement holds for the collection of towns $T_{1}, T_{2}, \ldots, T_{n-1}$, so that there is a unique town $T_{i}$ among them which cannot be swept away by any other of them. Thus we need to prove that in the full collection $T_{1}, T_{2}, \ldots, T_{n}$, exactly one of the towns $T_{i}$ and $T_{n}$ cannot be swept away. If $T_{n}$ cannot sweep $T_{i}$ away, then it remains to prove that $T_{n}$ can be swept away by some other town. This can be established as in the second paragraph of the proof of Claim 2. If $T_{n}$ can sweep $T_{i}$ away, then it remains to show that $T_{n}$ cannot be swept away by any other town. Since $T_{n}$ can sweep $T_{i}$ away, it also can sweep all the towns $T_{i}, T_{i+1}, \ldots, T_{n-1}$ away, so $T_{n}$ cannot be swept away by any of those. On the other hand, none of the remaining towns $T_{1}, T_{2}, \ldots, T_{i-1}$ can sweep $T_{i}$ away, so that they cannot sweep $T_{n}$ away as well. Comment 2. Here we sketch yet another inductive approach. Assume that $n>1$. Firstly, we find a town which can be swept away by each of its neighbors (each town has two neighbors, except for the bordering ones each of which has one); we call such town a loser. Such a town exists, because there are $n-1$ pairs of neighboring towns, and in each of them there is only one which can sweep the other away; so there exists a town which is a winner in none of these pairs. Notice that a loser can be swept away, but it cannot sweep any other town away (due to its neighbors' protection). Now we remove a loser, and suggest its left bulldozer to its right neighbor (if it exists), and its right bulldozer to a left one (if it exists). Surely, a town accepts a suggestion if a suggested bulldozer is larger than the town's one of the same orientation. Notice that suggested bulldozers are useless in attack (by the definition of a loser), but may serve for defensive purposes. Moreover, each suggested bulldozer's protection works for the same pairs of remaining towns as before the removal. By the induction hypothesis, the new configuration contains exactly one town which cannot be swept away. The arguments above show that the initial one also satisfies this property.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
In Lineland there are $n \geqslant 1$ towns, arranged along a road running from left to right. Each town has a left bulldozer (put to the left of the town and facing left) and a right bulldozer (put to the right of the town and facing right). The sizes of the $2 n$ bulldozers are distinct. Every time when a right and a left bulldozer confront each other, the larger bulldozer pushes the smaller one off the road. On the other hand, the bulldozers are quite unprotected at their rears; so, if a bulldozer reaches the rear-end of another one, the first one pushes the second one off the road, regardless of their sizes. Let $A$ and $B$ be two towns, with $B$ being to the right of $A$. We say that town $A$ can sweep town $B$ away if the right bulldozer of $A$ can move over to $B$ pushing off all bulldozers it meets. Similarly, $B$ can sweep $A$ away if the left bulldozer of $B$ can move to $A$ pushing off all bulldozers of all towns on its way. Prove that there is exactly one town which cannot be swept away by any other one. (Estonia)
|
We start with the same enumeration and the same observation as in Clearly, there is no town which can sweep $T_{n}$ away from the right. Then we may choose the leftmost town $T_{k}$ which cannot be swept away from the right. One can observe now that no town $T_{i}$ with $i>k$ may sweep away some town $T_{j}$ with $j<k$, for otherwise $T_{i}$ would be able to sweep $T_{k}$ away as well. Now we prove two claims, showing together that $T_{k}$ is the unique town which cannot be swept away, and thus establishing the problem statement. Claim 1. $T_{k}$ also cannot be swept away from the left. Proof. Let $T_{m}$ be some town to the left of $T_{k}$. By the choice of $T_{k}$, town $T_{m}$ can be swept away from the right by some town $T_{p}$ with $p>m$. As we have already observed, $p$ cannot be greater than $k$. On the other hand, $T_{m}$ cannot sweep $T_{p}$ away, so a fortiori it cannot sweep $T_{k}$ away. Claim 2. Any town $T_{m}$ with $m \neq k$ can be swept away by some other town. Proof. If $m<k$, then $T_{m}$ can be swept away from the right due to the choice of $T_{k}$. In the remaining case we have $m>k$. Let $T_{p}$ be a town among $T_{k}, T_{k+1}, \ldots, T_{m-1}$ having the largest right bulldozer. We claim that $T_{p}$ can sweep $T_{m}$ away. If this is not the case, then $r_{p}<\ell_{q}$ for some $q$ with $p<q \leqslant m$. But this means that $\ell_{q}$ is greater than all the numbers $r_{i}$ with $k \leqslant i \leqslant m-1$, so $T_{q}$ can sweep $T_{k}$ away. This contradicts the choice of $T_{k}$. Comment 1. One may employ the same ideas within the inductive approach. Here we sketch such a solution. Assume that the problem statement holds for the collection of towns $T_{1}, T_{2}, \ldots, T_{n-1}$, so that there is a unique town $T_{i}$ among them which cannot be swept away by any other of them. Thus we need to prove that in the full collection $T_{1}, T_{2}, \ldots, T_{n}$, exactly one of the towns $T_{i}$ and $T_{n}$ cannot be swept away. If $T_{n}$ cannot sweep $T_{i}$ away, then it remains to prove that $T_{n}$ can be swept away by some other town. This can be established as in the second paragraph of the proof of Claim 2. If $T_{n}$ can sweep $T_{i}$ away, then it remains to show that $T_{n}$ cannot be swept away by any other town. Since $T_{n}$ can sweep $T_{i}$ away, it also can sweep all the towns $T_{i}, T_{i+1}, \ldots, T_{n-1}$ away, so $T_{n}$ cannot be swept away by any of those. On the other hand, none of the remaining towns $T_{1}, T_{2}, \ldots, T_{i-1}$ can sweep $T_{i}$ away, so that they cannot sweep $T_{n}$ away as well. Comment 2. Here we sketch yet another inductive approach. Assume that $n>1$. Firstly, we find a town which can be swept away by each of its neighbors (each town has two neighbors, except for the bordering ones each of which has one); we call such town a loser. Such a town exists, because there are $n-1$ pairs of neighboring towns, and in each of them there is only one which can sweep the other away; so there exists a town which is a winner in none of these pairs. Notice that a loser can be swept away, but it cannot sweep any other town away (due to its neighbors' protection). Now we remove a loser, and suggest its left bulldozer to its right neighbor (if it exists), and its right bulldozer to a left one (if it exists). Surely, a town accepts a suggestion if a suggested bulldozer is larger than the town's one of the same orientation. Notice that suggested bulldozers are useless in attack (by the definition of a loser), but may serve for defensive purposes. Moreover, each suggested bulldozer's protection works for the same pairs of remaining towns as before the removal. By the induction hypothesis, the new configuration contains exactly one town which cannot be swept away. The arguments above show that the initial one also satisfies this property.
|
{
"resource_path": "IMO/segmented/en-IMO2015SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
ec35c816-a210-56e0-b52f-41c63ab44cc3
| 24,573
|
In Lineland there are $n \geqslant 1$ towns, arranged along a road running from left to right. Each town has a left bulldozer (put to the left of the town and facing left) and a right bulldozer (put to the right of the town and facing right). The sizes of the $2 n$ bulldozers are distinct. Every time when a right and a left bulldozer confront each other, the larger bulldozer pushes the smaller one off the road. On the other hand, the bulldozers are quite unprotected at their rears; so, if a bulldozer reaches the rear-end of another one, the first one pushes the second one off the road, regardless of their sizes. Let $A$ and $B$ be two towns, with $B$ being to the right of $A$. We say that town $A$ can sweep town $B$ away if the right bulldozer of $A$ can move over to $B$ pushing off all bulldozers it meets. Similarly, $B$ can sweep $A$ away if the left bulldozer of $B$ can move to $A$ pushing off all bulldozers of all towns on its way. Prove that there is exactly one town which cannot be swept away by any other one. (Estonia)
|
We separately prove that $(i)$ there exists a town which cannot be swept away, and that (ii) there is at most one such town. We also make use of the two observations from the previous solutions. To prove ( $i$ ), assume contrariwise that every town can be swept away. Let $t_{1}$ be the leftmost town; next, for every $k=1,2, \ldots$ we inductively choose $t_{k+1}$ to be some town which can sweep $t_{k}$ away. Now we claim that for every $k=1,2, \ldots$, the town $t_{k+1}$ is to the right of $t_{k}$; this leads to the contradiction, since the number of towns is finite. Induction on $k$. The base case $k=1$ is clear due to the choice of $t_{1}$. Assume now that for all $j$ with $1 \leqslant j<k$, the town $t_{j+1}$ is to the right of $t_{j}$. Suppose that $t_{k+1}$ is situated to the left of $t_{k}$; then it lies between $t_{j}$ and $t_{j+1}$ (possibly coinciding with $t_{j}$ ) for some $j<k$. Therefore, $t_{k+1}$ can be swept away by $t_{j+1}$, which shows that it cannot sweep $t_{j+1}$ away - so $t_{k+1}$ also cannot sweep $t_{k}$ away. This contradiction proves the induction step. To prove (ii), we also argue indirectly and choose two towns $A$ and $B$ neither of which can be swept away, with $A$ being to the left of $B$. Consider the largest bulldozer $b$ between them (taking into consideration the right bulldozer of $A$ and the left bulldozer of $B$ ). Without loss of generality, $b$ is a left bulldozer; then it is situated in some town to the right of $A$, and this town may sweep $A$ away since nothing prevents it from doing that. A contradiction. Comment 3. The Problem Selection Committee decided to reformulate this problem. The original formulation was as follows. Let $n$ be a positive integer. There are $n$ cards in a deck, enumerated from bottom to top with numbers $1,2, \ldots, n$. For each $i=1,2, \ldots, n$, an even number $a_{i}$ is printed on the lower side and an odd number $b_{i}$ is printed on the upper side of the $i^{\text {th }}$ card. We say that the $i^{\text {th }}$ card opens the $j^{\text {th }}$ card, if $i<j$ and $b_{i}<a_{k}$ for every $k=i+1, i+2, \ldots, j$. Similarly, we say that the $i^{\text {th }}$ card closes the $j^{\text {th }}$ card, if $i>j$ and $a_{i}<b_{k}$ for every $k=i-1, i-2, \ldots, j$. Prove that the deck contains exactly one card which is neither opened nor closed by any other card.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
In Lineland there are $n \geqslant 1$ towns, arranged along a road running from left to right. Each town has a left bulldozer (put to the left of the town and facing left) and a right bulldozer (put to the right of the town and facing right). The sizes of the $2 n$ bulldozers are distinct. Every time when a right and a left bulldozer confront each other, the larger bulldozer pushes the smaller one off the road. On the other hand, the bulldozers are quite unprotected at their rears; so, if a bulldozer reaches the rear-end of another one, the first one pushes the second one off the road, regardless of their sizes. Let $A$ and $B$ be two towns, with $B$ being to the right of $A$. We say that town $A$ can sweep town $B$ away if the right bulldozer of $A$ can move over to $B$ pushing off all bulldozers it meets. Similarly, $B$ can sweep $A$ away if the left bulldozer of $B$ can move to $A$ pushing off all bulldozers of all towns on its way. Prove that there is exactly one town which cannot be swept away by any other one. (Estonia)
|
We separately prove that $(i)$ there exists a town which cannot be swept away, and that (ii) there is at most one such town. We also make use of the two observations from the previous solutions. To prove ( $i$ ), assume contrariwise that every town can be swept away. Let $t_{1}$ be the leftmost town; next, for every $k=1,2, \ldots$ we inductively choose $t_{k+1}$ to be some town which can sweep $t_{k}$ away. Now we claim that for every $k=1,2, \ldots$, the town $t_{k+1}$ is to the right of $t_{k}$; this leads to the contradiction, since the number of towns is finite. Induction on $k$. The base case $k=1$ is clear due to the choice of $t_{1}$. Assume now that for all $j$ with $1 \leqslant j<k$, the town $t_{j+1}$ is to the right of $t_{j}$. Suppose that $t_{k+1}$ is situated to the left of $t_{k}$; then it lies between $t_{j}$ and $t_{j+1}$ (possibly coinciding with $t_{j}$ ) for some $j<k$. Therefore, $t_{k+1}$ can be swept away by $t_{j+1}$, which shows that it cannot sweep $t_{j+1}$ away - so $t_{k+1}$ also cannot sweep $t_{k}$ away. This contradiction proves the induction step. To prove (ii), we also argue indirectly and choose two towns $A$ and $B$ neither of which can be swept away, with $A$ being to the left of $B$. Consider the largest bulldozer $b$ between them (taking into consideration the right bulldozer of $A$ and the left bulldozer of $B$ ). Without loss of generality, $b$ is a left bulldozer; then it is situated in some town to the right of $A$, and this town may sweep $A$ away since nothing prevents it from doing that. A contradiction. Comment 3. The Problem Selection Committee decided to reformulate this problem. The original formulation was as follows. Let $n$ be a positive integer. There are $n$ cards in a deck, enumerated from bottom to top with numbers $1,2, \ldots, n$. For each $i=1,2, \ldots, n$, an even number $a_{i}$ is printed on the lower side and an odd number $b_{i}$ is printed on the upper side of the $i^{\text {th }}$ card. We say that the $i^{\text {th }}$ card opens the $j^{\text {th }}$ card, if $i<j$ and $b_{i}<a_{k}$ for every $k=i+1, i+2, \ldots, j$. Similarly, we say that the $i^{\text {th }}$ card closes the $j^{\text {th }}$ card, if $i>j$ and $a_{i}<b_{k}$ for every $k=i-1, i-2, \ldots, j$. Prove that the deck contains exactly one card which is neither opened nor closed by any other card.
|
{
"resource_path": "IMO/segmented/en-IMO2015SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
ec35c816-a210-56e0-b52f-41c63ab44cc3
| 24,573
|
Consider an infinite sequence $a_{1}, a_{2}, \ldots$ of positive integers with $a_{i} \leqslant 2015$ for all $i \geqslant 1$. Suppose that for any two distinct indices $i$ and $j$ we have $i+a_{i} \neq j+a_{j}$. Prove that there exist two positive integers $b$ and $N$ such that $$ \left|\sum_{i=m+1}^{n}\left(a_{i}-b\right)\right| \leqslant 1007^{2} $$ whenever $n>m \geqslant N$.
|
We visualize the set of positive integers as a sequence of points. For each $n$ we draw an arrow emerging from $n$ that points to $n+a_{n}$; so the length of this arrow is $a_{n}$. Due to the condition that $m+a_{m} \neq n+a_{n}$ for $m \neq n$, each positive integer receives at most one arrow. There are some positive integers, such as 1 , that receive no arrows; these will be referred to as starting points in the sequel. When one starts at any of the starting points and keeps following the arrows, one is led to an infinite path, called its ray, that visits a strictly increasing sequence of positive integers. Since the length of any arrow is at most 2015, such a ray, say with starting point $s$, meets every interval of the form $[n, n+2014]$ with $n \geqslant s$ at least once. Suppose for the sake of contradiction that there would be at least 2016 starting points. Then we could take an integer $n$ that is larger than the first 2016 starting points. But now the interval $[n, n+2014]$ must be met by at least 2016 rays in distinct points, which is absurd. We have thereby shown that the number $b$ of starting points satisfies $1 \leqslant b \leqslant 2015$. Let $N$ denote any integer that is larger than all starting points. We contend that $b$ and $N$ are as required. To see this, let any two integers $m$ and $n$ with $n>m \geqslant N$ be given. The sum $\sum_{i=m+1}^{n} a_{i}$ gives the total length of the arrows emerging from $m+1, \ldots, n$. Taken together, these arrows form $b$ subpaths of our rays, some of which may be empty. Now on each ray we look at the first number that is larger than $m$; let $x_{1}, \ldots, x_{b}$ denote these numbers, and let $y_{1}, \ldots, y_{b}$ enumerate in corresponding order the numbers defined similarly with respect to $n$. Then the list of differences $y_{1}-x_{1}, \ldots, y_{b}-x_{b}$ consists of the lengths of these paths and possibly some zeros corresponding to empty paths. Consequently, we obtain $$ \sum_{i=m+1}^{n} a_{i}=\sum_{j=1}^{b}\left(y_{j}-x_{j}\right) $$ whence $$ \sum_{i=m+1}^{n}\left(a_{i}-b\right)=\sum_{j=1}^{b}\left(y_{j}-n\right)-\sum_{j=1}^{b}\left(x_{j}-m\right) . $$ Now each of the $b$ rays meets the interval $[m+1, m+2015]$ at some point and thus $x_{1}-$ $m, \ldots, x_{b}-m$ are $b$ distinct members of the set $\{1,2, \ldots, 2015\}$. Moreover, since $m+1$ is not a starting point, it must belong to some ray; so 1 has to appear among these numbers, wherefore $$ 1+\sum_{j=1}^{b-1}(j+1) \leqslant \sum_{j=1}^{b}\left(x_{j}-m\right) \leqslant 1+\sum_{j=1}^{b-1}(2016-b+j) $$ The same argument applied to $n$ and $y_{1}, \ldots, y_{b}$ yields $$ 1+\sum_{j=1}^{b-1}(j+1) \leqslant \sum_{j=1}^{b}\left(y_{j}-n\right) \leqslant 1+\sum_{j=1}^{b-1}(2016-b+j) $$ So altogether we get $$ \begin{aligned} \left|\sum_{i=m+1}^{n}\left(a_{i}-b\right)\right| & \leqslant \sum_{j=1}^{b-1}((2016-b+j)-(j+1))=(b-1)(2015-b) \\ & \leqslant\left(\frac{(b-1)+(2015-b)}{2}\right)^{2}=1007^{2}, \end{aligned} $$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Consider an infinite sequence $a_{1}, a_{2}, \ldots$ of positive integers with $a_{i} \leqslant 2015$ for all $i \geqslant 1$. Suppose that for any two distinct indices $i$ and $j$ we have $i+a_{i} \neq j+a_{j}$. Prove that there exist two positive integers $b$ and $N$ such that $$ \left|\sum_{i=m+1}^{n}\left(a_{i}-b\right)\right| \leqslant 1007^{2} $$ whenever $n>m \geqslant N$.
|
We visualize the set of positive integers as a sequence of points. For each $n$ we draw an arrow emerging from $n$ that points to $n+a_{n}$; so the length of this arrow is $a_{n}$. Due to the condition that $m+a_{m} \neq n+a_{n}$ for $m \neq n$, each positive integer receives at most one arrow. There are some positive integers, such as 1 , that receive no arrows; these will be referred to as starting points in the sequel. When one starts at any of the starting points and keeps following the arrows, one is led to an infinite path, called its ray, that visits a strictly increasing sequence of positive integers. Since the length of any arrow is at most 2015, such a ray, say with starting point $s$, meets every interval of the form $[n, n+2014]$ with $n \geqslant s$ at least once. Suppose for the sake of contradiction that there would be at least 2016 starting points. Then we could take an integer $n$ that is larger than the first 2016 starting points. But now the interval $[n, n+2014]$ must be met by at least 2016 rays in distinct points, which is absurd. We have thereby shown that the number $b$ of starting points satisfies $1 \leqslant b \leqslant 2015$. Let $N$ denote any integer that is larger than all starting points. We contend that $b$ and $N$ are as required. To see this, let any two integers $m$ and $n$ with $n>m \geqslant N$ be given. The sum $\sum_{i=m+1}^{n} a_{i}$ gives the total length of the arrows emerging from $m+1, \ldots, n$. Taken together, these arrows form $b$ subpaths of our rays, some of which may be empty. Now on each ray we look at the first number that is larger than $m$; let $x_{1}, \ldots, x_{b}$ denote these numbers, and let $y_{1}, \ldots, y_{b}$ enumerate in corresponding order the numbers defined similarly with respect to $n$. Then the list of differences $y_{1}-x_{1}, \ldots, y_{b}-x_{b}$ consists of the lengths of these paths and possibly some zeros corresponding to empty paths. Consequently, we obtain $$ \sum_{i=m+1}^{n} a_{i}=\sum_{j=1}^{b}\left(y_{j}-x_{j}\right) $$ whence $$ \sum_{i=m+1}^{n}\left(a_{i}-b\right)=\sum_{j=1}^{b}\left(y_{j}-n\right)-\sum_{j=1}^{b}\left(x_{j}-m\right) . $$ Now each of the $b$ rays meets the interval $[m+1, m+2015]$ at some point and thus $x_{1}-$ $m, \ldots, x_{b}-m$ are $b$ distinct members of the set $\{1,2, \ldots, 2015\}$. Moreover, since $m+1$ is not a starting point, it must belong to some ray; so 1 has to appear among these numbers, wherefore $$ 1+\sum_{j=1}^{b-1}(j+1) \leqslant \sum_{j=1}^{b}\left(x_{j}-m\right) \leqslant 1+\sum_{j=1}^{b-1}(2016-b+j) $$ The same argument applied to $n$ and $y_{1}, \ldots, y_{b}$ yields $$ 1+\sum_{j=1}^{b-1}(j+1) \leqslant \sum_{j=1}^{b}\left(y_{j}-n\right) \leqslant 1+\sum_{j=1}^{b-1}(2016-b+j) $$ So altogether we get $$ \begin{aligned} \left|\sum_{i=m+1}^{n}\left(a_{i}-b\right)\right| & \leqslant \sum_{j=1}^{b-1}((2016-b+j)-(j+1))=(b-1)(2015-b) \\ & \leqslant\left(\frac{(b-1)+(2015-b)}{2}\right)^{2}=1007^{2}, \end{aligned} $$ as desired.
|
{
"resource_path": "IMO/segmented/en-IMO2015SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
33b4ec93-1e0c-57c2-b25d-69f13d712d69
| 24,587
|
Consider an infinite sequence $a_{1}, a_{2}, \ldots$ of positive integers with $a_{i} \leqslant 2015$ for all $i \geqslant 1$. Suppose that for any two distinct indices $i$ and $j$ we have $i+a_{i} \neq j+a_{j}$. Prove that there exist two positive integers $b$ and $N$ such that $$ \left|\sum_{i=m+1}^{n}\left(a_{i}-b\right)\right| \leqslant 1007^{2} $$ whenever $n>m \geqslant N$.
|
Set $s_{n}=n+a_{n}$ for all positive integers $n$. By our assumptions, we have $$ n+1 \leqslant s_{n} \leqslant n+2015 $$ for all $n \in \mathbb{Z}_{>0}$. The members of the sequence $s_{1}, s_{2}, \ldots$ are distinct. We shall investigate the set $$ M=\mathbb{Z}_{>0} \backslash\left\{s_{1}, s_{2}, \ldots\right\} $$ Claim. At most 2015 numbers belong to $M$. Proof. Otherwise let $m_{1}<m_{2}<\cdots<m_{2016}$ be any 2016 distinct elements from $M$. For $n=m_{2016}$ we have $$ \left\{s_{1}, \ldots, s_{n}\right\} \cup\left\{m_{1}, \ldots, m_{2016}\right\} \subseteq\{1,2, \ldots, n+2015\} $$ where on the left-hand side we have a disjoint union containing altogether $n+2016$ elements. But the set on the right-hand side has only $n+2015$ elements. This contradiction proves our claim. Now we work towards proving that the positive integers $b=|M|$ and $N=\max (M)$ are as required. Recall that we have just shown $b \leqslant 2015$. Let us consider any integer $r \geqslant N$. As in the proof of the above claim, we see that $$ B_{r}=M \cup\left\{s_{1}, \ldots, s_{r}\right\} $$ is a subset of $[1, r+2015] \cap \mathbb{Z}$ with precisely $b+r$ elements. Due to the definitions of $M$ and $N$, we also know $[1, r+1] \cap \mathbb{Z} \subseteq B_{r}$. It follows that there is a set $C_{r} \subseteq\{1,2, \ldots, 2014\}$ with $\left|C_{r}\right|=b-1$ and $$ B_{r}=([1, r+1] \cap \mathbb{Z}) \cup\left\{r+1+x \mid x \in C_{r}\right\} $$ For any finite set of integers $J$ we denote the sum of its elements by $\sum J$. Now the equations (1) and (2) give rise to two ways of computing $\sum B_{r}$ and the comparison of both methods leads to $$ \sum M+\sum_{i=1}^{r} s_{i}=\sum_{i=1}^{r} i+b(r+1)+\sum C_{r} $$ or in other words to $$ \sum M+\sum_{i=1}^{r}\left(a_{i}-b\right)=b+\sum C_{r} $$ After this preparation, we consider any two integers $m$ and $n$ with $n>m \geqslant N$. Plugging $r=n$ and $r=m$ into (3) and subtracting the estimates that result, we deduce $$ \sum_{i=m+1}^{n}\left(a_{i}-b\right)=\sum C_{n}-\sum C_{m} $$ Since $C_{n}$ and $C_{m}$ are subsets of $\{1,2, \ldots, 2014\}$ with $\left|C_{n}\right|=\left|C_{m}\right|=b-1$, it is clear that the absolute value of the right-hand side of the above inequality attains its largest possible value if either $C_{m}=\{1,2, \ldots, b-1\}$ and $C_{n}=\{2016-b, \ldots, 2014\}$, or the other way around. In these two cases we have $$ \left|\sum C_{n}-\sum C_{m}\right|=(b-1)(2015-b) $$ so in the general case we find $$ \left|\sum_{i=m+1}^{n}\left(a_{i}-b\right)\right| \leqslant(b-1)(2015-b) \leqslant\left(\frac{(b-1)+(2015-b)}{2}\right)^{2}=1007^{2} $$ as desired. Comment. The sets $C_{n}$ may be visualized by means of the following process: Start with an empty blackboard. For $n \geqslant 1$, the following happens during the $n^{\text {th }}$ step. The number $a_{n}$ gets written on the blackboard, then all numbers currently on the blackboard are decreased by 1 , and finally all zeros that have arisen get swept away. It is not hard to see that the numbers present on the blackboard after $n$ steps are distinct and form the set $C_{n}$. Moreover, it is possible to complete a solution based on this idea.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Consider an infinite sequence $a_{1}, a_{2}, \ldots$ of positive integers with $a_{i} \leqslant 2015$ for all $i \geqslant 1$. Suppose that for any two distinct indices $i$ and $j$ we have $i+a_{i} \neq j+a_{j}$. Prove that there exist two positive integers $b$ and $N$ such that $$ \left|\sum_{i=m+1}^{n}\left(a_{i}-b\right)\right| \leqslant 1007^{2} $$ whenever $n>m \geqslant N$.
|
Set $s_{n}=n+a_{n}$ for all positive integers $n$. By our assumptions, we have $$ n+1 \leqslant s_{n} \leqslant n+2015 $$ for all $n \in \mathbb{Z}_{>0}$. The members of the sequence $s_{1}, s_{2}, \ldots$ are distinct. We shall investigate the set $$ M=\mathbb{Z}_{>0} \backslash\left\{s_{1}, s_{2}, \ldots\right\} $$ Claim. At most 2015 numbers belong to $M$. Proof. Otherwise let $m_{1}<m_{2}<\cdots<m_{2016}$ be any 2016 distinct elements from $M$. For $n=m_{2016}$ we have $$ \left\{s_{1}, \ldots, s_{n}\right\} \cup\left\{m_{1}, \ldots, m_{2016}\right\} \subseteq\{1,2, \ldots, n+2015\} $$ where on the left-hand side we have a disjoint union containing altogether $n+2016$ elements. But the set on the right-hand side has only $n+2015$ elements. This contradiction proves our claim. Now we work towards proving that the positive integers $b=|M|$ and $N=\max (M)$ are as required. Recall that we have just shown $b \leqslant 2015$. Let us consider any integer $r \geqslant N$. As in the proof of the above claim, we see that $$ B_{r}=M \cup\left\{s_{1}, \ldots, s_{r}\right\} $$ is a subset of $[1, r+2015] \cap \mathbb{Z}$ with precisely $b+r$ elements. Due to the definitions of $M$ and $N$, we also know $[1, r+1] \cap \mathbb{Z} \subseteq B_{r}$. It follows that there is a set $C_{r} \subseteq\{1,2, \ldots, 2014\}$ with $\left|C_{r}\right|=b-1$ and $$ B_{r}=([1, r+1] \cap \mathbb{Z}) \cup\left\{r+1+x \mid x \in C_{r}\right\} $$ For any finite set of integers $J$ we denote the sum of its elements by $\sum J$. Now the equations (1) and (2) give rise to two ways of computing $\sum B_{r}$ and the comparison of both methods leads to $$ \sum M+\sum_{i=1}^{r} s_{i}=\sum_{i=1}^{r} i+b(r+1)+\sum C_{r} $$ or in other words to $$ \sum M+\sum_{i=1}^{r}\left(a_{i}-b\right)=b+\sum C_{r} $$ After this preparation, we consider any two integers $m$ and $n$ with $n>m \geqslant N$. Plugging $r=n$ and $r=m$ into (3) and subtracting the estimates that result, we deduce $$ \sum_{i=m+1}^{n}\left(a_{i}-b\right)=\sum C_{n}-\sum C_{m} $$ Since $C_{n}$ and $C_{m}$ are subsets of $\{1,2, \ldots, 2014\}$ with $\left|C_{n}\right|=\left|C_{m}\right|=b-1$, it is clear that the absolute value of the right-hand side of the above inequality attains its largest possible value if either $C_{m}=\{1,2, \ldots, b-1\}$ and $C_{n}=\{2016-b, \ldots, 2014\}$, or the other way around. In these two cases we have $$ \left|\sum C_{n}-\sum C_{m}\right|=(b-1)(2015-b) $$ so in the general case we find $$ \left|\sum_{i=m+1}^{n}\left(a_{i}-b\right)\right| \leqslant(b-1)(2015-b) \leqslant\left(\frac{(b-1)+(2015-b)}{2}\right)^{2}=1007^{2} $$ as desired. Comment. The sets $C_{n}$ may be visualized by means of the following process: Start with an empty blackboard. For $n \geqslant 1$, the following happens during the $n^{\text {th }}$ step. The number $a_{n}$ gets written on the blackboard, then all numbers currently on the blackboard are decreased by 1 , and finally all zeros that have arisen get swept away. It is not hard to see that the numbers present on the blackboard after $n$ steps are distinct and form the set $C_{n}$. Moreover, it is possible to complete a solution based on this idea.
|
{
"resource_path": "IMO/segmented/en-IMO2015SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
33b4ec93-1e0c-57c2-b25d-69f13d712d69
| 24,587
|
Let $S$ be a nonempty set of positive integers. We say that a positive integer $n$ is clean if it has a unique representation as a sum of an odd number of distinct elements from $S$. Prove that there exist infinitely many positive integers that are not clean.
|
Define an odd (respectively, even) representation of $n$ to be a representation of $n$ as a sum of an odd (respectively, even) number of distinct elements of $S$. Let $\mathbb{Z}_{>0}$ denote the set of all positive integers. Suppose, to the contrary, that there exist only finitely many positive integers that are not clean. Therefore, there exists a positive integer $N$ such that every integer $n>N$ has exactly one odd representation. Clearly, $S$ is infinite. We now claim the following properties of odd and even representations. $\underline{P r o p e r t y}$ 1. Any positive integer $n$ has at most one odd and at most one even representation. Proof. We first show that every integer $n$ has at most one even representation. Since $S$ is infinite, there exists $x \in S$ such that $x>\max \{n, N\}$. Then, the number $n+x$ must be clean, and $x$ does not appear in any even representation of $n$. If $n$ has more than one even representation, then we obtain two distinct odd representations of $n+x$ by adding $x$ to the even representations of $n$, which is impossible. Therefore, $n$ can have at most one even representation. Similarly, there exist two distinct elements $y, z \in S$ such that $y, z>\max \{n, N\}$. If $n$ has more than one odd representation, then we obtain two distinct odd representations of $n+y+z$ by adding $y$ and $z$ to the odd representations of $n$. This is again a contradiction. Property 2. Fix $s \in S$. Suppose that a number $n>N$ has no even representation. Then $n+2 a s$ has an even representation containing $s$ for all integers $a \geqslant 1$. Proof. It is sufficient to prove the following statement: If $n$ has no even representation without $s$, then $n+2 s$ has an even representation containing $s$ (and hence no even representation without $s$ by Property 1). Notice that the odd representation of $n+s$ does not contain $s$; otherwise, we have an even representation of $n$ without $s$. Then, adding $s$ to this odd representation of $n+s$, we get that $n+2 s$ has an even representation containing $s$, as desired. Property 3. Every sufficiently large integer has an even representation. Proof. Fix any $s \in S$, and let $r$ be an arbitrary element in $\{1,2, \ldots, 2 s\}$. Then, Property 2 implies that the set $Z_{r}=\{r+2 a s: a \geqslant 0\}$ contains at most one number exceeding $N$ with no even representation. Therefore, $Z_{r}$ contains finitely many positive integers with no even representation, and so does $\mathbb{Z}_{>0}=\bigcup_{r=1}^{2 s} Z_{r}$. In view of Properties 1 and 3 , we may assume that $N$ is chosen such that every $n>N$ has exactly one odd and exactly one even representation. In particular, each element $s>N$ of $S$ has an even representation. Property 4. For any $s, t \in S$ with $N<s<t$, the even representation of $t$ contains $s$. Proof. Suppose the contrary. Then, $s+t$ has at least two odd representations: one obtained by adding $s$ to the even representation of $t$ and one obtained by adding $t$ to the even representation of $s$. Since the latter does not contain $s$, these two odd representations of $s+t$ are distinct, a contradiction. Let $s_{1}<s_{2}<\cdots$ be all the elements of $S$, and set $\sigma_{n}=\sum_{i=1}^{n} s_{i}$ for each nonnegative integer $n$. Fix an integer $k$ such that $s_{k}>N$. Then, Property 4 implies that for every $i>k$ the even representation of $s_{i}$ contains all the numbers $s_{k}, s_{k+1}, \ldots, s_{i-1}$. Therefore, $$ s_{i}=s_{k}+s_{k+1}+\cdots+s_{i-1}+R_{i}=\sigma_{i-1}-\sigma_{k-1}+R_{i} $$ where $R_{i}$ is a sum of some of $s_{1}, \ldots, s_{k-1}$. In particular, $0 \leqslant R_{i} \leqslant s_{1}+\cdots+s_{k-1}=\sigma_{k-1}$. Let $j_{0}$ be an integer satisfying $j_{0}>k$ and $\sigma_{j_{0}}>2 \sigma_{k-1}$. Then (1) shows that, for every $j>j_{0}$, $$ s_{j+1} \geqslant \sigma_{j}-\sigma_{k-1}>\sigma_{j} / 2 . $$ Next, let $p>j_{0}$ be an index such that $R_{p}=\min _{i>j_{0}} R_{i}$. Then, $$ s_{p+1}=s_{k}+s_{k+1}+\cdots+s_{p}+R_{p+1}=\left(s_{p}-R_{p}\right)+s_{p}+R_{p+1} \geqslant 2 s_{p} $$ Therefore, there is no element of $S$ larger than $s_{p}$ but smaller than $2 s_{p}$. It follows that the even representation $\tau$ of $2 s_{p}$ does not contain any element larger than $s_{p}$. On the other hand, inequality (2) yields $2 s_{p}>s_{1}+\cdots+s_{p-1}$, so $\tau$ must contain a term larger than $s_{p-1}$. Thus, it must contain $s_{p}$. After removing $s_{p}$ from $\tau$, we have that $s_{p}$ has an odd representation not containing $s_{p}$, which contradicts Property 1 since $s_{p}$ itself also forms an odd representation of $s_{p}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $S$ be a nonempty set of positive integers. We say that a positive integer $n$ is clean if it has a unique representation as a sum of an odd number of distinct elements from $S$. Prove that there exist infinitely many positive integers that are not clean.
|
Define an odd (respectively, even) representation of $n$ to be a representation of $n$ as a sum of an odd (respectively, even) number of distinct elements of $S$. Let $\mathbb{Z}_{>0}$ denote the set of all positive integers. Suppose, to the contrary, that there exist only finitely many positive integers that are not clean. Therefore, there exists a positive integer $N$ such that every integer $n>N$ has exactly one odd representation. Clearly, $S$ is infinite. We now claim the following properties of odd and even representations. $\underline{P r o p e r t y}$ 1. Any positive integer $n$ has at most one odd and at most one even representation. Proof. We first show that every integer $n$ has at most one even representation. Since $S$ is infinite, there exists $x \in S$ such that $x>\max \{n, N\}$. Then, the number $n+x$ must be clean, and $x$ does not appear in any even representation of $n$. If $n$ has more than one even representation, then we obtain two distinct odd representations of $n+x$ by adding $x$ to the even representations of $n$, which is impossible. Therefore, $n$ can have at most one even representation. Similarly, there exist two distinct elements $y, z \in S$ such that $y, z>\max \{n, N\}$. If $n$ has more than one odd representation, then we obtain two distinct odd representations of $n+y+z$ by adding $y$ and $z$ to the odd representations of $n$. This is again a contradiction. Property 2. Fix $s \in S$. Suppose that a number $n>N$ has no even representation. Then $n+2 a s$ has an even representation containing $s$ for all integers $a \geqslant 1$. Proof. It is sufficient to prove the following statement: If $n$ has no even representation without $s$, then $n+2 s$ has an even representation containing $s$ (and hence no even representation without $s$ by Property 1). Notice that the odd representation of $n+s$ does not contain $s$; otherwise, we have an even representation of $n$ without $s$. Then, adding $s$ to this odd representation of $n+s$, we get that $n+2 s$ has an even representation containing $s$, as desired. Property 3. Every sufficiently large integer has an even representation. Proof. Fix any $s \in S$, and let $r$ be an arbitrary element in $\{1,2, \ldots, 2 s\}$. Then, Property 2 implies that the set $Z_{r}=\{r+2 a s: a \geqslant 0\}$ contains at most one number exceeding $N$ with no even representation. Therefore, $Z_{r}$ contains finitely many positive integers with no even representation, and so does $\mathbb{Z}_{>0}=\bigcup_{r=1}^{2 s} Z_{r}$. In view of Properties 1 and 3 , we may assume that $N$ is chosen such that every $n>N$ has exactly one odd and exactly one even representation. In particular, each element $s>N$ of $S$ has an even representation. Property 4. For any $s, t \in S$ with $N<s<t$, the even representation of $t$ contains $s$. Proof. Suppose the contrary. Then, $s+t$ has at least two odd representations: one obtained by adding $s$ to the even representation of $t$ and one obtained by adding $t$ to the even representation of $s$. Since the latter does not contain $s$, these two odd representations of $s+t$ are distinct, a contradiction. Let $s_{1}<s_{2}<\cdots$ be all the elements of $S$, and set $\sigma_{n}=\sum_{i=1}^{n} s_{i}$ for each nonnegative integer $n$. Fix an integer $k$ such that $s_{k}>N$. Then, Property 4 implies that for every $i>k$ the even representation of $s_{i}$ contains all the numbers $s_{k}, s_{k+1}, \ldots, s_{i-1}$. Therefore, $$ s_{i}=s_{k}+s_{k+1}+\cdots+s_{i-1}+R_{i}=\sigma_{i-1}-\sigma_{k-1}+R_{i} $$ where $R_{i}$ is a sum of some of $s_{1}, \ldots, s_{k-1}$. In particular, $0 \leqslant R_{i} \leqslant s_{1}+\cdots+s_{k-1}=\sigma_{k-1}$. Let $j_{0}$ be an integer satisfying $j_{0}>k$ and $\sigma_{j_{0}}>2 \sigma_{k-1}$. Then (1) shows that, for every $j>j_{0}$, $$ s_{j+1} \geqslant \sigma_{j}-\sigma_{k-1}>\sigma_{j} / 2 . $$ Next, let $p>j_{0}$ be an index such that $R_{p}=\min _{i>j_{0}} R_{i}$. Then, $$ s_{p+1}=s_{k}+s_{k+1}+\cdots+s_{p}+R_{p+1}=\left(s_{p}-R_{p}\right)+s_{p}+R_{p+1} \geqslant 2 s_{p} $$ Therefore, there is no element of $S$ larger than $s_{p}$ but smaller than $2 s_{p}$. It follows that the even representation $\tau$ of $2 s_{p}$ does not contain any element larger than $s_{p}$. On the other hand, inequality (2) yields $2 s_{p}>s_{1}+\cdots+s_{p-1}$, so $\tau$ must contain a term larger than $s_{p-1}$. Thus, it must contain $s_{p}$. After removing $s_{p}$ from $\tau$, we have that $s_{p}$ has an odd representation not containing $s_{p}$, which contradicts Property 1 since $s_{p}$ itself also forms an odd representation of $s_{p}$.
|
{
"resource_path": "IMO/segmented/en-IMO2015SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
11f5edaf-e572-54ea-b4c6-09c78659ddc4
| 24,591
|
Let $A B C$ be an acute triangle with orthocenter $H$. Let $G$ be the point such that the quadrilateral $A B G H$ is a parallelogram. Let $I$ be the point on the line $G H$ such that $A C$ bisects $H I$. Suppose that the line $A C$ intersects the circumcircle of the triangle $G C I$ at $C$ and $J$. Prove that $I J=A H$. (Australia)
|
Since $H G \| A B$ and $B G \| A H$, we have $B G \perp B C$ and $C H \perp G H$. Therefore, the quadrilateral $B G C H$ is cyclic. Since $H$ is the orthocenter of the triangle $A B C$, we have $\angle H A C=90^{\circ}-\angle A C B=\angle C B H$. Using that $B G C H$ and $C G J I$ are cyclic quadrilaterals, we get $$ \angle C J I=\angle C G H=\angle C B H=\angle H A C . $$ Let $M$ be the intersection of $A C$ and $G H$, and let $D \neq A$ be the point on the line $A C$ such that $A H=H D$. Then $\angle M J I=\angle H A C=\angle M D H$. Since $\angle M J I=\angle M D H, \angle I M J=\angle H M D$, and $I M=M H$, the triangles $I M J$ and $H M D$ are congruent, and thus $I J=H D=A H$. 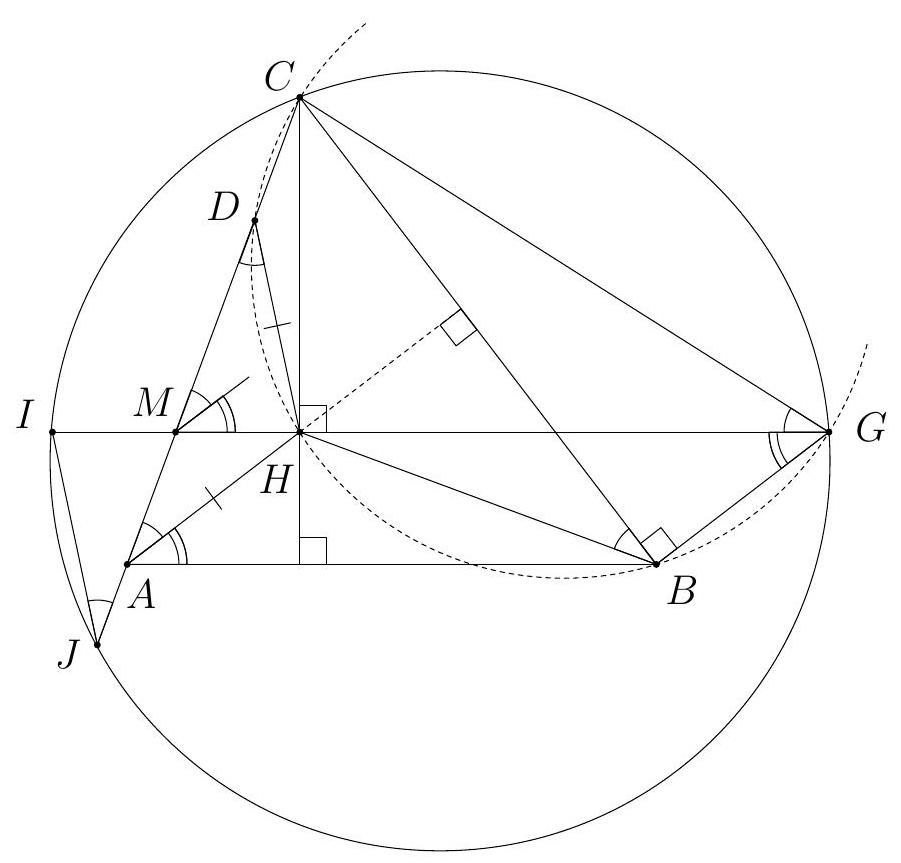 Comment. Instead of introducing the point $D$, one can complete the solution by using the law of sines in the triangles $I J M$ and $A M H$, yielding $$ \frac{I J}{I M}=\frac{\sin \angle I M J}{\sin \angle M J I}=\frac{\sin \angle A M H}{\sin \angle H A M}=\frac{A H}{M H}=\frac{A H}{I M} . $$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with orthocenter $H$. Let $G$ be the point such that the quadrilateral $A B G H$ is a parallelogram. Let $I$ be the point on the line $G H$ such that $A C$ bisects $H I$. Suppose that the line $A C$ intersects the circumcircle of the triangle $G C I$ at $C$ and $J$. Prove that $I J=A H$. (Australia)
|
Since $H G \| A B$ and $B G \| A H$, we have $B G \perp B C$ and $C H \perp G H$. Therefore, the quadrilateral $B G C H$ is cyclic. Since $H$ is the orthocenter of the triangle $A B C$, we have $\angle H A C=90^{\circ}-\angle A C B=\angle C B H$. Using that $B G C H$ and $C G J I$ are cyclic quadrilaterals, we get $$ \angle C J I=\angle C G H=\angle C B H=\angle H A C . $$ Let $M$ be the intersection of $A C$ and $G H$, and let $D \neq A$ be the point on the line $A C$ such that $A H=H D$. Then $\angle M J I=\angle H A C=\angle M D H$. Since $\angle M J I=\angle M D H, \angle I M J=\angle H M D$, and $I M=M H$, the triangles $I M J$ and $H M D$ are congruent, and thus $I J=H D=A H$.  Comment. Instead of introducing the point $D$, one can complete the solution by using the law of sines in the triangles $I J M$ and $A M H$, yielding $$ \frac{I J}{I M}=\frac{\sin \angle I M J}{\sin \angle M J I}=\frac{\sin \angle A M H}{\sin \angle H A M}=\frac{A H}{M H}=\frac{A H}{I M} . $$
|
{
"resource_path": "IMO/segmented/en-IMO2015SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
5dac3345-2c51-54d4-b3fd-89acbe58a012
| 24,600
|
Let $A B C$ be a triangle inscribed into a circle $\Omega$ with center $O$. A circle $\Gamma$ with center $A$ meets the side $B C$ at points $D$ and $E$ such that $D$ lies between $B$ and $E$. Moreover, let $F$ and $G$ be the common points of $\Gamma$ and $\Omega$. We assume that $F$ lies on the arc $A B$ of $\Omega$ not containing $C$, and $G$ lies on the arc $A C$ of $\Omega$ not containing $B$. The circumcircles of the triangles $B D F$ and $C E G$ meet the sides $A B$ and $A C$ again at $K$ and $L$, respectively. Suppose that the lines $F K$ and $G L$ are distinct and intersect at $X$. Prove that the points $A, X$, and $O$ are collinear. (Greece)
|
It suffices to prove that the lines $F K$ and $G L$ are symmetric about $A O$. Now the segments $A F$ and $A G$, being chords of $\Omega$ with the same length, are clearly symmetric with respect to $A O$. Hence it is enough to show $$ \angle K F A=\angle A G L . $$ Let us denote the circumcircles of $B D F$ and $C E G$ by $\omega_{B}$ and $\omega_{C}$, respectively. To prove (1), we start from $$ \angle K F A=\angle D F G+\angle G F A-\angle D F K $$ In view of the circles $\omega_{B}, \Gamma$, and $\Omega$, this may be rewritten as $$ \angle K F A=\angle C E G+\angle G B A-\angle D B K=\angle C E G-\angle C B G . $$ Due to the circles $\omega_{C}$ and $\Omega$, we obtain $\angle K F A=\angle C L G-\angle C A G=\angle A G L$. Thereby the problem is solved.  Figure 1
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle inscribed into a circle $\Omega$ with center $O$. A circle $\Gamma$ with center $A$ meets the side $B C$ at points $D$ and $E$ such that $D$ lies between $B$ and $E$. Moreover, let $F$ and $G$ be the common points of $\Gamma$ and $\Omega$. We assume that $F$ lies on the arc $A B$ of $\Omega$ not containing $C$, and $G$ lies on the arc $A C$ of $\Omega$ not containing $B$. The circumcircles of the triangles $B D F$ and $C E G$ meet the sides $A B$ and $A C$ again at $K$ and $L$, respectively. Suppose that the lines $F K$ and $G L$ are distinct and intersect at $X$. Prove that the points $A, X$, and $O$ are collinear. (Greece)
|
It suffices to prove that the lines $F K$ and $G L$ are symmetric about $A O$. Now the segments $A F$ and $A G$, being chords of $\Omega$ with the same length, are clearly symmetric with respect to $A O$. Hence it is enough to show $$ \angle K F A=\angle A G L . $$ Let us denote the circumcircles of $B D F$ and $C E G$ by $\omega_{B}$ and $\omega_{C}$, respectively. To prove (1), we start from $$ \angle K F A=\angle D F G+\angle G F A-\angle D F K $$ In view of the circles $\omega_{B}, \Gamma$, and $\Omega$, this may be rewritten as $$ \angle K F A=\angle C E G+\angle G B A-\angle D B K=\angle C E G-\angle C B G . $$ Due to the circles $\omega_{C}$ and $\Omega$, we obtain $\angle K F A=\angle C L G-\angle C A G=\angle A G L$. Thereby the problem is solved.  Figure 1
|
{
"resource_path": "IMO/segmented/en-IMO2015SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
489a2a54-aad2-5040-9d65-2229f462bc27
| 24,604
|
Let $A B C$ be a triangle inscribed into a circle $\Omega$ with center $O$. A circle $\Gamma$ with center $A$ meets the side $B C$ at points $D$ and $E$ such that $D$ lies between $B$ and $E$. Moreover, let $F$ and $G$ be the common points of $\Gamma$ and $\Omega$. We assume that $F$ lies on the arc $A B$ of $\Omega$ not containing $C$, and $G$ lies on the arc $A C$ of $\Omega$ not containing $B$. The circumcircles of the triangles $B D F$ and $C E G$ meet the sides $A B$ and $A C$ again at $K$ and $L$, respectively. Suppose that the lines $F K$ and $G L$ are distinct and intersect at $X$. Prove that the points $A, X$, and $O$ are collinear. (Greece)
|
Again, we denote the circumcircle of $B D K F$ by $\omega_{B}$. In addition, we set $\alpha=$ $\angle B A C, \varphi=\angle A B F$, and $\psi=\angle E D A=\angle A E D$ (see Figure 2). Notice that $A F=A G$ entails $\varphi=\angle G C A$, so all three of $\alpha, \varphi$, and $\psi$ respect the "symmetry" between $B$ and $C$ of our configuration. Again, we reduce our task to proving (1). This time, we start from $$ 2 \angle K F A=2(\angle D F A-\angle D F K) . $$ Since the triangle $A F D$ is isosceles, we have $$ \angle D F A=\angle A D F=\angle E D F-\psi=\angle B F D+\angle E B F-\psi . $$ Moreover, because of the circle $\omega_{B}$ we have $\angle D F K=\angle C B A$. Altogether, this yields $$ 2 \angle K F A=\angle D F A+(\angle B F D+\angle E B F-\psi)-2 \angle C B A, $$ which simplifies to $$ 2 \angle K F A=\angle B F A+\varphi-\psi-\angle C B A . $$ Now the quadrilateral $A F B C$ is cyclic, so this entails $2 \angle K F A=\alpha+\varphi-\psi$. Due to the "symmetry" between $B$ and $C$ alluded to above, this argument also shows that $2 \angle A G L=\alpha+\varphi-\psi$. This concludes the proof of (1).  Figure 2 Comment 1. As the first solution shows, the assumption that $A$ be the center of $\Gamma$ may be weakened to the following one: The center of $\Gamma$ lies on the line $O A$. The second solution may be modified to yield the same result. Comment 2. It might be interesting to remark that $\angle G D K=90^{\circ}$. To prove this, let $G^{\prime}$ denote the point on $\Gamma$ diametrically opposite to $G$. Because of $\angle K D F=\angle K B F=\angle A G F=\angle G^{\prime} D F$, the points $D, K$, and $G^{\prime}$ are collinear, which leads to the desired result. Notice that due to symmetry we also have $\angle L E F=90^{\circ}$. Moreover, a standard argument shows that the triangles $A G L$ and $B G E$ are similar. By symmetry again, also the triangles $A F K$ and $C D F$ are similar. There are several ways to derive a solution from these facts. For instance, one may argue that $$ \begin{aligned} \angle K F A & =\angle B F A-\angle B F K=\angle B F A-\angle E D G^{\prime}=\left(180^{\circ}-\angle A G B\right)-\left(180^{\circ}-\angle G^{\prime} G E\right) \\ & =\angle A G E-\angle A G B=\angle B G E=\angle A G L . \end{aligned} $$ Comment 3. The original proposal did not contain the point $X$ in the assumption and asked instead to prove that the lines $F K, G L$, and $A O$ are concurrent. This differs from the version given above only insofar as it also requires to show that these lines cannot be parallel. The Problem Selection Committee removed this part from the problem intending to make it thus more suitable for the Olympiad. For the sake of completeness, we would still like to sketch one possibility for proving $F K \nVdash A O$ here. As the points $K$ and $O$ lie in the angular region $\angle F A G$, it suffices to check $\angle K F A+\angle F A O<180^{\circ}$. Multiplying by 2 and making use of the formulae from the second solution, we see that this is equivalent to $(\alpha+\varphi-\psi)+\left(180^{\circ}-2 \varphi\right)<360^{\circ}$, which in turn is an easy consequence of $\alpha<180^{\circ}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle inscribed into a circle $\Omega$ with center $O$. A circle $\Gamma$ with center $A$ meets the side $B C$ at points $D$ and $E$ such that $D$ lies between $B$ and $E$. Moreover, let $F$ and $G$ be the common points of $\Gamma$ and $\Omega$. We assume that $F$ lies on the arc $A B$ of $\Omega$ not containing $C$, and $G$ lies on the arc $A C$ of $\Omega$ not containing $B$. The circumcircles of the triangles $B D F$ and $C E G$ meet the sides $A B$ and $A C$ again at $K$ and $L$, respectively. Suppose that the lines $F K$ and $G L$ are distinct and intersect at $X$. Prove that the points $A, X$, and $O$ are collinear. (Greece)
|
Again, we denote the circumcircle of $B D K F$ by $\omega_{B}$. In addition, we set $\alpha=$ $\angle B A C, \varphi=\angle A B F$, and $\psi=\angle E D A=\angle A E D$ (see Figure 2). Notice that $A F=A G$ entails $\varphi=\angle G C A$, so all three of $\alpha, \varphi$, and $\psi$ respect the "symmetry" between $B$ and $C$ of our configuration. Again, we reduce our task to proving (1). This time, we start from $$ 2 \angle K F A=2(\angle D F A-\angle D F K) . $$ Since the triangle $A F D$ is isosceles, we have $$ \angle D F A=\angle A D F=\angle E D F-\psi=\angle B F D+\angle E B F-\psi . $$ Moreover, because of the circle $\omega_{B}$ we have $\angle D F K=\angle C B A$. Altogether, this yields $$ 2 \angle K F A=\angle D F A+(\angle B F D+\angle E B F-\psi)-2 \angle C B A, $$ which simplifies to $$ 2 \angle K F A=\angle B F A+\varphi-\psi-\angle C B A . $$ Now the quadrilateral $A F B C$ is cyclic, so this entails $2 \angle K F A=\alpha+\varphi-\psi$. Due to the "symmetry" between $B$ and $C$ alluded to above, this argument also shows that $2 \angle A G L=\alpha+\varphi-\psi$. This concludes the proof of (1).  Figure 2 Comment 1. As the first solution shows, the assumption that $A$ be the center of $\Gamma$ may be weakened to the following one: The center of $\Gamma$ lies on the line $O A$. The second solution may be modified to yield the same result. Comment 2. It might be interesting to remark that $\angle G D K=90^{\circ}$. To prove this, let $G^{\prime}$ denote the point on $\Gamma$ diametrically opposite to $G$. Because of $\angle K D F=\angle K B F=\angle A G F=\angle G^{\prime} D F$, the points $D, K$, and $G^{\prime}$ are collinear, which leads to the desired result. Notice that due to symmetry we also have $\angle L E F=90^{\circ}$. Moreover, a standard argument shows that the triangles $A G L$ and $B G E$ are similar. By symmetry again, also the triangles $A F K$ and $C D F$ are similar. There are several ways to derive a solution from these facts. For instance, one may argue that $$ \begin{aligned} \angle K F A & =\angle B F A-\angle B F K=\angle B F A-\angle E D G^{\prime}=\left(180^{\circ}-\angle A G B\right)-\left(180^{\circ}-\angle G^{\prime} G E\right) \\ & =\angle A G E-\angle A G B=\angle B G E=\angle A G L . \end{aligned} $$ Comment 3. The original proposal did not contain the point $X$ in the assumption and asked instead to prove that the lines $F K, G L$, and $A O$ are concurrent. This differs from the version given above only insofar as it also requires to show that these lines cannot be parallel. The Problem Selection Committee removed this part from the problem intending to make it thus more suitable for the Olympiad. For the sake of completeness, we would still like to sketch one possibility for proving $F K \nVdash A O$ here. As the points $K$ and $O$ lie in the angular region $\angle F A G$, it suffices to check $\angle K F A+\angle F A O<180^{\circ}$. Multiplying by 2 and making use of the formulae from the second solution, we see that this is equivalent to $(\alpha+\varphi-\psi)+\left(180^{\circ}-2 \varphi\right)<360^{\circ}$, which in turn is an easy consequence of $\alpha<180^{\circ}$.
|
{
"resource_path": "IMO/segmented/en-IMO2015SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
489a2a54-aad2-5040-9d65-2229f462bc27
| 24,604
|
Let $A B C$ be a triangle with $\angle C=90^{\circ}$, and let $H$ be the foot of the altitude from $C$. A point $D$ is chosen inside the triangle $C B H$ so that $C H$ bisects $A D$. Let $P$ be the intersection point of the lines $B D$ and $C H$. Let $\omega$ be the semicircle with diameter $B D$ that meets the segment $C B$ at an interior point. A line through $P$ is tangent to $\omega$ at $Q$. Prove that the lines $C Q$ and $A D$ meet on $\omega$. (Georgia)
|
Let $K$ be the projection of $D$ onto $A B$; then $A H=H K$ (see Figure 1). Since $P H \| D K$, we have $$ \frac{P D}{P B}=\frac{H K}{H B}=\frac{A H}{H B} $$ Let $L$ be the projection of $Q$ onto $D B$. Since $P Q$ is tangent to $\omega$ and $\angle D Q B=\angle B L Q=$ $90^{\circ}$, we have $\angle P Q D=\angle Q B P=\angle D Q L$. Therefore, $Q D$ and $Q B$ are respectively the internal and the external bisectors of $\angle P Q L$. By the angle bisector theorem, we obtain $$ \frac{P D}{D L}=\frac{P Q}{Q L}=\frac{P B}{B L} $$ The relations (1) and (2) yield $\frac{A H}{H B}=\frac{P D}{P B}=\frac{D L}{L B}$. So, the spiral similarity $\tau$ centered at $B$ and sending $A$ to $D$ maps $H$ to $L$. Moreover, $\tau$ sends the semicircle with diameter $A B$ passing through $C$ to $\omega$. Due to $C H \perp A B$ and $Q L \perp D B$, it follows that $\tau(C)=Q$. Hence, the triangles $A B D$ and $C B Q$ are similar, so $\angle A D B=\angle C Q B$. This means that the lines $A D$ and $C Q$ meet at some point $T$, and this point satisfies $\angle B D T=\angle B Q T$. Therefore, $T$ lies on $\omega$, as needed.  Figure 1  Figure 2 Comment 1. Since $\angle B A D=\angle B C Q$, the point $T$ lies also on the circumcircle of the triangle $A B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $\angle C=90^{\circ}$, and let $H$ be the foot of the altitude from $C$. A point $D$ is chosen inside the triangle $C B H$ so that $C H$ bisects $A D$. Let $P$ be the intersection point of the lines $B D$ and $C H$. Let $\omega$ be the semicircle with diameter $B D$ that meets the segment $C B$ at an interior point. A line through $P$ is tangent to $\omega$ at $Q$. Prove that the lines $C Q$ and $A D$ meet on $\omega$. (Georgia)
|
Let $K$ be the projection of $D$ onto $A B$; then $A H=H K$ (see Figure 1). Since $P H \| D K$, we have $$ \frac{P D}{P B}=\frac{H K}{H B}=\frac{A H}{H B} $$ Let $L$ be the projection of $Q$ onto $D B$. Since $P Q$ is tangent to $\omega$ and $\angle D Q B=\angle B L Q=$ $90^{\circ}$, we have $\angle P Q D=\angle Q B P=\angle D Q L$. Therefore, $Q D$ and $Q B$ are respectively the internal and the external bisectors of $\angle P Q L$. By the angle bisector theorem, we obtain $$ \frac{P D}{D L}=\frac{P Q}{Q L}=\frac{P B}{B L} $$ The relations (1) and (2) yield $\frac{A H}{H B}=\frac{P D}{P B}=\frac{D L}{L B}$. So, the spiral similarity $\tau$ centered at $B$ and sending $A$ to $D$ maps $H$ to $L$. Moreover, $\tau$ sends the semicircle with diameter $A B$ passing through $C$ to $\omega$. Due to $C H \perp A B$ and $Q L \perp D B$, it follows that $\tau(C)=Q$. Hence, the triangles $A B D$ and $C B Q$ are similar, so $\angle A D B=\angle C Q B$. This means that the lines $A D$ and $C Q$ meet at some point $T$, and this point satisfies $\angle B D T=\angle B Q T$. Therefore, $T$ lies on $\omega$, as needed.  Figure 1  Figure 2 Comment 1. Since $\angle B A D=\angle B C Q$, the point $T$ lies also on the circumcircle of the triangle $A B C$.
|
{
"resource_path": "IMO/segmented/en-IMO2015SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
55deef0f-f9d6-52b9-909b-b7b8ecae9c51
| 24,609
|
Let $A B C$ be a triangle with $\angle C=90^{\circ}$, and let $H$ be the foot of the altitude from $C$. A point $D$ is chosen inside the triangle $C B H$ so that $C H$ bisects $A D$. Let $P$ be the intersection point of the lines $B D$ and $C H$. Let $\omega$ be the semicircle with diameter $B D$ that meets the segment $C B$ at an interior point. A line through $P$ is tangent to $\omega$ at $Q$. Prove that the lines $C Q$ and $A D$ meet on $\omega$. (Georgia)
|
Let $\Gamma$ be the circumcircle of $A B C$, and let $A D$ meet $\omega$ at $T$. Then $\angle A T B=$ $\angle A C B=90^{\circ}$, so $T$ lies on $\Gamma$ as well. As in the previous solution, let $K$ be the projection of $D$ onto $A B$; then $A H=H K$ (see Figure 2). Our goal now is to prove that the points $C, Q$, and $T$ are collinear. Let $C T$ meet $\omega$ again at $Q^{\prime}$. Then, it suffices to show that $P Q^{\prime}$ is tangent to $\omega$, or that $\angle P Q^{\prime} D=\angle Q^{\prime} B D$. Since the quadrilateral $B D Q^{\prime} T$ is cyclic and the triangles $A H C$ and $K H C$ are congruent, we have $\angle Q^{\prime} B D=\angle Q^{\prime} T D=\angle C T A=\angle C B A=\angle A C H=\angle H C K$. Hence, the right triangles $C H K$ and $B Q^{\prime} D$ are similar. This implies that $\frac{H K}{C K}=\frac{Q^{\prime} D}{B D}$, and thus $H K \cdot B D=C K \cdot Q^{\prime} D$. Notice that $P H \| D K$; therefore, we have $\frac{P D}{B D}=\frac{H K}{B K}$, and so $P D \cdot B K=H K \cdot B D$. Consequently, $P D \cdot B K=H K \cdot B D=C K \cdot Q^{\prime} D$, which yields $\frac{P D}{Q^{\prime} D}=\frac{C K}{B K}$. Since $\angle C K A=\angle K A C=\angle B D Q^{\prime}$, the triangles $C K B$ and $P D Q^{\prime}$ are similar, so $\angle P Q^{\prime} D=$ $\angle C B A=\angle Q^{\prime} B D$, as required. Comment 2. There exist several other ways to prove that $P Q^{\prime}$ is tangent to $\omega$. For instance, one may compute $\frac{P D}{P B}$ and $\frac{P Q^{\prime}}{P B}$ in terms of $A H$ and $H B$ to verify that $P Q^{\prime 2}=P D \cdot P B$, concluding that $P Q^{\prime}$ is tangent to $\omega$. Another possible approach is the following. As in Solution 2, we introduce the points $T$ and $Q^{\prime}$ and mention that the triangles $A B C$ and $D B Q^{\prime}$ are similar (see Figure 3). Let $M$ be the midpoint of $A D$, and let $L$ be the projection of $Q^{\prime}$ onto $A B$. Construct $E$ on the line $A B$ so that $E P$ is parallel to $A D$. Projecting from $P$, we get $(A, B ; H, E)=(A, D ; M, \infty)=-1$. Since $\frac{E A}{A B}=\frac{P D}{D B}$, the point $P$ is the image of $E$ under the similarity transform mapping $A B C$ to $D B Q^{\prime}$. Therefore, we have $(D, B ; L, P)=(A, B ; H, E)=-1$, which means that $Q^{\prime} D$ and $Q^{\prime} B$ are respectively the internal and the external bisectors of $\angle P Q^{\prime} L$. This implies that $P Q^{\prime}$ is tangent to $\omega$, as required.  Figure 3
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $\angle C=90^{\circ}$, and let $H$ be the foot of the altitude from $C$. A point $D$ is chosen inside the triangle $C B H$ so that $C H$ bisects $A D$. Let $P$ be the intersection point of the lines $B D$ and $C H$. Let $\omega$ be the semicircle with diameter $B D$ that meets the segment $C B$ at an interior point. A line through $P$ is tangent to $\omega$ at $Q$. Prove that the lines $C Q$ and $A D$ meet on $\omega$. (Georgia)
|
Let $\Gamma$ be the circumcircle of $A B C$, and let $A D$ meet $\omega$ at $T$. Then $\angle A T B=$ $\angle A C B=90^{\circ}$, so $T$ lies on $\Gamma$ as well. As in the previous solution, let $K$ be the projection of $D$ onto $A B$; then $A H=H K$ (see Figure 2). Our goal now is to prove that the points $C, Q$, and $T$ are collinear. Let $C T$ meet $\omega$ again at $Q^{\prime}$. Then, it suffices to show that $P Q^{\prime}$ is tangent to $\omega$, or that $\angle P Q^{\prime} D=\angle Q^{\prime} B D$. Since the quadrilateral $B D Q^{\prime} T$ is cyclic and the triangles $A H C$ and $K H C$ are congruent, we have $\angle Q^{\prime} B D=\angle Q^{\prime} T D=\angle C T A=\angle C B A=\angle A C H=\angle H C K$. Hence, the right triangles $C H K$ and $B Q^{\prime} D$ are similar. This implies that $\frac{H K}{C K}=\frac{Q^{\prime} D}{B D}$, and thus $H K \cdot B D=C K \cdot Q^{\prime} D$. Notice that $P H \| D K$; therefore, we have $\frac{P D}{B D}=\frac{H K}{B K}$, and so $P D \cdot B K=H K \cdot B D$. Consequently, $P D \cdot B K=H K \cdot B D=C K \cdot Q^{\prime} D$, which yields $\frac{P D}{Q^{\prime} D}=\frac{C K}{B K}$. Since $\angle C K A=\angle K A C=\angle B D Q^{\prime}$, the triangles $C K B$ and $P D Q^{\prime}$ are similar, so $\angle P Q^{\prime} D=$ $\angle C B A=\angle Q^{\prime} B D$, as required. Comment 2. There exist several other ways to prove that $P Q^{\prime}$ is tangent to $\omega$. For instance, one may compute $\frac{P D}{P B}$ and $\frac{P Q^{\prime}}{P B}$ in terms of $A H$ and $H B$ to verify that $P Q^{\prime 2}=P D \cdot P B$, concluding that $P Q^{\prime}$ is tangent to $\omega$. Another possible approach is the following. As in Solution 2, we introduce the points $T$ and $Q^{\prime}$ and mention that the triangles $A B C$ and $D B Q^{\prime}$ are similar (see Figure 3). Let $M$ be the midpoint of $A D$, and let $L$ be the projection of $Q^{\prime}$ onto $A B$. Construct $E$ on the line $A B$ so that $E P$ is parallel to $A D$. Projecting from $P$, we get $(A, B ; H, E)=(A, D ; M, \infty)=-1$. Since $\frac{E A}{A B}=\frac{P D}{D B}$, the point $P$ is the image of $E$ under the similarity transform mapping $A B C$ to $D B Q^{\prime}$. Therefore, we have $(D, B ; L, P)=(A, B ; H, E)=-1$, which means that $Q^{\prime} D$ and $Q^{\prime} B$ are respectively the internal and the external bisectors of $\angle P Q^{\prime} L$. This implies that $P Q^{\prime}$ is tangent to $\omega$, as required.  Figure 3
|
{
"resource_path": "IMO/segmented/en-IMO2015SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
55deef0f-f9d6-52b9-909b-b7b8ecae9c51
| 24,609
|
Let $A B C$ be a triangle with $\angle C=90^{\circ}$, and let $H$ be the foot of the altitude from $C$. A point $D$ is chosen inside the triangle $C B H$ so that $C H$ bisects $A D$. Let $P$ be the intersection point of the lines $B D$ and $C H$. Let $\omega$ be the semicircle with diameter $B D$ that meets the segment $C B$ at an interior point. A line through $P$ is tangent to $\omega$ at $Q$. Prove that the lines $C Q$ and $A D$ meet on $\omega$. (Georgia)
|
Introduce the points $T$ and $Q^{\prime}$ as in the previous solution. Note that $T$ lies on the circumcircle of $A B C$. Here we present yet another proof that $P Q^{\prime}$ is tangent to $\omega$. Let $\Omega$ be the circle completing the semicircle $\omega$. Construct a point $F$ symmetric to $C$ with respect to $A B$. Let $S \neq T$ be the second intersection point of $F T$ and $\Omega$ (see Figure 4).  Figure 4 Since $A C=A F$, we have $\angle D K C=\angle H C K=\angle C B A=\angle C T A=\angle D T S=180^{\circ}-$ $\angle S K D$. Thus, the points $C, K$, and $S$ are collinear. Notice also that $\angle Q^{\prime} K D=\angle Q^{\prime} T D=$ $\angle H C K=\angle K F H=180^{\circ}-\angle D K F$. This implies that the points $F, K$, and $Q^{\prime}$ are collinear. Applying PASCAL's theorem to the degenerate hexagon $K Q^{\prime} Q^{\prime} T S S$, we get that the tangents to $\Omega$ passing through $Q^{\prime}$ and $S$ intersect on $C F$. The relation $\angle Q^{\prime} T D=\angle D T S$ yields that $Q^{\prime}$ and $S$ are symmetric with respect to $B D$. Therefore, the two tangents also intersect on $B D$. Thus, the two tangents pass through $P$. Hence, $P Q^{\prime}$ is tangent to $\omega$, as needed.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $\angle C=90^{\circ}$, and let $H$ be the foot of the altitude from $C$. A point $D$ is chosen inside the triangle $C B H$ so that $C H$ bisects $A D$. Let $P$ be the intersection point of the lines $B D$ and $C H$. Let $\omega$ be the semicircle with diameter $B D$ that meets the segment $C B$ at an interior point. A line through $P$ is tangent to $\omega$ at $Q$. Prove that the lines $C Q$ and $A D$ meet on $\omega$. (Georgia)
|
Introduce the points $T$ and $Q^{\prime}$ as in the previous solution. Note that $T$ lies on the circumcircle of $A B C$. Here we present yet another proof that $P Q^{\prime}$ is tangent to $\omega$. Let $\Omega$ be the circle completing the semicircle $\omega$. Construct a point $F$ symmetric to $C$ with respect to $A B$. Let $S \neq T$ be the second intersection point of $F T$ and $\Omega$ (see Figure 4).  Figure 4 Since $A C=A F$, we have $\angle D K C=\angle H C K=\angle C B A=\angle C T A=\angle D T S=180^{\circ}-$ $\angle S K D$. Thus, the points $C, K$, and $S$ are collinear. Notice also that $\angle Q^{\prime} K D=\angle Q^{\prime} T D=$ $\angle H C K=\angle K F H=180^{\circ}-\angle D K F$. This implies that the points $F, K$, and $Q^{\prime}$ are collinear. Applying PASCAL's theorem to the degenerate hexagon $K Q^{\prime} Q^{\prime} T S S$, we get that the tangents to $\Omega$ passing through $Q^{\prime}$ and $S$ intersect on $C F$. The relation $\angle Q^{\prime} T D=\angle D T S$ yields that $Q^{\prime}$ and $S$ are symmetric with respect to $B D$. Therefore, the two tangents also intersect on $B D$. Thus, the two tangents pass through $P$. Hence, $P Q^{\prime}$ is tangent to $\omega$, as needed.
|
{
"resource_path": "IMO/segmented/en-IMO2015SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
55deef0f-f9d6-52b9-909b-b7b8ecae9c51
| 24,609
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.